Текст
А.Н.ПЛАНОВСКИЙ • В.М.РАММ
1.3.КАГАН
О Р О ИД IE [ [ ton
АППАРАТЫ
ХИМИЧЕСКОЙ
ТЕХНОЛОГИИ
I (К ХИМ ИЗ ДАТ
МП ГН В А • 19 Г) 2
A. H. ПЛАНОВСКИЙ*В. М. РАММ
С. 3. КАГАН
ПРОЦЕССЫ И АППАРАТЫ
ХИМИЧЕСКОЙ ТЕХНОЛОГИИ
ИЗДАНИЕ ВТОРОЕ,
ДОПОЛНЕННОЕ И ПЕРЕРАБОТАННОЕ
Допущено Министерством
высшего и среднего специального образования СССР
в качестве учебника для учащихся техникумов
ГОСУДАРСТВЕННОЕ НАУЧНО-ТЕХНИЧЕСКОЕ ИЗДАТЕЛЬСТВО
ХИМИЧЕСКОЙ ЛИТЕРАТУРЫ
МОСКВА 1962
Содержание
г а *Т
Кла :Иф,ДЦия (сортировка) материалов
2?ийИе све*»я................
3. Типы Д СИТОа ’ а^лиз • • ...................
* устрой™™; ‘ос“со6ы • • :
5. ГидравлическР *..............
стгецттал&ъ^ |
” ^”’"’TRe П(
Глава 4
ия , .
’ аг|ализ
>в........... ’ ‘ ' у ’
'Ссификация и воздушная сепараци!
86
8Ь
8Z
5
Дозирование и смешивание твердых материалов
1. Бункеры и затворы к ним................................
2. "Питатели........................................... •
3. Дозаторы............................................
4. Смесители твердых и пастообразных материалов...........
104
107
111
116
ГИДРОМЕХАНИЧЕСКИЕ ПРОЦЕССЫ
Глава 6
Основы гидравлики ’
1. Общие сведения....................................... • • 121Р
2. Основные физические свойства жидкостей..............». • 121₽,
3. Давление жидкостей...................................|. • 129f/
4. Материальный баланс потока (уравнения неразрывности ’|ю- J
тока) ......................................................• 13/j
5. Энергетический баланс потока (уравнение Бернулли) . . .| . . 13$
6 Режимы движения вязкой жидкости.......................L. . 14у
7. Элементы теории подобия................................h . 14&
8. Движение жидкостей по трубопроводам...................к, . 15!
9. Истечение жидкостей через отверстия и водосливы . . . .16
10. Пленочное течение жидкостей............................. 16*
11. Движение тел в жидкости...............................’j . 17
12. Движение жидкостей через зернистый и пористый слои . .У .17
13. Гидравлика кипящего (псевдоожиженного) слоя............| . 17!
х Г л а в а 7
Перемещение жидкостей и газов
1. Трубой'
nV
Содержание
5
12. Осевые компрессоры.......................................235
13. Вакуум-насосы............................................236
14. Сравнение и выбор компрессорных машин...................237
Глава 8
Разделение жидких неоднородных систем
1. Неоднородные системы и методы их разделения.............239
2. Разделение суспензий и эмульсий.........................241
А. Отстаивание
3. Общие сведения.............................................243
4. Скорость осаждения (отстаивания)...........................244
5. Устройство отстойников.....................................246
6. Расчет отстойников.........................................249
7. Осаждение в поле центробежных сил.........................251
Б. Фильтрование
8. Общие сведения...........................................252
9. Теория фильтрования......................................254
10. Устройство фильтров.....................................256
11. Фильтровальные перегородки..............................281
12. Сравнение и выбор фильтров..............................283
13. Промывка осадков........................................285
14. Расчет фильтров ."......................................286
В. Центрифугирование
15. Общие сведения............................................292
16. Устройство центрифуг......................................295
17. Сравнение, выбор и обслуживание центрифуг.................312
18. Расчет центрифуг..........................................314
Глава 9
Очистка газов
1. Общие сведения...............................................323
2. Устройство газоочистительных аппаратов......................325
3. Сравнение и выбор газоочистительных аппаратов...............344
Глава 10
Перемешивание
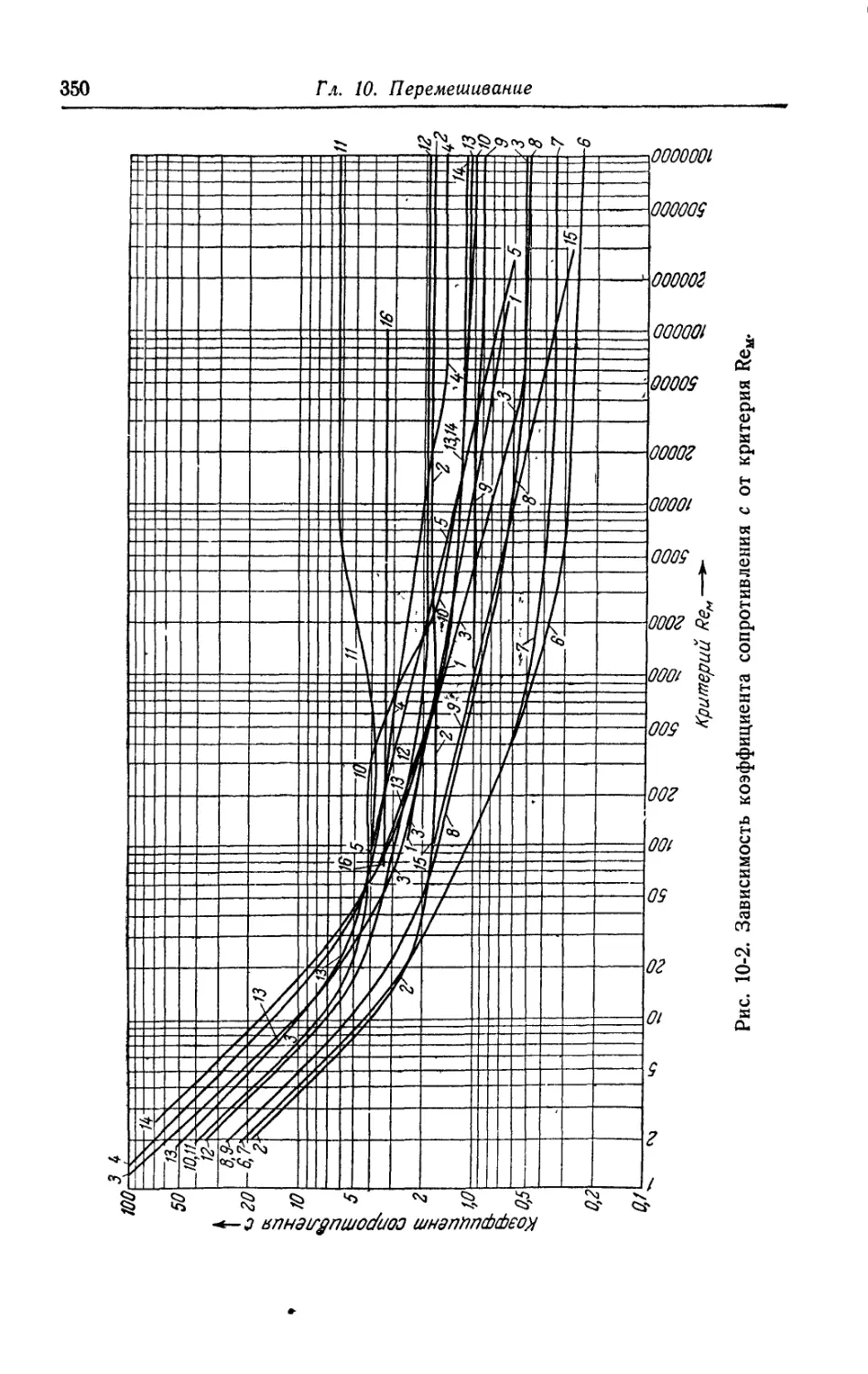
1. Общие сведения...........................................346
2. Расход энергии на перемешивание..........................347
3. Эффективность перемешивания.............................352
4. Устройство мешалок.......................................354
5. Перемешивание сжатым воздухом ........................ . 362
Содержание
ТЕПЛОВЫЕ ПРОЦЕССЫ
Глава П
Основы теплопередачи
. ’...........363
' 1. Общие сведения...................................... ... 364
2. Тепловой баланс ....................................... 368
3. Уравнения передачи тепла.............................. о71
4 Передана тепла через стенку .............................
5. Средний температурный напор..............................
6. Конвекция...............................................401
7. Лучеиспускание...........................................
8. Потери тепла в окружающую среду..........................wy
Глава 12
Нагревание и охлаждение
1. Общие сведения..........................................411
2. Способы нагревания и охлаждения.........................411
3. Устройство теплообменных аппаратов......................423
4. Сравнение н выбор теплообменных аппаратов...............438
5. Эксплуатация теплообменных аппаратов....................439
6. Расчет теплообменных аппаратов..........................440
7. Расчет теплообмена при конденсации пара.................456
8. Периодический процесс теплообмена.......................459
9. Теплообмен в кипящем (псевдоожиженном) слое.............460
10. Регенеративные и смесительные теплообменные аппараты . . . 464
Глава 13
Выпаривание
1. Общие сведения............................................467
2. Способы выпаривания......................................468
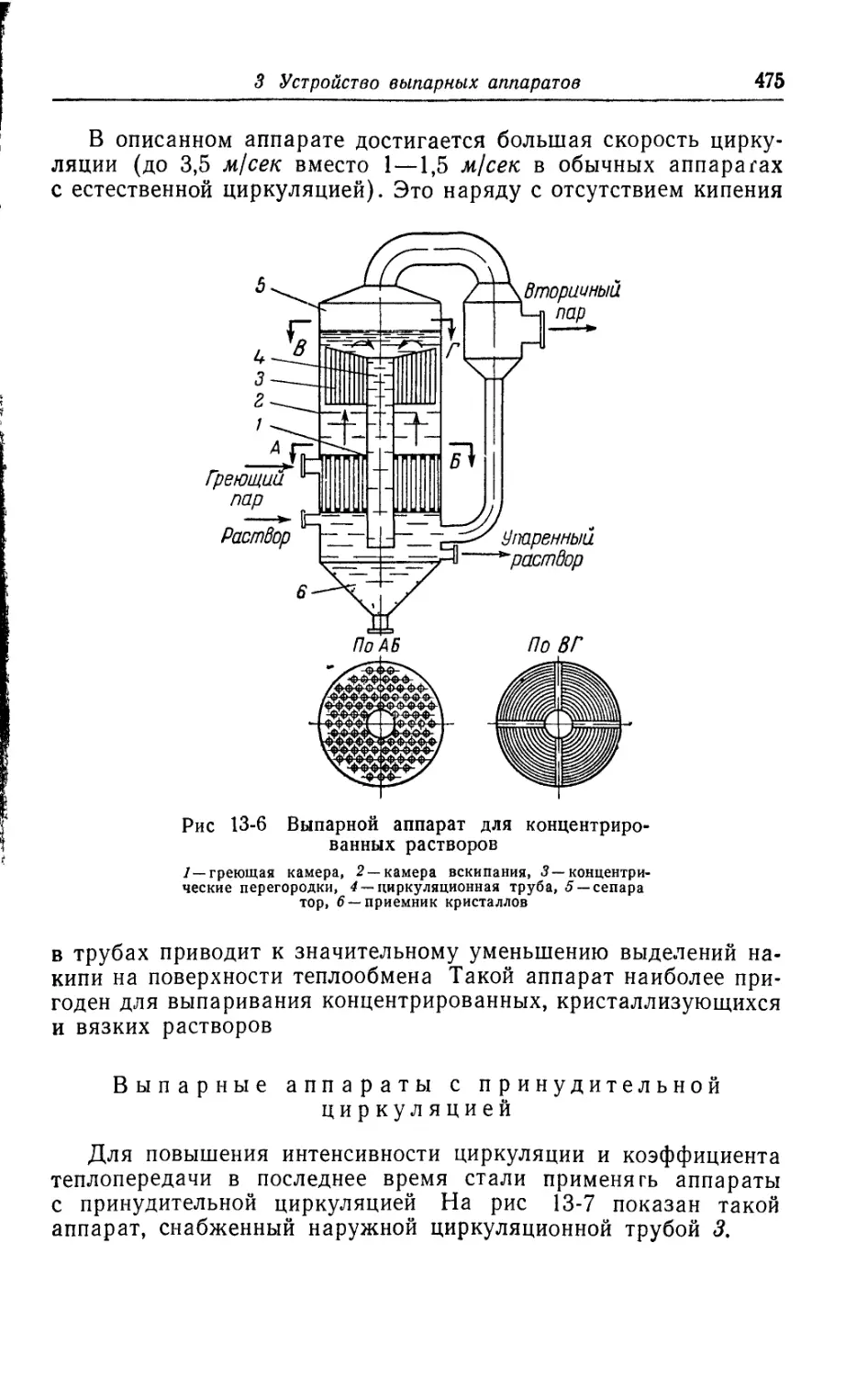
3. Устройство выпарных аппаратов............................469
4. Эксплуатация выпарных аппаратов..........................478
5. Расчет выпарных аппаратов................................479
6. Многокорпусные выпарные установки.........................488
7. Расчет многокорпусной выпарной установки.................496
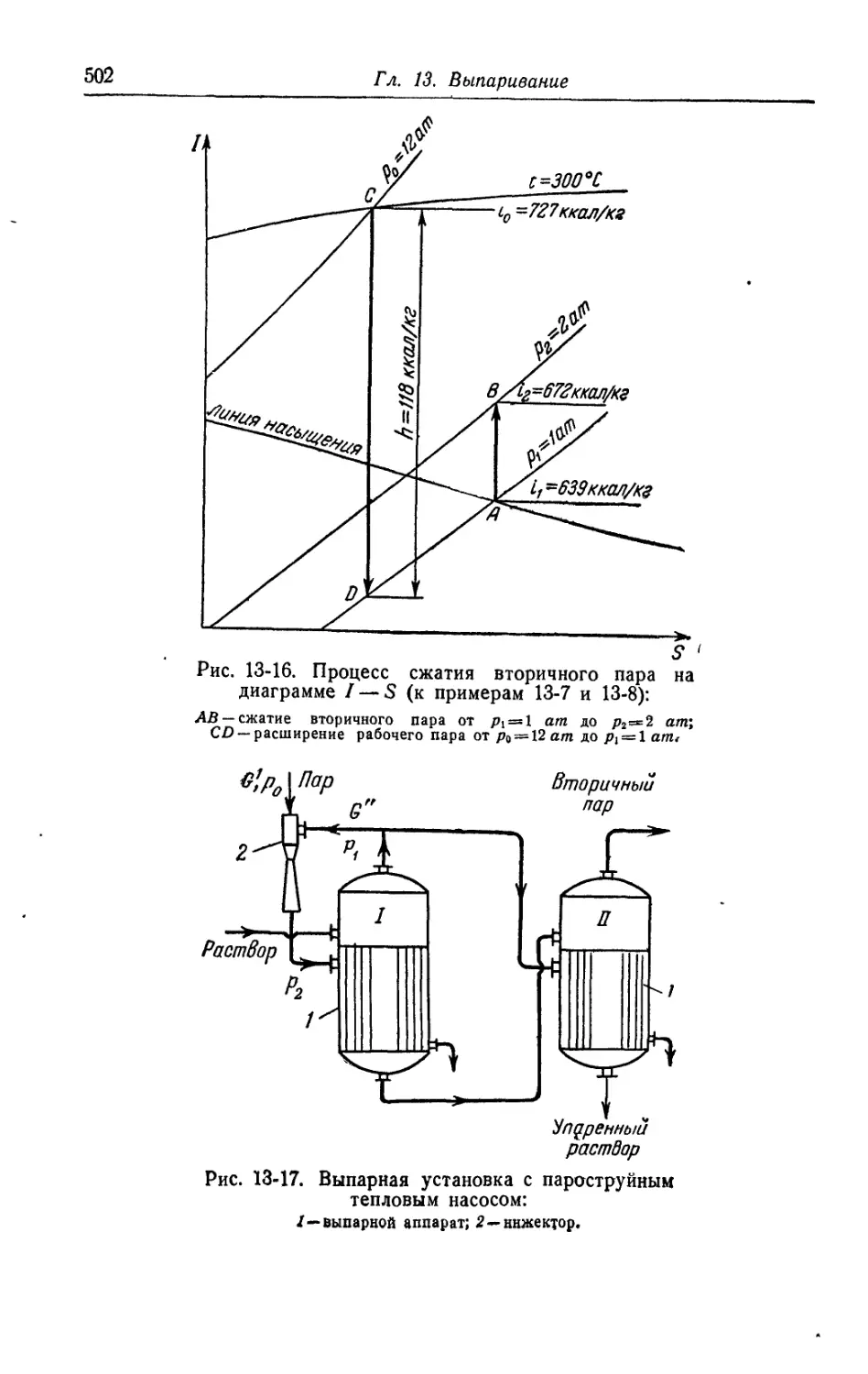
8. Выпарные установки с тепловым насосом....................501
9. Создание вакуума в выпарных установках...................505
Глава 14
Кристаллизация
I. Общие сведения................................................512
2. Устройство кристаллизаторов ................................ 514
3. Расчет кристаллизаторов .....................................519
Г л а в а 15
Искусственное охлаждение
1. Общие сведения...............................................523
2. Термодинамические основы получения холода................524
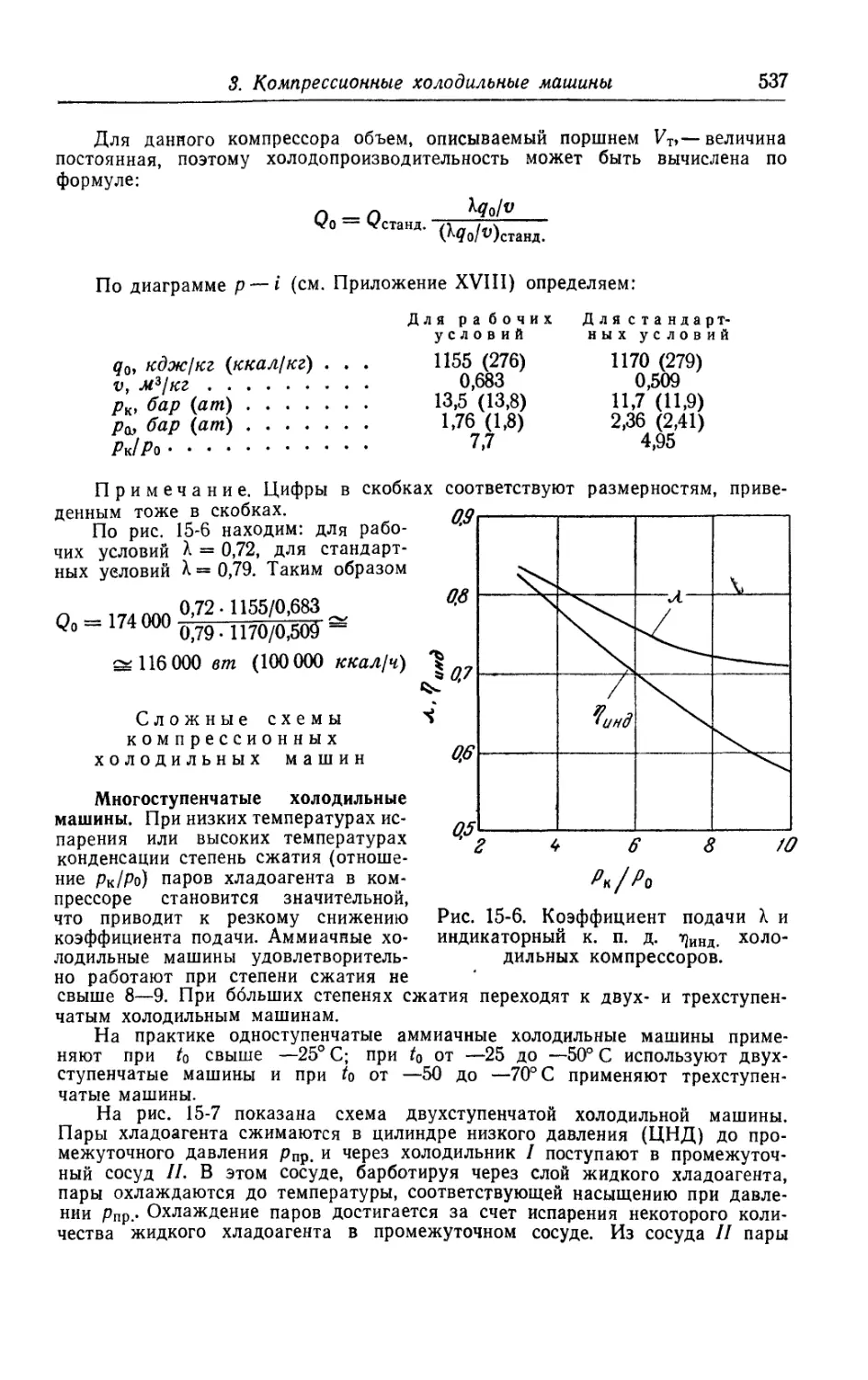
3. Компрессионные холодильные машины........................528
Содержание
7
4. Холодильные агенты Устройство компрессионных холодильных
машин ...................................................5Й0
5. Холодильные машины с затратой тепла на получение холода . . 542
6. Разделение газовых смесей и сжижение газов методом глубокого
охлаждения............................................. 545
МАССООБМЕННЫЕ ПРОЦЕССЫ
Глава 16
Теория процессов массопередачи
1 Общие сведения о массообменных процессах..............560
2. Способы выражения состава фаз......................". ."561
3. Равновесие между фазами...............................566
4. Материальный баланс процессов массообмена.............567
5. Уравнение массопередачи ............................. 570
6. Процесс массообмена между фазами......................573
7. Средняя движущая сила и методы расчета процессов массопере-
дачи ....................................................582
Глава 17
Абсорбция
1. Общие сведения............................................590
2. Физические основы процесса абсорбции.....................590
3. Устройство абсорберов .................................. 594
4. Десорбция.................................................605
5. Схемы абсорбционных установок........................... 606
6. Расчет насадочных абсорберов..............................608
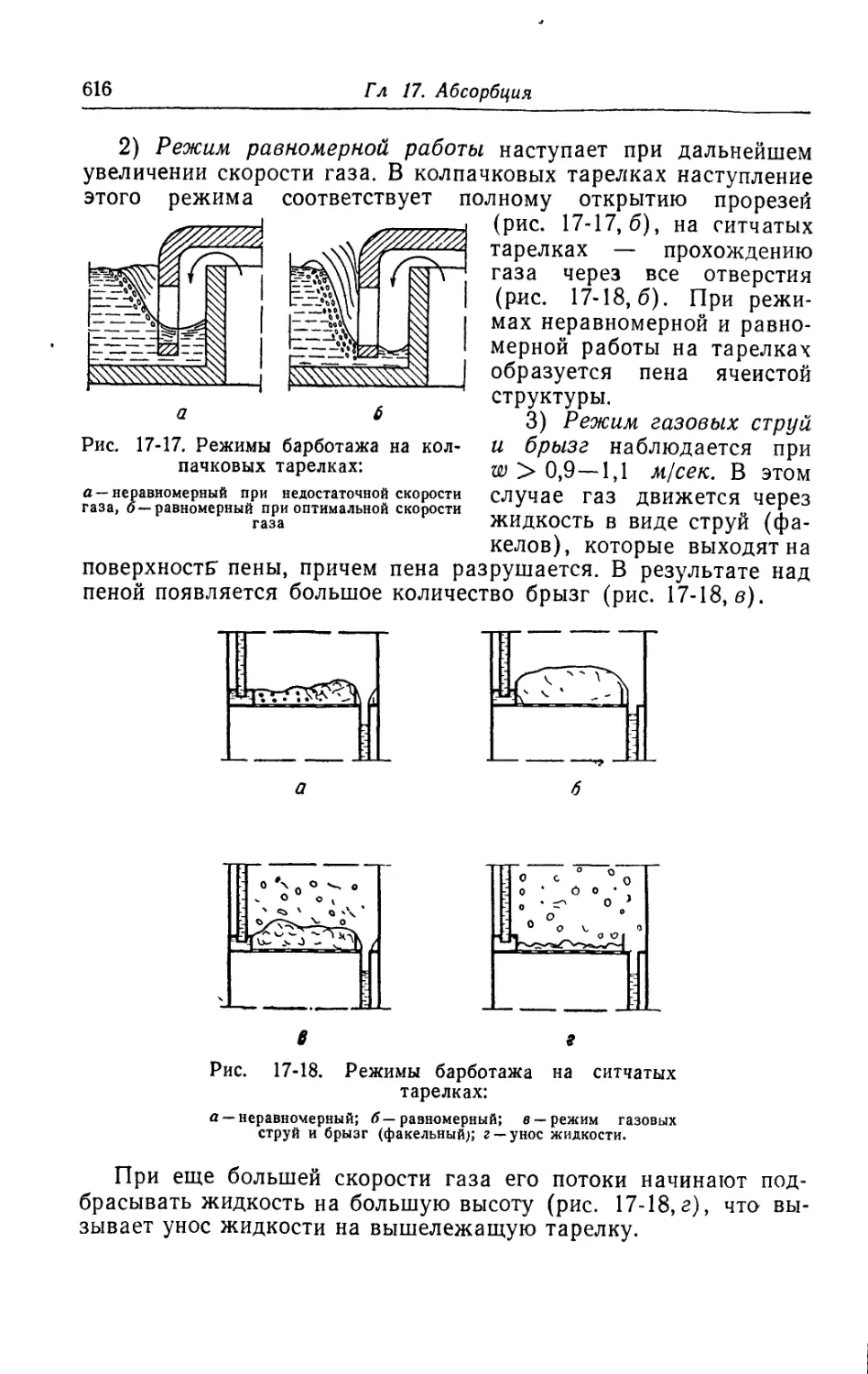
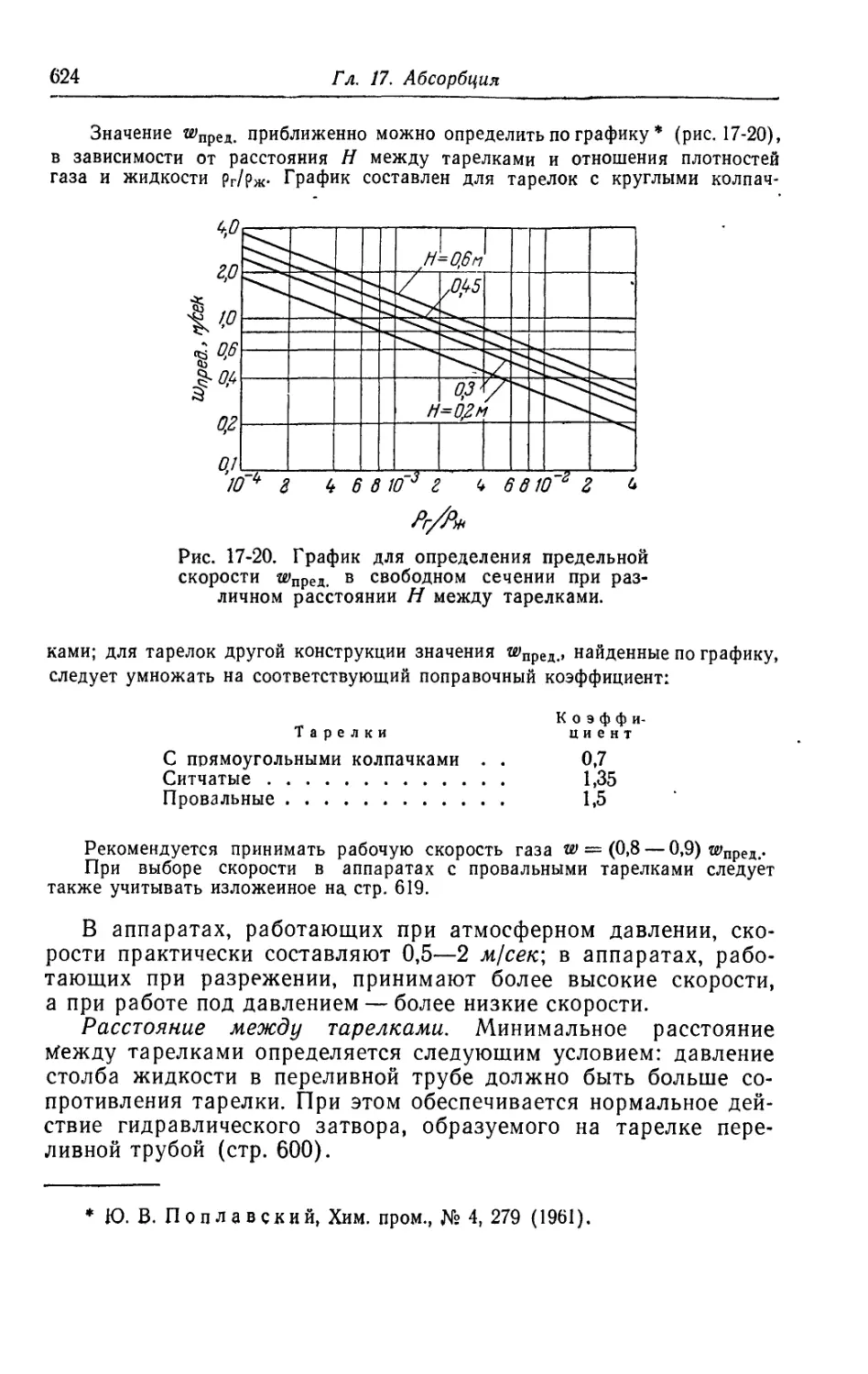
7. Расчет барботажных абсорберов.............................615
Глава 18
Экстракция
1. Общие сведения..............................................631
2. Физические основы процесса экстракции.......................632
3. Устройство экстракторов.....................................636
4. Схемы экстракционных установок..............................646
5. Сравнение и выбор экстракторов..............................649
6. Расчет экстракторов.........................................651
Глава 19
Ректификация
1. Общие сведения..........................................657
2. Основные свойства смесей жидкостей и их паров...........658
3. Материальный й тепловой балансы процесса ректификации . . 670
4. Схемы ректификационных установок........................683
5. Устройство ректификационных аппаратов...................688
6. Эксплуатация ректификационных установок.................689
7. Ректификация сжиженных газов............................690
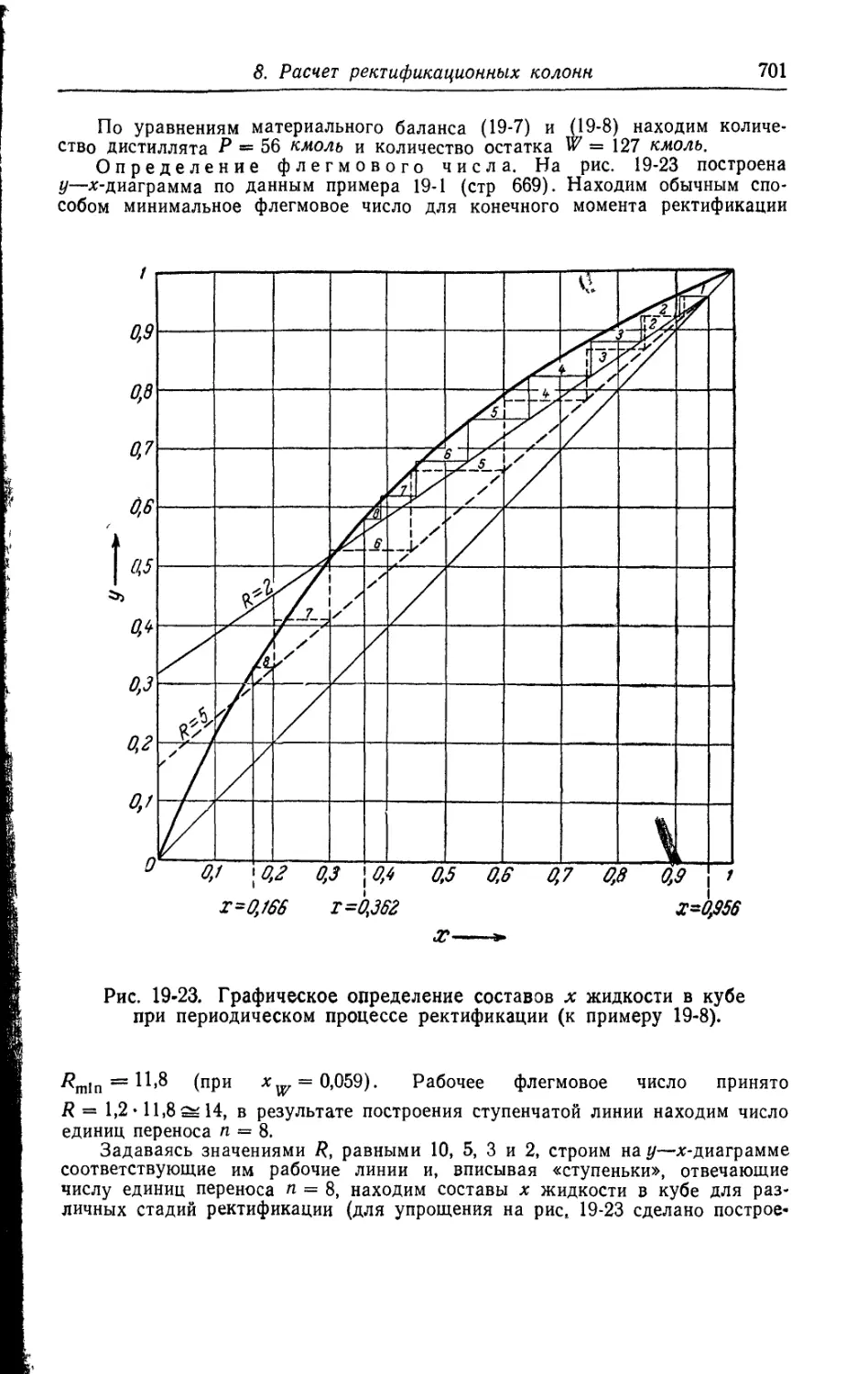
8. Расчет ректификационных колонн..........................692
9. Простая перегонка.......................................703
10. Специальные виды перегонки..............................708
8
Содержание
Глава 20
Адсорбция
1. Общие сведения................................................712
2. Теория адсорбции ............................................ 713
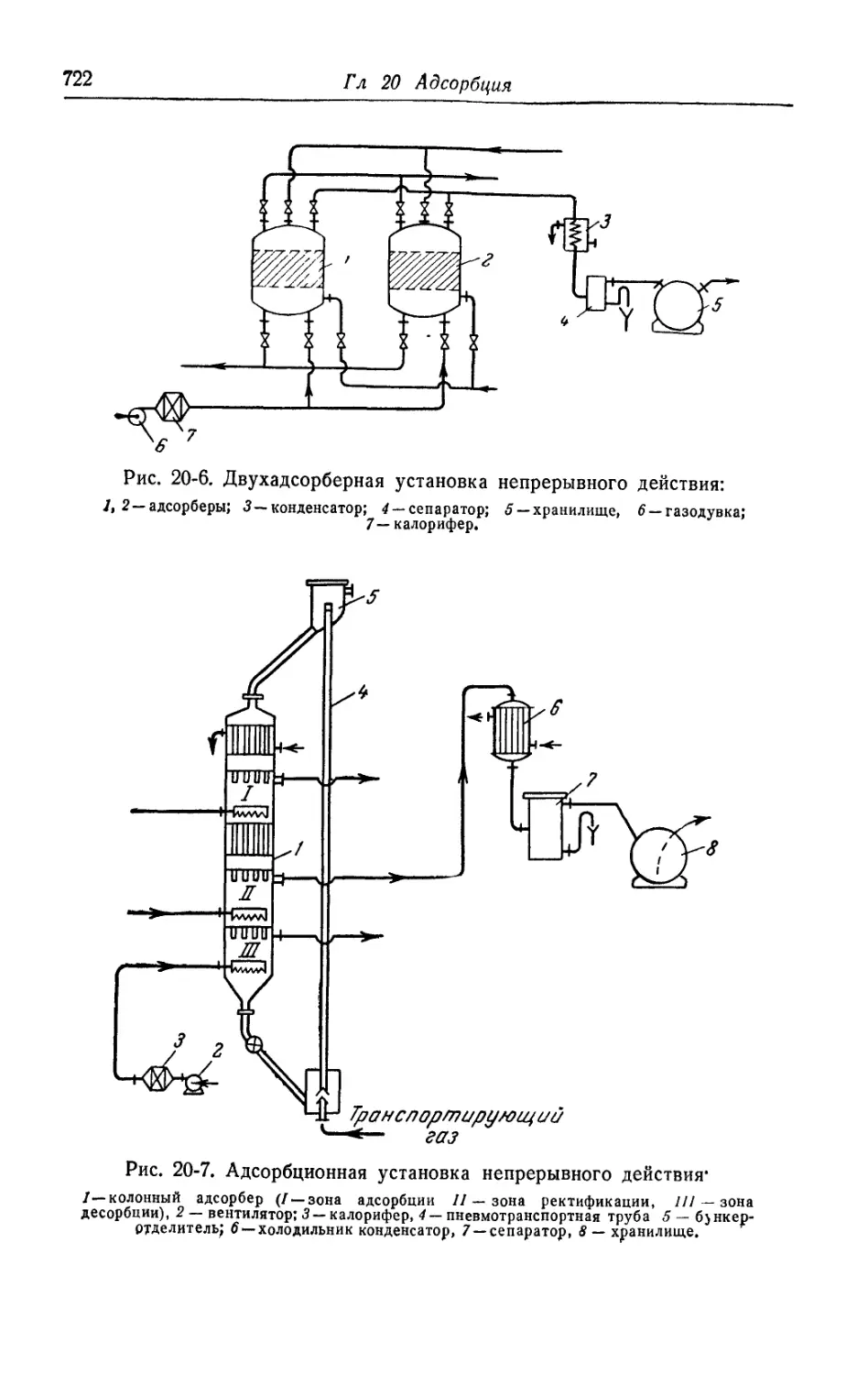
3. Устройство адсорберов.........................................717
4. Расчет адсорберов.............................................723
Глава 21
Сушка
1. Общие сведения...............................................731
2. Статика сушки................................................732
3. Свойства влажного газа (воздуха).............................736
4. / — х-диаграм-ма влажного воздуха............................739
5. Материальный и тепловой балансы процесса сушки...............743
6. Изображение процесса сушки на / — х-диаграмме................751
7. Схемы сушки..................................................753
8. Кинетика сушки...............................................757
9. Устройство сушилок...........................................765
10. Сравнение и выбор сушилок....................................783
11. Расчет сушилок...............................................785
12. Специальные способы сушки....................................797
Приложения
I. Плотность жидких веществ и водных растворов.........804
И. Вязкость жидких веществ и водных растворов...........806
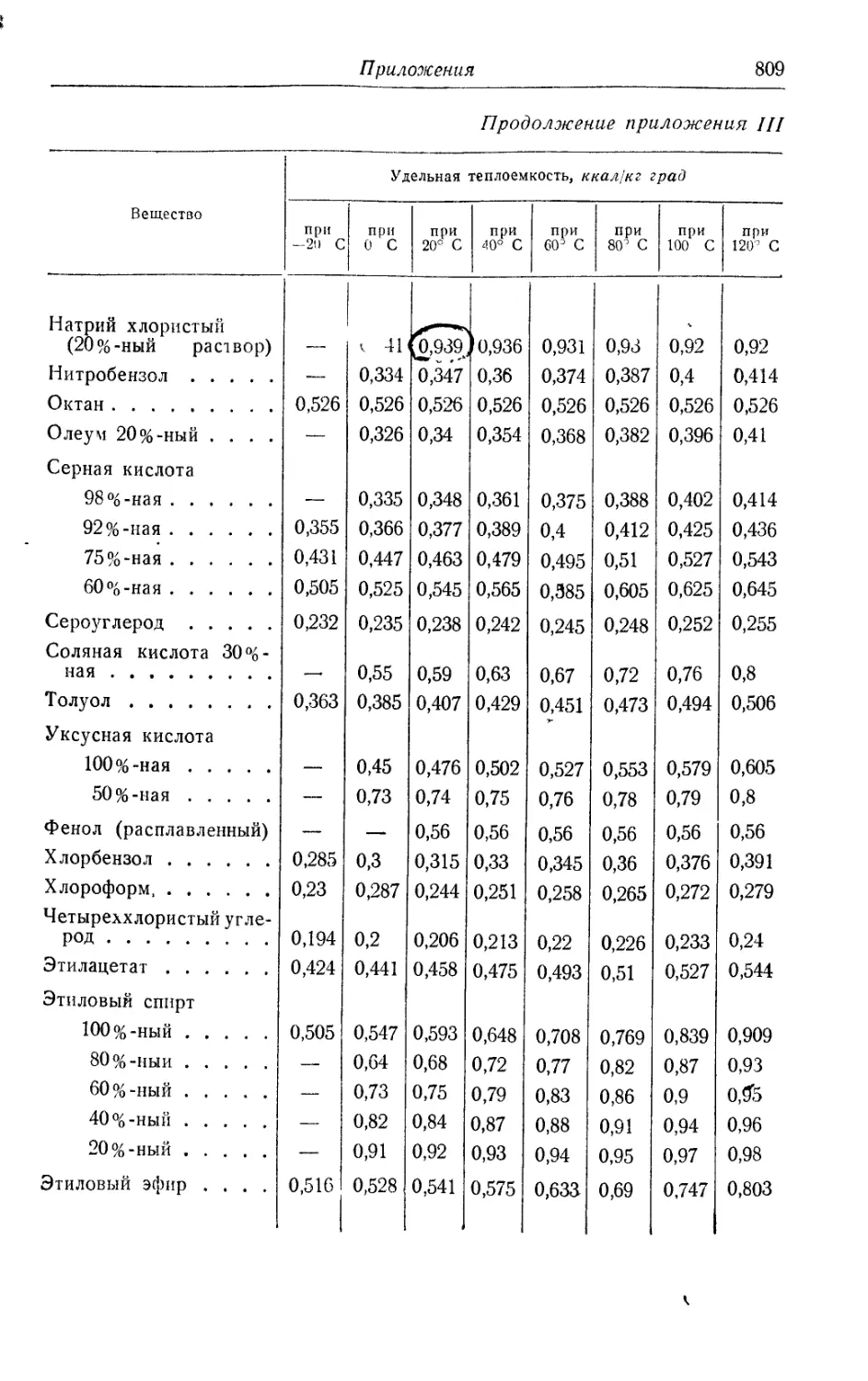
III. Удельная теплоемкость жидких веществ и водных растворов . . . 808
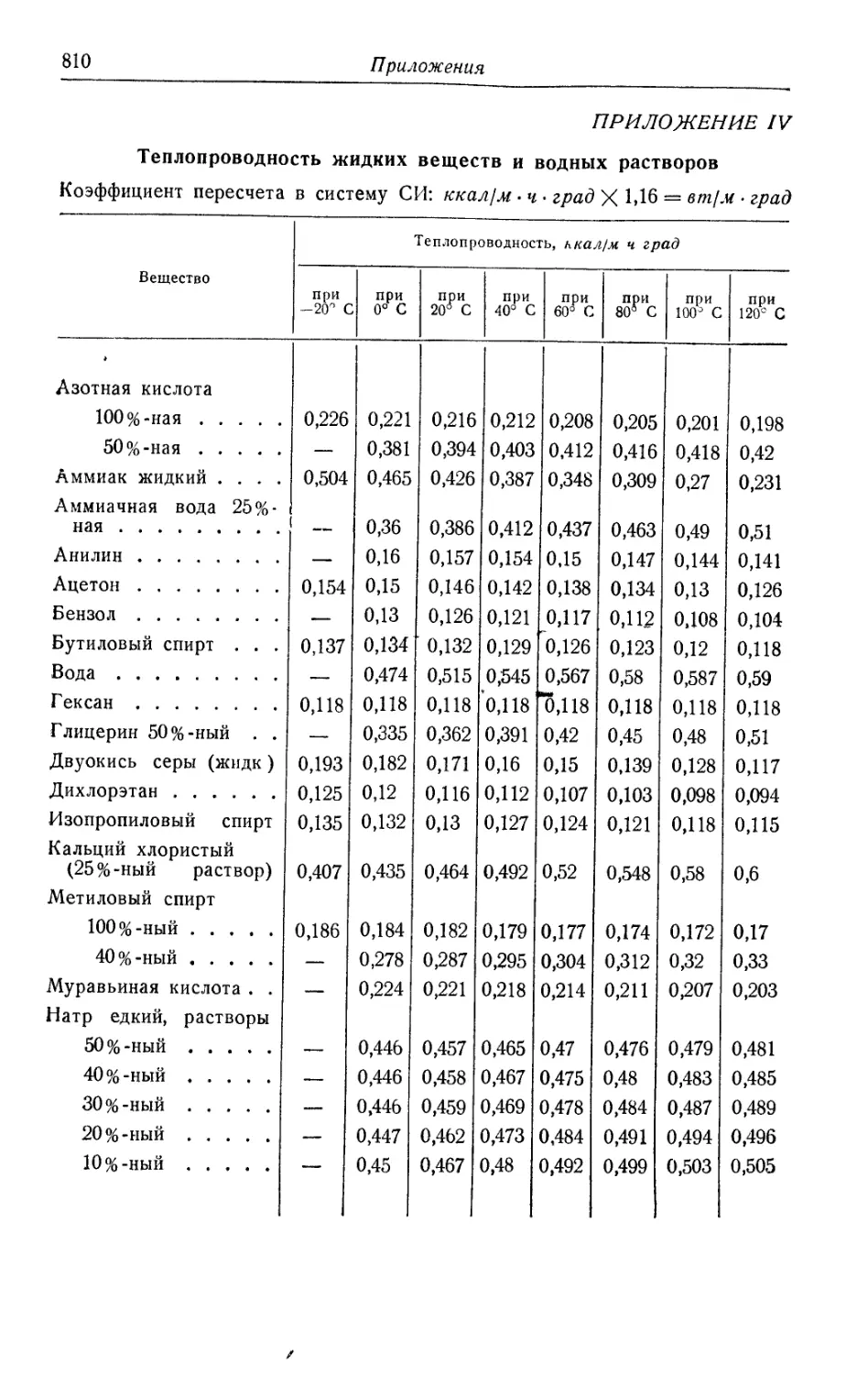
IV. Теплопроводность жидких веществ и водных растворов..810
V. Поверхностное натяжение жидких веществ и водных растворов . 812
VI. Коэффициент р объемного расширения жидких веществ и водных
растворов .............................................814
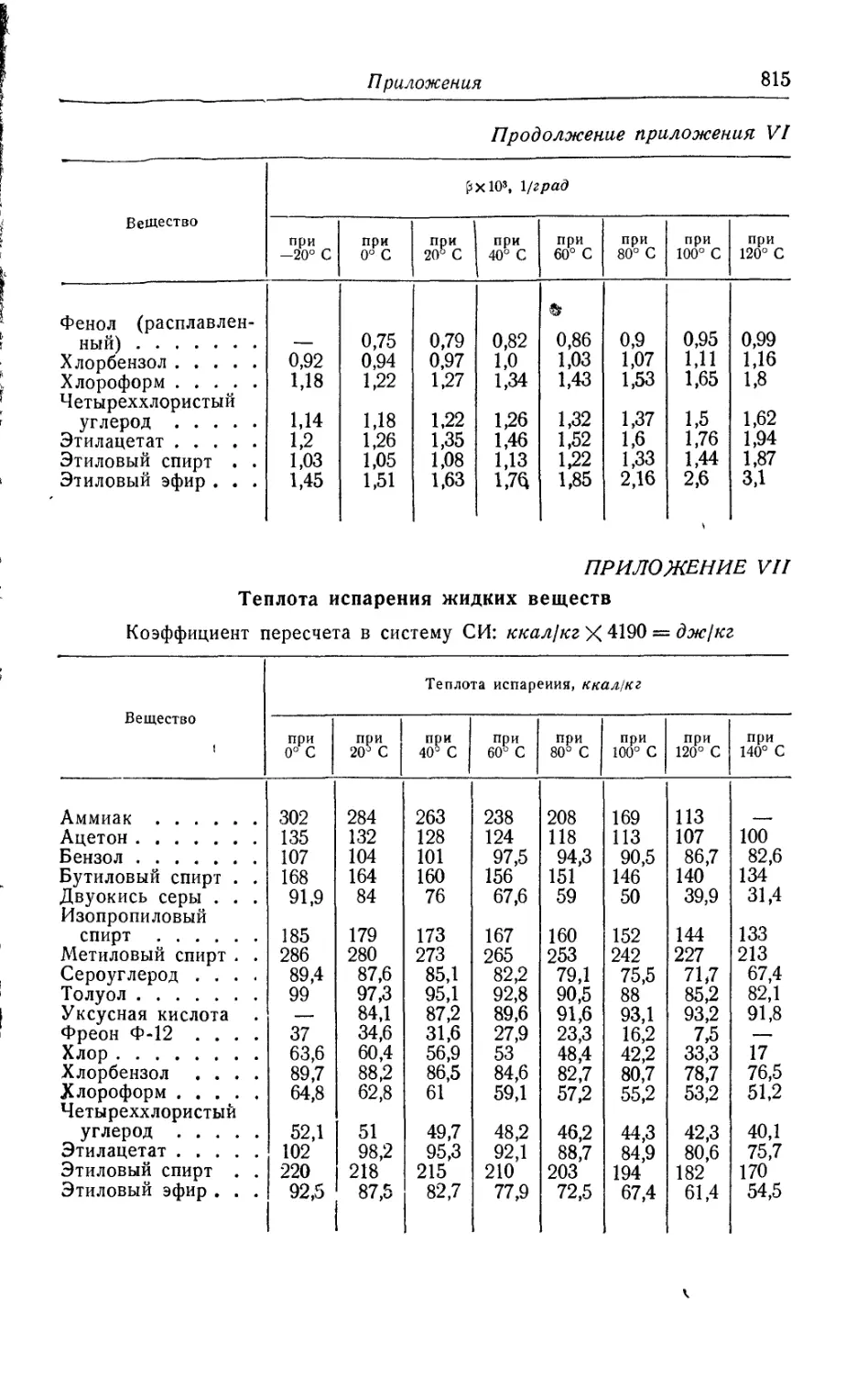
VII. Теплота испарения жидких веществ...............................815
VIII. Растворимость твердых веществ в воде и теплота кристаллиза-
ции <?Кр. ................................................816
IX. Температурная депрессия водных растворов при абсолютном дав-
лении 1 ат ......................... 817
X. Равновесные составы жидкости (х) и пара (у) в мол. % и темпе-
ратуры кипения (0 в °C двойных смесей при 760 мм рт. ст. . . 818
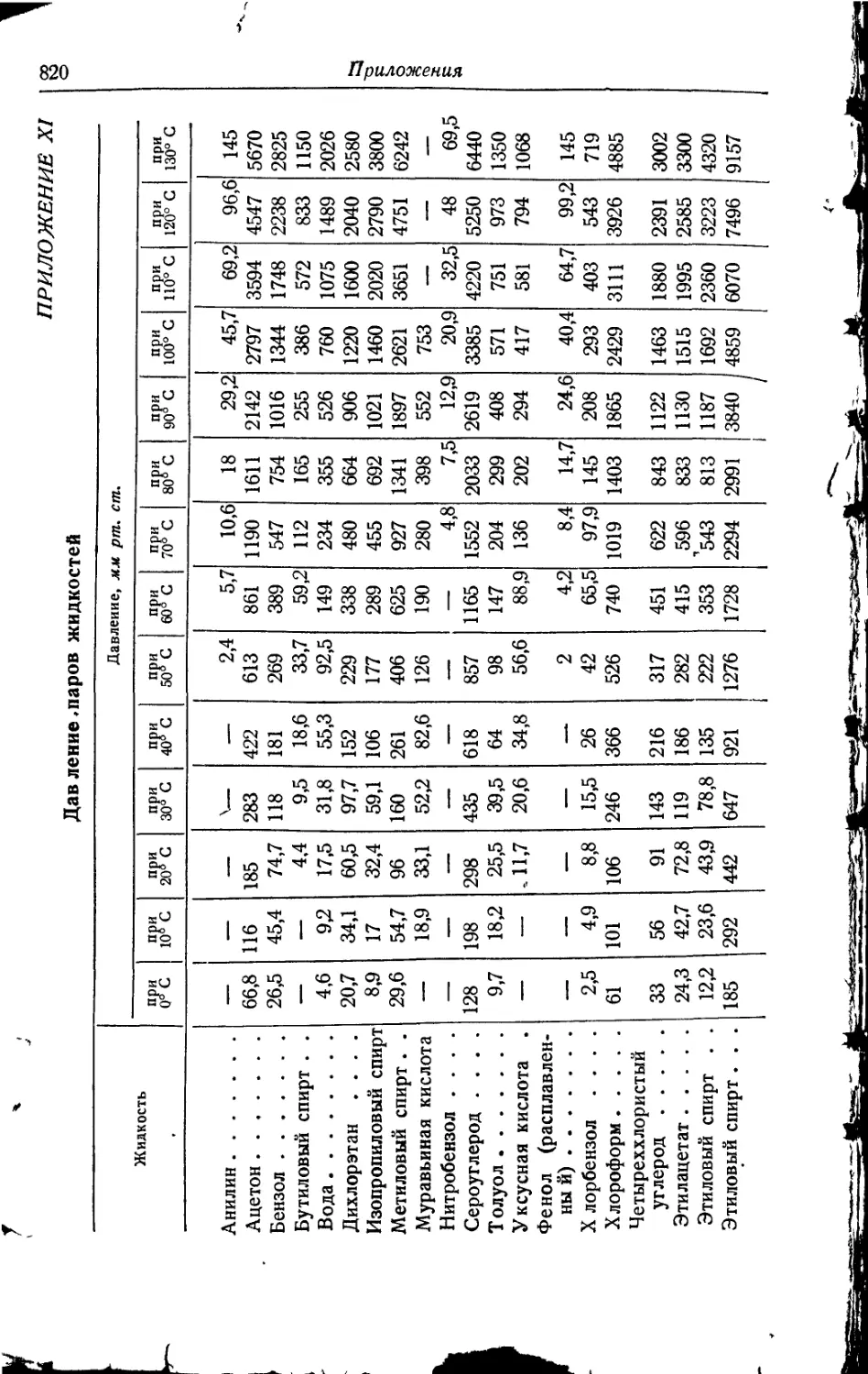
XI. Давление паров жидкостей.......................................820
XII. Параметры насыщенного водяного пара............................821
XIII. Удельная теплоемкость с (ккал/кг • град), вязкость ц (спз) и теп-
лопроводность А (ккал/м • ч/град) газов и паров...........822
XIV. Средняя объемная теплоемкость газов..............................825
XV. Коэффициенты диффузии D (в м2/сек) ............. 825
XVI. Значения коэффициента ф в формуле (17-1) растворимости газов
в воде....................................................826
XVII. Расчетные температуры to и относительная влажность <ро атмо-
сферного воздуха в различных районах СССР.................826
XVIII. Диаграмма р — i для аммиака (вклейка в конце книги)
XIX. Диаграмма / —х для влажного воздуха при 745 мм рт. ст. (вклейка
в конце книги)
Литература .............................. 828
Предметный указатель..................................................831
ПРЕДИСЛОВИЕ
Настоящая книга является вторым изданием учебника по
курсу «Процессы и аппараты химической технологии» для хими-
ческих техникумов. Она предназначена для учащихся технологи-
ческих и механических специальностей (техники-технологи и тех-
ники-механики химических производств).
К первому изданию учебник был подготовлен в соответ-
ствии с программами, разработанными. Управлением учебных
заведений Министерства химической промышленности СССР.
В раздел «Массообменные процессы» учебника авторы ввели
отсутствовавшую в программе главу «Экстракция», в этом же
разделе метод расчета высоты колонного аппарата по «теоре-
тическим тарелкам» был заменен более правильным методом
расчета по «единицам переноса».
Для более последовательного изложения учебного материала
холодильные процессы (умеренное и глубокое охлаждение) не
выделены в самостоятельную тему, а рассмотрены в разделе
«Тепловые процессы». В книгу не был включен раздел «Мате-
риалы химической аппаратуры», поскольку эти сведения доста-
точно полно освещаются в специальных учебных пособиях.
При подготовке книги ко второму изданию авторами вне-
сен в текст ряд изменений и дополнений, отражающих совре-
менный уровень развития теории основных процессов химической
технологии, и приведены описания новых конструкций аппаратов.
10
Предисловие
Одновременно были учтены замечания преподавателей Мо-
сковского и других химико-технологических техникумов, Ленин-
градского и Омского химико-механических техникумов, которым
авторы весьма признательны за высказанные ими советы и
пожелания по улучшению учебника.
Во втором издании книги раздел «Механические процессы»
дополнен сведениями о вибрационных транспортерах, пневма-
тическом транспорте в плотной фазе, дробилках и мельницах
для сверхтонкого измельчения, дозаторах для сыпучих мате-
риалов.
В главу «Основы гидравлики» включены разделы, посвящен-
ные движению тел в жидкости, течению жидкости через зерни-
стый и пористый слои, а также процессам, проводимым в кипя-
щем (псевдоожиженном) слое. Переработан расчет центрифуг,
описаны центрифуги новых типов (вибрационные и с выгрузкой
через сопла).
В разделе «Тепловые процессы» переработана методика рас-
чета теплообменных аппаратов, рассмотрены конструкции ин-
тенсивных теплообменников (пластинчатых, с оребренными по-
верхностями) и даны сведения о теплообмене в псевдоожижен-
ном слое.
В разделе «Массообменные процессы» полностью перерабо-
тана и расширена глава «Экстракция», уточнен метод расчета
барботажных абсорбционных и ректификационных колонн и опи-
саны некоторые новые типы аппаратуры (колонны с провальны-
ми тарелками, сушилки с кипящим слоем).
Все основные разделы книги дополнены примерами, иллю-
стрирующими применение методов расчета и расчетных фор-
мул.
В приложениях приведены справочные таблицы и диаграм-
мы, необходимые при выполнении расчетов по процессам и ап-
паратам. Кроме того, внесен ряд менее существенных изменений
и дополнений.
Содержание учебника соответствует программам, разра-
ботанным в 1962 г. Министерством высшего и среднего спе-
циального образования СССР для средних специальных учеб-
ных заведений.
Предисловие
11
В связи с тем, что в СССР с 1963 г. вводится как предпочти-
тельная Международная система единиц (СИ), излагаемый в
книге материал, формулы и расчеты приведены в соответствие
с этой системой. Одновременно в тексте и приложениях даны
указания по пересчету величин, выраженных в технической си-
стеме единиц, в систему единиц СИ. В примерах наряду с ве-
личинами, выраженными в системе единиц СИ, в скобках для
пояснения приводятся числовые значения этих величин в тех-
нической системе единиц.
Часть материала книги, выделенная мелким шрифтом, пред-
назначена для изучения данного курса по расширенной про-
грамме и может быть использована учащимися также при вы-
полнении курсовых проектов. Авторы предполагают, что препо-
даватели техникумов по мере прохождения учащимися курса
процессов и аппаратов будут давать указания об объеме мате-
риала, необходимом для усвоения учебной программы соответ-
ствующих специальностей, в зависимости от количества отведен-
ных на нее учебных часов.
В списке литературы, помещенном в конце книги, перечисле-
ны руководства и пособия, рекомендуемые для более глубокого
изучения различных разделов курса и для использования при
дипломном проектировании. Так, при выполнении дипломных
проектов желательно, наряду с данным учебником, использовать
в первую очередь следующие книги: А. Г. Касаткин, Основ-
ные процессы и аппараты химической технологии, 7-е изд., Гос-
химиздат, 1960; А. Н. Планов с кий, П. И. Н и к о л а е в, Про-
цессы и аппараты химической и нефтехимической технологии,
Гостоптехиздат, 1960; К. Ф. Павлов, П. Г. Романнов,-
А. А. Носков, Примеры и задачи по курсу процессов и аппа-
ратов химической технологии, 4-е изд., Госхимиздат, 1959;
И. И. Чернобыльский и др., Машины и аппараты химиче-
ских производств, 2-е изд., Машгиз, 1961.
Авторы выражают благодарность проф. П. Г. Романкову и
всему коллективу кафедры процессов и аппаратов химической
технологии Ленинградского технологического института им. Лен-
совета, а также канд. техн, наук В. И. Матрозову и преподава-
телям техникумов Е. А. Брацыхину и Л. С. Будыльской за цен-
12
Предисловие
ные указания, сделанные ими при рецензировании подгото-
вленной ко второму изданию книги, и с признательностью от-
мечают большую помощь, оказанную авторам канд. техн, наук
Л. Р. Стоцким его советами по пересчету учебного материала
в Международную систему единиц (СИ).
Все критические замечания читателей будут приняты авто-
рами с благодарностью.
Авторы
ВВЕДЕНИЕ
Предмет и задачи курса «Процессы и аппараты».
Классификация процессов
Современная химическая технология изучает процессы про-
изводства минеральных кислот и удобрений, щелочей и солей,
процессы синтеза разнообразных органических соединений из
природных газов и продуктов переработки каменного угля и
нефти, а также многие другие процессы химической переработки
синтетических и природных веществ. Несмотря на разнообразие
методов химической технологии, получение различных химиче-
ских продуктов связано с проведением однотипных физических
процессов (нагревание, охлаждение, перемешивание, фильтрова-
ние, сушка и т. д.), являющихся общими для большинства хими-
ческих производств. Аппаратурное оформление современных хи-
мико-технологических процессов также весьма разнообразно,
однако для одних и тех же целей в различных отраслях химиче-
ской технологии в большинстве случаев применяются сходные по
конструкции аппараты. «
В курсе «Процессы и аппараты» изучаются физико-химиче-
ские основы процессов, используемых во всех отраслях химиче-
ской технологии, а также рассматриваются принципы устройства
и методы расчета аппаратов, предназначенных для проведения
этих процессов. Выявление общих закономерностей протекания
различных процессов и разработка методов расчета аппаратуры
являются основными задачами науки о процессах и аппаратах
химической технологии.
Овладение этой наукой позволяет осуществлять в производ-
ственных условиях наилучшие (оптимальные) технологические
режимы, повышать производительность аппаратуры и улучшать
качество продукции; дает возможность разрабатывать более
рациональные технологические схемы и типы аппаратов при про-
ектировании новых производств, правильно оценивать результа-
ты лабораторных исследований и быстро реализовать их в про-
изводственных условиях.
Применяемые в химических производствах вещества обычно
измельчаются, транспортируются, нагреваются, охлаждаются,
14
Введение
реагируют друг с другом, причем взаимодействие их часто со-
провождается испарением, растворением и другими процессами,
связанными с переходом веществ из одной фазы в другую
(массообмен) или с образованием новых химических продук-
тов. Эти процессы подчиняются законам гидромеханики, тепло-
передачи, массопередачи и химической кинетики. В простейшем
случае процесс может быть охарактеризован лишь одним за-
коном, например законом движения жидкости, но чаще это
движение сопровождается теплообменом, массообменом и дру-
гими явлениями, т. е. протекает сложный процесс, зависящий
от целого ряда факторов, которые оказывают на ход процесса
совместное и часто противоречивое действие.
В курсе «Процессы и аппараты» изучаются принципы хими-
ческой технологии, основанные на законах гидромеханики, теп-
лопередачи и массопередачи, а также механики твердых тел
(измельчение и смешение). Процессы же химического взаимо-
действия подробно рассматриваются в курсах общей и спе-
циальной химической технологии.
В зависимости от закономерностей, характеризующих проте-
кание процессов, последние могут быть разделены на следую-
щие группы:
1. Механические процессы, применяемые для переработки
твердых материалов и подчиняющиеся законам механики твер-
дого тела. К таким процессам относятся: перемещение материа-
лов, измельчение, классификация (сортировка) материалов по
крупности, их дозировацие и смешивание.
2. Гидромеханические процессы, используемые при перера-
ботке жидкостей и газов, а также неоднородных систем, состоя-
щих из жидкости и мелко измельченных твердых частиц, взве-
шенных в жидкости (суспензий). Движение жидкостей, газов и
суспензий характеризуется законами механики жидких тел —
гидромеханики. К числу гидромеханических процессов относятся:
перемещение жидкостей и газов, перемешивание в жидкой сре-
де, разделение жидких неоднородных систем (отстаивание,
фильтрование, центрифугирование), очистка газов от пыли.
3. Тепловые процессы, связанные с теплообменом, т. е. пере-
ходом тепла от одного вещества к другому. К этим процессам
относятся: нагревание, охлаждение, процессы, протекающие с
изменением агрегатного состояния вещества, — испарение, кон-
денсация, плавление и затвердевание, а также процессы выпа-
ривания, кристаллизации и получения искусственного холода.
4. Массообменные процессы, заключающиеся в переходе
вещества (массы) из одной фазы в другую путем диффу-
зии. К этой группе относятся следующие процессы перехода
веществ:
Предмет и задачи курса «Процессы и аппараты»
15
а) из твердрй фазы в жидкую (растворение твердых ве-
ществ) или из жидкой фазы в твердую (кристаллизация);
б) из одной жидкой фазы в другую жидкую фазу (экстрак-
ция);
в) из жидкой фазы в газообразную (испарение жидкости, де-
сорбция растворенного газа из жидкости) или из газообразной
фазы в жидкую (конденсация пара из его смеси с газами, аб-
сорбция газа жидкостью);
г) из жидкой фазы в парообразную и одновременно из па-
рообразной фазы в жидкую (ректификация);
\у- д) из твердой фазы в газообразную (возгонка, десорбция
газов из твердых тел) или из газообразной фазы на поверх-
ность твердых тел (адсорбция газов твердыми телами).
Важнейшие массообменные процессы: сушка твердых мате-
риалов, ректификация и сорбция (поглощение газов жидкостя-
ми или твердыми веществами).
Указанные механические, гидромеханические, тепловые и мас-
сообменные процессы широко применяются в большинстве хи-
мических производств и потому называются основными процес-
сами химической технологии.
Процессы химической технологии проводятся периодически
или непрерывно. В периодическом процессе исходные вещества
загружаются в аппарат и реагируют или обрабатываются в нем,
после чего полученные продукты выгружают, и аппарат загру-
жают вновь. При этом все стадии процесса протекают во всем
объеме аппарата, но условия взаимодействия или обработки
веществ внутри аппарата — температура, давление, концентра-
ция и т. д. — изменяются во времени. В непрерывном процессе
загрузка аппарата и выгрузка производятся непрерывно. При
этом все стадии процесса протекают одновременно, но в разных
точках объема аппарата, причем в каждой его точке темпера-
тура, давление и другие параметры процесса остаются неиз-
менными во времени.
Применение непрерывных процессов позволяет значительно
повысить производительность аппаратуры, облегчает автомати-
зацию и механизацию производства и дает возможность улуч-
шить качество и однородность получаемых продуктов. Аппараты
непрерывного действия компактнее периодически действующих
аппаратов, требуют меньших капитальных затрат и меньших
эксплуатационных расходов. Благодаря этим серьезным досто-
инствам непрерывные процессы вытесняют периодические, кото-
рые применяются в настоящее время преимущественно в произ-
водствах небольшого масштаба и при разнообразном ассорти-
менте выпускаемой продукции.
16
Введение
Краткие исторические сведения
В древности и в средние века уже были известны различные
химико-технические процессы (фильтрование, выпаривание, пе-
регонка, сушка и др.), для проведения которых применялась
примитивная аппаратура.
С развитием химической промышленности в конце XVIII—
начале XIX вв. происходило совершенствование аппаратуры для
ранее применявшихся процессов; появились и новые процессы,
для осуществления которых создавались новые аппараты.
В начале XIX в. значительное развитие получили сахарная и
винокуренная отрасли промышленности, для которых были раз-
работаны различные аппараты, нашедшие затем широкое рас-
пространение. В этот период были созданы вакуум-выпарной ап-
парат (1812 г.), ректификационная колонна (1813 г.), фильтр-
пресс (1820 г.) и ряд других аппаратов, впоследствии значи-
тельно усовершенствованных.
Во второй половине XIX в. с развитием сернокислотной и га-
зовой промышленности приобретают распространение процессы
абсорбции и очистки газов, создаются и совершенствуются ап-
параты для этих процессов. В связи с необходимостью хранения
и перевозки скоропортящихся продуктов стала развиваться хо-
лодильная техника; сначала получили распространение воздуш-
ные холодильные машины (1845 г.), затем паровые компрес-
сионные холодильные машины (1874 г.).
В конце XIX — начале XX вв. с изобретением электроприво-
да и паровой турбины появилась возможность создания быстро-
ходных машин: центрифуг, центробежных насосов, турбоком-
прессоров.
В связи с значительным увеличением масштабов производ-
ства химической продукции большее внимание стали уделять
разработке непрерывных процессов. В этот период начинает раз-
виваться техника низких температур и высоких давлений. Раз-
рабатываются такие процессы, как глубокое охлаждение
(1895 г.), электрическая очистка газов (1906 г.), появляются
фильтры непрерывного действия (1904 г.).
После первой мировой войны химическая промышленность
стала одной из ведущих отраслей хозяйства, охватывающей мно-
гочисленные производства разнообразных неорганических и ор-
ганических продуктов, имеющих жизненно важное значение. Воз-
никли и получили промышленное применение процессы адсорб-
ции, экстракции, молекулярной дистилляции и др.
Отсутствие теории процессов и методов расчета аппаратов
длительное время задерживало внедрение аппаратуры прогрес-
сивных типов и приводило к излишним затратам средств и вре-
Краткие исторические сведения
17
мени. Лишь в начале XX в., в результате обобщения производ-
ственного опыта, начала развиваться теория процессов' и аппа-
ратов, которая достигла значительных успехов в последние де-
сятилетия. В настоящее время на основании теоретических рас-
четов и опытов, проведенных на модельных установках, в ряде
случаев можно правильно сконструировать и построить аппа-
раты промышленного типа. Однако еще остается большое ко-
личество неизученных и недостаточно исследованных вопросов.
Развитие химической техники неразрывно связано с интенси-
фикацией физических процессов, применяемых в химической тех-
нологии. Известно, что скорость ряда процессов возрастает с
увеличением скорости движения и поверхности соприкосновения
реагентов. Поэтому в последние годы в химической промышлен-
ности стали применять новые высокопроизводительные аппара-
ты, в которых скорости тепло- и массообмена возрастают во мно-
го раз благодаря тонкому распылению жидкостей, интенсивному
перемешиванию реагентов, проведению процессов в кипящем
(псевдоожиженном) слое твердого сыпучего материала и т. д.
В результате интенсификации технологических процессов,
внедрения непрерывных методов производства, автоматизации и
механизации значительно возросли производственные мощности
химической промышленности и неизмеримо повысился ее техни-
ческий уровень. В современных химических производствах ис-
пользуются низкие и высокие температуры (от —185° С при раз-
делении газовых смесей методом глубокого охлаждения до
+ 3000° С в электрических печах при производстве карбида каль-
ция), глубокий вакуум, высокие и сверхвысокие давления (от
0,0001 мм pm. cm. при разделении и очистке смесей высокомоле-
кулярных веществ до 1000 ат в процессах синтеза аммиака идо
2000 ат в производстве полиэтилена), большое применение по-
лучили различные катализаторы — вещества, значительно уско-
ряющие многие химические процессы. Достижения в области
мирного использования атомной энергии открывают широкие
перспективы для дальнейшего глубокого изучения и интенсифи-
кации химических процессов.
Успехи в области машиностроения и металлургии, освоившей
производство разнообразных сплавов (обладающих химической
стойкостью и высокой механической прочностью, устойчивых к
износу, к действию высоких температур), а также все расши-
ряющееся применение пластических масс в качестве конструк-
ционных материалов позволили значительно усовершенствовать
многие аппараты и машины, используемые в химической про-
мышленности. В частности, были созданы насосы для перекачи-
вания кислот, компрессоры для высоких давлений, высокопроиз-
водительные ректификационные колонны диаметром до 10 м и
2 Зак. 546,
18
Введение
высотой 50 м и более, представляющие собой сложные, полно-
стью автоматизированные агрегаты, и др. Достижения в области
сварки обусловили переход к цельносварной аппаратуре, кото-
рая почти полностью вытеснила клепанную — более громоздкую,
тяжелую и дорогую.
За годы Советской власти в нашей стране сделан гигантский
скачок от слабо развитой, технически отсталой химической про-
мышленности дореволюционной России к современной мощной
химической промышленности. В СССР построены десятки круп-
ных химических предприятий и реконструированы на новой тех-
нической основе старые химические заводы. Благодаря успехам
химического машиностроения отечественная химическая про-
мышленность оснащена мощной высокопроизводительной аппа-
ратурой и оборудованием. В настоящее время по объему про-
дукции химической промышленности Советский Союз занимает
второе место в мире.
В новой Программе партии, принятой XXII съездом КПСС,
в качестве одного из основных направлений технического про-
гресса на пути создания материально-технической базы комму-
низма предусмотрена глубокая химизация всех отраслей народ-
ного хозяйства. В течение ближайших 20 лет намечено резко
увеличить объем химической продукции, особенно быстро будет
развиваться производство синтетических материалов, минераль-
ных удобрений и химических средств защиты растений. Химиче-
ские процессы будут дополнять, а в ряде случаев заменять ме-
ханическую переработку.
Для осуществления грандиозных планов развития химиче-
ской промышленности Советского Союза необходимы дальней-
шая интенсификация и механизация производственных процес-
сов, разработка и создание новых высокопроизводительных ап-
паратов и машин, широкое применение автоматического контро-
ля и управления, быстрое внедрение в промышленность новей-
ших достижений науки и техники. В решении всех этих задач
важную роль должна сыграть наука о процессах и аппаратах
химической технологии.
Глава 1
ОБЩИЕ СВЕДЕНИЯ
1. Применение основных физических законов
к изучению процессов
Процессы химической технологии связаны с разнообразными
физическими и химическими явлениями. Однако большинство
этих процессов характеризуется сравнительно ограниченным чис-
лом физических законов. Применение основных законов физики
к изучению процессов химической технологии составляет теоре-
тическую основу курса «Процессы и аппараты». Так, на законах
сохранения массы и энергии основаны материальный и энерге-
тический балансы. Для большинства процессов весьма важное
значение имеют законы, характеризующие условия равновесия
процессов, а также законы, описывающие изменения в системах,
не находящихся в равновесии.
Материальный баланс. По закону сохранения мас°ы, количе-
ство веществ, поступающих на переработку (2Онач), равно коли-
честву веществ, получаемых в результате переработки (SGK0H.),
т. е. приход вещества равен расходу. Это можно представить в
виде уравнения материального баланса:
^нач. кон.
Для периодических процессов материальный баланс соста-
вляется на одну операцию, для непрерывных процессов — за
единицу времени, например за 1 ч.
Материальный баланс можно составить для одного аппарата,
для его части (пример составления баланса для части аппара-
та — см. стр. 568) или для группы аппаратов. В то же время
материальный баланс может быть составлен для всех перера-
батываемых веществ или только для одного из компонентов.
Рассмотрим, например, фильтрование суспензии. В результа-
те фильтрования получаются осадок и фильтрат В данном слу-
чае перерабатываемый материал состоит из двух компонентов:
твердого вещества и жидкости. Уравнение материального балан-
са можно составить либо для общего количества суспензии, либо
2*
20
Гл. 1. Общие сведения
для твердого вещества, либо для жидкости. Из этих трех урав-
нений независимыми будут только два. Так, уравнение мате-
риального баланса для общего количества суспензии полу-
чится, если сложить почленно уравнения материального баланса
для твердого вещества и для жидкости.
Энергетический баланс. По закону сохранения энергии, коли-
чество энергии, введенной в процесс, равно количеству ее, полу-
ченному в результате проведения процесса, т. е. приход энергии
равен расходу ее.
Энергия может вводиться в процесс и отводиться вместе с
участвующими в нем веществами или отдельно от них. Энергия,
вводимая и отводимая с веществами, состоит из внутренней, по-
тенциальной и кинетической энергии этих веществ (стр. 134).
К энергии, вводимой и отводимой из процесса отдельно от
участвующих в нем веществ, относятся: тепло, подводимое в ап-
парат путем его обогрева через стенку или электрическим то-
ком; механическая работа, затрачиваемая в насосе или компрес-
соре, а также тепло, теряемое аппаратом в окружающую среду.
Наиболее общим выражением энергетического баланса при-
менительно к процессам химической технологии является обоб-
щенное уравнение Бернулли (стр. 139).
Условия равновесия. Любой процесс протекает до тех пор,
пока не установится состояние его равновесия. Так, жидкость
перетекает из сосуда с более высоким уровнем ее в сосуд с бо-
лее низким уровнем до тех пор, пока уровни жидкости в обоих
сосудах не сравняются. Тепло передается от более нагретого
тела к менее нагретому до тех пор, пока температура обоих тел
не станет одинаковой. Соль растворяется в воде до тех пор,
пока раствор не станет насыщенным. Подобных примеров мож-
но привести бесчисленное множество. Условия равновесия ха-
рактеризуют так называемую статику процесса и показывают
пределы, до которых может протекать данный процесс.
Условия равновесия выражаются разными законами; к
ним относятся второй закон термодинамики и законы, характе-
ризующие соотношение между концентрациями компонента в
различных фазах системы.
Скорость процесса. Если какая-либо система не находится в
состоянии равновесия, то обязательно возникает процесс, стре-
мящийся привести эту систему к равновесию. При этом обычно
скорость процесса тем больше, чем больше отклонение системы
от состояния равновесия. Отклонение системы от состояния рав-
новесия выражает, таким образом, движущую силу г процесса.
Следовательно, чем больше движущая сила, тем больше ско-
рость процесса. По мере приближения к равновесию движущая
сила и скорость процесса уменьшаются, достигая нуля в состоя-
2. Общие методы расчета химической аппаратуры
21
нии равновесия. Вблизи состояния равновесия скорость процесса
весьма мала и продолжает уменьшаться при приближении к рав-
новесию, поэтому для его достижения требуется бесконечно
большое время. Однако обычно может быть сравнительно быст-
ро достигнуто состояние, столь близкое к равновесию, что прак-
тически его можно рассматривать как равновесное.
Для практических расчетов весьма важно знать скорость про-
цесса в различных его стадиях, или так называемую кинетику
процесса. Во многих случаях скорость процесса пропорциональна
движущей силе. Такая простая зависимость наблюдается при
фильтровании (стр. 178), при передаче тепла путем теплопро-
водности и конвекции (стр. 369 и 370), в процессах массопере-
дачи (стр. 570). В этих случаях уравнение скорости процесса
имеет следующий вид:
(1-1)
где N — количество вещества или тепла, передаваемое через по-
верхность F за время т;
К — коэффициент пропорциональности (коэффициент ско-
рости процесса);
А — движущая сила процесса.
В тепловых процессах через F обозначают поверхность тепло-
обмена, т. е. поверхность, через которую передается тепло
(стр. 363), в процессах массопередачи F — поверхность сопри-
косновения фаз.
Левая часть уравнения (1-1) представляет собой скорость
процесса.
Коэффициент скорости процесса К обычно находят из опыта,
расчетное определение его в ряде случаев представляет значи-
тельные трудности.
2. Общие методы расчета химической аппаратуры .
Основными задачами при расчете любого химического аппа-
рата являются:
1) определение расхода энергии, пара, воды и других тепло-
энергетических средств;
2) определение размеров аппарата, необходимых для обеспе-
чения заданной производительности, или, наоборот, определение
производительности аппарата по заданным размерам его.
Определение расхода теплоэнергетических средств произво-
дится на основании энергетического баланса аппарата. Наибо-
лее часто приходится определять расход пара и воды. Этот во-
прос подробно рассматривается на стр. 440.
22
Гл. 1. Общие сведения
Размеры аппарата определяются на основе данных о кине-
тике процесса. Исходя из этих данных, определяют время пре-
бывания обрабатываемого вещества в аппарате (продолжитель-
ность процесса), а из уравнения (1-1) находят необходимую по-
верхность F.
Рассмотрим основные случаи определения размеров аппара-
тов (количество перерабатываемого вещества V м3/сек счи-
тается известным).
1. Задано время пребывания вещества в аппарате т сек.
В этом случае определяется необходимая полезная емкость ап-
парата:
Кп. ~V?m3 (1-2)
2. Заданы время пребывания т сек и скорость прохождения
вещества через аппарат w м/сек. Площадь поперечного сечения
аппарата определяется по уравнению расхода (стр. 133):
s = (1-3)
Длина аппарата L, необходимая для соблюдения требуемого
времени пребывания в нем вещества, равна
м (1-4)
3. Заданы скорость w м/сек и поверхность теплообмена F м2.
Этот случай рассматривается при расчете теплообменных аппа-
ратов (стр. 444 и 448) .
4. Заданы скорость w м/сек и поверхность соприкосновения
фаз F м2. Этот случай рассматривается при расчете аппаратов
для массообмена, в частности при расчете насадочных колонн
(см. стр. 612).
Расчеты процессов и аппаратов часто вызывают у учащихся
значительные затруднения. Это объясняется некоторыми особен- ,
ностями таких расчетов, на которые мы считаем нужным обра-
тить внимание.
1. При решении математических задач даются коэффициен-
ты, характеризующие заданные величины, и внимание направле-
но на составление уравнения, которое имеет определенное реше-
ние. В расчетах процессов и аппаратов уравнение обычно из- «
вестно и основная трудность заключается в выборе значений тех
параметров, которые входят в расчетное уравнение. Некоторые
из них (например, характеристики физико-химических свойств
вещества) берутся по справочным таблицам, другие (например,
скорость прохождения вещества через аппарат) могут быть при-
няты более или менее произвольно, значения некоторых величин
3. Системы размерностей
23
(например, температуру стенки при тепловых расчетах) прини-
мают как ориентировочные и проверяют принятые значения их
в конце расчета. Следует также отметить, что большинство за-
дач по расчетам процессов и аппаратов не имеет однозначного
ответа — в зависимости от принятых величин могут получиться
различные размеры аппаратов. В этом случае при выборе того
или иного размера надо руководствоваться технико-экономиче-
скими соображениями.
2. Наличие готовых уравнений создает ложное впечатление
возможности механической подстановки в эти уравнения извест-
ных данных. При этом часто используют уравнения, которые не-
применимы к данному случаю. Поэтому необходимо всегда тща-
тельно обдумывать, каким именно уравнением следует восполь-
зоваться в том или ином случае.
3. Отдельные коэффициенты, данные промежуточных расче-
тов и конечные результаты должны иметь определенную степень
точности. Излишняя точность вычислений бесполезна — она
лишь увеличивает затраты времени и создает большую возмож-
ность допущения ошибок. В большинстве случаев достаточна
точность до трех значащих цифр, достигаемая на логарифмиче-
ской линейке, с помощью которой и следует производить все
расчеты.
4. Полученные путем расчета размеры должны быть округле-
ны в соответствии с действующими стандартами и нормалями.
Многие размеры берутся, исходя из конструктивных соображе-
ний.
3. Системы размерностей
При расчете процессов и аппаратов приходится пользоваться
различными данными о физических свойствах веществ (плот-
ность, вязкость и др.) и параметрами, характеризующими со-
стояние этих веществ (скорость, давление и др.). Все эти вели-
чины могут измеряться различными единицами.
В настоящее время применяется несколько систем единиц из-
мерения. В зависимости от принятой системы та или иная физи-
ческая величина имеет определенную размерность. Размерность
данной величины представляет собой ее выражение через ве-
личины, положенные в основу определенной системы единиц.
Основной системой единиц является Международная система
единиц — система СИ, принятая XI Генеральной конференцией
по мерам и весам в октябре 1960 г. В СССР, согласно ГОСТ
9867—61, система единиц СИ вводится с 1 января 1963 г. и
должна применяться как предпочтительная. Допускается также
применение систем СГС и МКГСС и некоторых внесистемных
единиц измерения.
24
Гл. 1. Общие сведения
В основу системы СИ положена система единиц МКС
(метр — килограмм — секунда), в которой за основные вели-
чины приняты единицы длины — метр (л<), массы — килограмм
(кг) и времени — секунда (сек).
Система СГС (сантиметр — грамм — секунда) отличается от
системы СИ тем, что за единицу длины принят сантиметр (см),
а за единицу массы — грамм (а). Эта система применяется глав-
ным образом для физических измерений.
Система МКГСС (метр — килограмм-сила — секунда) отли-
чается от системы СИ тем, что за основную величину вместо
единицы массы принята единица силы — килограмм-сила (кгс,
или кГ). Эта система применяется при механических измере-
ниях.
Стандартами допускается применение кратных и дольных
единиц измерения, образуемых путем умножения данной еди-
ницы на число 10 в определенной степени. При этом перед
наименованием величины пишут приставки, обозначающие соот-
ветствующую кратность или дольность данной основной едини-
цы. Например:
мега (Af) — 1 • 10е
кило (к) — 1 • 103
деци (д) = 1 • 10-1
санти (с) = 1 • 10~2
милли (м) — 1 • 10~3
микро (мк) — 1 • 10~6
Для тепловых измерений вводится четвертая основная вели-
чина — температура; единицей температуры является градус
(град). В зависимости от начальной точки отсчета различают:
абсолютную температуру (отсчет от абсолютного нуля), выра-
жаемую в градусах Кельвина (° К), и температуру по стоградус-
ной шкале (отсчет от точки плавления льда), выражаемую в гра-
дусах Цельсия (°C).
Рассмотрим единицы измерения некоторых величин, наибо-
лее часто применяемых в курсе «Процессы и аппараты».
Длина. Основной единицей длины является метр (м), а в си-
стеме СГС — сантиметр (см). Применяются также дольные еди-
ницы: дециметр (дм) и миллиметр (мм), а из внесистемных еди-
ниц—микрон (мк), причем:
1 м ~ 10 дм — 100 см == 1000 мм =1 • 106 мк
Площадь (и поверхность) в системах СИ и МКГСС имеет
размерность м2, в системе СГС — сл*2, причем 1 л*2 = 10 000 см2.
Объем в системах СИ и МКГСС имеет размерность ;и3, в си-
стеме СГС — см3. Из внесистемных единиц применяют литр (л),
приближенно равный 1 cbt3 (кубическому дециметру). При этом
1 м3=1 . Ю6см3^1000л
3. Системы размерностей
25
Время. Основной единицей времени во всех системах яв-
ляется секунда (сек). В качестве внесистемных единиц приме-
няют час (ч) и минуту (мин). Для выражения производительно-
сти установок и оборудования часто используют также непреду-
смотренные стандартами единицы времени: сутки и год.
Скорость в системе СИ, а также в системе МКГСС имеет
размерность м/сек, а в системе СГС — см/сек.
Ускорение в системе СИ, а также в системе МКГСС имеет
размерность м/сек? (метр на секунду в квадрате), а в системе
СГС — см/сек?.
Масса в системах СИ и СГС является основной величиной и
выражается соответственно в килограммах (кг) или граммах
(г). В системе МКГСС масса, как следует из основного закона
/ сила \
механики масса =------------ , имеет размерность:
\ ускорение / г г
г кгс • сек21
масса = -----—
L J
Единица массы, равная 1 кгс • сек?/м, иногда называется тех-
нической единицей массы (сокращенно т.е.м.). Часто приме-
няется также внесистемная единица массы — тонна (т). Между
размерностями массы в различных системах единиц существуют
следующие соотношения:
1 кг = 1000 г = ОД 02 кгс • сек2/м — 0,001 пг
В химической технологии массу часто выражают в молях
(моль) и киломолях (кмоль). Под киломолем (или молем) пони-
мают количество вещества в килограммах (или граммах), чис-
ленно равное молекулярному весу. Таким образом
1 кмоль == 1000 моль — М кг
где М — молекулярный вес *.
Сила является основной величиной в системе МКГСС, едини-
цей измерения силы служит килограмм-сила (кгс). Под кило-
грамм-силой понимают силу, сообщающую телу массой 1 кг
ускорение 9,81 м/сек?. На основании приведенного выше закона
механики (сила == масса X ускорение) сила в системах СИ и
СГС имеет размерность:
V кг • м д „ „ Г г • см 1
2 • в системе СИ -- в системе СГС
I Cc/v J [ СёК J
Единица силы, равная 1 кг-м/сек?, называется ньютоном (н);
единица силы, равная 1 г •см/сек?, называется диной (дин).
* В учебнике молекулярный вес в соответствии с принятой системой еди-
ниц СИ назван молекулярной массой.
26
Гл 1. Общие сведения
Сила 1 н сообщает телу массой 1 кг ускорение 1 м/сек2, сила
1 дин сообщает телу массой 1 г ускорение 1 см/сек2. Соотноше-
ние между единицами силы в различных системах следующее:
1 . Ю5 дин — 0,102 кгс
Вес (сила притяжения тела к Земле) определяется взвешива-
нием на пружинных весах и выражается в единицах силы («,
дин, кгс). Практически весом часто называют результат взвеши-
вания на рычажных весах, т. е. массу тела, и выражают его в
единицах массы (кг, г). В данной книге под весом тела будет
пониматься только сила притяжения его к Земле, выраженная в
единицах силы. Следует отметить, что вес тела в кгс и его масса
в кг выражаются одинаковыми числовыми величинами (ошибка
в случае приравнивания веса тела в кгс к его массе в кг не пре-
вышает 0,2%).
Работа (и энергия) равна произведению силы на путь (дли-
ну); размерность работы будет соответственно: ньютон-метр
(н-м)— в системе СИ, дина-сантиметр (дин • см) — в системе
СГС и килограмм-сила-метр (кгс • м) —в системе МКГСС. Еди-
ница работы, равная 1 н-м, называется джоулем (дж), единица
работы, равная 1 дин •см, называется эргом (эрг). Работа, рав-
ная 1000 дж, называется килоджоулем (кдж).
Широко распространены также внесистемные единицы рабо-
ты и энергии — ватт-час (вт • ч) и киловатт-час (квт-ч), а в
области тепловых измерений — калория (кал) и килокалория
(ккал).
Между различными единицами работы и энергии существуют
следующие соотношения:
1 дж — 0,001 кдж— 1 • 107 эрг = 0,102 кгс • м —
— 0,239 кал = 0,239 • 10-3 ккал
1 кет • ч = 1000 вт - ч — 3,6 • 106 дж = 3600 кдж —
= 367 000 кгс - м = 860 ккал
В системе СИ предусматривается одна и та же единица —
джоуль для измерения всех видов энергии, в том числе тепло-
вой. Это устраняет необходимость введения в расчетные форму-
лы дополнительных множителей для пересчета единиц измере-
ния различных видов энергии. Если же тепловая энергия изме-
ряется в ккал, то для перехода к единицам системы СИ или
МКГСС в расчетные формулы вводится делитель А (термиче-
ский эквивалент работы), равный количеству тепла, которое
соответствует данной единице работы (дж или кгс-м):
А = 0,239 • 10~3 ккал/дж = ккал/кгс - м
3. Системы размерностей
41
Мощность — работа, произведенная в единицу времени,—
имеет размерность: дж!сек — в системе СИ, эрг)сек — в системе
СГС и кгс • М/сек — в системе МКГСС. Единица мощности, рав-
ная 1 дж/сек, называется ваттом (вт). Величина, равная
1000 вт (или, что то же, 1 кдж/сек), называется киловаттом
(кет). Соотношение между единицами мощности следующее:
1 вт — 0,001 кет = 1 • 107 эрг!сек — 0,102 кгс • м/сек
Пересчет физических величин из одной системы единиц в дру-
гую можно производить, исходя из соотношения между основ-
ными единицами измерения:
1м—100 см 1кг—1000 г 1 кгс — 9,81 н
Так, например:
, , кг • м 1000 г • 100 см , г - см ЛГАГ.
1 =-----S3-----=100000—г- = 1000001Эии
1 дж — 1 н м — -^ёгкгс • м, или 0,102 кгс • м
У,01
Единицы систем СИ и МКГСС совпадают друг с другом,
если в размерность величины не входят единицы массы или си-
лы. Если же эти единицы входят в размерность, то для перехода
от системы МКГСС к системе СИ надо умножить числовое зна-
чение данной величины на 9,81, а в размерности заменить кгс
на н. Множитель 9,81 является коэффициентом перехода от ки-
лограмм-силы к ньютонам и имеет размерность н/кгс (или
дж/кгс • м). Этот множитель численно равен ускорению силы
тяжести на поверхности Земли.
Для обратного перехода от системы СИ к системе МКГСС
надо числовое значение величины разделить на 9,81, а в размер-
ности заменить кг (или н) на кгс'сек?/м (или соответственно на
кгс). Например, сила 80 кгс = 80 • 9,81 = 785 н.
В дальнейшем изложении авторы будут придерживаться си-
стемы единиц СИ. Учитывая, что в ранее изданной литературе
применяются другие системы единиц, в частности система
МКГСС, и в качестве единицы тепловой энергии используется
килокалория {ккал), в данной книге будут приведены соответ-
ствующие формулы пересчета и даны указания по преобразова-
нию основных уравнений в случае перехода к другим системам
единиц.
МЕХАНИЧЕСКИЕ ПРОЦЕССЫ
Глава 2
ПЕРЕМЕЩЕНИЕ ТВЕРДЫХ МАТЕРИАЛОВ
1. Общие сведения
В химических производствах приходится перемещать различ-
ные твердые материалы, являющиеся сырьем, полупродуктами
или готовыми продуктами. Для перемещения твердых материа-
лов в пределах завода или цеха применяются подъемно-транс-
портные устройства. Эти устройства составляют внутризавод-
ский транспорт предприятия.
Подъемно-транспортные устройства разделяются на следую-
щие группы:
1) устройства непрерывного транспорта, предназначенные для
перемещения материалов непрерывным потоком;
2) устройства периодического транспорта, предназначенные
для перемещения материалов отдельными порциями.
По направлению перемещения материала различают:
1) устройства для горизонтального (или слабонаклонного)
перемещения;
2) устройства для вертикального (или крутонаклонного) пе-
ремещения',
3) устройства для смешанного (пространственного) переме-
щения.
В зависимости от рода материала различают устройства для
перемещения сыпучих и штучных грузов.
К сыпучим материалам относятся порошкообразные и куско-
вые материалы, перемещаемые навалом.
К штучным грузам относятся изделия, имеющие определен-
ную форму (части машин, кирпич, металл), а также материалы,
упакованные в тару (мешки, бочки, барабаны, ящики).
Периодическая транспортировка осуществляется при помощи
вагонеток, подъемников, кранов и других устройств. Здесь рас-
сматриваются только основные устройства непрерывного транс-
порта (преимущественно для перемещения сыпучих материа-
лов), классификация которых приведена на стр. 29.
1. Общие сведения
29
Устройства непрерывного Типы
транспорта
2. Устройства непрерывного транспорта
для горизонтального перемещения
Ленточные транспортеры
Ленточный транспортер (рис. 2-1) состоит из бесконечной
ленты 3, непрерывно движущейся вокруг двух барабанов 1 и 8,
причем лента приводится в движение трением о поверхности ба-
рабанов.
Барабан 8 является приводным: он приводится в действие
электродвигателем через редуктор (или другую передачу) и при
30
Гл. 2. Перемещение твердых материалов
вращении тянет на себя верхнюю (груженую) часть ленты. Ба-
рабан 1 является натяжным и служит для натяжения ленты.
Натяжение ленты достигается тем, что барабан 1 установлен на
тележке, которая может перемещаться назад под действием ве-
са груза 10. Максимальное перемещение натяжного барабана
(ход натяжки) показано на рисунке. Чтобы предотвратить про-
висание ленты> под ней установлен ряд опорных роликов 4 и 9.
Рис. 2-1. Ленточный транспортер:
I — натяжной барабан; 2— загрузочная ворон-
ка; 3 —лента; 4, 9— опорные ролики; 5, 6— ба-
рабаны сбрасывателя; 7 —лоток; 8 — привод-
ной барабан; 10— груз для натяжения ленты.
Материал загружается на верхнюю ветвь ленты через загру-
зочную воронку 2 и перемещается при движении ленты к месту
разгрузки. Обычно оно находится у приводного барабана, т. е.
при огибании лентой барабана 8 материал сбрасывается с транс-
портера.
Разгрузка может быть осуществлена также в любом месте по
пути движения ленты при помощи сбрасывающего ножа или ба-
рабанного сбрасывателя.
Сбрасывающий нож представляет собой скребок, прегра-
ждающий движение материала и сбрасывающий его с ленты в
одну или обе стороны. Барабанный сбрасыватель состоит из
двух барабанов 5 и 6, которые изгибают ленту в виде буквы S.
Материал сбрасывается с барабана 6 и удаляется по лотку 7.
Сбрасывающий нож и барабанный сбрасыватель закрепляются
неподвижно или монтируются на тележке, которая может быть
установлена в любом месте.
Обычно применяют резино-тканевые транспортерные ленты,
состоящие из нескольких слоев резины и хлопчатобумажной
ткани. При транспортировании горячих материалов применяют
ленты, изготовленные из тонкой, термически обработанной стали.
Для увеличения производительности транспортера при пере’
2. Устройства непрерывного транспорта для гориз. перемещения 31
мещении сыпучих материалов рабочей ветви ленты придают же-
лобчатую форму путем применения роликов специального про-
филя. Как показано на рис. 2-1, нижняя ветвь ленты, не являю-
щейся рабочей, остается плоской.
Ленточные транспортеры применяются для горизонтального
или слабонаклонного (под углом к горизонтальной плоскости до
22°) перемещения сыпучих и штучных грузов при длине транс-
портирования до 150—200 м.
Скорость движения ленты для сыпучих материалов принимается от 0,5 до
2 м/сек-, более низкие скорости выбирают для легких мелкоизмельченных ма-
териалов (во избежание пыления при их перемещении), более высокие ско-
рости — для крупнокусковых материалов. Для штучных грузов принимают
скорость движения ленты 0,5—0,8 м/сек. Наиболее употребительные ленты
транспортеров имеют ширину 400, 500, 650, 800, 1000, 1200 и 1400 мм.
Пластинчатые транспортеры
Устройство пластинчатых транспортеров сходно с устрой-
ством ленточных транспортеров. Пластинчатый транспортер
(рис. 2-2) представляет собой бесконечную ленту, состоящую из
шарнирных цепей 1, к которым прикреплены пластины 2, не-
сущие перемещаемый материал. На шарнирах цепей располо-
жены ролики 3, которые катятся по направляющим 4, прикреп-
ленным к станине транспортера. Цепи транспортера огибают
звездочки 5 и 6, из которых одна приводная, а другая натяжная.
Загрузка материала может производиться в любой точке по
длине ленты, выгрузка осуществляется со стороны приводной
звездочки. При перемещении сыпучих материалов пластины
снабжаются бортами 7.
Пластинчатые транспортеры применяются для перемещения
материала на расстояние до 150 м. Если на пластинах постав-
лены поперечные перегородки, то угол наклона ленты к гори-
зонту может достигать 30—45°. Скорость движения ленты при-
нимается в пределах 0,2—0,6 м/сек.
Пластинчатые транспортеры дороже ленточных и применяют-
ся при перемещении крупнокусковых материалов или материа-
лов, имеющих высокую температуру, а также при перемещении
под большим углом, т. е. в тех случаях, когда ленточные транс-
портеры неприменимы.
Скребковые транспортеры
Скребковый транспортер (рис. 2-3) состоит из неподвижного
желоба 1, в котором движется бесконечная цепь 2 с прикреплен-
ными к ней скребками 3. Цепь приводится в движение при по-
мощи приводной звездочки 5; звездочка 7 является натяжной.
N3
Рис. 2-2. Пластинчатый транспортер:
/—цепь; 2 — пластины; 3— ролики; 4— направляющие; 5— натяжная звездочка; 6 — приводная звездочка; 7 —борт.
Гл. 2. Перемещение твердых материалов
2. Устройства непрерывного транспорта для гориз перемещения 33
На шарнирах цепи укреплены ролики 4, которые катятся по на-
правляющим 6.
Скребки при движении цепи захватывают и перемещают по
дну желоба поступающий материал, который разгружается либо
с другого конца желоба, либо через разгрузочное отверстие 9.
Рис. 2-3.-Скребковый транспортер:
/—желоб; 2— цепь; 3— скребки; 4 — ролики; 5— приводная звездочка;
6— направляющая; 7 —натяжная звездочка; 8 — загрузочный лоток; 9 — раз-
грузочное отверстие.
Преимуществами скребковых транспортеров, по сравнению с
ленточными, являются: 1) простота и дешевизна устройства,
2) удобство загрузки и разгрузки материала в любой точке,
3) большой угол наклона к горизонту (до 45°).
К недостаткам относятся: 1) повышенный расход энергии,
2) большой износ, 3) разрушение транспортируемых хрупких
материалов вследствие истирания.
Скребковые транспортеры применяются для перемещения
мелкокусковых и порошкообразных материалов на расстояние
до 60 м. Скорость движения принимается 0,25—0,75 м/сек.
Винтовые транспортеры
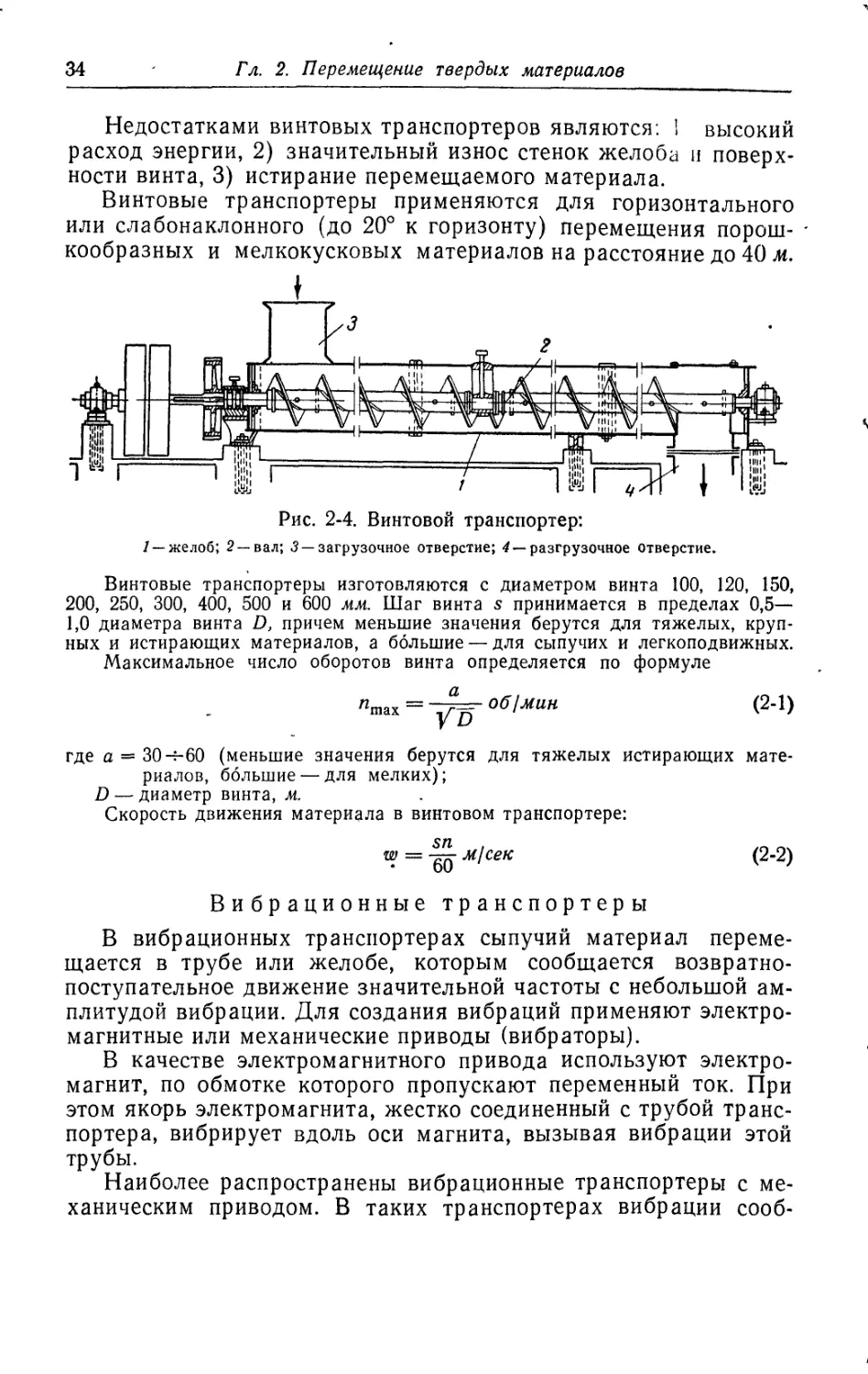
Винтовой транспортер, или шнек (рис. 2-4), представляет со-
бой закрытый желоб 1, в котором вращается винтообразный
вал 2 или вал, снабженный косо поставленными лопастями.
Перемещаемый материал поступает в желоб через загрузоч-
ное отверстие 3 и силами тяжести и трения о стенки желоба
удерживается от вращения вместе с винтом. Таким образом,
материал играет роль гайки для находящегося внутри него
винта и при вращении последнего перемещается вдоль желоба.
Выгрузка материала производится через отверстие 4, распо-
ложенное в дне желоба. Загрузка и выгрузка могут быть осу-
ществлены в любой точке по длине желоба.
К достоинствам винтовых транспортеров относятся: 1) ком-
пактность, простота и дешевизна устройства и обслуживания,
2) герметичность. Последнее особенно важно при перемещении
токсичных и пылящих материалов.
3 Зак 546.
34
Гл. 2. Перемещение твердых материалов
Недостатками винтовых транспортеров являются: 1 высокий
расход энергии, 2) значительный износ стенок желоба и поверх-
ности винта, 3) истирание перемещаемого материала.
Винтовые транспортеры применяются для горизонтального
или слабонаклонного (до 20° к горизонту) перемещения порош-
кообразных и мелкокусковых материалов на расстояние до 40 м..
Рис. 2-4. Винтовой транспортер:
1 — желоб; 2— вал; 3— загрузочное отверстие; 4— разгрузочное отверстие.
Винтовые транспортеры изготовляются с диаметром винта 100, 120, 150,
200, 250, 300, 400, 500 и 600 мм. Шаг винта s принимается в пределах 0,5—
1,0 диаметра винта D, причем меньшие значения берутся для тяжелых, круп-
ных и истирающих материалов, а большие — для сыпучих и легкоподвижных.
Максимальное число оборотов винта определяется по формуле
wmax
- об/мин
VD
(2-1)
где а = ЗО-т-60 (меньшие значения берутся для тяжелых истирающих мате-
риалов, большие — для мелких);
D—-диаметр винта, м.
Скорость движения материала в винтовом транспортере:
w = -gQ м/сек (2-2)
Вибрационные транспортеры
В вибрационных транспортерах сыпучий материал переме-
щается в трубе или желобе, которым сообщается возвратно-
поступательное движение значительной частоты с небольшой ам-
плитудой вибрации. Для создания вибраций применяют электро-
магнитные или механические приводы (вибраторы).
В качестве электромагнитного привода используют электро-
магнит, по обмотке которого пропускают переменный ток. При
этом якорь электромагнита, жестко соединенный с трубой транс-
портера, вибрирует вдоль оси магнита, вызывая вибрации этой
трубы.
Наиболее распространены вибрационные транспортеры с ме-
ханическим приводом. В таких транспортерах вибрации сооб-
2. Устройства непрерывного транспорта для гориз. перемещения
35
щаются трубе при помощи кривошипа или эксцентрика. Сущест-
вуют конструкции инерционных транспортеров, в которых вибра-
ции создаются вращением неуравновешенных масс (см. стр. 94).
При установке вибрационных транспортеров на площадках
или междуэтажных перекрытиях необходимо исключить переда-
чу вибраций строительным конструкциям здания или сооруже-
ния. Этому требованию удовлетворяют уравновешенные вибра-
ционные транспортеры. Схематично показанный на рис. 2-5
Рис. 2-5. Схема уравновешенного двухтрубного вибрационного транспортера:
1, 2 —транспортирующие трубы; 3 — рычаги-качалки; 4 —пружины; 5— стойки; 6 — эксцентрик;
7 —шатун.
уравновешенный двухтрубный вибрационный транспортер со-
стоит из труб 1 и 2, расположенных друг над другом, соединен-
ных между собой рычагами-качалками 3 и плоскими пружина-
ми 4. Качалки шарнирно крепятся к трубам и неподвижным
стойкам 5. Привод транспортера состоит из эксцентрика 6 и ша-
туна 7. Движение труб происходит попеременно: когда одна тру-
ба движется вперед, другая отклоняется назад. При движении
трубы вперед материал перемещается вместе с нею в том же
направлении; при движении трубы в обратном направлении (на-
зад) материал остается неподвижным, а труба как бы уходит
из-под него. В результате таких переменных движений труб
вибрационного транспортера происходит поступательное пере-
мещение материала относительно трубы в направлении, пока-
занном на рисунке стрелками.
К достоинствам вибрационных транспортеров относятся гер-
метичность, компактность, простота конструкции и надежность
работы, к недостаткам—сравнительно высокий расход энергии и
износ при перемещении истирающих (абразивных) материалов.
Вибрационные транспортеры являются весьма перспективным
видом подъемно-транспортных устройств. Обычно они предпо-
36
Гл. 2. Перемещение твердых материалов
чтительнее пластинчатых, скребковых и винтовых транспортеров
для перемещения горячих, пылящих и токсичных (ядовитых)
материалов, когда применение ленточных транспортеров нецеле-
сообразно. Для очень влажных и липких материалов вибрацион-
ные транспортеры не пригодны. Длина транспортеров дости-
гает 100 м при производительности до 250 т/ч.
Частоту вибраций (число оборотов эксцентрикового вала) выбирают та-
кой, чтобы частицы передвигались относительно желоба, а не качались вместе
с ним. Для этого число оборотов вала п должно быть больше минимального
числа оборотов nmln, определяемого по уравнению:
пт!п 30 V 2(14V0tga) об!мин
(2-3)
При большом числе оборотов частицы перемещаемого материала будут
подбрасываться над желобом, что приведет к увеличению его износа и исти-
ранию материала Чтобы избежать подбрасывания, число оборотов п не долж-
но превосходить некоторого максимального
значения nmax:
«max = 061мин (2"4>
Vrtga
В формулах (2-3) и (2-4)-
fo — коэффициент трения материала о же-
лоб в покое (примерно 0,5);
г — эксцентриситет, м (обычно 0,01—0,02);
а — угол между пружинами и вертикалью
(см. рис. 2-5).
Средняя скорость w передвижения ма-
териала по желобу составляет:
w = 0,23 nrftg а м!сек (2-5)
где f — коэффициент трения материала о
желоб (0,3—0,4).
Обычно величина w находится в пре-
делах 0,1—0,2 м/сек.
Рис. 2-6. Пневматический транс-
портный желоб:
/ — верхняя часть желоба; 2 —нижняя
часть желоба; 3— пористая плитка;
4 — матерчатый фильтр; 5 — уплотни-
тельная замазка.
/
через плитку, воздух проникает
Пневматические транспортные
желоба
Пневматический желоб (рис. 2-6) со-
стоит из двух частей 1 и 2, разделенных по-
ристой плиткой 3, на которой находится пе-
ремещаемый материал. В пространстве под
плиткой проходит сжатый воздух. Пройдя
в материал и разрыхляет его Вследствие
этого материал становится текучим, подобно жидкости, и перемещается по
желобу уже при небольшом угле наклона (но не менее 2,5°). Отработанный
воздух выходит в атмосферу через матерчатые фильтры 4, расположенные в
верхней части желоба.
Расход воздуха составляет приблизительно 1,5 мР/мин на 1 м? площади
желоба (при давлении 500 мм вод. cm.)t Расход энергии в 2—4 раза меньше,
чем в винтовых транспортерах,
3. Устройства непрерывного транспорта для верт. и смет, перемещений 37
Пневматические желоба применяются вместо винтовых транспортеров
и других устройств для перемещения порошкообразных и мелкозернистых
материалов на расстояние до 100 м. Преимущества таких желобов заклю-
чаются в простоте, отсутствии движущихся частей, герметичности и малом
расходе энергии. Основным недостатком является невозможность движения
материала с подъемом вверх.
3. Устройства непрерывного транспорта
для вертикального и смешанного перемещений
Элеваторы
Элеватор (рис. 2-7) состоит из бесконечной ленты или цепи 2
(лвнточный или цепной элеватор), на которой закреплены ков-
ши 3. Лента — в случае ленточного элеватора — огибает два ба-
рабана 1 и 6, расположенные один в
верхнем, другой в нижнем концах элева-
тора (верхний барабан приводной, ниж-
ний— натяжной). Цепи — в случае цеп-
ного элеватора — огибают две звездочки,
расположенные также в верхнем и ниж-
нем концах элеватора. Вал верхнего ба-
рабана (или звездочки) вращается в не-
подвижных подшипниках, тогда как вал
нижнего барабана (или звездочки) уста-
новлен в подвижных подшипниках, ко-
торые при помощи винта 5 можно пере-
мещать по вертикали, чем и достигается
натяжение ленты или цепи.
Все устройство заключено в кожух 4.
В нижней части кожуха имеется ворон-
ка 7, через которую загружается пере-
мещаемый материал. Далее материал за-
хватывается ковшами и поднимается на-
верх; при переходе через верхний бара-
бан ковши опрокидываются и материал
под действием центробежной силы и си-
лы тяжести высыпается в приемный же-
лоб 8. Таким образом, все поднимаю-
щиеся ковши элеватора движутся нагру-
женными, а все опускающиеся — порож-
Рис. 2-7. Элеватор:
/ — природной барабан; 2—
лента; 3—ковши; 4 — кожух;
5 —винт; б —натяжной бара-
бан; 7 —воронка; 8— прием-
ный желоб.
ними.
Элеваторы применяются для верти-
кального подъема порошкообразных и
кусковых материалов на высоту до 40 м.
Скорость движения ленты или цепи при-
нимается от ОД до 1,5 м]сек. Ленточные
38 Гл 2 Перемещение твердых материалов
элеваторы применяются при легких условиях работы (мелкий
и легкий материал, небольшая высота подъема); для тяжелых
условий работы (крупны# и тяжелый материал, большая вы-
сота подъема) применяются цепные элеваторы.
Для тяжелых крупнокусковых и истирающих материалов
применяются тихоходные элеваторы со скоростью движения
0,4—0,6 м!сек. При такой малой скорости выгрузка материала
происходит не под действием центробежной силы, а под дей-
ствием одной силы тяжести. Чтобы материал не падал обратно
в кожух элеватора, а поступал в приемный желоб, ковши распо-
лагают вплотную друг к другу (чешуйчатые элеваторы); в этом
случае материал при разгрузке скользит по задней стенке ниже-
расположенного ковша. Для облегчения разгрузки тихоходных
элеваторов их часто устанавливают наклонно под углом 45—70°
к горизонту.
Элеваторы изготовляют с ковшами шириной 135, 160, 200, 250, 350, 450,
600, 750 и 900 мм. Для хорошо сыпучих материалов применяют’ глубокие
ковши шириной 135—450 мм и емкостью 0,75—15 л, дня плохо сыпучих мате-
риалов— мелкие ковши шириной 160—450 мм и емкостью 0,65—15 л, для
крупнокусковых, абразивных и хрупких материалов — ковши шириной 160—
900 мм и емкостью 1,5—130 л (ковши чешуйчатых элеваторов)
Транспортеры с погруженными скребками
Транспортеры данного типа являются разновидностью скреб-
ковых транспортеров и отличаются от последних тем, что цепь
со скребками движется внутри закрытого желоба и скребки
погружены в транспортируемый материал, движущийся сплош-
ным потоком.
Транспортеры с погруженными скребками могут перемещать
материал по трассе сложного очертания (кривая или ломаная
линия) в горизонтальном, наклонном и вертикальном направле-
ниях без перегрузки в местах перегиба трассы, причем загрузка
и разгрузка транспортеров могут осуществляться во многих его
точках.
Габариты этих транспортеров меньше габаритов ленточных,
пластинчатых, скребковых и винтовых транспортеров. Расход
энергии значительно меньше, чем для скребковых и винтовых
транспортеров.
К недостаткам транспортеров с погруженными скребками от-
носится значительный износ рабочих деталей при перемещении
истирающих материалов. Для транспортирования липких и
комкующихся материалов эти транспортеры непригодны.
3. Устройства непрерывного транспорта для верт. и смет, перемещений 39
Пневматический транспорт
Пневматический транспорт осуществляется при помощи дви-
жущегося в трубопроводе воздуха, который увлекает переме-
щаемый сыпучий материал. Перемещаемый материал вводится
в трубопровод через загрузочные устройства, захватывается
струей движущегося воздуха и транспортируется к месту раз-
грузки.
В зависимости от концентрации перемещаемого материала в
смеси его с воздухом различают пневматический транспорт в
разреженной фазе (малая концентрация материала в смеси с
воздухом) и пневматический транспорт в плотной фазе (высо-
кая концентрация материала в смеси).
Пневматический транспорт в разреженной фазе осущест-
вляется при таких скоростях воздуха, при которых частицы ма-
териала увлекаются вместе с воздухом (стр. 180). В зависимо-
сти от размеров частиц и плотности перемещаемого материала
применяются скорости воздуха от 8 до 35 м/сек. Концентрация
материалов в смеси с воздухом составляет от 1 до 35 кг мате-
риала на 1 кг воздуха (обычно 10—25 кг/кг).
На рис. 2-8 показана схема всасывающей пневматической
установки. В трубопроводе 2 создается разрежение и воздух вса-
сывается в него вместе с перемещаемым материалом. Всасыва-
Рис. 2-8. Схема всасывающей пневматической
установки:
/—приемное сопло; 2— трубопровод, 3— разгружатель;
/ — фильтр; 5 — вакуум-насос; 6 — приемный бункер.
ние происходит через приемное сопло /; далее смесь воздуха с
материалом по трубопроводу 2 поступает в разгружатель 5, в
котором воздух отделяется от материала, поступающего затем в
приемный бункер 6. Разгружатели выполняются в виде
циклонов (стр. 327). Из разгружателя воздух поступает в
40
Г л. 2. Перемещение твердых материалов
фильтр 4, где от воздуха отделяются частицы материала, не
уловленные в разгружателе. Из фильтра воздух отсасывается
вакуум-насосом 5, который и создает необходимое разрежение
в системе.
Всасывающие пневматические установки применяются для
перемещения материала на расстояние до 100 м из разных мест
к одной точке разгрузки. Установки применимы при разреже-
ниях не более 0,5—0,6 ат.
Для перемещения материала на большие расстояния (до
300 м) из одного места по различным направлениям применяют
Рис. 2-9. Схема нагнетательной пневматической уста-
новки:
/ — компрессор; 2—трубопроводы; 3— питатель; 4 — разгружатели;
6 — фильтры; 6— приемный бункер.
нагнетательные пневматические установки (рис. 2-9). Компрес-
сор 1 нагнетает воздух в трубопровод 2, в который через спе-
циальный питатель 3 подается перемещаемый материал. Смесь
воздуха с материалом по трубопроводу 2 поступает в разгружа-
тель 4, где происходит отделение материала, после чего воздух
через фильтр 5 отводится в атмосферу. Избыточное давление
воздуха в нагнетательных установках достигает 3—4 ат.
Для перемещения материала на большие расстояния из раз-
ных мест к одной точке применяют смешанные пневматические
установки (рис. 2-10). Материал засасывается вместе с воздухом
через сопло 1 и по трубопроводу 2 поступает в разгружатель 3.
Воздух из разгружателя 3 через фильтр 4 всасывается компрес-
сором 5 и нагнетается в трубопровод 6, куда подается материал
из разгружателя 3. Далее смесь воздуха с материалом поступает
в разгружатель 7, откуда воздух направляется в фильтр 8. Пре-
имущества пневматического транспорта заключаются в про-
3. Устройства непрерывного транспорта для верт. и смет. перемещений 41
стоте, надежности, полной герметичности и компактности уста-
новок. Основными их недостатками являются повышенный рас-
Рис. 2-10. Схема смешанной пневматической установки:
1— приемное сопло; 2 —всасывающий трубопровод; 3, 7— разгружа-
тели; 4, 8~ фильтры; 5 —компрессор; б —нагнетательный трубо-
провод.
ход энергии по сравнению с расходом для механического транс-
порта, а также износ трубопроводов при перемещении истираю-
щих материалов.
Пневматический транспорт
применяется при перемещении
сухих порошкообразных и мел-
козернистых материалов. Для
перемещения влажных, липких
и крупнокусковых материалов
пневматический транспорт не-
пригоден.
Пневматический транспорт
в плотной фазе осуществляет-
ся в так называемых пневма-
тических подъемниках при ма-
лых скоростях воздуха (менее
10 м!сек) и высоких концент-
рациях перемешиваемого мате-
риала в смеси с воздухом
(120—250 кг!кг).
На рис. 2-11 показана схе-
ма пневматического подъемни-
ка непрерывного действия. Пи-
татель 1 непрерывно подает
Рис. 2-11. Пневматический подъемник
непрерывного действия:
7—питатель; 2—загрузочная камера; 3— по-
ристая перегородка; 4 — транспортный трубо-
провод; 5—разгружатель.
материал в загрузочную каме-
ру 2, в нижней части которой
расположена пористая перего-
родка 3. Сжатый воздух (избыточное давление 0,5—1,5 апг)
подается под пористую перегородку. В загрузочной камере
42
Гл. 2. Перемещение твердых материалов
материал увлекается воздухом и поступает вместе с ним в транс-
портный трубопровод 4, по которому передается в разгружатель 5.
Пневматические подъемники применяются для перемещения
материала на высоту до 25 м (одновременно возможно переме-
щение материала в горизонтальном направлении). Их основным
преимуществом является низкий расход энергии по сравнению с
расходом не только для описанных выше пневматических уста-
новок, но и для механического транспорта. Для перемещения
материалов в вертикальном направлении перспективно приме-
нение пневматических подъемников вместо элеваторов.
Гидравлический транспорт
В установках гидравлического транспорта материал вводится в струю
воды, перемещается вместе с ней до места назначения и здесь отделяется от
воды. Этот вид транспорта применим только для тех материалов, которые
не подвергаются изменениям под действием воды.
В низконапорных гидравлических установках материал смывается водой
низкого давления (до 5 am) и смесь материала с водой движется самотеком
по открытым каналам.
В высоконапорных установках вода подается под давлением 25—60 ат и
смесь материала с водой перемещается по трубам под избыточным давле-
нием 1,5—7 ат. В этих установках можно перемещать материал на расстоя-
ние свыше 1 км.
В смешанных установках материал перемещается в пределах цеха по от-
крытым каналам, из которых подается затем в высоконапорную установку
для передачи на большое расстояние.
4. Расчет устройств непрерывного транспорта
Производительность устройств непрерывного
транспорта
При определении производительности различают следующие случаи.
1. Материал перемещается в виде непрерывной струи (например, переме-
щение сыпучих материалов в ленточных, пластинчатых, скребковых и винто-
вых транспортерах). Если площадь поперечного сечения несущего органа, на-
пример желоба пластинчатого или винтового транспортера, равна S м2, а ско-
рость его движения w м/сек, то объем перемещаемого материала составит
Sw м2/сек.
Часовая производительность транспортера:
Q = 3600SwpHtf> m/ч (2-6)
где рн— насыпная масса * материала (масса единицы объема сыпучего ма-
териала), т/м?\
у — коэффициент заполнения, учитывающий неполную загрузку несущего
органа материалом.
* Эта величина в технической литературе до введения системы единиц
СИ называлась насыпным весом. В связи с переходом на систему единиц
СИ целесообразно называть эту величину насыпной массой.
4. Расчет устройств непрерывней) Транспорта
43
Для ленточных транспортеров площадь поперечного сечения материала,
лежащего на ленте, составляет при плоской ленте
5 = т^-(0,9В —0.05)2 м2
1о
где В — ширина ленты, м.
При желобчатой ленте величина S приблизительно в 2 раза больше.
Подставляя значение S в формулу (2-6), получим при <р = 1:
Q = с (0,9В — 0,05)2 огрн (2-7)
Коэффициент с для плоской ленты равен 200, для желобчатой ленты
с = 400.
Для пластинчатых транспортеров (с бортами у пластин), скребковых и
вибрационных транспортеров
S = Bh
где В — ширина пластин или желоба, м;
h — высота бортов у пластин или желоба (для вибрационных транспорте-
ров h — высота слоя материала в желобе), м.
Коэффициент заполнения составляет:
Транспортеры
Пластинчатые.....................0,5—1
Скребковые.......................0,5—0,9
Вибрационные.....................0,5—0,8
Меньшие значения (р принимаются для мелкокусковых, большие — для
крупнокусковых материалов.
Для винтовых транспортеров S = (D — диаметр винта, к). Подстав-
ляя в формулу (2-6) это значение S, а также значение w по уравнению
(2-2), получим:
tiD2
Q = 60 —4— sn рнср m/ч (2-8)
причем <р = 0,125—0,4 (меньшие значения берутся для тяжелых, крупных и
истирающих материалов, большие — для легких и порошкообразных).
2. Материал перемещается в ковшах (перемещение элеваторами). Про-
изводительность определяется по формуле:
Q = 3,6 т/ч (2-9)
где v — емкость ковша, л;
а — расстояние между ковшами, ти;
w — скорость движения, м/сек\
рн — насыпная масса материала, т/м3-,
<р—коэффициент заполнения ковшей (для порошкообразных материалов
0,75—0,95, для кусковых материалов 0,4—0,8).
3. Материал перемещается в виде штучных грузов. Если масса каждого
груза М кг и расстояние между грузами а м, то при скорости w м/сек про-
изводительность составит:
М
Q = 3,6— w m/ч (2-Ю)
44
Гл 2. Перемещение твердых материалоё
Мощность, потребная для устройств
непрерывного транспорта
Потребная мощность на приводном валу определяется по формуле:
Но = (АГ] 4- N2 4- JV3) Кз + Ni кет (2-11)
Работа, затрачиваемая на подъем материала, равна производительности
Q т/ч, умноженной на ускорение силы тяжести g м/сек2 и на высоту подъема
Н м, т. е. QgH кдж/ч. Тогда мощность, затрачиваемая на подъем материала,
будет равна
V __ QgH _ Q • 9>8Ш _
1 3600 “ 3 600 “ 367 Квт
(2-12)
Мощность, затрачиваемая на преодоление вредных сопротивлений при пе-
ремещении материала (трение материала о желоб и т. п.):
Н2 = -^-квт (2-13)
367
Мощность, затрачиваемая на преодоление сопротивления тягового органа
(ленты или цепи) при холостом ходе:
,, K2wL _ 1
ЛГ3 = квт (2-14)
Обозначения в формулах (2-11)— (2-14):
Q — производительность, т[ч\
Н — высота подъема, м\
L — длина транспортера, м;
w — скорость движения, м/сек\
К\ и — коэффициенты сопротивления, определяемые из опыта;
Кз — коэффициент запаса на неучтенные сопротивления;
Ni — мощность, затрачиваемая на работу сбрасывающего устройства, квт.
Мощность электродвигателя определяется по формуле:
(2-15)
’I
где К — коэффициент, учитывающий условия работы транспортера (К = 1,1—
1,4; меньшие значения выбирают при легких условиях);
>] — к. п. д. привода (0,6—0,85).
Для ленточных транспортеров К\ = 0,054, коэффициент Кч имеет следую-
щие значения при различной ширине ленты:
Ширина ленты, мм . 400 500 650 800 1000 1200 1400
К2 ................ 5,2 6,4 8 10,4 14 17 20,2
Коэффициент Кз определяется в зависимости от длины транспортера:
Длина транспортера, м . . . < 15 15—30 30—45 > 45
Кз......................... 1,2 1,1 1,05 1,0
I
Мощность Nt (в квт) находят по следующим формулам-
для сбрасывающего ножа: Nt = 0,01 QB (где В — ширина ленты, м);
для барабанного сбрасывателя: Nt — 0,225 (Ко—К4) + 0,005 Q;
для самоходного барабанного сбрасывателя: К4 = 0,275 (Ко— К4) Н-
+ 0.005Q + 0,4.
4. Расчёт устройств непрерывного транспорта
45
Для пластинчатых транспортеров Ki=O,ll, Кз = 1,1, а коэффициент Лг
определяется по формуле:
/<2 = 48В4-Л
где В — ширина пластин, м;
А = 52—80 (в зависимости от условий работы транспортера).
Для скребковых транспортеров Кз = 0, Кз = 1, а коэффициент К\ опреде-
ляется по табл. 1.
Таблица 1
Значения Ki для скребковых транспортеров
Транспортеры Производительность, тп/ч
4,5 9 18 27 36 45
Коэффициенты
С роликовыми цепями 2,25 1,7 1,3 1,1 1,05 0,7
С безроликовыми цепями 4,2 3,0 2,25 1,9 1,7 1,6
Для винтовых транспортеров Кз = 0, Кз = 1, К\ = 1,2—4 (меньшие значе-
ния — для неистирающих материалов, большие — для истирающих и липких
материалов).
Для вибрационных транспортеров Ki = 6—10, Кз = 0, Кз = 0.
Для элеваторов К\ = 0, Кз = 1,15, Кг = kQ, причем при расчете мощности
N3 по формуле (2-14) вместо L подставляют высоту подъема Н, а значения
k определяют по табл. 2.
Таблица 2
Значения k для элеваторов
Элеваторы Ковши • Производительность, тп/ч
< ю 10-25 25-50 50-100 >100
Ленточный Обычные 0,84 0,7 0,63 0,56 0,39
Чешуйчатые — — 0,58 0,53 0,48
Одноцепной Обычные 1,24 0,91 0,68 0,57 —
Чешуйчатые — 0,77 0,59 0,49 —
Двухцепной Обычные — 1,36 1,13 0,91 0,68
Чешуйчатые — — — 0,77 0,63
Пример 2-1. Определить ширину ленты наклонного ленточного транспор-
тера для перемещения фосфоритной муки; производительность Q = 160 пг/ч.
Решение. Насыпная масса фосфоритной муки рн= 1,6 m/м?, скорость
ленты w принимаем 0,75 м/сек. Выбираем желобчатую ленту и, решая урав-
нение (2-7) относительно В, находим необходимую ширину ленты:
В = ^1-0,05 = 0,056 /+ 0,05S0,7 м
46
Гл. 2. Перемещение твердых МатёрийЛОв
Принимаем ширину ленты В = 800 мм (ГОСТ 20—57).
Учащемуся предлагается убедиться, что при плоской ленте ее ширину
необходимо увеличить до 1000 мм.
Пример 2-2. Определить мощность электродвигателя для транспортера,
работающего в условиях, указанных в примере 2-1, если длина транспортера
L = 120 м, высота подъема Н = 15 м и сбрасывание производится при помо-
щи сбрасывающего ножа.
Решение. Мощность, затрачиваемую на подъем материала, опреде-
ляем по формуле (2-12):
.. 160-15
/V ] ~ —окт— ~ 6,53 кет
оО/
Мощность, затрачиваемую на преодоление вредных сопротивлений при
перемещении материала, находим по формуле (2-13) при К\ — 0,054:
КТ 0,054 -160 -120 _ __
N2 =--------ост----- — 2,82 Квт
36/
Мощность, затрачиваемая на преодоление сопротивления ленты при хо-
лостом ходе, определяется по формуле (2-14) при К2 = 10,4:
„ 10,4 - 0,75 • 120 о
М3 =--------ggy------= 2,55 кет
Мощность, затрачиваемая на работу сбрасывающего ножа:
N4 = 0,01 QB = 0,01 -160 - 0,8 = 1,28 кет
Мощность на приводном валу при Кз = 1:
No = (6,53 4- 2,82 4- 2,55) • 1 4- 1,28 s 13,2 кет
Мощность электродвигателя при ^ = 1,3 и = 0,85:
.. 13,2-1,3 оп
N == —— зй 20 кет
(J,oO
Пример 2-3. Определить производительность горизонтального ленточного
транспортера (для перемещения сульфата аммония) с плоской лентой шири-
ной В = 500 мм при скорости движения ленты w = 0,5 м/сек. Определить
также, насколько необходимо повысить скорость движения ленты для дости-
жения производительности транспортера Q = 30 т/ч.
Решение. Производительность транспортера по формуле (2-7) при на-
сыпной массе сульфата аммония ?н= 0,74 т/м3 составит:
Q = 200 • (0,9 • 0,5 — О,05)2 • 0,5 - 0,74 =11,8 т/ч
В соответствии с формулой (2-7) производительность транспортера про-
порциональна скорости ленты; следовательно, для повышения производитель-
ности до 30 т/ч необходима следующая скорость ленты:
30
w = 0,5 • 1,27 м/сек
1 1,0
С повышением Q и w возрастает потребная мощность, поэтому необходи-
мо проверить, достаточна ли мощность установленного электродвигателя.
Пример 2-4. Рассчитать горизонтальный пластинчатый транспортер с бор-
тами у пластин для перемещения колчеданного огарка; производительность
транспортера Q = 15 т/ч, длина L = 40 м, насыпная масса огарка рн= 1,8 т/м3.
4. Расчет устройств непрерывного транспорта
47
Решение. Выбираем скорость движения w = 0,5 м/сек. и принимаем
коэффициент заполнения ср =0,65. По формуле (2-6) находим площадь сече-
ния материала на транспортере:
Q
15
S 3600огрнср“ 3600-0,5-1,8-0,65 0,0071
Задаваясь шириной ленты В, можно определить высоту бортов h (или
наоборот). Принимая ширину ленты В = 400 мм, находим:
‘ , S 0,0071 ПП1О
й = -— = — — = 0,018 м
В 0,4*
Найденная высота бортов конструктивно мала, поэтому увеличиваем ее
до 40 мм.
Мощность, затрачиваемую на преодоление вредных сопротивлений при
перемещении материала, определяем по формуле (2-13) при К\ = 0,11:
.. KxQL 0,11.15-40 _1С
^2 = ----= °-18 квт
367
Мощность, затрачиваемую на преодоление сопротивления тягового органа
при холостом ходе, находим по формуле (2-14):
.. K2wL 99,2 -0,5-40
- ^ = -367- =-------367----
где = 48 В + А = 48 • 0,4 + 80 = 99,2.
Так как Ni = 0 и Nt = 0, то мощность на приводном валу по формуле
(2-11) при Кз — 1,1 составит:
No = (0,18 + 5,4) • 1,1 6,15 квт
Мощность электродвигателя при К = 1,2 и т] — 0,7:
КТ 6,15-1,2 1ПС
М = ——--------Ю,5 квт
Пример 2-5. Рассчитать горизонтальный винтовой транспортер для пере-
мещения антрацита (размеры кусков 25 мм)\ длина транспортера L = 40 м,
производительность Q = 20 т[ч.
Решение. В соответствии с размерами кусков перемещаемого мате-
риала принимаем диаметр винта D = 300 мм и шаг s = 0,87) = 0,8 • 300 =
= 240 мм. Принимая коэффициент заполнения ср = 0,3, определяем по форму-
ле (2-8) необходимое число оборотов винта при насыпной массе антрацита
Рн= 0,9 т/м3-.
Q
20
п “ 60 • 0,785D2spHcp 60 • 0,785 • 0,32 • 0,24 - 0,9 • 0,3 “ 73 об!М11н
Максимальное число оборотов по формуле (2-1) при а = 45:
45
nmax = = 82,5 об /мин
Таким образом, требуемое число оборотов меньше максимального. Принимая
Ki = 2,5, находим по формуле (2-13) мощность N2:
КТ 2,5-20-40
Л2 =------------= 5,45 квт
48
Гл. 2. Перемещение твердых материалов
Так как Ni = N3 — N4 = О и Кз = 1, то мощность на приводном валу
No = N2 = 5,45 кет. При К = 1,1 и "Q = 0,85 мощность электродвигателя со-
ставит:
кт 5,45-1,1
= кет
Пример 2-6. Рассчитать элеватор для перемещения фосфоритной муки,
производительность элеватора Q — 50 т/ч, высота подъема И = 15 м.
Решение. Выбираем ленточный элеватор с ковшами емкостью v —
= 4,5 л. Скорость ленты принимаем W— 1,25 м/сек, коэффициент заполнения
<р = 0,8. По формуле (2-9) определяем расстояние между ковшами при на-
сыпной массе материала рн = 1,6 т/м3-.
3,6vwpH? _ 3,6-4,5-1,25-1,6-0,8 9
а о — чп — 0,52 м
По табл. 2 для данных условий k — 0,63, откуда К2 = kQ = 0,63 • 50 =
= 31,5.
По формулам (2-12) и (2-14) рассчитываем мощность:
„ 50-15 о п.
М = - - = 2,04 кет
ои/
.. 31,5-1,25-15 1Д
Л^з = -----------=1,6 кет
Мощность на приводном валу ири N2 = N4 = 0 и Кз= 1,15 составит:
(2,04 +1,6)-1,15^4,2 кет
Мощность электродвигателя при ^ = 1,2 и ^ = 0,8 будет равна:
Л, 4,2 1,2
N = —fro— = 6,3 кет
и,о
Глава 3
ИЗМЕЛЬЧЕНИЕ ТВЕРДЫХ МАТЕРИАЛОВ
1. Общие сведения
Дробление и размол представляют собой процессы механи-
ческого измельчения твердых веществ. В результате измельче-
ния значительно увеличивается поверхность обрабатываемого
материала.
Применение твердых материалов, раздробленных на мелкие
куски (путем дробления) или измельченных в порошок (путем
размола), позволяет значительно ускорить растворение, обжиг,
химическое взаимодействие, т. е. различные процессы, проте-
кающие тем быстрее, чем больше поверхность участвующего в
них твердого вещества.
В настоящее время для измельчения материалов применяют
машины различных типов, начиная от крупных щековых дроби-
лок, дробящих глыбы материала объемом до 2 л!3, и кончая кол-
лоидными мельницами, измельчающими продукты на частицы
размером до 0,1 мк.
Дробление и размол характеризуются степенью измельче-
ния — отношением диаметра dH кусков материала до измельче-
ния к диаметру dK кусков после измельчения:
* = £ (3-1)
Куски исходного материала и куски или зерна, получаемые
в результате измельчения, не имеют правильной (симметричной)
формы. Поэтому на практике размеры кусков (dH и dK) опреде-
ляют размером отверстий сит, через которые просеивают сыпу-
чий материал, т. е. с помощью ситового анализа (стр. 86).
Измельчение производится в одну или несколько стадий.
Каждая машина, в зависимости от устройства, может обеспечи-
вать ограниченную степень измельчения, которая колеблется от
/ = 34-6 для щековых дробилок до i = 100 и более для мель-
ниц. Для достижения высоких степеней измельчения этот про-
цесс проводят в несколько стадий, используя последовательно
4 Зак. 546.
50
Гл. 3. Измельчение твердых материалов
соединенные дробильно-размольные машины, так как за один
прием (на одной машине) не удается получить кусков заданной
конечной крупности.
В зависимости от начального и конечного размера наиболь-
ших кусков условно различают следующие виды измельчения:
Измельчение dH, мм dK, ми
Крупное (дробление)
Среднее (дробление).
Мелкое (дробление) .
Тонкое (размол) . . .
Сверхтонкое (размол)
1500—150 250—40
250— 40 40—6
25—3 6—1
10—1 1—75 • 10-3
12—0,1 75 • 10"3—1 • 10"4
Крупное и среднее дробление производятся, как правило, су-
хим способом, мелкое дробление и размол — сухим или мокрым
способом (в водной среде). При мокром измельчении умень-
Рис. 3-1. Способы измельчения ма-
териалов:
а —раздавливание; б — удар; в —истирание;
г —раскалывание.
шается пылеобразование и ча-
стицы получаемого продукта
имеют более равномерные раз-
меры; кроме того, облегчается
выгрузка продукта.
Измельчение материалов про-
изводится раздавливанием, уда-
ром, истиранием и раскалыва-
нием. Схематически эти виды
усилий показаны на рис. 3-1.
Выбор того или иного вида механического воздействия зави-
сит от крупности и прочности материала. В зависимости от пре-
дела прочности при раздавливании (а) материалы условно де-
лят на следующие группы:
а, кгс/см2
а, Мн/м2
Твердые (гранит, диабаз и др.) .... Более 500
Средней твердости (известняк, камен-
ная соль, антрацит и др.)............... 100—500
Мягкие (уголь, глина и др.)............. Менее 100
Более 50
10—50
Менее 10
Обычно при измельчении материала комбинируются те или
иные усилия, например раздавливание и удар, истирание и удар.
Раздавливание применяют главным образом при крупном и
среднем дроблении, истирание — при тонком измельчении. В за-
висимости от физико-механических свойств материалов выби-
рают обычно следующие методы
Материал
Твердый и хрупкий
Твердый и вязкий
Хрупкий, средней твердости
Вязкий, средней твердости
измельчения:
Метод измельчения
Раздавливание, удар
Раздавливание
Удар, раскалывание и ис-
тирание
Истирание или истирание и
удар
1. Общие сведения
51
При выборе метода измельчения необходимо учитывать свой-
ства материала, например его склонность к комкованию, влаж-
ность и др.
Измельчение производится по двум основным схемам — в от-
крытом или замкнутом цикле. При работе по первой схеме весь
материал проходит через дробилку (мельницу) только один раз,
при работе по замкнутому циклу большая часть материала про-
ходит через дробилку (мельницу) многократно, так как мате-
риал с размерами кусков больше допустимого предела возвра-
щается на повторное дробление. Это достигается при соединении
дробилки или мельницы с устройствами для разделения измель-
ченного материала по крупности частиц — грохотами или клас-
сификаторами, описанными в главе. 4.
Типы машин
Виды
измельчения
Вибрационные мельницы и
дробилки
Сверхтонкое измельчение
Струйно-вибрационные мель-
ницы
Коллоидные мельницы
4*
52
Гл. 3. Измельчение твердых материалов
Измельчение в замкнутом цикле (стр. 83) позволяет значи-
тельно увеличить производительность установки и получить бо-
лее равномерный по крупности продукт.
Машины для измельчения (дробления и размола) делят на
дробилки и мельницы. Обычно мельницами называют машины
для тонкого и сверхтонкого измельчения, дробилками — маши-
ны для крупного, среднего и мелкого дробления, но такое де-
ление является весьма условным.
Классификация машин для измельчения по конструктив-
ным особенностям приведена на стр. 51.
2. Физические основы измельчения
По современным воззрениям, процесс деформации твердых тел заклю-
чается в том, что под действием внешних сил в наиболее слабых местах тела
образуются замкнутые или начинающиеся на поверхности мельчайшие тре-
щины. При прекращении внешнего воздействия трещинь! под действием мо-
лекулярных сил могут смыкаться («самозаживление»); при этом тело под-
вергается лишь упругой деформации. Разрушение тела происходит в том слу-
чае, когда трещины настолько увеличиваются, что пересекают твердое тело по
всему его сечению в одном или нескольких направлениях. В момент разру-
шения деформирующегося тела напряжение в нем превышает некоторое пре-
дельное значение, упругая деформация сменяется деформацией разрушения
и происходит измельчение.
Процессы измельчения связаны с значительным расходом энергии на об-
разование новых поверхностей, на преодоление внутреннего трения частиц
при их деформации во время разрушения и на преодоление внешнего трения
между материалом и рабочими частями машины.
Теория процесса измельчения устанавливает зависимость между энер-
гией, затраченной на измельчение твердого тела, и результатом измельчения,
т. е. размером кусков (зерен) продукта измельчения.
Теория измельчения основывается на двух гипотезах: объемной и поверх-
ностной.
Объемная теория. Эта теория была впервые предложена и доказана
В. Л. Кирпичевым в 1874 г.
Согласно объемной теории, расход энергии на дробление пропорционален
объему тела и, следовательно, отношение работ Л[ и Л2, затраченных на дроб-
ление двух тел, имеющих объемы V\ и У2, равно
Работа равна произведению силы Р на деформацию и по закону Гука
пропорциональна линейному размеру I тела, т. е. Л = Pal (а — коэффициент
пропорциональности). Объем тела пропорционален его линейным размерам и
может быть выражен зависимостью V = ЬР (Ь — коэффициент пропорциональ-
ности). Соответственно выражение (3-2) принимает вид:
откуда
Р]Л1Х Ы\
^2^2 ^2
р2 /2
(3-3)
2. Физические основы, измельчения
53
Таким образом, по теории Кирпичева для однородных твердых тел
усилия дробления пропорциональны квадратам их сходственных линейных
размеров или поверхностям тел, а произведенная работа пропорциональна
объемам или весам этих тел.
Поверхностная теория. Согласно этой теории, работа, затраченная на
дробление, пропорциональна поверхности кусков, образующихся при дробле-
нии. Поверхность материала при дроблении возрастает обратно пропорцио-
нально конечному размеру кусков dK, который, согласно зависимости (3-1),
равен -г-.
Тогда при одинаковой крупности кусков исходного материала получим
для различной степени дробления:
Л
-^1 _ Л (3-4)
^2 z2 z2 >
dH
т. е. работа, затрачиваемая на дробление, пропорциональна степени измельче-
ния материала.
Несмотря на то, что обе теории не отражают в полной мере всех явлений,
происходящих при дроблении, исследования, проведенные советскими учеными
(работы В. А. Баумана и др.), показали, что теория Кирпичева хорошо
согласуется с опытными данными при крупном и среднем дроблении, осуще-
ствляемом главным образом раздавливанием и ударом. Поверхностная теория
более соответствует процессам мелкого дробления и тонкого измельчения,
связанным с истиранием и иногда с раскалыванием материала.
Таким образом, обе гипотезы близки в определенных условиях к истине
и, следовательно, дополняют друг друга. Это нашло отражение в единой тео-
рии дробления, предложенной П. А. Ребиндером.
По Ребиндеру, работа, затрачиваемая на дробление, в общем случае
является суммой двух слагаемых:
A = akF + kW (3-5)
Первый член этого выражения представляет собой энергию, расходуемую
на образование новых поверхностей при разрушении твердого тела. Эта энер-
гия равна удельной поверхностной энергии а (приходящейся на единицу
поверхности тела), умноженной на поверхность ДА, образующуюся при раз-
рушении. Второй член уравнения выражает энергию деформации. Она равна
работе k упругой (и пластической) деформации на единицу объема твердого
тела, умноженной на часть объема тела ДУ, подвергшуюся деформации.
Уравнение (3-5) является частным выражением закона сохранения энер-
гии, согласно которому процесс дробления характеризуется переходом одного
из видов энергии твердого тела в другой. До разрушения тело обладает по-
тенциальной энергией, т. е. находится под действием внешних сил в состоянии
упругой деформации. В результате разрушения потенциальная энергия пере-
ходит в кинетическую, причем энергия деформации превращается в тепло и
рассеивается в окружающую среду.
При крупном дроблении величина вновь образующейся поверхности,
вследствие больших размеров исходного материала, сравнительно невелика.
Поэтому в данном случае второй член kkV уравнения (3-5) значительно пре-
вышает первый член аДА и расход энергии на дробление приблизительно про-
порционален объему твердого тела.
При тонком измельчении вновь образующаяся поверхность очень велика,
поэтому в уравнении (3-5), описывающем этот процесс, первый член во много
54
Гл 3. Измельчение твердых материалов
раз больше второго. В связи с этим расход энергии на измельчение прибли-
зительно пропорционален вновь образованной поверхности.
Теория Ребиндера хорошо согласуется с опытом, а описанные выше
объемная и поверхностная теории основываются на ней и могут рассматри-
ваться как частные случаи.
3. Щековые дробилки
Устройство щековых дробилок. В щековых дробилках мате-
риал поступает сверху и измельчается путем периодического
раздавливания между неподвижной и подвижной щеками. Раз-
рушение кусков материала происходит в основном вследствие
раздавливания их подвижной качающейся щекой. Продукт дроб-
ления свободно выпадает через нижнюю выпускную щель меж-
ду щеками.
Наиболее распространены щековые дробилки с верхней осью
подвеса подвижной щеки (рис. 3-2). Внутри станины 1, изготов-
Рис. 3-2. Щековая дробилка:
7 —станина; 2 —неподвижная щека (плита); 3 — боковая плита; 4 — плита;
5— подвижная щека; 6 — ось подвижной щеки; 7—главный (эксцентриковый)
вал; 8 — шатун; 9 — распорные плиты; 10 — тяга; 11— пружина; 12 — клинья;
13 — маховик.
ленной из чугуна или стального литья, находится неподвижная
щека 2 в виде рифленой плиты из износоустойчивого материала
(марганцовистая сталь, содержащая 12—14% Мп, или отбелен-
ный чугун). Такая же плита 4 укреплена на подвижной щеке 5,
качающейся на оси 6. С боков рабочее пространство дробилки
ограничено гладкими плитами 3.
Качание подвижной щеки 5 осуществляется при помощи ша-
туна 8, насаженного на главный (эксцентриковый) вал 7. Шатун
3. Щековые дробилки
55
соединен шарнирно с подвижной щекой посредством распорных
плит 9. Таким образом образуется коленчатый рычаг, при помо-
щи которого наибольшие усилия создаются в верхней части щек,
где происходит раздавливание наиболее крупных кусков мате-
риала. Натяжение в движущейся системе (щека, распорные пли-
ты, шатун) и обратное движение щеки достигаются с помощью
тяги 10 и пружины И. Ширина выпускной щели регулируется
путем перемещения одного из клиньев 12 по другому посред-
ством винта. На концах главного вала имеются маховики 13.
Привод главного вала осуществляется при помощи шки-
вов.
Для предохранения рабочих частей дробилки от поломки при
случайном попадании в нее кусков металла одну из распорных
плит изготовляют из двух частей. Обе части соединяют заклеп-
ками или болтами, которые срезаются при определенной нагруз-
ке, превышающей допустимую, и могут быть легко заменены но-
выми. Иногда предохранительной деталью
служит собственно распорная плита, сече-
ние которой рассчитывают с уменьшенным
запасом прочности.
Достоинства щековых дробилок: 1) про-
стота и надежность конструкции, 2) широ-
кая область применения (в том числе для
дробления крупнокусковых, материалов
большой твердости), 3) компактность,
4) легкость обслуживания.
Недостатки: 1) периодический характер
жении щек), 2) неполная уравновешенность
движущихся масс. Это последнее обстоя-
тельство является причиной шума, ударов
и сотрясений здания, где работают дробил-
ки. Поэтому их устанавливают на тяжелых
фундаментах и снабжают массивными ма-
ховиками.
Щековые дробилки со сложным движением щеки
стандартизованы (ГОСТ 7084—61). Характеристикой
щековых дробилок является ширина и длина загру-
зочного отверстия, которые указывают в обозначении
марки дробилки, например дробилка ЩС 60 X 90
имеет загрузочное отверстие 600 X 900 мм.
В химической промышленности наиболее распространены щековые дро-
билки с размерами загрузочного отверстия от 400X230 до 2100X1500 jwjw.
Расчет щековых дробилок. К числу основных параметров, характери-
зующих работу щековой дробилки, относятся: 1) угол а между щеками, на-
зываемый углом захвата (рис. 3-3), 2) оптимальная скорость, 3) производи-
тельность, 4) расход энергии.
t
воздействия на материал (только при сбли
Рис. 3-3. К расчету
щековой дробилки:
</н —начальный диаметр
кусков измельчаемого ма-
териала; е — минимальная
ширина выпускной щели;
5 —длина хода щеки;
Л —высота выпадающего
слоя измельченного мате-
риала.
56
Гл. 3. Измельчение твердых материалов
Угол захвата. От величины угла захвата зависит степень измельче-
ния, которая возрастает с увеличением а. Однако для того чтобы куски ма-
териала, поступающие в дробилку, не выталкивались из нее давлением щек,
необходимо, чтобы угол захвата не превышал 2?—удвоенного угла трения*
материала, т. е. должно соблюдаться условие a 2<р.
Это положение легко доказать, рассмотрев действие сил на кусок мате-
риала, зажатый между щеками дробилки (см. рис. 3-3).
На материал действуют давления щек Pi и Р, а также силы трения fPi
и fP (f — коэффициент трения). Проекции сил на горизонтальную и верти-
кальную оси:
Pi — Р COS а — fP sin а = 0 (3-6)
Р sin а — fP cos а — /Р] = 0 (3-7)
Определяя из уравнения (3-6) значение Р\ и подставляя его в уравнение
(3-7), после преобразований получим:
. 2/
gCt “ 1—/2
Как известно из механики, коэффициент трений равен тангенсу угла тре-
ния (/ = tg ?); следовательно
tga =
2tg?
1 — tg2 ?
= tg2T
а 2ср
Обычно принимают 15—22°.
Оптимальная скорость. При отходе подвижной щеки от непо-
движной (см. рис. 3-3) из дробилки под действием собственного веса выпа-
5
дает слой материала в виде призмы ABCD, имеющей высоту h — (s —
длина хода щеки, т. е. расстояние по горизонтали, на которое подвижная
щека перемещается параллельно самой себе). Если подвижная щека делает
п полных качаний в минуту, равных числу оборотов вала дробилки (об/мин),
то время отхода щеки т будет равно половине времени одного полного кача-
ния (направо и налево):
60 _ 30
п ~ п
2
сек
По закону свободного падения за время т призма выпадающего дробле-
ного материала пройдет путь
g-r2 _ g / 30 \2 _ 450g
2 2 \ п ) п2
Очевидно, выпадение материала из дробилки будет происходить свободно
при следующем условии:
s 450g
tg а п2
* Углом трения называется наибольший угол наклона плоскости к гори-
зонту, при котором тело, находящееся на плоскости, еще не скользит вниз.
3. Щековые дробилки
57'
откуда число полных качаний щеки, соответствующее наибольшей производи-
тельности дробилки, составит.
л 450g tg а
или
и <6651/"
Г S
об! мин
(3-8)
где s — длина хода щеки, см;
g — ускорение силы тяжести, см/сек2.
Производительность. Принимая а = 22° (tga~0,4), теоретиче-
скую производительность Q щековой дробилки можно определить по формуле
Q = 0,15pdcp s bn р т/ч (3-9)
где р — коэффициент разрыхления измельченного материала (р = 0,2—0,65, в
среднем~ 0,4);
dcp. — средний диаметр кусков измельченного материала, см;
s — длина хода щеки, см;
b — длина выпускной щели, cjw;
п — число оборотов в 1 мин;
р — плотность материала, кг/см3 *.
Как видно из рис. 3-3, средний диаметр кусков измельченного материала
_ (<? + s) + <? _
СР-— 2 “ 2
где е — минимальная ширина выпускной щели.
Расход энергии. Мощность, расходуемая на дробление (при
п об!мин), может быть приближенно рассчитана по формуле:
~2nb (d2 — d2K}
N = 2 340 0002? Квт
(3-10)
где a—предел прочности материала при сжатии, кгс/см2;
b — длины выпускной щели, см;
dn и dK — диаметры кусков исходного материала и продукта дробления, см;
Е — модуль упругости первого рода., кгс!см2.
Пример 3-1. Определить потребное число щековых дробилок для дроб-
ления рядового колчедана при Q = 30 т/ч. Средний диаметр кусков дробле-
ного материала dCp. = 40 лл,чкоэффициент разрыхления материала р = 0,25,
плотность материала р=5,2-10~3 кг/см3. Длина выпускной щели дробилки
b = 400 мм, длина хода подвижной щеки дробилки s = 25 мм.
Решение. Оптимальное число оборотов вала дробилки находим по
формуле (3-8):
tpp д / 0 4
п = 665 1/ —— = 6651/ = 266 об /мин
г s г 2,5
где tg a = tg 22° = 0,4.
Принимаем число оборотов вала п = 260 об/мин.
* Этой формулой можно пользоваться, выражая линейные размеры dc₽t,
s, b в м; при этом плотность должна быть выражена в кг/м3.
58
Гл 3. Измельчение твердых материалов
Производительность дробилки рассчитываем по формуле (3-9):
Qi = 0,15 • 0,25 • 4,0 • 2,5 • 40 • 260 • 5,2 • 10"3 = 20,2 т/ч
Потребное число дробилок составит:
Q 30 1 ло
т ~ Qt “ 20,2 “ 1,48
Устанавливаем две дробилки.
Пример 3-2. Определить мощность электродвигателей, которые следует
установить к дробилкам, работающим в условиях предыдущего примера,
если известно, что предел прочности рядового колчедана при сжатии
о = 1250 kzcIcm!1, а модуль его упругости Е = 350 000 кгс[см2. Диаметр наи-
больших кусков дробимого материала dH = 200 мм.
Решение. Потребляемую дробилкой мощность находим по формуле (3-10):
12502 • 260 • 40 (202 — 42)
N “ 2 340 000 • 350 000 ~ 9,5 квт
Принимаем запас мощности, равный 25%, тогда мощность электродвига-
теля составит:
== 1,257V = 1,25 • 9,5 = 12 квт
4. Конусные (гирационные) дробилки
В конусной дробилке (рис. 3-4) дробление происходит путем
непрерывного раздавливания и изгиба (излома) кусков материа-
ла дробящей головкой 1, выполненной в виде усеченного конуса,
при эксцентричном вращении ее в корпусе 2. Корпус дробилки
также имеет форму усеченного конуса.
Когда дробящая головка с одной стороны приближается к
корпусу, продукт дробления выпадает через уширяющуюся при
этом часть кольцевой щели между корпусом и головкой.
Различают конусные дробилки двух основных типов:
1) с головкой в виде крутого конуса — для крупного и сред-
него дробления;
2) с головкой в виде пологого конуса (так называемые гри-
бовидные дробилки) — для среднего и мелкого дробления.
Дробилки с крутым конусом. В конусной дробилке (рис. 3-5)
внутри стального литого корпуса 1 находится дробящая голов-
ка 2 в виде крутого конуса, которая закреплена на главном
валу 3. Вал подвешен сверху на крестовине 6, жестко скрепленной
с корпусом /, и укреплен на конической (или шаровой) втулке 7.
Поднимая или опуская вал с помощью гайки 8, можно регули-
ровать ширину выпускной щели дробилки. Нижний конец вала
свободно входит в стакан-эксцентрик 5, который приводится во
вращение посредством конической зубчатой передачи.
При холостом ходе вал с дробящей головкой не вращается
вокруг своей оси, а совершает круговое вращение (гирации) во-
4. Конусные (гирсщионные) дробилки
59
круг оси эксцентрика, описывая коническую поверхность с углом
при вершине, равным 8—12°. При дроблении, вследствие трения
о материал, вал и головка вращаются в направлении, противо-
положном вращению экс-
центрика, с меньшей ско-
ростью. При этом проис-
ходит непрерывное обка-
тывание дробящей голов-
кой материала, который
заполняет
пространство
Рис. 3-4. Схема конусной дро-
билки:
1 — дробящая головка; 2 — корпус дро-
билки (£>н— его нижний диаметр);
<3—привод; г —эксцентриситет глав-
ного вала (остальные обозначения
те же, что на рис. 3-3).
Рис. 3-5. Конусная дробилка для крупного
дробления (ККД):
/—корпус; 2 — дробящая головка; 3— вертикальный
(главный) вал; 4— броневая плита; 5 — стакан-эксцен-
трик; 6 — крестовина; 7 —коническая втулка;
8 — гайка.
между головкой и броневыми плитами 4, покрывающими вну-
треннюю поверхность корпуса 1.
В дробилках с крутым конусом достигается степень измель-
чения i = 5 — 6.
Конусные дробилки для крупного дробления (сокращенное обозначение
ККД) характеризуются размером загрузочной щели, ширина которой указы-
вается в обозначении марки дробилки (например, дробилка ККД-300 имеет
загрузочную щель шириной 300 мм).
Конусные дробилки для крупного дробления, изготовляемые Уралмашза-
водом, имеют ширину щели 300, 400, 500, 900 и 1500 мм.
60
Г л. 3. Измельчение твердых материалов
Грибовидные и короткоконусные дробилки. Грибовидная дро-
билка (рис. 3-6) отличается от описанной выше конусной дро-
билки формой головки и корпуса. Корпус 1 представляет собой
конус, расширяющийся в ту же сторону, что и пологий конус
дробящей головки 2, причем их стенки на определенной длине
параллельны и образуют узкую щель (зону параллельности).
Рис. 3-6. Грибовидная дробилка:
1— корпус; 2 — дробящая головка; 3 — станина;
4— пружины; 5 — шаровой подпятник; 6 —питающая
тарелка; 7 —основной вал.
Корпус 1 связан с стани-
ной 3 рядом пружин 4,
расположенных по его пе-
риметру.
Основной вал дробил-
ки установлен консольно
и опирается на подпят-
ник 5. На верхнем конце
вала установлена тарел-
ка 6, с которой куски ма-
териала равномерно сбра-
сываются в дробилку при
качаниях вала. Степень
измельчения регулируется
либо подъемом или опу-
сканием корпуса при по-
мощи специального ры-
чага, либо изменением
профиля плит, которыми
выложен изнутри корпус ।
дробилки.
В грибовидных дро-
билках достигается боль-
шая производительность и высокая степень измельчения
(i = Ю — 30) вследствие большого периметра и малой ширины
разгрузочной щели. Благодаря укорочению вала значительно
повышаются жесткость и надежность конструкции дробилки.
Грибовидные дробилки характеризуются наибольшим (ниж-
ним) диаметром дробящей головки и предназначаются главным
образом для среднего дробления.
Конусные дробилки для среднего дробления (сокращенное
обозначение КСД) характеризуются размером загрузочной
щели, ширина которой указывается в обозначении марки дро-
билки. По ГОСТ 6937—54 стандартизованы дробилки с шири-
ной щели 600, 900, 1200, 1650 и 2100 мм.
Конусные дробилки имеют следующие достоинства: 1) высо-
кая производительность вследствие непрерывности действия и
разрушения материала одновременно раздавливанием и изги-
бом, 2) спокойная уравновешенная работа (не нужен маховик),
4. Конусные (гирационные) дробилки
61
3) высокая степень измельчения (для грибовидных дроби-
лок).
Недостатки конусных дробилок (по сравнению со щековы-
ми): 1) более сложная и дорогая конструкция, 2) большая вы-
сота (особенно при крутом конусе), 3) более сложное обслужи-
вание.
Расчет дробилок с крутым конусом. Угол захвата. Для дробилок
с крутым конусом (см. рис. 3-4), как и для щековых, угол захвата « =
где <р — угол трения материала. Обычно принимается а = 21—23°.
Оптимальная скорость. Число оборотов, соответствующее наи-
большей производительности дробилки, определяется по формуле
n = 470j/~об/М11Н (3-11)
Где г — эксцентриситет главного вала на уровне низа дробящего конуса, см
(г = у , s — полный ход дробящего конуса, .
Производительность. Исходя из указанной выше величины угла
захвата, с достаточной точностью можно принять tgcti + tg«2 = 0,45.
Тогда производительность дробилки
Q = 0,755p.pn£>HrrfCp. т/ч* (3-12)
где р.— коэффициент разрыхления материала;
р — плотность материала, кг/см?-,
Da — нижний диаметр конического корпуса дробилки, см;
г — эксцентриситет главного вала, см;
^ср. диаметр кусков измельченного материала, см-.
, 2# 4- $ о .
^ср. =--2— (см- рис’ 3’4)
Расход энергии. Мощность для дробилок с крутым конусом опре-
деляется приближенно по теоретической формуле
Обозначения те же, что в формуле (3-10).
Пример 3-3. Выбрать конусную дробилку с крутым конусом для дроб-
ления 200 т/ч известняка, если максимальный диаметр кусков исходного ма-
териала dH = 300 мм, а средний диаметр кусков измельченного материала
Jcp = 60 мм.
Характеристика измельчаемого материала: плотность р=2,6«10~3 кг/см?;
степень разрыхления Р- = 0,4, предел прочности 1000 кгс/см2, модуль упру-
гости Е = 300 000 кгс/см2.
Решение. Принимаем угол наклона корпуса и дробящего конуса а, =
= аг = 12°40' (см. рис. 3-4). Тогда tg сц + tg аг — 0,45, Эксцентриситет г у
нижнего конца конуса принимаем 20 мм.
См. примечание на стр. 57.
62
Гл. 3. Измельчение твердых материалов
Число оборотов главного вала дробилки находим по формуле (3-11):
n = 470j/~ =223
об/мин
Принимаем округленно п = 220 об/мин.
Принимаем нижний диаметр корпуса дробилки = 1000 мм. Тогда про-
изводительность дробилки по формуле (3-12) составит:
Q = 0,755 • 0,4 • 2,6 • 10-3 • 220 • 100 • 2 • 6 = 207 т/ч
Потребляемая мощность рассчитывается по формуле (3-13):
хг 10002 • 220 • 100 (302 — 62) ое
N = 746 000 • 300 000 85 Квт
По рассчитанным значениям Q и N выбираем дробилку Уралмашзавода
марки ККД-500.
Расчет грибовидных дробилок. Оптимальная скорость Для нор-
мальной работы дробилки наименьшее число оборотов эксцентрика должно
соответствовать условию:
Рис. 3-7. К расчету грибовидной
дробилки:
3080 ,,
П -г... об мин
Vdk
(3-14)
dH~ начальный диаметр кусков измельчае-
мого материала; dK —конечный диаметр ку-
сков измельченного материала; £>к —диаметр
дробящего конуса; DQ — диаметр окружности,
на которой находится кусок материала, по-
ступивший в дробилку; / — длина зоны па-
раллельности стенок конусов.
где DK—диаметр дробящего кону-
са, см.
Формула (3-14) получена при
угле наклона образующей дробящей
головки, равном 41°, коэффициенте
трения f = 0,3 и длине зоны парал-
лельности I = 0,08 Dv (рис. 3-7).
Производительность. Тео-
ретическая производительность грибо-
видной дробилки:
Q = 0,015р.рш/к£)2 т/ч (3-15)
Расход энергии. Мощность
по формуле
где линейные размеры даны в см, а
плотность в кг/см3.
может быть ориентировочно определена
nDQd\
N== 89 700 Квт
(3-16)
где линейные размеры DQ и dH даны в см.
Формула (3-16) выведена для а -= 1500 кгс/см2, Е = 450 000 кгс/см2.
5. Валковые дробилки
63
5. Валковые дробилки
Устройство валковых дробилок. Эти дробилки состоят из
двух параллельных цилиндрических валков, которые, вращаясь
навстречу друг другу, измельчают материал главным образом
раздавливанием.
Валковая дробилка с гладкими
валками (рис. 3-8) состоит из стани-
ны 1 и валков 2 и 3. Валок 2 устано-
влен в подвижных подшипниках и мо-
жет перемещаться (подвижный ва-
лок). Подшипники валка 3 закреплены
неподвижно (этот валок является
неподвижным). Валок 2 удерживается
в определенном положении пружина-
ми 4. При попадании в дробилку куска
чрезмерно твердого материала пружи-
ны сжимаются, валки раздвигаются
и пропускают этот кусок без поломки
дробилки. Каждый из валков имеет
самостоятельный привод от ременного
шкива.
Для того чтобы куски измельчае-
мого материала втягивались вследст-
вие трения между валками, размер
кусков должен быть примерно в 20 раз
меньше .диаметра валков. Поэтому
/ — станина; 2~ подвижный валок;
3— неподвижный валок; 4 — пру-
жина; D — диаметр валка; /. — дли-
на валка; 2^ —зазор между вал-
ками.
гладкие валки применяются только для среднего и мелкого
дробления.
Валковые дробилки стандартизованы (ГОСТ 7243—54 и ГОСТ 8139—56).
Основной характеристикой валковых дробилок является диаметр D и длина
L валка. Эти размеры указываются в марке дробилки (например, дробилка
марки В-6-4 имеет D = 600 мм и L = 400 мм).
Для дробления хрупких материалов средней твердости (соли,
уголь и др.) применяют зубчатые валковые дробилки. Зубчатые
валки измельчают материал раскалыванием и отчасти раздавли-
ванием и могут захватывать куски с поперечником до 1/4—7г диа-
метра валка D. Для измельчения небольших кусков с размерами
примерно ’/ю—712 D используют валки рифленые или с мелкими
зубцами.
Двухвалковая зубчатая дробилка (рис. 3-9) имеет тихоход-
ные зубчатые валки 1 и 2, скорость которых w одинакова и со-
ставляет 1 —1,5 м!сек. Ведущий валок 1 имеет привод от ремен-
ного шкива через зубчатую передачу 3, причем вращение пере-
дается ведомому валку 2 через пару зубчатых колес 4 одинако-
64
Гл. 3. Измельчение твердых материалов
вого диаметра. При попадании в дробилку чрезмерно крупных
кусков валки раздвигаются, преодолевая натяжение пружин 5.
Быстроходные валки имеют непосредственный привод от ремен-
ной передами (w ~ 4 м/сек). Недостатком таких валков является
заметное переизмельчение материала.
Степень дробления на валковых дробилках для материалов
хрупких и средней твердости достигает i == 10—15, а размер
Рис. 3-9. Двухвалковая зубчатая дробилка:
1, 2—зубчатые валки, 3— зубчатая передача; 4— зубчатые колеса; 5 — пружина.
кусков продукта дробления колеблется от 10 до 5 мм (предель-
но до 2—3 мм). Для твердых материалов степень дробления
значительно ниже (1 = 3— 4).
Валковые дробилки широко применяются для дробления из-
вестняка, солей, мела, шамота и других материалов умеренной
твердости.
Достоинства валковых дробилок: 1) простота и компактность,
2) надежность в работе.
Недостатки: 1) выпуск плоских кусков (лещадок) измельчен-
ного материала (при гладких валках), 2) малая пригодность для
дробления материалов высокой твердости.
Расчет валковых дробилок. Угол захвата. На кусок материала А
(рис. 3-10), находящегося между валками, действует сила давления Р валка,
которая может быть разложена на составляющие Р sin а (по вертикали) и
Pcosa (по горизонтали). Сила Р вызывает силу трения fP, где f — коэффи-
циент трения скольжения между куском и валком. Эту силу также можно
5 Валковые дробилки
65
разложить на горизонтальную и вертикальную составляющие, как показано
на рис. 3-10.
Для втягивания куска между валками и его измельчения необходимо,
чтобы втягивающие силы 2fP cos а при вращении двух валков были больше
выталкивающих сил 2Р sin а, т. е. должно соблюдаться условие
откуда
или
2fP COS а > 2Р sin а
tga</
где <р — угол трения.
Из последнего выражения вытекает, что для захвата кусков материала
гладкими валками необходимо, чтобы угол захвата а был меньше угла тре-
ния материала <р:
а <р
Учитывая, что угол Р = 2а, можно
условие дробления материала предста-
вить в виде
В валковых дробилках угол захвата а
обычно принимают равным 18°.
Наибольший размер за-
хватываемых кусков По схеме
на рис. 3-10 можно определить наиболь-
ший диаметр d = 2г кусков, которые мо-
гут быть втянуты валками. Согласно
схеме
Р -j-e = (/? г) cos а Рис. 3-10. К расчету валковой
где R — радиус валка; дробилки.
е — половина зазора между валками.
Умножая обе части равенства на 2 и решая его относительно 2г, находим
наибольший диаметр кусков:
9 2/?(1 — cos a) +2g
cos а
(3-17)
или при сдвинутых вплотную валках (2е = 0):
п 2R (1 — cos а)
2г =----------------
COS а
Принимая а = 18° и подставляя в выражение (3-17) cos а =0,951, по-
лучим
2г -2R + 2e (3-18)
На практике наибольший диаметр кусков в 20—25 раз меньше диаметра
валков.
Скорость валков. Предельное число оборотов валков п находят,
исходя из недопустимости отставания материала от поверхности валков, ко-
торое приводит к снижению производительности дробилки, При этом
условии
п = 6161/ об (мин (3-19)
Г paHZ>
5 Зак 546
66
Гл. 3. Измельчение твердых материалов
где f— коэффициент трения материала о валок (f ~0,2);
р — плотность материала, кг/м3-,
dH — диаметр кусков исходного материала, м;
D — диаметр валка, м.
Обычно окружная скорость валков колеблется в пределах 3—6 м/сек
(не более 8 м/сек).
Производительность. Теоретическая производительность валко-
вых дробилок определяется по формуле
Q — 0,235p.p£ZMKn т/ч (3-20)
где Ц — коэффициент разрыхления измельчаемого материала ц = 0,2—0,3 (для
материалов средней твердости);
L — длина валка;
dK — диаметр кусков измельченного материала.
В формуле (3-20) все линейные размеры даны в см (плотность — в
кг/см3) *.
Расход энергии. Мощность, потребляемая валковой дробилкой,
складывается из расхода энергии на работу дробления, на трение материала
о валки и трение в подшипниках. Мощность валковых дробилок для средних
условий (а = 1250 кгс/см2, £ = 200 000 кгс/см2) можно приближенно опреде-
лять по формуле
.. LDn / , D2 \
ЛГ~ 35 300 \Т 24 000 ) Квт <3'21)
в которой все линейные размеры даны в см.
Пример 3-4. Выбрать ваДковую дробилку, определить число ее оборотов
и потребляемую мощность, если на измельчение поступает 70 т/ч материала
(плотность р=2,7-1О“3 кг/см3). Максимальный размер кусков исходного
материала rfH=40 мм, коэффициент разрыхления материала р-= 0,25. Тре-
буемый размер кусков измельченного материала dK = 10 мм.
Решение. Минимальный диаметр валков определяют из условия
у = 20—25; в данном случае необходимо, чтобы диаметр D валков был не
менее 20 • 40 = 800 мм. На основании этого условия и с учетом размера кус-
ков, поступающих на дробление, выбираем валковую дробилку с гладкими
валками Уралмашзавода типа 2ВГ—1000 X 400. Диаметр валков D = 1000 мм,
длина валков L = 400 мм. Зазор е между валками должен составлять:
е = dK = 10 мм.
Число оборотов валков находим по формуле (3-20):
Q 70 11П /Г/
п =-------------=--------------------5----------^110 об мин
0,235pPLDdK 0,235 • 0,25 • 2,7 • 10-3 • 40 • 100 • 1
Тогда окружная скорость валков составит:
~Dn 3,14-1-110 _0 .
w = -60“ =------60— “ 5’8 м/сек
что допустимо.
Потребляемая дробилкой мощность определяется по формуле (3-21):
40-100-110 / 4 , 1002 \
Л=~35300 U + 24000 ~30 Квт
* См. примечание на стр. 57.
6. Ударно-центробежные дробилки и мельницы
67
куски материала раздавливаются
Рис. 3-11. Молотковая дробилка:
/—плита; 2— корпус; 3— молоток; 4 — ротор;
5 — колосниковая решетка.
6. Ударно-центробежные дробилки и мельницы
Молотковые дробилки
В молотковой дробилке (рис. 3-11) измельчаемый материал
поступает сверху и дробится на лету ударами молотков 3, шар-
нирно подвешенных к быстро вращающемуся ротору 4. Мате-
риал отбрасывается молотками и разбивается о плиты 1, покры-
вающие корпус 2; кроме того,
и истираются на колоснико-
вой решетке 5. Измельчен-
ный материал выпадает че-
рез щели решетки. Степень
измельчения регулируется
изменением окружной ско-
рости молотков или ширины
щелей решетки.
Молотковые дробилки
для крупного и среднего
дробления измельчают ма-
териал главным образом
ударами молотков. При мел-
ком дроблении основное зна-
чение имеют раскалывание
и срез, а также истирание
материала на решетке. По-
этому £ля мелкого дробле-
ния применяют облегченные
заостренные молотки, вращающиеся с большой скоростью
(до 55 м/сек).
Молотки, плиты и решетку изготовляют из износоустойчивой
марганцовистой стали или углеродистой стали, наплавленной
твердым сплавом — сталинитом.
Молотковые дробилки различают по количеству роторов (од-
нороторные и двухроторные), а также по расположению молот-
ков в одной или нескольких плоскостях вращения (однорядные
и многорядные). Степень измельчения колеблется от i = 10— 15
в однороторных дробилках до i = 30 — 40 в двухроторных. Раз-
мер продукта дробления в однороторных дробилках составляет
10—15 мм (реже до 5 мм), в двухроторных 20—30 мм и более.
Для мелкого измельчения материалов небольшой твердости
(известь, охра, фосфориты и др.) применяют молотковые дро-
билки без колосниковой решетки, а также молотковые мельни-
цы, соединенные с воздушным сепаратором (стр. 102), в кото-
ром недоизмельченный продукт отделяется и затем возвра-
щается в мельницу.
5*
68
Гл. 3. Измельчение твердых материалов
В дробилках и мельницах, предназначенных для измельчения
мягких и вязких материалов, молотки часто закрепляют непо-
движно, что способствует истиранию и раскалыванию материала.
Такие дробилки и мельницы называются крестовыми.
Молотковые дробилки характеризуются произведением диаметра D на
длину L ротора; эти размеры указываются в обозначении марки дробилки
(например, дробилка марки М-6-4 имеет ротор диаметром D = 600 мм и дли-
ной L = 400 мм).
Однороторные молотковые дробилки по ГОСТ 7090—54 имеют следующие
размеры ротора (диаметр X длина): 300 X 200, 400 X 300, 800 X 600,
1000 X 800, 1000 X 1200, 1300 X 1600, 2000 X 1800 и 2000 X 3000 мм.
Производительность молотковых дробилок определяют по формуле
ЬГ№1 п2
Q= 3660-(,-l) (З-22)
где D — диаметр ротора, м;
L — длина ротора, м;
п — число оборотов ротора в минуту;
i—степень измельчения;
k — опытный коэффициент, величина которого зависит от конструкции
дробилки и твердости измельчаемого материала (обычно k = 4,0—6,2).
Мощность, потребляемая молотковой дробилкой, может быть приближенно
определена по эмпирической формуле:
2V = (0,1 0,15) iQ кет (3-23)
Пример 3-5. Имеется молотковая дробилка марки СМ-18. Диаметр ее
ротора D = 800 мм, длина L = 400 мм, ширина отверстий колосниковой ре-
шетки 13 мм, число оборотов ротора п = 950 об!мин. Мощность электродви-
гателя дробилки 20 кет.
Проверить, пригодна ли эта дробилка для измельчения 25 т/ч про-
дукта средней твердости, крупность кусков которого 100 мм. Диаметр кусков
дробленого продукта должен составлять 10 мм.
Решение. Степень измельчения продукта:
._ 100 _ ш
г- w -10
Производительность дробилки определяем по формуле (3-22):
п _ 4 • 0,82. о,4 • 9502 „ _ .
Q “ 3600 (io—1) ~ 28,5 m!li
Потребляемую мощность находим по формуле (3-23):
N = 0,1 • 10 • 28,5 = 28,5 кет
Следовательно, дробилка может быть использована на заданную произ-
водительность, но к ней должен быть установлен более мощный электродви-
гатель (N= 30 кет). Согласно каталогу привод дробилки рассчитан на такую
мощность электродвигателя.
Дезинтеграторы и дисмембраторы
Дезинтегратор (рис. 3-12) представляет собой ударную дро-
билку, в которой материал измельчается между двумя вращаю-
щимися роторами 1 и 2. Каждый ротор состоит из двух кольце-
7. Барабанные мельницы
73
При массе шара т, радиусе его вращения R угловой скорости <о, числе обо-
ротов барабана п центробежная сила Р, действующая на шар, составляет:
/ "П \2
Р = ma2R = m\-™] R
При этом допускается, что скорости движения шара и барабана равны,
a R равен внутреннему радиусу барабана, так как диаметр шара по сравне-
нию с диаметром барабана незначителен.
Сила тяжести "(вес) шара:
G = mg
где g — ускорение силы тяжести, м!сек2.
На рис. 3-15 шар изображен в момент его наибольшего подъема по стенке
мельницы, после чего он должен оторваться от стенки и свободно падать как
тело, брошенное со скоростью, равной
скорости барабана, под углом а к
горизонту (см. пунктир на рис. 3-15).
Угол подъема шара а, соответ-
ствующий этому моменту, опреде-
ляется из проекции сил на вертикаль-
ную ось:
Р cos а = mg
откуда
cos а —
mg
Р
mg
Wl\2
/30/
900
n2R
или
COS а
1800
n2D
(3-24)
где D — внутренний диаметр бараба-
на мельницы, м.
Найдем предельную, или «крити-
ческую», скорость, при которой шар
начнет вращаться вместе со стенкой.
Очевидно, шар не сумеет оторваться
от стенки, если, двигаясь вверх по ней,
в барабане, для которой а = 0, или cos
Рис. 3-15. К расчету барабанной
шаровой мельницы.
он достигнет самой высокой точки А
‘ = 1. В этом случае
1 =
1800
откуда
1800 42,4
«кр. = —об! мин
(3-25)
Фактически при этом числе оборотов шар еще не будет двигаться вместе
с барабаном вследствие своего скольжения относительно стенки и скольже-
ния одного ряда шаров относительно другого. Поэтому пкр., определяемое по
формуле (3-25), следует считать условной величиной, в долях которой выра-
жают наивыгоднейшее число оборотов мельницы.
74
Г л. 3. Измельчение твердых материалов
Обычно наивыгоднейшее число оборотов мельницы принимают равным
75% от пкр. и определяют по формуле
32
п = об! мин
Vd
(3-26)
Загрузка шарами. Короткие мельницы, независимо от способа их
разгрузки, заполняют шарами приблизительно на 40—45% объема барабана.
Размер шаров, загружаемых в барабан, зависит от наибольшего размера
кусков питания dH и размера частиц измельченного продукта dK и может
быть определен по формуле:
Ап = 6 (lgdK) уПЦ мм (3-27)
где dK выражено в мк, a dH— в мм.
Производительность и расход энергии. Производитель-
ность Q мельницы рассчитывается на выход частиц определенной крупности
и может быть ориентировочно определена по формуле:
Q = KVD0’6 т!ч (3-28)
где К — коэффициент пропорциональности, определяемый по табл. 3 (при раз-
грузке через диафрагму приведенные значения К следует умножать
V — объем барабана, м3;
D — диаметр барабана, м.
Таблица 3
Значение коэффициента К
Крупность исходного материала * мм Крупность измельченного материала *, мм
0,2 0,15 0,075
25 1,31 0,95 0,41
19 1,57 1,09 0,51
12 1,91 1,25 - 0,58
6 2,4 1,5 0,66
* Содержание в материале частиц крупностью, меньшей,
чем указано в таблице, составляет 85%.
Производительность зависит от многочисленных факторов: от свойств
материала, его крупности, степени измельчения, веса шаровой загрузки, раз-
меров мельницы и т. д. Поэтому более точно производительность мельницы
может быть определена только опытным путем.
Расход энергии на измельчение приближенно вычисляется по теорети-
ческой формуле
N — 6,\тш УD квт (3-29)
где тш—масса шаров, т;
D — внутренний диаметр барабана, м.
Из формулы (3-29) видно, что потребляемая мощность определяется
массой шаровой загрузки и диаметром барабана. Это объясняется тем, что
энергия расходуется в основном на подъем шаров в мельнице. Очевидно,
7. Барабанцые мельницы
75
Мощность, потребляемая при холостом ходе мельницы, незначительно отли-
чается от затраты мощности при работе с нагрузкой. Поэтому необходимым
условием экономичного измельчения является работа барабанной мельницы
при полной нагрузке.
Расход энергии на измельчение в однокамерных и многокамерных мель-
ницах определяется по эмпирической формуле
N = (С]/?!! + С2т2 + ...)/£> кет (3-30)
где m2... — массы шаров, загружаемых в каждую камеру, т;
D — диаметр барабана, м;
Clf С2 ... — коэффициенты, определяемые по табл. 4.
Таблица 4
Значения коэффициента С
Дробящие тела Степень заполнения камеры
0,1 0,2 0,3 0,4 0,5
Шары стальные большие . 11,9 11,0 9,9 8,5 7,0
» » малые . . 11,5 10,6 9,5 8,2 6,8
Цилиндры малые 11,7 10,0 9,2 8,0 6,0
Галька кремневая .... 13,3 12,3 11,0 9,5 7,8
Пример 3-6. Рассчитать шаровую мельницу с центральной разгрузкой,
размеры барабана которой D X L = 1500 X 3000 мм, если 85% кусков исход-
ного материала имеют диаметр dH = 25 мм, а 85% зерен измельченного про-
дукта имеют крупность менее 150 мк, насыпная масса стальных шаров
рш = 4100 кг/мг.
Решение. По формуле (3-26) число оборотов мельницы составляет:
32 ’ OR
п = .____- = 26 об мин
/1,5
Объем барабана мельницы:
Диаметр загружаемых шаров находим по формуле (3-27):
£)ш = 6 (1g 150) /25 = 65,3 мм
Принимаем Ош = 70 мм.
Принимаем степень заполнения барабана шарами = 0,4. Тогда масса
загружаемых шаров составит:
/пш = ?^бРш = 0,4 • 5,3 • 4100 = 8700 кг
Производительность (считая на измельченный продукт) согласно формуле
(3-28) равна:
Q = 0,95 • 5,3 • 1,5°>6 = 6,42 т/ч
Потребляемая мощность по формуле (3-29) составит:
N = 6,1 • 8,7 /IJ 65 кет
76
Гл 3. Измельчение твердых материалов
8. Ролико-кольцевые мельницы
Измельчение в кольцевых мельницах происходит путем раздавливания и
истирания материала несколькими мелющими телами (роликами или шарами),
которые катятся по внутренней
Рис. 3-16. Маятниковая ролико-
кольцевая мельница:
поверхности кольца (вкладыша) и прижи-
маются к ней центробежной силой или на-
тяжением пружин.
В маятниковой ролико-кольцевой мель-
нице (рис 3-16) ролики 1 свободно наса-
жены на трех — пяти маятниках 2, кото-
рые вращаются на общей крестовине. По-
ступающий в мельницу материал измель-
чается между роликами и поверхностью
кольца 5; измельченный материал уносится
струей воздуха в сепаратор (стр. 102),
встроенный в корпус мельницы (на рисунке
не показан).
Такие мельницы применяют для тонко-
го измельчения материалов, которые не мо-
гут быть обработаны в шаровых мельницах
вследствие налипания материала на шары
и футеровку барабана. К подобным мате-
риалам относятся различные пигменты и на-
1— ролики; 2— маятники; 3— кольцо.
полнители, например тальк, мел и др.
По сравнению с шаровыми мельницами
кольцевые более компактны и степень из-
мельчения в них может изменяться в широких пределах. Однако кольцевые
мельницы более сложны по конструкции и требуют больших эксплуатацион-
ных расходов.
9. Дробилки и мельницы для сверхтонкого измельчения
При увеличении частоты воздействий внешних сил на мате-
риал все меньшее количество трещин, образующихся в кусках
или зернах, успевает смыкаться («самозаживляться») и процесс
измельчения ускоряется. Поэтому с наименьшей затратой энер-
гии тонкое измельчение может быть осуществлено путем вибра-
ционного (высокочастотного) воздействия на материал, т. е. по-
средством весьма частых, но сравнительно слабых ударов по его
зернам. При таком воздействии происходит усталостное разру-
шение зерен измельчаемого материала.
Вместе с тем упругим деформациям и разрушению (или из-
носу) при измельчении подвергается не только измельчаемый ма-
териал, но и машина для измельчения—дробилка или мельни-
ца. Вес описанных выше дробилок и мельниц во много раз
превосходит вес измельчаемого материала, поэтому материалу
сообщается лишь незначительная доля всей энергии, затрачи-
ваемой на измельчение, и к. п.д. этих машин очень низок. Для
повышения эффективности измельчения необходимо возможно
больше уменьшить вес применяемой машины.
9. Дробилки и мельницы для сверхтонкого измельчения
77
Эти соображения были положены в основу созданных в по-
следние годы вибрационных мельниц, вибрационных, так назы-
ваемых отражательных дробилок, в которых происходит вибра-
ционное измельчение материала мелющими телами минималь-
ного веса, и струйно-вибрационных мельниц, работающих без
мелющих тел.
Вибрационные мельницы
На рис. 3-17 показана вибрационная мельница инерционного
типа. Цилиндрический корпус 1 мельницы, загруженный на 80—
90% объема мелющими телами (шарами) 2 и измельчаемым
материалом, вращается на валу 3, снабженном дебалансом. Де-
баланс расположен эксцентрично относительно оси вращения
Рис. 3-17. Вибрационная мельница инерционного типа:
1 — корпусу 2 — мелющие тела (шары); 3—вал с дебалансом; 4 — пружины;
5— электродвигатель; 6 — эластичная муфта.
мельницы; поэтому при вращении неуравновешенной массы ва-
ла с дебалансом (вибратора) возникают центробежные силы
инерции, вызывающие вибрации корпуса мельницы. При вра-
щении корпус вместе с загруженными в него шарами и мате-
риалом совершает колебания в плоскости, перпендикулярной к
оси вибратора, по траектории, близкой к круговой. Частота ко-
лебаний соответствует числу оборотов вала, которое изменяется
в пределах 1000—3000 об/мин при амплитуде колебаний, не
превышающей 2—4 мм. Под действием столь частых импульсов
и сложного движения мелющих тел (которые вращаются в сто-
рону, обратную направлению вращения вибратора, и одновре-
менно сталкиваются, вращаются и скользят) происходит весьма
интенсивное измельчение материала.
Для предотвращения передачи вибраций на пол помещения,
где установлена мельница, и на электродвигатель 5, корпус
78
Гл 3. Измельчение твердых материалов
мельницы опирается на пружины 4 и деревянные подкладки, а
электродвигатель соединен с валом эластичной муфтой 6.
При вибрационном измельчении значительная часть энергии,
расходуемой на измельчение, превращается в тепло, в резуль-
тате температура внутри мельницы может сильно повыситься,
что при измельчении ряда материалов недопустимо. Поэтому
вибраторы описанных мельниц непрерывно охлаждают водой,
циркулирующей через рубашку.
Вибрационные мельницы используют для сухого и мокрого
помола, причем в последнем случае степень заполнения корпуса
не превышает 0,75. Мельницы работают периодическим и непре-
рывным способом, непрерывнодействующие вибрационные мель-
ницы работают в замкнутом цикле с воздушным сепаратором.
В вибрационных мельницах целесообразно измельчать мате-
риалы с начальным диаметром зерен dH не более 1—2 мм до
конечного диаметра dK менее 60 мк. Прй сверхтонком измельче-
нии эффективность этих вибрационных мельниц в 5—30 раз пре-
вышает эффективность шаровых мельниц при значительно мень-
шем удельном расходе мощности.
Вибрационные мельницы конструкции ВНИИНСМ * изгото-
вляются с объемом корпуса 0,001, 0,005, 0,2, 0,4 и 1 м3. Мощ-
ность электродвигателя к мельницам колеблется от 4,5 до 75 кет.
Вибрационные (отражательные) дробилки
Эти дробилки (рис. 3-18) занимают промежуточное положе-
ние между вибрационными мельницами и мельницами без
мелющих тел. Поступающий в дробилку материал движется по ре-
шетке 1, на которой из него отсевается мелочь, после чего мате-
риал попадает на быстровращающийся валок 2, снабженный не-
большими лопатками (окружная скорость валка 12—70 м]сек).
Куски материала захватываются валком и с большой скоростью
отбрасываются на свободно подвешенный щиток 4, отражаясь
от которого, они сталкиваются с другими кусками. В небольшом
объеме, заключенном между решеткой /, цепями 5, валком 2 и
щитком 4, происходит интенсивное измельчение материала в ос-
новном вследствие соударений кусков материала. Взаимные уда-
ры кусков материала столь часты, что измельчение носит вибра-
ционный характер. За щитком 4 свободно подвешен щиток 5; в
пространстве между щитками, корпусом дробилки и валком 2
происходит окончательное измельчение отбрасываемых сюда бо-
лее мелких кусков материала. Такое двухстадийное измельчение
* Всесоюзный научно-исследовательский институт новых строительных
материалов.
9 Дробилки и мельницы для сверхтонкого измельчения
79
материала позволяет достигать в отражательных дробилках сте-
пени измельчения i = 20 — 50, причем получается однородный
продукт измельчения с минимальным содержанием мелочи.
Отражательные дробилки отличаются высокой эффектив-
ностью, малым удельным расходом энергии на измельчение, про-
Рис. 3-18. Вибрационная (отражательная)
дробилка:
1 — решетка; 2 — валок; 3, 4 — щитки; 5—цепи.
стотой устройства и малым весом, благодаря которому их можно
устанавливать на легких фундаментах и даже на перекрытиях
зданий.
Струйно-вибрационные мельницы
В этих мельницах энергия, необходимая для измельчения
частиц материала, сообщается струей перегретого пара или сжа-
того воздуха, вытекающей из сопла со звуковой и сверхзвуковой
скоростью.
В мельнице с плоской горизонтальной камерой (рис. 3-19) из-
мельчаемый материал подается инжектором 1 и поступает в пло-
скую размольную камеру 2 высотой 25—60 мм (диаметр камеры
1200 мм). В ту же камеру через сопла 3 вводится перегретый
пар (избыточное давление 7—35 ат) или сжатый воздух (избы-
точное давление 6—7 ат). Сопла 3 установлены под углом в
торцовой стенке размольной камеры на равных расстояниях
друг от друга. Частицы материала захватываются струей воз-
духа или пара, скорость которой может достигать 600—
800 м[сек, и направляются от периферии к центру камеры, за-
80
Гл. 3. Измельчение твердых материалов
тем другой струей воздуха или пара, пересекающей траекторию
движения частицы, последняя отбрасывается от периферии к
центру и т. д. Во время движения каждая частица многократно
сталкивается с другими частицами материала. При очень боль-
ших скоростях движения
происходит вибрационное
размеров частиц 3—6 мм
5
и весьма частых соударениях частиц
измельчение материала от начальных
до размеров 1—6 мк (для очень твер-
дых материалов начальный раз-
мер частиц ~200 мк).
По мере измельчения частиц
амплитуда их колебаний около
центральной трубы 4 уменьшает-
ся. Когда сила струи пара (или
Рис. 3-20. Струйно-ви-
брационная мельница с
вертикальной трубной
камерой:
Рис. 3-19. Струйно-ви-
брационная мельница с
плоской горизонтальной
камерой:
1 — инжектор; 2 — размольная
камера; 3— сопла; 4 — цен-
тральная труба; 5 —труба для
отвода отработанного газа;
6— приемник.
1 — инжектор; 2— размольная
камера; 3— сопла; 4 — пыле-
уловитель; 5 — труба для отвода
измельченного материала.
I
воздуха) превысит инерционные силы, действующие на частицу,
нисходящий поток газа выносит ее в трубу 4, по которой измель-
ченные частицы попадают в приемник 6. Наиболее мелкие ча-
стицы (содержание их 5—10% или меньше) увлекаются вос-
ходящим потоком отработанного газа, удаляемого по трубе 5, и
улавливаются в пылеуловителе-циклоне или мешочном фильтре
(см. главу 9).
В мельнице с вертикальной трубной камерой (рис. 3-20) из-
мельчаемый материал подается инжектором 1 в размольную ка-
меру 2, находящуюся в нижней части овального замкнутого кон-
г
tV
9. Дробилки и мельницы для сверхтонкого измельчения 81
тура (трубы). В камеру 2 через сопла 3 подают сжатый воздух
или перегретый пар; сопла расположены в два ряда так, что
струи воздуха (пара) перекрывают друг друга. Увлекаемые
струями частицы материала многократно сталкиваются и по ме-
ре измельчения поднимаются по левой ветви овального контура,
при этом скорость частиц достигает 150 м/сек. Проходя верхние
изгибы контура, частицы классифицируются по размерам.
В верхней части правой (нисходящей) ветви контура распо-
ложен инерционный пылеуловитель 4 в виде жалюзи из пластин
с переменным углом наклона. Измельченные до требуемого раз-
мера частицы проходят между пластинами и удаляются по тру-
бе 5, более крупные частицы задерживаются и отражаются от
пластин и по нисходящей ветви контура возвращаются на доиз-
мельчение. Кратность циркуляции частиц измельчаемого мате-
риала в мельнице 1500—2500.
В отличие от мельницы, показанной на рис. 3-19, в описанной
мельнице устранена возможность уноса недоизмельченных ча-
стиц с воздухом или паром. Данная мельница пригодна для
сверхтонкого измельчения (вплоть до 0,5 мк при размере ис-
ходных частиц 150 мк).
Достоинства струйно-вибрационных мельниц: 1) высокоэф-
фективное измельчение в сочетании с классификацией частиц из-
мельченного материала, 2) незначительный износ, так как из-
мельчаемый материал вводится в струи воздуха (пара) уже по-
сле истечения их из сопел.
Недостатки'струйно-вибрационных мельниц: 1) большой рас-
ход сжатого воздуха (или перегретого пара), температура и да-
вление которого должны быть постоянны, 2) необходимость весь-
ма равномерного питания исходным измельчаемым материалом.
Коллоидные мельницы
Помимо вибрационных мельниц, для сверхтонкого измельче-
ния применяются также коллоидные мельницы, которые по прин-
ципу действия напоминают ролико-кольцевые или ударно-цен-
тробежные мельницы. В коллоидных мельницах материал из-
мельчается, проходя через весьма малый (до 0,05 мм) зазор ме-
жду быстро вращающимся коническим роликом (ротором) и
расширяющимся кверху кольцом (статором) либо проходя ме-
жду расположенными по концентрическим окружностям пальца-
ми диска-ротора и корпуса мельницы. Коллоидные мельницы
работают при очень больших окружных скоростях ротора (до
125 м/сек) и применяются главным образом для мокрого из-
мельчения.
6 Зак. 546.
82
Гл. 3. Измельчение твердых материалов
10. Сравнение и выбор дробильно-размольных машин
Выбор дробилок и мельниц производят в зависимости от вида измель-
чения (см. стр. 50), а также от физико-механических свойств измельчаемого
материала (твердость, хрупкость, абразивность и др.).
Для крупного измельчения наиболее широко применяются щековые дро-
билки. Конусные дробилки обладают большей производительностью, чем ще-
ковые, требуют меньшего расхода энергии, дают более равномерный продукт
с меньшим содержанием мелочи и отличаются спокойной работой. Однако
вследствие более сложной конструкции, большего веса и большей стоимости
конусные дробилки целесообразно применять для крупного дробления только
при большой производительности, когда одна конусная дробилка может за-
менить две или более щековых. Во всех остальных случаях следует отдавать
предпочтение щековым дробилкам.
Валковые дробилки значительно уступают по производительности грибо-
видным, но при небольших производительности и степени из-мельчения целе-
сообразнее применять валковые дробилки, отличающиеся простотой, компакт-
ностью и надежностью работы. Для хрупких материалов наиболее пригодны
высокопроизводительные зубчатые валковые дробилки, простые по конструк-
ции и требующие небольшого расхода энергии.
Молотковые дробилки мало пригодны для измельчения очень твердых и
абразивных материалов (быстрый износ) или влажных материалов, содержа-
щих более 15% влаги (забивание решетки). Для влажных материалов неболь-
шой твердости более приспособлены дезинтеграторы.
Тонкое измельчение материалов (примерно до 100 мк) производится пре-
имущественно в шаровых мельницах. Ролико-кольцевые мельницы приме-
няются лишь для тонкого измельчения материалов небольшой твердости (на-
пример, для измельчения фосфоритов), а также для обработки материалов,
непригодных к измельчению в шаровых мельницах. Вследствие сложности
устройства ролико-кольцевые мельницы применяют значительно реже ба-
рабанных.
Вибрационные мельницы могут быть наиболее эффективно использованы
для получения высокодисперсных измельченных продуктов «£0 мк) при ус-
ловии их предварительного измельчения примерно до 2 мм в дробилках или
мельницах других типов. Вибрационные мельницы непригодны для измельче-
ния липких порошков и вязких паст.
Для сверхтонкого измельчения ряда материалов (каменный уголь, сухие
красители, двуокись титана и др.) перспективно применение струйно-вибра-
ционных мельниц, которые пока мало распространены.
11. Схемы измельчения
Дробление и особенно мелкое измельчение требуют большого расхода
энергии. Поэтому при выборе схем проведения этих процессов следует исхо-
дить из принципа: «Не дробить ничего лишнего». Практически это требование
сводится к тому, чтобы перед каждой операцией дробления отделять мелочь,
т. е. куски, равные (или меньшие) по крупности конечному продукту дробле-
ния, получаемому в данной дробилке. Таким путем удается уменьшить расход
энергии на дробление, хотя' одновременно возрастает стоимость оборудования.
В результате предварительного отделения мелочи избегают перегрузки и
износа дробилки, а также переизмельчения материала и получают продукт
равномерной крупности.
Как было указано выше, измельчение может проводиться в открытом и
замкнутом циклах.
При измельчении в открытом цикле куски материала проходят через дро-
билку (мельницу) только один раз, не возвращаясь в нее. Обычно в открытом
И. Схемы измельчения
83
цикле проводят крупное и среднее измельчение, если нет необходимости по-
лучать конечный продукт точных размеров. При наличии мелочи в исходном
материале его предварительно подвергают грохочению (рис. 3-21,а).
Исходный
материал
Крупный
(верхний)
продукт
I
Дробление
Грохочение (предварительное)
мелкий
(нижний)
продукт
а
Конечный
продукт
Исходный /
материал \
Исходный
----->---- материал
Y
Дробление
I
Грохочение (поверочное)
л г ।
Крупный Мелкий
(верхний) (нижний)
продукт продукт
_3
Рис. 3-21. Схемы измельчения в один прием:
а — по открытому циклу; б — по замкнутому циклу, 1 — грохот; 2 — дробилка.
При измельчении в замкнутом цикле дробилка (мельница) работает с
грохотом или классификатором, при помощи которого слишком крупный про-
дукт непрерывно возвращается для повторного измельчения в дробилку или
мельницу (рис. 3-21,6). Такая схема широко применяется при тонком измель-
чении, когда требуется однородность размеров конечного продукта. Работа
по замкнутому циклу позволяет снизить расход энергии на измельчение и по-
высить производительность дробилки (мельницы).
На рис. 3-21 изображены наиболее простые схемы измельчения в один
прием При измельчении в два приема (рис. 3-22) материал после щековой
дробилки поступает на поверочное грохочение, а затем направляется в валко-
6*
84
Гл 3. Измельчение твердых материалов
вую дробилку. Такая схема позволяет получать равномерный по крупности
продукт измельчения.
Количество материала, возвращаемого на повторное измельчение, при ра-
боте по замкнутому циклу («циркуляционная нагрузка») составляет 300—
600% от веса исходного материала.
Исходный
материал
верхний
продукт
Дробление J
(текован дробилка)
Грохочение (поверочное)
Дробление П
(валковая дробилка)
Нижний
продукт
Конечный
продукт
Рис. 3-22. Схема измельчения в два приема:
1 — щековая дробилка; 2 —грохот; 3— валковая дробилка.
Величина циркуляционной нагрузки при дроблении в замкнутом цикле
с предварительным грохочением определяется по формуле
х = —— (3-31)
7] —Г
где а — весовая доля крупных кусков в исходном материале;
т] — содержание крупной фракции в верхнем продукте грохота (к. п. д.
грохота);
г—весовая доля кусков крупнее заданного размера в продукте дроб-
ления.
При измельчении в замкнутом цикле с поверочным грохочением циркуля-
ционная нагрузка составляет:
х = ~~=7 <3’32)
В среднем весовая доля крупной фракции в дробленом материале равна:
для щековых и конусных дробилок г = 0,7, для грибовидных г = 0,4, для вал-
ковых г — 0,7—0,8.
Пример 3-7. На валковую дробилку, работающую в замкнутом цикле с
предварительным грохочением, поступает 15 т/ч исходного материала, со-
держащего 20% кусков, крупность которых меньше требуемого продукта
дробления (dK = 10 мм). После однократного прохождения материала через
11. Схемы измельчения
85
дробилку продукт дробления содержит 62,5% кусков размером > 10 мм,
к. п. д. грохота = 0,82.
Определить производительность дробилки и грохота.
Решение. Доля крупных кусков материала составляет: в исходном ма-
териале
а — 1—0,2 = 0,8
в продукте дробления г = 0,625.
Циркуляционная нагрузка валковой дробилки по формуле (3-31) равна:
0 8
Х = 0,82 — 0,625 = 4,1 ’ Т' е‘ 410 % .
Производительность валковой дробилки составляет:
фд = Gx = 15 • 4,1 = 61,5 mfu
Производительность грохота по питанию (количеству поступающего ма-
териала) :
Qr = фд + Q = 61,5 + 15 = 76,5 т/ч
Глава 4
КЛАССИФИКАЦИЯ (СОРТИРОВКА) МАТЕРИАЛОВ
1. Общие сведения
Разделение сыпучих материалов по размеру кусков или зерен
называется классификацией. Путем классификации сыпучая
смесь разделяется на классы, или фракции, ограниченные опре-
деленными пределами размеров кусков или зерен.
Применяются три вида классификации материалов:
1) грохочение — механическая классификация на ситах; че-
рез отверстия рабочей поверхности грохота проходят куски
меньше определенного размера, а остальные задерживаются на
поверхности и удаляются с нее;
2) гидравлическая классификация — разделение смеси на
фракции (классы) зерен, обладающие одинаковой скоростью
падения в воде;
3) воздушная сепарация — разделение смеси на фракции зе-
рен, обладающие одинаковой скоростью падения в воздухе.
Грохочение — наиболее универсальный способ классифика-
ции, применяемый для разделения материалов различной круп-
ности (примерно от 250 до 1 мм). При помощи гидравлической
классификации и воздушной сепарации можно разделять только
зерна крупностью менее 2 мм. Классификация применяется как
вспомогательная операция — для предварительной подготовки
материала к дроблению (удаление мелочи) или для возврата
слишком крупного материала на повторное измельчение, а так-
же как самостоятельная операция — для получения готового
продукта с заданным зернистым составом. В последнем случае
процесс классификации называется сортировкой.
Классификация широко используется для ситового анали-
за — определения зернистого состава материала.
2. Сита и ситовой анализ
Основной частью грохота является его рабочая поверхность, выполняемая
в виде проволочных сит (иногда шелковых) или решет из стальных листов с
штампованными отверстиями, или же решеток из параллельных стержней —
колосников.
3. Типы грохотов и способы грохочения
87
Проволочные сита представляют собой сетки с квадратными или прямо-
угольными отверстиями размером от 100 до 0,15 мм. При лабораторных рабо-
тах (ситовой анализ) применяют мелкие сита с отверстиями до 0,04 мм.
Согласно ГОСТ 3584—53 сита обозначаются номерами, соответствующими
размеру стороны отверстия (ячейки) сетки в свету, выраженному в милли-
метрах. Так, например, сито № 5 имеет квадратные отверстия с длиной
стороны 0,5 мм.
Раньше сита характеризовались числом ячеек, приходящихся на 1 погон-
ный дюйм сетки (число меш), либо числом отверстий на 1 см2 сетки. В таких
обозначениях не указывались размеры ячеек сита, которые зависят от тол-
щины проволоки. Таким образом, сита с одинаковым числом меш (или отвер-
стий на 1 см2) могут иметь разные размеры ячеек, что создает неудобства
при практическом применении.
Листовые решета изготавливают из листов толщиной 3—12 мм, в которых
штампуют круглые или продолговатые отверстия размером 5—50 мм (пре-
дельные размеры 1,6—125 мм)-, для уменьшения возможности забивания от-
верстий их делают слегка расширяющимися книзу.
Колосники представляют собой стержни трапецевидного сечения. Такая
форма удобна, так как облегчает прохождение материала через расширяю-
щиеся книзу зазоры между колосниками. В качестве колосников часто исполь-
зуют старые рельсы со срезанной подошвой
Определение зернистого состава сыпучих материалов производится при
помощи специального набора сит, размеры отверстий которых уменьшаются
от сита к ситу в постоянном соотношении Для выполнения ситового анализа
просеивают среднюю пробу материала. По окончании просеивания взвеши-
вают остатки материала на каждом из сит и зерна, прошедшие через нижнее
(самое тонкое) сито. Отношение полученных весов к навеске материала, взя-
той для анализа, дает содержание различных классов зерен в материале, т. е.
зерен, размеры которых ограничены определенными верхним и нижним пре-
делами.
Полученные в результате просеивания на сите продукты обозначаются
размером отверстий сита, полностью пропускающего зерна данного размера
(со знаком минус), и размером отверстий сита, полностью их задерживаю-
щего (со знаком плюс). Так, продукт, прошедший через сито с отверстиями
4 мм, обозначается —4 мм, а оставшийся на сите +4 мм.
Классы зерен обозначаются размерами сит, соответствующих предельным
размерам зерен или кусков данного класса. Если, например, данный класс
получен последовательно просеиванием на ситах № 4 и № 2, т. е. с отвер-
стиями 4 и 2 мм, то его обозначают так: —4+2 мм.
В результате ситового анализа определяют характеристику зернистости
материала, или его гранулометрический состав.
3. Типы грохотов и способы грохочения
Отделение кусков определенной крупности на грохоте проис-
ходит при движении материала относительно рабочей поверх-
ности грохота. Относительное движение материала создают ли-
бо на неподвижном грохоте, установленном под углом к гори-
зонту, ббльшим, чем угол трения материала, либо при движении
сита грохота в наклонной или горизонтальной плоскости.
Наклонные подвижные грохоты работают с помощью криво-
шипного или эксцентрикового механизма, сообщающего ситу
симметричное движение. В горизонтальных подвижных грохо-
тах ситу сообщаются при прямом и обратном ходе разные
88
Гл. 4. Классификация (сортировка) материалов
ускорения, причем несимметричность движения достигается
двумя путями: при помощи специальных устройств (шкивов с
неуравновешенными грузами, кулачков и др.) или с помощью
эксцентрикового механизма при установке грохота на наклон-
ных опорах или подвесках.
При определенной частоте качаний сита куски подбрасы-
ваются, это способствует расслоению материала, которое имеет
важнейшее значение для повышения эффективности грохочения,
и предотвращает забивание сита.
В результате грохочения получают два продукта: куски, про-
шедшие через сито, — просев (или нижний продукт) и куски, не
прошедшие через сито, — отсев (или верхний продукт).
Работа грохотов оценивается по двум показателям: 1) точ-
ность, или эффективность грохочения, 2) производительность
грохота.
Эффективность грохочения обычно характеризуется отноше-
нием веса полученного нижнего продукта к весу кусков того же
класса в исходном материале.
Производительность грохота определяется количеством мате-
риала в m/ч, получаемого с 1 м2 поверхности сита, и зависит от
физических свойств материала (плотности, формы и размера
кусков, влажности материала и т. д.), размеров сита, способа
подачи материала, скорости его движения и других факторов.
Вследствие трудности учета всех этих факторов производитель-
ность грохотов определяется по эмпирическим формулам.
Грохочение производится через одно сито или последователь-
но через несколько сит (многократное грохочение).
Исходный материал исходный материал исходный материал
а б 8
Рис. 4-1. Способы грохочения:
а —от мелкого к крупному; б— от крупного к мелкому; в —комбинированный способ.
Многократное грохочение проводится тремя способами:
1) от мелкого к крупному — через расположенные в одной
плоскости сита, размеры отверстий которых увеличиваются от
каждого предыдущего сита к последующему (рис. 4-1,а);
4 Устройство грохотов
89
2) от крупного к мелкому — через расположенные друг над
другом сита, размеры отверстий которых уменьшаются от верх-
него сита к нижнему (рис. 4-1, б);
3) комбинированным способом (рис. 4-1, в).
Грохочение от мелкого к крупному имеет ряд достоинств:
1) удобство наблюдения за ситами, а также ремонта и смены
сит (это очень важно, так как сита сравнительно быстро изна-
шиваются), 2) небольшая высота грохота и соответственно про-
изводственного помещения, 3) удобство распределения отдель-
ных сортов продукта по хранилищам.
Недостатки: 1) недостаточная четкость разделения материа-
ла на классы, так как отверстия мелких сит (первых по движе-
нию материала) перекрываются крупными кусками, 2) перегруз-
ка и повышенный износ мелких сит, 3) значительная длина гро-
хота.
" Достоинства грохочения от крупного к мелкому: 1) лучшее
качество грохочения вследствие отсева в первую очередь наибо-
лее крупных кусков, 2) меньший износ сит по той же причине.
Недостатки: 1) сложность ремонта и смены сит (кроме верх-
него), 2) большая высота грохотов; 3) неудобный отвод готового
продукта.
Недостатки первых двух способов грохочения удается в из-
вестной мере преодолеть при грохочении комбинированным спо-
собом.
4. Устройство грохотов
Барабанные грохоты
Цилиндрический барабанный грохот (рис. 4-2) представляет
собой открытый барабан цилиндрической, конической или мно-
гогранной формы, изготовленный из сетки или перфорированных
Рис. 4-2. Цилиндрический барабанный грохот.
листов. Барабан вращается на центральном валу, установлен-
ном на выносных подшипниках, либо на опорных роликах. При-
вод барабана осуществляется с помощью конической зубчатой
90
1л. 4. Классификация (сорт ировка) материалов
передачи, причем одна из шестерен укрепляется на валу, а в не-
больших грохотах — непосредственно на барабане.
Барабаны грохотов устанавливаются наклонно, под углом
4—7° к горизонту; конические барабаны, в которых свободное
перемещение кусков происходит благодаря самой форме бара-
бана, устанавливаются горизонтально. Отверстия в барабане
для прохода нижнего продукта в большинстве случаев увеличи-
ваются по ходу материала (грохочение от мелкого к крупному).
Многогранные грохоты, или бураты, применяются для срав-
нительно тонкого грохочения. Бурат имеет шестигранный бара-
бан, каждая грань которого представляет собой съемное пло-
ское сито. Барабан закрывается кожухом, из которого при рабо-
те грохота отсасывается пыль. Имеются бураты с горизонталь-
ными барабанами пирамидальной формы, расширяющимися к
разгрузочному концу. В буратах возможна быстрая смена каж-
дого из сит, составляющих лишь часть рабочей поверхности ба-
рабана.
Окружная скорость барабанных грохотов колеблется в пре-
делах 0,6—1,25 м/сек. (чаще всего 0,7—1 м/сек).
Достоинства барабанных грохотов: 1) простота конструкции
и обслуживания, 2) равномерное вращение.
Недостатки: 1) небольшая производительность на единицу по-
верхности сита, так как при грохочении используется только
’/в—Ve поверхности сита, 2) сильное крошение материала и зна-
чительное пылеобразование, 3) сравнительно легкая забивка сит
(материал не встряхивается), 4) большой расход металла на из-
готовление грохота.
Указанные недостатки столь существенны, что барабанные
грохоты постепенно вытесняются плоскими качающимися и ви-
брационными грохотами.
Число оборотов барабанных грохотов зависит от радиуса барабана R
(в ж) и обычно колеблется в пределах
8 14
п = (4-1)
Производительность барабанного грохота определяют по формуле:
Q = 0,72р.рни tg (2а) У R3h3 т/ч (4-2)
где р-— коэффициент разрыхления материала (0,6—0,8);
рн — насыпная масса материала, кг/м3\
а — угол наклона барабана к горизонту, градусы;
h — высота слоя материала в барабане, м.
Мощность, потребляемая грохотом, равна:
.. Rn (Gg 4- 13GM)
JV=—-2X <«>
где Gg и GM — соответственно масса барабана и загруженного материала, кг.
4. Устройство грохотов
91
Пример 4-1. Рассчитать число оборотов, производительность и мощность
электродвигателя барабанного грохота с барабаном размерами D = 1000 мм
и L — 3000 мм. Грохот установлен под углом к горизонту а ^7°, масса бара-
бана бб = 3200 кг, масса материала в барабане GM=84 кг.
Насыпная масса материала рн = 1400 кг/м3. Коэффициент разрыхления
материала ц = 0,7.
Решение. Число оборотов барабана при его радиусе R = = 0,5 м
рассчитываем по формуле (4-1):
14
п = г-___ 20 об/мин
/0,5
Принимаем высоту слоя материала в барабане h = 50 мм.
Производительность грохота определяем по формуле (4-2):
Q = 0,72 • 0,7 • 1400 • 20 tg (2 • 7) /б,53 - 0,053 = 13,9 т/ч
Мощность, потребляемую грохотом, находим по формуле (4-3):
.. 0,5 • 20 (3200 + 13-84) . _
N = —-------nr, nnn------ = 1,5 квт
29 200
Для учета потерь вводим к. п. д. ?] = 0,75, .тогда мощность электродвига-
теля составит:
аг м 1,5 о
Ад = — = тгтё- = 2 квт
т] 0>5
Плоские качающиеся грохоты
Грохоты этого типа весьма распространены. Плоский качаю-
опорах (рис. 4-3) состоит из
5
Рис. 4-3. Плоский качающийся гро-
хот на пружинящих опорах
1 — короб; 2 — сито; 3 — пружинящий стержень;
4 — эксцентрик; 5 —шатун.
щиися грохот на пружинящих
прямоугольного короба 1 с
ситом 2, которому сообщаются
качания от эксцентрикового
движущего механизма. При
качаниях грохота, обычно на-
клоненного к горизонту под
углом 7—14°, материал пере-
мещается вдоль сита. При
этом нижний продукт просеи-
вается, а верхний сбрасывает-
ся с разгрузочного конца гро-
хота.
В таких грохотах короб
устанавливается на 4—6 на-
клонных пружинящих стерж-
нях 3 (изготовленных из дере-
ва) и приводится в движение при помощи эксцентриков 4 дере-
вянного шатуна 5.
Наклон грохота, число оборотов вала и длина хода сита для
Достижения заданной производительности и требуемой точности
92
Г л. 4. Классификация (сортировка) материалов
разделения данного материала устанавливаются опытным пу-
тем. Обычно число оборотов вала в минуту составляет 300—500.
Плоские качающиеся грохоты применяются для классифика-
ции сухим и мокрым способом материалов с размером кусков
не более 50 мм.
Достоинства плоских качающихся грохотов: 1) большая про-
изводительность, чем для барабанных грохотов, и высокая чет-
кость грохочения, 2) компактность, удобство обслуживания и
ремонта (в частности, смены сит), 3) малое крошение материала.
Недостаток этих грохотов — неуравновешенность конструк-
ции, вызывающая сильные сотрясения зданий. По этой причине
плоские качающиеся грохоты нельзя устанавливать на верхних
этажах.
Число оборотов вала плоского качающегося грохота определяют по
формуле (2-4), исходя из условия, что подбрасывание кусков материала над
ситом недопустимо.
Скорость передвижения материала и производительность грохота опреде-
ляют соответственно по формулам (2-5) и (2-6).
Гирационные (эксцентриковые) качающиеся
грохоты
Схема качающегося гирационного грохота с круговыми ка-
чаниями в вертикальной плоскости показана на рис. 4-4. В стой-
ке рамы на шарикоподшипниках установлен вибратор — вал 1 с
1—вал-вибратор; 2—короб; 3—сито; 4 — пружины.
двумя эксцентриками и двумя противовесами. К валу симмет-
рично на подшипниках крепится короб 2 с ситом 3. Короб кон-
цами опирается на пружины 4 или на резиновые опоры. Эксцен-
триковый вал непосредственно сообщает коробу качательное
движение по окружности с амплитудой качаний, равной эксцен-
4. Устройство грохотов
93
триситету г вала. Вследствие быстроходности гирационных гро-
хотов их часто подвешивают на тягах с пружинами (амортиза-
торами) к потолочным балкам.
Достоинства гирационных грохотов: 1) уравновешенность
конструкции и спокойная работа при равномерном движении ко-
роба с материалом по круговой траектории, 2) большая произ-
водительность, 3) высокое качество сортировки.
Гирационные грохоты стандартизованы (ГОСТ 9148—59) и делятся на
грохоты нормальной конструкции (марки ГГ) и усиленной конструкции (мар-
ки ГГУ). В обозначении марки грохота указываются число сит и размеры
каждого сита (ширина X длина). Например, грохот марки ГГ-2—1,25x3
имеет два сита размером 1250 X 3000 мм каждое.
Пример 4-2. Рассчитать размеры плоского качающегося (гирационного)
грохота для сортировки 20 пг/ч материала с наибольшим диаметром кусков
D = 40 мм. Насыпная масса материала рн = 1,54 т/м3. Коэффициент трения
материала о сито f = 0,3. Коэффициент разрыхления материала р = 0,45. Диа-
метр отверстий сита d = 3 мм, угол наклона пружин грохота к вертикали
а = 20°. Эксцентриситет вала привода г = 15 мм.
Решение. Скорость вращения эксцентрикового вала рассчитываем по
формуле (2-4):
30 .Л_
п — --- --------= 407 об мин
/ 0,015 • tg 20° „
Скорость передвижения материала по ситу находим по формуле (2-5):
w = 0,23 • 407 • 0,015 • 0,3 • tg 20° = 0,153 м/сек
'Высоту h слоя материала наТрохоте принимаем равной 1,5 D;
h = 1,5 • 40 = 60 мм
для заданной производительности определяем пло-
на грохоте:
20
ЗбООо/рнр. = 3600 • 0,153 • 1,54 • 0,45 = 0,0525
Необходимая ширина грохота составляет:
R S 0,0525
В = Т = "ода-= 0,875 м
Принимаем округленно В = 1 м.
Согласно практическим данным, удельная производительность плоских
грохотов по питанию (при d = 3 мм) составляет ~7 м3/м2’Ч. Тогда площадь
сита равна:
Из уравнения (2-6)
щадь сечения материала
Q
S
Q = 20000
№, 7 • 1,5400 1,00 Л
и длина сита составляет:
_ F _ 1,86
В ~ 1
Принимаем с запасом L — 2,5 м. Таким образом, необходимо сито сле-
дующих размеров: L X В = 2,5 X 1 м; его площадь F = 2,5*1= 2,5 м2.
94
Гл. 4. Классификация (сортировка) материалов
Вибрационные (инерционные) грохоты
В вибрационных грохотах плоское и обычно наклонное сито
совершает при помощи специального механизма (вибратора)
частые колебания небольшого размаха. Число вибраций сита на-
ходится в пределах 900—1500 в 1 мин (иногда до 3600) при
амплитуде колебаний от 0,5 до 12 мм. Жесткая связь между эле-
ментами вибрационных грохотов полностью или частично отсут-
ствует, вследствие чего колебания сита в различных точках его
поверхности неодинаковы и зависят от угловой скорости вала,
упругости опорных пружин, движущейся массы грохота вместе
с материалом и других динамических факторов.
Вибрационные грохоты появились в промышленности только
25—30 лет тому назад, однако в настоящее время они успешно
вытесняют грохоты всех других типов. Это объясняется следую-
щими крупными достоинствами
вибрационных грохотов:
1) при высокой частоте коле-
баний сита его отверстия почти
не забиваются материалом, т. е.
устраняется недостаток, свой-
ственный грохотам других ти-
пов;
2) более высокая производи-
тельность и точность грохочения,
чем для грохотов других типов;
3) пригодность для крупного
и тонкого грохочения разнообраз-
ных материалов (в том числе вла-
жных и глинистых) с размерами
кусков и зерен от 250 до 0,1 мм\
4) компактность, легкость ре-
Рис. 4-5. Схема вибрационного
(инерционного) грохота:
1 — короб; 2 —сито; 3 — пружины; 4— вал;
5—шкив; 6— неуравновешенный груз
(дебаланс).
гулирования и смены сит;
5) меньший расход энергии, чем для грохотов других типов.
На рис. 4-5 показана схема вибрационного (инерционного)
грохота. Короб 1 и сита 2 установлены на пружинах 3. На стой-
ках и подшипниках вращается вал 4 (без эксцентриков) с двумя
шкивами 5, несущими неуравновешенные грузы 6 (дебаланс).
При вращении шкивов возникают центробежные силы инерции,
под действием которых коробу сообщаются вибрации. Траектории
точек короба и амплитуда его колебаний определяются динамиче-
скими факторами, перечисленными выше. Для вибрационных гро-
хотов требуется весьма равномерное питание материалом.
По такому же принципу работают электровибрационные гро-
хоты. Колебания сит в этих грохотах осуществляются посред-
4. Устройство грохотов
95
if ством электромагнита (соленоида), через обмотку которого про-
пускают переменный ток, или посредством специальных электри-
ческих вибраторов.
Производительность быстроходных вибрационных (инерционных) грохо-
тов может быть определена по эмпирической формуле:
Q = AF (55 + а) (60 4- b) fd м3/ч (4-4)
где А — коэффициент;
F — площадь сита, At2;
а — содержание нижнего продукта в исходном материале, %.;
b — содержание в нижнем продукте зерен размером меньше половины
отверстия сита, %;
d — размер отверстия, мм.
При сухом грохочении дробленого материала коэффициент А равен
0,00047 для горизонтального грохота и 0,00029 для наклонного грохота.
Производительность инерционных грохотов определяют также на основа-
нии опытных данных по удельной производительности сита в т/м2 • ч (см.
пример 4-4).
Наклонные вибрационные (инерционные) грохоты стандартизованы
(ГОСТ 8060—56).
Пример 4-3. Определить производительность горизонтального односит-
ного вибрационного (инерционного) грохота с размерами сита 1250 X 2500 мм
и размерами отверстий 7x7 мм. Содержание нижнего продукта в исходном
материале а = 40%, содержание в нижнем продукте зерен размером меньше
половины отверстия сита b — 15%.
Решение. Площадь сита грохота составляет:
F = 1,25 • 2,5 = 3,12 м2
«
Производительность грохота находим по эмпирической формуле (4-4):
Q = 4,7 • 10"4 • 3,12 (55 + 40) (60 %- 15) /7 == 27,7 м3/ч
Пример 4-4. Определить число двухситных вибрационных грохотов (пло-
щадь каждого сита Г = 3,75 м2), необходимое для разделения 90 т/ч угля
на следующие классы: 13—50; 6—13; 0—6 мм. Содержание класса 0—15 мм
в исходном угле а = 75%.
По опытным данным * удельная производительность верхнего сита
qB = 1,07 dB т/м2'Ч (при dB — 13 мм), производительность нижнего сита
qa = 1,38 dBm/M2-4 (при dH= 6 мм). К. п. д. верхнего сита = 68%. Коэф-
фициент неравномерности загрузки грохота k = 1,1.
Решение. Производительность грохота для верхнего сита может быть
определена по приближенной формуле:
QB = у = уу • 1,07 • 13 • 3,75 47,5 т/ч
Производительность грохота для нижнего сита по исходному углю:
_ 1 qaF_ 1 1,38 6-3,75 „ _ .
Qh ~ k ат\в ~ 1,1 ’ 0,75 • 0,68 “ 55,3 ml4
* Ф. Н. Булгаков, Дробление и грохочение угля, Углетехиздат, 1953,
стр. 85.
96
Гл 4 Классификация (сортировка) материалов
Требуемое число грохотов определяем по наименьшей производитель-
ности Q (т. е. для верхнего сита).
Необходимо установить два грохота.
5. Гидравлическая классификация
и воздушная сепарация
Процессы разделения зерен неодинаковой крупности на
классы по различной скорости их осаждения в жидкой и воз-
душной средах подчиняются общим законам осаждения твер-
дых тел (стр. 173 сл.).
Каждая фракция, отделяемая при классификации, предста-
вляет собой группу равнопадающих частиц, т. е. частиц, скоро-
сти падения которых в данной среде одинаковы.
Гидравлическая классификация осуществляется в горизон-
тальном или восходящем (и очень часто комбинированном) вод-
ном потоке. При этом скорость потока выбирают такой, чтобы
из классификатора выносились, т. е. направлялись в слив, ча-
стицы с размерами меньше определенной крупности, а в клас-
сификаторе оседали частицы больших размеров, обладающие
большей скоростью осаждения (нижний продукт). Как и грохо-
чение, водную классификацию можно проводить от крупного к
мелкому или от мелкого к крупному, а также комбинированным
способом.
При воздушной сепарации сопротивление воздуха движению
частиц значительно меньше сопротивления воды, так как по
сравнению с ней воздух обладает очень низкой вязкостью и ма-
лой плотностью. Поэтому частицы падают в воздухе во
много раз быстрее, чем в воде. Обычно осаждение производится
в горизонтальном или восходящем воздушном потоке.
Полученная при воздушной сепарации тонкая фракция (соот-
ветствующая сливу при водной классификации) всегда подвер-
гается осаждению в отдельном аппарате (циклоне), который
компонуется вместе с основным воздушным сепаратором.
Гидравлические классификаторы
Гидравлическая классификация производится под действием
сил тяжести либо в поле центробежных сил.
Для классификации продуктов измельчения, получаемых в
мельницах, работающих в замкнутом цикле, применяют глав-
ным образом спиральные и реечные механические классифика-
торы, в которых разделение происходит под действием сил тя-
5 Гидравлическая классификация и воздушная сепарация
97
жести. Такие классификаторы состоят из неподвижного корпуса
(корыта) и непрерывнодействующего транспортного устройства
для сбора и удаления песков — более крупных, осаждающихся
частиц, которые вновь подаются на доизмельчение в мельницу.
Спиральный классификатор (рис. 4-6) имеет наклонное ко-
рыто 1 полуцилиндрического сечения с насаженной на вал спи-
Рис. 4-6. Спиральный классификатор:
Z—наклонное корыто; 2—спираль; 3— nqpor.
ралью 2, частично погруженной в жидкость, и высоким поро-
гом 3, через который удаляется взвесь мелких частиц — слив.
Пески осаждаются в нижней части корыта и при помощи спира-
ли, делающей 2,5—17 об]мин, транспортируются в верхнюю
часть корыта и здесь выгружаются. Одновременно вращающаяся
спираль слегка перемешивает суспензию и пески, что облегчает
отделение мелких зерен от песков. Кроме односпиральных при-
меняются также двухспиральные классификаторы с двумя па-
раллельными спиралями в одном корпусе.
В реечных классификаторах пески удаляются при помощи
рам, совершающих возвратно-поступательные движения и снаб-
женных гребками (показаны на рис 4-7). По сравнению с
реечными спиральные классификаторы проще по устройству
7 Зак 546.
98
Г л. 4. Классификация (сортировка) материалов
и надежней в работе и, кроме того, могут выдавать более од-
нородный слив с большим содержанием твердого вещества. По-
этому спиральные классификаторы вытесняют реечные, особен-
но в крупных производствах.
Производительность спирального классификатора по пескам определяют
по формуле:
Q — 2,08mD3n • р т/ч
(4-5)
где т— число спиралей (т — 1 или 2);
D — диаметр спиралей, м;
п — число оборотов спирали в минуту;
р—плотность исходного материала, т/м3.
Для получения очень тонких сливов, содержащих преимуще-
ственно очень мелкие частицы, и достижения большой произво-
дительности по сливу используют спиральные классификаторы,
в которых большая часть спирали погружена в суспензию, а так-
же чашевые классификаторы.
Рис. 4-7. Чашевый классификатор:
/—конусная чаша, 2—сливной порог; 3 — патрубок для слива; 4 — криволинейные гребки;
5—патрубок для подачи суспензии; 6— реечный классификатор; 7 — гребки-рейки; 8 — порог
для удаления песков.
Чашевый классификатор (рис. 4-7) представляет собой агре-
гат, состоящий из двух классифицирующих устройств: верхне-
го — в виде конусной чаши 1 с медленно вращающимися криво-
5. Гидравлическая классификация и воздушная сепарация 99
Рис. 4-8. Гидроциклон:
7—корпус; 2—центральный (шламо-
вый) патрубок; 3— камера для слива;
4 — пескогая насадка; о —резиновый
вкладыш; 6— резиновый манжет.
линейными гребками 4 и нижнего — реечного классификатора 6.
Суспензия подается в чашу через патрубок 5. Слив, переливаясь
через порог 2, удаляется по патрубку <?; пески через отверстие в
дне чаши поступают в реечный классификатор 6, переме-
щаются гребками-рейками 7 и промываются водой, движущейся
противотоком к пескам, для удале-
ния увлеченных ими мелких частиц.
Промывные воды поднимаются че-
рез отверстия в дне чаши и удаля-
ются со сливом через порог 2, пес-
ки удаляются через порог 8.
В качестве центробежных клас-
сификаторов используют гидроцик-
лоны и центрифуги.
Гидроциклон (рис. 4-8) имеет
неподвижный корпус, состоящий из
нижней конической и верхней ци-
линдрической частей. Разделяемая
суспензия подается насосом (или
самотеком за счет напора столба
суспензии) под избыточным давле-
нием 0,3—2 ат через боковой патру-
бок в цилиндрическую часть кор-
пуса. Суспензия поступает в корпус
по касательной и потому начинает
в нем вращаться. При вращении по-
тока с большой угловой скоростью
более крупные твердые частицы
под действием центробежных сил
инерции отбрасываются к стенкам
гидроциклона. Возле стенок они
движутся по спиральной траекто-
рии вниз и в виде сгущенной сус-
пензии (пески) удаляются через
песковую насадку 4. Более мелкие
жидкости движутся во внутреннем
центрального (шламового) патрубка 2 и в виде тонкой взвеси
(слив) поднимаются по этому патрубку в камеру <?, откуда уда-
ляются через верхний боковой патрубок. При большой скорости
вращения потока вдоль оси гидроциклона образуется воздуш-
ный столб, давление в котором ниже атмосферного. Это воздуш-
ное ядро ограничивает с внутренней стороны поток мелких ча-
стиц в гидроциклоне.
Разделяющее действие гидроциклона можно регулировать,
изменяя глубину погружения шламового патрубка 2 и сечения
частицы и большая часть
спиральном потоке вокруг
7*
100
Гл. 4. Классификация (сортировка) материалов
песковой насадки 4. Насадки обычно являются сменными дета-
лями различного сечения или же предусматривается возмож-
ность регулирования сечения насадок. Один из сйособов такого
регулирования показан на рис. 4-8. При нагнетании воздуха или
масла в кольцевую полость резинового манжета 6 сечение на-
садки для прохода песков уменьшается. Таким способом воз-
можно автоматическое регулирование работы гидроциклона.
Для уменьшения износа корпус гидроцикл'она футеруют из-
нутри марганцовистым чугуном или плитками из каменного
литья (на рис. 4-8 футеровка не показана). В гидроциклонах
для разделения малоабразивных тонких суспензий корпус изго-
товляют из чугуна. Применяют также гуммирование корпуса и
быстроизнашивающихся деталей, т. е. покрытие их слоем изно-
соустойчивой резины; в песковых насадках часто устанавливают
резиновый кладыш 5 (рис. 4-8).
Для получения весьма тонких сливов применяют гидроцик-
лоны очень малых диаметров (до 10—15 мм), и для достижения
нужной производительности соединяют их в один агрегат (муль-
тигидроциклоны). По устройству и принципу действия гидроцик-
лоны и мультигидроциклоны аналогичны циклонам — аппара-
там, применяемым для очистки газов от пыли (стр. 327).
Гидроциклоны используют для классификации суспензий с
размерами частиц главным образом в пределах 15—100 мк. В
процессах тонкого измельчения гидроциклоны эффективно рабо-
тают совместно с мельницами в открытом и замкнутом циклах.
Центростремительные ускорения, сообщаемые потоку в гид-
роциклоне, во много раз превышают ускорение силы тяжести.
Поэтому несмотря на небольшие размеры, гидроциклоны имеют
высокую производительность, значительно большую, чем произ-
водительность механических классификаторов. От классифика-
торов других типов гидроциклоны выгодно отличаются
отсутствием движущихся частей. Перед механическими
классификаторами гидроциклоны обладают также следующими
преимуществами: 1) более тонкая сепарация по сравнению с
сепарацией, экономически выгодной в механических классифи-
каторах, 2) большая плотность слива, 3) отсутствие укрупнения
(флокуляции) мелких частиц.
Объемная производительность гидроциклона (по суспензии) может быть
определена по эмпирической формуле:
V 0,94dBX • dm У"Р м3/ч (4-6)
где dBX— наименьший диаметр входного патрубка (или эквивалентный диа-
метр в случае прямоугольного сечения), см\
dm — диаметр шламового патрубка, сж;
Р — избыточное давление перед входным патрубком, am.
5. Гидравлическая классификация и воздушная сепарация
101
Диаметр D цилиндрической части гидроциклона определяют из соотно-
шения D = (5 — 6)rfBX. Центральный угол конусной части гидроциклонов-
классификаторов принимают а = 20°. Диаметр песковой насадки dn может
быть определен в первом приближении из соотношения dn: = 0,3 — 0,43
и должен быть окончательно установлен при регулировании гидроциклона.
Избыточное давление на входе в гидроциклон зависит от расчетной
крупности разделения, соответствующей размерам отверстий сита dK, на кото-
ром суммарный остаток составляет 5%. Величина dK может быть рассчитана
по формуле
где /?74 — остаток на сите с отверстиями 74 мк, %.
Значения необходимого избыточного давления Р в зависимости от dK
(по В. А. Олевскому) приводятся ниже:
Крупность разделения dK, мк . . .
Содержание зерен размером меньше
74 мк в сливе р74, %.............
Избыточное давление Р, ат . . . .
0,417 0,285 '0,210 0,147
52 63 72 81
0,5 0,8 1,0 1,2
Для гидравлической классификации тонких частиц (до- 3—
15 мк) используют центрифуги, например сепарирующие центри-
фуги с шнековой выгрузкой (стр. 304).
Пример 4-5. Подобрать гидроциклон для классификации суспензии в ко-
личестве Q = 60 т/ч Плотность суспензии р = 1250 кг!м3. Содержание твердых
частиц диаметром меньше 74 м$ в сливе должно составлять 074 == 75%.
Решение. Определяем требуемый остаток на сите с отверстиями 74 мк:
Ru = ЮО — ₽74 == 100 — 75 = 25%
Необходимую крупность разделения, соответствующую размерам отвер-
стий сита dK, на котором суммарный остаток составляет 5%, рассчитываем
по формуле (4-7):
rfK = 74 / Y?* = 74 2,63 = 195 мк
Заданная объемная производительность гидроциклона по суспензии со-
ставляет:
IZ Q 60000 .о ,,
v=T = T255 = 4SMl't
По расчетной крупности разделения и заданному содержанию зерен клас-
са 74 мк в сливе ₽74 — 75% находим ориентировочно (интерполяцией данных,
приведенных выше) Р = 1,1 ат.
Зная объемную производительность и выбрав величину избыточного
давления Р, определяем из формулы (4-6) произведение диаметров входного
и шламового патрубков:
V 48
^вх^ш —------т=~ — ------т=- = 48,6 смг
0,94/Р 0,94/1,1
Выбираем диаметр входного патрубка dBX. = 50 мм.
102
Гл 4 Классификация (сортировка) материалов
Тогда диаметр гидроциклона будет равен
D s 5dBX = 250 мм
Диаметр шламового патрубка составит
48,6 48,6 о_.
dm — — 9,74 см
“вх °
Принимаем округленно с?ш= 100 мм
При выбранных значениях с?вх и dw по формуле (4 6) уточняем необходи
мое избыточное давление на входе в
Тонкая гидроциклон, которое должно быть
* “^фракция
° исходный
равно примерно 1 am
Воздушные сепараторы
Воздушные сепараторы де-
лятся на воздушно проходные
и воздушно циркуляционные
сепараторы
Воздушно-проходной сепа-
ратор (рис 4-9) обычно рабо-
тает в одном агрегате с мель-
ницей Измельченный материал
в потоке воздуха поступает со
скоростью ~20 м!сек, через па-
трубок 1 в кольцевое простран-
ство между корпусом 2 и вну-
тренним конусом 3 Вследствие
увеличения в этом простран-
стве проходного сечения ско-
рость воздушного потока сни-
жается в несколько раз и наи-
более крупные твердые части-
цы (грубая фракция) под дей-
материал
Рис 4-9 Воздушно-проходной сепа-
ратор
/ — входной патрубок 2—корпус 3— вну
тренний конус 4—патрубок для удаления
грубой фракции, 5 — лопатки, б—патрубок
для удаления тонкой фракции
ствием силы тяжести выпа-
дают из потока Через патру-
бок 4 они возвращаются на
доизмельчение в мельницу
Воздушный поток далее прохо-
дит через тангенциально уста-
новленные лопатки 5 При
этом потоку сообщается вращение и под действием возникаю-
щих центробежных сил инерции более крупные твердые частицы
отбрасываются на стенки конуса 3, опускаются по ним и уда-
ляются также через патрубок 4 Воздух вместе с тонкими взве-
шенными частицами отсасывается вентилятором (на рисунке
не показан) через патрубок 6 и подается в циклон, где твер-
5 Гидравлическая классификация и воздушная сепарация
103
дне частицы осаждаются, а воздух возвращается в мельницу
(при работе в замкнутом цикле) или удаляется наружу.
Работу сепаратора можно регулировать путем изменения
скорости воздуха или положения лопаток Воздушно-проходные
сепараторы Центрального котлотурбинного института (ЦКТИ)
изготовляются диаметром
от 500 до 4000 лш
Воздушно-циркуляцион-
ный сепаратор показан на
рис 4-10 Измельченный ма-
териал из воронки 1 посту-
пает на вращающийся рас-
пределительный диск (та-
релку) 4 Более тяжелые
частицы отбрасываются цен-
тробежной силой на стенки
внутреннего конуса 5, опу-
скаются вдоль его стенок
вниз и удаляются через па-
трубок 6 Мелкие частицы
подхватываются восходя-
щим потоком воздуха, цир-
куляция которого, показан-
ная на рисунке стрелками,
создается вентиляторным
колесом 2 Циркулирующий
пыле-воздушный поток про
ходит между поворотными
лопатками 8 Вследствие за-
кручивания потока и отра-
жения его от лопаток из по-
тока дополнительно отделя-
ются более крупные части-
цы, которые также удаля-
ются через патрубок 6
При переходе пыле воздушного потока из конуса 5 в корпус»?
сепаратора мелкие твердые частицы, стремящиеся сохранить на-
правление своего движения, выделяются из потока Этот процесс
аналогичен выделению пыли в центробежных пылеуловителях —
циклонах (стр 327) Мелкие частицы опускаются вдоль стенок
корпуса и удаляются через патрубок 7
Воздушно-циркуляционные сепараторы -совмещают функции
классификатора, пылеуловителя и вентилятора По сравнению с
воздушно-проходными сепараторами они более компактны и тре-
буют меньшего расхода энергии
франция
Рис. 4-10 Воздушно-ц&ркуляционный
сепаратор
1 — воронка, 2—колесо вентилятора, 3 — корпус
4— распределительный диск (тарелка), 5— вну-
тренний конус, (У—патрубок для удаления гру
бой фракции, 7—патрубок для удаления тонкой
фракции, 8— поворотная лопатка
Глава 5
ДОЗИРОВАНИЕ И СМЕШИВАНИЕ ТВЕРДЫХ
МАТЕРИАЛОВ
При проведении различных процессов необходима регуляр-
ная и равномерная подача измельченного материала в аппара-
туру; кроме того, часто требуется загружать исходные материа-
лы в определенной последовательности при заданном соотноше-
нии компонентов смеси (шихты).
Загрузка твердых кусковых и порошкообразных материалов
производится обычно из хранилищ (бункеров) при помощи пи-
тателей. Для подачи заданных количеств материала применяют
порционные и непрерывнодействующие дозирующие устройства
(дозаторы), причем в некоторых случаях одни и те же устрой-
ства служат для подачи и для дозирования материала (дозато-
ры-питатели) .
Во многих производствах для получения исходных смесей или
готового продукта отдельные компоненты смешивают в специ-
альных аппаратах — смесителях.
1. Бункеры и затворы к ним
Бункерами называются хранилища для сыпучих и кусковых
материалов емкостью до 100 ж1 * 3 и более. Большей частью бун-
керы имеют пирамидальную или коническую форму (рис. 5-1) и
изготовляются из стали, а также из железобетона и дерева. За-
грузка производится при помощи различных транспортных уст-
ройств, подающих материал в бункеры.
Выгрузка происходит через сужающееся книзу днище с вы-
пускным патрубкам, к которому крепится разгрузочное устрой-
ство — затвор или питатель.
Для равномерной и бесперебойной выгрузки материала из бункера yroi
наклона а его стенок к горизонту должен быть больше угла естественного
откоса материала (обычно а = 45—50°).
Чтобы устранить зависание или сводообразование материала, которое воз
можно вследствие его плохой сыпучести, смерзания или слеживания, в ниж
ней части бункера часто устраивают щели или отверстия для ручного шурова-
ния материала.
1. Бункеры и затворы к ним
105
В ряде случаев разрушение сводов в бункерах достигается с помощью
пневматического разрыхления (аэрирования) материала, к которому снизу
через пористые плитки или сопла подводится сжатый воздух. Для этой же
цели успешно используются механические вибраторы, устанавливаемые сна-
ружи на стенках стальных бункеров.
Рис. 5-1. Типы бункеров.
Для открывания и закрывания выпускных отверстий бункеров, а также
для грубого регулирования потока выгружаемого материала служат затворы.
В условиях химических производств
широко распространены плоские
(шиберные) и секторные затворы.
Плоские затворы деляется на
простые рычажные и реечные.
Рис. 5-2. Простой рычажный затвор. Рис. 5-3. Плоский реечный затвор:
/ — плоская задвижка; 2 —зубчатая рейка;
3— Шестерня; 4— цепное тяговое колесо.
Простой рычажный затвор (рис. 5-2) представляет собой горизонтальную
плоскую задвижку, скользящую в направляющих и открываемую при помощи
рычага, шарнирно подвешенного к бункеру. Такие затворы пригодны для
полной разгрузки любых материалов из Небольших бункеров за один прием
или для разгрузки легких, хорошо сыпучих материалов с некрупными кусками.
Плоский реечный затвор (рис. 5-3) состоит из плоской задвижки 1 с зуб-
чатой рейкой 2, находящейся в зацеплении с шестерней 3, и приводится* в
действие вручную при помощи цепного тягового колеса 4. Более мощные
106
Гл 5. Дозирование и смешивание твердых материалов
затворы этого типа приводятся в действие электродвигателем либо имеют пнев-
матический или гидравлический привод. Плоские затворы отличаются ком
пактностью, но при закрывании бункеров возможно защемление кусков (осо-
бенно в горизонтальных затворах) и крошение материала.
Рис. 5-4. Односекторный затвор:
Г —сектор; 2—корпус; 3 — рычаг; 4 — тяга.
Секторные затворы делятся на простые односекторные и
двухсекторные (челюстные).
Простой односекторный затвор (рис. 5-4) представляет со-
бой цилиндрический сектор 1, вращающийся на пальцах, за-
крепленных на боковых стенках корпуса 2, который имеет квад-
ратное сечение и крепится к отверстию бункера. Открывание и
закрывание производятся вручную посредством рычага 3 и тяги
4 с рукояткой. Чтобы облегчить закрывание затвора, на конец
рычага надет противовес. Такие затворы применяются преиму-
щественно в бункерах для хорошо сыпучих материалов с мел-
кими и средними кусками и могут использоваться для регули-
ровки подачи мелкокускового материала (до 50 мм) путем ча-
Рис. 5-5. Челюстной затвор:
/ — челюсти; 2—зубчатые секторы: 3 — рычаг; 4 — тяга.
стичного открытия разгрузочного
При больших размерах односекторных затворов требуется
продолжительное время на их открывание и закрывание.
2. Питатели
107
Поэтому для больших выпускных отверстий чаще приме-
няют челюстной затвор.
Челюстной затвор (рис. 5-5) состоит из двух секторов или
челюстей 1, которые соединены между собою зубчатыми секто-
рами 2, находящимися в зацеплении. Обе челюсти открываются
и закрываются одновременно при помощи рычага 3 с противове-
сом и шарнирно подвешенной тяги 4. Челюстные затворы лучше
приспособлены для частых открываний и закрываний бункеров
и регулирования подачи материала и применяются также в тех
случаях, когда нежелательно крошение материала, находящего-
ся в бункере.
2. Питатели
Питателями называются механические устройства для рав-
номерной подачи сыпучих и кусковых материалов в различные
аппараты — дробилки, сушилки, реакторы, печи и др. Питатели
подают материал из хранилищ (бункеров) непосредственно
в аппараты либо на транцпортеры и элеваторы, перемещающие
материал к приемным устройствам аппаратов. Питатели часто
используются также для регулирования подачи и для дозиро-
вания материалов.
Питатели с тягойыми органами
Ленточные питатели сходны с ленточными транспортерами
(стр. 29). Питатель состоит ив бесконечной резиновой ленты, на-
тянутой между приводным и натяжным барабанами и движу-
щейся со скоростью 0,1—0,25 м!сек. Питатели такого типа при-
меняют для подачи хорошо сыпучих, легких и неистирающих
материалов с размерами кусков не более 100—150 мм или тя-
желых, сыпучих и абразивных материалов (р>-1,2 тДи3) с раз-
мерами кусков не более 75 мм, а также для подачи влажных
материалов. В последнем случае для очистки ленты устанавли-
вают скребки.
Ленточные питатели применяются с лентами шириной 400, 500, 750, 900 и
1100 мм Производительность таких питателей достигает 300 м3/ч и более.
Пластинчатые питатели сходны с пластинчатыми транспор-
терами. Они снабжены стальной лентой, составленной из пере-
крывающих друг друга пластин данного профиля, жестко
укрепленных на бесконечных цепях. Цепи и стальная лента
движутся со скоростью 0,02—0,12 м!сек. Питатели такого типа
хорошо приспособлены для подаци тяжелых, крупнокусковых
материалов (в том числе абразивных и глинистых) с размерами
кусков, не превышающими обычно 400 мм; питатели надежно
работают, подвергаясь давлению материала, загруженного в
бункер, и нечувствительны к ударам.
108
Гл. 5. Дозирование и смешивание твердых материалов
Пластинчатые питатели стандартизованы (ГОСТ 7424—61) и делятся на
питатели- трех типов: для легких условий, для средних и тяжелых условий
и для особо тяжелых условий работы.
Питатели с колебательным движением
Лотковые питатели. Лотковый питатель (рис. 5-6) выпол-
няется в виде движущегося горизонтального стола с неподвиж-
ными боковыми бортами и задней стенкой, которые образуют
лоток 1.
Рис. 5-6. Лотковый питатель:
/ — горизонтальный лоток; 2—кривошипно-шатунный механизм.
При помощи кривошипно-шатунного механизма 2 стол со-
вершает возвратно-поступательное движение в горизонтальной
плоскости. При движении стола вперед материал перемещается
вместе со столом и ссыпается через его край. Одновременно на
освободившуюся часть поверхности стола из бункера насы-
пается новая порция материала. При обратном ходе стола ма-
териал, упираясь в стенку, проскальзывает по столу и частично
ссыпается через его край. Ход s стола составляет 200—250 мм,
число ходов 30—45 в 1 мин.
Такие питатели применяются для подачи сыпучих (но не
влажных и слеживающихся) материалов с размерами кусков
до 500 мм.
По ГОСТ 7010—54 качающиеся (лотковые) питатели делятся на два ти-
па: 1) подвесные питатели марки К для неабразивных, преимущественно лег-
ких материалов с насыпной массой до 1 т/м3, производительность 80—
360 м3/ч-, 2) питатели марки КТ для абразивных материалов с насыпной мас-
сой До 2,5 т/м3, производительность 10—50 м3/ч.
Пример 5-1. Определить производительность лоткового питателя; раз-
меры лотка В X h = 750 X 750 мм, радиус кривошипа г = 0,05 м, число обо-
ротов эксцентрика п — 50 об/мин. Коэффициент, учитывающий степень запол-
нения лотка и проскальзывание материала по нему (коэффициент подачи),
ф = 0,9. Насыпная масса подаваемого материала р = 800 кг/м3.
Решение. Производительность питателя определяется по формуле:
Q = V,V2rnBh^ (5-1)
Отсюда
Q = 0,12 • 0,05 • 50 • 0,75 • 0,75 • 800 • 0,9 120 т/ч
Плунжерные питатели подают материал путем проталкивания его по не-
подвижному желобу при помощи стального плунжера прямоугольного сече>
2. Питатели
109
ния, совершающего возвратно-поступательное движение (рис. 5-7). Плунжер 1
приводится в движение посредством эксцентрика 2 и тяги 3. Основное досто-
инство плунжерного питателя — точная дозировка материала. Однако вслед-
ствие сильного трения между материалом и поверхностью неподвижного же-
лоба такие питатели пригодны
только для хорошо сыпучих ма-
лоабразивных материалов.
Производительность питате-
лей ограниченна и колеблется в
пределах 2—8 м3/ч.
Маятниковые питатели
являются затворами, приво-
димыми в действие криво-
шипно-шатунным механиз-
мом. Такой питатель пред-
ставляет собой качающийся
Рис. 5-7. Плунжерный питатель-.
/—плунжер; 2— эксцентрик; 3— тяга; j —длина
хода плунжера.
на шарнире сектор или ло-
ток, который попеременно открыва*ет или закрывает выпускное
отверстие хранилища материала.
Применяются эти питатели только для подачи зернистых и
мелкокусковых материалов в установках малой производитель-
ности, когда не требуется точное дозирование.
Вращающиеся питатели
Рис. 5-8. Тарельчатый
питатель:
/ — тарелка; 2 — манжет;
3 — скребок.
Винтовые питатели мало отличаются от шнеков, описанных
выше (стр. 33). Для свободного прохода материала по желобу
вал винта не имеет промежуточных под-
шипников, поэтому длина перемещения
материала не превышает 1,5—2 м. Вин-
товые питатели применяются при подаче
тонкоизмельченных мелкозернистых и
мелкокусковых материалов, для которых
допустимо некоторое крошение. Абразив-’
ные материалы вызывают быстрый из-
нос желоба и винта питателя.
Производительность винтовых пита-
телей не превышает 20—30 лг3/ч.
Тарельчатые питатели. Тарельчатый
питатель (рис, 5-8) представляет собой
вращающуюся на вертикальной оси круг-
лую плоскую тарелку 1, над которой на-
ходится подъемный цилиндрический па-
трубок (манжет) 2. Манжет может пере-
мещаться вдоль горловины бункера. Материал, высыпающийся
на тарелку, располагается на ней слоем, имеющим форму усе-
но
Гл 5 Дозирование и смешивание твердых материалов
ченного конуса. Образующая конуса наклонена к вертикали под
углом, равным углу естественного откоса материала. При вра-
щении тарелки часть материала снимается с нее скребком 3
(иногда двумя скребками) и сбрасывается в приемное устрой-
ство. Положение скребков относительно тарелки можно изме-
нять. Подачу материала регулируют поднятием и опусканием
манжета или изменением положения скребка и глубины его
врезания в слой материала на тарелке.
Тарельчатые питатели широко применяются для подачи су-
хих, тонкоизмельченных, мелкозернистых и кусковых материалов
с размерами кусков не более 80—100 мм.
Применяются тарельчатые питатели с тарелками диаметром 600—2500 мм
(производительность 4—120 м3/ч); наиболее распространены питатели с та-
релками диаметром от 600 до 1250 мм
Пример 5-2. Определить число оборотов и производительность тарельча-
того питателя с тарелкой диаметром D = 1000 мм, установленного для равно-
мерной подачи колчедана в печь для обжига. Насыпная масса колчедана
р — 2250 кг/м3. Коэффициент трения колчедана о тарелку f 0,3, угол есте-
ственного откоса колчедана ?^45°. Высоту подъема h манжеты питателя
над тарелкой следует принять 70 мм
Решение Чтобы не происходило сбрасывания материала с тарелки под
действием центробежной силы, необходимо соблюдать следующее условие:
/ 7~ Г (И
п < 301/ 4 = 301/ 23 об/мин
т К Г 0,5
где п — число оборотов тарелки, об/мин*,
R — радиус тарелки, м.
Принимаем число оборотов тарелки п = 20 об/мин.
Производительность питателя определяется по формуле.
Q = 0,06 (кR + (5-2)
tg <Р \ 3tg<p / v 1
ГЛ ллС 0,072.20 - 2250 /о1. л- . 0,07\ .
Q = 0,06 • —----=-----13,14 • 0,5 -|- -5—г) а* 21 т/ч
1 \ о • 1 /
Лопастные (секторные) питатели. Лопастные питатели
(рис. 5-9) имеют лопастной барабан 1, состоящий из 3—12 сек-
торов (отсеков). Материал, поступающий через воронку 2, за-
полняет карманы, образуемые лопастями и торцевыми стенками
барабана, и периодически равномерно высыпается при враще-
нии барабана. Эти питатели пригодны преимущественно для по-
дачи тонкоизмельченных или кусковых материалов с размерами
кусков не более 50 мм. Изменением числа оборотов барабана
достигается точное регулирование подачи.
Лопастные питатели широко используются для дозирования
сыпучих материалов. Питатели устанавливают в сушилках, ци-
клонах и других аппаратах, разгрузка которых должна произво-
диться без подсоса наружного воздуха.
3 Дозаторы
111
Пример 5-3. Определить основные размеры барабана лопастного (сектор-
ного) питателя для подачи Q = 15 т/ч кускового материала в сушилку.
Насыпная масса материала рн= 1600 кг/м3, число секторов (отсеков) в бара-
бане /п 8, степень заполнения каждого сектора <р — 0,8, число оборотов
барабана л = 4 об/мин.
Рис. 5-9. Лопастной питатель:
/ — лопастной барабан; 2 —приемная воронка.
Решение. Площадь поперечного сечения f сектора определяем из фор-
мулы производительности питателя, принимая длину барабана L = 0,6 м:
Q — 0,06тп/£рнп<р т/ч (5-3)
откуда
f — Q____________________I*?_____________оо1 м2
1 ~ 0,06 • 8 • 0,6 • 1600 • 4 • 0,8 “ ’
Учитывая, что ~25% сечения барабана занято лопастями, находим об-
щую площадь сечения барабана.
1,25/п/= 1,25 • 8 • 0,01 = 0,1 м2
Диаметр барабана составляет:
гл „Л 0,1
= 1/ — 1/ л 7ос = 0,36 м
г тс г 0,785
Следовательно, размеры барабана питателя: Dxi = 0,36 X 0,6 м.
3. Дозаторы
Дозирование материалов производится объемным или весо-
вым методом, в некоторых случаях часть материалов дозируют
по весу, а часть — по объему (объемно-весовой метод).
Для дозирования объемным методом пользуются мерниками,
которые снабжены градуированными по объему шкалами, а так-
же барабанными, тарельчатыми, ленточными и другими пита-
112
Г л. 5. Дозирование и смешивание твердых материалов
телями, описанными выше. Объемный метод пригоден только
для дозирования порошкообразных материалов, имеющих по-
стоянный гранулометрический состав, и не склонных к слежи-
ванию и комкованию.
Дозирование материалов по весу является более точным.
Несмотря на относительно сложное устройство весовых дози-
рующих устройств, этот метод получает все более широкое рас-
пространение, причем применяются весовые дозаторы ручного,
полуавтоматического и автоматического действия.
В качестве ручных дозаторов употребляют весы различных
типов, на которых устанавливают весовой бункер с выпускным
отверстием, закрытым заслонкой. В дозаторах полуавтоматиче-
ского действия после взвешивания порции материала подача
его в бункер прекращается автоматически, но выгрузку мате-
риала из бункера производят вручную. Ручные и полуавтомати-
ческие дозаторы малопроизводительны, и в условиях крупных
непрерывнодействующих производств обычно применяют авто-
матические дозаторы, рассматриваемые ниже.
Автоматические весы
Автоматические весы предназначены для получения порций
сыпучего материала, имеющих определенный постоянный вес.
На рис. 5-10 показана схема действия автоматических весов
с открывающимся днищем ковша. Дозируемый материал посту-
пает через воронку 1 в ковш 2, в котором взвешивается порция
материала (рис. 5-10, а) По мере заполнения материалом ковш
опускается, одновременно опускается штанга 3, снабженная пру-
жиной, и через систему рычагов перемещает заслонку 4 в поло-
жение, показанное на рис. 5-10, а пунктиром. При этом через
узкую щель между заслонкой 4 и воронкой 1 материал тонкой
струей досыпается в ковш до требуемого веса, что облегчает
достаточно точное взвешивание порции материала, так как воз-
можно быстрое прекращение его подачи в ковш.
Ковш 2 подвешен на конце коромысла 5 весов и должен
уравновешиваться грузом 6. По достижении равновесия заслон-
ка 4 полностью перекрывает воронку 1 (рис. 5-10,6), в этот
момент рычаг 7 упирается в устройство9 (запирающее днище),
приподнимая его и освобождая днище. Под действием веса
материала оно откидывается и порция материала высыпается из
ковша (рис. 5-10, в). После опорожнения ковша днище закры-
вается под действием противовеса 8; при этом стержень запи-
рающего устройства. 9 ударяет по системе рычагов, при помощи
которых ковш поднимается кверху и затем снова заполняется
материалом.
4
Рис. 5-10. Схема действия автоматических весов:
8 Зак. 546.
а — дозирование; б— положение равновесия; в —выгрузка. 1 — воронка; 2— ковш; 3 — штанга; 4~заслонка; 5—коромысло весов; 6 — груз;
7—рычаг; 8— противовес; 9 — запирающее устройство.
I. Дозаторы ‘113
114
Гл. 5. Дозирование и смешивание твердых материалов
Весовые ленточные дозаторы
Весовой ленточный дозатор (рис. 5*11) применяется для авто-
матического непрерывного дозирования. Дозируемый материал
из бункера через воронку 1, не имеющую днища, поступает через
отверстие в боковой стенке воронки на ленту 4 транспортера,
натяжение которой регулируется роликом 3. На том участке
ленты, куда поступает материал, под лентой установлены опор-
ные ролики, 2, воспринимающие давление материала. Количество
Рис. 5-11. Весовой ленточный дозатор:
7 —воронка; 2 —опорный ролик; 3 — натяжной ролик; 4—лента транспортера; 5, 6 — заслонки;
7—отверстие; 8— коромысло весов; 9 — груз; 10 — регулирующий ролик; 11 — щетка.
материала, поступающего на ленту, регулируется заслонкой 5.
Перемещаясь на ленте, материал проходит через второе отвер-
стие 7, величина которого регулируется автоматической заслон-
кой 6, шарнирно соединенной с коромыслом 8 весов. Дозируе-
мый материал уравновешивается на ленте грузом 9, перемещаю-
щимся по коромыслу 8. Перед пуском дозатора производят его
регулировку для того, чтобы установить коромысло 8 в положе-
ние равновесия. Приподнимая заслонку 5, увеличивают подачу
материала (если коромысло, отклоняясь от положения равнове-
сия, опускается вниз), опуская заслонку 5, уменьшают подачу
материала (если коромысло поднимается вверх). При равновес-
ном положении коромысла материал дозируется равномерно, в
заданном количестве. После того как порция материала сбрасы-
вается с транспортера, лента 4 очищается щеткой 11. Скорость
ленты колеблется от 0,02 до 0,6 м/сек,.
Если вес материала на ленте чрезмерно увеличивается (сверх
нормы), ролик!<7 опускается, что приводит к подъему правого
плеча коромысла 8. Одновременно опускается левое плечо коро«
3. Дозаторы
115
мысла и связанная с ним автоматическая заслонка 6, что вызы-
вает уменьшение подачи материала до тех пор, пока порция его
не достигнет заданного веса. При недостаточном весе дозируе-
мого материала на ленте заслонка 6 поднимается и восстана-
вливается нормальная подача материала. В случае внезапного
значительного уменьшения веса материала на ленте дозатор ав-
томатически выключается.
Точность подачи мелкозернистых хорошо сыпучих материалов
ленточным дозатором колеблется в пределах ±1%.
Весовой ленточный дозатор с электрорегулированием. Основ-
ной частью такого автоматического дозатора непрерывного дей-
ствия (рис. 5-12) является ленточный транспортер 1, который
Рис. 5-12. Весовой ленточный дозатор с электрорегулированием:
/ — ленточный транспортер; 2 —опора; 3— электродвигатель; 4 — электровибрационный питатель;
5—коромысло весов; 6 — электрический регулятор.
может поворачиваться вокруг опоры 2. Транспортер приводится
в движение электродвигателем 3 через редуктор, установленный
на конце транспортера, другой конец которого соединен с весами.
Дозируемый материал подается на ленту электровибрационным
питателем 4. Вес материала на ленте транспортера уравновеши-
вается грузом, перемещающимся по коромыслу 5 весов, которое
соединено с питателем 4 электрическим регулятором 6.
В случае недостаточного поступления материала на транс-
портер левый его конец и соединенное с ним коромысло 5 ве-
сов поднимаются кверху. При этом регулятор 6 воздействует на
питатель 4, и подача дозируемого материала на ленту увеличи-
вается вплоть до восстановления равновесия коромысла. В слу-
чае избытка дозируемого материала на ленте левый конец
качающегося транспортера опускается и подача материала
уменьшается описанным выше способом.
8*
116
Тл. 5. Дозирование и смешивание твердых материалов
4. Смесители твердых и пастообразных материалов
Смешивание сухих сыпучих материалов и порошкообразных
веществ, а также густых и вязких масс и пастообразных мате-
риалов производится в смесителях разнообразных конструкций.
Смесители могут быть разделены на следующие группы: 1) сме-
сители с вращающимся корпусом; 2) смесители с вращающимися
лопастями различной формы; 3) циркуляционные смесители ин-
тенсивного действия.
К смесителям первой группы относятся барабанные смеси-
тели, применяемые для периодического и непрерывного смеши-
вания сухих порошкообразных веществ.
Барабанный смеситель (рис. 5-13) представляет собой ба-
рабан 1 с двумя бандажами 2, который вращается на роликах 5,
Рис. 5-13. Барабанный смеситель:
/—барабан; 2— бандажи; 3~спиральные перегородки; 4 — продольные полки; 5 — ролики;
6 — шнек.
делая 6—8 об/мин. Для лучшего смешивания материала на
внутренних стенках барабана укреплены косые спиральные
перегородки 3, а внутри него — несколько продольных полок 4
с перегородками. Загрузка и выгрузка материала производятся
при помощи шнека 6, который при загрузке вращается в одном
направлении, а при выгрузке — в противоположном. Направле-
ние вращения шнека изменяется посредством ручного приспособ-
ления.
Смесители барабанного типа являются тихоходными, цирку-
ляция смешиваемого материала в них малоинтенсивна и
4. Смесители твердых и пастообразных материалов
117
продолжительность смешивания значительна. Поэтому барабан-
ные смесители вытесняются аппаратами более интенсивного дей-
ствия.
Для непрерывного смешивания сыпучих, пластических и лип-
ких материалов применяют одновальные и двухвальные шне-
ковые смесители.
Двухвальный шнековый смеситель (рис. 5-14) состоит из
горизонтального корыта 1, в котором с неодинаковой скоростью
Рис. 5-14. Двухвальный шнековый смеситель:
/—корыто; 2 —вал; 3— перемешивающие лопатки; 4 — транспортирующие
лопатки; 5, 6 — воронки; 7 — лопастное колесо.
вращаются два параллельных вала 2 с лопатками (на рисунке
виден только один передний вал). На валах укреплены пооче-
редно прямые перемешивающие лопатки 3 и транспортирующие
лопатки 4, изогнутые по винтовой линии. Материал поступает
через воронку 5 и движется, перемешиваясь, вдоль переднего
вала 2, а затем передается лопастным колесом 7 на задний вал
и движется вдоль него в обратном направлении. Готовая смесь
выгружается через воронку 6. При закрытии этой воронки сме-
ситель может работать как аппарат периодического действия.
Для смешивания густых, весьма вязких (кашеобразных)
масс и сыпучих материалов широко применяются горизонталь-
ные двухвальные мешатели периодического действия с фасон-
ными лопастями.
Мешатель (рис. 5-15) выполнен в виде корыта 1, в котором
вращаются навстречу друг другу с различным числом оборотов
лопастные валки 2. Корыто снабжается откидной плотно закры-
вающейся крышкой и, если требуется, рубашкой для охлаждения
или нагревания материала. При вращении навстречу^друг другу
каждая из лопастей перемещает перемешиваемую массу в ко-
рыте к клиновидному седлу, которое разрезает ее на части. При
этом часть смеси подхватывается лопастью соседнего валка и
вминается в часть материала, перемещаемого этой лопастью.
Одновременное деление и вминание перемешиваемой массы
118
Гл. 5. Дозирование и смешивание твердых материалов
сопровождается ее перетиранием между лопастями и стенками
корыта, обнажением новых поверхностей массы и т. д. Таким
комбинированным воздействием достигается тщательное сме-
шивание густых и вязких масс.
По окончании смешивания выгрузка материала производится
опрокидыванием корыта посредством цепной передачи. На сво-
бодных концах цепей для облегчения подъема корыта подвеши-
ваются контргрузы 3. В мешателях некоторых конструкций ко-
Рис. 5.15. Двухвальный мешатель с фасонными лопастями:
/ — корыто; 2 —лопастные валки; 5—контргруз.
рыто опрокидывается при вращении подъемного винта, по кото-
рому перемещается вверх гайка, шарнирно связанная с задней
стенкой корыта.
Нормализованные конструкции мешателей разделяются по емкости ка-
рыта и максимальной мощности привода валков на мешатели малой, сред*'
ней и большой мощности.
Двухвальные мешатели с фасонными лопастями выпускаются с корытом
емкостью 5, 25, 100; 200, 400, 800 и 2000 л.
Смесители с вращающимися лопастями и неподвижным кор-
пусом также тихоходны. Вследствие небольшой скорости враще-
ния лопастей (п=10—50 об jмин) и одновременного воздей-
ствия лопастей лишь на небольшую долю объема обрабатывае-
мого материала смесители этого типа также не являются высо-
коэффективными аппаратами и смешивание в них довольно
длительно
ч 4. Смесители твердых и пастообразных материалов 119
Рис. 5-16. Циркуляционный сме-
ситель:
1 — корпус; 2—ротор; 3—масляная ру-
башка; 4—статор; о —электродвигатель;
6 — лопасти ротора.
В последнее время разработаны конструкции быстроходных
н смесительных аппаратов, в которых использован принцип интен-
сивной циркуляции смешиваемых материалов в распыленном
состоянии.
Для получения смесей порошкообразных веществ, главным
’S образом в производстве пластических масс, применяют смеси-
J ' тели, в которых обрабатываемые
1 'материалы подвергают аэрации,
чтобы смесь по своей подвижно-
сти приближалась к жидкости.
i’j В корпусе / циркуляционного
\ смесителя такого типа (рис. 5-16)
(( быстро вращается ротор 2 в виде
Г кольцевого диска с четырьмя ло-
Ъ пастями 6 (две верхние и две
4 нижние). Две верхние лопасти
.* при вращении ротора засасывают
воздух' из воздушной подушки,
создаваемой над перемешивае-
4 мым материалом. При проника-
нии некоторого количества воз-
4 духа в массу сыпучего материа-
* ла начинается циркуляция этого
материала в аппарате (напра-
вление циркуляции показано на
рисунке стрелками). Ротор вра-
щается внутри кольцевого непо-
- движного диска 4 с. пальцами
(статор). При прохождении ча-
стиц сыпучего материала между
ротором и статором в материале
зающие напряжения, способствующие эффективному смешива-
нию компонентов сыпучей смеси. Окружная скорость ротора не
превышает 40—60 м/сек, поэтому смешивание не сопровож-
дается измельчением материала, которое происходит в дезин-
теграторах (стр. 68).
Смесь удаляется двумя нижними лопастями ротора через
патрубок. Привод ротора осуществляется от электродвига-
теля 5.
Смешиваемый в таком аппарате материал нагревается
вследствие теплоты трения, выделяющейся при вращении ро-
тора. Если требуется дополнительный подогрев смешиваемо-
го материала, он может быть нагрет через стенку корпуса
смесителя, снабженного масляной рубашкой 3 с электрообо-
гревом.
создаются значительные сре-
120
Г л. 5. Дозирование и смешивание твердых материалов
й
Рис. 5-17. Смеситель центро-
бежного действия:
/—корпус; 2— конус; 3— свободно
вращающиеся лопасти; 4 — ножи,
5 — окна; 6 — скребок; 7 —тормоз
На рис. 5-17 показан смеситель центробежного действия,
в котором возможно тщательное смешивание сыпучих материа-
лов при относительно небольшом расходе энергии, обусловленном
малой длительностью смешивания и высокой производительно-
стью единицы объема аппарата. Смеситель состоит из корпуса /,
внутри которого вращается на вертикальной оси открытый полый
конус 2, обращенный большим основанием кверху. Смешивае-
мый материал перемещается по внутренней поверхности конуса
снизу вверх под действием центро-
бежных сил инерции, выбрасывает-
ся из конуса и образует взвешенный
слой, внутри которого происходит
интенсивное смешивание компо-
нентов. Частицы смеси опускаются
на днище корпуса и через окна 5
вновь поступают в конус 2. Таким
образом в аппарате создается ин-
тенсивная циркуляция сыпучего
материала, способствующая его бы-
строму и тщательному смешиванию.
При перемещении внутри кону-
са материал встречает на своем Пу-
ти ножи, укрепленные на свободно-
вращающейся раме с лопастями 3.
Лопастям сообщается часть кине-
тической энергии движущегося ма-
териала, благодаря чему они начи-
нают вращаться со скоростью, значительно меньшей скорости
вращения конуса 2. Лопасти 3 смешивают материал в коль-
цевом пространстве между конусом и корпусом смесителя и
направляют часть его в окна 5. Скорость вращения лопастей
регулируют тормозом 7. Чтобы устранить слеживание материала
возле днища корпуса, вместе с конусом 2 вращается наклонный
скребок 6. Смесь выгружается через люк, имеющийся в днище
корпуса смесителя.
В циркуляционных смесителях достигается более высокая од-
норпдность смеси, а продолжительность смешивания сокра-
щается в несколько раз по сравнению с длительностью смеши-
вания в смесителях других типов.
ГИДРОМЕХАНИЧЕСКИЕ ПРОЦЕССЫ
Глава 6
ОСНОВЫ ГИДРАВЛИКИ
1. Общие сведения
В химической промышленности широко распространены про-
цессы перемещения жидкостей, газов и паров по трубопроводам
(или через аппараты), процессы перемешивания, а также про-
цессы разделения смесей путем отстаивания, фильтрования и
центрифугирования. Все эти процессы связаны с движением по-
токов, которое описывается законами механики жидкостей —
гидромеханики. Поэтому перечисленные выше процессы хими-
ческой технологии называют гидромеханическими процессами.
Практическое приложение законов гидромеханики изучается
в гидравлике, которая делится на гидростатику (учение о равно-
весии жидкостей) и гидродинамику (учение о движении жидко-
стей). Законы движения жидкостей были открыты основополож-
никами гидравлики — Д. Бернулли (1700—1782) и Л. Эйлером
(1707—1783).
При изучении процессов и аппаратов химической технологии
законы гидродинамики используются главным образом для рас-
чета скорости и расхода жидкостей (газов, паров) по заранее
известной движущей силе — перепаду давления, или для реше-
ния обратной задачи — определения необходимой движущей
силы по заданной скорости движения или расходу жидкости.
Законы гидродинамики, составляющие основу гидромеханиче-
ских процессов, в значительной мере определяют также харак-
тер течения тепловых и массообменных (диффузионных) про-
цессов.
2. Основные физические свойства жидкостей
Движение жидкостей и газов характеризуется одними и теми
же законами при условии, что скорость газа меньше скорости
звука. Поэтому в гидравлике жидкостями называют как соб-
ственно жидкости, так и газы. В таком широком понимании тер-
мин «жидкость» употребляется в данной книге, причем под
жидкостями следует понимать вещества, обладающие текуче-
122
Гл 6 Основы гидравлики
стью, т. е. не способные сохранять свою форму и полностью за-
полняющие занимаемый ими объем.
При исследовании различных вопросов гидравлики вводят
понятие о реально не существующей, идеальной жидкости. Та-
кая жидкость абсолютно несжимаема и не обладает внутренним
трением между частицами (вязкостью). В действительности
жидкости в той или иной мере сжимаемы и обладают вязко-
стью; они называются реальными, или вязкими, жидкостями.
Реальные жидкости делятся на собственно жидкости, назы-
ваемые капельными, и упругие жидкости — газы, обладающие
сжимаемостью, или упругостью, т. е. способные изменять свой
объем с изменением давления. Сжимаемость капельных жид-
костей крайне незначительна; например, объем воды при увели-
чении давления от 1 до 100 ат уменьшается только на !/2оо пер-
воначальной величины.
Жидкости характеризуются следующими основными физиче-
скими свойствами: плотностью (и удельным весом), вязкостью
и поверхностным натяжением.
Плотность и удельный вес
Масса жидкости, заключенная в единице ее объема, назы-
вается плотностью и обозначается через р:
___ m г кг 1
p~'VL‘wTJ
(6-1)
где m — масса жидкости, кг;
V — объем жидкости, м3.
В системе единиц МКГСС размерность массы кгс-сек2/м
(стр. 25), соответственно размерность плотности в этой системе
единиц-
[р]=
кгс • сек2_f кгс • сек2
М-М3 J L ЛГ*
Удельным весом называется вес единицы объема жидкости
Т=Т-[£] <6-2’
где G — вес жидкости, н.
В системе единиц МКГСС вес выражается в кгс, соответственно размер-
ность удельного веса в этой системе единиц
2 Основные физические свойства жидкостей
123
Подставляя в выражение (6-1) значение т—-^ и заменяя
-у- через 7, легко убедиться, что удельный вес связан с плотно-
стью следующим соотношением:
7 = Pg (6-3)
где g — ускорение силы тяжести, м/сек2.
Плотность в системе СИ, выраженная в кг/м3, численно
равна удельному весу в системе МКГСС, выраженному
в кгс/м3. Однако это равенство будет соблюдаться лишь при
g — 9,81 м/сек2, так как удельный вес изменяется в зависимо-
сти от величины g ускорения силы тяжести, а плотность является
свойством вещества, не зависящим от действующей силы тя-
жести.
Плотность капельных жидкостей незначительно увеличи-
вается с повышением давления и обычно несколько умень-
шается с возрастанием температуры.
Плотность газов значительно изменяется в зависимости от
температуры и давления. Зависимость между температурой, дав-
лением и объемом газов определяется уравнением состояния:
„т/ mRT
ру=-тг
(6-4)
где р — давление, н/м2;
V — объем газа, м3;
m — масса газа, кг;
R — универсальная газовая постоянная, дж/кмоль • град;
Т — температура, °К;
М — молекулярная масса газа.
Из уравнения (6-4) следует, что
_ m RT _ ?RT
р~ V ' М “ М
(6-5)
Объем, занимаемый единицей массы тела, называется удель-
ным объемом. Так, если масса жидкости tn кг, то удельный
объем равен:
V г-и3!
<и = — —
m L кг J
Удельный объем является величиной, обратной плотности,
т. е. v = у- Соответственно этому уравнение (6-4) может быть
написано в следующем виде:
РТ
pv=-Jf (6-6)
124
Гл..б. Основы гидравлики
R
Универсальная газовая постоянная R, в зависимости от еди-
ниц измерения давления, имеет следующие значения:
Давление
н/м2 . . .
дж
кмоль • град
кгс м
8314
848
Объем газов часто приводят к их объему при нормальных
условиях (температура 0° С, давление 101 300 н/м2)*. Объем
газов при нормальных условиях (Уо) связан с их объемом при
фактических условиях следующим соотношением, которое можно
вывести из уравнения (6-4):
~ Ю1 300Т М
Пример 6-1. Удельный вес бензола в системе единиц МКГСС
Y = 880 кгс/м^ при 20° С. Определить плотность бензола при той же темпе-
ратуре в системе МКГСС и в системе СИ.
Решение. Плотность бензола в системе единиц МКГСС находим по
формуле (6-3):
р = — = 4^- — 89,7 кгс • сек2/м^
g 9,81 '
Плотность бензола в системе СИ численно равна его удельному весу:
р = Т = 880 кг/м2
Пример 6-2. Определить плотность газообразного аммиака при избыточ-
ном давлении рИзб. — 26 ат и 16°С.
Решение. Абсолютное давление составляет:
/? = 26 4~ 1 = 27 кгс/см2 — 265 • 104 н/м2
Молекулярная масса аммиака М = 17.
Согласно формуле (6-5), плотность аммиака равна
.... рМ _ 265-104-17 1й_ . 3
р “ RT 8314 (273 4-16)= 1,87 Кг/м
Вязкость
При движении реальной жидкости в ней возникают силы
внутреннего трения, оказывающие сопротивление движению.
Свойство жидкости оказывать сопротивление движению назы-
вается вязкостью.
Допустим, что жидкость движется по трубе параллельными
концентрическими слоями (рис. 6-1). Если некоторый слой имеет
* 101 300 н)м2 = 760 мм рт. ст.
2. Основные физические свойства жидкостей
125
скорость w, то соседний с ним слой имеет скорость w + \w.
Следовательно, слои движутся с относительной скоростью Aw.
Опыт показывает, что скорость слоев уменьшается от оси к стен-
кам трубы, причем возле стенок частицы жидкости как бы при-
липают к стенкам, т. е. скорость жидкости становится равной
нулю. Для перемещения каждого слоя относительно другого
надо приложить некоторую силу, пропорциональную поверхно-
сти соприкосновения слоев. Эта
поверхности F, называется на-
пряжением внутреннего тре-
ния:
' = Т (6-7)
причем согласно закону Нью-
тона
сила Т, отнесенная к единице
Рис. 6-1. К определению вязкости
жидкости.
477 | 1У+4 7Г
где ------градиент скорости по нормали, т. е. относительное
изменение скорости на единицу расстояния между
слоями по направлению, перпендикулярному к на-
правлению течения жидкости.
Входящий в уравнение (6-8) коэффициент пропорциональ-
ности ц зависит от физических свойств жидкости и называется
динамическим коэффициентом вязкости, или просто вязкостью.
т
Подставив в уравнение (6-8) т =~р, получим размерность
вязкости в системе единиц СИ:
г___
Aw
“Дп
м=
н "1_____Гн • сек ~1
Л{2 м/сек L м2 J
м
Учитывая, что размерность ньютона [«] ==['т|^г’] (стр. 25),
можно получить размерность ц в другом виде:
кг-м
В системе единиц СГС за единицу вязкости принимается
пуаз (пз) — вязкость жидкости, в которой сила величиной
1 дин перемещает слои жидкости поверхностью 1 см2 каждый,
находящиеся на расстоянии 1 см друг от друга, с относитель-
ной скоростью 1 см/сек, т. е.
г ,__Г дин • сек 1_Г г • см сек 1 Г г 1
~ L Fm2 J ~~ Гсёк2- * 7м2 j ~ [см • сек J
126
Гл. 6. Основы гидравлики
Единица вязкости, равная 0,01 пз, называется сантипуазом
(спз). В справочниках значения вязкости обычно приводятся
в спз.
В системе единиц МКГСС размерность вязкости
кгс ~ ____Г кгс • сек "I
2 м/сек ~ [ м2 J
м -------*
м
„ , кгс • сек
Вязкость, равная 1 ——» называется технической единицей вяз-
кости.
Для того чтобы вязкосгь, выраженную в единицах различных систем
размерностей, пересчитать в единицы системы СИ, следует соответствующие
значения вязкости умножить на следующие переводные множители:
кгс • сек • \н-сек~\
—Х9'81=Ч“
Так, при 20° С вязкость воды:
1 л 1 ло 1Л""4 • сек п ~ кг ~н • сек
и. = 1 спз = 0,01 пз = 1,02 • 10 4---s— — 3,6 --------= Ю ° 5—
г м2 м • ч м2
Отношение вязкости ц к плотности р жидкости называется
кинематическим коэффициентом вязкости, или просто кинема-
тической вязкостью
(6-9)
Размерность кинематической вязкости в системе единиц СИ:
V
н • сек/м21
кг/м3 J
кг • м сек
сек2 м2
~кг~
м3
Такую же размерность имеет кинематическая вязкость в си-
стеме единиц МКГСС:
" кгс • сек/м2 '
кгс • сек2
м*
2. Основные физические свойства жидкостей
127
Соответственно размерность вязкости в системе единиц СГС:
г , г см21
1 J [ сек J
Единица кинематической вязкости — стокс (ст) равна
1 см2/сек.. Единица кинематической вязкости, в 100 раз мень-
шая стокса, называется сантистоксом (сст).
Вязкость капельных жидкостей с повышением температуры
уменьшается, вязкость газов увеличивается. Изменение вязкости
в зависимости от давления незначительно и обычно не учиты-
вается (исключая область весьма высоких давлений).
Пример 6-3. Вязкость 40%-ного раствора едкого натра при 60°С соста-
вляет [х = 5,4 спз. Определить вязкость раствора в других единицах измере-
ния.
Решение. Вязкость раствора в системе единиц СИ:
jx = 5,4 10-3 = 0,0054
г м2
В системе СГС:
р =Д0054 • 10 — 0,054 г!см • сек (пз)
В системе МКГСС:
лллгх 1 ее 1л-4 кгс-сек *
[X — 0,0054 • g-gj- — 5,5 • ю —2
Если за единицу времени принять час (ч), то вязкость раствора соста-
вит:
р = 0,0054 • 3600 19,4 кг!м • ч
Вязкость пластичных жидкостей
Некоторые процессы химической технологии связаны с перемещением
жидкостей, которые, в отличие--от обычных вязких жидкостей, не следуют
закону Ньютона [уравнение (6-8)]. К числу таких жидкостей, называемых
пластичными, или неньютоновскими жидкостями, относятся растворы многих
полимеров, коллоидные растворы, густые суспензии и др. Эти жидкости при
малых напряжениях внутреннего трения т (в н[м2) не текут, а лишь изме-
няют форму. В условиях, когда т становится больше некоторого значения
т0 (т т0), начинается течение таких жидкостей.
Для пластичных жидкостей зависимость между напряжением внутреннего
трения и градиентом скорости по нормали имеет следующий вид:
Т — то == — 7)
До/
Ди
(6-10)
где т] — коэффициент пропорциональности, характеризующий пластические
свойства жидкости.
Различие между обычными вязкими и пластичными жидкостями видно
из рис. 6-2. На оси абсцисс этого графика отложены величины , на оси
ап
128
Гл. 6. Основы гидравлики
ординат — величины -с. В соответствии с уравнением (6-8) свойства вязкой
жидкости характеризуются прямой, проходящей через начало координат гра-
фика с наклоном, численно равным вязкости ц жидкости. Свойства пластич-
ной жидкости выражаются прямой, отсекающей на оси ординат графика
отрезок То и имеющей наклон, численно равный коэффициенту тр
Рис. 6-2. Зависимость между
До,
ти-т— для пластичных и вяз-
Ди
ких жидкостей.
Рис. 6-3. Зависимость между
До/
т и -д— для вязких, пластичных
Ди
и псевдопластичных жидкостей:
/—пластичная жидкость; 2—псевдо-
пластичная жидкость; 3~ вязкая
жидкость.
Вязкость пластичной жидкости не является постоянной: она уменьшается
с возрастанием напряжения т. Действительно, для некоторой точки А на ли-
нии пластичной жидкости вязкость последней равна тангенсу угла наклона
пунктирной линии, соединяющей точку А с началом координат. По мере
перемещения точки А вправо по прямой (см. точку А') угол наклона
пунктирной линии уменьшается.
Вязкость пластичных жидкостей выражается следующей формулой:
di0
6w
(6-11)
1
где d— диаметр трубопровода, м;
w*— средняя скорость жидкости в трубопроводе, м/сек.
Существуют также псевдопластичные^ жидкости, для которых зависимость
Д w
т и изображается кривой 2 (рис. 6-3), выходящей из начала координат
и асимптотически приближающейся к прямой 1, характеризующей пластичную
жидкость.
В отличие от пластичных жидкостей псевдопластичные жидкости начи-
нают течь при самых малых значениях т, но вязкость этих жидкостей изме-
няется от [До (при т == 0) до рте (при т->оо), приближаясь с возрастанием т
к вязкости пластичной жидкости.
3. Давление жидкостей
129
Поверхностное натяжение
Молекулы жидкости, расположенные на ее поверхности или непосредствен-
но у поверхности, испытывают притяжение со стороны молекул, находящихся
внутри жидкости, в результате чего возникает давление, направленное внутрь
жидкости перпендикулярно к ее поверхности. Действие этих сил проявляется
в стремлении жидкости уменьшить свою поверхность; на создание новой
поверхности требуется затратить некоторую работу.
Работа, необходимая для образования единицы новой поверхности жид-
кости при постоянной температуре, носит название поверхностного натяже-
ния и обозначается а. Эту работу измеряют в джоулях и относят к 1 л<2 по-
верхности.
Размерность поверхностного натяжения а в системе единиц СИ:
г . Г дж 1 Г « 1
w=L-55-J=L-ci?-J=ra
Размерность а в системе единиц СГС:
г 1 — Г эРг 1 — Г ^ин ' см 1 — Г 1
— L CM2 J “ L см2 J ~~ L CM J
Соответственно в системе единиц МКГСС размерность о = [кгс/м].
Зависимость между размерностями а в системах единиц МКГСС, СГС
и СИ:
Поверхностное натяжение можно рассматривать как силу, действующую
на единицу длины поверхности раздела жидкости и соприкасающейся с ней
среды.
3. Давление жидкостей
Жидкость оказывает давление на поверхность погруженного
в нее тела, а также на дно и стенки сосуда, в котором она за-
ключена.
Давление жидкости на единицу поверхности называется гид-
ростатическим давлением или просто давлением. Гидростатиче-
ское давление р представляет собой отношение
Р = 4 (6-12)
где Р — сила давления жидкости на поверхность F.
Если жидкость налита в.сосуд, то сила давления, действую-
щая на его дно, равна весу жидкости в сосуде:
P = FHpg
где F — площадь дна сосуда;
Н — высота столба жидкости;
р — плотность жидкости;
g — ускорение силы тяжести.
9 Зак. 546.
130
Гл. 6. Основы гидравлики
Следовательно, сила давления на дно не зависит от формы
и объема сосуда, и для данной жидкости определяется только
величиной площади дна и высотой столба жидкости в сосуде.
Согласно выражению (6-12), давление на дно сосуда со-
ставит:
FHpg и
P = —f—= H?g
(6-13)
Из выражения (6-13) следует, что давление жидкости на
дно сосуда равно весу столба жидкости высотой Н с площадью
основания, равной единице (F = 1).
В том случае, если давление над жидкостью равно ро, гидро-
статическое давление
P=Po + Hpg (6-14)
Давление на вертикальные или наклонные стенки сосуда не
является постоянным по всей высоте стенки. Поэтому гидроста-
тическое давление в каждой точке стенки рассматривают как
предел (11m) отношения силы давления ДР к элементарной пло-
щадке ДР (на которую она действует) при ДР, стремящейся
к нулю:
р=ИтГ^И (6-15)
Давление направлено по нормали к площадке, на которую
оно действует. Иначе силу давления можно было бы разложить
на составляющие, одна из которых вызвала бы перемещение
жидкости, что невозможно, так как жидкость находится в покое.
Кроме того, давление в жидкости одинаково по всем направле-
ниям, потому что через данную точку может проходить беско-
нечно большое число элементарных площадок, к которым при-
менимы приведенные выше положения.
Размерность давления в системе СИ — [н/м2], в системе
МКГСС — [кгс/м2]. Допускается также применение следующих
внесистемных единиц давления: бар (бар) *, техническая атмо-
сфера (апг, или кгс/см2), миллиметр ртутного столба (мм
рт. ст.) и миллиметр водяного столба (мм вод. ст.).
Раньше в качестве единицы давления применяли также физическую ат-
мосферу (атм), которая равна давлению столба ртути высотой 760 мм или
давлению столба воды высотой 760- 13,6 = 10330 мм, так как, плотность воды
в 13,6 раза меньше плотности ртути. Вес столба воды высотой 1033 см и пло-
* В системе СГС баром называли единицу давления, равную 1 дин!см?,
т. е. величину, в 10е раз меньшую, чем теперь В настоящее время эта редко
употребляемая единица давления называется барией, или микробаром
(мкбар).
3 Давление жидкостей
131
щадью 1 см? при удельном весе воды 0,001 кг/см? равен 1033 • 1 • 0,001 =
= 1,033 кгс)см?. Следовательно, физическая атмосфера соответствует давле-
нию 1,033 кгс/см?. Техническая атмосфера (ат) равна давлению в 1 кгс/см?,
что соответствует давлению столба ртуги высотой 735,6 мм
Соотношение между единицами давления в различных систе-
мах единиц следующее:
1 н/м2 — 0,102 кгс/м2 = 10,2 • 10-6 ат (кгс/см2) = 10-5 бар =
— 7,5 • 10-3 мм рт. ст.
1 бар = 10,2 • 103 кгс/м2 = 1,02 ат (кгс/см2) = 105 н/м2 = 750 мм рт. ст.
1 ат = 10 000 кгс/м2 = 98,1 • 103 н/м2 = 0,981 бар — 735,6 мм рт. ст.
Следует отметить, что давление, выраженное в мм вод. ст.,
численно равно давлению в кгс/м2.
Если давление над жидкостью выше
атмосферного, то жидкость находится
под избыточным давлением, равным
/^изб. /^абс. В
где Рабе.— абсолютное давление;
В — атмосферное, или баромет-
рическое давление.
Если давление над жидкостью ниже
атмосферного, то жидкость находится
при разрежении (в вакууме), равном
Рвак. == В Рабе.
Раньше давление, выраженное в технических
атмосферах, обозначали ата (абсолютное давле-
ние) и ати (избыточное давление).
Пример 6-4. В колонне (рис. 6-4) находятся
вода (плотность pi — 1000 кг/м3, высота слоя
h\ — 2 м) и несмешивающаяся с ней легкая
жидкость — бензол (плотность р 2 = 900 кг/м3,
высота слоя йг — 0,7 к). Абсолютное давление
над поверхностью жидкости в колонне р0 = 1,8 бар, атмосферное давление
В = 1 бар Определить показание ртутного манометра, установленного в
нижней части колонны.
Решение Выбрав плоскость сравнения О—О на уровне ртути в левом
колене манометра, устанавливаем, что давление столба ртути- в манометре и
атмосферное давление над ртутью уравновешиваются давлением столбов во-
ды и бензола и давлением над жидкостью в колонне:
Ро + Р1 gh 1 + р2gh2 = ррт.£/грт. -ф В
Выражая ро и В в н/м? и подставляя в эту формулу значение плотности
ртути ррТ. = 13 600 кг/м3 и ускорение силы тяжести g = 9,81 м/сек?, получим-
. 1,8-105 4-1000-9,81-2 + 900-9,81.0,7 — 1.105
«рт-----------------------13 600 9,81------------------= °’79 М
Таким образом, показание ртутного манометра составит ~790 мм рт. ст
9*
132
Гл. 6. Основы гидравлики
Пример 6-5. Вакуумметр, установленный на всасывающем патрубке на-
соса, показывает разрежение, равное Рвак.= 440 мм рт. ст., манометр на
нагнетательном патрубке того же насоса показывает избыточное давление
1,6 бар. Барометрическое давление В = 1 бар (750 мм рт. ст.). Определить
абсолютное давление жидкости во всасывающем и нагнетательном патрубках
насоса (в бар, ат, кгс/м? и н/м?).
Решение. Абсолютное давление во всасывающем патрубке:
рвс = В — Рвак. = 750 — 440 = 310 мм рт. ст.
Эта величина в’других системах единиц составляет;
310 П ЛЮ /Г
Рве. = 'узд' — 0,413 бар
Рве. = 735g- = 0,42 ат
Рве. — 3-10 • 13,6 = 4216 кге/м2
рвс = 0,413 • 105 н/м2
Абсолютное давление в нагнетательном патрубке:
рп = 1,6 -|- 1 = 2,6 бар
рн = 2,6 • 10,2 • 103 = 26,5 • 103 кге/м2
ра = 2,6 • 1,02 = 2,65 ат
^~рн = 2,6 • 105 н/м2
4. Материальный баланс потока
(уравнения неразрывности потока)
Скорости движения частиц жидкости неодинаковы по сече-
нию ее потока. Поэтому вводят понятие о средней скорости по-
тока всех частиц жидкости в сечении. Допустим, что в сечении
а б
Рис. 6-5. К выводу уравнений неразрывности
потока.
I—I трубы (рис. 6-5, а) все частицы имеют среднюю скорость
w, тогда за единицу времени они пройдут путь, равный w, и пе-
реместятся в сечение II—II. Объем жидкости, протекающей в
единицу времени через сечение I — I, будет равен объему V, за-
ключенному между сечениями /—/ и //—II, т. е. произведению
средней скорости w на площадь поперечного сечения 5 потока.
4. Материальный баланс потока (уравнения неразрывности потока) 133
Это произведение представляет собой объемный расход жид-
кости:
(6-16)
V—wS м3/сек
откуда средняя скорость
= м/сек (6-17)
о
Уравнение (6-16) носит название уравнения расхода. Ско-
рость, входящая в это уравнение, есть линейная скорость, т. е.
путь, проходимый жидкостью в единицу времени.
Массовая скорость W представляет собой количество жид-
кости, протекающее через единицу поперечного сечения потока,
в единицу времени, и определяется из соотношения
W= кг/м2 • сек
(6-18)
где G — массовый расход жидкости, кг/сек.
Зависимость между массовой и линейной скоростью можно '
установить, заменив в выражении (6-18) G через Vp (где р —
плотность жидкости в кг/м3) и подставив вместо -у его значение
из равенства (6-17). Тогда
(6-19)
Если скорости частиц жидкости не изменяются во времени,
ее движение считается установившимся. При установившемся
движении в каждом сечении потока постоянны не только ско-
рость, но и расход, температура, давление и плотность жидкости.
Вместе с тем при установившемся движении скорости потока
могут изменяться в пространстве, при переходе жидкости от
одного сечения к другому.
Рассмотрим установившееся движение жидкости, ограничен-
ной стенками любой формы, например движение в трубе пере-
менного сечения (рис. 6-5,6). Движущаяся жидкость сплошь
заполняет трубу, в которой, таким образом, нет пустот и разры-
вов потока. При переходе от сечения Si к сечению S2 скорость
жидкости будет изменяться, но по закону сохранения вещества
количество жидкости, поступающей в единицу времени через
сечение Si, будет равно количеству ее, протекающему через се-
чение S2, т. е. расход жидкости останется постоянным. В том
случае, если эти количества не были бы равны (например,
134
Гл. 6. Основы гидравлики
если поступающее через сечение Si количество жидкости превы-
шало бы ее количество, проходящее через сечение S2), жидкость
накапливалась бы в трубе, между сечениями Si и S2, и здесь
происходило бы возрастание ее плотности и давления, что при
установившемся движении невозмбжно.
Принимая массовые скорости жидкости в сечениях Si и S2
равными соответственно Wi и W2, можно написать
G = S1WZ1 = S2VVZ2 = const (6-20)
или
G = S^Wipi = S2-ze)2p2 = const (6-21)
где pi и p2 — плотности жидкости в сечениях Si и S2.
Для несжимаемой жидкости pi = р2 и уравнение (6-21) при-
нимает вид
V=S1‘Wl = S2iw2 — const (6-22)
Уравнения (6-20) — (6-22) представляют собой материаль-
ный баланс потока жидкости и называются уравнениями нераз-
рывности потока.
Согласно этим уравнениям, средние скорости жидкости в
различных сечениях трубопровода обратно пропорциональны
площадям этих сечений. Произведение скорости на сечение,
т. е. расход жидкости при установившемся движении, есть ве-
личина постоянная.
5. Энергетический баланс потока (уравнение Бернулли)
Удельная энергия жидкости
Жидкость, независимо от того, находится ли она в состоянии
покоя или движения, обладает некоторым запасом энергии, рав-
ным сумме внутренней, потенциальной и кинетической энергий.
Внутренняя энергия представляет собой энергию молекул
жидкости, всегда совершающих поступательные и вращательные
движения и потому обладающих кинетической энергией этих
движений. Скорость и, следовательно, энергия движения моле-
кул увеличиваются с повышением температуры. К внутренней
энергии относятся также потенциальная энергия молекул, зави-
сящая от сил притяжения между ними, и энергия внутримолеку-
лярных колебаний, которая определяется колебательным движе-
нием атомор, входящих в состав молекулы. Внутренняя энергия
обозначается через U и выражается в джоулях (дж).
Ж '
5. Энергетический баланс потока (уравнение Бернулли) 135
энергия давления в данном
о
Рис. 6-6. К определению потенциаль-
ной энергии жидкости.
Потенциальная энергия жидкости состоит из потенциальной
энергии давления и потенциальной энергии положения.
Общее выражение потенциальной энергии давления можно
получить, определив давление поршня на некоторый объем жид-
кости в сосуде (рис. 6-6). Если поршень находится под действием
D
груза Р, то жидкость находится под давлением р. = —, где s —
площадь поршня. Потенциал
случае равна потенциальной
энергии груза, представляю-
щей собой произведение Ph.
Заменяя Р через ps и учи-
тывая, что sh = V, получим,
что потенциальная энергия
давления равна pV, т. е.
произведению давления на
объем жидкости V.
Потенциальная энергия
положения определяется вы-
сотой z центра тяжести объ-
ема жидкости над некоторой
произвольно выбранной горизонтальной плоскостью О—О
(рис. 6-6), называемой плоскостью сравнения. Очевидно, потен-
циальная энергия положения равна Gz, где G — вес жидкости
в объеме V. Так как масса жидкости (g— ускорение
силы тяжестй), то потенциальная энергия положения рав-
на mgz.
Кинетическая энергия жидкости, движущейся со скоростью w,
, mw2
определяется по формуле —
Полная энергия жидкости равна сумме внутренней, потен-
циальной и кинетической энергий:
Е = U+p V-p mgz + (6-23)
Сумма внутренней и потенциальной энергий давления назы-
вается энтальпией (теплосодержанием) и обозначается "через I:
I = U-\-pV (6-24)
Соответственно
ством
полная энергия жидкости выражается равен-
Е — I^mgz-\-дж
(6-25)
136
Гл. 6. Основы гидравлики
Удельная энергия жидкости, т. е. энергия 1 кг жидкости,
может быть найдена делением обеих частей уравнения (6-23)
или уравнения (6-25) на массу жидкости т:
Eyii. = ii-\-ptv + gz-\-~- = i + gz-\-~ дж/кг (6-26)
где и — внутренняя энергия 1 кг жидкости, дж/кг;
v — объем, занимаемый 1 кг жидкости, м?/кг-,
i — энтальпия 1 кг жидкости, дж/кг.
Если и и I выражены в ккал, р — в кгс/м2, а Е — в кгс • м, то уравнение
(6-26) примет следующий вид:
С и I I
£уд-= Т + pv +
gZ ! W2
gc "Г 2^с
i . gz , w2 .
_ _L 2—l — кгс . м кг
A gc 2gc
где А —термический эквивалент работы (’/ш ккал/кгс • м);
gc—коэффициент перехода от джоулей к кгс-м, равный 9,81 кгС'М
(стр. 27).
Уравнение Бернулли
При движении жидкости по трубопроводу без дополнитель-
ного подвода энергии (источника работы или тепла) или ее от-
Рис. 6-7. Графическое изображение уравнения Бернулли:
а —для идеальной жидкости; б—для реальной жидкости.
вода удельная энергия жидкости, по закону сохранения энергии,
не будет изменяться. Поэтому при перемещении жидкости от не-
которого сечения I—I до сечения II—II (рис. 6-7) удельные
$
*
5. Энергетический баланс потока (уравнение Бернулли)
137
энергии жидкости в этих сечениях будут одинаковы:
+/ЗД + gZ\ 4- ~2~ == «24-P2^2 + gz2 4- ~2
Учитывая, что v = — , где р — плотность жидкости, получим
следующее выражение энергетического баланса:
2 2
4~ -----F gZ\ Ч--2~ ~ М2 4“ ~ Ч~ 4“
Pl z г2 z
(6-27)
Рассмотрим движение идеальной капельной жидкости
(рис. 6-7, а), для которой, как и для любой капельной жидкости,
pi = р2 = р. Идеальная жидкость движется без трения, поэтому,
при отсутствии подвода тепла, ее температура и внутренняя
энергия не будут изменяться. Следовательно, в данном случае
Ui = «2- Тогда уравнение энергетического баланса примет вид:
Р1 । _ I I W2
?g + 2g pg + 2g
(6-
Это уравнение, выражающее энергетический баланс движу-
щейся идеальной жидкости, называется уравнением Бернулли *.
В уравнении (6-28) член z, выражающий потенциальную
энергию положения жидкости, имеет размерность длины и на-
зывается геометрическим напором.
Член ~ выражает потенциальную энергию давления жидко-
сти и также имеет размерность длины:
I р I__Г н/м2 Я_____________Г кг • м!сек2 • м2 ~|
| pg I L кг/м3 • м!сек2 J L кг(м3 • м!сек2 J
=и
Энергия давления может быть измерена при помощи верти-
кальной пьезометрической трубки. Под действием давления жид-
кость поднимается в трубке на высоту которая назы-
вается пьезометрическим, или статическим напором.
* Уравнение (6-28) получается делением на g обеих частей уравнения
(6-27), выражающего энергетический баланс 1 кг жидкости, и, следовательно,
представляет собой энергетический баланс — кг жидкости.
138
Гл. 6. Основы гидравлики
Член выражает удельную кинетическую энергию движу-
щейся жидкости. Этот член, называемый скоростным, или ди-
намическим, напором, также имеет размерность длины:
г w21__Гм2/сек21_
L 2g J L м/сек2 J
Скоростной напор равен высоте, на которую может под-
няться струя жидкости, вытекающей вертикально вверх с на-
чальной скоростью w.
Таким образом, согласно уравнению Бернулли, при движе-
нии идеальной жидкости сумма геометрического, пьезометри-
ческого и скоростного напоров во всех сечениях потока является
постоянной величиной.
Рассмотрим уравнение Бернулли для реальной жидкости,
движущейся с трением. В этом случае при переходе жидкости от
сечения / — /до сечения //— // (рис. 6-7,6) часть удельной
энергии будет расходоваться на преодоление трения и других
сопротивлений. Потерянная при этом энергия превращается в
тепло, вследствие чего увеличивается внутренняя энергия жидко-
сти (при отсутствии теплообмена с окружающей средой). Из
уравнения (6-27) получим (при pi = р2 = р):
2 9
, Р\ Wi р9 W9
^I + y- + ^- = gz2+-^ + -^ + «2-M1 (6-29)
В уравнении (6-29) член и2 — и\ выражает увеличение вну-
тренней энергии 1 кг жидкости и равен удельной энергии, затра-
ченной на преодоление сопротивлений между сечениями трубы
/ — / и II— II. Таким образом, после деления уравнения (6-29)
на уравнение Бернулли для реальной жидкости можно напи-
сать в следующем виде:
- _1 w2 1- h
9g Г 2g A"2 2g Г rin
(6-30)
Член hn, как и другие члены уравнения (6'30), имеет раз-
мерность длины и называется потерянным напором.
Таким образом, согласно уравнению Бернулли, при устано-
вившемся движении реальной жидкости сумма геометрического,
пьезометрического, скоростного и потерянного напоров в каждой
точке любого сечения потока является постоянной величиной.
Все напоры имеют размерность длины, поэтому уравнение
Бернулли наглядно представлено графически (см. рис. §-7). Все
5. Энергетический баланс потока (уравнение Бернулли)
139
напоры будут изображаться отрезками вертикальной прямой, а
их сумма — вертикалью, проведенной от произвольно выбранной
плоскости сравнения 0—0 (нулевой уровень) до общей гори-
зонтальной плоскости N—N.
Если в рассматриваемых сечениях поместить открытые изо-
гнутые стеклянные трубки, один конец которых направлен по
оси потока, то высота подъема жидкости в трубках будет соот-
ветствовать сумме пьезометрического и скоростного напоров.
Для реальной жидкости отрезок hn (ём. рис. 6-7,6) будет харак-
теризовать величину потерянного напора при ее движении от
сечения /—/ до сечения II—II.
Сумма геометрического, пьезометрического и скоростного
напоров называется гидродинамическим напором. Если соеди-
нить уровни жидкости в стеклянных трубках, получим нисходя-
щую линию А—А (см. рис. 6-7,6), которая называется линией
гидродинамического напора, или линией падения напора.
Из рис. 6-7, б видно, что гидродинамический напор реальной
жидкости уменьшается в направлении ее движения на величину
напора, потерянного между начальным и конечным сечениями
потока.
Уравнение Бернулли является выражением одного из важней-
ших законов гидравлики, так как решение ее основных задач
связано с определением расхода энергии и вычислением работы
или мощности. Пользуясь уравнением Бернулли, определяют
скорость и расход жидкости, т. е. пропускную способность аппа-
ратов и трубопроводов. При помощи этого уравнения рассчиты-
вают также время истечения жидкости и ее полный напор.
Обобщенное уравнение Бернулли
В общем случае реальная жидкость движется по трубопроводу (рис. 6-8),
на котором расположены насос (или компрессор) 1, потребляющий работу L,
и источник тепла (теплообменник 2), при помощи которого к жидкости
подводится тепло Q. При этом воз-
можно возрастание энергии потока ме-
жду сечениями трубопровода /—I и
II—II.
Если при движении жидкости от
сечения /—/ до сечения //—// к ней
подводятся работа L и тепло Q, то
энергия жидкости на этом участке уве-
личится на L + Q. В этом случае энер-
гетический баланс потока выражается
уравнением
£1 + L + Q = £2 (6-31)
где Ег и £/— полная энергия жидкости
в сечениях I—I и II—II.
Выразив £i и £2 в соответствии
Рис. 6-8. К выводу обобщенного
уравнения Бернулли:
/—насос или компрессор; 2 —теплообмен-
ник; L — работа; Q — тепло.
140
Гл. 6. Основы гидравлики
с уравнением (6-26) и разделив обе части выражения (6-31) на массу
жидкости /и, получим уравнение энергетического баланса:
2 9
Wi Wo
ЛЧ-^Ч—?j" Ч~ Z Ч~ <7 = г’г Ч~ £г2 Ч—2" (6-32)
г L
где I = —— подведенная работа, отнесенная к 1 кг жидкости;
L
q —-----подведенное тепло, отнесенное к 1 кг жидкости.
Из уравнения (6-32) находим:
/ w2\( w\\
Z + 7 = уz2 + ^2 Ч—2~у — -|-gzx 4—2~у (6-33)
2 2
W9—
Z + <7 = 0г — Л) Ч~ S (z2 — zi) Ч-2- (6-34)
Согласно уравнению (6-34), работа, сообщаемая движущейся жидкости,
включая работу, эквивалентную количеству подведенного тепла, расходуется
на повышение энтальпии жидкости, на ее подъем (преодоление силы тяже-
сти) и на повышение кинетической энергии жидкости.
Если работа I выражена в кгс • м/кг, a q a i — в ккал/кг, то уравнение
(6-34) принимает следующий вид:
z , q — z0 । wl — wi
где Я — термический эквивалент работы (*/427 ккал/кгс • м); gc—коэффи-
циент перехода (стр. 136).
Обобщенное уравнение (6-34) может быть упрощено применительно
к различным частным случаям, рассмотренным ниже.
Движение капельной (несжимаемой) жидкости. Для несжимаемой жид-
кости = 02 = —- (где р — плотность жидкости); кроме того, согласно уравне-
р
нию (6-24), i = и + pv. Сделав подстановку в уравнение (6-33), получим:
(9 \ / 2 \
пп \ I D, I
и2 Ч-~ + gz2 Ч-/ — ( и1 + ~ Ч- Sz\ Ч-9- ) (6-35)
р / \ Р /
Повышение внутренней энергии складывается из подводимого тепла и
тепла, в которое превращается работа, затрачиваемая на преодоление сопро-
тивлений Лп, т. е. «2 — «1 = q + ghn.
Поэтому
(. 2 \ / 2 \
Рч W9 \ / Р\ ^1 \
~~ Ч- Sz2 Ч- Ч- J Ч- sha (6-36)
или
(6-37)
Таким образом, удельная работа I, потребляемая насосом, расходуется на
подъем 1 кг жидкости на высоту з2— Зь на повышение давления от р\ до рг,
на увеличение кинетической энергии жидкости и на преодоление сопротивле-
ний по пути движения жидкости.
5. Энергетический баланс потока (уравнение Бернулли) 141
Движение сжимаемой жидкости (газа). В большинстве случаев для
газов, ввиду их малой плотности, можно пренебречь разностью высот z2 — zb
так как она мала по сравнению с другими членами уравнения энергетического
баланса. Тогда общее уравнение (6-34) принимает вид
w2 —
' + ? = + (6-38)
В этом уравнении I представляет собой работу, затрачиваемую на сжатие
1 кг газа (в компрессоре).
Пример 6-6. Вода в количестве V = 16 подается под абсолютным
давлением pi = 3,5 бар (3,57 ат) по магистральному трубопроводу диаметром
di = 75 мм на охлаждение двух аппаратов I и II (рис. 6-9). Диаметр трубы
I
d2 на ответвлении к аппарату / составляет 25 мм, на ответвлении к ап-
парату // d3 = 46 мм. Абсолютное давление воды на входе в аппарат I р2 =
= 3,35 бар (3,42 ат). Разность геометрических высот z2— Z\ = Н\ = 1,4 м.
Определить скорость подачи и расход воды в каждом аппарате (сопротивле-
нием труб пренебречь).
Решение. Принимаем за плоскость сравнения горизонтальную пло-
скость, проходящую через ось 0—0 магистрального трубопровода.
Уравнение Бернулли (6-28) для идеальной жидкости и точек 1 и 2:
, , Pi , wi _ . Pi ,
1+P£ + 2£-*2+ pg + 2^
Разность статических напоров для точек 1 и 2:
рх-р2 _ (3,5 -3,35). 10б
Р£ “ 1000 • 9,81 “ ’
где р = Ю00 кг(м3 (плотность воды).
142
Гл. 6. Основы, гидравлики
Скорость воды в магистральном трубопроводе:
_ ^сек. _ V _ 16
Wi~ Sx “ — 3600.0,785 0.0752 “ 1 М/СеК
3600--ri-
4
Из уравнения (6-28) следует:
(2 \
Ру -Р<2 W1 \ / 12 \
*1 - *2 + J-^— + = (- 1 ’4 + 1 >5 + Т. 9,81') 2 • 9181 = 2)96
w2 = 1,72 м)сек
Расход воды на аппарат Г.
nd?
Vj = 3600 • w2S2 = 3600w2 = 3600 • 1,72 • 0,785 • 0,0252 s 3 м*/ч
Расход воды на аппарат II:
Vjj^V— V7 = 16 — 3=13 м3/ч
Скорость воды в трубе-ответвлении к аппарату II:
VI1 13 O1Q
W3~ Ttdl ~ 3600 - 0,785 - 0,0462 “ 2,18 М/
6. Режимы движения вязкой жидкости
При течении жидкости характер, или режим, ее движения
может быть ламинарным или турбулентным.
При ламинарном режиме, наблюдающемся при малых ско-
ростях или значительной вязкости жидкости, она движется па-
Рис. 6-10. Распределение скоростей в трубе при
различных режимах движения жидкости:
а —ламинарное движение; б—турбулентное движение.
раллельными струйками, не смешивающимися друг с другом.
Струйки обладают различными скоростями, но скорость каждой
струйки постоянна и направлена вдоль оси потока.
При ламинарном движении (рис. 6-10, а) скорость частиц
по сечению трубы изменяется по параболе от нуля у стенок
6. Режимы движения вязкой жидкости
143
трубы до максимума на ее оси. При этом средняя скорость жид-
кости равна половине максимальной куср. = 0,5 кумакс.- Такое
распределение скоростей устанавливается на некотором расстоя-
нии от входа жидкости в трубу.
При турбулентном режиме частицы жидкости движутся с
большими скоростями в различных направлениях, по пересекаю-
щимся путям. Движение носит беспорядочный характер, причем
частицы движутся как в осевом, так и в радиальном направле-
нии. В каждой точке потока происходят быстрые изменения ско-
рости во времени — так называемые пульсации скорости. Однако
значения мгновенных скоростей колеблются вокруг некоторой
средней скорости.
Но и при турбулентном движении (рис. 6-10,6) в очень тон-
ком граничном слое у стенок трубы движение носит ламинарный
характер. Этот слой толщиной 8 называется ламинарным погра-
ничным слоем. В остальной части (ядре) потока, вследствие пе-
ремешивания жидкости, распределение скоростей более равно-
мерно, чем при ламинарном движении, причем wcp. = 0,85 wmax.
Два различных режима движения и возможность взаимного
перехода одного режима в другой можно наблюдать, пропуская
в трубу воду с различными скоростями и вводя по оси трубы
тонкую струйку окрашенной жидкости. При малых скоростях
движения окрашенная струйка движется в воде, не перемеши-
ваясь с нею. С увеличением скорости воды окрашенная струйка
становится колеблющейся и по достижении некоторой критиче-
ской скорости полностью размывается, окрашивая воду. Резкое
изменение течения окрашенной струйки характеризует переход
ламинарного режима движения жидкости в турбулентный.
Опыты, проведенные в 1883 г. О. Рейнольдсом, показали, что
характер движения жидкости зависит от средней скорости w
жидкости, от диаметра d трубы и от кинематической вязкости v
жидкости. Переход одного вида движения в другой происходит
при определенном значении комплекса перечисленных величин,
названного критерием Рейнольдса:
Re = —-
(6-39)
Критерий Рейнольдса является безразмерной величиной, что
легко доказать, подставив входящие в него величины в одина-
ковой системе единиц, например в системе СИ:
На основе соотношений (6-9) и (6-19) могут быть полу-
чены различные выражения критерия Рейнольдса, которыми
144
Гл. 6 Основы гидравлики
пользуются в технических расчетах:
wd w dp Wd
Re — — —-= —
у р-р-
(6
где v — кинематическая вязкость;
р — плотность;
р- — динамическая вязкость;
W — массовая скорость.
Из этих выражений следует, что турбулентное движение воз-
никает с увеличением диаметра трубы, скорости движения и
плотности жидкости или с уменьшением вязкости жидкости.
Величина Re, соответствующая переходу одного вида движе-
ния в другой, называется критическим значением критерия Рей-
нольдса, причем для прямых труб ReKp. = 2300. Движение жид-
кости в прямых трубах при Re < 2300 является устойчивым ла-
минарным. При Re > 2300 движение турбулентно, однако
устойчивый (развитый) турбулентный характер оно приобретает
при Re > 10 000. В пределах Re от 2300 до 10 000 турбулентное
движение является недостаточно устойчивым (переходная об-
ласть).
Как будет показано ниже, в определенных условиях (движе-
ние твердых частиц в жидкости, движение жидкости через слой
насадочных тел и др.) переход одного вида движения в другой
происходит при значительно меньших значениях ReKp_. Однако
всегда существует определенный предел, соответствующий каче-
ственному скачку в характере движения жидкости, что является
яркой иллюстрацией одного из основных законов марксистской
диалектики — закона перехода количества в качество.
При движении жидкости в трубах или каналах некруглого
сечения в выражение критерия Re вместо диаметра подставляют
величину эквивалентного диаметра:
, — 45
^ЭКВ. - ~jY"
(6-41)
где S — площадь сечения потока;
П — периметр, смоченный жидкостью.
Пример 6-7. Определить характер движения жидкостей в теплообмен-
нике типа «труба в трубе» (рис. 6-11), если по внутренней трубе протекает
вода в количестве VB = 4,5 мР/ч при средней температуре 30° С, а в межтруб-
ном пространстве движется метиловый спирт в количестве GM = 5000 кг[ч,
средняя температура которого 50° С. Диаметры внутренней трубы: внутренний
dBH = 39,5 мм, наружный dH = 44,5 мм, Внутренний диаметр наружной трубы
теплообменника DBa «= 70 мм,
7. Элементы теории подобия.
145
Решение. Определяем сечения каналов для жидкостей:
V сечение внутренней трубы
1 s = __2±_ = 0,785 • 0,03952 = 0,001225 м2
4
г*
сечение межтрубного пространства
S2 = — 4) = 0,785 (0.072 — 0.04452) = 0,0023 м2
Рис. 6-11. К приме-
ру 6-7.
Скорости жидкостей в теплообменнике по уравнению расхода (6-17):
скорость воды
= 3600s, = 3600 • 6,001225 = 1,02 М,СеК
скорость метанола
... _ ________5000_________д-р MiceK
- 2 “ рм • 3600S2 ~ 765 • 3600 • 0,0023 U’79 1
где рм = 765 кг/м3 (плотность метанола при 50° С).
Определим характер движения воды в трубе по
величине критерия Рейнольдса:
R = *Мвн.Рв_ = = 50 000
(ЛВ 0,8 • 10"3
где рв — 995 кг!м3 (плотность воды при 30° С);
р.в — 0,8 • 10~3 н • сек)м2, или 0,8 спз (вязкость
воды при 30° С).
Таким образом, Rei > 10 000; следовательно,,движение воды в трубе раз-
витое турбулентное.
Чтобы определить значение критерия Рейнольдса в межтрубном простран-
стве, находим эквивалентный диаметр кольцевого канала, по которому проте-
кает метиловый спирт:
/ nD2K nd2 \
rf9KB. = = ....' д-Л = dbh.-= 0>07 - 0,0445 = 0,0255 м
11 чМй. Т“н)
Вычислим критерий Рейнольдса для межтрубного пространства:
R = rf3KB.pM_ = 0,79 • 0,0255 • 765 = 39 000
0,396 • 10" 3
где р.м = 0,396 • Ю"3 н • сек/м2, или 0,396 спз (вязкость метанола при 50° С).
Поскольку в- межтрубном пространстве Re > 10 000, то характер движе-
ния в нем метанола тоже развитый турбулентный. ч
' 7. Элементы теории подобия
Понятие о теории подобия
Движение жидкостей представляет собой сложное физиче-
ское явление, зависящее от многих факторов, всегда связанных
друг с другом, причем связь между ними выражает физический
10 Зак 546.
146
Гл. 6. Основы гидравлики
закон, характеризующий данное явление. Физические законы
могут быть представлены в виде математических уравне-
ний.
Во многих случаях уравнения, выражающие физические
законы, очень сложны и не могут быть решены известными
математическими методами. Поэтому для изучения различных
явлений, в том числе гидравлических, приходится прибегать
к эксперименту. При опытном исследовании трудности задачи
не исчезают, а переносятся на проведение опытов: необходимо
огромное число опытов, чтобы установить влияние на данное
явление каждого из многочисленных факторов, независимо от
других. Проведение опытов в аппаратах больших размеров (на-
туральной величины) весьма затруднительно и связано с боль-
шими затратами времени и средств. ,
Вместе с тем результаты проведенных опытов будут верны
только для тех условий, в которых они получены, и не могут
быть с достаточной надежностью распространены на явления,
аналогичные изученному, но происходящие в аппаратах, кото-
рые отличаются от испытанного. Таким образом, как чисто тео-
ретический, так и чисто экспериментальный пути часто недоста-
точны для решения задачи. В этих случаях плодотворным
методом исследования является применение теории подобия.
Теория подобия указывает, как надо ставить опыты и как
обрабатывать опытные данные, чтобы, ограничившись минималь-
ным числом опытов, иметь право обобщить их результаты и по-
лучить закономерности для целой группы подобных явлений.
Теория подобия позволяет с достаточной для практики точ-
ностью изучать сложные процессы на более простых моделях,
значительно отличающихся по размерам от аппаратов натураль-
ной величины.
Чтобы уяснить сущность теории подобия, надо ознакомиться
с подобием физических явлений.
Как известно, при подобии геометрических фигур отношение
сходственных сторон модели и натуры постоянно. Точно так же
при подобии физических явлений отношение между какой-либо
физической величиной для модели и для натуры одинаково во
всех сходственных точках.
Например, если в трубопроводах диаметрами di и rf2
(рис. 6-12) скорости жидкостей подобны, то отношение скоро-
стей и W2 по оси труб равно отношению скоростей tc»i и w2
в сходственных точках 1 и 2, т. е. — = —-• Это отношение
w2 w2
остается постоянным для всех сходственных точек в обоих тру-
бопроводах. Справедливо и обратное положение: если указанное
7. Элементы теории подобия
147
отношение постоянно для всех сходственных точек, то скорости
жидкостей в обоих трубопроводах подобны.
Однако движение жидкости в трубопроводе характеризуется
не только распределением скоростей, но и другими факторами:
вязкостью жидкости, ее плотностью и др. Как доказывается в
теории подобия, для того чтобы жидкость в трубопроводах диа-
метрами di и ds двигалась подобно, в их сходственных точках
должны быть равны некоторые безразмерные соотношения фи-
зических величин, влияющих на движение жидкости. Эти без-
размерные соотношения разнородных физических величин назы-
ваются критериями подобия
Рис. 6-12. К определению подобия движения
жидкостей.
Примером критерия подобия является рассмотренный ранее
(стр. 143) критерий Re. Если в двух трубопроводах критерии Re
равны, то движение жидкости в этих трубопроводах подобно.
Отсюда следует, что подобие движения жидкости может соблю-
даться в трубопроводах разных диаметров при течении в-них
разных жидкостей с различными скоростями, если только крите-
рии Re в этих'трубопроводах равны.
Движение жидкостей в двух трубопроводах будет поДобно в
том случае, если в подобных потоках будут постоянны отноше-
ния действующих в них сил. В потоке жидкости каждая частица
находится под воздействием сил давления, тяжести и трения.
Кроме того, в движущейся жидкости возникает сила инерции,
равная по величине, но обратная по знаку равнодействующей
перечисленных выше сил. В свою очередь сила инерции равна
произведению массы частицы на ее ускорение,
10*
148
Гл 6 Основы гидравлики
Постоянное отношение каждой из действующих сил к силе
инерции (или обратное отношение) характеризуется крите-
риями подобия, в которые входят следующие физические вели-
чины: w— средняя скорость жидкости, I — основной (опреде-
ляющий) линейный размер канала, по которому движется жид-
кость (например, для трубы — ее диаметр), Др — потеря давле-
ния (см. стр. 160), р—плотность жидкости, ц— вязкость жид-
кости.
В табл. 5 приведены выражения критериев гидродинамиче-
ского подобия, которые в сходственных точках натуры и модели
должны иметь одно и то же числовое значение.
Таблица 5
Критерии подобия гидромеханических процессов
Критерий Выражение критерия Физическое значение критерия
Кинематический крите- рий (критерий Рей- нольдса) Re = -^ (6-42) И Характеризует действие сил трения в подобных потоках и опреде- ляет режим движения жидкости
Гравитационный крите- рий (критерий Фруда) Fr = -^- (6-43) Характеризует действие сил тяжести в подоб- ных потоках
Критерий гидравличе- ского сопротивления (критерий Эйлера) Ей = (6-44) pW2 ' Характеризует действие сил давления в подоб- ных потоках
Поскольку все критерии являются безразмерными величина-
ми, входящие в них физические величины можно выражать в
любой, но одинаковой системе единиц измерения. В системах
единиц СИ и МКГСС выражают w в м/сек, I в м, g в м/сек2,
а р, ц и Др соответственно в следующих размерностях:
си мкгсс
р...................... кг/м3 кгс • сек2/м*
[л........................ н • сек/м2 кгс • сек/м2
или
кг 1м •сек
Ьр..................... н/м2 кгс/м2
Критерии Re и Fr составлены ив величин, определяющих рас-
пределение скоростей в потоке (to, Z, р й ц), и поэтому являются
основными или определяющими критериями гидродинамического
подобия. Если эти критерии в натуре и в модели равны, то су-
7 Элементы теории подобия
149
ществует одинаковое соотношение между действующими в по-
токах силами, независимо от различия в натуре и в модели
любых физических величин, входящих в критерии подобия.
При равенстве критериев Re, а также критериев Fr равенство
критериев Ей получается само собой, так как перепад давления
является следствием распределения скоростей в потоке.
Основные критерии Re и Fr иногда заменяют более сложны-
ми критериями Галилея (Ga) и Архимеда (Аг), полученными
сочетанием основных критериев:
критерий Галилея
Ga = ^ = ^ = < (6-45)
критерий Архимеда
А[=Оа^^=г'3?(ур)=<-(6-46)
Р (Л2 V2 р v 7
где р и pi — плотность жидкости в двух различных точках.
В критерии Ga исключена скорость жидкости, поэтому им
удобно пользоваться в тех случаях, когда трудно определить
скорость потока. Критерий Аг характеризует подобие при дви-
жении жидкости вследствие разных плотностей в различных точ-
ках потока, т. е. в условиях естественной конвекции (стр. 364).
При моделировании исходят из равенства только тех крите-
риев, которые отражают влияние сил, имеющих наибольшее зна-
чение для данных условий. Так, при вынужденном движении
жидкости (например, при перекачивании ее насосом) влияние
сил тяжести ничтожно мало и равенством критериев Fr в этом
случае можно пренебречь.
Таким образом, при подобии вынужденного движения долж-
на существовать зависимость между критериями подобия, ко-
торая в общей форме выразится функцией
Eu=/(Re, Ifd) (6-47)
где l/d — постоянное отношение линейных размеров, характери-
зующее геометрическое подобие труб.
Вид этой функции может быть установлен только опытным
путем. Для этого зависимость (6-47) представляют в степенной
форме:
Eu = CRe« (//</)“ (6-48)
и определяют коэффициент С и показатели степени п и m из
опытов.
Полученная количественная зависимость между критериями
подобия будет верна не только для условий опыта, но и для
150
Г л. 6. Основы гидравлики
любых других жидкостей при любых других скоростях и диа-
метрах труб, но при тех же пределах значений Re, что и в про-
веденных опытах.
Основы теории подобия были разработаны известным рус-
ским ученым В. Л. Кирпичевым еще в 1874 г. Позднее его идеи
были развиты в трудах ряда ученых, в том числе В. Нуссельта,
М. В. Кирпичева, А. А. Гухмана, И. Бэкингема и др. Их работы
дали возможность плодотворно использовать теорию подобия в
самых разнообразных отраслях техники.
По выражению М. В. Кирпичева теория подобия «стала
основой эксперимента; она осуществляет синтез теории и опыта».
ч
Физический смысл критериев гидродинамического
подобия
Поясним физический смысл рассмотренных выше гидродинамических кри-
териев подобия Re, Fr и Ей.
Пусть на элементарный объем жидкости в виде куба со стороной 1\ в
трубе / (см. рис. 6-12) действуют сила давления Pi, сила тяжести G] и сила
трения Ti (вдоль граней).
При рассмотрении подобия явлений имеют значение не абсолютные ве-
личины сил, а их соотношения. Поэтому в дальнейшем можно рассматривать
зависимость не между силами, а между пропорциональными им величинами.
Сила давления, действующая на противоположные грани выделенного эле-
ментарного объема жидкости, равна разности давлений pi — р? на эти грани,
умноженной на поверхность грани куба /f:
Л = (Л —Pz) 1\
Эта сила пропорциональна общему перепаду давления Др1 в трубе, а дли-
на стороны куба пропорциональна диаметру трубы di, который, как указыва-
лось, может быть принят в качестве основного (определяющего) линейного
размера.
Таким образом, силу давления можно выразить величиной, ей пропорцио-
нальной;
где знаком = обозначена пропорциональность величин.
Сила тяжести элементарного куба:
G] = pi£Z? или G^p^rf?
где Pi —плотность жидкости.
Сила внутреннего трения равна напряжению трения [см. формулу (6-8)],
умноженному на площадь трения Si:
О ,2 dWi
В данном случае Sj = /р а член можно заменить пропорциональ-
ной величиной -т2-, где — определяющая скорость, например средняя ско-
*i
рость во входном сечении трубы.
7. Элементы теории подобия
151
Тогда
2
1
т — I
Ti ~p.t -j- I
После сокращения и подстановки вместо 1\ определяющего размера d\
получим:
Л = |Л1 d'Wi
Сила инерции равна выделенной элементарной массе жидкости
m = pjZj (где pj—плотность жидкости), умноженной на ускорение. Ускорение
_ Z,
определяется приращением скорости w— — в единицу времени т, т. е.
Тогда сила инерции равна:
г • 13 Z i
/j = /ПЛ —PjZi
или
/2
т — 11 I2
Z.
Заменяя отношение — через иц и величину Zt через d1} представим силу
инерции пропорциональной величиной:
» Л = Р1®?^?
Очевидно, для модели (труба II, см. рис. 6-12) выражения соответствую-
щих сил будут:
^2 — ^^2^2 > ^2 — Р2^2« ^2 — ^2^2®2 и Л ~ P2W2^2
Теперь найдем постоянное отношение сил инерции к силам трения в по-
токе:
Л_ = = *MiPi =
Л н е
Легко видеть, что это безразмерное отношение представляет собой кри-
терий Рейнольдса.
Следовательно, режим движения в натуре и модели будет одинаков при
условии равенства критерия Рейнольдса в сходственных точках потоков:
Р1 __ W2^2P2 ,с .Q4
Отношение сил инерции к силам тяжести составит:
Л Pi^i
— —. —-— — ------ — Г Г ч
Gi Pi£rfi gdi
Постоянное и безразмерное отношение сил инерции к силам тяжести
представляет собой критерий Фруда. Таким образом, в сходственных точках
подобных потоков критерии Фруда равны:
2 9
^2
"gd^^'gd^
(6-50)
152
Гл. 6. Основы гидравлики
Отношение сил давления к силам инерции дает безразмерный комплекс
величин, носящий название критерия Эйлера:
Л Р1^1 Р1Ч
Для подобных потоков:
~ Д/>2
pH p2w|
(6-51) (
Таким образом, при наличии гидродинамического подобия определяющие
критерии Рейнольдса и Фруда должны иметь в сходственных точках подобных
потоков одинаковое числовое значение. В этом случае в натуре, и в модели
существует одно и то же соотношение между действующими в жидкости си-
лами, независимо от различия любых величин, входящих в критерий подобия.
Пример 6-8. Движение хлористого водорода в трубопроводе диамет-
ром 600 мм при 450° С изучается на модели (масштаб к натуре 1 : 10), через
которую продувается воздух при 20° С. Хлористый водород движется по тру-
бопроводу при помощи газодувки со скоростью 7 м!сек, плотность газа
Pi = 0,569 кг/м*, вязкость p-i = 0,0333-10~3 н> сек/м? (0,0333 спз). Определить:
1) условия гидродинамического подобия в трубопроводе и модели, 2) ско-
рость, с которой надо продувать воздух в модели для того, чтобы воспроиз-
вести в ней движение газа в трубопроводе.
Решение. В общем виде условие гидродинамического подобия выра-
жается уравнением (6-47). При вынужденном движении газа можно прене-
бречь влиянием сил тяжести на движение i аза и принять Eu = f(Re) (при гео-
метрическом подобии трубопровода и модели). Следовательно, чтобы газы в
трубопроводе и в модели двигались подобно, достаточно соблюдать условие
^етр. — Иемод.-
Обозначим соответствующие величины для трубопровода индексом 1 и
для модели — индексом 2, тогда условие гидродинамического подобия можно
написать так
1 1Р1 ^2^2р2
Р"1 ~~ р2
По заданию w = 7 Mjcen, d{ = 600 мм, d2 — ~ = 60 мм.
При 20° С плотность воздуха р2 = 1,2 кг)м\ вязкость воздуха fx2 =
= 0,018- 10-3 н-сек/м? (0,018 спз).
Из условия гидродинамического подобия следует, что необходимая ско-
рость воздуха в модели должна составлять:
w^iPi
w2 — —- —
Н
= 7-0,6-0,569 0,018 • 10~~3 _
rf2P2 О.ОЗЗЗ-Ю"3’ 0,06-1,2 ~
17,9 м!сек
8. Движение жидкостей по трубопроводам
Потеря напора на трение
При движении реальной жидкости по трубе или каналу про-
исходит потеря напора, которая складывается из сопротивления
трения о стенки и местных сопротивлений, возникающих при из-
менении направления или скорости потока.
8. Движение жидкостей по трубопроводам
153
Потерю напора на трение можно определить, рассмотрев
установившееся равномерное и прямолинейное движение по тру-
бопроводу некоторого объема жидкости, ограниченного сечения-
ми I—I и II—II (рис. 6-13).
На выделенный объем жидкости действуют:
1) силы давления p\S и piS, где S — площадь поперечного
сечения трубопровода, причем результирующая сил давления
или движущая сила перемещения жидкости составляет: Др —
= (Pi —р2);
Рис. 6-13. К определению потери напора на трение
в трубопроводе.
2) сила веса G = 'pgSlt где р—плотность жидкости, g—
ускорение силы тяжести, / — длина трубопровода между сече-
ниями I — I и // — 1Г,
3) силы трения, равные тП/, где т—напряжение сил трения,
П/ — произведение периметра на длину трубы, т. е. боковая по-
верхность трубопровода.
При равномерном и прямолинейном движении действующие
на жидкость силы находятся в динамическом равновесии. По-
этому проекция сил на направление движения потока равна
нулю:
(Pi — Рг) — ?gSl sin а — О
где а — угол наклона трубы к горизонту, причем sin а выра-
жается отношением
sin а == —Zx
Подставив в выражение проекции сил значение sin а и раз-
делив обе части равенства на pgS, после несложных преобразо-
ваний получим:
(Piv \
\р£ V ' v ?£•$
154
Гл. 6. Основы гидравлики
Левая часть этого равенства, согласно уравнению Бернулли
(6-30), есть не что иное, как потерянный напор hn, если учесть,
что жидкость движется по трубопроводу с постоянной скоро-
стью, т. е. Wi = W2.
Следовательно
, _________________________тП/
Как известно [см. выражение (6-41)], — —^кв- (д?9кв. — эк-
вивалентный диаметр трубы). Таким образом
Вместе с тем потерянный напор может быть выражен также
в виде доли скоростного напора:
= (6-53)
где £ — коэффициент пропорциональности.
Приравняв выражения (6-52) и (6-53), получим
4т I _ r w2
Pg ' ^экв. ~ 2^
откуда
_________________________ С ^ЭКВ. Р^2
4 ' / * 2
Обозначив ^~-в- через А, представим выражение для <г в сле-
дующем виде:
X pw2
Подставив его в формулу (6-52), найдем окончательное вы-
ражение потери напора на трение (в м столба жидкости):
, ___. I W2
п "d^'Zg
(6-54)
Для круглой трубы эта формула принимает вид
= (6-55)
Из формулы (6-55) видно, что потеря напора на трение про-
i W2
порциональна длине трубы I и скоростному напору и обрат-
но пропорциональна диаметру трубы d.
8. Движение жидкостей по трубопроводам
155
Коэффициент пропорциональности X называется коэффи-
циентом гидравлического сопротивления, или коэффициентом
трения.
Коэффициент трения X является безразмерной величиной и
зависит от режима движения жидкости, а также от шероховато-
сти стенок трубопровода.
При ламинарном движении значение коэффициента трения
зависит только от величины критерия Re и определяется по фор-
муле:
64
~ Re
(6-56)
В условиях ламинарного режима сопротивление движению
обусловлено силами вязкости, которые пропорциональны ско-
рости потока в первой степени.
При турбулентном движении X становится функцией не только
критерия Re, но и шероховатости стенок трубы. Шероховатость
труб оценивают по величине относительной шероховатости е,
равной отношению средней высоты k выступов на внутрен-
ней поверхности трубы (k — абсолютная шероховатость) к диа-
метру d трубы
е = А (6-57)
Для турбулентного движения значение X может быть опреде-
лено по следующей формуле:
_1. = _2]аГ-2-4-^У’9]
/X ZJ4 3,7 Ч Re J J
(6-58)
При относительно невысоких значениях критерия Re (примерно до
Re= 105) шероховатость мало влияет на сопротивление и первым слагаемым
в квадратных скобках можно пренебречь.
Тогда формула (6-58) упрощается-
X- = — 21g = 1,81g Re —1,5
i/\ \ Re / s
(6-59)
Для больших значений критерия Re, когда влияние шероховатости труб
на сопротивление становится определяющим, коэффициент трения X пере-
стает зависеть от Re и формула (6-58) принимает вид
1 о 1 3,7
- — 2lg~
/X 6
(6-60)
156
Гл. 6. Основы гидравлики
Рис. 6-14. Зависимость к от критерия Re.
8.- Движение жидкостей по трубопроводам
157
Абсолютная шероховатость изменяется по поверхности тру-
бы, поэтому для определения е пользуются некоторой условной
однородной шероховатостью k, средние значения которой, опре-
деленные из опыта, приводятся ниже:
Трубы
k, мм
Стальные новые...................... 0,06—0,1
Стальные, бывшие в эксплуатации
(с незначительной коррозией) .... 0,1—0,2
Стальные и чугунные, старые, загряз-
ненные ............................ 0,5—2
Чугунные новые и керамические . . . 0,35—1
График для определения X по формуле (6-58) в зависимости
k
от Re при различных значениях е = -у приведен на рис. 6-14.
Местные сопротивления
Потеря напора вследствие изменения скорости потока по ве-
личине или направлению происходит в местных сопротивлениях,
к числу которых относятся: вход и выход потока из трубы, вне-
запные сужения и расширения труб, колена, отводы, тройники,
диафрагмы, запорные и регулирующие устройства (краны, вен-
тили, задвижки и т. п.).
Отношение потери напора в местном сопротивлении (Лп) к
/ \ •
скоростному напору в нем называется коэффициентом
местного сопротивления и обозначается через £м.с..
Соответственно потеря напора в местном сопротивлении, вы-
раженная в метрах столба протекающей жидкости, определяется
по формуле
Лп = См.с.^ (6-61)
Коэффициенты местных сопротивлений определяются в боль-
шинстве случаев опытным путем. При расчетах их можно прини-
мать приближенно по табл. 6.
Значения См. с. в расширениях и сужениях относятся к скоростному на-
пору в узком сечении, т. е. потеря напора определяется по формуле
Лп = ^м. с. » гДе w — скорость в узком сечении.
158
Гл. 6. Основы гидравлики
Таблица 6 Коэффициенты местных сопротивлений ?м.с.
Местные сопротивления Коэффициент местного сопротивления с
Вход в трубу
при острой входной кромке i 0,5
при острой входной кромке и выступе трубы внутрь сосуда 1,0
Выход из трубы в сосуд большого объема . . 1,0
Внезапное расширение (£раСш.) \2 1 ; см. рис. 6-15
Внезапное сужение (Ссж.) См. рис. 6-15
Плавное закругление (отвод) при угле а = 90° и /? :> 3d 0,14; см. рис. 6-16
Колено (без закругления), а = 90° 1,1—1,3
Кран
при угле открытия а = 30—40° 4—11
при полном открытии 0,2
Задвижка параллельная
при степени открытия * h/d = 0,5 2,8
при полном открытии 0,1
Вентиль
нормальный бочкообразный 4,5—5,5
с обтекаемым корпусом 2,5—3,5
прямоточный с наклонным шпинделем . . . 0,8—1,6
* Степень открытия задвижки характеризуется отношением высоты /г живого сечения
к диаметру d трубопровода
Коэффициенты сопротивления в тройниках (рис. 6-17) определяются в
зависимости от отношения расхода жидкости в ответвлении УОтв. к общему
расходу Уобщ. в основном трубопроводе (магистрали) и приведены в табл. 7
8. Движение жидкостей по трубопроводам
159
St/S2
Рис. 6-15. Коэффициенты местных
сопротивлений при внезапном рас-
ширении и сужении трубы.
Рис. 6-16. Отвод.
Значения См. с. Gm или ^отв.) относятся к скоростному напору в маги-
м
с- V
страли, т. е. потеря напора йП = См.
, где wM—скорость жидкости в ма-
гистрали, определяемая по суммарному расходу жидкости до ответвления
(при разделении потоков) или по суммарному расходу при слиянии потоков
в тройнике.
Таблица 7
Коэффициенты местных сопротивлений в тройниках
Местные сопротивления Отношение расходов VQTB :^общ
0,0 0,2 0,4 0,6 0,8 1,0
Коэффициенты С
Втекание потока в магистраль (рис. 6-17, а) £отв. См —1,2 0,04 —0,4 0,17 0,08 0,30 0,47 0,41 0,72 1,51 0,01 0,60
Вытекание потока из магистрали (рис. 6-17, б) CqtB. 0,95 0,88 0,89 0,95 1,10 1,28
См 0,04 —0,08 —0,05 0,07 0,21 0,35
160
Гл. 6. Основы гидравлики
у
При определенном соотношении -««в тройнике коэффициент См. с. мо-
V общ.
Жет иметь отрицательное значение, так как при слиянии или разделении пото-
ков возможно всасывание жидкости и соответственно увеличение напора.
%отв
vo5m
^отв ^отв
♦
6
Рис. 6-17. Тройники:
а —втекание потока в магистраль (собирающий тройник); <5 —вытекание
потока из магистрали (распределяющий тройник).
Полная потеря напора
Полная потеря напора, как указывалось выше, складывается
из потери напора на трение и суммы потерь на местные сопро-
тивления:
аг 1 1 । V г A z > V г \ ™2
7/11 = Х~d ' 2F + 2j^M-c- V M CT* жиДкости
(6-62)
Из уравнения (6-30) при движении жидкости по горизон-
тальному Трубопроводу (Z1 = Z2) с постоянной скоростью
(йУ1 — w2) следует:
Р^Р^Н
pg pg 1 п
причем в данном случае hn — Hn, т. е. общей потере напора в
трубопроводе. Следовательно
Н„ = Г’'~Г1
pg
«
Разность pi — р2 представляет собой потерю давления в тру-
бопроводе и обозначается через Др. Таким образом
= «„pg = (х 4 + 2 С„. е.) = С н!м? (6-63)
где С = х4 + а„.с,
8. Движение жидкостей по трубопроводам
161
Аналогично потеря давления в трубопроводе только от трения может
быть выражена уравнением:
=hn?g = )~ • н/м2 (6-64)
Выражение (6-63) может быть представлено в следующем виде:
Др С
pw2 2
Левая часть этого выражения есть не что иное, как критерий
р Др
Ей = ——.
pw2
Таким образом, коэффициент сопротивления представляет собой величи-
ну, пропорциональную критерию гидравлического сопротивления Ей. Соглас-
но теории подобия, критерий Ей является функцией критерия Re и для гео-
метрически подобных систем связан с Re степенной зависимостью Eu = CRe”.
Заменяя Ей через -% , получим следующее обобщенное выражение коэф-
фициента сопротивления:
С = С Re71
(6-65)
где С и п — величины, определяемые из опыта.
При ламинарном движении пластичных жидкостей потеря давления может
быть определена по формуле (обозначения см стр. 127):
л „ _ чо/ Мо । \
6d
Для пластичных жидкостей устойчивый ламинарный режим движения
наблюдается при Re 2000, переходный режим соответствует 2000 < Re <
< 3000, при Re >3000 наступает турбулентный режим течения.
Потери давления при турбулентном движении можно определить по урав-
нению (6-64), причем при определении коэффициента трения X могут быть
использованы уравнения для вязких жидкостей. Однако для суспензий необ-
ходимо вводить в расчет вязкость только жидкой фазы. Для псевдопластич-
ных жидкостей надежные методы расчета потери давления пока отсутствуют.
Пример 6-9. По прямой трубе диаметром d = 50 мм движется жидкость
в количестве V — 7 м3/ч, потеря давления составляет 19 600 н/м2 (2000 кгс/м2).
Как изменится потеря давления в трубе, если расход жидкости V станет
равным 14 м3/ч, а диаметр трубы d будет увеличен до 100 мм?
Решение. Подставляя в уравнение (6-64) значение скорости из урав-
нения расхода w — AV/nd2, получим:
8 V2
. „ 1, сек.
Др = —5- II р.
те2 d5 г
Из этого уравнения видно, что при X == const потеря давления в прямой
трубе (на преодоление трения) прямо пропорциональна расходу жидкости'во
второй степени и обратно пропорциональна диаметру трубы в пятой степени.
Следовательно, при увеличении расхода жидкости V до 14 м3/ч, т. е. вдвое,
потеря давления увеличится в четыре раза:
Др = 19 600 • 4 ==• 78 400 н!м2 (8000 кгс/м2)
При увеличении диаметра трубы вдвое (от 50 до 100 мм) потеря напора
уменьшится в 25 раза:
Др = = 612,5 н!м2 (62,5 кгс!м2)
м2
П Зак 546.
162
Гл. 6. Основы гидравлики
Пример 6-10. Насос подает 19 500 кг[ч 98%-ной серной кислоты (плот-
ность р = 1830 кг[м?, вязкость р. — 0,035 Н'сек[м?, или 35 спз) со* скоростью
w = 1,5 м)сек в реактор, избыточное давление в котором составляет 0,687 бар
(0,7 ат). На всасывающей линии насоса имеется один вентиль, на нагнета-
тельной — два колена под углом 90° и вентиль. Длина всасывающего трубо-
провода Zi = 2 м, длина нагнетательного трубопровода h = 20 м. Высота
подъема жидкости Н = 7 м. Определить потерю давления во всасывающем и
нагнетательном трубопроводах и работу, потребляемую насосом.
Решение. Для заданных расхода и скорости кислоты требуется диа-
метр трубопровода d = 50 мм. Соответственно критерий Рейнольдса в этих
условиях составит Re = 3920. Следовательно, режим движения кислоты тур-
булентный.
С учетом коррозии труб при перекачивании кислоты принимаем их абсо-
лютную шероховатость равной k = 1 мм и определяем коэффициент трения X
по формуле (6-58):
Л_ = _ 2 Iff Г—1— 4- (Н
/Г g L 3,7• 50 3920 ) J
X = 0,059
По данным табл. 6 найдем сумму коэффициентов местных сопротивле-
ний:
S Д с. — £вх. 2СК0Л. -}- 2Свент. + £вых.
2 См.с. = 0,5+ 2 -1,3 Н- 2 - 5,5 4-1 = 15,1
Гидравлическое сопротивление всасывающего и нагнетательного трубо-
проводов определяем по формуле (6-63):
= (0,059 • + 15,1) -~’52 21830 = 879 н/м* (8620 кгс/м*)
где / = /j + /2 = 2 + 20 — 22 м.
Соответственно потеря напора во всасывающем и нагнетательном трубо-
проводах составит:
Лп рg ~ 1830 • 9,81 “ 0,049 М
Удельная работа, потребляемая насосом, может быть определена по урав-
нению (6-37). В данном случае Z\ = 0, wi = 0 и Z2 = Н =г 7 м, если выбрать
плоскость сравнения и точку 1 на уровне жидкости в нижнем (приемном)
резервуаре (см. рис. 7-3, а, стр. 188), а точку 2 — в месте подачи кислоты в
реактор. Тогда согласно уравнению (6-37) удельная работа равна:
О 6R7.105 1 ^2
9,81 • 7 + —т-бЪп + -Д- + 9,81 • 0,049 = 107,8 дж!кг
louU 2
Работа, потребляемая насосом за 1 ч-.
£ = 19 500 • 107,8 = 21 • 105 дж[ч
8. Движение жидкостей по трубопроводам
163
Мощность насоса:
ЛГ -21 • Ю5
3600 • 1000
= 0,58 квт
В приведенном расчете не учитываются потери энергии в насосе. Эти
потери рассматриваются в главе 7.
Истечение через трубопровод
которой
предста-
на
части,
простой
через
в котором под-
Рис. 6-18. Истечение через простой тру-
бопровод.
Рассмотрим движение жидкости через простой трубопровод,
т. е. трубу постоянного сечения без ответвлений,
имеются арматура (вентили, краны) и фасонные
вляющие собой местные сопротивления.
На рис. 6-18 показано истечение жидкости
трубопровод диаметром d и длиной L из сосуда,
держивается постоянный
• уровень Н. Определим рас-
ход жидкости через указан-
ный трубопровод. Выбрав
за плоскость сравнения ось
трубы, составим уравнение
Бернулли относительно то-
чек 1 и 2: +
+ ?g 2g ' п
где ра — атмосферное дав-
ление.
Подставляя вместо пП величину и произведя сокраще-
ния, получим следующее значение скорости истечения:
w —
2gH
1 + SC
м[сек
(6-66)
Объемный расход жидкости, или максимальная
способность трубопровода, по уравнению (6-16):
,, с -.Г 2gH 3/
V = wS = —г—1/ лг/сек
ъ г 1 -j- 24
пропускная
(6-67)
Трудность определения V состоит в том, что зависит от
коэффициента трения X, который в свою очередь является
функцией критерия Re. Определить же критерий Re можно толь-
ко, зная расход жидкости, который является искомой величиной.
Поэтому уравнение приходится решать подбором: принимают
значение скорости w и по ней определяют V, после чего находят
11*
164
Гл 6. Основы гидравлики
потерю напора, которая не должна превышать некоторой задан-
ной величины. Если принятая скорость слишком велика, произ-
водят пересчет до получения удовлетворительного совпадения.
Если поверхность жидкости в резервуаре оказывается под
давлением, создаваемым насосом или сжатым воздухом, то на-
пор Н в уравнении (6-67) определяется как сумма высоты стол-
ба жидкости в резервуаре и создаваемого давления, выражен-
ного в метрах столба жидкости.
9. Истечение жидкостей через отверстия
и водосливы
Истечение через отверстие при постоянном
уровне
Пусть жидкость вытекает при Н — const (рис. 6-19, а) через,
отверстие в днище сосуда. Составим уравнение Бернулли для
идеальной жидкости относительно сечений I—I и II—II, причем
сечение II—II примем за плоскость сравнения.
Рис. 6-19. Истечение через отверстие при
постоянном уровне жидкости в сосуде:
а —через отверстие в днище; б—через отверстие
в боковой стенке.
В сечении I—I геометрический напор zx = Н, а в сечении
II—II напор г2 = 0. Сосуд открыт, истечение через отверстие
происходит в пространство с атмосферным давлением; следова-
тельно, pi = р2. Скоростью в поперечном сечении сосуда, по
сравнению со скоростью в отверстии, можно пренебречь, т. е.
принять Wi = 0. Сделав соответствующие подстановки и сокра-
щения в уравнении (6-28), получим:
W2
2^
9. Истечение жидкостей через отверстия и водосливы
165
Следовательно, весь напор Н расходуется на создание скоро-
сти и, таким образом, теоретическая скорость истечения соста-
вляет:
<W,I = 'W2=i Vigfj (6-68)
При расчете истечения реальной жидкости надо учитывать
сжатие струи на выходе из отверстия и потерю напора.
Отношение площади сечения струи в месте наибольшего сжа-
тия $сж. к сечению s отверстия называется коэффициентом сжа-
тия струи:
6 = -^- (6-69)
Коэффициент сжатия е определяется опытным путем.
При истечении реальной жидкости должна быть учтена поте-
ря напора в местном сопротивлении — на входе в отверстие
/ w2 \
yha = (.-2^тогда уравнение Бернулли для сечений I—I нН—II
примет вид
1 ' ?£ ' 2g 2 ' pg ' 2g ' 4 2g
(6-70)
Считая a'i = 0, Zi = Я и 22 = 0, получим из этого уравнения
следующее выражение скорости истечения:
®=®’’=7ж/' 2g("+£Vi) (6'71)
Если же pi = Ра, выражение скорости истечения упрощается:
w = yf^V2gH (6-72)
Величина
1
П+С
называется коэффициентом скорости и
обозначается через <р. Коэффициент <р представляет собой отно-
шение действительной скорости истечения к теоретической; зна-
чение его определяется по опытным данным.
Таким образом, скорость истечения реальной жидкости:
w = ? y^gH
(6-73)
Зная скорость истечения, можно определить расход жидкости
через отверстие:
166
Гл. 6. Основы гидравлики
После подстановки в уравнение расхода значений sc*. и w из
формул (6-69) и (6-73) получим:
У= ecps /2g77 (6-74)
Произведение коэффициента сжатия струи е на коэффициент
скорости ф называется коэффициентом расхода и обозначается
через а. Следовательно
а = еср (6-75)
и уравнение расхода через отверстие получает следующий окон-
чательный вид:
Y=zsV2gH (6-76)
При истечении через отверстие в боковой стенке (см.
рис. 6-19, б) напор не будет одинаковым для всех точек по сече-
нию отверстия и уравнения (6-71) и (6-72), строго говоря, будут
применимы только для элемента сечения, высотой dH. В этом
случае расход жидкости может быть точно определен только пу-
тем суммирования, т. е. интегрирования элементарных расходов
по всему сечению отверстия. Однако в технических расчетах для
отверстия в тонкой боковой стенке можно с достаточной точно-
стью пользоваться теми же расчетными уравнениями, что и для
отверстия в дне сосуда. Лишь для отверстий больших размеров
следует учитывать изменения коэффициентов расхода, значения
которых приводятся в справочниках.
При истечении жидкости через короткий цилиндрический
патрубок (насадок) происходит дополнительная потеря энергии,
главным образом вследствие внезапного расширения струи в
патрубке. Поэтому скорость истечения жидкости через патрубок
меньше скорости ее истечения через отверстие в тонкой стенке.
Вместе с тем расход жидкости, вытекающий через патрубок,
больше, чем при истечении через отверстие,'так как струя в пат-
рубке сначала сжимается, а затем расширяется и вытекает, за-
полняя все его сечение. Поэтому коэффициент сжатия струи на
выходе из патрубка е = 1, что, согласно выражению (6-75), при-
водит к значительному возрастанию коэффициента расхода а и
соответственно к увеличению расхода жидкости.
Средние значения е, ф и а для различных случаев истечения
приведены в табл. 8.
Формулы (6-73) и (6-76) могут быть применены при расчете
истечения через отверстие в стенке, разделяющей два сосуда,
причем в данном случае Н представляет собой разность постоян-
ных уровней жидкости в сосудах^
9. Истечение жидкостей через отверстия и водосливы
167
Средние значения коэффициентов е, ? и а
Таблица 8
Вид истечения е <Р а
Через отверстие в тонкой стенке . . Через короткий цилиндрический па- 0,64 0,97 0,62
трубок Через короткий цилиндрический патрубок с хорошо закруглен- 1 0,82 0,82
ными краями 1 0,97 0,97
Истечение через отверстие при переменном уровне
В этом случае истечения напор жидкости уменьшается во времени. Соот-
ветственно уменьшается скорость жидкости, и время истечения ее оказывает-
ся больше времени истечения такого же объема жидкости при Н — const.
Если по всей высоте сосуда площадь его поперечного сечения постоянна,
время истечения жидкости через выпускное отверстие сечением s от уровня
Н\ до Hi составит:
сек
При полном опорожнении сосуда формула упрощается, так как Н2 — 0.
Для горизонтального цилиндрического сосуда (цистерны) диаметром D и
длиной L время опорожнения от уровня Hi до Н2 выражается формулой:
г = [/(D-Я,)» -V(D-//,)» J сек (6-78)
oaS У 2g
Для заполненной до верха цистерны время полного опорожнения через
малое отверстие в нижней точке ее сечения определяется по формуле:
4LD VD
ЗавУъУ
сек
(6-79)
где s — площадь поперечного сечения выпускного отверстия; D и L — диа-
метр и длина цистерны.
Пример 6-11. Мерник диаметром D = 1,2 м и высотой Н = 2 м опорож-
няют через штуцер в боковой стенке. Диаметр штуцера d = 19 мм, ось его
находится на высоте h = 60 мм от днища мерника. Определить продолжи-
тельность полного истечения жидкости из мерника, если он сообщается с ат-
мосферой и начальная степень заполнения мерника Р — 0,85.
Решение. Начальная высота столба вытекающей жидкости в мернике
над осью штуцера:
Нх = 0,85// — h == 0,85 • 2 — 0,06 = 1,64 м
При истечении через патрубок сжатие струи происходит внутри патрубка,
а его выходное сечение целиком заполнено жидкостью. Поэтому по табл, 8:
а = гср = 1 • 0,82 = 0,82
168
Гл. 6. Основы гидравлики
Площадь сечения мерника:
S = Д- = 0,785 • 1,22 = 1>13 М2
4
Площадь сечения штуцера:
$ = 2^1 = 0,785 • 0,0192 = 2,83-10"4 ж2
4
Продолжительность полного опорожнения мерника по формуле (6-77):
2.1ДЗ/Г64
т ........... д—rs==- = 2820 сек о* 47 мин
0,82-2,83.10"4/2-9,81
Истечение через водосливы
Водослив представляет собой поперечную стенку, имеющую
вырез прямоугольной (рис. 6-20, а) или треугольной формы
(рис. 6-20,6), через верхнее ребро которого, называемое греб-
нем, или порогом, переливается жидкость.
Рис. 6-20. Истечение через водосливы:
а — прямоугольный водослив; б—треугольный водослив.
Различают водосливы: с боковым сжатием, если ширина во-
дослива b меньше ширины канала В (рис. 6-20, а), и без боко-
вого сжатия, если 5 «= В. Водосливы называют не затопленными,
если Нп > h (рис. 6-20, а), и затопленными, если НП < h, где
h — уровень жидкости за водосливом, На — высота порога. Рас-
ход жидкости через прямоугольный водослив без бокового сжа-
тия определяется из формулы:
mb У2g Н*2 м3[сек
где tn— коэффициент расхода (может быть принят равным 0,63).
Тогда расход жидкости через водослив составит:
V= 0,42b ]/2g Н*/г м3/сек (6-80)
Для измерения относительно небольших расходов жидкости
часто применяют треугольные водосливы (рис. 6-20,6). Расход
10. Пленочное течение жидкостей
169
К'!..-'
жидкости через такой водослив (без бокового сжатия) соста-
вляет:
V— 0,32 ctg ₽ V2g м3/сек (6-81)
В большинстве случаев в треугольных водосливах угол
3 — 45°, при этом формула (6-81) упрощается:
V=l,4/f2,5 м3/сек (6-82)
Пример 6-12. Определить расход жидкости через борт тарелки баро-
метрического конденсатора (см. рис. 13-19, стр. 507), если ширина тарелки
Ъ = 850 мм, а напор жидкости над бортом тарелки И — 40 мм.
Решение. Рассматриваем борт тарелки как прямоугольный водослив
без бокового сжатия, так как ширина тарелки незначительно превосходит ши-
рину ее борта.
По формуле (6-80)
V = 0,42 0,85 V2 • 9,81 • 0,04^ = 0,0127 м*[сек = 45,6 м*1ч
10. Пленочное течение жидкостей
В ряде процессов химической технологии (ректификация, аб-
сорбция, тепловые и химические процессы) применяются аппа-
раты, в которых жидкость движется по поверхности в виде тон-
ких пленок, причем скорость процесса зависит от толщины плен-
ки и скорости ее течения.
Характер движения пленки определяется по величине крите-
рия Рейнольдса
ПА ^^ЭКВ.Р
пл- |Л
где w — скорость движения пленки;
d3K3. — эквивалентный диаметр пленки.
Если П — периметр поверхности, по которой движется плен-
ка, и 8 — толщина пленки, то площадь сечения пленки S = П8 и
эквивалентный диаметр пленки составляет:
d3KB. — “рр — pj~~ — 48 (6-83)
Подставляя значение rf9KB. в выражение RenJb, получим:
Измерить толщину и скорость движения пленки трудно, по-
этому обычно определяют количество жидкости, проходящее в
единицу времени через единицу длины периметра поверхности,
170
Гл. 6. Основы гидравлики
по которой течет пленка, или так называемую линейную плот-
ность орошения:
Г = - = w&p кг/м • сек (6-84)
где Q = wSp = wI15p— расход жидкости, кг/сек.
Критерий Кепл. выражается через линейную плотность оро-
шения следующим образом:
4Г
= v (6-85)
Г
Толщина пленки при стекании жидкости по вертикальной стенке
8 = (6-86)
Скорость стекания пленки по вертикальной стенке при равномерном сма-
чивании орошаемой поверхности
Г 3/"iV
w = -г— = 1/ м[сек (6-87)
ор г Зр.р ' ’
где g — ускорение силы тяжести, л/сек2;
р. — вязкость жидкости, н • сек/м2:
р — плотность жидкости, кг[м3.
При течении пленки жидкости по наружной поверхности горизонтальной
трубы длиной I м пользуются уравнением (6-85), определяя линейную плот-
ность орошения по формуле:
Г = кг]м • сек (6-88)
Цифра 2, введенная в знаменатель формулы (6-88), учитывает растека-
ние жидкости в обе стороны.
Пример 6-13. Определить критерий Рейнольдса, а также толщину и
скорость стекания водяной пленки по внутренней поверхности вертикальной
трубы диаметром d = 50 мм при расходе воды через трубу G — 400 кг/ч
(плотность воды р = 1000 кг)м\ вязкость [л == 0,85 • 10~3 н • сек/м2, или 0,85 спз).
Решение. Периметр трубы П = nd, поэтому линейная плотность оро-
шения равна:
Г = ае = 2550 кг/м • ч = 0,708 кг]м - сек
izd 3,14 • 0,05 ' '
Критерий Рейнольдса находим по формуле (6-85):
D 4 • 0,708 „ лп
Кепл =-----------ч — 3340
0,85 • 10-3
'ПЛ.
Толщина пленки вычисляется по формуле (6-86):
3 • 0,708 - 0,85 10~~3 „„ 10-з „
10и02-9,81 = °’57 ‘° *
11. Движение тел в Жидкости
171
Скорость стекания пленки определяем по формуле (6-87):
0,7082 • 9,81 . о. .
——:-------L-----= 1,24 м сек
3-0,85.10'3-1000
w =
Г
Это же значение w можно найти по формуле w = , что предлагается
проверить расчетом.
11. Движение тел в жидкости
Многие процессы химической технологии (отстаивание, пере-
мешивание жидкостей и др.) связаны с движением твердых ча-
стиц в жидкости или газе. В ряде процессов происходит движе-
ние жидких частиц (капель) в газе или жидкости, а также дви-
жение пузырьков газа в жидкости.
Движение твердого тела в среде жидкости или газа зависит
от сопротивления среды, которое направлено в сторону, обрат-
ную движению тела, и складывается из сопротивления сил тре-
ния и сил инерции.
а б
Рис. 6-21. Движение твердого тела
в жидкости:
а —ламинарный поток; б —турбулентный поток.
Сопротивление трения преобладает при небольших скоростях
и малых размерах движущихся частиц, а также при высокой
вязкости среды, т. е. в условиях ламинарного движения. В этом
случае поток плавно обтекает частицу (рис. 6-21, а) и вслед-
ствие трения скорость жидкости на поверхности частицы стано-
вится равной нулю (подобно тому, как при движении потока по
трубе скорость жидкости уменьшается до нуля у стенок трубы).
При турбулентном движении (рис. 6-21, б) под действием сил
инерции происходит отрыв струй от поверхности частицы,
172
Гл 6 Основы гидравлики
причем в пространстве за частицей возникают вихри. В области
вихрей создается разрежение, и при движении жидкости частица
должна преодолеть, кроме сил трения, разность давлений в ос-
новной массе жидкости и в зоне завихрений за частицей. При
турбулентном движении это сопротивление, обусловленное сила-
ми инерции, приобретает решающее значение.
Независимо от режима движения и формы твердого тела,
движущегося в жидкости, сила сопротивления R среды (в н)
может быть выражена в общем виде законом Ньютона:
(6-89)
где L — коэффициент сопротивления среды;
F—площадь проекции тела на плоскость, перпендикуляр-
ную к направлению его движения, ж2;
р — плотность среды, кг/м3-,
w — скорость, м/сек.
В случае движения шарообразных частиц закон сопротивле-
ния Ньютона выражается равенством:
(6-90)
где d — диаметр частицы.
В выражении (6-90) можно принять за коэффициент сопро-
тивления среды величину £у = ф. Тогда закон сопротивления
примет следующий вид:
(6-91)
откуда
(6'92)
Величина ф представляет собой критерий Ей и в соответствии
с общей зависимостью (6-47) является функцией критерия Re,
который в данном случае рассчитывается по диаметру d частицы
При движении шарообразных частиц зависимость коэффициента сопро-
тивления ф от критерия Рейнольдса Re может быть представлена следующими
уравнениями:
Характер движения Критерий
Рейнольдса
Ламинарный (уравнение Стокса) Re < 2
Промежуточный (уравнение Ал-
лена)........................ Re = 2-500
Турбулентный (уравнение Нью-
тона) ......................... Re > 500
= tyw2d2p
Коэффициент
сопротивления
_ 7,27
Reo.6
= 0,173
11 Движение тел в жидкости
173
Коэффициент сопротивления для частиц нешарообразной формы боль-
ше, чем для шарообразных, и зависит от критерия Re и коэффициента формы
(сферичности) Ф, который представляет собой отношение поверхности шара
/шар > имеющего такой же объем, что и частица неправильной формы, к дей-
ствительной поверхности f4 частицы
Ф = (6-93)
/ч
Ниже приведены значения коэффициента Ф для частиц различной формы
Форма частиц . . . Шар Куб Цилиндр Диск
(h = Юг) * (h = 0,1 г) *
Коэффициент Ф . . 1 0,806 0,69 0,32
* h — высота цилиндра (диска), г —радиус основания
Рассмотрим общий закон сопротивления на примере движе-
ния твердой частицы в неподвижной среде Пусть
массой m действует некоторая сила Р (рис 6-22)
В противоположную сторону действует сила сопро-
тивления среды Р. Поэтому уравнение движения
частицы имеет следующий вид:
Р — Р — та
где а — ускорение, с которым движется частица.
В исходный момент, когда скорость частицы
w — 0, сопротивление среды Р — 0 Однако как толь-
ко частица начинает двигаться, по мере нарастания
ее скорости увеличивается сила сопротивления сре-
ды и уменьшается ускорение а частицы Через ко-
роткий промежуток времени сила сопротивления
возрастает до величины Р = Р. За этот же период
ускорение уменьшается от ’ начальной величины
Р
а = ~ до а = 0 В момент, когда силы, действующие на частицу,
уравновешиваются, ускорение становится равным нулю, ско-
рость w частицы — постоянной, а движение ее — равномерным.
Эта постоянная скорость называется скоростью осаждения и
обозначается через Wq
Время, в течение которого частица достигает постоянной ско-
рости, теоретически равно бесконечности, так как возрастание
скорости при падении частицы все время замедляется; однако
практически скорость приближается к постоянной уже через ни-
чтожно малый промежуток времени (сотые доли секунды) после
начала падения.
Чтобы происходило осаждение твердых частиц, т е выделе-
ние их из жидкости или газа, действующая сила (сила тяжести,
на частицу
Рис 6-22
Действие сил
на твердую
частицу,
движущую-
ся в непо-
движной
среде.
174
Гл. 6. Основы гидравлики
центробежная сила и др.) должна быть равна или больше силы
сопротивления среды:
Р>$
Скорость осаждения может быть определена из уравнения
(6-91). Заменив в этом уравнении R на Р, найдем значения ско-
рости осаждения:
«в-94»
Коэффициент сопротивления ф зависит от критерия Re, в кото-
рыи входит искомая скорость осаждения w0^Re =—j* )’ °'
этому уравнение (6-94) решается только подбором; принимая
произвольно величину Re, определяют ф и находят по формуле
(6-94) величину w0, после чего рассчитывают действительное
значение Re. Расчет повторяют до совпадения расчетной вели-
чины Re с предварительно принятой.
Расчет упрощается, если исключить искомую скорость w0 из
выражения (6-91), умножив обе его части на Тогда, заменяя
Р-
R на Р, получим:
При падении частицы диаметром d под действием силы тя-
жести сила Р равна весу частицы в жидкости:
где g—ускорение силы тяжести, м/сек2.
Ртв. и Р — плотность частицы и среды, кг/м3.
Таким образом
фРе2 = 2rf3g(pTB,_-P)£. = "Аг
1 0|Л2 о
где Аг — критерий Архимеда (см. стр. 149).
Подставляя в это выражение значения ф по уравнениям Сток-
са, Аллена или Ньютона (стр. 172) и решая полученные урав-
нения относительно Re, найдем:
при Re < 2 или Аг <36 Re = 0,056 Аг (6-95)
при Re = 2-4-500 или Ar = 36^-83 • 103 Re = 0,152 Аг0-715 (6-96)
при Re > 500 или Ar>83-103 Re = 1,74 Аг0*5 (6-97)
12. Движение жидкостей через зернистый и пористый слои
175
Определив критерий Re по одной из приведенных формул (в
зависимости от величины Аг), легко найти скорость осаждения:
p Re
W°~ d?
(6-98)
В этой формуле w0 является скоростью осаждения единичной
частицы, при движении ее независимо от других частиц, в не-
ограниченном объеме (скорость свободного осаждения). Расчет
w0 при одновременном осаждении многих частиц приведен на
стр. 244.
Скорость осаждения нешарообразных частиц меньше, чем
шарообразных, и ее обычно определяют экспериментальным пу-
тем.
Если принять скорость осаждения шарообразных частиц с
гладкой поверхностью за w0, то для частиц другой (нешарооб-
разной) формы скорость осаждения приближенно можно счи-
тать равной 0,75 ау0-
При движении жидких капель в газе или жидкости, а также
пузырьков газа в жидкости уравнения для w0 усложняются
вследствие изменения формы капель или пузырьков при их дви-
жении.
Пример 6-14. Определить скорость осаждения твердых шарообразных
частиц суспензии, если диаметр частиц d — 25 мк, плотность ртв. = 2750 кг/м3.
Плотность жидкой фазы р = 1200 кг/м3, вязкость р = 2,4*10-3 н-сек/м2
(2,4 спз).
Решение. Определяем критерий Архимеда по формуле (6-46)
. (25 • 10”6)3 • 9,81 (2750 — 1200) 1200 _nn,Q7
(2,4-10-3)2 ’
В данном случае Аг < 36 (сМ. стр. 174), следовательно осаждение про-
исходит в области ламинарного движения.
' По формуле (6-95) определяем значение критерия Рейнольдса:
Re = 0,056 Аг = 0,056 • 0,0497 = 0,00278
Тогда скорость осаждения шарообразных твердых частиц по формуле
(6-98) составит:
Р Re = 2,4 • 10~? • 0,00278
dp “ 25•10-6• 1200
= 2,22-10-4 м/сек
или
w0 = 2,22 • 10~4 • 3600 = 0,8 м/ч
12. Движение жидкостей через зернистый и пористый слои
В химической технологии широко применяются аппараты, в
которых жидкость протекает через слой сыпучего материала (в
виде шариков, колец, кусков, зерен). Этот случай можно рас-
176
Г л. 6. Основы гидравлики
сматривать как течение через пористую среду, в которой жид-
кость движется по каналам (порам) между отдельными части-
цами сыпучего материала.
Основными характеристиками рассматриваемых слоев тако-
го материала являются удельная поверхность и свободный
объем (пористость). Удельной поверхностью называется поверх-
ность частиц материала, приходящаяся на единицу объема, за-
нятого слоем. Свободным объемом называют отношение пустого
пространства между частицами к объему, занятому слоем.
Чтобы определить сопротивление слоя (потерю давления),
можно воспользоваться уравнением (6-64), однако его непосред-
ственное применение затруднительно, так как скорость жидко-
сти в каналах w и их эквивалентный диаметр d3KB. трудно опре-
делимы. Поэтому в расчеты вводят фиктивную скорость w0,
т. е. скорость, отнесенную ко всему сечению аппарата.
Если поперечное сечение аппарата обозначить через S (в м2),
а высоту слоя через Н (в ж), то объем слоя будет SH, а объем
каналов SHe, где е — свободный объем. Примем, что длина ка-
налов I равна высоте слоя Н, тогда суммарное сечение каналов
SHs. с „
составит —pf- ~ Se. Произведение этого сечения на скорость w
в каналах равно объемному расходу, который в свою очередь
равен Sw0. Таким образом, Sew = Sw0, откуда скорость в ка-
налах составит:
w = (6-99)
Эту скорость w называют действительной скоростью (в отли-
чие от фиктивной), хотя такое название не точно, поскольку
фактическая длина каналов I больше высоты Н, а сечение кана-
ла меньше Se.
Общая поверхность каналов равна SHf, где f — удельная по-
верхность (в ж2/ж3). Разделив эту величину на принятую длину
каналов Н, получим их периметр Sf. Сечение каналов равно Se,
следовательно по формуле (6-41) эквивалентный диаметр кана-
лов составит:
4-
^экв. (6-100)
Подставляя значения w и d3KB. в формулу (6-40), получим
следующее выражение для критерия Рейнольдса при движении
жидкости через пористый слой:
_ wd3KB.P __ 4woP _ 4UZ ,
К Н- — fy. — /(х
где W — массовая скорость, отнесенная ко всему сечению аппа-
рата, кг[м2 • сек,
12. Движение жидкостей через зернистый и пористый слои
177
Подставляя значения w и с/экв. в уравнение (6-64), найдем
потерю давления в слое
= (6-102)
Значения X формулам: при течении через слои МОЖНО __ 220 Re __ п,б Re0'25 = 1,26 определить по (6-103) (6-104) (6-105)
при при при Re < Re = Re> 50 x
50 -и 7200 X
7200 X:
Объем частиц в 1 м3 слоя, очевидно, равен 1 —a, a объем час их поверхность f.
Если в 1 м3 «слоя имеется а ее поверхность составит m частиц, то средний 1 £ r.d3 4 m 6 f — f - ™d2 ,'4 m Ф :тицы будет равен:
где d — диаметр шара, имеющего такой же объем, что и частица;
Ф—коэффициент формы (стр. 173).
Разделив f4 на уч, получим:
А_ f _ 6
V4 1 — е Фс?
откуда
х . 6(1 — 8)
Подставляя это значение f в уравнения (6-101) и (6-102), получим:
= <6-106)
В этих уравнениях потеря давления и критерий Рейнольдса выражены
через диаметр частицы d и фиктивную скорость w0, причем величина Re0,
называемая модифицированным критерием Рейнольдса, равна:
w0 do
Re0 = - “ (6-108)
Iх
Приведенные выше уравнения применимы к фильтрованию
через пористую среду, широко используемому для разделения
жидких неоднородных систем (стр. 252). При фильтровании
движение жидкости обычно ламинарное, т. е. для этого процесса
178
Гл. 6. Основы гидравлики
применимо уравнение (6-103). Подставляя значения Л из этого
уравнения в уравнение (6-106) и заменяя Re по уравнению
(6-107), получим:
Др = 248
Г а2Ф2£3
Отсюда скорость жидкости при фильтровании составит:
Дрс?2Ф2е3 ,
W° ~ 248(1 —е)2 М!сек
Если площадь фильтра (поверхность фильтрования) равна
F м2, то количество жидкости V м3, проходящей через фильтр
за время т сек, составляет:
т/ г л г ^2ф2г3
И— w0A — IS.pF'z 248
или _____________
(б.1О9)
где
г, _ 248 (1 — е)2 pH
~ с?2Ф2е3
(R — сопротивление фильтрованию, н • се/фи3).
Из уравнения (6-109) видно, что скорость фильтрования
прямо пропорциональна движущей силе процесса, т. е. перепаду
давления на фильтре Др, и обратно пропорциональна сопротив-
лению фильтрования R. Сопротивление фильтрованию зависит
от свойств пористой среды (диаметр частиц d, коэффициент фор-
мы Ф, пористость s) и прямо пропорционально вязкости жидко-
сти ц и толщине пористого слоя Н.
Пример 6-15. Определить сопротивление слоя катализатора высотой
Н = 1,7 м в аппарате диаметром D = 2,5 м. Количество проходящего через
аппарат газа V — 8500 м3/ч, плотность газа р = 0,45 кг/м3, вязкость газа
р. = 0,294 • 10~4 Н’Сек!м2 (0,0294 спз). Удельная поверхность катализатора
f = 415 ju2/ju3, свободный объем £ = 0,43, число частиц катализатора в 1 м3
слоя tn = 106. Найти также коэффициент формы частиц катализатора и экви-
валентный диаметр каналов в его слое.
Решение. Площадь поперечного сечения аппарата S = 0,785 D2 =
= 0,785 • 2,52 = 4,9 м2. Фиктивная скорость газа в аппарате составляет:
V 8500 Л .оп . п
W° = 3600S “ 3600 • 4,9 “ °’482 М!
Критерий Рейнольдса вычисляем по формуле (6-101):
= _71
415.0,294- Ю-4
/5. Гидравлика кипящего (псевдоожиженного) слоя
170
В соответствии с значением Re коэффициент сопротивления определяем
по формуле (6-104):
, П.6 л
710,25
Сопротивление слоя катализатора находим по формуле (6-102):
. 4 • 1,7 • 415 • 0,45 • 0.4822 .ДЛ , „ ,
Др =---------г оз----------= 460 н!м2 (47 кгс/м2)
8 • 0,433
Эквивалентный диаметр каналов рассчитываем по формуле (6-100):
rf9KB = 4'?^3- = 0,00414 м
Для определения коэффициента формы Ф частиц найдем сначала диа
метр шара d, имеющего такой же объем, что и частица. Расчет ведем по
1 — nd3
уравнению———=—g— (стр. 177):
d = = 1Г =0.0103 ж
г кт т 3,14-106
0 __
Коэффициент формы находим посредством уравнения /=—v
(стр. 177), откуда
Ф= 6(1-0 _ 6(1—0,43)
fd ~ 415-0,0103 '
Предлагается далее вычислить по формулам (6-107) и (6-108) модифици-
рованный критерий Рейнольдса (Re0^76).
13. Гидравлика кипящего
(псевдоожиженного) слоя
За последние годы все большее распространение в химической
технологии получают так называемые процессы в кипящем слое.
При проведении таких процессов мелкораздробленные твердые
частицы находятся в восходящем потоке газа как бы в кипящем,
или псевдоожиженном, состоянии. Многие процессы (горение,
теплообмен, сушка, адсорбция), протекающие с участием твер-
дой фазы в псевдоожиженном состоянии, сильно ускоряются.
При небольшой скорости газа слой твердых частиц, через ко-
торый проходит газ, неподвижен (рис. 6-23, а) и движение газа
характеризуется закономерностями, рассмотренными в предыду-
щем, 12 разделе данной главы. С увеличением скорости газа
высота слоя твердых частиц начинает возрастать, и когда ско-
рость газа достигает критической величины, при которой сопро-
тивление слоя становится равным его весу, слой твердых частиц
приобретает текучесть и переходит в псевдоожиженное состоя-
12*
180
Гл. 6. Основы гидравлики
ние. При этом твердые частицы интенсивно движутся в потоке
газа и весь слой движущихся частиц напоминает кипящую жид-
кость, отделенную резко выраженной поверхностью от газа, про-
шедшего кипящий слой (рис. 6-23,6). В случае увеличения ско-
а б
Рис. 6-23. Движение газа в слое твердых частиц:
а —неподвижный слой; б—кипящий (псевдоожиженный) слой; в —унос твер-
дых частиц газом.
рости газа до некоторой новой критической величины, когда си-
ла гидравлического сопротивления частицы становится равной
уноситься потоком газа
(рис. 6-23, в). Это ис-
пользуется для пневмати-
ческого транспорта сыпу-
чих материалов (стр. 39).
Аналогичные явления на-
блюдаются и в том слу-
чае, если слой твердых
частиц находится'в пото-
ке капельной жидкости и
последовательно происхо-
дят описанные выше из-
менения скорости движе-
ния этбй жидкости.
На рис. 6-24 показано
ее весу, твердые частицы начинают
Рис. 6-24. Зависимость сопротивления слоя
твердых частиц от фиктивной скорости
газа.
изменение сопротивления слоя твердых частиц в зависимости
от скорости потока Wq. В области, характеризуемой неподвиж-
ным слоем (участок АВ), сопротивление слоя изменяется в соот-
ветствии с уравнением (6-106). Участок ВС соответствует кипя-
щему слою и характеризуется постоянным, не зависящим от
скорости сопротивлением. На участке CD, соответствующем
уносу частиц потоком, сопротивление снова возрастает с увели-
чением скорости.
13. ГиЗрабликй. кипящего (псевдоожиженного) слоя
181
Фиктивная скорость w'o, соответствующая переходу непо-
движного слоя в состояние псевдоожижения, называется скоро-
стью псевдоожижения, фиктивная скорость wo, соответствую-
щая началу уноса частиц, — скоростью уноса. Отношение рабо-
чей скорости Wo к скорости псевдоожижения
ф = (6-110)
w0
называется числом псевдоожижения и характеризует интенсив-
ность перемешивания частиц в
слое. Опытами установлено, что
шивание соответствует о = 2.
При дальнейшем возрастании
величины ю слой частиц ста-
новится неоднородным: проис-
ходит прорыв крупных пузы-
рей газа через слой (рис.
6-25, а) и начинается интенсив-
ное выбрасывание частиц над
поверхностью слоя. Пузыри
газа могут увеличиваться в
объеме и заполнять все сече-
ние аппарата. При этом кипя-
щий слой переходит в режим
так называемого поршневого
псевдоожижения (рис. 6-25,6);
слой разделяется на отдельные
части газовыми «пробками»,
кипящем (псевдоожиженном)
наиболее интенсивное переме-
Рис. 6-25. Неравномерное псевдоожи-
жение:
а—прорыв газовых пузырей; б— поршневсе
псевдоожижение.
часть слоя, находящаяся над
«пробкой», подбрасывается вверх, пузырь газа прорывается и
Происходит большой выброс твердых частиц. Развитию такого
процесса способствует увеличение размеров частиц, повышение
скорости газа и уменьшение диаметра аппарата. Режим порш-
невого псевдоожижения является нежелательным, так как при-
' водит к колебаниям сопротивления кипящего слоя и ухудше-
" Нию равномерности контакта между газом и твердыми части-
„цами.
? Сопротивление кипящего слоя равно весу твердых частиц в
.йслое Отв. н, деленному на площадь сечения аппарата S ж2.
fC)6beM, занимаемый слоем, равен SH, где Н — высота слоя в м.
} Если пористость (свободный объем) слоя равна е, то объем
/Жтвердых частиц в слое будет равен SH(]—s), а вес частиц с
да-учетом подъемной силы среды составит:
*04
°тв. = 5/7(1 ~ е) (Ртв< — р) g
Ж
182
Гл. 6. Основы гидравлики
где ртв. и р—плотность твердых частиц и среды, кг/м3',
g— ускорение силы тяжести, м/сек?.
Таким образом, сопротивление слоя можно выразить следую-
щей формулой:
= Н (Ртв. — р) g (1 — s) Н/м2
(6-111)
При увеличении фиктивной скорости w0 потока возрастают
как высота слоя Н, так и его пористость е. При этом (1 — е)
уменьшается, а произведение 77(1 —е) остается постоянным, по-
скольку сопротивление кипящего слоя не зависит от w0. Если
высота неподвижного слоя составляет Но, а его пористость ео, то
/7(1—е) =/7о(1—ео)- Отсюда пористость кипящего слоя воз-
можно представить следующим уравнением:
где К = jf-— отношение, показывающее, во сколько раз объем
кипящего слоя больше объема неподвижного слоя; К — назы-
вается коэффициентом расширения слоя.
Скорость псевдоожижения можно найти, приравняв сопротивление зер-
нистого слоя по формуле (6-106) к сопротивлению псевдоожиженного слоя по
формуле (6-111):
3 ^7/(1 — e0)p(wp)2
4 дГФе3
= 77(ртв. — р) g (1 — s0)
После преобразований получим:
> (₽<)’ = | Фе03 | Фе3 Аг
где Re0 — модифицированный критерий Рейнольдса, соответствующий скоро-
/
сти псевдоожижения ;
Аг — критерий Архимеда.
Подставляя в эту формулу значения X из уравнений (6-103), (6-104) или
(6-105) и решая полученные уравнения относительно Re0, найдем:
при Т Аг < 18500
ReJ = ----5°) (¥ Аг) (6-113)
при Аг = 18 500 -ь 1,1 • 108 Rep = °’2— (Т Аг)°<57 (6-114)
при Ф1 Аг > 1,1 • 108
ReJ = 1,03 (1ф (Ф Аг)0'5 (6-115)
где
Ф3е°
причем коэффициент Ф для частиц неправильной фор-
мы в среднем может быть принят 0,9.
13. Гидравлика кипящего (псевдоожиженного) слоя
183
Скорость уноса равна скорости осаждения и определяется по формулам,
приведенным на стр. 174.
Пористость слоя можно определить по приближенному уравнению:
/ 18Ren 4” 0,36Re« \0’21
•=(—~т,—-) (6-1I6)
Пример 6-16. Определить скорости псевдоожижения и уноса частиц диа-
метром а — 3,75 мм при следующих условиях: плотность твердых частиц
Ртв. = 1400 кг/м3; плотность газа р = 0,275 кг/м3; вязкость газа р- =
= 0,477-10~4 н-сек/м2 (0,0477 спз); пористость неподвижного слоя е0 = 0,4;
коэффициент формы Ф = 0,9.
Решение. По формуле (6-46) находим критерий Архимеда:
Аг _ 9>81 • 0.003753 • 0,275 (1400 — 0,275) = б(Ю
(0,477 10~4)2
откуда
Определяем величину Чг:
Ф3е« 0,93 • 0,43
Ф —_______--------------- = О 13
(1 —е0)2 (1-0,4)2 U’1J
Ф- Аг =0,13'87 600= 11 400
По формулам (6-113) и (6-97) находим:
Ке;=0Д040^^>11400 = 307
ReJ = 1,74 • 87 6ОО0,5 = 514
Отсюда скорость псевдоожижения составит:
, ReJ р 30,7 • 0,477 • 10~4
W°= dp = 0,00375-0,275 = 1,42 М,Сек
Скорость уноса будет равна:
„ Re"p 514-0,477. IO”4
Wo = dp = “0,00375 - 0,275 = 23,8 М,СвК
Пример 6-17. Для условий примера 6-16 определить сопротивление слоя
и коэффициент расширения, если высота неподвижного слоя Но = 0,4 м, а чис-
ло псевдоожижения «> = 2,75.
Решение. При « = 2,75 фиктивная скорость газа w0 = 2,75• 1,42 =
•= 3,9 м/сек, критерий Рейнольдса Reo = 2,75-30,7 = 84,5. По формуле (6-116)
_ / 18 • 84,5 + 0,36 • 84,52 \о,21
£ — | /?лл I —
87 600
Коэффициент расширения слоя находим по формуле (6-112):
К - - 1~~°’4 .....1 27
Л “ 1 —е “ 1 — 0,527 “ ’
Сопротивление слоя вычисляем по формуле (6-111):
Др = 0,4 (1400—0,275) 9,81 (1—0,4) = 3290 н/м2 (336 кгс/м2)
Глава 7
ПЕРЕМЕЩЕНИЕ ЖИДКОСТЕЙ И ГАЗОВ
1. Трубопроводы
Трубы и арматура
В химической промышленности применяются трубы: сталь-
ные (из углеродистых и легированных сталей), чугунные (из се-
рого чугуна и ферросилида), из цветных металлов (алюминия,
меди, свинца), керамические, из пластических масс (фаолита,
текстолита, винипласта, полиэтилена и др.), из стекла, а также
стальные с внутренним защитным покрытием (например, гум-
мированные).
Рис. 7-1. Способы соединения труб:
/ — фланцевое; б— сварное; в —на муфте. ►
Трубы соединяют посредством фланцев, сварки или на резьбе
при помощи муфт (рис. 7-1). Фланцы приваривают к трубе либо
надевают на резьбе. Фланцы чугунных труб отливаются заодно
с трубой. Трубы из хрупких материалов (ферросилид, керами-
ка), из цветных металлов и пластических масс изготовляют с
бортиками и соединяют на свободно вращающихся фланцах.
Плотность фланцевых соединений достигается посредством
прокладок, которые зажимаются между фланцами при помощи
болтов. При умеренных давлениях (в трубопроводах до ~40 ат)
прокладки изготовляют из мягких материалов — паронита, фиб-
ры, резины и др., при высоких давлениях — из металлов (мяг<
1. Трубопроводы
185
кой стали, меди, алюминия) или выполняют их в виде металли-
ческой оболочки с сердцевиной из мягкого материала.
Трубы соединяются на фланцах посредством разнообразных
фасонных частей (фитинги): колен, тройников, крестовин и др.
Для включения и выключения трубопроводов, а также регу-
лирования потока жидкости или газа на трубопроводах устана-
вливают арматуру: краны, вентили, задвижки.
Сальниковый кран (рис. 7-2, а) состоит из корпуса 1 и кони-
ческой пробки 3 со сквозным отверстием, притертой к гнезду
Рис. 7-2. Арматура трубопроводов:
а —сальниковый кран; б— нормальный вентиль; в —прямоточный вентиль; г —параллельная
задвижка, /—корпус; 2 —сальник; 3—коническая пробка; 4 — шпиндель; 5 —седло; 6— клапан;
7—параллельные диски; 8— клин.
корпуса и прижатой к нему сальником 2. В натяжных кранах
пробка прижимается к корпусу навертыванием гайки, что менее
надежно обеспечивает герметичность.
Краны имеют простое устройство, их можно быстро откры-
вать и закрывать; они отличаются также малым гидравлическим
сопротивлением. Недостатки кранов: возможность заедания или
прикипания пробки, нарушение герметичности (особенно при
движении по трубам жидкостей, содержащих взвеси), труд-
ность регулирования потока, так как сечение для прохода жид-
кости резко меняется при небольшом повороте пробки.
Краны изготовляют из чугуна, бронзы, керамики, пластмасс;
Их применяют на трубопроводах небольшого диаметра (до 50—
80 мм) при температуре до 100° С и давлении до 10 ат.
Значительно более герметичны в широких пределах давле-
ний и надежны в работе вентили и задвижки, отличающиеся,
кроме того, точностью регулирования потока.
186
Гл. 7. Перемещение жидкостей и газов
Нормальный вентиль (рис. 7-2, б) имеет бочкообразный кор-
пус 1, в котором перемещается на резьбе шпиндель 4\ к нижне-
му концу шпинделя крепится клапан 6. При закрывании вентиля
клапан плотно прижимается к седлу 5 корпуса.
Недостатки вентилей: более сложное устройство и больший,
чем для кранов, вес, непригодность при перемещении очень вяз-
ких жидкостей, большое гидравлическое сопротивление. Послед-
него недостатка лишены вентили с обтекаемой формой корпуса
и прямоточные вентили (рис. 7-2, в).
Диаметр прохода наиболее распространенных вентилей от
25 до 200 лш, они применяются при давлениях до 100 ат.
Параллельная задвижка (рис. 7-2, а) состоит из корпуса 7, в
котором перемещаются на шпинделе 4 параллельные диски 7,
между которыми имеется клин 8. При опускании дисков клин
прижимает их к уплотнительным поверхностям.
В клиновых задвижках на шпинделе вместо дисков переме-
щается двухсторонний клин.
Задвижки обладают малым гидравлическим сопротивлением,
легко открываются и закрываются, но громоздки. Диаметр про-
хода применяемых задвижек от 50 до 1000 мм при давлениях,
достигающих 100 ат.
Расчет трубопроводов
Диаметр трубопровода определяется по уравнению расхода
в объемных единицах:
V = 3600 Sw = 3600 w м3/ч (7-1)
или в единицах массы:
G = 3600 5дар = 3600 дар кг/ч (7-2)
где 5— площадь поперечного сечения трубопровода, м2-,
d — диаметр трубопровода, м;
w— скорость жидкости (газа), м/сек-,
р — плотность жидкости (газа), кг/м3.
Из формул (7-1) и (7-2) следует, что для определения диа-
метра трубопровода должен быть известен требуемый расход и
выбрана скорость движения жидкости или газа. С увеличением
скорости диаметр трубопровода, необходимый при данном рас-
ходе, уменьшается, но возрастает потеря давления и, следова-
тельно, расход энергии на перемещение жидкости (газа).
С уменьшением скорости расход энергии уменьшается, но увели-
чивается диаметр трубопровода и повышается его стоимость. Не-
которая оптимальная скорость соответствует минимуму эксплуа-
тационных расходов, т. е. сумме стоимости энергии, амортизации
2. Насосы и компрессорные машины
187
и ремонта. Однако определение оптимальной скорости сложно, и
обычно скорость выбирают по практическим данным (табл. 9).
Таблица 9
Скорости в трубопроводах
(ориентировочные данные)
Движущаяся среда Скорость, м/сек
Жидкости
При движении самотеком (конденсат и др.) 0,1—0,5
Вязкие (растворы солей и др.) 0,5—1
В трубопроводах насосов
всасывающих 0,8—2
нагнетательных ... 1,5—3
Газы
При естественной тяге 2—4
При небольшом давлении (в газоходах вентиляторов и др.1 4—15
При большом давлении (в нагнетательных трубопроводах
компрессоров) 15—25
Пары
Насыщенные при абсолютном давлении, ат
>1 15—25
1—0,5 20—40
0,5—0,2 40—60
0,2—0,05 60—75
Перегретые 30—50
Приняв скорость, определяют диаметр трубопровода по фор-
муле (7-1) или (7-2), после чего проверяют потери давления в
нем. Потери давления должны быть умеренными (ориентиро-
вочно 5—15% от давления нагнетания). Если эти потери чрез-
мерно велики, уменьшают скорость и производят соответ-
ствующий пересчет.
2. Насосы и компрессорные машины
(общие сведения)
Для перемещения капельных жидкостей служат насосы, для
перемещения и сжатия газов — компрессорные машины, или
просто компрессоры. Как насосы, так и компрессоры разде-
ляются на следующие основные типы: поршневые, центробеж-
ные, осевые, ротационные, струйные.
Поршневые насосы получили широкое распространение в
XIX в. G появлением быстроходных электродвигателей поршне-
188
Гл. 7. Перемещение жидкостей и газов
вне насосы стали вытесняться центробежными насосами, кон-
струкции которых достигли большого совершенства в течение по-
следних десятилетий.
В настоящее время отечественная промышленность выпускает
самые разнообразные гидравлические машины, в том числе про-
пеллерные насосы производительностью до 30 м,3!сек и более,
турбогазодувки производительностью до 4100 м31мин, компрес-
соры на давление до 1000 ат и многие другие машины.
3. Основные параметры насосов.
Высота всасывания
Основными параметрами, характеризующими работу любого
насоса, являются производительность, напор и мощность.
Производительность Q определяется объемом жидкости, по-
даваемой насосом в единицу времени, и выражается в м31сек,
м3!.мин, м3/ч, иногда в л/сек или л]мин.
Напор Н характеризует собой избыточную энергию I = gH
(сообщаемую 1 кг жидкости в насосе), которая определяется по
уравнению Бернулли (6-37).
Рис. 7-3. Схемы установки насосов:
а —всасывание с нижнего уровня; б— всасывание с подпором
на стороне всасывания. М — манометр; V — вакуумметр; Л —рас-
стояние между М и V по вертикали.
Из схемы насосной установки (рис. 7-3, а) видно, что гео-
метрическая высота подъема жидкости Нт (г2—Zi) составляет
7УГ =//вс,4-7/н (7-3)
Следовательно, геометрическая высота подъема жидкости
равна сумме высот всасывания и нагнетания. Соответственно
потеря напора складывается из потерь напора во всасывающем
и нагнетательном трубопроводах:
Ая = hBC% | ha
3. Основные параметры насосов. Высота всасывания
189
Разностью скоростных напоров в этих трубопроводах можно
пренебречь. Тогда, согласно уравнению (6-37), необходимый на-
пор насоса определится равенством
/7=/7г + ^|£!- + й.е. + Лн (7-4)
Следовательно, в общем случае напор затрачивается на
подъем жидкости на высоту Нг, преодоление сопротивлений в
трубопроводах Авс. -J- hH и разности давлений в напор-
ном и нижнем (приемном) резервуарах. Если давления в прием-
р2 — Pl г.
ном и напорном резервуарах равны, то р2 = Pi и —- г - = 0.
Насос может быть присоединен также ниже уровня жидкости в
нижнем резервуаре (рис. 7-3,6). В этом случае высота всасыва-
ния отрицательна (7/вс. < 0), так как насос работает с подпором
на стороне всасывания.
Напор выражают в метрах столба перекачиваемой жидкости.
В работающих насосах напор определяют по сумме показаний
манометра М и вакуумметра V, сложенной с расстоянием h по
вертикали между манометром и точкой присоединения вакуум-
метра (рис. 7-3, а).
Полезная мощность, передаваемая жидкости, равна энергии,
сообщаемой 1 кг жидкости (gH), умноженной на массовый рас-
ход жидкости Qp, где Q — объемная производительность на-
соса, м31сек-, р — плотность жидкости, кг/м3', g — ускорение силы
тяжести, м/сек2. Таким образом
М ~ QpgH Ml (7-5)
Мощность, потребляемая насосом, больше полезной мощно-
сти на величину потерь. Отношение полезной мощности насоса
к потребляемой называется полным коэффициентом полезного
действия (к. п.д.) насоса:
4 = ^- (7-6)
Отсюда потребляемая насосом мощность составляет:
7] 7]
ИЛИ
N=-T^Km (7-7)
190
Гл. 7. Перемещение жидкостей и газов
В системе МКГСС мощность, потребляемая насосом, определяется по
формуле;
кт <ЪН
N = ^7Kem
где y — удельный вес газа, кгс[м\
Полный к. п.д. является важной характеристикой насоса,
определяющей экономичность его работы. Полный к. п. д. пред-
ставляет собой произведение объемного к. п. д. (т]0), учитываю-
щего утечки жидкости через зазоры и сальники насоса, гидрав-
лического к. п. д. (т]г), учитывающего уменьшение напора
вследствие гидравлических сопротивлений, и механического
к. п. д. (^мех.)’ учитывающего потери на трение в насосе:
71 = 71о71г71мех. (7-8)
Величина зависит от конструкции и состояния насоса и для средних
условий колеблется в следующих пределах: т| поршневых насосов 0,7—0,9,
т| центробежных насосов 0,6—0,8. К- п. д. наиболее совершенных крупных
насосов достигает 0,93—0,95.
. Соглас-
затрачи-
Всасывание жидкости насосом происходит под действием
разности внешнего давления ро в приемном резервуаре и давле-
но Р\
ния pi на входе в насос или разности напоров —--—
Р S Р S
но уравнению Бернулли, разность напоров --------
вается на подъем жидкости на высоту всасывания f/Bc. (см.
рис. 7-3, а), на движение жидкости со скоростью w, т. е. создание
w2
скоростного напора и на преодоление гидравлических по-
терь во всасывающей трубе hBC_. Если жидкость засасывается из
открытого бака, то внешнее давление равно атмосферному
(р0 = Ра) и можно написать равенство:
Ра Pi — И I w2 I h
?g 9g ~ вс-^ 2g ' П'вс"
Чтобы происходило всасывание, давление pi должно быть
больше давления pt насыщенных паров жидкости при данной
температуре. Тогда с учетом приведенного выше равенства усло-
вие нормальной работы насоса выразится следующим образом:
откуда
н - Ра W2 U Я \
1 *вс. * Р£ \Р£ tg 1 /VBC. 1
(7-9)
(7-Ю)
4. Центробежные насосы
191
Из выражения (7-10) следует, что высота всасывания насоса
уменьшается со снижением барометрического давления ра и с
увеличением давления паров р(. Величина pt возрастает с по-
вышением температуры, поэтому при повышении температуры
жидкости допустимая высота всасывания уменьшается. Когда
давление pi становится равным р(, из жидкости начинают ин-
тенсивно выделяться пары и растворенные в ней газы. При этом
под действием противодавления р( паров и газов высота всасы-
вания снижается и может достигнуть нуля.
Высота всасывания уменьшается также при увеличении ско-
рости жидкости во всасывающей трубе и соответствующем воз-
растании потерь /гвс_. Обычно высота всасывания при перекачи-
вании холодных жидкостей не превышает 5—6 м\ при перемеще-
нии нагретых жидкостей она может быть значительно меньше.
Поэтому горячие, а также вязкие жидкости подводят к насосу
под некоторым избыточным давлением или с подпором на сто-
роне всасывания (рис. 7-3,6). Зависимость (7-10) является об-
щей для всех насосов, хотя процессы всасывания и нагнетания
существенно отличаются для насосов различных типов.
4. Центробежные насосы
Типы центробежных насосов
Центробежные насосы делятся на одноступенчатые и много-
ступенчатые.
На рис. 7-4 показан одноступенчатый насос. Центробежный
насос имеет рабочее колесо 1 с загнутыми назад лопатками, ко-
торое с большой скоростью вращается в корпусе 2 спиралеоб-
разной формы. Жидкость из всасывающего трубопровода 3 по-
ступает по оси колеса и, попадая на лопатки, приобретает вра-
щательное движение. Под действием центробежной силы давле-
ние жидкости увеличивается и она выбрасывается из колеса в
неподвижный корпус 2 и напорный трубопровод 4. При этом на
входе в колесо создается пониженное давление и, вследствие
разности давлений, жидкость из приемного резервуара непре-
рывно поступает в насос.
Без заполнения корпуса жидкостью колесо насоса при вра-
щении не может создать достаточной разности давлений, необ-
ходимой для подъема жидкости по всасывающей трубе. Поэтому
перед пуском в ход центробежный насос должен быть залит
жидкостью (если она не поступает в насос под напором). Чтобы
жидкость не выливалась из насоса и всасывающей трубы при
заливке насоса или его остановке, на конце всасывающей трубы
устанавливают приемный (обратный) клапан 5 с всасывающей
192
Гл. 7. Перемещение жидкостей и газов
сеткой. Одноступенчатые насосы предназначены для создания
небольших напоров — до 50 м.
Для высоких давлений применяются многоступенчатые насо-
сы (рис. 7-5), имеющие несколько колес 2, соединенных последо-
Рис. 7-4. Схема центробежного одно-
ступенчатого насоса:
1 — рабочее колесо; 2—корпус; 3 — всасы-
вающий трубопровод; 4 — напорный трубо-
провод; 5 — приемный клапан с всасывающей
сеткой.
вательно в корпусе 1. Напор, раз-
виваемый многоступенчатым на-
сосом, равен напору одного ко-
леса, умноженному на число ко-
лес. Жидкость из колеса попа-
Рис. 7-5. Схема центробежного
многоступенчатого насоса:
1 — корпус; 2—рабочие колеса; 3 — напра-
вляющие аппараты.
дает в кольцо из двух дисков 3 с лопатками, изогнутыми в сто-
рону, противоположную лопаткам рабочего колеса. Такое устрой-
ство называется направляющим аппаратом и предназначено для
уменьшения скорости (кинетической энергии) жидкости, которая
переходит при этом в потенциальную энергию давления.
Во многих насосах современных конструкций преобразование
скорости в энергию давления осуществляется без направляюще-
го аппарата — путем придания плавных очертаний спиральному
отводному каналу корпуса.
Центробежные насосы большой производительности изгото-
вляются с двухсторонним вводом жидкости в корпус насоса.
В химической промышленности насосы широко применяются
для перекачивания кислот, щелочей, рассолов и других вязких
жидкостей, часто содержащих твердые взвеси. Такие насосы из-
готовляются из коррозионностойких и износоустойчивых метал-
лических сплавов (например, хромоникелевые сплавы с присад-
кой титана или молибдена, кремнистые и высокохромистые чу-
гуны), для изготовления насосов применяются также пластиче-
ские массы (например, фаолит) и керамика.
4 Центробежные насосы
193
Чтобы свести к минимуму утечку перекачиваемой жидкости,
при конструировании таких насосов уделяется большое внима-
ние обеспечению надежного уплотнения вала. Для увеличения
срока службы сальниковых набивок их выполняют из специаль-
ных материалов (стеклянное волокно, фторопласт и др.), а так-
же стремятся более равномерно распределить нагрузку на коль-
ца набивки путем установки (в середине слоя набивки) пружины
или втулки (фонаря) с отверстием. Через это отверстие подают
под давлением жидкость, утечка которой допустима (вода, мас-
ло). Эта жидкость поступает в сальник под давлением, превы-
шающим давление жидкости, перекачиваемой насосом. Таким
способом предотвращают утечку рабочей жидкости, но часть по-
даваемой в сальник жидкости попадает внутрь насоса и смеши-
вается с перекачиваемой жидкостью. Применяют также торцо-
вые уплотнения вала в виде пары трения, например металличе-
ского и графитового колец, прижатых друг к другу пружиной.
Однако все описанные устройства для уплотнения вала не-
долговечны. Сальниковые набивки работают без замены не бо-
лее 300 ч, торцовые уплотнения — до 1000 ч, но они более дороги
и сложны в обслуживании, чем сальниковые уплотнения.
Более надежны бессальниковые насосы (рис. 7-6), в кото-
рых полностью устранена возможность утечки перекачиваемой
жидкости через уплотнение вала. Для предохранения от ударов
корпус 1 насоса помещен в чугунный кожух. Рабочее колесо 2
выполнено из кислотоупорной стали Для предотвращения
Рис. 7-6. Бессальниковый кислотоупорный насос из ферросилида:
/ — корпус; 2—рабочее колесо; 3 —добавочное колесо; 4— пружина; 5~ втулка.
13 Зак 546,
194
Гл. 7. Перемещение жидкостей и газов
Рис. 7-7. Погружной насос:
/—рабочее колесо; 2—всасывающий патрубок;
3—корпус; 4 — подшипники; 5— вертикальный вал;
6—напорные трубы; 7—нагнетательный патрубок.
утечки жидкости служит
объединенное с колесом 2
добавочное колесо 3,
снабженное радиальными
лопатками, которые на-
правляют протекшую за
колесо жидкость в по-
лость нагнетания насоса,
разгружая таким образом
сальник от воздействия
давления жидкости. Та-
кой гидравлический за-
твор действует только во
время работы насоса, в
случае же его остановки
утечка жидкости из на-
соса предотвращается
специальным уплотне-
нием, которое запирает
зазор между валом и кор-
пусом. Герметичность до-
стигается уплотнением
(посредством пружины 4)
конических поверхностей
удлиненной втулки рабо-
чего колеса 2 и фторопла-
стовой втулки 5. При
пуске насоса вал несколь-
ко перемещается влево
(в сторону всасывания)
и конические поверхности
указанных втулок отхо-
дят друг от друга, раз-
мыкая уплотнение.
Утечка перекачиваемой
жидкости устранена так-
же в погружном насосе
(рис. 7-7). Рабочее коле-
со 1 укреплено на ниж-
нем конце вертикального
вала 5, привод которого
размещен значительно
выше уровня жидкости в
резервуаре. Корпус 3 на-
соса погружен под уро-
4. Центробежные насосы
195
вень жидкости в этом резервуаре, из которого перекачивается
жидкость. Жидкость поступает в насос через патрубок 2, по-
дается в две симметричные напорные трубы 6, на которых под-
вешен корпус насоса, и далее отводится в патрубок 7. Насос
описанной конструкции предназначен для перекачивания сер-
ной кислоты; его подшипники 4 смазываются и охлаждаются
перекачиваемой жидкостью (кислотой).
Рис. 7-8. Герметический насос:
/—рабочее колесо; 2—ротор электродвигателя; 3—статор электродвигателя; 4— цилин-
дрическая оболочка (гильза).
Для перекачивания жидкостей, утечка которых недопустима
вследствие их химической агрессивности, токсичности или высо-
кой стоимости, например для перекачивания жидкого хлора,
разбавленной азотной кислоты, радиоактивных жидкостей при-
меняют герметические насосы (рис. 7-8). Их используют также
в случае необходимости работать при повышенном давлении на
стороне всасывания. Полная герметизация насоса достигается
путем установки рабочего колеса 1 непосредственно на валу ро-
тора 2 электродвигателя. Обмотки статора 3 электродвигателя
герметически отделяются от обмоток ротора 2 тонкой цилиндри-
ческой оболочкой 4 из немагнитной нержавеющей стали.
13*
196
Гл. 7. Перемещение жидкостей и газов
В таком экранированном электродвигателе сквозь гильзу пе-
редаются силовые линии магнитного поля статора. Заключенный
в оболочку ротор электродвигателя и подшипники погружены в
перекачиваемую жидкость, которая служит смазкой для под-
шипников и охлаждающей средой для ротора, при этом отпа-
дает необходимость в сальниковом уплотнении вала.
Разработаны также конструкции герметических насосов, в ко-
торых ротор и статор электродвигателя находятся в перекачи-
ваемой жидкости, обмотки и железо статора покрываются кис-
лотостойкой изоляцией. К достоинствам герметических насосов
относится также значительная компактность, обусловленная
лучшим охлаждением обмоток и уменьшением электрических
потерь.
Однако к. п. д. этих насосов несколько ниже, чем в обычных
центробежных насосах.
Пример 7-1. Серная кислота (плотность р = 1850 кг!м3) перекачивается
насосом в аппарат, работающий под избыточным давлением р — 2,45 бар
(2,5 апг). Выбрать насос для подачи кислоты в количестве Q — 150 м3/ч и
определить мощность электродвигателя к насосу. Геометрическая высота
подъема кислоты НГ = 15 м, гидравлическое сопротивление всасывающего
трубопровода Лвс. = 1,0 м столба кислоты, нагнетательного трубопровода
Лн = 4 м столба кислоты.
Решение. Определяем напор, развиваемый насосом, по формуле (7-4):
2 45 JO5
//=15+ттаг+1+4=33’5л
Насос выбирают по заданной производительности Q и напору Н, поль-
зуясь характеристиками насосов (см. стр. 201). Выбираем кислотоупорный
центробежный насос марки 6КХс-8.
При к. п. д. насоса т) = 0,65 находим мощность на валу насоса по фор-
муле (7-7):
150 -1850-9,81 -33,5
27 ~ 3600 • 1000 • 0,65
= 39 кет
Принимаем мощность электродвигателя с запасом 25%. Тогда его требуе,
мая мощность составит:
Njib. = 1.25W = 1,25 • 39 s* 49 кет
Пример 7-2. Насос, перекачивающий жидкость плотностью р =
» 1100 кг/м3, имеет производительность Q = 46,5 м3/ч. Избыточное давление
по манометру на нагнетательном патрубке насоса рм = 3,34 бар (3,4 ат), по-
казание вакуумметра на всасывающем патрубке рв = 0,45 бар (340 мм рт. ст.).
Расстояние между манометром и вакуумметром Лпр. — 300 мм, мощность на
валу электродвигателя N = 7 кет. Определить напор и к. п. д. насоса.
Решение. Определяем напор насоса по формуле:
4. Центробежные насосы
197
Полезная мощность насоса рассчитывается по формуле (7-5):
кт 46,5 • 1100 • 9,81 • 35,3 л о
збоо-1ооо 3=4,9 вт
Коэффициент полезного действия насоса:
Теория и характеристики центробежных
насосов
Основное уравнение центробежных машин. Частицы жидко-
сти в каналах рабочего колеса совершают сложное движение —
они перемещаются вдоль лопаток и одновременно вращаются
вместе с колесом. Соответственно различают:
.. яРл г.
1) окружную скорость вращения частицы и = -gg-, где и —
диаметр окружности вращения частицы, п — число оборотов ко-
леса в минуту;
2) относительную скорость w перемещения частицы по отно-
шению к лопатке.
Рис. 7-9. Движение жидкости в каналах колеса центро-
бежного насоса.
Абсолютная скорость с движения частицы равна геометриче-
ской сумме окружной и относительной скоростей и может быть
определена из параллелограмма скоростей (рис. 7-9).
Воспользовавшись уравнением Бернулли, определим полный
напор, развиваемый в колесе насоса.
Если принять за плоскость сравнения горизонтальную пло-
скость сечения колеса, то для точек на входе и выходе из него
Z1 = z2-
Допустим, что колесо неподвижно и жидкость движется че-
рез него с теми же относительными скоростями, что и во вра-
щающемся колесе. Тогда для невязкой жидкости баланс энер-
гии выражается уравнением:
Р\ । _ Р‘2 I w2
р + 2 р 2
198
Гл. 7. Перемещение жидкостей и газов
Во вращающемся колесе за счет работы центробежной силы
жидкости сообщается дополнительная энергия А, и уравнение
энергетического баланса приобретает вид:
. Pi , wi _ Р2 , w2
Р 2 ~ р +’ 2
(7-11)
Энергия, сообщаемая центробежной силой 1 кг жидкости
А
__ (О2 (/"[ + Г2)
~ 2
=4 (4-'I)
где со — угловая скорость колеса;
ri и гз — радиусы вращения.
Учитывая, что г2ы — и2 и fico = щ, получим:
2 2
«2 —«1
2
А =
(7-12)
Вводя найденное значение А в левую часть уравнения (7-11),
получим:
«2 — и1 ) Г1 t W1 Р2 , w2
2 -т* р 2 ~ р + 2
откуда
о О 9 9
Р2-Л __ ^1-^2 . «2~«1 п 1Qv
р *2 ' 2 V'1’5)
Согласно уравнению Бернулли, напор жидкости на входе в
колесо ина выходе из него при Z\ = составит:
Pi с?
Я1=—+-Л И
1 Р£ 1 2^
//2==а+/
2 Р£ 1 2^
Отсюда теоретический напор, развиваемый лопатками ко-
леса, равен:
н — И И —P2~Pl-L- С2‘"С1
— Т/2 — п{ — —— I 2^
Подставив значение из выражения (7-13),
i4 — Ц1 wi — w<2 с2 — С1
т~ ~2^ । 2^
(7-14)
получим:
2g
(7-15)
Примем, что жидкость движется через колесо с бесконечно
большим числом лопаток, т. е. все частицы движутся по подоб-
ным траекториям. Тогда, согласно рис. 7-9, зависимость между
скоростями частицы на входе в колесо и на выходе из него
определится соотношениями:
W2 — и2 + с\ — 2й1С1 COS ах -ай — М2 С2 ~ ^и2С2 C0S а2
4. Центробежные насосы
199
Вычитая из одного равенства другое, получим:
2 2 2 2 , 2 2 , z \
W1 — W2 = Hi — «2 + Ci — С2 + 2 («2^2 C0S а2 — И1С1 C0S а1)
Подставив Wj — в выражение (7-15) и произведя сокра-
щения, находим окончательное выражение теоретического на-
пора:
и Ц2С2 c0S а2 — “1C1 C0S а1 /7 1£\
Уравнение (7-16), называемое основным уравнением центро-
бежного насоса, было впервые выведено Л. Эйлером. Оно при-
менимо ко всем центробежным машинам, в том числе к турбо-
компрессорам, турбогазодувкам и вентиляторам.
Обычно жидкость поступает на лопатку колеса в радиальном
направлении, под углом ои =90°. Следовательно, cos ои — 0 и вы-
ражение (7-16) упрощается:
U-2^2 COS Otg
Из параллелограмма скоростей на выходе из колеса (см. рис.
7-9) видно, что c2cosa2 = u2— ^2oosp2, откуда
Un / w„ \
—r-cosM ' <7-18)
Фактический напор меньше теоретического, так как часть его
теряется на преодоление гидравлических сопротивлений внутри
насоса, а траектории частиц жидкости при конечном числе лопа-
ток неодинаковы. Поэтому фактический напор насоса равен:
77==77T7jre (7-19)
где 7jr — гидравлический к. п. д., равный 0,8—0,95;
е — поправочный коэффициент, учитывающий понижение
напора при конечном числе лопаток (величина s =
= 0,56 — 0,84).
Из выражений (7-16) и (7-18) следует: чем меньше угол а2
и больше угол р2, тем больше напор. При р2 > 90° и cos (32 < 0
теоретический напор имеет наибольшую величину. Однако с уве-
личением угла |32 значительно возрастают гидравлические поте-
ри. Поэтому центробежные насосы изготовляют с загнутыми на-
зад лопатками (р2 < 90°).
200
Гл. 7. Перемещение жидкостей и газов
Производительность насоса, соответствующая расходу жид-
кости на выходе из колеса при ширине его Ь2 (см. рис. 7-9), со-
ставляет:
Q == кП2&2е2г
(7-20)
где с2л— радиальная составляющая абсолютной скорости.
Кавитация. В случае местных падений давления в насосе ни-
же давления насыщенного пара жидкости при данной темпера-
туре из жидкости начинают выделяться пары и растворенные в
ней газы. Пузырьки пара, увлекаемые жидкостью по каналам
колеса в область более высоких давлений, быстро конденси-
руются. Жидкость мгновенно проникает в пустоты, образующие-
ся при конденсации пузырьков, что приводит к многочисленным
мелким гидравлическим ударам, сопровождающимся шумом и
сотрясениями насоса. Производительность, напор и к. п.д. насо-
са при этом резко падают. Описанное явление носит название
кавитации и приводит к
быстрому механическому
и химическому (от дей-
ствия выделяющихся га-
зов) разрушению на-
соса.
Чтобы избежать кави-
тации, повышают давле-
ние жидкости на входе в
насос, уменьшая высоту
всасывания или работая с
подпором. Кроме того, для
повышения стойкости к
кавитации колеса насосов
Рис. 7-10. Подобие треугольников скоростей, изготовляют из высоко-
прочных материалов.
Законы пропорциональности. С изменением числа оборотов
колеса насоса изменяются его производительность и напор. Если
при различных числах оборотов режимы работы насоса подоб-
ны, то будут геометрически подобны и треугольники скорости в
любых сходственных точках потоков, в том числе на выходе из
колеса (рис. 7-10). Из подобия треугольников следует:
, / , nD2nx
С2___ С2г __ и2 _ 60 _ П1 (7-91}
С2 С^т И2 гс£>2П2 П2
На основании выражений (7-20) и (7-21) можно
Qi С2г п1
Q2 л^2^2С2г С2т П2
написать:
(7-22)
4. Центробежные насосы
201
Из уравнения (7-22) следует, что изменение производительно-
сти насоса пропорционально числу оборотов.
Согласно формуле (7-17), напор изменяется ^пропорциональ-
но произведению скоростей с2 и и2, каждая из которых порознь
пропорциональна числу оборотов. Следовательно, изменение
напора пропорционально квадратам чисел оборотов:
/71
Я2 \ ^2 /
(7-23)
Потребляемая насосом мощность пропорциональна произве-
дению производительности Q на напор И (см. формулу 7-7).
Учитывая зависимости (7-22) и (7-23), получим:
Согласно этому соотношению, изменение потребляемой мощ-
ности пропорционально кубам чисел оборотов.
Зависимости (7-22) — (7-24) носят название законов пропор-
циональности. Практически они достаточно точны при изменении
чисел оборотов не более чем в два раза по сравнению с нор-
мальными.
Пример 7-3. Производительность центробежного насоса Qi =* 50 м3/ч, его
напор Н\ — 24 м Число оборотов п\ вала наеоса составляет 1450 об/мин-, по-
требляемая насосом мощность = 12 квт. Как изменится производительность
Q и напор Н насоса, если установить к нему электродвигатель, имеющий число
оборотов П2 — 750 об/мин?
Решение. В соответствии с формулой (7-23) производительность насоса
снизится и составит:
Q, = Q..^- = 80^ = 23,9^
Напор насоса, согласно формуле (7-23), станет равным
,, 14 (П1\2 ПЛ ( 750 \2 « Л
Отметим также, что при уменьшении числа оборотов мощности потреб-
ляемая насосом, уменьшится пропорционально отношению чисел оборотов в
третьей степени и достигнет Уг= 1,7 квт.
Характеристики центробежных насосов и сети. При испыта-
нии центробежных насосов, изменяя степень открытия задвижки
на нагнетательной линии, замеряют производительность Q, на-
пор Я, мощность N и вычисляют к. п.д. насоса т]. Полученные
при данном числе оборотов ((n = const) зависимости Q — Н,
Q — N и Q — т] наносят для наглядности на график, который на-
зывается характеристикой насоса (рис. 7-11,а).
202
Гл. 7. Перемещение жидкостей и газов
Из характеристики видно, что с увеличением напора при
п = const производительность Q насоса уменьшается. Лишь на
коротком начальном участке кривой Q — Н наблюдается незна-
чительное повышение напора с возрастанием Q, которое соответ-
ствует неустойчивой работе насоса, сопровождающейся толчка-
ми (гидравлическими ударами).
Для многих современных насосов кривая Q — Н не имеет
этого восходящего участка.
Максимуму кривой Q — т] соответствует нормальный режим
работы насоса при заданных Q, Н и п. При закрытой напорной
задвижке насос потребляет мини-
мальную мощность.
Снимая характеристики насо-
сов при различных числах обо-
Рис. 7-11. Характеристики центробежного насоса:
а —при п=const; б— универсальная характеристика (пунктирными линиями обозначены
кривые N—n при различных числах оборотов п от 2925 до 1230 об/мин).
ротов, получают ряд кривых Q—H, показанных на рис. 7-11,6.
Каждый насос обладает наибольшим к. п.д., которому соответ-
ствует определенная точка на каждой кривой Q — Н; при откло-
нении от этой точки в любую сторону кривой к. п. д. насоса
снижается. Соединяя между собой точки равных к.п.д. на всех
линиях Q — Н, наносят на диаграмму линии т] = const. Такая
диаграмма называется универсальной характеристикой насоса.
Согласно универсальной характеристике (рис. 7-11,6), при
п = 2925 об/мин, насос будет работать с наибольшим к. п. д.
(т] = 73%), давая производительность Q^0,02 м3/сек и напор
Н = 33 м, а при п = 1980 об/мин, Q = 0,014 мР/сек и Н 14,5 м
(наибольший к.п.д. т] ~ 69%).
При выборе насоса и числа оборотов необходимо, кроме соб-
ственной характеристики насоса, учитывать также характери-
4. Центробежные насосы
203
стику сети, т. е. трубопровода Й присоединенных к нему аппа-
ратов.
Характеристика трубопровода выражает зависимость между
расходом жидкости и напором, необходимым для ее движения
по трубопроводу. Этот напор складывается из геометрической
высоты подъема жидкости, равной сумме высот всасывания и
нагнетания Нг = Нвс-ф- Нн и высоты потери напора в трубопро-
воде, которую на основе зависимо-
стей (6-63) и (6-22) можно принять
пропорциональной квадрату расхо-
да жидкости:
hn = kQ?
где k — коэффициент пропорцио-
нальности.
Тогда характеристика трубопро-
вода выразится зависимостью
H=Hr-\-kQ2 (7-25)
Если нанести на один график
характеристики насоса и трубопро-
вода (рис. 7-12), то точка их пере-
сечения А, называемая рабочей точ-
кой, будет соответствовать наиболь-
шей производительности Qi, кото-
рую может дать насос, работающий
Рис. 7-12. Совместная харак-
теристика насоса и трубо-
провода.
на данный трубопровод. При дальнейшем увеличении произво-
дительности Q напор насоса станет меньше сопротивления'тру-
бопровода, и насос не сможет подавать жидкость.
Можно уменьшить производительность насоса и увеличить
напор, прикрыв задвижку на напорном трубопроводе, т. е. вводя
дополнительное сопротивление. При этом производительность
насоса снизится, например, до Q2, но часть напора насоса будет
бесполезно теряться на преодоление сопротивления задвижки
(отрезок ha3). Следовательно, увеличение напора насоса сверх
необходимого для преодоления сопротивлений сети нецелесооб-
разно.
Пример 7-4. Насос, имеющий характеристику, показанную на рис. 7-13,
подает жидкость в трубопровод, гидравлические сопротивления которого при
различных расходах жидкости составляют:
$,мЦсек............ 0,004 0,008 0,012 0,016 0,020 0,024 0,028 0,032
Ап, м столба жид-
кости ........... 0,2 0,77 1,7 2,9 4,5 6,5 8,7 11,4
Геометрическая высота подъема жидкости Нг ~ 10 м. Определить мак-
симальные производительность и напор насоса, потребляемую им мощность и
кпд. при работе на данный трубопровод.
204
Гл 7. Перемещение жидкостей и газов
Решение. Наносим на график (рис. 7-13) точки с ординатами Яг-}-ЛГ[,
соответствующими абсциссам Q:
О, лГЧсек . 0,004 0,008 0,012 0,016 0,020 0,024 0,028 0,032
Яг+Ап,ж. 10,2 10,77 11,7 12,9 14,5 16,5 18,7 21,4
Соединяя полученные точки, строим характеристику трубопровода
Q — И'. Пересечение характеристик насоса и трубопровода дает рабочую
точку А, по которой находим искомые величины- производительность
Q = 0,028 м3/сек, напор Н 18,8 м, потребляемую мощность N — 6,8 кеш;
к. п. д. насоса 76%.
Q, л/се*
Рис. 7-13. К примеру 7-4.
Параллельная работа центробежных насосов. Часто несколько центро-
бежных насосов параллельно работают на общий трубопровод.
Рассмотрим Случай параллельной работы двух одинаковых насосов
(рис 7-14). Для построения суммарной Характеристики насосов (кривая / 4-
+ //) следует взять несколько точек на характеристике каждого насоса и
сложить их абсциссы (производительность Q), оставляя неизменными орди-
наты, так как напор И определяется сопротивлением трубопровода и не ме-
няется.
Количество жидкости, подаваемой обоими насосами в нагнетательный
трубопровод, определится рабочей точкой А, которая является точкой пересе-
чения суммарной характеристики насосов и характеристики трубопровода (ли-
ния Т),
Легко видеть, что общая производительность параллельно работаю-
щих насосов всегда меньше суммы производительности этих насосов
2QZ при их работе независимо друг от друга на тот же трубопровод. Сум-
марная производительность насосов тем меньше удвоенной производительно-
сти одного из них, чем больше потери в трубопроводе, т. е. чем круче харак-
теристика трубопровода. Напор, развиваемый при параллельной работе на-
сосов, несколько больше напора каждого центробежного насоса.
4. Центробежные насосы
205
Рис. 7-14. Параллельная работа центробежных насосов I и II.
Работа центробежных насосов при перекачивании вязких жидкостей.
При значительной вязкости перекачиваемой жидкости увеличиваются потери
на трение и уменьшается напор насоса, а потребляемая им мощность возрас-
тает. С увеличением вязкости жидкости к. п. д. насоса снижается главным
образом из-за усиления трения жидкости о колесо насоса, т. е. вследствие
возрастания так называемых дисковых потерь.
Наиболее пригодны для перекачивания вязких жидкостей быстроходные
насосы без направляющего аппарата и с колесом малого диаметра, имеющим
небольшое число лопаток и большой угол выхода жидкости из колеса,
Регулирование и обслуживание центробежных
насосов *
Производительность насоса при постоянном числе оборотов
регулируют изменением открытия напорной задвижки, что свя-
зано, как указывалось выше, с добавочным расходом энергии.
Более экономично регулирование производительности насоса
путем изменения числа его оборотов. Однако такой способ регу-
лирования трудно выполним при осуществлении привода насо-
са от асинхронных двигателей переменного тока, так как онй
работают при постоянном числе оборотов. Поэтому регулирова-
ние с помощью напорной задвижки наиболее распространено.
Перед пуском насоса закрывают напорную задвижку, чтобы
не перегружать электродвигатель, открывают воздушные кра-
ники на корпусе насоса и заливают насос перекачиваемой жид-
костью. Насосы, работающие с подпором, заливают, открывая
задвижку на линии всасывания. Заливка центробежных насосов
производится одним из следующих способов:
1) из нагнетательного трубопровода путем открывания обвод-
ной задвижки;
206
Гл. 7 Перемещение жидкостей и газов
2) при помощи специального вакуум-насоса;
3) через воронку в корпусе насоса (в насосах малой произво-
дительности).
После заливки насоса закрывают воздушные краники и
включают электродвигатель. Пуск при закрытой задвижке дол-
жен быть кратковременным (не более 3 мин), так как иначе
насос может чрезмерно нагреться. Поэтому как только число
оборотов электродвигателя станет нормальным, а давление по
манометру будет соответствовать холостому ходу насоса, посте-
пенно открывают напорную задвижку и доводят производитель-
ность до заданной величины.
Для остановки насоса закрывают напорную задвижку и вы-
ключают электродвигатель.
5. Поршневые насосы
Типы поршневых насосов
Поршневые насосы по характеру действия делятся на насосы
простого, двойного, тройного и четверного действия, а по виду
привода — на приводные и прямодействующие. В зависимости
от конструкции поршня разли-
чают собственно поршневые
насосы и плунжерные насосы,
причем в последних поршень
непосредственно соприкасает-
ся с жидкостью либо отделя-
ется от нее эластичной непро-
ницаемой перегородкой (диа-
фрагмовые насосы).
Горизонтальный поршневой
насос простого действия (рис.
7-15) имеет цилиндр 1, в кото-
ром совершает возвратно-по-
ступательные движения пор-
шень 2. При ходе поршня
вправо в левой части цилиндра
Рис. 7-15. Горизонтальный поршневой
насос простого действия:
/ — цилиндр; 2—поршень; 3 — всасывающий
клапан; 4 — нагнетательный клапан; 5 — криво-
шипно-щатуиный механизм.
создается разрежение, вслед-
ствие чего открывается всасы-
вающий клапан 3, и жидкость
поступает в цилиндр. При об-
ратном ходе поршня (влево)
закрывается клапан 3 и открывается нагнетательный клапан 4.
С этого момента жидкость нагнетается насосом до прихода
поршня в крайнее левое положение. В начале следующего хода
поршня закрывается клапан 4, открывается всасывающий кла-
5. Поршневые насосы
207
пан 3 и цикл повторяется снова. Поршень насоса приводится в
движение кривошипно-шатунным механизмом 5, соединенным
через передачу с электродвигателем.
В плунжерном вертикальном насосе простого действия
(рис. 7-16) поршнем служит пустотелый стакан-плунжер 2, для
которого в отличие от поршня не требуется точной внутренней
обработки цилиндра; плунжер уплотняется при помощи сальни-
ка 3. При таком уплотнении цилиндр насоса мало изнашивается,
Рис. 7-16. Вертикальный плунжер-
ный насос простого действия:
/ — цилиндр; 2 —плунжер; 3 —сальник;
4—всасывающий клапан; 5 —нагнетательный
клапан.
I
Рис. 7-17. Диафрагмовый насос:
/ — цилиндр; 2 —плунжер; 3 —диа-
фрагма; 4 — всасывающий клапан;
5—нагнетательный клапаи.
а неплотности легко устраняются путем подтягивания или заме-
ны набивки сальника, без демонтажа насоса. Плунжерные на-
сосы приспособлены для работы при более высоких давлениях,
чем поршневые, и применяются для перекачивания загрязнен-
ных и вязких жидкостей. Поэтому в химической промышленно-
сти плунжерные насосы применяются чаще поршневых.
К числу поршневых насосов простого действия относится
также диафрагмовый насос (рис. 7-17), применяемый для пере-
качивания суспензий и химически активных жидкостей. Ци-
линдр 1 насоса и плунжер 2 отделены от перекачиваемой
жидкости эластичной перегородкой — диафрагмой 3 из мягкой
резины или специальной стали. При движении плунжера вверх
диафрагма прогибается под давлением жидкости вправо и
жидкость всасывается в насос. При обратном движении плун-
жера вниз диафрагма прогибается влево и жидкость вытес-
няется в нагнетательный трубопровод.
Насосы простого действия за двойной ход поршня (в обе сто-
роны) один раз всасывают и один раз нагнетают жидкость, т. е.
отличаются большой неравномерностью подачи.
208
Гл. 7. Перемещение жидкостей и газов
Рис. 7-18. Горизонтальный плунжерный
насос двойного действия:
/ — цилиндр; 2—плунжер; 3, 4— всасывающие кла-
паны; 5, 6 — нагнетательные клапаны. >
Горизонтальный плунжерный насос двойного действия
(рис. 7-18) имеет по два клапана с каждой стороны плунжера,
т. е. всего четыре клапана. При движении поршня вправо в ле-
вой части цилиндра происходит всасывание и одновременно в
правой его части — нагнетание жидкости. При обратном ходе
поршня всасывание происходит справа от поршня, нагнетание —
слева от него. Таким об-
разом, жидкость нагне-
тается за каждый ход
поршня и, следовательно,
производительность насо-
сов этого типа больше и
подача значительно рав-
номернее, чем в насосах
простого действия.
Разновидностью порш-
невых насосов двойного
действия являются пря-
модействующие паровые
насосы с приводом непо-
средственно от паровой
на одном штоке с порш-
машины, поршень которой находится
нем насоса. Обычно паровые насосы изготовляются в виде двух
сдвоенных насосов, расположенных рядом, причем управление
одним из насосов производится от штока другого.
Вследствие значительного расхода пара паровые насосы ис-
пользуются главным образом в таких установках, где по усло-
виям техники безопасности применение электрического привода
недопустимо или имеется дешевый отбросный пар (огне- и взры-
воопасные производства, подача воды в паровые котлы и др.).
Теория и характеристики поршневых насосов
Производительность. В поршневом насосе жидкость безот-
рывно следует за поршнем, занимая освобождаемый им объем.
Поэтому теоретически, без учета утечек внутри насоса, произво-
дительность поршневого насоса равна объему, описываемому
поршнем.
В насосе простого действия за один ход поршня (вправо или
вверх) засасывается объем жидкости, равный площади сечения
поршня F ж2, умноженной на длину хода поршня s м, но подачи
не происходит. При обратном ходе поршня теоретически вся за-
сосанная жидкость в количестве Fs м3 подается в нагнетатель-
ный трубопровод. Таким образом, за два хода поршня или за
один оборот вала объем подаваемой жидкости составляет Fs м3,
5. Поршневые насосы 209
При п оборотах вала в минуту теоретическая производитель-
ность насоса простого действия равна соответственно
QT = ^ л*3/сел: (7-26)
причем г= 4 , где D — диаметр поршня, м.
В насосе двойного действия за один ход поршня с одной сто-
роны его засасывается объем жидкости Fs м3, а с другой сто-
роны, где находится шток, имеющий площадь сечения f м2, вы-
тесняется (F— f)s м3 жидкости. При обратном ходе поршня
всасывается и нагнетается такой же объем жидкости, но в обрат-
ном порядке — со стороны, где происходило всасывание, жид-
кость нагнетается в количестве Fs м3, а с другой стороны поршня
всасывается (F— f)s м3. Таким об-
разом, за один оборот вала подача
насоса двойного действия составит:
(F—f)s-\-Fs = (2F—f)s м3
Следовательно, теоретическая
производительность такого насоса
при п об/мин равна:
QT — <2F-/).*” мз/сек (7.27)
т. е. почти вдвое превышает произ-
водительность насоса простого дей-
ствия.
Фактическая производительность
поршневого насоса меньше теоре-
тической из-за утечки жидкости через неплотности в клапанах,
поршне, сальниках и крышках. Все эти потери учитываются
объемным к. п. д. насоса ”п0-
Фактическая производительность насоса:
Q = QtVo
Для поршневых насосов, перекачивающих холодную воду,
= 0,9 (средний); при перекачивании очень вязких жидкостей
объемный к. п. д. значительно снижается (до т]0 = 0,3 и менее).
Зависимость между производительностью Q насоса и напо-
ром Н, т. е. характеристика поршневого насоса теоретически
изображается вертикальной прямой (рис. 7-19). Из графика
видно, что прбизводительность поршневого насоса — величина
постоянная, не зависящая от напора, и определяется только объ-
емом жидкости, вытесняемым поршнем. Практически вследствие
I Q= const
Г
Q
Рис. 7-19. Характеристика
Q — поршневого насоса.
14 Зак- 543.
210
Гл. 7. Перемещение жидкостей и газов
утечек жидкости через неплотности, увеличивающихся с воз-
растанием напора, зависимость Q—Н отклоняется от вертикали
(пунктирная линия на рис. 7-19).
Пример 7-5. Определить число оборотов вала поршневого насоса двой-
ного действия, имеющего диаметр поршня D — 160 мм, диаметр штока d —
= 50 мм, длину хода поршня s = 200 мм. Производительность насоса
Q = 25,2 м3/ч. Объемный к. п. д. нассса iq0 = 0,85.
Решение. По условию секундная производительность насоса соста-
вляет:
95 9
Q = -££ = °-007 м3/сек
ооии
Площадь сечения поршня:
tzD2
F = = 0,785 • 0,162 = 0,0201 м2
4
Площадь сечений штока:
f = = 0,785 • 0,052 = 0,00196 м*
4
Из формулы (7-27) производительности насоса (с учетом его объемного
к. п. д.) определяем число оборотов вала:
60 -Q 60-0,007
П “ (2F — /) stio (2 • 0,0201 — 0,00196) 0,2 • 0,85 = оо/мин
Неравномерность подачи и воздушные колпаки. Скорость поршня, при-
водимого в движение кривошипно-шатунным механизмом, изменяется по си-
нусоиде: скорость равна нулю в начале и в конце каждого хода (в так на-
зываемых мертвых положениях) и достигает максимума при среднем поло-
жении поршня. Жидкость безотрывно
следует за поршнем, поэтому подача
насоса изменяется в соответствии с за-
коном движения поршня.
Для смягчения гидравлических уда-
ров и увеличения равномерности по-
Рис. 7-20. Воздушные колпаки:
а —на всасывающем трубопроводе; б — на нагнетательном трубопроводе.
дачи на входе жидкости в насос и на выходе ее из насоса часто устанавли-
вают воздушные колпаки. Воздушный колпак (рис. 7-20) представляет собой
сосуд-буфер, в котором воздух сжимается при ускорении движения поршня,
т. е. при увеличении подачи, и расширяется при ее уменьшении. Соответствен-
но при подаче выше средней избыток жидкости поступает в колпак и уда-
ляется из него, когда подача становится ниже средней. Действие колпака на-
глядно прказаро на рис. 7-20 (справа), площадь ebf — объем жидкости, по-
5. Поршневые насосы
211
ступающей в колпак, площади ade и fgc — объемы жидкости, удаляющейся
из колпака в нагнетательный трубопровод (по оси абсцисс отложена s — длина
хода поршня, по оси ординат Q — подача жидкости).
Объем воздуха в колпаке гораздо больше объема поступающей жидко-
сти. Поэтому давление воздуха в колпаке при сжатии и расширении воздуха
изменяется незначительно, и движение жидкости в нагнетательном трубопро-
воде близко к равномерному.
Индикаторная диаграмма. В работающем насосе зависимость давления
на поршень от длины его хода устанавливают путем снятия индикаторной
диаграммы (рис. 7-21), которая вы-
черчивается специальным прибо-
ром — индикатором, присоединен-
ным к цилиндру насоса. Эта диа-
грамма дает возможность опреде-
лить индикаторную мощность, т. е.
мощность, сообщенную жидкости
поршнем, а также выяснить не-
нормальности в работе насоса.
На рис. 7-21 показана индика-
торная диаграмма нормально ра-
ботающего насоса простого дей-
ствия (с воздушными колпаками). рис 7.21. Индикаторная диаграмма
При всасывании (линия ао) давле- поршневого насоса (р — абсолютное
ние на поршень меньше атмосфер- г давление).
ного и равно Точка b со-
ответствует закрытию всасывающего клапана, после чего, при обратном дви-
жении поршня, давление быстро возрастает до величины рн (линия Ьс). На-
гнетание происходит по линии cd, ордината которой равна . После закры-
Ро
тия нагнетательного клапана (точка d) давление снижается до величины ро
по линии da.
Вследствие инерции клапанов при их открытии происходят колебания
давления, видные на диаграмме возле точек а и с.
Площадь диаграммы выражает в некотором масштабе индикаторную
мощность насоса, равную теоретической мощности [по формуле (7-5)], разде-
ленной на индикаторный к. п. д. (^инд. = ^о^г)-
Регулирование и обслуживание поршневых
насосов
Производительность поршневого насоса, имеющего привод от
двигателя с постоянным числом оборотов, регулируют посред-
ством вентиля или задвижки на перепускной линии, соединяю-
щей всасывающий и нагнетательный трубопроводы.
При помощи перепускной задвижки достигается плавное ре-
гулирование производительности, но оно связано с значительной
потерей энергии в задвижке.
Пуск насоса производится в такой последовательности:
1) открывают задвижку на всасывающем трубопроводе, за-
тем на нагнетательном трубопроводе и на перепускной линии
(если работа насоса регулируется перепускной задвижкой). Пуск
14*
212
Гл. 7. Перемещение жидкостей и газов
поршневого насоса при закрытой напорной задвижке недопу-
стим, так как это может вызвать аварию;
2) включают электродвигатель и, когда устанавливается нор-
мальное число оборотов насоса, медленно закрывают перепуск-
ную задвижку.
Для остановки насоса с приводом от электродвигателя от-
крывают перепускной вентиль, закрывают задвижку на всасы-
вающей линии и выключают электродвигатель, после чего за-
крывают задвижку на нагнетательной линии.
6. Насосы других типов
Пропеллерные (осевые) насосы
В корпусе 1 прЬпеллерного насоса (рис. 7-22) жидкость перемещается
вдоль оси вала 2 с помощью рабочего колеса 3, по форме близкого к гребно-
му винту. По выходе из колеса жидкость дви-
Рис. 7-22. Пропеллерный
насос:
1 — корпус; 2 —вал; 3—рабо-
чее колесо; 4 — направляющий
аппарат.
жется через направляющий аппарат 4, преобра-
зующий ее вращательное движение в осевое.
Гидравлические потери в таких насосах невелики.
Пропеллерные насосы быстроходны, компакт-
ны, просты по устройству и пригодны для пере-
качивания очень больших количеств жидкостей
(в том числе загрязненных) при небольших на-
порах.
В химической промышленности горизонталь-
ные пропеллерные насосы применяются для со-
здания циркуляции растворов в выпарных уста-
новках (стр. 476).
Пропеллерные насосы имеют характеристику,
отличающуюся от характеристики центробежных
насосов (при Q = О потребляемая пропеллерным
насосом мощность максимальная).
Пуск пропеллерных насосов производится
при открытой задвижке.
Вихревые насосы
В последнее время получили распростране-
ние вихревые насосы, пригодные для подачи не-
больших количеств жидкости (примерно до
40 м3/ч) при высоком напоре (до 250 м), в
2—5 раз превышающем напор, создаваемый цент-
робежным насосом при одинаковых окружных
скоростях. В вихревых насосах некоторых кон-
струкций возможно самовсасывание жидкости,
такие насосы могут при пуске откачивать (без
специальных устройств) воздух из всасывающего трубопровода до тех пор,
пока корпус насоса не будет залит рабочей жидкостью.
Вихревой насос (рис. 7-23) имеет рабочее колесо 2 с радиальными лопат-
ками, установленное концентрически в чугунном корпусе 1, который закрыт
спереди крышкой. В боковых стенках крышки и корпуса по обеим сторонам
колеса, укрепленного на валу 3, расположены кольцевые боковые каналы 4
6. Насосы других типов
213
и 5. На участке с центральным углом ~30° каждый канал перегорожен глухой
перемычкой, разделяющей напорную и всасывающую полости.
Жидкость поступает из всасывающего патрубка только на те лопатки ко-
леса 2, которые в данный момент перекрывают всасывающее окно 6 в стенке
корпуса. Пройдя по ячейкам колеса, жидкость увлекается в боковой канал
и движется по нему между всасывающим окном 6 и нагнетательным окном
7,
расположенным в крышке насоса. На участке канала, совмещенном с ок-
ном 7, жидкость вытесняется из ка-
нала и через колесо 2 проходит в
окно 7 и далее в нагнетательный
трубопровод.
При обтекании лопаток вращаю-
щегося колеса в жидкости происхо-
дя АЬ
Рис. 7-23. Вихревой насос:
/—корпус; 2—рабочее колесо; 3 — вал; 4, 5— кольцевые боковые каналы, 6 — вса-
сывающее окно; 7—нагнетательное окно.
дит интенсивное образование и разрушение вихрей, которые отрываются от
лопаток и передают энергию от жидкости, находящейся в ячейках колеса
(между лопатками), к жидкости, движущейся в боковом канале. Такому
переносу энергии сопутствует резкое возрастание напора жидкости в боковом
канале, одновременно происходит большая потеря энергии, что обусловливает
относительно низкий к. п. д. вихревых насосов (20—50%).
При пуске насоса в нем образуется кольцо жидкости, заполняющее внеш-
нюю часть колеса и боковые каналы. При этом у ступицы рабочего колеса
создается разрежение, благодаря чему воздух поступает из всасывающего пат-
рубка в насос. При вращении колеса давление в его ячейках повышается,
воздух сжимается и затем вытесняется в напорное окно жидкостью, посту-
пающей в насос.
Характеристика вихревых насосов значительно отличается от характе-
ристики центробежных насосов: с уменьшением производительности вихре-
вого насоса напор и мощность резко возрастают, достигая максимума при
Q = 0. Поэтому пуск описанных насосов производится при открытой за-
движке на нагнетательном трубопроводе.
Достоинства вихревых насосов: 1) возможность создания высоких напо-
ров; 2) простота и компактность конструкции; 3) простая конфигурация ко-
леса и корпуса, обусловливающая легкость их изготовления из коррозионно-
стойких материалов, трудно поддающихся литью л механической обработке;
4) возможность работы при меньших числах оборотов, чем в центробежных
214
Гл 7. Перемещение жидкостей и газов
насосах, приводящая к повышению стойкости основных частей насоса против
коррозии и эррозии
Недостатки вихревых насосов: 1) низкий к. п. д., 2) непригодность для
перекачивания вязких жидкостей и жидкостей, содержащих твердые взвеси.
Ротационные насосы
Рис. 7-24. Ротационный шестерен-
чатый насос:
/—корпус; 2 — шестерни.
Наиболее распространенным насосом ротационного типа является шесте-
ренчатый насос (рис. 7-24). В корпусе 1 вращаются навстречу друг другу две
шестерни 2, одна из которых приво-
дится во вращение от электродвигателя
черёз редуктор. Когда зубья шестерен
выходят из зацепления, в полости а
со стороны всасывающего патрубка со-
здается разрежение. Жидкость поступа-
ет в корпус, захватывается зубьями
шестерен и перемещается в направле-
нии их вращения. Когда зубья вновь
входят в зацепление, жидкость вытес-
няется через полость б в нагнетатель-
ный трубопровод.
Струйные насосы
В струйном насосе (рис 7-25) струя
рабочей жидкости — пара или воды —
вытекает с большой скоростью из соп-
ла 1 в камеру смешения 2 и увле-
кает путем поверхностного трения за-
сасываемую жидкость или газ. При
этом в камере 2 создается разрежение, достаточное для подъема жидкости из
приемного резервуара в насос. Засасываемая жидкость быстро смешивается
с рабочей, и смесь их поступает в конически расширяющуюся трубу — диф-
Засасываемая
жидкость
Рис. 7-25. Струйный насос:
1 — сопло; 2—камера смешения; 3 — диффузор.
фузор 3 В диффузоре скорость потока уменыпаегся, и, в соответствии с урав-
нением Бернулли, кинетическая энергия потока переходит в потенциальную
энергию давления, что приводит к сжатию засасываемого вещества до тре-
буемого конечного давления.
6. Носовы других типов
215
В пароструйных насосах, помимо смешения жидкостей и передачи энер-
гии перекачиваемой жидкости, происходит конденсация пара. Поэтому такие
насосы применимы только в тех случаях, когда допустимо смешение пере-
мещаемой жидкости с водой, образующейся при конденсации пара.
Струйные насосы применяются не только для нагнетания (инжекторы), но
и для отсасывания жидкостей (эжекторы). Пароструйные и водоструйные на-
сосы применяются также для смешения и нагревания жидкостей.
Монтежю
Монтежю (рис. 7-26) представляет собой вертикальный или горизонталь-
ный резервуар, в который жидкость подается самотеком и вытесняется сжа-
тым воздухом. Монтежю работает периодически. При заполнении корпуса 1
открывают кран-воздушник 6 и кран
2, через который поступает жид-
кость. При передавливании жидко-
сти краны 2 и 6 закрывают и откры-
вают кран 5 на нагнетательной тру-
бе 7, после чего через кран 3 пода-
Рис. 7-26. Монтежю:
/—корпус; 2—5— краны; 6 — кран-
воздушник; 7—нагнетательная труба.
Рис. 7-27. Воздушный подъемник
(эрлифт):
Z — труба для сжатого воздуха; 2—подъемная
труба; 3—смеситель; 4— зонт-отражатель;
5— резервуар.
ют сжатый воздух, вытесняющий жидкость. По окончании передавливания
закрывают кран 3 и сообщают монтежю с атмосферой, открывая кран 4.
Монтежю часто используют для перемещения химически активных и за-
грязненных жидкостей.
Воздушные подъемники
В воздушных подъемниках, или эрлифтах (рис. 7-27), сжатый воздух по
трубе 1 подводится снизу к подъемной трубе 2 и, поступая через смеситель 3,
распределяется в жидкости в виде пузырьков. Смесь жидкости и воздуха
имеет меньший удельный вес, чем жидкость, окружающая трубу 2, и по за-
кону сообщающихся сосудов поднимается вверх по этой трубе. На выходе из
трубы 2 смесь огибает зонт-отражатель 4\ при этом из смеси выделяется воз-
дух, а жидкость сливается в резервуар 5,
216
Гл 7 Перемещение жидкостей и газов
7. Сравнение насосов различных типов
В химической промышленности наиболее распространены
центробежные насосы, которые имеют значительные преимуще-
ства по сравнению с поршневыми. Достоинства центробежных
насосов: 1) равномерность подачи, 2) быстроходность (возможно
непосредственное соединение с электродвигателем), 3) компакт-
ность, 4) простота устройства, 5) возможность перекачивания
загрязненных жидкостей, так как в центробежных насосах име-
ются большие зазоры между кожухом и колесом и отсутствуют
клапаны. Кроме того, для установки центробежных насосов не
требуется массивных фундаментов.
Недостатки центробежных насосов: 1) несколько меньший
к. п. д., чем у поршневых насосов (на 10—15% ниже), 2) необхо-
димость заливки насоса и всасывающей трубы жидкостью перед
пуском насоса, 3) уменьшение производительности с увеличе-
нием напора, 4) резкое снижение к. п. д. при малой производи-
тельности.
В настоящее время центробежные насосы вытесняют поршне-
вые как в области больших, так и небольших подач при уме-
ренных давлениях.
Поршневые насосы применяют для перекачивания неболь-
ших количеств жидкости при высоких напорах, для перекачива-
ния высоковязких жидкостей, а также огне- и взрывоопасных
жидкостей (паровые насосы).
При очень больших подачах (до 30 м?[сек) и небольших на-
порах до (10—15 м) вместо центробежных насосов применяют
пропеллерные, отличающиеся простотой устройства, компактно-
стью и высоким к. п. д.
Шестеренчатые насосы наиболее пригодны для перекачива-
ния вязких, не содержащих твердых взвесей жидкостей при
больших давлениях (до 150 ат); однако производительность
таких насосов не превышает 0,1 м?[сек.
Струйные насосы, монтежю и воздушные подъемники отли-
чаются простотой устройства (отсутствие движущихся частей)
и могут быть изготовлены из химически стойких материалов, но
имеют низкий к. п. д. (не выше 20% для монтежю и 30—35%
для струйных насосов и воздушных подъемников).
8. Типы и основные параметры компрессорных машин
Типы компрессорных машин
Компрессорные машины по величине давления разделяются
на следующие группы:
1) низкого давления (избыточное давление до 0,1 ат) —
вентиляторы;
8 Типы и основные параметры компрессорных машин
217
2) среднего давления (избыточное давление 0’1—3 ат) без
охлаждения — газодувки-,
3) высокого давления (избыточное давление от 3 ат и вы-
ше) с охлаждением — компрессоры;
4) вакуумные (разрежение более 0,5 ат) — вакуум-насосы.
Несмотря на конструктивные отличия каждой группы машин,
принцип действия их одинаков. Поэтому газодувки, вентиляторы
и вакуум-насосы можно рассматривать как разновидности ком-
прессоров.
Компрессоры делятся на поршневые, ротационные, центро-
бежные, осевые и струйные; центробежные компрессоры назы-
ваются турбокомпрессорами и турбогазодувками. К центробеж-
ным и осевым компрессорам могут быть отнесены вентиляторы
Вакуум-насосы представляют собой компрессоры, в которых
газ засасывается при разрежении и выталкивается под давле-
нием несколько больше атмосферного.
Процессы сжатия газа
Работу, затрачиваемую на сжатие газа в компрессоре, можно
определить из обобщенного уравнения Бернулли (6-38). Обычно
не учитывают различия скоростей газа и w2 до и после
сжатия, т. е. полагают, что = w2. Тогда уравнение (6-38)
принимает вид:
l-\-q==i2— h (7-28)
Из этого выражения следует, что затраченная в компрессоре
работа / и подведенное к газу тепло q расходуются на увеличе-
ние энтальпии газа.
Теоретически процесс сжатия газа в компрессоре может быть
адиабатическим или изотермическим.
При адиабатическом сжатии тепло не подводится к газу и не
отводится от него, т. е. q = 0, и уравнение (7-28) принимает
вид:
l = i2 — (7-29)
В этом случае вся затраченная в компрессоре работа обра-
щается в тепло и расходуется на нагревание газа, вследствие
чего его энтальпия возрастает. При адиабатическом сжатии зна-
чительно повышается температура сжимаемого газа.
В изотермическом процессе газ сжимается при постоянной
температуре. В этом случае внутренняя энергия газа не изме-
няется («1 = w2) и соблюдается равенство piZ-ч = /№• Следовав
тельно, Ui + рхв\ = и2 + Р2^2, или i’i = i2, т. е. энтальпия газа при
218
Гл. 7. Перемещение жидкостей и газов
сжатии не изменяется. Соответственно уравнение (7-28) при-
нимает вид:
Z<? = О, или Z —— q (7-30)
Знак минус перед q указывает на отвод тепла. Таким обра-
зом, при изотермическом сжатии вся затраченная работа обра-
щается в тепло и отводится от газа, вследствие чего температура,
внутренняя энергия и энтальпия газа не изменяются. Следова-
тельно, при изотермическом сжатии газа необходимо охлаж-
дать компрессор, чтобы отводить тепло, эквивалентное затрачи-
ваемой работе.
Если, согласно системе единиц МКГСС, работа выражена в кгс • м, а эн-
тальпия в ккал!кг, то уравнение (7-28) принимает вид
А1 -|- (J = Z*2 — 1\
где А = V427 — термический эквивалент работы, ккал!кгс-м.
Соответственно для адиабатического процесса сжатия газа уравнение
(7-29) выразится следующим образом:
j__ г*2 — г‘1
“ А
Для изотермического процесса сжатия газа уравнение (7-30) запишется
в виде:
А1 = — q
Процессы сжатия газа наглядно могут быть изображены на
энтропийной, или тепловой, диаграмме Т — S (рис. 7-28).
На оси ординат этой диаграммы откладывается абсолютная температура
(Г), по оси абсцисс — энтропия (S). Как известно из термодинамики, энтро-
пия представляет собой некоторую функцию состояния тела, которая увели-
чивается при подводе к нему тепла, причем это увеличение тем меньше, чем
выше температура тела.
Приращение энтропии при подводе тепла q дж[кг составляет при обрати-
мом процессе:
тг
AS = J дж/кг • град (7-31)
Л
На Т—S-диаграмме нанесены линии, соответствующие постоянному да-
влению (изобары), и линии, соответствующие постоянной температуре (изо-
термы), которые изображаются горизонтальными прямыми. Линия АК.В яв-
ляется пограничной кривой. Область, лежащая ниже этой кривой, соответству-
ет влажному пару, ветвь ЛК — жидкости при температуре насыщения, ветвь
КВ — сухому насыщенному пару. Точка К является критической точкой. Сле-
ва от ветви ЛК находится область жидкости, справа от ветви КВ — область
перегретого пара. Так как испарение и конденсация жидкости протекают при
постоянных температурах и давлениях, то в области влажного пара изобары
совпадают с изотермами. Конденсация смеси влажных паров протекает при
переменной температуре, поэтому в таких случаях изобары в области влаж-
ного пара не совпадают с изотермами.
8. Типы и основные параметры компрессорных машин
219
Кроме того, на Т—S-диаграмме (рис. 7-28) нанесены линии постоянной
энтальпии (z = const). Энтальпия идеальных газов зависит только от темпе-
ратуры, и для таких газов линии i = const совпадают с изотермами. Энталь-
пия реальных газов зависит также
от давления и для них линии i =
= const не совпадают с изотермами.
Процессы сжатия газа в
компрессоре изображаются на
диаграмме Т—S следующим
образом. При адиабатическом
сжатии q = 0, следовательно
по формуле (7-31) Д8 = 0, т. е.
процесс идет без изменения
энтропии (8=const). Поэтому
процесс изображается верти-
кальной линией 1—2, причем
точка 1 характеризует состоя-
ние газа до сжатия и лежит рис 7.28. Диаграмма Т — S процесса
на пересечении изобары pi и сжатия газа.
изотермы Тг, точка 2 отвечает
состоянию газа после сжатия и лежит на изобаре, соответствую-
щей давлению рг.
При изотермическом сжатии процесс протекает при Т=const
и изображается горизонтальной линией /—2', причем точка 2',
характеризующая состояние газа после сжатия, лежит на изо-
баре Р2- Количество отводимого тепла q, согласно формуле
(7-31), составляет ТД8 и на рис. 7-28 выражается площадью за-
штрихованного прямоугольника а—1—2'—Ь, высота которого
равна 7\ а основание — изменению энтропии AS. В данном про-
цессе энтропия уменьшается, т. е. величина Д8 отрицательна.
Поэтому количество тепла будет также отрицательным, т. е.
процесс сопровождается, как указывалось выше, отводом тепла.
Та же площадь а—1—2'—b выражает работу изотермического
сжатия в тепловых единицах, а площадь а—2—2'—b на рис. 7-28
равна работе адиабатического сжатия.
Мощность компрессоров
Теоретическая мощность, затрачиваемая в компрессоре,
равна произведению его производительности на работу сжатия
газа
дг =___кнт
т 60-1000 Kfim
или
* г
^T==Tooo квгп
(7-32)
220
Гл 7. Перемещение жидкостей и газов
В этих уравнениях:
/ — теоретическая работа сжатия, дж!кг\
Q — производительность компрессора, м3/мин-,
р — плотность газа, кг/м3;
G — количество засасываемого газа, кг/сек.
Если теоретическая работа сжатия газа выражается в системе единиц
МКГСС (в кгс •м/кг), то теоретическая мощность, затрачиваемая компрессо-
ром, составит:
кт G (АГ)
W’ = ~860 Xm
где А — 1/ц7 ккал/кгс • м; G — кг/ч.
Для расчета теоретической мощности, потребляемой ком-
прессором, вместо определения величины / по Т—S-диаграмме
можно пользоваться следующими формулами:
при изотермическом сжатии газа
М == W 1п7Г квт (7-33)
при адиабатическом или политропическом сжатии газа
NT
т— 1
PiVl / Р2\ т
1000 [Дл/
квт
(7-34)
т
т— 1
где p2/pi — степень сжатия газа в компрессоре, равная отноше-
нию давления нагнетания pz (в н/м2) к давлению
всасывания pi (в н/м2)\
V— объем засасываемого газа, м3/сек\
т—показатель адиабаты или политропы (в зависимости
от характера процесса сжатия газа).
Наименьшая работа затрачивается при изотермическом сжа-
тии газа. Отношение мощности при изотермическом сжатии NH3.
к индикаторной мощности Мшд. (определяемой по индикаторной
диаграмме) характеризует совершенство теплового процесса в
компрессоре, работающем с охлаждением газа, и носит название
изотермического к. п. д. (^из.). Следовательно, индикаторная
мощность равна
= (7-35)
Чиз.
Для компрессоров, работающих без охлаждения газа, опре-
деляют отношение мощности при адиабатическом сжатии к ин-
дикаторной мощности. Это отношение представляет собой ади-
абатический к. п. д. (т]ад.)- Таким образом, индикаторная мощ-
ность составляет:
ДГад
7V™. = ^- (7-36)
9. Поршневые компрессоры
221
Величина адиабатического к. п. д. (^ад.) колеблется в пре-
делах 0,93—0,97. Он больше изотермического к. п. д. (т]из),
значения которого, в зависимости от степени сжатия и потерь
при всасывании и нагнетании, составляют 0,64—0,78.
Механические потери в компрессоре учитываются механиче-
ским к. п. д. CqMex.)« который представляет собой отношение
индикаторной мощности 2УИнд. к мощности на валу компрессора
Мф, причем т]мех. = 0,85 — 0,9.
Мощность на валу (эффективная мощность) равна:
= (7-37)
wex. r
9. Поршневые компрессоры
u t Типы поршневых компрессоров
Поршневые компрессоры по числу ступеней сжатия делятся
j ’ на одноступенчатые, двухступенчатые и многоступенчатые, а по
/ характеру действия — на компрессоры простого (одинарного)
у и двойного действия.
Одноступенчатые компрессоры изготовляются горизонталь-
ными и вертикальными; горизонтальные компрессоры являются
большей частью машинами двойного действия, а вертикаль-
ные — простого действия.
Одноступенчатый компрессор простого действия (рис. 7-29, а)
имеет цилиндр 1, который с одной стороны открыт, а с другой —
закрыт крышкой, в которой расположены всасывающий и нагне-
тательный клапаны 3 и 4. Поршень 2 соединен непосредственно
с шатуном 5. Такие компрессоры отличаются простотой устрой-
, ства — они не имеют сальника и ползуна (крейцкопфа).
й В одноступенчатых, компрессорах двойного действия (рис.
7-29,6) газ в цилиндре 1 сжимается по обе стороны поршня 2;
JV поэтому цилиндр снабжен двумя всасывающими клапанами 3
/С* и двумя нагнетательными клапанами 4. Устройство компрессо-
< ров двойного действия сложнее, но зато, при равном весе и рав-
V ной занимаемой площади, они дают вдвое большую производи-
тельность, чем компрессоры простого действия.
Для охлаждения сжатого газа цилиндр, а иногда и крышки
/ компрессоров снабжают водяными рубашками (на рисунке не
показаны). На коренной вал компрессора насажен маховик 8.
Для увеличения производительности одноступенчатых ком-
прессоров простого и двойного действия они изготовляются мно-
ь' гоцилиндровыми. В двухцилиндровом компрессоре простого дей*
ствия (рис, 7-29, в) поршни работают параллельно, привод
222
Гл. 7. Перемещение жидкостей и газов
поршней осуществляется от одного коленчатого вала с кривоши-
пами, сдвинутыми друг относительно друга на угол 90 или 180°.
Для сжатия газа до избыточного давления выше 4—5 ат
(максимум 7 ат) применяют многоступенчатые компрессоры с
двумя и более ступенями, причем газ' охлаждается в холодиль-
никах между ступенями сжатия.
Рис. 7-29. Одноступенчатые поршневые компрессоры:
а —одноцилиндровый простого действия; б — одноцилиндровый двойного действия;
в —двухцилиндровый простого действия. 1 — цилиндр; 2—поршень; 3 —всасываю-
щий клапан; 4 — нагнетательный клапан; 5—шатун; б —крейцкопф; 7 —кривошип;
8 — маховик.
Многоступенчатые компрессоры изготовляют с последователь-
ным расположением цилиндров (по одной оси) — системы тан-
дем (рис. 7-30, а) или с параллельным расположением цилинд-
ров — системы компаунд (рис. 7-30, б).
Двухступенчатые горизонтальные компрессоры часто изго-
товляют одноцилиндровыми со ступенчатым или дифференциаль-
ным поршнем (рис. 7-30,в). Газ первоначально сжимается в
цилиндре 1 одной стороной поршня 2, затем охлаждается в про-
межуточном холодильнике 9, из которого снова поступает в ци-
линдр по другую сторону поршня и сжимается до заданного ко-
нечного давления.
Горизонтальные компрессоры являются тихоходными (п = 80—300 об/мин).
Они соединяются с двигателем ременной передачей. Вертикальные компрес-
соры быстроходны (п = 300—350 об/мин и более) и соединяются с двигате-
лем либо непосредственно, либо через ременную, в частности клиноременную
передачу.
9. Поршневые компрессоры
223
Многоступенчатые горизонтальные компрессоры часто приводятся
в действие тихоходным электродвигателем, ротор которого насажен на вал
компрессора и служит одновременно маховиком.
Соединение компрессора с двигателем в один агрегат дает возможность
значительно уменьшить площадь, занимаемую машиной, причем для боль-
шей компактности цилиндры компрессора иногда располагают V-образно,
под углом друг к другу (рис. 7-30,г).
Рис. 7-30. Многоступенчатые поршневые компрессоры:
а —системы тандем; б— системы компаунд; в—с дифференциальным поршнем; г —с V-об-
разным расположением цилиндров, / — цилиндр; 2—поршень; 3 — всасывающий клапан;
4 — нагнетательный клапан; 5 —шатун; б —крейцкопф; 7 —коренной вал; 8 — маховик;
9 — промежуточный холодильник.
Сжатый газ из поршневых компрессоров направляется к ме-
стам потребления через газосборник (ресивер), служащий бу-
фером для смягчения толчков газа, неравномерно нагнетаемого
компрессором, и колебаний давления газа при неравномерном
потреблении. В газосборнике газ очищается от масла и влаги.
Характеристика работы поршневых
компрессоров
Индикаторная диаграмма. При испытании компрессора сни-
мается, как и для поршневого насоса, индикаторная диаграмма.
На рис. 7-31, а показана теоретическая р—У-диаграмма
одноступенчатого компрессора простого действия. На диаграмме
показаны: ab — линия всасывания, Ьс — линия сжатия, erf —ли-
ния нагнетания. В теоретическом процессе поршень компрессора
в крайних (мертвых) положениях (точки b и rf) вплотную под-
ходит к крышке цилиндра и всасывание начинается сразу же по
224
Г л. 7. Перемещение жидкостей и газов
окончании нагнетания. Вид кривой Ьс на диаграмме зависит ог
процесса сжатия газа (стр. 217).'
Рабочий процесс в реальном компрессоре (рис. 7-31, б) зна-
чительно отличается от теоретического. Между поршнем в мерт-
вом положении и крышкой цилиндра всегда остается некоторый
свободный объем, так называемое вредное пространство. По
окончании нагнетания остающийся в этом пространстве сжатый
Рис. 7-31. Индикаторные диаграммы:
а— теоретическая; б— рабочего процесса в компрессоре.
газ при обратном ходе поршня расширяется и всасывающий кла-
пан открывается лишь при снижении давления до давления вса-
сывания ро- Величина вредного пространства выражается долей
хода поршня и представлена на диаграмме отрезком VBp.
Практически сжатие газа протекает по политропе Ьс, харак-
теризующей реальный процесс с частичным отводом тепла. На
рис. 7-31,6 пунктиром показаны теоретические процессы сжатия
по изотерме (линия Ьс') и по адиабате (линия Ьс").
Как известно, площадь диаграммы выражает работу, совер-
шаемую в процессе сжатия газа. Легко видеть, что эта работа
будет наименьшей при изотермическом сжатии и наибольшей —
при адиабатическом. При охлаждении газа в компрессоре через
рубашку процесс сжатия приближается к изотермическому, при-
чем соответственно снижается расход энергии на сжатие газа.
Производительность компрессора. Из-за наличия в цилиндре
компрессора вредного пространства объем газа QBC., всасывае-
мый за один ход поршня, меньше объема Vn, описываемого
поршнем. Поэтому производительность компрессора уменьшает-
ся, причем отношение
= (7-38)
к п
называется объемным к. п. д. компрессора.
9 Поршневые компрессоры
225
Величина объемного к. п. д. отражает влияние вредного пространства
компрессора и определяется по формуле
Хэ — 1 с
£
т__।
(7-39)
где с — величина вредного пространства, выражаемая отношением объема
' вредного пространства к объему, описанному поршнем (с 3^0,03
0,08);
Р2
-— — степень сжатия газа;
Pi
т — показатель политропы (т = 1,2—1,4).
Объемная производительность компрессора уменьшается также вслед-
ствие потерь, которые не отражаются на индикаторной диаграмме Эти по-
тери вызываются утечками газа через неплотности в клапанах и подогревом
всасываемого газа при соприкосновении его с нагретыми стенками цилиндра
Вследствие подогрева газа его удельный объем увеличивается, а количество
всасываемого газа уменьшается.
Отношение объема газа, подаваемого компрессором (и приведенного
к условиям всасывания), к объему, описанному поршнем, называется коэф-
фициентом подачи и обозначается X.
Коэффициент подачи, учитывающий все потери производительности, мо-
жет быть представлен в виде произведения объемного к. п. д. Хо и коэффи-
циента Xi, учитывающего утечку газа через неплотности и подогрев его на
входе в цилиндр:
X = \0'kl (7-40)
Приближенно коэффициент подачи может быть определен по формуле.
Х = Х0 (1,01—0,02-^-) (7-41)
Теоретическая производительность поршневого компрессора
равна объему, описанному поршнем в единицу времени, и опре-
деляется по формулам (7-26) и (7-27), применяемым для рас-
чета теоретической производительности поршневых насосов.
Таким образом, если пренебречь площадью сечения штока,
фактическая производительность компрессора составит:
Q = \zFsn м3[мин (7-42)
где z— число всасывающих сторон поршня (для компрессоров
простого действия 2=1);
itD2
F — площадь сечения поршня, м2 (F — —%-, D—диаметр
поршня);
s — ход поршня, л-t;
п — число оборотов вала компрессора в 1 мин.
Для многоцилиндровых компрессоров величину Q, получен-
ную по формуле (7-42), следует умножить на число цилиндров.
Для многоступенчатых компрессоров F — площадь сечения
поршня первой ступени (низкого давления).
15 Зак 546.
226
Гл. 7. Перемещение жидкостей и газов
Пример 7*6. Одноступенчатый одноцилиндровый компрессор двойного
действия имеет внутренний диаметр цилиндра D = 500 мм, ход поршня
s = 500 мм, число оборотов вала компрессора п = 165 об/мин. Величина
вредного пространства с = 0,04.
Воздух сжимается в компрессоре от абсолютного давления р\ = 0,98 бар
(1 ат) до давления Рг = 3,92 бар (4 ат), температура засасываемого воздуха
= 20° С, его плотность р = 1,17 кг/м3.
Определить производительность компрессора и потребляемую им мощ-
ность, если адиабатический к. п. д. компрессора 7]ад. = 0,8, механический
к. п. д. ^мех. = 9.9-
Решение. Принимаем показатель политропы m — 1,2 и определяем
объемный к. п. д. по формуле (7-39):
Определяем коэффициент подачи компрессора по формуле (7-41):
Л = 0,915 (1,01 — 0,02 • у) = 0,85
Производительность компрессора рассчитываем по формуле (7-42):
Q = 0,85 - 2 - 0,785 • 0,52 • 0,5 -165 = 27,5 м*/мин
По Т — S-диаграмме для воздуха (стр. 554) энтальпия сжатого воздуха
/2 = 79,3 ккал/кг = 3,32 • 105 дж/кг, энтальпия исходного (атмосферного) воз-
духа /г = 42,5 ккал/кг — 1,78 • 105 дж/кг.
Работа адиабатического сжатия воздуха:
I = 12 — = 3,32 -105 —1,78 • 105 = 1,54 -105 дж/кг
Теоретическая мощность при адиабатическом сжатии по формуле (7-32):
1,54-105.27,5-1,17 QOK
^ад. кп . 1 пап 82,5 квт
60-1000
ад.
Определяем мощность, потребляемую компрессором:
Яад 82,5
W =----------' = n R nQ = 115 квт
Чад. • Чмех. °>8'0.9
Многоступенчатое сжатие. С увеличением степени сжатия
в одной ступени возрастают потери, связанные с сжатием газа
во вредном пространстве, и уменьшается к. п. д. компрессора.
Кроме того, происходит сильное нагревание газа и возрастает
расход энергии на его сжатие. Если известны величины сип,
то по формуле (7-39), приняв Ао — 0, можно найти предельную
степень одноступенчатого сжатия, при которой производитель-
ность компрессора падает до нуля.
Чтобы избежать чрезмерного повышения температуры газа
и повысить эффективность работы компрессора, применяют мно-
гоступенчатое сжатие, охлаждая газ в промежуточных холодиль-
никах между ступенями до температуры, возможно более близ-
кой к температуре газа, всасываемого в компрессор. Благодаря
9. Поршневые компрессоры
227
небольшой степени сжатия в каждой ступени уменьшается холо-
стой ход поршня при расширении газа во вредном пространстве
и соответственно увеличивается объемный к. п. д. компрессора.
При сжатии газа в двухступенчатом компрессоре затрачи-
вается меньше энергии, чем при сжатии в одноступенчатом ком-
прессоре, работающем в тех же пределах давления. Это можно
видеть из теоретической диаграммы, приведенной на рис. 7-32.
Сжатие в первой ступени происхо-
дит по адиабате ab от давления ро
до давления р\, охлаждение в про-
межуточном холодильнике — по пря-
мой Ьс до начальной температуры
газа, лежащей на изотерме асе. За-
тем газ сжимается во второй сту-
пени по адиабате cd до конечного
давления рг.
Таким образом, двухступенча-
тое сжатие протекает по ломаной
abed, которая ближе к изотерме,
чем адиабата abk, характеризую-
щая процесс сжатия газа в односту-
пенчатом компрессоре до того же
давления р2. Заштрихованная пло-
щадь bedk выражает выигрыш в
диаграма процесса многосту-
пенчатого сжатия газа в ком-
прессоре.
работе, достигаемый при двухступенчатом сжатии газа, по
сравнению с одноступенчатым.
С увеличением числа ступеней ломаная линия многоступен-
чатого сжатия все более приближается к изотерме и расход
энергии на сжатие уменьшается еще значительнее, но при этом
усложняется конструкция компрессора.
Поэтому число ступеней сжатия в компрессорах обычно не
превышает семи:
Степень сжатия
Число ступеней
5 10 80 120 > 120
1 2 3 4 5—7
’ Процесс сжатия в многоступенчатом компрессоре наиболее
экономичен, если степени сжатия во всех ступенях равны. По
этой причине, а также по конструктивным соображениям прини-
мается одинаковая степень сжатия х во всех ступенях. При п
ступеням сжатия она равна:
х = (7-43)
где рп и ро — конечное и начальное давление газа.
15*
228
Г л. 7. Перемещение жидкостей и газов
Регулирование и обслуживание поршневых
компрессоров
Регулирование компрессоров производится для изменения их производи-
тельности в соответствии с потреблением (расходом) сжатого газа при по-
стоянном давлении сжатия.
Регулирование при переменном числе оборотов легко осуществимо
только в компрессорах с паровым приводом и производится путем измене-
ния числа оборотов вала паровой машины.
В компрессорах с электроприводом регулирование производится при по-
стоянном числе оборотов различными способами.
Регулирование пропусками при всасывании осуществляют путем авто-
матического открытия всасывающих клапанов во время хода нагнетания,
если давление газа в газосборнике чрезмерно увеличивается. При этом газ
не сжимается, а выталкивается обратно во всасывающую трубу, и компрес-
сор работает с пропуском подачи. Регулятор давления выключает приспо-
собление, отжимающее клапан, когда давление в газосборнике снижается до
заданной величины.
Регулирование изменением величины вредного пространства осуще-
ствляют путем разделения пустотелой крышки цилиндра на отсеки, каждый
из которых соединяется с цилиндром через особый клапан. Клапаны откры-
ваются последовательно, вручную или автоматически с помощью регулятора
давления. При этом объем вредного пространства увеличивается, а произво-
дительность снижается. Такой способ регулирования проще предыдущего при
большом числе всасывающих клапанов.
Регулирование дросселированием возможно в одноступенчатых компрес-
сорах путем установки клапана на всасывающей трубе. При чрезмерном
давлении газа в газосборнике клапан опускается и перекрывает всасываю-
щую трубу. Такой способ регулирования связан с увеличением степени сжа-
тия газа и, следовательно, с увеличением расхода энергии. Он наименее
экономичен, так как сопряжен с потерей энергии на сжатие перепускаемого
газа.
При пуске компрессора подают смазку на трущиеся части, открывают
запорный вентиль на нагнетательном трубопроводе и подают охлаждающую
воду в рубашку компрессора, после чего включают двигатель.
При остановке машины все операции проводят в обратном порядке:
останавливают двигатель, прекращают подачу охлаждающей воды и смазки,
после чего закрывают вентиль на нагнетательном трубопроводе.
10. Ротационные компрессоры
Пластинчатый ротационный компрессор (рис. 7-33) имеет
цилиндрический ротор 1, который эксцентрично установлен вну-
три корпуса 2, снабженного водяной рубашкой. В радиальных
вырезах ротора свободно скользят пластины 3. При вращении
ротора пластины под действием центробежной силы выдвигаются
из прорезей и скользят по внутренней поверхности корпуса,
образуя замкнутые камеры. Объем камер увеличивается слева
от вертикальной оси корпуса и уменьшается справа от нее. Со-
ответственно этому газ засасывается через патрубок 4. затем
сжимается и нагнетается через патрубок 5. Абсолютное давле-
ние сжатия в одноступенчатых пластинчатых компрессорах —-
до 5 ат, в двухступенчатых — до 15 ат.
10. Ротационные компрессоры
229
Ротационный водокольцевой компрессор (рис. 7-34) состоит
из корпуса 1 и эксцентрично установленного в нем ротора 2
с лопатками (звездочки). Перед пуском корпус почти наполо-
вину заполняется водой, которая при вращении ротора отбрасы-
вается к стенкам корпуса, образуя около них вращающееся жид-
костное кольцо. Вследствие эксцентричности ротора простран-
ство, не заполненное жидкостью, делится лопатками ротора на
Рис. 7-33. Схема пластинчатого рота-
ционного компрессора:
1 — ротор; 2—корпус; 3— скользящие пластины;
4 — всасывающий патрубок; 5—нагнетательный
патрубок.
Рис. 7-34. Схема водокольцевого
ротационного компрессора:
1 — корпус; 2 —ротор; 3 — всасывающее
отверстие; 4 — нагнетательное отверстие.
ячейки неодинакового объема. В ячейки, объем которых увели-
чивается при вращении ротора, газ засасывается через отвер-
стие 3, затем сжимается в ячейках с уменьшающимся объемом
и выталкивается через отверстие 4 (отверстия 3 и 4 на рисунке
заштрихованы). Патрубки для входа и выхода газа распола-
гаются на торцовых крышках компрессора.
Водокольцевые компрессоры создают небольшое избыточное
давление (до 1 ат) и чаще используются в качестве вакуум-
насосов.
Для сжатия газообразного хлора применяют ротационные кольцевые
компрессоры с жидкостным поршнем, имеющие корпус эллиптической формы.
В качестве рабочей жидкости в них применяется концентрированная серная
кислота. При вращении ротора (ось которого совпадает с осью корпуса)
серная кислота, отбрасываемая под действием центробежной силы к стенкам
корпуса, образует жидкостное кольцо, следующее очертаниям стенок кор-
пуса. За один оборот ротора компрессора объем ячеек для газа дважды
увеличивается и дважды уменьшается вследствие эллиптичности жидкостного
кольца, играющего роль поршня, всасывающего и нагнетающего газ.
230
Гл. 7. Перемещение жидкостей и газов
11. Центробежные компрессоры
Центробежные вентиляторы
Типы вентиляторов. Центробежные вентиляторы делятся на
вентиляторы низкого давления (Р < 100 мм вод. ст.), среднего
давления (Р = 100—300 мм вод. ст.) и вентиляторы высокого
давления (Р = 300—1000 мм вод. ст.).
Центробежный вентилятор низкого давления (рис. 7-35)
имеет корпус 1, в котором вращается рабочее колесо 2, выпол-
ненное в виде широкого барабана с большим числом часто по-
ставленных лопаток. Воздух или газ поступает по оси колеса
Рис. 7-35. Центробежный вентилятор:
1 — корпус; 2 —рабочее колесо; 3— всасывающий патрубок; 4 — нагнетательный патрубок.
через всасывающий патрубок 3, захватывается лопатками и вы-
брасывается из корпуса через нагнетательный патрубок 4 в на-
правлении, перпендикулярном оси колеса.
Характеристика вентиляторов. Полное давление, развиваемое
вентилятором, представляет собой сумму статического давле-
ния рст. и динамического давления рдин.. Статическое давление
равно потере давления в трубопроводах и аппаратах, через ко-
торые движется газ во всасывающей и нагнетательной линиях.
Динамическое давление определяется по скорости-w газа в вы-
хлопном отверстии вентилятора:
pw2
Рд.т. 2
Таким образом, полное давление, развиваемое вентилятором,
составляет:
Р = Рсг. + ^Г Н1м2 (7’44)
где р — плотность газа, кг[м\
11. Центробежные компрессоры
231
Вентиляторы, как и центробежные насосы, имеют рабочую
характеристику, выражающую зависимость величин Р, N и г) от
объемной производительности Q при постоянном числе оборотов
(п — const) и постоянной плотности газа (р = const). Характе-
ристику устанавливают опытным путем, причем результаты ис-
пытаний обычно относят к постоянной плотности воздуха /?ст.
= 1,2 кг/м3, так как вентиляторы рассчитывают на стандартные
условия, т. е. на воздух, имеющий давление 760 мм рт. ст., тем-
пературу 20°С и относительную влажность 50% (стр. 736). По-
этому при подаче вентилятором другого газа величины /?ст. и 2УСТ.
пересчитывают на основе следующих соотношений:
и ^=^CT.-L (7-45)
Рст. гст.
При этом производительность вентилятора остается неизмен-
ной (Q = const). Для вентиляторов зависимость Q, Р nN от числа
оборотов выражается также соотношениями (7-22), (7-23) и
(7-24).
Рабочий режим вентилятора определяется по рабочей точке
пересечения его характеристики с характеристикой трубопро-
вода (стр. 203). Регулирование вентиляторов производится при
п — const изменением сопротивления трубопровода с помощью
задвижки или поворотной заслонки.
Выбор вентилятора. Вентиляторы ответственного производства выпу-
скаются сериями, охватывающими группы геометрически подобных вентиля-
торов, которые отличаются друг от друга диаметром колеса. Каждый вен-
тилятор серии имеет номер, соответствующий диаметру колеса в метрах,
умноженному на 10. Вид характеристики геометрически подобных машин
одинаков, поэтому выбрать вентилятор можно, пользуясь общей, или обезли-
ченной, характеристикой целой серии вентиляторов.
Характеристика, выражающая зависимость давления Р от скорости w
выхода газа из вентилятора, при различных значениях окружной скорости
и колеса, приведена на рис. 7-36. На характеристике нанесены также линии
постоянного к. п. д. т] и линия динамического давления рДин. По заданному
давлению Р подбирают w и и в области, близкой к максимальному к. п. д.,
после чего определяют сечение выхлопного отверстия вентилятора по
формуле:
5 — -2L J/2
^вых. — — м
где Q — объем газа, проходящего через вентилятор, м2/сек.
По табл. 10 находят диаметр D колеса, затем рассчитывают число обо-
/ 60и \
ротов вентилятора I п — 1 и потребляемую им мощность по формуле:
"’Жкет
где Р — полное давление, развиваемое вентилятором, н/м2.
232
Гл. 7. Перемещение жидкостей и газов
Таблица 10
Размеры серийных вентиляторов низкого и среднего давления
№ венти- лятора Он, м Ос, м *^вых.’ № венти- лятора Dh> м £) , м с’ 5ВЫХ.’ и2
2 0,20 0,22 0,026 11 1,10 1,21 0,775
3 0,30 0,33 0,058 121/я 1,25 1,375 1,000
4 0,40 0,44 0,102 14 1,40 1,54 1,255
5 0,50 0,55 0,160 15'/2 1,55 1,705 1,540
б’А 0,65 0,715 0,270 17 1,70 1,87 1,850
8 0,80 0,88 0,410 18'^ 1,85 2,035 2,190
g’/i 0,95 1,045 0,578 20 2,00 2,20 2,560
£>н —диаметр колеса вентилятора низкого давления.
Dc —диаметр колеса вентилятора среднего давления.
5ВЫХ —сечение выхлопного отверстия вентиляторов низкого и среднего давления.
Если развиваемое вентилятором давление выражается в единицах си-
стемы МКГСС (в кгс/м2), то формула (7-46) принимает следующий вид:
.v .
102т]
квт
Рис. 7-36. Обезличенная характеристика центробежных вентиляторов типа
„Сирокко1*:
а —низкого давления; б—среднего давления.
Пример 7-7. Выбрать вентилятор для отсасывания газа в количестве
Q = 8000 м3/ч (плотность газа р= 1.75 кг/мЛ), если сопротивление сети со-
ставляет Др = 637,6 н/м2 (65 мм вод. ст.) Определить также мощность, по-
требляемую вентилятором.
Решение. По условию Др < 100 мм вод. ст, следовательно, в данном
случае может быть использован вентилятор низкого давления. По характери-
стике (рис. 7-36, а), принимая максимальное значение к п д. т] = 0,57 для вен-
тиляторов низкого давления, находим рабочую точку А. Проводя из нее вер-
тикаль до пересечения с осью абсцисс, находим на этой оси значение ско-
11. Центробежные компрессоры
233
рости газа в выхлопном отверстии вентилятора: w = 15 м/сек. Тогда пло-
щадь сечения выхлопного отверстия составит:
5 — Q _ 8000 _ о 148 ич
двых- 3600- w'~ 3600-15 6
По табл. 10 выбираем вентилятор «Сирокко» № 5 низкого давления
(диаметр колеса D = 500 мм), который имеет ближайшее большее сечение
выхлопного отверстия (5ВЫХ.= 0,16 м2).
Скорость газа в выхлопном отверстии выбранного вентилятора составит:
Q 8000 .
W = QRAAC--- = ОДЛА Л1Й — 13’9 М С6К
36005вых> 3600 • 0,16
Находим по характеристике (рис. 7-36) рабочую точку А\, которой со-
ответствует окружная скорость колеса вентилятора и = 23,5 м/сек и к п. д.
т) = 0,557.
Определяем число оборотов вентилятора:
60 • и 60 • 23,5 плл
л=~пВ~== 3,14.0,5'900 0'7,Ж‘,,‘
Полное давление, развиваемое вентилятором, находим по формуле (7-44):
1 75.1.3 Q2
Р = 637,6 + 21О^~ = 806,6 н/м2
Мощности потребляемую вентилятором при подаче воздуха, определяем
по формуле (7-46):
.. 8000 • 806,6 _ оо
Nb = 3600 -1000 • 0,557 “ 3,22 Квт
Принимаем плотность воздуха рст. = 1.2 кг/м3 и пересчитываем по фор-
муле (7-45) мощность, потребляемую вентилятором:
1 75
W = 3,22 - -^2- = 4,7 квт
Турбогазодувки и турбокомпрессоры
Турбогазодувки и турбокомпрессоры не отличаются по прин-
ципу действия от центробежных вентиляторов, но вследствие
сжатия газа в ряде последовательно соединенных лопастных ко-
лес (ступеней) дают возможность достигать значительно более
высоких давлений.
Одноступенчатые турбовоздуходувки по существу являются
разновидностью вентиляторов высокого давления и нагнетают
воздух под избыточным давлением, не превышающим 0,3 ат.
На рис. 7-37 показана многоступенчатая турбогазодувка. Газ
через всасывающий патрубок 1 поступает в рабочее лопастное
колесо 2 первой ступени, проходит это колесо, а затем неподвиж-
ный кольцевой канал — направляющий аппарат 3. Далее газ
движется через обратный направляющий аппарат 5 с лопатками
и поступает в следующее рабочее колесо (второй ступени).
234
Гл. 7. Перемещение жидкостей и газов
Таким же образом газ последовательно проходит все колеса и
удаляется через патрубок 8.
Корпус турбогазодувки разделен на отдельные секции (сту-
пени) перегородками, или диафрагмами 4. Для уменьшения
утечки газа через щели между валом, рабочим колесом и корпу-
сом имеются лабиринтные уплотнения 6. Газ, проникающий че-
рез зазоры уплотнения, многократно расширяется в лабиринтах,
в результате чего давление его снижается до атмосферного.
Рис. 7-37. Многоступенчатая турбогазодувка:
1— всасывающий патрубок; 2—рабочие колеса I, II, III ступеней; 3 — направляющие аппараты
(диффузоры); 4 — диафрагма; 5 — обратные направляющие аппараты с лопатками; б —лабиринт-
ное уплотнение; 7—разгрузочный поршень; 8 — нагнетательный патрубок.
Вследствие разности давлений по обе стороны колес при
одностороннем входе в них газа, в турбогазодувке возникает
осевое давление. Оно уравновешивается упорным подшипником
и разгрузочным поршнем 7, который под действием разности
давлений стремится сдвинуться в сторону, противоположную
осевому давлению, и уравновесить его.
Турбогазодувки, в отличие от турбовоздуходувок, часто снаб-
жают специальными уплотнениями с масляными затворами (при
12. Осевые компрессоры
235
работе с токсичными и взрывоопасными газами), а также спе-
циальными кранами для удаления накапливающихся загрязне-
ний (например, смол) и для промывки машины.
Вследствие невысокой степени сжатия в турбогазодувках
число ступеней в них сравнительно невелико (3—4 ступени) и
газ не охлаждается между ступенями.
В турбокомпрессорах газ охлаждается при помощи внутрен-
ней водяной рубашки в виде сообщающихся камер, отлитых
в корпусе (в малых машинах), либо проходит через наружные
водяные холодильники.
Рабочие колеса турбокомпрессора делятся на ступени, в пре-
делах каждой ступени находятся колеса одного диаметра, от-
личающиеся друг от друга только по ширине. Диаметр и ширина
колес уменьшаются в соответствии с уменьшением объема газа
по мере его сжатия. При таком устройстве колес снижаются по-
тери на их трение о воздух.
12. Осевые компрессоры
Корпус осевого вентилятора (рис. 7-38) выполнен в виде короткого ци-
линдрического патрубка, в котором вращается рабочее колесо. Воздух дви-
жется прямотоком, т. е. вдоль оси вала. Вследствие прямоточного движения
газа и обтекаемой формы лопаток к. п. д. осевых вентиляторов значи-
тельно выше, чем для центробежных. Осевые вентиляторы могут работать
с реверсированием, т. е. с изменением напра-
вления потока воздуха на обратное.
Рис. 7-38. Осевой вен-
тилятор:
1 — корпус; 2 — рабочее колесо.
Рис. 7-39. Осевой компрессор:
/ — корпус; 2—ротор; 3— рабочие лопатки; 4 — не-
подвижные лопатки.
Осевой компрессор (рис. 7-39) представляет собой по существу много-
ступенчатый осевой вентилятор. В корпусе 1 вращается цилиндрический
ротор 2 с рабочими лопатками 3. Рабочие лопатки вращаются между закреп-
ленными в корпусе неподвижными лопатками 4, которые служат направляю-
щим аппаратом для газа при переходе его от одной ступени рабочих лопа-
ток к другой. Зазор между лопатками и корпусом незначителен (до 0,5 мм).
В осевых компрессорах достигается высокий к. п. д. и конечное избыточ-
ное давление газа до 6 ат. Эти компрессоры имеют непосредственный при-
вод от быстроходных газовых турбин.
236
Гл. 7. Перемещение жидкостей и газов
13. Вакуум-насосы
Отличительной особенностью вакуум-насосов является вы-
сокая степень сжатия газа. В вакуум-насосе, который создает
разрежение, равное 90% (остаточное давление р\ = 0,1 ат),
и сжимает газ до давле-
ния р2 = 1,1 ат, степень
сжатия составляет:
/7ар
I Конденсат
j Слив
Рис. 7-40. Пароструйный вакуум-насос:
J—пароструйные насосы; 2 —барометрические кон-
денсаторы.
й 0,1 11
всасывающая
линия
,В атмосферу
Повышение степени
сжатия связано со сни-
жением объемного к. п. д.
и производительности на-
соса. Для повышения объ-
емного к. п. д. вакуум-на-
сосы изготовляют с воз-
можно меньшим вредным
пространством.
Поршневые вакуум-на-
сосы отличаются от пор-
шневых компрессоров
двойного действия толь-
ко устройством органов
распределения. Вместо
клапанов эти насосы име-
ют золотник, при помощи
которого производится
попеременно всасывание
и выпуск газа. При золот-
никовом распределении
объем вредного простран-
ства незначителен и от-
сутствуют потери давле-
ния, связанные с откры-
тием клапанов.
Мокрые вакуум-насосы поршневого типа, отсасывающие жид-
кость вместе с газом, изготовляют е клапанным распределением.
Такие вакуум-насосы работают с меньшим числом оборотов и
имеют большее, чем сухие вакуум-насосы, вредное пространство,
вследствие чего создаваемое мокрыми вакуум-насосами разре-
жение меньше.
Работа адиабатического сжатия в поршневых вакуум-насосах
максимальна при остаточном давлении Pi = 0,324 ат, если при-
14. Сравнение и выбор компрессорных машин
237
нять приближенно давление сжатия р2 = 1 ат. Поэтому двига-
тель для поршневых вакуум-насосов выбирают исходя из наи-
большей потребляемой мощности, соответствующей указанному
выше значению Pi.
Водокольцевые вакуум-насосы широко распространены в хи-
мической промышленности. По устройству они не отличаются
от водокольцевых ротационных компрессоров (см. рис. 7-34,
стр. 229).
Пароструйные вакуум-насосы аналогичны описанным выше
струйным насосам (стр. 214). Вакуум, создаваемый одноступен-
чатым струйным насосом, не превышает 90%. Для достижения
более глубокого вакуума применяют многоступенчатые паро-
струйные вакуум-насосы (рис. 7-40), состоящие из нескольких
последовательно соединенных пароструйных насосов 1, между
которыми установлены конденсаторы 2. После каждой ступени
производится конденсация пара из паро-газовой смеси путем
смешения ее с охлаждающей водой. Таким путем устраняется
расход энергии на сжатие отработанного пара каждой предыду-
щей ступени в следующей.
Пример 7-8. Определить мощность, потребляемую вакуум-насосом, если
количество отсасываемого воздуха Vi = 435 м?/ч, давление всасывания
pi — 11 700 н/м? (1194 кгс/м?), давление нагнетания рг = 103 000 н/м?
(1,05 ат). Механический к. п. д. вакуум-насоса т]м = 0,9.
Решение. Принимая показатель политропы для воздуха m — 1,25,
теоретическую мощность, потребляемую вакуум-насосом, определяем по фор-
муле (7-34):
Г 1,25-1 т
1,25 11 700 - 435 / 103 000 \“W
Лт“ 1,25—1 ’ 3600-1000 |_\ И 700 ) ~ Квт
Фактическая мощность, потребляемая вакуум-насосом:
.. 3,87
N = —L — 4,3 квт
Чм 0,9
14. Сравнение и выбор компрессорных машин
Поршневые компрессоры, по сравнению с центробежными,
имеют недостатки, присущие всем поршневым машинам—тихо-
ходность, громоздкость, большой вес, необходимость установки
на массивных фундаментах. Однако изготовление центробежных
компрессоров, рассчитанных на небольшую производительность
и высокое давление, связано с значительными трудностями. По-
этому при избыточном давлении более 10 ат, а также при мень-
шем давлении и производительности до 100 м3/мин применяют
почти исключительно поршневые компрессоры. Наибольшее
распространение приобретают вертикальные поршневые ком-
238
Гл 7. Перемещение жидкостей и газов
прессоры, которые более быстроходны, компактны и обладают
большим к. п. д., чем горизонтальные поршневые компрессоры.
Центробежные компрессоры (турбогазодувки и турбокомпрес-
соры) применяют при умеренных давлениях ркз&. = 10—12 ат
и не более 30 ат для большой производительности, превышаю-
щей 50—100 мР/мин.
Ротационные компрессоры, по сравнению с поршневыми, об-
ладают теми же преимуществами, что и центробежные, отли-
чаясь еще большей компактностью и меньшим весом. К. п. д.
ротационных компрессоров выше, чем для турбокомпрессоров.
р,ат
Рис 7-41. Области применения воздушных ком-
прессоров и вентиляторов (р — избыточное да-
вление, ат):
7—5—число ступеней поршневого компрессора.
Ротационные компрессоры применяют при средней производи-
тельности (до 100 м3/мин) и избыточном давлении до 10 ат.
Большой компактностью и производительностью, а также вы-
соким к. п. д. отличаются осевые компрессоры, но создаваемое
ими избыточное давление не превышает 6 ат.
Выбор вакуум-насосов связан с глубиной создаваемого ими
вакуума. Мокрые поршневые вакуум-насосы дают разрежение,
равное 80—85%. Разрежение до 90—95% создают сухие поршне-
вые и водокольцевые вакуум-насосы, причем последним присущи
все преимущества центробежных машин перед поршневыми, но
они имеют низкий к. п. д. Для создания глубокого вакуума
(95—99,8%) применяют многоступенчатые пароструйные ваку-
ум-насосы.
Области применения воздушных компрессоров, воздуходувок
и вентиляторов показаны ориентировочно на рис. 7-41.
Глава 8
РАЗДЕЛЕНИЕ ЖИДКИХ НЕОДНОРОДНЫХ СИСТЕМ
1. Неоднородные системы и методы
их разделения
Под неоднородной системой понимают систему, состоящую из
различных фаз, например жидкости и твердых частиц, жидкости
и газа и т. д. Любая неоднородная система состоит из двух и
более фаз. Одна фаза, дисперсная, или внутренняя, находится
в мелкодисперсном состоянии; другая фаза, дисперсионная, или
внешняя, является сплошной, окружает отдельные частицы дис-
персной фазы и представляет собой среду, в которой распре-
делены частицы дисперсной фазы.
В зависимости от физического состояния фаз различают сле-
дующие неоднородные жидкие и газообразные системы:
Неоднородные Дисперсионная Дисперсная
системы (сплошная) фаза фаза
Суспензия........ Жидкость Твердое вещество
Эмульсия......... Жидкость Жидкость
Пена............. Жидкость Газ
Пыль, дым........ Газ Твердое вещество
Туман............ Газ Жидкость
Всякая неоднородная система характеризуется концентраци-
ей дисперсной фазы и размерами ее частиц.
Все системы, состоящие из жидкой и твердой фаз, в зависи-
мости от размеров частиц твердого вещества могут быть условно
разделены на четыре группы:
Системы Размер твердых
частиц мк
Грубые суспензии ... > 100
Тонкие суспензии . . . 0,5—100
Мути.................. 0,1—0,5
Коллоидные растворы . <0,1
Можно считать, что граница между суспензиями (взвесями)
и коллоидными растворами определяется появлением броунов-
ского движения твердых частиц. С возникновением броуновского
движения эти частицы не могут осаждаться под действием силы
тяжести.
240
Гл. 8 Разделение жидких неоднородных систем
Эмульсии состоят из несмешивающихся жидкостей и могут
расслаиваться под действием силы тяжести. Эмульсии приобре-
тают устойчивость лишь при очень незначительных размерах ка-
пелек дисперсной фазы (менее 0,4—0,5 мк) или при добавлении
стабилизаторов, например мыла. С увеличением концентрации
эмульгированного вещества в эмульсиях возможно обращение
фаз-, капельки дисперсной фазы сливаются друг с другом и об-
разуют сплошную фазу, в которой распределяются -капельки
жидкости, бывшей ранее дисперсионной фазой.
Пены, представляющие собой газо-жидкостные системы, по
своим свойствам близки к эмульсиям.
Неоднородные газовые системы образуются: 1) в результате
механического распределения частиц в газе (при дроблении
твердых материалов, распылении жидкостей и т. д.); 2) при кон-
денсации паров (газов) с переходом их в жидкое или твердое
состояние. В первом случае образуются пыли, а во втором —
соответственно туманы или дымы. Такие же системы могут об-
разовываться в результате взаимодействия между газами, со-
провождающегося образованием твердых или жидких веществ.
Пыли, дымы и туманы представляют собой аэродисперсные си-
стемы, или аэрозоли, и различаются размером взвешенных ча-
стиц:
Газовые системы Ориентировочный
размер частиц, мк
Механические (пыли) . . . 5—100
Конденсированные (дымы,
туманы)............. 0,3—5
Взвешенные частицы в газовых системах, особенно в конден-
сированных, могут во многих случаях, соединяясь друг с другом,
укрупняться (агломерироваться).
Выбор метода разделения неоднородных систем зависит глав-
ным образом от размеров взвешенных частиц. Применяются сле-
дующие методы разделения неоднородных систем: 1) осаждение,
2) фильтрование, 3) мокрое разделение.
Осаждение применяется главным образом для разделения
суспензий и пылей. Оно происходит под действием сил тяжести,
сил инерции (в том числе центробежных), электростатических
сил или звуковых волн.
Фильтрование осуществляется под действием сил давления
(разделение суспензий и отделение тонких пылей) или центро-
бежных сил (разделение суспензий на центрифугах).
Мокрое разделение применяют главным образом для очист-
ки газов (отделение пылей и туманов), но используют также при
обработке суспензий в комбинации с другими способами разде-
ления (промывка осадков при отстаивании и фильтровании).
2. Разделение суспензий и эмульсий
241
Таким образом, принципиально одни и те же методы приме-
нимы для разделения капельно-жидких и газовых неоднородных
систем.
2. Разделение суспензий и эмульсий
Основные параметры
Суспензии характеризуются весовым соотношением жидкой и
твердой фаз (Ж:Т). Это соотношение может быть выражено
через весовую долю х твердой фазы в суспензии
п = (Ж : Т) = ±=± (8-1)
Обозначив через рс и ртв< плотность суспензии и содержащей-
ся в ней твердой фазы, получим следующее выражение объем-
ной доли твердых частиц в суспензии:
х
„ Ртв. *Рс /о
q ~ т~—-—
1 Ртв.
Рс
Плотность рс определяют, исходя из того, что удельный
объем суспензии равен сумме объемов составляющих ее твер-
дой и жидкой фаз
Рс Ртв. рж
откуда
Рс = х
Ртв. Рж
где рж — плотность жидкой фазы.
Получаемый в результате разделения влажный осадок также
характеризуется отношением жидкой и твердой фаз:
где w — весовая доля жидкой фазы в осадке.
Аналогичные зависимости приложимы к эмульсиям, которые
состоят из двух жидких фаз Ж1 и Ж2 и соответственно характе-
ризуются отношением
«эм. == • ^^2
Вязкость суспензий и эмульсий определяется в зависимости от вяз-
кости р-о сплошной фазы и объемной концентрации q дисперсной фазы. Вяз-
кость разбавленных суспензий зависит от концентрации твердой фазы, но не
16 Зак 546,
242
Гл 8 Разделение жидких неоднородных систем.
зависит от размера твердых частиц и определяется по формуле А И Бачин-
ского
1* = М1 +4>5?) (8-4)
Вязкость эмульсий определяется по формуле
Р- = Но ------- (8-5)
1^1-1 *
V q
Материальный баланс разделения ' '
Рассмотрим материальный баланс разделения суспензий, как
наиболее распространенного процесса разделения жидких неод-
нородных систем.
Пусть Gc — количество разделяемой суспензии (в кг), Xi —
весовая доля твердой фазы в суспензии. В результате разделе-
ния получается осадок в количестве Goc кг с содержанием твер-
дой фазы %2 и влажностью w = 1 — Хг и жидкость, количество
которой равно 6Ж кг.
Тогда уравнения материального баланса будут иметь сле-
дующий вид:
для всей системы
Gc = Goc + Сж (8-6)
для твердой фазы
Gcxx — Goc х2 (8-7)
или
Осхг = Goc. (1 — w) (8-8)
Совместным решением уравнений (8-6) и (8-8) определяют
количество влажного осадка и количество жидкой фазы.
Пример 8-1. Определить объемную долю твердой фазы, плотность и вяз-
кость суспензии, если весовое соотношение жидкой и твердой фаз в суспен-
зии Ж Т = 6,7 Плотность твердой фазы рТв. = 3200 кг/м3, плотность жидкой
фазы рж= 1000 кг/м3 Вязкость жидкой фазы Цо = 0,001 н-сек/м2 (1 спз)
Решение Определяем весовую долю х твердой фазы в суспензии.
По условию
пс = Ж: Т = 1—= 6,7
с х
откуда
х = 0,13
Плотность суспензии по формуле (8-3) составит-
Рс = одз 1—одз = 1100 кг^9
3200 + 100Q
3. Общие сведения
243
Следовательно, объемная доля твердой фазы в суспензии по формуле
(8-2) равна
_ Хрс ___ 0,13 • 1100 __ q ЛДЛ7
q ~ “ 32оо “ 0,0447
По формуле (8-4) находим вязкость суспензии
|л = 0,001 (1 + 4,5 • 0,0447) 0,0012 н • сек!м* (1,2 спз)
А. ОТСТАИВАНИЕ
3. Общие сведения
Процесс осаждения под действием сил тяжести называется
отстаиванием.
Отстаивание суспензий протекает в несколько стадий, кото-
рые можно наблюдать, если тщательно перемешать разбавлен-
ную суспензию и поместить ее в стеклянный цилиндр (рис. 8-1).
Вначале твердые частицы рав-
номерно распределены в жид-
кости (рис. 8-1, а), но через ко-
роткий промежуток времени
они начинают осаждаться, при-
чем на дне цилиндра оседает
слой наиболее крупных твер-
дых частиц (рис 8-1,6, зона 4).
Над осадком образуется слой
сгущенной суспензии, в кото-
рой твердые частицы распола-
гаются настолько тесно, что
дальнейшее уплотнение слоя
Рис. 8-1. Схема процесса отстаивания:
а — д — стадии процесса. 1—4 — зоны системы.
возможно только путем вытеснения жидкости из промежут-
ков между частицами (зона стесненного осаждения 3). Выше
находится переходная зона, плотность которой уменьшается сни-
зу вверх по направлению к зоне исходной суспензии (зоне 2),
причем в обеих этих зонах частицы осаждаются свободно под
действием сил тяжести. Над зоной 2 расположен слой чистой
или осветленной жидкости (зона /). По мере отстаивания зоны/
и 3 возрастают (рис. 8-1, в, г), причем одновременно происходит
уплотнение зоны 3.
Отстаивание заканчивается, когда зона 2 и переходная зона
исчезают и завершается уплотнение сгущенной суспензии, что
соответствует полному разделению ее на осадок и осветлен-
ную жидкость (рис. 8-1,6).
Состояние, при котором переходная зона исчезла, но еще* не
началось уплотнение сгущенной суспензии (зоны 5), носит на-
16*
244
Гл. 8. Разделение жидких неоднородных систем
звание критической точки. При этом различают суспензии двух
типов:
а) суспензии, в которых скорость осаждения постоянна до
критической точки и затем уменьшается с уплотнением зоны 3;
б) суспензии, в которых скорость осаждения уменьшается с
самого начала отстаивания, причем не появляется четкой грани-
цы между осветленной жидкостью и сгущенной суспензией, т. е.
границы, соответствующей критической точке.
В процессе непрерывного отстаивания в аппарате образуются
те же зоны, что и при периодическом отстаивании, но эти зоны
не изменяются по высоте.
4. Скорость осаждения (отстаивания)
В главе 6 (стр. 173) был рассмотрен общий закон движения
тел в жидкости и определена скорость свободного осаждения
твердых частиц. С увеличением концентрации твердой фазы сус-
пензии сопротивление среды движению осаждающихся частиц
начинает зависеть не только от размера и формы частиц, но и
от концентрации твердой фазы в суспензии. Осаждение в огра-
ниченном объеме при большой концентрации твердой фазы, ко-
гда соседние твердые частицы при движении соприкасаются
друг с другом, называется стесненным осаждением. При стес-
ненном осаждении сопротивление движению твердых частиц
складывается из сопротивления среды и сопротивления, обус-
ловленного трением и ударами твердых частиц друг о друга.
Вследствие этого скорость стесненного осаждения всегда
меньше скорости свободного осаждения тех же частиц.
Объемная доля жидкости в суспензии составляет
£ = - Лж....
VTB.
где Уж — объем жидкости в суспензии;
1/тв. — объем твердых частиц в суспензии.
В концентрированных суспензиях жидкость движется по из-
вилистым каналам между твердыми частицами и сопротивление
среды является функцией е, которую обозначим Ф(е). Вместе с
тем движение твердых частиц под действием сил тяжести (при
отстаивании) является в большинстве случаев ламинарным. По-
этому, подставив в общую формулу (6-91) сопротивления
среды значение коэффициента Ф = (СТР- 172), полу-
чим частное выражение сопротивления среды R для ламинарной
области, или так называемый закон Стокса:
R = Зк
(8-9)
4. Скорость осаждения (отстаивания)
245
Соответственно сопротивление среды в условиях стесненного
осаждения может быть выражено следующим образом:
= жтт = (8-10)
'ст- Ф (е) Ф (е) v '
При плотности твердой фазы ртв. и плотности жидкой фа-
зы рж плотность суспензии можно определить по формуле
Рс == ®Рж I (1 ®) Ртв.
Разность плотностей Др твердой фазы и суспензии будет
равна:
Др — Ртв. Рс == Ртв. [®Рж I ®) Ртв.] (Ртв. Рж) ®
Подставляя значение Др в выражение силы тяжести Р
(стр. 174) и приравнивая Р сопротивлению среды R, получим:
nd3 , .3m d^w
6 S (Ртв. Рж) ® Ф
Откуда после сокращений находим скорость жидкости отно-
сительно твердых частиц. Она равна скорости движения твердых
частиц относительно жидкости
= (8.И)
Однако для расчета процесса отстаивания необходимо опре-
делить скорость движения твердых частиц не относительно жид-
кости, а относительно стенок аппарата (отстойника). При этом
следует учесть, что объемные скорости обеих фаз при осаждении
равны, так как объем твердых частиц, опускающихся вниз, вы-
тесняет вверх равный объем жидкости.
Пусть слой суспензии в- аппарате имеет площадь основания F
и высоту Н. Доля площади поперечного сечения слоя суспензии,
доступная для прохода жидкости, равна Fs. Путь, пройденный
в единицу времени вытесненной вверх жидкостью, или скорость
подъема жидкости, составляет:
Few
—p- = VW
Эта скорость равна искомой скорости осаждения w0 твердых
частиц:
W0 = £W
Подставляя в это выражение значение w из уравнения (8-11),
получим окончательную формулу :
w»-dig(l>iVMe2a>(£) (8’|2)
246
Гл. 8. Разделение жидких неоднородных систем
По опытным данным для шарообразных твердых частиц ве-
личина Ф(е) при е > 0,7 определяется по уравнению
Ф (е) = 10-1'82(1”*) (8-13)
Для высококонцентрированных суспензий, содержащих твер-
дые частицы шарообразной формы при е < 0,7.
1=±Ф(£) = 0,123 (8-14)
В более общей форме, т. е. для любой области осаждения,
уравнение (8-12) может быть выражено следующим образом:
= ^св.£2Ф (е) (8-15)
где дасв. — скорость свободного осаждения в данной области
осаждения.
Соответственно для суспензий при 0,7 с учетом выраже-
ния (8-14) скорость осаждения составит:
^0 = ^св. (8-16)
Пример 8-2. Определить скорость стесненного отстаивания суспензии
в условиях примера 6-14 (стр. 175), если содержание в ней твердой фазы
х = 30%. Плотность суспензии Рс — 1440 кг/м3, плотность твердой фазы
Ртв. = 2750 кг/м3.
Решение. В соответствии с формулой (8-2) объемная доля твердых
частиц в суспензии составляет:
£ = 1—0,157 = 0,843
По формуле (8-13) находим:
Ф(е) = Ю"1’82 0*157 = 10“0,286 0,52
Согласно примеру 6-14 скорость свободного осаждения о>о = 0,8 м/ч. Ско-
рость стесненного осаждения определяем по формуле (8-15)
w0 = 0,8 • 0,8432 • 0,52 = 0,3 м/ч
5. Устройство отстойников
Аппараты, применяемые для разделения суспензий, назы-
ваются отстойниками или сгустителями. Различают отстойники
периодического и непрерывного действия, причем непрерывно-
действующие отстойники делят на одноярусные, двухъярусные
и многоярусные.
Периодически действующие отстойники представляют собой
низкие бассейны без перемешивающих устройств. Отстойник за-
полняется суспензией, которая отстаивается в неподвижном
5. Устройство отстойников
247
Рис. 8-2. Одноярусный гребковый отстойник непрерывного
действия:
/ — цилиндрический резервуар; 2— кольцевой желоб; 3 — мешалка; 4 — труба
для подачи суспензии; 5 — диафрагмовый насос.
248
Гл 8. Разделение жидких неоднородных систем
состоянии. По окончании отстаивания спускают осветленную
жидкость и удаляют вручную или смывают водой осадок, после
чего вновь заполняют отстойник суспензией.
Наиболее распространены непрерывнодействующие одно-
ярусные гребковые отстойники (рис. 8-2). Отстойник представ-
ляет собой невысокий цилиндрический резервуар 1 со слегка
коническим днищем и кольцевым прямоугольным желобом 2
около верхнего края. В резервуаре имеется мешалка 3 с гребка-
ми, делающая 2,5—20 об/ч. Суспензия непрерывно подается
сверху через трубу 4. Осветленная жидкость стекает через верх-
ний желоб 2, сгущенная суспензия оседает на днище и медленно
перемещается гребками к центральному патрубку, через кото-
рый она откачивается диафрагмовым насосом 5. Содержание
жидкости в откачиваемом продукте колеблется от 35 до 55%.
Такие отстойники, рассчитанные йа очень большую произво-
дительность, часто снабжают мешалкой с краевым приводом в
виде радиальной фермы. Ось ее вращения совпадает с осью ап-
парата, а наружный край опирается на каретку с электродвига-
телем. Каретка движется по рельсам вдоль борта резервуара.
Кроме непрерывности действия, гребковые отстойники имеют
следующие достоинства: 1) равномерная плотность осадка и воз-
можность ее регулирования путем изменения производительно-
Цсходная
Рис 8-3. Двухъярусный отстой-
ник:
/ — верхнее отделение; 2 —нижнее
отделение; 3 — соединительная труба.
сти откачивающего насоса, 2) луч-
шее обезвоживание осадка при лег-
ком взбалтывании сгущенной сус-
пензии мешалкой, 3) механизация
процесса (один рабочий может об-
служить до 40 аппаратов).
Недостатком таких отстойников
является их громоздкость.
Значительно более компактны двухъ-
ярусные и многоярусные отстойники, пред-
ставляющие собой по существу несколько
отстойников, расположенных друг над
другом.
Применение таких отстойников особен-
но целесообразно в условиях холодного
климата, когда они должны устанавливать-
ся внутри зданий и надо наиболее рацио-
нально использовать производственную пло-
щадь.
В двухъярусных отстойниках верхнее или нижнее отделения работают
изолированно друг от друга (закрытый тип), либо сообщаются друг с другом
(открытый и сообщающийся типы).
В отстойнике, показанном на рис. 8-3, верхнее отделение / и нижнее от-
деление 2 соединены друг с другом трубой 3, которая опущена ниже уровня
сгущенной суспензии в отделении 2. Исходная суспензия подается раздельно
В оба отделения, сгущенный продукт откачивается только из нижнего отде-
6. Расчет отстойников 249
ления. Осветленная жидкость отводится из верхней части каждого отделения
отстойника
В описанном отстойнике давление столба более тяжелой суспензии урав-
новешивается давлением более высокого столба осветленной жидкости Из-
меняя высоту последнего, можно регулировать высоту столба сгущаемой сус-
пензии и распределение питания.
6. Расчет отстойников
Пусть в результате отстаивания в течение т сек суспензия
разделяется на слой сгущенной суспензии (шлама) и сЛой освет-
ленной жидкости высотой h м. При поверхности осаждения F м2
объем полученной осветленной жидкости составляет hF м3. Со-
ответственно объем осветленной жидкости, полученной в еди-
ницу времени, равен
м3/сек (8-17)
Осаждающиеся со скоростью w0 м/сек твердые частицы про-
ходят в 1 сек путь, равный оу0, а за т сек — путь w0~. В то же
время этот путь равен h м. Таким образом
wot = h
Подставив значение h в выражение (8-17), получим:
= м3/сек (8-18)
Из уравнения (8-18) видно, что производительность отстой-
ника пропорциональна поверхности осаждения и не зависит от
высоты отстойника.
Из этого уравнения находим необходимую поверхность от-
стаивания
v 2
F =—- м2
w0
Учитывая, что объем V осветленной жидкости при ее
составляет V = —— » получим:
Рж
р == G*
Рж^о
(8-19)
ПЛОТНОСТИ Рж KZjMZ
(8-20)
Количество суспензии, поступающей в отстойник, равно Gc кг/сек, весо-
вое содержание сухого вещества в ней составляет Xj долей.
В результате отстаивания все сухое вещество переходит в осадок, вес
которого равен разности количеств исходной суспензии и осветленной жид-
кости Ос — Ож.
Из уравнений (8-6) и (8-7) находим количество осветленной жидкости:
Ож = Gc
(8-21)
250
Г л. 8. Разделение жидких неоднородных систем
При подстановке значения вж в уравнение (8-20) получим:
М М2
Рж^О \ х2 /
(8-22)
Обозначив отношение весового содержания сухого вещества в суспензии
и осадке — =р, определим поверхность осаждения:
•^2
м‘ (8-23)
Рж^о
При выводе формулы (8-23) не учитывался характер движения жидкости
в отстойнике (возможность вихреобразований) и допускалось, что потоки
равномерно распределяются по всей площади аппарата. Для определения
необходимой поверхности отстаивания следует теоретическую поверхность,
рассчитанную по формуле (8-23), умножить на некоторый коэффициент, учи-
тывающий влияние неравномерности отстаивания, вихреобразований и дру-
гих факторов на реальный процесс отстаивания. Ориентировочно этот коэф-
фициент можно принять равным 1,3.
Соответственно поверхность осаждения, или площадь поперечного сече-
ния отстойника, определяют по уравнению:
1,3GC
Рж^о
(8-24)
В формулах (8-23) и (8-24) величина w0 представляет собой скорость
свободного осаждения наименьших твердых частиц. При стесненном осаж-
дении вместо ау0 подставляют wCT_.
Высоту отстойника обычно не рассчитывают, а принимают равной
до 2,5—3,5 м.
Пример 8-3. Определить производительность, поверхность и диаметр
непрерывнодействующего гребкового отстойника для осветления суспензии
в количестве Gc = 20 000 кг!ч. Концентрация твердой фазы в суспензии
Xi = 20%, концентрация сгущенной суспензии х2 = 50%, скорость осаждения
суспензии w0 — 0,5 м!ч, плотность жидкой фазы суспензии р = 1050 кг/м?.
Решение. Определяем производительность отстойника по твердой фазе:
GTB. = 20 000 • 0,20 = 4000 кг!ч
^сг.
Производительность отстойника по сгущенной суспензии:
GTB 4000 0ПЛЛ .
—— = x-g- = 8000 кг ч
х2 0,5
Соответственно производительность отстойника по осветленной жидкости
составит:
Ож = Gc — Gcr. = 20 000 — 8000= 12 000 кг!ч
Находим отношение содержания сухого вещества в суспензии и осадке:
р = = -|£ = 0,4
г х2 50
Определяем поверхность отстойника по формуле (8-24)
Р 1,3 - 20 000-(1-0,4) 2
Г “ 1050 0,5
7. Осаждение в поле центробежных сил
251
откуда диаметр отстойника составляет:
4 • 29,6
3,14
= 6,15 м
Принимаем с запасом D «= 7 м.
7. Осаждение в поле центробежных сил
Разделение неоднородных жидких систем может проводиться
также под действием центробежных сил, в этом случае происхо-
дит гораздо более интенсивное разделение, чем под действием
сил тяжести.
Рис. 8-4. Мультигидроциклон:
7, 2 — решетки; 3 — труба для подачи суспензии; 4— патру-
бок для удаления слива; 5 — патрубок для удаления песков.
Центробежное осаждение производится в гидроциклонах
(стр. 99) и в центрифугах, работа и устройство которых будут
описаны ниже.
Для более эффективного разделения твердой и жидкой фаз
применяют гидроциклоны специальных конструкций, например
мультигидроциклоны (рис. 8-4), аналогичные батарейным ци-
клонам — аппаратам, широко применяемым для очистки газов
(стр. 330). Мультигидроциклоны состоят из параллельно рабо-
тающих элементов (гидроциклонов) диаметром 10—150 лии. Ци-
клонные элементы сверху и снизу герметично закреплены
252
Гл 8 Разделение жидких неоднородных систем
в решетках 1 и 2. Суспензия поступает на разделение снизу по
трубе <5, осветленная жидкость — слив удаляется из циклонных
элементов через общий патрубок 4, сгущенная суспензия—пески
отводится через нижнюю камеру в общий патрубок 5. При ис-
пользовании циклонных элементов небольшого диаметра вели-
чина центробежных сил значительно возрастает (стр. 329).
Б. ФИЛЬТРОВАНИЕ
8. Общие сведения
Фильтрованием называют процесс разделения суспензий при
помощи пористой перегородки, пропускающей жидкость (филь-
трат) и задерживающей взвешенные в ней твердые частицы.
Различают следующие виды фильтрования:
1) фильтрование с образованием слоя осадка на фильтро-
вальной перегородке;
2) сгущение — отделение твердой фазы от жидкой не в виде
осадка, а в виде высококонцентрированной (сгущенной) суспен-
зии;
3) осветление — фильтрование жидкостей с незначительным
содержанием твердой фазы.
Можно условно считать, что фильтрование с образованием
осадка характеризуется содержанием в фильтруемой суспензии
более 1% объемн. твердой фазы, осветление—менее 0,1 %. Сус-
пензии, содержащие 0,1—1% твердой фазы, перед фильтрова-
нием желательно подвергать предварительному сгущению в от-
стойниках.
Фильтрование с образованием осадка наиболее распростра-
нено. В большинстве случаев твердые частицы в первые момен-
ты с начала фильтрования проходят через поры фильтровальной
перегородки, но вскоре накапливаются на ней, и через фильтр
начинает протекать только осветленная жидкость — фильтрат.
Таким образом, в этом процессе образующийся слой осадка
играет роль основной фильтрующей среды.
Фильтрование с образованием осадка наиболее часто прово-
дится при постоянном давлении, так как этот режим процесса
прост и удобен в практическом отношении. Однако при проведе-
нии процесса под постоянным давлением скорость фильтрования
с увеличением слоя осадка будет уменьшаться (стр. 255). Для
поддержания постоянной скорости фильтрования приходится уве-
личивать перепад давления на фильтре по мере протекания про-
цесса. В некоторых случаях фильтрование проводят при посто-
янной скорости, например в фильтрпрессах (стр. 259).
В процессе фильтрования очень вязких жидкостей с неболь-
шим содержанием мелких твердых частиц последние проникают
8. Общие сведения
253
в поры фильтровальной перегородки и задерживаются в них.
При этом на поверхности фильтровальной перегородки почти не
образуется слоя осадка. В таком процессе, называемом фильтро-
ванием с закупориванием пор, по мере задержки все большего
количества твердых частиц в порах фильтровальной перего-
родки ее сопротивление быстро возрастает и скорость фильтро-
вания уменьшается. Поэтому фильтрования с закупориванием
пор стремятся избежать, однако на практике фильтрование
иногда протекает с частичной закупоркой пор; возможно также
сочетание процессов фильтрования с образованием осадка и
с частичным закупориванием пор.
Ниже рассматривается только наиболее распространенный
процесс фильтрования с образованием осадка. '
Сгущение применяется для частичного отделения жидкой фа-
зы путем фильтрования, т. е. для той же цели, что и отстаивание
под действием сил тяжести. Однако сгущение путем фильтрова-
ния можно проводить в значительно более компактной аппара-
туре и получить более чистый фильтрат.
V Осветление жидкостей часто производится путем добавки
вспомогательны^ веществ в суспензию или создания намывного
слоя этих веществ на фильтре. <
В качестве вспомогательных веществ применяют кизельгур и
диатомит, а также бумажную массу, уголь, асбест, отбеливаю-
щую землю и др.
Эти вещества, накапливаясь на фильтре, задерживают
очень мелкие частицы осадка (диаметром 1 мк и менее), а неко-
торые из них, например отбеливающая земля и активированный
уголь, адсорбируют на поверхности мельчайшие твердые ча-
стицы.
Вспомогательные вещества добавляют в количестве 0,1—0,5%
(иногда до 2%) от веса суспензии и после промывки часто вновь
используют. Иногда вместо добавления в суспензию вспомога-
тельные вещества намывают в виде слоя небольшой толщины на
поверхность фильтра, что значительно облегчает отделение тон-
кодисперсных взвешенных частиц.
Фильтрование часто сопровождается осаждением частиц под
действием сил тяжести. Осаждение способствует фильтрованию,
если движение суспензии вследствие разности давлений и дви-
жение осаждающихся частиц совпадают по направлению, т. е.
если фильтровальная перегородка горизонтальна и находится
под слоем суспензии. В противном случае осаждение частиц
препятствует фильтрованию.
Получаемые при фильтровании осадки делятся на сжимае-
мые, частицы которых деформируются и размер пор умень-
шается с повышением давления, и несжимаемые, в которых
254
Гл. 8. Разделение жидких неоднородных систем
размер и форма частиц практически не меняются с изменением
давления. Кроме того, различают кристаллические, аморфные и
коллоидные осадки, причем аморфные и коллоидные осадки
отделяются от жидкости труднее кристаллических и являются
труднофильтруемыми.
Для более полного удаления из осадка находящейся в нем
жидкости (маточного раствора) осадки промывают. Иногда для
полноты промывки фильтрование проводят в двух последова-
тельно работающих фильтрах, осадок из первого фильтра сме-
шивают с промывной жидкостью и вновь отфильтровывают
{двухступенчатое фильтрование).
9. Теория фильтрования
При фильтровании происходит движение фильтрата через
слой осадка и фильтровальную перегородку. В слое осадка жид-
кость движется через поры — капиллярные каналы переменного
сечения и различной кривизны. Для такого движения жидкости
через слой справедливо приведенное на стр. 178 уравнение
(6-109). Как следует из этого уравнения, сопротивление фильт-
рованию R при прочих равных условиях уменьшается с возра-
станием пористости осадка и уменьшением вязкости фильтрата.
Величина R складывается из сопротивлений осадка /?ос. и
фильтровальной перегородки 7?пер.:
R~Roc 4~А*пер.
Сопротивление осадка пропорционально его толщине 8:
Яос. = г5 (8-25)
где г—коэффициент пропорциональности, называемый удель-
ным сопротивлением осадка.
Удельное сопротивление осадка представляет собой сопро-
тивление единицы объема осадка высотой 1 м, отложенного на
площади 1 м2, и может быть определено опытным путем. *
Из выражения (6-109) находим размерность сопротивления
фильтрованию:
г ___г hpF~ I_г н • м2 • сек 1_Г н • сек 1
им — |—у-J — [ Ж2.жз -J — мз J
Соответственно размерность удельного сопротивления осадка:
г 1 Г Roe 1 Г«- сек)м21 Г н • сек 1
и=t-г- J=L—5—1 =
Объем осадка, отложившегося на фильтре, можно выразить
как произведение площади F фильтра на толщину Посадка. Если
* В. А. Жужи ко в, Фильтрование, Госхимиздат, 1961, стр. 86 и сл,
9. Теория фильтрования
255
обозначить через и объем осадка (в м3), приходящийся на 1 м3
фильтрата, то объем осадка, отложившегося после образования
V м3 фильтрата, будет равен uV. Следовательно:
Fl = uV (8-26)
Отсюда толщина слоя осадка составляет:
Z = u-^ = uq (8-27)
q = м3!м3 (8-28)
Величина q представляет собой объем фильтрата, получае-
мого с единицы поверхности фильтра за время фильтрования т,
и называется удельной производительностью фильтра.
Подставив значение 8 в уравнение (8-25), найдем сопроти-
вление осадка:
/?ос. = ruq (8-29)
и получим следующее выражение для сопротивления фильтро-
ванию:
# = Roc. “+* Rncp. = ruQ + -ftnep. (8-30)
Из общего закона (6-109) движения через слой, разделив обе
части этого уравнения на Ft, можно найти скорость движения
жидкости через слой:
= 77 = y = • сек (8-31)
Как видно из уравнений (8-25) и (8-31), сопротивление R по
мере образования осадка и увеличения его толщины возрастает,
> а скорость фильтрования уменьшается. Перепишем уравнение
(8-31) в дифференциальной форме и подставим вместо R его
> значение по формуле (8-30). Тогда
ч W = ^=w~+R • (8-32)
li'ii гиЧ ^пер. ' '
# откуда
ruq Япер. ,
=-----------dq
Интегрируя это выражение в пределах от 0 до т и от 0 до q,
найдем продолжительность фильтрования:
<7 п
f ( ruq Япер \
о
256
Гл 8. Разделение жидких неоднородных систем
После интегрирования получим:
ruq2 Rn^.q
2Д/> \р СвК
(8-33)
Решая уравнение (8-33) относительно q, определим удельную
производительность фильтра:
( “^пер. \2 2 Др / /?пер. \
Я = У (—) + w (8-34)
Из уравнений (8-34) и (8-32) следует, что по мере протека-
ния процесса фильтрования величина q увеличивается, а ско-
рость процесса w соответственно уменьшается.
Промывка осадка соответствует фильтрованию при постоян-
ной высоте слоя осадка на фильтровальной перегородке.
Скорость промывки wnp. определяется по уравнению, ана-
логичному уравнению (8-32), и является постоянной. Следова-
тельно
—.—.—— м3!м2 сек (8-35)
ПР‘ ^пр.«? + ^пер. ' v }
(8-36)
где Дрпр.— перепад давления при промывке;
гпр. — удельное сопротивление осадка при промывке.
Величина гпр. определяется по формуле:
Р'Пр.
ГпР.=-~г
где (х и р-Пр. — вязкость фильтрата и промывной жидкости;
г—удельное сопротивление осадка при фильтрации.
Если расход промывной воды на 1 ж3 влажного осадка обо-
значить через L м3/м3, то объем промывной жидкости, получае-
мой с единицы поверхности фильтра, составит:
1/пр. = Luq м3/м2 (8-37)
По удельному объему промывной жидкости Vnp. и скорости
промывки wnp. можно определить продолжительность промывки:
т — Ипр- — LUq + гр„ /О ООЧ
гпр. w сек' (8-38)
2>Рпр.
пр.
10. Устройство фильтров
Промышленные фильтры разделяются по режиму работы на
фильтры периодического и непрерывного действия, а по величине
рабочего давления — на вакуум-фильтры и фильтры, работаю-
щие под давлением.
10. Устройство фильтров
257
Классификация фильтров по этим признакам и по конструк-
тивным особенностям приведена ниже:
Фильтры
Типы
Вакуум-фильтры
Периодического
действия
-> Нутч-фильтры открытые
Мешочные фильтры
Барабанные фильтры
Непрерывного
действия
Дисковые фильтры
Карусельные фильтры
Ленточные фильтры
Фильтры, работающие
под давлением
Периодического
действия
Патронные фильтры
Барабанные фильтры
Непрерывного
действия
Дисковые фильтры
17 Зак 546
258
Гл 8 Разделение жидких неоднородных систем
Нутч-фильтры
Различают два вида нутч-фильтров: 1) открытые, работаю-
щие при разрежении, 2) закрытые, работающие под избыточным
давлением до ~4 ат.
Открытый нутч-фильтр (рис.
угольный или цилиндрический а
8-5) Представляет србой прямо-
ппарат с фильтровальной пере-
городкой, расположенной не-
сколько выше его днища. Пе-
регородка состоит из пористых
керамических плиток или тка-
ни, уложенной на решетке. По-
сле заполнения фильтра сус-
пензией и включения вакуума
фильтрат проходит сквозь пе-
Рис. 8-5. Открытый нутч-фильтр:
/—корпус; 2 —фильтровальная перегородка
регородку, а осадок задержи-
вается на ней. После фильтрования осадок промывают (если
это необходимо) и удаляют из фильтра сверху вручную.
Достоинства открытых нутч-фильтров: 1) возможность тща-
тельной промывки осадков, 2) легкость защиты от коррозии,
3) простота и надежность конструк-
ции.
Недостатки: 1) малая скорость
фильтрования, так как разность
давлений практически не превы-
шает 0,75 ат, 2) громоздкость уста-
новки, 3) ручная выгрузка осадка.
Выгрузка осадка значительно об-
легчается и ускоряется в открытых
нутч-фильтрах с откидными днища-
ми и в опрокидывающихся нутч-
фильтрах. Откидное днище крепит-
ся к корпусу фильтра на болтах и
откидывается на шарнире. В опро-
кидывающихся нутч-фильтрах весь
корпус фильтра опрокидывается
вручную (при помощи червячного
устройства) либо посредством гид-
Рис. 8-6. Закрытый нутч^
фильтр:
/—корпус; 2—фильтровальная пере-
городка, 3 — люк.
равлического механизма.
В закрытом нутч-филътре, приведенном на рис. 8-6, фильт-
рование производится под давлением сжатого воздуха или
инертного газа. Осадок выгружают через откидное днище или
через боковой люк 3.
Достоинства закрытых нутч-фильтров: 1) значительная ско-
рость фильтрования, 2) возможность отделения трудно филь-
10 Устройство фильтров
259
труемых осадков, 3) пригодность для разделения суспензий,
выделяющих огнеопасные или токсичные пары.
Недостатком таких фильтров является ограниченная произво-
дительность, обусловленная тем, что изготовление их с большой
фильтрующей поверхностью
затруднительно, поскольку
аппараты работают под из-
быточным давлением.
Фильтрпрессы
Фильтрпресс (рис. 8-7)
состоит из ряда чередую-
щихся друг с другом плит 1
и рам 2. Плиты и рамы опи-
раются боковыми ручками
на параллельные брусья ста-
нины 5 пресса. На станине
имеются концевая непод-
вижная плита 3 и переме-
щающаяся на роликах под-
вижная плита 4. Между пли-
тами 3 и 4 при помощи спе-
циального устройства плот-
но зажимается комплект
плит и рам; между плитами
и рамами помещаются пере-
городки («салфетки») из
фильтровальной ткани. Сал-
фетки обычно навешивают-
ся на плиты и покрывают
их боковые поверхности.
Боковые поверхности
плиты фильтрпресса (рис.
8-8, а) по краям плоские и
гладкие и во внутренней ча-
сти рифленые. Желобки пли-
ты сообщаются с каналом в
нижней ее части, который
заканчивается краником
(или пробкой) для отвода
фильтрата. У верхней кром-
ки плиты расположены три
отверстия: центральное — для
них —
для промывной жидкости. Плита
прохода суспензии, два край-
покрыта салфеткой из
260
Гл. 8 Разделение жидких неоднородных систем
ткани, в салфетке прорезаны отверстия, совпадающие с отвер-
стиями плиты.
Полая рама фильтрпресса (рис. 8-8, б) помещается между
двумя плитами и образует камеру для осадка. Отверстия, имею-
щиеся в рамах, совпадают с отверстиями плит, благодаря чему
в фильтрпрессе создаются сквозные каналы для прохода суспен-
зии и промывной воды. Эти каналы заканчиваются у концевой
плиты. Канал для суспензии сообщается через отверстия с вну-
тренними полостями рам. Поэтому фильтруемая суспензия по-
ступает только внутрь рам фильтрпресса.
а 6
Рис. 8-8. Плиты и рамы фильтрпресса:
а —плита (справа разрез по фильтровальной плите, слева —по промывной плите);
б— рама.
Схема работы фильтрпресса показана на рис. 8-9.
Суспензия под давлением подается в фильтрпресс при по-
мощи насоса, монтежю или поступает под гидравлическим да-
влением из напорного бака. Фильтрат продавливается чере^
ткань, стекает по желобкам плит и через отводные каналы и
краники сливается в корыто, установленное на полу вдоль
фильтра. Из корыта фильтрат стекает в сборник или, если филь-
трат не представляет ценности, то выводится из процесса. Твер-
дые частицы осаждаются на ткани, причем наиболее часто филь-
трование ведется до заполнения рам осадком. Осадок промы-
вают (если это необходимо) или только продувают паром либо
воздухом для удаления жидкости. После этого плиты и рамы
раздвигаются и осадок частично падает под действием силы тя-
жести в сборник, установленный под фильтром. Остальную часть
осадка выгружают вручную лопаткой.
Для фильтрования, сопровождающегося промывкой осадка,
применяют фильтрпрессы, имеющие плиты двух видов: филь-
тровальные и промывные. Промывная плита 3 (рис. 8-9, а) отли-
чается от фильтровальной плиты 1 только тем, что в первой ка-
налы для воды соединены отверстиями с боковыми поверхностя-
ми плиты. При промывке (рис. 8-9,6) сливные краники про-
мывных плит закрываются. Вследствие этого промывная вода
10. Устройство фильтров
261
проходит через желобки про-
мывной плиты и покрывающую
ее ткань в осадок и движется
последовательно через слой
осадка, ткань и желобки филь-
тровальной плиты, после чего
сливается через краник. Рас-
положение промывных плит
видно из рис. 8-9, б, на кото-
ром стрелками показано дви-
жение промывных вод через
осадок.
Плиты и рамы фильтр-
прессов изготовляют из чу-
гуна или древесины.
В фильтрпрессах с дере-
вянными плитами и рамами
допустимо абсолютное давле-
ние до 5 ат, в фильтрпрессах
с чугунными плитами и ра-
мами — до 15 ат.
Сжатие плит и рам произ-
водится посредством винтово-
го, гидравлического или элект-
ромеханического зажимов.
При помощи винта со штур-
валом комплект рам и плит
зажимается вручную, что тре-
бует значительных физических
усилий. Таким способом труд-
Рис. 8-9. Схема работы фильтрпресса}
а —фильтрование; б—промывка осадка
7 — фильтровальная плита; 2 —рама, 3— про-
мывная плита.
но достичь плотного сжатия
при числе рам больше 30—35.
Электромеханический зажим действует от электродвигателя
через редуктор и зубчатую передачу. Зажим автоматически вы-
ключается по достижении определенного давления сжатия.
Гидравлический зажим (рис. 8-10) состоит из цилиндра /
и плунжера 2, который выдвигается давлением воды, нагнета-
емой в цилиндр, и упирается хвостовой частью (упорный
валик 3) в подвижную плиту 4, сжимая плиты и рамы.
Достоинства фильтрпрессов: 1) большая поверхность филь-
трования на единицу площади, занимаемой фильтром, 2) значи-
тельная движущая сила процесса (перепад давления); 3) воз-
можность контроля работы и отключения отдельных плит
(путем закрытия краника, через который вытекает мутный
262
Гл 8. Разделение жидких неоднородных систем
фильтрат), 4) простота и надежность эксплуатации благодаря
отсутствию движущихся частей.
Недостатки: 1) ручное обслуживание, 2) недостаточно полная
промывка осадка, 3) быстрый износ фильтровальной ткани вслед-
ствие частой разборки фильтра и работы его под давлением.
Рис. 8-10. Гидравлический зажим фильтрпресса:
7 —цилиндр; 2—плунжер; 5 — упорный валик; 4— подвижная
плита.
В СССР разработан автоматический камерный фильтрпресс
(рис. 8-11). Плиты 1 фильтрпресса расположены друг над дру-
гом горизонтально. Сверху каждая плита покрыта щелевым си-
том 3, над которым находится фильтровальная ткань 2, которая
представляет собой бесконечное полотно, перемещаемое систе-
мой роликов, работающих от общего привода. Снизу каждая
плита снабжена коническим днищем 4 с трубкой для отво-
да фильтрата. Зазор между фильтровальными плитами соста-
tO Устройство фильтров
2&3
вляет 25 мм, для уплотнения этого зазора при фильтровании
имеются специальные резиновые шланги 5, укрепленные на
нижней поверхности каждой плиты по ее периметру.
При подаче внутрь шланга воды под избыточным давлением
8—10 ат шланг раздувается и, как показано на рис. 8-11, при-
жимает фильтровальную ткань к плите. При этом шланг уплот-
Рис. 8-11. Автоматический камерный фильтрпресс:
/—плиты; 2 — фильтровальная ткань; 3 — щелевое сито, 4 — коническое днище, 5 — резиновый
шланг, 6, 7 —ножи; в—камера регенерации
няет зазор между соседними плитами и образует между ними
фильтровальную камеру. По завершении стадии фильтрования и
образования осадка снижают давление внутри шланга, при этом
шланг сжимается и между плитами образуется зазор, доста-
точный для свободного перемещения фильтровальной ткани со
слоем осадка, толщина которого составляет 5—20 мм.
При вращении системы роликов осадок на ткани выходит из
пространства междуz плитами и снимается ножами 6, в месте
огибания тканью роликов. Дополнительная очистка фильтро-
вальной ткани от осадка производится ножами 7. С последней
264
Гл 8' Разделение жидких неоднородных систем
(нижней) плиты ткань поступает в камеру регенерации 8, где
промывается и окончательно очищается скребками.
Фильтрование и промывка осадка производятся при избы-
точном давлении р < 6 ат. Все операции в процессе фильтро-
вания осуществляются автоматически.
Фильтрпрессы такой конструкции имеют фильтровальную по-
верхность F = 5—30 Л12.
Мешочные фильтры
Эти фильтры состоят из ряда вертикальных фильтроваль-
ных элементов (тканевые мешки, натянутые на каркасы), на-
ходящихся в горизонтальном или вертикальном корпусе.
Горизонтальный мешочный фильтр (рис. 8-12) представляет
собой цилиндрический, слегка наклонный аппарат, в котором
Рис. 8-12. Горизонтальный мешочный фильтр:
7- корпус, 2—фильтровальные элементы; 3— ролики, 4—съем-
ная крышка.
расположены 6—12 прямоугольных фильтровальных элементов 2.
Элементы жестко соединены с передней съемной крышкой 4 и
перемещаются вместе с ней на роликах 3 по рельсам, располо-
женным вдоль корпуса 1 аппарата. Отдельный элемент фильтра
(рис. 8-13) состоит из вваренной в полую раму 1 толстой метал-
лической сетки 2, этот каркас обтянут мешком 3 из фильтро-
вальной ткани.
10 Устройство фильтров
265
А
Рис. 8-14. Вертикаль-
ный мешочный фильтр
1 — корпус; 2 — фильтро
вальные элементы; 3 — кол-
лектор для отвода фильтра-
та, / — патрубок для вы-
грузки осадка.
г
Рама элемента имеет отводную трубку и краник для слива
фильтрата. Перед фильтрованием элементы вдвигают в корпус,
плотно закрепляют болтами съемную крышку и заполняют кор-
пус суспензией под давлением (ризб << 4 апг). Фильтрат проходит
через ткань и каркасы элементов, затем сливается через отвод-
ные трубки в общий желоб, установлен-
ный возле фильтра. Когда на ткани об-
разуется достаточный слой осадка, кор-
пус фильтра освобождают от суспензии
и промывают осадок водой под давле-
нием; промывные воды движутся по пути
фильтрата. После про-
мывки осадка сливают из
корпуса воду и просуши-
вают осадок сжатым воз-
духом. При помощи руч-
ной лебедки фильтро-
вальные элементы с
крышкой выдвигают из
корпуса и сбрасывают с
них осадок струей возду-
ха, подаваемого внутрь
элементов.
Отдельные операции
процесса фильтрования
осуществляются
фильтре при
автоматического
в этом
помощи
устрой-
ства.
Значительно более
компактен и удобен в
эксплуатации вертикаль-
ный мешочный фильтр
(рис. 8-14). В вертикаль-
ном корпусе 1 установле-
ны фильтровальные эле-
Рис 8-13. Элемент
горизонтального
мешочного филь-
тра:
/—полая рама; 2 — ме-
таллическая сетка;
3 — тканевый мешок;
4 — осадок.
менты 2, состоящие из каркаса в виде рифленой прямоуголь-
ной пластины, окаймленной трубчатой рамой. Каркас обтянут
снаружи фильтровальной тканью. Фильтрат отводится через
верхнюю чдсть каждой рамы, которая соединена с общим кол-
лектором 3, расположенным внутри фильтра. Осадок удаляется
сжатым воздухом или водой через патрубок 4 в коническом
днище корпуса.
Фильтр работает под избыточным давлением до 4 ат; аппарат
герметичен и не имеет движущихся частей.
266
Гл 8 Разделение жидких неоднородных систем
Горизонтальный мешочный фильтр с круглыми элементами (рис 8-15)
имеет корпус в виде двух полуцилиндрических половин 1 и 2, плотно соеди-
ненных откидными болтами 4, причем нижняя половина 2 может откиды-
ваться вниз на шарнире Фильтровальные элементы — диски 3 подвешены
параллельно друг другу в верхней половине корпуса Они представляют собой
Рис. 8-15. Горизонтальный мешочный фильтр с круг-
лыми элементами:
1 — верхняя половина корпуса; 2 — нижняя (откидная) половинд
корпуса, 3—фильтровальные элементы, 4 — откидные болты;
5— коллектор для отвода фильтрата, 6— противовес.
проволочные сетки, приваренные к круглой рамке и обтянутые фильтро-
вальной тканью Фильтрат и промывные воды отводятся через верхние па-
трубки элементов, которые соединяются с общим коллектором 5.
Описанный фильтр работает аналогично мешочному фильтру, показан-
ному на рис 8-12 Для удаления осадка нижнюю половину корпуса быстро
откидывают без затраты больших усилий, так как она уравновешивается про-
тивовесом 6 (см рис 8-15), а откидные болты имеют общую ось и поворачи-
1b Устройство фильтров
26?
ваются одновременно при помощи зубчатой передачи Осадок разгружается
под действием струи воздуха (поступает изнутри элементов) или смывается
водой, подаваемой через сопла, которые установлены на трубе Труба может
перемещаться над элементами, совершая возвратно-поступательные движения.
Мешочные фильтры, работающие под давлением, обладают
следующими преимуществами перед фильтрпрессами: 1) про-
мывка осадка при меньшем расходе воды, 2) меньший износ тка-
ни, 3) более легкое обслуживание, 4) большая производитель-
ность на единицу фильтровальной поверхности вследствие более
быстрой сборки фильтра, промывки и выгрузки осадка.
Недостатки этих фильтров: 1) сложность изготовления и бо-
лее высокая стоимость, 2) трудность контроля конечной толщи-
ны слоя осадка на элементах, 3) недостаточное перемешивание
суспензии (только путем ее рециркуляции); вследствие этого
при большой концентрации твердой фазы в суспензии осадок
неравномерно отлагается, что ухудшает его промывку,. 4) более
сложная замена ткани.
Патронные фильтры
Фильтры этого типа состоят из фильтровальных элементов
в виде узких, закрытых снизу вертикальных цилиндров (патро-
нов, или свечей), изготовленных из специальных материалов-
пористой керамики, угольной массы, прессованного кизель-
гура и др.
Эти фильтры работают по тому, же принципу, что и нутч-
фильтры под давлением: фильтрат продавливается снаружи че-
рез фильтровальную перегородку внутрь каждого элемента,
осадок остается на его наружной поверхности. Осадок сбрасы-
вается толчком жидкости или воздуха, которые подводятся из-
нутри патрона.
Патронные фильтры применяются главным образом в каче-
стве сгустителей.
На рис. 8-16 показана схема простейшего патронного филь‘
тра-сгустителя. Суспензия подается в корпус 1 через патрубок 3
под небольшим избыточным давлением, которое медленно авто-
матически повышается. Жидкость (фильтрат) проходит патрон 2
и удаляется через патрубок 4. Патрон (рис. 8-16, справа) обычно
имеет внутри сердечник в виде ребристой металлической трубы 8
с отверстиями 7. На трубу надевается гильза 9 из пористого ма-
териала.
По окончании фильтрования подача суспензии автоматиче-
ски прекращается и осадок сбрасываетея при резком увеличении
давления фильтрата внутри патрона. Затем давление снижают и
патрон промывают водой, движущейся изнутри патрона наружу,
268
Гл. 8. Разделение жидких неоднородных систем
Осадок в виде сгущенной суспензии удаляют при помощи ме-
шалки 5 через патрубок 6.
Обычно патронные фильтры состоят из нескольких десятков
фильтровальных элементов, заключенных в общем корпусе. Эти
фильтры часто снабжаются автоматическим управлением и мо-
гут работать без постоянного на-
блюдения.
Достоинства патронных филь-
тров: 1) компактность и герме-
тичность, 2) хорошее осветляю-
щее действие, 3) простота про-
мывки и осушки осадка и бы-
строе^ удаление его со всей филь-
Рис. 8-16. Патронный фильтр-сгуститель:
1 — кбрпус; 2— патрон; 3— патрубок для входа суспензии; 4— патрубок
для выхода фильтрата; 5— мешалка; 6 — патрубок для удаления осадка;
7 —отверстия для отвода фильтрата; 8 — ребристая металлическая труба
(сердечник); 9 — гильза-цилиндр.
трующей поверхности, 4) пригодность для фильтрования хи-
мически активных веществ, 5) легкость автоматизации процесса.
Недостатки: 1) возможность забивания фильтровальных
элементов мелкодисперсными осадками, 2) недоступность эле-
ментов для осмотра.
Барабанные фильтры
Барабанный ячейковый вакуум-фильтр с наружной филь-
трующей поверхностью (рис. 8-17 и 8-18) является наиболее
распространенным фильтром данного типа.
Полый барабан 1 с отверстиями на боковой поверхности, по-
крытый металлической сеткой и фильтровальной тканью, вра-
щается в корыте 2 с небольшой скоростью (0,1—2,6 об)мин).
Корыто заполнено суспензией, в которую погружено 0,3—0,4 по-
верхности барабана. Барабан разделен радиальными перегород-
ками на ячейки, каждая из которых через каналы в полой цапфе
вала 3 сообщается с распределительной головкой 4, прижатой
10. Устройство фильтров
269
к торцовой поверхности цапфы. Распределительная головка слу-
жит для последовательного соединения ячеек барабана с ли-
ниями вакуума несжатого воздуха. Погруженные в суспензию
Рис. 8-17. Общий вид и схема работы барабанного
вакуум-фильтра непрерывного действия с наружной
^фильтрующей поверхностью:
/—барабан; 2—корыто; 3 — главный вал; 4— распределительная
головка.
ячейки барабана сообщаются с вакуумной линией. Под дей-
ствием разности давлений снаружи и внутри барабана осадок
откладывается на его поверхности, а фильтрат отсасывается
внутрь барабана и удаляется через распределительную головку.
Рис. 8-18. Барабанный вакуум-фильтр непрерывного действия с наружной фильтрующей поверхностью:
/—барабан; 2 — корыто; 3—главный вал; 4— распределительная головка; 5 — трубки, 6 — лента для заглаживания трещин в осадке;
7—нож; 8—качающаяся мешалка.
:=>
Оо
Разделение жидких неоднородных систем
10. Устройство фильтров
271
Поверхность ячеек барабана, на которой откладывается оса-
док, называется зоной фильтрования (зона фильтрования /).
Когда соответствующие ячейки барабана выходят из суспензии,
осадок подсушивается при разрежении (зона просушки II). За-
тем осадок промывается водой, подаваемой через трубки 5 (см.
рис. 8-18), причем промывные воды отсасываются, как и филь-
трат, через распределительную головку. Вслед за промывкой в
этой же зоне (зона промывки и просушки III) осадок сушится
воздухом, который просасывается черёз слой осадка. После это-
го ячейки соединяются через распределительную головку с ли-
нией сжатого воздуха (зона отдувки IV). Воздух не только су-
шит, но и разрыхляет осадок, благодаря чему облегчается его
последующее удаление.
При подходе ячеек с просушенным осадком к ножу 7 прекра-
щается подача сжатого воздуха и осадок падает с поверхности
ткани под действием силы тяжести. Нож служит в основном напра-
вляющей плоскостью для слоя осадка, отделяющегося от ткани.
При дальнейшем вращении барабана ткань, освобожденная от
осадка, очищается путем продувки воздухом (зона регенерации
ткани V). Вслед за этим весь цикл операций, соответствующий
одному обороту барабана, повторяется снова. Между рабочими
зонами //, III, IV, V и I находятся небольшие мертвые зоны (на
рис. 8-17 не показаны). Это препятствует сообщению между со-
бой рабочих зон при переходе ячеек из одной зоны в другую.
Таким образом, на каждом участке поверхности фильтра все
операции — фильтрование, промывка, просушка, съем осадка и
очистка ткани — производятся последовательно одна за другой,
но участки работают независимо друг от друга и поэтому все
операции на фильтре проводятся одновременно, т. е. процесс
протекает непрерывно. По такому же принципу работают все не-
прерывнодействующие фильтры.
Чередование отдельных операций в ячейковом фильтре до-
стигается при помощи распределительной головки (рис. 8-19),
Неподвижный корпус 1 головки прижимается к ячейковой шай-
бе 3. Шайба вращается вместе с барабаном и имеет отверстия
по числу ячеек барабана. К корпусу головки крепится сменная
распределительная шайба 2, которая в случае износа может быть
заменена новой. В корпусе головки находятся четыре неоди-
наковые по величине камеры. Через наибольшую камеру / отса-
сывается фильтрат, через камеру II — промывные воды, а через
камеры III и IV подается сжатый воздух. Неподвижный корпус
головки прижимается к вращающейся шайбе 3 пружиной 4. Сус-
пензия подается в корыто со скоростью, равной скорости филь-
трования или несколько большей, постоянный уровень суспензии
в корыте поддерживается при помощи переливной трубы,
272
Гл 8 Разделение жидких неоднородных систем
В процессе фильтрования стремятся свести к минимуму оса-
ждение твердых частиц, которое происходит в направлении, про-
тивоположном движению фильтрата. Для предотвращения воз-
можности осаждения суспензия перемешивается в корыте ка-
чающейся мешалкой 8 (см. рис. 8-18). Чтобы не происходило
снижения вакуума из-за просасывания воздуха через трещины в
осадке, последний иногда заглаживают покровной лентой 6, дви-
Фильгпрат
жущейся благодаря трению
о поверхность осадка; одно-
временно осадок смачивают
через ленту водой. Для от-
жима влаги из осадка на
Рис. 8-19. Распределительная головка:
/ — неподвижный корпус; 2— распределительная шайба; 3—ячейковая шайба; 4 — пружина.
некоторых барабанных фильтрах установлены вибраторы в
виде свободно висящих на крестовинах отрезков труб, которые
при вращении отбрасываются центробежной силой и ударяют
по резиновому листу, покрывающему слой осадка.
Осадки снимают с фильтрующей поверхности различными
способами. При помощи ножа (рис. 8-20, а) снимают осадки
толщиной не менее 8—10 мм. Для-снятия более тонких слоев
(2—4 мм) применяют бесконечные шнуры, огибающие барабан
(рис. 8-20,6), с которых осадок сбрасывается при перегибе че-
рез валик. Тонкие и мажущиеся осадки снимают прижатым к
барабану вращающимся резиновым валиком (рис. 8-20, в), на
который переходит осадок и затем снимается валиком меньшего
диаметра. Снятие очень тонких слоев осадка (<2 мм) произво-
дится бесконечным сходящим полотном (рис. 8-20, а). Полотно
проходит через систему роликов, на первый ролик осадок нали-
ТО Устройство фильтров
273
пает и снимается с него ножом, после чего полотно промывается
и возвращается к барабану. Движение полотна осуществляется
вследствие его трения о поверхность барабана.
Рис. 8-20. Способы снятия осадка
/-ножом, (5—бесконечными шнурами, в —резиновым валиком, г —сходящим полотном
К числу достоинств барабанного ячейкового вакуум-фильтра
(см. рис. 8-17) относятся: 1) универсальность, т. е. пригодность
для обработки разнообразных суспензий, 2) возможность изго-
товления из материалов, стойких в химически активных средах,
3) легкость обслуживания.
В то же время фильтр обладает следующими недостатками:
1) небольшая фильтрующая поверхность и сравнительно вы-
сокая стоимость, 2) затруднительность тщательной промывки
и осушки осадка, 3) отдаленность распределительной головки
Рис. 8-21. Барабанный вакуум-фильтр с внутренней фильтрующей по-
верхностью:
/ — барабан; 2 — решетка; 3 — нож; 4— бандаж, 5— разгрузочный желоб, б — оросительная труба,
7—распределительная головка.
от фильтрующей поверхности, что приводит к задержке филь-
трата и промывных вод внутри барабана и усложняет их раз-
дельный отвод, т. е. получение неразбавленного фильтрата.
Барабанный вакуум-фильтр с внутренней фильтрующей поверхностью
(рис 8-21) имеет перегородку внутри барабана 1 в виде решетки 2, покрытой
18 Зак 546.
274
Гл 8 Разделение жидких неоднородных систем
фильтровальной тканью и установленной на некотором расстоянии от стенок
барабана Суспензия подается с открытого конца барабана (снабженного
закраиной), жидкость удаляется через распределительную головку 7, оса-
док сбрасывается в разгрузочный желоб 5 после отдувки воздухом и
снятия слоя ножом 3 Вращение барабана осуществляется при помощи бан-
дажа 4, который катится по опорным роликам В случае необходимости оса-
док промывается водой, подаваемой по трубе 6
В описанном фильтре осаждение твердых частиц совпадает по направле-
нию с движением фильтрата Поэтому на фильтровальной перегородке отла-
гаются в первую очередь более крупные частицы осадка, что облегчает филь-
трование (в фильтрах с наружной фильтрующей поверхностью сначала
отфильтровываются мелкие частицы, забивающие ткань)
В барабанных фильтрах с внутренней фильтрующей поверхностью про-
водится разделение грубых, быстро расслаивающихся суспензий При их раз*
делении не требуется тщательной промывки осадка
Рис. 8-22. Барабанный фильтр, работающий под давлением:
/ — барабан; 2—кожух, 3— патрубок для подачи суспензии; /—патрубок для подачи сжатого
воздуха; 5— цапфа вала, б—распределительная головка, 7—переливной патрубок; 8— валик;
9 — шнек
Барабанный фильтр, работающий под давлением (рис 8-22), имеет
ячейковый барабан 1 со сходящей тканью, заключенный в закрытый ко-
жух 2 Суспензия подается в кожух насосом или давлением сжатого воз-
духа через нижний патрубок 3 и отводится через переливной патрубок 7.
Сжатый воздух поступает сверху через патрубок 4 под тем же давлением,
что и суспензия (Ризб. = 2 — о ат). Фильтрат продавливается через поверх-
ность барабана и удаляется через пустотелую цапфу 5 и распредели-
тельную головку 6 Осадок сбрасывается с ткани при перегибе ее через
валик 8 с отверстиями, продуваемый изнутри сжатым воздухом Этим облег-
чается отделение осадка, который удаляется шнеком 9 Фильтры, работающие
под давлением, имеют ограниченную фильтрующую поверхность (примерно
до 9 м2) и отличаются сравнительной сложностью устройства
Дисковые вакуум-фильтры
Дисковый фильтр непрерывного действия (рис. 8-23) состоит
из 1—10 вертикальных дисков 1, укрепленных на горизонтальном
10 Устройство фильтров
Mb
полом валу. Вал с дисками вращается в корыте, имеющем фор-
му полуцилиндра с выступающими спереди узкими камерами
или карманами 2, число которых равно числу дисков. Диски при
Рис. 8-23. Дисковый фильтр непрерывного действия.
/_дИСКи; 2— карманы корыта, 3 —распределительная головка, 4 — скребки,
5 — трубки для подачи сжатого воздуха, 6 — труба для удаления фильтрата.
вращении по часовой стрелке входят в карманы и почти наполо-
вину погружаются в суспензию.
Каждый диск (рис. 8-24) состоит из плотно прижатых друг
к другу секторов 1 с рифлеными (иногда дырчатыми) боковыми
поверхностями. У основания сектора имеется полая обойма 2 с
дренажной трубкой 3, которая вставляется в соответствующее
отверстие вала и соединяет сектор с одним из продольных кана-
лов, на которые разделен полый вал. Снаружи каждый сектор
обтянут мешком из фильтровальной ткани, обвязанным вокруг
трубки 3. Секторы скрепляются друг с другом попарно длинны-
ми радиальными шпильками 4, ввинчиваемыми в тело вала и
имеющими на концах дугообразные накладки 5.
Таким образом, все секторы дисков, расположенные на одной
и той же образующей вала, соединяются общим продольным ка-
налом в нем. К одной из торцовых сторон вала плотно прижата
распределительная головка 3 (см. рис. 8-23), соединяющая ди-
ски с линиями вакуума и сжатого воздуха. Принцип действия
распределительной головки тот же, что и в барабанном фильтре.
Суспензия поступает в’камеры корыта снизу в таком количе-
стве, чтобы ее избыток сливался через переливной патрубок,
18*
276
Гл. 8. Разделение жидких неоднородных систем
При движении суспензия перемешивается, причем известное
перемешивающее действие оказывают диски.
Фильтрование происходит при вращении дисков, делающих
0,1—3 об!мин (иногда до 20 об/мин), фильтрат отсасывается че-
рез ткань, радиальные желобки секторов, обойму, дренажные
трубки, соответствующие каналы вала и камеры головки. В боль-
шинстве случаев за зоной фильтрования на диске следует зона
просушки и отдувки осадка воздухом, промывка осадка в диско-
Рис. 8-24. Сектор диска
непрер ывнодейст ву юще -
го фильтра:
/ — сектор; 2 —полая обойма;
3— дренажная трубка; 4 —
шпилька; 5 — накладка.
вых фильтрах»производится крайне ред-
ко. С обеих сторон каждого диска на
краях камер корыта установлены скреб-
ки 4 (см. рис. 8-23) или конические го-
ризонтальные валики. При продувке из-
нутри сжатым воздухом ткань на секто-
ре выпучивается, осадок разрыхляется и
сбрасывается, когда ткань проходит
между скребками. Осадок падает в про-
странство между камерами корыта и
поступает в желоб или на транспортер,
при помощи которого производится вы-
грузка. При снятии толстого слоя осадка
пользуются скребками вместо валиков,
причем скребки служат главным обра-
зом направляющей плоскостью.
Если нужна промывка осадка, к по-
верхности дисков подводятся радиаль-
ные трубки, через которые разбрызги-
вается вода; промывные воды отводятся
через отдельную камеру распределитель-
ной головки. Диски обычно изготовляют из древесины твердых
пород или же отливают из чугуна или цветных металлов.
Достоинства дисковых фильтров: 1) наибольшая фильтру-
ющая поверхность на единицу производственной площади по
сравнению с фильтрами других типов, 2) возможность удобной
замены отдельных дисков и ткани на них и соответственно мень-
ший расход ткани, 3) сравнительно небольшой расход энергии.
Недостатки: 1) плохая промывка осадков, 2) возможность
смешения промывной воды с суспензией в корыте фильтра; в
связи с этим дисковые фильтры работают, как правило, без про-
мывки осадка.
Разновидностью дискового вакуум-фильтра является тарельчатый вакуум-
фильтр, или план-фильтр (рис. 8-25), имеющий один горизонтальный пусто-
телый диск 1 значительного размера, вращающийся на полом вертикальном
валу 2 Диск имеет низкие борта и перфорированную поверхность, разделен-
ную на секторы-ячейки, которые покрыты фильтровальной тканью. Каждая
ячейка сообщается через каналы в вертикальном валу с распределительной
10. Устройство фильтров
277
головкой 3, находящейся под диском. За один оборот диска его ячейки по
следовательно соединяются с линиями вакуума и сжатого воздуха. Суспен-
зия подается на поверхность диска сверху. Осадок снимается ножом 4 после
почти полного оборота диска, т. е. возле места ввода суспензии.
Рис. 8-25. Тарельчатый вакуум-фильтр:
/ — горизонтальный пустотелый диск; 2—полый вал; 3 — распределительная головка; 4 — нож
для съема осадка.
Достоинства тарельчатого фильтра: 1) совпадение направления филь-
трата с направлением осаждения твердых частиц, 2) хорошая промывка
осадка, 3) возможность фильтрования
неоднородных суспензий. §
Недостатки' 1) громоздкость ус-
тановки, 2) небольшая фильтрующая
поверхность, 3) затруднительность
снятия осадка и очистки ткани.
Дисковый сгуститель (рис. 8-26)
представляет собой фильтр непрерыв-
ного действия, работающий под Дав-
лением и предназначенный для сгу-
щения суспензий. Внутри герметич-
ного кожуха 1 вращаются на валу 2
диски 3, устроенные аналогично ди-
акам вакуум-фильтров (см. рис. 8-24),
но целиком погруженные в суспен-
зию. Суспензия подается под давле-
нием через верхний патрубок, фильт-
рат удаляется из аппарата через по-
лости дисков, каналы в валу и рас-
пределительную головку 4. Осадок
отлагается на наружной поверхности
дисков и один раз за оборот вала
Рис. 8-26. Дисковый сгуститель:
/—кожух; 2—вал; 3 —диски; 4 — распредели
тельная головка; 5 —разгрузочный патрубок,
удаляется с каждого сектора диска
путем отдувки сжатым воздухом. В
результате отвода фильтрата и от-
дувки осадка внутри кожуха фильтра
собирается сгущенная суспензия, которая удаляется из него через клапан,
установленный в разгрузочном патрубке 5.
278 Гл- s- Разделение жидких неоднородных систем
Промывной,
раствор
Рис. 8-27. Карусельный фильтр:
а — общий вид; б —схема действия.
10. Устройство фильтров
279
Дисковые фильтры, работающие под давлением, аналогичны по устрой-
ству дисковым вакуум-фильтрам, но имеют герметически закрытый кожух,
внутри которого создается давление при помощи сжатого воздуха или газа.
Карусельные вакуум-фильтры
Карусельный фильтр (рис. 8-27) представляет собой горизон-
тальный вращающийся вакуум-фильтр непрерывного действия с
вращающейся кольцевой рамой, на которой шарнирно укрепле-
ны ячейки-противни. Каждый противень соединен гибким шлан-
гом с центральной распределительной головкой.
Все операции на каждом противне совершаются последова-
тельно (рис. 8-27,6). При вращении рамы с помощью зубчатой
рейки каждый противень заполняется суспензией, затем соеди-
няется с линией вакуума. После удаления маточного раствора
осадок можно многократно промывать (до пяти раз). После про-
мывки и осушки осадка противень переворачивается и осадок
сбрасывается в сборник. Далее ткань промывается и осушается,
после чего начинается новый цикл фильтрования.
Достоинства карусельных фильтров: 1) высокая производи-
тельность при разделении грубодисперсных суспензий, 2) весьма
тщательная промывка осадка, 3) длительный срок службы филь-
тровальной ткани (благодаря отсутствию съема осадка ножом)
и легкость ее замены, 4) низкие эксплуатационные расходы.
Рабочая фильтрующая поверхность карусельных фильтров
от 1,5 до 40 ж2.
Ленточные вакуум-фильтры
Ленточный фильтр непрерывного действия (конструкция
НИУИФ*), показанный на рис. 8-28, состоит из горизонтального
гладкого стола 2 (покрытого текстолитом для уменьшения тре-
ния), по которому скользит бесконечная резиновая лента 4, на-
тянутая между барабанами / и 5. Барабан 5 соединен с приво-
дом, задний барабан 1 может перемещаться в направляющих и
служит для натяжения ленты. Резиновая лента 4 имеет спе-
циальный профиль, рифленую рабочую поверхность. Лента снаб-
жена боковыми бортами, вдоль ее оси расположены отверстия,
которые при движении ленты сообщаются с тремя вакуум-ка-
мерами 3, расположенными под поверхностью стола 2. Вакуум-
камеры служат для отсоса фильтрата.
На резиновую ленту 4 надето бесконечное полотно 6 из филь-
тровальной ткани, кромки которой уплотнены круглым резино-
вым шнуром, вшитым в ткань и вдавленным в желобки рези-
новой ленты. Суспензия поступает на ткань по лотку 7.
* Научный институт по удобрениям и инсектофунгицидам.
280
Гл 8 Разделение жидких неоднородных систем
При движении ленты 4 и полотна 6 фильтрат отсасывается, а
осадок отлагается на ткани. Осадок промывается водой, посту-
пающей через трубки 8, просушивается в вакууме и сбрасы-
вается при перегибе полотна через барабан 5.
Для снятия липких осадков применяют пустотелый перфори-
рованный валик, в отверстия которого продувается сжатый воз-
дух, что облегчает отделение осадка от ткани. Иногда осадок
Рис 8-28. Ленточный фильтр непрерывного действия (конструкции
НИУИФ):
/ — натяжной барабан, 2 — стол; 3 — вакуум-камеры; 4 — бесконечная резиновая
лента, 5 — приводной барабан; 6— бесконечное полотно (фильтровальная ткань),
7—лоток для подачи суспензии; 8— оросительные трубки.
смывается с ткани струей воды. При обратном движении ткани
под столом она очищается (регенерируется) с помощью механи-
ческих щеток или паровых форсунок.
Ленточные фильтры снабжают приспособлениями для зати-
рания трещин в осадке и вибраторами для обезвоживания осад-
ка (по типу приспособлений, применяемых в барабанных филь-
трах).
Достоинства ленточных фильтров: 1) совпадение направле-
ний фильтрования и осаждения, 2) простота конструкции, в ча-
стности отсутствие распределительной головки, 3) хорошее раз-
деление фильтрата и промывных вод, 4) достаточные промывка
и обезвоживание осадка, 5) возможность обработки трудно-
фильтруемых материалов благодаря совершенному способу
съема осадка и регенерации ткани.
11. Фильтровальные перегородки
281
Недостатки: 1) небольшая поверхность фильтрования и не-
полное использование фильтровальной ткани, 2) большая про-
изводственная площадь, занимаемая фильтром, 3) износ ленты,
4) непригодность для обработки веществ, разрушающе дей-
ствующих на резиновую ленту, а также плохо смачивающих
резину и металл (смачивание необходимо для поддержания
достаточного вакуума).
Вибрационные фильтры
Для осветления тонких суспецзий могут быть использованы, кроме вспо-
могательных веществ (загрязняющих осадок), упругие колебания звуковых
и ультразвуковых частот.
Вибрационный (ультразвуковой) фильтр схематически показан на
рис. 8-29 Суспензия подается в нижнюю часть разъемного корпуса 1
фильтра через боковой штуцер и под-
нимается к фильтровальной перего-
родке 2, состоящей из двух жест-
ких решеток, между которыми за-
ложена фильтровальная ткань. Пере-
городка закреплена на резиновой
мембране 4, зажатой между верхней
и нижней частями корпуса фильтра.
Решетки перегородки 2 жестко со-
единены посредством вертикального
стержня 3 с излучателем 5 (магнито-
стрикционного или электромагнит-
ного типа), который заключен е
кожух 6, охлаждаемый водой Филь-
трат проходит сквозь фильтроваль-
ную перегородку, которой сооб-
щаются упругие колебания, посту-
пает в верхнюю часть корпуса аппа-
рата и отводится через верхний боко-
вой штуцер, осадок удаляется из ко-
нического днища фильтра через ниж-
ний штуцер. Описанный фильтр мо-
жет длительное время работать без
чистки и замены фильтровальной пе-
регородки.
Рис. 8-29. Вибрационный фильтр:
/ — корпус; 2 — фильтровальная перегородка;
3 — стержень электромагнитного вибратора;
4— резиновая мембрана, 5 — излучатель;
6— кожух излучателя.
11. Фильтровальные перегородки
Материал, применяемый в каче-
стве фильтровальной перегородки,
должен обладать следующими свой-
ствами’ 1) пористостью (размеры пор
должны быть такими, чтобы частицы
осадка задерживались на перегородке), 2) химической стойкостью к действию
фильтруемой среды, 3) достаточной механической прочностью, 4) теплостой-
костью при температуре фильтрования.
Наиболее распространены гибкие неметаллические перегородки, приме-
няемые в виде тканей или плетеных сеток, а также в виде перфорированных
листов.
282
Г$. 8. Разделение жидких неоднородных систем
Для нейтральных и слабощелочных сред (при температуре не выше
80° С) и для слабокислых сред (при кислотности не более 5% и температуре
не выше 40° С) применяют различные хлопчатобумажные ткани (бельтинг,
бязь, миткаль, диагональ и др.). В качестве подкладочного материала под
тонкие тканевые перегородки часто употребляют парусину. В ряде случаев,
главным образом в процессах фильтрования с закупориванием пор, в каче-
стве фильтровальных перегородок используют плетеные ленты из целлюлоз-
ных волокон (нетканые перегородки).
Для кислых сред, разрушающих хлопчатобумажные ткапп, фильтроваль-
ные перегородки изготовляют из шерстяных тканей, а также применяют
ткани из синтетических волокон. Шерстяные ткани (сукно, байка, войлок) из
овечьей шерсти сохраняют кислотостойкость при умеренных температурах
(не превышающих 60°С), более устойчивы к действию минеральных кислот
ткани из верблюжьей шерсти. Фильтровальные перегородки из шерстяных
тканей разрушаются в щелочных средах.
Ткани из синтетических волокон отличаются высокой химической стой-
костью, причем некоторые из них по ряду показателей (например, по проч-
ности, предельно допустимой температуре эксплуатации, отсутствию набуха-
ния) превосходят фильтровальные перегородки из материалов природного
происхождения. В качестве синтетических фильтровальных перегородок
используют поливинилхлоридные ткани, устойчивые к действию кислот и со-
лей при температуре не выше 60° С и ткани из волокна хлорин (перхлорви-
ниловые ткани), весьма стойкие в кислых и щелочных средах при темпера-
туре до 60° С. Успешно применяются также полиамидные ткани, отличаю-
щиеся высокой прочностью в сухом и влажном состоянии и устойчивые
к действию щелочей и разбавленных кислот. Кроме того, в качестве филь-
тровальных перегородок получают распространение химически стойкие ткани
из других синтетических волокон: виньона (сополимеры винилхлорида с ви-
нилацетатом или с акрилонитрилом), совидена, или сарана (сополимеры ви-
нилхлорида и винилиденхлорида), нитрона, или орлона (полиакрило-
нитрил), лавсана, называемого также териленом или дакроном (продукт
поликонденсации терефталевой кислоты и этиленгликоля). Некоторые из
этих тканей, например нитроновые или лавсановые, отличаются повышенной
теплостойкостью.
В последние годы начинают применять нетканые фильтровальные перего-
родки из механически связанных синтетических волокон. Такие перегородки
изготовляют путем перфорирования слоя волокон с последующей обработкой
жидкостью, вызывающей усадку волокнистого материала, или же путем про-
питки слоя волокон связующим веществом (синтетические полимеры, каучук)
с последующим прессованием при повышенной температуре.
При фильтровании химически агрессивных жидкостей употребляют также
тканевые перегородки из волокон минерального происхождения — асбестового
волокна (при небольшом перепаде давлений) и стеклянного волокна. Для
повышения срока службы фильтровальных перегородок из стеклянного во-
локна, плохо сопротивляющихся истиранию, под ткань подкладывают перфо-
рированные резиновые листы, а сверху покрывают металлической сеткой или
фильтровальной (непроклеенной) бумагой, чтобы предотвратить повреждение
ткани при снятии осадка.
Перфорированные резиновые листы с отверстиями 0,1—0,3 мм исполь-
зуются также самостоятельно в качестве фильтровальных перегородок. Рези-
новые перегородки отличаются теплостойкостью (до 90° С) и имеют гладкую
поверхность, что облегчает удаление осадка и очистку перегородки.
Гибкие металлические перегородки выполняются в виде перфорирован-
ных листов и сеток из стали, цветных металлов или их сплавов.
Широкое применение получили негибкие жесткие фильтровальные пере-
городки, состоящие из однородных частиц твердого материала (металл, кера-
12. Сравнение и выбор фильтров
283
мика, кизельгур, уголь, эбонит и др.), связанных между собой в результате
спекания. Спекание твердых частиц часто проводят в присутствии связую-
щего вещества. Описанные пористые негибкие перегородки, выпускаемые
в виде дисков, плиток и гильз (патронов), отличаются высокой прочностью
и хорошей кислото- и щелочестойкостью. Следует отметить, что очистка
таких перегородок от частиц осадка, проникших в их поры, затруднительна.
Из негибких жестких перегородок наиболее распространены керамиче-
ские перегородки, которые изготовляют путем смешения определенной фрак-
ции измельченного кварца или шамота со связующим веществом (например,
тонкодисперсным силикатным стеклом или феноло-формальдегидными поли-
мерами) и последующей термической обработки смеси. Керамические пере-
городки отличаются высокой стойкостью в кислых средах, но мало устойчивы
к действию щелочей.
В последнее время получают применение металлические негибкие филь-
тровальные перегородки, изготовляемые спеканием металлических порошков.
Перед спеканием порошки иногда предварительно прессуют или обрабаты-
вают на вальцах (для получения пористых лент). Перегородки из порошко-
образной углеродистой стали используются в нейтральных и щелочных
жидких средах, из порошкообразной нержавеющей стали — в кислых средах,
из порошкообразного никеля — в сильнощелочных средах.
Негибкие и нежесткие фильтровальные перегородки состоят из не связан-
ных жестко между собой твердых частиц и кусков зернистых материалов
(песок, гравий, кокс, уголь и др.), помещенных в виде насыпного слоя на
горизонтальной опорной решетке. Достоинствами таких перегородок
являются дешевизна и возможность тщательной промывки.
12. Сравнение и выбор фильтров
При выборе фильтра необходимо учитывать следующие
факторы: 1) цель процесса фильтрования — получение только
ценного осадка или только фильтрата, или одновременное по-
лучение осадка и фильтрата для дальнейшего использования;
2) свойства суспензии и осадка; 3) прочие условия процесса —
масштабы производства, простоту обслуживания, стоимость
аппарата, эксплуатационные расходы и др.
Фильтры непрерывного действия работают при коротких, цик-
лах фильтрования с автоматической промывкой и разгрузкой
осадка. Вследствие быстрой и непрерывной смены отдельных
операций скорость фильтрования в таких фильтрах значи-
тельно больше, чем в фильтрах периодического действия. Вместе
с тем преимущества фильтров непрерывного действия -могут
быть использованы в полной мере только при постоянном со-
ставе разделяемой суспензии и сравнительно крупном мас-
штабе производства.
Фильтры периодического действия работают при длинных
циклах фильтрования, так как частое повторение вспомо-
гательных операций (щягрузка, сборка фильтра, загрузка) рез-
ко снижает их производительность. Однако периодически дей-
ствующие фильтры сохраняют свое значение для небольших про-
изводств, особенно Ари разнообразном ассортименте продукции,
28-4
Гл 8. Разделение жидких неоднородных систем
когда требуется частое изменение режима фильтрования, а так-
же для отделения труднофильтруемых и требующих тщательной
промывки осадков.
Таким образом, в условиях большинства производств наибо-
лее эффективны фильтры непрерывного действия, несмотря на
их большую сложность и стоимость. Весьма важное значение
имеет легкость обслуживания этих фильтров.
Одной Из самых универсальных и простых конструкций филь-
тров периодического действия является фильтрпресс. Фильтр-
прессы наиболее пригодны для разделения небольших количеств
разнообразных суспензий в тех случаях, когда требуется полу-
чить достаточно обезвоженный осадок.
Еще более просты, но громоздки открытые нутч-фильтры,
которые применяются главным образом для отделения от жид-
кости легкоотфильтровываемых кристаллических веществ при
необходимости тщательной промывки осадка, а также для
фильтрования сильно агрессивных жидкостей (фильтры с ке-
рамической перегородкой).
Применение закрытых нутч-фильтров ограничено вследствие
их небольшой фильтрующей поверхности. В определенных ус-
ловиях (при давлении до 4 апг) эти фильтры более эффективны,
чем фильтрпрессы и мешочные фильтры, работающие под да-
влением.
Мешочные фильтры, работающие под давлением, приме-
няются главным образом для отделения ценного фильтрата
(осадок смывается водой) и мало пригодны для получения су-
хих, хорошо обезвоженных осадков. Мешочные фильтры с круг-
лыми элементами компактнее и удобнее в эксплуатации мешоч-
ных фильтров с прямоугольными элементами.
Патронные фильтры, в отличие от мешочных, имеют более
прочные фильтровальные перегородки из пористых твердых ве-
ществ (вместо тканевых перегородок). В фильтрах этого типа
получаются хорошо промытые и высушенные осадки, которые
быстро удаляются со всей фильтрующей поверхности. Патрон-
ные фильтры применяются также для сгущения и осветления
жидкостей.
Из фильтров непрерывного действия наиболее универсальны-
ми являются барабанные вакуум-фильтры, пригодные для одно-
временного получения хорошо промытого и высушенного осадка
и концентрированного фильтрата.
Дисковые вакуум-фильтры непрерывного действия служат
для фильтрования концентрированных суспензий, когда необхо-
дима большая фильтрующая поверхность, но не требуется
тщательной промывки осадка. Горизонтальные дисковые (та-
13. Промывка осадков
285
рельчатые) фильтры приспособлены для разделения быстро-
осаждающихся суспензий с большим содержанием твердой
фазы, при необходимости тщательной промывки осадка.
Ленточные непрерывнодействующие фильтры сочетают по-
ложительные качества нутч-фильтров с непрерывностью дей-
ствия. На ленточных фильтрах достигается четкое разделение
осадка и фильтрата и возможно разделение медленно филь-
трующихся и малоконцентрированных суспензий.
Барабанные и дисковые фильтры, работающие под давле-
нием, используются для разделения труднофильтруемых суспен-
зий и отделения твердой фазы от летучих жидкостей. Вслед-
ствие высокой стоимости, небольшой фильтрующей поверхно-
сти и сложности контроля эти фильтры имеют пока ограничен-
ное применение.
13. Промывка осадков
В большинстве случаев промывка производится путем вытеснения водой
маточной жидкости (фильтрата) из слоя осадка. Для обработки раствори-
мых в воде осадков в качестве промывной жидкости применяют разбавлен-
ные растворы солей и кислот (поваренной соли, хлористого калия, серной
кислоты и др.), а иногда — насыщенный раствор вещества, из которого со-
стоит осадок.
В фильтрах почти всех конструкций промывная вода движется по тому
же пути, что и фильтрат. Исключение составляют фильтрпрессы, в которых
промывная жидкость в первой половине толщины слоя осадка движется в на-
правлении, обратном движению фильтрата, а во второй половине толщины
слоя — в направлении, совпадающем с ним (см. рис. 8-9, стр. 261). Обратным
течением промывной жидкости осадок несколько разрыхляется, что способ-
ствует лучшей промывке.
Осадки, содержащие растворимые примеси, не могут быть равномерно
промыты способом вытеснения, так как вода, растворяя примеси, стремится
двигаться по каналам, образующимся в осадке. Поэтому такие осадки про-
мывают способом разбавления осадок размешивают с промывной жидкостью
в отдельном аппарате (промывателе), образующуюся суспензию снова от-
фильтровывают и промывают. Для равномерной промывки осадка заглажи-
вают образующиеся в нем трещины.
Иногда промывку проводят путем постепенного разбавления, повторяя
разбавление осадка и фильтрование несколько раз. Для лучшего растворения
примесей применяют также горячую промывку нагретой промывной
жидкостью.
Способом разбавления удается достаточно хорошо отмыть осадок. Од-
нако промывка вытеснением значительно проще и требует меньшего расхода
промывной жидкости. Обычно расход промывной жидкости значительно пре-
вышает объем фильтрата, удаляемого из осадка, и равен по меньшей мере
полуторному объему этого фильтрата.
Промывку всегда стремятся провести с минимальным количеством про-
мывной воды, что особенно важно, когда фильтрат представляет ценность и
разбавление удорожает его дальнейшую обработку.
Для сокращения расхода промывной жидкости часто проводя^ многосту-
пенчатую противоточную промывку на непрерывнодействующих фильтрах,
например ленточных (стр. 280) или карусельных (стр. 279). Так, при трех-
ступенчатой промывке в фильтре непрерывного действия на последний
286
Гл. 8. Разделение жидких неоднородных систем
участок зоны промывки (считая по движению промываемого осадка) по-
дают чистую промывную жидкость для окончательной промывки осадка.
Из этой последней ступени промывная жидкость поступает во вторую сту-
пень и из второй ступени направляется в первую ступень, где находится
еще не промытый осадок. При таком противоточном движении промывная
жидкость постепенно насыщается веществами, вымываемыми из осадка, и
средняя концентрация их становится значительно выше, чем в промывной
жидкости при одноступенчатой промывке. Это и обусловливает уменьшение
необходимого количества промывной жидкости.
Иногда многократную противоточную промывку осуществляют последо-
вательно на нескольких фильтрах (например, барабанных вакуум-фильтрах),
устанавливая между двумя соседними фильтрами приемный аппарат (сосуд)'
с мешалкой. Так, в случае промывки на трех фильтрах осадок с первого
фильтра перемешивают в приемном сосуде с промывной жидкостью из
третьего фильтра и фильтруют полученную суспензию на втором фильтре.
Осадок со второго фильтра перемешивают с чистой промывной жидкостью
И направляют на третий фильтр.
14. Расчёт фильтров
Процесс фильтрования проводится циклами. Каждый цикл
состоит из собственно фильтрования, промывки осадка и вспомо-
гательных операций (разгрузка осадка, подготовка фильтра к
следующему циклу и др.). Продолжительность цикла фильтрова-
ния составляет:
т = Т + Тпр> + Твсп. сек (8-39)
где т, тпр и твсп. — продолжительность собственно фильтрова-
ния, промывки осадка и вспомогательных
операций.
Если поверхность фильтра F м2, а удельная производитель-
ность его q мР/м2, то количество фильтрата, полученное за один
цикл, составит qF мг и часовая производительность фильтра (по
фильтрату) будет равна:
= м?1ч (8-40)
Из выражения (8-40) определяется необходимая поверхность
фильтра:
Q&T
3600? м<2 (8-41)
Если величина удельной производительности q фильтра зада-
на (или принята), то по уравнениям (8-33) и (8-38) находят т и
тпр_, затем определяют по уравнению (8-39) общую продолжи-
тельность фильтрования Т и по уравнению (8-41) — необходи-
мую поверхность F фильтра.
14. Расчет фильтров
287
Однако можно показать, что F принимает наименьшее значение при не-
котором оптимальном значении q, которое определяется по формуле:
Яот.
твсп.
ги
Ткр
(l+2Lu^.
\ р*
Ьр
^Рпр.
(8-42)
где р- и р.Пр. — вязкость фильтрата и промывной жидкости;
Ар и Дрпр. — разность давлений по обе стороны фильтровальной перего-
родки при фильтровании и промывке;
L — расход промывной воды, м3 на 1 м3 осадка;
и — объем осадка (в Л13) на 1 м3 фильтрата.
Величина 7опт. представляет собой наибольший объем фильтрата, полу-
чаемый с 1 м2 поверхности фильтра, т. е. соответствует максимальной произ-
водительности фильтра.
Во многих случаях сопротивлением фильтровальной перегородки можно
пренебречь, т е. принять 7?пер. = 0; тогда, складывая левую и правую
части формул (8-33) и (8-38), получим следующее выражение для тр— про-
должительности рабочих операций цикла фильтрования (собственно филь-
трования и промывки):
ruq2 гпо u2q2
’p = ’+’"p=W+£-^T (8’43)
Подставив в это выражение ^опт. по формуле (8-42), найдем:
т 4~ тпр. ~ твсп. (8-44)
т. е. производительность фильтра периодического действия максимальна,
когда сумма времени собственно фильтрования и промывки равна продолжи-
тельности вспомогательных операций.
При фильтровании на фильтрах периодического действия стоимость
вспомогательных операций (выполняемых вручную) выше стоимости соб-
ственно фильтрования и промывки. Поэтому частое чередование фильтрова-
ния и вспомогательных операций, определяемое соотношением (8-44), эконо-
мически невыгодно. Оптимальные условия работы фильтра могут быть най-
дены только путем технико-экономических расчетов. В первом приближении
оптимальным можно считать отношение
• твсп. —5 6
при котором производительность фильтра уменьшается только на 25—30%
против максимальной, а вспомогательные операции становятся достаточно
редкими.
В фильтрах непрерывного действия, наоборот, целесообразно часто чере-
довать фильтрование и вспомогательные операции, т. е. работать с корот-
кими циклами.
Как видно из формулы (8-34), объем фильтрата q, приходящийся на
единицу поверхности фильтрования, приблизительно пропорционален Vт ^если
7?пер. \
пренебречь величиной ——— у• Следовательно, производительность фильтра
УТ. 1
пропорциональна ----= - г С увеличением числа оборотов п фильтра
Т У Т
продолжительность фильтрования уменьшается и, следовательно, производи-
тельность фильтра увеличивается прямо пропорционально корню квадрат-
ному из числа его оборотов.
288
Гл 8 Разделение жидких неоднородных систем
Однако с повышением числа оборотов наряду с q уменьшается и тол-
щина слоя осадка &, так как S = uq [см. формулу (8-27)]. Поэтому число
оборотов фильтра можно увеличивать только до известного предела, так как
при малой толщине слоя затрудняется съем осадка.
Задавшись толщиной слоя осадка S, найдем:
V В
? = (8-45)
Для трудноотфильтровываемых осадков, обладающих большим сопроти-
влением г, как видно из формулы (8-34), величина q будет меньше, чем для
хорошо фильтрующихся. В соответствии с формулой (8-27) для трудноот-
фильтровываемых осадков будет меньше и толщина слоя осадка &. Вслед-
ствие этого при образовании таких осадков должно быть выбрано меньшее
число оборотов фильтра; соответственно более низкой будет производитель-
ность фильтра <2ф.
Продолжительность полного цикла фильтрования в ячейковом фильтре
непрерывного действия составит
(^ + ^пр.) ™
/ = ------;------- сек
ГПф + ^пр.
(8-46)
где тп, т.ф и шпр. — общее число ячеек, число ячеек зоны фильтрования и зоны
промывки.
Величинами m, и /ипр- задаются или принимают их по конструктив-
ным данным.
По продолжительности собственно фильтрования т определяется степень
погружения барабана:
(8-47)
Число оборотов барабана составляет:
п = 60 об)мин
(8-48)
Пример 8-4. Определить удельное сопротивление осадка и фильтроваль-
ной перегородки на основе следующих опытных данных:
Продолжительность Объем полученного Удельная производитель- т/<7
фильтрования фильтрата ность фильтра сек-м2[м'
(по фильтрату)
т, сек V, л м3/м3
70 10 0,2 350
225 20 0,4 562
455 30 0,6 758
770 40 0,8 962
Приведенные выше данные получены при фильтровании водной суспен-
зии в фильтре с фильтрующей поверхностью F = 0,05 м2 при постоянном
перепаде давления Др = 49 100 н/м2 (5000 кгс/м2) и температуре t — 20° С.
Объем осадка на 1 м3 фильтрата и = 0,01 мэ/м3.
Решение В соответствии с уравнением (8-33) получаем.
Т ГН । ^пер.
~q ~ 2 Др q Др
14. Расчет фильтров
280
По опытным данным, приведенным выше, строим график зависимости
t/q от q (рис. 8-30). Согласно графику тангенс угла а наклона опытной
прямой составляет:
ОТ----------------г-"------------
t 962 — 150 1П1.
0[8 - = 1014
Отрезок, отсекаемый прямой на оси
ординат, В = 150.
Определяем удельное сопротивление
осадка из выражения для т/<у:
2 Др +
Г =----— tg а —
U ь
= 2 '• 1014 9,9 109 « • сек/м*
Удельное сопротивление фильтро-
вальной перегородки:
Япер. = Др • В = 49 100 • 150 =
= 7,36 • 106 н • сек/м3
Удельная производительность
q, нЗ/мё
Рис. 8-30. К примеру 8-4.
Пример 8-5. Определить удельное
Сопротивление осадка и фильтровальной
перегородки для условий предыдущего
примера, если фильтрование ведется при
температуре t = 60° С.
Решение. В соответствии с выражением для сопротивления фильтро-
ванию (стр. 178) величина R пропорциональна (при. прочих равных усло-
виях) вязкости р- фильтрата (воды).
Следовательно
г60а С _ Ибр° Q
г20в с ^20° с
откуда
Н'йп0 с 0,47
Г6О° с = г20° с = 9,9 • 109 • -у- = 4,65 • Ю9 « • ceKfMi
Р-20° С 1
Аналогично для фильтровальной перегородки:
м*йло р 0,47
(/?пер.)бОо С = (*пер.)2(Г С ~~7,36 • W • -у- = 3,46 • W Н • СвК^
г20° С 1
Пример 8-6. Рассчитать объемную производительность по фильтрату
нутч-фильтра, в который загружается суспензия в количестве <?с = 2500 кг,
^одержание в ней твердой фазы х «= 10%. Получаемый осадок имеет влаж-
ность су = 60%, плотность фильтрата Рф = 1040 кг/м3.
Решение. Определяем количество твердой фазы, поступающей с су
спензией:
. GTB = Qcx — 2500 • 0,1 = 250 кг
Количество получаемого влажного осадка
G — 250 —
• 1 — w 1 — 0,6
19 Зак 546.
290
Гл. 8. Разделение жидких неоднородных систем
Количество получаемого фильтрата составит:
Сф = Gc — Оос. = 2500 — 625 = 1875 кг
Объем фильтрата:
G* 1875
у. —_____ =_____— 1 8 м3
ф р. 1040 ~ ’
Пример 8-7- Определить фильтрующую поверхность нуТч-фильтр а, рабо-
тающего в условиях предыдущего примера, если удельное сопротивление
осадка г= 13,24 • 109 н-сек/м^, удельное сопротивление фильтровальной пере-
городки 7?пер- = 56,9 • 106 «• сек!м3, плотность осадка рос. = И00 кг!м3.
Расход воды на промывку осадка L — 1,75 м3 на 1 м3 влажного осадка,
плотность фильтрата Рф = 1040 кг/.и3, его вязкость р.ф = 1,1 спз. Вязкость
фильтрата, получаемого при промывке, р.Пр. = 1 спз. Перепад давления по обе
стороны фильтровальной перегородки при фильтровании и промывке Др = ДрПр.=
= 1,96 бар (2 ат). Продолжительность вспомогательных операций на фильтре
Тзсп. == ^0 мин.
Решение. Определяем объем влажного осадка на 1 м3 фильтрата:
И = РосУф = ПОО-1,8 = 0,316 м3/м3
Находим удельную производительность фильтра по формуле (8-42):
9 опт. —
= 0,236 м3/м2
20-60
13,24 - Ю9 0,316 /
2-1,96-105
Продолжительность фильтрования по формуле (8-33) составляет:
13,24 -109 - 0,316 - 0,2362 , 56,9 • 106 • 0,236 спе , сп
2-1,96-Ю5 + 1,96 • 105 — 5954-69~ 665 сек
Определяем удельное сопротивление осадка при промывке по формуле
(8-36):
гпр = . 13,24 • 109 = 12,05 -109 н • сек1м*
Продолжительность промывки осадка рассчитываем по формуле (8-38):
1,75 • 0,316 • 0,236 (12,05 • 109 • 0,316 • 0,236 4- 56,9 • 10^) СЛП
тпр. =---------------------! ,96-105-------------------- == 640 сек
Продолжительность рабочей части цикла фильтрования:
tp = т 4- тпр- = 665 4- 640 — 1305 сек
Для Достижения оптимальных условий работы фильтра допускаем неко-
торое снижение его производительности, увеличивая тр в 4,6 раза, т. е. при-
нимая тр = 1305 • 4,6 = 6000 сек. Тогда общая продолжительность цикла
фильтрования составит
Т = т 4- тпр. 4- твсп_ = Тр 4- твсп# = 6000 4- 20 • 60 = 7200 сек — 2 к
Продолжительность операции собственно фильтрования увеличиваем про-
порционально увеличению тр:
т = 665 • = 3060 сек
loUu
14. Расчет фильтров
29-
Производительность фильтра:
V* 1,8
' Сф-у-у=0,9 м3)ч
Соответственно удельная производительность фильтра за один цикл со-
ставит по формуле (8-34):
Г~( 56,9• Ю6 \2 ! 2-1,96-105-3060
q ““ V \ 13,24 -109 • 0,316 ) + 13,24 -109 • 0,316
_______56.9 - 106 _ q 522 м3!м2
13,24 - 109 • 0,316 ~ '
Поверхность фильтра определяем по формуле (8-41):
РфТ 0,9 - 7200
р _ ф ~ Ъ К и2
~ 3600? ~ 3600 • 0,522 ’
Пример 8-8. Определить необходимую поверхность фильтрования и вы-
брать барабанный ячейковый фильтр непрерывного действия для фильтрова-
ния суспензии в количестве Gc = 200 т1сутки, содержание в ней твердой
фазы х = 20%, плотность твердой фазы рТв. = 2160 кг/м3. На фильтре отла-
гается слой осадка толщиной 8= 30 мм, влажность осадка w = 15% Осадок
подвергается промывке, расход воды на промывку составляет L = 1,85 м3 на
1 м3 влажного осадка.
Плотность получаемого фильтрата Рф = 1140 кг/м3, вязкость у = 1,7 спз.
Вязкость фильтрата при промывке упр, =’0,9 спз. Перепад давления при
фильтровании и промывке Др = 0,466 бар (0,475 ат). Удельное сопротивле-
ние осадка г = 2,35-109 н-сек/м*, фильтровальной перегородки /?пер.=
= 4,32 • 106 н • сек/м3.
Решение. Принимаем 20 рабочих часов фильтра в сутки (4 часа за-
трачивается на ремонт, смену и очистку ткани и т. д.). Тогда производи-
тельность фильтра по суспензии составит:
„ 200-1000 1АЛЛЛ
Ос =----------= Ю 000 кг ч
с 20 '
ос.
Аналогично расчету в примере 8-6, находим из материального баланса,
что производительность фильтра .по фильтр a iy Уф = 6,7 м3/ч, по осадку
Goc. 2360 кг]ч.
Определяем плотность осадка по формуле
Рос. = Ртв. (1 — ®) + рж® = 2160 (1 — 0,15) + 1000 - 0,15 = 1985 кг/м3
где рж — плотность жидкой фазы (воды), равная 1000 кг/м3.
Рассчитываем количество влажного осадка и, получаемого на 1 м3 филь-
трата:
и — ^ос- —______2360 q 177 м3!м3
РосУф 1985-6,7 м Iм
Определяем удельную производительность фильтра за цикл по фор-
муле (8-45):
= 0,169 м31м2
Продолжительность фильтрования находим по формуле (8-33)
2,35 • 109 • 0,177 • 0,1692 . 4,32 • 106 - 0,169 1по , 1е„
Х 2 • 0,466 • 105 + 0,466 • Ю5 ~ 128 + 15,7 “ 144 сек
19*
292
Гл. 8. Разделение жидких неоднородных систем
Удельное сопротивление осадка при промывке по формуле (8-36) со-
ставляет:
P4in 0,9
г = JZPl . ч = __ . 2,35 • 109 = 1,25 • 109 н • сек/м*
pi 1,7
Продолжительность промывки находим по формуле (8-38):
1,85 • 0,177 • 0,169 (1,25 • 109 • 0,177 • 0,169 + 4,32 • 106) _ -
’пр. — 0,466 • 105 Сек
Принимаем общее число ячеек барабана tn = 18, из которых в зоне
фильтрования находится л*ф = 6 ячеек и в зоне промывки лгПр. ~ 3 ячейки.
Тогда продолжительность полного цикла фильтрования по формуле (8-46)
составит:
(144 4-49,5)-18 „й_
Т = -----/, , о -= 387 сек
64-3
Определяем поверхность фильтра по формуле (8-41):
р — ' 387 4 26 м2
3600 4-0,169 ’
По нормалям НИИХИММАШ выбираем барабанный вакуум-фильтр
марки Б5-1,75/09 (F = 5 м2). Для выбранного фильтра определяем число обо-
ротов барабана по формуле (8-48):
п ==
-Д=- ^0,15 об!мин
оо/
Степень погружения барабана находим по формуле (8-47):
144
T = w = °,372
В. ЦЕНТРИФУГИРОВАНИЕ
15. Общие сведения
Наиболее распространенным способом разделения жидких
неоднородных систем под действием центробежных сил является
центрифугирование (или фугование), которое осуществляется в
машинах, называемых центрифугами. Основная часть центрифу-
ги— барабан (корзина) со сплошными или дырчатыми стенка-
ми, вращающийся с большой скоростью на вертикальном или
горизонтальном валу.
Различают следующие процессы разделения суспензий в цен-
трифугах: 1) центробежное фильтрование, 2) центробежное от-
стаивание, 3) центробежное осветление.
Центробежное фильтрование представляет собой процесс
разделения суспензий в центрифугах с дырчатыми барабанами
(рис. 8-31, а). Внутренняя поверхность такого барабана покрыта
фильтровальной тканью. Суспензия центробежной силой отбра-
15. Общие сведения
293
сывается к стенкам барабана, при этом твердая фаза остается
на поверхности ткани, а жидкость под действием центробежной
силы проходит сквозь слой осадка и ткань удаляется наружу
через отверстия в барабане.
Центробежное фильтрование в общем случае .складывается
из трех последовательно протекающих физических процессов:
1) фильтрования с образованием осадка, 2) уплотнения осадка,
3) удаления из осадка жидкости, удерживаемой молекулярными
силами.
Рис. 8-31. Центрифуги:
а — с дырчатым (фильтрующим) барабаном; б—оо сплошным (сепарирующим) барабаном.
/ — барабан; 2—кожух; 3 —труба для подачи суспензии.
При помощи центробежного фильтрования может быть до-
стигнута высокая степень обезвоживания осадка.
Центробежное отстаивание представляет собой процесс раз-
деления суспензий в центрифугах, имеющих барабаны со сплош-
ными стенками (рис. 8-31,6). Суспензия вводится в нижнюю
часть барабана и под действием центробежной силы отбрасы-
вается к стенкам. Непосредственно у стенок образуется слой
осадка, а жидкость образует внутренний слой и вытесняется
из барабана поступающей на разделение суспензией. Подни-
маясь кверху, жидкость переливается через закраину барабана
и удаляется наружу. При центробежном отстаивании происхо-
дят два физических процесса: 1) осаждение твердой фазы,
2) уплотнение осадка.
Центробежное осветление также проводится в сплошных ба-
рабанах и служит для очистки жидкостей, содержащих незна-
чительное количество твердой фазы. Этот процесс применяется
для разделения тонких суспензий и коллоидных растворов.
294
Гл 8. Разделение жидких неоднородных систем
По физической сущности центробежное осветление предста-
вляет собой процесс свободного осаждения твердых частиц в по-
ле центробежных сил.
В барабанах со сплошными стенками производится также
разделение эмульсий. Под действием центробежной силы компо-
ненты эмульсии в соответствии с плотностью располагаются в
виде разграниченных слоев: наружного слоя жидкости с боль-
шей плотностью и внутреннего слоя более легкой жидкости.
Жидкости выводятся из барабана порознь.
Таким образом, центрифугирование представляет собой по
существу процессы отстаивания и фильтрования в поле центро-
бежных сил.
Развиваемые при центрифугировании центробежные силы
оказывают на разделяемую жидкую систему гораздо большее
воздействие, чем силы тяжести и давления. Поэтому центрифу-
гирование является гораздо более эффективным способом меха-
нического разделения неоднородных жидких систем, чем отстаи-
вание и фильтрование.
Напряженность создаваемого в центрифуге поля центробеж-
ных сил характеризуется фактором разделения, который пред-
ставляет собой отношение центробежного ускорения к ускоре-
нию силы тяжести: „
Ф=-^ (8-49)
где w — угловая скорость вращения барабана, рад!сек\
г—радиус барабана, м\
g—ускорение силы тяжести, равное 9,81 м1сек?.
Чем больше фактор разделения, тем выше разделяющая спо-
собность центрифуги. Фактор разделения Ф может быть повы-
шен путем увеличения радиуса барабана и в еще большей сте-
пени — увеличением числа оборотов, поскольку величина Ф про-
порциональна квадрату числа оборотов (о2 — Однако уве-
личивать радиус и число оборотов можно только до известных
пределов, определяемых механической прочностью барабана.
Произведение фактора разделения Ф на поверхность F оса-
ждения твердой фазы в барабане центрифуги, обозначаемое S,
называется индексом производительности центрифуги-. *
S = Ф/7 м? (8-50)
Индекс производительности S представляет собой поверх-
ность осаждения отстойника или фильтра, в котором для данной
* В И Соколов, Современные промышленные центрифуги, Машгиз,
16 Устройство центрифуг
295
суспензии достигается та же производительность, что и в рас-
сматриваемой центрифуге. Величина S отражает влияние всех
конструктивных факторов, определяющих способность отстойных
и фильтрующих центрифуг к разделению суспензий или
эмульсий.
Центрифуги классифицируют по следующим признакам:
1) по величине фактора разделения; 2) по величине индекса про-
изводительности; 3) по режиму работы (периодический или не-
прерывный); 4) по способу выгрузки осадка; 5) по конструктив-
ным признакам.
Классификация центрифуг по фактору разделения, режиму
работы и способу выгрузки осадка приведена на стр< 296.
Механическая выгрузка осадка — основное условие непре-
рывной работы центрифуг, поэтому способ разгрузки является
важным признаком их классификации.
Исходя из конструктивных признаков, центрифуги различают
главным образом по расположению и способу закрепления вала.
По этому признаку центрифуги делят на вертикальные, горизон-
тальные и наклонные. Существует три вида вертикальных цен-
трифуг: стоячие (с подпертым валом), подвешенные на колонках
и висячие (с верхним подвесом главного вала). Горизонтальные
центрифуги с ножевым съемом осадка работают периодическим
способом, но поскольку в них возможна полная автоматизация
всех операций, они называются автоматическими центрифугами.
По технологическому назначению центрифуги разделяются на
три типа: 1) осветляющие — для очистки жидкостей от твердых
примесей, 2) разделяющие — для разделения суспензий и эмуль-
сий, 3) концентрирующие — для сгущения суспензий путем отде-
ления части жидкой фазы.
16. Устройство центрифуг
Центрифуги периодического действия с ручной
и гравитационной выгрузкой
Известны два типа центрифуг периодического действия с руч-
ной выгрузкой — центрифуги фильтрующего и отстойного ти-
пов. Суспензия загружается в барабан, находящийся в покое
или же вращающийся с рабочей или пониженной скоростью.
В последнем случае после загрузки барабана скорость его до-
водится до рабочей.
В фильтрующей центрифуге (см. рис. 8-31, а) жидкость
(фугат) проходит через фильтровальную ткань, металлическую
подкладочную сетку и удаляется через отверстия барабана 1 в
неподвижный кожух 2, окружающий барабан. Из кожуха фуга г
сливается в сборник.
296
Гл. 8. Разделение жидких неедцоредных систем
Нормальные центрифуги (Ф < 3500)
Сверхцентрифуги (Ф > 3500)
16. Устройство центрифуг
297
В отстойные центрифуги (рис. 8-31,6) суспензия загружается
на полном ходу; разделение происходит, как указывалось, при
движении жидкости вверх параллельно глухим стенкам бара-
бана, до образования осадка определенной толщины.
По окончании центрифугирования в глухом или дырчатом
барабане осадок промывают (если это необходимо) и некоторое
время ведут фугование для подсушки и уплотнения осадка, без
подачи суспензии. Затем выключают электродвигателе, останав-
ливают центрифугу тормозом и выгружают осадок вручную.
Ручная выгрузка осадка производится через верх или днище
барабана.
Нижняя выгрузка более удобна, но, как и верхняя, требует
большой затраты труда.
Таким образом, Цикл работы центрифуг складывается из ря-
да операций, перечень и ориентировочная продолжительность
которых приведены ниже:
Операция Продолжительность,
< мин
Разгон барабана ,.......... 0,5—1,0
Наполнение барабана........ 1,5—30
Центрифугирование.......... 2,0—40
Промывка осадка............ 0—20
Оодсушка осадка............ 20—25
Торможение................. 0,7—2
Разгрузка.................. 3—20
Полная продолжительность т цикла центрифуги с ручной вы-
грузкой определяется как сумма времени отдельных операций,
величина т колеблется в очень широких пределах — от 7 мин До
3 ч и более, в зависимости от свойств обрабатываемых ве-
ществ.
Если продолжительность цикла т мин известна, производи-
тельность центрифуги может быть определена по формуле:
, С = ^р-кг!ч (8-51)
где V —объем осадка, образующегося в барабане за один цикл
(объем, равный рабочей емкости барабана), ж3;
р — плотность осадка, кг]м3.
На рис. 8-32 показана трехколонная центрифуга с верхней
ручной выгрузкой. Барабан 1 центрифуги и станина 3, внутри
которой он вращается, подвешены при помощи тяг 4 на трех ко-
лонках 5; вибрация барабана воспринимается пружинами 6.
Благодаря такому устройству колебания барабана не пере-
даются через вал 2 и подшипники на станину и не вызывают ее
расшатывания.
298
Гл. 8. Разделение жидких неоднородных систем
Недостатки трехколонной центрифуги: 1) трудоемкая ручная
выгрузка осадка сверху, 2) малая доступность для осмотра
подшипников, привода и тормоза и возможность их коррозии
под действием проливающейся жидкости.
Рис. 8-32. Трехколонная центрифуга с верхней выгрузкой:
/—барабан; 2 — вал; 3 — станина; 4 — тяги; 5 — колонка, 6—пружина.
Этих недостатков в известной мере лишена висячая центри-
фуга с нижней выгрузкой (рис. 8-33). Барабан 1 такой центри-
фуги подвешен к нижнему концу вала 2, имеющего верхнюю
коническую или шаровую опору 3 (часто снабженную резиновой
прокладкой). Барабан не имеет глухого днища; боковая стенка
барабана соединяется внизу несколькими ребрами 4 с его втул-
кой. Разгрузочные отверстия, находящиеся между ребрами, во
время фугования закрывают съемным колпаком 5,’ подвешенным
на цепи. При выгрузке центрифуги колпак приподнимают или
извлекают из барабана и осадок проталкивают вручную вниз.
Достоинства висячей центрифуги: 1) устойчивость и некото-
рая свобода колебаний барабана, так как центр тяжести вра-
щающейся системы расположен ниже опоры вала и подшипни-
ков; кроме того, допустимо некоторое раскачивание барабана;
2) сравнительно легкая и быстрая выгрузка осадка; 3) опора
и привод не подвергаются коррозии.
Выгрузка осадка с минимальной затратой физического труда
достигается в саморазгружающихся центрифугах (рис. 8-34,
слева показана загрузка барабана, справа — выгрузка осадка).
16. Устройство центрифуг
299
Рис. 8-33. Висячая центрифуга с нижней вы-
грузкой:
/ — барабан; 2—вал; 3 — опора вала; 4— ребра барабана;
5 — колпак.
Рис. 8-34. Саморазгружающаяся центрифуга:
/ — барабан; 2 — вал; 3 — распределительный диск.
300 Гл 8 Разделение жидких неоднородных систем.
Осадок удаляется из них под действием сил тяжести гравита-
ционная выгрузка). Нижняя часть барабана 1 имеет коническую
форму с углом наклона, превышающим угол естественного
откоса материала. При остановке барабана осадок сползает с
его стенок и удаляется из центрифуги. Исходная суспензия за-
гружается на распределительный диск 3 при вращении бара-
бана с пониженной скоростью. В остальном саморазгружаю-
щиеся центрифуги не отличаются от висячих центрифуг с ниж-
ней выгрузкой.
Фильтрующие центрифуги с ручной и гравитационной вы-
грузкой имеют следующие достоинства сравнительно с аналогич-
ными центрифугами отстойного типа:
1) низкая конечная влажность осадка,
2) возможность тщательной промывки осадка.
Автоматические центрифуги периодического
действия с ножевым съемом осадка на ходу
В таких центрифугах загрузка и разгрузка происходят авто-
матически, без остановки или снижения скорости барабана. Раз-
грузка на ходу производится при помощи ножа, который пере-
мещается вверх и вниз независимо от барабана и срезает оса-
док. Подача суспензии, фугование и снятие осадка осуществ-
ляются последовательно друг за другом, смена и длительность
отдельных операций регулируются специальным автоматическим
устройством.
Продолжительность отдельных операций в автоматических
центрифугах составляет в среднем: наполнение т;н—0,5—2,5 мин,
центрифугирование — 0,4—0,5 мин, выгрузка тв — 0,7—5 мин.
Промывка и сушка осадка производятся только в случае необ-
ходимости. Продолжительность полного Цикла т меньше, чем в
центрифугах с ручной или гравитационной выгрузкой, и обычно
не превышает 10 мин, йо в отдельных случаях может достигать
160 мин и более.
Автоматические центрифуги с ножевым съемом осадка из-
готовляются только с горизонтальным валом.
Горизонтальная автоматическая центрифуга (рис. 8-35) имеет
дырчатый барабан 1, расположенный между подшипниками го-
ризонтального вала 2. Суспензия подается по трубе 3, ввод и
прекращение подачи суспензии производятся при помощи кла-
пана 4, работой которого управляет гидравлический (масляный)
цилиндр 5. Такой же цилиндр приводит в действие нож 6 для
снятия осадка, масло поступает под поршень цилиндра (при
подъеме ножа) или сверху поршня (при опускании ножа).
16. Устройстве центрифуг
301
‘ Ввод масла производится автоматически через определенные
промежутки времени с таким расчетом, чтобы действия ножа и
клапана координировались следующим образом:
1) подача суспензии — загрузочный клапан открыт, нож опу-
щен; 2) фугование — загрузочный клапан закрыт, нож опущен;
3) выгрузка осадка — загрузочный клапан закрыт, нож поднят.
Рис. 8-35. Горизонтальная автоматическая цен-
трифуга:
/ — барабан; 2— горизонтальный вал; 5 —труба для подачи
суспензии; клапан; 5 — масляный цилиндр; 6— нож;
7 —желоб, 8— пневматический молоток.
Осадок выгружается по крутому наклонному желобу 7 под
действием собственной тяжести; выгрузка облегчается благода-
ря частым ударам по желобу пневматического молотка 8, кото-
рый автоматически включается при подъеме ножа и выключает-
ся при его опускании.
Основные достоинства автоматических центрифуг: 1) устра-
нение непроизводительных затрат времени и энергии, связанных
с остановкой или торможением барабана для разгрузки, 2) пол-
ная автоматизация процесса. Недостатком таких центрифуг
является измельчение осадка при съеме его ножом.
302
Гл 8 Разделение жидких неоднородных систем
Центрифуги непрерывного действия
с выгрузкой пульсирующим поршнем
В центрифуги этого типа суспензия подается непрерывно,
осадок периодически выталкивается поршнем-толкателем из
дырчатого барабана, расположенного на горизонтальном валу
(рис. 8-36).
Внутри барабана 1 вдоль его оси перемещается поршень-
толкатель 2, который укреплен на конце штока 7. Шток нахо-
Рис. 8-36. Центрифуга непрерывного действия с выгрузкой пульсирующим
поршнем:
/ — барабан, 2 —поршень-толкатель; 3 — приемный конус; / — сито; 5 — полый вал; б—ползун;
7— шток; 8 — распределитель; 9 — цилиндр; 10— поршень; 77 —шестеренчатый насос; 12— кожух.
дится внутри полого вала 5, вращается вместе с ним и одновре-
менно совершает возвратно-поступательное движение. Суспен-
зия подводится в конус 3 и через отверстия в нем поступает в
барабан, покрытый изнутри металлическим щелевым ситом 4.
Слой осадка, отлагающийся на сите, перемещается поршнем-тол-
кателем 2 к открытому концу барабана, через который часть
осадка выгружается в кожух 12.
За каждый рабочий ход выгружается такое количество осад-
ка, которое соответствует длине хода поршня, равной примерно
7ю высоты барабана. Когда поршень движется в обратном на-
правлении, на освобождающейся при этом поверхности сита 4
образуется новый слой осадка. При следующем рабочем ходе
16. Устройство центрифуг
303
поршня из барабана выталкивается новая порция осадка и т. д.
Поршень-толкатель обычно совершает 10—16 ходов в минуту.
Направление движения поршня изменяется автоматически
посредством ползуна 6, который, перемещаясь с штоком 7, от-
крывает и закрывает переключающий клапан; через этот кла-
пан в золотник поступает масло. Золотник, в свою очередь, упра-
вляет поступлением масла в два распределителя 8. Масло, на-
гнетаемое шестеренчатым насосом 11, поступает через распре-
делители попеременно в правую и левую полости цилиндра 9 и
давит на поршень 10, вызывая возвратно-поступательное движе-
ние толкателя. В случае необходимости в барабан через спе-
циальную трубу подводится вода для промывки осадка, а в ко-
жухе устанавливаются раздельные патрубки для отвода фугата
и промывных вод.
Кроме непрерывности действия, основным достоинством опи-
санных центрифуг является меньшее измельчение осадка или
разрезание волокон, чем при выгрузке другими механическими
способами (ножом, шнеком).
Недостатки этих центрифуг: 1) загрязнение фугата осадком,
частично проходящим через отверстия сита, 2) значительный
расход энергии на перемещение осадка, 3) сравнительно быст-
рый износ фильтровальной перегородки.
Повышению производительности центрифуг непрерывного
действия, без снижения эффекта разделения, способствует уве-
личение длины барабана. В связи с этим в последнее время по-
лучили распространение центрифуги с пульсирующей выгруз-
кой осадка и многоступенчатым барабаном (рис. 8-37). Такая
центрифуга состоит как бы из нескольких последовательно
включенных центрифуг с пульсирующей выгрузкой осадка,
имеющих относительно короткие барабаны, смещенные друг от-
носительно друга (по общей оси). Разделяемая суспензия по-
следовательно проходит все барабаны, которые совершают воз-
вратно-поступательные движения вдоль оси. Торцовая кромка
одного барабана служит поршнем-толкателем для разгрузки
осадка из следующего барабана. Специальным поршнем-толка-
телем осадок выталкивается« только из барабана первой сту-
пени.
В центрифугах с многоступенчатым барабаном достигается
эффективное разделение трудноотфильтровываемых суспензий,
при разделении которых требуется продолжительное фугование.
Переходя из одной ступени в другую, осадок разрыхляется и
благодаря этому дополнительно подсушивается, что способ-
ствует повышению призводительности центрифуги. Одновремен-
но в таких центрифугах достигается более эффективная промыв-
ка осадка и лучшее разделение фугата и промывных вод, чем в
304
Гл 8 Разделение жидких неоднородных систем
одноступенчатых центрифугах. Удельный расход энергии в мно-
гоступенчатых центрифугах значительно меньше, чем в односту-
Сцспензия
Рис. 8-37. Многоступенчатая центрифуга непре-
рывного действий с пульсирующей выгрузкой
осадка:
/ — барабан первой ступени, 2 — барабар второй ступени;
3— барабан третьей ступени; 4 —барабан четвертой сту-
пени, 5—гидравлический привод, б—труба для подачи про-
мывной воды
пенчатых, так как значительная часть жидкости удаляется уже
в барабанах первых ступеней сравнительно малого диаметра.
Центрифуги непрерывногодействия сшнековой
выгрузкой
Выгрузка осадка при помощи шнека производится главным,
образом в Горизонтальных центрифугах отстойного типа
(рис. 8-38).
Глухой барабан 8 такой центрифуги имеет коническую или
цилиндрическо-коническую форму и вращается на полых цап-
фах 1. Внутри барабана 3 более медленно вращается шнек 5
с полым валом, цапфы которого находятся внутри цапф бара-
бана 3. Суспензия подается по трубе 6 и через отверстия 4 по-
ступает в наружный барабан. В некоторой части объема бара-
бана, у более широкого его конца, происходит отстаивание сус-
пензии (зона отстаивания), причем жидкость переливается через
окна 7 в торцовой стенке барабана, а осадок медленно переме-
16 Устройство центрифуг
305
щается шнеком к разгрузочным окнам 9 в противоположном
конце барабана. При движении осадка в незаполненной суспен-
зией части барабана 3 осадок дополнительно обезвоживается
(зона сушки).
Перемещение осадка происходит в результате того, что шне-
ковый барабан 5 делает меньше оборотов в 1 мин (на 1,5—2%),
чем барабан 3, вращаясь с ним в одинаковом направлении.
Рис. 8-38. Горизонтальная центрифуга непрерывного действия с шнековой
выгрузкой:
I—полая цапфа, 2— кожух, 3— барабан, 4 —отверстия для суспензии, 5 — барабан-шнек,
о — труба для подачи суспензии, 7—окно для фугата, 8—труба для подачи промывной воды;
9 —окно для выгрузки осадка
Такая разница скоростей вращения достигается при помощи
дифференциального редуктора В случае необходимости осадок
промывается в конц*е зоны етстаивания водой, подаваемой по
трубе 8. После подсушки осадок удаляется через окна 9 в не-
подвижный кожух 2, в котором имеются отдельные камеры для
отвода осадка и фугата. Режим работы центрифуги можно ре-
гулировать, изменяя продолжительность отстаивания и осушки
осадка (регулируя открытие окон), или изменяя числа оборо-
тов барабана и шнека.
Достоинства горизонтальных центрифуг с шнековой выгруз-
кой: 1) высокая производительность, 2) пригодность для разде-
ления суспензий с высоким содержанием твердого мелкоизмель-
ченного вещества, 3) пригодность для классификации^
20 Зак 546,
306
Гл. 8. Разделение жидких неоднородных систем
Недостатки: 1) высокий расход энергии на перемещение
осадка и на потери в дифференциальном редукторе, 2) значи-
тельное измельчение осадка, 3) загрязнение фугата мелкоиз-
мельченными частицами твердой фазы.
Центрифуги непрерывного- действия
с инерционной выгрузкой
Если угол наклона вертикального конического барабана к его оси больше
угла трения осадка, то последний под действием центробежной силы может
перемещаться вдоль образующей барабана к его основанию и удаляться
из центрифуги. Этот принцип положен в основу конструкций непрерывно-
действующих центрифуг с инерционной выгрузкой.
В современной центрифуге подобного типа (рис. 8-39) обрабатываемая
суспензия поступает сверху в конический фильтрующий барабан 1, внутри
Рис. 8-39. Непрерывнодействующая вер-
тикальная центрифуга с инерционной вы-
грузкой:
/ — барабан; 2 — тормозящий шнек; 3— кожух;
4 — канал для отвода фугата; 5 — канал для удаления
осадка.
которого вращается тормозящий шнек 2. Шнек вращается медленнее бара-
бана и потому замедляет движение осадка, перемещение которого опреде-
ляется скоростью вращения шнека относительно барабана. Таким способом
увеличивается продолжительность фугования и, следовательно, повышается
степень разделения. Обезвоживанию осадка способствует также утоньшение
его слоя по мере перемещения вниз. Осадок удаляется через канал 5, фугат
отводится из кожуха 3 через канал 4.
Способу выгрузки осадка центробежными силами присущи все достоин-
ства других способов непрерывной выгрузки (высокая производительность,
регулирование продолжительности процесса и др.). В то же время он лишен
многих их недостатков (загрязнение осадка фугатом, измельчение осадка,
значительный расход энергии). Поэтому разработке новых конструкций цен-
трифуг с инерционной выгрузкой уделяется много внимания.
Одной из новых эффективных конструкций центрифуг непрерывного дей-
ствия с инерционной выгрузкой являются вибрационные центрифуги. На
рис. 8-40 показана вертикальная вибрационная центрифуга с фильтрующим
барабаном / в виде усеченного конуса, обращенного большим основанием
16. Устройство центрифуг
Рис. 8-40. Вибрационная центрифуга непрерывного действия:
1 — фильтрующий барабан; 2—загрузочное устройство; 3 — головка; 4, 5 — резиновые буферы; 6, 7—ко-
жухи; приводной шкив; 9— шатун; 10— эксцентриковый вал.
ё
308 Гл 8 Разделение жидких неоднородных систем
кверху. Барабан приводится во вращение от электродвигателя с помощью
приводного шкива 8, который соединяется с основанием барабана через
резиновые буферы 5 При помощи эксцентрикового вала 10 и шатуна 9 (свя-
занного посредством резиновых буферов 4 с головкой 3, жестко соединенной
с барабаном) барабану сообщаются вибрации
Разделяемая концентрированная суспензия поступает в барабан через за-
грузочное устройство 2. Фугат проходит сквозь отверстия в стенках барабана
и удаляется из кожуха 6.
Под действием вертикальной составляющей центробежной силы и сил
инерции, обусловленных вибрациями барабана (угол его наклона меньше
угла естественного откоса осадка), осадок перемещается по стенкам бара-
бана вверх, через верхний открытый край барабана поступает в кожух 7
и затем удаляется из центрифуги
Вибрации барабана способствуют не только непрерывному перемещению
осадка вверх по стенкам барабана, но и лучшему отделению твердой фазы
от жидкой
Сверхцентрифуги
Для разделения тонких суспензий и эмульсий требуется воз-
действие весьма значительных центробежных сил. В этих слу-
чаях применяются сверхцентрифуги, которые делятся на трубча-
тые сверхцентрифуги и жидкостные сепараторы.
Трубчатые сверхцентрифуги. Трубчатая сверхцентрифуга
имеет глухой барабан в виде трубы небольшого диаметра (до
200 мм), который в несколько раз меньше ее длины. При такой
форме барабана удается значительно увеличить число его обо-
ротов, т. е. создать большую центробежную силу без чрезмер-
ного увеличения напряжения в стенках барабана. Так, если уве-
личить вдвое число оборотов п барабана в минуту и одновре-
менно уменьшить во столько же раз его диаметр Ь, то окружная
nDn
скорость w — -эд- и напряжение в стенках не изменятся, а цен-
тробежная сила (С — kDn2, где k — коэффициент пропорцио-
нальности) при удвоении числа оборотов увеличится в 4 раза,
а вследствие уменьшения вдвое диаметра уменьшится в 2 раза,
т. е. всего увеличится в 2 раза. Кроме того, в трубчатом бара-
бане удлиняется путь суспензии, благодаря чему улучшаются
условия отстаивания.
В трубчатой сверхцентрифуге (рис. 8-41) обрабатываемая
жидкость поступает внутрь быстровращающегося барабана 5
(« = 8000—45000об/мин) по трубке 1, ударяется об отража-
тель 2 и отбрасывается на стенки барабана. Чтобы жидкость
не отставала от стенок, в барабане установлена длинная кре-
стовина 4.
В головке 8 барабана имеются обособленные отверстия для
раздельного выхода тяжелой и легкой жидкости, в верхней
части барабана находятся две отдельные камеры для отвода
этих жидкостей. Тяжелая жидкость отводится через патрубок 6,
16 Устройство центрифуг
309
легкая — через патрубок 7. Вследствие большой скорости вра-
щения барабан трубчатых сверхцентрифуг подвешивается на
гибком валу 9 (веретене).
В разделяющих сверхцентрифугах (рис. 8-41, слева) в верх-
ней части барабана устанавливается сменная кольцевая диа-
фрагма для регулирования расстояния г0 от оси барабана до
поверхности слоя тяжелой
жидкости.
В осветляющих сверхцен-
трифугах осветленная жид-
кость удаляется через отвер-
Рис. 8-41. Трубчатая сверхцентрифуга:
/ — трубка для подвода суспензии; 2 — отражатель; 3— станина, /—крестовина; 5 — барабан,
б—патрубок для отвода тяжелой жидкости; 7—патрубок для отвода легкой жидкости;
<?—головка бдрабана; 9 — гибкий Вал: 10— привод.
етия в головке барабана, а осадок отлагается на стенках ба-
рабана и удаляется вручную после остановки центрифуги.
Достоинства трубчатых сверхцентрифуг: 1) высокая интен-
сивность разделения (развиваемая центробежная сила в
8—34 раза больше, чем в обычных центрифугах), 2) компакт-
ность и герметичность.
Недостатки: 1) периодическое разделение суспензий, 2) ма-
лая емкость, 3) ручная выгрузка осадка, 4) меньшая раздели-
тельная способность, чем для тарельчатых сепараторов (см.
ниже).
310
Гл. 8. Разделение жидких неоднородных систем
Жидкостные сепараторы. Эти сепараторы применяются для
разделения эмульсий, а также для осветления жидкости. Они
имеют большие, чем в трубчатых сверхцентрифугах, барабаны
(диаметр 150—300 мм) и меньшее число оборотов (5500—
10 000 об/мин).
Наиболее распространены тарельчатые сепараторы, в кото-
рых процесс центрифугирования ускоряется путем разделения
потока жидкости на тонкие слои без увеличения ее скорости.
Рис. 8-42. Тарельчатый сепаратор:
1— барабан, 2—конические тарелки; 3 — отверстия в тарел-
ках; 4 — канал для выхода легкой жидкости; 5 — труба для
подвода жидкости, 6 — канал для выхода тяжелой жидкости
Кроме того, в тарельчатых сепараторах разделившиеся жидко-
сти больше не соприкасаются и потому не могут вновь смеши-
ваться. Благодаря этому создаются благоприятные условия для
осветления жидкостей с малым содержанием твердой фазы (до
0,1 %) и для разделения эмульсий.
В барабане 1 тарельчатого сепаратора (рис. 8-42) находится
пакет конических тарелок 2. Разделяемая жидкость входит че-
рез трубу 5 и движется в полостях между тарелками, причем
16 Устройство центрифуг
311
на тарелки жидкость поступает через каналы, образованные
отверстиями 3.
При разделении более тяжелая жидкость направляется к
стенке барабана, движется вдоль нее и удаляется через кольце-
вой канал 6 в крышке. Легкая жидкость движется к середине
барабана, проходит между тарелками и питающей трубой 5,
после чего удаляется через край удлиненной горловины верхней
тарелки и поступает в канал 4. При осветлении жидкости твер-
дые частицы осаждаются на поверхности каждой тарелки (кро-
Рис. 8-43. Барабан сепаратора с гидравлической вы-
грузкой осадка:
1 — конусообразный барабан; 2— конические тарелки; 3 — сопла;
4—чаша; 5 — отверстия для ввода рециркулирующего тяжелого
компонента; б—коническая вставка; 7—кольцевой канал.
ме верхней), соскальзывают по ней и скапливаются возле сте-
нок барабана. Осветленная жидкость поднимается вверх и сли-
вается через край горловины верхней тарелки.
В настоящее время получают распространение тарельчатые
сепараторы непрерывного действия с гидравлической выгрузкой
сгущенной суспензии (тяжелый компонент) через сопла. Бара-
бан 1 такого сепаратора (рис. 8-43) образует конусообразную
камеру, в которой находится пакет конических тарелок 2. Сус-
пензия поступает через канал в конической вставке 6 в чашу 4
и проходит между тарелками. Здесь из суспензии выделяется
тяжелый компонент, который удаляется из барабана через соп-
312
Гл 8 Разделение жидких неоднородных систем
ла 5, расположенные по периферии барабана. Легкий компонент
удаляется через кольцевой канал 7. В некоторых случаях тяже-
лый компонент подвергается многократной сепарации, при ре-
циркуляции он возвращается в барабан снизу и поступает на
тарелки через отверстия 5 в чаше 4. Сепараторы такого типа
применяются для отделения твердых частиц катализатора в
процессах получения полимеров.
Преимущества тарельчатых сепараторов по сравнению с труб-
чатыми сверхцентрифугами: 1) более высокая степень разделе-
ния, 2) большая емкость барабана.
Недостатки: 1) сложность устройства, 2) трудность изгото-
вления сепараторов для переработки химически активных жид-
костей.
Кроме тарельчатых, применяются также менее интенсивные камерные
сепараторы периодического действия
В однокамерном сепараторе отсутствуют тарелки и разделение произво-
дится в полости вращающегося барабана (камеры), в нижнюю часть кото-
рого по трубе, проходящей вдоль оси барабана, подается суспензия или
эмульсия Труба имеет снизу конический раструб, на наружной поверх-
ности — несколько вертикальных ребер, препятствующих отставанию жидко-
сти от стенок барабана Компоненты разделяемой смеси отводятся сверху
через обособленные каналы по оси и периферии барабана
В многокамерном сепараторе в барабане имеется несколько цилиндриче-
ских вставок, образующих концентрические камеры, через которые последо-
вательно, от центра к периферии барабана, движется разделяемая смесь
17. Сравнение, выбор и обслуживание центрифуг
Центрифуги непрерывного действия производительнее перио-
дически действующих и обслуживание их значительно легче.
Поэтому центрифуги непрерывного действия все шире внедря-
ются в промышленность, постепенно вытесняя центрифуги пери-
одического действия. Последние сохраняют свое значение в про-
изводствах небольшого масштаба.
Фильтрующие центрифуги периодического действия с руч-
ной и гравитационной выгрузкой применяются для обработки
штучных, волокнистых и зернистых материалов. Достигаемая в
них конечная влажность осадка составляет менее 1 % для круп-
нозернистых веществ, 1—5% для среднезернистых и 5—40%
для мелкозернистых.
Отстойные центрифуги такого же типа применяются для раз-
деления труднофильтруемых суспензий Получаемые в отстой-
ных центрифугах осадки имеют влажность до 70% и выше, т. е.
значительно большую по сравнению с осадками в фильтрую-
щих центрифугах.
Более производительны автоматические центрифуги, которые,
несмотря на периодичность действия, занимают промежуточное
положение между периодически и непрерывно действующими ап-
17. Сравнение, выбор и обслуживание центрифуг
313
паратами. Вследствие съема осадка ножом автоматические цен-
трифуги не рекомендуется применять при разделении материа-
лов, для которых нежелательно измельчение зерен или разреза-
ние волокон. Для обработки таких материалов могут быть ус-
пешно применены центрифуги непрерывного действия с разгруз-
кой пульсирующим поршнем. Они пригодны для переработки
кристаллических и волокнистых материалов, быстро теряющих
влагу (например, сульфата аммония, целлюлозы и др.). При
этом содержание очень мелких частиц (диаметром менее.
150 мк) в разделяемой суспензии не должно превышать 10—20%*
количества твердой фазы.
Для непрерывной обработки суспензий с большим содержа-
нием мелкоизмельченных твердых частиц пригодны горизонталь-
ные центрифуги с шнековой выгрузкой. Эти центрифуги исполь-
зуются также в качестве классификаторов — для разделения зе-
рен по крупности или по плотности. Вертикальные центрифуги
с шнековой выгрузкой применяются главным образом для от-
деления твердых частиц средней крупности (руда, песок, уголь).
Центрифуги с инерционной выгрузкой весьма эффективны,
но пока еще мало распространены.
Сверхцентрифуги широко применяются для осветления лаков
и масел, для разделения весьма тонких суспензий и эмульсий.
Вследствие компактности и герметичности они удобны для об-
работки вредных, а также горячих жидкостей.
Жидкостные сепараторы применяются для обезвоживания
нефтяных продуктов, смол и растительных масел. Тарельчатые
сепараторы широко используются в молочной промышленности
(для отделения сливок от молока). Сепараторы хорошо приспо-
соблены для отделения тонкодисперсной твердой фазы и, по-
видимому, в ближайшем будущем найдут в химической промыш-
ленности более широкое применение.
Центрифуги являются быстроходными машинами, требую-
щими очень тщательного наблюдения и обслуживания.
После проверки готовности установки к работе центрифугу
пускают в ход, следя за тем, чтобы скорость вращения барабана
нарастала плавно, без рывков. При работе центрифуги следует
внимательно следить за вибрациями барабана и вала. Сильное
дрожание вала и колебания барабана (барабан «сильно бьет»),
указывают на неравномерное распределение загруженного мате-
риала в центрифуге или на значительный износ подшипников.
При эксплуатации центрифуг необходимо строго соблюдать
правила техники безопасности, так как нарушение их может
привести к аварии и травмам.
Для остановки центрифуги сначала выключают электродви-
гатель, затем плавно приводят в действие тормоз.
314
Гл. 8. Разделение жидких неоднородных систем
18. Расчет центрифуг
Технологический расчет центрифуг сводится к определению
их производительности и расхода энергии на центрифугирование.
Несмотря на сложность точного расчета производительности
центрифуг, в настоящее время разработан единый метод оценки
эффективности и производительности фильтрующих и отстой-
ных центрифуг. Этот метод, приводимый ниже, при наличии неко-
торых опытных данных позволяет определять производительность
центрифуг с достаточной для технических расчетов точностью.
Примем следующие обозначения:
R и /?н — внутренний и наружный радиусы барабана, м-,
L — длина барабана, м;
г0 — внутренний радиус кольцевого слоя суспензии в бара-
бане, м-,
F — — поверхность фильтрования суспензии в барабане, м2;
F' — 2nr0L — поверхность зеркала суспензии в барабане, м2-,
Q = т: (/?2 — г2) L — рабочий объем барабана, м3;
“ — угловая скорость барабана, рад/сек-,
тпит. — продолжительность питания барабана суспензий, сек-,
Рс и Рос. — плотность суспензии и влажного осадка, кг/м3-,
Ртв. и Рж — плотность твердой и жидкой фазы суспензии, кг1м3\
Др = ртв> — рж — разность плотностей фаз, ке/ти3;
р.ж — вязкость жидкой фазы суспензии, н • сек/м2.
Производительность центрифуг. Теоретическая производительность центри-
фуг определяется по общей формуле
Ут = aS м3!сек (8-52)
Для осадительных центрифуг а = w0 (w0—скорость осаждения частиц
твердой фазы под действием сил тяжести, см. стр. 173), для фильтрующих
центрифуг а ~ k (k — постоянная фильтрования, зависящая от свойств осадка
и определяемая опытным путем).
Производительность центрифуг обычно характеризуется объемом V
жидкости (фугата), удаляемого из барабана в единицу времени, однако при
малом содержании твердой фазы в суспензии производительность отстойных
центрифуг предпочтительнее определять по объему V суспензии, поступаю-
щему в барабан в единицу времени.
Индекс производительности 2 зависит от формы барабана центрифуги.
С достаточной для технических расчетов точностью значение 2 можно опре-
делять по формуле
2 = ср (8-53)
и2 (/? 4- г0) „ .
где ФСр. =---------------средний фактор разделения центрифуги;
- —2-----средний радиус слоя разделяемой суспензии,
включая слой осадка;
Л:р. = (# +го) — средняя поверхность разделения, м2.
18. Расчет центрифуг
315
Более точные формулы расчета S для центрифуг различных типов (по
В. И. Соколову) приводятся ниже:
Центрифуги Р асчетные
формулы
Фильтрующие с цилиндрическим барабаном . . £ =--------р-
900 In —
Отстойные с коротким цилиндрическим бараба- ЪппРЬГц
............................................ = " 900
Отстойные с коническим барабаном.............. S —
Фактическая производительность центрифуги меньше теоретической
вследствие скольжения жидкости относительно стенок барабана (до дости-
жения ею скорости вращения барабана), образования вихревых потоков,
затрудняющих оседание мелких частиц, а также вследствие перемешиваю-
щего действия шнека (в центрифугах с шнековой выгрузкой) и действия
других факторов. Поэтому фактическую производительность центрифуг опре-
деляют по формуле-
V = СаБ t (8-54)
где £ — показатель эффективности работы центрифуги, равный отношению
•фактической и теоретической производительности центрифуги.
Показатель эффективности работы центрифуги определяется по обобщен-
ной формуле:
C=^(Frll/(Rell))’(M’ (8-55)
V2
где Fru = - „ „ ---критерий Фруда для поля центробежных сил;
ч Т о
СО Гq/-*
Яец — -----критерий Рейнольдса для жидкости в барабане;
Z7C/" О|АЖ
А? Л
!---симплекс Архимеда.
Рж
По опытным данным, для отстойных центрифуг с короткими цилиндри-
ческими барабанами: А = 9, х = 0,1 у = —0,1, z = 2,04; для отстойных
центрифуг со шнековой выгрузкой: А = 9,52, х = 0,16, у — —0,151, z — 0,286
Подставляя выражение С подформуле (8-55) в уравнение (8-54) и решая
последнее относительно V, наводят производительность центрифуги.
Для определения производительности по формуле (8-54) необходимо
знать величину а, характеризующую проницаемость и соответственно сопро-
тивление осадка. Определение сопротивления осадка в условиях центробеж-
ного фильтрования затруднительно, но производительность промышленной
фильтрующей центрифуги можно рассчитать также, не зная физических
свойств осадка, но проводя разделение данной суспензии в лабораторных
условиях.
Производительность промышленной центрифуги периодического действия
может быть определена по уравнению:
V = A . гпит. (8-56)
где А — коэффициент, характеризующий сопротивление осадка.
316
Гд. 8. Разделение жидких неоднородных систем
По аналогии производительность лабораторной центрифуги (для которой
все величины обозначены индексом «л») определяется по уравнению:
Ил — "^Л • (тпит.)л
(8-57)
Разделив уравнение (8-56) на уравнение (8-57), находят производитель-
ность промышленной центрифуги за один цикл.
К=УЛ
, ^пит
2л (тпит.)л
(8-58)
Продолжительность питания тпит. центрифуги выбирают такой, чтобы
весь рабочий объем барабана заполнился осадком. Однако если к концу
заполнения барабана осадком значительно снижается скорость центрифугиро-
вания, для достижения максимальной средней производительности центри-
фуги следует принимать, что продолжительность подвода суспензии в бара-
бан должна быть равна общей продолжительности центрифугирования и вы-
грузки осадка:
тпит. = тц ~Ь твыг. (8-59)
Для определения производительности центрифуг непрерывного действия
может быть использовано уравнение (8-58) с исключением из него отноше-
ния ^ПИТ:-— t так как питание этих центрифуг осуществляется непрерывно.
(тпит.)л
Производительность промышленных центрифуг непрерывного действия,
производящих в основном отжим влаги из осадка (центрифуги с выгрузкой
пульсирующим поршнем), определяют, проводя предварительное центрифу-
гирование продукта в лабораторной центрифуге того же типа, при том же
факторе разделения, одинаковой толщине слоя суспензии, одинаковой длине
хода поршня и скорости его движения.
На основе лабораторных данных производительность промышленной
центрифуги по осадку рассчитывают по формуле
м3/сек (8-60)
После определения производительности проверяют соответствие влаж-
ности осадка заданной величине по формуле
\ “'н /
где wa— влажность осадка в начале центрифугирования, определяемая на
лабораторной центрифуге;
w и wn — конечная влажность осадка в промышленной и лабораторной
центрифугах.
' Расход энергии. Полный расход энергии в центрифуге периодического
действия складывается из следующих затрат мощности’
1) на сообщение кинетической энергии суспензии, поступающей на раз-
деление (при загрузке барабана), Nr,
2) на преодоление вредных сопротивлений — на трение в подшипни-
ках А^2 и трение барабана о воздух
3) на срез осадка (при выгрузке барабана), Nt-
Для автоматических и других периодически действующих центрифуг
расход энергии при отдельных операциях цикла различен:
18. Расчет центрифуг
317
при загрузке барабана
^заг = 1 + -^2 + ^з (8-62)
при отжиме Nотж. == 7V2 + -^з (8-63)
при выгрузке барабана (срезе осадка)
^ВЫГ. = ^2 + ^з + ^4 (8-64)
Затрата мощности (в кеш) на сообщение кинетической энергии суспен-
зии определяется по формуле.
=2й|^1(1_0'М)р»'-+Ч (8'65)
где —коэффициент заполнения рабочего объема барабана осадком;
/ f \2
ф = 1— 1-^-1 —отношение рабочего объема к полному объему барабана.
Слагаемое k в уравнении (8-65) определяется по следующим формулам:
для фильтрующих центрифуг
6 = (Л-В)Рж (8-66)
для отстойных центрифуг
/ г \2
А. = (Л-В)Рж^ (8-67)
В выражениях (8-66) и (8-67):
Л — ----Рс-объемная доля жидкой фазы в суспензии;
Ртв. Рж
В — — объемная доля жидкой фазы во влажном осадке.
Ртв. Рж
Плотность влажного осадка рос, (в кг/ж3) определяется по формуле,
аналогичной (8-3), а тпит. выражается в сек.
Расход энергии (в квт) на трение в подшипниках:
К* = 200(/ <8’68>
где Р — динамическая нагрузка на подшипники, зависящая от веса загру-
женного барабана и сил, возникающих вследствие его неуравнове-
шенности (дебаланса), н; г
d — диаметр цапф вала, м;
f — коэффициент трения (для подшипников скольжения f ~ 0,01, для
подшипников качения f ~ 0,002).
Динамическая нагрузка на подшипники определяется в зависимости от
статической нагрузки mg и фактора разделения по формуле:
Р = mg (1 + 0.002Ф) н (8-69)
где т — масса загруженного барабана, кг\
g — ускорение силы тяжести, .м/сек2.
Расход энергии (в квт) на трение барабана о воздух (при плотности
воздуха 1,3 кг/м3):
= 14,7 • 10~ W (г4 4- R4) (8-70)
318 Гл. 8. Разделение жидких неоднородных систем
Расход энергии (в кет) на срез осадка:
/8 (р~ А) а
Ni = 1,62 • 104тВЬ1Г. (8'71)
где I — длина режущей кромки ножа, мм;
8 — толщина слоя осадка, мм;
а — удельное сопротивление резанию, кгс/'мм2;
Ъыг. — время среза, сек.
В центрифугах непрерывного действия с выгрузкой осадка пульсирую-
щим поршнем мощность затрачивается на сообщение жидкости скорости
вращения барабана (Ni), на преодоление вредных сопротивлений — трения
в подшипниках и уплотнениях (Л/г) и трения барабана о воздух (Л/'з), на
выгрузку осадка поршнем-толкателем (Pt).
Расход энергии (в кет) на сообщение суспензии скорости вращения
барабана определяется по формуле
У|=^5Г (8’72)
где Gc — количество суспензии, поступающей на разделение, кг/сек.
Величины Л^2 и N3 определяются по формулам (8-68) и (8-70), а расход
энергии (в кет) на выгрузку осадка по формуле:
ТПосФ/гЛЛ (1+*) zn7o4
N* =------------------- (8-73)
В уравнении (8-73):
woc. =:7t(/?2—r2)Z,p0C— масса слоя осадка в барабане, кг;
In — длина хода поршня-толкателя, м;
f— коэффициент трения продукта о сито (для кри-
сталлических веществ f ~ 0,32—0,54);
6 = 0,75 — коэффициент, учитывающий деформацию осадка
при фильтровании;
х = 0,8 — 1,0 — отношение времени холостого (обратного) и ра-
бочего хода поршня.
В центрифугах непрерывного действия с шнековой выгрузкой осадка
расход энергии складывается из мощности, затрачиваемой на сообщение
кинетической энергии осадку и сливу (Ni), мощности, затрачиваемой на
преодоление вредных сопротивлений (Йг) — потерь в редукторе, трения
в цапфах шнека и трения барабана о воздух, а также мощности, затрачивае-
мой на транспортирование осадка внутри центрифуги (Мз).
Расход энергии на транспортирование осадка представляет собой в свою
очередь сумму энергии, расходуемой на преодоление составляющей центро-
бежной силы (направленной вдоль образующей барабана, к широкому его
концу), и энергии, расходуемой на преодоление сил трения осадка о стенки
барабана и о лопасти шнека.
Потери энергии в редукторе этих центрифуг значительны и изменяются
в широких пределах. Поэтому расход энергии в центрифугах с шнековой
выгрузкой пока не может быть с достаточной точностью определен расчетом.
Пример 8-9. Определить фактор разделения и индекс производительности
автоматической фильтрующей центрифуги АГ-1800 с барабаном следующих
размеров: внутренний радиус R = 900 мм, длина L = 700 мм, радиус борта
г = 650 мм. Число оборотов барабана п = 720 об/мин.
18. Расчет центрифуг
319
Решение. Угловая скорость вращения барабана составляет:
т.п 3,14-720 ,,
“ = “ЗУ-----------= 75,4 рад/сек
Определяем фактор разделения по формуле (8-49):
ф = =521
g 9,81
Находим рабочий объем барабана центрифуги (принимая Го = г):
Q = т (/?2 — г2) L = 3,14 (0,92 - 0,652) 0,7 s* 0,85 м3
По формуле для фильтрующих центрифуг с цилиндрическим барабаном
(стр. 315) определяем индекс производительности:
0,85 - 720* =15()0jf2
9W)-'"w
Пример 8-10. Рассчитать производительность и коэффициент заполнения
осадком центрифуги АГ-1800 (см. пример 8-9) при разделении суспензии
гипса с соотношением Т : Ж = 1 : 3. Плотность жидкой фазы суспензии
рж = 1000 кг/м3, плотность осадка . рос. = 1830 кг/м3, требуемая конечная
влажность осадка ауос. = 20% вес.
| Центрифугирование данной суспензии проводилось на лабораторной цен-
В трифуге такого же типа, имеющей следующую характеристику: радиус бара-
11 бана Рл — 215 мм, длина барабана £л==190 мм, рабочий объем
| йл = 10,6-10~3 м3. Индекс производительности + = 75 л*2.
| На лабораторной центрифуге при продолжительности питания
й (тпит.)л = 1 Мин было получено 32,5-10-3 .и3 фугата. Осадок с указанной выше
У конечной влажностью получался при отжиме в течение тц = 2 мин. Про-
Ж должительность выгрузки (среза) осадка составляла тВЬ1Г- = 1 мин.
Ж Решение. Для достижения максимальной средней производитель-
« ности промышленной центрифуги (стр. 316) принимаем:
| ^пит. = тц + твыг. =2+1=3 мин
е
£ Тогда продолжительность полного цикла центрифугирования составит:
7* = тпит. + тц + твыг> = 3 + 2 + 1 = 6 мин
Объем фугата, получаемого ц промышленной центрифуге за один цикл,
определяем по формуле (8-58): *
Уц = 32,5-10-3
.з.-=2дал,
10,6 • 10 3 1
Определяем производительность этой центрифуги:
у = А = 2^1 == о,375 м3!мин = 22,5 м3/ч
Согласно уравнению материального баланса по твердой фазе
(тос. + тж) -И — тое. (1 — woc.)
320
Гл. 8. Разделение жидких неоднородных сиСтеМ-
Количество влажного осадка, получаемого за один цикл, составит;
/ижАГ1 2250-0,25 1ЛОЛ
w ----= ---——___ = Ю20 кг
1 — woc — Xj I — 0,2 — 0,25
где тп — Урж= 2,25-1000 = 2250 кг — количество фугата, получаемого за один
цикл;
Т 1
X1 ~ t'^Р~Ж = 1 4J3 ~ — весовая доля твердой- фазы в исход-
ной суспензии.
Находим объем осадка, получаемого за один цикл:
^. = ^*- = -^• = 0.562
Рос. looU
Коэффициент заполнения барабана центрифуги осадком составляет:
У°с _ 0-562 _ 0 65б
ОС.
? 2 0,85
Пример 8-11. Определить мощность, потребляемую центрифугой типа
АГ-1800, при разделении суспензии плотностью рс — 1165 кг/м3. Плотность
жидкой фазы суспензии рж = 1000 кг/м?, плотность твердой фазы
тв. = 2300 кг/м3, плотность получаемого осадка рос. = 1830 кг/м* (см. при-
мер 8-10).
Наружный диаметр барабана центрифуги Дн = 1848 мм, длина бара-
бана 7.н= 780 мм, масса барабана = 3200 кг, диаметр цапф вала центри-
фуги d = 160 мм, число оборотов барабана п = 730 об/мин. Длина режущей
кромки ножа для съема осадка I — 680 мм. Внутренний радиус кольцевого
слоя суспензии в барабане г0 = 650 мм.
Решение. Определяем объемную долю жидкой фазы:
Л ртв. — Рс 2300 — 1165 л о_о
в суспензии А ~ - 2300 __ 1000 - 0,872
о Ртв, —Рос. 2300 — 1830 Л9Д1
в осадке В =± ртв. —рж ~ 2300—1000 “°’361
Находим значение k по формуле (8-66):
k - (А — В) Рж =* (0,872 — 0,361) • 1000 = 511
Отношение рабочего объема К полному объему барабана составляет:
Ф = 1 - (Го/Я)2 = 1 - = 0,479
Согласно примеру 8-9 для центрифуги типа АГ-1800 (внутренний радиус
барабана R — 0,9 -и) рабочий объем барабана 2 = 0,85 л3, фактор разделе-
ния Ф = 521.
По данным примера 8-10, принимаем продолжительность питания центри-
фуги ^пит. ~ 3 мин и коэффициент заполнения барабана осадком <р = 0,656.
Тогда мощность, затрачиваемая на сообщение кинетической энергии суспен-
зии, определится по формуле (8-65):
= °,65620542;13^f'°’9 Id — 0,5 0,656• 0,479) 1830 + 511)14,3 кет
18. Расчет центрифуг
321
Для определения расхода энергии на трение в подшипниках рассчиты-
ваем массу загруженного барабана:
m — Иц -j- m0C- — 3200 -J- 1020 — 4220 кг
Динамическая нагрузка на подшипники по формуле (8-69):
Р = 4220 • 9,81' (1 + 0,002 • 521) = 84 500 н
По данным примера 8-9 угловая скорость вращения барабана
© = 75Д рад/сек.
Принимая коэффициент трения f = 0,01 и учитывая, что обе цапфы вала
имеют одинаковый диаметр, находим расход энергии на трение в подшипни-
ках по формуле (8-68):
75,4 • 84 500 • 0,16 • 0,01
2000
= 5,1 квт
Определяем расход энергии на трение барабана о воздух по формуле
(8-70):
W3 = 14,7 • 10-6 • 0,78 • 75,43 (0,654 + 0,9244) = 4,46 квт
Объем слоя осадка в барабане центрифуги
‘'ое. = - ’,гос.£ = (^ - <)
откуда внутренний радиус слоя осадка-
г — л/~pt У/*. — 1/~о 92____________9’562.. q
roc. - V * V и’у ЗД4.0,7 м
Соответственно толщина слоя осадка:
8 = Р — гос. = 0,9 — 0,744 = 0,156 м
Принимаем время среза осадка твыг> = 60 сек и определяем расход энер-
гии на срез осадка по формуле (8-71):
680 • 156 (900 — 78) • 0,3
N' ==------1.62.- io 60------=26 квт
где 8 = 0,3 кгс/мм? — удельное сопротивление резанию.
Находим общий расход энергии для различных периодов цикла центри-
фугирования:
при загрузке барабана, по формуле (8-62)
^заг. = + N2 + W3 = 14,3 + 5,1*4- 4,46 23,9 квт
при отжиме влаги, по формуле (8-63)
ЛГОТЖ. = N2 + N3 = 5,1 -J- 4,46 s 9,6 квт
при срезе осадка, по формуле (8-64)
Мшг. = М + 4- М = 5,1 4- 4,46 + 26 = 35,6 квт
Пример 8-12. Для разделения 140 м3/ч суспензии предполагается исполь-
зовать центрифугу непрерывного действия типа НОГШ-600 с шнековой вы-
грузкой. Наибольший диаметр конического барабана центрифуги D — 600 мм,
длина барабана L — 1000 мм, число оборотов барабана п = 1400 об/мин.
21 Зак. 546.
322
Гл. 8 Разделение жидких неоднородных систем
Определить требуемое количество центрифуг типа НОГШ-600 для обеспе-
чения заданной производительности, если разделяемая суспензия имеет
следующую характеристику, плотность твердой фазы ртв. = 2300 кг/м3,
плотность жидкой фазы рж == 1000 кг/м3, вязкость жидкой фазы
р-ж = 9,71 • 10~4 н- сек/м2. Скорость осаждения суспензии w0 — 0,7 м!ч
Решение Радиус г0 свободной поверхности слоя жидкости в центри-
фуге принимаем 240 мм.
Определяем индекс производительности центрифуги по формуле для от-
стойных центрифуг с коническим барабаном (стр 315):
v=3.14.0,24L.1W.1=394 .
Находим показатель эффективности работы центрифуги по фор-
муле (8-55)
с = 9>52 { у2 \0,16 /_2Ъс_\“°'151 /lt\°’286 =
\ <^3 / \ 2*ГоРж / \ Рж /
= 9 52 / у2 У’16/___________________У -1000________\ -°>151 /2300 — 1000\0)286 _
~ ‘ \ 1472 • 0,243 • I3 ) \ 2 • 3,14 • 0,24 • 9,71 • 10~4 / \ 1000 / “
= 9,52 (O,4O2V0,32) (0,132 V-0’151) • 1,07 = 0,52V0’169
3,14-1400 1Л_ ,,
где w =--------—---- = 147 рад[сек.
Определяем производительность центрифуги по формуле (8-54)
V = O0S = 0,52V0’169 • - 394
Ovvv
V0’831 = 0,0398 м3!сек
откуда
V = 0,0206 м3!сек = 74,2 м3!ч
Требуемое количество центрифуг составляет.
140 - 1 88
74Д = 1’88
Устанавливаем две центрифуги типа НОГШ-600.
Глава 9
ОЧИСТКА ГАЗОВ
1. Общие сведения
Очистка промышленных газов от взвешенных в них твердых
частиц или жидких веществ проводится: 1) для улавливания
ценных продуктов, 2) для удаления примесей, отрицательно
влияющих на последующую обработку газа или разрушающих
аппаратуру, 3) для уменьшения загрязненности атмосферного
воздуха. В СССР обязательна очистка отходящих газов, содер-
жащих частицы золы, пыли и вредные примеси.
Загрязнение атмосферного воздуха отходящими газами про-
мышленных предприятий может быть устранено или сведено к
минимуму. Для этого необходимы:
1) рациональная организация технологических процессов —
применение таких способов производства и аппаратуры, при
которых атмосферный воздух загрязняется в наименьшей сте-
пени;
2) применение герметичных приспособлений для внутриза-
водского транспортирования пылящих или выделяющих газы
веществ;
3) разработка и внедрение промышленных способов исполь-
зования золы, огарка, шламов и других отходов производства,
загрязняющих воздух;
4) механизация производственных процессов и автоматизация
управления ими.
Примеси, содержащиеся в отходящих промышленных газах
в газо- или парообразном состоянии, извлекаются путем погло-
щения жидкостями (абсорбция, см. главу 17) или твердыми ве-
ществами (адсорбция, см. главу 20), а также путем каталитиче-
ского окисления или сжигания. Эти способы очистки газов спе-
цифичны для различных производств и в данной главе не рас-
сматриваются.
Очистка промышленных газов от взвешенных частиц произ-
водится осаждением под действием сил тяжести, инерционных
или электростатических сил, а также путем промывки и филь-
трованияь
21*
324
Гл 9 Очистка газов
Классификация пылеуловителей, применяемых для очистки
газов перечисленными способами, приведена ниже:
Способы очистки газов Аппараты
В ряде случаев для достижения требуемой степени очистки
газов применяются двухступенчатые и многоступенчатые уста-
новки, состоящие из газоочистительных аппаратов разных типов.
Иногда пылеочистители разных типов совмещают в одном агре-
гате»
2. Устройство газоочистительных аппаратов
325
Степень очистки газа в пылеулавливающем аппарате любого
типа (к. п. д. аппарата) определяется следующей зависимостью:
100 Л _А. А)100%
V 1*1 \ *'1*1/
где Ц и V2— объем газа на входе в газоочистительный аппа-
рат и выходе из него (при нормальных услови-
ях), ж3;
Xi и х2— концентрация пыли (тумана) в запыленном и очи-
щенном газе (при нормальных условиях), г/м3.
2. Устройство газоочистительных аппаратов
Пылеосадительные камеры
Отделение пыли в пылеосадительной камере (рис. 9-1) про-
исходит при движении запыленного газа с такой малой скоро-
стью, что частицы пыли успевают осесть под действием силы
тяжести прежде, чем газ вынесет их из камеры.
Рис. 9-1. Пылеосадительная камера:
/—камера; 2— перегородки (полки).
Время осаждения пыли будет тем меньше, чем меньше вы-
сота камеры. Поэтому внутри камеры 1 часто устанавливают
(на расстоянии 400—1000 мм друг от друга) параллельные го-
ризонтальные или наклонные перегородки (полки) 2, на которых
осаждается пыль при движении газа между перегородками. Та-
ким путем увеличивается поверхность осаждения и достигается
более равномерное распределение газа по ширине камеры.
Пылеосадительные камеры громоздки и малоэффективны;
они используются только для предварительной грубой очистки
газов и в настоящее время вытесняются газоочистительными ап-
паратами более совершенных типов»
326
Гл. 9. Очистка газов
Инерционные пылеуловители
В этих аппаратах очистка газа происходит под действием
инерционных сил, возникающих при резких изменениях напра-
вления газового потока с одновременным уменьшением его ско-
рости. При повороте потока взвешенные в газе твердые или жид-
кие частицы, стремясь сохранить направление своего движения,
удаляются из потока. Для эффективной очистки скорость газа на
входе в газоочиститель должна быть не менее 10—15 м/сек.
Жалюзийный золоуловитель (рис. 9-2) представляет собой
трубу 1 с решеткой 2 из наклонных перегородок. Взвешенные
в газе частицы золы,
проходя по трубе, уда-
ряются о поверхность
каждой перегородки и
отбрасываются от нее
'{Очищенный ч i в сторону, противопо-
Т______________^ч ложную движению ос-
к'дымососу новного потока газа.
Айль 8-
цинлон
Очищенный
газ
газ
Рис. 9-2. Жалюзийный золоуловитель:
/ — труба; 2 — наклонные перегородки; 3 —циклон.
Рис. 9-3. Конический жалюзийный
пылеуловитель:
1 — решетка; 2 — кожух.
В результате по одну сторону решетки собирается часть газа
(около 10% от общего количества), содержащая основную
2. Устройство газоочистительных аппаратов -
327
массу пыли, а по другую сторону — удаляется очищенный газ.
Газ, содержащий большое количество пыли, удаляется из золо-
уловителя и дополнительно очищается в циклонах 3.
По такому же принципу работает конический инерционный пылеуловитель
(рис. 9-3), решетка которого состоит из набора колец, установленных с зазо-
рбм 2—3 мм и немного перекрывающих друг друга. Газ движется сверху вниз,
многократно ударяясь о поверхность колец решетки и отражаясь от них.
При этом пыль отбрасывается к оси пылеуловителя и часть воздуха, обо-
гащенного пылью, выходит через нижнее узкое отверстие аппарата. Основная
масса газа, освобожденная от пыли, проходит через решетку и удаляется из
кожуха.
Достоинства инерционных пылеуловителей: 1) просто
та и компактность, 2) отсутствие
Недостатки: Г) невысокая степень
очистки (отделение только грубой пы-
ли), 2) сравнительно большое гидрав-
лическое сопротивление, 3) износ и за-
бивание решеток.
Центробежные
пылеуловители (циклоны)
Центробежные пылеуловители (ци-
клоны) широко распространены в про-
мышленности. Запыленный газ с зна-
чительной скоростью (20—25 м/сек),
поступая по касательной в корпус 1
циклона (рис. 9-4), приобретает вра-
щательное движение. При этом ча-
стицы пыли под действием центробеж-
ной силы отбрасываются в крайние
слои газа и движутся вместе с ними
вниз по спирали вдоль стенок цикло-
на. Взвешенные частицы пыли выно-
движущихся частей.
Очищенный
Рис. 9-4. Циклон:
1— корпус; 2— вводной патрубок
3— пылеотводящий патрубок
4 — выхлопная труба.
сятся через пылеотводящий патру-
бок 3. Газ, вынесший пыль из циклона, поднимается кверху и,
продолжая вращаться, образует вихрь, направленный по оси
аппарата к выхлопной трубе 4. К этому восходящему потоку
присоединяется некоторая часть газа из опускающихся вниз
внутренних слоев, имеющих малую концентрацию пыли. Газ из
этих слоев, достигнув нижнего края выхлопной трубы и дви-
гаясь в конической части корпуса, поворачивает к оси циклона,
как показано стрелками на рис. 9-4.
Таким образом, очистка газа в циклоне представляет собой
сложный аэродинамический процесс, при котором запыленный и
328
Гл. 9. Очистка газов
очищенный газ движутся вихреобразно в противоположных на-
правлениях. Пыль концентрируется во внешних слоях газа и пе-
реносится ими в сборник, причем образование множества мелких
вторичных вихрей затрудняет пылеотделение. Степень очистки
газа от пыли в циклонах зависит от геометрических размеров
и формы аппарата, свойств пыли (в первую очередь от склон-
ности ее к слипанию), скорости и степени турбулентности вра-
щающегося потока газа.
На рис. 9-5 показан циклон конструкции Научно-исследовательского ин-
ститута по санитарной и промышленной очистке газов (НИИОГАЗ). Кор-
пус 1 циклона имеет в верхней цилиндрической части крышку 2, согнутую
Рис. 9-5. Циклон конструкции НИИОГАЗ:
/ — корпус; 2— крышка; 3 — выхлопная труба;
4 — входной патрубок; 5— улитка; 6 — пылесборник.
по винтовой линии Шаг винтовой линии равен высоте прямоугольного вход-
ного патрубка 4. Выхлопная труба 3 часто соединяется с улиткой 5, служа-
щей для преобразования вращательного движения газа на выходе из циклона
в поступательное (газ может выводиться также прямо на выхлоп или через
колено) Нижняя коническая часть корпуса соединяется с пылесборником 6,
снабженным затвором.
2. Устройство газоочистительных аппаратов
329
Циклоны конструкции НИИОГАЗ имеют диаметр от 40 до 800 мм. Они
пригодны для очистки газов с содержанием пыли С400 г/м3 и при темпера-
туре газов до 400° С.
Такие циклоны часто устанавливаются параллельно, группами из 2, 3, 6
и 8 циклонов, с общим пылесборником и общими коллекторами для входа и
выхода газа. Газоочистительные установки, состоящие из циклонов конструк-
ции НИИОГАЗ, применяются для улавливания пыли из газов при нагрузках
по запыленному газу от 20 до 50 000 м3/ч.
Пример 9-1. Выбрать циклон для очистки от пыли отходящих газов ба-
рабанной сушилки, если расход газов V =*= 6500 м3/ч\ плотность газов
р 0,96 кг/м3.
Решение. Принимаем к установке циклон НИИОГАЗ типа ЦН-15.
Для циклонов этого типа рекомендуются следующие оптимальные соотноше-
ния перепада давления* Др (в н/м2) к плотности газа р (в кг/м3):
~ = 550—750. Принимаем = 700. Коэффициент сопротивления циклона
ЦН-15 С = 105.
Определяем диаметр циклона, приравнивая два выражения для скорости
газа в корпусе циклона:
4
Отсюда
V2 __ 2 Др
3600М РС
42 и
42
36002-2.2
D = 0,0158
65002•105
700
= 0,79 м
Устанавливаем циклон диаметром D == 0,8 м.
Фиктивная скорость газов в циклоне:
4 - 6500 0_ .
WcP-~ 3600 • 3,14 • 0,82 = 3>6
Определяем гидравлическое сопротивление циклона:
Cpw2 105 • 0,96 • 3,62
Др = —^-1— =--------------= 653 н/м2 (66,5 мм вод. ст.)
Из выражения центробежной силы С — -у— видно, что сте-
пень очистки газа в циклоне может быть повышена путем увели-
чения окружной скорости w или уменьшения радиуса г враще-
ния газа. Увеличение скорости связано с значительным возра-
станием сопротивления и усилением местных завихрений,
* Циклоны НИИОГАЗ, катауюг № 22А, Госхимиздат, 1961.
330
Гл. 9 Очистка газов
ухудшающих очистку. Поэтому для повышения эффективности
циклонов желательно уменьшение их диаметра и замена одного
циклона несколькими циклонами малого диаметра.
Такой принцип положен в основу устройства батарейного ци-
клона конструкции НИИОГАЗ и треста «Газоочистка» (рис. 9-6).
„ - Батарейный циклон состоит из
многих параллельно работаю-
Рис. 9-6. Батарейный циклон:
/ — корпус; 2 — газораспределитель-
ная камера; 3 — циклонные элементы;
4 — камера для обеспыленного газа;
5 — пылесборник.
щих циклонных элементов,
смонтированных в общем кор-
пусе. Запыленный газ, по-
ступая в 'корпус /, входит в
Рис. 9-7. Элемент бата-
рейного циклона:
/—корпус, 2 — направляющий
аппарат; 3— выхлопная труба.
газораспределительную камеру 2, ограниченную трубными ре-
шетками, в которых герметично укреплены циклонные эле-
менты 3. Очищенный газ удаляется через выхлопные трубы эле-
ментов в общую камеру 4, пыль собирается в коническом днище
циклона (пылесборник 5).
Каждый элемент (рис. 9-7) представляет собой циклон ма-
лого диаметра, отличающийся от обычного циклона главным
образом способом ввода запыленного газа. Газ поступает в эле-
мент не по касательной, а сверху—через кольцевое простран-
2 Устройство ёазйбчиСтительных аппаратов
331
ство между корпусом 1 и выхлопной трубой 3. Потоку газа со-
общается вращательное движение при помощи направляющего
аппарата 2, выполненного в виде винтообразных лопастей (вин-
та) или розетки с наклонными лопатками. Такой направляющий
аппарат установлен в кольцевом пространстве на входе газа в
каждый элемент.
Для нормального действия батарейного циклона все его эле-
менты должны иметь точно одинаковые размеры и работать в од-
них и тех же условиях (одинаковое сопротивление, равномерное
распределение газа).
Батарейные циклоны изготовляются с прямоугольным корпу-
сом и состоят из одной или нескольких секций.
В циклонах достигается значительно лучшая степень очистки
газов, чем в пылеосадительных камерах.
К числу недостатков циклонов относятся: 1) сравнительно
низкая степень очистки от тонкодисперсной пыли, 2) высокое
гидравлическое сопротивление и соответственно большой расход
энергии на очистку, 3) механическое истирание стенок части-
цами пыли, 4) чувствительность к колебаниям нагрузки.
Чтобы избежать снижения степени очистки, не следует умень-
шать нагрузку циклона по газу ниже нормальной. Кроме того,
температура поступающих на очистку газов должна быть на
15—20° С выше точки росы для того, чтобы предотвратить кон-
денсацию паров влаги из газа, приводящую к образованию
шлама, который оседает на поверхностях циклона.
Пример 9-2. Рассчитать батарейный циклон для улавливания пыли из
газа, количество которого Q = 4,17 м31сек, плотность газа р — 0,8 кг/jn3.
Решение. Выбираем батарейный циклон с элементами диаметром
D — 150 мм (завихряющее устройство — винт), коэффициент сопротивления
элемента С = 90. Принимаем отношение перепада давления в циклоне к плот-
ности газа —~ — 650 (для эффективной работы циклона это отношение
Р
должно быть в пределах 550—750)*.
Рассчитываем производительность одного элемента по запыленному газу:
о = 2^.1/"_ 1 ирг i/"ZZ
Мэл.- 4 ®ср,- 4 у рС -МШ у
Требуемое количество элементов циклона составляет:
Q Q _ 4,17 1/“'90“_fi9q
<?ЭЛ. “ 1ДЮ2 г Др ~ 1,11-0,152 V 650 ’
Согласно каталогу на батарейные циклоны принимаем количество эле-
ментов п = 64.
Определяем гидравлическое сопротивление циклона:
Др — 650р == 650 • 0,8 — 520 н/м2 (53 мм вод. ст.)
* Батарейные циклоны, каталог № 23А, Госхимиздат, 1961.
332
Гл 9 Очистка сазов
Механические вращающиеся сухие
пылеуловители
Механические вращающиеся, или ротационные, пылеулови-
тели представляют собой машины, которыми производятся одно-
временно перемещение воздуха и очистка его от пыли. Схема
устройства одного из распространенных пылеуловителей этого
типа, совмещающего функции вентилятора и пылеотделителя,
показана на рис. 9-8.
Рис. 9-8. Механический вращающийся сухой
пылеуловитель:
/—кожух; 2 — рабочее колесо; 3— патрубок для входа за пи-
ленного газа; 4— кольцевой приемник; 5— патрубок для
удаления пыли, б —бункер для пыли, 7—патрубок для
выхода очищенного газа.
В улиткообразном кожухе 1 вращается рабочее колесо 2,
имеющее форму вогнутого диска, на котором закреплены ло-
патки. Запыленный газ поступает по оси колеса через патру-
бок 3 и под действием сил инерции распределяется по узким
каналам между лопатками колеса. Частицы пыли, как более тя-
желые компоненты пылегазовой смеси, под действием центро-
бежных и кориолисовых сил прижимаются к диску и лопаткам,
скользят по ним от центра к периферии и через зазор между
диском колеса и кожухом поступают в кольцевой пылеприем-
ник 4. Отсюда обогащенная пылью смесь, содержащая лишь
3—5% газа, через патрубок 5 удаляется в бункер 6. Газ, вынес-
2 Устройство вазоочистительных аппаратов
333
ший пыль в бункер, где она оседает, направляется в корпус ап-
парата. Очищенный газ удаляется через патрубок 7.
Достоинства механических вращающихся пылеуловителей
1) высокая степень очистки мелкой пыли (до 5—8 лтк); 2) боль-
шая производительность; 3) компактность и простота эксплуа-
тации. Однако изготовление этих аппаратов весьма сложно
Рукавные фильтры
Рукавный фильтр (рис. 9-9) состоит из корпуса 1, в котором
находятся тканевые мешки 2 (рукава). Нижние открытые концы
рукавов закреплены на патрубках общей трубной решетки 3,
верхние концы снабжены крышками, подвешенными к общей
раме 4.
Рис. 9-9. Рукавный фильтр:
а —очистка газа, б —встряхивание и обратная продувка
рукавов. 1— корпус; 2 —тканевые мешки, 3 — трубная ре-
шетка; 4— рама; 5 — выхлопная труба; б—кулачковый меха
низм, 7 —шнек; 8 — секторный затвор.
Запыленный газ проходит изнутри рукавов наружу. При этом
пыль осаждается на внутренней поверхности и в порах ткани,
очищенный газ удаляется через выхлопную трубу 5. По мере
увеличения толщины слоя пыли сопротивление ткани возрастает.
Поэтому рукава периодически очищают встряхиванием при по-
мощи специального кулачкового механизма 6. В некоторых
фильтрах, наряду с механическим встряхиванием, рукава проду-
вают воздухом, пропускаемым в направлении, обратном движе-
нию очищенного газа.
334
Гл. 9. Очистка газов
На рис. 9-9, а показан рукавный фильтр во время очистки
газа, на рис. 9-9, б — при встряхивании и продувке рукавов.
Обычно встряхивание и продувка рукавов производятся через
каждые 5—8 мин и длятся 20—30 сек, причем переключение
фильтра в рабочее положение и на очистку рукавов осуществ-
ляются автоматически. Пыль падает в коническое днище и при
помощи шнека 7 через секторный затвор 8 удаляется из фильтра.
Запыленный газ просасывается через фильтр вентилятором
или подается под небольшим избыточным давлением, в послед-
нем случае исключается возможность подсоса воздуха через не-
плотности.
Рукавные фильтры состоят из нескольких секций и работают
непрерывно путем периодического отключения какой-либо одной
секции для разгрузки пыли. Последовательное отключение и
включение секций производится автоматически распределитель-
ным механизмом.
Производительность рукавных фильтров зависит от предель-
но допустимой (по величине гидравлического сопротивления)
удельной нагрузки ткани, определяемой объемом запыленного
газа в м3, проходящего через 1 м2 ткани в 1 ч. Удельная на-
грузка обычно не должна превышать 120—150 м3/м2'Ч.
Для изготовления рукавов применяют шерстяные и хлопча-
тобумажные ткани. Температура газа, очищаемого в рукавном
фильтре, ограничена определенными пределами. Верхний темпе-
ратурный предел определяется теплостойкостью ткани (80—90° С
для шерстяных тканей, 65° С для хлопчатобумажных), поэтому
газы перед поступлением в рукавные фильтры обычно охлаж-
дают. Нижний предел температуры газа должен быть по край-
ней мере на 10° С выше точки росы — температуры, при которой
происходит конденсация влаги из газа, иначе ткань быстро
увлажняется и замазывается грязью.
Достоинство рукавных фильтров — высокая степень очистки
газа от тонкодисперсной пыли; недостатки — сравнительно быст-
рый износ или закупорка ткани и непригодность для очистки
горячих и влажных газов.
В настоящее время для изготовления пылеочистных рукавов
начинают применять высокопрочные и более теплостойкие тка-
йи — шерстяную байку с добавкой капроновых волокон, синте-*
тические ткани из волокна орлон, ткани из стекловолокна,
причем в последнем случае возможна очистка газов при темпе-
ратурах до 400° С.
Нормализованные рукавные фильтры состоят из 3—12 секций. В каж-
дой секции имеется 8 рукавов диаметром 190 мм и длиной 2000 мм\ общая
фильтровальная поверхность такой секции 9,6 м\
2 Устройство газоочистительных аппаратов
335
Пример 9-3. Выбрать рукавный фильтр для улавливания окислов свинца
из отходящих газов трубчатой печи в производстве пигментов, если расход
газов Q составляет 1500 м3/ч.
Решение. Удельная нагрузка ткани по запыленному газу обычно ко-
леблется в пределах 48—120 м3/м2-ч. Учитывая тонкую дисперсность частиц
окислов свинца, принимаем удельную нагрузку на рукавную ткань
V = 54 м31м2 • ч *. Требуемая поверх-
ность фильтрования составит:
f=v- = 2fr=27’8 м2
Выбираем рукавный фильтр ти-
па МФУ завода им Воробьева с авто-
матическим встряхиванием рукавов
и обратной продувкой фильтроваль-
ной ткани. Фильтр имеет 24 рука-
ва с общей поверхностью фильтрова-
ния F = 28,8 ж2
Гидравлическое сопротивление
выбранного рукавного фильтра мо-
жет быть приближенно определено по
эмпирической формуле:
Др 0,03V1-28 = 0,03 =
= 5 мм вод. стп.
При значительной запыленности
ткани гидравлическое сопротивление
фильтра может возрасти во много
раз (см. стр. 344).
Масляные и п о р о л и то в ые Рис. 9-10. Ячейка масляного (висци-
газовые фильтры нового) фильтра:
„ „ 1 — коробка; 2 —насадка.
Для очень тщательной очистки
газов (главным образом воздуха)
применяются масляные (висциновые) фильтры, керамические поролитовые
фильтры и др.
масляный (висциновый) фильтр состоит из отдельных стандартных
ячеек-кассет размером 500 X 500 мм и толщиной 75 мм. Ячейка фильтра
(рис. 9-10) представляет собой металлическую коробку 1, закрытую с двух
сторон сетками. Коробка заполнена металлическими кольцами 2 или другой
насадкой, которая смачивается высоковязким висциновым маслом (смесь
машинного масла, глицерина и каустической соды). Ячейки устанавливаются
горизонтально или вертикально в стык друг с другом и образуют сплошную
фильтровальную перегородку Улавливаемая пыль прилипает к насадке, по-
этому каждую ячейку периодически вынимают, насадку очищают от пыли
промывкой и смачивают свежим маслом.
Степень очистки воздуха в масляных фильтрах достигает 99% при за-
пыленности 1—2 мг/м3 (при нормальных условиях). Допустимая нагрузка —
до 4000 м3[ч на 1 м2 поверхности фильтра.
*Г М Гордон, И. А Аладжалов, Г азоочистка рукавными фильт-
рами в цветной металлургии, Металлургиздат, 1956, стр. 102, 103.
336
Гл 9 Очистка газов
Поролитовые фильтры используются в химических производствах, для
которых по условиям технологического процесса необходим особенно чистый
воздух, например в производстве азотной кислоты окислением аммиака.
Поролитовый фильтр (рис 9-11) состоит из корпуса /, в котором нахо-
дится ряд керамических гильз 2, смонтированных на общей решетке 3. Запы-
ленный газ проходит внутрь гильз, пыль оседа-
ет на их наружной поверхности.
Рис. 9-11. Поролитовый
фильтр:
1 — корпус; 2 — гильзы; 3 — ре-
шетка.
Мокрые пылеуловители
Путем смачивания и поглощения ча-
стиц пыли жидкостью достигается высо-
кая степень извлечения пыли из газа.
Мокрая очистка газа особенно желатель-
на в тех случаях, когда необходимо ох-
лаждение газа независимо от его очистки.
При охлаждении влажного газа водяные
пары конденсируются на содержащихся
в нем пылинках, вследствие чего увели-
чивается вес пылинок и облегчается вы-
деление их из газа.
Выделение пыли в мокрых пылеуловителях происходит под
действием сил тяжести (при прямолинейном движении газа че-
рез аппарат) или под действием сил инерции (при резком из-
менении направления газового потока), или под действием цен-
тробежных сил (при вводе газа в аппарат с большой скоростью по
касательной к внутренней поверхности аппарата). В последнем
случае достигается наиболее тщательная очистка газа от пыли.
Смачивание и поглощение пыли водой производится при сте-
кании воды пленкой по внутренним стенкам аппарата, при раз-
брызгивании воды по всему объему аппарата или комбиниро-
ванным способом.
Предварительную очистку газов (в сочетании с охлаждением
их) проводят в полых скрубберах — башнях круглого или прямо-
угольного сечения. Запыленный газ движется в скруббере снизу
вверх, поглощающая жидкость распыляется форсунками, кото-
рые часто устанавливают на разных уровнях; при этом все се-
чение скруббера перекрывается распыляемой жидкостью. Для
уменьшения уноса брызг скорость газа в поперечном сечении
полого скруббера не должна превышать 1 —1,5 м/сек.
Несколько лучшая, чем в полых скрубберах, очистка газа до-
стигается в скрубберах с насадкой. В качестве насадки исполь-
зуют кусковой кокс и кварц, а также кольцевую и хордовую на-
садки. Орошение насадки производится через распределитель-
ные устройства. Скорость газа в насадочных скрубберах соста-
вляет 0,8—1,25 м/сек и более.
2 Устройство газоочистительных аппаратов
337
Для мокрой очистки газа при-
меняются также механические га-
зопромыватели — дезинтеграторы.
В таком дезинтеграторе быстро вра-
щается ротор в виде диска, на ко-
тором по концентрическим окруж-
ностям укреплены стержни. При
вращении ротора его стержни про-
ходят между неподвижными стерж-
нями, укрепленными на стенках кор-
пуса, и тонко распыляют жидкость
в газе. При этом жидкость смачи-
вает почти всю пыль, содержащую-
ся в газе, и удаляется вместе с нею.
Описанная машина совмещает
функции вентилятора и пылеотде-
лителя (подобно ротационному пы-
леуловителю при сухой очистке га-
за). Перед поступлением в дезин-
тегратор газ необходимо охладить
до 50—60° С, а по выходе из дезин-
тегратора — очищать от тумана. В
настоящее время дезинтеграторы
вытесняются более эффективными
пылеочистительными аппаратами—
электрофильтрами (стр. 339).
Мокрая очистка газов под дей-
ствием центробежных сил произво-
дится в циклонах, стенки которых
смачиваются непрерывно ’ стекаю-
щей по ним пленкой воды, а также
в центробежных скрубберах.
Центробежный скруббер конст-
рукции Всесоюзного теплотехниче-
ского института (ВТИ) им. Дзер-
жинского показан на рис. 9-12. За-
пыленный газ поступает в аппарат
через патрубок 2 по касательной к
стенке корпуса 1 и приобретает ин-
тенсивное вращательное движение.
Под действием центробежной силы
частицы пыли отбрасываются к стен-
кам скруббера и смываются плен-
кой воды, стекающей по стенкам.
При этом пыль не отражается от
Рис. 9-12. Центробежный скруб-
бер конструкции ВТИ:
/—корпус; 2—патрубок для входа
запыленного газа; 3— сопла; 4 — от-
верстие для удаления очищенного
таза; <5 —гидравлический затвор.
22 Зак 54$.
338
Гл 9 Очистка газов
стенок из-за местных завихрений, как это наблюдается в ци-
клонах.
Орошающая вода распределяется по стенкам через сопла 3.
Очищенный и одновременно охлажденный газ удаляется через
верхнее отверстие 4, степень открытия которого регулируется
дроссельной заслонкой, отработанная вода отводится через гид-
равлический затвор 5.
Достоинства
очистки в
поле
центробежного скруббера: 1) высокая степень
центробежных сил
при турбулентном движении
газа и жидкости, 2) низ-
кое гидравлическое сопро-
тивление, 3) простота уст-
ройства и экономичность
эксплуатации.
Одним из эффективных
аппаратов для мокрой га-
зоочистки является струй-
ный скруббер Вентури (рис.
9-13). Вода вводится в тру-
бу I через отверстия в ее
горловине 2 под избыточ-
ным давлением 0,3—1 ат и
тонко распыляется движу-
щимся с большой скоростью
потоком газа, который про-
тягивается через установку
при помощи вентилятора
Скорость газа в горловине
составляет 60—70 м/сек и
более. В расширенной части
трубы скорость потока снижается, тонко распыленная жидкость
увлажняет и поглощает частицы пыли. Вследствие этого ка-
пельки жидкости укрупняются и могут быть выделены из га-
зового потока в циклонном сепараторе 3. Вода отделяется от
шлама в отстойнике 4 и вновь подается в скруббер.
В описанном скруббере удается удалить из газа до 99% тон-
кодисперсной пыли (размеры частиц 1,5—0,5 мк).
Скруббер отличается простотой устройства и может быть ис-
пользован для очистки газов от тумана, например в производстве
серной кислоты.
Очищенный газ
9
вода
1
2
Л?
'Свежая
вода
' у UUUU |
Неочищенный
газ
^~Шлам
Рис. 9-13. Струйный скруббер Вентури:
7 —труба скруббер, 2 — горловина с отверстиями;
3 — циклонный сепаратор; 4 — отстойник; 5 — насос.
Высокая степень очистки топочных газов достигается в пенном пыле-
уловителе (рис 9-14) Газы поступают через патрубок 1 и, проходя через
мелкие отверстия решетки 2, вспенивают воду, подаваемую через штуцер 3
Благодаря значительной поверхности пена хорошо поглощает частицы золы
Отделившиеся от газа частицы золы уходят с водой, основная часть кото-
% Устройство ёазоочиСтитёЛьных аппаратов
339
рой (~80%) удаляется в виде пены через регулируемый порог 4 Остальная
вода сливается через решетку, а также испаряется и уносится в виде брызг
газами При пенной очистке получается значительное количество отработан-
Рис. 9-14. Пенный пылеуловитель:
1 — патрубок для входа запыленного газа; 2—решетка;
3 — штуцер для подачи воды; 4 — регулируемый порог.
ных кислых вод вследствие большого расхода воды и интенсивного погло-
щения слоем пены сернистого газа, обычно присутствующего в промышленных
топочных газах.
Электрофильтры
Действие электрофильтра основано на ионизации газа, т. е.
расщеплении его молекул на положительно и отрицательно заря-
женные ионы. Газ можно ионизировать в пространстве между
двумя электродами, к которым подведен электрический ток. Под
действием электрического поля в газе образуются ионы и сво-
бодные электроны, благодаря движению которых через газ на-
чинает протекать ток.
Если повысить разность потенциалов между электродами до
нескольких тысяч вольт, то скорость движения, а следовательно,
и кинетическая энергия ионов и электронов настолько возра-
стает, что при соударениях они расщепляют встречные молекулы
на ионы. В условиях ударной ионизации число ионов очень резко
возрастает и газ полностью ионизируется. При этом наблюдает-
ся потрескивание и слабое свечение газа («корона») вокруг про-
водника, который носит название коронирующего электрода.
Ионы и электроны, имеющие тот же знак, что и заряд корони-
рующего электрода, движутся к противоположно заряженному,
так называемому осадительному электроду.
22*
340
Гл. 9. Очистка газов
В электрофильтрах коронирующие электроды всегда присо-
единяются к отрицательному полюсу источника тока, поэтому
к осадительным электродам движутся только отрицательные
ионы и свободные электроны. Присоединяясь по пути к нейтраль-
ным молекулам, электроны превращают их также в отрицатель-
ные ионы.
При движении в запыленном газе или тумане отрицательные
ионы сообщают заряд пылинкам или капелькам жидкости и
увлекают их к осадительным электродам. Подойдя к осадитель-
ному электроду, частицы пыли (тумана) отдают ему свои за-
ряды и сбрасываются с электрода под действием собственной
тяжести или при встряхивании.
С увеличением напряжения сверх некоторой критйческой ве-
личины происходят проскоки искр, а затем электрический пробой
и короткое замыкание электродов. Во избежание этого в элек-
трофильтрах создают неоднородное электрическое поле, напря-
жение которого убывает по мере удаления от коронирующего
электрода. В этом случае почти весь слой газа между короной
и осадительным электродом играет роль изоляции, предотвра-
щающей искровой разряд между электродами. Неоднородность
поля достигается путем устройства электродов в виде проводов,
помещенных по оси труб в трубчатом электрофильтре или на-
тянутых между параллельными пластинами в пластинчатом
электрофильтре.
Электрофильтры работают только на постоянном электричек
ском токе, так как при переменном токе заряженные частицы
быстро меняют направление своего движения, вследствие чего
часть их не успевает осесть на электродах и выносится с газом
из электрофильтра. Питание электрофильтров осуществляется
постоянным током высокого напряжения (40—75 кв).
При отрицательной полярности тока, подводимого к корони-
рующим электродам, степень очистки газа увеличивается, так
как в этом случае допустимо более высокое напряжение без воз-
никновения искрового разряда между электродами.
Процесс отделения пыли в электрофильтре зависит от ее про-
водимости. Если пыль не проводит тока, осевший на электродах
слой пыли отталкивает приближающиеся одноименно заряжен-
ные частицы и при напряжении в слое, превышающем критическое,
у осадительного электрода появляется свечение — «обратная ко-
рона». Это явление значительно ухудшает процесс очистки газа.
Проводимость пыли обычно увеличивают путем увлажнения
горячего газа перед входом его в электрофильтр, не допуская,
однако, снижения температуры газа ниже точки росы. Очень хо-
рошо проводящая пыль мгновенно отдает свой заряд и, воспри-
нимая заряд электрода, отталкивается от него. Это также при-
2. Устройство газоочистительных аппаратов
341
водит к уносу газом части пыли и понижению степени очистки.
Наконец, при очень высокой концентрации пыли или тумана
большая часть ионов передает заряды пылинкам (или капель-
кам). В результате резко снижается скорость движения ионов
и, следовательно, уменьшает-
ся сила тока, так как скорость
заряженных тяжелых пыли-
нок значительно меньше ско-
рости ионов газа. При сниже-
нии силы тока до нуля очист-
ка полностью прекращается и
происходит так называемое
запирание короны.
Трубчатый электрофильтр
(рис. 9-15) представляет собой
вертикальную камеру 1, в ко-
торой установлены осадитель-
ные электроды 2, выполнен-
ные в виде круглых или ше-
стигранных труб. Чаще при-
меняют шестигранные трубы,
собранные в пакеты, имеющие
в плане форму пчелиных сот.
При такой форме электродов
достигается значительная ком-
пактность конструкции элек-
трофильтра. В качестве коро-
нирующих электродов служат
проволоки 3, натянутые по оси
осадительных труб. Корони-
рующие электроды сверху при-
креплены к раме 4, подвешен-
ной на изоляторах, а снизу
связаны общей рамой 5,
что предотвращает колебания
электродов.
Запыленный газ входит в
Очищенный
газ
Рис. 9-15. Трубчатый электрофильтр:
1 — вертикальная камера; 2 —осадительные
электроды; 3 — коронирующие электроды;
4, 5 —рамы; <5 —газоход для ввода газа;
7 —газораспределительная решетка; 8— газо-
ход для удаления очищенного газа.
электрофильтр через газоход 6.
Для равномерного распределения газа по трубам служит га-
зораспределительная решетка 7. Очищенный газ удаляется по
газоходу 3, а пыль собирается в нижней части электрофильтра
и периодически удаляется через отверстие в его днище.
В трубчатых электрофильтрах некоторых конструкций решет-
ка и осадительные электроды периодически встряхиваются при
помощи специальных молотков.
342
Гл. 9. Очистка газов
В пластинчатом электрофильтре (рис. 9-16) осадительные
электроды 2 представляют собой параллельные гладкие метал-
лические листы или натянутые на рамы сетки, между которыми
подвешены коронирующие электроды 3 в виде нихромовых или
Рис. 9-16. Пластинчатый электрофильтр:
1 — камера; 2 — осадительные электроды; 3— коронирующие электроды; 4,6—рамы; 5 — молотки;
7—газораспределительная решетка; 8 — пылесборник.
фехралевых проволок. Для очистки горячих газов применяют
осадительные электроды, имеющие форму волнистых листов
или прутков, что предотвращает их коробление.
Существуют вертикальные пластинчатые электрофильтры
(с движением газов снизу вверх) и горизонтальные (с горизон-
тальным ходом газов).
Для лучшей очистки газов применяют многопольные (трубча-
тые и пластинчатые) электрофильтры, состоящие из нескольких
2. Устройство газоочистительных аппаратов
343
Очищенный
Рис. 9-17. Схема акустического
газоочистителя:
/—агломерационная башня; 2— зву-
ковой генератор; 3 — циклон.
их столкновений и укпупнению
последовательно соединенных секций осадительных электродов,
т. е. нескольких электрических полей.
Очистка газа от влажной тонкодисперсной пыли и тумана
производится в мокрых трубчатых или пластинчатых электро-
фильтрах. В мокрых электрофильтрах очищаются газы, из' кото-
рых возможна конденсация влаги при охлаждении их до точки
росы. Трубы мокрых электрофильтров часто изготовляют из
свинца (фильтры для улавливания сернокислотного тумана) или
из графита и ферросилида (фильтры для очистки газов, обра-
зующихся при выпаривании серной кислоты). Коронирующие
электроды изготовляются из освинцованной проволоки и имеют
круглое или звездообразное сечение. Оседающая на электродах
влажная пыль периодически смы-
вается с них.
Преимущества трубчатых элек-
трофильтров перед пластинчатыми:
1) большая напряженность элект-
рического поля и соответственно
более высокая допустимая скорость
газа, 2) лучшее отделение трудно-
улавливаемой (например, плохо
проводящей) пыли из газов умерен-
ной влажности.
Недостатки: 1) трудность уда-
ления осевшей пыли, 2) громозд-
кость, больший расход металла,
3) сложный монтаж, 4) больший
расход энергии на единицу длины
проводов.
Акустические газоочистители
Очистка газов возможна также путем
воздействия на запыленный газ колебаний
звуковой и ультразвуковой частоты. Звуко-
вые (и ультразвуковые) волны вызывают
интенсивную вибрацию мельчайших частиц
пыли, что приводит к резкому увеличению
(агломерации) частиц. Отделение укрупненных частиц производится в
отдельно.м пылеуловителе, например в циклоне, последовательно соединенном
с акустическим газоочистителем.
На рис. 9-17 показана схема акустической установки для очистки газа
от сернокислотного тумана. Газ поступает в агломерационную башню 1
снизу, в верхней части башни находится звуковой генератор 2. Обработан-
ный в акустическом поле туман направляется в циклон 3, где газ отде-
ляется от жидкости. В такой установке степень очистки газа достигает 90%
при размере капелек тумана 0,5—5 мк.
Акустическую очистку газов проводят при частоте колебаний 2—50 кгц,
интенсивности звука 0,1—0,3 вт[см2 и продолжительности пребывания газз
344
Гл. 9. Очистка газов
в акустическом поле 1—4 сек. Описанный способ пылеулавливания приме-
ним для тонкой очистки горячих газов (до 550°С), а также химически агрес-
сивных и взрывоопасных газов.
Пылеулавливающие установки акустического действия отличаются про-
стотой и компактностью. Основные недостатки их: 1) высокий расход энер-
гии (о$ 0,7 до 2 кет • ч на 1000 м3 газа), 2) тяжелые условия труда обслу-
живающего персонала (при звуковых частотах).
В настоящее время акустические пылеочистители испытаны только
в полузаводском масштабе.
3. Сравнение и выбор газоочистительных аппаратов
Выбор аппарата для очистки газа зависит от многих факто-
ров. Главными из них являются: 1) свойства пыли (сухая, лип-
кая, гигроскопическая, волокнистая и т. д.) и размеры ее частиц,
2) влажность газа и начальное содержание в нем пыли, 3) тре-
буемая степень очистки газа.
В табл. 11 приведены некоторые ориентировочные данные,
характеризующие условия применения газоочистительных ап-
паратов различных типов, достигаемую в них степень очистки
газа и гидравлическое сопротивление аппаратов.
Таблица 11
Сравнительная характеристика газоочистителей
Типы аппаратов Начальное содержание пыли в газе мг/м* Размеры отделяемых частиц пыли мк Гидравли- ческое сопроти- вление мм вод. ст. Степень очйстки (к. п. д.) %
Пылеосадительные камеры Жалюзийные золоулови- — 100 и более — 40—60
тели 200—104 25 » » 90 60—75
Циклоны:
конические Более 1000 Более 15 40—70 90 и менее
батарейные — > 15 — 95 » »
Рукавные фильтры .... Более 200 2 и более 70—100 99,5» »
Висциновые фильтры . . . 100 и менее 10 » » — 99 » »
Мокрые скрубберы .... — 0,1 » » 40—80 90—99
Электрофильтры — 0,005 » » 99,5 и менее
Как следует из таблицы, инерционные пылеуловители и ци-
клоны пригодны для отделения сравнительно грубой пыли, при-
чем наименее эффективны жалюзийные золоуловители, а наи-
более — батарейные циклоны. Все эти пылеуловители пригодны
для очистки газов только от сухой, нелипкой и неволокнистой
пыли. Батарейные циклоны целесообразно применять вместо
обычных циклонов лишь при больших количествах очищаемого
3. Сравнение и выбор газоочистительных аппаратов
345
газа (например, батарейные циклоны, состоящие из элементов
диаметром 150 мм, при количестве газа не менее 7500 м^ч).
Более полная очистка газов может быть достигнута в рукав-
ных фильтрах, мокрых пылеуловителях и электрофильтрах.
Рукавные фильтры пригодны для очистки газов от тонкой
дисперсной пыли при температурах, которые ниже температуры
разрушения ткани, и для улавливания трудноувлажняемой пыли,
например сажи или окиси цинка. Эти фильтры не могут быть
использованы для очистки химически агрессивных газов, разру-
шающих ткань, и для отделения липкой и влажной пыли.
Мокрые пылеуловители применяются в тех случаях, когда
допустимо охлаждение и увлажнение газа, а отделяемая пыль
не является ценным продуктом. В этих условиях мокрые пыле-
уловители выгодно отличаются от электрофильтров простотой
конструкции и экономичностью. Применение мокрых пылеулови-
телей для очистки кислых газов связано с образованием боль-
шого количества кислых сточных вод и необходимостью их очи-
стки перед сбросом в водоемы.
Электрофильтры являются высокоэффективными пылеулови-
гельными аппаратами. Для очистки сухих газов используются
преимущественно пластинчатые электрофильтры, а для отделе-
ния трудно улавливаемой пыли и тумана (когда не требуется
встряхивания электродов), а также для наиболее полной очист-
ки — трубчатые электрофильтры. Применение электрофильтров
экономично только при больших объемах очищаемого газа.
Глава 10
ПЕРЕМЕШИВАНИЕ
1. Общие сведения
Перемешивание широко применяется в химической промыш-
ленности для приготовления суспензий, эмульсий и растворов
Посредством перемешивания достигается тесное соприкоснове-
ние частиц и непрерывное обновление поверхности взаимодей-
ствия веществ. Вследствие этого при перемешивании значи-
тельно ускоряются процессы массообмена, например растворе-
ние твердых веществ в жидкостях, процессы теплообмена и
протекание многих химических реакций ‘Перемешивание исполь-
зуют для ускорения абсорбции, выпаривания и других основных
процессов химической технологии
Наиболее распространенным способом перемешивания в жид-
ких средах является механическое перемешивание при помощи
мешалок, снабженных лопастями той или иной формы Помимо
механического перемешивания, применяют также перемешива-
ние сжатым воздухом. Иногда жидкости перемешивают много-
кратным перекачиванием их насосом через аппарат, т е путем
циркуляции в замкнутом контуре Оба последних способа тре-
буют сравнительно большого расхода энергии, а перемешивание
воздухом сопряжено также с возможным окислением или испа-
рением продуктов.
Основными характеристиками любого процесса перемеши-
вания являются расход энергии и эффективность перемеши-
вания
В различных процессах эффективность перемешивания опре-
деляется по-разному Например, при суспендировании эффек-
тивность перемешивания характеризуется равномерностью рас-
пределения твердых частиц в жидкости и скоростью достижения
достаточной равномерности Если перемешивание применяется
для интенсификации теплообмена, эффективность перемешива-
ния может определяться возрастанием коэффициента теплоот-
дачи (стр 370) в перемешиваемой среде
2 Расход энергии на перемешивание
347
2. Расход энергии на перемешивание
При вращении лопасти мешалки, как при обтекании жидко-
стью любого движущегося в ней тела (стр. 171), энергия затра-
чивается на преодоление трения, а также на образование и срыв
вихрей Сила сопротивления среды зависит от коэффициента со-
противления ф, который определяется по уравнению (6-92).
В данном случае (рис. 10-1)
d — диаметр лопасти мешалки и, по-
скольку скорость в точках лопасти, не-
одинаково удаленных от оси, различ-
на, йУср — некоторая средняя окруж-
ная скорость вращения лопасти.
Для лопасти любой формы между
средней скоростью и окружной ско-
ростью на конце лопасти существует
общее соотношение:
wcp = aw (Ю-1)
где w — окружная скорость на конце
лопасти,
а — коэффициент пропорциональ-
ности, постоянный для ло-
Рис 10-1 К определению
расхода энергии на пере-
мешивание
пасти данной формы.
Подставляя значение wcp в выражение (6-92) и принимая,
что R = Р (Р— сила, действующая на лопасть мешалки), по-
□ Г
D
лучим:
Ф
Р
pd2a2w2
(Ю-2)
Для преодоления сопротивления среды к валу мешалки дол-
жно быть подведено определенное количество энергии.
Мощность, необходимая для вращения лопасти, равна про-
изведению действующей силы на среднюю скорость вращения
лопасти:
W=Pwcp =Paw (10-3)
Окружная скорость на конце лопасти w = ndn (п — число
оборотов мешалки в 1 сек). Подставляя в выражение (10-3)
значения Р и ауср из выражений (10-2) и (10-1), получим:
N = фpd^a3w3 = фрб/2а3 (^ dn)3 или N= tyn3a3pd5n3
Обозначив произведение фи3а3 через с, получим окончатель-
ное выражение;
N—cd3n3p вт (10-4)
348
Гл. 10. Перемешивание
Входящий в уравнение (10-4) коэффициент с определяется из
опыта. Он зависит не только от формы лопасти и сосуда, в ко-
тором производится перемешивание, но и от критерия Re, по-
скольку в выражение величины с входит коэффициент сопро-
тивления ф, являющийся функцией Re. Таким образом
c=/(Re) (10-5)
Величина Re для мешалок выражается следующим образом:
wcp dp (aw) dp (an dri) dp nd2p
Re —----------:— ~--------=-----------= _
M fX fX [I [J.
Постоянный множитель ait можно исключить и определять
критерий Re для мешалок по формуле
Re« = ^ (10-6)
Г*
На рис. 10-2 приведены опытные значения с как функции от
ReM для мешалок различных типов при определенных отноше-
ниях диаметра D сосуда, высоты Н уровня жидкости в нем,
, л 1 D Н Ь\
ширины о лопасти и диаметра а лопасти мешалки 1-^--,
а также (для пропеллерных мешалок) при отношении шага винта
к диаметру сосуда -^-.равном 1 и 2. По рис. 10-2 определяют
значение с и, подставляя его в формулу (10-4), находят необхо-
димую мощность.
Однако величины с, полученные по графику, точны только
для мешалок, геометрически подобных тем, к которым относятся
соответствующие опытные данные. При отклонении от этого ус-
ловия расход энергии изменяется. Поэтому в случае отсутствия
геометрического подобия значение с, найденное по рис. 10-2,
надо умножить на соответствующие поправочные коэффициенты:
(Ю-7)
где а — отношение
рис. 10-2);
Р — отношение
рис. 10-2);
D » /
-j-для модельной мешалки (см. табл, к
для модельной мешалки (см. табл, к
b и Z—ширина и длина лопасти;
t — ширина перегородки;
АГ— число перегородок^
2. Расход энергии на перемешивание
349
Значения показателей степеней в выражениях поправочных
коэффициентов можно принимать по табл. 12.
Таблица 12
Значения показателей степеней в формулах (10-7)
Мешалки а А А т р г п
Лопастные без перегородок . Пропеллерные и турбинные 1Д 0,6 0,3 — — — —
без перегородок Пропеллерные с перегород- 0,93 0,6 —— 1,5 —— “— —
ками ; . . . . 0 0 1,7 0,3 0,4
Турбинные с перегородками . 0 0 — 1,5 — 0,3 0,4
При наличии в аппарате дополнительных устройств (змеевиков, труб
и т. д.), а также при сильной шероховатости стенок сосуда расход энергии
на перемешивание увеличивается. Некоторые опытные данные для сосудов
с змеевиками и отражательными перегородками на стенках приведены на
рис. 10-2. Для других устройств точных данных нет, грубо ориентировочно
можно вводить следующие поправочные коэффициенты к значению с:
Гильза для термометра.......
Труба ......................
Сосуд с сильно шероховатыми
стенками ...................
А =1,
Ар. — 1>
/ш =1,1-1,2
При пуске мешалки в ход энергия затрачивается не только на преодоле-
ние трения, но и на выведение жидкости из состояния покоя, т. е. на пре-
одоление сил инерции. Однако пусковая мощность превышает рабочую не
более чем в два раза и потребляется в течение очень непродолжительного
времени. Соответственно этому электродвигатель всегда выбирают по рабочей
мощности N мешалки, учитывая возможность кратковременного увеличения
крутящего момента на валу электродвигателя.
Пример 10-1. Выбрать электродвигатель для шестилопастной мешалки,
если диаметр каждой пары ее лопастей d — 1200 мм, а ширина лопастей
b — 100 мм. Число оборотов мешалки п = 40 об/мин.
Мешалка установлена в чугунном аппарате с шероховатыми стенками,
диаметр его D — 1700 мм. В аппарате перемешивается жидкость плотностью
р = 1300 кг/м3, вязкость жидкости р- = 0,03 «• сек/м2 (30 спз).
Высота столба жидкости в аппарате Н = 1700 мм, в жидкость погружена
гильза термометра.
Решение. Для определения режима перемешивания находим значение
критерия Рейнольдса для мешалки по формуле (10-6):
К м— р. ~~ 60-0,03 ~
По рис. 10-2 для модельной шестилопастной мешалки с характеристикой
D/d = 1,11, H/D — 1 и b/d = 0,066 величина коэффициента сопротивления
с д* 0,95,
Коэффициент сопротивления с
Гл. 10. Перемешивание
К рис. 10-2
№ кривой на рис. 10-2 Тип мешалки Характеристика мешалки при HID = 1
D/d bld s/d
1 Двухлопастная 3 0,25
2 То же 3 0,167 —
3 » » 2 0,885 —
4 » » 2 0,885 —
5 Шестилопастная 1Д1 0,066
6 Пропеллерная 3 — 1
7 То же 3 — 1
8 » » 3 — 2
9 » » 3 — 2
10 Открытая турбинная с 6 плоскими верти- кальными лопатками 3 0,2 (IId = 0,25) —
11 То же 3 0,2 (Z/rf = 0,25) —
12 Открытая турбинная с 8 плоскими наклон- ными лопатками 3 0,125
13 Закрытая турбинная с 6 лопатками .... 3 — —.
14 Закрытая турбинная с 6 лопатками и напра- вляющим аппаратом (статором) с 20 лопат- ками 3 .
15 Якорная 1,11 0,066 —
16 Дисковая с 6 лопатками 2,5 o.l —
Характеристика сосуда
Без перегородок
С 4 перегородками шириной 0,1 D
Без перегородок
Со змеевиком
= 1.М, d = 0,066d, t = 0,12d)
\ oM.
Без перегородок
To же
С 4 перегородками шириной 0,1 D
Без перегородок
С 4 перегородками шириной 0,1 D
Без перегородок
С 4 перегородками шириной 0,1 D
То же
Без перегородок
То же
С 4 перегородками шириной 0,1 D
352
Гл. 10. Перемешивание
Для мешалки, работающей в указанных выше условиях:
п/, 1700 1 ЛО „/п 1700 ъ 100 ППЙ_
D!d ~ 1200 “ 1,42> H^D ~ 1700 " b!d 1200 “ 0,0833
Поэтому вводим к величине с поправки, учитывающие отсутствие гео-
метрического подобия модельной и данной производственной мешалок:
. _/1,42 МЛ . _/0.0833 \о.з
Л? V 1,11 у ’2> Л \ одбб) 1,0
Кроме того, вводим поправочные коэффициенты на шероховатость сте-
нок аппарата /ш 1,15 и наличие гильзы термометра /г = М- Тогда
С1 = = °-95 • !'32 •1 • • 1,15 •1’1 - !’7
По формуле (10-4) определяем рабочую мощность, потребляемую ме-
шалкой:
/ 40 \з
Wp == с^п3? = 1,7 • 1,25 (--И • 1300 = 1960 вт
Принимаем к. п. д. передачи от электродвигателя к валу мешалки
iqM = 0,9, коэффициент запаса мощности (на случай возможных перегрузок)
f = 1,2 и определяем мощность электродвигателя:
.. 1960-1,2 __
^дв. — 1000.0 9 — 2>6 квт
3. Эффективность перемешивания
Эффективность перемешивания, определяющая качество
этого процесса, зависит от многих факторов, обусловливаемых
целью перемешивания (приготовление суспензии, ускорение хи-
мической реакции и т. д.), и до сих пор недостаточно изучена.
Равномерное распределение твердой фазы в жидкой при по-
лучении суспензий достигается при некотором числе оборотов
мешалки п0, при котором значение осевой составляющей ско-
рости потока равно или больше скорости осаждения &Уо наиболее
крупных твердых частиц, поэтому при получении взвесей твер-
дых частиц в жидкостях эффективность перемешивания можно
оценивать по некоторому определяющему числу оборотов п0 ме-
шалки. Значение п0 в зависимости от физических свойств твер-
дой и жидкой фаз определяют из уравнения *:
ReM = = С • Gas (£а)' (А)” (-у-)” (Ю-8)
где Ga = - —критерий Галилея;
d4 — диаметр твердой частицы;
Ртв. — плотность твердой фазы.
♦И. С. Павлушенко и др., ЖПХ, 30, 1160 (1957),
3. Эффективность перемешивания
353
Значения коэффициента С и показателей степеней в уравне-
нии (10-8) приводятся ниже:
Мешалки С k I m п
Пропеллерная . . . 0,105 0,6 0,8 0,4 1,9
Турбинная закрытая 0,25 0,57 0,37 0,33 1,15
Уравнение (10-8) пригодно для расчетов при весовом отноше-
нии твердой и жидкой фазы Т :Ж> 1 : 5 и высоте столба сус-
пензии Н = D. Оно выведено в результате обработки опытных
данных, соответствующих следующим условиям:
ReM = 7,3- 102 —3,8 - 105
Ga —3,5.106 — 7 - 1010
^- = (0,23— 8,25). Ю"3
D(d = 2 — 3
При эмульгировании эффективность перемешивания характе-
ризуется равномерностью распределения и размером капель
дисперсной фазы. Определяющее число оборотов п0 мешалки
при получении эмульсий взаимнонерастворимых жидкостей в
сосудах без отражательных перегородок можно найти по урав-
нению *
ReM = C-Ga0,01
/ z/pa \0,47 / Др \0,13
\ / \ Р /
(10-9)
где [х — вязкость сплошной (дисперсионной) фазы;
р — плотность сплошной фазы;
Др— разность плотностей фаз;
а — граничное натяжение между фазами.
Для пропеллерных мешалок значение С — 68,9, для турбин-
ных закрытых мешалок С = 62,9.
Уравнение (10-9) применимо в пределах следующих значе-
ний входящих в него величин:
ReM==3,4- 102 —2- 10б
Ga = l,74- 105— 1,24 • 10й
= 24,5 — 11,8 • 106
р.2
А =0,02 — 0,6
р
* И С Павлушей к о, А. В. Я нишевский, ЖПХ, 31, 1348 (1958).
23 Зак 546.
354
Гл. 10. Перемешивание
При выборе перемешивающих устройств следует отдавать
предпочтение той мешалке, которая потребляет при определяю-
щем числе оборотов по меньшую мощность.
Пример 10-2. В аппарате непрерывного действия необходимо равномерно
суспендировать твердые частицы в жидкости плотностью р = 1830 кг/м? и
вязкостью р. = 0,04 н-сек/м2 (40 спз). Наибольший размер твердых частиц
d4 = 1,5 мм. Плотность твердой фазы Ртв. = 2350 кг/м?. Диаметр аппарата
D = 1000 мм, высота жидкости в нем Н = D. Весовое соотношение твердой
и жидкой фаз в суспензии Т : Ж = 1 : 5. Выбрать мешалку и определить не-
обходимое число ее оборотов.
Решение. Учитывая высокую концентрацию твердой фазы в полу-
чаемой суспензии и относительно большой размер суспендируемых частиц,
выбираем закрытую турбинную мешалку. По нормали НИИХИММАШ диа-
метр d такой мешалки в аппарате диаметром D = 1000 мм составляет
300 мм.
Для расчета определяющего числа оборотов п0 мешалки находим значе-
ния безразмерных величин, входящих в правую часть уравнения (10-8):
Оа=ДУ£^^.^.9,81=
[л2 0,042
£^ = Ж = 1,28; Wl=0,005; А = М = 3,33
р 1830 а 0,3 а 0,3
Эти значения безразмерных величин находятся в пределах применимости
уравнения (10-8). Согласно этому уравнению
ReM = 0,25(57,1 • Ю')0’57 • 1,280’37 • 0,005°’33 • З.ЗЗ1’15 == 18 800
Рассчитываем определяющее число оборотов мешалки:
ReMp. 18 800 • 0,04 . _ _
п0 — = ~о 32". 1830 " = 4’^6 °б!сек “ 274 об1мин
Это число оборотов допустимо, так как по нормали для закрытой тур-
бинной мешалки данного размера число ее оборотов должно быть в пределах
250—350 об/мин.
4. Устройство мешалок
Механические мешалки разделяются по устройству лопастей
на следующие группы: 1) лопастные — с плоскими лопастями,
2) пропеллерные — с винтовыми лопастями, 3) турбинные.
4) специальные (якорные и др.)
Лопастные мешалки
Простейшие лопастные мешалки имеют две плоские лопасти,
установленные в вертикальной плоскости, т. е. перпендикулярно
к направлению вращения (рис. 10-3). Лопасти укреплены на
вертикальном валу, который приводится во вращение от зубча-
той или червячной передачи и делает 12—80 об/мин. Диаметр
лопастей составляет примерно 0,7 диаметра сосуда, в котором
вращается мешалка.
4. Устройство мешалок
355
При малых числах оборотов мешалки жидкость совершает
круговое движение, т. е. вращается по окружностям, лежащим
в горизонтальных плоскостях, в которых движутся лопасти.
В этих условиях отсутствует смешивание различных слоев жид-
кости и интенсивность перемешивания низкая.
Интенсивное перемешивание достигается в результате появ-
ления вторичных потоков и вихревого движения жидкости. Вто-
ричные потоки возникают под действием центробежных сил, вы-
вращения лопасти
зывающих движение жидкости в плоскости
от центра сосуда к его стенкам. Вслед-
ствие этого в центре сосуда возникает
пониженное давление, причем в область
пониженного давления всасывается
jzl.., .^я1Я!ча
Рис. 10-3. Лопастные мешалки:
а —стальная; б~ чугунная.
Рис. 10-4. Циркуляция
жидкости при переме-
шивании лопастными ме-
шалками.
жидкость из слоев, лежащих выше и ниже лопасти. В резуль-
тате в сосуде происходит циркуляция жидкости, показанная
стрелками на рис. 10-4. Вторичные потоки, складываясь с ос-
новным круговым движением жидкости, создают сложное дви-
жение, при котором происходит интенсивное перемешивание
отдельных слоев. Интенсивность перемешивания возрастает с
увеличением числа оборотов; однако еще быстрее увеличивается
мощность, потребляемая мешалкой.
При круговом движении жидкости на ее поверхности под дей-
ствием центробежной силы образуется воронка (рис. 10-4), глу-
бина которой возрастает с увеличением числа оборотов. Образо-
вание воронки ведет к ухудшению использования емкости сосуда.
Для каждого случая опытным путем можно найти оптималь-
ное число оборотов, при котором достигается необходимая эф-
фективность перемешивания. Дальнейшее увеличение числа обо-
ротов вызывает излишний расход энергии.
Вихревое движение жидкость приобретает при установке в
сосуде с мешалкой отражательных перегородок в виде верти-
кально поставленных полос (рис. 10-5). При обтекании жидко-
стью перегородок за ними образуется зона пониженного давле-
ния, в которой возникают вихри (стр. 171). При возрастании
числа оборотов вихри отрываются от перегородок и движутся
в направлении вращения лопасти. В случае дальнейшего
23*
356
Гл. 10. Перемешивание
Рнс. 10-5.
Перемешива-
ние жидко-
сти в сосу-
дах с пере-
городками.
увеличения числа оборотов возникает беспорядочное вихревое
движение жидкости, при этом вихри соударяются друг с другом
по всему объему жидкости. В этих условиях достигается высокая
равномерность и интенсивность перемешивания. В
то же время при наличии перегородок, препят-
ствующих вращению всей массы жидкости, резко
снижается глубина воронки. Обычно достаточно
четырех симметрично установленных радиальных
перегородок для улучшения перемешивания. Одна-
ко с установкой перегородок возрастает расход
энергии на перемешивание.
Для лучшего перемешивания всего объема
жидкости в сосуде на валу устанавливают не-
сколько пар горизонтальных лопастей, т. е. при-
меняют много лопастные, а также рамные мешалки
(рис. 10-6), состоящие из нескольких горизонталь-
ных и вертикальных, а иногда и наклонных пло-
ских лопастей. Рамные мешалки отличаются проч-
ностью и пригодны для перемешивания вязких
жидкостей.
Достоинства лопастных мешалок: 1) простота
устройства и дешевизна изготовления, 2) вполне
удовлетворительное перемешивание умеренно вяз-
ких жидкостей.
Недостатки: 1) малая интенсивность перемешивания вязких
жидкостей, 2) непригодность для перемешивания легко рас-
слаивающихся веществ.
Рис. 10-6. Рамная мешалка.
Основные области применения лопастных мешалок:
1) перемешивание жидкостей небольшой вязкости;
2) растворение и суспендирование твердых веществ, обла-
дающих малой плотностью;
4. Устройство мешалок
357
3) грубое смешение жидкостей.
Лопастные мешалки простого типа наиболее эффективны при
перемешивании маловязких сред (до 100 спз).
Для перемешивания жидкостей с вязкостью свыше 2500 спз
более пригодны рамные мешалки или лопастные мешалки в со-
судах с отражательными перегородками.
В указанных областях применения лопастные мешалки
обеспечивают хорошее перемешивание при небольшом расходе
энергии. Лопастные мешалки непригодны для быстрого раство-
рения, тонкого диспергирования, а также для получения суспен-
зий, содержащих твердую фазу большой плотности.
Диаметры лопастей нормализованных лопастных мешалок: 400, 500, 550,
700, 850, 950, 1000 и 1400 мм.
, Рамные мешалки выпускаются с рамами следующих размеров: 550X550;
650 X 600; 750X650; 950x850; 1140X900; 1340X950; 1540X1000; 1740X1200 льи
(первая цифра — диаметр рамы D, вторая — высота рамы Н).
Пропеллерные мешалки
Лопасти пропеллерных мешалок (рис. 10-7) изогнуты по
профилю судового винта, т. е. с постепенно меняющимся накло-
ном, почти от 0° у оси до 90° на конце лопасти. Вращаясь в жид-
кости, лопасти действуют наподобие винта, а жидкость, окру-
жающая пропеллер, как бы является гайкой и перемещается в
Рис. 10-7. Пропеллерная мешалка. .
направлении оси мешалки. Это осевое движение складывается с
круговым перемещением жидкости, благодаря чему возникает ее
винтовое движение. Если винтовая поверхность пропеллера пра-
вая, а вращение его происходит по часовой стрелке, то 'осевое
движение жидкости направлено вверх и в сосуде возникает цир->
куляция жидкости, показанная на рис. 10-7 (справа).
Пропеллер имеет обычно три лопасти, причем на вертикаль-
ном валу, в зависимости от высоты слой жидкости, устана-
вливают один или несколько пропеллеров. Диаметр лопасти
358
Гл. 10. Перемешивание
Рис. 10-8. Пропеллер-
ная мешалка с диф-
фузором.
пропеллера равен 0,25—0,3 диаметра аппарата. Скорость вра-
щения пропеллера составляет 160—1000 об/мин.
Пропеллерные мешалки создают более интенсивные осевые
потоки жидкости, чем лопастные, и, следовательно, более интен-
сивно перемешивают жидкость. Перемешивание пропеллерными
мешалками улучшается при установке в аппарате отражатель-
ных перегородок или диффузора — короткого цилиндрического
(иногда слегка конического) стакана, в
котором помещается пропеллер (рис. 10-8).
Диффузор направляет циркуляцию жидко-
сти в осевом направлении и благоприятно
влияет на перемешивание в аппаратах с
большим отношением высоты к диаметру,
а также в аппаратах с змеевиками и дру-
гими внутренними устройствами.
Эффективность перемешивания в аппа-
ратах большой емкости возрастает при
эксцентричной установке пропеллеров или
расположении вала пропеллерной мешалки
под углом 10 — 20° к вертикали.
Достоинства пропеллерных мешалок:
1) интенсивное перемешивание, 2) умерен-
ный расход энергии, даже при значительном числе оборотов,
3) невысокая стоимость.
Недостатки: 1) малая эффективность перемешивания вязких
жидкостей, 2) ограниченный объём интенсивно перемешиваемой
жидкости.
Пропеллерные мешалки применяются главным образом для
следующих целей:
1) интенсивное перемешивание маловязких жидкостей;
2) приготовление суспензий и эмульсий;
3) взмучивание осадков, содержащих до 10% твердой фазы,
состоящей из частиц размером до 0,15 мм.
Пропеллерные мешалки перемешивают жидкость быстрее и
интенсивнее лопастных мешалок, при умеренном расходе энер-
гии, превышающем, однако, расход ее для лопастных ме-
шалок.
Пропеллерные мешалки пригодны для проведения непрерыв-
ных процессов, но неприменимы для гомогенного смешивания,
для смешивания вязких жидкостей (ц более 6000 спз), а также
для смешивания жидкостей с твердыми веществами большой
плотности.
Нормализованные пропеллерные мешалки выпускают с диаметром про-
пеллера 150, 200, 250, 300, 400, 500 и 600 мм.
4. Устройство мешалок.
359
Турбинные мешалки
Турбинные мешалки бывают двух типов: открытые
(рис. 10-9, а и б) и закрытые (рис. 10-9,в), имеющие лопастное
в
Рис. 10-9. Турбинные мешалки:
а и б~ открытые; в —закрыта с направляющим аппаратом.
колесо с каналами (наподобие рабочего колеса центробежного
насоса). Турбинные мешалки работают при 100—350 об[мин и
производят интенсивное перемешивание жидкости.
Открытые турбинные мешалки представляют собой, по суще-
ству, усовершенствованную конструкцию простых лопастных
360
Гл 10. Перемешивание
мешалок. Вращение нескольких лопастей, расположенных под
углом к вертикальной плоскости, создает наряду с радиальными
потоками осевые потоки жидкости, что способствует интенсив-
ному перемешиванию ее в больших объемах. Интенсивность пе-
ремешивания возрастает при установке в сосуде отражательных
перегородок.
Закрытые турбинные мешалки обычно устанавливают внутри
направляющего аппарата, который представляет собой непо-
Рис. 10-10. Перемешивание
турбинной мешалкой.
движное кольцо с лопатками, изо-
гнутыми под углом 45—90° (рис.
10-9,в). Закрытые турбинные ме-
шалки создают преимущественно
радиальные потоки жидкости при
небольшой затрате кинетической
энергии. Образующиеся радиаль-
ные потоки жидкости обладают до-
статочно большой скоростью и рас-
пространяются по всему сечению
аппарата, достигая наиболее уда-
ленных его точек. Жидкость входит
в мешалку через центральное от-
верстие и выходит по касательной
к колесу. В колесе жидкость плав-
но меняет направление от верти-
кального (по оси) до горизонталь-
ного (по радиусу) и выбрасывает-
ся из колеса с большой скоростью.
При таком направленном и много-
кратно повторяющемся в единицу
времени движении жидкости дости-
гается быстрое и эффективное пе-
ремешивание ее во всем объеме
сосуда (рис. 10-10).
Для улучшения и ускорения перемешивания (что особенно»
важно в аппаратах непрерывного действия) применяют турбин-
ные мешалкц с лоцастями или колесами, расположенными на
различной высоте.
Достоинства турбинных мешалок: 1) быстрота перемешива-
ния и paQTBopeHHH, 2) эффективное перемешивание вязких
жидкостей, 3) пригодность для непрерывных процессов.
Недостатком турбинных мешалок является сравнительная
сложность и высокая стоимость изготовления.
Области применения турбинных мешалок:
1) интенсивное перемешивание и смешивание жидкостей раз-
личной вязкости, которая может изменяться в широких пределах
4. Устройство мешалок
361
(мешалки открытого типа до 105 спз, мешалки закрытого типа
до 5 • 105 спз);
2) тонкое диспергирование и быстрое растворение;
3) взмучивание осадков в жидкостях, содержащих 60% и бо-
лее твердой фазы (для открытых мешалок — до 60%); допусти-
мые размеры твердых частиц: до 1,5 мм
для открытых мешалок, до 25 мм для за-
крытых мешалок. ——
Нормализованные турбинные мешалки выпу-
скают с диаметром турбины 300, 400, 500 и 600 мм.
Специальные мешалки
Для перемешивания вязких жидкостей и пасто-
образных материалов применяют так называемые
якорные мешалки с лопастями, изогнутыми по фор-
ме стенок и днища сосуда (рис. 10 11). Якорные ме-
шалки очищают стенки аппаратов от налипающего
на них материала, благодаря чему улучшается тепло-
обмен и предотвращаются местные перегревы пере-
мешиваемых веществ
Барабанная мешалка (рис. 10-12) представляет
собой лопастной барабан в виде так называемого
Рис. 10-12. Барабанная
Рис. 10-11. Якорные мешалки.
мешалка.
беличьего колеса. Мешалки этой конструкции создают большую подъем-
ную силу и потому весьма эффективны при проведении реакций между
газом и жидкостью, а также при получении эмульсий, обработке быстро
расслаивающихся суспензий и взмучивании тяжелых осадков. Рекомендуемые
условия применения барабанных мешалок: отношение диаметра барабана
к диаметру сосуда от 1 : 4 до 1:6, отношение высоты жидкости к диаметру
барабана не менее 10.
362
Гл 10 Перемешивание
5. Перемешивание сжатым воздухом
Перемешивание маловязких жидкостей иногда производят
сжатым воздухом. Таким способом возможно лишь медленное
перемешивание при сравнительно большом расходе энергии;
кроме того, как указывалось, перемешивание воздухом может
сопровождаться нежелательным окислением или испарением
продуктов.
Обычно перемешивание сжатым воздухом проводят в аппара-
тах, снабженных барботером — трубой с отверстиями для вы-
хода воздуха, или в аппаратах, работающих по принципу воз-
душных подъемников (эрлифтов). В последнем случае жидкость,
смешанная с пузырьками воздуха, поднимается по центральной
трубе, расположенной по оси аппарата, и опускается в кольце-
вом пространстве между трубой и стенками аппарата. Таким
образом жидкость циркулирует в аппарате и перемешивается
в нем.
При расчете пневматических перемешивающих устройств определяют не-
обходимое давление и расход воздуха.
Давление воздуха находят по формуле-
+ нм2 (io-ю)
где Н—высота столба перемешиваемой жидкости, м,
рж и рв — плотность перемешиваемой жидкости и воздуха, кг/м3,
w — скорость воздуха в трубе (обычно ш = 20—40 м/сек),
С — сумма коэффициентов трения и местных сопротивлений,
р0— давление над жидкостью в аппарате, н/м2
При грубо ориентировочных расчетах, если длина воздушных трубопро
водов неизвестна, можно принимать потери в трубах равными ~20% от со-
противления столба жидкости//р«, т е вести расчет по формуле
Р = 1,2/7рж>? + Л «М2 (10-11)
Расход воздуха V на перемешивание (в пересчете на атмосферное давле-
ние) может быть определен по эмпирической формуле
V — kFP м3/ч (10-12)
где F— поверхность спокойной жидкости в аппарате до перемешивания, ;и2,
Р— давление воздуха, н/м2-,
k — опытный коэффициент, равный 2,4—6,0 в зависимости от интенсивно-
сти перемешивания (нижний предел — для слабого перемешивания).
ТЕПЛОВЫЕ ПРОЦЕССЫ
Глава 11
ОСНОВЫ ТЕПЛОПЕРЕДАЧИ
1. Общие сведения
При тепловых процессах тепло передается от одного вещества
к другому. Для самопроизвольного переноса тепла одно из этих
веществ должно быть более нагрето, чем другое. Вещества,
участвующие в процессе перехода тепла (теплообмене), назы-
ваются теплоносителями. Вещество с более высокой температу-
рой, которое в процессе теплообмена отдает тепло, будем на-
зывать горячим теплоносителем, а вещество с более низкой тем-
пературой, воспринимающее тепло, — холодным теплоносителем.
Существуют два основных способа проведения тепловых про-
цессов: путем непосредственного соприкосновения теплоносите-
лей и передачей тепла через стенку, разделяющую теплоноси-*
тели.
При передаче тепла непосредственным соприкосновением теп-
лоносители обычно смешиваются друг с другом, что не всегда
допустимо; поэтому данный способ применяется сравнительно
редко, хотя он значительно проще в аппаратурном оформлении.
При передаче тепла через стенку теплоносители не смешива-
ются и каждый из них движется по отдельному каналу; поверх-
ность стенки, разделяющей теплоносители, используется для пе-
редачи тепла и называется поверхностью теплообмена.
Различают установившийся и неустановившийся процессы
теплопередачи. При установившемся (стационарном) процессе
температуры в каждой точке аппарата не изменяются во вре-
мени, тогда как при неустановившемся (нестационарном) про-
цессе температуры изменяются во времени. Установившиеся про-
цессы соответствуют непрерывной работе аппаратов с постоян-
ным режимом; неустановившиеся процессы протекают в аппа-
ратах периодического действия, а также при пуске и остановке
аппаратов непрерывного действия и изменении режима их ра-
боты.
Передача тепла от одйого тела к другому может происходить
посредством теплопроводности, конвекции и лучеиспускания.
364
Гл. 11. Основы теплопередачи
Передача тепла теплопроводностью осуществляется путем пе-
реноса тепла при непосредственном соприкосновении отдель-
ных частиц тела. При этом энергия передается от одной ча-
стицы к другой в результате колебательного движения частиц,
без их перемещения друг относительно друга.
^Передача тепла конвекцией происходит только в жидкостях
и газах путем перемещения их частиц. Перемещение частиц обус-
ловлено движением всей массы жидкости или газа (вынужден-
ная или принудительная конвекция), либо разностью плотно-
стей жидкости в разных точках объема, вызываемой неравно-
мерным распределением температуры в массе жидкости или
газа (свободная, или естественная, конвекция). Конвекция всегда
сопровождается передачей тепла посредством теплопроводности.
Передача тепла лучеиспусканием происходит путем переноса
энергии в виде электромагнитных волн. В этом случае тепловая
энергия превращается в лучистую энергию (излучение), которая
проходит через пространство и затем снова превращается в теп-
ловую при поглощении энергии другим телом (поглощение).
Рассмотренные виды передачи тепла редко встречаются в
чистом виде; обычно они сопутствуют друг другу (сложный теп-
лообмен). Так, при передаче тепла через стенку перенос тепла
от горячего теплоносителя к стенке и от стенки к холодному
теплоносителю осуществляется конвекцией, а через стенку —
путем теплопроводности.
Потери тепла с нагретой поверхности в окружающую среду
происходят путем конвекции и лучеиспускания.
2. Тепловой баланс
Уравнение теплового баланса
Количество тепла, передаваемого в единицу времени от од-
ного тела к другому, называется тепловым потоком и выра-
жается в дж/сек, или вт, т. е. единицах мощности (стр. 27).
Значения теплового потока, выраженные в ккал/ч, для перевода
в вт надо умножить на коэффициент 1,16.
При теплообмене между теплоносителями происходит умень-
шение энтальпии (теплосодержания) горячего теплоносителя
ц увеличение энтальпии холодного теплоносителя. Пусть коли-
чество горячего теплоносителя, его начальная и конечная энталь-
пия равны соответственно G кг!сек, Zi и Л дж/кг, а количество
холодного теплоносителя и его начальная и конечная энтальпия
g кг/сек, t’i и 1’2 дж/кг.
Примем также, что количество тепла, передаваемого от горя-
чего теплоносителя к холодному, составляет Q вт (эта величина
%. Тепловой баланс
365
называется тепловой нагрузкой аппарата), а потери тепла в
окружающую среду равны Qn вт (рис. 11-1). Тогда уравнение
теплового баланса запишется в виде*
4-£4 = 4-£^2 4- Qn
Производя перегруппировку, получим:
Q (Л — Л) — £ (Аг — h) 4~ Qn
Величина
Qrop.= Q (Л
(11-1)
Рис. 11-1. Схема теплового
баланса.
представляет собой количество тепла, отданного горячим тепло-
носителем, а величина q
Qxo4. = £r(«2—А) (И-2)
количество тепла, сообщенное хо-
лодному теплоносителю.
Таким образом
Qrop.= Qxoji. Ч- Qn
т. е. тепло, отданное горячим тепло-
носителем, частично передается хо-
лодному теплоносителю и частично
расходуется на компенсацию потерь
в окружающую среду.
В теплообменных аппаратах потери тепла обычно невелики
(не более 2—3%) и ими можно пренебречь. Тогда уравнение
теплового баланса примет вид
Q = Qr»P.
Qxtxn.
или
Q = G(/1 —/2) = g(Z2—Z1)
(11-3)
Определение тепловой нагрузки при
нагревании и охлаждении без изменения
агрегатного состояния
Если в аппарате происходит охлаждение горячего теплоноси-
теля, то 1х = СТ\\ 12 = СТ2, где С — удельная теплоемкость
* При периодических процессах количества теплоносителей (G, g) и ко»
личества тепла (Q, Qn) рассчитывают в кг и дж на одну операцию,
366 Гл 11. Основы теплопередачи
горячего теплоносителя в дж/кг • град, а 7\ и Т2— температуры
теплоносителя * на входе в аппарат и на выходе из него.
Тогда ______________________________
0гор. = ОС(7'1-Г2)=ГДТ (11-4)
Аналогично при нагревании холодного теплоносителя
Рхол. == gc (t2 — tx) = <w А/ (11 -5)
где с — удельная теплоемкость холодного теплоносителя,
дж/кг • град-,
Л и t2 — температуры теплоносителя на входе в аппарат и на
выходе из него.
Величины ДТ = Тх— Т2 и &t = t2 — tx называются темпера-
турными перепадами и выражают изменение температуры теп-
лоносителей в процессе теплообмена (т. е. охлаждение горячего
и, соответственно, нагревание холодного теплоносителя). Произ-
ведения количества теплоносителя на его удельную теплоемкость
называются водяными эквивалентами (W = GC и w — gc).
Удельная теплоемкость — это количество тепла, сообщаемое
единице вещества (1 кг, 1 м3, 1 кмоль) для изменения его темпе-
ратуры на 1°С. Согласно Международной системе единиц СИ,
удельные теплоемкости выражены здесь в дж/кг • град. В спра-
вочных таблицах значения удельных теплоемкостей веществ
обычно приводятся в ккал/кг • град. Для перевода этих значений
в дж/кг • град их надо умножить на коэффициент 4190. Таким
образом, в системе СИ удельная теплоемкость воды будет
равна 4190 дж/кг • град (1 ккал/кг • град), удельная теплоемкость
воздуха составит 1000 дж/кг - град (0,24 ккал/кг - град).
При выводе формул (11-4) и (И-5) принято, что удельные теплоемкости
теплоносителей не зависят от температуры. Если удельная теплоемкость из-
меняется с температурой, то при определении энтальпии следует пользоваться
средними удельными теплоемкостями в пределах от 0°С до температуры
теплоносителя:
/i = С\ТХ, 12 = Л = ^1^ь ^2 ~ ^2^2
где С| и С2 — средние удельные теплоемкости горячего теплоносителя в
промежутке от 0° С до температур 7\ и Т2;
с( и с2 — средние удельные теплоемкости холодного теплоносителя в
пределах от 0°С до температур Л и
* В этой главе, а также в главах 12 и 13 мы будем пользоваться буквой
Т для обозначения температуры горячего теплоносителя в °C (а не в °К), за
исключением особо оговоренных случаев.
2. Тепловой баланс 367
В формулы (11-4) и (Н-5) следует подставлять средние удельные тепло-
емкости соответственно при температурах от Л до Та или от до Их
значения равны
_ Л — Т2 __— С2Т2
тх-т2- т{ — т2
С — 11 — С2^2 — С1^1
> ^2 ^2
Приближенно средняя удельная теплоемкость в пределах от 0°С до тем
пературы t равна истинной удельной теплоемкости при температуре » а
средняя удельная теплоемкость в промежутке от t\ до ti равна Истинной
удельной теплоемкости при температуре —1 .
Определение тепловой нагрузки
при изменении агрегатного состояния
При конденсации парообразного теплоносителя величины /1
и А в уравнении (11-1) представляют собой соответственно эн-
тальпию поступающего пара и уходящего конденсата. Если пар
поступает перегретым с температурой 1\, то величина GJ\ скла-
дывается из энтальпии жидкости при температуре насыщения Тн,
тепла, расходуемого на испарение жидкости и равного теплу
конденсации пара QK0HIl., а также тепла QneP.> необходимого для
перегрева пара, т. е.
GIi = ССжТп-]- Q
конд. + Qпер.
Величина /2 равна СЖТ2 (Т2—температура уходящего
конденсата). Тогда уравнение (11-1) после ряда преобразований
принимает вид:
Qrop. = ^(/i — /2) = Qnep.4~ Фконд. ^^охл. (11“6)
Тепло, отдаваемое при охлаждении перегретого пара, равно
теплу, затраченному на перегрев при его получении, и состав-
ляет:
Qnep. = GCn(T1-TH)
Тепло, отдаваемое при конденсации пара, равно теплу, расхо-
дуемому на испарение жидкости:
Рконд. == Gr
Тепло, отдаваемое при охлаждении конденсата, составляет;
Qovi- ~ GC^ (Тц Т2)
368
Гл 11 Основы теплопередачи
В этих уравнениях СП и Сж— удельные теплоемкости
пара и жидкости, дж/кг -град-, г — теплота испарения, дж/кг.
При конденсации насыщенного пара без охлаждения кон-
денсата
Ргор. = РкОНд —Gr (11-7)
Определение тепловой нагрузки при испарении холодного
теплоносителя рассмотрено в главе 13 (стр. 482).
3. Уравнения передачи тепла
Уравнение теплопередачи
Для протекания процесса передачи тепла необходимо нали-
чие некоторой разности температур между горячим и холодным
теплоносителями. Эта разность температур является движущей
силой процесса теплопередачи и называется температурным на-
пором. Если Т — температура горячего теплоносителя, a t — тем-
пература холодного теплоносителя, то температурный напор*
9 = 7' — /
Чем больше температурный напор, тем выше скорость пере-
дачи тепла, причем количество тепла, передаваемого от горячего
теплоносителя к холодному (т. е. тепловая нагрузка аппарата),
пропорционально поверхности теплообмена F, температурному
напору 9 и времени
' Q = kFfc (11-8)
Здесь k — коэффициент пропорциональности, называемый
коэффициентом теплопередачи и представляющий собой количе-
ство тепла, передаваемое через единицу поверхности в единицу
времени при температурном напоре, равном единице. Если Q
выражено в дж, F в м2, т, в сек и 0 в град, то коэффициент теп-
лопередачи имеет размерность
гм Г Q ~1 Г дж 1 _ Г вт I
I 1 L F-zQ J [ м2 • сек • град J “ L м2 • град J
Если Q выражено в ккал, а т в ч, то размерность коэффициента тепло-
передачи
... _ Г ккал ]
' J “ [м2 •ч •град J
Для перевода в вт/м2 • град значения k, выраженные в ккал/м2 - ч • град,
надо умножить на коэффициент 1,16.
* Для обозначения температурного напора в литературе вместо величины
О часто применяется величина Д/,
3 Уравнения передачи тепла
369
При непрерывных процессах под тепловой нагрузкой Q по-
нимают количество тепла, передаваемое за единицу времени
(вт); тогда уравнение (11-8) можно написать в виде:
Q = kFQ
(И-9)
В процессах теплообмена температуры теплоносителей и, сле-
довательно, температурный напор обычно изменяются; поэтому
при пользовании уравнениями (11-8) и (11-9) в них следует
подставлять некоторое среднее значение температурного напора
9ср. Определение величины 9ср. будет рассмотрено ниже
(стр. 378).
Уравнение теплопроводности
Если тепло переносится путем теплопроводности через стен-
ку, то, согласно закону Фурье, количество передаваемого тепла
пропорционально поверхности F, разности температур между
обеими поверхностями стенки 9СТ =/ст, — /Ст2, времени т и об-
ратно пропорционально толщине стенки 8:
lF(tcr — )т XFOcrT
___ \ Cl ] Cl .J г С!»
S в
(11-10)
где /ст, и /Ст2 — температуры поверхностей стенки.
Коэффициент пропорциональности % называется коэффици-
ентом теплопроводности (или просто теплопроводностью) и
имеет размерность
.л! г QS л г дж ] г вт 1
I * L /МСт. J L м • сек • град J [ м • град J
отличающуюся от размерности коэффициента теплопередачи
тем, что линейный размер (ж) входит в нее в первой степени.
Если Q выражено в ккал, а т в ч, то размерность теплопроводности
- __ Г ккал ~1
1 J ~ L м •ч •град J
причем значения К выраженные в ккал)м • ч • град для перевода в вт!м • град
надо умножить на 1,16.
Коэффициент теплопроводности представляет собой количе-
ство тепла, проходящее в единицу времени через единицу по-
верхности при разности температур 1°С на единицу толщины
стенки. Этот коэффициент зависит от свойств материала стенки
и от ее температуры. С повышением температуры теплопровод*
24 Здк 546,
370
Гл. 11. Основы теплопередачи
ность большинства твердых тел, а также газов возрастает, а
теплопроводность жидкостей (за исключением воды и некото-
рых других) уменьшается.
Приводим значения X (в вт/м • град) некоторых материалов, применяе-
мых для изготовления теплообменных аппаратов:
Сталь, чугун............. 45 Медь.................... 350
Сталь нержавеющая ... 17 Латунь................... 85
Алюминий................ 200 Свинец................... 35
Уравнение (11-10), называемое уравнением теплопроводно-
сти, отличается от уравнения теплопередачи (11-8) тем, что
вместо коэффициента теплопередачи k в него входит выраже-
ние -у.
о
Уравнение передачи тепла конвекцией
При передаче тепла конвекцией у поверхности стенки, вдоль
которой движется теплоноситель и через которую проходит
тепло, образуется ламинарный пограничный слой. Через этот
слой тепло передается путем теплопроводности, в то время как
за пределами слоя, в основной массе теплоносителя, темпера-
тура в каждом поперечном сечении почти постоянна (мало из-
меняется по мере удаления от стенки). Выравнивание темпера-
туры в основной массе происх'одит в .результате перемешивания
теплоносителя при движении отдельных его частиц. С повыше-
нием турбулентности потока перемешивание усиливается, что
приводит к уменьшению толщины пограничного слоя и увеличе-
нию количества передаваемого тепла.
Если разность температур между основной массой теплоно-
сителя и поверхностью стенки составляет 9част_, то количество пе-
редаваемого тепла, согласно закону Ньютона, пропорционально
поверхности стенки F, частному температурному напору 9част,
и времени т:
(11-11)
Q — а-^'®част.^
В этом виде уравнение передачи тепла конвекцией анало-
гично уравнению теплопередачи (11-8) с той лишь разницей,
что в последнее входит разность температур 9 между обоими
теплоносителями, а в уравнение (11-11)—частный температур-
ный напор 9част_, равный разности температур между теплоноси-
телем и стенкой. Величина а, входящая в уравнение (11-11),
называется коэффициентом теплоотдачи; он имеет такую же
размерность, как и коэффициент теплопередачи (вт/м2 • град),
4. Передача тепла через стенку
371
4. Передача тепла через стенку
Плоская стенка
Рассмотрим сложный процесс передачи тепла через плоскую
стенку от горячего теплоносителя к холодному. Характер изме-
нения температур показан на рис. 11-2. В слое горячего тепло-
носителя температура изменяется от Т до /ст.Р по толщине
стенки — от/стч до /ст.2 и в слое холод-
ного теплоносителя от /ст.2 до /.
Напишем уравнения передачи теп-
ла конвекцией от горячего теплоноси-
теля к стенке, путем теплопроводно-
сти через стенку и конвекцией от стен-
ки к холодному теплоносителю:
Q1 ---- а1‘^? (Т' /ст.])
Qct. — f F (Атч /ст
Q2 — (/ст.2 /)
где ai и аг — коэффициенты теплоот-
дачи от горячего тепло-
носителя к стенке и от
через плоскую стенку.
стенки к холодному теп-
лоносителю.
Поверхность теплообмена F равна поверхности стенки и при
плоской стенке является постоянной величиной.
При установившемся процессе количества тепла, передавае-
мые от горячего теплоносителя к стенке (Qi), через стенку (QCT.)
и от стенки к холодному теплоносителю (Q2), должны быть
равны между собой, т. е.
Q1 —• Qct. — Q2 — Q
Определим из уравнений (А) частные температурные на-
поры:
---?
®СТ. --- Ати At.j
avF
Q
Q — / _______/ — _Q_
u2 — ^ct.j *
(Б)
a2F
а из уравнения (11-9) общий температурный напор:
0 = = (В)
24*
Ж
Гл 11 Основы теплопередачи.
Отношение q^=~, представляющее собой количество тепла,
передаваемое в единицу времени через единицу поверхности, на-
зывают удельной тепловой нагрузкой, или плотностью тепло-
вого потока (размерность — вт/м2).
Величины Г1 = — и г2 = — > обратные коэффициентам тепло-
отдачи, называют тепловыми (термическими) сопротивлениями
при переходе тепла через пограничный слой теплоносителя,
л & а
Аналогично rCT = -j- будет тепловым сопротивлением стенки,
1 .
a r==~k------общим тепловым сопротивлением при переходе
тепла от одного теплоносителя к другому. Размерность тепло-
вого сопротивления — м2 • град]вт.
Вводя удельную тепловую нагрузку и тепловые сопротивле-
ния, уравнения (Б) можно написать в виде
= °ст. = ^ст.; 02=^2 (Г)
а уравнение (В) в форме
9 = 9г (Д)
Так как общий температурный напор равен, очевидно, сумме
частных температурных напоров (см. рис. 11-2):
6 = 01 -|- бст -|- 02
то, подставляя значения 9СТ,92 и 0 из уравнений (Г) и (Д),
после сокращения на q получим:
г = Г1 + гст -}-г2 (Е)
т. е. общее тепловое сопротивление равно сумме всех частных
тепловых сопротивлений.
Подставляя приведенные выше значения тепловых сопротив-
лений г, гх, гСТ' и г2 в уравнение (Е), находим
k cq 1 X 1 а2
или
* = T-4—Г (11-12)
__
Л 0^2
Это уравнение является весьма важным, так как позволяет
вычислить значение коэффициента теплопередачи k, если изве-
стны коэффициенты теплоотдачи ои и а2 обоих теплоносителей,
а также толщина 8 и теплопроводность X разделяющей их стенки.
4 Передача тепла через стенку
373
Если стенка состоит из нескольких слоев толщиной 8Ь 82, 83
с теплопроводностями М, Л2, ^з • (рис, 11-3), то тепловые сопро-
^1 ^2 &3
тивления слоев будут равны у-, -у, -у- ...» а тепловое сопро-
тивление всей стенки составит:
В этом случае уравнение (11-12) примет следующий вид:
(11-13)
Обратимся снова к уравнению (Е). Из него видно, что пол-
ное тепловое сопротивление г всегда больше каждого из сла-
гаемых:
г>О;
г > гст; Г>Г2
Подставляя значения теп-
ловых сопротивлений, получим:
2.
т;
£ 1
k а2
Соответственно для об-
ратных величин имеем:
< ар k < у ; k < а2
т. е. коэффициент теплопере-
дачи k всегда меньше любого
из коэффициентов теплоотда-
О X
Рис. 11-3. Передача тепла через
многослойную плоскую стенку.
чи ой и а.2-
Уравнение передачи тепла в форме выражения (Д) может
быть написано следующим образом:
?=-
(П-14)*
В этом виде, уравнение передачи тепла аналогично закону
Ома в электротехнике, причем температурный напор соответ-
ствует электродвижущей силе, тепловое сопротивление — элек-
трическому сопротивлению, а удельная тепловая нагрузка —
силе тока [ср. с уравнением фильтрования (8-31), в котором Ар
аналогично электродвижущей силе, R — электрическому сопро-
тивлению, w — силе тока]
£ 1 .
k а{ ’
k
i
6
374
Г л. 11. Основы Теплопередачи
Пример 11-1. Стенка печи состоит из трех слоев: 1-й внутренний слой —
шамотный кирпич толщиной = 120 мм; 2-й слой — изоляционный кирпич
толщиной да = 65 мм; 3-й слой — стальной кожух толщиной дз — 10 мм. Теп-
лопроводность слоев:
= 0,81 etnfM • град (0,7 ккал)м • ч • град)
Х2 = 0,23 etnfM • град (0,2 ккал!м • ч • град)
Х3 = 45 etnfM град (40 ккал{м • ч • град)
Температура в печи Т = 800° С, температура окружающего воздуха t =
= 30° С. Коэффициенты теплоотдачи с внутренней и наружной стороны печн-
ая 69,6 emfM^'Zpad (60 клал)м2 • ч • град) и а? = 13,9 etnfM2 • град
(12 ккал/м2 • ч • град). Определить потерю тепла с 1 м2 поверхности стенки и
коэффициент теплопередачи.
Решение. Находим тепловые сопротивления (в м2 • epadfetn):
горячего теплоносителя 1 “1 _ 1 _ “ 69,6 0,0144
г, =
1-го слоя стенки '"cTq __ 0,12 _ 0,81 0,148
2-го слоя стенки Г = ст.2 _&2 Х2 _ 0,065 0,23 = 0,28
3-го СЛОЯ стенки *3 0,01 0,00022
Гст.3 ^3 45
холодного теплоносителя
Общее тепловое сопротивление составит:
г = 0,0144 4- 0,148 4- 0,28 4- 0,00022 4- 0,072 0,515 м2 град^т
Плотность теплового потока, равную потере тепла с 1 м2 поверхности
стенки, определяем по формуле (11-14):
Т—t 800 — 30 , „ 1ОПП , , .
q = —-— = —0515— = 1495 etnfM2 (1290 ккал{м2 ч)
Коэффициент теплопередачи:
k = = 1,95 etnfM2 • град (1,68 ккал{м2 • ч • град)
Цилиндрическая стенка
При.неплоской стенке поверхности ее с обеих сторон будут различными
(7^1 и г2). в соответствии с этим уравнения (Б), приведенные на стр 371,
должны быть написаны следующим образом:
0!
Q . fl
477’ °ст-_
Q
а2^2
где /"ср. — средняя поверхность каждого из слоев стенки.
4. Передача тепла через стенку
375
Складывая почленно эти уравнения и приравнивая сумму к правой части
уравнения (В), получим:
1 1
kF a.f
откуда
_L_+_L_
hFср. а2^2
1
Л 5
k =
1
(11-15)
\ “lr 1 ср. а2‘ 2 /
В последнем уравнении общее тепловое сопротивление по-прежнему будет
г = ~ , а частные тепловые сопротивления составят:
ст.
2 ®2 ^2
a, F,
ср.
В уравнении (1'1-15) коэффициент теплопередачи относится к некоторой
расчетной поверхности F, за которую могут быть приняты величины А или Ег
или средняя поверхность Еср.
Для цилиндрической стенки отношение поверхностей можно заменить от-
ношением диаметров. Если расчетный диаметр равен dx (со стороны горячего
теплоносителя), то
1____________
в । dx
X ^Ср. а2^2
Если же за расчетный диаметр принять (со стороны холодного тепло-
носителя), то
k-
ai
ft = —-j-
и 2
1
В d2 L 1
X d.
(11-17)
Ср. а2
Средний диаметр слоя <7Ср. определяется в зависимости от наружного
(dHap.) и внутреннего (дВн.) диаметров по формуле:
^нар. ^вн.
2,з1е4Г
^ср.
вн.
(11-18)
Если т0 сРеДнелогаРифмическое значение dcpi по формуле
(11-18) можно заменить среднеарифметическим:
^нар. ^вн.
вн.
^ср.
(11-19)
(il-16)
2
Ввиду сложности формул для цилиндрической стенки при
расчете теплопередачи через тонкостенные трубы часто поль-
зуются формулой (11-13) для плоской стенки. При этом поверх-
ность теплообмена следует подсчитывать по тому диаметру, со
.стороны которого коэффициент теплоотдачи имеет меньшее
376
Гл. 11. Основы теплопередачи.
значение. Если же коэффициенты теплоотдачи ои и аг имеют
одинаковый порядок, то поверхность теплообмена следует опре-
делять по среднеарифметическому между диаметрами d\ и d2.
Пример 11-2. Определить коэффициент теплопередачи от газа, движуще-
гося по стальному трубопроводу, к окружающему воздуху. Наружный диа-
метр трубопровода dz = 1000 мм, толщина стенки 82 = Ю мм, теплопровод-
ность Х2 = 45 вт/м • град (40 ккал/м • ч • град). Трубопровод футерован изнутри
шамотным кирпичом; толщина футеровки о( = 65 мм, теплопроводность
= 0,81 вт/м-град (0,7 ккал!м • ч • град). Коэффициент теплоотдачи от газа
к стенке си = 11,6 вт/м1 2 * ч • град (10 ккал/м2 • ч-град), коэффициент теплоотда-
чи от наружной поверхности стенки к воздуху а3= 15,5 вт/м2-град
(13,4 ккал/м2 • ч . град).
Решение. Находим внутренний диаметр трубопровода:
dt = 1000 — 2 (10 4- 65) = 850 мм = 0,85 м
Средний диаметр слоя футеровки:
^i, ср = 850 65 = 915 мм = 0,915 м
Средний диаметр стальной стенки:
^2, ср = Ю00 — 10 = 990 мм — 0,99 м
Принимая за расчетный наружный диаметр d2 = 1000 мм (1 м), коэффи-
циент теплопередачи рассчитываем по формуле (11-17):
1 1 0,065 1 , 0,01 1 1 “
11,6 ’ 0,85 + 0,81 ' 0,915 ' 45 ’ 0,99 + 15,5
= 3,95 вт/м2 • град (3,4 ккал/м2 • ч • град)
Определение температуры стенки
При тепловых расчетах часто приходится определять тем-
ч пературы поверхности стенки, а в случае многослойной стен-
ки — также температуры на границах отдельных слоев.
Для определения этих температур в случае плоской стенки
воспользуемся приведенными на стр. 372 уравнениями (Г), ко-
торые в общем виде можно написать так:
9/ = ^ (11-20)
где — падение температуры на некотором участке толщины
стенки;
rt — тепловое сопротивление этого участка.
Для определения /ст-1 имеем уравнение:
г—/„.,=^1=4-
1
откуда
qrr = T -
I
(11-21)
4. Передача тепла через стенку
377
Аналогично
U, = / + ?r2 = / + ^ (11-22)
“2
Выражая плотность теплового потока через общий темпера-
турный напор
9 = | = Й0 (11-23)
получим следующие формулы для определения .температур по-
верхностей стенки:
(11-24)
(11-25)
Определим теперь температуры tx на границе слоев много-
слойной плоской стенки. Например, для границы слоев 2 и 3
(см. рис. 11-3) имеем:
Искомая температура согласно уравнению (11-20) составит:
tx = T — qrl (11-26)
Можно исходить также из температуры холодного теплоноси-
теля t, тогда
~ ix rt= if "Ь
и искомая температура составит:
= / + (11-27)
Аналогично можно найти температуры поверхностей цилиндрической
стенки, определяя q по расчетной поверхности, а тепловые сопротивления,
как указывалось на стр. 375. Так, для температур tCT f и / получим:
'ст.,3 г~
^.2 = * + <1Г2
Id Id
где г, = — • —г-; г2 ---т~>
atd{ а2 d2
Из уравнения (11-20) следует, что разность температур
ниже на том участке, на котором меньше тепловое сопротив-
378
Гл 11 Основы теплопередачи
ление rt. Поэтому, если один из коэффициентов теплоотдачи
велик по сравнению с другим (т. е. тепловое сопротивление
мало), то соответствующий частный температурный напор бу-
дет мал; другими словами, температура стенщ приближается
к температуре того теплоносителя, для которого а. выше.
Пример 11-3. Для условий примера 11-1 определить температуры обеих
поверхностей стенки печи, а также температуры на границах слоев.
Решение. Имеем.
tcr t = Т — qr^ = 800 — 1495 • 0,0144 = 778,4° С
/121 /ст s — qrzx= 778,4 — 1495 • 0,148 = 557,4° С
*2_3 = *1 —2 ~ ^Гст.2 = 557>4 — 1495 • °>28 = 138>4° С
*СТ.2 = *2—3 — <ГСт.3 = 138>4 — 1495 • 0,00022 = 138,1° С
Проверяем величину tCX2 по температуре холодного теплоносителя:
f = 14- = 30 4- 1495 • 0,072 = 138° С
Можно найти температуру на границе любых двух слоев, не прибегая
к последовательному определению температур на границах предыдущих
слоев. Например.
*!_2 = Т — q (rx 4- rCT J = 800 — 1495(0,0144 4- 0,148) = 557° С
или
^_2 = t + q (Г2 4- Гст з 4- rCT 2) = 30 4- 1495 (0,072 4- 0,00022 4- 0,28) = 557° C
Небольшие расхождения объясняются неточностью при расчетах с по-
мощью логарифмической линейки.
5. Средний температурный напор
При непрерывном процессе теплоносители всегда находятся
во взаимном движении, направления которого могут быть раз-
личны. Основными видами движения теплоносителей являются
прямоток и противоток.
При прямотоке оба теплоносителя движутся вдоль поверх-
ности теплообмена в одном и том же направлении; характер
изменения их температур показан на рис. 11-4, а.
При противотоке теплоносители движутся в противополож-
ных направлениях; характер изменения температур вдоль по-
верхности теплообмена зависит от соотношения между водя-
ными эквивалентами теплоносителей (рис. 11-4, б, в, г).
При прямотоке и противотоке средний температурный напор
определяется как среднелогарифмическое из значений макси-
мального (вшах) и минимального (9min) температурных напоров:
п _____ п
л _____ umax ит1п
°ср. о
2,3 1g
О min
(11-28)
5. Средний температурный напор
379
Если отношение <.2, то с достаточной точностью
°min
(ошибка менее 4%) можно пользоваться среднеарифметический
значением:
+ (П-29)
Уравнение (11-28) выводится следующим образом. Напишем уравнение
теплопередачи для элемента поверхности dF, через который передается коли-
чество тепла
dQ = k® dF (А)
Пусть на участке dF (рис. 11-4) изменения температур горячего и холод-
ного теплоносителей составляют dT и dt; тогда уравнения теплового баланса
для участка dF будут:
dQ— — WdT (Б)
dQ = + w dt (В)
где W и w — водяные эквиваленты горячего и холодного теплоносителя.
Как видно из рис. 11-4, Т при возрастании F уменьшается, т. е. изменение
температуры dT отрицательно, поэтому, чтобы dQ было положительной вели-
чиной, в правой части уравнения (Б) поставлен знак минус. Аналогично знак
Рис. 11-4. Характер изменения температур теплоносителей:
а —прямоток; б—противоток при W > w, в —противоток при W < w; г — притовоток при
W=w.
минус в правой части уравнения (В) соответствует противотоку, когда dt от-
рицательно (рис. 11-4,6), а знак плюс — прямотоку, когда dt положительно
(рис. 11-4, а).
Решая уравнения (Б) и (В) относительно dT и dt и производя вычита-
ние, получим
d^ = dT — dt = — dQ(~ т = —yldQ
л__ 1 - 1
где А — w + w .
Из последнего выражения определяем количество тепла:
380
Гл 11 Основы теплопередачи.
Подставляя значение dQ в уравнение (А), находим
kbdF = — -^1
А
откуда
dF =
rf0
Akft
Интегрируя это уравнение при постоянных k и А (последнее имеет место
при постоянстве удельных теплоемкостей С и с), получим
1 , 02 1.0!
Tj-lnV- =
Ak 0( Ak 02
p__ 1 f <Z0
Ak J 0
о
где ©i — значение разности температур при F — 0, а 02 — ее значение
величине поверхности, равной полной поверхности F.
В то же время
F = ... Q. .
&©ср
Приравнивая правые части выражений (Г) и (Д), находим.
Q 1 । ©1
£0ср “ Ak П 02
(Г)
при
(Д)
откуда
0 -
о,
02
Произведение AQ преобразуем следующим образом
~ (jw т = W T ~w ~ — + ^2““^
При противотоке
A? = (7’1-7’2)-(/2~<1) = (T1-/2)-(7’2-f1) = 8I-82
При прямотоке
ЛР = (7’1-7’2) + а2-/1) = (7’1-/1)-(7’2-/2) = 01-02
Таким образом, как при противотоке, так и при прямотоке
Л(? = 01—02
и средний температурный напор
О —
°СР “ , 0.
02
Переходя к десятичным логарифмам, получим формулу (11-28).
Формула (11-28) для определения среднелогарифмического
значения 6Ср> применима, если удельные теплоемкости обоих
5 Средний температурный напор
381
теплоносителей и коэффициент теплопередачи не изменяются
с температурой и все тепло, отдаваемое горячим теплоносите-
лем, сообщается холодному теплоносителю, причем отсутствуют
тепловые потери и не происходит выделения тепла вследствие
химической реакции
Среднелогарифмическим значением 0ср нельзя пользоваться,
если один из теплоносителей участвует в комбинированном про-
цессе (например, при конденсации пара с последующим охла-
ждением конденсата) В этом случае аппарат разделяется на
несколько зон и расчет ведется отдельно для каждой зоны
(стр. 456) Определение 9ср. ПРИ периодических процессах --
см главу 12, раздел 8.
При одинаковых начальных и конечных температурах тепло-
носителей (Г1, /ь Т2, /г) в случае противотока средний темпера-
турный напор выше (следовательно, поверхность теплообмена
меньше), чем в случае прямотока
Из рис 11-4 видно, что при прямотоке конечная темпера-
тура холодного теплоносителя (t2) всегда ниже конечной тем-
пературы горячего теплоносителя (Т2) При противотоке конеч-
ная температура холодного теплоносителя может быть выше
конечной температуры горячего. Следовательно, при одной и
той же начальной температуре холодного теплоносителя в слу-
чае противотока его можно нагреть до более высокой темпера-
туры, чем в случае прямотока Аналогично при одной и той же
начальной температуре горячего теплоносителя в случае проти-
вотока его можно охладить до более низкой температуры, чем
в случае прямотока Таким образом, расход охлаждающего или
нагревающего агента при противотоке может быть ниже, чем
при прямотоке Однако сокращение расхода теплоносителей
связано с уменьшением среднего температурного напора и уве-
личением поверхности теплообмена.
Как видно из приведенного сравнения, противоток выгоднее
прямотока Однако в двух случаях противоток и прямоток прак-
тически равноценны1
1) средний температурный напор значительно (более чем
в 5 раз) превышает температурные перепады теплоносителей,
2) водяные эквиваленты обоих теплоносителей сильно отли-
W W
чаются друг от друга (при — <0,05 и — >10), т. е. температур-
ный перепад одного из теплоносителей (с большим водяныхГ эк-
вивалентом) мал по сравнению с температурным перепадом
второго теплоносителя
Если водяной эквивалент одного из теплоносителей равен
бесконечности (температура этого теплоносителя йе изме-
няется), то между противотоком и прямотоком разницы нет.
382
Гл. 11. Основы теплопередачи
Пример 11-4. В холодильнике требуется охладить от температуры
Л =90°С до температуры 7’2 = 40° С G = 10000 кг/ч жидкости с теплоем-
костью С = 3350 дж/кг -град (0,8 ккал-кг • град). Начальная температура
охлаждающей воды 6 = 25°С, теплоемкость соды с = 4190 дж/кг-град
(1 ккал/кг - град). Коэффициент теплопередачи £=290 вт/м2-град
(250 ккал/м2 • ч • град). Определить необходимую^ поверхность теплообмена и
расход воды при прямотоке и противотоке.
Решение. Тепловую нагрузку рассчитываем по уравнению (11-4):
Q= Q = . 3350 (90 — 40) = 465 000 вт
r OOUU
При прямотоке конечная температура воды не может быть выше ко-
нечной температуры жидкости (40°С). Принимая = 35°С, находим из урав-
нения (11-5) расход охлаждающей воды:
Q 465 000 П1 . ,
ё~~ C(t2 — tx) “ 4190(35 — 25) - 11’1 Кг!сеК “ 40 000 Кг/Ч
Средний температурный напор при прямотоке равен
90 —> 40
25 —> 35
6j = 65 62 = 5
»ер. = -^ L = 23'4°С
2,3 IR- -f-
Необходимая поверхность теплообмена при прямотоке’
_ Q 465 000
fee,
'ср.
Если конечную температуру
чае прямотока, равной 35° С, то
ратурный напор составит:
90 —> 40
35 «— 25
290 • 23,4 “ 68,3 м2
воды при противотоке принять, как и в слу-
расход воды не изменится, а средний темпе-
6, = 55 62 = 15
0 55—15
°ср. — Ёк"
2,3 ig-
& 15
= 30,8° С
Необходимая поверхность теплообмена при противотоке:
„ 465000 _о _
F~~ 290-30,8 “ 52 М
Таким образом, при противотоке и одинаковом расходе охлаждающей
воды необходимая поверхность теплообмена меньше, чем в случае прямотока.
Кроме того, при противотоке температура ti может быть принята более вы-
сокой по сравнению с прямотоком; это позволяет сократить расход воды. Если
принять t2 = 50° С, то расход воды и средний температурный напор составят:
g— 16 000 кг/ч и 0ср. = 26,6° С, что предлагается проверить расчетом. При
этом необходимая поверхность теплообмена
465 000
290-26,6 -60'2 м
Следовательно, при противотоке можно значительно сократить расход
воды (в 2,5 раза) по сравнению с прямотоком и в то же время ограничиться
6. Конвекция
383
меньшей поверхностью. При дальнейшем повышении t2 расход воды еще боль-
ше снижается, но поверхность теплообмена возрастает. Если принять t2 —
= 55,5° С, то необходимая поверхность теплообмена при противотоке составит
68,3 Л12, т. е. будет такой же, как и в случае прямотока; расход воды при
этом будет равен 13 100 кг/ч (в 3,05 раза меньше, чем при прямотоке). Рас-
ход воды при противотоке может быть сокращен еще больше, но в этом слу-
чае уже потребуется большая поверхность теплообмена по сравнению с прямо-
током.
6. Конвекция
Общие сведения
Коэффициент теплоотдачи при передаче тепла конвекцией
определяется, с одной стороны, сопротивлением ламинарного
пограничного слоя, а с другой — сопротивлением при теплооб-
мене между основной массой теплоносителя и пограничным
слоем.
Ориентировочные значения коэффициентов теплоотдачи для
типичных процессов теплообмена приведены ниже:
Процессы теплообмена Коэффициенты теплоотдачи а,
вт/м^гра^
Нагревание и охлаждение газов (атмо-
сферное давление).................. 10—50
Нагревание и охлаждение органических
жидкостей.......................... 50— 1 500
Нагревание и охлаждение воды...... 200—10000
Кипение воды....................... 500—10 000
Конденсация водяных паров.......... 4000—15000
Конденсация паров органических жидко-
стей............................. 500— 2000
Основными факторами, определяющими величину коэффи-
циента теплоотдачи, являются Следующие:
1. Характер движения теплоносителя (ламинарный или тур-
булентный) и его скорость. С увеличением скорости теплоно-
сителя толщина ламинарного пограничного слоя уменьшается,
вследствие чего его тепловое сопротивление понижается, а коэф-
фициент теплоотдачи возрастает.
2. физические свойства теплоносителя (вязкость, теплопро-
водность, плотность7~удельная теплоемкость). Как правило, ко-
эффициент теплоотдачи увеличивается с понижением вязкости
и повышением теплопроводности, плотности и удельной тепло-
емкости. Так как физические свойства изменяются с температу-
рой, то коэффйциент теплоотдачи зависит от температуры теп-
лоносителя.
3. Размеры и форма поверхности теплообмена.
Таким образом, величина коэффициента теплоотдачи опреде-
ляется гидродинамическими, физическими и геометрическими
384
Гл. 11. Основы теплопередачи
факторами. Зависимость коэффициента теплоотдачи от этих фак-
торов весьма сложна и, как правило, не может быть установ-
лена теоретически!^ путем. Поэтому для определения коэффици-
ентов теплоотдачи прибегают к экспериментам, а опытные дан-
ные обрабатывают при помощи теории подобия, в результате
чего получают критериальные уравнения, выражающие зависи-
мость между критериями подобия (стр. 149).
Приложение теории подобия к передаче тепла конвекцией
показало, что этот процесс определяется рядом критериев, зна-
чения которых приведены в табл. 13.
Таблица 13
Критерии подобия при передаче тепла конвекцией
Критерий Формула Физический смь'сл кргуерия
Нуссельта Nu = -^- (11-30) Wl Re==-—- (11-31) Характеризует процесс тепло- обмена между теплоносите- лем и стенкой
Рейнольдса Характеризует гидродинами- ческий режим движения теплоносителя
Прандтля Pr = -^- (11-32)* Л Характеризует физические свойства теплоносителя
Грасгофа Gr== ^Р^-аст^ (11.33) Характеризует режим движе- ния теплоносителя при сво- бодной конвекции
* Выражение для критерия Рг составлено применительно к системе единиц СИ; при поль-
эовании системой единиц МКГСС критерий Рг = —— .
Все критерии подобия являются безразмерными и при вы-
числениях входящие в них величины можно брать в любой, но
обязательно в одинаковой системе единиц. При практических
расчетах мы будем пользоваться системой СИ (стр. 23). Тогда
величины, входящие в критерии, приведенные в табл. 13, будут
иметь следующие размерности:
а— коэффициент теплоотдачи, вт/м2 • град;
X—теплопроводность теплоносителя, вт/м. • град-,
Р- — вязкость теплоносителя, н • сек/м2;
с — удельная теплоемкость теплоносителя, дж/кг • град;
р — плотность теплоносителя, кг/м3;
р — коэффициент объемного расширения теплоносителя,
{/град;
6. Конвекция
385
W—массовая скорость теплоносителя, кг/м2-сек-,
I—определяющий геометрический размер, м;
g — ускорение силы тяжести, м/сек2 (g = 9,81 м/сек2)-,
бчаСт.—частный температурный напор, град.
В безразмерное™ приведенных в табл. 13 критериев подо-
бия нетрудно убедиться, подставив размерности входящих в
них величин. Например, для критерия Прандтля имеем:
н • сек дж
гр л м2 ' кг • град
м • град
кг - м - сек дж
сек2 - м2 кг- град
дж
сек • м • град
Г дж/сек • м • град "1
\дж/сек - м - град J
Безразмерность рассматриваемых критериев сохраняется и
при применении в качестве единицы тепла ккал вместо дж.
Однако если теплопроводность Л выражена в ккал/м • ч - град,
а вязкость р —в «• сек/м2, то в формулу для критерия Прандтля
необходимо ввести множитель 3600:
рг 3600р.с
При пользовании системой МКГСС уравнение (11-32) для
критерия Прандтля перестает быть безразмерным, так как по
структуре этого критерия удельная теплоемкость с в данном
случае должна быть отнесена к технической единице массы
(т.е.м.), а не к 1 кгс. Поэтому в системе МКГСС критерий
Прандтля имеет следующий вид (вязкость ц в кгс-сек/м2,
теплоемкость с в ккал/кгс • град, теплопроводность % в
ккал]м • ч • град):
Рг = 3600
Критерий Re, Рг и Gr являются определяющими, обуслов-
ливающими тепловое подобие. Критерий Nu представляет собой
определяемый критерий, зависящий от определяющих крите-
риев. Эта зависимость в общем виде может быть представлена
уравнением:
Nu=/(Re, Gr, Рг)
Определив' критерии Re, Gr и Рг, из критериального уравне-
ния находят значения критерия Nu, а затем вычисляют коэф-
фициент теплоотдачи из формулы (11-30):
a = yNu (Ц-34)
25 Зак. 546.
386
Гл. 11. Основы теплопередачи
При расчете физические константы теплоносителей берутся
при определяющей температуре, за которую принимается сред-
няя температура теплоносителя /т (стр. 443) или температура
пленки (пограничного слоя) /пл_, равная среднеарифметическому
температур стенки /ст. и теплоносителя:
. _ t-i /СТ.
*пл. 2
Тепловое подобие
Для выяснения условий теплового подобия и физического смысла крите-
риев подобия рассмотрим, в качестве примера, нагревание теплоносителя,
движущегося по трубе. Выясним условия подобия труб 1 и 2 (рис. 11-5) в
отношении передачи тепла конвекцией. Предпосылкой теплового подобия яв-
ляется геометрическое и гидродинамическое подобие. При соблюдении этих
условий отношение толщин пограничных слоев обеих труб равно отношению
Рис. 11-5. К выводу теплового подобия.
линейных размеров этих труб. Тепловое подобие заключается в том, что тем-
пературы в отдельных точках труб подобны, т. е. отношение разности темпе-
ратур между двумя любыми точками одной трубы к разности температур
между сходственными точками другой трубы является постоянной вели-
чиной
Пусть изменение температуры по толщине пограничного слоя составляет
для труб 1 и 2 соответственно 6j и 02> а температурный перепад теплоноси-
теля по длине труб Zi и /2— AZi и Л/2. Тогда условие теплового подобия
труб имеет вид
Условие геометрического и гидродинамического подобия труб / и 2 мож-
но написать следующим образом:
где и 82— толщины пограничных слоев труб 1 и 2;
1Х и /2 — длины этих труб.
Разделив уравнение (А) на уравнение (Б), получим:
ри Plu а
\ S, / ’ V /1 / \ 82 / • \ /2 /
(В)
6. Конвекция
387
Отношение разности температур между двумя точками к расстоянию ме-
жду этими точками называется температурным градиентом. Таким образом,
О'
отношение -у является температурным градиентом по толщине пограничного
слоя, а отношение ----температурным градиентом по длине трубы.
На основании уравнения (В) можно сказать, что условием теплового по-
добия труб 1 и 2 будет равенство отношения температурного градиента по
толщине пограничного слоя к температурному градиенту по длине трубы.
Это отношение обозначено через А.
Пусть плотность, удельная теплоемкость, теплопроводность и скорость
теплоносителя равны р, с, X и w, а площадь сечения и периметр трубы — 5 и
П. Тогда масса теплоносителя, протекающего через трубу в единицу времени,
будет и?5р, а количество сообщаемого ему тепла при нагревании на А/ со-
ставит wSpc At Такое же количество тепла передается путем теплопроводно-
сти через пограничный слой и равняется, на основании уравнения теплопро-
водности, П/ — О'. Таким образом
О
wSpc М = П/ у О' (Г)
Обозначая а = — (эта величина называется температуропроводностью)
?С S (
и заменяя отношение -yj- через эквивалентный диаметр rf9KB, трубы (rf9KB. =
45 \
==_р|_)» после преобразования уравнения (Г) получим
^-ЭКР- = 4 = 4А
а \ 8 / \ I /
Так как условием теплового подобия труб 1 и 2 является равенство от-
ношения А, то равенство для них величины —-—' также будет условием
1^ теплового подобия. Эта величина
Ре —:
а
называется критерием Пекле и характеризует отношение поперечного темпе-
ратурного градиента (по толщине пограничного слоя) к продольному (по
длине трубы).
Другим условием теплового подобия рассматриваемых труб является их
гидродинамическое подобие, т. е. равенство критериев Рейнольдса. При прак-
тических расчетах критерий Пекле заменяют критерием Прандтля
, Рг _ Ре „ 11С
Re а ” X
в который входят только физические константы теплоносителя (ч— кинемати-
ческая вязкость теплоносителя).
Таким образом, условием теплового подобия двух труб является равен-
ство для них критериев Re, а также критериев Рг.
Количество тепла, передаваемого через пограничный слой, было опреде-
лено выше как П1 -у 0'. Это же количество тепла можно выразить при
25*
388
Гл. 11. Основы теплопередачи
помощи уравнения конвекции как ШаОчастл где 0част< — частный температур-
ный напор, т. е разность температур между стенкой и теплоносителем. Сле-
довательно
П/ |= Ша6част
Сокращая обе части уравнения на П/0част, умножая на d3KBt и деля наХ,
получим:
а^экв. _ ^экв. . ®част.
X “ 8 ' 0'
Если написать такое уравнение для каждой из подобных систем, то пра-
вые части полученных уравнений будут одинаковы, так как при наличии гео-
метрического и гидродинамического подобия будет одинаковым отношение
—, а при наличии теплового подобия — и отношение . Следователь-
о о
но, будут равны и левые части этих уравнений, т. е. величина
Nu = -^^
А
называемая критерием Нуссельта, для подобных систем будет одинакова.
Таким образом, следствием теплового подобия является равенство для
подобных систем критерия Nu, причем можно написать:
Nu=/(Re, Рг)
При свободной конвекции движение теплоносителя определяется разно-
стью плотностей его холодных (Pi) и нагретых (р) частиц, и в число опре-
деляющих критериев входит критерий Архимеда [формула (6-46)].
Так как разность плотностей обусловлена разностью температур 0Част., то
Pi Р _ Q0
- — ричаст.
где р — коэффициент объемного расширения теплоносителя.
Подставляя это значение в выражение для критерия Архимеда, получим
критерий Грасгофа:
Рг gZ3 оп _______ Z3gp2ft64acT.
ur---роЧаст. — р
Выражение для критерия Нуссельта в данном случае запишется в виде
Nu = /(Or, Рг)
Теплоотдача при вынужденной конвекции
При вынужденной конвекции теплоноситель движется вдоль
поверхности теплообмена с определенной скоростью под дей-
ствием внешней силы, например силы тяжести или силы давле-
ния, развиваемого насосом, компрессором или вентилятором.
6. Конвекция
389
Движение теплоносителя по трубам и каналам. В этом слу-
чае для определения а пользуются следующими уравнениями:
устойчивое турбулентное движение (Re > 10000)
t Nu — 0,023Re°>8Pr°‘4 (11-35)
v переходное движение (Re = 2300—10000)
Nu = 0,008Re°’9Pr0’43 (1 1 -36)
ламинарное движение (Re < 2300)
Nu = a(Re Pr)0,2(Gr Pr)0>1 (11-37)
Множитель а в уравнении (11-37) имеет следующие значения.
а
Для горизонтальных труб................ 0,74
Для вертикальных труб при движении холод-
f ного теплоносителя вверх или горячего
вниз................................. 0,63
Для вертикальных труб при движении холод-
ного теплоносителя вниз или горячего
вверх.................................. 0,85
В уравнениях (11-35) — (11-37) определяющим геометрическим размером
служит внутренний диаметр трубы dB или эквивалентный диаметр канала
^экв. Определяющей температурой в уравнениях (П-Зб) и (11-36) является
температура /т, а в уравнении (11-37) темпер-атура /Пл. (стр. 386).
Движение теплоносителя вне труб. При движении теплоноси-
теля в кольцевом канале между двумя трубами (внутренний
диаметр наружной трубы D, наружный диаметр внутренней
трубы rfH) коэффициент а для теплообмена с поверхностью вну-
тренней трубы определяется по уравнению:
Nu = 0,023Re0>8Pr°’4 (~) (11 -38)
При движении в межтрубном пространстве кожухотрубных
теплообменников (стр. 424) ^отсутствие поперечных перегородок
Nu = 1,'16 ((Z9KB,Re)0'8Pr°.3’ (11-39)
(7/экв.— эквивалентный диаметр межтрубного пространства, л).
При наличии перегородок (сегментных или чередующихся
дисков и колец)~
Nu = O,2Re°*6Pr°'33 (11-40)
В уравнениях (11-38) — (11-40) определяющим геометрическим размером
является наружный диаметр трубы dH> а определяющей температурой — 1Т.
Скорость в выражении для критерия Re, входящего в уравнение (11-40),
подсчитывается по приведенному сечению (стр. 444)-,
6
390
Гл. 11. Основы теплопередачи
Перемешивание жидкости мешалкой. Для расчета а в сосудах с мешал-
ками пользуются уравнениями *:
при теплообмене со стенками сосуда
Nu = 0,36Re^67Pr0,33 (11-41)
при теплообмене со змеевиком
Nu = 0,87ReJ62 Рг0*33 (11-42)
В этих уравнениях критерий ReM определяется по формуле (10-6);
а определяющим размером для критерия Nu является диаметр сосуда D;
определяющей температурой служит tT.
Стекание жидкости пленкой. При стекании жидкости по наружной по-
верхности расположенных друг над другом горизонтальных труб с шагом по
вертикали, равным t, коэффициент а определяется по уравнениям:
при //dH = 1,7-2 NurM -= 0,005Re°’4 Рг0-4 (11-43)
при f/rfH = 1,3 NuUJI = O,OO2ReJfPr0’4 (11-44)
При стекании жидкости по вертикальной поверхности:
для турбулентного течения (ЁеПл. > 2300)
NunjI. = 0,01 (RenjI.Pr)0,33
для ламинарного течения (Кепл. < 2300)
/ s >0,33
Мипл = o,67Re»J1(pr-^-)
(11-45)
(11-46)
где Н—высота поверхности;
&прив. — комплекс, характеризующий толщину пленки (приведенная тол-
щина) и имеющий размерность длины:
/ и2 X0'33
= НУ (11-47)
\ г о /
В уравнениях (11-43) — (11-46) критерий Кепл. подсчитывается по фор-
муле (6-85), а критерий NunjI. — по определяющему размеру &Прив.> т. е.:
_ а / ц2 X0’33
^ипл. —
а&прив.
Г~
(11-48)
Определяющей температурой в уравнениях (11-43) и (11-44)' служит
температура /т, а в уравнениях (11-45) и (11-46) температура — £Пл>-
Пример 11-5. Определить коэффициент теплоотдачи при движении воды
по трубе с внутренним диаметром dB = 21 мм, если массовая скорость воды
№ = 400 кг/м2 • сек, а средняя температура составляет 28,5° С. Константы
воды при этой температуре:
вязкость...............р. = 0,835 • 10”3 н • сек!м2 (0,835 спз)
теплопроводность . . . . X == 0,613 втп]м • град (0,528 ккал]м • ч • град)
удельная теплоемкость . с = 4190 дж/кг • град (1 ккал/кг • град)
* Уравнения (11-41) и (11-42) приведены в несколько упрощенном виде.
6. Конвекция
391
Решение. Находим по формулам (11-31) и (11-32) критерии Рей-
нольдса и Прандтля:
Re = -400'0,021 ~ Ю ООО
0,835 -10'3
D 0,835 • 10"3 • 4190 _ _
РГ=?----- 0,613 ~^==5’7
Так как Re ^10 000, то для определения критерия Нуссельта применяем
уравнение (11-35):
Nu = 0,023 • 10 0000’8 • 5,7°>4 = 73,5
По формуле (11-34) вычисляем коэффициент теплоотдачи:
а = q '02 ~ 21$° вт1м2' гРа& (1850 ккал/м2 ч • град)
Пример 11-6. Определить коэффициент теплоотдачи при движении воз-
духа в межтрубном пространстве кожухотрубного теплообменника без попе-
речных перегородок. Внутренний диаметр кожуха D =•= 600 мм; наружный
диаметр труб dn = 38 мм; количество труб п= 121. Массовая скорость воз-
духа w = 36,1 кг/МР-сек, средняя температура tT = 185° С. Константы воз-
духа при этой температуре:
вязкость..............р = 0,253 • 10-4 н • сек/м2 (0,0253 спз)
теплопроводность . . . X = 0,0382 вт/м • град (0,0329 ккал/м • ч • град)
удельная теплоемкость с = 1030 дж/кг • град (0,245 ккал{кг • град)
Решение. Критерии Рейнольдса и Прандтля подсчитываем по форму-
лам (11-31) и (11-32):
Re = =54200
0,253 • 10"
р 0,253-IO-4.1030 _
РГ =-----ОДО85-------°'68
Площадь поперечного сечения межтрубного пространства составляет:
5мтр. = - J (D — nd§ = 0,785 (0,62 — 12 b 0.0382) = 0,146 м2
Периметр межтрубного пространства равен:
П = я (D + ndR) = 3,14 (0,6 4-121 • 0,038) = 16,3 м
Эквивалентный диаметр составляет:
4$мтр. 4-0,146
^экв.— р] 16 3 ~ 0,036 м
По формуле (11-39) находим:
Nu = 1,16 (0,036 • 54 200)0,6.0,680>за= 96
392
Гл. 11. Основы теплопередачи
Коэффициент теплоотдачи определяем из уравнения (11-34):
а = • 96 96,5 вт/м2 • град (83 ккал/м2 • ч • град)
Пример 11-7. Определить коэффициент теплоотдачи при движении мети-
лового спирта в межтрубном пространстве кожухотрубного теплообменника
с поперечными перегородками Наружный диаметр труб dn = 25 мм. Массо-
вая скорость спирта W = 168 кг/м2 • сек, средняя температура /т = 37,7° С.
Константы метилового спирта при этой температуре:
вязкость.............р. = 0,465 • 10“3 н • сек/м2 (0,465 спз)
теплопроводность . . . X = 0,208 в.п/м • град (0,179 ккал/м • град)
удельная теплоемкость с = 2660 дж/кг • град (0,634 ккал/кг • ч • град)
Решение. По формулам (11-31) и (11-32) имеем:
Re^ <* 0.025 50
0,465 • 10“3
р,_ 0,465 • 10“3 • 2660
----------ода----------5’9
Из уравнения (11-40) находим:
Nu = 0,2 • 9O5O0’6 • 5,90,33 » 86,8
По формуле (11-34) вычисляем коэффициент теплоотдачи:
а = • • 86,8 о* 720 вт/м2 • град (620 ккал/м2 • ч • град)
Пример 11-8. Определить коэффициент теплоотдачи от перемешиваемой
жидкости (60%-ная H2SO4) к змеевику в сосуде диаметром D = 1800 мм.
Диаметр лопасти мешалки d = 600 мм, число оборотов п = 120 об/мин Тем-
пература кислоты составляет 60°С. Константы 60%-ной H2SO4 при этой тем-
пературе:
плотность.............р = 1466 кг/м3
вязкость.............р. = 2,4 • 10“3 н • сек/м2 (2,4 спз)
теплопроводность . . X = 0,496 вт/м • град (0,427 ккал/м • ч • град)
удельная теплоемкость с = 2460 дж/кг • град (0,587 ккал/кг • град)
Решение. Вычисляем критерии ReM и Рг по формулам (10-6) и (11-32J:
d _ ”42р __ (120/60) • 0,62.1466
м“ Р “ 2,4.10“3
= 440 000
D 2,4 • 10"3 • 2460
Рг = —---------------
0,496
= 11,9
При определении критерия ReM число оборотов п выражено в об/сек,
поскольку вязкость р имеет размерность — н • сек/м3.
По формуле (11-42) находим критерий Nu:
Nu = 0,87 • 440 0000’62 • 11,90’33 = 6300
6. Конвекция
393
По уравнению (11-34) подсчитываем коэффициент теплоотдачи:
X хт 0,496 - 6300 . , , /1еЛЛ , , ..
а == — Nu =--------------= 1740 emlM* • град (1500 ккал{м2 • ч • град)
L) 1,о
Пример 11-9. Определить коэффициент теплоотдачи для наружной по-
верхности горизонтальных труб оросительного холодильника, орошаемых во-
дой. Длина верхней трубы I = 6 м; наружный диаметр труб da «= 76 мм; рас-
стояние между осями труб по вертикали t — 150 мм. Количество орошающей
воды g = 5000 кг/ч; ее средняя температура /т = 28,5е С. Физические кон-
станты воды при этой температуре см. пример 11-5.
Решение. Линейную плотность орошения вычисляем по формуле
(6-88):
Г = = 417 кг!м • ч = 0,116 кг)м • сек
2 • о
Из уравнений (6-85)' и (11-32) находим:
_ 4-0,116
л 0,835 -10“3
п 0,835-КГ3-4190 __
Рг =-----5313------= 5’8
Приведенную толщину пленки определяем по формуле (11-47) при
Р = 995 кг/мР;
Цо.зззло-ур33 5
°прив. - [ 9952.9>81 J , W м
t 150
Так как-j-= = 2, то расчет производим по уравнению (11-43):
NunjI. = 0,005 - 5550,4 • 5,7°-4 = 0,128
Коэффициент теплоотдачи вычисляем по формуле (11-48)':
а = —-—Иипл. = * 9у]?— = I860 вт[м2 • град (1600 ккал{м2 • ч • град)
8прив. ‘ 4,2 • 10
Теплоотдача при свободной конвекции
Свободная конвекция характеризуется движением отдельных
частиц теплоносителя, возникающим вследствие разности плот-
ностей нагретых и холодных частиц. Рассмотрим, например, не-
подвижную жидкость в сосуде, причем тепло подводится через
стенки этого сосуда. Частицы жидкости, соприкасающиеся со
стенками, нагреваются и становятся легче, в результате чего
они поднимаются вверх. На их место поступают холодные ча-
стицы, которые также нагреваются и поднимаются. В резуль-
тате возникает движение частиц жидкости — так называемые
конвекционные токи, направление которых показано на
рис. 11-6, а.
394
Гл. 11. Основы теплопередачи
Если жидкость охлаждается путем отвода тепла через стен-
ки сосуда, то частицы жидкости у стенки при охлаждении ста-
новятся тяжелее и опускаются вниз. В этом случае конвек-
ционные токи имеют напра-
вление, показанное на
рис. 11-6, б.
Чем интенсивнее тепло-
обмен, т. е. чем больше пе-
редается тепла, тем интен-
сивнее конвекционные токи.
Так как количество переда-
ваемого тепла пропорцио-
Рис. 11-6. Направление конвекционных нально частному темпера-
токов: турному напору, т. е. разно-
а — при нагревании; б —при охлаждении. СТИ Температур Между СТСН-
кой и теплоносителем (6част.)>
то интенсивность конвекционных токов и значение коэффи-
циента теплоотдачи определяются величиной 0част.‘
Для определения « при свободной конвекции пользуются следующими
уравнениями:
при ОгРг > 2 • 107
Nu = 0,135 (Gr Pr),/s
(11-49)
при ОгРг < 2 • 107
Nu = 0,54 (Gr Pr)0’25
(11-50)
В уравнениях (11-49) и (11-50) определяющей температурой является
температура /пл., а определяющим геометрическим размером наружный диа-
метр трубы (при свободной конвекции около горизонтальных труб) или
высота поверхности Н (при конвекции около вертикальных поверхностей).
Пример 11-10. Определить коэффициент теплоотдачи от вертикальной
стенки сосуда к воде при свободной конвекции. Высота стенки Н — 0,9 м.
Температура стенки /ст. = 35° С. Температура воды t = 21,5° С.
Решение. Средняя температура пленки:
j. t -f- 1ст. __ 21,5 35 л„0 р
*пл.= 2---------2 =
При этой температуре вода характеризуется следующими константами:
плотность .......................р = 995 кг/м2
вязкость........................[1 = 0,835 • 10-3 н • сек/м2 (0,835 спз)
теплопроводность.................X — 0,613вт/м-град (0,528 ккал!м-ч-град)
удельная теплоемкость............с = 4190 дж/кг • град (1 ккал/кг-град)
коэффициент объемного расшире-
ния ..........................§ = 0,00028 Х/град
Разность температур между стенкой и водой составляет:
Очаст. = *ст. — t = 35 — 21,5 = 13,5° С
6. Конвекция
395
Находим критерии Gr и Рг по формулам (11-33) и (11-32):
„ 0,93 • 9,81 • 9952 • 0,00028 • 13,5 , 1ПЭ
(0,835 • 10“3)2
п 0,835 • 10~3 • 4190 , _
Рг =-------ода-------=w
Произведение Gr • Рг =38,5 • 109 • 5,7 = 219 • 109. Так как Gr-Pr>2«107,
то критерий Нуссельта находим по формуле (11-49):
Nu = 0,135 (Gr • Рг)'3 = 0,135 (219 • 109)1/з = 810
Коэффициент теплоотдачи вычисляем ио уравнению (11-34):
а = А Nu = ‘ 81А s 555 ernfM2 • град (480 ккал!м2 • ч • град)
Н “,9
Теплоотдача при конденсации пара
При соприкосновении пара со стенкой, температура которой
ниже температуры насыщения пара, происходит конденсация
пара, причем конденсат осаждается на стенке. Различают пле-
ночную конденсацию, когда конденсат осаждается в виде сплош-
ной пленки, и капельную конденсацию, когда конденсат осаж-
дается в виде капель.
Капельная конденсация наблюдается в том случае, если кон-
денсат не смачивает поверхность стенки, а также при конденса-
ции пара с примесью масла и некоторых других веществ на по-
лированной стенке. В большинстве случаев происходит пленоч-
ная конденсация.
В случае пленочной конденсации а определяется по следую-
щим уравнениям:
при конденсации на наружной поверхности горизонтальных
труб
(11-51)
кепл.
при конденсации на вертикальных поверхностях:
Re„,,. <400 Nu„. = -^ (11-52)
ке„*
пл.
Вепл. > 400 NunjI. == (-R “-"Йо) (11 "53)
--------------+1580
В этих уравнения^ критерий Еепл. определяется по формуле* (6-85)\
а критерий НипЛ,—по формуле (11-48). В данном случае Г представляет
собой плотность стекания конденсата (в кз/м-сек), т. е. количество конден-
сата, приходящееся на единицу периметра поверхности в единицу времени.
396
Гл. 11. Основы теплопередачи
Для вертикальной поверхности высотой Н м с периметром П м количе-
ство отдаваемого тепла Unq равно произведению количества конденсирую-
щегося пара G кг/сек на теплоту испарения г дж/кг:
Wiq = Gr
откуда
r G дН
П ~ г
Тогда критерий Кепл. согласно формуле (6-85) запишется в виде:
Ке»л. = — (11-54)
Г'/
где q — плотность теплового потока, вт/м2.
Аналогично для г расположенных друг над другом горизонтальных труб
длиной I м и наружным диаметром dH м получим:
ndnlzq = Gr
откуда в соответствии с формулой (6-88)
г _ G _ ndKzq
21 ~~ 2г
Критерий Кепл. составит:
(11-55)
Если п — общее число горизонтальных труб в аппарате, а m — число
вертикальных рядов, то среднее значение z будет равно:
В уравнениях (11-51) — (11-53) физические константы конденсата бе-
рутся при определяющей температуре /Пл.> а теплота испарения г — при тем-
пературе насыщения пара. При конденсации перегретого пара в приведенные
уравнения вместо теплоты испарения подставляют разность энтальпии пара
и конденсата.
При конденсации внутри горизонтальных труб
(_ \ 0 3 / 7 \ 0,35
—(11-56)
Рп^./ \"в/
где а — 0,5 при конденсации паров воды и аммиака и 0,36 при конденса-
ции паров органических веществ;
а — поверхностное натяжение, н/м-,
рп — плотность пара, кг/м3-,
g — ускорение силы тяжести, м/сек2-,
I — длина трубы, м.
Критерий Иепл. находят из уравнения (6-85) или по формуле (11-55);
определяющим размером для критерия Nu является внутренний диаметр
трубы dB, определяющей температурой — /Пл.-
Пример 11-11. Определить коэффициент теплоотдачи при конденсации
водяного пара с абсолютным давлением 2,94 бар (3 ат) снаружи пучка гори-
зонтальных труб (наружным диаметром с?н = 25 мм) в зависимости от
6. Конвекция
397
удельной тепловой нагрузки. Количество труб в пучке п = 258, количество
вертикальных рядов т = 39.
Конденсат * (вода) при давлении 3 ат (температура конденсации
132,9° С) характеризуется следующими константами:
плотность...............р = 932 кг/м3
вязкость................[л = 0,206 • 10~3 н сек/м2 (0,206 спз)
теплопроводность . . . . X = 0,685 вт/м град (0,59 ккал]м • ч • град)
теплота испарения . . . г = 2170 • 103 дж/кг (517 ккал/кг)
Решение. Среднее число расположенных друг над другом труб;
п 258 _
Z = --= s 6,6
т 39
Критерий Рейнольдса находим по формуле (11-55)
RenJ1 - 2 3.14.0Л25.6.6.
0,206 • 10-3 • 2170 -103
Из уравнения (11-51) имеем:
кт 1,53 11,5
(0,00232^)А q4'
Приведенную толщину пленки рассчитываем по формуле (11-47):
__ Г (0^06. ю-у-!7_ 5
прив. — [ 9322.9,81 J ’
Коэффициент теплоотдачи вычисляем по уравнению (11-48):
X .. 0,685-11,5 463000
а —------Ыипл. =----------= ——22— вт/м2 град
Мив. 1,7.1О-У Vq
Так, например, при ^ = 28 800 вт/м2 (см. пример 12-7, стр. 448):
а — 463000 _ is iqq вт/м2 • град (13 000 ккал/м2 • ч • град)
У 28 800
Пример 11-12. Определить коэффициент теплоотдачи при конденсации
паров бензола снаружи вертикальных труб диаметром с?н — 38 мм Коли-
чество труб п = 211. Количество паров бензола G — 8500 кг/ч. Абсолютное
давление составляет 0,98 бар (1 ат). Константы бензола при 1 ат (темпера-
тура конденсации 80,2° С)*.
плотность..............р — 815 кг/м3
вязкость...............р = 0,317 • 10~3 н • сек]м2 (0,317 спз)
теплопроводность . . . X = 0,151 вт/м • град (0,13 ккал/м • ч • град)
удельная теплоемкость с = 1760 дж/кг • град (0,42 ккал/кг • град)
теплота испарения .../* = 395 • Ю3 дж/кг (94,3 ккал/кг)
* Свойства конденсата для упрощения расчета взяты не при‘темпера-
туре ^пл., а при температуре теплоносителя, что не вносит существенной по-
грешности.
398
Гл. Л. Основы теплопередачи
Решение. Плотность стекания конденсата равна:
Г О 8500 000 , Л АЛ Л I
г = = 3,14.0,038.211 = 338 «“/*•’ = «,094 кг/м . сек
По формулам (6-85) и (11-32) находим:
4 -0 094
RenjI =— "-—,-=1180
0,317 • 10~3
„г 0,317 • 10~3 -1760
РГ =-------0Д51------= 3’М
Так как Кепл. > 400, то расчет ведем по уравнению (11-53):
NT 1180 ПОЛО
Nu = -g-Ag ,11Qn—тйлГ---------= 0,248
6,25(1180 — 400) 158Q
3,68*/’ '1~
Приведенную толщину пленки рассчитываем по формуле (11-47):
/(0,317 •10-3)2\'/’ 5
6прив. - \ 8152.9 31 J - 2>48 • 10 М
Коэффициент теплоотдачи находим из уравнения (11-48):
X кт 0,151-0,248 , ,ч
а =--------Nunji. = —-----4^5- = 1510 вш1м2 • град (1300 ккал/м2 • ч. град)
8прив. 2,48 • 10
1ПЛ.
’ Теплоотдача при кипении жидкости
При кипении жидкости образуется пар, температура которого
равна температуре насыщения tn, определяемой давлением в
аппарате. Кипящая жидкость перегрета и в зависимости от ин-
тенсивности парообразования имеет температуру t, которая не-
сколько выше /н- Наибольший перегрев жидкости наблюдается
у обогреваемых стенок, причем отдельные точки поверхности
стенки (бугорки, шероховатости, пузырьки адсорбированных на
поверхности газов и т. д.) являются центрами парообразования,
т. е. местами возникновения пузырьков пара. Образующиеся
пузырьки быстро растут и, по достижении некоторого диаметра,
отрываются от поверхности и поднимаются вверх. При росте и
отрыве пузырька происходит охлаждение жидкости вблизи дан-
ного центра парообразования и следующий пузырек может об-
разоваться в этом центре только после того, как восстановится
необходимая степень перегрева жидкости. Описанный процесс
называется ядерным, или пузырьковым, кипением.
С увеличением плотности теплового потока усиливается пе-
регрев жидкости, в результате чего увеличивается число цент-
ров парообразования и частота отрыва пузырьков. Поэтому при
ядерном кипении коэффициент теплоотдачи возрастает с увели-
чением плотности теплового потока.
6. Конвекция
399
При некотором критическом значении плотности теплового
потока <7Кр. (для воды при атмосферном давлении примерно
1 200 000 вт/м2) число центров парообразования становится на-
столько большим, что отдельные пузырьки сливаются друг с
другом и образуют сплошную паровую пленку, отделяющую
жидкость от обогреваемой поверхности стенки; такое кипение
называется пленочным. При пленочном кипении коэффициент
теплоотдачи резко снижается, а разность температур между
стенкой и жидкостью становится весьма большой, что ведет к
перегреву стенки, которая (например, при обогреве горячими
топочными газами) может нагреться до недопустимых темпе-
ратур. По этой причине производственные аппараты работают
всегда в области ядерного кипения.
При расчетах можно пользоваться формулой:
1(0,6
NuKHn. = 54-^- (Ц-57)
причем критерий Нуссельта при кипении находят из уравнения:
NuK„„.=i/' (11-58)
а критерий К определяется выражением:
В формулах (11-58) и (11-59) приняты следующие обозначения:
q — плотность теплового потока, вт/м2;
г — теплота испарения, дж/кг;
а — поверхностное натяжение, н/м;
р — плотность жидкости, кг/м3
fpn—плотность пара, кг/м3;
w — произведение среднего диаметра пузырьков, возникающих при кипе-
’ нии, на число пузырьков, образующихся в единицу времени, м/сек.
Величина w при атмосферном давлении равна 0,078 м/сек, а при других
давлениях определяется по формуле:
/ ч1,1
w = 0,0781-^) (11-60)
\рп /
где ро — плотность пара при абсолютном давлении 1 ат, кг/м\
Пример 11-13. Определить коэффициент теплоотдачи при кипении
40%-ного раствора NaOH под абсолютным давлением 0,196 бар (0,2 ат).
Температура кипения раствора при этом давлении составляет 85° С. Кон-
станты раствора:
вязкость..................р. = 2,92 • 10-3 н • сек/м2 (2,92 спз)
теплопроводность..........К = 0,557 вт/м • град (0,48 ккал/м • ч • град)
удельная теплоемкость . .с — 3440 дж/кг • град (0,82 ккал/кг град)
поверхностное натяжение . а = 0,104 н/м (104 дин/см)
400
Гл 11 Основы теплопередачи
плотность.........................р = 1390 кг/м3\
теплота испарения при0,2а/и. . . . г = 2360- 10-3 дж/кг (563 ккал/кг)
Плотность водяного пара составляет.
при абсолютном давлении 0,2 ат . . рп = 0,128 кг/м2',
при абсолютном давлении 1 ат . . р0 = 0,579 кг/м2
Решение. По формуле (11-60) находим:
w = 0,078 =0,41 м/сек
Из уравнений (11-59) и (11-32) имеем:
К =___________q_________=
Л 0,128 • 2360 • 103 • 0,41 123 000
р _ 2,92 • 10~3 • 3440
0,557 ’
По формуле (11-57) определяем критерий Нуссельта:
гдл0,6
NuKHn =-----------------птг = 0,0198^°’6
123 0000'6-17,90,3
Коэффициент теплоотдачи вычисляем при помощи формулы (11-58):
° = >]/" ^-Наиш. = 0ДО|/’ -^^0,0198<Л'1 = 4</1'6
Так, например, при q = 18 400 вт/м2 (см. пример 13-5, стр 486).
а == 4 • 18 4ОО0,6 = 1450 вт/м2 • град (1250 ккал/м2 • ч • град)
Теплоотдача при непосредственном
соприкосновении теплоносителей
При охлаждении газов непосредственным соприкосновением
с жидкостью в насадочных колоннах коэффициент теплоотдачи
определяется по формуле:
Nu = a Re^’Rei’Pr?’33 (11-61)
где Rer и Иеж — критерии Re для газа и жидкости (стр. 608) j
Ргг—критерий Рг для газа.
Определяющим геометрическим размером для критерия Nu
является эквивалентный диаметр насадки [см. формулу (6-100)].
Множитель а при охлаждении сухого газа равен 0,01, при
охлаждении парогазовых смесей а — 0,17л1,15, где х— содержа-
ние пара в смеси (в объемных долях).
7 Лучеиспускание
401
Пример 11-14. Воздух охлаждается водой в башне с хордовой насадкой
при следующих условиях:
Воздух
Массовая скорость . 1Гг = 1,11 кг)м2 • сек
Средняя температура Т = 80° С
Вязкость ............р. = 0,208 10 4 н • ceKjM2 (0,0208 спз)
Теплопроводность . . ?. = 0,0305 вт1м • град (0,0263 ккал/м • ч • град)
Удельная теплоемкость с = 1000 дж!кг • град (0,24 ккал! кг • град)
Вода
Массовая скорость . 1^ж = 2,78 кг]м2 • сек
Средняя температура t =30° С
Вязкость..........р.ж = 0,8 • 10”3 н • сек!м2 (0,8 спз)
Хордовая насадка состоит из досок размерами 10 X 100 мм, расстояние
между досками (в свету) равно 20 мм Удельная поверхность насадки
f = 65 м2/м3, а ее свободный объем е = 0,68 Определить коэффициент тепло-
отдачи при непосредственном соприкосновении теплоносителей
Решение. Эквивалентный диаметр насадки рассчитываем по формуле
(6-100)-
, 4е 4-0,68 лллю .
^экв. — — 65 0,0418 м
Из уравнений (6-101), (17-9) и (11-32) находим критерии Rer, ₽еж и Ргг:
Rer = ^- = = 3280
/|.г 65-0,208. КГ*
= 4-2'78 =214
/[1Ж 65 - 0,8 -10"3
Рг 0,208 • 10-4 • 1000
РГг =-------ода----------- °’®84
Критерий Nu определяем по формуле (11-61) при а «0,01 (для сухого
газа):
Nu = 0,01 - 328O0,7 - 2140’7 - 0,684°'33 = 108
откуда
X кт 0,0305 -108 _о , „ , {RQ , . ,ч
а = -----Nu = —оо418— “ ™ вт1м ‘ гРа° (6° ккал]м2 • ч • град)
7. Лучеиспускание
Общие сведения
Лучеиспускание свойственно всем телам, при этом излуче-
ние энергии происходит непрерывно в результате сложных вну-
триатомных возмущений, интенсивность которых определяется
температурой тела. Лучистая энергия представляет собой энер-
гию электромагнитных колебаний с различными длинами волн.
402
Г л 11. Основы теплопередачи
В дальнейшем рассматривается лишь так называемое тепловое
излучение, которому соответствуют длины волн от 0,4 до 40 мк.
Такие лучи поглощаются телами, причем при поглощении их
лучистая энергия снова переходит в тепловую.
При попадании лучистой энергии на какое-либо тело погло-
щается лишь часть этой энергии; другая ее часть отражается,
а некоторая часть проходит сквозь тело. Тела, поглощающие
всю падающую на них лучистую энергию, называются абсолютно
черными. Тела, полностью отражающие падающую на них лучи-
стую энергию, называются абсолютно белыми, а тела, пропу-
скающие всю падающую на них энергию, — абсолютно прозрач-
ными.
Абсолютно черных, белых и прозрачных тел в природе не
существует. Практически прозрачными телами являются одно-
и двухатомные газы (воздух, азот, кислород, водород и др.).
Твердые тела и жидкости для тепловых лучей непрозрачны.
Поглощение и отражение лучистой энергии твердыми телами
в значительной степени зависит от состояния их поверхности:
гладкие и полированные поверхности обладают высокой отра-
жательной способностью; шероховатые поверхности, наоборот,
обладают высокой поглощательной способностью. Наиболее вы-
сокой поглощательной способностью, близкой к абсолютно чер-
ному телу, обладает сажа, которая поглощает 90—96% падаю-
щей на нее лучистой энергии.
Закон Стефана — Больцмана
Согласно закону Стефана — Больцмана, количество тепла Q,
излучаемого в единицу времени, пропорционально поверхности
излучающего тела F и четвертой степени его абсолютной тем-
пературы Т. Для технических расчетов этот закон можно запи-
сать в следующем виде:
« = С?Г(ж)4 (11-62)
где С — коэффициент пропорциональности, называемый коэф-
фициентом лучеиспускания.
Если Q выражено в впг, a F в м2, то размерность коэффици-
ента лучеиспускания
М = = [ М2. oKJ
Наибольшее значение коэффициент лучеиспускания имеет
для абсолютно черного тела:
С9 = 5,68 вт[м,2 • °К4
7. Лучеиспускание
403
Для других тел коэффициент лучеиспускания можно выра-
зить через коэффициент лучеиспускания абсолютно черного
тела:
С = eCs = 5,68е вт/м2 - °К4 (11 -63)
где величина е, называемая степенью черноты тела, представ-
ляет собой отношение коэффициента лучеиспускания данного
тела к коэффициенту лучеиспускания абсолютно черного тела.
Если Q выражено в
мерность
ккал[ч, то коэффициент лучеиспускания имеет раз-
— Г ккал 1
-1 м2 • ч • °K4J
причем для
абсолютно черного тела коэффициент лучеиспускания равен:
Cs = 4,88 ккал!м2 • ч • °К4
Закон Кирхгофа
Закон Кирхгофа устанавливает связь между лучеиспуска-
тельной и поглощательной способностью тела. Согласно этому
закону, поглощательная способность и степень черноты равны
между собой:
е = А (11-64)
где А — отношение поглощаемой телом лучистой энергии к об-
щему ее количеству, падающему на тело.
Из закона Кирхгофа следует, что лучеиспускательная способ-
ность тела тем выше, чем больше его поглощательная способ-
ность. Этим и объясняется наивысшая лучеиспускательная спо-
собность абсолютно черного тела, так как для него А = 1, а
следовательно, и е = 1.
Наоборот, тела, хорошо отражающие лучистую энергию,
сами излучают мало, а для абсолютно белого и абсолютно про-
зрачного тел лучеиспускательная способность равна нулю.
Значения степени черноты е для некоторых материалов приведены ниже:
Сталь окисленная...................... 0,82
Чугун окисленный...................... 0,96
Сталь нержавеющая................... 0,64—0,76
Медь................................ 0,57—0,87
Алюминий......................... 0,11—0,19
Железо оцинкованное, свинец . . . 0,28
Кладка кирпичная, штукатурка . . 0,93
Краска масляная................ 0,92—0,96
Краска алюминиевая............. 0,27—0,67
26*
404
Гл. 1). Основы теплопередачи
Теплообмен лучеиспусканием между телами
Тела не только излучают, но также поглощают и отражают
энергию, излучаемую окружающими телами.
Количество тепла, отданного телом с абсолютной температу-
рой Т\ окружающим его более холодным телам с абсолютной
температурой Т2, составляет:
(11-65)
где s — приведенная степень черноты системы;
F — условная расчетная поверхность теплообмена.
Если одно тело расположено внутри другого полого тела, то за услов-
ную расчетную поверхность принимают поверхность внутреннего тела F\,
а «приведенная степень черноты определяется по формуле:
1
(11-66)
где У7! и Р2— поверхности внутреннего и наружного тела;
£] и е2 — степени черноты внутреннего и наружного тела
Если поверхность Л мала по сравнению с поверхностью F2, то в фор-
муле (11-66) можно пренебречь вторым членом в знаменателе. Тогда
£ = #1 (11-67)
а расчетной поверхностью является F\.
Лучеиспускание газов
Значительной поглощательной и лучеиспускательной способ-
ностью обладают многоатомные газы, в частности двуокись уг-
лерода (СО2), водяной пар (Н2О), сернистый ангидрид (SO2),
аммиак (NH3) и др.
В отличие от твердых тел, газы способны поглощать и излу-
чать энергию лишь в определенных интервалах длин волн. Для
лучей с другими длинами волн газы прозрачны и энергия их
излучения равна нулю.
• В газах поглощение и излучение происходят во всем объеме,
вследствие чего поглощательная и лучеиспускательная способ-
ности газа зависят от формы газового слоя (т. е. от формы со-
суда, в котором находится газ), а также от его толщины и пар-
циального давления излучающего газа в газовой смеси.
Степень черноты газа определяется на рис. 11-7 и 11-8 (стр. 406) в за-
висимости от температуры газа и произведения р/, где р — парциальное дав-
ление излучающего газа в ат (парциальное давление равно полному абсо-
лютному давлению газовой смеси, умноженному на объемную долю данного
7. Лучёиспуекйние
405
газа в смеси), а / — средняя длина пути луча в м. Средняя длина пути луча
определяется в зависимости от формы и размеров газового слоя:
Форма и размеры газового слоя Средняя длина пути луча
Шар диаметром d........................ 0,6 d
Куб со стороной а...................... 0,6 а
Цилиндр бесконечной длины диаметром d 0,9 d
Плоский слой бесконечной длины толщи-
ной В.................................. 0,8 В
Пучок труб диаметром d (расстояние меж-
ду осями труб расстояние между
рядами t2)............................. 1,08 d f ~ — 0,785
Рис. 11-7. Степень черноты двуокиси углерода.
При других формах газового слоя среднюю длину пути луча находят по
формуле:
z 3,4У
(11-68)
Здесь V — объем газового слоя, м3; F — поверхность газового слоя, м2.
406
Гл. 11. Основы теплопередачи
При наличии в газовой смеси нескольких излучающих газов степень чер-
ноты смеси определяется как сумма степеней черноты отдельных газов. Так,
например, степень черноты смеси, содержащей СОг и НгО, будет равна:
ег = sCOa + ₽sH2O
Где р — поправочный коэффициент (см. вспомогательную диаграмму на
рис. 11-8).
Рис. 11-8. Степень черноты водяного пара
(на вспомогательной диаграмме, вверху, приведен поправочный коэффициент ₽ на парциаль-
ное давление водяного пара в ат).
Количество тепла, передаваемого путем лучеиспускания от газа к стенке,
определяется из уравнения
(11-69)
7. Лучеиспускание
407
Здесь Тт и Гст.— абсолютные температуры газа и стенки;
£*т>—эффективная степень черноты стенки, учитывающая
увеличение степени черноты стенки еСт. при наличии
• 6СТ. + 1 .
газового излучения, ест — —♦
ег и е' — степень черноты газа при температурах газа и стенки.
Совместная передача тепла конвекцией
и лучеиспусканием
Передача тепла лучеиспусканием обычно сопровождается
одновременной передачей тепла конвекцией. Пусть от стенки с
абсолютной температурой Тсг- тепло передается к среде с абсо-
лютной температурой Т (соответствующие температуры в °C бу-
дут /ст. И /) .
Тепло, передаваемое конвекцией, составит (ак — коэффи-
циент теплоотдачи при конвекции):
Qk = «kF(/ct.- /)
а тепло, передаваемое лучеиспусканием
«—MW ча1]
Общее количество передаваемого тёпла равно:
Q = Qk + Qa — ак^(/ст. — /) — (loo) ]
или
Второй член выражения, заключенного в квадратные скобки
(11-70)
называется коэффициентом теплоотдачи при лучеиспускании.
Таким образом
Q = (ак + ал) F (/Ст. ~ t) = а/7 (/ст. — /)
(И-71)
где общий коэффициент теплоотдачи (при совместной передаче
тепла конвекцией и лучеиспусканием)
<7 = ак-|-а4
(11-72)
408
Гл. 11. Основы теплопередачи
Как видно из выражения (11-71),- при совместной передаче
тепла конвекцией и лучеиспусканием можно пользоваться обыч-
ными формулами для передачи тепла конвекцией, подставляя
значение общего коэффициента теплоотдачи по формуле (11-72).
Пример 11-15. Определить количество тепла, отдаваемое топочными га-
зами стенкам труб из хромоникелевой стали. Наружный диаметр труб
dw — 57 мм; трубы расположены в шахматном порядке с шагом Л —150 мм,
расстоянием между рядами t2 — 130 мм. Средняя температура газов
4= 700° С, средняя температура стенок труб 4т. = 500° С, коэффициент тепло-
отдачи конвекцией ак= 17,4 вт/м2 • град (15 ккал/м2-ч-град). Состав топоч-
ных газов: 10% СОг и 5% НгО (по объему). Абсолютное давление 1 ат.
Решение. Эффективная степень черноты стенки:
' ест. + 1 0,7 4-1 ___
ест. = —’ = 2~ = °>85
где степень черноты еСт. = 0,7 (для хромоникелевой стали).
Парциальные давления СОг и НгО в газовой смеси составляют:
Рсог = 1 • 0,1 = 0,1 ат
Рц2о ~ 1 ’ Мб = 0,05 ат
Средняя длина пути луча равна (см. стр. 405):
/ = 1,08 0,057 — 0,785^ = 0,322 м
\ 57 . 57 /
Определяем произведения:
pCQl = 0,1 • 0,322 = 0,0322 м • ат Рц3о^= 0,05 • 0,322 = 0,0161 м • ат
По рис. 11-7 и 11-8 находим при 4 = 700° С
есо2 = °’08’ ₽енао = 1>04 • 0,037 = 0,0385
а при 4т. = 500° С
бСоа = 0,075; ₽eHj0 = 1,04 • 0,048 ₽ 0,05
Степень черноты газов при /г = 700° С составляет:
. ег== 0,08 + 0,0385 = 0,119
а при 4т. = 500° С:
е* = 0,075 + 0,05 = 0,125
Количество тепла, отдаваемого газами 1 м2 стенки путем лучеиспускания,
рассчитываем по формуле (11-69):
0л = 0,85 • 5,68.1 Го,119 У — 0,125 ( -7^\-°°-У1^3000 вт/м2
L \ 1UU / у Ivv / J
Коэффициент теплоотдачи лучеиспусканием равен:
__ Qji________ 3000 . к «
“л " F (tT — 4Т.) ~ 1 (700 — 500) ” 15 вт/м ’град
8. Потери тепла в окружающую среду
409
Общий коэффициент теплоотдачи находим из уравнения (11-72):
а = 17,4 15 as; 32,4 втп!м2 • град
Количество отдаваемого тепла (на 1 м2 поверхности труб) составляет:
q = a (tr — 4т.) = 32,4 (700 — 500) = 6480 вт/м2 (5580 ккал[т2 • ч)
8. Потери тепла в окружающую среду
Отдача тепла от поверхности аппарата в окружающую среду
происходит путем конвекции и лучеиспускания; поэтому при рас-
чете потерь тепла в окружающую среду следует пользоваться
уравнением (11-71), определяя общий коэффициент теплоотдачи
а по формуле (11-72). При расчете задаются температурой на-
ружной поверхности аппарата (/„.), а затем проверяют ее, как
указывалось выше (стр. 376).
При расчете потерь тепла аппаратом, установленным в помещении, для
определения общего коэффициента теплоотдачи можно применять следую-
щую приближенную формулу (при 4т. от 50 до 350° С):
а = 9,3 -|- 0,058 4т. впг[м2 • град (11-73)
Для уменьшения потерь тепла в окружающую среду аппа-
раты покрывают слоем тепловой изоляции, т. е. слоем мате-
риала с низкой теплопроводностью (теплоизоляционный ма-
териал). При нанесении тепловой изоляции увеличивается
тепловое сопротивление стенки и уменьшается температура ее
наружной поверхности. Этим достигается снижение потерь
тепла и улучшаются условия труда обслуживающего персонала.
Тепловой изоляцией покрывают наружные поверхности аппа-
ратов. Для предохранения стенки аппарата от воздействия очень
высоких температур изоляцию наносят с внутренней стороны
стенки.
Увеличение толщины изоляции ведет к возрастанию ее на-
ружной поверхности. Поэтому с увеличением толщины изоляции
. потери тепла уменьшаются лишь до известного предела. При
выборе толщины изоляции следует исходить из допустимых
потерь тепла или допустимой температуры стенки с учетом
стоимости самой изоляции.
Пример 11-16. Определить падение температуры газа, протекающего по
стальному футерованному трубопроводу в условиях примера 11-2, если длина
трубопровода составляет 150 м, количество (объем) газа при нормальных
условиях G— 10 000 мР/ч, удельная теплоемкость 1 м3 газа при нормальных
условиях С = 1340 ож/м3'град (0,32 ккал/.и3 • град), начальная температура
газа Ti = 500° С, температура помещения t = 10° С.
410
Гл 11 Основы, теплопередачи
Решение. Задаемся температурой наружной поверхности стенки
^ст.= 108° С. Тогда коэффициент теплоотдачи от наружной поверхности
в окружающую среду найдем по формуле (11-73):
а2 = 9,3 -j- 0,058 • 108 = 15,5 вт/м2 • град
Наружная поверхность трубопровода составляет;
F = 3,14 • 1.150 = 470 м2
Количество тепла, отдаваемого в окружающую среду, равно:
Q = а2Р (/ст. — t) = 15,5.470 (108 —10) 718 000 вт
В то же время
Q = GC(T1 —Г2) или 718000= -7♦ 1340(500— Т2)
oOUU
откуда
Т2^ 307°С
Средний температурный напор рассчитываем в данном случае по фор-
муле (11-29):
500 —> 307
10 ч-> 10 вср =,. ^90. + 29Z ~ 393 °с
490 297~
Для проверки /Ст. необходимо определить коэффициент теплопередачи,
который составляет k = 3,95 вт/м2 • град (см. пример 11-2).
Температуру стенки вычисляем по формуле (11-25):
з ОК
/ст =10-1- • 393 = 109,5 °C
1о,5
что близко совпадает с принятым значением /Ст.
Глава 12
НАГРЕВАНИЕ И ОХЛАЖДЕНИЕ
1. Общие сведения
В данной главе рассматриваются теплообменные аппараты
(теплообменники), применяемые для осуществления теплообмена
между двумя теплоносителями с целью нагревания или охлажде-
ния одного из них. В зависимости от целевого назначения
теплообменные аппараты называются подогревателями или хо-
лодильниками. Если процесс проводится для сообщения тепла
холодному теплоносителю, то участвующий в теплообмене горя-
чий теплоноситель будем называть нагревающим агентом. Если
же процесс состоит в отводе тепла от горячего теплоносителя,
то холодный теплоноситель, которому сообщается отводимое
тепло, будем называть охлаждающим агентом.
В ряде случаев целевое назначение имеют оба процесса —
нагревание холодного теплоносителя и охлаждение горячего.
Тогда теплообменные аппараты называют собственно тепло-
обменниками.
Часто в теплообменных аппаратах в процессе теплообмена
происходит изменение агрегатного состояния одного из тепло-
носителей: конденсация горячего или испарение холодного теп-
лоносителя. Аппараты, применяемые при конденсации горячего
теплоносителя, почти не отличаются от других теплообменных
аппаратов и поэтому рассматриваются в данной главе. Если
конденсация горячего теплоносителя является целевым процес-
сом, то эти аппараты называют конденсаторами. Аппараты для
испарения холодного теплоносителя (выпарные аппараты) бу-
дут рассмотрены в главе 13.
2. Способы нагревания и охлаждения
Нагревание паром
Нагревание водяным паром. Водяной пар является наиболее
распространенным горячим теплоносителем для нагревания до
температур 150—170° С.
412
Г л. 12. Нагревание и охлаждение
Преимущества водяного пара как нагревающего агента:
1) высокий коэффициент теплоотдачи, 2) большое количество
тепла, выделяемое при конденсации единицей количества пара,
3) возможность транспортировки по трубопроводам на значи-
тельные расстояния, 4) равномерность обогрева, так как конден-
сация пара происходит при постоянной температуре, 5) легкое
регулирование обогрева.
Обычно применяют насыщенный пар небольшого давления
(до 6—10 ат), иногда перегретый на 20—30°С. Применение пе-
регретого пара не дает особых преимуществ, так как теплота
перегрева невелика по сравнению с теплом конденсации, кото-
рое выделяется при нагревании насыщенным паром.
Целесообразно применение отработанного пара абсолютным
давлением 2—3 ат (после паровых турбин с противодавлением)
или отборного пара абсолютным давлением 6—7 ат (от турбин
с промежуточным отбором). Во многих случаях возможно ис-
пользование экстра-пара с выпарных установок (стр. 489).
Нагревание водяным паром производится путем примене-
ния так называемого острого или глухого пара. При обогреве
острым паром его вводят непосредственно в нагреваемую жид-
кость, и образующийся конденсат смешивается с нею. Ввод пара
в жидкость производится через трубу, опущенную ниже уровня
жидкости, или через барботер — трубу, снабженную большим
количеством мелких отверстий, расположенную также ниже
уровня жидкости. При использовании барботера одновременно
происходит перемешивание жидкости (стр. 362). В тех случаях,
когда разбавление жидкости или ее смешение с водой недопу-
стимо, обогрев острым паром непригоден.
При обогреве глухим паром обогреваемая жидкость не со-
прикасается с паром, а отделена от него стенкой, через которую
и передается тепло. Такой способ обогрева является наиболее
распространенным. При обогреве глухим паром необходимо,
чтобы он полностью сконденсировался в аппарате.
Совершенно недопустима работа теплообменника с пролет-
ным паром, т. е. с неполной конденсацией пара, когда из аппа-
рата отводится смесь конденсата и пара. При неполной конден-
сации пара расход его повышается.
Для удаления из аппарата конденсата без выпуска с ним
пара применяют специальные устройства — конденсатоотвод-
чики (водоотводчики).
При постоянном расходе пара и избыточном давлении до
7 ат употребляют подпорные шайбы, представляющие собой
диски с отверстиями в центре. Диаметр отверстия выбирают
так, что шайба пропускает только конденсат.
2. Способы нагревания и охлаждения
413
Наибольшее распространение имеют конденсационные горш-
ки (рис. 12-1). В корпусе 1 находится поплавок 2, представляю-
щий собой открытый стакан, в днище которого укреплен шток 4,
заканчивающийся сверху клапаном 5. К крышке горшка при-
креплена труба 3, всегда погруженная в конденсат. При запол-
нении корпуса горшка конденсатом поплавок всплывает и кла-
пан 5 закрывает выходное отверстие 6 для конденсата. При
Рис. 12-1. Конденсационный горшок с откры-
тым поплавком:
1— корпус; 2—поплавок; 3—труба; 4 — шток; 5— клапан;
6 — отверстие для выхода конденсата.
дальнейшем поступле-
нии конденсат начина-
ет переливаться внутрь
поплавка.
Когда в поплавке
наберется достаточное
Рис. 12-2. Схема уста-
новки конденсационного
горшка:
1 — теплообменник; 2 —конден-
сационный горшок; 3—обвод-
ной вентиль; 4 — трубка для
отбора проб конденсата.
количество конденсата, он опускается, клапан 5 открывает вы-
ходное отверстие и конденсат выдавливается из поплавка да-
влением пара через трубу 3 и отверстие 6. После удаления из
поплавка большей части конденсата поплавок снова всплывает,
клапан 5 закрывает выходное отверстие и начинается следую-
щий цикл работы горшка.
При установке конденсационных горшков обычно делается
обводная линия (рис. 12-2), чтобы теплообменник мог работать
при ремонте (отключении) горшка.
Нагревание парами высококипящих жидкостей. Для нагре-
вания до температур выше 150—170° С вместо водяного пара
высокого давления часто применяют пары высококипящих орга-
нических жидкостей или ртути. Из органических жидкостей наи-
414
Гл. 12 Нагревание и охлаждение
более распространена дифенильная смесь, содержащая 73,5%
дифенилового эфира (СбН5—О—С6Н5) и 26,5% дифенила
(C6Hs—С6Нб). Дифенильная смесь плавится и кипит при по-
стоянной температуре (температура плавления 12,3° С; темпе-
ратура кипения 258°С); выше 400°С начинается быстрое разло-
жение дифенильной смеси. Нагревание парами дифенильной
смеси применяется при температурах от 260 до 380—400° С; при
этом абсолютное давление паров доходит до 8—10 ат. Теплота
испарения дифенильной смеси при 300—350° С в 4—5 раз мень-
ше, чем для воды. Однако вследствие большой плотности паров
смеси количество тепла, выделяющееся на единицу объема пара,
для дифенильной смеси и воды примерно одинаково. Дифениль-
ная смесь горюча, но практически взрывобезопасна, вредное
влияние ее на организм человека незначительно. Коэффициент
теплоотдачи при конденсации паров дифенильной смеси равен
1400—1750 вт}м2 • град.
Пары ртути применяют для нагревания до 380—500° С. Ртуть
не горюча, но весьма токсична, что сильно затрудняет ее приме-
нение. Коэффициент теплоотдачи при конденсации паров ртути
составляет около 600 вт/м2 • град.
Пары высококипящих жидкостей получают в паровом котле,
обогреваемом топочными газами, и направляют в теплообмен-
ник, где они конденсируются. Конденсат возвращается в паро-
вой котел.
Нагревание горячими жидкостями
При нагревании горячими жидкостями чаще всего приме-
няется циркуляционный способ обогрева (рис. 12-3). По этому
способу находящийся в замкнутом пространстве жидкий нагре-
вающий агент циркулирует между печью или другим аппара-
том, где он нагревается, и теплообменником, в котором он отдает
полученное в первом аппарате тепло. Таким образом, нагреваю-
щий агент не расходуется, а служит лишь переносчиком тепла
от печи к теплообменнику. Нагрев горячего теплоносителя в
печи соответствует его охлаждению в теплообменнике (если пре-
небречь незначительными потерями тепла) и составляет 5—10° С.
Циркуляция может быть естественной или принудительной.
Естественная циркуляция (рис. 12-3, а) происходит за счет раз-
ности плотностей: нагретый охлаждающий агент вследствие
меньшей плотности поднимается вверх и поступает в теплооб-
менник, где он охлаждается, и затем снова возвращается в
печь. Для обеспечения циркуляции теплообменник должен быть
расположен выше печи на 4—5 м\ однако скорость циркуляции
незначительна (около 0,2 м{сек).
2 Способы нагревания и охлаждения
415
Принудительную циркуляцию (рис. 12-3,6) осуществляют
с помощью насоса. При этом отпадает необходимость в подъ-
еме аппарата и возможны более высокие скорости циркуляции,
что ведет к повышению коэффициента теплоотдачи. В то же
время установки с принудительной циркуляцией вследствие на-
личия циркуляционного насоса сложнее и менее надежны в
эксплуатации, чем установки с естественной циркуляцией.
а
Рис. 12-3. Схема циркуляционного обогрева жидким
нагревающим агентом:
а —обогрев с естественной циркуляцией, б —обогрев с принуди-
тельной циркуляцией. 7 —печь; 2 —теплообменник; 3—насос.
Другой способ нагревания горячими жидкостями заключает-
ся в применении обогревательных бань, представляющих собой
аппараты с рубашками, заполненными жидкими нагревающими
агентами. Рубашка нагревается топочными газйми, с помощью
электрообогрева или змеевика, по которому пропускается пар
высокого давления.
При нагревании горячими жидкостями нагревающими аген-
тами служат обычно вода или высококипящие органические
жидкости. Горячая вода, подогреваемая в водогрейных котлах
(обогреваемых топочными газами) или в теплообменниках —
бойлерах, обогреваемых паром, используется для нагревания
до 130—150° С. Однако в этих условиях предпочтительнее на-
гревание водяным паром. Иногда вода под давлением, близким
к критическому (225 ат), применяется для нагревания до 300—
350° С по циркуляционному способу. Такой способ нагревания,
называемый обогревом перегретой водой, связан с использова-
нием высоких давлений, что усложняет установку и сильно огра-
ничивает возможность применения различных типов теплооб-
менных аппаратов. Как нагревающий агент вода чаще всего
употребляется в виде отбросной горячей воды, например
конденсата из выпарных аппаратов или других теплообмен-
ных устройств. Использование конденсата для нагревания
416
Гл. 12. Нагревание и охлаждение
целесообразно особенно в тех случаях, когда его по каким-либо
причинам нельзя возвращать в котельную.
Из высококипящих органических жидкостей для создания
высоких температур применяют минеральные масла (до
250 —300° С), тетрахлордифенил (до 300° С), нафталин, глице-
рин, кремнийорганические соединения и др. Наибольшее распро-
странение имеет дифенильная смесь (нагрев без давления до
255° С, под давлением до 380—400° С), которая используется для
нагревания по4циркуляционному способу, а также для заполне-
ния обогревательных бань. Коэффициент теплоотдачи для жид-
кой дифенильной смеси в условиях естественной циркуляции
составляет 200—350 вт/м2 • град.
Из других жидких нагревающих агентов для заполнения обогреватель-
ных бань применяют расплавленные соли и металлы. Расплавленные соли,
обычно тройная нитрит-нитратная смесь (40% NaNOg, 7% NaNOa,
53% KNO3), используются для нагревания в пределах от 142° С (температура
плавления смеси) до 500—530° С. Расплавленные металлы (легкоплавкие ме-
таллы — свинец, висмут, кадмий, сурьма, олово и их сплавы) применяются
для нагревания от точки их плавления до температур порядка 1000° С.
Нагревание горячими газами
Горячие топочные газы, образующиеся при сжигании топ-
лива, применяют для нагревания до сравнительно высоких тем-
ператур (от 400 до 700—1000° С).
Схема обогрева топочными газами показана на рис. 12-4. То-
почные газы получаются в топке 1, в которой сжигается топливо
Воздух для
раздавления
Воздух для
горения г———
Топливо \ |
/ 2
Рис. 12-4. Схема обогрева топочными га-
зами:
/ — топка; 2—камера смешения; 3 —обогреваемый
аппарат; 4 — дымосос.
и куда подается необхо-
димый для горения воз-
дух. Из топки газы посту-
пают в камеру смешения
2, в которую подается воз-
дух для разбавления га-
зов и снижения их темпе-
ратуры. Регулированием
подачи воздуха в камеру
смешения устанавливает-
ся необходимая темпера-
тура газов перед обогре-
ваемым аппаратом. Прой-
дя обогреваемый аппарат 3, где они, охлаждаясь, отдают тепло,
газы отсасываются дымососом 4 и выбрасываются в атмосферу.
Недостатками этого способа обогрева являются: 1) низкий
коэффициент теплоотдачи; 2) малая объемная удельная тепло-
емкость газов (~ 1500 дж/м3-град), что вызывает необходи-
мость пропускания значительных объемов газа; 3) неравномер-
2. Способы нагревания и охлаждения
417
ный обогрев, так как отдача тепла газами связана с их охла-
ждением; 4) трудность регулирования обогрева; 5) загрязнение
нагреваемого вещества (при передаче тепла непосредственным
соприкосновением).
Вследствие большого объема и высокой температуры газов
транспортирование их затруднительно и сопряжено с потерями
тепла; поэтому топки для получения топочных газов распола-
гают в непосредственной близости от обогреваемого аппарата.'
Кроме топочных газов, полученных в специальной топке, ча-
сто используют отработанные газы (от печей, котлов и т. д.) с
температурой 300—500° С. Так как при применении отработан-
ных газов не требуется дополнительного расхода топлива, ис-
пользование их для нагревания весьма рационально даже в том
случае, если газы приходится транспортировать на некоторое
расстояние.
При расчете обогрева топочными газами определяют теплотворную спо-
собность топлива, расход воздуха на сжигание, количество и состав газо-
образных продуктов сгорания, а также температуру, развиваемую при сго-
рании топлива.
Теплотворная способность топлива. Теплотворную способность топлива
можно определить как опытным путем, так и расчетом. Для расчета низшей
теплотворной способности твердого и жидкого топлива пользуются формулой
Менделеева:
QH = [339С +-1030Н—109(0 —S) —25,117]. IO’ дж/кг (12-1)
где С, Н, О, S и 17 — содержание в топливе углерода, водорода, кислорода,
серы и влаги, вес. %.
Для газообразного топлива низшая теплотворная способность 1 м3 топ-
лива (здесь и далее расчеты ведутся на 1 м3 газообразного топлива, воздуха
и топочных газов, приведенных к нормальным условиям):
QH = [127СО + 108Н2 + 360СН4 + 598С2Н4 -}- 147H2S] • 103 дж/м3 (12-2)
где СО, Нг, СН4, С2Н4, H2S — содержание соответствующих химических со-
единений в топливе, объемы. %.
Расход воздуха на сжигание топлива. Теоретическим расходом воздуха
называется количество воздуха, необходимое для полного сгорания 1 кг топ-
лива, т. е. для сгорания содержащегося в топливе углерода, водорода и серы
соответственно в СОг, НгО и SO2.
Теоретический расход воздуха подсчитывается по уравнениям реакций
сгорания и для твердого и жидкого топлива составляет:
70 = 0.089С + 0.267Н + 0,033 (S — О) ж3/1 кг топлива (12-3)
Теоретический расход воздуха при сжигании газообразного топлива:
0,5(CO + H2) + 2CH4+3C2H4+l,5H2S-O2 _ 3 /1Q.
Ио =--------------------21-----------------— м /1 м топлива (12-4)
Для обеспечения полного сгорания воздух подается в избытке и действи-
тельный расход воздуха составляет:
где а — коэффициент избытка воздуха.
27 Зак. 546.
418
Гл. 12. Нагревание и охлаждение
Количество и состав топочных газов, В топочные газы переходят про-
дукты сгорания составных частей топлива (СО2, Н2О, SO2), весь содержа-
щийся в воздухе и топливе азот, поступающий с избыточным воздухом кисло-
род, а также водяные пары, приходящие с воздухом и образующиеся при
испарении влаги топлива Количества компонентов топочных газов, образую-
щихся при теоретическом расходе воздуха, для твердого и жидкого топлива
(в м3!кг топлива).
Ус02 = 0.0187С; ySO2 =0,007S
=O,797o + O,OO8N
VHj0 = 0,112Н + 0,0124 W + 1,61 Vox
Количества компонентов топочных газов, образующихся при теоретиче-
ском расходе воздуха, для газообразного топлива составляют (в м3/1 м3 топ-
лива):
УСО2 = 0,01 (СО2 + СО 4- СН4 -Н 2С2Н4)
VSO1 = 0,01H2S; VN1 = 0,791/(3 0,01N2
*Чо = О'01 (Н2 + 2СН4 + 2С2Н4 + H2S) + >'61 V+
где х— влarocoдержание воздуха, т. е. количество водяных паров в кг, при-
ходящееся на 1 кг поступающего сухого воздуха (стр. 737);
d — содержание водяных паров в газообразном топливе, кг/м3 сухого газа.
Общий объем топочных газов при сжигании топлива с избытком воз-
духа а равен сумме объемов соединений, получающихся при сгорании топ-
лива (при теоретическом расходе воздуха), плюс избыточное количество воз-
духа, составляющее (а—1) Vo. Таким образом, объем топочных газов на
1 кг или 1 jh3 топлива составит:
^топ. = ^СО2 + ^SO2 + ^N2 + ^Н2О + (“ — 0 м3 (12-5)
Энтальпия топочных газов, получаемых при сгорании топлива с избыт-
ком воздуха а, слагается из энтальпии продуктов сгорания при теоретиче-
ском расходе SVcT и энтальпии избыточного воздуха:
ZTon. = [2lZc+ (“-!) Vb] Т (12-6)
где Т — температура топочных газов:
SVc = (VcOj-f- VSOj) сСо2+ ^n2cn2 + 7Н2ОСН2О
Здесь cCOj, cn2> сН2О и св — средние удельные теплоемкости в пределах
температур 0 — Т° С 1 м3 СО2, N2, водяных паров и влажного воздуха, выра-
женные в дж!м3 • град
Тепловой баланс топки. На единицу количества топлива (1 кг или 1 м3)
в топку поступает тепло: 1) с топливом QT = Мт! 2) с воздухом — «VocB^B;
3) выделяется при сгорании QH (низшая теплотворная способность).
Здесь ст и /т— удельная теплоемкость и температура топлива, а св и /в —
удельная теплоемкость и температура поступающего воздуха.
Уходит из топки тепло- 1) с топочными газами /Топ.; 2) теряется в окру-
жающую среду, а также от неполноты сгорания (?пот.-
2. Способы нагревания и охлаждения
419
Уравнение теплового баланса топки:
QT 4" Qb + Qh — Aon + *?пот.
о — от
— Н V ПОТ. гл /Л т
Введем к. п. д. топки % =---------- и подставим значения QT, QB и /топ;
УН
V?» + СЛ + «VQcBtB = [ZKc +(« -1) VocJ Т (12-7)
К п. д. топки = 0,85 — 0,95.
Решая уравнение (12-7) относительно а находим избыток воздуха
в___ ^тОн Н~ ст^т (S Ус УрСв) Т (12 8)
V0(cBT-c'BtB)
необходимый для получения топочных газов с температурой Т
Расход топлива. Пусть энтальпия топочных газов на входе в обогревае-
мый аппарат и на выходе из него равна Л и /2 дж/кг топлива (для газо-
образного топлива дж/м9 топлива), тепловая нагрузка аппарата составляет
Q вт, потери в окружающую среду <2Пот нт
Тогда уравнение теплового баланса запишется в виде
B(/I-/2) = Q + Qn0T
откуда расход топлива
В — Q 4~ Qn°T.:. кг!сек (или м3]сек) (12-9)
/] — /2
Пример 12-1. Рассчитать количества продуктов сгорания подмосковного
угля марки Б (С = 29,4%; Н = 2,2%; 0 = 9,1%; N = 0,6%; S = 2,6%;
А = 23,6%; W = 32,5%)* и найти избыток воздуха для снижения температуры
топочных газов до 650° С Температура воздуха Цв = 7 8° у, влагосодержание
х = 0,0093 кг/кг Температура топлива От = _18°£ К. пГд. топки т)т = 0,9.
Решение Теплотворная способность топлива по формуле (12-1):
QH = [339 • 29,4 + 1030 - 2,2 109 (9,1 — 2,6) — 25,1 • 32,5] • 103 а
10 700 • 103 дж/кг (2560 ккал]кг)
Теоретический расход воздуха определяем по уравнению (12-3J:
VQ = 0,089 • 29,4 + 0,267 • 2,2 + 0,033 (2,6 — 9,1) s 3 м3]кг топлива
Количества продуктов сгорания при теоретическом расходе воздуха со-
ставляют на 1 кг топлива:
yCOj = 0.0187С = 0,0187 • 29,4 = 0,55 м3
ys0’2 = 0.007S = 0,007 • 2,6 == 0,018 м3
У^ = 0,79 Уо + 0.008N = 0,79 • 3 Ц- 0,008 • 0,6 = 2,37 м3
yHj0 = 0,112Н + 0,0124 W + 1,61 Уох = 0,112 - 2,2 +
+ 0,0124 • 32,5 +Д ,61 • 3 • 0,0093 = 0,694 м3
* А — содержание золы в топливе; W— влажность топлива.
27*
420
Гл. 12. Нагревание и охлаждение
Средние удельные теплоемкости с (от 0 до 650°С):
дж/мР-град ккал/м3-град
со2 2080 0,497
n2 1350 0,322
Н2О 1620 0,387
Таким образом, при 650° С
S Ус = (0,55 + 0,018) • 2080 + 2,37 • 1350 4- 0,694 • 1620 =
= 5500 дж/кг топлива (1,313 ккал/кг топлива)
Средняя удельная теплоемкость воздуха (от 0 до ГС):
при 650°С
св = 1390 дж/м3 • град (0,332 ккал/м3 • град)
при 18°С
с'в = 1320 дж/м3 • град (0,316 ккал/м3 • град)
Коэффициент избытка воздуха для снижения температуры до 650° С при
удельной теплоемкости угля ст = 1470 дж/кг’град (0,35 ккал/кг- град) вы-
числяем по формуле (12-8):
_ 0,9 • 10 700 • 103 + 1470 • 18 — (5500 — 3 • 1390) • 650
а~~ 3 (1390 • 650 — 1320 • 18) = d’34
Расход воздуха равен:
V — Уоа = 3 • 3,34 10 м3/кг топлива
Объем топочных газов находим из уравнения (12-5):
Утоп == 0,55 4- 0,018 4- 2,37 4- 0,694 4- (3,34 — 1) • 3 = 10,65 м3/кг топлива
Энтальпию топочных газов определяем по формуле (12-6):
Лоп. = [5,5 4- (3,34 — 1) • 3 • 1,39] • 103 • 650 =
= 9900 • 103 дж[кг топлива (2360 ккал)кг топлива)
Нагревание электрическим то ком
Электрическая энергия может быть использована для на-
гревания электрической дугой, нагревания сопротивлением и
диэлектрического нагревания.
Нагревание электрической дугой применяется в дуговых пе-
чах и дает возможность развивать высокие температуры (1500—
2000° С и выше). Различают печи с открытой и закрытой дугой.
В печах с открытой дугой пламя дуги образуется между элек-
тродами, расположенными над нагреваемым материалом, и
тепло передается путем лучеиспускания. В печах с закрытой
дугой пламя дуги образуется между электродом и самим нагре-
ваемым материалом. Дуговые печи не обеспечивают равномер-
ного обогрева и точного регулирования температур. Использу-
2. Способы нагревания и охлаждения
421
ются дуговые печи для плавки металлов, а также при получе-
нии карбида кальция и фосфора.
Нагревание сопротивлением производится непосредственным
пропусканием электрического тока через нагреваемое тело, либо
пропусканием тока через специальные нагревательные элементы,
от которых тепло передается нагреваемому телу путем лучеис-
пускания и конвекции. Чаще всего применяется второй способ,
который осуществляется следующим образом. Вокруг обогре-
ваемого аппарата размещают нагревательные элементы (не со-
прикасающиеся со стенками- аппарата), через которые пропу-
скается электрический ток; с наружной стороны нагревательных
элементов устраивается кожух, снабженный огнеупорной футе-
ровкой или изоляцией. Такой способ нагревания применяется
при температурах до 1000—-1100° С, дает равномерный обогрев
и обеспечивает точное регулирование температуры посредством
изменения напряжения электрического тока или путем включе-
ния и отключения части элементов.
К нагреванию сопротивлением относится нагревание индук-
ционными токами, которое производится следующим образом.
Аппарат окружают обмоткой, через которую пропускается пе-
ременный ток. При этом вокруг обмотки образуется перемен-
ное магнитное поле, индуцирующее в стенках аппарата элек-
тродвижущую силу. В результате в стенках аппарата возни-
кает электрический ток, который и прогревает их по всей тол-
щине.
Диэлектрическое нагревание, или нагревание токами высокой
частоты, основано на том, что при воздействии на диэлектрик
(непроводник электрического тока) переменного электрического
поля часть энергии затрачивается на преодоление трения между
молекулами диэлектрики и превращается в тепло; при этом ди-
электрик нагревается.
Величина диэлектрических потерь, а следовательно, и коли-
чество выделяющегося тепла, пропорциональны квадрату напря-
жения и частоте тока. Чтобы избежать высоких напряжений,
используют токи высокой частоты. Обычно применяют частоту
1 • 106— 100 • 106 гц при напряженности электрического поля
1000—2000 в/см. Для генерирования токов высокой частоты
пользуются ламповым генератором; полученные в генераторе
токи высокой частоты подводят к конденсатору, между обклад-
ками которого помещается нагреваемый материал.
Достоинствами диэлектрического нагревания являются: не-
посредственное выделение тепла в нагреваемом теле, что осо-
бенно важно для материалов с низкой теплопроводностью, к ко-
торым относится большинство диэлектриков; нагрев всей тол-
щи материала до требуемой температуры в течение короткого
422
Гл 12. Нагревание и охлаждение
промежутка времени без перегрева отдельных частей; легкое
регулирование процесса нагревания и возможность его полной
автоматизации.
Диэлектрическое нагревание применяется при прессовании
изделий из пластмасс, например из слоистых пластиков (тексто-
лит и др.), при склеивании древесины в производстве фанеры,
вулканизации каучука и др. Довольно широкое применение по-
лучило диэлектрическое нагревание в процессе сушки (стр. 799).
Охл аждение
В качестве охлаждающих агентов используют воздух и воду,
а для достижения низких температур — низкотемпературные
агенты.
Воздух применяется для естественного и искусственного
охлаждения, например, с помощью вентилятора. При естествен-
ном охлаждении нагретый теплоноситель охлаждается за счет
потерь тепла через стенки аппарата в окружающую среду. Ис-
кусственное охлаждение воздухом используется в поверхностных
или смесительных теплообменниках.
Охлаждение воздухом в поверхностных теплообменниках
применяется редко из-за низкого коэффициента теплопередачи
и значительного расхода энергии при работе вентилятора.
Смесительные теплообменники представляют собой аппараты
башенного типа, в которых охлаждаемый воздух движется снизу
вверх навстречу стекающей жидкости. При этом охлаждение
происходит не только за счет теплоотдачи, но в значительной
степени и за счет испарения части жидкости. Такие аппараты
широко используются для охлаждения воды и называются
градирнями.
Вода является наиболее распространенным охлаждающим
агентом. Ее достоинства: высокая теплоемкость, большой коэф-
фициент теплоотдачи и доступность.
Достигаемая степень охлаждения зависит от начальной тем-
пературы воды, которая в зависимости от местных условий и
времени года колеблется от 4 до 25° С. Мало изменяющуюся
в течение года температуру (8—15° С) имеет подземная (арте-
зианская) вода. Часто для охлаждения пользуются оборотной
водой, т. е. водой, охлажденной в градирне. В этом случае на-
гретая в теплообменном аппарате вода поступает на охлаждение
в градирню, после чего возвращается на охлаждение теплооб-
менного аппарата. При пользовании оборотной водой свежая
вода расходуется только на пополнение ее потерь вследствие
частичного испарения в градирне. Оборотная вода имеет высо-
кую температуру, достигающую летом 30° С.
3. Устройство теплообменных аппаратов
423
Охлаждение водой производят иногда путем непосредствен-
ного соприкосновения ее с охлаждаемым теплоносителем (на-
пример, охлаждают газы разбрызгиванием в них воды, см.
стр. 465), но чаще пользуются поверхностными теплообменни-
ками. Конечную температуру воды, во избежание выделения
растворенных в ней солей и образования накипи, принимают
обычно не выше 40—50° С.
Если температура охлаждаемой среды выше 100° С, приме-
няют испарительное охлаждение, при котором часть воды ис-
паряется. В этом случае расход воды резко снижается, а обра-
зующийся пар утилизируется.
Н изкотемпературные агенты используют для создания темпе-
ратур ниже 5—20° С, обычно не достижимых при охлаждении
водой. В качестве таких агентов применяют лед, охлаждающие
смеси (смеси льда с различными солями), холодильные рассолы
(растворы СаС12, NaCl и др.) и пары жидкостей, кипящих при
низких температурах. При охлаждении холодильными рассо-
лами и парами низкокипящих жидкостей пользуются холодиль-
ными установками, которые подробно рассмотрены в главе 15.
3. Устройство теплообменных аппаратов
По способу передачи тепла различают следующие типы теп«
лообменных аппаратов:
1) поверхностные, в которых оба теплоносителя разделены
стенкой, причем тепло передается через поверхность этой стенки;
2) регенеративные, в которых процесс передачи тепла от
горячего теплоносителя к холодному разделяется по времени на
два периода и происходит при попеременном нагревании и
охлаждении насадки т&члообменника;
3) смесительные, в которых теплообмен происходит при не-
посредственном соприкосновении теплоносителей.
Основные типы поверхностных теплообменных аппаратов
приведены на стр. 424.
В зависимости от агрегатного состояния теплоносителей раз-
личают аппараты для теплообмена:
1) между газами (подогреватели газов топочными газами,
газовые теплообменники и др.);
2) между паром и газом (паровые подогреватели для воз-
духа, пароперегреватели и др.);
3) между газом и жидкостью (холодильники для газов);
4) между паром и жидкостью (паровые подогреватели, кон-
денсаторы и др.);
5) между жидкостями (жидкостные холодильники, теплооб-
менники и др.)я
124
Гл 12 Нагревание и охлаждение
Спиральные
С поверхностью, образо-
ванной стенками аппарата
С оребренной поверх-
ностью теплообмена
Трубчатые теплообменники
Кожухотрубные теплообменники. Этот тип теплообменников
является одним из наиболее распространенных. Кожухотрубные
теплообменники состоят из пучка труб, концы которых закреп-
лены в специальных трубных решетках путем развальцовки,
сварки, пайки, а иногда на сальниках. Пучок труб расположен
внутри общего кожуха, причем один из теплоносителей (/) дви-
жется по трубам, а другой (//) — в пространстве между кожу-
хом и трубами (межтрубное пространство). На рис. 12-5, а
показан одноходовой теплообменник, в котором теплоноситель
движется параллельно по всем трубам. Многоходовые теплооб-
менники (рис. 12-5,6), работающие при смешанном токе
теплоносителей (стр. 442), применяют для повышения скорости
их движения в трубах.
На рис. 12-5,в показан теплообменник пленочного типа (вер-
тикально-оросительный), в котором жидкий теплоноситель не
заполняет всего сечения труб, а стекает пленкой по внутренней
3 Устройство теплообменных аппаратов
425
поверхности вертикальных труб. Жидкость направляется к стен-
кам труб специальными устройствами.
По конструкции различают теплообменники с неподвижными
трубными решетками, в которых обе решетки жестко прикреп-
лены к корпусу и трубы не могут свободно удлиняться (см.
рис. 12-5), и теплообменники с компенсирующими устройствами
(рис. 12-6), в которых трубы могут свободно удлиняться.
Рис. 12-5. Кожухотрубные теплообменники с неподвижными трубными
s решетками:
а — одноходовой; б— многоходовой, в —пленочный. 1 — кожух; 2 — трубная решетка;
3 — трубы; 4~ входная камера; 5 — выходная камера; 6 — продольная перегородка;
7—камера, 8 — перегородки в камерах.
В теплообменниках с неподвижными трубными решетками
при различном тепловом удлинении труб и кожуха возникают
температурные напряжения; поэтому такие теплообменники при-
меняют при небольшой (до 50° С) разности температур между
трубами и кожухом.
Компенсация неодинакового удлинения труб и кожуха до-
стигается установкой линзового компенсатора (рис. 12-6, а),
устройством подвижной трубной решетки (рис. 12-6,6, в и г),
применением U-образных труб (рис. 12-6, д), а такл^е закрепле-
нием труб в решетках на сальниках.
Теплообменники с подвижной решеткой имеют одну труб-
ную решетку, закрепленную в кожухе; вторая решетка подвижна
и может перемещаться внутри аппарата. В этих теплообменни-
426
Гл 12. Нагревание и охлаждение
Рис. 12-6. Кожухотрубные теплообменники с компенсирующими устройствами:
а —с линзовым компенсатором; б —с плавающей головкой закрытого типа, в —с плавающей
головкой открытого типа, г —с сальниковым компенсатором, д — с U-образными трубами,
/—кожух; 2 —линзовый компенсатор; 3-плавающая головка; 4 — сальник, 5 — U-образные
трубы.
3. Устройство теплообменных аппаратов
427
ках пучок труб можно вынуть из кожуха для осмотра и чистки
межтрубного пространства.
Теплообменники с U-образными трубами (рис. 12-6, д) яв-
ляются двухходовыми и имеют лишь одну трубную решетку; пу-
чок труб может быть вынут из кожуха, но очистка труб изнутри
затруднительна.
Рассмотренные теплообменники могут устанавливаться вер-
тикально или горизонтально, за исключением теплообменников
пленочного типа (рис. 12-5, в) и с
плавающей головкой открытого ти-
па (рис. 12-6, в), которые устанав-
ливаются вертикально.
Для повышения скорости дви-
жения теплоносителя в межтруб-
ном пространстве устраивают про-
дольные и поперечные перегородки.
Продольные пере? уродки приме-
няются в многоходовых теплообмен-
никах для разделения межтруб-
ного пространства на ходы (рис.
12-5,6).
Поперечные перегородки исполь-
зуются как в одноходовых, так и
в многоходовых теплообменниках.
Они бывают следующих видов:
а) сегментные перегородки
(рис. 12-7,/), представляющие со-
бой диски с вырезанными в виде
Рис. 12-7. Устройство попереч-
ных перегородок:
/ — сегментные перегородки; // — че-
редующиеся кольца и диски.
сегмента отверстиями;
б) перегородки в виде чередующихся колец и дисков
(рис. 12-7, //);
в) перегородки в виде сплошных дисков, перекрывающих
все сечение кожуха. В перегородках сделаны отверстия с диа-
метром на 1,5—2 мм больше, чем наружный диаметр труб. Эти
отверстия образуют кольцевые щели вокруг каждой трубы.
Увеличение скорости движения теплоносителя может быть
достигнуто и в элементных (батарейных) теплообменниках,
представляющих собой батарею из нескольких последовательно
соединенных друг с другом теплообменников.
Достоинства кожухотрубных теплообменников: 1) компакт-
ность; 2) небольшой расход металла; 3) легкость очистки труб
изнутри (за исключением теплообменников с U-образными тру-
бами).
Недостатками таких теплообменников являются: 1) трудность
пропускания теплоносителей с большими скоростями (этот
428
Гл. 12. Нагревание и охлаждение
недостаток в известной мере устраняется в многоходовых и эле-
ментных теплообменниках); 2) трудность очистки межтрубного
пространства и малая доступность его для осмотра и ремонта;
3) трудность изготовления из материалов, не допускающих раз-
вальцовки и сварки (чугун, ферросилид и др.).
Трубы в кожухотрубных теплообменниках обычно размещают по пери-
метрам правильных шестиугольников (рис. 12-8,/). Количество труб в каж-
дом шестиугольнике равно его порядковому номеру (считая от центра
аппарата), умноженному на 6. Таким образом, при а шестиуголь-
никах теоретическое количе-
ство труб с учетом центральной
трубы
д =14-6(1+24-3+... 4-а)«
=1+б1+£ а = 1 + за 4_ заг
Число труб по диагонали
шест угольника составляет b —
= 2g + 1.
Фактическое количество
труб может отличаться от тео-
ретического, так как трубы
Рис. 12-8. Способы разбивки труб:
I — по периметрам шестиугольников; II — по концен
трнческим окружностям.
размещают также в шести сег-
ментах между окружностью
и сторонами шестиугольника.
При стандартном диаметре ап-
парата не всегда можно раз-
местить теоретическое количество труб и приходится отказываться от уста-
новки крайних труб В многоходовых теплообменниках количество труб
уменьшают для размещения перегородок между ходами Фактическое коли-
чество труб находят вычерчиванием в масштабе их размещения Согласно
нормалям НИИХиммаша, в кожухотрубных теплообменниках количество
труб (наружный диаметр + = 25 мм, шаг t = 32 мм) составляет:
Наружный диаметр
кожуха1? мм
159...........
273 ..........
325 ..........
Количество труб при числе ходов
12 4 6
13 — — —
42 — — —
61 52 52 60
Нормализованные размеры других кожухотрубных теплообменников при-
ведены в табл. 14.
Иногда трубы размещают по концентрическим окружностям (рис. 12-8,//),
расположенным на расстоянии друг от друга, равном шагу труб t.
Шаг t разбивки труб (расстояние между осями соседних труб) прини-
мают 1,25—1,3 от наружного диаметра труб; при необходимости очистки
межтрубного пространства шаг может быть увеличен.
В многоходовых теплообменниках общее количество труб разбивают по
отдельным ходам так, чтобы в каждом ходе было одинаковое количество
труб. Для направления теплоносителя по ходам в камерах устраивают пере-
городки (рис 12-9,/—V/). Сплошными линиями показаны перегородки в пе-
редней камере (со стороны входа теплоносителя в трубное пространство),
3. Устройство теплообменных аппаратов
429
а пунктиром — в задней камере. Цифры обозначают последовательность хо-
дов: по нечетным ходам теплоноситель движется от передней камеры к зад-
ней, а по четным — от задней к передней.
Таблица 14
Нормализованные размеры кожухотрубных теплообменников
(dH — наружный диаметр труб, мм\ t — шаг труб, мм)
Вну- трен- ний диа- метр кожуха, мм dH=25, < = 32 Дн==38, < = 48 Дн = 57, < = 70
Количество труб при числе ходов
1 2 4 6 1 2 4 6 1
400 600 800 1000 1200 1400 121 283 511 823 1189 1639 110(80) 266 (186) 488 (392) 792 1152 1596 100 (76) 260 (176) 480(376) 788 1136 1572 • 102 258 486 768 1152 1596 121 211 361 511 703 ПО 196 342 488 676 104 204 336 484 688 114 204 336 510 684 97 163 241 317
Примечание. В скобках указаны количества труб для теплообменников с плаваю-
щей головкой при разбивке труб по квадратам. Длины труб (в м) выбираются из ряда: 1; 1,5,
2; 2,5; 3; 3,5; 4, 4,5; 5; 6
Рис. 12-9. Разбивка труб по ходам.
430
Гл. 12. Нагревание и охлаждение
Рис. 12-10. Теплообменник типа «труба
в трубе”:
/ — наружная труба; 2 —внутренняя труба; 3— калач.
«
а теплообменников
Теплообменники «труба в трубе». Теплообменники «труба
в трубе» (рис. 12-10) включают несколько расположенных друг
над другом элементов, причем каждый элемент состоит из двух
труб: наружной трубы 1 большего диаметра и концентрически
расположенной внутри нее трубы 2. Внутренние трубы элемен-
тов соединены друг с другом последовательно; так же связаны
между собой и наружные
трубы. Для возможности
очистки внутренние трубы
соединяют при помощи
съемных калачей 3.
Благодаря небольшо-
му поперечному сечению
в этих теплообменниках
легко достигаются высо-
кие скорости теплоноси-
телей как в трубах, так и
в межтрубном простран-
стве. При значительных
количествах теплоносите-
лей теплообменник со-
ставляют из нескольких
параллельных секций,
присоединяемых к общим
коллекторам.
труба в трубе»: 1) высо-
кий коэффициент теплопередачи вследствие большой скорости
обоих теплоносителей; 2) простота изготовления.
Недостатки этих теплообменников: 1) громоздкость; 2) высо-
кая стоимость ввиду большого расхода металла на наружные
трубы, не участвующие в теплообмене; 3) трудность очистки
межтрубного пространства.
Оросительные теплообменники. Оросительные теплообмен-
ники состоят из змеевиков, орошаемых снаружи жидким теп-
лоносителем (обычно водой), и применяются главным образом
в качестве холодильников. Змеевики выполняют из прямых го-
ризонтальных труб 3 (рис. 12-11), расположенных друг над
другом и последовательно соединенных между собой сваркой
или на фланцах при помощи калачей 2. Орошающая вода по-
дается на верхнюю трубу, стекает с нее на нижележащую трубу
и, пройдя последовательно по поверхности всех труб, стекает в
поддон 4, расположенный под холодильником.
Вода, орошающая трубы, частично испаряется (обычно испа^
ряется 1—2% от общего количества поступающей воды). При
этом часть отнимаемого от горячего теплоносителя тепла затра-
3. Устройство теплообменных аппаратов
431
чивается на испарение воды, расход которой в оросительных
холодильниках ниже, чем в холодильниках других типов.
Рис. 12-11. Оросительный теплообменник: &м?а
/—желоб для подачи воды; 2 — калач; 3 —труба; 4 — поддон.
Вследствие сильного испарения орошающей воды ороси-
тельные холодильники обычно устанавливают на открытом воз-
духе, снабжая их ограждением
в виде жалюзи во избежание
уноса воды ветром.
Достоинства оросительных
теплообменников: 1) понижен-
ный расход охлаждающей во-
ды; 2) простота устройства и
дешевизна; 3) легкость осмотра
и наружной очистки труб (при
соединении труб на фланцах
очистку нетрудно производить
и внутри).
Недостатки этих теплообмен-
ников: 1) громоздкость, 2) силь-
ное испарение воды, 3) чувстви-
тельность к колебаниям пода-
чи воды; при недостатке воды
нижние трубы не смачиваются
и почти не участвуют в теплооб-
мене.
Погружные теплообменники.
Рис. 12-12. Погружной теплообмен-
ник с цилиндрическими змеевиками:
1 — змеевик; 2 — сосуд.
Погружные теплообменники
состоят из змеевиков, помещенных в сосуд с жидким теплоно-
432
Гл. 12. Нагревание и охлаждение
сителем. Другой теплоноситель движется внутри змеевиков.
При большом количестве этого теплоносителя для сообщения
ему необходимой скорости применяют змеевики из нескольких
параллельных секций.
На рис. 12-12 показан погружной теплообменник, состоящий
из цилиндрических змеевиков 1, установленных в круглом со-
суде 2. Змеевик выполнен из концентрически расположенных
параллельных секций.
Преимущества погружных теплообменников: 1) простота из-
готовления; 2) доступность поверхности теплообмена для осмот-
ра и ремонта; 3) малая чувствительность к изменениям режима
вследствие наличия большого объема жидкости в сосуде.
Недостатки: 1) громоздкость; 2) неупорядоченное движение
Рис. 12-13. Пластинчатый тепло-
обменник.
(незначительная скорость)
жидкости в сосуде, в результа-
те чего теплоотдача снаружи
змеевиков происходит путем
свободной конвекции с невысо-
ким коэффициентом теплоотда-
чи; 3) трудность внутренней
очистки труб.
Пластинчатые
теплообменники
Пластинчатые теплообмен-
ники (рис. 12-13) имеют пло-
ские поверхности теплообмена.
Обычно такие теплообменники
. состоят из ряда параллельных
пластин, изготовленных из тонких металлических листов. Ка-
налы между пластинами сгруппированы в две системы: по од-
ной системе каналов движется горячий теплоноситель, по дру-
гой — холодный. Эти теплообменники весьма компактны, что
обеспечивает (при соответствующем выборе расстояний между
пластинами) пропускание обоих теплоносителей с значитель-
ными скоростями и приводит к достижению высоких коэффи-
циентов теплопередачи.
Будучи ограничены плоскими стенками, пластинчатые тепло-
обменники не выдерживают сколько-нибудь значительных да-
влений; кроме того, в этих теплообменниках трудно обеспечить
достаточную герметичность для предотвращения смешения теп-
лоносителей.
3. Устройство теплообменных аппаратов
433
Такие теплообменники используются для теплообмена между
газами при атмосферном давлении (главным образом для подо-
грева воздуха топочными газами). В последнее время теплооб-
менники подобного типа применяют для теплообмена между
газами в установках глубокого охлаждения (стр. 545).
Для теплообмена между жидкостями используют пластинча-
тые теплообменники фильтрпрессного типа. Они состоят из си-
стемы плит, похожих на плиты фильтрпрессов (стр. 259). По
каналам между плитами жидкости протекают так, что каждая
плита с одной стороны омывается первой жидкостью, а с дру-
гой стороны — второй жидкостью. Эти теплообменники рабо-
тают при избыточных давлениях до 10 ат, имеют высокий коэф-
фициент теплопередачи, отличаются большой компактностью,
легко поддаются разборке и чистке. Недостатком их является
большое число прокладочных соединений между плитами.
Спиральные теплообменники
Спиральные теплообменники (рис. 12-14) состоят из двух
спиральных каналов прямоугольного сечения, по которым дви-
жутся теплоносители I и II. Каналы образуются тонкими ме-
Рис. 12-14. Горизонтальный спиральный теплообменнике
1, 2 — листы; 3— разделительная перегородка; 4— крышки.
таллическими листами 1 и 2, которые служат поверхностью теп-
лообмена. Внутренние концы спиралей соединены разделитель-
ной перегородкой 3. Для придания спиралям жесткости и фи-
ксирования расстояния между ними служат прокладки. Система
каналов закрыта с торцов крышками <
434
Гл. 12. Нагревание и охлаждение
Горизонтальный спиральный теплообменник, показанный на
рис. 12-14, применяют для теплообмена между двумя жидко-
стями. Для теплообмена между конденсирующимся паром и
жидкостью используют вертикальные спиральные теплообмен-
ники (рис. 12-15); такие теплообменники применяют в качестве
Лар
I
£ис. 12-15. Вертикальный спи-
ральный теплообменник.
конденсаторов и паровых подогре-
вателей для жидкостей.
Преимущества спиральных теп-
лообменников: 1) компактность;
2) возможность пропускания обоих
теплоносителей с высокими скоро-
стями, что обеспечивает большой
коэффициент теплопередачи; 3) при
тех же скоростях гидравлическое
сопротивление спиральных теплооб-
менников меньше сопротивления
многоходовых кожухотрубных теп-
лообменников.
Недостатки: 1) сложность изго-
товления (требуется специальный
намоточный станок) и ремонта,
2) пригодность для работы под из-
быточным давлением не свыше 6 ат
(в отдельных случаях до 10 ат).
Нормалями предусмотрены спиральные теплообменники с поверхностью
теплообмена 15 м2 (ширина спирали 375 мм) и 30 м2 (ширина спирали
750 мм); ширина спирального канала 7 мм.
Теплообменники с поверхностью теплообмена,
образованной стенками аппарата
Для обогрева и охлаждения реакционных и других аппара-
тов часто осуществляют передачу тепла непосредственно через
их стенки, которые и служат поверхностью теплообмена. Приме-
нение этих аппаратов ограничено небольшой поверхностью теп-
лообмена (до 10 м2). Для повышения коэффициента теплоот-
дачи со стороны находящегося в аппарате жидкого теплоноси-
теля обычно перемешивают его с помощью мешалки.
Аппарат с рубашкой (рис. 12-16, а) является простейшим
представителем этой группы. Рубашка 2 крепится к корпусу 1
(путем приварки) или к фланцу аппарата (на болтах). По за-
мкнутому пространству между рубашкой и наружной поверх-
ностью корпуса пропускается нагревающий или охлаждающий
агент. Применение таких рубашек ограничено допустимыми из-
быточными давлениями, не превышающими 6—10 ат.
3 Устройство теплообменных аппаратов
435
Для избыточных давлений до 75 ат рубашку изготовляют из
листов с большим количеством выштампованных отверстий, при-
Ло Аб
Рис. 12-16. Аппараты с рубашками.
а —для низких давлений; б—для высоких давлений, / — корпус аппарата; 2 —рубашка.
чем кромки листов по периметру отверстий приваривают к кор-
пусу аппарата (рис. 12-16,6).
Аппараты с залитыми в стенки змеевиками (рис. 12-17, а) изготавливают
из чугуна, в стенки аппарата
Рис. 12-17. Устройство обо-
гревающих стенок:
а —аппарат с залитыми в стенки
змеевиками, б— аппарат с прива-
ренными снаружи змеевиками.
при отливке заливается стальной змеевик, по
которому пропускается нагревающий агент
с избыточным давлением до 250 ат Избыточ-
ное давление в аппарате не должно превы-
шать 6 ат Такие аппараты используются глав-
ным образом при обогреве перегретой водой.
Вследствие различного коэффициента удлине-
ния чугуна и стали достижение плотного со-
единения змеевиков с чугунной стенкой за-
труднительно, поэтому коэффициент теплопе-
редачи в этих аппаратах невысок.
Аппараты с приваренными снаружи зме-
евиками (рис 12-17,6) имеют стальные
змеевики, изогнутые в форме спирали или
состоящие из труб, расположенных по обра-
зующим цилиндрической поверхности аппа-
рата.
Теплообменники с оребренными поверхностями
теплообмена
Если коэффициент теплоотдачи для одного из теплоноси-
телей значительно ниже, чем для второго, то поверхность тепло-
обмена со стороны теплоносителя с низким а целесообразно уве-
личить по сравнению с поверхностью теплообмена со стороны
28*
436
Гл 12 Нагревание и охлаждение
другого теплоносителя. Это достигается в теплообменниках с
оребренными поверхностями теплообмена В таких аппаратах
поверхность теплообмена имеет на одной стороне различной
формы ребра. В трубчатых теплообменниках обычно использу-
ются поперечные или продольные ребра.
Поперечные ребра выполняют в виде круглых или прямо-
угольных металлических шайб, насаженных на трубу. Такое
оребрение широко применяется в пластинчатых калориферах,
Рис. 12-18. Пластинчатый калорифер:
1 — коробка, 2 —ребра.
показанных на рис. 12-18. Калориферы состоят из пучка ореб-
ренных труб, закрепленных в коробках 1. Применяют калори-
феры для подогрева воздуха, движущегося с наружной сто-
роны труб, паром или горячей водой, которые пропускаются по
трубам.
Продольные ребра используются обычно при движении теп-
лоносителя вдоль трубы и применяются для наружного оребре-
ния труб в теплообменниках с U-образными трубами и в теп-
лообменниках типа «труба в трубе» Трубы с продольными
ребрами изображены на рис. 12-19, а. Продольные ребра
плавникового типа (рис. 12-19,6) используются при движе-
нии теплоносителя в поперечном направлении относительно
труб.
3 Устройство теплообменных аппаратов
437
Рис. 12-19. Оребренные поверхности теплообмена:
а — тоуба с продольными ребрами, б —ребра плавникового типа, в-игольчатый теплообмен-
р J ник, г — пластинчато ребристый теплообменник.
438
Гл. 12. Нагревание и охлаждение
Иногда трубы оребряют с обеих сторон; в этом случае ребра
выполняют обычно в виде игл (игольчатые теплообменники), как
показано на рис. 12-19, в.
При оребрении пластинчатых теплообменников получаются
так называемые пластинчато-ребристые теплообменники, один
из типов которых показан на рис. 12-19, г.
4. Сравнение и выбор теплообменных аппаратов
Для достижения высоких коэффициентов теплопередачи теп-
лоносители следует пропускать через аппарат с большими ско-
ростями; однако при этом возрастает гидравлическое сопротив-
ление. Кроме того, для получения высокого коэффициента теп-
лопередачи поверхность теплообмена должна быть свободна от
загрязнений, а для удаления образующихся загрязнений она
должна быть доступна для очистки. При увеличении скорости
одного из теплоносителей коэффициент теплопередачи заметно
повышается лишь в том случае, если коэффициент теплоотдачи
со стороны другого теплоносителя достаточно высок, а тепло-
вое сопротивление стенки и загрязнений невелико. Так, если ко-
эффициент теплоотдачи в межтрубном пространстве значительно
ниже, чем в трубах (например, в межтрубном пространстве про-
ходит газ, а по трубам жидкость), то возрастание скорости в
трубах почти не влияет на величину коэффициента теплопере-
дачи; в этом случае следует увеличить коэффициент теплоот-
дачи в межтрубном пространстве, например, путем установки
в нем перегородок.
Для решения вопроса о том, какой из теплоносителей пропу-
скать по трубам и какой — с наружной стороны труб, надо
придерживаться следующих правил:
1) теплоноситель, из которого выделяются осадки, рекомен-
дуется пропускать с той стороны поверхности теплообмена,
с которой легче производить очистку;
2) для достижения большего коэффициента теплопередачи
теплоноситель с меньшим коэффициентом теплоотдачи следует
пропускать по трубам;
3) теплоноситель, оказывающий коррозионное действие на
аппаратуру, целесообразно пропускать по трубам, так как в
этом случае применение антикоррозийного материала необходи-
мо только для труб, решеток и камер; кожух же может быть
сделан из обычного материала;
4) для уменьшения потерь тепла теплоноситель с высокой
температурой целесообразно пропускать по трубам; в холо-
дильниках потери тепла уменьшают расход охлаждающего
5. Эксплуатация теплообменных аппаратов
439
агента, поэтому горячий теплоноситель следует пропускать с
наружной стороны труб;
5) теплоноситель с высоким давлением необходимо пропу-
скать по трубам, чтобы корпус не находился под давлением.
Кожухотрубные одноходовые теплообменники применяются при большом
объеме пропускаемого по трубам теплоносителя (например, в качестве газо-
вых теплообменников и при теплообмене между газом и жидкостью),
а также в качестве конденсаторов паров органических жидкостей. Использо-
вание их в других случаях обычно приводит к низкому коэффициенту тепло-
передачи.
Вертикально-оросительные теплообменники применяются главным обра-
зом как конденсаторы (пар движется в межтрубном пространстве, вода
стекает пленкой по трубам).
Кожухотрубные многоходовые и элементные теплообменники используются
в качестве жидкостных теплообменников и при теплообмене между конден-
сирующимся паром и жидкостью (конденсаторы пара, подогреватели жид-
кости). В последнем случае жидкость пропускается по трубам, а пар —
в межтрубном пространстве.
Теплообменники «труба в трубе» применяются при небольших количе-
ствах теплоносителя для теплообмена между двумя жидкостями, между
жидкостью и конденсирующимся паром, а также в качестве холодильников
для газов при высоких, давлениях.
Оросительные теплообменники используются как холодильники, в част-
ности для теплоносителей, оказывающих коррозионное действие на аппара-
туру и конденсаторы.
Погружные теплообменники применяются в качестве холодильников для
газов при высоких давлениях и для жидкостей, а также как конденсаторы и
подогреватели для жидкостей
Пластинчатые теплообменники используются длй теплообмена между
газами при низком давлении.
Пластинчатые теплообменники фильтрпрессного типа и спиральные тепло-
обменники при избыточных давлениях до 6—10 ат в ряде случаев предпочти-
тельнее аппаратов других типов при теплообмене между жидкостями, а спи-
ральные теплообменники — также при теплообмене между жидкостью и кон-
денсирующимся паром.
Теплообменники с оребренной поверхностью применяются главным обра-
зом для теплообмена между газом и жидкостью или паром, а также между
двумя газами. В некоторых случаях они используются в качестве жидкост-
ных теплообменников.
5. Эксплуатация теплообменных аппаратов
Эксплуатация теплообменных аппаратов заключается в регулировании
температуры и очистке их от загрязнений.
Регулирование режима работы теплообменных аппаратов. Регулирование
производится с целью поддержания необходимого температурного режима и
осуществляется путем изменения количества подаваемого агента (нагреваю-
щего или охлаждающего). Так, в подогревателях поддерживают требуемую
конечную температуру холодного теплоносителя регулированием подачи на-
гревающего агента.
Если нагревающим агентом служит водяной пар, то, прикрывая паровой
вентиль и уменьшая этим подачу пара, мы отнимаем от каждого килограмма
пара большее количество тепла, т. е. заставляем конденсат переохлаждаться.
Понижение температуры выхода конденсата приводит к уменьшению сред-
440
Г л. 12 Нагревание и охлаждение
него температурного напора в зоне переохлаждения и, следовательно,
к уменьшению количества тепла, сообщаемого холодному теплоносителю,
вследствие чего его конечная температура понижается. Для повышения ко-
нечной температуры холодного теплоносителя необходимо увеличить откры-
тие парового вентиля; тогда температура выхода конденсата будет возра-
стать. Повышение конечной температуры холодного теплоносителя и темпе-
ратуры выхода конденсата будет происходить до тех пор, пока последняя
не станет равной температуре насыщения пара. Дальнейшее открывание па-
рового вентиля бесполезно, так как, несмотря на увеличение подачи пара,
температурный напор останется без изменения и количество тепла, сооб-
щаемого холодному теплоносителю, не будет увеличиваться.
В холодильниках конечную температуру горячего теплоносителя поддер-
живают регулированием подачи воды (или другого охлаждающего агента):
с увеличением подачи воды ее конечная температура будет уменьшаться,
а средний температурный напор — увеличиваться, что вызовет повышение
количества тепла, отнимаемого от горячего теплоносителя, и понижение его
конечной температуры.
Если количества обоих теплоносителей являются определенными (на-
пример, в собственно теплообменниках), то регулирование температуры про-
изводится пропусканием части одного из теплоносителей по обводной линии
(минуя теплообменник).
Очистка теплообменных аппаратов. При использовании теплоносителей,
выделяющих осадки и оказывающих коррозионное действие на аппаратуру,
поверхность теплообмена покрывается слоем загрязнений, обладающих низ-
кой теплопроводностью, что снижает коэффициент теплопередачи. Очистку
аппаратов от загрязнений производят периодически. Продолжительность ра-
боты между очистками зависит от допускаемой степени загрязнения и от
скорости загрязнения поверхности теплообмена и может колебаться от не-
скольких дней до нескольких месяцев (и более).
Очистка аппаратов производится либо вручную, либо механическими
или химическими способами.
6. Расчет теплообменных аппаратов
При расчете определяют необходимую поверхность теплооб-
мена, расход нагревающих или охлаждающих агентов, кон-
структивные размеры и гидравлическое сопротивление теплооб-
менных аппаратов.
Определение тепловой нагрузки и расхода
нагревающих или охлаждающих агентов
Для определения расхода нагревающих или охлаждающих
агентов пользуются приведенным на стр. 365 уравнением тепло-
вого баланса: Qrop. = Qxon.- Если аппарат предназначен для‘на-
гревания, то тепловую нагрузку определяют по уравнению
(11-5), а расход нагревающего агента — по уравнению (11-4).
Если нагревающим агентом является пар, то его расход (при
условии, что пар поступает насыщенным, а конденсат удаляется
из аппарата при температуре насыщения) находят по уравне-
нию (11-7). Если же аппарат предназначен для охлаждения, то
6. Расчет теплообменных аппаратов
441
при вычислении тепловой нагрузки пользуются уравнением
(11-4), а расход охлаждающего агента рассчитывают по уравне-
нию (11-5). При определении расхода охлаждающего или нагре-
вающего агента необходимо знать его начальное (оно бывает
задано) и конечное (им обычно задаются) состояния. В соб-
ственно теплообменниках обычно известны количества обоих
теплоносителей, но из четырех температур, характеризующих их
начальное и конечное состояние Т2, ti, t2), даны лишь три;
четвертую, неизвестную температуру определяют, приравнивая
правые части уравнений (11-4) и (11-5).
Пример 12-2. Определить тепловую нагрузку и расход охлаждающей
воды в холодильнике для метилового спирта. Количество метилового спирта
0= 10 000 кг/ч, его начальная температура Т\ — 60° С, конечная тем-
пература 7'2 = 30° С, удельная теплоемкость С = 2680 дж/кг • град
(0,64 ккал/кг • град). Начальная температура охлаждающей воды Л = 25° С,
удельная теплоемкость с = 4190 дж/кг-град (1 ккал/кг • град).
Решение. Тепловую нагрузку находим по формуле (11-4):
Q = 22229.2680(60 — 30) = 223000 вт
ob(JU
Принимая конечную температуру воды /г = 32° С, определяем расход
воды по формуле (11-5):
8 = = 4190 (32 — 25) = 7,6 Кг,СвК = 27 400 Кг/Ч = 27,4 МЗ,Ч/
Пример 12-3. Определить тепловую нагрузку и расход пара в подогре-
вателе для 10%-ного раствора NaOH Количество раствора £ = 20 000 кг/ч,
его начальная температура Л = 85° С, конечная температура t2 =120° С,
удельная теплоемкость раствора с = 3860 дж/кг-град (0,92 ккал/кг • град).
Абсолютное давление греющего пара равно 2,94 бар (3 ат). Теплота испа-
рения водяного пара (при 3 ат) г = 2170* 103 дж/кг (517 ккал/кг).
Решение. Тепловую нагрузку вычисляем по формуле (11 5):
Q = • 3860 (120 — 85) 750 000 вт
OVvv
Расход пара находим по формуле (11-7):
G = — — 000 _ о,346 кг/сек = 1250 кг/ч
г 2170 • 103 '
Пример 12-4. Нитрозные газы в количестве 6 = 22 000 кг/ч охлаждаются
воздухом от температуры 7'1= 800° С. Количество воздуха £= 19 000 кг/ч,
его начальная температура Л — 20° С, конечная температура t2 = 350° С,
удельная теплоемкость с — 1030 дж/кг град (0,245 ккал/кё• град). Опре-
делить тепловую нагрузку и конечную температуру газов.
Решение. По формуле (11-5) рассчитываем тепловую нагрузку:
Q = • ЮЗО (350—20) = 1 790 000 вт
OOvv
442
Гл. 12. Нагревание и охлаждение
При средней удельной теплоемкости газов с «=1130 дж/кг -град
(0,27 ккал/кг- град) по формуле (11-4) имеем:
1 790000 = • ИЗО (800 — Т2)
ovUv
откуда Тг = 540° С.
Определение среднего температурного напора
передних температур теплоносителей
Если теплоносители движутся противотоком или прямотоком,
то средний температурный напор определяют по формуле
(11-28) или (11-29).
В многоходовых теплообменниках теплоносители движутся
вдоль части поверхности теплообмена противотоком и вдоль
другой ее части — прямотоком. Для такого вида движения
(смешанный ток) указанные формулы дают завышенные зна-
чения 6ср.-
Для расчета среднего температурного напора при смешанном токе
можно пользоваться следующими формулами:
1. Если теплообменник имеет один ход в межтрубном пространстве и
четное число ходов в трубах (простой смешанный ток, рис. 12-6,6), то
?31 + +
S 0J + 02 —+
2.
ходов
Если теплообменник имеет Af ходов в межтрубном
в трубах, кратное 2V (многократный смешанный
___________________/дл + д/2
СР'~ V9.41?^±£-^+^.
А — У^Тг+Ыг
пространстве и число
ток, рис. 12-5,6), то
(12-11)
В формулах (12-10) и (12-11) величины ДГ и М—температурные пере-
пады горячего и холодного теплоносителей; 6] и 02 — температурные на-
поры на входе и выходе теплообменника при работе противотоком с теми
же начальными и конечными температурами теплоносителей. Величина А
определяется по формуле:
Л’___ ,7___
К + ]/^2
Л = (0,-в2)
Nr._ N.~.
Vе.-у 02
При одинаковых начальных и конечных температурах теп-
лоносителей из всех видов движения наибольшее значение 9ср,
достигается при противотоке, а наименьшее — при прямотоке;
смешанный ток занимает промежуточное положение. При мно-
6. Расчет теплообменных аппаратов
443
гократном смешанном токе величина 6ср. больше, чем при про-
стом смешанном токе, и возрастает с увеличением N.
Если температура одного из теплоносителей не изменяется
в процессе теплообмена, то при любых видах их движения зна-
чения 6ср. одинаковы и находятся по формуле (11-28).
При расчетах пользуются средним значением коэффициента теплопере-
дачи, определяемым при средних температурах теплоносителей. Среднюю
температуру теплоносителя с меньшим температурным перепадом можно
вычислять как среднеарифметическую из начальной и конечной температур;
для теплоносителя с большим температурным перепадом средняя темпера-
тура находится из условия, что разность средних температур теплоносителей
равна среднему температурному напору.
Таким образом, средние температуры горячего (Тер.) и холодного (/ср.)
теплоносителей определяются из следующих соотношений:
при Д/ < ДГ 4р. = Гер. = /ср. + 0ср. (12-12)
при ДТ < М ГСр. = /ср. = Т'ср. - бср. (12-13)
Пример 12-5. Определить средний температурный напор при простом
смешанном токе, если в межтрубном пространстве движется горячий тепло-
носитель с начальной температурой Л = 60° С и конечной температурой
Т2 = 30°С, а по трубам — холодный теплоноситель с начальной температурой
6 = 25° С и конечной /2 = 32° С.
Решение. По формуле (12-10) находим:
0 ГЗО» + 7» Ср’ 9q. 28 4-5 4-1/302 + 72
32 ^.32 -25 т_725 2,3 Iff — 28 + 5 — V302 + 72
б, = 28 02 = 5
Пример 12-6. Определить средний температурный напор для условий
примера 12-5 при многократном смешанном токе, если число ходов в меж-
трубном пространстве N — 2.
Решение. Находим величину А:
А = (28 — 5) • =. 56,8 °C
/28 — / 5
Средний температурный напор рассчитываем по формуле (12-11):
оср.=---------___________________ с
Р 56,8-ьГ30"+7“
Z • Z.O 1 |'1~‘ г г ~ -
56,8 — /302 + 72
Путем расчета предлагается убедиться, что средний температурный на-
пор при N — 4 составляет 0СО. = 13,3° С, а при противотЪке 0ср. = 13,4° С.
Таким образом, в данном случае при N — 4 смешанный ток практически равно-
ценен противотоку, а при N = 2 только немного уступает ему,
444
Гл. 12. Нагревание и охлаждение
Определение сечений для прохода
теплоносителей
Диаметр и количество труб (или сечение каналов в пластин-
чатых и спиральных теплообменниках) необходимо выбрать так,
чтобы теплоносители двигались с требуемыми скоростями. Для
этого соответствующее сечение для прохода теплоносителя
(в м2) должно удовлетворять условию:
где G — расход теплоносителя, кг/сек-,
W — массовая скорость теплоносителя, кг/м2 • сек.
В то же время сечения для прохода теплоносителей связаны с конструк-
тивными размерами аппарата приведенными ниже соотношениями.
А. В трубчатых теплообменниках площадь поперечного сечения трубного
пространства составляет (в jw2):
где rfB — внутренний диаметр трубы, м; ,
е ( п\.
пх — число труб в одном ходе I пх = — I,
п— общее число труб в аппарате;
z— число ходов.
При расчете теплообменников «труба в трубе», а также оросительных и
погружных теплообменников в формуле (12-14) под пх понимают число
параллельных секций.
Б. Площадь поперечного сечения межтрубного пространства (в .м2)
определяется, в зависимости от его устройства, следующим образом.
1. В межтрубном пространстве без перегородок:
SMTp. = ^-(£>2 —
(12-15)
где D — внутренний диаметр кожуха, м;
4н — наружный диаметр труб, м.
Формула (12-15) применима и для теплообменников «труба в трубе»;
при этом п — 1.
2. В межтрубном пространстве, разделенном продольными перегородками
на N ходов:
_ к (D2-nrf2)
°мтр. — 4" ту
(12-16)
3. В межтрубном пространстве с поперечными перегородками расчет ве-
дут по приведенному сечению:
•^мтр.^Ф
прив.
(12-17)
6. Расчет теплообменных аппаратов
445
При этом SMTp. определяется по формуле (12-15), а коэффициент ф, учи-
тывающий сужение сечения ввиду наличия труб, находят по уравнению:
1
t
1 _ о,9 0^
,2
(12-18)
где t — шаг труб, м.
Приведенную длину пути теплоносителя между перегородками /прив. (на
рис. 12-7 показана пунктиром) определяют по формулам:
для сегментных перегородок
4
^прив. = A -j- — "д' Ъ (12-19)
для чередующихся колец и дисков
^прив. — 4
D 2 b
2 3 Г 2
(12-20)
Величины Миг обозначены на рис. 12-7. При условии одинаковой ско-
рости теплоносителя при поперечном (между перегородками) и продольном
(через вырезы в перегородках) движениях следует придерживаться следую-
щих соотношений:
для сегментных перегородок
6 = / 2Лф = (0,2 — 0,4) D
для чередующихся колец и дисков
, ,, D — 2/гф D
b = h* Р-4 <-2—г; Г = 2Л<’
Перед расчетом сечений для прохода теплоносителей выбирают скорости
их движения и диаметры труб.
В кожухотрубных теплообменниках целесообразно применять трубы не-
больших диаметров, так как при этом уменьшаются габариты аппарата.
Обычно используют трубы диаметром 16—38 мм-, для газов, загрязненных
и вязких жидкостей применяют трубы диаметром до 76 мм и более. Тру-
бами меньшего диаметра (5—16 мм) пользуются для теплоносителей, нахо-
дящихся под высоким давлением.
В теплообменниках «труба в трубе» применяют трубы диаметром
38—57 мм (при диаметре наружной трубы 76—108 мм), в погружных тепло-
обменниках— от 38 до 76 мм (и более), в оросительных теплообменниках —
трубы диаметром 50—100 мм.
Для жидкостей массовую скорость в трубах теплообменников принимают
равной 200—2000 кг]м? • сек, причем более низкие значения выбирают для
одноходовых кожухотрубных теплообменников, средние — для многоходовых,
элементных, погружных и оросительных теплообменников, а более высо-
кие — для теплообменников «труба в трубе» и каналов спиральных тепло-
обменников.
Для газов при атмосферном давлении массовую скорость принимают
в пределах 2—20 кг/м? • сек. При повышенном давлении допускаемая массо-
вая скорость газа увеличивается примерно пропорционально давлению; при
высоких давлениях (порядка 300 ат) она достигает 1000 кг[м1 • сек.
446
Гл. 12. Нагревание и охлаждение
Определение коэффициента теплопередачи
Коэффициент теплопередачи определяют по формуле (11-13).
Коэффициенты теплоотдачи рассчитываются по формулам, при-
веденным в главе И, раздел 6 (стр. 383 сл.).
При определении теплового сопротивления стенки у сле-
дует учитывать тепловое сопротивление загрязнений (табл. 15):
^загр.
^"загр. — “5
г лзагр.
Тогда
_____ г . 8 . "
^ст. — загр. “Г" у “Г Гзагр.
где г'агр и га — тепловые сопротивления загрязнений со сто-
роны горячего и холодного теплоносителей.
Таблица 15
Ориентировочные значения гзагр.
Теплоносители
Гзагр.» мг-град1вт
Вода
дистиллированная .................
морская ..........................
водопроводная, колодезная или озерная . .
речная хорошего качества
w < 0,9 м/сек ..............
w > 0,9 м/сек ..............
загрязненная
w < 0,9 м/сек ..............
w > 0,9 м/сек...................
Нефтепродукты
сырые ............................
чистые (в том числе масла минеральные) .
Органические жидкости, рассолы, жидкие хладо-
агенты (NH3, фреоны и др.).........
Водяной пар с примесью масла.........
Пары
органических жидкостей............
хладоагентов .....................
Воздух...............................
0,00009
0,00009 (0,00018)
0,00018 (0,00035)
0,00035 (0,00053)
0,00018 (0,00035)
0,00053 (0,00071)
0,00035 (0,00053)
0,0009
0,00018
0,00018
0,00018
0,00009
0,00035
0,00035
Примечание. Значения в скобках относятся к температуре воды >50° С или
к температуре горячего теплоносителя >115° С при водяном охлаждении.
6. Расчет теплообменных аппаратов
447
При определении коэффициентов теплоотдачи во многих слу-
чаях необходимо знать температуру стенки или удельную тепло-
вую нагрузку. Так как в начале расчета эти величины неизве-
стны, то ими задаются, а по окончании расчета пропреют по
соответствующим формулам (см. пример 11-16, стр. 409). Удоб-
нее всего при этом пользоваться графическим методом с по-
строением нагрузочной характеристики (см. пример 12-7).
Пример 12-7. Определить коэффициент теплопередачи для 10%-ного рас-
твора NaOH, нагреваемого в горизонтальном подогревателе. Избыточное
давление греющего пара составляет 2,94 бар (3 ат), температура Т =. 132,9° С.
Раствор проходит по стальным трубам диаметром 25/21 мм. Количество
труб п = 253. Массовая скорость раствора W = 412 кг/м2 • сек, средняя тем-
пература равна 106,2° С. Константы раствора при этой температуре:
вязкость.............р. = 0,64 • 10-3 н • сек/м2 (0,64 спз)
теплопроводность . . . . X = 0,715 впг/м • град (0,615 ккал/М'- ч • град)
удельная теплоемкость . . с = 3860 дж/кг - град (0,92 ккал/кг • град)
Решение. Значения Re и Рг находим по уравнениям (11-31) и (11-32):
Re
_ 412-0,021
“ 0,64 -10“3
= 13 500
Рг =
0,64 -10~3 • 3860
0,715
= 3,44
Так как Re > 10000, то расчет проводим по уравнению (11-35):
Nu = 0,023 -13 5ОО0,8 - 3,440’4 = 76
откуда коэффициент теплоотдачи для раствора
а2 = Nu = • 76 2590 вт/м2 • град (2230 ккал/м2 • ч • град)
(Ar g V Д/4& X
Определим теперь тепловое сопротивление стенки. Принимаем
гзагр == 0,00043 м2 • град/вт (со стороны раствора). Тогда при 8 = 0,002 м
и X = 45 вт/м • град (40 ккал/м • ч • град)
rCT = 14- /' = + 0,00043 = 0,000474 м2 - град/вт
их. Д' ddip.
Коэффициент теплоотдачи в межтрубном пространстве (для пара) опре-
делен для заданных условий в примере 11-11 (стр. 397) в зависимости от
плотности теплового потока q и составляет:
463000
а. = -
448
Гл. 12. Нагревание и охлаждение
Таблица 16
Определяемая величина Размерность q, вт/м2
25 000 30 000 35 000
463 000 emjM2 • град 15 800 14900 14200
г = _L _i_ 0,00086 ai м2 град/вт 0,000923 0,000927 0,00093
0ср. = qr град 23,1 27,8 32,6
q, в/п/м?
Рис. 12-20. Нагрузочная характе-
ристика подогревателя (к при-
t меру 12-7).
Однако величина q неизвестна; поэтому задаемся несколькими значе-
ниями q и определяем соответствующие значения и г, а затем — средний
температурный напор:
а / 1 Г I 1 \
0сР. = qr = q 1— + rCT. + — =
\ «I а2 /
= ?(^ +0,000474+^) =
== q ( — 4- 0,00086^
\ai /
Значения q, а также вычисленные
значения «1, г и 6Ср.> приведены в
табл. 16.
По данным таблицы строим так
называемую нагрузочную характеристи-
ку подогревателя (рис. 12 20), показы-
вающую зависимость между q и 6ср. В
рассматриваемом случае 0ср. — 132,9 —
— 106,2 = 26,7° С и соответствующее зна-
чение q по нагрузочной характеристике
составит 28 800 вт!м2 Таким образом,
коэффициент теплопередачи
q __ 28 800 _
k “ бср. ~ 26,7 “
= 1080 в/п/л/2 • град (930 ккал)м2 • ч • град)
Определение поверхности теплообмена и
основных размеров теплообменника
Необходимую поверхность теплообмена определяют из урав-
нения (11-9):
р=г (12-21)
б. Расчет теплообменных аппаратов
449
Поверхность теплообмена связана с конструктивными раз-
мерами аппарата; так, для трубчатых теплообменников вели-
чина F составляет (в Л12):
F=Tzdlti (12-22)
где d — диаметр труб, м;
I — длина труб, л;
п — количество труб.
При пользовании соотношением (12-22) поверхность тепло-
обмена подсчитывают по внутреннему, наружному или среднему
диаметру труб (см. стр. 375).
При расчете трубчатых теплообменников обычно задаются
диаметром труб (стр. 445), затем определяют число труб, ис-
ходя из необходимых сечений для прохода теплоносителей
(стр. 444) и, наконец, по уравнению (12-22) находят требуе-
мую длину труб.
Пример 12-8. Рассчитать одноходовой кожухотрубный теплообменник для
подогрева воздуха нитрозными газами в условиях примера 12-4, если абсо-
лютное давление газов составляет 6,5 ат, а абсолютное давление воздуха
равно 7 ат.
Решение. В примере 12-4 определена тепловая нагрузка
Q = 1 790 000 вт и конечная температура нитрозных газов Тг = 540° С. Сред-
ний температурный напор при противотоке составляет:
800----->540 450 + 520
350 <----20 V =--------2-----=485 с
450 520
Средняя температура газов:
Гср. = + 540 = 670 °C
Средняя температура воздуха [по формуле (12-13)]:
/со =670 — 485= 185 °C
По трубам пропускаем нитрозные газы и в соответствии с давлением
принимаем их массовую скорость № = 65 ке/м2 • сек-, тогда необходимое сече-
ние труб
ода4-"!
Выбираем трубы из хромистой стали диаметром 38/33 мм-, сечение одной
трубы равно 0,785* 0,0332 = 0,000855 м2, а количество труб
0,094
п~ 0,000855
По табл. 14 принимаем количество труб п = 121, тогда сечение труб
5тр = 121 "0,000855 = 0,103 м2 и массовая скорость
lF7 22 000 .
W “ 3600 • 0,103 “ 59,3 кг/м ' сек
29 Зак 546.
450
Гл. 12. Нагревание и охлаждение
Константы нитрозных газов (приняты по воздуху) при 670° С:
вязкость..............р. = 0,403 • 10-4 н • сек/м2 (0,0403 спз);
теплопроводность . . . . X = 0,065 впГм-град (0,056 ккал/м • ч град);
удельная теплоемкость . с = 1130 дж!кг-град (0,27 ккал)кг • град)
Критерии Re и Рг находим по формулам (11-31) и (11-32);
Re =
-^*.48 700
0,403 • 10~4
0,403- 10~4- ИЗО
0,065
Из уравнения (11-35) получаем:
Nu = 0,023 • 48 7ОО0,8 • 0,7°>4 = 112
откуда по формуле (11-34) находим коэффициент теплоотдачи:
otj = q’qII' • 112 = 220 вт/м2 • град (190 ккал)м2 ч • град)
При принятом количестве труб внутренний диаметр аппарата D = 600 мм
(см. табл. 14). Сечение межтрубного пространства 5мтр. = 0,146 м2 (см. при-
мер 11-6, стр. 391).
Массовая скорость воздуха-
.г. 19 000 . .
W ~ 3600 • 0,146 “ 36,1 Кг1м ’ СеК
При данных условиях коэффициент теплоотдачи для воздуха «2 ==
= 96,5 emlM^'epad (см. пример 11-6, стр. 392). Коэффициент теплопередачи
при 5 = 0,0025 ж и Х= 17 вт/ж-ерад (15 ккал/м < ч • град) составляет:
k — —:-----------------i— = 66 вт[м2 • град (57 ккал!м2 • ч • град)
1 » v.UUzd । 1
220 17 ^“9бУ
Поверхность теплообмена:
1790 000
66 • 485
55,7 м2
Длина труб при расчете F по среднему диаметру труб:
j 55,7 .
= 3,14-0,0355. 121 = ’ ° М
Принимаем I — 4,5 ж.
Пример 12-9. Рассчитать многоходовой теплообменник (с поперечными
перегородками в межтрубном пространстве) для охлаждения метилового
спирта в условиях примера 12-2 (стр. 441).
Решение. В примере 12-2 определены тепловая нагрузка Q = 223 000 am
и расход воды g = 7,6 кг!сек. Температурный напор для данного случая
(смешанный ток) составляет 0ср. =9,15°С (см. пример 12-5, стр. 443).
6. Расчет теплообменных аппаратов
451
Средняя температура воды:
/ср. = = 28,5 °C
Средняя температура метилового спирта:
Тср. = 28,5 + 9,15 37,7 °C
По трубам пропускаем воду, и принимаем ее массовую скорость
W — 600 кг/м2 • сек\ тогда необходимое сечение труб
V = w = 0’0127j'’
Выбираем стальные трубы диаметром 25/21 мм\ сечение одной трубы
равно 0,785 * 0,0212 = 0,000346 м2 и количество труб в одном ходе
0,0127 _
П' “ 0,000346 “
По т^бл. 14 выбираем двухходовой теплообменник с диаметром корпуса
400 мм и числом труб в ходе ni = 55; всего труб п = 2*55 =110. Тогда
площадь сечения труб
STP. = 55 • 0,000346 = 0,019 м2
и массовая скорость
w=w =400 кг,м2 *сек
При этих условиях коэффициент теплоотдачи для «2 = 2150 вт/м2-град
(см. пример 11-5, стр 390).
Площадь сечения межтрубного пространства
SMTp = 0,785 (0,42 _ по. 0,0252) = 0,0716 м2
Расстояние между поперечными перегородками принимаем h = 0,2 м.
При шаге между трубами t = 32 мм по формуле (12-18)^ находим:
Высота вырезанного сегмента
b = V2/гф = К2 • 0,2 • 0,487 = 0,13 м
Приведенную длину пути определяем по формуле (12-19):
4
/прив. = 0,2 + 0,4 — у.0,130,42 м
Приведенное сечение вычисляем по формуле (12-17):
_ _ 0,0716 0,2.0,487 _
*^прив. — 0 49 — 0,0166 м
Массовая скорость в межтрубном пространстве составляет:
IV/ О 10 000 1ео , о
W ~ Зприв. ~ 3600 • 0,0166 “ 168 Кг/М ‘ сек
29* '
452
Гл. 12. Нагревание и охлаждение
В данных условиях коэффициент теплоотдачи для метилового спирта
а] = 720 вт/м2 • град (см. пример 11-7, стр. 392).
Принимая тепловое сопротивление загрязнений со стороны воды
/"загр = 0,00018 м2 • град/вт, В = 0,002 я и Х=45 вт/м • град (40 ккал/м • ч -град),
находим коэффициент теплопередачи:
k=________________* 1
4)+ ^- + 0.000184
—— = 480 em/м2 • град (415 ккал/м2-ч • град)
2150
Необходимая поверхность
теплообмена:
223 000 сп_ „
480 • 9,15 “ 50,5 М
Длина труб при расчете по наружному диаметру:
1 __ 50,5 _ с
3,14 • 0,025 • 100 W М
Принимаем I = 6 м.
Пример 12-10. Рассчитать спиральный теплообменник для подогрева
g = 20000 кг/ч 10%-ного раствора NaOH от температуры Л = 50°С до тем-
пературы t2 — 85° С. Количество нагревающего агента (конденсат водяного
пара) G = 18 000 кг/ч, его начальная температура Т\ = 95° С.
Определение тепловой нагрузки и конечной темпера-
туры конденсата. Тепловая нагрузка при удельной теплоемкости рас-
твора с — 3860 дж/кг град (0,92 ккал/кг • град) составляет:
Q = •3860 (85 — 5°) = 750 000 вт
oOUU
При удельной теплоемкости конденсата С = 4190 С
(1 ккал/кг • град) находим его конечную температуру Т2 из выражения:
750000 = 18990 • 4190(95 — Т2)
ооОО
дж/кг • град
откуда Т2 = 59,2° С.
Определение
ператур теплоносителей.
95----->59,2
85<-----50/.
9Д
Средняя температура раствора:
Гср. - 2
10
температурного напора и средних те,м-
Средний температурный напор равен:
6ср. = --° + 9,2 = 9,6 °C
U85 =67,5 °C
ср.
Средняя температура конденсата:
Тср == 67,5 + 9,6 = 77,1 °C
Определение сечений каналов. Принимаем массовую ско-
рость конденсата = 1500 кг/м2 • сек, тогда необходимое сечение
18000 nnn-W и2
ЖООПбОО^0’00333 *
$1
6. Расчет теплообменных аппаратов
453
Полагая ширину канала b = 6 мм, находим ширину спирали:
„ $! 0,00333 _ кк_
в = т = -бда- = одал
Приняв рабочую ширину спирали В = 0,58 м, определяем сечение:
5! = 0,58 • 0,006 = 0,0035 м2
и массовую скорость
= 3600-0,0035 = 1400 Кг^ ' СеК
Для раствора принимаем такую же ширину канала, тогда массовая ско-
рость раствора
20000 1КЛП , „
“ 3600-0,0035 “ 1600 Кг1М ' СвК
Определение коэффициента теплопередачи. Эквива-
лентный диаметр канала:
<*экв. -4J = ^r = 2^ 2-0’006==0-012 М
2.D Z.D
Для конденсата константы составляют:
вязкость..................р = 0,373 • 10~3 н • сек/м2 (0,373 спз);
теплопроводность . . . . X = 0,67 вт/м • град (0,578 ккал/м • ч граду,
удельная теплоемкость . . с = 4190 дж/кг • град (1 ккал/кг • град)
Находим критерии Re и Рг для конденсата-
_ 1400 - 0,012 .КПАП
Re =---------~ 45 000
0,373 • 10~3
_ 0,373 • 10-3 • 4190 о
Рг =---------0,67------=2'32
Коэффициент теплоотдачи определяем по формуле (11-35):
Nu = 0,023 • 45 0000'8 • 2,320'4 = 170
откуда
а1 = = 9500 вт/м2 град (8200 ккал/м2 • ч • град)
Константы раствора:
вязкость..................р = 0,715 • 10-3 н • сек/м2 (0,715 спз);
теплопроводность..........X = 0,578 вт/м • град (0,498 ккал/м • ч • град);
удельная теплоемкость ... с — 3860 дж/кг • град (0,92 ккал/кг • град)
Отсюда критерии для раствора равны; Re = 26 900; Рг = 4,75; Nu = 152.
Тогда коэффициент теплоотдачи
“2 “ ~~^0 01278 = в,п!м2' гРад (6300 ккал/м2 • ч • град)
454
Гл. 12. Нагревание и охлаждение
При толщине стальной стенки 6 = 5 мм и тепловых сопротивлениях за-
грязнений гзагр. 0,00009 м2 • град/вт (со стороны конденсата) и
гзагр = 0,00027 м2 • град/вт (со стороны раствора), коэффициент теплопере-
дачи составляет:
k________________I_______________=
— 1 о схк 1
9S)o+ °'«ХХЮ+^+0,00027+^
= 1400 вт/м2 • град (1200 ккал/м2 • ч град)
Определение поверхности теплообмена. Поверхность
теплообмена равна:
Рабочая длина спирали *
, F 56 . 0
L ~ '2В ~ 2 • 0,58 “ 48,3 М
I
Шаг спирали при толщине листа 8 = 5 мм составляет:
t = 64-8 = 64-5= 11 мм
Начальный диаметр спирали принимаем d = 300 мм и определяем число
витков каждой спирали:
дг _ j Г । х2_____х _ । Г 2 • 48,3 13 j а_131—415
. nt + V 3,14.0,011 + 11
1 (d Л 1 /300 Л 101
где х— )“2\11 1J—13,1
Наружный диаметр спирали:
D = d4-2^-^8 = 3004-2-41,5-11 4-5 ^ 1220 мм
Гидравлическое сопротивление
“ теплообменников
Гидравлическое сопротивление теплообменников опреде- <•
ляется по формулам, приведенным на стр. 160 и сл. Выражая
в формуле (6-63) линейную скорость w через массовую скорость
W = wp, получим:
^ = (X4 + Ii:)'V н1м2 (12-23)
где X — коэффициент трения;
I — длина трубы, At;
d — диаметр трубы/ м;
2^—сумма коэффициентов местных сопротивлений;
W — массовая скорость, яа/ж2 • сек;
р — плотность, кг/м3.
* Определение размеров спиральных теплообменников см. В. М. Р а м м,
Теплообменные аппараты, Госхимиздат, 1948.
6. Расчет теплообменных аппаратов
455
| Значения коэффициентов местных сопротивлений приведены
j? в таблице 17.
Г Таблица П
I Коэффициенты местных сопротивлений £ в теплообменниках
Характер местных сопротивлений
С
Входная или выходная камера (удар и поворот)...........
Поворот (180°) между ходами или секциями...............
Вход в трубы и выход из них............................
Вход в межтрубное пространство и выход из него.........
Поворот в U-образных трубах ...........................
Поворот (180°) через перегородку в межтрубном простран-
стве ..................................................
Поворот (180°) через калач.............................
Поперечное движение в межтрубном пространстве (/и — чи-
сло рядов труб) .......................................
Круглые змеевики (п — число витков).....................
1,5
2,5
1
1,5
0,5
1,5
2
3m
Re0-* * 2
0,5/г
Пример 12-11. Определить гидравлическое сопротивление холодильника
для метилового спирта в условиях примера 12-9 (см. стр. 450).
Сопротивление труб. По трубам движется вода с массовой ско-
ростью W = 400 кг/м2'сек и плотностью р = 1000 кг/м3. Критерий Рейнольдса
Re = 10 000 (см. пример 11-5, стр. 390). Внутренний диаметр труб dB~ 21 мм,
длина труб / = 6 м. Число ходов N = 2.
Коэффициент трения находим по формуле (6-59):
Х = 7T,81g Re —1,5)2~ = (1,81g 10 000—1,5)2 0,031
' Коэффициенты местных сопротивлений определяем по табл. 17:
Вход и выход............... 2 (1,5 4-1) = 5
Поворот между ходами .... 2,5
• Итого . . . . С = 7,5
Гидравлическое сопротивление трубного пространства
/ 2-6 \ 4002
Др = (0,031 4- 7,5) • 2 1W 2000 н/м3 (205 кгс/м3)
Здесь перед значением длины труб поставлен множитель 2, так как вода
проходит последовательно по двум ходам.
Сопротивление межтрубного пространства. По меж-
трубному пространству движется метанол с массовой скоростью
w = 168 кг/м2-сек и плотностью р = 776 кг/м3. Критерий Рейнольдса
Re = 9050 (см. пример 11-7, стр 392). Общее число труб п= НО, число ря-
дов труб при поперечном движении между перегородками пг = 13 (найдено
путем вычерчивания расположения труб). Число поперечных ходов между
перегородками равно 30 (при длине труб I = 6 м и расстоянии между пере-
городками h = 0,2 м).
456
Гл. 12. Нагревание и охлаждение
Согласно табл. 17, коэффициент сопротивления при поперечном движе-
нии составляет (т = 13):
Г __ д О
9O5O0,2 “ ’
При 30 поперечных ходах коэффициент £= 30-6,3 = 189. Остальные
местные сопротивления равны:
Вход и выход...................... 2 • 1,5 = 3
Повороты у перегородок............ 29-1,5 = 43,5
Следовательно, S £= 189 + 3 + 43,5 = 235. Сопротивлением трения пре-
небрегаем. Гидравлическое сопротивление межтрубного пространства
Др = 235 • = 4270 н/м2 (435 кгс/м2)
7. Расчет теплообмена при конденсации пара
Если на конденсацию поступает насыщенный пар и конден-
сат не охлаждается, то расчет не вызывает затруднений (см.
примеры 12-3 и 12-7 на стр. 441 и 447). Если же пар поступает
перегретым, а конденсат охлаждается ниже температуры насы-
щения Тп, то соответственно трем стадиям процесса поверхность
Рис. 12-21. Характер изменения температур
теплоносителей при конденсации пара.
теплообмена разбивают на три зоны: 1) зона охлаждения пере-
гретого пара до температуры насыщения; 2) зона конденсации
(при постоянной температуре 7"н); 3) зона охлаждения конден-
сата до заданной температуры. Кривая изменения температур
теплоносителей вдоль поверхности показана на рис. 12-21 (при
противотоке между теплоносителями).
Расчет ведут отдельно для каждой зоны, определяя тепловые
нагрузки Qnep., QkohA. и Qoxji. (стр. 367), средние температурные
7. Расчет теплообмена при конденсации пара
457
напоры 9Пер., 9конд. и 9охл. и коэффициенты теплопередачи Лпер_,
Лконд. и ^охл.- После этого находят поверхности каждой зоны:
Qnep. Фконд
'пер. = h fl ’ ' конд. ~ 7 ft »
^перлпер ^конд.иконд.
Р _____ Фохл.
1 ОХЛ. h fl
"-охл.иохл.
и общую поверхность теплообмена:
F:==' ^пер. Ч- ^конд. ~Ь ^охл.
Расход охлаждающего агента вычисляется по общей тепло-
вой нагрузке Q = Qnep. Ч~ Фконд. Ч-Фохл. [см. формулу (11-5)].
Для определения температур охлаждающего агента при пере-
ходе его из одной зоны в другую (tx, /у) надо составить урав-
нения теплового баланса по зонам. При противотоке
Qnep. gC (^2 ^у)
Q конд. == gC (^у ^х)
Фохл. = gC (tx Ч)
По любым двум из этих уравнений находятся tx и ty.
Если температура стенки ниже температуры насыщения, то
конденсация начинается в зоне охлаждения перегретого пара.
Коэффициент теплопередачи при конденсации перегретого пара
определяют, как указано на стр. 396; при расчете температур-
ного напора за температуру горячего теплоносителя принимают
не температуру перегретого пара, а температуру насыщения.
Если пар поступает насыщенным или конденсат не охла-
ждается, то поверхность теплообмена разбивают на две зоны.
Пример 12-12. Определить поверхность конденсатора для конденсации
паров аммиака под абсолютным давлением 11,7 бар (11,9 am). Количество
паров G = 250 кг/ч. Пары поступают перегретыми с температурой Т\ = 100° С.
Теплота испарения аммиака г= 1145-103 дж/кг (274 ккал/кг). Удельная
теплоемкость жидкого аммиака Сж = 4770 дж/кг‘град (1,14 ккал/кг-град).
Конденсат охлаждается до Тг = 25°С. Температура охлаждающей воды
6 = 20° С. Коэффициенты теплопередачи по зонам:
&пер = 116 вт/м2 град (100 ккал/м2 • ч • град)
^конд. == 696 вт/м2 • град (600 ккал/м2 • ч • град)
^охл. = 232 вт/м2 град (200 ккал/м2 • ч • град)
Решение. По диаграмме р—i для аммиака (см. Приложение XVIII —
вклейку в конце книги) находим:
Температура насыщения Гн..........30° С
Энтальпия насыщенного пара 7Н .... 1470 • 103 дж/кг (350 ккал/кг)
Энтальпия Поступающих перегретых
паров 1Х....................... 1665-103 дж/кг (397 ккал/кг)
458
Гл 12 Нагревание и охлаждение
Определяем тепловые нагрузки по зонам:
250
Qnep. = G (Л - 4) = (1665 - 1470) • 103 = 13 600 вт
Сконд = Gr = . 1145.103 = 79 500 вт
Сохл. = GCX (Тн - Т2) = • 4770 (30-25) = 1660 вт
ооии
Общая тепловая нагрузка:
Q = 13 600 Ц- 79 500 4- 1660 94 800 вт
Принимая конечную температуру воды ti = 27° С, находим ее расход при
удельной теплоемкости с = 4190 дж/кг • град (1 ккал/кг • град)-
94 800
g = 4190(27 — 20) = 3’24 Кг,СеК = 11 700 кг1ч = П’7 м3/4
В случае противотока температуры воды при переходе из зоны охлажде-
ния конденсата в зону конденсации tx и из зоны конденсации в зону охла-
ждения перегретого пара ty определяем по уравнениям'
1660 = 3,24 - 4190 (tx — 20)
13 600 = 3,24 • 4190 (27 —/у)
откуда t х — 20,1° С и ty = 26° С
Рассчитываем температурные напоры по зонам:
в Л>не охлаждения перегретого пара
100------>30 р 73 — 4 поо£^
27 <----26 пер'
~73 4
в зоне конденсации
30-------->30 __ 9,9 — 4 _
26 <------20,1 конд. - 9 9
_____________ 2,31g
4 9,9
в зоне охлаждения конденсата
30-------->25 __ 9,9 — 5 _
20,1 <-----20 охл' “ „. 9,9 ~
2,31g —=—
-------------- О
Находим поверхности теплообмена по зонам:
р — 13 600 — 95 2
'’пер. - Пб.23,8 ~ ’
„ 79 500 п
^конд- 696 • 6,5 “ 7,6 М
~ 1660 ппо 2
“ 232 • 7,1^ “ 0,98 М
8. Периодический процесс теплообмена
459
Общая поверхность
F = 4,95 + 17,6 + 0,98 23,6 м*
При расчете предполагалось, что температура стенки в зоне охлаждения
перегретого пара выше температуры насыщения.
8. Периодический процесс теплообмена
Если температуры теплоносителей изменяются во времени, но в каждый
данный момент являются одинаковыми во всех точках аппарата, то средний
температурный напор определяют по формуле (11-28), а затем по формуле
(12-21) находят необходимую поверхность теплообмена. Это наблюдается,
например, при подогреве жидкости, находящейся в сосуде, путем пропуска-
ния по змеевику насыщенного пара: пар конденсируется при постоянной тем-
пературе, которая не изменяется в течение процесса, а температура жидкости
в каждый данный момент во всех точках сосуда одинакова.
Обычно при периодическом теплообмене температура одного из теплоно-
сителей изменяется не только во времени, но и вдоль поверхности теплооб-
мена. Пусть, например, в аппарате происходит периодическое охлаждение
теплоносителя от Л до температуры Т2, причем начальная температура охла-
ждающего агента равна Л. Конечная его температура будет непрерывно
изменяться по мере протекания процесса, при этом если в начальный момент
пределом нагревания является температура Л, то к концу процесса пределом
будет температура ?2 Таким образом, конечная температура охлаждающего
агента будет уменьшаться от /2 до
Средний температурный напор определяется по формуле
6 - Л"1
р- ОО1 Л—*! ’2,3 A 1g А
2>31gv—г S
12 — И
где
г,—
г,-4 T2-t2
Уравнение теплового баланса
Q = GC (7\ Т2) == gc (tit Срв —1\)
где средняя конечная температура охлаждающего агента
^2, ср. = 2е! + ^ср. 2,31g А
Аналогично, если при периодическом нагревании от температуры 6 до
температуры t2 конечная температура нагревающего агента изменяется от
до Т2 (при постоянной начальной его температуре 7\), то
(12-24)
(12-25)
(12-26)
2,31g
Г, —2i 2,3A 1g А
Л /2
где
л Ti-ti
Т2 —h **
460
Г л. 12. Нагревание и охлаждение
Уравнение теплового баланса в этом случае имеет вид
Q = gc (/2 - ^i) = GC (Г, - Т2, ср.) (12-28)
где средняя конечная температура нагревающего агента
^2, ср. = — ^ср. 2,31g Л (12-29)
Пример 12-13. Определить поверхность теплообмена, необходимую для
охлаждения 0 = 5000 кг раствора от температуры 71 = 80° С до темпера-
туры Т2 — 30° С. Охлаждение производится периодически за время х = 2 ч
при помощи воды с начальной температурой t\ = 25° С Удельная тепло-
емкость раствора С = 3560 дж/кг • град (0,85 ккал/кг - град); коэффициент
теплопередачи k = 290 вт/м"1 • град (250 ккал/м2 • ч • град).
Решение. Тепловую нагрузку находим по формуле (11-4):
Q = 5000 • 3560 (80 — 30) = 890 000 • 103 дж (212 000 ккал)
Конечную температуру воды в конце охлаждения (когда температура
раствора составляет 30° С) принимаем t2 = 28° С. Тогда
72-/, _ 30 - 25 _9,
Т2 —12 ~ 30 —28 ’
В то же время
откуда определяем конечную температуру воды в начале охлаждения
1'2 = 58°*С.
Средний температурный напор вычисляем по формуле (12-24):
_ 80-30 2,5- 1 _И7оГ
ср‘“ по» 80 — 25 ‘ 2,3 • 2,5 1g 2,5 ’
213'g 10=25-
Среднюю конечную температуру воды рассчитываем по формуле (12-26):
/2, ср. = 25 4- 13,7 • 2,31g 2,5 = 37,5 °C
Расход охлаждающей воды при ее удельной теплоемкости
с = 4190 дж/кг • град (1 ккал/кг • град) составляет'
Q 890 000-103
g = —77--“---ТТ = Hinn /от с-оёГ = 17 000 кг
с (^2, ср.4190 (37,5 — 25)
Необходимая поверхность теплообмена:
Q 890 000-103
~ Мср5 “ 290 • 13,7 • 2 • 3600 “
9. Теплообмен в кипящем (псевдоожиженном) слое
Аппараты с кипящим слоем (стр. 179) в последнее время ча-
сто применяют для проведения теплообмена, который в условиях
псевдоожижения значительно интенсифицируется. Теплообмен
Р Теплообмен в кипящем (псевдоожиженном) слое
461
можно осуществить либо между газом и находящимся в псевдо-
ожиженном состоянии слоем твердых частиц, либо между кипя-
щим слоем и теплообменной поверхностью.
Теплообмен между газом и твердыми частицами. Этот вид
теплообмена используют для нагревания или охлаждения твер-
дых частиц газом. Теплообмен может быть непрерывным или
периодическим. При непрерывном процессе твердые частицы
непрерывно вводятся в слой и такое же количество их выво-
дится из слоя. При интенсивном перемешивании в кипящем слое
температуры газа и частиц выравниваются по всему слою и мо-
гут быть приняты равными их конечным температурам Т2 и t2.
Тогда температурный напор равен разности конечных темпера-
тур 9 = Т2—t2 и уравнение теплопередачи (при нагревании
твердых частиц) можно написать в виде
Q = GC(7\~T2)==aF(T2—t2)
откуда конечная температура газа
Л = Л-(Л-<2) ьрг (12-30)
ГТ
где П = -5Г.
Здесь F — поверхность находящихся в слое твердых частиц,
которая определяется по формуле
где /птв. — масса твердых частиц, находящихся в слое, кг-,
Ртв. — плотность твердых частиц, кг/м3-,
d — диаметр частиц, м.
При периодическом процессе время (в сек), необходимое
для нагревания твердых частиц от температуры t\ до темпера-
туры t2, определяется по формуле
т = (1 + П) • 2,31g Tf-^ (12-32)
где 1\— начальная температура газа;
ств. — удельная теплоемкость твердых частиц, дж!кг-град.
Для определения коэффициента теплоотдачи а между газом и твердыми
частицами можно пользоваться уравнениями-
при Re0 <10 Nu = 0,00353ReQ,55/<o (12-33)
l j \0,45
при Reo = 3O—120 Nu = O,OlReo Ar°»175(-£-) (12-34)
wo /
при Re0 = 120 — 2500 Nu = O,O16ReJ-8Ar0’175 ' (12-35)
о
462
Гл. 12. Нагревание и охлаждение
Здесь Но — высота неподвижного (насыпного) слоя, м; — число псевдо-
ожижения (см. стр 181).
В этих формулах критерий Nu рассчитывается по диаметру частицы d\
определение критериев Reo и Аг см. стр. 177 и 149.
Коэффициент теплоотдачи а сравнительно невелик, что, од-
нако, компенсируется большой поверхностью частиц; поэтому
тепловые нагрузки в аппаратах кипящего слоя достигают очень
высоких значений.
Теплообмен между кипящим (псевдоожиженным) слоем и
теплообменной поверхностью применяют для подвода тепла к
слою или отвода тепла от него в реакционных, обжиговых и
других аппаратах. Для этого теплообменная поверхность в виде
змеевиков, труб и т. д. помещается внутри слоя или тепло пере-
дается через стенки аппарата с кипящим слоем.
С увеличением числа псевдоожижения (см. стр. 181) коэф-
фициент теплоотдачи значительно увеличивается, но лишь до
известного предела, который соответствует оптимальному ре-
жиму псевдоожижения. При дальнейшем увеличении числа
псевдоожижения коэффициент теплоотдачи снижается, что объ-
ясняется уменьшением концентрации твердых частиц в слое
вследствие перехода слоя из «плотного» состояния в «разбав-
ленное».
При расчете теплоотдачи между «плотным» слоем и теплообменной по-
верхностью можно пользоваться следующими приближенными уравнениями:
при теплообмене между слоем и помещенной в слой поверхностью
Reg’39
Nu = 2,15-----(12-36)’
fe3 -,0,61 ' '
(T^pJ
при теплообмене между слоем и стенками аппарата
/ Ren \°>47
Nu = 3,75 1g « ) (12-37)
где е — пористость слоя;
<л — число псевдоожижения.
Пример 12-14. Определить коэффициент теплоотдачи между топочными
газами и твердыми частицами в кипящем слое при следующих условиях:
скорость газов о0 = 3,8 м/сек-, диаметр твердых частиц d = 3,75 мм, их плот-
ность Ртв. = 1400 кг/м3-, высота неподвижного слоя Но = 0,2 м. Константы
газов при их температуре:
плотность..............р = 0,275 кг/м3-,
вязкость..............р. = 0,477 • 10-4 н • сек/м2 (0,0477 спз);
теплопроводность . . . . X = 0,161 вт/м • град (0,139 ккал/м • ч • град)
Решение. По формуле (6-108) рассчитываем критерий Рейнольдса:
п 3,8 • 0,00375 • 0,275 ЙО
Re0 = —---------------= 82
0,477 • 10 4
9. Теплообмен в кипящем (псевдоожиженном) слое
463
Критерий Аг = 87 600 (см. пример 6-16, стр. 183). В соответствии с най-
денным значением Reo для определения коэффициента теплоотдачи восполь-
зуемся уравнением (12-34):
Nu = 0,01 -82 - 87 600 °’175 (0,<Ю375 у1,45 = 0,97
Коэффициент теплоотдачи:
а = Nu = QQ(j375 • 0,97 = 41,7 вт/я2 • град (36 ккал/я2 • ч • град)
Пример 12-15. Определить производительность на 1 л*2 сечения аппарата
при нагревании твердых частиц в кипящем слое в условиях примера 12-14,
если начальная температура газов равна 71= 1050° С; начальная темпе-
ратура твердых частиц Л = 10° С, конечная температура частиц /г = 950° С,
удельная теплоемкость газов С = 1170 дж/кг • град (0,28 ккал/кг • град),
удельная теплоемкость частиц с = 1420 дж/кг -град (0,34 ккал/кг • град),
насыпная масса частиц рНас. = 850 кг/м3.
Решение. Масса твердых частиц на 1 м2 сечения при высоте не-
подвижного слоя Hq = 0,2 Л! и заданной насыпной массе:
титв. = 1 • 7/оРнас. = 0,2 • 850 = 170 кг/м2
Поверхность твердых частиц в слое на 1 м2 сечения при ртв. = 1400 кг/я3
находим по формуле (12-31):
р___ 6'170 — 273 я2 /я2
1400 • 0,00375 " '
Расход топочных газов на 1 м2 сечения:
G — wop = 3,8 • 0,275 1,04 кг/я2 • сек
Находим параметр П:
uF _ 41,7-273 __
GC 1,04-1170
Конечную температуру газов рассчитываем по формуле (12-30):
о .35
Тг = 1050 — (1050 — 950) • = 960 °C
Тепловая нагрузка на 1 я2 сечения составляет:
Q = GC (Тх — Т2) = 1,04 • 1170 (1050 — 960)
^110 000 вт/я2 (95000 ккал/я2 • ч)
Производительность по твердому веществу на 1 м2 сечения находим из
теплового баланса:
g = cfe-6) = ~ °’083 кг'м!- Сек = 300 ’
Отсюда нетрудно найти необходимый диаметр аппарата для любой за-
данной производительности.
Пример 12-16. Найти коэффициент теплоотдачи от слоя к внутренней
теплообменной поверхности для условий примера 12-14, если пористость
слоя 8 = 0,75.
464
Гл. 12. Нагревание и охлаждение
Решение. По уравнению (12-36) имеем:
090,39
Nu = 2,15-----------------= 3,75
Г 0,753 -|0-61
L(1-0,75)2]
откуда
а = ^-Nu = -q 13,75 — 161 вт/м2 • град (140 ккал/я2 • ч • град)
10. Регенеративные и смесительные теплообменные
аппараты
Регенеративные аппараты
В регенеративных теплообменниках в качестве насадки
применяют кирпичи, металлические листы, шары, алюминиевую
Холодный
теплоноситель
Гзрячий
теплоноситель
Рис. 12-22. Схема ре-
генератора с непо-
движной насадкой:
1, 2 — клапаны.
фольгу и т. п. В течение первого периода
(период нагревания насадки)- через аппа-
рат пропускают горячий теплоноситель,
причем отдаваемое им тепло расходуется
на нагревание насадки и в ней аккумули-
руется. В течение второго периода (период
охлаждения насадки) через аппарат про-
пускают холодный теплоноситель, который
нагревается за счет тепла, аккумулирован-
ного насадкой. Периоды нагревания и охла-
ждения насадки продолжаются от несколь-
ких минут до нескольких часов.
Для непрерывного осуществления теп-
лопередачи между теплоносителями необ-
ходимы два регенератора: в то время как в
одном из них происходит охлаждение горя-
чего теплоносителя, в другом нагревается
холодный теплоноситель. Затем аппараты
переключаются, после чего в каждом из них
процесс теплопередачи протекает в обрат-
ном направлении.
Схема соединения и переключения пары
регенераторов приведена на рис. 12-22. Пе-
реключение производится поворотом кла-
панов 1 и 2. Направление движения тепло-
носителей показано стрелками. Переклю-
чение регенераторов может производиться автоматически через
определенные промежутки времени; автоматизация безусловно
необходима при коротких периодах работы регенераторов.
10 Регенеративные и смесительные теплообменные аппараты
465
На рис. 12-23 показан регенератор с движущейся насадкой,
выполненной в виде металлических шаров. Через регенератор 1
пропускается горячий теплоноситель, причем насадка нагрева-
ется. Насадка непрерывно выгружается через затвор 3 и посту-
пает в- регенератор 2, через который пропускается холодный
теплоноситель. Из регенератора 2 насадка
затвор 4 и элеватором 5 вновь подается в
регенератор 1. Таким образом, переключе-
ние регенераторов отпадает, и тепло пере-
дается от горячего теплоносителя к холод-
ному при помощи насадки, непрерывно цир-
кулирующей через оба регенератора.
Достоинство регенеративного теплооб-
мена заключается в отсутствии
деляющей теплоносители, что
чаев упрощает конструкцию,
лучшему использованию тепла
работать с малыми разностями темпера-
тур между теплоносителями.
Недостатками регенеративного теплооб-
мена является необходимость переключе-
ния регенераторов (или транспортирования
насадки в регенераторах с движущейся на-
садкой) и невозможность избежать неко-
торого смешения теплоносителей.
Регенераторы применяются преимуще-
ственно при высоких температурах тепло-
носителей (более 500° С), когда поверхно-
стные теплообменники, ‘ вследствие низкой
стойкости металла в данных условиях, ма-
ло пригодны. В этом случае насадку реге-
нераторов выполняют из огнеупорного кир-
пича. Такие регенераторы широко приме-
няются для подогрева воздуха (или горючего газа) теплом
отходящих топочных газов.
В последнее время регенераторы получили распространение
для теплообмена' между газами (стр. 557) в области низких
температур (до —200° С); в качестве насадки применяется алю-
миниевая лента.
выгружается через
Рис. 12-23. Схема ре-
генератора с движу-
щейся насадкой:
I, 2—регенераторы; 3, 4—
затворы; 5 —элеватор.
стенки, раз-
в ряде слу-
приводит к
и позволяет
Смесительные аппараты
В смесительных теплообменниках передача тепла от горячего
теплоносителя к холодному теплоносителю происходит путем их
непосредственного соприкосновения. Такие аппараты довольно
3Q Зак 54Q.
466
Гл 12 Нагревание и охлаждение
часто используются для охлаждения газов и конденсации паров
при соприкосновении их с водой, а также для охлаждения
воды при помощи воздуха. К смесительным аппаратам относятся
также подогреватели для жидкостей с обогревом острым па-
ром (стр. 412). Наибольшее распространение имеют так назы-
ваемые конденсаторы смешения, предназначенные для конден-
сации водяного пара. Их устройство и работа будут рассмо-
трены ниже (стр. 506).
В смесительных теплообменниках, в которых происходит
соприкосновение газа и воды, наряду с теплообменом протекает
процесс массообмена, заключающийся либо в испарении воды
в газ, либо, наоборот, — в конденсации влаги из газа. Испаре-
ние воды (увлажнение газа) происходит при соприкосновении
с водой сравнительно сухого газа. При соприкосновении же
с водой газа с большим содержанием водяных паров происхо-
дит конденсация этих паров (осушка газа). Более подробно
процессы массообмена рассмотрены в главе 16.
Одним из основных факторов, определяющих работу смеси-
тельных аппаратов, является поверхность соприкосновения теп-
лоносителей, которая должна быть возможно большей. Для по-
лучения значительной поверхности соприкосновения в аппарате
либо помещается насадка, либо устраиваются полки, причем
жидкость постепенно перетекает с одной полки на другую, либо
жидкость распыливается на мелкие капли. Конструктивно такие
теплообменники оформляются обычно в виде колонн, не отли-
чающихся по своему устройству от скрубберов, применяемых
для очистки газов (стр. 336).
Глава 13
ВЫПАРИВАНИЕ
1. Общие сведения
При кипении растворов нелетучих веществ * в паровую фазу
переходит только растворитель. При этом по мере испарения
растворителя и удаления его в виде паров концентрация рас-
твора, т. е. содержание в нем растворенного нелетучего веще-
ства, повышается.
Процесс концентрирования растворов, заключающийся в
удалении растворителя путем испарения при кипении, назы-
вается выпариванием.
Большей частью из раствора удаляют лишь часть раствори-
теля, так как в выпарных аппаратах обычных конструкций упа-
ренный раствор должен оставаться в текучем состоянии. Пол-
ное удаление растворителя в таких аппаратах возможно в тех
случаях, когда растворенное вещество либо является жидким
(например, выпаривание растворов глицерина), либо при тем-
пературе процесса находится в расплавленном состоянии (на-
пример, выпаривание растворов аммиачной селитры или едкого
натра). Полное удаление растворителя из раствора возможно
также в некоторых аппаратах специальной конструкциии, на-
пример в распылительных сушилках (стр. 772).
В ряде случаев при выпаривании растворов твердых веществ
достигается насыщение раствора; при дальнейшем удалении
растворителя из такого раствора происходит кристаллизация,
т. е выделение из него растворенного твердого вещества.
Выпаривание широко применяется для повышения концен-
трации разбавленных растворов или выделения из них раство-
ренного вещества путем кристаллизации.
В промышленности в большинстве случаев выпариваются
водные растворы различных веществ; поэтому в дальнейшем
* Нелетучими веществами называют вещества, обладающие при темпера-
туре процесса ничюжно малым давлением пара, например большинство твер-
дых тел и некоторые высококипящие жидкости (серная кислота, глицерин
и др ).
30*
468
Гл. 13. Выпариваниё
рассматривается только выпаривание водных растворов. Од-
нако описываемые ниже выпарные аппараты и методы их рас-
чета применимы для выпаривания растворов с любыми раство-
рителями, а также для испарения чистых жидкостей.
2. Способы выпаривания
Для обогрева выпарных аппаратов применяют нагревающие
агенты, рассмотренные в главе 12 (стр. 411 и сл.). Наибольшим
распространением пользуется водяной пар. В некоторых слу-
чаях, когда необходимо проводить выпаривание при высокой
температуре, применяют топочные газы и высокотемпературные
нагревающие агенты (дифенильная смесь, перегретая вода,
масло); иногда используют электрический обогрев.
Нагревание выпариваемого раствора производится путем
передачи тепла от нагревающего агента через стенку, разде-
ляющую оба вещества, либо путем непосредственного соприкос-
новения веществ. Выпаривание путем непосредственного со-
прикосновения нагревающего агента с раствором применяется
только при обогреве топочными газами.
Выпаривание ведут как под атмосферным, так и под пони-
женным или повышенным давлением.
При выпаривании раствора под атмосферным давлением
образующийся так называемый вторичный (соковый) пар выпу-
скается в атмосферу. Такой способ выпаривания является наи-
более простым.
При выпаривании под пониженным давлением (при разре-
жении) в аппарате создается вакуум путем конденсации вто-
ричного пара в специальном конденсаторе и отсасывания из
него неконденсирующихся газов с помощью вакуум-насоса (по-
дробно о создании вакуума при выпаривании см. стр. 505).
Вакуум-выпарка позволяет снизить температуру кипения
раствора и применяется для выпаривания чувствительных к вы-
сокой температуре растворов (например, растворов органиче-
ских веществ), а также высококипящих растворов, когда темпе-
ратура нагревающего агента не дает возможности вести процесс
под атмосферным давлением. Использование вакуума позволяет
также увеличить разность температур между нагревающим
агентом и кипящим раствором, а следовательно, уменьшить по-
верхность теплообмена. Недостатком выпаривания в вакууме
является удорожание установки (дополнительные затраты на
конденсационное устройство) и ее эксплуатации (расход
воды на конденсатор, затрата энергии на вакуум-насос, рас-
ходы по обслуживанию, амортизация конденсационного
устройства). •
3. Устройство выпарных аппаратов
469
При выпаривании под повышенным давлением вторичный
пар может быть использован как нагревающий агент в подогре-
вателях, для отопления и т. п., а также для различных техно-
логических нужд. Выпаривание под давлением связано с повы-
шением температуры кипения раствора, поэтому применение
данного способа ограничено свойствами раствора и температу-
рой нагревающего агента.
Установки,состоящие изодиночного аппарата,вторичный пар
из которого не используется (при выпаривании под атмосферным
давлением или при разрежении) или используется вне аппа-
рата, называются однокорпусными выпарными установками.
Большим распространением пользуются многокорпусные вы-
парные установки, включающие несколько соединенных друг с
другом аппаратов (корпусов), работающих под давлением,
понижающимся по направлению от первого корпуса к послед-
нему. В таких установках можно применять вторичный пар,
образующийся в каждом предыдущем корпусе, для обогрева по-
следующего корпуса. При этом свежим паром обогревается
только первый корпус; образующийся в первом корпусе вторич-
ный пар направляется на обогрев второго корпуса, в котором
давление ниже, и т. д. Вторичный пар из последнего корпуса
поступает в конденсатор (если этот корпус работает при разре-
жении) или используется вне установки (если последний кор-
пус работает при повышенном давлении). Таким образом,
в многокорпусных выпарных установках осуществляется много-
кратное использование одного и того же количества тепла
(тепла, отдаваемого греющим паром в первом корпусе), что
позволяет сэкономить значительное количество потребляемого
свежего пара.
Многократное использование тепла возможно также в одно-
корпусных выпарных установках, если сжать вторичный пар при
помощи компрессора или пароструйного инжектора до давле-
ния, позволяющего применять пар для обогрева того же аппа-
рата, в котором этот пар образовался.
Выпарные установки с сжатием вторичного пара, называемые
аппаратами с тепловым насосом (или с термокомпрессией),
рассмотрены на стр. 501.
3. Устройство выпарных аппаратов
Общие сведения
Наибольшее распространение получили выпарные аппараты
с паровым обогревом, имеющие поверхность теплообмена, вы-
полненную из труб.
470
Гл. 13. Выпариваний
Выпарные аппараты с паровым обогревом состоят из двух
основных частей:
а) кипятильник (греющая камера), в котором расположена
поверхность теплообмена и происходит выпаривание раствора;
б) сепаратор — пространство, в котором вторичный пар от-
деляется от раствора.
Необходимость в паровом пространстве (сепараторе) соста-
вляет основное конструктивное отличие выпарных аппаратов от
теплообменников. В зависимости от характера движения кипя-
щей жидкости в выпарном аппарате различают:
1) выпарные аппараты со свободной циркуляцией;
2) выпарные аппараты с естественной циркуляцией;
3) выпарные аппараты с принудительной циркуляцией;
4) пленочные выпарные аппараты.
Выпарные аппараты со свободной
циркуляцией
В этих аппаратах неподвижный или медленно движущийся
раствор находится снаружи труб. В растворе возникают не-
упорядоченные конвекционные токи (свободная циркуляция),
обусловленные свободной конвекцией. К данной группе отно-
сятся аппараты, выполненные в виде чаш или котлов, поверх-
ность теплообмена которых образована стенками аппарата (см.
стр. 434). В настоящее время такие аппараты применяются ред-
ко, главным образом при выпаривании очень вязких жидко-
стей.
Змеевиковые выпарные аппараты аналогичны змеевиковым погружным
теплообменникам Греющий пар проходит по змеевику, а выпариваемая
жидкость находится снаружи. Змеевики полностью погружены в жидкость, .
Рис. 13-1. Выпарной аппарат
с горизонтальными трубами.
над уровнем которой остается объем, не-
обходимый для сепарации вторичного пара.
Эти аппараты работают неинтенсивно и
в настоящее время применяются лишь для
выпаривания вязких растворов при не-
больших масштабах производства, когда
не требуется большая поверхность тепло-
обмена Они могут быть использованы так-
же при применении греющего пара высоко-
го давления и при выпаривании агрессив-
ных жидкостей. В последнем случае зме-
евики изготовляются из химически стой-
кого материала, а внутренняя поверхность
аппарата снабжается защитным покрытием.
Выпарные аппараты с горизонтальными
трубами (пар пропускается по трубам,
жидкость — снаружи труб) могут быть из-
готовлены с значительными поверхностями
теплообмена — до 800 м2 и более (рис. 13-1).
Для компенсации удлинения труб и раз-
3 Устройство выпарных аппаратов
471
борки аппарата с целью очистки крепление труб в трубных решетках делают
на сальниках или применяют U-образные трубы.
Основным недостатком аппаратов этого типа является трудность очистки
межтрубного пространства, вследствие чего они непригодны для выпаривания
кристаллизующихся растворов. Кроме того, такие аппараты имеют невысо-
кий коэффициент теплопередачи, громоздки и требуют значительного коли-
чества металла для изготовления. В настоящее время они применяются редко
и вытесняются более совершенными конструкциями.
Выпарные аппараты с естественной
циркуляцией
Естественная циркуляция возникает в замкнутой системе, со-
стоящей из необогреваемой опускной (циркуляционной) трубы 1
(рис. 13-2) и обогреваемых подъемных (кипятильных) труб 2.
Если жидкость в подъемных трубах нагрета до кипения, то в
результате испарения части жидкости в этой
трубе образуется парожидкостная смесь, плот-
ность которой меньше плотности самой жидко-
сти. Таким образом, вес столба жидкости в
опускной трубе больше, чем в подъемных
трубах, вследствие чего происходит упорядо-
ченное движение (циркуляция) кипящей
жидкости по пути: подъемные трубы-* паро-
вое пространство->опускная труба-* подъ-
емные трубы и т. д. При циркуляции повы-
шается коэффициент теплоотдачи со стороны
кипящей жидкости и предохраняется поверх-
ность труб от образования накипи.
Для естественной циркуляции требуются
два условия: 1) достаточная высота уровня
жидкости в опускной трубе, чтобы уравнове-
сить столб парожидкостной смеси в кипятиль-
ных трубах и сообщить этой смеси необходи-
мую скорость; 2) достаточная интенсивность
Рис. 13-2. Схема
естественной цир-
куляции:
1 — циркуляционная
труба; 2 — кипятиль-
ная труба.
парообразования в кипятильных трубах, чтобы парожидкост-
ная смесь имела возможно малую плотность.
При небольшом уровне жидкости в опускной трубе паро-
жидкостная смесь не может подняться до верха кипятильных
труб; при этом не происходит циркуляции и работа аппарата
сопровождается резким снижением производительности и бы-
стрым покрыванием труб накипью. С повышением уровня жид-
кости возрастает скорость циркуляции и увеличивается коэф-
фициент теплопередачи. Однако возрастание коэффициента теп-
лопередачи происходит лишь при повышении уровня до неко-
торой определенной величины (оптимальный уровень), соответ-
ствующей покрытию кипятильных труб по всей их высоте
472
Гл. 13. Выпаривание
парожидкостной смесью. При дальнейшем повышении уровня
коэффициент теплопередачи несколько снижается, так как
вследствие возрастания давления внизу кипятильных труб жид-
кость начинает кипеть не в нижней их части, а немного выше.
Парообразование в кипятильных трубах определяется физи-
ческими свойствами раствора (главным образом вязкостью) и
разностью температур между стенкой трубы и жидкостью. Чем
I
Упаренный
раствор
Рис. 13-3. Выпарной аппарат
с центральной циркуляцион-
ной трубой:
/—корпус; 2— кипятильные трубы;
3— циркуляционная труба; 4 — сепара-
тор; 5 — отбойник.
ниже вязкость раствора и чем
больше разность температур, тем
интенсивнее парообразование и тем
больше скорость циркуляции. Для
достижения достаточной циркуляции
разность температур между грею-
щим паром и раствором должна
быть в среднем не ниже 7—10° С.
Оптимальный уровень жидкости
повышается с понижением разно-
сти температур и увеличением вяз-
кости раствора и находится опыт-
ным путем. Если при выпаривании
из раствора не выпадают кристал-
лы, оптимальный уровень обычно
составляет от ’Д до 3Д высоты ки-
пятильных труб.
Если при выпаривании из рас-
творов выпадают кристаллы (так
называемые кристаллизующиеся
растворы), уровень жидкости под-
держивают выше кипятильных труб
для того, чтобы, жидкость в них
перегревалась и закипала бы лишь
при выходе из труб в паровое про-
странство; при отсутствии кипения
в кипятильных трубах отпадает
главная причина выделения накипи.
Выпарной аппарат с центральной
циркуляционной трубой (рис. 13-3)
является одной из наиболее старых, но широко распростра-
ненных конструкций. Греющая камера состоит из ряда верти-
кальных кипятильных труб 2, обогреваемых снаружи паром. По
оси греющей камеры расположена циркуляционная труба 3 зна-
чительно большего диаметра, чем кипятильные трубы. Хотя в та-
ком аппарате циркуляционная труба обогревается снаружи паром,
раствор нагревается в ней значительно меньше, чем в кипятиль-
ных трубах. Это объясняется тем, что поверхность трубы пропор-
3. Устройство выпарных аппаратов
473
циональна ее диаметру, а объем жидкости в ней пропорционален
квадрату диаметра; таким образом, в циркуляционной трубе
объем жидкости на единицу поверхности трубы значительно
больше, чем в кипятильных трубах.
В аппаратах большой произво-
дительности вместо одной циркуля-
ционной трубы устанавливают не-
сколько труб меньшего диаметра.
Аппарат с центральной циркуля-
ционной трубой отличается просто-
той конструкции и легко доступен
для ремонта и очистки. В то же вре-
мя наличие обогреваемой циркуля-
ционной трубы снижает интенсив-
ность циркуляции.
По нормалям Главхиммаша аппараты
с центральной циркуляционной трубой вы-
полняют с поверхностью теплообмена 25,50,
100, 150, 250 и 350 м2; они снабжены кипя-
тильными трубами с наружным диаметром
38 или 57 мм (длиной от 2000 до 4000 мм)
и циркуляционной трубой диаметром около
‘/з диаметра аппарата
Выпарной аппарат с подвесной
греющей камерой показан на
рис. 13-4. Этот аппарат имеет грею-
щую камеру, снабженную кожу-
хом 2; роль циркуляционной трубы
выполняет кольцевой зазор между
корпусом аппарата и кожухом ка-
меры.
Греющий пар подводится в ка-
меру по трубе 4. Греющая камера
Греющий пар
Чпареннюй
раствор
Рис. 13-4. Выпаркой аппарат
с подвесной греющей камерой:
/—корпус; 2— кожух греющей ка-
меры; 3— кипятильные трубы; 4 — тру-
ба для подвода пара к греющей
камере.
может выниматься из аппарата для чистки и ремонта. В аппа-
рате имеются благоприятные условия для циркуляции, поскольку
кольцевое пространство со стороны корпуса не обогревается.
Недостатками являются усложнение конструкции и большие
габариты, так как часть площади сечения аппарата не исполь-
зуется из-за наличия кольцевого канала.
Аппараты с подвесной греющей камерой изготовляются с поверхностью
50, 75, 95 и 150 м2, кипятильные трубы имеют наружный диаметр 63,5 мм пои
длине оз 1300 до 1700 мм.
474
Гл 13 Выпариваниё
Выпарной аппарат с выносным кипятильником (риг 13-5)
широко применяется для выпарки кристаллизующихся и пеня-
щихся растворов и постепенно вытесняет аппараты других типов.
Аппарат имеет выносной кипятильник 1 и сепаратор 3 В ки-
пятильнике, состоящем из пучка труб, обогреваемых снаружи
паром, образуется парожидкостная смесь, поступающая в сепа-
ратор по трубе 2 В сепараторе происходит отделение вторичного
Рис 13-5 Выпарной аппарат с вы-
носным кипятильником
/—кипятильник, 2 —труба для парожидкост
ной смеси, 3 — сепаратор, 4 — циркуляционная
труба
пара от жидкости, которая по
циркуляционной трубе 4 воз-
вращается в кипятильник Тру-
бы кипятильника могут дости-
гать значительной длины (до
7 м), что способствует интен-
сивной циркуляции с увели-
чением длины труб возрастает
разность весов парожидкост-
ной смеси в них и жидкости в
циркуляционной трубе Распо-
ложение кипятильника отдель-
но от сепаратора удобно для
ремонта и чистки труб Часто
к сепаратору присоединяют
два или более кипятильников,
из которых один можно выклю-
чить для ремонта или очистки,
не останавливая всего аппа-
рата.
Аппараты с выносными кипятильниками выпускаются с поверхностью
100, 150, 250, 350 500, 700 и 900 м2, они имеют трубы с наружным диаметром
38 или 57 мм при длине от 3000 до 7000 мм
Выпарной аппарат для выпаривания концентрированных рас-
творов (рис 13 6), предложенный Р Е Левиным, состоит из
греющей камеры 1, над которой расположена камера вскипа-
ния 2 высотой около 3 м В верхней части камеры вскипания
размещены концентрические перегородки 3, образующие коль-
цевые каналы Из камеры вскипания парожидкостная смесь по-
ступает в сепаратор 5, откуда жидкость возвращается в грею-
щую камеру по циркуляционной трубе 4 через приемник для
кристаллов 6. В греющей камере происходит только подогрев
раствора, а кипит он в каналах между перегородками 3 Эти
перегородки упорядочивают поток вскипающей жидкости й пре-
пятствуют образованию пульсаций и вредных циркуляционных
юков в зоне кипения
3 Устройство выпарных аппаратов
475
В описанном аппарате достигается большая скорость цирку-
ляции (до 3,5 м!сек вместо 1 —1,5 м!сек в обычных аппаратах
с естественной циркуляцией). Это наряду с отсутствием кипения
Рис 13-6 Выпарной аппарат для концентриро-
ванных растворов
/—греющая камера, 2— камера вскипания, 3— концентри-
ческие перегородки, 4 — циркуляционная труба, 5 — сепара
тор, 6— приемник кристаллов
в трубах приводит к значительному уменьшению выделений на-
кипи на поверхности теплообмена Такой аппарат наиболее при-
годен для выпаривания концентрированных, кристаллизующихся
и вязких растворов
Выпарные аппараты с принудительной
циркуляцией
Для повышения интенсивности циркуляции и коэффициента
теплопередачи в последнее время стали применять аппараты
с принудительной циркуляцией На рис 13-7 показан такой
аппарат, снабженный наружной циркуляционной трубой 3.
476
Гл. 13. Выпаривание
Греющие
лар
Раствор
конденсат
2
Упаренный
раствор
Рис. 13-7. Выпарной аппарат
с принудительной циркуляцией:
/—кипятильник; 2— циркуляционный
насос; 3 — циркуляционная труба;
4 — сепаратор.
Циркуляция жидкости производится пропеллерным или цен-
тробежным насосом 2. Свежий раствор подается в нижнюю
часть кипятильника, а упаренный раствор отводится из нижней
части сепаратора. Уровень жидкости поддерживается несколько
ниже верхнего обреза кипятильных труб. Поскольку вся цирку-
ляционная система почти полностью заполнена жидкостью, ра-
бота насоса затрачивается не на
второу/шй подъем жидкости, а лишь на пре-
одоление гидравлических сопротив-
лений. Давление внизу кипятильных
труб больше, чем вверху, на вели-
чину давления столба жидкости в
трубах плюс их гидравлическое со-
противление. Ввиду этого на боль-
шей части высоты кипятильных
труб жидкость не кипит, а перегре-
вается по сравнению с температу-
рой кипения, соответствующей да-
влению в сепараторе. Закипание
происходит только на небольшом
участке верхней части трубы. Коли-
чество перекачиваемой насосом жид-
кости во много раз превышает ко-
личество испаряемой воды; поэтому
отношение массы жидкости к массе
пара в парожидкостной смеси, вы-
ходящей из кипятильных труб,
очень велико.
Принудительную циркуляцию
применяют также в аппаратах с
выносным кипятильником и в ап-
паратах других типов.
Скорость циркуляции жидкости
в кипятильных трубах принимают
равной 1,5—3,5 м/сек. Скорость
производительностью циркуляцион-
ного насоса и не зависит от уровня жидкости и парообразова-
ния в кипятильных трубах. Поэтому аппараты с принудительной
циркуляцией пригодны при работе с малыми разностями тем-
ператур между греющим паром и раствором (3—5° С) и при
выпаривании растворов с большой вязкостью, естественная цир-
куляция которых затруднительна.
Достоинствами аппаратов с принудительной циркуляцией
являются высокие коэффициенты теплопередачи (в 3—4 раза
больше, чем при естественной циркуляции), а также отсутствие
3 Устройство выпарных аппаратов
477
загрязнений поверхности теплообмена при выпаривании кри-
сталлизующихся растворов и возможность работы при неболь-
ших разностях температур.
Недостаток этих аппаратов — необходимость расхода энер-
гии на работу насоса.
Применение принудительной циркуляции целесообразно при
изготовлении аппарата из дорогостоящего материала (в этом
случае весьма существенно значитель-
ное сокращение поверхности теплооб-
мена вследствие повышения коэффи-
циентов теплопередачи), при выпари-
вании кристаллизующихся растворов
(сокращаются простои во время очист-
ки аппарата) и при выпаривании вяз-
ких растворов (что при естественной
циркуляции требует наличия большой
разности температур).
Пленочные выпарные
аппараты
В пленочных аппаратах раствор
движется вдоль поверхности теплооб-
мена в виде тонкой пленки.
Пленочные аппараты с вертикаль-
ными трубами (рис. 13-8) состоят из
пучка кипятильных труб, обогревае-
мых снаружи паром и присоединен-
ных вверху к сепаратору. Жидкость
подается снизу, причем уровень ее
поддерживается на V4—Vs высоты
труб. Остальная часть высоты труб
заполнена парожидкостной смесью,
Рис. 13-8. Пленочный вы-
парной аппарат:
/—кипятильник; 2 —сепаратор.
расслаивающейся на пленку жидкости
(около стенок) и пар (в центре). Трением о струю пара жидкая
пленка увлекается вверх; поэтому такие аппараты часто назы-
вают аппаратами с поднимающейся пленкой.
Пленочные аппараты обладают высоким коэффициентом
теплопередачи. Последний, однако, достигается лишь при опре-
деленном уровне жидкости, который устанавливается опытным
путем: при повышении уровня коэффициент теплопередачи сни-
жается; при понижении уровня уменьшается содержание
жидкости в парожидкостной смеси, что приводит к недостаточ-
ному смачиванию верхних концов труб и снижению активной
поверхности теплообмена. Ввиду однократного прохождения
478
Гл. 13. Выпаривание
жидкости через аппарат с значительной скоростью, для полу-
чения достаточно концентрированного упаренного раствора тре-
буются длинные трубы (обычно 6—9 л).
Недостатками вертикальных пленочных аппаратов являются
трудность очистки длинных труб и сложность регулирования
процесса при колебаниях давления греющего пара и начальной
концентрации раствора. Кроме того, для размещения пленочных
аппаратов необходимо строить производственные здания боль-
шой высоты.
Эти аппараты применяются для выпаривания пенящихся,
а также чувствительных к высокой температуре растворов; при
выпаривании очень вязких и кристаллизующихся растворов они
мало пригодны.
Пленочные аппараты изготовляются с поверхностью тепло-
обмена от 100 до 900 л2.
4. Эксплуатация выпарных аппаратов
Процесс выпаривания может производиться периодически или непре-
рывно. При периодическом, выпаривании в аппарат заливается определенное
количество раствора, который нагревается до кипения (период подогрева),
после чего начинается процесс выпаривания (период испарения воды). В про-
цессе выпаривания непрерывно повышаются концентрация и температура
кипения раствора, так как последняя зависит от концентрации (см. стр. 479).
По мере испарения воды уровень раствора в аппарате понижается. Выпари-
вание ведут до достижения заданной конечной концентрации раствора.
Понижение уровня раствора часто нарушает работу аппарата, поэтому
описанный способ проведения процесса обычно видоизменяют следующим
образом, начиная с момента закипания раствора, в аппарат непрерывно по-
дают слабый раствор в таком количестве, чтобы уровень раствора не изме-
нялся. При этом способе работы (выпаривание при постоянном уровне)
получаемый в конце операции упаренный раствор занимает тот же объем,
что и первоначально залитый в аппарат слабый раствор.
При непрерывном выпаривании уровень раствора и его температура не
изменяются во времени Раствор обычно находится в аппарате при своей
конечной концентрации (или очень близкой к ней); для устойчивой работы
в аппарате должно содержаться значительное количество жидкости, чтобы
поступление слабого раствора не снижало заметно концентрацию раствора,
находящегося в аппарате.
Для создания таких условий аппарат заполняют при пуске слабым
раствором и доводят его концентрацию до конечной путем периодического
выпаривания при постоянном уровне (или сразу заполняют аппарат концен-
трированным раствором), после чего переходят на непрерывную подачу сла-
бого раствора с отводом соответствующего количества упаренного раствора.
Пленочные выпарные аппараты применяются только для непрерывной
работы, они не содержат значительного объема раствора, который непре-
рывно протекает через аппарат, причем его концентрация и температура из-
меняются вдоль поверхности теплообмена.
При обслуживании выпарных аппаратов необходимо следить за поддер-
жанием уровня жидкости на определенной высоте (стр 471). В аппаратах
периодического действия уровень жидкости регулируется подводом слабого
5 Расчет быпарных аппаратов
479
раствора, а в аппаратах непрерывного действия — отводом упаренного рас-
твора. Количество слабого раствора в аппаратах непрерывного действия
поддерживается постоянным и регулируется в зависимости от концентрации
упаренного раствора’ если последняя понижается, то подачу слабого рас-
твора надо уменьшить, и наоборот. Для отбора проб упаренного раствора
на выпарных аппаратах устанавливают специальные пробные краны.
Процесс выпаривания сильно зависит от температуры, которая контроли-
руется термометром, измеряющим температуру раствора в аппарате, мано-
метры измеряют давление греющего и вторичного пара. Необходимый темпе-
ратурный режим устанавливается регулированием подачи греющего пара.
Кроме того, при обслуживании выпарного аппарата следят за правильным
отводом конденсата и неконденсирующихся газов. Конденсат отводится при
помощи конденсатоотводчиков (стр. 412). Для отвода неконденсирующихся
газов, содержащихся в греющем паре, в верхней части пространства для
греющего пара имеется трубка, через которую эти газы непрерывно или
периодически удаляются.
Периодически, по мере загрязнения поверхности теплообмена, выпарной
аппарат останавливают для очистки. Очистка производится путем промывки
или указанными выше способами (стр. 440).
5. Расчет выпарных аппаратов
Температура кипения растворов
Давление пара растворителя над раствором всегда ниже, чем
давление над чистым растворителем. Вследствие этого тем-
пература кипения раствора выше температуры кипения чистого
растворителя при том же давлении. Нап-ример, вода кипит под
атмосферным давлением при 100° С, так как давление ее пара
при этой температуре равно 1 а/п;для30% раствора NaOH дав-
ление водяного пара над раствором будет при 100° С ниже 1 ат,
и раствор закипит при более высокой температуре (117°С),
когда давление пара над ним достигнет 1 ат.
Разность между температурами кипения раствора (f) и чи-
стого растворителя (-О’) называется температурной депрессией-
b' = t — &
Температурная депрессия зависит от свойств растворенного
вещества и растворителя; она повышается с увеличением кон-
центрации раствора и давления. Определяется температурная
депрессия опытным путем (большинство опытных данных отно-
сится к температурной депрессии при атмосферном давлении).
Если известна температурная депрессия при атмосферном
давлении Да™-, можно найти депрессию и при других давлениях
по приближенной формуле Тищенко:
Т2
Д' = 16,2-у- Датм- (13-1)
где Т и г—абсолютная температура кипения (в °К) и теплота
испарения (в дж}кг) для воды при данном давлении.
480
Гл. 13. Выпаривание
/'г
Обозначая величину 16,2 — через k, получим:
Д' £Датм-
(13-2)
Значения k в зависимости
от давления приведены ниже:
Абсолютное
давление, ат 0,06 0,08
k............. 0,64 0,665
Абсолютное
давление, ат 0,6 0,8
k.............0,91 0,95
0,1 0,15
0,69 0,73
1 1,5
1 1,07
0,2 0,3
0,76 0,81
2 2,5
1,14 1,19
0,4 0,5
0,85 0,88
3 4
1,23 1,32
Повышение температуры кипения раствора определяется не
только температурной депрессией, но также гидростатической
и гидравлической депрессиями.
Гидростатическая депрессия вызывается тем, что нижние
слои жидкости в аппарате закипают при более высокой темпе-
ратуре, чем верхние (вследствие гидростатического давления
верхних слоев). Если, например, нагревать при атмосферном
давлении воду до температуры кипения в трубе высотой 10 м, то
верхний слой воды закипит при температуре 100° С, а нижний
слой, находящийся под давлением 2 ат, — при температуре
~120° С. В данном случае гидростатическая депрессия изме-
няется по высоте трубы от 0°С (вверху) до 20° С (внизу) и в
среднем составляет 10° С. Расчет гидростатической депрессии
в выпарных аппаратах невозможен, так как жидкость в них
(в основном в виде парожидкостной смеси) находится в движе-
нии. С повышением уровня жидкости в аппарате гидростати-
ческая депрессия возрастает. В среднем она составляет 1—3°С.
Гидравлическая депрессия учитывает повышение давле-
ния в аппарате вследствие гидравлических потерь при прохо-
ждении вторичного пара через ловушку и выходной трубопро-
вод. При расчетах Д'" принимают равной 1° С.
При кипении чистой воды температурный напор равен раз-
ности температуры греющего пара и температуры кипящей воды,
которая в этом случае равна температуре насыщения вторичного
пара. При кипении раствора температура насыщения вторичного
пара, соответствующая давлению в аппарате, не изменяется, а
температура кипения раствора повышается на величину депрес-
сии. Следовательно, на ту же величину депрессии уменьшается
и температурный напор. Таким образом, депрессия вызывает
потерю температурного напора, вследствие чего ее называют
температурной потерей. Полная депрессия Д равна сумме тем-
пературной, гидростатической и гидравлической депрессий:
Д = Д' + Д"-|- Д'" (13-3)
5. Расчет выпарных аппаратов
481
Температура кипения раствора t определяется, в зависимо-
сти от температуры насыщения вторичного пара О', по формуле:
/=л-4-д
(13-4)
Пример 13-1. Определить температуру кипения 40%-ного раствора NaOH
при абсолютном давлении 0,196 бар (0,2 ат).
Решение. Температурная депрессия для раствора при атмосферном
давлении Датм- = 28° С.Поправочный коэффициент k =« 0,76 (при 0,2 ат).
Следовательно, температурная депрессия при абсолютном давлении 0,2 ат
Д' = 28 • 0,76 = 21,3° С
Принимаем гидростатическую депрессию Д" = 3°С и гидравлическую
депрессию Д'" = 1°С. Полная депрессия
Д = 21,34-34-1 =25,3° С
Температура кипения воды при 0,2 ат составляет &«» 59,7° С. Темпера-
тура кипения раствора
t = 59,7 4- 25,3 = 85е С
Материальный баланс выпарного аппарата
Обозначим начальное (до выпарки) и конечное (после вы-
парки) количество раствора (в кг) через Gx и G2, его началь-
ную и конечную концентрацию (в весовых долях) через и а2
и количество выпаренной воды (в кг) через W. Тогда можно
написать уравнения материального баланса по всему количе-
ству вещества:
Gx — G2-\-W (13-5)
и по растворенному веществу:
G^ — G2a2 (13-6)
В приведенные уравнения входят пять величин; три вели-
чины должны быть заданы, а остальные две можно определить
из этих уравнений. Обычно бывают известны G\, а\ и а2, тогда,
решая совместно уравнения (13-5) и (13-6), находим:
> Gi#i
2 а2
(13-7)
(13-8)
W=Gl-G2^Gi(\-^
\ а2 /
Уравнение (13-8) дает возможность определить количество
выпаренной воды.
31 Зак 546.
482
Гл. 13. Выпаривание
Иногда бывают заданы Gb W и аг, тогда из уравнений (13-5)
и (13-6) вычисляют конечную концентрацию раствора:
03-9)
а из уравнения (13-5) находят G2.
Пример 13-2. На выпаривание поступает G\ = 25 000 кг/ч раствора NaOH
концентрацией а{ — 28 вес. %. Конечная концентрация раствора
<22 = 40 вес. %. Определить количество выпаренной воды и упаренного
раствора.
Решение. Количество выпаренной воды вычисляем по формуле (13-8):
W =25 000 (1 — ^ = 7500 кг/ч
Количество упаренного раствора составляет
О2 = 25 000 — 7500 = 17 500 кг/ч
Пример 13-3. На выпаривание поступает Gi—40 000 кг/ч раствора
koi центрацией а\ = 8 вес. %. Количество выпаренной воды
W = 18000 кг/ч, Определить концентрацию и количество упаренного рас-
твора
Решение. Концентрацию упаренного раствора находим по фор-
муле (13-9):
40 000 - 0,08 Л1._
° 40000-18000 ^ °'146’ или 14’6 вес %
Количество упаренного раствора-
G2 = 40000—18000 = 22000 кг/ч
Тепловой баланс выпарного аппарата
Составим уравнение теплового баланса выпарного аппарата
для выпариваемого раствора:
Приход тепла
Отдается нагревающим
агентом............ Q
С поступающим раство-
ром ..............
Расход тепла
С вторичным паром . . Wl
С уходящим раствором G2c2t
На дегидратацию . . . 0дег.
Потери в окружающую
среду............... Qn
Таким образом
Q4-GiCi/0= Wi+G2c2t -j- Qaer. + Qn (13-10)
где сх и c2 — удельные теплоемкости поступающего и уходя-
щего растворов, дж/кг • град',
t0 и I— температуры поступающего и уходящего раство-
ров, град',
i — энтальпия вторичного пара, дж/кг*
5. Расчет выпарных аппаратов
483
Теплота дегидратации представляет собой затрату тепла на
повышение концентрации раствора; она равна по величине и
обратна по знаку теплоте разбавления раствора. Таким образом,
если при разбавлении раствора водой выделяется тепло, то при
его концентрировании тепло поглощается. Обычно теплота деги-
дратации невелика и поэтому не учитывается.
Рассматривая поступающий раствор как смесь упаренного
раствора и испаренной воды, можно написать:
Gxc\t — О2с<^ 4- WcBt
откуда
G2c2 = G]C\ —
где св — удельная теплоемкость воды, дж}кг • град.
Подставляя значение G2c2 в уравнение (13-10), получим
Q = G]C\ (t — tQ) 4- W (i — cBt) 4- Qfler. 4“ Qn
Если пренебречь теплотой дегидратации и потерями тепла,
то предыдущее уравнение запишется в виде
Q = Gxcx (t -t0) 4- W (i - cBt) (13-11)
В этом уравнении член Gict(i—Zo) представляет собой рас-
ход тепла на подогрев поступающего раствора до температуры
кипения, а член W(i— cBt)—расход тепла на испарение воды.
Входящая в уравнение теплового баланса удельная теплоем-
кость раствора может быть подсчитана в зависимости от его
концентрации а по приближенной формуле
==^TBa-hcB(l — а) (13-12)
где ств,— удельная теплоемкость безводного твердого раство-
ренного вещества.
Энтальпия вторичного пара i принимается равной энтальпии
насыщенного водяного пара при давлении в аппарате и нахо-
дится по справочным таблицам.
Определив по уравнению (13-11) расход тепла на выпарива-
ние (тепловую нагрузку аппарата), вычисляют расход греющего
пара обычным способом (стр. 440).
В первом приближении, пренебрегая расходом тепла на по-
догрев раствора и приравнивая разность (г — cBt) к теплоте ис-
парения, можно найти, что расход греющего пара равен коли-
честву выпариваемой воды, т. е. с помощью 1 кг греющего пара
выпаривается 1 кг воды. В действительности, с учетом затраты
тепла на подогрев раствора, расход греющего пара выше и со-
ставляет 1,1—1,2 кг,
31*
484
Гл. 13. Выпаривание
Пример 13-4. Определить расход тепла и греющего пара на выпарива-
ние раствора NaOH. Количество поступающего раствора Gi = 25 000 кг/ч,
его начальная концентрация ai — 28 вес. %, конечная концентрация
а2 = 40 вес. %. Температура поступающего раствора'/о = 60° С. Абсолютное
давление в аппарате равно 0,196 бар (0,2 ат). Абсолютное давление грею-
щего пара составляет 1,37 бар (1,4 ат), его температура Т = 108,7° С.
Решение. При конечной концентрации температура кипения раствора
/ = 85°С (см. пример 13-1), а количество выпаренной воды W = 7500 кг/ч
(см. пример 13-2). Удельная теплоемкость 28%-ного раствора NaOH
G = 3560 дж/кг • град (0,85 ккал/кг • град). При 0,2 ат энтальпия вторичного
пара г = 2610’103 дж/кг (622 ккал/кг). Расход тепла при св = 4190 дж/кг X
X град находим по уравнению (13-11):
Q = • 3560 (85 - 60) 4- (2610 • 10’ - 4190 • 85)
ак 5 300 000 вт (4 560 000 ккал/ч)
Расход греющего пара при 1,4 ат и теплоте испарения г=2240* Ю3 дж/кг
(534 ккал/кг)
~ 5 300 000 .
D = 2240'Л03~ “ 2,37 1 = 8530 К
Определение поверхности теплообмена
Необходимая поверхность теплообмена выпарного аппарата
определяется по общему уравнению (12-21) в зависимости от
тепловой нагрузки Q. Температурный напор 9 принимается рав-
ным разности температуры насыщения греющего пара Т и тем-
пературы кипения раствора t, т. е.
Q^T — t
Коэффициент теплопередачи рассчитывается обычным спо-
собом (стр. 446); он зависит главным образом от удельной теп-
ловой нагрузки (т. е. в конечном счете от температурного на-
пора), от температуры и концентрации раствора. С повышением
концентрации раствора, а также с понижением температуры
возрастает вязкость, что приводит к уменьшению коэффициента
теплопередачи.
Коэффициент теплоотдачи со стороны кипящей жидкости в выпарных
аппаратах со свободной циркуляцией и в аппаратах с естественной циркуля-
цией при оптимальном уровне определяется по формуле (11-57). При этох1
высота оптимального уровня раствора /Опт., соответствующая наибольшему
значению а, рассчитывается по приближенной зависимост1Г
= 0,26 + 0,0014 (р - Рв) (13-13)
где Н—высота трубы, м;
Р и рв — плотность раствора и воды, кг/м3.
5. Расчет выпарных аппаратов
485
Рис. 13-9. Зависимость скорости
циркуляции от оптимального
уровня раствора.
Скорость циркуляции Доо (в м/сек) определяется в зависимости от отно-
шения - гр- по рис. 13-9.
п
В аппаратах с принудительной циркуляцией, учитывая, что на большей
части высоты труб жидкость не кипит, коэффициент теплоотдачи можно вы-
числить по формуле (11-35) для нагревания
жидкостей в трубах.
При расчете аппаратов с большим объ-
емом жидкости (аппараты с естественной,
свободной и принудительной циркуляцией)
физические свойства кипящей жидкости
и температуру ее кипения следует опре-
делять по конечной концентрации рас-
твора; в пленочных аппаратах эти вели-
чины находят по средней концентрации
раствора.
Пример 13-5. Определить поверхность
теплообмена выпарного аппарата с есте-
ственной циркуляцией для выпарива-
ния раствора NaOH в условиях примера
13-4.
Решение. Принимаем аппарат с вер-
тикальными трубами диаметром 33/38 мм;
количество труб п = 944 (пар движется сна-
ружи труб). Плотность стекания конденсата
по наружной поверхности труб (количество
составляет по формуле (6-84):
8530
г = ~з . q Q3g 944 = 76 кг/м ч — 0,021 кг/м • сек.
греющего пара равно 8530 кг/ч)
Константы для конденсата (воды) при 108,7° С:
плотность............р = 952 кг/м3;
вязкость.............р = 0,26 • 10-3 н • сек/м2 (0,26 спз);
теплопроводность . . X = 0,683 вт/м • град (0,589 ккал/м • ч • град)
Критерий Re пл. находим по формуле (6-85):
= 325
0,26 • 10"3
^епл.
Приведенную толщину пленки вычисляем по формуле (11-47):
_ / (0,26 • 10"3)2\'/з
ПРИВ- \ 9522 - 9,81 /
м
Так как Еепл. < 400, то расчет ведем по формуле (11-52):
N“-“^=°’27
Коэффициент теплоотдачи от конденсирующегося пара равен:
0 683
ai = Y • 0,27 — 9400 вт/м2 град (8100 ккал/м2 • ч • град)
486
Гл. 13. Выпаривание
Коэффициент теплоотдачи для кипящего раствора «2 = 4<7°’6 (см. при-
мер 11-13, стр. 399).
Поскольку плотность теплового потока неизвестна, то задаемся несколь-
кими значениями q и строим нагрузочную характеристику (рис. 13-10), как
Рис. 13-10. Нагрузочная характе-
ристика выпарного аппарата.
описано в примере 12-7 (стр. 447).
При ЭТОМ ПРИНЯТО ''загр. ~
= 0,00043 м2 • град/впг (со стороны рас-
твора) ; тогда полное тепловое сопротив-
ление при S =0,0025 м и X—45 вт/м • град
(40 ккал/м • ч • град) составляет:
_ 1 - 8 । л , 1 1 (
Г cq ‘ X +Гзагр.-Г а2 — 9400 +
+ + 0,000434-А = 0,0005924- —
40 ^*2 ^*2
Значения q, а также вычисленные
значения «2, г и 0ср. приведены в
табл. 18.
В рассматриваемом случае 0ср. =
= 108,7 — 85 = 23,7° С и соответствую-
щее значение q— 18 400 в/п/л12. Таким
образом, коэффициент теплопередачи
k = = 775 вт/м2 • град
2о,7
(или 670 ккал/м2 • ч • град)
Необходимая поверхность теплообмена (при Q = 5 300 000 вт) равна:
F=^0e 290 ^
7/0 • 2о,/
Длина труб при расчете F по внутреннему диаметру труб составляет!
/______29® _2 97 и
1 “ 3,14 • 0,033 • 944 - ’
Принимаем I = 3 м.
Таблица 18
Определяемая величина Размерность q, вт!м.г
15 000 20 000 25 000
«2 = 4?0-6 вт/м2 • град 1280 1520 1740
г = 0,000592 4 Л- м2 • град/вт 0,00137 0,00125 0,00117
0ср. = град 20,6 25 29,2
5. Расчет выпарных аппаратов
487
Найденный коэффициент теплопередачи соответствует оптимальному
уровню раствора, который рассчитывается по формуле (13-13) при плот-
ности раствора р =• 1390 кг/м3:
=х 0,26 4- 0,0014 (1390 — 1000) ag 0,8, или 80%
' откуда /Опт. — 3 • 0,8 = 2,4 м. Скорость циркуляции по рис. 13-9 равна
; о>о = 0,8 м/сек.
s Количество циркулирующего раствора
J ~dl
Сц=3600 nte>op = 3600 • 0,785 • 0,033» 944 • 0,8 • 1390 =± 3 230 000 кг/ч
$ Кратность циркуляции
i Gn 3230000 q ‘
ft “ 25 000
t Сепарация вторичного пара
f В паровом пространстве происходит отделение (сепарация) вторичного
? пара от выпариваемого раствора. При недостаточной сепарации наблюдается
4 унос в паропровод частиц жидкости (в виде тумана, отдельных капель или
§ пены) вместе с вторичным паром. Унос приводит к потере продукта. При
использовании вторичного пара в последующих корпусах или других нагре-
4 вательных аппаратах растворенное вещество, содержащееся в каплях рас-
твора, осаждается на поверхности теплообмена и загрязняет ее; конденсат
* пара также загрязняется растворенным веществом и становится непригодным
„ для питания паровых котлов.
< Величина уноса зависит от свойств выпариваемого раствора и интенсив-
Л ности парообразования. Низкое поверхностное натяжение и высокая вяз-
| кость раствора способствуют пенообразованию, т.“е. образованию тонких и
v стойких пленок жидкости вокруг пузырьков пара. Кристаллизующиеся рас-
( творы не склонны к образованию устойчивой пены. Присутствие в растворе
взвешенных частиц сообщает пене устойчивость. Для уменьшения ценообра-
зования к раствору иногда добавляют вещества, повышающие поверхностное
натяжение (например, масла); раствор, поступающий на выпаривание, под»-
вергают предварительному фильтрованию для удаления взвешенных веществ.
Унос может происходить и без образования пены в результате подбра-
сывания жидких капель в паровое пространство и механического захвата
частиц жидкости паром. Для предотвращения этого скорость вторичного
пара в паровом пространстве должна быть невелика, а высота паро-
вого пространства должна быть достаточно большой, чтобы увлеченные паром
капли жидкости осели под действием силы тяжести. Высоту парового про-
странства обычно принимают не менее 1,5 м, а при выпаривании сильно пе-
нящихся жидкостей — от 2,5 до 3 м.
Необходимый объем парового пространства V м3 находят по формуле:
W
(13-14)
где W — количество выпариваемой воды, кг/ч\
d — допустимое напряжение парового пространства (т. е. количество
выпариваемой воды на 1 м3 парового пространства), кг/м3’Ч.
Допустимое напряжение парового пространства зависит от давления и
способа ввода парожидкостной смеси, При вводе парожидкостной смеси
488
Гл. 13. Выпаривание
в паровое пространство ниже уровня раствора (например, в выпарном аппа-
рате на рис. 13-3 с уровнем раствора выше кипятильных труб) допустимые
напряжения меньше, чем в случае ввода смеси над уровнем
Значение d приближенно можно определить по формуле:
rf=/1/2rfa™- (13-15)
где rfaTM- — значение d при 1 ат, составляющее для чистой воды
2600 кг/ж2 • ч, а для растворов солей 1000 кг/м? • ч.
При выпаривании пенящихся растворов rfa™' уменьшают примерно в
2 раза.
Значения fi в зависимости от давления приведены ниже:
Абсолютное
давление, ат <С0,4 0,6 0,8 1 1,5 2 2,5 3 4
.......... 0,85 0,87 0,92 1 1,35 1,7 2,05 2,4 3,1
Значения /г в зависимости от уровня Hw раствора над точкой ввода
парожидкостной смеси в паровое пространство составляют:
м.................... 0 0,05 0,1 0,15 0,2 0,3 0,4 0,5
/2 ....................... 1 0,83 0,69 0,59 0,51 0,4 0,32 0,27
Для улучшения сепарации пара испарители снабжаются ловушками
(брызгоуловителями). Действие ловушек аналогично инерционным и центро-
бежным аппаратам для очистки газов (стр. 326 сл.); отделение брызг жид-
кости от пара происходит в результате резкого изменения скорости и напра-
вления движения пара или под действием центробежной силы.
6. Многокорпусные выпарные установки
Принцип действия
В многокорпусной выпарной установке вторичный пар ка-
ждого корпуса (кроме последнего) используется для обогрева
следующего корпуса. Давление от корпуса к корпусу умень-
шается так, чтобы температура кипения раствора в каждом кор-
пусе была ниже температуры насыщения пара, обогревающего
этот корпус.
Применение многокорпусных выпарных установок дает зна-
чительную экономию пара. Если приближенно принять, что с
помощью 1 кг греющего пара в однокорпусном аппарате выпа-
ривается 1 кг воды, то в многокорпусной выпарной установке
на 1 кг греющего пара, поступившего в первый корпус, прихо-
дится количество килограммов выпаренной воды, равное числу
корпусов, т. е. расход греющего пара на выпаривание 1 кг воды
обратно пропорционален числу корпусов.
Так, в двухкорпусной выпарной установке одним килограм-
мом греющего пара, поступившим в первый корпус, выпари-
вается в нем 1 кг воды, а образовавшимся при этом одним ки-
лограммом вторичного пара выпаривается во втором корпусе
еще 1 кг воды; таким образом, всего на 1 кг греющего пара
6. Многокорпусные выпарные установки
489
выпаривается 2 кг воды, а расход пара на 1 кг выпариваемой
воды составляет 0,5 кг. Аналогично можно найти, что расход
греющего пара на 1 кг выпариваемой воды в трехкорпусной вы-
парной установке составляет 0,33 кг, в четырехкорпусной —
0,25 кг и т. д.
Действительный расход греющего пара на 1 кг выпаривае-
мой воды несколько выше и в среднем составляет (в кг):
В однокорпусной выпарной установке ... 1,1
В двухкорпусной » » ... 0,57
В трехкорпусной » » ... 0,4
В четырехкорпусной » » ... 0,3
В пятикорпусной » ... 0,27
Вторичный пар, образующийся в каждом корпусе, можно не
целиком направлять на обогрев следующего корпуса, а частично
отводить на сторону и использовать для предварительного по-
догрева раствора, поступающего на выпаривание, или для дру-
гих технологических целей, не связанных с выпариванием. От-
водимый на сторону вторичный пар называется экстра-паром.
Экстра-пар может быть отобран из любого корпуса, кроме по-
следнего. Из последнего корпуса не производят отбора экстра-
пара, так как вторичный пар оттуда направляется в конденса-
тор; если же выпаривание ведется под давлением, вторичный
пар можно полностью использовать вне выпарной установки.
Преимущество отбора заключается в том, что возрастание
расхода греющего пара при отборе экстра-пара меньше, чем
количество отбираемого экстра-пара; целесообразнее отбирать
экстра-пар не из первых, а из последующих корпусов (стр. 497).
В многокорпусных выпарных установках экономия пара до-
стигается за счет увеличения поверхности теплообмена. Срав-
ним, например, однокорпусную и двухкорпусную установки, ра-
ботающие при одинаковой температуре греющего пара, равной
110° С и одинаковом вакууме в конденсаторе, соответствующем
температуре конденсации вторичного пара 50° С.
В этом случае, пренебрегая температурными потерями, по-
лучим для однокорпусной установки температурный напор
110 — 50 = 60° С. В двухкорпусной установке температура ки-
пения в первом корпусе должна быть выше 50° С и ниже 110° С;
примем ее равной 80° С, так что температурный напор в первом
корпусе будет ПО — 80 = 30° С, а во втором корпусе составит
80 — 50 — 30° С. Тепловая нагрузка каждого корпуса двухкор-
пусной установки в 2 раза меньше нагрузки однокорпусной
установки, температурный напор в каждом корпусе тоже в
2 раза меньше. Следовательно, поверхность каждого корпуса бу-
дет такой же, как поверхность однокорпусного аппарата. Полная
поверхность обоих корпусов двухкорпусной установки будет
490
Гл 13 Выпаривание
в 2 раза больше, чем поверхность однокорпусного аппарата. Об-
общая этот вывод, можно сказать, что поверхность многокор-
пусной установки больше поверхности однокорпусной в число
раз, равное количеству корпусов. Если учесть температурные
потери, то увеличение поверхности теплообмена многокорпусной
установки будет еще больше.
В приведенном примере температура кипения в первом кор-
пусе была выбрана произвольно для того, чтобы получить рав-
ные температурные напоры по корпусам. В действительности
температуры кипения по корпусам устанавливаются сами со-
бой в зависимости от поверхности отдельных корпусов и коэф-
фициентов теплопередачи в них. Если, например, в одном из
корпусов коэффициент теплопередачи понизится, то поступаю-
щий на обогрев этого корпуса вторичный пар из предыдущего
корпуса не будет полностью конденсироваться и давление (а
следовательно, и температура) в предыдущем корпусе повы-
сится, пока не установится новое распределение температур.
Таким образом, температуры в отдельных корпусах при ра-
боте установки не регулируются. Единственной возможностью
регулирования этих температур является изменение отбора экс-
тра-пара. При увеличении отбора экстра-пара из какого-либо
корпуса количество пара, поступающего на обогрев следующего
корпуса, уменьшится и температура в нем понизится.
Схемы многокорпусных выпарных установок
В зависимости от способа подачи раствора различают сле-
дующие основные схемы многокорпусных выпарных установок.
Схема с прямоточным питанием (рис. 13-11) имеет наиболь-
шее распространение. Слабый раствор подается в первый кор-
пус, из него поступает во второй, из второго в третий и т. д. Та-
ким образом, раствор и вторичный пар движутся в одном на-
правлении. Раствор переходит из одного корпуса в другой вслед-
ствие разности давлений в корпусах. Так как температура ки-
пения в каждом последующем корпусе понижается, то раствор
поступает во все корпуса (кроме первого) с температурой бо-
лее высокой, чем температура кипения. В результате раствор
охлаждается (член, входящий в уравнение теплового баланса
и выражающий расход тепла на подогрев раствора, будет от-
рицательным) и за счет отдаваемого при этом тепла испаряется
некоторое количество воды (самоиспарение). Однако при пи-
тании первого корпуса холодным раствором значительное коли-
чество греющего пара в этом корпусе затрачивается на подогрев
раствора. Поэтому при прямоточном питании целесообразно по-
давать в первый корпус предварительно подогретый раствор
6. Многокорпусные выпарные установки
491
(путем установки подогревателей, обогреваемых экстра-паром
или конденсатом).
Недостаток схемы с прямоточным питанием заключается в
том, что в последнем корпусе, где температура кипения самая
низкая, выпаривается наиболее концентрированный раствор.
Одновременное понижение температуры и повышение концен-
трации раствора приводит к повышению вязкости и снижению
Рис. 13-11. Схема трехкорпусной .выпарной уста-
новки с прямоточным питанием
(буквенные обозначения см стр 496 сл )
коэффициентов теплопередачи; поэтому в данной схеме коэф-
фициенты теплопередачи уменьшаются от первого корпуса к
последнему.
При схеме с противоточным питанием (рис. 13-12) слабый
раствор подается в последний корпус, из него в предпоследний
и т. д.; следовательно, раствор и вторичный пар движутся из
корпуса в корпус в противоположных направлениях. Так как
в этом случае раствор поступает из корпуса с меньшим давле-
нием в корпус с более высоким давлением, то для передачи
раствора между корпусами устанавливаются насосы.
При противоточном питании наиболее высокая концентра-
ция раствора достигается в первом корпусе, где и температура
кипения наибольшая. Поэтому значительного падения коэффи-
циента теплопередачи в корпусе с наиболее концентрированным
раствором не происходит и коэффициенты теплопередачи мало
изменяются по корпусам. Это является наиболее существенным
преимуществом противоточного питания перед прямоточным.
Кроме того, при противоточном питании количество воды, вы-
париваемой в последнем корпусе, меньше, чем при прямоточном
питании, что уменьшает нагрузку на конденсатор (при выпарке
402
Гл 13. Выпаривание
в вакууме). В отношении расхода тепла противоточное питание
выгоднее прямоточного при питании холодным раствором, но
уступает ему при питании горячим раствором.
Упаренный
раствор
Рис. 13-12. Схема трехкорпусной выпарной уста-
новки с противоточным питанием.
6,-Н2-Н3
Основным недостатком противоточной схемы является не-
обходимость в установке насосов между корпусами, что связано
с дополнительным расходом электроэнергии, усложняет уста-
новку и затрудняет ее регулирование.
Раствор
упаренный раствор
Рис. 13-13. Схема трехкорпусной выпарной уста-
новки с параллельным питанием.
При схеме с параллельным питанием (рис. 13-13) слабый рас-
твор подается одновременно во все корпуса, а упаренный рас-
твор отбирается из всех корпусов. Эта схема применяется редко,
6 Многокорпусные выпарные установки
493
главным образом при незначительном повышении концентрации
раствора и при выпаривании кристаллизующихся растворов, так
как передача их из корпуса в корпус в этом случае затрудни-
тельна вследствие возможного закупоривания перепускных тру-
бопроводов и арматуры.
Полезная разность температур и ее
распределение по корпусам
В многокорпусной выпарной установке сумма температур-
ных напоров для всех корпусов равна так называемой общей
полезной разности температур, т. е. разности температуры грею-
щего пара, поступающего в первый корпус (Г^, и температуры
насыщения вторичного пара из последнего корпуса ($„) за вы-
четом суммы температурных потерь по корпусам (SA):
0пол=01 + 02+ ... 4-бл=71~»л-ЕД (13-16)
где 62, 6п — температурные напоры для I, II, .... /г-го
корпусов;
£Д = Д14~ Дг 4~ ••• 4~ Ал
Др Д2, Дл— температурные потери в I, II, п-м
корпусах.
В справедливости соотношения (13-16) можно убедиться,
составив для каждого корпуса выражения для температурного
напора и сложив их. Так, для двухкорпусного аппарата
6i = 71 — /1 = 7Х — (&! 4- Д1)
62 = 7^2 — ^2 ~ Тч — (&2 4~ А2)
где tx и /2— температуры кипения в I и II корпусах;
71 и 72 — температуры греющего пара для I и II корпусов;
&1 и &2 — температуры насыщения вторичного пара в I и II
корпусах.
Складывая выражения для 01 и 02 и замечая, что 64 = Г2,
получим:
4- 62 — 7\ &2 (^i 4- ^2) — 7\ — &2 —
Как указывалось выше, общая полезная разность темпера-
тур распределяется по отдельным корпусам в соответствии с
поверхностями и коэффициентами теплопередачи в этих корпу-
сах. При расчете многокорпусной выпарной установки 6ПОЛ. целе-
сообразно распределить по корпусам так, чтобы поверхности
всех корпусов были одинаковыми, что упрощает и удешевляет
494
Гл. 13. Выпаривание
изготовление и обеспечивает взаимозаменяемость аппаратов и
их деталей при~ эксплуатации. Иногда 9ПОЛ. распределяют так,
чтобы общая поверхность всех корпусов была наименьшей.
Распределение 0Пол. ПРИ одинаковых поверхностях всех корпусов. В этом
случае /71 = F2 = ... = Fn = F. Полезная разность температур в каждом
корпусе составляет:
о _ Ql 1 . о _
61 “02“
Qz 1 . п ______Qn 1
k2 * F ’ •” п~~ kJ F
(A)
Складывая эти равенства, получим:
01+02+ ••• +0"=^(дг+’^М
fl - 1 V Q
«ПОЛ. - -р
(Б)
Определяя из равенства (Б) величину -р- и подставляя полученное зна-
(А), находим:
Qz Qn
бцол.» ~ VI-6ПОЛ>’ • • • = ' бпол. (13-17)
чение в уравнения
Qi
61 =
Распределение 6Пол. ПРИ наименьшей общей поверхности. Для этого слу-
чая разности температур в каждом корпусе должны удовлетворять следую-
щим соотношениям:
‘,==27Т'-:
т/- ^2 1/^~ Qn
02 = к'ч Г~сГ 0ПОЛ>’ "" * 0Л ” Г~с\ 0ПОЛ’ (13-18)
2/4 2/4
Распределение 6ПОЛ. при наименьшей общей поверхности и одинаковых
поверхностях всех корпусов. Можно показать, что соблюдение этого условия
возможно при равенстве разностей температур во всех корпусах, т. е.
е, = о,= ,,..ел=^
где п — число корпусов
Из уравнения (А) и (В) при этом условии следует:
Q\ = Qz _ _ On
k2 kД
Qi: Qz ’ ’ Qn — k\‘. k2‘. ... :kn
т. e. тепловые нагрузки корпусов должны быть прямо пропорциональны
коэффициентам теплопередачи в них. Это условие можно выполнить
только при определенном количестве отбираемого экстра пара; если
экстра-пар может найти применение, то данный способ распределения раз'
ности температур является наиболее целесообразным,
или
(B)
I Qn \
f kJ
6. Многокорпусные выпарные установки
495
Выбор числа корпусов
С увеличением числа корпусов повышается экономичность
установки. Однако число корпусов нельзя увеличивать беспре-
дельно, так как при этом уменьшается полезная разность тем-
ператур в каждом корпусе.
Пусть, например, разность температур (7\— &л) составляет
80° С, а температурные потери в каждом корпусе равны 10° С
(для простоты принимаем их равными для всех корпусов)-
Тогда при двух корпусах полезная разность температур соста-
вит 80 — 2 «10 = 60° С, а на каждый корпус (при распределении
9Пол. по корпусам поровну) будет 60 : 2 = 30° С.
Аналогично найдем, что полезная разность температур на
корпус составит:
в трехкорпусной установке
80-3-10 _
3 “
в четырехкорпусной установке
80-4-10 _
4 “
в пятикорпусной установке
80-5-10 _
5
16,7° С
10° С
Отсюда следует, что при применении аппаратов с естествен-
ной циркуляцией (принимая для каждого корпуса 6 = 10° С)
в данном случае можно установить лишь 4 корпуса, а при ис-
пользовании аппаратов с принудительной циркуляцией (при
6 = 5° С) — 5 корпусов. Дальнейшее увеличение числа корпусов
приводит к уменьшению полезной разности температур до 3,3° С
при 6 корпусах и до 1,4° С при 7 корпусах. При 8 корпусах ве-
личина 6Пол. становится равной нулю.
С увеличением температурных потерь и снижением разности
температур возможное число корпусов уменьшается. Для аппа-
ратов с принудительной циркуляцией оно выше, чем для аппа-
ратов с естественной циркуляцией.
Во многих случаях устанавливают меньшее число корпусов,
чем это возможно. Дело в том, что с увеличением числа корпу-
сов затраты на сооружение установки растут приблизительно
пропорционально числу корпусов, а расходы тепла умень-
шаются (стр. 489) сравнительно медленно. Так, например, При
496
Гл. 13. Выпаривание
переходе от двухкорпусной установки к трехкорпусной расход
пара на 1 кг выпариваемой воды уменьшается на 0,57—0,4 =
Рис. 13-14. Определение наи-
выгоднейшего числа корпусов.
= 0,17 кг, а при переходе от четы-
рехкорпусной установки к пятикор-
пусной на 0,3 — 0,27 = 0,03 кг.
Если отложить по оси абсцисс
число корпусов (рис. 13-14), а по
оси ординат — расходы на аморти-
зацию установки (линия АВ) и рас-
ходы на пар (кривая CD), то, скла-
дывая ординаты обеих линий, полу-
чим кривую MN, выражающую об-
щие расходы на выпаривание. Как
видно из рис. 13-14, кривая MN
имеет минимум, соответствующий
наивыгоднейшему числу корпусов,
при котором общие расходы будут
наименьшими.
На практике наиболее распространены выпарные установки
с 2—4 корпусами. Установки с числом корпусов более 5 встре-
чаются редко.
7. Расчет многокорпусной выпарной установки
Расчет многокорпусной выпарной установки довольно сложен; поэтому
вначале обычно производят приближенный расчет, а затем выполняют точ-
ный расчет.
Приближенный расчет. При этом расчете принимают, что на 1 кг грею-
щего пара приходится 1 кг выпариваемой воды, т. е. расход греющего пара
на каждый корпус равен количеству образующегося в нем вторичного пара.
Пусть в последнем корпусе выпарной установки с числом корпусов п выпа-
ривается Wn кг воды, а из предпоследнего (п—1)-го корпуса отбирается
£л_1 кг экстра-пара. Тогда в (п—1)-м корпусе должно выпариваться
Wn-{-Eri_l кг воды. При отборе из (п—2)-го корпуса Еп_2 кг экстра-пара
в этом корпусе должно выпариваться Wn-\~ Еп_2кг воды и т. д.
Таким образом, количества воды, выпариваемой по корпусам, соста-
вляют:
wn = wn
Wn^ = Wn-\-En^
IF„_2=U7„ + £„_i + £„_2
1Г2 = 1Гл + Е/1_1 + Ел_2+ ... +е2
1Г1 = и7л + £л_1 + £л_2+ ... +^2 + ^1
(13-19)
Складывая почленно эти уравнения, получим общее количество воды,
выпаренное в установке:
1Г = пГл+(п-1)^1 + (Л^2)£л„г+ ... 4-2^ + ^
7. Расчет многокорпусной выпарной установки 497
I Отсюда можно определить количество воды, выпариваемое в последнем
| корпусе:
I W — %) Еп-2 ••• %Е2 Ej (13-20)
и далее по уравнениям (13-19) рассчитать количества воды, ^выпариваемые
1 в каждом корпусе. При отсутствии отбора экстра-пара Wn — т. е. коли-
* чество выпариваемой воды по всем корпусам одинаково.
Расход греющего пара на первый корпус равен количеству воды, выпа-
' риваемой в этом корпусе, т. е.
* D = W = W — (п — \) Еп_{ — (п — ‘2.) Еп_2 — ... -2£2-£t
к 1 1 п . ~Г
I +Еп-1 + Еп-2+ ... +^-+^
< или
Из уравнения (13-21) следует, что расход греющего пара, затрачивае-
мого на получение экстра-пара, меньше, чем количество образующегося
экстра-пара. При этом расход греющего пара на получение экстра-пара
уменьшается по мере удаления точки отбора экстра-пара от первого корпуса.
Так, в четырехкорпусной выпарной установке (п = 4)
р1 = -т + 1^+т£2 + т£з
т. е. на 1 кг экстра-пара, отбираемого из первого корпуса, затрачивается
0,75 кг греющего пара, а на, 1 кг экстра-пара, отбираемого из второго и
третьего корпусов, — соответственно 0,5 и 0,25 кг греющего пара.
Точный расчет. Для определения расхода греющего пара на первый
корпус и количеств выпаренной воды по корпусам надо составить уравнения
теплового баланса для каждого корпуса и решить их совместно. Ниже при-
водятся эти уравнения в случае трехкорпусной установки с прямоточным
питанием (см. рис. 13-11):
для I корпуса Dtr = Glcl (£, —10) + G'i — cb^i)
для II корпуса (Wi—^i)(/i —cB&i) = (G1 —IT^Ca^ —^i) +
-|- 1^2 0*2 — CBf2)
для III корпуса (IF2 — E2)(i2 — cB&2) =
= (Gj - Wx - IT2) c3 (Z3 -12) + W3 (ia - cBt3)
(13-22)
В приведенную систему трех уравнений входят 4 неизвестных: Dlt Wlf
W2 и W3. Необходимое для решения системы четвертое уравнение имеет вид
W =
32 Зак 546.
498
Гл. 13. Выпаривание
В уравнениях (13-22), кроме обозначений, приведенных на рис. 13-11,
принято:
г — теплота испарения греющего пара для I корпуса, дж/кг;
с1г с2, с3— удельные теплоемкости раствора, поступающего в I, II и III кор-
пуса, дж/кг • град;
ii, г’г» г'з — энтальпии вторичного пара из I, II и III корпусов, дж/кг;
t\, h, h— температуры кипения раствора в I, II и III корпусах;
$i> ^2> — температуры насыщения вторичного пара из I, II и III корпусов;
t0 — температура раствора, поступающего на выпаривание;
св — удельная теплоемкость воды, дж/кг • град.
Разработаны более общие методы расчета многокорпусных выпарных
установок *, позволяющие вести расчет с той или иной степенью точности.
Пример 13-6. Рассчитать трехкорпусную выпарную установку с прямо-
точным питанием для выпаривания раствора NaOH. Количество поступаю-
щего раствора Gi = 13,9 кг/сек (50 000 кг/ч), его начальная концентрация
Oq = 0,1, конечная концентрация п3 = 0,4. Температура поступающего рас-
твора /о = 25° С; температура греющего пара для I корпуса 1\ = 140° С;
температура насыщения вторичного пара из III корпуса &з = 60°С. Отбор
экстра-пара производится для подогрева раствора.
Определение количества выпариваемой воды:
W = 13?9 (1 — = 10,4 кг/сек (37 500 кг/ч)
\ ид /
Определение расхода экстра-пара. Принимаем темпера-
туру подогрева раствора равной 115° С; тогда расход тепла на подогрев
Рпод. = 13,9 • 3860 (115 — 25) = 4 820 000 вт (4 150 000 ккал/ч)
где 3860 дж/кг-град — удельная теплоемкость поступающего раствора
(0,92 ккал/кг • град).
Так как параметры экстра-пара пока неизвестны, принимаем, что его
теплота испарения составляет 2260.103 дж/кг (540 ккал/кг), что соответ-
ствует абсолютному давлению 1 ат; тогда расход экстра-пара составит:
Е = 2260 Л05’ = 2,14 Кг{сек (770° Кг^
Это количество надо распределить между экстра-паром, отбираемым из
I корпуса (£i) и из II корпуса (£2). Распределение может быть сделано
более или менее произвольно, причем выгоднее, чтобы отбор из II корпуса
был больше, чем из I корпуса (стр. 497). Принимаем:
Е, =0,75 кг/сек (2700 кг/ч) Е2 = 1,39 кг/сек (5000 кг/ч)
Приближенный расчет. По уравнениям (13-20)) и (13-19)
U7—2£2 —Е, 10,4 — 2.1,39 — 0,75 , /ОПСА /ч
1Г3 =-------L --------= 2,29 кг/сек (8250 кг ч)
О о
W2 = 1Г3 4- Е2 = 2,29 + 1,39 == 3,68 кг/сек (13 250 кг/ч)
W{ = W — W2 — W3 = 10,4 — 3,68 — 2,29 = 4,43 кг/сек (16 000 кг/ч)
* М. А. Кичигин, Г. Н. Костенко, Теплообменные аппараты и вы-
парные установки, Госэнергоиздат, 1955; И. И. Чернобыльский, Выпар*
ные установки, Изд. Киевского университета, I960,
7. Расчет многокорпусной выпарной установки 499
Определяем концентрации раствора после I и II корпусов:
13,9-0,1
а2 - 13|9 _ 4 43 _ 3 08 ~
Определение полезного температурного напора и
распределение его по корпусам. Принимаем гидростатическую де-
прессию Д" = 2°С и гидравлическую депрессию Д'" =1°С. Температурные
депрессии находим при конечной концентрации раствора в каждом корпусе,
причем для III корпуса вносим поправку на давление. Для первых двух
корпусов, работающих под давлением, близким к атмосферному, поправкой
на давление пренебрегаем. Определенные таким путем температурные потери
составляют:
Д1=г8,4°С; Д2 = 14,7° С; Д3 = 24,3°С; 2Д = 47,4°С
Полезный температурный напор
6П0Л. = 140 — 60 — 47,4 = 32,6° С
или на корпус (при распределении поровну)
39 л
6j = 62 = 63 = —у-10,9° С
Распределение температур по корпусам приведено в табл. 19.
Таблица 19
Корпус Темпера- тура насыще- ния греющего пара °C Температура кипения раствора °C Температура насыщения вто- ричного пара °C Энтальпия кдж!кг (ккал!кг)
греющего пара вторичного пара
I 140 140—10;9 == 129,1 129,1— 8,4 = 120,7 2730 (653,3) 2710 (647,2)
II 120,7 120,7-10,9= 109,8 109,8—14,7 = 95,1 2710(647,2) 2670 (637,9)
III 95,1 95,1—10,9 ® 84,3 84,3—24,3 = 60 2670 (637,9) 2610 (623,5)
Точный расчет. Удельные теплоемкости поступающего в корпуса
раствора.
с, = 3860 дж!кг • град (0,92 ккал]кг • град}
с2 = 3770 дж]кг • град (0,9 ккал!кг • град)
с3 = 3690 дж]кг • град (0,88 ккал/кг • град)
Составляем уравнения теплового баланса:
D (2730 • 103 — 4190 • 140) = 13,9 • 3860 (129,1 — 115) +
+ (2710 • 103 — 4190 • 129,1)
(Wx 0,75) (2710 • 103 — 4190 • 120,7) = (13,9 — . 3770 (109,8 —129,1) +
+ W2 (2670 • 103 — 4190 • 109,8)
(UZ2 _ 1,39) (2670 • 103 — 4190 • 95,1) = (13,9 — Wx — 1Г2) • 3690 (84,3 — 109,8)
+ U73 (2610 • 103 — 4190 • 84,3)
4- W3 = 10,4
32*
500
Гл. 13. Выпаривание
Отсюда находим:
=4,17 Kzjcetc (15 050 кг/ч) 1Г2 = 3,7 кг{сек (13 350 кг!ч)
IF3 = 2,53 кг/сек (9100 кг!ч) £> = 4,65 кг/сек (16 750 кг!ч)
Перераспределение полезного температурного на-
пора по корпусам. Перераспределение производим из расчета одина-
ковых поверхностей корпусов. Для коэффициентов теплопередачи приняты <
следующие значения:
kx — 1620 вт!м2 • град (1400 ккал!м2 ч град)
k2 = 1275 вт]м2 град (1100 ккал[м2 ч град)
k3 = 695 вт/м2 • град (600 ккал[м2 • ч • град)
Тепловые нагрузки по корпусам:
Qx = 4,65 (2730 • 103 — 4190 • 140) = 9 970 000 вт (8 600 000 ккал{ч)
Q2 = (4,17 — 0,75) (2710 - 103 — 4190 • 120,7) = 7 540 000 вт (6 500 000 ккал/ч)
Q3 = (3,7 — 1,39) (2670 • Ю3 — 4190 • 95,1) = 5 260 000 вт (4 530 000 ккал{ч)
= 19 600
Находим отношения:
-§£ = 6150; -§1 = 5900; -§1 = 7550;
«1 ^2 «3
Температурные напоры по корпусам определяем из уравнения (13-17):
_ 6150 • 32,6 _ |q 2° с
“ 19 600
5900-32,6
02 “ 19 600 =9’8 С
63 = 32,6 — 10,2 — 9,8 = 12,6° О
Так как температурные напоры по корпусам мало отличаются от приня-
тых ранее, то пересчета можно не делать.
Определение поверхнопей теплообмена;
₽ 9 970 000 „пп „
Fl ~ 1620 • 10,2 600 М
р 7 540 000 Rnn ,
F2 = -T275T9J^ 600 м2
р 5260000 __ ,
Лз “ 695 • 12,6 = 600
Расчет подогревателей. Отбирается экстра-пар двух пара-
метров, поэтому устанавливаем два подогревателя, через которые раствор
проходит последовательно. Чтобы достигнуть возможно большего подогрева,
второй по ходу раствора подогреватель должен обогреваться экстра-паром
из I корпуса, имеющим более высокую температуру. Экстра-паром из II кор-
пуса обогревается раствор в первом по ходу раствора подогревателе.
Тепловая нагрузка первого подогревателя:
Q' = 1,39 (2720 • 103 — 4190 • 95,1) = 3 160 003 вт (2 720000 ккал!ч) =
= 13,9 • 3860 (Г — 25)
Отсюда температура раствора после подогревателя f = 84°С,
8. Выпарные установки с тепловым насосом
501
Тепловая нагрузка второго подогревателя:
Q" = 0,75 (2670 • 103 — 4190 • 120,7) = 1 650 000 вт (1 420 000 ккал{ч) =
= 13,9 • 3860 (t" — 84)
откуда температура раствора после подогревателя t" = 115° С.
Температура t" совпадает с принятой ранее (см. стр. 498), а темпера-
тура раствора после каждого подогревателя ниже температуры насыщения
экстра-пара, обогревающего подогреватель. Если эти условия не соблю-
даются, надо произвести пересчет, задавшись другой температурой подогрева
раствора и изменяя распределение отбора экстра-пара по корпусам.
8. Выпарные установки с тепловым насосом
Для сжатия пара приме-
раствор
Рис. 13-15. Выпарная уста-
новка с механическим тепло-
вым насосом:
7 —выпарной аппарат; 2 — турбоком-
прессор.
В выпарных аппаратах с тепловым насосом (или с термо-
компрессией вторичного пара) вторичный пар сжимается до
давления греющего пара и используется для обогрева того же
аппарата, в котором он образуется “
няют компрессоры или пароструй-
ные инжекторы. Таким образом в
тепловых насосах, или трансформа-
торах тепла, затрачиваемая извне
энергия используется для повыше-
ния температуры вторичного пара.
В механических тепловых насо-
сах пар сжимается с помощью тур-
бокомпрессора; при малых произ-
водительностях применяют ротаци-
онные компрессоры. На рис. 13-15
показана однокорпусная выпарная
установка с сжатием всего вторич-
ного пара в компрессоре. При пу-
ске аппарата раствор подогревается
свежим паром до кипения, после
чего выпаривание производится за
счет работы, затрачиваемой в комп-
рессоре (механическое выпарива-
ние). При этом теоретически добавки свежего пара не тре-
буется; на практике, в связи с расходом тепла на подогрев
раствора и потерями в окружающую среду, обычно добавляют
немного пара со стороны.
Мощность, затрачиваемую в компрессоре, находят по форму-
лам, приведенным на стр. 219 сл.; при этом работу сжатия
(в дж1кг) для адиабатического процесса определяют по фор-
муле (7-34). Эту работу можно найти также при помощи диа-
граммы I—S для водяного пара как адиабатический перепад
при сжатии пара от давления pi до давления р2 (рис. 13-16).
502
Гл. 13. Выпаривание
Рис. 13-16. Процесс сжатия вторичного пара на
диаграмме / — S (к примерам 13-7 и 13-8):
АВ — сжатие вторичного пара от Pi = l ат до ат;
CD —расширение рабочего пара от р9 —12 ат до Pi = l атг
Рис. 13-17. Выпарная установка с пароструйным
тепловым насосом:
1 — выпарной аппарат; 2 —инжектор.
8. Выпарные установки с тепловым насосом
503
В пароструйных тепловых насосах рабочий пар высокого
давления р0 расширяется в сопле инжектора и засасывает вто-
ричный пар давления pi; из инжектора выходит смесь паров
при некотором среднем давлении р2. При применении пароструй-
ного инжектора образуется избыток вторичного пара, который
может быть использован для обогрева последующих корпусов
многокорпусной выпарной установки (рис. 13-17).
Преимуществом пароструйных тепловых насосов перед ме-
ханическими является простота устройства, дешевизна и надеж-
ность в работе. Поэтому пароструйные насосы пользуются наи-
большим распространением.
Расход пара высокого давления в пароструйных насосах находят, исходя
из величины коэффициента инжекции (отношение количества засасываемого
пара G" к количеству рабочего пара высокого давления G'):
Коэффициент инжекции определяют по формуле:
и = ]/Г (13-23)
где h — адиабатический перепад при расширении рабочего пара от давле-
ния ро до давления pi, дж/кг-,
т]а—внешний к. п.д. инжектора, равный Ча = 4i42Ti3 (Ч1> Чг и чз — к. п.д.
сопла, камеры смешения и диффузора; при расчетах принимают
’ll = 0,9; 42 = 0,8; Чз = 0,7—0,8).
После сжатия в компрессоре или пароструйном инжекторе пар стано-
вится перегретым и, перед поступлением на обогрев аппарата, обычно про-
пускается через увлажнитель. В последний подается вода, которая, соприка-
саясь с паром и испаряясь за счет теплоты перегрева, переводит пар в насы-
щенное состояние.
Если на увлажнение поступает Gi кг!сек перегретого пара с энталь-
пией Л дж[кг и подается вода с температурой t и удельной теплоемкостью
св дж!кг • град, то после увлажнения, как можно вывести из теплового ба-
ланса увлажнения, количество насыщенного пара с энтальпией /2 дж/кг
составляет:
/ __Р i
О2 = Gi ~т---Л" (13-24)
/ 2 ~ Св*
Затраты работы на сжатие пара повышаются с увеличением
разности давлений, а следовательно, и разности температур на-
сыщения греющего и вторичного пара. При этом работа при-
близительно пропорциональна указанной разности температур.
Так как эта разность равна температурному напору плюс де-
прессия, то затрата работы возрастает с увеличением депрес-
сии раствора. На практике применение тепловых насосов целе-
сообразно при депрессии не более 10—12° С.
504
Гл. 13. Выпаривание
Пример 13-7. Рассчитать однокорпусную выпарную установку с тепло-
вым насосом (турбокомпрессор) при следующих условиях: количество выпа-
риваемой воды IF = 0,555 кг/сек, (2000 кг/^); тепловая нагрузка
Q— 1 390 000 вт (1 200 000 ккал/ч)\ абсолютное давление в аппарате
Pi = 0,98 бар (1 ат)-, абсолютное давление греющего пара Рг = 1,96 бар
(2 ат).
Решение. Расход греющего пара при теплоте испарения
г = 2210 - 103 дж/кг (527 ккал/кг) равен:
_ 1 390 000 _ „„„ . /ооол / \
D = ~2210~Лдт = 0,633 кг!сек <2280 кг!4^
При 1 ат энтальпия вторичного пара й = 2680‘103 дж/кг (639 ккал/кг)'.
По диаграмме I — S (рис. 13-16) находим, что энтальпия пара после сжатия
t*2 = 2820*103 дж/кг (672 ккал/кг), откуда адиабатический перепад при сжа-
тии пара
Z = 2820 • 103 — 2680 • 103 = 140 • 103 дж/кг 33 ккал/кг)
Мощность, затрачиваемая в компрессоре при сжатии 0,555 кг/сек вто-
ричного пара (при -^ад. = 0,93 и т)мех> = 0,85), составляет:
У =
0,555 • 140 • 103 л0
1000 • 0,93 • 0,85 = 98 Квт
Энтальпия греющего пара (насыщенный при 2 am) t = 2710-k yt/кг
(646,9 ккал/кг). Если на увлажнение сжатого пара подается вода с темпе-
ратурой t — 40° С, то количество греющего пара, образуемого из сжатого
вторичного пара при Г — is = 2820- 103 дж/кг и Л = * = 2710 • 103 дж/кг, на-
ходим по формуле (13-24):
_ 0,555 (2820 • 103 — 4190 • 40) л с_0 . ,олол ..
°2 “ 2710 • 103 — 4190 40 ~ 0,578 Кг1 еК (208° Кг1^
Количество добавляемого свежего пара равно 0,633 — 0,578 = 0,055 кг/сек
(200 кг/ч).
Пример 13-8. Определить расход рабочего пара на пароструйный инжек-
тор в условиях примера 13-7, если абсолютное давление рабочего пара
Ро = Н.8 бар (12 ат), а его температура составляет 300° С.
Решение. По диаграмме I — S (рис. 13-16) находим адиабатический
перепад при расширении рабочего пара до pi = 1 ат-.
/г = 494 • 103 дж/кг (118 ккал/кг)
При I — 140 • 103 дж/кг (см. пример 13-7), и принимая T]i = 0,9, т]2 — 0,8
и т]з = 0,8, по формуле (13-23), определяем коэффициент инжекции:
/ 4Q4.103
и = V 0,9 • 0,8 0,8 Г?.j”-, - 1 0,435
Г 140 • 10d
Энтальпия смеси паров после инжектора составляет:
+ 3040 103 -4- 0,435 • 2680 103 ол„л 1Л, , , .
i — —1 —----------/ -----------= 2930 • 103 дж/кг (700 ккал/кг)
1 —W 1 0,435
где i0 = 3040- 103 дж/кг (727 ккал/кг) —энтальпия рабочего пара;
Ц = 2680- 103 дж/кг (639 ккал/кг) —энтальпия вторичного пара.
Количество смеси после увлажнения должно равняться расходу грею-
щего пара, т. е. G2 = 0,633 кг/сек (2280 кг/ч)9
9. Создание вакуума в выпарных установках
505
Если температура и теплоемкость воды,, поступающей на увлажнение
смеси, равны t = 40° С и св = 4190 дж/кг -град, то из уравнения (13-24)
найдем количество увлажняемой смеси:
__ G2 (Z2 — св0 _ 0,633 (2710 • 103 — 4190 • 40) _
G1 Л — cBt 2930 • 103 — 4190 • 40 “
= 0,583 кг/сек (2100 кг/ч)
Расход рабочего пара
G' = = —j ^^'435 ~ 0’406 кг/сек (1460 кг/ч)
Количество засасываемого инжектором вторичного пара
G" = 0,583 — 0,406 = 0,177 кг/сек (640 кг/ч)
Остальное количество вторичного пара, равное 0,555—0,177’= 0,378 кг/сек
(1360 кг/ч), не подвергается термокомпрессии и может быть использовано
в последующих корпусах многокорпусной выпарной установки.
9. Создание вакуума в выпарных установках
х>илуум в выпарных установках создается в результате кон-
денсации вторичного пара в конденсаторах, охлаждает : во-
дой. ^Теоретически абсолютное давление в’конденсаторе должно
быть равно давлению насыщенного пара при температуре кон-
денсации. Однако в конденсатор вместе с паром поступает не-
которое количество воздуха, выделяющегося из выпариваемой
жидкости. Кроме того, воздух проникает через неплотности в
аппаратуре и трубопроводах; если конденсация производится в
конденсаторах смешения (путем непосредственного соприкосно-
вения с водой), воздух приносится с охлаждающей водой. В при-
сутствии воздуха давление в конденсаторе равно сумме парци-
альных давлений пара и воздуха, т. е. давлению насыщенного
пара плюс парциальное давление воздуха. Таким образом, ва-
куум в конденсаторе от подсоса воздуха ухудшается, и воздух
необходимо удалять при помощи вакуум-насосов. Обычно в
конденсаторах выпарных установок поддерживают абсолютное
давление, равное 0,1—0,2 ат (соответствует температуре кон-
денсации 45—60° С).
Устройство конденсаторов. Различают поверхностные кон-
денсаторы и конденсаторы смешения.
В поверхностных конденсаторах пар отделен от охлаждаю-
щей воды стенкой. Эти конденсаторы по устройству аналогичны
поверхностным теплообменникам (обычно применяются кожухо-
трубные конденсаторы) и используются в тех случаях, когда
конденсат необходимо сохранить в чистом виде.
506
Гл. 13. Выпаривание
В конденсаторах смешения пар конденсируется при непосред-
ственном соприкосновении с водой,.так что образующийся кон-
денсат смешивается с водой и удаляется вместе с ней. Вслед-
ствие простоты конструкции эти конденсаторы получили широ-
кое распространение и применяются во всех случаях, когда кон-
денсат не используется.
В зависимости от направления движения пара и воды кон-
денсаторы смешения разделяются на прямоточные и противо-
точные, а в зависимости от высоты расположения — на конден-
саторы низкого и высокого уровня.
Рис. 13-18. Прямоточный конденсатор.
Прямоточные конденсаторы применяются для выпарных уста-
новок небольшой и средней производительности и обычно разме-
щаются на низком уровне.
В этих конденсаторах (рис. 13-18) пар и вода движутся в од-
ном направлении (сверху вниз), а смесь воды и конденсата
откачивается насосом. Так как конденсатор расположен на низ-
ком уровне, то охлаждающая вода поступает в него не с по-
мощью насоса, а засасывается под действием имеющегося
в конденсаторе вакуума. Если абсолютное давление в конденса-
9. Создание вакуума в выпарных установках
507
Рис. 13-19. Противоточ-
ный барометрический
конденсатор.
I торе составляет 0,1—0,2 ат (т. в. вакуум равен 0,8—0,9 ат, что
1 соответствует 8—9 м вод. ст.), то ввод воды должен быть рас-
я положен не выше 5—6 м над уровнем засасываемой воды для
I того, чтобы обеспечить необходимый остаточный напор (2—3 м)
1 для распыливанйя воды при входе ее в
конденсатор. Воздух отсасывается ваку-
ум-насосом сверху, как показано н-а
рис. 13-18, или удаляется вместе с водой
и конденсатором при помощи специаль-
ного мокровоздушного насоса.
Противоточные конденсаторы приме-
шь няются для выпарных установок боль-
Г| шой производительности. Они распола-
1 j гаются обычно на высоком уровне, при-
F чем удаление смеси воды и конденсата
производится через опускную (баромет-
рическую) трубу. Высота столба жидко-
сти в барометрической трубе уравнове-
шивает атмосферное давление, и жидкость
вытекает из нее в сборник (барометриче-
ский ящик). Нижний конец барометриче-
ской трубы должен быть опущен ниже
( уровня жидкости в барометрическом
, > ящике, образуя гидравлический затвор,
J препятствующий засасыванию атмосфер-
' | ного воздуха в конденсатор. Высота ба-
\ рометрической трубы (стр. 510) должна
I1 быть не менее 1 м на каждые 0,1 ат раз-
режения; обычно эта высота составляет
10,5—11 м.
В таких конденсаторах, называемых
барометрическими (рис. 13-19), пар и
| - вода движутся в противоположных на-
[ правлениях (пар — снизу вверх, вода —
| ’ сверху вниз).
Причем для улучшения их соприкосновения в аппарате на
‘ различной высоте расположены тарелки или полки. Вода струй-
\ ками перетекает с одной тарелки на другую через отверстия по
всей поверхности тарелок; часть воды, кроме того, переливается
через борт тарелки, которым поддерживается определенный
уровень воды. Воздух отсасывается сверху, а смесь воды и кон-
денсата удаляется через барометрическую трубу.
Воду в конденсатор следует подавать под напором, так как
при высоком расположении ввода воды (на уровне 12—15 м)
j вакуум в конденсаторе недостаточен для ее засасывания.
508
Гл 13 Выпаривание
Преимуществами противоточных конденсаторов смешения по
сравнению с прямоточными являются меньший расход воды и
меньший объем отсасываемого воздуха (см. ниже). Достоин-
ством прямоточных конденсаторов является их компактность.
Если отработанная вода отводится из конденсатора в канали-
зацию, то предпочтение следует отдавать противоточным кон-
денсаторам, так как их громоздкость окупается простотой уда-
ления воды через барометрическую трубу. Если же отработан-
ная вода направляется в градирню для повторного использо-
вания, то для подачи воды необходимо устанавливать насос:
в этом случае в барометрической трубе нет надобности и при-
менение компактных прямоточных конденсаторов, установлен-
ных на низком уровне, может оказаться более целесообразным.
Расход воды на конденсацию пара. Расход воды опреде-
ляется из теплового баланса конденсатора и составляет:
кг'сек <13’25»
где G — количество конденсируемого пара, кг/сек;
i — энтальпия поступающего пара, дж/кг;
св— удельная теплоемкость воды, дж/кг • град;
/к — температура конденсата;
и t2— начальная и конечная температуры охлаждающей
воды.
В конденсаторах смешения tK —t2, поэтому
Г= к^ек (13-26)
Во всех случаях температура уходящей воды t2 должна быть
ниже температуры конденсации, соответствующей требуемому
давлению в конденсаторе. Разность между температурой конден-
сации и температурой уходящей воды в противоточных конден-
саторах смешения составляет 1—3° С, в то время как в прямо-
точных конденсаторах она достигает 5—6° С. Таким образом, в
противоточных конденсаторах обеспечивается более высокий на-
грев воды (f2 —и, следовательно, расход воды меньше, чем
в прямоточных конденсаторах.
Обычно расход воды в конденсаторах составляет от 15 до
60 л3 на 1 кг конденсируемого пара.
Определение основных размеров конденсаторов смешения. Диаметр кон-
денсатора определяют исходя из скорости пара, равной 35—55 м/сек. Необ-
ходимое число тарелок (полок) и расстояние между ними находят из расчета
принятого нагрева охлаждающей воды. Для определения нагрева воды
в одной ступени пользуются формулой:
Г — t' 0,029 / Н \0’7 /1ОП_Ч
lg т— t" ~~ Fj-0,2 \ rf3KB ) (13-27)
9. Создание вакуума в выпарных установках
509
Здесь Т—температура конденсации;
V и t" — температуры воды на входе и выходе рассматриваемой ступени;
Н—высота падения струи (высота ступени), .и;
^экв. — эквивалентный диаметр струи, м\
Fr — критерий Фруда для струи, рассчитанный по ^экв. и начальной
скорости истечения струи w м/сек (Fr = w2/grf3KB.)-
Если расстояние между тарелками одинаковое, то, пренебрегая измене-
нием количества воды в процессе конденсации, общий нагрев воды в конден-
саторе с N ступенями можно рассчитать по соотношению
Т — tx (Т— t'\N
T — t2~\T — t")
откуда необходимое число ступеней
. т~^
2 ’г_____________________________________/
N=-------(13-28)
Количество отсасываемого воздуха. Количество отсасываемого воздуха
зависит от качества монтажа и условий эксплуатации установки и не под-
дается точному расчету. Для его определения пользуются эмпирической
формулой
GB = 0,001 (0.025VT + 10G) кг/сек (13-29)
где W7 — расход охлаждающей воды, кг/сек-,
G — количество конденсируемого пара, кг/сек.
Для вычисления объема отсасываемого воздуха необходимо знать его
температуру и парциальное давление.
В прямоточных конденсаторах температура воздуха принимается равной
температуре уходящей воды, т е tB —t2, а в противоточных — определяется
по эмпирической формуле:
^ = ^+0,1 (^-fO + 4 (13-30)
Парциальное давление воздуха
Рв = Р-Ри (13-31)
где Р— общее давление в конденсаторе;
рп — парциальное давление пара, которое принимается равным давлению
насыщенного пара при температуре воздуха tB.
Объем отсасываемого воздуха вычисляется по уравнению состояния:
VB = .. 281°в (273±(в) м3/сек (13-32)
Рв
где 288 — газовая постоянная для воздуха, дж/кг - град-,
рв— парциальное давление воздуха, н/м2.
В прямоточных конденсаторах tB выше, чем в противоточных, и поэтому
объем отсасываемого из них воздуха тоже выше.
Для отсасывания воздуха из конденсаторов применяют поршневые и
водокольцевые вакуум-насосы (стр 236). Иногда (при большом вакууме,
а также для прямоточных конденсаторов) используются пароструйные на-
сосы-эжекторы. В случае применения поршневых вакуум-насосов после кон-
денсатора обязательно устанавливают ловушку для улавливания брызг воды
попадание которых в цилиндр вакуум насоса нарушает его работу.
ею
Гл. 13. Выпаривание
Определение размеров барометрической трубы, Диаметр барометрической
трубы определяют по обычным формулам гидравлики в расчете на про-
пускание смеси воды и конденсата в количестве (W + G) кг/сек. Скорость
в барометрической трубе w принимают до 2 м/сек.
Высота барометрической трубы (от дна конденсатора до уровня воды
в барометрическом ящике) рассчитывается по формуле
Н — -|~ 0,5 м
где Но — высота столба воды в трубе, необходимая для уравновешивания
атмосферного давления, ле;
НП — высота напора, необходимая для преодоления сопротивлений в
барометрической трубе и сообщения воде скорости w, м.
Высота 0,5 м прибавляется, чтобы избежать заливания водой парового
штуцера конденсатора при увеличении атмосферного давления.
Высота Hq зависит от разрежения b в конденсаторе (в мм рт. ст.) и
определяется по формуле:
Я. = 10,3 а ж
Принимая коэффициент сопротивления на входе в трубу £i = 0,5 и на
выходе = 1, высоту Нп находим по формуле
Яп = ^(1 + « + х")ж
где w — скорость в трубе, м/сек-,
к — коэффициент сопротивления трению;
d — диаметр трубы, м
Пример 13-9. Рассчитать противоточный барометрический конденсатор
смешения для выпарной установки (см пример 13-6, стр. 498). Температура
охлаждающей воды Л = 25° С.
Определение расхода воды. Температура конденсации соста-
вляет 60°С (равна температуре насыщения поступающего пара). Количество
поступающего пара (вторичный пар из III корпуса) G = 2,53 кг/сек
(9100 кг/ч), его энтальпия 1^2610-Ю3 дж/кг (623,5 ккал/кг). Температуру
уходящей воды принимаем на 3°С ниже температуры конденсации, т. е.
/2 = 60 — 3 = 57° С
Расход воды вычисляем по формуле (13-26) при св = 4190 дж/кг -град
2,53 (2610 -103 — 4190 • 57) ... . 1ft1 ППЛ . ... „
W = ————осч---------------- = кг сек, или 161 000 кг ч, или 161 м3 ч
4190 (57 — 25) '
Количество отсасываемого воздуха По формуле (13-29)
находим:
GB = 0,001 (0,025 • 44,7 + 10 - 2,53)« 0,026 кг/сек (95 кг/ч)
Температуру воздуха определяем по формуле (13-30):
tB = 25 4- 0,1 (57 — 25) + 4 = 32,2° С
Общее абсолютное давление в конденсаторе (при температуре конденса-
ции 60° С) Р = 0,203 кгс/см? = 19 900 н/м?-, парциальное давление водяного
пара (при £В=32,2°С) рП= 0,049 кгс/см? = 4800 н/м?. Парциальное давление
воздуха рассчитываем по формуле (13-31):
рв = 19 900 — 4800 = 15 100 н/м3
9. Создание вакуума в выпарных установках
511
Объем отсасываемого воздуха определяем по уравнению (13-32):
TZ 288 - 0,026(273 4-32,2) Л1е_ Л1 3.
V =--------1—le-inn -—= 0,152 м3/сек, или 9,1 м3/мин
1и 100
Устанавливаем ротационный водокольцевой вакуум-насос РМК-3 произ-
водительностью 12,8 м3/мин при разрежении 80%.
Определение основных размеров. Удельный объем насы-
щенного пара при 60° С равен 7,68 м3/кг-, отсюда объем пара составляет:
2,53 • 7,68 = 19,4 м3/сек
Площадь сечения конденсатора при скорости пара 35 м/сек равна
19 4
= 0,554 м*
Этой площади соответствует диаметр 0,84 м, принимаем диаметр 1000 мм.
Принимаем напор воды на тарелках (высоту бортов) h = 40 мм и диа-
метр отверстий в тарелках d = 8 мм. Тогда начальная скорость истечения
струи w и расход воды v через отверстие составят (при коэффициенте ско-
рости <f> = 0,97 и коэффициенте сжатия струи е = 0,64):
w = срV2gh = 0,97 /2-9,81-0,04 = 0,86 м/сек
v == ЗбООе ^4- w = 3600 • 0,64 - 0,785 • 0,0082 • 0,86 0,1 м3/ч
4 '
Необходимое число отверстий (при расходе воды 161 м3/ч)1
161 1ZJ1A
п = -Q-j- = 1610
Предлагается путем вычерчивания убедиться, что это количество отвер
стий можно разместить на площади тарелки (которая составляет около по-
ловины сечения аппарата) при шаге 16 мм.
Определяем критерий Фруда:
w3 0 862
Ег — _______________________ ' _Q 43
^“9,81-0,008 “ ’
Принимая высоту ступени Н = 800 мм, по формуле (13-27) получим:
- T-t' 0,029 /8ОО\0,7 _
'8 7=7 = ^ (т) = 0’463
Из уравнения (13-28) вычисляем необходимое число ступеней (при
Т = 60° С; h = 25° С; ti = 57° С):
60 — 25
При выполнении конденсатора по схеме, изображенной на рис. 13-19, за
ступень следует считать две смежные тарелки. Устанавливаем 6 тарелок,
расстояние между ними принимаем 400 мм.
Глава 14
КРИСТАЛЛИЗАЦИЯ
1. Общие сведения
Кристаллизация представляет собой процесс выделения
твердого растворенного вещества из его раствора (кристаллиза-
ция из раствора) или процесс выделения твердой фазы при за-
твердевании веществ, находящихся в расплавленном состоянии
(кристаллизация из расплава). Кристаллизация применяется
при производстве солей и ряда других веществ, а также для
получения твердых веществ в чистом виде путем их перекри-
сталлизации (растворение с последующей кристаллизацией).
Кристаллизация из растворов основана на ограниченной рас-
творимости твердых веществ. Раствор, содержащий максималь-
ное количество растворенного вещества в данном количестве
растворителя при определенной температуре, называется насы-
щенным; если раствор содержит большее количество раство-
ренного вещества, то он является пересыщенным; если же он
содержит меньшее количество растворенного вещества, то на-
зывается ненасыщенным. Пересыщенные растворы неустойчивы:
из них выделяется избыточное количество растворенного веще-
ства, т. е. происходит процесс кристаллизации. После выделе-
ния кристаллов раствор становится насыщенным. Этот насы-
щенный раствор, полученный в результате выделения кристал-
лов, называется маточным раствором, или маточником. Отделе-
ние маточного раствора от кристаллов производится центрифу-
гированием и другими методами, рассмотренными в главе 8.
Ненасыщенные растворы сами по себе устойчивы, но при
добавлении в такой раствор твердого вещества оно будет рас-
творяться до тех пор, пока раствор не станет насыщенным.
Твердое вещество находится в равновесии с насыщенным рас-
твором.
Растворимость равна концентрации насыщенного раствора
и зависит от температуры, а также от свойств растворяемого
вещества и растворителя. Для большинства твердых веществ
растворимость с повышением температуры возрастает, но для
некоторых веществ она с повышением температуры уменьшается
1 Общие сведения
513
или имеет при определенной температуре максимальное значе-
ние.
Для проведения процесса кристаллизации пользуются сле-
дующими способами создания пересыщенных растворов:
1. Охлаждение растворов применяют для кристаллизации ве-
ществ, растворимость которых заметно уменьшается с пониже-
нием температуры, а также для кристаллизации из расплавов.
2 Испарение части растворителя применяют для кристалли-
зации веществ, растворимость которых увеличивается или не-
значительно уменьшается с понижением температуры; испа-
рение производится при кипении раствора в выпарном аппа-
рате или путем испарения при температуре ниже точки ки-
пения.
3. Комбинированный способ заключается в одновременном
охлаждении и испарении части растворителя.
Кристаллизация может производиться также путем высаливания, т е.
добавления в раствор веществ, понижающих растворимость выделяемой
соли Такими веществами являются вещества, связывающие воду (кристал-
лизация сульфата натрия при добавлении спирта или аммиака), или соеди-
нения, содержащие одинаковый ион с данной солью (кристаллизация хло-
ристого натрия при добавлении хлористого магния, кристаллизация желез-
ного купороса при добавлении концентрированной серной кислоты).
Процесс кристаллизации состоит из двух стадий — образо-
вания зародышей кристаллов и роста кристаллов.
Образование зародышей может происходить путем самопро-
извольной кристаллизации. При этом оба процесса (образова-
ние зародышей и рост кристаллов) протекают одновременно.
Если скорость образования зародышей больше скорости их ро-
ста, получается* большое количество мелких кристаллов. Если
же скорость роста больше скорости образования зародышей,
получается меньшее количество крупных кристаллов. Изменяя
факторы, влияющие на скорость образования зародышей и ско-
рость их роста, можно регулировать размеры кристаллов. Бы-
строе охлаждение, перемешивание раствора, высокая темпера-
тура и низкий молекулярный вес кристаллов способствуют обра-
зованию зародышей и получению мелких кристаллов. Наоборот,
медленное охлаждение, неподвижность раствора, низкая темпе-
ратура и высокий молекулярный вес способствуют процессу ро-
ста и получению крупных кристаллов.
Кристаллизация может быть ускорена внесением затравки —
мелких частиц кристаллизующегося вещества, которые и явля-
ются зародышами кристаллов. В этом случае кристаллизация
происходит в основном за счет роста внесенных в раствор затра-
вочных кристаллов. Для получения крупных кристаллов число
затравочных кристаллов должно быть невелико.
33 Зак 546
514
Гл. 14. Кристаллизация
Размеры кристаллов имеют значение для последующей их
обработки. Крупные кристаллы легче высушиваются, отстаива-
ются, отфильтровываются, промываются и удерживают меньше
влаги при фильтровании и промывке. Мелкие кристаллы легче
растворяются и обычно чище, чем крупные, так как последние
часто содержат маточник с находящимися в нем примесями.
Во избежание слеживания следует получать либо крупные кри-
сталлы, либо мелкие кристаллы одинакового размера. Мелкие
кристаллы разной величины, особенно кристаллическая пыль,
способствуют слеживанию продукта.
2. Устройство кристаллизаторов
Простейшими аппаратами для кристаллизации являются
ящичные кристаллизаторы: они представляют собой открытые
прямоугольные ящики, в которых подвешиваются ленты или
нити. Кристаллизация происходит путем естественного охла-
ждения раствора и испарения части растворителя в воздух.
Основная масса чистых кристаллов осаждается на поверхности
лент или нитей и удаляется вручную. Примеси осаждаются на
дне ящиков и удаляются с маточником. Такие кристаллизаторы
работают периодически и неинтенсивно, отличаются громозд-
костью и требуют применения ручного труда.
В современных кристаллизаторах применяют водяное или
воздушное охлаждение, либо ведут кристаллизацию в ва-
кууме.
Кристаллизаторы с водяным охлаждением
В этих кристаллизаторах тепло от раствора к охлаждающей
воде передается через стенку, причем кристаллизация происхо-
дит вследствие охлаждения раствора. В случае необходимости
получения более низких температур, чем это возможно при во-
дяном охлаждении, применяют охлаждение при помощи холо-
дильных рассолов.
Кристаллизатор с мешалкой (рис. 14-1) состоит из сосуда /
в котором вращается мешалка 2. Охлаждающий агент (вод;
или рассол) движется по змеевику 3. Благодаря вращению ме
шалки выпадающие кристаллы не осаждаются на дне, .
остаются в растворе во взвешенном состоянии. Такие кристалли
заторы работают периодически или непрерывно. При периодич<
ской работе аппарат заполняют раствором; по окончании крр
сталлизаими производят разгрузку аппарата через патрубок
имеющий клапан (на рисунке не показан). При непрерывна
работе соединяют последовательно несколько аппаратов, пр
2. Устройство кристаллизаторов
515
чем раствор протекает из одного кристаллизатора в другой;
при этом раствор удаляется через боковой патрубок. Благодаря
простоте эти кристаллизаторы имеют широкое распространение.
Кристаллизаторы такого типа изготовляют иногда с рубаш-
ками (вместо змеевиков); чтобы устранить выпадение кристал-
лов на стенках аппарата (что
привело бы к ухудшению тепло-
передачи), лопасти мешалки снаб-
жают скребками или металличе-
скими щетками.
Применяют также горизон-
тальные кристаллизаторы с ме-
шалками; они состоят из корыта
водяной рубашкой. По всей
Вода
Вода
Рис. 14-2. Кристаллизатор с вынос-
ным холодильником:
/ — сосуд; 2, 5 —трубы для циркуляции рас-
твора; 3 — циркуляционный насос; / — холо-
дильник; б —труба для ввода раствора;
7 —ловушка.
Рис. 14-1. Кристаллизатор с мешал-
кой:
1 — сосуд; 2 — мешалка; 3 — змеевик; 4 — спуск-
ной патрубок.
длине корыта на горизонтальном валу расположена мешалка;
кристаллизуемый раствор подается к одному концу корыта и
движется к другому его концу, где и удаляется. Эти кристалли-
заторы часто соединяют друг с другом последовательно, распо-
лагая их для экономии места друг над другом.
Недостатками горизонтальных кристаллизаторов являются
их громоздкость и небольшая производительность.
Кристаллизатор с выносным холодильником (рис. 14-2) состоит из со-
суда / и трубчатого холодильника 4. Раствор поступает по трубе 6, а за-
33*
516
Гл. 14. Кристаллизация
тем по трубе 2 при помощи циркуляционного насоса 3 направляется в холо-
дильник 4, проходит по трубам холодильника (в межтрубном пространстве
движется вода) и возвращается в сосуд 1 по трубе 5. В холодильнике
происходит пересыщение раствора. Образующиеся кристаллы циркулируют с
раствором до тех пор, пока скорость их осаждения не станет больше ско-
рости движения раствора, после чего они осаждаются на дне сосуда 1. Та-
ким образом, в сосуде 1 происходит классификация кристаллов по крупности.
Величину кристаллов регулируют путем изменения скорости циркуляции
раствора и отвода тепла в холодильнике 4. Маточный раствор удаляется через
ловушку 7, в которой отделяются мелкие кристаллы.
Вращающийся кристаллизатор с внутренним охлаждением (вальцы)
применяется главным образом для кристаллизации расплавленных продуктов
/
Рис. 14-3. Вращающийся кристаллизатор с внутренним охла-
ждением:
/—барабан; 2 — корыто; 3 — полая цапфа; 4 — нож.
Кристаллизатор (рис. 14-3) состоит из вращающегося полого барабана 1,
нижней частью погруженного в корыто 2. В барабан через полые цапфы <3
подается охлаждающая вода. Кристаллизуемый продукт поступает в корыто
и кристаллизуется тонким слоем на наружной поверхности барабана. Кри-
сталлы снимаются с барабана ножом 4.
Кристаллизаторы с воздушным охлаждением
В таких кристаллизаторах охлаждение раствора произво-
дится путем непосредственного соприкосновения его с воздухом.
Вследствие этого одновременно с охлаждением происходит ис-
парение части растворителя в воздух.
Барабанный вращающийся кристаллизатор (рис. 14-4) пред-
ставляет собой цилиндрический аппарат /, несколько наклонен-
2 Устройство кристаллизаторов
517
ный к горизонту. Барабан опирается на две пары вращающихся
опорных роликов 2 и приводится во вращение при помощи зуб-
чатого венца 3. Раствор подается с одного конца барабана,
а кристаллы и маточный раствор выходят с другого конца.
Воздух нагнетается вентилятором и движется в барабане про-
тивотоком движению раствора.
В таких кристаллизаторах основное количество тепла отво-
дится от раствора за счет испарения части растворителя. Про-
изводительность кристаллизатора в значительной степени зави-
сит от температуры воздуха (зимой производительность выше,
Рис. 14-4. Барабанный вращающийся кристаллизатор:
/ — барабан; 2 —опорные ролики; 3 — зубчатый венец.
чем летом). Для усиления охлаждения барабан иногда оро-
шается снаружи водой, которая затем стекает в корыто, уста-
новленное под кристаллизатором.
Недостатком барабанных вращающихся кристаллизаторов
является их громоздкость.
Вакуум-кристаллизаторы
Если поместить раствор в замкнутый сосуд и создать в нем
вакуум, то по мере отсасывания вакуум-насосом паров раство-
рителя будет происходить охлаждение раствора, так как тепло,
необходимое для испарения растворителя, отнимается от рас-
твора. Охлаждение происходит до тех пор, пока температура
не станет равной температуре насыщенного пара при давлении,
установившемся в аппарате. Таким образом, в вакуум-кристал-
лизаторах происходит одновременное удаление части раствори-
теля (путем испарения в вакууме) и охлаждение раствора.
Простейший вакуум-кристаллизатор периодического действия
представляет собой герметический сосуд с мешалкой, в который
заливается раствор, после чего в аппарате создается вакуум.
По окончании охлаждения открывают воздушник, и в сосуде
устанавливается атмосферное давление. Затем маточный раствор
вместе с кристаллами удаляется через нижний патрубок. Для
создания вакуума обычно применяются пароструйные эжекторы,
отсасывающие из аппарата пары растворителя. Последние
518
Гл. 14. Кристаллизация
Кристаллы
Рис. 14-5. Вакуум-кристаллизатор
непрерывного действия:
/ — испаритель; 2—барометрическая труба;
3 — сборник; 4— насос; 5 —труба для ввода
раствора; 6 — циркуляционная труба.
в смеси с рабочим паром эжектора направляются затем в кон-
денсатор. Неконденсирующиеся газы отсасываются из конден-
сатора пароструйным эжектором или другим вакуум-насосом.
На рис. 14-5 показан вакуум-кристаллизатор непрерывного
действия. Испарение растворителя происходит в испарителе /,
из которого раствор по баро-
метрической трубе 2 поступа-
ет в сборник 3\ в этом сборни-
ке выпадают кристаллы, а рас-
твор насосом 4 по циркуляци-
онной трубе 6 возвращается в
испаритель. Отсасывание па-
ров растворителя осуществ-
ляется вакуум-насосом или
эжектором, как описано выше.
При непрерывной работе
обычно применяют многокор-
пусные вакуум-кристаллизато-
ры (рис. 14-6). Они состоят
из нескольких последователь-
но соединенных по ходу жид-
кости аппаратов, причем в пер-
вых корпусах испарение про-
исходит при меньшем ваку-
уме, а максимальный вакуум
достигается лишь в послед-
нем корпусе. При этом абсо-
лютное давление в аппарате
и температура раствора посте-
пенно уменьшаются от пер-
вого корпуса к последнему.
Перетекание раствора из кор-
пуса в корпус происходит за
счет разности давлений в
них.
В показанной на рис. 14-6 четырехкорпусной установке раз-
режение в корпусах (кристаллизаторах) 1 и 2 создается конден-
сатором 7, который разделен на две части перегородкой с ги-
дравлическим затвором, так что вода может перетекать из верх-
ней части конденсатора в нижнюю, а пар не может переходить
из одной части конденсатора в другую. Благодаря такому
устройству в нижней части конденсатора, к которой присоеди-
нен корпус /, поддерживается более высокое давление, чем
в верхней части, к которой присоединен корпус 2. Пары из
корпусов 3 и 4 отсасываются эжекторами 5 и 6 и сжимаются
3. Расчет кристаллизаторов
519
в них до давления, установившегося в верхней части конденса-
тора. Несконденсировавшиеся газы отсасываются из конденса-
тора 7 эжекторами 8 и 18, поступают в конденсатор 10, из
которого в свою очередь отсасываются эжектором 9, и посту-
пают в конденсатор 11. Из последнего газы отсасываются эжек-
Рис. 14-6. Схема многокорпусной вакуум-кристал-
лизационной установки:
1—4 — кристаллизаторы, 5, 6, 8, 9, 12. 13 — эжекторы; 7— кон-
денсатор; 10, // — промежуточные конденсаторы; // — сборник
для суспензии; 15 — насос.
тором /2, сжимаются в нем до атмосферного давления и выбра-
сываются в атмосферу. Таким образом, сжатие газов, отсасывае-
мых из конденсатора 7, производится в три ступени. В промежу-
точных конденсаторах 10 и И конденсируется рабочий пар, по-
ступающий из эжектора предыдущей ступени, вследствие чего
разгружается эжектор следующей ступени.
3. Расчет кристаллизаторов
Материальный баланс
Обозначим количество исходного раствора Gi кг, количе-
ство маточного раствора G2 кг, количество кристаллов 6кр. кг
и количество испаренного растворителя W кг.
520
Гл. 14. Кристаллизация
Содержание безводного кристаллизующегося вещества (в
вес. долях) в исходном растворе обозначим через ау в маточ-
ном растворе — через а2 и в кристаллах — через якр..
Если вещество кристаллизуется в безводной форме, то
пкр =1. Если же вещество кристаллизуется в виде кристалло-
гидрата, то акр. = Л^ез-~ > где УИбезв—молекулярная масса без-
водного вещества, а Л4кр>— молекулярная масса кристаллогид-
рата.
Уравнение баланса по всему количеству вещества:
+ W • (14-1)
по безводному кристаллизующему веществу:
Gi&i == ^2^2 Н~ ^кр.^кр. (14*2)
В кристаллизаторах с водяным или рассольным охлаждением
W = 0. В этом случае, зная Gh сц, а2 и акр_, совместным реше-
нием уравнений (14-1) и (14-2) находят О2 и GKp_.
В кристаллизаторах с удалением части растворителя (кри-
сталлизаторы с воздушным охлаждением, выпарные аппараты
с кристаллизацией вещества) задаются величиной W или GKp_,
после чего также можно совместно решить уравнения (14-1)
и (14-2).
В вакуум-кристаллизаторах W не может быть принято про-
извольно, а определяется совместным решением уравнений
(14-1) и (14-2) и уравнения теплового баланса.
Тепловой баланс
Для общего случая кристаллизации с охлаждением раствора
и удалением части растворителя имеем:
Приход тепла Расходтепла
С исходным раство-
ром ...............
Тепло, выделяющееся
при кристаллизации Окр> 0кр.
С маточным раствором G2c2t2
С кристаллами .... Окр. скр. t2
С испаренным раство-
рителем ............ Wi
Отводится с охлаж-
дающим агентом . . Q
Таким образом
+GKp.<7Kp. = G2c2^2 GKp сКр/2+ W7-4-Q (14-3)
где clf с2 и скр. — удельные теплоемкости исходного и маточ-
ного растворов и кристаллов, дж/кг • град;
— температура поступления исходного раствора;
/2 — температура маточного раствора и кристаллов.
3. Расчет кристаллизаторов
521
В уравнении теплового баланса (14-3), кроме приведенных
обозначений, принято:
i — энтальпия удаляемых паров растворителя, дж/кг-,
^кР.— теплота кристаллизации, дж на 1 кг кристаллов.
Теплота кристаллизации ^кр. вычисляется по закону Гесса,
который рассматривается в курсе физической химии. В ряде
случаев кристаллизация протекает с поглощением тепла; тогда
^кр. имеет отрицательное значение.
Рассматривая исходный раствор как смесь маточного рас-
твора, кристаллов и испаренной воды, можно написать:
Gxcxt = О2с2/4- (7кр скр t 4- WcBt •
откуда
I ^кр.^кр.^2
где св— удельная теплоемкость воды, дж/кг • град.
Комбинируя последнюю формулу с уравнением (14-3), по-
лучим:
Gp\ (^i — ^г) 4~ ^кр.^кр. ~W(i — + Q (14-4)
Член GiCi(/i — /2) представляет собой тепло, отдаваемое
раствором при охлаждении, а член W(t — cBt2) —тепло, затра-
чиваемое на испарение воды.
Если кристаллизация проводится без удаления части рас-
творителя (кристаллизаторы с водяным и рассольным охла-
ждением), то W = 0 и, как следует из уравнения (14-4), все
тепло, отдаваемое раствором при охлаждении и выделяющееся
при кристаллизации, отводится с охлаждающим агентом.
В вакуум-кристаллизаторах Q-0, и уравнение (14-4) при-
нимает вид
GiCi (^ — /2) 4- (?кр.?кр. — — cBt2) (14-5)
т. е, тепло, отдаваемое раствором и выделяющееся при кристал-
лизации, расходуется на испарение воды.
Определение основных размеров кристаллизаторов
Кристаллизаторы с водяным или рассольным охлаждением рассчитывают
как теплообменные аппараты, т. е. по найденной из теплового баланса теп-
ловой нагрузке Q определяют необходимую поверхность теплообмена. Раз-
меры аппарата вычисляют из условия размещения требуемой поверхности
теплообмена. В аппаратах периодического действия емкость аппарата рассчи-
тывают на одну операцию.
522
Гл 14. Кристаллизация
Методика определения размеров кристаллизаторов с воздушным охлаж-
дением и вакуум-кристаллизаторов еще не разработана и при выборе их
пользуются опытными данными. Для вакуум-кристаллизаторов поверхность
зеркала испарения можно принимать из расчета испарения 150 кг воды
в час с 1 м2 поверхности.
Пример 14-1. Рассчитать вакуум-кристаллизатор для раствора MgSCU-
Количество поступающего раствора Gi = 5000 кг/ч, содержание в нем суль-
фата магния ai = 0,27; температура раствора G = 50° С. Конечная темпера-
тура охлаждения t2 = 15° С.
Определение концентрации маточного раствора и
давления в аппарате Концентрация маточного раствора (насы-
щенного раствора при 15° С) а2 = 0,248. Для этой концентрации температур-
ная депрессия составляет 3°С. Температура насыщения паров растворителя
составляет:
15 — 3 = 12° С
При этом соответствующее абсолютное давление в аппарате равно
10,5 мм рт ст.
Составление и решение уравнений материального и
теплового балансов. Теплоемкость твердого сульфата магния
ств. — 945 дж/кг-град (0,226 ккал/кг град). По формуле (13-12) находим
теплоемкость поступающего раствора при св — 4190 дж/кг • град:
с{ = 945 • 0,27 4~ 4190 (1 — 0,27) = 3370 дж/кг град (0,805 ккал/кг • град)
Теплота кристаллизации для MgSCU'THaO составляет ^Кр. = 65700 дж/кг
(15,7 ккал/кг). Содержание MgSCU в кристаллах равно
120 A4QQ
лкр. — 246 “ ^>488
где 120 — молекулярная масса MgSCU;
246 — молекулярная масса MgSCU • 7НгО.
Энтальпия насыщенного водяного пара (при 12° С) i = 2520-103 дж/кг
(602,5 ккал/кг). По уравнениям (14-1), (14-2), (14-5) находим:
5000 = G2 + GKp. + W
5000 • 0,27 = G2 • 0,248 + GKp. • 0,488
5000 • 3370 (50 — 15) + GKp. • 65700 = UZ(2520 • 103 — 4190 • 15)
откуда
G2 — 4015 кг/ч
GKp. = 726 кг/ч
W = 260 кг/ч
Глава 15
ИСКУССТВЕННОЕ ОХЛАЖДЕНИЕ
1. Общие сведения
Для получения низких температур, недостижимых при охла-
ждении естественными охлаждающими агентами (вода, воздух),
применяют искусственный холод. Последний широко исполь-
зуется в химической промышленности (для сжижения паров и
газов, для разделения газовых смесей путем ректификации при
низких температурах, для кристаллизации, для отвода тепла\,
реакции и т. д.) и в других отраслях народного хозяйства (хра-
нение и перевозка пищевых продуктов, замораживание грунтов
при строительстве подземных сооружений, кондиционирование
воздуха и др.).
Наиболее старым способом искусственного охлаждения яв-
ляется применение холодильных смесей (смеси солей и некото-
рых других веществ с льдом), дающих при таянии низкие тем-
пературы. Так, смесь поваренной соли с льдом (22% NaCl)
дает температуру —21° С, смесь хлористого кальция с льдом
(30% СаС12) дает температуру —55°С.
В настоящее время для получения холода в технике приме-
няют следующие способы:
1. Испарение низкокипящих жидкостей. Так, например, если
испарять жидкий аммиак при абсолютном цавлении 2 ат, то он
охлаждается до температуры кипения при этом давлении (около
—20° С) и может служить охлаждающим агентом для получения
температур порядка —15° С. С понижением давления испарения
достигаются еще более низкие температуры.
2. Расширение сжатых газов в расширительной машине (де-
тандере). При этом газ совершает внешнюю работу за счет
уменьшения своей внутренней энергии, вследствие чего его тем-
пература понижается.
3. Дросселирование сжатых газов и паров. Дросселирова-
нием (мятием) называется такое расширение газа, когда давле-
ние его снижается вследствие протекания через сужение или
524
Гл. 15. ПскусстбенМё Охлаждение
другое препятствие (например, пористую перегородку); при
этом, в отличие от процесса в расширительной машине, расши-
рение происходит без совершения внешней работы. Дроссели-
рование обычно сопровождается понижением температуры
(стр. 526).
Условно различают умеренное (до температур порядка
—100° С) и глубокое (до температур ниже —100° С) 'охлажде-
ние. Для умеренного охлаждения применяют компрессионные,
абсорбционные и пароэжекторные холодильные машины. Для
глубокого охлаждения пользуются холодильными циклами, осно-
ванными на дросселировании и расширении газов в детандере.
2. Термодинамические основы получения холода
Минимальная работа для переноса тепла
кболее нагретому телу
Получение холода связано с передачей тепла, отнимаемого
от охлаждаемого тела, другому телу, имеющему более высокую
температуру, т. е. с переходом тепла от менее нагретого тела
к более нагретому. Согласно второму закону термодинамики,
такой переход сам по себе невозможен, так как сопровождается
уменьшением энтропии системы, в которой происходит тепло-
передача.
Нагревание сопровождается возрастанием энтропии, а охла-
ждение— уменьшением ее, причем в обоих случаях изменение
энтропии равно количеству переданного тепла Qo, деленному
на абсолютную температуру.
Если тепло передается от менее нагретого тела (с темпера-
турой То) к более нагретому (с температурой Т), то энтропия
первого тела уменьшается на а температура второго воз-
„ 1 о
Qo «
растает на при этом общее изменение энтропии
д5 = 7~%
„ / Qa Qo\
будет отрицательным )’т- е- такой процесс сам по
себе идти не может. Для его осуществления необходимо прове-
дение другого (компенсирующего) процесса, связанного с за-
тратой энергии и сопровождаемого возрастанием энтропии.
На практике получение холода основано на том, что рабочее
тело, так называемый холодильный агент (хладоагент), совер-
шает круговой процесс, на который затрачивается работа, обра-
щаемая в тепло и передаваемая более нагретому телу.
2. Термодинамические основы, получения холода
525
Если, например, для получения холода используется испаре-
ние аммиака, то его пары сжимаются в компрессоре до такого
давления, чтобы они могли быть сконденсированы при после-
дующем охлаждении водой. Например, при абсолютном давле-
нии 12 ат аммиак конденсируется при температуре около
+ 30° С, которая легко может быть достигнута водяным охлаж-
дением. При снижении давления (например, до 2 ат) получен-
ный после конденсации паров жидкий аммиак испаряется, отни-
мая от охлаждаемого тела тепло, необходимое для испарения
(теплота испарения). Затем пары аммиака снова засасываются
компрессором.
В данном случае компенсирующим процессом является сжа-
тие хладоагента в компрессоре с затратой механической энергии.
При этом энтропия более нагретого тела (воды, которой пере-
дается с хладоагентом тепло, отнимаемое от охлаждаемого
тела) возрастает на столько же, на сколько уменьшается энтро-
пия охлаждаемого тела, так как воде отдается не только тепло,
отнятое от охлаждаемого тела, но и тепло, в которое перешла
затраченная в компрессоре механическая работа. Таким обра-
зом, энтропия охлаждаемого тела по-прежнему уменьшается i^a
21, а энтропия воды возрастает на —°^!~L • Процесс возможен,
если энтропия системы не изменяется, т. е.
при у2- = —. Отсюда можно найти ми-
нимальную работу, затрачиваемую на по-
лучение искусственного холода:
L -Q (L-b
^мин. 'хО I т
_ ' 1 о
Уравнение энергетического баланса хо-
лодильной машины (рис. 15-1) имеет вид
Q0 + Z = Q (15-2)
где Q — тепло, отдаваемое хладоагентом
окружающей среде (воде).
Количество тепла Qo, отнимаемое от охлаждаемого тела, яв-
ляется холодопроизводительностью установки (в вт).
Отношение холодопроизводительности к затраченной работе
характеризует эффективность холодильной машины и назы-
вается холодильным коэффициентом-.
Рис. 15-1. Энергети-
ческий баланс холо-
дильной машины.
(15-1)
£ L
(15-3)
526
Гл. 15. Искусственное охлаждение
Холодильный коэффициент, который не следует путать с
к. п. д., обычно бывает больше единицы.
Необходимая мощность двигателя, приводящего в действие
холодильную машину, по уравнению (15-3) составляет вт
или
(15-4)
Количество тепла qo, отнимаемого 1 кг хладоагента от охла-
ждаемого тела, называется удельной холодопроизводитель-
ностью хладоагента, причем
Qo = Gqo (15-5)
где G — количество циркулирующего в установке хладоагента,
кг! сек.
Расширение газа без совершения внешней
работы (дросселирование)
Для рассмотрения процесса дросселирования воспользуемся
обобщенным уравнением Бернулли (7-28). При дросселирова-
нии газа не совершается внешней работы, т. е. I = 0.
Если дросселирование проводится адиабатически, то q = 0;
тогда по уравнению (7-28)
/2 — ix = о или = Z2
Таким образом, дросселирование является процессом, про-
текающим при постоянной энтальпии (Z = const).
Работа, совершаемая расширяющимся газом при дроссели-
ровании, расходуется на преодоление трения в дроссельном от-
верстии (сужении) и превращается в тепло, которое остается
в газе, вследствие чего энтальпия его не изменяется.
Постоянство энтальпии при дросселировании соответствует
в случае идеального газа и постоянству температуры, т. е. дрос-
селирование идеального газа протекает при постоянной темпе-
ратуре. При дросселировании реальных газов обычно происхо-
дит понижение температуры. Это явление называется дроссель-
ным эффектом (эффектом Джоуля—Томсона). Дроссельный эф-
фект считается положительным, если при дросселировании газ
охлаждается, и отрицательным, если газ нагревается.
Различают дифференциальный дроссельный эффект (пони-
жение температуры газа при уменьшении давления на 1 ат}
и интегральный дроссельный эффект (понижение температуры
газа при уменьшении давления от р^ до р2).
2. Термодинамические основы получения холода
527
В практических расчетах пользуются интегральным дрос-
сельным эффектом; этот эффект определяют при помощи диа-
граммы Т — S, на которой нанесены линии I = const. Двигаясь
вдоль кривой i = const из точки, характеризующей начальное
состояние газа, до изобары, соответствующей давлению рг,
легко определить температуру газа после дросселирования.
Причина изменения температуры реальных газов при дросселировании
заключается в том, что энтальпия этих газов, в отличие от идеальных, за-
висит не только от температуры, а также от давления. Внутренняя энергия
реального газа равна сумме кинетической энергии молекул cvT и внутрен-
ней потенциальной энергии ип:
и = cvT ип (15-6)
Внутренняя потенциальная энергия равна работе, которую надо затра-
тить, чтобы раздвинуть соприкасающиеся друг с другом молекулы, т. е.
работе, совершенной против сил притяжения (сцепления), действующих между
молекулами. Чем больше расстояние между отдельными молекулами, тем
больше внутренняя потенциальная энергия, так как тем больше работа, кото-
рая была затрачена для того, чтобы раздвинуть молекулы на это расстояние.
С увеличением давления расстояние между молекулами газа уменьшается,
а следовательно, уменьшаются внутренняя потенциальная энергия иП и вну-
тренняя энергия и. Уменьшение внутренней энергии равно работе, произведен-
ной силами сцепления при сжатии газа. у
Энтальпия реального газа, определяемая общим уравнением (6-24), мо-
жет уменьшаться или повышаться с увеличением давления в зависимости от
того, как изменяется с давлением величина pv.
Подставляя в уравнение (6-24) значение и из выражения (15-6), полу-
чим при дросселировании (й = i2):
4“ ип, I 4~/й*й = ИП, 2 ~i~P2V2
где индекс 1 относится к состоянию газа до дросселирования, а индекс 2
к его состоянию после дросселирования.
Обозначая иП> 2 — цП)! = Дип, находим:
^2)= ЛиП —P2V2) (15-7)
Член cv(Tt— Т2) представляет собой уменьшение внутренней кинетиче-
ской энергии газа в результате охлаждения от Т\ до Т%, а член Дип —уве-
личение внутренней потенциальной энергии газа, т. е. работу, совершаемую
против сил сцепления.
Таким образом, охлаждение газа при дросселировании происходит вслед-
ствие того, что газ при расширении совершает работу против сил сцепления,
причем его внутренняя потенциальная энергия увеличивается за счет умень-
шения части внутренней энергии, определяемой кинетической энергией моле-
кул.
Так как давление рз меньше р\, то «п, 2 больше ип, 1>т. е. член Д«п — ве-
личина всегда положительная. Член (pi^i — P2V2), представляющий собой ра-
боту, совершаемую газом при дросселировании, может быть как отрицатель-
ным, так и положительным. При этом возможны три случая:
1) P1V1 < p2v2, тогда правая часть уравнения (15-7) будет положитель-
ной и Т{ > Т'2;
2) PM > p2v2, причем Дип > (а*й — p2v2); тогда Т{ > Т2;
3) PiVj > p2v2, причем Дип < (pjVj — p2v2); тогда Т{ < Т2.
528
Гл. 15. Искусственное охлажоение
В первых двух случаях газ при дросселировании охлаждается, а в
третьем случае — нагревается.
Более подробный анализ показывает, что дроссельный эффект умень-
шается с повышением температуры газа и при некоторой, так называемой
инверсионной температуре становится равным нулю. При инверсионной тем-
пературе Aun = (Pivi—P2V2), так что правая часть уравнения (15-7) обра-
щается в нуль.
При температурах выше инверсионной дроссельный эффект будет отри-
цательным, т. е. газ при дросселировании нагревается.
Большинство газов имеет высокую инверсионную температуру и при
дросселировании в обычных условиях охлаждается. Исключение составляют
водород (инверсионная температура —73° С) и гелий (инверсионная темпера-
тура —243° С), которые при дросселировании в обычных условиях нагре-
ваются.
3. Компрессионные холодильные машины
Простейшей компрессионной холодильной машиной является
воздушная холодильная машина, в которой холод получается
путем расширения сжатого воздуха в детандере (стр. 554). Хо-
лодильный коэффициент этой машины очень низкий.
В настоящее время применяются исключительно паровые
компрессионные холодильные машины, впервые появившиеся
в 1834 г. В этих машинах холод получается путем испарения
низкокипящм жидких хладоагентов; сжатие паров хладоагента
производится в поршневых компрессорах или в турбокомпрес-
сорах.
Цикл идеальной компрессионной
холодильной машины
Наибольший холодильный коэффициент, т. е. наименьшая
говой процесс совершается
по обратному циклу Кар-
но (цикл идеальной комп-
рессионной машины), при-
веденному на диаграмме
Т—S (рис. 15-2). Точка/
изображает состояние
паров хладоагента перед
компрессором; в компрес-
соре / пары подвергаются
адиабатическому сжатию
(процесс при S = const,
линия 1—2). В конденса-
торе // происходит кон-
денсация паров при по-
стоянной температуре Тк
(линия 2—3). Из конденсатора хладоагент поступает в детан-
дер ///, в котором происходит адиабатическое расширение (ли-
затрата энергии, достигается, если
Рис. 15-2. Цикл идеальной компрессионной
холодильной машины:
/—компрессор; // — конденсатор; /// — детандер;
IV — испаритель.
3. Компрессионные холодильные машины
529
ния 3—4) с частичным испарением жидкости. Затем хладоагент
испаряется в испарителе IV при постоянной температуре То
(линия 4—/), возвращаясь к исходному состоянию (точка /).
Тепло, затрачиваемое на испарение хладоагента (равное хо-
лодопроизводительности 1 кг хладоагента), изображается пло-
щадью а—4—1—b—а и равно q0 = T0AS, а тепло, отводимое
в конденсаторе, изображается площадью b—2—3—а—b и
равно q = TKAS.
Затраченная работа (работа в компрессоре минус работа,
отданная в детандере), согласно уравнению энергетического
баланса (15-2), составляет:
I = Ч - ?о = (Г, - то) Д$ = q,
1 о
и изображается разностью площадей b—2—3—а—b и а—4—1—
—b—а, т. е. площадью 1—2—3—4—1. Полученное выражение
для работы совпадает с
уравнением (15-1).
Холодильный коэффици-
ент идеального цикла равен
В» = ^=--^-2-7 (15-8)
1 1 К 1 О
и не зависит от применяемо-
го хладоагента, а определя-
ется только абсолютными
температурами конденсации
(7\) и испарения (То).
На диаграмме Т — S хо-
лодопроизводительность и
работа изображаются пло-
Рис. 15-3. Диаграмма р — i:
щадями, измерение которых
НеСКОЛЬКО Затруднительно. 2—3—4—I—ЦИКЛ идеальной компрессионной
Пои Расчетах ПОЛЬЗУЮТСЯ холодильной машины; 3—4'—дросселирование;
“ Н J АВ — нижняя пограничная кривая; ВС — верхняя
ДИаграММОИ «давление — пограничная кривая,
энтальпия» (диаграмма
р — i), на которой холодопроизводительность и работа выра-
жаются прямолинейными отрезками.
На рис. 15-3 показаны основные линии диаграммы р — i. Ли-
нии р = const изображаются горизонталями, а линии i = const —
вертикалями. На диаграмме нанесены изотермы (линии t =
= const) и адиабаты (линии S = const). Линия АВС является
пограничной кривой, причем точка В соответствует критиче-
ской точке. Область ниже пограничной кривой соответствует
34 Зак. 546.
530
Гл 15 Искусственное охлаждение
влажному пару, выше этой кривой и левее точки В — жидкости,
а выше этой кривой и правее точки В — перегретому пару. В об-
ласти влажного пара линии t = const совпадают с горизонта-
лями (линиями р = const), а в области жидкости идут близко
к вертикали. На диаграмме р — i (рис. 15-3) показан также
цикл идеальной компрессионной машины. Линии сжатия (/—2)
и расширения (3—4) совпадают с кривыми S = const, а линии
конденсации (2—3) и испарения (4—/) изображаются горизон-
тальными прямыми, соответствующими давлениям конденса-
ции (рк) и испарения (р0).
Пример 15-1. Рассчитать холодильный коэффициент и расход энергии на
получение 1000 кдж (240 ккал) холода в идеальной компрессионной ма-
шине при температуре конденсации /К=+35°С и температуре испарения
t0 = —23° С
Решение. Абсолютная температура конденсации 7\ — 273 + 35 = 308° К,
абсолютная температура испарения То = 273 — 23 = 250° К По формуле (15-8)
находим холодильный коэффициент:
250
£и - 308 — 250 = ’
Расход энергии на получение 1000 кдж холода составляет:
1000 . 233
N ~ —г^ = 233 кдж или xstv; 0,065 квт • ч
4,о иОим
Практически на получение 1000 кдж холода расходуется 0,1—0,12 квт • ч
(0,4—0,5 квт • ч на 1000 ккал).
Цикл реальной компрессионной
холодильной машины
В цикле идеальной компрессионной холодильной машины,
как видно из рис. 15-3, точка 2 лежит на верхней пограничной
кривой (т. е. соответствует сухому насыщенному пару), а со-
стояние хладоагента перед компрессором соответствует влаж-
ному пару (точка /); температура жидкого хладоагента перед
детандером равна температуре конденсации (точка 3 лежит на
нижней пограничной кривой).
На практике вследствие сложности конструкции детандера
расширение хладоагента производят путем дросселирования с
помощью регулирующего вентиля; затем «влажный ход» ком-
прессора (работа его в области влажного пара) заменяется
«сухим ходом», т. е. компрессор засасывает сухой насыщенный
пар и сжатие происходит в области перегретого пара. Кроме
того, часто производят переохлаждение жидкого хладоагента
перед дросселированием, т. е. охлаждают его до температуры
более низкой, чем температура конденсации.
3. Компрессионные холодильные машины
531
На рис. 15-3 линиями 1—2—3—4'—1 представлен цикл хо-
лодильной машины с дросселированием хладоагента, отличаю-
щийся от цикла идеальной холодильной машины тем, что расши-
рение при дросселировании происходит по линии 3—4' (i = const).
По сравнению с идеальным циклом холодопроизводительность
уменьшается на величину отрезка 4—4', равного работе, отда-
ваемой в детандере. На эту же величину увеличивается затрата
работы. В соответствии с уменьшением холодопроизводительно-
сти и увеличением затрачиваемой работы холодильный коэффи-
циент снижается.
Рис. 15-4. Цикл реальной компрессионной холо-
дильной машины:
/—компрессор; // — конденсатор; /// — регулирующий вен-
тиль, IV— испаритель: V — насос для рассола; VI — аппарат,
потребляющий холод.
На рис. 15-4 показан цикл холодильной машины, работающей
на сухом ходу с переохлаждением жидкости. Точка 1, лежащая
на пограничной кривой и соответствующая давлению испарения
Ро, изображает состояние хладоагента перед компрессором. Ли-
ния 1—2 (направленная по S = const) изображает сжатие па-
ров хладоагента в компрессоре, причем точка конечного сжа-
тия 2 соответствует давлению конденсации рк. Линия 2—3
(горизонталь, соответствующая рк = const) изображает процесс
в конденсаторе, причем отрезок 2—2' выражает охлаждение пе-
регретых паров до температуры конденсации, отрезок 2'—3' со-
ответствует конденсации паров при постоянной температуре,
отрезок 3'—3 изображает процесс переохлаждения жидкости;
точка 3 лежит на изотерме, соответствующей температуре пере-
охлаждения /п.
Линия 3—4 (вертикаль, соответствующая i = const) выра-
жает процесс дросселирования от давления рк до р0, а линия
34*
532
Гл. 15. Искусственное охлаждение
4—1 (горизонталь, соответствующая р0 = const) — процесс ис-
парения хладоагента в испарителе.
Достоинствами сухого хода являются отсутствие гидравли-
ческих ударов, уменьшение потерь при теплообмене хладоагента
со стенками цилиндра и повышение коэффициента подачи ком-
прессора.
При отсутствии переохлаждения цикл изображается линиями
1—2—2'—3'—4'—1. Переохлаждение жидкого хладоагента по-
вышает холодопроизводительность на величину отрезка 4—4',
а расход энергии при этом не изменяется. Поэтому переохла-
ждение весьма выгодно, особенно при работе в области, близ-
кой к критическому состоянию.
Холод, получаемый в испарителе при испарении хладоагента,
может быть непосредственно передан охлаждаемой среде или
использован для охлаждения незамерзающих рассолов, которые
направляются затем в аппараты, потребляющие холод. Схема
рассольного охлаждения показана на рис. 15-4; рассол с по-
мощью насоса V непрерывно циркулирует между испарителем
IV и аппаратами VI, потребляющими холод.
В качестве рассолов применяют водные растворы хлористого
натрия и хлористого кальция. Температура замерзания рассола
должна быть на 3—5° С ниже температуры испарения /0. Рас-
творы хлористого натрия применимы при t0 до —16° С, а рас-
творы хлористого кальция — до—50° С.
Холодопроизводительность компрессионной машины в боль-
шой степени зависит от температур испарения (/0) и конден-
сации (tK). С понижением /о увеличивается удельный объем
паров хладоагента; поэтому масса засасываемых компрессором
паров (при одной и той же объемной производительности)
уменьшается, что приводит к снижению холодопроизводитель-
ности установки.
При повышении tK цикл изображается ломаной линией
1—2"—3"—4" (рис. 15-4); удельная холодопроизводительность
изображается при этом отрезком 1—4", меньшим, чем отрезок
1—4'. Таким образом, с повышением /к холодопроизводитель-
ность установки понижается.
Уменьшение холодопроизводительности при снижении темпе-
ратуры испарения и повышении температуры конденсации про-
Рк
исходит также вследствие увеличения степени сжатия что
Ро
в свою очередь вызывает уменьшение коэффициента подачи
компрессора. Одновременно увеличение степени сжатия приво-
дит к увеличению затраченной работы I и к уменьшению инди-
каторного к. п. д. компрессора.
3. Компрессионные холодильные машины
533
Так как холодопроизводительность зависит от условий про-
ведения холодильного цикла, то принято сравнивать работу
холодильных машин при стандартных условиях:
Температура конденсации......... tK = -f- 30° С
» переохлаждения ... /п = 4- 25° С
» испарения................... t0 — — 15° С
Эти условия приняты по предложению советских ученых
Международным институтом холода в 1938 г.
Пример 15-2. Построить холодильный цикл для фреона Ф-12 (стр. 540) и
определить холодильный коэффициент цикла при следующих условиях: темпе-
ратура конденсации tK = +35° С, температура испарения to = —23° С, темпе-
ратура переохлаждения ta = 27° С.
Решение. По заданным температурам tK, ta и t0 строим холодильный
цикл на диаграмме р — i (см. рис. 15-5, стр. 534) и определяем энтальпии:
/j = 562 • 103 дж!кг (134,3 ккал!кг)
i2 = 595,5 • 103 дж!кг (142,3 ккал!кг)
i3 = /4 = 444 • 103 дж)кг (106,1 ккал!кг)
Удельная холодопроизводительность Ф-12 равна:
qQ = /[ — = 562 • 103 — 444 • 103 = 118 • 103 дж!кг (28,2 ккал[кг)
Работа сжатия в компрессоре составляет:
I = 12 — i\ — 595,5 • 103 — 562 • 103 = 33,5 • 103 дж!кг (8 ккал!кг)
Холодильный коэффициент цикла:
118-10» ,,2
I ~ 33,5 • 103 —
По отношению к идеальному циклу (см. пример 15-1) к. п.д. составляет:
^..100 = 82%
Расчет паровых компрессионных холодильных машин
При расчете холодильной установки обычно бывают заданы холодопроиз-
водительность Qo вт, начальная температура охлаждающей воды и тем-
пература охлаждаемой среды. По этим данным надо прежде всего вы-
брать температуры конденсации, переохлаждения и испарения хладоагента
(^к» ^п» h).
Для определения tK и /п задаются степенью нагрева воды в конденсаторе
на 5—7° С и принимают /к на 7—8° С выше средней температуры воды, гп на
2—3°С выше начальной температуры воды. |
Температуру испарения выбирают на 5° С ниже температуры охлаждае-
мой среды (при рассольном охлаждении to принимают на 5° С ниже темпе-
ратуры охлажденного рассола, а охлаждение рассола в испарителе полагают
равным 2—3°С).
Зная tK, tn и t0 (а следовательно, и соответствующие давления рк 11 ра),
можно построить холодильный цикл на диаграмме р—i и найти удельную
холодопроизводительность хладоагента до и работу /.
534
Гл. 15. Искусственное охлаждение
Далее из формулы (15-5) определяют количество циркулирующего хладо-
агента G и объем хладоагента, засасываемый компрессором.
V = Gv м3/сек (15-9)
где v — удельный объем пара хладоагента перед компрессором, мР/кг (на-
ходится по диаграмме р — i для точки 1 или по таблицам для на-
сыщенных паров хладоагента).
Объем, описываемый поршнем компрессора-
у
Ут = -у M^jceK
(15-10)
где / —коэффициент подачи, определяемый по формуле (7-40).
Энтальпия, ккал/кг
Рис. 15-5. Диаграмма р — i для дифтордихлорметана (фреон Ф-12):
1—2—3—4 — холодильный цикл (к примеру 15-2).
Коэффициенты пересчета в систему СИ:
Давление..........am X 0,981 = 105 н!м2 = бар
Энтальпия.........ккал!кг х 4190 = дж/кг
3. Компрессионные холодильные машины
535
Теоретическую мощность, затрачиваемую в компрессоре на адиабатиче-
ское сжатие, рассчитывают по формуле (7-32).
Средние значения коэффициента подачи X и индикаторного (адиабати-
ческого) кпд. 1]инд. Для холодильных компрессоров можно определить по
рис 15-6, стр 537.
Механический к. п. д. в обычных условиях составляет — 0,8 — 0,85.
Действительный холодильный коэффициент холодильной установки:
е = ет1]инд.1]м (15-11)
где ет — теоретический холодильный коэффициент цикла ^ет = .
Количество тепла, отводимого в конденсаторе, определяется по формуле-
Qk = pQo + Mu. (15-12)
где р — поправочный коэффициент, равный 1,08—1,2;
TVaA.— адиабатическая мощность компрессора.
Пример 15-3. Рассчитать холодильную машину (хладоагент — Ф-12) для
охлаждения и сжижения 2 000 кг/ч хлора при следующих условиях:
Температура поступающего
газообразного хлора .... 30° С
Температура конденсации
хлора.................... —10° С
Удельная теплоемкость хлора 519 дж/кг • град (0,124 ккал/кг • град)
Теплота испарения хлора . . 282 • 103 дж/кг (67,4 ккал/кг)
Температура охлаждающей
воды..................... 25° С
Решение. Холодопроизводительность установки равна количеству
тепла, отводимого от хлора при его охлаждении и конденсации:
Qo = iSSS • 519 [30 — (-10)] + 1^-282 -103 = 168 000 вт (144 700 ккал/ч)
3600 3600
С учетом потерь холода в размере ~3%, принимаем Qo — 174 000 вт
(150 000 ккал/ч).
Температуру нагретого рассола, выходящего из конденсатора хлора, вы-
бираем —15° С (на 5°С ниже температуры конденсации хлора); тогда темпе-
ратура охлажденного рассола (при охлаждении его в испарителе на 3°С) со-
ставит —18° С, температуру испарения фреона принимаем на 5° С ниже, т. е.
t0 = —18 — 5 = —23° С.
Пусть вода нагревается в конденсаторе на 6° С; тогда температура ухо-
дящей воды составит 25 + 6 = 31° С, а средняя температура воды
—5 31 = 28° С
Температуру конденсации принимаем на 7° С выше средней, а темпера-
туру переохлаждения — на 2° С выше начальной температуры воды, т. е.
4 = 28 + 7 = 35 °C
/п = 25 + 2 = 27°С
Холодильный цикл для данных условий построен на рис. 15-5, найден-
ные значения qo и / см в примере 15-2.
Количество циркулирующего фреона находим по формуле (15-5)
G = — = — 1,48 кг/сек — 5320 кг/ч
qo 118 • 10J '
536
Гл. 15. Искусственное охлаждение
а его объем — из уравнения (15-9)
V = 5320 • 0,124 = 660 м3/ч
где v — 0,124 м3/'кг (см. рис. 15-5).
Адиабатическая мощность компрессора равна
х. GI 1,48-33,5-103
~ 1000 — 1000 ~ 49,5 квт
По р — i-диаграмме (см. рис. 15-5) определяем абсолютное давление
конденсации рк — 8,46 бар (8,63 ат) при tK = 35° С и абсолютное давление
испарения р0 == 1,34 бар (1,37 ат) при t0 = — 23° С. По рис. 15-6 при
— 6,3 находим коэффициент подачи X = 0,75 и индикаторный к. п. д.
Ро 1,о/
’’Зинд. — 0,69.
Необходимый объем, описываемый поршнем, составляет:
Ft=t=^“880 м3/ч
Л V,/ о
Подбираем по каталогу компрессор 2ФВ-35, для которого VT = 1038 м3/ч
при п — 360 об/мин.
Принимая механический к. п. д. компрессора т]м = 0,85, определяем эф-
фективную мощность:
49 5
Na^ = 0,69 • 0,85 ~ 85 Квт
При р = 1,1 количество тепла, отводимого в конденсаторе, вычисляем
по формуле (15-12)-
QK = 1,1 -174 000 + 1000 • 49,5 = 241 000 вт (209 000 ккал/ч)
Расход охлаждающей воды (при теплоемкости 4190 дж/кг • град);
W = = 9-6 кг/сек 35 000 кг/ч = 35 м3/ч
41Уи (о! — 20)
Количество циркулирующего рассола при его теплоемкости
2760 дж/кг • град (0,66 ккал/кг • град) и плотности 1250 кг/м3 составляет:
174 000 ЛЛ1Й7 □ . СЛ Ч/
8 ~ 2760 • 3 • 1250 “ °’0167 м 1сек = 60 ж /Ч
Зная тепловые нагрузки конденсатора (241 000 вт) и испарителя
(174 000 вт), а также количества охлаждающей воды и рассола, можно рас-
считать вспомогательное оборудование (конденсатор, испаритель, насос для
рассола).
Пример 15-4. Определить холодопроизводительность аммиачного компрес-
сора 4АУ-15 при /К=+35°С, /П=+27°С и to = —23° С, если его холодо-
производительность для стандартных условий составляет 174 000 вт
(150 000 ккал/ч) при и = 720 об/мин.
Решение. Из уравнений (15-5), (15-9) и (15-10) следует:
О -Zzkl
3. Компрессионные холодильные машины
537
Для данного компрессора объем, описываемый поршнем VT,— величина
постоянная, поэтому холодопроизводительность может быть вычислена по
формуле:
Qo — Фстанд.
fyo/v
(^о/^Останд.
По диаграмме р — i (см. Приложение XVIII) определяем:
Для рабочих
условий
Для стандарт-
ных условий
q0, кдж/кг (ккал/кг) . . . 1155 (276)
v, м3/кг........................... 0,683
Ас, бар (ат)...............
Ра, бар (ат)...................... 1,76 (1,8)
Рк/Ро............................... 7*7
1170 (279)
0,509
11,7 (11,9)
2,36 (2,41)
4,95
Примечание. Цифры в скобках соответствуют
денным тоже в скобках.
По рис. 15-6 находим: для рабо-
чих условий X = 0,72, для стандарт-
ных условий X = 0,79. Таким образом
Qo = 174 000
0,72 • 1155/0,683
0,79 • 1170/0,50^
~ 116 000 вт (100 000 ккал/ч)
Сложные схемы
компрессионных
холодильных машин
Многоступенчатые холодильные
машины. При низких температурах ис-
парения или высоких температурах
конденсации степень сжатия (отноше-
ние Рк/Ро) паров хладоагента в ком-
прессоре становится значительной,
что приводит к резкому снижению
коэффициента подачи. Аммиачные хо-
размерностям, приве-
Рис. 15-6. Коэффициент подачи X и
индикаторный к. п. д. 7]инд. холо-
лодильные машины удовлетворитель- дильных компрессоров.
но работают при степени сжатия не
свыше 8—9. При больших степенях сжатия переходят к двух- и трехступен-
чатым холодильным машинам.
На практике одноступенчатые аммиачные холодильные машины приме-
няют при t0 свыше —25° С; при t0 от —25 до —50° С используют двух-
ступенчатые машины и при to от —50 до —70° С применяют трехступен-
чатые машины.
На рис. 15-7 показана схема двухступенчатой холодильной машины.
Пары хладоагента сжимаются в цилиндре низкого давления (ЦНД) до про-
межуточного давления рпр. и через холодильник / поступают в промежуточ-
ный сосуд II. В этом сосуде, барботируя через слой жидкого хладоагента,
пары охлаждаются до температуры, соответствующей насыщению при давле-
нии рпр.- Охлаждение паров достигается за счет испарения некоторого коли-
чества жидкого хладоагента в промежуточном сосуде. Из сосуда II пары
538
Гл. 15. Искусственное охлаждение
засасываются в цилиндр высокого давления (ЦВД), где сжимаются до дав-
ления конденсации рк.
Далее пары поступают в конденсатор III, где они конденсируются. Жид-
кость, проходя через первый регулирующий вентиль (PBI), дросселируется
до давления рпр. и поступает в промежуточный сосуд. Часть хладоагента
в сосуде II, как указывалось выше, испаряется и поступает в цилиндр высо-
кого давления; остальная часть хладоагента дросселируется, проходя через
второй регулирующий вентиль (РВИ), до давления испарения ро и поступает
в испаритель IV, из которого пары засасываются в'цилиндр низкого давле-
ния.
На диаграмме (см. рис. 15-7) линия 1—2 изображает сжатие в ци-
— охлаждение паров в холодильнике,
а линия 3'—3 — охлаждение их в про-
межуточном сосуде.
Точка 3 лежит на пограничной
кривой и соответствует сухому на-
сыщенному пару при давлении рПр.
Линии 3—4, 4—5 и 5—5' изобража-
ют соответственно сжатие в цилиндре
ЦВД ЦНд
Рис. 15-7. Цикл двухступенчатой компрессионной холодильной машины:
/ — холодильник; //—промежуточный сосуд; /// — конденсатор; /^—испаритель.
высокого давления, процесс в конденсаторе и дросселирование в первом ре-
гулирующем вентиле. Точка 5' (состояние хладоагента после дросселирова-
ния) лежит в области влажного пара;
Рис. 15-8. Схема каскадного цикла:
1 — аммиачный компрессор; 2— фреоновый
компрессор; 3—испаритель фреона; /, 6 — ре-
гулирующие вентили; 5—конденсатор-испа-
ритель; 7—конденсатор аммиака.
для таких хладоагентов, как аммиак и
в промежуточном сосуде влажный пар
разделяется на паровую (состояние
характеризуется точкой 3) и жидкую
(состояние характеризуется точкой 6)
фазы. Линии 6—7 и 7—1 изображают
дросселирование во втором регули-
рующем вентиле и испарение.
Каскадный цикл. Для хладоаген-
тов с невысоким давлением конденса-
ции рк при низких температурах ис-
парения компрессор должен работать
со значительным вакуумом.
Современные поршневые ком-
прессоры могут работать при наи-
меньшем абсолютном давлении вса-
сывания 0,1 ат, что соответствует тем-
пературе испарения около —70° С
фреон Ф-12. Хладоагенгы с более вы-
соким давлением всасывания при низких температурах испарения имеют низ-
кую критическую температуру. Кроме того, для их конденсации необходимо
4 Холодильные агенты. Устройство компрессионных холодильных машин 539
применение высоких давлений; все это усложняет холодильную установку.
Поэтому при температурах испарения ниже —70° С применяют каскадный
цикл, в котором рабочими веществами являются два (или более) хладоагента
в различных интервалах температур. При этом холод, получаемый в верхней
ступени каскадного цикла, используется для конденсации хладоагента, при-
меняемого в нижней ступени. В верхней ступени осуществляют обычно двух-
ступенчатое сжатие, в нижней — одно- или двухступенчатое.
На схеме каскадного цикла (рис. 15-8), в верхней ступени рабочим веще-
ством служит аммиак (в интервале температур от +30 до —30° С), в ниж-
ней ступени — фреон Ф-13 (в интервале температур от —25 до —90°С).
Аммиачный испаритель является одновременно конденсатором для фреоно-
вого каскада (конденсатор-испаритель 5). Температура испарения аммиака
должна быть, разумеется, ниже температуры конденсации фреона.
4. Холодильные агенты. Устройство компрессионных холодильных машин
Холодильные агенты
Для получения холода в компрессионных машинах теоретически могут
служить пары любого вещества. Однако к хладоагентам предъявляется ряд
требований, значительно сокращающих возможное их число.
К хладоагентам для поршневых машин предъявляются следующие тре-
бования.
1) давление испарения Ро должно быть выше атмосферного или близким
к нему, так как легче предотвратить утечку хладоагента, чем подсос воз-
духа; при работе в вакууме абсолютное давление испарения должно
быть больше 0,1 ат\
2) теплота испарения хладоагента должна быть возможно больше, а
удельный объем его пара возможно меньше, что соответствует наименьшим
размерам поршневой холодильной машины;
3) температура замерзания хладоагента должна быть ниже температуры
испарения;
4) хладоагенты не должны обладать коррозионными свойствами и не
должны образовывать со смазочным маслом соединений, нарушающих нор-
мальную смазку машины;
5) хладоагенты не должны оказывать вредного действия на человече-
ский организм и должны быть безопасными в пожарном отношении.
Хладоагенты для турбокомпрессорных холодильных машин должны об-
ладать большим молекулярным весом (что позволяет строить турбоком-
прессоры с малым числом ступеней) и, в противоположность агентам
для поршневых машин, малой объемной холодопроизводительностью (чго
дает возможность строить турбокомпрессоры малой холодопроизводитель-
ности).
В поршневых машинах в качестве хладоагентов применяются аммиак,
сернистый ангидрид, двуокись углерода, хлористый метил, фреоны, а при низ-
ких температурах испарения (ниже —70° С) —пропан, этан и этилен.
Наиболее распространенным хладоагентом является аммиак, применяе-
мый при температурах испарения вплоть до —65° С. При использовании ам-
миака требуется сравнительно малый объем цилиндра машины; аммиак до-
ступен и легко обнаруживается при утечке. Недостатками аммиака являются
ядовитость, воспламеняемость и взрывоопасность в смесях с воздухом; под
действием аммиака медь и ее сплавы в присутствии влаги подвергаются
коррозии.
Двуокись углерода безвредна, при ее применении требуется наименьший
объем цилиндра машины. Недостатком СОг является высокое рабочее давле-
ние конденсации. Вследствие малых габаритов углекислотные машины исполь-
зуются в судовых установках.
540
Гл. 15. Искусственное охлаждение
В последнее время широкое распространение получили фреоны (фтор-
хлорпроизводные углеводородов жирного ряда), которые в большинстве слу-
чаев безвредны, не имеют запаха, взрывобезопасны и не горючи. Эти
достоинства фреонов имеют существенное значение в малых (бытовых и тор-
говых) холодильных установках и в установках для кондиционирования воз-
духа. Недостатком фреонов является их растворимость в смазочных маслах;
что обусловливает ряд особых требований как к самому маслу, так и к
схеме смазки.
Из различных фреонов основным агентом для поршневых машин (при
температурах испарения выше —7(ГС) является Ф-12 (CCI2F2). Фреоны Ф-13
(CCIF3) и Ф-22 (CHCIF2) применяются в низкотемпературных ступенях ка-
скадных циклов вместо пропана, этана и этилена. Фреон Ф-13 используется
также вместо двуокиси углерода в судовых установках.
В турбокомпрессорных машинах при температурах испарения выше
—20° С наиболее распространенными агентами являются дихлорметан и
фреон Ф-11 (CCI3F). При более низких температурах испарения (до —80° С)
применяется фреон Ф-12. В последнее время вместо дихлорметана исполь-
зуется фреон Ф-113 (C2CI3F3).
Устройство паровых компрессионных
холодильных машин
Компрессоры. Основными современными типами поршневых одноступен-
чатых холодильных компрессоров являются горизонтальные компрессоры
двойного действия и вертикальные прямоточные компрессоры простого дей-
ствия, а также компрессоры с угловым расположением цилиндров. Для
многоступенчатого сжатия применяют горизонтальные компрессоры с диф-
ференциальным поршнем. Двухступенчатое сжатие может быть получено
также соединением отдельных одноступенчатых компрессоров соответствую-
щих размеров. Аммиачные и фреоновые компрессоры (вертикальные и с уг-
ловым расположением цилиндров) изготовляются с холодопроизводитель-
ностью (при стандартных условиях}, от 8000 до 300 000 ккал/ч. Аммиачные
горизонтальные компрессоры изготовляются холодопроизводительностью
600 000 и 1 200 000 ккал/ч. При холодопроизводительности более 300 000 ккал/ч
целесообразно применение турбокомпрессоров.
Конденсаторы. Наиболее распространены элементные конденсаторы (из-
готовляются с поверхностью 8, 16, 20, 32, 40, 60, 80, 100 и 120 м2), ороситель-
ные конденсаторы с нижним подводом пара и промежуточным отводом кон-
денсата в нескольких местах по высоте (изготовляются с поверхностью 30,
45, 60, 75 и 90 м2) и вертикальные кожухотрубные конденсаторы ороситель-
ного типа с движением воды по трубам (изготовляются с поверхностью 50,
75 и 100 м2).
Ниже приведены практические коэффициенты теплопередачи k и удель-
ные тепловые нагрузки q (при температурном напоре 0Ср. = 5° С) для кон-
денсаторов различных типов:
Конденсаторы
k q
вт/м1-град вт/м?
Погружные............................... 175—230
«Труба в трубе» и элементные............ 900—1150
Кожухотрубные горизонтальные и вертикаль-
ные .................................... 700—900
Оросительные
с верхним подводом паров................ 230—300
с нижним подводом паров............. 800—1050
900—1150
4600—5800
4000—5200
1150—1400
4000—5800
4. Холодильные агенты. Устройство компрессионных холодильных машин 541
Испарители. Наиболее распространены вертикальнотрубные и горизон-
тальные кожухотрубные испарители с движением рассола по трубам. Вер-
тикальнотрубные испарители (рис. 15-9) состоят из трубчатых секций, поме-
щенных в бак /, в котором при помощи мешалки 2 циркулирует рассол.
Каждая секция выполнена из двух горизонтальных коллекторов 3, соеди-
ненных между собой изогнутыми на концах трубами 4 и вертикальными
трубами 5 большего диаметра. Жидкий хладоагент заполняет нижний кол-
лектор и большую часть труб. Циркуляция хладоагента происходит за
счет различного нагревания его в изогнутых и вертикальных трубах.
Жидкий
Пары
Рис. 15-9. Вертикальнотрубный испаритель:
1 — бак; 2— мешалка; 3—коллектор; 4— изогнутые трубы; 5 — циркуляционные
трубы; 6 — перегородка; 7 — отверстия в перегородке; 8 — маслоотделитель; 9 — изо-
ляция.
Вертикальнотрубные испарители изготовляются с поверхностью 20, 30,
40, 60, 90, 120, 160 и 200 м2.
Кожухотрубные испарители отличаются простотой, компактностью и за-
крытой системой циркуляции рассол’а; их недостатком является возмож-
ность замерзания рассола в трубах при остановке насоса. Многоходовые
кожухотрубные испарители изготовляют с поверхностью 50, 80 и 100 м2.
Ниже приведены практические коэффициенты теплопередачи k и удель-
ные тепловые нагрузки q (при 0Ср. = 5° С) для различных испарителей:
k q
Испарители вт/м2-град вт/м2
Погружные..........................
Вертикальнотрубные.................
Кожухотрубные:
одноходовые ......................
многоходовые...................
оросительные (для фреона) * . . .
230—300
520—650
350—400
400—450
450—580
1150—1500
2900—3500
1850—2100
2100—2600
2300—2900
* С орошением наружной поверхности труб жидким хладоагентом.
542
Гл. 15. Искусственное охлаждение
5. Холодильные машины с затратой тепла на получение
холода
Абсорбционные холодильные машины
В абсорбционных холодильных машинах рабочим агентом
служит водный раствор аммиака, причем аммиак является хла-
доагентом, а вода — поглотителем.
На рис. 15-10 показана схема абсорбционной холодильной
машины. В генераторе 1 за счет подогрева происходит выпари-
Рис. 15-10. Схема абсорбционной
холодильной машины:
1 — генератор; 2— конденсатор; 3— регу-
лирующий вентиль; 4— испаритель;
5— абсорбер; 6— перепускной вентиль;
7 —насос; 8 — теплообменник.
Для улучшения работы
вание водноаммиачного раство-
ра, в результате чего отгоняется
легкокипящий компонент — ам-
миак с некоторым количеством
паров воды. Пары аммиака из
генератора поступают в конден-
сатор 2, откуда жидкий аммиак
направляется в испаритель 4 че-
рез регулирующий вентиль 3, в
котором снижается давление ам-
миака. Из испарителя пары ам-
миака поступают в абсорбер 5,
где они поглощаются слабым
раствором, подаваемым из гене-
ратора через перепускной вен-
тиль 6. Тепло, выделяющееся при
поглощении аммиака, отводится
путем охлаждения абсорбера.
Концентрированный раствор, по-
лучающийся в абсорбере, пере-
качивается насосом 7 в генератор,
установки крепкий раствор, пере-
качиваемый из абсорбера в генератор, пропускают через тепло-
обменник 8, в котором он подогревается горячим слабым рас-
твором, поступающим из генератора в абсорбер.
Таким образом, в абсорбционную установку входят два аппарата (гене-
ратор и испаритель), в которые тепло подводится извне, и два аппарата
(конденсатор и абсорбер), из которых тепло отводится охлаждающей водой.
Тепловой баланс абсорбционной установки выражается уравнением
Рген. + Qo = Qk + Qa (15-13)
где Qrcn.— тепло, сообщаемое раствору в генераторе;
Qo — холодопроизводительность (тепло, подводимое в испарителе);
— тепло, отдаваемое в конденсаторе;
Qa — тепло, отдаваемое в абсорбере.
5. Холодильные машины с затратой тепла на получение холода 543
Холодильный коэффициент в данном случае представляет собой отноше-
ние количества полученного холода к теплу, затраченному в генераторе:
£ —
QreH.
Теоретическое значение е абсорбционной холодильной машины можно
найти из следующих соображений. Пусть абсолютная температура в генера-
торе равна Т'ген., а абсолютные температуры конденсации и испарения со-
ставляют Тк и Го. Так как в обратимом круговом процессе изменение энтро-
пии равно нулю, то
QreH. I Qo Qk Qa _________л
Т 1 т т v
л ген. л о -'к
На основании уравнения (15-13)
QreH. । Qo___ QreH. + Qo
'р "Т" 'г 'г
1 ген. 7 о 1 к
откуда можно определить
_1_______________________________________________1
_ Qo _____ гк гген-
QreH. J__________L ' (15-14)
Го Гк
Теоретический холодильный коэффициент абсорбционной машины уве-
личивается с повышением Тген. и То и уменьшается с повышением темпера-
туры Тк; он всегда ниже холодильного коэффициента обратного цикла Карно.
Хотя величина е для компрессионных машин значительно выше, чем холо-
дильный коэффициент абсорбционных машин, необходимо учесть, что ком-
прессионные машины расходуют электрическую энергию, а получение послед-
ней из тепловой энергии связано с низким к. п. д. тепловых двигателей.
Фактический расход тепла в абсорбционных и компрессионных машинах при-
мерно один и тот же. Поэтому выбор типа машины может быть произведен
только путем соответствующих технико-экономических расчетов.
Применение абсорбционных машин целесообразно при на-
личии в производстве отработанного тепла (отбросного пара,
отходящих топочных газов), а также при необходимости полу-
чения низких температур испарения (до —50° С), когда тре-
буются сложные многоступенчатые компрессионные установки.
Следует также отметить, что для абсорбционных машин
требуются меньшие затраты и менее сложное оборудование
(отсутствуют компрессоры); кроме того, они не имеют движу-
щихся частей, за исключением насоса для водноаммиачного
раствора.
Пример 15-5. Определить теоретический холодильный коэффициент аб-
сорбционной холодильной машины при температуре конденсации tK = +35° С
и температуре испарения
/ген. ’ 120 С.
/о = —23° С, если температура раствора в генераторе
544
Гл. 15. Искусственное охлаждение
Решение. По формуле (15-14) находим:
1 1
273 4-35 273 4- 120 Л
е =----р---------j---= 0,935
273 — 23 “ 273 4- 35
откуда к. п. д. машины по сравнению с идеальным холодильным циклом (см,
пример 15-1) составляет:
^•100 = 21,8%
Пароэжекторные холодильные машины
В пароэжекторных холодильных машинах хладоагентом слу-
жит вода. Достоинствами воды как хладоагента являются вы-
сокая теплота испарения (почти в два раза выше, чем у ам-
миака), безвредность и доступность. В то же время, обладая
Рис. 15-11. Схема пароэжекторной
холодильной машины:
/ — эжектор; 2 —испаритель; 3— конденсатор;
4, 6 — насосы; 5 — регулирующий вентиль;
7—аппарат, потребляющий холод.
низким давлением пара, вода
характеризуется чрезвычайно
низкими давлениями испаре-
ния, что требует работы при
значительном вакууме. Это,
наряду с большим удельным
объемом пара, делает воду не-
пригодной в качестве хладо-
агента для компрессионных
машин. Указанные недостатки
воды становятся малосущест-
венными при применении па-
роструйных эжекторов для
сжатия паров воды.
Схема пароэжекторной хо-
лодильной машины показана
на рис. 15-11. Рабочий пар вы-
сокого давления (3—6 ат) на-
правляется в сопло эжектора /, где он расширяется, причем его
давление падает до давления испарения (абсолютное давление
5—10 мм рт. ст.). В эжектор засасывается холодный пар из
испарителя 2, образующаяся смесь паров сжимается до давле-
ния конденсации (абсолютное давление 30—40 мм рт. ст.). Че-
рез испаритель и аппарат 7, потребляющий холод, при помощи
насоса 6 циркулирует вода. Часть этой воды, в результате от-
сасывания эжекторов водяных паров из испарителя, испаряется.
Тепло, необходимое для испарения, отнимается от остальной ча-
сти воды, вследствие чего она охлаждается. При этом охлажде-
6. Разделение газ. смесей и сжижение газов глубоким охлаждением 545
ние воды в испарителе происходит на столько же градусов, на
сколько она нагревается в аппарате 7.
Смесь паров, выходящих из эжектора, конденсируется в
конденсаторе 3. Для отсасывания воздуха из конденсатора при-
меняют двух- или трехступенчатую вакуум-эжекционную уста-
новку (на схеме не показана). Конденсат отводится из конден-
сатора насосом 4, причем часть конденсата через регулирующий
вентиль 5 вводится в испаритель для пополнения убыли цирку-
лирующей воды, происходящей вследствие ее частичного испа-
рения.
Тепловой баланс пароэжекторной холодильной машины выражается
уравнением
Q+Qo = QK (15-15)
где Q — тепло, затрачиваемое в котле на получение рабочего пара из кон-
денсата, возвращаемого в котел;
Qo — холодопроизводительность (тепло, отводимое от охлаждаемой
среды в аппарате 7);
QK — тепло, отводимое в конденсаторе.
Холодильный коэффициент пароэжекторной холодильной машины:
(15-16)
Теоретическое значение холодильного коэффициента определяется, как и
для абсорбционных холодильных машин, по уравнению (15-14).
Пароэжекторные холодильные машины применяются пре-
имущественно при сравнительно высоких температурах испаре-
ния (от —10 до +10°С), причем в этих условиях они обычно
экономичнее абсорбционных машин. Недостатком пароэжектор-
ных машин является трудность регулирования их работы, так
как пароструйный эжектор может эффективно действовать толь-
ко при полной нагрузке. Поэтому в случае необходимости ре-
гулирования устанавливают несколько параллельно соединен-
ных эжекторов; регулирование производят путем отключения
части эжекторов.
6. Разделение газовых смесей и сжижение газов
методом глубокого охлаждения
Общие сведения
Такие процессы, как смешение газов и испарение, протекают
с увеличением энтропии. Обратные процессы — разделение га-
зовой смеси и сжижение газов — сопровождаются уменьшением
энтропии. Так как энтропия изолированной системы самопроиз-
вольно уменьшаться не может, для осуществления этих процес-
35 Зак 546.
546
Гл. 15. Искусственное охлаждение
сов должна затрачиваться работа, которая, согласно уравнению
(7-28), равна:
• I = q -|- /2 — Л
*
где —q — тепло, отдаваемое окружающей среде;
й — энтальпия поступающего газа;
/2— энтальпия уходящих продуктов разделения или сжи-
жения.
Разность 7о = й — h, равная количеству тепла, отнимаемого
от поступающего газа, представляет собой требуемую холодо-
производительность.
Тепло, отдаваемое окружающей среде, составляет:
—q — T&S
где Т — абсолютная температура окружающей среды;
AS — увеличение энтропии окружающей среды.
Таким образом
l=TbS~qQ (15-17)
Минимальное значение работы I соответствует такому про-
цессу, при котором увеличение энтропии окружающей среды
равно уменьшению энтропии перерабатываемого газа. Мини-
мальная работа не зависит от способа проведения процесса и
определяется только свойствами газа и температурой Т.
Для осуществления процесса необходимо проведение холо-
дильного цикла, холодопроизводительность которого должна
быть равна заданной величине. Для разделения газовых сме-
сей и сжижения газов применяют так называемые циклы глу-
бокого охлаждения, в которых происходит дросселирование
газа или расширение его в детандере.
Если сжижается доля х газа, поступившего в установку, то
энтальпия сжиженной части газа будет равна IqX (й — энталь-
пия сжиженного газа в дж/кг), а энтальпия несжиженной части
составит z2( 1—х)\ отсюда требуемая холодопроизводительность
<7о = й — U’o* + h (1 — *)1
Для уменьшения затраты холода применяют рекуперацию
его путем теплообмена между поступающим газом и его несжи-
женной частью. При идеальном теплообмене й = й; тогда
= х (й — /0)
т. е холод расходуется только на сжижение продукта.
Ввиду неполноты теплообмена, а также вследствие притока
тепла из окружающей среды имеют место потери холода qn
и холодопроизводительность составляет
<70 = х(/1 — /0) 4 Qn. (15-18)
6. Разделение газ. смесей и сжижение газов глубоким охлаждением 547
Для разделения газовой смеси ее превращают в жидкость и
подвергают ректификации (стр. 690); при этом продукты раз-
деления получаются в газообразном состоянии. В данном слу-
чае х — 0 и <7о = <?п.> т- е- холод расходуется лишь на покрытие
потерь. При отсутствии потерь для разделения газовой смеси
не требуется затраты холода: процесс идет за счет рекупера-
ции запаса холода, полученного при пуске установки.
Минимальная работа для разделения газовой смеси (при —
l^=TtxS (15-19)
Согласно законам термодинамики, изменение энтропии при смешении
идеальных газов (при постоянной температуре) составляет:
А5 1п^ + у21п^+ = дж1«г-град (15-20)
где R— газовая постоянная (R = 8314 дж/кмоль • град);
М—молекулярная масса газовой смеси;
У(, у2, •••—молярные (объемные) доли компонентов в газовой смеси.
Можно показать, что минимальная работа разделения газовой ^смеси
равна работе изотермического сжатия компонентов смеси от давления, рав-
ного их парциальному давлению в смеси, до общего давления смеси.
Потери холода складываются из следующих статей:
1. Потери от недорекуперации холода. Эти потери вызваны тем, что об-
ратный газ, выходящий из теплообменника, имеет более низкую температуру,
чем поступающий в теплообменник сжатый газ. С обратным газом теряется
<7нед. ~ Sc
где g — количество обратного газа, кг/кг сжатого газа;
с — удельная теплоемкость обратного газа, дж/кг • град;
М — разность температур (недорекуперация) между поступающим в
теплообменник сжатым газом и уходящим обратным газом.
Обычно равна приблизительно 5° С; при использовании регенераторов
она может быть снижена до 3° С.
2. Потери в окружающую среду (от несовершенства изоляции). Эти по-
тери составляют 4200—8400 дж (1—2 ккал) на 1 м3 перерабатываемого газа.
Пример 15-6. Определить минимальную работу, затрачиваемую для по-
лучения 1 кг жидкого воздуха и разделения 1 кг воздуха на газообразные
кислород и азот (при абсолютном давлении 1 ат). Температура воздуха
равна 30° С (Г = 303° К).
Решение. По диаграмме Т — S находим: разность энтропии газообраз-
ного воздуха (при 1 ат и Т = 303° К) и жидкого воздуха AS = 3810 дж/кг • град
(0,91 ккал/кг • град); энтальпия газообразного воздуха й = 515* 103 дж/кг
(123 ккал/кг)-, энтальпия жидкого воздуха io = 93-103 дж/кг (22 ккал/кг).
Холодопроизводительность составляет-
qa = й — /0 = 515 • 103 — 92 • 103 = 423 • 103 дж!кг (101 ккал!кг)
Минимальная работа определяется по формуле (15-17):
I = Т AS — qa = 303 • 3810 — 423 • 103 = 730.103 дж!кг =
— 730 кдж!кг (174 ккал)кг)
или
730
Збдо 0,2 квгп • ч (на 1 кг жидкого воздуха)
35*
548
Гл. 15. Искусственное охлаждение
Изменение энтропии при образовании воздуха путем смешения газо-
образных кислорода и азота вычисляем по уравнению (15-20):
4S = I£ + *|П^) = —25^(°'211П 051 + °'79ln ок) =
= 147 дж!кг • град (0,0352 ккал!кг • град}
где М — молекулярная масса воздуха (М = 29);
У] — объемная доля кислорода в воздухе (t/i =0,21);
у2 — объемная доля азота в воздухе (У2 = 0,79).
Минимальная работа равна
I = Т AS = 303 • 147 = 44500 дж/кг = 44,5 кдж/кг (10,7 ккал/кг)
или
——= 0,0124 квт • ч (на 1 кг воздуха)
или
0,0124 • 1,29 s 0,016 квт-ч (на 1 м3 воздуха).
Отсюда минимальный расход энергии на получение 1 к3 газообразного
0,016
кислорода составляет, q ~ квт • ч.
Холодильные циклы без отдачи внешней
работы (с дросселированием газа)
Рассмотрим холодильный цикл с дросселированием газа
(рис. 15-12). Газ с давлением pi и абсолютной температурой Т{
изотермически сжимается в компрессоре / до давления р2 (ли-
Рис. 15-12. Схема холодильного цикла
с дросселированием газа:
/ — комп рессор; II — дроссельный вентиль;
ill — подогреватель.
ния 1—2), после чего, пройдя
дроссельный вентиль //, газ
расширяется до первоначаль-
ного давления рь а его темпе-
ратура снижается до Т3 (ли-
ния 2—3 при t2 — const).
Охлажденный газ нагревается
в подогревателе III до перво-
начальной температуры Т\ (ли-
ния 3—1 при pi = const), отни-
мая от охлаждаемой среды ко-
личество тепла, равное холодо-
производительности 1 кг газа:
*7о *7дрос.== й (15-21)
Таким образом, холодопроизводительность при дросселиро-
вании равна разности энтальпии газа (й—t2) До и после изо-
термического сжатия в компрессоре.
6. Разделение газ. смесей и сжижение газов глубоким охлаждением 549
Количество тепла, отводимого при изотермическом сжатии
газа, равно:
—q = Ту AS
где AS — изменение энтропии (длина отрезка 1—2).
Работа, затраченная в компрессоре на сжатие газа (при тем-
пературе Ту), согласно уравнению (7-28) составляет
^компр. Я 4“ G*2 Л) == Т' 1 ^дрос.
или с учетом к. п. д. компрессора т|к
t AS <7дрос.
^КОМПр. - ~
Чк
(15-22)
Температура после дросселирования может быть снижена
путем рекуперации холода. Для этого сжатый газ до поступле-
ния в дроссельный вентиль пропускают через теплообменник,
где охлаждают расширенным
газом перед его подачей в
компрессор из подогревателя.
Холодопроизводительность и
затрата работы на сжатие га-
за при рекуперации холода не
изменяются.
Используя дросселирова-
ние воздуха в сочетании с ре-
куперацией холода, К. Линде
разработал рассматриваемые
ниже циклы получения жидко-
го воздуха.
Цикл с простым дроссели-
рованием (рис. 15-13). Сжа-
тый в компрессоре / и охлаж-
денный до комнатной темпе-
ратуры воздух поступает в
теплообменник II в точке 2. Пройдя теплообменник, воздух
дросселируется до атмосферного давления и вновь направляется
в теплообменник, двигаясь противотоком по отношению к по-
ступающему сжатому воздуху. Дросселированный воздух ох-
лаждает сжаФый воздух, вследствие чего температура послед-
него перед дросселированием все более снижается, пока не
наступает частичное сжижение воздуха в точке 4. После этого
жидкий воздух выводится из системы и в теплообменник воз-
вращается лишь несжиженная часть воздуха.
На диаграмме Т — S линия 1—2 выражает изотермическое
сжатие воздуха в компрессоре, линия 2—3 — охлаждение
Рис. 15-13. Схема цикла с простым
дросселированием:
/ — компрессор; /7 —теплообменник; /77 —ре-
гулирующий вентиль; IV — сборник жидкого
воздуха.
550
Гл 15. Искусственное охлаждение
сжатого воздуха в теплообменнике (при постоянном давле-
нии р2), линия 3—4 — дросселирование (при i = const). Точка 4
изображает состояние воздуха после дросселирования. Она ле-
жит в области влажного пара, причем доля сжиженного воз-
духа х равна отношению отрезка 4—5 к отрезку 0—5, а точки
0 и 5 изображают состояние жидкого и несжиженного воздуха.
Линия 5—1 изображает нагревание несжиженной части воз-
духа (при постоянном давлении р\).
Из уравнений (15-18) и (15-21) холодопроизводительность
цикла составляет:
<7о = * (Zi — /0) + qn, = — i2 (15-23)
Рис. 15-14. Схема цикла с двукрат-
ным дросселированием:
/ — вспомогательный компрессор; //—ком-
прессор; /// — теплообменник; IV, V7 —регу
лирующие вентили; V — сборник промежуточ-
ного давления; VII — соорник низкого
давления.
Разность i\ — /2 возрастает с повышением давления сжа-
тия р2; поэтому данный цикл требует применения значительного
давления (около 200 ат) и
связан с большим расходом
энергии.
Цикл с двукратным дрос-
селированием (рис.15-14). Рас-
ход энергии на сжатие возду-
ха можно уменьшить, если
дросселирование сжатого воз-
духа производить до некоторо-
го промежуточного давления
(20—50 ат), направляя несжи-
женную часть в компрессор II,
где она снова сжимается до
высокого давления (200 ат).
Полученный в сборнике про-
межуточного давления V жид-
кий воздух для удаления его
из системы дросселируется до
атмосферного давления и что-
ступает в сборник низкого да-
вления У1Г, при этом испаряется часть жидкого воздуха. Испа-
ренный воздух и несжиженная часть воздуха после первого
дросселирования проходят через теплообменник ///, где нагре-
ваются и охлаждают воздух, сжатый до высокого давления.
Взамен жидкого и испаренного воздуха, удаляемых из си-
стемы, вводится такое же количество свежего воздуха, который
сжимается во вспомогательном компрессоре / до промежуюч-
ного давления.
На диаграмме Т — S линия 2—3 изображает сжатие в ком-
прессоре от промежуточного до высокого давления, линия
3—4 — охлаждение в теплообменнике, линия 4—5 — первое
6. Разделение газ. смесей и сжижение газов глубоким охлаждением 551
дросселирование, линия 7—2 — нагревание в теплообменнике не-
сжиженной части воздуха, линия 6—8 — второе дросселирование
и линия 9—1 — нагревание в теплообменнике воздуха, испарен-
ного при втором дросселировании.
Пусть на 1 кг поступающего в теплообменник воздуха высо-
кого давления подается М кг свежего воздуха (обычно
М = 0,2—0,5); тогда через первый дроссельный вентиль про-
ходит 1 кг, а через второй М кг йоздуха. В соответствии с этим
холодопроизводительность цикла составляет:
<7о = * (Z, — Zo) + ?п. = (Z2 — Z3) + М — Z2) (15-24)
Рис. 15-15. Схема цикла с предваритель-
ным охлаждением:
Z — компрессор; //—предварительный теплообмен-
ник; ///—аммиачный холодильник; IV — глав-
ный теплообменник; V — регулирующий вентиль;
V/ —сборник жидкого воздуха.
Первый член этого выражения (Z2 — Z3) представляет собой
холодопроизводительность, обусловленную дросселированием
1 кг воздуха от высокого давления до среднего, а член
М (Zi — Z2) — холодопро-
изводительность, обусло-
вленную дросселировани-
ем М кг воздуха от сред-
него давления до 1 ат.
Цикл с предваритель-
ным охлаждением. Даль-
нейшим усовершенство-
ванием холодильных цик-
лов с дросселированием
является предварительное
охлаждение сжатого воз-
духа холодом, получен-
ным в аммиачной холо-
дильной установке. Сжа-
тый воздух (рис. 15-15)
сначала охлаждается об-
ратным потоком несжи-
женной части воздуха в
предварительном теплообменнике II, а затем поступает в ам-
миачный холодильник III, где охлаждается за счет испарения
аммиака до температуры около —40° С. Далее воздух охлаж-
дается в главном теплообменнике IV, после чего дросселируется.
Несжиженная часть воздуха проходит через главный и предва-
рительный теплообменники. Назначение предварительного теп-
лообменника заключается в полном использовании холода не-
сжиженной части воздуха, которая в главном теплообменнике
может быть нагрета лишь до температуры охлаждения сжатого
воздуха в аммиачном холодильнике.
На диаграмме Т — S точка 2” соответствует охлаждению воз-
духа в предварительном теплообменнике, а точка 2' — его
552
Гл. 15. Искусственное охлаждение
охлаждению в аммиачном холодильнике. Точка Г, характери-
зующая состояние несжиженной части воздуха на выходе из
главного теплообменника, отвечает той же температуре, что и
точка 2'.
Холодопроизводительность цикла составляет:
<7о = x(Zi — Z0)-h Qn. = Zi —(15-25)
т. e. равна разности энтальпий несжиженного воздуха, уходя-
щего из главного теплообменника, и сжатого воздуха, поступаю-
щего в этот теплообменник.
Количество тепла, отнимаемого в аммиачном холодильнике,
составляет:
<7ам. = (— Z2) —• (Zi — Z2) + х (Zj — Z0 (15- 26)
т. e. равно разности холодопроизводительностей данного
(Zi — Z0 и простого (Zi — Z2) циклов плюс тепло х (Zi — Zi),
необходимое для охлаждения сжижаемой части воздуха от тем-
пературы засасываемого воздуха до температуры охлаждения
в аммиачном холодильнике при 1 ат.
Цикл с двукратным дросселированием и предварительным охлаждением.
Этот цикл является комбинацией циклов с двукратным дросселированием
и предварительным охлаждением.
Холодопроизводительность цикла:
Qo = * (q — + Qa = Й — *3) + M — i'2) (15-27)
Количество тепла, отводимого в аммиачном холодильнике, составляет:
Qzm. ~ [(*2 — *з) + — *2)] — [(г2 — гз) + М (z'i — /2)] -|- х (г\ — г\) (15-28)
т. е. равно разности холодопроизводительностей данного цикла и цикла
с двукратным дросселированием без предварительного охлаждения плюс
тепло т (4 — z’i). необходимое для охлаждения сжижаемой части воздуха от
темперагруы засасываемого воздуха до температуры охлаждения в аммиач-
ном холодильнике при 1 ат.
Здесь величины 1’2 и 1$ соответствуют точкам 2 и 3 на рис. 15-14, a /2
и z3 — энтальпии воздуха при температуре после аммиачного холодильника
и соответственно низком, среднем и высоком давлениях.
Пример 15-7. Определить дроссельный эффект для воздуха при расшире-
нии до абсолютного давления 1 ат от начальных абсолютных давлений 50
и 200 ат; начальные температуры равны +30° С (303° К) и —70° С (203° К).
Решение. При помощи диаграммы Т — S, двигаясь по линиям
i = const от точек, характеризующих начальное состояние воздуха, до изо-
бары р = 1 ат, находим температуру после дросселирования и затем опре-
деляем дроссельный эффект. Результаты вычисления дроссельного эффекта
при расширении до 1 ат сведены в табл. 20.
6. Разделение газ. смесей и сжижение газов глубоким охлаждением 553
Таблица 20
Дроссельный эффект при расширении до 1 ат
Начальное абсолютное давление воздуха ат Начальная температура воздуха Конечная температура воздуха °К Дроссельный эффект °C
50 303 291 12
50 203 175 28
200 303 268 35
200 203 120 83
Из данных, приведенных в табл. 20, видно, что дроссельный эффект воз-
растает с понижением начальной температуры воздуха и повышением его
начального давления.
Пример 15-8. Рассчитать работу, затраченную на получение 1 кг жид-
кого воздух&т для простого цикла с дросселированием Температур^ сжатого
воздуха Л = 30° С, абсолютное давление р\ = 1 ат Потери холода в окру-
жающую среду составляют 6500 дж/кг (1,55 ккал/кг) и от недорекупера-
ции 5000 дж/кг (1,2 ккал/кг), т. е. ^п. = 6500 + 5000 = 11 500 дж[кг
(2,75 ккал/кг). Коэффициент полезного действия компрессора т)к = 0,6. Из
диаграммы Т — S (рис. 15-16) следует: й —515-Ю3 дж/кг (123 ккал/кг)-,
i0 = 93. 103 дж/кг (22 ккал/кг).
Решение Принимаем рз = 200 ат и находим по диаграмме Т — S ве-
личину z2 = 481,5-103 дж/кг (115 ккал!кг).
Холодопроизводительность вычисляем по формуле (15-21):
= ^дрос> = — z2 — 515 103 — 481,5 • 103 = 33,5 • 103 дж/кг (8 ккал/кг)
Доля сжижаемого воздуха определяется из уравнения (15-23):
q0 — qa, 33,5- 103— 11500
й~ z0 “ 515-103 —93-103
= 0,052
По диаграмме T — S изменение энтропии при сжатии воздуха от 1 до
200 ат и Ti = 273 + 30 = 303° К составляет Д5 = 1560 дж/кг град
(0,372 ккал/кг- град). Отсюда работу в компрессоре находим по фор-
муле (15-22). v
Т, AS — «’„пос 303 • 1560 — 33,5 • 103
I = J-------..72P2L =---------------—--------------= 732 103 дж/кг =
’Ik
= 732
“ 0,6
732
кдж/кг, или I = 3QQQ = 0,203 квт • ч/кг
Удельная работа,
ставляет:
затраченная на получение 1 кг жидкого воздуха, со-
, I 0,203 _
Zy«- ~ х ~ 0,052 ““ 3,9 Квт ' 4
554
Гл. 15. Искусственное охлаждение
Абсолютная температура, °Н
Рис. 15-16. Диаграмма Т—S для воздуха.
Коэффициенты пересчета в систему СИ:
Энтропия...........ккал/кг • град х 4190 = дж/кг • град
Энтальпия..........ккал/кг х 4190=дж/кг
Давление.............ат х 0,981 = 106 н/м2—бар
Холодильные циклы с расширением сжатого
газа в детандере
При адиабатическом расширении газа тепло не подводится
и не отводится, т. е. q = 0, и уравнение энергетического ба-
ланса (7-28) принимает вид /ад. = /3—i2, откуда затрачивае-
мая работа
^ад. ~ (^*2' Z3)
где 12 и t3 —энтальпия газа до и после расширения, дж/кг.
6. Разделение газ. смесей и сжижение газов глубоким охлаждением 555
I Так как при расширении работа совершается самим газом,
? то I имеет отрицательное значение. По абсолютной величине
| работа, совершаемая при адиабатическом расширении газа,
1 равна:
11 ^ад. === ^2 J3
» При адиабатических условиях энтропия не изменяется (так
> как q = 0) и процесс расширения газа от давления р2 до р\
’ изображается на диаграмме Т — S вертикальной линией 2—3
(рис. 15—17): точка 2 изобра-
жает начальное, а точка 3 — ко-
' нечное состояние газа.
' Фактический процесс в детан-
* дере отклоняется от адиабатиче-
ского и изображается линией
.V 2—3'. Энтальпия газа после рас-
ширения будет при этом i3 и ра-
бота, отдаваемая в детандере, со-
ставит
^дет. ^2 i% == ^дет. (^2 ^*з) (15“29)
где к. п. д. детандера
12 13
---—
Рис. 15-17. Схема холодильного
цикла при расширении газа с
отдачей внешней работы:
I — компрессор; II — детандер; III — поло-
жа — греватель.
Рассмотрим цикл холодильной машины, показанный на
рис. 15-17. Газ засасывается компрессором I при давлении
и температуре Тх и сжимается изотермически до давления р2
(линия 1—2). Сжатый газ расширяется в детандере// до давле-
ния рх, охлаждаясь до температуры 7V Охлажденный газ на-
гревается в подогревателе Ill до первоначальной температу-
ры Тх (линия 3'—1 при pi = const), воспринимая тепло (холодо-
производительность 1 кг газа):
<7о —• ix is
где п и гз — энтальпия газа в точках 1 и 3'.
Прибавляя и отнимая i2 в правой части этого выражения
получим
<7о (i 1 ^2) 4“ О2 is) = Ялрос. ^дет. (15-30)
т. е. холодопроизводительность детандера равна сумме холодо-
производительности, соответствующей дроссельному эффекту
(<7дрос.К и работы, отдаваемой в детандере (/дет_).
556
Гл. 15. Искусственное охлаждение
Затрата работы на получение холода равна работе ком-
прессора Асомпр. [определяется по формуле (15-22)] за вычетом
работы, отданной в детандере, т. е.
/ = /К0МПр, /дет
(15-31)
Рис. 15-18. Схема
цикла
высокого
давления с детандером:
/ — компрессор // — детандер: ///—теплооб-
менник; IV — дополнительный теплообменник;
V — регулирующий вентиль; VI — сборник
жидкого воздуха.
При рекуперации холода путем теплообмена между газом,
поступающим в детандер, и расширенным газом холодопроиз-
водительность ^дрос. и работа в компрессоре не изменяются; од-
нако /дет. уменьшается и, следовательно, общая затрата работы
возрастает, а холодопроизво-
дительность qo уменьшается.
Цикл высокого давления
(цикл Гейландта). Сжатый до
давления ~200 ат воздух
(рис. 15-18) разделяется на
две части, из которых одна на-
правляется в детандер II, а
другая в теплообменник III и
далее в дополнительный теп-
лообменник IV.
Охлажденный в теплооб-
менниках воздух дросселирует-
ся и часть его сжижается. Не-
сжиженная часть проходит до-
полнительный теплообменник,
после чего смешивается с воз-
духом, расширившимся и охла-
дившимся в детандере. Эта
смесь охлаждает сжатый воз-
дух в теплообменнике III.
воздуха, проходящего через де-
тандер (величину М принимают 0,5—0,6), согласно уравнению
(15-30) имеем:
Обозначая через М долю
qQ = x (/\ — /0) + <7п = (/1 — 4) + (4 — /8) (15-32)
Первый член (z‘i— t2) выражает холодопроизводительность,
получаемую в результате дросселирования, а член М (i2 — i8) —
холодопроизводительность, соответствующую работе, отданной в
детандере. Коэффициент полезного действия детандера в усло-
виях данного цикла составляет ~0,7.
Цикл среднего давления (рис. 15-19). Сжатый до давления
25—40 ат воздух поступает в предварительный теплообменник
II, где охлаждается до температуры около —80° С (точка 3).
Затем часть воздуха поступает в детандер III, где, расширяясь
6. Разделение газ. смесей и сжижение газов глубоким охлаждением 557
до 1 ат, охлаждается до температуры порядка —140° С. Другая
часть воздуха охлаждается в главном теплообменнике IV и при
этом конденсируется. Жидкий воздух для удаления его из си-
стемы дросселируется до атмосферного давления и поступает
в сборник VI. Испаренная п
воздухом, выходящим из де-
тандера, проходит через глав-
ный и предварительный тепло-
обменники.
Обозначая через М долю
воздуха, проходящего через де-
тандер (Л4 принимают ~0,8),
находим холодопроизводи-
тельность цикла:
Яо = х (Zj — Zo) -I- qn, =
= (г\ — Z2) -|- М (Z3 — Z8) (15-33)
Недостатком данного цик-
ла является работа детандера
при низких температурах, что
приводит к снижению его
к. п. д. до 0,6—0,65.
Цикл низкого давления.
Недостаток цикла среднего да-
вления, заключающийся в низком к. п. д. детандера при работе
его в условиях низких температур, может быть устранен приме-
нением турбодетандера. П. Л. Капица разработал конструкцию
турбодетандера, обладающего высоким к. п. д. (^eT. = 0,8) при
низких температурах, что позволило снизить давление сжатого
воздуха и осуществить цикл низкого давления (Рабс. = 5,5—
6 ат}. Это в свою очередь сделало возможным применение для
сжатия воздуха турбокомпрессоров и использование регене-
раторов в качестве теплообменников. Принципиальная схема
цикла низкого давления такая же, как и схема цикла среднего
этом часть воздуха вместе с
Рис. 15-19. Схема цикла среднего
давления с детандером:
/—компрессор; //—предварительный тепло-
обмеиниик; /// — детандер; IV — главный
теплообменник; V — регулирующий вентиль;
VI — сборник жидкого воздуха.
давления.
Пример 15-9. Рассчитать работу, затрачиваемую на получение 1 кг жид-
кого воздуха, для цикла высокого давления с отдачей внешней работы в усло-
виях примера 15-8.
Решение. Принимаем р2 = 200 ат, М = 0,6 и находим по Т — S-диа-
грамме /2 = 481,5*103 дж!кг (115 ккал/кг) и i'8 = 268 • 103 дж/кг (64 ккал/кг).
При к. п. д. детандера т]дет. = 0.75 имеем:
z2 — /в 481,5 • 103 — /8
Тдет = —-------7- . ИЛИ 0,75 —--------------------5---
i2 — i8 481,5 • 103 — 268 • 103
откуда h == 321 • 103 дж/кг (76,7 ккал/кг), что соответствует /з =—160° С.
558
Гл 15 Искусственное охлаждение
Холодопроизводительность определяем по формуле (15-32).
q0 = it _ /2 + м (i2 — z8) = 515 • 103 — 481,5 • 103 + 0,6 (481,5 • 103 — 321 • 103) =
= 130 • 103 дж/кг (31,2 ккал!кг)
Доля сжижаемого воздуха составляет
130 Ю3 — 11 500 _
ix — Zo “ 515 • 103 — 93 • 103 “ ’
Работа сжатия I такая же, как и при простом цикле (см пример 15-8).
Работа, отдаваемая в детандере, при механическом кпд детанде-
ра т;м = 0,8
/дет = М (i2 — /8) т]м = 0,6 (481,5 • 103 — 321 • Ю3) • 0,8 =
77
— 77 • 103 дж/кг = 77 кдж/кг, или I = к™; = 0,022 кет • ч/кг
obUU
Таблица 21
Сравнение холодильных циклов сжижения воздуха
[при tx =30° С, ^пот = 11 500 дж/кг (2,75 ккал/кг), ijK = 0,6]
Циклы Абсолют- ное давление сжатия ат Холодо- произво- дитель- ность ккал/кг Доля сжижае- мого воздуха Расход энергии* (работа) 1 кет ч/кг Удельный расход энергии** (работа) , 1 = — кет ч х К п. д цикла
Простой с дрос- 200
селированием . С двукратным дросселирова- 8 0,052 0,203 3,9 0,051
нием (Л4 = 0,2) С предваритель- ным охлажде- 200/50 6 0,032 0,083 2,6 0,077
нием до —40° С С двукратным дросселирова- нием и предва- рительным охла- ждением до 200 16 0,157 0,208 1,33 0,15
—40° С (Л1=0,2) Высокого давле- ния с детанде- 200/50 12,2 0,113 0,087 0,77 0,26
ром (Л4 = 0,6) . Среднего давле- 200 31,2 0,282 0,181 0,64 0,312
ния (Л4 = 0,8) . Низкого давле- 40 15,3 0,124 0,126 1,02 0,196
ния 6 7,8 0,05 0,058 1,16 0,172
* На 1 кг перерабатываемою воздуха.
** На 1 кг жидкого воздуха.
6 Разделение газ. смесей и сжижение газов глубоким охлаждением 559
f
Удельная работа, затраченная на получение 1 кг жидкого воздуха,
равна:
Z —/дет 0,203 — 0,022
/ул. = ~= —0582— - °’64 кет 4
Сравнение холодильных циклов
В табл. 21 приведены данные, характеризующие расход энергии (работу)
и к п. д. для различных холодильных циклов при получении жидкого воздуха.
К. п д. цикла составляет 0,2//уд , где 0,2 квт • ч — минимальная работа полу-
чения 1 кг жидкого воздуха. Как видно из таблицы, наиболее выгодным
является цикл высокого давления с отдачей внешней работы Поэтому дан-
ный цикл и получил преимущественное распространение в установках для
производства жидкого воздуха и жидкого кислорода.
При разделении воздуха с получением газообразных кислорода и азота
наиболее выгодными являются цикл с двукратным дросселированием и
предварительным охлаждением и цикл среднего давления с отдачей внеш-
ней работы. В небольших установках применяют циклы с простым дроссе-
лированием. Цикл низкого давления с регенераторами не даА/ чистых про-
дуктов разделения и применяется при получении кислорода для технологи-
ческих нужд.
МАССООБМЕННЫЕ ПРОЦЕССЫ
Глава 16
ТЕОРИЯ ПРОЦЕССОВ МАССОПЕРЕДАЧИ
1. Общие сведения о массообменных процессах
В химической технике широко применяют массообменные
процессы: абсорбцию, экстракцию, ректификацию, адсорбцию
и сушку.
Абсорбция — избирательное поглощение газов или паров жид-
ким поглотителем (абсорбентом). Этот процесс представляет со-
бой переход вещества из газовой или паровой фазы в жидкую.
Экстракция — извлечение растворенного в одной жидкости
вещества другой жидкостью *. Этот процесс представляет собой
переход вещества из одной жидкой фазы в другую.
Ректификация — разделение жидкой смеси на компоненты
путем противоточного взаимодействия потоков пара и жидкости.
Этот процесс включает переходы вещества из жидкой фазы в
паровую и из паровой в жидкую.
'Адсорбция — избирательное поглощение газов, паров или
растворенных в жидкости веществ поверхностью пористого
твердого поглотителя (адсорбента), способного поглощать одно
или несколько веществ из их смеси. Этот процесс представляет
собой переход вещества из газовой, паровой или жидкой фаз в
пористый твердый материал.
Сушка — удаление влаги из твердых влажных материалов
путем ее испарения. Этот процесс представляет собой переход
влаги из твердого влажного материала в паровую или газовую
фазу.
Скорость перечисленных процессов определяется скоростью
перехода вещества из одной фазы в другую (скоростью массо-
передачи).
* К экстракции относят также процесс извлечения веществ из твердой
фазы в жидкую.
2 Способы выражения состава фаз
561
В большинстве процессов массопередачи участвуют три ве-
щества:
1) распределяющее вещество, составляющее первую фазу:
2) распределяющее вещество, составляющее вторую фазу;
3) распределяемое вещество, переходящее из одной фазы в
другую.
Распределяющие вещества не участвуют в процессе массопе-
редачи, а являются носителями распределяемого вещества.
Массообменные процессы обратимы, т. е. распределяемое
вещество может переходить из одной фазы в другую в зависи-
мости от концентрации этого вещества в обеих фазах и усло-
вий равновесия (стр. 566).
2. Способы выражения состава фаз
Весовой и молярный состав
В технике состав выражают обычно в весовых долях (или ве-
совых процентах), т. е. в виде отношения массв^ компонента в
данной фазе к массе всей фазы. Если масса фазы G, а масса со-
держащихся в ней компонентов А, В, С, ... составляют соответ-
ственно Ga, Gb, Gc, ..., то весовые доли компонентов будут:
О. Од Gr
аА = -Q-, ив — ~Q~, ас — ~q~ • • • (16-1)
причем + ••• — 1-
Во многих случаях состав выражают в молярных долях, т. е
в виде отношения числа киломолей компонента в данной фазе
к общему числу киломолей в этой фазе. Если всего в фазе со-
держится п кмоль, а число киломолей компонентов А, В, С, ...
составляет пА, пв, пс, ..., то молярные доли компонентов будут:
П. Ид п„
хА = ^-> хв = ~^> хс = ~^ ••• (16-2)
причем хА + хв-|-хс + ... =1.
Пересчет весового состава в молярный, или обратный пере-
счет, производится следующим образом. Пусть весовой состав
смеси аА, ав, а молекулярные массы компонентов
?Аа, Мв, Мс, .... Тогда в 1 кг смеси содержатся следующие
количества кмоль компонентов:
аА & в &с
па = ^г~-', nB = -1rf-; пс = -~...
А М, " М ’ с
U (л
а общее число кмоль составляет:
U Л а R ar VI а
п = пАА-пвАГпс-\- • •• = •” =
Л о G
36 Зак 546.
562
Гл. 16. Теория процессов массопередачи
По формуле (16-2) находим молярный состав смеси:
а. а „ а„
А в с
х _ МА . х _ Мв . __ Мс
Ха~ а'В у а_ ’ хс ~ у £ ’ * ’
2а м 2а м 2а м
или в общем виде для &-го компонента:
Если задан молярный состав смеси хА, хв, хс, то для
пересчета его в весовой состав надо найти массы компонентов
в 1 кмоль смеси:
= -МАхд, GB — Мвхв, Gc = Мсхс ...
и общую ее массу:
G = GA-\- GB-}~ Gc-\~... == МАхА-}-Мвхв-\- Мсхс-{-... =2 Mjc
По формуле (Ш-1) находим весовой состав смеси:
М .X .
__ А А .
2 Мх:
«л
ав
мвхв . „ _ Мсхс
%Мх’ с~~ %Мх
или в общем виде для k-ro компонента:
Mkxk
2 Мх
(16-4)
Знаменатель этой формулы, представляющий собой массу
1 кмоль смеси, называется средней молекулярной массой смеси:
М:р. — ^лхл4" ^вхв~5г ^схс “И ••• = 2 (16-5)
Состав смеси двух компонентов (двойные смеси) полностью
характеризуется содержанием в ней лишь одного из компонен-
тов. Пусть весовая и молярная доли этого компонента а и х.
Тогда весовая и молярная доли другого компонента (1—а) и
2. Способы выражения состава фаз
563
(1— х). Формулы (16-3) и (Ш-4) примут в этом случае сле-
дующий вид:
а
М,
а 1 — а
Mtx
а~ Afjx4-Af2(l— х)
где Mi и М2 — молекулярные массы компонентов.
(16-6)
(16-7)
Пример 16-1. Определить молярный состав и среднюю молекулярную
массу смеси бензола и толуола, содержащей 30 вес. % бензола.
Решение. Молекулярные массы компонентов: М\ = 78 (бензол) и
М2 = 92 (толуол). По формуле (16-6) находим молярную долю бензола
в смеси (при а — 0,3)
78 + 92 ’
Молярная доля толуола (1—х) = 0,664. Эту же величину можно найти
и по формуле (16-6), подставляя в нее весовую долю толуола а — 0,7, при
этом Mi = 92 и М2 = 78.
Средняя молекулярная масса смеси по формуле (16-5):
Л1ср. = 78 • 0,336 + 92 • 0,664 = 87,2
Пример 16-2. Определить весовой состав смеси, содержащей 20 мол %
этана, 35 мол % пропана, 15 мол. % бутана и 30 мол % изобутана.
Решение. Весовой состав определяем по формуле (16-4) и сводим
результаты расчета в табл. 22.
Таблица 22
Результаты расчета весового состава смеси
Компоненты Молекулярная масса Mk Молярная доля xk Mkxk Весовая доля a _Mkxk ft ZMx
Этан 30 0,20 6,0 0,126
Пропан 44 0,35 15,4 0,325
Бутан 58 0,15 8,7 0,183
Изобутан 58 0,30 17,4 0,366
Всего . . — 1,00 47,5 1,000
Объемная концентрация
Состав выражают также через массу компонента, содержа-
щегося в 1 Л!3 смеси (объемная концентрация). Объемная кон-
центрация С имеет размерность кг/м3.
36*
564
Гл. 16. Теория процессов массопередачи
Сумма объемных концентраций всех компонентов 2 С равна
массе 1 м3 смеси, т. е. плотности р. Таким образом, весовая до-
ля k-ro компонента смеси:
<h = ^- (16-8)
Парциальное давление компонентов газовых
смесей
Содержание компонентов газообразной смеси часто выра-
жают через парциальные давления. Под парциальным давле-
нием компонента понимают давление, под которым находился
бы данный компонент, если бы в отсутствие других компонен-
тов он занимал весь объем смеси при ее температуре.
Согласно закону Дальтона, полное давление Р газовой смеси
равно сумме парциальных давлений компонентов/^, рв, рс, ..
Р — Ра~*гРв~\~Рс~^~ •••
Как нетрудно убедиться, отношение парциального давления
компонента к полному давлению равно объемной доле компо-
нента в смеси. В самом деле, если парциальное давление k-ro
компонента pk, а объем газовой смеси V, то объем зани-
маемый этим компонентом при давлении Р, определится из со-
отношения pkV=PVk, откуда Vk = ^-,a объемная доля ком-
понента в смеси
uk у р
Так как 1 кмоль любых компонентов занимает при одинако-
вой температуре один и тот же объем, то объемная доля vk равна
молярной доле yk компонента в газовой смеси.
Таким образом
Ь = /г или pk = Pyk
(16-9)
Напишем уравнение состояния для 1 кг каждого компонента
газовой смеси:
_ RT
~ М*
где рк — парциальное давление k-ro компонента, н/м2\
Р—газовая постоянная (8314 дж/кмоль • град);
Mk—молекулярная масса компонента.
%. Способы выражения состава фаз
565
Отсюда определяем объем V смеси, в котором находится
1 кг k-ro компонента:
Объемная концентрация компонента Ck = -y, или
= (16-10)
Уравнение (16-9) устанавливает связь между парциальным
давлением и молярной долей, уравнение (16-10)—между пар-
циальным давлением и объемной концентрацией.
Пример 16-3. Смесь двуокиси углерода с воздухом содержит
15 объемн. % СО2. Определить содержание СОг в смеси в вес. %, парциаль-
ное давление СОг в смеси и объемную концентрацию СОг при 25° С и об-
щем (абсолютном) давлении Р = 19,6 бар (20 ат).
Решение. Для газовых смесей объемная доля компонента равна его
молярной; следовательно, молярная доля двуокиси углерода у = 0,15. Моле-
кулярные массы составляют: Mi = 44 (для СОг), М2 = 29 (для воздуха).
Весовую долю СОг находим по формуле (16-7)-
44 • О 15
а = 44-0,15 4-29(1—0,15) = °’212, ИЛИ 21,2 Вес' %
Парциальное давление СОг определяем по уравнению (16-9)
р = 19,6 • 0,15 = 2,94 бар (3 ат)
Объемная концентрация СОг по уравнению (16-10) составит,
_ 44-2,94-105 ео_ , ,
С 8314 (273 4- 25) 5,23 KzfM
Относительный весовой состав
Состав двойной смеси можно выразить в виде отношения
массы распределяемого компонента к массе носителя. Это от-
ношение называется относительным весовым составом. Связь
между относительным весовым составом X и весовой долей а
выражается следующ1&1 соотношением:
1 _ д’ ИЛИ Д = 1 (16-11)
При расчете состав газовой смеси, выраженный через парци-
альное давление компонента р, часто приходится пересчитывать
в относительный весовой состав. Это может быть сделано
следующим образом. Если общее давление смеси Р, то
566
Гл 16. Теория процессов массопередачи
парциальное давление носителя (Р — р): тогда уравнение со-
стояния для компонента будет иметь вид
и для носителя
где V— объем смеси, м3:
GK и Gn—количества компонента и носителя в объеме V, кг:
Мк и Мн— молекулярные массы компонента и носителя.
Деля первое-уравнение на второе, получим:
Р . Л1н
Р р GH AfK
Отсюда находим относительный весовой состав:
Qk _ ' р
Он Mi ’ Р—р
(16-12)
Пример 16-4. Найти относительный весовой состав смеси, рассмотренной
в примере 16-3.
Решение. По формуле (16-11) находим-
0 212
К = । о 21^ = кг С О2 на I кг в03ДУха
Если весовая доля не рассчитывалась, можно использовать формулу
(16-12):
44 2 94
Г = 29 ‘' 19'6 — 2 94 ~ 0,27 кг С°2 На 1 Кг ВОЗдУха
, 3. Равновесие между фазами
Подобно тому как передача тепла протекает лишь при от-
клонении от состояния равновесия, т. е. при наличии разности
температур между теплоносителями, так и переход вещества из
одной фазы в другую происходит при отсутствии равновесия
между фазами.
_ Пусть имеются две фазы G и L, причем распределяемое ве-
щество вначале находится только в первой фазе G и имеет кон-
центрацию У. Если привести фазы в соприкосновение, то распре-
деляемое вещество начнет переходить в фазу L. С момента
появления распределяемого вещества в фазе L начнется и
обратный переход его в фазу G.
Скорость обратного перехода будет увеличиваться по мере
повышения концентрации распределяемого вещества в фазе L.
В некоторый момент скорости перехода вещества из фазы G
4. Материальный баланс процессов массообмена
567
в фазу L и обратно станут одинаковыми. При этом установится
состояние равновесия между фазами, при котором явного пере-
хода вещества из одной фазы в другую происходить не будет.
В состоянии равновесия существует определенная зависи-
мость между концентрациями распределяемого вещества в
обеих фазах — любой концентрации X этого вещества в фазе L
соответствует равновесная концент-
рация его У * в фазе G:
Y*=f(X) (16-13)
Условие равновесия, выражен-
ное уравнением (16-13), позволяет
определить направление процесса.
Если рабочая концентрация У рас-
пределяемого вещества в фазе- G
больше равновесной (У> У*), ве-
щество будет переходить из фазы G
Рис. 16-1. Диаграмма К—X:
ОС — линия равновесия; АВ — рабо
чая линия.
в фазу L. Если же У < У *, веще-
ство переходит из фазы L в фазу G.
Равновесие между фазами мож-
но представить графически на
У — Х-диаграмме (рис. 16-1). На этой диаграмме по оси абс-
цисс откладывается концентрация X распределяемого веще-
ства в фазе L, а по оси ординат — его концентрация У в фазе G.
Кривая ОС, изображающая зависимость равновесной концен-
трации У* от X, называется линией равновесия.
Конкретные уравнения условий равновесия будут рассмотре-
ны при описании отдельных процессов.
4. Материальный баланс процессов массообмена
Рассмотрим схему движения потоков в противоточном ап-
парате для массообмена (рис. 16-2). В аппарат поступают фа-
зы G (например, газ) и L (например, жидкость). Пусть расход
носителя в фазе G составляет G кг/сек, а в фазе L равен L кг/сек.
Содержание распределяемого компонента, выраженное в виде
относительных весовых составов, в фазе G обозначим через У,
в фазе L — через X.
Предположим, что распределяемый компонент переходит из
фазы G в фазу L (например, абсорбируется из газовой смеси
жидкостью), причем содержание этого компонента в фазе G
уменьшается от У1 (на входе в аппарат) до У2 (на выходе из
аппарата). Соответственно содержание этого же компонента
в фазе L увеличивается от Х2 (при входе в аппарат) до Xi (на
выходе из аппарата).
568
Г л 16. Теория процессов массопередачи
Носители не участвуют в процессе массообмена; следова-
тельно, их количества G и L не изменяются по длине аппарата.
Тогда количество компонента, перешедшего из фазы G, соста-
вит:
M—GYl— GY2 = G (Yi—Y2) кг!сек
и количество компонента, перешедшего в фазу L:
М = LXx — LX2 = L (Хг — Х2) кг/сек
Оба эти количества равны, поэтому можно написать уравне’
ние материального баланса в следующем виде:
Рис. 16-2. Схема
движения потоков
в противоточном
аппарате для мас-
сообмеь а
M=G(Yl~Y2) = L(X1~X2) (16-14)
Отсюда находим соотношения между ко-
личествами носителя в обеих фазах:
L Г, — У2 ,
G ~ Xj — Х2 кг!кг
(16-15)
Рассмотрим произвольное сечение аппара-
та ММ, в котором составы фаз будут Y и X и
напишем уравнение материального баланса
для части аппарата, расположенной выше
этого сечения:
gy+lx2 = gy2-ylx
откуда
2 + ±(X-X2)=Y2 + l(X-X2) (16-16)
Уравнение (16-16), называемое уравнением рабочей линии,
выражает зависимость между неравновесными составами фаз
(У, X) в любом сечении аппарата.
Как видно из этого уравнения, на диаграмме У — X рабочая
линия представляет собой прямую с наклоном к оси абсцисс
под углом, тангенс которого равен I.
Подставив в уравнение (16-16) значение I из уравнения
(16-15), получим после простейших преобразований:
У—У2 _ Х — Х2
Yx-Y2 — Х[—Х2
Это выражение является уравнением прямой (см. рис. 16-1),
проходящей через точку А с координатами Хх, У1 и через точку В
с координатами Х2, Y2.
4. Материальный баланс процессов массообмена 569
На рис. 16-1 рабочая линия расположена выше линии равно*
весия, т. е. рабочие концентрации распределяемого компонента
4 в фазе G выше равновесных концентраций и компонент перехо-
дит из фазы G в фазу L. Если компонент переходит из фазы L
в фазу G, то рабочие концентрации в фазе G ниже равновесных;
< в этом случае рабочая линия расположена ниже линии равно-
весия.
К
Пример 16-5. Аммиак поглощается водой из газа (воздух) с начальным
г содержанием ЫН35объемн %, конечное содержание NH3 в газе 0,27 объемн. %.
Количество поступающего газа 10 000 м3/ч (при нормальных условиях). Об-
i" щее давление газа Р = 760 мм рт ст. Содержание NH3 в поступающей на
& абсорбцию воде 0,2 вес.%, удельный расход поглотителя I — 1,18 кг/кг Опре-
делить количество поглощенного аммиака, конечную концентрацию его в воде
| и построить рабочую линию данного процесса абсорбции.
Решение Количество инертного газа (воздуха) составляет (при нор-
м мальных условиях):
1’Г 10 000 (1 — 0,05) = 9 500 м3/ч
4 или
f G = 9500 • 1,29 12 300 кг/ч
где 1,29 — плотность воздуха при нормальных условиях, кг/м3.
, Относительные весовые составы газовой фазы определяем по формуле
(16-12), заменяя в ней величины давления на пропорциональные им объемные
содержания-
на входе
17 5
Г'=29'Т0бЬг=°Л»
на выходе
4 17 0 27
г,=й'Ж^27з1)да16
Количество поглощенного аммиака составляет:
М = G (Kj — Г2) = 12300 (0,0309 — 0,0016) = 360 кг/ч
Определяем расход воды:
L = IG = 1,18 • 12 300 = 14 500 кг/ч
Концентрация аммиака в поступающей на абсорбцию воде составит (в
относительных весовых единицах):
у ___ 0,002 «
Х2~п=оде=0,002
Конечную концентрацию аммиака в поглощающей воде определяем по
уравнению (16-15):
0,002+°'03W-°'0016 = 0,0268
/ 1. $ 1. о
Уравнение рабочей линии по формуле (16-16) имеет следующий вид:
Г = 0,С016 1,18 (X—0,002) = 1.18Х —0,00076
570
Г л. 16. Теория процессов массопередачи
Для построения рабочей линии на Y — Х-диаграмме (см рис. 16-5,
стр. 587) проводим прямую через точку А (X] — 0,0268, У] = 0,0309) и точку
В (Х2 = 0,002, У2 = 0,0016).
5. Уравнение массопередачи
При отклонении от состояния равновесия происходит пере-
ход вещества из фазы, в которой его содержание выше равно-
весного, в фазу, где содержание этого вещества ниже равно-
весного.
Скорость перехода вещества пропорциональна степени откло-
нения от равновесия, которую можно выразить как разность
концентраций — рабочей концентрации вещества в одной из фаз
и равновесной концентрации в ней данного вещества. Эта раз-
ность концентраций является движущей силой процесса массо-
передачи. Кроме того, скорость перехода вещества пропорцио-
нальна поверхности соприкосновения фаз.
Скорость перехода вещёства можно определить как коли-
чество вещества, переходящего в единицу времени из одной
фазы в другую. Тогда уравнение массопередачи можно напи-
сать в следующем виде:
M = KFb (16-17)
где М — количество вещества, перешедшего из одной фазы в
другою, кг/сещ
К — коэффициент пропорциональности, называемый коэф-
фициентом массопередачщ
F — поверхность соприкосновения фаз, м2]
А — движущая сила процесса массопередачи.
Уравнение (16-17) аналогично уравнению теплопередачи
(11-9): температурному напору соответствует движущая сила
процесса массопередачи, количеству тепла — количество веще-
ства, переходящего из одной фазы в другую, коэффициенту теп-
лопередачи — коэффициент массопередачи.
Движущая сила А может быть выражена в любых единицах,
применяемых для выражения составов фаз. При этом размер-
ность коэффициента массопередачи
г д-i_Г М 1 _____ Г_____кг_________1
‘ L Т’Д J L м2 • сек • (ед. движ силы) J
определяется единицами, принятыми для выражения движущей
силы.
Из этого уравнения следует, что коэффициент массопередачи
выражает количество вещества, переходящего из одной фазы в
5. Уравнение массопередачи
571
другую за единицу времени через единицу поверхности сопри-
косновения при движущей силе, равной единице.
Если движущая сила выражается в виде разности объемных
концентраций (кг/м3), то Д = С * — С, где С — фактическая кон-
центрация компонента в одной из фаз, С* — равновесная кон-
центрация компонента в той же фазе. Тогда уравнение (Ш-17)
примет вид
M = KcF(C* — C) (16-18)
причем размерность коэффициента массопередачи
кг
о Ы
м2 • сек • —v
м3
М 1
сек]
Если рабочая концентрация С в данной фазе выше равновес-
ной концентрации С*, вещество будет переходить из этой фазы
в другую фазу, а движущая сила будет равна разности факти-
ческой и равновесной концентрации (С —С*).
Движущую силу процессов массообмена, протекающих в га-
зовой фазе (например, при абсорбции), часто выражают через
разность парциальных давлений Д = р — р* (в w/ж2), где р —
фактическое парциальное давление компонента в газе, р* — пар-
циальное давление компонента в газе при равновесии его с жид-
костью. Размерность коэффициента массопередачи Кр, выра-
женного через разность парциальных давлений:
Связь между коэффициентами массопередачи Кс и Кр на
основании формулы (16-10) выражается соотношением:
Кр = -^ Кс сек/м (16-19)
Если движущая сила выражена через разность молярных
долей, коэффициент массопередачи будет равен:
(:гол.додя) , (16-20)
Если же движущая сила выражена в виде разности относи-
тельных весовых составов (кг/кг), то при небольших концен-
трациях компонента коэффициент массопередачи составит:
(16-21)
‘ м2 • сек —
кг
572
Гл. 16. Теория процессов массопередачи
В этих формулах:
7ИК и Мн — молекулярные массы компонента и носителя;
Afcp>— средняя молекулярная масса фазы;
— газовая постоянная (8314 дж/кмоль-граду
Т — абсолютная температура, °К;
Р — плотность фазы, кг/м3-,
Р—общее давление, н/ж2.
При практических расчетах за единицу времени часто при-
нимают ч, а за единицу разности парциальных давлений — am
или мм рт. ст. Тогда размерность коэффициента массопередачи
Кс будет м/ч, &КР— кг/м2 • ч> ат или кг/м2 -ч- мм рт. ст. Для
пересчета коэффициентов массопередачи в нужные значения
надо соответствующую величину коэффициента умножить на
следующие переводные множители:
м/сек X 3600 = м/ч
сек 1м X 3,53 • 108 = кг/м2 • ч • ат
сек/м X 4,8 • 105 = кг/м2 • ч • мм рт. ст.
кг/м2 • ч • мм рт. cm. X 735 == кг/м2 • ч • ат
Иногда коэффициент массопередачи относят к единице ра-
бочего объема аппарата (объемный коэффициент массопере-
дачи). В этом случае коэффициент массопередачи определяется
соотношением
= (16-22)
где f — поверхность соприкосновения фаз, отнесенная к единице
рабочего объема аппарата, м2/м3.
Размерность объемного коэффициента массопередачи при
движущей силе Д, выраженной в кг/м3:
Пример 16-6. Коэффициент массопередачи при водной абсорбции дву-
окиси серы из смеси ее с воздухом Кр = 9,35 кг/м* • ч • ат. Температура про-
цесса 20° С, общее абсолютное давление Р = 0,86 бар (0,878 ат). Определить
коэффициент массопередачи при выражении движущей силы через разность
парциальных давлений (мм рт. ст. и н/м2) и разности объемных концентра-
ций (кг/м3), молярных долей и относительных весовых составов.
Решение. Находим Кр для движущей силы, выраженной в ммрт. ст.
или н/м2: ,
Ко = — 0,0127 кг/м2 • ч • мм рт. ст:, или о = 2,65 • 10-8 сек/м
Р 735 3,53 • 108 '
Если движущая сила выражена в кг/м3, то по формуле (16-19)
КС^=~КР^ -8314(2ГС + 20) 2,65 • 10-8 = 0,00101 м/сек = 3,63 м/ч
где Мк — молекулярная масса SO2 (Мк= 64).
б. Процесс массообмена между фазами
573
Если движущая сила выражена в мол. долях, то по формуле (16-20)
К. = 0,86 • 105 • 2,65 • IO"8 == 0,00228 кг]м2 • сек (мол. доля) —
— 8,2 kzIm2 • ч (мол. доля)
Если движущая сила выражена в кг/кг, то по формуле (16-21)
К = 29' °ь846 ' --- 2,65 • IO"8 = 0,00103 кг/м2 • сек • (кг/кг) =
= 3,7 кг/м2 • ч • (кг/кг)
где 29 — молекулярная масса носителя (воздуха) Мн.
6. Процесс массообмена между фазами
Общие сведения
Различают два основных вида процессов массопередачи:
1) массообмен между жидкостью и газом (паром) или ме-
жду двумя несмешивающимися жидкостями;
2) массообмен между твердым телом и жидкостью, газом
или паром (стр. 581). /
Процесс переноса вещества из одной фазы в другую в пер-
следующим образом (рис. 16-3).
вом случае можно представить
Пусть концентрация распреде-
ляемого вещества в фазе G вы-
ше равновесной и вещество пе-
реходит из фазы G в фазу L.
Распределяемое вещество в
фазе G переносится к поверх-
ности раздела фаз, а в фазе L
переносится от этой поверхно-
сти. Перенос вещества в обеих
фазах осуществляется путем
молекулярной диффузии (т. е.
диффузии молекул через слой
носителя) и путем конвектив-
ной диффузии (т. е. движущи-
мися частицами носителя и
распределяемого вещества).
В каждой фазе различают
две области: ядро (основная
масса) и пограничный слой,
образующийся у поверхности
Поверхность
/? ппчНрпп гЬл.з
Рис. 16-3. Схема процесса массооб-
мена между жидкостью и газом или
между двумя несмешивающимися
жидкостями.
раздела фаз. Перенос распределяемого вещества в ядре фазы,
где обычно происходит интенсивное перемешивание, осуществ-
ляется преимущественно путем конвективной диффузии. Вслед-
ствие интенсивного перемешивания в ядре концентрация распре-
деляемого вещества в каждом сечении системы почти постоянна.
574
Гл 16. Теория процессов массопередачи
Пограничный слой является областью резкого изменения кон-
центрации распределяемого вещества. Перенос вещества в по-
граничном слое осуществляется путем конвективной и молеку-
лярной диффузии, причем по мере приближения к поверхности
раздела фаз происходит затухание конвективных потоков и воз-
растает роль молекулярной диффузии.
Концентрация распределяемого вещества в фазе G умень-
шается от величины У в ядре потока до величины Ур на границе
раздела фаз. В фазе L концентрация распределяемого вещества
уменьшается от величины Хр на границе раздела фаз до вели-
чины X в ядре потока. При установившемся процессе на грани-
це раздела фаз наблюдается равновесие, т. е. концентрации Yv
и Хр являются равновесными.
Молекулярная диффузия
При молекулярной диффузии, согласно закону Фика, количе-
ство диффундирующего через слой вещества пропорционально
поверхности слоя F м2, изменению концентрации по толщине
слоя Дсл. кг/м3, времени т сек и обратно пропорционально тол-
щине слоя 8 м. Таким образом
(16-23)
где D — коэффициент пропорциональности, называемый коэф-
фициентом диффузии.
Уравнение (16-23) называется уравнением диффузии. Оно
аналогично уравнению теплопроводности (11-10): разности тем-
ператур соответствует разность концентраций Дсл_, коэффициенту
теплопроводности — коэффициент диффузии D.
Из уравнения (16-23) определяем размерность коэффици-
ента диффузии:
кг • м
м2 • —т • сек
м3
Г Л£2 ~1
L сек J
Коэффициент диффузии выражают также в м2/ч. Для пере-
счета величины коэффициента диффузии из м2/ч в м2/сек надо
разделить данный коэффициент на 3600:
X з^о = м?/сек
Коэффициент диффузии зависит от свойств диффундирую-
щего компонента и среды, в которой происходит диффузия, а
также от температуры и давления.
6. Процесс массообмена между фазами
575
В справочных таблицах обычно приводятся коэффициенты диффузии Do
в газах при температуре То = 273° К и абсолютном давлении Ро =* 1 ат При
других абсолютных температурах Т и других абсолютных давлениях Р этот
коэффициент определяется по формуле
(16-24)
из которой видно, что коэффициент диффузии в газах обратно пропорционален
давлению и прямо пропорционален абсолютной температуре в степени 3/г-
Для определения коэффициента диффузии газа А в газе В (или, что то
же, газа В в газе А) при абсолютной температуре Т и абсолютном давлении
Р ат можно пользоваться следующей зависимостью:
0,0043 10~47'!1/2
P(VA +VB8)2
м2!сек
(16-25)
где иА и vB— молекулярные объемы газов А и В;
Л4А и Л1В—молекулярные массы газов А и В.
Молекулярные объемы определяются как сумма атомных объемов v эле-
ментов, входящих в состав соединений. Значения v приведены ниже:
Водород............................................. 3,7
Кислород
в метиловом эфире и сложных эфирах............... 9,1
в вмсших эфирах.................................. 11
в кислотах....................................... 12
в прочих соединениях ........................... 7,4
Азот
в первичных аминах............................. 10,5
во вторичных аминах............................ 12
в прочих соединениях........................... 15,6
Углерод............................................ 14,8
Сера............................................... 25,6
Хлор............................................... 24,6
Бром............................................... 27
Воздух.......................>..................... 29,9
Бензольное кольцо (вычитать) . . ................ 15
Нафталиновое кольцо (вычитать)..................... 30
Водород (Н2)....................................... 14,3
Коэффициенты диффузии в жидкостях значительно меньше, чем в газах.
Для приближенного определения коэффициентов диффузии в жидкостях
при 20° С можно пользоваться формулой
1 • 10~6 /~ 1
АВ У р (v'/> -f- vB/s)2 ' -^а
1
Л4В
м2!сек
(16-26)
где р — вязкость растворителя, спз-,
А и В — поправочные коэффициенты для диффундирующего вещества и рас-
творителя.
576
Гл. 16. Теория процессов массопередачи
Поправочные коэффициенты характеризуют отклонение свойств вещества
от свойств неассоциированных веществ, для которых этот коэффициент равен
единице. Для газов поправочный коэффициент А = 1. Для воды В = 4,7, для
метилового и этилового спирта В = 2, для ацетона В = 1,15.
Коэффициент диффузии в жидкости при данной температуре t находят
по соотношению
D = D20[l + H^ —20)] (16-27)
причем температурный коэффициент Ь определяют по формуле
0,2
i= к
где р — вязкость растворителя при 20° С, спз;
р — плотность растворителя, кг(м3.
Пример 16-7. Определить коэффициент диффузии паров бензола в воз-
духе при 40° С (313° К) и абсолютном давлении 1 ат.
Решение. Молекулярный объем для бензола (СбНб)
vA = 6 • 14,8 + 6 • 3,7 — 15 = 96
Молекулярный объем для воздуха vB = 29,9; молекулярные массы компо-
нентов: Л4а=78 (для бензола), 7ИВ= 29 (для воздуха). Подставляя все изве-
стные величины в формулу (16-25), получим:
_ 0,0043• 10"4 • 313а/а , Л 1 . 1 1П_4 ,. 2/ ч
D= l(96‘'.+ 29,9'/f" Г 78 + 29 = °’0866''° -«2/^ (0.0312 ж»/.)
Пример 16-8. Определить коэффициент диффузии двуокиси углерода в
воздухе при 25° С и абсолютном давлении Р = 20 ат
Решение. Коэффициент диффузии СО2 в воздухе при Ро = 1 ат и
То = 273° К равен Do = 0,138 • 10~4 м2!сек (0,0497 л2/ч). По формуле (16-24)
D = 0,138 • 10~4 • Х(-73О^25 УА = 0,0106 • 10"4 я2/сек (0,00283 м2/ч)
2\) \ Л о ]
Пример 16-9. Определить коэффициент диффузии аммиака в воде при
температуре 50° С.
Решение. Сначала определяем коэффициент диффузии при 20° С, под-
ставляя в формулу (16-26) значения А = 1, В = 4,7, р = 1 спз, оА = 15,6 +
+ 3 - 3,7 = 26,7 (для NH3); vB = 2 *3,7 + 7,4 = 14,8 (для воды),Л1А = 17 (для
NH3), Л4В= 18 (для воды): *
О 1-10-6 1,/~ТТГ-
20 1.4,7/ 1 (26,7‘/’+14,8</’)2 17 4 18
= 0,00244 • 10-6 я2/сек (0,0000088 м2/ч)
По формуле (16-27) при t = 50° С:
D = 0,00244 • 10~6 [1 + 0,02 (50 — 20)] = 0,0039 • 10~6 я2/сек (0,000014 м21ч)
те 0,02 — температурный коэффициент b при ц — 1 спз и р = 1000 кг/м3,
h = =0,02
/1000
6. Процесс массообмена между фазами
577
Конвективная диффузия
При конвективной диффузии количество вещества, переноси-
мого в единицу времени из фазы, отдающей вещество, к поверх-
ности раздела фаз (или от поверхности раздела фаз в фазу, вос-
принимающую это вещество), пропорционально поверхности F
и разности концентраций Дчаст. распределяемого вещества в фазе
и у поверхности раздела:
7И —рАДчаст. кг/сек
(16-28)
Разность концентраций Дчаст. является частной движущей си-
лой процесса, коэффициент пропорциональности р называется
коэффициентом массоотдачи.
Подобно тому как уравнения (16-17) и (16-23) аналогич-
ны уравнениям теплопередачи и теплопроводности, уравнение
(16-28) аналогично уравнению конвективного теплообмена
(11-11): коэффициент массоотдачи является аналогом коэффи-
циента теплоотдачи и учитывает перенос вещества путем моле-
кулярной и конвективной диффузии.
В зависимости от единиц, принятых для выражения Дчаст_,
коэффициент массоотдачи р имеет такие же размерности, как и
коэффициент массопередачи К.
Коэффициент массоотдачи зависит от гидродинамических,
физических и геометрических факторов и определяется экспери-
ментальным путем с обработкой данных при помощи теории
подобия.
Приложение теории подобия к процессам массопередачи по-
казало, что эти процессы определяются кинематическим крите-
рием Re и диффузионными критериями Nu' и Рг', являющимися
аналогами тепловых критериев Nu и Рг. Значения диффузион-
ных критериев приведены в табл. 23.
Таблица 23
Критерии подобия диффузионных процессов
Критерий Формула Физический смысл критерия
Диффузионный критерий Нуссельта М Nu' = (16-29) Характеризует процесс массопередачи у по- верхности раздела фаз
Диффузионный крите- рий Прандтля Рг'=-£-(16-30) Характеризует физиче- ские свойства среды
37 Зак 546
578
Гл. 16. Теория процессов массопередачи
Критерии подобия являются безразмерными, поэтому при
вычислениях входящие в формулу критерия величины должны
быть взяты в одинаковой системе единиц. При пользовании си-
стемой СИ все величины, входящие в формулы (16-29) и (16-30),
берутся в следующих единицах:
— коэффициент массоотдачи, м/сек-,
D — коэффициент диффузии, м2!сек-,
р. — вязкость, н • сек/м2',
р — плотность, кг/м3-,
I—определяющий геометрический размер, м.
При пользовании системой МКГСС величину р берут в кгс - сек1м2,
р — в кгс - сек2/м\ При этом за единицу времени для и D обычно прини-
мают ч, тогда формула (16-30) принимает следующий вид:
prz 3600р.
Критерии Re и Рг' являются определяющими, критерий
Nu' — определяемым. Зависимость между критериями выра-
жается в общем виде уравнением
Nu'=/(Re, Рг') (16-31
По найденному значению Nu' вычисляют коэффициент мае*
соотдачи при помощи формулы (16-29), из которой следует:
pc = 4-Nu' (16-32)
Пересчет рс в другие размерности коэффициента |3 произ-
водится аналогично пересчету коэффициента массопередачи по
формулам (16-19) — (16-22).
Конкретные зависимости критерия Nu' от Re и Рг' будут
приведены при рассмотрении отдельных процессов.
Подобие процессов массопередачи
Условия подобия процессов массопередачи можно вывести аналогично
условиям теплового подобия (стр. 386) Обозначив через Д' изменение кон-
центрации по толщине пограничного слоя и через ДС изменение концентрации
по длине (высоте) аппарата, можно написать условие подобия для двух
аппаратов (1 и 2) в следующем виде:
/ Ai \ / \ _ / ^2 \ \,
\ / \ А / \ \ ^2 /
Д'
Здесь у представляет собой 1радиент концентрации по толщине погра-
ДС .
ничного слоя, -градиент концентрации по длине (высоте) аппарата,
6. Процесс массообмена между фазами
579
Объем фазы, проходящий через аппарат в единицу времени, равен wS
(w — скорость фазы, S — площадь сечения аппарата). Если концентрация
фазы изменилась по длине (высоте) аппарата на АС, то количество вещества,
перешедшего в эту фазу, будет wShC. Такое же количество вещества пере-
дается путем диффузии через пограничный слой и, согласно уравнению диф-
фузии, составляет: П/у Д', где П — периметр пограничного слоя. Таким
образом
wS ЬС = П?-^- Д'
5 °
5
Заменяя у эквивалентным диаметром rf3KB_, получим:
и^экв, 4 /_ . .
Таким образом, условием подобия процессов массопередачи является ра-
венство отношения А или, что то же, равенство диффузионного критерия
Пекле:
р / _ ^ЭКВ.
re - D
Диффузионный критерий Пекле Ре' характеризует отношение поперечного
градиента концентрации (по толщине пограничного слоя) к продольному гра-
диенту (по длине или высоте аппарата).
При практических расчетах критерий Пекле заменяют диффузионным
критерием Прандтля:
Рг' = Л__ JL
Re D ~ PD
где — кинематическая вязкость фазы.
Условием подобия процессов массопередачи в двух аппаратах является
равенство критериев Re, а также критериев Рг'.
Количество вещества, передаваемого через пограничный слой, было опре-
делено как П/ у Д'. Это же количество вещества, согласно уравнению мас-
соотдачи (16-28), равно П/^сДчаст , где Дчаст—движущая сила массоот-
дачи (разность концентраций у поверхности раздела фаз и в ядре фазы).
Отсюда
ш -у д = п/рсдчасТе
или
М d Д
“С экв. _ экв. , част.
D “ S • Д'
Правая часть этого уравнения для подобных систем одинакова. Следова-
тельно, для них одинакова и левая часть, т. е. одинаков диффузионный кри-
терий Нуссельта:
NT ! ^С^ЭКВ
Nu' = ~^кв'
37*
580
Гл. 16. Теория процессов массопередачи
Связь коэффициента массопередачи и
коэффициентов массоотдачи
Рассмотрим переход вещества из фазы G в фазу L (см. рис.
16-3, стр. 573). Уравнение конвективного массообмена для
фазы G:
М = ^(К-Кр) (16-33)
для фазы L:
М==$2?(Хр~Х) (16-34)
где и р2—коэффициенты массоотдачи для фаз G и L;
F— поверхность соприкосновения фаз.
Пусть линия равновесия представляет собой прямую с тан-
генсом угла наклона, равным k, т. е.
Y*~kX
тогда на границе раздела фаз
Гр==^Хр
Таким образом, концентрации в фазе L можно выразить че-
рез концентрации в фазе 6:
хр=4 и
где У* — концентрация в фазе G, равновесная с концентра-
цией X в ядре фазы L.
Подставляя значения Хр и X в уравнение (16-34), получим:
Ж = (16-35)
Определим из уравнений (16-33) и (16-35) движущую силу
процесса:
у у ____ ^4 у у* _____
1 1Р-" ^F ’ Р ^F
Складывая почленно эти уравнения, получим:
г-г‘=^(^+к) (16'36>
Уравнение массопередачи для рассматриваемого случая
имеет следующий вид:
M — KF(Y— Г*)
или
(16-37)
6. Процесс массообмена между фазами
581
Приравнивая правые части уравнений (16-36) и (16-37), на-
ходим зависимость между коэффициентом массопередачи К и
коэффициентами массоотдачи pi и
К ~ 31 ' 32
(16-38)
Уравнение (16-38) аналогично уравнению (11-12), устана-
вливающему связь между коэффициентом теплопередачи k
и коэффициентами теплоотдачи ai и аг.
-В уравнении (16-38) член j- выражает сопротивление пере-
ходу вещества в фазе G, член ----сопротивление в фазе L.
2 1
Если коэффициент pi велик, то член у мал и, как видно из
уравнения (16-38), К = -у • В этом случае сопротивлением в
фазе G можно пренебречь.
При большом коэффициенте р2 член £- мал и, как видно из
Рг
уравнения (16-38), В этом случае сопротивлением в
фазе L можно пренебречь.
Уравнение (16-38) выведено при условии линейной зависи-
мости между равновесными концентрациями У* и X. В случае
отсутствия такой зависимости линия равновесия не будет прямой
и в качестве k надо брать тангенс угла наклона касательной
к линии равновесия в данной точке. При этом величины и Л
будут изменяться по длине аппарата. При расчетах берут сред-
нее значение k или же разделяют аппарат по длине на несколько
участков, считая k постоянным в пределах каждого участка.
Массообмен с участием твердой фазы
В твердой фазе конвекция отсутствует и перенос вещества
характеризуется уравнением массопроводности, аналогичным
уравнению молекулярной диффузии:
М = .^л.\ (16-39)
где х — коэффициент пропорциональности, имеющий размер-
ность коэффициента диффузии и называемый коэффи-
циентом массопроводности.
Если распределяемое вещество переносится из твердой фазы
в омывающую ее жидкую, газовую или паровую фазу, то в пре-
делах твердой фазы вещество перемещается вследствие
582
Гл. 16. Теория процессов массопередачи
массопроводности к границе раздела фаз и далее переносится в
омывающую фазу путем конвективной диффузии.
Перемещение вещества вследствие массопроводности яв<
ляется неустановившимся процессом. В начальный момент кон-
центрация вещества (У1) одинакова во всем объеме твердого
тела. В момент времени т средняя концентрация (У) ниже на-
чальной, причем распределение концентрации в твердом теле
неравномерно — в центре концентрация больше, у границы раз-
дела фаз — меньше. При т = оо концентрация выравнивается и
стремится к равновесной (У*).
7. Средняя движущая сила и методы расчета процессов
массопередачи
Движущая сила не остается постоянной по длине аппарата,
и при использовании уравнений, приведенных в разделе 5 дан-
ной главы, следует подставлять в них среднее значение движу-
щей силы. Ниже рассматриваются методы определения средней
движущей силы и расчета процессов массопередачи.
С р е д н е л о г а р и ф м и ч е с к а я движущая сила
Среднелогарифмическая движущая сила определяется по
формуле
(16-40)
2,3 lg I-
а2
где А1 и Аз — значения движущей силы на входе и выходе из
аппарата.
Формула (16-40) аналогична формуле (11-28) для средне-
логарифмического температурного напора.
При соотношении 2 > -А- > 0,5 можно с достаточной точ-
^2
ностью пользоваться среднеарифметическим значением (стр.379):
Среднелогарифмическое значение движущей силы точно
лишь в том случае, если линия равновесия и рабочая линия
являются прямыми, а коэффициент массопередачи сохраняется
постоянным по всей длине аппарата.
Линия равновесия часто значительно отклоняется от прямой.
В этих случаях, во избежание ошибок, следует пользоваться бо-
лее точным методом расчета, рассматриваемым ниже.
7. Средняя движущая сила и методы расчета массопередачи 583
Число единиц переноса
Обозначим рабочую высоту аппарата через Н м, площадь
поперечного сечения аппарата через S м2, удельную поверхность
соприкосновения фаз в единице объема аппарата через f м2/м3.
Тогда рабочий объем аппарата в м3 будет HS, а поверхность
соприкосновения фаз F = HSf. Подставляя это значение F в
уравнение массопередачи (16-17), получим:
M = KHSf^
Приравнивая это выражение к уравнению материального
баланса (16-14), можно написать
KHSf^ = G(Y.-Y2)
откуда рабочая высота аппарата составляет:
/у________________________ G —1^2
KSf * ДСр.
Множитель — — представляет собой изменение рабочих
^Ср
концентраций на единицу движущей силы и называется числом
единиц переноса:
п = -^=^- (16-41)
иср.
Одна единица переноса (п = 1) соответствует участку аппа-
рата, на котором изменение рабочих концентраций равно сред-
ней движущей силе на данном участке.
Множитель представляет собой высоту участка, соот-
ветствующего одной единице переноса, и называется высотой
единицы переноса (сокращенно ВЕП):
h = (16-42)
Таким образом, рабочая высота аппарата Н равна произ-
ведению числа единиц переноса на высоту единицы переноса:
H = nh (16-43)
При помощи уравнения (16-43) можно вести расчет процесса
массопередачи, если линия равновесия отклоняется от прямой,
а также в тех случаях, когда поверхность соприкосновения фаз
не может быть геометрически определена и потому непосред*
ственное применение уравнения (16-17) невозможно.
584
Гл. 16. Теория процессов массопередачи
Определение числа единиц переноса
Для определения числа единиц переноса пользуются графи-
ческим методом (рис. 16-4). Для этого на У— Х-диаграмме
проводят линию MN, делящую пополам отрезки ординат, за-
ключенные между рабочей линией и линией равновесия. Эти от-
резки ординат равны (У—У*) и выражают движущую силу
Рис. 16-4. Графическое определение числа единиц
переноса:
ОС —линия равновесия; АВ — рабочая линия; ДОЛГ—линия,
делящая пополам отрезки ординат между рабочей линией
и линией равновесия.
процесса. Затем через точку В на рабочей линии, соответствую-
щую состоянию фазы G на выходе из аппарата, проводят гори-
зонталь. Эту горизонталь, пересекающуюся с линией MN в
точке D, продолжают до точки Е, причем отрезок BE равен
удвоенному отрезку BD. Из точки Е проводят вертикаль EF до
пересечения с рабочей линией.
EF ВЕ
Из подобия треугольников BEF и BDK следует =
KL
Но по построению BE — 2BD и KD=-^-. Таким образом
рр___is Г) BE _ ^BD _____ „г
Ег KD BD 2 ’ BD
Ступенька BEF соответствует некоторому участку аппарата,
в котором изменение рабочих концентраций в фазе G равно EF,
а в фазе L соответствует ВЕ. Отрезок KL изображает среднюю
7. Средняя движущая сила и методы расчета массопередачи
585
движущую силу на этом участке. Так как изменение рабочей
концентрации ЕР по построению равно средней движущей
силе KL, то ступенька BEF соответствует одной единице пере-
носа.
Продолжая вписывать указанным выше способом ступеньки
до точки А, соответствующей состоянию системы на входе в ап-
парат, находим число единиц переноса (равное числу ступе-
нек), необходимое для достижения заданного изменения рабо-
чих концентраций между точками А и В.
Если между точками В и А не вписывается целое число полных ступенек,
то число единиц переноса, соответствующее последней неполной ступеньке,
равно отношению отрезка АР, ограничивающего неполную ступеньку, к верти-
кальному отрезку ST между рабочей линией и линией равновесия, проведен-
ному через середину основания неполной ступеньки. Так, для процесса массо-
др
обмена, графически представленного на рис 16-4, отношение = 0,65 и число
единиц переноса составляет 2,65
Если рабочая линия расположена ниже линии равновесия, то построение
ступенек ведут не слева направо, как описано выше, а справа налево, начи-
ная от точки А (см. пример 19-6, стр. 695).
Рассмотренный графический метод применим, если на уча-
стке, соответствующем одной ступеньке (см. рис. 16-4), линия
равновесия сильно не отличается от прямой. В противном слу-
чае отрезок KL не будет изображать среднюю движущую силу
на данном участке. В этом случае пользуются более точным
методом графического интегрирования, который заключается
в следующем.
На участке бесконечно малой высоты dh изменение концен-
траций составляет dY и движущая сила процесса—(У—У*).
Найдем для этой высоты число единиц переноса, представив
уравнение (16-41) в дифференциальном виде:
л- _ ~dY
Clll у __ у*
Знак минус обозначает убывание концентрации У.
Число единиц переноса по всей высоте аппарата получим,
проинтегрировав это уравнение в пределах изменения концен-
трации от У1 до Уг:
г,
f -у=уг (16-44)
У,
Интеграл в этом уравнении находят графически, для чего по
оси абсцисс откладывают значения У, а по оси ординат соот-
ветствующие значения у 3 у» и определяют площадь, ограни-
586
Гл. 16. Теория процессов массопередачи
ценную кривой, осью У и вертикалями, проведенными через
точки, абсциссы которых равны Уз и Уь Эта площадь и равна
искомому интегралу, т. е. числу единиц переноса. При расчете
необходимо учитывать масштабы построения. Если по оси абс-
цисс взят масштаб mi (единиц в 1 см), а по оси ординат — мас-
штаб т2 (единиц в 1 см), то число единиц переноса равно:
П = /ШхЩ
тцр. f—площадь, ограниченная кривой и соответствующими
абсциссами, см2.
Пример 16-10. Определить число единиц переноса при поглощении ам-
миака водой в условиях, описанных в примере 16-5 (стр. 569). Равновесные
концентрации У* при различных значениях X приведены в табл. 24 (расчет
данных — см. в примере 17-1, стр 593).
Решение. На рис. 16-5 изображена У — Х-диаграмма, на которой ра-
бочая линия построена, как указано в примере 16-5, а линия равновесия по-
строена по данным, приведенным в табл. 24. Из диаграммы находим значение
У* = 0,0236, соответствующее конечной концентрации t NH3 в жидкости
Xi = 0,0268 (точка W), и У* = 0,0009, соответствующее начальной концентра-
ции NH3, т. е. Х2 = 0,002 (точка М).
Движущая сила внизу абсорбера (на входе газа)
= 0,0309 — 0,0236 = 0,0073
вверху абсорбера (на выходе газа)
Д2 = 0,0016 — 0,0009 = 0,0007
Аср.
Среднелогарифмическую движущую силу определяем по формуле (16-40):
0,0073 - 0,0007 _оро289
о _ . 0,0073 0,00289
2,3 g 0,0007
Соответствующее число единиц переноса находим по формуле (16-41):
_ 0,0309 — 0,0016
п~~ 0,00289 = 1иД
Графическим методом, вписывая ступеньки (см. стр. 584), находим
п 6,85 (см. рис. 16-5).
Для определения числа единиц переноса методом графического интегри-
рования по рис. 16-5 для ряда значений X определены значения У и У*, а
также вычислены величины у •
Результаты расчета сведены в таблицу (табл. 24).
Таблица 24
X 0,002 0,005 0,01 0,015 0,02 0,025 0,03
у * 0,0009 0,0025 0,0057 0,0097 0,0147 0,0212 0,0284
У 0,0016 0,0051 0,0110 0,0169 0,0228 0,0287 0,0346
1 1430 385 189 139 122 134 162
У—У* • • • •
7. Средняя движущая сила и методы расчета массопередачи 587
Построив график зависимости от (Рис- 16-6) и определив пло-
щадь под кривой между точками Уз — 0,0016 иУ1 « 0,0309, находим f = 9,25 ent2.
При масштабе построения mj — 0,004 и тч = 200 число единиц переноса со-
ставляет:
п = 9,25 • 0,004 • 200 = 7,4
В данном случае при расчете по графическому методу и методу графи-
ческого интегрирования получаются близкие результаты, тогда как при рас-
чете по формуле (16-40) обнаруживается значительная ошибка.
Рис. 16-5. Графическое определение числа единиц переноса (к примеру
16-10) и минимального расхода поглотителя Zmin (к примеру 17-2, стр. 594).
588
Гл. 16. Теория процессов массопередачи
Рис. 16-6. Определение числа единиц переноса методом графического инте-
грирования (к примеру 16-10). Масштаб построения: — 0,004, /?г2 = 200.
Определение высоты единицы переноса
Подставляя в уравнение (16-42) значение из соотношения
(16-38), получим:
' О , AG __ G , h G L
fS^ “i" fS^ — * L ’ fS^
Величина
*. = 7^7 (16-45)
представляет собой высоту единицы переноса для фазы G.
Величина
= w (,6’46)
является высотой единицы переноса для фазы L.
7. Средняя движущая сила и методы расчета массопередачи
589
Таким образом
Л — /гг _ /г2
(16-47)
1 L
где /= Q--
Пример 16-11. Для условий примера 16-6 (стр. 572) найти высоту еди-
ницы переноса, если количество инертного газа (воздуха) G = 1750 кг/ч, диа-
метр аппарата (абсорбера) 1,8 м, удельная поверхность насадки в аппарате
(кольца керамические размером 25 X 25 X 3 мм) f = 200 м2/м3 (см. табл. 26,
стр. 598).
Решение. Площадь сечения аппарата:
S = 0,785 • 1,82 = 2,54 м*
Коэффициент массопередачи К, выраженный в кг/м2>4' (кг/кг), составляет
3,7 (см. пример 16-6). По формуле (16-42) находим высоту единицы переноса
. !750 _
3,7-2,54-200 -°’93 М
Глава 17
АБСОРБЦИЯ
1. Общие сведения
Абсорбцией называется процесс поглощения газа или пара
жидким поглотителем (абсорбентом). Обратный процесс — вы-
деление поглощенного газа из поглотителя — называется десорб-
цией.
В промышленности абсорбция с последующей десорбцией ши-
роко применяется для выделения из газовых смесей ценных ком-
понентов (например, для извлечения из коксового газа аммиака,
бензола и др.), для очистки технологических и горючих газов
от вредных примесей (например, при очистке их от сероводо-
рода), для санитарной очистки газов (например, отходящих га-
зов от сернистого ангидрида) и т. д.
В некоторых случаях десорбцию не проводят, если ’извлекае-
мый компонент и поглотитель являются дешевыми или отброс-
ными продуктами или если в результате абсорбции получается
готовый продукт (например, соляная кислота при абсорбции
хлористого водорода водой).
2. Физические основы процесса абсорбции
Равновесие между фазами
Растворимость газов в жидкостях зависит от свойств газа
и жидкости, от температуры и парциального давления раство-
ряющегося газа (компонента) в газовой смеси.
Зависимость между растворимостью газа и его парциаль-
ным давлением характеризуется законом Генри, согласно кото-
рому равновесное парциальное давление р* пропорционально
содержанию растворенного газа в растворе X (в кг/кг погло-
тителя)
= (17-1)
где ф — коэффициент пропорциональности, имеющий размер-
ность давления и зависящей от свойств растворенного
газа и поглотителя и от температуры (Приложение XVI).
2. Физические основы процесса абсорбции
591
Растворимость многих газов значительно отклоняется ог
закона Генри. Это относится главным образом к хорошо рас-
творимым газам, образующим растворы высокой концентра-
ции. При низких концентрациях раствора закон Генри обычно
хорошо соблюдается.
Для практических расчетов пол^уются полученными из
опыта значениями равновесного парциального давления газар*
и вычисляют равновесное содержание абсорбируемого компо-
нента в газовой смеси Kt по формуле (16-12)
¥* = ^'~р^~р* кг^кг инертного газа (17-2)
где Л4К и Л4Н— молекулярные массы абсорбируемого компонен-
та и инертного (неабсорбируемого) газа;
Р—общее давление газовой смеси.
По найденным значениям У* строят линию равновесия
(стр. 567).
При небольших значениях р*, по сравнению с Р, можно при-
ближенно написать, учитывая уравнение (17-1):
у* _ Р* _____ __ t, у /17
Y ~ Мп' Р Ма ' Р ~
, ЛЬ ф
где
В этом случае линия равновесия представляет собой прямую,
тангенс угла наклона которой равен k.
Материальный баланс
Материальный баланс абсорбера характеризуется уравне-
нием (16-14), в котором G — количество инертного газа, кг/сек\
L — количество поглотителя, кг!сек\ Y — содержание компонента
в газовой фазе, кг/кг инертного газа; X— содержание компо-
нента в жидкой фазе, кг/кг поглотителя.
Величина /, определяемая по уравнению (16-15), является
удельным расходом поглотителя (кг/кг инертного газа).
При полном извлечении компонента из газа его содержание
в газовой фазе на выходе из абсорбера было бы У2 — 0, а коли-
чество поглощенного компонента составило бы GY\. Отношение
количества фактически поглощенного компонента G(Yi — У2)
к количеству, поглощаемому при полном извлечении, назы-
вается степенью извлечения:
С(Г,-Г2) _ У.-К, У2
GY У! “ 1 К
(17-4)
592
Гл. 17. Абсорбция
Рабочая линия процесса абсорбции описывается уравнением
(16-16). На диаграмме Y — X она расположена выше линии
равновесия, так как при абсорбции содержание компонента в
газовой фазе больше равновесного. При десорбции, наоборот,
рабочая линия лежит ниже линии равновесия.
Чтобы построить рабочую линию, надо знать составы фаз на
входе в абсорбер (Х2, У1) и на выходе из него (A\, У2). По этим
составам строят точки А и В (см. рис. 16-1), а расход поглоти-
теля определяют по уравнению (16-15).
Однако обычно заданы только начальные составы газа и
жидкости (Уь Х2) и степень извлечения е. Заданным условиям
соответствует определенное значение У2, которое можно найти
по формуле (17-4) и таким образом построить точку В (рис.
17-1). В зависимости от удельного расхода поглотителя рабочая
Рис. 17-1. Определение минимального расхода погло-
тителя:
а —линия равновесия обращена выпуклостью вниз; б —линия равно-
весия обращена выпуклостью вверх.
ОС —линия равновесия; АВ — рабочая линия; А'В — пре-
дельное положение рабочей линии, соответствующее минимальному
расходу поглотителя.
линия будет поворачиваться около точки В, причем точка А
будет перемещаться по горизонтали, соответствующей орди-
нате Уь Положение А'В, когда точка А' лежит на линии равно-
весия (рис. 17-1, а) или когда рабочая линия касается линии
равновесия (рис. 17-1,6), соответствует минимальному расходу
поглотителя /тщ.
При минимальном расходе поглотителя движущая сила в
точке касания рабочей линии и линии равновесия равна нулю,
при этом требуется абсорбер бесконечно большой высоты. С уве-
личением удельного расхода поглотителя уменьшается требуемая
высота абсорбера, но возрастают расходы на десорбцию, на пе-
рекачивание поглотителя и т. д. Наивыгоднейший удельный рас-
ход поглотителя можно найти технико-экономическим расчетом.
2. Физические основы процесса абсорбции
593
Тепловой баланс
Если абсорбция ведется без отвода тепла или с неполным его отводом,
температура повышается вследствие выделения тепла при растворении газа
в жидкости. Повышение температуры ведет к повышению равновесного пар-
циального давления компонента и к сдвигу линии равновесия вверх. Движу-
щая сила при этом уменьшается и условия абсорбции ухудшаются.
Количество выделяющегося при абсорбции тепла составляет
Q = МФ = Ф£ (Xj — Х2) вт (17-5)
где Ф— дифференциальная теплота растворения (в дж/кг}, т. е. количество
тепла, выделяющегося при поглощении 1 кг компонента в растворе
данной концентрации;
М — количество поглощенного компонента, кг/сек.
Если абсорбция ведется без отвода тепла, можно считать, что все выде-
ляющееся тепло идет на нагревание жидкости:
Q = £c(/1-/2) (17-6)
где с — удельная теплоемкость жидкости, дж/кг • град-,
и t2— температуры жидкости на выходе из абсорбера и на входе в него.
Приравнивая правые части уравнений (17-5) и (17-6), получим уравнение
теплового баланса абсорбера, работающего без отвода тепла:
Ф (Х\—Х2} = с (t{~t2} (17-7)
Для части абсорбера, расположенной выше сечения, в котором состав
жидкости равен X, а температура t, это уравнение примет вид
Ф(Л-Х2) = с(/-/2)
откуда температура жидкости в любом сечении абсорбера при составе жидко-
сти X будет составлять:
Ф
t = t2 + ~(X-X2) (17-8)
При построении линии равновесия для каждого значения X надо опреде-
лить t по уравнению (17-8), а затем найти У* для этих значений X и t по
уравнению (17-2).
Пример 17-1. Построить линию равновесия процесса поглощения амми-
ака водой в условиях примера 16-5 (стр. 569), если температура поступаю-
щей воды /2 = 20°С, а коэффициент ф в уравнении (17-1) для раствора
аммиака в воде выражается формулой
, , 1922
1g Ф = 9,343--
где ф — в мм pm. ст., Т — температура раствора, °К.
Дифференциальная теплота растворения NH3 в воде Ф = 2070 • 109 дж/кг
(495 ккал/кг}.
Решение. Принимая теплоемкость жидкости (воды) с=4190 дж/кг • град
(1 ккал/кг • град}, находим по формуле (17-8) температуру жидкости:
2070 • 103
t = 20 + 419о (X — 0,002) = 19 + 495 X
где 0,002 — содержание NH3 в воде, поступающей на абсорбцию (Х2), см. при-
мер 16-5, стр. 569,
38 Зак. 546,
594
Гл. 17. Абсорбция
Задаваясь рядом значений X, находим температуру t и рассчитываем со-
ответствующие величины ф. Далее находим по уравнению (17-1) значения
р* и определяем У* по формуле (17-2):
Р* °’588/’
29 \ 760 — р* 760— /
где 17 и 29 — молекулярные массы NH3 и воздуха.
Результаты расчета сведены в табл. 25.
ца 25
0,02
0,025
0,
Та
X
0,002
0,005
0,01
0,015
t, °C 20 21,5 24 26,4 28,9 31,4 33,9 35,3
ф, мм рт. ст 605 658 742 855 945 1060 1200 1280
р *, мм рт. ст 1,2 3,3 7,4 12,8 18,9 26,6 36 45-
Y * 0,0009 0,0025 0,0057 0,0097 0,0147 0,0212 0,0284 0,037
Расчет числа единиц переноса по найденным значениям У* приведен в
примере 16-10 (стр. 586).
Пример 17-2. Определить минимальный удельный расход поглотителя
при абсорбции аммиака водой в условиях примеров 16-5 (стр. 569) и 16-10
(стр. 586).
Решение. На У — X диаграмме (см. рис. 16-5, стр. 587) строим точку
В с координатами (Хъ = 0,002, Уг = 0,0016) и точку А' на линии равновесия
с ординатой У1 = 0,0309. Абсцисса точки А' будет Х[ — 0,0318.
Минимальный удельный расход поглотителя составляет:
^мин. — tga —
2 0,0309 — 0,0016 ппск
— =------------------ = и,УОЭ
(2 0,0318 — 0,002
Принятый в примере 16-5 удельный расход поглотителя I — 1,18 больше
ZmIn в 1,2 раза. ;
3. Устройство абсорберов
При абсорбции процеоб массопередачи протекает на поверх-
ности соприкосновения фаз. Поэтому в аппаратах для поглоще-
ния газов жидкостями (абсорберах) должна быть "создана раз-
витая поверхность соприкосновения между газом и жидкостью.
По способу образования этой поверхности абсорбционные
аппараты можно разделить на поверхностные, барботажные и
распиливающие.
Поверхностные абсорберы
В абсорберах этого типа поверхностью соприкосновения фаз
является зеркало жидкости или поверхность протекающей жид-
кой пленки.
3. Устройство абсорберов
595
Абсорберы с соприкосновением фаз на поверхности зеркала
жидкости представляют собой сосуды, в которых газ проходит
над свободной поверхностью неподвижной или медленно проте-
кающей жидкости. Поверхность соприкосновения газа и жидко-
сти в таких аппаратах мала, поэтому обычно приходится уста-
навливать ряд последовательно соединенных абсорберов с про-
тивоточным движением газа и жидкости.
Для отвода тепла, выделяющегося при абсорбции, в абсорбе-
рах устанавливают змеевики, охлаждаемые водой или другим
хладоагентом, помещают абсорберы в сосуды с проточной во-
дой или орошают наружные поверхности стенок..
бер с водяным охлаждением:
1 — орошаемый элемент абсорбера; 2 — порог.
На рис. 17-2 показан абсорбер, стенки которого орошаются
охлаждающей водой. Абсорбер выполнен из ряда расположен-
ных друг над другом элементов 1, орошаемых снаружи водой,
наподобие оросительного холодильника. В каждом элементе
имеется порог 2, посредством которого поддерживается опре-
деленный уровень жидкости.
Поверхностные абсорберы малоэффективны и имеют ограни-
ченное применение, главным образом для абсорбции небольших
количеств хорошо растворимых газов (например, для поглоще-
ния хлористого водорода водой).
Пленочные абсорберы. К таким аппаратам относятся труб-
чатые абсорберы и абсорберы с листовой насадкой.
Трубчатый абсорбер (рис. 17-3) сходен по устройству с теп-
лообменником пленочного типа (стр. 424). Поглотитель посту-
пает на верхнюю трубную решетку, распределяется по трубам
и стекает по их внутренней поверхности в виде тонкой пленки.
38*
596
Гл 17. Абсорбция
Газ движется по трубам снизу вверх навстречу стекающей жид-
кой пленке. Для отвода выделяющегося при абсорбции тепла
по межтрубному пространству пропускают воду или другой
охлаждающий агент.
Газ
Рис. 17-3. Трубчатый пленочный аб-
сорбер.
Рис. 17-4. Абсорбер с листовой на-
садкой:
/ — насадка, 2— распределительные устрой-
ства для орошения насадки.
Абсорбер с листовой насадкой (рис. 17-4) представляет со-
бой колонну, в которой размещена насадка 1 в виде вертикально
установленных листов твердого материала (дерево, металл,
пластмассы и др.) или туго натянутых полотнищ ткани. Над
насадкой размещены распределительные устройства 2 для
орошения каждого элемента насадки с обеих сторон. Движение
жидкости и газа в этом аппарате происходит так же, как в
трубчатом абсорбере.
Насадочные абсорберы представляют собой колонны, загру-
женные насадкой — твердыми телами различной формы; при
наличии насадки увеличивается поверхность соприкосновения
газа и жидкости.
Наиболее распространена насадка в виде тонкостенных колец
высотой, равной диаметру, который колеблется в пределах
3 Устройство абсорберов
597
15—150 мм. Кольца беспорядочно засыпают в аппарат навалом
(рис. 17-5, а), либо укладывают правильными рядами, сдвину-
тыми друг относительно друга (рис. 17-5,6). Такая правильная
укладка практически возможна только при загрузке колец диа-
метром более 50 мм. Кольца изготовляют из антикоррозионных
материалов (керамика, фарфор), реже — из стали.
Широко применяют также хордовую насадку (рис. 17-5, в),
которая представляет собой ряд решеток из досок, поставлен-
ных на ребро, причем решетки сдвинуты друг относительно
друга на 45 или 90°,
Рис. 17-5. Насадки:
а —кольцевая навалом; б— кольцевая, правильно уложенная; в — хордовая.
В качестве насадок применяют также кокс и дробленый
кварц, засыпаемые в виде кусков размером 25—100 мм.
Основными характеристиками насадок являются удельная
поверхность и свободный объем (стр. 176). Характеристика не-
которых насадок приведена в табл. 26.
Жидкость стекает по поверхности насадки тонкой пленкой
и одновременно распределяется в слое насадки в виде капель
и брызг. При подаче жидкости на беспорядочно загруженную
насадку не достигается равномерное распределение жидкости
по сечению насадки на всей высоте ее слоя, так как плотность
засыпки насадки возле стенок всегда меньше, чем по оси аппа-
рата^ Вследствие этого жидкость растекается к стенкам, причем
на некотором расстоянии от верхнего уровня слоя орошение
центральной части насадки часто становится недостаточным.
Насадочный абсорбер показан на рис. 17-6. Насадка 1 опи-
рается на решетки 2, в которых имеются отверстия для прохо-
ждения газа и стока жидкости. Газ поступает в колонну снизу
и движется вверх противотоком по отношению к жидкости. По-
даваемая на насадку жидкость должна быть равномерно распре-
делена по сечению колонны. Для подачи жидкости применяют
желоба, дырчатые трубы и другие устройства.
598
Гл 17 Абсорбция
Характеристика насадок
Таблица 26
Вид и размеры насадки Удельная поверхность /, мЧм* Свободный объем е
Беспорядочно засыпанная Кольца керамические:
10 X Ю X 1,5 мм 440 0,7
15 X 15 X 2 мм 330 0,7
25 X 25 X 3 мм 200 0,74
50 X 50 X 5 мм Кокс кусковой: 90 0,785
25 мм 120 0,53
40 мм 85 0,55
75 мм Правильно уложенная Кольца керамические: 42 0,58
50 X 50 X 5 мм 110 0,735
80 X 80 X 8 мм 80 0,72
100 X 100 X Ю мм Хордовая деревянная (10 X 100 мм}, шаг в свету: 60 0,72
10 мм 100 0,55
20 мм 65 0,68
30 мм 48 0,77
В абсорбере, показанном на рис. 17-6, жидкость подается на
насадку при помощи распределительного стакана.? (брызгалка),
в котором имеется большое количество отверстий диаметром
3—6 мм. Жидкость поступает в распределительный стакан из
напорного бака или подается непосредственно насосом и выте-
кает из отверстий стакана отдельными струями.
Чтобы предотвратить растекание жидкости к стенкам, иногда
насадку засыпают не сплошь на всю высоту, а в виде отдельных
слоев, как показано на рис. 17-6. Высота отдельных слоев 1,5—
3 м. Для перераспределения жидкости и отвода ее от стенок
под каждым слоем насадки, кроме нижнего, устанавливают
направляющий конус 4.
Насадочные колонны — наиболее распространенный тип аб-
сорбера. Преимуществом их является простота устройства, осо-
бенно важная при работе с агрессивными средами, так как в
этом случае требуется защита от коррозии только корпуса ко-
лонны и поддерживающих насадку решеток, насадка же может
3 Устройство абсорберов
599
быть выполнена из химически стойкого материала (керамика,
фарфор). Другое преимущество насадочных колонн — более низ-
кое, чем в барботажных абсорберах, гидравлическое сопроти-
вление.
Однако насадочные колонны мало пригодны при работе с за-
грязненными жидкостями, а в случае малых количеств орошаю-
щей жидкости не дают удовлет-
ворительных результатов, так как
при низкой плотности орошения ¥
не достигается полная смачивае-
мость насадки. Кроме того, в
насадочных колоннах затруднен
отвод тепла, выделяющегося
при поглощении газа; отвод теп-
ла может быть осуществлен
только в выносных холодильни-
ках — путем рециркуляции по-
глотителя или путем промежу-
точного охлаждения (стр. 606).
Газ
Газ
Жидкость
г
Жидкость
Рис. 17-6. Насадочный абсорбер:
/ — насадка; 2— решетка; 3 — распреде-
лительный стакан (брызгалка); 4 — напра-
вляющий конус.
Барботажные абсорберы
В барботажных абсорберах
поверхность соприкосновения
фаз развивается потоками газа,
распределяющегося в жидкости
в виде пузырьков и струек. Та-
кое движение газа, называемое
барботажем, осуществляется в
тарельчатых колоннах с колпач-
ковыми, ситчатыми или проваль-
ными тарелками. Подобный же
характер взаимодействия газа и
жидкости наблюдается в наса-
дочных колоннах, работающих в
режиме подвисания (стр. 610).
Особенностью тарельчатых
колонн является ступенчатый ха-
рактер проводимого в них процесса (в отличие от непрерывного
процесса в насадочных колоннах) — газ и жидкость последова-
тельно соприкасаются на отдельных ступенях (тарелках) аппа-
рата.
* Плотностью орошения называется объем жидкости, проходящей через
единицу площади поперечного сечения колонны за единицу времени,
60Э
Гл. 17. Абсорбция
Рис. 17-7. Колонна
с колпачковыми
тарелками:
/ — тарелка; 2—па-
трубки; 3— колпачки;
4 — переливные трубы.
Колонны с колпачковыми тарелками. В колпачковых тарел-
ках газ барботирует через жидкость, выходя из прорезей
колпачков, расположенных на каждой тарелке. В прорезях газ
дробится на мелкие струйки, которые по выходе из прорези
почти сразу поднимаются вверх и, проходя через слой жидкости
на тарелке, сливаются друг с другом.
В колоннах с колпачковыми тарелками
(рис. 17-7) находятся тарелки 1 с патрубка-
ми 2, закрытые сверху колпачками 3. Нижние
края колпачков снабжены зубцами или проре-
зями в виде узких вертикальных щелей. Жид-
кость перетекает с тарелки на тарелку через
переливные трубы 4. Уровень жидкости на та-
релке соответствует высоте, на которую верх-
ние концы переливных труб выступают над
тарелкой. Чтобы жидкость перетекала только
по переливным трубам, а не через патрубки 2,
верхние концы патрубков должны быть вы-
ше уровня жидкости. Нижние края колпачков
погружены в жидкость так, чтобы уровень
жидкости был выше верха прорезей.
Газ проходит по патрубкам 2 в простран-
ство под колпачками и, выходя через отвер-
стия между зубцами или через прорези в колпачках, барботи-
рует через слой жидкости.
Чтобы газ не попадал в переливные трубы и не препятство-
вал таким образом нормальному перетоку жидкости с тарелки
на тарелку, нижние концы переливных труб опущены под уро-
вень жидкости. Благодаря этому создается гидрозатвор, предот-
вращающий прохождение газа через переливные трубы.
а
Рис. 17-8. Устройство колпачков:
а —круглый колпачок; б—прямоугольный колпачок.
По конструкции различают круглые колпачки (рис. 17-8, а) и прямоуголь-
ные колпачки (рис. 17-8,6). Круглые колпачки имеют диаметр 80—100 мм,
при работе с загрязненными жидкостями — до 200—300 мм. Ширина прямо-
угольных (туннельных) колпачков 70—150 мм.
3. Устройство абсорберов
601
Колонны с ситчатыми тарелками. Ситчатые тарелки
(рис. 17-9) имеют отверстия 1 диаметром 2—5 мм\ газ проходит
через отверстия и барботирует через слой жидкости на тарелке.
При нормальной работе колонны жидкость не протекает через
отверстия, так как она поддерживается снизу давлением газа.
Высота слоя жидкости на тарелке составляет 25—30 мм и
определяется положением верхних концов переливных труб 2.
Ситчатые колонны отличаются простотой устройства и вы-
сокой эффективностью. Основной их недостаток заключается в
том, что они удовлетворительно работают лишь в ограниченном
диапазоне нагрузок. При низких нагрузках,
когда скорость газа мала, жидкость проте-
кает через отверстия и работа колонны нару-
шается. При больших нагрузках гидравличе-
ское сопротивление тарелки сильно возра-
стает, причем наблюдается значительный унос
жидкости (хотя на ситчатых тарелках унос
меньше, чем на колпачковых тарелках). Дру-
гой недостаток ситчатых колонн состоит в
том, что отверстия в тарелках легко заби-
ваются.
Колонны с провальными тарелками. В
провальных тарелках отсутствуют перелив-
ные трубы, вследствие этого газ и жидкость
проходят через одни и те же отверстия.
Дырчатые провальные тарелки по устрой-
Рис. 17-9. Колонна
с ситчатыми та-
релками:
ству аналогичны ситчатым тарелкам И ОТЛИ- /-отверстия; 2-пе-
чаются ОТ НИХ ЛИШЬ отсутствием переливных реливная труба.
Труб.
Решетчатые тарелки (рис. 17-10, а) имеют отверстия в виде
фрезерованных щелей 1 шириной 3—4 мм. Иногда тарелки со-
бирают из полос, поставленных на ребро.
Трубчато-решетчатые тарелки являются разновидностью ре-
шетчатых. Решетку образует труба 2, изогнутая в плоскую спи-
раль (рис. 17-10,6), или ряд параллельных труб 2, присоеди-
ненных к коллекторам 4 (рис. 17-10, в). По трубам пропускают
охлаждающий агент для отвода тепла, выделяющегося при аб-
сорбции. Не занятую трубами площадь тарелки перекрывают
перфорированным листом 3, живое сечение» которого близко
к живому сечению решетчатой части тарелки.
Благодаря отсутствию переливных устройств провальные та-
релки проще тарелок других типов.
Преимуществами барботажных абсорберов являются хоро-
ший контакт между фазами и возможность работы при любом,
в том числе при низком, расходе жидкости. В барботажных
602
Гл 17. Абсорбция
абсорберах может быть осуществлен отвод тепла. Для этого на
тарелках устанавливают змеевики, по которым протекает охла-
ждающий агент, либо применяют выносные холодильники, через
которые проходит жидкость, поступающая с вышележащей та-
релки на нижележащую тарелку. Барботажные абсорберы по
Рис. 17-10. Решетчатые и трубчато-решетчатые тарелки:
а—решетчатая; б, в —трубчато-решетчатые, / — щели; 2—труба; 3— перфо-
рирований лист; 4 — коллекторы.
сравнению с насадочными более пригодны для работы с загряз-
ненными средами.
Основные недостатки барботажных абсорберов — сложность
конструкции и высокое гидравлическое сопротивление, связан-
ное при пропускании больших количеств газа с значительными
затратами энергии на перемещение газа через аппарат. Поэтому
барботажные абсорберы применяют преимущественно в тех слу-
чаях, когда абсорбция ведется под повышенным давлением, так
как при этом высокое гидравлическое сопротивление не суще-
ственно. к
3. Устройство абсорберов
603
Распиливающие абсорберы
В распиливающих абсорберах поверхность соприкосновения
фаз создается путем распыления жидкости в массе газа на мел-
кие капли. Такие абсорберы изготовляются обычно в виде ко-
лонн, в которых распыление жидкости производится сверху, а
газ движется снизу вверх. Применяются они главным образом
для поглощения хорошо растворимых газов.
Общая поверхность капель возрастает с увеличением плот-
ности орошения и с уменьшением их размера и скорости движе-
ния. Поэтому для эффективной работы абсорбера большая плот-
ность орошения имеет решающее значение.
Распыление жидкости производят механическими или пнев-
матическими форсунками и центробежными распылителями.
Механические форсунки (рис. 17-11, а) распиливают жидкость при избы-
точном давлении 2—200 ат, дают мелкий распыл (размер капель 50 мк
б
Рис. 17-11. Форсунки и распылители:
а —механическая форсунка; б —пневматическая форсунка; в —центробеж-
ный распылитель.
и менее), но легко засоряются и непригодны для распиливания суспензий,
загрязненных и вязких жидкостей.
Пневматические форсунки (рис. 17-11, б) работают под действием сжатого
воздуха или пара под избыточным давлением до 5 ат.
Центробежные распылители изготовляют в виде турбинок или дисков
(рис. 17-11, в), вращающихся с большой скоростью. Число оборотов дисков
4000—20 000 об/мин. Диски в отличие от форсунок могут‘распиливать сус-
пензии и загрязненные жидкости.
604
Гл. 17. Абсорбция
Преимуществами распиливающих абсорберов являются их
простота и дешевизна, низкое гидравлическое сопротивление и
возможность использования при абсорбции газов, сильно за-
грязненных механическими примесями.
К их недостатках относятся трудность применения загряз-
ненных жидкостей в качестве поглотителей, необходимость за-
траты энергии на распыление жидкости и применения больших
плотностей орошения, а также трудность регулирования коли-
чества подаваемой жидкости.
В последнее время получили распространение абсорберы
с распылением жидкости в быстро движущемся потоке газа
Рис. 17-12. Механический абсорбер:
1— корпус; 2— вал; 3 — сетчатые диски.
(скорость 20—80 м/сек). Такие абсорберы по устройству ана-
логичны струйным скрубберам Вентури (стр. 338) и отличаются
большой интенсивностью и высокой эффективностью. Их недо-
статками являются большое гидравлическое сопротивление и
прямоточное взаимодействие газа и жидкости, в связи с чем
эти абсорберы применяются в тех случаях, когда по условиям
процесса можно ограничиться 1—2 ступенями абсорбции.
К распыливающим аппаратам относятся также механические
абсорберы, в которых разбрызгивание жидкости производится
вращающимися деталями (рис. 17-12). Внутри неподвижного
корпуса / вращается горизонтальный вал 2, на котором наса-
жены сетчатые диски 3, частично погруженные в жидкость. При
вращении вала жидкость увлекается дисками и разбрызгивается
в виде мельчайших капель
4 Десорбция
605
Механические абсорберы достаточно эффективны; их недо-
статками являются сложность устройства и значительный рас-
ход энергии.
4. Десорбция
Десорбцию, или отгонку, т. е. выделение растворенного газа
из раствора, проводят одним из следующих способов: 1) в токе
инертного газа, 2) выпариванием раствора, 3) в вакууме. При-
меняется также комбинирование этих способов.
Отгонка в токе инертного газа (собственно десорбция) яв-
ляется процессом, обратным абсорбции. При соприкосновении
раствора с инертным газом растворенный газ переходит в газо-
вую фазу, так как парциальное давление газа над раствором
выше, чем в газовой смеси. Процесс ведут в насадочных или
барботажных колоннах, раствор подается в колонну сверху,
инертный газ — снизу; из нижней части колонны отводится ре-
генерированный раствор, из верхней — выделенный из раствора
газ в смеси с инертным газом.
В качестве инертного газа применяют большей частью воз-
дух. При этом выделенный из раствора газообразный компонент
получается не в чистом виде, а в виде смеси с воздухом. По-
этому данный способ отгонки применяется в тех случаях, когда
извлеченный из газов компонент (например, вредная примесь)
не используется или может быть использован при невысокой
концентрации.
Отгонка с инертным газом применяется также при обогаще-
нии газов, т. е. для получения более концентрированной газовой
смеси, чем исходная смесь, из которой данный компонент извле-
кают путем абсорбции.
При десорбции нерастворимых в воде газов в качестве инерт-
ного газа применяют водяной пар. Смесь выделенного компо-
нента с водяным паром по выходе из колонны направляется в
конденсатор, в котором водяной пар конденсируется, а выде-
ляемый компонент получается в чистом виде. Если компонент
имеет достаточно высокую температуру кипения (например,
бензол), он конденсируется вместе с водяным паром и отделе-
ние его от воды производится путем отстаивания.
Отгонка путем выпаривания раствора производится при по-
мощи обогрева глухим паром. При этом из раствора удаляется
не только выделяемый компонент, но испаряется также часть
растворителя.
Для разделения компонента и паров растворителя прибегают
к ректификации. Таким образом, по схеме процесса и применяе-
мой аппаратуре этот способ отгонки не отличается от ректифи-
кации (глава 19).
606
Гл. 17. Абсорбция
Отгонка в вакууме обычно комбинируется с отгонкой путем
выпаривания и применяется в тех случаях, когда при атмосфер-
ном давлении невозможно достаточно полное выделение компо-
нента из поглотителя. При отгонке в вакууме газообразный ком-
понент, выделяемый на установке, отсасывается вакуум-насосом.
5. Схемы абсорбционных установок
Схема с рециркуляцией поглотителя показана на рис. 17-13.
Вытекающая из абсорбера 1 жидкость насосом 2 через холо-
дильник 3 снова подается в абсорбер. Часть вытекающей из аб-
сорбера жидкости отводится из системы, а взамен подается со-
Газ
Рис. 17-13. Схема абсорбцион-
ной установки с рециркуляцией
поглотителя:
/ — абсорбер; 2 — насос; 3— холо-
дильник.
ответствующее количество свежего
поглотителя.
При рециркуляции свежий по-
глотитель смешивается с поглотите-
лем, уже насыщенным извлекае-
мым компонентом; таким образом,
содержание этого компонента в по-
ступающей на абсорбер жидкости
больше, чем при отсутствии ре-
циркуляции. В связи с этим умень-
шается движущая сила процесса
массопередачи и ухудшается извле-
чение компонента из газовой смеси.
Несмотря на отмеченные недо-
статки, абсорбция с рециркуляцией
поглотителя находит применение
благодаря тому, что в этом про-
цессе удается повысить плотность орошения и осуществить от-
вод тепла в выносном холодильнике.
Схема с последовательным соединением абсорберов показана
на рис. 17-14 и 17-15.
В схеме, представленной на рис. 17-14, абсорберы соединены
друг с другом противотоком; передача жидкости из одного аб-
сорбера в другой производится насосами. Тепло отводится в хо-
лодильниках, установленных на жидкостных линиях между аб-
сорберами (промежуточное охлаждение). Абсорбция, проводи-
мая по такой схеме, соответствует поглощению газа в одном аб-
сорбере, высота которого больше высоты каждого абсорбера во
столько раз, сколько абсорберов соединено последовательно.
На рис. 17-15 показана схема последовательного соединения
абсорберов при рециркуляции поглотителя в системе каждого аб-
сорбера В данном случае основное назначение рециркуляции—
увеличение плотности орошения. Абсорбционная установка в
5. Схемы абсорбционных установок
607
этой схеме сочетается с десорбционной. Насыщенный компонен-
том поглотитель из абсорбционной установки подается через
Рис. 17-14. Схема абсорбционной установки с последо-
вательным соединением абсорберов:
/ — абсорбер, 2 — сборник; 3—насос; 4 — холодильник.
теплообменник 5 в отгонную колонну 6. В теплообменнике по-
ступающая на десорбцию жидкость подогревается регенериро-
ДесорбироВанный
газ
Рис. 17-15. Схема абсорбционно-десорбционной
установки с рециркуляцией поглотителя в каж-
дом абсорбере.
/—абсорбер; 2 —сборник; 3 —насос; 4—холодильник;
5 — теплообменник, б —отгонная колонна.
ванным (освобожденным от компонента) поглотителем, выте-
кающим из отгонной колонны.
Регенерированный поглотитель, пройдя теплообменник,
охлаждается в холодильнике 4 и далее возвращается в абсорб-
ционную установку.
608
Гл 17 Абсорбция
6. Расчет насадочных абсорберов
Гидродинамика насадочных абсорберов
Движение газа и орошающей жидкости через слой насадки
характеризуется критериями Рейнольдса для газа (Rer) и для
жидкости (Кеж). Критерий Rer определяется по формуле
(6-101).
Обычно считают, что орошающая жидкость стекает по по-
верхности насадки в виде пленки; поэтому критерий Rex опре-
деляют по формуле (6-85). Линейную' плотность орошенйя Г
в насадочных колоннах определяют как отношение массовой ско-
рости жидкости №ж к периметру насадочных тел на 1 м2 по-
перечного сечения колонны. Этот периметр можно считать рав-
W
ным удельной поверхности насадки f. Тогда Г = ~у^ кг/м • сек.
Подставляя это значение Г в формулу (6-85), получим:
^ = 4^ (1^-9)
где |лж—вязкость жидкости, я «сек/м2;
Гж—массовая скорость жидкости, кг/м2-сек.
Гидравлическое сопротивление насадок. Гидравлическое сопротивление
сухой насадки определяется по формуле (6-102), причем коэффициент сопро-
тивления X имеет следующие значения:
Для беспорядочно засыпанных насадок
140
при ламинарном движении (Rer < 40) X = —— (17-10)
Кег
при турбулентном движении (Rer > 40) Х = —(17-11)
Rep2
Для правильно уложенных насадок X = —(17-12)
Rep
причем для кольцевой насадки а = 9,2, для хордовой насадки
а = 3.12 + 17-^Ь-(?рт)1'37 (17-13)
где </экв. — эквивалентный диаметр насадки, м [см. формулу (6-100)];
h — высота насадки в одном ряду, л;
t — расстояние между досками в свету,
s — толщина доски, м.
Гидравлическое сопротивление орошаемой насадки, через ко-
торую движется газ или пар, значительно больше сопротивле-
ния сухой насадки. Это объясняется тем, что некоторое коли-
6. Расчет насадочных абсорберов
609
чество жидкости задерживается в насадке вследствие смачива-
ния ее поверхности и скопления в узких криволинейных
каналах, образуемых соприкасающимися насадочными телами.
Количество жидкости, задерживающееся в единице объема
насадки, характеризует так называемую удерживающую способ-
ность насадки. Если жидкость задерживается в насадке, свобод-
ный объем насадки уменьшается, что приводит к увеличению
скорости газа, пропорционально квадрату которой возрасгает
сопротивление насадки.
Сопротивление орошаемой насадки (при плотности орошения менее
50 л<3/л<2 • ч) приближенно можно найти по формуле:
Др = Дрсух. (1 + kU)
(17-14)
где AjPcyx. — сопротивление сухой насадки;
U — плотность орошения, л<3/л<2 • ч (для удобства в практических
расчетах за единицу времени для размерности плотности оро-
шения принят час вместо секунды),
k — опытный коэффициент (для беспорядочно засыпанных и хордо-
вых насадок k = 0,06, для правильно уложенных кольцевых на-
садок k = 0,04).
Смачиваемость насадок,
следует учитывать неполное
чего в процессе массопере-
дачи участвует не вся по-
верхность насадки, а лишь
некоторая активная ее часть.
Это учитывается коэффици-
ентом, смачиваемости ф. Точ-
ных данных для определе-
ния ф в настоящее время еще
не имеется; при расчетах
ориентировочные значения
ф можно находить по рис.
17-16 в зависимости от отно-
шения tZ/^опт.’ где (70ПТ. —
оптимальная плотность оро-
шения (см. ниже).
1ри расчете насадочных колонн
смачивание насадки, вследствие
Рис. 17-16. Коэффициенты смачиваемо-
. и
стп ф при различном отношении -ту—:
б'ОПТ.
1 — на насадке из колец (навалом); 2 —на дере-
вянной хордовой насадке.
Максимальное смачивание на-
садки достигается при некоторой
оптимальной плотности орошения
t/опт.> при которой коэффициент
смачиваемости ф становится рав-
39 Зак 546.
610
Гл. 17. Абсорбция
ным единице При дальнейшем увеличении плотности орошения гр не изме-
няется. Оптимальная плотность орошения определяется по формуле
С70пт. = V м3)м2 ч (17-15)
где /— удельная поверхность насадки, лг2/лг3;
Ь — коэффициент, значения которого приведены в табл. 27.
Таблица 27
Значения коэффициента Ь
Процесс
Коэффициент Ь
м3/м-ч
Абсорбция аммиака водой ...................
Абсорбция паров органических жидкостей водой
Абсорбция паров органических жидкостей керо-
сином .....................................
Ректификация, испарение воды...............
0,158
0.093
0,024
0,065
Захлебывание насадок. Между газом и жидкостью, движу-
щейся по насадке, возникают силы трения, которые увеличи-
ваются с возрастанием относительной скорости движения газа
и жидкости. В случае противотока газа и жидкости силы тре-
ния, действующие на жидкость, направлены вверх, т. е. проти-
воположны направлению действия силы тяжести. Эти силы
трения возрастают с увеличением скорости газа до некоторого
предела, когда они становятся равными силе тяжести, действую-
щей на жидкость. При этом движение жидкости по насадке на-
чинает тормозиться потоком газа. Такой режим работы колон-
ны — режим подвивания начинается по достижении некоторой
предельной скорости газа, называемой пределом подвисания.
В этих условиях газ начинает барботировать через жидкость
(стр. 599), и поверхность соприкосновения между газом и жид-
костью значительно возрастает, что приводит к интенсифика-
ции процесса массообмена. Однако одновременно в колонне
резко увеличивается гидравлическое сопротивление.
При дальнейшем увеличении скорости газа силы трения газа
о жидкость становятся больше силы тяжести и начинается дви-
жение жидкости снизу вверх. Критическая скорость, соответ-
ствующая началу уноса жидкости газом, называется пределом
захлебывания. Начало захлебывания является верхней границей
работы колонн в режиме подвисания.
Скорость газа, соответствующую началу подвисания, можно определить
по уравнению
Re' = 0,045 Ar0*57 (-НМ0,43 (17-16)
\ №ж /
6. Расчет насадочных абсорберов
611
Здесь Rer— значение Rer, соответствующее началу подвисания;
Аг — критерий Архимеда [см формулу (6-46)], рассчитанный по
эквивалентному диаметру насадки и вязкости газа;
1Гг" и W* — массовые скорости газа и жидкости.
Пример 17-3. Определить сопротивление слоя правильно уложенной на-
садки из колец размером 50 X 50 X 5 мм. Высота насадки И = 11,5 м, плот-
ность орошения U = 7,2 м3/м2 • ч. Массовая скорость газа 1Т7 = 1,7 кг/м2 • сек,
температура газа 25° С.
Решение. Находим критерий Рейнольдса для газа по формуле (6-101):
Rer=^ =___________4-*'7 - .=3370 '
/|ЛГ 110-0,185-10“*
где f—удельная поверхность колец насадки (ПО м2/м3, см. таблицу 26,
стр. 598);
Р-г — вязкость газа (воздуха) при 25° С (0,185-10~4 н-сек/м2, или
0,0185 спз).
Коэффициент сопротивления определяем по формуле (17-12):
X
92
=0,44
33700’375
Сопротивление сухой насадки находим по формуле (6-102):
Х/7/рго$ 0,44-11,5-ПО-1,16-1,462
А^сух. = —873— =---------------------------= 432 «/^2 С44 ^гсМ2)
8 • 0,7353
где рг— плотность газа (воздуха) при 25°С (1,16 кг/м3);
е — £вободный объем насадки (0,735, см. табл. 26);
w0— фиктивная скорость газа:
WT 1>7 , AR ,
w0 = —L — т~гс" — Мб м сек
рг 1,16
Сопротивление орошаемой насадки рассчитываем по формуле (17-14):
Др = 432 (1 -f- 0,04 • 7,2) = 555 н/м2 (57 кгс/м2)
Пример 17-4. Определить скорость газа, соответствующую началу подви-
сания жидкости в колонне с насадкой из правильно уложенных колец разме-
ром 50 X 50 X 5 мм. Расход газа G= 12 300 кг/ч, расход жидкости
L = 14 500 кг/ч. Температура газа 25° С.
Решение. Для правильно уложенных колец указанного размера нахо-
дим по табл. 26: /=110 м2/м3, £= 0,735. Эквивалентный диаметр насадки
определяем по формуле (6-100):
4s 4 • 0,735 Л аос-т
^экв. — "у* — 110----0,0267 м
По формуле (6-46) определяем критерий Архимеда:
. _Л..Рг(Р«-Рг) 9,81 - 0.02673 -1,16(1000—1,16)
АГ---------?г = (0,185 10-*)2 '
где рг— плотность газа (воздуха) при 25°С (1,16 кг/м3);
рж— плотность жидкости (воды) при 25°С (1000 кг/м3);
рг—вязкость газа (воздуха) при 25° С (0,185-10~4 «• сек/м2, или
0,0185 спз).
39*
612
Гл. 17. Абсорбция
Находим значение Rer по формуле (17-16), заменяя в ней отношение
Wr G
на равное ему отношение -у-:
1УЖ L
Re^ = 0,045 Ar0-57 Y5'43 = 0,045(6,45 • IO8)0,57 = 4430
\ ж / \ оии /
Фиктивную скорость газа w0, соответствующую началу подвисания жид-
кости, вычисляем по формуле (6-101):
Re;/pr 4430-110-0,185.10"4
wo = 4рг = 4ЛД6 = 1,93 М/Сек
Ма с с опередача в насадочных абсорберах
При расчете насадочных абсорберов проще всего пользоваться
методом единиц переноса, определяя высоту единицы переноса
по формуле (16-47).
Высота единицы переноса для газовой фазы может быть определена по
следующей формуле:
Л1 = -^Ке»-м(Ргг7'.л< (17-17)
где е — свободный объем насадки;
ф— коэффициент смачиваемости насадки;
/— удельная поверхность насадки, м2/м3-,
Rer—критерий Рейнольдса для газа;
Ргг — критерий Прандтля для газа.
Значения коэффициента а, зависящие от вида насадки, приведены ниже:
Насадка а
Кольцевая.................. 8,13
Деревянная хордовая........... 6,58
♦
Высота единицы переноса для жидкой фазы может быть найдена по фор-
муле
*2 = И9вприв. Rei® (Pry»-5 м (17-18)
где 5прив. — приведенная толщина пленки, м [см. формулу (11-47)];
Реж и Ргж — критерии Рейнольдса и Прандтля для жидкости.
Определение основных размеров насадочных
абсорберов
Диаметр колонны определяется по принятой фиктивной ско-
рости газа и проверяется по. плотности орошения. Для достиже-
ния максимальной эффективности процесса целесообразно ско-
6. Расчет насадочных абсорберов 613
рость газа принимать равной или близкой скорости Wo,- соот-
ветствующей началу подвисания (стр. 610). Обычно принимают
рабочую фиктивную скорость газа w0 — (0,85 -ь 0,95) w^m/cck.
В тех случаях, когда необходимо малое гидравлическое со-
противление, принимают более низкую скорость газа.
По принятому значению w0 находят площадь сечения ко-
лонны:
= ЗбОО^о (17-19)
где Vr — расход проходящего через колонну газа, м3/ч.
Далее определяют плотность орошения:
U = м3/м?-ч (17-20)
о
где Уж —расход орошающей колонну жидкости, м3/ч.
Если плотность орошения мала по сравнению с (70пт., коэф-
фициент ф имеет низкое значение, т. е. насадка будет недоста-
точно смочена и использована неполностью. В этом случае сле-
дует применять насадку с меньшей удельной поверхностью,
чтобы снизить t/onT_.
Высота насадки определяется по уравнению (16-43). Опре-
деление числа единиц переноса п — см. стр. 584 сл.
Пример 17-5. Рассчитать насадочный абсорбер для поглощения аммиака
водой в условиях примеров 16-5 и 17-4. Насадка — правильно уложенные
кольца размером 50 X 50 X 5 мм.
Определение диаметра абсорбера. Принимаем рабочую фик-
тивную скорость газа Wo =® 0,85 w0:
w0 = 0,85 • 1,93 — 1,64 м/сек
где Wq— скорость, соответствующая началу подвисания (см. пример 17-4).
Расход газа при плотности рг =» 1.16 кг/м3 составляет:
.. а 12зоо ,,
Уг = —— = । = 10 600 м*1ч
Площадь сечения абсорбера по формуле (17-19) равна:
Уг 10 600
“ 3600w0 “ 3600.1,64 ~ ’
Этой площади соответствует диаметр абсорбера 1,52 м. Принимаем диа-
метр 1,6 м, соответствующий площади сечения S = 2,02 м2.
Определение коэффициента смачиваемости. Расход жид-
' кости при ее плотности рж — 1000 кг/м3 составляет:
„ L 14500 ...
“ Рж - 1000 “14,5 м
614
Гл. 17. Абсорбция
Находим плотность орошения по формуле (17-20):
^ = Ж = 7,2 м*1м2’4
Оптимальная плотность орошения по формуле (17-15) будет равна-
Uom. = bf = 0,158 • ПО = 17,4 м2/м2 ч
где b = 0,158 (см. табл. 27, стр. 610);
f = ПО м2/м3 (см. табл. 26, стр. 598).
7,2
Отношению /у— = = 0,415 соответствует коэффициент смачиваемо-
^ОПТ, 1'»*
сти ф — 0,45 (см. рис. 17-16, стр. 609).
Определение высоты единицы переноса для газовой
фазы. Массовая скорость газа составляет:
Wt ~~ 3600 3 “ 3600 • 2,02 “ 1,7 К^М ' Сек
Критерий Рейнольдса для газа Rer = 3370 (см. пример 17-3, стр. 6П)\
Диффузионный критерий Прандтля для газа при. 25° С определяем по фор-
муле (16-30):
Рг>_^= 0.185-10^
г ргг>г 1,16 • 0,195 • 10~4
где рг— вязкость газа (0,185-10-4 н • сек/м2, или 0,0185 спз);
рг—плотность газа (1,16 каЛи3);
Dr — коэффициент диффузии аммиака в воздухе (0,195-10-4 м21сек,
или 0,07 м2/ч)
При е = 0,735 (см. табл. 26) и а = 8,13 (см. стр. 612) определяем по
формуле (17-17) высоту единицы переноса для газовой фазы-
*1 = Re?’25 (Р<)’Л = 8о'435 °и^ ' 3370° 25 • 0.818*'- - 0.91 *
Определение высоты единицы переноса для жидкой
фазы Массовая скорость жидкости составляет:
. L 14 500 о ,
36003 “ 3600 - 2.02 2 Кг/М ‘ СвК
Находим критерий Рейнольдса по формуле (17-9):
fp* 110-0,85-10-3
где f—удельная поверхность насадки (110 jw2/jh3) ;
р.ж — вязкость воды при средней температуре 27° С (0,85 • 10~3 н-сек/м2,
или 0,85 спз)-
Диффузионный критерий Прандтля для жидкости при 27° С определяем
по формуле (16-30):
Рг' — _ 0,85 - Ю________ ggg
ж РжОж 1000 - 0,00208 • Ю-6
где рж — плотность жидкости (1000 кг/м3);
£>ж — коэффициент диффузии аммиака в воде (0,00208 • 10-6 м21сек,
или 0,075 • 10~4 м2[ч\.
7. Расчет барботажных абсорберов
615
Рассчитываем приведенную толщину пленки по формуле (11-47):
Г (0,85-Ю-3)2]''’ 10-5
’прив.—[ 1000= . 9,81 J -4,2 10
По формуле (17-18) высота единицы переноса для жидкой фазы:
h2 = 119 • 4,2 • 10~5 • 850,25 • 5650,5 = 0,407 м
Определение высоты единицы переноса. Средний наклон
линии равновесия определяем как наклон хорды, проведенной через точки М
и N (см рис. 16-5, стр. 587), ограничивающие рабочий участок линии рав-
новесия:
rj— Г2 0,0236 — 0,0009
k = Х{—Х2 = 0,0268 — 0,002 = 0,915
где У* и Kg — ординаты точек N и М. a Xi и Х2 — абсциссы этих точек.
По формуле (16-47) находим высоту единицы переноса:
ь 0 915
h = h, + 0,91 + -^-.0,407= 1,23 м
Определение высоты насадки. Число единиц переноса п = 7,4
(см. пример 16-10, стр. 586). Высота насадки по формуле (16-43) составляет:
7/ = п/г = 7,4- 1,23 = 9,1 м
С запасом 25% принимаем:
Н = 1,25 • 9,1 = 11,5 м
7. Расчет барботажных абсорберов
Гидродинамика барботажных абсорберов
При барботаже часть газа вследствие трения распыляется
в Жидкости, образуя пену, а часть жидкости увлекается газом
в виде брызг. При этом пространство над слоем жидкости на
тарелке заполняется пеной и брызгами, которые и создают раз-
витую поверхность соприкосновения фаз. Интенсивность пено-
и брызгообразования зависит в основном от скорости газа.
В зависимости от скорости газа различают следующие ре-
жимы работы барботажных тарелок:
1) Режим неравномерной работы, наблюдаемый при скорости
газа в свободном сечении колонны (между тарелками)
w < 0,5—0,6 м/сек. В колпачковых тарелках прорези колпачков
при такой скорости газа открыты не полностью (рис. 17-17,а).
В ситчатых тарелках при малых скоростях газа жидкость «про-
валивается» через отверстия, и газ проходит только через часть
отверстий. При повышении скорости газа «провал» жидкости по-
степенно прекращается, но тарелка продолжает работать в
неравномерном режиме (рис. 17-18,а).
616
Гл 17. Абсорбция
2) Режим равномерной работы наступает при дальнейшем
увеличении скорости газа. В колпачковых тарелках наступление
этого режима соответствует полному открытию прорезей
6
Рис. 17-17. Режимы барботажа на кол-
пачковых тарелках:
а —неравномерный при недостаточной скорости
газа, о —равномерный при оптимальной скорости
газа
(рис. 17-17,6), на ситчатых
тарелках — прохождению
газа через все отверстия
(рис. 17-18,6). При режи-
мах неравномерной и равно-
мерной работы на тарелках
образуется пена ячеистой
структуры.
3) Режим газовых струй
и брызг наблюдается при
w > 0,9—1,1 м!сек. В этом
случае газ движется через
жидкость в виде струй (фа-
келов), которые выходят на
поверхность" пены, причем пена разрушается. В результате над
пеной появляется большое количество брызг (рис. 17-18, в).
Рис. 17-18. Режимы барботажа на ситчатых
тарелках:
а —неравномерный; б— равномерный; в —режим газовых
струй и брызг (факельный); г —унос жидкости.
При еще большей скорости газа его потоки начинают под-
брасывать жидкость на большую высоту (рис. 17-18,г), что вы-
зывает унос жидкости на вышележащую тарелку.
7. Расчет барботажных абсорберов
617
Для достижения достаточной интенсивности барботажа скорость газа в
прорезях колпачков или отверстиях ситчатой тарелки не должна быть меньше
величины Wq, соответствующей началу режима равномерной работы и при-
ближенно равной
Wq = а У м/сек (i7-21)
где а — коэффициент, равный 1 для колпачковых тарелок и 0,67 для ситча-
тых тарелок,
g — ускорение силы тяжести, м/сек2,
С — коэффициент сопротивления (см ниже);
Рж и Рг — плотность жидкости и газа, кг/м3,
I — высота прорези (для колпачковых тарелок) или высота слоя жидко-
сти на тарелке (для ситчатых тарелок), м
Скорость газа в свободном сечении колонны w, в зависимости от скоро
сти iWj в прорезях или отверстиях, составляет.
W =
(17-22)
где у — живое сечение прорезей или отверстий (отношение их суммарной пло-
щади на тарелке к площади поперечного сечения колонны).
Гидравлическое сопротивление барботажных аппаратов. Гидравлическое
сопротивление Др барботажных тарелок складывается из сопротивления Api
сухой тарелки, сопротивления Дрг столба жидкости на тарелке, соответствую-
щего глубине барботажа, и сопротивления Дрз, обусловленного силами по-
верхностного натяжения жидкости
Таким образом
Д/>3 (17-23)
Сопротивление сухой тарелки
о
Рг^О
bpi = С —2~ н/м2
(17-24)
где рг — плотность газа, кг/м3,
w0— скорость газа в прорезях колпачка (для колпачковых тарелок) или
в отверстиях (для ситчатых тарелок), м/сек-,
С — коэффициент сопротивления, имеющий следующие значения для раз-
личных тарелок.
Тарелки С
Колпачковые....................... 4,5—5
Ситчатые
<в = 0,07 — 0,1................... 1,82
<Р = 0,15 — 0,2................... 1,45
Провальные
дырчатые....................... 2,1
решетчатые..................... 1,4—1,5
трубчато-решетчатые............ 0,9—1
618
Гл. 17. Абсорбция
Сопротивление столба жидкости на колпачковой тарелке (при полном от-
крытии прорезей):
Др2 = 1,3^рж (* + 4 + А*) н/м2 (17-25)
на ситчатой тарелке:
Др2 = 1,З^АРж (Ап + ДА) н/л/2 (17.26)
где g—ускорение силы тяжести, м/сек?;
k — отношение плотности пены к плотности чистой жидкости (при расче-
тах принимают k = 0,5);
Рж — плотность жидкости, кг/л<3;
е—расстояние от верхнего края прорезей до сливного порога, м;
I — высота прорези, м;
ДА — высота уровня жидкости над сливным порогом, м;
Ап — высота сливного порога, м.
Рис. 17-19. К расчету сопротивления столба
жидкости:
а —на колпачковой тарелке; б—на ситчатой тарелке.
Высоты Ап ДА и I и расстояние е показаны на рис. 17-19. Величина ДА
определяете} по формуле (6-80) истечения через водослив с учетом плотности
пены: »>
/ V \2/ч
ДНТ85ПГ) М
где Уж— объемный расход жидкости, м3/сек;
П — периметр сливной перегородки, м.
Сопротивление, обусловленное силами поверхностного натяжения:
4а
Др3 = _ (17-28)
где а — поверхностное натяжение, н/м;
d — диаметр отверстия в ситчатой тарелке или эквивалентный диаметр
прорези в колпачковой тарелке, м.
Сопротивлением сил поверхностного натяжения в колпачковых тарелках
обычно можно пренебречь.
Гидродинамика провальных тарелок. В провальных тарел-
ках при очень малых скоростях газа жидкость полностью про-
текает через отверстия. При повышении скорости газа жидкость
7. Расчет барботажных абсорберов
619
начинает задерживаться на тарелке и происходит барботаж газа
с образованием пены. При барботаже на провальных тарелках
газ движется пульсирующим потоком через часть отверстий,
через остальные отверстия протекает жидкость. При этом газ и
жидкость попеременно проходят через одни и те же отверстия.
На провальных тарелках, как и на тарелках других типов, обычно наблю-
даются три режима работы (стр. 615). Переход от одного режима к другому
описывается уравнением *:
lg Z = 1g Р£-=- • й16) = 1g в - 1,74 (-Et? (17-29)
° S \ £ d<p2 Рж ж / \ W7 / \ Рж /
где w — скорость газа в свободном сечении колонны, jw/сек;
g — ускорение силы тяжести, м/сек2-,
d— диаметр отверстий или эквивалентный диаметр щелей, м;
<р — живое сечение отверстий;
Рг и рж — плотность газа и жидкости, кг/м3-,
Р-ж — вязкость жидкости, спз;
U7r и — массовая скорость газа и жидкости, кг/м2-сек.
При скорости газа, соответствующей переходу от неравномерного к рав-
номерному режиму, В = 2,95, а при переходе к режиму газовых струй В — 10.
Высоту слоя пены на провальных тарелках можно определить посредством
следующих уравнений **:
при В < 2,95 Fr С0,067 = 3,25 • 10-3 Рж (17-30)
при В = 2,95 — 10 Fr 1ис°’067 = 1,1-Ю'3 В Рж (17-31)
при В > 10 Fr А.с°'067 = 11 • 10"3 Рж (17-32)
Здесь Fr — критерий Фруда, рассчитанный по скорости газа в отверстиях
(wo м/сек) и высоте пены (пи м)
С—безразмерная величина:
„ ^4Рж
с = — (17-33)
где U—плотность орошения, м3/м2-сек;
Рж — вязкость жидкости, н • сек/м2;
рж — плотность жидкости, кг/м3;
а — поверхностное натяжение, н/м.
Уравнения (17-30)—(17-32) применимы при диаметре d>3 мм. Для та-
релок при одновременном ф < 0,15 и d < 6 мм в любом В расчет ведут по
уравнению (17-31). Для тарелок при одновременном<р > 0,3 и d > 12 мм (дыр-
чатые тарелки) или d > 6 мм (решетчатые тарелки) и при любом В расчет
ведут по уравнению (17-32).
* А. Г. Касаткин, Ю. И. Дытнерский, Д. М. Попов, Хим.
пром., № 7, 482 (1961),
** Там же.
620
Гл 17. Абсорбция
Отношение плотности
найдено по уравнению *:
Сопротивление столба
пены к плотности чистой жидкости может быть
А _ °»21
Fr0-2/?
(17-34)
жидкости на тарелке определяется по уравнению:
Др2 = ^Рж^п н/м2 (17-35)
Пример 17-6. Определить сопротивление ситчатой тарелки при следую-
щих условиях: диаметр отверстия d = 0,002 м, живое сечение отверстий
? = 0,08, высота сливного порога йп = 0,025 м, плотность жидкости рж =
= 925 кг/м3, плотность газа рг =0,855 кг/м3, поверхностное натяжение о^=0,04 н/м
(40 дин/см), скорость газа в свободном сечении w = 0,94 м/сек, высота уро-
вня жидкости над сливным порогом АЛ = 0,02 м.
Решение. Скорость газа в отверстиях определяем по формуле (17-22):
w 0,94
К'" = Т= 0?б8 = ' м1сек
По формулам (17-24), (17-26) и (17-28) сопротивление при £=1,82:
0,855 • 11,72
Др, -=- С = 1,82-----------------= 107 н1м2 <10>9 кгс/м2)
Др2 = 1,3£йрж (Лп + АЛ) = 1,3-9,81-0,5-925 (0,0254-0,02) = 265 н/м2 (27 кгс/м2)
. 4а 4 • 0,04 ОЛ , , /о п ,
Др3 = — = о— .. = 80 н/м2 (8,2 кгс/м2)
Общее сопротивление тарелки:
Др = 107 4- 265 4- 80 s 450 н/м2 (46 кгс/м2)
Пример 17-7. Определить сопротивление провальной решетчатой тарелки
при следующих условиях- ширина щели b = 0,003 м, живое сечение ? = 0,12,
плотность газа рг = 0,855 кг/м3, плотность жидкости рж = 925 кг/м2, вязкость
жидкости р-ж = 0,45 • 10~3 н • сек/м2 (0,45 спз), поверхностное натяжение
а =0,04 н/м (40 дин/см). Отношение массовых скоростей жидкости и газа
1^ж/1Гг = 1,67. Скорость газа принимаем равной 0,8 от скорости, соответ-
ствующей переходу к режиму газовых струй. Определить также скорость газа,
соответствующую началу равномерной работы тарелки.
Решение Эквивалентный диаметр щели при ее длине I м (пренебре-
гая величиной Ь в знаменателе по сравнению с I).
л/h
d = ^2Ь = 2- 0,003 = 0,006 м
21 4~ 2Ь
Скорость газа w', соответствующую началу равномерной работы, опреде-
ляем посредством уравнения (17-29) при В = 2,95:
lg Z = 1g 2,95 — 1,74 - 1,67’'< = 0,47 — 0,827 = — 0,357 » T,643
\ iJZu /
* А Г Касаткин, Ю. И. Дытнерский, Д. М. Попов, Хим пром,
№ 7, 482 (1961),
7. Расчет барботажных абсорберов
621
Отсюда Z = 0,438. Скорость w' составляет-
Wf =
Zgd рж
Иж Рг
= 0,12
/0,438-9,81 0,006-925
0,450,16 • 0,855
= 0,675 м/сек
Аналогично находим скорость газа w", соответствующую переходу к ре-
жиму газовых струй при В = 10. IgZ = 0,173, откуда 2=1,49 и
w” = 1,24 м/сек.
Скорость газа в свободном сечении колонны:
w = 0,8 та)" = 0,8 • 1,24 = 0,99 м/сек
Скорость газа в отверстиях находим по формуле (17-22)
w
w0 = —
<Р
0,99 0 ,
= = 8»25 м/сек
Массовая скорость газа составляет:
U7r = wpr = 0,99 • 0,855 = 0,847 кг/м2 • сек
Массовая скорость жидкости составляет:
W
Wx = Тг = 1,67 • 0,847 1,41 кг/м2 • сек
W г
Плотность орошения равна:
U == = 1,53. Ю"3 мз/м2. cgK
Рж 925 '
По уравнению (17-33) находим величину С:
г <ЛжРж (1,53 • 10~3)6 (0,45 • 10~3)2 • 925
ga3 “ 9,81(0,04)3
Определяем коэффициент В при помощи уравнения (17-29):
z = . А. „о, 16 _ 0,992 - 0,855 0,1б _ 0 94
gdy2 рж Иж “ 9,81 -0,006-0,122-925 ’ ,У4
1g В = 1g Z + 1,74 = 1g 0,94 4- 0,827 = 0,801
\ Мчг / \ Рж /
откуда В ~ 6,3.
В соответствии с найденным значением В расчет высоты пены ведем по
формуле (17-31):
1,1 10~3В Рж _ 1,1 -10-3 -6,3 925
с0’067 Рг (3,89 • 10~ ^Л067 • 0,855
откуда высота пены составляет:
8,252
Hrt = ~gW = 9,81 • 110 0,063 м
Отношение плотности пены к плотности чистой жидкости определяем по
уравнению (17-34):
0,21 0,21
“ Fr02K? “ 110°-2/бД2 ’
622
Гл. 17. Абсорбция
Сопротивление столба жидкости на тарелке находим по формуле (17-35):
Др2 = 9,81 • 0,24 • 925 • 0,063 = 137 н/м2 (14 кгс/м2)
Сопротивление сухой тарелки и сопротивление, обусловленное силами по-
верхностного натяжения, находим по формулам (17-24) и (17-28) при £= 1,5:
ДЛ = 1,5 0,20 ^44 н/м2 (4,3 кгс/м2)
ДРз = ~о(Й64 = 27 н,м2 <2,7 кгс1м2>>
Общее сопротивление тарелки составляет:
Др = 44 -I- 137 + 27 = 208 н(м2 (21 кгс1м2)
Ма с с опередача в барботажных абсорберах
В барботажных аппаратах трудно определить истинную по-
верхность соприкосновения фаз, поэтому коэффициент массо-
передачи в этих аппаратах относят к единице площади тарелки.
Уравнение массопередачи для одной тарелки можно написать
в следующем виде:
Ж=С(Г'-Г") = ^тДСр.
где У', У"—концентрация газа перед тарелкой и после нее;
Кй — коэффициент массопередачи, отнесенный к единице
рабочей площади тарелки, кг/м2' ч • (кг/кг);
ST—рабочая площадь тарелки, л2 (площадь перфо-
рированной части для ситчатых тарелок или
площадь, на которой расположены колпачки).
Отсюда можно найти число единиц переноса по, соответ-
ствующее одной тарелке:
_ У'-У" _ K0ST
П° ~ ~Д^.~ ~ 7'36)
Число единиц переноса по на тарелку определяется в зависи-
мости от чисел переноса для газовой фазы rt\ и для жидкой
фазы «2 по уравнению
1 1 ь 1
= + (17-37)
где k — тангенс угла наклона линии равновесия;
I — удельный расход поглотителя.
7. Расчет барботажных абсорберов
623
Коэффициенты массоотдачи в барботажных абсорберах еще недостаточно
изучены; значения П1 и Пг можно найти, в зависимости от высоты пеныЛГпЛ£>
по формулам:
л1 = 1770Н°„'’|Л (17-38)
п2 = 1,26- 105/Л-4]/”
Z П f и
(17-39)
(17-40)
(17-41)
(17-42)
(17-43)
где Dr и Рж— коэффициенты диффузии в газовой и жидкой фазах, мДсек-,
w — скорость газа в свободном сечении колонны, м/сек-,
U — плотность орошения, ч3/л«2 • сек.
В настоящее время выведены уравнения для определения Нп на проваль-
ных тарелках (стр. 619) Для других типов тарелок достаточно надежные
уравнения для определения Нп отсутствуют и в этом случае значения п.\ и п?
можно найти в зависимости от сопротивления жидкости на тарелке по сле-
дующим формулам:
для колпачковых тарелок
пх = 0,01 w0,32 Држ -у-
_ щ/0,73
п2 = 0,61 • 10 4 —д— Ьрж
для ситчатых тарелок
П|=о,ооб83-^-.А.
«___________кр*________
2~ (69 200w — 14 500) U
где Држ — сопротивление жидкости на тарелке, н/м2 (Држ = Др2 -|- Др3);
ST — рабочая площадь тарелки, л«2;
S — площадь сечения колонны, л«2;
U — плотность орошения, рассчитанная по рабочей площади тарел-
ки, м3/м2 • сек-, - /
w—скорость газа в свободном сечении колонны, м/сек.
Определение основных размеров барботажных
абсорберов
Диаметр колонны определяют аналогично диаметру наса-
дочных абсорберов по принятой скорости газа w в свободном
сечении, площадь сечения находят по уравнению (17-19). При
выборе скорости w следует исходить из условий работы таре-
лок— в равномерном режиме или в режиме газовых струй и
брызг (стр. 616). Скорость w не должна превышать некоторого
предельного значения wnpea_, при котором резко увеличивается
унос брызг жидкости на вышележащую тарелку.
624
Гл. 17. Абсорбция
Значение ®Пред. приближенно можно определить по графику * (рис. 17-20),
в зависимости от расстояния Н между тарелками и отношения плотностей
газа и жидкости рг/Рж- График составлен для тарелок с круглыми колпач-
Рис. 17-20. График для определения предельной
скорости ®пред, в свободном сечении при раз-
личном расстоянии Н между тарелками.
ками; для тарелок другой конструкции значения ®Пред.> найденные по графику,
следует умножать на соответствующий поправочный коэффициент:
К о э ф ф и-
Тарелки циент
С прямоугольными колпачками . . 0,7
Ситчатые.......................... 1,35
Провальные.................... 1,5
Рекомендуется принимать рабочую скорость газа w = (0,8— 0,9) wnpea-.
При выборе скорости в аппаратах с провальными тарелками следует
также учитывать изложенное на стр. 619.
В аппаратах, работающих при атмосферном давлении, ско-
рости практически составляют 0,5—2 м!сек\ в аппаратах, рабо-
тающих при разрежении, принимают более высокие скорости,
а при работе под давлением — более низкие скорости.
Расстояние между тарелками. Минимальное расстояние
кГежду тарелками определяется следующим условием: давление
столба жидкости в переливной трубе должно быть больше со-
противления тарелки. При этом обеспечивается нормальное дей-
ствие гидравлического затвора, образуемого на тарелке пере-
ливной трубой (стр. 600).
Ю. В. Поплавский, Хим. пром., Ns 4, 279 (1961).
7. Расчет барботажных абсорберов
625
Данное условие соблюдается при
(17-44)
где Н — расстояние между тарелками,
Др — сопротивление тарелки, н/л<2;
рж — плотность жидкости, кг/;и3.
Практически расстояние между тарелками должно быть
больше высоты пены на тарелках. Во избежание уноса брызг
жидкости на вышележащую тарелку расстояние между тарел-
ками следует принимать тем больше, чем выше скорость газа
Рис. 17-21. Графическое определение ч^сла тарелок:
АВ —рабочая линия; ОС—линия равновесия; ЕВ —кинетическая
кривая.
в свободном сечении. Обычно расстояния между тарелками
принимают в пределах 0,2—0,6 м. В настоящее время стремятся
уменьшать расстояние между тарелками, что позволяет умень-
шить высоту колонн, особенно при большом числе тарелок, и
снизить их стоимость.
Число тарелок. С известным приближением можно считать,
что жидкость на тарелке полностью перемешана, т. е. имеет во
всех точках одинаковый состав X. Тогда изменение состава газа
на тарелке изобразится на Y — Х-диаграмме (рис. 17-21) верти-
кальным отрезком MN, равным {У'—Y"), где Y' и Y"—кон-
центрации компонента в газе на входе в тарелку и выходе из
нее. Равновесная концентрация Y* также постоянна на тарелке
40 Зак 546,
626
Гл 17 Абсорбция
и изображается точкой Q, лежащей на пересечении продолже-
ния отрезка MN с линией равновесия ОС. Определяя движущую
силу как среднелогарифмическую по формуле (16-40), найдем
число единиц переноса на тарелку:
V'__у*
п0 = 2,31g = — 2,31g (1 — Е) (17-45)
где Е — относительный коэффициент извлечения:
Y'-Y" _ MN лрл
. у' — у* — MQ (17-46)
представляющий собой отношение количества поглощенного на
тарелке компонента к количеству, поглощенному при достиже-
нии равновесия между газом и находящейся на тарелке жид-
костью.
Исходя из изложенного, число тарелок можно найти графи-
чески следующим путем. Определив Е из формулы (17-45), про-
водят на Y— Л'-диаграмме ряд вертикальных прямых MiQ[,
M2Q2 и т. д. и делят эти отрезки Л41Q1, M2Q2 и т. д. между рабо-
„ MN
чей линиеи и линиеи равновесия в отношении — Е. Через
найденные при этом точки N\, N2 и т. д. проводят линию EF,
называемую кинетической кривой. Далее, начиная от точки А,
соответствующей составу газа и жидкости на входе в аппарат,
вписывают между рабочей линией и кинетической кривой сту-
пенчатую линию из вертикальных и горизонтальных отрезкой,
как показано на рис. 17-21. Число вертикальных отрезков этой
ступенчатой линии между начальным и конечным составами
газа У1 и Y2 равно числу тарелок, необходимому для достиже-
ния заданного изменения состава газа.
Конструкция тарелок. При конструировании колпачков исходят из соблю-
дения равенства площадей:
S] = S2 = S3 = SK
где $i—площадь поперечного сечения газового патрубка;
s2 — площадь между верхним краем газового патрубка и колпачком, рав-
ная произведению периметра патрубка на расстояние по вертикали
от верхнего края патрубка до колпачка;
. s3 — площадь кольцевого пространства между газовым патрубком и кол-
пачком;
sK — площадь сечения прорезей одного колпачка.
При расчете ситчатых тарелок задаются диаметром отверстий и их живым
сечением <р, обычно <р = 0,08—0,2.
Высоту сливной перегородки принимают в пределах 20—50 мм. Площадь
сечения переливных труб рассчитывают, исходя из того, что скорость жидко-
сти в них не должна превышать 0,1—0,2 м/сек.
Вместо переливных труб часто применяют сливное устройство сегмент-
ного типа (рис. 17-22). При этом в тарелке вырезается сегмент, ограничен-
7. Расчет барботажных абсорберов
627
Таблица 28
Основные размеры колпачковых тарелок со сливными устройствами
сегментного типа
Диаметр КОЛОННЫ мм Тарелки с круглыми колпачками Тарелки с пргмоугольными колпачками
количество колпачков периметр перелива мм количество колпачков количество прорезей длина колпачка мм периметр перелива мм
1000 27 620 5 74 560 600
1200 33 835 6 94 710 700
1400 49 860 7 ПО 835 835
1600 63 1000 8 128 960 1030
1800 91 1200 9 144 1090 1200
2200 133 1500 11 180 1360 1490
2600 173 1950 13 216 1630 1780
3000 273 2070 15 250 1880 2070
Примечания. 1. В тарелках с круглыми колпачками газовые патрубки выполняются
из трубы 70 х 4 им; колпачки имеют наружный диаметр 100 им и 30 прямоугольных проре-
зей размером 4 х 20 мм каждая. 2. Для тарелок с прямоугольными колпачками указано коли-
чество прорезей в одном колпачке (с обеих сторон).
ный по хорде вертикальной перегородкой, выступающей
выше тарелки и образующей сливной порог. Вертикальная
перегородка опущена до нижележащей тарелки, но не-
много не доходит до нее.
В табл. 28 приведены основные размеры нормализо-
ванных колпачковых тарелок со сливными устройствами
сегментного типа.
Пример 17-8. Определить число тарелок барботажного
абсорбера (с ситчатыми тарелками) для поглощ' ния ам-
миака водой в условиях примеров 16-5 и 17-5. Диаметр
абсорбера 1,6 м, сопротивление жидкости на тарелке
ДРж = 343 н/м3 (35 кгс/м2).
Решение Площадь сечения абсорбера (при данном
диаметре) S — 2,02 м2. Скорость газа в свободном сече-
нии при расходе газа 10 600 м3/ч составляет.
10600 1 ЛА ,
W “ 3600 • 2,02 “ 1,46 м1сек
Рис. 17-22. Та-
релка со слив-
ным устройст-
вом сегмент-
ного типа.
Принимая рабочую площадь тарелки ST = 0,9 S и пре-
небрегая сопротивлением жидкой фазы, находим по фор-
муле (17-42) число единиц переноса на тарелку:
"» = " =0,00683-^-. А = 0,00683. .0,9=1,92
По формуле (17-45) находим относительный коэффициент извлечения:
Ig (1 - Е) = - _ -1А- = _ 0,835 = Г,165
40*
628
Гл. 17. Абсорбция
Отсюда 1 —Е =• 0,146, Е = 0,854.
Используя ранее приведенный график У — X (см. рис. 16-5, стр 587) к
примеру 16-10, строим кинетическую кривую (рис. 17-23) и, вписывая сту-
пенчатую линию, находим необходимое число тарелок, равное 8.
Рис. 17-23. График для определения числа тарелок (к примеру 17-8).
Пример 17-9. Определить размеры и сопротивление колпачковой тарелки
при следующих условиях: диаметр колонны D = 1 м, скорость газа в свобод-
ном сечении w — 1,1 м1сек, плотность газа рг — 0,65 кг/ж3, плотность жидкости
(вода) рж = Ю00 кг]м\ объемный расход жидкости Уж = 7,5 м51ч.
Выбор количества колпачков. Площадь сечения колонны со-
ставляет:
S = £ D2 = 0,785 • I2 = 0,785 мА
4
Принимая живое сечение <р = 0,1, находим общую площадь сечения па-
трубков:
Sn = <pS = 0,1 • 0,785 = 0,0785 мА
Выбираем круглые колпачки. При стандартных патрубках внутренним
диаметром da — 62 мм площадь сечения одного патрубка:
= 0,785 • 0,0622 s 0,003 м2
7. Расчет барботажных абсорберов
629
Количество патрубков и колпачков составляет:
Sn 0,0785
s, ~ 0,003 ~
По условиям разбивки колпачков принимаем пк = 27 (см. табл. 28).
Определение размеров колпачка. Площадь s2 (стр. 626) со-
ставляет:
s2 nd^h
где h — расстояние по вертикали от верхнего обреза патрубка до колпачка.
Из условия Si = s2 находим:
. $2 0,003 ЛЛ1С
h = = о Гн ллдо" = °>016 м = 16 мм
ndn 3,14 • 0,062
Площадь S3 (стр. 626) составляет:
53 = 0,785(4-0*)
где dK — внутренний диаметр колпачка;
Da — наружный диаметр патрубка.
Из условия $1 = хз находим (при Dn= 70 мм):
Г>2 _]—
п 0,785
0,003
0,785
0,093 м
Выбираем колпачки внутренним диам'етром 92 мм и наружным диамет-
ром DK = 100 мм. Прорези — прямоугольные, шириной Ь — 8 мм, высотой
I = 15 мм. Площадь сечения одной прорези:
$пр = Ы = 0,008 • 0,015 = 0,00012 м2
Из условия Si = sK (стр. 626) находим количество прорезей в колпачке:
„ _____£к_ _ в’вЗ ______ng
пр' “ $п₽. “ 0,00012 “
Общая ширина прорезей в одном колпачке составляет 25 • 8 = 200 мм, пе-
риметр колпачка равен 3,14*100 = 314 мм. Таким образом, расстояние между
прорезями составляет:
314 — 200 . _
—---------s4,5 мм
что можно считать достаточным (если по расчету это расстояние получается
слишком малым, надо увеличить высоту прорезей).
Определение скорости газа в прорезях. Фактическое жи-
вое сечение в прорезях колпачков на одной тарелке составляет:
So = лкипр snp. = 27 • 25 • 0,00012 = 0,081 м2
откуда
So 0,081
’ = Т = Ж = ™
Скорость газа в прорезях определяем по формуле (17-22):
— = -AU- = 10>7 м1свк
<р 0,103
w0 —
630
Гл. 17. Абсорбция
Находим по формуле (17-21) скорость, соответствующую полному откры-
тию прорезей, при С = 5 и а = 1
' рГ~, 1 9,81 • 1000 • 0,015 ,
= аи -у-' 1 — 1 • V ----г—лег ---- = 6>7 М сек
и г С рг г 5 • 0,65
Таким образом, принятое живое сечение вполне обеспечивает полное от-
крытие прорезей.
Определение сопротивления тарелки. Сопротивление су-
хой тарелки при С — 5 находим по формуле (17-24):
рХ 0,65 • 10,72
ДЛ = С 2^- = 5--------§----= 186 н/м2 (19 кгс!м^
Принимаем расстояние от верхнего края прорезей до сливного порога
е — 20 мм и периметр (ширину) сливной перегородки П = 0,6 м. Высоту уро-
вня жидкости над сливным порогом определяем по формуле (17-27) при
k = 0,5:
., / Уж \2/з / 7,5 \7з
“ \ 1.85ПЛ / “ \ 3600-1,85-0,6-0,5 ) = °’024 М
Сопротивление столба жидкости вычисляем по уравнению (17-25):
Др2 = 1,3 • 9,81 • 0,5 • 1000 ^0,02 + -|- 0,024^ = 328 н/м2 (33,5 кгс/м2)
Эквивалентный диаметр прорези (при полном ее открытии) составляет:
_ 46/ __ 4-0,008-0,015 _ПП1П,
экв- 2 (6 + Z) - 2 (0,008 + 0,015) “ U,U U£> М
Сопротивление, обусловленное силами поверхностного натяжения, опре-
деляем по уравнению (17-28), принимая для воды а = 73 • 10-3 н/м (73дин/см)
4 • 73 • 10-3
Дрэ = —0 0105— = 27 Н^м2 (2’8 кгс!м^
Общее сопротивление тарелки составляет:
Др = 186 -|- 328 27 540 н/м2 (55,3 кгс/м2)
Глава 18
ЭКСТРАКЦИЯ
1. Общие сведения
Экстракцией называют процессы разделения жидких смесей
и извлечения компонентов из твердых веществ при по'мощи
жидкого растворителя (экстрагента), избирательно растворяю-
щего только извлекаемые компоненты.
Экстракция из твердого вещества применяется для извлече-
ния масла из семян, канифоли, скипидара и других продуктов
из древесины и т. д. В химической технологии процессы
экстракции в системе твердое вещество — жидкость мало рас-
пространены.
Ниже будут рассмотрены процессы экстракции в системе
жидкость--жидкость, которые находят все более широкое при-
менение в различных отраслях химической технологии — в про-
изводстве синтетического каучука (например, для отмывки ди-
винила от ацетальдегида и других примесей), в производстве
капролактама и других продуктов органического синтеза, а так-
же при получении ядерного горючего, антибиотиков, в процессах
нефтепереработки.
Исходная жидкая смесь обрабатывается экстрагентом, кото-
рый не растворим или мало растворим в исходной смеси. В ре-
зультате взаимодействия экстрагента с исходным раствором
образуются: экстракт — раствор извлеченных из исходной смеси
компонентов в экстрагенте и рафинат — жидкая смесь, обеднен-
ная извлекаемыми компонентами и обычно содержащая некото-
рое количество экстрагента.
Разделение жидкой смеси методом экстракции складывается
из следующих процессов:
1) смешение исходной смеси с экстрагентом для создания
между ними тесного контакта;
2) разделение двух несмешивающихся жидких фаз (экст-
ракта и рафината);
3) регенерация экстрагента, т. е. удаление его из экстракта
и рафината.
632
Гл. 18. Экстракция
Ниже показана принципиальная схема процесса экстракции:
(без регенерации экстрагента):
Разделение жидких смесей экстракцией сложнее разделения
их ректификацией (см. главу 19), но во многих случаях
(стр. 658) применение экстракции более предпочтительно или
она является единственно возможным методом разделения
смеси. Иногда эти процессы разделения применяются совместно,
например при экстрактивной перегонке (стр. 709)'или для по-
вышения концентрации распределяемого вещества в растворе
перед ректификацией, которая осуществляется при этом с мень-
шим расходом тепла.
2. Физические основы процесса экстракции
Равновесие между фазами
В процессе экстракции растворенное в жидкой фазе веще-
ство распределяется между этой и другой жидкой фазой (экст-
рагентом) до достижения динамического равновесия. Состоя-
ние равновесия фаз при экстракции характеризуется законом
равновесного распределения, который выражают через коэф-
фициент распределения Кр, представляющий собой отношение
равновесных концентраций распределяемого вещества в экст-
ракте Y и рафинате X при данной температуре.
В простейшем случае /Ср есть величина постоянная
= х) и закон равновесного распределения имеет следую-
щий вид:
Y=KpX (18-1)
В данном случае линия равновесия в координатах У — X
является прямой ОС (рис. 18-1).
2. Физические основы процесса экстракции
633
отсутствии
взаимодей-
фазами.
Однако выражение (18-1) справедливо только при том усло-
вии, если исходный растворитель и экстрагент взаимно совер-
шенно нерастворимы и не происходит ассоциации или диссоциа-
ции молекул распределяемого вещества. Кроме того, данный
закон распределения при-
меним при
химического
ствия между
Практически экстрагент и
исходный растворитель
часто обладают некото-
рой взаимной раствори-
мостью. В этих случаях
,коэффициент распределе-
ния Лр зависит не только
от температуры, но и от
концентрации X распре-
целяемого вещества в ра-
финате, а закон равнове-
сия выражается в коор-
динатах Y—X кривой ОС'
(рис. 18-1), характери-
зующей зависимость
Y=f(X). Таким образом,
/Ср часто является величиной
циента распределения определяют опытным путем.
переменной, значения коэффи-
Если экстрагент частично растворим в исходном растворителе, то экстракт
и рафинат представляют собой взаимно насыщенные растворы, состоящие из
трех компонентов. Такие системы называются тройными. Кроме экстрагента
и извлеченного компонента (распределяемого вещества), экстракт содержит
также некоторое количество исходного растворителя. Рафинат состоит из
исходного растворителя и небольших количеств распределяемого вещества и
экстрагента.
Равновесие в тройных системах наглядно выражается при помощи тре-
угольной диаграммы (рис. 18-2). В этой диаграмме компоненты системы А,
В и С представлены точками, лежащими в вершинах равностороннего тре-
угольника (при этом длина каждой стороны треугольника принята за 100%).
а состав тройной смеси определяется точкой, лежащей внутри треугольника
(например, точкой М). Точки, лежащие на сторонах треугольника, выражают
составы бинарных смесей. Состав тройной смеси определяется длиной О1резков,
проведенных параллельно сторонам треугольника до пересечения с послед-
ними Так, точка М характеризует тройную смесь, состоящую из 35% компо-
нента А, 25% компонента В и 40% компонента С.
Перпендикуляры, опущенные на стороны треугольника из точки М, также
могут служить мерой содержания соответствующих компонентов в смеси.
С помощью треугольной диаграммы можно определить составы трехком-
понентной смеси жидкостей при изменении содержания в ней того или иного
компонента. Так, если в смеси, соответствующей точке М (см. рис. 18-2), бу-
дет увеличиваться содержание компонента В, то по мере его добавления
634
Гл. 18. Экстракция
составы образующихся растворов будут изображаться на диаграмме точками,
лежащими на прямой МВ и тем более близкими к вершине В треугольника,
чем богаче становится смесь компонентом В. Если же извлекать компонент В
из смеси, то ее составам будут соответствовать точки, лежащие на прямой
MD и тем ближе к стороне АС треугольника, чем меньше становится компо-
нента В в смеси. В смесях всех составов, отвечающих точкам, которые лежат
на прямой BD, при изменении содержания компонента В отношение количеств
остальных двух компонентов (4 и С) будет оставаться неизменным.
Пусть вершина A i реугольника соответствует исходному растворителю, вер-
шина В — распределяемому веществу, вершина С — экстрагенту, рбозначим
точкой S на стороне АВ треугольника состав исходной (двухкомпонентной)
смеси. В процессе экстракции исходная смесь сначала смешивается с экстра-
гентом. Процесс смешения изображается прямой CS, причем положение
точки М, отвечающей составу смеси, зависит от соотношения количеств сме-
шиваемых компонентов Д.ВиСь находится из пропорции:
ga + Gb
Gc MS
2. Физические основы процесса экстракции
635
В этом выражении G А, Gв, Gc—количества компонентов А, В, С в
смеси, а СМ и MS — длины отрезков прямой CS.
Полученная смесь расслаивается на две фазы: на экстракт Е—раствор,
обогащенный распределяемым компонентом В, и на рафинат /? — раствор,
обедненный компонентом В, причем составы экстракта и рафината находятся
в равновесии друг с другом. Линия, соединяющая точки равновесных соста-
вов экстракта и рафината, называется хордой равновесия, или конодой.
Наклон хорд равновесия определяется величиной коэффициента распре-
деления Кр, причем для процесса, показанного на рис. 18-2, Кр > 1. При
Кр < 1 хорды равновесия наклонены в обратном направлении, а при Кр = 1
хорды будут параллельны стороне АС треугольника.
Если содержание компонента В в смеси будет изменяться, то равновес-
ные составы рафината и экстракта будут лежать на концах других хорд
равновесия. Так, при добавлении компонента В к смеси, изображенной точкой
М, составы рафината и экстракта будут перемещаться на концы хорд RiEi,
R2E2 и т. д. При добавлении некоторой новой порции компонента В поверх-
ность раздела между фазами исчезает и система становится однофазной (го-
могенной). При этом хорда равновесия превращается в точку К, которая на-
зывается критической.
Положение хорд равновесия определяют опытным путем. Концы хорд
равновесия соединяют так называемой бинодальной кривой. Область, огра-
ниченная этой кривой, соответствует двухфазным (расслаивающимся) систе-
мам и является рабочей частью треугольной диаграммы. Область диаграммы,
лежащая вне этой кривой, соответствует гомогенной системе и поэтому для
расчета процессов экстракции неприменима.
Материальный баланс
Материальный баланс процесса экстракции соответствует
общему для массообменных процессов уравнению (16-14):
G(Y1-Y2) = L(Xi-X2) <
где G — количество реагента, кг!сек-,
L — количество исходного растворителя, кг1сек\
Г1 и Y2 — содержание распределяемого компонента в экстрак-
те и в экстрагенте, кг/кг экстрагента.
Хх и Х2—содержание распределяемого компонента в исход-
ном растворе и в рафинате, кг/кг исходного раство-
рителя.
Следовательно, расход экстрагента составляет:
(18'2)
Из уравнения материального баланса определяют удельный
расход экстрагента I = LIG.
Зависимость между составами экстракта и рафината выра-
жается рабочей линией (см. рис. 18-1), уравнение которой соот-
ветствует уравнению (16-16). Построение рабочей линии
636
Гл. 18. Экстракция
аналогично ее построению для процессов абсорбции (стр. 568).
Чтобы построить рабочую линию процесса экстракции, необхо-
димо знать состав исходного раствора и экстракта или рафи-
ната на выходе из аппарата.
Процессы экстракции проводятся чаще всего без подвода
или отвода тепла, при обычных (комнатных) температурах. По-
этому для расчета этих процессов не требуется составления теп-
лового баланса.
3. Устройство экстракторов
Предложено большое количество конструкций разнообраз-
ных экстракторов, однако в промышленности применяется лишь
ограниченное число типов экстракционных аппаратов.
По характеру изменения состава жидких фаз экстракцион-
ные аппараты можно разделить на две группы:
1) дифференциально-контактные экстракторы, в которых ха-
рактер изменения состава фаз близок к непрерывному;
2) ступенчатые экстракторы, в которых изменение состава
фаз происходит скачкообразно (ступенчато), в каждой ступени
осуществляется смешение и разделение (сепарация) фаз.
Экстракторы обеих групп могут быть классифицированы по
двум признакам:
а) по способу контакта между сплошной фазой, заполняю-
щей аппарат, и дисперсной фазой, распределяемой в виде ка-
пель в сплошной фазе. Контакт между фазами возможен за
счет собственной энергии потоков фаз (экстракторы без меха-
нических перемешивающих устройств), либо за счет подвода
энергии извне (механические экстракторы);
б) по виду сепарации фаз, которая может происходить
вследствие разности плотностей фаз (гравитационная сепара-
ция) либо под действием центробежных сил (центробежная се-
парация).
Экстракторы, в которых смешение и сепарация фаз проис-
ходят в поле центробежных сил, называются центробежными.
Классификация экстракционных аппаратов приведена на
стр. 637.
В этой классификации не отражены разновидности горизон-
тальных смесительно-отстойных экстракторов, различных по
конструкции перемешивающих устройств и по взаимному на-
правлению движения фаз после отстаивания (прямоток или
противоток)..
Промышленные экстракторы являются преимущественно ап-
паратами непрерывного действия. Лишь при лабораторных ра-
ботах (а иногда в производствах небольшого масштаба) исполь-
зуют экстракторы периодического действия.
3. Устройство экстракторов
637
638
Гл. 18. Экстракция
Распылительные экстракторы
Распылительный экстрактор представляет собой полую ко-
лонну, заполненную одной из жидкостей — сплошной (диспер-
сионной) фазой (на рис. 18-3 показан экстрактор, в котором
Тяжелая
жидкость
Поверхность
раздела /раз
сплошной фазой является тяжелая жид-
кость). Для создания большей поверхности
контакта фаз другая жидкость (дисперсная
фаза) распыляется при помощи распредели-
тельного устройства в сплошной фазе.
На определенном уровне капли дисперсной
фазы сливаются и образуют слой, отделен-
ный от сплошной фазы поверхностью раз-
дела. Уровень этой поверхности поддержи-
вают на нужной высоте (вверху, внизу
или посередине колонны), устанавливая
соответствующий уровень перелива через
нижнюю отводную трубу (на рисунке не
показана) или регулируя степень открытия
установленного на ней вентиля. Сверху и
снизу экстракционная колонна расширена,
что способствует лучшему отстаиванию
фаз.
Распылительные колонны обладают вы-
сокой производительностью, но мало эф-
фективны, что объясняется укрупнением ка-
пель дисперсной фазы и обратным переме-
шиванием, при возникновении которого кап-
ли дисперсной фазы увлекаются частицами
сплошной фазы (или наоборот), в результа-
те в колонне создаются местные циркуля-
Рис. 18-3. Распыли- ционные токи, нарушающие противоток
тельный экстрактор. фаз.
Колонные экстракторы с тарелками-
перегородками
В таких колоннах (рис. 18-4) для уменьшения обратного
перемешивания и для турбулизации потоков фаз установлены
перегородки в виде чередующихся друг с другом плоских ди-
сков (или тарелок) и колец. Расстояние между перегородками
75—150 мм и более.
Контакт между фазами осуществляется при обтекании пере-
городок дисперсной фазой в виде тонкой пленки (при коалес-
3. Устройство экстракторов
639
ценции капель) и при движении капель дисперсной фазы в про-
странстве между перегородками.
Тяжелая {
жидкость
Тяжелая
'жидкость
Легкая t
жидкости
Легкая^ t
жидкость
а
Рис. 18-4. Колонные экстракторы с тарел-
ками-перегородками:
а — перегородки в виде дисков и колец; б—пере-
городки в виде тарелок и колец.
Эффективность таких колонн низка (число единиц переноса
на тарелку 0,05—0,1), но может быть повышена при уменьше-
нии расстояния между тарелками.
Насадочные экстракторы
Насадочные экстракторы не отличаются по устройству от на-
садочных абсорберов, описанных в главе 17 (стр. 596).
Насадка, беспорядочно засыпанная на опорную решетку,
выполняет роль перегородок: она способствует многократному
дроблению и слиянию капель дисперсной фазы и сводит к мини-
муму обратное перемешивание.
В насадочных экстракторах насадку располагают в виде
слоев, помещенных на опорные решетки; расстояние между ре-
шетками 0,9—1,8 м.
По простоте устройства насадочные экстракторы прибли-
жаются к распылительным, но предельная производительность
их ниже, так как некоторая часть сечения колонны занята на-
садкой. Эффективность разделения в насадочных экстракторах
невысокая.
640
Г л. 18 Экстракция
Многоступенчатые смесительные
экстракторы
Наиболее распространенным аппаратом этого типа является
роторно-дисковый экстрактор (рис. 18-5). По оси колонны вра-
Рис. 18-5. Роторно-дисковый
экстрактор:
/ — вал, 2—плоские диски;
3—кольцевые переюродки;
4 — привод.
щается ротор—вал, на который наса-
жены плоские диски 2, перемешиваю-
щие жидкость. Колонна делится на
секции кольцевыми перегородками 3,
укрепленными на стенках аппарата,
причем диски находятся на середине
высоты каждой секции. Движущиеся
противотоком жидкие фазы смеши-
ваются в каждой секции и в некоторой
степени разделяются при обтекании
неподвижных кольцевых перегородок,
ограничивающих секции.
Производительность и эффектив-
ность описанных экстракторов зави-
сят от числа оборотов ротора, соотно-
шения размеров дисков и кольцевых
перегородок и расстояния между
ними, а также, как и в других экс-
тракторах, от соотношения расходов
фаз.
Достоинством роторно-дисковых
экстракторов является сочетание до-
вольно значительной производитель-
ности с высокой интенсивностью про-
цесса массопередачи.
Разновидностью аппаратов этого типа является колонный
экстрактор, в котором вместо плоских дисков установлены от-
крытые турбинные мешалки (стр. 359).
Пульсационные экстракторы
Пульсационный экстрактор (рис. 18-6) представляет собой
колонну с ситчатыми тарелками без патрубков для перетока
сплошной фазы. В колонне при помощи специального меха-
низма (пульсатора) жидкости сообщаются пульсации — колеба-
ния небольшой амплитуды (10—25 мм) и определенной часто-
ты. В качестве пульсатора чаще всего используют бесклапан-
ный поршневой насос, присоединяемый к днищу колонны
(рис. 18-6, а) или к линии подачи легкой жидкости (рис. 18-6, б).
При сообщении жидкости пульсаций происходит многократное
3 Устройство экстракторов
641
тонкое диспергирование одной из фаз, что обусловливает интен-
сивную массопередачу. Помимо ситчатых экстракторов, при-
меняются также насадочные пульсационные колонны.
Эффективный способ интенсификации процесса экстракции
путем сообщения жидкости пульсаций может быть использован
также в экстракционных аппаратах других типов.
Рис. 18-6. Пульсационные ситчатые экстракторы (А — тяжелая жидкость,
В — легкая жидкость):
а — пульсатор присоединен к днищу колонны; б — пульсатор присоединен к трубопроводу для
подачи легкой жидкости; в —пульсации передаются через мембрану; г —пульсации передаются
через сильфон; д — пульсации передаются через буферный слой воздуха (воздушную подушку).
Для надежного отделения механизма пульсатора от рабочей
среды при обработке химически агрессивных и радиоактив-
ных веществ применяют мембрану (рис. 18-6, в), сильфон
(рис. 18-6, а) или пневматическое устройство (рис. 18-6, д). В
последнем случае между поршнем пульсатора и колонной поме-
щают буферный слой воздуха, который попеременно расши-
ряется и сжимается, сообщая колебания жидкости в колонне.
41 Зак 546.
642
Гл 18 Экстракция
Центробежные экстракторы
При малой разности плотностей фаз достаточное увеличение
скорости капель дисперсной фазы, интенсивное смешение и раз-
деление фаз достигаются под действием центробежных сил пу-
тем увеличения эффективной разности плотностей фаз.
б
Тяжелая
жидкость
| легкая
жидкость
ввод тяжелой
жидкости
Отдод
левкой, жидкости
Рис 18-7 Центробежный экстрактор:
о —разрез аппарата; б— принципиальная
схема движения жидкостей 1 — барабан;
2—вал, 3— перфорированная перегородка
перфорация по всей перегородке не пока-
зана), 4 — каналы.
Наиболее распространен центробежный экстрактор, показан-
ный на рис. 18-7. Корпус аппарата представляет собой цилин-
дрический барабан /, быстро вращающийся на горизонтальном
валу 2 (1500—5000 об!мин). Внутри барабан разделен спираль-
3 Устройство экстракторов
643
ной перфорированной перегородкой 3 на каналы 4 прямоуголь-
ного сечения.
Контактируемые жидкие фазы подают с помощью насосов
через вал по обособленным каналам, тяжелая жидкость посту-
пает в барабан по его оси, лег-
кая жидкость подводится к пе-
риферии барабана. В бараба-
не жидкости движутся проти-
вотоком, они многократно сме-
шиваются, главным образом
при истечении через отвер-
стия в перегородке, и разделя-
ются под действием центро-
бежных сил. Рафинат и экс-
тракт удаляются также через
обособленные каналы вала.
Аппараты этого типа от-
личаются высокой интенсив-
ностью разделения.
Тарельчатые
экстракторы
В экстракторах с ситча-
тыми тарелками (рис. 18-8),
аналогичных ситчатым абсор-
берам (стр. 601), дисперсная
фаза многократно раздроб-
ляется при прохождении сквозь
отверстия ситчатых тарелок
(диаметр отверстий 2—9 мм)
Струйки дисперсной фазы рас-
падаются при этом на мел-
кие капли, которые образуют
слои над тарелками, если дис-
пергируется тяжелая жидкость,
или под тарелками, если диспергируется легкая жидкость.
Диспергирование происходит, когда гидростатическое давление
Легкая t
жидкости
Легкая
жидкость
Легкая
жидкость
Тяжелая
жидкость
Тяжелая
жидкость
Тяжелая
'жидкость
Рис. 18-8. Экстрактор с ситчатыми
тарелками.
слоя жидкости становится достаточным для ее прохождения
сквозь отверстия. Для стока сплошной фазы на тарелках имеют-
ся сливные патрубки. Расстояние между тарелками составляет
0,15—0,6 м.
При обработке жидкостей, содержащих твердые взвеси, при-
меняют ситчатые тарелки с вертикальными перфорированными
стенками; отверстия таких тарелок меньше засоряются твер-
дыми частицами.
41*
644
Г л. 18. Экстракция
Экстракторы с колпачковыми тарелками обычно обладают
низкой эффективностью. В некоторых случаях применяют экс-
тракторы с тарелками в виде вертикальных изогнутых перфо-
рированных пластин, расположенных каскадом (каскадные та-
релки), которые эффективнее обычных колпачковых тарелок.
Г оризонтальные смесительно-отстойные
экстр акторы
Экстрактор такого типа (рис. 18-9) представляет собой ци-
линдрический аппарат, разделенный перегородками на отсеки.
Каждый отсек состоит из камеры смешения (труба с внутрен-
ним погружным насосом) и отстойной камеры. Исходный рас-
твор, подаваемый в экстрактор, поступает по переливной трубе/
Рис. 18-9. Горизонтальный смесительно-отстойный экстрактор:
1— переливная труба для подачи раствора в камеру смешения; 2—труба для перетока экстра-
гента; 3— патрубок для подачи смеси в отстойную камеру; 4 — воронка для отвода экстракта;
5 — штуцер для подачи свежего экстрагента.
в первую по ходу раствора камеру смешения. В эту же камеру
по трубе 2 поступает из предыдущей ступени экстрагент, обо-
гащенный извлекаемым веществом. В камере смешения фазы
при помощи насоса перемешиваются, и смесь подается через
патрубок 3 на разделение в отстойную камеру. Отсюда экстракт
отводится из аппарата через воронку 4, а обедненный раствор
(рафинат) по переливной трубе направляется в следующую ка-
меру смешения, где снова смешивается с экстрактом, поступаю-
щим из предыдущей ступени, затем смесь направляется в сле-
дующую отстойную камеру. Смешение и разделение фаз повто-
ряется многократно, вплоть до последней ступени, где раствор
смешивается со свежим экстрагентом, поступающим через шту-
цер 5. Из этой ступени удаляется конечный рафинат.
Кроме конструкции экстрактора, показанной на рис. 18-9,
применяются горизонтальные смесительно-отстойные экстрак-
торы в виде батареи смесителей (с механическими мешалками)
и отстойников, чередующихся между собой и соединенных трубо-
3. Устройство экстракторов
645
проводами. Смесители и отстойники установлены каскадом,
причем тяжелая фаза движется через батарею аппаратов само-
теком, а легкая фаза перекачивается насосами. Иногда переме-
шивание производится непосредственно в насосах, служащих
смесителями и чередующихся с отстойниками.
Обычно в пределах каждой ступени экстракции жидкости
движутся прямотоком, а установка в целом работает при про-
тивотоке фаз (см. рис. 18-13, стр. 647).
Вертикальные смесительно-отстойные
экстракторы
К числу этих аппаратов относятся ящичные вертикальные
экстракторы, в которых установлены прямоугольные отстойные
камеры непосредственно одна над другой, а
для смешения фаз служат насосы, смонтиро-
ванные на боковых стенках отстойных камер.
Такие аппараты занимают значительно мень-
шую площадь, чем горизонтальные смеситель-
но-отстойные экстракторы. Кроме того, бла-
годаря прямоугольной форме отстойных ка-
мер удается уменьшить отношение высоты
камер к их сечению, что способствует ускоре-
нию отстаивания и приводит к большей ком-
пактности аппарата.
Разновидностью аппаратов этого типа яв-
ляется колонный экстрактор, показанный на
рис. 18-10. Колонна разделяется по высоте на
чередующиеся смесительные и отстойные сек-
ции, причем отстойные секции (каждая высо-
той 0,3 м и более) заполнены специальной на-
садкой в виде свернутой в рулон редкоплете-
ной сетки (площадь всех отверстий сетки со-
ставляет 97—98% ее общей площади). В сме-
сительных зонах перемешивание производит-
ся четырехлопастными мешалками, вращаю-
щимися на общем вертикальном валу, кото-
рый проходит по оси колонны.
Легкая Тяжелая
жидкостью жидкость
-М..
Легкая Тяжелая
жидкость жидкость
Рис. 18-10. Верти-
кальный смеси-
тельно-отстойный
экстрактор:
1 — мешалка; 2—на-
садка.
Вертикальные центробежные смесительно-отстойные
экстракторы
Такие аппараты представляют собой оверхцентрифуги (стр. 310), приспо-
собленные для разделения систем жидкость — жидкость. Наиболее распро-
странены многоступенчатые аппараты типа тарельвддых сепараторов, состоя-
щие из 3—4 тарелок (ступеней). Обе фазы поступают в экстрактор через
646
Гл. 18. Экстракция
каналы в вертикальном валу и движутся противотоком, последовательно сме-
шиваясь и разделяясь в каждой ступени в поле центробежных сил. Произво-
дительность таких экстракторов 0,3—6 м3/ч.
4. Схемы экстракционных установок
Одноступенчатая экстракция
Рис. 18-11. Схема одноступенчатой
экстракции:
1— смеситель; 2—сепаратор.
Принципиальная схема простейшего одноступенчатого про-
цесса экстракции показана на рис. 18-11. Фазы смешиваются
при помощи мешалки (или другим способом) в смесителе /,
после чего разделяются в сепараторе 2, из которого отводят
экстракт и рафинат. Далее
экстракт и рафинат поступают
на последующую переработку,
например в ректификацион-
ные колонны, для удаления
экстрагента. Регенерирован-
ный экстрагент поступает в
смеситель вместе со свежим
экстрагентом (регенерация экс-
трагента для упрощения на
схеме не показана).
Одноступенчатая экстрак-
ция может проводиться перио-
дически или непрерывно.
Составы получаемых экстракта и рафината равновесны друг
другу и сравнительно мало отличаются по содержанию распре-
деляемого компонента. Поэтому путем одноступенчатой экстрак-
ции не достигается достаточно полного извлечения экстраги-
руемого вещества. Значительно большая степень извлечения
возможна при использовании многоступенчатой экстракции,
которая наиболее широко распространена в технике.
Многоступенчатая экстракция
Процессы многоступенчатой экстракции проводятся только
непрерывным способом.
При многоступенчатой экстракции (рис. 18-12) рафинат, по-
лучаемый в одной ступени, смешивается в следующей ступени
со свежим экстрагентом. Таким образом, в каждую ступень
вводится свежий экстрагент, а из нее отводится экстракт. При
достаточном числе ступеней экстракции достигается высокая
степень очистки конечного рафината, который удаляется из по-
следней ступени.
4. Схемы экстракционных установок
647
Существенным недостатком этого способа экстракции яв-
ляется весьма большой расход экстрагента и соответственно
низкая средняя концентрация экстракта, который представляет
собой смесь жидкостей с постепенно убывающей концентрацией
извлекаемого вещества. Это затрудняет и удорожает регенера-
цию экстрагента.
Экстракт / Экстракт D Экстракт Ш
Рис. 18-12. Схема многоступенчатой экстракции:
I, II и ///—аппараты первой, второй н третьей ступени; / — смеситель;
2 — отстойник.
Высокая степень извлечения экстрагируемого вещества при
относительно малом расходе экстрагента достигается в наиболее
распространенном процессе противоточной многоступенчатой
Рис. 18-13. Схема противоточной многоступенчатой экстракции:
/, //, ///—аппараты первой, второй и третьей ступени; / — смеситель;
2 — отстойник.
экстракции. Исходный раствор и экстрагент поступают с про-
тивоположных концов аппарата; например, исходный раствор
подается в первую ступень, экстрагент — в последнюю ступень
(см. рис. 18-13). Соответственно из первой ступени удаляется
конечный экстракт, а из последней — конечный рафинат.
В этом процессе свежий экстрагент вступает в контакт с ра-
финатом, имеющим наименьшую концентрацию распределяе-
мого компонента, и после многократного контактирования
648
Гл. 18. Экстракция
в последовательных ступенях процесса насыщается извлекаемым
веществом. В результате требуемая степень экстракции дости-
гается при минимальном расходе экстрагента. Процессы проти-
воточной многоступенчатой экстракции проводятся в ряде сту-
пеней, состоящих из смесителей и отстойников (см. рис. 18-13),
либо в противоточной колонне (рис. 18-14), причем экстракт и
рафинат после подогрева направляются каждый в отдельную
экстрагент
Рис. 18-14. Схема противоточной многоступенчатой
эктракции с колонным экстрактором:
/ — колонный экотрактор; 2, 3— ректификационные колонны.
ректификационную колонну (см. главу 19). В качестве дистил-
лята в этих колоннах получается регенерированный экстрагент,
а в качестве остатка в одной колонне экстракт, в другой — ра-
финат.
При противоточной многоступенчатой экстракции в послед-
ней по ходу э-кстракт-а ступени экстракт контактируется с исход-
ным раствором. Поэтому наибольшая концентрация распреде-
ляемого компонента в экстракте является равновесной с кон-
центрацией его в исходном растворе.
В тех случаях, когда требуется более высокая концентрация экстракта,
применяют противоточную многоступенчатую экстракцию с флегмой
(рис. 18-15, а). Исходный раствор вводят в колонный экс-трактор на опреде-
ленном уровне и часть экстракта после удаления из него экстрагента в рек-
тификационной колонне возвращают в экстрактор в качестве флегмы.
Иногда для орошения кодонны используют часть рафината, которым на-
сыщают свежий экстрагент перед поступлением в колонный экстрактор.
5. Сравнение и выбор экстракторов
649
Как и в процессе ректификации (см. стр. 658), орошение колонны флег-
мой позволяет существенно увеличить степень извлечения экстрагируемого
компонента. Однако, в отличие от ректификации, при использовании флегмы
в процессе экстракции требуется соблюдение определенных условий: экстр-
агент должен быть лишь частично растворим в обоих компонентах исходного
раствора, а различие плотностей обеих фаз должно быть достаточно для их
движения противотоком в колонне.
Исходный
раствор г}
(компонент
ты/?+8}
Экстракт
(компо -
мент в}
“ X
Рис. 18-15. Схемы противоточной многоступенчатой экстракции:
о —с флегмой; б — с двумя растворителями. 1 — экстрактор; 2, 3 — ректи-
фикационные колонны.
Экстракт
(компонент Я)
Раствори -
тель 77
Растворитель 7
В некоторых случаях, например, если необходимо улучшить избирательное
действие экстрагента, применяют многоступенчатую экстракцию с двумя рас-
творителями (рис. 18-15,6). Растворители раздельно вводят сверху и снизу
колонны-экстрактора, раздельно (сверху и снизу) отводятся также соответ-
ствующие экстракты, в одном из которых растворен компонент Л, а в другом
компонент В исходного двухкомпонентного раствора.
5. Сравнение и выбор экстракторов
Дифференциально-контактные и ступенчатые экстракторы
без перемешивающих устройств (распылительные, тарельчатые,
ситчатые колонные экстракторы) отличаются сравнительно низ-
кой интенсивностью массопередачи. Это объясняется тем, что
в системах жидкость — жидкость разность плотностей фаз зна-
чительно ниже, чем в системах газ — жидкость или пар —
жидкость. Поэтому собственная энергия потоков, используемая
для контактирования фаз, в экстракционных аппаратах без пе-
ремешивающих устройств недостаточна для преодоления сил
650
Гл 18 Экстракция
поверхностного натяжения и интенсивного диспергирования
одной жидкости в другой. Несмотря на низкую интенсивность
массопередачи, эти аппараты, главным образом насадочные
экстракторы, получили распространение в промышленности бла-
годаря простоте их устройства, значительной производитель-
ности и пригодности для проведения процессов в химически
агрессивных средах.
В последнее время все более широко применяются экстрак-
торы с принудительным перемешиванием, в которых за счет
подвода к жидкости энергии из внешнего источника достигается
значительное увеличение поверхности контакта фаз и интенси-
фикация массообмена.
В производствах крупного м/асштаба, где необходима боль-
шая производительность, но требуется умеренное число единиц
переноса для разделения смеси, эффективны колонные экстрак-
торы с механическими мешалками, в частности роторно-диско-
вые экстракторы.
При любом числе единиц переноса, требующемся для раз-
деления смеси, и при необходимости обеспечить большую про-
изводительность эстракционной аппаратуры, пригодны горизон-
тальные смесительно-отстойные экстракторы. Однако для уста-
новки таких аппаратов требуется большая производственная
площадь, возрастающая примерно пропорционально необхо-
димому числу единиц переноса. В связи с этим наблюдается
тенденция к замене горизонтальных смесительно-отстойных экс-
тракторов вертикальными смесительно-отстойными (ящичными)
и колонными экстракторами различных типов.
Общим недостатком всех экстракторов с механическими ме-
шалками является затруднительность эксплуатации их при
обработке сильно химически агрессивных или радиоактивных
веществ. Этого недостатка лишены пульсационные (ситчатые и
насадочные) экстракторы, сочетающие большую производитель-
ность с высокой интенсивностью массопередачи. Пульсационные
экстракторы успешно применяются в процессах разделения и
получения редких и рассеянных элементов. Использование этих
аппаратов в многотоннажных производствах сопряжено с труд-
ностями, обусловленными необходимостью сообщения вибраций
значительным массам жидкости.
Центробежные экстракторы — компактные высокоэффектив-
ные аппараты, которые выгодно отличаются от экстракторов
других типов малым временем пребывания в них реагирующих
веществ и низкой удерживающей способностью х (стр. 651).
Эти экстракторы пригодны для обработки систем с малой раз-
ностью плотностей фаз, а также легко эмульгирующихся и легко
разлагающихся веществ, требующих быстрой экстракции (на-
6 Расчет экстракторов
651
пример, пенициллина и других антибиотиков). Недостатками
центробежных экстракторов являются относительно высокая
стоимость и большие расходы при их эксплуатации В настоя-
щее время созданы аппараты этого типа (см. рис. 18-7, стр. 642)
производительностью, превышающей 200 м3/ч, что делает воз-
можным использование их в многотоннажных производствах.
6. Расчет экстракторов
Расчет экстракционных колонн заключается в определении
их диаметра и высоты. Диаметр колонны определяют по ее пре-
дельно допустимой производительности, которая должна быть
несколько ниже производительности, соответствующей захлебы-
ванию колонны. Предельно допустимую производительность
можно рассчитать, исходя из характеристической скорости ка-
пель дисперсной фазы, т. е. скорости их осаждения в неподвиж-
ной сплошной фазе.
Обозначим:
Ус и Рд — объемные скорости сплошной и дисперсной фазы,
м?1м? • сек;
х—объемная доля дисперсной фазы, удерживаемой
в колонне (удерживающая способность);
е — доля объема колонны, свободного для прохода
жидкости (в насадочных экстракторах — свобод-
ный объем насадки);
— характеристическая скорость капель (при 1/с = 0
и 1/д->0), м{сек.
Обычно движение капель в колонне является стесненным.
Для стесненного осаждения в данном случае применима сле-
дующая зависимость:
Предельную производительность колонны по сплошной или
по дисперсной фазе при захлебывании (соответствующую хтах)
можно определить, продифференцировав Vc или Уд по х и при-
равняв производную нулю:
ПРИ ^ = ° ^=2еТОЛ.1(,-Хт.х) (18‘4)
при -^-=0 VC = BOTO(1— 2xmlI)(l — xmK)2 (18-5)
Исключая wQ из уравнений (18-4) и (18-5), получаем:
6b2
Гл 18 Экстракция
В этом уравнении b =*= — объемное соотношение дисперс-
ной и сплошной фаз.
Из уравнения (18-6) видно, что хтах не зависит от размера
капель и физических свойств жидкостей и является функцией
только объемного соотношения фаз b
Согласно уравнениям (18-4) и (18-5) для определения пре-
дельной производительности колонны, кроме величины хтах, не-
обходимо знать Wo Расчетные уравнения для определения w0
в экстракторах различных типов получают на основе обработки
опытных данных *
Для определения предельной производительности насадочных экстракцион-
ных колонн (с насадкой из колец) можно также пользоваться уравнением **
( Рд
1 I 0,835
X Рс /
VJ
0,078
(18-7)
1де рс и рд — плотность сплошной и дисперсной фаз, кг/м3,
Ар — разность плотностей фаз, кг/м3,
f—удельная поверхность насадки, м2/м3,
g— ускорение силы тяжести, м/сек2,
а — граничное натяжение между фазами, н/м
Производительность экстрактора обычно принимают на
20—40% ниже предельной производительности, соответствую-
щей состоянию захлебывания.
Рабочую высоту экстракционных колонн рассчитывают по
общей формуле (16-43) Высоту единицы переноса принимают
по опытным данным либо рассчитывают по формулам для экс-
тракторов различных типов.
Для насадочных экстракционных колонн приближенный расчет высоты
единицы переноса можно производить по формуле
h =
l,15rf3KB (Рг')
(Ve/Ид)*/’
(18-8)
где </экв — эквивалентный диаметр насадки, м,
Рг' — диффузионный критерий Прандтля
Пример 18-1. Определить диаметр непрерывнодействующего насадочного
экстрактора для извлечения уксусной кислоты из бензола водой (дисперсная
фаза — вода, сплошная фаза — бензол) Производительность экстрактора
Ус = 15 Л13/ч бензола, начальная концентрация уксусной кислоты в бензоле
х' = 100 кг/м3, конечная концентрация х" = 1 кг/м3 Концентрация уксусной
кислоты в экстрагенте (воде) на выходе из колонны у" = 250 кг/м3 Темпера-
тура t = 20° С
* Жидкостная экстракция, сборник статей под ред А Г Касаткина, Гос-
химиздат, 1958
** ВИНИТИ, Экспресс информация, Процессы и аппараты химических
производств, № 4, 1961.
6 Расчёт экстрактордё
653
Решение Определяем соотношение объемов сплошной и дисперсной
фаз, принимая, что исходный экстрагент не содержит уксусной кислоты
(У' = 0)
По уравнению материального баланса
У"-/ _ 250-0 _
уд “ х' — хг ~ 100 — 1 ’°
В качестве насадки выбираем керамические кольца размером
25 X 25 X 3 мм, удельная поверхность которых f — 200 м2/м3, свободный
объем е = 0,74 (см табл 26, стр 598)
Для определения объемной скорости сплошной фазы при захлебывании
экстрактора находим
рд — плотность дисперсной фазы (1000 кг/м3)-,
рс — плотность сплошной фазы (879 кг/м3),
а — граничное натяжение между фазами (^34 дин/см == 34 • 10-3 н/м}.
Объемную скорость сплошной фазы при захлебывании экстрактора вы-
числяем по уравнению (18 7)
1 + 0,875
V* 200 879 r-//200 0,74-34 Ю'3^ °'WS
9,81 0,743/ V1000 — 879 J \ 879 V* /
1,687 = vj 344 • 0,894 0,375 0,61 • 1,50
откуда
V^'344 =0,182
yc = 0,00708 м3/м2 сек
Принимаем скорость сплошной фазы на 20% ниже скорости, соответ-
ствующей захлебыванию
Ус = 0,8 • 0,00708 = 0,00566 м3/м2 • сек
Определяем площадь сечения экстрактора
S” 3600 0,00566 - 01737 м‘
откуда находим диаметр экстрактора
Г 0,737 4
V 3,14
= 0,969 м
Принимаем округленно D = 1 м,
654
Гл. 18. Экстракция
Пример 18-2. Определить высоту насадки экстрактора, работающего
в условиях примера 18-1.
Решение. По формуле (16-26) рассчитываем коэффициент диффузии
одной жидкой фазы (уксусной кислоты) в другую (бензол):
1 -10~6___________ Л 1________________1 _
АВ /(Г (у% + v^3)2 у МА Л4В
“ 1,38 • 1 • /ОД) (68,41/3 + 95,9‘/з)2 60 + 78 - 2,14 ’10 М ,СеК
где А — 1,38 (для уксусной кислоты);
В= 1,0 (для бензола);
vA = 14,8-2 + 3,7 • 4 12,2 = 68,4 (молекулярный объем уксусной кислоты); \
ив = 14,8 • 6 -|- 3,7 • 6 — 15 == 95,6 (молекулярный объем бензола);
р. = 0,6 • 10~3 н • сек/м2 — 0,6 спз (вязкость сплошной фазы — бензола).
Определяем величину диффузионного критерия Прандтля по формуле
(16-30):
рг' — ___ 0’6 ‘ Ю gig
рс£) 879-2,14-10-9
где рс — плотность сплошной фазы — бензола (879 кг/м3).
Эквивалентный диаметр насадки составляет:
. 4s 4-0,74 _m.o
^экв. — у — 20Q — 0,0148 м
Определяем высоту единицы переноса по формуле (18-8)
1,15rf„..B (Рг')2/з 1,15 • 0,0148 • 3192/з
h =-------экв v ’ =---------------------0,59 м
(Ус1Уя)/з 2,52^
По кривой равновесия, конечной концентрации уксусной кислоты в дис-
персной фазе (воде)
кислоты в сплошной
процесса на входе в
фазе):
у" соответствует равновесная концентрация уксусной
фазе (бензоле) х* = 20 кг/м3. Тогда движущие силы
экстрактор и выходе из него составят (по сплошной
Aj = ЮО — 20 = 80 кг/м3
Д2 = 1 — 0 = 1 кг/м3
Считая приближенно линию равновесия прямой, определяем среднюю
движущую силу процесса:
Лер. = А|~дг = - Л- = 17,7 кг/л’
2.3 'g £ 2.3 'И 7
Определяем число единиц переноса по формуле (16-41)
100—1
п = —jyy— = 5,6
Высота насадки составляет:
Н = hn = 0,59 • 5,6 = 3,3 м
Принимаем округленно высоту Н = 3,5 м.
6. Расчет экстракторов
655
Пример 18-3. Определить предельную производительность роторно-диско-
вого экстрактора диаметром D = 0,75 м для извлечения капролактама водой
из азеотропной смеси (стр. 664) бензол — циклогексан (сплошная фаза —
вода). Объемное отношение азеотропной смеси к воде b = = 0,25. Число
•'с
оборотов ротора п = 200 .об/мин. Внутренние размеры экстрактора: диаметр
дисков ротора Dp — 0,5 м, диаметр отверстий колец статора DK = 0,6 м, вы-
сота секции колонны h = 0,15 м.
Решение. Определяем приближенно характеристическую скорость ка-
пель дисперсной фазы по следующему уравнению *:
Vc _ n т9 ( Др \°«9/ g \(DK \2,3 / h \о,9 / Dp \2,7
о _u,ui^pj \Dpn2)\Dp) \Dp) \d)
Для условий примера: р.с = 1 • Ю-3 н-сек/м2 = 1 спз (вязкость сплошной
фазы — воды); а = 34,9 • 10-3 н/.w2 = 34,9 дин/см (граничное натяжение между
фазами); Др = 1000 — 827 = 173 кг/м3 (разность плотностей сплошной и дис-
персной фаз); g = 9,81 м/сек2 (ускорение силы тяжести); п = -^-=3,33
об/сек (число оборотов ротора).
Следовательно
w0 • 1 • 10-3 _ / 173 \о,9 / 9,81 \ / 0,6 \2.з / 0,15 \0,9 / 0,5 \2,7
34,9 . Ю-3 “ \ WOO J \ 0,5-3.332 Д 0,5 ) \ 0,5 ) \ 0,75 )
откуда характеристическая скорость капель составляет:
w0 = 0,419 - О,1730,9 -1,77 -1,22’3 - 0,3°-9 • 0.66727 = 0,0264 м/сек
По формуле (18-6) определяем объемную долю дисперсной фазы, удер-
живаемой в колонне при захлебывании:
_ /б2 + _ Зь (01252 8.0,25)1/2 — 3 • 0,25
Хтах - 4(1 — /,)--------------4(1 — 0,25) “’
Вычисляем по формуле (18-4) скорость дисперсной фазы, считая на всю
площадь поперечного сечения колонны. Принимаем долю объема, свободного
для прохода жидкости в роторно-дисковом экстракторе £ = 0,95. Тогда
УД = 2£w0x^ax (1 — xmax) = 2 0,95 • 0,0264 - 0,232 (1 — 0,23) = 0,002 м/сек
Соответственно скорость сплошной фазы составляет:
Гс = = 0,008 м/сек
Площадь сечения экстрактора:
K.D2
S = —= 0,785 • 0,752 = 0,441 м2
4
* Жидкостная экстракция, сборник статей под ред. Д. Г. Касаткина, Гос-
химиздат, 1958, стр. ИЗ.
656
Гл 18 Экстракция
Определяем предельную производительность экстрактора при захлебы-
вании
по дисперсной фазе
У'л = Уд5 = 0,002 • 0,441 = 8,8 • 10~4 м3/сек
по сплошной фазе
V' = 8>.LJ0 4 = 35 2.10“4 м3/сек
с 0,25
Учитывая приближенность уравнения, использованного для вычисления
характеристической скорости капель (уравнение было получено для колонны
диаметром 76 мм), рабочую производительность экстрактора принимаем рав-
ной 60% от предельной, рассчитанной без учета влияния вещества, распре-
деляемого между фазами Тогда
Ул = 0,6V' = 0,6 • 8,8 10“4 = 5,28 • 10“4 м3/сек
Ус = 0,6V' = 0,6 • 35,2 • 10“4 = 21,1 • 10“4 м31сек
Производительность экстрактора по обеим фазам составляет1
V = Уа 4- Гс = 5,28 • 10~4 %- 21,1 • 10“4 = 26,4 • 10~4 м3/сек 9,5 м3/ч
Глава 19
РЕКТИФИКАЦИЯ
1. Общие сведения
Для разделения смеси жидкостей обычно прибегают к пере-
гонке. Разделение путем перегонки основано на различной тем-
пературе кипения отдельных веществ, входящих в состав смеси.
Так, если смесь состоит из двух компонентов, то при испарении
компонент с более низкой температурой кипения (низкокипящий
компонент, сокращенно НК) переходит в пары, а компонент с
более высокой температурой кипения (высококипящий компо-
нент, сокращенно ВК) остается в жидком состоянии. Получен-
ные пары конденсируются, образуя так называемый дистиллят-,
неиспаренная жидкость называется остатком. Таким образом,
в результате перегонки НК переходит в дистиллят, а ВК — в
остаток.
Описанный процесс, называемый простой перегонкой, не
дает, однако, возможности произвести полное разделение ком-
понентов смеси и получить их в чистом виде. Оба компонента
являются летучими и потому оба переходят в пары, хотя и в
различной степени. Поэтому образующиеся при перегонке пары
не представляют собой чистого НК- Поскольку он вследствие
большей летучести испаряется в большей степени, чем ВК, то
пары обогащены НК по сравнению с содержанием его в исход-
ной смеси. Таким образом, в дистилляте содержание НК выше,
чем в исходной смеси, а в остатке, наоборот, содержание НК
ниже, чем в исходной смеси. В описанном явлении и заклю-
чается основное отличие перегонки от выпаривания. При выпа-
ривании, как указывалось (стр. 467), один из компонентов (рас-
творенное вещество) нелетуч, и в пары переходит только лету-
чий компонент (растворитель).
Для достижения наиболее полного разделения компонентов
применяют более сложный вид перегонки — ректификацию Рек-
тификация заключается в противоточном взаимодействии паров,
образующихся при перегонке, с жидкостью, получающейся при
конденсации паров.
42 Зак 54Q.
658
Гл. 19 Ректификация
Представим себе аппарат, в котором снизу вверх движутся
пары, а сверху (навстречу парам) подается жидкость, представ-
ляющая собой почти чистый НК. При соприкосновении подни-
мающихся паров со стекающей жидкостью происходит частич-
ная конденсация паров и частичное испарение жидкости. При
этом из паров конденсируется преимущественно ВК, а из жидко-
сти испаряется преимущественно НК. Таким образом, стекаю-
щая жидкость обогащается ВК, а поднимающиеся пары обо-
гащаются НК, в результате чего выходящие из аппарата пары
представляют собой почти чистый НК. Эти пары поступают
в конденсатор (дефлегматор), где и конденсируются. Часть кон-
денсата, возвращаемая на орошение аппарата, называется флег-
мой, другая часть — отводится в качестве дистиллята.
Процесс перегонки был известен еще в древности. Он полу-
чил значительное развитие в средние века, когда научились
получать этиловый спирт из продуктов брожения крахмала и
сахаросодержащих материалов.
В настоящее время перегонка и ректификация широко рас-
пространены в химической технологии и применяются для полу-
чения разнообразных продуктов в чистом виде, а также для раз-
деления газовых смесей после их сжижения (разделение воз-
духа на кислород и азот, разделение углеводородных газов
и др.). Однако при разделении чувствительных к повышенным
температурам веществ, при извлечении ценных продуктов или
вредных примесей из сильно разбавленных растворов, разделе-
нии смесей близкокипящих компонентов в ряде случаев может
оказаться более целесообразным применение экстракции
(глава 18).
2. Основные свойства смесей жидкостей
и их паров
Для понимания процессов перегонки необходимо ознако-
миться с некоторыми свойствами жидких смесей, в частности
с зависимостью давления пара, температуры кипения и состава
паров от состава жидкости. Мы ограничимся рассмотрением
свойств двойных смесей, т. е. смесей, состоящих из двух компо-
нентов. Свойства таких смесей проще всего изучать графиче-
ским методом при помощи диаграмм. Мы будем пользоваться
тремя видами диаграмм:
1) диаграмма зависимости давления пара от состава жидко-
сти (р — х- диаграмма);
2) диаграмма зависимости температур кипения и конден-
сации от состава жидкости и пара (t — х — у-диаграмма);
3) диаграмма равновесия, выражающая зависимость между
составами пара и жидкости (у— х-диаграмма).
2 Основные свойства смесей жидкостей и их парод
659
В зависимости от взаимной растворимости компонентов раз-
личают следующие типы двойных смесей:
1. Смеси взаимнорастворимых жидкостей, т. е. таких жидко-
стей, которые растворимы друг в друге в любых отношениях.
Эти смеси в свою очередь разделяются на три группы:
а) смеси жидкостей, в которых силы сцепления между мо-
лекулами обоих компонентов такие же, что и между молеку-
лами каждого из компонентов (идеальные смеси);
б) смеси с положительными отклонениями от закона Рауля
(см. ниже), в которых силы сцепления между молекулами НК
и ВК меньше, чем между молекулами каждого из компонентов;
в) смеси с отрицательными отклонениями от закона Рауля,
в которых силы сцепления между молекулами НК и ВК больше,
чем между молекулами каждого из компонентов.
2. Смеси жидкостей, нерастворимых друг в друге.
3. Смеси частично растворимых жидкостей.
(
Идеальные смеси
Парциальное давление пара каждого компонента идеальных
смесей зависит от температуры и содержания данного компо-
нента и пропорционально молярной доле данного компонента в
смеси. Эго соотношение называется законом Рауля и может
быть математически выражено следующим образом. Обозначим
через х состав жидкости, т. е. молярную долю НК в жидкой
смеси *, через />нк и />вк— парциальные давления паров НК и
ВК над смесью и через Рнк и Рвк—давления паров чистых
НК и ВК при данной температуре Тогда молярная доля ВК
в жидкой смеси будет (1—х). Следовательно
/7нк~^’нкЛ (19'0
/?вк=^>вкО х) (19-2)
т. е. парциальные давления паров компонентов равны произве-
дению давления пара чистого компонента на его молярную до-
лю в жидкости.
Полное давление пара над жидкостью равно сумме парци-
альных давлений компонентов:
Р = /^нк ^вк ~ ^нкх ^вк (1 х) (19-3)
* Здесь и далее в данной главе состав жидкости и паров всюду выра-
жается через содержание НК в смеси.
42*
660
Гл. 19. Ректификация
Эти уравнения можно выразить графически на р — лг-диа-
грамме (рис. 19-1), на которой по оси абсцисс отложен состав
жидкости х, а по оси ординат — давление пара р. Уравнения
(19-1), (19-2) и (19-3) изображаются прямыми линиями: пар-
циальное давление рнк —линией ОВ, парциальное давление
/?вк — линией AD, полное давление — линией АВ. Отрезок DB
(соответствующий абсциссе х — 1, т. е. чистому НК) равен Рнк,
а отрезок ОА (соответствующий абсциссе х ~ 0, т. е. чистому
Рис. 19-1. Диаграмма р— х для идеальной смеси.
ВК) равен Рвк- Описанное построение относится к некоторой
постоянной температуре; следовательно, линии АВ, ОВ и AD
являются изотермами.
Для определения температур кипения смесей различного со-
става надо построить ряд изотерм полного давления АВ, А{В[,
А2В2 ..., соответствующих температурам t, t\, t2 ... Далее про-
водят горизонтальную линию MN с ординатой, равной внеш-
нему давлению Р. В точке R пересечения изотермы АВ с линией
MN полное давление пара над смесью состава х, как видно из
рис. 19-1, равно внешнему давлению. Следовательно, эта смесь
закипит при температуре t, соответствующей изотерме АВ. Ана-
логично можно найти, чтс^при температурах Л, t2 ... будут ки-
петь смеси состава Xi, х2 ...
Для нахождения составов паров надо определить парциаль-
ное давление пара НК над жидкостью при температурах кипе-
ния. Покажем это на примере смеси состава х. Ордината /?нк
прямой ОВ, соответствующая абциссе х, представляет собой
парциальное давление пара НК; молярная доля НК в парах у
2. Основные свойства смесей жидкостей и их паров
661
составляет Найденные таким образом составы паров у
являются равновесными с соответствующими составами жидко*
сти х. ♦
Определив температуры кипения и составы паров для смесей
разного состава, можно построить t — х — у- и у — х-диаграммы.
На диаграмме t — х — у (рис. 19-2, слева) по оси абсцисс отло-
жены составы жидкости х и
паров £/; по оси ординат от-
ложены температуры t. От-
Рис. 19-2. Диаграмма t — х — у (слева)
и диаграмма равновесия у — х
(справа) для идеальной смеси.
кладывая по оси ординат температуры кипения ti, /2, h • - . для
смесей состава хь х2, *з • • • и соединяя точки А2, А3 ... плав-
ной кривой, получим линию АА1А2А3В, называемую линией ки-
пения. Далее откладываем по оси абсцисс составы паров
ylt У2, Уз .... соответствующие температурам ti, t2, t3 ..., и,
соединяя точки В\, В2, В3 ..., получаем линию ABiB2B3B, назы-
ваемую линией конденсации.
Ординаты линии кипения соответствуют температурам кипе-
ния смесей, составы которых выражаются абсциссами этой ли-
нии. Ординаты линии конденсации выражают температуры кон-
денсации паров, составы которых соответствуют абсциссам этой
линии. Чтобы найти состав пара для какой-либо смеси, надо от-
ложить на оси абсцисс состав этой смеси и из этой точки про-
вести вертикаль до пересечения с линией кипения; далее из точ-
ки пересечения надо провести горизонталь до пересечения с
линией конденсации. Абсцисса последней точки пересечения
выражает искомый состав пара.
Как видно из рис. 19-2, температуры кипения смесей ниже
температуры кипения чистого ВК (изображается ординатой
662
Гл. 19. Ректификация
точки В) и выше температуры кипения чистого НК (изобра-
жается ординатой точки Л), причем по мере увеличения в смеси
содержания НК температура кипения понижается.
Из рис. 19-2 видно также, что абсциссы линии конденсации
больше абсцисс линии кипения (при тех же ординатах), т. е.
содержание НК в парах больше содержания НК в жидкости;
иначе говоря, пары обогащаются НК. Это соответствует пер-
вому закону Коновалова, согласно которому пар обогащен тем
компонентом, при добавлении которого к жидкости повышается
полное давление пара.
При испарении смесей температура кипения не остается по-
стоянной, как при испарении чистых жидкостей. Так, смесь со-
става Xi начинает кипеть при температуре 6; состав паров при
этом будет г/ь Так как в пары переходит преимущественно НК,
то смесь обедняется этим компонентом и температура ее кипе-
ния повышается. Одновременно происходит изменение состава
паров в сторону понижения в них содержания НК- Кипение за-
канчивается при температуре /к, являющейся ординатой линии
конденсации при абсциссе xt; состав паров при этом будет
равен начальному составу смеси Xi, а состав жидкости бу-
дет хк.
Область между линиями кипения и конденсации является
двухфазной областью, в которой одновременно существуют жид-
кость и пар. Ниже линии кипения существует только жидкость,
выше линии конденсации — только пар.
На диаграмме равновесия (рис. 19-2, справа) по оси абсцисс
отложены составы жидкости х, по оси ординат — равновесные
с этими х составы паров у. Зависимость у от х выражена линией
равновесия. Кроме линии равновесия, проведена вспомогатель-
ная диагональ. Линия равновесия расположена выше диаго-
нали; следовательно, ординаты линии равновесия больше ее
абсцисс, т. е. пары обогащены НК. Чем ближе линия равнове-
сия к диагонали, тем меньше разница составов пара и жидкости
и тем труднее разделяется смесь при перегонке.
Следует’отметить, что диаграммы t — х — у и у — х построе-
ны при постоянном общем давлении (Р — const).
Смеси, отклоняющиеся от идеальных
Реальные жидкие смеси в той или иной степени отклоняются
от идеальных. Смеси химически сходных веществ мало откло-
няются от идеальных. Так, смеси жидких углеводородов (напри-
мер, бензола и толуола) практически могут рассматриваться
как идеальные.
2. Основные свойства смесей жидкостей и их паров
663
Неидеальные смеси не характеризуются законом Рауля. Как
указывалось выше, отклонения от закона Рауля могут быть по-
ложительными или отрицательными. Положительные отклонения
наблюдаются чаще. При положительном отклонении парциаль-
ные давления пара компонентов выше, чем
кона Рауля, и кривая 2 полного давления
выше прямой 1, соответствующей идеальной
тельном отклонении парциальные
давления пара компонентов ниже
соответствующих закону Рауля и
кривая полного давления 3 лежит
ниже прямой 1.
Если отклонения невелики, то на
диаграмме р — х они проявляются
лишь в том, что изотермы пар-
циальных и полного давлений изо-
бражаются не прямыми, а кривыми
линиями. Характер же диаграмм
t—х—у и у—х остается таким же,
как и для идеальных смесей.
При достаточно больших откло-
нениях на кривой полного давле-
ния появляется максимум (при по-
ложительных отклонениях) или ми-
нимум (при отрицательных откло-
нениях).
Согласно первому закону Ко-
новалова, поднимающаяся ветвь
полного давления пара (ветвь MAi
на кривой 4 и ветвь A2N на кри-
вой 5) соответствует обогащению пара НК, а опускающаяся
ветвь (ветвь AiN на кривой 4 и ветвь МА2 на кривой 5) —обо-
гащению пара ВК. Свойства таких смесей характеризуются вто-
рым законом Коновалова: максимуму кривой общего давления
пара соответствует минимум температуры кипения, а минимуму
кривой общего давления пара соответствует максимум темпера-
туры кипения.
На рис. 19-4 показаны диаграммы t — х — у и у — х для сме-
си этиловый спирт — бензол, обладающей минимальной темпе-
ратурой кипения при содержании этилового спирта 0,448 мол.
долей. В точке, абсцисса которой соответствует составу этой
смеси, линии кипения и конденсации сливаются в одну точку А,
а на диаграмме у—х линия равновесия пересекает в точке А
диагональ. Из этого можно заключить, что состав пара для этой
смеси такой же, как и состав жидкости.
это следует из за-
(рис. 19-3) лежит
смеси. При отрица-
Рис. 19-3. Диаграмма р — х
для смесей, отклоняющихся от
идеальных. Кривые полного
давления:
1 — для идеальной смеси; 2 —для смеси
с положительными отклонениями;
3 —для смеси с отрицательными от-
клонениями; 4 — для смеси с максиму-
мом полного давления; 5 — для смеси
с минимумом полного давления.
664
Гл 19 Ректификация
Такие смеси называются нераздельнокипящими или азео-
тропными смесями и обладают следующими особенностями:
1) азеотропная смесь имеет минимальную (как в данном
случае) или максимальную температуру кипения по сравнению
со смесями этих компонентов другого состава;
2) испарение азеотропной смеси, как и чистых веществ, про-
исходит при постоянной температуре,
3) азеотропная смесь испаряется без изменения состава.
Рис 19-4. Диаграммы t — х — у (слева) и равновесия (справа) для смеси
с минимальной температурой кипения (этиловый спирт — бензол).
Из рис. 19-4 видно, что пары смесей, содержащих менее
0,448 мол. долей С2Н5ОН (доазеотропные смеси), обогащены
НК, а пары смесей, содержащих более 0,448 мол. долей С2Н5ОН
(заазеотропные смеси), обогащены ВК. Таким образом, при пе-
регонке рассматриваемых смесей в дистиллят всегда переходит
азеотропная смесь, в остатке же при перегонке доазеотропных
смесей остается ВК (бензол), а при перегонке заазеотропных
смесей — НК (этиловый спирт). Абсцисса, соответствующая
азеотропной смеси, делит диаграммы на две половины, из кото-
рых левая (доазеотропные смеси) изображает смеси ВК с азео-
тропной смесью, а правая (заазеотропные смеси) — смеси НК
с азеотропной смесью.
На рис. 19-5 показаны диаграммы t — х — у и у — х для си-
стемы азотная кислота — вода, образующей азеотропную смесь
с максимальной температурой кипения при содержании
2 Основные свойства смесей жидкостей и их паров
665
0,378 мол. долей HNO3. Пары доазеотропных смесей, содержа-
щих менее 0,378 мол. долей HNO3, обогащены ВК (водой), пары
заазеотропных смесей обогащены НК (азотной кислотой). При
перегонке таких смесей в остатке всегда остается азеотропная
смесь. В дистиллят при перегонке доазеотропных смесей пере-
ходит ВК (вода), при перегонке заазеотропных смесей — НК
(азотная кислота).
Содержание НК (азотной кислоты)
мол доли
Рис. 19-5. Диаграммы i — х — у (слева) и равновесия (справа) для смеси
с максимальной температурой кипения (азотная кислота — вода).
Содержание НК (азотной кислоты)
В жидкости, пол. доли
Из сказанного можно сделать вывод, что разделение рассмо-
тренных смесей на два чистых компонента путем перегонки не-
возможно, так как одним из продуктов перегонки является азео-
тропная смесь. Для разделения азеотропных смесей прибегают
к специальным методам (стр. 709 сл.).
Азеотропные смеси не являются химическими соединениями.
Это подтверждается следующим: состав азеотропной смеси за-
висит от давления, таким образом, не соблюдается обязатель-
ный для каждого химического соединения закон постоянства со-
става. Так, например, смесь этиловый спирт — вода при абсо-
лютном давлении 760 мм рт. ст. образует азеотропную смесь,
содержащую 88,4 мол. % С2Н5ОН. При понижении давления со-
став азеотропной смеси изменяется в сторону повышения содер-
жания спирта, а при абсолютном давлении ниже 90 мм рт. ст.
азеотропная смесь вовсе не образуется.
Второй закон Коновалова показывает, что существование
азеотропных смесей является следствием особого характера
изменения зависимости общего давления пара от состава.
666
ft i 1 РеьтисЬикация
Образование азеотропных смесей при достаточно больших от-
клонениях от закона Рауля является примером перехода коли-
чественных изменений в качественные.
Смеси жидкостей, нерастворимых друг в друге
Совершенно нерастворимых друг в друге жидкостей не су-
ществует. Но в некоторых случаях (например, смеси бен-
зол— вода, сероуглерод — вода и др.) взаимная растворимость
жидкостей настолько мала, что практически их возможно счи-
тать нерастворимыми друг в друге. Нерастворимые жидкости
можно разделять отстаиванием, так как они расслаиваются,
причем в верхнем слое находится жидкость меньшей плотности,
в нижнем — жидкость с большей плотностью.
Парциальное давление пара каждого компонента не зависит
от присутствия второго компонента и равно давлению пара чи-
стого компонента при данной температуре:
/*нк ~ ^нк; ^вк = ^вк
Полное давление пара также не зависит от состава смеси
и определяется выражением
= + ^вк
Смесь кипит при такой температуре, при которой давление
пара, т. е. сумма (Рнк + ^вк), равна внешнему давлению. При
этой температуре парциальное давление пара каждого компо-
нента будет меньше внешнего давления, т. е. температура кипе-
ния смеси будет ниже температуры кипения каждого из компо-
нентов. Кроме того, температура кипения смеси нерастворимых
друг в друге жидкостей не зависит от состава этой смеси.
Определить температуру кипения такой смеси можно графи-
чески (рис. 19-6), построив кривые зависимости Рнк, ^вк и Р от
температуры. Линия АВ соответствует внешнему давлению. Абс-
цисса точки К пересечения прямой АВ с линией полного давле-
ния Р выражает температуру кипения смеси.
Из рис. 19-6, построенного для смеси бензол — вода, видно,
что при абсолютном внешнем давлении 760 мм рт. ст. темпера-
тура кипения смеси будет 69° С, тогда как температуры кипения
чистых компонентов равны соответственно 80° С (для бензола)
и 100°С (для воды).
Состав пара определяется соотношением
2. Основные свойства смесей жидкостей и их паров
667
и не зависит от состава жидкости. Величину Рнк при темпе-
ратуре кипения смеси находят непосредственно на диаграмме,
Рис. 19-6. График для определения температуры
кипения смеси жидкостей, нерастворимых друг
в друге
(бензол — вода).
Рис. 19-7. Диаграммы р — х, t — х — у и у — х для смеси жидкостей,
нерастворимых друг в друге (бензол — вода).
На рис. 19-7 показаны р — х-, t — к — у- и у — х-диаграммы
для смеси жидкостей, нерастворимых друг в друге. Линии пар-
циальных и полного давлений на р— х-диаграмме, линия кипения
на t — х — (/-диаграмме и линия равновесия на у — х-диаграмме
668
Гл. 19. Ректификация
изображаются горизонтальными прямыми. Линия конденсации на
t— х—//-диаграмме изображается кривой MAN.
Точка А соответствует азеотропной смеси с минимальной тем-
пературой кипения.
Смеси частично растворимых
жидкостей
Особенностью этих смесей является то, что в зависимости
от содержания компонентов жидкость может быть однородной
или состоять из двух несмешивающихся слоев.
Если, например, постепенно прибавлять к воде эфир, то вна-
чале эфир будет растворяться в воде и получится однородная
жидкость. Это будет продолжаться до тех пор, пока не обра-
зуется насыщенный раствор эфира в воде. После этого дальней-
шие порции прибавляемого эфира не будут растворяться, причем
жидкость разделится на два слоя, из которых один представляет
собой насыщенный раствор эфира в воде, а другой — насыщен-
ный раствор воды в эфире. Однако при последующем добавле-
нии эфира будет достигнуто такое соотношение между ко-
личествами воды и эфира в смеси, которое соответствует
растворимости воды в эфире. При этом жидкость снова станет
однородной и будет представлять собой насыщенный раствор
воды в эфире.
Эта жидкость будет оставаться однородной и при дальней-
шем прибавлении эфира.
Рис 19-8. Диаграммы t — х — у и у — х для смеси частично рас-
творимых жидкостей (вода — бутиловый спирт).
2. Основные свойства смесей жидкостей и их паров
669
Характер диаграмм р — х, t — х — у и у — х будет изменять-
ся в зависимости от того, является ли жидкость однородной или
состоит из двух слоев. В первом случае будут наблюдаться за-
кономерности, справедливые для смесей взаимно растворимых
жидкостей, во втором случае — закономерности, справедливые
для смесей жидкостей нерастворимых друг в друге.
На рис. 19-8 приведены диаграммы для смеси вода — бути-
ловый спирт. Область ОА соответствует растворимости НК в
ВК (т. е. воды в бутиловом спирте), область ВС — растворимо-
сти ВК в НК (т. е. бутилового спирта в воде). В области АВ
жидкость состоит из двух несмешивающихся слоев, полное да-
вление пара достигает при этом максимума. В соответствии с
вторым законом Коновалова область АВ соответствует мини-
мальной температуре кипения смеси. На этом участке располо-
жена точка, соответствующая азеотропной смеси с содержа-
нием 75,2 мол.°/о воды.
Построение диаграмм t—х—у и у—х
Для неидеальных смесей эти диаграммы могут быть по-
строены только на основании опытных данных.
Для идеальных смесей диаграммы можно построить путем
расчета, исходя из значений давления паров чистых компонен-
тов (Рнк и Рвк) при различных температурах. Для этого можно
воспользоваться уравнением (19-3). Решая его относительно х,
получим:
^--Рвк
^НК — ^вк
(19-5)
Таким образом, выбрав ряд температур (в пределах между
температурами кипения чистых компонентов), можно вычислить
состав жидкости, кипящей при данной температуре. Далее, опре-
деляя парциальное давление НК по формуле (19-1), находим
состав паров:
, /’нк ^нк-*
У— р — р
(19-6)
Пример 19-1. Построить диаграммы t — х — у и у — х для смеси бен-
зол — толуол при абсолютном давлении Р — 760 мм рт. ст.
Решение. Задаемся рядом температур, лежащих между температу-
рами кипения чистого бензола (80,2°С) и чистого толуола (110,4°С), находим
по таблицам давления паров чистых компонентов и определяем х и у по
формулам (19-5) и (19-6). Расчеты сводим в таблицу (табл. 29).
670
Гл. 19. Ректификация
Таблица 29
Расчет равновесия смеси бензол — толуол
t °C рнк чм рт. ст. рвк мм рт. ст. X — ^-^вк у“ р
рнк~рвк
80,2 760 300 760 760 -300 -300 1 760-1 760 “ 1
84 852 333 760- 852- — 333 „ —ЙУ = 0,823 — ООО 852 - 0,823 760 - 0,922
88 957 380 760- 957- -дао-0’659 957-0,659 760 0,830
92 1078 432 760- =^ = 0,508 1078 - 0,508 0,720
1078 760 ~
96 1204 493 760- ~ 493 _ q 070 1204 • 0,376 0,596
1204 — 493 U’ 760
100 1344 559 760- 1344 _ 559 - 0,256 1344-0,256 _ 760 0,453
104 1495 626 760- 1495 =0,155 — 020 1495 • 0,155 _ 760 0,304
108 1659 705 760- 1659 =4^ = 0,058 — /05 1659 - 0,058 _ 760 0,128
110,4 1748 760 760- 1748 — 760 1748•0 _ 760 0
3. Материальный и тепловой баланс процесса
ректификации
При ректификации исходная жидкая смесь делится на две
части: часть, обогащенную НК (дистиллят), и часть, обеднен-
ную НК (остаток). Непрерывная ректификация проводится
в аппаратах (ректификационных/колоннах), состоящих из двух
ступеней (рис. 19-9). Исходная смесь вводится в верхнюю часть
нижней ступени (исчерпывающая колонна 2). Здесь исходная
жидкая смесь взаимодействует в противотоке с паром, началь-
ный состав которого аналогичен составу остатка; в результате
происходит исчерпывание смеси, т. е. извлечение из нее НК и
обогащение ее ВК.
В верхней ступени (укрепляющая колонна /) пар, поступаю-
щий из нижней ступени, взаимодействует в противотоке с
жидкостью, начальный состав которой аналогичен составу ди-
стиллята; в результате происходит укрепление пара, т. е. обо-
гащение его НК-
3. Материальный и тепловой баланс процесса ректификации
671
Пар для питания ректификационного аппарата образуется в
кубе 3 путем испарения части жидкости, поступающей в куб,
жидкость для орошения аппарата (флегма) получается в де-
флегматоре 4 путем конденсации части пара, имеющего состав,
аналогичный составу дистиллята.
Тепло, необходимое для испарения смеси, сообщается ей
в кубе. В дефлегматоре производится отвод тепла, вследствие
чего поступающие в него пары полностью
или частично конденсируются. Дистил-
лят отводится из дефлегматора в жид-
ком или парообразном состоянии. Оста-
ток отводится из куба в виде жидкости.
Материальный баланс
Обозначим через F количество по-
ступающей на ректификацию смеси (в
кмоль!сек), через Р— количество полу-
чаемого дистиллята (в кмоль!сек), через
W — количество остатка (в кмоль/сек) и
через Хр, хР и xw — составы смеси, ди-
стиллята и остатка (в мол. долях НК).
Тогда уравнение материального ба-
ланса для всего количества смеси при-
мет вид
F=P-±W
(19-7)
и уравнение материального баланса для
НК
Рис. 19-9. Схема мате-
риального баланса рек-
тификационной колонны:
FxP = Рхр + Wxw
(19-8)
1 — укрепляющая колонна;
При ПОМОЩИ уравнений (19-7) И 2-исчерпывающая колонна;
/1Л гА ' ' 3—куб; 4 — дефлегматор.
(19-8) решаются все задачи, связанные
с определением количеств или составов
веществ, участвующих в процессе ректификации. Обычно за-
даны количество смеси F и составы xF, хР и xw. Количества
дистиллята Р и остатка W определяются совместным решением
уравнений (19-7) и (19-8).
Уравнения (19-7) и (19-8) применимы и при выражении ве-
личин F, Р и W в весовых количествах (в кг/сек). При этом
составы смеси, дистиллята и остатка должны подставляться в
уравнения в весовых долях (aF, ар, aw).
&71
Гл 19 Ректификация
Для дальнейшего изучения процесса ректификации сделаем
следующие допущения:
1. Молярные теплоты испарения обоих компонентов одина-
ковы; поэтому каждый киломоль сконденсировавшегося пара
испаряет 1 кмоль жидкости, вследствие чего количества подни-
мающегося пара и стекающей жидкости по высоте колонны
не изменяются, а изменяется лишь их состав. Следует отметить,
что молярные теплоты испарения (в дж/кмоль) различных ве-
ществ обычно близки друг к другу (в противоположность теп-
лотам испарения 1 кг вещества). Поэтому сделанное допущение
не приводит к значительной ошибке, если расчет процесса рек-
тификации вести не в весовых, а в молярных величинах.
2. Исходная жидкая смесь подается в колонну подогретой
до температуры кипения; следовательно, в колонне не расхо-
дуется тепло на нагревание смеси. В этих условиях количество
стекающей жидкости в нижней части колонны (ниже ввода ис-
ходной смеси) увеличивается на количество введенной смеси.
3. При конденсации пара в дефлегматоре не происходит из-
менения его состава; следовательно, состав пара аналогичен
составу дистиллята хр.
4. При испарении жидкости в кубе не происходит изменения
ее состава; следовательно, состав образовавшегося пара анало-
гичен составу остатка xw.
Обозначим через G и L количества паровой и жидкой фаз
(в кмоль/сек), через у\ и г/2— молярные доли НК в парах на
входе в колонну и на выходе из нее, через х2 и Xi — молярные
доли НК в жидкости на входе в колонну и на выходе из нее.
Рассмотрим произвольное сечение А — А в нижней или верх-
ней части аппарата (см. рис. 19-9). В этом сечении состав пара
у, а состав жидкости х.
Составим уравнение материального баланса по НК для ча-
сти аппарата, расположенной выше рассматриваемого сечения:
Gy ~= Gy 2 1-Х
откуда
—*) (19-9)
Аналогично, составляя материальный баланс по НК для ча-
сти аппарата, расположенной ниже сечения А — А, имеем':
Gy i -f- Lx = Gy + Lxv
откуда
У = У1 + ^(х~х1) (19-10)
Уравнения (19-9) и (19-10) являются уравнениями рабочей
линии процесса ректификации. По форме они аналогичны урав-
3. Материальный и тепловой баланс процесса ректификации 673
нению (16-16) и отличаются от него лишь тем, что количества
носителя заменены на общие количества фаз, а относительные
весовые составы — на молярные доли.
Количество поднимающегося пара G постоянно во всей ко-
лонне. Это количество пара образуется в кубе и поступает в де-
флегматор, откуда часть Ф возвращается в колонну в виде
флегмы, а остальная часть Р отводится в виде дистиллята. Та-
ким образом
О = Ф + Р
Отношение количества флегмы к количеству дистиллята
R = ^- (19-11)
называется флегмовым числом.
Следовательно, количество флегмы Ф = PR и количество
поднимающегося пара составляет:
G = P^+P = P(/? + l) (19-12)
т. е. на каждый киломоль дистиллята в кубе должно быть ис
парено (7?+1) кмоль остатка.
В укрепляющей колонне
количество стекающей жидко-
сти равно количеству флегмы:
£ = ф=Р/?
а состав пара на выходе из
колонны равен составу пода-
ваемой на орошение флегмы:
Уг = х2 = хР
Подставляя значения L, G,
у2 и х2 в уравнение (19-9), по-
лучим:
У=хр--^т(хр — х)
Рис. 19-10. Построение рабочей
линии ректификационной колонны:
А'В1 — рабочая линия исчерпывающей ко-
лонны; В'С'— рабочая линия укрепляющей
колонны.
или
X
У = 7? н- 1 Л + Я+1
Подставляя в уравнение (19-13) х = Хр, получим у=хр, т. е.
на у — х-диаграмме (рис. 19-10) рабочая линия укрепляющей
колонны проходит через лежащую на диагонали точку С' с абс-
циссой хР. Из уравнения (19-13) видно, что тангенс угла накло-
43 Зак 546.
674
Гл. 19. Ректификация
р
на рабочей линии tga= > а отрезок, отсекаемый на оси
ординат, составляет
(19-14)
Ь~ /?+1
В исчерпывающей колонне количество стекающей жидкости
L больше количества флегмы Ф на количество исходной жидкой
смеси F.
Р
Обозначая -р- = f, найдем для исчерпывающей колонны:
Составы поступающего в колонну пара и вытекающей из нее
жидкости равны составу остатка:
У1 — Xi — xw
Подставляя значения L, G, у\ и Xi в уравнение (19-10), полу-
чим:
У — xw Я4-1 (х xw)
или ____________________________
У = — (19-15)
Подставляя в уравнение (19-15) х = xw, получим у = xw,
т. е. рабочая линия исчерпывающей колонны проходит через
лежащую на диагонали точку А' с абсциссой xw.
Найдем абсциссу точки В' пересечения рабочих линий укреп-
ляющей и исчерпывающей колонн. Ордината этой точки, опреде-
ленная по уравнениям (19-13) и (19-15), будет одинаковой; сле-
довательно, можно приравнять правые части этих уравнений:
R , хр __ Я+/ /~1
Я 4-1 х-г ^4-1 “ я4-1 Х R+^Xw
Умножая обе части этой формулы на (Я 4- 1), получим пос-
ле приведения подобных членов:
хр —fx (f 1) xw
i-r £ F
Подставляя f = ~p- и решая уравнение относительно х, на-
ходим:
__ Рхр + (f — P)xw __ Рхр 4- Wxw __ Fx* _
х — р — р р —: XF
т. е. абсцисса точки В' равна составу исходной смеси хР.
3 Материальный и тепловой баланс процесса ректификации
675
На основании найденных соотношений можно построить на
у — х-диаграмме рабочие линии следующим образом (см. рис.
19-10). Откладываем на оси абсцисс точки А, В и С, соответ-
ствующие составам остатка xw, смеси хР и дистиллята хр,
проводим через эти точки вертикали АА', ВВ' и СС'. Далее, в
зависимости от принятого флегмового числа R, откладываем на
оси ординат отрезок OD, длина которого определяется по фор-
муле (19-14). Точку D на оси ординат и точку С' пересечения
вертикали СС' с диагональю соединяем прямой DC'. Точку В'
пересечения этой прямой с вертикалью ВВ' соединяем с точ-
кой А' пересечения вертикали АА' с диагональю. Отрезок В'С'
будет рабочей линией укрепляющей колонны, отрезок А'В' —
рабочей линией исчерпывающей колонны.
Пример 19-2. На ректификацию поступает смесь метанол — вода в коли-
честве F — 5000 кг/ч, содержащая метанола ар = 40 вес. %. Содержание ме-
танола в дистилляте ар=98,5 вес. %, в кубовом остатке а^=1,5 вес. %.
Определить количество дистиллята и остатка.
Решение По уравнениям материального баланса (19-7) и (19-8), со-
ставленным для весовых количеств, имеем:
5000 = Р 4- W
5000 • 0,4 = Р • 0,985 + W • 0,015
Совместным решением этих уравнений находим Р = 1985 кг/ч =
= 0,552 кг/сек, W = 3015 кг/ч — 0,838 кгIсек.
Минимальное и рабочее флегмовое число
Если изменять флегмовое число, будет изменяться и положе-
ние рабочих линий. При бесконечном флегмовом числе (колонна
работает «на себя», отбор дистиллята не производится) рабочая
линия совпадает с диагональю, так как при /? = оо отрезок b
обращается в нуль. Если уменьшать флегмовое число, рабочая
линия укрепляющей колонны будет поворачиваться около точки
С. При этом рабочая линия исчерпывающей колонны будет по-
ворачиваться около точки А и рабочая линия колонны последо-
вательно займет положения АВС, АВ'С, АВ"С и т. д. (рис. 19-11,
слева).
Однако уменьшать флегмовое число можно лишь до извест-
ного предела. Дело в том, что рабочая линия выражает неравно-
весный состав пара у, т. е. фактическое содержание в нем НК.
Составы пара у *, равновесные с жидкостью в каждом сечении
колонны, выражаются линией равновесия. Отрезки ординат ме-
жду линией равновесия и рабочей линией, равные разности
(у*— У)> выражают движущую силу процесса массопередачи,
а именно, процесса испарения НК из жидкости.
43*
6»
676
Гл. 19. Ректификация
Процесс ректификации может итти лишь в том случае, если
движущая сила положительна, т. е. у* > у. Поэтому положение
рабочей линии АВ"'С, при котором она выходит за пределы ли-
нии равновесия (т. е. на некотором участке у*<у), практически
невозможно. Крайним положением рабочей линии будет линия
АВ"С в положении, когда она соприкасается с линией равно-
весия в одной точке В". В этом случае ректификация возможна,
но так как в точке В" движущая сила равна нулю (у = у*), то
Рис. 19-11. Графическое определение минимального флегмового числа.
для проведения процесса потребуется колонна бесконечно боль-
шой высоты.
Положение рабочей линии АВ"С соответствует минимально-
му флегмовому числу Rmln. Из рассмотрения треугольника В”CD
видно, что длина отрезка CD равна (хр— ур), а длина отрезка
B"D равна (хР — xF\ Таким образом, тангенс угла наклона ра-
бочей линии составляет:
tga =
ХР~УР
Хр — Хр
В то же время (см. стр. 674)
tga =
^mln
^mln “1“ 1
Таким образом
3. Материальный и тепловой баланс процесса ректификации 677
Решая это уравнение относительно 7?min, находим:
р — _ хР~Ур (19-16)
•r\mln yF-xF
В этом уравнении yF—состав пара, равновесный с xF.
Величину /?mJn можно определить и графически (см.
рис. 19-11, слева). Для этого проводят прямую СЕ через точку
В" пересечения вертикали xF с линией равновесия и через точку
С на диагонали, соответствующую составу дистиллята хр. Изме-
рив отрезок Ьо, отсекаемый прямой СЕ на оси ординат, находят
fenin по формуле (19-14), откуда:
Лл»п = 4е~1 (19-17)
и0
Линия равновесия для некоторых смесей имеет такую форму,
что прямая СЕ на участке СВ" располагается выше линии рав-
новесия (рис. 19-11, справа). В этом случае прямую СЕ надо
провести через точку С как касательную к линии равновесия.
Минимальное флегмовое число соответствует, как указыва-
лось выше, бесконечно высокой колонне. С увеличением флег-
мового числа движущая сила массопередачи возрастает и тре-
буемая высота колонны уменьшается. При R = со нужна ко-
лонна наименьшей высоты. Таким образом, в отношении разме-
ров колонны выгодно работать с большим флегмовым числом.
В то же время с увеличением В возрастает расход тепла. Наивы-
годнейшее флегмовое число, при котором общие затраты мини-
мальны, может быть найдено путем технико-экономических рас-
четов. Обычно принимают значения рабочего флегмового числа
от /? = l,2/?min до R = 2,5/?mln.
Отношение рабочего флегмового числа к минимальному на-
зывается коэффициентом, избытка флегмы.
Пример 19-3. Для условий примера 19-2 (стр. 675) определить мини-
мальное флегмовое число.
Решение. На рис. 19-12 построена (по данным Приложения X) диа-
грамма равновесия для смеси метанол — вода при атмосферном давлении.
Выражая при помощи уравнения (16-6) составы исходной смеси х р, дистил-
лята хр и остатка xw в молярных долях, получим-
х =0,273; х = 0,973; х = 0,0085
Г r w
На У — х-диаграмме (рис 19-12) наносим точку А с координатами
xw ~?w~ 0,0085 и точку С с координатами хр == ур = 0,973; на кривой
равновесия наносим точку В' с абсциссой хр = 0,273. Йз точки С проводим
678
Гл. 19. Ректификация
Рж. 19-12. Построение рабочей линии и определение числа
единиц переноса (к примерам 19-3, 19-4 и 19-6).
3. Материальный и тепловой баланс процесса ректификации
679
через точку В' прямую до пересечения с осью ординат, отсекая на ней от-
резок Ьо = 0,515. Минимальное флегмовое число находим по формуле (19-17):
й- = -5Ж-1=0'89
Можно найти минимальное флегмовое число и без описанного построе-
ния по формуле (19-16):
0,973-0,643
mln 0,643 — 0,273 ’
где ордината точки В' равна ур = 0,643.
Пример 19-4. Для условий примеров 19-2 и 19-3 построить рабочую ли-
нию и определить количество поднимающегося в колонне пара, количество
флегмы, а также количество стекающей жидкости в укрепляющей и исчерпы-
вающей колоннах.
Решение. Принимаем коэффициент избытка флегмы 1,4, тогда рабо-
чее флегмовое число составит:
Я = 1,4Ят1п = 1,4 • W = 1,25
Отрезок, отсекаемый рабочей линией укрепляющей колонны на оси орди-
нат диаграммы равновесия, определяем по формуле (19-14):
0,973
Ь~ 1,25+1 ~'0,43
На рис. 19-12 построены (согласно указаниям, приведенным на стр. 675)
рабочие линии СВ для укрепляющей колонны и АВ для исчерпывающей
колонны. Количество поднимающихся даров находим по формуле (19-12):
G = р (R + 1) = 1985 (1,25 + 1) = 4470 кг/ч = 1,24 кг/сек
Количество стекающей жидкости в укрепляющей колонне равно коли-
честву флегмы и по формуле (19-11) составляет:
Ф = PR — 1985 • 1,25 = 2480 кг/ч = 0,69 кг/сек
Количество стекающей жидкости в исчерпывающей колонне:
L — Ф + F = 2480 + 5000 = 7480 кг/ч = 2,08 кг/сек
По рабочей линии (рис. 19-12) определяем состав пара в точке В (0,584),
соответствующий составу исходной смеси. Находим средний молярный со-
став пара в верхней части колонны:
0,584 + 0,973 _0?8
и в нижней части колонны:
0,0085 + 0,584 Л ,
2
Средний молярный состав пара в колонне:
0,78 + 0,3 Л ,.
У ср. =----------= 0,54
По t— х—«/-диаграмме (рис. 19-12) этому составу соответствует темпе-
ратура пара 82° С.
680
Г л. 19. Ректификация
Средняя плотность пара при этих условиях и абсолютном давлении
Р = 0,98 бар (1 ат) по уравнению состояния составляет:
МР 25,6 0,98 • 105 ЛОСС . з
Рн - RT - 8314 (273 + 83) = 0,855 кг/м
где М. = 25,6 средняя молекулярная масса пара, имеющего концентрацию уСр.
[определена по формуле (16-5)];
R = 8314 дж/кмоль • град — универсальная газовая постоянная.
Объемный расход пара составляет:
п 4470
Уп = — = лосе = 5220 м3/ч = 1,45 м3/сек
Рп
Плотность жидкости в верхней части колонны при среднем содержании
метанола
хср .= .^-73+-g'-9ra = 0,623
находим по формуле:
Р = ?нкхср. + Рвк 0 — *ср.) = 800 • °’623 + 1000 С1 — °>623) = 877 кг!м3
где рнк и рвк — плотность НК (метанола) и ВК (воды).
Аналогично плотность жидкости в нижней части колонны (при
*ср. = 0,14) р = 973 кг/л*3. Средняя плотность жидкости в колонне:
973 + 877 . 3
рж =--------------= 925 кг/м3
Объемный расход жидкости в верхней части колонны составляет:
Уж = = 2,83 м3/ч = 0,000785 м3/сек
Oil
Объемный расход жидкости в нижней части колонны равен:
Уж = = 7,7 м3/ч = 0,00214 м3/сек
UIO
Тепловой баланс
Составим уравнение теплового баланса ректификационной
колонны согласно схеме, изображенной на рис. 19-13:
Расход тепла
С паром, выходящим
из аппарата .......
С остатком ........
Потери в окружающую
среду .............
Приход тепла
Подводится в кубе . .
Со смесью...........
С флегмой...........
Q
Ф/Ф
G/
Wi
w
Qn
Таким образом:
Q +* Fip^\- Ф/ф = GI —|- Wiyy -j- Qn
(19-18)
где W, Ф — количества остатка и флегмы, кмоль/сек;
G — количество уходящих из аппарата паров, кмоль/сек;
/ — энтальпия паров, дж/кмоль;
ip, iw, 1ф—энтальпия смеси, остатка и флегмы, дж/кмоль.
3. Материальный и тепловой баланс процесса ректификации 681
Подставляя в уравнение (19-18) значения G и F по форму-
лам (19-12) и (19-7) и решая его относительно Q, получим:
Q = PR (/ - /Ф) + Р (/ - iF) + W (iw - iF) + Qn (19-19)
В этом уравнении член PR(I—/ф) представляет собой рас-
ход тепла на испарение флегмы, член Р(1 — iF)— расход тепла
на испарение дистиллята, член
^(/^— — расход тепла на
нагревание остатка.
Энтальпию жидкостей /ф, iw и
iF можно выразить в виде произ-
ведений соответствующих молярных
теплоемкостей (в дж/кмоль • град)
на температуры жидкостей:
1ф = Сф1ф', iw=cwtw\ ip — с pt f
Обычно в колонну поступает
флегма при температуре ее кипения,
тогда энтальпия пара составляет:
I~~ /ф -J- Г ф
где гф — теплота испарения флег-
мы, дж!кмоль.
При этом разность/ — /ф = гф и
член PR(I — гф)в уравнении (19-19)
может быть заменен на PRr*.
Рис. 19-13. Схема теплового
баланса ректификационной
колонны:
1—ректификационная колонна;
2 — куб; 3— дефлегматор.
В справочных таблицах обычно приводятся значения тепло-
емкостей и теплот испарения только для чистых веществ, поэто-
му для смесей пользуются правилом смешения:
с — ~I- ^вк 0 -*0
r = rHK.«+rBK(l-x)
где снк и £вк—молярные теплоемкости компонентов НК и
В К, дж/кмоль • град;
гнк и гвк — теплоты испарения НК и ВК, дж/кмоль;
х— молярная доля НК.
Приведенные выше расчеты могут производиться и с весо-
выми количествами, если энтальпия и теплоты испарения выра-
жены в дж/кг, удельные теплоемкости — в дж/кг • град, а со-
держание НК — в весовых долях.
В дефлегматоре происходит частичная или полная конден-
сация паров, поступающих из колонны.
682
Гл 19 Ректификация
При частичной конденсации в дефлегматоре конденсируется
лишь часть паров, требуемая для образования флегмы, а ос-
тальная часть (дистиллят) отводится из дефлегматора в паро-
образном состоянии. Тепловая нагруака дефлегматора в этом
случае составляет:
Рдеф. = Ф (/ - /ф) = РЯгФ (19-20)
При полной конденсации в дефлегматоре конденсируются
все поступающие в него пары. Часть полученного конденсата
возвращается в колонну в виде флегмы, другая часть отводится
в виде дистиллята Тепловая нагрузка дефлегматора при полной
конденсации составляет:
Рдеф =(Ф + /Э)(/-/ф) = /Э(/?+1)Гф (19-21)
Пример 19-5. Определить расход тепла для ректификации смеси мета-
нол — вода в условиях примеров 19-2 и 19 4 и найти тепловую нагрузку де-
флегматора, если в колонну смесь вводится при температуре ее кипения,
а в дефлегматоре происходит полная конденсация поступающих в него паров
Решение По данным Приложения X на рис 19 12 (внизу) построена
диаграмма t — х— у, по которой находим температуру кипения исходной
смеси (хF — 0,273) tp^ 79° С, температуру кипения дистиллята {хр = 0,973)
Zps65°C и температуру кипения остатка (х^, = 0,0085) ^ = 99° С
Для расчета удельных теплоемкостей и теплот испарения смесей 'мета-
нола с водой принимаем следующие значения удельных теплоемкостей и
теплот испарения чистых веществ (СНзОН и НгО)
для метанола
снк = 2680 дж)кг • град (0,64 ккал)кг • град)
гнк = 1090" Ю3 дж)кг (260 ккал)кг)
для воды
евк — 4190 дж!кг град (1 ккал[кг • град)
гвк — 2340 • 103 дж!кг (560 ккал!кг)
Расчет ведем на весовые количества
для дистиллята (флегмы) при ар = 0,985
Сф=2680 0,985 + 4190(1—0,985)^2680 дж/кг-град (0,64 ккал}кг • град)
гф = 1090 • 103 • 0,985 + 2340 • 103 (1 — 0,985) = 1100 • 103 дж!кг (264 ккал/кг)
для остатка при 0,015
cw— 2680 - 0,015 + 4190(1—0,015)^4140 дж/кг > град (0,99 ккал!кг • град)
для исходной смеси при ар = 0,4
ср = 2680 • 0,4 + 4190 (1 — 0,4) = 3580 дж!кг • град (0,856 ккал/кг • град)
Определяем расход тепла на испарение флегмы
Q* = РКГф = 0,552 1,25 • 1100 • 103 = 760000 вт (655000 ккал[ч)
4 Схемы ректификационных установок
683
Находим расход тепла на испарение дистиллята
<?д = р (Гф + Сф tp - Ср tp) = 0,552 (1100 • 103 +
+ 2680 • 65 — 3580 • 79) = 548000 вт (472000 ккал/ч)
Вычисляем расход тепла на нагревание остатка
<?»„ = w - СГ(р) = °'838 <4140 •99 - 3580 •79) =
= 110000 вт (94500 ккал/ч)
Общий расход тепла в кубе (без учета потерь в окружающую среду)
составляет
Q = 760000 + 548000 + 110000 1420000 вт (1222000 ккал/ч)
С учетом 5% потерь общий расход тепла
Q == 1,05 • 1420000^1490000 вт (1280000 ккал/ч)
Тепловую нагрузку дефлегматора определяем по формуле (19-21)*
<?Деф. = /> (Я + 0 гф = 0,552 (1,25 + 1) Н00 * Ю3 ==
= 1370000 вт (1180000 ккал/ч)
По найденным Q и 0деф. можно обычными способами расчета опреде-
лить расход пара в кубе и воды в дефлегматоре
4. Схемы ректификационных установок
Ректификация двойных смесей
Ректификацию можно проводить периодическим или непре-
рывным способом.
При периодической ректификации (рис. 19-14) смесь загру-
жается в куб 1 и нагревается паром, проходящим через змее-
вик 2. После того как смесь в кубе закипит, образующиеся пары
начинают поступать в колонну 3, откуда по трубе 4 направляют-
ся в дефлегматор 5, где конденсируются. Часть конденсата
(флегма) по трубе 6 стекает обратно в колонну, другая часть
(дистиллят) по трубе 7 поступает в холодильник 8 и отсюда
отводится в приемник дистиллята.
При таком процессе в колонне происходит укрепление паров,
а в кубе — исчерпывание смеси. Исчерпывание продолжается в
течение некоторого времени; когда достигается требуемый со-
став смеси, операция заканчивается и остаток отводится из куба.
По мере протекания процесса условия работы установки по-
степенно изменяются. В начале процесса в колонну поступают
из куба пары, богатые НК. В этот период нужно сравнительно
небольшое количество флегмы, чтобы выделить из паров содер-
жащийся в них ВК. В ходе процесса выходящие из куба пары
будут все более обогащаться ВК, и для выделения его из паров
684
Гл. 19. Ректификация
количество флегмы должно быть увеличено. Если же количество
флегмы оставить постоянным, будет возрастать содержание ВК
в дистилляте.
Остаток
Рис. 19-14. Схема рек-
тификационной установ-
ки периодического дей-
ствия:
1—куб; 2—змеевик; 3—ко-
лонна; 4 — труба для отвода
паров из колонны; 5 — дефлег-
матор; б —труба для возврата
флегмы; 7 —труба для отбора
дистиллята; 8 — холодильник.
Рис. 19-15. Схема ректификационной
установки непрерывного действия:
/ — теплообменник; 2 — укрепляющая колонна;
3 —исчерпывающая колонна; 4 — кипятильник;
5 —дефлегматор; 6— распределительный ста-
кан; 7 —холодильник; 8 — вентиль, регулирую-
щий отбор дистиллята.
При непрерывной ректификации )рис. 19-1&) смесь подается
в среднюю часть колонны через теплообменник обогреваемый
остатком или паром. В верхней части колонны Я. расположен-
ной выше точки ввода смеси, происходит укрепление паров.
В нижней части колонны 3, расположенной ниже точки ввода
смеси, происходит исчерпывание жидкости. Из исчерпывающей
колонны жидкость стекает в кипятильник (куб) обогреваемый
паром. В кипятильнике образуются пары, поднимающиеся вверх
по колонне; остаток непрерывно отводится из куба. Пары, вы-
ходящие из укрепляющей части колонны, поступают в дефлег-
матор 5, откуда флегма возвращается в колонну, а дистиллят
направляется в холодильник 7 (см. также стр. 686).
Преимущества непрерывной ректификации по сравнению с
периодической:
1) условия работы установки не изменяются в ходе процес-
са, что позволяет установить точный режим, упрощает обслужи-
вание и облегчает автоматизацию процесса;
4. Схемы ректификационных установок
685
2) отсутствуют простои между операциями, что приводит к
повышению производительности установки;
3) расход тепла меньше, причем возможно использование,
тепла остатка на подогрев исходной смеси в теплообменнике.
Благодаря перечисленным преимуществам в производствах
крупного масштаба применяют главным образом непрерывную
ректификацию, периодические процессы ректификации находят
применение лишь в не-
больших, неравномерно
работающих производст-
вах. ........
Ректификация
мно гок о мтгтттгетгттГ ых
смесей
Разделение многокомпо-
нентных смесей, как и двой-
ных, производится периодиче-
ски или непрерывно.
Периодическая ректифика-
ция проводится в одной колон-
не по схеме, показанной на
рис. 19-14, путем последова-
тельного ’ (по времени) отбора
отдельных фракций. При этом
наряду с фракциями, содержа-
щими чистые продукты, полу-
чается большое количество
промежуточных фракций, со-
держащих смеси различных
продуктов. Промежуточные
фракции собирают отдельно и
присоединяют к смеси, подавае-
мой на следующую операцию,
или по мере накопления -фРак'
ций подвергают их отдельной
ректификации, что сильно ус-
ложняет ведение процесса.
Для непрерывной ректифи-
кации многокомпонентных сме-
сей применяют установки, со-
стоящие из нескольких колонн.
В каждой колонне отделяется
одна из составных частей сме-
Рис. 19-16. Схемы разделения тройной
смеси:
1, 2—ректификационные колонны.
си или же смесь вначале раз-
деляется на более простые по составу смеси, из которых в последующих по
ходу процесса колоннах выделяются отдельные компоненты.
Количество колонн в установке должно быть на единицу меньше числа
компонентов в исходной смеси. Так, для разделения тройной смеси требуются
две колонны, причем процесс можно вести двумя способами. По одному спо-
собу (рис 19-16, а) в первой колонне 1 отгоняется НК, а остаток, состоящий
из смеси СК (компонент со средней температурой кипения) и ВК, передается
во вторую колонну 2, где происходит разделение остатка. По другому спо-
686
Гл. 19. Ректификация
собу (рис. 19-16,6) в первой колонне 1 отгоняется смесь СК и НК, которая
затем разделяется на второй колонне 2, а ВК переходит в остаток первой
колонны.
Ректификация под различным
давлением
В зависимости от температуры кипения разделяемых жидко-
стей ректификацию проводят под различным давлением. При
температурах кипения от 30 до 150° С обычно применяют ректи-
фикацию под атмосферным давлением. Ректификацию в ваку-
уме применяют при разделении высококипящих жидкостей для
снижения температур их кипения. Ректификацию под давлением
проводят при разделении жидкостей с низкой температурой ки-
пения, в частности при разделении сжиженных газов.
Давление в кубе всегда больше давления наверху колонны
на величину ее гидравлического сопротивления. Это имеет осо-
бенно большое значение для процесса ректификации, проводи-
мого в вакууме, так как в случае большого гидравлического
сопротивления колонны разрежение в кубе может оказаться не-
достаточным даже при очень глубоком вакууме наверху ко-
лонны. Поэтому гидравлическое сопротивление колони, рабо-
тающих при разрежении, должно быть возможно меньше.
Дефлегмация
Как указывалось (стр. 671), дефлегмацию ведут при частич-
ной или полной конденсации паров.
При частичной конденсации (рис. 19-17, а) в дефлегматоре
1 конденсируется часть паров, требуемая для образования флег-
мы. Остальная часть паров поступает в конденсатор 2, где об-
разует дистиллят, который затем охлаждается в холодильнике 3.
При частичной конденсации происходит некоторое обогащение
пара НК и получается'дистиллят с меньшим содержанием ВК,
чем в парах, выходящих из колонны. Частичная конденсация при-
меняется при простой перегонке (стр. 703). При ректификации
частичная конденсация также применяется часто, но в этом слу-
чае она не дает особых преимуществ, так как укрепляющее дей-
ствие дефлегматора незначительно.
При полной конденсации (см. рис. 19-15) поступающие из
колонны пары полностью конденсируются в дефлегматоре 5.
Конденсат стекает в стакан 6, где делится на две части. Одна
часть стекает в холодильник 7 и далее в сборник дистиллята.
Другая часть вытекает из стакана через переливную трубу и воз-
вращается в колонну в качестве флегмы. Количество отбирае-
мого дистиллята регулируется при помощи вентиля 5.
4 Схемы ректификационных установок
687
По другой схеме полной конденсации (рис. 19-17,6) дефлег-
матор 1 располагают ниже верха колонны. Конденсат отво-
дится в сборник 4. Флегма подается на орошение колонны насо-
сом 5. Дистиллят отбирается из сборника 4 или из напорной ли-
нии насоса.
Рис. 19-17. Схемы дефлегмации:
а —при частичной конденсации; б— при полной конденсации
(с подачей флегмы насосом), / — дефлегматор; 2—конден-
сатор; 3—холодильник; 4 — сборник; 5 — насос; 6 — трубка.
Трубка 6 сообщается с атмосферой (непосредственно или че-
рез гидравлический затвор) или, при ректификации в вакууме,
присоединяется к вакуум-насосу.
Основное преимущество полной конденсации заключается в
возможности более простого и точного регулирования процесса.
Использование тепла при ректификации
При ректификации тепло расходуется на испарение флегмы
и дистиллята, а также на нагревание остатка (стр. 681). Тепло
испарения отводится с охлаждающей водой в дефлегматоре, теп-
ло остатка теряется вместе с ним или отводится в холодильнике,
в котором обычно охлаждают остаток.
При непрерывной ректификации тепло остатка может быть
использовано для предварительного подогрева исходной смеси
до температуры кипения. Для этого горячий остаток пропускают
через теплообменник (см. рис. 19-15), в котором подогревается
смесь, поступающая на ректификацию. Можно также охлаждать
исходной смесью дефлегматор; нагретая в дефлегматоре смесь
поступает затем в теплообменник, где подогревается остатком.
Для подогрева смеси можно использовать и конденсат водяного
пара, обогревающего кипятильник колонны.
688
Гл. 19. Ректификация
В установках, состоящих из нескольких колонн, пары, выходящие из
одной колонны, могут быть использованы для обогрева кипятильника другой
колонны, который, таким образом, будет одновременно являться дефлегмато-
ром первой колонны. Для этого ректификацию в первой колонне надо вести
при повышенном давлении, чтобы выходящие из этой колонны пары имели
температуру более высокую, чем температура кипения жидкости в кипятиль-
нике второй колонны.
5. Устройство ректификационных аппаратов
Для ректификации применяют почти исключительно аппа-
раты колонного типа — насадочные и барботажные ректифика-
ционные колонны. По устройству они не отличаются от абсор-
беров аналогичного типа.
Насадочные ректификационные колонны. В таких колоннах обычно
применяется кольцевая насадка. Наиболее распространены кольца размером
25 X 25 X 3 мм. Отмеченные на стр. 599 недостатки насадочных абсорберов
несущественны при ректификации, так как в этом процессе не требуется
отвода тепла, а количество орошающей жидкости обычно достаточно велико.
В укрепляющей колонне количество жидкости меньше количества поднимаю-
щихся паров на количество отводимого дистиллята, в исчерпывающей же
колонне количество жидкости больше, чем в укрепляющей, на количество
вводимой смеси.
Неравномерное распределение жидкости по сечению колонны может при-
вести к недостаточно четкому разделению компонентов, особенно при боль-
шом диаметре колонны. Низкое гидравлическое сопротивление насадочных
колонн существенно лишь при ректификации в вакууме (стр. 686).
Насадочные ректификационные колонны применяются главным образом
небольшого диаметра (примерно до 1 л) а также при ректификации в ва-
кууме и для разделения химически агрессивных веществ.
Барботажные ректификационные колонны применяются с колпачковыми,
ситчатыми и провальными тарелками. Значительное сопротивление барботаж-
ных колонн при ректификации обычно несущественно (кроме процесса рек-
тификации в вакууме), так как вызывает лишь некоторое повышение давле-
ния и, следовательно, температуры кипения в нижней части колонны и не
связано с дополнительным расходом энергии.
Барботажные колонны являются наиболее распространенными ректифи-
кационными аппаратами благодаря возможности разделения в них компо-
нентов с любой степенью четкости Чаще всего применяются колонны с кол-
пачковыми тарелками. Колонны с ситчатыми и провальными тарелками при-
меняются при разделении незагрязненных жидкостей в установках, работаю-
щих с постоянной нагрузкой.
Теплообменные устройства ректификационных колонн (кубы и дефлегма-
торы) Куб периодически действующей колонны обычно выполняют в виде
вертикального или горизонтального котла с змеевиком для обогрева Емкость
куба должна быть рассчитана на количество всей смеси, перегоняемой за
одну операцйю.
В колоннах непрерывного действия куб служит лишь для испарения
части стекающей вниз жидкости и является, таким образом, кипятильником.
По устройству такие кипятильники сходны с кипятильниками выпарных ап-
паратов. При небольших поверхностях теплообмена применяют кипятильники
с обогревом при помощи змеевика или в виде горизонтальной трубчатки,
пронизывающей нижнюю часть колонны, причем греющий пар пропускается
по трубам (рис. 19-18, а).
6 Эксплуатация ректификационных установок
689
При больших поверхностях теплообмена применяют выносные кубы
с естественной циркуляцией теплоносителя (рис. 19-18,6), аналогичные по
устройству выпарным аппаратам с выносным кипятильником.
Дефлегматоры выполняются обычно в виде вертикальных или горизон-
тальных кожухотрубных теплообменников. Чаще всего вода проходит по тру-
Рис. 19-18. Устройство кипятильников рек-
тификационных колонн:
а —горизонтальная трубчатка; б— выносной кипя-
тильник.
бам, пары движутся в межтрубном пространстве. Иногда пары пропускают
по трубам, а воду — в межтрубном пространстве; в этом случае очистка
труб от накипи затруднительна.
6. Эксплуатация ректификационных установок
В работающей ректификационной колонне число тарелок или высота на-
садки — постоянные величины. Основными условиями достижения требуемой
степени разделения компонентов при ректификации являются: подвод соот-
ветствующего количества тепла в куб колонны и подача на ее орошение
необходимого количества флегмы. Оба эти условия неразрывно связаны друг
с другом. Изменяя подвод тепла в кубе и подачу флегмы, можно регулиро-
вать работу колонны.
Обычно степень разделения компонентов контролируется по температу-
рам в нижней и верхней частях колонны. Температура внизу колонны должна
соответствовать температуре кипения остатка, температура наверху ко-
лонны— температуре кипения дистиллята. Наряду с этим применяют и дру-
гие методы контроля (определение плотности, определение показателя пре-
ломления, химический анализ и др.).
Если, например, содержание ВК в дистилляте велико (температура на-
верху колонны выше нормы), необходимо увеличить подачу флегмы в ко-
лонну. При этом, однако, прежнего количества подводимого тепла в кубе
будет недостаточно и избыток флегмы не испарится в кубе, а перейдет
в остаток, в котором, таким образом, повысится содержание НК. Поэтому
рдновременно с увеличением подачи флегмы надо увеличить подвод тепла,
чтобы температура внизу колонны не стала ниже нормы.
Подачу флегмы регулируют изменением отбора дистиллята (стр. 686):
при частичной конденсации путем регулирования количества подаваемой
в дефлегматор воды, при полной конденсации при помощи вентиля на линии
отбора дистиллята. Подвод тепла в кубе регулируется изменением подачи
греющего пара.
Регулирование процесса ректификации производится также путем изме-
нения количества и состава подаваемой смеси При изменении количества
смеси меняется производительность установки и соответственно должны быть
отрегулированы подвод тепла в кубе и подача флегмы. Существенное влия-
ние оказывает изменение состава смеси. Если, например, содержание НК
в смеси уменьшилось, то уменьшится и его содержание в дистилляте; следо-
44 Зак 546,
690
Гл. 19 Ректификация
вательно, температура вверху колонны повысится Для сохранения требуе-
мого состава дистиллята надо уменьшить его отбор.
Отбор остатка регулируется обычно так, чтобы уровень жидкости в кубе
был постоянным. Если, вследствие увеличения подачи смеси или увеличения
содержания в ней ВК, уровень жидкости в кубе повышается, следует уве-
личить отбор остатка.
В колоннах непрерывного действия наиболее целесообразно применять
автоматическое регулирование, например, по следующей схеме
1) отбор дистиллята управляется регулятором температуры верхней
части колонны;
2) подача пара управляется регулятором температуры нижней части ко-
лонны;
3) отбор остатка управляется регулятором уровня жидкости в кубе.
При периодической ректификации регулирование процесса производят
путем увеличения флегмового числа с таким расчетом, чтобы состав дистил-
лята не изменялся. При этом по мере протекания процесса понижается ско-
рость перегонки, т. е уменьшается количество отбираемого дистиллята. Ко-
личество тепла, подводимого в единицу времени, и количество образующихся
паров остаются почти неизменными.
7. Ректификация сжиженных газов
Рис. 19-19. Схема раз-
делительного аппарата
одинарной ректифика-
ции:
/ — теплообменник; 2 — змее-
вик; 3— вентиль; 4— колонна.
Ректификацию сжиженных газов применяют для разделения
газовых смесей на составные компоненты и проводят ее при низ-
ких температурах, достигаемых при по-
мощи холодильных циклов (стр. 545 сл.).
Наиболее распространена ректифика-
ция воздуха для разделения его на кис-
лород и азот. При разделении воздуха
применяют аппараты одинарной и двой-
ной ректификации.
Разделительный аппарат одинарной
ректификации. На рис. 19-19 ноказана
схема простого цикла с дросселирова-
нием, в котором применен разделитель-
ный аппарат одинарной ректификации.
Аппарат представляет собой обычную
ректификационную колонну, куб кото-
рой обогревается сжатым воздухом, а ис-
ходная смесь подается на верх колонны.
Сжатый и охлажденный в теплообмен-
нике 1 воздух проходит по змеевику 2 и,
отдавая тепло кипящему в кубе жидкому кислороду, частично
конденсируется. Затем воздух дросселируется в вентиле 3 до
абсолютного давления 1,2—1,3 ат и подается на верх колонны 4.
В результате ректификации в кубе собирается ВК. (кислород),
из верхней части колонны отводится НК (азот).
В описанной установке получается чистый кислород, но азот
содержит до 7—10% кислорода, так как уходящий из колонны
7. Ректификация сжиженных газов
691
9''
пар находится в равновесии с поступающим в колонну жидким
воздухом. Это приводит к большим потерям кислорода: исполь-
зуется лишь 2/з кислорода, содержащегося в разделяемом воз-
духе, а !/з уходит с азотом, загрязняя его.
Разделительный аппарат двойной ректификации. Аппараты
двойной ректификации состоят из двух колонн (верхней и ниж-
ней), орошаемых азотной флегмой, со-
держащей ~95% N2. Флегма получается
в конденсаторе, служащем одновремен-
но кубом верхней колонны, в котором
кипит жидкий кислород. Таким образом,
тепло конденсации азотной флегмы пе-
редается кипящему кислороду. Посколь-
ку азот является НК, температуру его
кипения надо повысить, чтобы она пре-
вышала температуру кипения кислорода
в кубе верхней колонны. Для этого ниж-
няя колонна должна работать при
более высоком давлении, чем верх-
няя.
Чтобы повысить температуру кипе-
ния азота до температуры кипения кис-
лорода при атмосферном давлении
(—183° С), требуется абсолютное давле-
ние 3,6 ат. Практически абсолютное да-
вление в верхней колонне составляет
1,4—1,6 ат (это соответствует темпера-
туре кипения кислорода —180° С); в
нижней колонне абсолютное давление
примерно 6 ат (что соответствует темпе-
ратуре кипения азота —175° С). Таким
образом, разность температур конденси-
рующегося азота и кипящего кислорода,
необходимая для работы конденсатора,
составляет ~5°С.
На рис. 19-20 показана схема разделительного аппарата
двойной ректификации. Сжатый и охлажденный в теплообмен-
нике воздух, проходя по змеевику 1, конденсируется. Тепло
конденсации отводится жидкостью, кипящей в кубе 2. Из
змеевика воздух поступает в вентиль 3, где дросселируется до
давления ~6 ат, а затем идет в нижнюю колонну 4. В ре-
зультате ректификации, происходящей в нижней колонне, в
кубе 2 собирается обогащенная кислородом жидкость
(40—60% О2), наверху этой колонны — пары азота, содержа-
щие ~95% N2.
Рис. 19-20. Схема раз-
делительного аппарата
\двойной ректификации:
/—змеевик; 2 —куб; 3, 6,
9 — вентили; 4 — нижняя ко-
лонна, 5— карман; 7—конден-
сатор; 8~ верхняя колонна.
44*
692
Гл 19 Ректификация
Пары азота конденсируются в трубах конденсатора 7 за
счет испарения кислорода в межтрубном пространстве. Часть
полученной в конденсаторе азотной флегмы стекает в нижнюю
колонну, а часть собирается в кармане 5
В верхней колонне 8 производится ректификация жидкости,
собирающейся в кубе нижней колонны Эта жидкость подается
в верхнюю колонну через вентиль 6, сверху колонна орошается
азотной флегмой, поступающей из кармана 5 через вентиль 9.
В результате ректификации, происходящей в верхней колон-
не, сверху из нее выходит почти чистый газообразный азот, а в
кубе собирается чистый жидкий кислород, часть которого отво-
дится в жидком виде, а часть испаряется (за счет конденсации
азота в трубах конденсатора 7) и отводится в газообразном со-
стоянии.
В аппарате двойной ректификации получают кислород, со-
держащий не менее 99,3% О2, и азот, содержащий ~98% N2.
8. Расчет ректификационных колонн
Непрерывная ректификация
Расчет ректификационных колонн производится аналогично
расчету абсорберов При расчете следует иметь в виду, что
вследствие изменения температуры объем пара по высоте ко-
лонны изменяется при неизменном количестве пара (в кмоль).
Кроме того, количество стекающей жидкости в нижней части
колонны больше, чем в верхней.
В процессе взаимодействия пара и жидкости протекают од-
новременно два процесса массопередачи Первый процесс — ис-
парение НК из жидкой фазы и переход в паровую фазу, при-
чем содержание НК в паровой фазе у ниже равновесного со-
держания у*', движущая сила этого процесса равна (у* — у).
""Второй процесс — конденсация ВК из паровой фазы и переход
его в жидкую фазу, причем содержание ВК в паровой фазе
(1 —у) выше равновесного (1 — у*)-, движущая сила этого про-
цесса равна (1 — у) — (1 — у*) — у* — у.
Таким образом, движущая сила обоих процессов одинакова
и равна (у* — у)-, эта движущая сила изображается отрезком
вертикали между линией равновесия и рабочей линией и выра-
жается разностью концентраций в молярных долях. В соответ-
ствии с выражением составов в молярных долях (вместо относи-
тельных весовых составов) число единиц переноса определяется
уравнением:
где ЛСр выражено в молярных долях.
8 Расчет ректификационных колонн
693
Расчет процесса массопередачи при ректификации услож-
няется тем, что коэффициент массопередачи обычно значитель-
но изменяется по высоте колонны, увеличиваясь по направлению
к верху колонны. В соответствии с характером линии равнове-
сия процесса ректификации (см. рис. 19-2, стр. 661) тангенс
k угла наклона к ней касательной уменьшается с возрастанием
содержания НК в смеси, а уменьшение величины k согласно
уравнению (16-38) приведет к повышению коэффициента массо-
передачи К.
Расчет насадочных ректификационных колонн. Для насадоч-
ных колонн при скоростях паров ниже скоростей, соответствую-
щих подвисанию жидкости, высоту единицы переноса опреде-
ляют по формулам, приведенным на стр. 612. Наибольшее зна-
чение коэффициента массопередачи достигается при оптималь-
ной скорости паров, которая соответствует началу подвисания и
может быть определена по уравнению (17-16). Оптимальная ско-
рость изменяется по высоте колонны в соответствии с измене-
нием массовых скоростей пара и жидкости и их плотности.
Для определения диаметра колонны надо найти минималь-
ное значение оптимальной скорости Обычно она имеет мини-
мальное значение в нижней части исчерпывающей колонны. Од-
нако при большой молекулярной массе НК, а также при ректи-
фикации в вакууме, оптимальная скорость может иметь мини-
мальнц^значение в укрепляющей колонне или в верхней части
исчерпывающей колонны Поэтому следует определять опти-
мальную скорость в нескольких точках по высоте колонны
Высоту единицы переноса для колонн, работающих в режиме подвиса-
ния, можно определить по формуле
h = 28,6с?экв Re°r’2 (Рг;)0’65 м (19-22)*
где с?экв—эквивалентный диаметр насадки, м [см формулу (6-100)1,
Rer и Ргг — критерии Рейнольдса и Прандтля для пара
Расчет барботажных ректификационных колонн. Число единиц пере-
носа п0 на тарелку определяется по уравнению (17 37), причем числа единиц
переноса в паровой фазе п\ и в жидкой фазе для колпачковых и ситчатых
тарелок можно найти по формулам
Г) тр е
ni = ^(O>79Rer + nooo)lg.^.
п2 = 38 000^ £>ж(Рг')0,62
• 1/ ж \ ж/
у ж
(19-23)*
(19-24)*
* Эти уравнения получены преобразованием формул, приведенных
в книге А Н ПлановскогоиП И Николаева, Процессы и аппа-
раты химической и нефтехимической технологии, Гостоптехиздат, 1960.
694
Гл. 19. Ректификация
Обозначения в формулах (19-23) и (19-24):
£>г и — коэффициенты диффузии пара и жидкости, м2/сек,
w — скорость паров в свободном сечении, м/сек-,
Rer— критерий Рейнольдса для пара, рассчитанный по скорости
пара w в свободном сечении (причем определяющий раз-
мер 1=1 м);
Т—средняя абсолютная температура паров, °К;
Р— абсолютное давление в колонне, am-,
Ро — давление при нормальных условиях (Ро = 1 <w);
5Т— рабочая площадь тарелки, м2-,
S — площадь сечения колонны, м2-,
Уж—объемный расход жидкости, м3/сек-,
Ргж— диффузионный критерий Прандтля для жидкости.
Зная «о, находят по формуле (17-45) Е, представляющий собой в данном
случае коэффициент обогащения, т. е. отношение изменения молярной кон-
центрации НК на тарелке к изменению молярной концентрации этого компо-
нента, необходимому для достижения равновесия между паром и жидкостью
на тарелке. Число тарелок определяют графически, как описано на стр. 626.
Пример 19-6. Рассчитать насадочную ректификационную колонну непре-
рывного действия, работающую в режиме подвисания и предназначенную для
разделения смеси метанол—вода (см. пример 19-2).
Определение оптимальной скорости пара. Вследствие
большой разницы между количествами жидкости в исчерпывающей и укре-
пляющей колоннах, расчет ведем для каждой из этих колонн (по средним
составам, найденным в примере 19-4), учитывая, что колонны будут различ-
ного диаметра. Расчет ведется аналогично расчету в примере 17-4 (стр. 611).
Принимаем насадку из колец размером 15 X 15 X 2 мм (в навал)
с эквивалентным диаметром d3KB. = 0,0085 я.
Для исчерпывающей колонны:
Рж — плотность жидкости 925 кг/м3-,
рп — плотность пара 0,855 кг/м3,
рп — вязкость пара 0,11 • 10~4 н • сек/м2 (0,011 спз);
G — расход пара 1,24 кг/сек-,
L — расход жидкости 2,08 кг/сек.
По этим данным найден критерий Архимеда
Аг = 38,3 • 106
и рассчитано по формуле (17-16) значение Рег= 760, соответствующее опти-
мальной скорости w0 = 0,82 м/сек.
Аналогично для укрепляющей колонны (при L = 0,69 кг/сек и осталь-
ных величинах тех же, что для исчерпывающей колонны) определено
Re' = 1220 и Wq = 1,31 м/сек.
Определение диаметра колонны. Площадь сечения исчерпы-
вающей колонны при расходе паров 1,45 м3/сек (см. пример 19-4) и скорости
пара 0,82 м/сек составляет:
1 4Л
5 = -ОТ = 1-77
VjOZ
Соответственно диаметр колонны равен 1,5 м.
Аналогично для укрепляющей колонны найдены S = 1,11 .и2 и диа-
метр 1,2 м.
8. Расчет ректификационных колонн
695
Определение высоты единицы переноса. Находим по
формуле (16-30) диффузионный критерий Прандтля для пара при
£>г = о,27 • 10~4 м2/сек (0,097 л2/ч):
р,'__ _ 0,11 - 10________о 483
г РгРг 0,855-0,27-10-4 ’
По формуле (19-22) определяем высоту единицы переноса для исчерпы-
вающей колонны:
h = 28,6rf9KR Re°-2 (Рг'Г = 28,6 • 0,0085 - 760°’2 • 0.4830’65 = 0,57 м
□ Ко, 1 \ 1/
Аналогично для укрепляющей колонны h — 0,63 м.
Определение числа единиц переноса. Графическим мето-
дом (стр. 584) определено число единиц переноса: для исчерпывающей ко-
лонны 3,7, для укрепляющей колонны 8,3 (см. рис. 19-12).
Определение высоты насадки. Высота насадки для исчер-
пывающей колонны составляет:
3,7-0,57^2,1 м
для укрепляющей колонны:
8,3 • 0,63 5,2 м
Пример 19-7. Рассчитать ректификационную колонну непрерывного дей-
ствия с ситчатыми тарелками для разделения смеси метанол — вода (см. при-
мер 19-4, стр. 679)\
Выбор скорости пара Принимаем диаметр отверстий в та-
релке d — 0,002 м, живое сечение отверстий = 0,08 и высоту сливного по-
рога /?п = 0,025 м.
Принимая периметр (ширину) сливного порога П = 0,84 м, находим по
формуле (17-27) высоту уровня жидкости над сливным порогом в нижней
части колонны:
ДА =
( °>00214! \2/з
\ 1.85ПА? / 1,85 • 0,84 • 0,5/ ~
где —расход жидкости, равный 0,00214 м3/сек (см. пример 19-4).
Высота слоя жидкости на тарелке составляет:
Z = ha + Mi = 0,025 + 0,02 = 0,045 м
По формуле (17-21) определяем скорость пара в отверстиях, соответ-
ствующую началу равномерной работы тарелки:
w' = а~\/~ 4 • — z = °-67 Vтй ’ • °-045 = 10>8
и г С рп г 1,о2 и,ООО
где рж и Рп — соответственно 925 и 0,855 кг/м3 (см. пример 19-4);
1,82—коэффициент сопротивления С (стр. 617).
В верхней части колонны расход жидкости Ужи, следовательно, ДЛ и wG
будут меньше, т. е. найденное значение w0 = 10,8 м/сек обеспечит равномер-
ный режим работы на тарелках по всей высоте колонны. Скорость пара
в свободном сечении при — 10,8 м/сек -определяем по формуле (17-22):
iso — <?Wq = 0,08 • 10,8 = 0,86 м/сек
696,
Гл. 19. Ректификация
Принимая расстояние между тарелками Н = 0,2 м, находим по графику
на рис. 17-20 (стр. 624) предельную скорость в свободном сечении:
и'поед = 1,35 • 0,78 = 1,05 м/сек (при = 0,925 • 10~3)
F \ Рж 925 /
Принимаем рабочую скорость w = 0,9депреД1 = 0,9 • 1,05 = 0,94 м/сек. Эта
величина выше w', благодаря чему обеспечивается равномерный режим ра-
боты тарелок.
Определение диаметра колонны. Площадь сечения колонны
рассчитываем по формуле (17-19) при Vn = 1,45 м3/сек (см. пример 19-4):
1 45
s=w = 1'54-“2
Соответственно диаметр колонны D = 1,4 м.
Проверка принятого расстояния между тарелками.
При сопротивлении тарелки Др = 450 н/м2 (см. пример 17-6, стр. 620) нахо-
дим по формуле (17-44):
4 чп
0,2 > 1,8 - ” 0. или 0,2 > 0,09
925 • 9,о 1
Следовательно, принятое расстояние Н = 0,2 м достаточно для создания
гидравлического затвора.
Определение числа единиц переноса на тарелку для
паровой фазы. При р-г = 0,11 • 10~4 н-сек/м2 (0,011 спз) и рг =0,855кг/м?
критерий Рейнольдса для пара составляет:
= = 0,94.1-0,855 = 72 500
Нт о.н • кг4
Принимая отношение периметра переливного порога к диаметру ко-
П
лонны -р- = 0,6, находим центральный угол сегмента, занятого переливным
устройством:
s,"4 = 7> = 0’6
0ТКУДа 74 Я"
а = 73,о
Площадь, занятая сливным устройством, равна:
_ D2(r.a . \ 1,42 /3,14-73,8 . _„QO\ nnQ1 _
•^слив. — g у|80 $ п / — 8 \ 180 $ п 73,8 у » 0,081 м
Рабочая площадь тарелки составляет:
ST = S — 2$слив. = 1,54 — 2 • 0,081 = 1,38 м2
По формуле (19-23) находим число единиц переноса на тарелку при
Dr=0,27-10~4 м2/сек (0,097 м2/ч) и средней температуре пара 82°С (см.
пример 19-4):
Г> ТР 9
и. = (0,79 Rer + 11 000)
0,27-10"4 273 4-82 1,38
711 = —0Я------(0’79 • 72 500 + 11 000) —73 * = 2,3
8. Расчет ректификационных колонн
697
Определение числа единиц переноса на тарелку для
Жидкой фазы. При = 0,0036 • 10-6 м2]сек (0,13-Ю”4 м21ч),
Рж = 925 кг]м? и Н-ж — 0,44 • 10~3 н-сек1м2 (0,44 спз) находим по фор-
муле (16-30) критерий Прандтля для жидкости:
Ргж = —=-------------°’44-10 3 = 133
РжОж 925 • 0,0036 • 10“6
Пользуясь значениями объемных
мер 19-4), находим по формуле (19-24)
части колонны
расходов жидкости Уж (см. при-
числа единиц переноса для верхней
п, = 38 000 (Р4)0'62 = 38 000 о/)^7885 0,0036 • Ю"6 .133»’62 s 5
Аналогично для нижней части колонны Пг = 1,84.
Определение числа тарелок. Отношение I = -q- для верхней
части колонны составляет:
Для нижней части
, + + / 1,25 + 2,52 _
1,25 + 1 ’
где R— флегмовое число, равное 1,25 (см. пример 19-4);
, F 5000 п
f=~p = “1985” = 2,52 (см. пример 19-2).
Поскольку тангенс k угла наклона линии равновесия является перемен-
ным, определяем при помощи у — х-диаграммы (см. рис. 19-12, стр. 678) зна-
чения k для различных составов жидкости х, вычисляем «о по формуле (17-37)
и значения Е по формуле (17-45). Расчеты сводим в таблицу (табл. 30).
Таблица 30
X о,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9
k 3,2 1,6 0,81 0,61 0,5 0,46 0,4 0,4 0,4
1 1,67 1,67 0,555 0,555 0,555 0,555 0,555 0,555 0,555
По 0,68 1,05 1,37 1,53 1,63 1,67 1,73 1,73 1,73
Е 0,495 0,651 0,747 0,784 0,804 0,811 0,828 0,828 0,828
698
Гл. 19. Ректификация
Строим на у—х-диаграмме (рис. 19-21) кинетическую кривую и, вписы-
вая ступенчатую линию, находим число тарелок: для нижней части 8, для
верхней части 10.
Рис. 19-21. Графическое определение числа тарелок (к при-
меру 19-7).
Периодическая ректификация
При периодическом процессе ректификации в колонне про-
исходит только укрепление паров; поэтому всей колонне соот-
ветствует одна рабочая линия, определяемая уравнением
(19-13).
Состав жидкости в кубе непрерывно изменяется: в началь-
ный момент он равен составу исходной смеси xF, в конечный
момент — составу остатка xw. В соответствии с этим необходи-
мое число единиц переноса будет увеличиваться.
В реальной колонне число единиц переноса неизменно, по-
этому в ходе перегонки изменяется состав дистиллята. Число
единиц переноса, необходимое в начальный момент перегонки
для достижения заданной степени разделения смеси и получе-
8. Расчет ректификационных колонн
699
ния дистиллята требуемого качества, в дальнейшем будет уже
недостаточно. Вследствие этого качество дистиллята ухудшает-
ся, т. е. он обедняется НК.
Это видно из рис. 19-22, а, на котором показаны два поло-
жения рабочей линии — для начального, и конечного моментов
ректификации. Так как флегмовое число не изменяется
(R = const), то угловой коэффициент рабочей линии остается
без изменения, и все рабочие линии параллельны между собой.
Точки пересечения рабочих линий с диагональю соответствуют
составам дистиллята, который изменяется от (в начальный
момент) до Хр2 (в конечный момент). Число единиц переноса
при всех положениях рабочей линии остается одинаковым.
Рис. 19-22. К расчету периодической ректификации:
« — при постоянном флегмовом числе; б— при постоянном составе дистиллята.
Чтобы предотвратить изменение состава дистиллята в ходе
процесса ректификации, надо увеличивать флегмовое число. При
этом точка С (рис. 19-22, б) пересечения рабочей линии с диа-
гональю остается неподвижной, а рабочая линия поворачивает-
ся около этой точки в соответствии с изменением величины R. На
рис. 19-22, б показаны также два положения рабочей линии,
соответствующие начальному и конечному моментам ректифика-
ции. Число единиц переноса для всех положений рабочей линии
одинаково, флегмовое же число увеличивается от Ri (в началь-
ный момент) до R2 (в конечный момент).
При расчете процесса периодической ректификации (при хр= const) надо
обычным способом определить флегмовое число и число единиц переноса для
конечного момента ректификации. Далее задаются несколькими меньшими
значениями R, строят соответствующие положения рабочей линии и, вписы-
вая для каждого положения найденное ранее число единиц переноса, опреде-
700
Гл. 19. Ректификация
ляют составы х жидкости в кубе, отвечающие принятым значениям Р. Вы-
черчивают зависимость Р от х и графическим интегрированием находят сред-
нее флегмовое число:
?---- f Р dx
р хр~ xXI7 J
Г w V
При расчете процесса периодической ректификации (при Р — const) флег-
мовое число и число единиц переноса находят обычным способом — либо для
начального момента ректификации (по заданным хР( и Хр), либо для ее
конечного момента (по заданным Хр2 и х^). Затем задаются несколькими
промежуточными значениями хр, строят промежуточные положения рабочей
линии и, вписывая для каждого из них найденное ранее число единиц пере-
носа, определяют составы х жидкости в кубе, отвечающие принятым значе-
ниям Для определения количества остатка пользуются уравнением *
f
xw
Интеграл правой части этого уравнения определяют графически. Для
этого по оси абсцисс откладывают значения х, по оси ординат соответствую-
щие значения -------- и находят площадь, ограниченную кривой, осью х и
Хр х
вертикалями, проведенными через абсциссы xw и хр. Эта площадь равна
искомому интегралу.
Далее, на основании уравнения материального баланса (19-8), опреде-
ляют средний состав дистиллята:
v — ?хг ~ ^xw
Аналогично ведут расчет периодической ректификации и для процесса
в барботажных колоннах. В этом случае находят необходимое число тарелок
для конечного момента ректификации (при хр = const) и строят кинетические
кривые для каждого положения рабочей линии, определяя составы х жидко-
сти в кубе. Так же поступают и при Р — const с той разницей, что число та-
релок в этом случае можно определять либо для начального, либо для
конечного момента ректификации.
Пример 19-8. Рассчитать периодический процесс ректификации смеси
бензол — толуол в насадочной колонне при постоянном составе дистиллята
х= 0,956. Состав исходной смеси х„ = 0,335, состав остатка х,„ = 0,059.
р Г W
Количество загружаемой смеси г — 16 000 кг, температура загружаемой
смеси 30° С, продолжительность операции 24 ч.
Определение количества дистиллята и остатка. Ко-
личество смеси при средней молекулярной массе ее 87,3 составляет:
16000 1ОО
F = - 0^"а~ = 183 кмоль
о7,<5
* Это уравнение аналогично уравнениям (19-25) и (19-26) для процесса
простой перегонки, вывод которых приведен на стр. 704 сл.
8. Расчет ректификационных колонн
701
По уравнениям материального баланса (19-7) и (19-8) находим количе-
ство дистиллята Р = 56 кмоль и количество остатка w = 127 кмоль.
Определение флегмового числа. На рис. 19-23 построена
у—х-диаграмма по данным примера 19-1 (стр 669). Находим обычным спо-
собом минимальное флегмовое число для конечного момента ректификации
Рис. 19*23. Графическое определение составов х жидкости в кубе
при периодическом процессе ректификации (к примеру 19-8).
Pmin = И’8 (при xw~ 0,059). Рабочее флегмовое число принято
R = 1,2’11,8^14, в результате построения ступенчатой линии находим число
единиц переноса п = 8.
Задаваясь значениями R, равными 10, 5, 3 и 2, строим на у—х-диаграмме
соответствующие им рабочие линии и, вписывая «ступеньки», отвечающие
числу единиц переноса п = 8, находим составы х жидкости в кубе для раз-
личных стадий ректификации (для упрощения на рис, 19-23 сделано построе-
702
Гл. 19. Ректификация
Таким способом находим следующую зави-
ние лишь для Р = 5 и /? = 2 *.
симость между Р и х\
Рис. 19-24. Графическое определение среднего флегмового
числа (к примеру 19-8).
Вычерчивая зависимость Р от х, находим площадь, ограниченную кри-
вой, осью х и вертикалями, проведенными через абсциссы — 0,059 и
хр = 0,335 (рис. 19-24):
0,335
J ^=1з
0,059
Среднее флегмовое число, равное высоте прямоугольника KLMN, равно-
великого площади KL'M'N, составляет:
R - 1>54 -5 6
ср- 0,335 — 0,059 — ’
Определение расхода тепла. Расход тепла на подогрев смеси
от 30° С до температуры кипения смеси (97° С) составляет* **:
Qj = 183 • 157 • 103 (97 — 30) = 1930 106 дж (460 000 ккал)
(157 • 103 дж/кмоль • град — молярная теплоемкость смеси, 37,5 ккал!кмоль •
• град).
* При практических расчетах эти построения следует выполнять на
кальке, наложенной на диаграмму.
** В этом примере температуры определены по t — х — ^-диаграмме.
9. Простая перегонка
703
Расход тепла на процесс ректификации определяем по формуле (19-19),
пренебрегая теплопотерями (расчет ведем по среднему флегмовому числу):
Q = 56 • 5,6 • 29 800 • 103 + 56 (41 700 • 103 — 157 • 103 • 97) +
+ 127 (162 • 103 • 108 — 157 • 103 • 97) = 11 100 • 106 дж (2 650 000 ккал)
где 29 800 • 103 дж!кмоль — теплота испарения флегмы (7100 ккал!кмоль)',
41 700 • 103 дж!кмоль — энтальпия паров, выходящих из колонны при
82,5° С (9960 ккал!кмоль\,,
162 • 103 дж!кмоль • град — теплоемкость остатка (3%,'Т''Ккал1 кмоль • град)',
108° С — температура кубового остатка.
Определение расхода тепла и количества паров в
единицу времени. Принимая продолжительность подогрева смеси 4 ч
и продолжительность процесса ректификации 16 ч (остальные 4 ч произво-
дят загрузку и разгрузку куба), находим расход тепла в единицу времени
за период подогрева:
= 134 00,0 вт (115 000 ккал!ч)
OOUv • 4
и за период ректификации
ЧэдЛ'б" = 193000 вт (I66 000 ккал!ч)
Количество паров, поднимающихся по колонне в единицу времени, со-
ставляет:
P{R^ + i) 56(5,6 + l)
G = -----77---- = ----77---= 23,1 кмоль)ч
16
16
Дальнейший расчет (определение основных размеров и т. д.) ведут так
же, как для процесса непрерывной ректификации (стр. 694 сл.).
9. Простая перегонка
Схемы простой перегонки
При простой перегонке (рис. 19-25, а) смесь загружается
в куб 1, обогреваемый паром через змеевик или рубашку либо
топочными газами. После подогрева смеси до темпер aTJpS ки-
пения образующиеся пары отводятся из куба и конденсируются
в конденсаторе 2. Остаток удаляется из куба по окончании опе-
рации.
По мере испарения смеси содержание НК в дистилляте не-
прерывно уменьшается, максимальное содержание НК в дистил-
ляте — в начальный момент перегонки. При этом в случае на-
добности можно получать несколько дистиллятов (фракций)
различного состава, раздельно отводя их в соответствующие
сборники. Способ перегонки с разделением смеси на несколько
фракций, в различной степени обогащенных НК, называется
фракционной перегонкой.
704
Гл 19 Ректификация
Простая перегонка может проводиться при атмосферном да-
влении или при разрежении. В последнем случае неконденси-
рующиеся газы отсасываются из приемников дистиллята ваку-
ум-насосом.
Степень разделения компонентов может быть повышена при-
менением простой перегонки с дефлегмацией (рис. 19-25,6).
Рис. 19-25. Схема простой перегонки:
а — без дефлегмации; б —с дефлегмацией, / — куб; 2 — конденсатор;
3 — труба для возврата флегмы; / — дефлегматор.
В этом случае уходящие из куба 1 пары поступают в дефлегма-
тор 4, в котором конденсируются лишь частично. При частичной
конденсации конденсируется преимущественно ВК, а пары обо-
гащаются НК. Полученный в дефлегматоре конденсат (флегма)
возвращается в перегонный аппарат через U-образную трубу.?,
в которой образуется гидравлический затвор, препятствующий
выходу паров из куба, минуя дефлегматор. Не сконденсировав-
шиеся в дефлегматоре пары переходят в жидкую фазу в кон-
денсаторе 2, откуда и отводится дистиллят.
Простая перегонка без дефлегмации
При простой перегонке из аппарата отводится образующийся пар, кото-
рый каждый данный момент находится в равновесии с оставшейся
жидкостью
Пусть в некоторый момент количество жидкости в аппарате равно G,
а ее состав — к. За бесконечно малый промежуток времени количество
жидкости и состав ее изменятся и составят соответственно (G — dG) и
(х— dx). Количество образующегося за этот промежуток времени пара
равно уменьшению количества жидкости dG, а его состав у является равно-
весным с х. Содержание НК в жидкости к началу рассматриваемого проме-
жутка времени составляет Gx, а к концу (G — dG) (х — dx). Количество же
НК, перешедшего за этот промежуток времени в паровую фазу, равно ydG,
9 Простая перегонка
705
Таким образом, уравнение материального баланса по НК за рассматривае-
мый промежуток времени имеет следующий вид:
Gx = (G — dG) (х — dx) + у dG
Раскрывая скобки и пренебрегая членом dG dx,, представляющим собой
произведение двух бесконечно малых величин, получим:
G dx — (у — х) dG
или
dG _ dx V.
G ~ у — х
В начальный момент перегонки количество жидкости в аппарате равно
количеству начальной смеси F (состава хр), а в конечный момент — коли-
честву остатка W (состава xw). Таким образом, пределы интегрирования
будут: для левой части F и W, для правой части хр и xw> т. е.
F XF
С dG —С &х
J G ~~ j у — х
W xw
Выполняя интегрирование левой части и переходя к десятичным лога-
рифмам, получим:
XF
$ vh <19-25)
xw
Интеграл правой части уравнения (19-25) определяется графически.
Для этого по оси абсцисс откладывают значения х, а по оси ординат соот-
ветствующие значения _____х и находят площадь, ограниченную кривой,
осью х и вертикалями, проведенными через абсциссы х^ и хр: эта площадь
равна искомому интегралу. Расчет можно вести как в весовых, так и моляр-
ных величинах.
Простая перегонка с дефлегмацией
Уравнение (19-25) справедливо и для перегонки с дефлегмацией с той
лишь разницей, что во всех уравнениях состав пара у, равновйелйй с соста-
вом жидкости х, должен быть заменен на состав пара у', выходящего из
дефлегматора. Таким образом, уравнение (19-25) примет вид
F dx
2>31g> = f (19-26)
Xuz
Состав у' определяется из материального баланса дефлегматора. Пусть
количество флегмы Ф, а ее состав х', причем х' и у' находятся в равновесии
между собой. Количество пара, поступающего из перегонного аппарата в де-
флегматор, будет (Ф + Р), а состав этого пара у (равновесный с составом
жидкости х в аппарате). Тогда материальный баланс дефлегматора выра-
зится следующим уравнением:
(Ф -|- Р) у = Ру' + Фл'
706
Гл 19 Ректификация
1
Деля обе части этого уравнения на Р и вводя флегмовое число /?
Ф
вместо -р-, получим:
(R + l)y = y' + Rx'
Отсюда находим:
Я = (19-27)
На рис. 19-26 (слева) точка А изображает состояние пара перед дефлег-
матором, точка В — состояние пара после дефлегматора. Проведем через
точку А горизонтальную линию АС до пересечения с диагональю, точку С
соединим с точкой В, а из точки В проведем вертикаль BD до пересечения
с линией АС. Длина отрезка BD равна (у'— у), длина отрезка DC равна
(у — х'). Таким образом.
Сравнивая это выражение с уравнением (19-27), находим:
tga = /?
Следовательно, для построения точки В надо из точки А провести гори-
зонтальную линию до пересечения с диагональю, а через полученную на
диагонали точку провести прямую
под углом к оси абсцисс, тангенс ко-
торого равен R. Точка пересечения
этой прямой с линией равновесия
будет искомой точкой В, ордината
которой равна составу пара у' после
дефлегматора. Делая такое построе-
ние для различных значений х,
Пары из куба^
(Ф+РЦ/ ’
Дистиллят
I 77'
Рис. 19-26. К расчету перегонки с дефлегмацией.
вычисляют —т—— для этих значений, после чего графическим интегрирова-
у х
нием определяют интеграл правой части уравнения (19-26).
Пример 19-9. Определить количество дистиллята и остатка, а также
состав дистиллята при разделении смеси бензол—толуол путем простой пере-
гонки с дефлегмацией под давлением 760 мм рт ст Количество исходной
смеси F— 10 000 кг, флегмовое число R = 1,5, состав смеси ар = 0,3 вес.
доли, состав остатка aw = 0,18 вес доли
Решение. Откладываем на диаграмме равновесия* (рис. 19-27) по
оси абсцисс ряд значенйй а, проводим вертикальные отрезки до пересечения
* Построена по данным примера 19-1 (стр 669) с пересчетом молярных
составов в весовые.
9 Простая перегонка
707
с линией равновесия и горизонтальные отрезки до пересечения с диагональю.
Через полученные на диагонали точки проводим прямые под углом на-
клона а к оси абсцисс, тангенс которого равен заданному флегмовому числу
(tga=/?=l,5) Далее находим ординаты (Ь') пересечения этих прямых
с линией равновесия и вычисляем значения
а. .. . 0 0,1 0,2 0,3 0,4 0,5 0,6 0),7 0,8 0,9 1
Ь' . . . О 0,28 0,5 0,645 0,745 0,82 0,875 Ъ,915 0,95 0,98 1
. оо 5,56 3,33 2,9 2,9 3,12 3,64 4 66 6,67 12,5 оо
Ь —а
Рис. 19-27. К примеру 19-9.
Построив зависимость • от а (рис 19-27), находим площадь,
ограниченную кривой, осью а и вертикалями, проведенными через абсциссы
— 0,18 и ар = 0,3 С учетом масштабов построения определяем
0,3
0,18
da
b' —а
-0,37
45*
708
Гл 19 Ректификация
По уравнению (19-26) получаем:
2,3| w™ 0,37
W
откуда количество остатка W — 7050 кг.
Из уравнений материального баланса (19-7) и (19-8)
10 000 • 0,3 = 7050 • 0,18 4- PZ>'p
10 000 = 7050 + Р
находим количество дистиллята Р = 2950 кг и его средний состав
^ср. — 0,585 вес. доли.
10. Специальные виды перегонки
К специальным видам перегонки относятся перегонка с вве-
дением дополнительного компонента и так называемая молеку-
лярная перегонка. При введении дополнительного компонента
повышается давление пара НК и тем самым облегчается его
выделение из смеси. В качестве дополнительного компонента
применяют водяной пар (перегонка с водяным паром) или спе-
циальные растворители (экстрактивная и азеотропная пере-
гонка).
Перегонка с водяным паром
Перегонку с водяным паром применяют для выделения из
смесей высококипящих веществ, нерастворимых в воде (анилин,
скипидар и др.). При этом выделяемое вещество отгоняется
в виде азеотропной смеси с водой, температура кипения которой
ниже температуры кипения каждого из компонейтов (стр. 666).
Таким образом, температура кипения смеси всегда будет ниже
100° С и может быть еще более понижена пр.и ведении перегонки
в вакууме.
Так, например, скипидар, имеющий температуру кипения
160° С, будет перегоняться с водяным паром при температуре
95,5° С, при которой давление паров скипидара составляет
115 мм рпг. ст., а давление паров воды 645 мм рт. ст. (общее
давление 115 + 645 = 760 мм рт. ст.). Теоретическое содержа-
ние паров скипидара в их смеси с водяным паром составляет при
этом согласно формуле (19-4)
115 Л1К1
у ~ 760 0,151
Фактическое содержание паров скипидара в смеси несколько
ниже, так как водяной пар подается с избытком в коли-
честве 20—35%.
10. Специальные виды перегонки 709
Перегонку с водяным паром ведут в кубах, снабженных па-
ровой рубашкой или змеевиком для обогрева и барботером для
ввода острого пара. Выходящие из куба пары конденсируются
в конденсаторе.
Путем отстаивания или центрифугирования конденсат раз-
деляется на воду и отогнанный продукт.
Перегонку с водяным паром применяют также для выделе-
ния вещестд с низкой температурой кипения, например для вы-
деления бензола из каменноугольного масла.
Экстрактивная и азеотропная перегонка
Рис. 19-28. Схема экстрактивной пе-
регонки:
/ — экстракционная колонна: 2, / — дефлегма-
торы; 3 — отгонная колонна.
флегмой, поступающей из де-
Эти виды перегонки применяют для разделения компонентов
с близкими температурами кипения, а также для разделения
азеотропных смесей. Для повышения давления пара НК приме-
няют растворители избиратель-
ного действия, повышающие
давление пара НК в большей
степени, чем давление пара ВК.
Применяемый при экстрак-
тивной перегонке раствори-
тель менее летуч, чем разде-
ляемые компоненты, и уда-
ляется с остатком.
На рис. 19-28 показана схе-
ма экстрактивной перегонки
для разделения смеси бутана
(НК) и псевдобутилена (ВК),
растворителем служит ацетон.
Исходная смесь вводится в
среднюю часть экстракцион-
ной колонны /, ацетон — выше
ввода смеси.
Часть колонны выше ввода
ацетона орошается бутановой
флегматора 2, и служит для выделения из паров остатков аце-
тона. Остаток, представляющий собой смесь псевдобутилена и
ацетона, разделяется в отгонной колонне 3, причем псевдобути-
лен переходит в дистиллят, ацетон — в остаток. Из куба отгон-
ной колонны ацетон возвращается в экстракционную колонну.
При азеотропной перегонке применяют растворители, обра-
зующие с одним из компонентов азеотропную смесь с минималь-
ной температурой кипения. Следовательно, при азеотропной пе-
регонке растворитель удаляется с дистиллятом,
710
Гл. 19. Ректификация
На рис. 19-29 показана схема азеотропной перегонки для по-
лучения безводного этилового спирта из азеотропной смеси его
с водой. Дополнительным компонентом служит бензол, образую-
щий с водой азеотропную смесь с более низкой температурой
кипения (69°С), чем температура кипения азеотропной смеси
спирта с водой (78°С). Поэтому вся вода вместе с бензолом
переходит в дистиллят, а в
спирт
Рис. 19-29. Схема азеотропной
перегонки:
/—колонна; 2— конденсатор; 3— от-
стойник.
остатке получается безводный спирт.
Бензол отделяется от воды отстаи-
ванием и возвращается в процесс.
Если растворитель и отогнанный
компонент взаимнорастворимы, то
полученный при азеотропной пере-
гонке дистиллят подвергают пере-
гонке в отдельной колонне. При
этом в остатке этой колонны полу-
чают компонент, в ' дистилляте —
азеотропную смесь компонента и
растворителя, которую возвращают
в колонну азеотропной перегонки.
Основным преимуществом экст-
рактивной перегонки перед азео-
тропной является меньший расход
тепла, так как при экстрактивной
перегонке не требуется испарять
растворитель. Кроме того, для раз-
деления одной и той же смеси экст-
рактивной перегонкой можно ис-
пользовать различные растворители
и регулировать процесс изменением
количества вводимого растворителя.
Азеотропную перегонку удобно
применять при периодическом процессе, когда весь раствори-
тель загружают в куб вместе со смесью. На установках непре-
рывного действия азеотропную перегонку целесообразно приме-
нять при невысоком содержании отгоняемого компонента в сме-
си, так как в этом случае расход тепла на испарение раствори-
теля невелик.
Молекулярная перегонка
Молекулярную перегонку ведут в глубоком вакууме, соответ-
ствующем остаточному давлению 0,01—0,0001 мм рт. ст. При
таком вакууме молекулы легко преодолевают силы взаимного
притяжения, число ударов молекул друг о друга значительно
уменьшается, а длина свободного пробега молекул между со-
ударениями резко возрастает.
10 Специальные виды перегонки
7U
к Вануум'--
насосу
Остаток
Oamao&fa-
ющий
агент
Рис.
рата
Если расстояние между поверхностями испарения и конден-
сации меньше длины свободною пробега молекул, то отрываю-
щиеся от поверхности испарения молекулы НК непосредственно
попадают на поверхность конденсации и
улавливаются на ней. Расстояние между
поверхностями испарения и конденсации
составляет 20—30 мм-, разность темпе-
ратур между ними должна быть по-
рядка 100° С.
На рис. 19-30 показана схема про-
стейшего аппарата для молекулярной пе-
регонки. Внутри цилиндрического испа-
рителя 1 имеется спираль для электро-
нагрева разделяемой смеси. Цилиндри-
ческий конденсатор 2 снабжен рубаш-
кой 3, по которой движется охлаждаю-
щий агент. Исходная смесь подается
сверху по трубе в воронку 4 и стекает
пленкой по наружной поверхности испа-
рителя. Остаток удаляется снизу через
воронку 5, дистиллят, собирающийся на
внутренней поверхности конденсатора,
отводится также снизу по трубе 6. В
кольцевом пространстве между испари-
телем и конденсатором поддерживается
требуемый вакуум посредством насоса
глубокого вакуума, присоединенного к
патрубку 7.
Молекулярная перегонка применяется
для извлечения легколетучих ценных
компонентов, содержащихся в исходной
смеси в малых концентрациях, и для
тонкой очистки продуктов от вредных
примесей. Путем молекулярной перегон-
ки получают концентраты некоторых витаминов, безводные
пластификаторы, ценные компоненты тяжелых нефтяных фрак-
ций и др.
Молекулярной перегонке могут подвергаться только веще-
ства, достаточно устойчивые при температуре кипения, соответ-
ствующей глубокому вакууму.
19-30. Схема аппа-
для молекулярной
перегонки:
1— испаритель; 2-конденсатор;
3 — рубашка; 4, 5 — воронки;
6 —труба для вывода дистил-
лята, 7 —патрубок для при-
соединения вакуум-насоса.
Глава 20
АДСОРБЦИЯ
1. Общие сведения
Адсорбция представляет собой процесс поглощения газов,
паров или жидкостей поверхностью пористых твердых тел —
адсорбентов.
Процессы адсорбции являются избирательными и обрати-
мыми. Это значит, что каждый поглотитель обладает способ-
ностью поглощать лишь определенные вещества и не поглощает
(или поглощает лишь в незначительной степени) другие ве-
щества, содержащиеся в газовой смеси или растворе, а погло-
щенное вещество всегда может быть выделено из поглотителя
путем десорбции — процесса, обратного адсорбции.
Адсорбенты отличаются весьма высокой пористостью, вслед-
ствие чего их поверхность очень велика. Наиболее распростра-
ненными адсорбентами являются активированный уголь и гель
кремневой кислоты (силикагель), причем поверхность 1 г угля
колеблется от 200 до 1000 м2, силикагеля — до 500 м2 и более.
В некоторых случаях в качестве адсорбентов используют глины,
активированные серной кислотой. Адсорбенты применяются в
виде зерен размером 2—8 мм или в пылевидном состоянии (раз-
мер частицы 50—200 мк).
Процессы адсорбции протекают в неподвижном или переме-
щающемся слое зернистого адсорбента, или в кипящем (псевдо-
ожиженном) слое. В последнем случае адсорбенты могут нахо-
диться в виде «стационарного» слоя внутри аппарата или
циркулировать через аппарат. %
Адсорбция в слое движущегося адсорбента и особенно в ки-
пящем слое протекает значительно интенсивнее, чем в неподвиж-
ном слое, и может проводиться в более компактной аппаратуре.
Благодаря огромной удельной поверхности адсорбентов (по-
верхность на единицу объема) при адсорбции возможны очень
большие скорости поглощения и полное поглощение компонен-
тов, выделение которых путем абсорбции было бы невозможно
из-за малой концентрации их в смеси. Поэтому адсорбция яв-
2 Теория адсорбции
713
ляется эффективным способом разделения «бедных» смесей, со-
держащих незначительное количество поглощаемых веществ,
а также смесей, состоящих из компонентов, очень близких друг
к другу по химическим и физическим свойствам. —
Процессы адсорбции широко применяются для очистки и
осушки газов, для разделения смесей газов и паров, например
смесей газообразных углеводородов, для улавливания из паро-
газовых смесей паров ценных органических веществ (бензола,
бензина, ацетона и др.), или так называемой рекуперации ле-
тучих растворителей. Посредством адсорбции производят также
очистку растворов от примесей.
2. Теория адсорбции
Равновесие между фазами
При адсорбции молекулы газа или пара концентрируются
на поверхности адсорбента под влиянием молекулярных сил
притяжения. Этот процесс часто сопровождается химическим
взаимодействием, а также конденсацией пара в капиллярных
порах твердого адсорбента. Общепризнанной теории адсорбции
еще нет. Согласно широко распространенному взгляду, адсорб-
ция происходит под действием электрических сил, обусловлен-
ных взаимодействием зарядов молекул адсорбента и помещае-
мого вещества. По другой теории адсорбционные силы носят
химический характер и природа их объясняется наличием сво-
бодных валентностей на поверхности адсорбента.
Независимо от характера сил, вызывающих адсорбцию, при
достаточном времени соприкосновения фаз наступает адсорб-
ционное равновесие, при котором устанавливается определенная
зависимость между концентрацией адсорбированного вещества
X (в кг/кг адсорбента) и его концентрацией У в фазе, соприка-
сающейся с адсорбентом:
X—AY'ln (20-1)
где У — равновесная концентрация, кг/кг инертной части паро-
газовой смеси или раствора;
А и п — коэффициенты, определяемые опытным путем, причем
п^> 1.
Зависимость (20-1) соответствует определенной температуре
и изображается кривой, которая носит название изотермы ад-
сорбции.
Изотермы адсорбции некоторых веществ приведены на
рис. 20-1.
714
Гл. 20. Адсорбция
Концентрация адсорбируемого вещества в смеси при постоян-
ной температуре пропорциональна его давлению. Поэтому урав-
нение (20-1) может быть представлено в виде
Х=А^ (20-2)
где Л1 — коэффициент пропорциональности;
Р —равновесное давление поглощаемого вещества в паро-
газовой смеси.
Основными факторами, влияющими на протекание процесса
адсорбции, являются: свойства адсорбента, температура, давле-
ние, свойства поглощаемых веществ и состав фазы, из которой
они адсорбируются.
X, кг1/кг
Рис. 20-1. Изотермы адсорбции (при 20° С):
/ — для этилового эфира; 2 — для этилового спирта; 3 — для
бензола.
Равновесная концентрация X уменьшается с повышением
температуры и увеличивается с возрастанием давления. Таким
образом, адсорбция ускоряется при понижении температуры или
при повышении давления.
Те же’факторы влияют в обратном направлении на процесс
десорбции, проводимый обычно после адсорбции. Десорбция
ускоряется с повышением температуры адсорбента и снижением
давления над ним, а также при пропускании через адсорбент па-
ров, вытесняющих поглощенное вещество.
Адсорбенты характеризуются статической и динамической
активностью. После некоторого периода работы адсорбент пере-
стает полностью поглощать извлекаемый компонент и начи-
нается «проскок» компонента через слой адсорбента. С этогр
2. Теория адсорбции
715
момента концентрация компонента в отходящей парогазовой
смеси возрастает вплоть до наступления равновесия.
Количество вещества, поглощенного единицей веса (или
объема) адсорбента за время от начала адсорбции до начала
«проскока», определяет динамическую активность адсорбента.
Количество вещества, поглощенное тем же количеством адсор-
бента за время от начала адсорбции до установления равнове-
сия, характеризует статическую активность.
Активность адсорбента зависит от температуры газа и кон-
центрации в нем поглощаемого компонента. Динамическая ак-
тивность всегда меньше статической; поэтому расход адсор-
бента определяется по его динамической активности.
Материальный баланс процесса адсорбции
Процессы адсорбции проводятся периодически или непрерывно.
Если адсорбент движется через аппарат, адсорбция происходит непре-
рывно и материальный баланс процесса выражается уравнением (16-14),
общим для всех процессов массопередачи. Адсорбция в слое неподвижного
адсорбента является периодическим процессом, при котором концентрация
поглощаемого вещества в адсорбенте меняется во времени и в пространстве.
Примем, что газ (в количестве G за единицу времени), проходя за
время слой адсорбента высотой dH, изменяет свою концентрацию на ве-
личину dY и, следовательно, отдает количество вещества G dY dx. За это же
время концентрация поглощаемого вещества в элементе слоя увеличивается
на dX и количество вещества, поглощенного слоем высотой dH, составляет
S dH р dX, где S — площадь поперечного сечения адсорбента, р — насыпная
масса адсорбента. Тогда уравнение материального баланса будет иметь вид:
— GdYdi = SdH$dX
или
dY = — ^^dX (20-3)
G di '
Кинетика адсорбции
Адсорбция относится к процессам массообмена, протекающим с участием
твердой фазы, и описывается уравнением (16-39). Однако многочисленные
опыты показывают, что внутренним диффузионным сопротивлением самого
адсорбента можно пренебречь и проводить расчет процесса по уравне-
нию (16-28). Значения коэффициента массоотдачи ₽ можно определять по
следующим уравнениям:
1. Для зернистого адсорбента при ламинарном движении (Re < 30)
Nu; = 0,883 Re0’47 (Р/)0,33 (20-4)
при турбулентном движении (Re = 30— 150])
N< = 0,53 Re0’54 (Рг')0,3 (20-5)
В этих уравнениях определяющим геометрическим размером в крите-
риях Nur и Re является эквивалентный диаметр с?экв. [формула (6-10)].
716
Гл 20 Адсорбция
2. Для мелкозернистого адсорбента в кипящем слое ।
Nu^ = 46,25 • IO-6 ReJ>67 (20-6)
В уравнении (20-6) Reo определяется по формуле (6-108), a Nu^ по фор-
муле
где роб. — объемный коэффициент массоотдачи,-------------или-------;
л К2> СвК
м3 • сек —г
м3
d — средний диаметр зерна, м (являющийся также определяющим гео-
метрическим размером в критерии Re),
Dr — коэффициент диффузии в газовой фазе, м^свк
Пример 20-1. Определить коэффициент массоотдачи от паровоздушной
смеси (пары бензола в воздухе) к неподвижному слою адсорбента (активи-
рованный уголь) при 20° С, если свободный объем слоя е = 0,375, удельная
поверхность адсорбента f = 1630 м3/м3. Фиктивная скорость паровоздушной
смеси w0 = 10 м/мин = 0,167 м/сек *
Решение. Определяем эквивалентный диаметр слоя угля:
= --Тсэд 5 = 0,92 10-3 м
J 1UOV
Массовая скорость паровоздушной смеси составляет"
W ^£дРсм^ = °’167’1’2 = о,532 кг/м2 сек
е 0,375
где рем. — плотность паровоздушной смеси (1,2 ка/jn3).
Вычисляем критерий Рейнольдса для паровоздушной смеси
И^экв, 0,532 • 0,92 • 10~3 28
Исм. 1,75-10“ 5
где р.см.— вязкость паровоздушной смеси (1,75 • 10-5 н-сек/м^, или 0,0175слз).
Коэффициент диффузии паров бензола в воздухе при 0°С составляет:
Do = 0,77 • 10"5 м2/сек (0,0277 м2/ч)
Определяем по формуле (16-24) коэффициент диффузии паровоздушной
смеси при давлении Р = 0,98 бар (1 ат)
Dr = Do (^Y/2 = 0,77 • Ю"5 (273+ 20\8/* = о,861 • 10"5 м2/сек
Находим значение диффузионного критерия Прандтля:
Рг' = ^см- -= ^75 • 10 ~ 1 7
Рсм.^г 1,2 • 0,861 • 10"5 - ’
В соответствии с найденным значением Re определяем по формуле (20 4)
коэффициент массоотдачи от паровоздушной смеси к углю:
NuJ = 0,883 Re0'47 (Рг')0’33 = 0,883 • 280>47 • 1.70’33 = 5,05
откуда
или
DrNu' 0,861 • 10“5 • 5,05
ft = —1—£ = -------------------= 0,0472 м/сек
с аэкв. 0,92-10"3
0 = 1,2 • 0,0472 s 0,057 кг/м2 • сек
3 Устройство адсорберов
717
3. Устройство адсорберов
Для проведения процессов адсорбции применяются адсор-
беры следующих типов:
1) с неподвижным зернистым адсорбентом;
2) с движущимся зернистым адсорбентом;
3) с кипящим (псевдоожиженным) слоем мелкозернистого
адсорбента.
Паровоздушная
Рис. 20-2. Адсорберы с неподвижным зернистым адсорбентом:
а —вертикальный; б —горизонтальный, в — вертикальный с кольцевым слоем адсорбента.
/ — корпус; 2 —решетка; 3, 4, 5 —люки.
Адсорберы с неподвижным зернистым адсорбентом. Эти ад-
сорберы представляют собой полые вертикальные (рис. 20-2, а)
или горизонтальные (рис. 20-2, б) сосуды, в которых размещен
718
Гл. 20. Адсорбция
слой зернистого адсорбента. Иногда применяют адсорберы с
кольцевым слоем адсорбента (рис. 20-2, в).
Газовая (паровоздушная) смесь подается в корпус 1 адсор-
бера (рис. 20-2), проходит сквозь находящийся на решетке 2
слой адсорбента (на рисунке заштрихован), после чего уда-
ляется через выхлопной штуцер. По завершении адсорбции для
вытеснения поглощенного вещества из адсорбента в аппарат
подается перегретый водяной пар (или другой вытесняющий
агент), который движется в направлении, обратном движению
газа. Паровая смесь (смесь паров воды и извлекаемого компо-
нента) удаляется из аппарата и поступает на разделение в от-
стойник непрерывного действия или в ректификационную ко-
лонну. После десорбции сквозь слой адсорбента пропускают для
его сушки горячий воздух, который входит через паровой шту-
цер и удаляется через тот же штуцер, что и паровая смесь. Вы-
сушенный адсорбент охлаждается холодным воздухом, движу-
щимся по тому же пути, что и водяной пар, после чего цикл
поглощения повторяется снова.
Для адсорбции из жидкой фазы используют обычные
фильтрпрессы, рамы которых заполняют зернистым адсор-
бентом.
Адсорберы с движущимся зернистым адсорбентом. Эти ад-
сорберы представляют собой колонны, в которых зернистый ад-
сорбент движется самотеком сверху вниз, либо перемещается
при помощи специальных транспортных устройств (шнеки, эле-
ваторы). Адсорбер первого типа показан на рис. 20-3.
Газовая смесь, подаваемая в колонну через распределитель-
ную тарелку 3, поступает в адсорбционную зону / и поднимается
вверх. Адсорбент (гранулированный активный уголь) движется
по колонне под действием силы тяжести сверху вниз, противо-
током газовой смеси. В зоне / адсорбент поглощает более тяже-
лые компоненты газовой смеси, наиболее легкие, непоглощенные
газы (верхняя, или легкая фракция) удаляются из верхней
части зоны /. Далее адсорбент проходит промежуточную зону //
и поступает в зону десорбции ///, где движется по трубкам
теплообменника-десорбера 4, в межтрубном пространстве кото-
рого конденсируется греющий пар. Одновременно в трубки теп-
лообменника-десорбера подают перегретый острый пар для от-
дувки из адсорбента поглощенных тяжелых компонентов. Наи-
более тяжелые компоненты (нижняя, или тяжелая фракция)
удаляются из верхней части зоны III. Часть десорбированных
более легких компонентов в виде парогазовой смеси проходит
в промежуточную (ректификационную) зону //. Здесь парогазо-
вая смесь вытесняет из адсорбента часть поглощенных компонен-
тов, более легких, чем компоненты, десорбированные в зоне ///«
3. Устройство адсорберов
719
Эти вытесненные компо-
ненты отводятся из зоны
II в качестве промежуточ-
ной фракции.
Регенерированный в
зоне III нагретый адсор-
бент проходит через раз-
грузочное устройство 5,
регулирующее скорость
удаления адсорбента, и
через гидравлический за-
твор 6, предотвращающий
утечку острого пара с ад-
сорбентом. Далее адсор-
бент через регулирующий
клапан 7 поступает в
сборник 8, куда газодув-
кой 9 подается транспор-
тирующий газ (обычно
часть непоглощенных га-
зов легкой фракции). По
трубе-газоподъемнику 10
адсорбент подается то-
ком газа в бункер 1 и от-
сюда ссыпается в трубки
водяного холодильника 2,
где охлаждается, и снова
поступает в адсорбцион-
ную зону I. Для полного
восстановления активно-
сти адсорбента часть его
из бункера 1 направляет-
ся в теплообменник-реак-
тиватор 11, обогреваемый
топочными газами.
Рис. 20-3. Адсорбер с движу-
щимся зернистым адсорбентом:
/ — зона адсорбции; //—зона ректи-
фикации; ///-зона десорбции, /—бун-
кер; 2— холодильник; 3— распредели-
тельные тарелки; /-теплообменник-
десорбер; 5—разгрузочное устрой-
ство; 6 — гидравлический затвор;
7 — регулирующий клапан; 8— сбор-
ник; 9 — газодувка; 10 — труба-газо.
родъемник; 11 — теплообменник-реак
уиватор.
uuuUuuuu
3
Исходная
смесь
Промефср-й.
точная*" *
франция
тпппплпги
7яи/сеяая
франция
Лар
UUUUUUUU
ХПар
Я
720
Гл 20. Адсорбция
В трубках теплообменника-реактиватора при высокой тем-
пературе адсорбент продувается острым водяным паром и посту-
пает в сборник 8.
Распределительные тарелки 3 представляют собой трубные
решетки, к которым снизу присоединены короткие отрезки труб.
Тарелки служат для более равномерного распределения газа по
сечению колонны и уменьшения уноса частиц адсорбента газо-
вым потоком.
Адсорберы с кипящим (псевдоожиженным) слоем мелкозер-
нистого адсорбента. При проведении адсорбции в кипящем
(псевдоожиженном) слое адсорбента гидрав-
лическое сопротивление слоя является весьма
малым, поэтому можно создавать скорости
газового потока, в несколько раз большие, чем
в неподвижном слое адсорбента. Благодаря
сочетанию высоких скоростей газа с очень
развитой поверхностью фазового контакта
можно значительно интенсифицировать про-
цесс адсорбции. При интенсивном перемеши-
вании частиц в кипящем слое в нем проис-
ходит быстрое выравнивание температуры и
предотвращается' опасность перегрева адсор-
бента.
Следует, однако, отметить, что при сопри-
косновении газового потока на выходе из ки-
пящего слоя с отработанными насыщенными
частицами адсорбента может происходить ча-
Рис. 20-4. Одно-
ступенчатый ад-
сорбер с кипящим
(псевдоожижен-
ным) слъем адсор-
бента:
/—корпус; 2—распре-
делительная решетка;
3 — кипящий слой ад-
сорбента; 4 — труба
для выхода адсорбента.
стачная десорбция поглощенного вещества из
адсорбента. При интенсивном перемешивании
в кипящем слое происходит сильное истира-
ние твердых частиц адсорбента, в связи с чем
для проведения описанного процесса необхо-
димо применять адсорбенты, обладающие до-
статочной механической прочностью.
Адсорберы с кипящим слоем мелкозерни-
стого адсорбента делятся на одноступенча-
тые и многоступенчатые.
В корпусе 1 одноступенчатого адсорбера (рис. 20-4) имеется
распределительная решетка 2, через которую снизу подается
газ, приводящий мелкозернистый адсорбент в состояние кипя-
щего слоя.
Газ отводится через верхний штуцер. Адсорбент поступает
сверху и удаляется через трубу 4.
В аппарате поддерживается определенный уровень «стацио-
нарного» кипящего слоя адсорбента.
3 Устройство адсорберов
721
Многоступенчатый адсорбер представляет собой колонну
с тарелками в виде дырчатых или колосниковых решеток. Ад-
сорбент подается газодувкой на верх колонны и стекает по та-
релкам через переточные трубки противотоком к газовой смеси.
Газовая смесь, проходя через отверстия в тарелках, движется
противотоком к адсорбенту. Адсорбент выгружается снизу ко-
лонны через специальный затвор. Путем такой многоступенча-
той адсорбции достигается хорошее извлечение ценных компо-
нентов из «бедных» газов.
Схемы адсорбционных установок. Адсорбция производится
на установках периодического и непрерывного действия.
Рис. 20-5. Адсорбционная установка периодического действия:
/ — газодувка; 2 —газоход; 3— адсорбер; 4 — выхлопной газоход; 5 — конденсатор; 6 — тепло-
обменник.
На установке периодического действия (рис. 20-5) процесс,
проводимый в адсорбере, складывается из четырех последова-
тельных операций, или циклов: 1) поглощение (собственно ад-
сорбция), 2) отгонка поглощенного газа из адсорбента (десорб-
ция), 3) сушка адсорбента, 4) охлаждение адсорбента.
При адсорбции газовая смесь газодувкой 1 подается по газо-
ходу 2 в адсорбер 3, из которого удаляется через выхлопной
газоход 4. После насыщения адсорбента, определяемого по на-
чалу проскока поглощаемого компонента газа, производится
десорбция, при этом смесь отгоняемых па-ров направляется в
конденсатор 5, а затем в ректификационную колонну (на ри-
сунке не показана).
В установках такого типа, применяемых для улавливания
(рекуперации) паров летучих растворителей, сушку адсорбента
иногда проводят продувкой исходной паровоздушной смеси,
предварительно нагретой в теплообменнике 6 (на рисунке пока-
зан пунктиром), а охлаждение — холодной паровоздушной
смесью. Таким путем совмещают циклы сушки и охлаждения
адсорбента с циклом поглощения, что дозволяет сократить про-
должительность процесса,
46 Зак 54в,
722
Гл 20 Адсорбция
Рис. 20-6. Двухадсорберная установка непрерывного действия:
/, 2—адсорберы; 3 — конденсатор; 4 —сепаратор; 5 — хранилище, б —газодувка;
7— калорифер.
Рис. 20-7. Адсорбционная установка непрерывного действия1
7—колонный адсорбер (Z —зона адсорбции // — зона ректификации, 111 — зона
десорбции), 2 — вентилятор; 3— калорифер, 4— пневмотранспортная труба 5— б>нкер-
ртделитель; б —холодильник конденсатор, 7 —сепаратор, 8 — хранилище.
4 Расчет адсорберов
723
Для проведения адсорбции непрерывным способом приме-
няют установки, состоящие из двух или более адсорберов, кото-
рые поочередно включаются для адсорбции газа. На установке
из двух адсорберов (рис. 20-6) после насыщения адсорбента в
адсорбере 1 подачу газа переключают в адсорбер 2, а в адсор-
бере 1 проводят десорбцию, сушку и охлаждение, после чего
адсорбер 1 снова переключают на цикл поглощения, а адсор-
бер 2 — на десорбцию, сушку и охлаждение. При таком пере-
ключении достигается непрерывная адсорбция газа (хотя ка-
ждый из адсорберов работает периодически), так как все циклы
процесса в адсорберах проводятся последовательно друг за дру-
гом.
Установка для непрерывной адсорбции, показанная на
рис. 20-7, состоит из колонного адсорбера 1 с движущимся зер-
нистым адсорбентом, соединенного с вентилятором 2 и калори-
фером, нагревающим воздух, подаваемый для сушки адсор-
бента. Кроме того, адсорбер 1 соединяется с пневмотранспорт-
ной трубой 4, по которой высушенный адсорбент подается на
верх колонны в бункер 5, где отделяется от транспортирующего
его газа, и далее поступает в колонну 1. Смесь водяного пара
с вытесненным из адсорбента веществом поступает в холодиль-
ник-конденсатор 6, откуда конденсат направляется на разделе-
ние в сепаратор 7.
4. Расчет адсорберов
Адсорберы с неподвижным зернистым адсорбентом. Продол-
жительность Т полного цикла в адсорбере с неподвижным зер-
нистым слоем адсорбента (как и в любом адсорбере периодиче-
ского действия) складывается из времени собственно адсорб-
ции т, времени десорбции тд, в течение которого через адсорбент
продувают вытесняющий агент, и времени сушки и охлаждения
адсорбента тс. Величины тд и тс устанавливаются опытным пу-
тем, а их сумма составляет продолжительность вспомогатель-
ных операций:
Та ~F тс == твсп.
Таким образом
Т^ + ^всп. (20-7)
Для проведения адсорбции непрерывным способом приме-
няют установки, состоящие из нескольких адсорберов периоди-
ческого действия, в которых попеременно происходят адсорбция
и вспомогательные операции (десорбция и сушка). Число ад-
сорберов должно быть равным или кратным двум. Для работы
таких установок необходимо соблюдение условия
твсп. (20-8)
46*
724
Гл 20. Адсорбция
Приближенно продолжительность т собственно процесса ад-
сорбции можно определить, исходя из средней концентрации Xi
адсорбированного вещества в начальный момент времени и кон-
центрации Х2 этого вещества в конечный момент. Если масса
адсорбента в слое равна Gc кг, то количество поглощенного ве-
щества за один цикл составит:
M=Gc(X2~XJ кг (20-9)
Величина М может быть определена и по уравнению
М = wQS рсм. (— Г2) т кг (20-10)
где Wo — фиктивная скорость парогазовой смеси, м!сек\
S — площадь сечения адсорбера, м?\
Рсм. = плотность парогазовой смеси, яг/л3.
Приравнивая правые части выражений (20-9) и (20-10), по-
лучим:
__ Ос (^2--^1) /ЛЛ 1 1\
Х “ W0S Рсм. (^2-ГО СеК <20' 1 1)
Более точно т можно определить на основе следующего ана-
лиза работы слоя адсорбента.
Содержание X поглощенного вещества в адсорбенте изменяется во вре-
мени и по высоте слоя. Обозначим через У1— концентрацию поглощаемого
Рис. 20-8. Механизм адсорбции в слое неподвижного зернистого адсорбента
вещества в газе, поступающем на адсорбцию, через У2— минимальную кон-
центрацию вещества в газе, которую еще можно определить анализом.
Пусть Хс— концентрация вещества в адсорбенте, соответствующая У г, при-
чем концентрация Хс достигается в некоторый момент времени на высоте
слоя #1 (рис. 20-8).
Таким образом, практически можно считать, что в слое высотой по-
глощаемое вещество адсорбировано полностью.
По прошествии времени т2 от начала адсорбции концентрация поглощен-
ного вещества в начале слоя возрастает до Хг, причем на высоте слоя Яг
4. Расчет адсорберов
725
концентрация поглощенного вещества составляет Хс. Наконец, к мо-
менту времени т0 концентрация в начале слоя становится равной Хн, близ-
кой к концентрации Хр— равновесной с составом поступающего газа Уь
В этот момент концентрация адсорбента Хс и концентрация газа Y2 дости-
гаются на высоте слоя Но.
При дальнейшем протекании процесса адсорбции сечения слоя, соответ-
ствующие концентрациям Хс и Хи, будут перемещаться вверх, причем рабо-
тать в каждый данный момент будет только слой, заключенный между этими
сечениями. Так, в момент т3 работающим будет слой Н3— Н3.
Слой высотой Н3 (на высоте Н3 концентрация равна Хн) будет отрабо-
танным, а слой высотой Н — Н3 (на высоте Н3 концентрация равна Хс) еще
не будет работать
По скорости перемещения поверхности равных концентраций, соответ-
ствующих Хс (или перемещения фронта концентраций Хс), процесс адсорб-
ции может быть разделен на два периода:
1) период уменьшающейся скорости,
ограниченный временем т0 и высотой слоя
Но-,
2) период постоянной скорости (при
т > т0).
Зависимость скорости и (в м]сек.) пе-
ремещения фронта равных концентраций от
высоты слоя Н (в м) показана на рис. 20-9.
Величина, обратная скорости и, называет-
ся коэффициентом поглотительного дей-
ствия слоя и обозначается 1/u = k (в
сек/м). Величина k представляет собой
время насыщения слоя адсорбента высотой
1 м и определяется из уравнения мате-
риального баланса.
S • 1 • рнХн = GK, k
откуда
k = (2042)
Рис. 20-9. Зависимость скоро-
сти перемещения фронта рав-
ных концентраций от высоты
слоя адсорбента.
где S — площадь сечения адсорбера, м2-,
рн — насыпная масса адсорбента, кг/м3\
G — расход газа, кг/сек.
Зависимость времени адсорбции т от Н
жается прямой линией, тангенс угла наклона которой равен k. Соответ-
(рис. 20-10) при Н > Но выра-
ственно время поглотительного действия слоя выражается равенством
т = т0 4- (Н— Но) (20-13)
Впервые это уравнение было выведено Н. А. Шиловым применительно
к времени защитного действия слоя адсорбента в противогазах.
Величина т0 определяется из выражения
(20-14)
где К— коэффициент массопередачи, кг!м2 • сек-------;
/— удельная поверхность адсорбента, м2[м3,
726
Гл. 20. Адсорбция
Интеграл правой части выражения (20-14) определяется графически и
представляет собой площадь, ограниченную кривой изменения ------—, абс-
~ м
циссой Хн и крайними ординатами.
Высота работающего слоя адсорбента Но (в м) в момент времени т0
определяется в соответствии с общим уравнением (16-43):
Но = nh
где h — высота единицы переноса, м.
Рис. 20-10. Зависимость времени Рис. 20-11. Рабочая линия процесса
адсорбции от высоты слоя адсор- адсорбции,
бента.
Для определения числа единиц переноса п строят рабочую линию для
момента времени т0.
В соответствии с изложенным имеем:
dH 1 СУ,
— = и =-----==---------.
ах k sPhxh
Подставляя значение -у— в уравнение (20-3), получим уравнение рабо-
чей линии для момента^ времени т0
ау=-^ах
Хн
(20-15)
Уравнение (20-15) на У— Х-диаграмме (рис. 20-11) представляет собой
прямую ОА, проходящую через начало координат и имеющую тангенс угла
наклона -у—. Участок CD этой прямой, соответствующий изменению концен-
трации газа от Yi до У2, является рабочей линией для момента т0> когда
в начале слоя концентрация достигает Хн.
Подставляя значения k, х0 и HQ ъ уравнение (20-13), определяют время
работы слоя адсорбента высотой Н.
4. Расчет адсорберов
727
Площадь сечения адсорберов описанного типа определяют из уравнения
расхода:
S = — м2 (20-16)
где G — расход газа, кг/сек-,
w — фиктивная, т. е. отнесенная ко всему сечению адсорбера, скорость
газа, м/сек (обычно принимается в пределах 0,08—0,25 м/сек)-,
рг — плотность газа, кг/м3.
Пример 20-2. Определить продолжительность адсорбции паров бензола
из воздуха в адсорбере диаметром D = 2,5 м с неподвижным зернистым
слоем адсорбента при начальной концентрации паровоздушной смеси
У1 = 0,02 кг/кг воздуха. Адсорбент — активированный уголь с насыпной мас-
сой рн = 550 кг/м3. Высота слоя угля
в аппарате Н = 1,1 м, свободный
объем слоя е = 0,375, удельная по-
верхность адсорбента f = 1630 м2/м3.
Расход паровоздушной смеси VCM.=
= 0,818 м3/сек, ее плотность р =
= 1,2 кг/м3.
Рис. 20-13. К примеру 20-2.
Рис. 20-12. К примеру 20-2.
Решение. Площадь сечения слоя угля S = 0,785 • 2,52 = 4,9 л2.
Фиктивная скорость паровоздушной смеси составляет:
Рсм 0,818 Л1Й_
w0 ==-yg-= 0,167 м/сек
Весовой расход паровоздушной смеси:
Осм. — 1>2 • 0,818 = 0,982 кг/сек
По изотерме адсорбции (рис. 20-12) при У1 = 0,02 кг/кг воздуха
равновесная концентрация бензола в угле Л* = 0,24 кг/кг угля. Принимаем
концентрацию насыщения начального сечения слоя Хп = 0,98Х* = 0,235 кг/кг
угля.
Определяем продолжительность насыщения слоя угля высотой 1 м по
уравнению (20-12):
. SpHXH 4,9.550-0,235 _. ...
k OcmZi- 0,982 - 0,02 “3,24'10 сек!м
Находим время т0, в течение которого насыщается начальное сечение
слоя. Пользуясь формулой (20-14), вычисляем интеграл ее правой части
методом графического интегрирования. Принимаем ряд произвольных зна-
чений X (меньше Ан = 0,235 кг/кг угля). По изотерме адсорбции
728
Гл 20 Адсорбция
(см рис 20-12) определяем значения Y 1( соответствующие каждой величине X,
и строим график зависимости-------* от X (рис 20-13) на основании полу-
—
ченных данных, приведенных в табл 31
К расчету f —“7*
о П
Таблица 31
X * — ч 10 d У1 * у1~у1 1
$ у1-у1
0 0 0,02 0,02 50
0,05 1,65 0,02 0,01835 54,5
0,10 2,37 0,02 0,01763 56,8
0,15 3,54 0,02 0,01646 60,8
0,20 7,10 0,02 0,01290 77,6
0,235 15,70 0,02 0,0043 223
Площадь, ограниченная
тами, проведенными из точек
X
кривой, осью абсцисс и крайними ордина-
0 и Хн (см рис 20 13), составляет 41,3 слс2
С учетом масштабов построения
41,3 • 0,02 • 20 = 16,5
Согласно примеру 20-1, коэффициент мас-
соотдачи от паровоздушной смеси к углю
₽ = 0,057 кг/м2-сек Следовательно, время
т0 по уравнению (20-14) равно.
_рн Г dX _ 550-16,5
Т° $fJ у —Y* 0,057-1630 сек
о 1 1
Высота единицы переноса составляет
^СМ
0,982
0,057 • 1630 • 4,9
= 0,00216 м
Рис. 20-14. Определение Определяем число единиц переноса графи-
числа единиц переноса (к ческим способом (рис 20-14), принимая кон-
примеру 20-2). центрацию бензола в конце работающего слоя
адсорбента Хс= 0,01 кг/кг угля
Определяем значения ' х*ХХх в пРеделах изменения X от Хн =
= 0,235 кг/кг угля до Хс = 0,01 кг/кг угля (табл 32)
Методом графического интегрирования определяем по рис. 20 14 число
единиц переноса п = 4,6,
4 Расчет адсорберов
729
Таблица 32
К расчету
f dX
J Х* — Х
X X* Х*-Х 1
х*-х
0,01 0,025 0,015 66,7
0,05 0,165 0,115 8,7
0,10 0,21 0,11 9,1
0,15 0,217 0,067 14,9
0,20 0,24 0,04 25
0,235 0,245 0,01 100
Находим высоту Но слоя угля, который работает к моменту
H0 = nh = 4fi 0,00216 = 0,01 я
Определяем продолжительность адсорбции по формуле (20-13)
Т = ТО + k (Н— Но) = 98 + 3,24 -104 (1,1 — 0,01) = 3,54 104 сек 9,8 ч
Пример 20-3. Определить приближенным методом продолжительность
процесса адсорбции, проводимой в условиях примера 20 2, исходя из сред-
них значений концентраций адсорбированного вещества Х\ и Х2 (X! = 0)
Решение Определяем массу адсорбента в слое
Ос = ^ Г>2Ярн = 0,785 • 2,52 • 1,1 550 = 2970 кг
Принимаем Х2 как среднеарифметическую между Хн и Хс (см пример
20 2)
v 0,235 4-0,01 П1ОО ,
Х2 = ------10,122 кг{кг угля
По уравнению (20-11) продолжительность адсорбции составляет !
_ Ge№-X,) = ______2970(0,122 - 0)____
w0SPcM(r, —Г2) 0,167 4,9 1,2(0,02 — 0,001)
Величина т меньше рассчитанной точным методом (см пример 20 2) на
45%
Адсорберы со «стационарным» кипящим слоем адсорбента. В таких ад-
сорберах периодического действия, в отличие от адсорберов с неподвижным
зернистым слоем адсорбента, вследствие интенсивного перемешивания кон-
центрация поглощаемого вещества во всем слое адсорбента одинакова, яв-
ляется только функцией времени Х=/(т) и не изменяется по высоте аппарата.
При ооозначениях, принятых выше, уравнение материального баланса
по поглощенному веществу в данном случае имеет следующий вид.
G(Yx-Y2^ = SH^Xn
730
Гл. 20. Адсорбция
Пренебрегая У2 и учитывая выражение (20-12), определяем продолжи-
тельность адсорбции:
т = H=kH сек (20-17)
где рн — кажущаяся плотность слоя адсорбента в условиях псевдоожиже-
ния, кг/м3.
Адсорберы с движущимся зернистым адсорбентом. Площадь сечения
непрерывнодействующих адсорберов с движущимся зернистым адсорбентом
определяется по уравнению (20-16). Высота Н рабочей части аппарата скла-
дывается из высоты Яа зоны адсорбции, высоты НЛ зоны десорбции и вы-
соты Нс зоны сушки, через которые последовательно проходит адсорбент,
перемещаясь через аппарат:
Я=Яа + Яд + Нс (20-18)
Высота адсорбционной зоны определяется по формуле
«а = -X- (20-19)
где F — необходимая поверхность фазового контакта, определяемая по об-
щему уравнению массопередачи (16-17);
f — удельная поверхность адсорбента, м2/м3.
Можно принять, что высоты Лд и Нс относятся к Н, как продолжитель-
ности соответствующих операций тд и тс к общей продолжительности т про-
цесса, откуда
НС = Н^
Т X
Общая продолжительность процесса т может быть определена по урав-
нению
т = сек (20-20)
где L — расход адсорбента, м3/сек.
Адсорберы с циркулирующим кипящим слоем адсорбента. Пусть при
прохождении через аппарат кипящего слоя мелкозернистого адсорбента кон-
центрация поглощаемого вещества в нем за время т увеличивается от Х2
на входе в аппарат до Xi на выходе из него, причем в условиях установив-
шегося процесса Xi является величиной постоянной. Рабочий объем адсор-
бера обозначим через Уа м3. Тогда уравнение материального баланса по по-
глощаемому веществу примет вид
УаР (^-Х2) = /<Га/Дср.^
Откуда продолжительность адсорбции составляет:
Т = Р7- Х'.~Хг сек (20-21)
^ср.
кг
где К—коэффициент массопередачи, кг/м2 • сек
f— удельная поверхность адсорбента, м2/м3\
Дер — средняя разность концентраций поглощаемого вещества по высоте
адсорбера, кг/кг носителя.
Высота И адсорбера определяется по формуле (20-18).
Глава 21
СУШКА
1. Общие сведения
Тепловая сушка, или просто сушка, представляет собой про-
цесс удаления влаги из твердых влажных материалов путем ее
испарения и отвода образующихся паров. Сушка является наи-
более распространенным способом удаления влаги из твердых
и пастообразных материалов и проводится двумя основными
способами:
1) путем непосредственного соприкосновения сушильного
агента (нагретого воздуха, топочных газов) с высушиваемым
материалом — конвективная сушка\
2) путем нагревания высушиваемого материала тем или
иным теплоносителем через стенку, проводящую тепло, — кон-
тактная сушка.
Принципиальные схемы сушки этими способами показаны
на рис. 21-1.
Пар
Сушильный
Тепло
Отработанный
сушильный
агент
'Влажный материал
Стенка.
Теплоноситель-»
Влажный
материал
6
Рис. 21-1. Принципиальные схемы сушки:
а —конвективная; б—контактная.
Сушка производится также путем нагревания высушиваемых
материалов токами высокой частоты (диэлектрическая сушка)
или инфракрасными лучами (радиационная сушка).
В особых случаях применяется сушка некоторых продуктов
в замороженном состоянии при глубоком вакууме — сушка воз-
гонкой, или сублимацией.
732
Гл 21 Сушка
2. Статика сушки
При сушке процесс передачи вещества из одной фазы в дру-
гую (испарение жидкости) сопровождается процессом тепло-
передачи, при этом температуры фаз не одинаковы. Количество
тепла, передаваемое от газообразного сушильного агента к жид-
кости путем конвекции при температуре газа /, превышающей
температуру ft материала (жидкости), составит:
— — ft)
где а — коэффициент теплоотдачи.
Количество испаряющейся жидкости определяется уравне-
нием (16-17). Это количество жидкости переходит в виде пара
в газовую фазу и передает от жидкости к газу тепло, соответ-
ствующее теплоте испарения этой жидкости:
Q2 = Mr = rKF^ — p)
где г — теплота испарения;
р*— давление пара над жидкостью (при температуре '0);
р — парциальное давление пара в газовой фазе.
Всего передается тепла от газа к жидкости:
Q — Qi Qa
причем это тепло расходуется на нагревание жидкости.
По мере нагревания жидкости ее температура $ и давление
пара р* возрастают. В соответствии с этим Qi будет умень-
шаться, a Qa увеличиваться. Очевидно, наступит момент, когда
Qi будет равно Q2 и Q = 0, т. е. все тепло, получаемое жид-
костью от газа путем конвекции, будет возвращаться газу в виде
теплоты испарения жидкости После этого дальнейшее нагрева-
ние жидкости станет невозможным, и будет происходить испа-
рение ее при постоянной температуре (а следовательно, при по-
стоянном р*) до тех пор, пока не испарится вся жидкость.
Температура, принимаемая жидкостью при испарении ее
после достижения теплового равновесия (Q = 0), называется
температурой мокрого термометра и обозначается t м.
Это — температура термометра, шарик которого покрыт влаж-
ной тканью, с которой происходит испарение влаги. Температура
мокрого термометра определяется условием Qi = Q2, или
а(/~ Q = р)
где рм — давление пара над жидкостью при температуре
Определение /м из этого уравнения возможно только путем
подбора, так как рм является функцией /м. Другие методы опре-
деления tM будут рассмотрены ниже (стр. 742).
2 Статика сушки
733
Влажный материал может не только отдавать влагу путем
ее испарения в окружающую среду; при определенных условиях
он может также поглощать влагу из окружающей среды Для
проведения сушки необходимо знать условия, при которых ма-
териал способен отдавать влагу.
Среда, окружающая влажный материал, представляет собой
влажный воздух (смесь сухого воздуха и водяных паров) или
почти чистый водяной пар, содержащий небольшую примесь
воздуха, проникшего в сушилку через неплотности (при сушке
в вакууме).
Обозначим через рп парциальное давление водяного пара
в воздухе или давление чистого пара Для проведения сушки
давление паров влаги у поверхности высушиваемого мате-
риала ри должно быть больше рп, т. е. должно соблюдаться
условие
Рм>Рп (21-1)
' Из этого выражения видно, что сушка облегчается с воз-
растанием давления рм, которое тем больше, чем выше влаж-
ность материала и температура сушки; величина рм зависит
также от характера связи влаги с материалом (см. ниже).
При сушке в течение определенного времени влажность ма-
териала приближается к некоторому пределу, соответствующему
равенству
Рм=Рп (21-2)
Когда достигается это равенство, наступает равновесие в про-
цессе обмена влагой между материалом и средой. Этому состоя-
нию соответствует некоторая устойчивая влажность материала,
называемая равновесной влажностью, при которой процесс
сушки прекращается.
Равновесная влажность и, следовательно, протекание про-
цесса сушки зависят от свойств высушиваемого материала, ха-
рактера связи с ним влаги и параметров окружающей среды.
Связь влаги с материалом может быть механической, фи-
зико-химической и химической.
Механически связаны с материалом поверхностная влага и
влага, заполняющая крупные капилляры материала в резуль-
тате смачивания Эта влага (иногда называемая внешней) наи-
менее прочно связана с материалом и наиболее легко удаляется
из него.
Более прочно связана с материалом влага, которая погло»
щается поверхностью мелких капилляров (адсорбционная влага)
или проникает вследствие диффузии внутрь клеток материала
734
Гл. 21. Сушка
(структурная и осмотически связанная влага). Влагу, физико-
химически связанную с материалом, удалять из него значитель-
но трудней.
Влага, химически связанная с материалом (гидратная, или
кристаллизационная), в процессе сушки обычно не удаляется и
поэтому при расчете сушилок не учитывается.
Независимо от характера связи влагу, прочно связанную
с материалом, в отличие от внешней влаги называют гигроско-
пической. Эта влага не может быть полностью удалена из мате-
риала путем сушки. При сушке влажный материал отдает сна-
Относителъная
влажность воздуха %
Рис. 21-2. Кривые равновесной
влажности.
чала внешнюю влагу, затем часть
гигроскопической влаги, которая
может быть удалена при данной
температуре и влажности воздуха.
Вся влага, удаляемая из материала
в условиях тепловой сушки, назы-
вается свободной влагой.
Путем значительного увеличе-
ния температуры воздуха и сниже-
ния его относительной влажности
можно удалить еще некоторую часть
гигроскопической влаги. Эту часть
влаги, которую еще можно удалить
сушкой, часто называют связанной
влагой.
При прочих равных условиях
равновесная влажность тем выше,
чем больше давление водяного па-
ра в среде, окружающей влажный материал. Значения равно-
весной влажности wp (в % от веса абсолютно сухого материа-
ла) определяют опытным путем в зависимости от парциального
давления рП водяного пара в окружающей среде при постоянной
температуре материала, равной температуре среды. По опыт-
ным данным строят кривые равновесной влажности (рис. 21-2) *.
По этим кривым можно судить о том, будет ли происходить вы-
сушивание или увлажнение материала и до какой конечной
влажности возможно высушивание материала при данных пара-
метрах окружающей среды.
Пользуясь кривой равновесной влажности (рис. 21-3), рас-
смотрим изменение состояния материала в процессе сушки в за-
висимости от влажности материала и окружающей среды.
* Представленные на рис. 21-2 и 21-3 кривые показывают зависимость
равновесной влажности от относительной влажности воздуха (см. стр. 736
и сл.).
2. Статика сушки
735
Равновесная влажность, соответствующая полному насыще-
нию среды влагой, называется гигроскопической точкой мате-
риала (точка А на рис. 21-3). Эта точка характеризует предель-
ную влажность материала, при которой парциальные давления
пара в воздухе рП и непосредственно над поверхностью мате-
риала рм равны парциальному давлению насыщенного пара рн
при данной температуре:
Рп=Рм = Ра
Если влажность материала больше влагосодержания, соот-
ветствующего гигроскопической точке, материал находится во
Относительная в л а т н о с т ь <р, %
Рис. 21-3. Состояние материала в зависимости от его
влажности lFa и относительной влажности воздуха:
А —гигроскопическая точка.
влажном состоянии, при котором пары влаги над его поверх-
ностью насыщены (рм=рн)- Поэтому сушка протекает при лю-
бых параметрах окружающей среды, вплоть до ее полного насы-
щения.
Если влажность материала меньше влагосодержания, соот-
ветствующего гигроскопической точке, материал находится в
гигроскопическом состоянии, при котором пары влаги над его
поверхностью не насыщены (рм <рн). При таком состоянии ма-
териала сушка зависит от давления водяного пара в окружаю-
щей среде и возможна только при влажности материала,< пре-
вышающей равновесную (область сушки выше кривой wp рав-
новесной влажности, рис. 21-3, справа). В области ниже кривой
равновесной влажности материал не будет высушиваться, а, на-
оборот, поглощать влагу из окружающей среды (область сорб-
ции).
736
Гл 21 Сушка
Таким образом, сушка возможна как во влажном, так и в
гигроскопическом состояниях материала при условии, что его
влагюсодержание больше равновесного.
Во влажном состоянии материал имеет температуру, равную
температуре мокрого термометра (9- = /м), в гигроскопическом
состоянии температура материала больше /м, но ниже темпера-
туры окружающей среды (/м < < 4)- Когда достигается равно-
весная влажность, температура материала становится равной
температуре окружающей среды (& = /в)-
Процесс сушки зависит как от свойств материала, так и от
свойств окружающей среды. Поэтому для изучения процесса
сушки необходимо знать свойства влажного газа (воздуха) и
характер их изменения в процессе сушки.
3. Свойства влажного газа (воздуха)
Влажный воздух представляет собой смесь сухого воздуха
и водяных паров. В ненасыщенном воздухе влага находится в
состоянии перегретого пара, поэтому свойства влажного воздуха
с некоторым приближением характеризуются законами идеаль-
ных газов.
Количество водяных паров, содержащихся в 1 м3 влажного
воздуха, называется абсолютной влажностью воздуха. Водяной
пар занимает весь объем смеси, поэтому абсолютная влажность
воздуха равна массе 1 -и3 водяного пара, или плотности пара рп
в кг/jn3.
При достаточном охлаждении или увлажнении воздуха нахо-
дящийся в нем водяной пар становится насыщенным. С этого
момента дальнейшее понижение температуры воздуха или уве-
личение содержания влаги в нем приводит к конденсации из воз-
духа избыточного количества водяных паров. Поэтому количество
пара, содержащегося в насыщенном воздухе, является предельно
возможным при данной температуре. Оно равно массе 1 jh3 пара
в состоянии насыщения, или плотности насыщенного пара рн
в кг!м3. Отношение абсолютной влажности к максимально воз-
можному количеству пара в 1 jh3 воздуха, при той же температуре
и данном барометрическом давлении, характеризует степень на-
сыщения воздуха влагой и называется относительной влажностью
воздуха:,
(21-3)
т Рн
Плотность пара пропорциональна его парциальному давле-
нию в смеси при данной температуре, следовательно относи-
3 Свойства влажного газа (воздуха)
737
тельную влажность можно выразить отношением давлений:
<р=£ (21-4)
Рн
где Рп—парциальное давление водяного пара, соответствую-
щее его плотности рп;
ра — давление насыщенного пара при той же температуре.
При сушке меняются объем воздуха над влажным материа-
лом и абсолютная влажность воздуха, так как он отдает тепло,
необходимое для испарения влаги, и охлаждается, поглощая
влагу, испаренную из материала. Поэтому влажность воздуха
относят к величине, постоянной в процессе сушки, — к массе
абсолютно сухого воздуха, находящегося во влажном воздухе.
Количество водяного пара в кг, приходящееся на 1 кг абсо-
лютно сухого воздуха, называется влагосодержанием * воздуха
и обозначается х. Величина х характеризует относительный ве-
совой состав влажного воздуха.
Если Gn — масса водяного пара во влажном воздухе, а
Gc. в. — масса сухого воздуха в том же объеме, то согласно урав-
нению (16-12) влагосодержание (в кг/кг сухого воздуха) при
общем давлении Р составляет:
Qfl ____ -Мп t Рп
Qc. В. А1С. в. Р Рп
(21-5)
Из отношения (21-4) парциальное давление пара =
Подставляя значение рп и величины молекулярных масс сухого
воздуха и водяного пара УИС. в. и Мп в уравнение (21-5), полу-
чим следующую зависимость влагосодержания воздуха от его
относительной влажности:
<?Рп
Р — ЧРп
= 0,622
Р~ЧРп
(21-6)
Влажный воздух, как теплоноситель, характеризуется энталь-
пией 1 (теплосодержанием), равной сумме энтальпии сухого
воздуха и водяного пара:
7 = сс.в/-|-^п дж/кг сухого воздуха
(21-7)
где £с. в. — удельная теплоемкость сухого воздуха, дж/кг • град-,
t — температура воздуха, °C;
in— энтальпия перегретого пара, дж/кг.
* В литературе по сушке влагосодержание воздуха часто выражают так-
же в граммах водяного пара на 1 кг сухого воздуха и обозначают d г/кг.
47 Зак 546.
738
Гл 21 Сушка
Энтальпия пара определяется по эмпирической формуле:
/п==г0 + сп/ = (2493+1,97/) • 103 дж/кг (21-8)
где г0 = 2493 103 — постоянный коэффициент, примерно равный
энтальпии пара при 0°С;
са = 1,97 • 103 — удельная теплоемкость пара, дж/кг-град
(в условиях сушки может быть принята по-
стоянной) .
Подставив значение /п в выражение (21-7) и принимая удель-
ную теплоемкость сухого воздуха постоянной (1000 дж/кг-град),
найдем энтальпию влажного воздуха (в дж/кг сухого воздуха):
/ = Ю00/ + (2493 + 1,97/) • 103л (21-9)
или
/ = (1000+1,97 • 10+)/ + 2493 • 10+ (21-10)
В формуле (21-10) член (1000+1,97 • 103 х), равный (сс в +спл),
представляет собой удельную теплоемкость влажного воздуха
при влагосодержании х.
Если за единицу количества тепла принята ккал, то формула (21-8)
принимает вид
/п — 595 4- 0,47/ ккал/кг
Соответственно формула (21-9) принимает вид
I = 0,24/ (595 4~ 0,47/) х ккал/кг cjxqvq воздуха
где 595 — постоянный коэффициент, примерно равный энтальпии пара
при 0°С,
0,47 — теплоемкость пара, ккал/кг • град,
0,24 —- удельная теплоемкость сухого воздуха, ккал/кг • град.
Плотность водяного пара меньше плотности воздуха, по-
этому влажный воздух легче сухого, причем с увеличением
влажности масса воздуха уменьшается.
Рассмотрим некоторый объем влажного воздуха v, в котором
содержится 1 кг сухого воздуха и х кг водяных паров. Общее
давление воздуха Р, парциальное давление водяных паров рп.
По уравнению состояния объем v равен:
RT -8314 Г 288 Т о /О1 1П
'и = ~м---Ъ— = ~29"Б------= р — о" м/кг СУХОГО воздуха (21-11)
где R — универсальная газовая постоянная (8314 дж/моль-
• град);
/Ис. в. — молекулярная масса воздуха (29).
Величины Р,рс в. и рп в уравнении (22-11) выражены в н/м2.
Значения v приводятся в таблицах влажного воздуха.
4 I—х-диаграмма влажного воздуха
739
4. /—х-диаграмма влажного воздуха
Графический расчет сушилок ведут при помощи диа-
граммы влажного воздуха, впервые предложенной Л К- Рам-
зиным. Диаграмма (см. Приложение XIX) построена для баро-
метрического давления Р = 745 мм рт. ст., которое можно счи-
тать средним годовым давлением воздуха для центральных рай-
онов СССР. На осях координат диаграммы отложены два основ-
ных параметра влажного воздуха: влагосодержание х (ось абс-
цисс) и энтальпия I (ось ординат). Угол между осями координат
принят не прямым, как обычно, а тупым (135°); при этом влаго-
содержания х отложены в некотором масштабе на вспомогатель-
ной горизонтальной оси, на которую снесены значения х с на-
клонной оси абсцисс.
В соответствии с таким построением линии постоянного вла-
госодержания x = const изображаются на диаграмме вертикаль-
ными прямыми, а линии постоянной энтальпии I *=• const предста-
вляют собой наклонные прямые, параллельные оси абсцисс.
Кроме указанных линий на диаграмме нанесены: 1) линии
постоянных температур, 2) линии постоянной относительной
влажности, 3) линия парциального давления водяного пара
и 4) линии постоянных температур мокрого термометра.
Линии постоянных температур, или изотермы, t = const по-
строены на основе формулы (21-9), которая при t = const гра-
фически выражается прямой. Поэтому, определив I для х = О
и некоторого произвольного значения х, через полученные точки
проводят прямую t — const. Наклон изотерм увеличивается
с повышением температуры, так как при этом возрастает эн-
тальпия пара in [см. формулу (21-8)].
Линии постоянной относительной влажности ф = const по-
строены согласно формуле (21-6). Для нескольких температур
при ф = const определяют х и находят пересечение соответствую-
щих линий х = const и t = const. Соединяя полученные точки
плавной кривой, строят линию ф = const.
Линии ф = const образуют пучок кривых, сходящихся на оси
ординат в одну точку (х = 0, t = —273°С). При температуре
99,4° С, соответствующей барометрическому давлению 745 мм
рт. ст., эти линии имеют резкий перелом и идут вверх почти
параллельно линиям х — const. Это объясняется тем, что при
/>•99,4° С давление насыщенного пара ря равно барометриче-
скому давлению В = 745 мм рт. ст., для которого построена
диаграмма. Относительная же влажность, в соответствии с фор-
мулой (21-4), ф = -~, т. е. зависит только от парциального
давления пара рП и, следовательно, только от влагосодержа-
740
Гл 21 Сушка
ния х. Однако по более точной формуле (21-3) величина ф за-
висит не только от давления, но и от температуры; поэтому ли-
нии ф = const несколько не совпадают с линиями х = const.
Линия ф=1 (ф= 100%) показывает максимально возможное
содержание влаги в воздухе при данной температуре; она делит
диаграмму на области ненасыщенного воздуха и пересыщенного
воздуха, в котором влага распылена в виде мельчайших капель.
К пересыщенному воздуху неприменимы все зависимости, полу-
ченные для влажного воздуха, содержащего влагу в парообраз-
ном состоянии. Поэтому рабочей частью диаграммы является
область ненасыщенного воздуха, расположенная над линией
Ф = 1. При тупом угле между осями координат линия ф = 1 идет
сравнительно полого, площадь рабочей части диаграммы увели-
чивается, а кривые ф = const дальше отстоят друг от друга, что
облегчает пользование диаграммой.
Линия парциального давления водяного пара в воздухе по-
строена по уравнению (21-6) для различных влагосодержаний %,
причем шкала рп (в мм рт. ст.) помещена на правой ординате
диаграммы.
Процесс сушки связан с нагреванием, охлаждением и
увлажнением воздуха и со смешением воздуха разных пара-
метров.
Нагревание воздуха в поверхностном воздухоподогревателе
(калорифере) происходит без изменения его влагосодержания,
т. е. при x = const. На диаграмме (рис. 21-4, а) этот процесс изо-
бражается вертикалью, проведенной вверх от точки А, характе-
ризующей начальное состояние воздуха, до точки В, соответ-
ствующей его конечному состоянию после нагревания до задан-
ной температуры t\.
При нагревании воздуха возрастает парциальное давление
насыщенного пара рн и соответственно снижается относительная
влажность ф.
/ Охлаждение воздуха в поверхностном холодильнике изобра-
жается вертикалью BMi, направленной вниз (см. рис. 21-4, а).
Температура, отвечающая точке С\ пересечения вертикали с ли-
нией ф = 1, соответствует полному насыщению воздуха водя-
ными парами в процессе охлаждения при х = const и назы-
вается температурой точки росы. Охлаждение воздуха ниже
точки росы сопровождается конденсацией из него влаги, т. е.
осушкой воздуха. Осушение воздуха изображается линией CiC2,
совпадающей с линией ф = 1 и направленной влево от точки
росы до пересечения с изотермой, соответствующей конечной
температуре охлаждения воздуха.
Из выражения (21-6) видно, что при ф = 1 величина рн и
соответственно точка росы зависят только от влагосодержания л
4. I—х-диаграмма влажного воздуха
741
и общего давления Р, но не зависят от температуры и относи-
тельной влажности ф воздуха. На диаграмме точку росы нахо-
дят, как пересечение линии х — const, проведенной из точки,
соответствующей начальному состоянию воздуха, с линией ф = 1.
Рис. 21-4. Изображение основных процессов изменения состояния
воздуха на / — х-диаграмме:
а —нагревание и охлаждение воздуха; б— адиабатическое охлаждение воздуха; в— сме-
шение воздуха разных параметров.
Адиабатическое охлаждение воздуха происходит в том слу-
чае, если все тепло, необходимое для испарения влаги с поверх-
ности материала, поступает из окружающего воздуха как един-
ственного источника тепла. При этом процесс испарения (сушки)
протекает в адиабатических условиях — без потерь тепла и под-
вода его извне.
Воздух, отдавая тепло, охлаждается и одновременно погло-
щает пары влаги, в результате чего увеличиваются его влаго-
содержание х и относительная влажность ф. Температура испа-
ряющейся влаги постепенно устанавливается постоянной, рав-
ной температуре мокрого термометра /м (стр. 732).
Разность температур воздуха и испаряющейся влаги /м ха-
рактеризует способность воздуха испарять влагу, причем эта
разность по мере испарения влаги уменьшается и становится
равной нулю при температуре воздуха, равной /м; при этом
процесс сушки полностью прекращается.
Таким образом, температура мокрого термометра /м является
температурой воздуха, соответствующей его насыщению в адиа-
батических условиях. Поэтому ее называют также пределом
адиабатического охлаждения воздуха.
На диаграмме I — х (см. Приложение XIX) пунктиром на-
несены линии постоянных температур мокрого термометра
/м = const.
742
Г л. 21. Сушка
Температуру мокрого термометра находят как точку пере-
сечения линии tM = const с линией <р = 1 (точка С на рис. 21-4, б).
Изотерма, проходящая через эту точку, указывает значение tM.
Смешение воздуха разных параметров при отсутствии конденсации пока-
зано на рис. 21-4, в. Влажный воздух в состоянии А, содержащий 1 кг
сухого воздуха и имеющий параметры Xi и h, смешивается с воздухом
в состоянии В, который содержит п кг сухого воздуха и имеет параметры х2
и 12. Полученная смесь содержит п + 1 кг сухого воздуха и имеет пара-
метры Лом. и /см.. Зависимость между хсм_, /См. и параметрами компонентов
смести:
1-Л + л/2 = (п+1)/См- (21-12)
1 • Xj + пх2 ж» (п + 1) хсм. (21-13)
Эта зависимость выражается прямой линией. Соответственно на
/ — х-диаграмме (рис. 21-4, в) процесс смещения изобразится прямой линией,
проходящей через точки A (xi, Л) и В
(х2, h).
Точка С (хсм., /см.)> характеризую-
щая смесь, делит прямую АВ на отрез-
ки, обратно пропорциональные разностям
влагосодержаний:
АС: СВ = (хсм- л'|): (х2 -^см.)
причем координаты точки С определяют-
ся из выражений (21-12) и (21-13):
„ __ Х\ + ПХ2
- п +1
г __Л п/2
СМ-~ п + 1 ’
кг!кг сухого воздуха
(21-14)
дж!кг сухого воздуха
(21-15)
влагооодержанив 1
кг/нг сухого воздуха
Пример 21-1. Наружный воздух при
температуре to =15° С и относительной
влажности фо = 50% нагревается в ка-
лорифере до температуры t\ = 56° С.
Определить остальные параметры на-
ружного и нагретого воздуха и устано-
Рис. 21-5. К примеру 21-1.
вить, как влияет нагревание воздука
на его способность испарять влагу из
материала.
Решение. По заданным параметрам наружного воздуха to и <ро на-
ходим точку А на I — х-диаграмме (рис 21-5), характеризующую-состояние
наружного воздуха. Опуская из точки А вертикаль на вспомогательную ось
абсцисс диаграммы, находим влагосодержание воздуха х0 =•= 0,0054 кг/кг
сухого воздуха.
По линии / = const, проходящей через точку А, определяем энтальпию
воздуха /о = 6,8 ккал/кг сухого воздуха. Продолжая линию / = const до
пересечения с линией <р = 1 и проводя через точку их пересечения изотерму,
определяем температуру 'Мокрого термометра наружного воздуха /Мо -= 9,6° С.
Находим также парциальное давление водяного пара рп в наружном
воздухе. Для этого опускаем из точки А вертикаль до пересечения с линией
5. Материальный и Теплйвой балансы Cyulrtu
743
парциального давления водяного пара на диаграмме и, проводя из точки
пересечения горизонталь до правой ординаты диаграммы, находим:
Рп0 — 6,5 мм рт. ст.
Для определения параметров нагретого воздуха проводим из точки А
вертикаль до пересечения с изотермой Л = 56° С, точка пересечения В харак-
теризует состояние нагретого воздуха.
Аналогично определению параметров наружного воздуха определяем пара-
метры нагретого воздуха:
X] = х0 = 0,0054 кг/кг сухого воздуха
/1 = 16,7 ккал/кг сухого воздуха = 70 • 103 дж/кг сухого воздуха
Т1=0,05; /М1 — 23,5° С
Способность воздуха испарять влагу характеризуется разностью темпе-
ратур воздуха и мокрого термометра ta — tM:
для наружного воздуха
t0 — /Мо = 15 — 9,6 = 5,4° С
для нагретого воздуха
tx — = 56,0 — 23,5 = 32,5 °C
Таким образом, при повышении температуры воздуха от 15 до 56° С
его относительная влажность уменьшилась от <р0 — 50% до <pi = 5%
(в 10 раз), а способность воздуха испарять влагу возросла примерно в 6 раз.
5. Материальный и тепловой балансы сушки
Материальный баланс
Пусть количество влажного материала, поступающего в су-
шилку, равно G\ кг!сек, а его влажность вес. долей. В ре-
зультате сушки получается G2 кг/сек высушенного материала
(влажностью w2 вес. долей) и W кг/сек испаренной влаги.
Тогда материальный баланс по всему количеству вещества
выразится равенством:
G1 = G2-\- W кг/сек (21-16)
Баланс по абсолютно сухому веществу, количество которого
не меняется в процессе сушки:
O1(1_W1)==G2(1 _^2) (21-17)
Из этих уравнений определяют количества высушенного ма-
териала G2 и испаренной влаги W.
Для теплового расчета сушилки необходимо знать расход
воздуха на сушку, который определяется из баланса влаги.
Если на сушку расходуется L кг абсолютно сухого воздуха,
причем влагосодержание влажного воздуха на входе в сушилку
744
Гл. 21. Сушка
х0 кг/кг сухого воздуха, а на выходе из сушилки х2 кг/кг сухого
воздуха, то с воздухом поступает Lx0 кг влаги. Из материала
испаряется W кг влаги, с отработанным воздухом уходит Lx2 кг
влаги.
Следовательно, баланс влаги в сушилке выражается равен-
ством
Lx2 = Lx0 + IV
откуда расход воздуха составляет:
W
кг
Удельный расход воздуха (на 1 кг испаренной влаги), оче-
видно, составит:
(21-18)
Из выражения (21-18) видно, что удельный расход воздуха
зависит только от разности влагосодержаний отработанного и
свежего воздуха. Расход воздуха будет тем больше, чем выше
его начальное влагосодержание х0, которое определяется темпе-
ратурой и относительной влажностью воздуха. Поэтому расход
воздуха, при прочих равных условиях, будет возрастать с уве-
личением t0 и фо- Следовательно, расход воздуха на сушку в лет-
них условиях больше, чем в зимних, и устройства для перемеще-
ния воздуха (газодувки, вентиляторы) необходимо выбирать
по расходу воздуха в самый теплый месяц года.
Значения to и ф0 зависят от климатических условий района,
в котором работает данная сушилка. Средние значения этих ве-
личин в самый теплый и самый холодный месяцы года для раз-
личных районов СССР приводятся в справочных таблицах (см.
Приложение XVII).
Пример 21-2. Определить количество влаги, испаряемой за 1 ч из ма-
териала, поступающего на сушку в количестве G\ — 1235 кг/ч с начальной
влажностью ом = 77,5% (считая на общий вес). Влажность высушенного
материала ,^2 = 5%.
Решение. Производительность сушилки по высушенному материалу
в соответствья с формулой (21-17) составляет
G, (1 — 1235 (1 — 0,775)
1 — w2 1 — 0,05
= 293 кг!ч
5. Материальный и тепловой балансы сушки
745
По формуле (21-16) определяем количество влаги, испаряемой из мате-
риала за 1 ч:
W = Gi — G2^ 1235 — 293 = 942 кг/ч
Тепловой баланс
Составим тепловой баланс относительно тепла, переданного
сушилке (рис. 21-6), с учетом того, что количество подводимого
в сушилку тепла Q в общем случае слагается из тепла QH нагре-
вания сушильного агента (в воздухоподогревателе или топке)
и тепла фДОб.> сообщаемого дополнительно в сушильной камере.
Рис. 21-6. Принципиальная схема конвективной сушилки:
1— камера сушилки; 2—вентилятор; 3— воздухоподогреватель; 4— допол-
нительный воздухоподогреватель в камере сушилки.
Для составления баланса введем следующие обозначения
(в дополнение к принятым ранее):
с, св, с2 и ст — средние удельные теплоемкости сушильного
агента (на 1 кг сухого), влаги, удаляемой из
материала, высушенного материала и транс-
портных устройств сушилки, дж/кг' град-,
tQ и /2— температуры сушильного агента перед воздухо-
подогревателем и после сушилки, °C;
и &2 — температуры материала на входе и выходе из
сушилки, °C;
Gy — масса транспортных устройств, кг-,
1т и /т—температура транспортных устройств на входе и
выходе из сушилки, °C;
•О
и in — энтальпия водяного пара в свежем и отработан-
ном сушильном агенте, дж/кг,
746
Гл 21 Сушка
Баланс тепла может быть выражен следующим образом:
Приход тепла Расход тепла
С сушильным аген- Lct0 С сушильным
том агентом .... Lct2
С высушиваемым G2C2^l С высушенным G2C2^2
материалом . . . материалом . .
С влагой, испаряе- WcB^ С испаренной вла-
мой из материала гой
Физическое тепло Физическое тепло
транспортных GTcT нагретых транс-
устройств . . . портных
устройств . . . GTc/T
Подводимое тепло Q — Qn + Qao6. Потери тепла в
- окружающую среду Qn
Уравнение теплового баланса выражается равенством:
AfZ0 -|- Ч~ ~hQ —
= Lct<2~\- G2C2^2~\~ №1п-)- GTcTtT -|- Qn (21-19)
Решая уравнение (21-19) относительно количества подводи-
мого тепла, получим:
Q = Lc (/2 — to)~h W(i'a — £BHi)~h G2C2 (^2 — ^1) 4~
+ G^T(/;-/;) + Qn (21-20)
Из этого выражения видно, что подводимое в сушилку тепло
расходуется следующим образом:
1) потери тепла с уходящим сушильным агентом
At (/2 /0) Qyx.
2) на испарение влаги из материала
ir(Z''-cB»i)=QHcn.
3) потери тепла на нагревание высушенного материала
б?2С2 (®2 ^1) — Qm
4) потери тепла на нагревание транспортных устройств
G?Ct (Zt — /т) = Qt
5) потери тепла в окружающую среду Qn.
Соответственно уравнение (21-20) может быть записано так:
Q = Qyx. + Qncn. 4-Qm + Qt+Qh (21-21)
Для сравнения работы различных сушилок удобно вести теп-
ловые расчеты на 1 кг испаренной влаги. Разделив все члендо
5 Материальный и тепловой балансы сушки
747
уравнения (21-20) на W (общее количество испаренной влаги)
и обозначив удельный расход тепла и сушильного агента соот-
ветствующими строчными буквами, получим:
q — lc (/г — io) 4“ (*п — £в&1) 4~ <7м 4~ <7т 4~ —
=== *7уХ. 4" ^ЙСП. + 7м 4“ *7т 4“ Qn (21-22)
Преобразуем первые два члена правой части уравнения
(21-22), подставив значение теплоемкости влажного воздуха
е = £с в 4-сп-*о (стр. 738), а также значения /п и I по формулам
(21-8) и (21-18). Тогда
?,х + '7коп. = 1с (*2 ~ О + К — Св91) =
Г '
— I (бе в. 4“ £п-^о) (/г — io) 4—у —
или
<7ух. 4“ <7исп. — I [^с.в. (^2 — to) 4“ £п-^0 (^2 — i(j) 4“ in (-^2 — Xq) ] -— CB^i
Прибавив и отняв из правой части этого последнего выраже-
ния величину Го (стр. 738), проведем несложные преобразования:
<7ух. 4“ <7исп. ==-1 {^с в. (^2 — io) 4- Xq [(/"0 4- ^п^г)-
-— (го 4- ^nio)] 4“ (Х2 — Хо)| — Св&1 =
= I [се в. (^2 — to) 4“ Хо (in — in) 4“ in (Х2 — £())] — £в8т —
= I [(сс. в/г 4“ in-^г) — (се. в io 4~ in-^o)] — Св^т = I (Л —’ 7о) — Cb^i
Подставив полученное значение <?Vx. 4“ <7исп. в уравнение
(21-22), получим:
q = l(J2 — /о)4_<7м4_<7т4“<7п~ £b^i (21-23)
где <7 — 7н4-<7вдб.— сумма удельных расходов тепла в воздухо-
подогревателе и в сушилке.
Обозначив разность величин
(<7доб. 4- ^в®т) (<7м 4~ Qt 4~ Qn) === А
приведем уравнение (21-23) к виду
Z (/3 7q) qH А
Количество тепла 11\, вносимое сушильным агентом, равно
сумме тепла наружного воздуха IIq и тепла qa, сообщенного су-
шильному агенту в воздухоподогревателе:
/Л = Uq-}q*
748
Гл. 21. Сушка
Откуда Uq — II\ — qa, следовательно
//2— II х = Д
Вынося / за скобки и подставляя его значение из
(21-18), приведем полученное выражение к виду:
.<2.-/1
(21-24)
уравнения
Учитывая, что Хо = х\, получим окончательно:
= Д
(21-25)
Это выражение является основной формой теплового ба-
ланса конвективных сушилок.
Для контактных сушилок применимо уравнение теплового
баланса (21-20), в котором Lc(/2— А>) = 0, так как в таких су-
шилках воздух не является переносчиком тепла.
Входящая в уравнение теплового баланса величина А может
иметь положительное или отрицательное значение или же быть
равной нулю.
Как видно из уравнения (21-25):
при А > 0 энтальпия сушильного агента в сушилке возра-
стает, т. е. Л > Л;
при А < 0 энтальпия сушильного агента в сушилке умень-
шается, т. е. /2 < Л;
при А = 0 энтальпия сушильного агента остается неизмен-
ной, т. е. /2 — /ь
Последний случай соответствует сушке в адиабатических
условиях, которые возможны в сушилке, работающей без тепло-
вых потерь. В такой сушилке удельные потери тепла на нагре-
вание высушенного материала (<7И), транспортных устройств
(qT) и в окружающую среду (<?п)> а также добавочно вводимое
в сушильную камеру тепло (<7ДОб.) и энтальпия материала (СвОД
на входе в сушилку равны нулю:
<7п а== *7м <7т == ^доб. == == В (21 -26)
Такая сушилка называется теоретической. Процесс сушки
в ней протекает адиабатически при постоянной энтальпии воз-
духа / = const: испаряемая из материала влага вносит в су-
шильный агент ровно столько тепла, сколько он отдает, охла-
ждаясь, на испарение влаги. В соответствии с выражением
(21-7) в теоретической сушилке при уменьшении сс. в/ на та-
кую же величину возрастает xia, поэтому сумма обоих слагае-
мых остается постоянной (/ = const).
5. Материальный и Тепловой балансы cyulKu
749
В частном случае такие же условия сушки возможны и в
реальной сушилке, если приход тепла в ней (<7доб 4 gA) точно
равен тепловым потерям (7м4~7т4 т. е. А = 0.
Пример 21-3. Определить количество тепла, передаваемое топочными
газами высушиваемому материалу, из которого удаляется влаги
№ = 0,26 кг/сек Температура газов на входе в сушилку Л = 250° С, на вы-
ходе из сушилки t2 = 75° С. Начальная температура материала &i = 25°C.
Количество получаемого высушенного материала G2 = 0,08 кг/сек,
его температура $2 = 65° С. Теплоемкость высушенного материала
см = 1255 дж/кг -град (0,3 ккал/кг • град), теплоемкость испаренной влаги
(воды) св = 4190 дж/кг -град (1 ккал/кг • град).
Решение. Тепло, передаваемое газами материалу, расходуется на
испарение влаги (ОИсп.) и нагревание высушенного материала (QM).
Из уравнения (21-20) теплового баланса сушилки следует, что расход
тепла на испарение влаги из материала [с учетом выражения (21-8)] со-
ставляет:
= «'('» - Ml) = ’’Ч'о + с А - с,»,) =
= 0,26 [(2493 4 1,97 • 75).-103 — 4190 • 25] 659 000 вт
а расход тепла на нагревание высушенного материала равен:
Qm = О2см (&2 — М = 0.08 • 1255 (65 — 25) = 4020 вт
Общее количество переданного тепла составит:
Q = QHcn. + = 659 000 4 4020 s 663 000 вт (571 000 ккал/ч)
Пример 21-4. Определить расход топлива (подмосковный уголь марки Б)
в барабанной сушилке диаметром D — 1,6 м и длиной L = 10 м, производи-
тельность которой по высушенному материалу G2 = 8750 кг/ч Количество
влаги, испаряемой из материала, W = 1250 кг/ч. Сушка производится топоч-
ными газами, движущимися прямотоком с высушиваемым материалом. Тем-
пература топочных газов на входе в сушилку Л = 650° С, на выходе из нее
t2 = 100° С. Материал поступает в сушилку при температуре &i = 10° С и
удаляется из нее, имея температуру &2 = 90° С. Теплоемкость высушенного
материала с2 = 545 дж/кг • град (0,13 ккал/кг • град). Коэффициент тепло-
передачи от топочных газов в сушилке к окружающему воздуху через стенку
барабана, снаружи покрытую теплоизоляцией k = 0,895 вт/м2 • град
(0,85 ккал/м2 ч • град).
Решение. В соответствии с расчетом процесса горения подмосковного
угля (см. пример 12-1, стр. 419) при температуре топочных газов на входе
в сушилку t\ = 650° С энтальпия газов /1= 9900-103 дж/кг топлива
(2360 ккал/кг топлива); избыток воздуха а = 3,34.
Средние теплоемкости СОг, № и Н2О (пар) от 0 до 100° С составляют:
дж/мЛ-град ккал/м*-град
сСОг............................ 1720 0,411
cNj2............................ 1300 0,311
с ’ ............................ 1500 0,359
В дальнейших расчетах cSOj принимаем равным сСоа.
750
Гл 21 Cyiuita
Таким образом, при 100° С сумма произведений объема каждого компо-
нента топочных газов на его теплоемкость составляет (значения Vco2’
VNj и VHj0 взяты из примера 12-1)
S Ус = (0,55 + 0,018) • 1720 + 2,37 • 1300 + 0,694 -1500 =
= 5100 дж!кг топлива (1,22 ккал!кг топлива)
По формуле (12-6) определяем энтальпию топочных газов при
ti = 100° С, т е при температуре их на выходе из сушилки.
Л = Ус (а — 1) VocB] t2
I2 = [5100 + (3,34 -1) 3-1330] • 100 =
“ = 1444 • 103 дж!кг топлива (344 ккал!кг топлива)
где У0 = 3 м3!кг топлива — теоретический расход воздуха (см пример 12-1);
св = 1330 дж/м^'врад (0,317 ккал/м^ • град)—средняя теплоемкость
воздуха при температуре от 0 до 100° С.
Определяем расход тепла с уходящим сушильным агентом
QyXt = 12В = 1444 • 103В вт
где В — расход топлива, кг{сек.
Энтальпию водяного пара, содержащегося в газах на выходе из сушилки,
определяем по формуле (21-8)
Q = г0 + сп/ =<2493 + 1,970 • Ю3 = (2493 + 1,97 • 100) 103 =
= 2690 • 103 дж!кг (642 ккал!кг)
Расход тепла на испарение влаги из материала составляет
<?исп = — сЛ) = §|й (2690.103—4190-10)=920- 103а/и (793- \^ккал[ч)
Расход тепла на нагревание высушенного материала равен:
Qm = G2c2 (&2 — »i) = -S- • 545 (90 — 10) = 106 • 103 вт (91,3 • 103 ккалМ
uOvv
Средняя температура топочных газов в сушилке:
^=^±™= 375»С
Температуру окружающего воздуха О принимаем 25° С.
Тогда потери тепла сушилкой в окружающую среду составят:
Qn = kF6 (Ор — О) = 0,985 • 50,2 (375 — 25) = 17,3 • 103 вт (14,9 • 103 ккал!ч)
где Fg == nDL = 3,14 • 1,6 • 10 = 50,2 мг — боковая поверхность барабана
сушилки.
Тепловой баланс сушилки по уравнению (21-21):
Q = 1444 • 103В + 920 • 103 + 106 • 103 + 17,3 • 103 = 1444 103В + 1043,3 • 103
Расход топлива по формуле (12-9) составляет
Q __ 1444 • 103В 4 1043,3 • 103
В ~ Ц — 12~ 9900 103 — 1444 • 103 ’
В = 0,149 кг[сек = 536 кг[ч
6 Изображение процесса сушки на I—х-диаграмме
751
6. Изображение процесса сушки на /— лг-диаграмме
Для построения процесса сушки на I — х-диаграмме должны
быть заданы параметры воздуха начального состояния (обычно
/0, фо) и еще два параметра воздуха: и ф2), или (/i и Z2), или
(t2 и ф2).
Сначала строят для заданных условий теоретический процесс
сушки, который изображается в виде ломаной линии АВС
(рис. 21-7), отрезки которой па-
раллельны осям координат. Вер-
тикаль АВ изображает процесс
нагревания воздуха в воздухопо-
догревателе при х — const; ее
проводят из точки пересечения
линий А) = const и фо = const (точ-
ка Л) до пересечения с изотер-
мой ti = const (точка В). Нак-
лонная прямая ВС характеризу-
ет теоретический процесс сушки,
протекающий при постоянной
энтальпии / = const. Ее прово-
дят из точки В параллельно оси
абсцисс до пересечения с изотер-
мой /2 = const или с линией
ф2 = const (точка С).
Если заданы t0, фо и /2, ф2, по-
строение несколько изменяется:
из конечной точки C(t2, ф2) про-
водят линию / = const, а из на-
чальной ТОЧКИ A (tQ, фо) — линию
х = const до пересечения их в
точке В.
Построение процесса в реаль-
ной сушилке сводится к опреде-
Рис 21-7 Построение теорети-
ческого процесса сушки на
/ — х-диаграмме
лению наклона линии сушки. Эта линия также имеет началь-
ную точку В, но может отклоняться в ту или другую сторону от
линии теоретической сушки ВС в зависимости от знака вели-
чины А (рис. 21-8,а).
При А>0 энтальпия /2>Л и соответственно линия сушки
в реальной сушилке (BCi на рис. 21-8, а) пройдет выше ли-
нии / = const в теоретической сушилке (ВС на рис. 21-8, а).
При А < 0 энтальпия /2 < Л и соответственно линия сушки
будет более крутой и пройдет ниже I = const (линия ВС2 на
рис. 21-8,а).\Линич сушки в реальной сушилке соответствует
уравнению (21-25), в котором координаты 12 и х2 конечной точки
752
Гл 21 Сушка
могут быть заменены текущими координатами 1 и х любой про-
межуточной точки £, лежащей на этой линии:
(21-27)
На диаграмме разность 1 — Ц изображается отрезком Ее
в мм, умноженным на масштаб энтальпии (ккал/кг на
1 мм). Следовательно
I — f — Ee-uij
Рис. 21-8. Построение процесса сушки в реальной сушилке на / — х-диа-
грамме.
Разности влагосодержаний х— Xi на диаграмме соответ-
ствует отрезок ef (в мм):
х — хх = ef • тх
где тх— масштаб влагосодержания (кг/кг сухого воздуха на
1 мм).
Тогда
Ее т,
Д
ef-mx
nij
Обозначив отношение масштабов диаграммы через Л1,
получим:
£е = е/^- (21-28)
7 Схемы сушки
753
Пользуясь этой зависимостью, находят направление линии
сушки в реальной сушилке. Из произвольной точки е на линии
Л = const (рис. 21-8, а) проводят отрезок ef и определяют по
формуле (21-28) величину вертикального отрезка еЕ, который
откладывают от точки е вверх (при А > 0) или вниз (при А < 0).
4 Точка Е на конце отрезка Ее лежит на линии сушки в реаль-
ной сушилке. Поэтому линию сушки проводят, соединяя точку
3 B(xi, /1) с точкой Е и продолжая прямую BE до пересечения с
t линией t2 = const или <р2 = const. Конечная точка С\ (или С2)
I характеризует состояние воздуха на выходе из сушилки.
Если заданы два каких-либо параметра сушильного агента на выходе
из сушилки (например /2 и <р2), то на диаграмме / — х строят точку С2
* (рис 21-8,6), характеризующую состояние отработанного сушильного агента.
Из этой точки откладывают вверх (как показано на рисунке) или вниз вер-
тикальный отрезок С2С', выражающий разность /1 — А? энтальпии сушильного
агента на входе в сушилку и выходе из нее. Согласно уравнению (21-25)
/, — /2 = — д(х2 — %i) = —е ~ ’т/
где I =----------удельный расход сухого воздуха (на 1 кг испаренной
Х2 -К 1
влаги).
Отсюда
Если принять направление вверх от точки С2 за положительное, то при
Д < 0 отрезок С2С' также положителен и откладывается вверх, а при
Д >0 — вниз Из точки С' проводят линию 11 — const до пересечения
в точке В с вертикалью хо = const Соединяя точки В и С2, получают линию
1 сушки ВС2.
* 7. Схемы сушки
‘ Основным, или простым, процессом сушки воздухом назы-
j вают наиболее распространенный сушильный процесс, при кото-
; ром воздух нагревается только один раз в подогревателе’перед
1 сушилкой и однократно проходит через сушилку (рис. 21-9).
'j Рассматривая изменение параметров воздуха, можно видеть,
’ что при таком процессе воздух поступает в сушилку с низкими
Xi и <р1, а перепад температур воздуха 6 —t2 в сушилке значи-
* телен. Это обусловливает жесткие условия процесса, недопу-
л стимые при сушке некоторых материалов.
Более мягкие условия сушки и лучшее использование тепла воздуха до-
' стигаются при других схемах взаимодействия материала и сушильного
агента Главные из этих схем.
) 1) сушка с дополнительным подогревом воздуха;
2) сушка с промежуточным подогревом воздуха;
3) сушка с возвратом (рециркуляцией) части отработанного воздуха,
48 Зак 546
754
Гл 21 Сушка
В сушилке с дополнительным подогревом (рис 21-10) воздух нагре-
вается дважды сначала в подогревателе до температуры, зависящей от
свойств высушиваемого материала, а за-
тем дополнительно в сушилке Процесс
изображается ломаной линией АВ\С, в
наружном воздухоподогревателе подво-
дится тепло
L
Сушильная 4,^2
камера
Подогредатель воздуха
l I L
Ыаг-*-----М
I 1 । I
1
Чн
о. =
го CD М
и дополнительно в сушилке подводится
тепло (для простоты на рисунке изо-
бражен процесс в теоретической сушил-
ке)
<7доб. — 7. ________
Л-2 ----
В1В ..
—5— м
CD
Таким путем можно, снижая темпе-
ратуру подогрева воздуха перед сушил-
кой, значительно уменьшить перепад
температур 6 — tz в процессе сушки
В пределе все тепло, необходимое
для испарения влаги из материала, мож-
но подвести в самой сушилке (ли-
ния АС). Однако в этом случае температура воздуха будет очень низка и
сильно снизится способность воздуха испарять влагу, соответственно умень-
ч>
Рис. 21-9. Основной сушильный
процесс (схема сушилки и эпюры
изменения параметров воздуха)
шится производительность сушилки
Для лучшего использования тепла
воздуха следует нагревать его перед су-
шилкой до предельной температуры,
определяемой свойствами высушивае-
мого материала, например до темпера-
туры /j, соответствующей точке Д Как
видно из рис 21-10, без дополнительно-
го нагревания воздух пришлось бы на-
гревать в подогревателе перед сушилкой
до температуры Л, значительно превы-
шающей допустимую (точка В)
Уменьшить перепад температур при
испарении влаги из материала можно,
Рис. 21-10. Сушка с дополнительным подогревом воздуха в сушиль-
ной камере (схема сушилки и / — х-диаграмма процесса).
проводя сушку по несколько иной схеме, — в сушилке с промежуточным
подогревом воздуха (рис. 21-11). Обычно такие сушилки состоят из нескрль-
Z Схемы CyuiKtl
?55
ких последовательно соединенных секции (зон), между которыми устано-
влены воздухоподогреватели. На диаграмме 1—х (рис 21-11, внизу) про-
цесс в сушилке с промежуточным подогревом изображен ломаной ли-
нией АВ'С'В"С"В"'С.
Рис 21-11 Сушка с промежуточным подогревом
воздуха (схема сушилки и / — х-диаграмма про-
цесса)
В сушилке происходит ступенчатый подогрев воздуха (линии АВ', С'В",
С"В"'), вследствие чего создаются мягкие и гибкие условия сушки, так как
промежуточные температуры нагревания и степени насыщения воздуха мо-
гут быть выбраны в соответствии со скоростью испарения влаги из мате-
риала Благодаря постепенному нарастанию влагосодержания воздуха в та-
ких сушилках можно успешно высушивать материалы, для которых тре-
буются равномерные условия сушки при невысоких температурах.
48*
756
Гл. 21. Сушка
Как видно из рис. 21-11, при основном процессе сушки в сушилке, рабо-
тающей в тех же пределах изменения параметров сушильного агента, послед-
ний пришлось бы нагревать до температуры /3, определяемой точкой В, т. е.
до значительно более высокой температуры, чем в сушилке с промежуточ-
ным подогревом Л)-
В сушилке с частичной рециркуляцией воздуха (рис. 21-12) часть отра-
ботанного воздуха смешивается со свежим, полученная смесь нагревается
в воздухоподогревателе и поступает в сушилку. Процесс в сушилке изобра-
жается на / — х-диаграмме ломаной линией
ДМВ1С, причем точка А характеризует
состояние свежего воздуха, точка С — со-
стояние отработанного воздуха, точка М —
состояние смеси.
Линия AM изображает процесс смеше-
ния свежего и отработанного воздуха, ли-
ния MBi — нагревание смеси в воздухо-
подогревателе, линия В[С — испарение вла-
ги из материала (сушку).
Рис. 21-12. Сушка с частичной рециркуляцией воздуха (схема сушилки и
/ — х-диаграмма процесса).
Благодаря рециркуляции части воздуха достигается тот же эффект, что
и путем промежуточного подогрева — снижение разности температур Л —t2
в сушилке, т. е. происходит более равномерная сушка.
Обе схемы сушильного процесса — с промежуточным подогревом и с ча-
стичной рециркуляцией воздуха — имеют следующие преимущества по срав-
нению с сушкой по основной (простой) схеме:
1) при тех же пределах рабочего процесса (одинаковых to, <р0 и t2 ,<р2)
создается более равномерный и мягкий режим сушки, но расходы воздуха и
тепла не изменяются;
2) при одинаковых перепадах температур Л —12 повышается степень
использования воздуха в сушилке (увеличивается х2) и снижается расход
воздуха и тепла на сушку.
Кроме того, путем смешения свежего и отработанного воздуха в сушил-
ках с рециркуляцией получают (без затраты тепла на увлажнение) смесь
с высоким влагосодержанием хсм , что особенно ценно, если требуется сушка
материалов во влажном воздухе (дерево, керамические изделия и т. д).
В таких сушилках повышается также скорость воздуха, но одновременно
возрастает энергия, потребляемая вентилятором, увеличивается стоимость
установки
В промышленных сушильных установках применяются также другие ва-
рианты сушильного процесса, но все они представляют собой лишь комби-
нации схем, описанных выше.
8. Кинетика сушки
757
Сушка топочными газами производится обычно по схеме
основного процесса, реже — по схеме с рециркуляцией.
Для сушки применяют смесь топочных газов и воздуха, при-
чем газы, полученные в топке, разбавляют воздухом для пони-
жения их температуры до максимально допустимой при сушке
данного материала. По свойствам (плотность, теплоемкость
и др.) топочные газы близки к воздуху и отличаются от него
только большим влагосодержанием. Во многих случаях сушка
проводится с использованием отходящих газов промышленных
печей, котельных и других установок.
Основные достоинства сушки топочными газами по сравне-
нию с сушкой воздухом:
1) большая влагопоглощающая способность топочных газов,
во много раз превышающая влагопоглощающую способность
воздуха, так как температура газов значительно выше темпера-
туры нагрева воздуха в воздухоподогревателях;
2) меньший расход топлива (обычно на 10—25%), чем при
сушке воздухом, несмотря на то, что расход тепла на 1 кг ис-
паренной влаги при сушке топочными газами превышает соот-
ветствующий расход тепла в воздушных сушилках;
3) упрощение сушильной установки, так как отпадает необ-
ходимость в устройствах для нагревания воздуха.
Вместе с тем при сушке топочными газами возможно загряз-
нение высушиваемого материала и воздействие на него серни-
стых соединений, содержащихся в газах. Поэтому топочные
газы, используемые для сушки, получают путем полного сгора-
ния малозольных и малосернистых топлив и иногда подвергают
очистке перед входом в сушилку. В настоящее время сушка то-
почными газами находит все более широкое распространение.
8. Кинетика сушки
Для расчета сушилок необходимо знать скорость сушки, ко-
торая определяется количеством влаги W, испаряемой с еди-
ницы поверхности F высушиваемого материала за единицу вре-
мени. Таким образом, скорость сушки представляет собой отно-
шение:
w
и = кг!м? • сек (21 -29)
где т — время сушки, сек.
Зная скорость сушки, определяют продолжительность перио-
дического процесса сушки или поверхность высушиваемого
материала при сушке непрерывным способом и устанавливают
габаритные размеры сушильных аппаратов.
758
-*b
Гл. 21. Сушка
'дет"'
Скорость сушки, как массообменного процесса, следует ос-
новному уравнению массопередачи (16-17), согласно кото-
рому
.U=-^ = K^P. (21-30)
где К — коэффициент массопередачи;
Дср.— средняя движущая сила процесса.
Как видно из рассмотрения статики сушки (стр. 733), дви-
жущая сила процесса сушки определяется разностью давлений
Рм—Рп> т. е. разностью давления паров влаги у поверхности
материала рм и парциального давления паров в воздухе (или
чистого пара) рп.
Различают два периода сушки: период постоянной скорости
и период падающей скорости процесса.
В течение первого периода влага испаряется со всей поверх-
ности влажного материала так же, как она испаряется с зер-
кала испарения некоторого объема жидкости. В этом периоде
скорость сушки постоянна и определяется лишь скоростью
внешней диффузии, т. е. диффузии паров влаги с поверхности
материала в окружающую среду.
Во втором периоде скорость сушки определяется внутренней
диффузией — перемещением влаги изнутри материала к его по-
верхности. С начала второго периода поверхность подсохнув-
шего материала начинает покрываться коркой и поверхность
испарения влаги постепенно уменьшается, что приводит к уве-
личению сопротивления внутренней диффузии и к непрерывному
уменьшению скорости сушки.
В зависимости от толщины и структуры некоторых материа-
лов испарение влаги с их поверхности в конце второго периода
прекращается вовсе и происходит в глубине материала. Поэто-
му, в соответствии с характером удаления влаги, второй период
сушки часто складывается из двух стадий: стадии равномерно
падающей скорости и стадии неравномерно падающей скорости.
Двум основным периодам предшествует некоторый период
прогрева материала до температуры сушки.
Кинетика сушки определяется обычно путем взвешивания
образцов материала в начала сушки и через определенные про-
межутки времени. По весу образцов рассчитывают абсолютную
влажность* материала в различные моменты и строят кривую
зависимости абсолютной влажности wa от времени т, которая
* Абсолютной влажностью называется количество влаги в килограммах,
приходящееся на 1 кг абсолютно сухого материала.
8 Кинетика сушки
759
называется кривой сушки (кривая ABK\KiC на рис. 21-13). По
этой кривой можно определить скорость сушки.
Скорость сушки, характеризующаяся изменением абсолют-
ной влажности в единицу времени, может быть найдена для
Прогрей \ Постоянная |
мате- • скорость |
риала ! сушки j
Падающая
скорость
сушки
| Равно-
| весное
! состояние
Рис. 21-13. Кривая сушки материала и измене-
ние его температуры в процессе сушки.
каждого данного момента, как тангенс угла наклона кривой
сушки (например, tga2 для точки /С2 на рис. 21-13). Найденные
значения скорости сушки
наносят на график, как
функцию абсолютной
влажности, и получают
кривую скорости сушки
(рис. 21-14). Графиче-
ское изображение процес-
са в виде кривых сушки и
кривых скорости сушки
дает возможность устано-
вить различные периоды
его протекания.
Рассматривая кривые
на рис. 21-13 и 21-14,
можно различить пере-
численные выше периоды
Равно- Падающая Постоянная Прозрев
весное скорость скорость материала
состояние сушки сушки
Рис. 21-14. Кривая скорости сушки.
сушки материала.
Период прогрева материала (отрезок АВ на рис. 21-14) яв-
ляется, как правило, кратковременным и характеризуется
неустановившимся состоянием процесса. За этот период тем-
пература материала повышается до температуры мокрого
760
Гл 21. Сушка
термометра /м, но его влажность ^нач. снижается незначительно.
Скорость сушки возрастает и к концу периода прогрева дости-
гает максимальной величины.
В период постоянной скорости (прямолинейный отрезок ВК\)
скорость процесса является наибольшей, температура материала
/м = const.
Начальная точка К\ периода падающей скорости (отрезок
KiKzC) называется первой критической точкой, а влажность ма-
териала йУКр в этой точке — первой критической влажностью.
Период падающей скорости состоит, в свою очередь, из двух
стадий: равномерно падающей скорости (прямолинейный отре-
зок /СЛг на рис. 21-14) и неравномерно падающей скорости
(кривая К2С).
Точка К2 называется второй критической точкой, а соответ-
ствующая ей влажность материала — второй критической влаж-
ностью wKp.. К концу второго периода температура материала
повышается и достигает температуры воздуха tB или среды,
окружающей материал. Одновременно влажность материала
снижается до равновесной по всей его толщине. С момента до-
стижения равновесной влажности скорость сушки становится
равной нулю. При дальнейшем пребывании материала в сушил-
ке его влажность остается постоянной (отрезок CD на
рис. 21-13).
Для различных материалов отдельные периоды сушки могут
быть различны по времени или отсутствовать вовсе. Так, при
сушке плоских пластин процесс заканчивается этапом равномерно
падающей скорости (линия процесса АВК1К2 на рис. 21-14).
Длительность сушки материала достаточно точно можно
установить только опытным путем. Общую продолжительность
процесса определяют расчетом как сумму длительности сушки
в период постоянной скорости и длительности ее в период па-
дающей скорости, принимая, что падение скорости сушки во
втором периоде происходит прямолинейно.
Длительность сушки в отдельные периоды определяют по следующим
формулам:
в период постоянной скорости
Х1 = 7Г (W1 “ ) сек (21’31)
в период падающей скорости
т2 = (w'r. — w ) 2,31g —---- сек (21-32)
i Q \ кр- Р/ ь — Дор х <
8. Кинетика сушки
761
Соответственно общая продолжительность сушки может быть прибли-
женно определена по уравнению
1
Т Т2 = Q
w — W I
W,—W + 2,3(tt»' — Wo)1£~^----------------------Ч СвК (21-33)
1 кр. I ’ \ кр. Р/ ° --- W,, J
♦ р J
где w„ w2 и wp—начальная, конечная и равновесная влажность материала,
кг влаги на 1 кг сухого вещества;
wKp. — первая критическая влажность материала (в конце пер-
’ вого периода сушки).
Входящая в уравнение (21-33) величина С называется коэффициентом
сушки и выражается количеством кг испаренной влаги в сек, приходящимся
на 1 кг сухого вещества.
Обозначая количество испаренной влаги W кг, количество сухого веще-
ства в высушиваемом материале Осух. кг и время сушки т сек, получим,
с учетом уравнения (16-28), следующее выражение для коэффициента
сушки:
П7 ВЛД™х
С = = р/д «„-I (21-34)
'-'сухЛ '-'сух.т
кг
где ₽—коэффициент массоотдачи в газовой фазе, кг/м2 • сек • — ;
д f— удельная поверхность сухого вещества, м2/кг абсолютно сухого
вещества;
* ДСр. — средняя движущая сила, равная средней разности влагосодержа-
' ния воздуха в насыщенном и рабочем состояниях ДСр. = (** — х)ср.-
При переменных параметрах воздуха величина ДСр. с достаточной для
технических расчетов точностью может быть определена как средняя лога-
рифмическая разностей влагосодержания материала и воздуха в начале и
конце каждого периода сушки.
* Для определения ₽ можно пользоваться критериальным уравнением:
N< = HRe” (Pr;)°'33Qu0’135 (21-35)
И4
Определяющим размером при вычислении Nur и Rer является вели-
чина I — длина поверхности испарения по направлению движения сушиль-
ного агента.
Входящий в уравнение (21-35) критерий Гухмана Gu характеризует влия-
/ ние массообмена на теплообмен при одновременном протекании этих процес-
$ сов. Критерий Gu выражается формулой
| Ои=^г <21-36’
•% где г — теплота испарения влаги, дж/кг-,
О а — коэффициент теплоотдачи от воздуха, вт/м2 • град-,
$ t — температура воздуха, °C.
Величины А ил в уравнении (21-33) зависят от критерия Re:
* Re % . . 1—200 200—6000 6 000—70 000
I Л ... 0,9 0,87 0,347
$ п ... 0,5 0,54 0,65
Скорость сушки зависит также от направления движения су-
шильного агента относительно высушиваемого материала.
762
Гл. 21 Сушка
При прямотоке влажный материал на входе в сушилку со-
прикасается с свежим горячим воздухом; поэтому сушка вна-
чале протекает интенсивно, а затем замедляется, причем в конце
сушилки температура материала приближается к температуре
t2 отработанного воздуха.
При противотоке влажный материал вначале соприкасается
с отработанным воздухом, а высушенный материал — с свежим
горячим воздухом, поступающим в сушилку. Вследствие этого
сушка вначале идет медленно, в конце же влажность материала
быстро уменьшается, а его температура возрастает, прибли-
жаясь к температуре Ц сушильного агента, и может оказаться
выше допустимой для данного материала.
Поэтому при сушке топочными газами (или другим сушиль-
ным агентом, имеющим высокую температуру) применяют пря-
моток. Противоток предпочитают при сушке материала до низ-
кой конечной влажности, которая достигается в этом случае за
более короткое время.
Расчетом не учитывается ряд факторов, оказывающих боль-
шое влияние на продолжительность сушки, а именно: неравно-
мерное омывание материала воздухом, наличие «мертвых» зон,
Влажность W высушиваемого материала
Рис. 21-15. Изменение температур при
хрямотоке сушильного агента и высуши-
ваемого материала (t — температура су-
шильного агента, &2 — конечная темпера-
тура высушиваемого материала).
изменение температуры
материала и др. Поэтому
теоретическое время суш-
ки, полученное по форму-
ле (21-33), умножают на
поправочный коэффици-
ент, равный 1,5—2 и более.
Ввиду трудности рас-
чета динамики сушки
(диффузия влаги в раз-
личные периоды сушки,
скорость и продолжитель-
ность сушки) на практи-
ке часто ограничиваются
статическим расчетом по
средним данным, прини-
мая за исходную величи-
ну среднее количество
влаги, испаряемое в еди-
нице объема сушильной камеры (для конвективных сушилок)
или на единицу греющей поверхности (для контактных суши-
лок), т. е. величину напряжения сушилки по влаге А в кг!м3 • ч
или в кг!м2 • ч.
Изменение температуры сушильного агента и материала в
процессе сушки в зависимости ог влажности изображается кри-
8. Кинетика сушки
763
выми, приведенными на рис. 21-15, на котором показано из-
менение температур при прямотоке сушильного агента и высу-
шиваемого материала. В течение первого периода сушки тем-
пература материала постоянна и, как указывалось, равна тем-
пературе мокрого термометра /м. В соответствии с изменением
температур, показанным на рис. 21-15, можно, пользуясь общей
формулой (11-28), найти средний температурный напор для пер-
вого периода сушки:
где —начальная температура сушильного агента;
/2—температура сушильного агента в конце первого перио-
да сушки.
Соответственно находим температурный напор для второго
периода сушки:
02 ер. = (21 -38)
Г> о 1 Гм
где /2 — конечная температура сушильного агента;
&2 — конечная температура высушиваемого материала.
Средний температурный напор для всего процесса сушки
определяют по формуле:
9сР. = 9i сР. (1 — w) + 92cp.^ (21-39)
где т '_|_т-----отношение продолжительности сушки во вто-
ром периоде (т2) к общей продолжительности
сушки (ti + т2).
Величины Ti и т2 определяются соответственно по формулам
(21-31) и (21-32).
Соответствующие выражения для 01ср. и 02ср. могут быть
получены для противотока сушильного агента и высушиваемого
материала. При относительно высокой конечной влажности вы-
сушиваемого материала величина 0ср может быть определена
приближенно по уравнению
о Л — ^2
Cp^2.3lg^ (2Ь40)
*2 - -М
Пример 21-5. Определить среднюю разность температур между топоч-
ными газами и высушиваемым материалом (движущимися противотоком),
если количество материала, поступающего на сушку, G, — 1235 кг/ч
(0,343 кг/сек), его начальная влажность оч = 77,5% и конечная влажность
СУ2 = 5%.
764
Гл. 21. Сушка
По опытным данным, влажность материала в конце первого периода
сушки аУкр = 27,5%, равновесная влажность ®р = 0,025 кг!кг сухого веще-
ства. Температура мокрого термометра /м = 55° С, температура высушенного
материала &2 = 65°С, начальная температура газов Л = 250° С, конечная
температура газов = 75° С. Топливо — подмосковный уголь,
Решение. По уравнениям материального баланса (21-16) и (21-17)
Определяем количество высушенного материала G2 = 273 кг/ч (0,0758 кг/сек).
и количество испаренной из материала влаги W ~ 942 кг/ч (0,262 кг/сек.).
Пользуясь 1 — х-диаграммой (см. рис. 21-34, стр. 789), находим влагосо-
держание топочных газов на входе в сушилку Xi = 0,0907 кг/кг сухих газов
и влагосодержание отработанных газов хг — 0,159 кг/кг сухих газов.
Расход топочных газов по формуле (21-18) составляет / — 14,6 кг/кг
испаренной влаги, отсюда расход топочных газов
L = IW = 14,6 • 942 = 13 760 кг/ч (3,82 кг!сек)
Определяем влагосодержание топочных газов в конце первого периода
сушки по следующей формуле:
, Gjw,—0,343(77,5—27,5)
х' = х 1----= 0,0907 +---------
2 1 7,(100 — w ) 3,82(100 — 27,5)
= 0,153 кг/кг
Пользуясь 1 — х-диаграммой, по найденному значению х2 определяем
температуру топочных газов в конце первого периода сушки: t2 — 101° С.
Среднюю разность температур между топочными газами и высушивае-
мым материалом в первом периоде сушки находим по формуле (21-37):
й _ 250—101
1ср-“ о. 250-55
2’31gW^55
= 104° С
Средняя разность температур между топочными газами и материалом
во втором периоде сушки определяется по формуле (21-38):
ср. —
(101 —55) —(75 —65)
2,3 1g
101 — 55
75 — 65
= 23,6° С
Количество абсолютно сухого вещества, поступающего в сушилку с ма-
териалом:
G = 1235 (1 —0,775) = 278 кг/ч (0,077 кг/сек)
Влажность высушиваемого материала, в пересчете на абсолютно сухое
вещество, составляет:
77,5 q .- .
= Тлл—==-=- = 3,45 кг/кг сухого вещества
1Ш — 77,5
wKp = 0,61 кг/кг сухого вещества
w2 = 0,053 кг/кг сухого вещества
9. Устройство сушилок
765
В соответствии с уравнениями (21-31) и (21-32) определяем отношение;
т2
Х1 + т2
m —
ЛЛ^О2 1 0,61—0,025
(0,61 0,025) 2,3 1g 0,053 _ 0.025
По формуле (21-39) находим среднюю разность температур между су-
шильным агентом и высушиваемым материалом:
0ср = 104 (1 — 0,384) + 23,6 • 0,384 = 73° С
При расчете по приближенной формуле (21-40) получим:
_ 250 - 75 _ 770 Г
0С₽.- -250-55 '-77 G
2'3 '«"75=55-
77__73
Погрешность при приближенном расчете: 100----— = 5,5%
9. Устройство сушилок
Конвективные сушилки
> Камерные сушилки. В таких аппаратах сушка материала про-
изводится периодически при атмосферном давлении. Сушилки
имеют одну или несколько прямоугольных камер, в которых ма-
териал, находящийся на вагонетках или полках, сушится в не-
подвижном состоянии. Камеры‘загружают и выгружают через
дверь, причем вагонетки перемещают вручную или при помощи
лебедок.
Камерные сушилки обладают существенными недостатками,
к числу которых относятся: 1) большая продолжительность суш-
ки, так как слой высушиваемого материала неподвижен, 2) не-
равномерность сушки, 3) потери тепла при загрузке и выгруз-
ке камер, 4) трудные и негигиеничные условия обслуживания и
контроля процесса, 5) сравнительно большой расход энергии
из-за недостаточной полноты использования тепла сушильного
агента (особенно в конечный период сушки).
Разновидностью камерных сушилок является шкафная воз-
душно-циркуляционная сушилка (рис. 21-16), работающая с про-
межуточным подогревом и рециркуляцией части воздуха.
766
Гл. 21. Сурика
Нагретый в воздухоподогревателе 1 воздух подается венти-
лятором 2 в нижнюю часть камеры 3 сушилки и проходит в го-
ризонтальном направлении (слева направо) между противнями
с высушиваемым материалом, установленными на вагонетках 4.
Затем воздух проходит воздухоподогреватель 5 и движется через
среднюю часть камеры в противоположном направлении (справа
налево). В третий раз воздух нагревается в воздухоподогревате-
ле 6, после чего проходит слева направо через верхнюю часть ка-
Рис. 21-16 Шкафная воздушно-циркуля-
ционная сушилка:
/, 5> 6 — воздухоподогреватели; 2— вентилятор;
3— камера; 4— вагонетки; 7—шибер.
лок, связанные с периодичностью их
меры и удаляется из су-
шилки. Таким образом,
воздух в сушилке дви-
жется зигзагообразно че-
рез три зоны, дважды на-
греваясь и дважды меняя
направление своего дви-
жения в камере. Часть
отработанного воздуха
возвращают в сушилку,
регулируя его количество
при помощи шибера 7.
Работа по такой схе-
ме, как указывалось
(стр. 756), улучшает ис-
пользование тепла возду-
ха. Однако сушилке опи-
санной конструкции при-
сущи все другие недо-
статки камерных суши-
действия, ручным обслу-
живанием и сушкой материала в неподвижном слое.
Туннельные (коридорные) сушилки являются камерными
сушилками непрерывного действия, работающими при атмосфер-
ном давлении. Они состоят из сушильной камеры, представляю-
щей собой длинный закрытый коридор, в котором высушивае-
мый материал перемещается в вагонетках (вагонеточные сушил-
ки) или на бесконечной ленте (ленточные и петлевые сушилки).
Вагонеточные сушилки. В камере 1 туннельной ва-
гонеточной сушилки (рис. 21-17) медленно перемещаются ваго-
нетки 2 с высушиваемым материалом. Передвижение вагонеток
производится посредством лебедки 3, причем загрузка и выгруз-
ка вагонеток осуществляются с противоположных концов каме-
ры через двери 4, которые на время сушки герметически закры-
ваются. Со стороны выхода вагонеток в камере расположен вен- '
тилятор 5, при помощи которого воздух (или топочные газы)
просасывается через коридор, сушильный агент движется обыч-
9. Устройство сушилок
767
но противотоком движению материала. Нагревание воздуха про-
изводится в подогревателе 6. Коридоры туннельных сушилок
имеют значительную длину (до 50—60 м), часто эти сушилк i
строят с несколькими параллельными коридорами.
Рис. 21-17. Туннельная вагонеточная сушилка:
/—камера (коридор); 2 — вагонетки, 3 — лебедка; 4 — дверь; 5 — вентилятор;
6 ~ воздухоподогреватель.
Существенный недостаток туннельных сушилок — неравно-
мерность сушки вследствие расслоения нагретого и холодного
воздуха. Для более равномерной сушки повышают скорость
сушильного агента, но вследствие этого приходится увеличивать
длину коридора, чтобы время пребывания материала в сушилке
было достаточным.
Рис. 21-18. Ленточная сушилка:
1 — бесконечная (конвейерная) лента; 2— камера; 3 — циркуляционный вентилятор, 4, 5 —звез-
дочки, 6, 7—вентиляторы.
Ленточные сушилки. Основной частью ленточной су-
шилки (рис. 21-18) является горизонтальная бесконечная лен-
та 1, которая движется в камере 2. Материал поступает с одного
конца ленты и сбрасывается в высушенном виде с другого ее
768
Гл 21 Сушка
конца. Лента натянута между ведущей звездочкой 4 и ведомой
звездочкой 5, служащей для натяжения ленты.
Ленты изготовляют сплошными (из ткани) или сетчатыми
(из металлической сетки).
Как показано на рис. 21-18, сушилка обычно разделяется на
несколько зон (в данной сушилке их три), в каждой из которых
установлен вентилятор для создания циркуляции воздуха. В су-
шилках со сплошной лентой нагретый воздух движется над
слоем материала, противотоком его движению. В сушилках с
сетчатой лентой воздух проходит перпендикулярно плоскости
ленты — вверх или вниз. При такой поперечной продувке слой
материала Лучше разрыхляется, что ускоряет его сушку.
В одноленточных сушилках слой материала на ленте высы-
хает неравномерно: часть материала, обращенная к ленте (при
движении сушильного агента вдоль слоя материала), остается
более влажной. Поэтому часто применяют многоленточные су-
шилки, в которых материал пересыпается с одной ленты на дру-
гую. Благодаря многократному пересыпанию материала он луч-
ше омывается воздухом, при этом ускоряется процесс сушки и
уменьшается расход тепла по сравнению с его расходом в одно-
ленточных сушилках.
Петлевые сушилки В петлевых сушилках (рис. 21-19) произво-
дится сушка пастообразных материалов в движущемся тонком слое. Мате-
риал при помощи питателя 1 подается на бесконечную сетчатую ленту 2,
Рис. 21-19. Петлевая сушилка:
/ —питатель, 2—бесконечная сетчатая лента, 3— валки, 4 — молоток, 5— разгрузочный шнек;
6 — вентиляторы.
вдавливается в ее ячейки, проходя через обогреваемые паром валки 3, после
чего поступает на сушку в камеру сушилки, где движущаяся сетка образует
ряд петель. Высушенный материал сбрасывается при помощи молотков 4,
ударяющих по сетке, и падает в разгрузочный шнек 5 Циркуляция воздуха
производится вентиляторами 6, расположенными по обеим сторонам камеры.
769
Р Устройство суиШлок.
г> х подогре-
В сушилке имеется несколько зон Она работает с промежуточная рисунке
вом воздуха в воздухоподогревателях, расположенных в камере
не показаны), и частичным возвратом воздуха в зоны. ледующим
В петлевых сушилках достигается интенсивная сушка по %-ка с вы-
причинам 1) поверхность испарения влаги значительна, так как сторон,
сушиваемым материалом равномерно омывается воздухом с д^лнитеЛьно
2) сушка происходит в сравнительно тонком слое, 3) материал до^пастрески-
прогревается стенками металлической сетки, 4) по мере усадки 0 лверхности
вания материала в ячейках сетки создаются Дополнительные Р
испарения
г л с . л. 21-20)
Барабанные сушилки. Барабанная сушилка (р0 сдву-
представляет собой цилиндрический наклонный барабЛятся по
мя бандажами 3, которые при вращении барабана конца
опорным роликам 6. Материал поступает с приподнят^
Рис. 21-20. Барабанная сушилка:
лрные ролики;
/—топка; 2—питатель; 3—бандажи; 4 — барабан; 5 — зубчатый венец; 6 — о^^ка барабана;
7—циклон; 8—упорные ролики; 9 — шлюзовый затвор; 10—внутренняя нас^^
11 — дымосос.
барабана через питатель 2, захватывается винтовыми ВДОль
на которых он подсушивается, после чего перемещав о Осевое
барабана, имеющего угол наклона к горизонту до 0 ' $
смещение барабана предотвращается упорными роли14^оенней
Материал перемещается в сушилке при помощи В шо баоа-
насадки 10, равномерно распределяющей его по сече^? свойств
бана. Конструкция насадки зависит от размера кусков И
высушиваемого материала. шильный
Обычно в барабанных сушилках материал и еХэашается
агент движутся прямотоком, благодаря этому предот^"стопОНу
пересушивание и унос материала топочными газами РУ’
49 Зак 546
770
Гл. 21. Сушка
противоположную его движению. Для уменьшения уноса при
прямотоке скорость газов в барабане поддерживают не более
2—3 м{сек. Газы поступают'из топки /, примыкающей к бара-
бану со стороны входа материала и снабженной смесительной
камерой для охлаждения газов до нужной температуры наруж-
ным воздухом.
Высушенный материал проходит через подпорное устройство
в виде сменного кольца или поворотных лопаток, посредством
которого регулируется степень заполнения барабана, обычно не
превышающая 20—25% его объема. Готовый продукт проходит
через шлюзовый затвор 9, препятствующий подсосу наружного
воздуха в барабан, и удаляется транспортером (на рисунке не
показан).
Газы просасываются через барабан при помощи дымососа 11,
установленного за сушилкой. Для улавливания из газов пыли
между барабаном и дымососом включен циклон 7. При такой
• схеме установки барабан работает при разрежении (газы не
проникают в помещение через неплотности сушилки), при
этом значительно уменьшается износ вентилятора частицами
пыли.
Барабан приводится во вращение посредством зубчатого вен-
ца 5, который находится в зацеплении с ведущей шестерней, со-
единенной через редуктор с электродвигателем. Скорость враще-
ния барабана зависит от угла его наклона и продолжительности
сушки; обычно барабан делает 1—8 об!мин.
Наиболее распространенные конструкции внутренних наса-
док барабанов показаны на рис. 21-21.
Подъемно-лопастная насадка (рис. 21-21, а) применяется
для перемещения крупнокусковых и склонных к налипанию вы-
сушиваемых материалов.
Распределительные насадки — полочная (рис. 21-21,6) и
крестообразная (рис. 21-21, в) —применяются при сушке мелко-
кусковых и сыпучих материалов. При помощи таких насадок
обеспечивается многократное пересыпание материала и его тес-
ный контакт с сушильным агентом.
Промежуточная, или секторная, насадка (рис. 21-21, г) при-
меняется для перемещения крупнозернистых высушиваемых ма-
териалов, обладающих малой сыпучестью.
Ячейковая насадка (рис. 21-21, д) применяется в процессах
сушки тонкоизмельченных пылящих материалов. При пересы-
пании таких материалов в закрытых ячейках насадки дости-
гается интенсивное перемешивание частиц.
Барабанные сушилки нормализованы и выпускаются с барабанами диа-
метром 1200, 1400, 1600, 1800, 2000, 2200, 2400, 2800 мм и отношением длины
барабана к диаметру L : D = 3,5 — 7,
9. Устройство сушилок
771
Барабанные сушилки широко применяются для сушки сы-
пучих и мелкокусковых материалов (колчедан, уголь, фосфо-
риты, минеральные соли и др.).
Достоинства барабанных сушилок: 1) интенсивная и равно-
мерная сушка вследствие тесного контакта материала и сушиль-
ного агента, 2) большое напряжение барабана по влаге, дости-
гающее 100 кг/м3 • ч и более, 3) компактность установки.
Рис. 21-21. Внутренние насадки барабанов:
а—подъемно-лопастная; б—полочная; в —крестообразная; г —промежуточ-
ная (секторная); д — ячейковая.
Помимо барабанных конвективных сушилок (прямого дей-
ствия) с непосредственным соприкосновением материала и су-
шильного агента, применяются контактные барабанные сушилки
с передачей тепла от газов через стенку (стр. 778).
Пневматические сушилки. В пневматических сушилках мате-
риал сушится во взвешенном состоянии. Зернистый или кристал-
лический материал подается через питатель 1 (рис. 21-22) в вер-
тикальную трубу 6 длиной 10—20 м, в которую вентилятором 3
снизу нагнетается воздух, нагретый в подогревателе 2. Мате-
риал увлекается потоком воздуха, движущимся со скоростью
~40 м/сек, и выбрасывается уже высушенным в сборник-амор-
тизатор 8. В циклоне 5 высушенный материал отделяется от воз-
духа и удаляется через разгрузочное устройство 4. Воздух про-
ходит фильтр 7 и выводится в атмосферу. Продолжительность
пребывания. материала в сушилке составляет всего несколько
секунд; процесс протекает непрерывно.
49*
772
Гл. 21. Сушка
Достоинства пневматических сушилок: 1) весьма развитая
удельная поверхность соприкосновения материала и сушильного
=|=1 агента и, следовательно, быстрая интен-
8 сивная сушка, 2) возможность сушки ма-
териала при высоких температурах
Рис. 21-22. Пневматиче-
ская сушилка:
/ — питатель; 2—подогрева-
тель воздуха, 3— вентилятор;
4 — разгрузочное устройство;
5 — циклон; 6 — вертикальная
труба; 7 —воздушный фильтр;
8— сборник-амортизатор.
чательно очищается
сферу.
вследствие кратковременности пребыва-
ния его в сушилке, 3) простота и ком-
пактность установки.
Недостатки: 1) трудность регулиро-
вания процесса, 2) опасность взрыва при
сушке горючих пылящих материалов,
3) большой расход энергии.
Распылительные сушилки. Весьма
значительное укорение процесса сушки
достигается при увеличении поверхности
испарения влаги в сушилках, работаю-
щих по принципу распиливания жидких
растворов.
Распылительная сушилка непрерыв-
ного действия показана на рис. 21-23.
Исходный раствор (высушиваемый ма-
териал) распиливается в сушильной ка-
мере 1 посредством механической фор-
сунки 2. Сушильный агент — воздух за-
сасывается через фильтр 4 вентилятором
5 в газовый подогреватель 6, где на-
гревается топочными газами, поступаю-
щими из топки 8. Через регулируемые
щели 3 нагретый воздух входит в су-
шильную камеру и движется в ней па-
раллельным током с распыливаемым ма-
териалом.
Капли жидкости, омываемые со всех
сторон воздухом, в течение одной или
нескольких секунд теряют влагу и осаж-
даются в виде порошкообразных частиц
на дне камеры. Сухой порошок удаляет-
ся из сушилки при помощи скребков 9.
Отработанный воздух, проходя через
циклоны 7, очищается от пыли и
затем подается вентилятором 10 в
скруббер 11, орошаемый исходным рас-
твором. В скруббере воздух окон-
от остатков пыли и удаляется в атмо-
9 Устройство сушилок
773
Жидкость в распылительных сушилках диспергируется меха-
ническими или пневматическими форсунками или быстровращаю-
Рис. 21-23. Распылительная сушилка:
/ — сушильная камера, 2— механическая форсунка, 3— регулируемые щели для подвода
нагретого воздуха; 4 — воздушный фильтр; 5, 10 — вентиляторы, б —газовый подогреватель;
7—циклон; 8—топка, 9 — скребки; 11 — скруббер, 12—насос для подачи раствора на распыли-
• ванне; 13 — насос для подачи раствора на орошение скруббера
щимися горизонтальными дисками (центробежные распылители).
Некоторые типы распылительных дисков показаны на рис. 21-24.
Основные достоинства распылительных сушилок: 1) быстро-
та сушки, 2) низкая температура сушки, 3) возможность полу-
чения конечного продукта в виде тонкого порошка, не требую-
щего дальнейшего измельчения и обладающего хорошей раство-
римостью
Благодаря исключительно быстрой сушке температура высу-
шиваемого вещества в течение всего процесса остается близкой
к температуре испаряющейся влаги (50—70°С), несмотря на
значительно более высокую температуру сушильного агента, Это
774
Гл. 21. Сушка
особенно ценно при сушке материалов, чувствительных к дей-
ствию высоких температур.
Хорошая растворимость образующегося при сушке мелко-
дисперсного порошка в ряде случаев имеет большое значение
(например, при разведении водой сухого молока и некоторых
других порошкообразных продуктов).
Недостатки распылительных сушилок: 1) большие размеры
сушильной камеры вследствие малой скорости сушильного аген-
та и соответственно низкого напряжения камеры по влаге (2—
25 ка/ж3«ч), 2) значительный расход энергии и тепла, 3) слож-
ное оборудование сушильной установки (распыливающие и пы-
леулавливающие устройства).
Рис. 21-24. Типы распылительных дисков:
а —тарельчатый открытый; б— плоский закрытый с отверстиями; а —плоский закрытый
с зубьями; г—трехъярусный с перегородками и зубьями.
Сушилки с кипящим (псевдоожиженным) слоем. Эффектив-
ная сушка многих материалов возможна в кипящем слое.
Принципиальная схема сушки топочными газами в кипящем
(псевдоожиженном) слое показана на рис. 21-25. В камере
смешения 2 топочные газы смешиваются с воздухом, нагне-
таемым вентилятором /, и поступают в нижнюю часть сушилки,
представляющей собой цилиндрическую или прямоугольную
сушильную камеру 3 с газораспределительной решеткой 4.
Высушиваемый материал подается питателем 5 в верхнюю
часть камеры 3 и образует кипящий слой в восходящем
токе газа, проходящего сквозь отверстия решетки 4. Высушен-
ный материал пересыпается через порог 6 в сборник 7. Твердые
частицы, уносимые потоком сушильного агента, отделяются в
циклоне 8.
В кипящем слое происходит быстрое выравнивание темпе-
ратур твердых частиц и сушильного агента и достигается весь-
ма интенсивный тепло- и массообмен между твердой и газовой
фазами, в результате этого сушка заканчивается в течение
нескольких минут.
9 Устройство сушилок
775
При сушке в кипящем слое в качестве сушильных агентов
применяют топочные газы и воздух, сушку проводят в аппара-
тах непрерывного и периодического действия, причем непрерыв-
ная сушка производится в одноступенчатых и многоступенчатых
сушилках. В последнем случае достигается повышенная степень
использования тепла сушильного агента.
Рис. 21-25. Сушилка с кипящим (псевдоожиженным)
слоем:
/ — вентилятор; 2—камера смешения; 3 — сушильная калера; 4 — газо-
распределительная решетка; 5— питатель; 6— порог; 7— сборник;
8 — циклон.
На рис. 21-26 показана схема периодически действующей су-
шилки с кипящим слоем, пригодной для сушки крупнокристал-
лических и тонкоизмельченных (порошкообразных) материалов.
Образование кипящего слоя материала в такой сушилке осуще-
ствляется путем периодического кратковременного ввода су-
шильного агента (толчками-импульсами) в неподвижный слой
высушиваемого материала.
Сушилка имеет слегка конический, расширяющийся кверху
корпус 1 с наружным коллектором 2, к которому равномерно
по окружности присоединены газораспределительные головки 3.
Сушильный агент подается газодувкой 5 через подогреватель 4.
При введении сушильного агента импульсами (длительность по-
дачи примерно 1 сек) высушиваемый материал переходит в
ТГв
Гл 21 Сушка
состояние кипящего слоя, но после прекращения подачи газа
слой быстро становится неподвижным При таком ударном воз-
действии происходит быстрое перераспределение пустот и кана-
лов в слое, благоприятствующее испарению влаги из высуши-
ваемого материала. Продолжительность сушки и расход энер-
гии при сушке в импульсном кипящем слое значительно ниже,
чем в вакуум-сушилках.
Рис. 21-26. Сушилка периодического действия с им-
пульсным кипящим слоем1
/—корпус, 2— наружный коллектор, 3 — газораспределительная
головка, 4— подогреватель; 5 —газодувка.
Разновидностью сушилок с кипящим слоем являются аэро-
фонтанные сушилки (рис. 21-27) Влажный материал поступает
из загрузочного бункера /, подхватывается смесью воздуха с
топочными газами и поступает в камеру, или рюмку, 2. В ка-
мере материал интенсивно циркулирует до тех пор, пока высох-
шие частицы, как более легкие, уносятся газами в циклон 3.
Здесь газы отделяются от высушенного материала, который уда-
ляется через днище циклона.
Сушка в кипящем слое пригодна для обработки зернистых,
неслипающихся и мелкоизмельченных материалов В сушилках
9 Устройство сушилок
777
непрерывного действия размер твердых частиц высушиваемого
материала должен находиться в пределах от нескольких мм до
десятых долей мм
Достоинства сушилок с кипя-
щим слоем: 1) интенсивная суш-
ка, напряжение объема сушиль-
ной камеры по влаге может до-
стигать нескольких сот кг/м? • ч,
2) возможность сушки при высо-
ких температурах, которые могут
превышать допустимые для дан-
ного материала, вследствие крат-
ковременности его соприкоснове-
ния с сушильным агентом, 3) вы-
сокая степень использования
тепла сушильного агента, 4) воз-
можность автоматического регу-
лирования параметров процес-
са (в том числе времени пребы-
вания частиц материала в аппа-
рате).
Недостатки таких сушилок.
1) непригодность для сушки ма-
териалов, трудно поддающихся
псевдоожижению (например, ма-
териалы с высокой влажностью,
с крупными размерами частиц и
ское сопротивление, 3) истирание
частиц.
Рис. 21-27. Аэрофонтанная су-
шилка
7-бункер, 2- камера (рюмка), 3-циклон.
\ д), 2) высокое гидравличе-
и значительный унос твердых
Контактные сушилки
Вакуум-сушильные шкафы. Вакуум-сушильный шкаф
(рис. 21-28) является простейшей контактной сушилкой периоди-
ческого действия. Он представляет собой камеру 1 цилиндриче-
ского или прямоугольного сечения с рядом полых греющих
плит 2, обогреваемых изнутри паром, на которые устанавливают
противни с высушиваемым материалом. Пары влаги через шту-
цер 3 отсасываются при помощи вакуум-насоса в конденсатор,
где отделяются от воздуха
Несмотря на некоторые достоинства (простота устройства,
возможность одновременной сушки различных материалов),
вакуум-сушильные шкафы отличаются низкой производитель-
ностью (сушка в неподвижном слое, периодичность действия,
связанная с остановкой шкафа для загрузки и выгрузки, плохая
теплопередача вследствие образования воздушных прослоек
778
Гл. 21 Сушка
между противнями и плитами). В настоящее время вакуум-су-
шильные шкафы вытесняются сушилками более совершенных
типов.
Рис. 21-28. Вакуум-сушильный шкаф:
1— сушильная камера; 2—полые греющие плиты; 3—штуцер для соединения с вакуум-линией;
4 — съемная крышка.
Контактные барабанные сушилки непрямого действия. В ба-
рабанных сушилках непрямого действия (рис. 21-29) тепло пе-
редается высушиваемому материалу через стенку. Топочные
газы омывают барабан 1 снаружи и затем движутся по цилинд-
рическому газоходу 2, концентрически проходящему внутри ба-
рабана. Высушиваемый материал перемещается в кольцевом
Рис. 21-29. Барабанная сушилка непрямого действия:
1 — барабан; 2 —газоход.
пространстве между внутренней стенкой барабана 1 и газохо-
дом 2, не соприкасаясь с сушильным агентом. Такие сушилки
применяют в тех случаях, когда допускается высокотемператур-
ная сушка материала, но он не должен соприкасаться с топоч-
9. Устройство сушилок,
770
ними газами во избежание загрязнений продуктами неполного
сгорания и пылью.
Гребковые сушилки. Гребковая вакуум-сушилка (рис. 21-30)
представляет собой горизонтальный барабан /, снабженный па-
ровой рубашкой 2 и мешалкой в виде горизонтального полого
вала 3 с гребками. Высушиваемый материал загружается в ба-
рабан через верхний люк 4. Медленно вращающиеся гребки
Рис. 21-30. Гребковая сушилка:
1— барабан; 2— рубашка; 3 — вал с гребками;~4 — загрузочный люк; 5 — трубы („скалки")
б—разгрузочное отверстие.
(п ~ 8 об[мин) перемещают материал в обе стороны к крыш-
кам барабана, а затем обратно от крышек к середине. Для
этого направление вращения вала мешалки периодически из-
меняется при помощи специального устройства. Соседние лопа-
сти мешалки закреплены перпендикулярно друг другу; между
ними свободно уложены закрытые с концов трубы 5, которые
перекатываются при вращении барабана, способствуя лучшему
перемешиванию и измельчению материала. Сушилка соединена
с барометрическим конденсатором и вакуум*насосом.
Достоинства гребковых вакуум-сушилок: 1) ускорение суш-
ки, обусловленное перемешиванием материала, 2) легкость об-
служивания, 3) возможность получения высушенного продукта
в измельченном виде.
Недостатки: 1) периодичность действия, 2) сравнительная
громоздкость и сложность сушильной установки, 3) значитель-
ные эксплуатационные расходы (на смену гребков, ремонт ме-
ханизмов и т. д.).
В настоящее время внедрены в производство более эффек-
тивные гребковые сушилки периодического и непрерывного дей-
ствия, в которых сушка производится топочными газами, дви-
жущимися в барабане в одном направлении с высушиваемым
материалом. Эти сушилки работают при атмосферном давлении.
780
Гл. 21. Сушка
Вальцовые сушилки. Такие сушилки непрерывного действия
изготовляются одно- и двухвальцовыми и работают при атмо-
сферном давлении или при разрежении.
Одновальцовая атмосферная сушилка (рис. 21-31) предста-
вляет собой вращающийся барабан /, обогреваемый внутри па-
ром и частично погруженный в высушиваемый раствор, который
заполняет корыто 2, снабженное снизу паровой рубашкой. В ко-
рыте раствор перемешивается мешалкой 3 и наносится на ба-
рабан слоем толщиной до 2 мм. Тонкий слой материала успе-
вает высохнуть в течение одного оборота барабана и снимается
с его поверхности ножом 6. Высушенный материал падает в
шнек 5 и удаляется из сушилки. Пар поступает через полую цап-
фу барабана, паровой конденсат отводится изнутри барабана
через ту же цапфу по сифонной трубке 4.
В одновальцовых сушилках некоторых конструкций материал
наносится на барабан при помощи валика, распыливающего
жидкость, или нескольких валиков, намазывающих слой пасты
на барабан.
Для сушки пастообразных материалов используются одно-
вальцовые формующие сушилки, в которых материал подсуши-
вается в отформованном видеДстр. 783).
Двухвальцовая атмосферная сушилка (рис. 21-32) состоит
из двух барабанов-вальцов 1, вращающихся в кожухе 2 навстре-
чу друг другу (п — 2— 10 об{мин}. Жидкий или пастообразный
материал поступает в сушилку сверху и проходит зазор между
вальцами, величину которого можно регулировать, так как один
из вальцов имеет подвижные подшипники. Обычно зазор между
вальцами не превышает 1 мм.
Процесс сушки и съем высушенного материала происходят
так же, как в одновальцовой сушилке. Однако в двухвальцо-
вых сушилках количество влаги, испаряемой за единицу време-
ни с 1 м2 поверхности нагрева, меньше, чем в одновальцовых су-
шилках. Материал, снятый с вальцов, часто приходится досу-
шивать в шнековых досушивателях 3 и 4, снабженных паровыми
рубашками и мешалками. Окончательно высушенный материал
удаляется из досушивателей через патрубок 5.
Вакуумные одновальцовые и двухвальцовые сушилки отли-
чаются от соответствующих атмосферных сушилок главным об-
разом герметичным кожухом и вспомогательным оборудованием,
необходимым для работы при разрежении (сепаратор, конден-
сатор, вакуум-насос).
Для обогрева вальцов, кроме пара, применяют горячую воду
или высококипящие органические жидкости.
Достоинства вальцовых сушилок: 1) непрерывная сушка при
довольно высоком напряжении поверхности нагрева (до
9 Устройство сушилок
781
Рис 21-31. Одновальцовая сушилка.
/ —барабан; 2 — корыто; 3 — мешалка; 4 — сифолная трубка; 5 — шнек; б—нож.
782
Гл 21 Сушка
70 кг/м2-ч), 2) возможность сушки материалов, чувствительных
к действию высоких температур, в том числе пастообразных ма-
териалов, 3) экономичность сушки, обусловленная малыми по-
терями тепла с отработанным воздухом
Недостатки 1) сравнительно высокая влажность высушен-
ного продукта, 2) возможность перегрева материала
Вальцовые вакуумные сушилки, как и другие контактные су-
шилки, работающие при разрежении, несмотря на сложность
устройства и высокую стоимость, а также трудность контроля
Рис 21-32 Двухвальцовая сушилка
1— барабаны вальцы, 2—кожух, 3, 4 — досушиватели 5 — патрубок для отвода высушенного
материала, 6 — сифонная трубка, 7 —нож
их работы, довольно часто применяются в химических производ-
ствах Это объясняется специфическими достоинствами вакуум-
ных сушилок, к числу которых относятся 1) интенсивная сушка
при низких температурах, что важно при сушке материалов,
чувствительных к действию высоких температур, 2) безопасная
сушка взрывчатых и токсичных веществ, 3) чистота высушивае-
мого продукта, 4) возможность улавливания паров ценных рас-
творителей путем конденсации, 5) независимость процесса суш-
ки от атмосферных условий
Комбинированные сушилки
Вальцово ленточная и вальцово барабанная сушилки представляют собой
агрегаты из одновальцовой формующей сушилки и ленточной или соответ-
ственно барабанной сушилки
Одновальцовая формующая сушилка служит одновременно для предва-
рительной сушки пастообразного материала и формования его в виде пало-
чек, которые окончательно высушиваются в ленточной или барабанной су-
шилке
10 Сравнение и выбор сушилок
783
Вальцово ленточная сушилка (рис 21 33) имеет барабан / с кольцевыми
канавками шириной 6—12 мм, находящимися друг от друга на расстоянии
6—10 мм Исходный материал, поступающий через воронку 2, вмазывается
в канавки барабана при помощи прижимного валика 3
Материал подсушивается менее чем за один оборот барабана, дает
усадку и легко снимается гребенчатым ножом 4 При съеме отформованный
шнур материала ломается на короткие палочки которые по транспортерной
ленте 5 направляются в другую (ленточную или барабанную) сушилку для
досушивания
Рис 21-33 Вальцово-ленточная сушилка
/ — формующий барабан 2 —питающая воронка, 3 — прижимной
валик 4 — гребенчатый нож, 5 — транспортерная лента, 6 — ленточ-
ная сушилка
В одновальцовой формующей сушилке удаляется не более 30% влаги,
содержавшейся в исходном материале но процесс досушивания протекает
интенсивно вследствие большой поверхности испарения влаги с палочек,
приобретающих пористую структуру за время соприкосновения с горячей по
верхностью барабана В вальцово ленточных и вальцово барабанных сушил-
ках достигается интенсивная непрерывная сушка пастообразных материалов,
не чувствительных к действию температур до 100° С *
Недостаток этих сушилок — трудность очистки при частой смене вы
сушиваемых материалов (например, при сушке красителей разных марок)
10. Сравнение и выбор сушилок
Сушилки периодического действия отличаются низкой про-
изводительностью, громоздки и в большинстве случаев не удо-
влетворяют требованиям современной промышленности Сушка
в них производится в неподвижном толстом слое (вакуум-су-
шильные шкафы, шкафные воздушные циркуляционные сушил-
ки) или при перемешивании материала (гребковые вакуумные
сушилки)
Применение сушилок первого типа связано с необходимостью
затрат тяжелого физического труда, с потерями ценного продук-
та и загрязнением производственных помещений В случае при-
менения сушилок второго типа облегчается обслуживание су-
шилок, но продолжительность процесса остается значительной
Поэтому, как правило, вместо малопроизводительных суши-
лок периодического действия применяют сушилки непрерывного
784
Гл. 21 Сушка
действия, в которых достигается сокращение продолжительности
сушки и улучшается качество продукта и, кроме того, значи-
тельно облегчается обслуживание. Сушилки периодического дей-
ствия целесообразно использовать только в производствах не-
больших масштабов с разнообразным ассортиментом продукции.
Сушилки, работающие с использованием топочных газов, бо-
лее производительны и экономичны, чем воздушные сушилки.
При сушке топочными газами, благодаря ускорению процесса,
высокая температура газов не сказывается отрицательно на ка-
честве ряда ценных высушиваемых продуктов, которые удается
предохранить от загрязнения при полном сжигании топлива.
Важным фактором, влияющим на выбор сушилок, является
характеристика материала, подлежащего сушке (кусковой, сы-
пучий, пастообразный, жидкий).
Для сушки кусковых и сыпучих материалов, малочувстви-
тельных к действию высоких температур, применяются главным
образом барабанные и гребковые сушилки. Однако сушку мно-
гих сыпучих мелкоизмельченных материалов можно более эф
фективно проводить в сушилках с кипящим (псевдоожижен-
ным) слоем, 'в которых достигается более высокая производи-
тельность при значительно меньших габаритных размерах, чем
для барабанных сушилок.
Сушка пастообразных материалов связана с налипанием их
на стенки сушильных аппаратов и с образованием корки на по-
верхности высушиваемого материала, что приводит к резкому
увеличению длительности сушки. Наиболее пригодными для та-
ких материалов сушилками являются петлевые и вальцово-лен-
точные или вальцово-барабанные сушилки непрерывного дей-
ствия. В настоящее время проведены успешные опыты сушки
пастообразных материалов в сушилках с кипящим слоем.
Для сушки мелких партий разнообразных материалов ра-
ционально применение шкафных воздушно-циркуляционных су-
шилок.
Вакуум-сушилки, применяемые для сушки жидких и пасто-
образных материалов, сложнее по устройству и дороже атмо-
сферных сушилок. Поэтому применение вакуум-сушилок целе-
сообразно в тех случаях, когда атмосферные сушилки не могут
быть использованы, например при сушке быстро окисляющихся,
взрывоопасных или выделяющих токсические пары веществ.
Для высушивания жидких материалов применяют вальцо-
вые и распылительные сушилки, причем первые пригодны и для
сушки материалов густой консистенции. Вальцовые сушилки
компактнее распылительных, в них возможно более легкое ре-
гулирование температуры сушки (изменением давления греюще*
И Расчет сушилок 785
ДМ*
го пара) и ее продолжительности (изменением скорости враще-
ния вальцов). Однако распылительные сушилки весьма эффек-
тивны при необходимости получения порошкообразных мате-
риалов, не требующих последующего измельчения. Эффектив-
ность распылительных сушилок может быть повышена, а габа-
ритные размеры уменьшены при использовании в качестве
сушильного агента топочных газов.
В сушилках с кипящим (псевдоожиженным) слоем продол-
жительность пребывания материала в зоне сушки больше, чем
в пневматических сушилках, и, следовательно, достигается бо-
лее равномерная сушка материалов с частицами различных
размеров. Сушилки с кипящим слоем могут быть эффективно
использованы для сушки многих химических продуктов. Они вы-
годно отличаются* от сушилок других типов высокой производи-
тельностью, простотой устройства, компактностью, а иногда и
небольшим гидравлическим сопротивлением.
Для создания наиболее интенсивных режимов процесса
сушки желательно применение многоступенчатых или многосек-
ционных сушилок с кипящим слоем, в которых высушиваемый
материал последовательно проходит через секции аппарата,
причем в каждой секции материал и сушильный агент движутся
противотоком друг другу (ступенчатый противоток).
11. Расчет сушилок
Графо - аналити ческий расчет сушилок
В большинстве случаев расчет сушилок ведут графо-анали-
тическим способом с помощью /—х-диаграммьТ. Этот способ
прост, нагляден и дает достаточно точные для технических рас-
четов результаты.
Примером может служить расчет воздушной сушилки непре-
рывного действия, для которой заданы: количество материала,
поступающего в сушилку, Gi кг/сек, его начальная влажность
Wi % и конечная влажность w2 %. По этим данным, пользуясь
формулами (21-16) и (21-17), определяют количество влаги
W кг!сек, испаряемой в сушилке, а также находят производи-
тельность сушилки по высушенному материалу G2 = (Gi— W)
кг!сек. Затем вычисляют удельные потери тепла в сушилке и
определяют величину А = (^доб. + сЛ) — (qM + q? 4- qn). Далее
строят процесс сушки на I — х-диаграмме, как описано на
стр. 751. Определяют удельный расход I воздуха при помощи
формулы (21-18) и удельный расход тепла:
q = l(Ix— /0) ккал!кг испаренной влаги
Умножая I и q на W, находят суммарные расходы воздуха
и тепла на процесс сушки,
50 Зак 546
Гл 21 Сушка
Аналитический расчет сушилок
В некоторых случаях, например при малых перепадах тем-
ператур и влагосодержаний сушильного агента, расчет суши-
лок ведут аналитическим способом. Он точнее графо-аналитиче-
ского способа, но связан с более громоздкими вычислениями.
Аналитический метод расчета сводится к совместному реше-
нию основного уравнения теплового баланса (21-25), уравнения
влагосодержания (21-6) и уравнения (21-9) энтальпии влаж-
ного воздуха.
Если задана величина /2, то по формуле (21-9) находят /2
как функцию х2 и, подставляя полученное выражение для /2
в уравнение (21-25), определяют х2, а затем /2.
Если вместо t2 задано <f>2— относительное влагосодержание отработан-
ного воздуха, то совместное решение уравнений (21-25) и (21-7) приводит
к следующей зависимости-
/"-д 1
(1000 + 1,97 • (Л — *2) “ х2 —х0 (21-41)
причем
Уравнение (21-41) решают подбором. Принимая произвольно значение t2,
находят по справочным таблицам давление ра насыщенного водяного пара,
определяют энтальпию водяного пара в отработанном воздухе и подстав-
ляют найденные параметры в уравнение (21-41) до тех пор, пока его левая
и правая части не окажутся равными друг другу.
Пример 21-6. Определить расходы воздуха и тепла на сушку влажного
материала, поступающего в воздушную сушилку в количестве G\ = 2500 кг/ч
(0,694 кг]сек) при начальной влажности Wi = 20% и температуре &i — 10°С.
Материал высушивается до конечной влажности w2 = 5% и удаляется из
сушилки при температуре 92 = 80°С. Теплоемкость высушенного материала
с2 — 922 дж]кг • град — (0,22 ккал)кг • град).
Воздух поступает в сушилку при температуре t\= 160° С, на выходе из
сушилки он имеет относительную влажность ?2 = 80%. Удельные потери
тепла в окружающую среду составляют qn = 628 500 дж/кг (150 ккал/кг
испаренной влаги). Место установки сушилки — район Москвы
Решение. Определяем на основании формул (21-16) и (21-17) коли-*
чество влаги, испаряемой в сушилке.
W = Gx = 2500 • 4 = 395 кг/ч = 0,11 кг] сек
1100 — w2 100 — 5
Производительность сушилки по высушенному материалу составляет:
G2 = G} — W = 2500 — 395 = 2105 кг/ч = 0,585 кг/cetf
11. Расчет сушилок
787
Удельный расход тепла на нагревание высушенного материала равен-
= О2с2 (»2= 2105-922(80—10) = кг ккал) кг)
w о9э
Определяем величину Д (см стр 747), учитывая, что в сушилке отсут-
ствуют транспортные устройства и не производится дополнительный подвод
тепла в сушилку.
Д = сЛ — (<?м + 7п) = 4190.10 — (343 900 -% 628 500) =
= — 930 000 дж!кг (— 222 ккал!кг)
' Дальнейший расчет проводится раздельно для летних и зимних условий.
Летние условия
Средние параметры наружного воздуха для Москвы (в летнее время):
to = 18° С, <ро = 70% (см Приложение XVII)
На 1 — х-диаграмме (см. Приложение XIX) находим точку А, характе-
ризующую состояние наружного воздуха, и определяем его параметры:
х0 = 0,0092 кг]кг сухого воздуха
/0 = 41480 дж!кг сухого воздуха (9,9 ккал{кг сухого воздуха)
Проводим из точки А вертикаль хо = const до пересечения с изотермой
ti — 160° С в точке В, определяющей состояние воздуха на входе в сушилку:
xt = х0 = 0,0092 кг!кг сухого воздуха
= 187 300 дж)кг сухого воздуха (44,7 ккал)кг сухого воздуха)
Из точки В проводим линию теоретического процесса сушки Ц = const.
На этой линии берем произвольную точку е и проводим из нее горизонталь
до пересечения в точке f с линией х0 = Xi = conSt. Пусть длина отрезка
ef — 54 мм
Определяем отношение масштабов I — х-диаграммы:
/И; 0,1
П1 = -- — А— 500
тх 0,0002
и находим длину отрезка еЕ-
еЕ = ef± 54 • (~ 222) = - 24 мм
Tib u\J\)
Откладываем отрезок еЕ из точки е вниз (так как он отрицателен) и
через точки В и Е проводим прямую до пересечения с линией фг — 80%
в точке D, характеризующей состояние воздуха на выходе из сушилки:
х2 = 0,0436 кг! кг сухого воздуха
/2 = 154600 дж)кг сухого воздуха (36,9 ккал!кг сухого воздуха)
Определяем удельный расход воздуха по формуле (21-18)!
1 = л2 —х0 = 0,0436 — 0,0092 “29 кг1кг
60*
788
Г л. 21. Сушка
Тогда расход воздуха на сушку составит
L = IW = 29 • 395 11 500 кг/ч = 3,2 кг!сек
Удельный расход тепла на нагревание воздуха в калорифере равен:
q = — 70) = 29 (187 300 — 41 480) = 4230 • 103 дж!кг (1010 ккал!кг)
Расход тепла на сушку составляет:
Q = qW = 4230 • 103 • 395 — 1670 • 106 дж/ч = 0,464 • 106 вт (399 000 ккал/ч)
Зимние условия
Находим параметры наружного воздуха для зимних условий (см Прило-
жение XVII): tQ =—10,8°С, <р0 = 88%. На I — х-диаграмме (см Приложе-
ние XIX) состояние наружного воздуха характеризуется точкой Лк
х0 = 0,00136 кг!к г сухого воздуха
7' = — 7540 дж/кг сухого воздуха (— 1,8 ккал!кг сухого воздуха)
Произведя аналогичное предыдущему построение процесса на I — х-диа-
грамме (ломаная линия AiBiDt), получим:
х2 = 0,0365 кг/кг сухого воздуха
/2 = 137 000 дж/кг сухого воздуха (32,7 ккал/кг сухого воздуха)
Соответственно удельный и общий расходы воздуха на сушку в зимних
условиях составят
I = 28,5 кг/кг, L = 11 250 кг/ч = 3,12 кг/сек
Удельный и общий расходы тепла в этих условиях будут:
= 4920 -103 дж/кг (1175 ккал/кг)
Q = 1940 • 106 дж/ч = 0,54 • 10s вт (465000 ккал/ч)
Следовательно, в зимних условиях расход тепла значительно больше, чем
в летних условиях, а расход воздуха — несколько больше в летних условиях,
чем в зимних условиях.
Расчет газовых сушилок
Вследствие незначительной разности энтальпий топочных га-
зов и воздуха (не более 0,8%) при расчете газовых сушилок
можно пользоваться /—х-диаграммой влажного воздуха, по-
строенной для высоких температур. Тепло топочных газов вы-
деляется при горении топлива, поэтому изображение процесса,
аналогичного подогреву воздуха в воздухоподогревателе
(хо = Xi = const), в данном случае на диаграмме отсутствует.
Состояние топочных газов на входе в сушилку характери-
зуется точкой В (рис. 21-34), которая определяется как точка
11. Расчет сушйлок
789
пересечения линии заданной температуры газов 6 = const с ли
нией одного из параметров газов, например энтальпии Ц = const
которая может быть определена
по уравнению (21-9).
Положение точки В на I — х-
диаграмме может быть опреде-
лено также путем построения
процесса смешения топочных га-
зов со свежим воздухом (стр. 742).
Прц этом состояние смешивае-
мых топочных газов характери-
зуется топкой Т, состояние све-
жего воздуха — точкой А.
Дальнейшее построение про-
цесса сушки ведется так же, как
для воздушных сушилок. Это
можно видеть из рис. 21-34, на ко-
тором изображен процесс сушки
в газовой сушилке при Д < 0.
Расчет барабанных сушилок рис. 21-34. Построение процесса
г, , , сушки топочными газами на
Расчет процесса сушки в барабан- J / —х-диаграмме
ных сушилках производится по обычно- д р
му методу, принятому для воздушных
или газовых сушилок. При расчете определяются также число оборотов
рабана и мощность, потребная для его вращения.
Для определения числа оборотов барабана необходимо знать время т
пребывания материала в барабане:
т
УбРнФ
-7?-----сек
Gcp.
(21-42)
где Vq — объем барабана, jh3;
рн— насыпная масса материала, кг/м*-,
Ф— степень заполнения барабана;
Осо. — средняя марса материала, проходящего через барабан, кг/сек
Объем барабана Уб определяют, исходя из величины напряжения бара-
бана по влаге А кг/м? • ч, по формуле
W
Уб = -^л<з (21-43)
где 1У — общее количество испаряемой влаги, кг/ч (по материальному ба-
лансу).
Ориентировочные реличины напряжения барабана по влаге (опытные
данные) приведены в табл. 33.
Число оборотов барабана в 1 сек определяется по формуле
L
a~.D tga
(21-44)
700
Гл 21 Сушка
В уравнении (21-44):
D — диаметр барабана, ж;
bh L — длина барабана, ж;
а~~ЁГ (Ь — число падений частиц материала за один оборот
барабана; h—средняя высота падения, ж);
tga — тангенс угла наклона барабана.
Таблица 33
Напряжения барабана по влаге
Высушиваемый материал Влажность материала, % Температура, °C Напря- жение барабана А кг/м* ч Насадка барабана
началь- ная Wi конеч- ная w2 сушильного агента на входе Л матери- ала на выходе h
Аммиачная се- литра 1,5 0,5 100—120 60—70 4—6 Распредели- тельная
Солянокислый 6,5 0,2 106 60 7,5 —
анилин
Арсенат кальция 35—40 0,5 550—650 — 15 —
Бикарбонат на- 6-8 0,5—0,6 100—105 70—75 2,5 —
трия
Сульфат аммония 3—5 0,4 0,82 — 4,5 Подъемно-ло- пастная
Фосфориты 6 0,5 600 100 45—65 То же
Флотационный колчедан 12—16 2—4 600—650 80—90 60—70 Подъемно-ло- пастная и ячейковая
Значения а для насадок барабанов некоторых конструкций
приведены в табл. 34.
Таблица 34
Значения коэффициента а
Насадка Значения а при диаметре барабана, мм
1200 1600 2000 2400 2800
Подъемно-лопастная (см рис. 21-21, а) 1,2 1,2 1,2 1,2 1,2
Полочная (см. рис. 21-21, б) 0,6 0,5 0,43 0,375 0,336
Секторная (см. рис. 21-21, г): с 4 секторами 0,741 0,737 0,739 0,739 0,715
с 5 секторами 0,95 0,937 0,935 0,936 0,911
Ячейковая (см. рис. 21-21, д) 0,656 0,437 0,332 0,328 0,325
11 Расчет сушилок
791
Мощность N, затрачиваемая на вращение барабана, опреде-
ляется по следующей формуле:
N 0,078£)3Дрн<з/г кеш (21-45)
где п, — число оборотов барабана в 1 сек\
а— коэффициент, зависящий от вида насадки и степени
заполнения барабана (табл. 35).
Таблица 35
Значения коэффициента а
Насадка Значения а при степени заполнения барабана
0,1 0,15 0,20 0,25
Подъемно-лопасгная (см. рис. 21-21, а) 0,038 0,053 0,063 0,071
Полочная (см. рис. 21-21, 6} ... . 0,013 0,026 0,038 0,044
Ячейковая (см. рис. 21-21, д) ... 0,006 0,008 0,01 0,011
Пример 21-7. Рассчитать размеры барабана и мощность, потребную на
вращение барабанной газовой сушилки для сушки флотационного колчедана
в количестве Gi = 10000 кг/ч Начальная влажность материала Wi — 16%,
конечная влажность = 4%
Насыпная масса колчедана рн = 3300 кг!м3, теплоемкость высушенного
материала с2 = 545 дж[кг • град (0,13 ккал/кг • град}.
Степень заполнения барабана колчеданом 4 = 0,15, насадка барабана —
подъемно-лопастная.
Решение. По формуле (21-17) определяем производительность^ су-
шилки по высушенному материалу:
о2 = юооо = 8750 кг1ч = 2’43 кг!свк
Количество влаги, испаряемой в сушилке, составляет:
W = Gx — О2 = 10 000 — 8750 = 1250 кг!ч = 0,347 кг{сек
Согласно табл. 33, принимаем напряжение барабана сушилки по влаге
А 65 кг!м3-ч. Объем барабана по формуле (21-43) составит:
уб = 1^9 = 19,2 м*
о5
Принимая отношение длины барабана к его диаметру L . D == 6, опреде-
ляем диаметр барабана:
V6 = —— L = 0,78502.60 = 4,7103
Этот размер соответствует нормали (стр. 770),
792
Гл. 21. Сушка
Уточняем объем барабана:
Уб = 4,71 D3 = 4,71 -1,6з== 19,3 м3
и площадь его сечения:
TtD2
F = = 0,785 -1,62 = 2,01 м*
Длина барабана составляет:
£__Кб-213-96 Л
Г ~ 2,01 “9,ь
Принимаем округленно L — 10 м.
Находим среднюю массу материала, проходящего через барабан:
_ 0,4-02 10 000 4-8750 ,
Оср. —---2----~------2-----~ кг^ ~ 2’^ кг[сек
По формуле (21-42) определяем время пребывания материала в бара-
бане:
19,3-3300-0,15 t
Т = --------------- = 3660 сек
2,6
Принимаем угол наклона барабана а = 3° (tg а 0,052) и определяем
число оборотов барабана по формуле (21-44):
10
1,2 - 3660-1,6 - 0,052 - °’0274 об/сек&\,6 об!мин
где 1,2 — коэффициент а (см. табл. 34).
Мощность, потребная на вращение барабана, составляет по формуле
(21-45):
W = 0,078 • 1,63 -10 - 3300 - 0,053 • 0,0274 15,5 квт
где 0,053 — коэффициент <?, определенный по табл. 35.
Расчет распылительных сушилок
При расчете дисковых распылительных сушилок определяют
диаметр DK сушильной камеры, пользуясь Опытными данными
(рис. 21-35),* и требуемый объем сушильной камеры VK (в Л!3),
исходя из объемного коэффициента теплоотдачи ** аоб> (в
вт]м3 • град), который может быть найден по эмпирическому
уравнению:
«06=5,69X44-) (^J (21-46)
* Сушка в химической и легкой промышленности. Профиздат, 1958,
стр. 118—152.
** Объемный коэффициент теплоотдачи аОб. определяется количеством теп-
ла, передаваемого от горячего теплоносителя холодному при их непосред-
ственном соприкосновении в единице объема аппарата за единицу времени
при температурном напоре, равном 1° С.
11. Расчет сушилок
793
Здесь X — средняя теплопроводность сушильного агента, в
вт/м • град-,
G
q — р?- — объемная производительность сушилки по исход-
ному раствору (плотностью р кг/л13), приходящаяся
на 1 м2 сечения FK сушильной камеры, м3/м2-,
б/ср.— средний диаметр капель, м]
и wB — средние скорости сушильного агента и витания су-
хих частиц (при средней температуре сушильного
агента), м/сек.
Зная величины DK и VK, определяют высоту сушильной ка-
меры. Уравнение (21-46) применимо при dcp. = 46— 168 мк,
wr =0,19 — 0,35 м/сек, wB = 0,06 — 0,25 м/сек и температуре
сушильного агента в пределах 117—600° С.
Пример 21-8. Определить основные размеры камеры распылительной
сушилки для сушки суспензии красителя в количестве V — 1 м3/ч. Началь-
ное содержание жидкости в суспензии Wi = 77,5%, конечная влажность вы-
сушенного материалам = 5%, плотность суспензии рс = 1235 кг/м3.
Сушка производится топочными газами, движущимися прямотоком вы-
сушиваемому материалу. Температура газов на входе в сушилку Л = 250° С.
на выходе из сушилки /2 = 75° С. Температура суспензии на входе в су-
шилку &1 = 25° С, температура материала на выходе из сушилки &2 = 65° С.
Теплоемкость высушенного материала см=1255 дж/кг • град (0,3 ккал/кг- град).
Распыление производится центробежным диском диаметром дЛ — 250 мм,
делающим п= 12 000 об/мин (см. рис. 21-24, в). Средний размер образую-
щихся капель d = 35 мк.
Решение. Масса высушиваемой суспензии равна:
О — Vpc = 1 • 1235 = 1235 кг/ч
Количество испаряемой из материала влаги составляет W =? §42 кг/ч
(см. пример 21-2, стр. 744).
Количество тепла, передаваемого топочными газами суспензии: Q =*
— 663000 вт (571 000 ккал/ч, см. пример 21-3, стр. 749).
При средней температуре топочных газов /Ср.= 162,5° С их плотность
р = 0,82 кг/м3 и вязкость у- — 0,024 • 10~3 н • сек/м2 (0,024 спз).
По аналогии С примером 6-14 (стр. 175) находим Аг = 0,765, тогда по
формуле (6-95) Re — 0,0428, а скорость витания по выражению (6-98):
pi Re
№в = ——-
ар
0,024 • 10“3 • 0,0428
35 -10~6 • 0,82
0,036 м/сек
Определяем окружную скорость диска:
r.d^n 3,14 • 0,25 • 12 000
и ~ —60~ =----------60----------- 15? м!сек
По рие. 21-35 находим для данных Киа диаметр сушильной камеры
DK = 5,2 м. Отсюда площадь сечения камеры составляет:
Рк = 0,785£>2 =. 0,785 • 5,22 =* 21,2 м2
Согласно примеру 21-5 (стр. 764) расход топочных газов L = 13 760 кг/ч.
794
Гл 21 Сушка
Скорость газов в камере сушилки составляет
_ L _ 13760 ЛПО ,
Wr /\р - 3600 21,2 - 0,82.3600 “ 0,22 М,СвК
Полученные значения и wr близки к пределам применимости урав-
нения (21-46), а размер частиц сухого материала близок к нижнему пре-
делу </ср
2 6 Q ' Ю
Диаметр камеры, м
Рис. 21-35. Зависимость диаметра сушильной камеры распылительной
сушилки от ее производительности и окружной скорости распылительного
диска (рис. 21-24, в и г).
Производительность сушилки по высушиваемому материалу на 1 м2 се-
чения сушильной камеры составляет.
q = - 0,0471 м3/м2 - ч = 13,1 10“6 м3/м2 - сек
рсгк 12оО 21,2
Средняя теплопроводность топочных газов X = 0,0365 вт/м • град
(3,15- 10—2 ккал/м-ч • град). Тогда по уравнению (21-46) объемный коэффи-
циент теплоотдачи аоб от топочных газов к частицам материала
аоб
— 5,69 • 3,65 • 10“2
-13,1 • 10“6
1 \1.6 / 1 \0,8
35-10“® / \ 0,22 4-0,036/
аоб = 109 вт/м3 град (94,0 ккал/м3 • ч • град)
11 Расчет сушилок
795
'ср.
Согласно примеру 21-5 (стр. 765) средний температурный напор
0Ср. = 73° С.
Определяем объем сушильной камеры
Ук=с 83,5^
®об.®ср 199 • 73
Следовательно, высота камеры составляет:
Н = = Щ = 3,94 м s4 м
По конструктивным соображениям (учитывая величину диаметра камеры
сушилки) принимаем И = 6 м.
Расчет сушилок с кипящим
(псевдоожиженным) слоем
Расчет сушилок с кипящим (псевдоожиженным) слоем ве-
дут по уравнениям теплообмена, рассмотренным на стр. 461.
Исходя из скорости газа, при которой высушиваемый материал
переходит в состояние кипящего слоя (скорость псевдоожиже-
ния), а также из расхода сушильного агента, находят площадь
сечения сушильной камеры. Высотой неподвижного слоя мате-
риала задаются, проверяя последующим расчетом величину по-
верхности соприкосновения сушильного агента с частицами вы-
сушиваемого материала. Эта поверхность должна быть доста-
точной для передачи количества тепла, необходимого для про-
ведения сушки.
Расчет контактных сушилок
Расчет контактных сушилок ведут на основе уравнений теп-
лопередачи. При расчете вальцовых сушилок исходят из того,
что тепло передается от конденсирующегося пара стенке вальца,
через нее передается высушиваемому материалу, из которого
при этом испаряется влага, и пары диффундируют в окружаю-
щий воздух, передавая ему тепло испарения влаги.
Коэффициент теплоотдачи аисп, эквивалентный количеству
тепла, сообщаемого воздуху испаряющейся из материала вла-
гой, определяют из уравнения теплоотдачи:
б?г = аисп (О' /в) (21-47)
где G — скорость испарения влаги, кг/м2 • сек,’,
г—скрытая теплота испарения, дж}кг\
а — коэффициент теплоотдачи от испаряющейся из мате-
риала влаги к воздуху, вт/м2 • град\
& —температура поверхности высушиваемого материала,°C.
796
Гл. 21. Сушка
Скорость испарения влаги определяют по формуле:
G = 8,83 • 10* W (/в — /м) кг/м2 • сек (21 -48)
где фр—массовая скорость воздуха, к.г/м?'сек\
— 4) — разность температур воздуха и мокрого термо-
метра, °C.
Пример 21-9. Выбрать атмосферную вальцовую сушилку для сушки
G\ = 100 кг/ч пасты азокрасителя, имеющей начальную влажность W\ = 64%,
конечную влажность = 16% (считая на общий вес). Обогрев произво-
дится насыщенным водяным паром, абсолютное давление пара р = 2,45 бар
(2,5 ат), температура пара t— 126,2° С. Толщина пленки материала на валь-
цах 81 = 1 мм Скорость воздуха, продуваемого над поверхностью материала,
vB — 1,4 м/сек, средняя температура воздуха /в = 30° С, относительная влаж-
ность воздуха <рв = 40%.
Решение. По /— х-диаграмме определяем температуру мокрого тер-
мометра /м = 18° С, плотность воздуха р = 1,17 кг/м?. При абсолютном дав-
лении 0,98 бар (1 ат) скрытая теплота испарения воды г = 2263-103 дж/кг
(540 ккал/кг).
Принимаем температуру поверхности материала & = 72° С и определяем
по формуле (21-48) скорость испарения влаги:
G = 8,83• IO"4 V1,4-1,17(30— 18) = 0,0136 кг/м2 • сек
Коэффициент теплоотдачи аИСп. определяем из уравнения (21-47):
Gr 0,0136 • 2263 -103 , ,ft,0
“исп. = -а—г- =---------on---= 733 впг/м2 • град (632 ккал/м* • ч - град)
V tg I £ Ок/
Принимаем: коэффициент теплоотдачи от конденсирующегося пара
к стенке ai = 11 600 вт/м2 • град (10 000 ккал/м2 - ч • град), толщину чугун-
ного вальца 82 = 15 мм, коэффициент теплопроводности чугуна Х2 =
= 46,4 вт/м -град (40 ккал/м - ч - град), коэффициент теплопроводности пасты
М 0,7 вт/м - град (0,6 ккал/м - ч - град) и определяем коэффициент тепло-
передачи k от конденсирующегося внутри вальца пара к воздуху:
k — ----i----пТйтГ--nnTs-----Г~ ~ 31^ вш/м* - град (269 ккал/м2 • ч град)
X । XX jV/XJ X । XX । XX X । X
11 600 +-07”+ 46j + 733
Для проверки принятой температуры поверхности материала определяем;
общее термическое вопротивление:
™ = _L_JL
k~ 312
термическое сопротивление со стороны воздуха:
R - 1 - 1
в“«исп. 733
общую разность температур (между паром и воздухом):
6 = 126,2 — 30 = 96,2° С
Из соотношения
О YR
®част.
12. Специальные способы сушки
797
определяем разность температур между воздухом и материалом:
. 07?в 96,2-312 .10р
0част. = —= 733 — = 4! С
Тогда температура поверхности материала будет равна:
& = /в + 6Част. = 30 + 41=71°С
Следовательно, & достаточно близка к температуре, принятой для расчета.
Производительность сушилки по испаренной влаге [из формул (21-16) и
(21-17)]:
,r/ „ Wi — w2 100 / 0,64 — 0,16 \ лп1кп /
W = -у!-----—А------------= 0,0159 кг сек
1 1 — w2 3600 \ 1—0,16 )
Принимаем теплоемкость пасты сп = 3350 дж)кг • град (0,8 ккал/кг • град}
и определяем расход тепла на сушку (на подогрев материала и испарение
влаги):
Q = GlCn (& - /0) + Wr = ^6^-- (71 - 15) + 0,0159 • 2263 • 10’
Q = 41 200 дж!сек (35 400 ккал!ч)
где to — 15° С — начальная температура пасты.
Определяем рабочую поверхность нагрева вальцовой сушилки, вводя коэф-
фициент — 0,75, учитывающий, что часть поверхности вальца не сопри-
касается с высушиваемым материалом:
F — ®------------41 200 ~ 1 8 .и2
ktyF ~ 312-96,2.0,75 = ’
По нормалям выбираем одновальцовую сушилку с рабочей поверхностью
F = 1,8 м2 (диаметр вальца D = 600 мм, длина L — 1400 мм).
12. Специальные способы сушки
Радиационная сушка
Энергия, излучаемая инфракрасными лучами, значительно
превышает энергию излучения видимых лучей, имеющих длину
волны 0,4—0,8 мк. Поэтому при помощи инфракрасных лучей
(длины волн 8—10 мк) можно передать высушиваемому мате-
риалу большие количества тепла и достигнуть скорости испа-
рения влаги, во много раз превышающей скорость ее испарения
при конвективной или контактной сушке.
В качестве источников инфракрасного излучения применяют
электрические лампы (ламповые сушилки) либо экраны или
панели, обогреваемые газом (радиационные газовые сушилки).
В ламповой радиационной сушилке над поверхностью высуши-
ваемого материала (обычно перемещаемого в конвейере) уста-
навливают мощные осветительные лампы с отражательными
рефлекторами, направляющими лучи на поверхность мате-
риала, или специальные зеркальные лампы.
Б’олее равномерное нагревание (чем лампами) и меньший
расход энергии достигаются при использовании в процессе
798
Г л. 21. Сушка
сушки сплошных стальных, чугунных или керамических жаро-
упорных поверхностей, обогреваемых горячими газами. Нагрева-
ние излучающих поверхностей производится открытым газовым
пламенем (рис. 21-36, а) или продуктами сгорания газов, дви-
жущимися внутри излучателя (рис. 21-36,6). Для повышения
коэффициента теплоотдачи от газов применяют их рециркуля-
цию при помощи эжектора 8 (рис. 21-36,6), а для лучшего ис-
Рис. 21-36. Схемы радиационных сушилок с газовым обогревом:
а —открытым газовым пламенем; б— продуктами сгорания газов с их рецирку-
ляцией и регенерацией тепла, / — горелки; 2—излучатель; 3 — ленточный конвейер;
4 — выхлопная труба; 5 — подогреватель воздуха; о —вентилятор; 7—камера сгора-
ния, 8— эжектор.
пользования тепла отработанных газов их направляют на подо-
грев воздуха, поступающего в камеру сгорания 7. В газовых
радиационных сушилках тепло отходящих газов используют
также для подсушки исходного материала или окончательной
досушки высушенного материала.
Газовые сушилки проще и экономичнее ламповых.
В газовых радиационных сушилках применяют горелки со
светящимися раскаленными керамическими насадками, или реф-
лекторами (рис. 21-37).
Смесь газа и воздуха поступает по трубе 1 под избыточным
давлением 250—300 мм вод. ст. и сгорает, выходя из-под отра-
12. Специальные способы сушки
799
жателя газов 2. При этом раскаляется керамический рефлек-
тор 3 и создается интенсивный поток лучей, направленный
на поверхность высушиваемого материала. Интенсивное тепло-
вое действие инфракрасных лучей вызывает быстрое испарение
влаги из поверхностного слоя облучаемого материала, но воз-
дух, находящийся между
источником лучей и по-
верхностью высушиваемо-
го материала, практиче-
ски не нагревается.
Основные достоинства
радиационных сушилок:
1) быстрое удаление вла-
ги из тонкослойных ма-
териалов или лакокра-
сочных покрытий, 2) ком-
пактность устройства,
3) легкость регулирова-
ния температуры нагре-
ва, 4) незначительные
потери тепла в окружаю-
щую среду.
Недостатки этого спо-
соба сушки: 1) непригод-
г
Рис. 21-37. Керамическая горелка с рефлек-
тором:
/ — труба для подвода газов; 2 —отражатель газов;
3— рефлектор.
ность для высушивания толстых слоев материала, 2) неравно-
мерность нагрева высушиваемого материала, связанная с тем,
что, наряду с быстрым нагреванием поверхностного слоя, пере-
дача тепла во внутренние слои материала (за счет теплопро-
водности) происходит значительно медленней, 3) высокий рас-
ход энергии (1,5—2,5 квт-ч на 1 кг влаги).
Сушка инфракрасными лучами применяется главным обра-
зом для высушивания тонколистовых материалов или окрашен-
ных поверхностей (тонкая ткань, бумага, металлические дета-
ли, покрытые медленно сохнущими красками, и др.).
Исследования показывают, что для высушивания толстых
слоев материала, в частности пастообразных веществ, перспек-
тивно применение комбинированных способов сушки (радиаци-
онная и конвективная сушка или радиационная сушка и сушка
токами высокой частоты, см. ниже).
Сушка токами высокой частоты
Применение токов высокой частоты в определенных случаях
дает возможность значительно интенсифицировать процесс
сушки.
800
Гл. 21. Сушка
Сушка этим способом производится по следующей принци-
пиальной схеме (рис. 21-38). Переменный ток из сети поступает
в газотронный выпрямитель 2 и преобразуется в постоянный
ток высокого напряжения (4000—11 000 в), который питает лам-
повый генератор 3 высокой частоты. При помощи генератора
постоянный ток преобразуется в переменный ток высокой ча-
стоты (значительно больше 50 периодов в секунду). Ток подво-
дится к пластинам конденсатора 4, между которыми создается
поле высокой частоты.
Рис. 21-38. Схема сушки токами высокой частоты:
/ — сеть переменного тока; 2—газотронный выпрямитель; 3— генератор высокой
частоты; 4 — конденсаторы.
Высушиваемый неметаллический материал (диэлектрик) по-
мещается между пластинами конденсатора. Под действием элек-
трического поля возникает интенсивное колебание молекул ма-
териала, которые определенным образом располагаются в про-
странстве— происходит так называемая поляризация молекул.
Поляризация сопровождается трением между молекулами, на
что затрачивается часть электрической энергии поля, которая
превращается в тепло. Вследствие выделения тепла высушивае-
мый материал (диэлектрик) быстро нагревается. Интенсивность
нагревания зависит от частоты электрического поля (длины
волн) и его мощности, а также от свойств материала, так как
каждый материал наиболее быстро нагревается под действием
волн определенной длины.
Сушка токами высокой частоты обладает рядом существен-
ных достоинств, к числу которых относятся:
1) равномерное нагревание всей массы однородного мате-
риала в поле высокой частоты;
2) ускорение сушки в результате термодиффузии и электро-
осмоса в поле высокой частоты; перемещение влаги из глубины
материала к его поверхности за счет термодиффузии происхо-
12. Специальные способы сушки
801 J
дит в связи с тем, что температура на поверхности материала,
охлаждаемого окружающим воздухом, ниже, чем внутри мате-
риала;
3) избирательное удаление влаги из неоднородного по струк-
туре материала; путем подбора длины волн можно нагревать
отдельные части неоднородного материала практически без по-
вышения температуры остального материала;
4) улучшение качества сушки, так как при указанном выше
распределении температур, вызывающем термодиффузию,
уменьшается возможность образования корки на поверхности
материала и его коробления.
Вместе с тем сушка токами высокой частоты имеет серьез-
ные недостатки: 1) большой расход электроэнергии (не менее
2—3,5 квШ'Ч на 1 кг испаренной влаги), 2) сравнительная слож-
ность высокочастотной установки.
Поэтому описанный способ применяют главным образом в
тех случаях, когда сушка воздухом (или газами) дает неудо-
влетворительные результаты.
Сушка возгонкой (сублимацией)
Влагу можно удалить из твердых материалов путем возгонки (сублима-
ции), т. е. перевести влагу непосредственно из твердой фазы в паровую, ми-
нуя жидкое состояние.
Для сушки материала этим способом необходимо создать достаточно
большую разность температур между высушиваемым материалом и внешним
источником тепла. Такую разность темпера-
тур создают, высушивая материал в замо-
роженном состоянии при глубоком вакууме.
Например, сушка материалов, имеющих
температуру —15° С, должна проводиться
при остаточном давлении ^>1,4 мм рт. ст.,
соответствующем давлению водяного пара,
находящегося в равновесии с льдом. При
—50° С остаточное давление должно состав-
лять только 0,03 мм рт. ст.
В таких условиях влага испаряется из
материала, находящегося в замороженном
состоянии. Тепло, необходимое для испа-
рения влаги, передается из окружающей
среды через стенки сушильной камеры или
/ — сушильная камера; 2—конденса-
тор; 3 —вакуум-насос; 4 — компрес-
сионная холодильная установка;
5 — циркуляционный насос.
подводится от специальных подогревате-
лей. Схема установки для сушки сублима-
цией аналогична схеме работы обычной
вакуум-сушилки и отличается от последней
лишь тем, что конденсаторы сублимацион-
ных сушилок охлаждаются не водой, а холодильным рассолом, имеющим
температуру от —10 до —40° С.
Принципиальная схема сублимационной сушилки с компрессионной холо-
дильной установкой показана на рис. 21-39. Камера 1 сушилки сообщается
с конденсатором 2, к которому присоединен вакуум-насос 3 и холодильная
51 Зак. 546.
802 Гл 21 Сушка
установка 4 с насосом 5 для циркуляции рассола Для непрерывного удале-
ния из конденсатора образующегося в нем льда потребовалось бы значи-
тельное усложнение конструкции этого аппарата, поэтому обычно устанавли-
вают два конденсатора, которые попеременно работают и размораживаются.
Компрессионную холодильную установку в некоторых схемах сушки заме-
няют более компактной трехступенчатой пароэжекторной холодильной уста-
новкой (стр. 544).
Высушенные продукты, получаемые при сушке возгонкой, полностью со-
храняют свои качества (цвет, запах, растворимость, питательные свойства
и др ) и могут храниться длительное время.
В настоящее время этим сравнительно дорогим и сложным способом вы-
сушивают медицинские препараты, чувствительные к нагреванию и резко
ухудшающие свои качества при тепловой сушке (пенициллин, плазма крови
и др ), а также некоторые высококачественные пищевые продукты
ПРИЛОЖЕНИЯ
Для ряда чистых веществ и водных растворов в Приложениях приве-
дены основные физико-химические константы, которые наиболее часто
используются учащимися при расчетах по курсу «Процессы и аппараты».
Значения приводимых констант заимствованы из следующих источников:
Справочник химика, Госхимиздат, т. I, 1951, т. III, 1952; Техническая энци-
клопедия, Справочник физических, химических и технологических величин,
тт. I, V, VI, VII, X; С. С. Кутателадзе, В. М. Боришанский, Спра-
вочник по теплопередаче, Госэнергоиздат, 1959 и др.
В ряде случаев значения физико-химических констант при соответствую-
щих температурах и концентрациях получены путем интерполяции и экстра-
поляции справочных данных или расчетным путем.
ПРИЛОЖЕНИЕ I
Плотность жидких веществ и водных растворов
Вещество Плотность, кг)мъ
при —20° С при 0° С при 20° С при 40° С при 60° С при 80° С При 100° С при 120° С
Азотная кислота- 100%-ная 1582 1547 1513 1478 1443 1408 1373 1338
50%-ная — 1334 1310 1287 1263 1238 1212 1186
Аммиак жидкий 665 639 610 580 545 510 462 390
Аммиачная вода 25 % -ная — 918 907 897 887 876 866 856
Анилин — 1039 1022 1004 987 969 952 933
Ацетон 835 813 791 768 746 719 693 665
Бензол — 900 879 858 836 815 793 769
Бутиловый спирт . . . 838 824 810 795 781 766 751 735
Вода — 1000 998 992 983 972 958 943
Гексан 693 ЙТ‘ 660 641 622 602 581 559
Глицерин 50%-ный . . — 1136 1126 1116 1106 1006 996 986
Двуокись серы (жидк.) . 1484 1434 1383 1327 1264 1193 1111 1010
Дихлорэтан 1310 1282 1254 1224 1194 1163 1133 1102
Изопропиловый спирт . 817 801 785 768 752 735 718 700
Кальций хлористый (25%-ный раствор) . . 1248 1239 1230 1220 1210 1200 1190 U 80
Метиловый спирт 100%-ный 828 810 792 774 756 736 714 '690
40%-ный — 946 935 924 913 902 891 880
П риложения.
Продолжение приложения I
Вещество Плотность, кг/,и3
при — 20° С при 0е С при 20° С при 40° С при 60° с ПИИ 80 С при 100° С при 120° С
Муравьиная кислота . . — 1244 1220 1195 1171 1147 1121 1096
Натр едкий, растворы
50%-ный — 1540 1525 1511 1497 1483 1469 1454
40%-ньтй — 1443 1430 1416 1403 1389 1375 1360
30%-ный — 1340 1328 1316 1303 1289 1276 1261
20%-ный — 1230 1219 1208 1196 1183 1170 1155
10%-ный — 1117 1109 1100 1089 1077 1064 1049
Натрий хлористый
(20%-ный раствор) . . — 1157 1148 1139 ИЗО 1120 1110 1100
Нитробензол — 1223 1203 1183 1163 1143 1123 1103
Октан 734 718 702 686 669 653 635 617
Олеум 20%-ный .... Серная кислота — 1922 1896 1870 1844 1818 1792 1766
98%-ная — 1857 1837 1817 1798 1779 1761 1742
92%-ная 1866 1845 1824 1803 1783 1765 1744 1723
75%-ная 1709 1689 1669 1650 1632 1614 1597 1580
60%-ная 1532 1515 1498 1482 1466 1450 1434 1418
Сероуглерод 1323 1293 1263 1233 1200 1165 1125 1082
Соляная кислота (30%-
ная) 1173 1161 1149 1138 1126 1115 1103 1090
Толуол Уксусная кислота 902 884 866 847 828 808 788 766
100%-ная — 1072 1048 1027 1004 981 958 922
50 %-ная — 1074 1058 1042 1026 1010 994 978
Фенол (расплавленный) — — 1075 1058 1040 1022 1003 987
Хлорбензол 1150 1128 1107 1085 1065 1041 1021 995
Хлороформ 1563 1526 1489 1450 1411 1380 1326 1280
Четыреххлористый угле-
род 1670 1633 1594 1556 1517 1471 1434 1390
Этилацетат 947 924 901 876 851 825 797 768
Этиловый спирт
100%-ный 823 806 789 772 754 735 716 693
80%-ный — 857 843 828 813 797 783 768
60%-ный — 904 891 878 864 849 835 820
40%-ный — 947 935 923 910 897 885 872
20%-ный — 977 969 957 946 934 922 910
Этиловый эфир .... 758 736 714 689 666 640 611 576
Вязкость жидких веществ и водных растворов
Коэффициент пересчета в систему СИ: слзХЮ-3= н-сек/м2
ПРИЛОЖЕНИЕ II g
Вязкость, спз
Вещество при —20° С при —10° С при 0° С при 10° С при 20° С при 30° С при 40° С при 50° С при 60° с при 80° С при 100° С при 120° С
Азотная кислота 100%-ная 1,49 1,24 1,05 0,92 0,8 0,72 0,64 0,57 0,5 0,39 0,35 0,31
50%-ная — 4 3,05 2,4 1,88 1,55 1,28 1,07 0,9 0,68 0,53 0,44
Аммиак жидкий 0,258 0,251 0,244 0,235 0,226 0,217 0,208 0,199 0,19 — — —
Аммиачная вода 25%-ная .... — — — 1,72 1,3 1,05 0,855 0,71 0,6 0,42 0,32 0,23
Анилин — — 10,2 6,5 4,4 3,12 2,3 1,8 1,5 1,1 0,8 0,59
Ацетон 0,5 0,442 0,395 0,356 0,322 0,293 0,268 0,246 0,23 0,2 0,17 0,15
Бензол . — — 0,91 0,76 0,65 а,56 0,492 -0,436 0,39 -Д316 Д261_ -0^19
Бутиловый спирт 10,3 7,4 5,19 3,87 2,95 2,28 1,78 1,41 1,14 0,76 0,54 0,38
Вода — — 1,79 1,31 1,0 0,801 0,656 0,549 0,469 0,357 0,284 0,232
Гексан 0,479 0,426 0,397 0,355 0,32 0,29 0,264 0,241 0,221 0,19 0,158 0,132
Глицерин 50 % -ный — — 12 8,5 6,05 4,25 3,5 2,6 2 1,2 0,73 0,45
Двуокись серы (жидк.) 0,455 0,41 0,368 0,334 0,304 0,279 — — — — — —
Дихлорэтан 1,54 1,24 1,08 0,95 0,84 0,74 0,65 0,565 0,51 0,42 0,36 0,31
Изопропиловый спирт 10,1 6,8 4,6 3,26 2,39 1,76 1,33 1,03 0,8 0,52 0,38 0,29
Кальций хлористый (25 %-ный) 10,6 7 4,47 3,36 2,74 2,25 1,85 1,55 — — — —
Метиловый спирт 100%-ный 1,16 0,97 0,817 0,68 0,584 0,51 0,45 0,396 0,351 0,29 0,24 0,21
40 % -ный — — 3,65 2,54 1,84 1,37 — — — — — —
Муравьиная кислота — — — 2,25 1,78 1,46 1,22 1,03 0,89 0,68 0,54 0,4
Натр едкий, растворы 50% -ный — 46 25 16 8,03 5,54 3,97 3,42
40 %-ный — — — — 40 23 14 9.2 5,44 3,62 2,72 2,37
30 %-ный — — — — 13 9 6,3 4,6 3,4 2,16 1,82 1,71
Приложения
Натр едкий, растворы 20%-ный 10%-ный — 1 —
Натрий хлористый (20%-ныйрас-
1ВОр) — 4,08 2,67
Нитробензол — — 3,09
Октан 0,968 0,829 0,703
Олеум 20%-ный — — 95
Серная кислота
98%-ная — — 55
92%-ная 130 90 48
75%-ная 95 50 30
60 % -ная 20 15 10,5
Сероуглерод 0,556 0,488 0,433
Соляная кислота 30%-ная .... — — —
Толуол 1,06 0,9 0,768
Уксусная кислота
100%-ная — — —
50%-ная — — 4,35
Фенол (расплавленный) — —
Хлорбензол 1,48 1,24 1,06
Хлороформ 0,9 0,79 0,7
Четыреххлористый углерод . . . 1,9 1,68 1,35
Этилацетат 0,79 0,67 0,578
Этиловый спирт
100%-ный 2,38 2,23 1,78
80%-ный — — 3,69
60%-ный ......... — — 5,75
40%-ный — — 7,14
20%-ный — 5,32
Этиловый эфир 0,364 0,328 0,296
— 4,48 1,86 3,3 1,45 2,48 1,16 2 0,98 1,63 0,91 1,27 0,7 1,15 0,65 1,08 0,6
1,99 1,56 1,24 1,03 0,87 0,74 0,57 0,46 0,38
2,46 2,01 1,69 1,44 1,24 1,09 0,87 0,7 0,58
0,61 0,54 0,479 0,428 0,386 0,35 0,291 0,245 0,208
60 36,6 28,8 20,8 12,8 9 5,3 — —
37 25,8 17,1 12,9 9,46 7,5 4,1 2,7 2
32 23,1 15,6 11,8 8,4 6,7 3,8 2,5 1,95
20 13,9 10,6 8,1 5,9 4,6 2,8 1,9 1,45
7,7 5,52 4,08 3,42 2,8 2,4 1,5 1,07 0,9
0,396 0,366 0,319 0,29 0,27 0,25 0,21 0,19 0,17
2,1 1,7 1,48 1,3 — — — 1 —
0,667 0,586 0,522 0,466 0Д2 0,381 0,319 0,271 0,231
— 1,22 1,04 0,9 0,79 0,7 0,56 0,46 0,37
3,03 2,21 1,7 1,35 1,11 0,92 0,65 0,5 0,4
— 11,6 7 4,77 3,43 2,56 1,59 1,05 0,78
0,91 0,8 0,71 0,64 0,57 0,52 0,435 0,37 0,32
0,63 0,57 0,51 0.466 0,426 0,39 0,33 0,29 0,26
1,13 0,97 0,84 0,74 0,65 0,59 0,472 0,387 0,323
0,507 0,449 0,4 0,36 0,326 0,297 0,248 0,21 0,178
1,46 1,19 1,0 0,825 0,701 0,591 0,435 0,326 0,248
2,71 2,01 1,53 1,2 0,97 0,79 0,57 0,52 0,43
3,77 2,67 1,93 1,45 1,13 0,9 0,6 0,45 0,34
4,39 2,91 2,02 1,48 1,13 0,89 0,6 0,44 0,34
3,17 2,18 1,55 1,16 0,91 0,74 0,51 0,38 0,3
0,268 0,243 0,22 0,199 0,182 0,166 0,14 0,118 0,1
Приложения
808
Приложения
ПРИЛОЖЕНИЕ HI
Удельная теплоемкость жидких веществ и водных растворов
Коэффициент пересчета в систему СИ. ккал/кг • град ><4190 = дж!кг • град
Вещество Удельная теплоемкость, ккаткг град
при -20° С при 0° С при 20° С при 40° С при 60° С при 80° С при 100° с при 120° С
Азотная кислота 100%-ная 0,415 0,418 0,42 0,425 0.43 0,435 0,44 0,445
50%-ная — 0,667 0,68 0,693 0,71 0,73 0,74 0,76
Аммиак жидкий .... 1,08 1,1 1,13 1,16 1,22 1,3 1,37 1,48
Аммиачная вода 25 % - ная 1,03 1,03 1,04 1,06 1,08 1,1 1,13
Анилин — 0,477 0,487 0,498 0,508 0,519 0,529 0,54
Ацетон 0,49 0,505 0,52 0,535 0,55 0,566 0,581 0,596
Бензол . . . . . . . . — 0,39 0,413 0,436 0,46 0,483 0,506 0,52
Бутиловый спирт . . . 0,47 0,503 0,555 0,607 0,66 0,712 0,765 0,817
Вода — 1,01 0,999 0,99$ 1,0 1,0 1,01 1,02
Гексан 0,536 0,536 0,536 0,536 0,536 0,536 0,536 0,536
Глицерин 50 %-ный . . 0,85 0,85 0,84 0,84 — — —
Двуокись серы (жидк.) 0,313 0,317 0,327 0,342 0,363 0,389 0,42 0,457
Дихлорэтан 0,232 0,253 0,274 0,296 0,317 0,339 0,361 0,382
Изопропиловый спирт 0,525 0,564 0,635 0,706 0,777 0,847 0,917 0,987
Кальций хлористый (25 %-ный раствор) . . 0,678 0,69 0,702 0,71 0,73 0,74 0,75 0,76
Метиловый спирт 100%-ный 0,569 0,589 0,613 0,637 0,66 0,684 0,708 0,732
40 %-ный — 0,84 0,85 0,86 0,86 0,87 0,88 0,89
Муравьиная кислота . . — 0,469 0,49 0,511 0,531 0,552 0.573 0,593
Натр едкий, растворы 50%-пый — — 0,773 0,769 0,767 0,765 0,763 0,762
40 %-ный — 0,807 0,817 0,826 0,83 0,832 0,832 0,832
30%-ный — 0,824 0,84 0,856 0,865 0,869 0,869 0,869
20 %-ный — 0,842 0,862 0,875 0,882 0,886 0,888 0,888
10 %-ный — 0,882 0,9 0,912 0,918 0,922 0,924 0,926
Приложения
809
Продолжение приложения III
Вещество Удельная теплоемкость, ккал/кг град
при -20 С при 0 С при 20° С при 40° С при 60э С при 80° С при 100 С при 120° С
Натрий хлористый (2096-ный раствор) Нитробензол Октан 0,526 v 41 0,334 0,526 ^939^ 0,347 0,526 >0,936 0,36 0,526 0,931 0,374 0,526 0,93 0,387 0,526 0,92 0,4 0,526 0,92 0,414 0,526
Олеум 20%-ный .... Серная кислота — 0,326 0,34 0,354 0,368 0,382 0,396 0,41
98%-ная — 0,335 0,348 0,361 0,375 0,388 0,402 0,414
92 %-ная 0,355 0,366 0,377 0,389 0,4 0,412 0,425 0,436
75 %-ная 0,431 0,447 0,463 0,479 0,495 0,51 0,527 0,543
60 %-ная 0,505 0,525 0,545 0,565 0,585 0,605 0,625 0,645
Сероуглерод Соляная кислота 30%- 0,232 0,235 0,238 0,242 0,245 0,248 0,252 0,255
ная —• 0,55 0,59 0,63 0,67 0,72 0,76 0,8
Толуол Уксусная кислота 0,363 0,385 0,407 0,429 0,451 0,473 0,494 0,506
100%-ная — 0,45 0,476 0,502 0,527 0,553 0,579 0,605
50 %-ная — 0,73 0,74 0,75 0,76 0,78 0,79 0,8
Фенол (расплавленный) — — 0,56 0,56 0,56 0,56 0,56 0,56
Хлорбензол 0,285 0,3 0,315 0,33 0,345 0,36 0,376 0,391
Хлороформ, Четыреххлористый угле- 0,23 0,287 0,244 0,251 0,258 0,265 0,272 0,279
род 0,194 0,2 0,206 0,213 0,22 0,226 0,233 0,24
Этилацетат Этиловый спирт 0,424 0,441 0,458 0,475 0,493 0,51 0,527 0,544
100%-ный 0,505 0,547 0,593 0,648 0,708 0,769 0,839 0,909
80%-ныи — 0,64 0,68 0,72 0,77 0,82 0,87 0,93
60%-ный — 0,73 0,75 0,79 0,83 0,86 0,9 0,&
40%-ный — 0,82 0,84 0,87 0,88 0,91 0,94 0,96
20%-ный — 0,91 0,92 0,93 0,94 0,95 0,97 0,98
Этиловый эфир .... 0,516 0,528 0,541 0,575 0,633 0,69 0,747 0,803
810
Приложения
ПРИЛОЖЕНИЕ IV
Теплопроводность жидких веществ и водных растворов
Коэффициент пересчета в систему СИ: ккал/м • ч • град Х1>16 = вт)м • град
Вещество Теплопроводность, ккал/м ч град
при —20° С при 0° С при 20° С При 40° С при 60° С при 80° С при 100° С при 120° С
Азотная кислота 100%-ная 0,226 0,221 0,216 0,212 0,208 0,205 0,201 0,198
50 %-ная — 0,381 0,394 0,403 0,412 0,416 0,418 0,42
Аммиак жидкий .... 0,504 0,465 0,426 0,387 0,348 0,309 0,27 0,231
Аммиачная вода 25 % - ная i — 0,36 0,386 0,412 0,437 0,463 0,49 0,51
Анилин — 0,16 0,157 0,154 0,15 0,147 0,144 0,141
Ацетон 0,154 0,15 0,146 0,142 0,138 0,134 0,13 0,126
Бензол — 0,13 0,126 0,121 0,117 0,112 0,108 0,104
Бутиловый спирт . . . 0,137 0,134 0,132 0,129 0,126 0,123 0,12 0,118
Вода — 0,474 0,515 0,545 0,567 0,58 0,587 0,59
Гексан 0,118 0,118 0,118 0,118 мм» 0,118 0,118 0,118 0,118
Глицерин 50%-ный . . — 0,335 0,362 0,391 0,42 0,45 0,48 0,51
Двуокись серы (жидк) 0,193 0,182 0,171 0,16 0,15 0,139 0,128 0,117
Дихлорэтан 0,125 0,12 0,116 0,112 0,107 0,103 0,098 0,094
Изопропиловый спирт 0,135 0,132 0,13 0,127 0,124 0,121 0,118 0,115
Кальций хлористый (25%-ный раствор) 0,407 0,435 0,464 0,492 0,52 0,548 0,58 0,6
Метиловый спирт 100%-ный 0,186 0,184 0,182 0,179 0,177 0,174 0,172 0,17
40%-ный — 0,278 0,287 0,295 0,304 0,312 0,32 0,33
Муравьиная кислота . . — 0,224 0,221 0,218 0,214 0,211 0,207 0,203
Натр едкий, растворы 50 % -ный 0,446 0,457 0,465 0,47 0,476 0,479 0,481
40%-ный — 0,446 0,458 0,467 0,475 0,48 0,483 0,485
30 % -ный — 0,446 0,459 0,469 0,478 0,484 0,487 0,489
20 %-ный — 0,447 0,462 0,473 0,484 0,491 0,494 0,496
10 %-ный — 0,45 0,467 0,48 0,492 0,499 0,503 0,505
Приложения
811
Продолжение приложения IV
Вещество Теплопроводность, ккал/м ч-град
при —20° С при 0° С при 20* С при 40° С при 60° С при 80° С при 100° С при 120° С
Натрий хлористый (20%-ный раствор) 0,468 0,497 0,52 0,54 0,555 0,565 0,57
Нитробензол — 0,132 0,13 0,127 0,125 0,122 0,12 0,1
Октан 0,133 0,132 0,131 0,129 0,127 0,126 0,125 0,124
Олеум 20%-ный .... Серная кислота — 0,25 0,26 0,27 0,28 0,29 — —
98 %-ная — 0,264 0,284 0,294 0,306 0,324 0,334 0,344
92 %-ная 0,256 0,276 0,296 0,306 > 0,324 0,336 0,346 0,356
75%-ная 0,3 0,315 0,33 0,345 0,365 0,385 0,405 0,425
60 %-ная 0,33 0,35 0,37 0,38 0,4 0,43 0,45 0,47
Сероуглерод 0,15 0,146 0,142 0,139 0,133 0,129 0,125 0,121
Соляная кислота 30%- ная — 0,334 0,362 0,39 0,419 0,45 0,48 0,5
Толуол 0,125 0,121 0,117 0,113 0,11 0,106 0,102 0,098
Уксусная кислота
100%-ная — 0,152 0,149 0,145 0,141 0,138 0,134 0,13
50%-ная 0,27 0,298 0,326 0,355 0,383 0,41 0,44
Фенол (расплавленный) — —— 0,175 0,177 0,18 0,182 0,184 0,186
Хлорбензол 0,118 0,114 0,111 0,108 0,104 0,1 0,097 0,094
Хлороформ 0,13 0,122 0,114 0,105 0,097 0,088 0,079 0,071
Четыреххлористый углерод 0,113 0,107 0,101 0,095 0,089 0,083 0,077 0,071
Этилацетат Этиловый спирт 0,15 0,135 0,118 0,101 0,084 — — —
100%-ный 0,148 0,147 0,145 0,144 0,142 0,141 0,139 0,137
80%-ный ..... — 0,163 0,191 0,219 0,247 0,275 0,3 0,33
60%-ный — 0,215 0,243 0,27 0,298 0,326 0,35 0,38
40%-ный — 0,3 0,329 0,357 0,385 0,413 0,44 0,47
20%-ный — 0,384 0,412 0,44 0,467 0,495 0,52 0,55
Этиловый эфир .... 0,12 0,119 0,118 0,117 0,116 0,115 0,114 0,113
812
П риложения
ПРИЛОЖЕНИЕ V
Поверхностное натяжение жидких веществ и водных растворов
Коэффициент пересчета в систему СИ: дин/см X 10~3 = н/м
Вещество Поверхностное натяжение, дин/с м
при - 20° С при 0° С при 20° С при 40° С при 60° С при 80° С при 100° С при 1203 С
Азогная кислота
100%-ная 48,3 44,8 41,4 38,2 35,2 32,4 29,8 27,4
50 %-ная — 68,2 65,4 62,2 58,8 55,2 51,5 47,5
Аммиак жидкий .... 38 27 21,2 16,8 12,8 — — —
Аммиачная вода 25 % - ная — 65,7 62,9 59,7 56,3 52,7 49 45
Анилин — — 42,9 40,6 38,3 36 33,7 31,4
Ацетон 28,7 26,2 23,7 21,2 18,6 16,2 13,8 11,4
Бензол — 31,7 29 26,3 23,7 21,3 18,8 16,4
Бутиловый спирт . . . 28 26,2 24,6 22,9 21,2 19,5 17,8 16
Вода — 75,6 72,8 69,6 66,2 62,6 58,9 54,9
Гексан 22,6 20,5 18,4 16,3 14,2 12,1 10 7,9
Глицерин 50%-ный . . — 72,4 69,6 66,4 63 59,4 55,7 51,7
Двуокись серы (жидк.) 31 26,8 22,7 18,8 14,8 — — —
Дихлорэтан 37,8 35 32,2 29,5 26,7 24 21,3 18,6
Изопропиловый спирт 24,7 23,2 21,7 20,1 18,5 17 15,5 14
Кальций хлористый (25 %-ный раствор) 89,4 86,6 83,8 80,6 77,2 73,6 69,9 65,9
Метиловый спирт 100%- ный 26,6 24,5 22,6 20,9 19,3 17,6 15,7 13,6
Муравьиная кислота . . Натр едкий, растворы — 39,8 37,6 35,5 33,3 31,2 29 26,8
50%-ный — — 130 130 129 129 128 128
40 %-ный — — 108 108 107 107 106 106
30 %-ный — — 97 96,4 95,8 95,3 94,4 93,6
20 %-ный — — 85,8 85 84,7 83,2 81,3 79,6
10 %-ный — — 77,3 76,1 75 73 70,7 69
П риложения
813
Продолжение приложения V
Вещество Поверхностное натяжение, дин/см
при —20° С при 0° С при 20° С при 40° С при 60° С при 80° С при 100° С ПОИ 120° С
Натрии хлористый (20 % - ный раствор) .... 82,6 79,8 76,6 73,2 69,6 65,9 61,9
Нитробензол — 46,4 43,9 41,4 39 36,7 34,4 32,2
Октан 25,8 23,8 21,8 19,8 17,9 15,9 13,9 11,9
Серная кислота 98%-ная — 55,9 55,1 54,3 53,7 53,1 52,5 51,9
92%-ная 63 61,9 60,9 60,9 ‘ 60,3 59,7 59,1 58,5
75%-ная 74,1 73,6 73,1 72,6 72,1 71,6 7'1,1 70,6
60%-ная 77,3 76,7 76,1 75,4 74,5 73,6 72,7 71,8
Сероуглерод 38,3 35,3 32,3 29,4 26,5 23,6 20,7 17,8
Соляная кислота 30 % - ная — 72,6 69,8 66,6 63,2 59,6 55,9 51,9
Толуол 33 30,7 28,5 26,2 23,8 21,5 19,4 17,3
Уксусная кислота 100%-ная — 29,7 27,8 25,8 23,8 21,8 19,8 18
50 %-ная — 43 40 37 33 30 27 24
Фенол (расплавленный) — 43,1 40,9 38,8 36,6 34,4 32,2 30
Хлорбензол 38,4 36 33,6 31,1 28,8 26,5 24,1 21,8
Хлороформ 32,8 30 27,2 24,4 21,7 19 16,3 13,6
Четыреххлористый углерод 31 29,5 26,9 24,5 22 19,6 17,3 15,1
Этилацетат 29,5 26,9 24,3 21,7 19,2 16,8 14,4 12,1
Этиловый спирт 100%-ный 25,7 24 22,3 20,6 19 17,3 15,5 13,4
80 %-ный — 26 25 23 21 20 18 16
60 %-ный — 28 27 25 23 22 20 18
40 %-ный — 32 30 28 26 24 22 19
20 %-ный — 40 38 36 33 31 29 27
Этиловый эфир .... 22 19,5 17 14,6 12,4 10,2 8 6,1
814
Приложения
ПРИЛОЖЕНИЕ VI
Коэффициент 3 объемного расширения жидких веществ
и водных растворов
Вещество ЗхЮ\ Xjzpad
при —20° С при 0° С при 20° С при 40° С при 605 С при 80° С при 100° С при 120° С
Азотная кислота 50 %-ная 0,84 0,88 0,92 0,97 1,03 1,09
Аммиак жидкий . . 1,84 2,15 2,42 2,8 3,2 4,3 6,2 14,5
Анилин — 0,83 0,84 0,86 0,88 0,91 0,95 1,01
Ацетон 1,31 1,35 1,43 1,52 1,62 1,88 2 2,12
Бензол 1,18 1,22 1,26 1,3 1,37 1,43 1,57
Бутиловый спирт . . 0,83 0,85 0,88 0,91 0,94 0,98 1,03 1,09
Вода —0,06 0,21 .Л,39, 0,53 0,63 0,75 0,86
Гексан 1,16 1,22 1,37” 1,48 1,57 1,7 1,85 1,97
Двуокись серы (жидк.) 1,64 1,75 1,92 2,23 2,61 3,15 3,9 4,4
Дихлорэтан 1,07 1.П 1,16 1,21 1,26 1,31 1,37 1,44
Изопропиловый спирт 0,98 1,01 1,05 1,08 1,12 1,16 1,2 1,27
Кальций хлористый (25 % -ный рас- твор) 0,35 0,35 0,39 0,43 0,46 0,49 0,51 0,55
Метиловый спирт . . 1,09 1,14 1,19 1,27 1,3 1,42 1,61 1,81
Муравьиная кисло- та — 0,98 0,99 1,01 1,04 1,08 1,13 1,16
Натр едкий, раство- ры 50 %-ный .... 0,48 0,48 0,47 0,47 0,47 0,46 0,48
40 %-ный .... — 0,47 0,47 0,48 0,49 0,5 0,51 0,52
30 %-ный .... — 0,44 0,46 0,48 0,5 0,52 0,55 0,58
20 %-ный .... 0,41 0,45 0,48 0,51 0,55 0,59 0,63
10 %-ный .... 0,34 0,4 0,46 0,51 0,57 0,63 0,69
Натрий хлористый (20 %-ный раствор) 0,36 0,41 0,46 0,5 0,54 0,58 0,62
Нитробензол .... — 0,81 0,82 0,84 0,86 0,88 0,89 0,91
Октан 1,09 1,П 1,14 1,17 1,22 1,27 1,34 1,42
Серная кислота 98 %-ная .... 0,56 0,48 0,53 0,53 0,52 0,51 0,5
92 %-ная .... 0,58 0,58 0,58 0,57 0,56 0,56 0,55 0,55
75 %-ная .... 0,58 0,61 0,58 0,56 0,55 0,55 0,55 0,54
60 %-ная .... 0,58 0,58 0,56 0,55 0,55 0,54 0,53 0,53
Сероуглерод .... 1,13 1,14 1,19 1,28 1,41 1,6 1,84 2,05
Соляная кислота 30 %-ная 0,52 0,52 0,51 0,5 0,52 0,56 0,6
Толуол 1 1,04 1,07 1,11 1,17- 1,24 1,33 1,44
Уксусная кислота — 1,05 1,07 1,11 1,14 1,18 1,23 1,3
Приложения
815
Продолжение приложения VI
рхЮ3, \jzpad
Вещество при -20° С при 0° С при 20° С при 40° С при 60° С при 80° С при 100° С при 120° С
Фенол (расплавлен- ный) 0,75 0,79 0,82 & 0,86 0,9 0,95 0,99
Хлорбензол 0,92 0,94 0,97 1,0 1,03 1,07 1,11 1,16
Хлороформ 1,18 1,22 1,27 1,34 1,43 1,53 1,65 1,8
Четыреххлористый углерод 1,14 1,18 1,22 1,26 1,32 1,37 1,5 1,62
Этилацетат 1,2 1,26 1,35 1,46 1,52 1,6 1,76 1,94
Этиловый спирт . . 1,03 1,05 1,08 1,13 1,22 1,33 1,44 1,87
Этиловый эфир . . . 1,45 1,51 1,63 1,7П 1,85 2,16 2,6 3,1
ПРИЛОЖЕНИЕ VII
Теплота испарения жидких веществ
Коэффициент пересчета в систему СИ: ккал]кг X 4190 — дж)кг
Вещество Теплота испарения, ккал/кг
при 0° С при 20° С при 40° С при 60° С при 80° С при 100° С при 120° С при 140° С
Аммиак 302 284 263 238 208 169 113
Ацетон 135 132 128 124 118 113 107 100
Бензол 107 104 101 97,5 94,3 90,5 86,7 82,6
Бутиловый спирт . . 168 164 160 156 151 146 140 134
Двуокись серы . . . Изопропиловый 91,9 84 76 67,6 59 50 39,9 31,4
спирт 185 179 173 167 160 152 144 133
Метиловый спирт . . 286 280 273 265 253 242 227 213
Сероуглерод .... 89,4 87,6 85,1 82,2 79,1 75,5 71,7 67,4
Толуол 99 97,3 95,1 92,8 90,5 88 85,2 82,1
Уксусная кислота — 84,1 87,2 89,6 91,6 93,1 93,2 91,8
Фреон Ф-12 .... 37 34,6 31,6 27,9 23,3 16,2 7,5 —
Хлор 63,6 60,4 56,9 53 48,4 42,2 33,3 17
Хлорбензол .... 89,7 88,2 86,5 84,6 82,7 80,7 78,7 76,5
Хлороформ Четыреххлористый 64,8 62,8 61 59,1 57,2 55,2 53,2 51,2
углерод 52,1 51 49,7 48,2 46,2 44,3 42,3 40,1
Этилацетат 102 98,2 95,3 92,1 88,7 84,9 80,6 75,7
Этиловый спирт . . 220 218 215 210 203 194 182 170
Этиловый эфир . . . 92,5 87,5 82,7 77,9 72,5 67,4 61,4 54,5
ПРИЛОЖЕНИЕ VIII
Растворимость твердых веществ в воде и теплота кристаллизации qK^
(для обычных кристаллических форм)
оо
ст>
Коэффициент пересчета в систему СИ величины ^кр.: ккал/кг X 4190 = дж!кг
Вещество Растворимость, вес. % . <?кр / кал кг Количе- ство молекул кристал- лизацион- & ной ВОДЫ Темпера- турные пределы существо- вания кристалле гидратов °C
при 0° С при 10° С при 20° С при I 30° С при 40° С при 50° С при 60° С при 80° С при 100е С
СаС12 .... 37,3 39,4 42,7 50,1 53,5 56,9 57,8 59,5 61,4 20,8 18 < 29 8
Са (NO3)2 • 50,5 53,6 55,5 59,4 65,3 73 78 78,2 78,4 34,5 4 <_ 42,6
CuSO4 .... 12,9 14,8 17,2 20 22,8 25,1 28,1 34,9 42,4 11 5
FeSO4 .... 13,5 17 21 24,8 28,7 32,3 35,5 30,5 24 16,2 7 < 56,6
К2СО3 .... 51,9 52,2 52,8 53,4 53,9 54,8 55,9 58,3 60,9 2,3 1,5
КС1 22,2 23,8 25,5 27,2 28,7 30,1 31,3 33,8 36 59,7 Безв.
KNO, .... 11,6 17,7 24,1 31,5 39,1 46,2 52 62,8 71,1 83,2 Безв
MgCl2 .... 34,6 34,9 35,3 35,6 36,5 37 37,9 39,8 42,2 — 14,5 6
MgSO4 .... — 23,6 26,2 29 31,3 33,5 35 38,6 40,6 15,7 7 < 48 2
NH4C1 . . . 23 25 27,3 29,3 31,4 33,5 35,6 39,6 43,6 73,3 Безв
NH4NO3 . . . 54,2 59,1 63,9 70,8 74,8 78 80,4 86,2 91 79 Безв.
(NH4)2SO4 . . 41,4 42,2 43 43,8 44,8 45,8 46,8 48,8 50,8 18 Безв.
Na2CO3 . . . 6,4 11,2 17,8 29 32,8 37,2 31,7 30,8 30,8 55,7 10 < 32
NaCl 26,3 26,3 26,4 26,5 26,7 26,9 27,1 27,6 28,2 20,7 Безв.
NaNO3 .... 42,2 44,6 46,8 49 51,2 53,3 55,9 59,7 64,3 58,4 Безв.
Na2SO4 .... 4,5 8,2 16,1 29,1 32,5 31,8 31,3 30,4 29,9 58,2 10 < 32.4
Приложения
..... 1 ' *' —I —
ПРИЛОЖЕНИЕ IX i
Температурная депрессия водных растворов при абсолютном давлении 1 ат
Растворенное вещество / Концентрация раствора, вес. %
10 20 30 35 40 45 50 55 60 65 70 75 80 85 90 95
Температурная депрессия, °C
СаС12 . . . 1,5 4,5 10,5 14,3 19 24,3 30 36,5 43 50,7 60 75 — — — —
Ca(NO3)2 1,1 2,5 4,3 5,4 6,7 8,2 10 13,2 17,2 23 31,2 40,2 49,2 — — —
CuSO4 . . 0,3 0,6 1,4 2,1 3,1 4,2
FeSO4 . . 0,3 0,7 1,3 1,6
КС1 . . . . 1,3 3,3 6,1 8 — — — — — — — — — — — —
KNO3 . . . 0,9 2 3,2 3,8 4,5 5,2 6,1 7,2 8,5 10 11,6 13,7 — — — —
KOH . . . 2,2 6 12,2 17 23,6 33 45 60,4 78,8 100,5 126,5 155,5 190,3 225 — —
K2CO3 . . 0,8 2,2 4,4 6 8 10,9 14,6 19 24,2 31,4 — — — — — —
MgCl2 . . . 2 6,6 15,4 22 — — — — — — — — — — — —
MgSO4 . . 0,7 1,7 3,4 4,8 7 — — — — — — — — — —
NH4C1 . . 2 4,3 7,6 9,6 11,6 14 — — — — — — —
NH4NO3 . . 1,1 2,5 4 5,1 6,3 7,5 9,1 11 13,2 15,7 19 23 28 35,5 47,5 72,5
(NH4)2 so4 0,7 1,6 2,9 3,7 4,7 5,9 7,7 — — — — — — — —
NaCl . . . 1,9 4,9 9,6 — — — — — — — — — — — —
NaNO3 . . 1,2 2,6 4,5 5,6 6,8 8,4 10 12 14,5 17,9 — — — — — —
NaOH . . . 2,8 8,2 17 22 28 35 42,2 50,6 59,5 69 79,6 92 106,6 124 145,5 174,5
Na2CO3 . . 1,1 2,4 4,2 5,3 — — — — — — — — —
Na2SO4 . . 0,8 1,8 2,8 — — — — — 1 — — — — — — —
Приложения
1
ПРИЛОЖЕНИЕ X
Равновесные составы жидкости (х) и пара (.у) в мол. % и температуры кипения (О в °C
двойных смесей при 760 мм рт. ст.
Смесь X 0 5 10 20 30 40 50 60 70 80 | 90 100 Азео 1 'тропная / смесь 1
Азотная кислота — вода V 0 0,3 1 5 16 46 83 95,5 98,7 99,5 99,9 100 38,3
t 100 103,5 108,6 117,5 121,4 121,5 116 101,5 91,7 87,5 85,6 85,4 121,9 1
Аммиак — вода у 0 49 72 89,3 97,6 99,2 100 100 100 100 100 100
(735 мм рт. ст.) t 99,1 82,5 69,8 48 29,2 11,8 —4 —16,5 —24,5 —29,5 —32 —33,7 — / $
Ацетон — бензол у 0 14 24,3 40 51,2 59,4 66,5 73 79,5 86,3 93,21 100 '
t 80,1 78,3 76,4 72,8 69,6 66,7 64,3 62,4 60,7 59,6 58,8 56,1 — и съ
Ацетон — вода у 0 60,3 72 80,3 82,7 84,2 85,5 86,9 88,2 90,4 94,3 100 — а R Sxj
t 100 77,9 69,6 64,5 62,6 61,6 60,7 59,8 59 58,2 57,5 56,9 —
Ацетон — метиловый у 0 10,2 18,6 32,2 42,8 51,3 58,6 65,6 72,5 80 — 100 80
спирт t 64,5 63,6 62,5 60,2 58,7 57,6 56,7 56 55,3 55,05 — 56,1 55,05
Ацетон — этиловый у 0 15,5 26,2 41,7 52,4 60,5 67,4 73,9 80,2 86,5 92,9 100 1 —
спирт t 78,3 75,4 73 69 65,9 63,6 61,8 60,4 59,1 58 57 56,1 —
Бензол — толуол у 0 11,5 21,4 38 51,1 61,9 71,2 79 85,4 91 95,9 100 —
t 110,6 108,3 106,1 102,2 98,6 95,2 92,1 89,4 86,8 84,4 82,3 80,2 —
Бензол — уксусная кис- у 0 26 42 59 68,6 75 79 83 88 92,5 97 100 97,5
лота t 118,7 111,4 105,8 99 94 90,3 88 85,7 83,5 82 80,8 80,2 80
Вода — уксусная кис-. у 0 9,2 16,7 30,3 42,5 53 62,6 71,6 79,5 86,4 93 100 —
лота t 118,1 115,4 113,8 110,1 107,5 105,8 104,4 103,3 102,1 101,3 100,6 100 —f
... _ и цд Г\... — Г -X _ - т»—- , __ _ •
/ f 68,5
СЛ to Изопропиловый спирт — у 0 48,5, 53 60 64 66,5 68 68,4 70 77 83 100
вода t 100 84,4 82,5 81,2 81 80,6 80,5 80,4 80,5 81 82,3 82,4 80,4
Метиловый спирт — бен- у 0 38,5 50 56 58 59 60 61 62 66 75 100 61,4
зол t 80,2 66,9 61,1 58,6 58 57,8 57,7 57,6 57,6 58 59,6 64,9 57,6
Метиловый спирт—вода у 0 Ж- 41,8 57,9 66,5 72,9 77,9 82,5 87 91,5 95,8 100 —
t 100 923 87,7 81,7 78 75,3 73,1 71,2 69,3 67,6 66 64,5 -—
Метиловый спирт — эти- у 0 7,4 14,3 27,1 39,6 51,5 62,6 72,3 79,8 86,6 93,2 100
ловый спирт t 78,3 77,2 765 75 73,6 72,2 70,8 69,4 68,2 66,9 65,9 64,9 —
Муравьиная кислота — у 0 8 14,6 26 38 48,5 57,6 66 74,6 83,6 92,2 100 —
уксусная кислота t 118,1 116 115,4 112,8 110,7 108,8 107 105,4 103,9 102,5 101,4 100,8 —
Сероуглерод — ацетон у 0 19 29 46 53,3 57,5 60,5 61 68 72,2 78 100 61
t 56,2 51,2 48,3 43,5 41,3 40,3 39,6 39,3 39,3 39,6 40,9 46,3 39,3
Сероуглерод—четырех- у 0 13,2 24 42,3 54,4 64,5 72,6 79,1 84,8 90,1 95 100 —
хлористый углерод t 76,7 73,7 71 66 62,3 59 56,1 53,7 51,6 49,6 47,9 46,3 —-
Толуол — уксусная кис- у 0 15,5 25,5 37,2 46 54,1 57 61,5 66,5 71,8 81 100 62,7
лота t 118,1 111,3 108,9 105,6 103,3 101,7 100,8 100,6 100,6 100,9 102,6 110,8 100,6
Хлороформ —’бензол у 0 6,5 12,6 27,2 41 54,6 66 74,6 83 90,5 96,2 100 ——
t 80,6 80,1 79,6 78,4 77,2 75,9 74,5 '73,1 71 68,7 65,7 61,5
Четыреххлористыи уТ- лерод — этиловый У t fl 77,9 73,7 за 70,8 67,2 54 65,3 56,5 64,6 58,8 64 62 63,& 65,8 U 72,2 82,3 as,5 100 75,9 63 63,6
спирт
Этил ацетат —уксусная У 0 14,4 28,7 50,6 65,4 77 85,6 92 96,1 98,9 99,8 100 —
кислота t 118,1 77,1 —
Этиловый спирт — бен- У 0 18 28,6 36,8 40,5 43,5 46,5 49,5 53,5 60 71 100 44,8
зол (750 мм рт. ст.) t 79,7 74,3 71,2 69 68,2 67,8 67,8 68,3 68,9 70,1 72,6 78,1 67,8
Этиловый спирт — вода У 0 33,2 44,2 53,1 57,6 61,4 65,4 69,9 75,3 81,8 89,8 100 89,4
t 100 90,5 86,5 83,2 81,7 80,8 80 79,4 79 78,6 78,4 78,4 78,15
Приложения
7
\
со
ПРИЛОЖЕНИЕ XI
to
Дав ление«паров жидкостей
Жидкость Давление, мм рт. ст.
при (ГС при 10* С при 20° С при 30° С при 40* С при 50* С при 60° С при 70° С при 80* С При 90* С при 100° С при 110° С при 120° С при 130° С
Анилин 1 — \ 2,4 5,7 10,6 18 29,2 45,7 69,2 96,6 145
Ацетон 66,8 116 185 283 422 613 861 1190 1611 2142 2797 3594 4547 5670
Бензол 26,5 45,4 74,7 118 181 269 389 547 754 1016 1344 1748 2238 2825
Бутиловый спирт . . — — 4,4 9,5 18,6 33,7 59,2 112 165 255 386 572 833 1150
- Вода 4,6 9,2 17,5 31,8 55,3 92,5 149 234 355 526 760 1075 1489 2026
Дихлорэтан .... 20,7 34,1 60,5 97,7 152 229 338 480 664 906 1220 1600 2040 2580
Изопропиловый спирт 8,9 17 32,4 59,1 106 177 289 455 692 1021 1460 2020 2790 3800
Метиловый спирт . . 29,6 54,7 96 160 261 406 625 927 1341 1897 2621 3651 4751 6242
Муравьиная кислота — 18,9 33,1 52,2 82,6 126 190 280 398 552 753 — — - —
к Нитробензол .... — — — — — — — 4,8 7,5 12,9 20,9 32,5 48 69,5
Сероуглерод .... 128 198 298 435 618 857 1165 1552 2033 2619 3385 4220 5250 6440
1 Толуол 9,7 18,2 25,5 39,5 64 98 147 204 299 408 571 751 973 1350
г У ксусная кислота . Фенол (расплавлен- — — .11,7 20,6 34,8 56,6 88,9 136 202 294 417 581 794 1068
ны й) — — ——*• 2 4,2 8,4 14,7 24,6 40,4 64,7 99,2 145
- X лорбензол .... 2,5 4,9 8,8 15,5 26 42 65,5 97,9 145 208 293 403 543 719
Хлороформ Четыреххлористый 61 101 106 246 366 526 740 1019 1403 1865 2429 3111 3926 4885
углерод 33 56 91 143 216 317 451 622 843 1122 1463 1880 2391 3002
Этилацетат 24,3 42,7 72,8 119 186 282 415 596 833 ИЗО 1515 1995 2585 3300
Этиловый спирт . . 12,2 23,6 43,9 78,8 135 222 353 ’’543 813 1187 1692 2360 3223 4320
Этиловый спирт . . . 185 292 442 647 921 1276 1728 2294 2991 3840 / 4859 6070 7496 9157
Приложения
Приложения
821
ПРИЛОЖЕНИЕ XII
ч
Свойства насыщенного водяного пара
Коэффициенты пересчета в систему СИ: давление — д/пХ0,981 = бар;
энтальпия и теплота испарения — ккал]кг X 4190 == дж{кг
Температура °C Давление ат Плотность кг/м3 Энтальпия, ккал/кг Теплота испарения ккал/ кг
пара жидкости
0 0,00623 0,00485 597 0 597
5 0,00889 0,00679 600 5 595
10 0,0125 ' 0,0094 602 10 592
15 0,0174 0,0128 604 15 589
20 0,0238 0,0173 606 20 586
25 0,0323 0,021 608 25 583
30 0,0433 0,0304 610 30 580
35 0,0573 0,0396 613 35 578
40 0,0752 0,0512 615 40 575
45 0,0977 0,0654 617 45 572
50 0,126 0,0831 619 50 569
55 0,161 0,104 621 55 566
60 0,203 0,13 623 60 563
65 0,255 0,161 625 65 560
70 0,318 0,198 627 70 557
75 0,393 0,242 629 75 554
80 0.483 0,293 631 80 551
85 0,589 0.354 633 85 548
90 0,715 0,424 635 90 545
95 0,862 0,505 637 95 542
100 1,033 0,598 639 100 539
105 1,23 0,705 641 105 1 536
ПО 1,46 0,826 643 ПО 533
115 1,72 0,965 645 115 529
120 2,02 1Л? 646 120 52J
125 2,37 1,3 648 125 523
130 275 1,5 650 131 J?1SL
135 3,19 1,72 651 136 516
140 3,69 1,97 х 653 141 Ж
145 4,24 2.24 655 146 509
150 4,85 2,55 656 151 505
155 5,54 2,89 657 156 501
160 6,3 3,26 659 161 498
165 7,15 3,67 660 166 494
170 8,08 4,12 661 172 489
175 9,1 4,62 662 177 485
180 10,2 5,16 663 182 481
185 11,5 5,75 665 188 477
190 12,8 6,39 666 193 473
195 14,3 7,1 666 198 468
200 15,9 7,86 667 204 463
ПРИЛОЖЕНИЕ XIII
Удельная теплоемкость с (ккал!кг • град), вязкость р (спз) и теплопроводность X (ккал/м • ч • град)
газов и паров
Коэффициенты пересчета в систему СИ: удельная теплоемкость — ккал/кг • гра<?Х4190 = дж/кг • град;
вязкость — слзХЮ-3 = н • сек/м2; теплопроводность — ккал/м • ч • градус,16 = вт/м • град
§
Вещество Температура,°C
0 100 200 300 400 500 600 700 800
Азот с 0,248 0,249 0,251 0,255 0,261 0,266 0,272 0,277 0,282
р ' 0,0166 0,0208 0,0246 0,028 0,0311 0,0339 0,0366 0,039 0,0413
к 0,0209 0,0271 0,0331 0,0386 0,0436 0,048 0,0519 0,0552 0,058
Аммиак с 0,491 0,527 0,571 0,615 0,654 0,701 0,74 0,778 0,812
р 0,0091 0,0128 0,0165 0,0199 0,0234 0,0264 0,0293 0,0321 0,0348
к 0,0184 0,0255 0,032 0,0383 0,0444 0,0502 0,0554 0,0606 0,0655
Ацетилен с 0,39 0,449 0,495 0,528 0,553 0,578 0,598 0,617 0,634
р 0.0096 0,0127 0,0154 0,0178 0,0202 0,0223 0,0243 0,0261 0,0278
к 0,0149 0,0197 0,0238 0,028 0,0312 0,0343 0,0375 0,0403 0,0431
Ацетон с 0,3 0,367 0,427 0,483 0,534 0,58 0,618
р 0,0069 0,0094 0,0121 0,0147 0,0174 0,02 0,0228
к 0,0084 0,0149 0,0231 0,0332 0,0448 0,058 0,0728 — —
Бензол с 0,225 0,319 0,4 0,467 0,521 0,566 0,603
р 0,007 #6092 0,0121 0,0146 0,0172 0,0198 0,0223
к 0,0079 0,0149 0,0242 0,0358 0,0495 0,0657 0,0828 — —
Водород с 3,39 3,45 3,46 3,47 3,48 3,5 3,53 3,57 3,61
р 0,0084 0,0103 0,0121 0,0139 0,0154 0,0169 0,0183 0,0197 0,021
к 0,15 0,186 0,222 0,258 0,294 0,33 0,366 0,402 0,438
Приложения
Водяной пар с 0,444- 0,4^ 0,469 0,478 0,493 0,509 0,526 0,543 0,56
р 0,0085 0,0123 0,0161 0,0198 0,0232 0,0266 0,0299 0,0331 0,0361
к 0,0139 0,0206 0,0284 0,0373 0,0473 0,0584 0,0707 0,0842 0,0988
Воздух с 0,24 0,241 0,245 0,25 0,255 0,261 0,266 0,271 0,276
р 0,0218 0,0259 0,0294 0,0328 0,0357 0,0384 0,0411 0,0437
к 0,0276" 0,0338 0,0396 0,0448 0,0494 0,0535 0,0572 0,0606
Двуокись серы с 0,145 0,158 0,17 0,18 0,187 0,193 0,197 0,2 0,203
р 0,0121 0,0161 0,02 0,0238 0,0275 0,0313 0,035 0,0386 0,0421
к 0,0072 0,0106 0,0143 0,0182 0,0222 0,0264 0,0308 0,0353 0,0398
Двуокись углерода с 0,195 0,218 0,237 0,252 0,265 0,276 0,285 0,292 0,298
р 0,0138 0,0184 0,0226 0,0264 0,0299 0,0332 0,0362 0,0381 0,0418
к 0,0126 0,0196 0,0266 0,0336 0,0406 0,0472 0,0534 0,0592 0,0646
Кислород 0,219 0,223 0,23 0,238 0,245 0,25 0,255 0,259 0,263
р 0,0192 0,0244 0,029 0,0331 0,0369 0,0403 0,0435 0,0465 0,0493
к 0,0212 0,0283 0,035 . 0,0413 0,0473 0,0529 0,058 0,0626 0,0668
Метан с 0,517 0,585 0,67 0,758 0,843 0,921 0,992 1,06 1,11
р 0,0104 0,0133 0,0161 0,0185 0,0208 0,0227 0,0246 0,0265 0,0282
к 0,026 0,0355 0,0446 0,0536 0,0621 0,0704 0,0785 0,0864 0,094
Метиловый спирт с 0,341 0,412 0,477 0,536 0,591 0,643 0,693 — —
р 0,0088 . 0,0123 0,0157 0,0191 0,0226 0,0261 0,0296 —— —
- к 0,011 0,0188 0,0283 0,0394 0,052 0,066 0,0813 — —
Окись азота с 0,227 0,234 0,241 0,247 0,252 0,258 0,262 0,266 0,271
р 0,018 0,0229 0,0268 0,0306 0,034 0,037 0,04 0,0428 0,0453
к 0,0178 0,0236 0,0285 0,0328 0,0373 0,0412 0,045 0,0482 0,0513
Окись углерода с 0,248 0,25 0,253 0,258 0,264 0,27 0,276 0,282 0,0286
р 0,0166 0,0209 0,0246 0,0278 0,0309 0,0338 0,0363 0,0387 0,041
к 0,02 0,0259 0,0314 0,0366 0,0417 0,0465 0,0513 0,0559 0,0603
Сероводород с 0,238 0,247 0,258 0,269 0,282 0,294 0,305 0,316 0,326
р 0,0117 0,0161 0,0201 0,0241 0,0273 0,0304 0,0335 0,0365 0,0393
к 0,0103 0,0142 0,0177 0,0212 0,0241 0,0268 0,0296 0,0322 0,0346
1
- 1 t
Приложения
Продолжение приложения XIII
Вещество Температура, °C
0 100 200 300 400 500 600 700 800
Толуол с 0,246 0,337 0,418 0,489 0,548 0,598 0,638 •
Р 0,0066 0,0089 0,011 0,0132 0,0154 0,0175 0,0196 — —
Хлор с 0,225 0,236 0,242 0,246 0,248 0,25 0,252 0,253 0,254
р 0,0122 0,0168 0,021 0,0254 0,0287 0,0322 0,0356 0,0387 0,0416
X 0,0062 0,0085 0,0107 0,0129 0,0146 0,0164 0,0181 0,0197 0,0212
Хлористый водород с 0,191 0,191 0,192 0,193 0,196 0,199 0,203 0,207 0,21
Р 0,0132 0,0182 0,0229 0,0277 0,0313 0,0353 0,0388 0,0423 0,0456
Четыреххлористый с 0,124 0,14 0,148 0,153 0,156 0,159 0,161
углерод р 0,0092 0,0123 0,0153 0,0182 0,0212 0,024 0,0269
X 0,0052 0,0075 0,01 0,0126 0,0153 0,0182 0,0211 — —
Этилен с 0,336 0,415 0,493 0,572 0,65 0,729 0,808 0,886 0,965
р 0,0096 0,0127 0,0156 0,0182 0,0206 0,0228 0,0249 0,0268 0,0287
X 0,0141 0,0254 0,038 0,0511 0,0651 0,0794 0,0932 0,106 0,116
Этиловый спирт с 0,32 0,403 0,48 0,554 0,624 0,691 0,756
р 0,0079 0,0108 0,0137 0,0167 0,0197 0,0226 0,0257 —
X 0,0111 0,0198 0,0302 0,043 0,0574 0,0738 0,0924 — —
Этиловый эфир с 0,344 0,44 0,531 0,618 0,703 0,782 0,862
р 0,0069 0,0093 0,0117 0,014 0,0165 0,0188 0,0212 —
X 0,0112 0,0196 0,0303 0,043 0,0579 0,0743 0,093
Приложения
825
ПРИЛОЖЕНИЕ XIV
Средняя объемная теплоемкость газов от 0 до Г С
(на 1 я3 газа, приведенного к нормальным условиям)
Коэффициент пересчета в систему СИ: ккал!м3 • градХ4190 = дж!м3 • град
Температура t, °C СО2 N, о, Н2О (пар) Воз сухой дух влажный
Теплоемкость, ккал}м3 • град
0 0,387 0,310 0,312 0,356 0,311 0,316
100 0,411 0,311 0,315 0,359 0,312 0,317
200 0,432 0,311 0,319 0,362 0,313 0,319
300 0,449 0,312 0,324 0,367 0,315 0,321
400 0,464 0,315 0,330 0,372 0,318 0,324
500 0,479 0,318 0,335 0,378 0,321 0,327
600 0,492 0,321 0,339 0,384 0,324 0,331
700 0,503 0,324 0,343 0,390 0,328 0,334
800 0,514 0,327 0,347 0,397 0,331 0,337
900 0,523 0,330 0,350 0,403 0,334 0,341
1000 0,532 0,333 0,354 0,409 0,337 0,344
1100 0,540 0,336 0,356 0,416 0,340 0,347
1200 0,547 0,338 0,359 0,422 0,343 0,349
1300 0,553 0,341 0,361 0,428 0,345 0,352
1400 0,559 0,343 0,364 0,434 0,348 0,354
1500 0,565 0,346 0,366 0,439 0,350 0,357
ПРИЛОЖЕНИЕ XV
Коэффициенты диффузии D (в м2!сек)
Вещество В воздухе DxlO4 при 0° С и 1 ат В воде 0x106 при 20° С
Азот 0,122 0,00192
Аммиак 0,198 0,00183
Бензол 0,077
Водород 0,61 0,00305
Водяной пар 0,22 —
Двуокись серы 0,122 —
Двубкись углерода 0,136 0,00178
Кислород 0,175 0,00208
Метиловый спирт 0,132 0,00144
Окись углерода . . 0,211 —
Сероводород — 0,00161
Сероуглерод 0,088 ——
Толуол 0,071 —
Трехокись серы 0,094 —
826
Приложения
Продолжение приложения XV
Вещество В воздухе DxlO4 при 0° С и 1 ат В воде 0 x10е при 20° С
Уксусная кислота 0,00095
Хлор 0,124 0,00161
Хлористый водород 0,13 0,00274
Этилацетат 0,071 —
Этиловый спирт 0,102 0,00103
Этиловый эфир 0,078 —
ПРИЛОЖЕНИЕ XVI
Значения коэффициента ф в формуле (17-1) растворимости
газов в воде
Газ ф, ат
при 0° С при 10° С при 20° С при 30° С при 40э С при 50° С при 60° С
Аммиак . . . 0,274 0,485 0,823 1,36 2,15 • 3,36 5,06
Двуокись серы Двуокись уг- 1,48 2,24 3,67 5,72 8,03 11,2 16,3
лерода . . . 308 446 611 822 1060 1350 1800
Кислород . . . 14800 19000 23 200 27 700 31 300 34 500 37 100
Сероводород . 147 202 258 346 437 550 690
ПРИЛОЖЕНИЕ XVII
Расчетные температуры tQ и относительная влажность ?0
атмосферного воздуха в различных районах СССР
Город Зимой Летом
<о, °C То, % <о, °C То, %
Алма-Ата —8,6 87 22,1 56
Архангельск —13,3 88 15,3 79
Ашхабад —0,4 86 29,6 41
Баку 3,4 82 25,3 65
Владивосток —13,7 74 20,6 77
Воронеж —9,8 90 20,6 62
Волгоград —9.9 85 24,7 50
Горький —12,2 89 19,4 68
Днепропетровск —6,0 88 22,3 60
Ереван —5,8 89 25,0 50
Приложения
827
Продолжение приложения XVII
Зимой Летом
Город to, °C <ро» % to, °C <ро, %
Иркутск —20,9 —13,6 85 86 17,2 19,9 72 63
—6,0 89 19,3 69
Краснодар Красноярск Ленинград Луганск Львов —2,1 —18,2 —7,7 —7,0 —4,0 90 81 87 84 87 23,7 19,3 17,5 22,2 18,1 67 72 69 59 74
Минск —6,8 88 17,5 78
Москва —10,8 88 18,0 70
Новосибирск Одесса —19,3 —3,1 83 88 18,7 22,6 59 61
Омск - —19,6 85 19,1 70
Пермь Рига —16,0 —5,1 84 86 18,0 17,9 72 75
Ростов-на-Дону —6,1 89 23,7 59
Саратов Свердловск Таллин —11,3 —16,2 —7,1 84 84 89 2С,1 17,2 17,8 53 70 78
Ташкент —1,3 81 25,8 46
Тбилиси —0,1 80 24,6 51
Уфа —15,0 86 19,4 67
Харьков —7,7 88 20,6 65
Целиноград —17,0 85 20,3 59
Челябинск —16,2 84 18,6 72
ЛИТЕРАТУРА
Общая
1. А. Г. Касаткин, Основные процессы и аппараты химической техноло-
гии, 7-е изд., Госхимиздат, 1961.
2. А. Н. П л а н о в с к и й, П. И. Николаев, Процессы и аппараты хими-
ческой и нефтехимической технологии, Гостоптехиздат, 1960.
3. Я. Циборовский, Процессы химической технологии (перев. с польско-
го), Госхимиздат, 1958.
4. К. Ф. Павлов, П. Г. Р о м а н к о в, А. А. Носков, Примеры и задачи
по курсу процессов и аппаратов химической технологии, 5-е изд., Гос-
химиздат, 1961.
5. И. И. Чернобыльский, А. Г. Б о н д а р ь, Б. А. Г а е в с к и й, С. А. Го-
родинская, Р. Я. Ладиев, Ю. М. Тананайко, В. Т. Мирго-
родский, Машины и аппараты химических производств, 2-е изд.,
Машгиз, 1961.
6 А. Д. Д о м а ш н е в, Конструирование и расчет химических аппаратов,
Машгиз, 1961.
7. Дж. Перри, Справочник инженера-химика, Госхимиздат, т. I, 1937, т. II,
1947.
К разделу «Механические процессы»
1. М. А. Гурфинкель, С. Ф. Сорокин, Л. Г. Уликовский, Транс-
портные и погрузочно-разгрузочные машины в химической промышлен-
ности, Машгиз, 1960.
2. Л. Б. Левен с он, П. М. Цигельный, Дробильно-сортировочные ма-
шины и установки, Стройиздат, 1952.
3. М. А. Э й г е л е с, Обогащение неметаллических полезных ископаемых,
Промстройиздат, 1952.
4. В. И. Акунов, Современные вибрационные измельчители без мелющих
тел, Промстройиздат, 1957.
5 М. Л. Маргулис, Вибрационное измельчение материалов, Промстройиз-
дат, 1957.
6 В. А. Олевский, Конструкции и расчет механических классификаторов
и гидроциклонов, Госгортехиздат, 1960.
Литература
829
7. А. И. Поваров, Гидроциклоны, Госгортехиздат, 1961.
8. С. П. Орлов, Весовые дозирующие устройства, Машгиз, 1955.
К разделу «Гидромеханические процессы»
г
1. П. Г. Романков, Гидравлические процессы химической технологии, Гос-
химиздат, 1948.
2. Е. 3. Рабиневич, Гидравлика, 3-е изд., Физматгиз, 1961.
3. Н. 3. Френкель, Гидравлика, 2-е изд., Госэнергоиздат, 1956.
4 В. С. Яблонский, Гидравлика для нефтяных техникумов, 2-е изд.,
Гостоптехиздат, 1951.
5. И. Е. И де л ьч и к, Справочник по гидравлическим сопротивлениям, Гос-
энергоиздат, 1960.
6. М. Лева, Псевдоожижение (перев. с англ.), Гостоптехиздат, 1961.
7. Н. И. Сыромятников, В. Ф. Волков, Процессы в кипящем слое,
Металлургиздат, 1959.
8. Б. В. Канторович, Гидравлика, гидравлические и воздуходувные ма-
шины, Металлургиздат, 1950.
9. В. И. Киселев, Насосы, компрессоры и вентиляторы, Металлургиздат
1961.
10. А. М. Горшков, Насосы, Госэнергоиздат, 1947.
11. И. Г. Есьман, Насосы, Гостоптехиздат, 1954.
12. В. Е. Лисичкин, А. М. Горшков, Компрессорные машины, Госэнерго-
издат, 1948.
13. В. А. Ж У ж и к о в, Фильтрование, Теория и практика разделения суспен-
зий, Госхимиздат, 1961.
14. В. И. Соколов, Промышленные центрифуги, Машгиз, 1961.
15. В. И. Соколов, Д. Е. Ш к о р о п а д, Автоматические и непрерывнодей
ствующие центрифуги, Машгиз, 1954.
16. Г. М. Гордон, И. Л. Пей с а хов, Пылеулавливание и очистка газов,
Металлургиздат, 1958.
17. В. Н. У ж о в, Очистка отходящих промышленных газов, Госхимиздат,
1959.
18. В. Н. Ужо в, Очистка промышленных газов электрофильтрами, Госхим-
' издат, 1962.
19. В. В. Каф а ров, Перемешивание в жидкой среде, Госхимиздат, 1949.
К разделу «Тепловые процессы»
1. С. С. Кутателадзе, Основы теории теплообмена, 2-е изд., Машгиз,
1962.
2. М. А. Михеев, Основы теплопередачи, 3-е изд., Госэнергоиздат, 1956.
3. Т. Хоблер, Теплопередача и теплообменники (перев. с польского), Гос-
химиздат, 1961.
830
Литература
4. С. Н. Шорин, Теплопередача, Стройиздат, 1952.
5. С. С. Кутателадзе, В. М. Боришанский, Справочник по тепло-
передаче, Госэнергоиздат, 1959.
6. П. Д. Лебедев, А. А. Щукин, Промышленная теплотехника, Госэнер-
гоиздат. 1956.
7. А. В. Чечетки н, Высокотемпературные теплоносители, 2-е изд., Гос-
энергоиздат, 1962.
8. М. А. Кичигин, Г. Н. Костенко, Теплообменные аппараты и выпар-
ные установки, Госэнергоиздат, 1^55.
9. В. М. Р а м м, Теплообменные аппараты, Госхимиздат, 1948.
10. В. А. Андреев, Теплообменные аппараты для вязких жидкостей, Гос-
энергоиздат, 1961.
11. 3. В. Семи лет, Оросительные теплообменники химических производств,
Машгиз, 1961.
12. Н. Н. Егоров, Охлаждение газа в скрубберах, Госхимиздат, 1954.
13. Н. И. Гельперин, Выпарные аппараты, Госхимиздат, 1947.
14. И И. Чернобыльский, Выпарные установки, Изд Киевского универ-
ситета. 1960.
15. Н. С. Комаров, Холод, 5-е изд., Гизлегпищепром, 1953.
16. Л. М. Розенфельд, А. Г. Ткачев, Холодильные машины и аппараты,
Госторгиздат, 1955.
17. М. П. Малков, К. Ф. Павлов, Справочник по глубокому охлаждению
в технике, Гостехиздат, 1947.
К разделу «Массообменные процессы»
1. А. Г. Касаткин, А. Н. П л а н о в с к и й, О. С. Чехов, Расчет тарель-
чатых ректификационных и абсорбционных аппаратов, Стандартгиз,
1961.
2. В. М. Рам м, Абсорбционные процессы в химической промышленности,
Госхимиздат, 1951.
3. Жидкостная экстракция, Сборник статей под ред. А. Г. Касаткина,
Госхимиздат, 1958.
4. С. А. Б а г а т у р о в, Теория и расчет перегонки и ректификации, Гостоп-
техиздат, 1961.
5. Н. И. Гельперин, Дистилляция и ректификация, Госхимиздат, 1947.
6. В. Б Коган, Азеотропная и экстрактивная ректификация, Госхимиздат,
1961.
7. В. Б. Коган, В. М. Фридман, Справочник по равновесию между жид-
костью и паром в бинарных и многокомпонентных системах, Госхим-
издат, 1957.
8 В. И Матрозов, Аппаратура для молекулярной дистилляции, Машгиз,
1954.
Литература 831
9. Е. Н Серпионова, Промышленная адсорбция газов и паров, Госхим-
издат, 1956.
10 М. Ю. Лурье, Сушильное дело, 3-е изд., Госэнергоиздат, 1948.
11. Г. К. Фил он ен ко, П. Д. Лебедев, Сушильные установки, Госэнерго-
издат, 1952.
12. И И. Воронцов, Сушка в химических производствах, Госхимиздат,
1951.
13. М. В. Лыков, Сушка распылением, Пищепромиздат, 1955.
14. И. М. Федоров, Теория и расчет процесса сушки во взвешенном со-
стоянии, Гоёэнергоиздат, 1955.
предметный указатель
Абсолютная влажность 736, 758
Абсолютно белое и абсолютно чер-
ное тело 402, 403
Абсорбенты 542, 560, 590 сл., 606 сл.
Абсорберы
барботажные 594, 599 сл., 615 сл.
материальный баланс 591 сл.
механические 604, 605
насадочные 596 сл., 608 сл.
оросительные 595
пленочные 595, 596
поверхностные 594 сл.
распиливающие 594, 603 сл.
расчет 608 сл.
режимы работы 599, 610, 611,
615 сл.
с листовой насадкой 596
тарельчатые 599 сл., 615 сл.
тепловой баланс 593
трубчатые 595, 596
Абсорбционные установки 606 сл.
холодильные 524, 542 сл.
Абсорбция 15, 560, 590 сл.
Автоматические весы 112, 113
Адиабатические процессы
охлаждения воздуха 740, 741
расширения и сжатия газов
217 сл., 224, 226, 227, 236, 237,
526, 528, 529, 554, 555
сушки 748
Адсорбенты 560, 712 сл., 717 сл.
активность 714, 715
время поглотительного действия
725, 730
высота слоя 726, 730
коэффициент поглотительного
действия 725
Адсорберы 717 сл.
расчет 723 сл.
с движущимся зернистым адсор-
бентом 718 сл., 723, 730
с кольцевым слоем адсорбента
720, 721, 729, 730
с кольцевым слоем адсорбента
717, 718
Адсорберы
с неподвижным зернистым ад-
сорбентом 715, 717, 718, 723 сл.
Адсорбционные установки 715,721 сл
729, 730
Адсорбция 15, 560
изотермы 713, 714
материальный баланс 715
продолжительность 724 сл., 730
рабочая линия процесса 726
равновесие фазовое 713 сл.
Азеотропная перегонка 708 сл.
Азеотропные смеси 664 сл.
разделение 709, 710
Аллена уравнение 172, 174
Арматура трубопроводов 184 сл.
Архимеда критерий 149, 174, 175,
182, 183
Атмосфера техническая, физическая
130, 131
Баланс
материальный см. Материаль-
ный баланс
тепловой см. Тепловой баланс
энергетический см. Энергетиче-
ский баланс
Барабанные сушилки 784
конвективные прямого действия
769 сл.
контактные непрямого действия
"778, 779
расчет 789 сл.
Барабанные фильтры 284, см. также
Вакуум-фильтры
работающие под давлением 257,
274
расчет 288, 291, 292
Барботаж 362, 412, 599 сл., 615 сл.
Барботажные колонны
абсорбционные 599 сл., 615 сл.
ректификационные 688, 693 сл.
Барботеры
воздушные 362
паровые 412
Предметный указатель
833
Барометрическая труба 507 сл.
Барометрические конденсаторы 507
Бачинского формула 242
Бернулли уравнения 20, 136 сл., 163,
190, 197, 198, 217, 526
Бинодальная кривая 634, 635
Бункеры 104 сл.
Бураты 90
Вакуум-кристаллизаторы
материальный баланс 519, 520
многокорпусные 518, 519
непрерывного действия 518
периодического действия 517,
518, 521
расчет 519 сл.
тепловой баланс 520, 521
Вакуум-насосы 217
водокольцевые 237, 238
пароструйные 236 сл.
поршневые 236, 238
Вакуум-сушилки 777, 778, 801, 802
вальцовые 780 сл., 784, 785, 795
гребковые 779
сублимационные 801, 802
Вакуум-фильтры 256 сл.
барабанные 273, 274, 284
дисковые
горизонтальные 284, 285
непрерывного действия 274 сл ,
284
сгустители 277
ленточные 278 сл., 285
периодического действия 257,
258, 284
тарельчатые 276, 277
ячейковые 268 сл., 288, 291,
292
Вакуум-эжекторные холодильные
машины 544, 545, 802
Вентили 185, 186
Вентиляторы 216, 217
осевые 235
характеристика 230, 231
центробежные 230 сл.
Вентури скрубберы струйные 324,
338, 604
Весы автоматические 112, 113
Влагосодержание
воздуха 737, 739 сл, 744, 752,
786
материалов 735, 736
топочных газов 757, 764
Влажность
абсолютная 736, 758
влияние на скорость сушки 759
760
53 Зак. 546.
Влажность
критическая 760
относительная 736, 737, 744, 826,
827
равновесная 733 сл., 760
Вода
артезианская 422
вязкость 126, 806
давление паров 820
коэффициент объемного расши-
рения 814
—• теплоотдачи конвекцией 383
нагревающий агент 383, 415
оборотная 422
перегретая 415, 435
плотность 804
поверхностное натяжение 812
поглотитель в холодильных ма-
шинах 542
теплопроводность 810
удельная теплоемкость 808
хладоагент 383, 422, 423, 430,
431, 440, 506 сл., 514 сл., 544
Водоотводчики 412, 413
Водяной пар см. также Экстра-пар
вторичный см. Вторичный пар
глухой 412
коэффициент
диффузии 825
теплоотдачи 383
лучеиспускание 404, 406
нагревающий агент 411 сл, 468
острый 412
пролетный 412
степень черноты 406
физико-химические свойства 736,
821, 822, 825
Водяной эквивалент 366, 379, 381
Возгонка в сушке материалов 731,
801, 802
Воздух
влагосодержание 737, 739 сл.,
744, 752 сл., 7§6
влажность 736, 737, 744, 826,
827
диаграмма Т—S 554
нагревание и охлаждение 740,
741
очистка 323, 335, 336
расход на сушку 744
ректификация 690 сл.
сжатый, перемешивание 362
‘ сжижение 549 сл.
сушильный агент 753 сл.
физико-химические свойства 575,
736 сл., 786,''823, 825 сл,
хладоагент 422.
834
Предметный указатель
Воздухоподогреватели (Калорифе-
ры) 436, 740
Воздушная сепарация 86, 96, 102,
103
Воздушные колпаки 210
Воздушные подъемники 362
Вторичный пар 468, 469, 489 сл.
сепарация 487, 488
Выпаривание 467 сл., 657
непрерывное 478, 479
периодическое 478, 479
при отгонке (десорбции) 605,
606
Выпарные аппараты 474, 475
змеевиковые 470
материальный баланс 481, 482
пленочные 477, 478, 485
поверхность теплообмена 484,
485
расчет 479 сл.
с выносным кипятильником 474,
476
с горизонтальными трубами 470,
471
с греющей камерой 473
с паровым обогревом 469 сл.
с циркуляцией 470 сл., 475 сл.,
485
тепловой баланс 482 сл.
эксплуатация 478, 479
Выпарные установки
многокорпусные 469, 488 сл.
однокорпусные 469
питание 490 сл.
полезная разность температур
493, 494
расчет 495, 496 сл.
создание вакуума 505 сл.
с тепловым насосом (термоком-
прессией) 469, 501 сл.
Высота единицы переноса 583, 588,
589, 612, 614, 615, 652, 654, 693,
695
Вязкость
газов и паров 127, 822 сл.
единицы 125 сл.
жидкостей 124 сл., 806, 807
суспензий 241, 242
эмульсий 242
Газовая постоянная 123, 124
Газодувки 217, 233 сл., 238
Газоочистительные аппараты см. так-
же Фильтры и Циклоны
акустические 343, 344
дезинтеграторы 337
золоуловители 326, 338, 339, 344
Газоочистительные аппараты
инерционные 324, 326, 327, 344
камерные 324, 325, 344
пенные 324, 338, 339
пылеуловители 324, 326, 327 сл.,
332, 333, 336 сл., 343 сл.
расчет 329, 331, 335
скрубберные 324, 336 сл., 344
электрические 324, 339 сл., 344,
345
Газопромыватели 337 .
Газы
абсорбция 15, 560, 590 сл.
адсорбция 15, 560, 712 сл.
барботаж 599 сл., 615 сл.
вязкость 127, 822 сл.
десорбция 15, 590, 605, 606
диффузия 575, 576, 825, 826
дросселирование 523, 524, 526,
690, 691
ионизация 339
лучеиспускание 404 сл.
охлаждение 523 сл.
очистка 323 сл.
плотность 123, 124
разделение 545 сл.
растворимость 590, 591, 826
расширение 523, 524, 526 сл.
сжатие 217 сл., 526, 528, 529,
554, 555
сжиженные 545 сл., 690 сл.
теплоемкость 822 сл., 825
теплопроводность 822 сл.
топочные 416 сл., 757, 764
уравнения состояния 123, 124
эффект Джоуля—Томсона 526,
527, 553
Галилея критерий 149, 352, 353
Гейландта цикл высокого давления
556, 558, 559
Генри закон 590, 591
Гигроскопическая точка 735
Гидравлическая депрессия 480
Гидравлическая классификация 86,
96 сл.
Гидравлический транспорт 29, 42
Гидравлическое сопротивление
барботажных абсорберов 617,
618
коэффициент 154 сл., 608
насадок 608, 609
теплообменников 454 сл.
Гидродинамика 121, 133 сл., 152 сл.
абсорберов 608 сл., 615 сл.
провальных тарелок 618 сл.
Гидростатическая депрессия 480
Гидростатическое давление 129, 130
Предметный указатель
835
Гидроциклоны 99 сл., 251, 252
Глубокое охлаждение 524, 545 сл.
Глухой пар 412
Горшки конденсационные 413
Гравитационный критерий Фруда
148 сл.
Градиент
концентрации 578, 579
скорости по нормали 125, 127,
128
температурный 387
Градирни 422
Грасгофа критерий 384, 388
Графический расчет
минимального расхода поглоти-
теля 592
перегонки с дефлегмацией 706,
707
ректификации 698 сл.
скорости газа в барботажных
абсорберах 624
сушилок 785
флегмового числа 675 сл., 701,
702
числа единиц переноса 584 сл.,
678
числа тарелок 625, 626, 628, 698
Грохоты 83, 86, 87
барабанные 89 сл.
бураты 90
вибрационные 94, 95
гирационные 92, 93
инерционные 94, 95
коэффициент полезного действия
84
плоские качающиеся 91, 92
производительность 88, 90, 95
расход энергии 90, 91
расчет 90, 91, 93, 95, 96, 100 сл.
Грохочение 83, 84, 86, 88, 89
Гухмана критерий 761
Давление'
абсолютное 131
атмосферное 131
барометрическое 131
водяного пара 821
гидростатическое 129, 130
единицы 130, 131
жидкостей 129 сл.,
паров 658 сл., 735 сл., 820
избыточное 131
парциальное 564, 565, 590, 591,
659 сл., 735 сл.
Дальтона закон 564
Движущая сила процесса 20, 21
массопередачи 570 сл., 577, 579,
580, 582 сл., 606, 758, 761
Дезинтеграторы 68, 69, 82, 337
Депрессия
гидравлическая и гидростатиче-
ская 480
полная 480, 481
температурная 479, 480, 817
Десорбция 590, 592, 605 сл., 712, 714,
718 сл.
Детандеры 523, 524, 528 сл., 546 сл.,
554 сл.
Дефлегматоры 658, 671, 681, 682,
686 сл., 705 сл.
Дефлегмация 686, 687, 704 сл.
Джоуля — Томсона эффект 526, 527,
553
Диаграмма (ы)
двойных и тройных жидких сме-
сей 633 сл., 658 сл., 663, 667
индикаторные
компрессоров 223, 224
насосов 211
сжатия газа 218, 219, 227
состояния воздуха 527, 554
треугольная 633 сл.
фазового равновесия процессов
массопередачи 567 сл., 584 сл.,
592
холодильных циклов 528—538,
548—557
Диаметр эквивалентный 144, 169, 176
Дисмембраторы 69
Дистиллят 657, 670 сл.
Дифенильная смесь 414, 416
Диффузия
внешняя и внутренняя 758
газов, коэффициенты 575, 576,
825, 826
конвективная 573, 574, 577 сл.,
582
молекулярная 573 сл.
уравнение 574
Диффузоры 358
Доазеотропные смеси 664, 665
Дозаторы 104, 111 сл.
Дробилки •
валковые 51, 63 сл., 82, 84,
85
вибрационные 51, 78, 79
гирационные 51, 58 сл., 82, 84
грибовидные и короткоконусные
58, 60 сл., 82, 84
дезинтеграторы 68, 69, 82
дисмембраторы 69
крестовые 68
53
836
Предметный указатель
Дробилки
молотковые 51, 67 сл., 82
отражательные 51, 78, 79
производительность 57, 58, 61,
62, 66, 68, 69, 74, 75, 83
расход энергии 57, 58, 61, 62, 66,
82, 83
расчет 55 сл., 61, 62, 64 сл., 68
угол захвата 55 сл., 61, 64, 65
ударно-центробежные 51, 67 сл.
щековые 49, 51, 54 сл., 61, 82,
~~84 —
Дробление см. Измельчение
Дросселирование 523, 524, 526 сл.,
530 сл., 690, 691
Дроссельный эффект 526, 527, 553
Единицы
измерения 23 сл.
переноса (высота и число) 583,
588, 589, 612, 614, 615, 622,
652, 654, 678, 693, 695
Жидкие смеси
азеотропные (нераздельнокипя-
щие) 664 сл.
двойные
диаграммы 658 сл., 663, 667,
668
ректификация 683 сл.
свойства 818, 819
состав 562, 563, 818, 819
идеальные 659 сл.
отклоняющиеся от идеальных
662 сл.
правило смешения 681
разделение см. Разделение жид-
костей
тройные
ректификация 685, 686
диаграммы 633
фазовое равновесие см. Равнове-
сие фазовое
Жидкости,
взаимнорастворимые 659 сл.
вязкость 124 сл., 806, 807
давление 129 сл., 658, 735 сл.,
82J
идеальные 122, 137, 138
истечение см. Истечение жидко-
стей
капельные 122 сл., 140
кипение 398, 399
коэффициент объемного расши-
рения 814, 815
напряжение внутреннего трения
125, 127
Жидкости
неньютоновские (пластичные)
127, 128, 161
нерастворимые друг в друге 659,
666 сл.
плотность 122, 123, 804, 805
поверхностное натяжение 129,
812, 813
псевдопластичные 128, 161
расход 133, 139, 163, 168
режимы движения
ламинарный 142 сл, 155, 161,
171 сл., 348 сл., 383 сл., 608
переходный 144
турбулентный 142 сл., 155, 161,
171, 174 сл., 348 сл., 383 сл.,
608
скорость движения в трубопро-
водах 133, 187
температура кипения 479 сл., 660,
708 сл., 818, 819
теплопроводность 810, 811
теплота испарения 815
трение 152 сл.
теплоемкость 808, 809
удельная энергия 134 сл.
частично растворимые 659, 668,
669
Заазеотропные смеси 664, 665
Задвижки 185, 186
Закон(ы)
Генри 590, 591
Дальтона 564
Кирхгофа 403
Коновалова 662 сл.
Ньютона 125, 127, 172, 370
Рауля 659, 663
Стефана—Больцмана 402, 403
Стокса 244
Фика 574
Фурье 369
Затворы бункеров 105 сл.
Захлебывание
насадок 610, 611
экстракторов 651
Змеевики 430 сл., 435, 470, 690,
691
Золоуловители жалюзийные 326, 327,
344
Идеальные смеси 659 сл.
Извлечения коэффициент и степень
591, 626, 627, 646
Излучение тепловое см. Лучеиспу-
скание
Предметный указатель
837
Измельчение
в замкнутом цикле 51, 70, 78, 83
в открытом цикле 51, 82, 83
крупное 50 сл., 59, 82
мелкое 50, 51, 53, 67, 82
методы 50
мокрое 50, 72, 78, 81
сверхтонкое 50, 52, 76 сл.
среднее 50, 51, 53, 60, 67, 82
степень 49
сухое 50
схемы 51, 82 сл.
теории 52 сл.
тонкое 50, 51, 53, 76, 82, 83
Изоляция тепловая 409
Изотермическое сжатие газов 217,
224, 227, 526, 547 сл., 555
Изотермы
адсорбции 713 сл.
сушки 739 сл.
Инверсионная температура 528
Индикаторные диаграммы см. Диа-
граммы индикаторные
Индукционные токи 421
Инжекторы 215
Ионизация газов 339
Испарение жидкостей 367, 560,
671 сл., 732
теплота 672, 817
хладоагентов 523, 525, 528, 539
Испарители 528 сл., 541
Истечение жидкостей 163 сл.
время 139, 167
сжатие струи 165 сл.
скорость 165 сл.
через отверстия и водосливы
164 сл.
трубопроводы 163, 164
Кавитация 200
Калориферы 436, 740
Камеры пылеосадительные 324, 325,
344
Капицы цикл низкого давления 557
Карно цикл обратный 528, 543
Каскадный цикл 538, 539
Кинематический критерий см. Крите-
рий Рейнольдса
Кинетическая кривая 625 сл.
Кипение жидкостей 398, 399
Кипятильники 470, 473, 474, 476
Кипящий (псевдоожиженный) слой
в процессах адсорбции 710, 718,
719, 727, 728
коэффициент расширения 182
пористость 181 сл.
Кипящий (псевдоожиженный) слой
сопротивление 180 сл.
теплообмен 460 сл.
Кирпичева теория дробления 52, 53
Кирхгофа закон 403
Классификаторы гидравлические
производительность 98, 100
реечные 97, 98
спиральные 97
центробежные 99 сл., 101, 304,
313
чашевые 98, 99
Классификация материалов
воздушной сепарацией 86, 96,
102, 103
гидравлическая 86, 96 сл.
ситовая (грохочение) 83, 84, 86,
88, 89
Колонны абсорбционные
барботажные 599 сл.
гидравлическое сопротивление
608, 609, 617, 618
массопередача 612, 622, 623
насадочные 596 сл.
расчет 608 сл.
режимы работы 599, 610, 611,
615 сл.
тарельчатые 599 сл.
Колонны ректификационные 670,
690 сл.
барботажные 688, 693 сл.
насадочные 688, 693 сл.
рабочие линии 672 сл., 698 сл.
расчет 692 сл.
теплообменные устройства 671,
681, 682, 686 сл.
эксплуатация 689, 690
Колонны экстракционные 648
вертикальные смесительно-от-
стойные 637, 645
многоступенчатые смесительные
637, 640
насадочные 637, 639, 641, 652
пульсационные 637, 640, 641
распылительные 637, 638
расчет 651 сл.
тарельчатые 637 сл., 643, 644 '
Колпаки в&здушные 210, 211
Колпачки тарелок 599, 600, 615 сл.
Компрессионные холодильные маши-
ны 524
воздушные 528
идеальные 528 сл.
каскадный цикл 538, 539
многоступенчатые 537 сл.
паровые 533 сл., 540, 541
реальные 530 сл.
838
Предметный указатель
Компрессоры 216 сл., см также Тур-
богазодувки и Турбокомпрессоры
вертикальные 222, 540
горизонтальные 222, 223, 540
двойного действия 221, 222,
540
коэффициент полезного действия
220, 221, 224, 225, 535 сл.
многоступенчатые 222, 223, 540
мощность 219 сл.
одноступенчатые 221, 222
осевые 217, 235, 238
поршневые см. Поршневые ком-
прессоры
простого действия 221, 222
расчет 226, 232, 233
регулирование и обслуживание
228
ротационные 228, 229
струйные 217, 236 сл.
холодильных машин 524 сл, 540
центробежные 230 сл
Конвективная диффузия 573, 574,
577 сл., 582
Конвекционные токи 393, 394, 470
Конвекция 363, 364, 395 сл., 407 сл.
в кипящем слое 460 сл.
вынужденная 388 сл.
критерии подобия 384 сл.
коэффициенты теплоотдачи 370,
373, 383 сл., 407 сл., 446, 447,
453
свободная 393 сл.
уравнение передачи тепла 370,
371
Конденсатоотводчики 412, 413
Конденсаторы 411
барометрические 507 сл.
кожухотрубные 424, 425, 439,
540
оросительные 430, 431, 439, 540
поверхностные 505
погружные 431, 432, 439, 540
расчет 456 сл.
смешения 466, 506 сл.
тепловая нагрузка 540
«труба в трубе» 430, 439, 540
холодильных машин 540
элементные 439, 540
Конденсационные горшки 413
Конденсация
капельная 395
пленочная 395
полная 686, 687
расчет теплообмена 456, 457
частичная 686
Коновалова законы 662 сл.
Концентрация(и)
весовая 561 сл.
градиент 578, 579
молярная 561 сл.
объемная 563 сл.
рабочие 569, 582 сл.
Коэффициент (ы)
вязкости жидкости 124 сл
гидравлического сопротивления
154 сл., 608, 609
диффузии газов 574 сл., 825,
826
заполнения транспортеров 42,
43, 47, 48
избытка флегмы 677
извлечения 626, 627
инжекции 503
лучеиспускания 402, 403, 407
массоотдачи 577, 578, 581
массопередачи 570 сл., 581, 582
массопроводности 581, 582
местных сопротивлений 157 сл.,
455
объемного расширения 814, 815
поглотительного действия 725
подачи компрессоров 225, 537
полезного действия см. Коэффи-
циент полезного действия
разрыхления материалов 57, 61,
66
распределения 632, 633
расхода 166, 167
расширения кипящего слоя 182
сжатия струи 165 сл.
скорости 21, 165 сл.
смачиваемости насадок 609, 610,
613, 614
сопротивления 172 сл., 348 сл.
сушки 761
/ теплоотдачи 370, 373, 383 сл.,
407 сл., 446, 447, 453, 461 сл.,
792 795
теплопередачи 368, 369, 373, 446,
447
теплопроводности 369, 370
трения 56, 155, 172 сл., 454, 455
формы (сферичности) 173
холодильный 525, 526, 528, 529,
534, 542, 543, 545
Коэффициент полезного действия
газоочистительных аппаратов
325, 344
грохота 84
детандера 555 сл.
инжектора 503
компрессоров 220, 221, 224, 225,
535, 536, 537, 549
Предметный указатель
839
Коэффициент полезного действия
насосов 189, 190, 197, 202 209
211 ’
циклов сжижения воздуха 558,
559 ’
Краны 185
Кривые
бинодальная 635-
кинетицеская 625 сл
равновесной влажности 734 сл.
Критерий(И)
Архимеда 149, 174, 175, 182, 183
Галилея 149, 352, 353
Грасгофа 384, 388
Гухмана 761
Нуссельта 384, 385, 388 сл., 577,
578
Пекле 387, 579
подобия процессов
гидромеханических 147 сл.
массопередачи 577 сл.
тепловых 384 сл.
Прандтля 384, 385, 387, 577 сл.
Рейнольдса 143, 144, 147 сл,
169 сл., 176, 177, 315, 348, 352,
353, 384, 385, 387 сл.
Фруда 148 сл, 315
Эйлера 148 сл., 161
Кристаллизаторы
барабанные 516, 517
вакуумные см Вакуум-кристал-
лизаторы
материальный баланс 519, 520
основные размеры 521
расчет 519 сл.
с внутренним охлаждением
вальцы) 516
с водяным охлаждением 514 сл.,
520, 521
с воздушным охлаждением 516
520, 521
с выносным холодильником 515,
516
с мешалкой 514, 515 w
тепловой баланс 520, 521
ящичные 514
Кристаллизация 467, 512 сл.
Ламинарное движение 142 сл., 155,
161, 171 сл, 348 сл., 383 сл., 608,
715, 716
Линде циклы сжижения воздуха
549 сл.
Линейная плотность орошения 170
Лучеиспускание 363, 364, 401, 408
газов 404 сл.
коэффициенты 402, 403, 407
Массообмен -Я1
виды процессов 573 сл.,^581, 582
материальный баланс 567 сл.
теория процессов 560 сл.
Массопередача
в барботажных абсорберах 622
в насадочных абсорберах 612
движущая сила 570 сл., 577, 579,
580, 582 сл., 606, 758, 761
диаграмма фазового равновесия
567, 584 сл.
коэффициенты 570 сл., 581, 582
подобие процессов 577, 578, 579
при адсорбции 715, 716
при ректификации 692, 693
расчет процессов 582 сл.
скорость 560
уравнение 570 сл.
Массопроводности коэффициент 581,
582
Материальный баланс 19, 20
абсорберов 591 сл.
адсорбции 715
выпарных аппаратов 481, 482
кристаллизаторов 519, 520
потока 132 сл.
процессов массообмена 567 сл.
разделения суспензий и эмуль-
сий 242
ректификации 671 сл.
сушки 743 сл.
уравнение 19
экстракции 635, 636
Мельницы
барабанные 51, 70 сл, 82
вибрационные 51, 77, 78, 82
коллоидные 49, 51, 81
крестовые 68
маятниковые 76
молотковые 67
производительность 74, 75, 83
расход энергии 74, 75, 82, 83
расчет 72 сл.
ролико-кольцевые 51, 76, 82
стержневые 72
струйно-вибрационные 51, 77, 79
трубные 72
ударно-центробежные 51, 67 сл.
шаровые 71 сл., 82
Менделеева формула 417
Местные сопротивления 157 сл., 455
Мешалки
барабанные 361
дисковые 351
лопастные 349, 351, 354 сл.
пропеллерные 349, 351, 353, 357,
рамные 356, 357
840
Предметный указатель
Мешалки
специальные 361
турбинные 349, 351, 353, 359 сл.
якорные 349, 351, 361
Мешатели 117, 118
Монтежю 215, 216
Мощность 27 см также Расход энер-
гии на измельчение
грохотов 90, 91
компрессоров 221 сл.
насосов 188 сл., 201
транспортеров 44 сл.
элеваторов 44, 45, 48
Мультигидроциклоны 100, 251, 252
Нагревание
водой 415
водяным паром 411, 412, 468,469
горячими газами 416 сл., 461,
462
дифенильной смесью 414, 416
конденсатом 415, 416
обогревательными банями 415
парами высококипящих жидко-
стей 413, 414
ртутью 414
циркуляционное 414, 415
электрическим током 420 сл.
Напор
геометрический 137 сл.
гидродинамический 139
динамический 137 сл.
насосов 188 сл, 198 сл.
полный 139
потеря на трение 138, 139, 152 сл.
пьезометрический 137 сл.
скорое 1 ной 137 сл.
статический 137 сл.
температурный 368, 369, 371 сл.,
378 сл., 442, 443
Насадки
абсорберов 596 сл, 608 сл.
барабанных сушилок 770, 771
высота 613, 615
гидравлическое сопротивление
608, 609
движущиеся 465
захлебывание 610, 611
неподвижные 464
регенераторов 464, 465
ректификационных колонн 688,
693 сл.
свободный объем 598, 609
смачиваемость 609, 610
удельная поверхность 598, 608
удерживающая способность 609
экстракторов 639, 652 сл.
Насадочные колонны
абсорбционные 596 сл., 608 сл.
ректификационные 688, 693 сл.
экстракционные 637, 639, 641,
652 сл.
Насосы
бессальниковые 193, 194
вакуумные см. Вакуум-насосы
вертикальные 207
вихревые 212, 213
высота всасывания 188 сл.
герметические 195, 196
горизонтальные 206 сл.
двойного действия 208
диафрагмовые 207
индикаторная диаграмма 211
коэффициент полезного действия
189, 190, 197, 202, 209, 211
многоступенчатые 192, 193
мощность 188 сл , 201
напор 188 сл, 198 сл.
одноступенчатые 191, 192
осевые 212, 216
плунжерные 207, 208
погружные 194, 195
подъемники воздушные 215, 216
поршневые см. Поршневые на-
сосы
производительность 188, 189,
200, 201
пропеллерные 212, 216
простого действия 206, 207
прямодействующие паровые 208
ротационные 214
с направляющим аппаратом 192
струйные 214 сл.
тепловые 469, 501 сл.
центробежные см. Центробеж-
ные насосы
Неньютоновские (пластичные) жид-
кости 127, 128, 161
Нераздельнокипящие (азеотропные)
смеси 664 сл.
Нуссельта критерий 384, 385, 388 сл.,
577, 578
Нутч-фильтры 258, 259, 284
Ньютона
законы 125, 127, 172, 370
уравнение 172, 174
Объем (ы)
атомные 575
газов 124
молекулярные 575
свободные насадок 176, 181, 182,
598, 609
удельный 123
Предметный указатель
841
'Орошения плотность 170, 599, 603,
606 сл., 612, 613
Осаждение 240
в поле центробежных сил 251,
252
свободное 175, 244
скорость 173 сл. ».
стесненное 244, 245
Осветление жидкостей 252, 293, 294,
313
Относительная влажность воздуха
736, 737, 744, 826, 827
Отстаивание 243 сл., 293, 294
Отстойники
непрерывного действия 246 сл.
периодического действия 246,
248
расчет 249 сл.
Охлаждение 365, 366, 411
водой 422, 423
воздухом 422
глубокое 523, 524, 548 сл., 554 сл.
естественное 523
рассолами 423, 523, 532
умеренное 423, 523, 524, 528 сл.
Очистка газов 323 сл.
Пар водяной см. Водяной пар
Пекле критерии 387, 579
Пенные аппараты 324, 338, 339
Перегонка см. также Ректификация
азеотропная 708 сл.
молекулярная 708, 710, 711
простая 657, 703 сл.
с водяным паром 708, 709
экстрактивная 708 сл.
Перемешивание 390 см. также Ме-
шалки
механическое 346
расход энергии 347 сл.
сжатым воздухом 346, 362
эффективность 346, 352 сл.
Печи электрические 420, 421
Йитатели 104, 107 сл.
лотност ь
газов 123, 124
жидкостей 122, 123, 804, 805
суспензий 241
эмульсий 241
Плотность орошения 170, 599, 603,
606 сл, 612, 613
Пневматический транспорт 36, 37,
39 сл, 180
Поверхность
осаждения 249, 250
соприкосновения фаз 570, 594,
595, 599, 603, 615
Поверхность
теплообмена 21, 363, 368 сл., 448
удельная 176, 598, 608
фильтров 286, 287, 291, 292
Поглотители см. также Абсорбенты
и Адсорбенты
расход 590 сл.
рециркуляция 606 сл.
Пограничный слой 143
Подвисания режим 599, 610, 611
Подобие
гидромеханических процессов
147 сл.
критерии 147 сл., 384 сл., 577 сл.
процессов массопередачи 577,578,
579
теория 145 сл., 384
тепловых процессов 384 сл.,
578
треугольников скоростей 200
Подогреватели 411, 439, 466
нагрузочная характеристика 448
расчет 500, 501
Подъемники пневматические (воздуш-
ные) 41, 42, 215, 216, 362
Полезная разность температур 493
Политропическое сжатие газов 220,
224
Поршневые компрессоры 528, 539
индикаторная диаграмма 223,
224
коэффициент подачи 225, 226
— полезного действия 224, 225
многоступенчатые 222, 223, 226,
227, 540
одноступенчатые 221, 222, 540
производительность 224 сл.
регулирование и обслуживание
228
Поршневые насосы
диафрагмовые 207
индикаторная диаграмма 211
коэффициент полезного действия
209
плунжерные 206, 207
производительность 208 сл.
прямодействующие паровые 208
регулирование и обслуживание
211, 212
характеристика 209
Потери
напора на трение 138, 139, 152
тепла в окружающую среду 364,
409 сл., 547
холода 547
Правило смешения жидких смесей
681
842
Предметный указатель
Прандтля критерии 384, 385, 387,
577 сл.
Производительность
грохотов 88, 90, 95
дробилок .57, 58, 61, 62, 66, 68,
69, 74, 75, 83
классификаторов 98, 100
компрессоров 224 сл.
мельниц 74, 75, 83
насосов 188, 189, 200 сл, 208 сл.
сушилок 785, 786, 791 сл.
транспортеров 42, 43
фильтров 255, 256, 286, 287
центрифуг 314 сл.
элеваторов 43
Промывка осадков 254, 256, 285, 286
Противоток 378 сл., 762
Процесс (ы)
адиабатические см. Адиабатиче-
ские процессы
гидромеханические 14, 121 сл.
движущая сила 20, 21
изотермические 217 сл., 224, 227,
526, 547, 555
кинетика 21
массообменные 14, 15, 560 сл.,
563 сл., 581, 582
механические 14, 28 сл.
непрерывные 15
неустановившиеся 363
периодические 15
сжатия газа 217 сл, 548 сл.
скорость 20, 21
статика 20
тепловые 14, 363 сл.
условия равновесия 20
установившиеся 363
Прямоток 378 сл., 762
Псевдоожижение 181 сл., 462
Псевдоожиженный слой см. Кипя-
щий (псевдоожиженный) слой
Пылеосадительные камеры 325, 344
Пылеуловители
акустические 343, 344
инерционные 324, 326, 327, 344
мокрые 324, 336 сл., 344, 345
пенные 338, 399
расчет 329, 331
сухие 324, 332, 333
центробежные см. Циклоны
Рабочая линия процесса 568, 569,
582 сл., 585, 625, 626
абсорбции 591, 592
десорбции 592
ректификации 672 сл., 698 сл.
экстракции 635, 636
Равновесие фазовое 566, 567
при абсорбции 590, 591
при адсорбции 713 сл.
при ректификации 658 сл.
при экстракции 632 сл.
Равновесия линия 56/, 582 сл.
абсорбции 591 сл., 625, 626
ректификации 662
экстракции 632
Равновесная влажность 733 сл.
Разделение
газов 658
абсорбцией 590 сл.
адсорбцией 712 сл
глубоким охлаждением 545 сл.
ректификацией 690 сл.
жидких неоднородных систем 240
отстаиванием 243
фильтрованием 240, 252
центрифугированием 292 сл
жидкостей
ректификацией 632, 657 сл.
экстракцией 631 сл.
Разделения фактор 294
Размол 49 сл.
Распылители центробежные 603, 604
Рассолы холодильные 423, 523, 532
Растворимость 512, 513
газов 590, 591, 826
твердых веществ 816
Растворы 512, 513
выпаривание 467 сл.
коллоидные 239
температура кипения 479 сл.
теплота дегидратации и разбав-
* ления 483
Расход энергии
на измельчение 57, 58, 61г 62, 66,
74, 75, 82, 83
на перемешивание 347 сл.
при центрифугировании 316 сл.
Расчет
абсорберов 608 сл.
адсорберов 723 сл.
аппаратуры, общие методы 21,
22
выпарных аппаратов 479 сл.,
496 сл.
высоты единицы переноса 588,
589, 612, 614, 615, 652, 654, 695
газоочистительных аппаратов
329, 331, 335
графический см. Графический
расчет
грохотов 91, 91, 93, 95, 96, 100
дробилок 55 сл., 61, 62, 64 сл,
68
Предметный указатель
843
Расчет
компрессоров 22> 232, 233
конденсаторов 456 сл.
кристаллизаторов 519 сл.
массообменных процессов 582 сл.
мельниц 72 сл.
насосов 188 сл., 196, 197, 201,
203, 204, 210 '
отстойников 249 сл.
питателей 108, ПО, 111
ректификационных колонн 692
сушилок 785 сл.
теплообмена при конденсации
456, 457
теплообменников 440 сл.
транспортеров 42 сл.
трубопроводов 186, 187
фильтров 286 сл., 335
холодильных машин 533 сл.
центрифуг 314 сл.
циклонов 329, 331
числа единиц переноса 584 сл,
622, 678, 693, 695
экстракторов 651 сл. *
элеваторов 43, 45, 48
Расширение газов 523, 524
адиабатическое 526, 528, 529,
554, 555
Расширительные машины (Детандеры)
523, 524, 528 сл, 546 сл , 554 сл.
Раиля закон 659, 663
Рафинат 631
Ребиндера теория дробления 53, 54
Регенераторы (Теплообменники реге-
неративные) 423, 464, 465
Рейнольдса критерии см. Критерии
Рейнольдса
Ректификационные аппараты см. Ко-
лонны ректификационные
Ректификация 560, 632
воздуха 690 сл.
двойных смесей 683 сл.
использование тепла 687, 688
материальный баланс 671 сл.
I непрерывная 670, 671, 683 сл.,
' 690, 692 сл.
периодическая 683 сл., 690, 698
под различным давлением 686
сжиженных газов 690 сл.
схемы установок 683 сл.
уравнения рабочей линии 672 сл.
тепловой баланс 680 сл.
тройных смесей 685, 686
Сверхцентрифуги 296, 645
для сепарации жидкостей 310,645
трубчатые 308, 309
Сгустители
дисковые 277
патронные 267, 268
Сепараторы 470
воздушные 102, 103
жидкостные 296, 310 сл.
Сепарация
воздушная 86, 96, 102, 103
вторичного пара 487, 488
при экстракции 636
Сжатие газов
адиабатическое 217 сл, 224,
226, 227, 236, 237
диаграммы процесса 218, 219
изотермическое 217 сл., 224, 227,
526, 547 сл., 555
многоступенчатое 226, 227
политропическое 220, 224
Сжижение газов 523, 524, 545 сл
Ситовой анализ 86, 87
Скорость
истечения 165 сл.
коэффициент 165
линейная и массовая 133
массопередачи 560
осаждения (отстаивания) 173,
243 сл.
промывки осадков 256
процесса 20, 21, 169
псевдоожижения 181, 182
пульсации 143
сушки 757 сл.
уноса 181, 183
фильтрования 178
Скрубберы
насадочные 336
полые 336
струйные 324, 338, 604
центробежные 337, 338
Смачиваемость насадок 609, 610
коэффициент 613, 614
Смеси
азеотропные 664 сл.
идеальные 659 сл.
многокомпонентные, ректифика-
ция 685, 686
отклоняющиеся от идеальных
662 сл.
Смесители 104, 116 сл.
Смешанный ток 442, 443
Сопротивление
гидравлическое см. Гидравличе-
ское сопротивление
местное 157 сл.
осадка 254 сл.
слоя твердых частиц 180 сл.
среды 172 сл., 244, 245, 347
844
Предметный указатель
Сопротивление
тепловое 372, 446
трения 152 сл., 171
фильтрованию 178, 254 сл.
Степень
извлечения 591, 646
измельчения 49
очистки газов 344
сжатия 225, 227, 235
черноты 403 сл.
Стефана — Больцмана закон 402, 403
Стокса
закон 244
уравнение 172, 174
Суспензии 239
вязкость 241, 242
осаждение 243 сл., 251, 252
плотность 241
Сушилки
атмосферные 765 сл., 780, 784
аэрофонтанные 776, 777
барабанные см. Барабанные су-
шилки
вагонеточные 766, 767
вакуумные см. Вакуум-сушилки
вальцовые 780 сл, 784, 785
гребковые 779, 784
камерные 765 сл.
комбинированные 782 сл.
конвективные 765 сл
контактные 777 сл., 795 сл.
коридорные 766 сл.
ламповые 797
ленточные 767, 768
напряжение по влаге 762
непрерывного действия 766 сл,
771 сл., 776 сл., 780 сл., 784,
785
периодического действия 765,
766, 775, 776 сл., 783, 784
петлевые 768, 769, 784
пневматические 771, 772, 785
производительность по влаге 785,
786, 791 сл.
радиационные газовые 797 сл.
распылительные '467, 772 сл.,
784, 785, 792 сл.
расчет 785 сл.
реальная 751 сл.
с подогревом воздуха 754 сл.
с кипящим слоем 775 сл., 784,
785
сублимационные 801, 802
с рециркуляцией воздуха 756
терретическая 748, 751
туннельные 766 сл.
шкафные 765, 766, 784
Сушка 560
возгонкой (сублимацией) 731,
801, 802
диаграмма / — х 751 сл.
диэлектрическая 731, 799 сл.
инфракрасными лучами 731, 797
кинетика 757 сл.
конвективная 731, 745, 748, 762
контактная 731, 748, 762
коэффициент 761
материальный баланс 743 сл.
периоды 758 сл.
продолжительность 760, 761
радиационная 731, 797 сл.
скорость 757 сл.
статика 732 сл.
схемы 753 сл.
температурный напор 763 сл.
тепловой баланс 745 сл.
токами высокой частоты 731, 799
, топочными газами 757, 784
Тарелки
каскадные 644
колпачковые 599, 600, 615 сл.,
627, 644
провальные 601, 618 сл.
ситчатые 601, 615 сл., 640, 641
число 625, 626, 697 сл.
Тарельчатые колонны *
абсорбционные 599 сл.
ректификационные 688, 693 сл.
Температура
инверсионная 528
кипения жидкостей 479 сл., 660
708 сл., 818, 819
мокрого термометра 732, 736,
739 сл.
полезная разность 493 сл.
стенки, определение 376 сл.
теплоносителей 442, 443
точки росы 740
Температурная депрессия 479, 817
Температурный градиент 387
Температурный напор 368, 369, 371,
378 сл., 442. 443
Температуропроводность 387
Теория
измельчения (дробления) 52 сл.
подобия 145 сл., 384
фильтрования 254
Тепловая нагрузка 365 сл, 372, 483
испарителей 541
конденсаторов 540
теплообменников 440, 441
Тепловое подобие 384 сл., 578
Тепловое сопротивление 372, 446
66 02
П37
Книга является учебником для химических технику-
мов (для учащихся технологических и механических
специальностей). Она может быть использована также
в качестве пособия при курсовом и дипломном про-
ектировании.
В книге рассмотрена теоретические основы про-
цессов, описай^ конструкции типовых аппаратов и
методы их расчета, освещены вопросы обслуживания
аппаратов.
Материал изложен в объеме, предусмотренном учеб-
ными программами для химических техникумов.
ОПЕЧАТКИ И ИСПРАВЛЕНИЯ
(в части тиража)
ip. Строка Напечатано Должно быть
55 Рис 3—10 2е
35 4 снизу Qn = Gx Q^ = Qx
20 000 20 000
13 5 снизу 7-1,5400 * 7 • 1540
Q
i 3 сверху П~ Qh QB
i 12 сверху 9,81 кгс м 9,81 дж)кгс • м
1 13 снизу а диаметр или диаметр
20 сверху Ра ?g 2g t Ра , ?g 2g
3 7 снизу (z2— Zx) = г2 —2i
Al 6 ^верху Pct — Рст. ~
12 сверху H — рст “ ~ Р = Рст
Pct Рст.
255 7 сверху V 3/ 3 q = V ,, , sq=-p ж3/ж2
292 3 сверху P'np ГпР = ~4 Р'Пр Гпр
12 сверху F 67 •387 1 26 .,? 3600 4-0,169 ,2b „ 6,7 387 . ос , F ~ 3600 • 0,169 4’ 6 ж
16 сверху = 0Д5 об1мин do/ п = • 60 = 0,15 об!мин Оо7 9
392 9 сверху (0,179 ккал!м град) (0,179 ккал!м • ч • град)
10 сверху (0,634 ккал/кг ч град) (0,634 ккал]кг • град)
’393 14 сверху 5,8 5,7
409 4 сверху (5580 ккал!т2 ч) (5580 ккал!м2 • ч)
439 25 сверху туру и конденсаторы туру, и как конденсаторы.
462 8 снизу ’ <о0 w0
508 7 снизу 60 ж3 на 1 кг 60 кг на 1 кг
591 1 снизу G(Y}-Y2) GY G (Г, - Г2) GYi
715 25, 27, 29 Р рн
сверху
724 Формула Y2-Yi Yt-Y2
(20-11)
726 5 снизу Y Y, Хн
763 4 снизу противотоком) прямотоком)
На стр. 397 (16 строка сверху) неясно отпечатан показатель степени
1/3 выражения, заключенного в квадратные скобки.
Зак. 546 А. Н. Плановскии и др