Автор: Берман Г.Н.
Теги: математика учебное пособие свойства циклоиды техника и механика исторические экскурсы
Год: 1980
Текст
Г.Н. БЕРМАН
ПА
\
\
ИЗ ПРЕДИСЛОВИЯ
К ПЕРВОМУ ИЗДАНИЮ
Многие люди к математике относятся
с уважением, но без крайней необходимо-
необходимости предпочитают держаться от нее по-
подальше. Автор будет счастлив, если эта
книжка хотя бы в самой малой степени бу-
будет содействовать уничтожению этого
странного предрассудка.
Г.Н.БЕРМАН
ЦИКЛОИДА
ОБ ОДНОЙ ЗАМЕЧАТЕЛЬНОЙ
КРИВОЙ ЛИНИИ
И НЕКОТОРЫХ ДРУГИХ,
С НЕЙ СВЯЗАННЫХ
ИЗДАНИЕ ТРЕТЬЕ
МОСКВА «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ
ЛИТЕРАТУРЫ
1930
22.151.0
Б 50
УДК 513
Берман Г. Н.
50 Циклоида. —-М: Наука, 1980. —- Н2 с.—
20 к.
В брошюре Изложены в элементарной, чисто геомет-
геометрической форме, свойства циклоиды и некоторых других,
близких к нер, замечательных кривых Рассмотрены ча-
дачн из техники и механики, в коюрых появляются ис-
с^еЛуемые кривые. Б книге много исторических экскурсов.
Для учгщнхся старших классов средней школы, тех-
техникумов и ПТУ.
Георгий Николаевич Берман
ЦИКЛОИДА
М., 1980 г., 112 стр. с илл.
Редактор С. С. Рышков
Техн. редактор Я. В. Вершинина
Корректор Е. В. Сидоркина
ИБ J* 11600
Сдгно в набор 21.u8.79. Подписано к печати 05.02.80. Т 01058.
Бумага 84X1087.. тип. № 1. Литературная гарнитура. Высокая печать
Х'сл. печ. л. Р,88. Уч.-изд. л. 5,5. Тираж 108 000 экз. Заказ № 314.
Цена книги 20 коп.
Издательство «Наука»
Главная редакция физико-математической литературы
117071, Москва, Б-71, Ленинский проспект, 15
Ордена Трудового Красного Знамени Ленинградская типография № 2
имени Евгении Соколовой «Соызполиграфпрома» при Государственном коми-
комитете СССР по делам издательств, полиграфии и книжной торговли.
198052, Ленинград, Л 52, Из.\ыи ^Акии п.. n-аект, ?Э
ГЛАВА I
КРИВАЯ, РОЖДЕННАЯ КОЛЕСОМ
«Ехали медведи
На велосипеде...»
К. Чуковский.
Разговор двух велосипедистов
Мои друзья — девятиклассник Вася и студент-фи-
студент-физик Сергей — большие любители велосипедного спор-
спорта. Вот какой разговор произошел у них однажды по
возвращении с прогулки.
Сергей. Как ты думаешь, Вася, может ли вело-
велосипед обдать велосипедиста грязью, которая налипла
на заднее колесо машины и отскакивает от него?
Вася. Еще бы! Когда на грязной дороге случает-
случается замедлить ход, брызги всегда попадают в спину.
Сергей. А почему это так? Думал ли ты об
этом? Как, по-твоему, должен двигаться комочек
грязи, отделившийся от обода колеса? По какому
направлению?
Вася. Дай вспомнить. Нет, не помню...
Сергей. Ну так я тебе напомню. Если какая-
нибудь частица принуждена двигаться по кривой и
неожиданно получает свободу движения, она, по
инерции, будет двигаться в направлении касате1" чой
к траектории движения, сохраняя величину и направ-
направление скорости, которую имела в момент «освобож-
«освобождения». Ясно?
Вася. Не совсем. Я забыл, что такое траектория.
Сергей. Так называют кривую, по которой дви-
движется частица.
Вася. Да, верно! Теперь все ясно.
Сергей. Попробуй применить этот закон к на-
нашему случаю.
Вася. Зачем?
Сергей. Ты получишь неожиданный результат.
Вася. Ладно. (Подумав.) Путь комочка грязи
будет иметь такой вид (тут Вася начертил рисунок,
вроде нашего рис. 1, только велосипед у него полу~
чился гораздо хуже, чем нарисованный здесь). Зна-
Значит, комочек, отделившись, например, в точке А, бу-
будет двигаться в направлении касательной к ободу ко-
колеса и опишет вот эту кривую линию (показывает).
Рис. 1. Верно ли?
По такому же пути полетит камень, если его бросить
наклонно.
Сергей. Эта кривая называется параболой.
Вася (продолжая). Даже комочек, прилипший к
колесу сильнее и поднявшийся до положения В
(рис. 1), не догонит велосипедиста: он будет двигать-
ся вертикально. А выше комок грязи не подымется.
Ему помешает щиток.
Сергей. Что же будет, если велосипедист замед-
замедлит ход?
Вася. Велосипедист может даже совсем остано-
остановиться — все равно грязь на него не попадет... Что за
чепуха получилась! Ведь грязь-то еще как здорово
попадает на спину!
Сергей. Я говорил, что получится неожиданный
результат!
Вася. В чем дело? Не понимаю...
Сергей. Все дело в том, что ты неправильно
рассуждаешь. Давай, рассмотрим внимательнее два-
жение велосипедного колеса. Пусть это колесо катит-
катится направо. (Сергей нарисовал колесо, изображенное
на рис. 2 слева, и отложил от центра вправо стрелку
v.) Будем считать, что скорость велосипедиста v м/с,
а радиус колеса г м. Полный оборот колесо сделает
тогда, когда его центр продвинется вперед на длину
/
Рис. 2. Сложное движение велосипедного колеса.
всей окружности колеса, т. е. на расстояние, равное
2я/ (рис. 2). Обозначим время полного оборота через
х. Тогда получим:
за х секунд центр колеса пройдет 2кг метров,
за 1 секунду » » » v ».
Следовательно:
2ял
х = —— секунд.
Итак, один оборот колесо делает за —— секунд;
сколько же оборотов оно сделает в секунду?
Вася. Дай, я сам подсчитаю. Пусть у—число
оборотов колеса в секунду. Теперь нужно составить
пропорцию. Рассуждаем так:
, „ 1ш
1 ооорот колесо делает за секунд,
у оборотов колесо делает за 1 секунду.
Получается пропорция
1=0 = —:1
Так?
Сергей. Так!
Вася. Значит, У=-^г оборотов в секунду!
Сергей. Правильно! Мы видим, что колесо ве-
велосипеда совершает сложное движение: оно движется
поступательно с постоянною скоростью v м/с и при
v а
этом равномерно вращается, делая -^г оборотов в
секунду. Ну-ка, вспомни, как найти скорость точки,
принимающей участие в двух движениях?
Вася. Это я знаю! Нужно скорости обоих движе-
движений сложить по правилу параллелограмма.
Сергей. Верно! Рассмотрим теперь какую-ни-
какую-нибудь точку А на ободе колеса
в какой-то момент движения.
{Рис. 3.) Эта точка принимает
участие, во-первых, в посту-
поступательном движении, — зна-
значит, она имеет горизонталь-
горизонтальную скорость v м/с. Но эта же
точка участвует и во враща-
вращательном движении и имеет в
нем сбою, вторую скорость.
Как ее подсчитать?
Вася. Сейчас подсчитаю.
В одну секунду колесо делает
v-Лиг оборотов. При каж-
каждом обороте точка А на ободе
проходит путь, равный длине обода, т. е. 2лг метров.
Значит, за одну секунду, когда колесо сделает v
оборотов, точка А пройдет -$-
Рис. 3. Сложение скоро-
скоростей поступательного и
вращательного движе-
движений.
2яг
2nr = v метров. Вы-
ходит, что эта вторая скорость будет тоже v м/с.
Рис. 4. Путь комка грязи, отскочившего от колеса.
Сергей. Именно так. Скорость точки обода при
вращении колеса тоже равна v м/с; но скорость по-
поступательного движения направлена по горизонтали,
тогда как эта вторая скорость — по касательной к
ободу. Итоговая скорость будет направлена по диа-
гонали параллелограмма с равными сторонами (т. е.
по диагонали ромба), как это и видно на рисунке
{рис. 3, стрелка АВ). Ясно?
В ася. Да.
Сергей. Теперь, Вася, обрати внимание на ко-
комочек грязи, достигший положения С (рис. 4). Его
скорость будет составлена из горизонтальной скоро-
скорость, разной v, и вертикальной скорости, разной тоже v.
Итоговая скорость будет равна v у 2 (по теореме
Пифагора), а направлена она будет под углом 45° к
горизонту.
Комочек грязи будет двигаться, как камень, бро-
брошенный под углом в 45° к горизонту (па параболе,
изображенной штриховой линией на рис. 4). По инер-
инерции он и дальше сохранит горизонтальную состав-
составляющую скорости, равную v*). Догонит ли он вело-
велосипедиста?
Вася. Нет.
Сергей. А если велосипедист замедлит хоч?
Вася. Тогда грязь шлепнется ему на спину!
Сергей. Так на деле и бьшает?
Вася. Да. Третьего дня я вернулся с велосипед-
велосипедной прогулки весь в грязи.
Сергей. Значит, все ясно?
Вася (подумав). Ну, нет! По-моему, теперь все
окончательно запуталось! Ведь на рисунке (рис. 4)
видно, что скорость направлена не по касательной к
ободу колеса, а как-то наискось. Начали же мы раз-
разговор с того, что скорость комочка грязи должна
быть направлена по касательной к траектории движе-
движения. Ты сам сказал об этом.
Сергей. К траектории движения чего?
Вася. Соответствующей частицы обода, конечно!
Сергей. Совершенно верно! Она по касательной
к этой траектории и направлена.
Вася. Не понимаю. По-моему рисунки C и 4)
этому противоречат.
Сергей. Нисколько. Подумай.
Подумаем и мы вместе с Сергеем и Васей, на чем
основано это кажущееся противоречие. Подумаем, ка-
какую траекторию (какую кривую) описывает каждая
*) Д.пя упрощения расчетов здесь че учитывается сопротив-
сопротивление воздуха. Это не очень искажает результат.
частица обода велосипедного колеса при движении
велосипеда.
Центр велосипедного колеса равномерно движется
по прямой линии. Само колесо равномерно вращает-
вращается. Какую кривую описывает при этом каждая точка
обода колеса? Если бы центр был неподвижен, то все
точки колеса описывали бы окружности. Но центр
движется, и соответствующие окружности «разма-
«размазываются», «вытягиваются». Говоря геометрическим
языком, — выясним, какую кривую описывает каж-
каждая точка окружности, катящейся без скольжения по
прямой линии. Частица грязи будет двигаться по ка-
касательной не к ободу колеса, а по касательной к
зтой именно кривой. Эта-то кривая и называется цик-
циклоидой.
Что же такое циклоида?
Начнем с опыта. Выпилим из фанеры или выре-
вырежем из толстого картона круг, у самого его края
проколем шилом дырку и вставим в нее кусочек ка-
карандашного графита. Положив линейку на лист бу-
бумаги, будем катить вдоль нее наш кружок, плотно
4 Для,шла
Рис. 5. Пособие для демонстрации циклоиды
прижимая его к бумаге. Кусочек графита и начертит
нам циклоиду. На рис. 5 изображен демонстрацион-
демонстрационный прибор, которым пользуются на лекциях, когда
говорят о циклоиде. У вертикальной черной доски
сделана снизу горизонтальная закраина. По этой за-
закраине катится массивный железный обруч, вроде
тех, которые любят «гонять» малые ребятишки.
В толще этого обруча имеется отверстие, и туда
можно вставить кусок мела. Когда обруч катится по
закраине, мел описывает циклоиду. Рис. 5 дает пред-
представление о форме этой красивой кривой линии.
Построим теперь циклоиду «по точкам». Поста-
Постараемся сделать это возможно аккуратнее. Проведем
(рис. 6) прямую АВ и у левого ее конца начертим
круг радиуса а, касающийся нашей прямой АВ в
точке К. Проще всего поступить так: на расстоянии а
от прямой АВ провести прямую МР, ей параллель-
параллельную (эта прямая все равно нам еще понадобится).
Отметив недалеко от левого конца отрезка МР точку
Рис. 6. Построение циклоиды по точкам.
О, начертим окружность радиуса а с центром О. Эта
окружность непременно коснется прямой АВ. Точку
касания обозначим буквою К-
Теперь на прямой АВ отложим от точки К вправо
отрезок, равный длине окружности радиуса а.
Сделать это циркулем и линейкой точно, как извест-
известно, невозможно. Придется ограничиться приближен-
приближенным построением. Если радиус круга равен а, то его
окружность имеет длину 2ла, т. е. приблизительно
2
бус или 6,28 а. Допустим, что прямую МР мы
провели на расстоянии 4 см от прямой АВ. Значит,
у нас а = 4. Поэтому нам придется отложить на АВ
отрезок, равный 4-6,28, т. е. 25 см и 12 мм*). Конец
отрезка обозначим Л8.
Предположим теперь, что начерченный нами кру-
кружок катится по прямой АВ. Центр его перемещается
по прямой МР. Разделим отрезок OOS, равный КА8,
на восемь равных частей. Точка Оу (первая точка де-
деления) соответствует -^ полного оборота. Когда центр
О переместится в Оь радиус ОК повернется на
*) Чертеж на рис. 6 в этой книге сделан в масштабе 1:4 —
на нем а = 1 см. Мы советуем читателю сделать более крупный
чертеж, именно такой, о котором говорится в тексте (а = 4 см).
2 Г. Н. Бермаа
9
360° : 8 = 45°. Строим угол А\ОУК\, равный 45°, и от-
откладываем отрезок О\К\, равный ОК. Точка К\ дол-
должна принадлежать циклоиде. Штриховой линией изо-
изображено положение катящейся окружности, соответ-
соответствующее jr полного оборота.
Рассмотрим теперь точку О2 — центр круга, по-
2 1 „
вернувшегося на -g- = -^окружности. Делаем построе-
построение точно такое, как в предыдущем случае, только
360
угол А2О2К2 строим равным 2 .——.-=90°. Получим
принадлежащую циклоиде точку Къ Для построения
следующей точки циклоиды при центре О3 строим
яво
угол, равный 3 • -^—— = 135°, и откладываем отрезок
ОзКз, равный ОК.
Построение точек Ка, К*,, Кб, Ki ясно. Точка Ks со-
совместится, очевидно, с точкою Ав. Соединив все по-
полученные таким путем точки плавной кривою (от
руки), мы и получим циклоиду. Читатель сообразит
сам, как построить промежуточные точки, если полу-
полученная кривая покажется ему недостаточно плавной.
Можно с самого начала делить основной отрезок
(длину катящейся окружности) не на 8, а, например,
на 12 частей. Тогда вместо углов, равных 45е, 90е,
135° и т. д., придется строить углы, равные 30е, 60°,
90е, 120° и т. д. (Советуем читателю поупражняться
в построении циклоид разной величины, т. е. давая
разные значения радиусу а, и с помощью различного
числа вспомогательных точек деления.)
Заметим, что, подобно прямой линии, мы представ-
представляем себе циклоиду бесконечной кривой. Мы предпо-
предполагаем, что круг (его называют производящим кругом)
катится по прямой (направляющей прямой) неогра-
неограниченно долю. При этом получится кривая, состоя-
состоящая из бесконечного ряда арок (на нашем рис. 7
изображены две полные арки и часть третьей). От-
Отдельные арки соединяются в точках (остриях), в ко-
которых имеют общую (вертикальную) касательную.
Эти точки называются точками возврата циклоиды
(рис. 8). Они соответствуют самым низким положе-
положениям той точки на катящейся окружности, за кото-
которой мы следим и которая описывает циклоиду. Са-
Самые высокие положения находятся посредине между
10
точками возврата; эти «наивысшие» точки называют-
называются вершинами циклоиды (на рис. 6 одна из вершин
циклоиды находится в точке Ка, укажите все вер-
вершины на рис. 7). Отрезок прямой линии между дву-
двумя соседними точками возврата, равный 2яа, назы-
называется основанием циклоиды (точнее — основанием
одной арки циклоиды).
Рис. 7. Обшпй рид циклоиды.
Какие же задачи возникают при изучении цик-
циклоиды? Прежде всего, нужно дать ей чисто геомет-
геометрическое определение, независимое от механики. Да-
Веримп
Рис. 8. Элемент циклоиды (изображена одна арка).
лее, нужно изучить ее свойства, научиться проводить
к ней касательную, вычислять площадь, ограничен-
ограниченную аркой циклоиды и ее основанием, длину дуги,
объем тела, образованного вращением арки циклои-
циклоиды вокруг направляющей прямой. Попутно мы изу-
изучим кривые, родственные циклоиде, познакомимся с
чисто геометрическими их применениями и с приме-
применениями в смежных областях. Но прежде чем пе-
перейти ко всему этому, сделаем короткий историче-
исторический обзор.
Немного истории
Первым, кто стал изучать циклоиду, был Галилео
Галилей A564—1642)— знаменитый итальянский
астроном, физик и просветитель. Он же придумал
2- И
название «циклоида», что значит: «напоминающая о
круге». Сам Галилей о циклоиде ничего не писал, но о
его работах в этом направлении упоминают ученики
и последователи Галилея: Вивиани, Торичелли и дру-
другие. Торичелли — известный физик, изобретатель ба-
барометра-— уделял немало времени и математике.
В эпоху Возрождения не было узких ученых-специа-
ученых-специалистов. Талантливый человек занимался и филосо-
философией, и физикой, и математикой и всюду получал
интересные результаты и делал крупные открытия.
Немного позже итальянцев за циклоиду принялись
французы, назвавшие ее «рулеттой» или «трохоидой».
В 1634 году Роберваль — изобретатель известной си-
системы весов — вычислил площадь, ограниченную ар-
аркой циклоиды и ее основанием. Подробнее об этом,
а также об открытиях других ученых, связавших свое
имя с циклоидой, мы расскажем ниже. А сейчас уде-
уделим немного места, так сказать, предыстории циклои-
циклоиды, — замечательным исследованиям древних мудре-
мудрецов; мы увидим, что эти исследования имели к цик-
циклоиде известное отношение.
Великий античный философ — «отец логики» —
Аристотель из Стагиры C84—322 годы до н. э.),
занимаясь логическим обоснованием понятия движе-
движения, рассматривал, между прочим, следующий пара-
парадокс. Пусть кружок, изображенный на рис. 9 жирной
л м м1 в
Рис. 9. Парадокс Аристотеля.
линией, катится по прямой АВ. Когда кружок этот
сделает полный оборот, точка М вернется на прямую
АВ и займет положение М\. При этом, как мы знаем,
отрезок ММХ будет равен длине «жирной» окружно-
окружности. Рассмотрим начерченный кружок с центром О,
изображенный тонкой линией. Когда точка М придет
в положение Мь этот маленький кружок тоже сде-
сделает полный оборот и его точка К придет в положе-
положение К\. При этом в каждый момент времени какая-то
12
одна единственная точка маленькой окружности сов-
совмещается с единственной же точкой отрезка КК\.
Каждой точке окружности соответствует единствен-
единственная точка отрезка и каждой точке отрезка — един-
единственная точка окружности. Поэтому напрашивается
вывод: длина маленькой «тонкой» окружности равна
длине отрезка КК\ = ММи т. е. равна длине боль-
большой («жирной») окружности. Итак, круги различ-
различных радиусов имеют окружности одинаковой длины!
В этом и состоит парадокс Аристотеля.
Рис. 10. Взаимно одно-
однозначное соответствие.
Рис. 11. К парадоксу
Аристотеля.
Ошибка здесь в следующем. Из того, что каждой
точке окружности радиуса О К соответствует един-
единственная точка отрезка КК\, вовсе не следует, что
длина этой окружности равна КК\. Так, например,
на рис. 10 точки отрезка АВ приведены при помощи
лучей, проходящих через точку D, во «взаимно одно-
однозначное» соответствие с точками вдвое большего от-
отрезка СЕ, но никому в голову не придет утверждать,
что отрезки АВ и СЕ имеют одинаковую длину! Это
же относится не только к отрезкам прямых, но и кри-
кривых линий. Парадоксу Аристотеля можно придать
следующую, более грубую, а потому и более ясную
форму: рассмотрим две концентрические окружности
(рис. 11). На них «поровну» точек: соответствующие
точки соединены на рис. 11 прямыми линиями (ра-
(радиусами). И все же никто не станет утверждать, что
длины этих окружностей одинаковы.
Сравнение рисунков 6 и 9 приводит нас к очень
важному выводу. Возможны два типа качения ок-
окружности по прямой. Один тип имеет то свойство,
что в любой момент времени (при любом положении
13
производящего круга) длина душ К\АУ на рис. 6
равна длине отрезка КЛ\. Для др^юго тила качений,
изображенного на рис. 9, где малый круг радиуса ОК
катится по прямой КК\, это свойство не выполняется.
В первом случае говорят, что окружность катится
по прямой без скольжения. Во втором говорят,
что окружность не только катится, но и скользит
j,o пряЛшй АВ. Чтобы получить циклоиду, нужно рас-
рассматривать качение без скольжения. О кривых, кото-
которые получаются при качении со скольжением, мы
расскажем позже.
Аристотель рассматривал именно то движение, ко-
которое через 1900 лет привело Галилея к открытию
циклоиды; но он не заинте-
заинтересовался кривыми, кото- ~у*-
рые вычерчиваются точка- I
ми окружности катящегося ,}
м'[м
Рис. 12. Прямое движение пла-
планеты Марс.
Рис. 13. Попятное дви-
движение планеты Марс.
круга. Выдающийся астроном античности, живший
позже, — Птолемей Александрийский (II век н.э.) —
подошел к одной из «родственниц» циклоиды (так
называемой «эпициклоиде») значительно ближе.
Посмотрим теперь, какими нам представляются
движения планег, например Марса, по небесному
своду. Когда Земля и Марс расположены, как пока-
показано на рис. 12, и Земля из положения 3 переходит
в положение 5', а Марс — из положения М в М', то
наблюдателю на Земле будет казаться, что Марс
перемещается между звездами в направлении, обрат-
обратном движению часовой стрелки. Именно так
обычно и выглядит движение Марса. Но в противо-
противостоянии (рис. 13), когда Земля из положения 3 пе-
14
реходит в положение 3', а Марс—из положения М
в положение М', создается впечатление, что Марс
движется среди звезд по часовой стрелке. Эго
«попятное» движение планет было известно астроно-
астрономам уже в глубокой древности.
Знал о нем и Птолемей. Но он считал Землю не-
неподвижным центром Вселенной и считал, что все
планеты равномерно вращаются вокруг Земли. В его
времена считалось величайшим кощунством припи-
приписывать светилам некруговое и иеравномерное движе-
движение. Как же согласовать равномерное круговое дви-
движение с фактически наблюдаемым время от времени
(близ противостояний) «попятным» движением пла-
планет? Хитроумный Птолемей нашел следующий выход
из положения.
Рис. 14. Птспечеева система мира.
Он допустил, что каждая из планет движется рав-
равномерно по небольшому кружку, который он назвал
«.эпициклом» (слово «эпицикл» можно перевести по-
русски «надкруг»). Центр эпицикла в свою очередь
движется равномерно вокруг Земли. На рис. 14 изо-
изображена птолемеева система мира. Подбирая ра-
радиксы эпицикла и большого крута («деферента»),
Птолемей сумел хорошо согласовать свою теорию с
15
данными наблюдения. Даже полторы тысячи лет
спустя Коперник, поместивший в центр планетной
системы Солнце, не решился отказаться от равномер-
равномерных вращений: и у него планеты двигались по эпн-
гиклам, но центры эпициклов двигались не вокруг
Земли, а вокруг Солнца. Только очень тщательные
наблюдения и измерения Тихо Браге показали несо-
несостоятельность теории равномерных круговых движе-
движений и привели Кеплера к открытию неравномерного
эллиптического движения планет.
Что же представляли собою пути планет с точки
зрения Птолемея? Это были кривые, очень близкие
Рис. 15. Эпициклоида Птолемея.
в циклоиде. В случае циклоиды точка равномерно
вращается по окружности, а центр окружности, в
свою очередь, движется по прямой (читатель сооб-
сообразит сам, что при этом получится та же самая цик-
циклоида, что и при качении окружности по прямой).
У Птолемея точка движется по окр\жности, а се
центр движется также по окружности. Ясно, что по-
получится кривая, близкая по своим свойствам к цик-
циклоиде. Эту кривую называют эпициклоидой (рис. 15),
Мы о ней еще будем говорить.
ГЛАВА II
ВАЖНЕЙШИЕ СВОЙСТВА ЦИКЛОИДЫ
«На второе был подан пнрог
в форме циклоиды ..»
Дж. Свифт Путешествия Гулливера,
Касательная и нормаль к циклоиде
Наиболее естественным определением окружности
будет, пожалуй, следующее: «окружностью называет-
ся путь частицы твердого тела, вращающегося вок-
вокруг неподвижной оси». Это определение наглядно,
из него легко вывести все свойства окружности, а
главное, оно сразу рисует нам окружность, как не-
прерывную кривую, чего вовсе не видно из классиче-
ского определения окружности, как геометрического
места точек *") плоскости, равноудаленных от одной
точки.
Почему же в школе мы определяем окружность,
к? к геометрическое место точек? Чем плохо определе-
определение окружности с помощью движения (вращения)?
Подумаем об этом.
Когда мы изучаем механику, мы не занимаемся
доказательством геометрических теорем: мы считаем,
что уже знаем их — мы просто ссылаемся на геомет-
геометрию, как на нечто уже известное. Если и при доказа-
доказательстве геометрических теорем мы будем ссылаться
") То есть мюжества всех тех и только тех точек, которые
удовлетворяют заданному условию (здесь удаленности на за-
заданное расстояние от заданной точки).
17
на механику, как на нечто уже известное, то сде-
сделаем ошибку, которая называется «логический (по-
(порочный) круг»: при доказательстве предложения А
мы ссылаемся на предложение В, а само предложе-
предложение В обосновываем с помощью предложения Л.
Грубо говоря, Иван кивает на Петра, а Петр на Ива-
Ивана. Такое положение при изложении научных дис-
дисциплин недопустимо. Поэтому стараются, излагая
арифметику, не ссылаться на геометрию, излагая
геометрию, не ссылаться на механику и т. д. При
этом можно при изложении геометрии безбоязненно
пользоваться арифметикой, а при изложении меча-
ники — и арифметикой, и геометрией, лошческого
круга не получигся.
Определение циклоиды, с которым мы успели по-
познакомиться, никогда не удов четь фяло ученых: ведт>
оно опирается на механические понятия — скорости,
сложения движений и т. д. Поэтому геометры всегда
стремились дать циклоиде чисто геометрн\егкое оп-
определение. Но для того, чтобы дать такое определе-
определение, нужно прежде всего изучить основные свойства
I. жлоиды, пользуясь ее механическим on,j делением.
Выбрав наиболее простое и характерное из этик
свойств, можно положить его в основ) геометриче-
геометрического определения.
Начнем с изучения касательной и нормали к цик-
циклоиде. Чго такое касательная к кривой линии, каж-
каждый представляет себе достаточно ясно; точно оп-
определение касательной дается в к>рсах высшей
Рис. 16. Касательная и нормать к кривой.
математики, и мы его приводить здесь не б\дем. Ноп-
малью называется перпендикуляр к касательной, вос-
восставленный в точке касания. На рис. 16 изображена
касательная и нормаль к кривой АВ в ее точке М
Рассмотрим циклоиду (рис. 17). Кружок кати я
по прямой АВ. Допустим, что вер шкальный радикс
18
круга, проходивший в начальный момент через ниж-
нижнюю точку циклоиды, \спел повернуться на угол ф
(греческая буква «фи») и занял положение ОМ.
Иными словами, мы считаем, что отрезок М0Т состав-
составляет такую долю отрезка МСМ\, какую угол <р со-
составляет от 360° (от полного оборота). При этом
Ма Т
Рис. 17. Касательная к циклоиде.
точка Мо пришла в точку М. Точка М и есть интере-
интересующая нас точка циклоиды.
Стрелочка ОН изображает скорость движения
центра катящегося круга. Такой же горизонтальной
скоростью обладают все точки круга, в том числе и
точка М. Но, кроме того, точка М принимает участие
во вращении круга. Скорость МС, которую точка М
на окружности получает при этом вращении, направ-
направлена по касательной МС\ к окружности, т. е. перпен-
перпендикулярно к радиусу ОМ. Мы уже знаем из «разго-
«разговора двух вечосипедистов» (см. стр. 6), что скорость
МС по величине равна скорости МР (т. е. скорости
ОН). Поэтому параллелограмм скоростей в случае
нашего движения будет ромбом (ромб МСКР на
рис. 17). Диагональ МК этого ромба как раз и даст
нам касательную к циклоиде.
Теперь мы можем ответить на вопрос, поставлен-
поставленный в конце беседы Сергея и Васи (стр. 7). Комок
грязи, оторвавшийся от велосипедного колеса, дви-
жется по касательной к траектории той частицы ко-
колеса, от которой он отделился. Но траекторией будет
не окружность, а циклоида, потому что колесо не
просто вращается, а катится, т. е. совершает движе-
движение, состоящее из поступательного движения и вра-
вращения.
Все сказанное дает возможность решить следую-
следующую «задачу на построение»: дана направляющая
19
прямая АВ циклоиды, радиус г производящего круга
и точка М, принадлежащая циклоиде (рис. 17). Тре-
буетсл построить касательную МК к циклоиде.
Имея точку М, мы без труда строим производя-
производящий круг, в том его положении, когда точка на ок-
окружности попадает в М. Для этого предварительно
найдем центр О при помощи радиуса МО = г (точка
О должна лежать на прямой, параллельной АВ на
расстоянии г от нее). Затем строим отрезок МР про-
произвольной длины, параллельный направляющей пря-
прямой. Далее строим прямую МСЬ перпендикулярную к
ОМ На этой прямой откладываем от точки М отре-
отрезок МС, равный МР. На МС и МР, как на сторонах,
строим ромб. Диагональ этого ромба и будет каса-
касательной к циклоиде в точке М.
Это построение — чисто геометрическое, хотя по-
получили мы его, используя понятия механики. Теперь
мы можем проститься с механикой и дальнейшие
следствия получать без ее помощи. Начнем с простой
теоремы.
Теорема 1. Угол между касательной к циклои-
циклоиде (в произвольной точке) и направляющей прямой
равен дополнению до 90° половины угла поворота ра-
радиуса производящего круга.
Иными словами, на нашем рис. 17 угол KLT ра-
равен 90° — Z Л2'0Г или z. КМР = 90° — I". Это равен-
равенство мы теперь докажем. Для сокращения речи ус-
условимся угол <р поворота радиуса производящего
круга называть «основным углом». Значит, угол МОТ
на рис. 17 — основной угол. Будем считать основной
угол острым. Читатель сам видоизменит рассуждения
для случая тупого угла, т. е. для случая, когда катя-
катящийся круг сделает больше четверти полного обо-
оборота.
Рассмотрим угол СМР. Сторона СМ перпендику-
перпендикулярна к ОМ (касательная к окружности перпендику-
перпендикулярна к радиусу). Сторона МР (горизонталь) пер-
перпендикулярна к ОТ (к вертикали). Но угол МОТ, по
лсловию, острый (мы условились рассматривать пер-
первую четверть оборота), а угол СМР — тупой (по-
(почему?). Значит, углы МОТ и СМР составляют в сум-
сумме 180° (углы со взаимно перпендикулярными сторо-
сторонами, из которых один острый, а другой — тупой},
20
Итак, угол CMP равен 180° — ф Но, как известно,
диагональ ромба делит угол при вершине пополам.
Следовательно, угол КМР — 90° — ~, что и требова-
требовалось доказать.
Обратим теперь внимание на нормаль к циклоиде.
Мы говорили уже, что нормалью к кривой называет-
называется перпендикуляр к касательной, проведенный в точке
касания (рис. 16). Изобразим лев\ю часть рис. 17
крупнее, причем проведем нормаль ME (ME _L МК\
см. рис. 18).
Из рис. 18 следует, что угол ЕМР равен разности
углов КМЕ и КМР, т. е. равен 90° — Z. КМР. Но мы
Г В
Рис. 18. К теореме 2.
только что доказали, что сам }гол КМР равен 90° —
— ~. Таким образом, получаем:
Z РМЕ = 90° — Z. КМР = 90° — (90° ~ f) = f •
Мы доказали простую, но полезную теорему. Да*
Л им ее формулировку:
Теорема 2. Угол между нормалью к циклоиде
(в любой ее точке) и направляющей прямой равен
половине «основного угла».
(Вспомним, что «основным углом» называется
угол поворота радиуса катящегося круга )
Соединим теперь точку М («текущую» точку цик^
лоиды) с «нижней» точкой (Т) производящего круга
(с точкой касания производящего круга и направ-
21
ляющей прямой — см. рис. 18). Треугольник МОТ,
очевидно, равнобедренный (ОМ и ОТ — радиусы про-
производящего круга). Сумма углов при основании этого
треугольника равна 180° — ф, а каждый из углов
при основании — половине этой суммы. Итак,
Z-ОМТ = 90° ~ |--
Обратим внимание на угол РМТ. Он равен раз-
разности углов ОМТ и ОМР. Мы видели сейчас, что
Z.OMT равен 90°—~\ что касается угла ОМР, то
нетрудно выяснить, чему он равен. Ведь угол ОМР
равен углу DOM (внутренние накрест лежащие углы
Рис. 19. Основные свойства касательной и нормали к циклоиде.
при параллельных). Непосредственно очевидно, что
ZDOM равен 90° —ф. Значит, ZOMP = 90° — ф.
Таким образом, получаем:
Z РМТ = Z ОМТ - Z ОМР =
Получается замечательный результат: угол РМТ
оказывается равным углу РМЕ (см. теорему 2). Сле-
Следовательно, прямые ME и МТ сольются! Наш рис. 18
сделан не совсем правильно! Правильное расположе-
расположение линий дано на рис. 19.
Как же сформулировать полученный результат?
Мы сформулируем его в виде теоремы 3.
Теорема 3 (первое основное свойство
циклоиды). Нормаль к циклоиде проходит через
«нижнюю» точку производящего круга.
Из этой теоремы получается простое следствие.
Угол между касательной и нормалью, по определе-
определению, — прямой. Это угол, вписанный в окружность
22
производящего круга. Поэтому он должен опираться
на диаметр круга. Итак, ТТ\ — диаметр, и Т\ — «верх-
«верхняя» точка производящего круга. Сформулируем по-
полученный результат.
Следствие (второе основное свойство
циклоиды). Касательная к циклоиде проходит че-
через «верхнюю» точку производящего круга.
Воспроизведем теперь построение циклоиды по
точкам, как мы это делали на рис. 6. На рис. 20 ос-
основание циклоиды разделено на 6 равных частей;
Рис. 20. Циклоида — огибающая своих касательных.
чем число делений будет больше, тем, как мы знаем,
чертеж получится точнее. В каждой точке циклоиды,
построенной нами, проведем касательную, соединяя
точку кривой с «верхней» точкой производящего кру-
круга. На нашем чертеже получилось семь касательных
(из них две — вертикальные). Проводя теперь цик-
циклоиду от руки, будем заботиться, чтобы она действи-
действительно касалась каждой из этих касательных: это
значительно увеличит точность чертежа. При этом
сама циклоида будет огибать все эти касатель-
касательные *).
Проведем на том же рис. 20 нормали во всех най-
найденных точках циклоиды. Всего будет, не считая на-
направляющей, пять нормалей. Можно построить от
р\кн сгибающую этих нормалей. Если бы мы вместо
') Такая линия и называется «огибающей». Всякая кривая
линия есть огпбаюшая своих касательных.
23
шести взяли 12 или 16 точек деления, то нормалей на
чертеже было бы больше, и огибающая наметилась
бы ясней. Такая огибающая всех нормалей играет
важную роль при изучении свойств любой кривой ли-
линии. В случае циклоиды обнаруживается любопыт-
любопытный факт: огибающей нормалей циклоиды служит
точно такая же циклоида, только сдвинутая на 2а
вниз и на па вправо. С этим любопытным результа-
результатом, характерным именно для циклоиды, нам еще
придется иметь дело.
Свойства касательной и нормали к циклоиде были
впервые изложены Торичелли A608—1647) в его
книге «Геометрические работы» A644 год). Торичел-
Торичелли использовал при этом сложение движений. Не-
Несколько позже, но полнее, разобрал эти вопросы Ро-
берваль (псевдоним французского математика Жил-
ля Персонна, 1602—1672). Свойства касательной к
циклоиде изучал также Декарт; он изложил свои ре-
результаты, не прибегая к помощи механики.
Геометрическое определение циклоиды
Теперь мы дадим определение циклоиды как гео-
геометрического места точек, не пользуясь механикой.
Проще всего поступить так. Рассмотрим произволь-
произвольную прямую АВ (будем условно считать ее направ-
направление горизонтальным) и на ней точку Мо. Далее
рассмотрим всевозможные круги определенного ра-
радиуса, касающиеся этой прямой и расположенные по
одну сторону от нее. На каждом круге от точки Т ка-
касания его с прямой АВ отложим (в направлении к
точке Мо) дугу ТМ, по длине равную отрезку М0Т.
Геометрическое место точек М (взятых на всех упо-
упомянутых нами кругах) и будет циклоидой.
Неправда ли, какое тяжеловесное определение!
Насколько нагляднее определение с помощью движе-
движения! А в сущности, ведь ничего не изменено. Просто
слова из механики заменены словами из геометрии.
Выиграли мы при этом очень много: мы говорили
уже, что геометрические факты следует излагать, не
опираясь на механику, чтобы избежать в дальнейшем
«логического круга». Но многое мы и потеряли. Если
бы мы захотели, пользуясь только этим определе-
определением, вывести свойства касательной и нормали к цик-
24
лоиде, мы столкнулись бы с большими трудностям».
Недаром Торичелли и Роберваль не смогли их пре-
преодолеть и обратились к механике. Декарту в его чи-
чисто геометрическом изучении циклоиды помог им же
открытый необычайно мощный метод геометрических
исследований — метод координат *).
Установим еще одно важное свойство циклоиды и
попробуем именно его положить в основу изучения
этой кривой.
Рассмотрим треугольник МТТ\ (рис. 21), образо-
образованный вертикальным диаметром производящего кру-
круга, касательной к циклоиде и нормалью к ней. Угол
Л Но Е Г\ "~~~В
Рис. 21. Связь между «высотой» и наклоном касательной.
МТ{1, как вписанный в окружность, равен половине
центрального угла, опирающегося на ту же дугу, т. е.
равен |-. Проведем МК\\АВ и ME ± AB. ОтрезокМЕ
будет играть в дальнейшем значительную роль, по-
поэтому дадим ему имя и обозначение: будем называть
его «в ы с о т о ю» точки М циклоиды и обозначать
буквою h. Итак, высота точки М циклоиды — это рас-
расстояние ее от направляющей прямой.
Обратим внимание на угол КМТ. Он равен углу
МТ{Г (почему?). Из треугольника ТМТ\ получаем:
МТ = 2а sin %,
*) Об этом методе можно прочесть в замечательной книге
Л С Понтрягина «Метод координат» (М.: Наука, 1977).
3 Г. Н, Берман 25
а из треугольника ТКМ:
КТ = МТ sin f.
Сопоставляя эти результаты и замечая, что КТ — h,
получим окончательно:
ft = 2asin2-|.
Мы выразили высоту точки М через угол между
касательной в точке М и вертикалью (горизонталью
мы по-прежнему считаем направление прямой АВ).
Теперь выразим синус этого угла через «высоту». По-
Получим, очевидно:
где через k обозначена постоянная для данной цик-
циклоиды величина Л/ ¦%—• Полученный результат изло-
изложим словами.
Теорема 4. Синус угла между касательной к
циклоиде в точке М и вертикалью пропорционален
корню квадратному из «высоты» точки М.
Этим свойством обладает, очевидно, любая цик-
циклоида. Возникает вопрос: в какой мере это свойство
характеризует именно циклоиду: будет ли всякая
кривая, обладающая этим свойством, непременно
циклоидой?
Можно доказать, что это будет именно так, — что
верна и следующая (обратная) теорема:
Теорема 5. Если даны прямая АВ и точка М,
то единственной кривой, удовлетворяющей условиям
теоремы 4 и проходящей через точку М, будет цик-
циклоида.
При этом радиус производящего круга этой цик-
циклоиды связан с коэффициентом к, о котором гово-
говорится в теореме 4, следующим соотношением:
(Разумеется, расстояние точки М от АВ должно быть
меньше, чем 2а.)
Строгое доказательство этой теоремы средствами
элементарной математики очень громоздко, и мы его
приводить здесь не будем.
Теорема 5 — очень важная теорема. В физике и
технике часто приходится разыскивать кривую, удов-
удовлетворяющую тем или иным данным условиям. Мы
познакомимся в конце этой книжки с задачей, в ко-
которой требуется найти кривую линию, удовлетворяю-
удовлетворяющую условиям теоремы 5. Й в том, и во всех подоб-
подобных случаях мы можем быть уверены, что искомая
кривая — циклоида.
Если в условии теоремы 5 не оговорить, что иско-
искомая кривая проходит через наперед указанную точку
М, то получится не одна*), а бесконечное множество
циклоид, которые получаются друг из друга парал-
параллельным сдвигом по направлению прямой АВ (одна
из них проходит через точку М, другая — через Ми
третья — через М2 и т. д.). Это множество, или, как
Рис. 22. Семейство циклоид.
его называют, семейство циклоид изображено на
рис. 22.
Отметим еще одно, совершенно очевидное свой-
свойство циклоиды: ее арка симметрична относительно
перпендикуляра, восставленного в середине основа-
основания арки. А затем перейдем ненадолго к другой за-
замечательной кривой, которую изучал Роберваль; он
назвал эту кривую спутницей циклоиды.
Спутница циклоиды и ее разоблачение
Рассмотрим циклоиду (рис. 23). Из ее точки М
опустим перпендикуляр на вертикальный диаметр
производящего круга. Получим точку Р. Проделаем
такое построение для всех без исключения точек цик-
циклоиды (так, точке М2 будет соответствовать точка
Р% вершине циклоиды — сама вершина Р\, остриям —-
острия и т. д. Все это видно на рис. 23). Когда точка
*) Строго говоря, и при точном выполнении условий теоре-
теоремы 5 получается не одна, а две циклоиды. Читатели саки
пол'.'мают, почему это так и как расположена вторая циклоида.
3* 27
М опишет полную арку циклоиды, точка Р тоже опи-
опишет некоторую кривую. Вот эта-то кривая и назы-
называется спутницей циклоиды. Свойства «спутницы»
были изучены Робервалем. Он их использовал для
вычисления площади, ограниченной аркой циклоиды
и ее основанием. Но мы не будем систематически
^ Р.
Рис. 23. Спутница циклоиды.
изучать спутницу. Мы сделаем проще: постараемся
признать в ней нашу старую знакомую.
Рассмотрим циклоиду, точку М на ней и соответ-
соответствующую точку Р на спутнице (рис. 24). Центр про-
К - аср —~
Рис. 24. Спутница циклоиды — синусоида.
изводящего круга обозначим буквою Q. Тогда будем
иметь:
QP = QM cos Z. MQP == a cos A80° — ф) =
= — a cos ф = — a sin (90° — ф) = a sin (ф — 90°).
Начертим геометрическое место центров произво-
производящего круга (прямая Х\Х на рис. 24). От точки
Мо отложим по АВ отрезок М0К, равный — . Прове-
28
дем KY _L XiX. Точку пересечения Х\Х и KY обозна-
обозначим буквою О. Теперь все вспомогательные построе-
построения закончены, и мы можем без труда «выяснять лич-
личность таинственной спутницы», как принято писать
в приключенческих романах.
Отрезок M0R на направляющей прямой от острия
циклоиды (Мо) до точки прикосновения производя-
производящего круга (R) равен оф, где ф — основной угол
MQR, выраженный в радианах*). Отрезок OQ на
горизонтальной оси Х\Х (читатель узнал в прямых
ОХ и OY оси координат, которыми принято пользо-
пользоваться при вычерчивании графиков) равен M0R —
—М0К = а(ц>——J , а отрезок QP равен asmZPMQ,
т. е. равен синусу угла (<р—jj-J, умноженному на ра-
радиус а.
Итак, от точки О по горизонтали откладываются
отрезки, равные по длине дугам окружности, а по
Рис. 25. Построение синусоиды.
вертикали линии синусов соответствующих этим ду-
дугам углов. Мы узнаём известное из курса геометрии
построение обыкновенной синусоиды (рис. 25).
Итак, незнакомка разоблачена! Она оказалась
обычной синусоидой. Но «начало» этой синусоиды
(О) не совпадает с острием циклоиды: оно сдвинуто
на -у • а единиц вправо и на о единиц вверх.
Посмотрим внимательно на рис. 24 и мы сразу
увидим любопытное соотношение между соответ-
соответствующими друг другу точками М и Р циклоиды и
ее спутницы —синусоиды: отрезок МР между соот-
*) Так как M0R = длине душ MR. а длина душ окружности
равна сф, где <р — центральный угол, выраженный в радианах.
29
ветствующими точками циклоиды и ее спутницы ра-
равен полухорде производящего круга. (Хорда прово-
проводится параллельно АВ на расстоянии, равном рас-
расстоянию от АВ до точки М.)
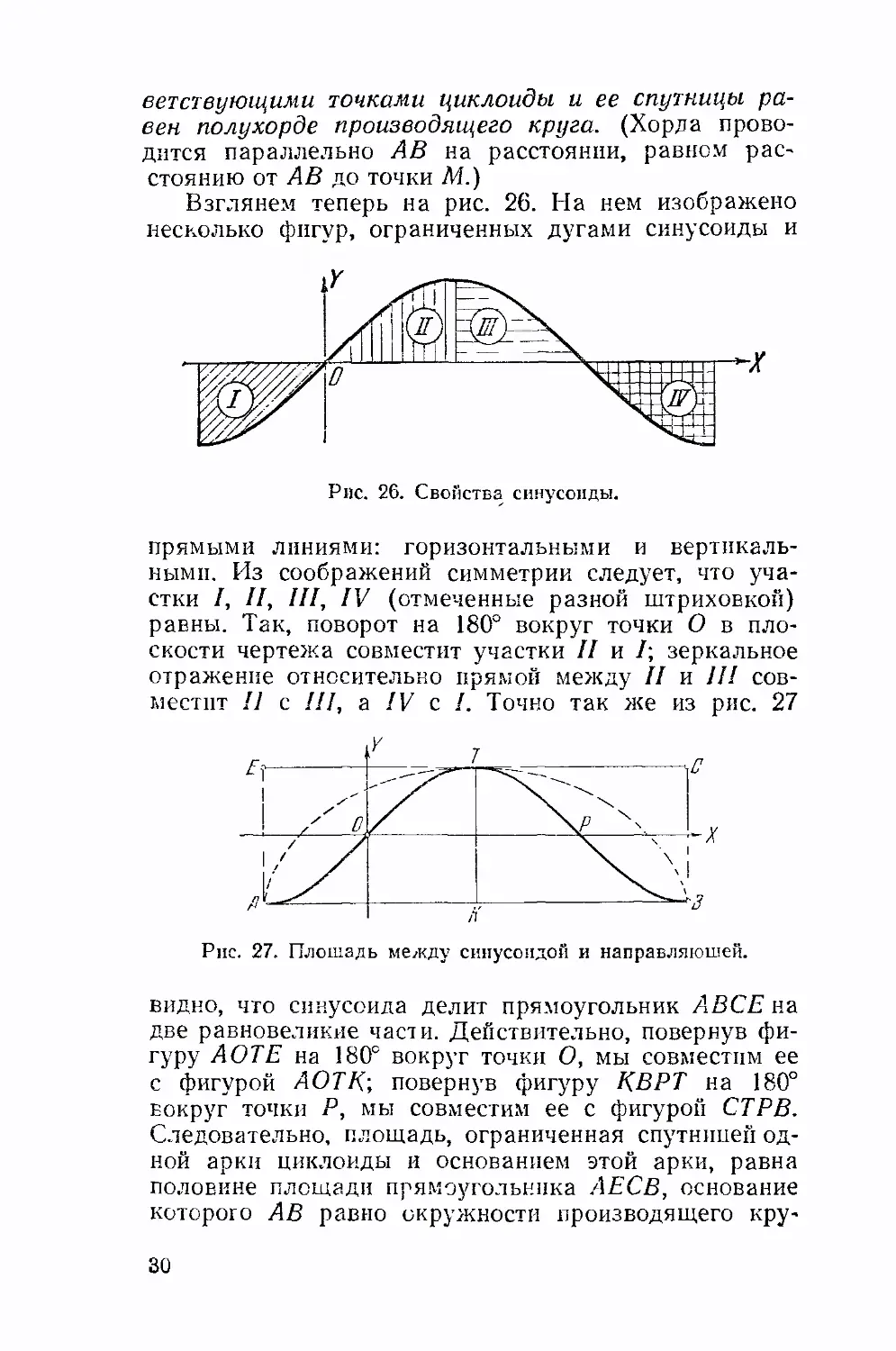
Взглянем теперь на рис. 26. На нем изображено
несколько фигур, ограниченных дугами синусоиды и
О
Рис. 26. Свойства синусоиды.
прямыми линиями: горизонтальными и вертикаль-
вертикальными. Из соображений симметрии следует, что уча-
участки /, //, ///, IV (отмеченные разной штриховкой)
равны. Так, поворот на 180° вокруг точки О в пло-
плоскости чертежа совместит участки // и /; зеркальное
отражение относительно прямой между // и /// сов-
совместит II с ///, а IV с /. Точно так же из рис. 27
Рис. 27. Плошадь между синусоидой и направляющей.
видно, что синусоида делит прямоугольник АВСЕ на
две равновеликие части. Действительно, повернув фи-
фигуру АОТЕ на 180° вокруг точки О, мы совместим ее
с фигурой АОТК; повернув фигуру КВРТ на 180°
Еокруг точки Р, мы совместим ее с фигурой СТРВ.
Следовательно, площадь, ограниченная спутницей од-
одной арки циклоиды и основанием этой арки, равна
половине площади прямоугольника АЕСВ, основание
которого АВ равно окружности производящего кру-
30
га, т. е. 2л«, а высота КТ — диаметру того же круга
Bа). Итак, площадь фигуры АОТРВК (рис. 27) рав-
равна 2л«-2а:2. Обозначив эту площадь буквою S, по-
получим формулу:
5
Словами это можно выразить так: площадь, ограни-
ограниченная спутницей одной арки циклоиды и ее основа-
основанием, равна удвоенной площади производящего круга.
Площадь циклоиды. Теорема Галилея
Теперь мы достаточно подготовлены к тому, чтобы
вычислить площадь, заключенную между аркой цик-
циклоиды и ее основанием. Первое упоминание о вычис-
вычислении такой площади имеется в трудах Вивиани и
Рис. 28. Двухлелесткозая
фигура Робервалл.
Торичелли. Они связывают это вычисление с именем
Галилея — своего учителя; поэтому теорему о пло-
площади циклоиды часто называют теоремой Галилея.
И Торичелли, и Вивиани при вычислениях площа-
площадей, ограниченных кривыми линиями, пользовались
особым приемом, который назывался «способом неде-
неделимых». Этот способ состоял в том, что криволиней-
криволинейную фигуру разбивали на бесконечно тонкие полоски
(«неделимые»), площади которых вычислялись срав-
сравнительно легко, а затем складывались. Этот прием
через полвека привел к изобретению интеграль-
интегрального исчисления*). Мы не будем следовать пути
*) Сущность этих методов доступно изложена ч интересной
и просто написанной книжке И. Б. А б е л ь с о н а «Рождение
логарифмов» (М.; Л.: Гостехиздат, 1948).
31
Торичелли и Внвкани, а изложим иной способ вычис-
вычисления площади — способ Роберваля (несколько уточ-
уточнив его).
Рассмотрим фигуру, ограниченную аркой циклои-
циклоиды и ее спутницей. На рис. 28 эта фигура, состоящая
из двух лепестков, обведена жирной линией. Займем-
Займемся вычислением ее площади.
Прежде всего, построим зеркальное отражение
правого лепестка фигуры относительно направляю-
направляющей прямой АВ (это отражение дано на рис. 28
штриховой линией). Перенесем затем эту штриховую
кривую налево вверх и приложим ее к левому ле-
пестгу так, чтобы дуги синусоид, ъходящие в контур
Рис. 29. Бо что превращается двухлепестксвая фигура.
каждого из лепестков, совпали. Получим выпуклую
фигуру, заштрихованную на рис. 28 и изображенную
отдельно на рис. 29. Установим важнейшие свойства
этой фигуры.
1. Выпуклая фигура М0РЬМ равновелика двухле-
пестковой фигуре, изображенной жирной линией на
рис. 28. Это видно из того, что она «составлена» из
тех же лепестков.
2. Любая горизонтальная хорда выпуклой фигуры
равна удвоенной хорде лепестка, находящейся на
том же расстоянии от АВ. Действительно, хорды СЕ
и РН (рис. 28) правого лепестка, равноудаленные от
линии центров, равны, так как равные им полухорды
производящего круга одинаково удалены от центра
(вспомним, что отрезок между соответствующими
точками циклоиды и ее спутницы равен полухорде
производящего круга, см. стр. 29). Значит, КТ =
= СЕ = РН = Р^Ну = TL.
Это дает важный результат: хорда МР выпуклой
фигуры (рис. 29) равна хорде производящего круга
32
СК, расположенной на том же расстоянии от направ-
направляющей прямой.
Рассмотрим теперь выпуклую фигуру Роберваля и
круг, касающийся тех же прямыхАВ и /lifii (рис.30).
Проведем ряд прямых, параллельных АВ и AiBu и
точки их пересечения с окружностью и с контуром
выпуклой фигуры соединим последовательно прямо-
прямолинейными отрезками, как показано на нашем чер-
чертеже*). Полученные таким образом вписанные много-
многоугольники {HLMNPQRSTK и HyUNhN&^T)
Рпс. 30. Многоугольники, вписанные в круг и в выпуклую
фигуру Роберваля.
мы будем называть «соответственными». Прямые, па-
параллельные АВ, разбивают «соответственные много-
многоугольники на ряд трапеций (и треугольников). Пло-
Площади «соответственных» трапеций в круге и в фигуре
Роберваля, например NPRS и NiPiRiSi, равны, по-
потому что у трапеций этих соответственно равны ниж-
нижние основания, верхние основания (соответственные
хорды) и высоты. На рис. 30 равновеликие «соответ-
«соответственные» трапеции покрыты одинаковой штрихов-
штриховкой.
Будем теперь неограниченно увеличивать число
«промежуточных» прямых, параллельных АВ, так
чтобы расстояние между любой соседней парой стре-
стремилось к нулю. Тогда в круге мы получим серию впи-
вписанных многоугольников, число сторон которых неог-
неограниченно возрастает, а каждая из сторон стремится
*) На этом чертеже надо представить себе также хорды
MN и ST окружности и хорды MiNi и SiTt фигуры Роберваля.
Но они так малы, что на глаз не отличимы от соответствующих
дуг.
33
к нулю. Мы знаем, что площади Sn этих многоуголь-
многоугольников имеют пределом площадь круга:
Urn Sn = па2.
Как будет себя вести при этом последовательность
многоугольников, вписанных в выпуклую фигуру Ро-
берваля? Площадь 2„ последовательных вписанных
многоугольников будет стремиться к площади 2 фи-
фигуры Роберваля. Известно, что если две переменные
величины сохраняют при всех своих изменениях соот-
соответственно равные значения и одна из них стремится
к определенному пределу, то к тому же пределу стре-
стремится и другая. Но каждый многоугольник, вписан-
вписанный в фигуру Роберваля, равновелик «соответствен-
«соответственному» многоугольнику, вписанному в круг. Поэтому
мы заключаем, что предел площадей многоугольни-
многоугольников, вписанных в фигуру Роберваля, равен пределу
площадей соответственных многоугольников, вписан-
вписанных в круг; а это значит, что площадь выпуклой фи-
фигуры Роберваля равна площади производящего
круга:
2 = па2.
Отсюда получаем немедленное следствие: пло-
площадь двухлепестковой фигуры (рис. 28) равна пло-
площади производящего круга.
Взглянем теперь на рис. 27. Площадь фигуры
АОТРВК.А, как мы видели, равна удвоенной пло-
площади производящего круга (площадь между спутни-
спутницей одной арки циклоиды и ее основанием, см.
стр. 31). Площадь двухлепестковой фигуры мы толь-
только что определили: она равна площади производящего
круга. Следовательно, площадь, ограниченная аркой
циклоиды и ее основанием, равна утроенной площади
производящего круга. Этот результат и известен под
названием «теоремы Галилея».
Дальнейшие свойства циклоиды
После площади естественно заговорить о длине
арки циклоиды и об объемах тел, порожденных вра-
вращением этой арки. Сначала поговорим об этих объ-
объемах.
Если арка циклоиды вращается вокруг своего ос-
основания, то она порождает поверхность, ограничи-
24
вающую яйцевидное тело, изображенное на рис. 31.
Разбив это тело на бесконечно тонкие слои, вписав
в эти слои цилиндрики (как это показано на нашем
чертеже) и сложив их объемы, Роберваль получил
Рис. 31. Яйцевидное тело вращения, порожденное циклоидой.
объем всего яйцевидного тела. Не будем повторять
его длинных, утомительных и не вполне строгих вы-
выкладок. В наше время высшая математика позволяет
Рис. 32. Репообразное тело вращения, порожденное циклоидой.
найти этот объем без труда. Сообщим готовый ре-
результат: объем тела, порожденного вращением арки
циклоиды вокруг ее основания, равен 5зт2а3. Вычио
64 2
лена и поверхность этого тела: она равна-д-зтаг.т. е.
более чем в 21 раз превосходит площадь производя-
производящего круга.
35
Роберваль рассматривал также другую поверх-
поверхность, порожденную вращением циклоиды. Он строил
зеркальное отражение арки циклоиды относительно
ее основания, и овальную фигуру, образованную
циклоидой и ее отражением, вращал вокруг оси КТ
(рис. 32). Площадь порождаемой при этом поверх-
поверхности вращения равна 32л2а2, а объем репообразного
тела, ею ограниченного, равен 12л3о3.
Немного позже знаменитый физик Паскаль опре-
определил объемы и центры тяжести тел, образованных
вращением частей циклоиды вокруг различных осей.
H At, Г
Рис. 33. Длина дуги циклоиды.
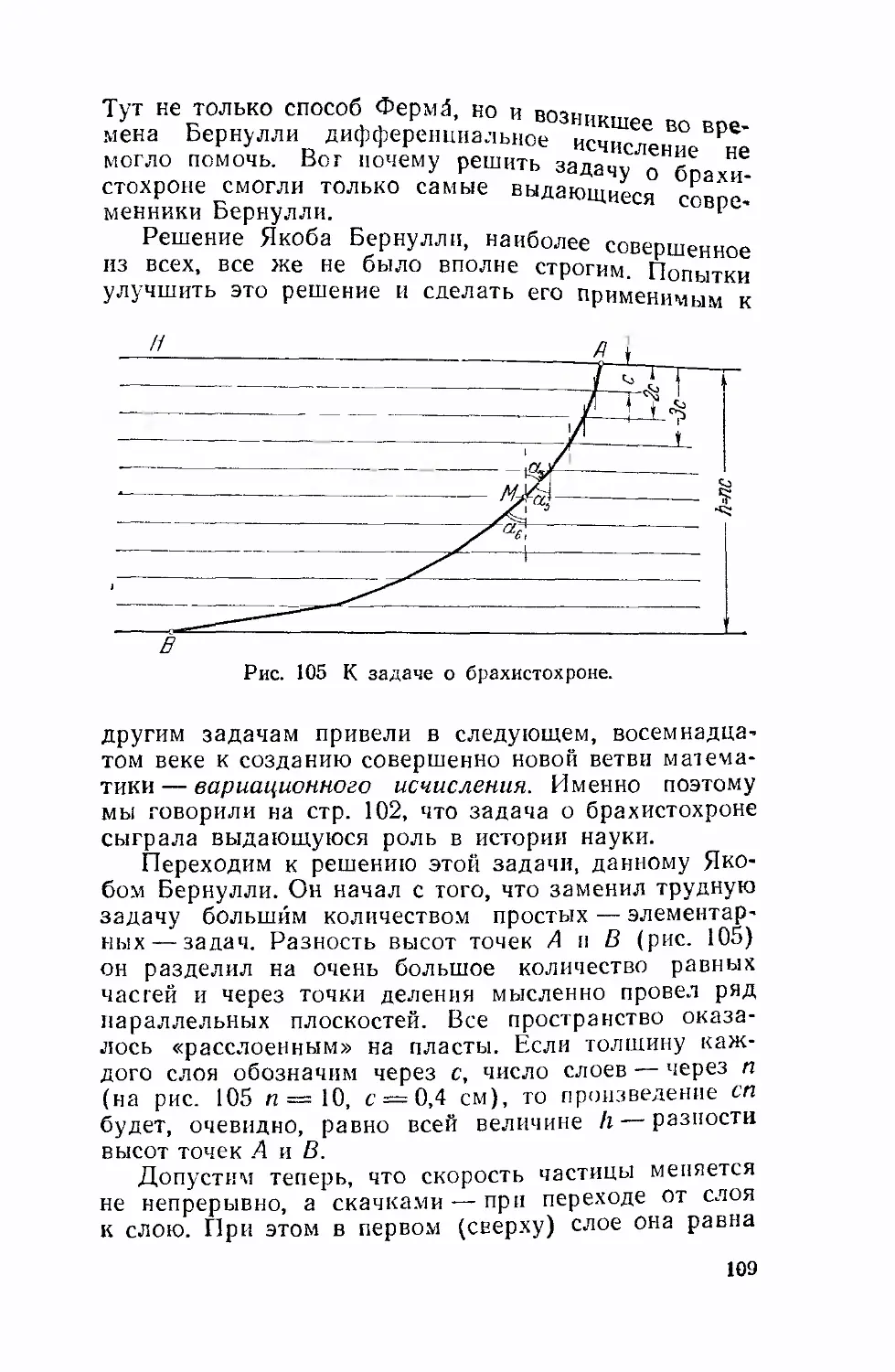
В 1658 году английский архитектор и математик
Рен, строитель знаменитого купола собора св. Пав-
Павла в Лондоне, определил длину дуги циклоиды. Его
открытие произвело тем большее впечатление, что в
то время задача вычисления длин дуг кривых линий
казалась необычайно трудной и была решена бук-
буквально для единичных кривых (для окружности, па-
параболы и некоторых спиралей). Дадим представле-
представление о том пути, по которому шел Рен, опуская под-
подробности доказательства. Впоследствии мы еще
вернемся к вычислению длины дуги циклоиды совер-
совершенно другим способом.
Рен исходил из механических соображений, напо-
напоминающих первые работы Торичелли и Роберваля.
Он рассматривал поворот катящегося (производя-
(производящего) круга на весьма малый угол а около точки Т
(рис. 33). При этом центр круга перемещается из
точки О в точку Ои так что угол ОТО\ равен как раз
а. На тот же угол повернется хорда ТМ, причем точ-
точка М, описав маленькую дужку циклоиды, перейдет
в точку Mi. Мы будем вместе с Реном считать угол а
столь малым, что дугу циклоиды ММ\ невозможно от-
отличить от дуги окружности радиуса ТМ с центром в
точке Т. Значит, длину циклоидальной дужки ММ\
мы будем считать равной МТ-а (предполагается, чго
угол а выражен в радианах). При этом мы созна-
тельно допускаем ошибку, но эта ошибка будет тем
меньше, чем меньше угол а, и в пределе ее влияние
сгладится.
При этом малом повороте треугольник ОМТ пе-
перейдет в треугольник 0<MiT. Сторона ОМ повернется
на тот же угол, что и сторона МТ; таким образом
угол между ОМ и M\Oi, т. е. угол MQMU будет ра-
вен а.
Начертим теперь левее на круге радиуса ОТ с
центром Р радиусы РК\\ОМ и РКЛОфи. Угол KiPK,
очевидно, равен углу а. Хорда /(Я[ параллельна и
равна отрезку касательной к циклоиде в точке М.
Хорда K\Hi не может сильно отличаться от отрезка
касательной к циклоиде в точке М\ — ведь при пере-
переходе от точки М к точке Mj производящий круг сме-
смещается очень немного. Рен допустил (хотя это и свя-
связано с некоторой неточностью), что хорда равна от-
резку касательной к циклоиде в точке Mi.
Угол КНК\ есть вписанный угол, опирающийся на
ту же дугу, что и центральный угол KPKi, равный а;
следовательно, Z/(Я/Ci =-|- Убыль длины хорды
МТ\ = КНх при переходе точки М в положение М\
равна без чувствительной погрешности отрезку K.L,
который в свою очередь можно считать равным ра-
радиусу НК, умноженному на угол KHKi (выражен-
(выраженный в радианах), т. е. равным НК • -^-или МТ • -^-.
Этой убыли длины хорды производящего круга со-
соответствует прирост дуги циклоиды, равный MMi,
т. е., как мы уже говорили, равный МТ-а. Мы полу-
получаем следующий результат: при малом повороте про-
производящего круга убыль длины хорды МТг вдвое
меньше приращения длины дуги циклоиды.
Это соотношение, конечно, не вполне точно; но
если мы возьмем поворот производящего круга на
180°, разобьем его на весьма малые части («элемен-
(«элементарные повороты» а), вычислим соответствующие
37
убыли хорд и приращения дуг, вычислим сумму всех
таких убылей и всех таких приращений и перейдем
к пределу, — то увидим, что полная убыль длины
хорды будет ровно вдвое меньше длины полуаркл
циклоиды. При этом хорда меняется от 2а (когда
точка М занимает самое низкое положение) до О
(когда точка М приходит в самое верхнее положе-
положение). Убыль длины хорды составляет 2а, следова-
следовательно, длина полуарки циклоиды равна 4а, а длича
всей арки — 8а.
Итак, «наводящие соображениям указывают, что
длина одной арки циклоиды должна равняться восо-
ми радиусам производящего круга. Результат неожи-
неожиданный: ведь даже для длины такой простой кривой,
как окружность, пришлось специально вводить ирра-
иррациональное число л, вычислить которое не так про-
просто. Длина же арки циклоиды выражается через ра-
радиус рациональным (даже целым) числом!
Чтобы придать нашим (вернее, реновскиы) наво-
наводящим соображениям доказательную силу, пришлось
бы рассмотреть целый ряд вспомогательных теорем.
Это сильно усложнило бы рассуждения и лишило им
их наглядности; поэтому мы эти детали опустили.
Сам Рен выполнил их достаточно аккуратно.
Читатель, вероятно, обратил внимание на следую-
следующие обстоятельства. Все рассуждения, связанные с
выводом формул площади циклоиды и длины ее ар-
арки, очень своеобразны и не похожи на соответствую-
соответствующие рассуждения в случае окружности. Если бы чи-
читатель взглянул на работы ученых XVII столетия,
посвященные какой-нибудь другой кривой, например,
параболе, он убедился бы, что их рассуждения тоже
приспособлены к специальному случаю и не похожа
ни на те, которые связаны с окружностью, ни на те,
с которыми мы встретились при изучении циклоиды.
Общих методов не было, каждое исследование требо-
требовало новых, иногда очень хитрых, приемов.
С другой стороны, читателю, вероятно, не нрави-
нравились постоянные указания на нестрогость доказа-
доказательств. Доказательства различных теорем, данные
учеными Возрождения, либо очень сложны и длинны,
либо носят скорее облик наводящих рассуждений,
чем строгих математических выводов. Очень часто
используется механика, хотя и в те времена казалось
38
желательным независимое от механики изложение
гегметрии.
А жизнь не ждала! Естествознание, техника, мо-
мореплавание, развьваясь, требовали единых геометри-
геометрических методов, доступных широким кругам специа-
специалистов-прикладников, а не только Галилеям и Паска-
Паскалям. И передовые ученые Возрождения все больше и
больше интересуются не решением отдельных задач,
а выяснением того, что же, собственно, объединяет
их сложные и хитроумные решения? Кавальери, Де-
Декарт, Ферма, Тейлор и другие математики пытаются
(¦1 крыть общие методы решения задач, связанных с
кривыми линиями и криволинейными фигурами. Ка-
Кавальери высказывает принцип, известный в наше
время любому десятикласснику. Декарт и Ферма
изобретают аналитическую геометрию: в ее основе
лежит связь между линией с одной стороны и урав-
уравнением с другой; простейшая форма этой связи в
наше время изучается в VIII классе («Таблицы «
графики»). Ферма, кроме того, изобретает общий
прием исследования касательных к разнообразным
кривым.
Все это завершается работами Ньютона и Лейб-
Лейбница, установившими замечательную связь между за-
задачами на построение касательных к кривым линиям
и вычислением площадей, ограниченных этими кри-
кривыми. Ньютон и Лейбниц разработали исключитель-
исключительно мощный и вместе с тем доступный метод решения
многих геометрических и механических задач, раз-
разросшийся затем в стройную дисциплину, называемую
математическим анализом (дифференциальное и ин-
интегральное исчисления). Но понадобилось еще пол-
полтораста лет, чтобы придать математическому анализу
ту строгость и убедительность, с которыми неразоыв~
но связано представление о математике.
ГЛАВА III
РОДСТВЕННИЦЫ ЦИКЛОИДЫ
«Как Вам доводится
Настасья Николавна?»
А, С. Грибоедов.
Укороченные и удлиненные циклоиды
Когда автор пьесы или романа хочет лучше оха-
охарактеризовать своего героя, он часто говорит о его
родных. В некоторых слу-
случаях знание родных и
знакомых позволяет пол-
полнее разобраться в харак-
характере человека. Мы тоже
на время оставим саму
циклоиду и перейдем к ее
ближайшим рэдичам. Ес-
Если производящий круг и
направляющая прямая
играют, в известном смы-
смысле, роль «родителей»
циклоиды, то кто же ее
братья и сестры?
Рис. 34. Движение внутренней
и внешней точек производяще-
производящего круга.
На рис. 34 изображен производящий круг, «гото-
«готовый к старту». Сейчас его точка Мо опишет красивую
циклоиду. А какая судьба ожидает точки Со и ?у?
Точка Со лежит не на окружности производящего
круга, а где-то внутри него. Точка Ео — внешняя точ-
точка, жестко связанная с катящимся кругом. Можно
40
вообразить, например, эту точку на ободе (реборде)
вагонного колеса, как это изображено на рис. 35. По-
Подобно внутренней точке, эта внешняя точка будет
двигаться вместе с колесом и опишет некоторую
кривую.
Этими кривыми, описанными внешними и внут-
внутренними точками катящегося круга, мы теперь зай-
займемся.
Шпага
Рис. 35. Как движутся точки рельсового обода?
Внутренняя точка производящего круга описы-
описывает при его движении кривую, называемую «укоро-
«укороченной циклоидой». Проведем через точку Со вспомо-
Рис. 36. Укорочгичая циклоида.
гательную окружность (рис. 36). Когда производя-
производящий круг катится по прямой АВ, маленькая окруж-
окружность будет катиться по прямой А'В', но ее качение
будет сопровождаться скольжением; мы говорили
уже об этом, когда разбирали парадокс Аристотеля
(стр. 12). Итак, можно сказать, что укороченная цик-
циклоида описывается точкою окружности круга, кото-
который катится по направляющей прямой со скольже-
скольжением.
4 Г. Н. Борман
41
Подобно этому, внешняя точка круга описывает
так называемую «удлиненную циклоиду». И на удли-
удлиненную циклоиду можно смотреть как на кривую, по-
порожденную точкой окружности катящегося круга. Но
это качение должно сопровождаться скольжением в
противоположном направлении.
Читатели сами придумают способы построения по
точкам укороченной и удлиненной циклоид. Нетрудно
сконструировать и демонстрационные приборы, по-
подобные изображенному на рис. 5. Мы не будем раз-
разбирать этого подробно и сразу нарисуем укорочен-
укороченную и удлиненную циклоиды «в готовом виде» (ри-
(рисунки 36 и 37). Укороченная циклоида отдаленно
напоминает синусоиду, а удлиненная представляет со-
собою красивую кривую с петлями. В наше время за
Рис. 37. Удлиненная циклоида.
укороченными и удлиненными циклоидами сохрани-
сохранилось имя «трохоиды», которым в старину француз-
французские ученые называли все кривые, связанные с каче-
качением круга по прямой, в том числе и обыкновенную
циклоиду.
Касательными к укороченным и удлиненным цик-
циклоидам занимались наши знакомые: Торичелли, Ка-
вальери, Роберваль, Декарт. Рен установил, что дли-
длина дуги этих кривых равна длине дуги некоторых эл-
эллипсов, которые нетрудно построить, если даны осно-
основания и производящие круги циклоид. Мы не будем
на этом останавливаться.
Скажем только два слова об известном шуточном
вопросе: какие точки железнодорожного вагона дви-
движутся в сторону, противоположную движению самого
вагона? Ответ теперь ясен: это будут нижние точки
ободьев (реборд) его колес (точка Е на рис. 38).
Если вагон катится направо, то нижняя часть обода
42
колеса смещается налево, причем направление дви-
движения самой нижней точки реборды противоположно
движению центра колеса.
Рис. 38. Ответ на шуточный вопрос.
Взгляните теперь на известную всем игрушку-^
«ваньку-встаньку». Она изображена на рис. 39. Ниж-
Нижняя часть болванчика имеет форму полушара, верх^
няя — нам безразлична. В нижнюю часть фигурки на*
лит свинец, а потому ее центр тяжести расположен
Рис. 39. Ванька-встанька.
очень низко (точка М на рис. 39). Если фигурку на-
наклонить, ее центр тяжести опишет дугу укороченной
циклоиды: ведь здесь, в сущности, мы имеем дело
с движением внутренней точки круга, катящегося по
прямой. Если наклоненную фигурку предоставить са-
самой себе, то она будет двигаться так, чтоб ее центр
43
тяжести возможно ниже опустился, а это и значит,
что «ванька-встанька» будет возвращаться к верти-
вертикальному положению (вставать).
Эпициклоиды
От родных сестер циклоиды перейдем к двоюрод-
двоюродным. Будем по-прежнему катить производящий круг,
но покатим его не по прямой, а по окружности дру-
другого круга, снаружи. В зависимости от соотноше-
соотношения между радиусами неподвижного и подвижного
Рис. 40. Эпициклоида с двумя заострениями.
(направляющего и производящего) кругов, будут по-
получаться различные, хотя и родственные кривые. Все
эти кривые называются эпициклоидами («надциклои-
дами»).
Начнем обзор эпициклоид с того случая, когда
радиус производящего круга вдвое меньше радиуса
круга направляющего. В этом случае получится кри-
кривая с двумя остриями, — «точками возврата» — изо-
изображенная на рис. 40. Если «неподвижный» радиус
больше подвижного в три, четыре или шесть раз, то
получатся кривые, изображенные, соответственно, на
рисунках 41, 42, 43.
44
Рис. 41. З-ициклоида с тремя Рис. 42 Эиициыон-а с че-
заострениями. тырьчя заострениями.
Рис. 43. Эпициклоида с шестью заострениями.
Те же ученые, которые изучили обыкновенную
циклоид}, установили правила для построения каса-
касательной к различным эпициклоидам, а также метри-
метрические свойства эпициклоид (т. е. их свойства, свя-
связанные с измерением длины их арок, ограниченных
ими площадей и т. д.). Выводы этих свойств очень
похожи на соответствующие выводы для обыкновен-
обыкновенной циклоиды; мы сообщим сразу готовые резуль-
результаты.
Рассмотрим направляющий круг с центром О
(рис. 44). Пусть Мо — точка возврата эпициклоиды с
Рис. 44. Касательная и нормаль к эпициклоиде.
тремя заострениями (рассуждения почти не изменят-
изменятся, если число заострений будет иным). Пусть, далее,
О) — центр подвижного (производящего) круга (сам
круг изображен на рис. 44 штриховой линией). По-
Построим соответствующую этому положению произво-
производящего круга точку М эпициклоиды. Если угол
OiOMo мы обозначим через ср, то угол ООуМ нужно
будет взять равным Зср (качение, разумеется, рас-
рассматривается без скольжения). Центр О{ движется в
направлении, перпендикулярном к ОО{; в этом дви-
движении принимает участие и точка М. Кроме того,
точка М принимает участие во вращении около цент-
центра О\. Точно те же соображения, что и в случае обык-
обыкновенной циклоиды, приводят к результату: каса-
касательная к эпициклоиде проходит через «наивысшую»
(Л), а нормаль — через «наинизшую» (В) точку про-
производящего круга.
46
Радиус производящего круга будем, как и дня
обыкновенной циклоиды, обозначать буквою а.
У обыкновенной циклоиды число а вполне ее опреде-
определяло (как, например, окружность вполне определя-
определялась своим радиусом). В случае эпициклоиды нужно
указать еще одно число: именно, нужно указать, во
сколько раз радиус неподвижного круга больше ра-
радиуса подвижного. Это число мы будем обозначать
буквою п. У эпициклоиды с двумя заострениями
п = 2, у эпициклоиды с десятью заострениями п = 10
и т. д. Для эпициклоид, изображенных на рис. 40, 41,
42, 43, числа п соответственно равны 2, 3, 4 и 6.
При этих обозначениях для длины одной арки
эпициклоиды с п заострениями получается следую-
следующая формула:
8 (+ l)
Обыкновенная циклоида, подобно прямой линии, бес-
бесконечна, и потому нельзя говорить о полной ее
Рчс 45. Плошгдь, смраничеииая эпициклоиаой.
длине. Эпициклоида, напротив, ограничена (как ок-
окружность). Поэтому, наряду с длиной ее арки, мож-
можно указать полную ее длину, которая, разумеется, в
п раз больше длины одной арки.
Длина всей эпициклоиды:
Точно так же, говоря о площади, можно дать фор-
формулу как для площади между одной аркой и непод-
неподвижным кругом, так и для всей площади, ограни-
ограниченной замкнутой кривой — эпициклоидой (проаая
47
циклоида не была замкнутой кривой и никакой пло-
площади сама по себе не ограничивала). Площадь между
производящим кругом и одной аркой будем обозна-
обозначать Si, а полную площадь, охваченную эпициклои-
эпициклоидой, S. Очевидно, S равно п раз повторенной площа-
площади Si плюс площадь неподвижного круга.
Вот формулы для Si и S:
На рис. 45 заштрихованы площади Si и S для
случая п = 3.
Сведем в одну табличку значения lu I, Si, S для
различных значений п, т. е. для эпициклоид с двумя,
тремя и т. д. заострениями. При этом заметим, что
h
1
Si
s
Эпициклоиды
с 2 заостре-
заострениями
12а
24а
4яа2
9ла2
с 3 заостре-
нпкгы
32
~з~а
32а
11 2
—г- яа2
о
12яа2
с 4 заостре-
заострениям.!
10а
40а
7 2
[ала2
с 5 заостре-
заострениям i
48
•— а
о
48а
17 2
lUi2
подвижные круги для всех эпициклоид предполагают-
предполагаются одинаковыми, а неподвижные возрастают вместе
с числом п заострений.
Видоизменим немного условия, при которых по-
порождается эпициклоида. Рассмотрим (рис. 46) круг
с центром О и будем предполагать, что по этому кру-
кругу равномерно движется центр другого круга, равно-
равномерно вращающегося. Какую кривую опишет при
этом точка окружности вращающегося круга?
Мы встречались с такой задачей в самом начале
этой книжки, когда шел разговор о птолемеевой си-
системе мира (стр. 14—16). Действительно, указанное
48
построение приведет нас к эпициклоиде Птолемея.
Но будет ли птолемеева эпициклоида «настоящей»
эпициклоидой? Нетрудно впдеть, что нет. Нужно по-
добрать специально соотношение между скоростью
точки О] и угловой скоростью вращения подвижного
круга, чтобы получить на-
настоящую эпициклоиду (по-
(попробуйте, читатель, сделать
такой расчет). При другом
соотношении между скоро-
скоростями подвижный круг бу-
дег катиться по штрихово-
штриховому кругу (рис. 46) со сколь-
скольжением, и вместо нормаль-
нормальных получатся укорочен-
укороченные или удлиненные эпи-
эпициклоиды (рис. 47, а а
47,6).
Вообразим теперь, что
на неподвижный обруч
(рис. 48) надет другой — подвижный — обруч, радиус
которого в 2, 3, вообще, в п раз больше радиуса не-
неподвижного обруча. Говоря геометрическим язчком,
Рис. 48. Пточемеева эпицик-
эпициклоида.
а) в
Рис. 47. Укороченные и удлиненные эпициклоиды.
скажем, что неподвижная окружность изнутри ка-
касается подвижной. Кривая, которую описывает точка
внешней окружности, катящейся по внутренней,
49
называется перщиклоидой. Но говорить о свойствах
перициклоид нет смысла: при более внимательном
Рис. 48. Перициклоида.
рассмотрении каждая перициклоида оказывается нз-
которой эпициклоидой.
Кардиоида. Конхоиды
Говоря об эпициклоидах, мы считали до сих пор,
что радиус неподвижного круга в несколько раз
больше радиуса подвижного (производящего) круга.
Но никто не может помешать нам рассмотреть и та-
такую эпициклоиду, у которой подвижный круг равен
неподвижному, т. е. такую, у которой п—1. Такая
эпициклоида называется кардиоидой. Итак, кар-
кардиоида — это траектория точки окружности, которая
катится без скольжения по неподвижной окружности
того же радиуса. Кардиоида изображена на рис. 49
(жирная линия). Слово «кардиоида» значит по-гре-
по-гречески «сердцевидная».
Относительно касатечьной и нормали к кардиоиде
говорить не приходится: ведь это — одна из эпицик-
эпициклоид (п = 1), а потому обладает всеми свойствами,
общими этим кривым. Заметим только, что в случае
кардиоиды углы O0OOi и ООХМ на рис. 49 равны.
Точно так же формулы для длины арки кардиои-
кардиоиды (она совпадает с длиной всей кривой) и для пло-
50
щади, ею ограниченной, получаются из формул на
стр. 47—49 простой подстановкой п= 1. Таким обра-
образом, получаем для кардиоиды:
/ = /i = 16а;
площади S\ и 5 изображены на рис. 50. Тело,
Рис. 49. Кардиоида.
а) б)
Рис. 60. Площадь кардиоиды.
полученное от вращения кардиоиды вокруг ее оси
симметрии (СЮ0 на рис. 49), напоминает помидор
(см. рис. 51); объем этого тела равен —g-зта .
Кардиоида обладает следующим замечательным
свойством. Соединим какую-нибудь точку М кардиои-
кардиоиды с ее «острием» Мо, как это изображено на рис. 52.
Обратим внимание на точку К
пересечения хорды ММ0 с не-
неподвижным кругом. Углы М0ОО\
и ОО\М равны (об этом мы толь-
только что упоминали — см. рис. 49).
Равны и радиусы ОМ0 и ОХМ.
Значит, хорда МйМ параллельна
отрезку ОО\, соединяющему
центры кругов. Точно так же
KO\\MOi. Поэтому отрезок КМ
равен отрезку ООи т. е. диамет-
диаметру неподвижного (и подвижного)
круга. Мы можем соединить
точку Мо (острие) с любой
точкой кардиоиды, и всегда от-
отсоединяющей острие и точку кривой,
между точкой кривой и точкой К
круга, будет равен диаметру произво-
Ркс. 51. Тело враще-
вращения, порожденное кар-
кардиоидой.
резок хорды,
заключенный
неподвижного
Рис. 52. Замечательное свой-
свойство кардпоьды.
Рис. 53.
Построение
диоиды.
кар-
дящего круга. Отсюда получается следующее построе-
построение кардиоиды. Начертим окружность радиуса а с
центром О и возьмем на ней произвольную точку М3
(рис. 53). Через точку Мо проведем пучок лучей (на
нашем чертеже изображено 7 лучей; чем больше взять
Б2
лучей, тем кривая получится точнее). От точек пересе-^
чения лучей с окружностью отложим вдоль каждого
луча в обе стороны отрезки, равные диаметру. Гео-
Геометрическим местом полученных таким способом то-
точек будет кривая, изображен-
изображенная жирной линией. Часть ее,
расположенная правее пря-
прямой АВ, на основании только
что сказанного, представляет
собою дугу кардиоиды. По-
Попробуйте, читатели, доказать,
что левая (штриховая) часть
«жирной» кривой дополняет
эту дугу до полной кардиоиды.
Оставим на время кардиои-
кардиоиду и займемся следующей
игрой. Пусть один из играю-
играющих станет на место, изобра- 0<(
женное на рис. 54 точкой О,
а остальные построятся перед
ним в прямолинейную шерен-
шеренгу, но каждый из них повернет-
повернется так, чтобы смотреть прямо
на своего командира. На чер-
чертеже играющие отмечены ко-
короткими черточками, а направ-
направление их взглядов — стрелоч-
стрелочками. Если командир скоман-
скомандует «кругом», а затем велит
каждому сделать ровно де-
десять шагов вперед, сохраняя
направление, то шеренга рас- Рис. 54. Коихоида пря-
строится: вместо прямой ли- мой линии,
нии получится своеобразно
изогнутая кривая. Эта кривая называется конхои~
дой Никомеда, по имени древнегреческого ученого,
изучавшего ее *).
Играющие могли расположиться сначала че по
прямой линии, а по некоторой кривой. Важно, чтобы
смотрели они прямо на командира и после команды
«кругом» сделали поровну шагов. И в этом случае
*) Точнее, это — только половина (одна ветвь) конхоиды
Ннкомеда. (Это будет ясно читателю, когда он прочтет еще не-
несколько строк.)
53
получается кривая, которая также называется кон-
конхоидой. Греческое слово «конхоида» значит «напоми-
«напоминающая раковину».
Дадим теперь точную геометрическую формули-
формулировку, пусть имеются некоторая кривая н точка О
(Эту точку мы будем называть «-полюсом»). Через
точку О проведем пучок лучей и на каждом луче от-
отложим равные отрезки в обе стороны от его точки
пересечения с данной кривой. Геометрическое место
концов этих отрезков даст новую кривую, которую
называют конхоидой исходной кривой относительно
данного полюса. Обратим внимание на небольшое
Рис. 55. Конхоиды различных кривых.
усложнение по сравнению с описанной только что иг-
игрой. Там — играющие шли в одну сторону; здесь —
отрезки откладываются по обе стороны от точек пе-
пересечения кривой с лучами. Поэтому всякая конхои-
конхоида будет состоять из двух ветвей, которые, впрочем,
иногда соединяются в одну кривую. Конхоида Нико-
меда (о которой говорилось выше и к которой нужно
присоединить ее левую половину, изображенную на
рис. 54 штриховой линией) является, таким образом,
конхоидой прямой линии.
На рис. 55 изображены (штриховыми линиями)
конхоиды различных кривых линий.
Читатель сообразит, что конхоидой окружности
относительно ее центра будет пара окружностей,
концентрических данной и одинаково удаленных от
нее (рис. 55, посредине).
Вернемся теперь к кардиоиде. Мы без труда за-
заметим, что кардиоида служит конхоидой окружно-
64
Рис. 56. Различные конхоиды одной и той же прямой.
Рнс. 57. Кардиоида и «улитки».
сти относительно точки, лежащей на окружности.
Чтобы в этом убедиться, достаточно взглянуть на
рис. 53.
Задавшись кривой линией и полюсом, мы можем
получить не одну конхсиду, а целое «семейство» кон-
конхоид, меняя величину откладываемого отрезка. Нз
рис. 56 изображено (разными штрихами) три конхон-
ды прямой линии АВ относшельно полюса О. (Каж-
(Каждая из них состоит из двух ветвей')
Если мы возьмем окружность и в качестве п )-
люса точку на ней, то кардиоиду получим только а
том случае, если будем откладывать отрезки, равнне
диаметру окружности. При других величинах отклч-
дываепых отрезков конхоидами будут удлиненные и
укороченные кардиоиды. Эти удлиненные и укорочен-
укороченные кардиоиды называются иначе улиткачи Паска-
Паскаля*). На рис. 57 изображены кардиоида (посредине)
и пара «улиток».
Кардиоида имеет различные применения в тех-
технике. В форме кардиоиды делают эксцентрики, ку-
кулачки у машин. Ею пользуются иногда при вычерчи-
вычерчивании зубчатых колес. Кроме того, она применяется
в оптической технике.
Гипоциклоиды
Если больший круг будет неподвижен, а меньший
будет катиться, касаясь его изнутри (рнс. 58), то
любая точка окружности этою меньшего круга опи-
опишет кривую, называемую гипоциклоидой («подцик-
лоидой»). Если радиус подвижного круга будет в
два. три, вообще в п раз меньше радиуса неподвиж-
неподвижного, то получится гипоциклоида с двумя, тремя, во-
вообще с п заострениями. Попробуйте, читатель, по-
построить самостоятельно гипоциклоиду с двумя за-
заострениями: вы получите любопытный результат. По-
Попытайтесь его сформулировать п доказать.
На рис. 59, а, б, в изображены гипоциклоиды с
тремя, четырьмя и шестью заострениями. Если каче-
качение внутреннего круга по внешнему будет сопровож-
сопровождаться скольжением, то будут получаться удлиненные
*) По имени французского математика Эгьепа Паскаля,
отца знаменитого физика и ма тематика Влеза Паскаля,
56
и укороченные гипоциклоиды, изображенные на ри-
рисунках 60 и 61.
Нормаль к любой гипоциклоиде в любсм ее то^ке
проходит через точку соприкосновения подыгкниго
и неподвижного кругов; касательная к гипоциклоиде
в любой ее точке проходит
через диаметрально противо-
противоположную точку подвижного
круга.
Если радиус подвижного
круга обозначим через а, ра-
радиус неподвижного — через па,
то для длины /[ одной арки ги-
гипоциклоиды, для длины / всей
гипоциклоиды, для площади Si
между одной аркой гипоцикло-
гипоциклоиды и неподвижной окруж-
окружностью, наконец, для oce"i пло-
площади S, ограниченной гипоциклоидой с п заострения-
заострениями, пслучим следующие формулы:
, 8 (и - 1).
Рис. 58 Гипоци<соича.
Зга —2
-а, 1 — 8(п—1)а,
-па", S = (п — 1) (п — 2) па2;
формулы эти напоминают соответствующие формулы
для эпициклоид (стр. 47—49).
Из всех гипоциклоид рассмотрим внимательнее
одну, именно, гипоциклоиду с четырьмя заострениями
(рис. 59,6). Ее называют иначе астроидой, что зна-
значит «звездообразная». Астроиду определяют обычно
не величиной подвижного радиуса а, а величиной не-
неподвижного, которую принято обозначать буквою/?.
Полагая в точько что дрнных формулах п = 4 и за-
заменяя а равной ему величиной -т-. получим дтя
астроиды:
7 —Ар /—en.
Ч~ 2 п' * —"А»
1 32 8 "
Итак, длина всей астроиды равна шести радиусам
неподвижного круга, а площадь, ею ограниченная, —¦
трем восьмым площади неподвижного круга.
57
о) 0
Рис. 59. Различные гипоциклоиды.
Рис. 6?. Удлиненные гипоциклоиды.
а) Ц
Рис. 61. Укороченные гипоциклоиды.
Рассмотрим внимательнее касательную А В к
астроиде в ее точке М (рис. 62). Как и у всех i ило-
циклоид, она проходит через точку Т, диаметрально
противоположную точке К касания подвижного и не-
неподвижного кругов. Если угол ОхОМ0 мы обозначим
буквою <р, то угол МО\К будет равен 4ф (почему?).
Углы при основании равнобедренного треугольника
ТО\М будут в сумме давать несмежный с ними внеш-
внешний угол 4ф, а каждый из них будет равен 2ф. Сумма
углов при основании ОВ треугольника ОТВ будет
0\ В' J
Рис. 62 Касательгая к астроиде.
равняться 2ф (все по той же теореме о внешнем угле
треугольника); но угол ТОВ равен ф (так мы сами
обозначили), следовательно, и угол ТВО будет тоже
равен ф; треугольник ОТВ — равнобедренный, и
ОТ = ВТ. Точно таким же образом убедимся, что
ТА = ОТ = ТВ.
Но ОТ — разность радиуса неподвижного и диа-
диаметра подвижного кругов — равна половине радиуса
кгподвижного круга, т. е. —• Следовательно, отрезок
касательной к астроиде, заключенный между двумя
взаимно перпендикулярными радиусами неподвиж-
неподвижного круга, проведенными в острия астроиды, равен
радиусу неподвижного круга, независимо от того, как
была выбрана точка М.
Это обстоятельство позволяет строить астроиду сле-
следующим путем. Чертим две взаимно перпендикулярные
59
прямые и проводим ряд отрезков длиною R, концы ко-
которых лежат на этих прямых. На рисунке 63 изобра-
изображено 12 таких отрезков (включая отрезки на самих
взаимно перпендикулярных прямых). Чем больше мы
проведем отрезков, тем точнее получим кривую. По-
Построим теперь от руки огибающую всех этих отрезков
(с огибающими мы уже имели дело на рис. 20). Этой
огибающей будет астроида.
Рис. 63. Астроида — огнбаю-
шая своих касат
Рис. С4. Тело вращения,
порожденное астроидой.
На рис. 64 изображено тело, ограниченное поверх-
поверхностью, порожденной вращением астроиды вокруг от-
отрезка, соединяющего ее противоположные острия.
Объем этого тела равен -j^-hF?3, а поверхность, его
ограничивающая, равна -g-nJi .
Вернемся теперь к вопросу, который мы предла-
предлагали самостоятельно разрешить читателям на стра-
странице 56 — в начале беседы о гипоциклоидах. Имен-
Именно, рассмотрим случай п = 2, т. е. гипоциклоиду с
двумя заострениями. Допустим, что центр подвиж-
подвижного круга занял произвольное положение О\
(рис. 65). Чтобы построить соответствующую точку
гипоциклоиды, нужно построить угол КО\М, вдвое
больший угла 0\ОМо. Но подвижный круг все вре-
время будет проходить через центр неподвижного. Угол
КОМ = а — вписанный в окружность подвшкного
60
Рис. 65. Теоре-а Коперника
круга, а угол КОХМ, равный 2сс, вдвое больший впи-
вписанного, т. е. центральный для той же окружности.
Поэтому точка М должна лежать на отрезке ОМ0.
Так будет для любого поло-
положения центра Oi, и мы по-
получаем замечательный ре-
результат: точка окружности,
катящейся без скольжения
по внутренней стороне
окружности вдвое большего
радиуса, движется по диа-
диаметру неподвижной окруж-
окружности. Эта теорема была
известна уже Копернику.
В этом случае гипоцик-
гипоциклоида, как говорят, «вы-
«вырождается» в прямолиней-
прямолинейный отрезок, дважды повто-
повторенный (точка М пройдет по диаметру из конца в ко-
конец в обе стороны). Если в формулах на стр. 57 мы
положим п = 2, то для площади S получим значе-
значение 0, а для длины всей
кривой» — 8а, т. е. дваж-
дважды повторенную длину
диаметра производящего
круга. Этого мы и долж-
должны были ожидать.
Предположим теперь,
что радиус а подвижного
круга раз навсегда уста-
установлен, а радиус непо-
неподвижного па неограни-
неограниченно возрастает. Иными
словами, положим, что п
принимает возрастающий
ряд значений: п = 3, п =
= 4, п = 5 и так далее —
до бесконечности. Кепо-
Рис. 66. Неограниченное ЕОзра-
стание радиуса неподвижной ДЕПЖНЫЙ круг бу ет прп
окружности. jJ }АК - г
этом все более и более
«выпрямляться» и стре-
стремиться к предельному положению — прямой АВ на
рис. 66. При этом гипоциклоида будет «разгибаться»
и в пределе превратится в обыкновенную циклоиду.
61
Посмотрим, что сделается при этом с формулами для
длины дуги одной арки гипоциклоиды и соответствую-
соответствующей площади. Для длины одной арки гипоциклоиды
мы имели:
8(я — 1) о« — 1
— а = 8а
= 8а f I — —
Когда п неограниченно растет, множитель в скобках
в правой части этого равенства стремится к единице,
потому что вычитаемое — стремится к нулю. Сле-
Следовательно, сама длина арки стремится при этом к
8а, т. е. к длине арки обыкновенной циклоиды.
Для площади мы имели формулу:
о 3« — 2
S
При неограниченном возрастании п правая часть
будет стремиться к Зла2, т. е. к площади, ограничен-
ограниченной аркой обыкновенной циклоиды и ее основанием,
Предлагаем читателям провести подобные рас-
рассуждения для эпициклоид.
Эпициклоиды с бесконечным множеством арок
До сих пор мы считали, что радиус неподвижного
круга в целое ччсло раз больше радиуса подвижного.
Но можно представить себе, что радиус неподвиж-
неподвижного круга в 1-г- или в З-g- раза больше чем радиус
подвижного. В случае эпициклоид можно рассматри-
рассматривать и тот случай, когда больший круг катится по
меньшему. Иными словами, отношение радиусов не-
неподвижного и подвижного кругов может быть дроб-
дробным числом, причем для гипоциклоид — это непра-
неправильная дробь, а для эпициклоид может быть кал
неправильной, так и правильной дробью.
На рис. 67 изображена эпициклоида, у которой
неподвижный радиус в полтора раза больше подвиж-
подвижного, т. е. n = -g- Нетрудно сообразить, что пол-
полному обороту подвижной окружности соответствует
на неподвижной окружности дуга 240°. Точка М опи-
опишет три петли прежде чем вернется в точку Мо.
62
Несмотря на свой необычайный, «запутанный» вит.,
эта кривая является самой настоящей эпициклоидой:
нормаль в каждой ее точке проходит через точку ка-
касания неподвижного и подвижного кругов, длина ее
арки и площадь между аркой и окружностью nsno i-
вижного круга вычисляются по формулам, приведен-
приведенным на стр. 47—48 (при п=="о~)'. только о всей пло-
площади, ограниченной этой
кривой, говорить нет
смысла: ведь полученные
арки будут несколько раз
пересекаться друг с дру-
другом.
На рис. 68, а, б, в и г
изображено несколько
эпициклоид и гипоцик-
гипоциклоид с различными дроб-
ными значениями числа п.
Рассматривая эти чер-
чертежи, нетрудно прийти к
следующему выводу. Ес-
Если отношение R : а ра-
радиусов неподвижного и
подвижного кругов эпи-
эпициклоиды равно несокра-
несократимой дроби — , то подвижный круг должен сделать
р оборотов (обегая при этом q раз неподвижную
окружность), для того чтобы точка М вернулась в
положение Мо. При этом кривая замкнется. Она бу-
будет с р остриями и с p(q— 1) точками самопересече-
самопересечения. На рис. 69 изображена эпициклоида, у которой
отношение р: q равно 5:ЗГт. е. п = — = ~з~)» ^ нее
5C—1)=10 точек самопересечения и 5 точек воз-
возврата. Точно так же у изображенной на рис. 70
эпициклоиды, у которой р : q = 2 : 3, имеется 2 точ-
точки возврата (острия) и 2C—1) = 4 точки само-
самопересечения. Наконец, у эпициклоиды, изображенной
на рис. 67, — три острия и три точки самопересечения,
как это и вытекает из общей формулы. Заметим, что
все эти эпициклоиды касаются изнутри круга, кон-
концентрического неподвижному кругу и имеющего
Рис. 67. Самопересекающаяся
эпициклоида.
63
радиус, равный сумме радиуса неподвижного и диа-
диаметра подвижного круга. Эти кривые лежат целиком
внутри кольца, образованного двумя концентри»
ческими окружностями.
а) Зтшци K
— " г"
б) SnuJuKJiouda, л=-у
е) Гипоциклоида, п J- г) Гипоциклоида, /?=-|
Рис 68. Эпициклоиды и гипоциклоиды при дробных эначеьпяч п.
Рассмотрим теперь наиболее интересный случай —¦
случай эпициклоиды, у которой отношение радиусов
подвижного и неподвижного кругов иррацио-
иррационально. На рис. 71 изображен неподвижный круг,
радиус которого равен диагонали квадрата, построен'
ного на радиусе подвижного круга. Иными словами,
отношение R:a = ^/2 есть число иррациональное.
Радиусы неподвижного и подвижного кругов — несо-
64
измеримы, и их отношение невозможно выразить ра*
циональным числом. Поэто.му эпициклоида, порож-
Рис. 69. Згицикчоида при
5
Рис. 70. Эпициклоида при
2
денная этими кругами, никогда не замкнется.
Конца ее петлям не будет. У нее будет бесконечное
число точек возврата и то-
точек самопересечения. На
рис. 71 изображена, разу-
разумеется, только часть этой
интересной кривой.
Мало тсго. Каша кривая,
делая бесконечное число пе-
петель, будет все плотнее и
плотнее заполнять кольцо,
образованное двумя концен-
концентрическими окружностями.
Заполнят ли точки кривой
все кольцо? Будет ли за
петлями ЭТОЙ кривой ЛИНИИ Рис- 7L Эпициклоида с не-
., * - ,, соизмери"ым отношечием
просвечивать бумага? Ины- радиусов подвижного и не-
ми словами, можно ли подвижного кругов,
утверждать, что наша кри-
кривая, сделав достаточное количество петель, пройдет
через любую, наудачу указанную точку кольца, на-
например, —точку Л? Очень хочется сказать, что да.
Но это, как оказывается, совсем не так. Суще-
Существуют точки кольца (и таких точек бесконечно
65
много!), через которые наша кривая не пройдет:
все-таки бумага будет просвечивать' При этом
вот что любопытно К любой то^ке кольца кривая
наша может подойти как угодно близко. Если мы от-
отметим произвольную точку А внутри кольца и выбе-
выберем какой-нибудь очень маленький отрезок, равный,
например, 0,001а, то наша кривая, сделав достаточ-
достаточное число петель, подойдет к точке А ближе чем на
это малое расстояние. Если мы зададимся расстоя-
расстоянием в 0,000 001 о или даже 0,000 000 001а, то и в
этих случаях кривая рано или поздно приблизится
к точке А ближе чем на такое расстояние. Эту мысль
выражают коротко, говоря, что точки кривой запол-
заполняют кольцо всюду плотно. Получается результат,
который может показаться парадоксальным: с одной
стороны, существуют—и притом в бесконечном ко-
количестве — точки кольца, недоступные кривой; а с
другой — точки кривой заполняют кольцо всюду
плотно'
Чтобы «раскрыть» этот парадокс, пришлось бы
прибегнуть к тому разбору понятия бесконечности,
о котором мы упоминали, когда речь шла о пара-
парадоксе Аристотеля (стр. 12). Здесь нет возможности
останавливаться на этом*). Заметим только, что су-
существуют и такие кривые линии, которые проходят
через все без исключения точки, находящиеся
внутри замкнутой линии — например, некоторого
квадрата. Наглядно представить себе это невозмож-
невозможно, но доказать существование таких кривых и изу-
изучить их свойства — вполне доступно для современной
математики.
Мы отошли от основной темы. Вернемся к ней —
перейдем от отвлеченных рассуждений к простым
чертежам, один взгляд на которые часто говорит нам
больше, чем самые строгие доказательства. Древние
индийские математики в своих геометрических рабо-
работах часто вместо доказательств давали наглядные
чертежи, снабдив их единственным словом, «смотрч' >
*) Эти вопросы рассматриваю~ея в отделе математики, ко-
который носит название «теории множеств».
ГЛАВА IV
ЭВОЛЮТЫ И ЭВОЛЬВЕНТЫ
«Куда на выдумки природа
таровата'»
И А Крылов.
Развертка (эвольвента) кривой
Мы рассказывали уже (на странице 36), как анг-
английский ученый Рен вычислил длину арки циклоиды.
Чтобы «наводящие» соображения Рена превратить в
строгое доказательство, при-
Ц-лось бы затратить слиш-
слишком много труда*). Пря-
Прямой путь здесь слишком
крут. Удобнее воспользо-
воспользоваться более длинным, но
«пологим» путем: он бы- Д
стрее приведет к цели. Этот
окольный путь связан с осо-
особой кривой — тоже своего
рода спутницей, — которая
имеется у ьаждой плавной
кривой, в том числе и у циклоиды. Эта «спутница»
носит название развертки данной кривой.
Рассмотрим выпуклую дугу АВ кривой линии
(рис. 72). Представим себе, что к дуге АВ в точке Л
Рис. 72 Развертка (эволь-
(эвольвента) кривой.
*) Методы, которыми доказываются такого рода теоремы,
относятся к интегральному исчис гению.
67
прикреплена гибкая нерастяжнмая нить такой же
длины, как сама дуга АВ, причем эта нить «навер-
«навернута» на нашу кривую и плотно к ней прилегает,
так что ее конец совпадает с точкою В.
Будем «развертывать» — распрямлять нить, держа
ее натянутой, так что свободная часть СМ нити будет
Бее время направлена по касательной к дуге АВ. При
и этих условиях конец нити
\ опишет некоторую кри-
вую. Вот эта-то кривая и
называется разверткой
1 или' по-латыни, эволь-
/// вентой исходной кривой.
Исходную кривую мо-
можно изготовить из жести
или из толстой проволо-
проволоки, прижать ее плотно к
Рис. 73. Точка лерешба Kf>n- бумаге, а к концу нити
вой и точка^возврата эзсль- Пр11ВЯЗаТь карандаш; то-
тогда этот карандаш ав-
автоматически вычертит
эвольвенту. Нужно только заботиться, чтобы нить,
к которой привязан карандаш, все время была туго
натянута.
Если дуга кривой не всюду выпукла в одну сто-
сторону, если она, подобно кривой АВ на рис. 73, имеет
точку С, в которой касательная к кривой переходит
с одной ее стороны на другую (такая точка назы-
называется точкой перегиба), то и в этом случае можно
говорить о разБертке кривой, но рассуждения придет-
придется немного усложнить.
Представим себе, что нить закреплена как раз в
точке перегиба С (рис. 73). Нить, сматываясь с дуги
ВС, опишет кривую BMP — развертку.
Теперь представим себе нить, намотанную на дугу
АС исходной кривой, но эта нить уже удлиненная:
в точке С к ней привязан кусочек нити СР. Сматы-
Сматывая удлиненную нить АСР с кривой СА, мы получим
дугу РНК, образующую вместе с дугой BMP единую
непрерывную кривую — непрерывную, но не
везде плавную: точке перегиба С исходной кри-
кривой будет соответствовать острие (точка возврата)
кривой ВМРНК: кривая ВМРНК и будет эвольвен»
той (разверткой) кривой ВСА.
68
Основные свойства развертки
При вычерчивании эвольвенты некоторой кривой
нить должна быть все время туго натянута. Благо-
Благодаря этому отрезок нити СМ всегда направлен по ка-
касательной к кривой в точке С (рис. 74). При движе»
нии нити конец карандаша как бы описывает неболь*
шую дугу окружности радиуса СМ с центром в С.
Правда, когда нить раз-
Еернется чуть-чуть боль-
больше и точка М перейдет в
точку К, конец каранда-
карандаша будет двигаться уже
по другой окружности,
именно — по окружности
с центром в Е. Эвольвен-
Эвольвенту можно представлять д
себе как окружность, ра-
радиус КОТОрОЙ все время Рис. 71. Основное свойство
меняется, а центр сколь- эвольвенты,
зит по кривой АВ. Но
в каждый момент времени точку касания можно счи-
считать центром бесконечно малой дуги окружности,
совпадающей с бесконечно малой дугой развертки.
Точку С так и называют — мгновенный центр, или
центр кривизны эвольвенты. Таким образом, всякая
кривая линия является геометрическим местом цент-
центров кривизны своей собственной развертки (эволь-
(эвольвенты).
Так как бесконечно малая дуга эвольвенты МК
«сливается» с бесконечно малой дугой окружности
радиуса СМ с центром в С, то касательная к эволь-
эвольвенте в точке М будет перпендикулярна к мгновен-
мгновенному радиксу СМ. Получается важный результат:
направление эвольвенты (т. е. касательной к ней)
перпендикулярно касательной ес исходной кривой.
Отсюда вытекает следствие: нормаль к развертке
служит касательной к исходной кривой.
Можно сказать и так: эвольвента пересекает все
касательные к данной кривой под прямым углом.
Это — очень важное свойство эвольвенты, и на нем
стоит задержаться. На рис. 75 изображена (сплош-
(сплошной линией) кривая АВ и несколько ее касательных
(в разных точках). На этом рисунке показано, что
69
найдется не одна, а бесчисленное множество кривых
(они начерчены штриховыми линиями), пересекаю-
пересекающих все эти касательные под прямым углом. Каждая
из этих кривых служит эвольвентой (разверткой)
кривой АВ. Действительно, если на кривую АВ на-
намотана нить, закрепленная в точке А, с карандашом
в точке В, то при разматывании этой нити карандаш
опишет кривую. Но карандаш можно было закрепить
в любой промежуточной точке
нити, например — в точках С, D,
Е и других, и тогда он описал бы
любую из штриховых кривых, пе~
ресекающих под прямым углом
касательные к кривой АВ. Все
эти штриховые кривые равно-
равноправны, и каждую из них можно
считать разверткой линии А В.
Этот результат можно сформули-
сформулировать так: плавная кривая
имеет не одну, а бесчисленное
_„ „ „ множество эвольвент.
7о. Семейство г,
эвольвент. Внимательный взгляд на
рис. 75 наводит нас еще на одну
мысль. Мы видим, что все развертки данной кривой
между собой «параллельны» — параллельны в том
смысле, что отрезки касательных к кривой АВ между
двумя развертками все между собою равны, совер-
совершенно так же, как отрезки перпендикуляров между
параллельными прямыми.
Практически наиболее важным будет следующее
свойство эвольвенты, непосредственно вытекающее нз
самого построения этой кривой. Длина дуги ВС
рис. 72 (на стр. 67) равна прямолинейному отрезку
СМ. Ведь кусок СМ нерастяжимой нити был плотно
навернут на дугу СВ. Отсюда вытекает следующая
теорема: длина дуги кривой линии равна отрезку ка-
касательной от точки касания до пересечения касатель-
касательной с соответствующей эвольвентой. Точнее, длина
дуги АВ равна отрезку касательной (в точке А) ме-
между точкою касания и эвольвентой, проходящей че-
через точку В.
До сих пор мы занимались следующей задачей:
дана кривая, найти (т. е. построить) ее эвольвенту.
Но можно поставить и обратную задачу: дана кривая;
70
найти другую кривую, для которой данная кривая
служит разверткой. Для решения этой новой, обрат-
обратной задачи воспользуемся тем, что нормаль к раз-
развертке является касательной к исходной кривой. Про-
Проведем несколько нормалей к данной кривой — эволь-
эвольвенте некоторой кривой, пока еще неизвестной. Чем
больше мы проведем нормалей, тем чертеж будет
точнее. На рис. 76 построено семь таких нормалей.
Кстати укажем удобный прием для построения
нормалей. Пусть нужно построить нормаль к кривой
В
Рис. 76. Как по эвольвенте найти саму кривую?
АБ (рис. 77) в точке М. Возьмем небольшое зеркаль-
зеркальце с ровным прямолинейным краем (еще лучше взять
блестящую металлическую линейку). Поставим это
зеркальце перпендикулярно к бумаге, гладким краем
вниз, так, чтобы этот гладкий край проходил через
точку М (правое положение зеркала на рис. 77). При
этом правая часть кривой отразится в зеркале, при-
причем в точке М получится излом (кривая и ее отра-
отражение встретятся в точке М под некоторым углом,
как это изображено на нашем чертеже — в точке/5).
Будем осторожно поворачивать зеркало, пока кри-
кривая и ее отражение не сольются в плавную линию
(без угла), как это изображено на нашем чертеже
справа — при точке М. Теперь можно смело провести
карандашом прямую по линейке — зеркалу: эта пря-
прямая и будет искомой нормалью.
Научившись строить нормали, вернемся к рис. 76,
на котором изображено семь нормалей. Остается
71
начертить кривую линию, которая касалась бы всех
этих нормалей — иными словами, огибающую
всех этих нормалей (вспомним, что уже на рис. 20
мы имели дело с огибающей нормалей). Ясно, что
наша первоначально взятая кривая будет разверткой
вновь построенной криоой. Поставленная задача, та-
таким образом, решена: мы по заданной кривой А В
построили такую новую
кривую, для которой сама
заданная кривая являет-
является эвольвентой.
Огибаюшая нормалей
служит важным вспомо-
вспомогательным средством при
изучении свойств кривой
линии. Ее называют эво-
Рис. 77. Построение нормали лютой данной кривой. Та-
с помощью зеркала. ким образом,' каждая
кривая является эволю-
эволютой собственной развертки, и, обратно, всякая кривая
является одной из разверток своей эволюты. Отноше-
Отношение между эволютой и эвольвентой с логической точ-
точки зрс-ния то же, что между, например, квадратом
числа и квадратным корнем: если число а есть квад-
квадрат числа Ь, то число Ь есть один из квадратных кор-
корней из числа а.
Мы видели, что всякая плавная кривая имеет
бесконечное множество «параллельных» между собой
эвольвент. Это было ясно из построения эвольвенты
с помощью натянутой нити*). Не так ясно обстоит
дело с эволютой. Для всякой ли кривой можно по-
построить огибающую семейства нормалей? Ученые
XVII века доказали, что для всех тех кривых, с ко-
которыми им приходилось иметь дело, существуют эво-
эволюты. Немного ниже мы докажем, что циклоида
имеет вполне определенную эволюту. Но как обстоит
дело в общем случае? Будет ли это справедливо для
любой кривой?
*) Придирчивая и строгая современная математика требует
доказательства столь очевидного предложения. Нужно отдать ей
справедливость, она не только требует, но и дает это доказа-
доказательство. Эти вопросы рассматриваются в том отделе высшей
математики, который называется «дифференциальная геометрия».
72
Ответить на подобные вопросы элементарная ма-
математика бессильна. Но высшая математика доказы-
доказывает, что каждая плавная кривая имеет
единственную эволюту. Исключение состав-
составляют только такие линии, все нормали которых либо
пересекаются в одной точке, либо такие, все нормали
которых параллельны между собою. Кривой, все
нормали которой пересекаются в одной точке, яв-
является окружность (нормалями к окружности служат
радиусы, которые, как известно, перпендикулярны к
касательным). Линией же, все нормали которой па-
параллельны между собой, является прямая: она сов-
совпадает с собственной касательной в любой точке и
нормалями к ней служат параллельные между собою
перпендикуляры, восставленные в различных точках
этой прямой. Окончательно общему предложению
можно дать следующую формулировку: любая плав-
плавная линия, кроме прямой и окружности, имеет одну-
единственную эволюту.
Развертка окружности
Можно ли в математической книге, хотя бы и в
популярной, говорить, например, о жуках? Оказы-
Оказывается, можно. Но начать
придется издалека.
Окружность, как мы
теперь знаем, не имеет
эволюты. Все ее нормали
пересекаются в одной точ-
точке — в центре. Иногда
говорят, что эволюта
окружности «вырождает-
«вырождается» в точку. Но зато
эвольвенту она имеет (в
чем, впрочем, большой
заслуги нет: ведь разверт-
развертку имеет всякая плавная
кривая). Эта эвольвента
оказывается близкой род-
СТВенницей ЦИКЛОИдаль- Рис. 78. Развертка окружности.
ным кривым.
Начнем с чертежа. Изготовим из фанеры кру-
кружок, укрепим его на бумаге, приклеим к нему нить и
73
навернем плотно эту нить на край нашего кружка. На
конце нити сделаем петельку, в которую просунем
острье карандаша (рис. 78). Если будем теперь «сма-
«сматывать» нить, то карандаш автоматически начертит
В
Рис. 79 Качение прямой по кругу.
эвольвенту. Нить, разумеется, должна быть туго на-
натянута, а карандаш плотно прижат к бумаге*).
Развертку окружности можно получить и иначе.
Рассмотрим неподвижный круг радиуса с н прямую
Рис 80. Простые качели.
АВ, касающуюся этого круга в точке Мо (рис. 79),
Если прямая АВ б\дет катиться без скольжения по
окружности, то точка Мо опишет, очевидно, разверт-
развертку окружности. Действительно, для любой точки М
*) Проще, но не так точно, можно начертить эвольвенту,
заменив кружок катушкой ниток и сматывая нитку с этой ка-
катушки, держа ее все время натянутой.
74
этой кривой катящаяся прямая КМ служит нор-
нормалью, и длина отрезка КМ равна длине дуги М0РК
неподвижной окружности.
Эвольвента круга является, таким образом, «цик-
«циклоидой, вывернутой наизнанку». В случае циклоиды
круг катится без скольжения по неподвижной пря-
прямой. В случае развертки круга прямая катится без
скольжения по неподвижной окружности.
На рис. 80 изображены простейшие качели. На
обрубок дерева положена доска АВ так, что ее сере-
середина касается обрубка. Что будет, если доску накло-
наклонить? Мы знаем, что она вернется в исходное поло-
положение, затем по инерции отклонится в другую сто-
сторону и будет качаться около положения равновесия.
При этом, разумеется, и доска, и обрубок должны
быть шероховатыми, иначе доска соскользнет в на-
направлении, указанном на чертеже стрелкой.
Почему доска будет возвращаться в исходное по-
положение? Это нетрудно сообразить. Известно, что
всякое тело движется под действием тяжести так,
что его центр тяжести опускается. Для ответа на
наш вопрос достаточно знать, по какому пути дви-
движется центр тяжести (середина) доски при неболь-
небольших ее отклонениях от положения равновесия.
Но это нам теперь ясно! Середина доски будет
описывать дугу развертки окружности. Эта часть
развертки изображена на рис. 80 штриховой линией.
Мы видим, что при небольших отклонениях доски ее
центр тяжести подымается, а потому доска будет
возвращаться к положению равновесия. Равновесие
будет, очевидно, устойчивым.
Родство развертки круга с цикчоидальпыми кри-
кривыми можно обнаружить и другим путем. Мы уже
говорили, что в случае эпициклоид или гипоцикюид
(рис. 66) неограниченное возрастание радиуса непод-
неподвижного круга при неизменном радиусе подвижного
приводит к циклоиде. Если мы обратимся к перицик-
лоиде (стр. 50) и, оставив неизменным радиус непод-
неподвижного круга, будем неограниченно увеличивать ра-
радиус подвижного, так сказать, «выпрямляя» его
(рис. 81), то перициклоида превратится в развертку
круга.
Мы не будем здесь приводить вывода формул для
длины дуги эвольвенты круга и площади ее сектора.
75
Приведем готовый результат (рис. 82). Для длины I
дуги М0М развертки и для площади S сектора MOMq
будем иметь;
Эти формулы интересны тем, что величину входя-
входящего в них угла приходится возводить во вторую и в
третью степень — обстоятельство, которое может
Рис. 81. Неограниченное увели-
увеличение подвижного круга.
Рис. 82. Длина дуги и пло-
площадь сектора эвольвенты круга.
смутить новичка. Подчеркиваем еще раз, что при
этом угол ф должен быть выражен непременно в
радианах. Если угол НОМ0 выражен в градусах
и равен, например, ас (а градусов равны <р радиа-
радианам), то формулы примут следующий вид:
/ =
1803
34 992 000
Обратим внимание читателей на то, что угол <р
радиан (или а градусов) — это угол НОМ0 нашего
чертежа, а вовсе не угол МОМ0 сектора эвольвенты!
Жук-математик
Возьмем бумажный кружок (рис. 83), разрежем
его от края к центру (например, по радиусу НО) и
свернем сектор НОК в трубочку, как показано на
76
рисунке. Трубочка получится очень аккуратная: ведь
она представляет собою коническую поверхность,
причем все образующие этой поверхности, как радиу-
радиусы одного и того же круга, между собою равны. Если
бы мы разрезали кружок так, как показано на
Рис. 83. Склеивание бумажного конуса.
рис. 84, то трубка получилась бы неаккуратная: об'
разующие конической поверхности были бы не равны
между собою.
Возьмем теперь листок, ограниченный не окруж-
окружностью, а какой-то другой плавной кривой, например,
такой, как изображено на рис. 85.^Если взять любую
точку внутри листка, например, точку О, сделать
разрез по ОН и свернуть трубку,
то трубочка получится плохая,
потому что образующие кониче-
конической поверхности будут разной
длины. И как бы мы ни выби-
выбирали точку О, нам хорошей
трубки получить не удастся, по-
потому что ни у какой кривой, кро-
кроме окружности, нет точки, рав-
равноудаленной от всех остальных
ее точек.
Что ж? Будем хитрить! Возьмем какую-нибудь
точку Я на краю листа (рис. 85) и наметим неболь-
небольшую дугу НК. Будем считать эту дугу дугой окруж-
окружности и найдем центр этой окружности. С этой целью
проведем в точках Н и К нормали. Точка пересече-
пересечения Т нормалей будет искомым центром. Далее, рас-
рассмотрим дугу КМ. Ее тоже можно без большой по-
погрешности считать дугой окружности, но центр этой
окружности не совпадет с Т; проведя нормали к
Рис.
84. Плохая
трубка.
77
н
Рис. 85. Как разрезать лист?
контуру листа в точках К и М, мы найдем точку их
пересечения Ти не совпадающую с точкою Т. Посту-
Поступая таким образом и дальше, мы получим точку Т2 и
вообще — целый ряд центров, около которых нужно
заворачивать листок, что-
чтобы полечить аккуратную
трубочку.
Остается сделать по-
последний шаг: перейти от
ломаной линии центров
TTiT2 ... к непрерывной
кривой, чтобы обеспечить
вполне гладкую трубочку,
свободную от зазубрин.
Ясно, что для этого до-
достаточно заменить лома-
ломаную ТТ\Т2 ..., звенья
которой соединяют точки
пересечения «соседних»
пар нормалей, плавной
кривой — огибающею этих нормалей, т. е. кривой
ТР, изображенной на рис. 86.
Но огибающей нормалей является, как мы знаем,
эволюта данной кривой.
Значит, для того чтобы
свернуть из листа наибо-
наиболее аккуратную трубочку,
нужно предварительно
разрезать лист сначала
по куску НТ норм&ли, а
затем — по эволюте ТР
его контура.
И вам, читатель, и
мне, и кому-нибудь еще
вряд ли понадобится
свертывать в трубки лнс-
ТОЧКИ б\маги (свертыва- Рис 86. Как избавиться от
ние папироски — «козьей зазубрил.''
ножки» — не в счег: при
этом ведь не нужно заботиться, чтобы все обра-
образующие были равной длины!). Поэтому практи-
практическая ценность разобранной нами сейчас задачи
ничтожна. Но вот что интересно: существует жук,
вернее, несколько пород жуков, которые изготовляют
78
для своего будущего потомства домик из листа, свер-
свертывая его в трубку. Эта трубка должна быть прочной
и аккуратной. Ее не должны растрепать ветры и лчв-
ни, она не должна своим живописным видом и вели-
величиной привлекать врагов. И наш жучок-листоверт
(жуки из родов Rhynchites, Byctiscus и др.) прекрас-
прекрасно решает сложную математическую задачу. Он про-
прогрызает лист по эволюте контура и лишь после этого
свертывает его. На рис. 87 изображен березовый ли-
стоверт (в натуральную величину) и разрезанный
(вернее, прогрызенный) им лист. На рис. 88 изобра-
Рис 87 Березовый листоверт
(натуральная величина).
Рис. 88. Виноградный листо-
листоверт и его трубка (увеличено
в 2 раза).
жен увеличенный в два рача виноградный листоверт
и его трубочка.
Разумеется, жучок-геометр решает эту далеко не
простую задачу совершенно бессознательно. В тече-
течение многих лет естественный отбор сохранял преиму-
преимущественно тех жучков, домики которых были особен-
особенно аккуратны. В результате возник инстинкт, пере-
передающийся по наследству из поколения в поколение.
Этот инстинкт заставляет насекомое, не зная геомет-
геометрии, решать сложную геометрическую задачу. Заме-
Заметим, что другое, более известное насекомое — пче-
пчела— тоже решает (бессознательно, разумеется) не
менее сложную задачу: построить соты так, чтобы
79
при заданном числе и емкости ячеек их поверхность
была наименьшей. При этих условиях достигается
наиболее экономное использование строительного ма-
материала (воска).
Развертка циклоиды. Длина дуги циклоиды
Разобранные примеры помогли нам привыкнуть
к новым понятиям эволюты и эвольвенты. Теперь мы
достаточно подготовлены, чтобы заняться исследова-
исследованием разверток циклоидальных кривых.
Изучая ту или иную кривую, мы нередко строили
вспомогательную кривую — «спутницу» данной кри-
-a/ztf-
т
[— а<р-Л~ apz-p) -
Рпс. 89. Циклоида и ее сопровождающая.
вой. Так, мы строили конхоиды прямой и окруж-
окружности, развертку окружности, синусоиду — спутницу
циклоиды. Теперь, исходя из данной циклоиды, мы
построим неразрывно связанную с ней вспомогатель-
вспомогательную циклоиду же. Оказывается, совместное изучение
такой пары циклоид в некоторых отношениях проще,
чем изучение одной отдельно взятой циклоиды. Та-
Такую вспомогательную циклоиду мы будем называть
сопровождающей циклоидой.
Рассмотрим половину арки циклоиды АМВ
(рис. 89). Нас не должно смущать, что циклоида эта
расположена непривычным образом («вверх нога-
ногами»). Проведем 4 прямые, параллельные направляю*
щей прямой АК на расстояниях а, 2а, За и 4а. По*
строим производящий круг в положении, соответ-
соответствующем точке М (на рис. 89 центр этого круга обо-
обозначен буквою О). Угол поворота МОН обозначим
через ф. Тогда отрезок АН будет равен аср (угол ф
выражен в радианах).
Диаметр НТ производящего круга продолжим за
точку Т до пересечения (в точке Е) с прямой Р'Р. На
ТЕ как на диаметре построим окружность (с цент-
центром О\). Построим касательную в точке М к цик-
циклоиде АМВ. Для этого точку М нужно, как мы знаем,
соединить с точкой Т (стр. 23). Продолжим касатель-
касательную МТ за точку Т до пересечения со вспомогательной
окружностью, и точку пересечения назовем М\. Вот
этой-то точкою М\ мы и хотим теперь заняться.
Угол МОН мы обозначили через ф. Поэтому угол
МТН будет равняться q/2 (вписанный угол, опираю-
опирающийся на ту же дугу). Треугольник ТО\Ми очевидно,
равнобедренный. Поэтому не только угол О\ТМ\, но
и угол TMiOi будут каждый равняться ф/2. Таким
образом, на долю угла ТО\М\ в треугольнике ТО\М\
остается ровно я — ф радианов (вспомним, что угол
180° равен я радианов). Заметим еще, что отрезок
НК равен, очевидно, а (я — ф).
Рассмотрим теперь окружность с центром О2, изо-
изображенную на рис. 89 штриховой линией. Из чертежа
ясно, что это за окружность. Если катить ее без сколь-"'
жения по прямой СВ, то её точка В опишет циклоиду
ВВ'. Когда штриховой круг повернется на угол я —
— Ф, центр О2 придет в точку Оь а радиус О2В зай-
займет положение ОуЩ. Таким образом, построенная
нами точка М] оказывается точкою циклоиды ВВ',
Описанное построение ставит в соответствие каж-
каждой точке М циклоиды АМВ точку М\ циклоиды
ВМ\В'. На рис. 90 это соответствие показано более
наглядно. Полученная таким путем циклоида и на-
называется сопровождающей. На рис. 89 и 90 циклои-
циклоиды, изображенные жирными штриховыми линиями,
являются сопровождающими по отношению к циклои-
циклоидам, изображенным жирными сплошными линиями.
Из рис. 89 видно, что прямая ММ1 является нор-
нормалью в точке М\ к сопровождающей циклоиде.
Действительно, эта прямая проходит через точку М\
циклоиды и через точку Т касания производящего
81
круга и направляющей прямой («наинизшую» точку
производящего круга, как мы говорили когда-то; те-
теперь она оказалась «наивысшей», потому что чертеж
повернут). Но эта же прямая, по построению, является
касательной к «основной» циклоиде АМВ. Таким об-
образом, исходная циклоида касается каждой нормали
сопровождающей циклоиды. Она является огибаю-
огибающей для нормалей сопровождающей циклоиды, т. с.
ее эволютой. А «сопровождающая» циклоида оказы-
оказывается просто-напросто эвольвентой (разверткой) ис-
исходной циклоиды!
Рис. 91 Соответствие между точками циклоиды и се сопровож-
сопровождающей.
Занимаясь этим громоздким, но в сущности про-
простым построением, мы доказали замечательную тео-
теорему, открытую голландским ученым Гюйгенсом. Вог
эта теорема: эволютой циклоиды служит точно такая
же циклоида, только сдвинутая.
Построив эволюту не к одной арке, а ко всей цик-
циклоиде (что можно, разумеется, сделать только мыс-
мысленно), зятем эволюту к этой эволюте и т. д., полу-
получим рис. 91, напоминающий черепицу.
Обратим внимание на то, что при доказательстве
теоремы Гюйгенса мы не пользовались ни бесконечно
малыми, ни неделимыми, ни приблизительными оцен-
оценками. Даже механикой мы не пользовались, хогя
употребляли иногда заимствованные из механики
выражения. Доказательство это совершенно в д} хе
82
тех рассуждений, которыми пользовались ученые
XVII века, когда хотели строго обосновать резуль-
результаты, полученные с помощью различных наводящих
соображений.
Из теоремы Гюйгенса получается сразу важное
следствие. Рассмотрим отрезок АВ' на рис." 89. Дли-
Длина этого отрезка равна, очевидно, 4а. Представим
себе теперь, что на дугу АМВ циклоиды намотана
шпъ, закрепленная в точке А и снабженная каранда-
карандашом в точке В. Если мы будем «сматывать»
иитъ, то карандаш будет двигаться по развертке
Рис. 91 Последовательные эволюты циклоиды.
циклоиды АМВ, т. е. по циклоиде ВМ^В'. Длина ни-
нити, равная длине полуарки циклоиды, будет, очевид-
очевидно, равна отрезку АВ', т. е., как мы видели, 4а. Сле-
Следовательно, длина / всей арки циклоиды будет равна
8а, и формулу / = 8а можно считать теперь достаточ-
достаточно строго доказанной.
Из рис. 89 можно увидеть больше: формулу ие
только для длины всей арки циклоиды, но и для дли-
длины любой ее дуги. Действительно, очевидно, что дли-
длина дуги MB равна длине отрезка ММ\, т. е. удвоен*
ному отрезку касательнойвсоотве1'сгь\ к. ел гочке цьк
лоиды, заключенному внутри производящего круга.
Точно такие же рассуждения и чертежи приведут
нас к эволютам эпициклоид и гип циклоид. Приведем
готовые результаты. Эволютой эпициклоиды
служит эпициклоида, подобная данной, с тем же
центром неподвижного круга, но повернутая на
\гол л/п радианов (т. е. 180 /п градусов), где
п — отношение радиуса неподвижного круга к ра-
радиусу подвижного. Отношение подобия равно -——.
Иными словами, если радиус неподвижного круга в
83
три, например, раза больше радиуса подвижного, то
з о
линейные размеры эволюты составляют -- . 2 ~~5~
соответствующих размеров самой эпициклоиды.
Рис. 92. Эволюта гипоциклоиды.
Эволютой гипоциклоиды служит гипо-
гипоциклоида, подобная данной, с тем же центром не-
неподвижного круга, повернутая, как и в случае эпи-
эпициклоиды, на угол л/п радианов. Но в отличие от
эволют эпициклоид, эволюта гипоциклоиды больше
самой кривой, причем отношение подобия равно
—Z~2 • На рис. 92 изображены астроида (п = 4) и
ее эволюта. Эволюта повернута относительно самой
астроиды на 180° : 4 = 45° и больше нее в два раза (по
линейным размерам, разумеется).
Понятия эволюты и эвольвенты — чрезвычайно
важные понятия как для самой геометрии, так и для
приложений. Гюйгенса подвела к его замечатель-
замечательной теореме как раз физическая задача. Об этой
физической задаче мы сейчас расскажем.
ГЛАВА V
ЛУЧШИЙ МАЯТНИК
«...Чтобы
не часы показывали время5
а чтоб время
честно
двигало часы.»
В. Маяковский.
Христиан Гюйгенс и его изобретение
«Славный Гугений» — так называл создатель рус-
ской науки Михаил Васильевич Ломоносов замеча-
замечательного голландского ученого Христиана Гюйгенса,
придав русское окончание латинизированной форме
его имени.
Гюйгенс A629—1695) был разносторонним уче-
ученым. Он был одинаково силен и в математике, и в
прикладной механике, и в оптике. Мы говорили уже,
что в эпоху Возрождения и в XVII веке такая раз-
разносторонность не составляла исключения.
Гюйгенс с одинаковым совершенством умел ис-
использовать и «неделимые» Торичелли и Кавальери,
н хитроумные соображения Декарта и Ферма, но все
полученные с помощью недостаточно обоснованных
приемов результаты он доказывал с непогрешимой
строгостью древних греков. Строгое и вместе с тем
изящное доказательство было его коньком. «Не так
важен результат, — говорил он, —- как безупречность
вывода и ясность доказательства».
85
Гюйгенсу принадлежит честь изобретения часов
с маятником. Он разработал их теорию и смастерил
первые такие часы. До сих пор часы с маятником
имеют самое широкое распространение в быту (стен-
(стенные часы — вспомним хотя бы ходики). Но значение
маятниковых часов гораздо больше: точнейшими ча-
часами, обеспечивающими службу времени в астроно-
астрономических обсерваториях, являются именно часы с
маятником*). Сочинение Гюйгенса «О маятниковых
часах» содержало целый ряд блестящих математиче-
математических открытий.
Кроме открытий в механике, физике, астрономии,
Гюйгенс получил ряд новых результатов в матема-
математике. Он обосновал важнейшие положения теории не-
непрерывных дробей; одновременно с Ферма и Паска-
Паскалем он заложил основу теории вероятностей; вычис-
вычислил площади поверхностей эллипсоида и параболои-
параболоида вращения. Ему принадлежит ряд замечательных
теорем об окружности, позволивших вычислить число
я с неслыханной в то время точностью. Наконец, ои
разработал учение об эволютах и применил его к ис-
исследованию циклоиды. Эти его исследования тесней-
теснейшим образом связаны с работой о маятниковых ча-
часах.
Часы с маятником. Почему плох обыкновенный
([фуговой) маятник?
«Однако ж прав упрямый Галилей!», — написал
А. С. Пушкин, имея в виду утверждение Галилея,
что Земля вращается вокруг Солнца. А мы расска-
расскажем о том, как этот великий борец за науку оказался
однажды неправ.
Наблюдая в храме за качающейся люстрой, Гали-
Галилей обнаружил, что время полного качания люстры,
т. е. время, по истечении которого она вернется в ис^
ходное положение (так называемый период колеба-
колебания), было одинаково и при больших размахах и
при малых. Это наблюдение привело Галилея к мыс-
мысли, что качающееся тело (маятник) можно исполь-
использовать для регулирования хода часов.
*) В то время, когда была написана эта книга. Сейчас «са-
«самые точные» часы — атомные.
86
Самому Галилею осуществить часы с маятником
ке удалось, а вскоре выяснилось, что его наблюде-
наблюдения были неточны. Более точные наблюдения пока-
показали, что период колебания маятника тем больше,
чем больше размах; но благодаря неизбежному тре-
трению оси и сопротивлению Еоздуха размах колебаний
обыкновенного маятника все время уменьшается, а
значит, будет уменьшаться и период его колебаний.
Часы с обыкновенным маятником — иначе называе-
называемым круговым маятником (потому что каждая точка
ею описывает дугу окружности), че могут идти верно.
Гюйгенс придумал, какое приспособление нужно
сделать круговому маятнику, чтобы у него был по-
постоянный размах (постоянная амплитуда, как гово-
говорят физики). Но он решил и другую интересную за-
задачу — ответил на вопрос, по какой кривой
должна двигаться точка, чтобы период
ее колебаний не зависел от амплитуды
(т. е. чтобы время качания не зависело от величины
размаха). Он придумал конструкцию, которая осу-
осуществила движение центра тяжести маятника по этой
кривой. Читатели догадались, конечно, что этой кри-
кривой оказалась циклоида: иначе зачем стали бы
мы говорить об этом в нашей книжке?
Начнем с приспособления, обеспечивающего вер-
верный ход часам с круговым маятником. Зубчатое ко-
колесо А (рис. 93) приводится во ьращение цепью с
гирькою В на конце. На ось этого колеса насажена
шестерня, наглухо с ним связанная (она не изобра-
изображена на рисунке). Эта шестерня и приводит в движе-
движение стрелки часов, а потому нужно, чтобы колесо А
двигалось равномерно.
Но гирька В, как и всякое тело, под действием
тяжести будет двигаться ускоренно, сообщая уско-
ускоренное же вращение колесу А. Устранить эго затруд-
затруднение должен маятник ММ.
Якорь С, лежащий в плоскости колеса А, наглухо
соединен с маятником ММ, сам маятник ММ лежит
за плоскостью чертежа и потому он начерчен пункти-
пунктиром. Якорь снабжен зубцами Н и К.
В момент, изображенный на рис. 93, колесо А
удерживается левым зубцом Н якоря С. Когда маят-
маятник качнется влево, зубец Н якоря отпустит захва-
захваченный зубец колеса, и колесо повернется, но только
87
на ползубца, потому что зубец К якоря попадет в
промежуток между зубцами ко теса и задержит его.
Когда иосле этого маятник снова качнется вправо,
зубец на этой стороне будет задержеи якорем. Итак,
при каждом полном качании маятника (туда и об-
обратно) колесо повернется ровно на один зубец, т. е.
на определенную долю окружности. Движение колеса
будет строго равномерным.
3>бцы якоря, как видно из рис. 93, срезаны наис-
наискось, так чго зубец колеса, который был задержан
Рис 93. Устройство часов с маятником.
якорем и снова отпушен, должен скользить по косой
поверхности зубца якоря. Вследствие этого якорь со-
сообщит маятнику небольшой толчок. Эти ритмические
толчки восполнят потерю энергии, которую маятник
расходует на преодоление трения и сопротивления
воздуха. Поэтому размах маятника (амплитуда коле-
колебания) не будет уменьшаться. Таким образом, гнря
сообщает энергию и колесам часов, и самому маят-
маятнику, — маятник же регулирует ход часов.
А если часы остановятся? Пустить в ход их не
трудно: достаточно поднять гирю и качнуть маятник.
Но при этом размах качания может оказаться дру*
гнм, и часы пойдут хотя равномерно, но неверно
(уйдут вперед или начнут отставать). Гюйгенс приду-
придумал приспособление, которое позволяет легко регули-
регулировать ход часов. Но Гюйгенса, как истинного уче-
ученого, заинтересовал вопрос: каков должен быть
«совершенный» маятник, маятник, время качания ко-
которого не зависит от величины размаха? О том, как
Гюйгенс решил этот вопрос и какую роль сыграла
при этом циклоида, — мы сейчас расскажем.
Таутохронная кривая Гюйгенса
Не пугайтесь, читатели, страшного греческого сло-
слова. «Таутохрона» значит попросту «равновремениая».
Так назвал Гюйгенс кривую, которую он начал ра-
разыскивать, т. е. такую кривую, по которой должен
двигаться центр тяжести маятника, для того чтобы
Л L
Рис. 94 К теории циклоидального маятника.
период его качания не зависел от величины размаха.
Поиски увенчались успехом: таинственная таутохро-
таутохрона оказалась незадолго перед тем изученной цикло-
циклоидой. При этом Гюйгенс проявил исключительное
остроумие. Достаточно сказать, что учение об эво-
эволютах было создано в процессе решения именно этой
задачи.
Гюйгенс рассуждал следующим образом*). Пред-
Представим себе желобок в форме циклоиды, как это изо-
изображено на рис. 94. По этому желобку катится тя-
тяжелый шарик М. Мы рассмотрим идеальный слу-
*) Мы излагаем рассуждения Гюйгенса, несколько упрощая
их и выражаясь современными терминами. При этом наше изло-
изложение более доступно, но очень теряет в выразительности, —
это лишь «. с живой картины список бледный».
89
чай, — тот случай, когда треиие и сопротивление воз-
воздуха отсутствуют.
Обозначим точки возврата циклоиды через Мо и
Мл, а радиус производящего круга через а. Начер-
Начертим круг радиуса а, касающийся циклоиды в верши-
вершине (круг с центром О) и производящий круг в поло-
положении, соответствующем точке М циклоиды (дан
штриховой линией). Допустим, что мы положили ша-
шарик в точку Mi желобка и отпустили его без толчка.
Под действием тяжести он покатится вниз. Изучим
его движение.
Какова будет скорость шарика, когда он опустит-
опустится до точки М циклоиды? Это нетрудно подсчитать.
Опустившись из точки Mi в точку М, шарик израс-
израсходует некоторое количество потенциальной энергии.
Эта потеря энергии равна произведению веса шарика
mg (т — масса шарика, g— ускорение силы тяжести)
на «потерю высоты», т.е. на разность выс^т шарика
в положениях М, и М, причем высоты отсчиты-
ваются от какого-то определенного уровня, напри-
например, от уровня земли. От какого уровня нн отсчиты-
отсчитывать высоты, разность их в нашем случае будет рав-
равна отрезку НМ. Итак, потеря потенциальной энергии
шарика будет равна mg-HM.
Но в силу закона сохранения энергии потерянная
потенциальная энергия шарика превратится в кине-
кинетическую энергию его движения, равную, как извест-
известно, —S— , если через v обозначить пока неизвестную
скорость шарика. Приравнивая эту кинетическую
энергию потерянной потенциальной, получим уравне-
уравнение
-g— = mg • НМ,
из которого сразу находим значение искомой скоро-
скорости
v =
Направление этой скорости тоже определить не-
нетрудно. Она будет направлена по касательной к цик-
циклоиде, т. е. по хорде ML (рнс. 94), где L — «наиниз-
«наинизшая» точка производящего круга.
Нас будет интересовать не столько сама скорость
v, сколько ее вертикальная проекция, т. е. «скорость
90
опускания шарика», скорость изменения его высоты.
Эту вертикальную проекцию лехко вычислить: она
равна и cos а, где а —угол между хордой ML и вер-
вертикалью. Хорда AT круга с центром О, очевидно, рав-
равна и параллельна хорде ML, а потому угол LMP ра-
равен )тл\ КАТ, что и отмечено на рис. 94. Итак:
овсрт — МР = v cos a = ^J2g • НМ cos а.
Неравномерное движен-ие по циклоиде, с которым
мы пока совершенно незнакомы, будем сравнивать с
равномерным движением по окружности, которое
подробно изучается в школе. С этой целью построим
вспомогательную окружность. Гюйгенс предложил
строить эту окружность так: через вершину А цик-
циклоиды проводится перпендикуляр AD (диаметр круга
с центром О), а через начальную точку Мх движения
шарика проводится параллель М\В к ее основанию.
Пусть точка пересечения этих параллели и перпенди-
перпендикуляра будет обозначена буквою В. Окружность,
построенная на АВ, как на диаметре, и будет иско-
искомой вспомогательной окружностью. Пока неясно, чем
именно она лучше других окружностей. Это выяс-
выяснится постепенно, при изложении хода мыслей
Гюйгенса.
Начнем с того, что вертикальную слагающую ско-
скорости движения шарика свяжем с элементами вспо-
вспомогательной окружности. Имеем:
МР = V2g • НМ cos a = V2S" • ВК cos а, W
потому что НМ = ВК. Из треугольника АКТ полу-
получим:
К 4
cos а = —tf-
/17
К 4
Но AT == 2а cos a, a потому cosa = -^—: , или
К А 2а соь а
cos « = -2a~ ' откУДа
¦у/АК
cos a = ¦
л] la
Подставим найденное значение косинуса в выра-
выражение для МР, отмеченное звездочкой (х). Пол\чнм:
МР = V2g • ВК cos a = -y/2g ¦ ВК • д/^Г =
91
Последний корень равен средней пропорциональ-
пропорциональной между отрезками ВК и АК, т. е. между отрез-
отрезками гипотенузы АВ треугольника ABC, на которые
последняя разделяется высотою С/С Но эта средняя
пропорциональная, по известной теореме о пропори
циональных линиях в прямоугольном треугольнике,
равна как раз высоте СК:
Поэтому для вертикальной составляющей МР ско-
скорости движения шарика по циклоиде получим окон-
чательно:
Величины а и g даны нам с самого начала и не
связаны ни с точкою М, ни с ее начальным положе-
положением М\. Таким образом, движение шарика по цик-
циклоиде вполне определяется хордою КС вспомогатель-
вспомогательной окружности, т. е. в конечном итоге положением
точки С на этой окружности.
Рассмотрим равномерное движение точки С по
вспомогательной окружности с угловой скоростью
V~g~ 360 1~
~ радианов в секунду, т. е. -^fty — градусов
в секунду. При этом скорость точки С но окружное! и
будет равна произведению радиуса окружности на
угловую скорость, выраженную в радианах (в секун-
секунду), т. е. равна
Чему равна вертикальная составляющая этой ско-
скорости? Иными словами, с какой скоростью опускает-
опускается точка С, с какою скоростью меняется ее расстоя-
расстояние от прямой МоМо при равномерном движении точ-
точки С по окружности? Это нетрудно подсчитать.
Скорость ш движения точки окружности направ-
направлена по касательной к окружности, т. е. перпендику-
перпендикулярно радиусу. Ее проекция на вертикаль равна са-
самой скорости w, умноженной на косинус угла р
(рис. 95). Но угол р равен, очевидно, углу КСО^-.
оба получаются путем вычитания угла О\СЕ из пря-
прямого угла. Косинус угла KCOi равен КС'. -к-АВ. Для
2
92
вертикальной проекции скорости равномерного дви-
движения по окружности находим:
Получается замечательный результат: когда точка
движется равномерно по окружности, ее проекция на
вертикаль движется точно так же, как проекция на
вертикаль шарика, катящегося по циклоиде. Проек-
Проекции обеих скоростей в любой момент времени равны
друг другу. Но отсюда следует, что точка окружности
из В в Л и шарик на циклоиде из М\ в А придут в
одно время. Это время легко определить. Мы гово-
говорили уже, что точка на вспомогательной окружности
1Т~
делает л/— радианов в секунду, иными словами,
на один радиан она повернется за А/-г- секунд, а
на л радианов (на полуокружность)—заяд/—.
Точно такое же время нужно и нашему шарику, что-
чтобы скатиться по циклоиде из точки М\ в точку А.
Такое же время понадобится ему, чтобы по инерции
подняться до точки М\, такое же — чтобы снова спу-
спуститься, и такое же — чтобы подняться и вернуться
в исходное положение (в точку М\). Значит, время
полного колебания шарика (период колебания) бу-
будет равняться 4
t = ¦
Это — весьма замечательная формула. Мы видим,
что период движения шарика по циклоидальному же-
желобку вполне определяется размерами желобка (ра-
(радиусом производящего круга циклоиды) и ускоре-
ускорением силы тяжести. Положение точки М\ на циклои-
циклоиде, ее расстояние от прямой МОМ'О не имеет никакого
значения. С какой бы точки циклоиды ни начинал
движения шарик, период его колебания будет один
и тот же.
Именно за это циклоиду называют «кривой рав-
равных времен» — таутохроной.
93
Забудем ненадолго маятник и посмотрим на
рпс. 95. На нем изображена ледяная гора, и не про-
простая ледяная гора, а изогнутая по циклоиде. На раз-
разной высоте (в пунктах К, Н, Р) стоят готовые к стар-
старту салазки. Одновременно по команде эти салазки
Рис. 95. «Таутохронная» гора.
начинают скользить. Кто первый достигнет цели? Не
спешите с ответом и не венчайте лаврами «спортсме-
«спортсмена» К- Лучше вспомните то, что сейчас было расска-
зано о движении по циклоиде. Тогда вам станет ясно,
что все трое достигнут точки А одновременно: ужас-
ужасное столкновение неизбежно!
Циклоидальный маятник
Гюйгенс задумался над тем, как использовать
таутохронное свойство циклоиды для устройства «со-
«совершенного» маятника? Обыкновенный маятник сде-
сделать совсем просто: достаточно привязать тяжелый
шарик к нитке и закрепить другой ее конец (рис. 96).
Центр тяжести маятника будет двигаться по окруж-
окружности. Нить можно заменить прочным тонким стерж-
стержнем. Но как заставить шарик маятника двигаться
таутохронно, не прибегая к желобкам и тому подоб-
подобным приспособлениям с большим трением? Как за-
заставить шарик на нити двигаться по
циклоиде? Размышляя об этом, Гюйгенс пришел
к понятиям об эволюте и эвольвенте.
Г4
Изготовим (например, из дерева) шаблон, состоя-
состоящий из двух одинаковых полуарок циклоиды, имею-
имеющих общую точку возврата О (рис. 97). Радиус про-
производящего круга циклоиды обозна-
обозначим, как всегда, через а. Шаблон
укрепим вертикально, и в точке воз-
возврата О привяжем нить, по длине
равную 4а — т. е. удвоенному диа-
диаметру производящего круга циклои-
циклоиды. Свободный конец нити Т снаб-
снабдим тяжелым шариком.
После того, что мы говорили об
эволютах и эвольвентах, ясно, что
шарик будет описывать при своем
движении развертку циклоиды
АСОЕВ, потому что нить будет на-
наматываться на шаблон (сравни
рис. 97 с рис. 89 на стр. 80). Но раз-
Еерткой циклоиды служит, как мы знаем, точно та-
такая же циклоида. Значит, кривая ВМТРА, по
которой движется шарик, будет циклои-
циклоидой, порожденной кругом радиуса а.
Рис. 96 Круговой
маятник.
К)
Рис. 97. Циклон чальиыЛ маятник.
Если мы поместим шарик в произвольную точку
М и предоставим самому себе, он начнет совершать
колебания, причем период этих колебаний не будет
зависеть от выбора точки М. Если даже, под влия-
влиянием трения и сопротивления воздуха, размах коле-
G5
баний будет уменьшаться, время колебания маятника
останется неизменным. Поистине этот маятник будет
таутохронным! Подумайте сами, как приспособить
такой маятник к регулированию хода часов.
Рассмотрим теперь
малые колебания маятни-
маятника по дуге Л В циклоиды
(рис. 98). Если эти коче-
бания очень малы, то
влияние направляющего
шаблона практически не
будет ощущаться и маят-
маятник будет двигаться поч-
почти как обыкновенный ма-
ягник длиною 1 = 4а,
подвешенный в точке О.
Путь А В циклоидального
маятника практически не
будет отличаться от пути
СЕ кругового маятника
длины 4а. Значит, и пе-
рчот, малых колебаний
обыкновенного кругового
маятника длиною I = 4а
не будет практически отличаться от периода циклои-
циклоидального маятника. Вводя в формулу
Рис. 98. Малые колебания кру-
кругового маятника.
с которой мы познакомились выше, вместо а равную
ему величину -т, получим выражение периода малых
колебаний кругового маятника через его длину:
Это — формула физики, известная любому школь-
школьнику.
Г Л А В А VI
УДИВИТЕЛЬНАЯ ЛЕДЯНАЯ ГОРА
«Посредине двора
Ледяная гора
Возвышается!»
И. Белоусов.
Задача о брахистохроне
На рис. 95 (стр. 94) изображена замечательная
ледяная гора: спортсмены, стартуюшне на разной вы-
высоте, прибывают к ее подножью в одно время. Но
возможна ледяная гора в некотором отношении еще
более замечательная, по крайней мере для математи-
математиков и физиков. Изучение этой горы сыграло важную
роль в истории науки, и потому она заслуживает упо-
упоминания.
Сознаюсь честно: никогда в юности мне не при-
приходил в голову вопрос — какова должна быть
форма горы, чтобы, скатываясь по ней,
совершить путь из Мо в А (рис. 95) в крат-
кратчайшее время? Ведь кратчайшим путем служит
прямая линия М0А. По ней и нужно двигаться! Ве-
Вероятно и читателям вопрос кажется очевидным и ма-
малоинтересным? Но это далеко не так. Здесь мы
встречаемся с одной из самых любопытных задач в
истории математики н на ней остановимся более под-
подробно.
Рассмотрим треугольник ABC (рис. 99). Гипоте-
Гипотенуза его АВ — ледяная гора, длина которой 20 мет-
«7
ров, высота ВС = 12 метров. Вычислим время, в те-
течение которого салазки скатятся с вершины В горы
к ее подножью А. При этом трение, как обычно, учи-
учитывать не будем.
В результате тщательных наблюдений Галилей
установил следующий закон: время движения тела по
наклонной плоскости под
действием одной тяжести
так относится к длине
пути, как время падения
с той же высоты к самой
высоте. Эту формулиров-
формулировку можно заменить такой,
вполне ей равносильной:
время, в течение которою
тело скатывается под
действием силы тяжести
по наклонной плоскости,
равно времени свободно-
свободного падения с той же вы-
высоты, деленному на син\с
угла между наклонной плоскостью и горизонтом. Чи-
Читатели без труда докажут равносильность обеих фор-
формулировок; для этого достаточно взглянуть внима-
внимательнее на рис. 99.
Галилей установил этот закон опытным путем. Но
его легко вывести из закона свободного падепия, при-
применяя правило разложения силы.
Итак, начнем с того, что вычислим время свобод-
свободного падения тела из точки В в точку С. Мы знаем,
что пройденный при свободном падении путь ВС вы-
выражается через ускорение силы тяжести (g =
= 9,81 м/с) и время t так:
Рис. 99.
Как быстрее ска-
скатиться?
Отсюда для времени t получаем:
t =
Л/8
2 V<3 = 0,32 • 4,90 = 1,57,
потому что
1 1
V9.81
= 0,32, а 2^/6" =4,90.
98
Теперь нетрудно найти время 7, в течение кото-
которого салазки скатятся по наклонной плоскости: для
этого достаточно разделить найденное значение
t A,57) на синус угла a I -jq = -=• J, или, что то же
5
самое, помножить t на — .
О
Получим:
7=1,57.| = 2,61.
Итак, салазки скатятся с горы за 2.61 секунды.
Допустим далее, что салазки из Б в Л катятся не
по горе ВА, а более сложным путем. Сначала они ка-
катятся по более крутой горе BE, а затем отрезок пути
ЕА — продолжают катиться по инерции со скоростью,
приобретенной за время спуска (которую легко вы-
вычислить). Путь из В в ? займет время, равное вре-
времени падения с высоты 12 м, деленному на синус
угла р (умноженному на -r-J, т. е. 1,57 • -^ = 1,96
секунды. К этому времени нужно добавить время
движения по инерции (на отрезке ЕА = 7 м). Ско-
Скорость, приобретенная салазками, когда они достигли
точки Е, вычисляется путем сравнения потерянной
потенциальной энергии (tngh) и приобретенной кине-
„ / mvl \
¦шческои I—5~1:
mgh = m\.
Откуда
v = ^Jigh = У& • V24 м/с.
Чтобы найти время движения салазок по инерции от
Е до А, нужно путь G метров) разделить на скорость
(л/g ' V24); ведь движение по инерции — равномер-
равномерное:
Складывая время «скатывания» по горе BE A,96 с)
и время движения по инерции @,46 с), получим об-
общее время движения по ломаной ВЕА. Оно оказы-
оказывается равным 1,96 + 0,46 = 2,42 с, т. е. оказывается
меньше, чем время спуска по наклонной ВА. Хотя
прямая АВ и является кратчайшим расстоя-
99
нием между В и А, но не она является линией
«наименьшего времен и»: с этой точки зрения
ломаная ВЕА является как бы «более короткой».
Оно и понятно: потеря в пути более чем вознаграж-
вознаграждается выигрышем в скорости, полученным за счет
большей крутизны спуска.
Эти соображения наводят на мысль, что самым
выгодным в смысле экономии времени будет, каза-
казалось бы, путь по ломаной ВСА: сначала салазки па-
падают вдоль отвесной горы ВС; далее небольшое
закругление (оно показано на рис. 99 пунктиром)
меняет по возможности плавно их направление; а по-
потом они катятся по инерции вдоль прямой СА, сохра-
сохранив большую скорость.
Не будем гадать, лучше займемся вычислением!
Время свободного падения салазок вдоль катета ВС
мы уже вычислили: ведь это — наше t, равное 1,57 с.
Скорость в точке С вычисляется из сравнения поте-
потерянной потенциальной н приобретенной кинетической
энергии: она равна д/g • д/24 , как мы тоже вычис-
вычислили. Поделив путь A6 м) на скорость, получим
время tcA-.
/Ci, = 16:(VF-V2f) = 0,32--|-2,45 = l,04 с.
Прибавив к этому время падения A,57 с), получим
полное время движения по ломаной ВСА:
*вса= 1.57+ 1,04 = 2,61 секунды.
Оказывается, что этот путь невыгоден: он — такой
же продолжительный, как путь по прямой ВА, и, зна-
значит, заметно дольше пути по ломаной ВЕА. Из трех
разобранных нами путей самым кратковременным
(хотя и не самым коротким) оказался путь по лома-
ломаной ВЕА.
Но является ли точка Е (рис. 99) «наивыгодней-
«наивыгоднейшей» точкой? Обеспечивает ли она наибольшую эко-
экономию времени? Или найдется некоторая точка М
(рис. 100), такая, что путь по ВМА, изображенный
штриховой линией ( ), займет еще меньше
времени? А может быть, вершина ломаной должна
лежать не на прямой СА, а где-нибудь внутри
треугольника ABC, и наивыгоднейшим по времени
100
л м
Рис. 100. Какой путь выбрать?
путем будет ломаная BDA, изображенная штрих-
пунктирной линией ( )? Или, наконец, реше-
решение даст кривая линия, изображенная пунктиром
( )? И как найти такую кривую?
Одним словом, возникает задача: через точки
Б н Л, лежащие на различной высоте над
уровнем з е м л и,
провести кривую
линию, при движе-
движении по которой под
j l :\ с т в и е м тяжести
тело пройдет из В
в А в кратчайшее
время. Искомую кри-
кривую назвали «брахисто-
«брахистохроной», т. е. «кривой
кратчайшего времени».
Если точки В и А лежат
на одной вертикали, то
брахистохроной является, очевидно, прямолинейный
отрезок. Но что будет, если точки Л и В не лежат на
одной вертикали, если они расположены как в разоб-
разобранной нами только что задаче о треугольнике?
В этом случае вопрос не ясен, а потому мы займемся
брахистохроной подробнее.
До сих пор мы говорили об ученых — Галилее,
Паскале, Робервале, Торичелли и других, — которые
своими работами подготовили создание Ньютоном и1
Лейбницем дифференциального и интегрального ис-
исчисления. Знаменитые братья Бернулли: Якоб
П654—1705) и Иоганн A667—1748) принадлежат к
иному поколению ученых. Они первые оценили могу-
могущество и красоту новых методов Ньютона и Лейб-
Лейбница и принялись энергично за их разработку и за
расширение области их применения. Они же были
первыми глашатаями новых идей в математике, пер-
первыми пропагандистами замечательных методов диф-
дифференциального и интегрального исчисления. Само
слово «интеграл» было введено в науку Якобом Бер-
Бернулли.
В 1696 году Иоганн Бернулли поставил задачу о
брахистохроне. Ниже мы расскажем, чем именно
трудна эта задача и почему она была особенно инте-
интересна. Иоганн Бернулли опубликовал ее без решения,
101
приглашая лучших математиков заняться ею. Чет-
гзеро ученых решили эту задачу: Лейбниц, Ньютон,
де-Лопиталь и Якоб Бернулли. Решение Якоба Бер-
нуллн было наиболее интересным и сыграло выдаю-
выдающуюся роль в истории математики.
Для того чтобы разобраться в вопросе о брахи-
брахистохроне, нам придется сделать экскурсию в сторону:
придется вспомнить кое-что из оптики.
Экскурсия в оптику. Хитрый jij ч света
Напомним формулировку задачи о брахистохроне.
Из всех кривых, соединяющих лежащие на различ*
ной высоте точки А и В, нужно выбрать такую, дви-
двигаясь по которой под влиянием только силы тяжести,
Рис. 101. Задача Ферма.
точка *) придет из более высокой в более низкую
точку в кратчайшее время.
Эта задача трудна. Рассмотрим предварительно
следующую, более легкую задачу: с корабля А
(рис. 101) требуется послать в город В гонца. Лодка
движется со скоростью v км/ч, пеший гонец делает
w км/ч. Расстояния a, b, m даны (рис. 101). На бе-
берегу КН нужно найти такое место М, чтобы гонец,
высадившись там, совершил весь путь АМВ в крат-
кратчайшее время.
*) Здесь речь идет не о чисто геометрической, а о мате-
материальной точке — точке, обладающей весом.
102
Близость этой задачи к задаче о брахистохроне —
очевидна. Но задача о брахистохроне гораздо слож-
сложнее: там нужно было найти не точку, а целую неиз-
неизвестную кривую. В новей задаче (будем называть
ее задачей Ферма) отыскивается только одна точка.
Более того: в задаче Ферма мы имеем дело только
с двумя значениями
скорости (и и w); в зада-
задаче о брахистохроне ско-
скорость точки меняется под
влиянием силы тяжести
непрерывно и принимает и
бесчисленное м н о - —
ж ест в о различных зна- — <
чений. ^- "~~Ss*~y- г - -" ~--~~ -—
Но и к решению зада- ^Л^^-^ fiy^^ZZ-Z^Z
чи Ферма мы приступим _, тг
не maw Ппежпе пяггмо- Рис- 102' Как принести водн с
не сразу, прежде рассмо нанмеиьшей „отерей времени?
трим один вопрос, кото-
которым почти 2000 лет назад занимался александрийский
ученый Герон (I век н. э.).
Представьте себе, что вы путешествуете с группой
товарищей. Часть вашей группы остановилась лаге-
лагерем в пункте А (рис. 102), другая часть — в пункте В.
Предположим, что вы находитесь в В, а ведерко
для воды ¦— в Л. Вы приходите в Л, берете ведерко,
а затем хотите зайти на берег НК реки, набрать воды
и вернуться в своп лагерь В. В каком пункте М бе-
берега вам нужно брать воду, чтобы путь из Л в В за-
занял кратчайшее время? Мы допустим, что с водой и
без нее вы двигаетесь одинаково быстро, и тогда воп-
вопрос физики можно будет заменить чисто геометриче-
геометрическим вопросом: найти кратчайший путь из Л в В
(с заходом на прямую НК).
Решается этот вопрос очень просто. Строим точку
Ви симметричную точке В относительной прямой НК
(иными словами, проводим ВС _L НК и на продолже-
продолжении ВС откладываем СВ\ = СВ). Возьмем теперь
любую точку Т на прямой НК. Совершенно очевидно,
что длины ломаных АТВ и АТВ\ равны, как бы ни
была выбрана точка Т. Кратчайшая ломаная типа
АТВ будет соответствовать кратчайшей ломаной типа
АТВ\. Для ломаных типа АТВХ вопрос ясен: соеди-
соединим А и В\ прямолинейным отрезком; «ломаная»
юз
u
-
Рис. 103. Закон Снеллиуса.
АМВ\ (т. е. прямая) будет кратчайшим расстоянием
между А и В\. Но тогда кратчайшей ломаной типа
АТВ (точки А и В — по одну сторону прямой Ш\)
будет ломаная АМВ, а искомой точкой — точка М
(точка пересечения прямой ЯД' и отрезка, соединяю-
соединяющего А с «зеркальным отражением» точки В).
Обратите внимание на то обстоятельство, что углы
ВМС и СМВ\ равны (почему?). Если через точку М
провести прямую ЕРА_НК,
то будут равны углы ЕМВ
иЕМА.
Допустим теперь, что мы
имеем дело не с берегом
Реки и экскурсантами, а с
поверхностью зеркала, ис-
источником света А и глазом
наблюдателя В (все тот же
рис. 102). Тогда наше реше-
решение задачи выразит извест-
ный из физики факт: угол
падения светового луча ра-
равен углу отражения. Эту же мысль теперь можно
сформулировать и так: при отражении световой луч
«выбирает» путь наименьшей длины. Этот результат
был впервые получен Героном Александрийским, а
потому последнюю формулировку закона отражения
принято называть теоремой Герона.
Через полторы тысячи лет после Герона были изо-
изобретены микроскоп и телескоп. Стремление усовер-
усовершенствовать эти приборы привело к усиленным заня-
занятиям геометрической оптикой, причем, естественно, в
центре внимания стал вопрос не об отражении, а о
преломлении света (в линзах). Было ясно, что в этом
случае не может быть и речи о кратчайшем пути лу-
луча АОВ (рис. 103). Но как должны быть связаны
углы аир, изображенные на рисунке 103, — об.этом
приходилось только догадываться. Голландскому уче-
ученому Снеллиусу A581 —1626) удалось опытным пу-
путем открыть закон, известный в наше время любому
школьнику: если луч попадает из среды А в среду В,
то отношение синусов угла падения и угла преломле-
преломления луча есть величина постоянная (равная отноше-
отношению показателей преломления среды В и среды А).
Уже ученые позднего Возрождения поняли, что разли-
104
чие коэффициентов преломления вызвано различием
скоростей света в разных средах. Если на рис 103
скорость света в верхней среде обозначим через v, в
нижней —через ш, то закон Снеллиуса можно будет
сформулировать так: синусы углов падающего и от-
отраженного лучей прямо пропорциональны соответ-
соответствующим скоростям света, — и записать так:
sin a: sin р = v : w.
Путь луча из Л в В через точку О не является
наименьшим по длине. Но, может быть, он будет
кратчайшим по времени? Французский математик
Пьер Ферми A601—1665) первый обратил внимание
на то, что в теореме Герона об отражении света мож-
можно говорить не о кратчайшем пути, а о наименьшем
времени (ведь скорость-то падающгго и отраженного
лучей одинакова!). А что, подумал Ферми, если и при
преломлении световой луч «выбирает» путь, соответ-
соответствующий кратчайшему времени? Это позволило бы
охватить отражение и преломление света единым об-
общим законом, положить в основу формулировки но-
новую, быть может, плодотворную идею!
И Ферма ставит задачу: пусть на рис. 103 ско-
скорость света над прямой МР равна v, под МР — рав-
равна w. Как должен двигаться световой луч, чтобы
прийти из Л в В в кратчайшее время?
Взглянем теперь на рис. 101 и сравним задачу
Ферми о луче света с задачей о гонце с корабля.
Сразу видно, что для математика — это одна и та же
задача. Поэтому-то задачу о корабле мы и назвали
задачей Ферма, хотя этот ученый кораблями никогда
не занимался. Мы можем теперь забыть и о кораб-
кораблях, и о лучах света, и говорить об отвлеченной за-
задаче механики: частица движется из Л в В, пересе-
пересекая прямую МР (рис. 103). Ее скорость над прямой
МР равна v, под прямой МР равна сс\ В какой точке
О путь частицы, состоящий из двух прямолинейных
отрезков, должен пересечь прямую МР, для того что-
чтобы время движения было наименьшим?
В чем здесь трудность? Возьмем задачу: даны ос-
основание равнобочной трапеции, ее периметр и угол
при основании; найти площадь. Это — обычная за-
задача, не слишком простая, но и не очень трудная, и
любой девятиклассник ее решит. Но видоизменим за-
105
дачу и рассмотрим такой случай: даны основание и
периметр равнобочной трапеции; как следует вы-
выбрать угол при основании, для того чтобы площадь
трапеции стала возможно большей? И вот из тысячи
школьников вряд ли найдется хотя бы один, который
сумеет решить эту новую задачу.
Практическая ценность задач такого рода (т. е«
таких, 1де нужно найти условия, при которых некото-
некоторая величина принимает наибольшее или наименьшее
Р ,Т
Н
М
Рис 104. Вывод закона Снеллиуса.
значение) — очевидна. В технике постоянно прихо-
приходится решать вопрос о самых экономных размера*
котла, о наивыгоднейшей форме крыла самолета и
т. п. Наука древних подобными вопросами почти не
занималась. Но перед учеными Возрождения стала
насущная задача: разработать простые способы ре-
решения такого рода задач — задач на максимум и ми-
минимум, как их называют.
Решить задачу о преломлении светового луча, не
зная закона Снеллиуса, очень трудно. Но допустим,
чго найденный из опыта закон Снеллиуса подсказал
нам решение. Тогда нетрудно доказать, что наша до-
догадка справедлива.
Этим мы теперь и займемся.
Пусть частица (или луч) движется прямолинейно
из точки А (рис. 104) к прямой И К, а затем от НК в
точку В, причем от Л до прямой НК движется со
скоростью v, а от прямой НК до точки В — со ско-
скоростью w. В какой точке С путь частицы (или луча
света) должен пересечь прямую НК, чтобы достичь
106
точки В в кратчайшее время? Докажем, что наикрат-
наикратчайшим по времени будет такой путь при котором
отношение синусов углов РСА и ВСМ будет равно
отношению скоростей v и ад.
Пусть АСВ— именно такой путь, т.е. пусть по ус-
условию (рис. 104)
sin a: sin р = v: ад.
Возьмем на НК произвольную точку F. Докажем, что
путь AFB займет больше времени, чем путь АСВ.
Сделаем подготовительное построение, которое
облегчит нам дальнейшие рассуждения. Опустим пер-
перпендикуляры из точки F на падающий луч и на на-
направление луча преломленного (эта оптическая фор-
формулировка годится и для решения задачи о движу-
движущейся частице). Иными словами, проведем FD Л С А
и FE JL ВТ. Угол DFC равен углу РСА (углу а), как
углы со взаимно перпендикулярными сторонами. По
той же причине угол CFE равен углу ВСМ (углу р).
Поэтому
CD . _ СЕ
sia sinp
Поделив эти соотношения одно на другое, поменяв их
местами и вспомнив, что (по закону Снеллиуса)
sin a : sin p = v : ад, получим:
CD sin a v CD СЕ
СЕ sinp и' v w '
Это и есть предварительный результат, который нам
нужно было получить. Переходим теперь к сравне-
сравнению времен, затрачиваемых на движение по путям
АСВ и AFB.
Для путей АСВ и AFB имеем соответственно:
АС СВ AF . FB
(на каждом прямолинейном участке для определения
времени равномерного движения делим путь на ско-
скорость).
Нужно доказать, что
АС . СВ ^ АГ , FB
t<h, т. е. что—+ — < — + —.
Преобразуем теперь выражение для t. Заменив АС
равной ему суммой AD -J- DC, получим:
AD + DC СВ _ АР DC СВ
Заменив —— равным ему отношением , получим;
, __ АР . СЕ СВ AD . BE
V W W V W
потому что СЕ -\- СВ — BE.
Остается последний шаг. Сравним отрезки AD и
AF. Первый — перпендикуляр, второй — наклонная к
DF. Следовательно, AD < AF. Точно так же ЕВ <<
<BF. Но если AD<AF, то-~<^. Точно так
BE ^ BF .„
же —— < ——. Мы получаем окончательно:
AD BE . AF . FB . ..
— + — < — + —' т. е. /<f,.
Итак, мы доказали, что время прохождения пути
АСВ меньше времени прохождения любого другого
пути. Теорема о падающем и преломленном лучах
доказана. А мы, тем самым, подготовлены к реше-
решению задачи о брахистохроне.
Снова циклоида!
Напомним формулировку задачи о брахистохроне
(кривой скорейшего спуска). По какому пути долж-
должна двигаться тяжелая часгица, чтобы под действием
одной только силы тяжести прийти из Л в Б
(рис. 105) в кратчайшее время? chn — совсем особая
задача. В задаче Ферма требовалось найти опреде-
определенное положение одной-единственной точки,
для которой рассматриваемая величина (время)
была наименьшей. В других задачах, подобных за-
задаче Ферма, требуется найти какое-то одно значение
некоторой величины, чтобы другая величина полу-
получила наибольшее или наименьшее значение. В задаче
же Иоганна Бернулли (задачу о брахистохроне по-
поставил, как мы помним, И. Бернулли) дело обстоит
рначе. нужно найти положение ие одной, и даже не
десятка, а бесконечного множества точек,
образующих непрерывную кривую линию.
108
Тут не только способ Ферми, но и возникшее во вое
мена Бернулли дифференциальное исчисление
могло помочь. Вог почему решить задачу
стохроне смогли только самые выдающиеся
менники Бернулли.
Решение Якоба Бернулли, наиболее совершенное
из всех, все же не было вполне строгим. Попытки
улучшить это решение и сделать его применимым к
Рис. 105 К задаче о брахистохроне.
другим задачам привели в следующем, восемнадца-
том веке к созданию совершенно новой ветви матема-
математики — вариационного исчисления. Именно поэтому
мы говорили на стр. 102, что задача о брахистохроне
сыграла выдающуюся роль в истории науки.
Переходим к решению этой задачи, данному Яко-
Якобом Бернулли. Он начал с того, что заменил трудную
задачу большим количеством простых — элементар-
элементарных—задач. Разность высот точек А и В (рис. 105)
он разделил на очень большое количество равных
частей и через точки деления мысленно провел ряд
параллельных плоскостей. Все пространство оказа-
оказалось «расслоенным» на пласты. Если толшину каж-
каждого слоя обозначим через с, число слоев — через п
(на рис. 105 п=10, с — 0,4 см), то произведение сп
будет, очевидно, равно всей величине h—разности
высот точек А и В.
Допустим теперь, что скорость частицы меняется
не непрерывно, а скачками — при переходе от слоя
к слою. При этом в первом (сверху) слое она равна
109
V\ = i/^gc, т. е. скорости, которую под действием силы
тяжести частица приобрела бы в конце пути через пер-
первый слой. Во втором слое она равна о2= -\/'2g • 2с >
т. е. равна той скорости, которую в конце второго
промежутка частица имела бы и при естественном
движении. Теперь ясно, какова должна быть скорость
в любом слое. Так, например, в четвертом слое она
будет »< = -\/2g • Ас и т. д. Частица будет двигаться
под действием тяжести по ломаной линии, причем
если п велико (а толщина слоя, следовательно, ма-
мала),— движение будет очень близко к естественному
движению по многоугольному желобку. Чтобы опре-
определить форму ломаной линии, дающей путь частицы
в случае приближенного, «скачкообразного» движе-
движения, нужно определить все углы при вершинах этой
ломаной.
Можно также определить углы, которые каждое
звено ломаной образует с вертикалью: эти углы
удобно обозначить через аи аг, аз и т. д. Номер под
альфой указывает, о каком слое идет речь (рис. 105).
Рассмотрим внимательнее поведение частицы на
границе каких-нибудь двух слоев, например, пятого
и шестого. Рассуждения и результат будут одина-
ковы и для любой иной пары смежных слоев. Чтобы
время следования по пятому и шестому слоям было
наименьшим, необходимо, чтобы синусы надлежащих
углов относились как скорости в пятом и шестом
слое (ведь здесь выполняются условия задачи Фер-
Ферма, а стало быть, будет справедлив закон Снеллиуса
в применении к частице). Итак, должно осуществ-
осуществляться равенство:
sin а5 : sin а6 = о5: о6>
но »5 = *\/2g • 5с, »6 = V2g ¦ 6с 1 потому
sin а^ л!^-ё ¦ 5с V5с sin а5 sin
ИЛИ
sina6 -y'2g-6c V6c V5c V6c
Повторив подобное рассуждение для всех пар смеж«
ных слоев, мы получим серию равенств:
sin ay sin <x3 sin щ
¦ — ¦ — • • • И Т. Д«
¦у/с
ПО
Иными словами, отношение синуса угла между лю-
быи. звеном ломаной и вертикалью к соответствую-
соответствующему расстоянию слоя от верхней плоскости (от пло-
плоскости АН на рис. 105) есть величина постоянная.
Искомая «ломаная кратчайшего времени» теперь
полностью определена. Ее можно построить ЗБено за
звеном, ьачиная с первого.
Следуя Якобу Еернулли, мы допустим то тол-
толщина с слоев неограниченно уменьшается, а число
слоев неограниченно растет. Тогда ломаный путь в
пределе перейдет в искомую кривую — в брахисто-
брахистохрону, — и задача будет решена.
Что при этом станет с направлением каждого зве-
звена ломаной? Оно перейдет в направление касатель-
касательной к искомой кривой. Таким образом, в любой точ-
точке брахистохроны отношение синуса угла меж,г/ ка-
касательной и вертикалью к корню квадратному из
«высоты» (из расстояния от точки кривой до гори-
горизонтали АН) будет постоянным.
Но ведь это свойство характеризует как раз цик-
циклоиду! Вспомним теоремы 4 и 5 на стр. 26. Един-
Единственной кривой, у которой направление касательной
в любой точке и расстояние от этой точки до данной
прямой связаны таким соотношением, является наша
старая знакомая! Ей мало быть таутохроной: она же
оказалась и брахистохроной.
Решение Якоба Бернулли, разумеется, несовер-
несовершенно. Не ясно, оправдан ли в этом случае предель-
предельный переход от ломаной линии к кривой. Есть и дру»
гие логические шероховатости. Но отказать Якобу
Бернулли в исключительной изобретательности и
остроумии никак нельзя. А развитие основной идеи
этого решения и привело в XVIII веке к созданию ва-
риационного исчисления.
ЗАКЛЮЧЕНИЕ
Подведем итоги. Мы познакомились с кривой, за-
замечательной во многих отношениях. Она — и след
точки обода катящегося колеса, она же — таутохрон-
ная кривая (кривая колебаний постоянного периода),
она же — брахистохрона (кривая быстрейшего спус-
спуска). Но этого мало. В наше время циклоидальные
кривые применяются при многих технических расче-
расчетах, и знание этих кривых облегчает изучение дета-
деталей машин. Не вдаваясь в подробности, упомянем,
что свойствами циклоидальных кривых пользуются
при построении профилей зубьев шестерен и во мно-
многих других технических вопросах. Даже с чисто при-
прикладной точки зрения кривые эти заслуживают са-
самого серьезного внимания.
Но у циклоиды есть и другие заслуги. Ею пользо-
пользовались ученые XVII века при разработке приемов ис-
исследования кривых линий, — тех приемов, которые
привели в конце концов к изобретению дифферен-
дифференциального и интегрального исчислений. Она же была
одним из «пробных камней», на которых Ньютон,
Лейбниц и их первые последователи испытывали
силу новых мощных математических методов. Нако-
Наконец, задача о брахистохроне привела к изобретению
вариационного исчисления, столь нужного физикам
сегодняшнего дня. Таким образом, циклоида оказа-
оказалась неразрывно связанной с одним из самых инте-
интересных периодов в истории математики.
ОГЛАВЛЕНИЕ
Глава I. Кривая, рожденная колесом
Разговор двух велосипедистов 3
Что же такое циклоида? 8
Немного истории \ . . 11
Глава II. Важнейшие свойства циклоиды
Касательная и нормаль к циклоиде 17
Геометрическое определение циклоиды 24
Спутница циклоиды и ее разоблачение 27
Площадь циклоиды. Теорема Галилея 31
Дальнейшие свойства циклоиды 34
Глава III. Родственницы циклоиды
Укороченные и удлиненные циклоиды 40
Эпициклоиды 44
Кардиоида. Конхоиды 50
Гипоциклоиды 56
Эпициклоида с бесконечным множеством арок 62
Глава IV. Эволюты и эвольвенты
Развертка (эвольвента) кривой 67
Основные свойства развертки 69
Развертка окружности 73
Жук-математик 76
Развертка циклоиды. Длина дуги циклоиды 80
Глава V. Лучший маятник
Христиан Гюйгенс и его изобретение 85
Часы с маятником. Почему плох обыкновенный (круго-
(круговой) маятник? 86
Таутохронная кривая Гюйгенса 89
Циклоидальный маятник 94
Глава VI. Удивительная ледяная гора
Задача о брахистохроне 97
Экскурсия в оптику. Хитрый луч света 102
Снова циклоида! . . . 108
Заключение 112
20 ноп.