Автор: Werke G.C.F.
Теги: algebra mathematica theoremata mathematica mathematicae superiores calculi integrales
Год: 1866
Похожие
Текст
CARL FRIEDRICH GAUSS WERKE
BAND JH.
CARL FRIEDRICH GAUSS
WERKE
DRITTER BAND
HERAUSGEGEBEN
VON DER
KÖNIGLICHEN GESELLSCHAFT DER WISSENSCHAFTEN
zu
GÖTTINGEN
1866.
DEMONSTRATIO NOVA
THEOKEMATIS
OMNEM FUNCTIONEM ALGEBRAICAM
RATIONALEM INTEGRAM
UNIUS VARIABILIS
FACTOEES EEALES PEIMI VEL SECUNDI GEADUS
RESOLVIPOSSE
QUAM PRO
OBTINENDIS SüMMIS IN PHILOSOPHIA HONORIBÜS
INCLITO PHILOSOPHORÜM ORDINI
ACADEMIAE IULIAE CAEOLIJSTAE
EXHIBUIT
CAßOLUS FRIDERICUS GAUSS
HELMSTADIT
APÜD C. G. FLECKEISEN. MDCCLXXXXIX.
DEMONSTRATIO NOVA THEOREMATIS
OMJSTEM FUJSTCTIOJSTEM ALGEBRAICAM RATIONALEM INTEGRAM
ÜNIÜS VARIABILIS
IN FACTORES REALES PRIMI VEL SECUNDI GRADUS RESOLVI POSSE.
1.
Quaelibet aequatio algebraica determinata reduci potest ad forraam
xm-{-Axm-l-{-Bafn-2-\- etc. -\-M= 0
ita ut m sit numerus integer positivus. Si partem primam huius aequationis per
X denotamus, aequationique X = 0 per plures valores inaequales ipsius x sa-
tisfieri supponimus, puta ponendo x — a, x = 6, x = y etc. functio X per
productum e factoribus x—a, x—6, x — y etc. divisibilis erit. Vice versa, si
productum e pluribus factoribus simplicibus x—oc, x — f>, x — y etc. functionem
X metitur: aequationi X = 0 satisfiet, aequando ipsam x cuicunque quanti-
tatum a, 6, y etc. Denique si X producto ex m factoribus talibus simplicibus
aequalis est (sive omnes diversi sint, sive quidam ex ipsis identici): alii factores
simplices praeter hos functionem X metiri non poterunt. Quamobrem aequatio
m11 gradus plures quam m radices habere nequit; simul vero pätet, aequationem
m}1 gradus paudores radices habere posse, etsi X in m factores simplices resolu-
bilis sit: si enim inter hos factores aliqui sunt identici, multitudo modorum di-
versorum aequationi satisfaciendi necessario minor erit quam m. Attamen con-
cinnitatis caussa geometrae dicere maluerunt» aequationem in hoc quoque casu m
radices habere, et tantummodo quasdam ex ipsis aequales inter se evadere: quod/
utique sibi permittere potuerunt.
4 DEMONSTRATIO NOVA THEOEEMATIS
2.
Quae hucusque sunt enarrata, in libris algebraicis sufficienter demonstran-
tur neque rigorem geometricum uspiam offendunt. Sed nimis praepropere et sine
praevia demonstratione solida adoptavisse videntur analystae theorema cui tota
fere doctrina aequationum superstructa est: Quamvis functionem talem ut X sem-
per in m factores simplices resolvi posse, sive hoc quod eum illo prorsus conspirat,
quamvis aequationem mtl gradus revera habere m radices. Quum iam in aequatio-
nibus secundi gradus saepissime ad tales casus perveniatur, qui theoremati huic
repugnant: algebraistae, ut hos illi subiicerent, coacti fuerunt, fingere quantita-
tem quandara imaginariam cuius quadratum sit — 1, et turn agnoverunt, si quan-
titates formae a-\-b\J—1 perinde concedantur ut reales, theorema non modo pro
aequationibus secundi gradus verum esse, sed etiam pro cubicis et biquadraticis.
Hinc vero neutiquam inferre licuit, admissis qüantitatibus formae a-\-b\j—1 ciü-
vis aequationi quinti superiorisve gradus satisfieri posse, aut uti plerumque ex-
primitur (quamquam phrasin lubricam minus probarem) radices cuiusvis aequatio-
nis ad formam a-\-b\J—1 reduci posse. Hoc theorema ab eo, quod in titulo
huius scripti enunciatum est, nihil differt. si ad rem ipsam spectas, huiusque de-
monstrationem novam rigorosam tradere. constituit propositum praesentis disser-
tationis.
Ceterum ex eo tempore, quo analystae comperti sunt, infinite multas ae-
quationes esse, quae nullam omnino radicem haberent, nisi quantitates formae
a-\-b\J—1 admittantur, tales quantitates fictitiae tamquam peculiare quantita-
tum genus, quas imaginarias dixerunt, ut a realibus distinguerentur, consideratae
et in totam analysin introductae sunt; quonam iure? hoc loco non disputo De-
monstrationem meam absque omni quantitatum imaginariarum subsidio absol-
vam, etsi eadem libertate, qua omnes recentiores analystae usi sunt, etiam mihi
uti liceret.
3.
Quamvis ea, quae in plerisque libris elementaribus tamquam demonstratio
theorematis nostri afferuntur, tarn levia sint, tantumque a rigore geometrico ab-
horreant, ut vix mentione sint digna: tarnen, ne quid deesse videatur, paucis
illa attingam. 'Ut demonstrent, quamvis aequationem
\- etc. +Jlf == 0
OHNEM FOTJCTIONEM ALGEBBÄICAM ETC. O
sive X — 0, revera habere m radices, suscipiunt probare, X in m faetoxes
simplices resolvi posse. Ad hunc finem assumunt m factores simplices <2?—~ a,
oc—6, x—y etc. ubi <x, 6, y etc. adhuc sunt incognitae, produciumque ex illis
aequale ponunt functioni X. Turn ex comparatione coeffieientium deducunt m
aequationes, exT quibus incognitas a, ö, y etc. determinari posse aiunt, quippe
quarum multitudo etiam sit m. Scilicet m — 1 incognitas eliminari posse, unde
emergere aequationem, quae, quam placuerit, incognitam solara contineat.' Ut
de reliquis, quae in tali argumentatione reprehendi possent, taceam, quaeram
tantummodo, unde certi esse possimus, ultimam aequationem revera ullam radi-
cem habere? Quidni fieri posset, ut neque huic ultimae aequationi neque propo-
sitae, ulla magnitudo in toto quantitatum realium atque imaginariarum ambitu
satisfaciat? Ceterum periti facile perspicient, hanc ultimam aequationem ne-
cessario cum proposita omnino idendcam fore, siquidem calculus rite fuerit insti-
tutus; scilicet eliminatis incognitis ö, y etc. aequationem
^+Aa^+Ba™-*-^ etc. +M = 0
prodire debere. Plura de isto ratiocinio exponere necesse non est.
Quidam auctores, qui debilitatem huius methodi percepisse videntur, tam-
quam aoßioma assumunt, quamvis aequationem revera habere radices, si non pos-
sibiles, impossibiles. Quid sub quantitatibus possibilibus et impossibilibus in-
telligi velint, haud satis distincte exposuisse videntur. Si quantitates possibiles
idem denotare debent ut reales, impossibiles idem ut imaginariae: axioma illud
neutiquam admitti potest, sed necessario demonstratione opus habet. Attamen
in illo sensu expressiones accipiendae non videntur, sed axiomatis mens haec po-
tius videtur esse: 'Quamquam nondum sumus certi, necessario dari m quanti-
quantitates reales vel imaginarias, quae alicui aequationi datae m11 gradus satisfaciant,
tarnen aliquantisger hoc supponemus; nam si forte contingeret, ut tot quantita-
quantitates reales et imaginariae inveniri nequeant, certe effugium patebit, ut dicamus
reliquas esse impossibiles.' Si quis hac phrasi uti mavult quam simpliciter di-
cere. aequationem in hoc casu tot radices non habituram, a me nihil obstät: at
si turn his radicibus impossibilibus ita utitur tamquam aliquid veri sint, et e. g.
dicit, summam omnium radicum aequationis afn-\-Aafn~i-\- etc. = 0. esse
= —A, etiamsi impossibiles inter ülas sint (quae expressio proprie signifrcat,
etiamsi aliquae deßciant): hoc neutiquam probare possum. Nam radices impossi-
6 DEMOHSTRÄTSO JfOVA fSOEOBEMATI&
biles, in tali sensu acceptae, tarnen sunt radices, et turn axioma illud nullo modo
sine demonstratione admitti potest, neque inepte dubitares, annon aequationes
exstare possint, quae ne impossibiles quidem radices habeant?*)
4.
Antequam aliorum geometrarum demonstrationes theorematis nostri recen-
seam, et quae in singulis reprehendenda mihi videantur, exponam: observo suf-
ficere si tantummodo ostendatur, omni aequationi quantivis gradus
- etc. + Jf = 0
sive X = 0 (ubi coefficientes A, B etc. reales esse supponuntur) ad minimum
uno modo satisfieri posse per valorem ipsius x sub forma a-A-b\J— 1 conten-
tum. Constat enim, X tunc divisibilem fore per factorem realem secundi gradus
xx—^ax-\-aa-\-bb, si b non fuerit =• 0, et per factorem realem simplicem
x— a, si b — 0. In utroque casu quotiens erit realis, et inferioris gradus quam
X; et quum hie eadem ratione factorem realem primi seeundive gradus habere de-
*) Sub quantitate imaginaria hie semper intelligo quantitatem in forma a + b\/—l contentam, quam-
diu b non est = o. In hoc sensu expressio illa semper ab omnibus geometris primae notae aeeepta est, ne-
neque audiendos censeo , qui quantitatem a-\-b\J—l in eo solo casu imaginariam vocare voluerunt ubi a = o,
impossibilem vero quando non sit a = o , quum haec distinetio neque necessaria sit neque ullius utilitatis. —
Si quantitates imaginariae omnino in analysi retineri debent (quod pluribus rationibus consultius videtur, quam
ipsas abolere, modo satis solide stabiliantur): necessario tamquam aeque possibiles ac reales speetandae sunt;
quamobrem reales et imaginarias sub denominatione communi quantitatum possibilium complecti mallem: con-
contra, impossibilem dicerem quantitatem, quae conditionibus satisfacere debeat, quibus ne imaginariis quidem
concessis satisfieri potest, attamen ita, ut phrasis haec idem significet ac si dicas, talem quantitatem in toto
magnitudinum ambitu non dari. Hinc vero genus peculiare quantitatum formare, neutiquam concederem.
Quodsi quis dicat, triangulum rectilineum aequilaterum rectangulum impossibile esse, nemo erit qui neget.
At si tale triangulum impossibile tamquam novum triangulorum genus contemplari, aliasque triangulorum pro-
prietates ad illud applicare voluerit, ecquis risum teneat? Hoc esset verbis ludere seu potius abuti. — Quam-
vis vero etiam summi mathematici saepius veritates, quae quantitatum ad quas speetant possibüitatem mani-
festo supponunt, ad tales quoque applieaverint quarum possibilitas adhuc dubia erat; neque abnuerim, huius-
modi licentias plerumque ad solam formam et quasi velamen ratiociniorum pertinere, quod veri geometrae
acies mox penetrare possit: tarnen consultius, scientiaeque, quae tamquam perfectissimum «laritatis et certi-
tudinis exemplar merito celebratur, sublimitate magis dignum videtur, tales libertates aut omnino proscribere,
aut saltem parcius neque alias ipsis uti, nisi ubi etiam minus exercitati perspicere valeant, rem etiam absque
illarum subsidio etsi forsan minus breviter tarnen aeque rigorose absolvi potuisse. — Ceterum haud negaverim,
ea quae hie contra impossibilium abusum dixi, quodam respectu etiam contra imaginarias obiiei posse: sed ha-
rum vindicationem nee Don totius huius rei expositionem uberiorem ad aliam occasionem mihi reservo.
OMNEM FÜXCTIONEM ALGEBBAICAM ETC. 7
beat, patet, per continuationem huius operationis functionem X tandem in facto-
res reales simplices vel duplices resolutum iri, aut, si pro singulis factoribus
realibus duplicibus binos imaginarios simplices adhibere mavis, in m factores
simplices.
5.
Prima theorematis demonstratio illustri geometrae d'Alembeet debetur, Re-
cherches sur le calcul integral, Histoire de T Acad. de Berlin, Annee 1746.
p. 182 sqq. Eadem extat in Bougainville, Traite du calcul integral, a Paris 1754.
p. 47 sqq. Methodi huius praecipua momenta haec sunt.
Primo ostendit, si functio quaecunque X quantitatis variabilis x fiat = 0
aut pro x = 0 aut pro x = oo, atque valorem infinite parvum realem positi-
positivum nancisci possit tribuendo ipsi x valorem realem: hanc functionem etiam va-
valorem infinite parvum realem negativum obtinere posse per valorem ipsius x vel
realem vel sub forma imaginaria p-\-q\J—1 contentum. Scilicet designante Q
valorem infinite parvum ipsius X, et u> valorem respondentem ipsius x, asserit
u) per seriem valde convergentem aQa-\-bQ -\-cQf etc. exprimi posse, ubi ex-
ponentes a, ö, 7 etc. sint quantitates rationales continuo crescentes, et quae adeo
ad minimum in distantia certa ab initio positivae evadant, terminosque, in qui-
bus adsint, infinite parvos reddant. Iam si inter omnes hos exponentes nullus
occurrat, qui sit fractio denominatoris paris, omnes terminos seriei reales fieri turn
pro positivo turn pro negativo valore ipsius Q; si vero quaedam fractiones deno-
denominatoris paris inter illos exponentes reperiantur, constare, pro valore negativo
ipsius Q terminos respondentes in forma p-\-q\J—1 contentos esse. Sed prop-
ter infinitam seriei convergentiam in casu priori sufficere, si terminus primus (i. e.
maximus) solus retineatur, in posteriori ultra eum terminum, qui partem imagi-
nariam primus producat, progredi opus non esse.
Per similia ratiocinia ostendi posse, si X valorem negativum infinite par-
parvum ex valore reali ipsius x assequi possit: functionem illam valorem realem
positivum infinite parvum ex valore reali ipsius x vel ex imaginario sub forma
p-\-q \/— 1 contento adipisci posse.
Hinc secundo concludit, etiam valorem aliquem realem finitum ipsius X
dari, in casu priori negativum, in posteriori positivum, qui ex valore imaginario
ipsius x sub forma p-\-q^J—1 contento produci possit.
8 DEMONSTBATIO NOVA
Hinc sequitur, si X sifc talis functio ipsius x, quae valorem realem V
ex valore ipsius x reali v obtineat. atque etiam valorem realem quantitate in-
infinite parva vel maiorem vel minorem ex valore reali ipsius x assequatur, eandem
etiam valorem realem quantitate infinite parva atque adeo finita vel minorem vel
maiorem quam V (resp.) recipere posse, tribuendo ipsi x valorem sub forma
p-{-q\l—1 contentum. Hoc nullo negotio ex praecc. derivatur, si pro X sub-
stitui concipitur V-\- Y, et pro x, v -\-y.
Tandem affirmat 111. d'Alembebt, si X totum intervallum aliquod inter duos
valores reales R, 8 pereurrere posse supponatur (i. e. turn ipsi R, turn ipsi 8,
turn omnibus valoribus realibus intermediis aequalis fieri), tribuendo ipsi x valo-
valores semper in forma p-\-q\J—1 contentos; functionem X quavis quantitate fi-
finita reali adhuc augeri vel diminui posse (prout 8^>R vel 8<aR), manente x
semper sub forma p-\-q\J—1. Si enim quantitas realis TJ daretur (inter quam
et R supponitur $ iacere), cui X per talem valorem ipsius x aequalis fieri non
posset, necessario valorem maximum ipsius X dari (scilicet quando 8^>R; mi-
nimum vero, quando 8<C_R), puta T, quem ex valore ipsius x, p~{-q\f—1,
consequeretur, ita ut ipsi x nullus valor sub simili forma contentus tribui posset,
qui functionem X vel minimo excessu propius versus U promoveret. Iam si in
aequatione inter X et x pro x ubique substituatur p-\-q\l—1. atque turn pars
realis, turn pars, quae factorem \J—t implicet, hoc omisso, cifrae aequentur:
ex duabus aequationibus hinc prodeuntibus (in quibus p, q et X cum constanti-
bus permixtae occurrent) per eliminationem duas alias elici posse, in quarum al-
tera p, X et constantes reperiantur, altera a p libera solas q, X et constantes
involvat. Qamobrem quum X per valores reales ipsarum p, q omnes valores ab
R usque ad T percurrerit, per praecc. X versus valorem U adhuc propius acce-
dere posse tribuendo ipsius p, q valores tales a-f-yy/—ltfi-\-$\/—i resp. Hinc
vero fieri x = a—^-j-(y-f-^)\/—*> i-e- adhuc sub forma p-\-q\J—1 esse, con-
contra hyp.
Iam si X functionem talem ut xm-\-Axm~l-\~Bxm~i-\-eXc.-\-M deno-
tare supponitur, nullo negotio perspicitur, ipsi x tales valores reales tribui posse,
ut X totum aliquod intervallum inter duos valores reales percurrat. Quare x
valorem aliquem sub forma p-\-q\j—1 contentum talem etiam nancisci potent,
nnde X fiat =0. Q. E. D.*)
*) Observare convenit, £11. d'Ai-embekt in sua huius demonstrationis exposüione consideratioaes geome-
OMNEM FUNCTIONEM ALGEBEAICAM ETC.
6.
Quae contra demonstrationem D^i$jcBEBTianam obiici posse
haec fere redeunt.
1. 111. d'A. nullum dubium movet de existentia valorum ipsius x, quibusva-
lores dati ipsius X respondeant, sed illam supponit, solamque formam istorum
valorum investigat.
Quamvis vero haec obiectio per se gravissima sit, tarnen hie ad solara dictio-
nis formam pertinet, quae facile ita corrigi potest, ut illa penitus destruatur.
2. Assertio, cd per talem seriem qualem ponit semper exprimi posse. certo
est falsa, si X etiam functionem quamlibet transscendentem designare debet (uti
d'A. pluribus locis innuit). Hoc e. g. manifestum est, si ponitur X = e^ sive
x = j—-£■ Attamen si demonstrationem ad eum casum restringimus, ubi X est
funetio algebraica ipsius x (quod in praesenti negotio sufficit) T propositio utique
est vera. . Ceterum d'A. nihil pro confirmatione suppositionis suae attulit; cel.
Boügainville supponit, X esse functionem algebraicam ipsius x, et ad inventio-
nem seriei parallelogrammum NEWTONianum commendat.
3. Quantitatibus infinite parvis liberius utitur, quam cum geometrico ri-
gore consistere potest aut saltem nostra aetate (ubi illae merito male audiunt) ab
analysta scrupuloso concederetur, neque etiam saltum a valore infinite parvo ip-
ipsius Q ad finitum satis luculenter explieavit. Propositionem suam, Q etiam va-
lorem aliquem finitum consequi posse, non tarn ex possibilitate valoris infinite
parvi ipsius Q concludere videtur quam inde potius, quod denotante Q quanti-
tatem valde parvam, propter magnana seriei convergentiam, quo plures termini
seriei aeeipiantur, eo propius ad valorem verum ipsius cd accedatuf, aut, quo
plurium partium summa pro cd aeeipiatur, eo exaetius aequationi, quae relatio-
nem inter cd et Q sive x et X exhibeat, satisfactum iri. Praeterea quod tota
haec argumentatio nimis vaga videtur, quam ut ulla conclusio rigorosa inde col-
ligi possit: observo, utique dari series, quae quantumvis parvus valor quantitati,
tricas adhibuisse, atque X tamquam abscissam, x tamquam ordinatam curvae speetavisse (seeundum
omnium geometrarum primae huius saeculi partis, apud quos notia funetionum minus usitata erat). Quia vero
omnia ipsius ratiocinia, si ad ipsorum essentiam solam respwäs, nuUis prineipiis geomeliicis, sed pure analyti-
cis innituntur, et curva imaginaria, ordinataeque imaginariae expressiones duriores esse iectoremque hodiex-
num facilius offendere posse videntur, formam repraesentationis mere analytiram hie adhibere maluu Haac
annotationem ideo-adieci, ne quis demonstrationem D'ALEMBE&Tianara ipsam cum hac succinefoexpositiaae com--
parans aliquid essentiale immutatum esse suspicetur.
2
10 DEMONSTEATIO KOVA, THEOEEMAIIS
secundum cuius potestates progrediuntur, tribuatur, nihilominus semper diyer»
gant, ita ut si modo satis longe continuentur, ad terminos quavis quantitate data
maiores pervenire possis#). "Hoc evenit, quando coefficientes seriei progressionem
hypergeometricam constituunk Quamobrem necessario denaonstrari debuisset, ta-
lem seriem hypergeometricam in casu praesentx provenire non posse.
Ceterum mihi videtur, 111. d'A. hie non recte ad series infinitas confugisse.
hasque ad stabiliendum theorema hoc fundamentale doctrinae aequationum haud
idoneas esse.
4. Ex suppositione, X obtinere posse valorem S neque vero valorem U,
nondum sequitur, inter S et U necessario valorem T iacere, quem X attingere
sed non superare possit. Superest adhuc alius casus: scilicet fieri posset, ut in-
inter S et U limes situs sit, ad quem accedere quidem quam prope velis possit X,
ipsum vero nihilominus numquam attingere. Ex argumentis ab ill. d'A. allatis
tantummodo sequitur, X omnem valorem, quem attigerit, adhuc quantitate
finita superare posse, puta quando evaserit = S, adhuc quantitate aliqua finita
Q augeri posse; quo facto, novum incrementum Qf accedere, tunc iterum augmen-
tum Q" etc., ita ut quoteunque incrementa iam adieeta sint. nullum pro ultimo
haberi debeat, sed semper aliquod novum accedere possit. At quamvis multitudo
incrementorum possibilium nullis limitibus sit circumscripta: tarnen utique fieri
posset, ut si incrementa Q, Q', Q" etc. continuo decrescerent, nihilominus summa
S-{-Q-\-Q'-\-&' etc. limitem aliquem numquam attingeret, quoteunque termini
considerentur.
Quamquam hie casus oecurrere non potest, quando X designat funetionem
algebraicam integram ipsius x: tarnen sine demonstratione, hoc fieri non posse,
methodus necessario pro incompleta habenda est. Quando vero X est funetio
transscendens, sive etiam algebraica fraeta, casus ille utique locum habere potest,
e. g. semper quando valori cuidam ipsius X valor infinite magnus ipsius x respon-
*) Hacce occasione obiter adnoto, ex harum serierum numero plurimas esse, quae primo aspectu maxime
convergentes videantur, e. g. ad maximam partem eas, quibus ill. Euleb in parte poster. Inst. Calc. Diff.
Cap. VI. ad summam aliarum serierum quam proxime assignandam utitur p. 441—47 4 (reliquae enim series
p. 475—478 revera convergere possunt), quod, quantum scio, a nemine hueusque observatum est. Quocdrca
magnopere optandum «sset, ut dilueide et rigorose ostenderetur, cur huiusmodi series, quae primo citissime,
dein paullatim lentius lentiusque convergunt, tandemque magis magisque divergunt, nihilominus summam
proxime -seram suppeditent, si modo non nimis multi termini capiantur, et quousque talis summa pro exaeta
tuto haberi possit ?
OMNEM FDNCTIONEM ALGEBBAICAM ETC. 11
det. Turn methodus D'ALEMBEETiana non sine multis ambagibus, et in quibusdäm
casibus nuHo forsan modo, ad principia mdubitata reduci ppsse videtur.
Propter has rationes demonstrationem DJALEMBEBTianam pro satisfaciente
habere nequeo. Attamen hoc non obstante verus demonstrationis nervus probandi
per omnes obiectiones neutiquam infringi mihi videtur, credoque eidem funda-
mento (quamvis longe diversa ratione, et saltem maiori circumspicientia) non so-
lum demonstrationem rigorosam theorematis nostri superstrui, sed ibinde omnia
peti posse, quae circa aequationum transscendentium theoriam desiderari queant.
De qua re gravissima alia occasione fusius agam; conf. interim infra art. 24.
7.
Post d'Alembertum'ÜI. Eulee disquisitiones suas de eodem argumento pro-
mulgavit, JRecherches sur les racines imaginaires des eqnations, Hist. de TAcad.
de Berlin A. 1749, p. 223 sqq. Methodum duplicem hie tradidit: prioris summa
continetur in sequentibus.
Primo ill. E. suseipit demonstrare, si m denotet quameunque dignitatem
numeri 2, funetionem x2m-+-B x2m~2-+- Cx2mr~3-\- etc. -J-Jf = X (in qua coeffi-
ciens termini seeundi est = 0) semper in duos factores reales resolvi posse, in
quibus x usque ad m dimensiones ascendat. Ad hunc finem duos factores assumit,
xm—uxm-l-}-axm-2-i-ßxm-3-i-etc., et xm-\-uxn)r-1-{-'kxm-2-\-iLxm-3 etc.
ubi coefficientes u, a, 6 etc. X, fi etc. adhuc incogniti sunt, -horumque produetum
aequale ponit funetioni X. Turn coefficientium comparatio suppeditat Im — 1
aequationes, manifestoque demonstrari tantummodo debet, incognitis u, a; fi etc.
X, [l etc. (quarum multitudo etiam est Im — 1) tales valores reales tribui posse. qui
aequationibus illis satisfaciant. Iam E. affirmat, si primo u tamquam cognita
consideretur, ita ut multitudo incognitarum unitate minor sit quam multitudo
aequationum. his secundum methodos algebraicas notas rite combinatis omnes
a, ß etc. X, {jl etc. rationaliter et sine ulla radicum extractione per u et coeffi-
coefficientes B, C etc. determinari posse, adeoque valores reales nancisei,, simulao u
realis fiat. Praeterea vero omnes at ß etc. X, {a etc. eliminari poterunt, ita ut
prodeat aequatio U = 0, ubi U erit funetio integra solius u et eoefficientium
cognitorum. Hanc aequationem ipsam per methodum eliminationis vulgärem evol-
vere, opus immensum foret, quando aequatio proposita X. = 0 est gradus ali-
2*
12 DEMONSTBATIO NOVA THEOREMATIS
quantum alti; et pro gradu indeterminato, plane impossibile (iudice ipsoE. p. 239).
Attamen hie suffieit, unam illius aequationis proprietatem novisse, scilicet quod
terminus ultimus in U (qui incognitam u non implicat) necessario est negativus,
unde sequi constat, aequationem ad minimum unam radicem realem habere, sive
u et proin etiam a, 6 etc. X, ja etc. ad minimum uno modo realiter determinari
posse: illam vero proprietatem per sequentes reflexiones confirmare licet. Quum
xm— uxm~~l-\-axm~-\- etc. supponatur esse factor funetionis X: necessario u
erit summa m radicum aequationis X = 0, adeoque totidem valores habere de-
bebit, quot modis diversis ex Im radieibus m excerpi possunt, sive per princi-
i i- -, • .. Im. Im— 1.2m — 2 m-\-\ -, tt-
pia calculi combmationum — — valores. Hie numerus sem-
r 1 . 2 . 3 . . . m
per erit impariter par (demonstrationem haud difficilem supprimo): si itaque po-
nitur =. 2k, ipsius semissis h impar erit; aequatio U = 0 vero erit gradus
2ÄÜ. Iam quoniam in aequatione X = 0 terminus seeundus deest: summa
omnium 2 m radicum erit 0; unde patet, si summa quarumeunque m radicum
fuerit -\-p, reliquarum summam fore —p, i. e. si -\-p est inter valores ipsius
u, etiam —p inter eosdem erit. Hinc E. concludit, U esse produetum ex k
factoribus duplieibus talibus uu—pp, uu—qq, uu — rr etc., denotantibus -\-p,
— P> ~\~Q> —q etc. omnes 2k radices aequationis U—Q, unde, propter mul-
titudinem imparem horum factorum, terminus ultimus in U erit quadratum pro-
dueti pqr etc. signo negativo aifectum. Produetum autem pqr etc. semper ex
coefficientibus JB, C etc. rationaliter determinari potest, adeoque necessario erit
quantitas realis. Huius itaque quadratum signo negativo aifectum certo erit quan-
titas negativa. Q. E. D.
Quum hi duo factores reales ipsius X sint gradus mtl atque m potestas
numeri 2: eadem ratione uterque rursus in duos factores reales \m dimensionum
resolvi potent. Quoniam vero per repetitam dimidiationem numeri m necessario
tan dem ad binarium pervenitur, manifestum est, per continuationem operationis
funetionem X tandem in factores reales seeundi gradus resolutam haberi.
Quodsi vero funetio talis proponitur, in qua terminus seeundus non deest,
puta x2m-\-Aocim~~l-\-Bxim~2^retc.-\-M, designante etiamnum 2 m potestatem
binariam, haec per substitutionem x = y transibit in similem funetionem
termino seeundo carentem. Unde facile concluditur, etiam illam funetionem in
factores reales seeundi gradus resolubilem esse.
Denique proposita funetione gradus wfa, designante n numerum, qui non
OM2JEM PUNCTIONEM ALGEBRAICAM ETC. 13
est potestas binaria: ponatur potestas binaria proxime maior quam n, = %m,
raultipliceturque functio proposita per Im—n factores siraplices reales quoseun-
que. Ex resolubilitate producti in factores reales seeundi gradus, nullo negotio
derivatur, etiam functionem propositam in factores reales secundi vel primi gra-
gradus resolubilem esse debere.
Contra hanc demonstrationem obiici potest
1. Regulam, secundum quam E. concludit, ex Im — 1 aequationibus
2m — 2 incognitas a, ß etc. X, ja etc. omnes ratiorialiter determinari posse, neu-
tiquam esse generalem, sed saepissime exceptionem pati. Si quis e, g. in art. 3,
aliqua incognitarum tamquam cognita spectata, reliquas per hanc et coefficien-
tes datos rationaliter exprimere tentat, facile inveniet, hoc esse impossibile, nul-
lamque quantitatum incognitarum aliter quam per aequationem m — tti gradus
determinari posse. Quamquam vero hie statim a priori perspici potest, illud ne-
cessario ita evenire debuisse: tarnen merito dubitari posset, annon etiam in casu
praesenti pro qiiibusdam valoribus m res eodem modo se habeat, ut incognitae
a, 6 etc. X, {jl etc. ex u, B, C etc. aliter quam per aequationem gradus forsan ma-
ioris quam Im determinari nequeant. Pro eo casu, ubi aequatio X. = 0 est
quarti gradus, E. valores rationales coefficientium per u et coefficientes datos eruit;
idem vero etiam in omnibus aequationibus altioribus fieri posse, utique explica-
tione ampliori egebat. Ceterum operae pretium esse videtur, in formulas il-
las, quae a, fi etc. rationaliter per u, JB, C etc. exprimant, profundius et gene-
ralissime inquirere; de qua re aliisque ad eliminationis theoriam (argumentum
haudquaquam exhaustum) pertinentibus/alia occasione fusius agere suscipiam.
2. Etiamsi autem demonstratum fuerit, cuiusvis gradus sit aequatio X = 0,
semper formulas inveniri posse, quae ipsas a, ß etc. X, [l etc. rationaliter per
u, B. C etc. exhibeant: tarnen certum est, pro valoribus quibusdam determinatis
coefficientium B, C etc. formulas illas indetermm&tas evadere posse, ita ut non
solum impossibile sit, incognitas illas rationaliter ex u, B, C etc. definire, sed
adeo revera quibusdam in casibus valori alicui reali ipsius u nulli valores reales
ipsarum ot, 6 etc. k, \l etc. respondeant. Ad confirmationem huius rei brevitatis
gratia ablego lectorem ad diss. ipsam E., ubi p. 236 aequatio quarti gradus fusius
explicata est. Statim quisque videbit, formulas pro coefficientibus ce, 6 indeter-
14 BEMONSTEATIO KOVA THEOBESfATIS
minatas fieri, si G=0 et pro u assumatur valor 0, illoramque valores non so-
lum sine extractione radieum assignari non posse, sed adeo ne reales quidem esse,
si fuerit BB—4Z> quantitas negativa. Quamquam vero in hoc casu u adhuc
alios valores reales habere, quibus valores reales ipsarura a. !j respondeant, fa-
cile perspici potest: tarnen vereri aliquis posset, ne huius düficultatis enodatio
(quam E. omnino non attigit) in aequationibus altioribus multo maiorem operam
facessat. Gerte haec res in demonstratione exacta neutiquam silentio praeteriri
debet.
3. HL E. supponit tacite, aequationem X = 0 habere Im radices, ha-
rumque summam statuit = 0, ideo quod terminus secundus in X abest. Quo-
modo de hac licentia (qua omnes auctores de hoc argumento utuntur) sentiam, iam
supra art. 3 declaravi. Propositio, summam omnium radicum aequationis alicu-
ius coefficienti primo, mutato signo, aequalem esse, ad alias aequationes appli-
canda non videtur, nisi quae radices habent: iam quum per hanc ipsam demon-
strationem evinci debeat, aequationem X = 0 revera radices habere, haud per-
missum videtur, harum existentiam supponere. Sine dubio ii, qui huius paralo-
gismi fallaciam nondum penetraverunt, respondebunt, hie non demonstrari, aequa-
tioni X = 0 satisfieri posse (nam hoc dicere vult expressio, eam habere radices),
sed tantummodo, ipsi per valores ipsius x subforma a-\-b\J—1 contentos satisfieri
posse: illud vero tamquam axioma supponi. At quum aliae quantitatum formae,
praeter realem et imaginariam a-\-b\J—1 coneipi neqiieant, non satis luculen-
tum videtur, quomodo id, quod demonstrari debet, ab eo, quod tamquam axioma
supponitur, differat; quin adeo si possibile esset adhuc alias formas quantitatum
exeogitare, puta formam F, F', F" etc.: tarnen sine demonstratione admitti non
deberet. cuius aequationi per aliquem valorem ipsius x aut realem, aut sub forma
a-\-b\J—1, aut sub forma F, aut sub F' etc. contentum satisfieri posse. Quam-
obrem axioma illud alium sensum habere nequit quam hunc: Cuivis aequationi
satisfieri potest aut per valorem realem incognitae, aut per valorem imaginarium
subforma a-\-b\J—1 contentum, aut forsan per valorem subforma alia hueus-
que ignota contentum, aut per valorem, qui sub nulla omnino forma continetur.
Sed quomodo huiusmodi quantitates, de quibus ne ideam quidem fingere potes
— vera umbrae umbra — summari aut multiplicari possint, hoc ea perspieuitata,
quae in mathesi semper postulatur, certo non intelligitur *).
*) Tota haec res multum illustrabitur per aliam disquisitionem sub prelo iam sudantem, ubi in argu-
OMNEM FUNCTIONEM ALGEBRAICAM ETC. 15
Ceterum conclusiones, quas E. ex suppositione sua elicuit, per has obieetio-
nes haudquaquam suspectas reddere volo; quin potius certus sum, illas per me-
thodum neque difficüem neque ab EüLEßiana multum diversam ita comprobari
posse, ut nemini vel minimus scrupulus superesse debeat. Solam formam repre-
heixdo, quae quamvis in inveniendis novis veritatibus magnae utilitatis esse possit,
tarnen in demonstrando, coram publico, minime probanda videtur.
4. Pro demonstratione assertionis, productum pqr etc. ex coefficientibus
in X rationaliter determinari posse, ill. E. nihil omnino attulit. Omnia, quae
hac de re in aequationibus quarti gradus explicat, haec sunt (ubi a, B, c, b sunt
radices aequationis propositae xk-\-Bxx-\- Cx-\-D = 0):
'On m'objectera sans doute, que j'ai suppose ici, que la quantite pqr etait
une quantite reelle, et que son quarre ppqqrr etait affirmatif; ce qui etait en-
core douteux, vu que les racines a, B, c, b etant imaginaires, il pourrait bien arri-
ver, que le quarre de la quantite pqr, qni en est composee, fut negatif. Or je re-
ponds a cela que ce cas ne saurait Jamals avoir lieu; car quelque imaginaires que
soient les racines a, B, c, b, on sait pourtant, qu'il doit y avoir a-j-&-|-c-|-b — 0:
ces quantites JB,C,D etant reelles. Mais puisque p = a-f-B, q = a-f-c,
r = a-f-b, leur produit pqr = (a-f-5)(a-f-c)(a-f-b) est determinable comme on
sait, par les quantites B, C, D, et sera par consequent reel, tout comme nous
avons vu, qu'il est effectivement pqr = — C, et ppqqrr = CC. On recon-
naitra aisement de meme, que dans les plus hautes equations cette m^me cir-
constance doit avoir lieu. et qu'on ne saurait me faire des objections de ce
coteV Conditionem, productum pqr etc. rationaliter per B, C etc. determi-
determinari posse, E. nullibi adiecit, attamen semper subintellexisse videtur, quum abs-
que illa demonstratio nullam vim habere possit. Iam verum quidem est in ae-
aequationibus quarti gradus, si productum (a-f-B)(a-f-c) (a-f-b) evoluatur, obtineri
aa(a-}-B-}-c-(-b)-}-aBc-(-aBb-}-acb-(-Bcb = —C, attamen non satis perspieuum
videtur, quomodo in omnibus aequationibus superioribus productum rationaliter
mento longe quidem diverso, nihilominus tarnen analogo, licentiam similem prorsus eodem iure usurpare
potuissern, ut hie in aequationibus ab omnibus analystis faetum est. Quamquam vero plurium veritatumde-
monstrationes adiumento talium fictionum paucis verbis absolvere lieuisset, quae absque his perquam diffieiles
evadunt et subtilissima artificia requirunt, tarnen Ulis omnino abstinere malui, speroque, paucis me satisfactu-
rum fuisse, si analystarum methodum imitatus essem.
*) E. per errorem habet C, unde etiam postea perperam statuk pqr — C.
16 I>E3fONSTJBATIQ ÜTOYA THEOEEMATIS
per coeffieientes determinari possit. Clar. de Foncenex , qui primus hoc obser-
vavit (Miscell. phil. math. soc. Taurin. T. I. p. 117), recte contendit, sine demon-
stratione rigorosa huius propositionis methodum omnem vim perdere, illam vero
satis difficilem sibi videri confitetur, et quam viam frustra tentaverit, enarrat*).
Attamen haec res haud difiiculter per methodum sequentem (cuius summam ad-
digitare tantummodo hie possum) absolvitur: Quamquam in aequationibus quarti
gradus non satis darum est, produetum (a-f-B)(a-f-c) (a-f-b) per cogfficien-
tes J5, C, D determinabile esse, tarnen facile perspici potest, idem produetum
etiam esse = (b-f-a) (B-f-c) (B-f-b), nee non = (c-f-a)(c-f-B)(c-f-b), denique
etiam = (b-f-a) (b-f-5) (byf-c). Quare produetum pqr erit quadrans summae
(a+B)(a+c)(o + b) + (B + o)F + c)F + b) + (c+o)(c+B)(c+b)+(b+o)(b+B)(b+c)f
quam, si evolvatur, fore funetionem rationalem integram radicum a, B, c, b ta-
lem, in quam omnes eadem ratione ingrediantur, nullo negotio a priori praevi-
deri potest. Tales vero funetiones semper rationaliter per coefficientes aequationis,
cuius radices sunt a, B, c, b, exprimi possunt. Idem etiam manifestum est,
si produetum pqr sub hanc formam redigatur:
i(a-fb—c—ii)x{(a+c- 6 — b)xiia+b — B — c)
quod produetum evolutum omnes a, B, c, b eodem modo implicaturum e,sse facile
praevideri potest. Simul periti facile hinc colligent, quomodo hoc ad altiores ae-
quationes applicari debeat. Completam demonstrationis expositionem, quam
hie apponere brevitas non permittit, una cum uberiori disquisitione de funetioni1
bus plures variabiles eodem modo involventibus ad aliam occasionem mihi reservo.
Ceterum observo, praeter has quatuor obiectiones, adhuc quaedam alia in
demonstratione E. reprehendi posse, quae tarnen silentio praetereo, ne forte cen-
sor nimis severus esse videar, praesertim quum praecedentia satis ostendere vi-
deantur, demonstrationem in ea quidem forma, in qua ab E. proposita est, pro
completa neutiquam haberi posse.
Post hanc demonstrationem, E. adhuc aliam viam theorema pro aequationi-
aequationibus , quarum gradus non est potestas binaria, ad talium aequationum resolutio-
nem reducendi ostendit: attamen quum methodus haec pro aequationibus quarum
*) In hanc expositionem error irrepsisse videtur, scilicet p. 118. 1. 5. loco characteris p (on choisis-
sait seulement celles oü entrait p etc.), necessario legere oportet, une wem« racine quelconque de lequa~
tion proposee, aut simile quid, quum illud miUum sensum habeat.
OMNEM FUNOTIONJEM ALGEBRAICAM ETC. tl
gradus est potestas binaria, nihil doceat, insuperque oranibus obiectionibus praecc.
(praeter qaartam) aeque obnoxia sit ut demonstratio prima generalis: liaud neeesse
est illam hie fusius explicare.
9.
In eadem commentatione ill. E. theorema nostrum adhuc alia via confir-
mare annixus est p 263, cuius summa continetur inhis: Proposita aequatione
xn~\-Aa/n~1-\-Bx!n~~2 etc. = 0 , hueusque quidem expressio analytica, quae ipsius
radices exprimat, inveniri non potuit, si exponens w>4; attamen certum esse
videtur (uti asserit E.), illam nihil aliud continere posse. quam operationes arith-
meticas et extractiones radicum eo magis complicatas, quo maior sit n. Si hoc
conceditur, E. optime ostendit, quantumvis inter se complicata sintsigna radica-
lia, tarnen formulae valorem semper per formam M-\~N\J—1 repraesentabilem
fore, ita ut M, N sint quantitates reales.
Contra hoc ratiocinium obiiei potest, post tot tantorum geometrarum labo-
res perexiguam spem superesse, ad resolutionem generalem aequationum algebrai-
carum umquam perveniendi, ita ut magis magisque verisimüe fiat, talem resolu-
resolutionem omnino esse impossibilem et contradictoriam. Hoc eo minus paradoxum
videri debet, quum id, quod vulgo resolutio aequationis dicitur, proprie nihil aliud sit
quam ipsius reduetio ad aequationes puras. Nam aequationum purarum solutio hinc
non docetur sed supponitur, et si radicem aequationis xm = H per y^ff expri-
mis, illam neutiquam solvisti, neque plus fecisti, quam si ad denotandam radicem
aequationis afl-\-Aocnr~x-\- etc. = 0 Signum aliquod exeogitares, radicemque huic
aequalem poneres. Verum est, aequationes puras propter facilitatem ipsarum ra-
radices per approximationem inveniendi, et propter nexum elegantem, quem omnes
radices inter se habent, prae omnibus reliquis multum praestare, adeoque neuti-
neutiquam vituperandum esse, quod analystae harum radices per signum peculiare de-
notaverunt: attamen ex eo, quod hoc signum perinde ut signa arithmetica addi-
tionis, subtractionis, multiplicationis, divisionis et evectionis ad di^nitatem sub
nomine expressionum analyticarum complexi sunt, minime sequitur cuiusvis aequa-
aequationis radicem per illas exhiberi posse. Seu, missis verbis, sine ratione sufiieienti
supponitur, ciiiusvis aequationis solutionem ad solutionem aequationum purarum
reduci posse, Forsan non ita difficile foret, impossibilitatem iam pro quinto gradu
omni rigore demonstrare, de qua re alio loco disquisitiones meas fusius proponam.
S
18 DEMONSTRATIO HOVA THEOREMATIS
Hic sufficit, resolubilitatem generalem aequationum, in illo sensu acceptam. ad-
huc valde dubiam esse, adeoque demonstrationem, cuius tota vis ab illa supposi-
tione pendet, in praesenti rei statu nihil ponderis habere.
10.
Postea etiam dar. de Foncenex, quum in demonstratione prima Euleki de-
fectum animadvertisset (supra art. 8 obiect. 4), quem tollere non poterat, adhuc
aliam viam tentavit et in comment. laudata p. 120 in medium protulit#). Quae
consistit in sequentibus.
Proposita sit aequatio Z=ö, designante Z functionem ml1 gradus in-
cognitae z. Si m est numerus impar, iam constat, aequationem hanc habere
radicem realem; si vero m est par, clar. F. sequenti modo probare conatur, ae-
aequationem ad minimum unam radicem formae p-\-q\/—1 habere. Sit m = 2ni,
designante i numerum imparem, supponaturque zz-\-uz-\-M esse divisor
functionis Z, Tunc singuli valores ipsius u erunt summae binarum radicum ae-
quationis Z = 0 (mutato signo), quamobrem u habebit m'^m~ — m' valores,
et si u per aequationem U= 0 determinari supponitur (designante U functio-
functionem integram ipsius u et coefficientium cognitorum in Z), haec erit gradus mtl.
Facile vero perspicitur, m fore numerum formae 2W~V, designante % numerum
imparem. Iam nisi m est impar, supponatur iterum, uu-\-u'u-\-M' esse divisorem
ipsius U, patetque per similia ratiocinia, u determinari per aequationem U'= 0.
ubi U sit iunctio ——— u gradus ipsius u. rosito vero —-—— = m » ent m
numerus formae 2n~~2i", designante i" numerum imparem. Iam nisi m" est im-
impar, statuatur uu'-\-uu-\-M" esse divisorem functionis U', determinabiturque
u" per aequationem U" — 0, quae si supponitur esse gradus m'"tl, m" erit nu-
numerus formae 2n~~si'". Manifestum est, in serie aequationum U = 0, U'=. 0,
U" = 0 etc. n^m fore gradus imparis adeoque radicem realem habere. Statue-
mus bre^dtatis gratia n = 3, ita ut aequatio TJ" ■=- 0 radicem realem u" habeat,
nullo enim negotio perspicitur, pro quovis alio valore ipsius n idem ratiocinium
valere. Tunc coefficientem M" per u" et coefficientes in ZT (quos fore functio-
nes integras coefficientium in Z facile intelligitur), sive per u" et coefficientes in
*) In tomo seeundo eorundem Miscellaneorum p. 337 dilucidationes ad hanc commentationem continen-
tur: attamen hae ad disquisitionem praesentem non pertinent, sed ad logarithmos quantitatum negativarum,
de quibus in eadem comm. sermo fuerat.
OMNEM FUNCTIONEM ALGEBEAICAM ETC. 19
Z rationaliter determinabilem fore asserit clar. de F., et proin realem. Hinc se-
quitur, radices aequationis u'u'-\-u"u'-{-M"= 0 sub forma p-{-q\J—1 conten-
tas fore; eaedem vero manifesto aequationi 27'== 0 satisfacient: quare dabitur
valor aliquis ipsius u sub forma p-\-q\J-7-l contentus. Iam coeffieiens M' (eodem
modo ut ante) rationaliter per u et coefficientes in Z determinari potest, adeoque
etiam sub forma p-\-q\J—1 contentus erit; quare aequationis uu-\-uu-\-M'
radices sub eadem forma contentae erunt, simul vero aequationi TJ =■ 0 satisfa-
satisfacient, i. e. aequatio haec habebit radicem sub forma p-\-q\J—1 contentam. De-
nique hinc simili ratione sequitur, etiam M sub eadem forma contineri, nee non
radicem aequationis zz-\-uz-\-M = 0, quae manifesto etiam aequationi propo-
sitae Z = 0 satisfaciet. Quamobrem quaevis aequatio ad minimum unam radi-
radicem formae p + q y—1 habebit.
11.
Obiectiones 1, 2, 3, quas contra Euleki demonstrationem primam feci (art. 8),
eandem vim contra hanc methodum habent, ea tarnen differentia, ut obiectio se-
eunda, cuiEüLERi demonstratio tantummodo in quibusdam casibus specialibus ob-
noxia erat, praesentem in omnibus casibus attingere debeat. Scilicet a priori de-
nionstrari potest, etiamsi formula detur, quae coefficientem M' rationaliter per u
et coefficientes in Z exprimat, hanc pro pluribus valoribus ipsius u necessario
indeterminatam fieri debere; similiterque formulam, quae coefficientem M" per
u" exhibeat, indeterminatam fieri pro quibusdam valoribus ipsius u" etc. Hoc
luculentissime perspicietur, si aequationem quarti gradus pro exemplo assumimus.
Ponamus itaque m = 4. sintque radices aequationis Z— 0, hae a, Ö, y, c.
Turn patet, aequationem U=Q fore sexti gradus ipsiusque radices —(a-f-6),
_(a+T), -(ot+g), -(Ö + y), —(Ö+g), —(T+g). Aequatio ZT = 0 au-
tem erit deeimi quinti gradus, et valores ipsius u' hi
g, 2a + y-f Bt 2ü-f a-f y, 26 + a + 8, 26 + y-f $,
Iam in hac aequatione, quippe cuius gradus est impar, subsistendum erit, habe-
bitque ea revera radicem realem a+6+y + ^ (quae primo coefficienti in Z mu-
tato signo .aequalis adeoque non modo realis sed etiam rationalis erit, si coefficien—
20 DEMONSTRATIO NOVA THEOREMATIS
tes in Z sunt rationales). Sed nullo negotio perspici potest, si formula detur,
quae valorem ipsius M' per valorem respondentem ipsius u rationaliter exhibeat,
hanc necessario pro u = a-\-16-\-~y-\-h indeterminatam fieri. Hie enim valor
ter erit radix aequationis V = 0, respondebuntque ipsi tres valores ipsius M\
puta (a-f-6)(y-f-&), (a-f-y)F-f-£)et (et + 8) F-f-y), qui omnes irrationales esse
possunt. Manifesto autem formula rationalis neque valorem irrationalem ipsius
M' in hoc casu producere posset, neque tres valores diversos. Ex hoc speeimine
satis colligi potest, methodum clar. de Foncenexü neutiquam esse satisfacientem,
sed si ab omni parte completa reddi debeat, multo profundius in theoriam elimi-
nationis inquiri oportere.
12.
Denique 111. La Geange de theoremate nostro egit in comm. Sur la forme
des racines imaginaires des equations, Nouv. Mem. de VAcad. de Berlin 177 2,
p. 222 sqq. Magnus hie geometra impriruis operam dedit, defectus in Euleki de-
monstratione prima supplere et revera praesertim ea, quae supra (art. 8) obiectio-
nem seeundam et quartam constituunt, tarn profunde perscrutatus est. ut nihil am-
plius desiderandum restet, nisi forsan in disquisitione anteriori super theoria eli-
minationis (cui investigatio haec tota innititur) quaedam dubia superesse videan-
tur. Attamen obiectionem tertiam omnino non attigit, quin etiam tota dis-
quisitio superstrueta est suppositioni, quamvis aequationem mtx gradus revera m
radices habere.
Probe itaque iis, quae hueusque exposita sunt, perpensis, demonstrationem
novam theorematis gravissimi ex principiis omnino diversis petitam peritis haud
ingratam fore spero, quam exponere statim aggredior.
13.
Lemma. Denotante m numerum integrum positivum quemeunque, funetio
sin cp. xm — sin m cp. rm~~1 x -\- sin (m — 1 )cp. rm divisibilis erit per oex—2 cos cp. rx -f- rr.
Demonstr. Pro m = 1 funetio illa fit = 0 adeoque per quemeunque facto-
rem divisibilis; pro m = 2 quotiens fit sin cp, et pro quovis valore maiori quo-
tiens erit sin cp. xm~% -f- sin 2 cp. r xm~~s -f- sin 3 cp. r r xm~!k -f- etc. -f- sin [m — 1 )cp. rm"~2.
Facile enim confirmatur, multiplicata hac funetione per xx—2coscp.r<z?-f-rr,
produetum funetioni propositae aequale fieri.
OMNEM FUNCTIONEM ALGEB^AICAM ETC. 21
14.
Lemma. Si qxiantitas r angulusque cp ita sunt determinativ ut habeantur ae-
quationes
rmcosmy-\-Arm~xcos(m —1) <p + Brm~%cos(m — 2) cp-f- etc.
-f-2rrrcos2cp-j-Z,rcoscp-f-lf == 0 . . [l]
n(m—l)<p + Brm~~2sm (m—2)cp-f- etc.
-*\~Krr sin 2 cp-{--L r sin cp = 0 . . [2]
functio xm + Axm~l -f Bxm~2 + etc. -{-Kxx+Lcc + M—X dimsibilis erit per
factorem duplicem xx — 2 cos cp. rx -f- n-, si modo r sin cp non = 0; si vero r sin cp = 0,
eadem functio divisibilis erit per factorem simplicem x—rcoscp.
Demonstr. 1/ Ex art. praec. omnes sequentes quantitates divisibües enint
per xx—2coscp.r<a?-f-rr;
sincp.r<2?m — sinmcp.rm<2? -f- sin(m—ljcp
A sincp. r xm~~x — Asin(m — 1) cp. rm~lx-\- A sin (m—2) cp. r
Ksiny.rxx
L sincp. rx
M sin cp. r
etc.
— jKTsin 2cp.rr<2?
— _Lsincp.r<z?
etc.
-f- ITsin cp. r3
-f-lfsm(—cp).r
Quamobrem-etiam summa harum quantitatum per xx — 2coscp.ra?-f-rr
divisibilis erit. At singularum partes primae constituunt summam sin cp . r X.;
secundae additae dant 0, propter [2]; tertiarum vero aggregatum quoque eva-
nescere, facile perspicitur, si [1] multiplicatur per sincp, [2] per coscp, pro-
ductumque illud ab hoc subducitur. Unde sequitur, functionem sin cp. r X di-
visibilem esse per xx—2coscp.r<2?-f-rr. adeoque, nisi fuerit rsincp = 0, etiam
functionem X. Q. E. P.
II. Si vero rsincp = 0, erit aut r = 0 aut sincp = 0. In casu priori erit
M== 0, propter [1], adeoque X per x sive per x — rcoscp divisibilis; in poste-
posteriori erit cos cp = +1, cos 2 cp =-f-1, cos3cp = +l et generaliter cosn cp = coscpw.
Quare propter [1] fiet X = 0, statuendo x = rcoscp, et proin functio X per
x—rcoscp erit divisibilis. Q. E. S.
ZZ »EMONSTRATIO NOVA THEOEEMAT1S
15.
Theorema praecedens plerumque adiumento quantitatum. imaginariarum de-
monstratur, vid. Euler Introd. in Anal. In/. T. I. p. 110; operae pretium esse duxi,
ostendere, quomodo aeque facile absque illarum auxilio erui possit. Manifestum
iam est, ad demonstrationem theorematis nostri nihil aliud requiri quam ut osten-
datur: Proposita functione quacunque X formae afn-\-Aafnr~1-\-Bafn~2-\- etc.
-{-Lx-\-M, r et cp ita determinariposse, ut aequationes [1] et [2] locum habeant-.
Hinc enim sequetur, X habere factorem realem primi vel secundi gradus; divisio
autem necessario producet quotientem realem inferioris gradus, qui ex eadem ra-
tione quoque factorem primi vel secundi gradus habebit. Per continuationem hu-
ius operationis X tandem in factores reales simplices vel duplices resolvetur. H-
lud itaque theorema demonstrare, propositum est sequentium disquisitionum.
16.
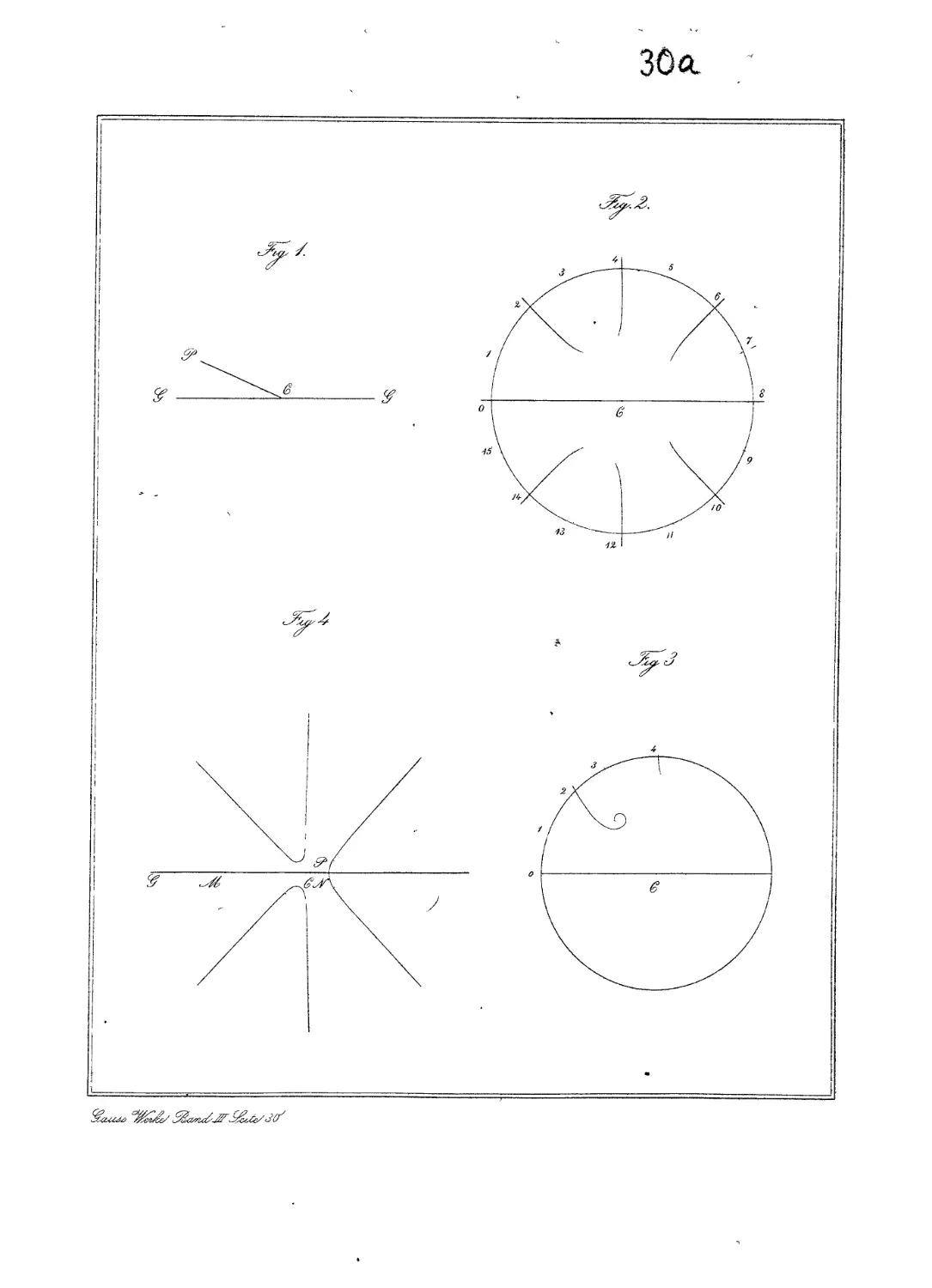
Concipiatur planum fixum infinitum (planum tabulae, fig. 1), et in hoc recta
fixa infinita GC per punctum fixum C transiens. Assumta aliqua longitudine
pro unitate ut omnes rectae per numeros exprimi possint, erigatur in quovis puncto
plani P, cuius distantia a centro C est r angulusque G CP = cp, perpendicu-
lum aequale valori expressionis
rmsinmcp-f- Arm~~lsin(m — 1)^+ etc. -f-Z/rsin^
quem brevitatis gratia in sequentibus semper per T designabo. Distantiam r
semper tamquam positivam considero, et pro punctis, quae axi ab altera parte
iacent, angulus cp aut tamquam duobus rectis maior, aut tamquam negativus
(quod hie eodem redit) speetari debet. Extremitates horum perpendiculorum (quae
pro valore positivo ipsius T supra planum aeeipiendae sunt, pro negativo infra,
pro evanescente in piano ipso) erunt ad superficiem curvam continuam quaquaver-
sum infinitam, quam brevitatis gratia in sequentibus superficiem primam vocabo.
Prorsus simili modo ad idem planum et centrum eundemque axem referatur alia
superficies, cuius altitudo supra quodvis plani punctum sit
rmcosmy-\-Arm~1 cos,(m—1)cp —{— etc. -}-Lrcos<p-\-M
quam expressionem brevitatis gratia semper per U denotabo. Superficiem vero
hanc, quae etiam continua et quaquaversum infinita erit, per denominationem
OMNEM MJNCTIONEM ALGEBBAICAM ETC. 23
superßciei secundae a priori distinguam. Tunc manifestum est, totum negotium in
eo versari, ut deraonstretur, ad minimum unam punctum dari, quod siöiul in
piano, in superficie prima et in superficie secunda iaceat.
17.
Facile perspici potest, superftciem primam partim supra planum partim in-
fra planum iacere; patet enim distantiam a centro r tarn magnam accipi posse,
ut reliqui termini in T prae primo rmsinmcp evanescant; hie vero, angulo cp rite
determinato, tarn positivus quam negativus fieri potest. Quare planum fixum ne-
cessario a superficie prima secabitur; hanc plani cum superficie prima intersectio-
nem vocabo Hneamprimam; quae itaque determinabitur per aequationem T= 0.
Ex eadem ratione planum a superficie secunda secabitur; intexsectio constituet
curvam per aequationem U=Q determinatam, quam lineam seeundam appel-
labo. Proprie utraque curva ex pluribus ramis constabit, qui omnino seiuneti
esse possunt, singuli vero erunt lineae continuae. Quin adeo linea prima sem-
per erit talis, quam complexam vocant, axisque G C tamquam pars huius curvae
speetanda; quieunque enim valor ipsi r tribuatur, T semper fiet = 0, quando
cp aut =0 aut =180°. Sed praestat complexum cunctorum ramorum per omnia
puneta, ubi T= 0, transeuntium tamquam unam curvam considerare (secundum
usum in geometria sublimiori generaliter reeeptum), similiterque eunetos ramos
per omnia puneta transeuntes, ubi U= 0. Patet iam, rem eo reduetam esse,
ut demonstretur, ad minimum unum punetum in piano dari, ubi ramus aliquis
lineae primae a ramo lineae secundae secetur. Ad hunc finem indolem harum li-
nearum propius contemplari oportebit.
18.
Ante omnia observo, utramque curvam esse algebraicam, et quidem, si ad
coordinatas orthogonales revocetur, ordinis m*1. Sumto enim initio abscissarum
in C, abscissisque x versus G, applicatis y versus P, erit x=-r cos 9, y = r sin cp,
adeoque generaliter, quidquid sit n,
ly !L^!=U»y>_ etc.,
= af-^iy-^+"T;-"l2;y *—/- etc.
Quamobrem turn T turn U constabunt ex pluribus huiusmodi ternainis axly\
24 BEMON&TEATTO NOTA THEOßEMATIS
denotantibus et, t! numeros integros positivos, quomm summa, ubi maxima est,
fit — m. Geteram facile praevideri potest, cunctos terminos ipsius T factorem
y involvere, adeoque lineam primam proprie ex recta (cuius aequatio y = 0) et
curva ordinis m — lü compositam esse; sed necesse non est ad hanc distinctio-
nem hie respicere.
Maioris momenti erit investigatio, an linea prima et seeunda crura infinita
habeant, et quot qualiaque. In distantia infinita a puneto C linea prima, cuius
aequatio sin m cp -|— sin {m — 1) cp —-j— sin {m — 2) <p etc. = 0, confundetur cum li-
linea, cuius aequatio sinmcp = 0. Haec vero exhibet m lineas reetas in puncto
C se secantes, quarum prima est axis GCG', reliquae contra hanc sub angulis
— 180, —180, —180 etc. graduum inclinatae. Quare linea prima Im ramos in-
finitos habet, qui peripheriam circuli radio infinito descripti in 2m partes aequa-
les dispertiuntur, ita ut peripheria a ramo primo secetur in concursu circuli et axis,
a seeundo in.distantia —180°, a tertio in distantia —180° etc. Eodem modo
m m
linea seeunda in distantia infinita a centro habebit asymptotam per aequationem
cosmep =r 0 expressam. quae est complexus m reetarum in puncto C sub aequa-
libus angulis itidem se secantium, ita tarnen, ut prima cum axe CG constituat
ansrulum —90°, seeunda angulum —90°, tertia anerulum —90° etc. Quare li-
nea seeunda etiam 2m ramos infinitos habebit, quorum singuli medium locum
inter binos ramos proximos lineae primae oecupabunt, ita ut peripheriam circuli
radio infinite magno descripti in punetis, quae —90°, —90°, —90° etc. ab axe
distant, secent. Ceterum palam est, axem ipsum semper duos ramos infinitos
lineae primae constituere, puta primum et m-f-ltum. Luculentissime hie ramo-
rum situs exhibetur in fig. 2, pro casu m = 4 construeta, ubi rami lineae seeun-
dae, ut a ramis lineae primae distinguantur, punetati exprimuntur, quod etiam
de figura quarta est tenendum *). Quum vero hae conclusiones maximi mo-
momenti sint, quantitatesque infinite magnae quosdam lectores offendexe pössint:
illas etiam absque infinitorum subsidio in art. sequ. eruere docebo.
19,
Theorema. Manentibus eunetis uf supra, eoc centro C describi poterit circidus,
*) Figura quarta construeta est supponendo X = xx—2zz-\- 3x-\- 10, in qua itaque lectores dis-
quisitionibus generalibus et abstractis minus assueti situm respectivum utriusque curvae in concreto intueri
poterunt. Longitudo lineae CG assumta est = lü (CN= 1,26255.)
OMNEM FUNCTIONEM ALGEBBAJCAM ETC. £5
in cuius peripheria sint Im puncta, in quibtis T= 0, totidemque, in quibus 27=0,
et quidem ita, ut singula posteriora inter hina priorum iaeeant.
Sit summa omnium coefficientium A, B etc. J8T, L, M positive acceptorum
= 8, accipiaturque JR simul ^>8\/2 et ]>1#): turn dico in circulo radio M
descripto ea, quae in theoremate enunciata sunt, necessario locum habere. Sci-
licet designato brevitatis gratia eo puncto huius circumferentiae, quod —45 gra-
dibus ab ipsius concursu cum laeva parte axis distat, sive pro quo cp = —45°,
per A); similiter eo puncto, quod —45° ab hoc concursu distat, sive pro quo
9 = — 45°, per C); porro eo, ubi cp = — 45°, per E) etc. usque ad (ßm—rl),
quod 45 gradibus.ab illo concursu distat, si semper versus eandem partem
progrederis, (aut — 45° a parte opposita), ita ut omnino 4 m puncta in peripheria
habeantur, aequalibus intervallis dissita: iacebit inter (8 m — l) et A) unum
punctum, pro quo T = 0; nee non sita erunt similia puncta singula inter C) et
E); inter G) et (9); inter A1) et A3) etc., quorum itaque multitudo 2m; eodem-
que modo singula puncta, pro quibus U= 0, iacebunt inter A) et C); inter
E) et G); inter (9) et A1), quorum multitudo igitur etiam =2m; deniqueprae-
ter haec 4 m puncta alia in tota peripheria non dabuntur, pro quibus vel T vel
U sit = 0.
Demonstr. I. In puncto A) erit mep = 45° adeoque
sm(m — l)<p + |sin(a» —2)f + etc.
•n
summa vero .Asin (m — 1) cp -f- -^ sin (m —2) <p etc. certo non poterit esse maior quam
S, adeoque necessario erit minor quam R\J^: unde sequitur, in hoc puncto valo-
valorem ipsius T certo esse positivum. A potiori itaque T valorem positivum habe-
habebit, quando mep inter 45° et 135° iacet, i.e. a puncto A) usque ad C) valor
ipsius T semper positivus erit. Ex eadem ratione T a puncto (9) usque ad A1)
positivum valorem ubique habebit, et generaliter a quovis puncto (8 Xr—|—1) usque
ad (8k-\-3), denotante k integrum quemeunque. Simili modo T ubique inter
E) et G), inter A3) et A5) etc. et generaliter inter (8 Ar+5) et (8Ar-f-7) valorem
negativum habebit, adeoque in omnibus his intervallis nullibi poterit esse = 0.
Sed quoniam in C) hie valor est positivus, in E) negativus: necessario alieubi
inter C) et E) erit = 0; nee non alieubi inter G) et (9); inter A1) et A3) etc.
*) Quando S > y/*, conditio prima seeundam 5 quando vero S < \/'i, seeunda primam injpüeabit.
4
26 DEMÖNSTEÄTIO NOVA THEOEEMATTS
usque ad mtervallum inter (8 m— 1) et A) incl., ita ut omnino in 2 m punctis ha-
beatur T = 0. Q. E. P.
II. Quod vero praeter haec 2m puncta, alia, hac proprietate praedita, non
dantur. ita cognoscitur. Quum inter (l) et C); inter E) et G) etc. nulla sint,
aliter fieri non posset, ut plura talia puncta exstent, quam si in aliquo interyallo
inter C) et E), vel inter G) et (9) etc. ad minimum duo iacerent. Turn vero ne-
cessario in eodem intervallo T alicubi esset maocimum, vel minimum, adeoque
^=0. Sed ~ = mRm~z(Rcosm^-{-n^Äcos(m — l)^-{-etc.) et cosmcp
inter C) et E) semper est negativus et ^>\Jir. Unde facile perspicitur, in toto
hoc intervallo -7— esse quantitatem negativam; eodemque modo inter G) et (9)
ubique positivam; inter A1) et A3) negativam. etc., ita ut in nullo horum inter-
vallorum esse possit 0, adeoque suppositio consistere nequeat. Quare etc. Q. E.S.
III. Prorsus simili modo demonstratur, U habere valorem negativum ubi-
ubique inter C) et E), inter (l l) et (J 3) etc. et generaliter inter (8&+3) et (8Är+5);
positivum vero inter G) et (9), inter A5) et A7) etc. et generaliter inter (8Är-f-7)
et (8Ä+9). Hinc statim sequitur, U= 0 fieri debere alicubi inter A) et C),
inter E) et G) etc., i. e. in 2m punctis. In nullo vero horum intervallorum fieri
poterit t— = 0 (quod facile simili modo ut supra probatur): quamobrem plura
quam illa 2 m puncta in circuli peripheria non dabuntur, in quibus fiat U= 0.
Q. E. T. et Q.
Ceterum ea theorematis pars, secundum quam plura quam 2m puncta non
dantur, in quibus T= 0, neque plura quam 2m, in quibus U = 0, etiam
inde demonstrari potest, quod per aequationes T= 0, 27= 0 exhibentur cur-
vae mtx ordinis, quales a circulo tamquam. curva secundi ordinis in pluribus quam
2m punctis secari non posse, ex geometria sublimiori constat.
20.
Si circulus alius radio maiori quam R ex eodem centro describitur, eodem-
eodemque modo dividitur: etiam in hoc inter puncta C) et E) iacebit punctum imum,
in quo T= 0, itemque inter G) et (9) etc., perspicieturque facile, quo minus
radius huius circuli a radio R differat, eo propius huiusmodi puncta inter C) et E)
in utriusque circumferentia sita esse debere. Idem etiam locum habebit, si cir-
circulus radio aliquantum minori quam R, attamen maiori quam S\j2 et 1, descri-
describitur. Ex his nullo negotio intelligitur, circuli radio R descripti circumferen-
OMNEM FÜNCTIOüiEM ALGEBRAICAM ETC. 27
tiam in eo puncto inter C) et E), ubi T= 0, revera seoari ab aliquaramo li-
lineae primae: idemque valet de reliquis punctis, ubi T — 0. Eodem mado pa-
tet. circumferentiam circuli huius in omnibus 2 m punctis, ubi U = 0, ab ali-
quo ramo lineae secundae secari. Hae conclusiones etiam sequenti modo exprimi
possunt: Descripto circulo debitae magnitudinis e centro C, in hunc intrabunt
2 m rami lineae primae totidemque rami lineae secundae, et quidem ita, ut bini
rami proximi lineae primae per aliquem ramum lineae secundae ab invicem sepa-
rentur. Vid. fig. 2, ubi circulus iam non infinitae sed finitae magnitudinis erit,
numerique singulis ramis adscripti curn numeris, per quos in art. praec. et hoc
limites certos in peripheria brevitatis caussa designavi, non sunt confundendi.
21.
Iam ex hoc situ relativo ramorum in circulum intrantium tot modis diversis
deduci potest, intersectionem alicuius rami lineae primae cum ramo lineae secun-
secundae intra circulum necessario dari, ut, quaenam potissimum methodus prae reli-
reliquis eligenda sit, propemodum nesciam. Luculentissima videtur esse haec: De-
Designemus (fig. 2) punctum peripheriae circuli, ubi a laeva axis parte (quae ipsa est
unus ex 2 m ramis lineae primae) secatur, per 0; punctum proximum, ubi ra-
mus lineae secundae intrat, per 1; punctum huic proximum, ubi secundus lineae
primae ramus intrat, per 2. et sie porro usque ad Am—t, ita ut in quovis puncto
numero pari signato ramus lineae secundae in circulum intret, contra ramus li-
lineae secundae in omnibus punctis per numerum imparem expressis. Iam ex geo-
metria sublimiori constat, quamvis curvam algebraicam, (sive singulas cuiusvis
curvae algebraicae partes, si forte e pluribus composita sit) aut in se redeuntem
aut utrimque in infinitum excurrentem esse, adeoque si ramus aliquis curvae al-
algebraicae in spatium definitum intret, eundem necessario ex hoc spatio rursus ali-
cubi exire debere#). Hinc concluditur J^cile, quodvis punctum numero pari signa-
*) Satis bene certe demonstratum esse videtur, curvam algebraicam neque alieubi subito abrumpi
posse (uti e. g. evenit in curva transscendente, cuius aequatio y = - ), neque post spiras infinitas in ali-
quo puncto se quasi perdere (ut spiralis logarithmica), quantumque scio nemo dubium contra hanc rem mo-
vit. Attamen si quis postqlat, demoustrationem nullis dubiis obnoxiam alia occasione tradere suseipiam. In
casu praesenti vero manifestum est, si aliquis ramus e. g. 2, ex circulo nulHbi exiret (fig. 3), te in circu-
circulum inter o et 2 intrare, postea cixca totum hunc ramum (qui in circuli spatio se perdere deberet) cireum-
meare, et tandem inter 2 et i rursus ex circulo egredi posse, ita ut nulHbi in tota via in lineam primam
ineideris. Hoc vero absurdum esse inde patet, quod in puncto, ubi in circulum ingressus es, superficiem
4*
,28 DEMONSTRATIO NOVA THEOEEMATIS
•turn (seur brevitatis caussa, quodvis punctum par) per ramum lineae primae cum
alio puncto pari intra circulum iunctum esse debere, similiterque quodvis punctum.
numero impari notatum cum alio simili puncto per ramum lineae secundae. Quam-
quam vero haec binorum punctorum connexio secundum indolem functionis X
perquam diversa esse potest, ita ut in genere determinari nequeat, tarnen facile
demonstrari potest, quaecunquü demum illa sit, semper intersectionem Jineae primae
cum linea secunda oriri.
22.
Demonstratio huius necessitatis commodissime apagogice repraesentari posse
videtur. Scilicet supponamus, iunctionem binorum quorumque punctorum parium,
et binorum quorumque punctorum imparium ita adornari posse, ut nulla inter-
sectio rami lineae primae cum ramo lineae secundae inde oriatur. Quoniam axis
est pars lineae primae, manifesto punctum 0 cum puncto Im iunctum erit.
Punctum 1 itaque cum nullo puncto ultra axem sito, i. e. cum nullo puncto per
numerum maiorem quam Im expresso iunctum esse potest, alioquin enim linea
iungens necessario axem secaret. Si itaque 1 cum puncto n iunctum esse sup-
ponitur, erit n<^2m. Ex simili ratione si 2 cum ri iunctum esse statuitur, erit
ri<^n, quia alioquin ramus 1...ri ramum \...n necessario secaret. Ex eadem
caussa punctum 3 cum aliquo punctorum inter 4 et ri iacentium iunctum erit,
patetque si 3, 4, 5 etc. iuncta esse supponantur cum ri', ri", ri'"etc., ri" iacere in-
inter 5 et n", ri'" inter 6 et ri" etc. Unde perspicuum est, tandem ad aliquod
punctum h perventum iri, quod cum puncto Ä-f-2 iunctum sit, et turn ramus.
qui in puncto A—j—1 in circulum in trat, necessario ramum puncta k et A-j-2 iun-
gentem secabit. Quia autem alter horum duorum ramorum ad lineam primam,
alter ad secundam pertinebit, manifestum iam est, suppositionem esse contra-
dictoriam, adeoque necessario alicubi intersectionem lineae primae cum linea se-
secunda fieri.
primam supra te habuisti, in egressu, infra; quare necessario alicubi in superficiem primam ipsam incidere de-
buisti, sive in punctum lineae primae. — Ceterum ex hoc ratiocinio principiis geometriae situs innixo, quae
haud minus valida sunt, quam principia geometriae magnitudinis, sequitur tantummodo, si in aliquo ramo li-
lineae primae in circulum intres, te alio loco ex circulo rursus egredi posse, semper in linea prima manendo, ne-
que vero, viam tuam esse lineam continuam in eo sensu, quo in geometria sublimiori accipitur. Sed hie suffi-
cit, viam esse lineam continuam in sensu communi, i. e. nullibi interruptam sed ubique cohaerentem.
OMKEM FUNCTIONEM ALGEBRAICAM ETC. 29
Si haec cum praecedentibus iunguntur. ex omnibus disquisitionibus expli-
catis colligetur, theorema, quamvis functionem algebraicam rationalem integram unkis
indeterminatae in factores reales primi vel secundi gradus resohi posse, omni rigore
demonstratum.
23.
Ceterum haud- difficile ex iisdem principiis deduci potest, non solum unam
sed ad minimum m intersectiones lineae primae cum secunda dari, quamquam
etiam fieri potest, ut linea prima a pluribus ramis lineae secundae in eodem puncto
secetur, in quo casu functio X plures factores aequales habebit. Attamen quum
hie sufficiat, unius intersectionis necessitatem demonstravisse, fusius huic rei bre-
vitatis caussa non immoror. Ex eadem ratione etiam alias harum linearum pro-
prietates hie uberius non persequor, e. g. intersectionem semper fieri sub angulis
rectis; aut si plura crura utriusque curvae in eodem puncto conveniant, totidem
crura lineae primae affore, quot crura lineae secundae, haecque alternatim posita
esse, et sub aequalibus angulis se secare etc.
Denique observo, minime impossibile esse, ut demonstratio praecedens, quam
hie principiis geometricis superstruxi, etiam in forma mere analytica exhibeatur:
sed eam repraesentationem, quam hie explieavi, minus abstraetam evadere cre-
didi, verumque nervum probandi hie multo clarius ob oculos poni, quam a de-
monstratione analytica exspeetari possit.
Coronidis loco adhuc aliam methodum theorema nostrum demonstrandi ad-
digitabo, quae primo aspectu non modo a demonstratione praecedente, sed etiam
ab omnibus demonstrationibus reliquis supra enarratis maxime diversa esse vide-
bitur, et quae nihüominus cum D'ALEMBEBriana, si ad essentiam speetas proprie
eadem est. Cum qua illam comparare, parallelismumque inter utramque explo-
rare peritis committo, in quorum gratiani unice subiuneta est.
24.
Supra planum figurae 4 relative ad axem C G punetumque fixum C de-
scriptas suppono superficiem primam et secundam eodem modo ut supra. Accipe
punetum quodeunque in aliquo ramo lineae primae situm sive ubi T = 0, (e. g.
quodlibet punetum M in axe iacens), et nisi in hoc etiam £7=0, progredere
ex hoc puncto in linea prima versus eam partem, versus quam magnitudo abso-
NOVA SHEOSgllATIS ETC.
Itifca ipsius TJ' deerescit. Si forte in puncto M valor absolutus ipsius TJ versus
utramque partem decrescit, arbitrarium est, quorsum progrediaris; quld vero fa-
ciendum sit, si TJ versus utramque partem crescat, statim doc^bo. Manifestum
est itaque, dum semper in linea prima progrediaris, necessario tandem te ad
punctum perventurum, ubi TJ =■ 0 , aut ad tale, ubi valor ipsius TJ fiat mini-
mum, e.g. punctum N. In priori casu quod quaerebatur, inventum est; in poste-
posteriori vero demonstrari potest, in hoc puncto plures ramos lineae primae sese in-
tersecare (et quidem multitudinem parem ramorum), quorum semissis ita compa-
rati sint, ut si in aliquem eorum deflectas (sive huc sive illuc) valor ipsius TJ ad-
hucdum decrescere pergat. (Demonstrationen! huius theorematis, prolixiorem
quam difficiliorem brevitatis gratia supprimere debeo.) In hoc itaque ramo iterum
progredi poteris, donec TJ aut fiat = 0 (uti in flg. 4 evenit in P), aut denuo
minimum. Turn rursus deflectes, necessarioque tandem ad punctum pervenies,
ubi sit Z7= 0.
Contra hanc demonstrationem obiici posset dubium, annon possibile sit, u£
quantumvis longe progrediaris, et quamvis valor ipsius U semper decrescat, ta-
tarnen haec decrementa continuo tardiora fiant, et nihilominus ille valor limitem
aliquem nusquam attingat; quae obiectio responderet quartae in art. 6. Sed haud
diflicile foret, terminum aliquem assignare, quem simulac transieris, valor ipsius
TJ necessario non modo semper rapidius mutari debeat, sed etiam decrescere non
amplius possit, ita ut antequam ad hunc terminum perveneris, necessario valor
0 iam affuisse debeat. Hoc vero et reliqua, quae in hac demonstratione addigi-
tare tantummodo potui, alia occasione fusius exsequi mihi reservo.
Principza quibus haecce demonstratio innititur deteximus Initio Octob. 17 97.
30cl
DEMONSTRATIO NOTA ALTERA
THEOREMATIS
OMNEM FUNCTIONEM ALGEBRAICAM
RATIONALEM INTEGRAM
UNIUS VARIABILIS
IJST FACTORES REALES PRIMI YEL SECUJSTDI GRADUS
RESOLVI POSSE
A U C T O E E
CAROLO FBJDERICO GAUSS
SOCIETATI REGIAE SCIENTIARUM TRADITA 1815. DEC. 7.
Commentationes societatis regiae scientiarum Grottingensis recentiores. Vol. in.
Gottingae mdcccxvi.
33
DEMONSTRATIO NOVA ALTERA THEOREMATIS
OMNEM FUNCTIOJSTEM ALGEBRAICAM RATIONALEM INTEGRAM
ÜNIÜS VARIABILIS
IN FACTOEES REALES PRIMI VEL SECUNDI GRADUS RESOLVI POSSE.
1.
Quamquam demonstratio theorematis de resolutione functionum algebraica-
rum integrarum in factores, quam in commentatione sedecim abhinc annis pro-
mulgata tradidi, turn respectu rigoris turn simplicitatis nihil desiderandum relin-
quere videatur, tarnen haud ingratum fore geometris spero, si iterum ad eandem
quaestionem gravissimam revertar, atque e principiis prorsus diversis demonstra-
tionem alteram haud minus rigorosam adstruere coner. Pendet scilicet illa demon-
demonstratio prior, partim saltem, a considerationibus geometricis: contra ea, quam hie
exponere aggredior, principiis mere analyticis innixa erit. Methodorum analyti-
carum, per quas usque ad illud quidem tempus alii geometrae theorema nostrum
demonstrare suseeperunt, insigniores loco citato recensui, et quibus vitiis laborent
copiose exposui. Quorum gravissimum ac vere radicale omnibus illis conatibus,
perinde ac recentioribus, qui quidem mihi innotuerunt, commune: quod tarnen
neutiquam inevitabile videri in demonstratione analytica, iam tunc declaravi. Esto
iam penes peritos iudicium, an fides olim data per has novas curas plene sit liberata.
2.
Disquisitioni principali quaedam praeliminares praemittentur, turn ne quid
deesse videatur, turn quod ipsa forsan traetatio iis quoque, quae ab aliis iam de-
5
34 DEMONSTRATIO NOVA ALTEEA THEOREMATIS
libata fuerant, novam qualemcunque lucem aifundere potent. Ac primo quidem
de altissimo divisore communi duarum functionum algebraicarum integrarum unius
indeterminatae agemus. Ubi praemonendum, hie semper tantum de funetionibus
integris sermonem esse: e qualibus duabus si produetum confletur, utraque huius
divisor vocatur. Divisoris ordo ex exponente summae potestatis indeterminatae
quam continet diiudicatur, nulla prorsus coefficientium numericorum ratione ha-
bita. Ceterum quae ad divisores communes functionum pertinent, eo brevius ab-
solvere licet, quod iis, quae ad divisores communes numerorum speetant, omnino
sunt analoga.
Propositis duabus funetionibus Y, Y' indeterminatae a?, quarum prior sit
ordinis. altioris aut saltem non inferioris quam posterior, formabimus aequationes
sequentes
F = qY' + F"
Y'=q'Y"-}-Y"
Y" = q" Y'"-\- Y""
etc. usque ad
ea scilicet lege, ut primo Y dividatur sueto more per Y'; dein Y' per residuum
primae divisionis Y", quod erit ordinis inferioris quam Y'\ tunc rursus residuum
primum per seeundum Y" et sie porro, donec ad divisionem absque residuo per-
veniatur, quod tandem necessario evenire debere inde patet, quod ordo functio-
functionum Y\ Y", Y'" etc. continuo decrescit. Quas funetiones perinde atque quo-
tientes q, q\ q" etc. esse funetiones integras ipsius x, vix opus est monere. His
praemissis, manifestum est,
I. regrediendo ab ultima istarum aequationum ad primam, funetionem
F(a) esse divisorem singularum praecedentium, adeoque certo divisorem commu-
nem propositarum Y, Y'.
II. Progrediendo a prima aequatione ad ultimam, elucet, quemlibet divi-
divisorem communem functionum Y, Y' etiam metiri singulas sequentes, et proin
etiam ultimam "Y^ . Quamobrem funetiones Y, Y' habere nequeunt ullum di-
divisorem communem altioris ordinis quam Y^\ omnisque divisor communis eius-
dem ordinis ut Y^ erit ad hunc in ratione numeri ad numerum, unde hie ipse
pro divisore communi summo erit habendus.
OMNEM FUNCTIONEM ALGEBKAICAM ETC. 35
III. Si yte) est ordinis 0, i.e. numerus, nulla tfunctio indeterminatae %
proprie sie dieta ipsas Y, Y' metiri potest: in hoc itaque casu dicendum est, has
funetiones divisorem communem non habere.
IV. Excerpamus ex aequationibus nostris penultimam; dein ex hac elimi-
nemus Y^~1^ adiumento aequationis antepenultimae; tunc iterum eliminemus
adiumento aequationis praecedentis et sie porro: hoc pacto habebimus
= +£
— —Je'
— _|_^" yd*-*) Je1
etc.
si funetiones k, k\ Je" etc. ex lege sequente formatas supponamus
k = 1
Je""=
etc.
Erit itaque
valentibus signis superioribus pro fi pari, inferioribus pro impari. In eo itaque
casu, ubi Y et Y' divisorem communem non habent, invenire licet hoc modo
duas funetiones Z, Z' indeterminatae oc tales, ut habeatur
V. Haec propositio manifesto etiam inversa valet, puta, si satisfieri potest
aequationi
ita, ut Z, Z' sint funetiones integrae iudeterminatae x, ipsae Y et Y' certo di-
divisorem communem habere nequeunt.
NOVA AMSERA OTEGEEMATIS
3
. Disquisitio praeliminaris altera circa transformationem functionum symme-
tricarum versabitur. Sint a, b, c etc. quantitates indeterminatae, ipsarum multi-
tudo m, designemusque per X' illarum summam, per X" summam productorum e
binis, per X'" summam productorum e ternis etc., ita ut ex evolutione producti
(pc—a){oc — b) [üc — c) . . . .
oriatur
—X'V^-f ^
Ipsae itaque X',X",X'"etc. sunt functiones symmetricae indeterminatarum a,b,c etc.,
i. e. tales, in quibus hae indeterminatae eodem modo occurrunt, sive clarius, ta-
les, quae per qualemcunque harum indeterminatarum inter se permutationem non
mutantur. Manifesto generalius, quaelibet functio integra ipsarum X. X", X'" etc.
(sive has solas indeterminatas implicet, sive adhuc alias ab a, b, c etc. indepen-
dentes contineat) erit functio symmetrica integra indeterminatarum a, b, c etc.
4.
Theorema inversum paullo minus obvium. Sit p functio symmetrica inde-
indeterminatarum a, b, c etc., quae igitur composita erit e certo numero terminorum
formae
denotantibus a, €, y etc. integros non negativos, atque M coefficientem vel de-
terminatum vel saltem ab a, b, c etc. non pendentem (si forte aliae adhuc indeter-
indeterminatae praeter a, b, c etc. functionem p ingrediantur). Ante omnia inter sin-
gulos hos terminos ordinem certum stabiliemus, ad quem finem primo ipsas in-
indeterminatas a, b, c etc. ordine certo per se quidem prorsus arbitrario dispone-
mus, e. g. ita, ut a primum locum obtineat, b secundum, c tertium etc. Dein
e duobus terminis
ci et
priori ordinem altiorem tribuemus quam posteriori, si fit
vel a>d, vel a = a'et !>>!)', vel a — d, € = €'ety>y', vel etc.
OMNEM FTOJCTIO2JEM ALGEBRAICAM ETC. S?
i. e. si e drfferentiis a — a', <6—6', y—y' etc. prima, quae non evanescit, posi-
tiva evadit. Quocirca quum termini eiusdem ordinis non differant nist respectu
coefficientis M, adeoque in terminum unrnn conflari possint, singulos terminos
functionis p ad ordines diverses pertinere supponemus.
Iam observamus, si Maab c* sit ex Omnibus terminis functionis p is,
cui ordo altissimus competat, necessario a esse maiorem, vel saltem non mino-
rem, quam €. Si enim esset €]>öc, terminus Mcfitfc1 , quem functio p,
utpote symmetrica, quoque involvet, foret ordinis altioris quam Ma^b^rf
contra hyp. Simili modo € erit maior vel saltem non minor quam y; porro y
non minor quam exponens sequens 8 etc.: proin singulae drfferentiae a — o\
6—y, y—h etc. erunt integri non negativi.
Secundo perpendamus, si e quotcunque functionibus integris indetermina-
tarum a, b, c etc. productum confletur, huius terminum altissimum necessario
esse ipsum productum e terminis altissimis illorum factorum. Aeque manifestum
est, terminos altissimos functionum X', X", X'" etc. resp. esse a, ab, abc etc. Hinc
colligitur, terminum altissimum e producto
p
X"
prodeuntem esse Mcfb^c1 ; quocirca statuendo p—p = p, terminus al-
altissimus functionis p' certo erit ordinis inferioris quam terminus altissimus functio-
functionis p. Manifesto autem p, et proin etiam p', fiunt functiones integrae symme-
tricae ipsarum a, b, c etc. Quamobrem p' perinde tractata, ut antea p, discer-
petur in p'-\- p", ita ut p sit productum e potestatibus ipsarum X', X", X'" etc. in
coefficientem vel determinatum vel saltem ab a, b, c etc. non pendentem, p" vero
functio integra symmetrica ipsarum a, b, c etc. talis, ut ipsius terminus altissi-
mus pertineat ad ordinem inferiorem, quam terminus altissimus functionis p'.
Eodem modo continuando, manifesto tandem p ad formam p -\-p'-\-p"-\-p'" etc.
redacta, i. e. in functionem integram ipsarum X', X", X'" etc. transformata erit.
5.
Theorema in art. praec. demonstratum etiam sequenti modo enunciare pos-
sumus: Proposita functione quacunque indeterminatarum a, h c etc. integra sym-
symmetrica p, assignari potest functio integra totidem aliarum indeterminatarum
l\l", V" etc. talis, quae per substitutiones Z' = X', /" = X", /'" — X'"etc. transeat
38 DEMONSTRATIO NOVA ALTERS THEOEEMATIS
in p. Facile insuper ostenditur, hoc unico tantum modoßeri posse. Supponamus
enim, e duabus fiinctionibus diversis indetermiaatarum l\ l", V" etc. puta turn
ex r, turn ex / post substitutiones V = X', l" = X", T'= X'"etc. resultare ean-
dem functionem ipsarum a, b, c etc. Tunc itaque r—/ erit functio ipsarum.
l', l", X" etc. per se non evanescens, sed quae identice destruitur post illas sub-
substitutiones. Hoc vero absurdum esse, facile perspiciemus, si perpendamus, r — /
necessario compositam esse e certo numero partium formae
quarum coefficientes M non evanescant, et quae singulae respectu exponentium
inter se diversae sint, adeoque terminos altissimos e singulis istis partibus pro-
deuntes exhiberi per
c. j+etc.
et proin ad ordines diversos referendos esse, ita ut terminus absolute altissimus
nullo modo destrui possit.
Ceterum ipse calculus pro huiusmodi transformationibus pluribus compen-
diis insigniter abbreviari posset, quibus tarnen hoc loco non immoramur, quum
ad propositum nostrum sola transformationis possibilitas iam sufficiat.
6.
Consideremus productum ex m(m — 1) factoribus
(a — b)(a — c)(a — d)
_x{b—a)(b—c)(b — d)
X(c—a)(c — b)(c—d)
X.{d—a)(d-—b){d—c)
etc.
quod per 7t denotabimus, et, quum indeterminatas «, b, c etc. symmetrice in-
volvat, in formam functionis ipsarum X', X", X'" etc. redactum supponemus. Trans-
Transeat haec functio in p, si loco ipsarum X', X", X'" etc. resp. substituuntur V, l", V" etc.
His ita factis, ipsam p vocabimus determinantem functionis
__ V
OMNE&t FUNCTIONEM ALGEBRAICAM ETC. 39
Ita e. g. pro m = 1 habemus
Perinde pro m = 3 invenitur
Determinans functionis y itaque est functio coefficientium V, l", V" etc. talis,
quae per substitutiones V = X', l" = X", V" = X'" etc. transit in productum ex
omnibus differentiis inter binas quantitatum a, b, c etc. In casu eo, ubi m = 1,
i. e. ubi unica tantum indeterminata a habetur, adeoque nullae omnino adsunt
differentiae, ipsum numerum 1 tamquam determinantem functionis y adoptare
conveniet.
In stabilienda notione determinantis, coefficientes fonctionis y tamquam
quantitates indeterminatas spectare oportuit. Determinans functionis cum coeffi-
cientibus determinatis
T= ar — Lcc^l+L''ar-2—L'"ar-*-)r etc.
erit numerus determinatus P, puta valor functionis p pro V = L\ l" = L",
V" = L'" etc. Quodsi itaque supponimus, Y resolvi posse in factores simplices
— C)
sive Y oriri ex
o = (a? — a){oc — b){x— c)
statuendo a =A, b = B, c— Cetc, adeoque per easdem substitutiones X', X", X'" etc.
resp. fieri Z/, L", U" etc., manifesto P aequalis erit producto e factoribus
(A-B)(A/-q(A~D)
x{B — A) (B — C){B—D)
X{C— A)(C—B) {C~D)
X(.D — A){D—B){D— C)
etc.
Patet itaque, si fiat P = 0, inter quantitates A7 B, C etc. duas saltem aequa-
les reperiri debere; contra, si non fuerit P = 0 , cunctas A, B, C etc. necessa-
rio inaequales esse. Iam observamus, si statuamus -^ =■ Y', sive
40 ' DEMONSTRATIO NOVA ALTERA THEOREMATIS
Y' = mxm~x — {m—\)L'xm-%+{m--^)Uxm-*—(m—Z)L"'ccm-i+ etc.
haberi
T = [x — B){x~ C)[x—D)
-f (x—A) (x—B) [x— C)
-f etc.
Si itaque duae quantitatum A, B, C etc. aequales sunt, e. g. A = B, Y' per
<z?— A divisibilis erit, sive Y et Y' implicabunt divisorem communem x—A.
Vice versa, si Y' cum Y ullum divisorem communem habere supponitur, neces-
sario Y' aliquem factorem simplicem ex his x — A, x—B, x— C etc. implicare
debebit, e. g. primum x—A, quod manifesto fieri nequit, nisi A alicui reliqua-
rum B, C, D etc. aequalis fuerit. Ex his omnibus itaque colligimus duo
Theoremata :
I. Si determinans functioms Y fit = 0, certo Y cum Y' divisorem commu-
communem habet, adeoque, si Y et Y' divisorem communem non kabent, deter-
determinans functionis Y nequit esse =0.
II. Si determinans functionis Y non est = 0, certo Y et Y' divisorem com-
munem habere nequeunt; vel, si Y et Y' divisorem communem kabent, ne-
cessario determinans functionis Y esse debet — 0.
7.
At probe notandum est, totam. vim huius demonstrationis simplicissimae in-
niti suppositioni, functionem Y in factores simplices resolvi posse: quae ipsa sup-
positio, hocce quidem loco, ubi de demonstratione generali huius resolubilitatis
agitur, nihil esset nisi petitio principii. Et tarnen a paralogismis huic prorsus si-
milibus non sibi caverunt omnes, qui demonstrationes analyticas theorematis prin-
cipalis tentaverunt, cuius speciosae illusionis originem iam in ipsa disquisitionis
enunciatione animadvertimus, quum omnes in formam tantum radicum aequatio-
num inquisivejint, dum existentiam temere suppositam demonstrare oportuisset.
Sed de tali proce<Jendi modo, qui nimis a rigore et claritate abhorret, satis iam in
commentatione supra citata dictum est. Qiiamobrem iam theoremata ai*t. praec,
OMNEM FÜJfCTIONEM ALGEBEAICAM ETC. 41
quorum altero saltem ad propositum nostrum non possumus carere, solidiori fun-
damento superstruemus: a secundo, tamquam faciliori initium faciemus.
Denotemus per p functionem
t.(x — h) (x—c) (x — d) . . . . ^
(a—by(a — Cy(a—dy
, tz(x — a) (x — c) (x—d)
* (b—ay(b—cy(b—dy...77
T.(x-a){x-b)(x-d)
~T~ (c—ay {c—by (c—dy
_, tz(x—a) (x—b) (x—c) .....
' (d-ay (d—by (d—c)\
-f- etc.
quae, quoniam iz per singulos denominatores est divisibilis, fit functio integra
indeterminatarum x, a, b, c etc. Statuamus porro ~ — u', ita ut habeatur
u' = (x—b)(x—c)(x—d)
—a)(a?—c)(w — d)
-\-(x—a)(x—b)(x—d)
-\-(x — a)(x—b)(x—c)
+ etc.
Manifesto pro x = a% fit po' = %, unde concludimus, functionem tt—po' in-
indefinite divisibilem esse per x — a, et perinde per x—b, x—c etc., nee non
per produetum u. Statuendo itaque
u
erit o functio integra indeterminatarum x, a, b, c etc., et quidem, perinde ut p,
symmetrica ratione indeterminatarum a, b, c etc. Erui poterunt itaque funetio-
nes duae integrae r, s, indeterminatarum x, l\ l", V" etc., tales quae per substi-
tutiones /'= X', /"= X", /"'== X'"etc. transeantin p, o resp. Quodsi itaque ana-
logiam sequentes, functionem
_ (m _ i) raT~2 + (m — 2) l"xm"s — {m — 3) W* -f etc.
i. e. quotientem diiferentialem -^ per y denotemus, ita ut y per easdem illas
6
42 DEMONSTRATIO KTOVA ALTEKA THEOKEMATIS
substitutiones transeat in o', patet, p — sy —ry per easdem substitutiones transire
in 7c — au — pt/, i. e. in 0, adeoque necessario iam per se identice evanescere
debere (art. 5): habemus proin aequationem itfenticam
p = sy-\-ry
Hinc si supponamus, ex substitutione /'=£', l"=L", lm= L'" etc. prodire
r = R, s = S, erit etiam identice
ubi quum 8, R sint functionis integrae ipsius a?, P vero quantitas determinata
seu numerus, sponte patet, Fet Y' divisorem communem habere non posse, nisi
fuerit P =z 0. Quod est ipsum theorema posterius art. 6.
9.
Demonstrationen! theorematis prioris ita absolvemus, ut ostendamus, in
casu eo, ubi Y et Y' non habent divisorem communem, certo fieri non posse
P = 0. Ad hunc finem primo, per praecepta art. 2 erutas supponimus duas
functiones integras indeterminatae x, puta fco et cpa?, tales, ut habeatur aequa-
tio identica
f
quam hie ita exhibemus:
sive, quoniam habemus
o'= (o?—6)(a? — c)[oc—d) ....
v &Ux—b){x — c)(x—d)
in forma sequente:
9<2?.(* — 6)(o?—c){oo—d) ....
Exprimamus brevitatis caussa
OMNEM FUNCnONEM ÄLGEBRAICAM ETC. . 4S
quae est functio integra indeterminatarum x, l\ l", V" etc.
per F[x% l\ l\ l'" etc.)
unde erit identice
i££2 , X', X", X'" etc.)
Habebimus itaque aequationes identicas [l"j
ya.{a — b)(a—c)(a—d) = l-f-.F(a, X', X", X'" etc.)
yb.{b — a){b—c){b — d) = 1+F(b% X', X", X"' etc.)
yc.{c — a){c—b){c — d) == i-\-F[ct X', X", X'" etc.)
etc.
Supponendo itaque, productum ex Omnibus
i+.F(fl, r, r, r etc.)
l+.FF, /', l", l'" etc.)
l+F(ct l\ l\ V" etc.)
etc.
quod erit functio integra indeterminatarum a, b, c etc.. l\ l", V" etc. et quidem
functio symmetrica respectu ipsarum a, b, c etc., exhiberi per
c!>(X', X", X'"etc., /', /", Tete.)
e multiplicatione cunctarum aequationum [l] resultabit aequatio identica nova [2]
Kya.yb.yc = <p(X', X", X'" etc., X', X", X'" etc.)
Porro patet, quum productum cpa.<pß.cpc. . . . indeterminatas a, b, c etc.
symmetrice involvat. inveniri posse functionem integram indeterminatarum
l', l", V" etc. talem, quae per substitutiones l'= X', l"= X", V" = X'"etc. transeat
in rf a.yb.yc . . . . Sit t illa functio, eritque etiam identice [3]
pt = w, v\ retc, /\ r, n
quoniam haec aequatio per substitutiones /'=X', l" =. X", r'=X'"etc. in identi
cam [2] transit.
Iam ex ipsa definitione functionis F sequitur, identice haberi
6*
44 DEMONSTRATIO NOVA ALTERA THEOREMATIS
F(x, L\ L", L'" etc.) = 0
Hinc etiam identice erit
l+l?(fl,I<lL"irete.) = 1
l + F{b,L',L", L'"etc.)= 1
l-\-F(ctL\L"t L'"etc.)= 1
etc.
et proin erit etiam identice
<p(A, K , k etc., _L, 1j , -L etc.) = 1
adeoque etiam identice [4]
<]>(/', r, r etc., i'. i", i'" etc.) = 1
Quamobrem e combinatione aeqiiätionum [3] et [4], et substituendo V =■ U,
l" = L", V" = L'" etc. habebimus [5]
si per T denotamus valorem functionis t illis substitutionibus respondentem.
Qui valor quum necessario fiat quantitas finita, P certo nequit esse =0. Q. E. D.
10.
E praecedentibus iam perspicuum est, quamlibet functionem integram Y
unius indeterminatae a?, cuius determinans sit = 0, decomponi posse in facto-
res, quorum nullus habeat determinantem 0. Investigato enim divisore communi
altissimo functionum Fet ,-, illa iam in duos factores resoluta habebitur. Si
da:
quis horum factorum #) iterum habet determinantem 0, eodem modo in duos facto-
factores resolvetur, eodemque pacto continuabimus, donec Y in factores tales tandem
resoluta habeatur, quorum nullus habeat determinantem 0.
Facile porro perspicietur, inter hos factores, in quos Y resolvitur, ad mi-
*) Revera quidem non nisi factor iste, qui est ille divisor communis, determinantem o habere potest.
Sed demonstratio huius propositionis hocce loco in quasdam ambages perduceret; neque etiam hie necessaria
est, quum factorem alterum, si et huius determinans evanescere posset, eodem modo traetare, ipsumque in
factores resolvere liceret.
OMKEM FUNCnONEM ALGEBRAICAM WTC. 45
nimum unum reperiri debere ita comparatum. ut inter factores numeri, qai eins
ordinem exprimit, binarius saltem non pluries occurrat, quam inter faetores nu-
numeri m, qui exprimit ordinem functionis Y: puta, si statuatur m = k. 2^, de-
notante k numerum imparem, inter factores functionis Y ad rninimum unus re-
perietur ad ordinem Je.2V referendus, ita ut etiam k' sit impar. atque vel v = ja,
vel v < {a. Veritas huius assertionis sponte sequitur inde, quod m est aggrega-
tum numerorum, qui ordinem singulorum factorum ipsius Y exprimunt.
11.
Antequam ulterius progrediamur, expressionem quandam explicabimus, eu-
ius introductio in Omnibus de functionibus symmetricis disquisitionibus maximam
utilitatem affert, et quae nobis quoque peropportuna erit. Supponamus, M esse
funetionem quarundam ex indeterminatis a, b, c etc., et quidem sit fi multitudo
earum, quae in expressionem M ingrediuntur, nullo respectu habito aliarum in-
determinatarum, si quas forte implicet ipsa M. Permutatis illis fi indetermina-
indeterminatis omnibus quibus fieri potest modis turn inter se turn cum m — fi reliquis ex
a, b, c etc., orientur ex M aliae expressiones ipsi M similes, ita ut omnino ha-
beantur
m{m—l)(m—1){m—3) (m — fA-f-1)
expressiones, ipsa M inclusa, quarum complexum simpliciter dicemus complexum
omnium M. Hinc sponte patet, quid significet aggregatum omnium Mt pro-
duetum ex omnibus M etc. Ita e. g. tu dicetur produetum ex omnibus a — b,
u produetum ex omnibus x—a, u' aggregatum omnium —^— etc.
Si forte M est funetio symmetrica respectu quarundam ex fi indetermi-
indeterminatis, quas continet, istarum permutationes inter se funetionem M non va-
riant, quamobrem in complexu omnium M quilibet terminus pluries, et quidem.
1.2.3 v vieibus reperietur, si v est multitudo indeterminatarum, quarum
respectu M est symmetrica. Si vero M non solum respectu v indeterminatarum
symmetrica est, sed insuper respectu v' aliarum, nee non respectu v" aliarum etc.,
ipsa M non variabitar. sive binae e primis* v indeterminatis inter se permutentur,
sive binae e seeundis v', sive binae e tertiis v" etc., ita ut semper
1.2.3 v. t. 2. 3 V. 1.2.3 v" etc.
»EMÖHSmAüüO TS0V& ALIERA THEOEEMATIS
permutationes terminis identicis respondeant. Quare si ex his terminis identicis
semper unicuiaa tantum retineamus, omnino habebimus
m(m — l)(ni'—2)(m—3) (m —
1.2.3 v. 1.2.3... ..v'. 1.2.3 v"etc.
terminos, quorum complexum dicemus complexum omnium M exclusis repetitioni-
repetitionibus, ut a compleani omnium M admissis repetitionibus distinguatur. Quoties nihil
expressis verbis monitum fuerit, repetitiones admitti semper subintelligemus.
Ceterum facile perspicietur, aggregatum omnium M, vel productum ex
omnibus M, vel generaliter quamlibet functionem symmetricam omnium M sem-
semper fieri functionem .symmetricam indeterminatarum a, b, c etc., sive admittan-
tur repetitiones, sive excludantur.
12.
Iam considerabimus, denotantibus u, x indeterminatas, productum ex omni-
omnibus u — [a-\-b)x-{-ab, exclusis repetitionibus, quod per £ designabimus. Erit
itaque Z> productum ex -fcm(m — 1) factoribus his
u — {a-\-b) x-\-ab
u — (a-\-c) x-\-ac
u—(a-\-d)x-\-ad
etc.
u — (b -f- c) x -f- b c
etc. .
u— (c-\-d)x-\-cd
etc. etc.
Quae functio quum indeterminatas a, b, c etc. symmetrice implicet, assignari
poterit functio integra indeterminatarum u, x, l', l", V" etc., per z denotanda,
quae transeat in 4, si loco indeterminatarum V ,V\V" etc. substituantur V, X",l'"etc.
Denique designemus per Z functionem solarum indeterminatarum w, x, in
quam z transit, si indeterminatis l\ l", V" etc. tribuamus valores determinatos
L\ L'\ L'" etc.
Hae tres functiones £, z, Z considerari possunt tamquam functiones inte-
grae ordinis \m[m — 1) indeterminatae u cum coefficientibus indeterminatis, qui
OMNEM FÜNCTJ0HEM ALGEBRAICAM ETC. 47
quidem coefficientes erunt .
pro £, functiones indeterminatarum x, a, b, e etc.
pro z, functiones indeterminatarum xy l\ l", V" etc.
pro Z^ functiones solius indeterminatae x.
Singuli vero coefficientes ipsms z transibunt in coefficientes ipsius L, per substi-
tutiones V = X', l" = X", V" = X'" etc. nee non in coefficientes ipsius Z per sub-
stitutiones V — L\ l" = L", V" = L'" etc. Eadem, quae modo de coefficienti-
bus diximus, etiam de determinantibus functionum £, z, Z valebunt. Atque in
hos ipsos iam propius inquiremus, et quidem eum in finem, ut demonstretur
Theorema. Quoties non est P=0, determinansfunetionis Z certo nequit
esse identice =0.
13.
Perfacilis quidem esset demonstratio huius theorematis. si supponere lice-
ret, Y resolvi posse in factores simplices
(cc — A){cc — B)(x—C)(cc—D)
Tunc enim certum quoque esset, Z esse productum ex omnibus u—(A-\-B)x-\-AB,
atque determinantem funetionis Z productum e differentiis inter binas quanti-
tatum
(J.-+-D) x—AD
etc.
(B-i-C)x—BC
etc.
(C-4- D)x— CD
etc. etc
Hoc vero productum identice evanescere nequit, nisi aliquis factorum per se iden-
identice fiat = 0» unde sequeretur, duas quantitatum A, J5, C etc. aequales esse,
adeoque determinantem P funetionis Y fieri .= 0, contra hyp.
48 DEMONSTEATIO NOVA ALTEEA
At seposita taK argumentatione, quam ad instar art. 6 a petitione principii
proficisci manifestum est, statim ad demonstrationem stabilem theorematis art. 1 2
explicandam progredimur.
14.
Determinans functionis £ erit productum ex Omnibus differentiis inter bi-
nas (a-\-b)x— ab, quarum differentiarum multitudo est
4tm(m — l)(£m(m — 1) — l) = ±{m-\-\)m(m—l)(m — 2)
Hie numerus itaque indicat ordinem determinantis functionis £ respectu indeter-
minatae x. Determinans functionis z quidem ad eundem ordinem pertinebit:
contra determinans functionis Z utique ad ordinem inferiorem pertinere potest,
quoties scilicet quidam coefficientes in de ab altissima potestate ipsius x evanescunt.
Nostrum iam est demonstrare, in determinante functionis Z omnes certo coeffi-
coefficientes evanescere non posse.
Propius considerando differentias illas, quarum productum est determi-
determinans functionis £, deprehendemus, partem ex ipsis (puta differentias inter binas
(a-\-b)x — ab tales, quae elementum commune habent) suppeditare
productum ex omnibus (a — b)(x — c)
e reliquis vero (puta e differentiis inter binas {a-\-b)x— ab tales, quarum ele-
menta diversa sunt) oriri
productum ex omnibus {a-\-b — c — d)x—ab-}-cd, exclusis repetitionibus.
Productum prius factorem unumquemque a — b manifesto m — 2 vieibus con-
tinebit, quemvis factorem x — c autem (m — l)(m — 2) vieibus, unde facile con-
cludimus, hocce productum fieri
Quodsi ita productum posterius per p designamus, determinans functionis 4 erit
__ ,-m—%^{m—\){tn— 2)
Denotando porro per r funetionem indeterminatarum xr V, l", V" etc. eam, quae
transit in p per substitutiones V = X', l" =■ \"y V" = X'" etc., nee non per JR
OMNEM PUBTCKOKEM ALGEBRAICAM ETC.
functionem solius oc, eam, in quam transit r per substitutiones V = Z/, l" =s L'\
V" ==z Zd" etc., patet determinantem functionis z fieri
determinantem functionis ^ autem
-pm—2 y(w—i)(m~2) jd
Quare quum per hypothesin P non sit = 0, res iam in eo vertitur, ut demon-
stremus, JR certo identice evanescere non posse.
15.
Ad hunc finem adhuc aliam indeterminatam w introducemus, atque pro-
ductum ex omnibus
(a -\- b—c — d) w -f- (a — c)(a — d)
exclusis repetitionibus considerabimus, quod quum ipsas a, b, c etc. symmetrice
involvat, tamquam functio integra indeterminatarum. w, X', X", X'" etc. exhiberi
poterit. Denotabimus hanc ftmctionem per f(w, X', X", X'" etc.). Multitudo illo-
rum factorum (a-^-b — c — d)w-\-{a—c){a—d) erit
= \m{m—l)(m — 2)(a»—3)
unde facile colligimus, fieri
/@, X', X", X'" etc.) = tcC^-2)^-3)
et proin etiam
/@, l\ l\ V" etc.) =
nee non
/@, L\ L\ U" etc.) =
Functio f(w, L', L", L'" etc.) generaKter quidem loquendo ad ordinem
%m[m—l)(m—2)(m—3)
referenda erit: at in casibus specialibus utique ad ordinem inferiorem pertinere
potest, si forte contingat, ut quidam coefficientes inde ab altxssima potestate ipsius
w evanescant: impossibile autem est, ut illa functio totasit identice = 0, quum
7
50 DEMONSTRATIO NOVA ALTERA'THEOREMATIS
aequatio modo inventa doceat, functionis saltem terminum ultimum non eva-
nescere. Supponemus, terminum altissimum functionis f(w, L\ L", U" etc.), qui
quidem coefficientem non evanescentem habeat, esse iW. Si igitur substituimus
w — x—a, patet, f(x—a, L', L", U" etc.) esse functionem integram indeter-
minatarum x, a, sive quod idem est, functionem ipsius x cum coeincientibus ab
indeterminata a pendentibus, ita tarnen ut terminus altissimus sit iW, et proin
coeiiicientem determinatum ab a non pendentem habeat, qui non sit =0. Per-
inde f(po — b, L\ L", L'" etc.), f{x — c, L\ JO\ L'" etc.) erunt functiones integrae
indeterminatae oc, tales ut singularum terminus altissimus sit iW, terminorum
sequentium autem coeflicientes resp. a b, c etc. pendeant. Hinc productum ex
m factoribus
f{x—at L\ L", L'" etc.)
f{x — b, L\ L", Lm etc.)
f{z — c,L\ L", Lm etc.)
etc.
erit functio integra ipsius x, cuius terminus altissimus erit Nm x™, dum termi-
terminorum sequentium coefficientes pendent ab indeterminatis a, b, c etc.
Consideremus iam porro productum ex m factoribus his
f{x — a, l\ l", V" etc.)
f{x—b, l\ l", Tete.)
f{x—c, V, r, Tete.)
etc.
quod quum sit functio indeterminatarum, x, a, b, c etc., l', l", V" etc., et quidem
symmetrica respectu ipsarum a, b, c etc., exhiberi poterit tamquam functio inde-
indeterminatarum x, X', X", X'" etc. l', l", V" etc. per
<p(a?, X', X", r etc., l\ l", Tete.)
denotanda. Erit itaque
<p(a?f X', X", X'"etc, X', X', X'"etc.)
productum ex factoribus
f{x — a, X', X", X'"etc.)
/(*—'6, x1, r, r etc.)
f(x—c, X', X", X'"etc.)
etc.
OMNEM FÜNCTIONEM ALÖEBEAICAM ETC. 51
et proin indefinite divisibilis per p, quum facile perspiciatur, quemlibet factorem
ipsius p in aliquo illorum factorum implicari. Statuemus itaque
<p(*. X', X", X'" etc., X', X", X'" etc.) = p <[>(*, X', X", X'" etc.)
ubi characteristica c[> functionem integram exhibebit. Hinc vero facile deducitur,
etiam identice esse
<p(*. L\ L", ZT etc., L', L", L'" etc.) = R^(x, L\ L'\ L'" etc.)
Sed supra demonstravimus, productum e factoribus
/(# — a, L\ L", L'" etc.)
fix— b, L\ L\ L'" etc.)
f{x — c,L\L",L'" etc.)
etc.
quod erit = cp [x, X', X", X'" etc., L', L", L'" etc.) habere terminum altissimum
Nmx™; eundem proin terminum altissimum habebit functio cp(<z?, U, L", 11" etc.,
U, L", L'" etc.) adeoque certo non est identice = 0. Quocirca etiam JR nequit
esse identice = 0, neque adeo etiam determinans functionis Z. Q. E. D.
16.
Theokema. Denotet <p(u, x)*) productum ex quotcunque factoribvs talibus, in
quos indeterminatae u, x Hneariter tantum ingrediuntur, sive cjui sint formae
a -{-fiu
etc.
sitporro w alia indeterminata. Tunc functio
indefinite erit divisibilis per <p (#,#).
*) Vel nobis non monentibus quisque videbit, signa in art. praec. introducta restringi ad istum
solum articulum, et proin significationem characterum tp, w praesentem non esse confundendam cum pristina.
52 DEMONSTRATIO NOVA ALIEBA THEOEEMATIS
Dem. Statuendo
cp (u, x) = (a -f- ö m -f- y<2?) Q
etc.
erunt Q, Q', Q"etc. functiones integrae indeterminatarum u, oc, a, 6, y,
a', 6", y" etc. atque
= 1Q+ &+*
'* dx
etc.
etc.
Substitutis hisce valoribus in factoribus, e quibus conflatur productum
puta in
a
«
7
etc. resp.
hi obtinent valores sequentes
etc.
OMKBM FUNCTIONEM ALGEBRAICAM ETC. BZ
quapropter Q erit productum ex v>(u,x) in factores
da: * du
etc. i. e. ex cp (u, x) in functionem integram indeterminatarum w, x, w, a, 'S, y,
a', t>\ j, a", $", f etc. Q. E. D.
17.
Theorema art. praec. manifesto applicabile est ad functionem £, quam ab-
hinc per
/(«, j?f X', X", X'" etc.)
exhiberi supponemus, ita ut
/{*+*.£, x-v-ru* ^.^^etc.)
indefinite divisibilis evadat per t,: quotientem, qui erit functio integra indetermi-
indeterminatarum u, x, w, a, b, c etc., symmetrica respectu ipsarum a, b, c etc.. exhibe-
bimus per
<[>(«,#, w, X', X",X'"etc.)
Hinc concludimus, fieri etiam identice
/(« + «>.^, x—w.^, l\ l", l'" etc.) =z<\>(u, x,w, l\ l",r etc.)
nee non
f(u+Wm*?t x — w.i£, L\ L\ U" etc.) = Ztyfa xt w, L', L\ IT etc.)
Quodsi itaque functionem. Z simpliciter exhibemus per F(u, x), ita ut habeatur
f{u, x, Lr, L", L" etc.) = F{u,x)
erit identice
F(u + w.±§, x-™^) = Zty{u, x, w, L\ L", V etc.)
54 DEMQNSTRATIO NOVA ALTEEA THEOKEMATIS
18.
Si itaque e valoribus determinatis ipsarum u, x, puta ex u = U, x = X,
prodire supponimus
d^ -y/ d^ TTT-/
J -Ä- 7 J *-'
ax au
erit identice
F(U+wX\ X — wU') = F{U,X).fy{U, X, w, L\ L", L" etc.)
Quoties V non evanescit, statuere licebit
X—x
unde emergit
xf-^, x) = F(^X).^Z7, X, ^=-*, r, i", i'" etc.)
quod etiam ita enunciare licet:
iur u =
-ffr-, Lt, Lt, Lt etc.)
Si in functione Z statuitur u = U-\- -jj, =^-, transibit ea in
19.
Quum in casu eo, ubi non est P = 0, determinans functionis Z sit
functio indeterminatae x per se non evanescens^ manifesto multitudo valorum de-
terminatorum ipsius x, per quos hic determinans valorem 0 nancisci potest, erit
numerus finitus, ita ut infinite multi valores determinati ipsius x assignarx pos-
sint, qui determinanti illi valorem a 0 diversum concilient. Sit X talis valor
ipsius x (quem insuper realem supponere licet). Erit itaque determinans functio-
functionis F(utX) non = 0, unde sequitur, per theorema II. art. 6, functiones
F(u,X) et «£3
habere non posse divisorem ullum communem. Supponamus porro, exstare aliquem
valorem determinatum ipsius u, puta U (sive realis sit, sive imaginarius i. e. sub
forma g-{-h\J—1 contentus), qui reddat F(u.X) = 0, i. e. esse F(U,X) = 0.
Erit itaque u — U factor indefinitus functionis F (u, X), et proin functio
•—^—- certo per u — U non divisibilis. Supponendo itaque, hanc functionem
OMJJEM FÜNCTIQNEM AL6EBEAICAM: ETC.
—g—' nancisci valorem U\ si statuatur u=U, certo esse nequit £T=0. Ma-
Manifeste autem TJ' erit valor quotientis differentialis partialis ■=— pro u=-U, x=^X:
quodsi itaque insuper pro iisdem valoribus ipsarum u, x valorem quotientis diffe-
differentialis partialis -^- per X' denotemus, perspicuum est per ea quae in art.
praec. demonstrata sunt, functionem Z per substitutionem
identice evanescqre, adeoque per factorem
indefinite esse divisibilem. Quocirca statuendo u = xxt patet, F{xx, x) divi-
sibilem esse per
■2L
XX
-\- jj, X ( U-\-
adeoque obtinere valorem 0, si pro x accipiatur radix aequationis
/y> /y> , I ., /y> / TT I \ —— A
du du | ttr & ' \ *-' i —Yr'i } ■ ■ "
i. e. si statuatur
— x' ± y^D uu'U'+ 4 j:x' J7r+ x'X')
quos valores vel reales esse vel sub forma g-\-h\J—1 contentos constat.
Facile iam demonstratur, pereosdem valores ipsius x etiam functionem Y
evanescere debere. Manifeste enim f{xxs x, X', X", X'"etc.) est productum exomni-
bus (a? — a)(x—b) exclusis repetitionibus, et proin = üm~1. Hinc sponte sequitur
f{xx, x, l', l\ V" etc.) =
f{xx, x, L\ L'\ 17 etc.) =
sive F(xx, x) = F™—\ cuius itaque valor determinatus evanescere nequit, nisi si-
mul evanescat valor ipsius Y.
20.
Adiumento disquisitionum praecedentium reducta est solutio aequationis
Y= 0, i. e. inventio valoris determinati ipsius x, vel realis vel sub forma
g-\-h\j—1 contenti, qui illi satisfaciat, ad solutionem aequationis F(u, X) = 0,
5ß DEMOKSTEAT1O NOVA ALTEEA THEOBEMATIS ETC.
sicjüidem determinans functionis Y non fuerit = 0. Observare convenit, si
omnes coefficientes in Y, i. e. numeri L\ U', 11" etc. sint quantitates reales,
etiam omnes coefficientes in F(u,X) reales fieri, siquidem, quod licet, pro X quan-
titas realis accepta fuerit. Ordo aequationis secundariae F(u, X) = 0 exprimi-
tur per numerum \m{m—1): quoties igitur m est numerus par formae I^k de-
notante Je indefinite numerum imparem, ordo aequationis secundariae exprimitur
per numerum formae 2tA~~1&.
In casu eo, ubi determinans funetionis Y fit = 0, assignari poterit per
art. 10 funetio alia 5) ipsam metiens, cuius determinans non sit =0, et cuius
ordo exprimatur per numerum formae 2V&, ita ut sit vel v<$i, vel v = ja. Quae-
libet solutio aequationis f) = 0 etiam satisfaciet aequationi Y= 0: solutio ae-
aequationis 2) = 0 iterum reducetur ad solutionem alius aequationis, cuius ordo
exprimetur per numerum formae 2V~1&.
Ex his itaque coUigimus, generaliter solutionem cuiusvis aequationis, cuius
ordo exprimatur per numerum parem formae 2^, reduci posse ad solutionem
alius aequationis, cuius ordo exprimatur per numerum formae 2^ä, ita ut sit
jt <C ja. Quoties hie numerus etiamnum par est, i. e. fi' non = 0, eadem me-
thodus denuo applicabitur, atque ita continuabimus, donec ad aequationem per-
veniamus, cuius ordo exprimatur per numerum imparem; et huius aequationis
coe'fiicientes omnes erunt reales, siquidem omnes coefiieientes aequationis primi-
tivae reales fuerunt. Talern vero aequationem ordinis imparis certo solubilem esse
constat, et quidem per radicem realem, unde singulae quoque aequationes antece-
dentes solubiles erunt, sive per radices reales sive per radices formae g~\-hsj—1.
Evictuni est itaque, funetionem quamlibet Y formae xm—Lxm~x-\-JU'afnr~2—
etc., ubi U, L" etc. sunt quantitates determinatae reales, involvere factorem in-
indefinitum x — A, ubi A sit quantitas vel realis vel sub forma g-\-h\J—1 con-
tenta. In casu posteriori facile perspicitur, Y nancisci valorem 0 etiam per sub-
stitutionem x = g—h \J— 1, adeoque etiam divisibilem esse per x — (g—h\J— 1),
et proin etiam per produetum xx—1gx-\-gg-\-hh. Quaelibet itaque funetio
Y certo factorem indefinitum realem prxmi vel secundi ordinis implicat, et quum
idem iterum de quotiente valeat, manifestum est, Y in factores reales primi vel
secundi ordinis resolvi posse. Quod deinonstrare erat propositum huius com-
mentationis.
THEOREMATIS
DE RESOLÜBILITATE FUNCTIONUM
ALGEBRAICAEUM INTEGRAEUM
IN FACTORES REALES
DEMONSTRATIO TERTIA
SUPPLEMEOTUM COMMENTATIOOTS PEAECEDENTIS
AÜCTOEE
CAEOLO FRIDERICO GAUSS
SOCIETATI EEGIAE SCIENTIARUM TEADITUM 1816. JAN. 30.
Commentationes societatis regiae scientiarnm Gottingensis recentiores. Vol. in.
Gottingae mdcccxvi.
THEOREMATIS DE RESOLÜBILITATE
FÜNCTIONUM ALGEBRAICARUM INTEGRARUM
IN FACTORES REALES
DEMONSTRATIO TERTIA.
SÜPPLEMENTUM COMMENTATIONIS PRAECEDENUS.
Postquam commentatio praecedens typis iam expressa esset, iteratae de eo-
dem argumento meditationes ad novam theorematis demonstrationem perduxerunt,
quae perinde quidem ac praecedens pure analytica est, sed principiis prorsus di-
versis innititur, et respectu simplicitatis illi longissime praeferenda videtur. Huic
itaque tertiae demonstrationi pagellae sequentes dicatae sunto.
1.
Proposita sit functio indeterminatae x haecce:
X = (z?w+^w-1+J5^2+C^3+ etc.
in qua coefficientes A, B, C etc. sunt quantitates reales determinatae. Sint r,
aliae indeterminatae, statuamusque
etc. +ircoscp+M = t
Bt*ri-2sm(m—2)<?
-\-Crm~ssin (m— 3)cp-}>etc. -f-irsin<j> = u
60 TBEOEEMA33S BE EISOLDBHJTAIE
cos (m—2)cp
cos (t»—3)cp-f~ etc. +i/coscp = *'
mrmsirim¥+(m-~l)Arm~'1sin(m—- \)y-\-(m— 2) Br'2 sin (m—2)cp
+ (*»—3)CV*""*sin(a»—3)cp-|-etc. +irsincp = u
mm r^cos m cp 4- (t» — 1 J A rm~4 cos (a» —-1) cp+(m—2J J^r"*-2 cos (m — 2) cp
+ (^--3JCr?n^3cos(^ —3)cp+etc. -j-Zrcoscp = f"
sin m cp+im—1 f^lr^ sin (m—1) 9 + (m — 2J J?^^ sin (m — 2) 9
-\-(m—äfCr™sin(a»—3)cp+ etc. -f-irsincp = u"
Factorem r manifesto e denominatore formulae ultimae tollere licet, quum
t\ u, t", u" per illum sint divisibiles. Denique sit JR quantitas positiva deter-
minata, axbitraria quidem, attamen maior maxima quantitatum
mAsJi, \J{mB\j2), y/(mC\]2), y/{mD\j2) etc.
abstrahendo a signis quantitatum A, B, C etc., i. e. mutatis negativis, si quae
adsint, in positivas. His ita praeparatis, dico, tt'-\-uu certo nancisci valorem
positivum, si statuatur r = JR, quicunque valor (realis) ipsi cp tribuatur.
Demonstratio. Statuamus
0+^i2m-1cosD5°+cp)+J5i2TO-2cosD50+2cp)
—1)cp)+McosD5°+^cp) = T
= U
■2)J5i2m-2cosD5°+2cp)
— 3) CiT-3cosD5°+3cp)+etc.+ii2cosD5°+(^—l)cp) — T
etc. 4-ii2sinD5°+(^—t)cp) = U'
patetque
I. T compositam esse e partibus
my/2
ALGEBRAICAEUM INTEGEARUM ETC.
[R -\-mAp.<
-f-
quas singulas, pro valore quolibet determinato reali ipsius 9, positivas evadere
facile perspicitur: Mnc T necessario valorem positivum obtinet. Simili modo
probatur, etiam Ut T\ V fieri positivas, unde etiam T T'-\- TJTJ' necessario
fit quantitas positiva.
II. Pro r = JR functiones t, u, f, u resp. transeunt in
Tcos D5°-f-^cp)+Z7sinD5°+^cp)
T sin D5°+^9)— CTcos D5°+^cp)
T'cosD5°+^cp) -f- ^'8^D5°+^9)
' y'sin D5a+a»«p) — U fcosD5°+a»<p)
uti evolutione facta facile probatur. Bünc vero valor functionis .tt'-\-uu, pro
r = K, derivatur = TT'-\- XJU\ adeoque est quantitas positiva. Q. E. D.
Ceterum ex iisdem formulis colligimus valorem functionis tt-\-uu, pro r=R,
esse TT-\-UU, adeoque positivum, unde concludimus, pro nuilo valore ipsius r,
singulis mA\J% \j(mB\]i)> ^(mC\/2) etc. maiori, simul fieri posse #==0, u = Q,
2.
Theoeema. Intra limites r ■=. 0 et r = R, atque cp = O et cp
certo exstant valores tales indeterminatarum r, cp, pro quibusßat simul t= 0 et u = 0.
Demonstratio. Supponamus theorema non esse verum, patetque, valorem
ipsius tt-\-uu pro cunctis valoribus indeterminatarum intra limites assignatos
fieri debere quantitatem positivam, et proin valorem ipsius y semper finitum. Con-
sideremus integrale duplex
ffydrdy
ab r = 0 usque ad r = R, atque a <p = 0 usque ad cp = 360° e^tensum»
quod igitur valorem finitum plene determinatum nanciseitur. Hie vaior, quem
TOEOEEMATIS DB
per Q denotabimus, idem prodire debebit^ sive integratio primo instituatur se-
secundum <p ac dein secundum r, sive ordine inverso. At habemus indefinite, con-
siderando r tamquam constantem,
tu'—ut'
•uu)
uti per differentiationem secundum cp facile confirmatur. Cönstans non adii-
cienda, siquidem integrale a cp = 0 incipiendum supponamus, quoniam pro
cp = 0 fit ?~u > = 0. Quare quum manifesto "~u > etiam evanescat pro
T r(tt-\-uu) ^- r(tt-{-uu) r
cp = 360°, integrale /y.dcp atp = ö usque ad cp = 360° fit = 0, manente r
indefinita. Hinc autem sequitur Q = 0.
Perinde habemus indefinite, considerando <p tamquam constantem,
fydr
tt + uu
uti aeque facile per differentiationem secundum r confirmatur: hie quoque con-
stans non adiieienda, integrali ab r = 0 ineipiente. Quapropter integrale ab
r ==■ 0 usque ad r =^ R extensüm fit per ea, quae in art. praec. demonstrata sunt,
= yyT jjjf adeoque per theorema art. praec. semper quantitas positivapro quo-
libet valore reali ipsius cp. Hinc etiam Q, i. e. valor integralis
J TT+UU QC?
a cp = 0 usque ad cp = 360°, necessario fit quantitas positiva*). Quod est ab-
surdum, quoniam eandem quantitatem antea invenimus = 0: suppositio itaque
consistere nequit, theorematisque veritas hinc evieta est.
3.
Functio X per substitutionem <2? = r(coscp-j-sincp.\/—l) transitin t-\-u\J—1,
nee non per substitutionem <2? = r(eoscp—sincp.y/—1) in t—u\J—1. Quodsi
igitur pro valoribus determinatis ipsarum r, <p, puta pro r = ff, cp = G, simul
provenit t = 0, u = 0 (qüales valores exstare in art. praec. demonstratum est),
X per utramque substitutionem
*) Utiiam per se manifestum est. Ceterumintegrale indefinitum facile eruitur =m<p+450 — arc.^tang—,
atque aliunde demonstrari potest (per se enim nondum obvium est, quemnam valorem ex infinite multis functioni
multiformi arc. tang. —s competentibus pro © = 360° adoptare oporteat), huius valorem usque ad © = 360Q
extensüm statui debere = mX 360° sive = 2mz. Sed hoc ad institutum nostrum non est necessarium.
FUNCTIONUM ALGEBRAICARÜM INTEGRARUM ETC. 63
x = g(co$G-+-smG.^—1), x = g(cosG—smG.^—1)
valorem 0 obtinet, et proin indefinite per
x—-g(cosG-±-sinG.\J—1), nee non per x—g(cosG—sinG.\J—1)
divisibilis erit. Quoties non est sin G = 0, neque g = 0, hi divisores sunt
inaequales, et proin X etiam per illorum produetum
xx — 2gcos G.x-\-gg
divisibilis erit, quoties autem vel sin G — 0 adeoque cos6r = + l, vel g = 0,
Uli factores sunt identici scilicet = x Ip g. Certum itaque est, tfunetionem X
involvere divisorem realem seeundi vel primi ordinis, et quum eadem conclusio
rursus de quotiente valeat, X in tales factores complete resolubüis erit. Q. E. D.
4.
Quamquam in praecedentibus negotio quod propositum erat, iam plene per-
funeti simus, tarnen haud superfluum erit, adhuc quaedam de ratiocinatione art. 2
adiieere. A suppositione, t et u pro nullis valoribus indeterminatarum r, <p in-
tra limites illic assignatos simul evanescere, ad contradictionem inevitabilem de-
lapsi sumus, unde ipsius suppositionis falsitatem conclusimus. Haec igitur con-
tradictio cessare debet, si revera adsunt valores ipsarum r, cp, pro quibus t et u
simul fiunt =0. Quod ut magis illustretur, observamus, pro talibus valoribus
fieri tt-\-uu = 0, adeoque ipsam y infinitara, unde haud amplius licebit, in-
integrale duplex ffydrdv tamquam quantitatem assignabilem tractare. Genera-
Generaliter quidem loquendo, denotantibus £, r\, C indefinite coordinatas punetorum in
spatio, integrale ffydrdy exhibet volumen solidi, quod continetur inter quin-
queplana, quorum aequationes sunt
i = o, t] = o, c = o, i = R, n = 360°
atque superficiem, cuius aequatio £ = y, considerando eas partes tamquam ne-
gativas, in quibus coordinatae £ sunt negativae. Sed tacite hie subintelligitur,
superficiem sextam esse continuam, qua conditione cessante, dum y evadit infi-
nita, utique fieri potest, ut coneeptus ille sensu careat. In tali casu de integrali
ffydrdo colligendo sermo esse nequit, neque adeo mirandum e&t, operationes
analyticas coeco calculo ad inania applicatas ad absurda perducere.
64 THEOREMATIS DE EBSOLUBHJTATE FÜNCTIONUM ETC.
Integratio Jydcp = ru^V*uu\ eatenus tantum est integratio vera, i. e. sum-
matio, quatenus inter limites, per quos extenditur, y ubique est quantitas finita,
absurda autem, si inter illos limites y alicubi infinita evadit. Si integrale tale
/rjdl, quod generaliter loquendo exhibet aream inter lineam abscissarum atque
curvam, cuius ordinata = r\ pro abscissa |, secundum regulas suetas evolvimus,
continuitatis immemores, saepissime contradictionibus implicamur. E. g. statuendo
1] = £=, analysis suppeditat integrale = C—r, quo area recte definitur, quam-
diu curva continuitatem servat; qua pro J = 0 interrupta, si quis magnitudinem
areae inde ab abscissa negativa usque ad positivam inepte rogat, responsum absur-
dum a formula feret, eam esse negativam. Quid autem sibi velint haec similiaque
analyseos paradoxa, alia occasione fusius persequemur.
Hie unicam observationem adiieere liceat. Propositis absque restrictione
quaestionibus, quae certis casibus absurdae evadere possunt, saepissime ita sibi
consulit analysis, ut responsum ex parte vagum reddat. Ita pro valore integralis
ffydrdy ab r = e usque ad r=ft atque a cp = JE7 usque ad cp = F ex-
tendendi, si valor ipsius j
pro r = e, cp == JE7 designatur per 6
r = e, cp = F 6'
r =/, y = E 6"
r =/, cp = i^ 6'"
per operationes analyticas facile obtinetur
Are. tang 6 — Are. tang 6'— Are. tang6"-f- Are. tangö'"
Kevera quidem integrale tunc tantum valorem certum habere potest, quoties y
inter limites assignatos semper manet finita: hie valor sub formula tradita utique
contentus, tarnen per eam nondum ex asse definitur, quoniam Are. tang. est funetio
multiformis, seorsimque per alias considerationes (haud quidem difficiles) decidere
oportebit, quinam potissimum funetionis valores in casu determinato sint adhi-
bendi. Contra quoties y alicubi inter limites assignatos infinita evadit, quaestio
de valore integralis ffydrdy absurda est: quo non obstante si responsum ab
analysi extorquere obstinaveris, pro methodorum diversitate modo hoc modo ülud
reddetur, quae tarnen singula sub formula generali ante tradita contenta erunt.
BEWEIS
EINES
ALGEBRAISCHEN LEHRSATZES.
Journal für die reine und ang. Mathematik herausg. von Ceelle. Band in.
Berlin 1828.
a
BEWEIS
EIJSTES ALGEBRAISCHEN LEHRSATZES.
Der Gegenstand dieses Aufsatzes ist der CABTEsische, gewöhnlich nach Hae-
eiot benannte, Lehrsatz über den Zusammenhang der Anzahl der positiven und
negativen Wurzeln einer algebraischen Gleichung mit der Anzahl der Abwechse-
Abwechselungen und Folgen in den Zeichen der Coefficienten. Man vermisst an den von
verschiedenen Schriftstellern versuchten Beweisen dieses Theorems die Klarheit,
Kürze und umfassende Allgemeinheit, die man bei einem so elementarischen Ge-
Gegenstande mit Recht verlangen kann, und eine neue Behandlung desselben scheint
daher nicht überflüssig zu sein.
Es sei X eine algebraische ganze Function von x von der Ordnung m,
nach absteigenden Potenzen von oc geordnet. Wir nehmen an (ohne Nachtheil
für die Allgemeinheit), dass das höchste Glied ocm sei, und das niedrigste von x
freie Glied nicht fehle; bloss die wirklich vorhandenen Glieder sollen aufgestellt,
also nicht die etwa fehlenden mit dem Coefficienten 0 angesetzt sein.
Wenn nicht alle Coefficienten positiv sind, so werden sie einen oder meh-
mehrere Zeichenwechsel darbieten. Es sei —Naf1 das erste negative Glied, das er-,
ste hierauf folgende positive ~{-Pxpt das erste hierauf folgende negative —Qxq
u.s.w. Es sind mithin m, n,p, q u.s.w. abnehmend^ ganze Zahlen; N,P, Q u.s.w.
positiv, und X erscheint so dargestellt
. . — Nxn . . 4-Pa?J»4~f- . . —Qaß— u.s.w.
9*
68 BEWEIS
Es werde X mit dem einfachen Factor x—a multiplicirt, wo a positiv
vorausgesetzt wird. Man sieht leicht, dass in dem Producte, af^1 einen ne-
negativen, x^1 einen positiven, xqJtl einen negativen Coefficienten u. s. w., also
das Product diese Form erhalten wird:
X{x — a) = x™+1. .. — iW+\ . . -\-P'ocV+x. . — Q'xq+l. . .
so dass N\ P', Q'u.s.w. positiv werden. Die Zeichen zwischen den aufgestell-
aufgestellten Gliedern bleiben zwar unentschieden: allein es ist klar, dass vom höchsten
Gliede bis zur Potenz xn~^1 wenigstens ein Zeichenwechsel, bis x^1 wenigstens
zwei, bis xq+1 wenigstens drei u. s. w. statt finden. Ist der letzte Zeichenwech-
Zeichenwechsel in X bei dem Gliede + Uxu, und bezeichnet man- den Coefficienten von
^m+i in x(x—a) durch + U', so wird V positiv sein, und bis zum Gliede
+ U'xu+1 haben dann wenigstens eben so viele Zeichenwechsel, wie in X sind,
statt gefunden. Das letzte Glied in X.(x—a) wird aber das Zeichen Ijl haben;
es muss also bis dahin wenigstens noch ein Zeichenwechsel hinzugekommen sein.
Wir schliessen also, dass X(x—a) wenigstens einen Zeichenwechsel mehr hat
als X.
Es sei nun X das Product aller einfachen Factoren, die den negativen und
imaginären Wurzeln einer Gleichung y = 0 entsprechen, also wenn a, 6, y u.s.w.
die positiven Wurzeln derselben Gleichung sind,
y = X(x—a)(x — 6)(a?—y) . . .
Es finden sich also nach vorstehendem Satze, in X{x—a) wenigstens ein Zei-
Zeichenwechsel, in X(x — a)(x—ff) wenigstens zwei, in X(x — a)(x—6)(a?—y)
wenigstens drei u.s.w. mehr als in X;. folglich werden, auch wenn in X gar kein
Zeichenwechsel vorkommt, in y wenigstens so viele Zeichenwechsel sein, wie po-
positive Wurzeln. Man sieht von selbst, dass wenn die Gleichung weder negative,
noch imaginäre Wurzeln hat, man X = 1 zu setzen hat, und dieser Schluss
seine Gültigkeit behält.
Es gehe y, wenn den Coefficienten der Potenzen x™^1, xm~~s, xm~5 u. s. w.
die entgegengesetzten Zeichen beigelegt werden, in y über; sämmtliche Wur-
Wurzeln der Gleichung y' = 0 werden dann den Wurzeln der Gleichung y — 0
entgegengesetzt sein. Es wird daher in y wenigstens eben so viele Zeichen-
Zeichenwechsel geben, als die Gleichung y == 0 negative Wurzeln hat.
ALGEBRAISCHEN LEHRSATZES. 69
Wir haben daher folgenden Lehrsatz:
Die Gleichung y = 0 kann nicht mehr positive Wurzeln haben, als es Zei-
Zeichenwechsel in y gibt, und nicht mehr negative Wurzeln^ als Zeichenwechsel in y
sind.
Diese Einkleidung des Theorems scheint die zweckmässigste zu sein, da sie
die grösste Einfachheit mit der umfassendsten Allgemeinheit vereinigt, und alle
Gestalten des Satzes > die nur unter besondern Bedingungen gelten, von selbst
daraus flies sen.
Wül man die Grenze der Anzahl der negativen Wurzeln unmittelbar an den
Zeichen der Coeflicienten von y erkennen, so wird es nothwendig, die unmittel-
unmittelbaren Zeichen Wechsel und Zeichenfolgen (bei Gliedern, wo die Exponenten von
x um eine Einheit verschieden sind) von den durch fehlende Glieder unterbro-
unterbrochenen zu unterscheiden. Offenbar wird jeder unmittelbare und jeder durch eine
gerade Anzahl fehlender Glieder unterbrochene Zeichenwechsel in y zu einer
ähnlichen Zeichenfolge in y, während ein durch eine ungerade Anzahl fehlender
Glieder unterbrochener Zeichen Wechsel in y auch in y ein ähnlicher. Zeichen-
Zeichenwechsel bleibt. Der zweite Theil des Theorems lässt sich daher auch so aus-
ausdrücken :
Die Anzahl der negativen Wurzeln der Gleichung y = 0 kann nicht grösser
sein, als die Anzahl der unmittelbaren und der durch eine gerade Anzahl fehlen-
fehlender Glieder unterbrochenen Zeichenfolgen, addirt zu der Anzahl der durch eine
ungerade Anzahl fehlender Glieder unterbrochenen Zeichenwechsel in y.
Fehlt in y gar kein Glied, so ist die Anzahl der negativen Wurzeln nicht
grösser, als die Anzahl der Zeichenfolgen.
Bezeichnet man durch A die Anzahl der unmittelbaren Zeichenwechsel,
und durch B die Anzahl der unmittelbaren Zeichenfolgen in y, so wird, wenn
kein Glied fehlt, A-\-B = m sein, also der Anzahl aller Wurzeln gleich. In-
Insofern diese Zeichen also bloss lehren, dass die Anzahl der positiven Wurzeln nicht
grösser als A, und die der negativen nicht grösser als B sein kann. bleibt es
unentschieden, ob oder wie viele imaginäre Wurzeln vorhanden sind. Weiss man
aber anders woher, dass die Gleichung keine imaginäre. Wurzeln hat, so muss
nothwendig A der Anzahl der positiven, und B der Anzahl der negativen Wur-
Wurzeln gleich sein.
Anders aber verhält es sich, wenn in y Glieder fehlen. Um mit Klarheit
70 BEWEIS EESTES ALGEBRAISCHEN LEHRSATZES.
zu übersehen, was sich daraus in Beziehung auf die imaginären Wurzeln schliessen
lässt, bezeichnen wir durch a die Anzahl der durch eine gerade, durch c die
Anzahl der durch eine ungerade Anzahl fehlender Glieder unterbrochenen Zeichen-
Zeichenwechsel; durch b und d resp. die Anzahl der durch eine gerade und ungerade
Anzahl fehlender Glieder unterbrochenen Zeichenfolgen in y. Man sieht leicht,
dass m — A—"B — a — b— c—d der Anzahl sämmtlicher fehlender Glieder, die
wir durch e bezeichnen wollen, gleich sein werde. Nun ist nach unserm Lehr-
Lehrsatze die Anzahl der positiven Wurzeln höchstens A-\-a-\-ct die Anzahl der ne-
negativen höchstens JB-J-fc-f-c, also die Anzahl aller reellen Wurzeln höchstens
A-{-B-\- a-\-b-\-2c = m-\-c—d—e
Es muss daher die Anzahl der imaginären Wurzeln wenigstens e — c -f- d sein.
Zählt man also alle fehlenden Glieder zusammen, jedoch so, dass man in
jeder Lücke zwischen einem Zeichenwechsel eine Einheit weniger, zwischen einer
Zeichenfolge aber eine Einheit mehr rechnet, als Glieder fehlen, so oft deren An-
Anzahl ungerade ist, so erhält man eine Zahl, der die Anzahl der imaginären Wur-
Wurzeln wenigstens gleich kommen muss.
BEITRÄGE ZUR THEORIE
DES
ALGEBRAISCHEN GLEICHUNGEN
VON
CARL FRIEDRICH GAUSS
Vorgelesen in der Sitzung der Königl. Gesellschaft der Wissenschaften am 16. Juli 1849.
Abhandlungen der Königl. Gesellschaft der Wissenschaften zu Göttingen. Band iv.
Göttingen, 1850.
12
73
BEITRÄGE ZUR THEORIE
DER ALGEBRAISCHEN GLEICHUNGEN.
Es werden in dieser Denkschrift zwei verschiedene die algebraischen Glei-
Gleichungen betreifende Gegenstände behandelt. Zuerst stelle ich den vor fünfzig
Jahren von mir gegebenen Beweis des Grundlehrsatzes der Theorie der algebrai-
algebraischen Gleichungen in einer veränderten Gestalt und mit erheblichen Zusätzen auf.
Der zweite Theil ist einer speciellen Behandlung der algebraischen' Gleichungen
mit drei Gliedern gewidmet, und enthält Methoden, nicht bloss die reellen, son-
sondern auch die imaginären Wurzeln solcher Gleichungen mit Leichtigkeit zu be-
bestimmen.
ERSTE ABTHEILUNG.
Die im Jahre 1799 erschienene Denkschrift, Demonstratio nova theorematis,
omnem functionem algehraicam rationalem integram unius variabilis infactores reales
primi vel secundigradus resolvi posse, hatte einen doppelten Zweck, nemlich er-
erstens, zu zeigen, dass sämmtliche bis dahin versuchte Beweise dieses wichtigsten
Lehrsatzes der Theorie der algebraischen Gleichungen ungenügend und illusorisch
sind, und zweitens, einen neuen vollkommen strengen Beweis zu geben. Es ist
unnöthig, auf den erstem Gegenstand noch einmal zurückzukommen. Dem dort
gegebenen neuen Beweise habe ich selbst Später noch zwei andere folgen las-
lassen , und ein vierter ist zuerst von Caücht aufgestellt. Diese vier Beweise beru-
10
<4 BEITRÄGE ZUR THEORIE
hen alle auf eben so vielen verschiedenen Grundlagen, aber darin kommen sie
alle überein, dass durch jeden derselben zunächst nur das Vorhandensein Eines
Factors der betreffenden Function erwiesen wird. Der Strenge der Beweise thut
dies allerdings keinen Eintrag: denn es ist klar, dass wenn von der vorgegebe-
vorgegebenen Function dieser eine Factor abgelöset wird, eine ähnliche Function von nie-
niederer Ordnung zurückbleibt, auf welche der Lehrsatz aufs neue angewandt wer-
werden kann, und dass durch Wiederholung des Verfahrens zuletzt eine vollständige
Zerlegung der ursprünglichen Function in Factoren der bezeichneten Art hervor-
hervorgehen wird. Indessen gewinnt ohne Zweifel jede Beweisführung eine höhere
Vollendung, wenn nachgewiesen wird, dass sie geeignet ist, das Vorhandensein
der sämmtlichen Factoren unmittelbar anschaulich zu machen. Dass der erste
Beweis in diesem Fall ist, habe ich bereits in der gedachten Denkschrift angedeu-
angedeutet (Art. 23), ohne es dort weiter auszuführen: dies soll jetzt ergänzt werden,
und ich benutze zugleich diese Gelegenheit, die Hauptmomente des ganzen Be-
Beweises in einer abgeänderten und, wie ich glaube, eine vergrösserte Klarheit
darbietenden Gestalt zu wiederholen. Was dabei die äussere Einkleidung
des Lehrsatzes selbst betrifft, so war die 1799 gebrauchte, dass die Function
afl-\-Aaft~1-\-Bafl~'2-\-u.. s. w. sich in reelle Factoren erster oder zweiter Ord-
Ordnung zerlegen lässt, damals deshalb gewählt, weil alle Einmischung imaginärer
Grossen vermieden werden sollte. Gegenwärtig, wo der Begriff der complexen
Grossen jedermann geläufig ist, scheint es angemessener, jene Form fahren zu
lassen und den Satz so auszusprechen, dass jene Function sich in n einfache
Factoren zerlegen lasse, wo dann die constanten Theile dieser Factoren nicht eben
reelle Grossen zu sein brauchen, sondern für dieselben auch jede complexen Wer-
the zulässig sein müssen. Bei dieser Einkleidung gewinnt selbst der Satz noch
an Allgemeinheit, weil dann die Beschränkung auf reelle Werthe auch bei den
Coefficienten A, B u. s. w. nicht vorausgesetzt zu werden braucht, vielmehr jed-
jedwede Werthe für dieselben zulässig bleiben.
1.
Wir betrachten demnach die Function der unbestimmten Grosse x
+ u. s. w. + Mx-\-N = X
wo A, B . . . . M, N bestimmte reelle oder imaginäre Coefficienten vorstellen.
DER ALGEBRAISCHEN GLEICHUNGEN, 75
Aus der Elementaralgebra ist der Zusammenhang zwischen den Wurzeln der Glei-
Gleichung X = 0 und den einfachen Factoren von X bekannt. Geschieht nemlich
jener Gleichung durch die Substitution x=p Genüge, so ist x—p einFactor
von X, und gibt es n verschiedene Arten, jener Gleichung Genüge zu leisten,
nemlich durch x = p, x = p\ x = p" u. s. w., so wird das Product (x —p)
(x—p)(x—p").... mit X identisch sein. Unter besondern Umständen kann
aber auch eine Auflösung, wie x=p, in X den Factor (x—pJ, oder (x—p)*
oder irgend eine höhere Potenz bedingen, in welchen Fällen man die Wurzel p
wie zweimal, dreimal u.s.w. vorhanden betrachtet.
Verlangt man also nur den Beweis, dass die Function X gewiss einen ein-
einfachen Factor zulasse, so ist es zureichend, nur das Vorhandensein irgend einer
Wurzel der Gleichung X = 0 nachzuweisen. Soll aber die vollständige Zerleg-
Zerlegbarkeit der Function in einfache Factoren auf Einmal bewiesen werden, so muss
gezeigt werden, dass der Gleichung X = 0 Genüge geleistet werden kann, ent-
entweder durch n ungleiche Werthe von x, oder durch eine zwar geringere Anzahl
ungleicher Auflösungen, wovon aber ein Theil die Charactere der mehrfach gel-
geltenden gleichen Wurzeln dergestalt an sich trägt, dass die Zusammenzählung al-
aller ungleichen und gleichen die Totalsumme = n hervorbringt.
2.
Das ganze Gebiet der complexen Grossen, in welchem die der Gleichung
X = 0 genügenden Werthe von x gesucht werden sollen, ist ein Unendliches
von zwei Dimensionen, indem, wenn ein solcher Werth x= t-\-iu gesetzt wird
(wo t immer die imaginäre Einheit \J—1 bedeutet), für t und u alle reellen
Werthe von — oo bis -f- oo zulässig sind. Wir haben nun zuvörderst aus die-
diesem unendlichen Gebiete ein abgegrenztes endliches auszuscheiden, ausserhalb
dessen gewiss keine Wurzel der bestimmten Gleichung X = 0 liegen kann.
Dies kann auf mehr als Eine Art geschehen: unserm Zweck am meisten gemäss
scheint die folgende zu sein.
Anstatt der Form t-{-iu gebrauche man diese
x = r(cosp-f-*sinp)
wonach zur Umfassung des ganzen unendlichen Gebiets der complexen Grossen 1
r durch alle positiven Werthe von 0 bis -f-oo, und p von 0 bis 360°, oder, was
10*
$6 « - BEITRÄGE <2P& THBOBEE
dasselbe ist, von einem beliebigen Anfangswerthe bis an einen um 360° grössern
Endwerth ausgedehnt werden muss.
Um für r eine Grenze zu, erhalten, über welche hinaus kein Werth mehr
einer Wurzel der Gleichung X = 0 entsprechen kann, setze ich zuvörderst die
Coefficienten der einzelnen Glieder von X in eine ähnliche Form, wie x, nemlich
A = a(cosa-f~*sina)
B = &(cos?)-f-£sint))
C = c(cosy-\-isiny) u.s.w.
wo also a, b, c bestimmte positive Grossen bedeuten sollen, abgesehen davon,
dass auch eine oder die andere darunter = 0 sein kann. Ich betrachte sodann
die Gleichung
^ —V/2.(arw-1 + &^-2 + crw-3+u.s.w.) = 0
welche, wie man leicht sieht, eine positive Wurzel hat, und zwar (Haeeiots Lehr-
Lehrsatz zufolge) nur Eine solche. Es sei R diese Wurzel, wo dann von selbst klar
ist, dass für jeden positiven Werth von r, der grösser ist als R, der Werth von
rn— ^2. (arn'~x-\-brnr~'2-\- cr**~3-j- u. s. w.) positiv sein, und dass dasselbe auch
von der Function
gelten wird, da dieselbe das rafache der erstem Function um
V/2. («r"-1 -f 2&r"-2+ 3crtt~s+ u. s. w.)
also um eine positive Differenz übertrifft.
.3.
Ich behaupte nun, dass die Grosse R geeignet ist, eine solche Grenze für
die Werthe von r, wie im vorhergehenden Artikel gefordert ist, abzugeben. Der
Beweis dieses Satzes ist auf folgende Art zu fuhren. *
Ich setze allgemein X = T-J- i Ut wo selbstredend T und U reelle Grossen
bedeuten, und zwar wird
^osßw — i) p-f.a)-}-$/»-* cos ((w —
-f- c i^~3 cos ((n — 3) p -f- y) + u. s. w.
DEE ALGEBRAISCHEN
»■— 3) p-f-7)-f u. s. w.
Man übersieht leicht, dass wenn fär r irgend ein positiver Werth grösser als M
gewählt wird, T nothwendig dasselbe Zeichen haben wird wie coswp, so oft
dieser Cosinus absolut genommen nicht kleiner ist als fy. Man braucht nemlich
nur T in folgende Form zu setzen
\/^ — u.s.w.
4-[H-cos«p—
±cos((»
+ [1 ±cos((n-d)9+1)]ci*-3
-j- u. s. w.
wo die obern Zeichen für den Fall eines positiven, die untern für den Fall eines
negativen cos n p gelten sollen, und wo der erste Theil des Ausdrucks auf (Jer
rechten Seite positiv ist, in Folge des im vorhergehenden Artikel gegebenen Satzes,
von den folgenden aber wenigstens keiner negativ werden kann. Auf ganz ähn-
ähnliche Weise erhellet (indem man in obiger Formel nur U anstatt T und durch-
gehends Sinus anstatt Cosinus schreibt), dass unter gleicher Voraussetzung in Be-
Beziehung auf r, allemal U dasselbe Zeichen hat wie sinnp, so oft dieser Sinus
absolut genommen nicht kleiner ist als fy. Es hat demnach in allen Fällen we-
wenigstens die eine der beiden Grossen T, U ein voraus bestimmtes positives oder
negatives Zeichen, und es kann folglich für keinen Werth" von p die Function
X == 0 werden. W. Z. B. W.
4.
Um das Verhalten von T und U in Beziehung auf die Zeichen und deren
Wechsel (bei einem bestimmten, JS überschreitenden, Werthe von r) noch mehr
ins Licht zu setzen, lasse man p alle Werthe zwischen zwei um 360° verschie-
verschiedenen Grenzen durchlaufen, wozu jedoch nicht 0 und 360°, sondern, indem zur
Abkürzung
45°
Ü>
n
78 BEITRÄGE ZÜE THEORIE
gesetzt wird, — u> und (8ä — 1)ü> gewählt werden sollen. Den ganzen Zwi-
Zwischenraum theile ich in An gleiche Theile, so dass der erste sich von —u> bis u>,
der zweite von u> bis 3u>, der dritte von 3u> bis 5u> u. s. w. erstreckt. Zuvör-
Zuvörderst hat man auch noch die Werthe der Differentialquotienten ^—, r- in Be-
Betracht zu ziehen, wofür man .hat
(w—l)«^-^^^—l)p-j-a) — (w
(n—Z) crn~3 sin ((n — 3) p -f- y) — u. s. w.
(—Z)crn~scos((n—3)p-f-y)-|-u.s.w.
Man erkennt daraus leicht, durch ähnliche Schlüsse wie im vorhergehenden Ar-
tikel und unter Zuziehung des Satzes am Schlüsse von Art. 2, dass j- immer
das entgegengesetzte Zeichen von sinwp hat, so oft dieser Sinus absolut genom-
genommen nicht kleiner ist als y/-f, dass hingegen ^- immer dasselbe Reichen wie
coswp hat, so oft der absolute Werth dieses Cosinus nicht kleiner ist als \J%.
Hieraus zieht man folgende Schlüsse.
In dem ersten Intervalle, d.i. von p = —u> bis p = -]-«>. ist T stets
positiv, U hingegen für den Anfangs werth negativ, für den End werth positiv,
mithin dazwischen gewiss einmal = 0, und zwar nur einmal, weil in dem gan-
ganzen Intervalle j- positiv ist.
In dem zweiten Intervalle ist U stets positiv, T zu Anfang positiv, am
Ende negativ, dazwischen einmal T = 0 und zwar nur einmal, weil in dem
ganzen Intervalle ^— negativ ist.
In dem dritten Intervalle ist T stets negativ, U einem Zeicljenwechsel un-
unterworfen , so dass einmal U = 0 wird.
Im vierten Intervalle ist U stets negativ, T einmal — 0.
In den folgenden Intervallen wiederholen sich in gleicher Ordnung diese
Verhältnissse, so dass das fünfte dem ersten, das sechste dem zweiten u. s. f.
gleichsteht.
5.
Aus der im vorhergehenden Artikel erörterten Folgeordnung der positiven
und negativen Werthe von T und U, die bei jedem über R hinausgehenden
DER ALGEBRAISCHEN GLEICHUNGEN. f§
Werthe von r Statt findet *), lässt sich nun folgern, dass innerhalb des Gebiets
der kleinern Werthe von r gewisse Kreuzungen in diesen Anordnungen vorhanden
sein müssen, die das Wesen unsers zu beweisenden Lehrsatzes in sich, schüessen.
Ich werde die Beweisführung in einer der Geometrie der Lage entnommenen. Ein-
Einkleidung darstellen, weil jene dadurch die grösste Anschaulichkeit und Einfach-
Einfachheit gewinnt. Im Grunde gehört aber der eigentliche Inhalt der ganzen Argu-
Argumentation einem höhern, von Räumlichem unabhängigen Gebiete der allgemeinen
abstracten Grössenlehre an, dessen Gegenstand die nach der Stetigkeit zusam-
zusammenhängenden Grössencombinationen sind, einem Gebiete, welches zur Zeit noch
wenig angebauet ist, und in welchem man sich auch nicht bewegen kann ohne
eine von räumlichen Bildern entlehnte Sprache.
6.
Das ganze Gebiet der complexen Grossen wird vertreten durch eine unbe-
unbegrenzte Ebene, in welcher jeder Punkt, dessen Coordinaten in Beziehung auf
zwei einander rechtwinklig schneidende Achsen t, u sind, als der complexen
Grosse $ = t+iu entsprechend betrachtet wird: bringt man diese complexe
Grosse in die Form x = r(cosp-|-«sinp), so bedeuten r, p die Polarcoordinaten
des entsprechenden Punkts. Der Inbegriff aller complexen Grossen, für welche
r einerlei bestimmten Werth hat, wird demnach durch einen Kreis repräsentirt,
dessen Halbmesser dieser Werth, und dessen Mittelpunkt der Anfangspunkt der
Coordinaten ist. Denjenigen dieser Kreise, für welchen r um eine nach Belie-
Belieben gewählte Differenz grösser als R ist, will ich mit K bezeichnen, und mit
(l), B), C) .... B m) diejenigen Punkte auf demselben, welchen die beziehungs-
beziehungsweise zwischen o> und 3u>, zwischen 5«> und 7u>, zwischen 9o> und ltu> u.s.f.
bis zwischen (8»—3)a> und (8m — l)u> liegenden Werthe von p entsprechen,
für welche nach dem 4. Artikel T = 0 wird. Man bemerke dabei, dass für die
Punkte A), C), E) u.s.w. U positiv, für die Punkte B), D), F) u.s. w. hingegen
negativ sein wird.
*) Es ist leicht zu zeigen, dass auch für den Werth r = R selbst eine gleiche Folgeordnung noch
gültig bleibt, nur mit der Einschränkung, dass dann in ganz speciellea Fällen ein Uebergangswerth von p>
(d. i. ein solcher, für welchen T oder U = 0 wird) mit einer der Grossen — cd, o», 3 o», 5 oj u. s. w. zusam-
zusammenfallen kann, während für alle grösseren Werthe von r jeder Uebergangswerth von p zwischen zweien die-
dieser Grossen Hegen muss. Ich halte mich jedoch dabei nicht auf, da für unsern Zweck zureicht, das Bestehen
jener Folgeordnung> von irgend einem Werthe von r an, nachgewiesen zu haben.
80 BEITRÄGE ZUR THEOEIE
7.
Die Gesammtheit derjenigen Punkte in unserer Ebene, für welche T po-
positiv ist, bildet zusammenhängende Flächentheile, wie schon von selbst erhellet,
wenn man erwägt, dass bei einem stetigen Uebergange von einem Punkte zu ei-
einem andern T sich nach der Stetigkeit ändert. Eben so bilden sämmtliche
Punkte, für welche T negativ wird, zusammenhängende Flächentheile. Zwi-
Zwischen den Flächentheilen der ersten Art und denen der zweiten liegen Punkte, in
welchen T = 0 wird, und nach der Natur der Function T können diese Punkte
nicht auch Flächenstücke, sondern nur Linien bilden, welche einerseits die ei-
einen , andererseits die andern Flächentheile begrenzen.
Der ausserhalb K liegende Raum enthält n Flächen der ersten Art, die mit
eben so vielen der zweiten Art abwechseln, und wovon jede, von einem Stück der
Kreislinie K an, zusammenhängend sich ins Unendliche erstreckt. Zugleich aber
ist klar, dass jedes dieser Flächenstücke sich über die Kreislinie hinaus in den
innerii Raum fortsetzt, und dass in Beziehung auf die weitere Gestaltung folgende
Fälle Statt finden können.
1) Das betreffende von einem Theile von K anfangende Flächenstück en-
endigt sich isolirt innerhalb der Kreisfläche; seine peripherische Begrenzung besteht
dann nur aus zwei zusammenhängenden Stücken, wovon eines ein Bestandtheil
von K ist, das andere innerhalb des Kreisraumes liegt. In der beigefügten Fi-
Figur, welche sich auf eine Gleichung fünften Grades bezieht und wo die Zeichen
von T in den verschiedenen Flächentheilen eingeschrieben sind, finden sich drei
der Flächen mit positivem T in diesem Falle; die eine hat die Grenzlinien 10.1
und 1.11.10; die zweite diese 4.5 und 5.12.4; die dritte 6.7 und 7.13.6.
Flächentheile ähnlicher Art mit negativem T finden sich zwei vor.
2) Das Flächenstück durchsetzt einfach die Kreisfläche dergestalt, dass es
mit einem an einer andern Stelle eintretenden Eine zusammenhängende Fläche
bildet. Die ganze peripherische Begrenzungslinie wird dann aus vier Stücken be-
bestehen , von denen zwei der Kreislinie K angehören, und die beiden andern dem
innern Räume, In unserer Figur findet sich dieser Fall bei dem durch 2.3;
3.0.8; 8.9; 9.11.2 begrenzten Flächenstück.
3) Das Flächenstück spaltet sich im innern Kreisraume einmal oder mehre-
reinale dergestalt, dass es mit noch zweien oder mehrern an andern Stellen ein-
eintretenden eine zusammenhängende Fläche bildet, deren ganze peripherische Be-
DEE ALGEBRAISCHEN GLEICHUNGEN. 81
grenzung dann aus sechs, acht oder mehrern Stücken in gerader Zahl bestehen
wird, die abwechselnd der Kreislinie und dem jnnern Baume angehören. In
unserer Figur tritt dies ein bei einem Flächentheile, dessen. Begrenzung durch
die sechs Stücke 3.4; 4.12.5; 5.6; 6.13.7; 7.8; 8.0.3 gebildet wird, in
welchem aber T negativ ist.
Bei einer vollständigen Aufzählung aller denkbaren Gestaltungen der in den
innern Kreisraum eintretenden Flächentheile würden den angegebenen Fällen
noch anderweitige Modificationen beigefügt werden müssen. Wenn z. B. ein sol-
solcher Flächentheil sich zwar in zwei Aeste spaltet, diese aber im innern Eaume
sich wieder vereinigen, so würde dieser Fall, jenachdem nach der Vereinigung
die Fläche im Innern ihren Abschluss findet, oder (ohne neue Theilung) sich bis
zu einer andern Stelle der Kreislinie fortsetzt, dem ersten oder zweiten Falle des
vorhergehenden Artikels zugerechnet werden können, indem die Gestaltung der
Fläche nur durch das Einschliessen einer nicht zu ihr gehörenden Insel modificirt
sein würde. Uebrigens würde es nicht schwer sein, strenge zu beweisen, dass
bei der besondern Beschaffenheit der Function T Modificationen dieser Art gar
nicht möglich sind: für unsern Zweck ist dies jedoch unnöthig, indem es nur auf
die Folge der Stücke der äussern Begrenzung jedes der in Hede stehenden Flächen-
Flächentheile (d. i. derjenigen, in welchen T positiv ist) ankommt.
Wir haben nemlich schon bemerklich gemacht, dass die Anzahl dieser Stücke
allemal gerade ist (zwei im ersten Falle des vorhergehenden Artikels, vier im
zweiten, sechs oder mehrere im dritten), wovon wechselsweise eines der Kreislinie
ÜT, eines dem innern Haume angehört. Ferner ist klar, dass wenn jene äussere
Begrenzungslinie immer in einerlei Sinn durchlaufen wird, wozu hier derjenige
gewälzt werden soll, in welchem die Bezifrungen der Punkte von K wachsen
(also, Beispiels halber in unserer Figur so, dass die Fläche immer rechts von der
Begrenzungslinie liegt), der Anfangspunkt und der Endpunkt eines der Kreislinie
angehörenden Stücks beziehungsweise durch eine gerade und die um eine Einheit
grössere ungerade Zahl bezeichnet sein wird, mithin der Anfangspunkt und der
Endpunkt jedes den innern Eaum durchlaufenden Stücks allemal beziehungsweise
durch eine ungerade und eine gerade Zahl.
Es steht also fest, dass von den n an einem mit einer ungeraden Zahl "be-
11
82 BEITRÄGE ZÜB THEORIE
zeichneten Punkte von K in den innern Raum eintretenden Linien, in denen
überall T= 0 ist, eine jede auf eine ganz bestimmte Art*) diesen Baum zusam-
zusammenhängend durchläuft, bis sie an einer andern mit einer geraden Zahl bezeich-
bezeichneten Stelle wieder austritt. Da nun, wie schon oben (Schluss des 6. Art.) bemerkt
ist, in ihrem Anfangspunkte den Werth von U positiv, am Endpunkte negativ
ist, so muss wegen der Stetigkeit der Werthänderung nothwendig in einem Zwi-
Zwischenpunkte V — 0 werden. Dieser Punkt repräsentirt dann eine Wurzel der
Gleichung X = 0; und da die Anzahl solcher Linien = n ist, so ergeben sich
auf diese Weise allemal n Wurzeln jener Gleichung.
9.
Wenn die gedachten Linien durch den Kreisraum gehen ohne ein Zusam-
Zusammentreffen mit einander, so ist klar, dass die so erhaltenen n Wurzeln nothwen-
nothwendig ungleich sind. Ein solches freies Durchgehen findet sich in unsrer Figur bei
den Linien von 3 nach 8, von 5 nach 4 und von 7 nach 6, und es gehören
dazu die durch die* Punkte 0, 12, 13 repräsentirten Wurzeln. Wenn hingegen
zwei solcher Linien, oder mehrere, einen Punkt gemeinschaftlich haben, so ist
zwar darum noch nicht nothwendig, aber doch möglich, dass dieser Punkt zu-
zugleich derjenige ist, in welchem U= 0 wird, in welchem Falle dann zwei oder
mehrere Wurzeln in Eine zusammenfallen, oder, wie es gewöhnlich ausgedrückt
wird, unter sich gleich sein werden. In unsrer Figur treffen die Linien 1.10
und 9.2 in dem Punkte 11 zusammen, und in demselben wird zugleich U= 0 ;
die Gleichung hat also ausser den schon aufgeführten drei ungleichen noch zwei
gleiche Wurzeln.
10.
Es bleibt nur noch übrig, nachzuweisen, dass wenn der eine Wurzel — p
*) Dass sie allemal einen ganz bestimmten Lauf hat, beruhet darauf, dass sie einen Theil der äussern
Abgrenzung einer Fläche, für welche T ein bestimmtes Zeichen hat, ausmachen soll: ich habe das positive
Zeichen gewählt, was an sich ganz willkürlich ist. So verstanden setzt sich z. B. die in l eintretende Linie
durch 11 nach 10 fort: als Theil der Grenzlinie einer Fläche, worin T negativ ist, würde die Linie 1.11
nach 2 fortgesetzt werden müssen. Spricht man hingegen nur von einer Linie worin T = o ist, ohne sie als
Theil der Begrenzung einer bestimmten Fläche zu betrachten, so würde eher 11.9 als natürliche Fortsetzung
von i.ii gelten können. Der hier gewählte Gesichtspunkt unterscheidet mein gegenwärtiges Verfahren von
dem von 17 99, und trägt wesentlich zur Vereinfachung der Beweisführung bei.
DEB ALGEBRAISCHEN GLEICEÜNGEN. &S
repräsentirende Punkt P in zweien oder mehrern Linien T = 0 zugleich liegt,
das Quadrat von x—p oder die der Anzahl jener concurrirenden Linien entspre-
entsprechende höhere Potenz in X als Factor enthalten sein wird. Der Beweis davon
beruhet auf folgenden Sätzen.
Man führe anstatt der unbestimmten Grosse x eine andere z ein. indem
man x = z-\-p setzt. Es gehe durch diese Substitution X in Z über, wo also
Z eine Function von z von gleicher Ordnung wie X von x sein wird, deren con-
stantes Glied aber fehlt. Indem man dieselbe nach aufsteigenden Potenzen von
z ordnet, sei das niedrigste nicht verschwindende Glied
= Kzm und Z =
wo £ die Form Lz-\-L'zz-\-L"#-\-u.s.Yr.-\-^s?>r*n haben wird,- endlich setze
man
z = s(cos<|>-f-tsin<!>)
Der reelle und der imaginäre Bestandtheil von z drücken die Lage jedes
unbestimmten Punkts der Ebene als rechtwinklige Coordinaten, und die Grossen
s, <j> die Polarcoordinaten ganz eben so relativ gegen den Punkt P aus, wie die
Bestandtheile von x, und die Grossen r, cp die relative Lage gegen den ursprüng-
ursprünglichen Anfangspunkt bezeichnen. Die Verbindung eines bestimmten Werthes
von s mit allen Werthen von <j> in einer Ausdehnung von 360° stellt also die
Punkte einer Kreislinie dar, die ihren Mittelpunkt in P hat und deren Halbmes-
Halbmesser = s ist.
Setzt man nun K = ^(cosx-f-^sinx), und folglich
Kzm = ksm (cos (mty -f- x) 4- i sin (m <j>+*))
so wird für ein unendlich kleines s die Grosse £, die wenigstens von derselben
Ordnung ist wie s, neben der 1 vernachlässigt, und mithin gesetzt werden dürfen
woraus erhellet, dass während ^ um 360° wächst, das Zeichen von T in m
Stücken der Kreisperipherie positiv, und in eben so vielen mit jenen abwech-
abwechselnden negativ ist, oder dass T in 2m Punkten =0 wird, nemlich für
6 = - (x — 9 0°), - (x+9 0°), ^ (x + 27 0°) u. s. w. Es gehen demnach von P zu-
&£ BEEFBÄGE ZUR THEORIE
sammen 2 m Linien aus, in denen T = 0 ist, oder wenn man sie paarweise so
verbindet, dass jede, wo, bei wachsendem ty, das Zeichen aus — in -j- über-
übergeht, zusammen mit der nächstfolgenden, wo der entgegengesetzte Uebergang
Statt findet, wie die Begrenzungslinie eines Flächentheils mit positivem T be-
betrachtet wird, so treffen in P überhaupt m dergleichen Begrenzungslinien zu-
zusammen.
Von der andern Seite ist klar, dass so wie Z unbestimmt durch zm und
durch keine höhere Potenz von z theilbarist, X den Factor (x—p)m, aber keine
höhere Potenz von x—p enthalten wird. Es ist also allemal, wenn p irgend
eine Wurzel der Gleichung X = 0 bedeutet, der Exponent der höchsten Po-
Potenz von x—p, durch welche X theilbar ist, der Anzahl der in P zusammen-
zusammentreffenden Begrenzungslinien für Flächen mit positivem T gleich, oder was das-
dasselbe ist, der Anzahl solcher an P zusammentreffender Flächen.
Uebrigens ist es leicht, der Beweisführung eine von Einmischung unendlich
kleiner Grossen ganz unabhängige Einkleidung zu geben, und zwar ganz analog
der Schlussreihe in den Art. 3 und 4. Es lässt sich nemlich einWerth von s nach-
nachweisen , für welchen, so wie für jeden kleinern, der ganze Cyklus aller Werthe
von cj> dieselbe abwechselnde Folge von m Stücken mit positivem T und eben-
sovielen mit negativem darbietet. Diese Eigenschaft hat die positive Wurzel der
Gleichung
0 =m\Ji — (m-\-l)ls—(m-\-2)rss — (m^-Z)rrss— u.s. w.
wo l, l\ V u.s.w. die positiven Quadratwurzeln aus den Normen diir c©Ba|>lexen
Grossen L, U, L" u. s.w. bedeuten, oder wo
L = l (cos X -{- i sin X)
ü= r(cosX'-HsinX')
L"= Z"(cos \"-\-isin X") u. s. w.
gesetzt ist. Ich glaube jedoch, die sehr leichte Entwicklung dieses Satzes hier
übergehen zu können.
Schliesslich mag noch bemerkt werden, dass bei der Beweisfiihrung in der
Abhandlung von 1799 die Betrachtung zweier Systeme von Linien erforderlich
war, das eine die Linien wo T= 0, das andere diejenigen wo £7= 0* enthal-
enthaltend , während in unserm jetzigen Verfahren die Betrachtung Eines Systems aus-
DER AMiEBBAISCHEKT GLEICHUNGEN. 8S
gereicht hat; ich habe dazu das System der Begrenzungslinien der FlaehentheHe
mit positivem T gewählt, es hätte aber eben so gut zu demselben Zweck,die Be-
Betrachtung der Begrenzungslinien der Flächen mit positivem, (oder negativem). U
dienen können.
ZWEITE ABTHEILÜNG.
11.
. Zur numerischen Bestimmung der Wurzeln solcher algebraischen Gleichun-
Gleichungen , die nur aus drei Gliedern bestehen, lassen sich verschiedene Methoden an-
anwenden, die hier einer Eleganz un,d Bequemlichkeit fähig werden, gegen welche
die mühsamen bei Gleichungen von weniger einfacher Gestalt unvermeidlichen
Operationen weit zurückstehen. Solche Methoden verdienen also wohl eine be-
besondere Darstellung, zumal da Gleichungen von jener Form häufig genug vor-
vorkommen.
Es gilt dies zunächst von der Entwicklung der Wurzeln in unendliche Rei-
Reihen. In der That lässt sich, jede, gleichviel ob reelle oder imaginäre, Wurzel ei-
einer Gleichung mit drei Gliedern durch eine convergente Reihe von einfachem
Fortschreitungsgesetz ausdrücken. Ich werde jedoch diese Auflösungsart aus meh-
mehrern Gründen von meiner gegenwärtigen Betrachtung ganz ausschliessen, und be-
bemerke hier nur, dass der Grad der Convergenz von dem gegenseitigen Verhalten
der Coefficienten abhängig, dass sie desto langsamer ist, je näher dies Verhalten
demjenigen kommt,, bei welchem die Gleichung zwei gleiche Wurzeln hat, und
dass in diesem Grenzfalle selbst sie schwächer ist, als bei irgendwelcher fallenden
geometrischen Progression. So bemerkenswerth auch diese Reihen in allgemeiner
theoretischer Rücksicht sind, so wird man doch, abgesehen von dem Falle, wo
ihre Convergenz eine sehr schnelle wird, in praktischer Beziehung immer den in-
directen Methoden den Vorzug geben, welche in den nachfolgenden Artikeln ent-
entwickelt werden sollen.
12.
Zur Auffindung der reellen Wurzeln benutze ich meine im Jahre 1810 zuerst
gedruckte Hülfstafel für Logarithmen von Summen und Differenzen, oder, wo
eine grössere Genauigkeit verlangt wird, als Logarithmen, mit fünf Zifern geben
8ß BEITRÄGE ZUR THEORIE
können, die ähnliche aber erweiterte Tafel von Matthiessen. Ich habe ein paar
specielle Anwendungen dieses Verfahrens schon früher bekannt gemacht, nemlich
zur Auflösung der quadratischen Gleichungen bei der 1840 erschienenen zwan-
zwanzigsten Ausgabe von Vega's logarithmischem Handbuch, und zur Auflösung der
cubischen Gleichung; welche bei der parabolischen Bewegung zur Bestimmung
der wahren Anomalie dient, in Nro. 474 der Astronomischen Nachrichten. An
letzterm Orte ist auch bereits die allgemeine Anwendbarkeit des Verfahrens auf
alle algebraischen Gleichungen mit drei Gliedern bemerklich gemacht. Obgleich
nun die Ausführung dieses ganz elementarischen Gegenstandes gar keine "Schwie-
"Schwierigkeiten hat, so wird man doch, bei der ziemlich grossen Mannigfaltigkeit der
Fälle, einer übersichtlichen Sonderung derselben, und der Zusammenstellung der
gebrauchfertigen Vorschriften ein paar Seiten gern eingeräumt sehen.
Anstatt jener logarithmischen Hülfstafeln kann man sich auch der gewöhn-
gewöhnlichen logarithmisch-trigonometrischen Tafeln bedienen: allein theils sind jene
im Allgemeinen für den gegenwärtigen Zweck von bequemerm Gebrauch, theils
gewähren sie doppelt so grosse Genauigkeit als die letztern. Ich würde daher die
Benutzung der trigonometrischen Tafeln für das in Rede stehende Geschäft auf
den seltenen Fall beschränken, wo man die durch siebenzifrige Logarithmen er-
erreichbare Genauigkeit noch zu überschreiten wünscht und dazu die bekannten
zehnzifrigen Logarithmen in Vlacq's oder Vega's Thesaurus verwenden kann.
Uebrigens sind, wenn man sich der Hülfslogarithmen bedient, doppelt so viele
Fälle zu unterscheiden, als wenn die trigonometrischen Logarithmen gebraucht
werden. Als ein Nachtheil darf dies jedoch nicht angesehen werden: denn wenn
einmal die vollständige allgemeine Classification vorliegt, ist es leicht, jedem con-
creten Falle sein Fach anzuweisen, und das eigentliche indirecte Geschäft ist so
viel leichter auszuführen, wenn das ganze Fach nur den halben Umfang hat. Aber
gerade aus jenem Grunde ist für die Auflösung durch trigonometrische Logarith-
Logarithmen die allgemeine Classification kürzer und bequemer darzustellen, und ich werde
sie daher vorausschicken, da sodann die Classification für die andere Auflösungs-
Auflösungsform sich daraus von selbst ergibt.
13.
Die Ausführung der Methode wird, unmittelbar, nur auf Bestimmung der
positiven Wurzeln einer vorgegebenen Gleichung gerichtet; die negativen ergeben
DER ALGEBRAISCHEN GLEICHUNGEN. Bf
sich, indem man dasselbe Verfahren auf diejenige Gleichung anwendet, welche
aus jener durch Einfuhrung der der ursprünglichen Unbekannten entgegengesetz-
entgegengesetzten Grosse entsteht.
Die Gleichung setze ich in die Form
= 0
wo m, n, e, f gegebene positive Grossen bedeuten. Diese Form umfasst eigent-
eigentlich, nach Verschiedenheit der Combination der Zeichen, vier verschiedene Fälle,
wovon aber der erste, wo beidemal die oberen Zeichen gewählt werden, ausfallt,
da offenbar die Gleichung
= 0
keine positive Wurzel haben kann. Uebrigens ist verstattet, vorauszusetzen, dass
m und n (worunter ganze Zahlen verstanden werden, obwohl die Anwendbarkeit
der Methode an sich davon unabhängig ist) keinen gemeinschaftlichen Divisor ha-
haben, indem auf diesen Fall jeder andere leicht zurückzuführen ist. Endlich werde
ich zur Abkürzung schreiben
Erste Form.
Indem man einen immer im ersten Quadranten zu nehmenden Winkel 6
einführt, so dass
j = sin 62, -j- = cos 62
wird, also (I)
=/sin62, afn=f-^, oen = etang6s
findet sich durch Elimination von x die Gleichung
aus welcher 6 bestimmt werden muss. Man erkennt leicht, dass der zweite Theü
dieser Gleichung als Function einer unbestimmten Grosse 6 betrachtet, von 0
88 BEITRÄGE ZUR THEORIE
bis oo wächst, während 6 alle Werthe von 0 bis 90° durchläuft, und dass es
also einen, und nur einen Werth von 6 gibt, der jener Gleichung Genüge leistet.
Nachdem derselbe gefunden ist, erhält man o? aus einer der Formeln I. Man be-
bemerke, dass 6 = 45° wird für X = 2W, und dass folglich 6 im ersten Octanten
zu suchen ist wenn X kleiner, im zweiten wenn X grösser ist als 2W.
Zweite Form.
Man wird hier setzen
faT*™ == sinö2, ex"" = cos Ö2
oder (I)
/ n e „m /cotangG'
"Ö* X ^Ö1 X ~
wonach also 6 aus der Gleichung
, sinO*"
zu bestimmen sein wird, was auf eine und nur auf eine Art geschehen kann: der
Werth von x findet sich sodann durch eine der Gleichungen I. Im ersten oder
zweiten Octanten liegt 6, jenachdem \ kleiner oder grösser ist als 2m.
Dritte Form.
Hier wird man setzen
- = sinö , -— = cos fr
e e
e
oder (i;
von welchen Formeln eine zur Bestimmung von x dienen wird, sobald der Werth
von 6 gefunden ist. Dieser ergibt sich durch Auflösung der Gleichung
Da das auf der rechten Seite stehende Glied dieser Gleichung, als Function einer
unbestimmten Grosse 6 betrachtet, sowohl für 6 = 0 als für 6 = 90° verschwin-
verschwindet, so muss dazwischen ein grosster Werth liegen, und da das Differential des
DEE ALGEBRAISCHEN GLEICHUNGEN. 80
Logarithmen dieser Function = B m cotg 6 — 2 n tang 6) d 6 ist, so findet der grösste
Werth Statt für 6 = 6#, wenn man \J— = tang 6* setzt. Es wird demnach jene
Function von 0 bis zu ihrem grössten Werthe, welcher offenbar
(m-
ist, zunehmen, und von da bis 0 abnehmen, während 6 von 0 zu b* und von
da bis 90° zunimmt. Der Maximumwerth ist daher jedenfalls grösser als der
Werth für 6 = 45°, d. i. grösser als ^^, den Fall ausgenommen, wo m = n,
und also -^-n selbst der Maximumwerth ist.
Man schliesst hieraus, dass jenachdem X grösser ist als
oder kleiner, der Gleichung X = cos62ttsin62jn gar nicht oder durch zwei ver-
verschiedene Werthe von 6 wird Genüge geleistet werden können. Im erstem Falle
hat die Gleichung xm'^ — exm-{-f= 0 gar keine (positive) Wurzel, im andern
zwei. In dem speciellen Falle, wo
ist, fallen beide Auflösungen zusammen, und die Gleichung hat zwei gleiche Wur-
Wurzeln, wofür man nach Gefallen eine der drei Formeln benutzen kann
Was übrigens in dem Falle, wo zwei Auflösungen wirklich vorhanden sind,
die Octanten betrifft, in welche die Werthe von 6 fallen, so sieht man leicht,
dass wenn X grösser ist als ^^, beide Werthe von 6 mit 6# in demselben Oc-
Octanten liegen, nemlich im ersten oder zweiten, jenachdem m kleiner oder grösser
ist als n: ist hingegen X kleiner als ^^, so wird der eine Werth von 6 im er-
ersten, der andere im zweiten Octanten zu suchen sein. In dem speciellen Falle,
wo X = y^, ist 45° selbst der eine Werth von 6, und der andere liegt in dem-
demselben Octanten wie 6#.
Es mag noch die aus dieser Zergliederung aller drei Formen sich leicht erge-
ergebende Folge bemerkt werden, dass unsere Gleichung (insofern wir annehmen, dass
m und n keinen gemeinschaftlichen Divisor haben) nicht mehr als drei reelle
Wurzeln haben kann, was auch aus andern Gründen bekannt ist.
90
züb theobie
14.
Die vorstehenden Vorschriften werden nun leicht in diejenigen umgeschmol-
umgeschmolzen , die der Anwendung der Hülfslogarithmen entsprechen, da diese A = log«.
B = log i, C = log c, betrachtet werden können wie die Logarithmen der Qua-
Quadrate der Tangenten, Cosecanten und Secanten der von 45° bis 90° zunehmen-
zunehmenden, oder, was dasselbe ist, wie die Logarithmen der Quadrate der Cotangenten,
Secanten und Cosecanten der von 45° bis 0 abnehmenden Winkel, also
a = tangö2, | = sinö3, - = cosÖ2
für die Werthe von 6 im zweiten Octanten, oder
- = tangö2, - = sinö2, | = cosö2
a ö c b
für die Werthe von 0 im ersten Octanten.
Die vollständigen Vorschriften vereinige ich in folgendem Schema, wo eben
so wie oben
gesetzt ist.
em+n
Erste Form.
Erster Fall. X>2W
= 0
■\ m-i-nin m n ^
—— "t~. oo ^^ , oc ^^^ ect
b * ec
Zweiter Fall X<2W
K — &
cn
fom+n *■
eh
Zweite Form.
—ear—f= 0
Erster Fall X>2'
Zweiter Fall X< 2m
DEE ALGEBRAISCHEN GLEICHUNGEN. 91
„n jtn v
— ac—-w
-— ~~j <*> —— ^c
7* * «+« »
Dritte Form.
— 0
Gar keine Auflösung.
Zweiter Fall T = v m }n
Zwei gleiche Wurzeln, zu deren Bestimmung eine der Gleichungen
„w+n fm ^n f(m +») ^ em
du , dU • üb — ~—
n ' en m-\-n
dient.
Dritter Fall y grösser als ^»^»— aber nicht grösser als 2m+", und zugleich
m grösser als n.
Zwei Wurzeln, für welche
Vierter Fall Für y dieselben Grenzen, wie im dritten Fall, aber m kleiner
als n.
Zwei Wurzeln, für welche
= c-ir = V'c
n
m
i
^w+n __ / ^m — /* „n — *_
. y grösser als 2m+n.
Zwei Wurzeln, wovon die eine durch die Formeln des dritten Falles, die
andere durch die des vierten bestimmt wird.
12*
BEITRÄGE ZUR THEORIE
Es mag noch bemerkt werden, dass im dritten Falle der Werth von a, wel-
welcher der einen Wurzel entspricht, kleiner als —, der zur andern Wurzel gehö-
gehörende grösser als ~ ist; im. vierten Falle verhalten sich die beiden Werthe von
a auf ähnliche Weise gegen —.
15.
Ueber die Anwendung dieser Vorschriften ist noch folgendes beizufügen.
Zur Bestimmung jeder Wurzel sind zwei Operationen auszuführen: zuerst
aus X den dazu gehörenden Werth von a (und damit zugleich den von b oder c)
abzuleiten; sodann, aus diesem.den Werth von x zu berechnen. Für jede die-
dieser beiden Operationen kann man unter drei Formeln wählen; ich ziehe in den
meisten Fällen die zuerst angesetzten vor. Bei allen diesen Rechnungen hat man
es gar nicht mit den Grossen X, a, b, c selbst, sondern nur mit ihren Logarith-
Logarithmen zu thun, Die erste Operation ist eine indirecte, und beruhet demnach in der
Regel auf mehrern stufenweise fortschreitenden Annäherungen, wobei es bequem
gefunden werden wird, zu Anfang Tafeln mit einer geringern Anzahl von Zifern
zu gebrauchen. Matthiessens Tafel hat bekanntlich sieben Decimalen: die mei-
meinige fünf; Enckb und Ursin haben sie mit vier Zifern abdrucken lassen, und wenn
man beim Anfange der Arbeit noch gar keine Kenntniss einer ersten groben An-
Annäherung mitbringt, wird man es vielleicht vortheilhaft finden, einen noch kür-
kürzern Extract der Tafeln mit nur drei Zifern auf einem besondern Blättchen vor
sich zu haben, etwa so:
A
0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1,0
B
0,301
0,254
0,212
0,176
0,146
0,119
0,097
0,079
0,064
0,051
0,041
A
1,0
1,1
1,2
1,3
1,4
1,5
1,6
1,7
1,8
1,9
2,0
B
0,041
0,033
0,027
0,021
0,017
0,014
0,011
0,009
0,007
0,005
0,004
A
2,0
2,1
2,2
2,3
2,4
2,5
2,9
3,0
B
0,004
0,003
0,003
0,002
0,002
0,001
0,001
0,000
DER ALGEBRAISCHEN GLEICHUNGEN.
16.
Als Beispiel mag die Gleichung
dienen, wo
6750
823543 '
480 = 0
y= 2,0863825
wird. Die Gleichung hat die erste Form, mithin eine positive Wurzel, und ge-
gehört, da X kleiner ist als 8, zum zweiten Fall. Die erste Operation besteht darin,
dass der Gleichung logy = 4A—dB Genüge geschehe, also, wenn man die
Rechnung mit drei Decimalen anfangt, dieser
2,086 = AA — dB
Ein flüchtiger Blick auf obige Tafel zeigt schon, dass A zwischen 0,5 und 0,6
zu suchen sei. Es wird nemlich
0,5
0,6
AA—dB
1,643
2,109
Fehler
— 0,443
+ 0,023
woraus sich auf einen genauem Werth 0,595 schliessen lässt. Eine neue Rech-
Rechnung nach den Tafeln mit fünf Decimalen, wo also logy =2,08638 zu setzen
ist, gibt
AA — dB
Fehler
0,595 2,08501 —0,00137
0,596 2,08961 +0,00323
woraus der noch genauere Werth 0,5953 erkannt wird. Endlich für sieben De-
Decimalen hat man
0,5952
0,5953
AA— dB
2,0859279
2,0863885
Fehler
— 0,0004546
+ 0,0000060
Zu dem Werthe A= 0,5953 muss also noch die Correction
60
4606
Einheiten
der vierten Decimale hinzukommen, in welcher Form ich sie beibehalte, da es,
wenn zur Bestimmung von x die erste Formel
BEITRAGE ZÜE TKEOEIE
X
c
gebraucht werden soll, nur darauf ankommt, den entsprechenden Werth von C
zu finden. Diesen erhält man, indem man zu dem neben A = 0,5953 stehen-
stehenden Werthe 0=0,6935705 die Correction — ^X798 hinzufügt, letztere
wie Einheiten der siebenten Decimale betrachtet, also
C
log/
0,6935695
2,6812412
7log<z? = 1,9876717
0,2839531
1,9228841
log<2?
x
Zur Auffindung der negativen Wurzeln wird man x == —*y schreiben und
die positiven Wurzeln der Gleichung
/—28/+480 = 0
aufsuchen. Diese gehört zur dritten Form, und da -=- = -~
grösser ist als
aber kleiner als 27= 128, zugleich auch m grösser ist als n, so
gilt der dritte Fall, oder es finden zwei Wurzeln Statt, zu deren Ausmittlung
der Gleichung
2,0863825
3J.+ 7J5
genügt werden muss. Aus der Schlussbemerkung des 14. Art. weiss man, dass
der eine Werth von A kleiner, der andere grösser sein muss als log|- = 0,12494.
Auch ergeben sich die Grenzen der Werthe von A sofort aus der obigen Tafel
mit dreizifrigen Logarithmen, nach welchen man erhält:
A
0,0
0,1
0,2
0,3
3J.-+-7J5
2,107
2,078
2,084
2,132
Fehler
4-0,021
— 0,008
— 0.002
4-0,046
Will man zur nähern Bestimmung zuerst vierzifrige Logarithmen gebrauchen, so
hat man zunächst für die erste Auflösung
DEE ALGEBRAISCHEN GLEICHUNGEN.
95
A
0,05
0,06
3J.+ 7J5
2,0869
2,0347
Fehler
+ 0,0005
— 0,0017
Sodann ergeben die fünfzifrigen Tafeln
Endlich
Hienach
0,052
0,053
die siebenzifrigen
0,0529
0,0530
wird
2,08667
2,08638
2,0863943
2,0863660
+ 0,00029
0
+ 0,0000118
— 0,0000165
A = 0,0529417
log/= 2,6812412
7logy = 2,7 341829
logy = 0,390597 6
—yz=x= — 2,4580892
Für die zweite Auflösung steht die Rechnung, auf ähnliche Weise geführt, fol-
gendermaassen:
A
0,19
0,20
3J.+ 7J5
2,0843
2,0868
Fehler
— 0,0021
+ 0,0004
0,197
0,198
0,1975
0,1976
2,08627
2,08654
2,0863805
2,0864082
— 0,00011
+ 0,00016
— 0,0000020
+ 0,0000257
A = 0,1975072
log/= 2.6812412
7logy = 2,8787484
logy = 0,4112498
x = —2,5778036
96 BEBPSÄGE ZÜE THEORIE
Die Gleichung, welche uns hier als Beispiel gedient hat, ist absichtlich so
gewählt, dass zwei ihrer Wurzeln wenig verschieden sind. In einem solchen
Falle sind, wie schon oben im Art. 11 bemerkt ist, die Reihen wegen ihrer sehr
langsamen Convergenz wenig brauchbar: auch bei der indirecten Auflösung ist
davon wenigstens eine schwache Analogie erkennbar, indem das Fortschreiten der
successiven Annäherungen bei den beiden negativen Wurzeln (welche eben die
wenig ungleichen sind) etwas träger ist, als bei der positiven. Ein wesentlicher
Unterschied ist aber der, dass die sehr langsame Convergenz der Reihen für sämmt-
liche Wurzeln eintritt, während bei dem indirecten Verfahren die, auch nur in
geringem Grade fühlbare, langsamere Annäherung lediglich bei den zwei wenig
verschiedenen Wurzeln vorkommt.
17.
Ganz verschieden von dem in den vorhergehenden Artikeln gelehrten Ver-
Verfahren ist dasjenige, welches zur Bestimmung der imaginären Wurzeln angewandt
werden muss. Im Allgemeinen ist die Bestimmung der imaginären Wurzeln auf
indirectem Wege deswegen weit schwieriger, als die der reellen, weil jene aus
einem unendlichen Gebiet von zwei Dimensionen herausgesucht werden müssen,
diese nur aus einem Unendlichen von Einer Dimension, und gerade darum ver-
verdient ein sehr umfassender besonderer Fall, wo man jene Schwierigkeit umgehen
und die Frage in dasselbe Gebiet versetzen kann, zu welchem die Aufsuchung
der reellen Wurzeln gehört, eine eigne Ausführung. Einen solchen Fall bieten
die Gleichungen mit drei Gliedern dar.
Da die Methode mit gleicher Leichtigkeit angewandt werden kann, die Coef-
ficienten der Gleichung mögen reell oder imaginär sein, so lege ich sofort die all-
allgemeine Form der Gleichung zum Grunde
X = <2?"*+n -f- e (cos g -f-1 sin g) xm -f-/(cos cp +1 sin cp) = 0
wo e und f positive Grossen bedeuten: für einen reellen, positiven oder negati-
negativen , Coefficienten ist dann der betreifende Winkel (g oder cp) entweder 0 oder
180°. Die Voraussetzung, dass m und n keinen gemeinschaftlichen Divisor ha-
haben , wird ohne Beeinträchtigung der Allgemeinheit auch hier beibehalten blei-
bleiben können. Eine der Gleichung Genüge leistende imaginäre Wurzel x = t-j-iu
setzt man in die Form »*(cos p -f-isin p), wobei es für unsern gegenwärtigen Zweck
DER ALGEBRAISCHEN GLE2CHÜNGEN. §7
vorteilhafter ist, die sonst gewöhnliche Bedingung, dass r positiv sein soll, hier
nicht zu machen, sondern anstatt derselben die, dass p immer zwischen den Gren-
Grenzen 0 und 180° genommen werden soll. In dem Fall, wo die Coefficienten der
Gleichung beide reell sind, kann man den Umfang der Werthe von p noch wei-
weiter auf die Hälfte verengen: denn da bekanntlich von den imaginären Wurzeln
einer solchen Gleichung je zwei zusammengehören, wie t-\-iu und t—iu, so
wird offenbar für die eine Wurzel jedes Paars der Werth von p zwischen 0 und
9 0° fallen, und man braucht durch das indirecte Verfahren nur diese zu bestim-
bestimmen, indem daraus die andere von selbst folgt durch Vertauschung von p mit
180° — p und von r mit —r.
18.
Das Wesen der Methode besteht in der Aufstellung einer Gleichung, welche
bloss p ohne r enthält. Um dazu zu gelangen, setze man die Gleichung X = 0
durch Division mit ihrem ersten Gliede in die Form
1 -f- e (cos g -f-1 sin g) x~n -f-/(cos cp -f- i sin cp) x~m~n = 0
oder
1 -f-er~w(cos(wp—g)—t sin(rcp—e))-{-fr~m~n(co$[(m-}-n)p—cp]—i sm[(m-\-n)p—<p])= 0
Da nun hier die imaginären Theile einander aufheben müssen, so hat man (I)
e sin (n p — s)
Auf ähnliche Art erhält man, wenn die Gleichung X = 0 mit ihrem zweiten
oder dritten Gliede dividirt, und erwägt, dass in beiden Fällen die imaginären
Theile der neuen Gleichungen einander aufheben müssen, die Gleichungen
/sin(wtp + e —<p)
sin (w p — e)
sin((»i + n)a—a
Man sieht, dass jede der drei Gleichungen (I) auch schon aus der Verbindung der
beiden andern abgeleitet werden kann. Eliminirt man aber r aus Verbindung
zweier r so erhält man (II)
13
98 BEHR&iGE Zim TBEOBm
? + s—<p)OTsin(wp — e)"
wo zur Abkürzung (eben so wie oben)
/ \
em+n — *■
gesetzt ist. Aus dieser Gleichung hat man die verschiedenen Werthe von p zu
bestimmen; den Werth von r, welcher jedem Werthe von p entspricht, findet
man sodann aus einer der Gleichungen (I), am besten aus der zweiten, rücksicht-
rücksichtlich der absoluten Grosse, wobei jedoch in dem Falle, wo m-\-n gerade ist, noch
eine der beiden andern Gleichungen zur Entscheidung des Zeichens hinzugezogen
werden muss.
19.
Die Auflösung der Gleichung II auf indirectem Wege wird man immer mit
Leichtigkeit beschaffen können, wozu noch die Berücksichtigung der folgenden
Bemerkungen beitragen wird.
1) Die Werthe von p liegen zwischen 0 und 180°; in dem Falle, wo die
Coe'fficienten der vorgegebenen Gleichung reell sind, braucht man nur die halbe
Anzahl, nemlich die zwischen 0 und 90° liegenden, einzeln aufzusuchen.
2) In dem einen wie in dem andern Falle wird man zuerst das betreifende
Intervall in die verschiedenen Unterabtheilungen scheiden, die sich durch die
Zeichenabwechslungen in den Werthen der auf der rechten Seite der Gleichung
II stehenden Function von p bilden. Die Uebergangswerthe von p können of-
offenbar nur solche sein, wo einer der Winkel «wp—(—s — <p, #p — e, (m-\-n)p — <p
durch 180° theilbar, und also jene Function selbst entweder 0 oder unendlich
wird. Von jenen Unterabtheilungen bleiben dann diejenigen, in welchen der
Werth der Function negativ wird, schon von selbst aus der weitern Untersuchung
ausgeschlossen.
3) Falls man nicht schon auf andern Wegen genäherte Werthe von p er-
erlangen kann, wird man sich das indirecte Durchsuchen der geeigneten Intervalle
dadurch sehr erleichtern, dass man auf ähnliche Weise, wie aus den Beispielen
des 16. Artikels zu. ersehen ist, die ersten Versuche nach abgekürzten Tafeln mit
wenigen Zifern ausführt, und in manchen Fällen möchte man wohl bequem fin-
»ER ALGEBRAISCHEN GLEICHUNGEN. 9®
den, zuerst nur die Sinuslogarithmen mit drei Zifern auf einem Blättchen- etwa
von Grad zu Grad verzeichnet zu diesem Zweck zu verwenden.
20.
Zu weiterer Erläuterung mag die Berechnung der imaginären Wurzeln der
oben behandelten Gleichung
B?7-f-28<2?4 —480 = 0
als Beispiel dienen. Nach der Bezeichnung des Art. 17 haben wir hier zuvörderst,
wie oben, m = 4, n = 3, e = 28, /= 480, und sodann weiter s = 0, cp = 180°.
Die Formeln I des Art. 18 werden demnach
4 480 sin 7 p
2 8 sin 3 p
7 480sin 4p
sin 3 p
und die Formel II
3 28 sin 4 p
sin 7 p
1 823543 sin7p7
X 67 50 ' sin 3 p3 sin
aus welcher Gleichung zwei zwischen 0 und 90° liegende Werthe von p zu be-
bestimmen sind, da die Gleichung X = 0 neben ihren drei bereits ermittelten re-
reellen Wurzeln noch zwei Paare zusammengehöriger imaginärer hat. Innerhalb
dieser Grenzen wird sin7p dreimal =0, nemlich für p = 25fGrad, 51f
Grad und 77-f Grad, wobei sin7p7 jedesmal sein Zeichen ändert; sin3p wird
einmal =0 für p = 60° gleichfalls mit Zeichenwechsel von sin 3 p3; endlich
sin 4 p wird einmal = 0 für p = 45°, aber ohne Zeichen Wechsel für sin 4 p4.
Erwägt man nun noch, dass der Werth von . sm37.p t «, für p = 0 dem Grenz-
^-> 7 sin 3 p3 sin 4 p* '
werthe ^ gleich zu setzen ist, so wird das Verhalten der Werthe jener Punction
in den sechs Unterabtheilungen des Zwischenraumes von 0 bis 90° in folgender
Uebersicht zusammengefasst:
100
p = 0 Grad
45
BEITRÄGE ZUM TBEOHIE
823543
6912
I
0
oo
oo
oo
60
77-f
90°
Man erkennt hieraus, dass sowohl im vierten als im sechsten Zwischen-
Zwischenräume nothwendig ein der Formel II Genüge leistender Werth von p liegen muss,
und eines Mehrern bedarf es für unsern Zweck nicht, da schon von vorne her fest
steht, dass es nur zwei solche Werthe gibt. Die Gleichung II setze ich in die Form
7logsin7p—3logsin3p — 4logsin4p = 8 = 2,0863825
Die Auffindung des zwischen 51f und 60 Grad liegenden Werthes durch
allmählige Annäherung vermittelst der Tafeln mit 3, 4, 5, 7 Zifern zeigt folgen-
folgendes Schema:
p
57°
58
57°
57
57°
57
57fl
57
40'
50
41'
42
41'41"
41 42
8
1,527
2,354
2,0624
2,2057
2,07658
2,09074
2,0862962
2,0865320
Fehler
— 0,559
+ 0,268
— 0,0240
+ 0,1193
— 0,00980
+ 0,00436
— 0,0000863
+ 0,0001495
Hieraus p = 57°4l'4t66, und ferner nach der zweiten Formel in I,
DER ALGHESBAISCHEN <HJE2CHDNGEN.
Iogsin4p =9,8891425»
Compl.log sin 3 p = 0,9193523
log(-~ 480) = 2,6£12412»
7 logr = 3,4897360
logr = 0,4985337
und damit
x = 4-1,68431594-2,6637914i
so wie die andere dazu gehörige Wurzel
x = 4-1,6843159 — 2,6637914*
Der andere zwischen 77-^ und 90° liegende Werth von p wird durch An-
Anwendung von Tafeln mit drei Decimalen als zwischen 86° und 87° liegend erkannt.
Die Rechnung in gleicher Gestalt wie im vorhergehenden Falle steht so :
P
86°
87
86° 10'
86 20
86 19
86 20
86°19'13"
86 1914
p = 86°19'1342
Iogsin4p = 9,4049540»
Compl.logsin3p = 0,0081108»
log(— 480) = 2,6812412»
7 logr = 2,0943060»
logr = 0,2991866»
Zieht man vor, r positiv zu haben, so braucht man nur zugleich für p den um
180° vergrösserten Werth 266°19'l342 anzusetzen. Die Wurzel selbst ist
X = — 0,1278113—1,9874234*
und die andere dazu gehörige nur im Zeichen des imaginären Theils davon ver-
verschieden.
8
1,885
2,533
1,9907
2,0946
2,08409
2,09447
2,0863229
2,0864970
Fehler
— 0,201
4-0,447
— 0,0957
4-0,0082
— 0,00229
4-0,00809
— 0,0000596
4-0,0001145
102 BETTfilGE ZUR THEORIE »EE AI^EBEAISCHEN GLEICHUNGEN.
Die sämmtlichen Wurzeln der Gleichung <a?7 4~ 28 #4 — 480 = 0 sind demnach
+ 1,9228841
— 3,4580892
— 2,5778036
4-1,68431594-2,6637914^
+ 1,6843159 —2,6637914£
— 0,12781134-1,98742341
— 0,127 8113 —1,9874234 £
Die Summe der Wurzeln 4-ö>°000005 ist so genau mit dem wahren Werthe 0
übereinstimmend, wie nur von dem Gebrauch siebenzifriger Logarithmen erwar-
erwartet werden durfte. In der andern Form hat man
log**
0,2839531
0,3905976
0,4112498
0,4985337
0,4985337
0,2991866
0,2991866
P
0
180
180
57
302
93
266
0
.41'
18
40
19
41"
18,
46,
13,
366
634
658
342
Die Summe der Logarithmen der Werthe von r findet sich = 2,6812411, gleich-
gleichfalls befriedigend genau mit dem Logarithmen von 480 übereinstimmend.
Es wird übrigens kaum nöthig sein zu erinnern, dass die in diesem so wie
die im 16. Artikel aufgestellten Rechnungen nur dazu bestimmt sind, den Gang
der Arbeit nach ihren Hauptmomenten zu erläutern, keinesweges aber für die
Form des kleinen Mechanismus der Operationen maassgebend sein sollen. Geüb-
Geübtere Rechner werden meistens vorziehen, nicht so viele Zwischenstufen anzuwen-
anzuwenden , als in jenen Beispielen geschehen ist. Ueberhaupt wird jeder in dergleichen
Arbeiten einigermaassen erfahrne die Einzelnheiten des Geschäfts leicht selbst in
diejenige Gestalt bringen, die den jedesmaligen Umständen und seiner eignen in-
individuellen Gewöhnung am meisten angemessen ist, und es kann hier nicht der
Ort sein, in solche Einzelnheiten weiter einzugehen.
ANZEIGEN.
Göttingische gelehrte Anzeigen. 1815 December 23.
Am 7, December wurde der Königl. Societät vom Herrn Prof. Gaüss eine Vor-
Vorlesung übergeben, überschrieben:
Demonstratio nova altera tkeorematis, omnem functionem algebraicam rationalem
integram unius variabilis in factores reales primi vel secundigradus resolvi posse.
Der hier ausgesprochene Lehrsatz, der wichtigste in der Theorie der Glei-
Gleichungen, hat bekanntlich mehrere der ersten Geometer vielfältig beschäftigt. Die
vornehmsten Versuche, einen vollkommen strengen Beweis davon zu geben, von
d'Alembekt, Etjler, Foncenex und Lagrange, sind von dem Verf. gegenwärtiger
Abhandlung bereits in einer vor sechszehn Jahren erschienenen Schrift zusammen-
zusammengestellt , und einer Prüfung unterworfen. So sehr man den Scharfsinn, welcher
jene Arbeiten auszeichnet, anerkennen muss, so ist doch nicht zu leugnen, dass
sie alle mehr oder weniger Lücken übrig lassen, wodurch die Beweiskraft zerstört
wird, und wenn gleich durch Lagrange's tiefeindringende Untersuchungen dem
grössten Theile jener Mängel abgeholfen worden ist, so können doch auch die Be-
Bemühungen dieses grossen Geometers eben so wie die scharfsinnige Art, wie spä-
später Laplace diesen Gegenstand behandelt hat, gerade von dem Hauptvorwurfe,
welcher alle jene versuchten Beweise trifft, nicht freigesprochen werden. Dieser
besteht darÄi, dass man die Sache so genommen hat, als sei bloss die Form der
Wurzeln zu bestimmen, deren Existenz man voraussetzte, ohne sie zu beweisen,
14
106 ANZEIGE. DEMONSTRATIO NOVA ALTERA THEOREMATIS OMNEM PÜNCTIONEM ETC.
eine Schlussart, die gerade hier bloss illusorisch, und in der That eine wahre
petitio principii ist. Alle die erwähnten Beweise sind rein analytisch, auch den
von d'Alembert nicht ausgenommen, obgleich er in einer geometrischen Einklei-
Einkleidung erscheint, die aber für die Sache selbst ganz gleichgültig ist; und man könnte
daher sich fast zu dem Schlüsse verleiten lassen, als sei jene Voraussetzung, de-
deren Unzulässigkeit übrigens den genannten Analysten selbst entgangen ist, bei
einer analytischen Behandlung gar nicht zu vermeiden gewesen.
Der Verf. vorliegender Abhandlung hatte in der oben erwähnten Schrift die-
diesen Gegenstand auf eine ganz verschiedene Art behandelt, und einen höchst ein-
einfachen neuen Beweis gegeben, welcher das Eigenthümliche hat, dass er sich zum
Theil auf die Geometrie der Lage gründet, und übrigens in Ansehung der Strenge
nichts zu wünschen übrig zu lassen scheint. Zugleich hatte er aber schon damals
erklärt, dass er keinesweges für unmöglich halte, auf rein analytischem Wege zu
einem vollkommen strengen Beweise zu gelangen, und sich die ausführliche Ent-
Entwicklung seiner Ideen auf eine andere Zeit vorbehalten. Andere Beschäftigun-
Beschäftigungen hatten ihn bisher von diesem Gegenstande abgezogen: die gegenwärtige Ab-
Abhandlung ist bestimmt, jene Zusage zu erfüllen.
Was nun diesen neuen Beweis selbst betrifft, so steht er dem erwähnten
frühern an Einfachheit und Kürze freilich sehr nach: allein dieser Umstand liegt
in der Beschaffenheit der subtilen Untersuchung selbst. Immer bleibt es ange-
angenehm, neben einem höchst einfachen, aber zum Theil auf Fremdartigem beruhen-
beruhenden Beweise des wichtigen Lehrsatzes, noch einen zweiten zwar langem und
künstlichem, aber für sich ganz selbstständigen zu besitzen. Eine Darstellung
der Hauptideen des neuen Beweises, wenn sie nur einigermassen befriedigend aus-
ausfallen sollte, würde übrigens bei weitem mehr Raum einnehmen, als der Zweck
dieser Blätter verstattet: wir müssen daher diejenigen, welche einen Hauptreiz
der Mathematik in der vollkommenen Klarheit ihrer Wahrheiten und der höch-
höchsten Strenge ihrer Beweise finden, auf den bald erscheinenden dritten Band der
Commentationen der Societät verweisen.
Göttingische gelehrte Anzeigen. 1816 März 2.
Nachdem die in diesen Anzeigen vom v. J. angezeigte Vorlesung des Herrn
Prof. Gauss bereits abgedruckt war, hatte derselbe bei fortgesetzter Beschäftigung
mit demselben Gegenstande das Glück, dasselbe Ziel noch auf einem ganz neuen
Wege zu erreichen. Er hat hierüber am 30. Januar der königl. Societät eine kleine
Abhandlung eingereicht, die die Aufschrift fuhrt :
Theorematis de resolubilitate functionum algebraicarum integrarum in factores reales
demonstratio tertia.
Die beiden frühern Beweise des wichtigsten Lehrsatzes in der Lehre von den
Gleichungen unterschieden sich dadurch, dass der erstere sehr kurz und einfach,
aber zum Theil auf geometrische Betrachtungen gegründet war, der andere hinge-
hingegen rein analytisch aber viel complicirter, so dass es unmöglich wurde, in dem en-
engen Räume dieser Blätter einen genügenden Auszug daraus zu geben. Dagegen
ist nun der gegenwärtige dritte auf gänzlich verschiedenen Principien beruhende
Beweis ebenfalls rein analytisch, übertrifft aber selbst den ersten so sehr an Ein-
Einfachheit und Kürze, dass wir hier ganz füglich alles Wesentliche desselben auf
wenigen Seiten mittheilen können.
Es bezeichne X die algebraische Function der unbestimmten Grosse x,
n.s. w.
14*
108 ANZEIGE. *
wo die Coefficienten A, B, C u. s. w. bestimmte reelle Grossen sind. Es seien
ferner r und cp zwei neue unbestimmte Grossen, und man setze
r™ cosm v + Ar™-X cos (m—l)v+JB r™-* cos (m — 2) © + CV*-3 cos (m — 3) © + u. s. w. = t
rmsinmto^rArm~xsia.{m — l)© 4-2?/JW-2sin(m—2)© + CV* sin(m—3)© + u.s.w. = m
mr^' cos m© + (m—i) -4 r cos (m— i) © + (»»-2M^ cos (m—2) © + (m—3) Cr1" cos (m— 3) © + u.s.w. = f
mr* sinmv-{-(m—tfAr™-1 sxa.{m—1)© + (m—2) JBr'2sin(m—2)© + (m—3) CrJW~3sln(m—3)cp 4- u.s.w. = u
mmr^cosmcp + («»—l)*Arm~icos(m— l)© + (m—2)^rm'2cos(m—2)© + (m—rfCr-* cos(m—3)© + u.s.w. = r
^—3)*CVw-3sin(m—3)© + u.s.w. = z<"
Der Factor r kann offenbar aus dem Nenner des Ausdrucks für y wegge-
schaift werden, da t\ u\ t", u" durch r theilbar sind.
Es sei ferner JR eine beliebige bestimmte positive Grosse, mit der einzigen"
Einschränkung, dass sie grösser sei als die grösste von folgenden
mÄ\/2, sJ(mBsj2), ty(mCsj2), >/{mDsji) etc.
abgesehen von dem Zeichen von A, B, C u.s.w., oder indem man alle als positiv
betrachtet.
Endlich mögen noch folgende Bezeichnungen Statt finden:
Rm cos 45° + AjB"8-1 cos D5° + ©) + 5Ü-2 cosD5° + 2 ©) + CS™-3 cos D5° + 3 ©) + u.s. w. = T
u.s.w. = U
—3)CÄm-3cosD5<>4-3©L-u.s.w.==T'
—3)
Nach allen diesen Vorbereitungen, welche wir der bequemern Uebersicht
wegen zusammengestellt haben, ergeben sich leicht nachstehende Folgerungen:
I. Die Grosse 'T ist nothwendig positiv, welchen Werth man auch immer
der Grosse cp beilege. Dies ist leicht zu übersehen, wenn man T in folgende
Form bringt:
u. s. w.
THEOEEMATJS DE BESOLÜBIUTATE FUJfCTIONDM ALGEBB. ETC.
da jeder Theil einzeln genommen nothwendig positiv wird. Auf ähnliche Weise
ist leicht zu beweisen, dass für jeden Werth von cp auch TJ, T\ U' nothwendig
positiv werden.
II. Für r = JR erhalten die Functionen £, u, t', il der Reihe nach fol-
folgende Werthe
Tcos D5°-f *»<$>)+ U sin D5°-f-*»<p)
Tsin D5°+m<p)— Z7cosD5°-(-mcp)
T'cos D 5° -f m cp) -f ZJ'sin D 5° -f m cp)
T'sin D 5° -f m cp) —- ZJ'cos D 5° -f m cp)
Hieraus folgt, dass für r — R, tt-\-uu = TT+ UU, tt'-\-uu'= TT'-\- Uü'
also beide nothwendig positiv werden.
III. Es kann also für keinen Werth von r, der grösser ist als jede der
Grossen mAsJi, \J(mB\/2), fy(mC\J2)u.s.w., zugleich t=.0xmdu = 0 werden.
Das Haupttheorem ist nun folgendes:
Innerhalb der Grenzen r = 0, r = R, und cp = 0, cp =360° {einschl.)gibt
es gewiss Werthe für r und cp, aus denen zugleich t= 0 und u= 0 wird.
Der Beweis davon wird auf folgende Art geführt. Wenn man annimmt, das
Theorem sei nicht wahr, so folgt, dass tt-\-uut für jede Werthe von r und cp
zwischen den angegebenen Grenzen immer positiv, und folglich y immer endlich
werden muss. Betrachten wir nur den Werth des doppelten Integrals
//^drdcp
von r = 0 bis r = R, und von cp = 0 bis cp = 360° erstreckt, der also eine
ganz bestimmte endliche Grosse haben wird. Dieser mit Q zu bezeichnende Werth
kann auf zwiefache Art gefunden werden, indem man entweder zuerst nach cp
und dann nach r integrirt, oder in umgekehrter Ordnung. Beide Wege müssen
nothwendig zu einerlei Resultate fuhren.
Nun hat man aber, wenn man r als beständig betrachtet, unbestimmt
tu'—ut'
r(tt + uu)
wie man sich leicht durch Diiferentiation versichern kann. Eine beständige Grosse
110 ANZEIGE.
ist bei der Integration nicht hinzuzufügen, insofern diese von cp =? 0 anfangen
soll, da für diesen Werth. offenbar
tu—ut' «
wird: und da eben dies für cp = 360° gilt, so ist der Werth von /ydcp, von
cp = 0 bis cp = 360° erstreckt, = 0, bei jedem Werthe von r. Hieraus
schliessen wir also Q = 0.
Von der andern Seite hat man, wenn man cp als beständig betrachtet, un-
unbestimmt
tt'+uu'
wie ebenfalls leicht durch die Differentiation nach r bestätigt wird. Auch hier
ist keine beständige Grosse hinzuzusetzen, insofern die Integration von r = 0
anfangen soll. Das Integral fydr, von r = 0 bis r = JR ausgedehnt, wird
folglich nach II
TT'+UU'
— tt+uu
also gewiss positiv für jeden Werth von cp. Hieraus wird demnach auch Q, d.i.
der Werth des Integrals
rTT'+UU'
J TT+UU ^
von cp = 0 bis cp ^= 360° ausgedehnt, nothwendig positiv "werden, welches mit
dem erstem Resultate in Widerspruch steht. Die Voraussetzung war folglich un-
unstatthaft , und dadurch ist die Wahrheit des Theorems selbst bewiesen.
Dass nun für jede Werthe von r und cp, welche zugleich t=Q und u = 0
geben,
r(coscp-f-sincpy/—1) und r(coscp — sincpy/—l)
Wurzeln der Gleichung X = 0 sind, oder dass die Function X dann entweder
den Factor der zweiten Ordnung
xx—2rcos<f.x-\-rr
(wenn weder r noch sincp verchwinden) oder den Factor der ersten Ordnung
x ip r
THEOBEMAUS DE EESOLUBILITATE FUtfCTIONUM ALGEBR. ETC. 111
(wenn entweder sin<p = O, also coscp —+ 1, oder r=0 wird) enthält, ist be-
bekannt genug, und braucht hier nicht erst weiter entwickelt zu werden. Was von
X so eben bewiesen ist, gilt nachher wieder von dem Quotienten, wenn X durch
jenen Factor dividirt ist, u. s. f., woraus die vollständige Zerlegbarkeit der Function
X in dergleichen Factoren erhellet.
Durch diese kurze Reihe von Schlüssen ist das eigentliche Ziel vollständig
erreicht. Nicht gefordert, aber doch gewünscht werden konnte noch eine Erläu-
Erläuterung, in wiefern der obige Widerspruch — der unvermeidlich war, wenn man
das Theorem als unwahr ansah — wegfalle, wenn man von der Wahrheit des
Theorems ausgeht. Der Verf. hat darüber einige Winke gegeben, die hier nur
kurz berührt werden können. Ist das Theorem wahr, so sind nicht mehr alle
Werthe von y endlich; es ist folglich nicht mehr ohne weiteres verstattet, ffydrdy
als eine wirkliche bestimmte Grosse anzunehmen, und man darf sich daher nicht
wundern, dass der blosse blinde Mechanismus des Calcüls, auf verschiedenen
Wegen widersprechende Resultate liefert. Die Analyse pflegt sehr häufig sich so
zu helfen, dass sie auf Fragen, die man ihr ohne Einschränkung vorlegt, obgleich
sie in-gewissen Fällen ungereimt sein können, nur halbbestimmte Antworten gibt.
So ist es bei der Bestimmung des Werthes des Integrals ffydrdy. Soll dasselbe
allgemein, von r = k bis r = l und von cp = K bis cp = L erstreckt wer-
werden , und bezeichnet man den Werth von j
für
r — k
r = k,
r=lt
r = /,
cp = K
cp ^^ 'j
cp = K
cp = L
durch
durch
durch
durch
0
6'
6"
6'"
so geben die analytischen Operationen für jenes Integral den Ausdruck
Are tg 6 — Are tg 6'—Are tg 0" -f Are tg 6'"
Das Integral hat in der That nur dann einen wahren Werth, wenn y innerhalb
der angegebenen Grenzen immer endlich bleibt: dieser wahre Werth ist dann un-
unter obigem Ausdruck allerdings begriffen, aber an sich dadurch noch nicht ganz
bestimmt, da die Function Are. tg. eine vielformige ist, und erst aus anderweitigen
(übrigens nicht schwierigen) Betrachtungen muss entschieden werden, welche
112 AN ZEIGE. THEOEEMATIS DE BESOLUBILITATE FUNCTIONEM ALGEBE. ETC.
Werthe dieser Function im bestimmten Fall zu nehmen sind. So oft hingegen
innerhalb der angegebenen Grenzen y irgendwo unendlich wird, ist eigentlich
die Frage nach dem Werthe von ffydrdy ungereimt; unterfängt man sich, diese
Ungereimtheit ignorirend, dennoch, sie zu beantworten, so darf man sich nicht
befremden lassen, auf einem Wege diese, auf anderm jene Antwort zu erhalten,
welche verschiedene Beantwortungen inzwischen allemal unter dem obigen halb-
halbbestimmten Ausdrucke begriffen sind.
Handschriftliche Bemerkungen,
Die Bedingung für R kann auch so gestellt werden, dass es grösser ist als l und als die absolute Summe
der Grossen A, B, C etc. in *Jl multiplicirt. Es sei diese absolute Summe = aA + gi? + Y C+ojD + etc.
so dass jeder der Coefficienten a, 6, f etc. entweder +1 oder — 1 wird. Dann ist der positive Werth von
T u. s. w. aus folgender Form klar
T= JB»1-1 cos 45°(.Ä— ^.(oA+ZB+iC+etcy+H'n-^aA-tA cos DS°+y))+£m-s(ZBlt+2?cosD 5°4-2<p))+ etc.
Lehrsatz. Sind ö, b, c . . . m, n die Wurzeln der Gleichung fx = o, a\ b\ c'. . . m die Wurzeln der
d f' x
Gleichung fx — o . wo f'x = ~-, und werden durch dieselben Buchstaben die entsprechenden Punkte in
piano bezeichnet, so ist, wenn man sich in a,b,c...m, n gleiche abstossende oder anziehende Massen denkt,
die im umgekehrten Verhältniss der Entfernung wirken, in a', b', c'.. . m' Gleichgewicht.
4JII
Nachrichten vo» der K. Gesellschaft der Wissenschaften zu Göttingen. 1849 Juli 30.
Die in der Sitzung der Königl. Gesellschaft der Wissenschaften am 16. Ju-
Julius von dem Geh. Hofr. Gauss gehaltene Vorlesung bezog sich auf die
Theorie der algebraischen Gleichungen.
Von der ausführlichen Denkschrift, die in Kurzem im Druck erscheinen wird,
geben wir hier nur folgenden Bericht.
Sie Jbesteht aus zwei Abtheilungen, deren jede einem besondern Gegen-
Gegenstande gewidmet ist.
Die erste Abtheilung beschäftigt sich mit dem Grundlehrsatz der Lehre von
den algebraischen Gleichungen, nemlich mit der Zerlegbarkeit jeder rationalen
bruchfreien algebraischen Function Einer veränderlichen Grosse in Factoren, wo-
worüber der Verf. schon im Jahre 1799 eine Denkschrift veröffentlicht hatte unter
dem Titel Demonstratio nova tkeorematis, omnem functionem algebraicam rationalem
integram unius variabilis in factores reales primi vel secundi gradus resolvi posse.
Diese Denkschrift hatte einen doppelten Zweck, zuerst, zu zeigen, dass die sämmt-
lichen bis dahin versuchten Beweise des ausgesprochenen Lehrsatzes ungenügend
und illusorisch waren, und zweitens, einen vollkommen strengen neuen Beweis
zu geben. Es würde unnöthig sein, auf den ersten Gegenstand noch einmal zu-
zurückzukommen: dagegen aber muss bemerkt werden, dass der Verf. jenem ersten
neuen Beweise späterhin noch zwei andere hat folgen lassen, die sich im 3. Bande
15
114 ANZEIGE.
der Commentationes recentiores unserer Societät befinden, und dass ein vierter von
Cauchy zuerst aufgestellt ist. Alle diese vier vollkommen strengen Beweise be-
beruhen auf eben so vielen ungleichen Grundlagen, darin aber kommen sie überein,
dass sie sämmtlich unmittelbar nur das Vorhandensein Eines Factors der betreifen-
betreifenden Function darthun. Der Strenge der Beweise geschieht hiedurch kein Eintrag.
Denn es ist klar, dass nach Ablösung dieses einen Factors von der vorgegebenen
Function eine ähnliche Function von niederer Ordnung zurückbleibt, auf welche
der Lehrsatz aufs neue angewandt werden kann, und dass aus der fortgesetzten
Wiederholung des Verfahrens zuletzt eine vollständige Zerlegung der ursprüngli-
ursprünglichen Function in Factoren der bezeichneten Art hervorgehen wird. Indessen ge-
gewinnt offenbar jede Beweisführung eine höhere Vollendung, wenn gezeigt wird,
dass sie geeignet ist, das Vorhandensein sämmtlicher einzelnen Factoren auf ein-
einmal unmittelbar anschaulich zu machen. Der erste Beweis ist wirklich in diesem
Falle, wie in der gedachten Denkschrift (Art. 23) bereits angedeutet, aber nicht
weiter ausgeführt war. Die gegenwärtige Abhandlung gibt nun diese Erweite-
Erweiterung, jedoch nicht in der Gestalt eines Zusatzes zu der Denkschrift von 1799,
sondern als Bestandtheil einer Umarbeitung derselben. Es wird nemlich der Be-
Beweis hier selbstständig von neuem aufgeführt, aber mit einigen wesentlichen Ab-
Abänderungen im Gange, wodurch eine bedeutende Vereinfachung gewonnen ist.
Verändert ist ausserdem auch die ganze Einkleidung, die bei der altern Schrift
absichtlich so gewählt war, dass alle Einmischung imaginärer Grossen gänzlich
vermieden werden konnte. Da jedoch die Beweisführung sowohl ihrem Ursprünge
als ihrem wahren Wesen nach mit der Conception der complexen Grossen im in-
innigsten Zusammenhang steht, was auch, seitdem diese in der Wissenschaft ein-
eingebürgert ist, aufmerksamen Lesern jener Denkschrift nicht entgangen ist, so
hat Verf. es für angemessen gehalten, jene erste Einkleidung jetzt fallen zu las-
lassen , und die Argumentation auf ihr eigentliches Feld zurück zu versetzen, deren
Grundbegriffe jetzt Jedermann geläufig sind, zumal da dadurch nicht bloss grössere
Einfachheit sondern auch noch etwas grössere Allgemeinheit gewonnen wird.
Die zweite Abtheilung ist den algebraischen Gleichungen mit drei Gliedern
gewidmet. Diese haben das Eigentümliche, dass von den zur numerischen Auf-
Auflösung der Gleichungen bestimmten Methoden einige bei jenen einer Geschmei-
Geschmeidigkeit und Eleganz fähig werden, von der ihre Anwendung auf Gleichungen von
weniger einfacher Gestalt sehr weit entfernt bleibt. Dies gilt namentlich von der
BEITRÄGE ZUR THEORIE DER ALGEBRAISCHEN GLEICHUNGEN. 115
Auflösung durch unendliche Reihen, und von der indirecten Methode. Es scheint
daher die Entwicklung dieser Methoden für die Gleichungen von jener Form eine
besondere Ausführung um so mehr zu verdienen, da das Vorkommen solcher
Gleichungen in der That ein sehr häufiges ist.
Die Auflösung durch unendliche Reihen hat jedoch der Verf. von seinem
gegenwärtigen Zweck gänzlich ausgeschlossen, und nur bemerkt, dass für jede
Wurzel einer solchen Gleichung, sei sie reell oder imaginär, eine convergente
und nach einem leicht erkennbaren Gesetz fortschreitende Reihe gefunden werden
kann. So schön aber auch diese Auflösungsart in allgemein theoretischer Bezie-
Beziehung ist, so wird man doch, wo es auf wirkliche praktische Anwendung ankommt,
den indirecten Methoden in allen den Fällen den Vorzug geben, wo jene Conver-
genz nicht eine sehr schnelle ist.
Diese indirecten Methoden nun sind der Gegenstand der zweiten Abtheilung.
Es handelt sich hier von zwei Methoden, denn das Verfahren, welches zur Be-
Bestimmung der imaginären Wurzeln erfordert wird, ist ganz verschieden von dem
für die reellen Wurzeln anzuwendenden. Von dem letztern hat der Verf. schon
bei andern Gelegenheiten ein paar Proben an besondern Fällen gegeben, und da-
dabei zugleich die allgemeine Anwendbarkeit des Verfahrens angedeutet. Obgleich
diese Generalisirung durchaus keine Schwierigkeit hat, so hat der Verf. doch ge-
geglaubt , dass man gern die gebrauchfertigen Vorschriften zusammengestellt sehen
würde, zumal weil die Anzahl der dabei zu unterscheidenden und einzeln zu be-
behandelnden Fälle nicht unbeträchtlich ist.
Die Auffindung der imaginäre^ Wurzeln auf indirectem Wege ist (insofern
nicht schon einigermassen angenäherte Werthe anderswoher bekannt sind) des-
deswegen viel schwieriger, als die der reellen, weil jene aus einem unendlichen Ge-
Gebiete von zwei Dimensionen herausgesucht werden müssen, diese nur aus einem
Unendlichen von Einer Dimension. Diese Schwierigkeit lässt sich bei den Glei-
Gleichungen von drei Gliedern durch einen einfachen sehr nahe liegenden aber wie es
scheint sonst bisher noch nicht benutzten Kunstgriff umgehen. Auch für diese
Aufgabe sind die zur Auflösung erforderlichen Vorschriften vollständig und in ge-
gebrauchfertiger Gestalt mitgetheilt.
Göttingische gelehrte Anzeigen. 1813 März 6.
Recherches matMmatiques ou diverses questions non resolues ou dont la solution
laisse quelque chose ä dSsirer. Par P. L. Coytiee. Premier memoire contenant
des observations g6ne'rales sur les equations algßbriques. Paris 1813. Chez Eberhardt.
A6 Seiten in Quart.)
Wenn wir die wortreiche, schwülstige Vorrede recht verstehen, so soll der
Zweck des gegenwärtigen Aufsatzes, und anderer, die ihm noch folgen sollen,
dahin gehen, allerlei nach des Verfassers Meinung usurpirte Resultate der Ana-
Analyse mit den Waffen der Synthese zu bekämpfen und umzustürzen. Aus dem
Ganzen der Schrift sieht man aber, dass der Verfasser eigentlich mit den Wör-
Wörtern Analyse und Synthese ihm eigenthümliche Begriffe verbindet, und bei jener
sich ein blosses blindes Zeichenspiel, bei dieser eine reelle anschauliche Erkennt-
niss denkt. Ein solches Unternehmen verdient allerdings Lob. wenn sich ein
solches blindes Zeichenspiel vorfindet, das sich den Namen Analyse anmasst; bei
den meisten Versuchen dieser Art aber, diesseit und jenseit des Rheins gemacht,
finden wir, dass die Blindheit nicht in dem Bekämpften, sondern in dem Bekäm-
Bekämpfenden lag. Wohin gegenwärtige Schrift zu rechnen sei. möge man aus dem
Inhalt, den wir kurz anzeigen wollen, beurtheilen.
Hauptsächlich ist die vorliegende Schrift gegen die Zerlegbarkeit der alge-
algebraischen Gleichungen in einfache Factoren gerichtet (schon in diesem Ausdrucke
liegt eine Unrichtigkeit, die sich freilich auch manche andere Schriftsteller haben
COYTTEE, EECHEECHES MATHEMATJQÜES ETC. 117
zu Schulden kommen lassen). Der Verfasser nennt dieselbe auch öfters das Theo-
Theorem von 1746 , ohne Zweifel, weil d'Alembeet um diese Zeit zuerst den Versuch,
eines strengen Beweises machte. Dass dieser JBeweis von d'Alembeet , eben so
wie die Beweise von Eulee, Foncenex, Lageange, keineswegs befriedige, darüber
haben wir schon vor 14 Jahren an einem andern Orte unser Urtheil erklart, und
eben so müssen wir freilich, unserer Ueberzeugung nach, von Laplace's und La-
geange's spätem Arbeiten über denselben Gegenstand urtheilen. Allein in diese
Beweise selbst lässt sich unser Verfasser gar nicht ein: seine Bemerkungen sind
ganz anderer Art, und nicht gegen die Beweise, sondern gegen den Lehrsatz
selbst gerichtet. Er behauptet nemlich (um ;nur bei dem einfachsten Fall einer
quadratischen Gleichung xx—2ax-\-b = 0 stehenzubleiben), x — [a-\-\J(aa — b)]
sei gar kein einfacher Factor, weil x—[a-\-\j(aa — b)] =■ 0 gar keine Gleichung
der ersten Ordnung, sondern eine wahre quadratische Gleichung sei. Man möge
vor die Wurzelgrösse das Zeichen -f-, oder das Doppelzeichen + schreiben, im-
immer drücke sie beide Wurzeln zugleich aus. Jede Gleichung stelle eigentlich die
Relation zwischen zwei veränderlichen und einer beständigen Lineargrösse dar, die
Classification der Gleichungen und die Classification der Curven nach Ordnungen
müsse aufs genaueste zusammenhangen, die Gleichung x — [a-\-\J(aa—b)) — 0
als identisch mit der Gleichung xx—2ax-\-b — 0 betrachtet, und also erstere
so gut, wie letztere, zur zweiten Ordnung gezählt werden. Diese Behauptungen
machen den Inhalt der Schrift aus, und zeigen uns nichts, als die Verworrenheit
der Begriffe des Verfassers. Die gemeine Algebra kennt gar keine veränderlichen
Grossen, sondern bloss unbekannte und bekannte. Das Wurzelzeichen \J hat ei-
eigentlich in der mathematischen Zeichensprache eine doppelte Bedeutung (und
dies ist allerdings eine kleine Unvollkommenheit); \]A soll entweder definirt wer-
werden, eine Grosse, deren Quadrat = A, oder die positive Grosse, deren Quadrat
= A, insofern A positiv ist. Es hängt von dem Analysten ab, wie er das Zei-
Zeichen gebrauchen will, und ein denkender, vorsichtiger Analyst wird sich immer
klar bewusst sein. und sich immer so ausdrücken, dass auch dem Leser kein
Zweifel übrig bleibe, ob das Zeichen in unbestimmter oder in bestimmter Bedeu-
Bedeutung gebraucht sei. Gleichungen werden, wie wir schon oben andeuteten, gar
nicht in Factoren zerlegt, sondern Functionen einer veränderlichen Grosse. Also
nicht die Gleichung xx—2ax-\-b = 0, sondern die Function xx—%ax-\-k
wird in die Factoren x — \a-\-\J[aa — b)}, x—[a—sj(aa—b)] zerlegt, und inso-
118 ANZEIGE. COYTIER, RECHERCHES MATHEMATIQUES ETC.
fern man darin bloss x als veränderlich betrachtet, nennt man dieselben Facto-
ren der ersten Ordnung. Immerhin mag der Verfasser, wenn er die Gleichung
xx— 2ö#-f-& = 0 als Ausdruck einer Curve, und a oder b als veränderlich
betrachtet, den Factor x — \a-\-\j(aa— bj] einen Ausdruck der zweiten Ord-
Ordnung nennen, er bestreitet dadurch keine Wahrheit, sondern nur die Schicklich-
Schicklichkeit einer Benennung in einem Fall, worin man sie nicht gebraucht, und nie ge-
gebraucht hat.
Den meisten mathematischen Lesern dieser Blätter werden freilich diese
Erörterungen überflüssig sein; wir glaubten aber doch die Begriffe des Verfassers
etwas entwickeln zu müssen, damit Niemand sich durch den Titel der Schrift ver-
verleiten lasse, neue Aufklärungen darin zu erwarten, wozu dem Verfasser die er-
ersten Elemente zu fehlen scheinen.
Göttingische gelehrte Anzeigen. 1833 Februar 25.
Analyse des equations determinees par Fodeeee. Premiere partie. Paris 1831.
Chez Firmin Didot freres. (XXIV und 258 S. in Quart.)
Nach dem Entwurf des Verfs. sollte dieses Werk aus zwei Abtheilungen be-
bestehen , und die erstere ausser einer allgemeinen Uebersicht des Ganzen die bei-
beiden ersten Abschnitte, die zweite Abtheilung hingegen die fünf übrigen Ab-
Abschnitte enthalten. Der Verf. wurde den Wissenschaften durch den Tod entris-
entrissen , als der Druck eben angefangen war. Indessen fand sich die ganze erste
Abtheilung, die wir hier durch dip Besorgung des Hrn. Naveer erhalten, so gut wie
vollständig ausgearbeitet vor, während der Rest von der Vollendung noch weit
entfernt war: man muss dies um so mehr bedauern. da aus der allgemeinen Ue-
Uebersicht hervorgeht, dass manche interessante Untersuchungen dafür bestimmt
waren. Hier müssen wir, mit Uebergehung dessen, was wir zu erwarten gehabt
hätten, wenn dem Verf. ein längeres Lieben zu Theil geworden wäre, uns auf die
Anzeige von dem einschränken, was wir wirklich erhalten haben.
Der Zweck des Werks ist, die numerische Auflösung der bestimmten alge-
algebraischen Gleichungen in einen ganz sichern und möglichst einfachen Gang zu
bringen, namentlich die Anzahl der reellen und imaginären Wurzeln mit völliger
Bestimmtheit auszumitteln, jene einzeln in feste Grenzen einzuschliessen und die
stufenweise zu beliebiger Schärfe zu führende Annäherung zu ihren Werthen ganz
methodisch anzuordnen. Die Hauptgrundlage des Ganzen bildet ein dem Verf.
120 ANZEIGE.
eigenthumlich.es Theorem, welches als eine glückliche Generalisirung von Des-
caetes Lehrsatz (gewöhnlich nach Haeeiot benannt) zu betrachten ist, und, dem
Wesen nach, in Folgendem besteht. Es sei X eine geordnete ganze algebraische
Function von x (mit lauter reellen Zahlen coefficienten); ferner a, a zwei beliebige
bestimmte ungleiche reelle Grossen, und zwar a — a positiv; durch die Substi-
Substitutionen x = y-\-a> x = y-\-d gehe X in die gleichfalls geordneten Functio-
nen Y, Y' über, in welchen die Coefficienten resp. g, g' Zeichenfolgen enthal-
enthalten: der ausnahmliche Fall, wo einer oder mehrere Coefficienten verschwinden,
wird hier der Kürze wegen bei Seite gesetzt. Dies vorausgesetzt, kann die Glei-
Gleichung X. = 0 innerhalb der Grenzen x — a, x = d nicht mehr als g—g
reelle Wurzeln enthalten, oder noch bestimmter, wenn die Anzahl der reellen
Wurzeln zwischen jenen Grenzen =X ist, so ist allemal g — g — \ entweder
= 0 , oder eine gerade positive Zahl. Ist demnach die Differenz g—g, welche
niemals negativ sein kann, = 0, so gibt es zwischen jenen Grenzen gar keine
reelle Wurzel; wird g—g = 1 , so enthalten die Grenzen eine reelle Wurzel
und nicht mehr; ist endlich g—g = 2. so bleibt einstweilen noch ungewiss,
ob zwei reelle Wurzeln zwischen den Grenzen liegen oder gar keine. Anstatt
zweier Grenzen a, d kann man eine grössere Anzahl auf ganz ähnliche Art be-
behandeln , und solche so wählen, dass erstlich der kleinsten eine Function Y mit
blossen Zeichenwechseln, der grössten eine mit blossen Zeichenfolgen entspricht,
also wenn die entsprechenden Zahlen der Zeichenfolgen der Reihe nach mit
g, g, g", g'"u. s.f. bezeichnet werden, die erste, dieser Zahlen = 0, die letzte
der Ordnungszahl der Gleichung gleich wird; und zweitens, dass sämmtliche ein-
einzelne Differenzen g—g, g"—g\ g"—y'u.s.w. nur entweder = 1 oder = 2
werden Dadurch werden dann sämmtliche reelle Wurzeln dergestalt zwischen
Grenzen eingeschlossen, dass in jedem einzelnen Intervall entweder eine liegen
muss, oder zwei liegen können. Wie im letztern Fall auf ganz methodische Art,
nöthigenfalls durch weitere Verengung der Grenzen zur Entscheidung gebracht
wird, ob die zwei reellen Wurzeln wirklich vorhanden sind, oder fehlen, kann
hier des beschränkten Raumes wegen nicht näher ausgeführt werden. Wir be-
bemerken nur, dass so oft dieser letzte Fall eintritt, es allemal innerhalb solcher
Grenzen einen Zwischenwerth gibt, für welchen in der Function Y ein Coeffi-
cient vor dem letzten ausfällt, während der vorhergehende und folgende gleiche
Zeichen haben. Foukiee nennt solche Stellen kritische: jede solche kritische
FOÜBDSß, ANALYSE DES EQVATIONS DETERMESEES. 121
Stelle bedingt demnach das Fehlen von zwei reellen Wurzeln: wenn aber Fou-
hier sich zugleich so ausdrückt, dass jedesmal zwei solche ausfallende reelle Wur-
Wurzeln imaginär werden, so können wir diesen Ausdruck nicht ganz billigen, da er
leicht zu einer Misdeutung Veranlassung geben könnte. In der That ist es zwar
wahr, dass die Gleichung X = 0 zusammen gezählt genau so viele Paare imagi-
imaginärer Wurzeln enthält, als solche Ausfalle oder kritische Stellen vorkommen: al-
allein die Werthe aller imaginären Wurzeln sind an sich eben so bestimmte Grossen
wie die reellen, und jener Ausdruck kann daher leicht so gedeutet werden, als
ob jeder bestimmten Lücke ein bestimmtes Paar imaginärer Wurzeln angehörte, was
jedoch nicht nur von Fouiuer nicht nachgewiesen ist, sondern so lange, als tie-
tiefer eindringende Untersuchungen diesen interessanten Punkt noch nicht in helles
Licht gesetzt haben, zweifelhaft bleiben muss. Uebrigens soll hiermit nicht ge-
gesagt werden, dass Fourier selbst den Ausdruck so verstanden habe; wir möchten
eher das Gegentheil annehmen, und fast vermuthen, dass er über das Dasein oder
Nichtdasein eines solchen bestimmten Zusammenhanges ungewiss geblieben, und
absichtlich einer offenen Erklärung über den verfänglichen Ausdruck ausgewichen
sei. Ueberhaupt hat Fouriek in das Wesen und die Berechnung der imaginären
Wurzeln in diesem Werke sich gar nicht eingelassen, und es bleibt daher noch
ein weites Feld zu bearbeiten übrig.
Einem so gewandten Grössenforscher, wie Fourier war, konnte es. einmal
im Besitz jenes schönen Lehrsatzes — und nach den von Herrn Naveer mitgetheil-
ten Notizen ist jener in diesem Besitz schon seit sehr langer Zeit gewesen — nicht
schwer fallen, auf demselben die Anordnung der Technik der numerischen Auf-
Auflösung der Gleichungen zu begründen, und diese Entwicklung ist mit grosser
Vollständigkeit und Ausführlichkeit gegeben. Geübtere Leser möchten vielleicht
eine etwas gedrängtere Darstellung und die Wegschneidung mancher Wiederho-
Wiederholungen vorziehen, dem weniger geübten werden die vielen gut gewählten und aus-
ausführlich behandelten Beispiele willkommen sein. Jedenfalls sichert dieses Werk
Foureer's Namen auch in diesem Theile der Grössenlehre einen ehrenvollen Platz,
den er in andern schon längst behauptet.
J2Z
All
DISQUISITIONES GENERALES
CIRCA SERIEM INFINITAM
(a+l)ÖF+l) ,
1.2 -7G+.)"+
PAKS PRIOR
A ü C T O E E
CAROLO FRIDEBJCO GAUSS
SOCIETATI EEGIAE SCIENTIARUM TEADITA 1812. JAN. SO.
Commentationes societatis regiae scientiarmn Gottingensis recentiores. Vol. n.
Gottingae mdcccxhi.
16*
DISQUISITIONES GENERALES
CIRCA SERIEM INFINITAM
, I «6 r i a(<*-HNF+*)rr I a(a + l)(»4-2NF + i)F + 2) « , ,
i-»T '1.2. y(y + i) ' 1.2.3. y(y+i)(y + 2) "^
PARS PRIOR.
1.
Series, quam in hac commentatione perscrutari suscipimus, tamquam functio
quatuor quantitatum a, ß, y, x spectari potest, quas ipsius elementa vocabimus,
ordine suo elementum primum a, secundum €, tertium y, quartum x distin-
guentes. Manifesto elementum primum cum secundo permutare licet: quodsi ita-
que brevitatis caussa seriem nostram hoc signo F(a, fi, y, x) denotamus, habe-
bimus F(ß, a, y, x) = F(a, <6, y, x).
2.
Tribuendo elementis a, fi, y valores determinatos, series nostra in functio-
nem unicae variabilis x transit, quae manifesto post terminum 1 — a1^111 vel
1—tf1™11 abrumpitur, si a — 1 vel # — 1 est numerus integer negativus, in ca-
sibus reliquis vero in infinitum excurrit. In casu priori series exhibet functionem
algebraicam rationalem, in posteriori autem plerumque functionem transscenden-
tem. Elementum tertium y debet esse neque numerus negativus integer neque
= 0, ne ad terminos infinite magnos delabamur.
126 ~ disqüisitiones geneeales
3.
Coefficientes potestatum x™, xm+i in serie nostra sunt ut
adeoque ad rationem aequalitatis eo magis accedunt, quo maior assumitur m. Si
itaque etiam elemento quarto x valor determinatus tribuitur, ab huius indole
convergentia seu divergentia pendebit. Quoties scilicet ipsi x tribuitur valor rea-
lis, positivus seu negativus, unitate minor, series certo, si non statim ab initio,
tarnen post certum intervallum, convergens erit, atque ad summam finitam ex
asse determinatam perducet. Idem eveniet per valorem imaginarium ipsius x
formae a~\-b\j—1, quoties aa~\-bb<C\. Contra pro valore ipsius x reali uni-
tateque maiori, vel pro imaginario formae a -f- b \J— 1, quoties aa~\- b b ^> 1, se-
series si non statim tarnen post certum intervallum necessario divergens erit, ita ut
de ipsius summa sermo esse nequeat. Denique pro valore x = 1 (seu generalius
pro valore formae d~\-b\J—1, quoties aa-\-bb = 1) seriei convergentia seu di-
divergentia ab ipsarum a, <6, y indole pendebit, de qua, atque in specie de summa
seriei pro x =■ 1, in Sect. tertia loquemur.
Patet itaque, quatenus functio nostra tamquam summa seriei definita sit,
disquisitionem natura sua restrictam esse ad casus eos, ubi series revera conver-
gat, adeoque quaestionem ineptam esse, quinam sit valor seriei pro valore ipsius
x unitate maiori. Infra autem, inde a Sectione quarta, functionem nostram al-
tiori principio superstruemus, quod applicationem generalissimam patiatur,
4.
Differentiatio seriei nostrae, considerando solum elementum quartum x
tamquam variabile, ad functionem similem perducit, quum manifesto habeatur
L } = jF(a-{-l, ü+1, y+1, x)
Idem valet de differentiatioiübus repetitis.
5.
Operae pretium erit, quasdam functiones, quas ad seriem nostram reducere
licet, quarumque usus in tota analysi est frequentissimus, hie apponere.
g
CIRCA SKRfKM IHMMTAM 1 4":p~<#4- ETC.
ubi elementum € est arbitrarium.
II. (#4-M)»4-(#__„)»=
III. (*4-tf)»4-^ — 2tnF(—n, <o, 2«), — j)
denotante to quantitatem infinite parvam.
IV. (t+u)*-(t-u)* = 2rc*-1«.F(-1H*-K, -4-»-H. f, f
V. (f+ii)*—*" = n*"-1«^! —», 1. 2, -^D
VI. l0g(l4-') =r ^A, 1, % —t)
VII.
VIII. ^ = F{1, *, i, ^) = l + '-F(l. *, 2,1) = i+*4-4-«JP(if *, 3, i) etc.
denotante e basin logarithmorum hyperbolicorum, k numerum infinite magnum.
IX.
denotantibus Je, Je numeros infinite magnos.
XI. sin t = tF(k, k\ f, —2L)
XII. cost = F{k,kr,i-,—-^,)
XIII. t = sin f. ^(-J-, -J-, f, sin t2)
XIV. # = sin*, cost .F(l, 1, f, sin*2)
XV. t = tang f. F{i-, 1, f, — tang *2)
XVI. sin^# = nsint. Ffon+t* —inJrh h
XVII. sinnt = rcsint cost F(\n-\-\, —fn-\-\, f, sinf3)
XVIII. sinw^ = nsmt. cos^^—4-»-{-l, —4-«+4-, i> —t
XIX. sinw^ = wsin*. cosr* ^(-fw-f 1, 4-»+^, f, — tang*2)
XX. cosnt = Ffcn, —£rc, f, sin*2)
XXI. cosra* = cos*. F{±n-\-$, — £»-h£, 1, sinf2)
XXn. coswf = cos*Äi?(—iw, —i»+^,^—tang*2)
XXin. cosrc* = cosr^^n+i, i», i, —tang*3)
. DISQDISITIONES GENEBALES
6. *
Functiones praecedentes sunt algebraicae atqae transscendentes a logarith-
mis circuloque pendentes. Neutiquam vero karum caussa disquisitionem nostram
generalem suscipimus, sed potius in gratiam theoriae tfunctionum transscenden-
tium altiorum promovendae, quarum genus amplissimum series nostra complecti-
tur. Huc, inter irifinita alia, pertinent coefficientes ex evolutione functionis
^Ö_|_JJ — Sö&coscp)—** in seriem secundum cosinus angulorum cp, 2cp, 3cp etc.
progredientem orti, de quibus in specie alia occasione fusius agemus. Ad formam
seriei nostrae autem illi coefficientes pluribus modis reduci possunt. Scilicet sta-
tuendo
(aa-\-bb — 2abcosv)~n = Q — J.-j-2vl'coscp-|-2 J/'cos2cp-|-2^"'cos3<p--|- etc.
habemus primo
A =a-*nF(n,ntl,£)
Ä = na-*^bF(nt n-\-1, 2, ^)
n+ 2, 3, **}
1 • j2 • o
etc.
Si enim aa-\-bb—2«&coscp consideratur tamquam productum ex a — br in
a—bf~l (designante r quantitatem coscp-f-sincp.y'—1), fit Q aequalis producto
ex a~2n
in
in
1 ! bt
a
1 Y>
1 a
»(i
i
*(«
i
. 2
t+l) _
. 2
«(« +
1 .
»(» +
1 .
l)(f
2 ;,
iH
?,
* + 2)
. 3
» + 2)
. 3
b*r3
ös
J3r-
a3
-f- etc.
- -f- etc.
Quod productum quum identicum esse debeat cum
valores supra dati sponte prodeunt.
Porro habemus secundo
circa sereem; mwmr&M 1-f %-\- etc.
iaabb
Ä = »(aa + 66)—'aii^(i»+i, *»+ 1, 2,
Tertio fit
Ä = •(a+6)r»-»fljli'(»+i, f, 3,
M, 7,
etc.
Denique fit quarto
a i 7\ ——2m Tn/ * a Aub
A = B(«-&)-2»-2a4J?(.+l, f 3, -j^
(+f, 7,
etc.
Valores illi atque hi facile eruuntur ex
^^( . 4,
etc.
qui valores facile deducuntur ex
^+^(-f ^+ etc.
etc.
17
D1SQUISITI0NES G&NERALES
SECTIO PRIMA.
Relationen inier functiones contiguasi
7.
Functionem ipsi F(a, fi, y, x) contiguam vocamus, quae ex illa oritur, dum
elementum primum t secundum, vel tertium unitate vel augetur vel diminuitur,
manentibus tribus reliquis elementis. Functio itaque primaria F(a. 6, y, x) sex
contiguas suppeditat, inter quarum binas ipsamque primariam aequatio persim-
plex linearis datur. Has aequationes, numero quindecim, hie in conspectum
produeimus, brevitatis gratia elementum quartum quod semper subintelligitur = x
omittentes, funetionemque primariam simpliciter per F denotantes.
[I] 0 = (y— 2a—(fi — a)%) F-+-a(l — x) F(a-+-\ ,fi,y) — (y — a) F(a—:
[2] 0 =
[3] 0 =
[4] 0 =
[5] 0 = (y — a — l)F-+-aF(a-+-l,f),y) — (y — l).F(a,6,y — 1)
[6] 0_-=
[7] 0 =
[8] 0 =
[9] 0 =
[10] 0 =
[II] 0 =
[12] 0 =
[13] 0 =
-[14] 0 = F—1—(y—a—1
[15] 0 =
Ecce iam demonstrationem haram formularum. Statuendo
—2) __ ^
1.2.3 m . y(y-H) (Y + w — 0
CIECA SERIEM INFINIT AM 1 -f- ~ X + ETC.
erit. coefficiens potestatis x™
in F a(ß-\-m —
in JP
in 2*>(
in F(
coefficiensautem potestatis af"^1 in .F(a+1,6, y), seu coefficiens potestatis x
in #.F(+,,y)
= m(y-\-m — \)M
Hinc statim demanat veritas formularum 5 et 3; permutando a cum 6, oritur
ex 5 formula 12, atque ex his duabus per eliminationem 2. Perinde per ean-
dem permutationem ex 3 oritur 6; ex 6 et 12 combinatis oritur 9, hinc per
permutationem 14, quibus combinatis habetur 7; denique ex 2 et 6 eruitur 1,
atque hinc permutando 10. Formula 8 simili modo ut supra formulae 5 et 3,
e consideratione coefficientium derivari potest (eodemque modo, si placeret, omnes
15 formulae erui possent), vel elegantius ex iam notis sequenti modo. Mutando
in formula 5 elementum a in a—1, atque y in y-f-l, prodit
0 = (y — a+\)F(a— i,6,
Mutando vero in formula 9 tantummodo y in y+1, fit
0 = (a— 1— (y-%)F(a,6,T+l)+(T-a+l)F(a— t,
E subtractione harum formularum statim oritur 8, atque hinc per permu-
permutationem 13. Ex 1 et 8 prodit 4, hincque permutando 11. Denique ex 8 et 9
deducitur 15.
9.
Si a — a, b"—6, y'—y, nee non d'—a, 6"—ß. y"—y sunt numeri in-
tegri (positivi seu negativi), a funetione F(a,fity) ad funetionem F(d,W,y),
et perinde ab hac usque ad funetionem F(a\ß", y") transire licet per seriem si-
milium funetionum, ita ut quaelibet contigua sit antecedenti et consequenti, mu-
mutando scilicet primo elementum unum e.g. a continuo unitate, donec a F(a, ö, y)
perventum sit ad F(a',f>,y), dein mutando elementum seeundum, donec perven-
132 DISQUISmONES GENEEALES
turn sit ad F(a\ 6',y), denique mutando elementum tertium, donee perventum sit
ad F(d,f)',y), et perinde ab hac usque ad _F(a", 6",y"). Quum itaque per art.7
habeantur aequationes lineares inter functionem primam, secundam atque tertiam,
et generaliter inter ternas quascunque consequentes huius seriei, facile perspici-
tur, hinc per eliminationem deduci posse aequationem linearem inter functiones
F(atfi,y), F(a\f)',y')t F(d\ 6",y"), ita ut generaliter loquendo e duabus functio-
nibus, quarum tria elementa prima numeris integris differunt, quamlibet aliam
functionem eadem proprretate gaudentem derivare liceat, siquidem elementum
quartum idem maneat. Ceterum hie nobis sufficit, hanc veritatem insignem ge-
generaliter stabilivisse, neque hie compendiis immoramur, per quae operationes ad
hunc finem necessariae quam brevissimae reddantur.
10.
Propositae sint e. g. functiones
inter quas aequationem linearem invenire oporteat. Iungamus ipsas per functio-
functiones contiguas sequenti modo:
F(a, ^y) = F
F(a + 2, Ö + 2, y -f 2) = F"""
Habemus itaque quinque aequationes lineares (e formulis 6, 13, 5 art. 7):
I. 0 = {y — a—\)F— (y — a — 1—ß)F'— 6A — x)F"
II. o = y.F'— y(l—x)F"— (y — a —
IH. 0=yjF"— (y — a—\)F'"~ (a-\-l)FMr
IV. 0 = (y — a — \)F'"— (y—a — 2 — $)F""— (€ + 1) (l—x)FmH
V. 0 =
Ex I et Il'prodit, eliminando F
CIßCA SEEIEM INFIXITAM 1-|- -—<£ + ETC. 133
VI. o=TF— 7A—x)F"— G — a—6 — l)wFm
Hinc atque ex III, eliminando F"
VII. o=yF-(T-a-l-
Porro ex IV atque V, eliminando F
VIII. 0 = (T-f l)F"'—(y+lJF^+^ + lJ
Hinc atque ex VII, eliminando F"",
IX. • 0=
11.
Si omnes relationes inter ternas functiones F(a, 6, y), F(a-f-X, 6-f-{x,
F(a-\-X, 6+ji, y+v), inquibus X, {x,*v, X', jx', v' vel =0 vel = +1 vel = — 1,
exhaurire vellemus, formularum multitudo usque ad 325 ascenderet. Haud in-
utilis foret talis collectio, saltem simpliciorum ex his formulis: hoc vero loco suf-
ficiat, paucas tantummodo apposuisse, quas vel ex formulis art. 7, vel si magis
placet, simili modo ut duae priores ex Ulis in art. 8 erutae sunt, quivis nullo
negotio sibi demonstrare poterit.
[16]
[17]
[18] f
[19] F(tt|Ö + l, T + i)-F(a,Ö,7) = ^=^F(a+l, 6 + 1, y+2)
[20] ^(a+l,6,7 + l)~F(a,Ö,7) = ^^F(a+l,Ö + l,7+2)
[2i] F(a-l,6+l,r)-F(«,6,y) = (-^=^F(a, 6+1,7+1)
[22] ^l>
[23] F(a —1,6+1,T)-F(a+1, 6 — 1,7) = ^=-^F(a+l,6+1,
134 DISQDISITIONES GENEBALES
SECTIO SECUNDA.
Fraetiones contmuae.
12.
Designando
61, x)
F<*t,l*) per
fit
,z) — F (%*,*[, x) —
et proin, dividendo aequationem 19 per -F(ct,€—{—1,y—}—1,<2?),
7,*) 7G+0
sive
et quum perinde fiat
etc., resultabit pro G (a, €, y, a?) fractio continua
1
ex
1 " Tx
1
i— etc.
ubi
YG + 0 U G+0G+2)
C
etc., cuius lex progressionis obvia est.
Porro ex aequationibus 17, 18, 21, 22 sequitur
CIRCA SEBIEM INFXNITAM t-{~ ~CC-\- ETC.
[27] *(«+i.«.T.*)_
G(a+1, 6, y, x)
F(a—l, 6+1, T,a)
7 a , ,y,s
unde, substitutis pro functione £r eius valoribus in fractionibus continuis, totidem
fractiones continuae novae prodeunt.
Ceterum sponte patet, fractionem continuam in formula 25 abrumpi, si e
numeris a, 6, y — a, y — 6 aliquis fuerit integer negativus, alioquin vero in in-
finitum excurrere.
13.
Fractiones continuae in art. praec. erutae maximi sunt momenti, asserique
potest, vix ullas fractiones continuas secundum legem obviam progredientes ab
analystis hactenus erutas esse, quae sub nostris tamquam casus speciales non sint
contentae. Imprimis memorabilis est casus is, ubi in formula 25 statuitur 6 =. 0,
unde F(aif>iy,x) = lt adeoque, scribendo y—1 pro y
[30] F{a,l,y) = l-f--^<H
i
l— etc.
ubi
a
a — T
~ G + 0G + *)
_
l
__ 2(y + 1 —a)
etc.
136 DISQTHSITIONES GENEKALES
14.
Operae pretium erit, quosdam casus speciales huc adscripsisse. Ex formula
I art. 5 sequitur, statuendo t = 1, € = 1
[31] (!+«)» = -i-
. nu
—— u
u
1—-^-^
3. 4
2 (« — 2)
etc.
E formuKs VI, VII art. 5 sequitur
[32] log(l-H) = ^
Ä<5
1+*'
1 -f- etc.
[33] iÄor»"t- «'
*> ^
_«
5.7
1— etc.
Mutando hie signa — in -f- prodit fractio continua pro arc. tang t.
Porro habemus
[34] e* = l— t
1+ü
TZ**
1— etc.
CIRCA SEBEEM ISTFINFTAM t-f" j^ <2?-f- ETC.
j-q k] j, sin t cos t
i .2 . ,»
sinr
i.3
—'— mit2
3.5
3.4 . ._
sinr
— sin*2
7.9
5.6 . ..
sinl'
1— etc.
Statuendo a = 3, y = f, e formula 30 sponte sequitur fractio continua
in Theoria motus corporum coelestium art. 90 proposita. Ibidem duae aliae fractio-
nes continuae prolatae sunt, quarum evolutionem hacce occasione supplere visum
est. Statuendo
5. 8
1 . 4
1 x etc.
11.13
fit 1. c. x—£ = —^^r = ——-—, adeoque
35 Q 35
2
—XX
> 3>5
QAr — X
35
quae est formula prior: posterior sequenti modo eruitur. Statuendo
1 . 4
X
JR _ t 7.9
5.8
3. 6
11. 13
l
. 7.10
1 x etc.
13.15
erit per formulam 25
-i — GU, f, -J-, x), atque ^ =
Hinc
18
138 DISQUISmONES GENEßALES
QFfc -fc f, x) =
sive permutando elementum primum cum secundo
QFfc h h *) = F{- h f, -f-, x)
Sed per aequationem 21 habemus
unde fit Q = JR—-f-a?, quo valore in formula supra data substituto prodit
quae est formula posterior.
Statuendo in formula 30, a —-, ob — —ynt, fit pro valore infinite
magno ipsius y
[36] F{™,l,y,—ynt) = 1—mt-\-m(m--\-n)tt—m(m-{-n){m-}-2n)ts-{- etc.
1 + 3 « £ etc.
SJECTIO TERTIA.
De summa seriei nostrae statuendo elementum quartum = 1, ubi sirnul quaedam aliae functiones
transscendentes discutiuntur.
15.
Quoties elementa et, 6, y omnia sunt quantitates positivae, omnes coeffi-
cientes potestatum elementi quarti x positivi evadunt: quoties vero ex Ulis ele-
mentis unum alterumve negativum est, saltem inde ab aliqua potestate xm omnes
eoefiieientes eodem signo aifecti erunt, si modo m aeeipitur maior quam valor ab-
solutus elementi negativi maximi. Porro hinc sponte patet, seriei summam pro
CIRCA SERDSM DTPIHITAM
1 H °~X-\- ETC.
x = 1 finitam esse non posse, nisi cogffieientes saltem post certum terminum in
infinitum decrescant, vel, ut secundum morem analystarum loquamur, nisi coefii-
ciens termini otf° sit = 0. Ostendemus autem, et quidem, in gratiam eoram,
qui methodis rigorosis antiquorum geometrarum favent, omni rigore,
primo, coefiicientes (siquidem series non abrumpatur), in infinitum crescere,
quoties fuerit a~\-^—y—1 quantitas positiva.
secundo, coefficientes versus limitem finitum continuo convergere, quoties
fuerit a-f-6—y—1 = 0.
tertio, coefficientes in infinitum decrescere, quoties fuerit a-\-G—y—1
quantitas. negativa.
quarto, summam seriei nostrae pro x = 1, non obstante convergentia in
casu tertio, infinitam esse, quoties fuerit a-f-6 — y quantitas positiva vel ^=0.
quinto, summamyeioßnitam esse, quoties a-\-f>— y fuerit quantitas ne-
negativa.
16.
Hanc disquisitionem generalius adaptabimus seriei infinitae M, M', M", M'"etc.
3f' 3£" Jif'" • * ♦
ita formatae, ut quotientes -^, -^-, jpr etc. resp. sint valores fractionis
etc.
tl + at1-1 -j- b 1?-* + ctx-3 + etc.
pro t = m, t = m-\-l, t = m-\-2 etc. Brevitatis caussa huius fractionis nu-
meratorem per P, denominatorem per p denotabimus: praeterea supponemus,
P, p non esse identicas, sive differentias A—a, B—b, C—c etc. non omnes
simul evanescere.
I. Quoties e differentiis A—a, B — b, C—c etc. prima quae non evanes-
cit est positiva, assignari poterit limes aliquis l, quem simulac egressus est valor
ipsius t, valores functionum P et p certo semper evadent positivi, atque P^>p.
Manifestum est, hoc evenire, si pro l accipiatar radix maxima realis aequatio-
nis p(P—p) = 0; si vero haec aequatio nullas omnino radices reales habeat,
proprietatem illam pro omnibus valoribus ipsius t locum habere. Quapropter in
serie ~, ^7, ^ etc. saltem post certum intervallum (si non ab initio) omnes tex-
texmini erunt positivi atque maiores unitate; quodsi itaque nullus neque = % ne-
que infinite magnus evadit, perspicuum est,
18*
140 BISQÜISITIONES ÖENEEALES
seriem M, M', M", M'" etc. si non ab initio tarnen post certum intervallum
omnes suos terminos eodem signo affectos continuoque crescentes habituram esse.
Eadem ratione, si e differentiis A — a, B—b, C—c etc. prima quae non
evanescit est negativa, series M, M\ M", M'"ete. si non ab initio tarnen post
certum intervallum omnes suos terminos eodem signo affectos continuoque de-
crescentes habebit.
II. Si iam coefficientes A, a sunt inaequales, termini seriei M, M\ M", M'"
etc. ultra omnes limites sive in infinitum vel crescent vel decrescent, prout diffe-
rentia A — a est positiva vel negativa: hoc ita demonstramus. Si A—a est
quantitas positiva, accipiatur numerus integer h ita, ut fiat h(A — a)^>l, statua-
turque *-* = tf, J£- = N\ *£. = N", *£ = W etc., nee non tP» = Q,
(t-\-l)pk = q. Tunc patet, ^, ^, ^7 etc. esse valores fractionis — ponendo
t = m, t = m-\-l, t — m-\-2 etc., ipsas Q, q vero esse funetiones algebraicas
formae huius
i- etc.
q = ^Ä+»_|_(Äa+i)^A+ etc.
Quare quum per hyp. differentia hA—(ha-\-\) sit quantitas positiva, ter-
termini seriei N, N', N", Nr" etc. si non ab initio tarnen post certum interval-
intervallum continuo crescent (peri); hinc termini seriei mN, (m-\-l)N', (m-\-2)N",
(m-\-3)Nm etc. necessario ultra omnes limites crescent, et proin etiam termini
seriei M, M', M", M'"etc., quippe quorum potestates exponente h illis sunt ae-
quales. Q.E. P.
Si A—a est quantitas negativa, accipere oportet integrum h ita,, ut
h(a—A) fiat maior quam 1, unde per ratiocinia similia termini seriei
mMh, (m-{-\)Mth, [m-\-1)M"h, (m-{-3)Mr"h etc.
post certum intervallum continuo decrescent. Quamobrem termini seriei Mh,
M'h, M"h etc. adeoque etiam termini huius M, M\ M", M"r etc. necessario in
infinitum decrescent. Q. E. S.
III. Si vero coefiieientes primi A, a sunt aequales, termini seriei
Mt M\ M", M'" etc. versus limitem finitum continuo convergent, quod ita de-
demonstramus. Supponamus primo, terminos seriei post certum intervallum con-
continuo crescere, sive e differentiis B — b, C—c etc. primam quae non .evanescat
g
CIRCA SEMEM EJITNITAM 1 + —<2?+ ETC. 141
esse positivam. Sit h integer talis, ut h-\-h—B fiat quantitas positiva, sta-
tuamusque
m^f = N, M' (=±i)* = JV', M- (=£)* = W etc.
atque (tt—l)hP = Q, t?hp = q, ita ut -^, -^-etc. sint valores fractionis —
ponendo t = mt t = m-\-\ etc. Quum itaque habeatur
g == tk+2h+Atk+zh-1-{-bik+2j>-2 etc.
atque per hyp. B—h—b sit quantitas negativa, termini seriei JV, JV', JV", JV'" etc.
post certum saltem intervallum continuo decrescent, adeoque termini seriei
Mt M\ M", M'" etc., qui Ulis resp. semper sunt minores, dum continuo crescunt,
tantummodo versus limitem finitum convergere possunt. Q. E. P.
Si termini seriei M, M\ M", M'" etc. post certum intervallum continuo
decrescunt, accipere oportet pro h integrum talem, ut h-\-B—b sit quantitas
positiva, evinceturque per ratiocinia prorsus similia, terminos seriei
)\ M\-^-)\ M"(*±±)h etc.
post certum intervallum continuo crescere, unde termini seriei M, M\ M"etc,
qui illis resp. semper sunt maiores, dum continuo decrescunt, necessario tantum-
tantummodo versus limitem finitum decrescere possunt. Q. E. S.
IV. Denique quod attinet ad summam seriei, cuius termini sunt Mt M\
M'\ M'"etc., in casu eo, ubi hi in infinitum decrescunt, supponamus primo, A—a
cadere inter 0 et —1, sive -4+1 — a esse vel quantitatem positivam vel = 0.
Sit h integer positivus, arbitrarius in casu eo, ubi A-\-l — a est quantitas posi-
positiva, vel talis qui reddat quantitatem h-\-m-\-A-\-B—b positivam in casu eo
ubi A-\-l—a = 0. Tunc erit
—1)) = ^+* + (J.+l — m — h)iK~{-(B~A{m-{-h~-l))t^~l etc.
p(t— (j»+ä)) = ^+1-\-{a — m—ä)^ + F—a{m-\-h))^~1 etc.
ubi vel A-\-\ — m — h—[a—m — h) erit quantitas positiva, vel, si haec fit =0,
saltem B— A(m-\-h—1) — F — a(m-\-hj) positiva erit. Hinc (per i) pro quan-
titate t assignari poterit valor aliquis l, quem simulac transgressa est, valores
fractionis P^,'7^?'^~1^ semper fient positivi atque unitate maiores. Sit n integer
142 DiSQuisrrioNES generales
maior quam l simulque maior quam h, sintque termini seriei M, M\ M", M"'etc.
qui respondent valoribus t = m-\-n, t = m-\-n-\-l, t = m-\-n-\-1 etc., hi
N, N\ N\ N'"etc. Erunt itaque
(»4-1—h)N' (n + 2—h)N" (n+3—h)N"r
etC
(n—h)N ' (» + i—h)N' ' (n+2— h)N" etC'
quantitates positivae unitate maiores, unde
adeoque summa seriei N-\-N'-\-N"-\-Nm-\- etc. maior summa seriei
(rc_MjV(—,+ / , + -r^^—i- + —r^—i+ etc.)
^ i ^n—h ' «4-1—h ' «4-2—ä ' «4-3—h ' >
quotcunque termini colligantur. Sed posterior series, crescente terminorum nu-
mero in infinitum, omnes limites egreditur, quum summa seriei l-4"-j-~t"T+-i-+ e^c
quam infinitam esse constat etiam infinita raaneat, si ab initio termini 1-j—|- -f-3- -f-etc.
H-^iziuä rescin(^antur- Quare summa seriei JV-f-JV'+iV'r+JVrw'-f- etc., adeo-
adeoque etiam summa huius M-]~M'-\-M"-\-Mm-\- etc., cuius pars est illa, ultra
omnes limites crescit.
V. Quoties autem A—a est quantitas negativa absolute maior quam uni-
tas, summa seriei M-\-M'-\-M"-\-M'"-\- etc. in infinitum continuatae certo
erit finita. Sit enim h quantitas positiva minor quam a—A—1, demonstrabi-
turque per ratiocinia similia, assignari posse valorem aliquem l quantitatis t,
ultra quem fractio , ,__ . semper adipiscatur valores positivos unitate mino-
res. Quodsi iam pro n accipitur numerus integer ipsis l, m, A-f-1 maior, ter-
minique seriei M, M', M", M'"etc, valoribus t = n, t = n-{-l, t — n-\-2 etc.
respondentes, designantur per N, N', iV"etc., erit
^ n ' ^- w(«4-l)
adeoque summa seriei N-\-N'-\-N"-f- etc., quotcunque termini colligantur, mi-
minor producto ex N in summam totidem terminorum seriei,
1 _|_ * —&—1 1 (»-A —1)(« —A) _, (« — h-l)(n-h)(n — h + i) >
' •« "T" »(» + 1) ' n(n4-1) («4-2)
Huius vero summa pro quolibet terminorum numero facile assignari potest; est
scilicet
terminus primus = ^-^- — "~~ —1
CIRCA SEBEBM INJFINITAM 1 -f- ~ X + ETC.
-■ , • n — l (n — h — l)(n — h)
summa duorum terminorum = —=■ ~± -
n hn
. - . • n — l (n—h — l)(n — h)(n — h+l) ,
summa tnum terminorum = — ^ A n -^lj etc.
h h n (n + l)
et quum pars altera (per II) formet seriem ultra omnes limites decrescentem,
summa illa in infinitum continuata statui debet = ^~. Hinc N-\-N'-\-N" etc.
in infinitum continuata semper manebit minor quam Ä~ » e^ proin M-\-M'-\-M"
etc. certo ad summam. finitam converget. Q. E. D.
VI. Ut ea, quae generaliter de serie Mt M\ M" etc. demonstravirnus, ad
coefficientes potestatum xm, xm+1, x™^2 etc. in serie F(atfi,y,x)t applicentur,
statuere oportebit 1=2, A = a-f-ö, B = aß, a = y-f-1, b = y, unde quin-
que assertiones in art. praec. propositae sponte demanant.
17.
Disquisitio itaque de indole summae seriei F(at ß,y,l) natura sua restrin-
gitur ad casum, quo y — a — 6 est quantitas positiva, ubi illa summa semper
exhibet quantitatem finitam. Praemittimus autem observationem sequentem. Si
coefficientes seriei \-\-ax-\-bxx-\-ca?s-\- etc. = 8 inde a certo termino ultra
omnes limites decrescunt, productum
A—x)S = \-{-(a—\)x-\-(b — a)xx-{-(c — b)x*-{- etc.
pro x = 1 statuere oportet = 0, etiamsi summa ipsius seriei S infinite magna
evadat. Quoniam enim collectis duobus terminis summa fit = a, collectis tri-
bus = b, collectis quatuor = c etc., limes summae in infinitum continuatae
est = 0. Quoties itaque y — a — 6 est quantitas positiva, statuere oportet
(l—x) F(a, 'S, j —1, x) = 0 pro x = 1, unde per aequationem 15 art. 7 habebimus
), sive
[37] J?(a,6,
Quare quum perinde fiat
et sie porro, erit generaliter, k denotante integrum positivum quemeunque
DISQUISITIONES GENEBALES
F(a. fi, y, 1) aequalis producto ex F(a, 6, y -f- k, 1)
in (y —a)(y4-l_a)(y_|_2 — O) (y -f k — 1 — Ct)
in (y —6)(y+l_tf)(y+2_,tf)....(y+*—1-6)
diviso per productum
in (y — a — 6)(y-f-l — a — Ö)(y + 2 — a — 6) . . . (y-j-*— l_a
18.
Introducamus abhinc sequentem notationem :
ubi k natura sua subintelligitur designare integrum positivum, qua restrictione
U.(k,z) exhibet functionem duarum quantitatum Jc,z prorsus determinatam. Hoc
modo facile intelligetur, theorema in fine art. praec. propositum ita exhiberi posse
(a ?> y \) — n(*»T-i)-n(*,T-«—8-*) Ft -z
[ato,y, i) — n(*,T—o-i).n(*,Y-6-i) ^ ' '
19.
Operae pretium erit, indolem functionis H(ktz) accuratius perpendere.
Quoties z est integer negativus, functio manifesto valorem infinite magnum ob-
tinet, simulac ipsi k tribuitur valor satis magnus. Pro valoribus integris
ipsius z non negativis autem habemus
n(£,0) = 1
1 . 2
1.2.3
etc. sive generaliter
\ 1.2.3
[40]
CffiCA SEKIEM INMNITAM 1 ,4~-^-#-4- ETC.
1 1 -Y '
Generaliter autem pro quovis valore ipsius z habenras
[41]
i +
[42]
k
adeoque, quum Ei A, z) = -^j^,
, nZ+l oZ+l ,Z+l
\1 2 3 4
20.
Imprimis vero attentione dignus est lime$, ad quem pro valore dato ipsius
z functio Ei (Ar, z) continuo converget, dum k in infinitum crescit. Sit primo h
valor finitus ipsius k maior quam z, patetque, si k transire supponatur ex h in
A-f-1, logarithmum ipsius Tl(ktz) accipere incrementum, quod per seriem con-
vergentem sequentem exprimatur
g(l-M) ■ g(l—gg) ■ Z(l+g3) | g(l—**)_■_ f
t~r rl)S~r '
2(Ä+1)S t
Si itaque A: e valore h transit in h-\-n, logarithmus ipsius W{k,z) accipiet in-
incrementum
-f- etc.
quod semper finitum manere, etiamsi n in infinitum crescat, facile demonstrari
potest. Quare nisi iam in H(h,z) factor infinitus aifuerit, i. e nisi z sit nume-
rus integer negativus, limes ipsius II (Ar, z) pro k = oo certo erit quantitas fi-
nita. Manifesto itaque Ei (oo, z) tantummodo a z pendet, sive functionem ipsius
z ex asse determinatam exhibet, quae abhinc simpliciter per Uz denotabitur.
Definimus itaque functionem n z per valorem producti
i . 2 . 3 k . 1?
(g + Ä)
19
146 DISQÜIS1TI0NES GENERALES
pro k = oo, aut si mavis per limitem producti infiniti
Z+l 1SB+Z) ' 2ZC+Z)
21.
Ex aequatione 41 statim sequitur aequatio fundamentalis
[44] I1
ünde generaliter, designante n integrum positivum quemcunque
[45] 11B?+») = Br+i)Br+2)Br+3) (z-\-n)X\z
Pro valore integro negativo ipsius « erit valor functionis Ei z infinite magnus; pro
valoribus integris non negativis habemus
ÜO = 1
m = i
Ü2 = 2
Ü3 == 6
Ü4 == 24 etc.
atque generaliter
[46] Uz z= 1.2.3 z
Sed male haec proprietas functionis nostrae tamquam ipsius definitio venditaretur,
quippe quae natura sua ad valores integros restringitur, et praeter functionem
nostram infinitis aliis (e. g. cos2tc2.]1z, costc«21*II2 etc., denotante tc semiperi-
pheriam circuli, cuius radius = 1) communis est.
22.
Functio n (Ar, z), etiamsi generalior videatur quam Ei z, tarnen abhinc no-
bis superflua erit, quum facile ad posteriorem reducatur. Colligitur enim e com-
binatione aequationum 38, 45, 46
[47]
Ceterum nexus harum functionum cum iis, quas dar. Keamp facultates nu-
CIRCA SEEIEM INFESITAM 1 -4- — tf-\- ETC. 147
merieas nominavit, per se obvius est. Scilicet facultas numerica, quam hie auetor
per abIc designat, in signis nostris est
Sed consultius videtur, functionem unius variabilis in analysin introducere, quam
functionem trium variabilium, praesertim quum hanc ad illam reducere liceat.
23.
Continuitas funetionis Uz interrumpitur, quoties ipsius valor fit infinite
magnus, i. e. pro valoribus integris negativis ipsius z. Erit itaque üla positiva
a z = —1 usque ad z — oo, et quum pro utroque limite Uz obtineat valorem
infinite magnum, inter ipsos dabitur valor minimus, quem esse = 0,8856024
atque respondere valori z= 0,4616321 invenimus. Inter Limites z =—1 et
z =—2, valor funetionis Uz fitnegativus, inter z =—2 atque z = —3
iterum positivus et sie porro, uti ex aequ. 44 sponte sequitur. Porro patet, si
omnes valores funetionis Uz inter limites arbitrarios unitate differentes e. g. a
z = 0 usque ad z == 1 pro notis habere liceat. valorem funetionis pro quovis
alio valore reali ipsius z adiumento aequationis 45 facile inde deduci posse. Ad
hunc finem construximus tabulam, ad ealcenj huius sectionis annexam, quae ad
figuras viginti exhibet logarithmos briggicos funetionis Uz, pro z= 0 usque ad
z = 1 per singulas partes centesimas summa cura computatos, ubi tarnen mo-
nendum, figuram ultimam vigesimam interdum una duabusve unitatibus erro-
neam esse posse.
24.
Quum limes funetionis F(a, €, y -f- k, 1), crescente k in infinitum, mani-
festo sit unitas, aequatio 39 transit in hanc
r48l F(a $y D — n(r-i).n(Y-a-8-i)
t4i>J x-^a, o,y, i) — n(T-a-i).n(Y—6—i)
quae formula exhibet solutionem completam quaestionis, quae obiectum huius
sectionis constituit. Sponte hinc sequuntur aequationes elegantes:
3.4§ DKQÜISITIOKES GEKEßALES
[49] F[a&yt 1) = F{— a, —% T—a — % 1)
[50] F{a.$,y,l).F(— a, 6,y — a, 1) = 1
[51] F{a,^y,l).F{a,- — 6,T — 6, l) = 1
in quarum prima y, in secunda y—€, in tertia y — a debet esse quantitas po-
sitiva.
25.
Applicemus formulam 48 ad quasdam ex aequationibus art. 5. FormulaXIII,
statuendo t = 90° = |-tu, fit 4-TC = ^(t> t> f> !)» siye aequivalet aequationi
notae
x . , 1.1 ^. t.t.3 |^ 1.1.3.5 .^
TTC _ !-(-___{_—--^_(_______(_ etC.
Quare quum per formulam 48 habeatur jF(f, |-, |-, 1) = ^ ^ , atque sit
no = 1, Ui = iii{— i), fit 7u = (n(—f)J
[52] n(-±) - v/^
[53] U^ = isJ%
Formula XVI art. 5, quae aequivalet aequationi notae
. • . «{««—1) • j3 , n(nn—l)(nn—9) • ,5 ,
smnt = nsmt \—--^smr-|—^-——^-——Jsmf— etc.
atque generaliter pro quovis valore ipsius n locum habet, si modo t limites
— 90° et -f--90° non transgrediatur, dat pro t = -%-tz
01112 n (-1-»). n \n
unde deducitur formula elegans
= Jnit sive statuendo w = 1z
[55] n(— z).U(z—1) = -r
nec non scribendo z -f--f Pr0
[56] - • n(
CIRCA SKBTKM DTFINITAM , 1 -\~^üß-\- BTC»
E combinatione formulae 54 cum definitione functionis Ei sequitur, -^~
* sin z ~
esse limitem producti infiniti
(l . 2 . 3 . 4 .... kf
(l.— zz)D—zz) (9 —zz) .... (kk — zz)
crescente k in infinitum, adeoque
sin^Tt = ztz(\—zz){\—")A—") etc. in inf,
similique modo ex 56 deducitur
coszTu = A — Azz)(l ")(t — -^) etc. in inf.
formulae notissimae, quae ab analystis per methodos prorsus diversas erui solent.
26.
Designante n numerum integrum, valor expressionis
nnzU (k, z).Il(k,z—-). II(ä, z——) n(k,z-^—^)
n n n
U(nk, nz)
rite collectus invenitur
A.2.3.... &)WM**
~~ 1.2.3 nk. JfcK"-1)
adeoque a z est independens, sive idem manebit," quicunque valor ipsi 2;.tribua-
tur. Exhiberi poterit itaque, quoniam n(&, 0) = U{nk, 0) = 1, per productum
Crescente igitur k in infinitum, nanciscimur
-).n(z—-) n(z—
Unz \ n>-"\ n'' y n> v n '
Productum ad dextram, in se ipsum ordine factovum inverso multiplicatum, pro:
ducit, per form. 55,
K T. Tt «_ BTt)W-1
.1 .2 . 3 * * " * . n—l n
sin—« sin-n sm-r sin tz
n n n n
Unde habemus theofema elegans
150 3WSQUISTFI0NES GEKERALES
()n()n(ü^il)
\jn
27.
Integrale fxK~1(l—a^ydx, ita acceptum, ut evanescat pro # = 0, ex~
primitur per seriem sequentem, siquidem X, ja sunt quantitates positivae:
Hinc ipsius valor pro x = 1 erit
-+v
Ex hoc theoremate omnes relationes, quas ül. Euler olim multo labore evolvit,
sponte demanant. Ita e. g. statuendo
/dx a /• xxdx t>
W^) — ** J v'(i-*4) ~
erit 4 = n-i^. B = üiinfcil = n<-W), adeoque AB = tx. gf,
mul hinc sequitur, quoniam 11^.11 (—i-)=^Ti = ^'
Valornumericusipsius J., computanteStieling,habetur = 1,3110287771 4605987,
valor ipsius B, secundum eundem auctorem, =0,5990701173 6779611, ex
nostro calculo, artificio peculiari innixo, = 0,5990701173 6779610372.
Generaliter facile ostendi potest, valorem functionis Ylz, si z sit quanti-
tas rationalis = —, denotantibus m, [i integros, ex ja—1 valoribus determi-
natis talium integralium pro x = 1 deduci posse, et quidem permultis modis
diversis. Accipiendo enim pro X numeram integrum atque pro v fractionem, cu-
ius denominator = ja, valor illius integralis semper reducitur ad tres Uz, ubi z
est fractio cum denominatore = ja; quodvis vero huiusmodi Uz vel ad O( ),
vel ad Il(—£), vel ad Ei(—-) etc. vel ad ü(—^—^) reduci potent per for-
mulam 4 5, siquidem z revera est fractio; si enim z est integer, Uz per se con-
stat. Ex illis vero integralium valoribus, generaliter loquendo, quodyis U(— —),
p
CIRCA SEEIEM rNPINTTAM 1-{-—-tf-\- ETC. . J&&*
si m<^\l, per eUminationem erui potest*). Quin adeo semissis talium integra-
lium sufficiet, si formulam 54 simul in auxilium vocamus. Ita e. g. statuendo
r— .u -p — ni-n(-f) p_
Hinc propter ü^-= ^-E[(—^), habemus
n(—f-) = </F25 CJDEF)
Formulae 54, 55 adhuc suppeditant
yy it D sin-^Tt
sin-^7:' F sinfTt
ita ut duo integralia D, E, vel E et F sufficiant, ad omnes valores ü(—•£),
ü(—-§-) etc. computandos.
28.
., , f , nx.nv .f . . f r >S~l*-*T**
ötatuendo y=vx, atque fi=l, xnft ,-r erit valor integralis
ab ,y = 0 usque ad ^ = v, sive valor integralis fy1 A—^) dy inter eosdem
limites = xn(X4-vi r=: l (form. 47), siquidem v denotet integrum. Iam cres-
cente v in infinitum, limes ipsius ü(v,X) erit = FIX, limes ipsius A — —)
autem e~y, denotante e basin logarithmorum hyperboiicorum. Quamobrem si
X est positiva, y sive Ü(X — 1) exprimet integrale fyk~i^'~ydy ab y = 0 us-
que ad y = co, sive scribendo X pro X — 1, ÜX est valor integralis
ab y = 0 usque ad y = oo, si X-f-1 est quantitas positiva.
Generalius statuendo ^ = £a, aX-f-ot—1 = €, transit Jyxe~ydy in
faze~z dz, quod itaque inter limites z = 0 atque z = oo sumtum exprime-
tur per n(—- —1)
sive
Valor integralis JsP e~z dz, a: = (l usque ad z = oo fit = -
si modo a atque €-f-l' sunt quantitates positivae (si utraque est negativa, in-
*) Haec eliminatio, si pro quantitatibus ipsis logarithmos introducimus, aequationibus tantammodo ii^
nearibus applicanda erit.
»TSQÜlSiTIONES GENEBALES
tegrale per g v* exprimetur). lta e. g. pro € = 0, a = 2, valor integra-
lis fe~wdz invenitur = ta
.HL Eieleb pro summa logarithmprum log 1 -f-log 2 -f- log 3 -f-etc. -f- logz
eruitseriem {z-\-\)\ogz — z +1^2^+^ _ _^_ _j_ _i_ _ etc.
ubi & = ^, SS = -g*^, (S; = -JT etc. sunt numeri Beenoüluani. Per hanc-itaque
seriem exprimitur log Eis:; etiamsi enim primo aspectu haec conclusio ad valores
integros restricta videatur, tarnen rem propius contemplando invenietur, evolu-
tionem ab Euleeo adhibitam (Instit. Calc. Diif. Cap.vi. 159) saltem ad valores posi-
tivos fractos eodem iure applicari posse, quo ad integros: supponit enim tantum-
modo. functionem ipsius z, in seriem evolvendam, esse talem, ut ipsius dimi-
nutio, si z transeat in z—1, exhiberi possit per theorema Tatloei, simulque ut
eadem diminutio sit = log£. Conditio prior innititur continuitaü functionis, ad-
eoque locum non habet pro valoribus negativis ipsius z, ad quos proin seriem il-
lam extendere non licet: conditio posterior autem functioni logüsr generaliter
competit sine restrictione ad valores integros ipsius z. Statuemus itaque
[58] l^nz = («+i-)lo&2?-Ä+^log2ic+14s-^ + ^?-f^?+ etc.
Quum* hinc quoque habeatur
etc.
atque per formulam 57, statuendo n = 2,
<«^ 1»^. zS o. 4« öS o • u* o zZ V.ö.IZ öS
Hae duae series pro valoribus magnis ipsius z al> initio satis promte con-
vergunt, ita ut summam approximatam commode satisqae exacte colligere liceat:
attamen probe notandum est, pro quovis valore dato ipsius z, quantumvis magno,
praecisionem limitatam tantummodo obtineri posse, quum numeri Beknoulliani
seriem hypergeometricam constituant, adeoque series illae, si modo satis longe
extendantur, certo e convergentibus divergentes evadant. Ceterum negari uequit,
theoriam talium serierum divergentium adhuc quibusdam difficultatibus premi, de
quibus forsan alia occasione pluribus commentabimur.
1%
C1BCA SKBFEM JNFDttTAM 1 -j X 4- ETC.
1 l .y '
30.
E farmula Ä8 sequitur
~ z+ 1 z + 2 z+3 z-
, z) z + i+to z + 2+u) z+3
unde sumtis -logarithmis, in series infinitas evolutis, prodit
[60]
>5r0
- (
. -f
Series, hie in o> multiplicata, quae, si magis placet, ita etiam exhiberi potest,
e terminorum multitudine finita constat, crescente autem k in infinitum, ad li-
mitem certum, converget, qui novam functionum transscendentium speciem nobis
sistit, in posterum per ^z denotandam.
Designando porro summas serierum sequentium, in infinitum extensarum,
7r + G+i? + (i+iM + etc'
L
etc.
resp. per P, Q, R etc. (pro quibus signa functionalia introducere minus neces-
sarium videtur), habebimus
\ß\\ lQgFI{24-.«)) = logllz-f <oty*z-f £<oü>P—iüKQ4-i<o4ß— etc.
Manifesto functio *Fz erit functio derivata prima functionis logülz, adeoque
Perindeerit P=^, Q-^ +^
20
154 I>ISQDISmONES GENERAIiES
31.
Functio Wz aeque fere memorabilis est atque functio II^, quapropter in-
signiores relationes ad illam spectantes hie colligemus, E differentiatione aequa-
tionis 44 fit
[63] V(r+1) =
unde
[64] V(f+n) = Vx+^z + ,-L. + ^ + etc.
Huius adiumento a valoribus minoribus ipsius z ad maiores progredi, vel a ma-
ioribus ad minores regredi licet: pro valoribus maioribus positivis ipsius z funetio-
nis valores numerici satis commode per formulas sequentes e differentiatione ae-
quationum 58, 59 oriundas computantur, de quibus tarnen eadem sunt tenenda,
quae in art. 29 circa formulas 58 et 59 monuimus:
L«*] ** = !«*•+f. - n-, + ff ~ w + etc-
[66] ¥(,-+) = logs+^ - ^ + J£ - etc.
Ita pro z = \0 computavimus
Wz = 2,3517525890 6672110764 743
unde regredimur ad
Wo = —.0,5772156649 0153286060 653#)
Pro valore integro positivo ipsius z fit generaliter
T67J Wz = ^o + l+-|--f-i+etc. -f-
Pro valore integro negativo autem manifesto Wz fit quantitas infinite magna.
*) Quum hie valor inde a figura vigesima discrepet ab eo qaem computavit clar. Mascheeo^i in Adno-
tat. ad EtTLEKi Calculum Integr., adhortatus sum. Feidekicum Beenhabdum Gothofeedum Nicolai , iuvenem
in calculo indefessum, ut computum illum. repeteret ulteriusque extenderet. Invenit itaque per calculum du-
plicem, scilicet descendens tum a z = 5 0 turn a z = 100, %
^"O =— 0,5772156049 0153286060 6512090082 4024310421
Eidem calculatori exercitatissimo etiam debetur tabulae ad finem huius Sectionis annexae pars altera, exhibens
valores funetionis Wz ad i 8 figuras (quarum ultima haud certa), pro omnibus valoribus ipsius z a o usque ad
l per singulas partes centesimas. Ceterum methodi, per quas utraque tabula construeta est, innituntur par-
tim theorematibus quae hie traduntur, partim calcuH artifieiis singularibus, quae alia oceasione proferemus.
CIRCA SEEIEM INFINITAM 1|
32.
Formula 55 nobis suppeditat log II (— z) -j- log II (z—1) = log iz — log sin z ic,
unde fit per diiferentiationem
[68] W (— z) — W(z — 1) =
Et quum e definitione functionis W generaliter habeatur
[69] Wx— Wy= — ^j + ^ — ^f-2-h—^2 — ^-3+ etc'
oritur series nota
1 1.1 i . 1 1 , ,
lucotangzir = ; f- — \- etc.
0 z 1—a ' i + s 2 — s • 2+s 3—s '
Simili modo e differentiatione formulae 57 prodit
170] ¥*+¥(* —JL) + V(*_jL)+etc.
adeoque statuendo sr = 0
[71] qf(_l) + *P(_l) + l{f(_2
Ita e. g. habetur
*(_.|.) = f 0 —2log2 = —1,9635100260 2142347944 099, unde porro
W% — +0,0364899739 7857652055 901.
33.
Sicuti in art. praec. W(—4-) ad ^0 et logarithmum reduximus, ita gene-
generaliter W(—^), designantibus m, n integros, quorum minor m, ad ¥0 et loga-
rithmos reducemus. Statuamus — = o>, sitque cp alicui angulorum u>, 2u>,
3u) . . . . in—l)u) aequalis; unde 1 = coswcp = cos 2wcp = cos 3wcp etc.,
coscp = cos(»+l)? == cos(w-f-2)cp etc., cos2cp = cos(w-f~2)9 etc., nee non
coscp-f-cos2cp-f-cos3cp-f-etc. -\-cos{n — Ijo-f-1 = 0. Habemus itaque
coscp. ^-H? = —w cos cp-f-cos cp. log 2 — ^—cos(w-f~^)?~f~cos?-^°ol'— e^c-
cos 2 cp. ty* ^^ = — ycos 2cp -|- cos 2cp. log 2 — ~-^ cos(w+2) cp-f-cos 2cp.logf — etc.
cos 3 cp. W ^=^ = — - cos 3©+cos 3©. log 2 J-cos (»4-3) cp 4- cos 3cp. logf — etc.
etc. usque ad
156 ' BIS^t^EEIOSKS GENERALE&
I)cp.log2 — ^-j-cosBw—l)cp
-\-cos(n — l)cp.logf-— etc.
W 0 =—-^coswcp-f-log2—^cos2%cp-f-log#— etc.
atque per summationem
—1)9. V(—^
= — ^(coscp -f-|-cos 2cp-}--^cos 3cp-j-t cos 4 <p -f- etc. in infin.)
Sed habetur generaliter, pro valore ipsius x unitate non maiori,
log(l — 2<z?coscp-f-##) = —2(<2?eoscp-f-i<z?#cos2cp-}--!-<2?3cos3cp-f-
quae quidem series facile sequitur ex evolutione log(l—ra?)-f-log(l——), deno-
tante r quantitatem cos cp -j- sj— 1 • sin cp. Hinc fit aequatio praecedens
[72] coscp.f ^4-cos2cp.^^ + cos3cp.W^+etc. -f-cos(» — l)cp.^(— 1)
= — W 0 -\-in log B — 2 cos cp)
Statuatur in hac aequatione deinceps cp=ru), cp=2u), cp = 3u) etc. usque ad
cp — {n — l)o), multiplicentur singulae hae aequationes ordine suo per cos«wo>,
cos2mu>, cos 3 ma) etc. usque ad cos (n — l)mu>, productorumque aggregato adii-
ciatur aequatio 71
lw i^ i^_j_ etc. ^
Quodsi iam perpenditur, esse
1 -f-c°sw««).cos^a)-f-cos 2wo), cos 2&a>-f-cos 3ma) .cos 3Ajo)
-f- etc. -j-cos(w — l)mw.co$(n.— i)k<a = 0
denotante Ä aliquem numerorum 1, 2, 3 ....(»— 1) exceptis Ms duobus m at-
atque n — m, pro quibus summa illa fit =£w, patebit, ex summatione illarum
aequationum prodire, post divisionem per y,
[73] <jr(_
2logw-j-cosMw.logB — 2cosu))-(-cos 2mw.logB — 2cos2u>)
2 — 2 cos 3u))-f-etc. -
Manifesto terminus ultimus huius aequationis fit = cosmto.logB — 2cosa>), pen-
CIRCA SKRTKM INFtNITAM l-\-^-3ß-\- ETC. 157
ultimus <= cos 2mm.logB — 2cos 2<o) etc., ita ut bini termini semper sint ae-
quales, excepto, si n est par, termino singulari cos y.mo>logB— 2cosyo>),
qui fit = -|- 2 l°g2 Pro m P^» vel = —2 log 2 pro m impari. Combinando
iam cum aequatione 7 3 hanc
^ ( ) — W{ ) = ic cotang — ic
habemus, pro valore impari ipsius w, siquidem m est integer positivus minor
quam n
IT.
4-cos^^. logB — 2cos—)-f-cos!l^.logB — 2cos—)+ etc.
j_cos ("-0™" # iOorB — 2 cos ^—^)
Pro valore pari ipsius w autem
[7@ W( ^ —
log2
ubi signum superius valet pro m pari, inferius pro impari. Ita e. g. invenitur
— 3log2, V(— i) = ^0— 4-7U— 3log2
v/i-ilog3, W{— $ = Wo-$TzsJi-
Ceterum combinatis his aequationibus cum aequatione 64 sponte patet, Wz
generaliter pro quovis valore rationali ipsius z, positivo seu negativo per Wo at-
que logarithmos determinari posse, quod theorema sane maxime est memorabile.
34.
Quum, per art. 28, FIX sit valor integralis fyKe~yd.y1 ab y — 0 usque
ad y — oo, siquidem X-j-1 est quantitas positiva, fit differentiando secundum X
dllX d/vle-Vdy f \ _
-sr = dx =fre
sive
[76] nX.^X = fyle~ylogt/.d.2/> ab ^ = 0 usque ad y = oo
158 DISQÜISITIONES GENER ALES .,
Generaiius statuendo^ = £a, aX-f-a—1 = 6, valor integralis yz6e~-z log z dz,
a 2 = 0 nsque ad z = oo, fit
a a
siquidem simul 6-f-l atque a sunt quantitates positivae, vel aequalis eidem
quantitati cum signo opposito, si utraque ö—j—1, cc e'st negativa.
35.
At non solum productuna IIX.WX, verum etiam ipsa functio WX per in-
integrale determinatum exhiberi potest. Designante k integrum positivum, patet
* Ou
valorem mtegralis J i__x~• d<3?, ab x = 0 usque ad oo = 1
1 y^ 1 j^ 1 ^^ , ^
esse
Porro quum valor integralis f(— TZ^) ^^ generaliter sit = Const. -f- log ^—,
idem inter limites x = 0 atque <2? == 1 erit = logA:, unde patet, valorem in-
integralis S = J*A ~f__— "np)^^ inter eosdem limites esse
1 * 1 f
quam expressionem denotabimus per Q. Discerpamus integrale S in duas partes
Pars prima f^E^-dx, statuendo x =■ yk mutatur in
j i—yk y
unde sponte patet, illius valorem ab x = 0 usque ad x = t, aequalem esse
valori integralis
J i=p
inter eosdem limites. quum manifesto literam y sub hac restrictione in x rau-
tare liceat. Hinc fit integrale 8, inter eosdem limites
Hoc vero integrale, statuendo <a^ = z, transit in
CIRCA SERIEM INFINITAM
1 -j X -f- ETC. 159
quod itaque inter limites z = 0 atque z = 1 sumtum aequale est ipsi Q. Sed
crescente k in infinitum, limes ipsius Q est Wk, limes ipsius —- est 0. limes
i
ipsius k(l — «)t vero est log- sive — logz. Quare habemus
[77] ^
a2=0 usque ad 2r = 1.
36.
Integralia determinata, per quae supra expressae sunt functiones FIX, FIX.WX,
restringere oportuit ad valores ipsius X tales, ut X-J-l evadat quantitas positiva:
haec restrictio ex ipsa deductione demanavit, reveraque facile perspicitur, pro
aliis valoribus ipsius X illa integralia semper fieri infinita, etiamsi functiones
FIX, nX.^X finitae manere possint. Veritati formula 77 certo eadem conditio
subesse debet, ut X-f-1 sit quantitas positiva (alioquin enim integrale certo in-
infinitum evadit, etiamsi functio ^X maneat finita): sed deductio formulae primo
aspectu generalis nullique restrictioni obnoxia esse videtur. Sed propius atten-
denti facile patebit, ipsi analysi, per quam formula eruta est, hanc restrictio-
nem iam messe. Scilicet tacite supposuimus, integrale fjz^&oc cui aequale
-—k 6.x substituimus, habere \dloxem.ßnitum, quae conditio requint,
ut X-f-l sit quantitas positiva. Ex analysi nostra quidem sequitur, haec duo
integralia semper esse aequalia, si hoc extendatur ab x = 0 usque ad x = 1—o>,
illud ab x= 0 usque ad x= A — ia)k, quantumvis parva sit quantitas o>, modo
non sit = 0: sed hoc non obstante in casu eo. ubi X-f-1 non est quantitas posi-
positiva , duo integralia ab x = 0 usque ad eundem terminum x = 1 — <o extensa
neutiquam ad aequalitatem convergunt, sed potius tunc ipsorum differentia, de-
crescente o> in infinitum, in infinitum crescet. Hocce exemplum monstrat, quanta
circumspicientia opus sit in tractandis quantitatibus infinitis, quae in ratiocinüs
analyticis nostro iudicio eatenus tantum sunt admittendae, quatenus ad tjieoriam
limitum reduci possunt.
DISQÜIS1TI0NES GBNERALES
37;
Statuendo in formula 77, z = e~u, patet, illam etiam ita exhiberi posse
Wk = —J ( i__e_M) dw, ab m=oo usque ad m — 0, r. e.
[78] WX=f(^ ^z^;)^M' ab « = 0 usque ad w=oo.
(Perinde valor ipsius FIX in art. 28 allatus, mutatur statuendo ^""^ = 0, in se-
quentem
IIX = /(log-J-) du, a o = 0 usque ad o = l)
Porro patet e formula 77, esse
[79] <FX — W\l= /^£^d^, a z = 0 usque ad sr = 1
ubi praeter X-f-1 etiam fi+1 debet esse quantitas positiva.
Statuendo in eadem formula 77, z = ua, designante a quantitatem positi-
vam, fit
du> ab %=0 usque ad u=l
et quum perinde statui possit, pro valore positivo ipsius 6,
y> K=i I (— y-) dw
patet, fieri
6
ffu — u . <tu+
sive
6x+6~l
integralibus semper ab m = 0 usque ad «=l extensis. Sed ponendo X = o,
integrale posterius indefinite assignari potest; est scilicet ^ log^^), si eva-
* 1"™" * 1/r _
nescere debet pro u = 0; quare quum pro u = 1 statuere oporteat —-R = ~
ent integrale log-g =J —^~—du, ab u= 0 usque ad m= 1, quod theorema
olim ab ill. Eüler per alias methodos erutum est.
CIRCA SEREEM INF1NITAM
cc6
z
o.oo
O.OI
O.O2
O.O3
O.O4
O.O5
O.O6
O.O7
O.O8
O.O9
O.IO
O.II
O.I2
0.13
0.14
0.15
0.16
0.17
0.18
0.19
O.2O
0.21
0.22
0.23
0.24
0.25
0.26
0.27
0.28
0.29
0.30
0.31
0.32
0.33
0.34
035
0.36
0.37
0.38
0.39
0.40
041
0.42
0.43
044
0.45
0.46
0.47
0.48
0.49
0.50
log uz
0.0000000000 0000000000
9.9975287306 5869172624
9.9951278719 8879034144
9.9917964208 8883589748
9.9905334004 0842900595
9.9883378587 9012046216
9.9862088685 5581945437
9.9841455256 3523567773
9.9821469485 3403172902
9.9802122775 3951136603
9.9783406739 6180754713
9-9765313194 0866250820
9.9747834150 9201128963
9-9730961811 6469083029
9.9714688560 8569966779
9.9699006960 1252903489
9.968390974219175 27943
9.9669389805 3852656982
9.9655440208 2789424567
9.9642054164 5653136262
9.9629225038 1404835193
9.9616946338 3869862929
9.9605211715 6456577252
9.9594014956 8673884734
9-9583349981 4361387302
9.9573210837 1550754011
9.9563591696 3881435774
9.9554486852 3498063412
99545890715 5360828076
9-9537797810 2903856417
9.9530202771 4980077695
9.9523100341 4034352140
9.9516485366 5449703876
9.9510352794 8014390879
9.9504697672 5460261315
99499515141 9025401627
9.9494800438 0996487612
9.9490548886 9188515282
9.9486755902 2321722697 .
9.9483416983 6257525751
9.9480527714 1057187897
9.9478083757 8828733374 !
9.9476080858 2329302469
9-9474514835 4291742066
9.9473381584 7445730981
9.9472677074 5205163055
9.9472397344 2994856529
9.9472538503 0190930853
9.9473096727 2650396072
9.9474068259 5806639475
99475449406 8308573196
Tz
— 0.5772156649 01530861
0.5608854578 68674498
0.5447893104 56179789
0.5289210872 85430502
0.5132748789 16830312
0.4978449912 99870371
0.4S26259358 14825705
0.4676124198 67553632
0.4527993380 01712885
0.4381817634 95334764
04237549404 «076796
0.4095142760 71694248
O-3954553339 34292807
0.3815738268 38792064
0.3678656106 07749546
0.3543266779 76279272
0-3409531528 32261794
0.3277412847 48392299
0.3146874437 88860621
0.3017881155 74610030
0.2890398965 92188296
0.2764394897 32192051
0.2639837000 44220200
0.2516694306 96100107
0.2394936791 25936794
0.2274535333 76265408
0.2155461686 00265182
0.2037688437 30623157
0.1921188983 02221732
0.1805937494 20369178
0.1691908888 66799656
0.1579078803 36141874
0.1467423567 95996017
0.1356920179 64169332, ,
0.1247546278 97003946
0.1139280126 83088296
O.IO32IOO582 36977615 s
0.0925987081 87861259
0.0820919618 58406487
0.0716878723 29281510
0.0613845445 85116146
0.0511801337 37897756^
0.0410728433 24024375^
00310609236 71447052
0.0211426703 33530475'
0.0113164225 86445845
- 0.0015805619 87083418^
4-0.0080664890 11364893 y
0.0176262683 88849468^
0.0271002758 35486201,
0.0364899739 78576520
21
162
DISQUISITIONES GENEBALES CIBCA SEEIEM INFESHTAM ETC.
z
0.50
0.51
0.52
0.53
0.54
o-55.
0.56
0.57
0.58
0.59
0.60
0.61
0.62
0.63
0.64
0.65
0.66
0.67
0.68
0.69
0.70
0.71
0.72
0.73
0.74
0.75
0.76
0.77
0.78
0.79
0.80
0.81
0.82
0.83
0.84
0.85
0.86
0.87
0.88
0.89
0.90
0.91
0.92
0.93
0.94
0.95
0.96
0.97
0.98
0.99
1 00
log Ila i
9.9475449406 8308573196
9.9477236538 6182228429
9.9479426085 749455°35i
9.9482014538 7500065798
9.9484998446 4251966174
9.9488374414 4659973817
9.9492139104 0978143536
9.9496289230 7706494873
9.9500821562 8891076887
9.9505732920 5807738191
9.9511020174 5015512544
9.9516680244 6766136244
- 9.9522710099 3756789859
9.9529106754 0213704917
9-953586727° "94797Ö74
9.9542988754 2799988466
9.9550468357 1178337730
9.9558303272 3821579829
9.9566490735 9634064632
9.9575028024 9869525351
9-958391H56 9225480685
9.9593141388 7186450668
9.9602712215 9607519880
9.9612622372 0530119641
9.9622869327 4222223320
9.9633450588 7435456829
9.9644363698 1871920339
9.9655606232 6853798084
9.9667175803 2189101417
9.9679070054 1227146665
9.9691286662 4097614416
9.9703823337 1127271250
9.9716677818 6428658993
9.9729847878 1655271065
9-974333i3J6 9917940601
9.9757125965 9857361442
9.9771229684 9867851092
9.9785640362 2467644771
9.9800355913 8811182162
9.9815374283 333901363°
9.9830693440 8561111078
9.9846311382 9969520321
9.9862226132 1076437381
9-9S78435735 8573930651
9.9894938266 7611664682
9.9911731821 7189109803
9.9928814521 5658844947
9.9946184510 6337679375
9.9963839956 3222432515
9.9981779048 6807320161
0.0000000000 0000000000
4-0.0364899739 78576520^
O-O457967895 61914496^
0.0550221145 79551622^
0.0641673073 66077154^
0.0732336936 45365776.,
0.0822225675 39644344
0.0911351925 40635189^
0.0999728024 44444623^
0.1087366022 51781439
0.1174277690 35011042^
0.1260474527 73476253'
0.1345967771 58445210,-
C.1430768403 68980212^,
0.1514887158 19958383^
0.1598334528 83415463'
0.1681120775 84327804
0.1763255932 71894293^
0.1844749812 67329607.,
0.1925612014 89132418
0.2005851930 56747012^
0.2085478748 73493948^
0.2164501461 89604789^
0.2242928871 46157521^
0.2320769593 00672792I
0.2398032061 35096466^.
0.2474724535 46861164"
0.2550855103 23688336^
0.2626431686 02762795
0.2701462043 14883540"
0.2775953776 14168016''
0.2849914332 93861542^
0.2923351011 88779580
0.2996270965 64887544'^
0.3068681204 96501033
0.3140588602 31568639^
0.3211999895 45479708^
0.3282921690 83820641^
O-335336O466 94485409^.
0.3423322577 49528903^,
0.3492814254 57J35499.
0.3561841611 64059720
0.3630410646 48881123 ..
0.3698527244 06401469^,
0.3766197179 23498793^
0.3833426119 46740214
0.3900219627 42043086
0.3966583163 46662402
04032522088 13771306^
04098041664 49890838^
0.4163147060 45414956
0.4227843350 98467139
METHODUS NOVA
INTEGRALIUM VALORES
PER APPROXIMATIONEM INTENIENDI
AÜCTOEE
CAROLO FBJDERICO GAUSS
SOCIETATI REGIAE SCIENTIARUM EXHDBITA 18U. SEPT.
Commentationes societatis regiae seientiarum Gottingensis recentiores. Vol. in.
Gottingae mdcccxvi.
21'
METHODÜS NOVA
INTEGRALIUM VALORES
PER APPROXIMATIONEM INVENEENDI.
1.
Inter methodos ad determinationem numericam approximatam integraliiim
propositas insignem tenent locum regulae, quas praeeunte summo Newton evolu-
tas dedit Cotes. Scilicet si requiritur valor integralis fydx ab x=g usque ad
x = h sumendus, valores ipsius y pro his valoribus extremis ipsius x et pro
quotcunque aliis intermediis a primo ad ultimum incrementis aequalibus progre-
dientibus, multiplicandi sunt per certos coefficientes numericos, quo facto pro-
ductorum aggregatum in h —g ductum integrale quaesitum suppeditabit, eo ma-
iore praecisione, quo plures termini in hac operatione adhibentur. Quum prin-
cipia huius methodi, quae a geometris rarius quam par est in usum vocari videtur,
nusquam quod sciam plenius explicata sint, pauca de his praemittere ab instituto
nostro haud alienum erit.
2.
Sit n-\-l multitudo terminorum, quos in usum vocare placuit, statuamus-
que h—g = A, ita ut valores ipsius x sint g, g-\—, g-\ , g-\-— etc. us-
usque ad #+A, respondeantque iisdem resp. valores ipsius y hi A, A, A, A" etc.
usque ad A^: denique ponatur indefinite x = g-{-&t, ita ut y etiam spectari
possit tamquam functio ipsius t. Designemus per Y functionem sequentem
166 METHODUS NOVA INTEGKALIDM VALOBES
a (nt—l)(nt—2)(nt—3). . . . (nt—«*
^. (_x) (_2). (_3).... (_wy
nt.(nt~*-%}.{nt—3) (nt— n)
1 .(-1) (-2) (l-n)
nt.{nt— l). (nt— 3) (nt—«)
Y. ü (—l) B —»)
nt.(nt—i). (nf— 2) (nt—«)
T. £ l C — n)
-f- etc.
\A(n) nt(nt—\).(nt — 2) (nt—n
-f" * ».(»—1) (» — 2) l
sive S , ubi repraesentante [i singulos integros 0,1,2,3...»,
nt(nt—l)(nt—2)(nt—3) .... (nt—»)
nt— fj.
valor ipsius T pro w # = ji.
Manifestum erit, 1^ exhibere functionem algebraicam integram ipsius t ordinis n,
atque eius valores pro singulis n-\-l valoribus ipsius t, puta °>-^>~> — 1
aequales esse valoribus ipsius^. Porro patet, si Y' sit functio alia integra pro
iisdem valoribus cum y conspirans, Y'—Y pro iisdem evanescere, adeoque per
factores tt t——, t — —, t t—1 et proin etiam per eorum productum
(quod est ordinis. n-\-l) divisibilem esse, unde patet, Y', nisi prorsus identica sit
cum F, certo ajd altiorem ordinem ascendere debere, sive Y ex omnibus functio-
nibus integris ordinem n haud egredientibus unicam esse, quae pro iUis n +1
valoribus cum y conspiret. Quodsi itaque y, in seriem secundum potestates
ipsius t progredientem evoluta, ante terminum qui implicat t^1 omnino ab-
rumpitur, cum Y identica erit: si vero saltem tarn cito convergit, ut terminos se-
quentes spernere liceat, functio Y inter limites t = 0, t =£ 1 sive x = g, x== h
ipsius y vice tfungi poterit.
3.
Iam integrale nostrum fy&oc transit in kfydt a t = 0 usque ad t = 1
sumendum, cuius loco perea, quae modo monuimus,.adoptabimus hfY&t. Evol-
ifcaque T^ in
p+ etc.
erit fTitydt, a„-^:=0 usque ad *=1, . . .
PEE APPROXTM ATIONEM INVENIENDI.
qua quantitate posita = M^E^\ erit integrale quaesitum
= b(AR+ÄR'+A"R"+AmRm-t- etc. -M
Exempli caussa apponemus computum. coöfficientis E" pro w = 5. Fit hie
T" = 55^—13.54/4 + 59.5V—107.52^H-60.5.#
"Jf" = 2XlX(-l)x(-2)x(-3) = -12
Hinc -1212"= ^-1625 + ^-^4-150 = -^, adeoquei?'=ü
6 '43' 12' ^- 144"
144"
Computus aliquanto brevior evadit, statuendo 2t.—1 = u. Tunc fit
(nu-{-n)(nu + n—2){nu-\-n—4)...(nu—n-\-\){nu — n-\-2)(nu — n)
Ponamus
(nnuu — rui).(nnuu—(n — 2)*).(nnuu—(n—i)*) .(nnuu—(n—6)*)
nnuu — (n — 2 p.)*
ubi numerator desinere debet in ... (nnuu— 9)(nnuu — 1), si n est impar, vel
in ... (nnuu — 4)ww, si n est par, eritque
Iam integrale fT^dt a t = 0 usque ad t = 1 aeeeptum aequale est integrali
.
ab u = — 1 usque ad u = -f" 1.
Statuendo itaque
l/ü*) = aun~x-{-gw"-3+TW»-5-f aww-74. etc.
(sponte enim patet, potestates w", w"~4, w" etc. abesse), integralis pars
J ^— evasesöet pro valore impan ipsius n, pars altera J 2n+t vero
pro valore pari, tmde integrale fT&dt fiet pro n pari
V UrlJ_ + _JL_j *—^etc.)
168 -METHODUS NOVA ÖJTEGEALIÜM VALOKES
pro n impari autem
In exemplo nostro habetur
U"={2buu—25)B5mw—9) = 625w4 — 8h0uu-+- 225 , adeoque
—1212" = —^A25—8^+225) = —ff ut supra.
Observare convenit, fieri ü(n~^ = U^\ adeoque /T(n~^dt = ±
signo superiore valente pro n pari, inferiore pro impari. Quare quum facile per-
spiciatur, perinde haberi M("~ti = + M^\ semper erit BP^-v) = !&&, sive e
coefficientibus R, R', R".... ]£n) ultimus primo aequalis, penultimus secundo
et sie porro.
4.
Valores numericos horum coefficientium a Cotesio usque ad n =. 10 com-
putatos ex Harmonia Mensnrarum huc adscribimus.
Pro n = 1 sive terminis duobus.
R = Jx = 4^
Pro n = 2 sive terminis tribus.
R = R" = %, 22'= f
Pro w = 3 sive terminis quatuor.
12 = 22" = i, R'=R"= f
Pro w = 4 sive terminis quinque.
t> r>"" •?• T>' ZV" •! c X>" 9
Pro w = 5 sive terminis sex.
R = 12V = ^, 12' = 12"" = ff, 12" = 12'" = TVv
Pro n = 6 sive terminis septem.
12 = Än= AV, Ä'= 12V= ^, 12" = 12IV = ^fö-, 12"' = T*fe
Pro w = 7 sive terminis octo.
^ ;= 12ra= ^-l^-, 12'=: 12VI^ tVWt, ä"= 12v='^o-5 ä"= 12""= W¥W
Pro w = 8 sive terminis novem.
12 = 12VIII=: &a V ?
PEß APPJBOXIMATIONEM INVENDSNDI.
Pro n = 9 jsive terminis decem.
B" =# = &#&
Pro n = 10 sive terminis undecim.
-r*k -r^k Y -r^k f tu IY ■»%, #/ ■»%, /fTT
#J f "f ß A fi T Lß f * o C K ? K t-ß1 7J'1"
IC = IC = XsVtW' ■**' =-— -"- ——: ~TiTW8W- 2t = XL
t>'// -pvii ,... piv t>vi a «o « r>v
JtC = x£ = ^247% , -tt = xt = — HoaT' 2t
rT'
5.
Quum formula M^AR-{-ÄR'-\-ÄIg+Ä'Il" + etc. -|-^(w)i2(w)) integrale
ab oc = €f usque ad <2?=^-f-A, sive integrale Afydt & t = 0 usque
ad t = 1 exacte quidem exhibeat, quoties y in seriem evoluta potestatem f"
non transscendit, sed approximate tantum, quoties y ttltraprogreditur, superest,
ut errorem, quem inducunt termini proxime sequentes, assignare doceamus. De-
Design emiis generaliter per U>m) differentiam inter valorem verum integralis ff1 dt
a t = 0 usque ad t = 1, atque valorem ex formula prodeuntem, ita ut sit
k = 1 —R — R'—R"—R'— etc. —BW
kr= i — ^ W
k= ^
k"'= i—.i
etc.
etc.
etc.
etc. Patet igitur, si y evolvatur in seriem
etc.
diiferentiam inter valorem verum integralis fydt atque valorem approximatum
formulae exprimi per
Kk -f K'k'+ K"W-\- K'"k"'+ etc.
Sed manifesto k, Je, k" etc. usque ad kfö sponte fiunt = 0 : correctio itaque for-
formulae approximatae erit
K(n+1) tfn+i) _|_ K(n+2) fcn+2) _j_ R(n+S) ^(«+8) _|_ etc.
Indolem quantitatum ^"^1, ^w+2) etc. infra aecuratius perscrutabimur; hie
sufiieiat, valores numericos primae aut seeundae', pro singulis valoribus ipsius n,
apposuisse, ut gradus praecisionis, quam formula approximata aifert, inde aesti-
mari possit.
22
170 METHODUS NOVA INTEGRALIÜM VALORES
Pro n = 1 habemus Je'= —£. k'" =— ±, k""=—
Pro n= 2 invenimus k'"= 0, #'"= — TfD-, &v = —
Pro valore pari ipsius n ubique hie fieri animadvertimus k^1^ = 0, ac
praeterea ^("+3^ = OljiI ^(»+2). pr0 valore impari ipsius w autem ubique prodit
£(»+2) __ n±_l ^(w+1)> Ratio horum eventuum facile e considerationibus sequenti-
bus depromitur.
Designemus generaliter per l^ differentiam inter valorem verum huius in-
tegralis f(t—i)mdt a t=0 usque ad t=l. atque valorem eura, quem for-
mula approximata profert, ita ut habeatur
etc.
integrali a t = 0 usque ad t = 1 aeeepto. Manifeste pro valore impari ipsius
m evanescet turn valor verus integralis turn valor approximatus: erititaque l'= 0,
V" =0, ly = 0, lm = 0 etc. sive generaliter J(m) = 0 pro valore impari ipsius wz.
Pro valore pari autem ipsius m, formulae tribuiraus formam hanece
si simul fuerit n par; vel hanc
^+(ri2'(-4ri2"+ etc.
si simul fuerit n impar.
PER APPBOXIMATIONEM INVENEENDI. 171
Si igitur per evolutionem ipsius y in seriem secundum potestates ipsius
t — £ progredientem prodit
y = L+L'{t—t) + LH(t-tf+ir{t—t)*+ etc.
correctio valori approximato integralis fydt a t= 0 usque ad t = 1 appli-
canda erit
T 7 I T"l" I T'H'l"" I T^'j^1 ( i.
±il-\-L/1 -\-L l -\-Jb l -\- etc.
aut potius, quum l^ necessario evanescat pro yalore quovis integro ipsius m
haud maiori quam n, correctio erit
pro w pari, vel
pro w impari.
Facillime iam correctiones l(m) ad täm) reducuntur et vice versa. Quum
enim habeatur
(t - i)m = tm — im. r^+i. ^^ r~2+ etc.
erit
Et perinde fit /
ÖM+ etc.
Ex posteriori formula eiicientur termini, ubi l afficitur indice impari: utraque
autem continuanda est tantummodo usque ad indicem n-\-\ (inclus.). Manifesto
itaque habebimus
pro n pari
__ ^±1. /(«+2)
pro n impari
unde demanant observationes supra indicatae
22
METHODUS HOVA,l»TEGEAIiIÜM VALOBES
Generaliter itaque loquendo praestabit, in applicanda methodo Cotesiana
ipsi n tribuere valorem parem, seu terminorum multitudinem imparem in usum
vocare. Perparum scilicet praecisio augebitur, si loco valoris paris ipsius n ad
imparem proxime maiorem ascendamus, quum error maneat eiusdem ordinis, licet
coefficiente aliquantulum minori affectus. Contra ascendendo a valore impari
ipsius n ad parem proxime sequentem, error duobus ordinibus promovebitur, in-
superque coefficiens notabilius imminutus praecisionem augebit. Ita si quinque
termini adhibentur, sive pro n = A, error proxime exprimitur per
vel per —WwtL6; si statuitur n = 5, error erit proxime
—ttWö"-^6' adeoque ne ad semissem quidem prioris depressus: contra faciendo
n — 6, error fit proxime = — mri-sir-^8 vel = — -^-^L8, praecisioque tanto
magis aucta, quo citius series, in quam functio evolvitur, iam per se convergit.
7.
Postquam haecce circa methodum Cotesii praemisimus, ad disquisitionem
generalem progredimur, abiiciendo conditionem, ut valores ipsius x progressione
arithmetica procedant. Problema itaque aggredimur, determinare valorem inte-
gralis fydx inter limites datos ex aliquot valoribus datis rpsius y, v«l exacte vel
quam proxime. Supponamus, integrale sumendum esse ab x — g usque ad
x = g -|- A, introducamusque loco ipsius x aliam variabilem t = ^^, ita ut
integrale kfy&t a £=0 usque ad t — 1 investigare oporteat. Respondeant
n-\-\ valores dati ipsius y hi A, Ä, A", A'" A^ valoribus ipsius t inaequali-
bus his a, a, a", a"— dn\ designemusque per Y functionem algebraicam inte-
gram ordinis n hancce:
4 (^—«') {t — a") {t — a").... {t — a(n))
(a — a')(a — a")(a—a'") (a — a(n))
, ./ (t — a) (l — a")(t — a'").... (t — aW)
~T~ " (a'~ a) (a1- u") (a1— a'").... {a1— a(*))
— a'")....
-4-A" (^ —«) #-
■ ' (a"—a)(a"—a'){a"—a'")....(a"—a(n))
-f- etc.
1 Ain) (t—a) (t — a') (t — a").... (t—ai11-1))
1 ^- (a(») _ ö) (a(w) _ ö'j(ap) _ a" j (a{») _ o(»-i))
Manifesto valores huius functionis, si t alicui quantitatum «, a, a\ d" a^m
aequalis ponitur, coincidunt cum valoribus respondentibus functionis y, unde per
PEE APPEOXIMATJOXEM INVENIENm. If 3
inde ut in art. 2. concludimus, Y eum y identicam esse» quoties y qaoqne üit
functio algebraica integra ordinem n non transscendensr aut saltem ipsius y vice
fungi posse, si y in seriem secundum potestates ipsius t progredientem conversa
tantam convergentiam exhibeat, ut terminos altiorum ordinum negKgere üceat.
Iam ad eruendum integrale fYdt singulas partes ipsius Y consideremus.
Designemus productum,
(t—a){t—a)(t—a")(t—a'").... [t—cfa)
per T, fiatque per evolutionem hums producti
. T = t^+aP-t-dt^ + art*-*-^ etc.
Numerator fractionis, per quam, in parte prima ipsius Y, multiplieata est A, fit
= -?—; numeratores in partibus sequentibus perinde sunt -—,, ;—7,, -—m etc.
Denominatores vero nihil aliud sunt, nisi valores determinati horum numeratorum,
si resp. statuitur t = a, t =d, t = a", t = d" etc.: -denotemus hos denomina-
denominatores resp. per M, M', M", M'" etc., ita ut sit
V— AT \ A'T \ A"T I etc ' I A(n)T
X Mit—a) ' M'(t — a')~l~M"(t—a") ' CtU' "" M{n)(t— ain))
Quum fiat T =■ 0, pro t = a, habemus aequationem identicam
/+1+o» + a'/-1 + a"/-2+ etc. -faW = 0
adeoque
T= tn+i -an+i +a(tn-an) + a\tn~i-a^ + a''^ — «""')+ etc. '
Hinc dividendo per t — a fit
T .» i .»—1 i .»—2 , 3.«—3 , ,
= t -\-at -\-aat -\-a t -j- etc.
i .»-1 , j(»—2) , .»—3 , >
-\-at -\-aatK J-\-aaat -f- etc.
»-2 , ..,..,»-3 et(j , a,fl»-2
-faV*~3 -f-'etc.
-f- etc. etc.
n—i
If 4 Mmmmm nota" jntegeaodm valobes
Valor huius functionis pro t =a colligitur
(_2)aV-3+ etc.
j rp
Hinc M aequalis valori ipsius -rj pro t= a, uti etiam aliunde constat. Perinde
M', M", M'", etc. erunt valores ipsius -^ pro t = a, t = a", # = «'" etc.
Porro invenimus valorem integralis f^i, a ^ = 0 usque ad ^ = 1,
1 , a aa . az . . »
+ 7 + »-=I + »-=i+ etc. +fl
JÜ J^ J^ etc. +0C«"-1
++
, a' , a'o , > , / «—2
H -+ etc. -{-aa
"_»—3
-f- etc. etc.
-\ 1- etc. -\-a'a
1 «— 2 ' '
quos terminos ordine sequenti disponemus:
+ etc. +
+ etc. +a(l|-2))
-f etc. +a(w~3))
ir[a -{-aa -{-aa -f- etc. -\-a> J)
-f- etc.
Sed manifesto eadem quantitas prodit, si in producto e multiplicatione functio-
functionis T in seriem infinitam
.— 3
etc.
orto, reiectis omnibus terminis, qui implicant potestates ipsius t exponentibus
negativis (sive brevius, in producti parte ea, quae est functio integra ipsius t)
pro t scribitur a. Supponamus itaque. fieri *)
*-{- etc.) = T"+ T"
*) Vix opus erit monere, characteres T, T', T" alio sensu hie aeeipi, quam in art. 2.
PER APPEOXMATIOHE34 ÖTVENJEKDI. , IT 5
ita ut T' sit functio integra ipsius t in hoc producto contenta, T" vero pars al-
tera t scilicet series descendens in infinitumque excurrens. Quo facto valor inte-
gralis fjzra a £ = 0 usque ad t = 1 aequalis erit valori functionis T' pro
t = a. Quodsi itaque valores determinatos functionis
T
{"■■"■ \
Kit
pro t = a, t = a, t = a", t — a'" etc. usque ad £ = d-n) resp. per 12, R\ R",
R'" l&n) denotamus, integrale fYdt a t = 0 usque ad £ == i fiet
i"-\- etc.
quod per A multiplicatum exhibebit valorem vel verum vel approximatum inte-
gralis fy&x ab x = g usque ad x = g -j- A.
9.
Hae operationes aliquanto facilius perficiuntur, si loco indeterminatae t in-
troducitur alia u = 1t — 1. Scribimus quoque brevitatis caussa b = 1a—1,
b'= 1a — 1, b" =■ 2 a"—1 etc. Transeat T, substituto pro t valore ^-M-f-^-, in
^5+j, sive sit
U = {u - 6) (« — b') (u — b") .... {u—bn)
Erit itaque -r- = i • t— , adeoque Mt M', M" etc. valores determinati ipsius
-£• -r-> si deinceps statuitur u = b, u = b', u = b" etc.
2W dM ' r
Quum series t~x-\-±t~2-{-%t~*-{-±t~k-\- etc. nihil aliud sit quam
7^~i: Per substitutionem ^ = i-M+-J- necessario transibit in
2m—1 -f-f w~-f-f u~h-\-\vT1 -f- etc. Quodsi itaque statuimus
ita ut CT sit functio integra ipsius u in hoc producto contenta, U" vero pars al-
tera, puta series descendens infmita, patet esse
T+T" = + [&
Sedmanifesto T\ tamquam functio integra ipsius t, per substitutionem t =
necessario funetionem integram ipsius u producet: contra T", quae non continet
nisi potestates negativas ipsius t, per eandem substitutionem tantummodo potesta-
1T6
tes negativas ipsius u gignet. Quara ob rem V nihü aliud erit quam 2" T' per
haue substitutionem transformata, ac perinde 27" produeta erit ex 2" T". Nihil
itaque intererit, sive in -^r substituamus t = a, sive in -5-^ faciamus
u =z b, unde colli^mus, R, JR', JB", i2'" etc. etiam esse valores determinatos
Jjr
funetioms ■, TT pro u =■ b. u = i', w = i", m ■= i'w etc.
Um ;
10.
Antequam ulterius progrediamur, haecce praecepta per exemplum illustra-
bimus. Sit n = 5, statuamusque a = 0, d =■ \, a" = J-, «'"= -|, «""=■ -f-, a'""=l.
Eünc fit
Multiplicando per f1 -f- 4- ^~+^- ^~3 -f-^ ^~ + etc. obtinemus
■* —~ ^ T^ "T~(T^ Y?^ I 75J«f 7'5 0 <T
Valores itaque coefiieientium JS, ^', ^", ^'", JS"", JR'"" exprimuntur per funetio-
nem fraetam
6ts—
in qua pro ^ deineeps substituendi sunt valores 0, 4-, J-, f, ^, 1. Aliquanto bre-
vior est methodus altera, quae suppeditat b = — 1, b' = — f, b" — — -§-, Ä'" = £,
unde -R. ^', ^" etc. erunt valores funetionis fraetae
pro u = — i, u~ —f, m=: —-|- etc. Utraque methodus eosdem numeros pro-
fert, quos in art. 4. ex Harmonia Mensurarum tradidimus. Ceterum in casu
tali, qualem hocce exemplum sistit, ubi a, d. a" etc. sunt quantitates rationa-
les, valores denominatoris -^ commodius in forma primitiva computantur, puta
(ö —'«')(a — d').(a—d")....(« — a^) pro t = a ac perinde de reliquis. Idem
valetdedenominatore ~, quipro w = 6 fit =(b-~b')(b—b")(b—b'")....(b—bM).
PEE APPEOXIMATIONEM: ENVENIENPI.
11.
Quoties a, d, a" etc. vel ex parte vel omnes snnt irrationales,. utilis erit
transformatio functionis fractae, ex qua numeros JR, R', R" etc. derivamus, in
functionem integram: principia talis transformationis, quum in libris algebraicis
non inveniantur, hoc loco breviter explicabimus. Propositis scilicet tribus functio-
nibus integris Z, C, C indeterminatae' z, quaeritur functio integra, quae fractae
Y vice fungi possit, quatenus pro z accipitur radix quaecunque aequationis £'== 0.
Supponemus autem, £ pro nullo horum valorum ipsius z evanescere, sive quod
eodem redit, £ atque C .nullum divisorem communem indeterrainatum implicare.
Exponentes potestatum altissimarum ipsius z in £ atque t,' per k, k' denotabimus.
Dividatur sueto more £ per £', donec residui ordo infra k' depressus sit;
statuatur residuum = ^, eiusque ordo = k", ita ut ^2^' sit residui terminus
altissimus; divisionis quotientem ponemus = f-. Perinde ex divisione functionis
rm . . , o'
C,' per L," prodeat residuum yr ordinis k"\ quotiens fr; dein rursus e divisione
functionis 4" per 4'" prodeat residuum -^- ordinis k"" atque quotiens ^ et sie
porro, donec in serie functionum £", tf". ^""etc., quae singulae terminum suum
altissimum coefficiente 1 affectum habebunt, perveniatur ad tjP) = 1. Hoc tan-
dem evenire debere facile perspicitur, quum quaelibet functionum C, U £'\ Vetc.
cum praecedenti divisorem communem indeterminatum habere nequeat, adeoque
certo divisio absque residuo fieri nequeat, quamdiu divisor fuerit ordinis maioris
quam 0. Habebimus igitur seriem aequationum
im \ii f ii n f in
K 4 p 4
\ii f ii n
= K 4 —p
f lim \ in f m ni f im
4> = k 4) —p 4>
etc. usque ad
£(m) __ ^(w—2) £(m-2) (m—2)^(m—l)
ubi T, 4'". r'".--.C(w) sunt funetiones integrae ipsius z ordinis k'\ k"\ k""...../Jm);
numeri k', k", k'" kW continuo decrescentes usque ad ultimum k^ = 0:
p>p,p\ p'"etc. quoque funetiones integrae ipsius z ordinis k—k', k'—k'\ k"—k'",
V—#""etc. (excepto casu, ubi k<C.k\ in quo manifesto statui debet p = 0).
His ita praeparatis formamus secundam seriem functionum integrarum ipsius
z, puta T], ?]', Tj", T]'" TjH. Et quidem statuemus i) = 1, i)' = 0, reliquas vero
23
178 METHODÜS NOVA INTEGEALUBl VALOEES
singulas e binis praecedentibus per eandem legem derivamus, per quam functio-
nes £, £', £", £'" etc. inter se nexae sunt, scilicet per aequationes
T]'""= X'"t]'"— fx[" etc. usque ad
T](m) =
Manifesto r\"= X hie est ordinis 0; r\" =■—\p ordinis k'—k", et perinde se-
quentes r\"\ r["" etc. resp. ordinis k'—k'", k'—&""etc, ita ut ultima tj(b') ascen-
datadordinem k'— k^^.
Porro consideremus tertiam funetionum seriem, £ — £i]» C,'—C,r\, t,"—Cyi\"i
L,'"—£u]'"etc, inter cuius terminos quosvis ternos consequentes manifesto similis
relatio intercedet, scilicet
4""_ 4n"" = x"D"- Crj") -vT"- W)
Iam prima harum funetionum fit = 0, seeunda =£>': hinc facile colligitur, sin-
singulas per £' divisibiles fore.
Hinc autem nullo negotio sequitur, loco fractionis y adoptari posse funetio-
nem integram Zrfm\ quatenus quidem ipsi z non tribuantur alii valores nisi qui
sint radices aequationis £'=0: manifesto enim differentia C1—^7!"8) pro ^^
valoreipsius z necessario evanescit, quum 1 — £r](m) —£(m)—£i(](m) per C,' sit di-
visibilis.
Loco funetionis Zrf™) etiam adoptari poterit eius residuum ex divisione per
£' ortum, cuius ordo erit inferior ordine funetionis £'.
Ceterum hocce residuum commodius per algorithmum sequentem immediate
eruere licet. - Formentur aequationes sequentes
Z =q'ü' +Z'
Z' =q't;' -\-Z"
Z" = q'" £'"-{-Z'"
Z'"= q-'T+Z"" etc. usque ad
PER APPEOXIMATIONEM DfVENIENDL lf 0
scilicet deinceps dividendo Z per £', dein residuum primae divisionis Z' per £",
turn residuum secundae divisionis per L,'" ac sie porro. Quum residuum semper
ad ordinem inferiorem pertineat quam divisor, ordo functionum Z\ Z'\ Zw, Zrmetc.
erit resp. inferior quam k', k'\ k"\ k"" etc.; ultima vero Z^ necessario fit = 0,
quum divisor L}m^ sit = 1. Habemus itaque
tr+ etc. +?(m)£(m)
Quatenus autem pro z solae radices aequationis £' = 0 accipiuntur, fit 4'== 0,
£" = £tj", 4'"= £*]'"» C""= £*]"" etc., unde sub eadem restrictione erit
| = ^"r|"+^"r]'"+/"r]""+ etc. +jO»)ijH
Ordo vero huius expressionis necessario erit infra ^:': quum enim ordo quotien-
tium q", q", q""etc. esse debeat infra k'—k", k"~ k'", k'"—k""etc., ordo singu-
larum partium q"rf, q"'f\\ q""y\"""etc. erit infra £'— >t", >t'— k"\ k'—k"" etc.
Denique adhuc observamus, si forte inter valores indeterminatae z, quos in
z
fractione y substituere oporteat, rationales cum irrationalibus mixti reperiantur,
magis e re fore, illos ab his separare atque hos solos in aequatione C'= 0 com-
prehendere. Pro rationalibus enim valoribus calculi compendio opus non erit; pro
irrationalibus autem calculus tanto simplicior erit, quo minor foerit gradus tfunctio-
nis integrae, ad quam fractam. reducere licet.
12.
Ecce nunc exemplum transformationis in art. praec explicatae. Proposita
sit functio fracta
in qua z indefinite repraesentat radices aequationis
Si hie omnes septem radices complecti vellemus, ad funetionem integram
sexti ordinis delaberemur. Manifesto autem pro valore rationali z = 0 compu-
tus fractionis obvius est, datque valorem ^^-: quapropter seposita hac radke in
aequatione sexti gradus subsistemus:
23*
180
MEISOBUS NOYA ÜSTEGBATJÜM VALORES
quo pacto facile praevidemus orturam esse functionem integram quarti ordinis.
Iam ex applicatione praeceptorum praecedentium prodeunt sequentia:
■fllf
•f ntt
V
V'
Y] =
Y] =
tt
T] =
zz — -f-
1
H
— H7
l
0
tt
P = V3
3 9 O O
o o ^>
w
" A
9 == T
Hinc tandem derivatur functio integra fractioni propositae aequivalens
1_ 5 7 3 -y -y f T 9 4- 7
13.
Ad determinandum gradum praecisionis, qua formula nostra integralis
JRJ.4-JR'J.'4-JR"J."+ etc. +JR(nU(n) gaudet, statuamus generaliter
m+ etc.
ita ut &(m) sit diiferentia inter integralis ff71 dt a, t = 0 irsque ad t=\ sumti
valorem verum atque approximatum. Habebimus itaque, singulis fractionibus in
series evolutis,
PEE APPEOXIMATIONEM INVENIENDI. 181
etc-
—*')r*+(-i—rjr^+f-i- —Är'^r^-f. etc.
+ijr4+ etc. —6
si statuimus
6 = kr* + k'r*+k"r* + kmf-* + etc.
sive potius (quum iam sciamus, k, k\ k", k'" etc. usque ad ]£$ sponte evanescere
debere)
e = *(*+or(»+*)+Ä(»+*)r(»+»)+Ä(»+»)r(»+*)+ etc.
Multiplicando per T fit
T( + ^+t4^>+ etc. +J^) = T'+ T- TB
+ ^
Pars prior huius aequationis est functio integra ipsius t ordinis n, eiusque valo-
res determinati pro t = a, t = a, t= a" etc. resp. fiunt MR, M'R', M"R"etc.:
quapropter, quum eadem valeant de functione T\ uti ex ipso modo numeros
JR, ß', JK" etc. determinandi perspicuum est, necessario illa pars prior aequatio-
aequationis identica esse debet cum T", adeoque T"= T6. Oritur itaque 6 ex evolu-
tione fractionis -^-, quo pacto coefficientes 1cn \ Je1 ' etc. quousque libet de-
terminari poterunt. Quibus inventis correctio valoris nostri approximati integra-
lis fy&t erit
si series, in quam evolvitur y, est
y = K+K't+KHtt+Kmt-\- etc.
14.
Si magis placet, correctionem exprimere per coefficientes seriei secundum
potestates ipsius t—4- progredientis
illa erit
182 METHODUS NOVA INTEGBAIilüM VALOEES
si generaliter per /H exprimimus correctionem valoris approximati integralis
f(t — lr)mdt. Hae correctiones l(m) cum correctionibus k£m) nexae erunt per ae-
quationem
lim) = ^(m)_imA.(m-l) + i.^^Il^-2)__i.m.m-l.m-2^(m-3) ,
X. • A 1 • ^ « 3
Quo vero illas independenter eruere possimus, perpendamus, functionein 0 per
substitutionem t = \u-\- \ transire in
1k{u~x — w~2-f- u~s— u~k-\- etc.)
+ 4^'(m~2 — 2w~3-f 3w~4— 4M~54-etc.)
-f 8 ¥ {u~3 — 3 w~4 -f 6 w~5 —-10 w~6 + etc.)
-f 16 F'(w~4— 4 w~5 4-1 0 u~6 — 2 0 w~7 -f etc.)
-f- etc.
sive in
+ D+iAr'— i^)w~4+ etc.
sive in
2/m~1 + 4 /'w~2 + 8Tw +16r"w~4-f etc.
sive denique , quum a priori sciamus, l, l\ l", V" etc. usque ad l^n) sponte eva-
nescere, in
At 6 = -y ; quare quum Tt T" per substitutionem t = 4ru-\-± transeant in
-j[^, —, (art. 9), functio 0 per eandem substitutionem transibit in ^-. Quodsi
itaque seriem ex evolutione fractionis -^ oriundam per Q designamus, erit
Q = 2"+1^"+1)ii"("+2)+2"+2/("+2)i|-("+8)+ 2w+3/(w+3)W-^+4) + etc.
quo pacto coefiicientes rn \ rn 2^etc. quousque lubet erui poterunt.
Ita in exemplo art. 10 invenimus
Q =—
PER APPROXIMATIONEM INVEN1ENDI. I8S
adeoque correctio valoris approximati integralis
„ _5A»»
T3 7 £ 0 0 00 0'
15.
Coeffreiens K^) functionis ^ in seriem evolutae fit, per theorema Taylori,
aequalis valori ipsius
sive
1.2.3....»» d
pro £ = 0 sive a? = g; perinde cogfftciens Z/m) est valor eiusdem expressionis
pro t = % sive w=0 sive % = (jr-\-4rk: utrique coefficienti ordinem m tribue-
mus. Generaliter itaque loquendo integratio nostra usque ad ordinem n inclus.
exacta erit, quicunque valores pro at d, a".. . . «^ accipiantur. Attamen hinc
nüiil obstat, quominus pro valoribus harum quantitatum scite electis praecisio ad
altiorem gradum evehatur. Ita iam supra vidimus, in methodo Cotesh i. e. pro
a — 0, a = —, a" = —, d" = ~ etc. praecisionem sponte ad ordinem n-{-\ inclus.
extendi, quoties n sit numerus par. Generaliter patet, si valores a, d, a, d"etc.
ita fuerint electi, ut in functione T" vel U" ab initio excidat terminus unus plu-
resve, praecisionem totidem gradibus ultra ordinem n promotum iri, quot termini
exciderint. Hinc facile colligitur, quum multitudo quantitatum quas eligere con-
ceditur sit n-\-l, per idoneam earum determinationem praecisionem semper ad
ordinem 2w-f-l inclus. evehi posse, quo pacto adiumento w-f-1 terminorum eun-
dem praecisionis ordinem assequi licebit, ad quem attingendum 2w-j-l vel 1n-\-1
terminos in usum vocare oporteret, si Cotesii methodum sequeremur.
16.
Totum hoc negotium in eo vertitur, ut pro quovis valore dato ipsius n functio-
nem T eruamus formae ^*+1-f-a^-f-a'^"-}-«"^ etc. itaque comparatam, ut
in producto
f etc.)
evoluto potestates f\ f~2, r~3.. . . f~(w+1) omnes nanciscantur coefficientem 0;
aut si magis placet, functionem U formae ur^'x-\-16un-\-16'un~~x-\~16"ut^~%-\- etc.,
cuius productum per u~l -f- -^w~-f- ^ m~5-f- -f u~7-f- etc. liberum evadat a potesta-
184 METH0DUS XOVA INTEGBALIÜM VALOEES
tibus vT1, u~2, u~3, u~k. . .. vT^1). Modus posterior aliquanto simplicior erit:
<juum enim facile perspiciatur, coefficientes ipsius U, ut conditioni praescriptae
satisfiat, alternatim evanescere debere, sive statui fi = 0, €"= 0, t>"" = 0 etc.,
laboris dimidia fere pars iam absoluta censenda erit. Evolvamus casus quosdam
simpliciores.
I. Pro n = 0, coefficiens unicus ipsius f~x in producto
(f+a)(r*4-ir*++r*_|_ etc.)
evanescere debet. Qui quum fiat =£-\-a, habemus a = —^, sive T=t—£.
Perinde U= u.
II. Pro n = 1, determinatio ipsius T pendet a duabus aequationibus
0 =
0 =
unde deducimus a = —1, a' = -f-^, sive T=tt—£-(-£. Determinatio functio-
nis U unicam aequationem affert
unde ^' =—-f, sive U = uu — 4-.
III. Pro w = 2, functio T determinatur adiumento trium aequationum
0 =
0 =
0 =
unde nanciscimur a=—f, a = -§-, ot"^=— ^V, adeoque T^=ts—%tt-{-%t—2V
Ad determinandam U unica aequatio sufficit
unde 6' = —|- sive TJ =. us — -§-w.
Attamen hunc modum, qui calculos continuo molestiores adducit, hie ul-
terias non persequemur, sed ad fontem genuinum solutionis generalis progre-
diemur.
PEE APPROXIMATIONEM INVENIENDI. 185
17.
Proposita fractione continua
w-\—-
w'"-\- etc.
constat, fractiones continuo magis appropinquantes inveniri per algorithmum
sequentem. Formentur duae quantitatum series, F, V, F", V" etc.,
W, W, W\ W" etc. per hasce formulas
F =±l 0 TF = 1
F' = v W = wW
V" = w'V +v'V W" = w'W +v'W
V" = w" V"+1?" F' W7"' = w" W" +v"W
V"" = ww F'"+1?'" F" W'" = w'" W'"-\- v'" W
etc. eritque
W
V"
W-\ r
W
V" v
W"' , »'
et sie porro. Praeterea constat, vel facile ex ipsis aequationibus praecedentibus
confirmatur, esse
VW ~V'W =—v
VW" —V"W =-\-vv
W — V W = —vvv
Flll TXT'IH TTUll TTTIH i ' " '"
W —v W = -\-vvv v
etc. Hinc perspieuum est, seriei
vv' , vv'v" vv'v"v'" ,
L_ I
'W"\W"W'" w'"W""\
24
v
tewmnum pnmum esse = -^
V"
summam duorum termmorum pnmorum = ^7
V'"
summam tnum termmorum pnmorum = —f^
v""
summam quatuor termmorum pnmorum = ^7-,
et sie porro; quocirca series ipsa vel in infinitum vel usque dum abrumpatur con-
tinuata ipsam fractionem continuam 9 exprimet. Simul hinc habetur differentia
V V" V"
inter 9 atque smgulas iractiones appropinquantes ^7, ^, -^7, etc.
E formula 33 art. 14 Disquisitionum generalium circa seriem inßnitam mu-
tando t in —, facile obtinemus transformationem seriei
fj-i-f M*7-f- etc.
in fractionem continuam sequentem
1
u-
u —
2.2
3. ä
U-
3.3
5.7
U-
4.4
TTäi
— etc.
ita ut habeatur
v = l, v'=r —i, v"= -A, v'"= — A-. ^""= —H- etc.
w = w' = w" = w'" = w"" etc. = w.
Hinc pro F, F\ F", F" etc. fF, TF', TF", W" etc. nanciseimur valores se
quentes
F = 0, TF = 1
F = 1, TF' =«
F"=«, TF" ==««—■J.
F" = m-A, TF'" = us—iu
F""= k3 -ff«, TF"" = u'
Vy = w4 —^tt«4-^r, TFV = w5—
= u6 — |-^--t-ff§ww — tHIt, TF™ = w7—f|-w5+-fH-^3—^V« etc
PER APPBOXBfATlONEÄ INVEN1ESDL
Leviattentione adhibita elucet, singulas F. V, V", F'"etc. W, W, W", W'"ebc.
fieri functiones integras indeterminatae u; terminum altissimum in V("b fieri
umr~\ potestatesque um~2, «"*-*, u™"* etc. abesse; terminum altissimum vero in
WW fieri um, atque abesse potestates u1"^1, u™^3, u™-* etc. Per ea autem, quae
supra demonstravimus, erit
O___J I 1 _i 2_.J . 2.2.3.3 . 2.2.3.3.4.4 ,
Y JF JF'' 3 W W" ' 3 . 3 . 5 W" W"~T~ 3.3.5.5.7 W'"W"" "+" 3 . 3 . 5 . 5 . 7 .7.9 W""W'""~^~ eW*
ac proin generaliter
F<w) 2.2.3.3 m.m
? W(M) 3 . 3 . 5 . 5 .... B m — l)B«t +1) W(m) JTAW+1)
_j 2.2.3.3 (wi-H)(m+l)
"T~3.3.5.5 B«t + l)B»»4-3) W(m+l) W(m+t)
-f- etc.
Si lgitur cp — -^^ in seriem descendentem convertitur, eius terminus primus erit
2.2. 3. 3.... m .mu-(*m+t)
3. 3 . 5. 5 . .. .Bm—l)Bm+l)
Productum vero 9 W^ compositum erit e functione integra V^ atque serie
infinita, cuius terminus primus
2.2.3.3
3.3.5.5 B«t—l)Bffl+l)
Hinc igitur sponte inventa est functio U ordinis n-\-\\ quae conditioni in
art. praec. stabilitae satisfacit, scilicet ut productum 9 U liberum evadat a po-
testatibus vT1, w~2, m m~^x\ Scilicet non est alia quam W^^, simul-
que patet, U' aequalem fieri ipsi F^+1), nee non terminum primum ipsius
ü" esse
__ 2.2.3.3 (w+1)(w+1) _(»+2)
3.3.5.5 B+l)B» + 3)
Quodsi igitur pro b, b', b" p*' aeeipiuntur radices aequationis W^n+l' = 0,
valoresque coefneientium J2, R', R" Rr> per praeeepta supra tradita eruun-
tur, formula nostra integralis praecisione gaudebit ad ordinem 1n-\-\ ascen-
dente, eiusque correctio exprimetur proxime per
1 . 2.2.3.3 (n-H)(»-H) rBn+2) __ 1.1.2.2.3.3 («
2sn+t* 3.3.5.5 Bw+l)Bn+3) 2.6.6.10.10.14 Dn+ 2)D »
24
#
188 METHODDS NOVA INTEGEAUÜM VALOEES
18.
Disquisitiones art. praec. functiones idoneas 27< pro singulis valoribus nu-
meri n invenire quidem docent, sed successive tan turn, dum a valoribus minori-
bus ad maiores transeundum est. Facile autem animadvertimus, has functiones
generaliter exprimi per
, (n + i)n(n —l)(n — 2) „3 (n + i)n(n—i)(n — 2)(w — 3)(w-4) r)r_b
' 2 4Bw + l)Bw — 1) 24 ßBw+l)Bw —1)BW—3)
_
2.Bw+i) ' 2. 4Bw + l)Bw — 1) 2.4. ß.Bw+l)Bw —1)BW—3)
-f- etc.
sive etiam, si characteristica F ad normam commentationis supra citatae uti-
mur, per
Haecce inductio facile in demonstrationem rigorosam convertitur per methodum
vulgo notam, aut, si ita videtur, adiumento formulae 19 in comment. cit. Functio
U, si magis placet, etiam ordine terminorum inverso, exprimi potest per
pro n pari, valente signo superiori vel inferiori, prout \n par est vel impar
aut per
pro n impari, valente signo superiori vel inferiori, prout \(n-{-i) par est vel impar.
Functio ZT expressionem generalem aeque simplicem non admittit: facile
tarnen ex ipsa genesi quantitatum V, V, V" etc. colligitur, terminum ultimum
ipsius V pro n pari fieri
i_ 2.2.4.4.6.6 n.n
— 3.5.7.9.11.13 (in —l) Bw +1)
signo superiori vel inferiori valente, prout \n par est vel impar.
Functio TJ" ■= yW^ '—pK^+O^ cuius terminum primum iam in art.
praec. assignare docuimus, etiam per algorithmum recurrentem evolvi potest,
quum manifesto generaliter habeatur
cpfF" — V" = w'^W — V) +ff{yW —V)
9W" —V" = w"(fW" — V") 4-v"(yW — V)
&W— V")
PER APPROXIMATK»?EM INVENIENDJ, 189
etc. adeoque eo quem tractamus casu
Ita invenimus
7 +etc.
' — F'= iw~2+ i^~4+ ^w"~6+ -J-ir-8-f etc.
<?W"—V"= ^u-s+ThrU-S-i- ä^+^^m-9 + etc.
10+ etc.
etc. quas series ita quoque exhibere licet
etc.)
etc.)
etc. Hanc inductionem sequentes habebimus generaliter
U" = <%W^n ' — ]7v»+1) aequalem producto ex
2.2.3.3.4.4 (»-frl).(»+l) u—{n+i)
3.3.5.5.7.7.9 B » + 1) B W + 3)
in seriem infinitam
(» + 2)(» + 3)ni__% . (n + 2)(n + 3)(n+i)(n+!,) 4 ,
I n ä (c. „ 1^ K\ fa „ 1_ ij\ ** I *
2B«+5)
aut si magis placet in i?(|-»+l, I-w+t, »+•!■. w~2). Haec quoque inductio
facillime ad plenam certitudinem evehitur vel per methodum vulgo notam vel ad-
iumento formulae 19 in commentatione saepius citatae.
19.
Quum sufficiat, functionum T, U alterutram nosse, posterioris determi-
nationem tamquam simpliciorem praetulimus. Quae quemadmodum evolutioni
seriei u~l-\-^-u~s-\-^u~5-\- etc. in fractionem continuam innixa est, per ratio-
cinia simüia ex evolutione seriei t~1-{-^t~2-\-^t~s-\-^t~i-\- etc. in fractionem
continuam
190
METHOBÜS üfOVA INTEGRÄLIÜM VALOEES
V ""^™"
1—■
1 —:
t—
1— etc.
derivare potuissemus algorithmum ad determinandam functionem T pro valori-
bus successivis numeri n. Ad eandem vero conclusionem pervenimus perpen-
dendo, T nihil aliud esse quam -^ seu -, si pro u scribitur 1t—1, quo
pacto functiones successive pro T adoptandae habebuntur per algorithmum se-
quentem:
W = 1
etc. Per inductionem hinc resultat generaliter
■ (n+iy.nn m-\ {n + \f.nn.{n—\f m-2 ■ f
"> 1.2.B» +2) B»+i)f i . 2. 3. B»+ 2)B» + l). 2» ' L
sive T= tn+iF(— (m+1), — (»+l), — 2(»+l), f), cui inductioni facile
est demonstrationis vim conciliare. Si magis arridet, T ordine terminorum in-
verso etiam per
± ,:;?;.>:,V::::|
exprimi potest, ubi Signum superius valet pro n impari, inferius pro pari. Si-
mili denique modo generaliter T" aequalis invenitur producto ex
1 .1 .2.2.3.3
3
2 .6. 6. 10. 10. 14 D »-t-2). D »4-6)
in seriem infinitam
t , (-2)s !_■_
1~ri.B»4-4)t "T"l.2.B»4-4)B»4-5)
,_2 ■ (n+ 2J, (n+ ^(n+ 4J
6 ' 1 . 2. 3 . B» + 4)B »+ 5) B »4- 6)
sive in
PER APPEOXIMATIONEM INVENIEüfDI. 1901
20.
Quum in functione U potestates un, un~~ , un~i etc. absint, e radicibus
aequationis U = 0 binae semper erunt magnitudine aequales sigiais oppositae,
quibus pro valore pari ipsius n adhuc associare oportet radicem singularem 0. In-
ventis radicibus, valores coefficientium R, R', R" etc. secundum methodum art. 11
habebuntur per functionem integram ipsius u, quae pro valore impari ipsius n
erit formae
«—1 , / «—3 i // «—5 , ,
yu -f-yw H~7^ -f-etc.
pro valore pari autem, si excluditur coefficiens radici u — 0 respondens, formae
ju -\-yu -f-yu + etc.
Exemplum art. 12 ipsam hanc reductionem exhibet pro n = 6. Manifesto igitur
valoribus oppositis ipsius u semper respondent coefficientes aequales. Ceterum
in casu eo, ubi n est par, coefficiens radici u = 0 respondens facile generali-
ter a priori assignari potest. Habebitur hie coefficiens, si in ~rjf substituitur
u = 0. Valorem numeratoris V pro u = 0 iam in art. 18 tradidimus, valor
denominatoris autem ibinde erit
I
— 3.5.7.9.11
, 3.5.7 (»+0 I 3.3.5.5.7.7
it («+3)(«4-5) B
adeoque coefficiens quaesitus
/ 2.4.6.8 « x2
^3.5. 7.9.,.'..(»-f-l)'
21.
Functio -integra ipsius u coefficientes R, R', R" etc. repraesentans in eo
quem hie traetamus casu etiam independenter a methodo generali art. 11 erui
potest sequenti modo. Differentiando aequationem
zr u"
V~ v —~ü~
substituendo dein -^- = -—-—, ac multiplicando per TJJJiuu — 1), obtinemus
J MKEHODUS NOVA ÖJTEGBAUÜM VALOKES
Termini huius aequationis ad laevam manifesto constituunt functionem integram
ipsius u: itaque necessario in parte ad dextram coefficientes potestatum ipsius u
cum exponentibus negativis sese destruere debent.
Sed -j—~ producit seriem infinitam incipientem a termino
fl.2.3.4
— W.3.5.7 B
qua igitur per (uu — \)TJTJ multiplicata nihil aliud prodire poterit nisi quanti
tas constans
/1-2.3,4 l»fiA-
M . 3. 5.7 BW+1)-'
Hinc colligimus *)
IU. /1.2. 3.4 (« + l)v2
\u ' M . 3.5.7 BW+1)''
divisibilem esse per U, quamobrem functioni fractae ,„. , quae coefficientes
R, R\ R" etc. suggerit, aequivalebit functio integra
W.2.3.4 («TÖ ' '[UU '
Loco huius functionis, quae est ordinis 2 n -f- 2, manifestoque solas potestates
pares ipsius u implicat, adoptari poterit residuum ex eius divisione per U ortum,
quod erit ordinis n, seu n — 1, prout n par est seu. impar. Si vero in casu priori
coef&cientem eum, qui respondet radici u = 0, excludere malumus, loco illius
functionis eius residuum ex divisione per — ortum adoptabimus, quod tantum-
modo ad ordinem n — 2 ascendet.
22.
Ut praesto sint, quae ad appljcationem methodi hucusque expositae requi-
runtur. adiungere visum est, pro valoribus suecessivis numeri n, valores nume-
ricos turn quantitatum a, a, a" etc., turn coefficientium JR, R'. R" etc. ad sede-
cim figuras computatos, una cum horum logarithmis ad decem figuras.
J TT •
*) Simul hiiiCj petitur demonstratio, quod U cum divisorem indeterminatum communem habere
d«
nequit, neque adeo aequatio U = o radices aequales.
PES APmOXIMATIQNEM INVENIENDI.
I. Terminus umts, n = G.
?7=w, ^'=1, T=t— i, T—U
a = 0,5
12= 1
Correctio formulae integralis proxime = i^-L".
II. Termini duo, n = 1.
27=«« —4-, Z7'=w
T=tt—t-\-i, T' = t — i
a = 0,2113248654 051871
«'=0,7886751345 948129
12 = R' — 4-
Correctio proxime = -j-^J/"'
IIT. Termini tres, n — 2.
U=us— fu, Zr = uu—£g-
a = 0,1127016653 792583
a' = 0,5
207417
Correctio proxime = a 810 0 -Lvl.
IV. Termini quatuor, n = 3,
a = 0,0694318442 029754
a = 0,3300094782 075677
«"=0,6699905217 92^323
«'"= 0,9305681557 970246
R = R'"= 0,1739274225 687284 log. = 9,2403680612
JR'= R" = 0,3260725774 312716 log. = 9,5133142764
Horum coefficientium expressio generalis —-i^^^ + t!
Correctio proxime = 44|0<tX
25
194 MPTHOJHJS NOVA TOTEGHBAIOTM VALOßES
V. Termini quinque, n = 4.
£7 = rf
TJ'—ulk
T = ^
« = 0,0469100770 306680
«' = 0,2307653449 471585
ö = 0,5
«'" = 0,7692346550 528415
«""=0,9530899229 693320
JR = JR"" = 0,1184634425 280945 log. = 9,0735843490
JR' = JR'" =0,2393143352 496832 9,3789687142
R" = ^g. — 0,2844444444 444444 9,4539974559
Expressio generalis horum coefficientium, excluso R",
Correctio proxime = 6 9
VI. Termini seoo, n = 5.
a = 0,0337652428 984240
d = 0,1693953067 668678
«"=0,3806904069 584015
«'"=0,6193095930 415985
«""= 0,8306046932 331322
«'""=0,9662347571 015760
R = R""'= 0,0856622461 895852 log. = 8,9327894580
R'= JR""= 0,1803807865 240693 9,2561902763
R'= 22'"= 0,2339569672 863455 9,3691359831
Coefficientium expressio generalis
—ÄV«4
Correctio proxime = 110 ü\ 0 8 8 Xx"
PEE APPROXIMATIVEM INVENIENDI. 105
VII. Termini septem, n — 6. .
a = 0,0254460438 286202
a' = 0,1292344072 003028
a" = 0,2970774243 113015
a = 0,5
«""=0,7029225756 886985
«'""= 0,8707655927 996972
«"""=0,9745539561 713798
12 = R""" = 0,0647424830 844348 log. == 8,8111893529
JR' = E"" =0,1398526957 446384 • 9,1456708421
R'—R' =0,1909150252 525595 9,2808401093
R'"= vVW= 0,2089795918 367347- 9,3201038766
Horum coefficientium, JR'" excluso, expressio generalis
Correctio proxime =; -
23.
Coronidis loco methodi nostrae efficaciam ob oculos ponemus computando
valorem integralis
dz
/
logx
ab x = 100000 usque ad #=200000.
I. Ex termino uno habemus &RA = 8390,394608
AJR-4 =4271,810097
II. Ex terminis duobus fit... kR'Ä =4134,144502
Summa = 8405,954599
äRA = 2390.572772
= 3729,064270
TTT ^ . . .,
III. Ex terminis tnbus ,
\LR"Ä = 2286,599733
'Summa = 8406,236775
25*
METHODUS JTOVA INTEG^RAIJUM VALOBES PER APPKOXIMATIONEM INVENIENDI.
IV. Ex terminis quatuor
V. Ex terminis quinque
VI. Ex terminis sex
VII. Ex terminis septem,
LRA
LR'Ä
Aii"i"
kR'"A!"
Summa
= 1501,957053
= 2763,769240
= 2711,454637
= 1429,062040
= 8406,242970
= 1024,879445
kR'Ä = 2041,833335
= 2386,601133
' = 1980,509616
"= 972,419588
Summa = 8406,243117
= 741,912854
=r 1545,757256
= 1976,737668
' = 1950,466223
'"= 1488,588550
= 702,780570
Summa = 8406,243121
= 561,1213804
= 1202,0551998
" = 1621,6290819
L/ff= 1753,4212406
i""= 1584,9790252
v = 1152,0681116
w= 530,9690816
Summa = 8406,2431211
E calculis clar. Bessel valor eiusdem integralis inventus est =8406,24312.
ANZEIGEN.
Göttingische gelehrte Anzeigen. 1S12 Februar 10.
Die logarithmischen und Kreisfunctionen, als die einfachsten Arten der
transscendenten Functionen, sind diejenigen, womit sich die Analysten am mei-
meisten beschäftigt haben. Sie verdienten diese Ehre sowohl wegen ihres steten Ein-
Eingreifens in fast alle mathematische Untersuchungen, theoretische und practische,
als wegen des fast unerschöpflichen Reichthums an interessanten Wahrheiten, den
ihre Theorie darbietet Weit weniger sind bisher andere transscendente Functio-
Functionen bearbeitet, die sich auf jene nicht zurückführen lassen, sondern als eigne
höhere Gattungen betrachtet werden müssen, die nur in speciellen Fällen mit je-
jenen zusammenhängen. Und doch sind manche solcher Functionen nicht minder
fruchtbar an interessanten Relationen, und daher dem, welcher die Analyse um
ihrer selbst willen ehrt, nicht minder wichtig; so wie ihr häufiges Vorkommen
bei mancherlei andern Untersuchungen sie dem empfehlen muss, der gern erst
nach practischem Nutzen fragt. Professor Gauss hat sich mit Untersuchungen
über dergleichen höhere transscendente Functionen schon seit vielen Jahren be-
beschäftigt, deren weit ausgedehnte Resultate das Gesagte bestätigen. Einen, ver-
hältnissmässig freilich nur sehr kleinen, Theil derselben, der gleichsam als Ein-
Einleitung zu einer künftig zu liefernden Reihe von Abhandlungen angesehen wer-
werden kann, hat er am 30. Januar unter der Aufschrift
Disquisitiones generales circa seriem inßnitam
'l.y ' 1.2.7.7+1 l i.2.3.yfl + 2 '
Pars prior,
198 ANZEIGE.
als eine Vorlesung der königl. Gesellschaft der Wissenschaften übergeben, wor-
woraus wir hier die Hauptmomente des Inhalts anzeigen wollen.
Die transscendenten Functionen haben ihre wahre Quelle allemal, offen lie-
liegend oder versteckt, im Unendlichen. Die Operationen des Integrirens, der Sum-
mationen unendlicher Reihen, der Entwickelung unendlicher Producte, ins Un-
Unendliche fortlaufender continuirlicher Brüche, oder überhaupt die Annäherung an
eine Grenze durch Operationen, die nach bestimmten Gesetzen ohne Ende fort-
fortgesetzt werden — diess ist der eigentliche Boden, auf welchem die transscenden-
transscendenten Functionen erzeugt werden, oder wenn man lieber sich eines andern Bildes
bedienen will, diess sind die eigentlichen Wege, auf welchen man dazu gelangt.
Zu einem Ziele führen gewöhnlich mehrere solcher Wege: die Umstände und die
Zwecke, welche man sich vorsetzt, müssen bestimmen, welchen man zuerst oder
vorzugsweise wählen will. Die Reihe, welche den Gegenstand gegenwärtiger Ab-
Abhandlung ausmacht, ist von einer sehr umfassenden Allgemeinheit. Sie stellt,
je nachdem die Grossen a, t>, 7 (welche nebst «2? der Verfasser durch die Benen-
Benennungen erstes, zweites, drittes, viertes Element unterscheidet, so wie er, Kürze
halber, die ganze durch die Reihe dargestellte Function mit den Zeichen F(a, <6, y, cc)
bezeichnet) so oder anders bestimmt werden, algebraische, logarithmische, tri-
trigonometrische oder höhere transscendente Functionen dar, und man kann behaup-
behaupten, dass bisher kaum irgend eine transscendente Function von den Analysten un-
untersucht sei, die sich nicht auf diese Reihe zurückführen Hesse. Eine grosse
Menge von Wahrheiten, welche in Beziehung auf solche schon in Betrachtung ge-
gezogene Functionen schon aufgefunden sind, lassen sich aus der allgemeinen Na-
Natur der durch unsere Reihen dargestellten Function ableiten, und schon um dess-
willen würden Untersuchungen darüber die Aufmerksamkeit der Geometer->verdie-
nen, obwohl diess nur als Nebensache, und die Eröffnung des Zuganges zu neuen
Wahrheiten als Hauptzweck zu betrachten ist. Gegenwärtige Abhandlung ent-
enthält nur erst die Hälfte von den allgemeinen Untersuchungen des Verfassers, de-
deren zu grosser Umfang eine Theilung nothwendig machte. Hier gilt eben die
Reihe selbst als Ursprung der transscendenten Functionen, welche in dem wei-
weitern Verfolg der Arbeit aus einer allgemeiner anwendbaren Quelle werden abge-
abgeleitet, und aus einem höheren Gesichtspunkte betrachtet werden. Die erstere
Erzeugung mac^it, ihrer Natur nach, die Einschränkung auf die Fälle nothwen-
nothwendig, wo die Reihe convergirt, also wo das vierte Element «2?. positiv oder negativ,
DISQÜISITIONES GENERALES CIRCA SERIEM INFINITAM ETC. 199
den Werth 1 nicht überschreitet: die andere Erzeugungsart wird diese Beschrän-
Beschränkung wegräumen. Allein eben die erstere Erzeugungsart fuhrt schon zu einer
Menge merkwürdiger Wahrheiten auf einem bequemern und gleichsam mehr ele-
elementarischen Wege, und desswegen hat der Verf. damit den Anfang gemacht.
Diese erste Hälfte der Untersuchungen zerfallt in drei Abschnitte, welchen
einige allgemeine Bemerkungen voraus geschickt sind. Um eine Probe von der
ausgedehnten Anwendbarkeit der Reihe zu geben, sind auf dieselbe zuvörderst
23 verschiedene Reihenentwickelungen algebraischer, logarithmischer und tri-
trigonometrischer Functionen zurück geführt, so wie, als ein Beispiel höherer
transcendenter Functionen, die Coefficienten der aus der Entwickelung von
[aa-\-bb—2 ab cos v)n entspringenden, nach den Cosinus der Vielfachen von cp
fortschreitenden, Reihe, und zwar letztere auf drei verschiedene Arten.
Der erste Abschnitt beschäftigt sich mit den Relationen zwischen solchen
Reihen von der obigen Form, in welchen die Werthe eines der drei ersten Ele-
Elemente um eine Einheit verschieden, die Werthe der drei übrigen hingegen gleich
sind. Dergleichen Reihen nennt der Verf. series contiguae, im Deutschen könnte
man sie etwa verwandte Reihen nennen. Jeder Reihe F(a, <6, y, oo) stehen also
sechs verwandte zur Seite, nämlich F(a-\-1, ^, y, ob), F(a—1, <6, y, <z?), F(a, <5-f-l, y, a?),
F(a, tf — 1, y, oj), F(a, tf, y-f-1, oo), F(a, #, y—1, ob), und es wird hier gezeigt,
dass es zwischen der ersten und je zweien der verwandten eine lineare Gleichung
gibt. Fünfzehn Gleichungen entspringen auf diese Weise. Es folgt hieraus das
wichtige Theorem, dass, wenn d—a, a"—a, <6'—1>, <6"—6, y'—y, y"—y,
ganze Zahlen sind, auch zwischen F(a, *>, y, üß), F(d, *>', /, x), F(a", t>", y", ob),
eine lineare Gleichung Statt findet, und also, allgemein zu reden, aus den Wer-
then zweier dieser Functionen der Werth der dritten abgeleitet werden kann. Ei-
Einige der einfachsten oder sonst merkwürdigen Fälle hat der Verf. hier noch be-
besonders zusammengestellt.
Der zweite Abschnitt gibt Verwandlungen in continuirliche Brüche, und zwar
für die Quotienten
F(a, 6+1, T-H'*) -Ffa 6+1, T, x) F(a-l, 6+1,7,*)
F(a, g, y, x) ' F(a, 6, y, x) ' F(a, 6, Y, x)
auf welche sich noch drei andere durch die offenbar verstattete Vertauschung der
beiden ersten Elemente zurück führen lassen. Von diesen Lehrsätzen sind fast
alle bisher bekannte Entwickelungen in continuirliche Brüche nur specieUe Fälle.
200 * ANZEIGE.
Vorzüglich merkwürdig ist der Fall, wo man in der zweiten Entwickelung ß = 0
setzt. Es folgt daraus ein Lehrsatz, welchen wir seiner umfassenden Anwend-
Anwendbarkeit wegen hier beifügen. Die Function F(a, 1, y. j?) oder, was einerlei ist,
die Reihe
„ . cc . a.a-f-1 . a. a 4-1. a + 2 q , ,
14--.2H ^mqcA ^ -f- jr + etc.
i Y Y-Y-H ' Y-Y+1-Y + 2
gibt den continuirlichen Bruch
- etc.
wo die Coefficienten a, b, c, d etc. nach folgendem Gesetze fortschreiten
a 7 Y—a
Y Y(Y + O
(a + l)T r]
"~ ( + 0(T + 2) ~
(Y+2)(Y+a)
Hiernach lassen sich z.B. die Potenz eines Binomium, die Reihen für log(t + «r),
log -^-, für Exponentialgrössen, für den Bogen durch die Tangente oder durch
den Sinus u. a. in unendliche continuirliche Brüche verwandeln. Auch beruhen
hierauf die in der Theoria motus corporum coelestium gegebenen Verwandlungen in
solche Brüche, deren Beweise hier von dem Verfasser nachgeholt werden.
Bei weitem den grössten Theil der Abhandlung nimmt der dritte Abschnitt
ein, in welchem von dem Wertlie der Reihe gehandelt wird, wenn man das vierte
Element = l setzt. Nachdem zuvörderst mit geometrischer Schärfe bewiesen,
dass die R^ihe für x = 1 nur dann zu einer endlichen Summe convergire, wenn
y — a—ß eine positive Grosse ist, führt der Verf. diese Summe, oder F{a,ß,y, 1)
auf den Ausdruck n;T ' V/"t"' zurück, wo die Charakteristik II eine
ü(y — a—l).U(Y — o —l) .
eigene Art transcendenter Functionen andeutet, deren Erzeugung der Verf. auf
ein unendliches Product gründet. Diese in der ganzen Analyse höchst wichtige
Function ist im Grunde nichts anders als Eulers inexplicable Function
Ylz = 1 .2.3.4 z
DISQÜISITIONES GENERALES CffiCA SER1EM INFJNITAM ETC. 201
allein diese Erzeugungsart oder Definition ist, nach des Verf. Urtheil, durchaus
unstatthaft, da sie nur für ganze positive Werthe von z einen klaren Sinn hat.
Die vom Verf. gewählte Begründungsart ist allgemein anwendbar, und gibt selbst
bei imaginären Werthen von z einen eben so klaren Sinn, wie bei reellen, und
man läuft dabei äurchaus keine Gefahr, auf solche Paradoxen und Widersprüche
zu gerathen, wie ehedem Hr. Kramp bei seinen numerischen Facultäten, die sich,
wie man leicht zeigen kann, auf obige Function zurückführen lassen, aber zur
Aufnahme in die Analyse weniger geeignet scheinen, als diese, da jene von drei
Grossen abhängig sind, diese nur von Einer abhängt, und doch als eben so allge-
allgemein betrachtet werden muss. Der Verf. wünscht dieser transscendenten Function
Uz in der Analyse das Bürgerrecht gegeben zu sehen, wozu vielleicht die Wahl ei-
eines eigenen Namens für dieselbe am beförderlichsten sein würde: das Hecht dazu
mag demjenigen vorbehalten bleiben, der die wichtigsten Entdeckungen in der
Theorie dieser der Anstrengungen der Geometer sehr würdigen Function machen
wird. Hier ist von dem Verf. bereits eine bedeutende Anzahl merkwürdiger, sie
betreffender, Theoreme zusammen gestellt, wovon ein Theil als neu zu betrachten
ist. Der Raum verstattet uns nicht, in das Detail derselben hier einzugehen: nur
das eine heben wir davon aus, dass der Werth des Integrals yV"—1(l —x^ydx von
x = 0 bis x = 1 leicht auf die Function II zurückgeführt werden kann, und
dass alle die von Euler für dergleichen Integrale zum Theil mühsam gefundenen
Relationen sich mit grösster Leichtigkeit aus den allgemeinen Eigenschaften jener
Functionen ableiten lassen, so wie umgekehrt allemal Hz, wenn z eine Ratio-
nalgrösse ist, sich durch einige solche bestimmte Integrale darstellen lässt.
Nicht weniger merkwürdig ist die aus der Differentiation von IIz entsprin-
entspringende, gleichfalls transscendente, Function, oder vielmehr
d log uz duz
dz Uz.dz
welche der Verfasser mit Wz bezeichnet hat, und die gleichfalls eine besondere
Benennung verdiente. Von den zahlreichen merkwürdigen Eigenschaften dieser
Function, welche in der Abhandlung aufgestellt sind, fuhren wir hier nur die
Eine an, dass allgemein Wz — Wti, wenn z eine rationale Grosse ist, auf Loga-
Logarithmen und Kreisfunctionen zurückgeführt werden kann; W0 selbst aber ist die
bekannte, von Euler und Andern untersuchte, Zahl 0,5772156649 . . . . negativ
genommen, welche der Verfasser hier, nach einer von ihm selbst geführten Rech-
26
ANZEIGE.
nung, auf 23Decimalen mittheilt, wovon die letzten von Maschekojni's Bestimmung
etwas abweichen. Uebrigens hängen sowohl EU, als Wz, mit mehreren .merk-
.merkwürdigen Integralen für bestimmte Werthe der veränderlichen Grosse zusammen.
Diesem dritten Abschnitte ist noch eine unter der Aufsicht des Professors
Gaüss von Hrn. Nicolai mit grösster Sorgfalt berechnete Tafel für log IIz und für
¥z beigefügt, worin das Argument z durch alle einzelnen Hunderttheile von 0
bis 1 fortschreitet; aus der Theorie dieser Functionen ist klar, dass man auf diese
Werthe von z alle andere leicht zurück führen kann.
Göttingische gelehrte Anzeigen, lSi4 September 26.
Der königl. Societät wurde am 16. September von dem Prof. Gaüss eine Vor-
Vorlesung eingereicht überschrieben:
Methodus nova integraUum valores per approooimationem inveniendi.
Unter den verschiedenen Methoden zur genäherten Bestimmung der Inte-
Integrale , oder wie es in der Sprache der altern Analysten hiess, zur genäherten Qua-
Quadratur krummliniger Figuren, ist die Newton - CoTEgische, welche sich auf die In-
Interpolationsmethode gründet, eine der brauchbarsten. Newton hatte eine Auflö-
Auflösung der Aufgabe gegeben, durch eine beliebige Anzahl gegebener Punkte eine
parabolische Curve zu ziehen, deren immer leicht ausführbare Quadratur dann
näherungsweise die Stelle der Quadratur der eigentlich vorgegebenen durch jene
Punkte gehenden Curve vertreten kann, und zwar desto genauer, je mehr Punkte
man in Anwendung bringt. Newton hatte es indessen bei dieser allgemeinen An-
Andeutung bewenden lassen und nur gleichsam beispielsweise für den Fall von vier
in gleichen Zwischenräumen liegenden Ordinaten A, B, C, D den genäherten
Flächenraum zwischen der ersten und letzten, wenn deren Entfernung = R ist,
durch (-&A-{-fB-}-fC-\-i-D)Ii angeführt. Cotes, welcher für sich, und noch
ehe Newtons Schrift Methodus differentialis erschienen war, schon im Jahre 1707
ähnliche Untersuchungen angestellt hatte, wurde durch die zierliche Form, in wel-
welcher Newton das Endresultat in obigem Beispiele dargestellt hatte [pulcherrima et
METHODDS NOVA INTEGEALIDM VALÖBES PER APPEOXIMATIONEM EfVENIENDl. 20S
utilissima regula nennt es Cotes) bewogen, diese Vorschriften weiter und bis auf
den Fall von 11 Ordinaten auszudehnen. Immer erscheint so der verlangte
Flächenraum in der Gestalt des Products der Basis, oder der Entfernung der
äussersten Ordinaten, in die Summe der durch bestimmte Zahlcoeffieienten mul-
tiplicirten Ordinaten, und zwar haben zwei gleich weit vom Anfang und Ende
abliegende Ordinaten allemal gleiche Coefficienten. Diese Quadraturcoefficienten
bis zu dem Fall von 11 Ordinaten gibt Cotes am Schluss der Abhandlung de me-
thodo differentiali^ welche einen Theil der Harmonia mensurarum ausmacht, ohne
sich über das Verfahren, wodurch er sie berechnet hat, weiter zu erklären. Viel-
Vielleicht hat man es dieser anspruchlosen Kürze, womit bloss das Endresultat dar-
dargestellt ist, zuzuschreiben, dass diese schöne und zweckmässige Methode von den
Analysten weniger gekannt und benutzt zu sein scheint, als sie es verdient.
Bei dieser Methode liegt durchaus die Voraussetzung gleicher Abstände zwi-
zwischen den Ordinaten zum Grunde. Allerdings scheint beim ersten Anblick diese
Voraussetzung am einfachsten und natürlichsten zu sein, und es war noch nicht
in Frage gekommen, ob es nicht demungeachtet noch vortheilhafter sein könne,
Ordinaten in ungleichen Abständen zum Grunde zu legen. Um diese Frage zu
entscheiden, musste zuerst die Theorie der Quadraturcoefficienten in unbeschränk-
unbeschränkter Allgemeinheit entwickelt, und der Grad der Genauigkeit des Resultats be-
bestimmt werden. Es zeigte sich, dass die Bedingungen, wovon dieser Grad der
Genauigkeit abhängt, von der Art sind, dass man dieselbe durch zweckmässig
gewählte Ordinaten in ungleichen Abständen allerdings verdoppeln kann, so dass
man mit einer beliebigen Anzahl gehörig gewählter Ordinaten eben so weit reicht,
als mit der doppelten Anzahl von Ordinaten in gleichen Abstanden. Diese Un-
Untersuchungen , nebst der vollständigen Theorie der zweckmässigsten Auswahl der
Ordinaten, der dabei anzuwendenden Quadraturcoefficienten und der Bestimmung
des Grades der Genauigkeit, welchen dieses Verfahren gewährt, machen den
Hauptinhalt der vorliegenden Abhandlung aus.
Aus der kurzen Entwickelung der Theorie der CoTEsischen Quadraturcoeffi-
Quadraturcoefficienten , welche der Verf. vorausschicken zu müssen glaubte, berühren wir hier
nur dasjenige, was den Grad der Genauigkeit betrifft, welchen die dadurch ge-
gefundenen genäherten Integrale haben. Vor allen muss hier bemerkt werden, dass
die Anwendbarkeit dieser Methode, eben so wie das Interpoliren, auf der Vor-
Voraussetzung beruhe, dass die Ordinaten innerhalb des zu quadrirenden Raumes
26*
204 AUFZEIGE.
sich durch eine convergirende Reihe darstellen lassen. Es sei x die Absscisse, y
die Ordinate, und das Integral fydx werde von x = g bis x = h verlangt.
Man fahre statt x eine andere veränderliche Grosse ein, indem man etwa
x ■= g-\-{h—g)t, oder auch x = -!t(g-\-h)-{-%{h—g)u setzt. Hier muss also
y sich durch Reihen wie
a + dt -i-d'tt 4-aV -f- etc.
oder
gg'g"g'V-}- etc.
darstellen lassen, die convergiren, jene, wenigstens so lange t, diese so lange u
nicht grösser wird als 1. Man mag daher Kürze wegen den Coefficienten d und 6'
die Ordnung 1, den Coefficienten a" und ö" die Ordnung 2 u.s.w. beilegen. Diess
vorausgesetzt, wird gezeigt, dass die Fehler, denen man sich bei der CoTESischen
Methode aussetzt, zwar immer von einer höhern Ordnung werden, je grösser die
Anzahl der zum Grunde gelegten Werthe von y ist, jedoch so, dass eine unge-
ungerade Anzahl und die zunächst grössere gerade Anzahl immer Fehler von einer-
einerlei Ordnung hervorbringen. So ist für drei Ordinaten der Fehler sehr nahe
= Thrih—9) a""' fö** ^er Ordinaten nahe = T-^- (k—g)d'"; sodann für
fünf Ordinaten nahe = jr^ss (Ä—^)a" und für sechs Ordinaten nahe
= T*Vjnr(Ä—g)&1 u.s.f. Man sieht hieraus, dass es im Allgemeinen vortheil-
haft sein wird, bei Anwendung der CoTESischen Methode eine ungerade Anzahl von
Ordinaten zu benutzen.
Der Verf. geht hierauf zu der allgemeinen Untersuchung über, wo die Ein-
Einschränkung , dass die Ordinaten gleiche Abstände von einander haben, wegfällt.
Sind hier A, Ä, A" u.s.w. die Werthe von y. die entsprechenden Werthe von t
hingegen a, a, a"u. s. w., oder l, b', b" u. s. w. die entsprechenden Werthe von u, und
ihre Anzahl w-j-1, so wird das genäherte Integral wiederum die Gestalt haben
(*-^)Ei+B'4'+B'4''+ etc.)
wo -ß, -R', -ß" u.s.w. Zahlcoefficienten sind, die unabhängig von der Function y
bloss durch a, d,a"u.s.w., oder durch b,b\ b"u.s.w. bestimmt werden. Die Un-
Untersuchungen <les Verf. geben für diese Bestimmung folgendes Resultat. Es sei
T=(t—a){t—d){t--df)
METHODÜS NOVA INTEGRALIÜM VALOEES PER APPBOXIMATKHSEEM INVEIHENDI.
Aus der Multiplieation dieser ganzen Function von tr welche auf die Ordnung
n-\-\ steigt, in die unendliche Reihe, welche den Logarithmen von ^- vor-
vorstellt, nemlich
*+etc.
ergebe sich das Product J"-f- T", so dass J" die darin enthaltene ganze Funetion
von t bezeichnet, so wie T" die übrige mit negativen Potenzen von t ins Unend-
Unendliche fortlaufende Reihe, Diess vorausgesetzt, ergeben sich die Qua4raturcoefli-
cienten R, Rf, R" u.s.w., wenn man in ^-^- für t der Reihe nach die "Werthe
a, a, u" u. s. w. substituirt. Auf eine ähnliche und noch etwas bequemere Art
leitet man jene Coeffieienten aus b, b', b" u. s. w. ab, indem man die Function
durch U, ihr Product in die unendliche Reihe
l*~5-{- etc.
durch TJ'-\~ TJ" bezeichnet (so dass TJr die darin enthaltene ganze Function von
u vorstellt), und dann in -^- für u der Reihe nach die Werthe b, b\ b"n. s. w.
substituirt. Statt der gebrochenen Functionen -^r, -^- lassen sich auch ganze
Functionen von t und u finden, welche die Stelle von jenen vertreten können,
und für deren Bestimmung der Verf. eine allgemeine Methode entwickelt.
Der Grad der Genauigkeit der Integrationsformel hängt nun von der Be-
Beschaffenheit der Reihe T" oder TJ" al>. Im Allgemeinen ist der Fehler zwar von
der Ordnung w-f-l; allein wenn von den ersten Gliedern jener Reihen einige
ausfallen, so wird der Fehler von einer höhern Ordnung, so dass wenn T" erst
mit der Potenz t~m oder TJ" mit der Potenz vT™ anfangt, der Fehler von der
Ordnung n-\-m wird.
Hieraus ergab sich nun, dass in so fern die Werthe a, a, «"u.s.w., oder
b, b\ b" u. s. w. willkürlich gewählt werden können, diese sich so bestimmen las-
lassen müssen, dass die ersten n-\-\ Glieder von T" oder TJ" wirklich ausfallen;
wovon die Folge sein wird, dass der Fehler der Integrationsformel auf die Ord-
Ordnung 2w + 2 kommt. Die Untersuchung schreitet demnach zu der Bestimmung
derjenigen Functionen T und TJ, für jeden Werth von n, fort, wodurch der
angegebenen Bedingung Genüge geleistet wird. Der beschränkte Raum erlaubt
206 ANZEIGE. METHODDS NOVA INTEG^ALTCM VALOKES ETC.
uns nicht, in das Einzelne dieser Untersuchung hier einzugehen: wir bemerken
also hier nur, dass diese Ftmctionen ein sehr einfaches Fortschreitungsgesetz be~
folgen, und in genauem Zusammenhange stehen mit der Entwicklung der Reihen
4- i-ir5+^u~7 4- etc.
in continuirliche Brüche, die der Verf. in einer frühern Abhandlung [Disquisitiones
gener ales circa seriem infinitam \-\- —x-\-etc.] gegeben hat.—- Offenbar gibt dem-
demnächst die Auflösung der Gleichung T= 0 oder U=0 die Werthe von a, a, cl'vl.s.w.
oder b, b', b" u.s.w., und die Werthe der Quadraturcoefficienten werden nach den
allgemeinen Hegeln bestimmt, die in diesem Falle noch,besondere Vereinfachun-
Vereinfachungen vertragen. Uebrigens werden allerdings in den meisten Fällen sowohl die
Werthe von a. a, a'u.s. w. als die Quadraturcoefficienten Irrationalgrössen. Diess
ist indess an sich sehr gleichgültig, sobald nur ihre numerischen Werthe ein für
allemal mit einem angemessenen Grad von Genauigkeit berechnet sind. Ist diess
der Fall, so wird die Anwendung dieser Methode auf irgend eine Anzahl von Or-
dinaten wenig oder gar nicht mehr Mühe machen, als die Anwendung der Co-
TEsischen Methode auf eine eben so grosse Anzahl, da hingegen letztere auf eine
doppelt so grosse Anzahl angewandt werden müsste, um ungefähr dieselbe Ge-
Genauigkeit des Eesultats zu geben, wie erstere.
Um für die Anwendung dieser neuen Methode nichts zu wünschen übrig zu
lassen, hat der Verf. noch die numerischen Werthe von a, a, «"u.s.w., so wie
von R, R\ B," u. s.w., auf 16 Decimalen berechnet, mitgetheilt, zugleich mit
den BRiGGischen Logarithmen der letztern auf 10 Decimalen, alles bis zu dem
Fall von sieben Ordinaten. In diesem letzten Fall wird der Fehler der Integra-
Integrationsformel nahe = 1766^jro-a^, woraus man abnehmen kann, dass in den
meisten in der Ausübung vorkommenden Fällen schon eine geringere Anzahl zu-
zureichen wird. Um die Anwendung der Vorschriften und ihre verhältnissmässige
Schärfe noch mehr zu versinnlichen, ist als Beispiel die Berechnung von
von x = 100000 bis oc =■ 200000 beigefügt, wo schon bei der Anwendung von
vier Werthen der Fehler nur tttö-öWfö- des Ganzen ist, und bei einer grössern
Anzahl sich in den unvermeidlichen Fehlern verliert, die selbst die grössern Lo-
Logarithmentafeln hoch übrig lassen.
20?
NACHLASS.
DETERMINATIO SERDEI NOSTRAE
PER AEQUAT1ONEM DIFFERENTIALEM SECÜNDI ORDINIS.
38.
Statuendo brevitatis causa F(a, 6, y, x) = P, habemus per art. 4
atque hinc differentiando denuo
Hinc aequatio IX art. 10 suppeditat
[80] 0 = aÖP-(T-(
Haecce aequatio differentio - differentialis tamquam definitio exactior functionis
nostrae considerari potest; sed quoniam P = F(a, fi, y, x) non est integrale com-
pletum sed particulare tantum (quod constantes non accesserunt), adjicere oportet
conditionem, ut P incipiat a valore 1 pro «2? = 0 simulque pro eodem valore
. . . dP a8 , ddP 6(8
ipsius üb supponatur ^- = - atque -^
Ita pro quovis valore ipsius a?, ad quem a valore x = 0 per gradus con-
tinuos transiisti, ita tarnen, ut valorem a? =■ 1, pro quo x — xx-=^ 0, non atti-
geris, P erit quantitas perfecte determinata; sed manifesto hoc modo ad valores
reales ipsius x positivos unitate majores pervenire nequis nisi transeundo per va-
$08 #
lores imaginarios, quod quam infinitis modis diversis absque continuitatis praeju-
dicio fieri possit, hinc nondum liquet, annon eidem valori ipsius x plures, quin
adeo infinite multi valores discreti ipsius P respondeant, sicuti in pluribus functio-
nibus transscendentibus magis notis evenire constat. Sed de hoc argumento in
posterum fusius loqui nobis reservamus, quum hoc loco casus is potissimum, ubi
x accipitur infra vel saltem non ultra unitatem positivam, atque P aequalis sum-
mae seriei F(a, f>, yt x) tractetur.
39.
Scribendo in aequatione 80, 1—y pro x, transit ea in hanc
quae habet formam similem ut illa. Hinc statim prodit aliud integrale particulare
P = F(a, 6, a+tf-}-1 — y,y) = F(a, ö, a+ö+l—7, 1—x)
unde per principia nota sequitur integrale completum aequationis 80,
[81] P=MF(a, ß,y,ai)-\-NF(a, ö, a + ö-fl—y, 1—a?)
denotantibus M% N constantes arbitrarias.
Ceterum obiter hie observamus, ad formam aequationis 80 facile reduci
posse aequationem generaliorem
0 =
Sunto enim radices aequationis 0 = D-\-Ey-\-Fyy hae. y ■= a, y z=zb,
sive D-\-Ey-\-Fyy indefinite aequalis produeto F(j/—a) C/—b) patetque sta-
tuendo H~~ ^^ % atque determinando a, ö, 7 ita ut fiat
o — a ^- •
illam transire in aequationem 80.
40.
Adiumento aequationis differentialis 80 eruere licet complura theoremata
maxime memorabilia circa seriem nostram, turn generalia turn magis specialia, ne-
que dubitamus, quin multa plura atque graviora adhuc lateant, ulterioribus curis
servata. Quae hactenus nobis revelare contigit, hie in conspectum producemus.
DETEEMEtfATIO SEEEEI NOSTEAE PEE AEQÜATIONEM DIffEmEMTIALEM ETC.
Statuamus P == (l—^P\ eritqtte
Quibus valoribus in aequatione 80 substitutis prodit dividendo per A
0 =P'j
Determinemus [i ita, ut multiplicator ipsius P' per 1—x divisibilis evadat, quod
fiet vel statuendo {i = 0 vel [i = y — a--ö. Suppositio prior nihil no\d doce-
ret, sed valor posterior substitutus producit
sive
quae prorsus eandem formam habet ut aequatio 80. Quare quum pro «2? = 0,
manifesto fiat P = 1 atque -^- = {i = VJ ^ ^, patet ipsms integrale
esse P = F(y — a, y—€, y,<2?), ita ut generaliter habeatur
[82] F{y — a, y-$, y, oc) = (\-a>)a+^F(a, Ö, T, co)
Hinc petenda est transformatio seriei
A i 2.8 ■ 3.8.10 . 4.8.10.12 3 , ,
in
(l-^)-f (i + ^ + i^L^+ etc.) = (i_^
quam in Ephemeridibus Astronomicis Berolinensibus 1814 p. 257 [Zusatz zu
Art. 90 und 100 der Theoria motus] sine demonstratione indicaveramus.
41.
Statuamus porro P = <#P', ita ut fiat
27
quibus valoribus in 80 substitutis, fit dividendo per
0 = P'{aGa: — G—(a+6+l)<2?)jA —A —«r)^— ja)}
da;8 ^ J
Multiplicator ipsius P in hac formula fit divisibilis per oß statuendo ja = 0 vel
fji = 1 — y; valor posterior producit
0 = P'faö + a+ö+l — 2y — ay—
BT(
Comparando hanc aequationem cum 80, cuius forma prorsus similis est, patet
quae illic fuerant P, a, ö, y hie esse P', a-f-1—y, ö-f-1 — y, 2 — y: quare
quum illius integrale completum assignaverimus, manifestum est, P' contentam
fore sub formula
P'= MF{a+\—y, ö + l—y, 2 — y, ce)
-\-NF{a-\-\— y, ö-j-1— y, a+ö+1 —y, 1 — a?)
denotantibus M, N quantitates constantes, sive
[83] F{a, ö, y, co) = If^^^a+l — y, ö+l—y, 2 —y,
+ + 7, \ — 3C)
ubi constantes Jkf, 2V ab elementis a, ö, 7 pendebunt.
42.
Ex aequatione 82 sequitur
F(a+1—7, ö+i—7, 2—7, a?) = A — üßy-«-*F(l — a, 1 — fi, 2—7, ob)
F(a-\-l—7, ö + i_7, a + ö+1 —7, l—#) = ^"^(a, ö, a+ö+1 —7, 1— oc)
unde statuendo
^ =/(a, ö, 7), —f = #(a, ö, 7)
DETERMINATIO SERIEI UOSTRAE PER AEQÜATIONEM DJPFPEUENTIALEM ETC.
aequatio 83 fit
F{a, ß, a + Ö+1 —7, 1—x)
= /(a, ß, y)F(a, 6, y, ob)
(a, ß, y)(i—^-«-«^-Y^i-a, i_S, 2
Eidem aequationi adiumento formulae 82 hanc quoque formam tribuere licet
7,
a, Ö. T)(l -^Y—6 Fft—a, y—ß, y, co)+g(a, ß, yy^a+l —7, Ö-fl -T, 2-T,
sive dividendo per ^1""^ mutandoque resp. a, ö, y in a-f-1 — y, ö—j—1—y, 2 —
F(a, ß, a+Ö+1—y, l —*)
— 7, 2—y)F(a, ß, y, ce)
Quae quum identica esse debeat cum formula praecedenti, habemus
g{a, ß,y) = f(a+l—y, tf+1—y, 2—T)
itaque
[84] F{a, ß, a-f-ö-f-1 — y, 1 — a?)
—a, 1 — 6, 2—
43.
Iam ut indolem functionis f(a, ß, y) eruamus, statuamus x = 0. Tunc
patet, esse F(a, ß, y, 00) = 1. «a?1"* = 0, quoties quidem 1 — y fuerit quantitas
positiva. Sed per aequationem 48 habemus
tm -e 1^1. *\ n(a+6
F{at ß, a+6 + l—T, 1) = n(r-
Quare sub eadem restrictione demonstratum est, fieri
Hanc vero formulam generalem esse, ita demonstramus.
27
NACHLASS.
Diifferentiando aequationem 84 provenit
= ~/(a, ö, y)F(a+t, 6 + 1, 7+1, w)
+/(a+ i^t,ö-h1 -T, 2—T)(l -a?)^"-Ma?"T j(A -fj( 1 -<37)-(T-a-%J^ 1 -a, 1 -6, 2-?,a?)
(l^1g)-a, 2-6, 3 —y, ^) j
Sed per formulam IX art. 1 0 fit mutando a, 6, 7 in —a, —ö, 1—y
A— T)B—T)i^(—a,— ö, 1-T,<37)=:B—T)(i-Y+(a+ö—1)^A— a, 1— 6,2-T,#)
+ A— a)(l — ö)(<2? — xx)F{1 — a, 2—ö, 3 — y, x)
unde aequatio praecedens transit in hanc
—7, l-ar)
«+l—Trg+l—T> 2—T)(l—^-tt-g-1<a?-^(—a,—g, I — t,*
Mutando autem in aequatione 84, a, Ö, y m a+1, ö+l,
T, t +1 — T, 1 — t) A - ^)^-8 so-!F(— a, ~ Ö, j — T, a?)
Quare quum facile perspiciatur, has duas aequationes identicas esse debere, fit
generaliter
sive mutando a, ö, y in « — 1, f> — 1, y — 1
etc. unde facile concluditur, esse generaliter pro quovis valore integro ipsius k
DRTERMINATIO SERIEI NOSTRAE PER AEQUATIONEM DIFFERENTIALEM ETC.
Sed quoties 1 — (y— k) sive k-}-\—y est quantitas positiva, demonstravimus
esse (formula 85)
J{a—K,O — K,i K) — n(a-Y)nF— T)
Quare quum k, quidquid sit y> semper accipi possit tantus, ut k-\-\—y evadat
quantitas positiva, eritgeneraliter
f(a $ y) _ n(«
j\u, u, y n(a
et proin
ita ut formula nostra fiat
[86] F(a, ö,
sive nmtata y in a-(-6-(-1-—
[87] J?(a, ö,T, I— x)
Si magis placet, scribere licet
in forraula 86
pro A — x)T-*-*F{\ — a, 1 —ö, 2 — 7,^) ^(a+t —y, ö+1 —y, 2 — y, jr)
in formula 87
pro (\ — ccf^F{\ — a, 1 — 6, y-f-i — a — ö, x)....F(j — a, y — ö, y+l — a—6,
44.
Quoties itaque elemento quarto in aliqua. Serie sub forma nostra contenta
valor tribuitur inter 0,5 et 1, convergentiae lentiori per formulas praecedentes
remedium affertur, quippe quae illam in duas alias sejies simües dispescunt,
NACHLASS.
eo eitius eonvergentes, quo tardius illa convergebat. Sed excipere oportet casus
speciales, ubi haec transformatio non succedit, quoties scilicet in serie transfor-
manda differentia inter elementtim tertium summamque duorum elementorum pri-
morum fit numerus integer. Si enim in formula -86 y est = 0 vel aequa-
lis numero negativo integro, manifesto F(a, fi, y, x) fit series inepta (art. 2)
atque factor II (y—2) infinitus; si vero y est integer positivus unitate major
jP(l—a, l — 6, 2—y, a?) atque F(a-\-\—y, ö-j-1 — y, 2—y, <2?) fiunt series in-
eptae et II(—y) infinitus; denique si y = 1 duae series transformatae F(a, f>,y,#)
atque F(i—a, 1 — f>, 2—y,<2?) vel F(a-\-\—y, 6-f-l— y, 2—y, oo), quae ideo
cum jP(a.6,y,<2?) identica evadit, hocce quidem incommodo non laborant, sed
nihilominus transformatio nullius est usus, quum utraque series transformata per
coefficientem infinitum II (—1) multiplicata sit. Operae itaque pretium erit osten-
dere, quomodo in his quoque casibus convergentia lentior in citiorem mutari possit.
45.
Sit k numerus integer positivus (sive etiam = 0) designemusque k-\-\
primos terminos seriei F(a, 6, y, ce) per X. Terminus sequens erit
1.2. s....*+i.
qui etiam ita exhiberi potest
n(r-i) n(a+^)n(g+^)
D(o—1HF—l) *
similique modo termini sequentes. Hinc colligitur
x n(o + 6 —r)(ü(—r) -w-M .& N . •
I. n(a-T)n^) • F& °> 7' ^ expnmi posse per
si pro t omnes valores 0, 1, 2, 3 etc in infinitum substitui concipiuntur.
Simili modo F{a-\-\—y, ö-f-1— y, 2—y, oc) exprimi potest per
t perinde ut ante determinato, adeoque quum sit II(l — y) = A — y)H(—T) at"*
que ü(y—1) == —(l — y)Il(y — 2), patet esse
DETERMINATIO SEBIEI NOSTEAE PER AEQJTATIONEM »IFFERBOTIALEM ETC«
D(«—1HF—1) x -r^a-t-i y, o-f-j y, z y
ü(a—1I1F—t)ü(a-
Hinc formula 86 etiam ita exhiberi potest:
F(a, ö, a-f-ö-f-1 y, 1 ai)
Haecce expressio protinus ostendit, singulas differentias, quae sunt sub signo 2,
fieri =0, si supponatur y = —Je, sed quum hie simul fiat II(y—1) quan-
titas infinite magna, produetum finitum evadere posse patet. Cuius valorem ut
per quantitates finitas exprimamus, statuamus primo y-f-Ä = cd, unde fit
= 11@
sive
11 (T ~1) = ,(,-i)(,-2". ...(«,-*)
üei summa vertitur itaque in eo, ut videamus, quid fiat
.l-H-Yj
si tu in infinitum decrescat. Per principia nota autem hinc resultat
d_7
dY
si brevitatis caussa statuimus
= u
solamque y tamquam variabilem spectamus. Sed hinc fit
Hinc colligitur pro y = — k
[88] F{a, ö,
—i)(—2) (—
^^
ubi
4- etc.
atque
j i_ ^
1 i 1 1_ x
O+-Ä+8 "■ 6+Ä+S Ä + 4 3'
etc.
signumque superius vel inferius accipiendum est, prout k est numerus par vel
impar.
46.
Hoc itaque modo .F(a, 6, a+6 + 1—-y, t — a?) tmnsmutatur, si y est 0
vel integer negativus. Casum y == -|-l prorsus simili modo tractare possumus,
sive brevius statuera possumus in ratiociniis praecedentidus k = —1 , unde X
prorsus evanescit atque obtinemus:
DETEEMDTATIO SEEEEI NOSTEAE PEE AEQÜATIONEM DIFFEEENTIALEM ETC.
[89J F(a, ö, a+ö, 1 — #)
.2.3.1.2.3
+ etc.]
ubi
^^ C' + ""^' etc-
Ita e. g. pro et = 4-, ö = 4- obtinemus (cfr. form. 52, 71)
[90] J?(*,±, 1, 1-a)
1 4N1.1.3.3.5.5.7.7 4. , v
+)+ te}
^6+etc.}
Denique casum tertium, ubi y est integer positivus unitate maior, seorsim
tractare haud necesse est, quum sit
F(a, Ö, a-hö-f-l— y, 1—*) = a^^a+l —y, 6+1 — y, a+Ö+1—y, 1—
transformatioque seriei F(a~{-1~-y, 6-f-l—.y, a-|-ö-}-l—y, 1 — oc) pro y>»l
ad casum primum sponte reducatur.
47.
Transimus ad alias transformationes, inter quas primum locum obtineat
sübstitutio ob = —^-. Hinc fit dx = —-,—~, adeoque
^ = —j-(l—yf, differentiando denuo fit
d^ = -(l-^Jd|f+2(l-^)dP, adeoque
28
218 NACHLASS.
Quibus valoribus substitutis transit aequatio 80 in hanc
0 =
Ut vero obtineamus aequationem ipsi 80 simüem, statuamus P= (l—yY^*\ unde
ddP
Quibus substitutis fit post divisionem per A—yY
0 = P'
Determinemus [i ita, ut multiplicator ipsius P' per 1—y divisibilis evadat,-
quod fiet statuendo vel {i = a vel ja == ö. Valor prior mutat aequationem prae-
cedentem in hanc
0 = a(g
sive
0 = «(r_«)P'_(r_(r_
cui ita satisfaciendum est, ut fiat pro y = 0, P'= 1 atque ^— = a^Y~ \ Hinc
autem deducitur P'=F(a,y — fi,yty) adeoque habetur
[91] F(a, Ö, y, Ä) = (l-^)aP(a, y-Ö, r,y) = (l-^P(a. y-Ö, y, -^)
Si pro {i valorem alterum ö adoptavissemus, prodiisset prorsus simili modo
[92] F(a, Ö, y,^) = (l-*)"*p(ö, y-a, y, -^)
quae formula quoque e praecedenti per solam permutationem elementorum a, ß
sponte sequitur. Adiumento formulae modo inventae valores serierum nostrarum
pro valoribus negativis elementi quarti semper ad valores similium serierum pro
valoribus positivis elementi quarti interque 0 et 1 sitis redacitur, quum fiat
. F(a, Ö, y, -x) = (l-\-xr*F(a, y- Ö. y,
DETERMJNATIQ SEEIÖ HOSTRAE PEB AEQÜATJ0KE8C
48.
Operae pretium erit ostendere, qnomodo adiumento fcransformationum
82,91 omnes formulae in art. 5 collectae perfacile e solo tbeoremate binomiali
deduci possint. Protinus enim inde sequuntur formulae I — IV. Formu-
Formulae VI—IX hinc sponte sequuntur, si e* spectatur tamquam limes potestatis
A+-^-)* vel (l — 4)""*, atque log# tamquam limes ipsius i(a?r—1), erescente i
in infinitum. Porro ex
coswcp-f"V—l.sinwcp = (cos <p-f-V—l.sin<p)w
> — \f—1 .sinwcp = (coscp—\j—1 .sincp)Ä
sequitur per subtractionem et additionem formula XVIII et XXII atque hinc
per formulam 82 statim XIX et XXIII; hinc rursus per formulam 91 deducun-
tur XVI, XVII, XX et XXI. Statuendo t pro nt atque n infinitum ex XVI et
XX sequuntur XI et XII; statuendo vero n infinite parvum ex XVI—XVHI
sequuntur XIII—XV.
49.
Ex substitutione oc = — simili modo evadit
y
0 =
Statuendo dein P = y*P\ fit
I. 0 = P'(aÖ —
Ut multiplicator ipsius P' per y divisibilis evadat, statui debet vel ja = a vel
jjt == ö; valor prior producit, *
II. 0 = P'a(T-a-l)^^-'(g-a-l-(T-2a
cuius integrale particulare M
P'= JP(o,« + l—7, a+l—Ö,y)
28
220 TSACELAS&.
Satisfit igitur aequationi I per integrale particulare
P = yaF{a, a+i — y, a+1 — ß,y)_
et perinde valor alter ja = ö suppeditat alterum integrale particulare
unde integrale completum habetur
designantibus .A, 23 constantes, quae vero non sunt arbitrariae sed penitus de-
terminatae, quum P non sit integrale completum aequationis 80, sed particu-
particulare tantum. At ne determinatio valorum constantium A, B in. ambages inuti-
les nos deducat, eandem aequationem alio modo per ea, quae iam evolvimus, de-
ducemus.
Statuendo in aequatione 91 ——^— = 1—z, mutandoque in aequat. 86
ß in y — ö, y in a-f-1 — ß, x in z, colligetur
T,
Sed per aequatt. 91, 92
F(a, T— Ö, ct+1 —tf, «) = A— «^^(a, a+1 — y, a + l —Ö, —1~
—a, «) = A—z)-*F(ß, Ö+l — y, Ö+l—a, —^
His substitutis, nee non 2 = , 1—z = — , — = —, habemus
1—x 1 — x 1—z a;
[931 *■(«, g, 7,,) = ggl^ngl'^-»)-*^«. «+i-r. «+1-«. 7
— i)n(a— 6—1
a, -
quae convenit cum aequatione supra inventa, si statuatur
4 _n(Y
^1 — n(
DETEEMINATIO SEB3EI NOSTRAE. PER AE^fFATIOlSEM mFFERSamALEtt ETC.
ubi notandum, esse
(—lN =
designante Tz indefinite integrum imparem quemcunque.
50.
Per aequationem 93 valor functionis nostrae pro valoribus elementi quarti
unitate maioribus ad casum eum reducitur, ubi elementum quartum unitate mi-
minus est. Simul patet, valoribus elementi quarti negativis, unitate maioribus,
semper unum valorem realem functionis F respondere, positivis vero tunc tan-
tum respondere posse valorem realem functionis, si a et ö sint vel integri vel
fractiones rationales, quarum denominatores sint impares; in casibus reliquis
F(a, 6, yi &) pro valore positivo ipsius x unitate maiore tantummodo valores ima-
ginarios admittit.
51.
Relationes inter plures functiones F hactenus evolutae omnes lineares fue-
runt: adiicimus aliam diversi generis. Sit
P = F(a, Ö, y, co)
Q = a:l-tF{a + \—y, €+1 — y, 2 — y, »)
R = F(a, $, a+ö+1 — y, 1—co)
ita ut P, Q. -ß sint tria integralia particularia aequationis 80, sive sit
L 0 = aÖP-G-
II. 0 -
III. 0 =
Multiplicando aequationem primam per Q, secundam per P, fit subtrahendo
A / / , ^ , -v \QdJP—PdQ , , NQddP-PddQ
0 =(T_(a+ö_|_i)Ä)^___—2+fr—a,a!J ^—Jf
Haec v^ro aequatio per a?T*(l—x)a+&~i multiplicata integrabilis evadit atque
suppeditat
NACEH&ASS.
[94] A = *T A _ ,}-+*+«-T
Prorsus simili modo habetur
[95] -B =
[96] C =
Constantes ^4, J5, C facile determinantur per methodum sequentem.
Pro #=0, fit P=i; porro tfQ = a?F(a-\-l—t,fi-\-l—y« 2—Y» ^)
fit = 0 pro «2? = 0; ipsius differentiale autem per dx divisum, puta
^ fit =1; hinc colligitur ~^=i—y Pr0 ^=0, adeoque
Ut vero etiam B et C determinemus, resumamus aequationem
quae differentiata dat
Multiplicando primam per -^, secundam per Q, fit subtrahendo
Qdi2—i2dQ ., ^ xQdP —PdQ ,
^ = /(a, 5, y) ä^ adeoque
Similiter multiplicata aequatione priore per -r-, posteriore per P, subtractio dat
d^ =/(«+1—Y' ö+l-TT, 2 —T) d^
adeoque
Si magis placet, hae tres aequationes etiam ita exhiberi possunt, ut functio-
nes derivatae ^-, -^, -^- per functiones finitas exprimantur; ita e. g. fit for-
mula 96,
DETEBMINATIO SERffil NOSTBAE PER AEQÜATIONEM DIFFERENTIALEM ETC. 22$
[97] -F{a, ß, a + tf + 1-—y, 1—
52.
Denotando ftmctionem F(—et,—ß, 1—^x) per S, erit
0 =
Combinata hac aequatione cum I art. praec. fit
o = «
quae est integrabilis atque suppeditat
Const. = aß PS—[x—^^)^*^
Valor quantitatis constantis sponte demanat = aß ex x = 0. Si formam fini-
tam mavis, habes
[98] F{a, ß, y, x)F{—a, —ß, l —y, a?)
^ —a, 1 — ß, 2 — ^x) = 1
Transformando hie singulas quatuor funetiones secundum fonnulam 82 ac
dein scribendo y — a> Y—^ Pr0 a» ^» na^ebis
[99] {\—x)F{a,ß,^x)F{\ — a, 1—ß, l—^,x)
Quaedam theoremata specialia.
53.
Relätiones omnes quas hactenus eruimus eatenus sunt generalissimae, quod
elementa a, ß, y nullis circumscribuntur conditionibus. Praeterea autem plures
alias invenimus, quae conditiones speciales inter elementa a, ß, y supponunt :
multo vero plures sine dubio adfcuc latent, easque ipsas quas hie trademus for-
tasse ex altioribus prineipiis derivare in posterum licebit.
224c KACHLASS.
Statuamus primo in aequ. 80, x = *y , unde
da- — d«/ 4{)
adeoque
dP __ dP _
da: dy " 4(t —
ddP_,dP (i + yK , dP B-y)(i+y)'dy
d« udy *4(i—y)"dy 2A— y)8
ddP__ddJ> (l + yN ■ B—y)(l + g)' dP
dar8 ~" dy8 -töCl-y)8" 8(l-y)s ' dy
Hinc fit aequatio illa
0 =
ddP y(l+i/)8 yB—y)(|+y) dP
dy8 ' 4 2(i-y) 'dy
sive
0 = 4afi(l—
0 = 4oö(l—
Statuendo P = A-f-^) Q, hinc deducitur
I. 0 = 2aBö—Y-f-Ba-}-l — i)y)Q
Iam supponendo esse 6 = a-f-^-, haec aequatio induit formam sequentem
0 =
ddQ
cuius integrale est
= F{2a,
DETEEMINATIO SERIEI NOSTRAE PEB AEQÜATIQNEM DISTiaSENTIALElf ETC.
ita ut resultet ,
[100] ^ if^
54,
Si loco relationis 6 = a-f--|-, hanc adoptamus f = 26, aequatio I art.
praec. fit
0 = 2oBo+l
(\ \ddQ
yv- yy)
Iam statuendo yy — «, fit
dQ =2 dQ
dy «^ dz
ddQ . ddQ , 2dQ
0 = a(a + 4—6)Q
' ' dz
cuius integrale quum sit
Q = ^(a, a+|- — 6, 6 + ±, s)
habemus
[101] (l+#a^(>, a+4-~6, 6 + *,^ = ^(a, «, 26,
55.
Statuamus secundo a? = 4^ — 4^, unde
dF dP
da; dy ' 4(l—2y)
ddP ddP l _i_df 1
da;2 Hy" 16(t—2y)8~l dy * 8(l—2y)s
unde aequatio 80 fit
29
5JACHLASS,
0 = 4a€P
ddP
Ut in membro secundo fractionem auferre liceat, statuere oportet -( = «x —J— 6 —f- -|-,
unde prodibit
0 == 4a6P
— {y—yy)^f
cuius integrale est
P = F{2ai 26, a + y)
unde habemus
[102] J?(a, 6, a + 6 + ±, 4y — 4yy) = J?Ba, 26, a+
Si in bac aequatione y mutareraus in 1 —y, prodiret inde
F{a, 6, a-f-6-K, 4y—4yy) = .PBa, 26, a
unde sequi videtur paradoxem
a, 26, a + 6 + 4-.y) = i^Ba, 26, a + 6
quae aequatio certo est falsa. Quod ut solvamus, meminisse oportet, quod probe
distinguendum est inter duas significationes characteristicae F, quatenus scilicet
vel repraesentat functionem, cuius indoles exprimitur per aequationem differen-
tialem 80, vel solam summam seriei infinitae. Posterior, quamdiu ejementum
quartum inter —1 et -j-1 situm est, semper exhibet quantitatem ex asse de-
terminatam, sed cavendum est, ne hos limites excedas, quum alioquin nulla pror-
sus significatio supersit. Prior vero significatio repraesentat functionem genera-
lem, quae quidem secundum legem continuitatis semper mutatur, si elementum
quartum fluxu continuo mutatur. sive ipsi välores reales sive imaginarios tribuas,
si modo semper valores 0 et 1 evites. Hinc patet, in posteriori sensu functionem
pro aequalibus elementi quarti valoribus (transitu seu potius reditu per quantita-
tes imaginarias facto) valores inaequales adipisci posse, e quibus is quem series F
DETERMINATIO SF.RTET NOSTRAE PER AEQUATIONEM DIFFERENTIALEM ETC.
repraesentat unicus tantum est, adeoque jieutiquam est contradictorium, quod,
dum aliquis valor functionis jF(at 6. a4-^>4~ih ^y— ^yy) es^ aequalis ipsi
FBa, 26, a-f-6-f-4-,#), alius valor fit = FBa, 26, a-f-6-j-^-, 1—y) foretque aeque
absurdum, hinc aequalitatem horum valorum concludere, ac si ex Are. sin 4-= 30°,
Are. sin 4-= 150° concluderes 30° = 150°.— Si vero characteristicam JP acci-
pimus in significatione minus generali, scilicet, ut tantummodo repraesentet sum-
marn seriei F, ratiocinia ea, per quae aequationem 102 eruimus, necessario suppo-
nunt, y tantummodo eousque a valore 0 crescere, donec evaserit x =. t, i. e. usque ad
y=\. In hoc ipso puneto autem covtinuitas seriei P = F(a, 6, a -f- 6 -f- ^-, Ay — Ayy)
interrumperetur, quum manifesto ^— e valore positivo (finito) subito ad negati-
vum saliat. Itaque in hac significatione aequatio 102 extensionem ultra limites
y = % — \J± usque ad y = 4- non patitur. Si mavis, eandem aequationem ita
quoque exhibere potes
[103] j?(a,6,a + 6-H-,ff) = FBa, 26,
sive ita
[104] F{a,po, a+S-K, I—a?) = FBa, 26, a
unde tamquam corollarium sequitur (formula 48)
n(a_
II(a4-g
56.
Ex applicatione formulae 87 ad aequationem 104 sequitur
[106] FBa, 26, a ^
unde patet, seriem
2^B0, 26, a+ ^
exhiberi posse per seriem
Bl^pt A***1!**1^ etc.
statuendo brevitatis caussa
29
228 NACBLASS.
Hinc colligere licet, esse
[107]
Quodsi cui haec conclusio haud satis legitima videatur, (quam tarnen extra
omne dubium collocare haud difficüe foret) ad eandem aequationem sequenti modo
pervenire possemus. Ex aequatione 87 fit
FBa, 26,a+6+i, 1±^) = Ci^Ba, 26, a+6+1-, i=^) .
+ D(^)*-a-«J?(l —2a, 1— 26, f— a—6, i=^)
statuendo brevitatis caussa
° • n(a — 6 — i)n(g— a — ■§) ' -17 nBa—l)nBg—1)
Ex aequatione 104 autem facüe deducitur
F{\— 2a, 1_26,|— a —6fi=^ = J?(± —a,± —6,1— a-6, i_
statuendo brevitatis caussa
Hinc rursus sequitur per aequationem 82
j?(l_2a,l —26,1—a-6, 1=^)
His substitutis colligitur statuendo
AC-^-DE22a+2&-1 = Jf, ^C+DG?22a+2g-1 = iV
o, 26, a l±^
convenit cum aequatione 107. Iam possemus quidem e sola natura
functionis U derivare M=A, N=—B, quum per aequ. 55, 56 facüe demon-
stretur, esse
p cos(a—6)g _Z)^2sc+3(?-i 2sina-sing7T D(?22B+2|?" 2cosaitcosgr
cos(a-f-g)z' Ä cos(a4-g)- ' £ cos
DETERMDfATIO SEBJEI NOSTKAE PER AEQUATIONJEM DIFFERENTIALE^; ETC.
sed hoc labore ne opus quidem est. Patet enim, statuendo x = 0, fieri debere
M= FBa, 26, 0+6 + 4-, 4.) = A
differentiando vero illam aequationem prodit
°°~* ■ \ 1 « 2^B o+l, 26+1, a + 6+f, i-^~)
«4-64.1 ' IIaII6
_n(a4-g-i-)n(-i)__ _n
n(o—1I1F—1)
57.
E combinatione aequationum 106, 107 habemus itaque
[108]
= 2^Ba, 26, a+6 + 4-, l=^) + 2^Ba, 26, a
[109]
= 2^Ba, 26, a + 6+i, i^)_.PBa, 26, a
-, f,
unde statuendo a? = 0 prodit
^^a+l, 26+1, a+6+f, i)
Mutando in aequatione 109 a in a — 4-, 6 in 6 — ^-, facile videbis, inde prodire
= FBa-1, 28—1, a+8—i, l+^)-F{ia-\, 28-1, a+6—i,
BEMERKUNGEN.
In der Handschrift bildet die Deierminatio seriei nostrae per aequationem dijferentialem etc. den zwei-
zweiten Theil einer Abhandlung, die den Titel führt, 'Disqui&itiones generales circa functiones a serie inßnita
1 -|—— x 4- etc. jpendentes auctore Cabolo Feiedesico Gauss sodetati regiae traditae Nov. l Sl l.' Der erste
Theil ist nach einer weitern Ausführung der Einzelheiten in die 1812 Jan. 30 veröffentlichte bekannte Ab-
handlung übergegangen. Dabei sind aus 27 Artikel 37 geworden, und die 65 numerirten Gleichungen bis
zu 7 9 vermehrt. An jene schliessen sich die Nummern der Artikel und Gleichungen des zweiten Theils in
der Handschrift an, zur Bequemlichkeit des Lesers hat man sie aber nach denen der veröffentlichten Ab-
Abhandlung sich fortsetzen lassen und auch auf diese die vorkommenden Citate bezogen.
Das Handexemplar der gedruckten Abhandlung Disqu. gen. circa seriem etc. enthält zu Art. 28 die
Aufzeichnung
+ 00
Die beste Definition von II ist dass IIm = fe(m+i)xe~e da;
ferner die Gleichung 5 8 auch noch in dieser Form
[58] log 11« = (a + *)log2—a + 3log2w + 4.*P + ^f Q+^.iÄ + TVtS+etc.
die unmittelbar aus 61, 62 und 57 abgeleitet werden kann.
In einem Notizbuche ist mit Hülfe der Gleichung 58 unter der EuiEB'schen Form der Werth von
logII(lo-H") und daraus der von log Ui zu 9,7173075 — I7°ie'5793« und 11« = + o, 4980156—0,1549496»
berechnet (nach dem Jahre 1847).
Der Art. 4S ist hier so wiedergegeben, wie er nach vielfachen Durchstreichungen von Worten und
ganzen Sätzen in der Handschrift gelesen werden muss; nach Absicht des Verfassers dürften aber wohl
noch die Worte 'e solo theoremate binomiali' fortzulassen sein.
Schekikg.
ANZEIGEN.
Göttingische gelehrte Anzeigen. 1815 Juli i.
Der Königl. Societät ist durch Hrn. Prof. Gauss eine handschriftliche Ab-
Abhandlung des Hrn. Prof. Ppaff in Halle vorgelegt, überschrieben:
Methodus generalis, aequationes differentiarum partialium, nee non aequaüones
differentiales vulgäres, utrasque primi ordims, inter quoteunque variabiles,
complete integrandi.
Die Lehre von den partiellen Differentialgleichungen des ersten Grades ver-
verdankt bekanntlich Lagrange zwei wichtige Erweiterungen, nemlich die allgemeine
Integration derselben, wenn sie entweder, bei einer beliebigen Anzahl veränder-
veränderlicher Grossen, die partiellen Differentialquotienten bloss linearisch enthalten,
oder ohne Einschränkung in Rücksicht der Form, wenn der veränderlichen
Grossen nur drei* sind. Ueber diese beiden Fälle war man eigentlich bisher noch
nicht hinausgegangen, und das von Lagrange bei den partiellen Differentialglei-
Differentialgleichungen dreier veränderlicher Grossen angewandte Verfahren würde bei einer
grössern Anzahl besondere Schwierigkeiten haben. Wir haben es daher als eine
merkwürdige Bereicherung der Integralrechnung anzusehen, dass es dem scharf-
scharfsinnigen Verfasser der vorliegenden Abhandlung gelungen ist, die allgemeine In-
Integration der partiellen Differentialgleichungen des ersten Grades für jede Anzahl
von veränderlichen Grossen zu finden. Er hat bei dieser Untersuchung exnea ei-
232 ANZEIGE.
genthümlichen Weg gewählt, und sie an einen andern nicht weniger interessan-
interessanten Zweig der Integralrechnung angeknüpft, nemlich an die Lehre von den ge-
gewöhnlichen Differentialgleichungen (des ersten Grades) zwischen mehr als zwei
veränderlichen Grossen, deren wahre Natur bekanntlich erst Monge uns kennen
gelehrt hat, obwohl die Integration derselben von diesem Geometer nur für die
einfachsten Fälle vollendet ist. Von dieser Gattung von Differentialgleichungen
giebt Hr. Pfaff die allgemeine Integration, und die der partiellen Differential-
Differentialgleichungen erscheint dann nur als eip. besonderer Fall von jener. Bei diesen
Untersuchungen wird die allgemeine Integration der Differentialgleichungen von
jedem Grade zwischen zwei veränderlichen Grossen vorausgesetzt, welches ganz
in der Ordnung ist, eben so wie man in den höhern Theilen der Mathematik die
allgemeine Auflösung der algebraischen Gleichungen postulirt.
Wir glauben den Freunden der höhern Mathematik einen angenehmen
Dienst zu erweisen, wenn wir sie durch gegenwärtige Anzeige in den Besitz die-
dieser schönen Erweiterung der Integralrechnung setzen. Freilich würde ein Aus-
Auszug aus der 144 Quartseiten starken Abhandlung, in welchem wir dem Verfasser
Schritt für Schritt folgen und nichts Wesentliches übergehen wollten, die Gren-
Grenzen des uns vergönnten Raumes weit überschreiten. Wir wollen daher versuchen,
indem wir uns bloss an die Sache halten, in einer etwas veränderten Darstellung
das Wesentliche so herauszuheben, dass Kenner sich dasselbe vollkommen an-
aneignen können.
Als die Hauptoperation des ganzen Geschäfts muss angesehen werden die
Reduction eines Differentialausdrucks
Q = pdx-\~p'dx'~\-p"dx"-{- etc. -\-p^n~~^dx^n~~^
wo jeder der Coefficienten p, p, p" u. s. w. Function der veränderlichen Grossen
x, x\ x" u. s. w. ist auf die Form
Q — \(qdy-\-q'dy'-\-q'dy"~\- etc. -f-q(n~2^dg(n~~J}
&o dass X,^,y,y'u. s.f. Functionen von x. x',x"n. s. w. seien, hingegen q, q, ^"u.s.f.
Functionen von y, y, y"u.s.w., und dass die Anzahl der letztern veränderlichen
Grossen um eine kleiner sei, als die Anzahl der veränderlichen Grossen x, x\ x'u.s.f.
Diese Verwandlung, welche wir Kürze halber mit (I) bezeichnen wollen,
beschränkt sich auf den Fall, wo n eine gerade Zahl ist; wir werden weiter un-
PPAPP. METHODOS GENERA US AEQÜATIONES DIPPEBENTIAEDM ETC. 233
ten entwickeln, wie sie ausgeführt werden müsse, und sie, um die Uebersicht
nicht zu stören, hier einstweilen voraussetzen.
In dem Fall, wo n eine ungerade Zahl ist, würde die Verwandlung I nur
unter speciellen Bedingungen zwischen den Coefficienten p, p\ p". . . möglich
sein; allgemein aber lässt sich in diesem Falle Q auf die Form
p*dx-irMqdy + <jdy + q'dy"+ etc.
bringen. Man sehe nemlich einstweilen x in Q als constant an, und verwandle
unter dieser Voraussetzung nach (I)
p'dx'+j)"dx"+p"dx"-±- etc. -f-y-^da^
wo nunmehr die Anzahl der veränderlichen Grossen x', x", x". . . gerade sein
wird, in
l(qdy + qdy'+q"d/'-f- etc. ~\-q(n~s)dy(n~s)) = \Q'
Hier werden also q, q, q" u. s. w. Functionen von y, y', y"u. s. w. sein, diese hin-
hingegen , eben so wie X, Functionen von x, x, x", x". . .., von welchen Grossen
jedoch die erste x als constant behandelt werden muss, um aus der Entwicke-
lung von XQ'
g
p'dx'~\~p"dx"~\-p'"dx'"~\- etc.
zu erhalten. Das Glied, welches noch hinzukommt, wenn beijener Entwicklung
auch x als veränderlich betrachtet wird, ist
£ + «'•£+etc.) Xd»
Man hat daher, um die obige Form zu erhalten, nur
zu setzen. Diese Verwandlung von Q in p*dx-{-'kQ', welche auf ungerade Wer-
the von n beschränkt ist, wollen wir mit II bezeichnen. Offenbar kann dieselbe
Reduction abermals auf Q' angewandt und
etc.
30
2M ANZEIGE.
gesetzt werden, und so abermals Q"= r*dz-f-X"Q'" bis man zuletzt auf einen
Ausdruck kommt, der bloss Eine veränderliche Grosse enthält. Dadurch ist also
Q auf die Form
p*dx~\-lq*dy~\-l'k'rdz~\- etc.
gebracht, oder auf die Form
Pdx~\-Qdy-{- Rdz-\- etc.
wo die Anzahl der veränderlichen Grossen x, y, z u. s. w. = -%-(n-\-\), und wo die
sämmtlichen n Grossen y, z u. s. w. P, Q, R u. s. w. Functionen von x, x, x"u. s. w.
sein werden. Diess Reductionsverfahren mag durch III bezeichnet werden.
Wendet man diess Verfahren III in dem Fall, wo ursprünglich eine gerade
Anzahl veränderlicher Grossen vorgegeben war, auf den durch die Reduction I
erhaltenen Ausdruck
qdy~\-q'dy'~\-q"dy"~\- etc.
an, so kommt dadurch
Q = pdx+p'dx'-\-p"dx"-\- etc. +/w-1Ww~t) in die Form
Qdy~\-Rdz~\- etc.
so dass die Anzahl der veränderlichen Grossen y, z u. s. w. = \n wird, und alle
n Grossen Q, R u. s. f. y, z u. s. f. Functionen von x, x, x" u. s. w. werden.
Diese Reduction werde mit IV bezeichnet.
Diese allgemeine Transformabilität der Differentialausdrücke nach III und
IV ist ein eben so neuer als merkwürdiger Lehrsatz, der sich zwar in der Ab-
Abhandlung des Hrn Pf äff nicht ausdrücklich ausgesprochen findet, aber sich leicht
aus den dortigen Untersuchungen folgern lässt.
Es lassen sich nun daraus die Auflösungen der im Eingange dieser Anzeige
erwähnten Aufgaben mit Leichtigkeit ableiten.
1) Um die Differentialgleichung
0 = pdx~\-pdx'~\-p"dx"~\- etc.
oder ■ 0 = Q
PF ÄFF. METHODUS GENERALI& AEQUATIONES DIFFEEENTIAEÜM ETC. 235
zu integriren, wo p, p, p" u. s. w. gegebne Functionen der n veränderlichen
Grossen x, x, x"vl.s.w. sind, wird man, wenn n gerade ist nach IV
Q = Qdy~\-Rdz~\-Sdu~\- etc.
machen, wo Q, y. R, z, S, u u. s. w. zusammen n gegebne Functionen von x, x, x"
sein werden. Die Differentialgleichung
0 = Qdy-{-Rdz-{-Sdu-{- etc.
wird also der vorgegebnen gleichgeltend und ihre allgemeinste Integration in 'fol-
'folgendem System von 4-w Gleichungen enthalten sein :
= <p(y, z, u etc.), '. *?(**"•••) = » d^j^ = i
du
wo <p eine willkürliche Function vorstellt, und die Differentialquotienten, wie
sich von selbst versteht, partielle sind. In so fern vermittelst der Gleichung
0 = y(y,z,u etc.) die Grosse y sich durch die übrigen bestimmen lässt, kann
man die Auflösung auch durch folgende Gleichungen darstellen:
y = ty (z, U . . . .)
d<b(z, u. . . .) H
~ dl Q
d'b(z,u . . . .) ^
du Q
U. S. f.
Genau genommen wäre indessen diese Auflösung weniger allgemein, da die will-
willkürliche Function v[y,z, u . . . .) auch solche unter sich begreift, in welchen y
nicht mit vorkommt.
2) Zur Integration derselben Differentialgleichung in dem Falle, wo n un-
ungerade ist, wird man 12 nach III in folgende Form setzen
Q = Pdx-{-Qdy-{-Rdz-{- etc.
wo P, Q, y, R, z u.s.w. zusammen n gegebne Functionen von x, x, x"u. s.w.
sein werden. Die allgemeinste Integration der Differentialgleichung Q = 0 be-
beruhet dann auf folgendem System von i[n-{-l) Gleichungen:
30*
236 ANZEIGE.
3) Die allgemeine Integration einer gegebnen partiellen Differentialgleichung
des ersten Grades, d. i. einer endlichen Gleichung zwischen den partiellen Diffe-
Differentialquotienten
dar / da* // da; m n
d^=^ w=P> d^'=P • u-s-f-
und x, x, x", x"u. s. w. (wo x eine erst zu bestimmende Function der m ver-
veränderlichen Grossen x\ x", x'"u. s. w. vorstellt) ist nichts anders, als die allge-
allgemeine Integration der gewöhnlichen Differentialgleichung
0 = — dx-{-pdx'-{-p"dx"-{-p"dx'"-\- etc.
Da nemlich vermöge jener endlichen Gleichung eine der Grossen p',p",p"'\i.s.w.
z.B. p als Function der übrigen p", p" u. s. w. und x, x, x", a/"u.s. w. darge-
dargestellt werden kann, so ist die eben angegebne Differentialgleichung als eine zwi-
zwischen den 2 m veränderlichen Grossen x, x, x" u. s. w. p", p'" u. s. w. zu betrach-
betrachten , in welcher die Differentiale dp", dp"u.s.w. mit dem Coefficienten 0 be-
behaftet sind. Um also die Integration auszuführen, wird man den Differential-
Differentialausdruck
— dx+p'dx'+ p"dx"-{-p'"dx'"-{- etc.
auf die Form
Rdz-{- Sdu+ etc.
bringen, wo die 2 m Grossen Q, y, R. z, S. u u. s. w. bekannte Functionen von
x, x\ x" p", p'" sein werden. Die Integration ist sodann in demselben
System von Gleichungen wie oben A) enthalten, und wenn man sich aus ihnen
p", p"u. s. w. eliminirt denkt, bleibt Eine endliche Gleichung zwischen x, x, x",x"
etc. zurück. Die wirkliche Elimination kann freilich nur ausgeführt werden, in so
fern für cp bestimmte Functionen angenommen werden; allein dieser Umstand be-
beruhet auf der Natur des Problems und nicht auf der Unvollkommenheit der Ana-
Analyse , welche, so lange sie beim Allgemeinen stehen bleibt, die Auflösung nur in
jener Form geben kann.
Uebrigens sieht man von selbst, dass auf ähnliche Art die Integration meh-
mehrerer neben einander bestehender partieller Differentialgleichungen in unsrer Ge-
Gewalt ist.
Es bleibt uns jetzt nichts weiter übrig, als nur noch eine allgemeine Me-
PFAFF. METHODUS GEJSTERALIS AEQUATIONES DIFFERENTIAKUM ETC.
thode für die oben mit (I) bezeichnete Transformation anzugeben. Was für
Functionen von x, x, x" u. s. w. auch immer für y, y', y" u. s. w. angenommen
werden, so ist klar, dass, wenigstens allgemein zu reden, durch Elimination die
Grossen x, x", a/"u. s.w. sich als Functionen von x, y, y, y"u. s. w. werden dax-
daxstellen lassen, deren Differentiation n — 1 Gleichungen hervorbringen wird:
dx' = %dx +a'dy -f-6'd/-}-T'd/' + etc.
dx" = £"dx+a"dy +%"dy'+fdy"+ etc.
dxm= £'"dx+a'"dy + V"dy + fdy"+ etc. u.s.w.
Hier sind also die Coefficienten £', £", 4'" u. s. w. a, a", a!" u. s. w. Functionen von
x, y, y, y" u. s. w., und in dieser Beziehung werden wir ihre partiellen Differen-
Differentialquotienten nach x durch Einschliessung in Klammern unterscheiden: offen-
offenbar können jene Grossen auch als Functionen von x, x, x", x'"u. s. w. angesehen
werden, in welcher Beziehung wir den partiellen Differentialquotienten nach x
ohne Klammer schreiben wollen, so dass (-^—) wohl von -=— unterschieden wer-
den muss. Dasselbe gilt von (%^) und ^~ u.s.w. Damit nun Q nach Substitu-
Substitution jener Werthe von dx, dx", dx"u.s.w. die vorgeschriebene Form erhalte,
muss offenbar erstlich dx herausfallen, also folgende Bedingungsgleichung [1]
Statt finden:
0 =p+p'i'+p'V+pmim+ etc.
Ferner sollen die Coefficienten von dy, dy, dy" u. s. w. nemlich
pV+/a"+/'a'"-}-etc. == A
. = B
= C, u.s.w.
die Form \q, \q\ Xq"u.s.w. erhalten, so dass q, q, q"u.s.w. bloss Functionen
von y, y, y"u. s. w. werden; damit diess geschehe, müssen wir zweitens haben [2]:
Nun ist aber
;d^)H_i>-(d^:)+etc.
^n-r 1 I Je \(i* / I
238 ANZEIGE.
Substituirt man hier
^da;' dy ' (da; ' dy
und subtrahirt
, d£' „ dl" ,
welche Gleichung entsteht, wenn man [l] nach y differentiirt, so wird
Da man nun ferner hat
-etc.
(jf) = jf+«'• J?+fi*-3$+ etc. u. .. w.
dy da; ' da; ' da;
dp' r dp' . „ dp' , ,„ dp'
.x^ + a . ; + etc., u. s. w.
da;" ' da/' '
so wird nach diesen Substitutionen
""" i'"_i_ etc.
werden, wo
k' =A,0) * -f (l,2)£"-j-(i,3)£'"-f etc.
k" = B,0)-f-B,1L' # -f-B,3L'"-f-etc.
F'=C,0)+C,l)C'+C.2)|"— * + etc.
u. s. w. wenn man Kürze halber allgemein
dpW dpi")
dx(v) dzO*)
durch (ji,v) bezeichnet, so dass allgemein (jx, ji) = 0, und (v,ji) = :—(ja. v) wird.
Ferner sieht man leicht, dass auch
"-4-k'"t'"-4- etc.
PFAFF. METHODUS GENEBALIS AEQUATIONES DIFFEBENTIABÜM ETC. 239
u.s.w. wird, und dass folglich den Gleichungen [2] werde Genüge geleistet wer-
werden, wenn k', k", k'" u.s.w. resp. den Grossen p\ p", p"u. s. w. proportional wer-
werden. Setzt man übrigens noch
k = * H-@,l)C/H-@,2)Cw+@,3)C*+ etc.
so hat man die identische Gleichung
0 = *+ k'i'+k"i"+K"i'"+ etc.
aus welcher mit [1] verbunden leicht gefolgert wird, dass auch k der Grosse p
proportional sein muss; diese letztere Proportionalität kann die Stelle der Glei-
Gleichung [1] vertreten. Mit Hülfe der n — 1 Gleichungen
IV IV IV IV
- = — = -r, = -fr, = U. S. W.
p p p' p
können nun die bisher unbekannten Functionen i\ i", i'"u. s.w., deren Anzahl
gleichfalls n—1 ist, bestimmt werden; jedoch zeigt eine nähere Betrachtung,
dass diese Bestimmung nur für gerade Werthe von n ausführbar ist; für unge-
ungerade n wird allemal, sobald die Grossen £', £", £"' u.s.w. bis auf eine eliminirt
sind, diese von selbst herausfallen und bloss eine Bedingungsgleichung zwischen
p, p, p" u. s. w. übrig bleiben. In diesem Umstände liegt der Grund, warum die
Verwandlung (I) auf gerade Werthe von n beschränkt werden muss.
Die Bedingungen der Verwandlung I sind also jetzt darauf zurückgeführt,
dass die partiellen Differentialquotienten (^-), (j^~). (^r)u-s-w-' ^n s0 ^ern
x',x",x"vl s.w. als Functionen von x, y, y, y" u.s.w. betrachtet werden, die jetzt
als bekannte Functionen von x, x\ x" u. s. w. dargestellten Werthe £', |", i'" u.s.w.
erhalten. Diess lässt sich auch so ausdrücken: In so fern y, y, y" u.s.w. als
constant und also x\ x", x"u. s. w. bloss als Functionen der veränderlichen Grosse
x betrachtet werden, muss folgenden n—l Differentialgleichungen Genüge ge-
geleistet werden
dx = i'dx, dx" =- i"dx, dx'" = i'"dat, u. s. w.
oder wenn man die ursprünglichen Gleichungen vorzieht, aus deren Combination
diese eigentlich entstanden waren, folgenden:
240 ANZEIGE.
^).d^+^.darH- etc.
p p
?. d*"+ Üi!) dx"-{- etc.
p
= u. s. w.
Die Integration dieser Gleichungen gehört aber in das Gebiet der gewöhn-
gewöhnlichen Integralrechnung, und wird hier vorausgesetzt; sie wird, allgemein zu re-
reden, n—1 von einander unabhängige Constanten enthalten H, H', H", H'"vl. s. w.,
die als gegebne Functionen von x, x", x"'u. s.w. erscheinen, so dass man n—1
endliche Gleichungen erhält
H=X, B'=X\ H"=X", u.s.w.
wenn X, X\ X"u.s.w. diese Functionen vorstellen. Es erhellt also aus dieser
Analyse, dass den vorgeschriebenen Bedingungen Genüge geleistet sein wird,
wenn man eben diese Functionen für y, y', y" u. s. w. wählt, oder
y^X, y=X\ y"=X", u.s.w.
setzt.
Eine Bemerkung wollen wir hier noch beifügen. Wir haben mit Vorbedacht
gesetzt, dass die Integration, allgemein zu reden, n — 1 von einander unabhängige
Constanten gebe. In speciellen Fällen nemlich, d. i. wenn die Coefficienten
p, p, p" u.s.w. so beschaffen sind, dass obige n—1 Differentialgleichungen nicht
von einander unabhängig sind, sondern eine schon aus Combination der übrigen
abgeleitet werden kann, gilt diess nicht mehr: hier wird auch die Bestimmung
von i', |", 4'"u.s.w. durch Elimination nicht mehr ausführbar sein. Dieser Fall
müsste eigentlich als Ausnahme besonders behandelt werden; wir begnügen uns
indessen hier um so mehr mit einer kurzen Andeutung, wie man sich dabei ver-
verhalten könne, da der Verf. ihn nicht berührt hat. Man braucht nemlich an die
Stelle der einen von obigen Differentialgleichungen, die schon in den andern ent-
enthalten ist, nur irgend eine andere willkürliche in diesen noch nicht enthaltene
linearische Gleichung zwischen dx, dx, dx"u.s.w. zu setzen, um das vorige an-
anwenden zu können. Am bequemsten wird es immer sein, eines von diesen Diffe-
rentialien = 0 zu setzen, oder eine von den veränderlichen Grossen x, x',x"\i.s. w.
PRASSE. LOGARITHMISCHE TAFELN. 241
als constant zu behandeln, z.B. «2?, wenn nicht zufällig da? = 0 schon aus den
vorhandenen Gleichungen folgt. In diesem Fall wird eine von den Integralglei-
Integralgleichungen sein
und wenn man y = x setzt, so lässt sich zeigen, dass in dem verwandelten Aus-
Ausdrucke von Q allemal von selbst q = 0 wird.
BEMERKUNGEN ÜBER LOGARITHMENTAFELN.
Monatliche Correspondenz, herausg. vom Freih. v. Zach. 180 2 Nov.
2.
Zu dem S. 497 des vorigen Heftes gegebenen Verzeichniss aller Druckfeh-
Druckfehler der Stereotype-Ausgabe der CALLET'schen logarithm. Tafeln hat Dr. Gauss die
Güte gehabt, noch folgende Errata anzuzeigen:
Log. Sin. de Seconde en Seconde 4° 15' 5" sin 8. 8 69009 6 lies 8.8700096
4 15 6 sin8.8690379 — 8.8700379
Log. Sin. de 10 en 10 Secondes Are 21° 27' 20" lies 21° 27' 30".
Für 33° unten statt 59 Deg. lies 56 Deg. (nur in einigen Abdrücken).
Göttingische gelehrte Anzeigen. 18M Mai 25.
Logarithmische Tafeln für die Zahlen, Sinus und Tangenten, neu geordnet
von Moritz von Prasse, ordentlichem Professor der Mathematik zu Leipzig. ,80 Sei-
Seiten in Octav. Leipzig. In Commission bei P. J. Besson.
Diese Tafeln enthalten dasselbe. was die beliebten kleinen Tafeln von La-
lande haben, nemlich die Logarithmen aller Zahlen bis 10000, und die Logarith-
31
242 ANZEIGE.
men der Sinus und Tangenten für alle einzelnen Minuten des Quadranten; alles
auf fünf Decimalen. Allein Hr. v. Prasse hat dieses bei einem nicht viel grössern
Format auf den dritten Theil der Seitenzahl reducirt, indem er die bei den grössern
Tafeln übliche Einrichtung anwandte, immer je zehn Logarithmen in Eine Zeile,
und die ersten Ziffern nur Einmal anzusetzen, wobei aber alle Differenzen haben
wegbleiben müssen. Es scheint also hierdurch an Bequemlichkeit wieder verlo-
verloren zu gehen, was an Kürze gewonnen wird. Da indessen hierüber nur nach
wirklichem Gebrauche geurtheilt werden kann, so hat Rec., der sich an die klei-
kleinen LALANDE'schen Tafeln gewöhnt hat, diese eine Zeitlang bei Seite gelegt, und
sich der vorliegenden zu bedienen versucht. Er hat gefunden, dass jene kleinen
Unbequemlichkeiten von demVortheile, viel weniger blättern zu müssen, beiden
Logarithmen der Zahlen, die hier auf 31, bei Lalande auf 111 Seiten stehen,
merklich überwogen werden, und er bedient sich daher dieser neuen Tafeln gern.
Nicht so hat er es bei den trigonometrischen Tafeln gefunden, die hier 40, bei
Lalande 90 Seiten einnehmen, besonders desswegen, weil bei Hrn. v. Prasse die
Bogen von 0 bis 90 Grad fortlaufen, und daher die Sinus und Tangenten von den
Cosinus und Cotangenten getrennt sind. Diess ist um so beschwerlicher, da die
Fälle so sehr häufig sind, wo-man z. B. von einem Bogen den Sinus und Cosinus
zugleich nöthig hat, oder wo man, ohne den Bogen selbst zu brauchen, aus dem
Sinus oder der Tangente den Cosinus verlangt. Hier würde er also allemal die
LALANDE'schen Tafeln vorziehen, und er hätte gewünscht, dass Hr. v. Prasse lie-
lieber jede Seite noch einmal in der Mitte durch eine Horizontallinie getheilt hätte,
um jene unangenehme Trennung zu vermeiden, wobei die Zusammendrängung in
den kleinen Raum doch hätte Statt finden können.
Ausserdem unterscheiden sich diese Tafeln noch dadurch, dass allemal die
letzte Ziffer eines jeden Logarithmen, wenn sie vergrössert worden ist, mit einer
andern Schrift gesetzt ist. Hr. v. P. glaubt dadurch grössere Genauigkeit bei den
Rechnungen befördern zu können. Allein da man doch meistens in der Ausübung
nur mit Logarithmen zu rechnen hat, die interpolirt werden müssen, so kann
man nicht ohne Beschwerde auf jenen Umstand Rücksicht nehmen, und so oft
man glaubt, dass die nur auf eine halbe Einheit in der fünften Decimale zuver-
zuverlässigen Logarithmen nicht genug genaue Resultate geben können, so thut man
besser, grössere Tafeln mit sechs oder sieben Decimalen anzuwenden. Rec. kann
daher diese Einrichtung, die, allgemein zu reden, allerdings die Genauigkeit der
.PRASSE. TABLES LOGABITHMIQUES.
Rechnung zu verdoppeln dienen kann, nicht für sehr nützlich anerkennen, zumal
da die Cursivzahlen neben den andern dem Auge unangenehm, und hin und wie-
wieder nicht scharf genug sind. Sonst ist der Druck nett; nur werden diejenigen,
die dergleichen Tafeln viel brauchen, stärkeres Papier wünschen.
Göttingische gelehrte Anzeigen. 1814 December 19.
Tables logarithmiques pour les nombres, les sinus et les tangentes, disposees
dans un nouvel ordre par M. de Prasse , professeur des mathematiques ä Berlin (zu
Leipzig) corrigees et precedees dune introduction traduite de l'allemand et accom-
pagnee de notes et d'un avertissement par M. Halma 1814. Paris. 80 Seiten. Preis
Ein Frank.
Ein neuer Abdruck der geschmeidigen von PßASSE'schen Tafeln, welche wir
in diesen Blättern [1811 Mai 25] angezeigt haben. Unser dortiges Urtheü über
die von dem französischen Herausgeber unverändert beibehaltene Anordnung der
Tafeln haben wir durch einen drei Jahre länger fortgesetzten Gebrauch derselben
in allen Stücken bestätigt gefunden. In Ansehung der Schönheit des Drucks und
Papiers scheint uns die Französische Ausgabe der Deutschen eher nachzustehen;
doch sind mehrere Druckfehler der letztern hier berichtigt. Wenn man übrigens
bei einem Werke dieser Art, das der verstorbene von Prasse gewiss nicht Gewin-
Gewinnes halber, sondern zum Dienste der Wissenschaft auf seine Kosten unternahm,
auch nicht weiter untersuchen will, in wie fern Hr. Halma zu einem neuen Ab-
Abdrucke berechtigt war, so kann man doch nicht umhin, sich zu wundern, dass
derselbe, aus Besorgniss seinerseits wieder nachgedruckt zu werden, die einzel-
einzelnen Exemplare mit seinem JSfamenszuge bezeichnet hat, und die Nachdrucker ge-
gerichtlich zu belangen droht.
244 ANZEIGE.
Monatliche Correspondenz, herausg. vom Freih. v. Zach. 1812. Nov.
Tafel zur bequemern Berechnung des Logarithmen der Summe oder Differenz
zweier Grossen, welche selbst nur durch ihre Logarithmen gegeben sind. Von Herrn
Prof. Gauss.
Je weiter sich beständig die Geschäfte der rechnenden Astronomen ausdeh-
ausdehnen , desto wichtiger wird ihnen jede, wenn auch an sich nur kleine Erleichte-
Erleichterung derselben. Die Monatliche Correspondenz hat sich hierin schon vielfältige
Verdienste erworben, indem sie mancherlei Tafeln aufgenommen hat, deren klei-
kleiner Umfang nicht verstattete, sie besonders herauszugeben. Ich lege daher gern
in derselben eine kleine Tafel nieder, die freilich nicht eigentlich astronomisch
ist, aber besonders doch den rechnenden Astronomen willkommen sein wirql, und
die etwa in Zukunft sehr zweckmässig mit einem neuen Abdruck der kleinen La
LANDE'schen Tafeln verbunden werden könnte. Das Geschäft, was sie erleich-
erleichtern soll, kommt bei astronomischen Rechnungen alle Augenblick vor; es erfor-
erfordert sonst ein dreimaliges, oder wenn man eine leichte Verwandlung anwendet,
doch nothwendig ein zweimaliges Aufschlagen in den Logarithmen-Tafeln, was
hier auf ein einziges gebracht wird. Die Idee dazu hat Leonelli, so viel ich weiss,
zuerst angegeben: allein seine Meinung war, eine solche Tafel für Rechnungen
mit 14 Deeimalen zu construiren, und gerade dies kann ich nicht zweckmässig
finden. Sie würde bei einer solchen Ausdehnung einen grossen Folioband füllen,
ihre Berechnung würde eine ungeheuere Arbeit und Zeit erfordern, und sie würde
fast nie von Nutzen, und immer nur von wenig Nutzen sein, da so scharfe Rech-
Rechnungen so selten — in der eigentlichen practischen Astronomie nie — vorkom-
vorkommen , dass die verhältnisstnässig doch nur kleine Erleichterung die Construction,
ja nicht einmal den Ankauf einer solchen Tafel belohnen würde. Ich habe diese
Tafel zu meinem eigenen Gebrauch für Rechnungen mit 5 Deeimalen, die in der
Ausübung die häufigsten sind, schon vor vielen Jahren construirt, und die, wenn
auch jedesmal kleine, doch wenn sie viele Tausendmale wiederkehrt, sehr erheb-
erhebliche Erleichterung, hat mir die darauf gewandte Mühe bereits reichlich ersetzt.
Es wäre zu wünschen, dass jemand sich der Arbeit unterzöge, eine ähnliche Ta-
Tafel in 10 oder 1 00 mal so grosser Ausdehnung für Rechnungen mit 7 Deeimalen zu
TAFEL ZUR BEQUEMERN BERECHNUNG DES LOGARITHMEN DER SUMME ETC.
construiren, die als ein sehr schätzbares Supplement den gewöhnlichen Logarith-
Logarithmen-Tafeln beigefügt werden könnte.
Die Einrichtung der aus drei Columnen bestehenden Tafel ist sehr einfach.
Die erste Columne A geht von 0 bis 2 durch alle Tausendtheile, von da bis 3,4
durch alle Hunderttheile, und von 3, 4 bis 5, 0 durch alle Zehntheile; mit 5,0
kann die Tafel für 5 Decimalen als geschlossen angesehen werden, da die zweite
Columne für diesen und für grössere Werthe von A verschwindet, und die Zah-
Zahlen der dritten Columne denen der ersten gleich werden. Setzt man eine Zahl
der ersten Columne A = logm, so ist in der zweiten Columne B = W(l-4-^
und in der dritten Columne C ■= log(l-f-m), so dass immer C = A~\-B. Man
kann also auch die Zahlen der drei Columnen als die doppelten Logarithmen der
Tangenten, Cosecanten und Secanten der Winkel von 45° bis 90° betrachten.
Die Anwendung davon ist nun folgende:
I. Aus den Logarithmen zweier Grossen a, b den Logarithmen der Summe
zu finden.
Es sei Yoga der grössere Logarithm., man gehe mit loga — logb in die
Columne A ein, und nehme daneben entweder aus der zweiten Columne B, oder
aus der dritten Columne C. Man hat dann
oder ' log(a-f-i) = log&-f-C
II. Aus den Logarithmen zweier Grossen a, b den Logarithmen der Differenz
zu finden.
Erstens, ist die Differenz der Logarithmen loga — log b grösserals 0,30103,
so suche man dieselbe in C, wodurch man hat
log(a — b) — loga — B
oder log [a — b) = log b-\-A
Zweitens, ist loga — logb kleiner als 0,30103, so suche man es in B. wo-
wodurch wird
log(a — b) = loga—C
oder log(a—b) = log b—A
246 ANZEIGE.
Es gibt daher bei jeder Aufgabe zwei Auflösungsarten; man thut aber wohl,
sich an eine bestimmte zu gewöhnen, um sich den Gebrauch der Tafel desto leich-
leichter mechanisch zu machen. Mir ist dies bei der jedesmal zuerst angesetzten Ma-
Manier am bequemsten gefallen.
Beispiele:
I. Aus loga = 0,36173 und logb = 0,23045 den Logarithmen der Summe
zu finden, sucht man 0,13128 in A, wobei man findet
B 0,24033 C 0,37161
loga 0,36173 log& 0,23045
log(a-f b).. 0,60206 0,60206
II. Aus loga = 0,89042, und logb = 0,24797 den Logarithm. der Dif-
Differenz zu finden. Da loga — logb = 0,64245 grösser als 0,30103, so sucht
man es in der Columne C, woneben man findet
B 0,11227 A 0,53018
loga 0,89042 logb 0,24797
log(a —6). . 0,77815 0,77815
III. Aus loga = 0,25042, log& = 0,19033 den Logarithmen der Diffe-
Differenz zu finden. Hier gibt loga — logb =0,06009 in J3 aufgesucht
C 0,88871 A 0,82862
loga 0,25042 log& 0,19033
_____________ 9,36171
Göttingische gelehrte Anzeigen. 1817 October 4.
Abgekürzte Logarithmisch - Trigonometrische Tafeln, mit neuen Zusätzen zur
Abkürzung und Erleichterung trigonometrischer Rechnungen, herausgegeben von Joh.
Pasqüich, Director der Königl. Ofner Sternwarte. Leipzig. In der Weidmannschen
Buchhandlung 1817. XXXII und 228 Seiten in Octav. (Auch mit Lateini-
Lateinischem Titel.)
PASQÜICH, ABGEKÜEZTE LOGARTTHMISCHE TAFELN. 247
Kleinere logarithmische Tafeln, mit fünf Decimalen, sind bei denjenigen,
die viel mit Zahlenrechnungen zu verkehren haben, besonders bei den Astrono-
Astronomen,- sehr beliebt, weil in derThat die Fälle, wo sie ausreichen, häufig, ja die häufi-
häufigeren, sind, und durch ein bequemes Format und eine massige Grosse die Arbeit
sehr erleichtert wird. Die kleinen netten' LALANDE'schen und die PßASSE'schen
Tafeln sind in Jedermanns Händen; bei letztern ist das Zusammendrängen in ei-
einen kleinen Raum so weit wie möglich getrieben, zum Theil aber allerdings auf
Kosten der Bequemlichkeit. Die Herausgabe der vorliegenden auch nur auf fünf
Stellen gehenden Tafeln ist, wie in der Vorrede berichtet wird, durch den von
Gauss in der monatlichen Correspondenz 1812 geäusserten Wunsch veranlasst,
dass die daselbst zuerst abgedruckte Tafel zur bequemen Berechnung der Loga-
Logarithmen der Summen und Differenzen einer neuen Ausgabe der LALANDE'schen Ta-
Tafeln einverleibt werden möchte. Der neue Abdruck dieser Hülfstafel in gegen-
gegenwärtiger Sammlung wird denjenigen angenehm sein, denen der erste Abdruck
nicht zu Gebote stand, oder denen der Gebrauch derselben in der M. C. zu be-
beschwerlich war. Ausserdem zeichnet sich diese Sammlung noch durch eine neue
von Hrn. Pasqdich berechnete den trigonometrischen Tafeln beigefügte Hülfsta-
Hülfstafel aus, deren wir unten mit mehrern erwähnen werden.
Die Logarithmen der Zahlen gehen, wie bei Lalande und von Pbasse bis
10000, und sind, so wie bei jenen, hier in ihrer natürlichen Ordnung gedruckt.
Doch vermisst man ungern ein Paar Erleichterungsmittel, welche bei den LALAN-
LALANDE'schen Tafeln Statt finden; es sind nemlich theils die Differenzen nicht beige-
beigefügt, theils die untersten Logarithmen jeder Spalte oben in der nächstfolgenden
nicht wiederholt. In den PßASSE'schen Tafeln findet man zwar diese Bequemlich-
Bequemlichkeit auch nicht, allein dort werden sie durch den kleinen Raum der Tafel mehr
als ersetzt, da jene auf 24 Seiten eben dasselbe liefern, was bei Pasqdich auf 56
Seiten eines beträchtlich grössern Formats steht. Dies scheinen zwar nur Klei-
Kleinigkeiten , und sie sind es auch für alle, die nur dann und wann einmal Loga-
Logarithmen aufzuschlagen haben, aber nicht für solche, die Logarithmen-Tafeln be-
beständig zur Hand haben müssen.
In den trigonometrischen Tafeln enthält immer jede Seite zur linken die
Logarithmen der Sinus, Cosinus, Tangenten und Cotangenten, und zwar so,
dass je drei Seiten zwei Grade fassen. Diese Einrichtung, welche durch das ge-
gewählte Format und die Schrift herbeigeführt wurde, scheint uns etwas unbequem;
248 ANZEIGE.
wir hätten entweder ein kleineres Format, immer mit einem halben Grad auf der
Seite, oder ein etwas weniges längeres mit kleinerer Schrift, so dass ein ganzer
Grad auf die Seite gekommen wäre (wie in Shebvtns Tafeln) vorgezogen. Von die-
diesen Logarithmen sind immer nur die vier, drei oder zwei letzten Ziffern, so lange
die vorgehenden ungeändert bleiben, abgedruckt, wodurch dem Copiisten, dem
Setzer und dem Corrector die Arbeit erleichtert wurde, und die Tafeln ein rein-
reinlicheres Ansehen erhalten: dem ungeachtet können wir diese Einrichtung bei
Tafeln, die zum täglichen Gebrauch bestimmt sind, nicht unbedingt billigen, da
das Auge immer die, wenn auch nur kleine, Mühe hat, in der Columne erst in
die Höhe zu gehen, und die übrigen Ziffern zu finden. Die Differenzen der Lo-
Logarithmen findet man hier sogleich mit 60 dividirt; eine Einrichtung, welche auch
in einigen andern Tafeln gewählt ist, in der Absicht, das Interpoliren zu erleich-
erleichtern. Ob diese Erleichterung wirklich Statt findet, oder nicht, wird von der Ge-^
wöhnung des Rechners abhängen. B,ec. findet in dieser Beziehung die Lalande-
schen Tafeln, wo die ganzen Differenzen angesetzt sind, wenigstens nicht unbe-
unbequemer. Bei der Kleinheit der Zahlen, mit denen zu operiren ist, macht ein
etwas geübter Rechner die zum Behuf des Interpolirens nöthigen Operationen
leicht im Kopfe, und findet fast immer diesen oder jenen Local-Vortheil zu be-
benutzen Gelegenheit. Dabei hat man noch die angenehme Gewissheit, sein Inter-
Interpolations-Resultat so scharf zu erhalten, als es möglich ist; bei der von Hrn. Pas-
qüich gewählten Einrichtung hingegen ist, allgemein zu reden, der Fehler des
Interpolirens etwas grösser, welches indessen ausführlicher zu entwickeln hier
nicht der Ort ist.
Die Seite zur rechten enthält bei den trigonometrischen Tafeln die Quadrate
der Sinus, Cosinus, Tangenten und Cotangenten, welche zur Erleichterung des
Interpolirens dienen sollen, wenn man aus dem Logarithmen eines Sinus, Cosi-
Cosinus , einer Tangente oder Cotangente den Logarithmen einer der drei andern tri-
trigonometrischen Functionen verlangt, ohne den Bogen selbst nöthig zu haben.
Diese Operation kömmt allerdings äusserst häufig vor, und das gewöhnliche Ver-
Verfahren erfordert beim Interpoliren eine Multiplication und eine Division, wo mit
Hrn. Pasqüich's Hülfstafel eine Multiplication ausreicht. Es ist nemlich, für das
Interpoliren hinreichend genau,
PASQUICH. ABGEKÜRZTE LOGABITHMISCHE TAFELN.
Alog cos9 = — tangcp2. Alog sincp
A log tang cp = — A log cotang cp = A -f- tang <ps). A log sin <p
A log sin cp = — cotang cp2. A log cos cp
A log tang cp = — A log cotang cp = — A -f- cotang cp2). A log cos cp
A log sin cp = cos cp2. A log tang cp = — cos cp2. A log cotang cp
A log cos 9 = — sin cp2. A log tang cp = sin cp2. A log cotang cp
Inzwischen muss Rec. gestehen, dass er dem ungeachtet das gewöhnliche Verfah-
Verfahren zum Interpoliren nicht bloss eben so bequem, sondern sogar bequemer fin-
findet. Theils wird es immer erst einige Mühe kosten, sich die obigen sechs For-
Formeln so mechanisch zu machen, dass man sie ohne alles Besinnen oder ohne ein
besonderes Blatt neben sich zu legen, richtig anwendet; theils ist es beschwer-
beschwerlich, den Multiplications-Factor erst auf der andern Seite aufzusuchen, oder viel-
vielmehr zusammen zu suchen, da die oben erwähnte Trennung der ersten und letz-
letzten Ziffern auch hier beim Abdruck gewählt ist; endlich hat man bei dem ge-
gewöhnlichen Verfahren es immer nur mit kleinen Zahlen zu thun, mit denen man
leicht im Kopf rechnet, da hingegen die Quadrate in PASQUictfs Tafeln mit fünf
Deciinalen angesetzt sind, die man freilich nicht alle braucht, aber die gerade des-
deswegen, wie jeder erfahrne Rechner weiss, störend sind. Ausserdem können wir
hier nicht unerwähnt lassen, dass das gewöhnliche Verfahren, allgemein zu reden,
schärfer ist, als diese künstlichere Interpolation (die Gründe dieser Behauptung,
von der man vielleicht bei einer weniger genauen Prüfung gerade das Gegentheil
glauben könnte, würden für diesen Ort zu weitläuftig sein). Wir begnügen uns
das Gesagte bloss durch ein Beispiel zu erläutern. Soll zu log cos cp = 9,92478
der log tang cp gesucht werden, so findet man den Prpportionaltheil aus Pas-
quich's Tafel durch die Berechnung von 4x(l-f-2,4170) = 13,668 oder am näch-
nächsten = 14, also log tang cp ==. 9,80850, während die gewöhnliche Methode den
Proportionaltheil eben so bequem durch die Entwicklung von 4X2S = 12f, am
nächsten =12, und den gesuchten Logarithmen = 9,80848 gibt. In diesem
Beispiele ist auch das Resultat der gewöhnlichen Methode das schärfere; in an-
andern Fällen kann auch das umgekehrte Verhältniss Statt finden, aber im Durch-
Durchschnitt wird der Vortheil in dieser Beziehung auf Seiten des gewöhnlichen Ver-
Verfahrens sein. Uebrigens wollen wir nicht in Abrede stellen, dass dieser Theil
der Tafel, wenn auch das Interpoliren nicKt dadurch gewinnt» doch zuweilen für
250 ' ANZEIGE.
andere Zwecke angenehm sein könne; allein die Bequemlichkeit logarithmischer
Handtafeln, die man zum täglichen Gebrauch bestimmt, verliert natürlich in dem-
demselben Verhältniss, als ihr Umfang vergrössert wird. Wir bemerken noch, dass
in dem ersten Grade die trigonometrischen Logarithmen von 10 zu 10 Secunden
bis 56 Minuten, und in den vier letzten Minuten von 20 zu 20 Secunden ange-
angesetzt sind.
Die GAUssische Tafel für die Logarithmen der Summen und Differenzen ist
ganz unverändert abgedruckt. Inconsequent scheint es uns aber zu sein, wenn
der Verf. in der Einleitung den Nutzen einer ähnlichen Tafel mit sieben Decima-
len in Zweifel zieht. Ist anders eine solche Tafel zweckmässig eingerichtet, so ist
ihr Nutzen bei scharfen Rechnungen gerade eben so gross. als der Nutzen der
hier wieder abgedruckten Tafeln bei Rechnungen mit fünf Decimalen: bei den
kleinern Tafeln, eben so wie bei den grössern, wird der dadurch zu erhaltende
Zeitgewinn natürlich nur solchen Personen fühlbar, die viel zu rechnen haben.
Wir haben jetzt bald die Erscheinung einer solchen grössern Tafel, von einer ge-
geschickten Hand berechnet, zu erwarten.
Göttingische gelehrte Anzeigen. 1819 Januar 30.
[E. A. Matthiessen.] Tafel zur bequemern Berechnung des Logarithmen der
Summe oder Differenz zweier Grossen, welche selbst nur- durch ihre Logarithmen ge-
gegeben sind. Altona 1818. Bei J. F. Hammerich. Einleitung 33 S. Die Tafeln
212 S. in Quart. (Titel und Einleitung auch in lateinischer Sprache.)
Bei etwas ausgedehnten Rechnungen ist jede Abkürzung schätzbar; auch
solche Hülfsmittel, die bei einer einmaligen Anwendung nur einen kleinen Vor-
theü gewähren, werden durch oft wiederkehrende Benutzung wichtig. Ein sol-
solches Erleichterungsmittel ist eine im Jahr 1812 in der monatlichen Correspondenz
zuerst gegebene Hülfstafel, um aus den Logarithmen zweier Grossen unmittelbar
die Logarithmen ihrer Summe oder Differenz abzuleiten: man erreicht dadurch
mit Einem Aufschlagen, wozu man sonst ein dreimaliges oder wenigstens zweima-
zweimaliges nöthig hätte. Im Besitz einer solchen Tafel wird man mit Vortheil manche
MATTHTESSEN. TAFEL ZUR BEQUEMEKN BERECHNUNG DES LOGAREEHMEN ETC. 251
Formeln in ihrer ursprünglichen Gestalt beibehalten können, denen man sonst
wohl, durch Einführung von Hülfswinkeln, eine zur Rechnung bequemere Form
zu geben sucht. Die erwähnte Tafel war nur für Rechnungen mit fünf Deeimalen
bestimmt: eben weil solche Rechnungen am häufigsten vorkommen, lag dies Be-
dürfniss am nächsten. Der bei Bekanntmachung derselben geäusserte Wunsch,
dass jemand sich der Mühe unterziehen möchte, eine ähnliche Tafel in grösserm
Umfange und mit sieben Deeimalen zu berechnen, hat die vorliegenden Tafeln
veranlasst, deren Verfasser, Hr. Mathiessen, sich durch diese mühsame Arbeit
ein Recht auf den Dank aller derer erworben hat, die viel mit logarithmischen
Rechnungen zu thun haben. Die Vorrede gibt Nachricht von der Methode, de-
deren sich der Verfasser zur Berechnung bedient hat, und von seiner lobenswerthen
Sorgfalt, die Tafel auch in der letzten Ziffer durchgehends zuverlässig zu machen.
Bei Tafeln dieser Art ist auch die äussere Einrichtung keinesweges gleichgültig.
Der Verf. hatte anfangs eine Anordnung im Sinn, deren Zweck war, die Tafel in
den möglich kleinsten Raum zusammenzudrängen. Allein da die ganze Bestim-
Bestimmung der Tafel nur dahin geht, die Rechnungen zu erleichtern, so würde jene
ganz verfehlt werden, wenn die Anordnung der Tafel zu künstlich wäre, und eine
beschwerliche Aufmerksamkeit erforderte. Der Verf. entschloss sich daher bei
reiferer Ueberlegung mit Recht, jene wenn gleich sinnreiche Anordnung bei Seite
zu setzen, und statt derselben eine einfachere zu wählen, obgleich der Umfang
des Bandes dadurch beträchtlich vergrössert wurde. Vielleicht wird mancher,
der die Tafeln gebraucht, mit uns wünschen, dass der Verf. hierin lieber noch
etwas weiter gegangen wäre, und die Columne B und C jede vollständig hätte
abdrucken lassen, deren vier letzte, beiden gemeinschaftliche, Ziffern nur einmal
dastehen. Der Ueberblick würde dadurch noch bequemer geworden sein, und
das Format wäre auch dadurch nicht vergrössert, wenn etwas kleinere Schrift ge-
gewählt wäre, welches ohne Nachtheil, vielleicht selbst mit Vortheil für das gefäl-
gefällige Ansehen, hätte geschehen können. Auch die fast zu strenge Oekonomie mit
den Ziffern, wo in der Regel nur die vierte abgedruckt ist, so lange die vorher-
vorhergehenden ungeändert bleiben, und mit den Proportionaltheilen, die immer nur
Einmal angesetzt sind, und also zuweilen ein Zurück- oder Vorausblättern nöthig
machen, thut der Bequemlichkeit einigen Eintrag. Endlich hätten wir gewünscht,
dass der letzte Theil der Tafel S. 2 i 2 in einer zehnmal, grössern Ausdehnung ge-
gegeben wäre, um die zweiten Differenzen unmerklich zu machen; es wäre dazu
32*
252 ANZEIGE.
nur Eine Seite mehr erforderlich gewesen. Alle diese Bemerkungen, die zum
Theil mit auf individueller Gewöhnung beruhen mögen, sollen das Verdienstliche
dieser Arbeit keinesweges schmälern, welches gewiss von allen anerkannt wird,
die von derselben Gebrauch zu machen Gelegenheit nehmen werden.
Astronomische Nachrichten, herausg. v. Schumachee. Nr. 24. Beilage 2. 1822 Dec.
Gaüss an Schumachee.
Göttingen 1822. Nov. 25.
Den von Herrn Professor Encke geäusserten Wunsch Logarithmentafeln mit
6 Ziffern betreffend, habe ich schon öfters gehegt, und Sie werden sich gewiss
vielfaltigen Dank erwerben, wenn Sie solche veranlassten. Alles, was Herr Encke
über das Aeussere und Innere sagt, unterschreibe ich als meine eigene Meinung,
nur die Proportionaltheile scheinen mir überflüssig, und alles Ueberflüssige scha-
schadet dem leichten übersichtlichen Gebrauch. Bei solchen Dingen hängt freilich
manches von individueller Gewöhnung ab; indessen wenn einige, die Gebrauch
von Tafeln machen, anders gewöhnt sind als ich, so sind doch auch wohl andere
eben so gewöhnt; und daher berühre ich noch einen Umstand, nemlich die Ab-
Abänderung der 4ten Ziffer für die Logarithmentafeln. Sie kennen die Einrichtung,
die in dieser Beziehung in Callet's Tafeln gemacht ist, und einige haben dies als
eine Verbesserung betrachtet. Ich gestehe, dass ich der entgegengesetzten Mei-
Meinung bin, und die regelmässige Abtheilung von 5 zu 5 Zeilen durch horizontale
Striche, wie sie in Sherwest's und andern Tafeln ist, für etwas, bei häufigem Ge-
Gebrauche viel wesentlicheres und bequemeres halte, daher ich mich der Callet'-
schen Logarithmen auch niemals bedienen mag. Bei meiner vieljährigen Praxis
weiss ich auch nicht einen einzigen Fall, wo der Gebrauch der SHEEwiN'schen Ta-
Tafeln mich bei der 4ten Ziffer zu einem Rechnungsfehler verleitet hätte, daher ich
auch auf die Sternchen bei Vega und andern Tafeln gar keinen Werth lege, und
des bessern Papiers und der schönern Ziffern wegen, mich lieber an die Sheewtn'-
schen halte. Wer auf solche Warnungszeichen einen Werth setzt, kann sich
leicht in seinem Exemplare an den betreffenden Stellen rothe oder grüne Punkte
machen. —
BABBAGE, TABLE OF LOGABITHMS.
Göttingische gelehrte Anzeigen. 1S2S Januar 19.
Table of logarithms oftke natural numbers, from 1 to 108000, by Charles
Babbage. Stereotyped. London. Printed for J. Mawman. 1827. 202 S. gr. 8.
Dieser neue Abdruck der Logarithmentafeln zeichnet sich vor andern durch
eine geflissentlichere Beachtung kleiner Nebenumstände aus. Wer nur von Zeit
zu Zeit einmal veranlasst wird, einige Logarithmen in den Tafeln aufzusuchen,
verlangt von ihnen hauptsächlich nur möglich grösste Correctheit. Allein für an-
andere , denen die Tafeln ein tägliches Arbeitsgeräth sind, bleiben auch die gering-
geringfügigsten Umstände, die auf die Bequemlichkeit des Gebrauchs Einfluss haben
können, nicht mehr gleichgültig. Farbe, Stärke und Schönheit des Papiers;
Format; Grosse, Schärfe und gefälliger Schnitt der Typen: Beschaffenheit der
Druckerschwärze; Anordnung der Zahlen, um das was man sucht ohne Ermü-
Ermüdung des Auges schnell und sicher zu finden; Vorhandensein von allem, was man
braucht-, aber auch Abwesenheit von allem, was man nicht brauchen mag, und
was sonst die leichte Uebersicht nur stören würde, alle diese Umstände erhalten
eine gewisse Wichtigkeit bei einem Geschäfte, welches man täglich hundert mal
wiederholt. Freilich hängt dabei manches von der Individualität des Rechnenden
und von seiner Gewohnheit ab, so dass nicht wohl Eine Ausgabe allen am besten
gefallen kann; dem Kurzsichtigen ist ein grosses Format beschwerlich, und er
zieht kleinere Typen vor, während es sich bei dem Weitsichtigen umgekehrt ver-
verhält; der weniger geübte Rechner legt einen Werth auf diesen oder jenen Zusatz,
welchen der geübtere, der mehrere Theile der Operationen ohne Anstrengung im
Kopf macht, lieber wegwünscht, weil alles Ueberflüssige nur störend wirkt. In-
Inzwischen gibt es doch auch allgemeingültige Regeln. Der Herausgeber der vor-
vorliegenden Tafeln hat in der Vorrede ein Dutzend solcher Vorschriften zusammen-
zusammengestellt, die er aus der Vergleichung vieler Logarithmentafeln abgeleitet hat, und
die meistens sogleich von selbst einleuchten, obwohl einige davon nur unter Ein-
Einschränkungen anzuerkennen sein möchten.
Was die gegenwärtige Ausgabe der Logarithmentafeln am meisten von. an-
andern unterscheidet, ist, dass sie auf farbiges (gelbes) Papier abgedruckt ist: man
gewöhnt sich daran bald, und findet es, besonders zum Gebrauche bei Licht, an-
254 ANZEIGE.
genehmer als weisses. Die Anordnung ist im Wesentlichen die gewöhnliche.
Nach einem Wechsel der dritten Ziffer ist für die übrigen Logarithmen in dersel-
derselben Zeile die vierte Ziffer mit andern Typen, etwa halb so gross wie die übrigen,
gesetzt. Für Eef., der überhaupt auf solche Warnungszeichen wenig Werth setzt,
haben diese Typen, auch nach einem Gebrauch von ein paar Monaten, noch nicht
das fremdartig Störende verloren, und er würde den in Vega's Tafel gebrauchten
Sternchen, oder den Punkten, die in die bessern Exemplare von Taylok's Tafeln
eingedruckt sind, den Vorzug geben. Sternchen hat der Herausgeber desswegen
nicht gebrauchen wollen, weil sonst die Columnen zu breit geworden, und dann
für die Verwandlung der Zahlen, als Secunden betrachtet, in Grade, Minuten
und Secunden kein Raum geblieben wäre. Referent würde diese Verwandlungs-
columne (eben so eingerichtet, wie man sie aus Callet's Tafeln kennt) gern ent-
entbehrt haben; ein geübter Rechner wird nicht, einer so leicht selbst im Kopfe zu
machenden Verwandlung wegen, erst die Tafeln aufblättern; zweckmässig ist es
aber, dass der Herausgeber diese Columnen wenigstens durch eine starke Linie
von der Logarithmentafel geschieden hat. Endlich ist der Fall wo die letzte Zif-
Ziffer eine Vergrösserung erlitten hat, (weil der weiter fortlaufende Logarithm als
achte Ziffer 5 oder eine grössere gehabt haben würde) durch einen unter diese sie-
siebente Ziffer gesetzten Punkt ausgezeichnet; diese Einrichtung ist wenigstens bes-
besser, als die von Prasse gewählte, durch Typen von anderer Form; doch behalten
auch so einige Ziffern noch etwas unangenehm Fremdartiges, was nach unserer
schon bei Anzeige der PßASSE'schen Tafeln in diesen Blättern [1811 Mai 25] er-
erwähnten Ansicht durch den Nutzen nicht aufgewogen wird.
Uebrigens lassen Typen und Papier bei dieser Ausgabe der Logarithmenta-
Logarithmentafeln nichts zu wünschen übrig, und auf die Correctheit ist die ausgezeichnetste
Sorgfalt verwandt. Bei einer Ausgabe, wo auf die kleinen- die Bequemlichkeit
des Gebrauchs angehenden Umstände so viel Sorgfalt verwandt ist, fallt die spär-
spärliche Ansetzung der Proportionaltheile auf; häufig muss man, um diejenigen zu
finden, die man eben braucht, voraus- oder zurückblättern.
HASSLEE. TABÜLAE LOGARTTHMICAE ETC. 255
Göttingische gelehrte Anzeigen. 1831 März 31.
Tabulae logarithmicae et trigonometricae notis septem decimalibus expressae.
In forma minima. Purgatae ab erroribus praecedentium tabularum cura F. K. Hass-
Hasslee. New York. G. C. und H. Carvill.
Diese transatlantische Ausgabe der Logarithmentafeln zeichnet sich durch
eine ganz vorzügliche Nettigkeit des stereotypisch ausgeführten Drucks aus. Sie
enthält, durchgehends auf sieben Decimalstellen, die Logarithmen der Zahlen
bis 100000, die Logarithmen der Sinus, Tangenten, Cosinus und Cotangenten
im ersten Grade durch alle Secunden, in den beiden folgenden von zehn zu zehn
Secunden, und für alle übrigen Grade des Quadranten von dreissig zu dreissig
Secunden. Ausserdem die natürlichen Sinus und Tangenten durchgehends von
dreissig zu dreissig Secunden. Und diess alles in dem Raum von 312 Seiten in
klein Octav oder gross Duodez. Eine solche Zusammendrängung war freilich nur
durch sehr kleine Typen zu erreichen, welche, bei aller Schönheit, doch wohl
für die meisten nicht kurzsichtigen Augen zum täglichen Gebrauch fast zu klein
sein möchten. Auf die Correctheit scheint eine ganz besondere Sorgfalt gewandt
zu sein, wenigstens ist uns bei dem eine Zeitlang versuchten häufigen Gebrauch,
gar kein Druckfehler aufgestossen.
Vega und Hüls se. Sammlung mathematischer Tafeln. 1840.
Auflösung quadratischer Gleichungen in der Form, dass nicht die Coefßcienten
der Gleichung selbst, sondern deren Logarithmen gegeben sind, und dass man auch
nicht ihre Wurzeln selbst [oder eine derselben), sondern vielmehr deren Logarithmen
zu anderweitiger Benutzung nöthig hat.
Die Ausführung dieses Geschäfts, bloss mit Hülfe der gewöhnlichen Loga-
Logarithmentafeln, erfordert nothwendig ein vierfaches Aufschlagen in denselben; man
reicht mit einem zweifachen Aufschlagen aus, wenn man entweder die trigonome-
trigonometrischen Logarithmentafeln oder die Tafeln für Logarithmen von Summen und
256 ANZEIGE.
Differenzen benutzt; man reicht mit einem einfachen Aufschlagen aus, wenn letz-
letztere Tafel, wie hier, durch die Zusatzcolumnen D, JE und F erweitert ist.
Die vierte Columne, D, enthält B-\- C, die fünfte, JE, enthält A-\- C,
die sechste, F, enthält B— A. Nehmen wir an, dass die Zahlen selbst, denen
die Logarithmen A, B, C zugehören, beziehungsweise a, b, c sind, so enthielte
also die vierte Columne die Logarithmen von bc, die fünfte die von ac, die
sechste die von —.
a
Es mag noch darauf aufmerksam gemacht werden, dass die Logarithmen in
der sechsten Columne F, welche bis zu A = 0,208 positiv sind, von A = 0,209
an negativ werden (S.640); es ist ziemlich gleichgültig, ob sie in dieser negati-
negativen Form oder, wie hier, durch ihre Complemente angesetzt werden; also könnte
z.B. für A = 0,367 unter F stehen —0,21180 oder, wie hier, 9,78820.
Für die Anwendung dieser Zusatzcolumnen auf die Auflösung der quadra-
quadratischen Gleichung
pxx-\-qx-\-r = 0
selbst müssen vier verschiedene Fälle unterschieden werden, nemlich
I. p und r haben gleiche Zeichen und — ist nicht kleiner als 4;
II. p und r haben gleiche Zeichen und — ist kleiner als 4;
III. p und r haben entgegengesetzte Zeichen und —— ist grösser als 2;
IV. p und r haben entgegengesetzte Zeichen und —— ist kleiner als 2.
Der Fall, wo —p— = 2 ist, kann sowohl zu III. als zu IV. gezählt werden.
Im Falle II. sind die Wurzeln imaginär, in den übrigen erhält man jede der
beiden Wurzeln auf eine doppelte Art. Durch folgendes Schema ist alles leicht
zu übersehen, wobei
— = h — = a
gesetzt ist, theils zur Abkürzung, theils weil die Rechnung wirklich in dieser
Form am bequemsten geführt wird.
II.
III.
IV.
_1_ h
ff
ff
9
h
9
h
7
<4
= flC =
a
j
e
f
JEkste Wurzel.
h
Imaginär.
-\-ha = — —
c
_4_ h - 9
* a b
Zweite Wurzel.
, h
9b —
Imaginär.
' a
-\-ga= —hb
VEGA. THESAURUS LOGARITHMOKÜM. 257
Die Beweise der Vorschriften wird sich jeder leicht selbst entwickeln kön-
können. Ein Beispiel des Gebrauchs mag zum Ueberfluss noch hergesetzt werden.
Es sei gegeben logp = 0,69897
logq = 0,84510
logr = 0,77815n
Also logÄ = 0,14613
logg — 9,93305 n
log(— |) = 9,78692
Man sieht sogleich, dass hier der Fall IV. statt findet und also 9,78692 in
der. sechsten Columne unter B — A oder F zu suchen sein wird. Was von der
Tafel (S. 643) hier nöthig wäre ist nur Folgendes:
o,
0,
A
367
368
0,
0,
B
15520
15489
B—A oder
9,78820
9,78689
F
Zu i^=^9,78692 gehört also
A — 0,36798 = loga, woraus log ^ — 9,7781 5 , log^a = 0,30103n oder
a 1:
B — 0,15490 =log&, woraus log (—-f) = 9,77815, log(—Ä6) = 0,30103 n.
Astronomische Nachrichten. Nr. 756. 1851. Mai 2.
Einige Bemerkungen zu Vega's Thesaurus Logarithmorum, von Herrn
Geheimen Hofrath Gauss.
Der Thesaurus Logarithmorum von Vega ist bekanntlich seinem grössten
Theile nach ein neuer Abdruck der grössern VLACQ'schen Logarithmentafeln. In
der Vorrede führt Vega eine nicht unbeträchtliche Anzahl von Fehlern im Origi-
Original an, die er verbessert hat, mit dem Zusatz, dass er ausser diesen noch eine
sehr grosse Menge von Unrichtigkeiten an der letzten Ziffer der Logarithmen be-
berichtigt habe, zu dem Betrage von einer, zwei, drei, vier Einheiten. Mit glei-
gleicher Sorgfalt seien auch die neu hinzugekommenen Tafeln (namentlich also die in
33
258 VEGA. '
den beiden ersten Graden für alle einzelnen Secunden angegebenen Logarithmen
der trigonometrischen Grossen) berechnet, geprüft und berichtigt. Vega scheint
nun mit der Hoffnung sich geschmeichelt zu haben, dass auf diese Weise seine
Tafeln fast fehlerfrei geworden seien, und verspricht, um zu vollkommen fehler-
fehlerfreien Tafeln zu gelangen, für die erste Anzeige jedes etwa noch stehen gebliebe-
gebliebenen Fehlers, der zu falscher Rechnung Anlass geben könne (jpro sphalmatibus cal-
culum turbantibus) eine Prämie von einem Ducaten zu bezahlen. Ob diese vom
1sten October 1794 datirte Ausgelobung jemals Folge gehabt hat, ist mir nicht
bekannt.
Es ist mir zweifelhaft, ob Vega sich ganz klar gemacht habe, was für Feh-
Fehler als möglicher Weise zu falschen Rechnungen Anlass gebend betrachtet wer-
werden sollten. Für alle Tafeln, welche bestimmt sind, theoretisch feststehende
irrationale Grossen darzustellen, gilt bekanntlich der Grundsatz, dass die Tabu-
largrösse dem wahren Werthe allemal so nahe kommen soll, als bei der gewähl-
gewählten Anzahl von Decimalstellen möglich ist, und es darf folglich die Abweichung
niemals mehr als eine halbe Einheit der letzten Decimale betragen. Jeder Ver-
stoss gegen diese strenge Norm ist ein Fehler, der möglicherweise einen sich auf
die strenge Uebereinstimmung verlassenden Rechner zu einem unrichtigen Resul-
Resultate verleiten kann. Lässt man diese strenge Auslegung fahren, und mischt in
sein Urtheil eine Rücksicht auf Erheblichkeit der Unrichtigkeit ein, so verirrt
sich die Entscheidung in das Gebiet der Willkühr. Der schon vorhin erwähnte
Umstand, dass Vega selbst von Correctionen an den ViACQ'schen Tafeln spricht,
die nur eine Einheit in der letzten Stelle betrugen, und dass er vollkommene Feh-
Fehlerfreiheit wie sein Ziel bezeichnet, scheint allerdings darauf hinzudeuten, dass
er die strenge Auslegung im Sinne gehabt. Auch habe ich den ersten Theil des
Thesaurus, der die Logarithmen der laufenden ganzen Zahlen enthält, bei sehr
vielen gelegentlich gemachten Vergleichungen mit mehrstelligen Bestimmungen
immer sehr correct gefunden.
Es sind seit jener Zeit bei mehrern andern logarithmischen Tafeln, in der
Absicht ihre Correctheit zu vervollständigen, ähnliche Ausbietungen von Preisen
für die erste Anzeige von Fehlern in den Zahlen gemacht: ich weiss jedoch nicht,
ob dieselben einen Erfolg gemacht haben, mit Ausnahme des bei Tauchnitz in
Leipzig 1847 von Köhler herausgegebenen logarithmisch-trigonometrischen Hand-
Handbuchs. Der Verleger dieser Tafeln versprach bei dem ersten Erscheinen, für die erste
THESAURUS LOOAE1THMOBÜM.
binnen einer gesetzten Frist eingesandte Anzeige eines jeden Fehlers, welcher
falsche Resultate veranlassen könne, einen Louisd'or zu bezahlen, und nach ei-
einem gedruckten Bericht vom t. Juli 1848 ist diese Prämie für vier zur Anzeige
gebrachte Fehler wirklich ausgezahlt. Was nun dabei eine ehrende Erwähnung
verdient, ist der Umstand, dass dem einen tiieser Fehler jene Qualification nur
unter Anerkennung obiger strengen Auslegung zugesprochen werden konnte. Es
war nemlich der Logarithm von 103000, welcher, auf 12 Stellen genau,
= 5,012837224705
ist, in den ersten Abdrücken mit acht Ziffern
= 5,01283723
angesetzt, während die principmässig abgekürzte Zahl 5,012837 22 ist. Es ist
zu wünschen, dass in künftig vorkommenden ähnlichen Fällen, diese Entschei-
Entscheidung als Präcedenz respectirt werde.
Bekannte sich Vega zu derselben strengen Auslegung, so hätte es ihm leicht
gehen mögen, wie dem König Shiram, dessen Kornkammern nicht ausreichten,
dem Erfinder des Schachspiels die ihm zugesagte Belohnung zu gewähren.
Dass die von Vega ausgebotene Belohnung, unter jener Voraussetzung, ihm
theuer zu stehen kommen konnte, lässt sich schon, ohne alles Nachrechnen, aus
einem Umstände erkennen, der leicht zu bestätigen, jedoch meines Wissens an-
anderweit noch nirgends zur Sprache gebracht ist. Dieser Umstand besteht darin,
dass in der Tafel für die Logarithmen der trigonometrischen Grossen die Zahlen
der Sinuscolumne fast ohne Ausnahme*) der Summe der Zahlen der Cosinusco-
lumne und der Tangentencolumne genau gleich sind. Da alle diese Zahlen nur
abgekürzte Werthe der irrationalen genauen Grossen sind, so ist klar, dass bei
streng richtiger Abkürzung jene Gleichheit nicht Statt finden wird, in allen den
Fällen, wo die Abweichungen von den genauen Werthen in der zweiten und drit-
dritten Columne gleiche Zeichen haben, und ihre Summe mehr als eine halbe Ein-
Einheit der letzten Decimale beträgt. Man übersieht leicht, dass bei einer grossen
*) Ich habe grosse Strecken der Tafel in dieser Beziehung prüfen lassen: allein unter Tausenden von
Fällen ist nur eine einzige Ausnahme gefunden, nemlich bei dem Bogen 27°54'o". Ich kann jedoch diese
Ausnahme, sowie etwanige andere, wenn dergl. noch hie und da vorkommen sollten, nur einem Versehen,
und nicht einem Vorsatze zuschreiben.
33*
260 VEGA.
Menge von Fällen dieser Ausnahmefall durchschnittlich einmal unter vieren vor-
vorkommen wird, was sich bei wirklicher Abzählung in solchen siebenziffrigen Ta-
Tafeln , wo auf die Richtigkeit der letzten Ziffer mit -Sorgfalt gehalten ist, bestätigt
findet (Es hat z. B. eine solche Abzählung in den erwähnten Komischen Ta-
Tafeln an den 900 einzelnen Minuten von 30°0' bis 44°59' genau 225 solcher Fälle
ergeben, welche vollkommene Uebereinstimmung allerdings für zufällig zu hal-
halten ist). Vega's Thesaurus enthält die Logarithmen der Sinus, Cosinus und Tan-
Tangenten von 22680 Bogen. Unter der Voraussetzung also, dass alle Zahlen in
zweien dieser Columnen scharf nach dem Princip abgekürzt seien, wird man, mit
einer geringen Unsicherheit im Mehr oder Weniger, in der dritten Columne 5670
Logarithmen erwarten dürfen, die um eine Einheit unrichtig angesetzt sind. Für
den Preis von so vielen Ducaten würden wohl befähigte Personen zur vollständi-
vollständigen Neurechnung bereit gewesen sein.
Welche zwei Columnen die ursprünglichen sind, wird man aus der Ver-
Vergleichung mit anderweitigen auf mehr als zehn Stellen zuverlässigen Bestimmun-
Bestimmungen erkennen können, schon an wenigen Bögen und mit Gewissheit, wenn die
Voraussetzung der strengen Richtigkeit der ursprünglichen Columnen zutrifft, im
entgegengesetzten Fall aber an einer etwas beträchtlichem Menge wenigstens mit
überwiegender Wahrscheinlichkeit.
Einiges hiezu dienliche findet man schon fertig vor am Schluss der Deci-
maltafeln, welche Hobest und Idelee 1799 geliefert haben, und die zwar nur mit
sieben Ziffern abgedruckt sind, aber in der Handschrift auf doppelt so viele vol-
vollendet waren. Es werden daselbst 138 fehlerhafte Logarithmen des VEGA'schen
Thesaurus angezeigt, von denen 127, um genau gesetzmässig zu werden, einer
Correction von einer Einheit in der zehnten Stelle bedürfen, 10 einer Correction von
zwei Einheiten, und eine drei Einheiten. Von den 127 fallen 49 auf Sinus, 35
auf Cosinus und 43 auf Tangenten; die übrigen 11 Correctionen, von 2 oder 3
Einheiten, beziehen sich blos auf Tangenten. Die betreffenden Bögen sind die
mit 27 Minuten messbaren, und die nicht mit angeführten sind diejenigen, wo
die Logarithmen keiner Correctionen bedurften. Es hätten übrigens diese Ver-
Vergleichungen auch ohne die HoBERT-lDELER'schen handschriftlichen Tafeln gemacht
werden können, da die allgemein verbreiteten CALLET'schen Tafeln die Logarith-
Logarithmen der Sinus und Cosinus auf 14 Ziffern für alle Tausendtheile des Quadranten
enthalten. Wenn man aus diesen auch noch das Nöthige für alle Bögen unter
THESAÜBUS LOGARITHMOBÜM. 261
zwei Grad entlehnt, die durch 5'24" aber nicht durch 27' messbar sind, so ge-
gewinnt man die Vergleichung VEGA'scher Logarithmen von 118 Bögen mit schär-
fern Bestimmungen, wovon die Resultate in folgendem Abxiss (I) zusammenge-
zusammengestellt sind:
0
1
2
3
Sin.
65
53
Cos.
75
43
Tang.
54
53
10
i
Die Bedeutung dieser Zahlen, z. B. der in der letzten Columne ist, dass unter
118 Tangenten-Logarithmen 54 richtig angesetzt sind, 53 einer Correction von
einer Einheit in der zehnten Stelle bedürfen, 10 einer Correction von zwei Ein-
Einheiten , und einer der Correction von drei Einheiten. Es folgt hieraus schon ent-
entschieden, dass keine Columne der VEGA'schen Tafel durchaus richtig angesetzt
ist, und mit überwiegender Wahrscheinlichkeit, dass die Tangenten-Logarithmen
die abgeleiteten sind, durch die einfache Subtraction der Zahlen der Cosinusco-
lumne von denen der Sinuscolumne. ,
Die Verfasser der erwähnten Decimaltafeln hätten übrigens doppelt so viele
Vergleichungen aus ihrer Handschrift geben können. Man kann sich aber eine
noch viel grössere Ausbeute verschaffen, wenn man die höchst schätzbare Tafel
von Beigg's (in der nach dessen Tode von Gelubrand 163S herausgegebenen Tri-
gonometria Britannica) benutzt, welche die Logarithmen der Sinus und Cosinus
für alle Hunderttheile der gewöhnlichen Grade auf 14 Ziffern liefert, und aus
welcher Callet die oben erwähnten Zahlen entlehnt hat. Sie enthält das Mate-
Material, um Vega's Tafeln bei 1060 Bögen, also zusammen 3180 Logarithmen, prü-
prüfen zu können. Ich selbst habe mich jedoch darauf beschränkt, .diese Prüfung
an 81 Bögen oder an 243 Logarithmen, von 14°O' bis 18°0' vorzunehmen, wovon
das Resultat hier folgt (II):
0
1
2
Sin.
29
52
Cos.
56
25
Tang.
36
42
3
262 VEGA.
Wirft man die Gruppen A} und (II) zusammen, so jedoch, dass man die
beiden gemeinschaftlichen Bögen nur einmal in Rechnung bringt, so erhält man
fax 190 Bögen folgende Ausbeute (III):
Sin. Cos. Tang.
0 89 126 87
1 101 64 90
2 12
3 1
Will man diese Zahlen zu einer Abschätzung des Verhältnisses zwischen den
richtigen und unrichtigen Logarithmen anwenden, so muss man erst noch einen
kleinen Abzug machen. Es ist in (I) der Logarithm des Sinus von 4 5° zweimal
gezählt, nemlich zugleich auch als log cos45°; es ist ferner in der Tangentenco-
lumne auch der Logarithm der Tangente von 45° mitgezählt, der doch rational
ist. Dasselbe gilt von (III) und man muss daher, zu obigem Zweck, das Resul-
Resultat davon so aussprechen, dass unter 56& geprüften irrationalen*Logarithmen 301
sich als richtig, und 267 als unrichtig ausgewiesen haben. Dürfte man dies Ver-
hältniss als durchschnittlich zutreffend betrachten, so würden unter den 68038
irrationalen Logarithmen des VEGA'schen Thesaurus (indem man, wie billig, die
Cotangenten nicht mitzählt) nach der Wahrscheinlichkeit etwa 31983 fehlerhafte
anzunehmen sein.
Wahrscheinlich ist aber diese Zahl noch bedeutend zu klein. Ich finde in
meinen Papieren die vor längerer Zeit und zu andern Zwecken auf 14 Ziffern ge-
gemachte Berechnung der trigonometrischen Logarithmen für ein paar Gruppen von
Bögen, die nicht sprungsweise, sondern in denselben Intervallen wie die VEGA'-
VEGA'schen Tafeln, fortschreiten, woraus wenigstens hervorgeht, dass obiges Resultat
(III) noch keinen richtigen Maassstab für die Ungenauigkeit dieser Tafeln abgibt.
Während bei jenen 190 Bogen kein einziger Fall vorkommt, wo der Logarithm
eines Sinus oder eines Cosinus um mehr als eine Einheit verbessert werden müsste,
sind solche Fälle gar nicht selten bei denjenigen Bögen, die nicht in der Trigono-
metria Britannica vorkommen, und wo also das zur Vergleichung nöthige erst
durch besondere Rechnung herbeigeschafft werden muss. Ich füge daher die Re-
Resultate jener Rechnungen hier bei, da sie dazu dienen können, unserer Vorstel-
Vorstellung von dem Grade der Ungenauigkeit der Zahlen in Vega's Thesaurus eine fe-
festere Haltung zu geben.
THESAURUS LQGAKITHMOBUM.
Die Vergleichung der Zahlen im Thesaurus bei den 21 Bögen von 15°38'20"
bis 15°4l'4O" mit den schärfer berechneten hat ergeben (IV);
0
1
2
3
4
Sin.
4
9
6
2
Cos.
12
8
1
Tang.
1
8
6
4
2
Die Fälle, wo die grössten Abweichungen vorkommen, sind:
15°40'20", wo die Correctionen +3, —1, +4
15 41 30, wo folgende +3, 0,+4
an die Logarithmen des Sinus, des Cosinus und der Tangente angebracht wer-
werden müssen.
Ebenso hat die Vergleichung der VEGA'schen Zahlen bei den 9 3 Bögen, von
1°19'52" bis 1°21'24" mit schärferer Rechnung folgende ergeben (V):
0
1
2
3
4
Sin.
38
39
15
1
Cos.
30
56
7
Tang.
17
41
22
11
2
Die grössten Abweichungen finden Statt bei den Bögen l°20'l 0" und l°20'l 5";
und die nöthigen Correctionen betragen bei ersterm — 2, -f-l. —4, bei dem an-
andern — 2, +2, —4.
Die Gruppen IV und V haben nicht gleichen Ursprung, da die Zahlen des
Thesaurus zu der Gruppe IV aus Vlacq's Trigonometria Artificialis genommen sind,
die andern hingegen zu den neu hinzugekommenen gehören, welche unter Vega's
Leitung und Aufsicht von dem Lieutenant Doefmund berechnet sind. Nach obi-
obigen Abrissen erscheinen die letztern wie etwas weniger ungenau als die erstem,
wiewohl die Gruppe IV zu wenig zahlreich ist, um ein sicheres TJrtheil zu begrün-
begründen. Jedenfalls folgt aus dem Zusammenwerfen beider Gruppen eine Schätzung
ANZEIGE.
für die Totahmgeiiauigkeit der Tafeln, die eher etwas zu günstig sein wird, als
umgekehrt. Aus dieser Vereinigung folgt, für 114 Bögen (VI):
0
1
2
3
4
Sin.
42
48
21
3
Cos.
42
64
8
Tang.
18
49
28
15
4
Es sind also hier unter 342 Logarithmen nur 102. die keiner Verbesserung be-
bedürfen, gegen 240 ungenaue. Nach diesem Verhältniss würde man unter den
68038 irrationalen Logarithmen 47746 ungenaue erwarten können.
Die Summe der Quadrate der Abweichungen findet sich für die Sinus 159,
für die Cosinus 96, für die Tangenten 360. Als mittlern Fehler mag man also
annehmen für die Sinus 1,18, für die Cosinus 0,92, für die Tangenten 1,78.
Man kann hienach nicht zweifeln, dass die Tangenten-Logarithmen die abgeleite-
abgeleiteten sind.
Dass die Zahlen der Cosinuscolumne weniger ungenau sind, als die der Si-
nuscolumne, rührt wohl ohne Zweifel wenigstens theilweise, daher, dass bei den
erstem die zur Ausfüllung erforderlichen Interpolationsmethoden einfacher aus-
ausfallen, möglicherweise können indess noch andere Ursachen mitgewirkt haben,
worüber sich nur unsichere Vermuthungen aufstellen lassen würden.
265
NACHLASS.
THEORU INTERPOLATIONIS
METHODO NOYA TRACTATA.
Peobleäia. Invenire summam seriei
a^ b»
(a — b)(a — c)(a — d){a—e) . . . "> (b~a) (b — c)(b— d)(b — e) . . .
I
(c — a)(c—b)(c— d) (c — e) . . . "T" (d—a)(d-b){d- c)(d-e) . . .
(e—a){e-L){e-c){e-d).
i ö. 6, c, rf, e äww^ m quantitates diversae, atque n numerus integer quicunque
positivus, negativus sive etiam 0.
Solutio. Faciendo brevitatis caussa
(a — b)(a — c)(a— d)(a —e) . . .
(c — a){c — b){c — d)(c- e) . . .
\
(rf— a)(d — b)(d— c)(d—e). . .
ita ut summa quaesita, quam per Sn denotabimus fiat =a
manifestum est, si oe exprimat quantitatem indeterminatam, ex evolutione ag-
gregati
34
266 NACHLASS.
^Tx + i=rfi + etc-
in seriem secundum potestates ipsius # ascendentem, prodire
8P-\-8}x-\-&xx-\-&£-\- etc. in infin.
Statuatur A—ax){\ — 6a?)A — coc){\ — da?)... — Q, eritque Q functio
integra indeterminatae ob , ad ordinem mtum ascendens; PQ autem fiet functio
integra ordinis m — lü puta =
a(l—fto?)A — cae){\—doc). . .
—coc) . . .
etc.
+ etc.
Qua propius considerata, patebit, per substitutionem «2? = — omnes partes prae-
ter primam evanescere, hanc vero abire in
Simili modo per substitutionem ob ==■ y evanescent omnes partes praeter se-
cundam, quae fit = —j^. Perinde per substitutiones a? = y, oo = ^ etc.
transit PQ in —•> ^i etc. Hinc vero sequitur, PQ — x?m~1 per omnes has sub-
substitutiones valorem 0 obtinere, quod fieri nequit, nisi fuerit identice = 0. sive
PQ = xm~l\ alioquin enim aequatio PQ — a?tl~~~1 = 0, quae non maioris quam
m—lü ordinis est, m radices diversas —, -r-, —, -? . . . haberet.
Iam sit
Q = 1 — Aco-\-Boßüß— Cx*-\- i)«2?4— etc.
nempe A summa quantitatum a, b, c, d. . .; JB summa productorum e binis;
C summa productorum e ternis etc., patetque, quum ex evolutione fractionis
—Q- — P prodire debeat
etc.
primo: esse debere 8° = 0, Sl = 0, £2 = 0 etc. usque ad Sm 2=0#), tunc
*) Haecce solutionis pars iam ab ill. Euusbo tradita est, per methodum a nostra aliquantum disere-
pantem. Insi. Calc. Jntegr. T. II pag. 432.
THEORIA ESTEKPOLATIONIS MBTHOBO NOVA TKACTATA.
vero fieri S™ = 1, Sm = A, tande:mque terminos ulteriores tamquam mem-
bra seriei recurrentis per legem sequentem determinari:
Sm = A
= ASm—BSm
etc.
Facile quidem hinc colligitur S™*1 esse = aa-\-bb-\-cc-\- . . . -\-B sive sum-
mam quadratorum cum summa omnium productorum e binis diversis quantitatum
a, b, c, d. . ,; sed quo clarius perspiciatur, quonam modo termini sequentes ex
elementis a, b, c, d. . . formentur, observamus -= esse productum e seriebus
\-\-aöß-\-aaxoc -\-c?xz -A- etc.
1 + boo-f- bboßüß -j-ö3«^-!- etc
\-\-'coß-\-ccoßüß -}-c3<2?3-}- etc.
\-\-dx-\-ddocoß-\-dzx?-\- etc.
etc.
Hoc vero productum est = ^a^b^c*... X<z?x+fX+v'\ ubi exponentibus X, ja, v...
omnes valores integri a 0 usque in infin. tribuendi omnibusque quibus fieri potest
modis combinandi sunt. Quocirca ut in serie, in quam -^ evolvitur, eius ter-
termini, qui continet afr^1~m, coefficientem obtineamus, numerum w-j-1 — m omni-
bus quibus fieri potest modis in n partes integras X-f-^-j-v-f-.. (inter quas etiatn
pars 0 admittitur) discerpere oport'et, omnibus quoque permutationibus harum
partium permissis; atque tunc singula producta a.b^cs... in summam colligere,
quae erit coefficiens quaesitus, simulque = Sn. Levi attentione adhibita pate-
bit, huic regulae prorsus aequivalere sequentem: Ex m quantitatibus a,b,c,d...
omnes combinationes w-f-1 — m elementorum colligendae, admissis repetitioni-
bus, et singulae tamquam producta considerandae, quorum aggregatum erit =.Sn.
Quare erit ut supra $m+1 summa omnium productorum e binis quantitatum
a, b, c, d. . . turn diversis turn identicis; Sm+2 summa omnium productorum e
ternis diversis seu identicis etc.
Nihil iam superest, nisi ut summam progressionis nostrae pro valoribus ne-
gativis ipsius n definire doceamus. Ad quem finem partem primam summae Ä"™"*,
puta 7 ^7—%t 5T— sub hanc formam ponemus
1 (a—b){a—c)(a — d) .. . u
34*
4- 1 >c1*1
4
— abcd...
n 1Wl t\fi 1
ubi signum superius vel inferius adoptandum est, prout m impar est vel par, si-
milisque transformatio etiam ad partes reliquas applicari poterit. Quamobrem si
per characterem T designetur expressio, quae perinde ex —, T, —, -j . . oritur,
tpm+n-s a 0 C u
ut S ex a, b, c, d..., manifesto fiet S~~n = + -=—=-—. Hoc itaque modo hie
casus ad praecedentem reduetus est, fitque
$~~3 aequalis producto ex ~\~ ahcd— in summam omnium productorum e binis
quantitatum —, -r, —, -j... diversis aut identicis etc.
2.
Applicabimus disquisitionem praecedentem ad eum casum, ubi quantitati-
bus a, b, c, d valores imaginarii tribuuntur: hac ratione ad quasdam insignes re-
lationes perfacile perveniemus, quae alia methodo tractatae maiores difficultates
obiicerent. Sit E basis logarithmorum naturalium, * quantitas imaginaria \J—1;
consideremus loco quantitatumrealium a,b,c... imaginarias Eia, Ezh, JEW, Elf...
et E~ia, E~ib, E~ic, E~id..., statuamusque
l~
= S , atque
+ etc. = V
jpirib
jpinc
jpiind
rjßtä _Er*aV_Er*<2 E^)(l
jß-ina
l
B*).. .
JE'd)'"
E*) .. .
■**)... '
—zb ,,_ "p1 — zd\
-™-E-*«)...
THEORIA INTERPOLATIOUIS METHODO NOVA TRACTATJl. 269
Designando itaque multitudinem quantitatum a, b, c, d . . . per m> erunt
8°, S1, S2. . . Sm~2, nee non T°, T\ T2 . . . Tm~~2 omnes = 0; porro
Sm-t _. Tm-x __x.Sm summa quantitatum Eia, Ea, JS* Eid ; S™*1
summa produetorum omnium e binis diversis seu identicis; S™*2 summa pro-
duetorum e ternis etc.; et perinde valores summarum Tm, Tm+1, T™*2 etc. e
quantitatibus E~ia, E~ib, E^6, E~id. . . formandi erunt.
Iam quum constet, esse Elx-\-E~ix = 2cos#, Eix—E~ix = lismoc, fa-
cile perspicietur, valorem expressionis i-(Sn-\- T-Ä), qui pro w=0, 1, 1...m — 2
fit = 0, pro m = m — 1 autem = 1, pro n — m fieri
= cosa-j-cos£>-|-cosc-|-cos£?. .. .
similiterque fieri -|-(>Sm+1-f- T™*1) summam cosinuum omnium angulorum, qui oriun-
oriuntur addendo binos ex his a, b, c, d.. diversos seu identicos; -^■(Sm^'2-\- T*1^*2) summam
cosinuum omnium angulorum, qui oriuntur addendo ex iisdem ternos etc. Perinde
erit —Yi— — ° pro » = 0,1, 2...m—1; porro = sina-f-sinb-\-sinc-f-sind-\-..
pro n — m: et similiter -= erit summa sinuum omnium angulorum, qui
oriuntur addendo ex his a, b, c, d... binos diversos seu identicos; :
summa sinuum omnium angulorum, qui oriuntur ex iisdem, ternos combinando etc.
Summarum Sn> Tn partes nunc propius considerabimus. Est
perinde
Eia_Eic = 2iE^a+chmi-(a-c) etc.
Quamobrem in Sn partis primae denominator fit
statuendoque a-\-b-\-c-\-d-\- ... = s, haec pars ipsa
B i)™-1 sin * (a — b) sin t (a — c) sin \ (a — d).
Simili modo habetur
unde tandem pars prima summae Tn provenit
270 '
4. jc?-
B f)«-1 sin-g-(a — Ä)sin£ («—c)sin£(a — d)...
ubi signum superius vel inferius valet, prout m impar est vel par. Quam cum
parte prima summae Sn addendo, sive ab eadem subtrahendo, concludimus fieri
primo pro valore impari ipsius m partem primam summae i-(Sn-\- Tn)
a—| s)
Bi')8*~*'sin J-(a — b)sin%(a — c)sin \{a — d). . .
partem primam summae ——.—
sin((w4-l—%m)a — fs)
— b)sin-£(a — c) sin^(a — d)...
secundo pro valore pari ipsius m partem primam summae %{ßn-\- Tn)
2"*-1 im~z sin i (a — b) sin h (a — c) sin£ {a — d)...
Sn_Tn
partem primam summae ——r—
—cos((w + l-—£m)a —-Js)
(a — d)...
Manifeste partes sequentes expressionum i-(Sn-{- Tn), ——{— primae prorsus
analogae erunt, atque inde per solam commutationem characteris a cum b,c,d...
orientur. Iam designando per k angulum arbitrarium ponendoque w-f-l — £m = X,
adiumento formularum
cos(ka-}-k) =
= cos (k-\-±s) sin (ka—
haud difficile perveniemus ad summationem serierum sequentium
cos (X a 4- Ti)
sini(a—J)sinf (a — c)sin£(a^—d). . .
, cos (X b 4- k)
' sin*-(£—a)sin%(b—c)sin^F — d). . .
■ cos (X c 4- ä)
•~sin^(c—a)sin^(c—£)sin£(c — d).. .
+ . tM ,.C0s/^t^ „ ,- + etc. ^ Ul
1 smi(d-^-a)s].n^(d—b)smi(d—c)... '
atque
THEOBIA INTEBPOLATKÖHS MEEHODO NOVA TKAGTATA.
| Olli ^/^ t/ ""f" /fc I
t sin (X c -+- h)
_i sin(Xa?-fr-&) , . T/-X
—I : 7^ r—: t-= T •■■. — 1— GLC. —— V
' sin £ (a—a) sm£ (a—o) sm £ (a— c)... '
Casus primus, si m est impar.
In hoc casu X debet esse non numerus integer sed fraetione 4- affectus sive
numeri imparis semissis. Ad valores negativos ipsius X non opus est respicere,
quum habeatur cos (—la-\-k) = cos(Xa—k) atque sin(—\a-\-k) === — sin(Xö—Je),
adeoque summatio pro valore negativo e summatione pro opposito positivo per so-
lam mutationem ipsius k in —k sponte demanat: haec observatio manifeste
etiam in casu sequenti valebit. Iam patet facile, pro n = 0, 1, ... m—2, sive
pro X = —%m-\-\, —\m-\-1, . .. \m—1, sive ut valores negativos omittamus,
pro X = \, J-, -f-.. . \m—1 fieri turn UK — 0, turn V1 = 0; porro
-\-co&($-s-\-k-\-d)-\- etc.j
Vim+1 = {2i)m~l jsinD-Ä+it+a) + 8in(-J-Ä+it+6)+8in(i-*
+ sin D- s+k+rf)+ etc.}
m prO(jucto ex Bz)m"~1 in summam cosinuum vel sinuum
omnium angulorum, qui oriuntur addendo ^^-f- ^ cum binis angulorum a, byc, d
diversis seu identicis; fj^m+3 yel Vim+S aequalem produeto ex Bi)m~l in
summam cosinuum vel sinuum omnium angulorum, qui oriuntur addendo %s-\-k
cum ternis ex iisdem etc. Ceterum vix opus erit admonere, potestatem quanti-
tatis imaginariae i cum exponente pariter pari fieri ===== —|— 1, cum impariter
pari = —1.
Casus seeundus, si m est par.
In hoc casu X debet esse numerus integer, fitque pro X = O,l,2...-$-0i — 1
turn Ux=0, turn Fx= 0. Porro erit
— 2
—1 -w—2 •
i s
-\-sin(%s-{-k-{-d)-{- etc.}
COS (±
etc.j
etc. aequalis producto ex 2m im in summam sinuum omnium
angulorum, qui oriuntur addendo ^s-\-k cum binis, ternis etc. angulorum a, b, c
diversis seu identicis; V^m , Us etc. aequalis producto ex —2m~~1 im~2
in summam cosinuum omnium angulorum, qui oriuntur addendo %s-\-k cum
binis, ternis etc. eorundem angulorum.
3.
Sit X functio indeterminatae oc huius formae
etc.
quae non excurrat in infinitum, sed abrumpatur, neque ultra terminum. qui con-
tinet ctT egrediatur, ita ut multitudo coefficientium non sit maior quam m.
Tunc si pro m valoribus diversis ipsius «2?, puta a, b, c, d... valores correspon-
dentes ipsius X sunt cogniti. puta = A, J5, C, D... ex his valor ipsius X va-
lori alicui alii ipsius oc respondens sequenti modo concinne eruetur. Sit t va-
valor novus ipsius x, atque T valor respondens ipsius X, ita ut sequentes m-\-l
aequationes locum habeant
A = a-^-^a-\-^aa~\-ha^-f-.. .
B = *
C = a
etc.
THEOBIA INTEBPOLATIONIS METHODO NOVA TEACTATA. $7%
Multiplicentur hae aequationes resp. per
(a — Ä)(a—c)(a — d)....{a — t)
1
(b—a)(b— c)(b—d)....(b—t)
1
(c — a)(c — b)(c — d) (c — t)
i
(d-a) (d—b) (d—c) ....(d-t)
etc.
prodeatque inde per productorum additionem
A
*
^ (b — a)(b—c)(b — d)...(b — t)
~f~ (c — a)(c — b)(c — d).. . (c — t)
"T~ (d— a) (d— i) (d— c) .. . (d— t)
-f- etc.
rp
\ (t — a){t—b)(t — c)(t—d) . . .
Tunc ex art. 1, ubi m idem denotabat, quod hie nobis e&t m-\~\, facile conclu-
detur, fieri TT=0; quamobrem multiplicando per (t—a){t—b)(t—c)...prodit
ii I ■■ .. . ■ i -M~S
~~^~ (c — ä) (c—b)(c — d).. . C
1 (d— a)(d—b)(d— c). ..
-}- etc.
4.
Formula in art. praec. inventa, ita comparata est, ut sponte sine omni cal-
culo pateat, si pro t quantitatum a, b, c, d.. aliqua in illa substituatur, valorem
respondentem A, B, C, D.. inde prodire. Neque hoc solo respectu sese commen-
dat: certo enim ad usum practicum longe commodissima est, saltem quotiesuni-
35
274 • ' ' " " NACHLASS.
cus tantum valor ipsius X e valoribus datis computandus est. Quando plures
sunt eruendi, transformatio sequens formulae nostrae nonnunquam praeferri
poterit
4- (t a) (t b) ( (a_Ä)(a_c) + (j_aj(j_cj + (c_a)(c_j))
-\-{t—a) (t b) (t c) ({fL_h)(fl_c){fl_d) -f- (b—a)(b—c)(b—d)
-f- etc.
(quae ex formula art. 3 facillime derivatur, si in hac multitudo quantitatum
a,b,c,d... ab una a ad duas a, b, inde ad tres a, b, cetc. successive increscere
concipitur et quisque valor ipsius T hoc modo oriens a sequenti subtrahitur).
Ponantur coefficientes
■—i -f- n—^, 7—iw \ -h 7i—r/i—\ -4" 7 w—r; etc. = A!, A" etc.
a—b ' D — a)' (a—*)(« — c) ' (o—a)D—c) ' (c — a)[c — b) '
porro designetur per Br, B" etc. id, quod fit ex Ä, A" etc. si pro a, b, c..
resp. scribitur b, c, d... atque pro A, B, C... resp. J3, C, D...; similiter de-
designetur per C, C" etc. id quod fit ex Ä, A"etc., si pro a,b,c... resp. substi-
tuitur c,d,e... et pro -4, .B, C... resp. C,D,E... et sie porro. Tunc habebimus
A—B -D' B — C „r C — D
A =
Än
XX. *—
a — o o — c c—d
A'—B' jy» B'—C „„ C'—B'
a — c * o — d ' c— e
A,„ A"—B" r>„, B"—C" n,„ C"—B"
^ — a — d ' D ~ ~T^-T~' ° — c-f • •
etc.
atque
T =^ Ä-\-A\t— a)~\-A"(t—a)(t— b)-\-Ä"(t—a){t — b){t—
Multitudo quantitatum A', B', C etc. hie computandarum erit m — 1, multitudo
quantitatum A", B", C" etc. erit m—2 et sie porro.
5.
Sequens quoque mutatio formulae art. 3 non sine fruetu in usum vocari
poterit. Sit 36 funetio integraarbitrariaindeterminatae #, neque tarnen alterioris
THEORIA INTERPOL ATIOtflS METHODO NOVA TRACTATA.
quam m—lti ordinis; atque %, 23, (S. 2) Z eius valores pro
resp. Tunc per art 1 erit
o= a
a_J)(a — c)(a—d).. . (a — t)
— t)
_tf) . . . (p—t)
^ (d— a)(d— i)(d — c) . . . (d — t)
-f- etc.
Hinc facile deducitur
«-6)(<-c)(<-
"i (a — b){a—c)(a —
b){a—c)(a — d). . .
(<-g)(^-&)(<-^)... /r,_(rN
"T"(c — a)(c — i)(c — d)... ^ *~J
. (< — g) (t — b){t — c) .. . ,j, (t^
~r'{d~a) (d—b){d— c) .. . { -'
+ etc.
Quodsi functio 1 ita eligitur, ut valores functionis X hi A, B, C, D... prope
per illam repraesententur, hoc lucramur, ut coefficientes ra_h\ra_Cc\,a_d\ " e^c-
per quantitates parvas multiplicandi sint. Potest etiam pro X quantitas constans
assumi, e. g. una ex his A, JB, C, D...; in quo casu pars una e valore ipsius
T excidet. Aiit ita determinari potest 36, ut duae pluresve harum quantitatum
per 36 repraesententur, in quo casu totidem partes ex T excident.
6.
Quae praecedunt, suppositioni innituntur, functionem X ultra potestatem
xm~1 non egredi, sive differentiam m^™ una cum superioribus evanescere, in
quo casu methodus interpolationis rigorose vera est. Si vero illa suppositio locum
non habet, interpolatio eo tantummodo tendit, ut loco functionis X functio sim-
plicissima eruatur, per quam valoribus propositis A, B, C,.D... satisfiat. Iam
ut errorem, qui a neglectis differentiis superioribus nascitur, diiudicare possimus,
35*
sin*termiai ia X post potestateo» «asP M ^«t^ -f-va?"^1 -f- etc. Eri4 itaque ia art
non. W = 0, sed ut ex art. 1 sequitur, PF = jt -f- v («-4~ ^-f- £-4^ ^4- •
Hinc valori ipsius T illic tradito adhuc adiici debet
(*— a)(#—*)(<—c)(<—d)^ ^><\\j.-\-v(a-!rb-{-jc->rd+ ... +t)-\- etc.j
7.
Casus in praxi maxime frequens est, ubi a, b, c, d... progressionem arith-
meticam constituunt. Ponendo intervallum = 1, ita ut sit b = ö-f-1, c = a~\- 2
etc., formula art. 4 fit
+ (*-!) (£-
+ etc.
sive
ubi A\ Ä\ AI" etc. computantur per algorithmum sequentem
4'= £—.4, ^'= C—£, C'= D— C etc.
= B'— J.', 2JT= CT—B\ IC"=.D'—C etc.
= ^"— ^'r, 3B'" = C"— B", 3 CT = D"— er etc.
etc., quae formula cum vulgata interpolationis formula per differentias omnino
convenit,
8.
Si pro satis multis valoribus ipsius x in serie arithmetica progredientibus
a, a*4-l» «r^2 .. . valores respondentes fimctionis X cognitä snni, ut seriem w
valprum successivorum ipsins x ad lubitum eligere liceat ad computum ipsius T:
quaestio odtor, quomam valores ad bunc fiaem praeferre maxime praestet, siqui-
dem plures quam m adMbere sive ultra differeutiam m—l^01 egredi nolimais?
THEORIA INTERPOI^TIOIiLS. HKTHODO NOVA TBACTATA. 25BT
Manifeste hoc ita est decidendum, ut error a differentia nP ordinis oriundus fiat
quam minimus; hie vero error fit
= (t-a)(t—a—i)(t-a-2).... (t-a^
si adhibentur termini ad x = a, a-f-1, a-f-2,.. .a-\-m—1 pertiaentes, vel
= (*_a—1)(f—a-2)(*—a~3).... (t-a-m)-^^—-
si adhibentur termini ad x = ö-f-1, ö-f-2, a-}-3,.. . a-\-m pertinentes, vel
—a){t-a — 1) . . . (*-«--» + 2) t.,. *_„
si adhibentur termini ad <r = ö — l,«,«^1»-^^ — 2 pertinentes, designando
per A differentiam "ordinis mü, quae siquidem ad differentias superiorum ordinum
non respicitur, hie tamquam constans considerari potest. Quodsi igitur m termini
ad x = a, ö+1, ö+2, . .. a-\-m — 1 pertinentes maxime idonei sunt, ex illis
tribus expressionibus prima debet esse minima adeoque sine respectu signi t— «<
vel saltem non ^>t — a—m, nee non t—a-}-i^> vel saltem non <^t—a—m-\~\.
Ex conditione priore facile deducitur, t—a—m esse debere quantitatem negati-
vam inter —{-m et —oo sitam, unde t—a iacebit inter -\-%m et —oo; ex
conditione posteriore autem erit t—a-\-\ quantitas positiva atque inter %m et
-f-oo sita; quare t—a iacebit inter %m—1 et \m. Hinc sequitur, si m fue-
rit numerus par, valores ad interpolationem adhibendos ita eligendos esse, at
prior semissis ab una parte. posterior ab altera termini quaesiti iaeeant; si autem
m fueritimpar, termini ii sunt eligendi, quorum medius quaesito iaceat quam
proximus. Quoties in hoc casu / est exaete medius inter duos valores consecu-
tivos ipsius jy, respectu erroris a neglecta diiFerentia mü ordinis generaliter lo-
quendo nihil intererit, sive terminus quaesito praecedens sive sequens pro medio
adhibendorum adoptetur.
9.
Exempla. I. Invenire oporteat log. sin24°30', si logarithmi sinuum per sin-
gulos gradus habentur, ita ut differentiae quartae et superiores negl%antur. In
hoc itaque casu secundum praecepta art. praec. adhibebimus logarithmos sinuum
areuum 23°, 24°, 25°, 26°, quibus per A, B, C, D designatis provenit per for-
mulam art. 3 logarithmus quaesitus
278 NACHLASS.
cuius valor numericus ex
A = 9,5918780
B = 9,6093133
C = 9,6259483
D — 9,6418420
eruitur 9,6177271.5; tabulae dant 9,6177270.
Quodsi hie loco log. sin 23°, logarithmum sin 270=_E=9,6570468 ad-
hibuissemus, formula
dedisset 9,6177267.37 5.
Formula art. praec. pro hoc casu dat errorem ex neglecta differentia quarta
A oriundum = tJ-^-A, si A, B, C, D, contra = —ttitA, si -B» C A -E ad"
hibentur; qui error valori calculato adiieiendus est. In exemplo nostro habetur
A = —0,0000066; correctio hinc calculata utrumque computum cum tabulis
conciliat.
II. Sit tempus novilunii 16 Junii 1806 e longitudinibus solis et lunae pro
singulis diebus computandum, ita ut differentiarum usque ad quartam incl. ratio
habeatur. Habentur in ephemeridibus Parisiensibus pro meridie vero loci se-
quentes
1806 Junii 14
15
16
17
18
longit. solis
82
83
84
85
86
°39'l2"
36 30
33 48
31 7
28 24
longit. lunae
53(
67
81
96
111
}19'l5
29 4 3
59 52
44 9
35 30
Sunt hie valores dati ipsius oc differentiae inter longitudinem solis et lunae, va-
lores respondentes ipsius X tempora, quae inde a meridie 1 6 Junii numerabun-
tur; quaeriturque valor ipsius X valori x = 0 respondens. Fit igitur
THEOEIA INTEEPOLATIONIS METHODO NOVA TEACTATA. 279
a~— 29°19'57" =— 105596" A = — 2
&=_16 6 47 = — 58007 £=—1
c = — 2 33 56 = — 9236 C= 0
d = -\-ll 13 2 =+ 40382 D = -fl
e = -\-2h 7 d =+ 90426 JS == +2
* = 0
Hinc computatur
(aZb)(a-c)(a-d)(a-e) = +0,0149084
— —0,1050660
+ 0,9624567
— a)(c — b)(c — d)(c — e)
1S~1»~*i = +0,1434435
—c)(d — e) ' '
~l(<~f! = -0,0157429
(e — a)(e — b) (e—c) (e —
His coefficientibus#) per —2, —1, 0, 1, 2 resp. multiplicatis, productorum summa
fit =+0,1872069; quare novilunium erit 16Junii, 4h29'34 temp. ver.
Paris, sive 4h29'4l temp. med.; Connaissance des tems habet 4h27'42".
10.
Sit X functio arcus indeterminati oc huius formae
a-j-a'cos<2?+a"cos2<2?-|-a'"cos3<»-|- etc.
etc.
quae non excurrat in infinitum, sed cum cos moc et %\n.moc abrumpatur, ita
ut multitudo coefficientium (incognitorum) sit 2m+l. Pro totidem valoribus di-
versis ipsius x, puta a, b, c, d etc. dati sint valores respondentes functionis X,
puta A, B, C, D .. . (Ceterum valores ipsius x, quorum differentia est periphe-
ria integra sive eius multiplum, manifesto hie pro diversis haberi nequeunt). Ex
his datis quaeritur formula pro valore T, quem functio X pro quoeunque alio
valore ipsius oc, puta t nanciscitur. Habentur itaque im-^-i aequationes
*) Confinnationi calculi inservit obs,ervatio ex art. 5 sine negotio derivanda, summana harum coefficien-
tium esse debere = i.
280
A = aH-a'cosö4~a"cos2ö + a'"cos3a+ etc-
H-ö'sin«4-ö"sm2a+ö'"sin3a+ etc.
i? = a-|-a'cps6+a"eos2Z>+a'"cos3&-j- etc.
H-ö'sin&+ö"sin2& + ö'"sin3&+ etc.
C = et-j- et' cos c+a" eos 2 c -{- a'"cos 3 c -\- etc.
-j-ö'sine+ö"sin2c + 6'"sin3c + etc.
D = a-|-a'cosd-j-a"cos2d-{-a'"cos3d-f- etc.
-j-ö'sind+ö"sin2d-+-öwsin3<H- etc.
etc.
T= a-f a'cos*-}-a"cos2*-|-a'"cos3£+ etc.
etc.
Multiplicando has aequationes resp. per
in-|-(ö—öjsinf (a—c)sinf (a— d) sin-*-(ö—t)
l
sinf(&—ö)sin%(b — c)sinf (b—d).. ..sin|(& — t)
__ ^
sin |-(c—a)sin^(c—b)sxn$(c—d)... .sin%(c — t)
1
—c)... .sin£ (d — t)
etc.
sin£ (t—a)sin %(t — £)sin£ (t — c)sin^-(< — d) . . .
addendoque producta prodeat
sin£ (a — b)sirt%(a — c)sin.${a — d) ... .sin-§-(o — t)
_]__ *
1 sini(i—a) sinA(i — c)sin^(& — d) sin|(£ — t)
■ £
•^ sin^ (c — a) sinf (c — i)sin % (c— d)... . sin £ (c — t)
• sin% (d ~ a) sin £ (d—b) sin %(d—c) sin$(d—t)
-f- etc.
' sin£ (t — a) sin%(t~b) sia±(t — c)sin* (t — d)....
THEORIA INTERHXLATIO3SIS MEIHODO NOVA TEACTA^A«
Tunc ex art. 2, ubi m idem erat, quod hie est %m~\-% adeoque easus se-
eundus locum habet, fit W = 0; quamobrem multiplicando per
—d) .. .
prodit
*
rp sin-fr(£—&)sinf (t — c)&ua.£(t—d) . ...
sin■£(a—b)sin-J-(a—c)sm£(a — d)....
■ sin£(<—-a)sin|(£—c)sinf(<—d).... jn
"■ sin | (ö—a) sin^ (b—c) sin £ (b— d) ...,
t sin.^-(t — a)sin%(t — J)sin-|-(^ — d) . . .. sy
•"sin ^(c — a)sin-|-(c — J)sin|(c—d) ....
i^ sin ^ (t—a)sinf(# — J)sin^(<—c). . . . j\
* sin%(d—a)sin£{d—b)sj.n$(d—c) ....
+ etc.
Quum haec formula indefinite pro valore quoeunque ipsius t locum habeat, ma-
nifestum est, si produeta sinuum in numeratoribus in cosinus sinusque areuum
multiplicium evolvantur, id quod provenit cum
a+ a!cost-f-a"cos21~\-a"cos 31-\- etc.
etc.
identicum esse debere, unde coefficientes a, a, 6", a", ö" etc. innotescent.' Cete-
rum formula pro T, ut hie exhibita est, ita est comparata, ut sponte et sine eal-
culo pateat, siibstitutis pro t resp. a, b, c, d etc. valoribus propositis A, J5, C,D
etc. probe satisfieri.
11.
Si multitudo valorum datorum A, B, C, D etc. unitate minor esset, quam
supposuimus, puta = Im, hi non sufficient ad determinationem 1m-\-i coef-
iicientium incognitorum, nisi inter eos relatio aliqua cognita fuerit. In hoc ita-
que casu expressio generalis pro T aliter exhiberi nequit, nisi ita, ut eonstan-
tem incognitam implicet. Ratiocinia art. praee. He adhiberi non possunt, quo-
niam summatio W =■ 0, ex art. 2 petita, suppositioni innixa est, nmMtudinem
quantitatum A, B .. . T esse parem. Formula quidem in art. praec. pro T in-
venta valoribus A, 1$ etc. generaliter satisfeeit, sive horum multitudo par sit
sive impar: sed levi attentione perspicitur, ex evolutione produetorum e sinubus
prodire, in nostro casu, expressionem propositae non similem, sed hmm formae
etc.
"sinf t-\- etc.
Quamobrem pro lioc casu viam aliam ingredi oportebit.
Multiplicetur X per cos (£#-{-Ar), proditque, si termini ultimi in X sta-
tuuntur am cos ma;-\-fim sin mce
-f-£ et'cos (£■# — Ar)+£a"cos(f x — k)+id"cos(jt<v—Ar)-f-
-|-_-amcos ((m—i)x — k)
' sin(f <
d?— Ar)+4-ö'" sin (f.» —
m((«i—i)a? — Ar)
Iam si in hae expressione pro «27 successive substituitur a, 6, c, d 1, quod
inde provenit resp. per
sin£(a-i)sin£(a-<
sin£(&—a)sin£ (b — <
sm*(e-a)sm*(e—1
etc.
i
1
1
1
1
4z(a — d)..
$(b — d)..
%(c — d)..
.. sinf {a — t)
..sixi\{b — t)
sin£ (t — a) sin £ (tf — b) sin £ (rf — c)sin%(t — d) . . . .
multiplicatur, productorumque aggregatum = W ponitur: ex iis, quae in art. 2,
(in casu priori, ubi m idem erat, quod hie est 2w-f-l) tradidimus, facile sequi-
tur, haberi
J&x. altera vero parte erit
THEOSIA INTERPOLATION^ METHODO NOVA TRACTATA.
a — b) sin ±(a — c) sin ±(a — d) sin£(a — t)
, .8 cos (j b -f- 1e)
' sin$(£ —a)&vai(b — c)sin$F — d) sin£(£—t)
• C
' sin^(c — a)sin|(c—
)sin|(c— 6)sin£(c — d) sin^(c — t)
_l J>cos(j d + k)
' sin^(rf— a)sin4-(d--&)8ini(rf — c)
-f- etc.
, Tc
' sin|(^ — a)sin %(t — 4)sin^-(^ — c)sin^(^ — d). . . .
Quodsi iam quantitatem k, quae prorsus arbitraria est, = — % t ponimus,
summam autem a-\-b-\-c-\-d-\- ... = s (exclusa t), prodit, multiplicando per
sinf (t—a) sin ±(t—b) sin ±(t—c)sin^[t—d)
■^ sin t.F — a)sini(i —
' si
sin|-(c—a)smj(e-6)sin^-(c — d)
sinj-ft —a) sin |-(<-&) sin j-(^-c)
7:
-f- etc.
+ 22w-1rmsin4-(f—a)sin*(*—&) sini{t—c) sin-|-(#—rf) ...
Circa haue formulam quasdam adhuc annotationes adiicimus
I. Est i2m = 4-1« vel — *» P^out w par est vel impar.
II. Quum formula indefinite pro quovis valore ipsius t valeat, necessario,
evolutis sinuum productis in sinus et cosinus areuum multiplicium, cum formula
pro X, si pro x scribitur t, identica erit, i. e. cum
a-j-a'cos£-f~a"c0S2£+ etc.
HI. Determinantur itaque omnes coefficientes a, a, fi\ a", f>" etc. per quan-
titates cognitas, atque unicam incognitam amcos^-^-f'^msini-^ quamobremr si
qua inter illos relatio insuper datur, omnes ex asse facile poterunt assignari.
36*
284 NACHLASS.
IV. Quodsi autem tantummodo expressio eiusdem formae ut
-{-$'sint-{-$"sin2t-i- etc.
quaeritur (sive cum hac identica sit, sive non), per quam valores propositi
A, B, C, D etc. repraesententur, sipro t resp. a,b,c,d etc. substituitur: quantitas
amcos%s-{-fimsiR-Jts ex incognita arbitraria evadit, quam si placet etiam = 0
statuere licebit; reveraque formula nostra pro T ita comparata est, ut absque
calculo sponte pateat, hacce eam proprietate praeditam esse.
12.
Operae pretium erit, transformationem ei analogam, quam in art. 4 expli-
cavimus, etiam ad formulas art. 10 et art. praec, si ibi a^cos^s-f-ö^sin^-s = 0
ponitur, applicare, quo pacto hos duos casus diversos sub formula unica compre-
hendere licebit. Crescat itaque multitudo quantitatum a, b, c, d . . . successive
ab una a, ad duas a, b, deinde ad tres a, b, c etc.: evolvatur alternis vicibus
per artt. 10 et 11 valor, quem t pro singulis his suppositionibus nanciscitur, tan-
dem quisque valor a proxime sequente subtrahatur, sequenti modo:
A
sm|-(a — b) l ^ i ' sin^(o — a)
—c)
c) * . sin-§-(£ — a)sinj-(^—c) -n. sin$(t—a)s]n%(t — b)
a — c) ~~r~sin£(£ — a)sin^(i—c) "■ sin|(c — a)sin^(c— b)
etc.
Hie differentia inter valorem primum et secundum fit
b)\r£^
'! Umi(a—b)
Differentia inter valorem secundum et tertium
— ".in'fr gW
°)\sini(a-b)sini(a-c)^~ siniD-a)siniD^"T" sin £(c-a) sin J (C-&}$
Quae operatio si ultra continuatur, facile emergit lex generalis. Scilicet sta-
tuendo
THEORU INTEKPOLATKMSIS METHODO NOVA TKACTATA.
A' fL I
sin % [a — o) ' si
a—c) | JBcos$(b—c) . C
A"= - x ■ , - . • -y •
A ttt ^L i -ö
_l | -P
« /y l * cm ■! i^ /vicin X. i ii Äi ein 1 / J /»\
^w/ Acos%(a — e)
sin^-(a—b) sin £ (a — c)sin ^ (a — d) sin ^(a— e)
. -5cos^(i — e)
' si
+
+
— ö) sin|-(& — c) sin ^(b — d) sin -^D — e)
Ccos^(c — e)
:^-g)
1 si
sin % (e — a) sin £ (e — b) sin £ (e — c) sin ^ (e — d)
etc. fiet
sin■!-(#—a)c
-|- ^1" sin-l- (#—a) sin ^- (t—b)
-f- ylw sin -I- (t — a) sin |- (t — b) sin 4- (t— c) cos£(t—d)
-\-Am8w.±(t—a) sini-(t—b) sm{-(t—c) sin-J-(#— d)
-+-Ä1 sin^- (t— a) sin-J-(#—6) sin 4- (£— c)sin-f(#—d) slnf(f— e) cos £ (t—/)
+Ä11 sin i(t—a) sin -f (t—b) sin f (t—c) sin -f (t — d) sin i(t—e) sin £ (*-—/)
-f- etc.
quae progressio ad totidem terminos continuanda est, quot valores funetionis X
dati sunt.
Coefficientes A'} Ä\ Ä", Ä'" etc. etiam per algorithmum sequentem com-
putari possunt. Designetur per B', B", B'", B"" etc. id quod illi resp. fiunt, si
a, A, b, B, c, C, d, D etc.
resp. mutantur in
b, B, c, C, d, D, e, E etc.
Porro transeant
Ä, A", A", A'"etc. in C\ C", Cr", C"" etc. vel in D\ &', D"', W etc. etc.
si
286 NACHLASS.
a, A, b, B, c, C, d, D etc.
resp. mutantur in
c, C, d, D, e, E, f, F etc.
vel in
d, D, e, E, f F, g, G etc.
etc.
Tunc erit
etc«
sin}(a — c) ' sm{(i—d)
A" cos$(a — c) + A' s,]n$(a — c) —J3 " j*n, B" cos % {b — d) 4-^/sin^(&— d)—C"
JS"'cos j(b—/) — C"
A""co*j(a — e) + ^"'sinj(a — e)—B"" Rv
.vi __ ^vcos^(a-ff) — #v ^vi £vcos$(b~h)-
sn^(a 5»)
sin£(a — h)
etc.
Lex formationis hie satis ob via es t, si modo observetur, numeratores in valori-
bus pro A", A"\ A"", Ä1, Ayl etc. (valor pro Ä ab hac regnla excipiendus est)
alternis vicibus e duabus vel tribus partibus constare.
13.
Theoeema. Si X est funetio arcus x formae (F)
a-\-dcosx-\-a"cos 2x-\-a!"cosZx-\- etc.
+ ö'sinB?-4-ö''sin2#-f-6'''sin3<2?-|- etc.
vel huius formae (G)
y cos-f-^-|-7'cos f Qß-\-y" cosfüß~\- etc.
in%üß-\- etc.
positoque 00 ==■ a, valor funetionis X fit =0: erit X divisibilis per sin^{oß—a),
quotiensque in casu priore formae G, in posteriore formae F.
Demonstratio. Casus prior. Si in funetione X pro quavis parte cosnoc
substituitur cosw«2?—cosna, pro quavis parte sinw<z? autem sinw<z?—sinwa,
THEORIA INTEBPOLAIONK METHODO NOVA TKACTATA.
denique pro a, a—a sive 0, manifestum est, partes determinatas hoc modo ad-
iunctas, mutuo se tollere adeoque functionem X hoc modo noa variari. Singu-
lae vero partes ipsius X nunc per sin£(#—a) divisibiles £runt, puta
cos nx — cos na e\ ' /f < \
7 r- == —2 sinn» — 4-)
(a; — a) vv ii
i(( )
— etc.
— 2 sin ((■£# -f- (n
-f- etc.
-f- 2 cos (|- <2? -f- (»—£) a)
Uterque coefficiens manifesto ad formam G reduci potest, quamobrem etiam tota
X per sin\{oß—a) divisibilis, quotiensque ad formam G reducibilis est. Q.E.D.
Casus posterior. Si in functione X pro quavis parte cosnoe (desig-
nante iam n non ut ante integrum, sed integri imparis semissem) substituitur
cosw#—cos4-(<2?—a)coswa, pro quavis parte sinw<z? autem sinw<2?—cos^-(a?—a)sinna,
manifestum est, partes, quae hoc modo functioni X accedunt, mutuo se tollere,
adeoque X non variari. Singulae autem partes ipsius X nunc per sin\ [ob—d)
divisibiles erunt, puta
— 2 sin ((» — |) oo-\- f a)
— etc.
— 2sin(<2?-f-(»—l)a)
— sinna
sin mx—cos 4- (x — a) sin n a . A // ,\ i < \
^{x_a) '* = +2cos((n —*)ar-|-ia)
+ 2 cos ((n—|) x -f- f a)
+ 2 cos ({n — |.} 07+fa)
+ etc.
+ 2 cos (#+(»—1)«)
+ coswö
288 NAGHLASS.
ut per multiplicationem facile confirmatur. Uterque quotiens est formae F. Quam-
obrem functio tota X. per sin£(#— a) divisibilis, quotiensque ad formam F
reducibilis erit. - Q. E. D.
14.
Theobema. Si functio X formae F vel G pro pluribus valoribus diversis*)
ipsius x, puta a, b, c, d etc. fit — 0, per productum
sin^{x—ajsin^-^—6)sin^.(a; — c)sin£(a?—d) ....
divisibilis, quotiensqpe vel eiusdem formae erit ut X vel diversae, prout multitudo
valorum a, b, c, d . . . . par est vel impar.
Demonstr. Ponatur X = X' sin £ («2?—a), sitque M valor ipsius X' pro
00 z=.b. Hinc Msm^b—a) erit valor ipsius X pro x =. b, qui quum esse de-
beat = 0, necessario erit M = 0. Quare X' divisibilis erit per sin^-(<z? — b)
et simili ratione quotiens hinc oriundus per sin £(<2?—c), et sie porro. Quare X
divisibilis erit per productum
sin£(a?—a)sin£(<z? — &)sin£(a;—c)sin^(a?—d) ... Q. E. D.
Altera theorematis pars tarn obvia est, ut demonstratione opus non sit.
Ceterum aeque obvium est theorema inversum, si X per productum
sin£(a? — a) sin £(<z? — b) sin£(a? — c)sin|(«2? — d) ....
divisibilis sit, ipsius valorem fieri = 0, si ipsi «2? aliquis valorum a, b, c, d etc.
tribuatur.
15.
Ex theoremate praec. sequitur, si funetionis X, formae F, valores pro
x ■=■ a, b, c, d etc. resp. sint A, B, C, D etc., quamvis aliam similem funetionem
arcus x, quae iisdem valoribus satisfaciat, sub ibrmula X--\~PY contentam esse
debere, ubi per P designamus productum
sin ^ ix — a) sin £ (x — b) sin ^{x —- c) sin £■ [x — d) etc.
per Y autem funetionem indefinitam arcus x% quae sit vel formae F vel formae
*) Adiecta e'adem restrictione, quam in art. vo exhibuimus.
THEOKIA INTERPOLATIONIS METHODO NOVA TBACTATA.
G, prout multitudo valorum a, b, c, d etc., quam per p. designabimus, par est
vel impar. Iam observamus:
I. In artt. 10, 11, 12 eruere docuimus fanctionem X ordinis mtl (ie. ulfcra
cos ma? et sinm<z? non,progredientem), quae ja valoribus propositis A,B,Ct Detc.
satisfaciat, ita ut m sit = ^fi — •§■, vel ^-ft, prout p impar est vel par. Pro-
ductum P manifesto est ordinis -|{iü. Quando itaque {i impar est, adeoque Y vel
ordinis £ü vel altioris, erit PY ordinis adminimum ^p-f-^1 adeoque ordinis al-
tioris quam X, unde colligitur, functiones alias quam X, quae iisdem valoribus
propositis satisfaciant, non dari, nisi ordinis altioris. Quando vero ja est par,
PY tunc tantummodo fit ordinis ^fi*1, si pro Y accipitur quantitas definita;
quare in hoc casu infinite multae quidem functiones similis formae et ordinis ut
X dantur, quae iisdem valoribus satisfaciunt, omnes autem sub forma X-^-hP
comprehensae erunt, designante h quantitatem definitam. Eaedem conclusiones
ex methodo, per quam in artt. 10,11 functionem X derivavimus, sponte sequuntur.
II. Vice versa autem, si quae functio X' aliunde innotuisset, quaeomni-
bus quidem valoribus propositis A, B, C, D etc. satisfacit, sed ad altiorem quam
opus est ordinem ascendit, functionem Y ita determina]?e licebit, ut X'-\-PY
ad ordinem £{i — ^tum vel £fitum (prout fi impar est vel par) deprimatur. Sint
termini summi in X', Kcosna?-\-Lsinnx\ in P, A:cos^-{i<2?-|-/sin|-{iB?, accipian-
turque pro terminis summis in Y hi
Hinc calculo facto invenietur, coefficientes ipsorum cosnß et sin not in ^
fieri = 0, siquidem fuerit n^>^^\ similique modo ex terminis summis functio-
nis evolutae X'-f-Pp (qui erunt ordinis n—l11) definientur termini proxime
inferiores in Y (ordinis n—^-{i—lü). Haec operatio eousque repetenda erit.
donec X'-{~PY depressa sit ad ordinem non altiorem quam 4-ja, adeoque ad
ordinem 4{i — 4-tum, quando [i impar est, ad ordinem 4-^tum, quando {i par est.
Ulterius hanc depressionem non patere, nullo negotio perspicitur.
III. In casu itaque priore (quando [i impar est) hoc modo necessario ad ean-
dem functionem X perveniemus, quam per methodum supra traditam e valori-
valoribus datis A, B, C, D etc. eruissemus. In casu posteriore autem methodus modo
exposita suppeditat functionem, quae quidem eiusdem ordinis erit, cuius est
functio, per methodum art. 12, sive per methodam art. 11, si terminus
37
290 NACHLASS.
= 0 ponitur, oriunda, attamen ab hac diversa esse potest. Sit functio illa X",
haec X'": adeoque X'"'= X"-f-AP, designante h quantitatem definitam. Po-
namus terminos summos in X" esse K'cos ^ [tx-\-Lr sin ^iloj; in X'" autem
JST"cos^-{ia?-f-Z/"sin4-{i<2?, ita ut sit K"— K'-\-hk, L" = L'-\-hl. Iam non dif-
ficile est, ex art. 11 vel ex art. 12 demonstrare, si aggregatum a-\-b-\-c-\-d-\- etc.
designetur per s, esse K" cos% s-\-L" sin %s = 0, unde deducitur
+
K'l-L'k
i ja. tu»,« -J-L sin^s
K=
Haud difficilius demonstratur, esse
7. i COS-§-S j [
K cos i«-(-' sin £ s
K'l-L'k
y ;——j-. COS4-Ä
ubi Signum superius valet, quando |-[jl est par, inferius, quando est impar.
Quare in valoribus modo traditis pro K" etL" denominator fit =4:^ adeoque
K" = (K'sin^s — L'cos^-s)sm^-s
L" = — [K' sin |- s — L' cos {- s) cos ^- s
16.
Hactenus tales functiones consideravimus, in quibus turn cosinus turn sinus
adsunt: saepissime vero aut hi aut Uli absunt, quae functionum genera seorsim
tractare conveniet. Utrumque quidem casum ad casum generalem hucusque con-
sideratum reducere liceret; attamen etiam magis e re esse videtur, hanc disquisi-
tionem ad problema art. 3 reducere.
Primo, si constat, omnes coefficientes f)', ß", f>"'etc. in functione X (art. 10)
esse = 0, multitudo incognitarum ad m-f-1 diminuitur, et proin pro tot valo-
valoribus diversis ipsius 00 valores respondentes functionis X novisse sufficit. Quo-
niam vero in hoc casu valor functionis X non mutatur, si pro Oß substituitur —oß,
manifestum est, non solum tales valores ipsius oß, quorum differentia peripheriae
vel multiplo peripheriae aequalis est. sed tales quoque, quorum summa est 0 vel
peripheriae vel multiplo peripheriae aequalis, pro diversis non esse habendos. Aut
generaliter, ut duos valores ipsius x pro diversis habere liceat, cosinus inaequa-
THEORIA INTEBPOLATIONIS METHODO NOVA TBACTATA. 291
les habere debent. Quibus ita intellectis sint m-f-1 valores dati functionis X
hi A, B, C, D etc., valoribus ipsius x his a, b, c, d etc. respondentes, quaeri-
turque expressio generalis pro valore T, quem functio pro x = 0 adipiscitur.
Quum functionem X in casu nostro etiam sub formam
-r-{--r'cosx-{-f(cosxJ-{-f'(cosxf-\- etc. -hym(cos<2?)m
reducere liceat, habebimus per art. 3
rp (costf—cosb) (cost — cosc) (cos #— cosrf)... 4
(cosa — eos b) (cos a — cos c) (cosa — cos d)...
, (cos t — cos a) (cos t — cosc) (cos t — cos d)... t>
1 (cosb — cos a) (cos b — cos c) (cos b — cos d).. .
■ (costf—cosa)(cos# — cos£)(cos£ — cos^)... p
"■ (cosc — cosa) (cosc — cosi)(cosc— cosd)...
! (cos t — cosa) (cos t— cosi) (cos t — cos c). .. j-v
"* (cosd — cosa)(cosd— cosb) (cosd — cosc). ..
-f- etc.
Secundo, si omnes coefficientes a, a, a", a'" etc. evanescunt, multitudo in-
cognitarum erit m, sufficitque adeo, valores functionis X pro totidem valoribus
diversis ipsius oß novisse. Quum valor functionis X pro x = — t ex valore pro
x = -f-1 sponte sequatur (per solam mutationem signi in oppositum), etiam hie
tales valores pro diversis haberi nequeunt, unde facile colligitur, hie perinde ut
in casu praec. eos tantummodo valores ipsius x pro diversis agnosci, quorum co-
sinus sunt inaequales. Praeterea quum valor functionis X pro x= 0, 180°, 360°
etc. et generaliter pro tali valore ipsius x, cuius sinus est = 0, sponte fiat ;= 0,
adeoque iam ex natura problematis datus sit, talem valorem inter m datos non
numerari supponimus. Iam quum constet, esse
sin nx
= 2cos(w — l)<2?-f-2cos(w — 3)<z?-f-2cos(ft— 5)a?-f-. . . -f-2cos<a?
pro valore pari ipsius n, atque *
= 2cos(w — i)<2?-f-2cos(w — 3)#-}-2cos(rc — 5)a?-f- • • -}-2cos
■yr
pro valore impari ipsius w, facile concluditur -— ad formam
sinx
etc. -f ^(cos,*?)™-1
37 *
KACHLASS.
xr
reduci posse, adeoque, quum valores funetionis ^ pro oe = a, b, c, d... fiant
= -r—, -T-T, -r~, -r—i. .. ., haben per eundem art. 3
sin a sin o' sin c sin d *■
rp sin t (cos t — cos&)(cos# — cosc) (cos t — cosd)... *
sin a (cos a — cos b) (cos a — cos c) (cos a — cos d). . .
! sintf (cos< — cosa)(eos#—cosc) (cos< — cosd) • • • t>
1 sin b (cos i — cos o) (cos i — cos c) (cos i — cos d). . .
1 sine (cosc —cosa) (cosc — cosi)(cosc — cosd) . . .
, sin # (cos # — cos a) (cos £ — cos b) (cos # — cos c) . . . yv
y
^ sind(cos<tf—cosa)(cosd— cosi)(cos^—cosc) . . .
-f- etc.
Ceterum in utroque casu formula pro T cura funetione X identica erit, mutando
t in «2?, quoniam illa indefinite pro valore quoeunque ipsius t valet.
17.
E prineipiis algebraicis facile conclusio petitur, si, pro casu priore art. praec.
produetum
(cos t — cosa) (cos t—cos b) (cos t—cos c) (cos t — cos d) etc.
pro posteriore autem produetum
sint(cos t—cosa) (cost—cos&) (cost—cosc)(cos t— cos</) etc.
per P designetur, quamvis funetionem ipsi X. similem, quae iisdem valoribus
A, B, C, D etc. pro at= a, b, c, d etc. satisfacit, necessario sub forma X-j-PF
contentam esse debere, ubi Y est funetio indefinita arcus «2? formae
7 ~^~ 7 cos x ~H l"cos 2 x H~ 7'" cos s x ~t" etc-
Theorema inversum, scilicet quamlibet funetionem sub forma X~\-PY conten-
contentam illis valoribus satisfacere, sponte patet. Porro manifestum est, produetum
P esse ordinis m-\-ltl, adeoque proxime altioris quam X; quamobrem aliafunetio
ipsi X similis quae iisdem valoribus satisfaciat non datur, nisi ex ordine altiore
quam X.
Vice versa, si quae funetio X', ipsi X similis quidem, sed altioris ordinis,
aliunde innotuit, quae valoribus datis A, B, C, D etc. satisfacit. funetionem F,
eius quam tradfdimus formae, ita determinare licet, ut X'-f-PF ad ordinem
THEORIA INTEEPOLATIONfö METHODO NOVA TEACTATA.
mtum deprimatur, unde necessario functio X ipsa, quae e valoribus A, B, C, D etc.
per methodum art. praec. eruitur, prodire debebit. Quum methodus terminum
summum functionis Y atque inde deinceps inferiores evolvendi, tamquam casus
specialis e methodo in art. 1 5, II tradita peti possit, non opus est, huie rei hie
diutius inhaerere.
18.
Omnesdisquisitiones praecedentes superstructae sunt conditioni, X esse pro-
gressionem cum cosinu sinuquearcus moß abruptam. Quae conditio si locum non
habet, tot valores ipsius X, quot cognitos esse hactenus assumsimus, manifesto non
sufficiunt ad determinationem completam, expressioque pro T in variis quos con-
sideravimus casibus tradita, correctione opus habebit, a coefficientibus sequentibus
in X pendente et per summationes artt. 1 et 2 facile assignabili. Quodsi autem
series X, sive in infinitum excurrat sive uspiam abrumpatur, tantopere convergit,
ut partes post cosm<2? et sinm<z? sequentes pro evanescentibus haberi possint,
etiam illam correctionem negligere licebit, adeoque valorem T saltem proxime
verum nacti erimus. Quomodocunque vero haec se habeant, T certo funetionem
verae similem simplicissimam exhibet, per quam omnibus valoribus propositis sa-
tisfieri potest.
19.
Impriniis frequens, maximaque adeo attentkme dignus -est casus iste, ubi
valores arcus a?, pro quibus valores functionis X dati sunt, progressionem arith-
meticam constituunt, in qua terminorum differentia aequaüs est coefficienti, ex
divisione peripheriae integrae in totidem partes quot sunt termini orto, ita ut si
progressio ultra terminum postremum continuaretur, termini primi peripheria in-
tegra aueti rursus deinceps prodituri essent. Postquam itaque disquisitionis ge-
neralis praeeipua momenta in praecedentibus absolvimus, hunece casum, ubi
termini dati quasi periodum completam constituunt, coronidis loco seorsim copio-
sius traetabimus. Antequam vero hanc disquisitionem ipsam aggrediamur, duo
lemmata erunt praemittenda.
Lemma Peimum. Si arcus a, b, c, d etc., quorum multitudo est fi, constituunt
progressionem arithmeticam, in qua terminorum differentia i—a = c — b = d—c
etc. est = , produetum ex ja factoribus P =
204 NACBLASS.
sin-|-(£— a) sin4-(t—b)sin-f-(t—c) sin4- (t— d) etc.
fit = 4^ sm^^~ , «fo Signum swperius vel inferius valet, prout p par est vel impar.
Demonstr. Potest quidem hoc theorema facile ex alio ab ill. Eulero in In*
trod. in Anal. Infin. I, §.240 tradito derivari; ne quid vero hie desiderari vi-
deatur, demonstrationem aliam paucis hie explicabimus.
I. Si produetum P primo ponitur sub formam
— b— 180°)cos!-(*—c— 180°)cos£(£— d— 180°) . . .
atque tunc secundum algorithmum sinuum notum in aggregatum cosinuum evol-
vitur, facile perspicietur, inde prodire functionem vel formae F vel formae G
(art. 13) ad ordinem 4-{itum ascendentem, terminumque summum fieri
—a—*—c — ^— etc- —
— ö—360°) + 90°)
= — 2-^siniji(*— a — 360°)
= —^t-iSin-§-[!(£—a)cosfiX 180°
signo superiore pro valore pari ipsius [i valente, inferiore pro impari.
II. Quum sin -f- ji(t—a) fiat =0, si ipsi t aliquis valorum a. b, c, d etc.
tribuitur, per theorema art. 14 erit sin^-ji(f—a) per produetum P divisibilis;
quotiens autem necessario erit quantitas definita =h, quoniam sin^-{i(^—a) etP
eiusdem sunt ordinis. Manifesto autem (per I) ex aequatione P = ysin£[i(£—a)
sequitnresse h =J^.^-\ adeoque P= =jZsin^~a) Q. E. D.
Lemma Secundum. Si arcus a, b, c, d . . . eodem modo se habent, ut in lern-
mate primo, produetum ex (i factoribus
(cos t — cos a) (cos t— cos b) (cos t— cos c) (cos t—cos d).. .
Demonstr. Quum fiat
THEOBIA INTEIffOLATIOlSFIS'METHODO NOVA mACTATA. 205
cos*—cosa = 2sin£(£—a)sin^-(—t—a)
cost—cos b = 2sin-|-(£—Z>)sin-£-(—t—b)
—cosc= 2sin^(£—c)sin4-(—t—c)
—cosd = 2sin£(£—d)sin-|-(—t—d)
etc.
productum ex Ms factoribus fit, per lemma primum
—a) —sinjt^— t—a)
9{ji _ pg
— -, ?<^ -j- 2
sin^[i(<—a)sin^i>.(— t—a) co&pt—co&y.a (~\ ~I? T\
2-s^ 2-^ZZI 14. &. U.
Quum habeatur
sin|-{i(^—d) = —sin-|-{i(f—b) = sin^-ji(f—c) = —sin^-{i(f—d) etc.
nee non cosfia = cos{i6 = cosjic = cos{i£? etc.: manifestum est, productum
in lemmate primo fieri etiam
— b) -pginjuC*— c)
nec non productum in lemmate secundo fieri etiam
COS[A<—COSfAC COS\).t — COSpd ,
^i^~ i^1 e
20.
Consideremus primo casum generalem art. 10, ubi X est formae
a -f- a cos «3? -f- a"cos 2 a? + a'"cos 3«3? -f- ...-}- a^ cos moo
atque fi = 2m-f-l. Hie igitur erit
unde substituendo a pro f
sin-^-(a — b)sni%{a — c)sin.^(a—d).. . = ^
296 NACHLASS.
Hinc in formula art. 10 pro T, fit coeiüciens ipsius A
= -(l+2cos(f—a)-\- 2cos2(£—«)-|-2cos3(f—«)+ . -. 4-2cosm(£— a))
Simili modo fit
smi(t—a)smi{t—c)smi{t—d)...= —
atque
sin 4- F — a) sin £ F — c) sin-|- F — rf)... = — ^~
Hinc coefficiens ipsius B in formula pro T fit
= -A + 2cos (# — 6) + 2 cos 2 (#—b) 4- 2 cos 3 (t — b) -f ... -f- 2cosm (t — b))
Prorsus similes erunt coefficientes ipsorum C, D etc., unde tandem concluditur,
fieri
T= ±(A + B+C+D+...)
r
4" — {Acosa -\-Bcosb -\-Ccosc -\-Dcosd 4---*)cos^
[*
4"—
4" —
4- -£■ (-4 sin 2a4- -Bsin 2 6 4- Csin 2 c4-D sin 2 ^4~ •. •) sin 21
4" etc.
4~—
4~ —
Quum haec formula cum
a4-a'cosH-6'sin*4-a"cos2^ö"sin2*-r- etc. -+■ a.(m)cos m t + fi(m) sin mt
identica esse debeat, valores coefficientium a, a, f>'. a", ö" etc. hinc protinus
habentur.
21.
Si progressio pro X cum terminis cos ma? et sin ma? non abrumpitur, sive
in infinitum excurrat. sive finita sit, valor pro T in art. praec. inventus incom-
THEOEIA DfTEEPOLATIONIS METHODO NOVA TßACTATA. 29Z
pletus erit, itemque valores singulorum coefficientium et, a, €', a", fi" etc. ibi
traditi correctione opus habebunt. Haec autem commodius per methodum sequen-
tem quam per summationem art. 2 determinatur. Ante omnia observamus, esse
cos n a -f- cos n b -f- cos nc-\- cos w d-\-... = pcosna
sin n a-\-sin nb-\-sin nc-\-sin n d-\-... = psinna
quoties n est integer per [i divisibilis; contra
... = 0
quoties n est integer per fi non divisibilis. Pro casu priore res per se clara est;
pro posteriore sit summa prima = P, secunda = Q, unde facile deducitur
Pcosn(b — a)—Qsinn(b — a) — P
Psmn(b — d) -f- Qco&n (b — a) = Q
Multiplicando aequationem primam per cosn(b—d)—1, secundam per smn(b—a),
fit addendo delendoque quae mutuo se destruunt
2PA — cos n(b—a)) = 0
Similiter multiplicando aequationem primam per sin n(b—a), secundam per
1 — cos n (b — d), provenit addendo
2Q(l — cosn(b — a)) = 0
Iam pro casu quidem priore (ubi n per [i divisibilis est, et proin cosn{b — a) = l)
hae aequationes identicae sunt, pro posteriore autem (ubi n per p non est divisi-
divisibilis, adeoque cosn(b — a) = cos — x 360° non potest esse =1) consistere ne-
queunt, nisi fuerit P = 0 et Q = 0.
Iam ponamus, post terminos amcosmx-\-fim sinma? in expressione functio-
nis X sequi
+^ +-}- etc
-}- etc.
valorem vero (incompletum), in suppositione, has partes nonadesse, pro T in
art. praec. inventum, esse
38
298 NACHLASS.
'cos t-\- y"cos
'sin t'+B" sin 2 t+Bm sin
itaut habeatur y = —{A-\-B-\- C-\-D-\- etc.) etc. Substituantur pro A, B, C, D
etc. valores sui, puta
A = a-^ a' cos a~\-a" cos 2 a-{-...-{- am cos ma-\- am+t cos (m -\-"i) a...
+ ö'sina + ö"sin2fl4-... + öfBsin»ifl + öm+1sin(»8-f-1)«...
etc.
fietque (per summationem modo traditam)
y = a4-a^coslXß + a2'acos2flß4~a3'acos3[J<tf 4" etc-
+ 6f*sin pa4-62f*siii 2 p«4- f>3fJ<sin 3 jia4- etc.
y = a'4-(atA-14-a^+1)cos[ia4-(a2'a-14-a2'a+1)cos2;i,«4- etc.
_|_ (gi*->_|_ giH^) sin {ia4- (S*^14- S2^1) sin 2 fi.« 4- etc.
Ö^Jcosjia — (^-1_g2fA+1)cos2ji«— etc.
a^+1) sin|xa — (a2^1 — a^+1) sin 2 pa — etc.
y" = a- («f*-2 4- a'a+2) cos {i a 4- (a2'a~2 4- a2'a+2) cos 2 ji a 4- etc.
«+2) sin {i a 4- F2'a~2 4- Ö2^+2) sin 2 ji a 4- etc.
cos2jifl— etc.
(a — a^+2) sin jxa — (a2^ — a2^+2) sin 2{ia — etc.
etc. usque ad
ym= am4- («'a-m4- a^+m)cos [i«4- (a2tJ-m4-a2>a+m) cos 2 jiä4- etc.
sin jifl+ (g8J^M4-ö*M+°l) sin 2 {i a 4- etc.
cos 2 ^^ _ etc>
— a^+m)sin pa— (a2'a~m—a2^ sin 2 pa — etc.
Si itaque progressio tantopere convergit. ut am+1, ßm+\ otm+2, gTO+2 etc. negligi
possint, valores y, y, h' etc. pro veris a, a', ö' etc. accipere licebit.
22.
Transimus ad casum alterum art. 11, ubi progressio X quidem eadem ma-
net ut in art. 20, multitudo valorum datorum autem unitate minor est, quam
multitudo coefficientium incognitorum, puta = 2 m = p. Hie habetur
THEOBIA INTERPOLATIQMS METHODO NOVA TRACTATA.
c)sm^-(t—d)...
— a)co&£(t—a)
-lsin4-(rf — a) s *
^i{t—a)-{-cosf(t—a) + cosf(t — a) + . .. + cos^=-l(/— a))
2(£—tf)-}-2cos2(*—a)-}-2cos3(*—a) + ... -f 2 cos(m — 1 )(*—
-\- cos m[t—a))
Quare in formula art. 11 pro T coefficiens ipsius A fit
a)-f-2 cos 2 (£— «)-}-
-f- 2cos(m—\){t—a)-\-cosm(t—a))
Et prorsus süniles expressiones (mutato tantummodo a in b, c, d etc.) pro coeffi-
cientibus ipsorum B, C, D etc. inveniuntur. Denique pars ultima ipsius T
— d)... x{a
fit
= —i2msmm{t— a)\am cos (ma-\- Bm —1)90°) -}-6m sin (ma + Bm-1)90°)
—a)(am$inma — f)mcosma)
Hinc tandem colligitur
r
-\- — (A cos a-\-B cos 6 -f- Ccos c -f-D cos ^-f- etc.) cos/
-f-— (-4sin« -f-B sin 6-f- Csinc-|-Dsind-|-etc.)sin£
+ -(^4cos2ö-|-5cos2 6-|- Ccos 2 c-f-Dcos 2 <?-[-etc.) cos2 £
+ — (-4 sin 2 a + J5 sin 2 6+ Csin 2 c-|- D sin 2 d-{- etc.) sin 2 t
-f- etc.
-j—- (Acos.ma~\-Bcosmb-\- Ccosmc-j-Dcosm^-f-etc.)cosmt
^ — (A&inma-^-Bsinmb-^- Csin m c -j- D sin m^-f- etc.) sin mt
-f-(amsinma — ömcos?wa)(sinmacosm£— cos^asinmf)
Quae expressio, si, rescissa parte ultima, per
etc. -{-jmcosmt'
etc. -+-$msinmt
38*
300 NACHLASS.
exhibetur, omnes coefficientes y, y, $', y", $" etc. praecise eosdem valores ha-
bere patet, ut in art. praec., ubi erat [i = 2m-f-l, exceptis duobus ulti-
mis ym, $m, qui illic duplo erant maiores. Porro liquet, omnes coefficientes
a, a\ a"...am-\ t\ Ö"...^ Ulis y, y, y".. .y»-\ S', S"... S™ resp. aequa-
les adeoque cognitos fieri, inter Ultimos amßm autem haberi aequationes
am =■ ym-\-(amsmma—ö
— f)mcosma)cosma
quae tarnen (ut ex natura problematis praevidere licebat) non sufficiunt ad deter-
minationem completam coefficientium am, f)m. Scilicet quum fiat
cosma = —cosmb = cosmc = —cosmd etc.
atque sinma = —sinmb = sinmc = —sinmd etc.
adeoque ym = ^~ {A — B+ C—D+ etc.)
^i—J5_|_ c—2>-f- etc.)
facile perspicitur, utramque aequationem contentam esse sub unica
amcosma-|-ömsinmö = -(A — B+ C— D-\- etc.)
Aliam itaque insuper relationem inter am et öm datam esse oportet, ut utrum-
que coefficientem penitus assignare liceat.
23.
Si progressio -X cum cosma? et sinma? non abrumpitur, valor ipsius T
in art. praec. inventus incompletus erit, coefficientesque y, y\ B' etc. a veris
a, a, ö' etc. diversi erunt. Et quidem facile perspicitur, si coefficientes termi-
norum sequentium in X per eosdem characteres denotentur, quibus in art. 21
usi sumus, pro y9 y\ ^'etc. usque ad ym~\ S™-l prorsus eosdem valores prodire,
quos illic eruimus; duos Ultimos autem fieri
ym = 4-am+4-(amH-a3m)cosJixa-}-^(a3m-}-a5Wi)cos2jia+ etc.
j— etc.
a5m)sin 2jia— etc.
THEOEIA INTEEPOLATIONIS METHODO NOVA TEACTATA. 301
In hoc itaque casu coefficientes y, y', $', y", B" . . . y™^1, ß"*"-1 pro veris
a, a', ß', a", ß".. . am~\ ö^ adoptare licet. quatenus sequentes a*"*1, #m+1etc.
negligi possunt; ad Ultimos vero ym, $m nisi ipsi pro negligendis haberi possunt,
haec conclusio non est extendenda.
24.
Per disquisitionem inde ab art. 20 traditam eo pervenimus. ut propositis jx
valoribus functionis X arcus indeterminati #, periodum completam formanti-
bus, functionem (X') =
sin #-}-£" sin 1x-\- . . . -\-Bmsmmx
quae illis omnibus satisfaciat, assignare possimus, ita, ut numerus m, ordinem
huius functionis exprimens sit vel = |-{i—^ vel = -|-{i, prout {i impar est vel
par. Ex artt. 15, 19 concluditur, quamvis aliam simüem functionem, quae iis-
dem valoribus satisfacit, sub forma X'-f- Fsin^-^^—a) contentam esse debere,
ubi Y functionem indefinitam arcus ce exhibet formae G vel F (art. 1 3), prout jx
impar est vel par. In casu priore praeter X' functio alia similis non datur, iisdem
valoribus satisfaciens, nisi ex ordine altiore, unde X' cum X identica erit, si
constat X ordinem mtum non egredi. In casu posteriore autem infinitae quidem
aliae similes functiones ordinis wü iisdem valoribus satisfaciunt, omnes tarnen in
eo convenient, quod sub forma X'-f-hsinm{ce — a) contenti erunt, designante
h quantitatem definitam: quamobrem, si constat X ordinem mtum non egredi,
saltem X et X' aliter quam in coefficientibus ipsorum cos mce et sin moo
non discrepabunt; in functione X' autem inter hos coefficientes aequatio
jmsinma — hmcosma = 0 locum habebit. Porro patet, si qua functio X" si-
similis formae ut X', quae iisdem valoribus satisfaciat, aliunde constet, iisdem sa-
tisfieri per functionem quam cunque X"-f- Y&m-%-\L(a? — a), atque Y ita deter-
minari posse, ut haec functio ordinem mtum non egrediatur. Ad hunc finem ob-
servamus, si qua pars ipsius Y exhibeatur per Kco&{x.üß-\-k), designante K
coefficientem definitum, k arcum definitum, x numerum vel integrum vel fractione
\ affectum (prout fi par vel impar) — ad quam formam singulae partes reduci
possunt, si cosinus et sinus eiusdem arcus contrahuntur — pars respondens pro-
ducti Fsin|ji(,27 — ä) exhibebitur per
302 STACHI/ASS.
sive quod eodem redit per
L sin (X#-f-/)— Z/sin((A—
designante X integrum. Quocirca in X" pro quavis parte Lsin (kat-\-l) sub-
stituere licebit hanc Xsin((X— \l)z>-\-1-\-[ui) et simili ratione pro hac rursus
Zsin((X—2{i)<2?-f-Z-f-2[i.«) porroque Zsin((X—3[i),2?-}-Z-}-3jixa) etc. Ut similis
conclusio ad cosinus extendatur. sufncit observatio, cosinus pro sinubus prodire,
si modo pro / scribatur /-f-90^. Hinc colligitur, si in X" occurrat terminus
Z,cosX<r, designante X integrum maiorem quam ^ft, qui proin sub formam
X = vfi-j^X' poni potest, ita ut v sit integer atque X' non maior quam ^\l, pro
isto termino substitui posse
et similiter pro termino tali Z/sinX«2? substitui poterit
= L sinv [iacosX^-f- L cosv
Hoc modo manifesto functio X" deprimetur ad aliam, ordinis certo non maioris
quam ^-{iü.
Per hanc itaque operationem X" semper transibit in ipsam X', quoties jx
impar est; in casu altero autem, ubi [i par est, certo in functionem talem, quae
tantummodo in coefficientibus ipsorum cosmx et smmat a functione X' diversa
esse potest. Ut ex illis coefficientibus coefficientes respondentes in X' deducan-
tur, methodus generalis art. 15 adhiberi potest, ex qua sine negotio sequitur, si
in illa functione termini ultiini sint Kcosmx-\-Lsmmx, pro his substitui de-
bere, ut functio X' prodeat,
(K cos ma-\-L sin m a) cos ma cos m x
-f- (K^cos m a -\- L sin ma) sin ma sinmx
Hi terminifiunt = Kco&mx -\-L sin moc, si inter iTetZ/aequatio K&mma—Lcosma
locum habet, ut per calculum facile confirmatur: tunc igitur illa functio cum X'
omnino iam identica est.
THEOKIA INTERPOLATION METHODO NOVA TEACTATA.
25.
Si functio X cum terminis cosm#, sinmar non abrumpitur, sed nlterms
excurrit, coefficientesque terminorum sequentium adhuc nimis considerabües sunt,
ita ut ipsos negligere non liceat, coefficientes y, y', $' etc. in functione X', quae
{i valoribus functionis X periodum completam formantibus, pro x = a, b,c, d etc.
satisfacit, notabiliter a coefficientibus respondentibus a, et', ö'etc. discrepabunt.
Quodsi itaque pro periodo ce = a,b, c,d etc. periodum aliam [i terminorum,, puta
pro oc = a, b\ c, d' etc. simili modo tractamus, functionemque mü ordinis, his
novis valoribus functionis X. satisfacientem evolvimus, et perinde ut X' per ex-
pressionem
exhibemus: pro coefficientibus y, y', ^'etc. iam valores nanciscemur, ab iis, quos
ante invenimus, notabiliter diversos. Hinc intelligitur, quo pacto hos coefficien-
coefficientes tamquam variabiles spectare liceat, et quidem, quum ex artt. 21, 23 singulos
perinde per arcum \xa determinari pateat, ut valores priores per arcum ja«, sin-
guli coefficientes considerari poterunt tamquam functiones arcus incieterminati y,
similiter ut X est functio arcus oc. Iam supponamus, fiv = tu valores functio-
functionis X periodum integram formantes, pro
cü = a, a, a", .. . b, b', b", . . . c, c, c", . . . d, d', d" .. . etc.
cognitos esse, ita ut sit
d— a-}-^3600. a"~ a-h|a60° etc. *
b = «_|-^3600 = a-hJ-360o, b' = a+^360° = a'-f -360° etc.
c
-360° = a-h-360° etc.
JA
patetque, hanc periodum iz terminorum in v periodos {i terminorum pro
ob = a, b, c, d etc.
«2? = d, b\ c', d' etc.
oc = a, b", c'\ d" etc.
etc.
discerpi posse. Quodsi itaque eo quo docuimus modo pro singulia periodis functio
304: NACRXASS-
X' evolvitur, nanciscimur v valores singulorum coefficientium y, y', §' etc., qui
hisce deinceps valoribus ipsius y respondent
y=pa, y = \±a — {ia-}-^-3600, y = pa" = {!«-}--^-360° etc.
adeoque periodos completas v terminorum formant. Quocirca, per methodum no-
stram, singuli coefficientes y, y, $' etc. per expressionem talem
g-f-s'cos^-f-e"'cos2y-\- .... -f-
exhiberi poterunt, ita ut sit n vel = £v — £ vel = -|-v, prout v impar est vel
par. Manifestum est, talem expressionem eundem valorem ex substitutione
y = jab, {ic, ]xd etc. obtinere, quem obtinet ex y = [xa; nee non eundem ex
y = {!&', {ic, {ic?' etc , quem obtinet ex y = <^d et sie porro. Quamobrem si in
Y-f-Y'cos<2?-j-Y"cos2<2?-|- etc.
etc.
pro singulis coefficientibus y, y', $' etc. hae funetiones arcus indeterminati y sub-
stituuntur, prodibit functio Z, duos arcus x, y involvens, transibitque Z in
eam funetionem X', quae e periodo prima dedueta est, si pro y aliquis valorum
{ia, {iö, {ic, {i^etc. substituitur; sivero pro y aliquis valorum \xa, pb', {ic', pd'etc.
aeeipitur, transibit Z in eam funetionem, quae eruta est e periodo seeunda. Hinc
tandem colligitur, si in ^pro^ statim scribatur jji<2?, ita ut functio solius x pro-
deat (X"), hanc ita comparatam fore, ut pro omnibus tc valoribus ipsius x, va-
valoribus propositis funetionis X satisfaciat.
26.
Si methodus artt. 20, 22 ad omnes tc valores propositos immediate sine prae-
via discerptione in v periodos minores applicata esset, prodiisset functio (X'") or-
dinis -^t: — ^1 vel ^-tc*1, prout tc impar vel par, quam cum funetione X" iam
comparabimus. Quum haee posterior, si rite redueta est, manifesto ad ordinem
{AW-j-mtum ascendat, tres casus distinguemus.
I. Quando turn {i turn v est impar, erit pn-f-m = -J-pv—it — if* — i-
unde patet, X" cum X'" prorsus identicam esse debere.
IT. Quando {i par est, v impar, fit pn-\-m = ^-{iv = ^iz, adeoque X" eius-
XHEOBIA INTERPOLATION» METHODO NOVA TEACTATA. 305
dem ordinis ut X'". Sufiicit itaque utriusque functiorüs terminos Ultimos com-
parare. Haud difficile perspicitur, hos terminos Ultimos in X" prodire unice ex
terminis ymcosm<2?-f-<$msinm<z?, et quidem ex iis terminis eoefiicientium y"*, £5"\
qui continent cosny et sinny sive cospnx et &in\Lnx. Sint hi termini
in ym . . . . kcospnx-\-l smpnx
in 3m . . .. k'cos }inx-\-Vsva.\Lnx
produceturque hinc in X"
(k cos {i n x -f- / sin fi n x) cos m x-\- (k'cos {i n x -f- /'sin {i n x) sin m x
unde prodeunt termini ordinis [iw-j-m11 sequentes
•f (A*—//)cos({i»4"Äl)«2?4-4-(^+^/)siii({i»4-«w)a?
Iam haud difficile quidem ea? formatione coefficientium demonstrari potest T esse
(k—/')sin({iw-f-m)a = (l-\-k) cos {\in-\-m)a
praeferimus tarnen methodum sequentem, quae concinnior videtur. Ex art. 24 se-
quitur, esse
ymsin|-t^ — (^cos^ = 0
turn si pro y substituitur pa, atque pro ym, £m valores ex periodo prima deducti;
turn si pro y substituitur jia', atque pro ym, $m valores ex periodo secunda de-
ducti etc. Quodsi itaque pro ym, $m expressiones, quae erutae sunt indefinitae
substituuntur, ita ut y^sin-J-y — ^mcos^ fiat functio arcus y formae G ad
ordinem n-{-% = £v ascendens, haec pro omnibus v valoribus ipsius y his
[ia, \ia, pa" etc. fiet = 0, adeoque per art. J4 per
sin4-(y — jia)sin-^-(y — ji«') sin^-(y — {ia") etc.
divisibilis, hinc etiam per sin£v(y — jia) et proin formae Asin-fv(y — jia), ita ut
h sitquantitas definita. Quamobrem termini ultimi functionis ymsinfy—
evolutae esse debebunt
omnes vero antecedentes evanescere: iüos vero fieri patet
39
306 NACHLASS.
Quocirca erit ^{k— V) = hcos-^tza = Acos-|-([i.w-f-m)a
-f-m)fl Q. E. D.
Haec vero aequatio ipsissimum erit criterium coefficientium ultimorum functionis
X.'", ut in art. 24 ostentum est: quare in hoc quoque casu functio X" cum X'"
prorsus identica erit.
HL Quando v par est. fit \Ln-\-m = %Tz-\-m, adeoque X" ordinis altio-
ris quam X'". Facile autem perspicitur, omnes terminos in X", qui ordinem
4-7ctmn transcendunt, provenire unice ex iis terminis singulorum coefficientium
-y', B\ y", S" etc., qui continent cosny et sinny sive cos{iw<3? et sin{iw<2?. Sint
hi termini, in expressione pro coefficiente aliquo y^ vel <^ kcoS[t.na}-\- /sinjixw<2?,
ex quibus producitur in X"
{kcos {iw<2?-f- /sin{iWB?)cosXB? in casu primo
vel (&cos[iw<z?-|-/sinfJt.w<z?)sinX(Z? in casu secundo
unde
%kcos ({i n -f- X) «2?-f- % /sin (jaw -f- X) «2?
in casu primo atque
in casu secundo. Per art. 24 autem substituere oportet pro cos([i.w-f-X)# sive
cosD-7c-f-X)<2?, cos7cacosD-ic—X)«2?-f-sin7c«sin(^-7c — X)a?; jatque pro sin({iw4-X)<2?
sive sin^Tc-f-X)^, sinicdrcosQ-TC—X)oß—cos7casinD-7c — X)#. Quare habebimus
in casu primo
in casu secundo autem
THEOEIA INTERPOLATIONIS HETHODO KTOVA TEACTATA. 307
Sed ex aequatione ksia-^Tza = Icos^iza, quae in utroque casu iater k et l lo-
cum habere debet (art. 24), nullo negotio deducitur
= k
■$■A-{-ksimza — Icosiza) = /
Hinc tandem colligitur, pro iis partibus in X", quae ex terminis ultimis
kcos ny -f- Isinng
cuiusvis coefficientis -y^ vel $~ producerentur, designante X indicem maiorem
quam 0 , statim substitui posse
kcosD-Tc — X)a?-f-1 sin(£tc — X)«2? in casu priore vel
/cos(^-tc — X)B?—k sin (-J-ic — X)a? in casu posteriore
Hoc modo loco functionis X", quae ad ordinem ^-7c-f-^tum ascenderet, aliam
X"" nanciscimur, quae ordinem -f7ctum non egreditur. Mhil itaque superest,
nisi ut coefficientes cosinus et sinus arcus 4-tu<2?, qui manifesto in hac functione
iidem manserunt ut in X", cum coefficientibus respondentibus in X'" compare-
mus. Levi attentione autem perspicitur. hosce terminos unice produci ex coeffi-
ciente primo y, et quidem ex ultimis eius terminis; qui si per kcosny-\-teinny
exhibentur, illi erunt kco&^Tzx-^-lsin^TZQe, adeoque necessario identici cum
respondentibus in X'". Hinc itaque colligitur, functionem X"", quae per prae-
cepta modo tradita loco functionis X" obtinetur, cum functione X'" prorsus iden-
ticam fieri.
27.
Pro eo itaque casu, ubi multitudo valorum propositorum functionis X, pe-
periodum integram formantium, numerus compositus est = tc = [iv, per parti-
tionem illius periodi in v periodos {i terminorum eandem functionem cunctis va-
loribus datis satisfacientem eruere in artt 25, 26 didicimus, quae per applicatio-
nem immediatam theoriae generalis ad periodum totam prodiret: illam vero me-
thodum calculi mechanici taedium magis minuere, praxis tentantem docebit.
Nulla iam amplius explicatione opus erit, quomodo illa partitio adhuc ulterius ex-
tendi et ad eum casum applicari possit, ubi multitudo omnium valorum proposi-
propositorum numerus e tribus phiribusve factoribus compositus est, e. g. si numerus ja
39 *
308
NACELASS.
rarsus esset compositus, in quo casu manifeste quaevis periodus [i terminorum
in plures periodos minores subdividi potest. Ceterum ex pluribus aliis annota-
tionibus applicationi practicae inservientibus hie sequentes tantummodo attinge-
mus. Valores talium aggregatorum
JLcosXa-f-.BcosX6-f-CcosXc-f-X)cosXd-f- etc. = p
AsinXa-f-BsinXb-f- Csin\c-{-DsinXd-f- etc. = q
(ubi ut in praecedentibus, supponimus b— a — c—b = d c etc. = — 360°= A)
saepius, siquidem nondum est a = 0, comraodius determinantur per- formulas
J._}-,BcosXA-f-Ccos2XA-f-Dcos3XA -f- etc. = P
5sinXA-|-Csin2XA-|-Dsin3XA + etc. = Q
p = Pcosa— Qsina, q = Psina-f- Qcosa, sive etiam faciendo -y = tangep,
^^ = E' Perhas i? = -ßcos(cp-}-ö), q =
28.
Exemplum. In commercio literario a clar. barone de Zach edito, vol. X
p. 188 invenitur tabula, limitem borealem et australem zodiaci Palladis exhibens.
Utriusque limites declinatio tamquam functio periodica ascensionis rectae specta-
tur, quae in tabula illa per singulos quinque gradus progreditur. Ad illustra-
tionem disquisitionum praecedentium applicationem ad limitem borealem hie fa-
ciemus, cuius itaque declinatio nobis erit X, ascensio reeta «2?. Excerpimus ex
tabula illa periodum sequentem 12 terminorum
Oß
0°
30
60
90
120
150
180
210
240
270
300
330
6°48'Bor. = -f- 408'
1 29 4" 89
1 6 Austr. . . — 66
0 10 Bor + 10
5 38 4" 338
13 27 4" 807
20 38 4238
25 11 -f-15*1
26 23 4583
24 22 -|- 1462
19 43 4183
13 24 4"
THEORIA INTEBPOLATIONiS MEEBODO NOVA TRACTATA.
309
Distribuamus hanc periodum primo in tres periodos quatemorum tenninorum
a = 0°
b = 90«
c — 180«
d == 270«
In formula
fit itaque
B' = %
af = 30«
&' == 120«
c' =210«
d' = 300«
= + 408
= + 10
== + 1238
= + 1462
-f- B' sin üb -f- S " sin 2 <z?
= 779',5
cos a+B cos b+C cos c + D cos d) =.+(A—C) =
b-t- Csinc+Dsind) — i(B — D) =
= 0
89
338
511
183-
a
b"
c
d"
= 60»
= 150«
= 240«
= 330«
A"
B"
er
D"
= —
= +
= +
; 1
66
807
1583
804
415',0
726',0
C—D)
et similiter pro periodo seeunda ac tertia. Hoc modo emergit
Pro periodo
ubi y = 4 oc
1
i
B'
T"
B"
prima
seeunda
tertia
0«
120«
240«
+ 779,5
-1-780,2
+ 782,0
415,0
404,5
413,5
726,0
721,4
713,3
+ 43,5
-f- 9,9
+ 11,7
0
17,1
20,3
Hie porro exhibetur y per formulam
+fG79,5 + 780,2cos 120« + 782,0 cos 2 40«) cos 4.2?
+ fG80,2sin 120«+782,0 sin 240«) sin4a;
sive per
780,6— I,lcos4#— l}0sin4<2?, et perinde
y per —411,0— 4,0cos4<z?+ 5,2 sin 4 x
B' per —720,2— 5,8cos4«2? —. 4,7sin4«3?
y" per + 21,7+ 21,8cos4«3?— I,isin4a?
B" per — 1,1+ I,lcos4<37+21,6sin4«37
Quibus valoribus in X' substitutis prodit formula 12 valores prop'ositos exhibens
310
NACBLASS.
+ 780,6
— 411,0cos<2? —720,2sin<2?
+ 43,4cos2<2?— 2,2sin2<2?
— 4,3 cos 3«2?+ 5,5 sin 3 «2?
— I,lcos4<2?— 1.0sin4«2?
+ 0,3 cos 5,2?— 0,3 sin 5,2?
+ 0,1 cos 6 <2?
Distribuamus secundo eandem periodum in quatuor periodos ternorum termino-
rum, quibus singulis itaque per formulam primi ordinis
X' = Y+ycoSB?+S'sin<2?
satisfaciendum erit. Hie invenitur
Pro periodo
prima
seeunda
tertia
quarta
ubi y = 3 x
0°
90°
180°
270°
1
+ 776,3
4-786,0
4-785,0
4-775,0
i
— 3,68,3
— 414,5
— 453,0
— 408,2
— 718,8
— 676,0
— 721,1
— 765,0
unde dedueuntur formulae, sub quibus y, y, B' exhibentur sequentes:
y +780,6— 4,3cos3«2?+ 5,5 sin 3 «3?+ 0,1 cos 6w
y — 411,0+4 2,3 cos 3a?— 3,2sin3«37+0,3cos 6<2?
$'. . . . —720,2+ I,2cos3C7+44,5sin3<37+0,3cos6«37
His valoribus in y-\- ycos<2? + S'sin<z? substitutis, partibusque ultimis in 7,7', £'
quae cos6<2? continent, seeundum praeeepta art. 26 traetatis, prorsus eadem for-
mula eruitur, ad quam supra pervenimus.
29.
Supersunt casus, ubi in funetione X vel cosinus vel sinus soli adsunt, quos
in artt. 16, 17 generaliter traetavimus. Supponemus, ut in praecc., datam esse
periodum fi terminorum, puta X ^= A, B, C, D etc. pro x = a, b, c, d etc.
Duo vero casus Mc probe distinguendi sunt. Aliter enim traetari debet
lm0 casus, ubi a est complementum alicuius valorum sequentium b, c. detc.
ad 360° vel ad 0 vel ad multiplum peripheriae. Sit hie terminus a-\—360°,
THEORIA INTERPOL ATIONIS METHODO NOVA THACTATA. 311
atque a+-360°-{-a = Ix 360°, sive a = (ji/ — k)~. Quare in hoc casu a
per — divisibüis erit, adeoque sin{ia==0; porro habetur b = (ji/—&-J-2)—,
atque sin[i£> =0, et perinde de sequentibus c, d etc. Supponendo itaque, a
esse minorem quam —, sed non negativum (quod permissum est, quum ab omni-
bus a, b, c, d etc. multiplum proxime minus totius peripheriae subtrahere et ex
residuis minimum, quod proprietate illa praeditum erit pro periodi initio accipere
liceat), eritvel a = 0, atque b = i-3600, c — -360°, d=-360° etc.; vel
° b ° °r d /
I* ' f* f* p-
aliter 2 casus, ubi non est complementum ullius valorum sequentium
b, c, d etc. ad 360° vel 0 vel multiplum peripheriae. Hie a non erit divisibüis
180° T • T 7
per —, adeoque smjia = smjio — smfic = smfidf etc. non = 0.
In casu posteriore methodus generalis art. 16 statim applicari potest. In
priore autem ex valoribus a, 6, c, d etc. (quos infra 360° reduetos esse supponi-
mus), omnes antea reiieere oportet, qui sunt majores quam 180°, quippe quorum
complementa ad 360° inter reliquos reperiuntur; insuperque, quando adsunt,
valores 0 et 180°, si in funetione X sinus soli oecurrunt: sed quoniam applica-
tio methodi generalis hac ratione minus concinna evaderet, hunc casum alio modo
infra absolvemus. Initium iam ab illo casu faciemus, ubi sinjia non est =0.
30.
Sit primo X funetio formae
a+a'cos<z?+a"cos2<z?-}-a'"cos3<z?-J- . .. -\-an cos nec
unde esse debebit [i = n-\-\. Hie habetur per lemma seeundum art. 19
(cosf—cosb)(cost—cosc)(cost—cos«?) etc. = 2i^X^~^^^
ji([a—2)acos2^4~e^c- + 2sinacos(fi—l)t\
Facüe scilicet confirmatur, produetum ex aggregato seeundae partis huius aequa-
tionis per cos£—cosa fieri = sin a (cos [i t—cos ja«). Quare fit quoque, scri-
bendo a pro t
(cosö — cosfe)(cosa—cosc)(cosa — cos«?)etc. = 2„_tri^ jsin^a-|-2sin([i—l)acosa
2)öcos2a-f- etc.
Aggregatum in hac expressione fit = {isinjia, ut inde manifestum est, quod
312 NACHLASS.
terminus secundus = sin pa -f- sin (fi — 2) a
ultimus = sinfia—sin({i—2)a
porro terminus tertius = sin[iö + sm({jL—4)a
terminus penultimus = sinjia—sin({i—4)a
etc.
Hinc colligitur, coefficientem ipsius A in formula art. 16 pro T fieri
i— l)flcos£-f-2sin([i— 2)acos2£-j-etc. -j-2 sin a sin (|i—l)t\
Prorsus similes expressiones proveniunt pro coefficientibus ipsorum B, C, D
etc., mutando tantummodo a in b, c, d etc. Quamobrem statuendo
2 i
etc.
e ^(A sin a-\-B sin b-\- Csinc+Dsin^+ etc.)
erit
T — e + e cos f + £"cos 2 #+ £wcos 3 ^+ etc. + £w cos w t
Quum haec formula generaliter pro valore quocunque ipsius t valere debeat, ne-
cessario cum X identica fiet, mutata t in cc, adeoque coefficientes e, e', e" etc.
ipsis a', a', a" etc. resp. aequales.
31.
Quum per praecepta supra explicata fünctio X' formae
y -f- y'cos x -f- y"cos 2 x-\-....-}- ym cos m a;
quae omnibus {i valoribus propositis satisfaciat, et in qua sit m = %p — \ vel
\y., prout |i impar est vel par: operae pretium est, hanc functionem cum functione
modo inventa
c4-£'c0S<2?-f-£"C0S2<2?-|-£'"cOS3<2?-|- . . . -f" S-f1 COS ({X—\H0
THEOEIA DJTERPOLATIOMS METHODO NOVA TEACTATA. S'IS
comparare, quam per X" exprimenius. Comparando valores coefficientium
y, y', $', y", 8" etc. in artt. 20, 22 traditos cum valoribus coefficientium e, e', e"etc.
modo inventis, invenitur
e =y
t = Y —S'cotangfia, e^"* = ^'cosecjia
e" = y" — S"cotang pa , e^2 = ^"cosec (ia
zm= Y"~^"cotang ji« ,
etc. usque ad
Factor 4- ipsis gm et ^~m praepositus tunc tantummodo valet, quando {i par
est, omittique debet, quando [i est impar. Quo pacto, in casu posteriore, ubi
ja — m =. m-\-\ manifesto omnes jx coefficientes e, e', z etc. per y, y', ^' etc.
determinati sunt; in priore vero, ubi m = fi—m, pro coefficiente e2fA valores
duos 2y^—2§*ficotjifl, 2^cosec{ia habemus, quorum aequalitatem ex ae-
quatione y^sin-J-jia = S^cos-J-jia facile perspicere, et pro quibus igitur etiam
hunc y^ — 6^cotg[ia-|-^'acosec{ia adoptare possumus.
Hinc facile deducitur, esse in utroque casu
X"— (X'— S'sina?— S"sin2<2? — Swsin3<2?— etc! — S
-£mcosm«2?)
cos([A — m)üß)
Hinc patet, X" ex X' deduci, si pro quovis termino B1 sinX«3? substituatur
— cotgjia $^ cosX«2?-|-cosec{ia B cos({i — X)<2?
sive
— S^cos [AacosXa; 4- S^cos^ — \)x
__
cuius praecepti comparationem cum iis, quae in art. 24 explicata sunt, lectoribus
linquimus.
32.
Si functio X cum cosnx non abrumpitur, sed ulterius excurrit, terminis
sequentibus per a^cosfi^-f-a^^cos^-f-l)^-!- etc. expressis, habebimus
40
314 NACHLASS.
e = a-f-a.Peospa-f-ct2fAcos2pa-\- etc.
e' = -^— j a' sin \ia -f- a?+1 sin 2 jix« -f- a2fA+1 sin 3 jix a -f- etc.
— a2'"" sin jixa — tf^ sin 2 juta — a4fA-1 sin 3 \ia — etc.}
e" = -J— ja"sinjixa4-a!J-+2sin2^ö-}-a2fX+2sm3iix+ etc.
— a2[A~2 sin jix a — a3[A~2 sin 2 jix « — a4'"" sin 3 jix a — etc. j
etc.
~l = ~-^ {af* sinjha + a2'*"'1 sin 2 jha + a3^ sin 3 pa -f- etc.
— a^1 sin p a—a2[A+1 sin 2 jix a — a3'a+1 sin 3 jix a — etc. j
ex quibus formulis iudicari potest, quatenus differentiam coefficientium e, e\ e"etc.
a veris a, a', a" etc. negligere liceat. In hoc itaque casu functio X" non erit
X ipsa, cum qua tarnen in eo convenit, quod omnibus p valoribus propositis sa-
tisfacit. Omnes autem similes functiones his valoribus satisfacientes sub forma
X"-\- Y(cos}iaj—cosjixa) contenti erunt, designante Y functionem indefinitam
arcus ob eiusdem formae ut X, scüicet a sinubus liberam. Functio X" erit
unica ordinis \i—l*1: quaevis alia similis valoribus datis satisfaciens ad or-
dinem altiorem ascendet. Quodsi talis functio X.'" aliunde constaret, omnes
similes functiones, per quos valores dati repraesentantur, in hac quoque forma
X'"-\-Y(cos}xa}—cosjixa) contenti erunt, poteritque Y ita determinari, ut functio
ad ordinem jut—1tum depressa prodeat, quae erit ipsa X". Methodus vero fa-
cillima ad hunc finem videtur esse, si primo ex X'" derivetur X' per art. 24 at-
que hinc X" per art. 31. Sit itaque terminus quicunque in X'" -LcosX<z?, pona-
turque X = ^jn-f-X', ita ut sit X'<^jix atque k integer. Tunc per art. 24 pro
illo termino scribi debebit in X'
LcoskpacosHaj — .Lsin&jixasinX'«??, si X'^^ju,, neque vero X' = 0
si X'^>4-^
si X'=4-jix
Bünc autem prodit in X", per art. praec. in casu primo
in casu secundo
cos (jh—X')a? — ism(A;-|-1)jixöcotgjixacos(jix—X')a?
-f- L sin (k -f-1) jix a cosec \i a cos X',2?
THEORIA INTEEPOLATIOJOS METHOJDO NOVA. TBACTATA. " 315
in casu tertio
L cos £ n a cos (k■+■£■) \i a cos 4- jix «2? — Lsm^
^)\iacosec\iacos
quae expressio in omnibus tribus casibus reducitur ad
Quoties autem X'=0, habemus in X' simpliciter Lcosk\ia, qui termi-
nus sine variatione in X" retinetur.
33.
Sit secundo X functio formae
ö'sin(Z?-f-ö''sin2«z?-f-ö"'sm3<z?-|- etc. -f-öwsinw«2?
unde esse debebit \i = n. Hie fit, ex art. 30, coefficiens ipsius A in formula
seeunda art. 16 pro T
+ etc.
-f-2sinacos {\i — \)t)
= sinag B cos (fi—1) a sin t -f- 2 cos (ju,— 2) a sin 21-f- 2 cos (jix— 3) a sin 31-\- etc.
-f- 2 cos a sin (jix—1) ^ -f- sin jtx ^)
Prorsus similes expressiones pro coefficientibus ipsorum J5, C, D etc. pxodeunt,
mutato tantummodo arcu a in b, c, d etc. Quamobrem faciendo
C = —-■ lAcos(a—1 )a-f-Bcos(a—1)&4- Ccosia—\)c~\-DcosUi—1)
ix sin txa *■ ^ ^
* _^_— ) a /^/^o f ii S) irt I J-? /^i%o f ii _^ 0 l/l I f/*^ö /|| _^.__9 )/• I / f /*/\o
w , i -CL OiJÖ l /Üb " JZi itl/ I » * l/Ug l /Üb £* \U \ Ks \j\J(j \ fjv £ /O I JL* KsKJto
p.sin[j.a? u / i m y i \i y i
; (jh— 3)& + Ccos (]Lt— 3)c -|- B cos
etc.
C^"^ —^—|JLcosa + 5cos^4- Ccosc-4-Dcosd+ etc.
fj.sinfj.af ' '
£a =i —v—i-4—\~ B-\*- C~\-D-\- etc. |
erit
T = C'sin t -f- C'sin 2^-4- C'sin 3 ? -4- etc.
Quum haec formula generaliter pro valore quocunque ipsius t valeat, necessario
40*
316 NACHLASS.
cum X identica erit. mutando t in a?, unde coefficientes £', £", £'" etc. ipsis
#', ö", #'" etc. resp. aequales erunt.
34.
Si ut in art. 31 omnibus valoribus propositis per functionem talem
X'= y-f-y'cos<2?-f-y"cos2#-f- etc. -±-ymcosma?
etc.
satisfactum est, existente m = £jix — f vel = 4-fx, prout jix impar vel par est,
comparatio huius functionis cum hac
X"= C'sina?+4"än2a?-}-4'''siii3a? + etc.
quam in art. praec. eruimus, hasce aequationes suppeditant:
C? = y cosec {xa
C = S'-f-y' cotgjixa, O"* = y'cosec jixö
C" = g"-|-y" cotg jixa, C^2 = Ycosecixa
etc. usque ad
ubi factor 4- coefficientibus Cm, C[A'~W praepositus pro eo tantum casu valet, ubi jix
par est, pro altero vero, ubi ju impar est. omitti debet. In casu itaque posteriore
ubi jix — m = m-j-1, pro quovis coefficiente C', C" etc. valorem unum per y, y', y"
etc. et ^', 8" etc. habemus; in priore vero, ubi fi — m = m, pro coefficiente CT'a
duos aequales, pro quibus etiam valor S2f*-j-y¥[Acotg/xa-j-ys'acosecjixö adoptari
potest. Hinc colligitur
X"= X'—y — y'coS(Z?—y"cos2<z?— etc. —y
■4-cotgjixa(y'sinC7-|-y"sin2C7-4-y'"sin3^-|- etc. -|- ym sin m 00)
-h cosec jixa(y sin jix<»+y'sin(]Lt—l)#-f-y"sin(jix— 2) a? 4-etc. -|-y^~msin(fx—m)oe)
Quamobrem ex X' producitur X", scribendo pro y, y cosec \ia sin p x
et, pro quovis termino yl cos X«2?
THEORIA DJTERPOLATIONIS METHODO NOVA TRACTATA. 317
,—\)ce sive l-
quod praeceptum lectores cum iis, quae in art. 24 tradidimus, ipsi comparent
35.
Si functio X cum sin n oo non abrumpitur, sed ulterius excurrit, terminis
sequentibus per fra+1 sin (ji -f-1) oo -f- &a+2 sin (fi -f- 2) oo etc. expressis, habebimus:
etc.
sin ^fl _|_ g^u-i sin 2 jix a + a4^ sin 3 \i a ~\- etc. j
etc.
Jlxa-}- etc.}
etc.
etc.}
etc. Pro coefficiente ultimo autem
0"= ^-(^sinjixa + ^2tAsin2iixa-}-^tAsin3iixa4- etc.)
0
Hae formulae ostendunt, quatenus differentia inter X et X" negligi possit.
Haec posterior formula simplicissima erit inter omnes similes, per quas \i valori-
bus propositis satisfit; hae vero omnes in formula X"-j- l^sin<2?(cosjix<2? — cosjixö)
contentae erunt, designante Y, ut in art. 32 functionem indefinitam arcus «2? a
sinubus liberam. Et generaliter, si X'" est functio quaecunque eiusdem formae
ut X, i. e. solos sinus continens, per quam fjb valoribus datis satisfit, formula
X'"-|-l;'sin<z?(cosjix<z? — cosjixa) omnes huiusmodi functiones continebit, quae si Y
rite detenninatur, ad ordinem jutum deprimi potest, quo pacto necessario functio
X" ipsa prodire debet. Prorsus simili modo utin art. 32 regula generalis sequens
ad hunc finem eruitur: Pro quovis termino in X'" tali jLsinX«z?, ubi X estmaior
quam jix, substituere oportet in X", faciendo X = £jix-|-X', ita ut k\i sit jnul-
tiplum ipsius \i proxime minus quam X adeoque X' inter limites 1 et jix incl.
situs, terminos
sin kos-j-L —.—^— sin (ix — k)os
sui[j.a Ki '
qui, quoties fit X'—fi, ad unum L^—.^sinjix<# reducuntur.
318 NACHLASS.
36.
Transformationes in art, praec. atque in art. 32 traditae concinnius ex theo-
remate quodam generali deduci possunt» quod quum per se quoque satis elegans
sit, paucis hie adhuc attingemus.
Theoeema. Designantibus X, X', X" numeros integros quoseunque. [i numerum
integrum, qui differentias inter illos, X'—X, X"—X', X — X" metitur (e. g. unitatem),
x arcum indefinitum, a arcum definitum: funetiones
P = sin (X'— X") a cos X «2? -f- sin (X"— X) a cos k'x -f- sin (X — X') a cos k"x
Q = sin (X'— X") a sin X x -f- sin (X"— X) a sin k'x -\- sin (X — X') a cos )"x
per cos{jl<27—cosfia erunt divisibiles.
Demonstr. Quando X per [i divisibilis est, ideoque etiam X', X" per [i di-
divisibiles erunt, facile confirmatur, valorem ipsarum P, Q, si substituatur x = a,
esse identice = 0; quare P non mutabitur, si pro
cosX«2? substituitur cosXa? — cosXa
cos X',2? cos X'<z? — cosX'a
cos Yoe cos X"B? — cos X"a
neque Q, si pro
sm Xx substituitur sin kx ; !-—
sinu sinX<2? = —
sina
Sed hae sex expressiones per cosfia?—cospa divisibiles sunt, quod pro va-
lore positivo ipsius X de prima et quarta ostendisse sufficit. Scilicet facile per
multiplicationem confirmatur, esse
sin fia (cosXa? — cosXa)
== (cos{iB? — cosjaö) 12 sin ja <z cos (X— ja) x -f- 2 sin 2jiacos(X— 2ji)<2?
-f-2sin3{iöCOs(X—3{i)<2?-f- etc. -f-2sin(X —
sin pa sin X«2? — sin ka sin px
= (cos[i<z? — cosfia) |2sin{iasin(X— p)x-\- 2sin2{i«sin(X — 2{i)<r
-|-2sin3{iasm(/v—3 jx)cj?—{- etc. -f-2sin(X—p.)
Casus, ubi X est negativus, ad hunc sponte reducitur. Hinc patet, funetiones
THEORIA INTERPOLATIONEN METHODO NOVA TRACTATA. 319
P, Q ex partibus per cospai—cosji« divisibiles compositas, ideoque ipsas quo-
que per hunc divisorem divisibiles esse.
II. Quando X per [i non est divisibilis, sit / numerus integer arbitrarius
per {i divisibilis, ponaturque X = /-f-Q, X'—/'-f-ö, X" =£"-}-6^ unde etiam
/', /" per {i divisibiles erunt. Iam patet, si ponatur
sin(/'—l")acoslx-\-sm(r—/)acosZ'<z?4-sin(£—V)acosl"x = P'
sin(/'— l")asm lx-\- sin(/"— /)a sin l'oß-f- sin (/— /')« sin l"x = Q'
fieri
P = P'cosÖd?—Ö'sinÖd?, Q == P'sinÖ^-}-
atque functiones P', Q', quippe quae sub casum primutn iam absolutum per-
tinent, per cos[i<z?—cospa divisibiles: hine manifesto etiam P et Q per
cos[A<z?—cosfia divisibiles erunt. Q. E. D. Ceterutn demonstratio casus primi ita
perfecta est, ut non sine quibusdam explicationibus applicari possit, quöties
sin{i.a = 0; tunc vero fit P= 0, Q = 0, ita ut demonstratione omnino non
opus sit.
Quodsi itaque ponitur X—"k'=kp, X—X/' = (Ä-f-l){i, patet, per cosjjuz? — c
divisibiles esse
sin jia sinXB?—sin (A;-|-l) [ia sin X'«??-}- sin Arjia sin (X'— ja) «2?
adeoque etiam
> sin(A-f-l)!J'fltcos^'a; — sinA[jiacos([ji. — V)x
sin ;x a
. ^ sin (Ä-f-l)^« sin X'ar + sinÄ[xasin([ji.—V)x
sin ;x a
unde ratio substitutionum in artt. 32, 35 statim elucet: quotiens enim ex divi-
sione posteriore e solis sinubus constabit, adeoque manifesto denuo per sin<z? di-
divisibilis erit.
37.
In artt. 30—36 supposuimus, sinjia non esse = 0: superest itaque, ut
easdem disquisitiones pro eo casu resumamus, ubi sin fi a = 0. Hie statim sup-
, ISO0
ponemus, esse a = 0, vel a = —.
320 NACHI.ASS,
Sit primo X functio formae
etc. -\-yncosnx
adeoque multitudo eoefficientium incognitorum = \-\-n. Iam scimus, ex omni-
bus valoribus propositis functionis X eos reiici debere, qui respondent valori
ipsius maiori quam 180°: quatuor itaque casus hie sunt distinguendi:
1) quando \i par, atque a = 0, erit 180° välor 4- jx-f-1tus ipsius x; quare
quum sequentes reiici debeant, remanent valores £[i-f-l. Hinc esse debebit
2) quando fi par, atque a = —. valor £p ipsius x erit 180 ;
sequentes, qui fiunt maiores quam 180°, reiieiendi sunt. Hinc esse debebit
n = |[i — 1.
3) quando fi impar est, atque a= 0, fit valor ^ jx —f-^-tus = 180° -, et
4) quando fi impar est, atque a = ^-, fit valor ip- + itus = 180 : se-
sequentes in utroque casu reiici debent, adeoque erit n = ^{i—^.
Iam quoniam methodus in praecc. adhibita ad casum praesentem, ubi pars
valorum datorum a periodo completa antea rescindenda esset, non sine quibus-
dam ambagibus applicari posset, methodum sequentem praeferimus.
Si per praeeepta artt. 20, 22 functio formae
y-f-y'cosx-j-y"cos2x-f- etc. -\--ymcosmx
-j— 8'sin <2? —j— ^"sin 2o? —}— etc. -\-timsin mx
investigatur, per quam omnibus (jl valoribus datis satisfit. et in qua m = ^-{i — £
vel = ^{Jt, prout (jl impar est vel par, coefficientes £', 8", §"' etc. sponte fient
= 0. Nullo enim negotio patet, in expressione tali
nXd-|- etc.
fieri vel partem primam = 0, atque ultimam =. —Bsin\b, penultimam
= — CsinXc, antepenultimam =—DsinXd etc. puta quando a=-0; vel ulti-
ultimam = — J.sinX«, penultimam =—^sinX6, antepenultimam ==■ — CsinXcetc,
quando a = , quum pro talibus valoribus ipsius x, quorum alter alterius
complementum ad 360° est, valores functionis X aequales sint. Quamobrem
functio
Xr = Y-f~Y'cos#-|--y'cos2(Z?--}- etc,
THEOKIA INTERPOLATIOMS METHODO NOVA TRACTATA.
in qua coefficientes y, y, y" etc. determinantur per formulas
y =j(A + B+C+D+etc.)
y' = — (^Lcosö -f-^cos^ -j-Ccose -^-Dcosd -f- etc.)
y"= ~(Acos2a-{-Bcos2b-{-Ccos2c-{-Dcos2d-}- etc.)
etc., ultimus autem, quando [i par est atque adeo m = ^\l, per hanc
ym = — (A cos ma-\-B cos mb-\-Ccos mc-{-JD cos md-\- etc.)
necessario cum functione X identica erit, siquidem haec non est gradus altioris
quam supra definivimus. Namque in casibus 3 et 4 X est ordinis 4-jx — £ü, i.e.
eiusdem ut X' et proin per art. 24 cum X' identica. In casu primo X esteius-
dem ordinis ut X' et in casu secundo non maioris, quare turn hie turn illic omnes
termini saltem usque ad ordinem ^-{i—1tum in utraque functione convenient
(art. 24). Terminos ordinis ^{iü in his funetionibus quoque convenire debere.
inde per eundem art.24 patet, quod in X aequatio conditionalis Ksinma =.Lcosma
locum habet; scilicet fit L =. 0 , atque in casu primo sinma = 0, in secundo,
ubi X ad ordinem ^-{i—1 tantummodo ascendit, K = 0. Ceterum in casu
secundo X' ordinis altioris esse videtur quam X, sed in hoc casu terminus or-
ordinis ^{iü in X' quoque evanescit, quum fiat
yia = ^(J.cos90°-|-J5cos27a04-Ccos4500-}-Dcos6300-h etc.) = 0
ita ut in hoc quoque casu X' revera sit ordinis m — lü sive ^{i—lu.
Si funetio X cum termino cos nai non abrumpitur, sed ulterius exeuxrit:
denotatis terminis sequentibus per an+lcos[n-\-\)oe-\-an+2cos(n-\-2)w-\-etc. erit
per artt. 2t, 23
= ö +a** 4-er* -f- etc.
etc.
etc.
Y'= a'"+a'a-ä + a^ä+a:!'"i+a!!^+ etc.
et sie porro usque ad ultimum ym, quando {i impar est, vel ad penultimum
180*
ym~\ quando ji par est; signum inferius hie valet, quoties a = -—, adeoque
41
322 NACHLASS.
in casu 2 et 4, superius in casu t et 2; denique pro ultimo habebitur in casu.
primo
■f1 = am+a3m + a5m-h etc.
in casu secundo autem ym = 0. Hae aequationes ostendunt, quatenus differen-
tiam inter fiinctiones X et X' negligere permissum esse possit. Haec posterior
functio inter omnes, quae [i valoribus propositis satisfaciunt, simplicissima erit,
quae omnes sub forma X'-f- Fsin(|-px—^y-a) contenti erunt, quae in casu
1 et 3 ad X'-f- Fsin^-fi^, in casibus 2 et 4 vero ad X'-f- Fcos^\lx reducitur.
Manifeste autem, si haec expressio eiusdem formae esse debet ut X i. e. a sinu-
bus libera, Y esse debet
in casu primo formae ^sin<2? -\-gsm2a!-\-(jr"smSa?-{- etc.
in casu secundo formae g -\-gcosx -\-g"cos 2 x -f- etc.
in casu tertio formae ^sin^#-j-ysinf tf-f-ysinJ-^-j- etc.
in casu quarto formae ^cos ^x-\-g'co&%x-\-g"co&%x~\- etc.
Et generalius, designante X" functionem quamcunque ipsi X similem. quae {i va-
valoribus propositis satisfacit, omnes huiusmodi formae sub formula X'-j-F^sin^-fi^
vel X"-f-Ycos^-fitf contentae erunt, ubi Y functionem indefinitam eius, quam
modo docuimus formae designat. Hoc ita perficere licet, ut sie functio ad ordi-
nem £ji, J-{i — 1, ^-{i — £, f{i — 4£ depressa prodeat, quae manifesto cum X'
identica erit. Regula autem generalis pro reductione talis funetionis X" ad X'
ex art. 24 facile deducitur. Pro quovis termino LcosXx in X" substitui debet
in X', facto X = A:{i+X', ita ut )/ non sit maior quam ffi, terminus -f-Z<cosX'd?,
ubi signum inferius aeeipiendum est. quoties simul a = atque k par, su-
perius in casibus reliquis; denique quoties in casu secundo, i. e. pro a = —
et valore pari ipsius fi, evadit X' = £ji, pro Lcos\x statim poni debet 0 in
X', sive terminus ille omnino negligi.
39.
Si secundo functio X est formae
etc.
adeoque multitudo coefficientium incognitorum = n, etiam multitudo valorum
THEORIA INTEBPOLATIOMS METHODO NOVA TEACTATA.
datorum, subductis superfluis, esse debebit = n, ut ad coefficientium determi-
nationem completam sufficiant. Iam quum ut superflui in hoc casu reiiciendi sint
valores functionis X ii, qui respondent valori ipsius x maiori quam 180° nee
non valori 0 et 180°, habebimus pro quatuor casibus supra distinetis:
1. quando fi par, a = 0, erit n = ^p — 1
_ j ISO0
2. quando [i par, a — , erit n = £[i
3. quando [i impar, a = 0. erit n = ^p—-^
4. quando {i impar, a = , erit n = 4-{i—-fr
Iam prorsus simili modo ut in art. 37 , in funetione
etc.
-f- 8'sin m-\-8"sin 2 x -f- etc. -f- 8m sin mx
ad normam artt. 20, 22 eruta, quae omnibus [i valoribus satisfacit, et in qua m
vel = -^{i—^. vel = 4{x, coefficientes y, y', y" etc. sponte evanescent. Quum
enim in serie ~4, B, C, D etc. vel termini ultimi ordine retrogrado in casu prae-
senti vel fiant = —B, — C, —D etc. vel = —A, —B, — Cetc, prout a— 0,
ISO0
vel = —, insuperque pro illo casu A = 0, manifesto
Aco&\a-\-Bcos\b-\-CcosXc-f-DcosX^-f- etc.
pro quovis valore ipsius x erit = 0. Quamobrem funetio X' =
etc.
in qua coefficientes &', $", ^'"etc. determinantur per aequationes
&' =—(Asina -{-Bsinb -\-Csinc -{-Dsind -f- etc.)
8" = -{Asin2a-{-Bsm2b-{-Csm2c-{-Dsm2d-±- etc.)
8'"= -Dsin3a-|-.Bsm3&-}-Csin3c-}-Dsin3d-}- etc.)
etc., ultimus autem. quando {i par est, adeoque m — f fi, per hanc
^ 6-|- Csinmc-|-X)sinm</-f- etc.)
necessario cum X identica erit, quod eodem modo, ut in art. 37, faeüe demon-
stratur. Ceterum funetio X' in casu primo, ubi a = 0, jt par, revera ad or-
41*
$24: . . - « - NACHLASS.
dißem .g-f*.—1 töntum ascendit,. quum fiat
gwt~i-(^lsin04-J5sinl800-|-Gsiii3600+Dsiii5400+ etc.)
= 0
40.
Si functio X non est ordinis w*1, ut supposuimus, sed ulterius excurrit, ae-
quationes sequentes docebunt, quomodo differentia inter X' et X a coefficienti-
bus sequentibus pendeat (v. artt. 21, 23)
*i«+i etc.
etc.
etc.
et sie porro usque ad ultimum $m vel penultimum 3IMf, prout [i impar
est vel par; signa superiora hie valent, quando a = 0, inferiora, quando
a = : denique pro ultimo habetur in casu A) Sm = 0, in casu B) vero
! etc Omnes functiones periodicae, per quas
{i valoribus propositis satisfit, et ex quibus X' est simplicissima, sub forma
X'-\- Ysin [y^oo — % (jl a) sive generalius sub forma X"-\- Ysin D- fi cd — % \t a) con-
tentae erunt, designante X" funetionem talem quameunque, quae formula pro
casu 1 et 3 ad X"-f-Fsin^-{iB?, pro casu 2 et 4 autem ad X"-\-Ycos4z]ix redu-
citur; Y vero, siquidem alias functiones non consideramus, nisi quae ipsi X
sunt similes, i. e. e solis sinubus compositae, necessario debet esse:
in casu 1 formae g-\-g'co&x -\-g"co&1oe-\- etc.
in casu 2 formae ^sin«*? -\-gsiin. 100~{-g"sin%üß-\- etc.
in casu 3 formae ^cos4-(Z?-f-ycosf-#-f-ycosJ-«2?-|- etc.
in casu 4 formae ^sin-^-j-ysinf <2?-f-ysinf-(Z?-|- etc.
Funetionem Y hie ita determinare licebit, ut prodeat functio ad ordinem
£[i—1, £{1, -^{i—4-, -^-fjt—|- depressa, quae cum X' necessario identica erit.
Pro reduetione funetionis X" ad X' regula generalis sequens habetur:
Quivis terminus in X" talis Lsin\x = isin^jix+X')^, transmutetur aut
in +XsinX'«2? (quoties a= 0, vel k par), aut in ipZ/sinX',2? (quoties nee a = 0,
nee & par, i. e.« quoties simul a = ^- atque A: impar): denique quoties in casu
THEORIA INTEBPOLATIOMS METHODO NOVA TEACTATA.
primo i.e. pro a = 0, et valore pari ipsius \l evadit X' = 4-ji,.termintis
omnino destruatur.
41.
Quum omnes casus speciales in artt. 29—40 considerati ad casuin genera-
lem in artt. 20—28 absolute reducti sint, omnia artificia, per quae in hoc casu
calculus abbreviatur, qualia in artt. 25, 26, 27 explicavimus, etiam ad illos
applicari poterunt. Quamobrem non opus erit, huie disquisitioni immorari, cui
sequens exemplum ad artt. 39, 40 pertinens, finem imponet.
Aequatio centri pro novo planeta Iunone, adhibita excentricitate 0,254236,
calculata est per methodum indirectam per singulos denos gradus, ut sequitur
Anomalia media
0°
10
20
30
40
50
60
70
80
90
100
110
120
130
140
150
160
170
180
= X
360°
350
340
330
320
310
300
290
280
270
260
250
240
230
220
210
200
190
180
—
0
3°
7
11
14
18
21
23
26
27
29
29
28
26
23
19
13
7
0
Aequatio
50'
38
20
52
12
16
58
14
58
3
20
41
55
55
35
57
16
+-
380
21,47
8,79
48,06
49,21
17,02
42,92
55,85
52,36
?8,13
33,68
2,10
22,77
2,70
0,79
40,52
58,33
Centri =X
0
138380
27501,47
40808,79
53568,06
65569,21
.... 76577,02
86322,92
. . . . 94495,85
100732,36
104608,13
. . . . 105633,68
103262,10
. . . . 96922,77
86102:70
.... 70500,79
50260,52
26218,33
0
Discerpimus hanc periodum 36 terminorum in sex minores senorum termi-
norum; valores seni functionis X in singulis periodis contenti exhibebuntur per
formulam talem
Y -f-"/cos «2? -f- y"cos 2 x -f- y "cos 3 x
326 NACHLASS.
ubi pro coefficientibus y, y', ft etc. valores sequentes invenimns:
Periodus
prima
secunda
tertia
quarta
quinta
sexta
y=6z
0°
60
120
ISO
240
300
T
*0
4-56'
+ 56,
0
— 56,
— 56,
'205
115
115
205 i
0
217 57
■217,467
0
■217,467
■217,757
0
+ 76l71
+ 760,805
0
— 760, 805
— 761,671
— 1528,S25
— 1527,397
0
+1527,397
+ 1528,825
—103830,lt,5
— 103937,346
— 104151,314
— 104258,100
— 101151,314
— 103937,346
+ 15406,638
+ 1584.1,387
+ 16709,402
+ 17142,684
+ 16709,402
+ 15841,387
0
— 832,667
— 2645,530
— 3525,740
— 2645,53ft
Singuli coeffieientes y, y', y", y'", d\ £", $'" rursus sub formam talem
g-f-g'cos6#-|-g"cos 1 2#-|-s'"cos I Sa?
reducentur: nullo vero negotio perspicitur, pro quatuor prioribus evanescere de-
bere g, g', g", g'"; et pro tribus posterioribus, £', C,", 'Q". Hoc modo invenitur
y = -f- 64",848sin6#-f-0",052sin12a;
y =— 25l",277sin6a;— 0",l 67 sin 1 2ar
y" = -f- 879",002sin6a;-f 0",500sinl2ar
-Ym— — 1764",511sin6a;— 0",824sin J 2xc
g7 = —104044",264-|- 2J 3",968cos 6^+0",132cos 12a;-}-0",000 cos iSx
8"=-f- 16275",15ü— 86S",020cos6a; — 0",489cosl2#—0",003cos 18a;
762",868cos6^-f-0",819cosl2<2?-}-0",002coslS3r
His valoribus pro y, y' etc. substitutis, praeceptisque art. praecc. observa-
tis, prodit functio sequens pro aequatione centri, in qua singuli coeffieientes intra
centesimam minuti seeundi partem exaeti sunt.
—10404464 sina;
-f- 16275,150 sin2ar
— 3527,378 sin 3a?
+ 873,511 sin4xc
— 232,622 sinöa;
-|- 64,848 sin6a;
— 18,655 sin!x
+ 5,491
— l43
+ 0,494 sin 10a:
— 0,149 sin 1 Ix
-f-0,052 sinl2xc
— 0,017 sinl3a;
-f 0,006 sinl4a;
— 0,004 sin 15a?
-j-0,003 sinie«
THEORIA INTERPOLAtTONIS METHODO KOVA TRACTATA. 327
Hoc modo manifesto calculus ita se habet, ac si pro arcu x alius x — x—a
introduceretur. Saepenumero etiam calculus magnopere sublevari potest, si pro
functione X alia X—36 adhibetur, ubi pro 36 functio quaelibet ipsi X simüis
assumi potest, modo ordinem -J-fi— £tum pro valore impari vel ordinem -^-ft1^111
pro valore pari ipsius [i non egrediatur, et in casu posteriori coefficientes ter-
minorum cos^^lx et sin^-ji^ (siquidem eo ascendit) teneant debitam rationem
(cos^iia: sm^-pa). Manifestum est, si valores functionis 36 pro x = a. b, c, d etc.
sint resp. 9K, 55, S, 2) etc., fore valores functionis X — 36 pro iisdem valoribus
resp. A — $[, B—55, C—(£, JD — © etc.; si porro functio Z hisce valoribus sa-
tisfaciens per praecepta praecedentia investigatur, functio 36 -\-Z identica erit
cum ea, quae ex applicatione directa horum praeceptorum ad valores ipsius
functionis X prodiret. Semper autem functionem 36 ita determinare oportet, ut
valores propositi functionis X prope per illam exhibeantur, quo pacto quantita-
tes A — 5T, B — $8, C—(E, D—2) etc. parvae et ad calculum magis tractabiles
evadent. Ceterum pro 36 etiam quantitas constans assumi potest, e. g. haec
—(A-\-B~{- C-f-D-f- etc.), quae functionis quaesitae partem invariabilem con-
stituit.
32?
BEMERKUNGEN.
Die vorliegende Abhandlung über Interpolation ist die wiederholte Ausarbeitung einer Untersuchung,
von welcher ein früherer Entwurf im October 180 5 begonnen zu sein scheint. Sie enthält die Methoden, die
bei der Berechnung der Ausdrücke für die durch Störungskräfte hervorgebrachten Aenderungen der Ele-
Elemente einer Planetenbahn vielfach angewandt worden sind. Dieser Ausmittelung der Störungen steht ein an-
anderes Verfahren zur Seite, das direct die Werthe der Bahnelemente für einzelne Zeitpunkte ergibt und das,
wie aus den im vorgefundenen handschriftlichen Nachlasse aufgezeichneten schliesslichen Formeln hervorgeht,
auf folgenden Principien beruht.
Bilden die Werthe des Arguments, für welche die Werthe der Function gegeben sind, eine arithme-
arithmetische Reihe, und hat man ein Argument x eingeführt, das bei jenen Werthen wie die ganzen Zahlen
fortschreitet, bezeichnet die gegebenen Werthe mit fx, führt deren aufeinanderfolgende Differenzenrei-
Differenzenreihen ein:
/(* + !)-/* =/'(*+!), ft(x + l)-fi(x-i)=f*x, f*(z + l)-f'x =f*(x+*)vi.*.f.
ferner deren mit beliebigen Anfangsgliedern beginnende Summenreihen /''(x+l), f~'x, f~3(x -hf)u.s. f.
für welche
-f-'x u.s.f.
endlich die Mittelwerthe der aufeinander folgenden Glieder der so entstandenen Reihen nemlich
= J/f (x + i) + i/1 (x-
also in übersichtlicher Anordnung zusammengestellt folgendes System von gegebenen und daraus zunächst
berechneten Werthen
M.W. II. Summe, i M.W. I.Summe
/"•*
BEMERKUNGEN.
gegeb. W. M.W.
I. Differ.
/ *+*)^
M.W.
'C.-0
II. Differ. M.W.
/8(*-i)
so gibt Art. 4, wenn man ls für t, a, b, c, d, e . . resp. x-\-t, x, x + i, x—l, x-\-'l, x — 2 2S für
t, a, b, c, d, e . , resp. x-\-t, x, x—t, x + i, x—2, x-\-2... setzt, 3S aus den entsprechenden Seiten der
beiden so erhaltenen Gleichungen die halbe Summe bildet, 4S aus denselben Gleichungen, nachdem zu-
zuvor in der zweiten x + i und t — i resp. für x und t gesetzt ist, die halbe Summe bildet und 58 in
der zuletzt erhaltenen Gleichung t = f macht, folgende Gleichungen für die durch Interpolatation zu be-
bestimmenden Werthe cf(x+t) und ®(x + i) derjenigen Function ox, die bei jedem ganzzahligen Werthe
von x der gegebenen Grosse fx gleich wird:
9 It • O
&
n».n»
Die Coefficienten von /"* in der dritten, vierten und fünften Gleichung sind gleich den Coefficienten von
sin2£a> cosB£ — l)oo . .
Bi"sina>)** in den Reihenentwickelungen resp. für cos2^a>-f-t , i j-isinB1<—l)oo
, cos oo cosoa
und nach Potenzen der Grosse 2»sino>.
cos oo
42
3 SO BEMERKUNGEN.
Setzt man nun
•^flfrnr/6*
indem man als Coefficienten von /"* in diesen vier Gleichungen die Coefficienten nimmt, die bei den
Entwicklungen resp. für —-—, —: , , noch Potenzen von 2 2 sin to entstehen,
'2i@ 2tu COS to 4 to to 4 to to COS to
so sind $(«+ i)> ®xi ^xi ^(^+i) die besonderen Werthe solcher Functionen Q>(x-\-t), ^{x-\-1),
für welche die Gleichungen
t t
Statthaben, sie werden also bestimmten Integralen von y{x-\-t)&.t und <i>(x+ t).&t.ät gleich, wenn
man die Anfangswerthe der Summenreihen f~l(x—|), f~l{x+ §).., f~zx, f~z{x-\-\).. auf geeignete
Weise ausgewählt.
Die Ableitung der Reihen für <t> und V aus der dritten und vierten der obigen Gleichungen für
<p (x -j- t) erhält man unmittelbar, wenn man die Integrationen so ausführt, dass zunächst die Ausdrücke für
0(Ä + i) —<&(*—0, <D(* + 0 —**, V(x + i) — 2Wx + V(x-i) und V(*+#)— 2^(a;+ ») + W(x- j)
entstehen.
SCHEKING.
DETERMINATIO ATTRACTIONIS
QUAM IN PUNCTUM QÜODVIS POSITIONIS DATAE
EXERCERET PLANETA SI EIÜS MASSA
PER TOTAM ORBITAM
RATIONE TEMPORIS QUO SINGULAE PARTES DESCRIBUNTUR
ÜNIFORMITER ESSET DISPERTITA
A ü C T O R E
CAROLO FRIDERICO GAUSS
SOCIETATI REGIAE SCIEü^IARUM EXHIBITA 1818. IAN. 17.
Commentationes societatis regiae scientianim Gottingensis recentiores. Vol. iv.
Gottingae mdcccxviii.
42
333
DETERMNATIO ATTRACTIONIS
QUAM IN PUNCTUM QUODVIS POSITIONIS DATAE
EXERCERET PLAN ETA SI EIXjJS MASSA
PER TOTAM ORBITAM
RATIONE TEMPORIS QUO SINGÜLAE PARTES DESC^EBUNTUR
UNIFORMITER ESSET DISPERTITA.
1.
Variationes saeculares, quas elementa orbitae planetariae a perturbatione
alius planetae patiuntur, ab huius positione in orbita sunt independentes, atque
eaedem forent, sive planeta perturbans in orbita elliptica secundum Kepleei leges
incedat, sive ipsius massa per orbitam eatenus aequabiliter dispertita concipiatur,
ut orbitae partibus, alias aequali temporis intervallo descriptis, iam aequales mas-
sae partes tribuantur, siquidem tempora revolutionum planetae perturbati et per-
turbantis non sint commensurabilia. Theorema hoc elegans, si a nemine hucus-
que disertis verbis propositum est, saltem perfacile ex astronomiae physicae prin-
cipiis demonstratur. Problema itaque se offert turn per se, turn propter plura ar-
tificia, quae eius solutio requirit, attentione perdignum: attractionem orbitae pla-
planetariae , aut si mavis. annuli elliptici, cuius crassities infinite parva, atque se-
secundum legem modo explicatam variabilis, in punctum quodlibet positione datum
exacte determinare.
2.
Denotando excentricitatem orbitae per e, atque puncti cuiusvis in ipsa ano-
maliam excentricam per E, huius elemento dJS respondebit elementum anoma-
liae mediae (l — ecosJS)djG; quamobrem elementum massae ei orbitae portiun-
culae, cui respondent illa elementa, tribuendum, erit ad massam integram, quam
pro unitate accipiemus, ut A — ecosE)dE ad 2%, exprimente tc semicircumfe-
3S4 DETEEMINATIO ATTRACTIONIS
rentiam circuli pro radio 1. Statuendo itaque distantiam puncti attracti a puncto
orbitae = p, attractio ab orbitae elemento producta erit
(l— ecosJS)dJS
Designabimus semiaxem maiorem per a, semiaxem minorem per b, atque
illum tamquam lineam abscissarum, centrumque ellipsis tamquam initium adopta-
bimus. Hinc erit aa—bb = aaee, abscissa puncti orbitae = acosJS, ordi-
nata = bsinE. Denique distantiam puncti attracti a piano orbitae denotabimus
per C, atque coordinatas reliquas axi maiori et minori parallelas per A et B. His
ita praeparatis, attractio elementi orbitae decomponetur in duas axi maiori et mi-
minori parallelas atque tertiam piano orbitae normalem, puta
){\ — ecosJS)dE -, >
h— ecosJE)dE
i —<?cosJS)dJS
ubi p = \J((A — acosEJ-{-(B—bsmEJ+CC).
Integratis hisce differentialibus ab E = 0 usque ad E= 360°, prodibunt
attractiones partiales i, t], C, secundum directiones, directionibus coordinatarum
oppositas, e quibus attractio integra composita erit. et quas per methodum no-
tam ad quaslibet alias directiones referre licebit.
3.
Rei summa iam in eo versatur, ut introducta loco ipsius E alia variabili,^
quantitas radicalis in formam simpliciorem redigatur. Ad hunc finem statuemus
■p a -{- a'cos T-f- a"sin T ' T? ^ ~^~ ^'cos T -\-?> "sin T
COS Jh Y + Y'cosrfY"smr' Sin-Ü Yt^cosr+fsiiTT
ubi autem novem coefficientes a, a\ a" etc. manifesto non sunt penitus arbitrarii,
sed certis conditionibus satisfacere debent, quas ante omnia perscrutari oportet.
Primo observamus, substitutionem eandem manere, si omnes coefficientes per
eundem factorem multiplicentur, ita ut absque generalitatis detrimento uni ex ipsis
valorem determinatum tribuere, e. g. statuere liceret y = 1: attamen concinni-
tatis caussa omaes novem aliquantisper indefiniti maneant. Porro monemus, ex-
QÜAM IN PUNCTDM QUOJDVIS POSUIONIS DATAE EXERCEBET PLANETA ETC.
335
cludi debere valores tales, ubi a, a', a" vel 6", <&', 6"' ipsis y, y, y" resp. pro-
proportionales essent: alioquin enim E haud amplius indeterminata maneret. Ne-
queunt igitur y'a!'—y'a', y'a.—ya", ya!—y'a simul evanescere.
Manifesto coefficientes a, a', a" etc. ita comparati esse debent, ut fiat in-
indefinite
(a+a'cos r+a"sm Tf \
— (y+ycos T-|-y"sm Tf )
unde necessario haec functio habere debet formam
£(cosr2-}-sinT2 — l)
Hinc colligimus sex aequationes conditionales
— aa —öö -4-YY = k }
— a'a" —
— a"a—
— aa —
Y=: — k
/= 0
= 0
= 0
(I)
Ab his aequationibus pendent plures aliae, quas evolvere operae pretium
erit. Statuendo brevitatis caussa
y — (t&'y — dtf— od'ß'y = e . .
e combinatione aequationum (I) facile derivantur novem sequentes:
gtf'=:-H&(/a—cTy)
gy = — Ar(a"Ö— tfwa)
"=— k(afi' —ßa)
(III)
33ß DETERMHJATIO ATTRACTIONIS
E tribus primis harum aequationum rursus deducimus hanc:
= _ k($ Y— i*y — k(ya"~ a'y" J + k(d 6"— 6'a"J
cui aequivalens est haee:
gg = k{—dd—ß'$'+Yy)[—a"a''—$"$"+ff)~k(—aW'
quae adiumento aequationum 2, 3, 4 in (I) mutatur in hanc:
gg = £3 (IV)
Aeque facile ex aequationibus (I) derivantur hae:
— a'«')
> (V)
Exempli caussa evolutionem primae adscribimus, ad cuius instar reliquae
facile formabuntur. Aequationes 4, 2, 3 in (I) scilicet suppeditant
- (aa — Ar)(a"a"—Ar)
quae aequatio evoluta protinus ipsam primam in (V) sistit.
Ex his aequationibus (V) concludimus, valorem k — 0 in disquisitione
nostra haud admissibilem esse; hinc enim omnes novem quantitates 6'y"—y'6"etc.
necessario evanescerent, i. e. coefficientes a, a', a" turn ipsis ö, 6', f>". turn ipsis
y, y', y" proportionales evaderent. Hinc etiam, propter aequationem IV, quan-
titas g evanescere nequit; quamobrem k necessario debet esse quantitas positiva,
siquidem omnes coefficientes a, a', a" etc. debent esse reales. Combinatis tribus
aequationibus primis in (III) cum tribus primis in (V), hae novae prodeunt, quae
manifesto a valore ipsius k non evanescente pendent:
QÜAM IN PÜNCTÜM QÜQDVIS POSITIONIS DATAE BXERCEEET PLANETA ETC. §37
a a—a a'— a"a" = — k
(VI)
}
Combinatio reliquarum easdem produceret. His denique adiungimus tres sequentes:
— Yct—faT = 0 } (VII)
quae facile ex aequationibus III derivantur; e. g. secunda, quinta et octava sup-
peditant:
gÖy-8ÖY— e^Y= —ky(iar—cCf)—kftfa—ary) — kY{ya!—ay)= 0
Manifesto hae quoqiie aequationes ab exclusione valoris & = 0 sunt dependentes #).
Quoniam, ut iam supra monuimus, omnes coefficientes a, a, a" etc. per
eundem factorem multiplicare licet, unde valor ipsins k per quadratum eiusdem
factoris niultiplicatus prodibit, abhinc semper supponemus
quo pacto necessario quoque erit vel s = -f-t vel g = —1. Patet itaque, no-
vem coefficientes a, a, a" etc., inter quos sex aequationes conditionales adsunt,
ad tres quantitates ab invicem independentes reducibiles esse debere, quod qui-
dem commodissime per tres angulos sequenti modo efficitur:
a = cositangiV
ß = sinZ/tangiV
y = seciV
a = cosZ/CoslfseciV+sinZ/sinlf
6' = sin L cos M sec iVIjI cos L sin M
y = coslftangiV
a" = cosLsinMsecN^ZsmLcosM
ß"= sin L sin 3/sec JV-f- cos Zcos Jkf
y'= sinlftangiV
*) Forsan haud superfluum erit monere, nos analysin praecedentem consulto elegisse atque alii deri-
vationi relationum III—VII praetulisse, quae quamquam aliquantulum elegaatior videretur, tarnen, accurate
examinata, quibusdam dubiis obnoxia inventa est, quae non sine ambagibus removere licuisset.
43
338
DETERMINATIO ATTRACTIONIS
ubi signorum ambiguorum superiora referuntur ad casum g = -|~ 1, inferiora ad
casum g = —1. Attamen tractatio analytica ad maximam partem elegantius
sine usu horum angulorum absolvitur. Ceterum haud difficile foret, significatio-
nem geometricam turn horum angulorum, turn reliquarum quantitatum auxilia-
rium in hac disquisitione occurrentium assignare; hanc vero interpretationem ad
institutum nostrum haud necessariam lectori perito explicandam linquimus.
4.
Si iam in expressione distantiae p pro cos E et sin E valores supra assumti
substituuntur, illa in hanc formam transibit:
'cosT- +G"sin Ta + 2.ffcos Tsin T +1H'sin T + 2 H"cos T)
ubi coefficientes a, a', a" etc. ita determinabimus, ut salvis sex aequationibus
conditionalibus
— aa —
y
1
/= 0
= o
= o
— a a — ö c
adeoque etiam reliquis inde demanantibus, fiat
quo pacto problema generaliter loquendo erit determinatum. Quodsi itaque de-
nominatorem ipsius p per t denotamus, transire debet functio trium quantita-
quantitat, tcosE, tsinE haec
mEf— 2aAt.tcosE— 2bBt.tsinE
per substitutionem
tcosE
tsinE
t
a
a cos T-{-a" sin T
os T+fi"sinT
y-|-y'cosr-hy"sinr
QÜAM IN PÜNCTÜ.M QUODVIS PQSITJONJS DATAE EXERCERET ETC.
m
Manifesto hoc idem est, ac si dicas, functionem trium indeterminatarum %, y, z
hanc (W)
aaxx-\-bbyy-\-{AA-\-BB-\-CC)zz—1aAxz—elbByz
per substitutionem
in functionem indeterminatarum u, u', u hanc
Guu+G'uu+G"u"u"
transire debere. At quum ex his formulis, adiumento aequationum [l], facile
sequatur
u = —ax —
u' = a'<2?-}-öy—Y21
u = ax-f-oy — y z
manifesto functio W identica esse debebit cmn hac
G(—ax-
unde habemus sex aequationes
aa =,
bb =
GrG'i'-\-
■fzf
bB =
} [2]
0 =
Ex his duodecim aequationibus [1] et [2] incognitas nostras G, G\ G", a, et', a"
etc., determinare oportebit.
43*
B4rO DETERMINATK) ATTRACTJONIS
5.
E combinatione aequationum [1] et [2] facile derivantur sequentes
— aaa-\-^aA = aG
unde fit porro
Ultimam sie quoque exhibere possumus
AA BB CC__
Perinde e combinatione aequationum [1] et [2] deducimus
a'aa—y'aA = a'G'
atque hinc
d = -£~ , . . [6]
o ■ — — . . 7
AA , BB £C |-8-|
et prorsus simili modo
"- aa — G" l*-
> [io]
Patet itaque, G, — G', — G" esse radices aequationis
QÜAM IN PUNCTÜM QÜODVIS POSITIONIS DATAE EXESCERET PLANETA BTC. 3Ü
quae rite evoluta ita se habet
x3—(AA + BB+CC—aa — bb)xx-\-{aabb—aaBB—aaCC—lbAA —-UCC)x
— aabbCC= 0 [13]
Iam de indole huius aequationis cubicae sequentia sunt notanda.
I. Ex aequationis termino ultimo —aabbCC concluditur, eam certe ha-
bere radicem unam realem, et quidem vel positivam, vel, si C = 0, cifrae ae-
qualem. Denotemus hanc radicem realem non negativam per g.
II. Subtrahendo ab aequatione 12, ita exhibita
„ 4.4-* , BBx , nn
aa -{- x '
hanc-
AAg .^ -5-5^
et dividendo per x —g, oritur nova, duas reliquas radices complectens
aaAA . bbBB
(aa+x)(aa+g) * (bb+x)(bb + g)
quae rite ordinata et soluta suppeditat [14]
aaAA , bbBB ,, , ,., ,, aaAA , bbBB^ \ iaabbAABB
130 — ^tzt"T" iu„ aa oo±\i\\aa ob—„„,„ -r hhj_„) ~r
aa+g ' bb + gJ ' (a a
Haec expressio, quum quantitas sub signo radicali natura sua sit positiva, vel
saltem non negativa, monstrat, etiam duas reliquas radices semper fieri reales.
III. Subtrahendo autem ab invicem aequationes istas sie exhibitas
bb-\-g
et dividendo per g — #, prodit aequatio duas reliquas radices continens in hacce
forma:
a AAgx , BBgx
" ~~ (aa+g)(aa+x)~r (bb
cui manifesto, si g est quantitas positiva, per valorem positivum ipsius x satis-
fieri nequit. Unde concludimus, aequationem nostram cubicam radices positivas
plures quam unam habere non posse.
342 BEHäBMiNATIO ATTBACTIONIS
IV. Quoties itaque 0 non est inter radices aequationis nostrae, aderunt
necessario radix una positiva cum duabus negativis. Quoties vero C = 0, adeo-
que 0 una radicum, reliquas coraplectetur aequatio
ooüß — (AA-{-BB—aa— bb)oo-\-aabb— aaBB— bbAA = 0
unde hae radices exprimentur per
±(AA + BB— aa —bb)±i\J((AA — BB — aa + bbf+4AABB)
Tres casus hie iterura distinguere oportebit.
Primo si terrainus ultiraus aabb — aaBB — bbAA est positivus (i. e. si
punctura attractum in piano ellipsis attrahentis intra curvam iacet), ambae radi-
radices , quum reales esse debeant, eodem signo affeetae erunt, adeoque quum simul
positivae esse nequeant, necessario erunt negativae. Ceterum hoc etiam inde-
pendenter ab iis, quae iam demonstrata sunt, inde concludi potest, quod coef-
ficiens medius, quem ita exhibere licet
(aabb-aaBB—bbAA)(- + ±) + ^^ + a-^
\ IKaa ' ob' ' aa l ob
manifesto in hoc casu sit positivus.
Secundo, si terminus ultimus est negativus, sive punetum attractum in piano
ellipsis extra curvam situm, necessario altera radix positiva erit, altera negativa.
Tertio autem, si terminus ultimus ipse evanesceret, sive punetum attractum
in ipsa ellipsis circumferentia iaceret, etiam radix secunda fieret = 0, atque tertia
bbAA aaBB
aa bb
i. e. negativa. Ceterum hunc casum, physice impossibilem, et in quo attractio
ipsa infinite magna evaderet, a disquisitione nostra, hocce saltem loco, exclu-
demus.
7.
Ad determinandos coeificientes y, y\ y", ex aequationibus 1, 3, 4, 6, 7, 9, tO
invenimus •
QÜAM IN PÜNCTUM QÜODVIS POSITIONIS DATAE UXEECERET PLANETA ETC.
aA
bb+G
aA
aA
bB
[15]
Ex his aequationibus rite cum 5, 8, 11 combinatis etiam sequitur:
./ G
Y 4-CC
AG' ,
[aa— G'-
t"= V-
, BG'
^bb—G
G"
na-"
^8 1 CC
[16]
Hae posteriores expressiones ostendunt, nullara quantitatum G, G\ G" negati-
vam esse posse, siquidem y, y, y" debent esse reales.
In casu itaque eo, ubi non est C = 0, necessario G aequalis statui de-
bet radici positivae aequationis JB, patetque adeo, —G' aequalem esse debere
alteri radici negativae, atque — G" aequalem alteri *); utram vero radicem pro
— G\ utram pro —G" adoptemus, prorsus arbitrarium erit.
Quoties C = 0, punctumque attractum intra curvam situm, duas radices
negativas aequationis 13 necessario pro —G' et—G" adoptare et proin G=^0
statuere oportet. Quoniam vero in hoc casu formula prima in 16 fit indetermi-
nata, formulam primam in 15 eius loco retinebimus, quae suppeditat
y =
bb
Quoties autem pro C = 0 punctum attractum extra ellipsin iacet. aequa-
*) Proprie quidem ex analysi praecedenti tantuxnmodo sequitur, — G' et — G" satisfaeere de-
debere aequationi 13, unde dubium esse videtur, annon liceat, utramque — G' et — G" eidem radici
negativae aequalem ponere, prorsus neglecta radice tertia. Sed facile perspicietur, siquidem aequatio-
aequationis radix secunda et tertia sint inaequales, ex —G'= — G" sequi y' = Tf", a'= a"> g' = g"> et Pr°Jo
-—na"—g'g-YY' = — a'a'—6'6'+yY = *> ^0^ aequationi quartae in [l] est contrarium, Conf. quae
infra de casu duarum radicum aequalium aequationis 13 dicentur.
344 . DETERJONATIO ATTRACTIONIS
tionis 13 radix positiva statuenda est = G, atque vel negativa = — G\ et
G"= 0, vel radix negativa = — G", et G' — 0; coefficientem y" vel y' vero
inveniemus per formulam
i
*^ aa ' bb '
Ceterum in casu iam excluso, ubi punctum attractum in ipsa circumferen-
tia ellipsis situm supponeretur, coefficientes y et Y' ve^ T et l" evaderent infiniti,
quod indicat, transformationem nostram ad hunc casum omnino xton esse appli-
cabilem.
Quamquam formulae 15, 16 ad determinationem coefficientium ^» t'« T'
sufficere possent, tarnen etiam elegantiores assignare licet. Ad hunc finem mul-
tiplicabimus aequationem [5] per aabb — GG, unde prodit, levi reductione facta,
aa-\- G
Sed e natura aequationis cubicae fit
summa radicum G— G'— G" = AA-\-BB-\-CC—aa — bb
productum radicum GG'G" = aabbCC
Hinc aequatio praecedens transit in sequentem:
aaAA{bb^ bbBli{aa+G) G,G„_G,G_G,_Gtl w _
aa-\- G ' bo-f- G ' ' ' '
quam etiam sie exhibere licet
Hinc valor coefficientis y e formula prima in [15] transmutatur in sequentem:
Per analysin prorsus similem invenitur
i i\aa — G j (bb
V 7"» i ni \t /"<"
[aa — 6
n i{aa—G"){bb — G")
QÜAM IN PUNCTÜM QD0BV1S POSITIONIS DATAE EXEBCEBET PLANETA ETC 345
Postquam coefficientes y, y\ y" inventi sunt, reliqui a, t, a\ t\, ot", f
inde per formulas 3, 4, 6, 7, 9, 10 derivabuntur.
9.
Signa expressionum radicalium, per quas y, t'» T" determinavimus, ad lu-
bitum accipi posse facile perspicitur. Operae autem pretium est, inquirere, quo-
modo Signum quantitatis g cum signis istis nexum sit. Ad hunc finem consi-
deremus aequationem tertiam in III art. 3.
quae per formulas 6, 7, 9, 10 transmutatur in hanc:
abABjf
e1 (aa— G')(bb— G") (aa—G")(bb~G')
ab{aa — bb)AB(G"— G')-{f
(aa — G')(aa~ G")(bb— G')(bb — G")
Sed e consideratione aequationis 13 facile deducimus
{aa-{-G)(aa — G'){aa— G") = aa{aa — bb)AA
(bb+G)(bb—G')(bb—G") = —bb(aa — bb)BB
Hinc aequatio praecedens fit
S • ab{aa — bb)AB
quae combinata cum aequatione 17 suppeditat
/ n tab{aa — bb)AJB
"^ ^ (G + Gr)(G + G")(G1— G")
Hinc patet, si pro — G' electa sit aequationis cubicae radix negativa ab-
absolute maior, simulque coefficientes y> T'•> t" omnes positive accepti sint, g idem
signum nancisci, quod habet AB, idemque evenire, si his quatuor conditioni-
bus, vel omnibus vel duabus ex ipsis, contraria acta sint, oppositum vero, si uni
vel tribus conditionibus adversatus fueris. Ceterum sequentes adhuc relationes
notare convenit, e praecedentibus facile derivandas:
44
346 DETERMTSTATIO ATTBACTIONIS
zaabAAB
zabbAJBJB
.g ab AB
t^>t abAJB
a o = —
abAJB
10.
Forraulae nostrae quibusdam casibus indeterrainatae fieri possunt, quos
seorsim considerare oportet. Ac primo quidera discutieraus casum eum. ubi ae-
quationis cubicae radices negativae —G', —G" aequales fiunt, unde, per for-
mulas 18, 19, coefficientes 7,7" valores infinitos nancisci videntur, qui autem
revera sunt indeterrainati.
Statuendo in formula 14, g = G, patet, ut duo valores ipsius oc, i. e. ut
— q' et — G" fiant aequales, necessario esse debere
ä t> n. 11 aaAA , bbBJB „
AB = 0, aa—bb r^+rrr^^ö
aa-{-G ' 004-G
Hinc facile intelligitur, quum aa — bb natura sua sit vel quantitas posi-
tiva, vel = 0 , esse debere
77 aaAA • . /~i aaAA
aa — bb =.—^-^ , sive aa-{-Gr = - 7^
afl-f-fr flfl — ob
Substituendo hos valores in aequatione 14 , fit
G' = G" == &&
Substituendo porro valorem # = —&& in aequatione cubica 13, prodit
Quoties haec aequatio conditionalis simul cum aequatione B = 0 locum habet,
casus, quera hie traetamus, adducitur. Et quum fiat
sy aaAA aaCC
G = rr — da — —j-r-
aa—bb ob
QÜAM m PUNCTUM QÜODVIS POS1TIONIS DATAE EXEECEßET PLANETA ETC.
formula 17 suppeditat
* aabbAA laaCC+actbb
1 V (aa — bfyiaaCC+b*) V aaCC+bl
ac dein formulae 3, 4
— bb) -jbbA /bb(aa — bb\ , b'AA
V V
/bb(aa — bb\ ,
V aaCC + b* V
aA a(CC+bb) V aaCC + b* V (CC+bb)(aaCC + b*
Valores coeffieientium "/,"/' per formulas 18, 19 in hoc casu indeterminati
raanent, atque sie etiam valores coefficientiura reliquorum a, ö', a", 6". Nihi-
lominus per unura horum coeffieientium omnes quinque reliqui exprimi possunt,
e. g. fit per formulam 6
aa — bb
ac dein
g'=v/(i-«'«'+7Y). Y'=\/G7->-7Y). *=£&> S"=v/(i-«v+TY)
Sed concinnius hoc ita perficitur. Ex
YY = l+aa, aa'= yy', 1 = dd-\-t'~&'—yy
sequitur
Quapropter statuere possumus
'6'= cos/, y — asin/, a'— ysin/
Dein vero e formulis
invenimus
a" = — gy cos/> ^" = gsul/\ t" == — gö cos/
Valor anguli f hie arbitrarius est, nee non pro lubitu statui poterit vel g = -f-1
vel g = — 1.
11.
Si G', G" sunt inaequales, valores coeffieientium y% y\ i" per formu-
formulas 17, 18, 19 indeterminati esse nequeunt, sed quoties aliqua quantitatum
44*
348 DETEEMmATIO ATTRACTIONIS
aa—G', bb — G\ aa—G'\bb—G" evanescit, valor coefficientis a, fi', a", 7"
per forrnulam 6, 7, 9, 10 resp. indeterminatus manere primo aspectu videtur,
quod tarnen secus se habere levis attentio docebit.
Supponumus e. g., esse aa—G'= 0, fietque, per aequationem 18, y'—0>
nee non per aequationem 7, ö'— 0 (siquidem non fuerit simul aa =- bb)
unde necessario esse debet a'= +1. Si vero simul aa = bb, formula, quae
praecedit sextam in art. 5, suppeditat a'A-{-fi'B = 0, quae aequatio cum
da'-\-6'fir = 1 iuneta, producit
\J(AA+BB)
Hae expressiones manifesto indeterminatae esse nequeunt, nisi simul fuerit
A = 0, B = 0; tunc vero ad casum in art. praec. iam consideratum delaberemur.
12.
Postquam duodeeim quantitates G, G', G", a, a, a", fi. fi\ fi'\ y, y\ y" com-
plete determinare doeuimus, ad evolutionem differentialis dJS progredimur.
Statuamus
t = t-|-y'cos T+f sin T [20]
ita ut fiat
^cos^; = a + a'cos T+owsin T [21]
f8in.E = ö+öcos T-}-ö"sinr [22]
Hinc dedueimus
= cos-Ed.£sin,E—sin_Ed. tcosE
— cos.EF"cos T— ö'sin T)d T— sin^(a"cos T—a'sin T)dT
adeoque
tt&E= (a6"— a"Ö)cos Td T+(a'6~6'a)sin Td T+[a'6"—ß'a)d T
= g/cos Td T-4-gY"sm Td T-|-gYd r=:: g^d T
sive
/d^ = sdT [23]
Observare convenit, quantitatem t natura sua semper positivam esse, si
coefficiens y sit positivus, vel semper negativam, si 7 sit negativus. Quum enim
sit (Y'eosX4-7"sinTJ-}-(Y"cos T—fsin TJ = tY+yY = YT^1» erit semper
QUAM IN PÜNCTUM QUOBVIS POSEFIONIS DATAE EXERCEBET PLANETA ETC.
T+y"sux Tt sine respectu signi, minor quam y- Hinc coneludimust quo-
ties gy sit quantitas positiva, variables E et T semper sinml creseere; quoties
autem gy s^ quantitas negativa, necessario alteram variabilem semper decrescere,
dum altera augeatur.
13.
Nexus inter variabiles E et T adhuc melius illustratur per ratiocinia se-
quentia. Statuendo sjfty — l) = 8, ita ut fiat ^3 == aa-f-^ö = y't'+y't"' ex
aequationibus 20, 21, 22 deducimus
"sin T)
Perinde ex aequationibus 21, 22 sequitur
*(asin.E—tf COS.E) = g(Y'sin T— y"cos T)
Hae aequationes, statuendo
nanciscuntur formam sequentem:
s(T— M))
tsin(E—L) = esin(T-M)
unde fit per divisionem, propter
Jf) = g(Y4-^)tang4-(E—L)
Hinc non solum eadem conclusio derivatur, ad quam in fine art. praec. de-
ducti sumus, sed insuper etiam patet, si valor ipsius E crescat 360 gradibus, va-
lorem ipsius T tantundem vel crescere vel diminui, prout gY sit vel quantitas
positiva vel negativa. Ceterum statuendo $ = tangiV, y == sec -^ manifesto erit
350 ©EHSEMEfATIO ATTRACTIONIS
14.
E eombinatione aequationum 20, 21, 22 cum aequationibus art. 5 obtinemus:
at(A~acosE) = a G— a G'cos T—a"G"sm T
bt(B — bsinE) = tG— ß'G'cos T— 6"G"sin T
Statuendo itaque brevitatis gratia
(aG — a'G'cos T—a"G"sm T)(i — ea+{t'—ea)cos T+{f—ea)sm T) = aX
(ßG—$'G'cos T—$"G"sin T)(i—ea-\-tf—ea')ooa T+[f—ea!')sm T) = bY
C(T-|-T'cos T-}-Y"sin T)(t — ea-\-{Y—ea)cos T+{f—ea")sm T) = Z
fit
,. eXdT , eYdT ,<,
Sed habetur
t9 == ±\/{G+ G'cos T2+ G"sin T2)
signo superiore vel inferiore valente, prout t est quantitas positiva vel negativa
(p enim natura sua semper positive accipitur), i. e. prout coefficiens y est positi-
vus vel negativus. Hinc
ubi signum ambiguiim a signo quantitatis yg pendet.
Ut iam valores ipsarum £, j\, C obtineamus. integrationes differentialium
exsequi oportet, a valore ipsius T, cui respondet E = 0, usque- ad valorem,
cui respondet £=360°, sive etiam (quod manifesto eodem redit) a valore ipsius
T, cui respondet valor arbitrarius ipsius E, usque ad valorem, cui respondet va-
lor ipsius E auctus 360°; licebit itaque integrare a T=0 usque ad T== 360°,
quoties gy est quantitas positiva, vel a T =■ 360° usque ad T = 0, quoties gy
est negativa. Manifesto itaque, independenter a signo ipsius gy, erit:
2 7T (G + G' cos 2'2 + G " sin Ts)i
r £dr
*^ 2 {G + G'os Ts + G"sin 2'?)l
^ 2 t:(G+G'cos 2TS + G"sin T3)§
integrationibus a T=0 usque ad T= 360° extensis.
QDAM IN PONCTÜM QÜODVIS POSITIONIS DATAE EXEECERET PLAKETA ETC. 351
15.
Nullo negotio perspicitur, integralia
C cos Td T
J (G4-G'cos2'34-G"sinT3)f
/• sin Td T
•' (G 4- G'cos T8 4- G"sin T3)l
f cos2'sinTdT
^ (G4-G'cosTa4-G"sinrs)f
a T = 180° usque ad T = 360° extensa obtinere valores aequales üs, quos
nanciscantur, si a T = 0 usque ad T = 180° extendantur, sed signis oppo-
sitis affectos; quapropter ista integralia a T= 0 usque ad T = 360° extensa
manifesto fiunt =0. Hinc colligimus. esse
/!
— ea)aG—(y — ea')a'G'cos T3—(f— ea")^TG"si
2 7:a(G 4- G'cos Tz 4- G"sin
((t_«o)t 4- (y'— ea')v'cos T34- (f— ea")Y"sin Tz) Cd T
2 7t (G 4- G' cos Tz 4- G" sin T3)f
integralibus a T= 0 usque ad T== 360° extensis. Quodsi itaque valores in-
tegralium, eadem exten sione acceptorum,
cosT3dT
2iü((fi + G')cos Tz + (G4- G")sinT3)f
* 2 7i (
2 7i ((G + G') cos Tz 4- (G 4- G") sin T8)f
per P, Q denotamus, erit
— ea)aG—(f— ea")a"G")Q
ea)ßG— (/
ea)y
quo pacto problema nostrum complete solutum est.
352 ' DETEEMßJATIO ATTBACTIONIS
16.
Quod attinet ad quantitates P, Q, manifesto quidem utraque fit
l
quoties G' = G", in omnibus vero reliquis casibus ad transscendentes sunt re-
ferendae. Quas quomodo per series exprimere liceat, abunde constat. Lecto-
ribus autem gratum fore speramus, si hacce occasione determinationem harum
aliarumque transscendentium per algorithmum peculiarem expeditissimum expli-
cemus, quo per multos iam abhinc annos frequenter usi sumus, et de quo alio
loco copiosius agere propositum est.
Sint m, n duae quantitates positivae, statuamusque
m = ■£(«»-}-«), ri = \J
mn
ita ut m\ ri resp. sit medium arithmeticum et geometricum inter m et n. Me-
Medium geometricum semper positive accipi supponemus. Perinde fiat
m" = % im> -f- ri), n" = \J m'ri
III A I II " I II \ /// / // //
m = i-(m -\-n ), n =.-\Jmn
et sie porro, quo pacto series m, m, m", m" etc., atque n, ri, ri', ri" etc. versus
limitem communem rapidissime convergent, quem per ja designabimus, atque
simpliciter medium arithmetico -geometricum inter m et n vocabimus. Iam demon-
strabimus, — esse valorem integralis
p dT
J 2-it\/(mmcosTz + nnsin T%)
a T = 0 usque ad T= 360° extensi.
Demonstr. Supponamus, variabilem T ita per aliam T exprimi, ut fiat
+ 2msinT's
perspicieturque facile, dum T a valore 0 usque ad 90°, 180°, 27 0°, 360° augea-
tur, etiam T (etsi inaequalibus intervallis) a 0 usque ad 90°, 180°, 270°, 360°
crescere. Evolutione autem rite faeta, invenitur esse
dr dr
(m'm! cos T's + n'ri sin T'2)
QÜAM IN PÜNCTÜM QUODVIS POSITIONIS »ATAE EXERCEEET PLANETA ETC. SS3
adeoque valores integralium
rin'sin Trt)
si utriusque variabilis a valore 0 usque ad valorem 360° extenditur, inter se ae-
quales. Et quum perinde ulterius continuare liceat, patet, his valoribus etiam
aequalem esse valorem integralis
de
y/({i. (x cos 08 + {a {a sin 08)
Sa
a 6 = 0 usque ad 9 = 360°, qui manifeste fit = -. Q. E. D.
17.
Ex aequatione, relationem inter T et T' exhibente,
im — n)sin T.smT'2 = 2msinT'—(m-\-n)sin T
facile deducitur
\J(mmcos T2-\-nnsin T2) = m—(m—n)smT.sinT'
\J(m'm'coa T'2+ «Vsin T2) = ,wcotang T. tang T
atque hinc, adiumento eiusdem aequationis,
sin T. sin T.\J(mm cos T2 -\-nnsin T2) +m'(cos T2 — sin T2)
— cos T. cos T.\J(mmcos r'a+»Vsin T'2)—£(«»—w)sin T2
Multiplicata hac aequatione per
dT d2"
v/(mmcosr8 4-wwsinr8) v^(»»'»»'cos T**4-»Vsin 5TS)
prodit
wr(cosr»-sinT»)dr __ _
(
y/(m'm'co*r* +wVsinrs)
Multiplicando hanc aequationem per ^^, substituendo w'(m — n) =%(mm-L-nn),
(m—nf — 4(mm—nn), sin T'2 = 4-— |-(cos T'2—sin T'2), et integrando, a va-
valoribus T et T' = 0 usque ad 360°, habemus:
__ 2(m'm-nn') , / W_ / /-. /» (cos T'8-sin r8)dT
_ _ t-z\mm nn)J 2 „ s/(m'm'cos T'* + nn sin T'
sin T'
45
354 DJCTRBMTHATIO ATTEACTIÖMS
Et quum integrale definitum ad dextram perinde transformare liceat, manifesto
integrale
/» (cosT8 — sinr3)dr
J 2iz sj[mmcos T9 + nn sinTs)
exprimetur per serjem infinitam citissime convergentem
2 (m'm— n'ri) + 4 (m"m"— n"n") 4- 8 (m'"m'"-— n'"n'")+ etc. v
(mm—nn)\i. y.
Calculus numericus commodissime per logarithmos perficitur, si statuimus
^\]{mm — nn) — \, £\/(m'm'—nri) = 1', i\J(m"m"—n"n") = l'r etc.
unde erit
\ r A.A. \ i/ AA \ rrr XA . ,
a. = —, A r^ —77, A.= —jjj- etc. atque
m m m u
2A'X'4-4X"X- sX'"A'"-t- etc.
18.
Per methodum hie explicatam etiam integralia indefinita (a valore variabilis
= 0 inchoantia) maxima concinnitate assignare licet. Scilicet, si T" perinde
per m', n', T' determinari supponitur, uti T' per m. n, T, ac perinde rursus
T'" per m", n", T" et sie porro, etiam pro quovis valore determinato ipsius T,
valores terminorum serie T, T', T", T'" etc. ad limitem 8 citissime convergent,
eritque
J
äT
\J(mm cos T* + nnainTs) jx
p (cosT8—sinT*)dT vö _, X'cos Tsin T'-f- 2X"cos T'sin T"+ 4X'"cos r'sin T'"+ etc.
J y/ (m m cos Ta + n n sin Ts) jT ' ~lCk ~
8ed haec obiter hie addigitavisse sufläciat, quum ad institutum nostrum non
sint necessaria.
19.
Quodsi iam statuimus m = ^[G-\- G'), n = \j(G~\~ G"), valores quanti-
tatum P, Q facile ad transscendentes ji, v reducentur. Quum enim P, Q sint
valores integralium
QÜAM IN PÜNCTDM QÜODVIS POSITIONIS DATAE JEXEECERET PI^ANETA ETC. 355
cos T* d T/•sin TadT
f cos T* d T /•
J 2n(mmcosT24-wwsinT2)f' ^
a T= 0 usque ad T= 360° extensorum, primo statim obvium est, haben
mmP-\-nnQ = £- [24]
Porro fit
(cosT8 —sinr8)dr , (mmcos 3T3 — wwsin T8)d T (mmcosT* —wwsin T*)dT
7:v/(m>ncosT84-wwsmT2) •" 27r(TOTOCos T8 + wwsinT8)! 7i(>nmcos T8 + nnsin T8)l
j cos Tsin T
= d.
it y/(mm cos T8 4-wwsin Ts)
Integrando hanc aequationem a T = 0 usque ad T = 360°, prodit
— --{-mmP—nnQ =0 [25]
E combinatione aequationum 24, 25 denique colligimus
T)
35?
ANZEIGE.
Göttingische gelehrte Anzeigen. ISIS Februar 9.
Am i7ten Januar übergab Hr. Hofr. Gaüss der Königl. Societät eine Vor-
Vorlesung:
Determinatio attractionis, quam in punctum quodlibet positionis datae exerceret
planeta, cuius massaper totam eins orhitam, ratione temporis, quo singulae partes
describuntur, uniformiter esset dispertita.
Vermöge eines, vielleicht bis jetzt noch von niemand ausdrücklich ausge-
ausgesprochenen , aber aus den Gründen der physischen Astronomie leicht zu bewei-
beweisenden Lehrsatzes, sind die Säcularveränderungen einer Planetenbahn durch die
Störung eines andern Planeten dieselben, der störende Planet mag seine ellipti-
elliptische Bahn nach Keplers Gesetzen wirklich beschreiben, oder seine Masse mag
auf den Umfang der Ellipse in dem Masse vertheilt angenommen werden, dass
auf Stücke der Ellipse, die sonst in gleich grossen Zeiten beschrieben werden,
gleich grosse Antheile an der ganzen Masse kommen: vorausgesetzt, dass die Um-
Umlaufszeiten des gestörten und des störenden Planeten nicht in rationalem Verhält-
Verhältnisse zu einander stehen. Die Aufgabe, welche den Gegenstand dieser Abhand-
Abhandlung ausmacht, nemlich die nicht genäherte, sondern genaue, nicht von massi-
massiger Excentricität der Ellipse abhängige, sondern allgemeine, Bestimmung der An-
Anziehung , welche ein elliptischer Ring von unendlich kleiner und nach obigem
358 ANZEIGE.
Gesetze unveränderlicher Dicke gegen einen jeden Punkt im Räume ausübt, ist
daher für die physische Astronomie von hohem Interesse. Inzwischen ist sie nicht
weniger auch in rein mathematischer Hinsicht merkwürdig, wegen der mancher-
mancherlei Kunstgriffe, welche ihre vollständige Auflösung erfordert.
Von der Auflösung selbst ist es nicht wohl thunlich, hier einen Auszug zu
geben. Der Verf. hat eine rein analytische Behandlung gewählt; Kenner, welche
ihr mit Aufmerksamkeit folgen, werden leicht die geometrischen Correlate der
einzelnen in der Untersuchung vorkommenden Grossen, und die Umschmelzbar-
keit in eine geometrische Form wahrnehmen. Hier mag es genügen, nur das
Endresultat anzuführen. Drei unbekannte Grossen G, G', G" werden durch
die Wurzeln einer cubischen Gleichung bestimmt, aus deren Beschaffenheit sich
beweisen lässt, dass sie alle Mal drei reelle Wurzeln habe. Die nach einer be-
beliebigen Richtung zerlegte Anziehung des elliptischen Ringes wird sodann durch
einen Ausdruck von der Form pP-\-qQ dargestellt, wo p und q algebraisch
von G, G', G" abhängen, P und Q hingegen die bestimmten Werthe der In-
Integrale
cos Ts . d T
2 tc (mm cos T% -\-nnsin Ts)y
/• sin T* . d T
J 2 tz (mm cos T* + nnsinT2)l
bedeuten, wenn die Integrationen von T = 0 bis T=360° = 2tc ausgedehnt
werden, und wo
m = \J(G+G'), n = \/{G+G")
Da diese Integrale im = n ausgenommen) transscendenter Natur sind, und be-
bekannter Massen mit andern in der Perturbationsrechnung vorkommenden vielbe-
vielbehandelten Transscendenten zusammenhängen, so konnte die Auflösung, nachdem
sie bis auf diesen Punkt geführt war, als vollendet angesehen werden. Der Ver-
Verfasser hat indessen diese erste sich ihm darbietende Gelegenheit benutzt, um die
ersten Linien eines neuen Algorithmus zu geben, dessen er sich schon seit einer
langen Reihe^ von Jahren zur Bestimmung dieser Transscendenten bedient hat, und
worüber er in Zukunft eine ausgedehnte zu vielen merkwürdigen Resultaten füh-
führende Untersuchung bekannt machen wird. Hier können nur die Hauptsätze,
mit Uebergehung der Beweise angeführt werden. Wenn man aus zwei gegebe-
DETEßMJNATlO ATTRACTIONIS, QUAM IN PÜHCTÜM QUODLIBET POSWSONIS ETC.
nen positiven Grossen m und n, andere rri, m", m"u.s. w., n\ n", ri"«.s.w. nach
folgenden Gesetzen ableitet:
m = ^-{m -\-n), ri = \Jmn
m" = J- (rri -f- w'),- »" = \/ ?wV
m"'= 4-(m"+w"), »'"= J»Vu. s. w.
d. i. wenn m, n resp. das arithmetische und geometrische Mittel zwischen m
und n ist; eben so m", ^" das arithmetische und geometrische Mittel zwischen
m und ri u. s. f.: so nähern sich die Glieder sowohl der Reihe m, m\ m", m'"vL. s. w.,
als die der Reihe n, ri, ri', ri" u. s. w. äusserst schnell einer gemeinschaftlichen
Grenze = {x, welche der Verfasser das arithmetisch-geometrische Mittel von
m und n nennt. Offenbar ist fi zugleich das arithmetisch-geometrische Mittel
von m und ri, oder überhaupt von je zweien zusammengehörigen Gliedern der
beiden Reihen. Der Verfasser beweist nun, dass — der Werth des Integrals
r *1 '
J 2 tz \/(mm cos T2+ nn sin T%)
ist, wenn die Integration von T= 0 bis T== 360° ausgedehnt wird. Man
wird leicht sehen, dass diess auch auf folgende Art hätte ausgesprochen werden
können: Wenn die Entwicklung der Function
\/ (a -f- g cos d»)
die Reihe
A-\-Bcosty-}-Ccos2<l)-\-DcosZ<b-\- etc.
gibt, so ist allezeit -j das arithmetisch-geometrische Mittel der beiden Grossen
V/(a-f-6) und v'(«~ö).
Ein zweites eben so wichtiges Theorem ist, dass wenn man die Summe der
unendlichen jederzeit sehr schnell convergirenden Reihe
(mV—^'V'')-f- u. s.w.
wo die Zahlencoefficienten eine geometrische, Progression bilden, == (mm—»w)v
setzt, der Werth des Integrals
^s + nnsin Ts)
360 ANZEIGE. ÖETERMINATIO ATTBACT1ONIS, QÜAM IN PÜNCTCM QUODLIBET POSITIONIS ETC.
von T= 0 bis T= 360° erstreckt, = —— wird. Offenbar ist denn hier-
hierdurch auch der zweite Coefficient obiger Reihe bekannt, nemüch B = — —
wenn man m = \J(a-}-6), n = \J(a—€) gesetzt hat. Alle folgenden Coeffi-
cienten C, D, u. s. w. aber werden bekanntlich durch die beiden ersten A und B
algebraisch und einfach bestimmt. Für die numerische Berechnung der Grossen
mm—riri, m"m"—ri'ri'u.s. w. wird in der Abhandlung selbst noch ein besonderes
sehr bequemes Verfahren gelehrt.
Die Anwendung auf die Transscendenten der gegenwärtigen Untersuchung
gibt endlich noch die einfachen Ausdrücke
1—v
Aufmerksamen Lesern wird es nicht entgehen, wie viele interessante Auf-
Aufgaben , die mit den hier betrachteten Transscendenten zusammenhangen, durch
den erklärten Algorithmus mit grösster Leichtigkeit aufgelöst werden. Als ein
Beispiel führen wir hier die Rectification der Ellipse an. Setzt man ihre halbe
grosse Axe = m, die halbe kleine Axe = n, so wird die Peripherie
= VI | m'm'_ 2 (m"m"— n"n") _ 4 (m"W— n'"n") — 8 (m""m""— n""n"") — u. s. w. j
Ein anderes Beispiel gibt die Dauer der Pendelschwingungen bei endlichen Bo-
Bogen, welche sich zu der Dauer der unendlich kleinen Schwingungen verhält, wie
die Einheit zu dem arithmetisch-geometrischen Mittel zwischen 1 und dem Co-
Cosinus von einem Viertel des ganzen Schwingungsbogens.
Schliesslich mus noch bemerkt werden, dass der Verf. diese Resultate, so
wie er sie schon vor vielen Jahren unabhängig von ähnlichen Untersuchungen
Lageange's und Legendee's gefunden hat, in ihrer ursprünglichen Form darstellen
zu müssen geglaubt hat, obgleich sie zum Theil aus den Entdeckungen dieser Geo-
meter leicht hätten abgeleitet werden können, theils weil jene Form ihm wesent-
wesentliche Vorzüge zu haben schien, theils weil sie gerade so den Anfang einer viel
ausgedehntem Theorie ausmachen, wo seine Arbeit eine ganz verschiedene Rich-
Richtung von der der genannten Geometer genommen hat.
NACHLASS.
[ARITHMETISCH GEOMETRISCHES MITTEL.]
PAUS I.
DE ORIGINE PROPRIETATIBUSQUE GENERALIBUS NÜMERORUM
MEDIORUM ARITHM. GEOMETRICORÜM.
1.
Sint | j' y j,/ j,„ | duae progressiones quantitatum ea lege formatae, ut
quilibet ipsarum termini correspondentes sint media inter terminos antecedentes,
et quidem termini progressionis superioris media arithmetica, progressionis inferio-
ris geometrica, puta
a]=4r(a+b), b'=\Jab, a"=i{a'+V). V=sja% a"=$(a"-{-b"), b'"=\ja"b" etc.
Supponemus autem, ipsos a, b esse reales positivos, et pro radicibus quadraticis
ubique accipi valores positivos; quo pacto progressiones quousque libuerit produci
poterunt, omnes ipsarum termini erunt plene determinati valoresque positivos rea-
reales nanciscentur. Porro prima hie se fronte offerunt observationes sequentes:
I. Si a = b, omnes utriusque seriei termini erunt = a = b.
II. Si vero a, b sunt inaequales, erit (a—b')[a'-\-b')—^(a — bf, unde
concluditur b'<^a, et perinde erit b"<^a", b'"<^d" etc., i. e. quivis terminus se-
seriei inferioris minor erit quam correspondens superioris. Quocirca in hoc casu
supponemus, esse etiam b<^a.
III. Eadem suppositione erit a<^a, b"^>b; a"<^a, b"^>b'etc-, progressio
itaque superior continuo decrescit, inferior continuo crescit; hinc manifestum est,
utramque habere limitem; hi limites commode exprimuntur per «°°, &00.
ttt t. • «'—b' (a — b) a — b •, r i/ ^* * / i\
IV. Demqueex —^^^L.^^^^ sequitur a—b<i(a--b),
eodemque modo erit a"—b"<O-(a — b') etc. Hinc concluditur, a—b, a—b',
46
362 NACHLASS.
a"— b", d"— b'" etc. constituere progressionem continuo decrescentem atque ipsius
limitem esse = 0. Hinc a™ =bcß , i.e. progressio superior et inferior eundem
limitem habebunt, quo illa semper manet maior, haec minor.
Hunc limitem vocamus numerum medium arithmetico-geometricum inter a et b,
et per M(a, b) designamus.
2.
Radices aequationis xx—1ax-\-bb = 0 erunt reales positivi, siquidem
a>_b; medium arithmeticum inter has radices erit a, geometricum b\ designata
itaque una radice (et quidem maiore si sunt inaequales) per 'a, altera per '6, pote-
rit 'a spectari tamquam terminus progressionis superioris terminum a praece-
dens, eodemque modo 'b tamquam terminus progressionis inferioris ante b. Si-
militer designando
aequationis xx—2 'ax-\- 'b 'b = 0 radicem maiorem per "a minorem per "b
xx— 2 "ax -f "b "b = 0 '"a '"b
xx—2'"ax+'"b'"b = 0 ""a ""b
poterunt 'a, "a, '"a etc. spectari tamquam continuatio progressionis superioris ver-
versus laevam, atque 'b, "b, '"b etc. tamquam continuatio progressionis inferioris, ita
ut iam habeantur duae progressiones utrimque in infinitum continuabiles
. . . . a, a, a, a, a, a, a , a , a (i)
tun ini "x ir, r, T.' r" ri" T."" /TT\
.... ö, 6, o, o, o, o, o , o , o (II)
Quivis itaque terminus progressionis (I) erit maior quam correspondens se-
riei (II); series illa a laeva ad dextram continuo decrescit, a dextra ad laevam
crescit: haec a laeva ad dextram continuo crescit sensuque contrario decrescit.
Versus dextram utraque series eundem limitem habet; versus laevam autem (I)
super omnes limites crescit, (II) habet limitem 0 (nisi omnes utriusque progres-
progressionis termini sunt aequales). Nam 'a = a-\-\j(aa—bb)\ 'b — a — \j[aa — bb);
hinc 'da— 'b'b = 4a\J{aa — bb)>4(aa— bb), similiterque "d'a— T&>4(V«-~'b'b)
etc., unde patet, seriem aa — bb,'da—'b'b, "d'a—"b"b etc. et proin etiam hanc
ö, 'a, "a etc. quemvis limitem superare posse; -r = — <C~ similiterque -^<C— e^c-
i. e. -^- infra quemvis limitem deprimi potest augendo ipsum n, adeoque lim es
seriei b, 'b, "b etc. = 0.
DE OßIGINE NUMERORÜM MEDIOSÜM AßlTHM. GEOMETBICORÜJIf ETC.
Ex definitione nameri medii arithmetieo-geometrici tarn manifestum est, ut
explicatione ampliore iam non opus sit, sequens
Theoeema. Numerus medius inter terminos quoscunque carrespondentes pro-
gressionum I, II idem est atque inter a et b.
3.
Quo clarius perspiciatur, quanta rapiditate series (I) et (II) ad dextram
versus limitem suum approximent, et quomodo versus laevam illa crescat, haec
decrescat, exempla quaedam hie sistimus:
Eocemplum 1. a = 1, b = 0,2
'""a =15,83705 47919 02
'"a = 7,91897 73959 512
"a = 3,95948 86986 4971
'a = 1,97979 58971 13271 23927 9
a = 1,00000 00000 00000 00000 0
d = 0,60000 00000 00000 00000 0
d' — 0,52360 67977 49978 96964 1
d"— 0,52080 54052 86123 66484 5
dm— 0,52080 16381 12999 95414 3
ay = 0,52080 16381 06187
Hie av, by in 23a demum figura discrepant; yb est minor quam ^
""a, ya, yia etc. sensibüiter formant progressionem geometricam, cuius exponens = 2.
""b = 0,00000 00000 00000 00005 7
'"b = 0,00000 00013 481
"b = 0,00010 30955 7682
'b = 0,02020 41028 86728 76072 1
b = 0,20000 00000 00000 00000 0
V = 0,44721 35954 99957 93928 2
b" = 0,51800 40128 22268 36005 0
V" = 0,52079 78709 39876 24344 0
b""— 0,52080 16380 99375
by = 0,52080 16381 06187
a =
a =
a —
a =
a =
a =
a" =
a =
d"=
1
4,35538
7,17769
3,58885
1,80000
1,00000
0,80000
0,78729
0,78724
0,78724
2913
14569
43819
00000
00000
00000
83346
71015
71007
Eooemplum 2.
307
99831
00000
00000
00000
20741
63456
8
75712
00000
00000
00000
68851
92796
a
7
0
0
0
8
7
= 1
""b
'"b
"b
'b
b
b'
b"
V
b""
, b = 0,6.
= 0,00000
= 0,00001
= 0,01114
= 0,20000
= 0,60000
= 0r77459
= 0,78719
= 0,78724
= 0,78724
00000
73070
56180
00000
00000
66692
58685
70999
71007
00168
00000
00000
41483
06172
8
46*
24287
00000
00000
S7703
16741
3
0
0
6
6
364
NA€HLASS,
Eüßemplum 3. a = 1,
m
a
"a
"a
a
a
d
a
a
'"a
"a
'a
a
d
a"
25,19190 722
-12,59595 36116 78
: 6,29797 68125 07655 42373 4
: 3,14919 33384 82966 75407 2
: 1,60000 00000 00000 00000 0
: 1,00000 00000 00000 00000 0
= 0,90000 00000 00000 00000 0
= 0,89721 35954 99957 93928 2
= 0,89721 14321 16346
: 0,89721 14321 15042
Exemplum 4. a
:19,17024 37557 69475 31905 0
: 9,58512 18783 51017 67266 3
; 4,79262 77923 78537 18223 7
2,41421 35623 73095 04880 2
: 1,41421 35623 73095 04880 2
r 1,20710 67811 86547 52440 1
■ 1,19815 69480 94634 29555 9
: 1,19814 02347 93877 20908 3
1,19814 02347 35592 20744 1
""b
'"b
"b
'b
b
b'
b"
b'"
b""
b = 0,8.
0,00000
0,00000
0,00040
0,05080
0,40000
0,80000
0,89442
0,89720
0,89721
0,89721
00000
00133
98644
66615
00000
00000
71909
92687
14321
14321
0
367
58278 08440 9
17033 24592 8
00000 00000 0
00000.00000 0
99915 87856 4
32734
13738
15042
""b = 0,00000 00009
'"b = 0,00013 37064
"b =z 0,03579 93323
'b = 0,41421 35623
b — 1,00000 00000
V — 1,18920 71150
b"'= 1,19812 35214
b'"= 1,19814 02346
bm= 1,19814 02347
32560
06056
67652
73095
00000
02721
93120
77307
35592
02627 6
69181 0
95745 7
04880 2
00000 0
06671 7
12260 7
20579 8
20743 9
4.
Habeantur praeter progressiones
duae aliae
III iii in iir
. . . a, a, a, a, a, a , a . . .
ini in in 7 ii rn rni
... o, o, 6, b, b, b , 6 ...
//' ii i i n in
. . . c, c, c, c, c, c , c . . .
. . .'X "d,
d, d\ d", d"\ . .
simili modo formatae; supponamusque, duos terminos in posterioribus duobus in
prioribus^proportionales esse, e. g. a:b — c:d, sive a;c = b:d = 1 :n. Tunc
omnes termini in I ad terminos in III, omnesque in II ad terminos in IV (simi-
liter relative ad a, b, c, d siti ac sitos) in eadem ratione erunt, puta
DE ORIGDÜE NUMERORUM MEDIORUM ARITHM. GEOMETRICOßUM ETC.
c=na, c"=nd\ c'"=nd", 'c ='an, dv=nbv, yd = ybn
Hinc facile deducitur, etiam limitem serierum I, II, fore ad limitem serierum
III, IV ut 1 ad n, sive generaliter M(na,nb) =nM.(a,b). Erit itaque generali-
ter M(a,6) = a}
5.
Problema. Exprimere medium arithmetico-geometricum inter numerum unitate
maiorem \-\-oß et unitatem, per seriem secundum potestates ipsius x progredientem.
Sol. Quum M(l,l) = l, supponamus
M(l-H*.l) = l + Ä^ + ÄV+AV + Ä^^+etc
ita ut ti, h", h"\ h"" sint coefficientes constantes ab x non pendentes. Sit
«2? = 2t-\-tt, eritque
J, 1).
Quare häbebitur
"{21-\- ttf + K"{11-\- ttf + etc.
(^+ etc.
Hinc prodeunt aequationes
4h" + h'=4rh'
SÄ'" 4-4Ä"= 0
16Ä"- 12Ä"r4- h"=±h"
32ÄV 4- 32F- 6Ä'"=-iÄ"
71 4- 80Av 4- 24Ä"- K"
256 Ävm4- 448 Äv- 240 Ä™4- 40 li 4- A"
etc. unde fit
Quare
a^ ^6 etc.
Ceteriim nullo negotio perspicitur, medium inter 1 et numerum unitate minoren*
KACHLASS.
Quum hi coefficientes legem obviam non exhibeant, has series praetergredimur,
aliamque viam tentamus, quae successum feliciorem praestabit.
6.
Pboblema. Exprimere medium ar. g. inter \-\-x et 1 — x per seriem secun-
dum potestates ipsius x progredientem.
SoL Quum habeatur
1\ / a *
^
statim habetur e serie art. praec. substituendo ibi —^- pro x
Mf1^!^'1) = l4-^+f^+f^3+-H^4+if^+fH^6+ etc.
atque hinc
üb) = 1 — jrxx—-jfV^4—-r^x6-{- etc.
Coefficientes huius seriei etiam independenter a serie art. praec. per metho-
dum sequentem erui possunt. Ponatur x = eritque
Quare statuendo
M(l+a?, 1 — a?) = l-f-a^^-f-o^ + y^+^^8-}- etc.
(nam potestates ipsius x cum exponente impari non adesse sponte patet) habebitur
Hinc prodeunt aequationes
i -f- 4 a = 0 unde a = —
4a — 48Ö-|-647 = 0 7 =
_4a-}-96Ö—3207+256g = Ö g = -TH
etc. etc.
In hac quoque serie coefficientes legi simpHci non subiecti suntr at si unitas per
illam seriem dividitur, prodit
DE ORIGINE NUMERORUM MEDIORUM ARITHM. GEOMETRICOEUM ETC. 36V
etc.
ubi primo aspectu videmus, coefficientes esse quadrata radicum ■£•, 4-.f, 4-.-f-.-i-,
•r-T-ih-ir, adeoque secundum legem persimplicem progredi. Sed methodus, per
quam ad hanc conclusionem pulcherrimam pervenimus, inductionis tantummodo
vim habet; quam ad certitudinis gradum evehere in disquisitionibus sqq. nobis
proponimus.
7.
Supponendo
l +^+B* C^ etc.
2 £
atque ut in art. praec. x = —^ habemus
Cf^r I)^)^ etc.
s-}- etc.
unde emergunt aequationes
4 A = 1
16J5 = 4
— 64-B+ 64C= 4
— 164+160B— 384 C+256D = J5 etc.
atque hinc 4 = ±, 5 = ^-.^, C7 = i.TV.H. -D = i.iV.tt--H. ut supra:
sed legis ratio hinc operosius deduceretur: quare methodum sequentem praeferi-
mus. Ex aequatione
demanant aequatione« sequentes:
1 = 1 [1]
0=1— 44 [2]
A.= 1 — 124+ 16 J5 " [3]
0 = 1—244+ SOB— 64 C ^ [4]
B = 1 — 404+240-B— 448C+ 256D [5]
0 = 1 — 604 + 560-B— 1792C+2304D— 1024jEJ [6]
368 NACHLASS.
ubi coefficientes facile subiiciuntur formulae generali: scilicet aequatio n^ erit
ubi M erit vel = 0 (quando n par), vel aequalis termino i-(w + l)t0 seriei
1, ,4, JB, C, D etc. (quando w impar). Iam ex his aequationibus sequentes no-
vas deducimus*).
[2], 0=1— AA
4 [3]— [1], 4^1 — 1 = 3— 48^L+ 645
9[4]_4[2], 0 = 5— 200J+ 7205— 576G
16[5]— 9[3], 16-B— 9^ = 7— 532^1-|- 3696-B— 7168C-}- 4096D
25 [6]—16[4], 0 = 9—1116J.+ 12720J5 —43776C+57600D—25600^
etc., ubi coefficientes legi generali facile subiiciuntur. Scilicet aequatio nta erit
a r> sy n+l.n.n—l.»—2.7»« —
16 O X —; : :
, v
ubi factorum progressio obvia est (puta praeter factores simplices in singulos coef-
coefficientes ingreditur factor duplex talis knn — kn -\-±[kk—1)). Hae aequationes
siraplicius sequenti modo exhibentur, singularum membris ad dextram in binas
partes discerptis (praeter aequ. priraam, quae immutata retinetur) •
0 = 1 — 4-4
4-4 — 1 = J3— L
0 = {5— 180-4+ 400-B
— 20J.+ 3205-576G}
J.= |7— 504J.+ 2800-B— 3136G
— 28^1+ 8965— 4032C+4096D!
0 = J9 — 1080-4+10800J5— 28224G+ 20736D
— 36J.+ 19205—15552Ü+36864D— 25600^
*) Signa derivationis esplicantur in Disquisitionibus Arithmeticis art. 162.
**) L, et N hie sunt vel utraque = o (quando n impar), vel resp. terminis %ntis,
1, A, B, C, D, JE etc. aequales.
DE OßIGINE NÜMERORUM MEDIORUM ARITHM. GEOMETRICORDM.
scilicet generaliter aequatio m1*
nnN—(n—\fL
3.4^^^-}-5.16^
2
+
1 . 2.3.4
1 . 2 ... 6
,»+l .n.n—i.n—2.54
1.2.3.4.5.6
' r 2
1
k— 5
1 2
.n +
. 2
.1*
2
. 3
*-7
2
•
Jfc-
2
•
7
ft—8
2
Ä—1
Ä-l
•*( !)
1 . 2
designante A: indefinite quemvis imparem, sint ita
0 = 1—4Ä
4A—1 = 3A — 4Ä) — 4(9^1— 16J3)
0 = 5A— 4-4)— 20(9^1— 16^)-}-16B5^—36C)
16^— 9-4 = 7A — 4Ä)— 56(9^1 — 1 6^)+ 112B5^— 36 C) — 64D9 C— 64D)
0 = 9A — 4-4)—120(9^1— 16J5)-}-432B55— 36 C) — 576D90— 64j>)
+ 256(8li>—
etc. et generaliter aequ. n**
nnN—(n —
t—l .n-\-i.n.n—1.»—2
1 ! 2^ .3.4 '. ~
B5J5—36C)
— 64
2»—1 .
2 .»—3
3 .4.-5
64D)-h etc.
ubi legis obviae universalitas e calculo sponte demanat. Hinc vero perspicuum
est, fieri necessario
0= 1—4-4, 0 = 9^i—16.B, 0 = 25-B—36Cr 0 = 49 C— 641), 0 = 8lD
etc. in inf. adeoque
ä«c J9(wto 3» inßnitum. Q. E. D.
in.
47
370 NAC3HLASS.
8.
Si statuimus
fit
atque
unde sponte sequitur
aadd^ , „«dy , l/ ddy
sive
Hoc itaque modo media nostra arithmetico-grometrica ad quantitates integrales
revocata sunt, solutionemque particularem huiusce aequationis differentio - diffe-
rentialis subministrant.
Eiusdem aequationis int. compl. est M(i,x t-J^~t~M(i x)'
Sit <p angulus indefinitus, eritque valor integralis /*coscp2dcp, a cp = 0 us-
que ad cp = 7c, ut vulgo notum est, =^-tü; eodem modo fit valor integralis
JcoscpMcp inter eosdem limites ^=^-.|-7ü; valor integralis /*coscp6dcp = J-.-f-.-g-Tc
etc. — denique, ut sponte patet, Jd <p = tu. Hinc perspicuum est, valorem in-
integralis
/dcpxfl + i^cos^-l-^-.f^coscp^^.l-.-l-^coscp6-!- etc.)
sive huius / ,,1_a.Jco 8), fieri = tc^ , si sumatur a cp = 0 usque ad <p = tc,
spectando quantitatem «2? tamquam constantem.
Quodsi functio -1Ft ^ in seriem talem evolvi supponatur,
y(l—xxcoscp"') rr
P-{-2 Qcos2cp-|-2i2cos4cp-|-2>S'cos6cp+ etc.
ita ut coefficientes P, Q, JB, Setc. a sola «3? pendeant: valor integralis supra tra-
diti completus erit
Pcp+Qsin2cp+4-JBsin4cp-|--|-/Ssin6cp-|- etc. +Const.
DE ORIGINE NUMEROBUM MED1OKUM ABTTHM. GEOMETBICOBUM. 371
adeoque valor intra limites ante allatos, — P<p, unde y = P. Iam observamus,
quura sit — = M(l-f-<2?, 1—x) fieri quoque — = M(l, sj(l—##)). Hinc facil-
lime derivatur sequens theorema generalius: Si expressio talis -jg— ^ = W
in seriem secundum cosinus angulorum 29, 49, 69 etc. progredientem evolva-
tur, cuius terminus constans designetur per P; valores maximus et minimus ipsius
W autem (puta , ° . et —^ denotentur per v, v: erit — medium arithme-
tico-geometricum inter — et —,. Proxime quidem ratiocinia praecedentia pro eo
tantumraodo casu valent, ubi y es^ quantitas positiva: sed facillime ad eura quoque
casum extenduntur, ubi y est negativus. In hocce enira casu fit W=,(* ^ ^
ponendo <j> = 90 — 9; unde ^ med. inter ^- et ^°~Yl Ut supra. Ceterum
nullo negotio patet, idem theorema sine ulla mutatione etiam ad expressiones ta-
leS v/(g+Ycoscp) extendi, puta ut Term/Const> fiat
valor max. valor mirum.
huiusmodi enim functiones reducentur ad formam ,(g_ ° ^, ei de qua
modo diximus prorsus similem, si scribatur 9 = 2<j>#).
Denique monemus, in sequentibus demonstrationem multo generaliorem
eorundem theorematum ex principiis magis genuinis datum iri; praetereaque mox
etiam omnes reliquos coefficientes Q, R, S etc. per methodos aeque expeditas
eruere docebimus. Hoc loco haec disquisitio eam quoque utilitatem praestabit,
ut iis, qui dum veritatum aetemarum sublimitatem atque divinam venustatem non
sapiunt, earum pretiutn ex solo usu, qui inde in partes matheseos applicatae re-
dundare potest aestimare noverunt, — hasce investigationes cariores reddat. Quan-
tae enim utilitatis sit evolutio coefficientium P, Q, JK, S etc. tarn rapida, ut ea
quae ex his principiis promanat, in astronomia physica sive theoria perturbatio-
num planetarum, nemo ignorat.
*) Ceterum ex praecedd. sponte sequitur, si plures expressiones tales r- ita comparatae
sint, ut ipsarum valores extremi aequales sint: terminos constantes ex ipsarum evolutione prodeuntes necessa-
rio aequales fieri, etiamsi omnes reliqui coefficientes valde discrepent.
PARS II.
DE FÜNCTIONIBUS TRANSSCENDENTIBUS QUAE EX DIFFERENTIATIONE
MEDIORUM ARITHMETICO-GEOMETRICORUM ORIUNTUR.
Sint
oc, x', oc", oc'".... (I)
h, y, y, /'..-•
series perinde formatae ut series in art. 1., puta ut quivis terminus in j^j sit
medium {^JjJJ^J^ j inter duos terminos praecedentes, adeoque occo=yco = M(oc,y):
patetque, omnes has quantitates et proin etiam ipsarum limitem esse functiones
duarum variabilium «2?, y, atque variari, simulacque harum alteruter aut uterque
mutationem patiatur. Hic nobis de solis mutationibus infinite parvis sermo erit.
Fit itaque
et perinde
dg" = \y—,. da?'+ \—, dy' etc.
Hoc modo differentialia omnium terminorum in I et II per differentialia ipsarum
x% y adiumento substitutionum exhiberi possent: sed lex progressiones magnopere
obscura hinc prodiret. Quam ut clarissime ob oculos producamus, sequentibus
scribendi compendiis utemur: Scribemus
DE FÜNCTIONIBÜS TRANSSCENDSIIISBUS ^ÜAE EX ÖO'EESENTIA'FIONE ETC
s',4f -, d
ytf~^Y * '
dy d
y y»
unde statim prodit
da; dy da;' dy' , da;" d«"
X y y» tf y> — y» *'f y''
et prorsus simili modo
r=s+#££., r=f+tfC^L etc.
Perinde fit
" i ^ x ar'jj y ' £ xx ^ ' * z yx ** ' *if \ x /
eodemque modo g" = %g'x~f , g"' = \g"x ~„?- etc. Nee non hinc patet esse
/=/+/, /"=:/-j-/4-/ f' = f+g'+</'+g'" ete. Nullo negotio perspici-
tur, seriem —, —, — etc. celemme infra omnes limites decre&cere, quamobrem
habebimus per seriem infinitam rapidissime convergentem
= 0
^_ 2dM(a;,y)
y<» — M(x,y)
_£_L-d^+ f^-^jx ji—>i^'-^+ ete.| sive
+ dfx(i-iX-^-^-^- etc.)}
Calculum aliquantum commodiorem nanciscimur sequenti modo: Fit
x—x' x-y (x — yf (x + yJ— ixy x'x'—y'y1*}
x x + y xx — yy xx—yy xx—yy
unde promanat
,. t . . x'-x" x"x"—y"y" xn—x"' x'"x'"-y"Y' +
*) et pennde —- = 4———y-r-r, —^,— = *~ttt,—hrtr etc*
; v x" x'x'—yy' x'" x"x"—y"y"
374 NACHLASS.
Ut computus maxima facilitate per logarithmos confici possit, sequentes formulas
adiicimus, ex algorithmo serierum I. II sponte demanantes :
(xx-yy) = 16//; , xx-yy = ltJJ} etc.
quae simul protinus ostendunt, quanta velocitate series nostrae convergere debeant.
Si magis arridet, etiam sequentes formulae poterunt adhiberi:
x'x—y'y = i{x—y)\ x"x"—y"y"= i{x—yff etc.
10.
Rapiditatem convergentiae harum serierum monstrabunt exempla sequentia :
I. Sit x = s/2, y = 1 (Conf. art. 3). Hie habetur xx—yy = 1
I(x'x —yy') =£{x —yf =0,0857864376 2690
4(x"x" — y"y") = [x —yf = 0,.. .3203980 4927
8 {x"'x"r —y'y") = 2 (x" —y"f = 0 22 3462
16 (x""cc""—y""y"") = 4(a/"—y'") = 0,
Summa =0,0861068379 10
Hincfit dM(<2?,^)=M(C7,^)x j^X 1,0861068379...+^X0,9138931621...}
sive in numeris = d^X 0,460082 +d^X 0,5474860839
II. Sit
«2?= 5,202778 + 2,784072 = 7,986850, y = 5,202778 — 2,784072 = 2,418706
ubi x, y sunt distantiae maximae et minimae Iovis et Cereris (neglecta excentri-
citate planorumque inclinatione). Quare
x = 7,9868500 y = 2,4187060 #«2? — // = 59,
X = 5,2027780 / = 4,395207 2(x'x —y'y) = 1,28
x" =. 4,7989925 y" = 4,781975 4(<2?V — /'/') =
x'"= 4,7904838 /"= 4,790476 S(xV—y'"y'") =
x""— 4,790480
11.
Faeile iam etiam coefficientes sequentes serie
37ST
FORTSETZUNG DER UNTERSUCHUNGEN
ÜBER DAS ARITHMETISCH GEOMETRISCHE MITTEL.
[Die weiteren Untersuchungen von Gauss über das Arithmetisch geometri-
geometrische Mittel sind so unvollständig, nur in den Endformeln, und mit so wechseln-
wechselnder Bezeichnung niedergeschrieben, dass fast alle Übersicht fehlen würde, wenn
der Abdruck nur jene Formeln ohne nebenhergehende Erläuterung wiedergäbe.
In den folgenden Artikeln habe ich die im Nachlasse gefundenen Stellen hervor-
hervorgehoben und durch solchen Gedankengang verbunden, wie er vielleicht die Ver-
Veranlassung gewesen ist, dass Gauss die betreffenden Resultate unter einem erkenn-
erkennbaren gemeinsamen Gesichtspunkte aufgestellt hat.]
12.
[An mehren Stellen bedient sich Gauss neben den in den vorhergehenden
Artikeln betrachteten beiden ursprünglichen Reihen von Grossen («, b), welche
sich auf dasselbe arithmetisch geometrische Mittel beziehen, auch noch einer
dritten Reihe von Grossen (c), die mit jenen durch die Gleichung aa= bb-{-cc,
welche für jeden gemeinsamen Index der drei Glieder (a,b,c) gilt, zusammen-
zusammenhängt. Nach den Festsetzungen in Art. 2 können die Gleichungen zur Berech-
Berechnung der rück- und vorwärts folgenden aus «, b, c abgeleiteten Grossen in die
Form gebracht werden:
376 NACHJUASS«
. . "a = 'a-\-'c, ra = a-\-cx a, 2d = a-\-b, 2a" = d-
"b = a 'c 'b = a c b b'b' ab h"b" 'h'
. . V'c = 4Vc, Vc = 4ac, c, 2c=a—b, 2c" = d—b', . .
Hieraus ergibt sich unmittelbar dass, während
U(a,b) = M{an,bn) = M(na,nb) = limam= Iim6m für m = oo
ist,
M(a, c) = 2»M(an, cn) = 2-"M(na, nc) = lim^ == lim^ für m = oo
wird und sich damit die dem ersten Beispiel in Art. 3 angefügte Bemerkung, dass
die na, n+1a, n+2a etwa wie die Glieder einer geometrischen Reihe mit dem Quo-
Quotienten 2 zunehmen als allgemein gültig erweist, ferner dass für den im Bei-
Beispiel 4 Art. 3 berechneten Fall a = b\/2 = c\J2 bei jedem n: na~2n.an,
nb = 2n.cn, nc= 2n.bn ist.
Die Art der Annäherung jener Grossen an ihre Grenz werthe ergibt sich aus
den folgenden R^ihenentwickelungen
M(a,6) = an — cn+1 — cn+2— . . . —cn+m— . . .
M{a,b) = 6u + cn+1 — cn+2— . . . —cn+m— . . .
M (a, c) = 2~n . na — 2-"-1. n+1b — 2~n~2 . n+2b
M (a, c) = 2~*. nc + 2-*-1. n+ib
M(fl)if= /./-K.c11-
M{a,bJ =^ bn.bn +%cn.cn —
U(a,cJ = 2-3w.nc.nc + 4-2-2K.n6.n$ — f 2
M{a,cf = 2-2w.na.na—f 2-2w.n6.n^—f
ARITHMETISCH GEOMETRISCHES MITTEL. Sff
\jM{a,c) = sli-n.^a
(«, c) = v/2~*. nc
2 * M(«, c) 2n ö cn 2"
2 'M(a, c) :
ic M («,«)_ ilmyo^ . J_lrt„,!ü? , . 3 ,_,-*«*«
In den vier letzten Gleichungen ist ^- statt der für beständig wachsendes m
geltenden Grenzwerthe beziehungsweise von
ö c ' M(ma,mc)-10&4fiV Mr«,mc) g
das ist statt des Grenzwerthes von M(l,e)log— für bis zur Null abnehmende
positive Werthe des e gesetzt. Es folgt nemlich zunächst aus jenen Gleichun-
Gleichungen, in welchen, wie die Relationen
leicht erkennen lassen, die zu logarithmirenden Werthe, so bald sie alle reell
sind, vom zweiten Gliede der Reihe an beständig bis zur Einheit hin abneh-
abnehmen, dass die gesuchte Grosse eine völlig bestimmte und z. B., wenn man
a = b\Ji =cv/2 setzt, eine zwischen den Grenzen ■§• log 2 und ^ log 2 einge-
eingeschlossene Grosse ist. Die obigen Gleichnngen gelten auch für complexe Wer-
Werthe der Veränderlichen, wenn man n = 0 setzt und diejenigen Werthe der
logma, logmc, log«, logb, logc, logöm, log&m zu Grunde legt, welche durch
stetige Änderung derselben aus den reellen Grossen folgen. Nimmt man nun
als ein System (a,b,c) das der Bedingung ß = b\/2 = c\J2 unterworfene und
aus reellen Grossen bestehende, ferner als anderes System (a, #, y) dasjenige,
für welches a = c, ß = b\J—: 1, y = a -= b\Jl = c^2 ist und die durch Wur-
Wurzel-Ausziehung zu bestimmenden Werthe von fim und my positive reelle Theile
erhalten, so kann man ein drittes veränderliches System (A,B,C) aufstellen,
welches von dem einen (a, b, c) zu dem andern (a, *>, y) stetig übergeht, und zwar
ni. 48
378
NACHLASS.
so, dass bei diesem Übergang keine der Veränderlichen mA, mC, A,B, C, Am,Bm
den Werth Null berührt oder einen negativen reellen Theil erhält. Die letzte
jener Gleichungen, n gleich Null gesetzt, gilt also sowol für das System (a,b,c)
wie für (a, ö, y) und da
M(a,tf) = ^(i_}-V/_t)M(a,6), M(a,T) = M(a,c) = M(a,6)
ist, wird ^-^—* =l°g^—*; es hat also tu die gebräuchliche Bedeutung als Ver-
Verhältniss-Zahl der Länge des Umfangs eines Kreises zu dessen Durchmesser.
Mit Hülfe dieser Betrachtung lässt sich auch die Richtigkeit der folgenden
von Gaüss aufgezeichneten Bemerkung erweisen, der ich die hier benutzte Be-
Bezeichnungsweise zu Grunde lege und ein von Gaüss berechnetes Beispiel folgen
lasse:]
Die Arithmetisch - Geometrischen Mittel gestalten sich anders, wenn man für
ein b', b", b'". . den negativen Werth wählt: doch sind alle Resultate in folgender
Form begriffen:
l l , 4 ik
Wl[a,b) M^i}~f~M(a,c)
[wo k eine ganze reelle Zahl bedeutet.]
Beispiel für einen imaginären Werth des A. G. Mittels
a = 3.0000000 log . . 0.4771213
b = 1.0000000 0.0000000
a = 3.0000000 log . . 0.4771213-
c = 2.8284270 0.4515450
a = 2.0000000
b' = 1.7320508
a" = 1.8660254
b" .=. 1.8612098
a'" = 1.8636176
b'" = 1.8636159
a""= 1.8636167
0.3010300
0.2385606
0.2709175
0.2697953
0.2703568
0.2703564
0.2703566
\.a
\:c
T-"a
= 2.9142135
= 2.9129510
= 2.9135822
0.
0.
0.
4645214
4643332
4644273
ARITHMETISCH GEOMETRISCHES MITTEL.
a =
b =
a =
V =
a =
b" =
Cl =
&'"^=
im
a =
jim
ay =
6V =
ivl =
3.0000000
1.0000000
2.0000000
— 1.7320508
0.1339746
+ 1.8612098z
0.0669873 +0.9306049*
0.3530969 +0.3530969z
0.2100421 +0.6418509*
0.2836930 +0.6208239»
0.2468676 +0.6313374z
0.2470649 +0.6324002z
0.24699625 + 0.63 18688 z
0.24699625+0.6318685*
0.24699625+ 0.63 186865 z
1 1 0 'S^fi'SO 1 0
log .
-1.3728
. 0.4771213
o.oooooao
0.3010300
0.2385606
9.1270225
0.2697953
9.9698876
9.6984089
9.8295254
9.8341482
9.8311572
9.8318368
9.8314971
9.8314970
9.83149705
7 7 A ■»* 1
M(a,b)
0
360°
0
180°
0
90°
85°
45
71S
65
68
68
68
68
68
1 4*
52'
0
52
26
38
39
39
39
39
58"
0
46.
29.
36.
37.
6.
6.
6.
10
58
05
05
82
95
93
94
13.
[Die Differentiale erster Ordnung der einzelnen Glieder des vollständigen
Algorithmus eines arithmetisch geometrischen Mittels sind in Artikel 9 auf zweier-
zweierlei Weise zu einander in Beziehung gesetzt. Die eine umfasst nur die Differen-
Differentiale der Logarithmen der Quotienten jener Grossen, sie ergibt sich aus der wie-
wiederholten Anwendung der beiden Relationen aa = bb-4-cc, —,=■ ^r, und
" c a—o
kann durch Benutzung der im vorhergehenden Artikel gewonnenen E-esultate zu
einer Werthbestimmung des Differentials vom Quotienten zweier zusammenge-
zusammengehöriger arithmetisch geometrischer Mittel erweitert und so dargestellt werden,
dass — dlog-^r, welches mit A bezeichnet werden mag, für jedes positive und
negative n, wenn nemlich ein negativer nachstehender Index n als gleichbedeu-
gleichbedeutend mit einem voranstehenden positiven Index von gleicher absoluter Grosse
gedeutet wird,
NACHLASS.
— 1 _J_dW- — 1 _J_d W- — 1 -1-dloff- - dW
— 2« * anan luo ia 2W ' &n&a U 1Ug a11 2" * cncn U g &n 2 * M(o, &). M{a, c) U 1Ug M(a, b)
ist. Die andere Beziehung erstreckt sich auch mit auf die Differentiale der Lo-
Logarithmen von zweigliedrigen Producten, sie folgt aus b'b' = ab und 'c'c =
in der Form
d log («m. bm) = d log (am+1. fcm+l) — A. 2m+1. cm+1
d log (ma. mc) = d log f^a. m+Jc) + A. ^ .
und ergibt, wenn man m bis zur unendlichen Grenze wachsen lässt, die in
Artikel 9 aufgestellte Gleichung und die dieser entsprechende nemlich:
2dlogM(ö,c) = dlog(na.\)—
Hieraus kann durch Elimination der Differentiale mit Hülfe des oben ge-
gefundenen Ausdrucks für A die Gleichung
±M(a,b)M(a,c) = . . - 2
abgeleitet werden, welche Gaüss neben der im vorigen Artikel wiedergegebenen
ersten Gleichung für j jjt~t aufgezeichnet hat, ohne den Weg, auf welchem
sie gefunden waren, anzudeuten.]
14.
[Für die vollständigen Differentiale zweiter Ordnung findet man unmittel-
unmittelbar aus den Ausdrücken für A, dass jedes mit gemeinsamen Index behaftete Sy-
System von Gliedern a, b, c die drei Gleichungen
j-dlogj.dloga = f d(|-dlogj)
erfüllt. Multiplicirt man darin die Zähler und Nenner unter den zweimal zu
differentiirenden Logarithmen der Reihe nach mit a, b, c und löst alle Logarith-
ABITHMETISCH SEOMBTBE5CHES MITTEX. 381
men von Quotienten in Differenzen von Logarithmen auf, so ersieht man leicht,
dass der Ausdruck
j d logan.d logbn — ±d( j d log«n&n)
der mit D bezeichnet werden soll, seinen Werth nicht ändert, wenn man statt
an und bn setzt: an und c oder: ba und cn. Nimmt man das Mittel der bei-
beiden letzten so entstandenen Ausdrücke und berücksichtigt, dass
d logan-f d logbn = 2 d log&n+1
ist, so folgt, dass man in jenem Ausdruck ohne dessen Werth zu ändern statt
der beiden genannten Grossen auch cn und 6n+1 setzen kann und ferner,
wenn man in diesem wieder dlogc11 durch ^-dlogan+l-|-4-dlogcn+1 ersetzt,
dass man mit demselben Erfolge a und 6n+1 statt an und bn setzen kann.
Es ist also der Werth jenes Differential-Ausdrucks unabhängig von n und dem-
demnach gleich
D = ±d\ogbn.dlogc*
= ±d\ogcn.d\ogan
Setzt man a als unveränderlich voraus, so wird
D = Äbbcc = —bbdlogb = ccdlogc
und es entsteht die in Artikel 8 aus der Reihenentwickelung abgeleitete für
" und * b) als Werthe von {i geltende Differentialgleichung
ddji — x*d^ — AA66cc.{i = O
aus welcher sich nach den Untersuchungen in der Abhandlung ' Determinatio se-
riei nostrae per aequationem differentialem secundi ordinis' auch wieder die Dar-
Darstellung durch die GAüssischen Reihen:
l)
S82 ffACHLASS.
und als specielle Fälle der dortigen Gleichungen [90] und [96] der oben Art. 12
gefundene Grenzwerth von M A, e) log — und die im vorigen Artikel aufgeatellte
Differentialgleichung erster Ordnung zwischen M(«, b) und M(a,c) ergeben.]
15.
[Die Differentialgleichung zweiter Ordnung für die Glieder der Reihe des
arithmetisch geometrischen Mittels nimmt eine Form an, in welcher sie Differen-
Differentiale nur von Quotienten der Veränderlichen enthält, wenn man mit einer belie-
beliebigen Grosse e den Ausdruck D-f-d(-^ d löge)-f--^ (dlögeJ bildet, dieser wird
nemlich
— \/(eea b ). dfo-^. d^— )
ein Ausdruck, dessen Werth also unabhängig von n ist und sich auch nicht än-
ändert, wenn man bn und cn oder cn und an statt an und bn setzt. Derselbe ver-
verwandelt sich für beständig wachsende positive und für negative n in
dM^fil und in -
dagegen für n gleich Null und für a, b, c als besondere Werthe von e bezie-
beziehungsweise in -\-Abbcc, —kccaa, —kaabb.
Setzt man also zur Abkürzung
so wird mit Rücksicht auf die Gleichung für A in Art. 13:
1 d \\ _ 11 A{ * A » \ — rr A( 1 AU
ogy pp> r*p* ^dlogy ' qq> p*q* ^dtegy * f r>
und von gleicher Form werden die Ausdrücke des -M(a,cf in
t/ a J_f_ i/_J— _ M(q>C)
VM(a,c)' VM(a,c)' VM(a,c)' 7tM(a;i)
Die Elimination von je zwei der drei Grossen p, q, r ergibt
16 1 -. / l H—^ 1 — 0
AEITHMETISCH GEOSDETBISCHES MITTEL.
als Differentialgleichung sowol für p als auch für q und für r, das ist für
v/t.,?■ ,,, v/,,, ,. und J^c a\ and ebenso auch, wenn man —rc 'a>f? = logg
VM(fl,4)' v M(a,b) v M(a,b) M(a,b) *
statt logy darin gesetzt denkt, als Differentialgleichung für \/M * ,, ^/ * e)
16.
[Die Darstellung der Quotienten der Grossen a, b, c, M(a,b), M(a,c) durch
Reihen, die nach Potenzen von y* oder z* fortschreiten, lässt sich mit Hülfe
der Fundamentalsätze des hier zu untersuchenden Algorithmus z. B. in folgender
Weise ausführen.
Nach der Definition von y und dem in Art. 1 2 für den rückwärts verlän-
verlängerten Algorithmus aufgestellten Satze wird:
also nach den Gleichungen in Art. 12 der Grenz werth von fy~~2 . s/M(°l ha für ein
immer wachsendes n, oder was dasselbe ist, der Grenzwerth von 4?y~~i r(y),
wo r {tf) statt v/m7^T) gesetzt ist« ^Gr ^s zur ^u^ abnehmendes positives y*
gleich der Einheit.
Bezeichnen wir noch v/m^) und Vm^ durch P(v) und ^W» so folgt
aus aa = 66 + cc und den beiden Gleichungen für \/M(a,5) in Art. 12
p(y) =
Die Eeihen für pt q, r, welche nach ganzen Potenzen von y* fortschrei-
fortschreiten und diesen Bedingungen genügen, findet man, so weit man die Entwicke-
lung ausführt von der Form:
g
p(y)=
q(y)=
r(y) =
BTACHLASS.
Bass das hier angedeutete Gesetz für die Bildung der Glieder das allge-
allgemein gültige ist, scheint Gauss unter Anderem auch auf folgende Art bewiesen
zu haben. Neben den entsprechenden Gleichungen, welche sich auf Reihen mit
zwei Argumenten beziehen und weiter unten in Art. 23 und 25 Platz finden wer-
werden, hat Gauss sich die Aufzeichnung gemacht:]
Zur Theorie der Zerlegung der Zahlen in vier Quadrate.
Das Theorem: das Product zweier Summen von vier Quadraten ist selbst eine
Summe von vier Quadraten, wird am einfachsten so dargestellt:
es seien l, m, X, ja, X\ ja' sechs complexe Zahlen, so dass X, X' und fi, fi' sociirt sind.
Durch N bezeichne man die Norm. Es ist dann
[und also auch
N [(n+n^n^— ntJ-H(— n+n^n^+n Jj
-f- N {(n + nt — nu-\- nj — i{-\-n — n^ ntt-\- nj \
Hieraus lassen sich leicht die beiden folgenden Sätze ableiten, in welchen
verschiedene Darstellungen einer Zahl durch eine Summe von vier Quadratzahlen
sich beziehen auf die verschiedenen Werthensysteme der vier Wurzeln mit Be-
Berücksichtigung sowol der Zeichen als auch der Reihenfolge der Wurzeln, worin
ferner unter den geraden Zahlen auch die Null mit begriffen wird.
Ist das Vierfache einer Zahl von der Form 4&-f-l durch vier ungerade
Quadratzahlen darstellbar, so ist sie selbst halb so oft durch eine ungerade und
drei gerade Quadratzahlen darstellbar, und umgekehrt, ist eine Zahl in der letz-
letztern Weise darstellbar. so ist ihr Vierfaches doppelt so oft in der ersten Weise
darstellbar.
Ist das Vierfache einer Zahl von der Form 4Ä-j-3 durch vier ungerade
Quadratzahlen darstellbar, so ist sie selbst halb so oft durch eine gerade und
drei ungerade Quadratzahlen darstellbar und umgekehrt, ist eine Zahl in der letz-
letztern Weise darstellbar, so ist ihr Vierfaches doppelt so oft in der erstem Weise
darstellbar.
Mit Hülfe dieser beiden Sätze lässt sich unmittelbar beweisen, tlass die
obigen Reihen der Gleichung r(yf =^p{yf—q[yf genügen, und femer durch
ARITHMETISCH GEOMETRISCHES MITTEL. .
die wiederholte Anwendung dieser Relation, dass, wenn man nach dem Schema
r+1 = V- p -1 = 2 *'• (/L- (O4 = (?7
aus den Werthen der Quadrate der beiden ersten Reihen, nemlich pp und qq^
als Anfangsglieder die Glieder des Algorithmus eines arithmetisch geometrischen
Mittels für positive gerade Indices bildet, auch
wird. Durch Übergang zu dem Grenzwerthe von n entsteht also nach Art. 12:
17.
[Aus den im vorhergehenden Artikel abgeleiteten Eigenschaften der durch
die dort auigestellten Reihen definirten Functionen p, q, r folgt, dass, wenn
a, bt c drei die Gleichung aa = bb-\-cc erfüllende Grossen sind, sie in die Form
gesetzt werden können
b = M(a,b).(qy)\ c =
und dass dann — = —„\ ' { sein muss. Setzt man nun noch
■r M (a, c)
a = M(a,c).(_p«)8,
so wird
Der durch die Vereinigung dieser beiden Darstellungen sich ergebende Satz
ist von Gauss so ausgesprochen, dass die Functionen
+ . . +2«
loga M(a,c) ie
den Gleichungen
in. 49
386 . NACHLASS.
genügen, worin die Quadratwurzeln mit solchen Zeichen zu nehmen sind, dass
der reelle Theil positiv ist.
Aus dieser und der anderen von ihm aufgezeichneten Eigenschaft derselben
Functionen, dass nemlich
ist, scheint Gauss den folgenden Satz abgeleitet zu haben:]
1 7 .
Es seien a, Ö, y, B ganze reelle Zahlen, aB—fiy ==■ 1, °*7~ '. = t'.
Wir unterscheiden 6 Fälle, jenachdem nach dem Modulus 2
a = 1 1 10 10
ö = 0 1 Olli
Y = o o l l l l
0^1 1 1 1 00
Es ist dann
= ft Qt dtt dtt £U Ißt
!' = £it «ß* £i# «ß# 31 # ^^
hdtf = dtt dtt %t
[worin X für die Factoren der drei Functionen $ß, &, dt im Allgemeinen verschie-
verschiedene Werthe hat.]
Ist hier t = ^±^, f = i±±l!, —d=bb — ac = b'b'—a'c', so geht die
Form (a,b,c) in (a,b',c) über durch die Transformation (_~°).
Zusammenhang zwischen den Formen des negativen Determinanten —p und
den summatorischen Fwnctionen.
Sind nemlich die Formen (a,b,c) (AtB, C) aequivalent, so ist die Function J
in Betracht zu ziehen wo ft = fu so wol wenn -^ ganze Zahl als wenn t = —
Jeder Glosse entspricht dann ein bestimmter Werth von ^*
ARITHMETISCH CHSOMETJBISCHJES MITTEL.
18.
[Mit dem Algorithmus des arithmetisch-geometrischen Mittels hat Gauss
einen andern in Verbindung gebracht, welcher ebenfalls wie jener von zwei ge-
gegebenen Grossen, die hier a und ö bezeichnet werden sollen, ausgeht und auf
eine solche Form zurückgeführt werden kann, dass viele Analogien mit jenem
sich zeigen, wenn nemlich
4da = (a -HJ, b'b' = ab, u. s. f.
4 da! = (a+öf, b'V = a$, u. s. f.
gesetzt wird. Ebenso wie die bisherigen Untersuchungen durch Einführung der
die Gleichung aa = bb-\-cc erfüllende Grosse c bedeutend übersichtlicher
wurden, wird hier eine entsprechende Vereinfachung der Formeln erreicht, wenn
man y durch die Gleichung aa ==■ bfi-\-cy und h durch
bc(by—cfi) = ca{ay — ca) = ab(ba—aß) = abch
so wie y11, 8n durch dieselben Gleichungen, nachdem allen Zeichen der Index n
gegeben ist, einführt. Unter den zwischen diesen Grossen bestehenden Relatio-
Relationen finden die folgenden bei der Untersuchung dieses Algorithmus vielfache An-
Anwendung :
a + 6 f — h a—6 f + h a + Y 6 + 8 a — f 6 — 8
a-\-b e ' a—b e ' a-f-e b ' a—e c
= TT— ÜB = i
Die Grenzwerthe der Glieder in den sieben Reihen von Grossen a, b, c,a, €, y,
lassen si^ auf diese vier zurückfahren:
388 NACHLASS.
k = M(a, b) = lima11 == Iim6n
•k M (a, i)
Wenn a und 6 und alle Grossen an, bn, positiv sind, so nehmen ^ und
von den Werthen j, und ^|? beständig bis zur Einheit ab; es ergeben also
die vorstehenden Ausdrücke einen bestimmten Werth für x. Das Gleiche folgt
für K], wenn y, 8 und alle cn und 6n positiv sind, aus
V//4V| Vfc
wenn aber B negativ ist aus der von Gauss angewandten Substitution
y'— = tang ü. \Jj = tang V. \/^ = \J(taag ü. tang V) = tang ü'
y^^' = tang2 U'.\Jj. = tang2 V\\J% ^
Y Ü"F'
^ = tar*g4 Zr.>j£ == tang4 F"^^ = V/(tang4Z7".tang4F") = tang4f7'"
"= 2F'"
+Fn= 2Fn+1
weil dann
sin Z72 = £=*, cos C72 = - 1,
Cd CO.
siaF^—8, cos F2 = |{, ^
ist, und diese Gleichungen auckgeltenrwenn a*,'}j\e£«€i\
statt a, b, c, a, f>, y, S, U, V gesetzt werden, so dass also '
sich ergibt. • ■ • :
ARITHMETISCH GEOMETRISCHES MITTEL.
Für 8 = 0 verschwinden alle £n und es wird
Vergleicht man die Grenz werthe k,y, x, yj, », zu denen man gelangt, wenn
man bei der Bildung des combinirten Algorithmus von den Grossen a, b, a, fi
ausgegangen ist, mit den Grenzwerthen k\ y\ x', r[, u, zu denen man gelangt,
wenn man bei solchem Algorithmus von den bestimmten zuvor erhaltenen Grossen
d, b', d, fi' als Anfangsglieder ausginge, so ersieht man unmittelbar, dass
# = £, y=yy, -|; = ||, ij'=tjif}, u = 2u
sein muss und dass durch die nach diesem Gesetze gebildeten Gleichungen die
den an, 6n, an, ön entsprechenden Grenzwerthe Ä11, ^n, xn, k]h, wn sich ergeben
Aus den Gleichungen von der Form:
e' a — b c' y' /«— °\2 c' a' ,-\ — 8.2
folgt, dass, wenn alle Glieder des Algorithmus positiv werden, y, yx\ und — klei-
kleiner als die Einheit sind.
Die von Gauss angegebene Methode zur Bestimmung des Grenzwerthes für
Un und Fn und ebenso die Bestimmung von -£ mit Zuhülfenahme jener Win-
Winkel führt bei Rechnungen mit Zahlen sehr rasch zum Ziele. Weniger bequem
für Zahlenrechnungen sind die obigen Formeln zur Bestimmung eines reellen t]
und des zugehörigen j. Dieser Umstand wird die Veranlassung gewesen sein,
wesshalb Gauss den Algorithmus: ]
TV
2
A'+JS'
u. §. f» [mit dem Gi-enzwerthe]
h — b V a£'y a'B"y a"B" ' V amB'" ' ' "
[aufgestellt hat, welcher sich auf den obigen zurückführen lässt, wenn man
A = a, B= fi setzt, weil dann
390
wird. Die Bestimmung eines reellen kj ist in Gauss Aufzeichnungen durch eine
Lücke unvollendet gelassen, sie ergibt sich aber, wenn man aus C = y, und
D = 8 denselben Algorithmus wie eben aus A und J5 bildet, denn dann sind:
^T' — b y aB'y a'D"y a"D"'y a!"J>4" ' ' '
und diese Grossen C, D nähern sich rasch dem Werthe -^\Jf8, während y° und
8a zugleich entweder bedeutend wachsen oder abnehmen, sobald -iry*v\ sich von
der Einheit unterscheidet.]
19.
[Die Beziehungen zwischen den Differentialen der zu untersuchenden Grossen
sind besonders einfach, wenn a und b ungeändert bleiben; es ergibt sich dann
unmittelbar aus den Bedingungsgleichungen zwischen Gliedern mit gleichem In-
Index, dass der Ausdruck ^^\f°^^.ä\og^ seinen Werth nicht ändert, wenn
darin der Reihe nach a, ö, y, 8 statt ö, y, 8, a gesetzt wird. Die beiden so er-
erhaltenen Ausdrücke können zu einem dem erstem entsprechenden Ausdruck für
den Index w-j-1 vereinigt werden, der Werth dieses Ausdrucks ist also auch
unabhängig vom Index n. Durch Übergang zur Grenze und durch Vergleichung
mit den Differentialen der auf verschiedene Weise gebildeten Quotienten er-
ergibt sich
eine Relation, weiche also immer gilt, wenn die Indices der a, b, c, a, ö, y, 8, %
um gleich viel Einheiten vermehrt werden. Hieraus folgt der von Gaüss ange-
angezeichnete Satz:]
J s/iaaänU^-^bb oo&ü2) J
\J{aa cos
ARITHMETISCH GEOMETRISCHES MITTEL. -391.
et
{Mit Hülfe der Gleichung für dloggg lassen sich durch wiederholte An-
Anwendung derselben unmittelbar die Reihen für die Differentiale der einzelnen
Grossen a, f>, y, B aufstellen, für ein negatives B entsteht:
7 dlog — 7 dlog— 7 dlog— . _, , dlog—
* LJL t o/o^oF' — h — — h * 1 /7SmF — - Jt- — hm
= c'sin 2 F'+c" sin 22F"+c'"sin23F"'-f . . .]
20.
[Die Differentiale zweiter Ordnung» welche auf die Grosse t] als einzige
unabhängig Veränderliche sich beziehen, können unmittelbar durch Differentia-
Differentiation der Differentialgleichung erster Ordnung hergeleitet und die Bestimmung
ihrer Werthe in der Weise dargestellt werden, dass die Ausdrücke von der Form
Füüil
L dlogT) J
,. a6
d log.7ä
dlogt)
für die mit irgend welchem gemeinsamen Index hehafteten a, Ö, y, $ verschwin-
verschwinden, in welcher Reihenfolge die et, 6, y, B auch darin eingesetzt sein mögen.
Multiplicirt man Zähler und Nenner unter dem zweimal zu differentiirenden Lo-
Logarithmus mit t>, .ersetzt aö durch b'fi' und die Derivirten erster Ordnung durch
ihre Werthe so erhält man für zwei aufeinander folgende Indiens:
und hieraus durch wiederholte Anwendung dieser Gleichung und mit Zuhülfe
nähme der in Art. 13 für d log M (a, b) gefundenen Reihe die Gleichung
dlog— ddlog— ddlog —
k * M ac y x , ,««5
ddlog— ddlog— „
— --.- o« aco
%
(dlog-qf TMj =
welche ihre Gültigkeit behält, wenn a, b, c, a, 6, y, B, x, y, T] mit irgend einem
gemeinsamen von Null verschiedenen Index behaftet werden.
392 UACHLASS.
Durch die Vereinigung dieses Resultats mit der im vorigen Artikel gefun-
gefundenen Entwickelung von d log — ergibt sich die von Gadss gefundene Werthaus-
Werthausmittelung des Integrals:]
fs/(aasinU2+bbcosU2)dU = f t^üt^L -
jyK ' ; J (aacosV* + bb&inV*)%
u \n'„' 9/V A/V" 8/'V" }
+ c'siu 2 F'— c"sin 4 F"— cnr sin 8 V'"~ c""sm 16 V""— . . .
21.
[Bildet man die Gleichungen zwischen den Derivirten der a, ö, y, B nach
der Grosse y als unabhängig Veränderliche, so müssen dieselben Coef&cienten
dieser Derivirten entstehen, wie in den Gleichungen für die Differentiale nach ij
und da die letztern Gleichungen in solche Form gebracht werden können, dass
die Verhältnisse zwischen den Derivirten von Quotienten bestimmt werden, so
müssen die erwähnten Coefficienten auch diesen Derivirten umgekehrt proportio-
proportional sein. Ersetzt man sie durch deren reciproken Werthe, so ersieht man, dass
auch die übrigen Glieder jener Gleichungen durch solche Derivirten dargestellt
werden können und zwar so, dass der Ausdruck von der Form
.dlogy _
für einen beliebigen gemeinsamen Index der Zeichen a, t>, y, &, x, y, rj seinen
Werth nicht ändert, in welcher Reihenfolge man auch die Grossen a, 6, y, §
mit einander vertauscht. Vergleicht man diesen Ausdruck, welcher sich auf
T' S' ^y bezieht, mit demjenigen für \, = j|, ^-,, rj'= ij-rj, y = yy und
beachtet, dass nach Art. 19
[dlog|-"| dlog-1 dlog|; Fdlog-1
dlogirjj dlogY) dlogT) ' Ldiog^J
-^ dlogy
dlogirj d logt)
ist, so ergibt sich, dass der Werth jenes Ausdrucks auch unabhängig von dem
Index der Zeichen «, ö, y, B, y^y, rj und, wie aus den Grenz werthen folgt, gleich
Null sein muss.
ARITHMETISCH GEOMETRISCHES MITTEL.
Um die Derivirte. nach y von jeder einzelnen der vier Grossen a, 6, y, $
zu bestimmen. wird zunächst erforderlich sein, jenen Ausdruck so zu verwan-
verwandeln , dass er nur zwei der Grossen enthält. Dies kann z. B. mit Hülfe der im
vorhergehenden Artikel bestimmten nach ij genommenen zweiten Derivirten der
Quotienten geschehen, so dass also alle Ausdrücke
,, a a aS ,. a
dlog -p d dlog-s- dlog— dlog-s-
6 6 1 v.% 6
dlogy (dlogt))8 ^ dlog7) dlogig
verschwinden, in welcher* Reihenfolge a, 6*, y, Z mit einander auch vertauscht
werden und welcher gemeinsame Index ihnen und den Zeichen y, x, tj gege-
gegeben werde. Ersetzt man %- durch -»Iva6* durch Ä'6' und nach dem vorherse-
0 00 % t ~
henden Artikel
v_ ,,, 6' r,, 6612
durch
so ersieht man, dass der Ausdruck
dlog— ddlog—
% x
d logy (d log tq)8 * L d log 7)
seinem Werthe nach ungeändert bleibt, nicht nur, wie eben gefunden, wenn #
mit a oder y oder 8 vertauscht wird, sondern auch wenn diesen Grossen zu-
zugleich mit y, x, Tj ein beliebiger gemeinsamer Index gegeben wird. Ftr einen
beständig wachsenden Index verschwindet der Werth des Ausdrucks und durch
Multiplication mit i\J ^- entsteht demnach
1. o
dlogy (dlogi))8
als partielle Differentialgleichung für jede der Grossen a, ö, y, 8.]
22.
[Alle Glieder des Algorithmus sind ihrem Werthe nach abhängig von vier
Grossen, als solche dürfen a, b, a, 6* angenommen werden, aber auch k, y, x, i]
weil diese unabhängig von einander sich ändern können. Sämmtliche Gleichun-
Gleichungen zwischen den Gliedern der Reihen lassen sich in solche Form bringen, dass
sie sowol in Bezug auf a, b, c, . . an, bn, cn, k als auch in Bezug auf
in. 50
394 NACHLASS.
± L l —
Jf *' Jfe» * • • •
homogen sind. Die Verhältnisse zwischen diesen letzteren hangen also nicht von
k und x, sondern allein von y und rj ab, wir können also
setzen und aus den Betrachtungen in Art. 18 folgt dann, dass diese Functionen
P, Q, R, S dieselben bleiben, wenn a, 6\ y, 8, x, y, rj mit einem beliebigen
Index versehen werden. Aus demselben Artikel folgt auch, mit Benutzung der
in Artikel 15 gebrauchten Bezeichnung, für die mit einem gleichen Index behaf-
behafteten a, b. c, y
(a,b)
> i) = qy = \/i
S(y, 1) = 0
ferner als Gleichungen, welche denjenigen entsprechen, durch die die Grossen
7 und 6* bestimmt wurden:
qqrr{qqRR—rrQQ) = rrpp(ppRR — rrPP)
= ppqq(qqPP—jppQQ) = ppqqrrSS
PP+QQ ££ — 88 PP—QQ JtJR+SS
p(yy) ri.yy) " r(yy)
PP + RJß QQ + SS PP—RJß QQ — SS
pWy) qWy) '
und als Gleichungen, die das Bildungsgesetz des Algorithmus darstellen :
2r (yy).P(yy,riri) = RR-SS
worin alle Functionen, neben denen kein Argument geschrieben ist, sich auf die
einfachen y und rj beziehen.
ARITHMETISCH GEOMETRISCHES MITTEL.
Zur Berechnung der Werthe der Functionen» welche gegebenen Werteten
von ~ = %£ und U oder V zugehören, erhält man aus der GAussischen Fonael
für H oder x, wenn man zur Abkürzung
(«nsin 2n Unf+ {b* cos 2" I7nJ = &nfcaAnA
setzt, die Gleichungen:
,sm
Die Bestimmung der Grossen k, y, x, yj als Grenzwerthe lässt erkennen,
dass, bei geeigneter hier noch zulässiger Wahl der Vorzeichen der Functionen
P, Q, -R, S, für bis zur Null abnehmende Werthe von y, y v\, — die Ausdrücke
sich dem Grenzwerthe Eins nähern, dass aber für ein beständig abnehmendes y
und ein endliches reelles u die Ausdrücke
PC.«*).
jenen Grenzwerth haben.
Die Functionen P, Q, JK, »Ä haben reelle Werthe für ein complexes r\*
von der Form etu und bleiben bis auf iS, welches nur sein Zeichen wechselt,
ungeändert, wenn man u in —u verwandelt, es ist also
2a.
[Bildet man denselben Algorithmus wie vorher für et, G, y, $, jetzt für
., J5, C, D und macht A = y, J5 = S, so wird offenbar für jedes «, -4n= ya,
^= gB, Cn~ an, 1^= ^1 und also für die Grenzwerthe JT, H, welche den
50*
NACHLASS.
x, xi .entsprechen: T = T. vs. M, T«*iq = T, demnach bestehen die Functio-
nalgleichungen
i i l i
-B(y>— ) 8(.t/> —) P{.y —) ö{y» —)
Macht man aber JL = 6, 5 = a, so wird 0= — 8, D = — -y und für
jedes w, welches gleich oder grösser als Eins ist: An— an, 5n= €n, Cn= yn,
D = Bn, man erhält also:
Q(y> ~~iü -P(y> — i) '*ß(y> —^) iR{y> —^) «
Setzt man endlich 2\jA!'=^a-\-\Jß, 2\/C"=\/a—\/ö, so wird für jedes
n> 1
also:
= QQ—88, (^)(^i
(/)8(/ = 2
wo wieder diejenigen Functionen, denen keine Argumente beigefügt sind, sich
auf die einfachen y und i] beziehen.
Der so erhaltene neue Algorithmus, bei welchem man von den Functionen
P, Q, JS, $ mit den Argumenten y, i] übergeht zu den Functionen mit den Ar-
Argumenten yy, Tj, ist offenbar der von Gaüss in Art. 16 der Determinatio attractio-
nis quam in punctum quodvis positionis datae exerceret planeta etc. angewandte.
Die Relationen zwischen den Functionen, welche sich auf die beiden belie-
beliebigen Werthe I, tj des zweiten Arguments beziehen, und denjenigen Functionen
mit den zweiten Argumenten £tj und — lassen sich auf verschiedene Weise mit
AETTHMETISCH ÖEOlffiTKlSeBES MITTEL.
Hülfe des für oc, 6 aufstellten Algorithmus ableiten, Die Methode, för wel-
welche die Entwickelungen am wenigsten weitläufig sind, ist wol diejenige, welche
sich auf Functionen bezieht, in denen neben den zweiten Argumenten £^ und
— als erstes Argument auftritt das Quadrat von dem ersten Argument der Functio-
Functionen , welche £, i\ als zweites Argument haben.]
24.
[Bei dem Algorithmus des arithmetisch-geometrischen Mittels ergeben die
durch Rückwärts-Verlängerung entstehenden Glieder mit Hülfe der Gleichungen
die Glieder «n, cn. &n die ebenso von a, c abhangen, wie «n, bn, c11 von a, b.
Vertauscht man dem entsprechend bei dem combinirten Algorithmus gleichzeitig
b mit c und ö mit y, lässt a ungeändert, so wechselt B nur sein Zeichen, wir
erhalten also einen Algorithmus, der ebenso von a, c, <x, y abhängt wie der bis-
bisher betrachtete von a, b, a, ß wenn wir setzen
<xo==(X' 7o = ö' öo = T' K = — *
und so fort bis zu den Grenzwerthen :
lima = limc = M(a, c) = l
n n \ * /
1nl « M (q, c)
Vfi^e «MC«,*) —^
Es sind also a, y, ö, —B ebensolche Functionen von /, s, X, C, wie a, l>, y, B von
k, y, x, Tj und da y allein von y und i\ abhängt und zwar auf dieselbe Weise
wie j von i] und y, so muss für —^ = j~j,
398 NACHLASS.
sein, wobei aus&er T auch noch C als Function von y, v\ zu bestimmen ist und
zwar C so, dass y, t\, C der Reihe nach mit z, C, i\ vertauscht werden können,
also so, dass
lOg» IT
IT
r]J, (logg2] = ?[(logC)',(log7i)a]
wird.
Für die P, Q, JR als Quadratwurzeln aus —, —, -1- sind hier gleiche Vor-
zeichen genommen, weil nach Art. 18 1] und C zugleich den Werth 1 annehmen
und also nach Art. 22 und 17
1__ ^ rz_ qz_ .r^togy ./ «
(z, l)—py—qy — ry — \ n " V_lo
logz
wird und hier dasjenige Vorzeichen der Quadratwurzel gilt, für welches der reelle
Theil positiv wird.
Lässt man die zweiten Argumente C, i\ sich in ihre reciproken Werthe ver-
verwandeln, so bleiben P, Q, R ungeändert und 8 wechselt nur sein Zeichen, es
ist also
)
und eine entsprechende Bedingung gilt für y als Function von i], C. was durch
die oben aufgestellte Form der <p Function angedeutet sein soll.
Transformirt man in der Gleichung, durch welche T eingeführt ist, die
P, Q, jR, 8 in der Weise, dass die Argumente z, C, y, i] einmal in z, —C, y, —
dann in \Jz, C, yy, i\t\ übergehen, und berücksichtigt, dass
pjz_ ___ r^z __ qtfz, _ / —logyy __ / tt
pyy q.yy ryy V * »—lo
ist, so erhält man
A
ARITHMETISCH GEOMETRISCHES MITTEL. 399
und daher
logy « __ i
ic logz -^- * logC
Worin das Vorzeichen der Quadratwurzel so zu nehmen, dass der reelle Theil
derselben positiv wird, das Vorzeichen von + i p^|j aber so, dass der reelle Theil
dieses Ausdrucks negativ wird.]
25.
[Aus den Functionalgleichungen für P, Q, R, St welche bei der Verwand-
Verwandlung des zweiten Arguments i] in seinen reciproken Werth, bei der Zeichenän-
Zeichenänderung desselben und bei der Multiplication desselben mit dem ersten Argument
y Statt finden, so wie aus den bekannten Werthen der Functionen für i] = 1
oder auch aus der in Art. 21 für die allgemeinen Functionen aufgestellten par-
partiellen Differentialgleichung folgt, dass wenn P, Q, R, 8 sich in Reihen nach
ganzen wachsenden Potenzen von y* und rf entwickeln lassen, diese
Q Cjmi) = i -y(i\ + vr1) +/ V+ir2) - / (t + *r*)+/*(V+n'') —h •
sein müssen.
Dass durch die Reihen P, Q multiplicirt in den Grenzwerth \JH die Grossen
\JA, \JB dargestellt werden, auf welche der von Gauss benutzte am Schluss des
Art. 18 wiedergegebene Algorithmus sich bezieht, ist im handschriftlichen Nach-
Nachlasse als besonderer Lehrsatz ausgesprochen und zugleich bemerkt, dass]
NACHLA&S.
U =
y^cosf tt-J-y3"cosftt + y ^ cosf w Hhy f cosf u-\- , .
jy, y% sin« —^ i
tang u — —
COS7W-J- . .
j. rt tt" y$ &ha.2u — y% sin 6 u + y * sin 1 bu—y^ sin 1 4m+ . .
tang 2 u = — 1 J2 ^5
y* cos2zi +y*
[wird. Für den Satz, dass die Reihen P, Q den Functionalgleichungen genügen,
welche den besprochenen Algorithmus bestimmen, und welche oben in Art. 22
zusammengestellt sind, hat Gauss ausser dem Beweise, der sich auf die Verwand-
Verwandlung jener Reihen in unendliche Producte stützt und der in der unten folgenden
Abhandlung 'hundert Theoreme über die neue Transscendente' enthalten ist,
wahrscheinlich auch noch einen andern Beweis geführt, wie er sich leicht aus
den oben in Art. 16 gemachten Andeutungen ergibt.]
26.
[Bezeichnen wir, abweichend von der in den vorhergehenden Artikeln be-
befolgten Weise, die ersten Derivirten der Functionen P(y,ij), Q(y,i)), jR(^,k}),
iS(y,i]) nach der Grosse logt] als unabhängige Veränderliche mit P', Q\ R\ S'
und die zweiten Derivirten nach derselben Grosse mit P", Q", R'\ S'\ ferner die
ersten Derivirten der Functionen py, qy, ry nach logy als unabhängig Verän-
Veränderliche mit p, q, r, so folgt aus den für a, b, c, a, G, y, § gefundenen Differen-
Differentialgleichungen :
qr'—rq' __ p r'— rp' __ qp'—pq' ___ ±
qrp°- 4
PS'—SP' QS'—SQ' HS'-SS' QR'—RQ' __ PR'—RP' QP'—PQ'
ppQR ' qqPR rrPQ ppPS qqQS rrBS l
P'P'—PP" . . 2222 Q'Q'—QQ" . SS
hipprr =iPprr
R'R'—RR" , . PP S'S'—SS" . QQ
^^'= SS±PPrr
4 (r
ARITHMETISCH GEOMETRISCHES MITTEL. 401
ddP dP
(dbgTj)8 dlogy»
welch letzterer Gleichung jede der Functionen P, Q, JR, S genügt Die vorher-
vorhergehende mehrfache Gleichung zwischen den ersten und zweiten Derivirten der
Functionen nach der Grosse logK] findet sich, soweit sie sich auf P und 8 be-
bezieht, in Gaüss handschriftlichem Nachlasse an einer von den übrigen Unter-
Untersuchungen dieser Functionen getrennten Stelle. Es sind dort P, S, pt r in einer
für diese specielle Entwickelung etwas bequemeren Form als die hier benutzte
durch ihre Reihen definirt, und es heisst dann,] so wird
pp =
hier ist noch zu bemerken [wovon jedoch der Beweis tiefer liegt)
also
S'S'—SS" . ,PP . SS
noch findet man
Das Quadrat des zweiten Factors im andern Theile der vorstehenden Glei-
chung wird
Der erste Factor wird
Zusammen wird, reductis reducendis
ni. 51
(PS'-SP'f = i-{p{yyf^-r{yyf]\p{yy)P(yy,xiri)-T(yy)R(yy,'n'n)\><
XJp(yy)r(yy)PP-lp(yy)*-r(yyf]SS\
Setzt man also
—is jp(yy)*-r(yyY
P V 2p{yy)r{yy)
so wird
j 2dÖ
dcp =
cos 6 = -
P
x P V 1p{yy)r{yy)
403
Media Arithmetico-Geometrica inter unitatem et sinus singulorum semigrandum.
1 r
1 z
11 3
1 4
II 5
1! 6
I 7
1 8
II 9
!
0.256340z
0.2890201
0.3122942
0.3312018
0-3475041
0.3620469
0.3753082
10.3875870
0.3990846
ro j 0.4099431
11
12
13
15
16
r7
'18
r9
20
21
22
23
24
*5
26
27
28
29
3°
3i
3*
33
34
35
* 36
37
38
39
40
41
11 42
n 43
1! ^
I 45
!
O.42O2673
O.43OI365
O.4396124
O.4487447
O.457573O
O.4661299
O.4744428
O.4825346
O.49O4248
O.49813OI
O.5O5665I
O.5I3O424
O.52O2728
O.5273662
O.53433«
O.54«753
0-5479055
O.554528O
O.56IO483
O.5674713
O.5738O16
O.58OO433
O.5862OOI
O.5922755
O.5982726
O.6O4I943
O.6IOO433
O.6I5822O
O.62I5325
O.627I77O
O.6327574
O.6382757
O.6437334
O.649I3I9
O.6544727
9.4O88168
9.46O928O
9.4945639
9.52OO926
9.54O9599
9.5587648
9.574388I
9.5883692
9.6OIO65O
9.6127236
9.6235256
9.6336062
9.643O699
9-65I9994
9.6604604
9.6685069,
9.6761838
9-6835285
9.69O5724
9.6973428
9.7O3863O
9.7IOI532
9.71623II
9.722I122
9.7278105
9-7333379
9.7387057
9-7439*35
9.7490002 j
9-7539439
9.7587617
9.7634604
9.7680459 ■
9.7725238 1
9.7768991
9.7811766
9.7853606
9.7894551
9.7934638
9.7973902 j
jl
9.8012372 1
9.8050084
9.8087060
9.8123330
9.8158914
45
46
47
48
49
50
51
5*
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
7°
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
9°i
0.6544747
0.6597572
0.6649867
0.6701622
0.6752849
0.6803558
0.6853757
0.6903457
0.6952666
0.7001389
0.7049637
0.7097416
0.7144731
0.7191589
o-7237995
0.7283955
0.7329474
o-7374556
0.7419207
0.7463429
0.7507228
0.7550605
O-7593567
0.7636114
0.7678251
0-77*998*
0.7761305
0.7802227
0.7842750
0.7882874
0.7922602
0.7961936
0.8000879
0.8039432
0.8077596
0.8115373
0.8152764
0.8189771
0.8226396
0.8262639
0.8298501
0.8333983
0.8369086
0.8403811
0.8438159
0.8472131
9.8158914
9.8193842
9.8228129
9.8261799
9.8294870
9.8327361
9.8359287
9.8390666
9.8421514
9.8451842
9.8481668
9.8511003
9-8539859
9.8568248
9.8596183
9.8623672
9.8650728
9.8677359
9-87O3575
9.8729384
9.8754796
9.8779818
9.8804458
9.8828724
9.8852623
9.8876162
9.8899348
9.8922186
9.8944684
9.8966845
9.8988678
9.9010187
9.9031377
9.9052254
9.9072821 '
9.9093085
9.9113049
9.9132718
9.9152096
9.9171188
9.9189996
9.9208526 ||
9.9226780 |j
9.9244763
9.9262477
9.9279927
90
9i
92
93
, 94
95
| 96
97
98
99
100
; 101
1102
IOC
104
105
106
107
108
109
HO
III
112
«3
114
«5
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
J34
135
0.8472131
0.8505727
0.8538947
0.8571793
0.8604265
0.8636364
0.8668089
0.8699442
0.8730422
0.8761030
0.8791266
0.8821131
0.8850624
0.8879746
0.8908497
0.8936878
0.8964887
0.8992526
0.9019793
0.9046691
0.9073217
0.9099373
0.9125158
0.9150572
0.9175616
0.9200288
0.9224590
0.9248520
0.9272080
0.9295268
0.9318084
0.9340529
0.9362602
0.9384303
0.9405632
0.9426588
0.9447172
0.9467383
0.9487221
0.9506687
0.9525779
0.9544497
0,9562842
0.9580812
0.9598409
0.9615631
9.9279927
9.9297114
9.9314043
9-933°7r7
9-9347I38
9.9363309
9-9379*34
9.9394914
9.9410352
9.9425552
9.9440514
9.9455243
9.9469739
9.9484006
9.9498045
9.9511858
9.9525448
9.9538817
9.9551966
9.9564897
9-95776I3
9-959OIIS
9.9602404
9.9614483
9.9626352 |
9.9638014 1
9.9649471
9.9660723
9.9671772
9.9682619
9.9693266
9.9703715
9.9713965
9.9724020
9.9733880
9-9743545
9.9753018
9.9762299
9.9771390
9.9780292
9.9789005
9-979753O
9.9805870
9.9814023
9.9821992
9.9829778
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
r75
176
177
178
179
180
0.9615 631
0.9632479
0.9648951
0.9665049
0.9680772
0.9696119
0,9711090
0.9725685
O-97399O5
O-9753748
0.9767214
0.9780304
0.9793016
0.9805352
0.9817310
0.9828890
0.9840094
0.9850919
0.9861366
0.9871434
0.9881125
0.9890438
0.9899369
0.9907923
0.9916098
0.9923894
0.9931310
O-9938346
0.9945004
0.9951281
0.9957178
0.9962696
0.9967833
0.9972591
0.9976968
0.9980965
0.9984581
0.9987817
0.9990672
0.9993147
0.9995241
0.9996954
0.9998287
0.9999239
0.9999800
1.0000000
9.9829778
9.9837381
9.9844801
9.9852041
9.9859100
9.9865979
9.9872680
9.9879202
9.9885547
9.9891715
9.9897707
9.9903523
9.9909165
9 9914632
9.9919925
9.9925045
9.9929992
9.9934767
9-9939371
9.9943803
9.9948064
9-995«55
9.9956075
9.9959826
9.9963408
9.9966821
9.9970065
9.9973141
9.9976049
9.9978790
9.9981363
9.9983769
9.9986008
9.9988080
9.9989986
9.9991725 1
9.9993298
9.9994706
9-9995947
9.9997022
9-9997932
9.9998677
9.9999256
9.9999669
9.9999917
co.ooooooo
51
ELEGANTIORES INTEGRALIS f dx PROPRIETATES.
Valorem huius integraüs ab ce = 0 usque ad <a? = 1 semper per 4- es de-
signamus. Variabilem % respectu integralis per Signum sin lemn denotamus, re-
respectu vero complementi mtegralis ad \m per cos lemn. Ita ut
sin lemn f$~^ = *, cos lemn (im —/^if^) = *
Variabilis x tamquam radius vector curvae, integrale autem tamquam curvae ar-
cus respondens considerari potest, curva vero erit ea quam Lemniscatam dixe-
runt Haec suflficiunt ad intelligenda quae sequuntur.
cos lemn(a±b) = l
sin lemn (— a) = — sin lemn a > cos lemn (—a) = cos lemn a
sin lemn km =z= a sin lemn (&-J-£) es = +1
cos lemn km = -j-1 cos lemn (ife 4-4.) 03 = 0
LEMNISCATISCHE FÜN.CHONEN I.
405
k denotante numerum integrum quemcunque positivum seu negativum, signum
superius sumendum quoties k est par, inferius quoties est impar.
sin lemn cp =
sinlemn2<p =
sinlemn3y =
sm Iemn4<p =
sinlemnöcp =
suilemn«? ==
= sc[\-\-cc)-~p.
—5*4—
5 —
1—12s4
1_2s4-j-5«8' 1+52«4—
».»»—l.BU + 6 4 »'—13»4+36»»-j-420.».n»+1 8
60 10080
».».
1 -\
cos lemn 9
cos
= c
12
1—2cc — c4 1 — 2ss—
1008»
cos lemn3<p
cos Iemn4cp
1—4*S—6S4—
l—Sss—I2g4-t-8s6— 38a8 — 8at0— 12a18 + 8a14
1_|_8ss_12s*_8s« — ss^ + s«1«—12*«*-8***
[4-]
1.3
1.3.51 13 . 1.3.5.7
sm lemn cp
1 5 , 19 11 13 i_ 211 17
— <p -r ^ 9 156Oo ^ • ¥
1607 21
60
10080
156Oo
3536000
318240000
259459200
20748433305600»
1.2.3.4.5
36 9_. 552 13 l_ 515< 17 . &1^<848
1....9 ^ "• 1..., 13 ^ ' 1.... 17 r ' 1....21 *
12
1.2.3.i
10080
19958400
43589145«000
1....8
1....12
coslemncp = l-
2 T t
24 *
NACHLASS.
1 240* 1 40320
—I— Q
-5-4151347200 1
61 co10
>»+
403200 r
4171
6974263296(
' 159667200
CD16
H0 Y
42
Formulae pro P, Q, pt q in infinitum continuatae quavis convergentia data
citius convergunt, formula autem pro sin lemncp diverget, si cp ponetur ^>-r^
sive cp4]> — ,"" formula autem pro cos lemncp diverget, si cp^>cs
Einige neue Formeln die Lemniscatischen Functionen betreffend.
Essei
-.* l^i ,3 16,3.71 io f3.7.111
Man hat dann 99 = #<a?-f-.-ar + -—.-«2? + t-x-tt--
Es sei # = sin lemn cp, y = sin lemn <L, 2- = sin lemn (cp -f- cj>)
so hat man
l + xxyy x\J{\ — y<t)
—ixy + y^fi — 3a)y/(i—y*) l — xx — yy—xxyy
J \n£. — *(i+yV(i-**
V zz (l + xxy
(l + xxyy)(xx —
(l—
V v. t
l-\-xxyy
— xx)s/(\—yy)
LEMNISCATISCHE FDNCTIONEN I.
4ÖZ
Die einfachste Manier sin lemn <p in eine Reihe nach Potenzen von <p zu
entwickeln scheint folgende zu sein: man hat
setzt man also
(sin lemn<f)~2 = <f
und folglich
(sinlemn(l+«)(f)-2 = — £i<p(l — 4ct<p4
also
sin lemn <p2 = — 2 t (sin lemn A -j- *) <p)~~2 + (sin lemn <p)~~2
man hat also
hieraus
5ct= 1
3277T]=818aC — 2026e-j-38y£
5
1
2
4875
82875
2
■ 242409375
4
19527421875
223
1
5
1
2
3.5«
3.5«
9.5»
3f.5'
3.57.
>
.13
.13.17
.13.17
4
13*.17.2»
223
1
«5
1
3ȣ
— = 4 , , . = ^
44815433203125 3*.5» 13*.17*.2» 9180
Die Grenze des Verhältnisses zweier aufeinander folgender Glieder ist"
B,6220 . .L:1 =47,27:1
408 ^ NACHLASS.
Sehr nahe ist
92 168 ß 124
BÖJ
i l « l » l 12 l iß l s
= logcp cp cp cp cp cp
ÖT 60 T 4200T 321750* 19890000T 1180968750*
22 24
* # *
1756255921875
i 1 4 i * 8 1 12 i 127 16
= losrcp cp H cp cp -4 cp
&T 10T ' 300T 48751 I 9945000T
20
p
cp Hcp cp -4 cp cp
10T ' 300T 48751 I 9945000T 3453125»
89 24
CP
+ 89 24
CP
1454456250T
Die Coäfficienten a, fi, 7 u. s. f. lassen sich auch vermittelst folgender Glei-
Gleichung bestimmen
Die bequemste Art log cos lemn cp in eine Reihe zu entwickeln ist fol-
gende. Es ist
hieraus ergibt sich
logcoslemn^
6044 26 20824792 30
44890625 iP 527240390625 r
2 5 36 9 . 552 13 , 5136 47 , 5146S48 21
^ -^ +^ +^ +^
1 5 1 9 . 23 J3^ 107 j
4,5,5™ 32.9. 5. P '123.81 .25.7.11.73^ * 2O4S. 24S , 125 . 49 . 11 . 1$ . 17 »
1
8192.729.625.49.11.13.17.19T
LEMNISCATISCHE »DKCTIONEN. I.
= + 2.6220575$
— 2.0656648 fys
— 0.5811918 $9
+ 0.024547 5 <J;13
+ 0.0001890 <j>17
+ 0.0000620 <J>21
=?= +1.2453446 =
ddlogQ
QQ
Die Halbirung geschieht sehr bequem so
cos lern ncp = tangw
sinlemncp = y/cos 2 m
coslemn^) = y/tang-|-D50+w)
sinlemn<f = \/tang-^D50 — u)
sin lemn(<f + »^) = r (cos i? + i sin v)
sin lemn <f2 = tang $
sin lemncp2 = tangW
sin (p + 4)
V^(cos 2 <S> sin 2 *F) — v^(sin 2 <t> cos 2 V)
Es sei
sin lemn J. ^= j?, sin lemn J5 =^, sin lemn l^T_i =
so ist
A4-Oa =
r—y
in. 5,2
410 NACELASS.
sin lemn —H-—
sin lemn A — sin lemn B
. j A-\~B sin lemn A + sin lemn B
pp= QQ—PP, qq= QQ + pp
P(a—b).Q(a + b) = Pa. Qa.^(QbA—P&4)—.
P{a — b). P{a + b) = P«2. Qb2— Qa2. Pb2
Q(a — b).Q(a-\-b) =
« — b).q{a + b) =pa2.Pb2-\-qa2. Qb2
— b).Q(a-\-b) = qa.qb. Qa.Qb—pa.pblPa.Pb
— b).P(a-\-b) = qa.pb.Pa.Qb+pa.qb. Qa.Pb
= Q
= 2PQ\/(Qi — Pi)
= Q4 + P4
= Q4 — 2QQPP—P
3Q8P—6Q4P5—P9
Q9 +6Q5P4—3QP8
—PP).(Q*— 4Q6PP— 6Q4P4—
(Q4+4Q6PP— 6Q4P4-f4QQP6-|-P8)
4).(Q12— 5Q8P4— 5Q4P8+P12)
Q16+20Q12P4—26Q8Ps+20Q4P12 + P16
Q16— SQHPP—12Q12P4— SQ'^^SStfP^S^P10— 12Q4P12
= Qlß-\-$QuPP— 12Q?*PA+SQ?»I»+ZSGP*— 8Q6P10— 12Q4P12
LEMNISCATISGHE FUNCTIONfiN I.
= iPy
= QQ — iPP
i)PQ4 —P5
Q(i + 20?= Q5 —A+20 QP
01" Q16—B0+120P5Q12 —
+ A2
Q(l+40? =
.l)(nn-4)(Wn+75)(|J)
. Pm>12
i)<j> = 0<°—D—Zi)ffPP— B—4J)ß<iP4+D+2»)ß4P6— C+4jH0P8— iP10
52*
412
NACHLASS.
■ nn.nn—l , n.nn—\ .nn—4
==(l-f in)PQnn —
^ 12 ■ 60
n.nn—l. l + in.n— ii -,
60
Unter den Zahlen y = x, 2o?-^—1, 1x-\-i, 2x— 1, 2x— i ist immer we-
wenigstens eine (oder drei oder alle), die die Auflösung der Congruenz \—y4 = zz
nach irgend einem Modulus möglich macht.
sin lemn X =
sinlemnF =
sinlemn^=2
— Ixyz{xx + yy + zz—xxyyzz) + x\J{ 1 —?/*). y/(l — z*). (l —«/j/gz+zzzs+ara^y)
+^A — a:*). \J(\ — z4). (l +Hzz~a:a:zz+:ra;!/2/)
sin lemnfX-f-F-hZ) = wA "~**}' ^(l"^'(l +w»+««-«w)
^ i i / l + 2 j/yzz -J- 2araaz + Ixxyy + j/*z*"+*a24 + #*2/*— 2ar*»/?/ia—2a:a:?/*z2—2xxyyz*
Ist cp-f-<p'~T?" = 0, sin lemn cp = a? cos lemn cp = y
sin lemn cp' = x cos lemncp' = y'
sin lemn cp" = #" cos lemn cp' = y"
so ist
y"
1+4."
5
9
13
17
25
50 <»4
G_ 4i)xs-\
2Si)x8-
125<»8+ 300 xn —
für <3?4 = -f und ^4 = —1
werden diese Functionen respective den Quadraten und Würfeln
von 1 — i —2 —2 — 2i
gleich für M = 5 9 13
17
25
3 5 [aa+b bf—3 3 6 {a-{-bif-\-^Q{aa-\-bb)\.
Qaa+bb—8 p 8
DE CÜRVA LEMNISCATA.
Posito integrali
sinum lemniscaticum ipsius
1.
, a x = 0 usque ad x = s, = cp,
s = sin lemn cd.
dicimus
2.
Valor integralis ab x = 0 usque ad <*? = 1 est = 1.3110287771 4605987
secundum Stirling, qui valor a nobis usque ad figuram undecimam verus in ven-
tus est, utentibus formula: arc sin lemn ^-j- 2 arc sin lemn £ (Edler habet
1.311031). Potestates nuius numeri, cuius duplum semper per öS designabimus,
has invenimus
320.7
1 ..
2 . .
4 . .
5 . .
6 . .
8 . .
9 . .
12 . .
13 . .
. . 1.3110287771
. . 1.7187964545
.. 2.9542612520
. . 3.8731215170
. . 5.0777737656
. . 8.7276595451
. . 11.4422128208
. . 25.7837864151
. . 33.8032859402
4605990680
0509311.7
1927863.4
0712625 4
5251025.3
8251569.0
59
41749
5
414 NACHLASS.
log brigg^es = 0.1176122226 9692.2
log hyp-g-eö = 0.2708121550 7159155410 6425
loghypsj =0.9639593356 3153686352 36577
Sinum lemniscaticum ipsius D-es— a) cosinum lemniscaticum ipsius a
dicemus.
3.
Aequationis
integrale completum invenitur hoc
A — xx
x\J — -4- W
i + yy
i+xx
,1 22 1 Vtl
l—arj/v7—
l + xx l + yy
Sed eiusdem aequat. integrale est
arc sin lemn<2?-f-arc sin lemny = c
unde sequitur C esse functionem ipsius c. Ut appareat qualis, ponamus y =. 0,
turn fit C=x, c = arc sin lemn #, quare erit c = arc sin lemn C, sive
C = sin lemn c. Hinc si sin lemnj» = ce, sin lemn q = y, erit
1 — XX 1
sin lemn (p-\-q) =
Hinc posito p = %m, q — —a, fit propter
sin lemn (— a) = — sin lemn a, sin lemn^- öj = .1
1 / l— sin lemno*
cos lemn a = y
v
Forma autem praecedens transit in hanc
LEMNISCATJSCHE PDNCTIONEN H. 415
■■ / ! \ sin lemn » cos lemn o 4-sin lemn o cos lemn «
sin lemn (p -f- q) = _ . , . . -,— ,——
K* -!— *' l + sm lemn j» sm lemn q cos lemn^p cos lemn q
1 / _» \ cos lemn^j cos lemnq + sin lemnp sin lemnq
\* H. "/ t -+- sin lemn^) sin lemnj cos lemn^j cos lemny
[Spätere Bemerkung:]
I. a-j-ö-j-y = 180° [= es]
Setzt
sin lemn a = tang a, cos lemn a = cos A
sin lemn ^ = taug b, cos lemn tf =■ cos B
sin lemn y = tang c, cos lemn y = cos C
so sind ös, b, c, A, B, C Seiten und Winkel eines sphärischen Dreiecks, wo
sinA sini? sinC ,
sin a sin b sin c V
II. ct-f ö-f-y = 90° [= -J-UI]
Setzt
sin lemn a = cos a, cos lemn a = — tang A
sin lemn ?> = cos b, cos lemn ö = — tang 5
sin lemn 7 = cos c, cos lemn 7 — — tang C
so sind wieder a, b, c, A, B, C Seiten und Winkel eines sphärischen Dreiecks,
in welchem
sin.5 sinC /t
sinJ sine » 2
Si valores s [= sin — <p], qui reddunt ipsum sin lemn cp = 0 seeundum
regulas notas productum infinitum generare concipiuntur, nee non valores ipsius
s, qui reddunt ipsum sin lemn<p = 00, quorum primum sit P<p, seeundum Q<p,
permissum erit (id quod rigorose demonstrare possumus) ponere
sin lemn <p = ^f
erit vero
4 8-6
4 S S
4 S S
4SS \ /. 4SS \ /. 4SS
a =
Simili modo positis
r . 4SS \ / .
1— (Z7V ■ -»^«)A
4 SS
4SS
erit
cos lemn <p = —
[5.]
[werden die an einem andern Orte untersuchten Reihen Seite 405 d. B.
resp. mit $<p, £)<f, ^<f, q<f bezeichnet, so ist:]
LEMNISCATISCHE FÜNCTIONEN. II. 4:13
[«•]
Ex expressionibus supra allatis sequittir
sin lemn co =
-*"
+ etc.
cos lemn <p =
Hinc vero sequitur
/ u. / ja \2 cos 2 © . / w. \s cos 3 ©
= 2 I^ cosyC) 5 +( )
log Q ty es = — -J- log 2 4- A^
logJPcpcs = 4-log 2—i
— ^COS2(j^- *JIn?ZTCOS4<J;TU —^^^COSÖ^TU— ..
cos 2
= ilog2—-^ic-J-log cos^ic
g
log sin lemn epcö = log2 — -j^-f-log sin<|>tu
in. 53
418
= —0.0847742372 7
-j-0,0865895371 57
— 0.0018674144 52
+ 0.0000537996 86 cos6^tc
— 17436 71 cos8(^tc
-f- 602 81
— 21 71
-j- 81 COS14^TC
— 3
logP^es =
— 0.1770251853 2
— 0.0037418731 98 cos2^tu
— 34873 54 cos4<J;tc
— 43 42 cos6<J;7u
— 6 ^
[8.]
sinlemncLos = j»***— m
4-Tt -1t , -4Tt
ll2e 00824"^+ 2«
i/- = 0.9135791381 5611682140 724259
2*~i7: = 0.911 &762555 3199247S53 1842589456 058838833
2e~~^ = 0.0017028766 8561031607 1704906
2^~¥7r= ." 59 3851399312 9644497731 18
«~V* = 3867 4050599*
LEMNTSCATISCHE PDNOTIONEN. U. 419
0.0864278365 2754449954 8835474343 4560225514
0.0000069746 8471241799 0983550387 96535
105109703 5201288
295807
[9.]
sin lemn <b 55 ui
- 4 (e~ilz — e~l(yK-\- e~1S7: — . . .) sin 3 ty tc
[10].
sin lemn <}/öS = tangwrc
tz du = cscoslemnc}>ös.d^
cos lemn ty ® = ^ \
+ e 2 «* -j-e
1
p
1 -j- 1p cos cp -f- Ipp cos 2 cp -j- . . . = -—
\-p — 2CO8Cp
1 2 p COS <p -f- 2 J9J9 COS 2 <p . . . = -—-
1
—p
(
^) cos <p +j» cos 3 <p + . . . = —
2 sin <L tz , ^, om Y ,.
7c = arc tang — — arc tane — *—.
° iir -*7c c' «t — \
e —6 e —6
(— -\-pJ—4 coscp*
P
. 2sin«p
. . = are tang ——*—
53
[11.]
*
2* cos|-it
J
2* sin |-n:
,71 7T
v— v—
E_ 7? — ro
, -D — —
2 cosf tz 2
0.3522376226 6118372314 = A
0.3535519576 3585935635 =
0.0013155679 2352259042 — 2Ae 2?
0.0000012329 5741446398 = iBe~^
0856752170 =
1494 =
[12.]
Variae* Summationes serierum absconditae.
i
i-
U2«+Ä2wJ
i r 2 "i2
r 2 -18 r 2 -12 ■ _,,!
''' T
2-|2
kO 2.2. ,55
5 \- . . . = ■*- —
*7c , -4-7T' ' fit + e—|tt ' ^ tt
6°
LEMNISCATISCHE FÜNCTIOKEN H.
4Stl
[13.]
Rechnungen zur Lemniscata gehörig.
sin lemn-$• esJ j2 = \A\Jh — 30
j (sin lemn f(ö
j(sinlemnfcsJ — (sin lemn-f-esJJ = 10^/5 — 22
4- (sin lemn % csL+ \ (sin lemn i esL = 6 \J 5 —13
= 0.4164078649 9873817845 5042012387
(sin lernn-f-esL—i(sin lemnf ffiLj4 = 340 — 152^5
daraus Radix
also
(sin lemni®L
(sin lemn-|03L
(sin lemn^esJ
(sin lemn-l-eöJ
65741
=0.1176674200 3196614580 5602352846 01228
0.3430268503 0761971797 7310507555 85731
= 0.0733810146 9111846047 7731504831 80010
= 0.7594347153 0635789643 2352519943 51472
= 0.2708893033 8999814497 30710
= 0.8714555153 9155336074 646029
[14.]
Lemniscatische Function.
/dx
v/(i—**)
Es verhalte sich 1 x
wie /> ^
und 1 X
wie P Q
\/(l— xx)
r
8
so verhalten sich die
entsprechenden Grossen
NACHLASS.
wie ppPP-\-qqQQ
oder pqRS— rsPQ
oder prPR-\-qsQS
oder psPS—qrQR
pqRS-\-rsPQ
qqPP—ppQQ
qrPS+psQR
qsRR+prQS
prPR — qsQS
qrPS—psQR
ppRR—qqSS
rrPP—ssQQ
rsRS—2pqPQ
psPS-\-qrQR
qsPR—prQS
2pqPQ+rsRS
ssPP+rrQQ
=ppSS+qqRR
Es sei
sin lemn X. = ao
sin lemn Y' = y
sin lemn Z = #
und X, F, i/ so von einander abhängig, dass
= 0
Man setze JxocaX = FX
und FX+FY+FZ = u
Aus früher vorgekommenen Formeln folgt
xx—zz = yz^(l — x*) —xy\J(\ —
yy—zz = xz\J(l— /)— xy\j{\—
Aus
xxdx
zzdz
o —
v/(i—y*)
. i
folgt
== d.xyz
LEMNISCATISCHB FBNCTIONEN. II.
42$
also
u = xyz
Es ist folglich
F(a -f- b) = -Fös —j—J^6—sin lemn a. sin lemn b. sin lemn (a-f-b)
Setzt man
^ = Ga
so ist
G(a-\-b) = Ga-\-Gb — sin lemn a. sin lemn b. sin lemn (a+2>)
- dQa
~ Qa.da
[15.]
05 . _I i_l! * i 1-3.5.7 1 _, 1.3.5.7.9. 11 1 ^, v /2
71 ^ ' 4.4* 9 ' 4.4.8.8*81 ' 4.4.S.S.12.12* 7Ü ' * */ V 3
Ö 2 /1 l , 1.3.5 1 ,1.3.5.7.» 1 _, 1.3.5.7 . 9.11.13 1 , \ /
it Ö5 ^ 4 ' 3 "'4.4.8* 27 '4.4.8.8.12 ' 243 ' 4. 4 . 8 . 8 .12 .12 .16 ' 2187 ' ' '* »
erit
Ponendo
M(l,coscp)
[16.]
= -ZV—J— a cos 2 <p -{- i cos 4 cp -f-
= 1.393203
= 0.581803
= 0.309601
= 0.209449
= 0.157960
= 0.126704
— cos 2 9) = -f-0.220635
+ 0.636620 cos2<p
+ 0.318310 cos4<p
+ 0.2122Q7 COS69
+ 0.159155 cos8cp
.127324 coslO«p
424 „ NACHEASS.
3.3.7.7.11 .11.15
/3.3.7.7.11 .11.15 ya <) &&
^2.4.6.8.10.12.14 * * *' Ü7T
5-5 9-9 13.13 x2 4
i/5-
8.10 ' 12.14 ' * '^ 53ö5
4.
5.
3
2
6
5
.S.
.9.
4
S
10.
9.
7
6
12.
13.
$
9
14
13 "
11
10
12
13 ' *
[17.]
Demonstratio. Ponatur
eritque, posito x(x*—l)~ — (Zx*— 1)^+«»/ = 12, 12 = 0
Hinc etiam
0=^^ + 12; necnon o
unde fit, evolutione facta
0 = ^(
sive ponendo tt = u
cui aequationi invenitur respondere
LEMNISCATI3CHJ5 FUNCTIONEN. II.
Iam quum
z = 0 usque ad 2; = 1, fit, pro oß = 1,
71 2 7t V
adeoque
Valor seriei
fit
4 /y d<pd^
T.TiJJ y/(i — cosy'cos^*
a <f = 0 usque ad <p = 90° et a <); — 0 usque ad ^ = 90°. Faciendo itaque
cos cp cos 4» = cos 0, idem valor fit
_ _L ff
d<pdo
19* — cos«*)
et quidem ab ü = ö usque ad o = 90° et a 9 = 0 usque ad <p = 0. Deni-
que statuendo 9 + 0 =/> ° — 9 =#> erit expressio nostra
_2_ /»/» d/. d;
TtTt«A/ t/sinfsi
ab ^ = 0 usque ad # = 90° et a f = g usque ad /= 180°—^r. Sed haud
difficulter probatur integrale eundem valorem nancisci, si sumatur ab f = 0 us-
usque ad /= 90° et a g = 0 usque ad ^ =r 90°, unde ipsius valor deducitur
= 2 —
7t IC
uti supra.
hl 54
[17.]
Sammlung von Rechnungen,
vornehmlich solchen, bei denen von meinen Methoden, die Factoren grosser
Zahlen zu finden, und von den WoLPBAMschen Logarithmentafeln Gebrauch ge-
gemacht ist.
Erste Rechnung für e~rL = A
Durch eine vorläufige Näherung war schon bekannt, dass A bis auf die
14te Figur 0,0432139182 6377 sei, folglich ll.lO10^. sehr genau 4753531008
= 128*243.152827. Es fragte sich also, ob die Zahl 152827 sich noch in ein-
einfache Factoren zerlegen lasse.
Die Division mit kleinen Primzahlen gelang nicht; man musste also zu
künstlichen Methoden seine Zuflucht nehmen. Hier fand sich nun, indem man
die Zahl selbst sowohl als verschiedene ihrer Vielfache mit den nächsten Quadra-
ten verglich, unter andern, dass
2 6772=152 mod. 1 52827
woraus man sogleich schloss, dass
11042=3800, 33853 = 3800
und mithin die Zahl 152827 keine Primzahl sei, weil sonst die Quadrate zweier
Zahlen, die beide kleiner als die Hälfte von jener sind, unmöglich congruent
sein könnten (Disqu. Arr. art. .). Durch die in diesem Werke gelehrte Me-
Methode (art ) fanden sich nun die Factoren der Zahl 152827, nemlich 67.2281.
Man war also gewiss, dass sich der hyperbolische Logarithme von
N= 128.243.67.2281.H^.IO0
aus den vorhandenen Tafeln bestimmen lasse und zugleich dass derselbe von dem
gegebenen Logarithmen, —7c, nur in der 10ten Decimalstelle abweichen könne.
Die zu dieser Differenz gehörige Absolutzahl brauchte also blos berechnet und
mit N multiplicirt zu werden, um A zu erhalten,
— Iog2281— \Qg21i4 — Iog972 — ~ __
LEMNISCATISCH? PÜ^CTIONEN. II.
Durch die WoLPSAMsche Tafel war; - . v
[Zur Abkürzung g—logA -j-21 35.10~13) =' S'i' 8 — -log(l +1443.10~17)= ^"gesetzt.]
10 log 10
= 23,0258509299 4045684017 9914546843 6420760110 14886288.
logll = 2,3978952727 983.7054406 1943577965 1292998217 06853937
25,4237462027 3882738424 1858124808 7713758327 21740225
1.2281= 7,7323692222 8438803081 0466064812 2168095619 53159812
1.2144= 7,6704285221 9069260675 6232603654 6055909444 33,575023
1.972= 6,8793558044 6043907581 0690427528 9816593884 53057834
tc= 3,1415926535 8979323846 2643383279 5028841971 69399375
25,4237462025 2531295184 0032479275 3069440920 09192044
$= 0, 2 1351443240 1825645533 4644317407 12548181
£'= 0 1443242 4616770530 2204949495 65316893
£"= 0 .* 242 4616770634 3329449495 6431533124
-£-£"£"= 0 29393 8324222063
/'= .1, 242 4616770634 3329478889 4755755187
/== 1 1443242 4616770634 3679351089 4781097632
el = 1 2 1351443242 4619851957 0236156393 853651221t
11-4 = 0,4753531009 0149474751 8595108889 008*240330 0920791693 5
A = 0,0432139182 6377224977 4417737171 7280112757 2810981063
Um sich von der Richtigkeit dieses Resultats durch eine zweite Rechnung
zu versichern, multiplicirte man die Zahl A durch 599.108, wodurch sich ergab
2588513703,999957.., so dass man also eine sehr leichte Rechnung übrig hatte,
wenn die Zahl 2588513704 sich in Factoren kleiner als 10000 zerlegen Hess.
Nach angestelltem Versuch fand sich 2588513704 = 8.7.17.2719027. Es kam
also darauf an, ob 2719027 eine Primzahl sei. Man fand, dass —1848 gewiss
ein quadratischer Rest von 2719027 sein müsse, wenn diese Zahl eine Primzahl
sei, und dass sie in diesem Fall einmal unter der Form %xx-\- 616yy enthalten
sein müsse und umgekehrt, dass sie durch diese Form entweder gar nicht oder
mehr als einmal müsse dargestellt werden können, wenn sie zusammengesetzt sei.
Allein die Exclusionsmethode lehrte, dass jene Zahl wirklich nur einmal unter
der Form Zxx-\- 616yy enthalten sei, nemlich 2719027 = 3 1972-f-616.652,
54*
&$ " * KACHODASS.
woraus also mit Gewissheit folgte, dass 2719027 eine Primzahl und folglich die
versuchte Methode diesmal nicht anwendbar sei.
Nach einigen andern vergeblichen Versuchen kam man endlich auf folgen-
folgenden, der besser gelang. Die Zahl A multiplicirt mit 1014 gab 4321391826377,25
und die Zahl 4321391826375 zerfiel in die Factoren 125.81.13.32831087. Dass
die Zahl 32831087 keine Primzahl sei, folgte daraus, dass sie nicht unter der
Form xx-\- 190yy enthalten war; man wandte also die erste der in den Disqui.
Arr. gelehrten Methoden darauf an, wodurch sich entdeckte, dass sie das Pro-
duct aus 373.8819 sei.
Zweite Rechnung filr e K — A
59.109J. fand sich sehr genau '== 2549621178 = 54.13.3631939. Die Zahl
3631939 zerfiel in die Factoren 1091.3329 (welche aus
3631939 = 40.2322-j-19.2792 = 40.3002+1 9.412
gefunden waren). Also
59-4. = ?02 109t 3329 10-9^1ogl0+log59-log702-logl091-log3329-^ = ^
Aus Wolframs Tafel fand sich [S—log(l —17157.10~14) = 8\ ^ff-f-fcS^e gesetzt]
C9l.lO= 21,2767341630 5358884383 8076907840 7221315900 86602341
C.l. 59= 5,9224625560 9428054938 3949626280 3023759366 53210670
1.702= 6,5539334040 2581111965 6455273791 0722868232 39752589
1.1091= 6,9948499858 3307081851 1895817110 3840806982 08318537
1.3329= 8,1104272375 7502494295 2021653586 1576658324 67001597
tu= 3,1415926535 8979323846 2643383279 5028841971 69399375
— £= 0 1 7156951280 5042661888 1414250778 24285109
8'= 0 48720 9675470563 5420349120 2333831382
e= 0, 1186866339 3606594227
/= 1 48720 9675470563 6607215459 5940425609
1—eä= 0 1 7156951279 0324613026 9032989386 4786573955
59^.= 2,5496211775 6256273669 0646493131 9526652679 5847882752 6
A= 0,0432139182 6377224077 4417737171 7280112757 2810981063 6
LEMNISCATISCHE FCTNCTIONEN. U.
Zugleich kann man aus der Übereinstimmung beider Rechnungen schliessen,
dass die Logarithmen von 2, 3, 5, 11, 13, 59, 67, 1091, 2281, 3329 in der
WoLFEAMschen Tafel bis auf die letzte Figur richtig sind.
Doppelte Berechnung von e~~** = A.
Erste Rechnung.
Da man durch eine schon vorher angestellte Rechnung wusste, dass der
Werth von A bis auf die letzte Zifer =0,4559381277 6599 sei, so war
19.131.A oder 2489^.= 1134,8300000095oder 248900^. sehrgenau =113483.
Man fand 113483 = 283.401 aus
113483 = 3112_|-58.172 = 792+58.432
und hiemit
2489 A = 113483 10~2 ^log10-log283-log401 + log2489-i. = ^
Aus Wolframs Tafeln erhielt man
[wenn zur Abkürzung
g_log(l-}- 8428.10~15) = h'
gesetzt wird]:
$= 0 842825208 2107272461 7421888198 29069513
S' = 0 25208 2142788053 7419892695 5615344103
•£.S'S'= 317727033 5630835760
1-S« = 267
e* = 1 25208 214278S053 7737619729 1246180130
e6 = 1 842825208 2142790178 3220613906 2965706721
2489^1
=1134,8300000095 6463331037 8102578065 2249279282 5372958193
A = 0,4559381277 6599623676 5921294728 0294194166 04366
'Zweite Rechnung für e~** ■== A
113A wurde gefunden 51,52100843755. Die Zahl 515210084852 zer-
zerfiel in die Factoren 27.131072.145583. Endlich erhielt man aus
4.145583 = 4373+163.492 = 7632+163
145583 = 197.739 mithin
[und wenn 6— log(l+4576.10~15) = B' gesetzt wird]
B = 0 4575948387 0747214839 8399455217 14190720
— B' = 0 51612 8205796360 1919946163 4337976121
-f-i-S'#=: 0, 1331941624 0928492341
1 — /== 0 51612 8205796360 0588004539 3409483780
eh= 1 4575978387 1794180021 9145023046 2961445343
113^=51,5210084375 5757475454 9106304267 3243940900 3220627240 5
A= 0,4559381277 6599623676 5921294728 0294194166 0436523820
e~~*% ;= 0,4559382 =? 367 1.54.23.10
Dritte Rechnung für e~T% = A.
455938128 = 144.3166237 Die Divisoren der Zahl 3166237 fand man,
indem man die Periode der reducirten Form A, 1779, —1396) entwickelte, in
welcher die Form (—1897, 530, 1521)-die sechste war. Hieraus
A1 + 28.1779)* =E 1521 = 392, und 3166237 = 107.127.233
A = 455938128.l0-9^9logl0-ilt-log45593Sl2S = Ne*
[und B — log(l— 513.10~12) = 8' gesetzt]:
— B = 0 5 1323578556 7221212746 8124092623 9185579000
— S'=0, 23578543 5636712701 8105102450 7737514264
'= 27797 3858291971 9406911797
— -fg'8 = 21 8473957577
1 — / = 0 23578543 5636684904 4246810500 6804560044
1 — e} = 0, 5 1323578543 5515726975 9430616940 9818422176
LEMNISCATISOBE FÜ2JCTIONJSN n. $31'
Berechnung von e~xlz = A.
Durch Näherung war bereits gefunden A = 0,0008514383 42805. Nun
fand sich 8514383436 = 4.9.1 3.19.307.3119, mithin sehr genau. - . .
A = 4.9.t3.19.307.31J9..10~ls
aus Wolfbams Tafel
13loglO— Iog3119— log 1842— log 1482— fw = 3
[und
S — log(l —9335.10~13) = £', S'— log(l— 285.10-") = S"
gesetzt]:
— £ = 0 9 3352850560 8342583868 5326823995 3184946898 8
— B' = 0 2850517 2631458732 9539039720 5781872612 0
— S" = 0, 517 2631458326 8289039720 5396053412 0
4-£"£" = 0, 133780 5810183616 8
1 —/" = 0, 517 2631458326 8288905939 9585869795 2
1 — / = 0, ...2850517 2631458326 6814705974 3354407457 0
1 —/ =0 9 3352850517 2604848748 03000424947639127186 6
A = 0,0008514383 4280515803 5852453295 4846487994 1872486024
8176915
e~l'sz satis exacte =. 4.11.13.29.3593.7~1.10~10
Ecce iam computum pro eiiz.
Per logarithmos brigg. invenimus praeter propter e*K = 4,810484.
Est vero 48104847 = 2293.37.7.81 et
Iog81.259.2293+7 log 10 + 4-ic
= —0 15214 7666454820 0537824776 3190
numlog= 1 — 0 15214 7550690316 7468363738 6798
eilz-= 4,8104773809 6535165547 3044648993 1536
. Computus secundus pro e*%~
Invenimus 481047 7 3 SOS = 19 549 7.133.7. 1 ß superest itaque ut utrum sit
195497 numerus non primiLS investigetur. Tentamus itaque aequaüonem
195497 =
Lim.» =111, Excl. valores x =
195497 = 442+193561 = 762-f-189721 = 3562 + 68761 = 3642-{-63001
= 3642H-25l2 quare 195497 est prim.
VsW — 3 + t+4^+^f = 4,8104773824 4 . .
1 1 ö ö
TT—-f-T^ = —0,... 3 0703542806 9410475204 9155
5 • 5 oö1
numlog=l — 0 3 0703542802 2275098164 7660
Computus pro e~~^
e~^ praeter propter = 0,20787957 = 7151.19.17.9.10""8
Iog5t.57.7151
= —0, 305 5019697961 8740193606 8277
numlog^=l —0 305 5019651296 1477199011 4138
Investigatio divisorum numeri 2078795763 = 99.20997937,005
20997937 = 1848.342-f-43432 numerus primus
Computus secundus pro «"*"
ll.e~ilz = 2,286675339858378
228667536 = 81.16.176441
176441 = 880<2?<r-j-y# = 73,2417
H.»4»+8l°g10-**
= — 0 88 0825474705 3269478285 7110
Hll
VARIA IMPBIMIS DE INTEGRALI
du
7C ZCOSÜ _ 7T 7CCOS» t
: PH /g
l v Msin»
£6@=: ±-\ ?**** , 4rin8** U. .1
I LJLÖ5 I 05 {S Qj' Qj' ' I
I Q3 ■ QJ fl5 i flj I
6 -J- 6 fi -|- 6 J
H^cLqs = v/Mcosv. [_1 —1— ^ ro 2cos2cpTc-J-e ro
= \Jcotgv.\JMcosv. \_e
r —i— t: — i— n i
. \_e ro 2sin^n; — e ro 2 sin3<J;TC-f- . J
2 — w —2— ic 3 — ic —3—7t
o ® ^^ >> 05 05 (D
m' s' cy
r. —4—r — 4— r.
Terminus constans
e
tz —4 — ir
55
434 nachlass.
Problema. Summare seriem
XX ^ X8 XiS T X3*
05'
2 sin*»
r — * —7t i»05 u
05'
cos6c|;tc+ . .
^ ro'^ 9ö5'7t 25S5'7t
V sin *
Si
supponitur producere
producet
7) ••• = *•
ZUR THEORIE DER NEUEN TRANSSCENDENTEN. I.
Si ex quadrato prodit
erit
* ' x* aa ' xx a
• i"f n rt ' <r rr n ' nur. ' !T.!r. '
2 — 1t —2—
x = e ro
\-x**a*) . . . A—~)(i —~)A —^5 )
' x a2/v aa/ a*
aa aa aa
>)* . . .
Observatio
Med. inter 1 et y/ 2 — 1
Med. inter l etv/Bv/2
1-21 = <J*
Msin756 /
M sin 15° V
55*
tu.]
ZUR THEORIE DER TRANSSCENDENTEN FÜNCTIONEN GEHÖRIG.
L J
Es sei 2^""a(*"^)8 = T% indem für k alle ganzen positiven und negativen
Zahlen gesetzt werden, und
T = ^L+2Bcos(üP+2Ccos2(oP+2Deos3(oP+ etc.
so ist
A==fTdo>, B =/jTcos(üP.dü>, C = /rcos2<oP.d«>,
D =/Tcos3(üP.d(o, u.s.w.
alle Integrale von u> = 0 bis <o == 1 ausgedehnt. Es ist aber klar, dass jene
Integrale zwischen diesen Grenzen mit den Integralen
jy-atmöd(o, yV-aüKöcos(oP.d(o, JV-aüKöcos2(oP.d(o, fe~aCi<ocos3o>P.do>, etc.
übereinkommen, wenn diese von <o = — oo bis to = -j-°° ausgedehnt wer-
werden. Da nun allgemein
cos ntuP
. — ctoaoo+iwroP , . —atooi—inmP . 4a )
nnPP, . um. ,
/ —a(oo ]
e 2a
ZUR THEORIE DER NEUEN TRANSSCENDENTEN. II.
so folgt leicht, dass
nmz-
lw = « a \J —
V et
folglich
T = \J-.\\-\-1e a cos<oP-f-2e a cos2<oP-{-2e a cos3ct>P-j- etc.
In einer andern Form so ;
TtZ —4^ -WS:
. 2 € a
Allgemeiner:
— \] — .2e a
Oder, aa' = uit und —aty = w'^ gesetzt,
cos B^ + 2(o)(ü'tc — isin B^ + 2 (o) w
= \/-.Sra'(^4 jcos 2 kiöiz— »sin 2
9 —
a sin3(oP-}- etc.
Man kann den Lehrsatz auch so ausdrücken:
ändert den Werth nicht, wenn t in \ und m in —u verwandelt wird.
t
[2-]
Man setze
xtn.l—x»*1 ■ ar»".! — aw+1.t x .
T etC-
= P— Q
' XACHfcASS.
Man suche zuerst diese Differenz, indem man das erste, zweite, dritte Glied
n. s. w. der Reihe Q von dem ersten, zweiten, dritten Gliede der Reihe P ab-
abzieht, so kommt
■n _J ■ s*. 1—g» . xzn.\ — xn. \-xn+± . x3n.t — xn.t — x%+1.i—xn+s
l + xn ' l + x>l.l + xn+t~T~ \ + xn.l + xn+\\ + xn+s ' 1-f «".l+a"*.!+**•+«. 1+ 3"+« • etC*
1-f «".
Wir bezeichnen diese Reihe durch 9 (#,»}.
Man suche ferner jene Differenz JR, indem man das erste, zweite, dritte
Glied u. s. w. der Reihe Q von dem zweiten, dritten, vierten u. s. w. der Reihe
P abzieht, so wird
■n x2n+± xan+2. l — :rn+1 xm+s.i—xn+i.l — xn+2
oder offenbar
folglich
Dieser Schluss ist allgemein, so lange w^>l, man hat demnach unter die-
dieser Einschränkung
9 (*.*)= 1—<»3w+1-f-^4w+4 —<»6w+94-<»8w+16— etc.
hingegen ist für den Fall n = 0 das letzte Glied von Q nicht als verschwin-
verschwindend zu betrachten. Setzt man es = T, so wird der erste Werth von R um
T kleiner sein als der zweite, also
T= 1 —a?9(a?,l) —9(#,0)
oder
9(a?,0) — 1—.a?cp(a?, 1) — T = 1 — x+rf—aP+x16 — . . —T
also da
9 {x, 0) = £
und
rt/t» ! —« l—xx l — a;3 l — #* ,
so wird*
ZUR THEORIE DER NECEN TEANSSCENDENTEN. II.
.i=f! etc. = 1 — 2<a?-l-2<a?4—2<r4-2<a?16— etc
der erste Theil ist hier
— 1 __ r 1 — i?3 1 — i?5 1 — r7 etc
— «—oß.i — jc .i jc . l «3? etc.
'"** i=
• 1+ira.'1+x3 etc.
= A— ar)*(l — xx){Y — rff{\— ^{X—tfYiX—x6) etc.
Bezeichnen wir noch
1 —2#-l-2<a?4— 2j?9+2,3?16etc. mit
so wird offenbar
[3.]
Zieht man auf ähnliche Weise von der Reihe
die Reihe
a*l x"*g x2"!J^+Slgw+a . g3M.l — g**g.l — j^+*.l — a^6 .
ab, so erhält man einmal
1—x" , a*.l—a*. t — a^+2 _, xsn. t — a*.l— tf1** . \—
und zweitens
Man hat also, den Fall n — 0 ausgenommen,
folglich
- etc.
dagegen hat man für den Fall n = 0
&(#,0) = l-f-^ + ^3^^, 2)—l~x '^^»tZ^ e*c*
440
folglich
*'\ZC'"- = l + *-f *3"M6-f *10-f etc.
1 — X. 1 X*. 1 X* . . .
Wir bezeichnen
1—x.l— xx.1 — xz etc. mit [x]
so ist:
. , , 3 , 6 i j. 1 — xx. i. — xx.X — x6 . . . [xxY
1 -\-x-\-x -\-xb-\- etc. = ä s = L-r~
1111 l — x . 1—#. l — a;5 . . . [a;]
1—^*1 — XX. \ — X3
[*][**]
)(|
etc. =
[xf = \ — %o)-\-bx!i — 7x6-\-$x10— etc
folgt leicht aus
±)»»_y_^)«»+ etc.}
wenn man ^ = 1-J-eo setzt und daraus die Bedingungsgleichungen bildet.
ZUR THEORIE DER 22EUEN TRANSSCENDENTEN. H.
[5.]
Zu den Hauptsätzen in dieser Theorie gehört folgendes Theorem.
Bezeichnet man
Po 2äPa 49Pa 12lP<x 16«Pa
[e^-e^-e ^+e *r + * *+..}.Va durch
so ist
Diese Function ist ein Maximum für a = 1, wo ihr Werth
= 0,7682255 = 4 = fo.^*
^2.^1,19814.. *
ferner ist
oder [a] = -j-^
logx
_
Es sei
so ist
P P 1 Sa
a]e 2i
[6-]
Die Siebentheilung führt auf folgende Gleichung
» rl — 2x+ 2a:*— . .-&
Ll + 2ar + 2Ä*+ . J
A —
Ll+2ar +2ar*4- . J
iu. 56
. i{ , 16-32Ü /5 30 Aj , 32— 64&& j3 20 -j- 768 && — 768&*
343 ' 2401 16807
, 48—2144ÄÄ + 6144Ä*—4096. b*i 1
' 823543 T 823543
,3 20Äe+788Ä4—768 Ä2 T?2
49 34
_, 48Ä7—2144 &s-f 6144 &3—4096Ä tj 1 ~
_| 823543 823543
Wenn man in der ersten Gleichung statt bb, 1 — bb und statt A, — A
setzt, so wird sie nicht geändert.
[7-]
Für die Dreitheilung hat man
a b \ = t
A B -A = T
T3(*)T* = 0
oder
(T—tf= U>(t—t*){T—Tz)
A^ 3t — ts+T(l— Ztt)
T 3[jT(i—tt) + t{\.—TT)~\
Setzt man T = tangiV, t = tangw, so ist
3 sin B N— 2 nf = 4 sin (iV-f 3 n). sin C N-\- n)
sin(iV^—wL = sin 4 n. sin 4 JV
Esinn 2sin(iV+3») sinB.ZV—in)
acosN bsiaN 3sinBiV—2»)
[8.]
Zum Beweise der schönen Lehrsätze der Reciprocität wird folgendes dienen
I. Das Product aus allen
ist das Product aus allen
ZUR THEOSIE DEK NEUEN TRANSSCEMDENTEN. IL
I in,
also
. JV-YJ
a
. 2V
sin — it
— t>
a
1-
2 (N 7) ) _
-e a
— — n«
— ^ a
2j
1 6
2-
a
—itt
i-e
II. Sollen aber blos für k die ungeraden Zahlen gesetzt werden, so ist
jenes Product
2 2a i + e a Ta
N tz ~~ * ' N . — * N .
cos— — ——it t —it t
«2 i+e a
Setzt man also N = k'a', so wird der Werth jenes Products, wenn man
a'r.i Tjiti
c -^^— oo unci c — u
setzt,
folglich das Product aus allen Werthen für k' alle ungeraden Zahlen gesetzt
Es seien m, n zwei beliebige, positive reelle Grossen und X reell oder
imaginär, man setze
so ist das Product aus allen
für k und # alle ungeraden ganzen Zahlen gesetzt, obigem zu Folge
56*
v '«" [arafj*
Offenbar ist aber obiges Product auch, das Product aus allen
kmi + k'n
also, wenn man
n \ .
IC —TZt
e m =*', em =
setzt, so ist jenes Product
folglich diese beiden Ausdrücke einander gleich, oder
-. i + a*y.i+ —. .. l + x'y'. 1 +-,.
\-\-x . l+ar.i + a:3 . 1 + ar3... 1 + ar' . l + a:'. 1 + a:'3 . 1 + a:'3 . . .
Diese Schlüsse bedürfen einer Verbesserung (alle geradezu noch einen con-
stanten Theil im Nenner).
[9.]
x-\- 4xa--\- 9a^ + l6a:16+ . . x Ixx _, 3 a;8 y
. . T^x~x T^x1 ' 1 — x* ' * *
* I ** | *" I IT
also
+) +
I. aus der Differentiation des Logarithmen des Ausdrucks durchs Product.
Wird I. entwickelt in
x-\- xz -j- o? + x1 + . . .
und die verticalen Reihen einzeln summirt, so entsteht II.
ZDE THEOEIE DES NEUEN TRANSSCENDENTEN. H.
—20!*+. .L ==
+
Die Reihen
p= 1+2^ + 2^+etc., ± = t
q=l—2<» + 2<»4— etc., — = u
werden durch Differentialgleichungen am einfachsten auf folgende Art ausge
drückt
X&t .; Xdt' .// X&t" .;
da; ' da; ' da;
a;d« / xdu' » x&u" ,
u u u
[in.]
[ZUR THEORIE DER NEUEN TRANSSCENDENTEN.]
Die Theoreme in Beziehung auf diejenigen Reihen und unendlichen Pro-
ducte, welche zu der Theorie der Arithmetisch Geometrischen Mittel gehören,
ordnen wir so:
11 _ w 1 - np np 1 —. *¥$ 1 __ ^ . r^i
2. l + ^.l-J-^^.l + ^.l + ^4 . . . = ^
3. 1—x.l — x* . 1 — x5. 1 — <»7 . . . = =W=
4. 1 + a?. l + <»3 . l + <»5. 1 + A?7 . . . = jft^r
Pv f <m —> <- -I
6. 1 +<»y. \-\-x*y. 1 +*5y . . . l-f-^.1 + oc*y~l. \
evolvitur in seriem
7 also F^? — (t-*)*^—*)'(i-^)'... _ M
. cuäu x-«* _ 12 + 2.29+ — ^
ZUR THEORIE DER NEUEN TBANSSCENDENTEN. IH. . 44:7
yp t + xx . 1 + a;* . l + a?t0 ... [#*]* *
9. ' [xx] Fx = [xs] Fx* = [x*2] Fx16 = [x™] Fx<* = etc. =
10. 1 * jH 1~X\iXZ\ZXl
44- _ [«]' _ l+ar.l-arar.l+a;«.!-^..
Andere Beweise dieser Sätze.
Wenn man in 6 statt y, xy schreibt, so wird
+xhyy. l-\-x6yy . . . \-\-xxy~2.
oder
12. y + i.l + ^^yy.l+^Vy-t+^Vy • • • l+xxy-*A+x^y-2A-\-x6y
[xx]x*
Anderer Beweis
oder
14.
15.
16.
17.
18.
19.
Anderer Beweis
(!-»•+«••
(l+2»+2**
(I + S- + J*1
Anwendung auf arithm. gepm. Mittel.
20. a =
a"
etc. etc.
c = \][aa — bb)
c = ^ad - KV) = i(— i) = £ = ^, v
c" = v/(O»a"-i» J") = *(rf-y) = ^
^(bb ) ±(b)
c ^
etc. etc.
=7^1^] W etc'
Setzt man in 6 statt x, xz und statt y, —x, so wird
.1—ajlo.l—a?16... 1 — ^.1—*8.1—o;14...
oder
23. [«] = l — x—xx-\-x5-\-x7 — xi2—xl5-\- etc.
Anderer Beweis.
Man setze in 6 statt x, a?3 und statt y, -\-x, so wird
ZUR THEORIE DER NEUEN TBANSSCENDENTEN. HI
24. l-+-x-\-xx-\-xs-\-x7-\-xli-\-xl5-\-etc. =
Man setze in 6 statt x, x3 und statt y, xxy, so wird
oder statt x, x3 gesetzt
also
25.
26. x—xA—x^+x^+x^—etc. = a?f 1 — x\ 1— a?15.1— a?21.1—x**
Da nun
so ist
MI» U/ ~"~ ov ~~~ i
tt «*» «41
'5"-|-a?'*i-fa?'^"-|- etc.]
ferner folgt aus 24, wenji man statt x, x* setzt, weil
28. 1—2
also aus der Verbindung von 27 und 28
iii. 57
29. i—f<+ .
— i_^.1—«>. l-*15 ...JL j^«.2^+*v+*V _2*v—etc.
ferner folgt aus 23
#* X» —«2?» + <2? »-{-..= XT[üf\
also
30. 1f +
= l—ar.i—V.l — <2?15...-^-j^ — x* —oe* -\-x 8 -\-x 8 — ..
•ZT
Aus der Summation von 29 und 30
31. {1—2<a?-|-2<a?4 — 2./+..} + jl — 2<a?3-{-2#12— 2<»27+..}
= 1—<»3.1—<a?9.1—o?15 .. . ^[x^—x^—x^^x^^-x1^—. .}
Aus der Summation von 28 und 30
32. jl
= 1—<2?3- 1 <2?9. 1—<2?15 . . .-IS^+^ + ^
Setzt man in 6 statt x> x6 und statt y, <»y, so wird
i+
Man hat demnach die Zerlegungen in Factoren
33. A — 2<a?3-|-2<a?12— 2a^+
= 2[.r36].l— <2?3.1 — aP.
34. A —
.1—xK X — x1..
35. (f + ++) + ( + +f
= 2[<»36]. l+<»3. l+<»9.1-j-a?15.. . 1— a?15. l—a*. l—a?1
36. 31227
ZUR THEORIE DER NEUE» TBJUSSSCENDEMXS, UL
Hieraus ergeben sich zugleich die Factoren des letzten Theils in 31.
Aus der Subtraction von 28 und 30
37. A — 2<z9+2<zM —2a?84-..)-- (l
= 2.1—<**. 1—a?. 1 — ^.. ^(^H-^ + af^-f.,/^-}- ..)
Setzt man in 6 statt x, x6 und statt y, #5y, so wird
Also die Zerlegung in Factoren
38. (i_2<5S6 81
39.
40.
41. ( + j++
)A—xA — xnA— xx\\—
Aus der Subtraction von 29 und 30 folgt
42. A —2«3+2a;12—2«27+ . .) —A—2a? + 2aj*— . .)
I » — *i Ü. Ü5
= 2.1— x3. l—x9A—x15. . .-i.(a;T — a;8 — a?»-fa;8 +a; 8 — ..)
Woraus die Zerlegung des letzten Gliedes dieser Gleichung in Factoren folgt.
Aus der Multiplication von 34 und 39 folgt
43. (i_2*3-f 2*12 — 2ar7-f . .J — A
Ebenso aus der Multiplication von 36 und 41
57
452
44.
.1 - *7. 1 - a?"
Also der Quotient
(l— 2a8+2sli8—2s*7 + . .)*■—Q—
/
1—a;\3/i —
und das Product
45b. {A — 2a?3-f 2<»12— ..J — A
Aus 28 4-130 folgt
46. A — 2^+ 2a?36— . .) —«A— 2a?3-f 2a?12— . .)
Nun findet man aus 6 nach dem, was zwischen 22 und 23 gezeigt ist
l6 112
~
Also
... l-~. 1-f-'. l — £... l+a?6.1—a?12. l-f a?18
2 Z %
Daher die Zerlegung in Factoren
47. A— 2a?3-j-2a?12— . .) — i{\—
= i—a?.l —a?3.1—a?5.. . 1 — ^. 1-j-a?3.1 —o?6.1-j-ar*. ..
'a?. l+ia?a?. 1—ia?4.1 — ia?5.1-j-ia?7.
ZUR THEOBEB DER NEUEST TK1NSSCENDENTEN. JU, rÄn
und ferner
48. A — 2.3
XI — ^#. 1—ixx. 1-j-t.r4.l-j-»,a?5.l— ix7.1—ix*...
= l-j-^.l-j-^.l-j-.»5. .. 1—i.l—x*.l— af.i — x9.
XI — ix.\-\~ixx.\ — ixk. 1 -f-ix5. . .
50.
Xl+»*. 1 — ixx. 1 -f-t<a?4.1 —
Also aus der Multiplication von 47 und 48
51. A—
= 2A— <a?J(l — a?3J(l — <»5J...
= 2A— o?J(l—^*JA — x5f. . .
X(l— a?f{\—xXif... \-\-xx.
und aus der Multiplication von 49 und 50
52. (l + 2^r3+2a?12+. .J-l-(l-l-2<27+2<»4+
32 *5J. . . (l
. \-\-x\ \-\-x*. 1 + a;
und der Quotient
ITACHIiASS
und das Product
54. |(l-2a>3 + . .
Aus Formel 23 folgt
55. x+x*+x™-\-.. =
•§- Exponent = D —
Aus Formel 26 folgt
56. 4?3+*27+*75+.. =
oder x*. l-\-x8.1+a;16. l-\-xu. . . = A, x2 = <* gesetzt
55.
56.
Nun folgt aus der Factorenzerlegung in 24 sehr leicht, wenn man statt x, it
statt y, i setzt
Also aus 55 — 56
57. (* +
Und so sehr leicht
58.
= xA-\-xx.l—
Also durch Multiplication
ZUE THEORIE DES NEUEN TRA2JSSCENDENTEN. IH. 455
59. (^
Eben so folgt aus der Factorenzerlegung in 24, wenn man statt ce, t und
statt y, —i setzt
also
60. (a;+a;9+a;25+ .. .J-f^+ar'+a^-h . ..)
= xA-\-ixx.\ — ixi0A-\-ixuA— ia?2. . . l-\-x\ l+x16.. . 1—o?t5\ 1— a?w. . .
und eben so
61.
= xA — ixx. 1 + tV0.1 —tV*. l + to^.. . l+<»8. l+<a?16... 1 —a?12.1— a?24
Also durch Multiplication
62. (^ + ^+^H- . . .f-H^ + ^-h . .)*
Also Product von 59 und 62
63.
Durch Multiplication von 62 und 44 folgt
64. {(^+aj*+a.V+..
Durch Multiplication von 59 und 44
456 NACHLASS.
65. |(^ + ^+a.¥+ # .J_(a?f+(^
X j( +
= 4^
Man hat ferner
r, —
**
die Fünf- Theilung \aAhB\
ia—A V* AA — BB BB
\4 __.
j
\hA — aj aa — bb ' bb
B—b Y I AA — BB AA
sB — bf aa — bb ' aa
a — A 5.5 — b a..aB
B~^h sA—H V O
(a -,Ä) FA — af= 2bQAabb{aa — bb)
{B— b){5B — bM= 2h6Baab(aa — bb)
[a —Af{hA—a) = 2b§AaBB(AA—BB)
(B— bf{bB — b) = 25 SAAbB (AA—BB)
WM
ZUR THEORIE DER NEUEN JSANSSCEKDENTEN.
457
Zu der Theorie der Fünftheilung gehören folgende Theoreme. Wir be-
bezeichnen \-{-xy. \-\-a?y. \-\-o^y . .. 1+ —. 1+— • H— • . • durch (#,y), so ist
y y y
[69] (
wo P, Q von y unabhängig.
Also
oder
Ferner für y = — ax
(~, n rt r\ I v> r>\ A
I iJL « ^^"~ CX ULiA/ I • l w • ^^^ <A/ I — \J
d. i.
P =
/J~"i\xxY
Nun ist
Also
und unser Theorem
70.
x
ui.
58
458
oder
(Man kann auch leicht die Reihe, wodurch P multiplicirt ist, = 0 machen,
durch y = ix)
Den Satz 70 kann man auch so enonciren
72. (a?,.a).(a?,€) = W= {(##, a6).(# «3?, -|) -{-#«(##, aß xx).(xx,
Hieraus folgt
hieraus ferner
73. (* et).(«.
Nun ist
(*«*, —%xt).(%xi, tx2)
(— x*, xx) (— a", — x) + g (— arB, — a;8) (— arh, ar*)
(— x*,xx)(— x*, — ar) — ar(— x*, — a:8) (— arB, x*)
Woraus der erste zu beweisende Satz von selbst folgt. Ebenso ist
l4-2ar +2ar4 + ... l — tx. l—ttx. 1—eax. l —e*ar. \-\-txx. l + eexx. l + e3xx. l -\-t*xx
. 1+ ear. 1 + eear. l + e3ar. 1 + £4#- i—sxx.i — ttxx.i.— saxx. 1—t^xx
1—e4. 1 — e8 (/a:'5', iex*). (ix*, ieea:8)
ee — es.e — e4 (—x,—e8ar).f—x, e) — ear(—x,saxx)(—ar,—ear)
.e+e** (—ar, —e3ar).(—ar, e)+ear(—ar, £3xx)(—x, —tx)
— e4 (x,z*x).(x, —e) + e8(ar, — e3)(x, ex)
+ e + ee+ e8 + e4 ' (x, z*x).(x, — z)—zz (x, — e3)(ar, ex)
Woraus der zweite zu beweisende Satz von selbst folgt.
ZUB THEORIE DER NEUEN TBANSSCENDENTEN. m.
(*,») = 2
(•. 1) =
Man hat also
Durch die Entwickelung von (x,yf erhält man
also für y = — tx
A — ee)sfc4 = Qx~*\e—ee — (e — ee)<r#— . . .)
oder
Zx*.0 = Q(t—^ —^+^m+^*— ...) = [xx]Q
also
Durch Entwickelung von (x,y). (x, —yf erhält man
Man folgert hieraus leicht, dass man setzen darf
T(x,yf+ ü(x,y) (x, -yf = (a?,ys)
so dass T und U Functionen von x. Um sie zu bestimmen setzen wir
58*
460 NACHLASS.
1) y = # so wird r(*,*)? = (*».*») oder T
2) y = —£# so wird T(a?, — s<rJ = Z7(#, +s^?J
oder
oder
r — _ ^
oder
folglich
y rfo—y) i3 j_ rrfo-y)
L (ar,y) J ^ («, y)
L (ar,y)J
also
[xxY r(ar, -y)n3_ o [o:6]4 (*, -y)
a?ar]*r(ar,-y)i8 [^6? (ar,-y)
rt2]2L (ar,y)
[IV.]
HUNDERT THEOREME ÜBER DIE NEUEN TRANSSCENDENTEN.
1.
Es sei
\.an — a an — \.an—a.an —
an—l . . an—\.an — a an — \.an—a.an — aa *
'"T" a — l ' ' a — l .öö-l ' rr"T" ö-i.öö_i.ö»_i '
■ an—i.an — a.an — aa.an~a*
+
indem wir n, a, t ganz unbestimmt lassen. So oft w eine ganze nicht negative
Zahl ist, bricht die Reihe offenbar ab und besteht aus w-f-1 Gliedern, auch sind
dann, wie wir in der Abhandlung Summatio quarundam serierum singularium ge-
gezeigt haben, alle Coefficienten ungebrochne Functionen von a. Ist aber n ge-
gebrochen oder negativ, so findet beides nicht Statt.
Indem man T mit \-{-ant multiplicirt erhält man
T.(x+a»t) = i + ^^l^l^1w""r
v ' ; ' a—i
a—i.jj-i.s«-!
Indem man also in T das Element n als veränderlich ansieht, und sich
des Functionalzeichens 8 bedient, dass
T= Sn
wird man haben
Hieraus folgt das 1. Theorem.
4S2 NACHLASS.
Wenn n eine gomze positive Zahl bedeutet, ist
a—l ' a —l.aa—l ' a —l. aa —l .o3 — l
aat)(l-{-a3t) . . .
2.
Wenn wir T auf folgende Art schreiben
l—a ' l — a l—aa ■ l—a l—aa l — a"
' l—a ' l—aa ' l—a3 ' l — a* ' '
wo die Exponenten von a die Trigonalzahlen sein werden, so erhellet, dass das
letzte Glied sein wird
a^nn~n)tn =/
wenn wir a^n~i't = y setzen. Die ganze Reihe wird dann, indem wir das
letzte Glied mit dem ersten, das vorletzte mit dem zweiten etc. zusammenfassen,
für ein gerades n
. l—on l—o"-1 l — ain+t s-.±n.$n—l An
■" 1—O * 1—OO **i af«
indem das mittelste Glied isolirt stehen bleibt. Bezeichnen wir dasselbe durch
A und setzen a = xxn so wird die Reihe
u.s.w. welche Reihe aus -J-(»—J—2) Gliedern besteht und dann abbricht.
Unser Product (i+*)(l-|-fl*)(l+flfl*).. (l+a"^) hingegen verwan-
verwandelt sich
ZUR THEORIE DER NEUEN TRANSSCENDENTEN. IV. 4$$
Das Product der ersten Hälfte der Factoren
wozu noch die übrigen kommen
Da nun
, 1
1
1—ara: ' 1—x* ' 1—a;* * " 1— x" ' i
wird, so verwandelt sich das erste Theorem in folgendes zweite: fSur ein gerades
n wird:
etc.
1 — XX 1 X*- 1
3.
Ist n ungerade, so stellt sich die Reihe so dar:
j . . . a ^
Machen wir wie vorher ös = <3?<r und setzen das Glied, welches hier das letzte
ist, = -Ba?*.(y*-{-y~*), so wird die Reihe
*nacbi«ass.
welche Reihe aus ±(n-\-l) Gliedern besteht und dann abbricht. Von unserm
Product stellen wir die ersten \{n—1) Factoren so dar
wozu noch kommt
Da nun
— a*+5 l —gn+7 ' i—arn
1—xx "l—x3- *1—a:6 * ' l —
1—XX ' ' ' 1—X*1'1 ' Ann
•ZT
so ergibt das erste Theorem folgendes dritte :/#r ein ungerades n ist
*) 4-15^ • *v (y" +^-l) + etc-
1 — xx l—a:4 l—x6 1 — i
4.
Wenn man n ins unendliche wachsen lässt, so verwandeln sich die Rei-
Reihen und Produete des zweiten und dritten Theorems in unendliche Reihen und
Produete. In dieser Gestalt ist das vierte Theorem
^ etc. ininf.
Und DAS FÜNFTE
^^^^^^^1 etc. in inf.
xx) A— xA) (\~x6) . .
ZUE THEORIE DES STEUER TEANSSCENDENTEN. IV. &&>
5.
Die Functionen, welche durch das vierte und fünfte Theorem in unendliche
Producte entwickelt werden, sind von grosser Wichtigkeit, und es wird gut sein
sie hier durch besondere Functionalzeichen zu bezeichnen. Wir schreiben
daher
P(x,y) = l + ^(^+y-*) + ^(yy4.y-2) + ^(y3+^-3)+ etc
R{x,y) = #^+y~^+*V+y~f) + *V(/+y~*) + etc.
zugleich auch
Q(x,y) = \-af(j+tf-*)+a*üy+y-*)-a>tf+f*) + etc.
wo also Q{x,y) = P(—x,y) = P(x,—y) wird. Der einfachste Werth, welcher
y beigelegt werden kann, ist 1 und da die demselben entsprechenden Werthe un-
unserer Function von besonders grosser Wichtigkeit sind und häufig vorkommen
werden, so schreiben wir der Kürze wegen statt P(x, 1), Q(x, 1), R(x, 1) schlecht-
schlechtweg Px, Qx, Rx. Wir bemerken noch, dass wo ein Exponent sich blos auf
das Argument einer Function bezieht, dieses durch Klammern bezeichnet wird
wie P(x3), ohne Klammern ist immer vorauszusetzen, dass es sich auf die
Function bezieht, also Px3 so viel bedeutet wie (Pxf. Also
Px = 1-|-2<a?+2#4-l- .
Qx = l — 2a? 4-2 x*—.
Rx = 2o?*
Endlich wollen wir durch das Functionalzeichen F in dieser Abhandlung das un
endliche Product ausdrücken
Fx — (l—x)(\—xx)(\—x3)(l—xA) . . .
In diesen Zeichen erscheinen die beiden letzten Theoreme so
4. P(*.y)
5. jR(*fy) = *
Und so ist offenbar
6. Q^) = (x
lii. 59
KACHfcASS.
ferner indem man y =■ 1 setzt
7. Px = (l + ,a?J(l — *a)(l-+-**)*A — ^4)(*1+<»5KA—x6) . . .
8. Qx = (i—*)*(i —^)(i_«»)*(i—ä*)A —^)*A—«•) . . .
9.
Substituirt man hier 1-f—«a? = !_**, l-f-#3 = —^u.s.w. so verwandeln diese
Ausdrücke sich in folgende
10. Px = ;
12.
hieraus ergibt sich ferner
13.
14. Px.Rx = 4r(R\JxJ oder was dasselbe ist
JL iA/ iA/ * JLv vU iA/ ——• ~rr \ -*•%/ <A/ J j JLV iA/ iA/ ■—
K^fiA/ iA/ \ JLvcv / ——• tw . l JL iA/ J Ciloiy
15. Jr X = y'' j === y7 i === y7 —
ferner
16.
17. P<»— Qa; = 2R(xi)
Also durch Multiplication nach 14
18. (Pxf — [Qxf == 2(J2<»^J
Bedeutet ferner i die imaginaire Grosse \j— 1, so wird
19. Px-\-iQx— (l + t)Q(ta?)
20. Px—iQx = (l — *)P(ta?)
Also durch Multiplication
ZÜE THEORIE DES IJEDEN TBjLNSSCENDENTEN. IV.
21. (Pxf+(Qxf = 2 (Pxxf
und aus der Multiplication von 18 und 21 mit Zuziehung von 14
22. {Pxf — (Qxf = (RxY
Man sieht also, dass (Pxxf das arithmetische Mittel zwischen (Pxf und
(Qxf ist, und da nach 13. die Grosse (Qxxf das geometrische Mittel zwischen
denselben Grossen vorstellt und da (Theor. attract. el. p.) wenn zwei Grössen-
reihen
m, m\ m", m'". . .
w, n\ ri\ n" . . .
so verbunden sind, dass m^ immer das arithmetische n& das geometrische
Mittel zwischen m^"^ und w^—1) ist, man die gemeinschaftliche Grenze das arith-
arithmetisch geometrische Mittel von m, n oder von irgend ein Paar zusammengehö-
zusammengehörigen Grossen der beiden Reihen nennt, so ergibt sich das höchst wichtige
Theoeem B3):
Das Arithmetisch Geometrische Mittel zwischen (Pxf und (Qxf ist alle-
allemal = 1.
Nach dem, was wir am angezeigten Orte bewiesen haben, ist also auch
24. das Integral
von <p = 0 bis <p=2tc ausgedehnt = 2tc oder auch von <p = 0 bis y —
wenn Je irgend eine ganze Zahl bedeutet, =.^kiz.
6.
Um den Zusammenhang des Algorithmus des arithmetisch geometrischen
Mittels mit unsern Functionen noch weiter zu entwickeln, bemerken wir zuvör-
zuvörderst, dass wenn
— = ¥^i und m =i ilPx*> m.= |xQ«2?2, mm—nn =
gesetzt wird, man hat
59*
46*8 ■ NACHLASS.
m = |x(P<»«rJ, n = p{Qxxf, mm —riri = \i\i{Rxxf
m" = ti(Px<)\ n" = |x(Q,a?4J, m" m" —n"n" =
»-= |x(Pa?8J, w'" = 2
u. s. w. oder allgemein
und dass offenbar jx das arithmetisch geometrische Mittel zwischen m und n
selbst ist. So bald wir also den Werth von x, welcher vorgegebenen Werthen
von m und n entspricht, zu bestimmen im Stande sind, werden wir jedes Glied
der Reihen
m, m, m . .
n, n\ n" . .
unmittelbar darstellen, auch die Reihen interpoliren und rückwärts fortsetzen
können. Das nächstliegende Mittel x zu bestimmen ist folgendes.
Man sieht leicht, dass die Glieder der Reihe
Rx'
sich dem x immer mehr nähern, so dass x die Grenze derselben ist. Man hat
also
x — "" h'K • ä" * ä"' * • •
Nun ist aber nach 14
Ä /'P™*»\2 nnH «n — — Pr4 — — (~Pv$\* Ä" — fP»1^
-77 ^=^ [JrXX) unu so y»> — jtU/ , 7,,, — ^jl <*> ) , -,,,„ — \jtul j
Also
x =
ZUR THEORIE DER NEUEN TRANSSCENDENTEN. IV.
wir haben folglich
25. X = mm-nn
wofür man auch schreiben kann
_ mtn-nn /m«U /m^U /m^'U
* 16m'm" '\m"f '\m""f \mv]
Da die Glieder ?ra', w", m'" sich äusserst schnell der Gleichheit nähern so
erhält man x mit grösster Bequemlichkeit.
Allgemeines Theorem A827 Aug. 6)
P(x,ty).P(x,j) = P(xx%tt).P{xx,yy)-\-R(xx,tt).R(xx%tjy)
[2-]
Durch Zerlegung in Factoren bestätigt sich leicht,
gesetzt:
also durch Addition
P(
P(«, 1)—
also
ZUR THEOBIE DER NEUEN TBANSSCENDENTEN. V.
P{x,xt) = -±-R(xtt)
R(x,xt) =z-L.p(x,t)
x*\]t
P[x, \J.P(x,yf = Q(x, lJ. Q(x,yy+R(x, \f.
P[x%y).Q{x,y) = Q{xx, 1). Q{xx,yy)
f l).P(Mtyjf)
x, \).R{xx,yy)
x\ i)—P(x\ l)j.
[3.] '
P{x\ 1) = P, Q(x\ 1) = Q, R(x\ \) =
pqr\P[x\yz) = MR.P(x,y)s+ZPQR.P(x,y). Q(x,yf
ZpPQR =7*Q—qsR
SqPQR = r*P—psR
ZrPQR=p*Q—qsP
ü Q— q r
rR qQ pP
= 4 + 24a;a;+24a;
= $P(xx, 1) P{x6,1) — 4 Q(xx, 1) Q(a?6,1) ? wurde dann sein
472 . ...-.- KACHLASS,
So wie
durch R(x,y) bezeichnet ist, so wollen wir noch
durch S(x,y) bezeichnen. Man hat dann
iS(x,y) = R(x,—y)
, 1).
R{x,y) .S{x,z) -\-S(x,y).R{x,z) = iS{x^
R{x,y).S(x,z)—S(x,y).R(x,z) = <LS(xx,-).Q(xx,yz)
Setzt man
wo Ä alle ganzen Zahlen bedeutet, so sind die Theoreme enthalten in
ZUB THEORIE DER NEUEN TEANSSCENDENTEN. V.
auch ist
(8,a) = (8,— et)
[5.]
Man setze
COS U
P(x,y) r
y = cosM-f-«sin«
dann ist
P (x,y) d 6 = pq Q (x,y) d u
, _ dQ __ dG
i/(»4—r4cos02) t/(»4i
?, xy), 8{x%tf) = x*y* Q{x% xy)
Setzt man
sin <L = — cos 6
pp
so wird
— — • p/ ;, sin 9 = —. p; :
p P(ar, y) ~ p P{x,y)
[6-]
P(x,y).P(x,z) = P(
R{x,y).R{x,z) =
ui. 60
[7.]
fe) .P(x,y)-S(x,e).Q(x,y)
R(x,e5).P(x,y)-8(x,e5).Q(x,y)\
worin s7 = i. Zum Beweise dient, was sich leicht nachweisen lässt:
P(x, sy). P(x, j) = P(xx,yy). P{xoo, tt)-\-Il(xa),yy). Rixx, ee)
__ P(x,y)>+Q(x,y)* p[ > P(*,y)*-Qfr,y)* -p/ n
P/ X2 J2(ar, s)
[8.]
xdg
x&r
4# 3— 4<»4— 6^— 8x6 — Sx7
4r'= SS
Coefficient von x2 a c '' wenn a, b> c .. Primzahlen, wird
aa+1— l b6+t — i c7+i — i
a — l * b — l * c — l
[worin ftr jene drei Reihen folgeweise] A = 2ft(— l)^1, A = 2^, ^= 8C
ZUR THEORIE DER NEUES TRANSSCENDENTEN. V. £75
Ap — Aq=rk ' ' ' '
A r — 4p = qk
Ar—Aq = p*
dpx d»ar4 da:
d^£ dyg" __ d« r*qq(pp —
4ar* PP99— hPPQQ
[9.]
Bei der 5Phc- ist (Aug. 29)
pp — PP = A.\J^ ,
qq—QQ = —A.\J±,
ä rr—RR = A.\/^,
AB = —2ppPP+2qqQQ-\-2rrRR = [\6pqrPQR]*, ^ = IM
B=2*.
}
(pqr?1
also
r q
Siehe weiter unten [Art. 11.]
Für die Ableitung dient u. a.
P(x\xA).P(ar>, —XX) = P(xl\—xx
P{x\—x*).P(x\xx) = P(a?*0,— j?*
60
also durch Multiplication
{Fx™)
was mit <? identisch ist, nemlich
Auch beweist man leicht
[10.]
Bei der Trisection ist noch, p, P etc. in voriger Bedeutung genommen
und P(^, 1) = P° gesetzt
=^_ 4 («')*
j
Allgemein wenn P(a?, i), Q(o?, l) gegeben sind und P(<»n, l), Q^, l) ge-
gesuchtwerden, wo % ungerade, sind dem P(#*\ 1) coordinirt +y/^-.^(ä?^", 1)
oder Jzi\J—'P{#~fr, 1). je nachdem w von der Form 4Ar—|—1 oder 4Ar—1 ist.
Die Gleichung findet sich leicht aus Entwickelung der Summe der geraden Po-
Potenzen der ra-f-1 Wurzeln.
tu.]
Setzt man
ZUR THEORIE DER SEÜEN «RANSSCENDEOTEN. V.
so ist auch
Setzt man hier y = 1, so erhält man
woraus die Gleichung weiter zurück [Art. 9] folgt
0 =
daraus
A — r
ppqqr*
[12.]
Theobem. Wenn der imaginäre Theil von t und -J- zwischen —i und
-{-i liegt, so ist der reelle Theil von
\Pt)
positiv. 1 + **
Geometrisch zu beweisen
Raum für t und —
Unter dieser Bedingung ist also das arithmetisch geometrische Mittel
zwischen
indem man immer das geometrische Mittel zwischen m, n so nimmt, dass ^^
einen positiven reellen Theil hat,
Ein solches Mittel nennen wir das einfachste Mittel.
Ist das einfachste AG. Mittel zwischen «i, w, — jt, das zwischen
m, \jimm—nn), == t» so ist ^ der Canon des Verhältnisses - , nemlich
KACHI.ASS.
m_ lQt\Z
n — \Pt)
dann ist das einfachste A G. Mittel zwischen m und — n
und der dazu gehörige Canon
t
Die Gleichung
(if =
hat immer Eine und nur Eine Auflösung in dem Räume
Es sei a& — €y=l, a = 8= 1 (mod.4), ö, y gerade
dann ist
[13.]
Fünftheilung
c = \j(aa—bb) C = \/(AA—BB)
2v = —aA+bB-\-cC
4« = aa — 6aA+hAA = — (W— 6JJ5 + 5J5J5) = — (cc —6cC+5 CC)
ZUR THEORIE DES NEUEN TEANSSCENDENTEN. V.
Die Elimination auf eine Gleichung
\Ja-\-\Jb-\-\Jc+\Jd = 0
angewandt, gibt
0 = 2(a4 — 4a36 — 2aabb-\-4aabc — Hiabcd)
[14.]
Die 7plication beruht auf
[a sin (<f-f-J.)-f-6 sin C <f 4-B)]2 sin
[15.]
Bei der Trisection hat man
./ 9 « ./G
gesetzt,
proportional
3 cos 9 sin <p3
°—<p)s
3 cosF0°—9) sinF0°—<p)
cosF0° — <pKsinF0°—
3cosA20°— <p)sin(l20° — <
cosA2ü°—(fKsinA200—<
[16.]
Wenn innerhalb einer begrenzten Figur überall
ddF , ddF_
&x* *+" dy* —
an der Grenze hingegen F constant = ^4. ist, so ist nothwendig auch im gan
zen Räume V = A
Beweis. Es sei dM ein Element der Fläche und
Wäre V nicht constant, so wäre offenbar das Integral positiv. Allein das Inte
gral ist auch
durch den Umfang der Figur ausgedehnt, also =0. Da dies mit dem Vorigen
im Widerspruch steht, so ist die Voraussetzung unzulässig.
Ähnliches findet mit drei Unbestimmten Statt.
Es lassen sich hieraus manche schöne Folgerungen ziehen.
Ein Punkt kann innerhalb eines hohlen Raumes nicht im stabilen Gleich-
Gleichgewicht sein, wenn nicht innerhalb des ganzen Raums gar keine Wirkung Statt
findet, weder im Fall der Abstossung, noch der Anziehung.
[17.]
Dass in der Peripherie einer Gleichgewichtsfigur keine negative Theile sein
können, beweist sich so. Gesetzt AB wäre negativ, so wäre V—A (A Werth
von V in der Peripherie) auswendig neben AB positiv, neben den andern Thei-
len negativ. Es wird daher einen endlichen Raum geben, wo dies positive gilt;
er sei innerhalb ABCDE; dann wäre er aber, da er an der Grenze 0 ist, in
diesem Räume constant, welches ein Widerspruch.
Dieselbe Schlussart lässt sich auf drei Dimensionen anwenden.
Bei drei Dimensionen findet, für die Fläche s, wo V = Const., noch das
schöne Theorem statt, dass l^-ds, wenn p normal gegen s, =4izM, wo M
ganze Masse (vermuthlich allemal die in einer solchen Fläche eingeschlossene
Masse, also ungerechnet die draussen liegende).
Vermuthlich ist der Satz ivx jede einhüllende Fläche gültig, ohne dass V
'constant zu sein braucht.
Es seien zwei einander einschliessende Flächen, in denen V constant ist,
nemlich resp. V = A, V=B, dW ein Element des Raumes zwischen beiden,
p die Anziehungskraft in jedem Punkte, dann ist
wenn M die Masse im innern Räume, wobei angenommen ist, dass im Räume
W keine anziehende Masse ist.
PENTAGRAMMA MIRIFICUM.
ni.
61
482
cos 1 = sin 2. sin 5
cos 2 = sin 3 . sin 1
cos 3 = sin 4 . sin 2
cos 4 = sin 5. sin 3
cos 5 = sin 1 . sin 4
1 = cos 1 . tang3 . tang4
= cos 2. tang 4. tang 5
= cos 3. tang 5. tang 1
= cos 4. tang 1. tang 2
= cos 5. tang 2 . tang 3
8. —dl = d2.cos4-J-d5.cos3
9. —d2 = d3.cos5-j-dl .cos4
10. —d 3 = d 4. cos 1 -\- d 2. cos 5
11. —d4 = d5.cos2-f-d3.cosl
12. —d5 = dl.cos3-j-d4.cos2
Die Elimination von d 5 aus 8 und 12 gibt
d 1 . sin 32 = —d 2. cos 4 -f- d 4 . cos 2. cos 3
Die Elimination von d3 aus 9 und 10 hingegen
d 2. sin 52 = —dl. cos 4 -f- d 4. cos 1 . cos 5
Das ebne Fünfeck, welches die Centralprojection jenes sphaenschen auf
eine beliebige Ebne bildet, hat die Eigenschaft, dass die von den einzelnen Win-
Winkelpunkten zur gegenüberstehenden Seite gezogenen Normalen sich in Einem
Punkte schneiden (im Augenpunkte). Zugleich sind die Producte der beiden
Stücke, in welche jener gemeinschaftliche Durchschnittspunkt jede Normale
theilt, für alle gleich.
PENTAGRAMMi. MSOHCUlf.
cos A = et, cosi?=ö, cosC=y,
Um die Eckpunkte in ganzen complexen Zahlen ausgedrückt zu erhalten,
seien p, p\ p", p"\ p" fünf complexe ganze Zahlen, und zwar
p =. a-j-bi, p =■ a-j-b'i, etc.
Man setze
a'a'"+bW= A,3), a"a""+b'V" = B,4) u.s.w.
und nehme für die Eckpunkte
A,3) B, 4)|»f B, 4)C,0)/, C,0) D,1)/, D,1)@,2}/", @,2)(l, 3)/"
= q> q\ q", q"\ q""
also
q =
Es ist dann
u. s. f.
q'—q = (bd— aZ»/)B,4)(r— d"i) = — (bd— ab')B,A)p"i
u. s. f.
61
484 NACHLASS.
Der Schnitt von qq mit oq'" hat die complexe Zahl =
^ — o'"o'- ä'"ä'" jt u' 6- w*
Das oben erwähnte Product wird
[3.]
Die Relationen zwischen den Seiten des sphärischen Fünfecks so
Quadrate der Gleichungen
Tangenten Secanten Cosecanten
a yö —
u> 5. 8e
7 ea *±
1 Y
aß
T
6_Y
£
ö et ö
0
Diese Gleichungen sind nicht unabhängig, es ist nemlich identisch:
'—ea) = ej
und auf ähnliche Weise wird die fünfte aus dreien der übrigen abgeleitet.
Aus zweien der Grossen a, fi, y, 8, e folgen die übrigen
f. i + g+T ^ HJ l + « ^ l + e
U ay* ° o ' T aß —l ' ° aTHi
X 1 + a l+a £ ^
. __ £+Y . ___ >-H°-HS . 1 + 6 «, _ l + a
6 * '. - *y -a8 ' S a6-^l ' ° «137
Beispiel .
S =5
cos2
f
i
i
sin2
f
1-
i
i
74°
39
54
65
30
33'
13
44
54
0
S6
54
7
19
0
Schöne Gleichung
Der Inhalt des sphärischen Pentagons ist 360° weniger Summe der Seiten.
Setzt man die Summe = 8 und
so wird:
A
B
[4.]
Axx-\-Byy-\-Czz-\-tayz-\-1bxz-\-1cxy
{A—G)a-\-
aD—G) — &cja= \b(B—G) — ac\$ = \c(C—G)
hc l ac i _£i___ _L_ 1 A
— G)-ac~t~ c(C— G) — ab"*". .— U
a(A — G) — bc'ibiB — G)-ac~t~ c(C— G) — ab
(A— G)(B—G)(C— G) + 2abc = aa(A—G)+bb{B~- G) + cc(C~ G)
/g(^g) —Se
"
NACHLASS.
Setzt man
so wird indefinite
jaD—<*?) —&cj \b{B—x)—ac) \c{C—x) — ab\Q
= —abc(x—G)(x—G'){x—G")
Differentiirt man und setzt nach der Differentiation x = G, so wird
{a{A—G) — bc} \b{B—G)—ac\\c(C—G) — ab}
— G")
woraus
G')(G— O")
Die Schlüsse bedürfen einer Abänderung, wenn eine der Grossen a, £* c
verschwindet. Die obige erste Gleichung für G wäre dann eine identische.
[5.]
Gleichung der Punkte der Kegelfläche, in welcher die Punkte (l) B) C) D) E)
liegen, Spitze des Kegels im Mittelpunkt der Kugel zugleich Anfangspunkt der
Coordinaten. Achse der x geht durch den Punkt C), also Ebene der yz geht
durch (l) und E), Achse der y geht durch A)
C)
D)
E)
@
B}
X
1
cosl
0
0
cos 5
y
0
0
cos 3
1
cos 4
z
0
sinl
sin 3
0
—cos3 .sin5
Gleichung
(z. cqs 1 — x. sin \) (z, cos 3 —y. sin 3) cos 2 = xy
PENTAGBAMMA MKIFICUM.
oder
zz = oßzsj
Durch Veränderung der Coordinatenflächen lässt sich dieselbe in die Yoiya.
bringen
zz = Lx'a;-{-Myy
Löst man die Gleichung auf
welche eine negative (G) und zwei positive Wurzeln (G\ G") hat, so wird
Gz'z'+ GW-f- G"y'y = 0
Für obiges Beispiel
*B*— lJ = 20{* —1)
Wurzeln —2,1973145, +1,06931815, -4-2,1279965
Setzt man
aÖröNe = «> und V/(-
so wird
^ = 4 ^ COS tj> . y7 C 0>-j- 1)
Das Verhalten der cubischen Gleichung
(welche man am bequemsten mit Webdenbach's Tafel auflöst, wo für J~ = y
gesucht werden muss — = aöy^e, wonach dann 2t—1 = — wird) über-
übersieht man durch folgende Tafel
48a
NACHLASS.
t
oo
+ 10
+ 8
+ 7
-*- 6
+ 4
+ 3
+ 2
oo
+ 400.9
+ 325.1
+ 257.1
+ 197.2
+ 145.2
+ 101.2
+ 65.3
+ 37.5
+ 18
+ 1-8
+ 1.7
+ 1.6
+ 1.5
+ 1.4
+ 16.6
+ 15.2
+ 14.0
+ 12.9
+ 12.0
+ 11.34
t
+1.0 oo
..... negativ
—1.0 oo
— 1.618034 + 11.0901699
— 2
— 3
+ 1.309017 +11.0901699 —4
+ 1.3 +11.09 —5
+ 1.2 +11.76 —oo
+ 1.1 +15.84
+ 16.7
+ 36.7
+ 64.8
.+ 100.8
oo
Damit also drei reelle Wurzeln Statt finden, muss aÖY£e>11.0901699
—^ sein, die Grenzwerthe für t sind also: +1.309017 = Uli und
1.618034 =
oder —
2
[6].
A, B, C, D, E die Winkelpunkte des Polygons
a, b, c, d, e Pole der Diagonalen
0, 1, 2 die drei Hauptachsen entsprechend den Wurzeln G, G', G" der
Gleichung
H)t~li)Z = (tang-4B. tangB C. tang CD.tangD^.tangEAf
wo für G die negative Wurzel genommen werden mag; so dass
Guu-\—\~G'uu-\~ G"u"u" = 0
wenn u die Coordinaten irgend eines der Punkte A, B, C, D, E bedeuten,
also zugleich uu-\-uü-\-uu = 1.
Die Quelle der Hauptsätze ist in den zwei Gleichungen enthalten
I.
II.
cos 0 A. cos Ob =
cos 0 A. cos 0 C =
lff—s
G')(G—G")
Die Gleichung I. repräsentirt 30 Gleichungen, die II. hingegen. 15 d&alle
Permutationen der Achsen und der Winkelpunkte erlaubt sind. Noeh zierlicher
(in den anfänglichen Bezeichnungen, wo a = tangCD?u.s.w.)
|cos0C.cos,0d = l?
UosOD.cosOc =*
II. eosOi?.cosO.E = 4
Die zehn Gleichungen I. können nur für neun gelten, weil die Multiplica-
Multiplication von fünfen dasselbe Resultat gibt wie die Multiplication der fünf übrigen.
Es muss also zwischen den 10 Grossen 2t, a, 33, B etc. vier Bedingungsgleichun-
Bedingungsgleichungen geben, welche am zierlichsten so dargestellt werden
öbc(£=eeb2), y c b £) = et a e(£ u. s. w. oder auch
6ci2l(S =ybS33), ybSBS) = Se<£<£ u. s. w.
Es ist aber
cos 0 A" = —rr. a = -^ = -«r- u. s. w., cos0dr = — u. s. w.
PO
1843. April 20. Die excentrischen Anomalien cp, <j>\ cp", cp"', cp"" der Punkte
A, J5, C, D, E sind durch die Gleichungen verbunden (G als negativ betrachtet)
cos} (9'"— ?") ~~ 6?" ' Sm ? ' eso j (9'"-<p") o»-cos?
/
cos i (9'-9"") — V6^_,
Die Relationen zwischen den Winkeln cp°, <p', cp" sind am einfachsten auf
folgende Art darzustellen, \jG._x = 6, \lG*_x = ^ gesetzt, wird 6tj =
ta"g i(?'—?"") tapgj(9"—»*■) tang j (9'"— o') tangf (<?""— 9") tang £ (9*— 9'")
tang *(9"'— 9") tang j (9""— 9'") tang i (9»— 9"") tangj-^'— 9*) tang^(<p*—o')
fur |l+i gibt es einen ähnlichen Ausdruck, der sich hieraus leicht ableiten lä&st.
5tq—t ö
111. 62
490
NACHLASS. PE3STTAGRAMMA MIRIFICUM.
In Zahlen
<p° = 50° 29' 20" 80° 54' 55"
cp' = 92 56 38 55 49 27
cp" = 162 8 U 83 48 52
<p"'=260 34 22 64 29 16.5 21 13 39
<p""=291 6 47 74 57 29 34 35 48
log tang log tang log A
49° 13' 4" 0.79616 0.06418 9.81007
15 16 12.5 0.16814 9.43617 9.182
59 41 16.5 0.96505 0.23313 9.97901
0.32127 9.58931 9.33515
0.57068 9.83871 9.
0.73196 = log
[8.]
Die cp, cp', cp", cp'", cp"" sind nichts anders als die Amplituden zu fünf trans-
scendenten Argumenten, welche um fK zunehmen (in der Bedeutung von Jacobi
p. 31) und wo der Modulus h
G'G' G"G"
/_J L
4 G"G" GG
Sinti., COS|X = \/ —
' G^G' GG G'G' GG
Das transcendente Argument selbst, unbestimmt genommen, ist
r xdy—y&z 4 / G'G'~~G~G
G'G' GG
in der Bezeichnung von Jacobi gebraucht so dass Acp = \J(l—kk sincp2),
es sind
die drei Grossen
Acp0
ebenso
tangi(cp"_cp°)
Acp'
u. s. w.
propositional
den Zahlen
oder
tang amf K
tang
1
BEMERKUNGEN.
In diesem dritten Bande von Gauss Werken habe ich alle Abhandlungen und Aufsätze aus dem
Gebiete der allgemeinen Analysis und zwar speciell aus der Theorie der algebraischen Functionen, der
GAusssischen Reihen und der Elliptischen Functionen, so wie einige Mittheilungen das PFAirsche Theorem
und die Construction von Logarithmentafeln betreffend vereinigt. Sie bestehen aus -einer Boctordissertation
(früher in Quart gedruckt); aus früher veröffentlichten Abhandlungen: fünf in den 'Contmentationes societa*
tis regiae sdentiarum Qottingensis' (Quart), einer in den 'Abhandlungen, der königlichen Gesellschaft der
Wissenschaften zu Göttingen' (Quart) und einer im CsEixEschen 'Journal für reine und angewandte Mathe-
Mathematik' (Quart); ferner aus sechs Anzeigen eigner Abhandlungen in den 'Gb'ttingittchen Gelehrten Anzeigen
und Nachrichten1 (Octav); aus zwölf Mittheilungen über nicht eigne Schriften in den * GötÜngischen ge-
gelehrten Anzeigen' (Octay) (von Gadss nicht unterzeichnet aber in Betreff seiner Autorschaft durch die Acten
der Göttinger Universitäts-Bibliothek verificirt), in der 'Monatlichen Correspondenz zur Beförderung der JErd-
und Himmels - Kunde herausgegeben vom Freiherrn von Zach' (Octav), in den 'Astronomischen Nachrichten
herausgegeben von Schümacheb' (Quart); und auch aus zwei Erläuterungen in der 'Monatlichen Correspondenz'
und in Vega's 'Sammlung von Hü'lfstafeln' (Quart) zu den GAUssischen Additions- und Subtractions - Loga-
Logarithmentafeln, Diese Tafeln selbst habe ich hier nicht abdrucken lassen, weil sie sehr verbreitet sind und
das Format dieser Werke zum Gebrauche solcher Tafeln unbequem sein würde.
Bei der Redaction habe ich dieselben Grundsätze befolgt wie in den frühem Bänden. Zur bessern
Übersicht der Gegenstände in einem so umfangreichen Bande sind die Hauptlenrsätze auf gleiche Weise
durch den Druck ausgezeichnet. Zum leichtern Gebrauch sowohl der altem Ausgaben als der vorliegenden
habe ich bei den Verweisungen auf Schriften, die nicht in diesem Bande selbt sich finden, statt des Ortes der
Veröffentlichungen die eignen Titel so wie statt der Nummer der Seite die der Artikel angegeben. Auf
Seite 20 in Zeile 15 und 16 ist gemäss einer handschriftlichen Bemerkung 'objectionem secundam etquar*
62*
492 BEMEKKBNGEST.
tarn' statt 'objeetionetn tertiam et quartam' und in Zeile 19 ebenso 'objectionem tertiam' statt ' objeddonem
primam' gesetzt. Ausserdem unterscheidet sich die vorliegende Ausgabe von den frühern derselben Schrif-
Schriften nur durch die Berichtigung einiger Druckfehler,, wobei ich zum Theil die GAussischen Original-Manu-
scripte benutzen konnte.
Aus dem Handschriftlichen Nachlasse habe ich aufgenommen: die den Seiten 30 und 112 beigefüg-
beigefügten Noten, den zweiten Theil der Abhandlung ' Disquisitiones generales circa seriem infinitam etc,', eine
ausführliche Abhandlung über Interpolation mit einigen in meinen Bemerkungen Seite 328 u. f. erläuterten
Zusätzen, und eine Reihe von Abhandlungen, die sich auf die Elliptischen Functionen beziehen.
Die Handschriftlichen Aufzeichnungen habe ich hier wie auch früher bis auf Berichtigung von uner-
unerheblichen Schreibfehlern unverändert abdrucken lassen und meine Einschaltungen, die mit Ausnahme der
' Fortsetzung der Untersuchungen über das arithmetisch-geometrische Mittel' nur in kurzen Sätzen bestehen,
durch [Einklammerung] abgesondert. Die geschichtlichen Angaben und erforderlichen Zusätze für den Nach-
lass über hypergeometrische Reihen und Interpolation habe ich in den jenen Abhandlungen unmittelbar
folgenden Bemerkungen zusammengestellt.
Die Redaction der GAtissischen Arbeiten über Elliptische Functionen wurde Seitens der Königlichen
Gesellschaft der Wissenschaften zu Göttingen von Riehanjn gewünscht und ihm zu dem Zwecke die Hand-
Handschriften übergeben. Leider hat er weder eine schriftliche noch mündliche Mittheilung aus diesen seinen.
Studien hinterlassen. Erst nach dem bedauernswerthen allzufrühen Tode Rtrmanms und nachdem der vor-
vorliegende dritte Band bis auf jenen Theil gedruckt war, konnte ich die GAussischen Handschriften zu mei-
meiner Bearbeitung übernehmen.
Gaüss hat von seinen Untersuchungen der Functionen, die wir jetzt die Elliptischen nennen, nur ei-
einen Theil veröffentlicht: eine Anwendung dieser Theorie auf die höhere Arithmetik in der Summatio qiutrun~
datn serierum singularium 180S September und eine Anwendung auf die Bestimmung der Säcularstörungen
der Planeten in der Detertninatio attractionis, quam in punctum quodvis positionis datae exerceret planeta, s»
ejus massa per totam orbitam ratione temporis, quo singulae partes descrtbuntnr, uniformiter esset dipertita, 1818
Januar. Den grössern Theil hat er niedergelegt in einigen unvollständigen Entwürfen zu Anfängen verschie-
verschiedener Abhandlungen und in zahlreichen zwischen andern Arbeiten sehr zerstreuten Aufzeichnungen einzelner
Formeln. Diese im handschriftlichen Nachlasse befindlichen Untersuchungen habe ich hier in einzelnen
Gruppen zusammengestellt jenachdem sie vom Algorithmus des Arithmetisch-Geometrischen Mittels oder ei-
einem anderen diesem analogen und mit diesem in Verbindung gesetzten Algorithmus ausgehen oder aber
sich auf die speciellen Lemniscatischen Functionen beziehen oder endlich die Darstellungen der allgemeinen
Functionen durch Producte als wesentliches Hülfsmittel gebiauchen. Die Untersuchung des Pentagramma
mirißcum bildet eine Anwendung der Fünftheüung der ganzen Elliptischen Integrale.
Die Abhandlung mit den beiden Abschnitten de origine ptoprietatibusque generalibus numerorutn me-
diorum arithmetico - geomeiricoritm und de functionibvs transscendentibus quae ex differentiatione mediorum
arithmeticQ-geometrieorux* orüntiur bildet die erste und zwar eine sehr sorgfältig geschriebene Aufzeichnung
in einem Handbuche, welches» wie der Titel besagt, von dem Jahre isoo an benatzt ist. DU» Besch&fägUÄg
mit diesem Gegenstande wird aber schon in einer viel frühern Zeit begonnen haben; nach Mittheilungen
über eine mündliche Äusserung von Gatjss, scheint er im Jahre 1794 die Beziehungen zwischen den arithme-
arithmetisch-geometrischen Mitteln und den Pptenzreihen, in denen die Exponenten mit den Quadrat-Zahlen fort-
fortschreiten , gekannt zu haben.
Die Formeln für den in Art. 18. Seite 38 9. aufgenommenen Algorithmus, der die von Gauss ein-
eingeführten neuen Transscendenten mit den Quadrat-Werthen der beiden Argumente zurückführt auf die Traas-
scendenten mit den einfachen Argument-Werthen, folgen in einem Handbuche unmittelbar auf eine astrono-
astronomische Rechnung an deren Schlüsse steht 'geendigt d. 2. May iS0 9*. Die Aufzeichnungen der anderen Un-
Untersuchungen über das Arithmetisch-Geometrische Mittel befinden sich theils auf einzelnen nicht datirten
Blättern, theils erscheinen sie in den Handbüchern wegen ihrer Kürze an einigen, früher zu grösserer Über-
Übersichtlichkeit zwischen verschiedenartigen Arbeiten leer gelassenen, Stellen niedergeschrieben und erlauben
keine sichere Zeitangabe.
Wie schon in Art. 12 bemerkt, habe ich geglaubt zur Annehmlichkeit für den Leser diese sehr zer-
zerstückelten Uutersuchungen durch eine zusammenhängende Darstellung vereinigen zu müssen selbst auf die
Gefahr hin, hier einige Entwickelungen hinzustellen, die von Gacsb nicht ausgeführt worden sind, wie
z. B. die Ableitung der Differentialgleichung für das Arithmetisch-Geometrische Mittel ohne die Reihen*-
Entwickelung und die Darstellung durch bestimmte Integrale vorauszusetzen^ eine Ableitung,, die sich an
die in Art. 10. ausgeführte Untersuchung anschliesst und sich von der von Herrn Bobchabdt gegebenen
ersten derartigen Ableitung unterscheidet. Die in Art. 17. angeregte Frage über den Zusammenhang zwi-
zwischen den binaren quadratischen Formen mit negativen Determinanten und den von Gadss gefundenen
neuen Transscendenten findet ihre vollständigste Erledigung durch die Untersuchungen des Herrn- Kbon-
eckeb über diesen Gegenstand. • * '
Für die Lemni&catiscken Funetionen besitzen wir die von Gadss in einem Handbuche verzeichnete
Zeitbestimmung 'Functiones Lemniscaticas considerare coeperamus 17 97. Januar. $.' Von den im Nach--
lasse vorhandenen Aufzeichnungen scheint nach Papier und Form der Handschrift zu urtheilen, die auf
einem besonderen Blatte stehenden und hier von mir mit 1, 2, 3, 4 bezeichneten Artikel der ersten Gruppe
der Untersuchungen über die Lemniscatischen Funetionen die früheste zu sein. Die folgenden hier auf-
aufSeite 406—412 unter der gemeinsamen von Gaübs an mehreren Stellen gebrauchten Überschrift: 'Einige neue
Formeln die Lemniscatischen Funetionen betreffend' zusammengestellten Aufzeichnungen derselben ersten
Gruppe gehören einer ungleich spätem Zeit an, die darin enthaltenen Resultate sind auch wohl viel früher
gefunden und theils zur Gedächtnissprobe, theils in dem Streben recht elegante Formeln zu erhalten von
Neuem niedergeschrieben und zwar in zwei Handbüchern, von denen das eine im 'November iSOl' das andere
'im Mai ISO9 angefangen' ist. Die Funetionen sin. lemn. so wie cos. lemn. bezeichnet Gadss überall durch
die aus der Zusammenziehung von s und * so wie von wund l gebildeten "Schiiftzüge. - Da diese bis jetzt
nicht in Druckzeichen vorhanden sind, so habe ich sie m'eT durch die Worte selbst ersetzt. ' • '
4r94 BEMERKUNGEN.
i
Von den Untersuchungen, welche sich vorzugsweise auf die Darstellung der-<Lemniscatischen Functio"
nen durch unendliche Producte und durch trigonometrische Reihen beziehen und welche ich als eine zweite
Gruppe zusammengestellt habe, bilden die ersten vier Artikel die Scheda prima eines nach der Angabe
des Titelblattes im Juli 17 9S begonnenen Notizbuches. Die Artikel l, 2, 3 sind von Gauss selbst num-
merirt, dann folgt im selben Hefte unmittelbar der Inhalt von Art. [4.] [5.] Seite 415, und hienach mit
vielfachen Unterbrechungen durch Astronomische Untersuchungen der Theil der in Art. [ 17.] Seite 43ri auf-
aufgenommenen Rechnungen, der mit lateinischem Text erläutert ist, und die einzelnen Theile des Inhalts
von Art. [6.] [7.] Seite 417,418. Der Inhalt von Art. [s.] [9.] [io.] Seite 418, 419, Art.[i5.] [16.]
Seite 423—425 findet sich zerstreut in einem 17 99 November angefangenen Notizbuche. Die Aufzeichnun-
Aufzeichnungen der übrigen Untersuchungen gehören, vielleicht mit Aussehluss der FünftheiLung des ganzen lemnisca-
tischen Bogens Art. [13.], wohl einer spätem Zeit an und befinden sich, ausser den in Art. [14.] wiederge-
wiedergegebenen und in ein Handbuch nach dem 20. Febr. 1817 eingetragenen Summationsformeln für das Lemnisca-
tische Integral der zweiten Art, alle auf einzelnen Blättern.
Die der Zeit nach erste unter den im Handschriftlichen Nachlasse erhaltenen die allgemeinen El-
Elliptischen Functionen betreffenden Aufzeichnungen ist wohl die im November 17 99 begonnene auf Seite
433—435 abgedruckte Abhandlung Zur Theorie der neuen Transscendenten I. die sich in einem Notiz-
Notizbuche dessen Titelblatt die Aufschrift 'Varia, imprimis de Integrali 1 —; :—rr, Novembr. 17 99'
3 v/O + ^sin«-)
trägt, zwischen Untersuchungen über ganz verschiedenartige Gegenstände zerstreut befindet.
Die Abhandlung II. mit der Überschrift lZur Theorie der transscendenten Functionen gehörig' folgt
in einem Handbuche unmittelbar nach den in der Theoria motus corporum coelestium wiedergegebenen
Hülfstafeln. Diese Untersuchungen, insbesondere die auf die Siebentheilung bezüglichen, werden wohl
dem Jahre 18OS angehören und die Veranlassung zu einer Mittheilung an Schumacher gewesen sein.
Die Abhandlung III. mit den Eingangs-Worten 'Die Theoreme in Bezug auf diejenigen Reihen und
unendlichen Producte, welche zu der Theorie der Arithmetisch-Geometrischen Mittel gehören, ordnen wir
so:' Seite 446—460 folgt in einem Handbuche unmittelbar nach einer astronomischen Rechnung, der die
Bemerkung beigefügt ist 'geendigt den 28. April 1S09'.
Die Abhandlung IV. 'Hundert Theoreme über die neue Transcendente' Seite 461 — 469 steht auf
einzelnen Blättern ohne irgend eine Zeitangabe,
Die Abhandlung V. Seite 47 0—480 mit den Eingangsworten 'Allgemeines Theorem' enthält die bei-
beiden Zeitangaben 1827 Aug. 6. und Aug. 2 9. Der letzte Theü dieses Aufsatzes bildet wohl eine der frü-
hesten Vorarbeiten von Gadss für seine 'Allgemeinen Lehrsatze in Beziehung auf die im verkehrten Ver-
Verhältnisse des Quadrats der Entfernung wirkenden Anziehungs- und Abstossungskräfte' und lassen vermu-
then, dass.er den Zusammenhang dieses Gebietes mit einem anderen Gebiete der Analysis, nemlich der
Theorie der Functionen mit complexen Argumenten erkannt habe, ein Zusammenhang welcher Bisxaw?
auf ein so fruchtbares Gebiet der Forschung geführt hat.
Die Untersuchung des Pentagramma mirificum, eines sphärischen Fünfecks, dessen fünf Diagonalen
Quadranten sind, befindet sich an zwei getrennten Stellen in einem Handbuche, auf einem besonde-
besonderen Blatte der Art. [4.]. Das, was ich hier als Art. [1.] und [2.] bezeichnet habe, ist vor dem 23. Ja-
Januar 1S36 geschrieben, das andere enthält in Art. [7.] die Zeitangabe 1343 April 20.
Zwischen den unter Nr. I. zusammengestellten Untersuchungen über die neuen Transscendenten be-
befindet sich auch der Anfang einer Abhandlung mit der Überschrift 'Motus solidi a nullis tnribus soläci-
tati'. Das Problem ist dort bis zu dem bei der bekannten Auflösung auftretenden elliptischen Integral
geführt, so dass zu vermuthen steht, Gadss habe erkannt, dass die Gleichungen zur Bestimmung dieser
Bewegung mit Hülfe der neuen Transscendenten in endlicher Form erscheinen.
Die Aufzeichnung der hier unter V. zusammengestellten Untersuchungen über die neuen Trans-
Transscendenten, mit den Zeitangaben 1827 August 6 und August 29 ist wohl durch die jAcoBischen Briefe
an Schumacher datirt aus Königsberg von 1S27 Juni 13 und Aug.2 deren ersterer die algebraischen Glei-
Gleichungen für die Dreitheilung und Fünftheilung elliptischer Integrale der andere die Gleichung zwischen den
trigonometrischen Tangenten der Argumente für die Transformation beliebigen Grades gibt, veranlasst
worden. Diese beiden Briefe sind in der im Monat September 1827 ausgegebenen Nr. 123 der 'Astrono-
'Astronomischen Nachrichten' veröffentlicht, aber im Original zuvor an Gadss mitgetheilt worden, wie aus den
GAussschen Briefen an Schumacher vom 4. und 19. Aug. 1827 hervorgeht. Die Beweise jener Jacobi-
schen Lehrsätze hat dieser selbst durch einen aus Königsberg vom 18. November 1827 datirten in der im
Monat December 1827 ausgegebenen Nr. 127 der 'Astronomischen Nachrichten' abgedruckten Briefe an
Schumacher veröffentlicht.
Zu dieser Zeit war noch nicht, aber doch im selben Jahre, durch das zweite Heft des zweiten Bandes
des CRELLEschen Journals für reine und angewandte Mathematik die Abhandlung von A«*x 'Recherches
sur les fonctions eüiptiques §. I. — §. VII.' erschienen, und dieses war wohl diejenige Arbeit Abels , von
der Gauss am 30. Mai 1S2S an Schumacher schreibt, 'die, Ihnen gesagt, mir von meinen eignen Unter-
Untersuchungen wol * vorweggenommen hat, und mit diesen zum Theil selbst bis auf die gewählten bezeich-
bezeichnenden Buchstaben übereinstimmt*.
Auf dieselbe Arbeit bezieht sich wohl die folgende Stelle eines Briefs von Crelle an Abel vom
is. Mai 1828: — — Voici ce que m'ecrit Mr. Gauss de Goettingue que j'avaia egalement prie de m'en-
voyer quelque chose sur les fonctions eiliptiques dont il s'occupe, comme j'ai appris, plus de 30 ans. *D'au-
tres occupations m'empechent pour le moment de rediger ces recherches. Mr. Abel m'» prevenu au moins
d'un tiers. II vient d'enfiler precisement la meme route dont je suis sorti en 17»8. Ain» je ne m'etonne
nullement de ce que, pour la majeure partie, il en soit venu aux m£mes resultats. Comme d'aüleurs dans
sa deduction il a mis tant de sagacite de penetratien et d'elegance, je me crois par cela m&ae dispens6
■de la redaction de mes propres recherches.' — —
496 BEMERKUNGEN.
Auch über Legesdre besitzen wir einen Ausspruch von -Gadss. In einem Briefe ohne Datum schreibt
er an Olbebs 'Sie verlangten, in Ihrem letzten Briefe [wahrscheinlich derjenige 'Bremen d. 16. Aug. lSW,
Empfangen den 25. Aug.' bezeichnete; die Briefe aus jenen Monaten sind: O. an G. Juli 17. — G. an
O. Aug. 2. — G. an O. der hier im Auszuge mitgetheilte ohne Datum — O. an G. Nov. 2. — G. an
O. Dec. 2.], allertheuerster Freund, mein Urtheil über Mossottis in- den Mailänder Ephemeriden gege-
gegebene Methode die Bahnen von H. K. zu berechnen. Als ich Ihnen neulich schrieb, war mir der Gegen-
Gegenstand nicht gegenwärtig genug, ob ich gleich jenen Aufsatz früher so weit gelesen hatte, dass ich ein
Urtheil darüber vorläufig gefasst hatte. In jenem Augenblicke erlaubte mir meine Zeit nicht, mich gleich
wieder gehörig in die Sache hineinzustudiren, und ich überging daher Ihre Anfrage. Seitdem habe ich
nun wieder Anlass genommen, jenen Aufsatz noch einmal zu lesen , und in den eigentlichen Geist weiter
einzudringen, und ich will heute eine Stunde dazu anwenden mich mit Ihnen über diesen Gegenstand zu
unterhalten.'
'Geneigt, wie ich von jeher gewesen bin, jeden neuen originellen oder genialen Gedanken mit
Liebe aufzunehmen*), wurde ich von der wirklich neuen Idee in Mossottis Aufsatz bei meiner ersten
Lecture frappirt.' — —
*) 'Ich brauche Ihnen wohl nicht zu sagen, dass die neuliche wunderliche Recension von Legendre's
JExercices de calcul Integral in unsern G. A. [Göttingische gelehrte Anzeigen 1817 August w.] nicht von
mir ist, da dieses Werk so manches der oben erwähnten Art enthält.'
Es verdient noch besonders ausgesprochen zu werden, dass in Bezug auf die Theorie der TheiLung
des Lemniscaten-Bogens der Handschriftliche Nachlast nichts enthält, als was der vorliegende Abdruck an
Hülfssätzen dazu darbietet, während in dem Werke 'Disquisitiones arithmettcae', welches Juli 1801 aus-
ausgegeben worden, Art. 335 der Sectio septima, de aequationibus circuli sectiones detinientibus, gesagt wird
— 'Ceterum principia theoriae, quam exponere aggredimur, multo latius patent, <juam hie extenduntur.
Namque non solum ad funetiones circulares, sed pari successu ad multas alias funetiones transscendentes
C dx
applicari possunt, e. g. ad eas quae ab integrali I -j- jt pendent, praetereaque etiam ad varia con-
J v (i x )
gruentiarum genera: sed quoniam de illis funetionibus transscendentibus amplum opus peculiare paramus,
de congruentiis autem in continuatione disquisitionum arithmeticarum copiose traetahitur, hoc loco solas
funetiones circulares considerare visum est.' —
Abel und Jacobi haben Gauss' Untersuchungen über die Elliptischen Functionen nicht vorgefunden,
sie mussten dieses Gebiet der Wissenschaft von Neuem entdecken.
Die speciellen Beziehungen zwischen den Arbeiten von Gadss in diesem Gebiete der reinen Analysis
und den Arbeiten von Anderen werde ich in einer besondern Schrift im Zusammenhange mit einer Ge-
Geschichte der gesammten wissenschaftlichen Thätigkeit von Gauss darzustellen versuchen, wahrend ich in
diesen seinen eignen Werken angeschlossenen Bemerkungen nur die betreffenden actenmässigen Thatsachen
aufgenommen habe.
Gottingen im Juni 1S6S.
Schebing.
INHALT.
GAÜSS WERKE BAND III. ANALYSIS.
• ALGEBRAISCHE FUNCTIONEN.
Abhandlungen.
Demonstratio nova theorematis omnem functionem algebraicam rationalem in-
tegram unius variabilis in factores reales primi vel secundi gradus re-
solvi posse 17 99 Seite 1
Demonstratio nova altera theorematis omnem functionem algebraicam rationa-
rationalem integram unius variabilis in factores reales primi vel secundi gradus
resolvi posse 1815 Dec. . . — 31
Theorematis de resolubilitate functionum algebraicarum integrarum in facto-
factores reales demonstratio tertia. Supplementum commentationis praecedentis 1816 Jan. . . — 57
Beweis eines algebraischen Lehrsatzes 1828 — 65
Beiträge zur Theorie der algebraischen Gleichungen • . . 184 9 Juli . . — 71
Anzeigen eigner Abhandlungen.'
Demonstratio nova altera theorematis omnem functionem algebraicam ratio-
rationalem integram unius variabilis in factores reales primi vel secundi gra-
gradus resolvi posse 1815 Dec. . . — 105
Theorematis de resolubilitate functionum algebraicarum integrarum in facto-
factores reales demonstratio tertia 1S16 März . . — 107
Beiträge zur Theorie der algebraischen Gleichungen 1849 Juli . . — 113
Anzeigen nicht eigner Schriften.
Cot-teek. Recherches math&natiques 1813 März . . — 116
Foubdek. Analyse des equations determin^es 1833 Febr. . . — 11»
GAUSS' REIHE.
Abhandlungen.
Disquisitiones generales circa seriem infinitam
+ 2NF +
t a.6x *(* + i)W + l)xx
1 -T 1-2.y(y+i)
Pars prior 1812 Jan. . . — 123
Hl. 63
498 . INHALT.
Methodus nova integralium valores per approximationem inveniendi . . . 1 si4 Sept. . .Seite 163
Anzeigen eigner Abhandlungen.
Disquisitiones generales circa seriem infinitam etc. Pars prior 1812 Febr. . . — 197
Methodus nova integralium valores per approximationem inveniendi . . . 1814 Sept. . . — 202
Nachläse.
Determinatio seriei nostrae "per aequationem differentialem secundi ordinis . — 207
Bemerkungen zu dieser Abhandlung — 230
MITTHEILUNGEN ÜBER VERSCHIEDENE SCHRIFTEN.
Peaff. Methodus generalis, aequationes differentiarum partialium, nee non
aequationes differentiales vulgäres, utrasque primi ordinis, inter quot-
eunque variabiles, complete integrandi 1815 Juli . . — 231
Caixet. Tables logarithmiques 1802 Nov. . . 241
Prasse. Logarithmische Tafeln für die Zahlen, Sinus und Tangenten . . 18t l Mai . . — 241
Prasse. Tables logarithmiques pour les nombres, les sinus et les tangentes 1814 Dec. . . — 24 3
Gadss. Tafeln zur bequemern Berechnung des Logarithmen der Summe oder
Differenz zweier Grossen, welche selbst nur durch ihre Logarithmen ge-
gegeben sind 1812 Nov. . . — 244
Pasqüich. Abgekürzte Logarithmisch-Trigonometrische Tafeln 1817 Oct. . . — 246
[Matthtessen.] Tafel zur bequemern Berechnung des Logarithmen der Summe
oder Differenz zweier Grossen, welche selbst nur durch ihre Logarith-
Logarithmen gegeben sind lsi9 Jan. . . — 250
Logarithmentafeln mit sechs Ziffern 1822 Dec. . . — 252
Babbage. Table of logarithms of the natural numbers 1828 Jan. . . — 253
Hasslee. Tabulae logarithmicae et trigonometricae 1831 März . . — 255
Vega und Hülsse. Sammlung mathematischer Tafeln .. .. ..1840 — 255
Vega. Thesaurus Loganthmorum 1851 Mai . . — 257
INTERPOLATION.
Nachlass.
Theoria interpolationis methodo nova traetata — 265
Bemerkungen zu dieser Abhandlung — 328
ELLIPTISCHE FUNCTIONEN.
Abhandlung.
Determinatio attractionis,. quam in punetum quodvis positionis datae exerceret
planeta, si eius massa per totam orbitam ratione temporis, quo singulae
partes describuntur, uniformiter esset dispertita ISIS Jan. . . — 331
Anzeige der vorhergehenden Abhandlung 1S18 Febr. . . — 357
Nachlass.
De origine proprietatibusque generalibus numerorum mediorum arithmetico-geometricorum.
Art. 1—8 — 361
DiHALT.
De functionibus transcendentibus quae ex differentiatione mediorum arithmetico-geometrico-
rum oriuntur. Art. 9— ll Seite 372
Fortsetzung der Untersuchungen über das arithmetisch-geometrische Mittel. Art. 12—26. . — 375
Tabula. Media anthmetico-geometrica inter unitatem et sinus singulorum semigradum . . — 40$
Lemniscatische Functionen (I.) dargestellt durch Potenz- Reihen — 404
Lemniscatische Functionen (II.) dargestellt durch unendliche Producte'und durch trigonome-
trigonometrische Reihen • — 413
Zur Theorie der neuen Transscendenten
I. Anfange der der Untersuchungen über die neuen Transscendenten — 433
II. Zur Theorie der transcendenten Functionen gehörig — 436
III. Neue Anordnung der Theoreme in Bezug auf diejenigen Reihen und unendlicheq Pro-
ducte, welche zu der Theorie der arithmetisch-geometrischen Mittel gehören .... — 446
IV. Hundert Theoreme über die neuen Transscendenten — 461
V. Allgemeine Theoreme — 47 0
Pentagramma mirificum — 481
Bemerkungen — 401
Zwei Steindrucktafeln zu Seite 30 und 102.
GOTTINGEN,
GEDRÜCKT IN DER DIETERICHSCHEN UNIVERSITÄTS- DRUCKEREI
W. FB. KAESTNEB.