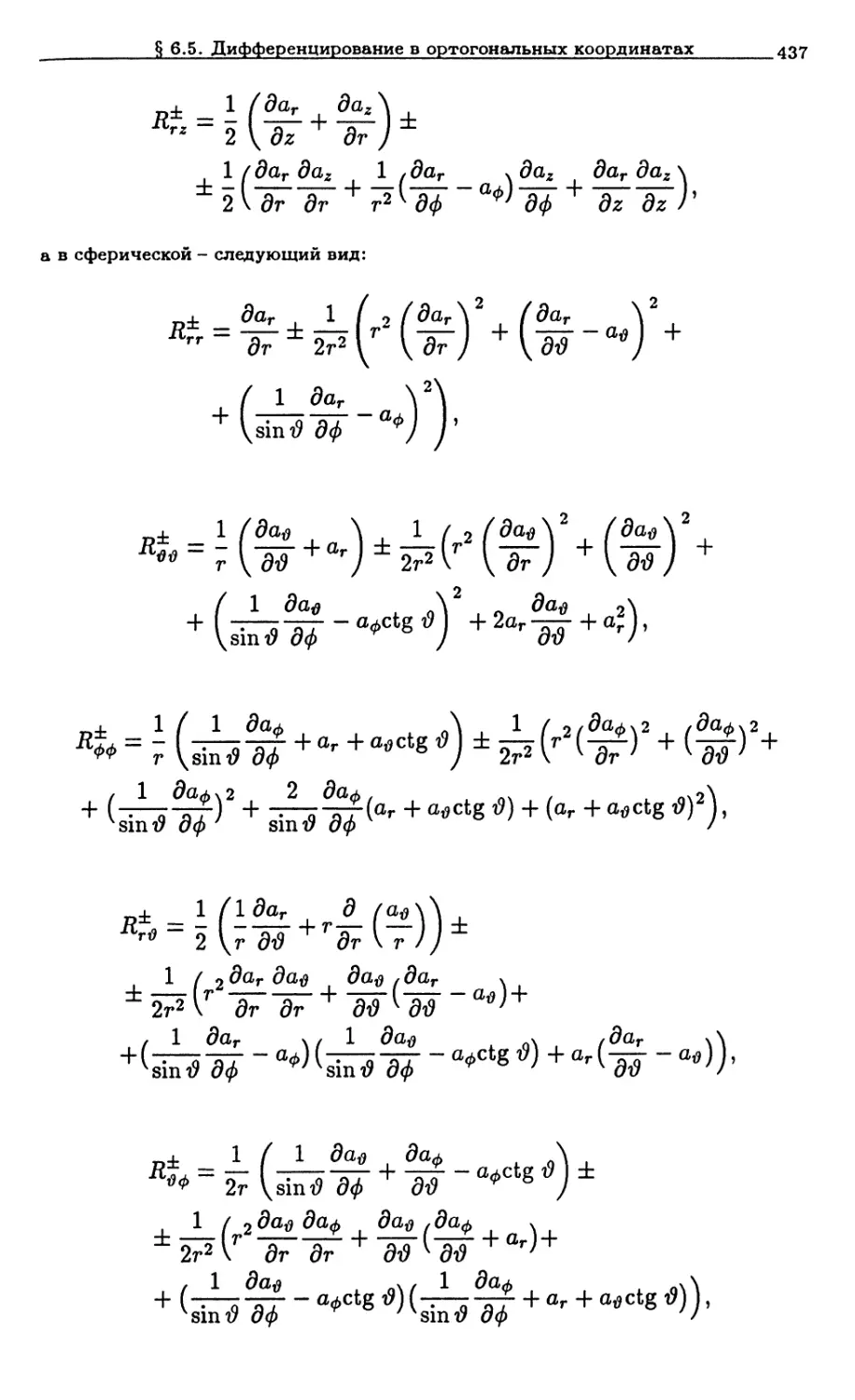Автор: Димитриенко Ю.И.
Теги: математика естественные науки физико-математические науки математическая физика
ISBN: 5-06-004155-7
Год: 2001
Текст
Ю.И. ДИМИТРИЕНКО
Тензорное
исчисление
Рекомендовано учебно-методическим объединением вузов
по университетскому политехническому образованию
в качестве учебного пособия для студентов
высших учебных заведений, обучающихся
по физико-математическим и машиностроительным специальностям
Москва
«Высшая школа» 2001
УДК 501
ББК 22
Д 46
Рецензенты:
кафедра сопротивления материалов, динамики и
прочности машин Московского авиационного института
(завкафедрой, д-р физ.-мат.наук, профессор А.Г.Горшков);
д-р физ.-мат.наук, профессор Д.В.Тарлаковский
Димитриенко Ю.И.
Д46 Тензорное исчисление: Учеб.пособие для вузов. -М.: Высш.
шк., 2001. - 575 с; ил.
ISBN 5-06-004155-7
Учебное пособие охватывает основные разделы тензорного исчисления,
используемые в механике и электродинамике сплошных сред, механике
композитов, кристаллофизике, квантовой химии: алгебру тензоров, тен-
тензорный анализ, тензорное описание кривых и поверхностей, основы тен-
тензорного интегрального исчисления. Изложена теория инвариантов, теория
индифферентных тензоров, задающих физические свойства сред, теория
анизотропных тензорных функций,а также основы тензорного исчисления
в римановых пространствах и пространствах аффинной связности.
Для студентов и аспирантов высших учебных заведений, обучающих-
обучающихся по физико-математическим и машиностроительным специальностям.
УДК 501
ББК 22
ISBN 5-06-004155-7 © «Издательство«Высшая школа», 2001
Оригинал-макет данного издания является собственностью издательства «Высшая
школа», и его репродуцирование (воспроизведение) любым способом без согласия изда-
издательства запрещается.
ОГЛАВЛЕНИЕ
Предисловие 5
Истоки тензорного исчисления 7
Введение 13
Глава 1. ТЕНЗОРНАЯ АЛГЕБРА 17
§ 1.1. Локальные векторы базиса. Якобиевы и мет-
метрические матрицы 17
§ 1.2. Векторное произведение 29
§ 1.3. Геометрическое определение тензора и алгеб-
алгебраические операции с тензорами 35
§ 1.4. Алгебра тензорных полей 52
§ 1.5. Собственные значения тензора 59
§ 1.6. Симметричные, кососимметричные и ортого-
ортогональные тензоры 62
§ 1.7. Физические компоненты тензоров 70
§ 1.8. Тензоры высших рангов .... 73
§ 1.9. Псевдотензоры 80
Глава 2. ТЕНЗОРЫ НА ЛИНЕЙНЫХ ПРО-
ПРОСТРАНСТВАХ 87
§ 2.1. Линейное n-мерное пространство 87
§ 2.2. Матрицы n-ого порядка 97
§ 2.3. Линейные преобразования п-мерных про-
пространств 109
§ 2.4. Сопряженное пространство 118
§ 2.5. Алгебра тензоров на n-мерных линейных
пространствах 124
§ 2.6. Внешние формы 143
Глава 3. ГРУППЫ ПРЕОБРАЗОВАНИЙ . . 157
§ 3.1. Линейные преобразования координат .... 157
§ 3.2. Группы преобразований в трехмерном евкли-
евклидовом пространстве 171
§ 3.3. Симметрия конечных тел 175
§ 3.4. Матричные представления групп преобразо-
преобразований 195
Глава 4. ИНДИФФЕРЕНТНЫЕ ТЕНЗОРЫ И
ИНВАРИАНТЫ 201
§ 4.1. Индифферентные тензоры 201
§ 4.2. Число независимых компонент индифферент-
индифферентного тензора 214
§ 4.3. Симметричные индифферентные тензоры . . 226
§ 4.4. Скалярные инварианты 238
§ 4.5. Инварианты симметричного тензора второго
ранга 250
Глава 5. ТЕНЗОРНЫЕ ФУНКЦИИ 267
§ 5.1. Линейные тензорные функции 267
§ 5.2. Скалярные функции тензорного аргумента . 295
§ 5.3. Потенциальные тензорные функции 308
| 5.4. Квазилинейные тензорные функции 317
§ 5.5. Спектральное представление тензоров второ-
второго ранга , 328
§ 5.6. Спектральные представления квазилиней-
квазилинейных тензорных функций 346
§ 5.7. Непотенциальные тензорные функции .... 359
§ 5.8. Дифференцирование тензорных функций по
тензорному аргументу 376
§ 5.9. Скалярные функции нескольких тензорных
аргументов 379
§ 5.10. Тензорные функции нескольких тензорных
аргументов 395
Глава 6. ТЕНЗОРНЫЙ АНАЛИЗ 401
§ 6.1. Ковариантное дифференцирование 401
§ 6.2. Дифференцирование тензоров второго ранга 410
§ 6.3. Свойства ковариантных производных .... 414
§ 6.4. Ковариантные производные второго порядка 419
§ 6.5. Дифференцирование в ортогональных криво-
криволинейных координатах 424
Глава 7. ГЕОМЕТРИЯ КРИВЫХ И ПО-
ПОВЕРХНОСТЕЙ 439
§ 7.1. Кривые в трехмерном евклидовом простран-
пространстве 439
§ 7.2. Поверхности в трехмерном евклидовом про-
пространстве 449
§ 7.3. Кривые на поверхности 468
§ 7.4. Геометрия в окрестности поверхности .... 483
§ 7.5. Уплощенные поверхности в IR3 490
Глава 8. ТЕНЗОРЫ В РИМАНОВЫХ ПРОС-
ПРОСТРАНСТВАХ И ПРОСТРАНСТВАХ
АФФИННОЙ СВЯЗНОСТИ 495
§ 8.1. Римановы пространстэа 495
§ 8.2. Пространства аффинной связности 507
§ 8.3. Риманово пространство с аффинной связнос-
связностью 515
§ 8.4. Тензор Римана-Кристоффеля 522
Глава 9. ИНТЕГРИРОВАНИЕ ТЕНЗОРОВ . 535
§ 9.1. Криволинейные интегралы от тензора ... 535
§ 9.2. Поверхностные интегралы от тензора .... 544
§ 9.3. Объемные интегралы от тензора 550
Приложение. Энергетические и квазиэнерге-
квазиэнергетические пары тензоров .... 554
Сйисок литературы 567
Предметный указатель 569
ПРЕДИСЛОВИЕ
Возникновению тензорного исчисления в современном его виде мы
обязаны прежде всего Риччи, который в конце XIX века предложил
математический аппарат для операций над "системами с индексами".
Хотя сами эти "системы" были обнаружены раньше - при исследо-
исследовании неевклидовых геометрий Гауссом, Риманом, Кристоффелем и
при исследовании упругих тел Коши, Эйлером, Лагранжем, Пуассо-
Пуассоном (см. об этом раздел "Истоки тензорного исчисления"), именно
Риччи разработал удобную компактную систему обозначений и поня-
понятий, которая широко используется в настоящее время в самых различ-
различных областях механики, физики, химии, кристаллофизики и других
науках.
В настоящее время тензорное исчисление продолжает развиваться,
появляются новые направления, переосмысливаются некоторые ранее
введенные понятия. Именно поэтому, несмотря на имеющуюся учеб-
учебную литературу по тензорам (см. список литературы), потребность
в изложении этих вопросов достаточно актуальна. Для иллюстра-
иллюстрации сказанного приведем лишь один пример. Как это ни покажется
странным, на вопросы: "Можно ли представить себе тензор второго
ранга столь же наглядно, как и вектор в трехмерном пространстве?"
и "Что такое диада?" - ответ скорее всего затруднятся дать многие
искушенные читатели, знакомые с тензорами.
Данная книга предназначена читателю, начинающему знакомство
с методами тензорного исчисления, именно поэтому в ней во введении
изложено знакомое из школьной программы понятие вектора как гео-
геометрического объекта в трехмерном пространстве, на основе которого
затем дано "геометрическое" же определение тензора. Это определе-
определение позволяет "увидеть" сам тензор и основные операции с ним. И
лишь после такого знакомства дано формальное определение тензоров
в абстрактных n-мерных пространствах.
Автор надеется, что книга будет полезна также и специалистам,
прежде всего в области механики сплошных сред, физики твердого
тела, кристаллофизики, квантовой химии, поскольку кроме указан-
указанных глав для начинающих, в ней содержатся многие недостаточно, на
наш взгляд, освещенные в литературе вопросы теории тензоров, "за-
"задающих физические свойства" (в книге они названы индифферентны-
индифферентными), теории инвариантов тензоров относительно кристаллографичес-
кристаллографических групп, теории тензорных функций, теории интегрирования тен-
тензоров.
Предисловие
Книга построена по "математическому принципу": в ней имеются
определения, теоремы, доказательства и упражнения в конце почти
каждого параграфа. Начало и конец доказательств выделены значка-
значками Ў и А соответственно.
При изложении материала отдано предпочтение безиндексной фор-
форме записи тензоров, которая при определенных навыках позволяет
быстро и компактно записывать различные соотношения в механи-
механике и физике, не заслоняя при этом физическую суть явлений. В то же
время везде, где это уместно, даны соответствующие компонентная и
матричная формы записи тензорных соотношений.
Автор считает своим приятным долгом поблагодарить заведующе-
заведующего кафедрой механики композитов МГУ им.М.В.Ломоносова, профес-
профессора Б.Е.Победрю, под влиянием идей которого в значительной сте-
степени возник замысел этой книги; заведующего кафедрой "Сопротив-
"Сопротивление материалов, динамика и прочность машин" МАИ, профессора
А.Г.Горшкова и профессора Д.В.Тарлаковского за ряд ценных заме-
замечаний, высказанных при рецензировании книги, а также профессо-
профессоров МГТУ им.Н.Э.Баумана В.В.Феоктистова, С.П.Ерковича и доцен-
доцента А.Н.Щетинина, советы и рекомендации которых помогли автору
при написании нескольких разделов книги.
Автор благодарен кандидату физико-математических наук
И.Д.Димитриенко за подготовку оригинал-макета книги и ее редак-
редактирование.
Автор
ИСТОКИ ТЕНЗОРНОГО ИСЧИСЛЕНИЯ*
Исторически тензорам предшествовали векторы, матрицы и "сис-
"системы с индексами". Еще Архимед, живший в 287-212 гг до н.э.,
складывал силы, действующие на тело, по правилу параллелограмма,
т.е. интуитивно вводил особые объекты, которые характеризуются не
только величиной, но и направлением. Этот основополагающий шаг
в сторону разработки векторного исчисления долго оставался един-
единственным: голландский математик и инженер С.Стевин A548-1620),
который считается создателем понятия векторной величины, факти-
фактически переоткрыл еще раз закон сложения сил по правилу паралле-
параллелограмма. Этот же закон формулировал и И.Ньютон A642-1727) в
своих "Началах" наряду с законами движения тел.
Следующий важнейший с современной точки зрения шаг был сде-
сделан только в XIX веке ирландским математиком У.Р.Гамильтоном
A805-1865), который, занимаясь теорией кватернионов-гиперкомплек-
сных чисел, в 1845 году ввел сам термин "вектор" (от латинского
"vector" - несущий), а также термины: "скаляр", "скалярное произ-
произведение", "векторное произведение", - и дал определение этих опера-
операций. В эти же годы Г.Грассманом A809-1877) была создана теория
внешних произведений (само понятие введено в 1844 году), известная
в настоящее время как алгебра Грассмана. Англичанин У.Клиффорд
A845-1879) объединил подходы Гамильнона и Грассмана, окончатель-
окончательная же связь кватернионов, алгебры Грассмана и векторной алгебры
была установлена только в конце XIX века Дж.У.Гиббсом A839-1903).
Само геометрическое изображение вектора как отрезка со стрелкой
также устойчиво появилось впервые, по-видимому, у Гамильтона, а
в 1853 году французский математик О.Коши A789-1857) ввел в об-
обращение понятие радиус-вектора и соответствующее ему обозначение
г.
В XIX веке математики стали активно использовать еще один объ-
объект - предшественник тензоров - матрицы. Первое появление матриц
связывают с древнекитайскими математиками, которые во II веке до
н.э. применяли их для записи систем линейных уравнений. Мат-
Матричная запись алгебраических уравнений и само современное матрич-
матричное исчисление было развито английским математиком А.Кэли A821-
*Этот краткий исторический очерк ни в коей мере не претендует на полноту
изложения всей истории развития тензорного исчисления и связанных с ним наук,
его целью является лишь знакомство начинающего читателя с этапами разра-
разработки и именами ученых, усилиями которых было создано современное тензорное
исчисление.
Истоки тензорного исчисления
1895), который, в частности, в 1841 году ввел используемое и сейчас
Ь
обозначение для определителя:
Многие основополагающие
с d
результаты в теории систем линейных алгебраических уравнений бы-
были получены немецким математиком Л.Кронекером A823-1894).
В течение все того же XIX века в разных областях математики
появляются "системы с индексами". В алгебре это, например, квад-
квадратичные формы, теорию которых разабатывали А.Кэли, С.Ли A842-
1899) и другие, в геометрии - квадратичные дифференциальные фор-
формы, которые в настоящее время известны как первая и вторая квадра-
квадратичная форма поверхности и квадрат длины элементарного отрезка.
Основоположником теории поверхностей по праву считают выдаю-
выдающегося немецкого ученого К.Ф.Гаусса A777-1855). Многие важней-
важнейшие результаты в этой области были установлены Б.Риманом A826-
1866), который развил теорию поверхностей на случай п измерений,
Э.Бельтрами A835-1900), Ф.Клейном A849-1925), Г.Ламэ A795-1870).
Выдающаяся роль принадлежит Э.Б.Кристоффелю A829-1900), кото-
который в 1869 году, рассматривая преобразования квадратичных форм
ds2 = ?) |/ dfit/dx^dx^, впервые обнаружил тензорный закон их преоб-
преобразования, а также ввел понятие производных от векторных величин,
которые преобразуются по тензорному закону (сейчас их называют
ковариантными производными).
Возникшая еще в XVIII веке усилиями крупнейших математиков и
механиков: Л.Эйлера A707-1783), Ж.-Л.Лагранжа A736-1813),
П.Лапласа A749-1827), С.Пуассона A781-1840), О.Коши A789-1857),
М.В.Остроградского A801-1861) - наука о движении и равновесии уп-
упругих тел (теория упругости), стала еще одним источником появления
"систем с индексами" - компонент напряжений и деформаций. Ком-
Компоненты напряжений обозначали как ХХ) Ху) Xz, YX) Уу, Y2) Zx, Zy,
Z2 и подразумевали под ними проекции сил, действующих на гранях
элементарного кубика, на оси координат. Операции над такими сис-
системами с индексами были весьма громоздки, содержали многочислен-
многочисленные повторения с точностью до круговой замены обозначений. Однако
только в конце XIX века удалось понять внутреннее единство формул,
содержащих "системы с индексами", и найти новый математический
аппарат, сделавший операции с ними компактными и удобными.
Впервые для векторых величин эту задачу удалось решить амери-
американскому физику и математику Дж.У.Гиббсу, который создал вектор-
векторную алгебру с операциями сложения, скалярного и векторного умноже-
умножения, показав ее связь с теорией кватернионов и алгеброй Грассмана.
Кроме того Гиббс создал современный векторный анализ - теорию
дифференциального исчисления векторных полей и сам "язык" век-
векторного исчисления, в котором используется как компонентная, так и
безиндексная форма записи соотношени. В частности, им были даны
удобные представления для операций дивергенции и ротора вектор-
Истоки тензорного исчисления
ных полей. Эти выдающиеся результаты Гиббса можно сравнить с
введением алгебраической символики Ф.Виетом A540-1603), которую
используют вот уже 400 лет. Созданные Гиббсом векторная алгеб-
алгебра и анализ также прочно вошли в современную физику и механику,
а его лекциям "Элементы векторного анализа в изложении для сту-
студентов", выпущенным в 1881-1884 гг. и представляющим, по сути,
первый учебник по векторному исчислению, фактически следуют все
соответствующие современные курсы.
Гиббс был большим энтузиастом в распространении векторного ис-
исчисления в различных областях точных наук, в частности, именно
им была дана современная векторная запись уравнений электромаг-
электромагнетизма Дж.К.Максвелла A831-1879), сам же Максвелл использовал
метод кватернионов. Хотя не обошлось без критики сторонниками
этого метода, векторное исчисление Гиббса было активно воспринято
физиками, и с начала XX века теория Максвелла практически всеми
используется в форме Гиббса.
Однако в тех областях науки, где возникают системы с большим
числом индексов, чем у векторов (более одного): в геометрии, в теории
упругости, в кристаллофизике, - векторное исчисление Гиббса оказа-
оказалось бессильным, и он сам, например, при записи уравнений теории
упругости в 1889 году использовал все те же обозначения Хх, Ху, Х2,
Yx и т.д.
Проблему обобщения векторного исчисления на системы с произ-
произвольным числом индексов удалось решить итальянскому математику
Дж.Риччи A853-1925), который в своих работах 1886-1901 гг. соз-
создал новый аппарат, названный им абсолютным диффенциальным ис-
исчислением, для алгебраических и дифференциальных операций с "ко-
вариантными и контравариантными системами порядка Л (так Рич-
чи называл компоненты тензоров ?Г1Г2...ГЛ и жГ1Г2*"Гл). Самим Рич-
чи с помощью этого аппарата были установлены основополагающие
результаты в дифференциальной геометрии n-мерных пространств.
Исчисление, созданное Риччи, оказало настолько сильное влияние на
геометрию и физику, что некоторое время оно даже называлось "ис-
"исчислением Риччи". С некотроыми изменениями оно широко исполь-
используется и в настоящее время.
Применение теории абсолютного дифференцирования для римано-
вых пространств было осуществлено другим выдающимся итальянс-
итальянским математиком Т.Леви-Чивита A873-1942), коллегой и соавтором
Риччи в нескольких основополагающих работах. Им, в частности,
было введено правило свертывания индексов, введен символ ?*•**, но-
носящий его имя и играющий наряду с символом Кронекера 8ij важ-
важнейшую роль в тензорном исчислении. Исключительно важную роль
сыграло введение Леви-Чивитой понятия параллельного переноса век-
векторов и тензоров в римановых пространствах.
Для зарождавшейся на рубеже XIX и XX веков теории относитель-
до Истоки тензорного исчисления
ности аппарат абсолютного дифференциального исчисления оказался
весьма удобным и многообещающим, и в то же время дальнейшее
развитие этого исчисления происходило совместно с разработкой фи-
физических основ этой теории. Так в 1913 году А.Эйнштейн A879-1955)
совместно с М.Гроссманом применяет абсолютное дифференциальное
исчисление к теории относительности и теории гравитации, а в 1916
году в замечаниях к своей статье он предлагает "ради простоты" про-
пропускать знак суммы в тех случаях, когда суммирование идет по дваж-
дважды повторяющимся индексам. С тех пор это правило стало широко
применяться и в настоящее время называется соглашением Эйнштей-
Эйнштейна о суммировании.
Новое исчиление примерно в тоже время начали применять в тео-
теории упругости и кристаллофизике для описания свойств кристаллов.
Здесь прежде всего следует назвать немецкого ученого В.Фойгта, ко-
который и ввел в 1898 -1903 гг. сам термин "тензор" (от латинского
"tensus" - напряженный) именно для описания механических напря-
напряжений. Фойгт одним из первых дал матричное представление ком-
компонент тензоров второго и четвертого рангов, задающих физические
свойства различных типов кристаллов. Термин "тензор" был активно
воспринят не только в теории упругости, но и в геометрии и физике,
для обозначения ковариантных и контравариантных систем. Так, на-
начиная с 1913 года, в своих работах Эйнштейн использует этот термин.
Дальнейшее развитие тензорного исчисления в начале XX века осу-
осуществлялось многими учеными, среди которых назовем уже упоми-
упоминавшегося Т.Леви-Чивита, голландского математика Я.Схоутена, ко-
которые выпустили соответственно в 1927 и в 1924 гг. первые специали-
специализированные учебники по тензорному исчислению. Книга Я.Схоутена
называлась "Исчисление Риччи" (Der Ricci-Kalkul). В ней и в по-
последующих книгах он, в частности, упорядочил правила расстановки
индексов у тензоров, а также предложил некоторые геометрические
образы тензоров.
Тем не менее, как и в случае векторного анализа, не обходилось
и без определенной критики появивишегося тензорного исчисления,
главным образом сводившейся к тому, что расшифровка тензорных
формул требует дополнительных усилий при анализе тех или иных
физических соотношений (заметим, что такая критика иногда выска-
высказывается и до сих пор). Однако затраты на овладение тензорным
аппаратом с лихвой окупаются при дальнейшей работе с ним.
Важную роль сыграли работы выдающегося немецкого математи-
математика Г.Вейля A885-1955), который вместе с О.Вебленом развил под-
подход к определению тензора на основе рассмотрения квадратичных
форм, тем самым оформив "алгебраический" способ введения тензо-
тензоров. Много сделали для развития теории тензоров Б.Вильсон, выпус-
выпустивший в 1913 году широко известный учебник по векторному ана-
анализу, Ф.Мурнаган, который, в частности, ввел обобщенные символы
Истоки тензорного исчисления
Кронекера, Э.Картан, разработавший теорию внешних дифференци-
дифференциальных форм, Р.Вайценбек, Д.Витали, которые наряду с Э.Картаном
и Я.Схоутеном разработали теорию пространства абсолютного парал-
параллелизма, Дж.Л.Синдж, Т.Томас, З.Аппель, Л.Эйзенхарт, Л.Витерн-
бен, а также И.С.Сокольников и А.Дж.Мак.-Коннел, написавшие пре-
превосходные учебники по тензорному анализу. Успехам в применении
тензоров для задач теории упругости мы во многом обязаны Л.Брил-
люэну и А.Ляву.
Значительный вклад в развитие тензорного исчисления внесли рос-
российские ученые: П.К.Рашевский, А.П.Широков, В.Ф.Каган, Н.Е.Ко-
чин, Н.Е.Ефимов, И.Н.Векуа, Б.Е.Победря, В.В.Лохин и многие дру-
другие. Так И.Н.Векуа разработал теорию ковариантного дифференци-
дифференцирования в комплексных криволинейных координатах, а Б.Е.Победря
ввел спектральное представление тензоров и на его основе существен-
существенно развил теорию нелинейных тензорных функций.
Важным шагом стало введение безиндексной формы записи тензор-
тензорных соотношений, которая появилась в середине XX века в исследова-
исследованиях по механике сплошных сред Р.Ривлина, Дж.Эриксена, В.Нолла,
Дж.Адкинса, А.Грина, Дж.Смита, К.Трусделла, А.И.Лурье. Безин-
дексная форма, введенная для векторов еще Гиббсом, позволила за-
записать специальным математическим языком все физические законы
в простой, компактной и объективной (т.е. независящей от выбора
системы координат) форме, в которой индексы "не заслоняют" физи-
физической сути законов. Современное тензорное исчисление использует
все три упоминавшиеся формы записи соотношений: компонентную,
безиндексную и матричную.
Тензорное исчисление в настоящее время тесно связано с другими
областями математики, в частности, с теорией инвариантов, теорией
групп и теорией представлений, теорией индифферентных тензоров.
Теория алгебраических инвариантов, возникшая еще в XIX веке, в
настоящее время находит широкое применение в механике и физике.
Теория групп, у истоков которой стоял Э.Галуа A811-1832), в XIX
активно применялась в естественных науках для описания свойств
симметрии кристаллов. С ее помощью были установлены 32 кристал-
кристаллографические группы, в 1848 году Бравэ нашел 14 трансляционных
групп, соответствующих решеткам кристаллов, которые получили
его имя. В 1890-1894 гг. российским ученым Е.С.Федоровым и неза-
независимо от него А.Шенфлисом были выведены 230 пространственных
групп симметрии кристаллов. После создания теории представлений
групп, разработанной, главных образом, Г.Фробениусом A849-1918),
И.Шуром A885-1955), У.Бернсайдом A852-1927), было установлено,
что теория групп имеет фундаментальное значение для квантовой
физики. В настоящее время теория представлений является одним
из бурно развивающихся разделов математики. Некоторые методы
теории представлений, используемые при описании свойств индеффе-
12 Истоки тензорного исчисления
рентных тензоров, изложены в данной книге.
Теория индифферентных тензоров (или иначе тензоров с внешней
симметрией - по А.В.Шубникову, или еще иначе материальных тен-
тензоров, задающих физические свойства: упругость, тепловое расшире-
расширение, теплопроводность, пьезоэлектрический эффект, электропровод-
электропроводность и многие другие) активно начала развиваться в XX веке вслед за
основополагающими работами Фойгта. Весомый вклад в эту область
внесли российские ученые А.В.Шубников и его ученики, Ю.И.Сиро-
тин, Н.В.Белов, И.С.Желудев, Ф.И.Федоров, П.Бехтерев, Н.Г.Ченцов,
С.Г.Лехницкий, М.П.Шаскольская. Усилиями этих и многих других
ученых теория описания линейных свойств анизотропных сред (крис-
(кристаллов,1 монокристаллов, композиционных материалов, древесины и
других) была в значительной степени завершена. Тем не менее мно-
многие важные вопросы остались до сих пор невыясненными, так только
в 1983-1984 гг. польскому ученому Я.Рыхлевскому удалось привести
тензор четвертого ранга модулей упругости к диагональному виду и
исследовать его свойства.
Примерно с середины XX века была начата активная разработка
теории нелинейных тензорных функций и функционалов, основы ко-
которой восходят к знаменитой теореме Гамильтона-Кэли. Эта теория
позволяет описывать такие нелинейные свойства сред, как эффекты
анизотропной пластичности, ползучести, нелинейной вязкости и вяз-
копластичности, нелинейной диффузии, диаграммы намагниченнос-
намагниченности, нелинейные оптические свойства и др. Основополагающие ре-
результаты в этой еще только развивающейся области были получены
Р.Ривлином, Ф.Смитом, А.Спенсером, А.Грином, Дж.Адкинсом. Ими
были установлены представления, главным образом, скалярных или
алгебраических функций от тензоров для различных групп симмет-
симметрии. Иной более общий подход, основанный на построении тензор-
тензорных базисов, был применен российскими учеными: Ю.И.Сиротиным,
В.В.Лохиным, Б.Е.Победрей, Г.Н.Малолеткиным и В.Л.Фоминым. В
настоящей книге этому перспективному направлению посвящена вся
пятая глава.
В заключение подчеркнем, что тензорное исчисление является не-
необходимым инструментом большинства новых развивающихся естес-
естественнонаучных направлений в физике, механике, квантовой химии,
кристаллофизике. В частности, такие увлекательные проблемы со-
современности, как разработка квантовой теории относительности, те-
теории объединенных полей, теории наноструктур и другие, решаются
главным образом методами тензорного исчисления.
ВВЕДЕНИЕ
А. Геометрическое определение вектора
Тензорное исчисление является развитием векторного исчисления,
поэтому прежде всего напомним простейшие определения векторов и
операций с ними.
Используя аксиоматику элементарной геометрии (в которой введе-
введены понятия точки, прямой, отрезка, длины, угла и др.)» вектором а
называют направленный отрезок, соединяющий некоторые две точки
О и М пространства. Одну из точек (О) называют началом, а другую
(Л<) - концом вектора. Графически векторы изображают стрелками
(рис.0.1). Длиной вектора а называют расстояние между его началом
и концом, которое обозначают как |а|. Прямую, проходящую через
вектор а, называют линией действия вектора.
Данное выше определение называют геометрическим, так как оно
вводит вектор а как некоторый геометрический объект. Существуют
и другие определения вектора, которые будут рассмотрены далее.
Рис. 0.1. Геометрическое опреде-
определение вектора
Рис. 0.2. Геометрическое пред-
представление операции сложения векто-
векторов
Используя геометрическое определение, можно ввести операцию
сложения двух векторов а и Ь, имеющих общую точку начала О:
суммой двух таких векторов называют вектор с = а + Ь, совпадаю-
совпадающий с диагональю параллелограмма, построенного на векторах а и Ь,
и началом которого является та же точка О (рис.0.2).
Важную роль играет нулевой вектор О, который при сложении с
любым вектором а дает снова a: a -f 0 = а.
Геометрически определяют и вторую операцию с вектором - умно-
умножение вектора а на вещественное число ф: такое произведение фа.
есть вектор, лежащий на той же прямой, что и а, но имеющий длину
ф\а.\ и направление, совпадающее с направлением а, если ф > О, и
противоположное к нему, если ф < 0 (рис.0.3).
Введение
i|/a3 v|/<0
PliC. 0.5. Геометрическое пред- Рис. 0.4* Геометрическое пред-
представление умножения вектора на ставление скалярного умножения
число векторов
Третья основная операция с векторами - это скалярное умножение
пары векторов а и Ь, которую определяют как вещественное число,
равное произведению длины вектора а, длины вектора b и косинуса
угла между ними (рис.0.4), и обозначают как
ab = |a||fr|cosy>. @.1)
Ненулевые векторы а и b называют ортогональными, если их ска-
скалярное произведение равно нулю:
а.Ь = 0. @.2)
Из @.1) и @.2) следует, что угол (р между ортогональными векто-
векторами равен 90°, поэтому они геометрически изображаются так, как
показано на рис.0.5.
Важную роль играет система трех взаимно ортогональных векто-
векторов ехе^ез единичной длины, линии действия которых лежат на трех
взаимно перпендикулярных прямых (рис.0.6). Эту систему называют
ортонормированным (декартовым) базисом.
Произвольному вектору а всегда можно поставить в соответствие
диагональ прямоугольного параллелепипеда, ребра которого лежат на
линиях действия векторов е,-, имеющих общее начало с вектором а
(рис. 0.7). Поэтому а всегда можно представить в виде суммы векто-
векторов базиса е,-:
а = агег + а2е2 + а3е3. @.3)
Это соотношение можно записать иначе:
a = a*et, @.4)
здесь по повторяющимся индексам происходит суммирование (прави-
(правило Эйнштейна).
Введение
.15
Соотношения @.3), @.4) называют разложением вектора по бази-
базису, а числа а% - координатами вектора а в базисе е,-.
Je3
а
е2
PliC. 0.5. Ортогональные векторы Рис. 0.6. Декартов базис
Рис* 0.7. Разложение вектора по де-
картову базису
Если выбрать другой ортонор-
мированный базис е( с общим на-
началом в точке О, то относитель-
относительно него можно построить свой па-
параллелепипед с вектором а по ди-
диагонали. Тогда а можно предста-
представить в виде суммы векторов ба-
базиса е[:
а=а"е;., @.5)
где числа а" являются компо-
компонентами вектора в базисе ej,
причем, вообще говоря,
а"" ф а1'.
Из @.4) и @.5) следует важное свойство векторов - их инвариант-
инвариантность (т.е. независимость от выбора базиса), в то же время компо-
компоненты векторов могут изменяться.
Б. Изображение физических величин векторами
Итак, вектор, введенный выше геометрическим способом, имеет
три признака: точку начала, длину и направление. Многие величины,
описывающие физические объекты, характеризуются теми же призна-
признаками и могут быть изображены векторами. При этом длина вектора
равна числовому значению физической величины, измеренной в опре-
определенном масштабе. Таковы например: радиус-вектор, описывающий
положение материальной частицы вещества относительно некоторой
выделенной геометрической точки; скорость движения этой частицы;
сила, действующая на нее, момент силы и многие другие. Говорят,
16 Введение
что множество всех векторов, изображающих какую-либо физическую
величину, образует векторное пространство, если в этом множестве
разрешены операции сложения и умножения на число. Если разреше-
разрешена также и операция скалярного произведения, то такое множество
образует евклидово пространство (более строгие определения будут
даны далее).
В. Три категории векторов
Векторы, изображающие физические величины, можно разделить
на три категории: свободные, скользящие и закрепленные.
Если векторная физическая величина не меняется при переходе из
одной точки пространства в другую, то она описывается свободным
вектором. Свободные векторы можно складывать и умножать, даже
если они не имеют общего начала. Для этого надо предварительно,
не меняя длин и направлений этих векторов, совместить их точки на-
начала. Свободными являются, например, векторы ё, декартова базиса:
за точку их начала можно выбрать произвольную точку О.
С помощью скользящих векторов изображают векторные физичес-
физические величины, не изменяющиеся при переходе в любую точку прямой,
совпадающей с направлением физической величины. Для осущест-
осуществления операций сложения и умножения скользящие векторы можно
переносить параллельным переносом только вдоль линии их дейст-
действия. Скользящим является, например, вектор силы, действующей на
материальную точку.
Закрепленные векторы изображают векторные физические вели-
величины, определенные только в данной конкретной точке пространства.
Такими являются, например, вектор скорости движущейся матери-
материальной точки, момент силы, радиус-вектор х, описывающий поло-
положение материальной точки относительно некоторой геометрической
точки О и др.
В дальнейшем мы будем рассматривать в основном свободные век-
векторы.
ГЛАВА 1
ТЕНЗОРНАЯ АЛГЕБРА
§ 1.1. Локальные векторы базиса. Якобиевы и
метрические матрицы
1.1.1. Координаты и локальные векторы базиса
Введем в трехмерном пространстве прямоугольную декартову сис-
систему координат х\ г — 1, 2, 3 с началом в точке О, тогда каждой точке
пространства Ai будет взаимнооднозначно соответствовать радиус-
вектор х с началом в точке О и концом в точке М (рис.1.1). Выбе-
Выберем такой ортонормированный базис ё,, у которого линии действия
векторов совпадают с осями Ож1, а начало - с точкой О декартовой
системы координат. Такой базис будем называть декартовым. Со-
Согласно соотношению @.4), радиус-вектор х всегда можно разложить
по базису ё,:
х = х%, A.1)
где хх - координаты точки М. в декартовой системе координат.
Трехмерное пространство, в котором существует единая для всех
точек прямоугольная декартова система координат, называют трех-
трехмерным евклидовым.
Введем криволинейные координаты Xх, которые связаны с хх функ-
функциями вида:
х* = х*{Х>). A.2)
Тогда радиус-вектор точки М. может быть представлен как функция
координат X*:
х = х(Х*). A.3)
Будем далее предполагать, что функции A.2) непрерывно диффе-
дифференцируемы и взаимнооднозначны, тогда их можно обратить:
Х*=Х*{х{). A.4)
Ввиду дифференцируемости функций A.3) можно ввести производ-
производные:
Rj=dx/dXj, A.5)
18.
Глава 1. Тензорная алгебра
X
X
Рис. 1.1. Положение точки про-
пространства М. в декартовой системе
координат
Рис. 1,2. Локальные векторы ба-
базиса в криволинейной системе коор-
координат
которые снова образуют векторы, называемые локальными вектора-
векторами базиса (рис. 1.2). Эти векторы Rj направлены по касательным к
координатным линиям Xj = const в точке М с координатой A.3).
В отличие от ё,-, векторы базиса R,- меняются при переходе от одной
точки М к другой М!.
Заметим, что хотя формально ё, и R,- определялись в разных точ-
точках, их можно привести к одной точке, так как векторы ё, являются
свободными.
1.1.2. Якобиевы матрицы
Можно связать векторы базисов R,- и ё,-.
Из A.5) и A.1) находим выражение:
A.6)
где введен объект с двумя индексами
С?. = дх>/дх\
A.7)
Такие объекты всегда можно записать в виде матрицы, т.е. упо-
упорядоченной таблицы 3x3:
A.7')
§1.1. Локальные векторы базиса 19
Матрицу A.7) называют матрицей преобразования или якобиевой
матрицей.
Заметим, что порядок расположения элементов в матрице сущест-
существенен: далее везде первый индекс у Q3{ будем полагать меняющимся
при переходе от одной строки к другой, а второй - от одного столбца
к другому.
Определение 1.1. Определителем (детерминантом)
матрицы QJ{ A.7') называют число
det (Q\) = Q\Q\Q\ - Q\Q\Q\ - Q22Q\Q\-
- Q\Q\Q\ + Q\Q\Q\ + Q\Q\Q\. {Щ
В силу взаимной однозначности функций A.4), в любой точке Xх
детерминант якобиевой матрицы всегда отличен от нуля:
0. A.8')
Такие матрицы называют невырожденными.
Определение 1.2. Обратной kQ%j называют такую матрицу
Plj, которая удовлетворяет соотношениям:
n#fc = QV,PW'b A-9)
где 6%к -смешанный символ Кронекера:
* AЛО)
Обратную матрицу будем также иногда обозначать как
Рх. = (О1^) = (Q"I^. Для всякой невырожденной матрицы всегда
существует обратная.
Введем также ковариантный символ Кронекера Ski и контравари-
антный символ Кронекера 6кг, значения которых совпадают с 8хк:
?;!=*: <iu'>
Для якобиевой матрицы QXj A.7) обратная якобиева матрица име-
имеет вид:
A.11)
20 Глава 1. Тензорная алгебра
где X* являются функциями A.4). С помощью P%j можно выразить
векторы декартова базиса ё* через R,-. Домножая A.6) на Р*к, полу-
получаем
ё* = Р\Щ. A.12)
1.1.3. Метрические матрицы
В силу ортонормированности векторов ё,-, их скалярное произведе-
произведение можно записать с помощью символов Кронекера:
ё*.ё,-=4у. A.13)
Тогда скалярное произведение векторов R,- с помощью уравнений
A.6) и A.13) можно представить в виде:
R,- • R, = Я\ Qljek • е, = Q\ QljSki = дц. A.14)
Определение 1.3. Матрица дц, введенная по формуле A.Ц), на-
называется метрической или фундаментальной.
Определитель метрической матрицы обозначим следующим обра-
образом:
O*,)J. A.15)
Метрическая матрица, очевидно, является симметричной по индек-
индексам г, j; ее определитель можно записать через компоненты явным
образом (согласно A.8)):
det (gij) = 011022033 - 011023 ~ 022013 - 033012 + 2012013023- A.16)
В силу A.8') всегда 0^0, поэтому для дц всегда существует об-
обратная метрическая матрица gkl:
Непосредственной подстановкой выражения дц = Qki Ql -8к\ в A.17)
можно убедиться в том, что обратная метрическая матрица д%* выра-
выражается через обратную матрицу Якоби:
A.18)
1.1.4. Векторы взаимного базиса
С помощью g%i определяем векторы локального взаимного базиса
R1:
R'=0'*R*. A.19)
§1.1. Локальные векторы базиса 21
Очевидно, что верны обратные соотношения:
R, = SfRt = 9к1дцКк = guR1. A.19')
1.1.5. Правила расстановки индексов
В тензорном исчислении существуют правила расстановки индек-
индексов у различных объектов, некоторые из них уже использовались вы-
выше.
А. Объекты могут иметь верхние (контравариантные), нижние (ко-
вариантные) и смешанные индексы. Например, из уже введенных
объектов нижними индексами обладают:
верхними:
Ski, gij, R\
смешанными:
Пк. Pi Л*.
Число индексов, как будет показано в дальнейшем, может быть, в
принципе, любым.
У объектов со смешанными индексами иногда используют обо-
обозначение Q*t- или Q*/» чтобы подчеркнуть, что к - первый индекс,
а г - второй (или наоборот -Q'k%.)> Если порядок индексов не имеет
значения, то применяется также запись индексов "один над дру-
другим", например, 8\.
Б. Складывать, вычитать и приравнивать (т.е. подвергать действию
операций со знаками "+","— "и" =") можно только объекты с
одинаковыми индексами, т.е. должны совпадать: число, обозначе-
обозначение и расположение (верхний-нижний) индексов у объектов. Поря-
Порядок же расположения индексов может быть различным. Например,
правильными записями являются:
неправильными
В первом случае нарушено обозначение индексов, во втором - рас-
расположение, в третьем - число и расположение.
В. Во всех других операциях могут участвовать объекты с неодинако-
неодинаковыми индексами, например, в скалярном произведении A.14) у R,-
и Rj обозначения индексов разные, и их число у каждого объекта
22 Глава 1. Тензорная алгебра
не совпадает с числом индексов у д^. Однако объекты (R,- • Ry) и
gij уже связаны операцией " = ", поэтому индексы их должны быть
согласованы с правилом Б. В дальнейшем будут введены и другие
операции.
Г. В операциях умножения, как обычного числового, так и скалярного
(а также векторного и тензорного, которые будут введены ниже),
повторяющиеся индексы должны располагаться следующим обра-
образом: один вверху - другой внизу, например:
ж'е,- =
причем считается, что по этим повторяющимся индексам идет сум-
суммирование от 1 до 3 (в трехмерном пространстве).
Повторяться могут и индексы у одного и того же многоиндексного
объекта, например
i
В этом случае также по этим индексам идет суммирование. Далее
будет показано, что суммирование индексов у одного объекта - это
частный случай операции скалярного умножения (свертки).
Повторяющиеся индексы "взаимно уничтожаются" в формулах с
операциями сложения и приравнивания (см. правило Б), т.е. пра-
правильными будут, например, следующие записи:
а + Ь\ = с/, (ур* = А1"*, а{Р/ + V = с\
поэтому повторяющиеся индексы еще иначе называют немыми, а не-
неповторяющиеся - свободными индексами.
Д. Умножение на метрические матрицы gij или д^ приводит, соответ-
соответственно, к "опусканию" или "подниманию" индексов. Это свойство
называется "жонглированием индексов", оно, в частности, исполь-
использовано при определении локальных векторов базиса A.19), вообще
же
Е. Особый случай представляет декартовая прямоугольная система
координат. Если в A.14) в качестве R,- взять R,- = ё,-, то на ос-
основании A.13) получим:
9ij = Sij,
т.е. метрическая матрица в декартовом базисе - единичная, еди-
единичной же будет и обратная метрическая матрица: д1* = 6**.
§1.1. Локальные векторы базиса 23
Тогда векторы базиса, взаимного к ё,-, можно вычислить согласно
A.19):
ei=gi^j=Si^j, A.20)
т.е. ё1 = <Jljej = ei и т.д., тогда ё1 и ё, совпадают. Однако для
того чтобы сохранить правило А расстановки индексов, будем для
обозначения равенства этих векторов использовать формулу A.20).
Точно также в дальнейшем будем поступать со всеми объектами,
относящимися к декартовому базису: вводим верхние и нижние ин-
индексы согласно правилам Л, понимая, что численное значение ве-
величины от этого не изменяется.
Этим объясняется необходимость использования различных сим-
символов Кронекера <J,j, 51* и <Jj-, значения которых одинаковы. Соглас-
Согласно этому же правилу можно определить ковариантные и контрава-
риантные якобиевы матрицы:
численные значения компонент которых равны между собой (Qu =
Q\, Ql2 = Q\ И Т.Д.).
Тогда выражения для метрических матриц A.14) и A.17) можно
записать в виде:
ян = Q\ Qkj, gij = P\Pik = Р<кР{.
Подставляя A.17) и A.6) в A.19), находим связь R* сё1:
R,- = pimpkn>QJk%. = pi.yy ei = Qi. R.-( A.2i)
которая, очевидно, отличается от связи A.6) векторов основного
базиса R,- с ej.
Ж. В операциях дифференцирования считается, что производная по
объекту с верхним индексом дает объект с нижним индексом и на-
наоборот:
это правило использовано, например в A.5), а обратное - в A.18).
То же самое правило перемены индексов относится и к операции
взятия обратной матрицы (см., например, A.17)).
3. Для обозначения индексов применяются малые латинские буквы
(г, j, Aj, /, га, п и др.). В этом случае, если не оговорено особо, пред-
предполагается, что индекс пробегает значения 1, 2, 3.
24 Глава 1. Тензорная алгебра
Иногда в качестве индексов используют также индексные объек-
объекты, например: ii, ^2» *з? В этом случае получаются многоярус-
многоярусные индексные объекты:
однако, как и в предыдущем случае, такая запись означает, что
каждый из г*1,г2 и др. пробегает значения 1, 2, 3.
Если хотят подчеркнуть, что индексы пробегают только два зна-
значения, например, 1 и 2, то для них часто используют заглавные ла-
латинские буквы:
a,, &', Q7,, J,J = 1,2.
Греческие буквы в качестве индексов часто используют для того, что-
чтобы применять повторяющиеся индексы, по которым нет суммирова-
суммирования:
Qaa> 9aa, a = 1, 2, 3.
Кроме того, в целях придания компактности формулам греческие ин-
индексы используют в формулах с циклической перестановкой индексов,
например, вместо трех формул
можно применить одну
где предполагается, что а,/3,7 пробегают значения от 1 до 3, но все
они не равны и меняются циклическим образом: если a = 1, то /3 = 2,
7 = 3; если a = 2, то /3 = 3, 7 = 1; если а = 3, то /3 = 1, 7 = 2.
1.1.6. Векторное поле
Пусть теперь в каждой точке х пространства определен вектор а,
меняющийся, вообще говоря, при переходе от одной точки х к другой
х'. В этом случае говорят, что определено векторное поле а(х). В
каждой точке х вектор а можно представить разложением по декар-
тову базису в виде A.1):
а = аа"ё,- A.22)
где аг - компоненты вектора в базисе ё,.
В силу инвариантности вектор а можно представить в локальном
базисе R,-, определенном в данной точке х:
a^a'R,-, A.23)
§1.1. Локальные векторы базиса
.25
а также во взаимном базисе:
а = a'Rt = ofgaK1 = a/R/,
при этом выполнены соотношения:
а = a'e,- = a'R, = a,R' = a'Q'^e,.
A.24)
A.25)
Отсюда получаем связь компонент вектора а в различных системах
координат х' и Xх:
а1' = Q>-\ а? = Р>. а1.
A.26)
Величины at называют ковари-
антными компонентами век-
вектора в базисе R*. Они связа-
связаны с а\ называемыми контра-
вариантными компонентами в
базисе R, (рис. 1.3), соотноше-
соотношениями:
щ = дцаг.
A.27)
Рис. 1.3. Ковариантные и контравари-
антные компоненты вектора а
Очевидны и обратные соотно-
соотношения:
а' = </%.
A.27')
Подставляя A.14) и A.26) в A.27), получаем связь ковариантных
компонент а, и а* в различных базисах:
i = Qkiak, ak =
A.28)
Заметим, что векторы базисов и компоненты векторов в этих бази-
базисах преобразуются различным образом (формулы A.6), A.26) и A.21),
A.28)).
1.1.7. Операции с векторными полями
Теорема 1.1. Сумма двух векторных полей а и Ь, определенных
в одной точке х, образует векторное поле, причем
а + Ъ = a'Rt- + b*Ri = (a1" + b'")R,-.
A.29)
Доказательство очевидно, так как в каждой точке х векторные поля
- это просто векторы, которые можно складывать.
26 Глава 1. Тензорная алгебра
Теорема 1.2. Скалярное произведение двух векторных полей а и
Ъ равно сумме произведений их компонент в основном и взаимном
базисах:
Ў В самом деле, используя представление A.24) для а и Ь, а также
определение метрической матрицы A.14) и правило Д, получаем
а • Ъ = a'R, • VRj = а'Ь%- = а'Ь{ = <цЬ\ А A.30)
Теорема 1.3. Скалярное произведение вектора самого на себя
представляет собой длину вектора \а\:
\а\ = (а • аI/2 = (а'«цI/а = (а'а,I/2. A.31)
Ў Так как а1 и а,- совпадают, то с помощью двукратного применения
теоремы Пифагора убеждаемся, что а%щ = \а\2. Но из A.26) и A.28)
получаем:
а*<ц = PikakQjiaj = a% = \а\2. А
Косинус угла ф между векторами а и b через координаты вычис-
вычисляем следующим образом:
™+= A32)
Упражнения к § 1.1.
Упражнение 1.1.1. Показать, что
=gij.
Упражнение 1.1.2. Доказать формулы A.15) и A.18).
Упражнение 1.1.3. Показать истинность формулы
Упражнение 1.1.4. Доказать формулу A.18).
Упражнение 1.1.5. Доказать, что R1 • Rfc = 6%к.
Упражнение 1.1.6. Используя определение A.8;), показать, что для двух
произвольных матриц А%j, BXj выполнено:
det {А';В\) = det (A'^det (В\).
^_____ § 1.1. Локальные векторы базиса 27
Упражнение 1.1.7. Используя результаты упр. 1.1.6 и A.9), показать, что
для матрицы QXj и ее обратной PXj справедлива формула:
det (Q'j) = 1/det (Р)).
Упражнение 1.1.8. Показать, что при переходе из одной криволинейной
системы координат Xх в новую криволинейную систему координат X •*, опреде-
определенную как
'<" ( i)
локальные векторы базисов R,- и R{ = dx/dXfJ и компоненты произвольного
вектора а в этих базисах связаны соотношениями:
где Q. i — дХ'Э IдХг - матрица преобразования из Xх в XfJ. а Р.1^, =
= ЭХ1 /дХ1т - обратная матрица:
Р» глгп _ s)i ртп _ с»
тУ j ~ Ч m? j -0 у
Здесь аг и а!х - компоненты вектора а в различных базисах:
а = a'R,- = a"R; = a.R1 = a^R".
Упражнение 1.1.9. Показать, что при переходе из системы координат Хг
в Xft, метрические матрицы преобразуются следующим образом:
9'{j = Щ ¦ Щ = РТ P'jgmi, g'ij = R" • R° = Q'
Упражнение 1.1.10. Используя результаты упражнений 1.1.8 и 1.1.9, по-
показать, что векторы взаимного базиса R*, ковариантные компоненты вектора A{
преобразуются при переходе из одной криволинейной системы координат в другую
следующим образом:
R" = Q'raRTO, R'" = P';'R", сц = <У^, а'т = Р\пщ.
Упралснение 1.1.11. Для цилиндрической системы координат (см.рис. 1.4)
определены соотношения A.2) вида
Ж1 = 7*COS <^>, X2=rsill<^, X3 =: Z,
где X = V (полярный радиус точки М на плоскости Ох Х~)у Х~ = ф (поляр-
(полярный угол точки М на плоскости Ох X"), X "=¦ Z (осевая координата) - цилинд-
цилиндрические криволинейные координаты; показать, что якобиевы матрицы QXj и Р%:
имеют вид:
/соъф —гътф 0
Q'j = I sin^ гсойф 0
V 0 0 1
28.
Глава 1. Тензорная алгебра
Рис. Ц. Цилиндрическая система Рис. 1.5. Сферическая система ко-
координат ординат
Упражнение 1.1.12. Для сферической системы координат (см. рис. 1.5)
определены соотношения A.2) вида
х1 = г sin д cos ф, х2 = г sin д sin ф, ж3 = г cos д,
где X = Г (радиус точки М), X =¦ $ (меридиональный угол), X = ф
(азимутальный угол) - сферические криволинейные координаты; показать, что
якобиевы матрицы Q* и Р* имеют вид:
^ r costf cos <? —^
Q%j = J sin i9 sin ф r cos д sin ф r sin д cos ф I ,
\ cos?9 —rsini9 0 /
Р) =
sin д cos ф
A/r) cos#cos<^>
sin д sin ^
0
Упражнение 1.1.13. Показать, что для цилиндрической системы координат
векторы локального базиса имеют следующий вид:
R2 = —rsin^ei 4- r cos 0ёг, R3 =
а для сферической системы координат:
Ri = sin д cos ^ei + sin $ sin фё2 + cos #ё"з,
R2 = r cos д cos <^>ei + r cos # sin ^ёг — r sin ?9ёз,
§1.2. Векторное произведение 29
R.3 = (— si
Упражнение 1.1.14. Показать, что для цилиндрической системы координат
метрические матрицы g%j, д%^ и детерминант д имеют вид:
A 0 0
О г2 0
0 0 1
а для сферической системы координат:
о
о
0 0 l/(r2sin2tf)
д = г4 sin2
Упражнение 1.1.15. Показать, что для цилиндрической системы векторы
взаимного локального базиса имеют вид:
R1 = Ri = cos фё\ + sin фё2<>
R2 = ^-R2 = -- sin фёх + - cos фё2, R3 = R3 = ёз;
а для сферической системы координат:
R1 = Ri = sin d cos фё\ + sin d sin фё2 + cos дёз,
R2 = — R2 = - cos d cos фёг + - cos d sin фё2 si
г г
1 „ 1
2 ' 2 qR3 = —Г—« (
r2 sin v г sin v
COS
§ 1.2. Векторное произведение
1.2.1. Символы Леви-Чивиты
Определение 1.4. Векторное произведение векторов а. и
Ь, обозначаемое как axb, представляет собой следующий вектор:
axb = у/^е^ка1ЫКк = ^р€^ка^Кк. A.33)
у/9
30 Глава 1. Тензорная алгебра
Здесь €ijk, €%зк - символы Леви-Чивиты:
0, если есть совпадающие индексы,
1, если индексы различны и образуют четную
Uiks e'jn — { подстановку,
— 1, если индексы различны и образуют нечетную
подстановку,
A.34)
а д — det |</,j|.
Важную роль играют комбинации символов Леви-Чивиты с у/д.
Например, из A.33) следует:
:€gmignjgik. A.35)
у/9
Непосредственно можно проверить, что
еу*«У*=в, eijkei"n=6lj6?-6lkS?, e^1 = 2S\, A.36)
а также
€ijkTij = О, A.37)
где Tij - компоненты произвольной симметричной матрицы, для ко-
которой Tij — Tj{.
Умножая A.35) на б'-7*, получаем явное выражение детерминанта д
метрической матрицы через ее компоненты:
У = \^kemnlgmignjykl. A.38)
Формулу A.38) можно применить к любой матрице Alj, а не только
к метрической, тогда получим:
det (А',-) = ^*€-»'А'гаА'„А*,. A.39)
Принимая за определение детерминанта det {Alj) формулу A.8'), в
справедливости A.39) можно убедиться непосредственно, расписывая
покомпонентно суммы по всем индексам.
Формулу A.39) можно представить в несколько ином виде, если
расписать покомпонентно только один из символов Леви-Чивиты:
det (A'j) = ^€ijk(A{AiAl - А[А{Ак2 +
^{l i{k Й. A.40)
§ 1.2. Векторное произведение 31
Поскольку по индексам г, j, к справа идет сумирование, то меняя мес-
местами пары индексов, убеждаемся, что все шесть слагаемых в правой
части равны между собой, поэтому
det(Aij) = €ijkAiaAjpAk1, афрфчфа, а,0,7= 1,2,3, A.41)
где а, /3,7 образуют любую четную подстановку. При нечетной под-
подстановке следует поменять знак.
Еще один способ записи этой формулы таков:
det (Л'>шп/ = eijkA*mA?nAl A.42)
В его справедливости также легко убедиться непосредственно распи-
расписав по индексам т,п,1.
Опускание или поднятие индексов приводит к объектам el<;fc, е?к и
т.п., которые уже не являются константами:
€ijk = €4mgmk, €{\=ъткдт* и т.п. A.43)
Покажем некоторые важные свойства векторного произведения.
1.2.2. Смешанное и двойное векторные произведения
Определение 1.5. Последовательное применение операций век-
векторного, а затем скалярного умножения для трех векторов
(а х Ъ) • с = с • (а х Ь) A.44)
называется смешанным произведением.
Смешанное произведение, очевидно, приводит к образованию ска-
скаляра (р:
(р = с • (а х Ь) = y/geijkdVc*. A-45)
Определение 1.6. Двойным векторным произведением
называется вектор d, образованный из трех векторов a, b и с сле-
следующим образом:
d = а х (Ь х с).
Используя определение A.33), находим компоненты d:
d = -±-&kai(y/gelmjbl<r]B.k = {^к€1т]а{Ь1ст)Кк = dkRk. A.46)
у/9
Используя вторую формулу в A.36), преобразуем A.46) к виду:
d=(-6i,6lm+6im6?)aib'cmB.k =
= (-а,Ь'ск + ambkcm)Rk = (а • с)Ь - (а • Ь)с. A.47)
Таким образом, приходим к формуле:
а х (Ь х с) = (а • с)Ь - (а ¦ Ь)с. A.48)
32.
Глава 1. Тензорная алгебра
1.2.3. Ортогональность ахЬсаиЬ
Теорема 1.4. Вектор axb ортогонален ка«Ь (рис. 1.6).
Ў В самом деле,
axb
(а х Ь) • а =
e2jia1a2+
+ €2j3a2a3
ax + e3j2a3a2)b> =
e2ji)a1a2+
e3ji)a1a3+
Puc. 1.6. К выводу свойств + F2i3 + e3j2)a2a3jy =
= 0 • fr> = 0, A.49)
векторного произведения
Т.К. €ij2 = ~€2ji И Т.Д. А
1.2.4. Длина |а х b|
Теорема 1.5. Длина вектора |ах Ь| равна площади S параллело-
параллелограмма, построенного на векторах а и Ъ (рис. 1.6):
S = |з.||Ъ|sinV = |а х Ь|.
A.50)
Ў Поскольку S является скалярным инвариантом, то его значение не
зависит от выбора системы координат, в которой он рассчитывается.
Выберем специальную систему координат R{, в которой:
Тогда
|а|2 = 9ija}a? = gnala\
S =
^b2\y/l -cos2V'.
Вычислим cos^ из определения скалярного произведения векторов
A.32):
а- b = |а.||Ь|cos-0-
Отсюда
/911922 |ax62| Jgng22
§ 1.2. Векторное произведение ___33
011022 у 011022
Здесь использовано определение коэффициента обратной матрицы
зз 1/
9 = -@11022-
0
Тогда выражение для S принимает вид:
5 = -
011022
Вычислим а х b во введенной системе координат:
а х Ь =
таким образом утверждение A.50) доказано. А
Если обозначить п - единичный вектор нормали (п • п = 1) к пло-
площадке S параллелограмма, то соотношения A.49) и A.50) можно пред-
представить в виде:
n5 = axb. A.51)
Это соотношение будем часто использовать в дальнейшем.
1.2.5. Геометрический смысл векторов
взаимного базиса
Рассмотрим векторное произведение векторов базиса Rn x Rm и
воспользуемся определением A.33), в котором а = R^R,- и b =
Rn x Rw = y/g€ijk8ijtnRk = уД€пткКк, A.52)
в частности
Отсюда следует геометрический смысл векторов взаимного базиса
Ra: это векторы ортогональные к координатной плоскости, натяну-
натянутой на векторы R^, R-^ (a ф /3 ф 7).
1.2.6. Вычисление объема
Умножим скалярно на R, обе части уравнения A.52):
R,- • (К„ х Rm) = y/genmkRk • R,- = y/genmi = y/g€inm. A.54)
2 Тензорное исчисление
34 Глава 1. Тензорная алгебра
Рассмотрим частный случай:
Rx. (R2 x R3) = ^6123 = y/g. A.55)
Покажем, что у/д это объем |V|, построенный на векторах R,. Ис-
Используя свойства скалярного и векторного произведений, получаем:
(R2 x R3) = |Ri||R2 x
= |Ri| costs' = hS= |V|, A.56)
здесь S - площадь параллелограмма, лежащего в основании паралле-
параллелепипеда, построенного на векторах R,-, a h — |R,| cos^ ~ его высота.
Учитывая, что R, = Q\ej и gij = Q*Qjk, имеем
д = det tin) = det (QkQk) = det (Qf)det (Qk) = l^rl2- A-57)
Таким образом, имеем равноправные соотношения:
-- 1та1- A-58)
Упражнения к § 1.2.
Упражнение 1.2.1. Доказать формулы A.36) и A.37).
Упражнение 1.2.2. Доказать, что
Упражнение 1.2.3. Доказать, что
R' х Ы =
Упражнение 1.2.4. Доказать, что
Упражнение 1.2.5. Показать, что
R,- х R1' = 0.
Упражнение 1.2.6. Доказать, что циклическая перестановка не меняет ре-
результата смешанного произведения:
(а х Ь) • с = (с х а) • b = (b x с) • а.
§ 1.3. Геометрическое определение тензора 35
Упражнение 1.2.7. Показать, что
axb = —b х а, а х а = 0.
Упражнение 1.2.8. Показать, что если е, - три ортогональных вектора
единичной длины, то
е, х е, =efc, г ф j ф к = i.
Упражнение 1.2.9. Используя определение A.34), показать непосредствен-
непосредственно, что из A.38) следует A.16).
§ 1.3. Геометрическое определение тензора и
алгебраические операции с тензорами
1.3.1. Графическое изображение векторов
и операций с ними
Для векторов, называемых также тензорами первого ранга, сущест-
существует наглядное графическое изображение.
Графически вектор а, соединяющий точки ОиМ, изображен на
рис. 0.1 (см. Введение). Наличие стрелки в точке М указывает на
то, что точка О - начальная, а точка М - конечная.
Операции сложения векторов с = a-fb "по правилу параллелограм-
параллелограмма" и скалярного умножения a-b = |a||6|cosy> также можно наглядно
изобразить графически (см. рис.0.2 и 0.4).
То же самое относится и к умножению вектора на число (см.
рис.0.3), а также к разложению вектора а по базисным ортонорми-
рованным векторам е,- (рис. 1.7 для векторов на плоскости), которое
позволяет графически изобразить и компоненты вектора а1 в базисе
ё, как проекции вектора а на ё,-.
Можно также изобразить графически компоненты вектора а в неор-
тонормированном базисе R,-:
a = al'R,- = al-R>a. A.59)
Ковариантные компоненты а,- - это ортогональные проекции ащ
вектора а на R,*, умноженные на длину R,-:
аа = a- Ra = |а||Ла|со8^а = aRoi\Ra\. A.60)
Векторы взаимного базиса Ra можно изобразить графически с по-
помощью свойства (см. упр. 1.1.5) их скалярного произведения с векто-
вектором основного базиса. Для двумерного случая имеем:
R2-R1 = 0, Ri-R2 = 0, Ri-R^l, R2 • R2 = 1, A.61)
36.
Глава 1. Тензорная алгебра
ат
i
е2
>а2
г-
а/
а1
А
/
Ri
aR,
Рис. 1.7. Графическое изображе-
ние компонент вектора в ортонорми-
рованном базисе
Рис. 1,8. Геометрическое пред-
ставление ковариантных компонент
вектора в ортонормированном базисе
т.е. вектор R1 ортогонален к R.2, a R2 - к Ri, а длины этих векторов
вычислим по длинам |Д|
1
а = 1,2,
A.62)
где (р - угол между Ri и R2 @ ^ (р ^ тг). Напомним, что в плоскос-
плоскости левый базис нумеруется по направлению против часовой стрелки,
такая же ориентация сохраняется и для векторов взаимного базиса.
После построения векторов R', ортогональными проекциями на них
можно изобразить графически ковариантные компоненты а% вектора
а:
аа = а • Ra = aRa |Да|,
где фа - угол между векторами а и Ra
= \a\ cos4>Q
A.63)
1.3.2. Геометрическое определение тензора
Дадим теперь подобное геометрическое определение для нового
объекта - тензора второго ранга. Вначале рассмотрим для нагляд-
наглядности тензоры в двумерном евклидовом пространстве.
Определение 1.7. Тензором второго ранга Т в двумер-
двумерном евклидовом пространстве назовем упорядоченную совокупность
четырех векторов, выпущенных из одной точки, два из которых
фиксированы (одинаковы для всех тензоров), а два других произволь-
произвольны (индивидуальны для каждого тензора).
§ 1.3. Геометрическое определение тензора
.37
Рис. 1.9. Геометрическое пред-
представление векторов взаимного ба-
базиса
Рис. 1.10. Геометрическое представле-
представление ковариантных и контравариантных
компонент вектора
При графическом изображении
фиксированные векторы выделяются
жирными стрелками (рис. 1.11).
Упорядочение четырех векторов, обра-
образующих тензор Т, производится следу-
следующим образом: первым и третьим счи-
считаются два фиксированных вектора ei
и ез, вторым и четвертым - два инди-
индивидуальных а и Ь.
Для определенного таким образом тен-
тензора Т введем специальное обозначение:
Рис. 1.11. Геометрическое
представление тензора второго
ранга
Т = [eiae2b].
A.64)
В евклидовом пространстве в качестве фиксированных векторов е/
удобно выбрать векторы базиса ё/.
1.3.3. Операции с тензорами
Введем теперь операции с тензорами вида A.64), т.е. графические
правила вычисления суммы и скалярного произведения.
А. Сложение двух тензоров
Определение 1.8. Суммой двух тензоров
Т = [eiae2b] и В = [eice2d] A.65)
38.
Глава 1. Тензорная алгебра
Рис. 1.12. Графическое вычисление суммы
двух тензоров
называется тензор S, у которого индивидуальные векторы являют-
являются суммой соответствующих векторов от тензоров Т «В:
A.66)
Таким образом, графическое правило сложения двух тензоров за-
заключается в сложении соответствующих индивидуальных векторов
по правилу параллелограмма и неизменности двух фиксированных
векторов, в результате снова образуется объект вида A.64) (рис. 1.12).
Б. Скалярное умножение тензора на вектор
Определение 1.9. Скалярное умножение тензора Т на
вектор с справа представляет собой вектор d, образуемый путем
сложения двух фиксированных векторов е\ и ег, умноженных пред-
предварительно на скалярные произведения с с индивидуальными векто-
векторами aub;
Т • с =
• с = ei(a • с) +
с) = d.
A.67)
Графический способ построения такого вектора d вытекает из опре-
определения и показан на рис. 1.13.
Скалярное умножение тензора Т на вектор с слева дает вектор f,
представляющий собой сумму индивидуальных векторов а и Ь, пред-
предварительно умноженных на скалярное произведение с с фиксирован-
фиксированными векторами ei и ёг:
с • Т = с • [eiae2b] = (с • ei)a + (с • ё2)Ъ = f. A.68)
Графическое построение вектора f показано на рис. 1.14.
§ 1.3. Геометрическое определение тензора
-39
Рис. 1.13. Графическое вычисле- Рис. 1.Ц. Графическое вычисле-
вычисление скалярного произведения тензора ние скалярного произведения вектора
на вектор на тензор
Рис. 1.15. Графическое вычисление произ-
произведения тензора на скаляр
В. Умножение тензора на скаляр
Определение 1.10. Умножение тензора Т на скаляр (р пред-
представляет собой тензор (рТ, индивидуальные векторы которого по-
получаются умножением соответствующих векторов а«Ь тензора
Т на <р:
ipT = p[eiae2b] = [ei(pa)e2(pb)]. A.69)
Графическое изображение тензора (рТ становится очевидным: надо
просто умножить оба индивидуальных вектора а и b на число (р (рис.
1.15).
1.3.4. Компоненты тензора
Определение 1.11. Компонентами тензора Т называют
40.
Глава 1 ¦ Тензорная алгебра
двойные скалярные произведения тензора Т слева и справа на век-
векторы базиса ё/ :
= е/ • Т • ej = е/ • [eiae2b] • ej.
A.70)
Т12а2-
Вычислим сначала скалярное произве-
произведение справа, пользуясь правилом
A.67), а затем скалярное произведение
слева A.68), в результате получаем:
Ти = ei • (ei(а • ei) + ё2(Ь • ei)) =
+ bie2) = ai. A.71)
Здесь dj и bj - компоненты векторов а
и b в базисе ё/:
а = aJe/ = a/eJ
Ри С, 1.16, Геометрическое
представление компонент тензо-
тензора второго ранга
Аналогично получаем
12 — ei • i. • е2 — ei • [С]
Ъ = Ь1ё1 = Ь1ё1. A.72)
(Напомним, что поскольку базис ё/ -
декартов, то все а/ и а1 совпадают).
(ех(а • е2) + е2(Ь • е2)) = ег • (а2ех + Ь2е2) = а2>
A.73)
Tfei = е2 • Т • ei = 6i, T22 = е2 • Т • е2 = Ь2.
Таким образом, доказана следующая теорема.
Теорема 1.6. Компоненты Tjj тензора Т совпадают с соот-
соответствующими компонентами его индивидуальных векторов aj и
h
Теорема позволяет графически изобразить компоненты тензора
(рис. 1.16).
1.3.5. Компоненты тензора в новом базисе e'j
Выберем теперь произвольный базис R/, связанный с е'Т якобиевой
матрицей (см. A.6)):
R/ = 0J/ej, A.74)
и вычислим компоненты тензора Т в этом базисе по правилам A.70);
= R/ • Т • Rj = R/ • [ёдеЬ] • Rj =
A.75)
§ 1.3. Геометрическое определение тензора
-41
е2=Ь
Рис. 1.17. Графическое изображение базис-
базисных тензоров
Здесь мы используем свойства:
R/ • eL =
а • Rj = a*eK • Rj
A.76)
тогда с учетом определения A.73) компонент тензора в декартовом
базисе из A.75) получаем:
Ти = QuQKjdK + Q2iQKjbK =
= QliQKj f1K + Q2jQKj T2K = QLi QKj
A.77)
т.е. компоненты тензора Т A.70) преобразуются подобно компонентам
вектора A.28). Такое правило преобразования компонент называют
тензорным законом.
1.3.6. Базисные тензоры
Произвольный тензор второго ранга может быть представлен в ви-
виде суммы некоторых фиксированных тензоров - базисных тензоров.
Такие базисные тензоры Т(и) образуем, выбирая в качестве пары
векторов (а и Ь) нуль-вектор 0 и какой-либо базисный вектор ё/:
A.78)
, TBi) = [ei0e2ei],
= [eiOe2e2], T(i2) = [eie2e20].
42.
Глава 1. Тензорная алгебра
Рис. 1.18, а. Графическое разложение тен-
тензора второго ранга по базисным тензорам
а, I
1 ?
1
Рис. 1.18, б. Графическое разложение век-
вектора по базисным векторам
Графически базисный тензор Т(ц), следуя общему правилу, естест-
естественно изобразить как "двойную стрелку" из векторов ei, одна из кото-
которых проведена "жирной" линией, а вторая, соответствующая вектору
а - простой.
Действие же нуль-вектора 0 на вектор, стоящий слева, дает изоб-
изображение "нуль", т.е. никак не изображается.
Тогда базисный тензор ТB2) будет изображен двойной стрелкой
векторов ё2, тензор ТA2) - совокупностью только двух векторов ei
и ё2 = а, причем ёх изображается жирной стрелкой, а ёг - простой,
т.к. в данном случае он выступает в роли индивидуального вектора
а. Тензор TBi) также изображается совокупностью двух векторов
ei = b и ёг, где ёг показан жирной стрелкой, а ёх - простой (рис.
1.17).
1.3.7. Разложение тензора по базисным тензорам
Теорема 1.7. С помощью операций сложения и умножения на
число, введенных в п.1.3.3, можно всякий тензор Т представить
как сумму четырех базисных тензоров:
). A.79)
Ў В самом деле, используя правила A.66) и A.69), получаем:
[ei'(aiei)e20] + [ei(a2e2)e20] + [ei0e2(Mi)] + [ёхОё2(Ь2ё2)] =
= [ei(aiex + o2e2)e2(biei + 62ё2)] = [§iae2b] = Т. А A.80)
§ 1.3. Геометрическое определение тензора
-43
С помощью формулы A.79) можно графически представить разложе-
разложение тензора Т по базисным тензорам: это есть сумма четырех опи-
описанных в п. 1.3.6 базисных тензоров (рис. 1.18, а).
Это изображение является аналогом графического изображения для
разложения вектора а по базисным векторам (рис. 1.18, б).
Используя теорему 1.6, разложение A.79) можно записать с помо-
помощью компонент тензора TIJ:
T = f/JT(/J). A.81)
Здесь, как и всегда в декартовой системе координат, TIJ совпадают
1.3.8. Единичный тензор
ё2=ь
Рис. 1.19. Графическое
изображение единичного
тензора,
Если в качестве индивидуальных векторов
а и b выбрать базисные векторы ei и ё2, то
получим единичный тензор Е:
Е = [eieie2e2].
A.82)
Графическое изображение этого тензора
есть совокупность двух "двойных стрелок"
из векторов ёх и ё2 (рис. 1.19).
Учитывая свойство A.80), единичный тен-
тензор всегда можно представить в виде суммы
двух базисных тензоров:
Е =
B2),
A.83)
а скалярное умножение Е на всякий вектор с, согласно A.67) и A.68),
дает снова вектор с:
Е • с = [eieie2e2] • с = ei(ei • с) + ё2(с • ё2) = ciei -f с2ё2 = с, A.84)
с • Е = (с • ei)ei + (с • ё2)ё2 = с,
как и должно быть для единичного тензора.
1*9.12. Скалярное умножение тензоров
Определение 1.12. Скалярное умножение тензора Т на
шензор В слева представляет собой тензор S, индивидуальные век-
шоры которого образованы суммой индивидуальных векторов тен-
тензора В, умноженных предварительно на скалярное произведение век-
торов тензора Т с базисными ё/:
S = Т • В = [eiae2b] • [eice2d] = [eia'e2b'], A.85)
44.
Глава 1. Тензорная алгебра
fT I e2
i.iJO. Графическое изображение ска-
скалярного произведения тензоров
а' = (а • ei)c -f (a • e2)d, b' = (b • ei)c -f (b • e2)d.
Это определение и формула A.85) дают способ графического изоб-
изображения скалярного произведения тензоров, его пример приведен на
рис. 1.20.
Компоненты векторов а' и Ь' связаны с компонентами векторов а,
b и с, d соотношениями:
5ц = а'г = а
A.86)
-f
= 6'2 =
Если в качестве тензора В (или Т) выбрать единичный тензор, то
получим, согласно A.82) и A.85), тензор Т (или В):
Т • Е = [eiae2b] • [eieie2e2] =
= [ei(uiei + a2e2)e2(biei + Ь2ё2)] = [eiae2b] = Т, A.87)
как и должно быть.
Определение 1.13. Двойным скалярным произведением
тензоров Т и В называют число (р, вычисляемое следующим обра-
образом:
(р = Т--В = [eiae2b] • -[eice2d] = a • с + b • d. A.88)
Двойное скалярное произведение обозначают двумя точками.
1.3.10. Транспонированный тензор
Рассмотрим теперь некоторые важные типы тензоров.
§ 1.3. Геометрическое определение тензора
.45
а2
Рис. 1.21. Графическое изображение транспо-
транспонированного тензора второго ранга
Определение 1.14. Транспонированным к Т называют
тензор Т", который имеет в каком-либо базисе ё/ "перевернутые"
компоненты:
Т'и = ТЛ. A.89)
Транспонированный тензор обозначают как Т' = Тт.
Для графического изображения транспонированного тензора Т" сле-
следует взять значение а2 = Т\2 с его знаком и отложить по оси ёх,_-
получим компоненту с\ = Т21. Затем следует взять значение_Т21 = Ъ2
с его знаком и отложить по оси ё2 - получим компоненту Т[2 = d\.
Далее строятся векторы с и d с компонентами:
c2
= а.2, d2 = b2,
A.90)
которые и являются индивидуальными векторами транспонированно-
транспонированного тензора Т":
Тт = Г = [eice2d]. A.91)
Пример построения транспонированного тензора Т' показан на рис.
1.21.
1.3.11. Симметричный тензор
Определение 1.15. Симметричным называют такой тен-
тензор, транспонированный к которому совпадает с исходным:
лп/ ПП-^1
A.92)
Для того чтобы при графическом изображении Т' выполнялось это
свойство, необходимо у исходного тензора потребовать равенство ком-
компонент:
Т12 = Т21, A.93)
46.
Глава 1. Тензорная алгебра
Рис. 1.22. Графическое изображение сим-
симметричного тензора второго ранга
т.е. чтобы проекция вектора а на вектор ё2 по абсолютной величине
и знаку совпадала с проекцией вектора b на ei:
a2 = h. A.94)
Пример такого симметричного тензора изображен на рис. 1.22.
1.3.12. Обратный тензор
Определение 1.16. Тензор В называют обратным к Т, если
его скалярное произведение на Т дает единичный тензор. Такой
тензор В обозначают как Т:
ТТ =Е.
A.95)
Если в формуле A.85) тензор S является единичным, то тензор В
представляет собой тензор, обратный к Т. Найдем его индивидуаль-
индивидуальные векторы с и d. Из A.85) имеем:
Т • Т-1 = [eiae2b] • [eice2d] = [eieie2e2] = Е, A.96)
или
(а • ei)c + (а • e2)d = ёь (Ь • ёх)с + (Ь • e2)d = ё2. A.97)
Переходя к компонентам, получаем систему четырех уравнений для
нахождения ci, с2 и di, J2:
A.98)
+ d2d2 = О,
+ b2di = 0,
+ b2d2 = 1
§ 1.3. Геометрическое определение тензора
.47
Э2=а1/А
с1=Ь2/Д
PliC. 1.25. Графическое изображение об-
обратного тензора
решая которую, находим
ci = 62/А, с2 = -а2/А, di = ~&i/A, d2 = ai/A, A = ai62-a26i.
A.99)
Формулы A.96), A.97) позволяют графически изобразить тензор
Т. Для построения его индивидуальных векторов end необхо-
необходимо их компоненты выбрать по A.99), пример такого графического
изображения приведен на рис. 1.23.
1.3.13. Ортогональный тензор
Определение 1.17. Ортогональным называют тензор Т,
обратный к которому тензор Т совпадает с транспонированным
Пусть Т г имеет вид:
1 = [elCe2d],
A.100)
где компоненты ci, c2 и di, d2 вычисляем по A.99). Но если он сов-
совпадает с транспонированным, то эти же компоненты должны удовле-
удовлетворять уравнениям A.90), т.е. должны выполняться соотношения:
«ц = Ь2/А,
Г a>i = Ь2/
а2 = -bi/A,
6г = ai/Д
A.101)
относительно компонент ai,a2 и 6i,62.
Решение этой системы имеет следующий вид:
02
— Sill <p
J
48.
Глава 1. Тензорная алгебра
Рис, 1.24» Графическое изображе- Рис. 1.25. Трехмерный тензор в
ние ортогонального тензора графическом изображении
где (р - произвольное число.
Таким образом, если тензор Т - ортогональный, то его индивиду-
индивидуальные векторы а и b имеют компоненты A.102), т.е. длина этих
векторов - единичная: |а| = |Ь| = 1, и они взаимно ортогональны:
• b =
а262 = 0.
A.103)
Эти свойства позволяют дать графическое изображение ортого-
ортогонального тензора Т: все его четыре вектора ёх, а, ё2 и b лежат на
единичном круге и являются попарно ортогональными: ei _L ё2, a _L b
(рис.1.24).
1.3.14. Геометрическое определение тензора
в трехмерном пространстве
Вернемся теперь к трехмерному пространству.
Определение 1.18. Тензором второго ранга Т в трехмерном
евклидовом пространстве назовем объект:
Т = [eiaie2a2e3a3],
A.104)
представляющий собой упорядоченную совокупность шести векто-
векторов, из которых три ё±, ё2 и ёз - фиксированы, а три другие: ai, а2
и аз - индивидуальны для каждого трехмерного тензора.
Графическое изображение такого тензора Т показано на рис. 1.25,
где фиксированные векторы изображены жирными стрелками, а ин-
индивидуальные - простыми.
С объектами вида A.107), очевидно, можно ввести такие же опера-
операции, как с двумерными тензорами: сложение двух тензоров и умно-
умножение тензора на число
Т + В =
+ [eibie2b2e3b3] =
bi)ea(a3 + Ь2)ё3(а3 + b3)], A.105)
§1.3. Геометрическое определение тензора 49
(рТ = p[eiaie2a2e3a3] = [ei(?>ai)e2(v?a2)e3(pa3)],
скалярное умножение тензора Т на вектор аналогично A.67) и A.68):
з
Т • с = [eiaie2a2e3a3] • с = ]Р ёа(аа • с),
а=1
з
с • Т = с • [ё1а1ё2а2ёзаз] = ]>^(с • ёа)аа, A.106)
а=1
скалярное умножение тензоров Т и В аналогично A.85):
Т • В = [eiaie2a2e3a3] • [eibie2b2e3b3] = [eiCie2c2e3c3], A.107)
где
Ce = ?(ae-e/,)b/5; A.108)
/3=1
а также двойное скалярное прозведение тензоров:
з
*р = Т • В = [eiaie2a2e3a3] • -[ёх^ёгЬгёзЬз] = ^ (аа • ё/3)(Ь/3 • ёа).
а,/3=1
A.109)
Компоненты тензора Т в базисе ё,- по аналогии с A.70) вводим
следующим образом:
ЗЬ=в,--Т.ё;, A.110)
тогда из A.104) и A.110) получаем
2;,-=а,--ё,-. A.111)
Единичный тензор в трехмерном пространстве по аналогии с A.82)
вводим следующим образом:
Е = [ё1ё1ё2ё2ёзёз]. A.112)
1.3.15. Диады
По аналогии с A.78) можно определить базисные тензоры T(tJ) и в
трехмерном пространстве. Введем для них специальные обозначения:
ё2 0 ej = T{2j) = [ё10ё2ёуё30], A.113)
ё3 0 ё^- = TCj) = [ёхОёгОёзё^].
Знак 0 называют знаком тензорного произведения.
50 Глава 1. Тензорная алгебра
Определение 1.19. Диадным базисом называют набор ба-
базисных тензоров, записанный в виде A.113)f а каждый тензор e,-0ej
в отдельности называют базисной диадой.
Определение 1.20. Операцию, которая сопоставляет вектор-
векторному базису е,- диадный базис е,- 0 ej, определенный по формулам
A.113), называют тензорным произведением базисных векторов.
Поскольку базисные диады являются тензорами, но только специ-
специального вида, их можно складывать и умножать на число, однако при
этом будет получаться, вообще говоря, уже не новая диада, а какой-то
новый тензор, например:
ei 0 ё2 + ё2 0 ё2 = Т" = [ё1ё2ё2ё2ёз0],
р(ё2 0 ё;) = Т" = [ёхОёз^ё^ёзО].
Рассмотрим теперь операции скалярного умножения диад.
Теорема 1.8. Порядок выполнения операций тензорного и ска-
скалярного произведений векторов базиса можно менять местами:
(ei 0 ej) • efc = ё, 0 (ej • в*) = <Jj*e,-, A.114)
ё* • (ё. 0 ej) = (ё* • ё,-) 0 ej = Skiej.
Ў В самом деле, из определения A.113) и формулы A.67), обобщенной
на трехмерный случай, следует, например, для г = 1:
(ei 0 ej) • ё* = [eieje20e30] • ё* =
= ei(ej • ё») + ё2@ • efc) + ё3@ • efc) = ei(Jjfc, A.115)
и аналогично из A.68) получаем:
ё, • (ёх 0 ej) = ё,- • [eieje20e30] =
= (ё,- • ei)ej + (ё,- • ё2H +'(ё,- • ё3H = Snej. A.116)
Для г = 2 и г = 3 доказательство аналогично. А
Теорема 1.9. Скалярное и двойное скалярное произведения двух
диадных базисов вычисляются следующим образом:
(ё,- 0 ej) • (ё* 0 ei) = Sjkei 0 ё/, A.И7)
(ё,- 0 ej) • .(ё* 0 ё|) = SjkSu. A.118)
Ў Для доказательства первого соотношения используем определение
A.85), обобщенное на трехмерный случай, например, для г = 1, к = 2:
(ei 0 ej) • (ё2 0 ei) = [eieje20e30] • [ei0e2e/e30] =
= [eia^e20e30] = S2je1 0 ё/, A.119)
_ §1.3. Геометрическое определение тензора ___51
где
aj/ = (ei • ei)° + (ei * ёг)ё/ + (ej • ё3H = S2jeh
Для остальных ink доказательство аналогично.
Соотношение A.118) доказываем, используя определение A.109)
двойного скалярного произведения тензоров, например, для г = 1,
(ei ® ej) • -(ei <g> ё/) = [ёхё^ёгОёзО] • [ёхё/ёгОёзО] = (ej • ei)(e/ • ei)+
+ (ej • ё2)@ • ei) + (ej • ё3)@ • ёх) = iyiu, A.120)
и аналогично для остальных ink. А
Теорема 1.10. Всякий тензор Т второго ранга можно предста-
представить разложением по диадному базису:
Т = Г'ё,®ё,-, A.121)
где TIJ совпадают с Tij.
Ў Учитывая, что базисные диады ё,- ® ej суть базисные тензоры
A.113), доказательство этой теоремы аналогично приведенному для
теоремы 1.7. А
Разложение A.121) поясняет смысл введения диадного базиса: срав-
сравнивая A.121) и @.4), нетрудно заметить, что диадный базис - это об-
обобщение понятия векторного базиса на случай тензоров второго ранга.
Пусть теперь имеется два вектора а = а'ё, иЬ = Ь*ё».
Определение 1.21. Диадой векторов а и Ь называется тен-
тензор, образованный суммированием базисных диад с коэффициентами
a ® b = а'У'ё. ® ej. A.122)
Если в A.122) подставить разложения векторов а и b по базису ё,-,
то получим важное следствие о возможности вынесения коэффициен-
коэффициентов из-под знака тензорного произведения:
аФ"ё,- <g> ej = (а%) ® (Vej). A.123)
Теоремы 1.9, 1.10 и формулы A.122), A.123) открывают возмож-
возможность выполнения операций с тензорами в форме A.121) без исполь-
использования их явного вида A.104). При этом от формы A.121) всегда
можно вернуться к A.104).
Действительно, пусть имеется тензор Т, представленный в диад-
ном базисе своими компонентами. Сгруппируем представление A.121)
следующим образом:
Т = ei ® ai + ё2 ® а2 + ё3 ® а3, A.124)
52 Глава 1. Тензорная алгебра
где векторы а,-, г = 1,2, 3, определим как
ai = Тпё! + Т12ё2 + Т13ё3, а2 = Т21ёх + Т22ё2 + Т23ё3,
а3 = t31ei + Т32ё2 + Т33ё3. A.125)
Сравнивая представления A.124) и A.104), заключаем, что инди-
индивидуальные векторы а,- в A.104) определяются формулами A.125), а
саму символическую запись A.104) можно понимать как упорядочен-
упорядоченную совокупность шести векторов ei, аь ё2, а2, ё3, аз, связанных
последовательно операциями: 0, +, 0, +, 0.
Несложно проверить, что для такого представления A.124) тензоры
действительно складываются и скалярно перемножаются по правилам
A.66), A.105) и A.108).
§ 1.4. Алгебра тензорных полей
1.4.1. Поле тензора второго ранга
Пусть теперь в каждой точке х пространства имеется тензор второ-
второго ранга Т, меняющийся, вообще говоря, при переходе от одной точки
к другой. В этом случае говорят, что определено тензорное поле Т(х).
Из определения 1.18 следует, что в каждой точке х тензор Т(х):
• является инвариантным, т.е. не изменяется относительно любых
преобразований координат, порождаемых уравнениями A.4),
• имеет в любом диадном базисе двухиндексные компоненты, напри-
например, в декартовом диадном базисе TIJ (см. A.121)).
В каждой точке х могут быть образованы следующие диадные ба-
базисы:
ё,-®ёу, R'eiy, R'<g>R;, R,-®Rj. A.126)
Например, локальный диадный базис R,- 0 Ry можно образовать сум-
суммированием декартова диадного базиса ё& 0 ё/ с якобиевыми матри-
матрицами согласно определению 1.21 и соотношению A.6):
R, ® R; = Q\ Q'jek ® ё». A.127)
Из свойства инвариантности тензора Т вытекает, что при переходе
от декартовых координат хг к прозвольным криволинейным Xх тен-
тензор Т не изменяется, поэтому его можно представить разложением по
локальному диадному базису:
Ri, A.128)
где TtJ называются контравариантными компонентами тензора Т.
§ 1.4. Алгебра тензорных полей
.53
Из A.121), A.127) и A.128) следует правило преобразования ком-
компонент тензора при переходе из декартова диадного базиса ё,- 0 ёу в
локальный R,*® Ry (т.е. при переходе из системы координат ж1 в I1):
fij = TklQiQjn Tkl = Т>Р*\ Р). A.129)
Ковариантными компонентами тензора TJ-y называют его компонен-
компоненты в базисе R* 0 W, они связаны с Т1-* с помощью метрической мат-
матрицы:
1 A.130)
Теорема 1.11. Единичный (метрический) тензор Е можно пред-
представить следующим образом:
Е = ё* 0 ё, = R' 0 R, = gijRi 0 R, = 0,-yR1' 0 Rj, A.131)
T Действительно, используя определения A.112) и A.113) для Е и
диадного базиса ё,- 0 ёу, в силу правила A.J.05) сложения тензоров
получаем первое равенство в A.131). В справедливости второго ра-
равенства легко убедиться, если подставить вместо R,- и R1 выражения
A.6), A.19) и воспользоваться формулой A.18). Остальные равенства
в A.131) следуют из A.19). А
Из A.131) следует, что ковариантные компоненты метрического
тензора Е совпадают с матрицей gij в базисе R' 0 RJ, а контрава-
риантные - с обратной матрицей дх*.
Если тензор имеет в какой-либо системе координат нулевые ком-
компоненты, то из A.129) и A.130) следует, что будут нулевыми и ком-
компоненты в любой другой системе координат. Такой тензор называют
нулевым и обозначают как 0 - нуль-тензор.
1.4.2. Алгебраические операции с тензорными полями
Из определения A.105) и представления A.128) следует, что сумма
двух тензоров есть тензор, компоненты которого равны сумме компо-
компонент этих тензоров в одном и том же диадном базисе:
Т + В = {Tij + Bij)Ri 0 Rj. A.132)
С помощью теорем 1.8, 1.9 и соотношений A.127) легко доказать
следующие правила скалярного умножения локальных диадных бази-
базисов:
(R,- 0 R,) • R* = R,- 0 (Ry
(R,- 0 Ry) • (Rfc 0 R|) = gjkRi 0 R/, A.133)
(R,- 0 Ry) • -(Rjb 0 Rf) = gjkga.
54 Глава 1. Тензорная алгебра
Пусть имеется тензорное Т(х) и векторное а(х) поля, тогда для
каждой точки х операцию A.106) скалярного умножения а на Т со-
согласно A.133) можно представить следующим образом:
а • Т = a'R, • TjkRj 0 R* = a'T^R,- • R, 0 R* =
k = a'TfRk = c*R* = с A.134)
Эта операция образует вектор с с компонентами с* = агТк в локаль-
локальном базисе R*.
В соотношениях A.134) мы воспользовались тем, что сами компо-
компоненты тензора Т*к при фиксированных j и к являются скалярными
объектами, и их можно переставлять в любое место, в данном случае
их удобно перенести к аг, чтобы явным образом появилось скалярное
произведение R, • Ry = g^. Этот прием широко будет использоваться
в дальнейшем. Заметим, что порядок следования векторов, связанных
какими-либо операциями, вообще говоря, менять нельзя.
Скалярное и двойное скалярное умножение двух тензорных полей
согласно A.107), A.109) и A.133) можно представить в виде:
Т • В = Т'В* 0 R, • Bk!Rk 0 R/ = TlBklRi 0 R/, A.135)
Т • В = TijKi 0 R, • -BHRfc 0 R; = TijR{ • gjkBklRi = TlkBkl. A.136)
Скалярное умножение векторов или тензоров называют также опе-
операцией свертки.
Имеют место следующие правила перестановки порядка скалярного
умножения трех тензоров второго ранга (см. упр. 1.4.3):
(А • Т) • В = А • .(Т • В) = В • А • Т = Т • В . А. A.137)
Определение 1.22. Векторным произведением вектора
на тензор второго ранга (слева и справа соответственно) называ-
называют тензоры следующего вида:
а х Т = a,R' x TjmW 0 Rm = -L€^kaiTjmRk 0 Rm, A.138)
/9
T x а = TjmRj 0 Rw x a,-R" = 4=€w'*Tiwol-Ri 0 Rk.
Транспонированный тензор АТ в трехмерном евклидовом прост-
пространстве вводят аналогично определению 1.14:
А = AijRi 0 R,, AT = AijRj 0 R,- = AjiR{ 0 R^ A.139)
§1.4. Алгебра тензорных полей 55
Следствием A.134) и A.139) являются следующие многократно ис-
используемые соотношения с тензорами второго ранга:
аА = Ата, (А • В)т = Вт • Ат. A.140)
Квадратом тензора, кубом тензора и вообще п-ой степенью тен-
тензора А называют следующие тензоры:
А-А = А2, А-А-А = А3, А-...-А = Ап. A.141)
Из A.122) и A.127) следует, что векторы а и b всегда можно раз-
разложить по любому диадному базису, т.е. представить в виде суммы
диад векторов базиса:
а 0 b = а% 0 Vej = a'VR,- 0 R, = a'bjR1' 0 Rj. A.142)
1.4.3. Детерминант тензора
Ранее в §1.1 было введено понятие детерминанта (определителя)
матрицы A*j по формуле A.8).
Определение 1.23. Детерминантом тензора Т называют
детерминант его смешанных компонент, взятых в каком-либо ба-
базисе:
detT=det{Tij). A.143)
Детерминант тензора, определенный таким образом, не зависит от
того, в каком именно базисе взяты компоненты Tlj. В самом деле,
пусть имеется две системы координат Xх и Xй с локальными базиса-
базисами R,- и RJ-, a TXj и T'j - компоненты тензора Т в этих базисах:
Т = Т1)К{ 0 Rj = T1) RJ 0 R'>, A.144)
тогда, используя правила преобразования компонент тензора (см.
упр. 1.4.6), получаем
= det (P'fc)det (Q'j)det {T'f ) = det (T'f ) A.145)
- свойство инвариантности детерминанта, т.е. независимости его от
системы координат (здесь использованы результаты упр.1.1.6, 1.1.7).
Используя теперь формулу A.39), выражение для детерминанта
тензора можно представить с помощью символов Леви-Чивиты:
det T = ^к€тп1ГтТ\Т) . A.146)
56 Глава 1. Тензорная алгебра
Алгебраическим дополнением для компоненты Тгт называют мат-
матрицу Л,т вида:
АГ = \^ь^п1Т^Ткг . A.147)
Вычислим произведение Тга и Л,т:
А{тТа = ^€тп|ГвТ'пТ*, . A.148)
Если а ф т, то по свойствам символа emnl индекс а должен совпадать
с п или /. Пусть, например, а = п, тогда в A.148) возникает свертка
€ijk с симметричной матрицей ТгаТ*а, что по A.37) неминуемо даст
нуль:
^T^T) = 0. A.149)
То же самое получаем при а = I. Следовательно, произведение A.148)
при афт всегда равно нулю.
Вычислим теперь произведение A.148) при а = т, преобразуя его
следующим образом:
А(аГа = 1ео*е^Га(Т>,Т* - Т'7Г*,), афЦф1фа. A.150)
Заметим, что по греческим индексам суммирования нет, и для а, /3,7
всегда соответствует четная подстановка индексов из {1,2,3}. Тог-
Тогда €а^7 = 1, и можно расписать явным образом и свертку с другим
символом Леви-Чивиты. В результате получим:
А{аГа = \
Таа
а
^ - Т« Т^) = det (Г;). A.151)
Сравнивая формулы A.151) и A.8), нетрудно увидеть, что при любых
значениях а = 1,2,3 выражения A.151) действительно всегда образу-
образуют детерминант матрицы det (Т^).
Таким образом, объединяя оба случая а = m и а ф т, получаем
свойство алгебраического дополнения:
(AmT'a) = Cdet Т. A.152)
§ 1.4. Алгебра тензорных полей 57
Если тензор Т является неособенным, т.е. det T ф О, то для него
существует обратный тензор Т (определенный по A.96)):
Т^Т^Е, A.153)
или в компонентной записи
{Т-%1С 0 W • TklRk 0 R/ = R* 0 Rb A.154)
(T^^T^R* 0 R/ = R* 0 Rfc,
отсюда
(T-1),^'^^. A.155)
С помощью свойства A.152) алгебраического дополнения могут
быть вычислены компоненты обратного тензора (см. упр. 1.4.1).
Используя результаты упр. 1.4.1, можно показать, что для обратной
матрицы д%3 имеет место формула:
,« = l-g-, A-156)
где частная производная dg/dgij совпадает с алгебраическим допол-
дополнением элемента gij.
Обращение скалярного произведения тензоров производится следу-
следующим образом (см. упр. 1.4.3):
(A-BJ-^B^. A.157)
1.4.4. Тензорные признаки
Пусть имеются компоненты Ти некоторого объекта. Для того что-
чтобы установить, являются ли они компонентами тензора, можно попы-
попытаться проверить выполнимость тензорного закона A.129) при пере-
переходе из одной системы координат в другую. Такой способ называется
прямым тензорным признаком.
Однако можно поступить по-другому, если компоненты TIJ учас-
участвуют в каком-либо алгебраическом тензорном уравнении с другими
компонентами BtJ, CIJ и др., про которые известно, что они являются
компонентами тензора, например:
или
TijBjk = Cik. A.158)
58 Глава 1. Тензорная алгебра
Тогда без непосредственной проверки можно утверждать, что TIJ то-
тоже являются компонентами тензора. Такой способ называется обрат-
обратным тензорным признаком.
Справедливость обратного тензорного признака для операций сло-
сложения очевидна, проверим операцию свертки. Используя A.129), пе-
перейдем в A.158) в новую систему координат:
TijPkt Qmj Blm = Р\Р%Csp. A.159)
Домножая на Qn{ Q*fc, получаем:
Qni Q\Pki Qmj TijBlm = Qn{ Qmj Т>Вгт = Cnt. A.160)
Отсюда находим, что действительно при переходе в новую систему
координат:
tnm = Qni Qmj T*>, A.161)
таким образом, TIJ преобразуются по тензорному закону.
Упражнения к § 1.4.
Упражнение 1.4.1. Показать, что если тензор Т имеет компоненты
T = i;iRt'®Ri,
то компоненты обратного тензора Т имеют следующий вид:
гр-1 __ (Т~1\ ir>« <о> т> . (Т'г\ i — г- J*PT mT п
J. — \± ){ Л. Q9 Лл \1 }{ — 2detX П Р "
Упражнение 1.4.2. Показать, что
Упражнение 1.4.3. Доказать формулы A.137), A.140) и A.157).
Упражнение 1.4.4. Показать, что для произвольного тензора X второго
ранга и вектора а имеет место соотношение:
а • Т • а = a <g> a • Т.
Упражнение 1.4.5. Показать, что всякая диада а 0 Ь является особенным
тензором:
det (а 0 Ь) = 0.
§ 1.5. Собственные значения тензора 59
Упражнение 1.4.6. Показать, что при переходе из одной криволинейной
системы координат Xх в другую X1х компоненты тензора Т преобразуются сле-
следующим образом:
Ц = Рк- Цт, Т!j = Р* <?,Tfe', Т* = Q\Q\Tkl.
У пр ажнение 1.4.7. Показать, что векторное произведение тензора на вектор
можно представить в виде:
Т х а = y/g€ijkTmjakRm 0 R1".
§ 1.5. Собственные значения тензора
1.5.1. Определение собственных значений тензора
Определение 1.24. Собственными значениями Аа, Аа и
собственными векторами еа, еа тензора второго ранга А
называют такие числа (вообще говоря, комплексные) и тройки век-
векторов (вообще говоря j комплексно-значных), которые обеспечива-
обеспечивают выполнение условий:
А • еа = Ааеа, еа . А = Ааеа, а = 1, 2,3. A.162)
Если известны компоненты А1 • тензора А в некотором базисе Rt:
0 0
А = AxjRi 0 RJ, а левый и правый собственный базисы еа, еа пред-
представлены в виде разложения по этому базису:
° К
еа = КЪ, е" = Q",R'f A.163)
то уравнения A.162) можно записать в компонентном виде:
(A'j - А«^)К = 0, (A'j - \а6Г)С}ао A.164)
и представляют собой системы линейных уравнений для определения
0 . о
PJa и Qaj при фиксированном а. Ненулевые решения этих систем
существуют только при тех Аа, Аа, которые обеспечивают равенство
нулю определителей:
det (A'j - Ав^.) = 0, det (Ах) - \а6х)) = 0. (Ы65)
Глава 1. Тензорная алгебра
Поскольку Аа и Аа охватывают все множество корней этих уравнений,
то, очевидно, что
Аа = Аа, A.166)
а единственное уравнение в A.165) представляет собой уравнение
третьей степени относительно Аа:
V{Xa) = det (A - АаЕ) = det (А*; - Аа^) = 0 A.167)
и называется характеристическим уравнением.
Так как (А — АаЕ) - тензор, то его собственные значения Аа не
зависят от того, в какой системе координат они определены, т.е. из
A.167) следует, в частности, что
det fa - XaSij) = 0, det {Aij - XQgij) = 0, A.168)
еще одно доказательство этого факта будет дано в п.4.5.3.
1.5.2. Свойства собственных векторов
Собственные векторы еа и еа определяются неоднозначно, дейст-
действительно, если еа - собственный вектор, то кеа - тоже собственный
вектор (к ф 0). Для устранения неоднозначности обычно собственные
векторы нормируют:
ев-еа = 1, а =1,2,3. A.169)
Собственные векторы еа и е^ - взаимно ортогональны. В самом де-
деле, умножая первое уравнение в A.162) на еР слева, а второе - справа
о
на е
-ea) A.170)
получаем, что должно выполняться соотношение
(Ав-А/,)е"-еЛ = 0. A.171)
Откуда при некратных корнях Аа ф А^ следует, что
У-^=^в. A.172)
§1.5. Собственные значения тензора
1.5.3. Разложение тензора по собственному базису
Тензор А может быть представлен разложением по собственному
базису:
А = А*&®е>. A.173)
Умножая A.173) слева и справа на еа и е^, на основании A.170) и
о
A.172) получаем, что матрица Alj - диагональная, и ее ненулевые
значения совпадают с собственными значениями:
А р = Аа<??, А = у j Ааеа % е . A.174)
а=1
1.5.4. Разложение обратного тензора по
собственному базису
Пусть теперь А - неособенный тензор: det А ф О, тогда для него
имеет место формула A.153):
А-1-А = Е. A.175)
Умножим слева и справа это соотношение на собственный вектор е^:
А" • А • е^з = Е • е^ = е/з,
а затем подставим сюда вместо А его разложение A.174) по собствен-
собственному базису:
^=е^ A.176)
а=1 а=1
Здесь мы использовали свойство ортонормированности A.172).
Перенося Ар в правую часть, получаем окончательно:
А-г.ер = \р%. A.177)
Из этого выражения следует, что собственные векторы обратного тен-
тензора А" совпадают с собственными векторами исходного тензора А,
а собственными значениями у А* являются А71. Тогда тензор А
также можно представить разложением по собственному базису в ви-
виде:
А-^^А-^Ое*. A.178)
а=1
62 Глава 1. Тензорная алгебра
1.5.5. Разложение тензорных степеней по
собственному базису
Рассмотрим теперь квадрат тензора А2 A.141):
А2 = А • А = X) Е А«*« ® *° * Х№ ® «" = Е А^° ® •"- (
а=1/3=1 а=1
т.е. собственными значениями тензора А2 являются А2, а собствен-
собственные векторы совпадают с еа. Очевидно, что имеет место следующая
теорема.
Теорема 1.12. Для любого целого п, как отрицательного, так и
положительного, имеет место разложение п-ой степени для тен-
тензора второго ранга:
а=1
§ 1.6. Симметричные, кососимметричные и
ортогональные тензоры
1.6.1. Симметричные и положительно-определенные
тензоры
Согласно определению 1.15, тензор Т называется симметричным,
если
Т = ТТ. A.181)
Для симметричного тензора матрица его компонент в любом диад-
ном базисе является симметричной:
Т = TijRi 0 Rj, Tij = Tj\ Tij = Tji. A.182)
Определение 1.25. Положительно определенным назы-
называется тензор Т, для которого
а-Т-а = Т*Ч-су >0 A.183)
для любого а = a,-R' ф 0.
Для симметричного тензора Т результат скалярного умножения на
вектор а слева и справа одинаков (см. A.140)):
Та = аТт =а-Т, A.184)
§ 1.6. Симметричные и ортогональные тензоры
-63
в частности, если а = еа - левый собственный вектор, то для сим-
симметричного тензора он, очевидно, совпадает с правым: еа = еа (ср.
с A.162)). Таким образом, существует единственный собственный
триэдр еа всякого симметричного тензора, являющийся ортонорми-
рованным, в силу A.172):
еа-ер=8ар. A.185)
Теорема 1.13. Собственные значения Аа симметричного тензо-
тензора Т всегда вещественны.
Ў Действительно, если бы Ai, например, был бы комплексным:
где i = л/—1L то ему соответствовал бы комплексно-сопряженный
корень Аг = Ai = А'х — iA", а им соответствовали бы комплексно-
сопряженные собственные векторы:
1 о' .о" о 1 о' .о" о'," , .
ei = -75(ei+lei)' e2 = -^(e1-ie1), |ex | = 1, A.186)
о о
скалярно перемножая которые, получаем, что ei • ег = 1, что проти-
противоречит взаимной ортогональности собственных векторов: ei *в2 = 0.
А
Симметричный тензор Т, подобно A.174), можно представить раз-
разложенным по собственному базису:
з
Т = TijRi 0 R, = Y^ A«ea 0 ea, A.187)
a=l
где компоненты в собственном и локальном базисах связаны следую-
следующим образом (см. A.163)):
AaK^Q. A-188)
a=l
Теорема 1.14. Для симметричного положительно-определен-
положительно-определенного тензора Т все собственные значения положительны:
Ха > 0. A.189)
64 Глава 1. Тензорная алгебра
Ў Действительно, если Т - положительно определен, то из A.183) и
A.188) следует, что должно выполняться:
a«J>0, а'а = Р*а<ц A.190)
а=1
для всех а'а, а это возможно только при Аа > 0. А
Со всяким симметричным тензором Т можно связать центральную
поверхность второго порядка, называемую тензорной поверхностью.
Для этого по компонентам Tij составляется квадратичная форма:
hrijXiXj = / = const, A.191)
которая в трехмерном пространстве координат Xх образует либо эл-
эллипсоид, либо гиперболоид, либо их вырождение.
Подставляя A.188) в A.189), получим, что квадратичную форму
можно привести к диагональному виду:
3
•/ \2
Ха(Х'аJ, A.192)
а=1 " а=1
если ввести новые - собственные координаты:
Х'а = PiaX\ Pia = P*aflf,'*. A.193)
Если Т - положительно-определенный, то в силу A.189) все собст-
собственные значения положительны, и поверхность, описываемая уравне-
уравнением
1 3
/=2^Aa(X«J = C°nSt' AЛ94)
a=l
представляет собой эллипсоид, главные направления которого совпа-
совпадают с направлениями осей собственных координат Х'а.
Если все собственные значения совпадают: Аа = А, а = 1,2,3,
то уравнение A.194) является уравнением сферы, для которого все
направления - главные.
Симметричные тензоры второго ранга А и В называются соосны-
о
ми, если их собственные базисы еа совпадают
з з
А = S Аа*<*0 ®а> в = S Ва*<*0 ^»' AЛ95)
a=l a=l
§ 1.6. Симметричные и ортогональные тензоры 65
при этом собственные значения Аа и Ва различны; если же Аа = Ба,
то тензоры А и В совпадают А = В.
Скалярное произведение соосных тензоров А и В образует симмет-
симметричный тензор
(А.В)Т = А-В, A.196)
поэтому это скалярное произведение - коммутативно, т.е. перестави-
переставимо:
А В = ВА. A.197)
1.6.2. Кососимметричные тензоры
Определение 1.26. Тензор ft называют ко с о симметрич-
симметричным, если
П = -пТ. A.198)
Всякий произвольный тензор А всегда можно представить в виде
суммы симметричного и кососимметричного тензоров:
A = T + ft, A.199)
где
T = i(A + AT), П=1-(А-АТ).
Обозначим компоненты кососимметричного тензора ft в базисе
R, <g> Rj как
n = n'''R,-®Ri9 A.200)
тогда
П1' = -Uij. A.201)
Из определения следует, что диагональные компоненты QIJ равны ну-
нулю: Qaa = 0, и тензор ft имеет только 3 независимые компоненты, по-
поэтому на основе всякого кососимметричного тензора можно построить
вектор со, называемый вектором, сопутствующим кососимметричному
тензору (или аксиальным вектором):
и = w,R\ ы{ = -\y/geiikuik. A-202)
Теорема 1.15. Кососимметричный тензор и сопутствующий
ему вектор связаны следующим соотношением:
H = wxE. A.203)
3 Тензорное исчисление
Глава 1. Тензорная алгебра
Ў Действительно, по определению ц>:
n = -jz€ijkUjgnk*R.i 0 Rn =
л/9
0 R* = У**сцрп'*Ъ 0 Rfc -
= fif*Rt 0 Rk = П. A.204)
Здесь использовано определение векторного произведения A.33) и
свойства A.36). А
Найдем собственные значения кососимметричного тензора. Свой-
Свойство кососимметричности A.201), означает, что его компоненты Пи
образуют следующую матрицу:
/ 0 ft12 -fi13\
П* = -fi12 0 fi23 . A.205)
\ fi13 -П23 0 /
Составляя характеристическое уравнение A.167):
V{\) = flfdet {Uij - \gij) = -Л(А2 -fa;2) = 0, A.206)
находим собственные значения:
Ai = —1CJ, Л2 =^ 1CJ, A3 = 0,
u* = 4 ( S wl9aa + 2(a;ia;2^12 + W2W3023 + ^3^i(/13) J . A.207)
\a=l /
1.6.3. Ортогональные тензоры
Согласно определению 1.17, тензор О называется ортогональным,
если
От = О. A.208)
Для ортогонального тензора всегда выполнено соотношение:
ОТ.О = О.ОТ = Е. A.209)
Введем компоненты тензора О в локальном диадном базисе:
O = 0liRi®Ri, A.210)
§ 1.6. Симметричные и ортогональные тензоры
тогда
О . От = O'jO,! R, 0 W • R/ 0 R* = O^OjRi ®Rfe =
= E = ^Rt-0Rfe, A.211)
или
O'jOj = Ofcj = б1'^ = 4. A.212)
Из A.212) следует, что на девять компонент тензора О наложены
шесть связей, следовательно, произвольный ортогональный тензор
имеет не более трех независимых компонент.
Определитель ортогонального тензора равен ±1, так как
1 = det (Е) = det (От • О) = det (От) • det (О) = (det (О)J, A.213)
откуда
det (О) = ±1. A.214)
Бели выбрать некоторый базисный триэдр R, и применить к нему
преобразование с помощью ортогонального тензора О, то получим
новый базисный триэдр RJ:
A.215)
который обладает следующими свойствами.
• Метрические матрицы д^ и gij совпадают. В самом деле,
д'ц = R(. • R^ = R, • О • От • R,- = R,. R,- = дФ A.216)
• Углы rpij между базисными векторами R,- и соответствующие углы
ф\± между RJ одинаковы. Действительно, по A.32) и A.14):
(L217)
• Длины векторов не изменяются:
A-218)
Это означает, что преобразование A.215) произвольного триэдра,
осуществляемое с помощью ортогонального тензора, происходит
"жестким" образом - без изменения углов и длин, т.е. это преобразо-
преобразование поворота вокруг некоторой оси с вектором сз, которое может со-
сопровождаться зеркальным отражением относительно некоторой плос-
плоскости, если det О = — 1. Если же det О = 1, то происходит собственно
поворот.
68 Глава 1. Тензорная алгебра
Выберем два вектора ci и сг в плоскости, ортогональной векто-
вектору сз, для определенности положим |са| = 1. Поскольку тензор О
осуществляет поворот вокруг оси с вектором сз, то сз не изменяется:
с'3 = От • сз = сз, A.219)
а векторы q и сг поворачиваются в своей плоскости "жестким обра-
образом" на некоторый угол tp:
c'Q = OT.ca, A.220)
так что
с^ = ci cos tp + сг sin у?, с'2 = —ci sin у? + сг cos (p. A.221)
Очевидно, что cfa также будут ортонормированы.
Тогда тензор О можно представить в виде
ввс^ A.222)
а=1 а=1
Подставляя сюда A.221), получаем:
О = ci 0 (ci cos ip + c2 sin tp) + C2 (—ci sin ip + c2 cos tp) + c3 0 сз =
= (Ci 0 Ci + C2 ® C2) COS tp + (Ci 0 C2 — C2 0 Ci) sin tp + C3 0 C3 =
= Ecosy?-fc3 0 сзA — cosy>) — E x c^smtp. A.223)
Здесь мы воспользовались свойствами векторного произведения, при-
приведенными в упр. 1.2.7, 1.2.8.
Таким образом, всякий ортогональный тензор О всегда можно
представить в виде A.223).
Вычислим теперь собственные значения ортогонального тензора.
Из A.223) следует, что в базисе са тензор О имеет компоненты:
0 / cosy? sin у? 0\
(О1,) = -sin у? cosy? 0 . A.224)
V 0 0 1/
Составляя характеристическое уравнение A.167), получаем
7>(А) = det (О1',- - А*}) = A - А)(А2 - 2Acosy> + 1) = 0, A.225)
откуда
А3 = 1, Ai = е-1*, А2 = eiv?, A.226)
таким образом, доказана следующая теорема.
_ § 1.6. Симметричные и ортогональные тензоры 69
Теорема 1.16. Ортогональный тензор всегда имеет одно дей-
действительное собственное значение, равное 1, и два, вообще говоря,
комплексных.
Из A.219) следует, что собственный вектор, соответствующий зна-
значению А = 1, совпадает с с3, т.е. е3 = е3 = с3. Два других собст-
собственных вектора являются, вообще говоря, комплексными, их находим,
записывая разложение A.174) тензора О по собственному базису:
О = e-^ei 0 е1 + е*е2 ® е2 + с3 0 с3 = (ех 0 еЧ
+ е2 0 е2) cos <р - i(ei 0 е1 - е2 0 е2) sin <p + с3 0 с3. A.227)
Сравнивая A.227) и A.223), находим
ех = е2 = i=(Cl - ic2), °e2 = S1 = -~(С1 + ic2). A.228)
Упражнения к § 1.6.
Упражнение 1.6.1. Показать, что если в двойном скалярном произведе-
произведении двух тензоров А и В один из тензоров симметричен, то второй тоже можно
симметризовать:
А--В = Т--В, и В = ВТ, где Т= ^(А + Ат).
Упражнение 1.6.2. Показать, что для кососимметричного тензора из A.201)
следует Q{j = —^'и но для смешанных компонент, вообще говоря, это соотно-
соотношение не имеет места.
Упражнение 1.6.3. Показать, что скалярное умножение кососимметричного
тензора ft на произвольный вектор а можно представить в виде:
Упражнение 1.6.4. Показать, что соотношение A.203) для кососимметрич-
кососимметричного тензора можно также представить в виде:
Упражнение 1.6.5. Показать, что собственные векторы еа, соответствую-
соответствующие собственным значениям Ла кососимметричного тензора ffc, могут быть пред-
представлены в виде:
е3 = е3 = —, е1 = е2 = -=(сх - ic2), е2 = е1 = -Wei + ic2),
70 Глава 1. Тензорная алгебра
где Ci и С2 - некоторые вещественные нормированные векторы \са\ = 1.
Упражнение 1.6.6. Показать, что всякий кососимметричный тензор ГЪ яв-
является особенным, т.е. det (П) — 0.
Упражнение 1.6.7. Показать, что если два векторных базиса Rt и R,
связаны с помощью ортогонального тензора Q:
то тензор Q можно представить в виде тензорного произведения векторов базиса
- исходного R,- и конечного R/1, полученного ортогональным преобразованием:
Q = R, ® R".
Упражнение 1.6.8. Показать, что если имеются два ортонормированных
базиса С^ и Са, связанных соотношениями:
с'х = ci cos ф + С2 sin ф, с'2 = —ci sin ф -f C2 cos ф, Сз = ез, 0 ^ ф ^ 2тг,
то эти два базиса также можно связать с помощью некоторого ортогонального
тензора Q: с!а =¦ Q • Са. Найти компоненты этого тензора в базисе Са.
§ 1.7. Физические компоненты тензоров
1.7.1. Ортонормированный базис
В ортогональных системах координат ОХк метрическая матрица
является диагональной:
ГО 1фз f911 ° ° \
дц = R, • Rj = { ' / . , т.е. 9ij = 0 д22 0 .
A.229)
Введем обозначения для ее компонент:
=#a, a -1,2,3, A.230)
где На называют параметрами Ламе.
Определитель д в ортогональных координатах имеет вид:
д = det {9ij) = (Я!Я2ЯзJ. A.231)
Обратная матрица дх* тоже является диагональной, и ее коэффици-
коэффициенты вычисляются следующим образом:
A.232)
Введем единичные векторы локальных базисов eQ и е°:
ео = Ra/|Ra| = Ra/V^, e° = Ra/|Ra| = Ra^^, A.233)
§ 1.7. Физические компоненты тензоров
71
где обозначены длины векторов базиса
|Ra| = (Ra • RaI/2 = (gQQI/2 = —!= = 4--
В силу
ea =
= e ,
получаем, что единичные векторы базиса ea и ea совпадают.
Очевидно также, что еа - ортогональны между собой:
= Q.
A.245)
A.236)
т.е. базис еа является ортонормированнглм.
Векторы базиса еа направлены по нормали к координатным по-
поверхностям Ха = const и по касательным к координатным линиям
Ха в сторону их возрастания.
1.7.2. Компоненты тензоров в ортонормированном базисе
Произвольные вектор а и тензор Т можно представить в ортонор-
ортонормированном базисе следующим образом:
а = a'R,- =
a = с^е,- = a,R' =
a=l
a=l
A.237)
a=l/3=l
Здесь введены компоненты вектора Яф,
ортонормированном базисе е,-:
т?" =
или с использованием параметров Ламе:
и тензора
A.238)
A.239)
72.
Глава 1. Тензорная алгебра
Рис. 1,26. Ортонормированный ба- Рис. 1,27. Ортонормированный ба-
базис в цилиндрической системе коор- Зис в сферической системе координат
динат
Определение 1.27. Компоненты тензора Т$ и вектора Яф в ор-
тонормированном локальном базисе е, называются физически-
физическими.
Из A.238) следует, что так же, как и в декартовом базисе ё,, все
компоненты Т^, Тф,^, Т^ совпадают.
Упражнения к § 1.7.
Упражнение 1.7.1. Показать, что для цилиндрической системы координат:
#1 = 1, #2 = Г, #з = 1,
а для сферической:
Упражнение 1.7.2. Показать, что для цилиндрической системы координат
(см. упр.1.1.11, 1.1.14) ортонормированный базис еа имеет следующий вид:
= er =
= ez,
причем в каждой точке М, вектор ег направлен вдоль радиальной полупрямой,
соединяющей ось Oz и точку М., вектор Ъф - по окружности вокруг оси Oz, a
е2 - вдоль прямой, параллельной Oz (см.рис. 1.26).
Упражнение 1.7.3. Показать, что для сферической системы координат (см.
упр.1.1.12, 1.1.13 и 1.1.15) ортонормированный базис еа имеет следующий вид:
= er = sin д cos <^>ei -f sin d sin <^в2 + cos т9ез,
§ 1.8. Тензоры высших рангов 73
е2 = е# = cos тЗ cos фе\ + cos д sin <?е2 — sin
е3 = еф = — sin <?ei + cos <?
причем в каждой точке М вектор ег направлен вдоль радиальной полупрямой,
исходящей из начала координат, вектор в$ - по касательной к меридиану,
по касательной к параллели (см. рис. 1.27).
§ 1.8. Тензоры высших рангов
1.8.1. Геометрическое определение тензора n-го ранга
Кроме рассмотренных тензоров нулевого (скаляры), первого (век-
(векторы) и второго рангов, "геометрическим" способом, т.е. в форме
A.104), можно ввести тензоры произвольного n-го ранга (где п - на-
натуральное число).
Определение 1.28. Тензором п-ого ранга пП в трехмерном
евклидовом пространстве назовем объект
пП = [ё1П"Л51ё2пЛ12ёзп'Пз], п ^ 2, A.240)
представляющий собой упорядоченную совокупность трех фиксиро-
фиксированных векторов базиса ё,- и трех тензоров (п — \)-го ранга nfl,-,
индивидуальных для каждого тензора nfl.
Это определение, очевидно, является рекуррентным: тензор п-го
ранга определяют через тензоры (п — 1)-го ранга. Из A.240) при п =
2 получаем определение A.104) тензора второго ранга. При п = 3
получаем тензор третьего ранга:
3П = [ёхПхёгПзёзПз], A.241)
где Г)},- - тензоры второго ранга.
Операции сложения и умножения на число для тензоров A.240) вво-
вводим аналогично A.105):
ПТ = [ё'41-1
= nS,
<рпп = ф™-1^] = [e'V1-1^)]. A.242)
Базисные тензоры также введем рекуррентным способом, исполь-
используя знак тензорного произведения ®. Для п = 3 имеем:
ei ® ё,- ® ej = 3T(ltj) = [eiT(o)e20e30],
ё2 ® et- ® ei = 3TBti) = [ei0e2TW)e30], A.243)
ё3 ® ё,- О ei = 3TCti) = [ei0e20e3T(o)].
Здесь T(tJ) - базисные тензоры A.113) второго ранга, а 0 - это нулевой
тензор второго ранга.
74 Глава 1. Тензорная алгебра
Определение 1.29. Набор A.243) базисных тензоров третьего
ранга называют триадным базисом.
Каждая базисная триада ё& 0 ё,- 0 ej при фиксированных &, г, j, как
и всякий тензор третьего ранга, представляет собой совокупность 27
векторов.
Продолжая построение A.243) рекуррентным способом, приходим
к определению базисных тензоров n-го ранга, которые обозначим сле-
следующим образом:
ei ® ё,-а ® ... ® ё,п = [ё1п-1Т(,-2...,п)ё2п-10ё3п-10],
ё2 0 ё,-2 0 ... 0 ё,п = [ein-1Oe2n-1T(l-2...ln)e3n-1O], A.244)
ё3 ® ё,-а ® ... ® ё,п = [ё1п-10ё2п-10ёзп-1Т(|-2...,п)].
Здесь п"Т(,-2...,п) - базисные тензоры (п — 1)-го ранга, п"0 - нуль-
тензор (п — 1)-го ранга.
Определение 1.30. Набор базисных тензоров A.244) называют
полиадным базисом, а сами тензоры etl 0 ... 0 ё,п при фикси-
фиксированных i\.. ,in -базисными полиадами.
Имеет место аналог теоремы 1.7 и 1.10: всякий тензор n-го ранга
пП можно разложить по полиадному базису:
пП = fi'1 "'"ё^ 0 ... 0 ё,п, A.245)
где П*1—1п - компоненты тензора в полиадном базисе.
Поскольку базисные полиады являются тензорами n-го ранга, то их
можно складывать и умножать на число. Кроме того для них можно
ввести обобщенную операцию скалярного произведения.
Определение 1.31. Скалярным k-кратным произведением
двух базисных полиад n-го и т-го рангов называют базисную полиаду
( п — 2k)-го ранга:
(etl 0 ... 0 ein)^^(ejl 0 ... 0 ejm) = etl 0 ...
к
• • • ® ejmSinjiSin-ij* • • -un-n+iin+fc» A.246)
причем l^k^nuk^m.
Заметим, что если бы мы также, как и в п. 1.3.14, ввели скалярное
произведение сначала для объектов A.240), то формула A.246) пред-
представляла бы собой уже теорему, обобщающую теоремы 1.8 и 1.9 (см.
упр. 1.8.9).
§ 1.8, Тензоры высших рангов 75
Определение 1.32. Тензорным произведением базисных поли-
ад п-го и т-го рангов называют базисную полиаду (п + т)-го ранга:
(ё|Ч 0 ... 0 ё,-п) 0 (ё,-п+1 0 ... 0 ё,п+т) = etl 0 ... 0 ё,-п+т. A.247)
1.8.2. Поле тензора n-го ранга
Пусть теперь в каждой точке х трехмерного пространства опреде-
определен тензор n-го ранга nfl(x).
По определению тензор n-го ранга является инвариантным объек-
объектом, тогда его можно представить разложением по локальному поли-
адному базису:
ПП = fl^-^R,-, 0 R,-2 0 ... 0 R,n, n ? 1, A.248)
где flll###ln - компоненты тензора n-го ранга в локальном полиадном
базисе Rtl 0 ... 0 R,n.
Компоненты тензора пП при переходе из декартовой системы ко-
координат х% в криволинейную систему Xх преобразуются следующим
образом:
а при переходе из криволинейной системы Xх в другую криволиней-
криволинейную Xfx таким образом:
^•••\+,..,„ = П •¦¦р% Qik%+1 ¦ ¦ ¦ Q\ ^jl-%,..u • (i-250)
Примером тензора третьего ранга является тензор Леви-Чивиты,
определяемый как
^Ri 0 R^- 0 Rb A.251)
у/9
Заметим, что сами символы Леви-Чивиты €,^, е**к не являются
компонентами тензора, т.к. не преобразуются по тензорному закону
A.250).
Примером тензора четвертого ранга является единичный тензор
четвертого ранга А, определяемый как
А = - (R,- 0 R' 0 R1' 0 R/ + R,- 0 R' 0 R/ 0 R1') =
= AijklRi ® R,- ® Rjt ® R,. A-252)
76 Глава 1. Тензорная алгебра
Компоненты этого тензора в ковариантном тетрадном базисе имеют
вид:
Aijkl = -{gikgjl + gilgik). A.253)
1.8.3. Транспонирование тензора n-го ранга
Обобщением операции транспонирования A.139) на случай тензора
n-го ранга является введение объекта
пп(т1...тп) _ Qi^.in^^ 0 R ^ 0 _ 0 R.n f A.254)
Ш1...т„ G {l,...n}, ii...»n € {1,2,3},
где (mi... my... rrin) - некоторая подстановка. Индекс щ в этой под-
подстановке указывает на то, что вектор базиса R,m. находится на j-ом
месте в полиаде
Таким образом, для тензора n-го ранга существует п! транспони-
транспонированных тензоров.
Перенумеровав индексы у диадных векторов R,m. в A.254) так,
чтобы эти векторы нумеровались по возрастающей, получим альтер-
альтернативное представление транспонированного тензора n-го ранга:
пп(т1...тп) = n^i-'-nR^ 0 R,2 0 . .. 0 R^, A.255)
где (w\.. .Wj .. .гуп) ? {1.. .n} - обратнаяк (mi.. ,щ .. .mn) подста-
подстановка (поэтому для нее используем букву гу, похожую на переверну-
перевернутую т). Число Wj в этой подстановке указывает на то, что индекс iWj
компоненты тензора пП находится на j-ом месте, т.е.
Найти обратную подстановку можно, например, записав подста-
подстановку в матричном виде, поменяв затем верхнюю и нижнюю строки и
переставив столбцы так, чтобы в верхней строке получился ряд 1... п:
/1 ... j ... п \ /mi ... mj ... гпп\ ^
\тг ... mj ... тп) \ 1 ... j ... п )
'•• k '•• nV A.256)
i ... Wk ... WnJ V
Элементы исходной и обратной подстановки, очевидно, связаны со-
соотношениями:
j = Wmj или k = mWk Vi,fce{l...n}. A.257)
§ 1.8. Тензоры высших рангов
Вообще же подстановку с элементами (тп{1 ...rriik . ..га,п) называют
произведением подстановок с элементами: (mi.. . m,-.. .тп) и
(ii...ifc...»n).
Подстановка (m-i... ran) называется ортогональной, если она сов-
совпадает со своей обратной подстановкой (wi.. .wm):
Wj=rrij) j = l...n или j = mmj Vj = l...n. A.258)
Для ортогональной подстановки формулу A.255) можно записать в
виде:
"fllmi-ra«) = П|>яч-¦'¦»• R.^ 0 ... 0 R,n. A.259)
Например, для тензора четвертого ранга 4П:
4П = fi'—'R,, ® R,-, ® R,-s ® R,-4 A.260)
можно ввести следующие обобщенные транспонированные тензоры:
ftD321) = nti."au.-4R.4
4 2
A.261)
ПC142) =fi«i«2»V4R.80R.i0R.40R.2 =fl^.(iUR|.ieR.aeR.|gR.4j
A.262)
и так далее. В первом случае подстановка D321) является ортого-
ортогональной, а во втором случае C142) - нет.
1.8.4. Симметрирование тензора n-го ранга
Среди тензоров четвертого ранга важную роль играют тензоры,
обладающие симметрией компонент следующего вида:
т.е. удовлетворяющие соотношениям:
4^A234) __ 4^B134) 4^A234) = 4^A243) 4^A234) = 4
A.264)
Такие тензоры являются аналогом симметричного тензора второго
ранга, и поэтому называются симметричными тензорами четверто-
четвертого ранга.
Из произвольного тензора второго ранга А можно образовать сим-
симметричный тензор Т путем операции симметрирования:
Т = -(Ат + А) = ~(А<21> + А<12>). A.265)
78 Глава 1. Тензорная алгебра
Аналогичная операция симметрирования для произвольного тензора
четвертого ранга имеет следующий вид:
4С = *Ф = (
+ ft<3412> + ft<3421> + ft<4312> + ft<4321>). A.266)
Тензор
4C = C'218'4!^ ® ... ® R,4, A.267)
очевидно, обладает симметрией компонент A.263).
Симметричный тензор четвертого ранга может быть образован и
другими перестановками, например, если тензор 4П сам обладает дву-
двумя первыми условиями симметрии A.264) (по индексам 1, 2, а также
3 и 4), то тензор
4Ф = - Dft<2314> + 4ftC214) + 4П<1432) + 4П<4132>) A.268)
обладает полной симметрией компонент A.263).
Иногда применяется также симметричный тензор шестого ран-
ранга 6П, обладающий симметрией индексов внутри каждой пары и по
парам:
6^A23456) __ 6^B13456) __ 6^A24356) = 6^A23465) q 269)
6ПA23456) = 6^A25634) = 6^E63412) = 6^C41256) и т д
Из произвольного тензора шестого ранга 6П можно образовать сим-
симметричный тензор путем введения операции симметрирования, напри-
например, следующим образом:
6С = 6П<-> = —
A.270)
Здесь операция 6П^'I2 означает симметрирование вида A.266) по че-
четырем индексам гз^Ч^Ч^в при фиксированных индексах ii,22» стоя-
стоящих на пятом и шестом местах и т.п.
Тензор 6С вида A.270) обладает симметрией компонент типа
A.269).
§ 1.8. Тензоры высших рангов ___79
Упражнения к § 1.8.
Упражнение 1.8.1. Показать, что операция Свертки двух тензоров чет-
четвертого ранга
1'31'"'4!^ ® ... ® R,4, 4П<2) = nWi-i'R^ ® ... ® Ri4,
т.е. скалярное умножение по всем четырем индексам приводит к образованию
следующего скаляра:
Упражнение 1.8.2. Показать, что для симметричного тензора второго ранга
Т имеет место соотношение:
Т®Т Д = Т2-Е.
Упражнение 1.8.3. Показать, что для всякого тензора второго ранга Т и
четвертого ранга П имеет место соотношение:
т • -4п • т = т ® т • • • -4п.
Упражнение 1.8.4. Показать, что для произвольных тензоров второго ранга
А, В, С, 13 имеют место соотношения:
(А • В) • -(С • D) = (D ® В)<3214> • • • -(С ® А) =
= (В ® D)<1432> • • • -(С ® А) = (D ® В)<1432> • • • -(А ® С) =
Упражнение 1.8.5. Показать, что квадрат симметричного тензора Т можно
представить в виде:
Т2 = А • Д • • • -Т ® Т.
Упражнение 1.8.6. Показать, что если тензор ft обладает двумя первыми
условиями симметрии A.264), то
Упражнение 1.8.7. Показать, что векторное произведение вектора на про-
произвольный тензор 71-го ранга имеет вид:
а х пП = —€ijilaiUji:i { Rtl <
V9
80 Глава 1. Тензорная алгебра
Упражнение 1.8.8. Показать, что имеет место следующая формула пере-
перестановки множителей в скалярном произведении:
a.
Упражнение 1.8.9. Дать определение Aj-кратного скалярного произведения
тензоров 71-го ранга в форме A.240), а затем вывести формулу A.246) в качестве
следствия.
§ 1.9. Псевдотензоры
1.9.1. Общие замечания о псевдотензорах
Из общего определения тензора, данного в п. 1.7.1, следует, что не
всякий объект с индексами является тензором, а только обладающий
свойством инвариантности, т.е. компоненты которого при переходе
из одной системы координат в другую преобразуются специальным
образом - по закону A.129).
Выше мы уже встречались с объектами, которые не преобразуются
по тензорному закону, и, следовательно, не являются компонентами
каких-либо тензоров, в частности, это относится к символам Леви-
ЧИВИТЫ €ijk-
Однако, оказывается, существует ряд объектов, которые преобра-
преобразуются по закону, "близкому" к тензорному A.129), но несколько от
него отличающемуся. Такие объекты играют важную роль в тензор-
тензорном исчислении, и их объединяют в отдельный класс - псевдотензо-
псевдотензоров.
Рассмотрим примеры псевдотензоров, а затем сформулируем об-
общий закон преобразования их компонент.
1.9.2. Определитель метрической матрицы
Метрические матрицы gij и g%i являются компонентами тензора
(см. упр.1.1.9), и поэтому преобразуются при переходе из одной криво-
криволинейной системы координат Xх в другую Х'х по закону (см.
упр.1.1.9):
(fit = Р™ Plj9mi. A.271)
Вычислим определитель матрицы д'^:
д' = det (^-) = (det (Pm{ )Jdet (gml) = (det (Pmt )Jg, A.272)
или, вводя обозначение для определителя якобиевой матрицы:
Д = det (Qmi ), A.273)
§ 1.9. Псевдотензоры 81
получаем, что
V?=±A\/7. A.274)
Поскольку всегда должно выполняться условие у/д > 0, то формула
A.274) имеет вид:
Vfl = |A|\/7- A-275)
Таким образом, важнейший скаляр у/д не является инвариантом
при любых преобразованиях координат A.2) (для инвариантов долж-
должно было бы выполняться равенство \fg* = у/д) и, следовательно, не
является тензором ранга 0.
1.9.3. Векторное произведение
Рассмотрим произвольный вектор с, образованный с помощью век-
векторного произведения двух векторов а и Ь:
c = axb = у/деика{Ь'Кк = скКк. A.276)
Всюду ранее мы использовали такие векторы как "истинные век-
векторы", т.е. преобразующиеся по тензорному закону A.26) ранга 1.
Это действительно так, если только преобразование координат A.2)
не меняет ориентации координатных осей, т.е. может быть получено
непрерывно из тождественного преобразования. Если же ориентация
осей меняется, то нарушается непрерывность преобразований, и век-
векторное произведение перестает быть тензором ранга 1. Покажем это.
Распишем векторное произведение A.276) покомпонентно:
3 + е132а3Ь2) = ^д(аЧ3 - а3Ь2) и т.д.. A.277)
В общем виде три такие формулы можно представить следующим
образом:
са =
а = 1,2,3, A.278)
и индексы а,/3,7 образуют четную подстановку.
При переходе в новую систему координат Х'% это выражение при-
примет вид:
A.279)
<4 =
где с'а, а'Р, Ь'~< - компоненты векторов с, а и b в системе координат
X", которые связаны с а&, Ь соотношениями:
a = Ql}ia\ 6'^=Q7^ A.280)
g2 Глава 1. Тензорная алгебра
(для векторов а и b мы предполагаем выполнение тензорного закона).
Тогда, подставляя A.280) и A.275) в A.279), получаем:
Очевидно, что выражение в скобках отлично от нуля только при
г ф j и меняет знак на противоположный при замене i на j, т.е. это
компоненты кососимметричного тензора, тогда A.281) можно пред-
представить следующим образом:
с'« = Ш ВЯ'Ж - Я\ОРЛ**Г ~ <ГЪ% A.282)
а = 1,2,3; рфафифр, р,а,и = 1,2,3,
где индексы />, сг, и снова образуют четную подстановку.
Однако величины
Ч (тЧ и> Ч (тЧ w
являются дополнительными минорами для элементов Рра обратной
якобиевой матрицы, поэтому
^@№и-0\Я*ш) = Рра> Р= 1.2,3; а =1,2,3 A.283)
(формула для определения компонент обратной матрицы).
Тогда A.282) принимает вид:
или с учетом формулы A.278), в которой индексы а,/3,7 следует за-
заменить на р,сг,а;, получаем
A.285)
- искомую формулу для преобразования компонент векторного произ-
произведения. Из A.285) следует, что векторное произведение двух "истин-
"истинных" векторов (или их еще называют полярными векторами), являет-
является "истинным" вектором только при непрерывных преобразованиях,
когда Д > 0. В общем случае формула преобразования компонент век-
векторного произведения отличается коэффициентом А/|А|, т.е. знаком
§ 1.9. Псевдотензоры 53
от обычного тензорного закона. Такие векторы называются аксиаль-
аксиальными или псевдовекторами.
1.9.4. Символы Леви-Чивиты
Выше уже упоминалось, что символы Леви-Чивиты е,-^, efJ* не яв-
являются компонентами тензора третьего ранга. Установим закон их
преобразования при переходе из одной системы координат в другую.
Для этого воспользуемся формулой A.42), которую применим к яко-
биевой матрице Qlji
A*mn/ = Q'mQ^Q'i *;*, A = det (Q1,.). A.286)
Эту формулу фактически можно рассматривать как закон преобразо-
преобразования символов Леви-Чивиты. Очевидно, что этот закон не совпадает
с тензорным из-за наличия коэффициента Д.
Умножая A.286) слева и справа на yjg, с учетом A.274) получаем
формулу для преобразования компонент y/geijk*
VF A-287)
Совершенно аналогично можно получить обратную формулу:
Р1 Р" P
щ A-288)
а также формулу для компонент (/)ik
Из соотношений A.288) и A.289) следует, что при непрерывных
преобразованиях, когда Д > 0, компоненты ^/ge^ju и {\/^/д)е%^к пре-
преобразуются по тензорному закону, а при Д < 0 - нет.
1.9.5. Смешанное произведение
Смешанное произведение трех истинных векторов a, b и с можно
представить в виде:
V?=(axb)-c = d-c = dic\ d = а х b = d.R1'. A.290)
Вычислим его в системе координат Xх и Х'\ используя формулу
A.285) для преобразования компонент векторного произведения:
у' = 4с" = щР{ ЬС2\ск = AdiC* = jL9. A.291)
Глава 1. Тензорная алгебра
Таким образом, смешанное произведение, вообще говоря, не является
"истинным" скалярным инвариантом относительно любых преобра-
преобразований координат A.2), его инвариантность имеет место только при
непрерывных преобразованиях A.2), когда 6 > 0.
Укажем на одно кажущееся противоречие. Если в качестве векто-
векторов a, b и с взять векторы базиса Ri, R2 и R3, то получим объем
R3 = ^ A-292)
и согласно A.291)
</= V? = щл/9- A-293)
Но для преобразования у/д при переходе из Xх в Х1х у нас имеется так-
также формула A.274), которая, очевидно, отличается от закона A.291).
На самом же деле, противоречия между A.293) и A.274) нет. Фор-
Формула A.274) указывает связь смешанных произведений различных век-
векторов базиса у/д* = (R'x x R'2) • R3 и ^/д = (Ri x R2) • R3; в то время
как формула A.293) устанавливает связь между смешанными произ-
произведениями одних и тех же векторов, но вычисляемых в различных
системах координат Xх и X", т.е. формула A.293) для связи у/д* и
у/д неприменима, если только базисы R,- и RJ не совпадают.
1.9.5. Общее определение относительных
тензоров и псевдотензоров
Дадим теперь общее определение для объектов, преобразующихся
по законам, "близким" к тензорному.
Определение 1.33. Относительным тензором п-го
ранга называется объект пП, имеющий в полиадном базисе пред-
представление вида:
пП = Ull-im tm+1...tnRtl ® ... <g> R,m <g> Rim+1 <g>... <g> RS A.294)
компоненты которого при переходе из одной системы координат Xх
в другую Х1х преобразуются по закону:
х=Д/|А|. A.295)
Таким образом, в законе преобразования A.295) участвуют два чис-
числа: я и w, причем я может принимать значения только 1 или -1, a w
- некоторое целое число, которое может быть и отрицательным. При
этом различают четыре класса:
§ 1.9. Псевдотензоры 85
• если и = 1, a w ф О, то пП называется относительным тензором
п-го ранга веса w;
• если х = 1, а ги = О, то nfl называется тензором п-го ранга (или
истинным тензором);
• если,** может принимать значение -1, а ги = О, то nfl называется
псевдотензором п-го ранга;
• если ус может принимать значение -1,аги^0,топГ1 называется
относительным псевдотензором п-го ранга веса w.
Очевидно, что определение, данное выше, для истинного тензора
п-го ранга совпадает с определением тензора п-го ранга в § 1.7.
Сравнивая теперь законы преобразования A.275), A.285), A.289) и
A.291), получаем, что
• у/g является относительным тензором нулевого ранга (относитель-
(относительным скаляром) веса w = — 1;
• векторное произведение двух истинных векторов а х b является
псевдотензором первого ранга (т.е. псевдовектором);
• смешанное произведение трех истинных векторов а-(Ьхс) является
псевдотензором нулевого ранга (т.е. псевдоскаляром);
• тензор Леви-Чивиты е с компонентами ^/g€{jk является псевдотен-
псевдотензором третьего ранга.
Обратные соотношения для компонент относительных тензоров,
очевидно, имеют вид:
im+l—Jn
• = я\А\-Р\ ...P'?m g'"^ -<?'"i.nWW"-+....u- A-296)
Если мы рассматриваем только непрерывные преобразования ко-
координат A.2), то Д > 0, х = 1, и псевдотензоры преобразуются как
истинные тензоры, а относительные псевдотензоры веса w как отно-
относительные тензоры веса w.
Это обстоятельство фактически всюду использовалось выше при
операциях с векторными, смешанными произведениями и тензорами
Леви-Чивиты.
В заключении этой главы приведем еще один показательный при-
пример. В п.1.9.4 было показано, что объект €, у которого компоненты
в любом базисе имеют вид y/gtijk является псевдотензором. Если же
мы введем объект €, компоненты которого определим равными e%jk
в любом базисе, то согласно A.286) такой объект является относи-
относительным псевдотензором веса и = 1. Наконец, если ввести объект €,
компоненты которого определить в любом базисе равными A€tJ-fe, гДе
Д = det (Qlj), a Q*j матрица преобразования из фиксированного ба-
базиса R' в произвольный, то согласно той же формуле A.286) объект
€ будет истинным тензором.
86 Глава 1. Тензорная алгебра
Упражнения к § 1.9.
Упражнение 1.0.1. Показать, что двойное векторное произведение трех
истинных векторов h= (ахЬ) ХС является истинным вектором, используя при
доказательстве представление:
d = a x b
и формулы A.285) и A.289).
Упражнение 1.9.2. Показать, что для произвольного относительного век-
вектора а и относительного тензора Т формулы представления в различных базисах
следует записывать в виде (ср. с упр. 1.1.8):
а = a,R' = x\A\w^RH, Т = ТИ1С ® R> = х\А\"ГцК* ® R*,
где
или в виде:
а = ojR" = лг'|ДГ«'а,К', Т =
ГЛАВА 2
ТЕНЗОРЫ НА ЛИНЕЙНЫХ ПРОСТРАНСТВАХ
В первой главе был дан геометрический способ введения тензора,
основанный на аксиомах элементарной геометрии. Рассмотрим теперь
несколько иной, "формальный", способ введения тензоров, используя
теоретико-множественное понятие линейных пространств.
Оба подхода для трехмерных евклидовых пространств совершенно
эквивалентны, в то же время геометрический способ, по-видимому,
более нагляден при первом знакомстве с тензорами, а "формальный"
является более общим, применимым даже в случаях, когда не опреде-
определены понятия скалярного произведения и длины векторов.
§ 2.1. Линейное n-мерное пространство
2.1.1. Определение линейного (векторного) пространства
Определение 2.1. Линейным (или его еще называют век-
векторным или аффинным) пространством С называют неко-
некоторое множество, элементы которого объявляются как векторы
и обозначаются также, как и обычные трехмерные векторы - ма-
малыми жирными буквами а, Ь, с и т.п., и на котором заданы две
операции: сложения и умножения на число.
А) Операция сложения однозначно каждой паре векторов a, b из С
ставит в соответствие элемент а + Ь, также принадлежащий С и
называемый суммой векторов.
Б) Операция умножения на число s каждому элементу а из ? ставит
в соответствие элемент за Е ?, который называется произведением
вектора на число.
Если s принадлежит множеству комплексных чисел, то С назы-
называется комплексным линейным пространством, если 5 принадлежит
множеству действительных чисел, то С - действительное линейное
пространство.
Введенные операции сложения и умножения для любых векторов а,
Ь, с из С должны удовлетворять следующим аксиомам:
1°. а + Ь = Ь + а.
2°. (а + Ъ) + с = а+(Ь + с).
3°. Существует нулевой элемент 0 Е ?, такой, что для каждого а Е С:
а + 0 = а.
gg Глава 2. Тензоры на линейных пространствах
4°. Существует противоположный элемент (—а) Е С для каждого а Е
?, такой, что
(-а) =0.
5°. s(a + b) = sa + sb.
6°. (si + 5г)а = 5ia + s2a, где si и $2 - числа.
7°. si(s2a) = Ei52)a.
8°. Произведение любого элемента а Е С на число 1 равно а, т.е.
1 • а = а.
Разностью двух векторов а и b называют сумму векторов а и (—Ь),
и обозначают ее а — Ь.
Из этих аксиом следует, что с векторами в n-мерном пространстве
производятся те же действия и по тем же правилам, что и с обычными
векторами трехмерного пространства.
Однако понятие "вектора" в линейном пространстве С шире, ^.ем
обычного трехмерного вектора, как геометрического объекта. Напри-
Например, множество всех полиномов от одной переменной, степень которых
не выше заданного числа п, будет формально удовлетворять всем ак-
аксиомам 1°...8° и образует линейное пространство, если в качестве
"векторов" (т.е. элементов пространства С) принять сами полиномы
(см.упр. 2.1.3).
Несложно проверить, что множество всех тензоров пП заданного
ранга п в трехмерном евклидовом пространстве также удовлетворяет
всем аксиомам 1° ... 8° и, следовательно, образует линейное простран-
пространство, "векторами" (т.е. элементами) которого являются тензоры nfl.
Другие примеры линейных пространств будут даны ниже, а пока
рассмотрим некоторые их общие свойства.
2.1.2. Линейная зависимость
Определение 2.2. Линейной комбинацией векторов
ai...an линейного пространства С с коэффициентами s1 ...sn на-
называется сумма вида:
5fa,- = 5xai + ... + snan,
которая, очевидно, также образует элемент из С.
Линейная комбинация - тривиальная, если все 5* равны нулю.
Система векторов ai... ап из С называется линейно зависимой, ес-
если существует равная нулю нетривиальная линейная комбинация этих
векторов, т.е.
$4 = 5% + ... + зпа„ = 0, B.1)
где среди s% существует хотя бы один ненулевой коэффициент.
^^___ §2.1. Линейное n-мерное пространство gg
Если же любая нетривиальная линейная комбинация этих векторов
ai... an E С не равна нулю, то такая система векторов называется
линейно независимой.
Некоторые из свойств линейно зависимых векторов приведены в
упр.2.1.3- 2.1.5.
2.1*3. Базис в линейном пространстве
Определение 2.3. Базисом в линейном пространстве С назы-
называют упорядоченную конечную систему векторов ei ...en, которая
• является линейно независимой;
• каждый элемент а Е С есть линейная комбинация этой системы:
а = а'е,-, i=l...n. B.2)
Коэффициенты аг линейной комбинации называются компонента-
компонентами вектора а в базисе е,-.
Упорядоченность означает, что каждый вектор в базисе имеет опре-
определенный номер. Изменяя нумерацию векторов е,, получаем различ-
различные базисы.
Часто, когда базис е,- в пространстве С фиксирован, то вместо век-
векторов a, b из С используют координатные столбцы векторов в этом
базисе:
¦¦(!)¦ ь-?)-
Иногда применяют также запись в виде координатной строки, тог-
тогда рядом с а ставят значок транспонирования Т:
ат = (а1...оп). B.4)
Очевидно, что компоненты суммы (или разности) векторов равны
сумме (или разности) компонент этих векторов:
а + Ь = (а|" + Ь|>.'. B.5)
То же самое утверждение справедливо для координатных столбцов
векторов, поэтому координатные столбцы можно складывать, вычи-
вычитать и составлять из них линейные комбинации.
Теорема 2.1. Векторы ai...am - линейно зависимы тогда и
только тогда, когда линейно зависимы их координатные столбцы.
Ў В самом деле, если ai... am - зависимы, то для них существует не-
нетривиальная линейная комбинация, равная нулю, которая с помощью
определения B.3) может быть переписана для коордиантнх столбцов,
откуда следует их линейная зависимость. В обратную сторону дока-
доказательство аналогично. А
Из этой теоремы, очевидно, следует, что векторы ai... am линей-
линейно независимы тогда и только тогда, когда линейно независимы их
координатные столбцы.
90.
Глава 2. Тензоры на линейных пространствах
Теорема 2.2. Любые т координатных столбцов ai.. .am длиной
п < т - линейно зависимы.
Ў Будем далее полагать, что среди ai... am нет нулевых координат-
координатных столбцов, так как в противном случае, согласно упр.2.1.4, столб-
столбцы были бы линейно зависимы и теорема была бы доказана.
Применим метод математической индукции. При п = 1 координат-
координатные столбцы являются просто числами а*...^, и требуется найти
не все нулевые коэффициенты 51...5т, чтобы выполнялось условие
B.1):
Так как среди а} нет нулевых, то B.6) будет выполнено, если выбрать
коэффициенты з2 ... sm произвольным образом (но чтобы хоть один из
них был бы ненулевым), аз1- следующим образом:
1 ?_ / 2 1 • I л"» 1 ^ -/ Г) A7)
агК 2 ¦¦¦ т)т ¦ К- )
Пусть теперь теорема 2.2 верна для случая п и m > п, докажем, что
она справедлива и при n-flHrn>n-fl.
Условие B.1) будет иметь вид:
а\
\
B.8)
= 0, го>п+1.
Рассмотрим последнюю строку в B.8). Среди чисел aj+1...(
имеется хотя бы одно ненулевое, так как в противном случае все
столбцы имеют длину п(т>п+1>п),и теорема по индукции
будет доказана.
Пусть ненулевым является, например, а?+1 (к ? {1...ш}), тогда
выберем коэффициент sk следующим образом:
1
ап+1
B.9)
где все остальные з1... sm - произвольные.
Подставим теперь это значение sk в B.8) и соберем слагаемые при
одинаковых s1... s*", $fc,... sm. Если отбросить последние координа-
координаты а|*+1, то в результате этих операций получаем следующие столб-
столбцы:
„*-i
B.10)
§ 2.1. Линейное n-мерное пространство 91
где
Длина этих столбцов равна п, а их число mi = т— 1 > п (т.к. т >
п + 1). По предыдущему шагу индукции эти столбцы всегда линейно
зависимы, и можно найти ненулевые координаты s1.. .зк~1зк ... sm,
обращающие B.10) в нуль, что и доказывает теорему. А
Теорема 2.3. Если в линейном пространстве имеется базис из
п векторов, то все другие базисы в этом пространстве состоят
также из п векторов.
Т Предположим противное. Пусть в пространстве С имеется два ба-
базиса ei... еп и е[ ... е^ разной размерности: примем для определен-
определенности m > п. Тогда можно векторы е{ разложить по базису ei.. .еп:
B.11)
где е\ - коэффициенты разложения.
В результате получим т координатных столбцов длиной п (n < m),
которые, в силу теоремы 2.2, являются линейно зависимыми. Тогда,
в силу теоремы 2.1, будут линейно зависимыми и векторы е^.. .е^,
что невозможно, так как они образуют базис. Это противоречие и
доказывает теорему. А
Используя эту теорему, можно ввести следующее определение.
Определение 2.4. Линейное пространство С, в котором суще-
существует базис из конечного числа векторов п, называютп-мерным,
а число п -размерностью пространства.
Размерность пространства обозначают либо формулой dim С = п,
либо индексом: Сп. Размерность нулевого пространства по опреде-
определению полагают равной нулю, поскольку в нем нет базиса (нулевой
вектор является линейно зависимым).
Бесконечномерным называют пространство, в котором для любого
натурального числа п существует п линейно независимых векторов.
Далее будем рассматривать только n-мерные пространства.
Теорема 2.4. В п-мерном пространстве всякая упорядоченная
система п линейно независимых векторов является базисом.
Ў Действительно, пусть в пространстве С имеется п линейно неза-
независимых векторов ai...an, но эта система не образует базис, т.е.,
согласно определению, найдется вектор а Е ?, который не является
линейной комбинацией ai... ап. Тогда в С существует система из
71 + 1 линейно независимых векторов ai.. .апа, по которой можно об-
образовать п + 1 координатных столбцов длиной п. Но, в силу теоремы
92 Глава 2. Тензоры на линейных пространствах
2.2, эти столбцы, а, следовательно, и система ai.. .апа должны быть
линейно зависимыми. Таким образом, наше предположение приводит
к противоречию. А
Теорема 2.4а. В п-мерном пространстве всякая упорядоченная
линейно независимая система из т < п векторов может быть до-
дополнена до базиса.
Ў Для доказательства рассмотрим в пространстве С линейно незави-
независимую систему ai.. .aw (m < п). Эта система не является базисом,
так как пространство С - n-мерное, значит, в нем существует базис
из п векторов, и, согласно теореме 2.3, только из п векторов. Тогда
найдется такой вектор а, который не выражается через ai... aw, и
значит можно образовать систему т + 1 линейно независимых векто-
векторов ai... ama. Если ra-fl < п, то доказательство можно продолжать
до тех пор, пока не получим п линейно независимых векторов, ко-
которые, согласно теореме 2.4, являются базисом и включают в себя
векторы ai... am. A
2.1.4. Линейные подпространства
Определение 2.5. Непустое множество С1 элементов из линей-
линейного пространства С называют линейным подпространст-
подпространством, если
1° для любых элементов а и b из С1 их сумма а + b также принад-
принадлежит С1;
2° произведение любого & ? С на произвольное число s также при-
принадлежит С.
Каждое линейное пространство С содержит, по крайней мере, два
подпространства: нулевое, состоящее только из элемента 0, и само
пространство С. Эти подпространства называют несобственными, а
все остальные - собственными.
Если выбрать в С некоторую систему векторов ai... am, то множес-
множество С всех линейных комбинаций этих векторов называют линейной
оболочкой системы векторов ai... am. Это множество ?' образует ли-
линейное подпространство в ?, так как любая сумма или произведение
на число линейных комбинаций векторов ai... am снова даст некото-
некоторую их линейную комбинацию.
Теорема 2.5. Всякое подпространство С1 п-мерного линейного
пространства С имеет размерность т ^ п, причем при т = п под-
подпространство С! совпадает с С.
Ў Если С1 - нулевое пространство, то его размерность по определению
равна нулю, и так как n ^ 0, то теорема будет доказана. Для нену-
ненулевого пространства ?', начиная с любого ненулевого вектора аЕ?',
можем построить базис методом, изложенным в доказательстве тео-
теоремы 2.4а. Число векторов в этом базисе не может быть больше п,
так как всякая система линейно независимых векторов из С будет
§2.1. Линейное п-мерное пространство 93
линейно независимой в ?, а значит, согласно теореме 2.2, может со-
содержать не более п векторов. Если базис в ?' действительно содержит
п векторов, то любой вектор из ? можно разложить по этому базису
(в противном случае мы смогли бы построить базис из п + 1 вектора
в ?, что невозможно), это и означает, что ?' совпадает с ?. А
Теорема 2.6. Если построить базис ei...en в п-мерном про-
пространстве С таким образом, чтобы векторы е\.. .ew (т ^ п) об-
образовывали базис подпространства ?' в ?, то все векторы из С и
только они будут иметь нулевые компоненты ат+1 = ... = ап = О
в этом базисе ех ... еп.
Т В самом деле, если вектор а Е ? имеет нулевые компоненты
am+1,... , ап, то он раскладывается по базису ei... em, и значит при-
принадлежит ?'. Очевидно и обратное: если а принадлежит ?', то он
раскладывается по ei.. .em:
тогда если ввести компоненты aw+1 = ... = ап = 0, то линейная
комбинация а = ^У!=1а%е* будет являться разложением а по базису
ei... еп, а в силу единственности разложения вектора по базису (см.
упр.2.1.6), это будут единственно возможные компоненты а1.. .ап. А
2.1.5. Сумма подпространств
Пусть имеется два подпространства С и С" линейного простран-
пространства ?.
Множество всех векторов а, принадлежащих одновременно ?' и ?",
называют пересечением линейных подпространств и обозначают ?'П
?".
Определение 2.6. Множество всех векторов а, представляю-
представляющих собой сумму sl = a'-fa", где a! G ?', а" Е ?", называют суммой
линейных подпространств и обозначают как С + С".
Теорема 2.7. Пересечение С (Л С" и сумма С1 Л-С11 двух линейных
подпространств из ? сами являются линейными пространствами в
?.
Доказательство теоремы оставим в качестве упражнения 2.1.14.
Определение 2.7. Прямой суммой двух линейных подпрос-
подпространств ?' и С" из С называют их сумму ?' + ?", в случае если
пересечение подпространств ?' П ?" - нулевое подпространство.
Прямую сумму обозначают как ?' ф ?".
Каждый элемент а Е ?/0?"можно разложить единственным обра-
образом в виде суммы а = a'-fa", где а' Е ?', а" Е ?". В самом деле, пусть
Глава 2. Тензоры на линейных пространствах
существует еще одно разложение а = Ь' + Ь", где Ь' ? ?', Ь" ? ?".
Тогда существует вектор (а' — Ь;), принадлежащий ?', и одновремен-
одновременно, в силу а' — Ь' = Ь" — а", принадлежащий ?", т.е. а' — Ь' ? С П С".
Но поскольку ?'П?" - нулевое подпространство, то а' = Ь' и а" = Ь".
2.1.6. Евклидовы п-мерные пространства
Дадим теперь обобщение использованного ранее в первой главе по-
понятия трехмерного евклидова пространства.
Определение 2.8. Вещественное линейное пространство назо-
назовем евклидовым ?п, если в нем определена операция скалярно-
скалярного умножения, которая любой паре векторов а«Ь сопоставля-
сопоставляет вещественное число, обозначаемое как а-b, и которая обладает
следующими свойствами:
1° а • b = Ь • а;
2° (a + b)-c = a-b + b-c;
3° (*а)-Ь = в(а-Ь);
4° а • а ^ О (причем равенство достигается только если а = 0^;
где s - произвольное действительное число.
Длиной вектора а называют число: |а| = (а • аI/2.
Имеет место неравенство Коши-Буняковского:
a-b^|a||b|, B.12)
доказательство которого следует из соотношения:
(ра + 9Ъ) • (ра + 9Ъ) = Р2\а\2 + 2pqa • Ь + q*\b\2 ^ 0. B.13)
Здесь р и q - произвольные числа, в качестве которых можно выбрать:
р = |6|2, q = — а • Ь, что и приведет к неравенству B.12).
Векторы а и b называют ортогональными, если а • b = 0.
Систему векторов ах ... ат в евклидовом пространстве называют
ортогональной, если любые два вектора этой системы ортогональны.
Теорема 2.8. Любая ортогональная система ненулевых векто-
векторов линейно независима.
Ў Для доказательства предположим противное, т.е. существует ор-
ортогональная линейно зависимая система векторов ei.. .em, для кото-
которой sxai + ... + 5maw = 0. Умножая это соотношение скалярно на
произвольный вектор а,-, получим, в силу ортогональности, что все
слагаемые в сумме обращаются в нуль, кроме 5*|а,| = 0. Так как а,
- ненулевой, то, в силу аксиомы 4°, |а,| ф 0 и, следовательно, s% = 0.
Поскольку индекс i был произволен, то все коэффициенты s% = 0, что
противоречит условию B.1) линейной зависимости. Это противоре-
противоречие и доказывает теорему. А
Ортогональная система ei.. .еп, все векторы которой имеют еди-
единичную длину |е,| = 1, называется ортонормированной.
§2.1, Линейное п-мерное пространство 95
Теорема 2.9. В п-мерном евклидовом пространстве существу-
существует ортонор мир о ванная система из п векторов,
V Докажем эту теорему по индукции. Если п = 1, то выбрав нену-
ненулевой вектор а, образуем из него вектор единичной длины: е = а/|а|.
Тогда теорема будет справедлива. Предположим теперь, что в каж-
каждом (п — 1)-мерном евклидовом пространстве существует ортонор-
мированный базис и перейдем к n-мерному евклидовому простран-
пространству ?п • Выберем в нем произвольный базис ai... ап, тогда линей-
линейная оболочка векторов ai.. . an_i, согласно п.2.1.4, образует (п — 1)-
мерное евклидово пространство ?^_i, и по индукции в ?/п_1 сущест-
существует ортонормированный базис ei.. .en_i. Введем далее вектор а!п =
ап - 5iei — ... — sn_ien_i, где коэффициенты si...sn_i определим по
формулам: s,- = an • е,-, и на его основе построим вектор en = ajj/|ajj.
Длина этого вектора еп равна единице, и он ортогонален ко всем век-
векторам ei.. .en_i, что легко проверяется непосредственно. Тогда сис-
система векторов ei.. .en_ien будет ортонормированной. Теорема дока-
доказана. А
Метод построения, использованный при доказательстве, называют
методом ортогонализации Грама-Шмидта.
Пусть теперь имеется n-мерное евклидово пространство, тогда в
нем можно выбрать базис ei... еп и ввести матрицу gij из попарных
скалярных произведений:
Я,, =et-e,, i,j = l...n, B.14)
эта матрица называется фундаментальной или матрицей Грама.
Если для базиса ei... еп фундаментальная матрица является еди-
единичной:
{?' %*h »\j = l,...,n, B.15)
> * = 3,
то такой базис называется ортонормированным, где <JtJ- - n-мерный
символ Кронекера.
Из теорем 2.8 и 2.9 следует, что в n-мерном евклидовом простран-
пространстве ?п существует линейно независимая ортонормированная система
п векторов, которая, согласно теореме 2.4, является ортонормирован-
ным базисом в ?„.
Упражнения к § 2.1.
Упражнение 2.1.1. Доказать, что линейное пространство С с аксиомами
*¦ • . .8 обладает единственным нулевым вектором 0, а противоположный эле-
элемент (—а) для всякого a G С также является единственным.
Упражнение 2.1.2. Доказать, что для любого вектора а Е С и любого к
имеют место соотношение:
Оа=0, (-1)а=-а, кО = 0.
96 Глава 2. Тензоры на линейных пространствах
Упражнение 2.1.3. Функция Рт(х) называется TIOAUHOMOM или целой
рациональной функцией от аргумента Ху если она может быть представлена в
виде
i=0
где Xх означает i-ую степень числа X из области определения функции, 771 - нату-
натуральное или 0, к{ - действительное (или комплексное) число (кт ф 0). Доказать,
что множество всех полиномов Рт (х) степени не выше заданной 771 ^ 71 образует
линейное пространство.
Упражнение 2.1.4. Доказать, что любая система ai .. . ап векторов ли-
линейного пространства ?, включающая в себя нулевой вектор, является линейно
зависимой.
Упражнение 2.1.5. Доказать, что каждая подсистема линейно независимой
системы из С сама является линейно независимой.
Упражнение 2.1.6. Показать, что компоненты пг вектора а Е ? в базисе
et определяются однозначно.
Упражнение 2.1.7. Доказать, что множество всех тензоров второго ран-
ранга, введенных геометрическим способом по формуле A.104) с операциями A.105),
образует линейное пространство.
Упражнение 2.1.8. Доказать, что множество всех квадратных 71-мерных
матриц образует линейное 71-мерное пространство.
Упражнение 2.1.9. Показать, что скалярное произведение векторов аи Ь
из ?п можно представить в виде:
a-b =
где а% и W - их компоненты в некотором базисе е,-. Если же этот базис ортонор-
мированный, то
a=l
Упражнение 2.1.10. Доказать, что в 71-мерном пространстве любая линейно
независимая система из 71 векторов является базисом.
Упражнение 2.1.11. Доказать, что множество всех непрерывных функций
одной независимой переменной X, определенных на отрезке [0, 1], образует линей-
линейное пространство.
Упражнение 2.1.12. Доказать, что пространство всех непрерывных функ-
функций одной переменной, определенных на отрезке [0, 1], является бесконечномер-
бесконечномерным.
Упражнение 2.1.13. Множество IRn, элементами которого являются упо-
упорядоченные совокупности 71 произвольных действительных чисел (ж ,. .. , Жп),
называется арифметическим пространством. Доказать, что IRn является
71-мерным линейным пространством.
Упражнение 2.1.14. Доказать теорему 2.7.
Упражнение 2.1.15. Пусть С1 и С11 - два линейных пространства размер-
размерности 71 и 771. Доказать, что
dim (?' + С") = dim С + dim С" - dim (С П С").
§ 2.2. Матрицы п-го порядка
§ 2.2. Матрицы n-го порядка
2.2.1. Определение матриц n-го порядка
В трехмерном пространстве в первой главе мы использовали толь-
только квадратные матрицы размером 3x3, например, для обозначения
компонент тензора: Ах^ i,j =1, 2, 3. Действия с п-мерными вектора-
векторами требуют введения матриц большей размерности.
Матрицей размером т х п называется совокупность из тп чисел,
расположенных в виде таблицы из т строк и п столбцов:
,А\ А\ ... А\
А\ А2, ... А\
12 " ' B.16)
т лт
А
\А х 2 п
Далее будем рассматривать в основном квадратные матрицы, для
которых т = п:
B.17)
Будем также говорить, что эти матрицы имеют порядок п и исполь-
использовать для них обозначение А%^ где i,j пробегают значения 1...П,
либо просто обозначение А (с помощью заглавной нежирной буквы).
Числа A%j , составляющие матрицу, называют элементами матрицы.
Две матрицы одинакового размера т х п называют равными, если
равны их соответствующие элементы.
Заметим, что матрицы n-го порядка могут быть составлены из
элементов и с другой структурой индексов:
А11
•
Anl
. . .
...
(А/
Апп j
1
) =
\
/
(A
iA
l
l
l
(Aij) =
... v
'¦
... A"
B.18)
Вообще говоря, все эти матрицы различны, однако если имеется ин-
информация о том, что значения элементов матрицы не зависит от рас-
расположения индексов i,j (верхний или нижний), то все четыре мат-
Рицы B.17), B.18) равны между собой. Так, например, обстоит де-
Ло, когда Аг j - компоненты тензора в трехмерном декартовом базисе.
Тензорное исчисление
Глава 2. Тензоры на линейных пространствах
Будем далее, если это не оговорено особо, полагать, что такая инфор-
информация у нас имеется.
2.2.2. Основные операции с матрицами
С матрицами n-го порядка можно определить те же самые опера-
операции, что и с трехмерными, например, транспонирование матрицы Ат:
B.19)
Сумма двух матриц n-го порядка А и В есть матрица С n-го по-
порядка с компонентами: Clj = A*j + BXj.
Нулевая матрица - это матрица с нулевыми компонентами. Про-
Противоположная матрица (—А) - это матрица с компонентами (—А% • ).
Умножение матрицы на число sA образует матрицу n-го порядка с
компонентами {sA%j).
Перечисленные свойства позволяют сделать вывод о том, что мно-
множество всех квадратных матриц порядка п образует линейное про-
пространство ?, "векторами" которого являются сами матрицы (см. упр.
2.1.8).
Матрица А является симметричной, если она совпадает со своей
транспонированной: А = АТ.
Матрица А называется кососимметричной, если А = —Ат.
Единичная n-мерная матрица Еп имеет единицу на главной диаго-
диагонали и нулевые остальные компоненты:
B.20)
Матрица А называется ортогональной, если ее умножение на свою
транспонированную матрицу АТ дает Еп:
А-Ат = Еп. B.21)
Определение 2.9. Скалярным произведением (или прос-
просто произведением) матриц А и В n-го порядка называется матрица
С n-го порядка с компонентами Clj = A1 kBkj , где i^j,k— 1.. .п, а
по к идет суммирование.
§ 2.2. Матрицы n-го порядка 99
Произведение матриц А и В можно записать и таким образом:
А\
А-В =
А\В\
Дп
Л 1
,АпкВ\ ...
т.е. каждый элемент матрицы С"у есть результат умножения коорди-
координатной строки (А\ ... Ахп) на координатный столбец (В1^ .. .Bnj ) .
Скалярным произведением матрицы А размером тхп на коорди-
координатный столбец а = (а1...а71O называется координатный столбец
b = (б1—6т)т, компоненты которого вычисляются по формуле:
V, i=l,...n, B.23)
или
/Ь*\ (А\ ... А\\ /а>\
B.24)
или иначе
Ь = А.а. B.25)
Определение 2.10. Скалярное умножение квадратной матрицы
А п-го порядка на координатную строку Ьт = (б1.. .6П) слева и на
координатный столбец а = (а}...ап)Т справа образует билиней-
билинейную форму (скаляр):
у>(Ь,а) = Ьт.Л.а, B.26)
Иначе ее можно записать следующим образом:
ijaiV, B-27)
или
Аи ... А1п \
B.28)
Ап1 ... А„п
Если матрица А - симметричная, то билинейная форма также сим-
симметрична: v(b, а) = (р(&, Ь) (верно и обратное утверждение).
100 Глава 2. Тензоры на линейных пространствах
Определение 2.11. Квадратичной фор мой называется вы-
выражение вида B.26) - B,28) при а = Ь, т.е. ф(а) = ат • А • а.
Матрица А n-го порядка называется положительно определенной,
если ее квадратичная форма всегда положительна:
А • а = ^ AyaV > 0 B.29)
= ат
для любого ненулевого вектора а из рассматриваемого пространства
2.2.3. Детерминант и обратная матрица
Детерминант (определитель) матрицы А n-го порядка введем ре-
рекуррентным способом: детерминантом матрицы первого порядка, со-
состоящим из одного числа «А1, назовем само это число; детерминантом
матрицы n-го порядка п > 1 назовем число
а=1
где М\ - детерминант матрицы размерности (п — 1), получаемой
из А вычеркиванием первой строки и второго столбца (а = 1...п).
Вообще, такой детерминант M*j матрицы, полученной из А вычер-
вычеркиванием г-ой строки и j-ro столбца называется минором элемента
Нетрудно убедиться, что введенный ранее детерминант трехмерной
матрицы A.8) полностью удовлетворяет определению B.30).
Формула B.30) называется разложением детерминанта по первой
строке, вообще же детерминант может быть представлен разложением
по г-ой строке или по j-ому столбцу (см. упр. 2.2.1).
Детерминант может быть непосредственно выражен через элемен-
элементы матрицы (см. упр. 2.2.2):
(-lI'1-'-^1,-^^...^, B.31)
где сумма определяется по всем подстановкам (ii...in) из п чисел
A...П).
Число N = |z'i... г„ | называется знаком перестановки и равно об-
общему числу элементарных перестановок (при которых меняются мес-
местами два соседних числа), приводящих подстановку i\...in к тож-
тождественной A...п).
§2.2. Матрицы n-го порядка _101
Если детерминант матрицы А отличен от нуля: det А ф О, то
можно определить обратную матрицу Л, которая при умножении
на А дает единичную матрицу:
А-А-1=А-1-А = Еп. B.32)
Если рассматривать матрицу А n-го порядка как совокупность ко-
координатных столбцов или координатных строк, то можно сформули-
сформулировать следующую теорему.
Теорема 2.10. Система координатных столбцов или строк
матрицы А линейно независима тогда и только тогда, когда
Доказательство можно найти, например, в [4].
Для матрицы А размером тхп самый большой порядок, для кото-
которого существуют отличные от нуля миноры, называют рангом мат-
матрицы и обозначают rang A.
Имеет место следующая теорема, доказательство которой приво-
приводится в курсе линейной алгебры, например, в [4].
Теорема 2.10а. Ранг матрицы А равен максимальному числу ли-
линейно независимых строк или столбцов этой матрицы.
2.2.4. Блочные матрицы
Любую матрицу А размером тхп можно разбить на матрицы
меньшего размера (блоки) с помощью горизонтальных и вертикаль-
вертикальных "перегородок", идущих вдоль всей матрицы. Например, для мат-
матрицы 3x3:
B.33)
где Aij - элементы матрицы (г, j = 1,2,3), a Aut (и, t = 1,2) - это уже
блоки-матрицы меньшего размера:
An = {Ац), М2 = {А12, Ai3),
*"=(?)• *¦=(? ?)• B34)
102.
Глава 2. Тензоры на линейных пространствах
Вообще же разбиение произвольной матрицы А на блоки A%t (и =
1.. .р) можно записать следующим образом:
А =
ill
1ml
... А,
где
(An .
:
:
\Ар1
¦. 1
Ant
|
Л1Л
:
¦A-pq/
A\q =
B.35)
Aut =
B.35')
"ran
Блочная форма матрицы задается двумя
(mi.. .mp_i|p), (щ .. .ng.
перегородок:
B.36)
где mi.. .mp^i - индексы элементов матрицы AtJ-, соответствующие
горизонтальным "перегородкам", а щ .. .ng_i - вертикальные перего-
перегородки блоков, р и q - число блоков в столбце и в строке.
Для рассмотренного выше примера матрицы 3x3 имеем:
И
Наиболее эффективно введение блочной формы для матрицы, когда
отдельные ее блоки имеют существенно различные элементы. Тако-
Таковы, например, блоки из нулевых элементов, или блоки в виде единич-
единичных матриц.
§ 2.2. Матрицы n-ого порядка
.103
Теорема 2.11. Операции сложения и умножения с блочными
матрицами формально совершаются по тем же правилам, что и
действия с обычными матрицами.
Т А) Сумма двух матриц А и В размером тх п одинаковой блочной
формы, т.е. с одинаковыми массивами перегородок:
А =
Ац
i
Apl
.. 1 Alq
;
Apq
в =
Ац
в1я
;
Bpq
. B.37)
является матрица С размером m x n с той же блочной формой:
С = А + В =\ : 1 ••. I ! • B.38)
Ац + Вц
;
Др1 + вр1
...
Аи + Ви
:
Apq + Bpq
Б) Произведением двух блочных матриц А к В с размерами тх п
и п х к соответственно:
А =
(An | ...
Upi
..
..
... 1 ...
;
Ant
l
...
*
;
...
A\q >
:
Apq J
В =
St.
B.39)
блочная форма которых имеет массивы перегородок:
А: (т1...титр-1\р) (пг.. .nfng_i|g), B.40)
В : (пг .. .ntriq-xlq) (кг .. .kvks-i\s),
(т.е. число столбцов в каждом блоке Aut равняется числу строк в
блоке Btv, а также совпадают число q блоков в строке матрицы А
104.
Глава 2. Тензоры на линейных пространствах
и число блоков г = q в столбце матрицы ?), является матрица С
размером га х к:
•t
(Си
;
I
\cpl
...
!
I
...
. . .
!
:
Cu\
:
Cps)
B.41)
с массивом перегородок
(m1...mump-i\p) (кг .. J
причем каждый блок Си1, (п = 1»..р, v
формуле:
9
!«**-i|e), B.42)
= 1... s) вычисляется по
B.43)
(Умножение блоков происходит по обычному правилу умножения мат-
матриц).
Доказательство утверждения А) очевидно, так как матрицы А и
В складываются поэлементно независимо от той или иной блочной
формы.
Для доказательства утверждения Б) достаточно расписать выра-
выражение для элемента матрицы С,&, выделив из него суммы элементов,
принадлележащих блокам:
jBjk = {АцВ1к + ... + AinlBnik) + ...
-i+l к + - - - + А{пВпк) =
Я
t=l
B.44)
Если элементы dk соответствуют блоку Cuv (т.е. i = rau-.i +
l...mtt, fc = nt,_i + l...nt;), то в скобках в последнем выражении
будет в точности стоять произведение элементов блоков Aut • Btv, a
суммирование будет идти по числу блоков: t — 1.. .q. Здесь принято,
что п0 = 1, nq = п. Утверждение доказано. А
Если матрица А имеет отличными от нулевых только блоки Ац ...
... Лрр, а р = д, то она называется квазидиагопальпой. Такая матрица
§ 2.2. Матрицы n-ого порядка
.105
содержит блоки только на главной диагонали:
/Аи
0
0
\ о
0
Aii
0
0
0
0
• .
0
0 \
0
П
Арр/
B.45)
При умножении квазидиагональных матриц перемножаются соответ-
соответствующие блоки, т.е. в суммах B.43) имеется по одному слагаемому,
и будет снова образована квазидиагональная матрица.
2.2.5. Треугольные матрицы
Матрица L n-ого порядка называется верхней треугольной, если
все ее элементы V^ ниже главной диагонали равны нулю: Lx j = 0, г >
j. Такая матрица имеет вид:
L =
(L\ L\ ...
0 L\ ...
\ О
О
B.46)
Квадратная матрица L называется нижней треугольной, если рав-
равны нулю все ее элементы выше главной диагонали: L'j = 0, г < j,
т.е.
L =
L\ 0
0
0
B.46')
ТП
L 2
Теорема 2.12 (Теорема Холецкого). Всякая симметричная,
положительно определенная матрица А n-ого порядка может быть
единственным образом представлена в виде произведения двух мат-
матриц:
A = L-LT, B.47)
где L - нижняя треугольная матрица с положительными диагональ-
диагональными элементами, a LT - верхняя треугольная матрица.
Ў Доказательство проведем методом математической индукции. Для
71 = 1 матрица А имеет один положительный элемент .Аи, поэтому
матрица L также состоит из одного элемента: Ьц — у/Ац.
106.
Глава 2. Тензоры на линейных пространствах
Предположим, что теорема верна для матриц (п — 1)-го порядка, и
рассмотрим симметричную, положительно определенную матрицу А
п-го порядка. Ее всегда можно представить в блочной форме:
ill
i т \ / А22 ... А2п
, где А22 = I : •.. :
\Ап2 ... Атп.
B.48)
где Ац = Ац - положительный элемент, b = Ai2 = (Ai2 .. .Ain)T -
координатный столбец длины (п — 1), А22 - симметричная, положи-
положительно определенная матрица (п — 1)-го порядка.
Блочную матрицу B.48) можно записать в виде произведения трех
новых блочных матриц:
А =
о
где En-i - единичная матрица порядка (п — 1), а
B.49)
Я = А22 -
Ац
B.50)
- симметричная матрица, т.к. А22 - симметрична и b • bT - симмет-
симметричная матрица (п — 1)-го порядка (см.упр. 2.2.5).
Справедливость соотношения легко установить непосредственным
перемножением блочных матриц по правилу B.43).
Выберем теперь некоторый ненулевой координатный столбец а
(п — 1)-го порядка, образуем по нему столбец n-го порядка:
с =
B.51)
(заметим, что ат • b - скаляр (см.упр. 2.2.5)), а затем составим квад-
квадратичную форму:
А-с= [-
B.52)
Так как А - положительно определена, то из B.52) следует, что и
Н будет также положительно определенной. Тогда по предположению
§ 2.2. Матрицы n-го порядка
.107
индукции она имеет треугольное представление Н = ?#•?#, где ?# -
треугольная матрица (п — 1)-го порядка с положительной диагональю.
Подставляя это представление в B.52), получаем:
А =
л/АЦ
О
ткъТ
= L-I?
B.53)
Bn-i
где L - треугольная матрица n-го порядка с положительной диаго-
диагональю:
L-
ткъ
B.54)
Существование представления B.47) доказано.
Предположим, что существуют две различные матрицы L и V,
удовлетворяющие представлению B.47), которое может быть записа-
записано в элементном виде:
ДЛЯ
B.55)
а=1
а=1
Выразим из этой формулы отдельно диагональные элементы мат-
матрицы L, а затем остальные ее элементы:
/3-1
а=1
a=l
1
L/зр'
B.56)
Эти формулы позволяют найти элементы матрицы L, причем един-
единственным образом:
B.57)
L31 = 4*Lt L32 = ^-(A32-
А А
, L33 =
и т.д.
108 Глава 2. Тензоры на линейных пространствах
Знак " +" перед корнем выбираем из-за положительности L$$ по усло-
условию.
В силу единственности решения уравнений B.56), проводя анало-
аналогичное построение для матрицы ?', получим те же самые выражения
для ее элементов L\^ что и доказывает теорему. А
Приведенное доказательство является конструктивным: формулы
B.56) позволяют найти матрицу L по матрице А.
Упражнения к § 2.2.
Упражнение 2.2.1. Используя оределение B.30), методом математической
индукции доказать, что детерминант 71-мерной матрицы можно представить в
виде:
а=1
C=1
где а + /3 = 1... П.
Упражнение 2.2.2. Методом математической индукции доказать формулу
B.31).
Упражнение 2.2.3. Методом математической индукции доказать, что для
71-мерных матриц выполнено равенство:
det A = det AT.
Упражнение 2.2.4. Показать, что из B.25) следует формула умножения
матрицы на координатную строку:
Упражнение 2.2.5. Доказать, что скалярное умножения координатной стро-
строки на столбец дает скаляр, а столбца на строку - матрицу 71-го порядка:
/аЧ1 ... аЧп
aT-b = ?V&°, аЬт = : •. :
°=1 КаГЬ1 ... апЬп,
Упражнение 2.2.6. Методом математической индукции доказать, что мат-
матрица, обратная к верхней (нижней) невырожденной треугольной матрице, является
также верхней (нижней) треугольной.
Упражнение 2.2.7. Показать, что для матриц 71-го порядка имеют место
соотношения:
(А-В)т = ВТ -Ат, А-(В
зуя теорему
B.14) всегда
det gij ф 0.
Упражнение 2.2.8. Используя теорему 2.10, доказать, что для фундамен-
фундаментальной матрицы, определенной в B.14) всегда выполнено соотношение:
§ 2.3. Линейные преобразования n-мерных пространств Ю9
§ 2.3. Линейные преобразования п-мерных
пространств
2.3.1. Определение отображения и линейного преобразования
Вернемся к рассмотрению линейных пространств.
Определение 2.12. Если имеет место закон, который каждому
элементу а G М ставит в соответствие единственный элемент
Ъ G Af, то говорят, что имеется отображение Л множества
М в множество Af, которое обозначают как Л: М —> Af, или в
виде зависимости:
Ь = А(а), *еМ, ЪеАГ. B.58)
Отображение B.58) называют сюръективным, если для каждого
b G Af существует а G М такой, что /(а) = Ь. Отображение B.58)
называют инъективным, если из ai ф а2 следует, что /(ai) ф /(аг),
где ai,a2 G АЛ. Если отображение одновременно сюръективно и инъ-
ективно, то его называют взаимнооднозначным (биективным).
Если М и Af - два линейных пространства С и С1 размерности
пит, оба вещественные или оба комплексные, то B.58) определяет
отображение Л: С —> С пространства С в ?'. В этом случае отобра-
отображение B.58) называют также оператором, действующим из ? в С.
Если С1 есть пространство вещественных (или комплексных) чисел,
то B.58) называют функционалом. Вектор Ь, определяемый по B.58),
называют образом а, а вектор а - прообразом Ь.
Определение 2.13. Если отображение B.58) удовлетворяет
следующим условиям:
1° A(ai -f &2) = ^(ai) + A{a2)> для любых ai, аг G С,
2° A(sa.i) = 3A(a), для любого a G С и любого вещественного (или
комплексного) s (однородность степени 1),
то его называют линейным (или линейным оператором).
Если С и С совпадают, то линейное отображение B.58) называют
линейным преобразованием.
2.3.2. Матрица линейного преобразования
Пусть имеется линейное n-мерное пространство ?п, тогда в нем
можно выбрать базис из п векторов: ei... еп. Если над Сп осуществ-
осуществляется линейное преобразование Л: Сп —> ?п> то выбранному базису
будет соответствовать единственный набор из п векторов: А(е\)...
-..Л(еп). Поскольку векторы Л(е,) также принадлежат ?„, то их
можно разложить по базису ei.. .еп:
Х-е,-, ;=1...п, B.59)
tnl
Глава 2. Тензоры на линейных пространствах
где А% j - коэффициенты разложения. Эти коэффициенты образуют п-
мерную квадратную матрицу, называемую матрицей линейного пре-
преобразования.
Так как при фиксированном г коэффициенты A3i образуют коорди-
координатные столбцы (Аг{ ...Ап{ )Т векторов Л(е,), то можно также ска-
сказать, что матрица линейного преобразования имеет в качестве столб-
столбцов координатные столбцы векторов -А(е,) в базисе е,-.
Выберем теперь произвольный элемент aG?n, ему будет соответ-
соответствовать образ b = Л(а), также принадлежащий Сп. Разложим а и b
по базису ei... еп, в котором мы ввели матрицу линейного преобра-
преобразования А\:
b = Vejy a = а'е,-. B.60)
Согласно свойствам 1°, 2° линейного преобразования, имеем:
b = А(в) = А(а{е{) = а{А{е{) = а*А'{е; = b*eif B.61)
откуда получаем:
Ь> = А\а\ B.62)
т.е. компоненты любого вектора а и его образа b всегда связаны
линейно с помощью матрицы линейного преобразования. Поэтому го-
говорят, что линейное преобразование полностью определено своей мат-
матрицей.
2.3.3. Замена базиса
Очевидно, что матрица линейного преобразования определена не-
неоднозначно: выбирая различные базисы в B.59), будем получать, во-
вообще говоря, различные матрицы А^. Однако все такие матрицы
будут обладать некоторыми общими свойствами. Укажем их.
Пусть имеется два базиса е,- и е(- в пространстве ?п, тогда каждый
из векторов одного базиса можно разложить по другому базису:
e^S^-ey, i=l... п. B.63)
Компоненты разложения S\ представляют собой матрицу n-го поряд-
порядка:
(S\ ... S\
5= : •-. : , B.64)
J
столбцы которой являются координатными столбцами векторов е(- в
базисе е,-. В силу теоремы 2.1, столбцы такой матрицы 5 линейно
независимы и по теореме 2.10 имеем:
det 5^0,
§ 2.3. Линейные преобразования n-мерных пространств щ
т.е. матрица 5 - невырожденная.
Тогда существует обратная матрица 5", и, умножая B.63) на S,
получим:
ej = (S-1)'^. B.65)
Если имеется произвольный элемент a ? ?п, тогда его можно раз-
разложить как по базису е,-, так и по ej:
а = а'е,- = а"е{ = а'^е* = а1'^)*^. B.66)
В силу единственности разложения вектора по базису, получаем
а* = S'y', а* = E-1)>J', г = 1.. .п. B.67)
Заметим, что полученные ранее для трехмерного евклидова простран-
пространства аналогичные формулы преобразования компонент и векторов ба-
базиса (см. упр.1.1.8) представляют собой частный случай соотношений
B.65), B.67), так как эти соотношения, вообще говоря, не предпола-
предполагают введения систем координат.
Пусть теперь имеется линейное преобразование Л: Сп —> Сп. Вы-
Выберем снова два базиса е, и е(- и построим по B.59) для каждого мат-
матрицу линейного преобразования: A%j и А1% у Эти матрицы связывают
компоненты ах вектора а ? Сп и его образа b согласно B.62):
V =А\а\ Ь'*=А''{ан. B.68)
Но а% и а", а также V и 6/<7 связаны матрицей перехода 5, тогда
получаем:
V> = (S-1)'^ = (S^YtA'to* = {S^YiA^S^ a'1. B.69)
Сравнивая со второй формулой в B.68), получаем формулу изменения
матрицы линейного преобразования при замене базиса:
A't^iS-iY.A1^ B.70)
или
А' = S'1 ¦ А ¦ S. B.71)
112.
Глава 2. Тензоры на линейных пространствах
2.3.4. Инвариантные подпространства
Определение 2.14. Если имеется линейное преобразование Л ли-
линейного пространства С, то в С можно выделить подпространст-
подпространство С, называемое инвариантным относительно А, для каждого
элемента которого а Е С образ -А(а) также принадлежит С!.
Очевидно, что нулевое подпространство, а также само С являют-
являются инвариантными относительно любых линейных преобразований.
Каждое же подпространство будет инвариантным относительно тож-
тождественного преобразования.
Пусть имеется п-мерное линейное пространство ?п, задано линей-
линейное преобразование Д, относительно которого инвариантно некоторое
771-мерное подпространство Ст в Сп (m ^ п). Тогда можно выбрать
базис ei...em в ?т, а затем дополнить его векторами em+i...en,
не принадлежащими ?т, до базиса в Сп. Разделим теперь матрицу
линейного преобразования Л на четыре матрицы:
А =
/ Л1
( А г
А1 ..
А"» ••
¦ А\
лт
л m
¦ А"»
П1 + 1 ' *
Лт
дт+1
"^ т+1
дп
171 + 1 ' *
• А\
дт
л п
¦ А"»
дп
А п
B.72)
где Ац имеет размерность тхт, Аи — тх (n—m), A21 — (п—т) хгп,
а А22 — (п — т) х (п — т). Покажем, что матрица А21 - нулевая. В
самом деле, матрицы Ац, А21 образованы первыми т столбцами мат-
матрицы А, которая представляет собой, согласно B.59), координатные
столбцы векторов A(ei)... A(em). Но так как Ст - инвариантное под-
подпространство, a ei...em ? ?m, то A(ei)... А(ет) также принадлежит
Ст и, следовательно, согласно B.59) их компоненты разложения Axj
(j = 1... m, i = m -f 1... n) по базисным векторам em+i... en равны
нулю. Таким образом, матрица А имеет вид:
А =
B.73)
Верно и обратное утверждение: если матрица А линейного преобра-
преобразования в каком-нибудь базисе ei.. .еп имеет вид B.73), то линейная
§ 2.3. Линейные преобразования n-мерных пространств цд
оболочка векторов ei... em образует инвариантное подпространство.
Действительно, из определения B.59) и B.73) следует, что
А^е,-, B.74)
t=i
т.е. образы A(ei)... А(ет) векторов ei.. ,em есть линейная комбина-
комбинация этих же векторов, а значит и образ любой линейной комбинации
векторов ei... em будет снова их линейной комбинацией.
Таким образом, доказана следующая теорема.
Теорема 2.13. Матрица А линейного преобразования Л имеет
блочный вид B.73) в базисе ei...en тогда и только тогда, когда
линейная оболочка векторов ei.. .ет, т ^ п, является инвариант-
инвариантным подпространством относительно Л.
2.3.5. Собственные векторы
Если инвариантное подпространство Ст имеет размерность m = 1,
то его базис состоит из одного вектора не равного нулю (обозначим
его е), а всякий элемент а из С\ имеет вид ахе, где а1 - число. В
Q
силу инвариантности ?i, образ вектора е также принадлежит С\ и,
следовательно, для А(е) существует такое число А, что
А(е) = Ае. B.75)
Имеет место обратное утверждение: если для некоторого вектора
Q
е выполнено условие B.75), то оно будет выполнено для любого век-
Q
тора а из подпространства ?i, образованного линейной оболочкой е,
поэтому С\ инвариантное подпространство.
Определение 2.15. Ненулевой вектор е, удовлетворяющий
B.75), называется со бете енным в ектор ом преобразования Л,
а число А - собственным значением.
о о
Выбирая в Сп некоторый базис е,-, вектор е и его образ А(е) можно
разложить по этому базису:
п п
. *. B.76)
Подставляя B.76) в B.75), получаем матричную запись этого условия:
А\У = \е\ B.77)
Глава 2. Тензоры на линейных пространствах
С использованием обозначений для координатных столбцов е =
= (е1.. .еп)т можно также переписать B.77) в виде:
А-е=Ае. B.78)
Условие B.78) при п = 3 естественно совпадает с условиями A.162).
Также как и в трехмерном прстранстве, рассматривая B.77) как ли-
линейную комбинацию линейно зависимых столбцов матрицы A%j с не-
нетривиальными коэффициентами е-7, из теоремы 2.10 получаем:
V{\) = det (A*; - \ti)) = 0 B.79)
- характеристическое уравнение для нахождения собственных значе-
значений Л.
Характеристическое уравнение представляет собой полином п-ой
степени относительно Л, который обычно записывают в виде:
7>(А) = J2(-l)%\\ B.80)
1 = 1
где Ь{ - коэффициенты полинома, причем
п
Ьп = 1, Ьп_! = ? А\, Ьо = det (Л1,.). B.81)
В трехмерном случае константы &о, &1 и h (см. далее формулу
D.156) в гл.4) совпадают, соответственно, с третьим, вторым и пер-
первым инвариантами h{A), h{A), h{A), построенными из компонент
матрицы Axj.
В случае произвольного п, константы 6,- также являются инвари-
инвариантами - они не зависят от выбора базиса в пространстве ?п. Дейст-
Действительно, если записать матрицу линейного преобразования в базисе
ej, а затем найти характеристическое уравнение 'Р'(А), то получим
согласно B.71):
V'{\) = det {A' - ЛЕ) = det (S • А . 5 - ЛЕ) =
= det{S-1-{A-XE)-S) =
= det S • det (A - ЛЕ) • det 5 = P(A), B.82)
т.е. характеристический полином V(X) не зависит от выбора базиса,
а значит являются инвариантами и его коэффициенты Ь{.
2.3.6. Приведение матрицы преобразования
к блочному виду
Сформулируем теперь теорему, которая потребуется нам в даль-
дальнейшем.
§ 2.3. Линейные преобразования n-мерных пространств
.115
Теорема 2.14. Пусть существуют т линейно независимых соб-
собственных векторов ei...em линейного преобразования А, соответ-
соответствующих собственному значению А, тогда матрицу преобразова-
преобразования Alj, определенную в произвольном базисе ei...en, с помощью
невырожденного преобразования S можно привести к блочному ей-
ду А':
А1 — Я"*
-/1 — tj
/А
B.83)
где Aftj - матрица линейного преобразования Л в базисе е[.,,егп,
а е(- = SJiej> здесь также обозначены: Ет - единичная матрица
размера тхт, А'12 ~ матрица тх(п — т), А'12 ~ матрица (п — т)х
(п — т).
Т В самом деле, так как ei.. .em - линейно независимы, то их можно
выбрать в качестве первых га векторов базиса е(-: е( = е,- (г = 1.. .т).
Дополняя их векторами е'т+1.. .е'п до базиса в ?п, запишем матрицу
А1 преобразования Л в этом базисе. Найдем первые т координатнх
столбцов этой матрицы:
Л(е;.) = A(h) = Ае, = Ае{, г = 1...т;
^e'j. B.84)
1 = 1
В силу единственности разложения вектора по базису, находим:
н
<\6}, j = l...m,
• \ 0, j = m+l...n,
B.85)
Откуда получаем вид B.83) матрицы А1 в базисе ej. Этот базис,
как следует из B.63), связан некоторой невырожденной матрицей 5 с
базисом е,-. Но тогда, в силу B.71), матрицы А и А1 линейного преоб-
преобразования Л в базисах е,- и е(- действительно связаны соотношением
B.83), что и доказывает теорему. А
П6_ Глава 2. Тензоры на линейных пространствах
Теорема 2.15. Если две матрицы А1 и А" двух линейных преоб-
преобразований имеют одинаковые собственные векторы ei.. .em, соот-
соответствующие одному и тому же собственному значению А, то они
могут быть приведены к блочному виду B,83) с помощью одного и
того же преобразования 5.
Ў Действительно, обе матрицы А' и А", согласно теореме 2.14, мож-
можно привести к виду B.83) в базисах е( и е" (г = 1.. .п). Причем га
первых векторов в этих базисах совпадают: е( = е" = е,-. Если мы
выберем совпадающими и остальные векторы е( = е" (г = ra-f 1... п),
то матрицы Аа и Аь изменятся только в блоках А22 и А22, сохранив
в целом блочный вид. Но тогда оба базиса е( и е" полностью совпа-
совпадают, и они будут связаны с исходным базисом е,- одним и тем же
преобразованием 5, что и требовалось доказать. А
2.3.7. Свойства собственных векторов
Характеристический полином B.80) имеет п корней Л, среди кото-
которых могут быть и комплексные, и кратные корни. Каждый собствен-
собственный вектор соответствует только одному собственному значению.
Теорема 2.16. Каждому собственному значению А матрицы А
линейного преобразования может соответствовать несколько ли-
линейно независимых векторов, при этом их число га не может пре-
превышать кратности s собственного значения А = \q.
Ў Для доказательства этого факта воспользуемся теоремой 2.14, со-
согласно которой матрицу А в данных условиях можно привести к блоч-
блочному виду B.83) в некотором базисе е^ .. .е'п. Поскольку характерис-
характеристический полином V(X) не зависит от базиса, вычислим его в базисе
V{\) = det (А' - ХЕ) = (Ао - A)mdet (А!22 - A#n_m). B.86)
Здесь мы для вычисления детерминанта воспользовались формулой
разложения по первому столбцу, а Еп-.т - единичная матрица разме-
размером (п — ш) х (п — т). Поскольку det (А'22 — \Еп-т) также может
иметь корень Ао, то из B.86) следует, что общая кратность 5 корня
Ао, вообще говоря, больше, чем число m. A
Сформулируем в конце этого раздела еще две теоремы.
Теорема 2.17. Все собственные векторы, принадлежащие одно-
одному и тому же собственному значению, вместе с нулевым вектором
о
образуют линейное инвариантное подпространство С.
Ў Действительно, нетрудно проверить, что для таких векторов аксио-
аксиомы линейного пространства выполняются, например, если А • е, = Ае,
§ 2.3. Линейные преобразования n-мерных пространств цу
(г = 1,2), то А • (ei + е2) = A(ei + е2), а также А • (set) = A(set).
Инвариантность этого подпространства также очевидна, так как об-
образ собственного вектора Л(е,) = Ле,- также является собственным
вектором A(Xei) = А(Ае,). А
о
Теорема 2.18. Если в Линейном подпространстве С выбрать ба-
о о
зис ei...em, то линейная оболочка любой системы (к ^ га) век-
о' о' ^ о о
торов e1.,.ek, составленной из векторов базиса ei...em, также
о о
образует инвариантное подпространство С в С.
Т В самом деле, пусть вектор а является линейной комбинацией вида:
а = ]Ct=ia'^i> тогда его образ А(а) = А(а*е{) = Aa*et- = Ла также
является линейной комбинацией векторов е^.-вд. и, следовательно,
о
принадлежит С\ А
2.3.8. Изоморфные пространства
Между разными линейными пространствами возможны определен-
определенные соответствия.
Определение 2.16. Два линейных пространства С и С называ-
называют изоморфными, если существует линейное взаимнооднознач-
взаимнооднозначное отображение А: С —> С'.
Следующая теорема дает условие существования изоморфных про-
пространств.
Теорема 2.19. Два конечномерных линейных пространства изо-
изоморфны тогда и только тогда, когда совпадают их размерности.
Ў Пусть пространства С и С! имеют одинаковую размерность. Выбе-
Выберем в них базисы е,- и е(- соответственно. Построим отображение Д:
С —> С - следующим образом. Всякому элементу а = а'е,- из С по-
поставим в соответствие элемент b = a*ej, имеющий те же координаты
а1, но только в базисе е{. Очевидно, что всегда b ? ?', так как он
представляет собой линейную комбинацию векторов е{ из С1. Это ото-
отображение b = Л (а) = А(а*е{) = ахе\ является линейным и инъектив-
ным, так как если А{ъ\) = Л(а2), то A(a.i) — Л(аг) = (а\ - аг2)е\ — О,
и в силу линейной независимости е(- неминуемо следует а\ = аг2, а зна-
значит ai = а2. Кроме того, отображение b = Д(а) сюръективно ввиду
того, что, наоборот, по всякому вектору b = а*е\ G С всегда можно
найти вектор а = а*е,- из ?. Таким образом, построено взаимноодно-
взаимнооднозначное отображение Д: С —> С, что по определению 2.16 означает
изоморфность пространств С и ?'.
В обратную сторону. Пусть пространство С имеет размерность п и
существует взаимнооднозначное отображение А: С —> С. Выберем
Глава 2. Тензоры на линейных пространствах
в С базис е,- (г = 1...п) и покажем, что система е( = Л(е,) (г =
1... п) линейно независима. Пусть противное: существуют ненулевые
коэффициенты з1: s%ef{ = 5'Д(е,) = 0'. Но тогда, так как 0' - нулевой
вектор из ?', являющийся образом нулевого вектора 0 из ?, в силу
линейности Л получаем: Д(з'е,) = Л@). Поскольку отображение А
- инъективно, это возможно только если s'e,- = 0, что противоречит
тому, что е,- - базис в С. Следовательно, е( - линейно независимы.
Поскольку отображение Л сюръективно, всякий элемент b ? С! яв-
является образом некоторого вектора а = а'е,- Е ?, но тогда b = Л(в) =
Д(а*е,-).= а'Д(е,) = a'ej, т.е. он может быть всегда представлен в ви-
виде линейной комбинации векторов ej. Таким образом, построен базис
е(- в ?', состоящий из п векторов. Следовательно, размерности С и С1
совпадают. А
Упражнения к § 2.3.
Упражнение 2.3.1. Методом математической индукции доказать, что систе-
система собственных векторов, принадлежащих попарно различным собственным зна-
значениям, является линейно независимой.
§ 2.4. Сопряженное пространство
2.4.1. Линейные функционалы
Рассмотрим два линейных пространства Сп и ?', одно из которых
(С) совпадает с пространством вещественных чисел Е, и предполо-
предположим, что задано линейное отображение /: Сп —> Е, обозначаемое
как
Ь = /(а), ае?„, ЬеШ B.87)
и называемое, согласно п.2.3.1, линейным функционалом на Сп. Со-
Согласно определению 2.13, линейный функционал удовлетворяет двум
аксиомам:
1° /(ai + а2) = /(ах) + /(а2), для любых аь а2 G Сп,
2° /(sai) = s/(a), для любого а ? Сп и любого «ЕЕ.
Выберем некоторый базис ei... еп в ?п и разложим по нему про-
произвольный элемент а из Сп: а = а'е,-. Тогда значение функционала /
(т.е. образ а) можно представить следующим образом:
/(а) = /(а'е.) = а'/(е.-) = а'/*, B.88)
где обозначены /,- = /(е,-) - образы векторов е,-. Эти числа /,- G Е не
зависят от элемента а, а определяются только базисом е,- и функцио-
функционалом /, поэтому назовем их компонентами функционала f.
Формула B.88) составляет содержание следующей теоремы.
2.4. Сопряженное пространство ___119
Теорема 2.20. Любой линейный функционал на Сп можно пред-
представить в виде разложения B.88), где /,- - компоненты функциона-
функционала, являющиеся значениями функционала на некотором базисе Сп.
Согласно п.2.3.2, каждому линейному отображению Л : Сп —> Сщ
соответствует матрица отображения А размером га х п. Для линейно-
линейного функционала эта матрица имеет размеры 1хп, т.е. представляет
собой координатную строку длиной п. Согласно определению, эта
строка состоит из значений функционала на базисных векторах из
?п, т.е. это строка компонент функционала:
fT = (Л •••/») = (/(ei).../(en)). B.89)
Согласно теореме 2.20, каждому линейному функционалу / на Сп со-
соответствует координатная строка f3*. С другой стороны, каждая стро-
строка fT, умноженная на координатный столбец а произвольного вектора
а из ?п., согласно формуле B.88) образует функционал, который мож-
можно записать в виде
/(a)=fT.a = /ia', B.90)
где компоненты а1 для всех аЕ?п берутся в одном и том же базисе
ei...en. Несложно установить, что такой функционал B.89) будет
линейным. Таким образом доказана следующая теорема.
Теорема 2.21. Множество С* всех линейных функционалов на
Сп изоморфно множеству координатных строк длиной п.
Введем на множестве С* следующие операции.
Определение 2.17. Суммой линейных функционалов f и g на
Сп называют линейный функционал h, который всякому а ? Сп ста-
ставит в соответствие число /i(a) = /(а) + g(a), а про из в едением
функционала f на число s Gl называют функционал д, который
каждому а ? Сп ставит в соответствие число g(a) =¦ sf(a).
Теорема 2.22. Множество ?* всех линейных функционалов на
Сп с введенными на нем по определению 2.17 операциями сложения
и умножения на число образует п-мерное линейное пространство.
Ў Согласно теореме 2.21, существует взаимнооднозначное отображе-
отображение множества ?* во множество координатных строк длиной п. При
этом из представления B.90) и определения 2.17 следует, что для вся-
всякого а ? Сп сумма двух функционалов h = f + g соответствует сумме
координатных строк t1 + gT, так как
а произведение д = sf соответствует строке sf3", так как
120 Глава 2. Тензоры на линейных пространствах
Поскольку множество координатных строк длиной п является ли-
линейным n-мерным пространством (см. упр.2.1.13) и для него выпол-
выполнены все аксиомы 1°.. .8°, то они будут выполнены и для операций
в ?*, следовательно, С* является линейным пространством. В силу
теоремы 2.21, оно изоморфно n-мерному пространству координатных
строк, и по теореме 2.19 С* имеет размерность п. А
Определение 2.18. Линейное пространство С* всех линейных
функционалов на Сп называют сопряженным пространст-
пространством по отношению к Сп.
2.4.2. Базис сопряженного пространства
Выберем теперь в пространстве Сп некоторый базис ei.. .еп, тогда
для всякого вектора а из Сп имеет место разложение а = а'е,. Введем
набор п линейных функционалов на Сп специального типа
е'(а)=а\ B.91)
т.е. каждый г-ый функционал ех (а) сопоставляет всякому а из Сп его
г-yip компоненту (число).
Очевидно, что функционалы B.91) действительно обладают свой-
свойствами1 линейности. Если в качестве а в B.91) выбирать векторы
базиса е,-, то получим, что
е'(е,-) = ^, B.92)
так как компоненты векторов е;- в том же базисе равны 6lj.
По аналогии с B.89) образуем координатные столбцы, состоящие
из значений функционалов е* (а) на векторах еу при фиксированном г.
е' = (е'(е1),...е'(еп))Т. B.93)
Тогда произвольный функционал / из ?*, согласно B.88) и B.91),
можно представить в виде разложения по функционалам е1... еп:
/ = e'7,=fT-e,
а соответствующий ему координатный столбец f - в виде разложения
по координатным столбцам е1:
Таким образом, е1,.. .еп действительно образуют базис в простран-
пространстве координатных столбцов, а функционалы е1,.. .еп - базис в С*.
Заметим, что построенный базис е1,... еп зависит от выбора базиса
ei,...en в Сп.
§ 2.4. Сопряженное пространство
Определение 2.19. Базисы е(- в Сп и е1х в ?* называют взаим-
взаимными (или биортогональными), если они удовлетворяют соотно-
соотношению
eft"(ej) = S'j. B.94)
Очевидно, что построенные выше базисы е1 и е,- являются взаим-
взаимными в силу соотношения B.92).
Элементы f пространства координатных столбцов, соответствую-
соответствующего пространству ?*, сопряженному к ?п, называют также кова-
риантными векторами или ковекторами (поэтому в соответствии с
общими правилами индексы у ковариантного базиса е1 стоят вверху).
2.4.3. Замена базиса в сопряженном пространстве
Пусть в пространстве Сп имеется два базиса е, и е(, связанных со-
соотношениями B.63). Построим для каждого из них соответствующие
функционалы е1 и е" по формуле B.91):
е'(а) = а', е"(а) = а", B.95)
где a = а*е,- = а"е(- - произвольный вектор из ?п. Используя формулу
B.67) связи компонент а" = E~)lJa'7, получаем:
е'Ча) = (S-^y = (S-^y (a). B.96)
Если ввести координатный столбец, состоящий из значений функ-
функционалов е" (а) на векторах е;-:
e" = (e"(ei)...e"(en))T, B.97)
то из B.96) получим следующие соотношения между е" и е':
е"' = E-%.е*, е> = Sj{ e'1'. B.98)
Компоненты произвольного функционала / из С* в базисах е1 и е"
вводим по формулам B.88):
/,=/(е,), Л = /(е|.). B-99)
Тогда из соотношений
/(а) = /Ке,) = a4i = /(а"е{) = а«Я = а*^1?;/*, B.100)
получаем
122 Глава 2. Тензоры на линейных пространствах
связь компонент функционала / в различных базисах е* и е".
Таким образом, координатные столбцы базисов е" и е1 сопряжен-
сопряженного пространства ?*, взаимных к базисам ej и е, пространства ?„,
связаны между собой соотношениями B.98), а координаты произволь-
произвольного функционала / из С* в этих базисах е" и е1 связаны формулами
B.101).
2.4.4. Пространство, сопряженное с евклидовым
пространством
Между элементами Сп и С* можно установить взаимнооднозначное
соответствие (изоморфизм), которое будет зависеть от выбора базиса.
Однако если Сп является евклидовым пространством ?„, то изомор-
изоморфизм может быть установлен независимо от базиса, что позволяет
отождествить пространства ?п и ?*.
В самом деле, поскольку в ?п определено скалярное произведение,
то зафиксировав некоторый элемент b G ?п, получим линейный функ-
функционал
/(а)=Ь-а, Va??n. B.102)
Меняя Ь, будем получать различные функционалы /. Следователь-
Следовательно, можно ввести отображение ф: ?п —> ?*, где / = V(b) = b • а,
b G ?n, / G ?*. Следующая теорема позволяет установить, что это
отображене взаимнооднозначно.
Теорема 2.23 (теорема Рисса). Всякий линейный функционал
f на евклидовом пространстве ?п можно однозначно представить
в виде скалярного произведения B.102), где Ь - некоторый элемент
из ?п.
Т Выберем некоторый базис е, в ?п, тогда, согласно теореме 2.20,
всякий линейный функционал / можно представить в виде B.88), где
а = а'е,- - произвольный вектор из ?П1 a /,- - компоненты функцио-
функционала /. С помощью этих компонент всегда можно образовать вектор
b = 6'ei, выбирая Ь1 = gt;i fj, где д1* - матрица, обратная к фундамен-
фундаментальной B.14):
9ij9jk = 6\. B.103)
(Эта матрица всегда существует, TaKKaKdet (gij) ф 0 (см. упр.2.2.8)).
Этот вектор b и будет искомым элементом из ?п, обеспечивающим
возможность представления B.102), так как для всякого a G ?п (см.
упр.2.1.9):
b • а = gijaW = а{д^к}к = а*/,- = /(Ь).
Для доказательства единственности представления B.102) предпо-
предположим противное, что существуют два различных вектора bi,b2 ?
?п, такие, что /(а) = bi • а и /(а) = Ьг • а. Тогда можно образовать
разность /(а) — /(а) = (bi — Ьг) • а = 0. Поскольку это соотношение
§ 2.4. Сопряженное пространство __123
выполнено для любого аб5п,то, следовательно, должно выполняться
равенство bi = Ьг, что противоречит сделанному допущению. А
Согласно определению 2.12 и теореме 2.23, введенное отображение
ф: ?п —У ?„ является взаимнооднозначным и не зависит от базиса в
?п. Следовательно, ?п и ?* - изоморфны, и их можно отождествить:
?* = ?п, в этом смысле ?п называют "самосопряженным".
Ввиду отождествления ?п и ?* можно не делать различия между
вектором Ь, однозначно определяющим функционал / и координат-
координатным столбцом функционала /. Тогда соотношение B.90) можно пред-
представить в виде B.102):
/(a)=f.a, B.104)
где f уже элемент из ?п.
В частности, формула B.92), связывающая векторы базисов е,- и е*
в форме B.104), запишется следующим образом:
ei(ej)=ei-ej=Sij, B.105)
т.е. е,- и е7 взаимно ортогональны.
После отождествления ?п и ?* всякий элемент из ?* можно разло-
разложить по базису из ?п, например: е1 = е|<7еу. Подставляя эту формулу
в B.105), получаем
е* • е, = etkekej = etkgkj = 8х ^
т.е. etk - это матрица, обратная фундаментальной: е1-7 = дх*. Та-
Таким образом, в евклидовом пространстве сопряженный базис связан с
исходным с помощью соотношений:
е' = <7'4-, e,-=ffye»\ B.106)
Соотношение B.106) позволяет переходить от разложения произ-
произвольного элемента а ? ?п в основном базисе е,- к разложению во вза-
взаимном и наоборот:
а = а*е,- = ax'gikek = акек. B.107)
Ковариантные а,- и контравариантные а1 компоненты связаны соот-
соотношениями:
а%'=д1как, ak=gkia\ B.107а)
Формулы B.106), B.107) и B.107а) при п = 3 полностью экви-
эквивалентны соответствующим соотношениям из §1.1 для трехмерного
евклидова пространства.
124 Глава 2. Тензоры на линейных пространствах
§ 2.5. Алгебра тензоров
на n-мерных линейных пространствах
2.5.1. Отношение эквивалентности
Далее нам потребуются некоторые сведения из теории множеств.
Приведем их.
Рассмотрим два некоторых множества М и ЛЛ
Определение 2.20. Декартовым произведением
множеств М и М называется множество, состоящее из всех воз-
возможных упорядоченных пар элементов fab), где а ? М и Ь ? ЛЛ
Такое множество обозначим как М х N.
Аналогично вводят понятие декартова произведения п множеств
Mi. ..М„ и обозначают его Mi х ... х Мп, а также n-t/ю декартову
степень множества М, которую обозначают следующим образом:
Мп = М х ... х М (п штук).
Примером является арифметическое пространство Еп, элементы ко-
которого представляют собой упорядоченные наборы вещественных чи-
чисел (х1.. .жп), и которое можно рассматривать как n-ую декартову
ГТАТТАТТи» ШП ГО>*- V ГО>*- V V ТО*
I* 1\?11Сх1Ъ. Ж. — Ж. Л Ж. А ... А Ж .
В множестве М часто необходимо найти эквивалентные в некото-
некотором смысле элементы.
Говорят, что на множестве М задано отношение эквивалентнос-
эквивалентности между его элементами, если определено некоторое правило, уста-
устанавливающее эквивалентность (неразличимость) элементов a, b ? М
между собой. Отношение эквивалентности обозначают знаком "~",
а элементы а, 6, связанные отношением эквивалентности, обозначают
как а^Ьи называют эквивалентными.
Отношение эквивалентности удовлетворяет следующим аксиомам
для любых а, Ь, с ? М:
1° а ~ а (рефлексивность);
2° если а ~ Ь, то b ~ а (симметричность);
3° если а~ЬиЪ~с, тоа~с (транзитивность).
Определение 2.21. Подмножество всех элементов из М} экви-
эквивалентных фиксированному элементу а ? М называют классом
эквивалентности, содержащим а и обозначают его как [а].
Всякий элемент из класса эквивалентности [а] называют предс-
представителем класса [а].
Теорема 2.24. Любой класс [а], где а ? М однозначно опре-
определяется любым своим представителем; иначе говоря, для любых
a, b ? М их эквивалентность а ~ b равносильно совпадению их
классов: [а] = [Ь].
Ў В одну сторону: пусть а ~ Ь, тогда выберем произвольный элемент
с ? [а]. Из определения 2.21 следует, что с ~ а, но тогда в силу 3°
§2.5. Алгебра тензоров на n-мерных линейных пространствах ^25
должно быть с ~ Ь, т.е. с ? [Ь]. Таким образом, любой элемент,
принадлежащий [а], принадлежит и [Ь], значит [а] С [Ь]. Однако если
выбрать произвольный элемент d ? [b] то d ~ b, а, следовательно, в
силу транзитивности d ~ а, поэтому [Ь] С [а]. Это означает, что [а]
и [Ь] совпадают: [а] = [Ь].
В обратную сторону: пусть [а] = [Ь], тогда а ? [Ь], по определению
2.21 это означает, что а ~ b. A
Имеет место еще одна важная теорема.
Теорема 2.25. Множество ж„(М) всех классов эквивалентнос-
эквивалентности по отношению ~ разбивает все множество ЛЛ на непересекаю-
непересекающиеся подмножества.
Т В самом деле, пусть имеется множество 7r^(Ai) всех классов эк-
эквивалентности, но какой-либо элемент а ? М не попадает в тг^(Л1).
Тогда можно образовать еще один класс эквивалентности, состоящий
из одного этого элемента: [а] = а; аксиомы 1° 3° для него бу-
будут выполнены. Так как по предположению а $ п„(М), то и [а] не
принадлежит тг^(Л1). Но это противоречит условию теоремы, что
тт~(М) содержит все классы из М. Полученное противоречие дока-
доказывает, что все элементы ЛЛ входят в тг^(.М).
Покажем теперь, что различные классы эквивалентности не пересе-
пересекаются. Пусть противное: имеются различные классы [а] и [Ь] такие,
что [а] О [Ь] ф 0. Тогда можно выбрать элемент с такой, что с ? [а] и
с ? [Ь]. Но тогда с ~ а и с ~ Ь, а значит в силу 3° а ~ b и по теореме
2.24 [а] = [Ь], что противоречит допущению о различии этих классов.
^
2.5.2. Фактор - пространство
Пусть теперь отношение эквивалентности задано на линейном про-
пространстве ?, при этом аксиомы 1° - 3° дополним еще двумя: для
любых a, b и с ? С
4° если а ~ Ь, тоа + с~Ь-Ьс;
5° если а ~ Ь, то аа ~ ab.
Применяя теорему 2.25, получим, что пространство С можно раз-
разбить на непересекающиеся классы эквивалентности:
С= U [а]. B.108)
а(Е?
Между этими классами можно определить операции сложения и ум-
умножения на число:
• суммой классов [а] + [Ь] называют класс [a -f b] элементов, эквива-
эквивалентных сумме a -f b;
• произведением класса [а] на число s называют класс [sa] элементов,
эквивалентных элементу 5а, т.е.
[a] + [b] = [a + b], s[a] = H. B.109)
126 Глава 2. Тензоры на линейных пространствах
Определение 2.22. Множество всех классов эквивалентности
линейного пространства С называют фактор-пространст-
фактор-пространством, [С] пространства С.
Очевидно, что имеет место следующая теорема.
ТЕОРЕМА 2.26. Фактор-пространство [С] линейного простран-
пространства С само является линейным пространством по отношению к
операциям B.109).
Заметим, что хотя согласно B.108) объединение элементов всех
классов [а] тоже образует все пространство ?, фактор-пространство
[С] не совпадает с ?, так как его элементами являются сами классы.
В силу эквивалентности элементов в классе, класс можно отождеств-
отождествлять только с одним из его представителей, что мы и будем делать в
дальнейшем.
2.5.3. Тензорное произведение линейных пространств
Рассмотрим два линейных пространства Сп и Ст. Образуем из
них множество ?Пт> представляющее собой n-ую декартову степень
от декартова произведения Сп х ?т, т.е.
Спт = {Сп х Ст)п. B.110)
Согласно определению 2.20, элементами множества Спт являют-
являются упорядоченные наборы А длиной Bп), составленные из элементов
пространств Сп и ?т, т.е.
А = (а,-ЬИ) = (aibWa2bM .. .anb^) , B.111)
где a,- Е Cn, b^ Е Cm (i = l,...n). Индекс у векторов Ь^ взят в
скобки, чтобы не путать их с элементами сопряженного пространства.
Наборы вида B.111) будем далее называть векторными наборами.
Введем операции сложения и умножения на число векторных набо-
наборов (a;bM) из множества Спт.
Два векторных набора назовем однотипными, если они имеют оди-
одинаковые векторы а,- Е Сп или bW e Cm (t = 1.. .п).
Определение 2.23. Суммой двух однотипных элементов мно-
множества Спт называют следующие наборы:
(a,-bW) + (а,-сИ) = (a,(bW + с")), B.112а)
Пр о из в едением элемента множества СПт «я число s называют
наборы вида:
§ 2.5. Алгебра тензоров на n-мерных линейных пространствах ^27
Из определений B.111) и B.112а) для однотипных элементов сле-
следует, что
(а,-ЬМ) = (а,-сМ) ^> bW = с™, i=l...n, B.113)
Введем на множестве Спгп отношение эквивалентности следующим
образом.
Определение 2.24. Элементы А иВ множества Спт называют
эквивалентными, если выполнено хотя бы одно из условий:
а) элементы А и В состоят из одних и тех же пар векторов
aibM,...anblnl, но упорядоченных, вообще говоря, различным об-
образом;
б) один элемент может быть получен из другого с помощью опера-
операции B.1126);
в) все пары векторов aib^,...anbfn' и порядок их расположения у
элементов А и В совпадают, кроме тех пар, у которых один из
векторов - нулевой вектор 0.
Приведем примеры элементов А и В пространства ?зз (п = 3),
эквивалентных согласно правилам а), б) и в) соответственно:
А = (а^МазЬМазЬИ) - (a3bMa2bMaibw) = В, B.114)
А = (^)
(Ы1]^[2]И) = В, s ф О,
А = (ai0a2bM0bP]) - @Ь^а2Ь^а30) = В.
Несложно убедиться, что введенное отношение эквивалентности удов-
удовлетворяет аксиомам 1° - 3° (см. упр.2.5.1).
Выбирая некоторый элемент А ? Спт с помощью правил а) - в), на-
находим все эквивалентные ему элементы, в результате получаем класс
эквивалентности [А] элемента А.
Перебирая все элементы А ? ?nm, получаем множество всех клас-
классов эквивалентности множества ?nm, которое, аналогично определе-
определению 2.22, назовем фактор-пространством [СПт] множества Спт.
Для [Спт] вводят специальное обозначение.
Определение 2.25. Тензорным произведением линейных
пространств Сп и Ст размерности пит называют фактор-прос-
фактор-пространство п-ой декартовой степени от декартова произведения
пространств Сп х Ст по отношению к введенной в определении 2.24
эквивалентности и обозначают его как
Сп®Ст = [Спт] = [(Сп х Ст)п], B.115)
где ® - знак тензорного произведения.
Глава 2. Тензоры на линейных пространствах
Определение 2.26. Элементы Т множества Сп®Ст называют
тензорами на линейных пространствах Сп и Ст и обо-
обозначают следующим образом:
Т = [А] = [a,-bW], B.115а)
где a, G ?п, ЬИ G Ст, А Е ?Пт.
2.5.4. Диадный базис
Построим теперь в множестве Сп 0 Ст специальную систему эле-
элементов (т.е. классов). Для этого выберем некоторый базис ei.. .еп в
Сп и базис hi.. .hm в ?m, и построим на их основе следующие систе-
системы векторов в Сп и Ст:
а,=е„ B.116)
Подставляя эти векторы при фиксированных j и А; в наборы B.111),
получим систему из пт элементов пространства Спт:
A(iJb) = (ei-bg) = (ei(^ihJb)). i = l...n, * = l...m. B.117)
Укажем свойства этой системы.
Теорема 2.27. Все элементы системы B.117) принадлежат раз-
различным классам эквивалентности [Ау*)] пространства СПт по от-
отношениям а), б) и в).
Доказательство теоремы рекомендуем проделать в качестве упраж-
упражнения 2.5.2.
Введем для классов эквивалентности элементов Ау*) специальное
обозначение:
ej®hk = [ei(PJhk)]. B.П8)
Назовем эти классы базисными диадами (сравните с A.113)).
Важную роль играет следующая теорема.
Теорема 2.28. Класс эквивалентности [a,-bM] любого элемента
a,-bW из Спт можно представить в виде линейной комбинации клас-
классов элементов системы B.117):
п т
[А] = [a,-bW] = ??T'fc[Ay*)], BЛ19)
где Т*к - коэффициенты.
Поскольку классы [А] и [Ау*)], согласно определениям 2.25 и 2.26,
являются тензорами второго ранга, то с учетом обозначения B.118)
получим еще одну формулировку теоремы 2.28.
§2.5. Алгебра тензоров на n-мерных линейных пространствах ^29
Теорема 2.28а. Любой тензор Т = [А] на линейных простран-
пространствах Сп и Ст можно представить в виде линейной комбинации
базисных диад:
T = Tjkej®bk. B.120)
Прежде чем доказать теорему 2.28, сделаем два замечания. Во-
первых, согласно B.109) и теореме 2.26 нами определены три вида
действий с классами: их сложение, умножение на число и переход к
новому классу, содержащему элемент из данного класса. Во-вторых,
по определению B.109) сложение классов - это класс элементов, экви-
эквивалентных сумме элементов из ?nm, которая, в свою очередь, опреде-
определена правилами B.112) не для всех элементов из ?пга, а только для
однотипных. Следовательно, складывать можно только классы, со-
содержащие однотипные элементы из Спт. В частности, все элементы
системы B.117) однотипные, поэтому сложение их классов в формуле
B.119) правомерно.
Т Выберем произвольный элемент (а,1>М) из Спт и представим его
класс в виде суммы классов однотипных элементов:
[а,-ЬМ] = [aibWa20.. .anQ] + ... + [ах0 .. .а„ЬМ .. .anQ]+
+ ...+ [а10...ап_10апЫп)]. B.121)
В этих классах элементы имеют только по одной, вообще говоря,
ненулевой паре векторов aabtal, a остальные - это пары вида aQ0.
Разложим теперь векторы аа и Ь^ по базисам: аа = а^е;, Ь^ =
bakhk, тогда каждый класс в сумме B.121) можно представить следу-
следующим образом:
m n
... 0hn] = ? ]? b^a^O .. .е,-Ь* .. .en0] =
k=lj=l
fcrrljrrl
Здесь мы применили теорему 2.24 для замены элемента в классе на
эквивалентный (фактически поменяли пары а,0 на Oh,-, а затем пары
Oh, на е,0).
Подставляя B.122) в B.121), получаем
m n
Т = [a,bU] = J2 ? <ЬаЧ- ® hfc, B.123)
fc=lj,a=l
5 Тензорное исчисление
130 Глава 2. Тензоры на линейных пространствах
что совпадает с выражением B.120), причем
i6afc- A BЛ24)
a=l
Следствием этой теоремы является еще одно важное утверждение.
Теорема 2.29. Тензорное произведение Сп 0 Ст линейных про-
пространств Сп и Ст размерности пит само является линейным
пространством размерности пт.
Т Действительно, с помощью теоремы 2.28 появляется возможность
складывать классы неоднотипных элементов из Спт: для этого надо
предварительно эти классы представить в виде B.123), а затем уже
складывать, используя правила сложения B.112) для классов одно-
однотипных элементов:
= (aj{bik + dV'*)e; ® h, = [ejWtV* + djiCik)hk)] B.125)
Несложно проверить, что эти операции с элементами пространства
?>п ® ?>т удовлетворяют аксиомам 1° - 8° линейного пространства,
откуда следует, что Сп ® Ст - линейное пространство. Установим
теперь его размерность.
Для этого заметим, что базисные диады B.218) являются элемен-
элементами пространства Сп ® Ст, а набор всех базисных диад еу ® h*
(j = 1... п, к = 1... га) образует линейно независимую систему в
этом пространстве. В самом деле, предположим, что нашлась такая
ненулевая система коэффициентов Tjfc, для которой выполнено соот-
соотношение
Tjkej®hk = 0. B.126)
Выбирая некоторых представителей классов, получаем из B.126) и
B.118):
0 = Г>>,(*'>*)) = (е.-(Г'*Ь*)) = (е.-Ь<«'>). B.127)
Откуда на основании B.115) получаем Ы1) = ТгкЪк = 0, но это проти-
противоречит тому, что hi.. .hm - базис в ?m. Таким образом, базисные
диады еу ® h^ образуют линейно независимую систему в Сп ® Ст.
Кроме того, на основании теоремы 2.28а, любой элемент из Сп 0 Ст
линейно выражается через них, а значит, на основании определения
2.3, ej (8) hfc - базис в пространстве Сп <g> Cm, называемый диадным
базисом. Число элементов в диадном базисе равно пга, откуда на
основании определения 2.4 получаем, что
dim (Сп (8) Ст) = пт. А B.128)
§2.5. Алгебра тензоров на 71-мерных линейных пространствах ^31
Поскольку ej 0 h* - базис, то естественно назвать коэффициенты
Г7* в B.120) компонентами тензора в этом диадном базисе.
2.5.5. Тензоры высших рангов
Построим теперь рекуррентную последовательность тензорных
произведений линейных пространств.
Шаг г = 1. Выберем пространства Ст и Сп совпадающими: Ст =
= Сп (n = m), тогда из определения 2.25 получаем тензорное произ-
произведение Сп ® Сп, элементами которого являются тензоры Т, которые
на основании B.120) можно представить в виде:
Т = Tikei <g> efc, г, Jb = 1...n, B.129)
так как в данном случае базисы е,- и h* совпадают. Такие тензоры
называют тензорами второго ранга на линейном пространстве Сп.
Шаг1 г = 2. Поскольку, на основании теоремы 2.29, Ст <8> Сп также
является линейным пространством, то его можно выбрать в качестве
пространства Ст в определении 2.25. Базис hi... hm этого простран-
пространства Ст состоит из га = п2 элементов, в качестве которых можно
взять базисные диады е,- <g> еу (i,j = 1.. .п). Обозначим их следую-
следующим образом:
h/(n-i)+* = ej ® efc, j, k = 1.. .п. B.130)
Тогда из определения 2.25 получим
Сп®Ст=Сп®Сп®Сп B.131)
снова линейное пространство, элементами которого являются тензо-
тензоры третьего ранга, которые на основании B.120) можно представить
в виде:
3T = Tl"*e,-®hfe, г=1...п, fc = l...m, т = п2. B.132)
Вводя трехиндексные компоненты
TW = T,-,i(n-i)+/? {-г = lj#eeTlj B.133)
с учетом B.130) получаем:
3T = Tyiei®ei®e|. B.134)
Тензоры е,- ® ej ® е/, как и ранее в главе 1, назовем базисными триа-
триадами. Выстраивая далее аналогичным образом рекуррентную после-
последовательность, на шаге г = к — 1 придем к fc-кратному тензорному
произведению линейных пространств
= Сп ® Сп ® ... ® Сп, т = п*-1. B.135)
132 Глава 2. Тензоры на линейных пространствах
Элементами пространства СТп являются контравариантные тен-
тензоры k-го ранга, которые можно представить в следующем виде:
*Т = Т1"*-^ ® ... ® e,-fc, B.136)
где е,^ <g>.. ,<g>etAf - базисные полиады, a Ttl"tft - компоненты тензора
в этом полиадном базисе.
2.5.6. Тензоры на сопряженном пространстве
Выберем теперь в определении 2.25 в качестве Сп и Ст сопряжен-
сопряженные к ним пространства ?* и С*т с базисами ег...еп и h1..^.
Элементами тензорного произведения ?* ® ??, являются тензоры ви-
вида:
Т = [а'Ьи]. а'еС ЬИ€С. B-137)
где (а'Ь[,]) - векторные наборы вида B.111), а [ ] - класс эквива-
эквивалентности по отношениям, аналогичным к приведенным в определе-
определении 2.24.
Для тензоров типа B.137) остаются справедливыми теоремы 2.27
- 2.29, в частности, сопряженные базисные диады имеют вид:
е^®п* = [е'У,.п*)], B.138)
и разложение произвольного тензора B.137) по базисным диадам при-
принимает вид:
Т = Тце*®Ъ!, B.139)
где
Тц = а\Ьл B.140)
- компоненты тензора Т в сопряженном диадном базисе, причем
а'=а'У, byjrzfyh'. B.141)
Если построить рекуррентную последовательность тензорных про-
произведений, аналогично построенной в п.2.5.5, то на шаге г = к — 1
придем к линейному пространству вида:
С"п®...®С*п, B.142)
к
элементами которого являются
к
Т = З^.-лпв1'1 ® •. • ® eik B.143)
- тензоры fc-ro ранга, называемые ковариантными тензорами.
§2.5. Алгебра тензоров на n-мерных линейных пространствах 133
Если же, начиная с шага г = р (где р < к) данной рекуррентной
последовательности в качестве пространства Ст снова выбирать Сп,
то на шаге г = к — 1 придем к следующему линейному пространству:
®.y®Cnj Я = к-р, B.144)
р я
элементами которого являются
кТ = 2;.l...>+l"'lV* 0 ... ® е1* ® е,р+1 ® ... ® е,-„ B.145)
- тензоры fc-ro ранга, называемые смешанными или ко-контравари-
антными тензорами.
На основании теоремы 2.29 заключаем, что размерность простран-
пространства Тп определяется по формуле:
dim ТП(Р9) = п*+«. B.146)
Для всех трех типов тензоров B.136), B.143) и B.145) вводят еди-
единую классификацию.
Определение 2.27. Тензорами типа (p,q) называют элемен-
элементы линейного пространства Тп , где р ^ 0, q ^ 0 (целые числа).
Таким образом, ковариантные тензоры B.136) - это тензоры типа
(fc,0), где р = к, q = 0; контравариантные тензоры B.143) - это тен-
тензоры типа @, fc), где р = 0, q = к\ а смешанные B.145) - это тензоры
типа (р, q) с р > 0, q = к - р > 0.
2.5.7. Изменение компонент тензоров
при замене базиса
Пусть теперь в пространстве Сп выбран новый базис е(, связанный
с базисом е,- матрицей преобразования 5^ (см. B.63) и B.65)).
Поскольку е{ G Сп, то на его основе можно образовать базисные
Диады ej <g> е^, которые, очевидно, также являются тензорами, т.е.
элементами из Тп •
Установим связь между ej <g> efk и ej ® е^. Для этого воспользуемся
формулой B.116), в которой в качестве векторов а, и Ы^ выберем:
а,- = е'{ = 5',еь B.147о)
bjg = ^e'fc = (^5'ь)е,, t, j, * = 1.. .п. B.1475)
134 Глава 2. Тензоры на линейных пространствах
Тогда из B.118) находим:
e'j ® е'к = [еН^)] = S'^e, ® ег. B.147)
Откуда получаем
e'j <g> е'к = S'j&bei <g> е,. B.148)
Очевидно, что имеют место обратные соотношения:
е, ® е,- = (S-'Y, (S-1)^ e'j ® e'fc. B.149)
Произвольный тензор Т из Тп \ согласно теореме 2.28а, можно
разложить по всякому диадному базису, проделаем это для базисов
е^- <g>e'fc и e/<g>e,-:
Т = T'jke'j ® е'к = T'^S'jS^ei в е, = Г7е,- в е,. B.150)
Отсюда получаем связь компонент Т'-7* и Т1' в разных базисах:
lk. B.151)
Выберем теперь в сопряженном пространстве ?* два базиса е" и
е1, связанные матрицей преобразования S'^ по формулам B.98). Об-
Образуем на основе этих базисов базисные диады е7 ® е* и е'-7 ® e/fe,
являющиеся элементами пространства Тп •
Разложим тензор е" ® e/fc по диадному базису е7 ® е* с помощью
формул B.137) - B.141), в которых в качестве ковекторов а1 и Ьед
выбираем
at' = e/t' = E-1)t'jeJ', B.152)
Тогда получим
= [e/t'((j/e/fc)] = (S-1)^. бЦБ^ е* в е'. B.153)
В результате приходим к соотношению между сопряженными ба-
базисными диадами:
efj в e/fc = (S-1)',.^-1)*!^ в е'. B.154)
Если выбрать произвольный тензор Т из пространства Тп , то его
можно разложить по формуле B.139) как по диадному базису е1 <g> efc,
так и по е" 0 e/fc, тогда с учетом B.143) получим:
Т = З^е* ® e/fc = T;,E-1)i,(S)*, ef" «e' = ^e1" в е'. B.155)
§2.5. Алгебра тензоров на n-мерных линейных пространствах 135
В силу единственности разложения по базису элементов линейного
пространства, в итоге имеем:
T^T^S-'y^S-1)", B.156)
соотношение между компонентами тензора из Тп в различных со-
сопряженных диадных базисах.
Вообще же для тензоров из пространства Тп имеет место следу-
следующая теорема.
Теорема 2.30. Базисные полиады в пространстве Тп {р ^ 0,
д^О) при замене базиса в порождающем их пространстве Сп:
е" = S'te/ и сопряженном к нему пространстве Сп: e/l = (SI ^е?
преобразуются следующим образом:
...Sjkike?1 <8> ... (8) е7'" ® е7"^1 ®...®е*\ B.157)
Компоненты произвольного тензора кТ типа (p,q) при такой заме-
замене базисов преобразуются следующим образом:
iil...tp -P Ji!---^ J «рь ip+i---^ ikxn-ip
B.158)
Идея доказательства аналогична приведенной выше для случаев
р:=2,д=:0ир = 0,д = 2, детали доказательства оставляем в качестве
упр.2.5.4.
2.5.8. Операции с тензорами
А) Сложение
Поскольку все введенные выше тензоры являются элементами со-
соответствующего линейного пространства Тп (р ^ 0,g ^ 0), то их
можно складывать с себе подобными и умножать на число, например
*Т + *В = Г1-1^ ® ... ® eik + Bil"'ikeix ® ... ® eik =
л ^'^ei, ® ... ® e,-fcl B.159)
Б) Транспонирование
Для каждого тензора кТ fc-ro ранга можно ввести транспониро-
транспонированные тензоры подобно тому, как это было сделано в евклидовом
пространстве (см. п. 1.8.2):
*т(т1...тО = Til"-ikeim ® ... ® е,-т , B.160)
136 Глава 2. Тензоры на линейных пространствах
т1...тк е {1...А;}, *i... ife G {l...n},
где (mi... rrik) - некоторая подстановка.
В) Тензорное произведение
Для тензоров из Тп можно определить операцию тензорного про-
произведения.
Определение 2.28. Тензорным произведением двух тен-
тензоров тТ т-го ранга и *В к-го ранга из пространств Тп и Тп q
( q = m,'p' + q' = к):
mT = TiltaAp i''+t-'"e1"* ® ... ® e*' ® e,-p+l ® ... ® e,m, B.161)
e,-
,-fc,
называется тензор (к + т)-го ранга
= rp 'p+l-'mD «m+p' + l—в'т+*е11 (О,
•^ii-ip «m+i...iTO+p# c чу-"
... 0 e1'" О etp+1 ® ... ® e,-TO ® et'-+1 ® ...
...®et'm+P'®etm+p4i®...®elfc+m, B.162)
являющийся элементом пространства Тп ® Тп q .
Гу Симметрирование
Если для тензора fcT типа (р, д) выбрать группу из г верхних (или
только нижних) индексов, причем г ^ р, то с помощью транспони-
транспонирования в этой группе индексов можно получить г! тензоров *Т^ с
учетом исходного. Здесь а — (mi... г... т,-.. Л ... т*) - соответству-
соответствующая подстановка, полученная из тождественной A... г.. .j ... Z ...&),
в которой г, I... (всего fc—r штук) не меняются. Тогда суммированием
этих тензоров получим новый тензор типа (р, q)
*TW = :L J^TW. B.163)
Очевидно, что применение операций транспонирования в группе из
тех же г индексов к самому тензору кТ^ не изменяет его:
Такие тензоры называют симметрированными по группе индексов.
Примеры операций симметрирования приведены в 1.8.3.
Если же сам тензор кТ типа (р, q) совпадает с любым из своих
транспонированных тензоров в группе из г индексов, т.е.
кгт\ кгт\(<т)
то его называют симметричным тензором по группе индексов а.
§2.5. Алгебра тензоров на n-мерных линейных пространствах ^37
Теорема 2.31. Множество всех тензоров кТ типа (p,q), сим-
симметричных по одной и той же группе а из г индексов, образует
линейное пространство Sna, причем Sna С Тп •
Т Действительно, поскольку операции транспонирования и сложения
(или умножения на число) тензоров переставимы, то для любых двух
тензоров кТ и *В, симметричных относительно группы индексов сг,
их сумма (и произведение на число) тоже является симметричной от-
относительно той же группы а:
(кТ + кВ)^ = кТ^ + кВ^ = кТ + кВ,
(«*Т)<*> = 8*ТМ = 8кТ.
Так как все симметричные тензоры кТ € Sn<? являются также и
просто тензорами типа (р, д), то, очевидно, что Sn* С Тп . А
Д) Альтернирование
Обозначим через \а\ количество инверсий в каждой подстановке и
образуем сумму, аналогичную B.163), но меняя знак перед каждым
кТ^а\ в результате получим
r!~. - Bлб4)
- тензор, который изменяет знак при любых перестановках в группе
индексов а:
• РЧУЧ II. РЧ
B.165)
Такие тензоры *Т^ называют ко со симметричными по группе ин-
индексов «г, а операцию преобразования кТ —У кг^[а) называют аль-
альтернированием. Примеры кососимметричных тензоров приведены в
п.1.6.2.
2.5.9. Скалярное произведение тензоров
в евклидовых пространствах
Если пространство евклидово (Сп = ?п) , то в силу его самосопря-
самосопряженности (?п = ?*) все линейные пространства Тп — ?п совпа-
совпадают для р и q таких, что р + q == к. Поэтому можно рассматривать,
например, только пространства ?п ' = ?п К
Для тензоров из этого пространства ?п можно ввести дополни-
дополнительно операцию жонглирования индексами (опускания или подня-
поднятия).
138 Глава 2. Тензоры на линейных пространствах
Е) Опускание или поднятие индексов
Всякий тензор кТ можно представить различными способами в ос-
основном е, и взаимном е1 базисах с помощью фундаментальной матри-
матрицы Qij и ее обратной дх*:
P+1k B.166)
где
rpii...ik = /xi»i...«p ip+tjp+i ikjk
Кроме того, поскольку в ?п определено скалярное произведение,
тензоры из ?п можно скалярно перемножать.
Ж) Скалярное умножение
Определение 2.29. Скалярным k-кратным произведением
тензоров тТ и 'В из пространств ?п и ?п называют тензор
m4-l—k *~л i-i(m+/—k)
Г1 С из пространства Сп -
2.5.10. Независимые компоненты тензоров
Рассмотрим произвольный тензор fcT из некоторого подпростран-
подпространства Т? С 7п , & = Р + 5 ^ который в некотором полиадном базисе
имеет вид:
Т = Т- . V®...®e'®eJi®...®e«.
Образуем из компонент 3Jl>ttl- Jl*"<7<* этого тензора каким-либо об-
образом координатный столбец (Т1.. .Т1.. ,Tfc°)T. Один из способов
образования такого столбца приведен далее в п.4.2.1. Число ко = np+q
- это общее число компонент тензора fc-ro ранга, ко = dim Tn •
Говорят, что среди компонент T{i { Jl'"jq тензора имеется только
к'о независимых, если существует матрица D%j размером (ко — к'о) х
§2.5. Алгебра тензоров на n-мерных линейных пространствах 139
fco, ранг которой равен (ко — Ajq), такая, что имеют место (ко — kf0)
соотношений:
Д«'/рт=0, t=l...(*o-*i). B.167)
Числом независимых компонент тензора feT из 7^' называют чис-
число к'о для тензора с максимально возможным количеством ненулевых
компонент.
Теорема 2.32. Число к'о независимых компонент тензора кТ из
некоторого подпространства Т'п С Ы равно размерности этого
подпространства:
ко = dim % ^ fc0.
Ў Рассмотрим произвольный тензор кТ из 7^. Так как 7^ - линейное
пространство, то в нем можно выбрать базис fcAE), s = 1.. .i\T, из N
тензоров, где N = dim 7^', и разложить кТ по этому базису:
?), B.168)
где Т(*) - коэффициенты разложения. Если образовать координатный
столбец (Т1.. .Тко)т из компонент Т: , <71*"<7</ тензора кТ в некото-
ром базисе е1 и столбцы (ЛКх ...Л^°х)т из компонент Ats\iltm.iJl'"J4
базисных тензоров ЛА(Л), то B.168) можно записать в виде:
N
Г = Y,Ai(s)T{s\ i= l..-Ао- B.168а)
3 = 1
Столбцы А1(8\ образуют матрицу размером ко х TV, причем
rang (A\s\) = N, так как это координатные столбцы из компонент
N базисных тензоров. Тогда существует квадратная матрица А1^
порядка iV, образованная из А*,х вычеркиванием ко — N строк и пе-
перенумерацией оставшихся строк, у которой det А\8\ ф 0. Из вычерк-
вычеркнутых строк образуем матрицу А\ х размером (ko-N)xN. Обозначим
(Т1.. .TN)T координатный столбец, образованный из (Т1.. .Тк°)т вы-
вычеркиванием элементов с теми же номерами, что и при формирова-
формировании матрицы А\у Из вычеркнутых же элементов образуем столбец
(Т1.. .Т*°)т. Тогда соотношение B.168а) можно разбить на две груп-
группы:
8=1 3=1
140 Глава 2. Тензоры на линейных пространствах
В силу невырожденности матрицы А\х из первой группы найдем:
т(8) = ?f=i^ie)Ti> гДе Ц8) ~ матрица, обратная к A\g). Подстав-
Подставляя Т(*) во вторую группу соотношений, получаем:
N N
fi - Е Е AU^]TJ = 0. i = 1... (*о - ЛГ). B-169)
,=i;=i
Если снова образовать единый координатный столбец
/ml fj\i mko\T /ml /тпко—Nml mN\T
то соотношение B.169) можно переписать как
D^T* = О, i = 1... (*0 - W), B.169a)
где D*j - блочная матрица размером (ko—N) х ко вида D = (Eko-N |-A)>
а #, = Ef=i EjLi \)A(;\ i = l...{ko-N)tj = l...N,a Eko-N
- единичная матрица порядка ко — N. Так как матрица Dlj имеет,
очевидно, ранг (ко—N), то из B.169а) и B.167) следует, что среди ком-
компонент T{i { Jl'"Jq независимых не более N штук, т.е. к'о ^ N (слу-
(случай к'о < N возможен, если существуют и другие соотношения кроме
B.169а), связывающие компоненты тензоров из 7^'). Однако тензор кТ
с максимальным числом компонент fcg, который удовлетворяет только
условиям B.169а), будет обладать и разложением B.168), т.е. также
принадлежит пространству 7^'. Для этого тензора существует только
ко = N независимых компонент, что и доказывает теорему. А
В качестве примера подсчитаем число независимых компонент kf0
тензоров, симметричных только по первым двум индексам, т.е. при-
принадлежащих подпространству 5я?? , где а = B1345...fc), к = р+ q.
Так как компоненты тензоров этого подпространства связаны соот-
соотношением: Tiii:i Jl'"jq = Thii ijl'"jq , в которых только A/2)(п2+
+п)пр~2+я различных, то получаем, что
2.5.11. Полилинейные формы
С понятием тензора типа (р, q) связан еще один часто используемый
объект, обобщающий понятие линейного функционала.
Пусть Сп - линейное пространство, а Сп - сопряженное к нему про-
пространство. Рассмотрим декартово произведение пространств вида:
Mpq = Сп х ... х Сп х Сп х...хС*п.
§2.5. Алгебра тензоров на 71-мерных линейных пространствах 141
Определение 2.30. Функционал
/ = /(аь...,ар,Ь\...,Ь*) B.170)
от р векторов а,- и q векторов Ь1, осуществляющий отображение
/: MPq —> Ш1, называют полилинейной формой типа {p,q)
на Сп, если он является линейным по каждому из аргументов.
Полилинейная форма типа A0) - это линейный функционал, т.е.
ковектор, а полилинейная форма типа @1) - это по определению век-
вектор из Сп.
На множестве полилинейных форм обычным образом можно опре-
определить операцию сложения: суммой двух форм / и <р одного типа
(р, q) называют функционал ф = f + ip, значения которого равны сум-
сумме значений / и ip при каждом значении набора аргументов из Aipq.
Аналогично определяется умножение полилинейной формы на число.
Теорема 2.33. Множество всех полилинейных форм типа (р, q)
на Сп является линейным пространством.
Доказательство, заключающееся в проверке того, что операции сло-
сложения форм и умножения их на число сохраняют тип формы, остав-
оставляем в качестве упр.2.5.4.
Выберем теперь базис е, в пространстве ?„, и взаимный к нему
базис е1 в С*п. Тогда, раскладывая произвольные векторы а,- и ковек-
торы Ь*, являющиеся аргументами формы B.170), по этим базисам, в
силу линейности / по аргументам, получаем
= ai'...eJrb)|...*Jf/ll..jFil"J', B.171)
где обозначены коэффициенты
4....V '''¦"''' = /(*„.-. ,е,-„е>\... ,е»"«), B.172)
называемые по аналогии с линейными функционалами (см. B.88))
компонентами полилинейной формы.
Имеет место следующая теорема.
Теорема 2.34. Компоненты полилинейной формы f B.170) типа
{Р)Я)> определенные в базисе е,- из Сп связаны с компонентами в
другом базисе е(- = SJ{ e/ следующими соотношениями:
f'i,..ip ''-'¦' = S\ ...S\ (S~lrh {S-l)*\fklmki)''-'' . B.173)
142 Глава 2. Тензоры на линейных пространствах
Ў Определяя координаты формы / в новом базисе е(- согласно правилу
B.172), получаем в силу линейности формы по аргументам:
..., S\
ekp, (S)\ e\
ekp, (S-l)\ e
*)\ f(ekl,... , efcp) e'«,... , e'«),
что и доказывает теорему. А
Сравнивая соотношение B.173) с формулой B.158), заключаем, что
компоненты /tl_,- n'q являются компонентами тензора типа (р, д),
заданного на пространстве ?„. Таким образом, полилинейной форме
/ типа (р, q) на Сп соответствует тензор типа (р, q) на Сп:
kF = fiiuaAp il~'*eil ® ... О е1'* в eh О ... в eig, .р + ? = *.
2.5.12. Сравнение геометрического и алгебраического
определений тензора
Сравним теперь два подхода к определению тензора: "геометричес-
"геометрический" (определение 1.18) и "алгебраический" (определение 2.25). В ос-
основе первого лежит аксиоматика элементарной геометрии в трехмер-
трехмерном евклидовом пространстве, а второго - теоретико-множественные
аксиомы линейного пространства. Формальные выражения для тен-
тензоров A.104) и B.115а) в этих подходах практически совпадают для
случая i = 1,2,3. Введенные в A.104) скобки "[ ]" как простое обозна-
обозначение, в рамках алгебраического подхода получили свое обоснование
- это класс эквивалентности на введенном множестве векторных на-
наборов a,-bM. Более того, если пространство Сп является евклидовым
?з> то определения A.104) и B.115а) вводят один и тот же объект.
Тензорные законы преобразования компонент тензоров A.250) и
B.158) при замене базисов 1Ц = Р^-R,- (упр.1.1.8) и е(- = S^e, (со-
(соотношение B.62)) соответственно также совпадают, если положить
Pli = 51,-, СУ,- = (Р-% = (S-1)^., м = 1,2,3.
Упражнения к § 2.5.
Упражнение 2.5.1. Доказать, что введенные в определении 2.24 отношения
эквивалентности удовлетворяют аксиомам 1° -3° из п.2.5.1.
Упражнение 2.5.2. Доказать теорему 2.27, непосредственно образуя для
каждого элемента A(jk) его класс эквивалентности [-^(jfc)] с помощью правил
а) - в) из определения 2.24 и показывая, что никакие другие элементы системы
B.117) не принадлежат этому классу.
§ 2.6. Внешние формы _143
Упражнение 2.5.3. Используя определение 2.30, показать, что полилиней-
полилинейную форму типа A,1) можно отождествить с линейным оператором, действую-
действующим из Сп в Сп.
Упражнение 2.5.4. Доказать теоремы 2.30 и 2.33.
§ 2.6. Внешние формы
2.6.1. Свойства операции альтернирования
Если операция альтернирования B.164) осуществляется по всем ин-
индексам тензора, то будем ее обозначать следующим образом:
кг?Ш = JL \^ (_1ym1...mfc|T(m1...mfc)# B.174)
' (rai...mfc)
Теорема 2.35. Операция альтернирования B.174) тензоров кТ
из Тп или Тп обладает следующими свойствами:
__ / ^\\mi...mk\kr^[A] B.175)
= / 2>\|mi...mfc|ferp[A] B.176)
B.177)
где альтернирование Т^ осуществляется по B.164) в группе пер-
первых г ^ к индексов, т.е. а = (mi... mrr + 1... к).
Т Используя определение B.174), получаем
= 2^ (-1) х
(»i...tfc)
_ (_1)\т1...тк\Т[А]ш B.178)
Здесь мы применили два свойства подстановок:
а) если суммирование идет по всем возможным подстановкам
(*i--.ifc), то подстановка каждого слагаемого может быть умно-
умножена на одну и ту же некоторую подстановку mi... га*;
б) знаки трех перестановок i\... г&, mi... m* и гШ1 ... imk связаны со-
соотношениями:
.•*mfc| = |*i---*fc mi...mfc
B.179)
144 Глава 2. Тензоры на линейных пространствах
Доказательство соотношения B.176) проводится аналогично. Со-
Соотношение B.177) доказываем следующим образом:
_ ± Y^ (_lj\mi...mr\^_y\ml...mr\kr?[A] _ кг^[А]^ B.180)
Здесь было использовано свойство линейности операции альтерниро-
альтернирования, а также свойство B.176). А
Из B.177), в частности, следует, что
2.6.2. Свойства кососимметричных тензоров
Рассмотрим тензоры fcT G 7n или Тп \ кососимметричные по
всем индексам, т.е. удовлетворяющие соотношению:
fciji(mi...mfc) __ / ^\|mi...
для всех подстановок индексов а = (mi... )
Такие тензоры называют кососиммегпричными.
Перейдем в B.182) к компонентам тензора типа @,fc):
Г11-'Чт1 ® • • • О etmfc = (_i)|mi.»m*lTil...ue.i в ... ® e|-fc. B.183)
Применяя правило A.255) перемены индексов у полиадного базиса
rpiWl...iWft _ (_1)|m1...mfc|rt1...t^ B.184)
затем меняя еще раз индексы согласно A.257) и умножая правую и
левую части на (—l)lmi-m*l? получаем окончательно
rpimi.'.imk _ ^_ij|m1...rafc|2rti...ifc# B.185)
Аналогичную формулу можно установить для тензоров типа (fc, 0):
ТгМ1...гя„ = (-lI1-1"*1^,..^. B.186)
Формулы B.185) и B.186) представляют собой содержание следую-
следующей теоремы.
§ 2.6. Внешние формы 145
Теорема 2.36. Тензоры кТ типа @,fc) и (fc,0) кососимметпричны
тогда и только тогда, когда кососимметричны их соответствую-
соответствующие компоненты, т.е. выполнены условия B.185) и B.186).
Сравнивая B.185) и B.184), заключаем, что для кососимметричных
тензоров любая подстановка индексов совпадает со своей обратной:
rpiWl...iWk =rpiml...imk^ B.187)
Операция альтернирования не изменяет кососимметричного тензо-
тензора fcT, так как
Теорема 2.37. Множество всех кососимметричных тензоров
типа (p,q) на Сп образует линейное пространство Лп , причем
д (pq) q-{pq)
Т Действительно, если fcT и fcB являются кососимметричными, то
любая их линейная комбинация тоже кососимметрична, так как
(-l)kl (sxkT + s2kB). B.189)
Но поскольку все кососимметричные тензоры - это тоже тензоры, то
2.6.3. Внешние произведения векторов
Для кососимметричных тензоров удобно использовать специальную
операцию - внешнее произведение.
Определение 2.31. Внешним произведением векторов
ai Е Сп (г; = 1.. .q) называют альтернирование их тензорного про-
произведения и обозначают его следующим образом:
Л ... Л aq = (ai ® ... ® &q)[A]. B.190)
146 Глава 2. Тензоры на линейных пространствах
Аналогично определяют внешнее произведение ковекторов Ьг ? ?*
(г=1...р);
Ь1 Л ... Л Ы> = (Ь1 0 ... 0 Ър)М. B.191)
Выражения, стоящие в левой части B.190) и B.191), называют
внешними формами типа @, q) и (р, 0) соответственно (используют
также название поливекторы или д-векторы и р-векторы).
Из B.190), например, при к = 2 получаем
Л аг = ~(ai 0 а2 - аг 0 ai), B.192)
а при к = 3:
1,
ai Л аг Л а3 = ~(ai 0 а2 0 аз + а2 0 аз 0 ai + аз <8> ai ® аг —
6
— ai 0 аз (8> а2 — аз (8> а2 (8> ai — а2 (8> ai (8> аз).
Из свойства B.175) следует, что внешние формы B.190) и B.191)
являются кососимметричными тензорами типа @,д) и типа (р, 0) со-
соответственно. Заметим, что обратное, вообще говоря, неверно (см.
упр.2.6.1).
Внешние формы являются линейными по каждому из векторов:
ах Л ... Л {з)Ък) Л ... Л aq = ^ s*(ах Л ... Л Ьк Л ... Л ад), B.193)
где s* - коэффициенты, что немедленно следует из линейности q-
кратного тензорного произведения по каждому вектору:
ai О ... О (в}Ь,-) 0 ... 0 aq = skj (ai 0 ... О bfc О .
и линейности операции альтернирования B.174).
Напомним, что согласно определению B.161) тензорное произведе-
произведение векторов и ковекторов вводят следующим образом:
ах 0 ... 0 aq = а^ .. .a^e^ 0 ... 0 eiq, B.194)
b1 0 ... 0 bp = b^ ...Щре?1 0 ... 0 e7'*,
где а,« = а)кеь и Ы = Цке*к, а е,- и е* базисы в ?п и С*п.
Подставляя B.194) в B.190) и B.191), с учетом свойства линейнос-
линейности B.193) приходим к следующей теореме.
§ 2.6. Внешние формы j.47
Теорема 2.38. Внешнее произведение векторов а,- ? Сп и ковек-
торов Ы ? ?* можно представить в виде разложения по внешним
произведениям базисных векторов е,- и е1 соответственно:
ai Л ... Л а, = а^ .. .<#etl Л ... Л е,-„ B.195)
Ь1 Л ... Л Ьр = Й ...Й е*1 Л ... Л «Л.
л Jp
Используя явное выражение B.174) для операции альтернирования,
из B.190) и B.191) получаем разложение внешней формы по полиад-
ному базису:
aiA.-.Aa^ = -у ^ (-l)^mi"'m^(arni ® ... ® am J =
= а1'1"*^ ®...®eig, B.196)
где коэффициенты а*1***1* имеют вид:
l)l(mi...mg)|aji а*я_ =
B.197)
vax ... aq
Здесь мы использовали определение B.31) детерминанта матрицы
размером q x q.
Для внешнего произведения ковекторов получаем аналогично:
Ь1 А ... А Ьр = bjl.,,jpeil (8)... О е*', B.198)
где
1
Ji-jp р|
Рассмотрим внешние произведения векторов базиса е,-, тогда так
как е,- = Sjej, из B.186) получаем
где в соответствии с B.197) обозначены коэффициенты:
- ft
к Эр
Этот символ называют обобщенным символом Кронекера.
Докажем еще одно важное свойство внешних форм.
148 Глава 2. Тензоры на линейных пространствах
ТВОРВМА 2.39. Векторы а, € Сп (i = 1.. .q) линейно зависимы
тогда и только тогда, когда их внешнее произведение равно нулю:
aiA...Aag = O. B.199)
Такое же утверждение имеет место и для линейно зависимых ко-
векторов Ы ? С*п:
^Л.-.ЛЫ'ггО. B.200)
Ў В одну сторону. Пусть выполнено условие B.199), тогда в силу
B.197) определители матриц, составленные из их коэффициентов рав-
равны нулю. Но тогда в силу теоремы 2.10 координатные столбцы каж-
каждой из этих матриц линейно зависимы, а, следовательно, один из них
с номером j можно выразить через все остальные:
где не все з% нулевые. Поскольку это соотношение выполнено для
всевозможных значений i\.. .ig, то оно будет выполнено и для набора
(aj .. .a")T. Но это означает, что
т.е. векторы ai... а9 - линейно зависимы.
В обратную сторону. Пусть ai... а9 линейно зависимы, тогда най-
найдутся не все нулевые s% такие, что для некоторого а^ имеет место
соотношение B.201). Подставляя это выражение во внешнюю форму
B.199), в силу ее линейности по каждому из векторов, приходим к
(q — 1) внешним формам, у которых имеется по два одинаковых век-
вектора, т.е. ai Л ... Л а,- Л а,- Л ... Л ад. Но поскольку каждая внешняя
форма является кососимметричным тензором, то она должна менять
знак при любых перестановках ее векторов. Однако если поменять
местами у полученных форм одинаковые векторы а,- и а,-, то, очевид-
очевидно, что знак формы не изменится, значит все эти формы есть нулевой
тензор.
Доказательство утверждения B.200) проводится аналогично. А
2.6.4. Представление кососимметричных тензоров
с помощью внешних форм
Рассмотрим теперь кососимметричные тензоры кТ и *В типа @, q)
и типа (р, 0). Имеет место следующая теорема.
§ 2.6. Внешние формы _149
Теорема 2.40. Всякий кососимметричный тензор кТ типа @, к)
на Сп можно разложить по внешним формам базисных векторов
е, ? Сп:
kT _ Tii..ikeii ® ... ® e,-fc = *! Y^ Til'ikeh Л ... Л elfc, B.202)
а всякий кососимметричный тензор fcB типа (А;,0) на Сп - разло-
разложить по внешним формам базисных векторов е1 ? Сп:
kB = B,-l...*fce1 0 ... <g> eik = к\ ]Г вп^ье*1 Л ... Л etfc. B.203)
Здесь суммирование идет лишь по тем комбинациям индексов
ii.. .г*, которые расположены в порядке возрастания, например, для
тензора типа @,2) на С$ имеем:
Т = Т^7е{г (8) е,-2 = 2(Т12ех Л е2 + T13ex Л е3 + Т23е2 Л е3). B.204)
Ў Прежде всего заметим, что если тензор кТ - кососимметричен, то
в силу B.188) и определения B.190) его можно представить в виде:
kT = rpi^.i^^ ® ... ® e,-fc = *ТМ = Т1-^ Л ... Л e,-fc, B.205)
то же самое справедливо и для тензора кВ.
Согласно теореме 2.39 в суммах в правой части соотношения B.205)
отличны от нуля только слагаемые с различными индексами ii.. .г*.
Зафиксируем одно такое слагаемое, у которого индексы располагают-
располагаются в порядке возрастания:
Ttl'tkeil Л ... Л etfc, г*1 < ... < г* нет суммирования. B.206)
Но тогда все остальные слагаемые с такими значениями индексов
%\.. .ik (а их fc!), но взятыми в другом порядке, отличаются от сла-
слагаемого B.206) двойной перестановкой: у коэффициентов Г11"*1* и у
формы etl Л ... Л etfc. В силу кососимметричности и формы, и коэф-
коэффициентов (см. B.185)), при таких двойных перестановках знак сла-
слагаемого B.206) не будет меняться. Таким образом, в суммах B.202)
действительно находится к\ различных сумм B.206). А
Из теоремы 2.40 следует, что если ранг кососимметричного тензора
кТ больше размерности пространства к > п, то такой тензор всегда
нулевой. Действительно, при к > п в формах B.202) всегда будут
повторяющиеся векторы, что в силу теоремы 2.39 влечет за собой
обнуление всей правой части соотношения B*202).
Если же к = п, то упорядочение индексов i\ < ... < in возмож-
возможно только одним способом, поэтому в B.202) остается только одно
слагаемое:
nT = nlT1-1^! Л ... Л е„. B.207)
150 Глава 2. Тензоры на линейных пространствах
Теорема 2.41. Внешние формы
etl Л ... Л eiq, 1 ^ п < ... < iq ^ n B.208)
образуют базис пространства Ап кососимметричных тензоров
типа (О,^) на Спу а внешние формы
е*1 Л ... Л е1'", 1 ^ ч < ... < ip ^ п. B.209)
образуют базис пространства Апр •
Ў Поскольку из теоремы 2.40 следует, что всякий кососимметричный
тензор можно представить в виде разложения по соответствующей
системе форм B.208) или B.209), то нам остается показать только
линейную независимость систем B.208) и B.209).
Предположим противное: система B.208) линейно зависима, тогда
найдутся такие не все нулевые коэффициенты Т'1***1*, определенные
ТОЛЬКО При 1 ^ 2*1 < . . . < iq ^ П, ЧТО
Г1"^е,1Л...Ле,-9 = 0. B.210)
Тогда переходя с помощью формулы B.196) к тензорному произведе-
произведению векторов, получаем
= ?.?. S
ii<".<iq (mi».m,)
B.211)
Поскольку все ii ...ig не равны между собой, то, очевидно, что в
суммах B.211) все полиады e,mi <g>.. .®е,-те различны между собой. Но
тогда условие B.211) означает, что эти полиады линейно зависимы,
что неверно, так как они входят в полиадный базис etl 0 ... ® etn. A
Определение 2.32. Формы B.208) и B.209) называют базис-
базисными внешними формами в Anq и An соответственно.
2.6.5. Изменение компонент кососимметричных тензоров
при замене базиса
Выберем два базиса е,- и е(- в ?п, связанные соотношением B.62):
§ 2.6. Внешние формы
Образуем из векторов е{ базисную форму е^ Л ... Л e-fc и восполь-
воспользуемся формулой B.196):
(mi...mfc)
..ifcil""i4.®---®ei». B-212)
где обозначены коэффициенты:
sfc
Поскольку слева в B.212) стоит внешняя форма при фиксирован-
фиксированном наборе z'i... ifc, то выражение справа является кососимметричным
тензором типа @,fc), и к нему можно применить теорему 2.40, тогда
получаем окончательно формулу преобразования внешних форм типа
@, к) на ?„ при замене базиса в Сп:
S.W»il""'4-.A...Ae,v B.214)
Аналогичным образом можно установить соотношение между
внешними формами ковекторов е" и е1 из ?*:
еЛ...ЛеНк = J2 5ll"'llri1...ifceJlA"-AeJfc' B-215)
ii<...<jfc
где
Рассмотрим теперь кососимметричный тензор кТ типа @, к) на ?п
и представим его в виде разложения B.202) по базисным внешним фор-
формам е^ Л...Лefik и etl Л...Лetfc, а затем воспользуемся соотношением
B.214I:
кТ = к\ Y^, Т'{*~Лке'{1 Л ... Л е\к =
B.217)
152 Глава 2. Тензоры на линейных пространствах
Отсюда получаем соотношение между компонентами кососиммет-
ричного тензора:
Ttil-ikSil_ihjl'"jk. B.218)
Аналогично устанавливаем связь между компонентами тензора
..л= ? ^...^'""'V*-
Таким образом, мы доказали следующую теорему.
Теорема 2.42. Базисные внешние формы типа @,fc), определен-
определенные на Сп, преобразуются при замене базиса в Сп по соотношениям
B.2Ц), а формы типа (fc, 0) - по B.215). Кососимметричные тензо-
тензоры kT ? Лп преобразуются при такой замене по формулам B.218),
а тензоры кТ ? А„ - по формулам B.219).
Заметим, что соотношение B.219) не противоречит тензорному за-
закону преобразования B.158), а является только иной формой его за-
записи для кососимметричных тензоров.
2.6.6. Случай к = п
Рассмотрим кососимметричные тензоры кТ из пространств An и
Л(пО) п п
п на Ln, ранг которых равен размерности пространства ?п.
Тогда из теоремы 2.40 получаем:
nT = jnw.e^ ® ... ® etn = n!T12-nei Л ... Л е„, B.220)
так как возможна только одна комбинация индексов^ 1 ^ zi < ...
... < in ^ п - это тождественная подстановка. Таким образом, такие
кососимметричные тензоры ПТ определяются только одной компонен-
компонентой Т12—п, все остальные, получающиеся перестановкой индексов, на
основании B.185) выражаются следующим образом:
2п"те1..лтея = (_1)|m1...mn|T12...ne B.221)
Это соотношение можно записать иначе, если ввести компоненты п-
мерных символов Леви-Чивиты:
аг..лп и 6fl-In =
__ Г (—1I*1—^1, если все индексы i\.. .г„ различны;
B.222)
О, если имеются совпадающие индексы.
§ 2.6. Внешние формы ^53
Тогда B.221) будет эквивалентно следующему соотношению:
rpii...in = €ii...inrpl2...n *2 223)
Кососимметричный тензор ПТ типа (п, 0) на Сп также имеет толь-
только одну1 независимую компоненту Ti2...n> а все остальные выражаются
следующим образом:
Th...in = eh...inT12...n, B.224)
и, следовательно,
nT = nlT^.ne1 Л ... Л еп. B.225)
Из формул B.220) и B.225) следует, что для тензоров из Л« и
Лп существует только по одной базисной внешней форме: eiA.. .Леп
ие1Л...Леп.
В силу формул B.214) и B.215) эти внешние формы преобразуются
по следующему закону при замене базиса в Сп и ?* соответственно:
е^Л.-.Ле^ = AeiA...Aen, е;1Л...Ле/п = -^е1Л...Леп, B.226)
где
A = det (ffj). B.227)
Действительно, так как при к — п в суммах соотношений B.214) и
B.215) остается только по одному слагаемому 51фшшП1#шфП и 51***'i.#.n, то
вычисляя по B.213) и B.216) эти коэффициенты:
B.228)
убеждаемся в истинности формул B.226).
Единственные независимые компоненты Ti...n и Т1'п кососиммет-
ричных тензоров согласно теореме 2.30 преобразуются при замене ба-
базиса следующим образом:
Ti...n = Д11..п, Т1-" = It'1-". B.229)
2.6.7. Внегпнее произведение кососимметричных
тензоров
Рассмотрим обобщение операции B.190) внешнего произведения
векторов.
154 Глава 2. Тензоры на линейных пространствах
Определение 2.33. Внешним произведением кососиммет-
ричных тензоров РТ ? An и *В ? Ап назовем альтернирование
их тензорного произведения:
рТЛ*В = (рТ ® *В)М. B.230)
Так как РТ ® *В является тензором (р + fc)-ro ранга, то мы мо-
можем записать выражение B.230) в компонентах, используя определе-
определение B.174):
..•®elmp®eimp+i®...®eimp+fc, B.231)
где
pT = TfW'e,-1®...®el-p,
fcB = B^'-^ej, ® ... ® eifc, B.232)
Поскольку в правой части B.230) стоит альтернированный тензор,
то согласно B.175) РТ Л *В будет кососимметричным. Тогда в пра-
правой части выражения B.230) можно переобозначить индексы с учетом
формул B.187):
(p + k)\
•. ¦ ® е,-р ® е|р+1 ® ... ® eip+k. B.233)
Ввиду кососимметричности этого тензора, его можно преобразо-
преобразовать согласно теореме 2.40:
ip+Ae^ A...Aet-p+fc, B.234)
здесь введено обозначение для коэффициентов:
«m
p+fc
B.235)
§ 2.6. Внешние формы 155
Теорема 2.43. Введенная операция B.230) внешнего умножения
кососимметричных тензоров обладает следующими свойствами:
однородность
kB), sGl1, B.236)
дистрибутивность
л *в _ pTi л *в + рТз л *В) B.237)
Л (fcBi + *В2) = рТ Л *Bi + рТ Л *В2, B.238)
Л *В) Л qC = рТ Л (*В Л 9С), B.239)
B.240)
Т Свойства B.236) - B.238) непосредственно вытекают из определе-
определения B.230).
Для доказательства B.239) представим левую часть этого выраже-
выражения в виде:
{рТ Л кВ) Л qC = ({рТ Л кВ) ® *С)[Л], B.241)
и рассмотрим тензор под знаком альтернирования:
^ (l)^T ^ fcB)(m,...mP)
* (mi...mr)
B.242)
где г = р -f fc.
Здесь альтернирование "[а]и берется по группе из первых г индек-
индексов тензора pT®fcB®9C согласно определению B.164).
Но тогда, подставляя B.242) в B.241), с учетом свойства B.177)
получаем
{рТ Л кВ) Л qC = {pT ® кВ 0 «C)W. B.243)
Совершенно аналогично можно доказать, что
рТ Л (*В Л 9С) = {рТ (8) fcB (8) «С)[Л]. B.244)
Глава 2. Тензоры на линейных пространствах
Сравнивая B.243) и B.244), убеждаемся в истинности соотношения
B.239),
Для доказательства утверждения B.240) заметим, что
i... ® e,-fc+p ® etl ® ... ® etfc =
Тогда согласно свойству B.176) получаем:
••»*1*В ЛРТ, B.246)
но так как
то от B.246) приходим к B.240). А
Операции внешнего умножения и сложения кососимметричных тен-
тензоров, удовлетворяющих свойствам B.236) - B.240), позволяют по-
построить на пространствах Л« {к = 0,1,2,...) или Лп '
(к = 0,1,2,...) алгебраический объект, называемый алгеброй Грае-
смана. Заметим, что в п.2.6.4 было установлено, что ненулевых косо-
симметричных тензоров в пространствах Лп и Лп при к > п нет,
Лп*°> = О, ЛП°*> =0, к > п. B.247)
Упражнения к § 2.6.
Упражнение 2.6.1. Доказать, что кососимметричный тензор из А\ на
и
Т = ех Л е2 + е3 Л е4
не может быть представлен в виде внешней формы типа @, 2), т.е. в виде Т =
а ЛЬ, гдеа,Ь ? А-
Упражнение 2.6.2. Доказать, что
(е,-, Л ... Л е1р) Л (е|р+1 Л ... Л etp+j = (е.^ Л ... Л etp+j.
Упражнение 2.6.3. Показать, что обобщенный символ Кронекера обладает
следующими свойствами в Сп:
{п(п — 1)... (п — т -f 1), т < п,
*' ' t'i...tm •l«»»*m*
0, т> п,
ГЛАВА 3
ГРУППЫ ПРЕОБРАЗОВАНИЙ
Вернемся теперь в трехмерное евклидово пространство К3, и рас-
рассмотрим линейные преобразования координат в нем. Множество та-
таких преобразований может образовывать особую алгебраическую
структуру - группу. Вообще теория групп, у истоков которой стоял
блистательный французский математик XIX века Э.Галуа, в настоя-
настоящее время является одним из важнейших разделов алгебры. Группы
широко применяются не только в математике, но и в механике, фи-
физике, квантовой химии, кристаллофизике и др. В данной главе мы
познакомимся с понятием группы на примере групп линейных преоб-
преобразований в К3.
§ 3.1. Линейные преобразования координат
3.1.1. Формы представления линейных преобразований
координат
В евклидовом пространстве Е3 рассмотрим частный случай преоб-
преобразований координат A.4).
Линейное преобразование координата определим как
X* = А\ х* + Aj, х* = B{jXj + B\ C.1)
где А3{ и A*, B*j и BJ не зависят от х% и ХК Преобразование C.1)
называют также аффинным.
В случае центральных преобразований: А1 = В% = 0. Каждому ли-
линейному центральному преобразованию соответствует матрица А1;-,
являющаяся обратной к В1 •:
А<^к = А\В<; = 61 C.2)
Будем далее также использовать матричное представление преоб-
преобразований C.1) с помощью матриц 3x3:
(А\ А\ А\\
(А',)=\А\ А\ А\\. C.3)
\А\ А\ А\)
158.
Глава 3. Группы преобразований
х t010]
@10)
С. 5.i. Обозначения кристалло- Рис. 3.2. Обозначения кристалло-
кристаллографических осей графических плоскостей
Кроме того для описания линейных преобразований иногда удобно
использовать кристаллографические оси, проходящие через начало
координат О и вектор h:
Для таких осей используют обозначения: [h}h2hz], а кристаллографи-
кристаллографические плоскости, ортогональные к этим осям h, обозначают круглы-
круглыми скобками: (Л1 Л2Л3). Например, сами координатные оси Оха в этих
символах будут обозначены как [100], [010] и [001]. Ось, проходящую
через главную диагональ куба, обозначим как [111] и т.п. (рис.3.1).
Если h% принимают отрицательные значения, то в этом случае над
ними сверху ставится черта, например [110]. Примеры кристаллогра-
кристаллографических плоскостей приведены на рис.3.2.
Рассмотрим важные частные случаи центральных преобразований.
3.1.2. Важнейшие линейные преобразования
1) Унимодулярными называют преобразования, определитель матри-
матрицы которых A*j не меняет знака:
det {А*;) = 1 (или- 1).
C.4)
2) Ортогональными называют преобразования, которым соответству-
соответствует ортогональная матрица А
A.212)):
• (для нее выполняются условия
и Я',В,.'=#, C-5)
§3.1. Линейные преобразования координат 159
согласно результатам п. 1.6.3, ортогональное преобразование - это по-
поворот вокруг какой-либо оси или отражение относительно какой-либо
плоскости.
3) Собственно ортогональными называют преобразования, для кото-
которых одновременно выполнены условия C.4) и C.5).
4) Преобразованием трансеерсальной изотропии называют преобра-
преобразование поворота вокруг оси Ох$ на произвольный угол $, матрица
A*j которого имеет вид:
(cos ф ьтф О \
- sin ф cos ф О 1 , где 0 < ф < тт. C.6)
О 0 1/
Для этой матрицы выполнены соотношения:
А^А{к = б1 A3i=6f, А<3 = 6'3.
Ось Охз в этом случае называют осью бесконечного порядка (или
осью трансверсальной изотропии).
Подставляя C.6) в C.1), получаем соотношения между "старыми"
хх и "новыми" -X координатами (рис.3.3):
X1 = cos фх1 + sin фх2, X2 = - sin фх1 + cos фх2, X1 = ж3. C.7)
Рассмотрим далее частные случаи преобразования трансверсаль-
трансверсальной изотропии.
5) Тождественное преобразование, которому соответствует единич-
единичная матрица:
/1 0 0\
(А*,-) = Е = 0 1 0 , C.8)
\0 0 \)
означает поворот на угол ф = 0 или 2тг.
6) Преобразование поворота на угол ф = тг/2 вокруг оси Ох3:
C.9)
Преобразование поворота на угол ф = -кII вокруг осей Ох\ и 0x2
определяется аналогично:
/1 0 0\ /0 0 -Г
Ql12 = 0 0 1 , Ql12 =01 0 | . C.10)
Vo-io/ Vioo
160.
Глава 3. Группы преобразований
Х3=Х3
I
::::::::::!Ту?!т*
X2=X2
PtJC. 5.5. Преобразования
Puc. 3.4' Преобразование зеркаль-
зеркального отражения R\
7) Преобразование поворота на угол ф = 2тг/3 и ф = -2тг/3 вокруг оси
Ох3:
-1/2 г/3/2 0\ /-1/2 -\/3/2 0\
^.) = 5Х = -л/3/2 -1/2 0 , 52 = г/3/2 -1/2 0 .
0 0 1/ \ 0 0 1/
C.11)
8) Преобразование зеркального отражения относительно плоскостей
0 @х1хз и Ох\Х2 определяется, соответственно, матрицами:
C.12)
'j) = Й1 = I 0 1 0 I ,
' 1 0 0
Д2 = ( 0 -1 0 ,
,0 0 1
при этом одна из осей меняет свое направление на противоположное,
а две другие не изменяются (рис.3.4).
Девять независимых преобразований
В, Ql'2, Ra,S^ a = 1,2,3; 7 = 1,
C.13)
играют ключевую роль в описании свойств симметрии тел (см. далее
§3.3): кристаллов, композиционных материалов и т.п. Суперпозицией
§3.1. Линейные преобразования координат
этих девяти преобразований можно построить еще двенадцать важ-
важнейших преобразований:
С = Д1-Д2-Дз а,/3= 1,2,3; /3 ^«, C.13а)
где индексы а,/3 выбираем круговой перестановкой: (а,/3) = A,2),
B,3) и C,1), т.е.
Ti = RzQl'\ T2 = R&l12, T3 = B2Q^/2.
Здесь и далее операции транспонирования ( )т и умножения (•)
матриц соответствуют операциям действий с тензорами второго ран-
ранга A.135) и A.139):
А\ А\ А\\
А\ А\ А\ , C.14)
А\ А\ А\)
а также
(Д1-Д2Г, = (Д1)Ч(Д3)*,-. C-15)
Напомним, что в декартовой системе координат хг матрицы Агк и
Af совпадают (см. п. 1.1.5.Б), т.е. А^ = А12 и т.д.
Запишем матрицы преобразований C.13а) явным образом.
9) Матрицы Qa определяют преобразование поворота на угол —тг/2
вокруг оси 0ха:
(зле)
Ю) Матрицы Da определяют преобразование поворота на угол тг во-
вокруг оси Оха:
/10 0
(Aij) = Dl= 0-10
\0 0 -1
^ Тензорное исчисление
162.
Глава 3. Группы преобразований
[ill]
Рис. 3,5. Преобразование отраже- Рис. 3,6, Преобразование попорота
ния Тз Мг
/-1 0 0 \ /-1 0 0\
?>2 = 0 1 0 , ?>з = 0 -10. C.17)
\ 0 0 -1/ V ° ° V
11) Каждая матрица Тр определяет преобразование отражения отно-
относительно плоскости, проходящей через ось Ох^ и равнонаклоненной к
двум другим координатным осям Оха, Ох1:
/1 0 0\ /0 0 1\ /0 1 0\
Ti = 0 0 1 , Г2 = 0 1 0 , Гз = 1 0 0 ) . C.18)
\0 10/ \1 0 0/ \0 0 1/
Ось Ох& при этом преобразовании остается на месте, а оси Оха и Ох1
меняются местами (рис.3.5).
12) Матрицы М7 определяют преобразования поворота на угол ^-2-п/Ъ
вокруг оси [111], при этом изменяется нумерация всех трех координат-
координатных осей Ох*:
'0 1 0>
М1 = ( 0 0 1
1 0 0.
'о о Г
М2 = ( 1 0 0
0 1 0.
C.19)
Поворот всех координатных осей происходит в плоскости A11) (рис.
3.6).
13) Матрица С определяет преобразование инверсии (т.е. централь-
центрального отражения) относительно начала координат:
C.20)
§ 3.1. Линейные преобразования координат 163
Все перечисленные матрицы J57, Qq , Да, QZ* , Ах, Т/з, М7, С
образованы из элементов {0,1 и — 1}. Всего же ортогональных матриц
с такими элементами имеется только 50 штук. Оставшиеся 29 матриц
образуются суперпозицией из матриц C.13а):
RaTa, DaTp, DaM1, ДаМ7, CTQ, CM1 C.21)
a,/3= 1,2,3, 7=1,2.
(Три матрицы RQTp = QV при аф /З уже учтены при введении мат-
матрицы Qp , а три матрицы RpTQ = Qa - при введении поворотов
фГ . Далее для обозначения поворотов на ±тг/2 будем использовать
именно эти матрицы: RQTp и RpTQ).
С помощью же матриц 57 можно образовать еще 14 матриц:
CS-f, Да57, ?>aS7, a = 1,2,3, 7=1,2- C.22)
Итого имеется множество из 64 матриц C.13), C.13а), C.21) и C.22).
3.1.3. Тензоры линейных преобразований
С точки зрения теории линейных пространств, изложенной во вто-
второй главе, центральное преобразование координат C.1) соответствует
замене декартова базиса ё,- на новый ортонормированный базис е,-:
е,- = B^ej, ё,- = А^еи C.23а)
где В\ - обратная к Alj матрица.
Якобиевы матрицы Q3{, P*j на основании формул A.7) и A.11), а
локальные векторы базиса R,- и RJ на основании A.6) и A.19) вычис-
вычисляются для линейных преобразований C.1) следующим образом:
Q{j = Д1,., Р) = A'j, К{ = е,- = В\ё,-, R« = е{ = А*;**. C.236)
Векторы локальных базисов R,- и R1 для случая линейных ортого-
ортогональных преобразований координат обозначим далее как е,- и е*.
Если матрица Alj ортогональна, то базисы е1 и е,- также ортого-
ортогональны и совпадают, и
дц = В\ Bkj = Sijt gij = А\А*> = J«.
В самом деле, если выбрать в пространстве Е3 вектор х с коорди-
координатами хх в базисе ё,-, то в новом базисе е,- он будет иметь координаты
Х\ так как согласно C.1) и C.23) имеем: х = ж'ё,- = хгА\е± =
164 Глава 3. Группы преобразований
Сравнивая формулы C.23) с B.63), устанавливаем, что в рассмат-
рассматриваемом случае матрица S%j перехода от одного базиса к другому,
введенная в п.2.3.3, суть
причем ё, = е(-. Однако если Slj была введена нами для произвольных
базисов, то в данной главе и в последующих матрица A1 j связывает
специальный фиксированный декартов базис ё, с ортогональным ба-
базисом е,-.
Тогда можно образовать тензор второго ранга
Q = 4>>ie''®el-, C.24)
который называется тензором линейных преобразований.
Если матрица Alj - ортогональная, то в силу C.5) и A.70) тен-
тензор Q - тоже ортогональный. Для него транспонированная матрица
совпадает с обратной, поэтому получаем:
QT =В*&®ё>. C.25)
Таким образом, каждой из 64 ортогональных матриц преобразо-
преобразований C.8) - C.22) соответствует тензор линейных преобразований.
Будем эти тензоры обозначать той же буквой, что и матрицы, т.е.
Е, О;л/\ Ra, Sa и т.д.
Тензор Е, определенный таким образом, очевидно, действительно яв-
является метрическим тензором.
3.1.4. Изомерные тензоры
В формулах C.1) в качестве исходных для линейных преобразова-
преобразований были выбраны декартовы прямоугольные координаты хх в базисе
ё,. Однако это необязательное условие, линейное преобразование с
матрицами А3{ вида C.4) - C.22) можно построить для произвольных
прямоугольных координат Хп:
Xj =Aj{Xft\ Х'* = В^Х*.
Пусть линии действия ортогональных векторов е(- совпадают с ося-
осями системы координат Х'\ а векторы е,- - с Xх. Тогда с помощью
базиса е(- можно образовать тензор линейных преобразований Q':
Q'z^e'J'eeJ. C.25a)
§ 3.1. Линейные преобразования координат
.165
Рис. 3.7. Преобразование отражен Рис. 3.8. Преобразование JD2T1 по-
ния JD3T3 ворота с отражением
Вообще говоря, тензоры Q' и Q - различны, хотя компоненты у них
одинаковые.
Определение 3.1. Тензоры, обладающие одинаковыми компонен-
компонентами, но отнесенные к различным базисам, называют изомер-
изомерными.
Таким образом, каждый тензор линейных преобразований Q связан
с конкретной системой координат ж1, в то время как матрица преоб-
преобразований Alj может связывать различные пары систем координат.
Везде далее, если не оговорено специальным образом, будем считать,
что A*j относится к декартовой системе координат Охг с базисом ё,,
т.е. полагаем, что имеет место формула C.1).
Упражнения к § 3.1.
Упражнение 3.1.1. Показать, что матрицы DaTa имеют вид:
о о -Г
D2T2 = | 0 1 О
-10 0
и определяют преобразование отражения относительно плоскости, проходящей че-
Рез ось Оха и ось h с hQ = 1, hp = /l7 = -1 (рис.3.7). Здесь и далее во всех
Упражнениях а, /3, 7 меняются циклическим образом.
166.
Глава 3. Группы преобразований
Mm]
Рис. 3.9. Преобразование D2T1 по- Рис. 3.10, Преобразование поворота
ворота с инверсией D\ M\
Упражнение 3.1.2. Показать, что матрицы DpTQ имеют вид:
о о -Г
D3T2 = | 0 -1 0
1 0 0
и определяют преобразование поворота на угол ф = 7г/2 вокруг оси Оха с после-
последующим зеркальным отражением относительно плоскости, ортогональной к Оха
(рис.3.8), а матрицы 1)аТр имеют вид:
о о г
DiT2 = | 0 -10
-10 0,
'0 -1 0
D2T3 = | 1 0 0
О 0 -1
и определяют аналогичные преобразования с углом ф = — 7г/2.
Упражнение 3.1.3. Показать, что матрицы DpTQ и DQTp определяют од-
одновременно и преобразование поворота на угол ф = Ц11г/2 соответственно вокруг
оси Оха с последующей инверсией относительно точки О (рис.3.9).
§ 3.1. Линейные преобразования координат
.167
Рис. 3.11. Преобразование поворота Рис. 3.12. Преобразование поворота
DM CT3l
Упражнение 3.1.4. Показать, что матрицы DaMa имеют вид:
0 1 0 \ /0 0 1'
= 0 0 -1 , D2M2 =10 0
-1 0 0 / \0 -1 0,
и определяют преобразование поворота на угол ф = ^2тг/3 вокруг наклонной оси
h [111] (рис.3.10)
Упражнение 3.1.5. Показать, что матрицы DQMp имеют вид:
0 0 1\ /0—1 0
=|-1 0 0 , ?>3А/1 = [ 0 0 -1
0-10/ \ 1 0 0
и определяют преобразование поворота на угол ф = d:27r/3 вокруг оси h [111],
а матрицы DpMQ имеют вид:
о -1 о\ / о о -Г
= [ 0 0 1, D3M2 =1-10 0
-1 0 0/ \ 0 1 0
и определяют преобразование поворота на угол ф — :f27r/3 вокруг оси h [111]
(рис.3.11).
Упражнение 3.1.6. Показать, что матрицы CTQ имеют вид:
-1 0 0 \ / 0 0 -1'
= ( 0 0 -1 , СТ2 = 0 -1 0 j ,
0-10/ V -1 о о
168.
Глава 3. Группы преобразований
(Ill)
X1
Рис. 3.13. ПреобразованиеСМ\ по- Рис. З.Ц. Преобразование R\M\
ворота с отражением поворота с отражением
0-10
СТз = | -1 0 0
0 0 -1
и определяют преобразование поворота на угол ф — 7Г вокруг оси h с hQ = 0,
hp = 1, /l7 = —1 (рис.3.12).
У 3.1.7. Показать, что матрицы СМа имеют вид:
0 -1 0 \ / 0 0 -Г
= 0 0 -1 , СМ2 =1-10 0
-1 0 0/ \ 0 -1 0
и определяют преобразование поворота на угол ф = ^ртг/3 вокруг оси h[lll] с
последующим зеркальным отражением относительно плоскости A11) (рис.3.13).
Упражнение 3.1.8. Показать, что матрицы RQMa имеют вид:
/0 -1 0\ /00 1'
RXMX = 0 0 II, R2M2 =-100
VI 0 0/ V 0 1 0
и определяют преобразование поворота на угол ф = ^ртг/3 вокруг оси h[lll] с
последующим зеркальным отражением относительно плоскости A11) (рис.3.14).
Упражнение 3.1.9. Показать, что матрицы RQMp имеют вид:
0 0 -1
i?iM2 =10 0
о 1 о
§ 3.1. Линейные преобразования координат
.169
Рис. 3,15. Преобразование R$Mi Рис. 3.16. Преобразование R2M1
поворота с отражением поворота с отражением
и определяют преобразование поворота на угол ф = ±тг/3 вокруг оси h[lll] с
последующим зеркальным отражением относительно плоскости (Ш) (рис.3.15),
а матрицы RpMQ имеют вид:
/0 1 о \ /о о г
R2MX =0 0 -II, R3M2 =10 0
\1 0 0 / \0 -1 0,
и определяют преобразование поворота на угол ф — ^ртг/3 вокруг оси h[lll] с
последующим зеркальным отражением относительно плоскости A11) (рис.3.16).
Упражнение 3.1.10. Показать, что матрицы 22аТа имеют вид:
'О 1 О
Д3Тз = | 1 О О
,0 0 -1
и определяют преобразование поворота на угол ф = 7Г вокруг оси h с hQ '= 0,
/1^3 = /i-y = 1 (рис.3.17).
Упражнение 3.1*11. Показать, что матрицы Дз5"«у определяют преобразо-
преобразование поворота вокруг оси Ох на угол ф = ±2тг/3 с последующим отражением
относительно плоскости поворота @01).
Упражнение 3.1.12. Показать, что матрицы RiSi, R1S2, R2S1 и R2S2
определяют преобразование зеркального отражения относительно плоскостей
Aд/30), Aл/30), (л/310), (\/310), соответственно (рис.3.18).
^Праж:нение 3.1.13. Показать, что матрицы D^S^ определяют преобразо-
преобразование поворота вокруг оси Ох на угол ф = ±7г/3.
170.
Глава 3. Группы преобразований
Д1Т1
. 5.17. Преобразование поворота Рис. 3.18, Преобразование отраже-
(ШО)
Рис, 3.19. Преобразование поворота
Упражнение 3.1.14. Показать,
что матрицы DiSij D1S2, D2S1 и
D2S2 определяют преобразование пово-
поворота на угол ф = 7г/2 вокруг осей h:
[1л/зо], [iV5o], [V310] и [Узю], со-
ответственно (рис.3.19).
Упражнение 3.1.15. Показать,
что матрицы CiS-y определяют преобра-
h[lY3] зование поворота на угол ф = d:27r/3
вокруг оси Ох с последующей инвер-
инверсией относительно точки О.
Упражнение 3.1.16. Показать, что матрицы С57 определяют также пре-
преобразование поворота на угол ф = Т^/З вокруг оси Ох с последующим зер-
зеркальным отражением относительно плоскости поворота @01), 7 = 1» 2.
Упражнение 3.1.17. Показать, что матрица поворота Q3 C6) имеет сл6"
дующие собственные значения:
А! = е1*, А2 = е-1*, А3 = 1.
Упрахснение 3.1.18. Показать, что матрицы 7? имеют следующие собст-
собственные значения:
Ао,/3 = 1> ^7 = ""!» а =1,2,3.
Упражнение 3.1.19. Показать, что матрицы Мр имеют следующие собст-
собственные значения:
1 .лД
А/з = 1, А7|в = --±1—.
§ 3.2. Группы преобразований в евклидовом пространстве
§ 3.2. Группы преобразований
в трехмерном евклидовом пространстве
3.2.1. Определение группы
Рассмотрим теперь не одно, а множество преобразований коорди-
координат C.1). Оказывается, что эти множества могут обладать опреде-
определенной симметрией, например, образовывать группу.
Определение 3.2. Множество М называют группой G, если
в нем определена операция умножения
а.ЬеМ —у с = а-ЬеМ, C.26)
которая обладает следующими свойствами:
1° ассоциативность
(а -6) -с = а- (Ь-с),
2° существует левая единица, т.е. такой элемент е ? М, что
е- а = а,
3° для любого а существует левый обратный элемент а ? М та-
такой, что
а • а = е.
Группу G называют коммутативной (или Абелевой), если
а-Ь=Ь-а. C.27)
Если группа имеет конечное число элементов, то ее называют то-
точечной (или конечной); если бесконечное, то - непрерывной.
3.2.2. Сингонии, классы и группы симметрии
Поскольку у нас определено произведение двух матриц Alj и В3к
~ это матрица С\ с компонентами Сгк = A1 jBJk, определена единич-
единичная матрица &у. Alj6Jk = A\, и для всякой невырожденной матрицы
существует обратная: А1 ^{А~1)\ = 5к, то множества матриц могут
образовывать группы.
Оказывается, что из 64 преобразований, описываемых матрицами
C.13), C.13а), C.21) и C.22), можно образовать 32 точечные груп-
группы преобразований, эти группы объединяют в 7 систем (сингонии),
сингонии состоят из одного или двух классов.
172 Глава 3. Группы преобразований
I. Триклинпая сингопия (триклинный класс Е):
группы: Gi = {#}, G2 = {Е, С}.
II. Моноклинная сингония (моноклинный класс (М)):
группы: G3 = {Я, Дз}, G4 = {Я, ?>3}, G5 = {Е, С, Д3,
///. Ромбическая сингония (класс ортотропии (О)):
группы: G6 = {E,RUR2,D3}, G7 = {E,DQ},
{}
IV. Тетрагональная сингония:
тетрагональный класс (Т):
группы: G9 = {Е, ?>3, #7Тз}, Сю = {Е, D3i RyT3}, j = 1,2;
Gn = {E, С, Дз, ?>з, ЯуТ3, ?>7Тз};
класс квазитрансверсальной изотропии (К3):
группы: G12 = {E, DQ, T3, ^aT3}, Gi3 = {Я, Л7, ^з, Т3>
, Gi4 = {^, Da, CT3, ДаГз}, G15 = {Е, С, i?a> i3a> 2з
СТз, ЛаТз^аТз} а = 1,2,3.
V. Ромбоэдрическая (гпригональная) сингония:
Л-ромбоэдрический класс (А):
группы: Gie = {JB, 57}, Gi7 = {Я, 57, С, С57};
В-ромбоэдрический класс (jB):
группы: Gi8 = {??,57, Ль ВД}, Gi9 = {^,57,
G20 = {Я, 57, С, С5 5}
VJ. Гексагональная сингония (гексагональный класс
G21 = {E,S^, Д3Лз57}, G22 = {i?,57, ?>3,^з57};
G23 = {i?, 57, С, С57, Д3, Дз57, ?>з,
= {??, 57, Д2, Д257, Д3,
7
G26 = {Я, 57, Ль fliS7l Д2, Д257, ZK
G27 = \Е, 57, С, С57, Да, RQSly DQ, i)a57},
7 = 1,2; а= 1,2,3.
V7/. Кубическая сингония (класс квазиизотропии (К)):
G28 = {E,Da,M1,DaM~f},
G29 = {Е, С, Да, Д,, М7, GMa, ДаМ7, DaM7},
G31 = {Я, Da, CTa, ДаТ^, М7,
G32 = {Е) С, Да,1)а,Та,СТа,
М7, СМ7, ДаМ7, ?>аМ7}.
В скобках указано обозначение класса J57, М, О, Т, Хз, -^, ^з,
Я.
§ 3.2. Группы преобразований в евклидовом пространстве
.173
Непрерывных групп, называемых также текстурами, существует
7 штук, объединенных в 2 класса.
Класс трансе ерсальной изотропии
Сзз = {Q& 0<Ф< 2тг}; G34 = {Qt, О < ф < 2тг;
G35 = {Qt 0 < ф < 2тг; ЗД*};
G36 = {Qt 0 < ^ < 2тг; ?>7Q*};
G37 = {Qt 0 < ф < 2тг; ?>7Q*, EaQ*} 7 = 1,2.
Класс изотропии (/):
i ° < ^ X < 2тг,0 < 0 < тг};
{^> 0 < Ф> X < 2тг, 0 < в < тг; ^}
Здесь обозначена матрица поворота С}фХв на углы ф, х и 0 вокруг
осей Ож,-, ее компоненты имеют вид:
+ сфзхсв -зфзх + сфвхсв -сфзв | , C.28)
ев
где с = cos, 5 = sin.
Матрица Q% поворота на угол ф вокруг оси Ох^ определяется по
C.6).
Определение 3.3. Подгруппой Ss epynnuGs называется под-
подмножество элементов группы Gs, которое само образует группу
относительно той же операции умножения, которая определена в
G
Отношение групп 5, и G8 в этом случае обозначают S8 С Gs.
Максимальной группой в классе называют такую G,, для которой
выполняется соотношение Gi С Gs для всех групп из данного класса.
Максимальные группы в классах показаны в табл.3.1.
Таблица 3.1
Класс
Максимальная
группа
Класс
Максимальная
группа
Е
G3
м
G5
0
Gs
т
Gn
Кз
Аз
Вз
G20
К
(?32
Тз
G3<
I
<?39
174 Глава 3. Группы преобразований
Эти группы иногда называют соответственно названию класса: Gs
- моноклинная группа, G& - группа ортотропии, <?34 - группа транс-
версальной изотропии и т.д.
Группа изотропии G39 совпадает с полной группой ортогональных
преобразований /, содержащей все ортогональные матрицы C.5) (см.
упр.3.2.8).
3.2.3. Оси анизотропии
Поскольку с каждым преобразованием координат C.1) можно свя-
связать как матрицу преобразований А3{, так и тензор Q линейного пре-
преобразования, то введенным выше группам преобразований Gs
(s = 1,.. .39) соответствуют не только группы матриц А*{, но также
группы, составленные из соответствующих тензоров преобразований.
Буквенные обозначения для элементов этих групп одинаковы и соот-
соответствуют обозначениям п.3.2.2.
Так как тензоры линейных преобразований определены нами по
формуле C.24) в некотором фиксированном базисе, например ё,, то
и группы тензоров преобразований будут отнесены к тому же базису,
который называют кристаллофизическим базисом, а линии действия
векторов этого базиса называют осями анизотропии.
Далее, если не оговорено специальным образом, подразумевается,
что группы тензоров преобразований отнесены к декартову базису ё,-.
3.2.4. Симметрическая группа
Множество всех подстановок (mi... rrin) длиной п также образует
группу, поскольку в этом множестве имеется единичный элемент -
тождественная подстановка A2...п), определены произведение под-
подстановок (см. п.1.8.2): (mi.. .mn)(ii... г„) = (mtl ... mtn) и обратная
подстановка (mi.. .mn)(wi.. .wn) = A2 .. .п). Эту группу называют
симметрической.
Упражнения к § 3.2.
Упражнение 3.2.1. Показать, что множества преобразований, представлен-
представленных в п.3.2.2, действительно являются группами, т.е. удовлетворяют определению
3.2.
Упражнение 3.2.2. Показать, что внутри классов имеют место следующие
отношения групп:
Vi GiCG,-, г = 1,...32; G,- С G5, i = 3,4,5;
G,CG8, 2 = 6,7,8; G.CGn, 2 = 9,10,11;
г = 9,... 15; G16 С Gi7, G{ С G20 г =16,...20;
i С G27, г = 21,.. .27; G, С G32, г = 28,... 32;
§ 3.3. Симметрия конечных тел _175
Gi С <?37, г = 33,.. .37; G38 С G39.
Упражнение 3.2.3. Показать, что
Упражнение 3.2.4. Показать, что группа G34 является максимальной по
отношению ко всем группам точечных классов, а G37 является максимальной ко
всем группам (?,-, i = 1,. . . 37.
Упражнение 3.2.5. Показать, что все линейные невырожденные (det Alj ф
0) преобразования, определяемые по C.1) образуют группу линейных преобразо-
преобразований.
Упражнение 3.2.6. Показать, что все нелинейные невырожденные преоб-
преобразования координат, определяемые формулами A.4), образуют группу криволи-
криволинейных преобразований.
Упражнение 3.2.7. Показать, что множество всех унимодулярных преоб-
преобразований C.4) образуют группу, называемую Собственной унимодулярной
()
()
Упражнение 3.2.8. Показать, что все ортогональные преобразования C.5)
образуют группу, называемую полной группой ортогональных преобразо-
преобразований. Показать, что эта группа совпадает с группой изотропии G39 = -f •
Упражнение 3.2.0. Показать, что собственно-ортогональные преобразова-
преобразования образуют группу, которая называется группой собственно-ортогональ-
НЫХ преобразований (/о)* Показать, что эта группа совпадает с группой
С 1
з8 о
Упражнение 3.2.10. Показать, что множество всех преобразований C.4), в
которых допускается как +1, так и — 1, образуют группу, называемую полной
унимодулярной (U).
Упражнение 3.2.11. Показать, что из определения 3.2 следует, что левая
единица является также и правой единицей, а левый обратный элемент является
также и правым обратным.
§3.3. Симметрия конечных тел
3.3.1. Симметричные тела
До сих пор мы рассматривали свойства только самих преобразо-
преобразований координат C.1). Пусть теперь в пространстве Ш3 определена
некоторая ограниченная замкнутая область V. Будем называть ее
далее конечным телом V.
Тело V называют неоднородным (составным или кусочно-однород-
кусочно-однородным), если для него введено разбиение на конечное число замкнутых
областей VJ, общими точками которых могут быть только точки на
их границах. Если же для области V такое разбиение не введено, то
будем называть тело V геометрически однородным или просто одно-
однородным.
176.
Глава 3. Группы преобразований
Без ограничения общности будем
рассматривать далее тела, обра-
образующие связные множества. Ес-
Если введена некоторая система ко-
координат хх, то каждой точке тела
М G V можно взаимнооднозначно
поставить в соответствие коорди-
координаты х% ? V, т.е. ввести биектив-
биективное отображение
<р : V —> V С М3.
Однако такое отображение не
единственно возможное. Перехо-
Переходя к новой системе координат Xх,
получим другое отображение <рх-
V —У Vx С М3, где Vx ~ область
изменения координат Xх точек
MeV (рис.3.20).
Исследуем как связаны между собой образы тел V и Vx, если сис-
системы координат хх и Xх связаны ортогональными преобразованиями
C.1).
При таких преобразованиях каждая точка М тела с координатами
ххм в области V имеет координаты XЗм в области Vx» причем рассто-
расстояние s между любыми двумя точками М и Л/\ принадлежащими V, в
областях V и Vx не меняется, так как
Рис, 3.20. Преобразование тел при
ортогональных преобразованиях коор-
координат
Q=l
Q=l
C.29)
а=1
согласно свойству C.5). Это означает, что при ортогональных преоб-
преобразованиях область V преобразуется в область Vx как жесткое целое
в пространстве Е3.
Определение 3.4. Будем говоришь, чтпо тело V обладает сим-
симметрией (является симметричным) относительно ортого-
ортогонального преобразования C.1)f если образ тела V до и после такого
преобразования неотличим (т.е. области V и Vx совпадают).
Если тело V - неоднородное, то для его симметрии необходимо,
чтобы области V% и Vix совпадали.
Тело может быть симметричным относительно нескольких преоб-
преобразований.
§ 3.3. Симметрия конечных тел
.177
Рис. 3,21. Пример оси симметрии Рис. 3.22. Пример оси симметрии
четвертого порядка третьего порядка
Определение 3.5. Будем говорить, что тело является сим-
симметричным относительно группы Gs, если оно симмет-
симметрично относительно каждого преобразования в этой группе.
3.3.2. Оси симметрии
При ортогональных преобразованиях, как было показано в п. 1.6.3,
образ тела V может либо поворачиваться вокруг некоторой оси, либо
зеркально отражаться относительно некоторой плоскости или центра.
В первом случае det (Alj) — 1, во втором - det (Alj) — — 1. Возможно
также совместное действие этих преобразований.
Анализируя приведенные в п.3.1.2 матрицы Аг j ортогональных пре-
преобразований, нетрудно заключить, что в рассмотренных выше то-
точечных группах присутствуют позороты только на углы: тг/3, тг/2,
B/3Oг, тг и 2тг, т.е. на 2тг/п, где п =1, 2, 3, 4 и 6. Поворот на 0°
эквивалентен повороту на 2тг. Вообще же для конечных тел возмож-
возможны повороты и на другие углы, при которых имеет место симметрия.
Обоснование, почему в группах G5, s = 1.. .32, присутствуют только
указанные повороты, мы дадим в п.3.3.11.
Поворот на углы 2эт и 0° является тождественным преобразованием
и описывается матрицей Е. Матрицы Аг^ соответствующие другим
углам поворота, указаны в п.3.1.2.
Если тело V - симметрично относительно преобразования поворота
на угол 2тг/п, то говорят, что оно обладает осью симметрией п-ого
порядка.
На рис.3.21 изображено неоднородное тело, имеющее вертикальную
ось симметрии четвертого порядка. Тело, изображенное на рис.3.22,
имеет ось симметрии третьего порядка h[lll], равнонаклоненную к
178.
Глава 3. Группы преобразований
Рис. 3.23. Оси симметрии для
куба с шаром внутри
Рис, 3.24- Оси симметрии бесконечного
порядка для конуса, цилиндра и шара
координатным осям Ох1.
Одно и то же тело может иметь несколько осей симметрии. Так куб
с шаром внутри имеет четыре оси третьего порядка, направленные по
главным диагоналям куба, три оси четвертого порядка, нормальные
к каждой паре параллельных граней, и шесть осей второго порядка,
проходящих через середины ребер, противолежащих по отношению к
центру куба (рис.3.23). Символически эти оси изображены следую-
следующим образом:
• п = 2, А п = 3,
¦ п = 4, Ш п = 6.
Для них также используют название главные оси симметрии.
В непрерывных группах Тз-класса возможны повороты на произ-
произвольный угол относительно оси 0ж3, а в группах изотропного класса
- относительно любой оси. Такие оси называют осями бесконечного
порядка. На рис.3.24 показано, что, например, тело V в виде кону-
конуса имеет одну ось бесконечного порядка, а шар - бесконечное число
таких осей.
3.3.3. Плоскости симметрии и центр симметрии
Если тело V является симметричным при преобразованиях отраже-
отражения относительно некоторой плоскости, то говорят, что оно обладает
плоскостью симметрии.
Преобразование отражения относительно плоскостей Ох^х1 описы-
описывается матрицами RQ (см. §3.1).
Последовательное отражение относительно трех координатных
плоскостей приводит к преобразованию инверсии, являющейся отра-
отражением относительно точки О - центра симметрии. Это преобразо-
преобразование описывает матрица С.
§ 3.3. Симметрия конечных тел _179
Если тело V является симметричным при преобразованиях инвер-
инверсии, то его называют центрально-симметричным. На рис.3.21 изобра-
изображено тело, имеющее плоскость симметрии, а на рис.3.23 - центрально-
симметричное тело.
3.3.4. Зеркально-поворотные и инверсионно-
поворотные оси
Комбинация поворота на угол 2тг/п вокруг какой-либо оси и отра-
отражения относительно плоскости поворота называется зеркально-пово-
зеркально-поворотным преобразованием. Если тело V является симметричным от-
относительно такого преобразования, то говорят, что оно обладает зер-
зеркально-поворотной осью п-ого порядка. Комбинацию оси бесконеч-
бесконечного порядка и ортогональной к ней плоскости зеркального отражения
называют зеркально-поворотной осью бесконечного порядка.
Если тело V является симметричным при преобразованиях поворо-
поворота на угол 2тг/п вокруг какой-либо оси с последующим отражением
относительно центра О, то говорят, то тело обладает инверсионно-
поворотной осью п-ого порядка.
3.3.5. Соответствие между элементами симметрии и
матрицами преобразований
Оси и центр симметрии, а также плоскости отражения называются
элементами симметрии. Каждую матрицу Alj ортогонального пре-
преобразования можно отнести к одному из элементов симметрии. Ни-
Ниже, на основании результатов п.3.1.2 и упражнений к §3.1, приведена
таблица 3.2 соответствия между матрицами преобразований Alj то-
точечных групп Gs и элементами симметрии, здесь а ф /3 ф 7 ф р,
а,/3=1,2,3,7,/>=1,2.
3.3.6. Классы сопряженных элементов
Рассмотрим теперь вопрос о том, какие из элементов симметрии
входят в каждую группу Gs • Для этого вначале выясним возможность
переставимости операций умножения матриц в группах или, что то
же самое, о переставимости операций симметрии. Если для любой
пары матриц преобразований Аг^ Ю^ из группы Gs их произведение
переставимо:
А-К = К-А, VA,KeG,, C.30)
то такая группа, как было отмечено в п.3.2.1, называется коммута-
коммутативной.
Однако свойством коммутативности обладают только некоторые
группы преобразований Gs (какие именно будет указано ниже). Для
некоммутативных групп Gs целесообразно ввести некоторое разделе-
разделение элементов группы на классы сопряженных элементов. Покажем
как это можно осуществить.
180.
Глава 3. Группы преобразований
Таблица 3.2.
Элемент симметрии
1. Ось симметрии 71-ого
порядка (поворот):
71 = 1 (тождественное
преобразование)
71 = 2
71 = 3
71 = 4
71=6
2. Плоскость симметрии
(зеркальное отражение), 771
3. Зеркально-поворотные оси
71-ого порядка:
4. Инверсионно-поворотные оси
71-ого порядка:
71= 1
71= 3
71 = 4
5. Центр симметрии С
Матрицы преобразований А'•
Е
DQ, CTQ, RQTQ
D$S-f
XLq , JL q , UCX J-Q.') -*t-y >Jp
CMa, RqMq , RQMp, CS-y
С
cs1
с
Перепишем операцию коммутативности C.30) в виде:
C.31)
или, учитывая, что А и К - ортогональные матрицы, получим:
Кт - А • К = А. C.32)
Проверку коммутативности группы Gs можно проводить следую-
следующим образом: выбирать поочередно элементы А из группы (для не-
непрерывных групп надо указать некоторое правило перебора всех эле-
элементов) и составлять произведения Кт • А • К со всеми остальными
элементами группы.
Если окажется, что для некоторого К ? G8 выполнено
КТАК =
C.33)
§ 3.3. Симметрия конечных тел
то группа G8 является некоммутативной. Однако, поскольку резуль-
результат произведения - Р, очевидно, всегда будет принадлежать группе
Gs\ после того как К пробежит всю группу СЛ, можно объединить
все получившиеся значения Р в одно множество ? вместе с А. Это
множество называют классом сопряженных элементов группы. Если
теперь менять сам элемент А, пробегая всю группу Ge, то эта группа
окажется разбитой на несколько классов ?,-.
Оказывается, что в каждый класс сопряженных элементов попада-
попадают только однотипные матрицы А, т.е. те, которым соответствуют,
например, повороты на угол тг/2 или только на угол 7г/3, или только
плоскости симметрии, поэтому разбиение группы на классы полезно
при рассмотрении симметрии тел.
3.3.7. Пример нахождения класса сопряженных
элементов
Рассмотрим пример построения классов сопряженных элементов
(не следует их путать с классами симметрии Е, М, О и др.) для
^-ромбоэдрической группы Gi&. Эта группа (см. п.3.2.2) состоит из
шести элементов:
Gis = {E, Si, S2, Ri, RiSi, RiS2}. C.34)
Зафиксируем элемент Si и вычислим его произведение R^ • Si • Ri.
Умножая матрицы, получим:
/-1 0 0\ / -1/2 V3/2
Rf.Si.Ri= 0 1 0 -v^/2 -1/2 О
\ 0 0 1/ \ 0 0
/-1/2 -V3/2 0\
= V3/2 -1/2 0 = S2, C.35)
\ О 0 1/
-1
0
0
0
1
0
°\
0 =
1/
т.е. группа Gis удовлетворяет условию C.33) и является некоммута-
некоммутативной. Продолжим перебор элементов группы, учитывая при этом,
что Si = S5T:
Здесь учтена ортогональность всех матриц в группах Gs. Используя
результат C.35), получаем:
(Ri • Si)T . Si • (Ri • Si) = S[ • {R* • Si • Ri) • Si = S2 • S2 • S^ = S2)
(H.i-S2)T-Si-(RrS2) = S^.(Rf-SrRi)-S2 = S2, E-Si = Sb C.37)
132 Глава 3. Группы преобразований
Таким образом, все произведения вида C.33), где А = Si для всех К
из группы Gi8 дают только две матрицы: снова Si или S2. Следо-
Следовательно, класс сопряженных элементов, порождаемый элементом Si
состоит из двух элементов: Si = {Si, S2}.
Аналогичным способом несложно проверить, что класс, порождае-
порождаемый элементом S2, совпадает с Е\.
Зафиксируем теперь элемент Ri и вычислим для него произведение
C.33):
/-1/2 -уД/2 0\ /-1 О О'
S[ • Ri • Si = К/3/2 -1/2 0 0 10
\ о о 1/ \ о о 1,
/ -1/2 л/Ъ/2 0\ /1/2 \/3/2 0\
х -V3/2 -1/2 0 = уД/2 -1/2 0 = RiS2. C.38)
\ 0 0 1/ V 0 0 1/
Используя этот результат, далее находим:
S2 • Ri • S2 = S2 • Si • Ri • Si = Ri • Si,
(Ri • Si) • Ri * (Ri * Si) = Si • Ri * Ri • Ri * Si = Ri • S2, C.39)
^X\.l * 02J • JtCi * ^JtCi • O2j == »^2 • JtCi • JtCi • JtCi • 02 == xtl ' Oi,
Таким образом, все произведения вида C.33) для А = Ri в груп-
группе Gi8 дают либо Ri, либо R1S2, либо RiSi. Следовательно, класс
сопряженных элементов ?г» порождаемый элементом Ri, имеет вид:
?2 = {Ri, R1S1, R1S2}. Несложно проверить, что для элементов RiSi
и R1S2 классы сопряженных элементов будут совпадать с 5г»
Хотя единичный элемент Е всегда в тройном произведении даст
самого себя:
Кт . Е • К = Кт • К = Е,
его тоже можно отнести в самостоятельный класс - ?з-
Итак, мы установили, что группа Gis состоит из трех классов.
Запишем этот факт следующим образом:
Gie = {/S*/?i/?2/} = {/E/S1,S2/R1,R1S1,R1S2/},
отделяя классы сопряженных элементов наклонными чертами.
Посмотрим теперь, какие элементы попали в классы ?,-. Обеим
матрицам Si и S2, как следует из табл.3.2, соответствует ось симмет-
симметрии третьего порядка Ох3, Обозначим такой класс ?\ = 2C$Z. Трем
матрицам Ri, R1S1 и RiS2 из класса ?2, как следует из табл.3.2 и
упражнения 3.1.12, соответствуют плоскости симметрии A00), A\/30)
§ 3.3. Симметрия конечных тел
.183
и A\/30), пересекающиеся друг с другом под углом тг/3 и параллель-
параллельные одной и той же оси Ох3. Такой класс обозначим как ?2 =¦ Зстд.
3.3.8. Разбиение групп на классы
Для всех групп Gs (s =¦ 1...39) можно произвести разбиение на
классы сопряженных элементов указанным выше способом. Если в
какой-то группе Gs все классы ?,- окажутся состоящими только из
одного элемента, то это означает, что данная группа является комму-
коммутативной. Тем не менее, ради общности для коммутативных групп
также используют одноэлементные классы ?,.
Многие классы ?, встречаются в разных группах Gs, поэтому для
классов вводят специальные обозначения, по которым можно восста-
восстановить соответствующие элементы симметрии. Эти обозначения при-
приведены в табл.3.3, где Спх, Cny, Cnz - ось симметрии Ож1, Ох2, Ож3,
соответственно, имеющая n-ый порядок.
Таблица 3.3.
Обозначение
класса соп-
сопряженных
элементов
/С2х/С2у/
Сгг1
/с3г/си
/<WCi/
ISolSU
ls6*ISlzl
Элементы
группы в
классе
/Di/D2/D3/
/fc/ft/
/D3S1/D3S2/
jR3Si/R3S2l
/DlT3/D2T3/
/CS2/CS!/
Элементы
симметрии
одна ось.симметрии
второго порядка в
каждом классе
Оха,а = 1,2,3
одна ось симметрии
третьего порядка Ох
одна ось симметрии
четвертого порядка Ох
одна ось симметрии
шестого порядка Ох
одна зеркально-пово-
зеркально-поворотная ось третьего
порядка Ох
одна зеркально-поворотная
ось четвертого порядка Ох
одна зеркально-поворотная
ось шестого порядка Ох
Характер
матрич-
матричного пред-
представления
Х(А)
класса
-1
0
1
2
-2
-1
0
184.
Глава 3. Группы преобразований
Таблица 3.3. (продолжение)
зс2
2С2г
2C2d
6C2d
зс2Л
3C2ft
4C3ft
4С&
8С3
2С3г
2С4,
6C4d
456h
45б5Л
85б
-Dl,I>2
ДзТз.СТз
¦й<Да,СТа
?>2,?>2S7
M2,Z)QM2
JMi,A,ATl
M7,?>aAf7
Д1Т3, Л2Т3
Да^/3
СМ2,ДаМ2
СМьЛаМ1
СМ7,ДаМ7
три оси второго
порядка 0жа, а = 1, 2, 3
две оси второго
порядка Ох , Ож
две диагональные оси
второго порядка [111], [НО]
шесть диагональных осей
второго порядка по две в
каждой координатной плос-
кости [011], [011], [101],
[101], [ПО], [110]
три оси симметрии
второго порядка в одной
плоскости под углом 7Г/3:
[010], [V310], [\/ЗЮ]
три оси симметрии
второго порядка в одной
плоскости под углом 7г/3:
[100], [1\/30], [1ч/30]
четыре оси симметрии
четвертого порядка
[in], [Hi], [Hi], [Ш]
четыре оси симметрии
четвертого порядка
одна ось симметрии
второго порядка Ох
одна ось четвер-
четвертого порядка Ох
три оси четвертого
порядка Оха
четыре зеркально-поворотные
оси третьего порядка
[ш], [Hi], [ill], [Ш]
четыре зеркально-поворотные
оси третьего порядка
-1
-1
-1
-1
-1
-1
0
0
0
1
1
0
0
§ 3.3. Симметрия конечных тел
.185
Таблица 3.3. (продолжение)
2S±Z
654
253г
/сГХ/(Ту/(Т2/
Зстл
3G
2а2
2ad
6crd
?>iT3,?>2T3
DQTp
Дз57
/Л1/Л2/Л3/
Д1, Дх57
Лг, Лг^-у
Ла
Лх, Лг
Т3,?>зТз
TQ, ?>аТа
две зеркально-поворотные
оси четвертого порядка
Ох1, Ох2
три зеркально-поворотные
оси четвертого порядка
OxQ
одна зеркально-поворотная
ось Ох3
одна плоскость симмет-
симметрии, ортогональная Оха
три плоскости симметрии
под углами 7Г/3, па-
параллельные оси Ох :
A00), A\/30), (Ь/30)
три плоскости симметрии
под углами 7г/3, па-
параллельные оси Ох :
@10), (V310), (л/310)
три плоскости симметрии,
ортогональные Оха
две плоскости симметрии,
ортогональные Ох , Ож
две диагональные плос-
плоскости симметрии
(НО), (Ш)
шесть диагональных плос-
плоскостей симметрии
-1
-1
-1
1
1
1
1
1
1
1
В табл.3.4 приведены элементы симметрии для непрерывных
групп.
Здесь индексы а, /3 пробегают значения 1,2,3, причем всюду а ф /3;
индекс 7 принимает значения 1, 2. Буквы С означают оси симметрии,
S - зеркально-поворотные оси, а - плоскости симметрии. Цифра в
нижнем индексе означает порядок оси, буквы x,y,z в индексе означа-
означают координатные оси Ожа, буква h - признак гексагональной системы,
индекс d указывает на диагональные плоскости. Цифры перед буква-
Ми С, 5 и а означают число элементов в классе. Цифры в верхнем
индексе, например, С\г указывают на то, что преобразования симмет-
симметрии, описываемые матрицами данного класса, также можно получить
186.
Глава 3. Группы преобразований
трехкратным применением операции С*2 (повороты на —тг/2 и тг/2,
соответственно).
Наклонные черты отделяют один класс от другого. Разъяснение
объекта х(-А) будет дано в §3.7.
Заметим, что одни и те же матрицы в разных группах могут обра-
образовывать классы сопряженных элементов, а могут - нет.
Таблица 3.4-
Класс
сопря-
сопряженных
элементов
Сзоо
(ТЗф
Гф
ct
Coo
Я"оо
Элементы
группы в
классе
Qi
QiRz
R-tQi
D.Qt
Яф\в
Яа?}фхО
Элементы
симметрии
одна ось Ох бес-
бесконечного порядка
одна зеркально-по-
зеркально-поворотная ось Ох
бесконечного
порядка
одна плоскость
симметрии
одна ось вто-
второго порядка
одна произвольная
ось бесконеч-
бесконечного порядка
одна произвольная
плоскость
симметрии
Характер
матрич-
матричного пред-
представления
Х(А)
класса
2 COS ф + 1
2 cos ф — 1
1
-1
СО80 + A+
cos0) cos($ + х)
В табл.3.5 представлены классы всех групп Gs (s = 1...32), при
этом использованы обозначения классов из табл.3.3.
В этой же табл.3.5 приведены обозначения для групп симметрии,
часто используемые в литературе, - это международные (по Герману-
Могену) и по Шубникову. В этих обозначениях цифры указывают
порядок осей симметрии, т - наличие плоскостей симметрии, знаки
"/" или ":" означают, что плоскость симметрии перпендикулярна оси
симметрии, а отсутствие этих знаков означает, что она параллельна.
§ 3.3. Симметрия конечных тел
.187
Таблица 3.5.
Син-
гония
I.
Трик-
линная
П.
Монок-
Моноклинная
III.
Ромби-
Ромбическая
IV.
Тетра-
гональ-
гональная
Класс
сим-
симметрии
Е
Трик-
линный
м
Монок-
Моноклинный
0
Ортот-
ропный
т
Тетра-
гональ-
гональный
к3
квази-
транс-
версаль-
ноизо-
троп-
ный
Группа симметрии Gs
но-
номер
S
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
междуна-
международные
обозна-
обозначения
1
1
m
2
2/m
mm2
222
mmm
4
4
4/m
4 2m
4mm
422
4/mmm
обозна-
обозначение
по Шуб-
никову
1
2
m
2
2:m
2- m
2:2
m* 2* m
4
4
4:m
4* m
4:2
4:2
m*4:m
Классы
сопряженных
элементов
в группе
/Е/
/E/I/
/E/az/
/E/C2z/
/E/I/
/C2z/az/
/E/C2z/
/crx/cry/
/E/C2x/
/C2y/C2z/
/E/I/
/C2x/C2y/
C2z/crx/
/E/C2z/
/SiZ/S\z/
/E/C2l/
jC^zjC\zj
/E/I/C^l
/E/2StJC2z/
2C2z/2ad/
/E/C2z/2C4z/
2ad/2az/
/E/C2z/2C2J
2C2d/2Ci-J
/E/I/C2z/
/2C2Z/2C2d/
(Tz/2az/2ad/
188.
Глава 3. Группы преобразований
Таблица 3.5. (продолжение)
V.
Ромбоэд-
Ромбоэдрическая
(триго-
нальная)
VI.
Гексаго-
Гексагональная
VII.
Куби-
чес-
ческая
А
-Л-ромбо-
-Л-ромбоэдрический
в
jB-ромбо-
эдрический
я
Гексаго-
Гексагональный
К
Квази-
изо-
троп-
ный
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
3
3
Зт
32
3 т
6
6
6/т
6 т2
622
бтт
6/ттт
23
тЗ
43т
432
3
6
3* т
3:т
6- т
3:т
6
6:т
т*3:т
6:2
6*т
т*6:т
3/2
6/2
3/4
3/4
/Е/С32/С1/
/E/I/C32/Cl/
Se/Se/
/E/2C3z/Sah/
/E/2C3z/SC2h/
/E/I/2C3z/
ЗС2Л/256/3GЛ/
/E/C3z/Cl/
S32/S3z/crz/
/E/C3z/C&
c2jc6l/cl/
/E/I/C3l/Cl/
/С2,/С6г/С12/
/SlJS62/S3i/
/sLM/
/E/2C32/iC2h/
/35з,М/3(тЛ/
/E/2C3z/
/2С6г/С2г/
/ЗС2Л/ЗС2Л/
/Е/2С3г/2Сб1/
2/E/I/2C3z/
/2С6г/С2г/
/ЗС2Л/3G2Л/
/2C6z/2S3z/
/Е/ЗС2/
/4ClJ4C3h/
/E/I/
/ЗС2/4С|Л/
4C3h/45|h/
/E/2C2/BC3/
/6S4/6Gd/
/ IP 10 /~* 1Q /~* 1
1 •" / OU2/ О^З/
§ 3.3. Симметрия конечных тел
.189
Таблица 3.5. (продолжение)
трансвер-
сально-
изотроп-
ный
i
изот-
изотропный
32.
33.
34.
35.
36.
37.
38.
39.
m3m
ОО
ОО/т
ОО т
ОО 2
оо/тт
оо/оо
ООООт
6/4
ОО
ОО:т
ОО- т
ОО : 2
пгОО : т
оо/оо
Оо/оО:т
/Е/1/ЗС2/
/8C3/6C4d/
/6C2d/856/
/Сзоо/
/Сз<х,/сгзф/
/Сзоо/<Тф/
/Сзоо/Ct/
/Coo/
/Coo AW
Результат представленного выше разбиения групп на классы со-
сопряженных элементов можно оформить в виде следующей теоремы.
Теорема 3.1. Тело V симметрично относительно группы Gs
тогда и только тогда, когда оно обладает элементами симметрии,
входящими в соответствующую группу Gs.
Т Доказательство очевидно, так как выше мы установили взаимно-
взаимнооднозначное соответствие между группами Gs матриц преобразова-
преобразований из п.3.2.2 и группами из элементов симметрии, приведенных в
табл.3.5. А
3.3.9. Тела с периодической структурой
В механике и физике важную роль играют такие конечные тела V,
которые, периодически повторяясь, заполняют собой все пространство
Ш3. Рассмотрим их.
Определение 3.6. Периодической структурой Ру назы-
называют объединение всех образов Vn<* некоторого тела V, полученных
с помощью отображений ф^: V —У Vn* С К3, обладающих следую-
следующими свойствами:
1° каждое фпа задается трансляционным преобразовани-
преобразованием координат:
x° =
a = 1,2,3,
C.40)
где Xt% G V, Xх ? Уп<», аа - числа, называемые периодами, па -
целые числа (п1,?^2,?^3);
замкнутые области Vnc и Vnp при па ф п^ могут иметь общими
только граничные точки;
190.
Глава 3. Группы преобразований
Рис. 3.25, Периодическая структура
Ру кристалла с примитивной решет-
решеткой
Рис 3.26. Ячейка периодичности
дисперсно армированного композици-
композиционного материала с примитивной ре-
решеткой
3° объединение всех Vn<* покрывает Ш3, т.е. УХ% ? Е3 3Vn<*: Xх Е
Vna.
Координаты -X71 могут быть, вообще говоря, криволинейными, в
этом случае говорят, что Ру является криволинейной периодической
структурой. Если же Х1х - прямолинейные (не обязательно ортого-
ортогональные), то их называют кристаллографическими координатами.
Числа аа полагают фиксированными, а па - переменными, меняя
которые, получаем различные отображения фп<* тела V. Трансля-
Трансляционные преобразования C.40) представляют собой частный случай
линейных преобразований C.1), когда Alj = Sj и Аа = пааа. Тело V,
образующее периодическую структуру, называют ячейкой периодич-
периодичности.
Очевидно, что не всякое конечное тело V может образовывать пе-
периодическую структуру. В физике и механике чаще всего рассмат-
рассматривают ячейки периодичности в виде выпуклых многогранников. Ес-
Если в вершины такого многогранника V поместить атомы кристал-
кристалла (рис.3.25), полагая, что геометрически они соответствуют точкам
пространства, а все остальное пространство считать "пустотой", то
соответствующую периодическую структуру Ру называют кристал-
кристаллом с примитивной решеткой. Из таких ячеек периодичности (ре-
(решеток) состоят реальные кристаллы различных веществ. Аналогом
кристаллической решетки является периодическая структура, в кото-
которой многогранник V представляет собой неоднородное тело со сферо-
образными подобластями Vi, центры которых располагаются в вер-
вершинах многогранника (рис.3.26). Если эти подобласти Vi рассмат-
рассматривать как наполнитель, а остальное пространство многогранника V
как матрицу, то такую периодическую структуру называют дисперс-
§ 3.3. Симметрия конечных тел
но армированным композиционным материалом также с примитив-
примитивной решеткой.
3.3.10. Решетки Бравэ
Существует всего только семь различных примитивных решеток,
представляющих собой параллелепипеды, длины ребер которых рав-
равны периодам сц,а2>аз> а, углы между ними - 61,62,63. Все они изоб-
изображены на рис.3.27, там же указаны соответствующие значения пе-
периодов а, и осевых углов 6,-. Названия этих решеток являются произ-
производными от формы образованных ими тел, например, три различных
угла 6,- в каждой вершине дали основание для названия триклинной
решетки; решетка с одним только из 6,- непрямым углом названа мо-
моноклинной и т.п.
Кроме примитивных, существуют более сложные решетки, содер-
содержащие'"точечные" атомы (или сферообразный наполнитель) в центре
пары противолежащих граней (базоцентрированные решетки), или
в центре всех граней (гранецентрированные решетки), или в цент-
центре симметрии решетки (объемноцентрированные решетки). Ока-
Оказывается, что различных решеток, обладающих соответствующими
симметриями, существует еще семь штук: базоцентрированные мо-
моноклинная и ромбическая; объемноцентрированные ромбическая, те-
тетрагональная и кубическая, и гранецентрированные ромбическая и ку-
кубическая. Все они показаны на рис.3.27.
Совокупность из четырнадцати примитивных и перечисленных не-
непримитивных решеток называют решетками Бравэ.
Заметим, что для гексагональной и ромбоэдрической сингоний су-
существуют дополнительные часто используемые решетки. Объеди-
Объединив три примитивные решетки гексагональной сингоний, получим но-
новую уже непримитивную решетку, в основании которой лежит шес-
шестиугольник.
Для ромбоэдрической сингоний существует дополнительная непри-
непримитивная решетка с соотношением параметров как у гексагональной
(ai = а,2 ф аз, 61 = 62 = 90°, 6з = 120°), но с двумя дополнительны-
дополнительными внутренними "точечными" атомами, расположенными на главной
Диагонали с координатами X'3 = аз/3 и 2аз/3 (рис.3.28,6). Объединив
три такие решетки, получим, как и для гексагональной сингоний, еще
одну решетку, имеющую в основании шестиугольник (рис.3.28,в).
3.3.11. Симметрии решеток Бравэ
Совпадение названий семи примитивных решеток с названиями
гРУпп G,, объединенных в семь сингоний, объясняет следующая тео-
Рема.
Теорема 3.2. Решетки Бравэ каждой сингоний являются сим-
симметричными относительно групп G, из одноименной сингоний.
* Очевидно, что доказательство достаточно провести только для мак-
192.
Глава 3. Группы преобразований
Сингония
Решетки
Примитивная
Базоцентри-
рованная
Объемно-
центриро-
Гранецен-
трирован-
ная
Ириклинная
II Моноклинная
ах*аг*аъ*а{
0, = 02 = 90" * въ
III Ромбическая
вх = в2 = 9Ъ = 90°
IV Тетрагональ-
Тетрагональная
а, = а2 * аг
V Ромбоэдричес-
Ромбоэдрическая
VI Гексагональ-
Гексагональная
0t=e2= 90е, 03=12Ов
VII Кубическая
вг=въ= 901
Ж.
---¦-¦4
\
ш
Рис. 3.27. Решетки Бравэ
§ 3.3. Симметрия конечных тел
Л 93
б)
Рис. 3.28. Дополнительные решетки для гекса-
гексагональной (а) и ромбоэдрической (б) и (в) сингоний
X'2
симальных групп в каждом классе, тогда для остальных групп, яв-
являющихся подгруппами максимальной группы, теорема также будет
верна.
Введем кроме кристаллографических координат Xх еще одни - пря-
прямоугольные декартовы координаты хх с базисом ё,-, называемым в
соответствии с п.3.2.3, кристаллофизическим базисом. Точку О на-
начала координат х% поместим в центр симметрии решеток, что всегда
возможно, так как у всех решеток она имеется и расположена на пере-
пересечении главных диагоналей. Оси Охх направим следующим образом:
сингоний:
• триклинная, моноклинная: Ох3 1 (O'XflX'2), Ox2 \\ ОХп\
• ромбическая, тетрагональная: Охх || O'Xfx;
кубическая
• ромбоэдрическая, гексагональная: Ox3 J_ (O'XflXf2), Ox2 \\ OX12,
где || означает параллельность, a J_ - ортогональность оси к плоскос-
плоскости. Для ромбоэдрической и гексагональной сингоний выбираем ре-
решетки с шестигранником в основании (рис.3.28).
Используем представление группы Gs с помощью элементов сим-
симметрии, приведенных в табл.3.5, и покажем, что решетки являются
симметричными в построенных осях Ох1.
Триклинная решетка, очевидно, симметрична относительно груп-
группы С?2, так как в ней только один элемент симметрии - центр сим-
симметрии.
Нетрудно убедиться, что моноклинная решетка, у которой единст-
единственный непрямой угол в$ лежит в плоскости сг2, ортогональной оси
Ох3, будет симметричной относительно этой плоскости. Поскольку
четыре грани этой решетки параллельны оси Ох3, а две другие пред-
представляют собой параллелограмм, через пересечение диагоналей кото-
которого проходит ось Ох3 (см. рис.3.27), то эта ось будет осью симметрии
второго порядка решетки.
7 Тен:
'зорное исчисление
194 Глава 3. Группы преобразований
Проверяя таким образом все решетки на симметричность относи-
относительно элементов симметрии из табл.3.5, убеждаемся в справедливос-
справедливости теоремы. Подробный анализ остальных решеток оставим в качест-
качестве упр.3.3.1. А
Докажем теперь обещанную ранее теорему, объясняющую, почему
в точечных группах Gs содержатся повороты только на углы 0, тг/4,
тг/3, тг/2 и тт.
Теорема 3.3. Решетки Бравэ могут иметь оси симметрии
только п-го порядка, где п=1, 2, 3, 4 и 6.
Т Пусть имеется некоторая ось симметрии ОХ n-го порядка тела V,
образованного одной из решеток Бравэ. Тогда при любом повороте во-
вокруг этой оси на угол у>, сохраняющем симметрию, каждая из вершин
решетки (например, точка А на рис.3.29) перейдет снова в вершину
(например, в точку j4i), причем отрезок АА\ будет лежать на прямой
Zi2, параллельной плоскости поворота ?. Если мы осуществим еще
один поворот на угол (р в плоскости ?, то рассматриваемая вершина
перейдет в новую вершину - точку Лг, причем отрезок А\А2 также
будет лежать на прямой /23? параллельной плоскости ?. Так как при
повороте вокруг оси расстояния от точек до оси не меняются, то при
одном и том же угле поворота (р получаем, что \AAi\ = \AiA2\. Осу-
Осуществляя п поворотов на угол (р вокруг оси О-Х", получаем, что все
точки А\... Ап лежат в одной плоскости ?', параллельной плоскости
поворота Е, и образуют правильный п-угольник.
Но поскольку все А\...Ап - вершины решетки Бравэ, то у нее в
одной плоскости могут лежать только четыре или шесть вершин. Так
как фиксированная вершина при поворотах переходит не обязательно
во все остальные, лежащие с ней в одной плоскости ?', то имеются еще
две возможности образования правильного n-угольника: при п =2 и
3. Присоединяя тождественное преобразование с (р = 0, окончательно
получаем: п =1, 2, 3, 4 и 6. А
3.3.12. Периодические структуры для непрерывных групп
Примеры тел, симметричных относительно непрерывных групп Gs,
s = 33...39, приведены на рис.3.27. Периодическая структура мо-
может быть построена и для этих групп, однако ячейку периодичнос-
периодичности в этом случае следует рассматривать как область, ограниченную
только в одном направлении, например, по х3: 0 ^ ж3 ^ аз/2. В
результате получим слой (рис.3.30) или неоднородную ячейку перио-
периодичности в виде системы нескольких слоев. Преобразование трансля-
трансляции C.40) этой ячейки осуществляются только в направлении ОХ3:
X3 = X'3 -Ь паз, где аз - период. Такая ячейка периодичности явля-
является симметричной относительно групп трансверсально-изотропного
класса.
Ячеек периодичности, ограниченных хотя бы по одному направле-
направлению, симметричных относительно групп изотропного класса не су-
существует.
§ 3.4. Матричные представления групп преобразований
.195
ilil
Рис. 3.29. К выводу теоремы 3.3 Рис. 3.30. Ячейка периодичности
трансверсально-изотропной периоди-
периодической структуры
Упражнения к § 3.3.
Упражнение 3.3.1. Доказать теорему 3.2 для ромбической, тетрагональной,
кубической, ромбоэдрической и гексагональной сингоний.
§ 3.4. Матричные представления групп
преобразований
3.4.1. Тензорное произведение матриц
В п.3.2.1 мы ввели понятие группы преобразований G,, и каждому
ортогональному преобразованию координат в трехмерном простран-
пространстве поставили в соответствие матрицу A*j размером 3 х 3, в резуль-
результате получили группы Gs (s = 1,... 39) из матриц 3x3. Однако это не
единственный способ такого соответствия. Каждому преобразованию
можно поставить в соответствие тензорное (или прямое, или его еще
называют кронекеровским) произведение матриц AtljlA**j3 или двой-
двойное тензорное произведение AXl ^А*2 ^Ах* ^, или, вообще, полиадное
произведение матриц A%lji ...Atnjn. При этом в качестве Л*;- в этих
произведениях выбирается та или иная матрица из групп G\... Сзэ-
Такие тензорные произведения играют важную роль в теории ин-
индифферентных тензоров (см. далее гл.4).
Полиадное произведение матриц в данном случае удобно рассмат-
рассматривать не как компоненты тензора ранга 2п, а как матрицу размером
Зп х Зп. Будем обозначать такие матрицы рекуррентным способом:
введем .последовательность матриц Л*1), А^2\ ... Л<п) размерами 3x3,
З2 х З2, ... Зп х Зп соответственно, которые имеют следующий вид:
196 Глава 3. Группы преобразований
матрица первого уровня
А<»> = (АA)\,) = (A'j), C.41)
матрица второго уровня
АB) = {AB)i
9x9
Здесь каждый элемент, например, А\А^ есть матрица А'^ Cx3),
элементы которой умножаются на А\:
(А\А\ А\А\ А\А\\
А\А^ = А\А\ А\А\ А\А\ . C.43)
3X3 I /tl ЛЗ jl /|3 \\ \Ъ }
\Л2Л1 Л 2Л 2 Л2Л3/
Тогда матрица .А^") п-го уровня имеет вид:
C.44)
ее размерность 1x1, где Z = 3".
Формула C.44) для матрицы А*") n-го уровня может быть симво-
символически записана как тензорное произведение матрицы А = А^ на
матрицу А^") (п — 1)-го уровня:
А<п> = А<х> ® А*"*. C.45)
Очевидно, что матрица А^") связана с матрицей первого уровня по-
лиадным произведением n-го уровня:
C.46)
п штук
поэтому будем говорить, что матрица А^ n-го уровня, образованная
таким способом порождена матрицей А. Саму матрицу А первого
уровня будем называть порождающей матрицей.
§ 3.4. Матричные представления групп преобразований 197
3.4.2. Матричные представления группы
Рассмотрим теперь не одну, а множество матриц А^ размером
3x3, принадлежащих какой-либо группе СЛ, тогда соответствующие
матрицы А(п) п-го уровня образуют некоторое множество ?>" матриц
размером Зп х Зп.
Теорема 3.4. Множество D" матриц А^ образует группу,
Т В самом деле, вычисляя скалярное произведение двух матриц А^ и
#(п), порожденных двумя матрицами 4,ffGG,, по правилам обыч-
обычного перемножения матриц B.22) получаем:
, C.47)
т.е. матрицы А^п~г\ Я^) и матрицы Asn Hlt перемножаются не-
независимо.
Для матриц первого уровня имеем:
(ЛA).#A)) = (^#^). C.48)
Таким образом, снова получаем матрицу А^ -Я^ того же строения,
что и исходные А^п\ Н^п\ порождающая ее матрица AljHJk также
принадлежит группе Gs. Следовательно, операция произведения мат-
матриц п-го уровня C.47) отображает множество J9" в себя.
Если в качестве Я';- выбрать обратную к Агj матрицу В%-^ то по
правилу C.47) перемножения получим, очевидно, единичную матрицу
размером Зп х Зп:
C.49)
Эту же матрицу можно получить из C.44), если в качестве A%j взять
Sj. Умножение такой матрицы Е^ на А^п\ очевидно, будет всегда
Давать А^п\
Если A*j (i,j = 1,2,3) - ортогональные матрицы, то все матри-
матрицы -4 '• (i,j = 1.../) также будут ортогональными. Это следует
из формулы перемножения матриц C.47), если в качестве Н(п) взять
193 Глава 3. Группы преобразований
матрицу, порожденную транспонированной матрицей Hlj = Af. Та-
Таким образом, множество D" матриц n-го уровня А^ действительно
образует группу. А
Итак, одной и той же группе Gs ортогональных преобразований
C.1) можно поставить в соответствие различные группы D" матриц
при разных п, называемые матричными представлениями группы Gs
n-го уровня.
Заметим, что, вообще говоря, матричные представления можно
ввести для произвольной группы G8, не относящейся к группам ли-
линейных преобразований координат.
3.4.3. Изомерные матричные представления
Пусть теперь имеется некоторая невырожденная матрица 5 того
же порядка I = Зп, что и матрица А^п\ Тогда, образуя с каждым из
элементов А^ группы D" новую матрицу Z-ro порядка
АЦп) _ 5-i . А(п) . s^ det s ф 0) C.50)
получим еще одно множество матриц А'^ n-го уровня. Это множес-
множество также образует группу D?n, так как произведение двух матриц
А'(п) и #'(п) вида C.50) снова есть матрица вида C.50):
Л'(п).н>(п) = (s-^H-S^S-^tf^.S) = S^-iA^-H^yS. C.51)
Выбирая в качестве Н'^ матрицу, обратную к А'(п\ получим эле-
элемент (л4/(п))~1 - обратный к А'(п\ который, очевидно, тоже имеет
вид C.44).
Группа матриц D'sn дает еще одно матричное представление п-го
уровня группы Gs.
Определение 3.7. Матричные представления D^ и D'J1, элемен-
элементы которых связаны соотношением C.50) называют изомерны-
ми (или эквивалентными).
3.4.4. Приводимые и неприводимые представления
Для одной и той же группы Gs можно построить бесконечное число
матричных представлений. Выше мы привели два способа их постро-
построения: с помощью тензорного произведения матриц C.46) и с помощью
невырожденного преобразования C.50). Укажем еще два способа, на-
назовем их третьим и четвертым.
Пусть имеется некоторое матричное представление группы Gs с
помощью матриц На n-го порядка и второе представление той же
3.4. Матричные представления групп преобразований
.199
группы с помощью матриц Ва га-го порядка. Тогда можно образо-
образовать квазидиагональные матрицы Са (п + га)-го порядка, в которых
На и Ва являются блоками (см. B.45)):
Са =
'На
О
Ва
C.52)
Перемножение квазидиагональных матриц (см. п.2.2.4) снова дает
квазидиагональную матрицу, поэтому все матрицы Са, построенные
по C.52), дают еще одно матричное представление группы G8.
Вообще говоря, из конечного числа к матричных представлений с
помощью матриц На, Ва, ... , Ра различного порядка можно всег-
всегда образовать новое матричное представление Са с использованием
квазидиагональных матриц вида:
(На
0
0
\ 0
0
Ва
п
0
0
0
• .
0
0 \
0
п
Ра)
C.53)
Четвертый способ является комбинацией третьего и второго: вы-
выбирая произвольную невырожденную матрицу S того же порядка, что
и Са, образуем новые матричные представления группы Gs:
С'а = S-1
Ca-S, det
C.54)
Матрицы Са в этом представлении, вообще говоря, уже не будут ква-
квазидиагональными.
Дадим теперь следующую классификацию.
Определение 3.8. Матричное представление группы G8, матри-
матрицы Са которого имеют квазидиагональный вид C.53) с количеством
блоков более одного, называют при в еденным.
Приведенное представление распадается на конечное число к мат-
матричных представлений с матрицами Яа, Ба, ... , Ра> меньшего, чем
Са порядка.
Определение 3.9. Матричное представление, матрицы Са ко-
которого не имеют квазидиагонального вида, но могут быть приведе-
приведены к нему с помощью невырожденного преобразования C.54), назы-
называют приводимым.
Если оке матричное представление не имеет квазидиагоналъно-
го вида и не может быть приведено к нему с помощью какого-либо
невырожденного преобразования C.54), то такое представление на-
называют неприв одимым.
В этой связи возникает задача: пусть имеется некоторое матрич-
матричное представление группы G8; требуется установить является ли оно
200 Глава 3. Группы преобразований
приводимым, и если да, то требуется найти его квазидиагональный
вид с максимально возможным количеством блоков (т.е., иначе гово-
говоря, найти все его неприводимые представления). Как будет показано
далее в гл.4, эта задача непосредственно связана с нахождением числа
к независимых компонент тензора.
3.4.5. Характеры матричных представлений
Определение 3.10. Характером матрицы А^ размером3n x
Зп называют сумму ее диагональных компонент (след), и обознача-
обозначают его следующим образом:
л(п); , / = 3". C.55)
1 = 1
Характером матричного представления n-го уровня для группы
Gs называется множество (конечное или континуальное) характеров
•всех матриц n-го уровня А^ данной группы:
xDn))...xDn))---xDn))' G, = {4n),...4n),-..4n)}> C-56)
где р - общее число элементов в группе (для конечных групп), непре-
непрерывные группы будут рассмотрен далее в гл.4.
Учитывая структуру C.44) матриц А^ можно установить соотно-
соотношения между характерами матриц n-го и первого уровня:
^ ,,-2>) и т.д., C.57)
т.е. получаем
Х(АЫ) = Х"(А). C.58)
На этом мы закончим краткое знакомство с теорией представлений
групп, более подробно о них можно узнать, например, из [21].
Упражнения к § 3.4.
Упражнение 3*4*1 • Показать, что характеры матричных представлений
X(i4) групп GSy 5 = 1... 38, вычисляются согласно данным табл.3.3 и 3.4.
Упражнение 3*4*2* Показать, что характеры матричного представления
( группы Стзэ = I имеют вид:
Х{А) = сов(ф-х){1-совв)(-1)т+соа0, если A{j € {ЯуЯфхв}, 7 = 1,2;
Х{А) ~ COs(<f> - х)A + COS^) - COsfl, если А*; € {Я,зС)фхв}-
ГЛАВА 4
ИНДИФФЕРЕНТНЫЕ ТЕНЗОРЫ И ИНВАРИАНТЫ
§ 4.1. Индифферентные тензоры
4.1.1. Принцип Неймана
Выше в §3.3 были рассмотрены способы описания только геомет-
геометрической симметрии тел. Реальные физические тела могут обладать
определенным физическими свойствами (например, упругостью, сжи-
сжимаемостью, теплопроводностью, тепловым расширением и т.п.), кото-
которые описываются некоторыми тензорами ПП. Эти физические свой-
свойства также могут обладать определенной симметрией, т.е. зависеть
определенным образом от преобразования координат. В этом случае
говорят, что тела обладают анизотропией физических свойств.
Связь между геометрической симметрией и симметрией физических
свойств устанавливает принцип Неймана, который говорит о том, что
группа элементов симметрии любого физического свойства должна
иметь подгруппу элементов геометрической симметрии.
Рассмотрим теперь способы описания симметрии физических
свойств тел, которые определяются некоторым тензором nfl. Нач-
Начнем с формул преобразования компонент этого тензора при линейных
преобразованиях C.1).
4.1.2. Преобразование компонент тензоров при линейных
преобразованиях координат
При линейных преобразованиях C.1) формулы A.129) и преобразо-
преобразования компонент filJ произвольного тензора ft второго ранга имеют
вид:
пк1 = А\А'^. D.1)
Аналогичным образом преобразуются компоненты любого тензора
n-ого ранга ПП:
пП = п'1' ine{l 0 ... 0 е,-п = пA"Лпё{1 0 ... 0 ё,п п > 1,
П1"*-»'» = Uh"jnAi)i . ..А\. D.2)
202 Глава 4. Индифферентные тензоры и инварианты
4.1.3. Определение индифферентных тензоров
Определение 4.1. Если при любых линейных преобразованиях ко-
координат C.1) компоненты 0,%1"Лп некоторого тензора п?1 в базисе
ё,- не изменяются, т.е.
QI-1...U = Ql"i...U п > 1? D.3)
то такой тензор nffc называется индифферентным относи-
относительно преобразований C.1).
Определение 4.2. Если условие D-3) неизменяемости компо-
компонент п%1~%п выполнено только для некоторой группы Gs линейных
преобразований C.1), то такой тензор nfl называется индиффе-
индифферентным относительно группы Gs, а группу Gs в этом случае
называют группой симметрии тензора п?1.
Не все компоненты индифферентных тензоров являются независи-
независимыми, т.к. между ними существуют зависимости, вытекающие из
D.2) и D.3):
№-•** = uil-^Afj\ ...А\пп п ^ 1. D.4)
В частности, индифферентным является сам тензор линейных пре-
преобразований Q, компоненты которого совпадают с матрицами преоб-
преобразований (см. п.3.1.3):
<} = А*;ё>®ё>. D.5)
В самом деле, используя формулы C.23), перейдем в новый базис:
Q = А*;У®ъ = А^А\ Bjmem®ek = Ak{ ^ет®ел = А\ е|#®е*. D.6)
Отсюда и следует, что компоненты тензора Q в базисах ё,- и е,- сов-
совпадают.
Используя тензор линейных преобразований Q, можно сформули-
сформулировать условие индифферентности тензора.
Теорема 4.1. Тензор пП является индифферентным относи-
относительно группы Gs, если и только если скалярное умножение на лю-
любой тензор линейных преобразований Q из группы G9 не изменяет
значений этого тензора пП, т.е.
Q)
B»-1.2n-3f... ,3,1,2,4,... ,2
Т Покажем эквивалентность формулировок D.4) и D.7). Тензор
Q ® ... ® Q имеет следующие компоненты:
Q®...®Q = Ailki ... А*%пек1 ® etl ® ... ® ё*» ® ё1п, D.8)
4.1. Индифферентные тензоры 203
тогда D.7) в компонентном виде записывается следующим образом:
п^-'^ёг, .. .ё,п = uh'"jneh ® ... ® ein •... • А\ ... Ainknekn <g>...
<g> ё*3 <g> ё*1 <8) etl ® ё,-а 0 ... 0 ё,п = О'1-'»^1'^ . ..А\ х
х 8fc .. .<5?etl ® ... ® ё,-т = Й*-'»^ ... А^ё,-, 0 ... ® ё,-п. D.9)
Сравнивая в этом равенстве первое и последнее выражения, очевидно,
получаем, что формула D.9) будет выполнена тогда и только тогда,
когда выполнена формула D.4), что и требовалось доказать. А
Получим теперь с помощью D.7) условие индифферентности век-
вектора а:
а = a Q или а* = о?А{^ (A*;) G Gs D.10)
и тензора второго ранга Т:
Т = Т - .(Q ® Q)C124) или fij = TklA\ А\. D.11)
Это выражение можно также представить в виде (см. упр.4.1.7):
T = QT.T.Q. D.12)
4.1.4. Изомерные группы симметрии
Понятие D.3) индифферентности тензора, а также альтернативные
формулировки D.4) и D.7), непосредственно связаны с фиксированной
системой координат ж1, к которой отнесена группа симметрии. Совер-
Совершенно аналогично можно определить тензоры, индифферентные от-
относительно группы G,, отнесенной к другой ортогональной системе
координат X'* (см.п.3.1.4 и 3.2.3):
ПЛ'1-«'« =п'1"л'», D.13)
где п'%1"'%п - компоненты тензора ПП в системе координат Х/%:
пп = fi''1-'^ ® ... 0 ejm = П1'1-1"»^ ® ... ® е,Л. D.14)
Тогда формулировка D.4) будет иметь вид:
ПЛ'1-»'« = п'^"^А\ ... Ainjn, D.15)
а формулировка D.7) примет вид:
пп = ПП •... (Q/0...0Q/j1 D.16)
204 Глава 4. Индифферентные тензоры и инварианты
где Q' - тензор линейных преобразований группы G,, определенный
в базисе е'1 (формула C.25а)).
Для тензора второго ранга это соотношение имеет вид:
T = Q'TTQ'. D.17)
Один и тот же тензор nfl, индифферентный относительно группы
G,, связанной с одной системой координат х\ вообще говоря, не бу-
будет индифферентным относительно группы G,, связанной с другой
системой координат Х1х.
Если двум группам симметрии G, и G's соответствуют тензоры
линейных преобразований Q и Q', которые являются изомерными
(см.п.3.1.4), то такие группы также называют изомерными. Изомер-
Изомерным группам соответствуют, очевидно, одни и те же матрицы преоб-
преобразований А1 ^, но различные оси анизотропии. Далее к обозначениям
групп симметрии, у которых оси анизотропии отличаются от осей
координат Ох\ будем добавлять знак "/".
4.1.5. Группа симметрии произвольного симмет-
симметричного тензора второго ранга
В этой связи установим группу симметрии произвольного симмет-
симметричного тензора второго ранга Т.
Как было установлено в п. 1.6.1, для Т всегда существует три ве-
вещественных собственных значения Аа и три ортонормированных соб-
о
ственных вектора еа:
т.е.
a=l
таким образом, Т в базисе еа имеет диагональный вид.
Выберем в качестве осей анизотропии линии действия векторов
е'а = еаи покажем, что все матрицы из группы ортотропии Gs: i?, С,
Ra и jDa, a = 1,2,3 (см. п.3.2.3) сохраняют без изменения компоненты
ij
Т"' = Л'>',Т'*', А\ е {Е, С, RQ, DQ). D.18)
В самом деле, поскольку все указанные матрицы, включая T/IJ, - диа-
гональны, то это соотношение можно переписать в виде:
Т'^ = (А%JГ^. D.18а)
Но, в силу ортогональности матриц из группы Gs: (^^J = 1? и,
следовательно, соотношения D.18а) и D.18) всегда выполнены.
Таким образом, доказана следующая теорема.
4.1. Индифферентные тензоры 205
ТЕОРЕМА 4.2. Произвольный симметричный тензор второго ран-
ранга обладает группой симметрии G'8, принадлежащей к классу орто-
тропии, оси анизотропии которой совпадают с собственными на-
направлениями тензора.
4.1.6. Тензорный базис
Теорема 4.3. Множество всех тензоров п-го ранга, индиффе-
индифферентных относительно фиксированной группы преобразований Gs,
образует конечномерное линейное пространство размерности
Т Действительно, множество всех тензоров n-го ранга в евклидовом
пространстве Ш3 согласно теореме 2.29 образует линейное простран-
пространство 7з размерности т = п3. Множество всех индифферентных
тензоров n-го ранга Zg является подмножеством Тз . Очевидно,
что это множество Zg само является подпространством, так как сум-
сумма (nHi + nf&2) любых двух индифферентных относительно одной и
той же группы Gs тензоров nfti и п^2 тоже индифферентна, тоже
самое относится и к произведению тензора ПП на число. Поскольку
размерность подпространства Т$ Е 7з не может превосходить раз-
размерности пространства 7з , то, следовательно, dim Ig = к ^ Зп =
= m = dimT3(n). A
Следовательно, в пространстве Zj существует базис nfl(p) P =
1... fc, называемый тензорным базисом, такой, что любой индиффе-
индифферентный тензор ПП фиксированного ранга п можно представить в виде
разложения по этому базису:
w n?l D.19)
/3=1
или
к
^Jn = E^%'n' DЛ9а)
7=1
где 7/з - коэффициенты разложения.
4.1.7. Образующие и направляющие тензоры
Тензоры, входящие в тензорные базисы ППG) для различных п,
взаимосвязаны между собой: для одной и той же группы преобразова-
преобразований Gs существует минимальный набор тензоров О,7 7 = 1, 2,.. .&,,
на основе которого с помощью только операций тензорного умноже-
умножения, сложения и транспонирования образуются все тензоры ППG) для
206 Глава 4. Индифферентные тензоры и инварианты
любого п > 1. Эти тензоры О,7, имеющие, вообще говоря, различный
ранг, называют образующими тензорами группы Gs.
Образующие тензоры О,7 обладают следующими свойствами:
• все они являются индифферентными относительно фиксированной
группы преобразований Gs (группы симметрии);
• любой тензор, являющийся индифферентным относительно группы
Gs может быть образован из тензоров О,7 с помощью операций
тензорного умножения, транспонирования и сложения.
Образующие тензоры можно разложить по любому базису, напри-
например, по* локальному R,:
°'М = О\$netl ® ... ® ё,.т = Ofcj'-R,-, ® ... Ru, D.20)
з = 1...39, 7 = l...fc,,
где Ог$\"\п - компоненты образующих тензоров в декартовом базисе
ё,-, a O*/"jln - в произвольном локальном базисе R,-. "Все образующие
тензоры О,G), в свою очередь, выражаются только через 17 тензоров,
называемых направляющими тензорами. Перечислим их:
векторы:
ёв, D.21)
тензоры 2-го ранга:
ё* = ёа 0 ёа, Е, hQ = ёр 0 ё7, D.22)
тензоры 3-его ранга:
з
€, Td= ^ ёа®ё/30ё7,
а,/3,7=1
Озл = ei ® (ei ® ei - ё2 ® ё2) - ё2 ® (ёх О ё2 + ё2 ® ёх), D.23)
тензоры 4-го ранга:
з
D3d = ё3 ® D3/», ОЛ = ^ ёа ® ёа ® ёа ® ёа, D.24)
а=1
ТЛ = ё\ ® ё| + ё| ® ё§ + ё§ 0 ef, а ф р ф 7 ^ а, a,j9,7 = 1,3,
тензор 6-го ранга:
D.25)
§ 4.1. Индифферентные тензоры 207
Используются также тензоры
т
ё7 - ё7 <g> ё/з. D.26)
Компоненты этих направляющих тензоров в декартовом базисе ёа
имеют следующий вид:
а=1
4^ ^ D-27)
а=1
Компоненты направляющих тензоров в произвольных криволиней-
криволинейных координатах Xх приведены в упр.4.1.5.
4.1.8. Образующие тензоры различных групп
симметрии
Направляющие тензоры являются индифферентными по отноше-
отношению к разным группам Gs линейных преобразований декартовых ко-
координат хх. Ниже приведены образующие тензоры групп G\.. .G29>
составленные из направляющих тензоров.
!• Триклинная сингония
OlG) = {§7) *1 = 3,
О2Ы = {§2,Па} fc2 = 6, a = 1,2,3, /3 = 1,2. D.28)
"• Моноклинная сингония
о
°зG) = {§/8' ёз) fcs = 3; О4G) = {ё3, с, П3, ё^} к4 = 5;
О5Ы = {Е,П3,ё^} fc3 = 4. D.29)
208 Глава 4. Индифферентные тензоры и инварианты
III. Ромбическая сингония
= {ё3, Е, ё?} fc6 = 4, О7G) = {Е,€,ё^} к7 = 4,
{ё?} *8 = 3. D.30)
IV. Тетрагональная сингония
| = 4, O10W = {E,e3,e,Oh} k10 = 4;
fcu =4; О12G) = {E,e|,Td} ft12 = 3;
D.31)
= {E,e3,Oft} fti3 = 3, 2
V. Ромбоэдрическая сингония
§ k17 = 4,
fcis = 3, O19G) = {E,e§,?,D3ft} fci9 = 4,
D.32)
O20G) = {E,e§,D3<i} ^20 = 3.
VI. Гексагональная сингония
O21G) = {E, ё|, n3, D3h}, O22G) = {E, ё3, с, D6h},
O23G) = {E, ё|, n3, D6h}, O24G) = {E, Ц, D3h},
O25G) = {E, 4, c, D6h}, O26G) = {E, ё3, D6h}, D.33)
O27G) = {E,e|,D6h}.
VII. Кубическая сингония
C>28G) = {E, €, Th} fc2s = 3, O29G) = {E, Th} fc2g = 2,
O30G) = {E,Td} fc3o = 2, О31G) = {Е,е,ОЛ} k31 = 3, D.34)
O32G) = {E,Oh} fc32 = 2.
Класс трансверсальной изотропии
ОззG) = {Е, ё3, с}, О34G) = {Е, ё|, п3}, О35G) = {Е, ё3},
О36G) = {Е, ё|, ?}, О37G) = {Е, 4). D.35)
§ 4.1. Индифферентные тензоры
.209
Класс изотропии
а -
D.36)
4.1.9. Симметричные направляющие и образующие
тензоры
Важный случай представляют симметричные тензоры второго ран-
ранга Т и четвертого ранга П, при этом симметрия тензора четвертого
ранга понимается как выполнение следующих условий (см. п.1.8.4):
j 0 Rk 0 R,, T = TijR{
= uijlk =
D.37)
Все симметричные тензоры Т и П, являющиеся индифферентны-
индифферентными (по условию D.3)) относительно группы симметрии G5, выража-
выражаются линейно через тензорный базис в виде D.19). Тензорный ба-
базис симметричных тензоров в каждой группе строится из симметрич-
симметричных комбинаций образующих тензоров О5G), а те, в свою очередь, -
из симметричных комбинаций направляющих тензоров. Укажем эти
симметричные тензоры (табл.4.1).
Табл. 4.1. Симметричные направляющие тензоры
Векторы:
Тензоры 2-го
Тензоры 4-го
ранга:
ранга:
oQ =
И II $>
®ер, е
0
а. Е
Здесь введена операция (•) симметрирования тензора 4-го ранга:
a D^d 4' означает транспонированный тензор четвертого ранга (см.
о
п. 1.8.3). Тензор Оа образован симметрированием тензора Па:
Oa = ha + ha. D.39)
В декартовом базисе ё,- эти тензоры имеют следующие компоненты:
210
Глава 4. Индифферентные тензоры и инварианты
(ОЛ)«« =
а=1
ks[ - sks2)
D.40)
+ sk2s[),
636{)(8k62 + 6k6[)
+ S2S{)(Sk83 + SkS[) + F{6{ -
534)(SkS[ ~
6k6'2),
(D3p' = (
+ (S[S{ - Р2
+ S35i)(8kS[ - Sk8l2) - {&2&{ + 6{38>2)Fк82 + SkS[)+
6<26{)Eк62
8k83).
Для симметричных тензоров четного ранга образующие тензоры
О4G) одинаковы внутри каждого класса и совпадают с образующими
тензорами максимальных групп в классах (табл. 4.2).
Табл. 4i%- Симметричные образующие тензоры классов
Е
М
0
т
К:
А
В
Н
К
Тъ
I ¦
- триклинный класс
- моноклинный класс
- класс ортотропии
- тетрагональный класс
з - класс квазитрансвер-
сальной изотропии
- ромбоэдрический класс
- ромбоэдрический класс
- гексагональный класс
- класс квазиизотропии
- класс трансвер-
сальной изотропии
- класс изотропии
^-JjE/G) — \eQj
ОоG) = {ё|}
ОтG) = {Е? ёз? Од, оЕзл}
Oj^3G) = {Е,ёз, Од}
ОдG) = {E,e§,D3,ft3d}
OBG)={E,ei,D3}
.ОЯG) = {Е,ё§}
ОкG) = {Е,ОЛ}
ОТЗG) = {Е,ё§}
О/G) = {Е}
На основе этих образующих тензоров строятся тензорные базисы
для индифферентных симметричных тензоров второго и четвертого
рангов. Эти тензорные базисы будут приведены ниже в гл.5.
§ 4.1. Индифферентные тензоры 211
4.1.10. Симметричные направляющие тензоры
третьего ранга
Для тензоров третьего ранга 3П также можно ввести понятие сим-
симметрии. Наиболее часто в механике и физике встречаются тензоры,
обладающие симметрией по второму и третьему индексам:
или Uijk = Uikj, D.41)
где
3?1 = UijkRi 0 Rj 0 Rb
Далее тензоры третьего ранга, обладающие такими свойствами,
будем называть симметричными.
Тензорный базис D.19) для индифферентных симметричных тензо-
тензоров третьего ранга строится из представленных ниже симметричных
комбинаций направляющих тензоров D.21) - D.25):
ёа, ё2, T\f, Бзл,
ЕЛ = Е 0 ё3 + (Е 0 ё3)A32), B3d = Td • ё2 + (Td ¦ ё§)<132>, D.42)
OQd = e • ё| + (с • ё2)A32>, АЗЛ =
Для этих тензоров имеют место следующие соотношения (см.
упр.4.1.4):
В3<* = ei 0 Oi + ё2 0 О2,
OQff = e/3 0O/3 -ё70О7, а,/3,7 = 1,2,3, афРфчфа,
АЗЛ = ei 0 О3 + ё2 0 (ё\ - ё2), D.43)
Яза = ei 0 О2 - ё2 0 Оь N3d = 2ё3 0 (ё| - ё?) - R3<f.
Компоненты этих направляющих тензоров в декартовом базисе ёа
имеют следующий вид:
Ё}>к = 5<Ч* + 8ikSl В&к = б[D8* + 6}36к2) + Si(S{Sk3 + ф*),
0% = Ъ(#Л + Ф") - W% + *j?), D-44)
212 Глава 4. Индифферентные тензоры и инварианты
Построение из этих направляющих тензоров конкретных тензор-
тензорных базисов для различных групп симметрии Gs будет выполнено
далее в гл.5.
Упражнения к § 4.1
Упражнение 4.1.1. Доказать, что если симметричный тензор второго ран-
ранга X имеет только два различных собственных значения, например, Ai ф Л2,
А2 = Аз, то его группой симметрии является С?з4> принадлежащая к классу Т$
о
трансверсальной изотропии с осью трансверсальной изотропии вдоль ei.
Упражнение 4.1.2. Показать, что если собственные значения симметрич-
симметричного тензора второго ранга X все равны между собой, то его группа симметрии
совпадает с G39» принадлежащей к классу изотропии (полная группа ортогональ-
ортогональных преобразований).
Упражнение 4.1.3. Показать, что направляющие тензоры D.27) являются
индифферентными относительно соответствующих групп преобразований.
Упражнение 4.1.4. Доказать справедливость формул D.43).
Упражнение 4.1.5. Показать, что в криволинейной системе координат Xх
направляющие тензоры D.27) имеют следующие компоненты:
ёа = p;r,-, в* =
Е = ff«R,- ® Rj, ila = (Р
-
Td = У] P^P'R,- ® R,- ® Rfc,
? - НН) -
= (PlzP{{P$P[ - Р^Р'г) - W(PM + HP'S)
°h =
0=1
Упражнение 4.1.6. Показать, что имеют место следующие соотношения
между направляющими тензорами:
а=1
Упражнение 4.1.7. Доказать, что из D.11) следует D.12).
4.1. Индифферентные тензоры 213
Упражнение 4.1.8. Показать, что если компоненты тензора четвертого
ранга ft удовлетворяют условиям симметрии D.37) в какой-либо системе коор-
координат Ж1, то в любой другой системе координат Xх1, полученной невырожденным
преобразованием также будут выполнены эти же условия симметрии.
Упражнение 4.1.9. Доказать, что если тензор пП - индифферентен, то
любой транспонированный тензор п Л(то1"-т») тоже является индифферентным.
Упражнение 4.1.10. Используя единственность решения уравнения
Т • Т"~ — Е, доказать, что если симметричный невырожденный тензор вто-
второго ранга Т индифферентен относительно какой-либо группы Gs, то обратный
к нему тензор Т~ также будет индифферентным относительно той же группы
G,.
Упражнение 4.1.11. Используя единственность решения уравнения
4С • • С"" = А, доказать, что если тензор С является симметричным и ин-
индифферентным относительно группы Gs, то обратный к нему тензор С также
будет индифферентным относительно той же группы Gs.
Упражнение 4.1.12. Показать, что из D.27) и табл. 4.1 следуют формулы
D.40) для симметричных направляющих тензоров в декартовой системе коорди-
координат.
Упражнение 4.1.13. Записать в произвольной криволинейной системе ко-
координат компоненты симметричных направляющих тензоров Оз, Г&3/1, JT&3<2 и
D
Упражнение 4.1.14. Доказать, что тензор D3, определяемый по D.38),
обладает условиями симметрии D.37).
Упражнение 4.1.15. Показать, что ненулевыми компонентами тензора D3
являются
?^311 = 1, U1322 = Д2312 = -1.
Упражнение 4.1.16. Показать, что тензор D3<f, определенный по D.38),
обладает следующей симметрией компонент:
Упражнение 4.1.17. Показать, что единичный тензор четвертого ранга А
A.252) можно выразить через направляющие тензоры:
3
А = ^ ёа <g> ё/з 0 ёа 0 ё/з + ёа 0 ё^ 0 ёа =
а,/3=1
Упражнение 4.1.18. Показать, что тензор ПзЛ» определяемый по D.40),
обладает условиями симметрии D.37) и имеет только две отличные от нуля ком-
компоненты:
Щн - 1, \lzh - -1.
Упражнение 4.1.19. Показать, что если какие-либо компоненты, например,
контравариантные D.3), сохраняются при линейных преобразованиях, то любые
Другие: ковариантные, смешанные - также сохраняются при тех же преобразова-
преобразованиях.
Упражнение 4.1.20. Доказать, что если неособенный тензор второго ранга
А индифферентен относительно группы Gs, то обратный к нему тензор Т"~
также индифферентен относительно той же группы Gs.
214 Глава 4. Индифферентные тензоры и инварианты
§ 4.2. Число независимых компонент
индифферентного тензора
Выше в пп.4.1.7 - 4.1.10 мы указали способ построения тензорного
базиса D.19) в пространстве 1$ индифферентных тензоров - с помо-
помощью образующих тензоров групп. Однако открытым остался вопрос
о числе к - размерности пространства Х^1 для различных п. Это
число fc, очевидно, совпадает с числом элементов в тензорном базисе
D.19), а также согласно теореме 2.32 - с числом независимых компо-
компонент тензора ППЕ Х$ .
Формулы для числа к могут быть установлены с помощью теории
матричных представлений групп, о которой говорилось в §3.4. Выводу
этих формул посвящен данный раздел.
4.2.1. Векторное представление компонент тензоров
Рассмотрим произвольный тензор n-го ранга пП с компонентами
Qt!...tn в декартовой системе координат Ох%. Образуем из этих ком-
компонент координатный столбец из / = Зп элементов:
a(n) = (a[n))...a'(n))T, / = 3". D.45)
Компоненты этого столбца aL\> • • -а\п\ определим рекуррентным об-
образом: представим столбец n-го уровня а(п) как совокупность трех
столбцов (п — 1)-го уровня ajjl_14 (ii = 1, 2, 3) длиной З1*:
afn) = (a(J-l)»afJ-l)>a?J-l))i D-46)
а столбец ^„х) ~ как совокупность трех столбцов (п — 2)-го уровня
aji!!2) и т.д.:
а(п-1) "~ Va(n-2)'a(n-2)'a(n-2)/>
аB) — Va(l) >a(l) >аA) )•
Координатные столбцы первого уровня а'Л''Лп~1 имеют длину, равную
трем, и состоят из компонент тензора fi11**'71:
*i,...in-i = 1,2,3.
§ 4.2. Число независимых компонент индифферентного тензора 215
Знак "Т" здесь, как и ранее, означает транспонирование - превраще-
превращение столбцов в строки. Будем говорить, что координатный столбец
а(п) порожден компонентами тензора ft*1—ln.
Приведем пример формирования координатного столбца аB) ука-
указанным способом для тензора второго ранга ft с компонентами ^
D.49)
4.2.2. Линейное преобразование А^
Очевидно, что множество всех координатных столбцов а(п) задан-
заданного уровня образует линейное пространство С^ размерности /_= Зп.
При линейных преобразованиях координат C.1) компоненты fi11—ln
преобразуются по формуле D.2):
Jl Jn
D.50)
С помощью матрицы А^ n-го уровня, введенной по C.44), и коорди-
координатных столбцов а(п) n-го уровня это соотношение можно записать в
матричном виде:
а'(п) = Л<">.а(п), D.51)
где а'/ч - координатный столбец вида D.45), порождаемый компонен-
компонентами П11—1п тензора ft в системе координат Xх.
Соотношение D.51) определяет линейное преобразование Л^ I-
мерного линейного пространства С^ координатных столбцов а(п) в
себя, а матрица А^ n-го уровня есть матрица Z х I этого линейного
преобразования.
4.2.3. Индифферентные векторы n-го уровня
Если тензор nfl является индифферентным относительно какой-
либо группы Gs ортогональных преобразований в трехмерном про-
пространстве, то его компоненты fitl#-*n не меняются при любых преоб-
преобразованиях вида D.50) (см. формулу D.7)):
Qii...u = а\...А\п'1"*», D.52)
где Alj - произвольная матрица третьего порядка из группы Gs.
С помощью матричной записи D.51) соотношение D.52) можно
представить следующим образом:
(п) =
(п). D.53)
216 Глава 4. Индифферентные тензоры и инварианты
Определение 4.3. Вектор а(п) 1-мерного пространства С^п\
удовлетворяющий D*53) для любых матриц А™ из группы D™, на-
назовем индифферентным вектором п-ого уровня относи-
относительно D™ .
Этот вектор, очевидно, порожден компонентами индифферентного
тензора ft11-1".
Сравнивая формулу D.53) с соотношением B.78) для собственных
векторов матрицы А линейного преобразования, получаем, что ин-
индифферентный вектор а(п) является собственным вектором, соответ-
соответствующим собственному значению А = 1, для каждой матрицы
А{ап)
а
Если же собственное значение А = 1 имеет кратность s, то, согласно
теоремам 2.16 и 2.17, все собственные векторы матрицы А^п\ соответ-
соответствующие этому значению, образуют инвариантное подпространство
Са размерности т^«в пространстве С^п\ В этом подпространстве
Са можно выбрать базис е^ .. .е\?\ тогда всякий индифферентный
вектор а(п) будет выражаться через него.
Пусть теперь среди этих векторов е^ .. .em имеется к векторов
(к ^ га), которые являются собственными одновременно для всех мат-
матриц Ah' из группы D" (число к может быть равно и нулю). Эти к
векторов не обязательно совпадают с первыми e^n . ..ejj. , поэтому
о(п) о(п)
обозначим их как ег ,... ек .
Согласно теореме 2.18, линейная оболочка из них также образует
о
о
инвариантное fc-мерное подпространство С^ в С^п\ Назовем его ин-
индифферентным подпространством. Тогда любой индифферентный
о
вектор а(п), принадлежащий Оп\ можно представить в виде суммы
этих векторов:
к м
/8=1
Формула D.54) является матричным аналогом формулы D.19) раз-
разложения индифферентного тензора nft по тензорному базису группы
Gs. Поэтому если мы найдем число элементов в базисе e^n , ...ej.n ,
то найдем и искомое число к независимых компонент тензора пП.
4.2.4. Приведение матричного представления
к квазидиагональному виду
о
Рассмотрим подробнее введенное подпространство ?(п). Поскольку
о(") о(п) i -
его базис ег ,... ек образует систему А: линейно независимых векто-
векторов, которые соответствуют одному собственному значению А = 1
§ 4.2. Число независимых компонент индифферентного тензора 217
для любой матрицы А^ из ?>", то, согласно теореме 2.14, существу-
существует невырожденное преобразование 5, которое приводит матрицу А^
к блочному виду B.83):
S =
D.55)
где Ek - единичная матрица k-то порядка, A'l2 ~ матрица размером
к х (I — fc), Af22 ~ квадратная матрица (I — fc)-ro порядка.
Если вектор а(п) является индифферентным относительно всех
матриц Аа группы jD", to вектор
а(п) = 5-а(п) D.56)
будет индифферентным относительно всех блочных матриц А^п\ так
как
А1(п) • а'(п) = S-1 • А^ • S • S-1 • a(n) = 5 • а(п) = а'(п), D.57)
т.е.
D.58)
Теорема 4.4. Матрицу А^ можно привести не только к блоч-
блочному, но и к квазидиагональному виду.
Т Для доказательства рассмотрим матрицу 5 • 5Т /-го порядка.
Эта матрица является симметричной и положительно-определенной,
так как E" • S~1T)T = 5 • 5"Т, тогда, согласно теореме 2.12,
ее можно представить в виде произведения неособенной треугольной
матрицы L на ее транспонированную:
s-i . S-1T = L.LT^ det L ф 0> D.59)
С помощью этой матрицы L 1-го порядка введем новый вектор
a'^I^.a'^G-1-^) D.60)
и новую матрицу
А"М = L-1 ¦ Л'<"> • L = G-1 • AW • G, D.61)
где
G = S-L. D.62)
218_
Глава 4. Индифферентные тензоры и инварианты
Покажем, что А"(п) тоже имеет блочный вид D.55). Представляя мат-
матрицу L в блочном виде, по правилу B.43) перемножения блочных мат-
матриц действительно получаем:
0
0
Ек |
L22
In
L221
±11
I L
12
-422
V 0 | 122.
А-12 — L22 \
A'2'
D.63)
22
где jCh и L^1 - верхние треугольные матрицы размером к х к (см.
упр.2.2.6); ?22 и L22 - верхние треугольные матрицы размером (/ —
к) х (I - fc); Z^1, Z12 и
= Ь^
^
12 •
^
- матрицы размером к х (I — fc), а А^ = Х^1 * ^22 • ?22 ~ матрица
A-к)хA-к).
Матрица G - ортогональная, так как
G-GT = 5-Z.E-?)T = 5-?.ZT.5 = 5.5-1.5-1T-5=^n). D.64)
Тогда и А"(п) является ортогональной матрицей, поскольку А^11^ -
ортогональная (см. п.3.4.2). В самом деле, умножая А"^ на свою
транспонированную, получаем:
Ап(п) . А„(п)т = ((?-i. A(n) . G). (G-i
= G ¦ A(n) • G • GT ¦ A(n>T • G~1T =
= G ¦ ^W • A(")T • G~1T = G'1 ¦ G
D.65)
Учитывая блочную структуру D.63) и ортогональность матрицы
А"{п\ получаем:
АН
г22,
7пТ 7пТ
^22 ' ^22
D.66)
§ 4.2. Число независимых компонент индифферентного тензора 219
Последнее равенство в D.66) возможно только если А = 0 и
^22 " ^22* = En-ki т.е. матрица А"^ действительно имеет квази-
квазидиагональный вид:
Ек
О
О
Ло'
D.67)
22,
причем А'22 - ортогональная матрица, а Ей - единичная матрица к-то
порядка. Теорема доказана. ^
Поскольку у нас имеется группа D™ матриц Аа , то, согласно до-
доказанной теореме, каждую матрицу можно привести к квазидиаго-
1л ап\ с о(п) °(П)
нальному виду D.67), причем поскольку базис ег ,...efc является
общим для всех Аа , то единичная матрица Ей в D.67) имеет один
и тот же порядок к. Согласно теореме 2.15, матрица преобразования
5, а, следовательно, и матрица G, определяемая по S однозначно (см.
теорему 2.12), является общей для всех матриц Аа . Это означает,
что все матрицы Аа из jD" одним невырожденным преобразовани-
преобразованием G - Аа • G могут быть приведены к квазидиагональному виду
(аналогично C.54)). В соответствии с классификацией п.3.4.4, та-
такое матричное представление Аа группы Gs является приводимым.
Фактически мы доказали следующую теорему.
Теорема 4.5. Если в С^ имеется некоторое подпространство
о
С размерности к ^. I, элементы которого являются индифферент-
индифферентными относительно всех матриц из матричного представления Аап
группы Gs, то это матричное представление приводимо.
При этом число неприводимых матричных представлений размер-
размерности 1 (т.е. число диагональных элементов-блоков в единичной мат-
матрице Ek), содержащихся в приводимом, равно числу fc.
4.2.5. Приведенное матричное представление
Каждой матрице Аап' из jD" можно поставить в соответствие ква-
квазидиагональную матрицу Аа^ = G • Аап^ • G. Множество D"n всех
таких матриц Аа образует группу, изомерную с jD", и, согласно
классификации п.3.4.4, образует приведенное матричное представле-
представление группы Gs.
о
Теорема 4.6. Размерность подпространства ?"'п), индиффе-
индифферентного относительно группы D's , равна размерности к подпро-
о
Сгъранства С^п\ индифферентного относительно D".
220 Глава 4. Индифферентные тензоры и инварианты
0(п) 0(п) о
Т Для доказательства выберем базис ег ,... ек в Оп) и образуем на
его основе векторы по формуле D.60):
CW^, -I,-*. D-68)
Эти векторы будут инвариантными относительно группы Ds , так
как
D.69)
Они являются также и линейно независимыми. Поэтому линейная
0//(п) о
оболочка из векторов е, образует подпространство С"^п\ индиф-
индифферентное относительно 2?" , его размерность не меньше к. Пусть
0//(п) " 0//(п)
существует еще один вектор ек+1 линейно независимый с е,- и ин-
индифферентный относительно jD, , тогда найдется вектор efc+1 =
^ °"(п) - - о(п) /• 1 м
= G-e^+1, линейно независимый с е,- (г = 1... к) и индифферентный
относительно D»\
л(п) о(») _ (п) о"(») /(п) х о"(»)
^v ; ' ek+i -AK f'G' ek+i =G-A i >-G • G • efc+1 =
^ w/Гп) °"(n) ^ °'/(n) o(n) ia n^
= G • A"W • efc+1 = G • efc+1 = efc-+1, D.70)
oW o()
что невозможно, так как система е1 ... ек по предположению со-
содержит максимальное число таких векторов. Полученное противоре-
о
чие доказывает утверждение, что размерность подпространства ?"(п)
равна к. А
4.2.6. Свойство ортогональности матричных представлений
0//(п) о"(п) °
Рассмотрим теперь базис ег .. .ек подпространства С"^пК По-
Поскольку элементы пространства С^ - координатные столбцы, то
„ о"(")
каждый е,- имеет вид:
е,- =(ef- ,...,е,- ) , i=l...fc, D.71)
где ei можно рассматривать как компоненты в некотором базисе
et- (г = 1.../) пространства С^ (см. упр.4.2.1).
§ 4.2. Число независимых компонент индифферентного тензора 221
Введем новую систему к векторов b| , обнулив в D.71) компоненты
при j — fc+ I,.../:
b[n) = (е- П ,...,е-/П ,0, ...,0)T, i=l,...fc. D.72)
Эта система b| , очевидно, является линейно независимой и индиф-
индифферентной относительно группы Ds , так как
t 0, t>k.
Здесь мы учли квазидиагональный вид D.67) матрицы А11^.
Рассмотрим далее в этом параграфе только точечные группы, со-
состоящие из конечного числа р элементов.
Введем еще один произвольный ненулевой вектор следующего вида:
c<"> = @,...0,c*+\...c')T D-74)
и образуем с его помощью сумму:
р
а=1
где суммирование идет по всем элементам группы Da'.
В силу квазидиагональности формы D.67) матрицы А" , вектор
b(n) будет иметь нулевыми первые к компонент, как и с(п). Этот
вектор t>(n) будет индифферентным относительно группы Ds :
?) п) •с(п) = ЕА°{п) ¦с(п)=ь(п)'
а=1 а=1
так как в силу свойств группы, произведение элементов группы всегда
дает снова элемент группы.
Вектор b^n), очевидно, является линейно независимым с базисом
btn^ (г = l,...fc). Тогда получается, что мы построили линейно не-
независимую систему из к -f 1 векторов, индифферентных относительно
группы Da , т.е. принадлежащих С"^п\ Но, согласно теореме 4.6,
это невозможно, следовательно, вектор Ып) должен быть равен нулю:
Ь<п> = 0. D.77)
222 Глава 4. Индифферентные тензоры и инварианты
Если ввести обозначение для ненулевой части вектора с^п' как
с' = (cfc+1,... ,с')т, то получим новый вектор размерности (I — &),
и условие D.77) с учетом D.75) и D.67) примет вид:
р
Л22а с — и> V*'10)
а=1
где А'зза - матрицы (I — к)-го порядка.
Соотношение D.78) должно выполняться для любых ненулевых
векторов с', очевидно, что это возможно только если
А'2'2а = 0. D.79)
а=1
Это соотношение называют свойством ортогональности матрич-
матричных представлений. Фактически оно является следствием некоторых
более общих соотношений ортогональности представлений, более де-
детальное изложение которых можно найти, например, в [3, 7, 30, 39,
43].
4.2.7. Вывод формулы для числа к
Из свойства ортогональности D.79), в частности следует, что ха-
характер суммы матриц А'^а равен нулю:
р
() D.80)
а=1
Тогда, вычисляя характер суммы матриц Аа из Ds , получаем
*(? <(п)) = ? х(Ек) +х(? %и) = Е * = Рк, D.81)
а=1 а=1 а=1 а=1
так как характер единичной матрицы Ей равен к.
Теорема 4.7. Характеры изомерных матричных представлений
совпадают.
Т Справедливость этой теоремы следует из того, что все коэффици-
коэффициенты характеристических полиномов V(X) изомерных матриц совпа-
совпадают (см. п.2.3.5), а след матрицы является одним из этих коэффи-
коэффициентов. А
Используя теорему 4.7, в D.81) переходим к характерам матриц
л(п)
Аа и получаем окончательно следующую основную теорему.
§ 4.2. Число независимых компонент индифферентного тензора 223
Теорема 4.8. Число к независимых компонент тензора пП лю-
любого п-го ранга, индифферентного относительно точечной группы
GSf вычисляют по следующей формуле:
). D.82)
Это число к равно размерности пространства 2% индифферент-
индифферентных тензоров п-го ранга.
Характеры х{Аа ) матриц п-го уровня можно вычислить по ха-
характерам х(Аа) матриц Аа первого уровня, согласно формуле C.58).
4.2.8. Случай непрерывных групп
Для непрерывных групп изложенное выше доказательство также
остается справедливым, но в формулах D.75) и D.82) перебор всех
элементов группы путем суммирования должен быть заменен интег-
интегрированием по непрерывным подгруппам.
Рассмотрим группы G33 • • • G37 класса трансверсальной изотропии
(см. п.3.2.2). Каждая группа содержит несколько континуальных
множеств (К штук), каждый элемент которых соответствует точке
на отрезке 0 ^ ф ^ 27г:
Например, для группы Сзз- /С = 1, А[х](ф) = Q^ для группы G34:
К = 2 и А[х](ф) = фз> А[2]{Ф) = Фз-^з и Т-Д- Тогда каждой из этих
матриц можно поставить в соответствие матрицы п-го уровня:
$i> D-84)
а также квазидиагональные матрицы:
|5п)' г, t = l...K. D.85)
В результате получим непрерывные группы jD, .
Тогда вектор b^n), по аналогии с D.75), строим следующим обра-
образом:
()еГ$)() D-8б)
Следствием равенства нулю D.77) этого вектора является соотноше-
соотношение, аналогичное D.78):
:0. D.87)
224 Глава 4. Индифферентные тензоры и инварианты
Свойство ортогональности, записанное для характеров D.80), прини-
принимает в данном случае вид:
А г ~
Е/ х№т(Ф))*Ф = 0. D.88)
Переходя к характерам матричного представления из группы D*s ,
получаем:
К" К"
Е Г *и йп) ww = Е Г
Е Г *и й ww = Е Г ы^ = ***¦ D-89)
«=о Jo t=o Jo
Отсюда, переходя к характерам матриц Ащ (<^), получаем утвеждение
следующей теоремы.
Теорема 4.9. Число к независимых компонент тензора п?1, ин-
индифферентного относительно непрерывных групп трансверсаль-
но-изотропного класса вычисляют по формуле:
Х\^ D.90)
Характеры матриц А$ (ф) можно вычислить по характерам мат-
матричного представления А^](ф) групп Gs:
Х(А$(ф)) = Хп(Аф)), t = l...K, 0<:ф<^2ж. D.91)
Рассмотрим теперь изотропный класс.
Каждый элемент группы (?,, s = 38,39, из этого класса соответ-
соответствует некоторой точке из множества [0,2тг] х [0,2тг] х [0, тг] в трехмер-
трехмерном пространстве:
D.92)
таких континуальных множеств в каждой группе G,, s = 38, 39, име-
имеется К штук. По этим элементам группы Gs строим матрицы п-го
уровня Ащ(ф,(р,в) и А'/г](ф,<р, в). Вектор b^n) строится следующим
образом:
Ь(П) = Е / ' / /'42П)(^Ч>*в)«м0М<1<р<1ф. D.93)
^io io Jo lJ
Проделывая еще раз все выкладки, получаем формулу для числа к.
§ 4.2. Число независимых компонент индифферентного тензора 225
Теорема 4.10. Число независимых компонент индифферентного
тензора п-го ранга относительно групп изотропии вычисляют по
формуле:
k= ^T,fj fj [х{А^{ф,<р,в))в\пвс1в<1Ч><1ф. D.94)
Характеры рассмотренных матриц вычисляются следующим обра-
образом:
{$ >,в)). D.95)
Упражнения к § 4.2.
Упражнение 4.2.1. Показать, что если матрица А = А^ ' определена
в декартовом трехмерном базисе ё," (i = 1,2,3), то матрица линейного пре-
преобразования А^п', порожденная ей, будет определена в Z-мерном базисе векто-
векторов е^ , . . . , е^ (I = Зп) пространства ?^п', каждый элемент которого ег-
[г = 1, . . ./) есть координатный столбец, порожденный компонентами полиады
etl 0 ё,'2 ® . . . 0 ё|п в трехмерном пространстве Ш .
Упражнение 4.2.2. Показать, что базис ej (г = 1, . . .Z), введенный в
упр.4.2.1, можно представить рекуррентным образом:
(п) (п) -17
где
(п)Т _ (п)Т _ / (n-l)lT (n-lJT (n-lKT\
(n-l)jT __ / (n-2)j,lT (n-2)i,2T (n-2)j,3T\
e»i...»n — Vet'i...in 'e»i...in »eii...in />
Здесь введена функция % — i\i\ . . .^n)> устанавливающая соответствие между
трехмерными индексами 1\ . . . in =¦ 1, 2, 3 и /-мерными i = 1 . . . / (/ = Зп).
У^Пралснение 4.2.3. Показать, что функцию % = i(ii . . . in) можно записать
явным образом:
i =
- 1) + 3"~2(г1 - 1) + ... + З1^.! - 1) + in.
Тензорное исчисление
226 Глава 4. Индифферентные тензоры и инварианты
Упражнение 4.2.4. Используя формулу упр.4.2.3, показать, что для случая
П = 2 функция I = i(i\ ... in) связывает девятимерные индексы с трехмерными
следующим образом:
»= A2 3 4 5 6 7 8 9),
hi2 = A1,12,13,21,22,23,31,32,33).
Упражнение 4.2.5. Показать, что векторы е) , построенные по формулам
упр.4.2.2, имеют явный вид:
и образуют базис в пространстве
?'п'.
§ 4.3. Симметричные индифферентные тензоры
4.3.1. Число независимых компонент индифферентных
симметричных тензоров
Формулы D.82), D.90) и D.94) позволяют установить число незави-
независимых компонент любого тензора n-го ранга, индифферентного отно-
относительно группы G,, по характерам х{Аа ) приводимого матричного
представления. Вычисление этих характеров достаточно сложно, поэ-
поэтому, пользуясь формулами D.91), C.58) и D.95), переходят к харак-
характерам неприводимого представления групп х(^а)- Однако эти фор-
формулы D.91), C.58) и D.95) верны, только если тензор ПП не обладает
никакой симметрией по индексам. Если же такая симметрия имеется,
то число независимых компонент тензора уменьшается, и указанные
формулы следует уточнить.
Суть этого уточнения в следующем. Для индифферентного тензо-
тензора nfl, обладающего какой-либо симметрией по компонентам, следует
составить индифферентный вектор а(п), а потом еще один вектор 8(п),
суммируя совпадающие вследствие симметрии компоненты. Размер-
Размерность вектора S(n) при этом будет уже меньше, чем размерность а(п),
т.е. q <? Зп.
Матрица n-го уровня А^п\ соответствующая индифферентному
вектору S(n) будет также иметь уменьшенный порядок q. Эта матри-
матрица А(п) строится из соответствующей матрицы А^ путем суммиро-
суммирования строк, отвечающих совпадающим компонентам вектора а(п), и
__ § 4.3. Симметричные индифферентные тензоры 227
исключением соответствующих строк и столбцов. (Можно поступить
наоборот: к столбцу j матрицы А^ добавить столбцы з, ?, и,..., если
компоненты вектора а?х = ajx = a?n) = • • • совпадают из-за симмет-
симметрии, а затем исключить в матрице А^ строки и столбцы с номерами
Sit,u, Хотя матрица А^ при этом получится, вообще говоря,
другая, но ее характер будет совпадать с х(^п'))*
Заметим, что построение матрицы А^ по матрице А^ отличает-
отличается от операции симметрирования по группе индексов B.163), поэтому
для таких матриц А^ будем использовать термин - симметриз о ван-
ванная матрица n-го уровня.
Если теперь образовать множество всех построенных таким обра-
образом матриц А(п) для одной и той же группы Gs и одного и того же
вектора S(n), то получим еще одно матричное представление группы
(?,, которое будет, очевидно, приводимым.
Для этого матричного представления А^ будут справедливы все
выводы пп.4.2.4 - 4.2.8, а также формулы D.82), D.90) и D.94). Под-
Подсчет числа независимых компонент тензора ПП, обладающего сим-
симметрией компонент, сведется к определению характеров приводимого
представления х{Аа ) (а Для непрерывной группы характеров
$ через характеры
4.3.2. Симметричные индифферентные тензоры
второго ранга
Формулы связи х{Аа ) и х{Аа) для случая симметричного тензора
второго ранга ft:
ft = ft , f2tlt2 = Ut2%1 (n = 2)
можно легко установить непосредственным вычислением характеров.
Покажем это.
Вначале образуем индифферентные векторы а(п) и S(n), имеющие
размерности З2 = 9 и 6 соответственно:
JT _ /IT ЛТ „ЪТ\ _ /Qll О12 О13 О21 О22 О23 О31 О32 О33\
и
af2) = (Й11, fi12 + Й21, fi13 + Й31, П22, П23 + fi32, П33).
Матрица AW будет иметь вид C.42).
Тогда соотношение D.51) индифферентности в явном виде запи-
228.
Глава 4. Индифферентные тензоры и инварианты
шется следующим образом:
п12
п13
п21
п22
п23
п31
п32
\а33/
/П"\
я12
)
п22
п23
п31
п32
\п33/
D.97)
где
А\ А\ .
А^ =[ А2 А2 А2
\А3 A3 Alt
Просуммируем теперь строки 2и4, Зи7, 6и8в векторах и в матрице,
а затем исключим из матрицы столбцы 4, 6 и 7. В итоге получим
соотношение индифферентности для симметризованного вектора SB):
аB) = Л<2>-аB), D.98)
или в явном виде, выписывая только члены главной диагонали:
\ /А{А{ \ / П" \
п22
(А\А\
А\А\ +А\А\
А\А3+
A%A-t-\- АоАъ
2Л3
A\A\J \
U12 + U21
п13 + п31
U22
U23 + п32
/
D.98')
Вычислим характер симметризованной матрицы
ХAB>) = (А\J + (А2J + (А3J + А\А\ + А\А3 + А2А3+
+ А12А2 + А3А2 + А13А31.
Комбинируя слагаемые в том выражении, получаем:
D.99)
= 1{А\ + А2 + А3J + \{А\А\ + А\А\ + А\А3 + А2А\+
+ А2 А2 + А2 А3 + А\А\ + А3 А2 + А3 А3.
Откуда окончательно получаем следующую теорему.
D.100)
§ 4.3. Симметричные индифферентные тензоры 229
Теорема 4.11. Характеры матричного представления группы
Gs, образованного с помощью симметризованных матриц второго
уровня А^2', связаны с характерами матричного представления А
первого уровня той же группы Gs следующей формулой:
1 )^ D.101)
Формула D.101) является аналогом формулы C.58) на случай сим-
симметричного тензора второго ранга.
Если теперь подставить D.101) в D.82), или D.90), или D.94), то
можно подсчитать число независимых компонент симметричного тен-
тензора второго ранга, индифферентного относительно различных групп
симметрии.
4.3.3. Симметричные индифферентные тензоры
третьего ранга
Рассмотрим теперь индифферентный тензор третьего ранга 3П,
симметричный по второму и третьему индексам:
или ft1'11'21'8 = ft1'11'21'8, D.102)
тогда п = 3, / = З3 = 27. Соответствующий ему индифферентный
вектор а(з) имеет 27 компонент, запишем их рекуррентным способом,
используя обозначения из п.4.2.1:
аC) - laB)>aB)>aB))> aB) -\аA) '°A) >аA) Ь
a(i)aT = (П1'11'21, ft'11'22, n'll'a3). D.103)
Симметризованный вектор аC) имеет 18 компонент, которые ре-
рекуррентным способом можно записать следующим образом:
s'B) = (n'lU. nil12 + и'1". o<l13 + nil31. n<l22, fiil23 + nil32,
Условие D.53) индифферентности вектора а(з) также записываем ре-
рекуррентным образом:
= Л?ЛB) ^IA(^) Л|ЛB) а\2) , D.105)
\?() |B> ЙB) V/
230.
Глава 4. Индифферентные тензоры и инварианты
где
\
А\
\AlAW
D.106)
Сравнивая D.103) и D.104), легко заметить, что симметрирование
тогда в симметризованном
в D.106), а матрица Лл3' в
производится только для векторов a!L,
виде должна быть записана матрица
D.105) останется без изменения:
А\А\
А\А\+ А\А\
А\А33+ AfAj
2 2
А3А\ I \ W*33 I
D.107)
т.е. в симметризованном виде матрицы А^ в соотношениях D.98) и
D.107) совпадают. Это означает, что совпадают и их характеры, т.е.
х{АB)) можно вычислить по формуле D.101). Так как в соотношении
D.105) замена матрицы А^ на симметризованную А^ происходит
одинаково во всех блоках матрицы А^2\ получаем следующую теоре-
теорему.
Теорема 4.12. Характеры матричного представления группы
Gsy образованного с помощью симметриз о ванных матриц третье-
третьего уровня А^3\ связаны с характерами матричного представления
первого уровня А той же группы Gs следующей формулой:
D.108)
Формула D.108) совместно с формулой
DЛ09)
а=1
(или аналогичными формулами D.90) или D.94)) позволяют вычис-
вычислить число независимых компонент симметричного индифферентного
тензора третьего ранга 3П по характерам х{Аа) матричного пред-
представления группы G,.
§ 4.3. Симметричные индифферентные тензоры 231
4.3.4. Симметричные индифферентные тензоры
четвертого и более высокого рангов
Используя формулы C.58) для тензоров без симметрии, D.101) для
симметричного по паре индексов тензора второго ранга и D.108) для
симметричного по одной паре индексов тензора третьего ранга, мож-
можно установить следующие рекуррентные зависимости характеров сим-
симметричных тензоров.
Теорема 4.13. Пусть имеется индифферентный относительно
группы Gs вектор п-го уровня а(п). Тогда
1° если на (т — 1)-ом уровне векторы а(^"\1п"т+1 имеют какую-либо
симметрию, а на т-ом уровне у вектора ft/J^V**" не появляется
новых видов симметрии, то характеры симметриз о ванных мат-
матричных представлений группы Gs на этих уровнях связаны следу-
следующим образом (т ^ п):
2° если на (т — 2)-ом уровне векторы ajj^jj) m+2 имеют какую-либо
симметрию, а на т-ом уровне у вектора ^\1^%п~т появляется до-
дополнительно только симметрия по двум "новым индексам"
гп_т+1, г„_т+2> то характеры матричных представлений на
этих уровнях связаны следующим образом:
х{А{т)) = -(х2(А) + x(A))x(A(m~2)); D.111)
3° если на т-ом уровне векторы a|jTln~m имеют какую-либо сим-
симметрию, а на уровне 2т <С п вектор аBт)П~2т симметРичен по
группе индексов гь .. .гп_2т, *n-2m+ii • • -in-m, rno характеры
матриц на этих уровнях связаны следующим образом:
х(А{2т)) = ^(Х2М(ГО)) + Х(А^2). D.112)
Ў Доказательство утверждения D.110) осуществляется также, как и
вывод формулы D.108) для тензора третьего ранга, а утверждения
D.111) - аналогично доказательству формулы D.101).
Для доказательства формулы D.112) рассмотрим случай тензоров
четвертого ранга 4П, обладающих симметрией по парам индексов:
D.113)
232.
Глава 4. Индифферентные тензоры и инварианты
тогда п = 4, т = 2, и представим соответствующий индифферентный
вектор аD) с помощью двухиндексных элементов
D-П4)
где индексы i\ и г^ пробегают значения от 1 до_9, каждое из этих зна-
значений соответствует паре индексов у тензора ftlll2ts'4 (см. табл.4.3).
Таблица J^.3. Значения (ji) и соответствующие им пары
)
(ii)
(«i,t2)
i
ii
2
12
3
13
4
21
5
22
6
23
7
31
8
32
9
33
Тогда матрицу А^ также можно представить с помощью кронеке-
ровского произведения матриц А^ размерностью 9x9:
81x81
D.115)
где А^2) имеет вид C.42). В справедливости такого представления
легко убедиться непосредственно, расписывая компоненты матрицы
Л'4' через матрицы А^. Соотношение индифферентности D.53) с
учетом обозначений D.114) и D.115) будет иметь вид:
"B)
"B)
О19
"B)
"B)
O29
"B)
Q91
"B)
UBVB>
21
D.116)
§ 4.3. Симметричные индифферентные тензоры
.233
где
D.116')
tB)9
Сравним теперь соотношения индифферентности D.97) и D.116).
Очевидно, что они отличаются только размером матриц и векторов:
в D.97) матрица имеет размер 9 х 9, а в D.116) - 81 х 81. Более то-
того, симметризация соотношения D.111) осуществляется точно также,
как и в D.97) - суммированием строк, соответствующих компонентам
ftjj2 с ji ф 32, и исключением соответствующих столбцов. В резуль-
результате получим симметрированное соотношение индифферентности:
аD) =
•аD),
D.117)
явная форма которого в точности повторяет симметрированное соот-
соотношение D.98') только для большей размерности:
/ .BI .BI
аD) =
\
.BI .BJ
2 .BJ
2Л 2
.BK .BJ
.B)9 .B)9
D.119)
где
аD) =
D)
19
91
О"\Т
Здесь, как и в D.98'), мы выписываем только члены на главной диа-
диагонали, поэтому, очевидно, характер такой матрицы А^ можно вы-
вычислить по формуле, аналогичной D.101):
D.119)
Отметим, что формула D.119) не зависит от конкретных значений
и порядка матрицы А^2\ Поэтому если матрицу А^ заменить на
234 Глава 4. Индифферентные тензоры и инварианты
симметризованную А^2\ то формально результат D.119), очевидно,
не изменится:
\ ). D.120)
Матрица А^\ полученная таким образом, будет соответствовать ком-
компонентам индифферентного тензора ft*1'2'**4, симметричного уже не
только по парам индексов, но и внутри каждой пары: ii,Z2 и гз,г4,
что и доказывает формулу D.112) для случая п — 4.
Для п > 4 справедливость теоремы можно показать таким же спо-
способом. А
Для компонент симметричного тензора четвертого ранга ft'112'3'4,
т.е. удовлетворяющего соотношениям D.37), формулу D.120) можно
преобразовать, если учесть, что х(^2'2) = х{А2^)> и воспользовать-
воспользоваться формулой D.101):
2 \ >). D.121)
Приводя подобные, получаем следующую теорему.
Теорема 4.14. Характеры матричного представления группы
Gs, образованного с помощью симметриз о ванных матриц четвер-
четвертого уровня А^\ соответствующих индифферентному тензору 4П
с условиями D*37), связаны с характерами матричного представле-
представления первого уровня А следующей формулой:
2Х(А2)х2(А) + ЪХ2{А2) + 2Х(А4)). D.122)
Эта формула вместе с D.82) (или D.90), D.94) для непрерывных
групп) позволяет установить число независимых компонент индиф-
индифферентного тензора четвертого ранга 4П, обладающего симметрией
компонент вида A.263).
4.3.5. Расчет независимых компонент тензоров
с помощью характеров матричных представлений
Для того чтобы воспользоваться формулами D.82), D.90) или
D.94), нужно вычислить характеры х(А) матриц А%^ входящих в
группы симметрии G8. Вычисления можно сократить, если учесть,
что характеры всех матриц, принадлежащих к одному и тому же клас-
классу ?s сопряженных элементов группы Gs, равны. Поэтому достаточно
вычислить характер х(^) только одной какой-либо матрицы из клас-
класса.
Например, для матриц A%j из моноклинной группы Gs имеем:
Х(А) = х(Е) = 3, D.123)
§ 4.3. Симметричные индифферентные тензоры 235
Х(С) = -3, х(Яз) = -1, х(Дз) = 1, Р = 4.
Тогда по формулам D.82) находим число независимых компонент ин-
индифферентного вектора (тензора первого ранга п — 1):
= ;[C + (-3) + (-1) + 1) = 0, D.124)
т.е. индифферентных векторов относительно данной группы не су-
существует.
По формуле D.101) находим характеры х(А^) симметризованных
матриц второго уровня группы G$:
= 6, х(С<2>) = \{Х\С) + Х(С2)) = iC2 + 3) = 6, D.125)
= \(X2(D3) +Х(Р1)) = 1A + 3) = 2, х(Лз) = \A + 3) = 2.
Тогда по формуле D.82) находим:
к = \ {х(ЁМ) + Х(С<2)) + хФ?]) + х(Д?°)) = 1F + 6 + 2 + 2) = 4
D.126)
- число независимых компонент симметричного тензора второго ранга
П'1'2, индифферентного относительно моноклинной группы.
По формуле D.108) находим характеры х(-А^) симметризованных
матриц третьего уровня группы G5:
Х{Е{3)) = 6 • 3 = 18, х(СC)) = -3 • 6 = -18,
??3) 43)) = 1-2 = 2, D.127)
тогда по формуле D.108) находим:
к - \
= 1A8-18-2 + 2) = 0, D.128)
т.е. индифферентных симметричных тензоров третьего ранга для
данной группы нет.
Наконец, по формуле D.122) находим характеры симметризован-
симметризованных матриц четвертого уровня:
= 1C4 + 2 • 3 - З2 + 3 • З2 + 2 • 3) = 21,
о
236
Глава 4. Индифферентные тензоры и инварианты
= i((-3L + 2 • 3 • (-3J + 3 • З2 + 2 • 3) = 21, D.129)
О
) = ?((-1L + 2 • 3 • (-1J + 3 - З2 • +2 • 3) = 5,
О
= ?A4 + 2 • 3 • I2 + 3 • З2 + 2 • 3) = 5.
О
По формуле D.82) находим:
к= ^B1 + 21
5) = 13
- число независимых компонент симметричного тензора четвертого
ранга ft'1*2*»14, индифферентного относительно моноклинного класса.
Таблица 4-4- Число к независимых компонент векторов и сим-
симметричных тензоров второго, третьего и четвертого рангов, индиф-
индифферентных относительно различных групп симметрии
Син-
гония
Трик-
линная
Моно
клин-
ная
Ром-
биче-
бическая
Тет-
раго-
наль-
ная
Класс
сим-
симметрии
Е
Трик-
линный
м
Моно-
клин-
клинный
0
Орто-
троп-
ный
т
Тет-
раго-
наль-
ный
Группа
Gs
1
2
3
4
5
6
7
8
9
10
11
век-
векторы
п=1
3
0
2
1
0
1
0
0
0
1
0
Числе
сим.
тен-
тензоры
2-го
ранга
6
4
3
2
к
сим.
тен-
тензоры
3-го
ранга
18
0
10
8
0
5
3
0
4
4
0
сим.
тен-
тензоры
4-го
ранга
21
13
9
7
§ 4.3. Симметричные индифферентные тензоры
.237
Син-
гония
Ром-
биче-
бическая
Гек-
саго-
наль-
ная
Куби-
чес-
ческая
Класс
сим-
симметрии
Къ
Ква-
ЗИИЗО-
троп-
ный
А
Ромби-
Ромбический
в
Ромби-
Ромбический
н
Гек-
саго-
наль-
ный
К
Ква-
ЗИИЗО-
троп-
ный
Тран-
свер-
саль-
ноизо-
троп-
ный
Изо-
троп-
тропный
Группа
Gs
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
век-
векторы
п=1
0
1
0
0
1
0
1
0
0
0
1
0
0
0
1
0
0
0
0
0
0
1
0
1
0
0
0
0
Число
сим.
тен-
тензоры
2-го
ранга
2
2
2
2
1
2
1
к
сим.
тен-
тензоры
3-го
ранга
2
3
1
0
6
0
4
2
0
2
4
0
1
1
3
0
1
0
1
0
0
4
0
3
1
0
0
0
сим.
тен-
тензоры
4-го
ранга
6
7
6
5
3
5
2
238 Глава 4. Индифферентные тензоры и инварианты
Подобные вычисления можно проделать для всех остальных групп
симметрии G,, используя для этого данные из табл.3.3 и 3.4, в ко-
которых приведены характеры матричного представления х(А) классов
сопряженных элементов симметрии для всех групп симметрии Gs.
Итог этих вычислений подведем следующей теоремой.
ТЕОРЕМА 4.15. Число к независимых компонент векторов и сим-
симметричных тензоров второго, третьего и четвертого рангов (т.е.
удовлетворяющих соотношениям D-37) и D.41))> индифферентных
относительно групп симметрии Gs s = 1...39, определяется в со-
соответствии с табл.4-4-
Это число к совпадает с числом элементов тензорного базиса
D» 19) в соответствующем пространстве индифферентных тензо-
тензоров.
Для тензоров четных рангов число к одинаково для всех групп
в рамках класса симметрии (см. табл.4.4). Этим обстоятельством,
главным образом, и обусловлено выделение в сингониях понятия клас-
класса симметрии.
§ 4.4. Скалярные инварианты
Кроме индифферентных тензоров, сохраняющих свои компоненты
при определенных преобразованиях, в механике и физике широко при-
применяют скалярные функции от тензоров, также не изменяющиеся при
линейных преобразованиях координат.
4.4.1. Определение скалярных инвариантов
Определение 4.4. Скалярным инвариантом тензора пП
п-го ранга относительно группы преобразований Gs называют
функцию /(•>: Т3(п)—>МХ
/E) = 1^{П) = J<'>(fifW"), D.130)
от компонент тензора П'1—•» в некотором базисе ё,-, не изменяю-
изменяющуюся при любых преобразованиях в данной группе Gs, т.е.
j(')(n«"i.«u) = /W(JV'i-'n). D.131)
Здесь
Замечание 1. Данное определение включает в себя задание кристал-
лофизического базиса ё,- или осей анизотропии. Фиксируя группу Gs
§ 4.4. Скалярные инварианты 239
матриц преобразования и меняя базис на е(-, получим другие инвари-
инварианты /(*)(П;|1—tn) тензора пп = ft'll*lne(i <g> ...® e(n относительно
изомерной группы симметрии G',.
Далее, если не оговаривается особо, полагаем, что инварианты рас-
рассматриваются в базисе ё,.
Замечание 2. Согласно определению 4.4, скалярный инвариант тен-
тензора можно рассматривать и как функцию j('): 7з —*" ^Х> и> пос"
ле фиксирования кристаллографического базиса ё,-, как функцию /'*):
Шк —> М1, ставящую в соответствие набору компонент ftll<tn тензо-
тензора в базисе ё,- вещественное число. Здесь к = Зп - число компонент
тензора, равное размерности пространства 7^. Оба эти подхода эк-
эквивалентны.
Замечание 3. Если у тензора nfl не все компоненты ft'1* iln явля-
являются независимыми (например, когда тензор пП - симметричный по
какой-либо группе индексов сг, т.е. принадлежит подпространству
5з"° = Sr?/ С 7з ), то число к будет меньше, чем Зп. В этом слу-
случае, будем всегда полагать, что аргументами функции /(*)(П11—1п)
являются только к независимых компонент тензора ПП. Набор этих
компонент П* 1шп представляет собой элемент пространства ]Rfc, и для
него будем применять обозначение fifl-ln E Rk.
4.4.2. Независимые инварианты
Инвариантов относительно фиксированной группы Gs У каждого
тензора п ft существует бесконечное множество (любой инвариант, ум-
умноженный на число - тоже инвариант), поэтому выделяют функцио-
функционально независимые инварианты тензора (будем их называть также
просто независимыми). Дадим их определение.
Определение 4.5. Отображение f : Ег —> Ш1 (г ^ 1) назы-
называют тривиальной функцией от г аргументов и обозначают
как /(/i,...Ir), где (i"i,.. .Jr) G Кг, если существует такая область
W С Кг, что для любых несовпадающих элементов (Д,.../г) С W и
{1{ ,.../*) С W, их образы совпадают:
f(h>...IT) = f(ri>...rr). D.133)
Соответственно, функция /(Д,... , /г) - нетривиальная, если в лю-
любой области W С Шг всегда найдутся несовпадающие элементы
(Д,... , /г) С W и (/J, ...,/*) С W, образы которых также не сов-
совпадают.
Определение 4.5 применимо для функций /, непрерывных во всем
Кг. Если же / является непрерывно дифференцируемой в1г, то для
нее справедлива следующая теорема.
240 Глава 4. Индифферентные тензоры и инварианты
Теорема 4.16. Пусть функция f(Ii,... 1Г) непрерывно дифферен-
дифференцируема в W, тогда она является тривиальной в том и только
в том случае, когда существует область 1У С Мг, в которой все
ее частные производные тождественно равны нулю: df /dip = 0
(/3=1,....г).
Т Действительно, если / - тривиальная, то существует область W',
в которой выполняется D.133) для любых 1р ф 1% из W. Тогда для
всякого фиксированного набора (i"i,... , 7^,... , /г) можно образовать
функцию
значение которой равно нулю, а предел при 1р —> 1? совпадает с
частной производной:
lim T,gfi{Ii,...,Ir) = df/dIp=O.
В силу построения, этот предел всегда равен нулю во всей W.
Наоборот, если у функции / все частные производные равны ну-
нулю в некоторой области W, то / является константой в W. Тогда,
очевидно, что D.133) всегда выполнено. А
Следствие. Из этой теоремы следует, что непрерывно дифферен-
дифференцируемая функция / является нетривиальной тогда и только тогда,
когда fl любой области 1УСМгв какой-либо точке найдется хотя бы
одна не равная нулю частная производная df/dlp ^0, A G {1,... , г).
Примером тривиальной функции является тривиальная линейная
комбинация (см. п.2.1.2) инвариантов / = si/i-K . .-fsr/r, для которой
выполнение условия D.133) эквивалентно тому, что sQ = 0, а —
1,...г.
Определение 4.6. Если для системы скалярных инвариантов
IQ(n?l), а — 1,.. .г, тензора п?1 относительно группы Gs существу-
существует нетривиальная функция /(Д,.. .1Г), тождественно равная нулю
при всех значениях компонент Q%1'"in:
f(l1{Uii'~i*)...Ir{Uii~-i»))=0, Vfi1-1"», D.134)
то такую систему инвариантов называют функционально за-
зависимой.
Определение 4.7. Систему скалярных инвариантов /a(nfl).
а = l,.k.r, тензора nfl относительно группы Gs называют функ-
функционально независимой, если для любой нетривиальной функ-
функции /(/i,... /г) от этих инвариантов найдутся такие значения ком-
компонент П|1#п, что
f (^(Й'1-1"-) ...Jr(Q'--'»)) ф 0. D.135)
§ 4.4. Скалярные инварианты ___241
Эти определения обобщают понятие линейной независимости эле-
элементов системы (см. упр.4.4.1).
Будем далее полагать, что инварианты 1а(п%1—%п) и соответству-
соответствующие функции /(Д,... , Jr) принадлежат одному классу: либо не-
непрерывных, либо непрерывно дифференцируемых функций в соответ-
соответствующих пространствах.
4.4.3. Условия функциональной независимости у
инвариантов
Сформулируем теперь достаточное условие независимости системы
инвариантов.
Теорема 4.17. Пусть имеется тензор nfl, принадлежащий про-
пространству 7з , причем dim Т$ = к <С Зп, рассмотрим инвариан-
инварианты этого тензора IQ(U%1'"ln), a = 1,...г, относительно некото-
некоторой группы Gs, которые являются непрерывно дифференцируемыми
функциями IQ : Шк —У Ш1. Тогда при г <J к система инвариантов
/i,... Jr функционально зависима в том и только в том случае, если
для любого Й1'1-1'» G V
<г,
а пр« г > к система инвариантов Ii,...Ir всегда функционально
зависима.
Т Пусть инварианты /а, а — 1,...г, функционально зависимы, тог-
тогда согласно определению 4.6 существует нетривиальная непрерывно
дифференцируемая функция /(ii(fill##*ln),.. ./г(Й|1ш#Лп)), равная нулю
для любого Й|1#ф>1п G Mfc. Дифференциал df такой функции также
тождественно равен нулю в М*, следовательно,
=»
В силу независимости приращений еШ11"*1" (см. замечание 3 из
п.4.4.1) из D.137) получаем, что должно выполняться соотношение:
Так как / - нетривиальная, тов силу следствия из теоремы 4.16 в со-
соотношении D.138) при любых ft*1—1»1 найдутся не все нулевые коэффи-
коэффициенты 5//5/а, тогда D.138) выражает собой линейную зависимость
242 Глава 4. Индифферентные тензоры и инварианты
всех г координатных строк матрицы (dIa/dUll-~tn). Следовательно,
максимальное число независимых строк этой матрицы всегда меньше
г. По теореме 2.10а, отсюда следует, что ранг такой матрицы также
всегда меньше г. В одну сторону теорема доказана.
В обратную сторону. Предположим, что имеет место D.136), но
инварианты 1а - функционально независимы. Тогда, согласно опре-
определению 4.7, длявсякой нетривиальной функции /(Д,... /г) найдутся
такие значения П*1—1», что выполняется соотношение D.135).
Выберем в качестве такой функции линейную функцию / = c\I\ -f
.. .-fcr/r, где ci,... , сг - произвольные не все нулевые числа. Но тогда
дифференциал такой функции будет отличен от нуля:
df = J^Cadla^O D.139)
а=1
при любых ненулевых dIQ. Следовательно, рассматривая IQ как функ-
функции от Qtl#tn, имеем
а=1
В силу произвольности dU%1'%n (так как dIQ в D.139) также произ-
произвольны), получаем, что имеют место следующие соотношения:
а=1
Таким образом, мы показали, что для любых не всех нулевых ко-
коэффициентов cQ имеют место соотношения D.141), означающие, что
все г строк матрицы (dIQ/dU%l'"tn) линейно независимы.
Если г > А, то получаем, что имеются г линейно независимых строк
длиной fc, что согласно теореме 2.2 невозможно. Следовательно, пред-
предположение о независимости инвариантов Д,.../г - ложно. Если же
г <С fc, то согласно теореме 2.10а независимость всех г строк матрицы
д1а/д?1%1"Лп означает, что
но это противоречит условию теоремы, следовательно, инварианты
Д,... 1Г - функционально зависимы, и в этом случае теорема доказана.
А
С помощью теоремы 4.17 можно указать достаточные условия не-
независимости инвариантов, которыми будем пользоваться далее.
§ 4.4. Скалярные инварианты
.243
Теорема 4.18. Пусть имеется система инвариантов /а(пП) (где
а = 1,...г иг ^ к) тензора пП относительно группы Gs С I, яв-
являющихся непрерывно дифференцируемыми функциями. Выполнение
каждого из следующих условий является достаточным для функцио-
функциональной независимости этой системы инвариантов:
1° подсистема из г — 1 инварианта 1а (а = 1,.. .г, а ф /?) данной
системы является независимой, а инвариант 1р зависит хотя бы
от одной компоненты П1*"*1», от которой не зависят остальные
инварианты;
2° каждый из инвариантов 1а (а = 1,...г) зависит хотя бы от
одной компоненты П*1—1п, от которой не зависят остальные ин-
инварианты.
Ў Докажем п. 1°.
Образуем матрицу частных производных (dIQ/dUll'"%n) в условиях
теоремы:
dip
5ft1-1
f
к
о
г
0
0
¦р-
Согласно этим условиям столбец, соответствующий индексам
3
> • • «гп
у , у
состоит из нулей кроме элемента в /3-ой строке:
Вычеркивая из этой матрицы /?-ую строку и несколько столбцов,
включая (il.. .г*)-ый, получаем матрицу (д1а/дп%1"ЛпУ частных про-
производных размером (г — 1) х (к — 1), которая содержит все производные
244 Глава 4. Индифферентные тензоры и инварианты
от инвариантов /а, а = 1.. .г, а ф C. Так как эти инварианты неза-
независимы, то эта матрица имеет ранг
га = rang I -—г—r- 1 > r — 1
согласно теореме 4.17. Но так как в ней только (г—1) строк, то т = г.
Значит, вычеркиванием (к — г) столбцов в матрице {dIQ/dQ%1"'tnY
можно найти невырожденную матрицу (dIa/dUll'"tn)" (r — 1)-го по-
порядка.
Тогда, вычеркивая те же самые столбцы в матрице (dIQ/d?ltl'"tn),
придем к матрице (д1а/д?1%1"ЛпУ" r-го порядка, содержащей /?-ую
строку и столбец, соответствующий индексам гJ ... г*. Вычислим де-
детерминант этой матрицы, используя разложение по указанному
(ij .. .г* )-ому столбцу. Тогда получим
det (dla/dW1-*»)"' = det {д1а/дП*1"*")" ф О,
так как по условию теоремы с ф 0 и det (д1а/дп%1"Лп)" ф 0. Отсюда
следует, что
rang (dla/dff1"**)'" = rang {д1а/дП*1"л*)" = г.
Согласно теореме 4.17 это означает, что вся система инвариантов
/i... Ir - функционально зависима. Для случая 1° теорема доказа-
доказана.
Рассмотрим случай 2°. Выберем вначале два инварианта, к ним
применимы условия п.1°. Следовательно, они независимы. Далее при-
присоединяем к системе третий инвариант - снова оказываются приме-
применимы условия п.1°, и система трех инвариантов будет независима.
Продолжая этот процесс до г-го инварианта, очевидно, получим неза-
независимость всей системы г инвариантов. Теорема доказана. А
Сформулируем еще одну теорему, которая нам потребуется при
подсчете независимых инвариантов тензоров.
Теорема 4.19. Если в некотором базисе е,-, полученном из ё,- с
помощью матрицы A3i, принадлежащей некоторой группе симмет-
симметрии Gs: ё,- = A3iejf где А3\ Е Gs, тензор nft = п%1'Лпе{1 0 ... 0 е,-п
имеет р ненулевых компонент, то число г функционально независи-
независимых инвариантов этого тензора относительно той же группы Gs
не может быть больше р: г ^ р.
Т Действительно, пусть имеется набор из г скалярных инвариантов
тензора ПП относительно группы Gs: IQ = IQ(Q%1'"tn) с осями анизо-
анизотропии, направленными по ё,-. Так как данная матрица А3{ Е Gs,
§ 4.4. Скалярные инварианты 245
то функции IQ = ia(fitl'"ln), a = 1...г, также будут инвариантами
тензора пП вследствие соотношения:
По условию теоремы /а(?}и"-1п), а = 1...Г, - независимы, тогда и
система Ja(fill'"fn), a = l...r, - функционально независима. Но со-
согласно теореме 4.18, число г не может быть больше ранга матрицы
dla/dU11'*1! а так как ft'1*1" имеет только р ненулевых компонент,
то ранг этой матрицы не может быть больше р, т.е.
г <? rang (д1а/дп{1'"{п) <? р. А
4.4.4. Функциональный базис
Определение 4.8. Система из г скалярных инвариантов ц'({1)
(где 7 = 1...г) тензора nil относительно группы преобразований
G$ называется функциональным базисом независимых инва-
инвариантов тензора относительно группы преобразований Gs, если
- она является функционально независимой,
- любой иной, не входящий в эту систему, скалярный инвариант
тензора пП относительно этой же группы преобразований Gs
может быть представлен в виде функции от этих инвариантов
4>
Функциональный базис, очевидно, всегда является не единствен-
единственным.
Заметим, что скалярные инварианты D.130) могут быть установ-
установлены для любого тензора ПП, не обязательно являющегося индиффе-
индифферентным.
Из теоремы 4.18 следует, что число г функционально независимых
инвариантов не может быть больше числа к - независимых компонент
тензора ПП. Независимые скалярные инварианты /7(ПП) относитель-
относительно группы G$ могут быть образованы с помощью операции свертки
направляющих тензоров О7 в данной группе с данным тензором "Пи
его тензорными степенями nfl<g>nft и nft®nft®nft.
Такие инварианты называют полиномиальными. Реально в механи-
механике и физике другие, неполиномиальные инварианты используют край-
крайне редко, и здесь они далее не рассматриваются.
Заметим также, что когда говорят о независимых инвариантах и
компонентах тензора ПП, фактически неявно предполагают, что этот
тензор имеет максимально возможное число ненулевых и различных
между собой компонент. В частном же случае тензоры могут при-
принимать любые значения, например, все компоненты тензора ft'1-1*
могут быть равны между собой, но это отнюдь не означает, что у
тензора одна независимая компонента и один инвариант. Поэтому
246 Глава 4. Индифферентные тензоры и инварианты
везде далее будем использовать понятие независимых инвариантов и
компонент тензора с учетом этого допущения.
4.4.5. Неприводимые инварианты
Иногда ограничивают вид зависимости между инвариантами и рас-
рассматривают только полиномиальные соотношения между ними, при
этом если какой-либо инвариант может быть представлен в виде поли-
полинома (т.е. суммы степеней) от других инвариантов, то его называют
приводимым. В противном случае его называют неприводимым.
Если выбран набор из п скалярных инвариантов тензора ft отно-
относительно группы Gs, которые обладают следующими свойствами:
- являются неприводимыми,
- любой иной, не входящий в этот набор инвариант можно предста-
представить в виде полинома от этих инвариантов,
то такой набор называют минимальным целым рациональным бази-
базисом.
Очевидно, что число элементов р минимального рационального ба-
базиса и число г элементов полного набора функционально независимых
инвариантов, вообще говоря, различны, причем г <С р, а р может быть
больше к. В самом деле, возможна ситуация, когда соотношения меж-
между инвариантами являются полиномиальными, но ни один из них не
может быть выражен в виде полинома от других инвариантов. Та-
Такие соотношения называются сизигиями. В то же время из сизигии
какой-либо инвариант Ц*' можно выразить как неполиномиальную
функцию от других инвариантов, тогда он заведомо не будет входить
в полный набор функционально независимых инвариантов. Однако
Ц* останется неприводимым и войдет в целый рациональный базис
(если, конечно, он не выражается полиномиально из других каких-
либо еще соотношений).
Примером такой сизигии является, например, полиномиальное со-
соотношение между инвариантами Д и /г:
all + bhh + cl\ = О,
где a,b, с - числа. Очевидно, что в общем случае ни Д, ни Д нельзя
выразить в виде полинома друг от друга, и в то же время Д или
Д можно выразить в виде неполиномиальной функции от Д или Д.
Другие примеры сизигий будут приведены в упражнениях к §4.4.
Далее нас будут интересовать в основном функционально незави-
независимые инварианты.
Наиболее часто в механике используют инварианты векторов и сим-
симметричных тензоров второго ранга, т.е. п =1 и 2. Рассмотрим их.
4.4.6. Инварианты вектора
Независимые скалярные инварианты вектора а — а,е,- относитель-
относительно группы Gs могут быть образованы с помощью операции скалярного
§ 4.4. Скалярные инварианты 247
произведения вектора а с образующим вектором ОG) (тензорами раз-
размерности п = 1) соответствующей группы G5, а также скалярного
произведения тензора а 0 а с образующими тензорами второго ранга
О,G). При этом число г независимых инвариантов вектора не может
превышать г ^ к = 3.
Исходя из перечня D.27) направляющих векторов и тензоров, по-
получим, что указанным выше способом можно построить только сле-
следующие инварианты вектора а:
о
а-ёа = аа, a<g>a--Е = |a|2, a<g>a--ё2 = а2 , a<g>a- -ftQ = dpa^.
D.142)
В зависимости от принадлежности направляющих тензоров той
или иной группе' G,, получаем из набора D.142) инварианты векто-
вектора ц относительно данной группы Gs. Ниже приведены инвариан-
инварианты вектора а, построенные указанным способом для всех групп Gs,
з=1, ...39.
В скобках выписана явная запись инвариантов через компоненты
а, вектора в базисе ё,.
/. Триклинная сингония
Gi : /iX) = аёа = аа, а = 1,2,3, г = 3; {аьа2,а3} D.143а)
B) ° B) °
G2 • /| = а • fti • а = аоаз, Ц = a • ^2 • a = «хаз,
43) = |a|2, г = 3; {а2а^ а^з, |а|2}
Я. Моноклинная сингония
G3: /J3)=a.e/3=d/3, /3=1,2;
43) = а • ё§ • а = а§, г = 3; {аь а2, а§}
G4: /J4)=a.e2.a = a2, /3^1,2;
44) = а • ё3 = а3> г = 3; {а2, а2, а3} D.1436)
G5: /J5)=a.e2.a = a2, /3=1,3;
4 = а • п3 • а = aia2, г = 3; {af, aia2, a2}
Я/. Ромбическая сингония
G6: jJ6)=a.e».a = a^, 46)=а-ёз = аз,
/3 = 1,2, г=3; {а?, а|,о3}
G,, s = 7,8: i4f) = a.e*-a = o|, а = 1,2,3, г = 3;
{б?, а|, а§} D.143b)
IV. Тетрагональная сингония
Gs, s = 9,11,12,14,15 : l[$) = a • Е • a = |a|2,
4")=а.ё2.а = а1, г = 2; {а?, о|}
248 Глава 4. Индифферентные тензоры и инварианты
Gs, s = 10,13: /|4) = |а|2, 7<')=а-ё3 = а3; {|а|2,а3}D.143г)
V. Ромбоэдрическая сингония
G,, 5=16,18: /{4) = |a|2, 4''= а3, г = 2; {|а|,а3}
G,, s = 17,19,20 : l['] = |a|2, l[s) = й2, г = 2; {|а|2,а2}
D.143д)
VI. Гексагональная сингония
G,, 5 = 21,23,24,25,27: 1['] = \&\2, 1{2'] = ag, r = 2; {|а|2,а|}
G,, 5 = 22,26 : l[s) = |a|2, J<f) = a3, r = 2; {|а|2, а3}D.143е)
V7J. Кубическая сингония
G,, з = 28,.. .32 : l[s) = |а|2, г = 1; {|а|2} DЛ43ж)
VTJ/. Трансе ерсалъная изотропия
G,, s = 33,35 : j}#) = |а|2, /^ = *>, г = 2? {1а12' °з}D.143з)
G,, 5 = 34,36,37: l\a) = |а|2, 4'> = а2, г = 2; {|а|2, а2}
/X. Изотропия
G,, 5 = 38,39: 45) = |а|2, г = 1; {|а|2} D.143и)
Очевидно, что для тех групп, у которых инвариантами являются
длина вектора |а| и а§, также инвариантом является и длина проекции
вектора на плоскость Oeie2: \/(aiJ + (U2J, но этот инвариант не
является независимым.
ТЕОРЕМА 4.20. Функциональный базис независимых инвариантов
вектора а относительно группы Gs С I состоит из г элементов,
где
- г = 1 для группы G, изотропного и кубического классов;
- г = 2 для групп G8 тетрагональной, ромбоэдрической, гексаго-
гексагональной, кубической сингоний и трансе ер сально-изотропного
класса;
- г = 3 для остальных групп Gs С I.
В качестве функционального базиса могут быть выбраны инвари-
инварианты D.143).
Ў Рассмотрим изотропный класс и произвольный вектор а = a*ej.
Тогда можно построить новый ортогональный базис е,-, одним из век-
векторов которого, например ез, будет вектор а = е3. Поскольку все
ортогональные базисы связаны ортогональными матрицами преобра-
преобразований, то найдется такая матрица Alj G /, что ё,- = A3{ej. Но
в базисе е,- вектор а имеет только одну ненулевую компоненту аз-
Следовательно, выполнены условия теоремы 4.19, а значит число не-
независимых инвариантов вектора а не может быть более одного. Но
один инвариант всегда существует, это, например, длина вектора |а|,
так как
|а|2 = (Ja'Si, = А\А\ака18^ = dkdl8kl.
§ 4.4. Скалярные инварианты 249
Следовательно, г = 1.
Рассмотрим теперь трансверсально-изотропный класс. Для про-
произвольного вектора а опять введем новый базис е, с помощью спе-
специальной матрицы Axj вида C.6), где угол ф выберем из условия:
tg ф — а2/а1; причем ё* = А\ъ3-. В базисе е, вектор а имеет толь-
только две ненулевые компоненты: fli и а3. Поскольку такая матрица
AXj принадлежит к группе Тз, то снова оказываются выполненными
условия теоремы 4.19, и, следовательно, для группы Тз число г ^ 2.
Но два независимых инварианта всегда существуют - это, например,
инварианты D.143з). Независимость следует из теоремы 4.18 п.2°,
так как у инварианта /^ = |а|2 имеются компоненты вектора а,, не
входящие в инвариант Ц — а>з (или а^).
Доказательство теоремы для групп из классов Т, Аз, Дз, -Н"» К и
Кз оставим в качестве упражнения 4.4.4.
Для групп из классов Е, М и О теорема будет доказана, если мы
установим независимость трех инвариантов (максимально возможное
число: г = к = З1) в системах D.143а), D.1436) и D.143в) соответ-
соответственно. Но независимость этих инвариантов IQS\ а = 1, 2,3, относи-
относительно групп G,, s — 1,3, ...8, очевидно, вытекает из теоремы 4.18,
так как выполнены условия п.2°. Для доказательства независимости
инвариантов 1а , ос = 1,2, 3, составим матрицу частных производных:
2а3
Очевидно, что существуют такие значения aj, что определитель этой
матрицы
Д = det [dialда1') = 2a3(a^ + a\ - а\)
отличен от нуля, например, при ai = a<i — a3 = 1, получаем Д = 2.
Следовательно, rang (dIQ/dd%) = 3, и в соответствии с теоремой 4.17
делаем заключение о независимости инвариантов 1а , ее = 1, 2, 3.
Независимость инвариантов 1а относительно остальных групп
G5, s — 9,.. .32, легко установить с помощью теоремы 4.18 п.2°. А
Упражнения к § 4.4
Упражнение 4.4.1. Показать, что система линейно зависимых инвариантов
является и функционально зависимой; если же система функционально независи-
независима, то она и линейно независима.
Упражнение 4.4.2. Показать, что абсолютные значения компонент вектора
(а'^а а) = 1^а| (а = 1, 2, 3) являются инвариантами относительно группы
(-Т2 (т.е., что выполнены условия D.131)), однако они не являются независимыми,
т.к. выражаются через полный набор инвариантов следующим образом:
I, а,/9,7= 1,2,3;
250 Глава 4. Индифферентные тензоры и инварианты
Д = G<2O<2O<2)I/2.
Упражнение 4.4.3. Показать, что скаляр
является инвариантом относительно группы (?з> но не является функционально
гC)
независимым, т.к. выражается через i-у :
Упражнение 4.4.4. Доказать теорему 4.20 для групп из классов Т,
Я, К3 и К.
§ 4.5. Инварианты симметричного тензора
второго ранга
4.5.1. Пространство симметричных тензоров
, Рассмотрим теперь симметричные тензоры второго ранга Т, т.е.
удовлетворяющие условию A.181).
Согласно теореме 2.31, множество всех симметричных тензоров
второго ранга в М3 образует линейное пространство S$ , являюще-
являющееся подпространством в 7з .
4.5.2. Построение инвариантов симметричного тензора
Функционально независимые скалярные инварианты симметрично-
симметричного тензора второго ранга Т с компонентами
T^fijei^ej D.144)
в базисе ё,- относительно группы симметрии Gs, принадлежащей к не-
некоторому классу, могут быть построены с помощью операций сверт-
свертки симметричных образующих тензоров ОG) (см. табл.4.2) данного
класса симметрии с самим тензором Т, либо его тензорными степеня-
ми Т2, .Т 0 Т и Т 0 Т 0 Т, Т3.
Исходя из перечня (см. табл.4.1) направляющих симметричных
тензоров получим,, что указанным выше способом можно построить
следующие скалярные инварианты тензора Т:
Т ¦ -Е = Гц + ?22 + Тзз, Т • О3 = 2Т12 D.145)
§ 4.5. Инварианты симметричного тензора 251
- линейные инварианты, образуемые сверткой Т с направляющими
векторами ёа или тензорами второго ранга ё^, Е и Оз:
Т2 • Е = 2» + Т22 + Т23 + 2G* + Т|3 + Т23),
Т2 • -О3 = 2(fuf12 + f12t22 + Г13Г23),
Т2 • -ё2 = Т2! + Т22 + Т23, (Оз • Т) • -(ё2 • Т) = 2Г13Т2з,
(ё2 • Т) • -(ё2 • Т) = Та23, (Е - ё3) • Т • -(ё2 • Т) = Т23 + Т2з, D.146)
Т <g> T • • • Oh = f2! + f222 +1323,
Т ® Т • • • -D3 = 4(T13(tu - Таз) - 2Т12Т23),
Т ® Т • • • -Пзл = 4Т12(Тц - Т22),
Т ® Т • • • -n3d = 4(Т2з(Тц - Т22) + 2Ti2Ti3)
- квадратичные инварианты, образуемые сверткой квадрата тензора
Т2 или Т ® Т с направляющими тензорами второго ранга Е, Оз, ё2
или четвертого ранга О/,, D3,
Т3--О(а), T2®T-..-4O(Q), (T2-O(Q))..(T-OW)T,
(Т • О(в)) • (Т • От) ¦ .(Т • OW)T, D.147)
(Т.-4О(а)).(Т-О(/3))..(Т-Оы)т,
(T.O@))-(T--40(/J))..(T..40G))T и т.п.
О(в) G {Е, Оз, ё2 }, 4O(Q) = {Oh, D3, Пзл, Пм}
- кубические инварианты, образуемые сверкой куба тензора Т3 с на-
направляющими тензорами второго ранга Е, Оз и ё2, или третьей сте-
степени тензора Т®Т®Т с направляющими тензорами четвертого ранга.
Среди последних наиболее распространенными являются инвари-
инварианты:
(Т • ОЬ) • (Т • -Oh) ¦ .(Т • -О„) = Тй + Т*2 + Т33з, D.148)
Т2 ® Т • • • .О„ = 2» + Т32 + f Зз + Тц(Т?2 + Т23) + T22(fl2 + f 23)+
Сформулируем теперь теорему, из которой следует, что все введен-
введенные скаляры D.145) - D.148) действительно являются инвариантами.
252 Глава 4. Индифферентные тензоры и инварианты
Теорема 4.21. Любой скалярный полином тензора второго ранга
Т;
/(Т) = 2иО—^ T0...0T, n ^ 1,
2n n
где 2пО - тензор Bп)-го ранга, индифферентный относительно
группы Gs, является скалярным инвариантом тензора Т относи-
относительно той же группы Gs.
Ў Запишем выражение для / в базисе ё,, совпадающем с осями ан-
анизотропии тензора 2пО = Otl#l2netl <g>... ® ё,-п:
а также в базисе е,-, связанном с е,-, ортогональной матрицей A%j Е Gs
Откуда получаем, что скаляр /(Т) удовлетворяет условию D.131) и,
следовательно, является инвариантом относительно группы Gs. A
4.5.3. Главные инварианты тензора
Наиболее часто применяют инварианты, образованные с помощью
метрического тензора Е:
Ji(T) = Т • Е, Д(Т2) = Т2 • Е, D.149)
/х(Т3) = Т3 • Е = I* + Т32 + Т33з + 3(tn(t22 +123) + T22{Tl2 + Г|3)+
которые, очевидно, являются инвариантами относительно любой
группы преобразований (?,, т.к. метрический тензор входит в чис-
число образующих тензоров каждой группы.
Вводя определитель симметричного тензора Т по формуле A.8'):
det Т = Tii?22?33 - ?ц?!з - Г221?з - Т33Т22 + 2Т12Т13Т23, D.150)
непосредственной проверкой нетрудно установить, что
det (Т) = ^ (J3(T) - 3Ji(T)J2(T2) + 2Д(Т3)) , D.151)
§4.5. Инварианты симметричного тензора 253
откуда следует, что определитель тензора также является инвариан-
инвариантом относительно любой группы Gs.
На основе инвариантов D.149) и D.150) введем так называемые
первый, второй и третий главные инварианты:
\ - Д(Т2)) = Тг1Т22 + ТцТзз + t22t33 - Т>2 - Т& - Т223,
I3(T)=det (T). D.152)
Остальные скаляры в D.145) - D.148) являются инвариантами от-
относительно уже не произвольной группы (класса) симметрии G,, а
только той, к которой принадлежит образующий тензор ОG), с помо-
помощью которого образован данный инвариант.
Теорема 4.22. Собственные значения Аа симметричного тензо-
тензора Т также являются инвариантами относительно всех классов
симметрии.
Ў В самом деле, если Аа - собственные значения Т:
(Т - AQE) • eQ = 0, D.153)
то можно составить характеристический полином:
V{\) = det (T - АЕ) = det {% - Щ), D.154)
тогда
Т{\) = (Тп - Л)(Т22 - Л)(Т33 - А) - (Гц - Л)Т|3 - (Т22 - А)ТХ23-
- (Тзз - А)!* + 2Т12Т13Т23 = det(T) - А2^ + Т222 + Цг)-
- A(Tut22 + Т„Гзз + Т|2Т33 - Т\2 - flz - 2?з) - А3 =
= /з(Т) - А/2(Т) + А2/Х(Т) - А3. D.154а)
С другой стороны, полином Т{\) можно представить через его кор-
корни Ао:
V{\) = (А: - А)(А2 - А)(А3 - А) = -А3 + А2(АХ + А2 + А3)-
А2А3) + AiA2A3. D.155)
Сравнивая эти два представления, находим связь между Ао и ин-
инвариантами /а(Т):
/3(Т) =
D.156)
254 Глава 4. Индифферентные тензоры и инварианты
Откуда следует, что Аа, как и Л*(Т) инвариантны относительно лю-
любого класса симметрии.
Так как 1^(Т) не зависят от системы координат, то из D.156) кроме
того следует, что собственные значения тензора Аа также не зависят
от системы координат. А
4.5.4. Теорема Гамильтона-Кэли
Поскольку Аа являются собственными значениями тензора Т, то
характеристический полином V(X) при каждом А = Аа обращается в
нуль. Тогда из D.154а) имеем:
\3a=Ii{T)\2a-I2(T)\a+h{T), a =1,2,3. D.157)
о
Тензор Т можно разложить по собственному базису еа согласно
A.173):
3
Т = ? Ааеа <g> еа. D.158)
а=1
Рассмотрим теперь тензорные степени Т2 и Т3. В силу A.180), для
Т2 и Т3 имеет место аналогичное разложение:
л = 2,3. D.159)
а=1
Заменим теперь в разложении для Т3 коэффициенты А3 их выра-
выражениями D.157):
Т = Д(Т) ? Х2аеа ® еа - J2(T) ? AQea ® е«+
а=1 а=1
3
+ .Х. /с\ Хек />1 1 /?л\
еа 0 е . D.160)
а=1
Если тензор Т неособенный, то, умножая D.160) на Т, получаем
Г2 - Ji(T)T + /2(T)E). D.161)
Если воспользоваться представлениями D.158) и D.159), то придем к
Т3 = h(T)T2 - /2(Т)Т + /3(Т)Е D.162)
- уравнению, которое по форме аналогично характеристическому
уравнению D.157), если вместо Аа поставить сам тензор Т. В этом
состоит утверждение следующей теоремы.
___ $4.5. Инварианты симметричного тензора 255
Теорема 4.23 (Гамильтона-Кэли). Неособенный тензор удов-
удовлетворяет своему характеристическому уравнению.
Из D.162) следует важный вывод: любую тензорную степень Тп
(п > 3) можно выразить только через первые две степени: Т2, Т и Е,
например
Т4 = Т3 • Т = /!(Т)Т3 - /2(Т)Т2 + /з(Т)Т =
= h (ДТ2 - /2Т + 13Е) - /2Т2
= (J? - /2)Т2 - (hl2 - 1з)Т + J
и т.д.
4.5.5. Функциональные базисы независимых инвариантов
симметричного тензора второго ранга
Среди всего множества инвариантов представляет интерес выде-
выделение полного набора функционально независимых инвариантов для
каждого класса симметрии.
Ниже приведены функциональные базисы независимых скалярных
инвариантов 1а симметричного тензора Т, построенные с помощью
наборов D.145) - D.148) и соответствующие фиксированному классу
симметрии (Gs). В скобках представлено явное выражение инвариан-
инвариантов {l[8\ .../г } через компоненты TJj тензора Т в базисе ё,.
(Е) - триклинный класс:
{Гц, Т22, Тзз, Т23, Ты, t12}. D.163)
(М) - жонокл«нкый класс:
а = 1,2,3; j|M) = 1Т •-О3,
{tu, Т22, Тзз, Т12, Г»,. Т13Т23}. D.164)
(О) - класс ортотропии:
T.-el а=1,2,3; /<° > = (ef • Т) • • (ё§ • Т),
256 Глава 4. Индифферентные тензоры и инварианты
{Гц, ?22, Тзз, Т23, t23, fi2T13f23}. D.165)
(Т) - тетрагональный класс:
т®Т----ПЗЛ, 4T)=det(T),
{Гц+Г22, Тзз, 2?з + Г|з, Tfi + Tla, ^(Гц-Ти), det (T)}. D.166)
(^з) - квазитрансверсально-изотропный класс:
=4Т), а=1,...4,б;
{Гц + Т22, Тзз, Т23 + f|3, Т& +1222) T!2,, det (T)}. D.167)
(Л) - ромбоэдрический класс:
/() = (Е-ё).Т--(ё.Т), 7<) = i
r(>l)_T2..F т(АJ 9Т(А) г(Л) _ 1
Т22, Тзз, Т13 + Т23, Т1з(Тц - Т22) —
2 + 2Т!22, Т23(ТП - Т22) + 2T12Ti3}. D.168)
(В) - ромбоэдрический класс:
J?*>=#\ в=1...б; 4B)=det(T),
{Тц + Т22, Т33, Т23 + Т23, Т13(Тп - Т22) - 2Т12Т23,
Т2! + Т222 + 2Т22, det (T)}. D.169)
__ § 4.5. Инварианты симметричного тензора 257
(К) - квазиизотропный класс:
l[Q) = T..E, I{2Q) = T®T----Oh, 4«> = I (та-.Е-.#
= Т2
= Т2 ® Т • • • Oh - 4Q), 4Q) = det (T),
{Гц + Г22 + Тзз, Т\х + Т\2 + Т3231 Т22 + Т23 + Т223, 2?х + Т232 + 3^,
? + 2?з) + Г22B?2 + Т223) + Т33(Т% + f23), det (T)}. D.170)
(Н) - гексагональный класс:
{Гц + Т22, Тзз, Т23 + Т223, Т2! + Т22 + 2Т22, det (T)}. D.171)
(Тз) - трансеерсалъно-изогпропный класс:
43)=4Я), о = 1...5. D.172)
(/) - класс изотропии:
/) 7 = 1,2,3. D.173)
Теорема 4.24. Для симметричного тензора второго ранга Т
функциональный базис независимых инвариантов относительно
группы Gs С I состоит из г элементов, где
- г = 3 для групп Gs изотропного класса,
- г = 5 для групп Gs трансверсально-изотропного и гексагонально-
гексагонального классов,
- г = 6 для всех остальных групп Gs полной ортогональной группы
I.
В качестве этих функциональных базисов соответствующих групп
Gs могут быть выбраны наборы инвариантов D.163) - D.173).
Ў Как и ранее будем для определенности полагать, что все рассматри-
рассматриваемые группы Gs соответствуют осям анизотропии, направленным
по векторам базиса ё,-. Тогда определения D.131), D.132) скалярных
9 Тензорное исчисление
258 Глава 4. Индифферентные тензоры и инварианты
инвариантов тензора второго ранга Т = Т^ё,- ® ej можно записать
следующим образом:
\^ МА^ GG,, а = 1,.. .г <С 6.
D.174)
Поскольку Т - симметричен, то у него имеется не более шести неза-
независимых компонент ftJ (г, j = 1,2,3), поэтому согласно теореме 4.17
для всех групп Gs (s = 1... 39) число г ^ к = 6.
Рассмотрим группы Gs из класса изотропии I. Согласно теореме
1.13, симметричный тензор Т имеет три вещественных собственных
значения А,- и ортогональный собственный базис е,. Тогда сущест-
существует ортогональная матрица А% у, связывающая е,- с ёу: ej = А* уе,*.
Поскольку соотношение D.174) в изотропном классе имеет место для
о
любых ортогональных матриц, то в качестве <А* • можно выбрать А% j.
о ° . о . -. .
Так как в базисе е, матрица компонент Т%3 = А% tl A7 jxT%l31 - диаго-
диагональная, из D.174) получаем: 1^\тз) = li^(Ai, А2, А3), а = 1,...г.
Отсюда следует, что любой инвариант 1а изотропного класса мо-
может быть представлен как функция только трех скаляров - А,-. Но
согласно теореме 4.22, Аа(Ти") сами являются инвариантами тензора
Т. Следовательно, они образуют функциональный базис в классе /,
а значит г = 3. Вместо А,- в качестве базиса можно выбрать главные
инварианты Л*(Т), которые связаны с А,- соотношениями D.156).
Рассмотрим теперь тпрансверсалъно-изотропный класс Тз. Пред-
Представим тензор Т в виде суммы двух тензоров: Т = Ti -f Тг, где
Тг = {Ti3Sj3 + Tj38i3 - T33Si3S3'3)ei 0 ёу, D.175)
Т2 = Т*'ё,- 0 ej = fIJej 0 ej, I, J = 1,2.
Тензор Т2 является симметричным и по теореме 1.13 имеет вещест-
вещественные собственные значения, но ненулевых из них только два: Ai и
А2, - в силу структуры самого тензора. Тогда собственные, векто-
0 0
ры ei, e2 тензора Т2 будут лежать в плоскости векторов ei, ё2, ор-
ортогональной к оси трансверсальной изотропии Ох3. Следовательно,
о .
существует ортогональная матрица А% j вида
о о >
cos ф sin ф О
такая, что ё,- = A\ej, причем ез =
§ 4.5. Инварианты симметричного тензора
259
mi 7 ° ° °
Тензор Тг = ?2 e,- 0 e, в базисе е, диагоналей, поэтому
Txj = A%kA\Tkl = Y?x=i^c*u%q8jq, а тензор Ti в этом базисе сохра-
сохраняет свою структуру:
0
СОБф
о
— sin^
0
О
сойф
0
sin<i
о
sin<^
о
cos<^
0
О
— sin<^
о
COS<^
0
0
1
0
0
О О Т13
П П Т23 I v
.U U i \Х
rpl3 f 23
где Т13 = cos Jt13 + sin фТ23, Т23 = cos фТ23 - sin фТ13, Т33 = Т33.
о
Тогда тензор Т в базисе е,- имеет следующий вид:
о . о . _
Tij = А* кА> ,Тк1 = Т? + Т% =
О Т13>
А2 Т23
т.е. содержит только пять ненулевых компонент. Поскольку матрица
о
преобразования А1 к принадлежит к группе Тз, то у нас оказывают-
оказываются выполненными условия теоремы 4.19, согласно которой число не-
независимых инвариантов тензора Т не может превышать пяти. Для
доказательства теоремы нам остается только показать, что сущест-
существуют пять независимых инвариантов относительно Тз-класса. Ниже
мы покажем, что таковыми являются, например, инварианты D.172).
Доказательство теоремы для Я-класса оставим в качестве
упр.4.5.13.
Для остальных классов симметрии, поскольку г = 6, т.е. совпа-
совпадает с максимально возможным числом инвариантов, нам достаточно
построить в каждом классе хотя бы одну систему из шести функцио-
функционально независимых инвариантов. Такие системы построены в D.163)
- D.173). То, что эти системы являются инвариантами, следует из
теоремы 4.21. Покажем их независимость.
В классах Е, М и О системы инвариантов D.163), D.164) и D.165)
являются независимыми, так как каждый из инвариантов содержит
хотя бы одну компоненту Т1-7, которая не входит в остальные инвари-
инварианты системы, и тем самым выполнено условие 2° теоремы 4.18.
Для доказательства независимости системы инвариантов D.166) в
260.
Глава 4. Индифферентные тензоры и инварианты
Т-классе составим матрицу частных производных:
f 1
0
0
2Гц
Tia
0
0
0
0
Тц - T2
Bl2
0
0
2T13
0
2 0
JE?i3
1
0
0
2T22
-Tl2
Б22
0
0
2T23
0
0
В2з
0
1
0
0
0
B-
D.176)
Здесь введено обозначение для производных: Bij = 5(det T)/3TIJ =
det T(T),j. Вычисляя определитель этой матрицы, находим
Д = det (д1а/дТ>) = 4(Тц - Т22J(Т23В13 - Т13В23).
Поскольку всегда существуют такие 7^-, что Д ф 0, например, при
D.177)
получаем Д = -468), то rang (д1а/дТ%з) — 6, из теоремы 4.17 следует
независимость системы D.166).
Аналогичным образом, составляя матрицу частных производных
{dla/dT1*), доказываем независимость систем из шести инвариантов
D.167) - D.170).
Матрицы частных производных для if, T3 классов и класса изо-
изотропии соответственно имеют вид:
\dfijj
/ 1 0 0 1 0 0 \
0 0 0 0 0 1
0 0 2T13 0 2t23 0
2TU 4T12 0 2T22 0 0
\ Вц В\2 B\3 B22 B23 B33 /
ц
0 0
-2f12 -2Ti
В13
B22
0 1
-2t23 (T11 + T22)
B23 B33
Вычеркивая в первой матрице четвертый столбец, а во второй -
четвертый, пятый и шестой столбцы, получаем матрицы пятого и
§ 4.5. Инварианты симметричного тензора 261
третьего порядка соответственно. Убеждаясь, что определители этих
матриц для случая D.177) отличны от нуля:
#, Тз-классы Д = 8ti_2(T23JBi3 - Т13Д23) = -208,
Т-класс Д = 2(Т13?12 - Т12В13) = 26,
находим ранги этих матриц: 5 и 3, соответственно. Применяя еще
раз теорему 4.17, отсюда делаем вывод о независимости систем инва-
инвариантов D.171) - D.173). А
В силу теоремы 4.24, все другие скаляры из D.145) - D.147), явля-
являющиеся тоже инвариантами относительно данной группы G,, могут
быть выражены в виде некоторой функции от инвариантов ц соот-
соответствующего функционального базиса.
В частности, второй и третий главные инварианты всегда можно
выразить через ц' любого класса. Другие примеры приведены в
упражнениях к данному разделу.
4.5.в. Запись инвариантов в криволинейных
системах координат
Выше была использована запись инвариантов вектора а и тензора
Т через их компоненты в декартовом базисе ё,. Однако ничто не
мешает записать эти инварианты с помощью компонент a,- hIJj в
произвольной системе координат:
а = a,-Rf" = a'R,-, T = Т{ jR{ <g> R,.
Очевидно, что достаточно записать только неповторяющиеся ин-
инвариантные комбинации. Для вектора из D.142) следует
аа = а • ёа = <цР^ \а\2 =
а=1
а2а = *Ъ*.-ё2а = ща>РМ?, D.178)
= a® a- -Sla = aiajPtpQ'j, а ф C ф уа; а,/3,7= 1,2,3.
Переход от записи в базисе ёа к записи в криволинейной системе
координат с базисами R,- и R7, очевидно осуществляется с помощью
одной из формул: ёа = P^R,- = QfR*.
Для симметричного тензора второго ранга инварианты, участвую-
участвующие в полных наборах, можно записать подобным образом:
таа = т{ '"ад?, j j
f13f23 = T/Tb'PiQlpbQf, D.179)
262 Глава 4. Индифферентные тензоры и инварианты
Г12?1зГ23 = Г, iTjTj PiQJPfQfPFQl
fu + f22 = Т^(Щ + Р1Я]).
При записи инвариантов в криволинейной системе координат более
удобно использовать именно смешанные ко-контравариантные компо-
компоненты TJJ, в частности из-за того, что первый, второй и третий ин-
инварианты при этом не изменяются:
3
Л(Т) = Тц + Т22 + Тзз = ? TiJp«Qj = Т1г + Т22 + тз3, D.180)
а=1
/2(Т) = \ {тцъ - j?(t)) = \
J3(T) = det (f«) i
= det (Ij'jdet (Pjj)det (Qy) = det C;^").
Здесь учтены формулы перехода: ёа = QfW, a также взаимообрат-
ность якобиевых матриц: P^Q) = Sj.
4.5.7. Запись инвариантов в физических компонентах
Часто возникает необходимость связать запись инвариантов в де-
декартовой системе координат и в физических компонентах. Переход к
физическим компонентам осуществляется с помощью формул A.238).
Очевидно, что инварианты |а|2, /а(Т) не изменяют своего вида и в
физических компонентах:
T?o, D.181)
а=1
= det
где
а = Оф.-е,-, Т = Тф/е,- 0 е,, D.182)
а е,- - физический (ортонормированный) базис криволинейной системы
координат.
4.5. Инварианты симметричного тензора
.263
Остальные инварианты в физических компонентах записываются
следующим образом:
з
Е
/3,7=1
/3=1
Гр?Я5> DЛ83)
е,<г=1
Инварианты тензора имеют вид:
3
/3,7=1
3 3
3 3
/
р^й7 9(ТСГ
?j<7=1
и т.д.
D.184)
Упражнения к § 4.5.
Упражнение 4.5.1. Используя соотношение между /*у(Т) и собственными
значениями Ла положительно-определенного тензора Т, а также свойство
/2(Т) - 3/2(Т) = 1- ((Ах - А2J + (А2 - АзJ + (Аз - А^2),
показать, что имеют место следующие неравенства для инвариантов:
; 3/31/3(Т), /2(Т) ^ 3/32/3(Т),
72(Т) ? 3/2(Т).
204 Глава 4. Индифферентные тензоры и инварианты
Упражнение 4.5.2• Показать, что второй и третий инварианты /2(Т),
/з(Т) выражаются через полный набор инвариантов моноклинного класса следу-
следующим образом:
_ т(м)(т(М) т(ми АМ)Т(М) AM)
am)
(М) Т(М)
(AM) \ 2
h \ AM)JMJ
Am) am) I -ii ^ ~
J4 h /
AM)AMJ cyAM)
— h Js + ZIe »
а скаляр Т23 также является инвариантом относительно М-класса, т.к.
Ф2 _ АМJ /Т(М)
-^23 — ^6 /i5
Упражнение 4.5.3. Проверить, что скаляр
является инвариантом относительно ортотропного класса О (т.е. проверить вы-
выполнение условий D.131)), но уже не является независимым, т.к. выражается
АО)
через полный набор инвариантов 1^ :
Т2 _ t{OJ/(t(O)t(OU
i2i /Н h )
Упражнение 4.5.4. Показать, что скаляры |Ti2|, ТцТ22, \Тц — Т22|,
а также ^(Т) выражаются через полный набор инвариантов тетрагонального
класса i :
1/2
АТJ
AT) _ Ц
3 ог(т)_ г(т>2'
и поэтому являются инвариантами относительно (Т) -класса.
§ 4.5. Инварианты симметричного тензора 265
Упражнение 4.5.5. Показать, что скаляры ТцТ22, |Тц — Т221 и /г(Т) вы-
ражаются через полный набор /у if з~класса и поэтому являются инвариантами
относительно квазитрансверсально-изотропного класса; в частности
Упражнение 4.5.6. Показать, что скаляры ТцТ22 - Т^, (Тц - )
-j-4T^2, T11 ~Ъ~ -^22 ~Ъ~ 2^12, а также /г(Т) выражаются через полный набор ин-
(А)
вариантов А-ромбоэдрического класса Ху :
(т„ - т22J + ат
-L D
и поэтому являются инвариантами относительно (А)-класса.
Упражнение 4.5.7. Показать, что скаляры ТцТ22 — Т?2, (Тц —
-j-4T^2> a также /2(Т) выражаются через полный набор инвариантов В-ромбоэд-
рического класса .Ту :
Упражнение 4.5.8. Показать, что скаляры Т11Т22 + T22T33
T11T22T33, а также Хг(Т) выражаются через полный набор инвариантов
К -квазиизотропного класса /-у :
Iq = ТпТ22 + Т22Т33 + Т„Тзз = i(/|QJ - 4Q)),
AQ)
266 Глава 4. Индифферентные тензоры и инварианты
и являются инвариантами относительно (JRf )-класса.
Упражнение 4.5.9. Показать, что скаляры ТцТ22 — Т*2, {Тц — Т22J +
4Т12, а также /г(Т) выражаются через полный набор инвариантов Н и Тз клас-
классов Ху или /<у таким же образом, как показано в упражнении 4.5.7, и являются
инвариантами относительно (Н) и (?з) классов.
Упражнение 4.5.10. Проверить непосредственно, что инварианты 1± и
ig удовлетворяют условиям D.131).
Упражнение 4.5.11. Используя формулу D.162), доказать, что /з(Т) всег-
всегда можно представить в виде:
1з(Т) = ^ (Д(Т3) - lf(T) + Zh{T)h(T2)) .
Упражнение 4.5.12. Показать, что формула D.162) имеет место также и
для несимметричного тензора Т.
Упражнение 4.5.13. Доказать теорему 4.24 для Я-класса.
Упражнение 4.5.14. Используя метод, описанный при доказательстве тео-
теоремы 4.24, доказать независимость систем инвариантов D.167) - D.170).
ГЛАВА 5
ТЕНЗОРНЫЕ ФУНКЦИИ
§ 5.1. Линейные тензорные функции
5.1.1. Определение тензорной функции
Рассмотрим два тензора nS и тТ n-го и га-го рангов, принадлежа-
принадлежащие пространствам 7з (Ж3) и 7^ (М3) соответственно. В механике
и физике большую роль играют законы соответствия между различ-
различными тензорами, называемые тензорными функциями.
Определение 5.1. Отображение пространства тензоров
7з (ffi3) в пространство 7з (К3) называют тензорной функ-
функцией и обозначают как пТ : 7^(т)(К3) —у 7^(п)(М3) или в виде
зависимости:
ns = nF{mT) vmTer3(m\ nseT3(n). E.1)
Кроме формального установления закона соответствия тензоров п S
и тТ, запись E.1) содержит утверждение, что тензорная функция не
меняется при переходе из одной системы координат в другую при пре-
преобразованиях координат A.2) в М3, т.е. если записать компонентное
представление функции E.1) в каком-либо базисе, например в R,-:
то при переходе в любой другой базис R( = Р3{ Rj это представление
можно записать следующим образом:
Здесь обозначены компоненты тензоров в базисах R,- и RJ-:
nS = 5'1-'"R,-l ® ...® R,n = 5"'l-'-R{l 8...8R!,,
mT _ TJi...imKji ® ... ® R_.m = т'л-imR/^ 0 # # _ e r^^
"J^ = ^'i-'-R,-, ® ... <g> R,n = jF'^-nR^ ® ... <g> R'in.
Глава 5. Тензорные функции
Учитывая правило (см. A.250)) преобразования компонент тензора
при переходе из системы координат Xх в Х'х:
5*i...u = д«'^ . ,,Q{inSk""kn, Tfii-im = Q%\ . ..Q{jmTjl-jm E.5)
и подставляя E.2) и E.3) в E.5), получаем:
Q% •..QilnFkl'"kn{Til"jm) = Ffil-in{Qjlh ...Q^T'1-'-). E.6)
Таким образом, фраза о неизменяемости тензорной функции при
переходе из одной системы координат в другую означает, что компо-
компонентное представление этой функции преобразуется по закону E.6).
5.1.2. Индифферентные тензорные функции
Важную роль в механике играют тензорные функции, компонент-
компонентное представление которых сохраняется при переходе от некоторой
фиксированной системы координат Хп = хг в другую Х%, получаю-
получающуюся путем линейного преобразования C.1):
Я1'"'* =Я1"Л\ E.7)
где f%l'"Xn - компонентное представление функции nT в декартовой
системе координат хх.
Определение 5.2. Тензорные функции E.1), удовлетворяющие
условию E.7), называют индифферентными.
Подставляя E.7) в E.3), E.2), получаем, что если в системе коор-
координат хх тензорная функция связывает компоненты SXl'"Xn и Т*1*"*т с
помощью соотношений:
то компоненты тензоров nS и тТ в системе координат Xх будут свя-
связаны теми же самыми функциями:
Определение 5.3. Если функция пТ E.1) удовлетворяет свой-
свойству E.7) не для всех преобразований координат C.1), а только для
тех, которые образуют некоторую группу Gs, то такая тензорная
функция называется индифферентной относительно
группы Gs.
Группу Gs в этом случае называют группой симметрии тензорной
функции пТ.
Не все компоненты индифферентной тензорной функции являются
независимыми, в силу E.6) и E.7) между ними имеются связи:
A%r..AilnFkl'''kn{fjl-jm) = Fil'''in{AJl ...A'^t'1 •••'"). E.9)
Здесь соотношение E.6) записано для линейных преобразований C.1),
для которых якобиевы матрицы имеют вид C.236).
§5.1. Линейные тензорные функции 269
5.1.3. Определение линейной тензорной функции
Определение 5.4. Тензорную функцию E.1) называют линей-
линейной, если она удовлетворяет двум условиям:
• тензорная функция от суммы двух тензоров mTi и тТ2, принад-
принадлежащих 7зm , есть сумма тензорных функций от каждого из
этих тензоров:
• тензорная функция от произведения тензора тТ Е 7з «я ве-
щественное число А ф О есть произведение числа на тензорную
функцию оттТ:
{mT) = \пГ(тТ). E.11)
Наиболее часто в механике встречаются центрированные тензор-
тензорные функции, т.е. удовлетворяющие условию:
n.F(m0) = n0, E.12)
здесь т0 и п0 - нуль-тензоры га-го и n-го рангов.
Теорема 5.1. Всякая линейная центрированная тензорная функ-
функция может быть представлена в виде:
E.13)
где п+тП - некоторый фиксированный тензор (п -f т)-го ранга из
у-(п+т)
В отличие от nS и тТ, являющихся переменными, тензор n+mfl
не меняется и характеризует данную линейную тензорныю функцию.
Будем называть его тензором, задающим линейную функцию.
Т Для доказательства теоремы 5.1 выберем в качестве базисов 7з и
7з полиадные базисы: Rtl 0...0R,n и W1 ®... 0RJm, и разложим
по ним nS и тТ. В силу линейности E.10) имеем
..jmR?1 ® ... в Rim) =
Разлагая теперь тензоры "^(R71 <g>... <g> RJm) no полиадному базису
в 7зП':
<g>... <g> RJm) = fl1!—*nii—i^R^ 0 ... <g> Rtn? E.14a)
270 Глава 5. Тензорные функции
находим коэффициенты разложения fi*i—**ii—im? которые являются
компонентами некоторого тензора (п + га)-го ранга.
В самом деле, возьмем другой базис R( = Р\ Kj и проведем в нем
те же самые построения. Тогда получим, что
0 ... 0 Rfjm) =
Откуда, заменяя базис, находим
Сравнивая E.14а) и E.146), убеждаемся, что fi1*—•»+*» преобразуются
по тензорному закону. Тогда всегда можно выбрать тензор n+mft,
компоненты которого в базисах R, и RJ- имеют вид:
п+тп = nf"i-t"-+mRl-10... 0 Rt-n+m = п'{1-^+гпК^ ^... ^ R;.n+m,
и который удовлетворяет E.13). А
Тогда компонентное представление линейной тензорной функции
E.13) будет иметь вид:
С*1—*п — qpi\-»in = П«1-«п+тФ. . (К 1 К\
Поскольку fi'1—tn по определению есть компоненты тензора, то, оче-
очевидно, что условие E.6) для линейной функции E.13) будет всегда
выполнено при любом тТ.
5.1.4. Примеры линейных функций
С помощью одного и того же тензора n+mfl можно построить, во-
вообще говоря, несколько различных тензорных функций. В самом деле,
переобозначив в E.13) индексы п —У га, a (n -f га) —у п, получим:
E.16)
п = 0,1,... ; га = 0,1,... , п.
Отсюда следует, что при фиксированном п, меняя га от 0 до п, можно
построить п -f 1 различных тензорных функций.
Например, при п = 0 получаем из E.16) обычную скалярную:
S UW
§5.1. Линейные тензорные функции 271
Для п > 1 вместо mS и n"mT используем обозначения, которых
придерживаемся везде в тексте: скаляры °S и °Т обозначим как 5 и
W; векторы *S и гТ обозначим как s и а; тензоры второго ранга 2S
и 2Т обозначим как S и Т. Для тензоров ПП, задающих линейную
функцию примем далее обозначения:
Тогда при п = 1 из E.16) имеем две линейные функции, которые
во введенных обозначениях имеют вид:
m = О, S = с • а (или S = с%п{);
m=l, s = cW (или s1' = cW). E.18)
При п = 2 имеем три функции:
m = 0, 5 = К • Т (или 5 = KijWji);
77i=l, s = K-a (или sx = K%iaj); E.19)
m = 2, S = KW (или &> = i
При п = 3 имеем четыре функции:
m = 0, 5 = 3М • • • 3W (или S = y
m = 1, s = 3М • Т (или s{ = M^kTkj). E.20)
77i = 2, S = 3M-a (или Sij = ^*
m = 3, 3S = 3MW (или
При n = 4 имеем пять функций:
m = 0, 5 = 4C • • • -4W (или 5 = C^klWikji);
m = 1, s = 4M - - • 3W (или в* = CijklWlkj). E.21)
m = 2, S = 4C - -T (или Sij = CijklTlk);
m=.3, 3S = 4C-a (или '^* ^'
m = 4, 4S = 4CW (или
5.1.5. Индифферентные линейные тензорные функции
Рассмотрим теперь линейные тензорные функции E.16), которые
являются индифферентными относительно некоторой группы Gs.
Подставляя E.16) в E.7), получаем, что если линейная индиффе-
индифферентная функция в исходной системе координат х% имеет вид:
5'l-'™=ft>l->"Tim+1..,n, E.22)
то в любой другой системе координат Xх, получающейся из ж1 с помо-
помощью линейного преобразования C.1), соответствующего данной груп-
группе С?,, эта функция будет иметь вид:
272 Глава 5. Тензорные функции
т.е. компоненты тензора ПП при таких преобразованиях не изменя-
изменяются:
jyi...in+m = jyi-f»+»\ E.23)
Сравнивая E.23) с D.3), заключаем, что имеет место следующая
теорема.
Теорема 5.2. Тензор пП, задающий линейную индифферентную
относительно группы Gs тензорную функцию E.16), является ин-
индифферентным относительно той же группы Gs.
Если подставить E.15) и E.23) в соотношение E.9); то получим
Й**-*»^ ... Ainkn = ft'1-1'" V (A*k) е Gs. E.24)
Это соотношение означает, что между компонентами индифферент-
индифферентного тензора существуют зависимости (см. также D.4)).
Условие индифферентности E.24), согласно п.4.1.3 (формула
D.7)), можно записать с помощью тензора линейных преобразований
Q, определенного формулой D.5):
П?1 = Пп • . . . -(Q 0 . . . 0 Q)Bn-l,2n-3,...3,l,2,4 2n)?
где
Например, условия индифферентности вектора с и тензора второго
ранга К, третьего ранга 3М и четвертого ранга 4С будут иметь вид:
с = с. Q, 3М = 3М • • • (Q 0 Q 0 Q)E31246>,
4С = 4С . . . .(Q 0 Q 0 Q 0 Q)G5312468)>
Из теоремы 5.2 следует, что для описания индифферентной ли-
линейной тензорной функции достаточно рассмотреть соответствующий
индифферентный задающий тензор nfl.
Для индифферентных относительно фиксированной группы преоб-
преобразований Gs тензоров, как было установлено в п.4.1.6, существует
разложение по тензорному базису D.19) в пространстве 1$ ':
E>25)
/3=1
или
к
^yS E.26)
/3=1
__ § 5.1. Линейные тензорные функции 273
где пП(р) - тензорный базис для группы G,, а 7/3 - коэффициенты раз-
разложения. Этот тензорный базис может быть организован с помощью
образующих тензоров группы 0sG) (см- п.4.1.8).
Подставляя E.25) в E.16), получим первое представление линей-
линейной индифферентной тензорной функции (через тензорный базис):
/3nft(/3)-n~mT. E.27)
/3=1
Вторым представлением индифферентной линейной тензорной
функции назовем компонентное представление, например, в декарто-
декартовом базисе ё,-:
"-«-iim+l...u. E.28)
/3=1
Заметим, что в этих представлениях одна линейная функция отли-
отличается от другой только значениями констант 7/3 (в рамках одной
группы симметрии G,).
Соответствующие представления E.25) и E.26) будем называть
первым и вторым представлениями задающего тензора пП.
Укажем далее тензорные базисы ПП^ и представление задающего
тензора пП для различных групп симметрии, ограничиваясь наиболее
распространенными в механике значениями п =1, 2, 3 и 4. Будем при
этом использовать символику E.17).
5.1.6. Индифферентные линейные векторные функции
Как было отмечено в п.4.1.8, тензорные базисы могут быть постро-
построены с помощью только образующих тензоров Os(<y) группы Gs. Рас-
Рассмотрим случай индифферентных тензоров первого ранга (векторов):
гП — с, т.е. в E.25) положим п = 1. Тогда в тензорный базис 3П(/з)
могут входить только образующие тензоры групп из наборов D.28) -
D.36) рангом не выше п = 1. Если таких образующих тензоров нет в
какой-либо группе Gs, то индифферентной линейной векторной функ-
функции в этой группе нет. Соответствующие компоненты с1 задающего
вектора в этом случае будем полагать равными нулю.
В табл.5.1 даны вторые представления E.26) задающего вектора с
линейной функции для разных групп симметрии.
Максимальное число ненулевых констант 7/3 У линейной векторной
функции равно 3 и достигается в группе G\. Для групп Gs s = 4,
б, 10, 13, 16, 18, 22, 26, 33, 35 имеется только одна константа 7> а
для (?з - две. Для остальных групп Gs не существует соответствую-
соответствующих ненулевых индифферентных линейных тензорных функций, что
отражено в E.25) как с* = 0.
274 Глава 5. Тензорные функции
Таблица 5.1.
I. Триклинная сингония
П. Моноклинная сингония
G3: ё = Тф=110%, G4: ?=74. <?5 : с* = 0.
III. Ромбическая сингония
G6: с1 = 7<%, G?,8 : ? = 0. E.29)
IV. Тетрагональная сингония
G9,n,i2,i4,i5 : ? = 0, Оюдз : с1 = 7^3-
V. Ромбоэдрическая сингония
<?1б,18 : с1 = 74» ?17,19,20 : с1' = 0.
VI. Гексагональная сингония
^21,23,24,25,27 : С1 = 0, ^22,26 '• С1 = 7^3'
VII. Кубическая сингония
G28...32 : ? = 0.
VIII. Трансверсалъная изотропия
<2зз,35 : с1' = 7*31 ^34,зб,37 : с1 = 0.
IX. Изотропия
<?38,39 : ? = 0.
5.1.7. Индифферентные линейные функции второго ранга
Рассмотрим случай линейных функций E.16) при п = 2, причем
кроме условия индифферентности E.23) будем считать выполненны-
выполненными условия симметрии для задающих тензоров 2П = К, т.е.
К = КТ или Kij=Kji. E.30)
Для случая п = 2 часто используется еще одно, третье представ-
представление задающего тензора К -в матричном виде:
/К11 К12 К13\
(К) = К22 К23 . E.31)
\сим. К33/
Матричное (третье) представление линейной тензорной функции
второго ранга может быть также введено для функций вида E.19) при
т=1:
\ /К11 К12 К13\ /аЛ
s2) = \ К12 К22 К23 а2 , E.32)
J3) \К13 К23 К33) \а3/
где введены компоненты векторов s и а в виде координатных столбцов
в базисе ё,-.
§5.1. Линейные тензорные функции 275
Максимальное число независимых компонент у симметричного тен-
тензора второго ранга равно 6, так как на 9 возможных комбинаций из
К-7 наложены 3 условия симметрии E.30):
К12 = К2\ К13 = К31, К23 = К32. E.33)
Условие E.30) с г = j, очевидно, образует тождества.
Индифферентность тензора К по отношению к той или иной группе
симметрии Gs приводит к появлению дополнительных условий E.24):
= KklA\A\, \/{А\) е G8 E.34)
на компоненты K%i и число к независимых компонент еще уменьшает-
уменьшается. Это число к может быть определено с помощью теории характеров
матричных представлений (см. теорему 4.15 и табл.4.4).
Тензорный базис О5G) E.25) симметричных индифферентных тен-
тензоров второго ранга К будет состоять только из симметричных обра-
образующих тензоров рангом выше второго. Эти тензоры содержатся в
табл. 4.2. Заметим, что они одинаковы для разных групп Gs в пре-
пределах фиксированного класса.
Ниже даны первое, второе и третье представления задающего тен-
тензора К для различных классов, а также используемые образующие
тензоры.
Триклинный Е-класс {еа}:
з
К = 2_^ 7аеа ® еа + 74^1 ® &2 + ^2 ® ei) -f 75(©1 ® еЗ + €
а=1
i<8>e2),
к** = X; 7а^^а + 74(^4 + 4*i)+75D4 + 44)+7бD4 + 44),
а=1
/л:» к» 71 74 75
(К") = К12 К" К™\ = [ 74 72 76 • E-35)
Моноклинный М-класс {е
з з
к = Е -**е«+^°з. Rij = Е т«W+^(ад+w, E.36)
а=1 а=1
276 Глава 5. Тензорные функции
Ортотропный О-класс
з
E.37)
Т - тетрагональный, К$ - квазитрансверсалъноизотропный, А,В-
ромбоэдрические, Н - гексагональный, Тз - трансверсальноизотроп-
ный классы {Е, ез}:
К = 71 (Е-е§)-
Ю> = I 0 71 О I • E-38)
\0 0 та/
JK" - квазиизотропный, I - изотропный классы {Е}:
0\
E.39)
Для групп симметрии ^-класса у тензора К достигается макси-
максимальное число независимых констант - 6; для групп М-класса - 4;
для ортотропного класса - 3; для групп классов Т, К$, А, В, Н и Тз -
2 константы, и для групп К и /-классов - одна независимая константа.
Если тензор К невырожден, то соотношения E.19) при га = 2 и
E.32) можно обратить:
а = L- s,
где L - симметричный тензор, обратный к К и имеющий матричное
представление:
( ii2 ^13 \
L_i2 L22 L23 ,
?23 ?33 /
причем
K-L = E
§5.1. Линейные тензорные функции 277
или
Используя результаты упр.4.1.8, получаем, что если К - индиффе-
индифферентен относительно какой-либо группы симметрии, то и L - индиф-
индифферентен относительно той же самой группы Gs. Это означает, что
обратный тензор L для каждого класса симметрии будет иметь ту же
структуру E.35) - E.39), что и тензор К.
5.1.8. Индифферентные линейные функции третьего ранга
Для индифферентных линейных тензорных функций третьего ран-
ранга (формулы E.16), п = 3) задающим тензором является тензор треть-
третьего ранга 3П = 3М (формулы E.17) и E.20)). Будем далее считать
его симметричным (см. п.4.1.10), т.е.
3М = 3М<132> или Mijk = М'Ч E.40)
Наличие симметрии E.40) приводит к сокращению числа макси-
максимально возможных независимых компонент М**к: из З3 = 27 компо-
компонент остаются только 18 штук, так как условия E.40) накладывают
9 ограничений на компоненты.
Условия индифферентности E.24) тензора 3М по отношению к
группам симметрии G$:
еще уменьшают число независимых компонент (см. табл.4.4).
Для симметричного тензора третьего ранга также можно дать
матричное представление, для этого расположим его независимые
компоненты в виде матрицы 3x6:
/М111 М122 М133 V2M123 уДМ131 уДМ112'
CМ) = М211 М222 М233 уДМ223 уДМ231 уДМ212
3x6 \м311 м322 м333 V2M323 уДм331 уДм312
E.42)
Появление коэффициентов уД в этой матрице позволяет записать
линейную функцию третьего ранга E.20) при т = 1 также в матрич-
матричном виде:
{ s } = CМ){Т}, E.43)
llx3J v 3x6/llx6J' v ;
где { s }и{Т}- координатные столбцы из компонент вектора s и
llx3J llx6J
симметричного тензора Т, построенные следующим образом:
^li \
Т22
Тзз
{ s } = Is2 , { Т } =
llx3J 1-3 '
E.44)
\уДТ12/
278.
Глава 5. Тензорные функции
Если координатные столбцы { } имеют различные размеры, как
в данном случае, то в матричной записи указывается их размер. Эк-
Эквивалентное для E.43) и E.20) компонентное представление линейной
функции третьего ранга имеет вид:
? =MijkTjk.
E.45)
Хотя для тензоров третьего ранга не существует понятия обратно-
обратного тензора, однако аналогом обратной к линейной функции третьего
ранга E.20) т = 1 можно считать функцию E.-20) при т = 2:
S = 3М<231> • а,
E.46)
где S - симметричный тензор второго ранга. Его компонентное (вто-
(второе) представление имеет вид:
а матричное (третье):
ij =Mkijak)
{ S } = CM)T{ a },
llx6J V 6x3; llx3J
E.47)
E.48)
или
\
s22
s33
V2S23
V2S31
Min M2n M311 \
M122 M222 M322
M133 M233 M333
V2M123 V2M223 V2M323
V2M131 V2M231 V2M331
\V2M112 V2M212 V2M312
E.49)
Обозначение CМ)Т здесь, означает, что к матрице CМ) применено
транспонирование.
Тензор 3М и в случае линейной функции E.46) обладает симмет-
симметрией вида E.40). Сравнивая матричные представления E.43) и E.49),
легко заметить, что введение в матрицы CМ) и CМ)Т коэффициен-
коэффициентов л/2 позволило сохранить структуру столбцов { } и матриц ( ) в
"обратной" функции E.49) (см. упр. 5.1.4).
Если тензорные функции E.43) и E.46) индифферентны относи-
относительно какой-либо группы G,, то соответствующий тензор 3М можно
представить разложением E.25) по тензорному базису данной группы.
Тензорные базисы групп строятся с помощью направляющих тензо*
ров, приведенных в п.4.1.10.
§5.1. Линейные тензорные функции 279
Как и для тензоров первого ранга, ненулевые индифферентные тен-
тензоры третьего ранга существуют не во всех группах G,. Ниже при-
приведены по три представления (тензорное, компонентное и матричное)
ненулевых индифферентных тензоров 3М в тензорном базисе различ-
различных групп и классов симметрии. В фигурных скобках указаны обра-
образующие тензоры О,G) групп.
(Е) -Триклинный класс
Группа Gi {ёа, а = 1,2,3}:
з
3М = ^2 (<*ё + d3+e ® ёЦ + d6+e ® ё2 + dQ+(e2
3М = ^2 (<*аёа + d3+QeQ ® ёЦ + d6+Qea ® ё2 + dQ+Q(e2Q
а=1
? ® ё7 + (ё2 ® ё7)<132>) + d15+aea ® О„),
а,/3,7=1,2,3;
а=1
E-50)
(
d8 d2 d5 y/2du y/2d17
d6 d9 d3 V2d15 y/2d12
/M111 M122 M133 V2M123 л/2М131 V2M112>
= M211 M222 M233 x/2M223 V2M231 V2M212
\M311 M322 M333 x/2M323 л/2М331
Здесь da - константы разложения по тензорному базису.
Индексы в формуле E.50) и далее следует расшифровывать следую-
следующим образом: если в сумме по а значение а = 1, то/3 = 2,7=:3; если
а = 2, то /? = 3, 7 = 1; если а = 3, то /3 = 1, 7 = 2. Таким образом,
тензор 3М в данной группе имеет максимальное число независимых
компонент - 18.
280 Глава 5. Тензорные функции
(М) -Моноклинный класс
Группа G3 {ei,e2,e§}:
2
3М = ^2 (dae2Q ® eQ + d2+QeQ <g> ё§ + ^4+а(ё§ <8> ёа + (ё§ <8> ёа)<132))+
а=1
^6) а,/3=1,2; а^А E.51)
а=1
/di d7 d3 0 0 ^9 \
CM) = \d8 d2 di 0 0 V2d10 =
V 0 0 0 V2d6 V2d5 0 /
/Mni M122 М13Э 0 0 V2M112
= m2U m222 m233 о о л/ш2
V 0 0 0 V2M323 y/2M313 0
Тензор 3М имеет 10 независимых констант da.
Группа G4 {ej, ё?, ё3, Oad, a = 1,2,3}:
3 2
3M = J] (<*«ё3 ® ё2 + d3+aOad)+? d6+Q (ё2 ® ё3 + (ё2
l l
( )
a=l a=l
а=1
2
а=1
000 \^(d6 - db) V2d7 0
CM) =000 V5de л^(^4 - de) 0
i d2 cf3 0 0 V^(d5-
0 0 О лДм132 лДЙ131 0
= 10 0 0 л/2М232 v^M231 0
М311 М322 Ж333 0 0 л/Ш312
§5.1. Линейные тензорные функции 281
Тензор 3М имеет 8 независимых констант.
(О) -Оргпотропный класс
Группа G6 {ё?,ё|,ё3}:
3М = "? d«e* ® ё' + Е d3-f a (ё? ® ё§ + (ё*
а=1 а=1
+ <?Ф?)> E-53)
а=1 а=1
000 0 у/Ыь 0
CМ) =000 л/2^5 0 0 =
i d2 d3 0 0 0
0 0 0 0 v^M131 0
0 0 0 V^M232 0 0
М322 мззз 0 0 0
Тензор.3М имеет 5 независимых констант.
Группа G7{Oad,a = l,2,Z}:
з з
3М =
а=1 а=1
E.54)
/0 0 0 y/2(d3-d2) 0 0
CМ) =000 0 V2(di - da) 0
\0 0 0 0 0 V2(d2-d1)l
Тензор 3М имеет 3 независимые константы.
(Т) -Тетрагональный класс
Группа Gq:
3М =
"к = (dt + d») _Г #аф$ + &%) + d1Si3F{6k2 + S'25k)+
a=l
(^<J3fc+4**) - si Ф*+4**))+
i E.55)
282 Глава 5. Тензорные функции
/О 0 0 V2(d! + d2) л/5(«и-4з) 0
CМ) =10 0 0 -V2{d4 - d3) уЭД + d2) 0
\-2d3 2d3 0 0 0 V
/0 0 0 уДЙ123 V2M131 0
= 0 0 0 -V2M131 \/2M123 0
\M311 M322 M333 0 0
Тензор 3М имеет 4 независимые константы. Определение тензоров
Td, B3d, N3d и R3d дано в п.4.1.10.
Группа
3М = diEh + d2e3 ® Е
i 3i3
- 8Цб1бк + 6{6к)), E.56)
/00 0
CM) =00 0 y/2di -V2d4 0
\d2 d2 di + d2 + d3 0 0
Тензор 3М имеет 4 независимые константы.
(K3) -Квазитрансверсалъно-изотропный класс
Группа Gi2:
3М = dxTd + d2B3d,
^ ^(J^* + ^*) + <*х4(ф* + ^*), E.57)
/0 0 0 V2(di + d2) 0 01
CM) =000 0 y/2{dx + d2) 0
\0 0 0 0 ^
Тензор 3М имеет 2 независимые константы.
Группа G\3:
3М = dxEh + d2e3 ® E
Mijk = di(^'4 + Sik533) + d2S3Pk + d3S3SiS^, E.58)
§ 5.1. Линейные тензорные функции ___283
0 0 0 V2dx 0\
CМ) = ( 0 0 0 V2dx 0 0 =
,d2 d2 di + d2 + d3 0 0 0 /
0 0 0 0 л/2М131 0х
0 0 0 \/2М13г О О
М311 М311 М333 0 0 0,
Тензор 3М имеет 3 независимые константы.
Группа Gii'.
3М = dO3d,
E.59)
6{6к3)),
CМ) =
/о
0
\0
0
0
0
0
0
0
V2d
0
0
0
-y/U
0
0
0
0
Тензор 3М имеет 1 независимую константу.
(А) -Ромбоэдрический класс
Группа
3М = diEh + d2e3 ® Е + d3e3 ® ё§ + d4O3d + d5D3h + d6A3h,
+ 46*) + (d6Si + d5S[)(S{Sk - ф|), E.60)
( 0 \/2d4
CM) = d6 -de 0 y/Ui
d2 d2 dx+d2 + d3 О О
Тензор 3М имеет 6 независимых констант.
(В) -Ромбоэдрический класс
Группа (?18=
3М = d!Eh + d2e3 ® E + d3e3 ® |
Mijk = di(^f| + Sik4) + d28\S>k + d3S3S}3Sk+
+ d4(б[(б{8к - S{Sk) - 82{S{8k + S{Sk)), E.61)
234 Глава 5. Тензорные функции
(d4 -d4 0 0
0 0 0 л/&1
d2 d2 dx+d2 + d3 0
Тензор 3М имеет 4 независимые константы.
Группа Gig:
3М = d1O3d
+ Si5k2) - 8'2фк + S{Sk)) +
d2(8[(б{бк - б{8к) - S2(S{Sk2 + 5{5к)), E.62)
(d2 -d2 0 V2d1 О О
0 0 0 0 -V2d1 -V2d2
0 0 0 0 0 0
Тензор 3М имеет 2 независимые константы.
(if) -Гексагональный класс
Группа (?2i:
Mijk = {d2S[ - di4)(*l*2 + *2*i) + №4 + di«i)(«{^i - Ф2)> E-63)
(dx -dx 0 0 0 л/2е/2
d2 d2 0 0 0 -V2di
0 0 0 0 0 0
Тензор 3М имеет 2 независимые константы.
Группа G22: тензор 3М имеет такой же вид, как и для группы Gio, и
содержит 4 независимые константы.
Группа
3М =
M^k = d{siF{6k - S{Sk) - 62(S{Sk + 6}26к)), E.64)
Id -d 0 0 0 0
CM) = I 0 0 0 0 0 -
\0 0 0 0 0 0
Тензор 3М имеет 1 независимую константу.
Группа G2$: тензор 3М имеет такой же вид, как и для группы Gi4, и
содержит 1 независимую константу.
§5.1. Линейные тензорные функции 285
Группа &2б: тензор 3М имеет такой же вид, как и для группы Gi3, и
содержит 3 независимые константы.
(К) -Кубический класс
Группы G28 « Сзо-
3М = dTd,
ед E.65)
а=1
C
М) =
0
0
\о
0
0
0
0
0
0
V2d
0
0
0
y/2d
0
0
0
V2d
Тензор 3М имеет 1 независимую константу.
(Тз) -Трансверсалъно-изотропный класс
Группа G33- тензор 3М имеет такую же структуру, как и для группы
Gio, и содержит 4 независимые константы.
Группа G35: тензор 3М имеет такой же вид, как и для группы G13, и
содержит 3 независимые константы.
Группа G36- тензор 3М имеет такой же вид, как и для группы Gi4, и
содержит 1 независимую константу.
Для всех остальных групп (?,, в том числе для всего изотропно-
изотропного класса (/) индифферентными тензорами третьего ранга являются
только нулевые тензоры:
/0 0 0 0 0 0\
CМ) =000000. E.66)
\о о о о о о/
5.1.9. Индифферентные линейные функции
четвертого ранга
Если задающий тензор четвертого ранга 4С связывает симметрич-
симметричные тензоры второго ранга S и Т, то его компоненты в любом базисе,
в частности в декартовом, обладают симметрией вида:
gijki = Qjiki и gijki = Qij\hm E.67а)
Кроме того, будем полагать выполненным условие симметрии по па-
парам индексов (см. D.37)):
Qijkl = Qklij E.676)
286.
Глава 5. Тензорные функции
Первая группа соотношений E.67а) содержит 27 независимых урав-
уравнений для С*-7*': каждой из 3 пар неповторяющихся индексов (г, j) =
A2,23,13) соответствует 9 пар индексов (Ы) A1,22,13,31,21,...).
Вторая группа соотношений содержит 18 независимых уравнений:
каждой из 3 пар неповторяющихся индексов (А:,/) = A2,23,13) соот-
соответствует только 6 пар индексов A1,22,33,12,13,23), так как пере-
перевернутые пары B1,31,32) уже учтены в первой группе соотношений.
Третья группа соотношений содержит 15 независимых уравнений:
первой паре индексов A1) соответствует 5 соотношений со всеми дру-
другими парами (кроме перевернутых B1, 32, 31), т.к. они уже учтены
в первой и второй группе), второй паре A2) - уже 4 соотношения и
т.д., т.е. всего 5+4+3+2+1=15 соотношений.
Эти соотношения имеют место для любой группы симметрии. Од-
Однако, для частных случаев число независимых компонент еще сокра-
сокращается и определяется теоремой 4.15. Здесь же мы иным способом
доказали частный случай этой теоремы.
ТЕОРЕМА 5.3. Тензор четвертого ранга 4С Е 7з , обладающий
симметриями вида E.67а) и E.676), имеет не более 21 независимой
компоненты.
Для тензора четвертого ранга с типом симметрии E.67) третье
(матричное) представление вводится с помощью матрицы 6x6:
/С1111
?1122
?2222
СИМ.
?1133
?2233
?3333
^?3323
2?2323
V2C1113
V2C2213
V2C3313
2?2313
2?1313
У2С-2212
V2C3312
2С-1212
2С1212
2С1212 .
E.68)
Введем также представление для компонент симметричных тензо-
тензоров S и W с помощью координатных столбцов:
{S}
1x6
511
?22
5зз
л/2523
n/2513
KV2S12/
{Т}
1x6
т11 \
\/2Т
il3
E.69)
тогда для линейной тензорной функции четвертого ранга E.21) m = 2
можно дать третье (матричное) представление:
= DC){T}.
1x6 6x6 1x6
E.70)
§ 5.1. Линейные тензорные функции
.287
Тензорный базис О,G) E.25) для индифферентного тензора чет-
четвертого ранга 4С, обладающего симметрией E.67), будет состоять из
симметричных образующих тензоров, представленыых в таблице §4.2.
Так же как и для тензора второго ранга, тензорный базис одинаков
для всех групп Gs в пределах фиксированного класса.
Ниже даны первое, второе и третье представления тензора чет-
четвертого ранга 4С, индифферентного относительно различнх классов,
а также образующие тензорных классов, участвующие в этих пред-
представлениях.
Е - Триклинный класс {ёа}:
з
4С =
а=1
а 0 О1 + Ог 0 ё*)
ee ® °з + О3 0 el)
0 ё* +
ё*
ё* + ё* 0 ejj) + Аб+аОа 0 Оа+
(^ 0 О2 + О2 0 ё*)+
А18+а(О/3 0 О7 + О7 0 О
а=1
18+Q
% + SkJp) + {8% +
рфыфуфр, p,W,i/,/i,a,ft7=l,2,3. E.71)
Индексы в формуле E.71) выбираются следующим образом: если,
например, а = 1, то /3 = 2, 7 = 3, и, следовательно, i/ = 1, /i = 3 и
р= 1, w = 2.
В матричном представлении тензор С имеет общий вид E.68) и
содержит максимальное число независимых констант -21:
Аб А5
А2 А4 \/2Ац
Аз V^A12
сим. 2А7
\/2Ai6\
2A2i
2A8
\/2A18
2A2o
2A9
E.72)
288-
Глава 5. Тензорные функции
М - Моноклинный класс {е1,е2,
з
а=1
О3 + О3 0 ё2)
ё7
Оа
О2 + О2
а=1
DС) =
/
\
/
\
1 /X*ХЗ 1 Х*?.?\/Х&х'
+ (<Мз + d3^l)(d2d3 J
?1111 ^«1122
с2222
СИМ.
Ai Аб As
A2 A4
Аз
сим.
?1133
?2233
?3333
0
0
0
2А7
0
0
0
0
0
0
2?2323 2С2313
2(
0 лДХг
0 ч/гА!
0 \/2Ai
2А13 0
2А8 0
2А9
э\
1
2
1
V2C1112\
у/2С2212
^?3312
0
0
2?1212 J
E.73)
Индифферентный относительно моноклинного класса тензор 4С
имеет 13 независимых констант.
Заметим, что среди тензоров Оа только Оз является априори ин-
индифферентным относительно М-класса, однако тензоры четвертого
ранга Оа 0 Оа, Oi 0 О2 + О2 0 Oi (a = 1,2) также индифферент-
индифферентны (см. упр.5.1.2), поэтому их использование в качестве тензорного
базиса для тензора 4С правомерно.
О - Ортотропный (ромбический) класс {ё2}:
® ё*
а=1
А6+аОа ® Ов),
§5.1. Линейные тензорные функции
.289
а=1
DС) =
афрф-1
/С1111 с1122
?2222
СИМ.
\
/ \\ Аб As
А2 А4
Аз
сим.
?1133
?2233
?3333
0
0
0
2А7
«•Р.
0
0
0
7
2?2323
0
0
0
0
2А8
0
0
0
0
0
—
1,2,3,
0
0
0
0
2?1313
\
•
0 \
0 '
0
0
0
2С1212)
2А9/
Индифферентный относительно ортотропного класса тензор 4С
имеет 9 независимых компонент.
Заметим, что как и в М-классе, тензоры Оа (а = 1,2,3) не явля-
являются индифферентными относительно О-класса, однако как показано
в упр.5.1.2, тензоры четвертого ранга Оа 0 Оа уже индифферентны
относительно О- класса.
Т - Тетрагональный класс {Е, ё§, О/,,
4С = AXE 0 Е
+ A4(Oi 0
А3(Е 0 ё
О2 0 О2) + А5ОЛ
2АбА
As
E.75)
а=1
Тензорное исчисление
290
Глава 5. Тензорные функции
/С1 С1112
0 =
?1111
СИМ.
\
/Л1 + А5Ч-2Аб Ai
Ai + А5Ч- 2А6
сим
\
?1133
?1133
?3333
'•I ¦*
'•I ¦*
А'
0
0
0
2С2323
Аз
Аз
2А4
0
0
0
0
2С2323
0
0
0
+
2Аб
V2C1112
-V2C1112
0
0
0
2?1212
0
0
0
0
2А4 + 2А6
\
—
/
V^A7 \
-\/2А7
0
0
0
2А6 /
А' = Ai + А2 + 2А3 + А5 + 2А6.
Тензор 4С в Т-классе имеет 7 независимых компонент. Выраже-
Выражение для компонент Q%k приведено в п.4.1.9 (формулы D.40)). Тензор
Oi®Oi-fO20O2 является индифферентным относительно Т и Ку
классов в силу результатов упр.5.1.3.
Кз - Квазитпрансверсалъно-изотропный класс {Е, ё§, Од}:
4С = AiE ® Е + А2ё§ ® ё§ + А3(Е ® ё| + ё§ <
+ A4(Oi ® Oi + О2 ® О2) + А5ОЛ + 2А6А,
Cijhl =
E.76)
а=1
DС) =
,^>11и (J1122 с1133 О
?1111 ?1133 О
?3333 Q
сим. 2С2323
О
О
О
О
2?2323
о \
о
о
О
О
Ai Ai + A3 О
А5+ 2А6 Ai + A3 О
А' О
сим. 2А4 + 2Аб
О
О
О
О
2А4 + 2А6
л/2А7
О
О
О
2А6
§5.1. Линейные тензорные функции
291
Тензор 4С имеет 6 независимых компонент.
А - Ромбоэдрический класс {Е, e3)D3) Пза}-
4С = AiE 0 Е + А2ёз 0 §з + А3(Е 0 ё§ + ё§ 0
+ A4(Oi 0 Ог + О2 0 О2) + A5D3 + 2А6А
Cijkl = Ai^'J*1
E.77)
/С1111 С1122 С1133 л/2С1123 л/2С1113
?1133 ^^?1123 ^^?1113
4пч
Ч "
3333
сим.
0
2С2323
0
0
2?2323
\/2А7
Ai+.Аз
А"
сим.
0
2А4 + 2А6
А" = Ai + А2 + 2А3 + 2Аб.
DlJkl
0
\
0
~2С1113
2С1123
с1111-с1122/
0
0
0
-2А5
2А7
2А6
\
Выражения для компонент тензоров DlJkl и О%?1 представлены в
D.40). Тензор 4С в данном классе имеет 7 независимых компонент.
Тензор Oi 0 Oi -f O2 0 О2 в силу результатов упр.5.1.3, является
индифферентным относительно А и В- ромбоэдрических классов.
В - Ромбоэдрический класс {Е, e§, D3}:
4С = AiE 0 Е
+ A4(Oi 0
ё| 0 ё§ + А3(Е 0 ё§ + ё§ 0
О2 0 О2) + A5D3 + 2А6Д,
А4
6k38l2)
6к8[))
E.78)
ю*
292
Глава 5. Тензорные функции
/?1111 ?1122 ?1133
V
) =
?1111 ?1133
?3333
СИМ.
\
/А! + 2Аб Ai
Ai -Ь 2Аб
сим.
\
0
0
0
2?2323
А1 + А3
А^Аз
А"
^?1113
-у/2С1ПЗ
0
0
2?2323
0
0
0
2А4 + 2А6
0
0
0
_2?ШЗ
0
С1111 - С
\/5а5
-л/2А5
0
0
2А4 -Ь 2Ag
1122 у
0 \
0
0
-2А5
0
2А6
/
Тензор 4С в данном классе имеет 6 независимых компонент.
Н - Гексагональный класс и Тз - Трансе ерсалъно-изотропный класс
1
4С =
ё|
E + А2ё| ® ё^ + А3(Е <8» ё| + ё|
® Ох + О2 ® О2) + 2А5А,
= Аг
DС) =
E.79)
/С1111
\
/Аг+ 2
\
?1122
?1111
СИМ.
Ai -
?1133
?1133
?3333
\l
f 2A5
сим.
0
0
0
2?2323
Ai + Аз
Ai + А3
А'"
0
0
0
0
2?2323
0
0
0
2А2 + 2А5
?1111
2А2
0
0
0
0
0
—
0
0
0
0
+
—
?1122 )
0 N,
0
0
0
2А5 0
2А5>
А'" = Ai + А2 + 2А3 + 2А5.
§ 5.1. Линейные тензорные функции
.293
Тензор 4С в данном классе имеет 5 независимых компонент.
К - Кубический (квазиизотропный) класс {Е, Од}:
4С = AiE ® Е + 2А2А + А3ОЛ,
з
Cijkl = Ах W + A2(W + SilSjk) + Аз
E.80)
а=1
) =
/?1111 ?1122 ?1122
?1111 ?1122
С1111
СИМ.
\
/A! + 2A2 + A3 Ai
Xi + 2A2 +
сим.
\
0
о
0
2?2323
А3
Ai +
0
0
0
0
2?г2323
4
i
Ai
Ai
2А2 + А3
0
0
0
0
_0
0
0
0
2А2
—
Ч
0
0
0
0
2А2
0 \
0
0
0
0
2А2У
Тензор 4С в данном классе имеет 3 независимые компоненты.
- Изотропный класс:
А2(
E.81)
Dс) =
2А2
2А2
сим.
Аг
Ai
+ 2А2
0
0
0
2А2
0
0
0
0
2А,
0
0
0
0
0
Тензор 4С в данном классе имеет 2 независимые компоненты.
Упражнения к § 5.1.
Упражнение 5.1.1. Доказать, что если тензор С обладает симметрией
вида E.67) в какой-либо системе координат, то в любой другой системе координат
эта симметрия сохраняется.
294.
Глава 5. Тензорные функции
Упражнение 5.1 «2. Показать, что имеют место следующие соотношения:
Ог 0 О2 + О2 0 Oi = 4(О3 0 ё§)н,
Оа0Оа=4(ё*0ё§)", а = 1,2,
из которых следует, что хотя тензоры Oi и О2 не являются индифферентными
относительно М-класса, но образованные выше из них тензоры четвертого ранга
уже iVf-индифферентны.
Упражнение 5.1.3. Показать, что имеют место следующее соотношение:
О2 0 О2 = 4(О3 0
- ё§ 0 ё\,
из которого следует, что данный тензор четвертого ранга является индифферент-
индифферентным относительно Т, .Кз-классов, хотя Оа таковыми не являются.
Упражнение 5.1.4. Показать, что если в матричных представлениях E.42)
и E.49) симметричного тензора третьего ранга убрать у 2, то в соответствующей
линейной функции E.43) и "обратной" функции E.49) векторы {S} и {Т} будут
иметь вид:
/ Гц \ /5й\
Тзз
1/2Т23
1/2Гз1
М/2Т12/
533
531
523
\S12J
т.е. структура матричной записи будет различной в прямой и "обратной" функ-
циях.
циях.
Упражнение 5.1.5. Показать, что если для матрицы (С) использовать не
E.68), а следующее определение:
Dс) =
6*2222
то ему соответствуют векторы {S} и
структуру:
/5U\
522
5зз
512
513
6*2212
С*3312 Сз313 6*3323
C*i212 C*i213 С*1223
C*1313 Cl323
С*2323 /
имеющие различную между собой
\2е2з/
§ 5.2. Скалярные функции тензорного аргумента
295
а обратная к ней матрица ( П) в этом случае принимает вид:
/Пни
DП) =
V6x6;
П2222 П2233 2П2212 2П2213 2П2223
Пзззз 2П3312 2П3313 2П3323
сим. 4П1212 4П1213 4П1223
4IIi3i3 4IIi323
4П232з/
т.е. имеет отличную от ( С) структуру (поэтому предпочтительным является
матричное представление E.68)).
§ 5.2. Скалярные функции тензорного аргумента
5.2.1. Определение скалярной функции
Рассмотрим теперь нелинейные тензорные функции, определение
которых дано в п.5.1.1. Начнем с рассмотрения частного случая, когда
в формуле E.1) тензор nS имеет нулевой ранг п = 0:
s =
E.82)
Определение 5.5. Тензорную функцию вида E.82) называют
скалярной функцией тензорного аргумента.
Компонентное представление такой функции в базисе R, имеет вид:
j~jm). E.82а)
В силу E.6) при переходе от одной системы координат Xх к другой
Х'х значение скалярной функции не меняется:
h. .. QiL Th...im)
E 83)
Определение 5.6. Скалярная функция E.82) называется ин-
индифферентной относительно группы линейных пре-
преобразований Gs, определяемых по C.1), если вид самой функции
-7) не изменяется:
E.84)
при переходе из системы координат х% в Xх, причем
296 Глава 5. Тензорные функции
С использованием тензора линейных преобразований Q = А1 ^
(см. пп.4.1.3 и 5.1.5), условие индифферентности E.84) скалярной
функции E.82) можно записать в виде:
/(таТ) = /(mT^.^;(Q 0 ... 0 Q)B"-l,2n-3 3,l,2,4,...,2n)^ E.84a)
Например, для скалярной функции от вектора это условие имеет вид:
/(a)=/(a-Q), E.85a)
а для скалярной функции от тензора второго ранга:
/(T) = /(QT-T-Q). E.85tf)
Подчеркнем, что из определения E.83) следует, что вид функции /(Т)
может меняться при переходе в новую систему координат, но не ме-
меняется значение этой функции, а из E.84) следует, что и вид функции
/(Т) не должен меняться. Например, если скалярная функция - это
просто компонента вектора в базисе Rt: s = /(а) = а3, то-при переходе
в декартов базис ё, эта функция будет иметь другой вид f'(a%) = Afax,
но значения этих функций будут совпадать:
в силу того, что а% - компоненты вектора. Однако индифферентной
такая функция /(а) будет только относительно некоторых групп сим-
симметрии, например Тз.
Из определения E.84) следует, что все скалярные инварианты
/7(тТ) относительно группы Gs, в том числе инварианты ц\ опре-
определенные в п.4.5.3, являются индифферентными функциями относи-
относительно той же группы Gs. Так например, длина вектора: 5 = /(а) =
|а| = l[ '(а) - индифферентна относительно группы (?зэ = -Г-
5.2.2. Дифференцирование скалярной функции
по тензорному аргументу
Важную роль в механике играют формулы дифференцирования
скалярной функции E.82) по тензорному аргументу.
Пусть имеется компонентное представление E.82а) функции /. Вы-
Вычислим дифференциал от этой функции, как от функции многих пе-
переменных:
^.i». E.87)
Производные df/dT^"^m образуют компоненты некоторого тензора,
который обозначим как
§ 5.2. Скалярные функции тензорного аргумента 297
Определение 5.7. Тензор E.88) называется тензором производ-
производной скаляра f no тензорному аргументу или просто тензором
произв одной.
Очевидно, что т/т является тензором того же ранга, что и тТ.
Введем еще один тензор, называемый дифференциалом тензора
d(mT), который обладает компонентами
d{mT) = dTji'~jmRjl <g>... <g> Rim. E.89)
Транспонирование этого тензора дает следующий объект:
d(mT)(m...l) = dTjl'~jmRjm <g> ... <g> Rix. E.90)
Преобразуем теперь выражение E.87) следующим образом:
Здесь использовано свойство: R,- • R-7 = Sj. Используем теперь опреде-
определение введенных тензоров df/dT и d(mT), тогда придем к следующей
теореме.
Теорема 5.4. Дифференциал скалярной функции E.82) от тен-
тензорного аргумента представляет собой выражение вида
# = т/т-...-<*(шТ)(т"л>. E.92)
Например, если т = 2, то формула E.92) имеет вид:
df = fT..dTT. E.93)
Для симметричного тензора Т функцию / необходимо представить в
виде:
\ E.94)
тогда формула E.87) для дифференциала примет вид:
а тензор производной E.88) можно записать следующим образом:
* = \ш^0Ri+Rj*R<) = \(wj + ^)Ri0Ri- E-96)
298 Глава 5. Тензорные функции
Таким образом, для вычисления производной от скаляра / по сим-
симметричному тензору надо вначале вычислить частную производную
df/dTij по всем девяти компонентам без учета симметрии Т1-7, а затем
у результата дифференцирования 9//5Т1-7 поменять индексы г f* j и
сложить обе производные с коэффициентом 1/2.
Из E.96) следует, что производная скаляра по симметричному тен-
тензорному аргументу является симметричным тензором:
(/т)Т = /т, если Т = ТТ. E.97)
5.2.3. Дифференцирование инвариантов вектора
Рассмотрим случай, когда в качестве скалярной функции выбраны
инварианты Ц (а) вектора а, рассмотренные в п.4.4.6:
/(a)=jW(a), E.98)
где s - номер группы симметрии G,, а у - номер инварианта в соот-
соответствующем полном наборе.
Вычислим производные по а от различных инвариантов jfy (а),
приведенных в D.142).
Инвариант /,. (а) = |а|2.
Вычислим сначала частные производные:
-^\а\2 = —(атапдтп) = 8?ат + 5?ап = 2aiy
а затем составим вектор согласно E.88):
\а\1 = ^- = 2a,R«' = 2а, E.99)
который и дает искомое выражение для производной от инварианта.
Инварианты Ц (в) = a2Q.
Вычислим частные производные по декартовым компонентам:
да* ~ да?( ' ~ '' °'
(по а суммирования нет), и составим вектор согласно E.88):
-^ = 26?ааё{ = 2&aea. E.100)
Ов.
§ 5.2. Скалярные функции тензорного аргумента 299
Инварианты Ц (a) = aQ.
Частные производные и производная от инварианта имеют вид:
^ , ^ = <$,.оё,. = ёа. E.101)
Инварианты ц (в) = aQap, <хф @.
Частные производные и производная от инварианта имеют вид:
+ ааер. E.102)
Инварианты |а|2, а\ и dQap квадратично зависят от компонент а,-,
поэтому можно вычислить производные от них по симметричному
тензору a 0 a = a2.
Все эти инварианты можно рассматривать как линейные тензор-
тензорные функции от а2, поэтому получим общую формулу для производ-
производной линейной скалярной функции от симметричного тензора Т:
T--Cl = TmnUnrn, E.103)
где П - некоторый фиксированный тензор. Тогда
1* ~ 2 9ТЧ( ' пт ~
ОТ1* ~ 2
\ 8?)Ппт = \(Ппт + птп),
и, следовательно, имеет место следующая теорема.
Теорема 5.5. Тензор производной от линейной скалярной функ-
функции E.82) от симметричного тензора второго ранга Т вычисляют
по формуле:
-^(Т ¦ -П) = i(finro + Umn)Rn ® Rm = i(n + Пт). E.Ю4)
Если Т - несимметричен, то
А(Т..П) = П. E.105)
Используя формулу E.104), получаем, что
300 Глава 5. Тензорные функции
(.ЛИ)
5.2.4. Дифференцирование главных инвариантов
тензора второго ранга
Выберем теперь в качестве скалярной функции / первый главный
инвариант Д(Т) тензора второго ранга Т и его степеней Тп и вычис-
вычислим их производные по Т.
Производные инварианта Д(Т) = Е--Т находим, используя E.105):
Ji(T)T = E. E.107)
Далее вычисляем частные производные от Д(ТП), п =2 и 3:
= ¦SJijVmkTnl9»k9lm) =
= 22},,
^ 5. E.108)
Тогда производные от инвариантов имеют вид:
h(Т2)т = 2TJtRf' ® Ш = 2ТТ, Д (Т3)т = ЗТ/'^.Я1' ® RJ' = ЗТ2Т.
E.109)
Таким образом, имеет место следующая теорема.
ТЕОРЕМА 5.6. Выражения для тензора производной от первого
инварианта степеней тензора Т имеют следующий вид:
Ji(T)T = Е, Д(Т2)Т = 2ТТ, /i(T3)T = 3TT2. E.110)
Выберем теперь в качестве скалярной функции / второй и третий
главные инварианты /2(Т) и /з(Т) тензора Т.
Согласно D.151) и D.152) (см.п.4.5.3) эти инварианты можно вы-
выразить через Д:
'з(Т) = ^(Т) - 3h(T)h(T2) + 2h(T3)), E.111)
§5.2. Скалярные функции тензорного аргумента 301
Дифференцируя E.111) по Т, с учетом E.110) получаем:
/з(Т)т = ТТ2-Ji(T)TT + EJ2(T), /2(Т)Т = ЕЛ(Т)-ТТ. E.112)
Используя следствие D.161) (см.п.4.5.4) формулы Гамильтона-
Кэли, можно также записать E.112) в виде:
= /з(Т)т = h(T)T~\ E.113)
5.2.5. Формулы дифференцирования линейных, квадратич-
квадратичных и кубичных инвариантов тензора второго ранга
относительно различных групп симметрии
В данном разделе получим формулы для дифференцирования ска-
скалярной функции /(Т), в качестве которой выбираем инварианты /*
симметричного тензора Т второго ранга относительно различных
групп симметрии G,:
ДТ)=Ц(Т). E.114)
Как было показано в п.4.4.4, полные наборы независимых инвари-
инвариантов всех групп симметрии G8 s = 1... 39 могут быть получены с
помощью свертки тензорных степеней Т,Т®ТиТ®Т®Т. Тогда
можно считать, что любой из инвариантов Ц(Т) может быть пред-
представлен в виде либо линейной функции:
/ = Т--П, E.115)
либо квадратичной функции:
/ = T®T....4ft, E.116)
либо кубической функции:
/ = Т®Т®Т 6П, E.117)
где nft, п = 2,4,6 - некоторые индифферентные в группе Gs тензоры,
составленные из образующих тензоров этой группы.
Производная от линейной функции E.115) была получена выше:
А(Т..П) = 1(П + ПТ). E.118)
Для вычисления производной от квадратичной и кубической функ-
функций, найдем их частные производные с учетом правила расшифров-
расшифровки скалярного произведения тензоров высших рангов, приведенного в
302 Глава 5. Тензорные функции
упр.1.8.1:
/гпТПП rphlО \ — (грТПП | /тгТОТЛЧ (rpkl i Т^^АО
1 / \
= — ( (и,- д.* + 0,- 0?- )(Т* + Т ) + (о,- 0.* + 0|*0* Jv-f1 ~Ь -* ) ) ^(Ьт ==
= lTj(g'kglt+g"gtk)(Ulkj
4 \
+ (ff' "У" + «/SVm)(fi,i»m +
+ (Rn 0 Rm + Rm 0 Rn)(fi,jnm + tijinm) ) • E.119)
Здесь произведение обратных метрических матриц представлено в ви-
виде:
gtmgtn = R" ® R' • R" 0 Rm, и т.д.
Составляя теперь выражение для тензора производной E.88) от ска-
скалярной функции, получим
А(Т 0 Т ... -4П) = ^(T™T*'fi*nw)R'' 0 R* =
или, используя определение операции симметрии A.266), получаем
следующую теорему.
Теорема 5.7. Тензор производной от скалярной квадратичной
функции симметричного тензора второго ранга вычисляют по фор-
формуле:
^(Т 0 Т - - --.4П) = 2Т - .4П<*> = 24ft<-> ¦ -Т. E.120)
Второе равенство справедливо ввиду симметрии Т и 4ffc(').
Если тензор 4ffc - симметричный, т.е. удовлетворяет условиям
A.264), то из E.120) получаем:
—(Т 0 Т • • • -4ft) = 2Т • -4ft = 24П • -Т. E.121)
дТ
§ 5.2. Скалярные функции тензорного аргумента 303
Если квадратичный инвариант имеет структуру вида:
¦ / = (А • Т) • -(В • Т) = Т 0 Т • • • -(А 0 В)A432> E.122)
(см.упр.1.8.4), где А и В - симметричные тензоры, то формула E.120)
принимает вид:
А ((А • Т) • -(В • Т)) = 2(А ® В)" • Т, E.123)
где вторая операция симметрирования [•] определяется по A.268).
Для нахождения тензора производной от кубической функции
E.117) необходимо вычислить частную производную:
¦ пр.№пт = i ((ты + т
+ (r + г-)рт + T"9)(np,iinm + npqijnm)+
+ (Tnm + Tmn)(Tkl + T'*)(njm.nm + Uijlknm), E.124)
Переходим к ковариантным компонентам, разбивая каждое из трех
слагаемых в E.124) еще на 2, например,
((g'kgH + 9>19гк){9а*9Ьр + ff
(9ак9Ы + 9al9bk)(9'q9tp + 9>p9tq))
Далее представляем произведение метрических матриц в виде
свертки двух тензоров четвертого ранга, причем для одного из них
(например, левого) фиксируем расположение индексов, например:
9ak9bl9sq9tp = R' 0 R* 0 Ra 0 R6 • • • -R' 0 Rfc 0 Rp 0 R9.
Проделав эти операции, подставим итоговое выражение частной про-
производной E.124) в тензор производной, в результате получим:
^(Т ® Т ® Т 6П) = JL
- —т ® т
Или, используя обозначение операции симметрирования (см. A.270)),
получаем следующую теорему.
304 Глава 5. Тензорные функции
Теорема 5.8. Тензор производной от скалярной кубической
функции от симметричного тензора второго ранга имеет вид:
(т®Т®ТП) = ЗТ®Тп =3ftT®T. E.125)
дТ
Тензор 6ffc{'} является симметричным тензором шестого ранга
(см. A.269)). Если же исходный тензор 6П уже является симмет-
симметричным, то из E.125) следует, что
—(Т 0 Т 0 Т 6П) = 36ft ... Т <g> Т. E.126)
с/Т
5*2*6. Тензоры производной от инвариантов
тензора второго ранга относительно
различных групп симметрии
Применяя формулу E.118) к линейным инвариантам Ц{Т) разных
групп симметрии, получим следующие тензоры производной от ли-
линейных инвариантов:
дт(Т)
Остальные линейные инварианты классов совпадают с указанными
выше, например:
г@) _ т(М) _ т(Е) AM) __ АЕ) AT) _ JA) __ АЕ)
if) = ij*) = 4Л), 4Q) = '1Л и т.п., E.127')
поэтому совпадают и их тензоры производной.
Применяя формулу E.123) к различным квадратичным инвариан-
инвариантам групп симметрии Gs (п.4.5.5), получаем после расшифровки опе-
операции симметрирования [•]:
-§f- = ^((ё? • Т) • -(ё| • Т)) = -О2 ® О2 • -Т, E.128)
Я/(М) Я 1
-^- = зт((^ • т) • "(Оз • Т)) = -(О! ® О2 + О2 0 Ох) • -Т
§ 5.2. Скалярные функции тензорного аргумента
.305
- для моноклинного класса;
8
" = df((ё^ ' Т) ' '(ё' * Т)) = 2Ql 0 Ol' Т EЛ29)
для ортотропного класса;
^ ёз) • Т • •(§§ • Т)) = 2((Е - ё§) ® ё»)И • -Т =
(°®° + O®O)T
= 2(Ofc - ё| ® ё|) • -Т = 2(ё? ® ё? + ё| ® ё|) • -Т, E.130)
ат гат1 ; зт 2 дт 2 ат
= (А - i(Oi ® Oi + О2 ® О2) - Ofc) • -Т,
1 Я
- для тетрагонального и квазитрансверсально-изотропного (кроме
д1(р /дТ) классов;
и1Ъ _
дт "
- для Л-ромбоэдрического и Б-ромбоэдрического (кроме дц /дТ)
классов;
•Т E.132)
306 Глава 5. Тензорные функции
- для квазиизотропого класса;
^Г = ~~И~ = F' « = 1,2,з,
ат " ат " зт (
- для гексагонального и трансверсально-изотропного классов.
Различных кубических инвариантов во всех группах симметрии
всего три:
/з(Т), /|Q) и 40)=4О)- E-134)
Тензор производной от третьего главного инварианта уже был вычис-
вычислен в п.5.2.4:
2МЕ1 E.135)
(для симметричного тензора Т).
Для вычисления тензора производной от l[ ' представим его в виде
E.117) и воспользуемся формулой E.126):
l[Q) = (Т • -О„) • (Т • -О,,) • (Т • -Oft) = Т ® Т 0 Т 6О„, E.136)
dI(Q)
где тензор 6ОП является симметричным тензором шестого ранга и
имеет следующий вид:
з
б
On = (Oft . Oft). -Oft = ? S^S^S^ei, 0 ... 0 ё,-в. E.137)
a=l
Еще один кубический инвариант имеется в классах сртотропии и
АО)
квазиизотропии Ц }, его можно представить в виде:
ё5-Т) = T0T0T (ё?®ё2®ё§)A65432). E.138)
Используя формулу E.125), получаем:
= з((ё? 0 ё\ 0 eD^^y •. • .Т 0 Т. E.139)
§5.2. Скалярные функции тензорного аргумента 307
Можно показать (см.упр.5.2.3), что тензор шестого ранга, участву-
участвующий в этом выражении, представим следующим образом:
, t Oa 0 Од 4- Од 0 Oa) 0O7 = Om, E.139a)
a,/3,7=l
тогда
^r = 36Om-...T®T. E.140)
Упражнения к § 5.2.
Упражнение 5.2.1. Доказать справедливость формулы E.136), записывая
компонентные представления тензоров O/j и Оп.
Упражнение 5.2.2. Доказать справедливость формулы E.139).
Упражнение 5.2.3. Записывая явное компонентное представление тензоров,
показать, что тензор E.139а) имеет следующие компоненты:
(ё2 ® ё2 ® e2)(i65432) = R^M'S^SifSi'ei, 0 ... <8> ё,в.
Применяя операцию симметрирования {•}, доказать справедливость формулы
E.139а).
Упражнение 5.2.4. Используя определение E.88) тензора производной, по-
показать, что имеют место правила дифференцирования скалярных функций по тен-
тензору, совпадающие с обычными правилами дифференцирования:
d (f) = ¦?
Упражнение 5.2.5. Доказать, что
д
j-{T2 ¦ -П) = ((П ® Е)A423> + (П ® Е)D123>) • Т = П ¦ Т + Т • П,
если Т иП- симметричные.
308 Глава 5. Тензорные функции
§ 5.3. Потенциальные тензорные функции
5.3.1. Определение потенциальной тензорной функции
Определение 5.8. Тензорная функция EЛ) или E.2) называет-
называется потенциальной, если существует скалярная функция ф(пТ)
тензорного аргумента, называемая потенциалом, тензор произ-
производной от которой совпадает с этой функцией:
"S = nr(nT) = ^. E.141)
Очевидно, что для потенциальных тензорных функций тензоры nS
и ПТ имеют одинаковый ранг.
В компонентах формула E.141) имеет вид:
^i:(TJl-ja)- E-142)
При переходе от одной криволинейной системы координат Xх в дру-
другую Х'х компонентное представление потенциальной функции соглас-
согласно E.3) изменяется следующим образом:
$,...,. = ^..,„(Т"--'») = JgL-t E.143)
где
Su.-.i^Cri.-.Q^S^...^ T^"=P{\ ...Р^Т", E.144)
причем в силу инвариантности тензорной функции E.141) имеют мес-
место следующие соотношения:
W &Ф kn Tl/Zx.-./nN
E.145)
5.3.2. Индифферентные потенциальные тензорные
функции
Согласно общему определению E.8), индифферентная тензорная
функция не меняет свой вид при переходе из одной системы координат
х% в другую Xх, осуществляемом в рамках определенной группы Gs
преобразований, например линейных. Применительно к потенциаль-
потенциальной тензорной функции, это свойство индифферентности относитель-
относительно группы G8 записывается следующим образом: если имеет место
соотношение
& EЛ46)
§ 5.3. Потенциальные тензорные функции
.309
в декартовой системе координат Ох\ то при переходе в другую сис-
систему координат Xх, получающуюся с помощью линейного преобра-
преобразования в группе G,, характеризуемого матрицами Ах ^ и Вх ^ вид
зависимости S{1...in от T-Ь—i» в новой системе координат не меняется
и определяется формулой E.142).
Очевидно, выполнена следующая теорема.
Теорема 5.9. Если скалярная функция ф(Т^"^п) является ин-
индифферентной относительно группы Gs, т.е. для нее выполнена
формула E.84) из п. 5.2.1:
ф^г.-п) = ф{А^ ...а^З*'-*-), \/{Ajk} e G., E.147)
то потенциальная тензорная функция E.142) также является ин-
индифферентной относительно группы G8.
Условие E.145) для компонент индифферентной потенциальной
функции имеет вид:
причем в левую часть необходимо после дифференцирования подста-
подставить соотношение:
E.149)
5.3.3. Представление потенциальной функции
в тензорном базисе
Теорема 5.10. Индифферентная относительно группы G8 ска-
скалярная функция ф(пТ) всегда может быть представлена как функ-
функция полного набора функционально независимых скалярных инвари-
инвариантов Ц8\пТ) относительно той же группы симметрии:
ф{пТ) = ф{1^{пТ)), у=1...г. E.150)
Т В самом деле, если скалярная индифферентная функция -0(nT) не
выражается через инварианты /.у (ПТ), то ее саму можно рассматри-
рассматривать как еще один независимый скалярный инвариант тензора nT, a
это противоречит полноте набора ц*\ Таким образом, представление
E.150) всегда возможно. А
Вычислим теперь тензор производной от ф E.150) и подставим его
в E.141), тогда получим:
Й;в4')в"т"
3io Глава 5. Тензорные функции
Перепишем это соотношение в следующем виде:
HW(nT), E.152)
г
7=1
где введены обозначения для тензоров производной от инвариантов:
и скалярных функций:
4>i = |р E.154)
которые, очевидно, удовлетворяют условиям взаимности:
Запись E.152) называется представлением потенциальной тензор-
тензорной функции в тензорном базисе.
В самом деле, любая потенциальная тензорная функция E.141) мо-
может быть представлена в виде разложения E.152), причем в рамках
одной и той же группы симметрии Gs одна функция отличается от
другой только коэффициентами у>7, а тензоры пЩ8' не изменяются.
Так как полный набор инвариантов Ц8' строится с помощью образу-
образующих тензоров групп пщ' и тензорных степеней от ПТ, то и ПН7
зависит от этих же самых тензоров.
Установим далее эти тензоры пЩ8' для п = 1 (векторные функ-
функции) и п = 2 (тензорные функции второго ранга) и различных групп
симметрии.
5.3.4. Потенциальные векторные функции
Рассмотрим случай п = 1, тогда потенциальная функция E.141)
имеет вид:
s = /(a) = ^, E.156)
где ф является функцией инвариантов вектора относительно группы
G,:
¦ф = фA^{а)) 7= !•••*•• E.157)
Представление E.151) для векторной функции имеет вид:
5.3. Потенциальные тензорные функции
.311
где
Используя теперь выражения для вектора производной дц /да,
полученного в п.5.2.3, запишем представление E.158) векторной функ-
функции относительно различных групп симметрии G,.
Триклинная сингония:
s = ?7=1
s = Yl~t=i
Моноклинная сингония:
G3: s =
, аз)ё7,
E.159)
а,/3,7=1,2,3.
Ромбическая сингония:
E.160)
E.161)
Сингонии:
тетрагональная
ромбоэдрическая
гексагональная
трансверсальная изотропия
s = 2<pia + ?
G$ = 9, 12, 14, 15
G8 = 17, 19, 20
G, = 21, 23, 24, 25, 27;
G8 = 34, 36, 37;
E.162)
Сингонии:
G, = 10, 13;
Gs = 16, 18;
G, = 22, 26;
G, = 33, 35;
Кубическая сингония, изотропия G8 = 28,... , 32,38,39:
тетрагональная
ромбоэдрическая
гексагональная
трансверсальная изотропия
s = 2 + ё
E.163)
E.164)
312^ Глава 5. Тензорные функции
5.3.5. Общее представление потенциальных тензорных
функций второго ранга
Рассмотрим теперь случай п = 2, тогда потенциальная функция
E.141) имеет вид:
S = *4T) = |?, E.165)
где S и Т - симметричные тензоры второго ранга, а ф - скалярная
функция, зависящая от инвариантов тензора Т относительно группы
G,:
V' = VD')(T)). 7=1--г. E.166)
Представление E.152) для функции второго ранга имеет вид:
|fe) E.167)
7=1
где
E.168)
В качестве инвариантов ц'(Т) выберем полные наборы инвариантов
различных классов, приведенные в п.4.5.5.
Как было показано в п.5.2.5, все эти инварианты являются либо
линейными:
4J)(T) = Т - -ftW, 7=1..-™, E.169)
либо квадратичными:
4')(Т) = Т®Т--.-41Ц»), 7 = *»+!..•«, E-170)
либо кубическими:
4'>(Т) = Т®Т®Т 6ft7*), 7 = 9 + 1. ..г, г^б, E.170а)
где щ\ *щ' и бщ' - тензоры, построенные с помощью образующих
тензоров групп, am- число линейных инвариантов, rri2 = q — т -
число квадратичных инвариантов, гпз = г — q - число кубических
инвариантов в группе.
Тензоры производной от этих инвариантов вычисляются в п.5.2.5
(формулы E.105), E.120) и E.125)), и в общем виде могут быть запи-
записаны следующим образом:
<'K-> • .Т, 7 =
§ 5.3. Потенциальные тензорные функции 313
7 = Я + 1... г. E.171)
Тогда представление E.167) можно записать в виде:
S = 5^p7ftW+2 ? y>74ft^<-> •-Т + 3 ? ^76П^,
7=1 7=m+l 7=9+1
E.172)
Ъ = р7(/<*>(Т),... ,/W(T)) = ^y. E.173)
C7i-y
Подчеркнем, что тензоры ft7 , 4П7 "' и 6ft}'*'' не зависят от тен-
тензора Т, а меняются только при переходе от одного класса симметрии
к другому. Таким образом, доказана следующая теорема.
Теорема 5.11. Всякая потенциальная тензорная функция E.165)
второго ранга, индифферентная относительно некоторой группы
G8, может быть представлена в виде разложения E.172) по тен-
тензорным степеням: Е, Т и Т 0 Т - не выше второй степени.
Для одной и той же группы Ga одна потенциальная функция E.165)
отличается от другой только коэффициентами у?7, которые являются
скалярными функциями E.173) инвариантов /7 (Т).
5.3.6. Потенциальные тензорные функции второго
ранга относительно различных групп G8
Запишем теперь представление E.172) потенциальной тензорной
функции для каждого класса симметрии. Будем исходить из пред-
представления E.167), в которое подставим выражения для тензоров про-
производной дц* /дТ каждого класса симметрии, полученные в п.5.2.6.
Представление тензорной функции E.172) запишем в безиндексном
виде и в компонентной форме в декартовом базисе ё,-.
(Е)-Триклинный класс (гп =¦ 6, rri2 = 0, гпз = 0):
з
S =
7=1
(ЪЦ \% W)а ф/Зф-г фа,
7=1 ^
314 Глава 5. Тензорные функции
(М)-Моноклинный класс (га = 4, га2 = 2, газ = 0):
S = У>7ё* + -у>4Оз + x(Wo2 0 О2)+
7=1 г г
® О2 + О2 0 Oi) + y>7(Oi 0 Oi)) • -Т,
7=1
x (S[Si + SiS{) + (v>6T13 + <Р7Т23)F'2б1 + 6l34), E.175)
У*7 = у?7(Тц, T22, T33, T12, T13, T13T23, Tf3).
(О)-Ортотропкый класс (т = 3, m2 = 2, тз = 1):
s = У2 V7e? + о (^Ol ® °i + ^O2 ® O2 + <p7O3 ® O3)
7=1 L
6, E.176)
7=1
, T22, T33, f|3, Т?з, f12f13f23,2?
(T)-Тетрагональный класс (т = 2, m2 = 3, m3 = 1):
S = {<pi + #>2/2)(E - el) + (<p2 + I2<p6)el+
+ O2 ® O2) + 2<p4{el 0 ej + ё
i a) • -T + y>6T2, E.177)
§5.3. Потенциальные тензорные функции 315
ij + (<р2 - Vi -
<Ъ = у>7 (Гц + Т22, Т33, Т?з + 2», 2?i + ^!2> 2?а. ^(Гн - Т22)).
(Кз)-Квазитпрансверсалъно-пзотпропный класс (гп = 2, Шг = 3,
т3 = 1):
S = {(pi + /2Ы(Е - ё§) + (<р2 + /2?>б)ё§ + (j*>3(Oi ® Oi + О2 ® О2)+
- -(Ox ® Oi + О2 ® Оа) - Оь)-
E.178)
5ij + (<p2 -Щ-
(S[S33 + 6'36{)f13)
V>7 = v7 (Гц + t22, f33) 2?3 + T|3, Г2! + Ij'j, T22, detT).
(А)-Ромбоэдрический класс (m = 2, m2 = 4, m3 = 0):
S = y>i(E - ё§) + р2ё| + (^(Oi ® О! + O2 ® O2) + -
+ 2у>5(Д - -(d ® Oi + O2 ® Oa) - ё^ ® ё2) + +-у>бПз<1) • -T,
{<p2 -tp!- 2<p5f33)S3Si+
12633 + 6{3632){(<р3 - 2у>5)Т23 - <P4T12 + ^(Тц - Т22)) +
(б[б{ + 6'36{)((<р3 - 2<ръ)Т13 + ?i(Tii - Т22)
E[б{ - 4<52)(^4Т13 + <p6f23)+
[4 4 E.179)
= V7 (Гц + Г22, Тзз, Г{з + Т23, Т13(Тц — Т22) —
2! + Т% + 2Т22, Т23(Тп - Г22) + 2Т12Т13).
316 Глава 5. Тензорные функции
(В)-Ромбоэдрический класс (то = 2, то2 = 3, тоз = 1):
S = (y?i + /2Уб)(Е'- ё2) + {<р2 + |
2 (Ы°1 ® Oi + О2 0 О2) + 2
2<р5(А - -(Ох ® Ох + О2 ® О2) - ё§ ® ё|) - ip&h д) • Т + у?6Т2,
6ij + (<р2 -91-
Т13 + ^(Гц - Т22))F[6}3 + 6<36{)B(<р4 - <p5)f13+
- S28{) - T23(S[Si + SiS{)) +
* кк*, E.180)
,Тзз, T13 + T23,
класс (m = 1, m2 = 2, TO3 = 3):
S = (vi + /2Ve)E + Bу>2ОЛ + ^3(A - Ofc - ve/iA) • -T+
6„ + 3^56Om + <p6A ¦ A) • • • -T ® T,
- ч>ъ
E.181)
= ^ (Tu + f22
3u + 3» + 2». ТгзТиТю, det T).
(H)-Гексагональный и (Т3)-Трансверсалъно-изотропный классы
(то — 2,гп2 = 2, тоз = 1):
S = (у>1 + /2?>5)(Е - ё2) + {tp2 + 12<рь)ё1 + (^3@! ® Ох + О2 ® О2)+
- -(Ox ® Oj + О2 ® О2) - ё23 ® ё2 -
§5.4. Квазилинейные тензорные функции 317
+ (S[6i + 6{36{)Т13)+
+ B<р4 - htpjf" + <p5fikfki, (
4>t = <Py (Тц + f22, T33, 7% + f>3, j» + T|2 + 23» , det T).
A)-Изотропный класс (т — 1, m2 = 1, тз = 1);
S = (ipi+ h<p2 + /2у>з)Е - [f2 + h<P3)T + ^3T2, E.183)
Sij = (<pi + h<p2 + <Рз)& - (<P2 + h<fi3)Tij + <pzfikfki,
Функции у>7 во всех соотношениях E.174)-E.183) потенциальны,
т.е. удовлетворяют соотношениям взаимности:
E.184)
Сделаем ряд замечаний к представленным выше выражениям.
1. В двух классах симметрии, Af-моноклинном и О-ортотропном, по-
потенциал -0, а, следовательно, и коэффициенты у>7, удобно рассмат-
рассматривать как функции не шести, а семи инвариантов (среди которых,
естественно, только шесть независимых): в М-классе добавлен ин-
инвариант Ц ' = Т223, а в О-классе - инвариант Ц ' = Т^. В этом
случае выражения для потенциальных функций StJ(Tfc/) становят-
становятся симметричными: в Af-классе - по отношению к индексам 1 и 2,
а в О-классе - по отношению ко всем трем индексам.
2. Инварианты Д и /2, входящие в представленные выше тензорные
функции, всегда могут быть выражены через инварианты 1^ со-
соответствующего класса симметрии (см. упражнения к §4.5).
Упражнения к § 5.3.
Упражнение 5.3.1. Исходя из общего представления E.172) потенциальных
тензорных функций и формул п.5.2.6 для тензоров производных dl\$ /9T, до-
доказать справедливость представлений тензорных функций для различных групп
G8, приведенных в п.5.3.6.
§ 5.4. Квазилинейные тензорные функции
5.4.1. Определение квазилинейных функций
Рассмотрим потенциальную тензорную функцию второго ранга
E.165). Как было показано в п.5.3.5, ее всегда можно представить
в виде разложения E.172) по тензорному базису относительно каждо-
каждого класса симметрии.
318 Глава 5. Тензорные функции
Определение 5.9. Частный класс тензорных потенциальных
функций E.141), для которых разложение E.172) по тензорному ба-
базису содержит только тензорные степени не старше первого по-
порядка, т.е. Е и Т:
J2 ^4*Ч'><-> •-Т, E.185)
7=1
называется классом к в аз илине иных потенциальных функ-
функций.
Из E.172) и E.185) следует, что для квазилинейных потенциальных
функций:
дф
<P-! = qJ- = V, 7 = 9 + 1,-¦-,г, E.186)
т.е. потенциал зависит, вообще говоря, не от всего набора инвари-
инвариантов Ц3' данной группы G,, а только от линейных и квадратичных
инвариантов:
1> = 1>(ll(T),...,Iq(T)). E.187)
Заметим, что, вообще говоря, понятие квазилинейности, или иначе
тензорной линейности, может быть распространено и на непотенци-
непотенциальные тензорные функции, об этом пойдет речь в § 5.7.
5.4.2. Квазилинейные функции различных
классов симметрии
Рассматривая разложения потенциальных функций по тензорному
базису для различных классов симметрии, представленных в п.5.3.6,
нетрудно заметить, что для некоторых классов тензорные функции
являются квазилинейными, без дополнительных допущений вида
E.187). Очевидно, что это те классы, у которых потенциал ф не
зависит от кубических инвариантов. Итак, для
- триклинного (#),
- моноклинного (М),
- тетрагонального (Т),
- А-ромбоэдрического (А)
классов потенциальные функции являются квазилинейными, и их раз-
разложения E.172) и E.185) по тензорному базису совпадают.
Остальные классы содержат кубические инварианты. Ниже приве-
приведены разложения квазилинейных тензорных функций по тензорному
базису для этих классов.
(О)-Ортотропный класс:
(О7 0 О7) • -Т), E.188)
7=1 1
§ 5.4. Квазилинейные тензорные функции 319
& = ? №4 + \
2
(Кз)-Квазитрансверсалъно-изотропный класс:
S = у?х(Е - %1) + <р2ё1 + (-?>3(О! ® Oj + О2 ® О2)
+ ё| ® ё|) + (A
(О: ® Ох + О2 ® О2) - Ол)) • -Т, E.189)
= ^i^ + (<р2 -91-
F{6i + 636{)f13)
Ъ = <ру (Ги + Т22, Т3з, Т^з + Т22з, Тп + Т|2, Т?2).
)-Ромбоэдрический класс:
S = vi(E - ё|) + <р2ё1 + (y>3(Oi ® Oi + О2 ® О2) + -
О2 ® О2) - ё^ ® ё^)) • -Т, E.190)
^ = y>7 (fn + Т22,Гзз, Ti23 + T23, f13{fn - f22) - 2T13T23,
(К)-Квазиизотпропный класс:
S = piE + Bу?2ОЛ + у>з(А - ОЛ) • -T, E.191)
a=l
320 Глава 5. Тензорные функции
-til + -*22 + ^33) -ь 11 + -^22 •" -^331 -^13 • ^23 + 1\2)ш
(Н)-Гексагональный и (Тз)-Трансверсально-изотропный классы:
.--(Oi®Oi + O2®O2)-e|®e|))--T, E.192)
Р7 = ^7 (Гц + Т22, ТЬз, Г^з + Т223, Т2! + Т222 + 2Т22).
(I)-Изотропный класс:
E.193)
Для ортотропной квазилинейной функции потенциал ф и коэффи-
коэффициенты у>7 7 — 1» • • • »6 зависят от шести независимых инвариантов,
в число которых не входит кубический инвариант
5.4.3. Представление квазилинейных функций с помощью
тензора четвертого ранга
Квазилинейные функции можно сделать действительно совпадаю-
совпадающими по форме с соответствующими линейными тензорными функци-
функциями, описанными в п.5.1.9. Для этого следует преобразовать функции
(рч таким образом, чтобы можно было выделить симметричный тензор
четвертого ранга 4С при Т в квазилинейных функциях п.5.3.6 и 5.4.2.
Проделаем эти операции для каждого класса, начиная с изотропного.
(I)-Изотропный класс:
В формуле E.193) введем две новые функции Ai и А2, зависящие от
инвариантов Д, J2:
Ai(/i,/2) = 92 + т1, A2(Jb J2) = -2p2, E.194)
h
§ 5.4. Квазилинейные тензорные функции 321
тогда расшифровывая линейный инвариант Ji = Е • -Т, преобразуем
E.193) к следующему виду:
S = AiIxE + 2А2 А - Т = (AiE 0 Е + 2А2 А) - Т =
= 4С--Т, E.195)
где тензор четвертого ранга 4С определен по формуле E.81). Однако,
в отличие от линейной тензорной функции, для квазилинейной функ-
функции коэффициенты Ai, A2 уже не константы, а некоторые функции
инвариантов Д, J2.
(К)-Кубический класс:
В формуле E.191) введем три новые функции:
Ai = 7i, А2 = -у>3, Аз = 2y>2-y>3, E.196)
/i 2
тогда E.191) можно преобразовать следующим образом:
S = Ai/iE + BА2А + А3ОЛ) • Т =
= (AiE <g> E + 2А2А + А3ОЛ) ¦ -Т = 4С ¦ -Т. E.197)
Тензор 4С здесь совпадает с соответствующим тензором E.80).
(Н)~Гексагональный и Т$-Трансеерсалъно-изотропный классы:
Представим функции <рг...<р4 в формулах E.192) следующим об-
образом:
^ = А1A<Я>Ч-4Я)) + А31<Я\
92 - п - 2^4Я) = A2/f > + Аз(/!Я) + 4Я)), E.198)
А4 = (рз - Ч>\, ^4 = А5,
где А1...А5 функции инвариантов l[HK..l[H\ тогда E.192) можно
представить в виде:
S = (Al(/f > + /f >) + Аз4Я))Е + (А,4Я) + Аз(/{Я) + 4Н)))ё1+
+ (A4(Oi 0 Oi + О2 ® О2) + 2А5 А) • -Т. E.199)
Расшифровывая линейные инварианты 1{ + Ц = Е • -Т,
/2 = Т • -§з, получаем:
S = (AiE 0 Е + А2ё§ 0 ё§ + А3(Е 0 ё| + ё§
+ A4(Oi ® Oi + О2 ® О2) + 2А5А) • -Т = 4С ¦ -Т. E.200)
11 Тензорное исчисление
322 Глава 5. Тензорные функции
Тензор 4С совпадает с соответствующим тензором E.79).
(В)-Ромбоэдрический класс:
Введем шесть функций Ai... Аб от инвариантов Ц \ представляя
функции <pi...<p$ в формулах E.190) в виде:
} + X3(l[B) + 4В)), E.201)
<Рз - 4>ь = А4, <р* = 2А5, ч>ъ = Аб.
Тогда после расшифровки линейных инвариантов l[ +4 = Е- «Т,
Ц = Т • -ёз, приводим E.190) к виду:
S = (AiE 0 Е + Л2ё| 0 el + А3(Е 0 ё§ + %\ 0 Е)+
+ A4(Oi 0 Oi + O2 0 О2) + A5D5 + 2А6А) - -Т = 4С • -Т. E.202)
Тензор 4С также совпадает с соответствующим тензором E.78).
[А)-Ромбоэдрический класс:
Семь функций Ai... А7 от инвариантов Ц вводятся в формулах
E.179) следующим образом:
) + 4А)), E.203)
^з - 4>ь = А4, у?4 = 2А5,
4>ь = Аб, у?б = 2А7.
Тогда аналогично E.202) приводим E.179) к виду:
S = 4С • -Т, E.204)
где тензор 4С определяется формулой E.77).
(Кз)-Квазитрансверсалъно-изотропный класс:
Шесть функций Ai... Аб от инвариантов ц ' вводятся в формулах
Eч 189) следующим образом:
§ 5.4- Квазилинейные тензорные функции 323
E.205)
тогда формулу E.189) можно привести к виду E.204), в которой тен-
тензор 4С определяется формулой E.76).
(Г)-Тетрагональный класс:
Семь функций Ai... А7 от инвариантов ц вводятся в формулах
E.177) следующим образом:
?>2 - Pi - 2^4Т) = A2/f> + A3jf \ E.206)
Ч>ъ~Ч>ь = 2А4, 2у?4 - 4>ь = А5,
У?5 = 2Аб, у?б = 2А7,
тогда функцию E.177) можно привести к виду E.204), в котором тен-
тензор 4С определяется формулой E.75).
(О)-Ортотпропный класс:
Девять функций Ai... А9 от инвариантов Ц ' вводятся в формулах
E.188) следующим образом:
фа, а,/3,7 =1.2,3;
= 2Аб+а. E.207)
Тогда расшифровывая линейные инварианты Ц ' = Т • -ё^, приводим
E.188) к виду:
з
S = ?(AQ4°> + А3+7/Г + А3+/з4О))ёа + Аб+а(Оа 0 Ов) • -Т =
а=1
3
= Х1(Лаё« 0 ё« + А3+7(ё^ ® Ц + Ц 0 ё|) + Аб+а(Оа 0 Оа) ' "Т =
= 4С . -Т. E.208)
Здесь тензор 4С определяется формулой E.74).
324 Глава 5. Тензорные функции
(М)-Моноклинный класс:
Тринадцать функций Ai... А13 от инвариантов Ц ' вводятся в фор-
формулах E.175) следующим образом:
з
у>4 = 2 ? А9+а/?м> + 4А94М), у>5 = А8, E.209)
а=1
?>6 = Ai3, <Р7 = А7,
Расшифровывая линейные инварианты 1а = Т • -е^, l\ =
= A/2)Т • -Оз, преобразуем выражение E.175) к виду:
з
а=1
¦Ь Аб+а(Оа 0 Оа) + Ai3(Oi 0 О2 + О2 0 Oi)) • -Т =
1 ®а + Аз+а(в^ 0 ё7 + ё7 0 ё^) + Аб+аОа 0 Оа +
а=1
0 O3 + O3 0 %D) + Aii(Oi 0 O2 + O2 0 Oi)) • -T =
= 4C.-T. E.210)
Тензор 4С совпадает с тензором четвертого ранга, определяемым по
формуле E.73).
(Е)-Триклинный класс:
Двадцать одна функция Ai... А21 от инвариантов /{ ... ц 'в фор-
формулах E.174) вводятся следующим образом:
<Ра = \ЛЕ) + Аз+,4Я) + As-w/W + 2A9+a/f }+
з
a = 2 Y,
E.211)
афрфчфа, a,/3,7=l,2,3.
Расшифровыв?1Я линейные инварианты/a =Т--ё|, /з+„ = |T"Oa,
убеждаемся, что выражение E.174) действительно можно привести к
виду E.204), в котором тензор 4С выражается по формуле E.71).
§ 5.4. Квазилинейные тензорные функции 325
5.4.4. Потенциалы линейных тензорных функций
Представление с помощью тензоров четвертого ранга позволяет
легко получить из квазилинейной обычную линейную тензорную
функцию с образующим тензором 4С, нужно только все AQ положить
константами.
Получим выражение для потенциалов ф, которые соответствуют
линейной тензорной функции с образующим тензором 4С из п.5.1.9
для каждой группы. Для этого вспомним, что
и воспользуемся соотношениями между у>7 и Аа, введенными в п.5.4.3.
(Е)-Триклинный класс:
Из E.211) имеем:
' + 2УАзи+б+аС, E.213)
_^_ = 2^\- .-- г(В)л.О1... f(*> J.O\.- -r(?) j.01.. f(?)
Решением этой системы уравнений является скалярная функция от
т(Е)
инвариантов ц :
3 ,
a=l
которая и является потенциалом линейной тензорной функции в три-
клинном классе, а. фо - постоянная интегрирования.
Тензор производной от этой функции имеет вид:
— - и • -1, id.Jioj
где тензор 4С определяется формулой E.71).
326 Глава 5. Тензорные функции
(М)-Моноклинный класс:
Решением дифференциальных уравнений E.212) с правой частью
из E.209) является следующая скалярная функция:
з -
ф~^МХа1а +Аз+а//з Ji +2Хт1г +2А8/5
+ 2А94М J + 2А9+а4М ]l[M) + 2А134М}) + Фо. E.216)
Тензор производной от этой функции дает линейную функцию E.215)
с тензором 4С, определяемым по E.73).
(О)-Ортотропный класс:
Потенциал линейной функции имеет вид:
* = Е (I Х{°J + Аз+а4ОLО) + 2AeWiS) + *>• E-217)
\ ?, " /
а=1
Тензор производной от этой функции образует линейную функцию
E.215) с тензором 4С E.74).
Частные производные дф/дЦ приводят к формулам E.207), в
которых все Аа следует положить константами.
(Т)-Тетрагональный класс:
Потенциал линейной функции имеет вид:
т — 7> v 1 1 ' 2 2 / ^3-^1 -^2 ^^4-*з ^б-'д *"
+ О \ /Л ' I \ Г\ ) I л/. /Г fti Q\
Для того чтобы тензор производной от этой функции привел к ли-
линейной функции E.215) с тетрагональным тензором 4С, определяе-
определяемым по E.75), необходимо положить:
А2 = А2 + 3Ai + 2А3 + А5 + 2Аб, А3 = А3 + Аь E.219)
~ ~ 1
А4 = A4 + Аб, As = -\ь + Аб-
В этом случае частные производные у?7 = дф/дЦ приводят к
формулам E.206), в которых все Аа также следует считать констан-
константами.
§ 5.4. Квазилинейные тензорные функции 327
(Кз)-Квазитрансверсалъно-изотропный класс:
Потенциал имеет вид E.218), но А7 = 0:
ф = l
А5 J^} + 2Аб/^) + ^о. E.220)
Тензор производной от ф приводит к тензору 4С в виде E.76), а
частные производные дф/дЦ приводят к формулам E.205).
(А)-Ромбоэдрический класс:
Потенциал линейной функции имеет вид:
ф = i(A{4
+ 2А54Л) + Аб4Л) + 2А74Л) + Л, E-221)
А2 = А2 + 3Ai + 2А3 + 2Аб, А3 = Ai + А3, А4 = А4 + Аб.
Тензор производной от ф образует линейную функцию с образую-
образующим тензором 4С в форме E.77), а частные производные дф/дЦ
приводят к формулам E.203).
(В)-Ромбоэдрический класс:
Потенциал имеет вид E.221), в котором А7 = 0:
ф = lix
4В) 4В)^о, E.222)
А2 = А2 4- 3Ai + 2А3 + 2Аб, А3 = Ai + А3, А4 = А4 + Аб,
ему соответствует тензор четвертого ранга 4С E.78) и коэффициенты
E.201).
(Н)-Гексагональный иТ^-Трансверсально-изотропный классы:
Потенциал имеет следующий вид:
^Г f o, E.223)
А2 = А2 ч- 3Ai + 2А3 + 2А5, А3 = Ai + А3, А4 = А4 + А5,
328 Глава 5. Тензорные функции
ему соответствует тензор четвертого ранга 4С E.79) и коэффициенты
E.198).
(К)- Квазиизотропный класс:
Потенциал имеет вид:
+ = |а»^> + (Л2 + ^LQ) + 2A2/<Q) + *,, E.224)
ему соответствует тензор 4С E.80) и коэффициенты у>7 E.196).
(/)- Изотропный класс:
Потенциал имеет вид:
ф = i(Ai + \2)ll - А2/2 + V>o, E.225)
ему соответствует тензор 4С E.81) и коэффициенты у?7 E.194).
С использованием тензора четвертого ранга 4С потенциал ф для
линейных потенциальных функций всех классов симметрии можно
представить в виде:
ф= 14С...-Т®Т + ^0. E.226)
В самом деле, рассматривая ф как скалярную функцию квадратичного
типа E.116), можем вычислить тензор производной согласно E.121):
-^ = 4С<*> • Т = 4С • Т = S, E.227)
аТ
так как 4С является симметричным тензором четвертого ранга. Та-
Таким образом, E.226) действительно является потенциалом для всех
линейных функций E.227).
§ 5.5. Спектральное представление тензоров
второго ранга
5.5.1. Определение спектрального представления
Для квазилинейных потенциальных функций можно дать еще одну
форму представления, основанную на так называемом спектральном
представлении тензоров. Дадим определение этих представлений.
Рассмотрим пространство симметричных тензоров второго ранга
B)
__ § 5.5. Спектральное представление тензоров 329
Теорема 5.12. Пространство S$' можно разбить на прямую
сумму ортогональных подпространств V(Q), инвариантных относи-
относительно некоторой группы преобразований G8, являющейся подгруп-
подгруппой полной ортогональной группы преобразований Iq:
Si2) = V(i) Ф ... 0 Р(„), Gs С /о. E.228)
Иначе говоря, любой симметричный тензор второго ранга Т можно
представить суммой
(в)> п<6, E.229)
а=1
где каждый тензор Р(а) обладает следующими свойствами:
1° (прямая сумма подпространств) P(Q) является симметричным тен-
тензором второго ранга, принадлежащим подпространству V{a)\
2° (ортогональность подпространств) Р(а) ~ взаимно-ортогональны,
Р(в)--Р(я = 0, если афC; E.230)
3° (инвариантность подпространств) P(Qj является индифферентной
тензорной функцией относительно группы преобразований G,, т.е.
QT • Р(О)(Т) • Q = P(a)(QT • Т • Q), E.231)
где Q - тензор линейных преобразований, соответствующий группе
преобразований G,;
4° тензор Р(а) является линейной тензорной функцией от Т:
Р(а) = Р(а)(Т)=4Г(а)--Т, а=1...п. E.232)
Заметим, что формула E.231) действительно определяет линейное
преобразование подпространства V(Q) в себя, если ее переписать в
виде:
(Q 9 Q)<2431) • -Р(о) = P'(e)l P(e)l P'(Q) € Vlay E.231a)
Поскольку P/Qv = P(aj(QT • T • Q) тоже принадлежит V(a)i т0 *Р(а) ~
действительно инвариантное подпространство относительно преобра-
преобразования E.231а). А так как E.231а) имеет место для любого Q G G,,
то V(Q) - инвариантно относительно группы преобразований.
Возможность представления E.229) тензора Т докажем ниже кон-
конструктивно, т.е. построив в пп.5.5.3 - 5.5.8 эти представления для
различных групп симметрии.
330 Глава 5. Тензорные функции
Определение 5.10. Представление E.229), обладающее свойст-
свойствами 1° - 4°> называют спектральным представлением
симметричного тензора второго ранга.
Впервые спектральное представление E.229) было установлено
Б.Е.Победрей.
Тензоры Р(а) называются обобщенными девиаторами или р-тензо-
рами, причем 4Г(а) - некоторые постоянные тензоры четвертого ран-
ранга, не зависящие от Т, а только от образующих тензоров О,G) группы
симметрии Ga.
Среди этих 4Г(а) имеются приводимые, т.е. полученные тензорным
произведением некоторого симметричного тензора второго ранга а(а):
4Г(а) = -уа(а) 0 а(а), а = 1.. .т < п. E.233)
аа
Для тензоров 4Г(а) и а(а) вводятся инварианты:
Г^а) = 4Г(а) ¦ ¦ ¦ .4Г(а), а = т + 1...п, E.234)
— ( \г^2 -
Из условия индифферентности функции Р(а)(Т) следует, что тен-
тензоры 4Га и а(а) должны быть индифферентны сами, т.е. должны
удовлетворять условиям D.7), D.12):
QT.a(a).Q = а(а), 4Г(а) = 4r(a)....(Q0Q0Q0Q)G5312468), E.235)
или в компонентном виде:
а(а) = а^)ё,- 0 ej, а^ = а^А*кА^ , E.236)
4Г(а) = Г 'Л')Л4ё,1 0 ё,-2 ® ё,а 0 ё,-4, Ца)*4 = Г/'а)"'4^1'1-! • • -^t4-4^
где Агк - произвольная матрица преобразований из группы G8.
5.5.2. Инварианты, связанные со спектральным
представлением
Введем с помощью тензоров Р(а) инварианты тензора Т, обозначим
их в отличие от инвариантов, введенных в §4.1, как YQ{T). Для тех
Р(а), у которых 4Г(а) является приводимым, инвариант YQ вводится
как
Ув(Т) = —а(а) ¦ -Т, а = 1.. .т, E.237)
аа
§5.5. Спектральное представление тензоров 331
причем из E.232) и E.233) следует, что
Р(а) = ^-Ya&{a), E.238)
а скаляр E.237) называется спектральным линейным инвариантом.
Для остальных Р(а), а = ra-fl...п инварианты вводятся формулой
Y (Т) — (Vi ч . -Р/ Л1/2 E 2Ш
и называются спектральными квадратичными инвариантами. Заме-
Заметим, что для линейных инвариантов E.237) также справедлива фор-
формула E.239).
С учетом E.238), разложение любого тензора второго ранга Т
E.229) может быть представлено в виде
п
__ Т)+ Y1 Р(а)(Т)' E'24°)
а=1 **а а=т+1
Отметим два важных свойства спектральных разложений, которые
будут использоваться в дальнейшем.
Умножая скалярно Р(а) на Т, с учетом представления E.229) и
ортогональности Р(а) получаем:
п
Р(а) * *Т = ЕРИ ' *((>) = РИ ' "РИ = Уа' *=1".". E-241)
/3=1
Рассмотрим теперь скалярный квадрат тензора Т • -Т и подставим
вместо Т спектральное разложение E.229), тогда с учетом ортого-
ортогональности Р(сф получим:
") * 'Р(/з) = S Р(")" *Р(а) = ? У' E'242)
а,/3=1 а=1 а=1
т.е. сумма квадратов всех спектральных инвариантов Ya всегда об-
образует один и тот же инвариант - след от квадрата тензора:
a=l
332 Глава 5. Тензорные функции
5.5.3. Спектральное представление для класса
изотропии
Т Докажем теперь теорему 5.12.
Покажем, что введенные в п.5.5.1 спектральные представления су-
существуют. Начнем с класса изотропии - (I).
Образующий тензор О5G) в этом классе только один (см.п.4.1.8) -
это тензор Е. Тогда существует только один тензор второго ранга
а(а), a ot(i) - его инвариант:
аA) = Е, т = 1, аA) = (Е • -ЕI'2 = >/3. E.244)
Спектральный линейный инвариант определяется следующим выра-
выражением:
iLLT). E.245)
Сооответствующий ему тензор P(i) определяется формулой E.238):
^ | E.246)
Второй обобщенный девиатор строим следующим образом:
РB) = Т - i/iE. E.247)
Соответствующий ему тензор 4ГB) имеет вид:
4ГB) = А- ^Е0Е. E.248)
о
В декартовой системе координат тензоры а.^ и 4ГB) имеют вид:
а'({} = с*1''', ах = л/г, E.249)
f |J2{' = -(SikSjl + SuSjk) - -SijSkl.
Других обобщенных девиаторов в этом классе нет, т.е. число п = 2
для класса изотропии.
Покажем, что построенные таким образом тензоры Р(а) являются
обобщенными девиаторами.
§ 5.5. Спектральное представление тензоров 333
Проверим справедливость формулы E.229). В самом деле, склады-
складывая тензоры Р(а)> получаем:
Т = b/lE + (Т - ^ДЕ) = РA) + РB). E.250)
Проверим ортогональность Р(Х) и РB)> т.е. справедливость E.230):
Р() * -РB) = 5/lE " '(Т - ^ = S(J " J'lE " 'Е) = °
т.к. Е • Е = 3.
В компонентной записи Р(а) тензоры имеют вид:
i .. ..
Т'3 = % + S\i) = -ZW + РЦу E.253)
Представление E.253) называют разбиением тензора на шаровую и
девиаторную части.
Спектральный квадратичный инвариант определяем по E.239):
УB) = (РB).-РB)I/2. E.254)
Этот инвариант называют интенсивностью тензора Т, вычислим
его в декартовой системе координат:
з
Tl = Y* = PijPij = 53 Р«« + 2(Pi22 + Р12з + Р2з)- E-255)
а=1
но Pij = fij - A/3)TkkSij, поэтому
Рп = Гц - \(fu + f22 + Тзз) = | ((Г„ - T22) + (Гц - Гзз)),
Ргг = \ ((Г22 - Ги) + (Т22 -
Рзз = I (№з - Гц) + (Тзз - Г22)), E.256)
Pl2 = Ti2, Р13 = Т13, P23 = Т2з.
334 Глава 5. Тензорные функции
Тогда, подставляя E.256) в E.255), после приведения подобных членов
получаем
Tl = | ((Гц - Т22J + (fu - ТззJ + (Т22 - Т33J+
E.257)
часто используемое представление второго спектрального инварианта
в декартовой системе координат.
5.5.4. Квазиизотропный (кубический) класс
Как показано в п.4.1.8, в квазиизотропном If-классе также имеется
только один образующий тензор второго ранга - это Е, поэтому в
спектральном представлении число ш= 1 и
a(i) = Е, аг = л/3, m = 1. E.258)
Следовательно, первый обобщенный девиатор Р^) такой же, как и в
классе изотропии:
РA) = -^ПаA), E.259)
v3
где
Yi(T) = ^=h(T). E.260)
Однако, по сравнению с /-классом, в квазиизотропном случае су-
существует еще один дополнительный образующий тензор четвертого
ранга - это О& (см.п.4.1.8), следовательно, появляется возможность
построения еще одного девиатора:
РC) = Т - ОЛ • Т. E.261)
Второй девиатор при этом принимает вид:
РB) = Т - РA) - РC) = ОЛ • Т - -i=YiE. E.262)
Соответствующие тензоры 4Г(а) выражаются следующим образом:
4ГB) = Oh - ^Е ® Е, 4ГC) = А - О„. E.263)
Следовательно, общее число обобщенных девиаторов для квазиизо-
квазиизотропии - п = 3.
§5.5. Спектральное представление тензоров 335
Проверим, что P(Q) обладает всеми свойствами E.230) - E.232).
Свойство E.232) очевидно, так же как и индифферентность всех функ-
функций Р(а)(Т), так как тензоры 4Г(а) состоят только из индифферент-
индифферентных относительно К- класса образующих тензоров Е, Аи О/,.
Покажем взаимную ортогональность P(Q), используя свойство
E.241):
- А) = о,
a=l
P(i) • -PB) = P(i) • -T - P(i) • -P(i) = hh - h) = 0, E.264)
PB) • -PC) = (T - Oh ¦ -T) • -(Oft • T - i/xE) =
/Л 1 1 \
= I V^ (t2 —T2) — -i2 + -i21 = о
Спектргшьные квадратичные инварианты имеют вид:
УC) = Т • (Т - Oft • -Т) = Т2 • Е - Ол • -(Т ® Т) = 2ICQ),
УB) = Т • .(Oft • -Т - ^ДЕ) = ОЛ • .(Т 0 Т) - i/2. E.265)
Запишем теперь обобщенные девиаторы и инварианты в компонен-
компонентах:
р^ = 7z6ii' р™ = % ^f- " $%Y*6i*' E'266)
а=1
Тензоры 4Г(а) имеют следующие компоненты:
а=1
336 Глава 5. Тензорные функции
1
Г(з)г/*/ = Г{&ik&jl + SuSjk) - 22 SiaSjaSkaSla- E.267)
1 а=1
Линейный Yi и квадратичные Уг, Уз инварианты
Yx = -bffcb Уз = \/ЭД2 + f 23 + TI3I/2 E.268).
У2 = 4=(№i - Т22J + (Гп - ТззJ + (Т22 - Т33JI/2.
Матричное представление обобщенных девиаторов:
1 0 0\ / 0 • Г1а 0 \
1 ° » PC)«i = Т12 _° Т23
0 0 1 \Т13 Т23 0
О О
PB)ij = ? | О 2Т22 - Гц - Т33 О
О 2Тзз-Т11-Т22/
E.269)
5.5.5. (Й')-Гексагональный и (Тз)-Трансверсально-
изотропный классы
В этом классе существует два образующих тензора второго ранга
О(,O (см.п.4.1.8) - это Е и ё2, поэтому можно образовать два тензора
а(в):
и аB) = Е-ё|, m = 2, E.270)
причем их инварианты принимают следующие значения:
O(i) = ё3 ® ё3 • -ё3 ® ё3 = |ё3|4 = 1, E.271)
а22) = (Е - ё3 ® ё3) • -(Е - ё3 ® ё3) = 3 - 2ё3 • ё3 + 1 = 3 - 2 + 1 = 2.
Им соответствуют линейные спектральные инварианты тензора Т:
У1(Т) = Т-.ё2, у2 = -Ьт--(Е-ё2) E.272)
и обобщенные девиаторы Р(а)
® ё3, РB) = 4=Уг(Е - ё3 ® ё3). E.273)
_ §5.5. Спектральное представление тензоров 337
Полное число ортогональных подпространств V[a) B данном слу-
случае равно п = 4, а оставшиеся два р-тензора вычисляют следующим
образом:
Р(з) = Т - -^У2(Е - ё§) + Y&1 - (Т • ё§ + ё§ • Т), E.274)
Тензоры 4Г(з) и 4ГD), соответствующие этим девиаторам имеют
следующий вид:
4ГC) = Л - -(Е - ё§) 0 (Е - %1) - ё\ 0 ё\ - -(Oi 0 Ог + О2 ® О2),
4ГD) = -(Oi 0 Oi + О2 0 О2). E.275)
То что эти тензоры соответствуют девиаторам E.274), проверяется
непосредственно умножением 4Г(а) на Т, при этом следует учесть
очевидное соотношение:
Т • ё§ + ё\ • Т = Bё| 0 ё| + J(Oi 0 Ог + О2 0 О2)) • -Т. E.276)
Справедливость E.229) следует из построения тензоров E.273) и
E.244).
Проверим ортогональность Р (<*)'•
РA)"РB) = ™ё30ё3.-(Е-ёз0ёз) = ^(|ёз|2~|ё3|4) - 0, E.277)
т.к. |ё§| = 1. Аналогично можно установить ортогональность других
тензоров Р(а)-
Запишем выражения для двух спектральных квадратичных инва-
инвариантов:
- 4Ух(Т • ё! + ё| • Т) • -ё| + 4Y?. E.278)
Учитывая, что
(Т.ё|)--(Т-ё2) = (ёз-Т.ё3J = У12,
(Т.ё1).-ё1 = (ё§.Т).-ё1 = У1, E.279)
338 Глава 5. Тензорные функции
получаем
У42 = 2ё| • Т2 + 2УХ2 - 8УХ2 + 4УХ2 = 2(ё2 . Т2 - У*). E.280)
Выражение для инвариантов Уз получим с помощью соотношения
E.242):
У32 = /i(T2) - У2 - У22 - У42. E.281)
Запишем компоненты тензоров a(Q) и Г(а) в декартовой системе
координат:
aB) = V^, E.282)
Выражения для обобщенных девиаторов произвольного симметрич-
симметричного тензора Т имеют вид:
Гц
-ill -/22
№'i4;i + &*2&зг) + Гзз^з^уз - №з^з +
E.283)
Инварианты Уа тензора Т вычисляются следующим образом:
1 - Гц + Г22
У2 = -j=Tij(8ij - Si3Sj3) = —¦-=—,
§5.5. Спектральное представление тензоров 339
г3 — -/»j-t 1 j — I33 — 9 vilx + i22/ ~ ^iJfc3^Jk3 + ^-^-33 =
= г lUn - ^22) + 4T12J, E.284)
\/2 OfHT1 ПН rni \ О(ПН% 1 ПН^> \
м — ?\1кг±къ — i-гг) — -Ч-мз + -'гз)-
Матричное представление обобщенных девиаторов имеет вид:
/0 0 0 \ f ,ф /1 0 О1
PA)>i =00 0 , РШ = П^ 22 0 1 0 j , E.285)
\0 0 Тзз/ \0
'(Ги-Т22)/2 Т12
Т12 (Т22 - Тц)/2 0 | ,
0 0 0
/0 0 Т13
РD)у = 0 0 Т23
\Ti3 t23 0
5.5.6. (^з)-Квазитрансверсально-изотропный класс
В этом классе так же, как и в Я-классе, имеется два образующих
тензора, Е и ё|, но число индифферентных тензоров четвертого ранга
увеличивается на один за счет тензора Од. Следовательно, в данном
классе числа тип имеют следующие значения:
m = 2, п = 5, E.286)
т.е. имеются два тензора а(а) и три тензора 4Г(а) четвертого ранга.
Тензоры а(а) аналогичны соответствующим тензорам в (Я) и (Т3)-
классах:
a(i) = ё§, аB) = Е - ё§, сц = 1, о2 = 2. E.287)
Линейные спектральные инварианты также остаются без измене-
изменений:
У1 = Т--ё2, у2 = -2=Т--(Е-ё2). E.288)
Соответствующие девиаторы имеют вид:
РA) = Пё2, PA) = -Ly2(E-e2). E.289)
340 Глава 5. Тензорные функции
Тензоры 4Г(а) для данного класса имеют вид:
4ГC) = О„ - ё| 0 ё| - ±(Е - §1) ® (Е - ё§),
4ГD) = -(Oi 0 Qi + O2 0 О2), E.290)
4ГE) = А - Ол - -(Oi 0 Oi + О2 (8» О2).
Соответствующие им обобщенные девиаторы выражаются следую-
следующим образом:
РD) = Т.ё§ + ё1.Т-2Г1ё§, E.291)
Р(б) = Т-Ол-.Т-Т.ё1-ё1.Т + 2У1ё^
Здесь учтено свойство E.276).
Введенные таким образом обобщенные инварианты обладают все-
всеми свойствами E.230) - E.232) р-тензоров.
Поскольку девиатор РD) такой же, как и для (Я)-класса (см.
E.274)), то и соответствующий ему инвариант сохраняет свой вид
E.280):
У42 = 2(Т2--ё1-У12). E.292)
Вычислим инвариант У32:
У22 = РC) • -Р(з, = Т ¦ -Oft ¦ .Ол • -Т = +УХ2 + У22 - 2УХТ • Oh • -ё2-
- 4=У2Т • -Ofc ¦ -(Е) - ё2) = Ол • • • -Т 0 Т - Y? - У22. E.293)
л/2
Пятый инвариант находим из E.243):
У52 = /!(Т2) - 2Т2 • -ё§ - Oh • • • -Т 0 Т + 2У!2. E.294)
В декартовой системе координат тензоры a(Q) и 4Г(а) имеют вид:
= 1) пB) = у/%, E.295)
а=1
§5.5. Спектральное представление тензоров _341
1 1
ГD)г/Ы = Г №"йз + ^k3)Sj3 + X
1
2
Обобщенные девиаторы симметричного тензора Т имеют вид:
Р .. — ^11 + ^22 /С С С С N
= fnSj3 + fj35i3 - 2Т3з<Ы;з, E.296)
/Tl I /XI
Матричное представление этих девиаторов имеет вид:
0 0 0
PA)ij =00 0 , P{2)ij =01
0 0 Тзз/ \0 0
(Тц-Т22)/2 0 0\
0 (Т22 - Гц)/2 0 , E.297)
0 0 0/
0 0 Т13\ / 0 Т12 0\
у =10 0 Г23 , РE)« = ^12 ° ° '
Т13 Т23 0 / \ 0 0 0/
Линейные инварианты тензора Т совпадают с линейными инвари-
инвариантами в (Тз)-классе:
Yi = Тзз, Y2 = 4=(Tii + Г22). E.298)
v2
Квадратичные инварианты в (^з) имеют вид:
T~i2 \1/2 у _ л/0|77,о| /ГС OQQ\
23/ ' 5 — V ^|-l 121 - \O.?%7VJ
342 Глава 5. Тензорные функции
5.5.7. Ортотропный класс
В этом классе имеется три индифферентных симметричных тензо-
тензора второго ранга: ё^, общее же число обобщенных девиаторов макси-
максимально и равно шести, т.е.
т = 3, п = 6. E.300)
Тензоры а(а) и 4Г(а) имеют вид:
а(а) = ё*, а = 1,2,3, а(в) = 1, E.301)
4Г(а) = -Оа_3 0 Оа_3, а = 4,5,6.
Обобщенные девиаторы определяются следующим образом:
Р(а)=Уаё^, а =1,2,3, E.302)
где
YQ = Т • -ё* E.303)
- линейные спектральные инварианты, а также
Р(в) = ^Оа^з(Т • .Ов.з), а = 4,5,6. E.304)
Проверим, что все свойства р-тензоров E.229) - E.232) выполнены.
Спектральное представление E.229) проверяем, переходя к компо-
компонентной записи:
? Р(«) = Е (У«ё« + ^°«+з(Т • -Оа+3)) =
а=1 а=1
3
а=1
Индифферентность функций Р(а)(Т) - очевидна, т.к. все тензоры
®а> Оа 0 Оа индифферентны относительно класса ортотропии.
Взаимная ортогональность Р(а) вытекает из ортогональности век-
векторов базиса ёа:
Р(а) • -Р(/з) = ё« - -ё^ = 0э а ф /3, а,0= 1,2,3, E.306)
§ 5.5. Спектральное представление тензоров _343
Р(а)" '^(р+з) = ёа • -Ор = ёа 0 ёа • -(ё7 0 ё<$ + ё«$ 0 ё7) =
= 2(ёа-ё7)(ёв-ё*) = 0, а,/3,7,* = 1,2,3,
Р(а+з) • -Poj+з) = Оа • О^ = 0, а#/3, а,/3= 1,2,3.
Квадратичные спектральные инварианты определяются по форму-
формулам E.241):
Уа2 = Р(а)--Т=Л(Т--Оа_3J, а = 4,5,6. E.307)
Запишем также все введенные тензоры в декартовой системе коор-
координат:
O(a).j- = SiaSja, a — 1,2,3, аа = 1;
WU SbWS **) фРффа- E.308)
Обобщенные девиаторы и инварианты имеют вид:
Л«)У = rea*o*io, a = 1,2,3; РD)у = 2\2(*a*,-2 + ^2^1),
Р(ъщ = ftatfnSjs + 6а6ц), P{6)ij = f23(Si2Sj3 + 6i3Sj2), E.309)
,=Tee, a = 1,2,3; Y4 = л/2|Г12|, П
Обобщенные девиаторы имеют следующее матричное представле-
представление:
/Гц 0 0\ /0 0
P{1)ij = 0 0 0, Р(а)у = 0 Т22 0
\ 0 0 0/ \0 0 0
/0 0 0 \ / 0 Т12 0\
РC)у =00 0 , РD)у = Ти 0 0 , E.310)
\0 0 Тзз/ V 0 0 0/
/ 0 0 Т13\ /0 0 0
РEH- = О О О , Р(в)у = О О Т23
\Т13 0 0/ \0 Т23 О
5.5.8. Триклинный класс
В этом классе имеется шесть индифферентных симметричных тен-
тензоров второго ранга: eQ ® ёр, следовательно, все числа шип совпа-
совпадают и равны шести:
тп ^ Ti = б, E.311)
344 Глава 5. Тензорные функции
а обобщенные девиаторы являются линейными. Тензоры a(Q) имеют
вид:
а(а) = ё?, а = 1,2,3, а(в) = 1, E.312)
»(а+3) = g (ё/3 ® ё7 + ё7 ® ё/з) = 2 Оа' а(«+3) = 1-
Спектральные инварианты определяются по формулам:
Ya = Т • -ё» = /<?>, У3+а = ^Т • Оа = /?>,, а = 1,2,3. E.313)
Поэтому обобщенные девиаторы имеют вид:
Р(а) = Yael PC+Q) = ^3+аОа, а = 1, 2, 3. E.314)
Очевидно, что все свойства р-тензоров выполняются при таком по-
построении.
В декартовой системе координат введенные объекты имеют следу-
следующий вид:
а,/3,7=1,2,3, афрфчфа, E.315)
а также
^(a)ij = Ya&iaSja> P(a+3)ij = ^^{^i^h + &П^р)- E.316)
Спектральные инварианты имеют вид
Ya = Таос, ос — 1,2,3,
П = |Т2з|, Y5 = |Т13|, Уб = |Т12|. E.317)
Матричное представление обобщенных девиаторов также очевидно:
каждая матрица (P(Q)ij) имеет одну ненулевую компоненту тензора Т:
/Гц 0 0\ /0 0 0>
P(i)ij = 0 0 0, P{2)ij = 0 Т22 0
\ о о о/ \о о о,
/0 0 О
PC)ij =00 0 , Рш = 0 0 t23 I , E.318)
V0 0 Т ^
§5.5. Спектральное представление тензоров 345
о т12 о>
PF)ij = Т12 О О
V 0 0 0
5.5.9. Сравнение спектральных инвариантов Ya
с инвариантами групп ц
Для триклинного класса спектральные инварианты Ya и 1а \ вве-
введенные в п.4.5.5, как было показано в п.5.5.8, совпадают.
Для остальных рассмотренных классов: (/), (Я), (Тз), (if), (^з) и
(О), - число спектральных инвариантов Ya на один меньше, чем ин-
инвариантов ц\ причем отсутствует кубический инвариант в каждом
классе. В классе ортотропии - это ц ' = Т12Т13Т23, а в остальных -
это /3 = detT.
Этот результат естественней, так как само построение инвари-
инвариантов YQ предполагает, что могут возникнуть либо линейные, либо
квадратичные инварианты. Вспомним теперь результаты §5.4, где
было получено, что в построении квазилинейных тензорных функций
участвуют как раз линейные и квадратичные инварианты.
Таким образом, применение спектральных инвариантов является
еще одним (весьма удобным, как будет показано в §5.6) способом для
описания квазилинейных функций.
На этом мы закончили доказательство теоремы 5.12, показав, что
спектральное разложение E.229) существует для классов: (Е), (О),
(*з), (К), (Я), (Тз) и (/).
Заметим, что квадратичные спектральные инварианты YQ по опре-
определению E.239) являются положительно определенными формами от
fiji т.е. YQ > 0, а = т + 1,... ,п, поэтому для остальных классов:
(М), (Т), (А) и (Б)-классов, у которых имеются квадратичные инва-
инварианты, но не являющиеся положительно определенными (см.п.4.5.5),
спектральные разложения не построены. А
Упражнения к § 5.5.
Упражнение 5.5.1. Показать, что из взаимной ортогональности тензоров
Р(а) следует
4Г(а) • -4Г№ = 0, а
346 Глава 5. Тензорные функции
§ 5.6. Спектральные представления квазилинейных
тензорных функций
5.6.1. Спектральное представление двух тензоров
Спектральное представление, введенное в §5.5, обладает важным
свойством: оно одинаково в рамках одной и той же группы симмет-
симметрии Ga для всех симметричных тензоров. Это означает, что если
имеются два симметричных тензора S и Т второго ранга и фикси-
фиксирована группа симметрии G,, то спектральные представления этих
тензоров записываются следующим образом:
i3
' T=Epi3>
а=1 а=1
где Pjaj и Р}а\ - обобщенные девиаторы тензоров:
E.320)
Из представления E.320) следует, в частности, что тензоры PJ! и
(Т)
PL/ взаимно ортогональны:
Спектральные инварианты тензоров Т и S обозначим следующим
образом:
Jjj; E.322)
Среди них имеются по га линейных инвариантов, для которых
уРП уE)
(«) = -f-fi(«)' PC = -f-«4«). «=!.••"»• E-323)
§ 5.6. Спектральные представления квазилинейных функций 347
5.6.2. Спектральное представление приращения
потенциала
Пусть теперь два симметричных тензора S и Т связаны потенци-
потенциальной квазилинейной функцией:
S = Т{Т) = |^, E.324)
где ф - потенциал.
Составим дифференциал от функции ф, рассматривая ее как ска-
скалярную функцию от Т (см.E.93)):
# = |~-<*Т. E.325)
Здесь учтено, что Т - симметричный тензор. Если теперь подставить
E.324) в E.325), то получим условие потенциальности в виде:
йф = S • .(Л*. E.326)
Подставляя теперь в E.326) спектральные представления E.319)
тензоров S и Т, получим в итоге
а=1
Дифференциал тензора dP)} определен в п.5.2.2 и представляет
собой симметричный тензор:
где P!JQ[ ' - компоненты девиатора:
E-328)
?; $,-®R,-. E.329)
Очевидно, что тензоры dP\l будут взаимно ортогональны к P)J
фр )
), что и учтено в E.327).
Формула E.327) называется спектральным представлением при-
приращения потенциала квазилинейной функции.
348 Глава 5. Тензорные функции
5.6.3. Вывод спектрального представления
квазилинейной функции
Как было показано в п.5.4.1, потенциал ф квазилинейной функции
может зависеть только от линейных и квадратичных инвариантов
тензора Т. Выберем в качестве этих инвариантов спектральные ин-
инварианты YQ(T) относительно какой-либо группы симметрии G3:
E.330)
Тогда
Дифференциал dY& вычислим следующим образом:
лу(Т) __ jy(TJ __ I /с ооп\
но Yq ' является, согласно E.239), квадратичной скалярной функци-
функцией от Р/а\» поэтому ее дифференциал вычисляем по E.93) и E.123):
V()
dY(TJ __ <>*<* . .р(т) _ 2р(т) я ,р(т)
Q ~" (т) («) "" («) И'
Q
Подставляя E.333) и E.332) в E.331), получаем:
г ^ Р(т) • .^Р(
а=1 г« C/Ja
Подставляя теперь E.334) в E.327), имеем:
П1 W р(г) рE)\ . .р(Т) _ п
a=l r« 0*a
В силу независимости приращений девиаторов из E.335) вытекает
следующий результат.
Теорема 5.13. Обобщенные девиатпоры двух симметричных тен-
тензоров второго ранга, связанных квазилинейной потенциальной функ-
функцией E.324), пропорциональны друг другу:
рE) _ ?><> р(Т) _ 1
^ § 5.6. Спектральные представления квазилинейных функций 349
Коэффициенты пропорциональности являются скалярными функ-
функциями от спектральных инвариантов Yq ':
E.337)
и У ос
Соотношения E.336) называют спектральным представлением
квазилинейной тензорной функции E.324). Это представление впер-
впервые было установлено Б. Е. Побед рей.
Подставляя в первые га соотношений E.336) выражения E.323),
получаем:
P ?$ E.338)
Умножая оставшиеся соотношения E.336) при а = т+1.. .п скалярно
сами на себя, с учетом определения E.322) квадратичных инвариан-
инвариантов получаем, что соотношения E.338) имеют место и для оставшихся
индексов а =¦ т + 1.. .п. Здесь учтено, что (ра ^ 0.
Если подставить E.336) в E.319), то получим еще одно представ-
представление квазилинейной функции:
^)S- E-339)
а=1 *ог
Поскольку первым а = 1... га обобщенным девиаторам соответству-
соответствуют линейные инварианты E.237), то это соотношение можно перепи-
переписать с учетом E.238):
(Т) y(TU п (у(Т) y(Th , .
у. ) Е ЫЪ у, )(т)
(а) Е р {
а=1 а а=т+1 *ос
На практике используют одно из трех представлений квазилинейной
функции E.324):
¦ E.340), которое называют полным спектральным представлением;
¦ E.336), E.337), называемые укороченным спектральным пред-
представлением (т.е. не, выписано явное выражение S ~ Т);
¦ E.338), являющееся соотношением между инвариантами, когда не
выписывают явным образом даже соотношения между обобщенны-
обобщенными девиаторами.
Очевидно, что все эти представления эквивалентны.
350 Глава 5. Тензорные функции
5.6.4. Спектральное представление линейной
тензорной функции
Если тензорная функция E.324) - линейная, то, как было показа-
показано в п.4.4.4, потенциал ф представляет собой сумму квадратичных
инвариантов тензора Т и квадратов линейных инвариантов. С ис-
использованием спектральных инвариантов потенциал ф для линейной
функции имеет вид:
* = *> + * ? адРУ^-Ь ? CaaYP\ E.341)
а,/3=1 а=ш+1
где Сар - константы.
Подставляя это выражение в E.338) получаем, что линейные инва-
инварианты связаны только с линейными, квадратичные - с квадратич-
квадратичными:
а=1
CaQYlT\ о = го + 1...п. E.342)
Подставляя теперь E.342) в E.336), имеем
PJJ} = Caep?J, а = то+1...п. E.343)
Если же подставить E.342) в E.340), то получим полное спектраль-
спектральное представление линейной тензорной функции:
у
а,/3=1 а а=ш+1
Наконец, если в E.344) подставить определение E.237) линейных
инвариантов и E.232) девиаторов, то линейную функцию приведем к
явному виду:
т ~ п
S = ( Е ^Т"а(«) ® а(^> + Е С°а%с)) ¦ Т = 4С • -Т, E.345)
а,/3=1 а ^ а=т+1
где
а=т+1
§ 5.6. Спектральные представления квазилинейных функций 351
является тензором четвертого ранга, задающим линейную функцию.
В силу единственности линейной функции, это тот же самый тензор,
который был введен в п.5.1.9.
Формула E.346) устанавливает связь между 4С и двухиндексными
константами Са/з-
Получим обратные к E.346) соотношения. Образуем для этого
свертку тензора 4С с тензорами A/(а7а$))аG) 0 а^), а затем с 4Г(а).
Тогда, учитывая результаты упр.5.5.1:
Саа*Г(а) аG) 0 8цд) = 0, С* = 771+1 . . . П, <у,6 = 1...ГП, E.347)
(О, если (а,/3) ф (<у,6),
а,/3,7, Я = 1...Ш,
Са/з«аа^ если (ое,)9) = (Т»*)»
4Г 4Г _ / °> еСЛИ а Ф А
(аГ " (/3) " I VI, если а =/3, а,/3 = m + 1.. .п,
и из E.346) получаем:
), o,/3=l...ro,
п l' ^
Далее рассмотрим спектральное представление тензорных функ-
функций, индифферентных относительно различных классов симметрии.
5.6.5. Спектральное представление изотропных
тензорных функций
Пусть квазилинейная тензорная функция E.324) является изотроп-
изотропной, т.е. индифферентной относительно класса изотропии.
Тогда спектральные представления E.319) тензоров Т и S имеют
вид E.250):
S = р<5) + i/i(S)E, Т = Р<т> + iri(T)E, E.349)
о о
где Р^5) и Р(т' - девиаторы.
Спектральные инварианты тензоров вычисляются следующим об-
образом (см. E.245), E.255)):
Yf) = ^/i(T), УгE) = ^i(S), E.350)
352 Глава 5. Тензорные функции
Соотношения E.338) между инвариантами представляют собой две
функции от двух аргументов:
Укороченное спектральное представление E.336) изотропной квазили-
квазилинейной функции имеет вид:
Полное же спектральное представление имеет следующий вид:
S = 1(МТ«,УР) - ЫТа,УГ)^г)Е + Щ^1т. E.353)
Частным случаем являются соотношения E.351), в которых линей-
линейные инварианты связаны линейно, а квадратичные - нелинейно:
[ уE) _ зкгуСг)
E.354)
здесь К и G - константы, a w(Tu) - нелинейная функция А.А.Ильюши-
А.А.Ильюшина, удовлетворяющая условию w@) = 0.
Тогда укороченное спектральное представление E.354) принимает
вид:
Если функцию ш(Ти) выбрать в виде:
,ф. /О, Ти ^ 2",
I [\ — 1?\ ('1 — ^Т* /Т1 ^^ Т1 *^ пг1* /л ^«» jl ^ 1 \
то функция Su = 5И(ТИ) является кусочно-линейной:
2G(l-(l-fc)(l-(T7T«)))Tu, Т„^Т*. E57)
§ 5.6. Спектральные представления квазилинейных функций 353
5.6.6. Трансверсально-изотропные функции
Пусть теперь функция ^(Т) - трансверсалыю изотропная, т.е.
G$ = T3. В этом случае четыре инварианта тензоров S и Т имеют
вид (см.п.5.5.5):
Yx -Т. е3, Y2 --j=T (E-e3) = -^,
У3(ТJ = Т2 • Е - (Т • -ЕJ + \{УР + Т • -ЕJ - 2Т2 • -ё2, E.358)
F3EJ = S2 • -Е - (S • -EJ + i(FxE) + S • -EJ - 2S2 • -ё2, E.359)
F4EJ = 2(S2--e2-yi(sJ).
Соотношения E.338) между четырьмя инвариантами Y<i и Yd
представляют собой четыре функции от четырех аргументов:
YW = <pisHY}T)...Y}T\ a = l,...,4. E.360)
Полное спектральное представление E.340) с учетом E.270) имеет
вид:
s = n(Yp. ..yP)-4 + ±myP •. .у4(Т))(е - 4)+
Р(
r^f5(з)
В случае линейной трансверсально изотропной функции все <ра ли-
нейно выражаются через инварианты Y} ':
Ч>1 = СцУ1(Т) + С12У2(Т), ^2 - С12У1(Т) + С22У2(Т), E.362)
где CQiC - константы.
12 Тензорное исчисление
354 Глава 5. Тензорные функции
В декартовой системе координат линейное соотношение E.361) име-,
ет вид:
C12TNi36j3 + (%^зз + ^ff^ Fп6ц + Si2Sj2)+
^(SnSjl + Si2Sj2) + f33Si3Sj3 - Ti3Sj3 - fj36i3)+
+ Tj3Si3 - 2T338i38j3). E.363)
Сравнивая это представление с выражением E.21) Sij = CijkiTkl
для различных случаев: Т33 ф 0, остальные f{j = 0; Тц ф 0т осталь-
остальные Tij = 0; Т13 ^ 0, остальные TJ; = 0, находим связь четырехин-
дексных компонент Cijkt с двухиндексными Сар:
O2233 = ^1133 = —/=-> ^1111 = ^
= 2С2323 — С44, 2С1212 = Сзз- E.364)
Рассмотрим пример нелинейной трансверсально-изотропной функ-
функции.
В простейшей модели функция (ра имеет вид:
Vi = Cu(l-Wl(YiT)))YiT) + С12У2(Т),
<Рг = C^yf) + С22A - а;2(У2(Т)))У2(т), E.365)
V3 = С33A - а;з(У3(Т)))У3(Т), V* = С«A - w4(Yp))Y}T\
т.е. имеется только четыре нелинейные функции ljq(Yq ^), зависящие
от одного своего аргумента.
Аналитическое задание этих функций можно осуществить также с
помощью кусочно-линейных функций:
{0 у(
где Т* - пределы пропорциональности, а ка = C'Qa/CQa - отношение
тангенсов углов наклона функций о;а(Уа ) в нелинейной и линейной
областях.
§5.6. Спектральные представления квазилинейных функций 355
5.6.7. Ортотропные функции
Рассмотрим ортотропные функции E.324). В этом случае тензоры
S и Т имеют по шесть инвариантов (см.п.5.5.7):
a = 1,2,3; E.367)
Y(TJ = i (Т • -(ё2 ® ё3 + ё3 ® ё2)J = 2Т|3,
П = \ (Т • -(ei <8> ё3 + ё3 ® ёх)J = 21*3>
YP2 = i (Т • •(§! ® ё2 + ё2 ® ei)J = 2Т22,
a = 1,2,3; E.368)
^ ё3 ® ё2)J = 25|3,
= I (S • .(ёх ® ё3 + ё3 ® ёОJ = 2523,
Уб<5>2 = I (S ¦ -(ex 0 ё2 + ё2 0 ёх)J = 2522,
соотношения между которыми имеют общий вид E.338), т.е. пред-
представляют собой шесть функций от шести аргументов.
Полное спектральное представление E.340) имеет вид:
S = ? MYP .. .yf >)ё2 + ? Ы?^Т)-?Р)Г%- E-369)
а=1 а=3 *о
В декартовой системе координат это соотношение имеет вид:
з
Si,- = Y, ЫУР ¦ • .YP)fQQSiQ6ja + <p4(YP .. .У6(Т))?12(<Ы,-2+
УР)Т13Fп6^ + 6а6ц)+
Si2Sj3 + 6i3Si2), E.370)
где
P f a = 1,2,3;
a=l
}T) = л/2|Т12|, П(Т) = v^|T13|, YP = л/2|Т23|. E.371)
356 Глава 5. Тензорные функции
В случае линейной функции <ра линейно выражаются через инва-
инварианты УХ(Т>,..., У6(Т):
Vi = CnY}T) + C12yP + C13Y3(T\
= C12Y}T) + C22Y2{T) + C23YP, E.372)
(Т) P + C33Y{T\
3\
<p4 = с44у4(т) , (T)
Простейшая нелинейная модель ортотропной функции предполага-
предполагает, что
4>х = }) P P
4>г = C12y}T) + C22YP + C23YP, E.373)
<Ръ = C13YP + C23Y2(T) + C33(l - ЦУ3(Т)))У3(Т\
<pa = Caa(l - u>a(YP))Yp, a = 4,5,6,
т.е. имеем четыре функции одного аргумента uQ(Ya ), вид которых
может быть выбран также как E.366).
5.6.8. Квазитрансверсально-изотропные функции
Для квазитрансверсально-изотропной функции (ра тензоры Т и S
имеют по пять инвариантов yj ' и Yq ' (а = 1,... 5), которые можно
выразить по формулам E.288), E.293) и E.294). Из этих инвариантов
два являются линейными: Ya (a = 1,2) и три - квадратичными:
Уа(Т) (а = 3,4,5).
Соответствующие тензоры а(а) (а = 1,2) можно определить из
формул E.295).
Тогда полное спектральное представление E.340) для квазитранс-
квазитрансверсально-изотропной функции имеет вид:
(rF\ (rP\
m №з^'з + Tj3Si3 — 2T338C5j3)+
Y3
di2<>j2) +
+ Тззйз^/3 ~ Ti2(8ii5j2 + Si2
(Лк ( J , ... ier I —
7^1 ¦Ll2\fiiiuj2 ~т 0i20ji). @.O/4J
§ 5.6. Спектральные представления квазилинейных функций 357
Инварианты Ya (а = 1,... , 5) в декартовой системе координат
имеют вид E.298), E.299).
В простейшей нелинейной модели квазитрансверсально-изотроп-
ные функции (ра выбирают следующим образом:
) + С22У2(Т), E.375)
-ua(YP)Y^T), a = 3,4,5,
где Сар - константы, a ua(Ya ) - нелинейные функции. Согласно
степенной модели выбираем их в виде:
0 I^qT'| < Y*
1 V0 _ |v(T) ^
\Ja Га
{О I^q| < Y
(\yP\-kX' \y\Iy- E-376)
I/
где У^, У<° и па - константы модели.
Рассмотрим частный случай плоского состояния, когда часть ком-
компонент тензоров Т и S равна нулю:
?-з = О, Т13 = Т23 = 0, г = 1,2,3, E.377)
а остальные компоненты отличны от нуля (заметим, что компонента
Тзз может быть отлична от нуля). Тогда инварианты и девиаторы
имеют вид:
У2 = E11
У4E) = 0, У5E) = V2\S12\; E.378)
, У2(Т) = -^ (Т11 + Т22),
|, У4(Т) = 0, У5(Т) = V2\f12\, E.379)
E &) Л? = ^12' остальные pgj4 = О,
E.380)
= Г1Я, остальные Pgi = 0-
E.381)
358 Глава 5. Тензорные функции
Укороченное спектральное представление (соотношение E.336)
между девиаторами) для тензорной функции E.374) и плоского со-
состояния приобретает вид:
Sn + S22 =
5ц - 522 = C33 ( 1 - 1 |A""Vaal ) ) (Гц - T22), E.382)
Часто необходимо иметь запись тензорной функции не в осях анизо-
анизотропии Ож,-, а в осях Ож(-, повернутых вокруг оси Ожз в плоскости
квазиизотропии на угол ф. Тогда Т[^ и S\j в этой повернутой системе
координат связаны с Т^' и Sij соотношениями:
Тц = Рк{ J* rkh Sij = Рк{ Р\ #kj% E.383)
где
(cos ф Бтф 0 \
-sin^ cos^ О I C.384)
О 0 1/
- матрица поворота, или в явном виде:
Тц = Т'Х1 cos2 ф + Ц2 sin2 ф - Т[2 sin 2ф,
Т22 = Т[г sin2 ф + Т'22 cos2 ф + Т'12 sin 2ф, E.385)
Соотношения E.382) в повернутых осях примут вид:
(S'n ~ S'22) cos 20 - 2S'12 sin 2ф = C33(l - «зAз(Т)))х
- T^2) cos 2^ - 2T{2 sin 20), E.386)
25^2 cos 20 = 2C55A - а;5(У5(Т)))х
x ((Т[г - Ц2) sin 20 + 2Tf2 cos 20).
Здесь
\/2F3(T) = |(T{: - T^2) cos20 - 2T^2 sin 20|,
V2YP - |(T^ - T'22) sin20 + 2T^ cos 20|. E.387)
___ § 5.7. Непотенциальные тензорные функции 359
Важный частный случай представляют соотношения E.386) при
ф = тг/4:
S'u =
S'22 - С22{Т'1Х + Т22),
Ъ E 388)
~ S>22 = Сьь
(\ - а-5 (|Т"^г|
таким образом соотношения E.388) являются двойственными к
E.382), записанным в осях анизотропии Охг.
§ 5.7. Непотенциальные тензорные функции
5.7.1. Представление непотенциальных функций
в тензорном базисе
Наиболее часто в механике и физике применяются рассмотренные
выше потенциальные тензорные функции, однако в ряде случаев
встречаются также функции, не обладающие потенциалом тр. Рас-
Рассмотрим эти функции.
Теорема 5.14. Пусть имеется тензорная функция EЛ) второго
ранга, являющаяся индифферентной относительно некоторой груп-
группы G8 (т.е. для нее выполняются условия E,8) и E.9)), но, вообще
говоря, не обладающая свойством потенциальности E.Ц1):
S = Г(Т) E.389)
или
Sij = Pj{fkI)} E.390)
где S и Т - симметричные тензоры второго ранга, тогда эту тен-
тензорную функцию всегда можно представить в виде суммы:
aHW, E.391)
a=l
где фа - скалярные индифферентные относительно Gs функции ин-
инвариантов тензора Т:
a = l...n, E.392)
а тензоры На являются либо тензорами-константами:
l...m, E.393)
360 Глава 5. Тензорные функции
либо линейными тензорными функциями от Т;
Т, а = m + 1...q, E.394)
либо квадратичными тензорными функциями:
, a = q + l...n. E.395)
Число п, очевидно, не может быть больше 6.
Тензоры
Н$\ 4Н<,1) и 6Н^2) E.396)
являются индифферентными тензорами относительно группы Gs и
состоят из образующих тензоров группы Gs-
Подставляя E.392) - E.395) в E.391), получим представление не-
потенциальной функции в тензорном базисе:
т q
а=1 а=т+1
п
•••Т®Т. E.397)
Докажем теорему 5.14 и возможность представления E.397) кон-
конструктивным способом, т.е. указав метод построения тензоров На ,
4На1) и 6На2). Этому посвящены пп.5.7.2 - 5.7.5.
5.7.2. Триклинные тензорные функции
Т Рассмотрим вначале тензорную функцию E.390), индифферентную
относительно триклинного ^-класса.
Для тензора S, как для всякого симметричного тензора, можно за-
записать его представление в диадном базисе, выбирая в качестве век-
векторов базиса ё,-, с которыми связана группа симметрии G$:
S = Sijei ®ej = Pj{fkl)ei 0 ё,. E.398)
Если этот тензор S зависит от тензора Т, то компоненты 5IJ в
этом представлении являются функциями от компонент Tkl\ что и
отражает второе равенство в E.398).
Введем теперь обозначения:
фа = Taa(fkl), E.399)
), a,/3,7-1,2,3, а ф C ф ъ
§5.7. Непотенциальные тензорные функции 361
тогда E.391) можно записать в виде:
1
Q), E.400)
о=1 1
где ОQ — ёр 0 ё7 + ё7 0 ёр (см. табл.4.1).
Сравним теперь это представление E.400) с представлением E.174)
в тензорном базисе для потенциальной тензорной функции, индиффе-
индифферентной относительно ^-класса. Формальные записи этих представ-
представлений совпадают, причем в E.174) коэффициенты y>Q, а = 1.. .6, яв-
являются скалярными индифферентными потенциальными функциями
инвариантов тензора Т относительно i?-класса, т.е. зависят от всех
компонент Tij.
В представлении E.400) фа также согласно E.399) зависят от всех
шести компонент Tkl. Если кроме того мы потребуем от тензорных
функций E.390) индифферентности только относительно триклинно-
го класса, то функции E.399), очевидно, будут скалярными функци-
функциями, индифферентными тоже относительно ^-класса. В самом деле,
при переходе из декартовой системы координат хг в другую Хг, по-
получаемую с помощью линейного преобразования C.1) с матрицей Вг^
соотношения E.399) преобразуются согласно E.9) следующим обра-
образом:
B\B\Thlk*{fili*) = Р1**{В*1 Bhhfhh). E.401)
Но для триклинного класса Blj = 5*j, поэтому соотношение E.401)
превращается в тождество и выполняется всегда, следовательно, (pQ
будут индифферентными скалярными функциями.
Таким образом, существует единственное отличие между E.174) и
E.400): в первом случае функции (pQ потенциальны, т.е. удовлетво-
удовлетворяют условиям взаимности E.184), а в E.393) функции фа - вообще
говоря, нет. Они являются произвольными функциями инвариантов
тензора Т в триклинном классе:
Фа = Фа (Т11,Т22,Тзз,Т2з,Тз1,Т12) E.402)
Следовательно, представление E.400), полученное без каких-либо
предположений, является общим представлением для индифферент-
индифферентной относительно ^-класса тензорной функции. Из него, в частности,
следует, что если функция E.390) потенциальна, то коэффициенты
(ра не произвольны, а удовлетворяют условиям взаимности E.184).
Если теперь в E.400) обозначить тензоры как
?k ^Oa, a = 1,2,3, E.403)
то, очевидно, представление E.400) будет в точности совпадать с
E.391). Отсюда следует, что для триклинного класса представление
362 Глава 5. Тензорные функции
E.391) действительно существует, причем линейные и квадратичные
тензорные функции в нем отсутствуют:
0, т = п:=6. E.404)
5.7.3. Доказательство представления функций
в тензорном базисе
Докажем теперь возможность представления E.397) для тензорных
функций из следующих классов симметрии: М, О, Т, Кз, А, В и К,
исключая пока трансверсально-изотропный (Тз), гексагональный (Н)
и изотропный (/) классы.
Выберем для каждого из этих классов функциональный базис неза-
независимых инвариантов тензора Т:
4*)=/W(T), a = l...r. E.405)
Число г этих инвариантов относительно указанных выше классов, как
следует из теоремы 4.24, максимально и равно шести.
Данные инварианты являются линейными, либо квадратичными,
либо кубическими функциями от Т (см. E.169), E.170)). Введем
обозначения: т - число линейных и (q — га) - число квадратичных
инвариантов.
Дифференцируя инварианты E.405) по Т, получим тензоры про-
производной (см.п.5.2.2), для которых введем обозначения:
Н«) = ^Г' * = 1>""п> п = г = 6. E.406)
Используя правила дифференцирования инвариантов E.171), полу-
получим, что
Hi') = г4^0 • -Т, a = m + l,...,g, E.407)
Н?> = 36fl(,'>H • • • -Т ® Т, a = q + 1,... ,n.
Введем обозначения для тензоров-констант:
,...,e, E.408)
Как было показано в п.5.2.6, для всех групп симметрии тензоры
П(а\ *п(аз) и 6Sl(d\ а, следовательно, и Н^0), 4Н^1) и 6нк2) являют-
являются индифферентными относительно соответствующих групп Gs. Это
означает, что и тензорные функции E.407) также индифферентны.
§ 5.7, Непотенциальные тензорные функции 363
Кроме того, тензоры Ш* , ос = 1.. .п, для фиксированной группы
Gs - линейно независимы. В самом деле, в противном случае можно
было бы выразить какой-либо тензор через все остальные:
а=1
*3
Но согласно E.406), тогда имело бы место соотношение между инва-
инвариантами:
?' - Е *« > = const>
а=1
что противоречит условию о независимости 1а -
Поскольку Щ являются симметричными тензорами второго ран-
ранга, то их можно всегда представить в декартовом базисе:
Н?> = #;Ч- 0 ё,-, а = 1.. .п. E.409)
Используя тензоры ё^ и Оа, это представление можно записать
подобно E.400):
....6, E.410)
/3=1
где обозначены компоненты тензора:
Нар = ЙМ, /3=1,2,3, E.411)
тт л гг23 тт лг>31 тт л тт 12
На E.410) можно смотреть как на систему шести линейных уравне-
уравнений относительно шести неизвестных тензоров ё^ и О^, /3 = 1,2,3.
Поскольку тензоры Н« - линейно независимы, то решение такой сис-
системы существует и его можно записать в виде:
б
ё|| = ?^«Н?>, E.412)
а=1
&>, /3 = 1,2,3,
а=1
364 Глава 5. Тензорные функции
где коэффициенты фар зависят от Нар и, следовательно, являются
функциями HXJ, а значит и от компонент Т1-7 тензора Т:
. E.413)
Однако, вообще говоря, фар не являются функциями инвариантов
)
()
Используем теперь для тензора S представление E.400) в декарто-
декартовом базисе и подставим в него выражение E.412):
S = Е Е (*>«*<*Н?* + \<Ра+зФа+зфЯ{;Л . E.414)
Вводя обозначения для коэффициентов
6
6 / 1 \
= Е ( ^«^ + 2 ^a+3^a+3j/3) ' ^ = 1'''6)
a=l ^ '
E.415)
из E.414) получаем искомое представление E.391).
Коэффициенты фр в этом представлении действительно являются,
в отличие от (ра и фар, индифферентными скалярными функциями от
Т, так как HJ^ (Т) и сама S(T) по условию - индифферентные функ-
функции. Тогда фр всегда можно считать зависящими от инвариантов
1{а8){Т) в виде E.392).
Таким образом, возможность представления тензорной функции в
виде E.391), а также теорема 5.14 доказаны.
Подставим теперь выражение E.407) в E.397). В результате полу-
получим:
a=l a=m+l
. E.416)
Сравнивая это выражение с E.172), убеждаемся в их формальном
сходстве, однако в E.172) функции (ра не произвольны, а потенци-
потенциальны, т.е. удовлетворяют условиям взаимности E.184). На фа в
E.416) этого ограничения нет.
Итак, показано, что произвольная непотенциальная, вообще говоря,
тензорная функция E.390), индифферентная относительно группы G,,
§ 5.7. Непотенциальные тензорные функции
-365
может быть представлена в тензорном базисе в виде квадратичной
функции E.416).
5.7.4. Непотенциальные тензорные функции для
различных классов симметрии
Для конкретных классов симметрии: Е, М, О, Т, Кз, А, В и К
- представление E.416) формально совпадает с соответствующими
представлениями E.174) - E.181) для потенциальных функций, одна-
однако функции (ра в них уже, вообще говоря, непотенциальны.
Учитывая произвольность непотенциальных функций (ра в E.174)
- E.181), выражения для тензорных функций в некоторых классах
можно упростить, обозначая комбинации из y>Q, стоящие при индиф-
индифферентных тензорах, новой буквой. Ниже представлены непотенци-
непотенциальные тензорные функции различных классов, преобразованные та-
таким образом.
(Е)-Триклинный класс: вид тензорных функций совпадает с E.174).
(М)-Моноклинный класс: вид тензорных функций совпадает с E.175).
(О)'Оргпотропный класс: вид тензорных функций совпадает с E.176).
(Т) - Тетрагональный класс:
S = фгЕ + ф2%\ + (^3(Oi 0 Oi + О2 0 О2)+
® ё1
+ Ф*№А + *$)(Гц - Т22) + 2Т12F[6{ - 6
(Кз)-Квазитрансверсалъно-изотропный класс:
S = V>iE + ф2%\ + (v>3(Oi 0 О: + О2 ® О2)+
+ ЫА ® ё? + ё| 0 ё^) + V-sA) • -Т + VeT2
Глава 5. Тензорные функции
(А)-Ромбоэдрический класс (т = 2, т2 = 4, т3 = 0):
S = фгЕ + ф2%\ + (фз(О1 ® Oi + О2 ® О2)+
ф5 А +
и - Гаа))D4 + $4) + (#А +
п - Т22) + 2ф6Т12) + 2F\6{ - 62632)(ф4Т13 + ф6Т23)+
+ 2(б[4 + 6{2б{)(ф6Т13 - ф4Т23).
(В)-Ромбоэдрический класс:
S = ф{Е + ф2%1 + (ф3{О! ® Ох + О2 0 О2)+
= фг№ + ф25ъ5{ + 2(ф3Т23 - фАТХ2)(й& + &36{)+
Bф3Т13 + ^4(Гц -122)) F[6i + 6'36{)
2фА{Т13E[5{ - 628{) - Т23F[6{ + 526{))
(К)-Квазиизотропный класс:
S = ^iE + {ф2А
А) • • • -Т 0 Т,
а=1
Все скалярные функции ф1 в этих формулах являются функциями
соответствующих инвариантов Ц*'(Т). Однако, в отличие от потен-
потенциальных функций у>7, это могут быть любые наборы независимых
§ 5.7. Непотенциальные тензорные функции 367
инвариантов в классе, не обязательно те, которые представлены в
E.174) - E.183), так как для непотенциальных тензорных функций
базисные тензоры На , вообще говоря, не связаны с инвариантами
5.7.5. Трансверсально-изотропные и гексагональные
тензорные функции
Эти два класса симметрии отличаются от остальных, рассмотрен-
рассмотренных выше, тем, что функциональный базис независимых инвариантов
Ц (Т) у них состоит из пяти, а не из шести элементов. Поэтому если
тензорный базис Н« выбирать только из тензоров производной от
инвариантов, то этот базис может оказаться неполным.
Действительно, для Тз-класса тензоры Н« , построенные указан-
указанным способом, имеют вид:
Hi = Е — ё3,
Н2 = §з, т = 2,
Н3 = ^ (Oi 0 Ох + О2 0 О2) • Т, E.417)
Н4 = BА - (Oi 0 Oi - О2 0 О2) - 2ё| 0 ё§) • Т\
К ним можно присоединить еще один тензор Не, являющийся квад-
квадратичной тензорной функцией:
Нб = (Е 0 Е 0 ё2)A46352>... .т 0 Т. E.418)
В декартовых компонентах эти тензоры имеют вид:
H[j = 6" - S'3Si Щ
а* = (б<28{+4^)т23
H{j = 2(f*> - Т336(з - H3j), E.419)
= fikfkj - hf* + I2Sij, Й$ = T3fj3.
Все шесть тензоров являются линейно независимыми, в чем мож-
можно убедиться непосредственно, составив определитель матрицы Нар
размером б х б с компонентами E.411), а в качестве НЩ использовав
E.419). Этот определитель, очевидно, будет отличен от нуля, если
368 Глава 5. Тензорные функции
компоненты тензора Т1-7 взять как максимально возможные (см. за-
замечание к п.4.4.4).
Заметим, однако, что все инварианты, образованные из тензора Нб,
например:
в • •& = 1 3li3, t±e • -е3 — i33,
Нб..Т = Г3^3Т;7, E.420)
уже не являются независимыми и выражаются через /} ... /5 (см.
упражения к §4.5).
Тем не менее тензор Н6, являясь индифферентным относительно
Т3-класса (что следует из индифферентности Е и ё3 в E.418)), замы-
замыкает систему E.417) базисных тензоров На и делает возможным при-
применение далее всей процедуры выражения тензоров ё2 и Оа согласно
E.412). В итоге для трансверсально-изотропной тензорной функции
E.390) доказываем возможность представления E.414) и, следователь-
следовательно, E.3.91) и E.397).
В явном виде это представление будет иметь вид:
S — ^iE + Ф2&3 H~ (Фз{®1 0 Oi + O2 0 O2)+
•T + V5T2 + Ve(E ® E <g> ё§)<146352) • • • -T ® T, E.421)
или в компонентах
где все фа являются функциями пяти инвариантов, например Ц ':
Фа = Фа (Гц + Т22,Т33,ТЪ + Т23,Т?г + t222 + 2f22,det T) , E.422)
Сравнивая E.421), E.422) с E.182), находим, что в отличие от других
рассмотренных выше классов симметрии, различие между потенци-
потенциальными и непотенциальными трансверсально-изотропными функци-
функциями заключается не только в том, что (ра в E.182) потенциальны, а фа
в E.421) - нет. Для непотенциальной функции появляется еще одно
квадратичное слагаемое и, соответственно, дополнительная функция
Все проделанные выше построения, а также итоговое представле-
представление E.421) и E.422), справедливы и для случая гексагональной тензор-
тензорной функции, поскольку тензор Нб является, очевидно, индифферент-
индифферентным и относительно if-класса. На этом завершим доказательство те-
теоремы 5.14, оставив изотропный случай как отдельное утверждение.
А
§ 5.7. Непотенциальные тензорные функции 369
5.7.6. Теорема об инвариантах тензоров,
связанных тензорной функцией
Перед тем как перейти к изотропным тензорным функциям, уста-
установим связь между инвариантами /7(Т) тензора Т и инвариантами
/7(S) тензора S относительно одной и той же группы Gs, если эти
тензоры связаны, вообще говоря, непотенциальной тензорной функци-
функцией E.389), индифферентной относительно Gs.
Каждый из инвариантов /7(Т), 7 =: 1 • • -г> является, как было от-
отмечено в п.5.2.1, скалярной тензорной функцией, индифферентной от-
относительно группы G,, т.е. удовлетворяет условию E.856):
/7(Т) = /7(QT ¦ Т • Q), VQ e {G,}, E.423)
где Q - тензор линейных преобразований из группы Gs.
Построим теперь некоторый инвариант /^(S) тензора S относи-
относительно той же группы Gs. Знак "/" означает, что структура зави-
зависимости /^ от S может отличаться от любой из функций /7(Т), но из
инвариантности /^ вытекает, что
/7(S) = /7(QT • S • Q), VQ G {G5}. E.424)
Так как S является функцией от Т, то /7(S) можно рассматривать
как некоторую скалярную функцию от Т:
4(S) = /;(:F(T)) = /;(T). E.425)
Покажем, что эта функция /7(Т) также является индифферентной
относительно Gs. Используем свойство индифферентности функции
E.389), которое можно записать в виде:
QT ¦ Г{Т) • Q = F{QT • Т • Q). E.426)
Тогда инвариант /^ при линейных преобразованиях в группе G$ пре-
преобразуется следующим образом:
; • Т • Q)) = /;(QT • Т • Q), E.427)
т.е. удовлетворяет свойству E.423). Но всякая скалярная функция от
Т, индифферентная относительно G5, является по определению инва-
инвариантом относительно этой группы.
Таким образом, доказана следующая теорема.
370 Глава 5. Тензорные функции
Теорема 5.15. Если два тензора S и Т связаны индифферентной
относительно G3 тензорной функцией E.389), то любой инвариант
от одного тензора /^(S) является одновременно инвариантом дру-
другого тензора Т относительно той же группы симметрии G8.
5.7.7. Теорема о соосности тензоров, связанных
•изотропной тензорной функцией
Теорема 5.16. Пусть два симметричных тензора S и Т связа-
связаны тензорной функцией E.389), являющейся индифферентной от-
относительно изотропного класса I (такие функции будем называть
изотропными), тогда эти тензоры S и Т являются соосными (см.
п. 1.6.1), т.е. имеют один и тот же собственный базис.
Т Как было показано в п.4.1.5, всякий симметричный тензор Т обла-
обладает группой симметрии Gg, принадлежащей к классу О-ортотропии,
причем оси анизотропии е^ совпадают с осями собственного базиса
еа. Иначе говоря, Т индифферентен относительно О'-класса, т.е. для
него выполняются соотношения D.17):
Т = Q/T - Т • Q', VQ' G {G'9}, E.428)
где Q' - ортогональный тензор линейных преобразований из группы
о
ортотропии G9 с осями анизотропии вдоль еа.
Составим теперь тензор: Q^ • S • Q' и преобразуем его следующим
образом:
Q^ . S • Q' = Q^ - Jc-(T) - Q' = ^(Q^ • T • Q') = F{T) = S. E.428')
Здесь учтено, что ^(Т) - изотропная функция, следовательно, для нее
второе равенство в строке имеет место для произвольного ортогональ-
ортогонального тензора, в том числе и для Q'.
Из соотношения E.428') следует, что тензор S индифферентен от-
относительно той же группы ортотропии Gr9. Но ортотропный тензор
второго ранга, как было установлено в п.5.1.7, имеет диагональный
вид в осях анизотропии, а значит оси анизотропии е' = е, совпада-
совпадают с собственными направлениями тензора S в силу единственности
последних.
Таким образом, действительно собственные базисы тензоров S и Т
совпадают* А
5.7.8. Представление изотропной функции
в тензорном базисе
Рассмотрим вновь тензорную функцию E.389), предполагая ее ин-
индифферентной относительно класса изотропии. Поскольку тензоры S
§ 5.7. Непотенциальные тензорные функции _371
и Т, связываемые этой функцией, соосны, то их можно записать в
едином собственном базисе:
з з
S = ]Г 5аеа 0 еа, Т = ^ TQeQ 0 eQ. E.429)
а=1 а=1
Выберем в качестве базисных тензоров HQ следующие:
з з 2
Нх = Е = ? eQ 0 ев, Н2 = Т = ? TaeQ 0 eQ, E.430)
a=l a=l
a=l
Поскольку при изучении инвариантных характеристик мы рассмат-
рассматриваем тензоры с максимально возможными ненулевыми и различны-
различными компонентами (см.п.4.4.4), то эти тензоры На всегда будут линей-
линейно независимыми. Тогда так же, как это было проделано в п.5.7.3,
можно рассматривать E.430) как систему линейных уравнений отно-
относительно трех тензоров eQ 0 ea. Найдем эти тензоры:
E.431)
/3=1
причем коэффициенты фар зависят только от Та, которые являются
инвариантами тензора Т:
Фар = ^(/i(T),/2(T),/3(T)). E.432)
Подставляя далее тензоры E.431) в E.429), получим представление
тензора S по базисным тензорам Н^. Оно состоит из трех слагаемых:
S = фгЕ + ф2Т + ^3Т2, E.433)
где
з
YafiSa. E.434)
a=l
Поскольку фар являются функциями от инвариантов тензора Т, а соб-
собственные значения Sa тензора S согласно теореме 5.15, всегда можно
считать функциями от J7(T), то функции фр - тоже есть функции от
инвариантов тензора Т:
E.435)
Таким образом, доказана следующая теорема.
372 Глава 5. Тензорные функции
Теорема 5.17. Всякая изотропная тензорная функция E,390),
связывающая симметричные тензоры второго ранга, может быть
представлена в виде E.433), который является частным случаем
представления в тензорном базисе E.397).
Представление E.433) отличается от представлений в других клас-
классах: оно содержит только три базисных тензора. Функции фр E.435),
вообще говоря, не являются потенциальными.
5.7.9. Полиномиальные изотропные тензорные
функции
Рассмотрим непотенциальную изотропную тензорную функцию от
несимметричного тензора Т, а именно полиномиальную функцию, об-
образованную тензорными степенями:
оо
S = JF(T) = с0Е + С1Т + с2Т2 + с3Т3 + ...= ? спТп, E.436)
п=0
где под Т° понимается метрический тензор Е, а сп - константы.
Теорема 5.18. Функция E.436) является изотропной.
Т Действительно, так как при замене Т на QT • Т • Q, где Q - про-
произвольный ортогональный тензор, тензорные степени преобразуются
как
(QT . Т • Q)n = (От • Т • О) • QT • Т • Q •,.. • QT • Т • Q =
п
= QT • ТТ- ... Т Q = QT • Тп • Q,
а, следовательно, полиномиальная функция E.436) удовлетворяет ус-
условию E.9):
71=0
= QT • ( ? СпТп) Q = QT Г(Т) • Q. А E.437)
\п=0
Записывая тензор Т в собственном базисе A.174):
з
Т = Y, A«e« ® eQ, E.438)
§5.7. Непотенциальные тензорные функции 373
любую целую степень Тп также можно представить в виде диагональ-
диагонального тензора в том же базисе A.180):
E-439)
а=1
Тогда полиномиальная функция E.436) может быть представлена
в виде:
s = Е (Е с»А«)°е°® °е° = Е /(АЛ ®|а< E-44°)
а=1 \п = 1 / а=1
где
оо
?>АП. E.441)
Таким образом, всякой полиномиальной изотропной тензорной функ-
функции .F(T) E.436) может быть сопоставлена обычная функция /(А),
которая имеет аналогичную структуру, если аргумент Т заменить на
А.
Очевидно, что верно и обратное утверждение: по всякой полино-
полиномиальной обычной функции можно образовать изотропную тензорную
функцию E.440).
Используя это свойство изотропных функций, можно построить
тензорные функции - аналоги элементарных функций. Для этого на-
надо представить эти функции разложением в степенные ряды E.441) в
окрестности точки А = 0, сходящиеся в некотором интервале |А| ^ Ао,
а затем, заменяя А на Т, построить тензорную, функцию - аналог
E.440).
Например, функция "синус от тензора" будет иметь вид:
п=0
а":
T-iT3 + iT5 + ... = f;?i^IT2»+1, E.442)
0 ^ ''
"косинус от тензора"
"логарифм от тензора":
Л f-Un-l
-Тп, E.444)
„=о п
374 Глава 5. Тензорные функции
'экспонента от тензора":
00 1
n!
S = ехр Т = 2J ZTTn- E-445)
n=0~
Для экспоненты от тензора, очевидно, выполняются свойства обыч-
обычной экспоненты, например:
п=0
п=0
оо .
= 53 ^(Т? + пТ?-1 • Т2 + ... + nTi ¦ Т!?-1 + Т5) =
hT>)= exp Ti •ехр Тг- E-446)
\п=0 " / \п=0
Транспонируя E.440), устанавливаем важное свойство полиноми-
полиномиальной функции:
ST = (:F(T))T = Г(ТТ). E.447)
Пусть теперь тензор Т = ft - кососимметричен, тогда по E.447):
(ехр П)т = ехр пт = ехр (-ft). E.448)
Умножая теперь ехр ft на транспонированный к нему, по E.448) и
E.446) получаем:
ехр ft • (ехр ft)T = ехр ft - ехр ftT = ехр (ft - ft) = E, E.449)
таким образом, экспонента от кососимметричного тензора образует
ортогональный тензор.
Вернемся теперь снова к полиномиальному представлению E.436) и
воспользуемся теоремой Гамильтона-Кэли (см. п.4.5.4), которая спра-
справедлива в том числе и для несимметричных тензоров Т (см.
упр.4.5.12). Согласно этой теореме, любую тензорную степень Тп
выше второй: п > 2, можно выразить через Т2, Т и Т° = Е. Тогда
из представления E.436) вытекает следующая теорема.
Теорема 5.19. Всякую изотропную тензорную полиномиальную
функцию E.436) всегда можно представить в виде:
S = Г(Т) = (р0Е + (ргТ + (р2Т2, E.450)
§ 5.7. Непотенциальные тензорные функции 375
где (ра - скалярные функции от инвариантов тензора Т;
V>« = VPa(/l(T),/2(T),/3(T)). E.451)
Сравнивая E.450) с формулой E.433), которая была выведена для
симметричных тензоров, получаем, что разложение изотропной тен-
тензорной функции по базису Т2, Т и Е возможно и для несимметрич-
несимметричных тензоров, но только для полиномиальных функций E.436). Заме-
Заметим, что для симметричных тензоров условие полиномиальности не
использовалось.
Условие полиномиальности является существенным, так например,
линейная изотропная тензорная функция
s = 4c -т,
связывающая несимметричные тензоры S и Т (где 4С - тензор чет-
четвертого ранга, индифферентный относительно полной ортогональной
группы и не обладающий симметрией вида A.264), не является поли-
полиномиальной и не может быть представлена в виде E.450).
Пусть теперь известен вид E.436) полиномиальной функции !F(T)
с коэффициентами с,. Найдем функции (ра E.451) в соответствую-
соответствующем представлении E.450). Для этого подставим разложение E.438)
тензора Т по собственному базису в E.450):
S = Г(Т) = Y, fa + ?>iAa + ч>г\1) еа 0 еа. E.452)
а=1
Сравнивая E.452) с представлением E.440) функции E.436), получа-
получаем, что должны выполняться равенства коэффициентов при собствен-
собственном тензорном базисе:
+ ?>гА* = /(Аа), а = 1,2, 3, E.453)
где функция /(Аа) определяется по E.441).
На E.453) можно смотреть как на систему трех линейных уравне-
уравнений относительно <ра. Определитель этой системы имеет вид:
Д =
1 Ах А?
1 А2 \\
1 Аз XI
= (Ai-A2)(A2-A3)(A3-Ai) E.454)
и называется определителем Вандермонда.
Как и ранее при рассмотрении тензорных базисов в п.5.7.4, мы
предполагаем, что тензор Т содержит максимально возможное чис-
число ненулевых и различных компонент. Тогда все Аа отличны от нуля
376 Глава 5. Тензорные функции
и различны. Следовательно, А ф О и существует решение системы
E.453) относительно (ра:
- А§) + /(А2)(А| - А?) + /(А3)(А? - А*)), E.455)
<р2 = _^ДАхЯАз - А2) + /(A2)(Ai - Аз) + ДАз)(А2 - Ах)).
Поскольку Аа являются инвариантами тензора Т и выражаются через
Л(Т), /2(Т) и /3(Т) (см. D.156)), то и y?Q являются функциями /а(Т).
§ 5.8. Дифференцирование тензорных функций
по тензорному аргументу
5.8.1. Определение производной от тензорной
функции по тензорному аргументу
В §5.2 было введено понятие тензора производной т/т для скаляр-
скалярной функции s = /(mT) от тензорного аргумента. В механике часто
возникает необходимость определения производной от произвольной
тензорной функции
по тензорному аргументу тТ. Введем эти производные.
В компонентной записи функция E.456) в базисе R,- имеет вид:
Всегда можно вычислить дифференциал этой функции, рассматривая
ее как обычную функцию многих переменных:
С помощью производных дТХх"Лп/дТ*1'"*т можно определить сле-
следующий объект:
® Rh ® • • • ® Rim. E-459)
называемый тензором производной тензорной функции по тензор-
тензорному аргументу. Очевидно, что (n+m)ST является тензором и имеет
ранг (n + m).
§ 5.8. Дифференцирование по тензорному аргументу .377
Составим теперь дифференциал тензора dnS, используя определе-
определение E.89):
cTS = dS1-1"*!^ 0 ... 0 Rln, E.460)
и подставим в него E.459). Преобразуем получившееся выражение
следующим образом:
... <g> Rjm ..... Rkm 0 ... 0 R^dT*1-**. E.461)
Используя определение E.459) тензора производной, этому выраже-
выражению можно придать следующий вид:
- ... .(*(тТ)(т"л), E.462)
где й(™Т)(т**л) - транспонированный тензор от дифференциала Т
(см. E.89) и E.90)).
Формула E.462) дает инвариантное определение производной тен-
тензора функции по тензорному аргументу. Фактический способ опреде-
определения этой производной дает формула E.459).
В частном случае, если и — т = 2, то формула E.462) принимает
вид:
dS = 4ST"dTT, E.463)
где 4St - тензор четвертого ранга, определяемый по E.459):
ST = I^-R,- 0 Ri 0 R* 0 R' = Ip^R1' 0 Rj 0 R* 0 R'. E.464)
5.8.2. Дифференцирование функций от симметричного
и кососимметричного тензоров
Если Т - симметричный тензор, то также как и для скалярной
функции (см. §5.2) необходимо симметризовать аргумент функции
hTkl + Tlk)\ ,
E.465)
378 Глава 5. Тензорные функции
а затем, после вычисления производных в E.464) по каждой из девяти
компонент, учесть симметрию Tkl = Tlk.
Формула E.459) в этом случае примет вид:
1 В7' •
ST = ^]jfnRi ® Rj ® (R* ® R/ + R/ ® R*)- E-466)
Если Т - кососимметричный тензор, то необходимо вместо E.465)
ввести следующий аргумент:
Sij _ ЯУ / * (ум _ т'*) j , E.467)
а затем, после вычисления производных в E.464), учесть кососиммет-
рию Тк1 = -Т1к.
Формула E.459) в этом случае примет вид:
ST = ~!%Rf' ® Rj ® (Rfc ® R' - R' 0 Rfc). E.468)
5.8.3* Производная произведения скалярной и
тензорной функций
Пусть ^(Т) - скалярная функция, a S(T) - тензорная функция от
одного и того же тензора. Вычислим тензор производной от их про-
произведения, применяя определение E.464) для функции (^S), в резуль-
результате получим:
х R1' 0 Rj 0 R* 0 R' = S 0 фт + <0ST. E.469)
Здесь мы использовали определение E.88) тензора производной от ска-
скаляра фт, определение E.464), а также применили обычное правило
дифференцирования произведения функций.
Подставляя E.469) в E.463), получим выражение для дифференци-
дифференцирования произведения скалярной и тензорной функций:
= (S 0 ^т + tfST) • 'dTT. E.470)
5.8.4. Производная произведения тензоров
Подставим в определение E.464) вместо S произведение S • В, где
S = JF(T) и B = G(T) E.471)
§ 5.9. Скалярные функции нескольких тензорных аргументов 379
- тензорные функции от одного и того же тензора Т. Тогда получим
(S • В)т = ^|ы №roGmi)R'' ® & ® R* ® R' =
i >n5 ) R®R'®R®R
1" 0 Rn • R
1' 0 Rn ® Rp ® Rg • -R/ ® Rfc • R
-R, 0 R*) 0 Rk <g> R'. E.472)
Здесь несколько раз использовано свойство S^Sf =¦ Rp 0 R9 • -R/
Последнее выражение можно переписать следующим образом:
(S-B)t = ((ST • -R/ 0 Rfc) • В + S • (Вт • -R/ 0 Rfc)HRfc0R'. E.473)
Таким образом, формальное правило дифференцирования произведе-
произведения функции для тензорных функций уже видоизменяется.
Используя свойство
Rfc 0 R' • -dTT = Rk 0 R' • -R,- 0 RjdTij = dTkl
и выражение E.473), получим для дифференциала от произведения
тензорных функций следующее выражение:
d(S • В) = (ST • -dTT) - В + S • Вт • -dTT. E.474)
§ 5.9. Скалярные функции нескольких
тензорных аргументов
5.9.1. Определение скалярной функции
нескольких тензорных аргументов
В механике, кроме рассмотренных выше скалярных функций одно-
одного тензорного аргумента, иногда применяются скалярные функции,
аргументами которых являются одновременно несколько тензоров:
()(),...m^T(n)), E.475)
где ШаТ(а) - тензор ранга mQ, или в компонентном представлении:
s = f (^Y^S^y^,...^-"») . E.476)
380 Глава 5. Тензорные функции
Определение 5.11. Отображение декартова произведения п
пространств тензоров 7^ (М3) (к = 1,...п) в пространстве Ш1
называют скалярной тензорной функцией от п тензор-
тензорных аргументов и обозначают как /: 7^ х ... х 7з —> ^г
или в виде зависимости E.475).
При переходе из одной системы координат Xх в другую Х'г значе-
значение такой скалярной функции не меняется:
= /' (q
... Q\t a-,...,
) E>477)
В то же время вид функции / при таких преобразованиях может ме-
меняться.
5.0.2. Индифферентные скалярные функции
нескольких тензорных аргументов
Определение 5.12. Если при любых линейных преобразованиях
вида (ЗА) относительно группы G$ вид самой функции f не меняет-
меняется, то такую скалярную функцию E.475) называют индифферент-
индифферентной относительно группы Gs:
где компоненты тензоров преобразуются следующим образом:
I(a) ~"i(a) Л к1'"Л fcma' а-1...П,
E.479)
5.9.3. Совместные инварианты нескольких
тензоров
Индифферентная относительно некоторой группы G$ скалярная
функция нескольких тензорных аргументов, очевидно, является ин-
инвариантом относительно данной группы Gs. Построенные таким об-
образом инварианты называются совместными инвариантами тензо-
тензоров Ш1Т(!).. .ШпТ(п) относительно группы преобразований Gs. Бу-
Будем обозначать их буквой J(roiT(i).. .ШпТ(„)).
Среди всех совместных инвариантов п тензоров относительно дан-
данной группы G8 можно выделить функционально независимые.
§ 5.9. Скалярные функции нескольких тензорных аргументов 381
Определение 5.13. Систему совместных инвариантов
Ja{t(^''imi...^'im^)9a=l...r9 тензоров т>ТA).. .m»T(n) отно-
относительно группы G8 называют функционально независимой,
если для любой нетривиальной функции /(Ji,... Jr) от этих инвари-
инвариантов найдутся такие значения Т/Л'"*™1,.. .Т1КЛгПп , что
/wiHfi) шии1(п) ;»---JrU(i) •••i(n) ))ru'
В противном случае система совместных инвариантов называется
функционально зависимой.
Определение 5.14. Система функционально независимых сов-
совместных инвариантов, с помощью которой функционально может
быть выражен любой другой совместный инвариант относитель-
относительно той же группы G8, называется функциональным базисом
совместных инвариантов тензоров WlT(x).. . ШпТ(п).
Замечание 1. Также как и скалярные инварианты одного тензора
(см. замечания 1 - 3 к определению 4.4), совместные инварианты
J(T/t11r*lmi .. .Т^Г*тп) можно рассматривать как функции вида J:
Шк —> К1, где к = ki + ... + кп, а ка - число независимых компо-
компонент тензора т^у1 то«. Такой подход позволяет формально применить
уже доказанные результаты пп.4.4.2 - 4.4.4 для случая совместных
инвариантов, просто формально увеличив число компонент тензоров.
Теоремы 4.17 - 4.19 при этом также имеют место для совмест-
совместных инвариантов, если под компонентами П*1—1* подразумевать набор
компонент всех п тензоров: (fi1'1-1"*) = (TAlj"lmi,... , Т^тп).
Из теоремы 4.17, примененной для совместных инвариантов, выте-
вытекает следующее утверждение.
ТЕОРЕМА 5.20. Число z независимых совместных инвариантов
miT(i).. .ШпТ(п) в функциональном базисе не может быть больше
суммарного числа к независимых компонент всех этих тензоров:
где ка - число независимых компонент тензора ШаТ(а).
Если же, как и в случае инвариантов одного тензора (см.п.4.4.5),
способ выражения одного совместного инварианта через другие огра-
ограничен полиномиальными соотношениями, то число р неприводимых
совместных инвариантов (т.е. тех, которые не выражаются поли-
полиномиально через другие), образующих минимальный рациональный
базис, может быть больше к.
В дальнейшем нас будут интересовать только функционально не-
независимые совместные инварианты.
382 Глава 5. Тензорные функции
5.9.4. Функциональные базисы совместных инвариантов
двух симметричных тензоров
Рассмотрим наиболее частый для механики сплошных сред случай
- совместных инвариантов двух симметричных тензоров Т и В вто-
второго ранга:
j\8) = J(8) (Т, В), 7 = 1 • • • *> в = 1... 39. E.480)
Тогда, согласно теореме 5.20, максимальное число z элементов в функ-
функциональном базисе совместных инвариантов относительно какой-либо
группы Gs, являющейся подгруппой полной ортогональной группы /,
не превышает к =. 12:
z ^ 12.
Совместные инварианты j\s , также как и инварианты одного тен-
тензора, могут быть образованы с помощью операций свертки направля-
направляющих тензоров О7 в данной группе с каждым из тензоров Т и В, а
также их тензорными степенями: Т2, В2, Т • В и т.п.
Инварианты каждого из тензоров Ц*'(Т) и ц (В) также могут
входить в функциональный базис совместных инвариантов. Однако
простое объединение таких инвариантов ц'(Т) и Ц* (В) даже в слу-
случае, когда их по шесть штук, относительно той или иной группы Gs
не обязательно образует функциональный базис совместных инвари-
инвариантов.
Ниже приведены функциональные базисы независимых совместных
инвариантов двух тензоров для различных классов симметрии, в скоб-
скобках представлены явные выражения совместных инвариантов через
компоненты Tij и Bij тензоров в декартовом базисе ё,-.
(Е)-Триклинный класс:
E.481)
Ъ, ц, Д22, зз» 2з^ i3? 12}, z — 12.
(М)-Моноклинный класс:
т(м) _ ИМ)(В\ /9-1 4 fi
i, Т22, Т33, Т12, Т23, Т13Т23, -Вц, -022,
З13В13, -В1зВ2з}» 2 = 12
§ 5.9. Скалярные функции нескольких тензорных аргументов 383
(О)-Ортпотропный класс:
a = l,...6; 4Й = 4О)(В), /3 = 1,2,3,6,E.483)
3 • Т) • -(ё§ • В), jg> = (ё2 • Т) • .(§1 • В),
, Т22, Тзз,Т2з, Т{з, Ti2Ti3T23^ Вц, В22, Вы,
3, B12B13B23}, z = 12.
(Т)- Тетрагональный класс:
|^iT)), /3=1,2,3,
= T 0 В • • • -О„ - 4Т) (ТLТ) (В), E.484)
{Гц + Т22, Т3з, 2?з + ^1з. Т1!! + ^222. Т12{Ти - Гзз), det T,
\ T22B22,
^ ((Гц - Т22)В12 + (В„ - B22)f12)}, z = 12.
(Кз)-Квазитпрансверсалъно-изотпропный класс:
4K)=I{QK)(T), а=1,...6; 4S=4K)(B), /3=1,2,3,
J<f > = T ® В • • • -Oh - 4K)(TLK) (B), E.485)
AK) _ ! /T R 9 r(K) r(K) r(iC) .(Я-Л
J12 ~ 2 V ° ~ 2 / '
{Гц + T22, T33, 2\23 + f223, f1!2! + T222, f^, det T, Bn + B22,
^ -Bi3 + ^23> Г13В13 + T23B23, T11B11+T22B22, T12B12}.
{А)-Ромбоэдрический класс:
^ 'A)), /3 = 1,2,3,
384
Глава 5. Тензорные функции
Т22,
=
4Т®В
Т23,
E.486)
D3,
7?' = -Т®В-
— Т22) — 2Т12Т23,
1 _ _ _
323-023? ^{Вгз{Тц — Т22)
1 _
- (Т2
(В)-Ромбоэдрический класс:
j
{Гц + T22, f33, 2\2з + Т|3,
detT, Вц + В22
— Т22)) -
BГ)-АГвазиизотропмый класс:
4-
Т13В12}.
), /3=1,2,3,
E.487)
- Т22) - 2Т12Т23,
Т2
22
Т13В13 + T23B23, -
B\
E.488)
4 = твв....о», j = |(t..b-/),
J^> = (Т • -Oh) • (Т • -Oh) ¦ -(В • -Ofc), J<f > = Т2 0 В • • • -О„ -
¦/<?> = (В2 ® Т) • • • -Oh - (В • •(>„) • (В • -Oh) • -(Т • -Он),
{Тп + Т22 + Тзз, Т2! + Т\2 + Т323, 2\22 + Т?3 + ^223, T?i +1232 + 3
2Т22(Т22 + Т23) + Тзз(Т23 + f23), detТ, Вп+
T22J322 + T33B33, 2\2Bi2 + Ti3-Bi3 +
зз, В„(Т22 + Т23) + 522(Т22 + Т*3)
f2з), ТП(В22 + В\3) + %г{В\г + Щз) + Т33(В213 + В223)}.
§ 5.9. Скалярные функции нескольких тензорных аргументов 385
(Н)-Гексагональный класс:
4Н) - 1(аИ) (Т), а = 1,... 5; 4н> = /f) (В), /3 = 1,... , 4, E.489)
№ = ((В - ё!) • Т) • -(el ¦ В), 4? = Т В - 2JW
+ 2rf2, detT,
22 + 2J512,
+ B22T22 + 2Ti2Bi2}, г = 11.
(Тз)-Трансверсально-изотропный класс:
43)=4Я). а = 1,...11, г =11. E.490)
A)-Изотропный класс:
4J)=/a(T), 4Je = /a(B), а = 1,2,3, E.491)
47) = Т - -В, J<7) = Т2 • -В, 4Т) = Т • -В2,
{Г,., i((r,J-T^,), detT, B\, ±{(В\J-В';В*{), detB,
Теорема 5.21. Функциональный базис совместных инвариантов
двух симметричных тензоров второго ранга относительно одной и
той же группы G8 С / состоит из z элементов, где
- z = 9 для групп Ga изотропного класса;
-2 = 11 для групп Тз и Н классов;
- z = 12 для всех остальных групп Gs С /.
В качестве функциональных базисов могут быть выбраны совмест-
совместные инварианты E.481) - E.491).
Т Рассмотрим изотропный класс.
Выберем такую ортогональную матрицу Аг^ которая преобразует
базис ё,- в собственный базис е,- тензора Т, т.е. ё,- = A\ej. Так как Т
- симметричный, то в этом базисе он имеет три ненулевые веществен-
вещественные компоненты: Таа = А*\ Аа- ТХК Поскольку базис е,-, вообще гово-
говоря, не является собственным базисом тензора В, то он в этом базисе
имеет шесть компонент Вх* = AxkA\ Bkl. Следовательно, всего набор
(TIJ', В1*) содержит девять ненулевых компонент. Поскольку матрица
13 Тензорное исчисление
386 Глава 5. Тензорные функции
AXj G /, то оказываются выполненными условия теоремы 4.19 с учет,
том замечания 1 из п.5.9.3. Из этой теоремы следует, что 2^9. Но
девять совместных независимых инвариантов относительно /-класса
существуют - это, например, набор E.491). Первые шесть инвариан-
инвариантов Ja в нем, очевидно, независимы по теореме 4.18 (п.1°) с учетом
замечания 1 из п.5.9.3. Доказательство независимости всей системы
инвариантов E.491) можно осуществить с использованием теоремы
4.17 тем же методом, который был использован при доказательстве
теоремы 4.24.
Рассмотрим теперь класс Тз.
Для тензора Т, как было показано при доказательстве теоремы 4.24,
о .
всегда можно найти чгакую матрицу А%j E Тз, что этот тензор в ба-
зисе е,-: ё,- = А7,^-, - будет иметь только пять ненулевых компо-
компонент. Поскольку тензор В в этом базисе, вообще говоря, будет иметь
все шесть ненулевых компонент, то общее число ненулевых компо-
компонент (Tij',jBij") в базисе е, равно 11. Тогда по теореме 4.19 z ^ 11.
Но одиннадцать независимых совместных инвариантов действитель-
действительно существуют - это, например, набор E.490). Независимость этого
набора можно показать, вычислив ранг матрицы частных производ-
производных dJa/dTx^, dJa/dB1^ и воспользовавшись теоремой 4.17.
Для остальных классов число z максимально и равно 12. Поэтому
достаточно найти двенадцать независимых совместных инвариантов
в каждом классе. Такие инварианты приведены в наборах E.481) -
E.488). Доказательство их независимости аналогично рассмотренно-
рассмотренному выше и основано на использовании теоремы 4.17. А
5.9.5. Сизигии для совместных инвариантов
Подчеркнем еще раз, что если ограничить возможность выраже-
выражения одних инвариантов через другие только полиномиальными соот-
соотношениями (т.е. в виде сумм и произведений сверток целых степе-
степеней тензоров), то число неприводимых инвариантов в каждом классе
расширится. Про те совместные инварианты, которые построены в
виде полиномиальных соотношений тензоров Т, В с участием образу-
образующих тензоров ОG) классов, но могут быть разрешены относительно
функционального базиса инвариантов только как некоторые неполи-
неполиномиальные функции, говорят, что они образуют сизигии. Такие сов-
совместные инварианты, очевидно, не входят в функциональный базис,
но могут входить в целый рациональный базис.
Рассмотрим примеры таких сизигий для некоторых классов сим-
симметрии.
Для триклинного .Е-класса функциональный базис нескольких тен-
тензоров может быть образован без совместных инвариантов, поэтому
нет необходимости его рассматривать.
В М-классе можно образовать инварианты, например, инвариант
¦#23^23, не входящий в функциональный базис. Очевидно, что он мо-
§5.9. Скалярные функции нескольких тензорных аргументов 387
жет быть выражен через этот базис неполиномиальным образом:
АМ)_Й ф _ (Т13Т23)(Т13В23) 4М)Л?]
J13 -ВгъТгг jr^ =
откуда получаем сизигию:
4М)№ - jWjg> = 0. E.493)
Для ортотропного О-класса можно образовать, например, инвари-
инварианты Б23, Б23, которые выражаются через функциональный базис не-
неполиномиальным образом:
АО) й Ф (Ti2T13f23)(B12B13B23) J^jj?
Лз = Bl2Tl2 = (f»B13)(f23B23) = -]М]?У
т(ОJ
т(°) -_ 52 __ J10
J14 — -°23 ~ (о)
и также образуют сизигию.
Покажем, что для тетрагонального Т-класса следующие инвариан-
ты можно выразить через функциональный базис Ц \ и, следователь-
следовательно, они не являются независимыми:
т(т) (Ф
1 = (Т
- B22h
" ^22
E.495)
Для первых трех инвариантов достаточно расписать явным обра-
образом следующие произведения инвариантов из функционального бази-
базиса:
j[TLT) - 4V = (Гц + Т22)(Вц + В22) - ТцВц - Т22В22 =
= J
*4V - 4ТLТ) = 2(ТцВц + Б22Т22) - (Гц + Т22)(Вц + В22) =
= (Тц - Т22)(БП - Б22) = 4г\ E-496)
388 Глава 5. Тензорные функции
= (Bu-B22)(fn-f22) Bu - В22
2jf > - J[TJ 22?x + 2f|2 - (Гц + T22J fn - f22
Таким образом, скаляры J{8', J\^} и J\b} также являются инвариан-
инвариантами относительно Т-класса, но уже зависимыми. Поскольку j[s' и
j{4' выражаются полиномиально через функциональный базис, толь-
только последнее из соотношений E.495) образует сизигию.
IT)
Для доказательства функциональной зависимости J^6 выпишем
выражение для четырех инвариантов:
j[T) = Тц.+ ?22, j{T) = Т^ + f%2, E.497)
J7 =^11+^22, Jn = Til-Вц + Т22В221
и рассмотрим этот набор как систему четырех уравнений относитель-
относительно компонент Тц, Т22, 5ци ^22« Выразим из третьего уравнения Вц
и, подставляя его в четвертое уравнение, находим:
ЛТ) _ АТ)ф Т^Т.о 7(т)
^22 - —= = , ^11 - — . E.498)
-*22 — -ill -i22 — ^11
Возводя в квадрат эти уравнения, а затем складывая друг с другом,
с учетом первых двух уравнений системы E.497), получим:
т(Т) _ 1 (, AT) АТ)ф ,2 , / AT) АТ)ф
(T22 — ТпУ \
1 {TJ - 27(T) 7(T) 7(T)
) 7(T) 7(T) -4- 7(TJ T(T)) (*>
AT) ATJ
— 7
- искомое соотношение, показывающее функциональную зависимость
(Т)
инварианта J^6 .
Такой способ доказательства функциональной зависимости какого-
либо инварианта, при котором входящие в его структуру компоненты
тензоров предварительно находятся из системы уравнений, состав-
составленной из инвариантов функционального базиса, содержащих те же
компоненты, назовем компонентным методом. Этот метод можно
эффективно применять для различных классов симметрии.
Для доказательства функциональной зависимости j[7* составим
систему:
4Т) = T12(Tn-T22), 2jg] = {f11-f22)B12 + {B11-B22)f12 E.500)
§5.9. Скалярные функции нескольких тензорных аргументов 389
и выразим из нее В\2'-
4ит)- <5-5И>
Домножая это выражение слева и справа на (В и — #22) > с учетом
E.497) получаем окончательно:
4V = В12{Ви - Вгг) = Bj[? - jg^PvP- E.502)
Поскольку J$ } образует сизигию, то E.502) также представляет со-
собой сизигию.
А-класс. Среди совместных инвариантов А-ромбоэдрического класса
рассмотрим следующий:
j[? = ТцВц + Т22Б22 + 2Т12?12. E.503)
Используя компонентный метод, покажем, что инвариант E.503) мож-
можно функционально выразить через базис А-класса. Рассмотрим сис-
систему двух уравнений, составленную из инвариантов базиса Л-класса:
— Т22) + Ti3(J5ii - В22) — Т12В23 — Т23В12,
ii - Т22) + Т23(Вц - B22) + T12B13 + T13B12 E.504)
j5
и выразим из нее В\2 и (Ви — В22):
2?Ц —
А) - (А) ~ А - С - \
2 2 ) '
— ^— I «>ll — r-^l3Ull - -*22; -Т J-12&23 -Г ^2Э^12 I ?
-U3 \ ^ /
E.505)
А = (Гц - Т22)Т13 + 2Т12Т23, С = 2Т12Т13 - Т2з{Тц - Т22).
Подставляя эти выражения в E.503), получаем окончательно соотно-
соотношение
Аг' = \(Тц + Т33){Вп + В22) + 1(Ги - T23)(J5u - В22)+
E-506)
3go Глава 5. Тензорные функции
которое образует сизигию.
5.9.6. Дифференцирование скалярных функций
нескольких тензорных аргументов
В механике важную роль играют частичные дифференциалы от
скалярной функции E.476) по одному из тензорных аргументов:
{1,...»}. E.507)
(к)
Определение 5.15. Тензором частной производной
скалярной функции от п тензоров по к-ому тензорному ар-
аргументу называют следующий тензор:
Этот тензор имеет тот же ранг, что и аргумент-тензор ткТ^)- С
учетом E.508) и определения E.89) дифференциала тензора, частич-
частичный дифференциал скалярной функции можно представить в виде,
аналогичном E.92):
dkf = mkhw • • • • • rf(»*T(i))<""-1). E.509)
Для случая тензоров второго ранга (га* = 2) эта формула имеет
вид:
dkf = fT{k)..dTjk), fee {1,2}. E.510)
Полный дифференциал от скалярной функции E.476) представляет
собой сумму частичных дифференциалов:
4f(TO*TA,...т»т(п)) =
к=1 fc=l
E.511)
Например, для случая скалярной функции двух тензоров (п = 2) вто-
второго ранга имеем:
d/(T, В) = /т • -<ЙГТ + /в • -сШт. E.512)
Если тензоры Т и В - симметричные, то вычисление тензоров произ-
производной /т и /в должно осуществляться по правилам E.94) и E.96).
§ 5.9. Скалярные функции нескольких тензорных аргументов 391
5.9.7. Дифференцирование совместных инвариантов
Рассмотрим в качестве скалярной функции / E.475) совместные
инварианты / = Ja двух тензоров Т и В относительно какой-либо
группы G,. Очевидно, что если совместный инвариант содержит ком-
компоненты только одного тензора, то тензоры производных от них бу-
будут совпадать с соответствующими тензорами производных обычных
инвариантов /а . Поэтому вычислим производные только от инвари-
инвариантов Ja из функциональных базисов классов, приведенных в п.5.9.4,
которые содержат компоненты обоих тензоров Т и В. Возможны два
вида таких инвариантов:
/=(Т®В)....4П E.513)
- квадратичный совместный и
бП E.514)
- кубический совместный, где 4Пи6П- индифферентные относитель-
относительно группы G3 тензоры.
Для вычисления тензора частной производной /в, рассмотрим
тензор Т как фиксированный, тогда скалярные функции E.513) и
E.514) можно свести к линейной относительно В:
/ = B..ft, П = *П-Т E.515)
и квадратичный относительно В:
/ = (В 0 В) • • • 4П, 4П = бП • -Т. E.516)
Тогда, используя правила E.118) и E.120) дифференцирования ли-
линейных и квадратичных функций, получаем:
E.517)
а также
^¦(Т ® В <8> В 6П) = А (в ® В • • • -4П) = 24П<-> • -В. E.517')
Если совместный инвариант E.517) имеет структуру вида:
/ = (А - Т) • -(С - В) = (Т 0 В) • - - -(А 0 С)'1432», E.518)
где А и С - симметричные тензоры второго ранга, то формула E.517)
принимает вид:
А ((А • Т) • -(С • В)) = i ((А ® С)<1432> + (А ® С)<4132>) • -Т.
E.519)
392 Глава 5. Тензорные функции
5.9.8. Частные производные от совместных
инвариантов функциональных базисов
Применим полученные правила для вычисления тензоров частных
производных от совместных инвариантов функциональных базисов в
различных классах симметрии.
В триклинном классе нет инвариантов, содержащих компоненты
обоих тензоров.
В моноклинном классе есть один такой совместный инвариант:
НгаП = ^((ё? •т)' -(ё§ •в)) = \ ((ё> ®
+ (в? 0 ё§)D132)) • -Т = i(O2 ® О2) • Т E.520)
в силу симметрии Т.
В ортотропном классе два аналогичных инварианта:
^§ = ±{Ог 0 О!) - Т, ^- = ±(О2 0 О2) • -Т. E.521)
Для тетрагонального класса имеем
т(т) 1 ,
= - (((Е - el) <g> ё*)<1432) + ((Е - i
2 Vu 3J Ъ) u
л ,1
дВ 2
Для Кз-класса:
Я j(K) 1 / 1
В~ = 2 (Л " 2(Ql ® °i + °2 ® Ог) - Ofc ) • -Т. E.523)
Для Л-класса:
д№ 1.
О2 ® О2) • -Т,
§5.9. Скалярные функции нескольких тензорных аргументов 393
Для В-класса:
дТ{В) 1 dJ{B)
^ (О0О + О®О)Т ^
1
^ = (О10О1 + О2®О2)Т, ^=-D3--T, E.525)
ов 4 ов 4
(В) / ,
g-= f Д--(
Для квазиизотропного Jf-класса:
7 яг 1
8 -С Т 9 - (А ОП Т
= Oft • .((T • .Oh) • (T • -О,,)) = (T • -Oft) • (T • -Oh), E.526)
^g- = Oft • -T2 - (T • -Oft) • (T • -Ofc),
= В • Oft • T + (T • -О,,) • В - (T • -Oft) • (Oft • -B).
дВ
Для гексагонального (Я) и трансверсально-изотропного (Тз) клас-
классов:
а /(Я) 1
(d 0 Oi + О2 ® О2) • -Т,
^- = (A - i(Oi 0 Oi + O2 0 O2) - eg ® e2) • T. E.527)
дВ \ 2 )
Для изотропного класса:
Т()
9
= T В + В Т,
394 Глава 5. Тензорные функции
Упражнения к § 5.0.
Упражнение 5.9.1. Показать, что следующие скаляры можно выразить
через функциональный базис совместных инвариантов М-класса:
,2 J>
(МJ Т(МJ Т(М)
13
j(M)
j(MJ
j(M)
AM)
J12
rn2 __
J23 ~ (M) ' ^23 ~ -(M)T
^5 «'ll
,(M) f(M)
^6 ^11
AM)
J5 ^11
Упражнение 5.9.2. Показать, что следующие скаляры являются инвариан-
инвариантами относительно О-класса, и их можно выразить через функциональный базис
этого класса:
j(OJ j{O) j(O) j(OJ
12 = т(ОJ j(OJ » "°13 = ,(O) "
^10 ^11 ^5
Упражнение 5.9.З. Показать, что следующие скаляры являются инвариан-
инвариантами относительно Кз-кп&сс&, и их можно выразить через функциональный базис
этого класса:
2 _ X U r(KJ 9 j(K) j(K) j(K) f(KJ JK)
Упражнение 5.9.4. Показать, что следующие скаляры являются инвариан-
инвариантами относительно Л-класса, но их можно выразить через функциональный базис
этого класса:
Лб = ^1з{Вц — В22) — ^BuB23i Ju = -623(^11 - ^22) + 2J5i2jBi3.
Упражнение 5.9.5. Показать, что следующие скаляры являются инвариан-
инвариантами относительно 5-класса, но их можно выразить через функциональный базис
этого класса:
Лз =Вп +2?22+ 2Bi2 J = Вх
ц — В22) —
Упражнение 5.9.6. Показать, что следующие скаляры являются инвариан-
инвариантами относительно jFC-класса, но их можно выразить через функциональный базис
этого класса:
AQ) — 52 ,52 ,52 т(^) __ 52 ,52 ,52
J15 - ^11 + ^22 + -^33» ^14 -^12 + ^13+^23»
AQ) _ 53 ,53 , 53
§ 5.10. Тензорные функции нескольких тензорных аргументов 395
§ 5.10. Тензорные функции нескольких
тензорных аргументов
5.10.1. Определение тензорной функции
нескольких тензорных аргументов
Кроме скалярных функций вида E.475) в механике применяют так-
также тензорные функции нескольких тензорных аргументов.
Определение 5.16. Отображение декартова произведения п
пространств тензоров 7з , fe = 1...П, в пространство Т$ на~
зывают тензорной функцией п тензорных аргументов
и обозначают как тТ : T3(mi) x ... х Г3(Шп) —У Т3(ш) или в виде
зависимости:
), VmSGT3(m), rafcTwGT3W,
E.529)
k = l...n.
В компонентном представлении, например, в базисе R,- простран-
пространства Ж3 такие функции имеют вид:
^ .. .3*у*-) . E.530)
При переходе из одной системы координат Xх в другую Хп значе-
значения такой функции меняются по тензорному закону:
= Р\ ...J*7m Tqi...qm (T(V-,... ,T('n'j"'m") • E-531)
Определение 5.17. Тензорную функцию E.530) называют ин-
индифферентной относительно группы G3) если вид функции не
меняется при всех преобразованиях в этой группе:
?i1...im = Fil...imt E.532)
где Tix,,,im - компонентное представление тензорной функции в де-
декартовой системе координат хг = X'1 с осями, совпадающими с
осями анизотропии.
Из E.531) и C.45) следует, что для индифферентной тензорной
функции нескольких аргументов выполняются условия:
E.532')
395 Глава 5. Тензорные функции
5.10.2. Псевдопотенциальные тензорные функции
нескольких тензорных аргументов
Для тензорных функций нескольких тензорных аргументов введем
понятие псевдопотенциальности, которое, вообще говоря, отличается
от обычного понятия потенциальности тензорной функции.
Определение 5.18. Псевдопотенциальной или потен-
потенциальной по к-ому тензорному аргументу называют
функцию вида E,530), для которой существует скалярная функция:
E.533)
тензор частной производной от которой по k-ому аргументу сов-
совпадает с функцией E.530):
§j E-534)
или в тензорном виде
(T(fc)...TO»T(n)). E.534')
Из определения псевдопотенциальной тензорной функции следует,
что ранг га тензора S совпадает с рангом аргумента тТ(д.).
Очевидно, что если скалярная функция E.533) является индиффе-
индифферентной относительно группы G,, то соответствующая ей псевдопо-
псевдопотенциальная тензорная функция также является индифферентной от-
относительно G8.
5.10.3. Представление псевдопотенциальной тензорной
функции в тензорном базисе
Рассмотрим псевдопотенциальную тензорную функцию E.534'), за-
зависящую от двух симметричных тензоров:
S = *(T,B) = J|. E-535)
Индифферентную относительно группы G8 скалярную функцию
^(Т, В) всегда можно представить как функцию от полного набора
совместных инвариантов Ja(T, В) из функционального базиса отно-
относительно той же группы симметрии:
V>(T, В) = VD5)(T, В)), 7 = 1 ¦ • ¦*• E.536)
Обозначим z - число совместных инвариантов J7 в функциональ-
функциональном базисе группы G$, а г - число инвариантов J7 одного тензора Т
§ 5.10. Тензорные функции нескольких тензорных аргументов 397
относительно этой группы G8. Будем далее полагать, что инвариан-
инварианты 1-у{Т) полностью входят в набор J7: J7 = «/7(Т), 7 = 1.. .г. Тогда
от тензора В зависят только J7, для которых *у = r+l...z.
Вычисляя тензор частной производной от ф, получаем, что псевдо-
псевдопотенциальную функцию E.535) можно представить в виде:
•А дф »4" ,5537)
Также как и для функции одного тензорного аргумента, введем тен-
тензорный базис:
dJ{i)
и скалярные функции
dJ
= ЯГ' 7 = 1-*-г E.538)
7 = I--*-r. E.538')
77Г'
Тогда получим следующую теорему.
Теорема 5.22. Всякую псевдопотенциальную тензорную функ-
функцию E.535), индифферентную относительно группы G8, можно
представить в виде разложения по тензорному базису Н7 :
() E.539)
7=1
Если тензорная функция является потенциальной по другому аргу-
аргументу
S = ^(T,B) = ||, E.540)
то формально для нее можно получить точно такое же представление,
однако вид тензоров Н7 и их число при этом могут отличаться.
5.10.4. Псевдопотенциальные тензорные функции
для различных классов симметрии
Выберем в качестве совместных инвариантов J7 G = 1.. • z) функ-
функциональные базисы, приведенные в п.5.9.4, тогда, используя резуль-
результаты вычисления тензоров частных производных 9J7!|.r/9B, содер-
содержащиеся в п.5.9.8, найдем базисные тензоры Н7 . В итоге получим
следующие представления E.539) для различных классов симметрии.
393 Глава 5. Тензорные функции
(Е)-Триклинный класс: представление E.539) совпадаете E.174).
(М)-Моноклинный класс:
s = Y>7e2 + VK + I
7=1 ^ 2^ 4
\ 1
+ <P7Oi 0 Oi • -Т + ~^e(Oi 0 О2 + О2 0 Oi) • -В, E.541)
/ 2
(О)-Ортотропный класс:
з -
S = J2 ^ё7 + 4 (^4Gl 0 Ol
7=1
0 О3) • -Т + Зу>66Ото • • • В 0 В, E.542)
класс:
S = (y>i + у>7/2(В))Е + (^2 - <pi)el + -<
Z
(Кз)-Квазитпрансверсалъно-изотпропный класс:
S = (vi + ?>7/(В))Е + ( )ё +
+ О2 ® О2)
О2 ® О3) • -(узВ + ^Т) + Bv?5(Oh - ё| ® ё|) + -<р6Пзн) • -Т-
E.543)
jr}^ = det В.
р3В + Т)
^ А) • -Т - y>7/i(B)B + ^B2, E.544)
= det В.
$ 5.10. Тензорные функции нескольких тензорных аргументов .-399
(А) -Ромбоэдрический класс:
S = y>i(E - 4) + {<Р2 - 12(В)<р7)ё1 + -(d ® Oj + О2 ® О2) • -(у3В+
+ (у - 9у)т) + {<Р7А + 5VsD3 + -?<p6Sl3d) ¦ -Т, E.545)
(В)-Ромбоэдрический класс:
(<р2 - к - ^6/2(В))ё1 + -(Oi
О2 ® О2) • • (у>3В + (у - ?>б)т) + (у>б А + -?>5D3) • -Т-
E.546)
«ласе:
S = (^ + vt/2(B))E + (^ - Ц)Оп ¦ -Т + ^
+ (V4 - *»в)(Т • -О,,) • (Т • -Од) + ipbOh ¦ -Т2+
(о,, • -т) + (т • -ofc) • в - (т • -ofc) • (в • -оь))+
E.547)
(Д')-Г'ексагомальный и (Тз)-Трансверсалъно-изотропный классы:
S = {<pi + ?>б/2(В))Е + (р2 - Ч>\ ~
+ (у - V5)T) +
E.548)
2 (°i ® °i + °2 ® О2) • • (vsB + (у
400 Глава 5. Тензорные функции
(/) -Изотропный класс:
S = (<pi + (p2h(B) + ^з/г(В))Е - (<р2 + y?3/i(B))B
+ <р5Т2 + <р6(Т В + В Т) + у?7(Т2 В + В2 Т), E.549)
=у>7G<'\...,
В этих представлениях кроме функциональных базисов совместных
инвариантов J^ G = I...2) добавлено еще по одному инварианту
</{з (для Н- и Тз-классов - это j[2 ^), которые являются зависимыми,
однако их введение обеспечивает возможность предельного перехода
к функции одного тензорного аргумента S = !F(T) = ^"(Т, Т), если
положить В = Т.
Если же такой предельный переход не учитывается, то все функ-
функции у>7> соответствующие инвариантам j\*3 : ipj — дф/д^83\ можно
положить равными нулю. Для Н и Тз классов то же самое относится
к функции (ре = дф/д^2 •
Добавочные инварианты имеют вид:
jM = j[? = (elT)..(el.B),
4V = W = W = AT = A? = det В, E.550)
Для изотропного класса добавочные инварианты не вводятся.
ГЛАВА в
ТЕНЗОРНЫЙ АНАЛИЗ
Большинство законов физики и механики записывают с помощью
дифференциальных соотношений между тензорными величинами.
Так как эти законы должны быть "объективны", т.е. не зависеть от
выбора системы координат, то и дифференцирование тензоров должно
учитывать это свойство. Оказывается однако, что обычные частные
производные от компонент тензора не являются компонентами какого-
либо другого тензора, поэтому применяют специальное ковариантное
дифференцирование тензоров, которому и посвящена настоящая гла-
глава.
§ 6.1. Ковариантное дифференцирование
в.1.1. Символы Кристоффеля
Пусть в пространстве Ш3 кроме декартовой системы координат
0х% имеется некоторая криволинейная система координат Xх A.2),
и задано некоторое тензорное поле пП(ж), которое в силу A.3) мож-
можно рассматривать как тензор-функцию от криволинейных координат
пЩХх).
Рассмотрим простейший случай такого поля - локальные векторы
базиса R,-.
Поскольку система координат Хк (хг) криволинейная, то локальные
векторы базиса
действительно зависят от координат, т.е. имеется векторное поле
k
Рассмотрим производные векторов базиса дИг/дХ^. Поскольку
при фиксированных значениях г и j объект дК{/дХ^ тоже является
вектором, то его можно разложить по векторам базиса Rj:
dRi/dXj = r*.R*. F.1)
Коэффициенты разложения Г^- называют символами Кристоффеля
{коэффициентами связности), они симметричны по нижним индек-
402 Глава 6. Тензорный анализ
сам: Г^. = Г?, т.к.
3R,- дх 6Rk
F.2)
дХк дХ<дХк дХ*'
Символы Кристоффеля не являются компонентами тензора, при пе-
переходе из одной системы координат в другую они преобразуются по
закону, отличному от тензорного (см. упр.6.1.1). Вычислим произ-
производные от векторов взаимного базиса: дКк/дХ\ Для этого продиф-
продифференцируем соотношение между R; и R* (см. упр. 1.1.5):
тогда
9Ki
Умножая это уравнение тензорно на R1, получаем:
dRj/dXk = -r?fcR\ F.3)
в.1.2. Связь Г*, с gij
Оказывается, что Г^- связаны с матрицей д^. В самом деле, диф-
дифференцируя A.14), имеем:
Вдц _dRiRj_
или с учетом обозначения F.1):
J|i- = rj-fcR, • Ry + R,- • Tljk ¦ R, = Т\кдн + Т'^дц. F.4)
Меняя индексы i и fc, получим:
||f = rUi,-+r>/. F.5)
Меняя в F.4) индексы j и fc, получаем аналогично:
^ ^ 1 F.6)
Складывая F.5) и F.6) и затем вычитая из полученного выражения
уравнение F.4), получаем с учетом симметрии символов Кристоффеля
dgik dg{j . . .
+ Tijgu - Т\кди - T!jk9il = 2Г^/Ь F.7)
Умножая левую и правую части на A/2)<7*т, придем к теореме.
§ 6.1. Ковариантное дифференцирование 403
ТЕОРЕМА 6.1. Символы Кристоффеля Г™ определяются только
метрической матрицей gij:
_ 1 km
9
dgik d9ij \
Отсюда видно, что в декартовой системе координат, где gij = const,
* = о.
Часто используют формулу, связывающую символы Кристоффеля
dgim dgkj _ dgkm\ _ 1 imdgim . .
dxk + ьх™ dx* ) ~ 29 dxk' " '
Вычислим также с учетом формулы A.156) производную от g =
det (g{j) no Xk:
- FЛ0)
Из F.9) и F.10) получаем, что
fcm~ 2gdXk ~ /
6.1.3. Символы Кристоффеля первого рода
Умножая Г™- на gmk согласно правилам жонглирования индексами,
получим
Г,;* = T?j9mk F.12)
~ полностью ковариантные символы, называемые символами Крис-
Кристоффеля первого рода. Для Г?] в этом случае используют название
символов Кристоффеля второго рода.
Из F.8) и F.12), очевидно, следуют соотношения между Г,^ и мет-
метрической матрицей:
ih_ дд& dgij\
+ dx> " эх*) '
6.1.4. Градиент скаляра
Пусть имеется скаляр y>(Xfc), заданный как функция координат
точки М с координатами Хк.
404 Глава 6. Тензорный анализ
Определение 6.1. Градиентом скаляра назовем вектор,
определенный следующим образом:
k FЛ4)
Здесь V - символ Гамильтона, называемый набла- оператор ом, ко-
который трактуется как действие символического вектора:
^, F.15)
Введем также обозначения для компонент разложения вектора У7<р
по базису Rfc:
h F.15')
- получим ковариантную производную скаляра, которая, очевидно,
совпадает с обычной частной производной.
Для векторов и тензоров такого совпадения, как увидим, далее, уже
нет.
6.1.5. Ковариантные производные компонент вектора
Рассмотрим теперь произвольное векторное поле a.(Xk), заданное
в IR3 и вычислим его производные по Хк:
За da'R,- да1 _ , <9R,
дхк ~ дхк ~ дхк '" дхк~
) jl FЛ6)
Величина, стоящая в скобках, называется ковариантной производной
от контравариантных компонент вектора и обозначается как
^ aT^. F.17)
Ковариантную производную от ковариантных компонент векто-
вектора определяют как
Тогда производную от самого вектора а можно представить в виде:
^г = V*a'"Rj = R'Vfcfly. F.19)
Контравариантной производной от, соответственно, ко- и контра-
контравариантных компонент вектора называют следующие величины:
и V"V = gmkVkaj. F.20)
§ 6.1. Ковариантное дифференцирование 405
в. 1.в. Набла-оператор и градиент вектора
Определение 6.2. Набла-оператором (градиентом)
в ектора а называют тензорное произведение векторов взаимного
базиса Rk и частных производных да./дХк :
V 0 а = R* 0 ^ = R* 0 RjVkaj. F.21)
Раскроем физический смысл градиента вектора.
Вычислим дифференциал вектора da, рассматривая его как прира-
приращение вектора а, обусловленное переходом из точки М с координата-
координатами Хк в близкую точку Mi с координатами Хк -f dXk:
^X"- F-22)
Если в качестве а выбрать радиус-вектор х, то получим:
^k k F.23)
Умножим F.23) слева и справа на R,-, тогда
R1' • dx = R1' • RkdXk = R1' - RmgmkdXk =
= gimgmkdXk = 6idXk = dX\ F.24)
Следовательно, F.22) можно преобразовать следующим образом:
da{Xk) = dx-Rk -^ = dx • Rk
= dx • VkajRk ® Rj = dx • V <g> a. F.25)
В итоге получим:
da = (V 0 а)т • dx. F.26)
Таким образом, градиент вектора (V 0 а)т связывает приращения
вектора а с соответствующими приращениями радиуса-вектора х при
переходе от материальной точки Хк к Хк 4- dXk.
Для тензора (V 0 а)т на основании F.15) справедливо следующее
формальное представление:
да
(V ® а)т = а ® V = j-g ® Rfc = VkajRj ® Rfc. F.27)
406 Глава 6. Тензорный анализ
Теорема 6.2. Градиент вектора V®a является тензором вто-
второго ранга, а ковариантные Vt-oJ', Vt*Oj и контравариантные V'oj,
V'a-7 производные являются компонентами этого тензора.
Т То, что V 0 а - тензор, следует, например, из F.26) по обратному-
тензорному признаку. Следовательно, при переходе из одной системы
координат Xх в другую Х1х его компоненты преобразуются по тензор-
тензорному закону. Но из F.21) следует, что его компонентами являются
V,'aj, V,aJ и Va^, Vctj в соответствующих базисах:
V ® а = V.-aj-R1' <g> R7 = V.a'R' <g> R, = V'cyR,- <g> Rj = VVR,- <g> R,.
F.28)
Следовательно, в отличие от частных производных даг/дХк и
dcij/dXk, ко- и контравариантные производные являются компонен-
компонентами тензора. ^
Поскольку физические законы описываются, как правило, инва-
инвариантными дифференциальными уравнениями, то в них используют
именно ковариантные (а не частные) производные.
в.1.7. Ротор вектора
Определение 6.3. Ротором вектора а называется вектор,
определенный следующим образом:
V х а = R1 х -^ = rot а = 2w. F.29)
Используя определение A.33) векторного произведения, находим
компоненты ротора:
V х а = —e^V.-ajR*. F.30)
л/9
Вектор u> называют вектором вихря. Как всякий вектор, образо-
образованный векторным произведением двух полярных векторов, и> явля-
является аксиальным вектором, т.е., вообще говоря, псевдовектором (см.
§1.9). Кроме того, с*> является вектором, сопутствующим некоторому
кососимметричному тензору ft, который по A.203) можно образовать
следующим образом:
1 . . За
П = Ехо) = -Rt ®R'xRJ:
¦i* •((*•&) "-с1 ¦*>&)=
jj 6.1. Ковариантное дифференцирование _407
Здесь использовано свойство A.48) двойного векторного произведения,
а также определение F.21) градиента вектора.
Кососимметричный тензор П, определенный формулой F.31), назы-
называют тензором вихря, с его помощью транспонированный градиент
вектора всегда можно представить в виде:
(V®a)T=e + ft, F.32)
где
e = def аЕЕ ^ (V ® а+(V ® а)т) F.33)
- симметричная часть, называемая линейным тензором деформации
над а.
Подставляя разложение F.32) в F.26), получаем формулу Гелъм-
голъца:
da = (V <8> а)т • dx = Т • dx + ft • dx = Т • dx + u> x dx, F.34)
которая определяет приращение вектора а в окрестности точки М
через тензоры линейной деформации и вихря.
в. 1.8. Дивергенция вектора
Определение 6.4. Дивергенцией вектора а. называют следу-
следующий скаляр:
v • а = Ri * 4^ = v«a* = div a. F.35)
С учетом F.11) и F.17) выражение F.35) можно представить в
виде:
L^ F.36)
в.1.9. Набла-оператор — самостоятельный вектор
Набла-оператор V можно формально рассматривать как самосто-
самостоятельный вектор, компонентами которого являются операторы кова-
риантной или контравариантной производной:
V = R*Vfc. F.37)
Для набла-оператора справедливыми являются все операции умноже-
умножения и сложения, как для обычных векторов. Например, легко прове-
проверить, что формулы для градиента F.21), ротора F.29) и дивергенции
F.35) будут справедливы при формальном умножении V на вектор а:
V <8> а = R*Vfc <g> ajRj = VkajRk <g> R,-,
408 Глава 6. Тензорный анализ
V . а = R* V* • ajRj =. VkajRk • R, = V*a*, F.38)
V x a = R*Vfc x a'Rj = V*a'R* x R, = vfc*imVfcajRm.
В отношении Vk действуют обычные правила перемещения компо-
компонент векторов в любое место по отношению к знакам операций ®, •
или х. Однако V* нельзя перемещать по отношению к компонентам
других векторов, так как по определению V* действует на стоящий
справа от него символ компоненты тензора (напомним, что обычные
компоненты в тензорах и их произведениях можно перемещать друг
относительно друга).
Формула F.14) для градиента скаляра тоже может быть получена
формальным путем, так как согласно F.15') Vk<p = д(р/дХк.
При формальном подходе можно произвести операции умножения
F.38) в обратном порядке:
а 0 V = ajRj <g> RkVk = R, <g> RkajVk)
а - V = ajRj • R*Vfc = R, • RkajVk = a'V,-,' F.39)
ax V = ajRj x R*Vfc = Rj x R^V 4
V9
Здесь мы опять поступаем с V* как с обычными компонентами век-
вектора, однако перестановка по отношению к а\ как указывалось выше,
недопустима.
Чтобы формальные операции F.39) не потеряли смысл при их рас-
расшифровке в физических соотношениях, справа от операций F.39) обя-
обязательно должен стоять какой-либо тензор, вектор или скаляр.
Таким образом, "странные", на первый взгляд, операции умноже-
умножения F.39) являются вполне допустимыми и используются в дальней-
дальнейшем. Для них применяют следующие названия: правый градиент
вектора, правая дивергенция вектора и правый ротор вектора.
6.1.10. Нелинейные дифференциальные операции
над вектором
Все рассмотренные выше дифференциальные операции над векто-
вектором: V х а, V • а и def а - являются линейными, однако в механике
широко применяются и нелинейные дифференциальные операции.
Наибольшее распространение имеют четыре такие операции:
lef± (а) = def а ± J(V 0 а) • (V 0 а)т,
которые называют левым положительным (или отрицательным)
тензором деформаций над а и
ref± (а) = def а ± ^(V ® а)т • (V 0 а)
_____ §6.1. Ковариантное дифференцирование 409
правым положительным (или отрицательным) тензором деформа-
деформаций над а.
Компоненты этих тензоров в базисе R,- имеют следующий вид:
lef-t (a) = x(Vg-aj + Vja,- ± V,-afcVja )R* 0 RJ,
2
ref± (а) = i(Vfa, + Vj-a,- ± Vfca.V^a^R1' 0 R>.
Упражнения к § 6.1.
Упражнение 6.1.1. Используя формулы F.8) и F.13), а также результаты
упр.1.1.9, доказать, что символы Кристоффеля при переходе из системы координат
Xх в Х'% преобразуются следующим образом:
Q2 у/га
pfc — рк /лт s\n р/7 , и л рк
,jfc = Qmi Qnj Q kTfi;i
Упралснение 6.1.2. Используя формулу F.8), показать, что в цилиндри-
цилиндрической системе координат ненулевые символы Кристоффеля второго рода имеют
вид:
^ = r ¦ 21
¦*¦ 21 =
а ненулевые символы Кристоффеля первого рода имеют вид:
Tl22 = Г, Г221 = — Т.
Упражнение 6.1.3. Показать, что в сферической системе координат нену-
ненулевые символы Кристоффеля второго рода имеют вид:
Т\2 = -г, Г?3 = -г sin2 tf, Г§з = - « sin M>
а символы Кристоффеля первого рода имеют вид:
2,« - 1 2 •
Г221 = -г, Г3з1 = -г sin2 0, Г332 = - 2 r2 sin 2t9'
Г122 = г, Г133 = г sin219, Г2зз = g г2 sin M-
410-
Глава 6. Тензорный анализ
Упражнение в.1.4. Показать, что дифференциал скаляра <р(Хк) можно
представить в виде
dip = V(p • dx.
Упражнение 6.1.5. Показать, что в декартовой системе координат градиент
скаляра имеет вид:
а=1
Упражнение в. 1.6. Показать, что
V<g>x = E, V-x = 3, Vxx = 0.
Упражнение 6.1.7. Показать, что в декартовой системе координат формулы
F.18) для градиента, F.35) - для дивергенции и F.29) - для ротора вектора имеют
вид:
дак дсц
Vfl da=
rot a =
a=l
Упражнение 6.1.8. Показать, что ротор вектора F.29) можно представить
в виде символического определителя:
1
X
rot а = ——
л/9
Ri
Vi
ai
R2
v2
a2
R3
v3
где Vt- умножается на dj слева, а правый ротор F.39) - в виде:
axV =
Ri R2 R3
al a2 a3
Vi V2 V3
где Vt умножается на CLj справа.
§ 6.2. Дифференцирование тензоров второго ранга
6.2.1. Ковариантные производные тензора
Определим ковариантные производные тензора второго ранга.
Для этого вычислим производную от тензора Т(Хк)} заданного как
__ S 6.2. Дифференцирование тензоров второго ранга 411
функция от криволинейных координат Хк:
ш
R,- ® R,- = ЪГ'Ъ ® R,-. F.40)
Здесь введено обозначение ковариантной производной контравари-
антных компонент тензора второго ранга:
Ковариантные производные ковариантных компонент тензора
определяют как
дТ-
? TmjT?k - TimT?k, F.42)
а ковариантную производную смешанных компонент тензора следу-
следующим образом:
L ТрГ - ГтГ%. F.43)
Умножая ковариантные производные на обратную метрическую мат-
матрицу дктп, получим контравариантные производные:
F.44)
в.2.2. Дифференциал тензора
По аналогии с дифференциалом вектора определим дифференциал
тензора n-го ранга ЙПП, рассматривая его как приращение тензора
71П, обусловленное переходом из точки «M(X*) в близкую точку с ко-
координатами Xk + dXk:
*хкт F-45)
Используя формулу F.24), получим
Яп г)
<Гп = dx-Rk® —? = dx • V 0 ПП. F.46)
Здесь введено обозначение для градиента тензора n-го ранга
Яп о
V ® "П = Rfc ® ^j- = Vfcfl'^-'-R* ® R,- в ... в Rn. F.47)
412 Глава 6. Тензорный анализ
Теорема 6.3. Градиент тензора п-го ранга, определенный по
F.4V> представляет собой тензор (п -f 1)-го ранга, а ковариант-
ные VfcO11***'11 it контравариантные Vfcnfl*#*tn производные являются
компонентами этого тензора в соответствующих базисах.
Т Доказательство аналогично доказательству теоремы 6.3 и основано
на соотношении F.46). ^
В силу этой теоремы, ко- и контравариантные производные тензо-
тензоров при переходе из одной системы координат в другую преобразуются
по тензорному закону.
6.2.3. Дивергенция тензора
Определение 6.5. Дивергенцией тензора второго ранга
V • Т называют следующий вектор:
дТ
V • Т = R* . j^ = У,Т'>К, = div T. F.48)
Дивергенцию тензора с учетом F.41) и F.11) можно представить в
виде
V • Т =
*1
или иначе
V-T =
>- F-50)
Оба эти представления F.49) и F.50) часто используют в механике.
6.2.4. Ротор тензора
Определение 6.6. Ротор тензора второго ранга Т опреде-
определяют следующим образом:
V х Т = R1' х ^г = rot Т. F.51)
Используя формулу A.138) для векторного произведения вектора и
тензора, находим компоненты V х Т:
V х Т = 4=€°'* V«'Ti'R* ® R/ = у/9ЪкЧ'Т>!11к 0 R/. F.52)
у/9
§6.2. Дифференцирование тензоров второго ранга 413
в.2.5. Ковариантные производные метрической
матрицы
Если в качестве T{j выбрать метрическую матрицу </tJ, то из F.42)
и F.8) получим:
- 1 ki9mj A kj9rni -
dgkj dgki \ 1 / d9ij dgki dgkj \_
то есть
V^y = 0, V*^ = 0. F.54)
Отсюда и из A.38) следует, что
^^' = 0. F.55)
Таким образом, мы доказали следующую теорему.
Теорема 6.4 (Риччи). Ковариантная производная метрической
матрицы и ее определителя g равны нулю.
Из теоремы Риччи следует, что при всех операциях ковариантного
дифференцирования р,у, gxi и g можно считать константами и выно-
выносить из-под знака ковариантной (но не частной!) производной.
Упражнения к § 6.2.
Упражнение 6.2.1. Показать, что правый ротор тензора имеет следующие
компоненты:
В = Т х V = В1тК{ ® Rm = BimRi ® Rm,
Bim = y/getnikTi'V*, Bim =
V9
правая дивергенция тензора имеет компоненты:
а = Т • V = a'Ri = a'R,, a,- = Т{kVk, a1 = TikVk,
и правый градиент:
3П = Т ® V = O^R,- ® Rj ® Rfc, ^ ij
6.2.2. Используя формулу F.52), показать, что если Т - сим-
симметричный тензор, то двойная свертка его ротора с метрическим тензором дает
нуль:
414 Глава 6> Тензорный анализ
Упражнение 6.2.3. Используя формулы F.52) и F.31), показать, что если
П - кососимметричный тензор, то двойная свертка ?го ротора с метрическим
тензором выражается следующим образом:
/i(V x(l)EE..Vxfi = -2V • u>,
где LO - вектор, сопутствующий П.
§6.3. Свойства ковариантных производных
6.3.1. Ковариантное дифференцирование сумм
Из определения ковариантных производных F.17) и F.41) следует
аддитивность операции ковариантного дифференцирования:
F*56)
(Гт + Bim)Tjmk = VfcT^' + VfcB0', F.57)
mk
тоже самое относится, очевидно, ко всем другим комбинациям индек-
индексов.
Из аддитивности ковариантных производных следует аддитив-
аддитивность набла-оператора во всех рассмотренных операциях: градиенте,
дивергенции и роторе. Например, для векторов имеем:
V ® (а + Ъ) = V,-(aJ" + V)R{ <g> R, = V <g> а + V <g> b,
V x (a + b) = -Lcy*Vi{aj + bj)Rk = Vxa + Vxb, F.58)
y/9
( ) i() . b.
Аналогичные правила справедливы и для тензоров:
V ® (Т + В) = Vk(Tij + Bij)Rk <g> Rt- ® Rj = V <g> T + V ® B,
Vx(T + B) = VxT + VxB, F.59)
V • (T + B) = V • T + V • B.
§6.3. Свойства ковариантных производных 415'
6.3.2. Дифференцирование произведений вектора и
тензора на скаляр
Ковариантные производные произведения скаляра ф(Хк) на другой
скаляр <р(Хк), вектор а или тензор П вычисляют по формальным
правилам дифференцирования произведения классических функций.
В самом деле, согласно определениям F.15'), F.17) и F.41):
F.60)
тк + TimTjmk) = <рЧкТ** + Т*Чк<р.
Аналогичные формулы имеют место и для других комбинаций ин-
индексов.
Образуем теперь с помощью этих формул градиент произведения
скаляров:
F.61)
градиент, ротор и дивергенцию произведения скаляра на вектор:
V <g> ((ра) = Vk((pa{)Rk 0 R,- = Vtp 0 а + tpV ® а, F.62)
V х [<ра) = — e'^Vi^JR* =
V • (<pa) = Vt(^af) = V^> • а + <pV • a,
скаляр
, F.63)
а также градиент, ротор и дивергенцию произведения скаляра на тен-
тензор:
V • (<рТ) = V<p • Т + <pV • Т.
6.3.3. Дифференцирование произведений двух векторов
Вычислим, используя определение F.43), ковариантную производ-
производную от произведения компонент двух векторов а и Ь:
% + a'Vfc^. F.64)
Глава 6. Тензорный анализ
Используя эту формулу, найдем градиент скалярного произведения
двух векторов:
V(a • Ь) = Vk{a%)Rk = Чка{КкЬ{ +
= Vfca'R* 0 R, - bjRj + VkVRk 0 Rt • <цВ? =
= (V 0 а) • Ь + (V 0 Ь) • а. F.65)
Формально эту операцию можно было бы записать как V 0 (а • Ь),
однако для градиента скаляра знак тензорного произведения обычно
не используется.
Аналогично вычисляем градиент векторного произведения двух
векторов:
V 0 (а х Ь) = \?т{у/деука*Ы)Кт 0 R* =
= у/9Ък{{Чта')Ы WvmV)Rm- 0 R* =
= (V 0 а) х Ь - (V 0 Ь) х а. F.66)
Здесь использовано свойство F.28), а также свойство векторного про-
произведения тензора на вектор (см. упр. 1.4.7).
Вычислим теперь две возможные дивергенции векторного а х b и
тензорного a0b произведений (очевидно, что дивергенцию от скаляра
а • b образовать невозможно):
V • (а х Ь) =
=
= (V x a) - b - (V x b) • a, F.67)
а также
V • (a 0 b) = Vk{akbj)Rj = (Vkak)VRj + akVkVRj =
= (V • a) 0 b + a • V 0 b. F.67')
Наконец, вычислим два возможных ротора от векторного и тензор-
тензорного произведений векторов:
V х (а х Ь) = e'"''*eimnVt-(am6n)Rfc =
= ((Vna*Nn + a*Vn6n - bkVwam - a'V.-b*) Rk =
= b • V 0 а + a(V • b) - b(V • a) - a • V 0 b, F.68)
§ 6.3. Свойства ковариантных производных 417
здесь использованы определения векторного произведения A.33) и ро-
ротора F.30), а также свойство A.36) символов Леви-Чивиты;
V х (а 0 Ъ) = 4=*°'*^,-(а;Ьто)К* 0 Rm =
л/9
с(\?щ)Кк 0 bmRm - -Le^ajVibmRk 0 Rm =
л/9 л/9
= (V х а) 0 Ь - а х (V 0 Ь). F.69)
6.3.4. Дифференцирование произведений вектора на
тензор
Убедимся вначале, что правило ковариантного дифференцирования
формально сохраняется и для произведений компонент тензора Т и
вектора а:
a,-
= (VfcT'J)a, + Т^ка'. F.70)
Пользуясь этим правилом, вычислим градиенты от скалярного про-
произведения тензора на вектор:
V 0 (Т - а) = Vt(Tifcafc)R1' 0 R,- = (У,Г^)К1' 0 R,- 0 Rfc • amRm+
+ V.-afcR1' 0 TjkKj = (V 0 T) • а + (V 0 а) . Тт, F.71)
и
V 0 (а - Т) = V.VTj^R' ® Rfc = V.-o^R1" 0 Kj • TmfcRm 0 R*+
+ V.Tj-fcR1' 0 Rk 0 Rj • amRm = (V 0 a) • T + (V 0 TT) • a. F.72)
Вычислим дивергенцию от скалярного произведения тензора на
вектор:
V • (Т • а) = V,(Iu.afc) = (V,-Ta>fc + T'fcV,afc =
= (V-T)-a + T--(V®a)T, F.73)
V • (a • T) = Vi{akTki) = (V • TT) • a + T • -V 0 a,
и дивергенцию от векторного произведения:
V . (Т х а) = Vi(> pj
л/9
L = (V • Т) х а + (Тт • V) х а, (Q.74)
+
л/9
14 Тензорное исчисление
418 Глава 6. Тензорный анализ
V . (а х Т) = V,- (-^€
_ 1 ^(ViTjk)Rkam = (V x а) • T - а • (V х Т). F.75)
у/9
Здесь использовано формальное определение набла-оператора как век-
вектора, а также формулы F.51) для ротора тензора.
Вычислим также роторы от скалярного произведения тензора на
вектор:
V х (Т • а) = ^
V9
= (V хТ)-а-(Тх V)T-a, F.76)
V x (a-T) = -Le'i'v.-KT? )R* = --^-e^T'] V,omRfc+
y/9 V9
+ _Le*i* (v,-T7 )Rfcam = (V k TT) • a - (TT x V) • a, F.77)
и роторы от векторного произведения тензора на вектор:
V х (Т х а) = €y*€/m«V,-B}mon)Rfc ® R1 =
= ^е/то„ (^ey*V«TiW) a"R* ® R' "
x a"Rfc ® R' = (V x T) x а - (TT x V) x a, F.78)
V x (a x T) = e''fcemnjV,(amr; )Rk ® R; =
= (-VroamTfc, + V.-o'T*, - a1'V,Tfc, + akViT,) Rfc ® R' =
= -(V • a)T + (V®a)-T-a-V®T + a®V-T. F.79)
Эти правила широко используют при безиндексной записи уравнений
механики.
§ &.4. Ковариантные производные второго порядка 419
6.3.5. Дифференцирование произведения тензоров
Рассмотрим два тензора Т и В и покажем, что ковариантные про-
производные от произведений их компонент также вычисляются по пра-
правилам формального дифференцирования произведения классических
функций:
^Г;Втп ) + (Г) It - Т\Т^)Втп +
+ T) (В>пГ?к - В"! T'km) = (УЛГу )Bmn + Г,- VkBmn . F.80)
Свертывая по индексам j и га, получаем отсюда, в частности:
* * F.81)
Вычисляя теперь с помощью F.81) дивергенцию от скалярного про-
произведения Т • В:
V • (Т • В) = V*(T*- Bjn)Rn = (VkT) )BjnRn + T) VkBjnRn =
= (VfcT*. )Rj • B'nRs <g> Rn + T) Rj <g> Rfc • -У,Б*ПК* <g> Rm ® Rn =
= (V • T). В + TT ..V 0 B, F.82)
получаем компоненты вектора.
§ 6.4. Ковариантные производные второго порядка
6.4.1. Двукратное дифференцирование скаляров
Рассмотрим теперь операцию двукратного ковариантного диффе-
дифференцирования, и начнем с двукратного применения набла-оператора
к скалярному полю <р(Хк).
Однократное применение оператора V к <р приводит к градиенту
скаляра F.14), представляющего собой векторный объект, поэтому
при повторном применении V возникнут три объекта: градиент от
градиента, дивергенция от градиента и ротор от градиента. Рас-
Рассмотрим первый случай:
л / а.- \
F.83)
Дифференцируя произведение в скобках по частям, получаем с уче-
учетом F.3) выражение для градиента от градиента скаляра:
420 Глава 6. Тензорный анализ
представляющего собой симметричный тензор второго ранга. Если в
определении F.83) использовать обозначение F.15') и F.21) для кова-
риантных прозводных, то получим альтернативное F.84) представле-
представление:
= R* 0 A" (Vk<pRk) = V,(V^)R* ® R*. F.85)
Сравнивая F.85) и F.84), находим выражение для вторых ковари-
антных производных скаляра:
В силу того, что первая ковариантная производная скаляра совпадает
с частной прозводной (см. формулу F.15')), мы получили правило не-
независимости вторых ковариантных производных скаляра от порядка
дифференцирования.
Дивергенцию от градиента скаляра определим следующим обра-
образом:
Дифференцируя по частям выражение в скобках, получаем:
T
F*88)
т.е. эта операция образует скаляр, называемый часто лапласианом
над (р. Запись лапласиана через ковариантные производные имеет
следующий вид:
VV = V • V^ = If • A- {Vk<pRk) =
= V.V^R' • Rfc = V.-VV = VV,^. F.89)
Ротор от градиента скаляра вычисляют следующим образом:
Переходя к ковариантным производным, получаем:
V х V<p = -L€«i*v.-V^Rfc = 0, F.91)
/9
§6.4. Ковариантные производные второго порядка 421
так как символ Леви-Чивиты сворачивается по двум индексам с сим-
симметричным тензором V,-Vj9? (см. A.37)), т.е. ротор от градиента
скаляра всегда равен нулю.
6.4.2. Двукратное дифференцирование векторов
Двукратное применение набла-оператора V к вектору а приводит
к образованию различных тензоров:
A,VG{®,x,-}, F.92)
в зависимости от сочетания знаков операций Л и V тензорного, вектор-
векторного и скалярного умножения (здесь Л не является знаком внешнего
умножения).
Переходя в F.92) сначала для одного набла-оператора, а затем для
другого к ковариантным производным, с учетом F.16) и F.47) полу-
получим:
F.93)
- представление в тензорном базисе набла-операции второго порядка
над вектором.
Теорема 6.5. В пространстве М3 ковариантные производные от
компонент вектора и, вообще, тензора любого ранга являются пе-
перестановочными при двукратном дифференцировании:
1-1'». F.94)
Т Образуем разность ковариантных производных:
ViVfcfl1-1"* - VfcV.-n'1-1'* = Mikil'"in.
В декартовой системе координат всегда имеем Mik%l"'*n = 0, так как в
ней Г^ = 0, и ковариантные производные совпадают с частными. Но
согласно теореме 6.3, ковариантные производные тензоров являются
компонентами тензора, тогда в произвольной системе координат Xх
имеем
JLf «l...«n __ /)»' f)k' pt'i ptn «f
Mik — Ч хЧ к r ,-j • • •r t'n
«1—fn __
откуда следует F.94). ^
Рассмотрим наиболее часто используемые сочетания операций Л и
V в F.93).
422 Глава 6. Тензорный анализ
Дивергенцию от градиента вектора получим, если в F.93) знак Л
заменим на " •", знак V на 0:
Да = V • V 0 а = V.-VfcOfR1' • R* 0 Rj = V, Уо/КЛ F.95)
В результате получаем вектор, для которого используется также на-
название лапласиан вектора.
Градиент от дивергенции вектора получаем при обратном соче-
сочетании знаков скалярного и тензорного произведений:
V <8> V • а = V.-Vtaj-R1' 0 R* • Rj = VtVfca*Rt-. F.96)
Ротор от ротора вектора получаем из F.93), выбрав в качестве
V и Л знак векторного произведения:
V х (V х а) = V.-VfcayR1' x (R* x Rj) =
= -L^^V.-Vfcaj-R1" х Rm = ек>те{тпЧ*ЧкцКп. F.97)
у/9
Используя свойство A.36) символов Леви-Чивиты, а также F.95) и
F.96), получаем:
rot rot а = V х (V х а) = E*5? - 8*8*п)ЧкЧ*а;Кп =
= Vn V'aj-R" - V.-Va^R1' = V 0 V • а - Да. F.98)
Дивергенция от ротора вектора всегда дает нуль:
div rot а = V • (V х а) = V.-VfcdjR1' • (R* x R') =
л/9 y/Q
в силу свойства F.94) перестановочности ковариантных производных
и свойства A.37).
Ротор от градиента вектора также есть нулевой тензор:
V х V 0 а = Vt-V^R1' xRk® Rj = -^-€tfciVt-ЧыцИт 0 Rj = О,
у/9
F.100)
в силу того же свойства A.37) символов Леви-Чивиты, свернутых по
двум индексам с симметричными производными V,-Vfc.
При перестановке операций получаем уже ненулевой тензор - гра-
градиент от ротора вектора:
V 0 V х а = ViVfcaj-R1" 0 R* x R»' = -iz6fci-VtVfcaiRm. F.101)
у/9
§ 6.4. Ковариантные производные второго порядка 423
в.4.3. Двукратное дифференцирование тензоров
второго ранга
Двукратное применение набла-оператора к тензору второго ранга
Т приводит к образованию следующих тензорных объектов:
V Л VV Т = R* Л -?-? (кк V j?A Л, V Е {0, х,.}, F.102)
с различными сочетаниями знаков операций Л и V.
Общее базисное представление этих тензоров имеет следующий
вид:
V Л VV Т = ViVfcTj-mR1" Л R* V Rj <g> Rm. F.103)
Градиент от дивергенции тензора представляет собой снова тен-
тензор второго ранга:
V 0 V • Т = V.VfcT^R1' 0 Rm.
Тензорами второго ранга также являются дивергенция от гради-
градиента тензора^ называемая лапласианом тензора:
AT = V • V 0 Т = V.-V'Tj-mR1' 0 Rm, F.104)
и ротор от ротора тензора:
V х (V х Т) = VtVfcTimR'' х (R* х W) 0 Rm =
= ек'пеш V VfcTimR* 0 Rm. F.105)
Используя свойство A.36) символов Леви-Чивиты, получаем, что
V х (V х Т) = {5k5j - SfSijV'VkTjmR* 0 Rm = VjV$TjmRs 0 Rm-
- V* VfcT,mR* 0 Rm = V 0 V • T - AT. F.106)
Важную роль в механике играет несовместность тензора Т:
Ink Т = V х (V х Т)т = -eijkemnlViVmTjnRk 0 R/, F.107)
являющаяся тензором второго ранга.
Дивергенция от ротора тензора аналогично F.99) образует нуле-
нулевой вектор:
div rot T = V • (V х Т) = VtVfcTimR* • (Rk x Rj) 0 Rw =
= 4=**inVnV*TimRTO = 0. F.108)
424 Глава 6. Тензорный анализ
Перестановка операций в F.108) приводит к ротору от диверген-
дивергенции тензора:
V х (V • Т) = V.-Vfcl* R1' х Rm = -L€imjVtVfcT^RJ'. F.109)
л/9
В отличие от вектора, для тензора определена операция дивергенции
от дивергенции, образующая скаляр:
div div T = V • (V • Т) = V, VfcT'*. F.110)
Упражнения к § 6.4.
Упражнение в.4.1. Используя формулы F.93) и F.95), показать, что
V • (V <g> а)т = V 0 V • а.
Упражнение 6.4.2. Доказать, что для ротора от ротора вектора порядок
следования операций существенен и
(V х V) ха = 0.
Упражнение 6.4.3. Доказать, что
E-.VxV<8>T = Vx V/i(T) = 0, /i(T) = E • -Т.
Упражнение 6.4.4. Доказать, что
Е • -V 0 V <g> T = V.-Vfc/iOTJR1" <8> R*.
Упражнение 6.4.5. Показать, что тензор Ink T, определяемый по F.107),
является симметричным, если симметричен Т.
§ 6.5. Дифференцирование в ортогональных
криволинейных координатах
6.5.1. Символы Кристоффеля второго рода
в ортогональных координатах
Криволинейные ортогональные координаты Xх часто применяют
при решении различных задач механики. В этом случае переходят
от безиндексной записи уравнений к компонентной. Поэтому полезно
записать основные дифференциальные операторы, введенные выше, в
ортогональных координатах Xх. Начнем с символов Кристоффеля.
§6.5. Дифференцирование в ортогональных координатах 425
Если Xх ортогональны, то дц и дх* - диагональны (см. §1.7), и
формулы F.8) для символов Кристоффеля примут вид:
г<* - ^а (9кр , dgkg dgQp\ __ 1 QQdgQQ /
а"" 2д \дх« + дх? дх><)- 2д эхр ' t
а^/3, а,/3= 1,2,3,
Т.К. <5fa/3 = 0.
Напомним, что по повторяющимся греческим буквам суммирования
нет. Переходя к параметрам Ламе gQQ = if^, gQQ = I/^q? получаем:
Г^ = -L-Z^l?L = _Г±1?.. F.112)
При другом сочетании индексов получим:
F.113)
При полностью совпадающих индексах из F.8) имеем:
dgQQ\ _ 1 ааддаа __ I dHQ
)д -^J^^
При всех неравных индексах символы Кристоффеля равны нулю:
-°- FЛ15)
Итак, получили следующие выражения для символов Кристоффеля
второго рода:
_ 1 дНа _ Нр дНр _ 1 дНа /
_ 1 дНа _ Нр дНр _
426 Глава 6. Тензорный анализ
в.5.2. Производные от векторов ортонормированного
базиса
Часто в различных задачах механики необходимо иметь значения
прозводных от векторов ортонормированного базиса: деа/дХ^. Вы-
Вычислим их, используя определения A.233) и F.1):
deQ д /Ra\ I 3Ra I
на) щ
(= JL
эх? \на) щ ex? на
Используем теперь свойства F.116) символов Кристоффеля:
деа _ (га 1 дНЛ 1 - 1 _ 1 дЩ
дХ? ~Уае~н: дХ? ) HQKa + l a^H~aP ~ НаЩдХ"^
F.118)
^4 ^v \ -w^ ^^O
dxa
l и л. а ± и IIQ
Слагаемые в скобках равны нулю в силу F.116). Возвращаясь снова
к ортонормированному базису, имеем окончательно:
dHa
дх?
Обе эти формулы, очевидно, можно объединить в одну:
в.5.3. Дифференциальные операции с векторами
в ортогональных координатах
Вектор а, согласно A.237), всегда можно представить в ортонор-
мированном базисе еа:
з
а = a'R,- = ]Г афаеа, аа = афа/На. F.121)
а=1
§ 6.5. Дифференцирование в ортогональных координатах 427
А* Градиент вектора
Запишем формулу F.21) для градиента вектора V ® а в базисе еа,
используя A.235), F.121):
дХа
е"®!й7- FЛ22)
а,/3=1 а а,7=1
Во вторую сумму подставим формулу F.120), поменяв в ней предва-
предварительно индексы круговой перестановкой: а —у 7> P —* а> 7 —^ &•>
тогда получим:
F.123)
Учитывая свойство символа ?а-р получаем окончательно:
7
F.124)
Для дальнейшего анализа введем следующие обозначения:
афа дНа _ 1 у-
ЖЩШ* a = Z^
тогда компоненты градиента вектора можно представить в следую-
следующем виде:
з
V<g>a= Y1 (аа0 + <*а02а)ев®е0. F.126)
а,/3 = 1
Б. Ротор вектора
Приведенный выше для градиента вектора вывод полностью со-
сохраняется, если знак ® заменить на знак векторного произведения х,
поэтому для ротора вектора имеем:
а,/3=1
428 Глава 6. Тензорный анализ
Поскольку еа х еа = 0, а еа х е^з = е7 (а,/3,7 образуют четную
подстановку), то в этой сумме ненулевыми являются слагаемые толь-
только при а ф /3. Это означает, что второе слагаемое в скобках вообще
пропадает. Тогда
з
V х а = Z) (а«Р ~ аР°) е7> афрф-уфа, F.128)
7=1
где при каждом 7 индексы а,/?,7 образуют четную подстановку.
Подставляя вместо аар их выражения F.125), после приведения по-
подобных получаем окончательно:
Fm)
В. Дивергенция вектора
Для дивергенции воспользуемся формулой F.36), а также A.231),
в результате получим:
Г. Лапласиан скаляра
Если в формуле F.130) в качестве а выбрать градиент скаляра
а = VV>, то получим формулу для лапласиана скаляра:
Д. Линейный тензор деформаций над а
Используя определение F.33) линейного тензора деформаций над
вектором а и складывая формулу F.126) со своей транспонированной,
получаем:
Гв.)Т) = 1 у („„ + «„ +26,а)е ®е,
а,/3=1
F.132)
§ 6.5. Дифференцирование в ортогональных координатах 429
Если обозначить физические компоненты этого тензора как ?а/з, то с
учетом обозначений F.125) получим:
з
е = У j ?a^ea®e0, F.133)
а,/3=1
где
ф 1 дафа 1 дНа 1 дНд
ф
аа ~ на дх? + нанр ех^а^ + нащ dx-iа<5п"
((
щ дхр \нJ + на дхр{ нр
Е. Левые тензоры деформаций над a
Получим представление нелинейных дифференциальных операто-
операторов, определенных в п.6.1.10, в частности левых тензоров деформаций
над а. Для этого вычислим скалярное произведение градиента F.124)
на свой транспонированный:
(V ® а) - (V ® а)т =
з з
= ]Г (аа/з + SapaQ)eQ <g> e^ • ]Г (аер + 5?ра?)ер ® е? =
а,/3 = 1 е,р=1
3
^а^ + ^а»? + Яаа?а + 8Q?a>l I еа ® ее. F.135)
=1
Складывая этот тензор с линейным тензором деформаций, получаем
окончательно:
lef±(a) = def а ± -(V 0 а) • (V 0 а)т =
1 3
7=1
F.136)
430 Глава 6. Тензорный анализ
Ж. Правые тензоры деформаций над а
Аналогичным образом вычисляем вначале вспомогательный тен-
тензор:
з
аа0 + S<*pa<*)ep ® еа • ]Г (а?р + 8?ра?)е? 0 ер =
а,/3=1 е,р=1
3
( e^ ® ер, F.137)
/3,р=1 \а=1 /
а затем находим правые тензоры деформаций:
ref±(a) = def а ± -(V ® а)т • (V 0 а) =
- 3 3
= - 22 (аа/з + а/За + 2SQpaQ ±
а,/3=1
+ аа/з^а + а^аа^ + 2Ja^3^J jea ® e^. F.138)
7=1
в.5.4. Дифференциальные операции с тензорами
в ортогональных координатах
Согласно A.237), тензор второго ранга в ортогональном базисе име-
имеет вид:
Т = Т*Ъ ® Rj = У) Тфа/}еа 3
-А. Дивергенция тензора
Вычислим наиболее часто применяемую в механике операцию - ди-
дивергенцию тензора в базисе еа. Воспользуемся формулой F.49):
?
• <6ЛМ»
jj 6.5. Дифференцирование в ортогональных координатах 431
А = tfi#itf3.
Преобразуем это выражение с учетом формулы F.120) дифферен-
дифференцирования векторов базиса е^, в результате получим:
1 Л д (А \ 1 X А / 1 8На
!>7е7, F.140)
7=1
где
{ дх<* [на 1ау + нщ V
F.140')
Если расписать все девять слагаемых в сумме F.140), то выраже-
выражение F.140') можно также представить в виде:
1 / Л
hl = А \дХ
' (б
аа + НаШ
(два слагаемых в F.140) в круглых скобках при а = 7 взаимно уни-
уничтожаются).
J5. Лапласиан вектора
Выберем теперь в качестве тензора Т градиент вектора Т = V<g>a,
дивергенция такого тензора дает лапласиан вектора а. Найдем его
компоненты в базисе еа:
= ]P c7e7.
7e7.
7=1
Используя формулу F.140), где в качестве Та1 следует взять
7 + йа-уйси получаем
{HHZ) ±Р±±а- FЛ42)
432
Глава 6. Тензорный анализ
Упражнения к § 6.5.
Упражнение 6.5.1. Используя формулу F.120) и результаты упр.1.6.1, по-
показать, что для цилиндрической системы координат отличны от нуля только сле-
следующие производные от векторов ортонормированного (физического) базиса:
дег
деф
для сферической системы - следующие:
дег дег
е
Те
= —er
деф
де# деф
Упражнение 6.5.2. Показать, что формула F.129) для ротора вектора мо-
может быть записана в виде символического определителя:
1
д/дх1 д/дх* д/дх3
Н2аф2 Я3аф3
rot a =
Упражнение 6.5.З. Показать, что формула F.129) для ротора в цилиндри-
цилиндрических координатах имеет вид:
даг
а в сферических - следующий вид:
V х а -
^ е
дф) г
1/1 даг д(гат)
д{га-в) даг
Упражнение 6.5.4. Показать, что формула F.130) для дивергенции в ци-
цилиндрической системе координат имеет вид:
_ 1 д , ч 1 даф daz
V • а = -—{гаг) + -—f- + -^-,
гдгх ; г дф dz
а в сферической системе координат - следующий вид:
д ( • о ч даф\
г2 дгк }
rsintf
+
§6.5. Дифференцирование в ортогональных координатах 433
Упражнение 6.5.5. Показать, что формула F.131) для лапласиана скаляра
ф в цилиндрической системе координат имеет вид:
1 д ( дф\ 1 д2ф д2ф
г2 дф dz2 '
а в сферической системе координат - следующий вид:
дф\ 13/. дф\ 1 д2ф\
дг ) sin д дд \ дд ) sin2 д дф2 )
Упражнение 6.5.в. Показать, что формулы F.134) для компонент линейного
тензора деформаций SQp в цилиндрической системе координат имеют вид:
даг 1 дпф аг да2 да2 даг
дг ^ г дф г dz dr dz
а в сферической системе координат - следующий вид:
даг 1 да$ аг
?гг — —— Sflfl ^^ Г~Г Г ч
от г ov r
__ 1 даф аг cLectgd _ 1 даг
vv rsmd дф г г г дд дг
дг rsind дф г
1
rsmd дф г дд г
Упражнение 6.5.7. Показать, что в цилиндрической системе координат
формулы F.140 ) для компонент 0-у дивергенции тензора второго ранга Т имеют
вид:
_ 1 дгТ„ 1 дТфГ дТ1Г Тфф
г ~ г дг г дф dz r '
_ 1 дгТГф 1 дТфф дТ,ф Тфг
^ г or г дф dz т
__ 1дгТГ2 t 1дТфх dTzz
Vz — п I 7Г~1 I п ?
г or г дф dz
434.
Глава 6. Тензорный анализ
а в сферической системе координат - следующий вид:
1д 2 1 ( 9 (.,т ,,дТф
г2 or rsmv \ov
+
(
г2 дг
dfl ф J
6.5.8. Показать, что в цилиндрической системе координат
матрица аар F.125) и па имеют вид:
*) =
/«11
/
«21
I
«12
«22
«32
«23 I =
«33/
/ даг
1 дат а±
дат
даф
~дг
' гЖ
daz \
гЖ
Si = 0, a2 = aT/r, a3 = 0,
а в сферической системе координат - следующий вид:
К/з) =
\д
даг
да#
дг
да± ч
д
\ г sin ti
а^ 1 да
г г sin tf ~B
аг = 0, а2 = аг/г, й3 = [ar/r) + (a#/r)ctg д.
Упражнение 6.5.9. Используя результаты упр.6.5.8 и формулу F.136), по-
показать, что компоненты левого тензора деформаций L = 1е?± (а) в цилиндри-
цилиндрической системе координат имеют вид:
9а
да
г± _1Эо0 аг 1 //д«г
§ 6.5. Дифференцирование в ортогональных координатах 435
2 (даЛ2 (даА2\
± _ да2 1 ((даА2 (даЛ2 (да
f 1 даг д /о>ф\\ 1 /даг .даг
дпф /даф \ daz daz\
± -
Г2 " 2 \"зГ +17) 21 + +
а в сферической — следующий вид: '
даЛ2 ,(даф\2
) +Ы
2
I +
436 Глава 6. Тензорный анализ
даг
¦г— (-4 I ±
¦д +
1 /flar / 1 даг аф\ да* ( 1
2r\dr \rsind дф r ) dr Vsintf
Упражнение 6.5.10. Используя результаты упр.6.5.9 и формулу F.138),
показать, что компоненты правого тензора деформаций R = ref-f- (а) в цилинд-
цилиндрической системе координат имеют вид:
и± _ даг . 1 1(даЛ\ Aдаг аф\2 (даЛ2\
Кгг ~ ~fo * 2 \\~fc ) +{г1ф~Т) +\д1) )'
даф\2
2агдаф (аг\\
г2 дф \г ) )'
± _ 1 /5аг 5 /аф\\ 1 (дат даф
г*~ 2\дф + дг\г)) 2\дгК дг~
go^, даг ат даг \
dz dz "г2 дфГ
§ 6.5. Дифференцирование в ортогональных координатах 437
± _ 1 /во, даЛ
гг ~ 2 V dz + дг )
1 /даг daz I /3ar -. даг даг да2 \
а в сферической - следующий вид:
даг 1 ( 2(даЛ2 (даг V
\sini
даг
>-дф~пф
l_daL ±(<±\\
г д$ +Гдг\г))±
1 / 2 даг дав | да.0 (даг
± 1 ,2^ + ^^ +
2г2 V дг дг дд к дд '
438 Глава 6. Тензорный анализ
Д ( .
дг\г))
( _ s даф
2т-2 v дг дг + ^ а^ tf;
/ 1 да2 w 1 даф .
ГЛАВА 7
ГЕОМЕТРИЯ КРИВЫХ И ПОВЕРХНОСТЕЙ
§ 7.1. Кривые в трехмерном евклидовом
пространстве
7.1.1. Способы задания кривых
Данная глава посвящена тензорному описанию кривых и поверх-
поверхностей в пространстве Ш3.
Напомним, что положение одной точки М в трехмерном евкли-
евклидовом пространстве в гл.1 определялось с помощью радиуса-вектора
Определение 7.1. Кривой С в Ш3 называют непрерывное ото-
отображение отрезка [?1^2] из R1 в пространство Ш3, т.е. С : [?1^2] G
3
Иначе говоря, множество точек, об-
образующих кривую С в трехмерном
евклидовом пространстве, определя-
определяется с помощью вектор-функции
(рис.7.1):
или трех обычных функций:.
от одного аргумента, где ? - некото-
Рый параметр (не обязательно вре-
мя)- Такой спосо6 определения кри-
вой в прострайстве называется пара-
параметрическим.
Понятие непрерывности отображения С уместно, поскольку в ев-
евклидовом пространстве Ш3 определена метрика (т.е. расстояние меж-
между точками). Тогда xl(?) являются непрерывными числовыми функ-
функциями.
Кривую С можно также задать с помощью двух функций от трех
Рис. 7.1. К определению кривой
d пространстве М3
440 Глава 7. Геометрия кривых и поверхностей
аргументов - координат х1:
*^> = 0' G.2)
Такой способ называется неявным.
Если кривые являются гладкими (непрерывными и без изломов), то
вектор-функции G.1) или функции G.2) являются непрерывно диффе-
дифференцируемыми, по крайней мере один раз.
В дальнейшем будем предполагать существование и непрерывность
тех производных, о которых говорится в тексте.
За положительное направление кривой ?, по определению, выбира-
выбираем направление, соответствующее возрастанию параметра ?.
7.1.2* Длина дуги кривой
Две соседние точки М и М! с радиусами-векторами х(?) и х(? -Н
Д?), находящиеся на кривой ?, соединены малым вектором Ах
(рис.7.2):
х@- G.3)
XJ
Устремляя Д? —> О, получим эле-
jy( dx ментарный радиус-вектор dx, ко-
"""" ' ' торый связывает бесконечно близ-
близкие точки М. и М! на кривой С.
Из определения dx следует, что он
направлен по касательной к кри-
кривой С. Также по касательной к С
->. направлен и вектор скорости дви-
2 жения по кривой dx/d^.
Длина элементарного вектора |dx|
численно равна расстоянию ds
между бесконечно близкими точка-
точками М и М! на кривой С:
Рис. 7.2. К определению длины
дуги кривой ds = \dx\ = (dx • dxI/2, G.4)
величина ds называется элементарной длиной дуги кривой С.
Очевидно, что ds является функцией параметра ?, тогда можно
определить функцию s(?) как
= /
G.5)
^ §7.1. Кривые в евклидовом пространстве 441
называемую длиной дуги кривой ?, которая соединяет точки Aio и М.
(расположенные на кривой С уже произвольным образом) с радиуса-
радиусами-векторами х(?0) и х(?).
Подставляя G.4) в G.5), получаем явное представление для длины
дуги:
7.1.3. Векторные характеристики кривой
Элементарную длину дуги ds G.4) можно записать в ином виде:
<Ь = \щ\<Ц. G.7)
С помощью этого соотношения между дифференциалами ds и d?,
можно перейти от параметра ?, характеризующего движение по кри-
кривой ?, к параметру з - длине дуги.
Тогда все характеристики кривой можно рассматривать как функ-
функции длины дуги з. Например, само задание кривой в виде G.1) можно
представить следующим образом:
Х = х(«), 8!^ 8^82, G.8)
или
х* = *'•(*),
где справа стоят, конечно, уже другие функции по сравнению с G.1).
Также от вектора скорости движения по кривой (dx/d?) можно пере-
перейти к вектору (dx/ds):
%
Вектор
t = dx/ds G.10)
называется единичным вектором касательной к кривой ?. Также как
и (dx/c^), он направлен по касательной к ?, и в силу соотношения
М-?-?¦'. P.U)
действительно имеет единичную длину.
Дифференцируя вектор t по з, получаем
442 Глава 7. Геометрия кривых и поверхностей
- вектор кривизны кривой ?.
Этот вектор ортогонален вектору t. В самом деле, дифференцируя
по з соотношение t • t = 1, имеем
откуда, в силу независимости скалярного произведения от порядка
множителей, получаем:
rc-t = 0. G.14)
Поскольку t направлен по касательной к кривой С в некоторой точке
М, то вектор л, в силу G.13), направлен по нормали к ? в той же
точке.
Определение 7.2. Кривизной кривой С в точке Ad называ-
называют длину вектора к в этой точке и обозначают как к.
Выражение для к через декартовы координаты, согласно G.12) и
G.8), имеет вид:
Величина
Д=1/* G.16)
называется радиусом кривизны кривой С в точке АЛ. Из определений
G.15) и G.16) ясно, что к и R - всегда неотрицательны.
Единичный вектор
v = Rk, G.17)
называется вектором главной нормали к кривой.
С помощью v и t можно построить вектор
b = txi^, G.18)
называемый единичным вектором бинормали. В силу свойства A.49)
векторного произведения, он ортогонален t и v, и в силу A.50) дейст-
действительно имеет единичную длину.
В силу свойств (см. упр.1.2.7) векторного произведения, из G.18)
следуют также формулы:
и = -t х Ь, t = i/xb. G.18')
§ 7.1. Кривые в евклидовом пространстве
.443
7.1.4. Сопровождающий трехгранник
Рис» 7.3. Сопровождающий трехгран-
трехгранник пространственной кривой С
Таким образом, в каждой точ-
точке М кривой С имеется три
взаимно ортогональных еди-
единичных вектораt,i/Hb, кото-
которые образуют тройку векто-
векторов, называемых сопровож-
сопровождающим трехгранником про-
пространственной кривой С
(рис. 7.3).
При движении вдоль кривой
С сопровождающий трехгран-
трехгранник движется как твердое те-
тело.
Определение 7.3. Плоскость, проходящую через точку М. кри-
кривой С и содержащую векторы t ии, называют соприкасающей-
соприкасающейся; плоскость, содержащую векторы tub, называют спрямляю-
спрямляющей, а плоскость, содержащую векторы и иЬ, — нормальной.
7.1.5. Кручение кривой
Если вся кривая С лежит в одной плоскости (плоская кривая), то
эта плоскость совпадает с соприкасающейся плоскостью.
Для плоской кривой единичный вектор бинормали b постоянен, т.е.
не меняет не толькб единичную длину, но и направление, поэтому
db/ds = 0.
Для неплоской кривой эта производная отлична от нуля: db/ds ф
0, и характеризует отклонение кривой от плоской формы. Поэтому
вектор
т = db/ds G.19)
называют вектором кручения.
Дифференцируя G.18), с учетом G.12), G.19) получаем:
—
T-KXV+tX—.
Так как векторы к и и по G.17) - коллинеарны,
. А/
т = t х -—.
G.20)
= 0, поэтому
G.21)
По свойству векторного произведения из G.21) следует, что т ортого-
ортогонален вектору t. С другой стороны, поскольку b - единичный вектор,
444 Глава 7. Геометрия крирых и поверхностей
то дифференцируя соотношение b • b = 1, получим аналогично G.13)
и G.14), что b ортогонален dh/ds = т. Таким образом, т ортогонален
b и t, следовательно, коллинеарен вектору нормали и:
т = -ти, G.22)
где т - коэффициент пропорциональности.
Определение 7.4. Коэффициент пропорциональности г между
вектором кручения т и вектором и главной нормали к кривой С,
взятый с обратным знаком называют кручением кривой С.
В отличие от кривизны &, кручение г может быть как положитель-
положительным, так и отрицательным. Обратная к нему величина
RT = 1/г
называется радиусом кручения.
Получим выражение для кручения т.
Умножая G.22) скалярно на и, имеем с учетом G.21):
"- (?-2з)
Подставим сюда вместо и его выражение G.17) через вектор кривизны
к,:
dlRk) n fdR „*Л „
г = -t х , } • Rk, = -t х —к + Л-г- • Rk =
ds \ds ds)
Л. G.24)
= R^(tXK)KR(tx ^
ds \ ds
Так как вектор (t x к) ортогонален гс, то первое слагаемое в G.24) рав-
равно нулю. Во втором слагаемом в G.24) согласно свойству смешанного
произведения векторов (см. упр.1.2.6) получим:
r = tf(tx«).^. G.25)
ds
Подставляя вместо t и к их выражения G.10), G.12) через радиусы-
векторы к, имеем
§7.1. Кривые в евклидовом пространстве 445
Заметим, что смешанное произведение в G.26) представляет собой
объем параллелепипеда, построенного на векторах ^, ^f и ^f, поэ-
поэтому G.26) можно представить в виде:
G-26;)
7.1.6. Формулы Френе
Формулы Френе-Серре позволяют выразить производные от векто-
векторов сопровождающего трехгранника через сами векторы t, b и и. Из
G.12) и G.17) следует первая формула Френе-Серре:
^ = ки. G.27)
аз
Из G.19) и G.22) вытекает вторая формула Френе:
Дифференцируя первую формулу G.18') с учетом G.27) и G.28),
получаем:
dv
— = -ки xb + rtx^. G.29)
as
Еще раз используя формулы G.18) и G.18'), получаем третью форму-
формулу Френе-Серре:
^ = -kt + тЪ. G.30)
аз
На формулы Френе-Серре G.27), G.28), G.30) можно смотреть как
на дифференциальные уравнения относительно векторов t, и и Ь, тог-
тогда если известны две функции
к = fc(s), t = t(s), 5o^3^3i, G.31)
то с помощью формул Френе-Серре можно полностью определить кри-
кривую С с точностью до положения в пространстве.
Такой способ задания кривой С называют естественным.
7.1.7. Механический смысл формул Френе
Рассмотрим движение по кривой С от точки s = з0. Если при дви-
движении длину дуги s трактовать как "время", то величины (dt/ds),
[dh/ds) и [du/ds) - есть "скорости" изменения векторов сопровожда-
сопровождающего трехгранника.
446.
Глава 7. Геометрия кривых и поверхностей
Согласно первой формуле Френе
G.27) за малое "время" Аз измене-
изменение вектора t на величину
At =
происходит в направлении нормали
и. Кроме того, вектор At, представ-
представляющий собой разность
t(S+AS)
Рис. 7.4' К определению меха-
механического смысла формул Френе
пересекает касательную с направля-
направляющим вектором t(s). Отсюда следу-
следует, что At лежит в соприкасающейся
плоскости, содержащей векторы и и
t(s) и ортогональной вектору бинор-
бинормали b (рис.7.4).
Иначе говоря, в течение малого "времени" Аз изменение вектора
касательной t происходит путем вращения в спрямляющей плоскости,
т.е. вокруг оси бинормали Ь(з), называемой мгновенным положением
бинормали.
Абсолютная угловая скорость этого вращения \(dt/ds)\ согласно
G.27) равна кривизне:
Совершенно аналогично из второй формулы Френе G.28) можно
показать, что бинормаль b в течение малого "времени" Аз вращается
вокруг мгновенного положения касательной t(s) с угловой скоростью
равной кручению т:
!§! = * G-33)
Так как сопутствующий трехгранник движется как жесткое целое
вдоль кривой ?, а оси бинормали и касательной при этом испытыва-
испытывают мгновенное вращение с угловыми скоростями г и i, то в целом
трехгранник вращается с суммарной угловой скоростью
|ы| = у/т2 + к2 G.34)
вокруг оси, направление которой определяется вектором Дарбу.
о> = тЬ + кЪ. G.35)
§ 7.1. Кривые в евклидовом пространстве
.447
7.1.8. Уравнения касательной, нормали и бинормали
с координатами хг = ж0 на кривой
Если зафиксировать точку
?, то уравнение касательной к кривой, проходящей через эту точку
/Ло и содержащую вектор касательной в этой точке to, будет иметь
вид (см. рис.7.5):
м
Рис. 7.5. К выводу уравнения каса-
касательной к кривой С
х - хо = (t0, G.36)
или в декартовых координатах
х{ - 4 =
G.37)
Здесь ж0, tl0 фиксированы для
точки Л4о> х% - переменные, а ?
- переменный параметр.
Совершенно аналогично запи-
записываются уравнения нормали
х - х0 =
G.38)
и бинормали
к кривой С в точке
х - хо =
G.39)
Упражнения к § 7.1.
Упражнение 7.1.1. Разложим векторы сопровождающего трехгранника t,
V и Ь по векторам неподвижного декартова базиса ё,*:
Показать, что для декартовых компонент t,-, V{ и Ь% имеют место выражения через
компоненты радиуса-вектора:
аз /г аз- к as as*
Упражнение 7.1.2. Показать, что из формул Френе G.27), G.28) и G.30)
следуют уравнения для координат векторов сопровождающего трехгранника:
448 Глава 7. Геометрия кривых и поверхностей
Упражнение 7.1.3. Используя формулы Френе из упр.7.1.1, доказать, что
если вдоль кривой С кривизна к = О, то эта кривая С суть прямая линия.
Упражнение 7.1.4. Используя упр.7.1.1, доказать, что если вдоль кривой С
кручение Т = 0, то эта кривая С суть плоская кривая.
Упражнение 7.1.5. Показать, что из G.9) выражение для параметра
имеет вид:
d/di = |х|,
где X = dx/d?.
Упражнение 7.1.6. Используя результат упр.7.1.5, показать, что если кри-
кривая С задана в виде G.1), то из G.16) и G.18) следует такое выражение для
кривизны k:
к = |х X х|/|х|3.
Упражнение 7.1.7. Показать, что выражение для fc, представленное в
упр.7.1.6, может быть также записано следующим образом:
* =
_ |х||х| — (х -хJ
|х|3
Упражнение 7.1.8. Используя результаты упр.7.1.5 и 7.1.6, показать, что
если кривая С задана в виде G.1), то из G.26) можно получить следующее выра-
выражение для кручения:
__ X X X • X*
"~ |х х х|2
Упражнение 7.1.0. Показать, что для кривой С, представляющей собой
винтовую Линию, для которой уравнения G.1) имеют вид:
= asin?, ж3 = Ь?, а>0
(если Ь > 0, это правая винтовая линия; если Ь < 0 - левая), длина дуги S
пропорциональна ?:
S =
Упражнение 7.1.10. Показать, что для винтовой линии кривизна к и кру-
кручение Т постоянны и равны:
а Ь
= 2 +
Ь2' Т = а2 + Ъ2 '
Упражнение 7.1.11. Показать, что из G.9) и G.27) следует формула:
.. .. S2
х = st + —и,
называемая формулой разложения ускорения движущейся точки на тангенциаль-
тангенциальную и нормальную составляющую.
§ 7.2. Поверхности в евклидовом пространстве 449
Упражнение 7.1.12. Доказать, что если три вектора а, Ь и С лежат в одной
плоскости (ортогональной некоторому вектору I/), то
а х b • с = 0.
Показать, что это выражение эквивалентно следующему:
V а2 а3>
det | б1 Ь2 Ь3 | = 0.
с1 с2 с3
§ 7.2. Поверхности в трехмерном евклидовом
пространстве
7.2.1. Способы задания поверхностей
Определение 7.5. Пусть w - открытая область в двумерном
пространстве Ш2, тогда поверхностью S в трехмерном про-
пространстве Ш3 называют отображение S: w —> Ш3, которое за-
задается с помощью вектор-функции
х = х(Х\ X2), {Х\Х2) е w С Ш2 G.40)
или с помощью трех числовых функций
х* = х{(Х\Х2), « = 1,2,3, G.41)
зависящих от двух аргументов X1 и X2.
Эти X1, X2 представляют собой криволинейные координаты на по-
поверхности S. Соотношения G.40) или G.41) выражают параметричес-
параметрический способ задания поверхности.
Три функции G.41) предполагаются однозначными, непрерывными
и имеющими непрерывные производные до второго порядка в некото-
некоторой области изменения аргументов X1', I = 1,2.
Здесь и далее в этой главе заглавные латинские буквы в индексе
пробегают значения от 1 до 2: /, «7, JFC, X = 1,2, а малые латинские -
как обычно от 1 до 3: г, j, fc, Z = 1, 2, 3.
Поверхность Е можно задать также неявным способом с помощью
одной функции трех аргументов - координат х1:
Ф(ж') = 0. G.42)
Если подставить функции G.41) в G.42), то получим тождество.
15 Тензорное исчисление
450.
Глава 7. Геометрия кривых и поверхностей
7.2.2. Локальные векторы базиса и метрическая
матрица на поверхности
Подобно тому как в гл.1 вводились локальные векторы базиса R,
для пространства М3, введем два локальных вектора базиса р/ на
поверхности:
Р1 = дх/дХ1.
G.43)
Эти векторы направлены по ка-
касательной к координатным лини-
линиям X1 = const поверхности Е.
Компоненты локальных векто-
векторов pi в декартовом базисе ё,
обозначим как р\\
91 = р}е,-.
G.44)
Рис. 7.0. Поверхность в трехмер-
трехмерном евклидовом пространстве
Введем метрическую матрицу
поверхности:
913 = 91 • 9з,
G.45)
которая имеет размер 2x2.
Определитель метрической матрицы ди отличен от нуля:
полагаем, что
д = det (ди) = 0ц022 - i
> 0, 022 > О, 0П022 - 012 > °-
G.46)
Для 0/j существует обратная метрическая матрица поверхности
0/J с компонентами:
-11 _ 922 -22 _ 0И -12 _ 012
0 — ~^~"» 0 — ~^г-, 0 — ^г-,
0 0 0
причем
~Т'91К = «
Здесь J1^ - двумерный символ Кронекера:
'д^^'птт^ —
1фК.
G.47)
G.48)
G.49)
§ 7.2. Поверхности в евклидовом пространстве 451
Векторы взаимного локального базиса поверхности р1 введем сле-
следующим образом:
Р1 = 9UPJ- G.50)
7.2.3. Тензоры на поверхности
Определение 7.6. Плоскость ?$, содержащую векторы pj, опре-
определенные для точки Мо поверхности S, называют касательной
плоскостью к поверхности Е в точке
Рассмотрим вектор а = а'ё,-, который лежит в касательной плос-
плоскости Е$, в данной точке Л^о* Тогда его можно разложить по базису
9V-
а = о. pi.
Теорема 7.1. Множество всех векторов а = а'ё,-, лежащих в
касательной плоскости Е$, в фиксированной точке Мо поверхности
S с радиусом-вектором х образует линейное пространство ?*(х)-
Это пространство называют также касательным линейным про-
пространством.
Т Действительно, сумма двух векторов а и b из касательной плоскос-
плоскости Е$ всегда может быть представлена в виде а + b =• (а1 + bI)pj =¦
с1 pi Е Е*, произведение вещественного числа Л на а также образует
вектор Ла = (\aI)pi, лежащий в касательной плоскости. Свойства 1°
- 8° линейного пространства очевидны, dim А(х) = 2. А
Тогда к пространству А(х) можно применить весь аппарат, изло-
изложенный в §2.5, в частности, образовать множество векторных набо-
наборов (aibia2b2), где а/ Е А(х)> ^/ Е ?*(х)> ввести на этом множестве
операции B.112) сложения и умножения на число и дать определение
тензора, аналогичное определению 2.26.
Определение 7.7. Тензорным касательным простран-
пространством Тп (А(х)) называют тензорное произведение линейного
пространства Ct(x) на себя:
) = А(х) ® А(х), х Е S.
Переходя от одной точки х поверхности S к другой х', получа-
получаем различные тензорные касательные пространства. Определение 7.7
корректно, поскольку операция тензорного произведения вводится со-
согласно определению 2.25 как фактор-пространство n-ой степени (здесь
п = 2) декартова квадрата пространств: ?*(х)®?*(х) = [(А(х)хА(х)J]
по отношению к введенной в определении 2.24 эквивалентности. А
согласно теореме 2.29, 7п (?«(*)) действительно является линейным
пространством, причем dim 73—4.
452 Глава 7. Геометрия кривых и поверхностей
Базисные диады в Тп (А(х)) введем аналогично B.118):
pJ®pK = [plftjPK)],
или явным образом:
Pi ® Р\ = [Р1Р1Р2О], Pl®p2 = [plP2p2<>],
p2®Pl = [pl0p2pl], Р2® Р2~
Определение 7.8. Тензорами второго ранга на поверхно-
сти А(х) называют элементы тензорных касательных прост-
пространств Тп (А(х))> определенных для каждой точки х поверхности
?.
Согласно теореме 2.28а, всякий тензор А на поверхности можно в
данной точке М представить разложением по диадному базису:
А = AIJ pi 0 pj.
Аналогично вводят тензоры высших рангов.
В силу положительной определенности gjj, все касательные про-
пространства Ct(x) будут евклидовыми, тогда, согласно п.2.5.9, сопря-
сопряженные пространства ?*/. совпадают с ?*(х)> и для тензоров на по-
поверхности А(х) в каждой точке х Е Е кроме операций сложения, умно-
умножения на число и транспонирования определены операции скалярного
умножения и поднятия-опускания индексов с помощью матриц ?]и и
9IJ.
Также как и для трехмерного евклидова пространства с помощью
векторов локального базиса pj и р1 можно определить различные диа-
дные базисы:
Pi®Pj, P*®Pj, Р*®р\ /,,/ = 1,2,
с помощью которых тензор на поверхности А можно представить в
виде:
А = AIJpi <8> pj = Аир1 ®pJ = A*3pi ® pJ.
Тензоры на поверхности представляют собой инвариантные объ-
объекты, не меняющиеся при переходе из одной криволинейной системы
координат X1 в другую X1'.
Правило преобразования компонент векторов локальных базисов и
тензоров при переходе из X1 в X1' также сохраняется:
G.51)
§ 7.2. Поверхности в евклидовом пространстве
_453
Б:
Метрический тензор на поверхности Е определяют по аналогии с
= дир1
р3 = gIJpi
= pI® pj.
Заметим, что хотя локальные базисы р/, р1 и метрические матрицы
дн ljIJ
ljIJ формально введены по аналогии с R,-, R1,
д%* -
трехмер-
трехмерд ^
ными объектами, но, вообще говоря, их соответствующие компоненты
различны, так как поверхностные объекты определены для функций
G.40) специального вида.
7.2.4. Касательные плоскости и вектор нормали
Получим уравнение касательной плоскости Е* в точке Мо с коор-
координатами хг0.
Выберем произвольную точку М с координатами ж*, лежащую в
касательной плоскости Е* к точке Мо (рис.7.7), тогда три вектора х—
Х(ь Р\ и р2 лежат в одной плоскости Е$. Определитель, составленный
из компонент этих векторов, будет равен нулю (см. теорему 2.10):
X Хг\ X Хп
р\
р\
А
А
Р\
Р\
= 0
G.52)
Рис. 7.7. К выводу уравнения каса-
касательной плоскости
или в векторном виде
(х - хо) х Р1. р2 = 0. G.53)
Разрешая G.52) относительно ко-
координат х% 1 получим уравнение
плоскости Е*, касательной в точ-
точке х%0
х%0:
где
р\р\ -
G.54)
= р\р\ - р\р\-
G.55)
В уравнении G.54) х*0 - фиксированы, а хг - переменные.
Нормалью к поверхности S называется прямая, проходящая через
точку М поверхности и ортогональная к касательной плоскости Е*
454 Глава 7. Геометрия кривых и поверхностей
поверхности в этой точке АЛ. Очевидно, что единичный вектор нор-
нормали п ортогонален векторам pj; определим его как
п = —-=.pi х р2. G.56)
V9
Используя определение A.33) векторного произведения, можно по-
показать (см. упр. 8.2.1), что формула G.56) эквивалентна следующей:
п=- г, G.56а)
|pixp2|
откуда вытекает, что вектор п действительно единичный:
п • п = 1.
Если зафиксировать точку Мо на поверхности S, то уравнение нор-
нормали, проходящей через эту точку Л4о и содержащей вектор по, будет
иметь вид:
х - х0 = ?п0 G.57)
или
х* - 4 = ?<. G.58)
Здесь хг0 и rig - фиксированы, хг - переменные, а ? - переменный пара-
параметр.
7.2.5. Первая квадратичная форма поверхности
Рассмотрим кривую С на поверхности Е. Уравнение этой кривой
можно записать в параметрическом виде:
*'=*'¦ (О
в криволинейных координатах Xх поверхности, или в декартовых ко-
координатах:
2
Возьмем две близкие точки М и М1 с радиусами-векторами хих',
лежащие на этой кривой С (рис.7.8). Эти две точки связаны вектором
Ах = х' — х. Переходя к пределу, получим элементарный радиус-
вектор dx, связывающий две бесконечно близкие точки М и М1 по-
поверхности. Согласно G.40) и G.43) для dx имеем выражение:
dx = pjdX1. G.59)
Длина элементарного радиуса-вектора есть дифференциал длины
дуги ds кривой С:
ds2 = \dx\2 = dx-dx. G.60)
Подставляя G.59) в G.60) для квадрата дифференциала длины дуги
ds2, получим
ds2=gudXJdXJ. G.61)
§ 7.2. Поверхности в евклидовом пространстве
.455
Рис. 7.8. К определению элемен- Рис. 7.9. К определению элемен-
элементарного радиуса-вектора, связываю- тарной площадки поверхности
щего две близкие точки поверхности
Определение 7.9. Квадратичную форму G.61) называют пер-
первой квадратичной формой поверхности, a Tjjj — коэффи-
коэффициентами первой квадратичной формы.
7.2.6. Элементарная площадка поверхности
Рассмотрим на поверхности Е в окрестности точки М малую пло-
площадку, ограниченную двумя парами близких координатных линий X1
(рис.7.9). Переходя к пределу, получим, что пары точек М, Mi и М,
М2 соединены элементарными радиусами-векторами dxi и dx2, при-
причем
dxQ = pQdXQ, a = 1,2 G.62)
(здесь суммирования по а нет).
В предельном переходе описанная малая площадка превращается в
параллелограмм, площадь которого бЕ, согласно A.51), вычислим по
формуле:
ndE = dxi х dx2. G.63)
Вычислим длину векторов, стоящих справа и слева в G.63), учиты-
учитывая формулы G.62), G.56), а также тот факт, что |п| = 1. В итоге
получим
dE = |pi x P2\dX1dX2 = y/7jdX1dX2 G.64)
~ выражение для элементарной площадки поверхности.
456.
Глава 7. Геометрия кривых и поверхностей
7.2.7. Угол между двумя кривыми на поверхности
Пусть на поверхности Е имеются две кривые, пересекающиеся в
точке М. и заданные параметрически:
х = х {X\i),X\i)) , х = х
G-65)
Тогда элементарные радиусы-векторы, выпущенные из точки
вдоль этих кривых, согласно G.58) имеют вид:
dx =
dx' = PldXfI.
G.66)
Косинус угла х между векторами dx и dx' находим, используя ска-
скалярное произведение векторов:
dx-dx'
gjjdXJdX/J
{gKLdXKdXLI/2{gMNdXfMdXfNI'2'
G.67)
Если в качестве параметра ? в G.65) выбрать длину дуги, то выра-
выражение G.67) с учетом G.11) можно упростить:
_ dX1 dX'J
fl/J — _.
7*2.8. Вторая квадратичная форма поверхности
АП
G.68)
Для двух близких точек поверхнос-
поверхности М и Л!', связанных радиусом-
вектором Дх, рассмотрим векторы
нормали пип' (рис. 7.10) и опреде-
определим элементарный вектор нормали
dn как предельное положение раз-
разности нормалей:
Лп = п; — п.
Подобно G.59) для элементарного
вектора нормали имеем:
Рис. 7.10. К определению элемен-
элементарного, вектора нормали
где обозначены производные вектора нормали:
дп
= UjdX1,
G.69)
G.70)
§ 7.2. Поверхности в евклидовом пространстве 457
Составим теперь скалярное произведение dn и dx, с учетом G.59)
и G.69) имеем:
-dx • dn = bjjdXJdXJ. G.71)
Здесь введено обозначение для скалярного произведения:
bu = -pi-nj. G.72)
Определение 7.10. Выражение G.71) называют второй квад-
квадратичной формой поверхности, a bjj - коэффициентами второй
квадратичной формы.
Представим выражение G.72) для Ьи в несколько ином виде.
Вспомним, что векторы pi, определенные в некоторой точке М, на-
направлены по касательным к кривым на поверхности Е, совпадающим
с координатными линиями X1 — const. Тогда р/ будут ортогональны
вектору нормали п, выпущенному из той же точки, т.е.
Р1 • п = 0. G.73)
Обозначим вторую производную от радиуса-вектора как
_ ЬР1 дЧ
Тогда дифференцируя G.73) по XJ, получим
pjj • n = -pi • nj = 6/j, G.75)
или с учетом G.74):
blJ = дШх* •п> G'76)
Из этого выражения, очевидно, следует симметричность коэффициен-
коэффициентов второй квадратичной формы поверхности 6/jr.
Подставим в G.75) вместо п его определение G.56), тогда выраже-
выражение дли коэффициентов Ьи примет вид:
Ьи = -i=Pij • Р\ х р2- G.77)
V9
7*2.9. Псевдотензоры на поверхности
Рассмотрим теперь кроме координат X1 на поверхности Е еще одни
криволинейные координаты Хп. Тогда в каждой точке М. поверхнос-
поверхности мы имеем два локальных базиса р/ и р'Т, связанных соотношением
458 Глава 7. Геометрия кривых и поверхностей
G.51), две метрические матрицы gjj и *д'и = р\ • р*3, между которыми
имеется следующая связь:
дХк дХь
и два набора коэффициентов второй квадратичной формы:
_ 32х pi х р2
13 ~ дХ'ЭХ1 ' |р! хР2\'
Pi х Р'2
,77fU
G<78)
Вычисляя по этим формулам детерминанты р и р', находим:
где A =
Векторное произведение р[ х р'2 преобразуем с учетом определений
A.33) и G.44):
/ #_ Ч4-к_ дх{ дх> кдХ! дХ3
Pi*P2- ey*Pift e - е0*
Здесь учтено, что ра х ра = 0 (а = 1,2). Подставляя полученное
соотношение в выражение для bjj, получаем формулы преобразования
при переходе к новой системе координат:
__ |А| д2х дХК дХь Р1хр2
13 "" Д dXKdXL дХ'1 dX'J ' \Р1 х Р2\
\b\dX'1 dXIJ
G.79)
Согласно введенной в п.1.9.6 классификации, скаляр yfg являет-
является относительным тензором веса и = — 1, а коэффициенты второй
квадратичной формы образуют симметричный псевдотензор второго
ранга:
В = Ъир1 ® р3 = Ь13pi <g> pj. G.80)
§7.2. Поверхности в евклидовом пространстве 459
7.2.10. Деривационные формулы
В каждой точке поверхности Е была определена тройка векторов
pi, P2, п, которая называется сопровождающим трехгранником по-
поверхности. Деривационные формулы Гаусса-Вейнгартена описывают
изменение векторов сопровождающего трехгранника.
Рассмотрим эти векторы:
Их всегда можно разложить по векторам какого-либо базиса, напри-
например, по сопровождающему трехграннику:
Ьиъ, G.81)
n/ = cjpj + dm, G.82)
где Fjj, Ь/j, с/ и dj - коэффициенты разложения. Установим вид этих
коэффициентов.
Умножая G.81) скалярно на п, в силу ортогональности pj is. n по-
получаем:
п = Ьи. G.83)
Сравнивая G.83) с G.75), находим, что bjj - это коэффициенты второй
квадратичной формы:
Ьи = Ьи. G.84)
Умножая G.81) скалярно на рь, с учетом G.45) и G.73) получаем:
Ри ¦ PL = T?j9kl = Тт. G.85)
Продифференцируем теперь G.45):
PiL-pj + Pi-pjL = ^i. G.86)
Меняя в G.86) индексы J f* X, получим:
Pu-PL + Pi-PJL = ^f. G.87)
Если поменять в G.86) индексы / <->• i, то
. &gjL /7 одч
PL/ PJ + PL* PJI = -Qxf- G*88)
Глава 7. Геометрия кривых и поверхностей
Учитывая симметрию рн, из G.86) - G.88) и G.85) получим:
1 {ддть dgJL ддц\
2 [dX? + 1ХГ " «FJ = P/J ' PL =
- выражение для коэффициентов Г/л,.
Если сравнить G.89) с выражением F.13) для символов Кристоф-
феля Tijk, то увидим сходство этих формул с точностью до замены
трехмерных индексов на двумерные. Таким образом, коэффициенты
Tjjjj G.89) естественно определить как двумерные символы Кристоф-
феля первого рода.
Символы второго рода получаются умножением на обратную мет-
метрическую матрицу:
Tu = TIJLg --g (_ + _-_). G.90)
Умножая теперь формулу G.82) скалярно на п, получаем:
nj-n^d/. G.91)
Но так как п • п = 1, то
nj-n^O, G.92)
поэтому
di = 0. G.93)
Наконец, умножая G.82) на рк, получаем:
niPK = cJjgJK. G.94)
Используя определение G.72) коэффициентов б/я-, из G.94) выражаем
/
с
/:
с/ = -pJirbK/ = -Ь/, G.95)
где 6/ - смешанные коэффициенты второй квадратичной формы.
Подставляя теперь G.84), G.93) и G.95) в G.81), G.88), получаем
следующую теорему.
Теорема 7.2. Изменение векторов сопровождающего трехгран-
трехгранника описывается следующими соотношениями для производных:
Ъ„п,
n/ = -bjpj.
§7.2. Поверхности в евклидовом пространстве 461
Соотношения G.96) называют деривационными формулами, первая
из которых была установлена Гауссом, а вторая - Вейнгартеном.
7.2.11. Ковариантное дифференцирование на поверхности
Заметим, что в случае трехмерного пространства символы Крис-
тоффеля T!-j вводились согласно F.1) как коэффициенты разложения
производной dRi/dXi по локальному базису R,, а формула F.8) связи
Г*у с метрической матрицей gij была установлена в виде следствия.
Для случая двумерной поверхности аналогичное разложение F.1)
не существует; как следует из деривационных формул G.96), дву-
двумерное дифференцирование локальных векторов базиса pj приводит
к разложению по трехмерному базису р/,п. Поэтому за определе-
определение двумерных символов Кристоффеля Г^ более естественно принять
формулу G.90), являющуюся в точности аналогом трехмерного соот-
соотношения F.8), тогда деривационные формулы G.96) будут их следст-
следствием. Это и было проделано в п.7.2.10.
Далее с помощью двумерных символов Кристоффеля можно опре-
определить ковариантную производную от компонент вектора на поверх-
поверхности Е.
Определение 7.11. Ковариантной производной на по-
поверхности от контравариантных и ковариантных компонент
вектора называют следующие величины:
V/»' = |? + fjKa\ Vraj = |* - г* ejf, G.97)
а от контр авариантных и ковариантных компонент тензора вто-
второго ранга - следующие:
dTIJ ~ ~
+ T^T*1 + TJKLTIL, G.98)
Здесь aj и TIJ - компоненты вектора и тензора на поверхности:
а = а1Рт = а7Р/, Т = Тир1 ® pJ = TIJPl ® pj. G.99)
Аналогично определяются ковариантные производные на поверхности
от других компонент.
Если в качестве Т взять метрический тензор Е, то будут иметь
место бажные формулы, являющиеся аналогом формулы Риччи F.54)
в трехмерном случае.
462 Глава 7. Геометрия кривых и поверхностей
Теорема 7.3. Ковариантная производная на поверхности от
компонент метрического тензора на поверхности равна нулю:
VKgIJ = О, VkQij = 0, VKg = 0, G.100)
Доказательство этой теоремы оставим в качестве упр.7.2.3.
Дифференцирование векторов и тензоров на поверхности отлича-
отличается от трехмерного случая. В самом деле, например:
да __ д{атР1) _ да1
да1
dXKi
bIKn) = {VKaJ)pi + а7Ь/л:п, G.101)
т.е. частная производная от вектора а на поверхности уже не является
"вектором на поверхности".
7.2.12. Условия интегрируемости
Вернемся теперь вновь к деривационным формулам G.96) и посмот-
посмотрим на них как на систему дифференциальных уравнений относитель-
относительно векторов сопровождающего трехгранника р/, п. Очевидно, что эта
система будет переопределена: она содержит пять векторных уравне-
уравнений относительно трех векторных неизвестных, значит ее решение
существует не всегда. Поскольку система имеет первый порядок про-
производных относительно р/, п, то условием ее интегрируемости будет
равенство вторых смешанных производных:
*>¦ - *» G.102)
92° дЧ G.103)
dxJdxK ~ дхкдх1'
Вычислим эти производные. Дифференцируя G.96), получаем:
= ~EPl + ^hPLK + ^Fn + bijn.K, G.104)
Подставляем сюда выражение для рьк и пк из G.96), тогда имеем
д (дТм \
( # + Ггй ЪЬ%\ рм+
G.105)
§ 7.2. Поверхности в евклидовом пространстве 463
L-bJjbjKn. G.106)
Подставляя теперь G.105), а также формулы G.105) с заменой индек-
индексов J <->• if, в условие интегрируемости G.102), получаем уравнение,
которое должно выполняться при любых рм и п. Тогда приравнивая
коэффициенты при рк и п нулю, получаем условие интегрируемости
G.102) в виде:
IJ . pL pM U1 IK pL pM __
G.107)
0. G.108)
Подставляя G.106) в G.103) и приравнивая коэффициенты при pj
и п нулю, получаем вторую группу условий интегрируемости:
dbK -j м ~j м /
~ "дХ^ мк J "" м/ ^ "" l
0. G.110)
Введем обозначение:
5
кл — ^к ~ ^jj-j + Lи1 lk
\M
Компоненты Л^-j/ м являются компонентами тензора 4R четвер-
четвертого ранга на поверхности Е (см.упр.7.2.16), называемого тензором
кривизны поверхности или тензором Римана-Кристоффеля:
4R = %JX Mp^ ®pJ ®р* ®рм = RkjimPK ®PJ®PT® P
Полностью ковариантные компоненты тензора кривизны Rkjil
вычисляем путем умножения G.111) на метрическую матрицу:
Rkjil = RkjiM9ml. G.112)
С учетом G.111), G.112), формулы G.107) можно представить в
виде:
= Rkjil- G.113)
464 Глава 7. Геометрия кривых и поверхностей
Уравнения G.108) с учетом определения G.98) ковариантной произ-
производной и симметрии символов Кристоффеля Tjfcj = Г^к можно пред-
представить в виде:
ЧкЪи - VjbIK = 0. GД14)
Заметим, что G.113) содержит всего одно тождественно не равное
нулю уравнение:
Ь\2 ~ ЬцЬ22 = ^1212, G.115)
а G.114) - два таких уравнения:
Vi&/2 - Vjbn = 0, /=1,2. G.116)
Уравнение G.115) называется уравнением Гаусса, а G.116) - уравне-
уравнениями Петерсона-Кодацци.
Рассмотрим теперь две оставшиеся группы условий интегрируе-
интегрируемости G.109) и G.110). Уравнения G.110) выполняются всегда, при
любых комбинациях индексов, в чем можно убедиться непосредствен-
непосредственно, перейдя к ковариантным компонентам:
9JM(biMbjK - ЪкмЬл) = 0. G.117)
В уравнениях G.109) также перейдем к ковариантным компонентам
Ь/j, произведем дифференцирование по частям и сгруппируем слага-
слагаемые следующим образом:
дЬш
LM
9
=0. G.118)
Учитывая свойства G.100) метрической матрицы, выражения в скоб-
скобках во втором и третьем слагаемых преобразуем следующим образом:
|^ G.119)
тогда G.118) будет иметь вид:
Сравнивая G.120) с G.108), заключаем, что условие интегрируе-
интегрируемости G.120), а значит и G.109), удовлетворяются, если только вы-
выполнены условия G.108).
Таким образом, условия G.109) и G.110) не вносят никаких новых
уравнений дополнительно к уравнениям Гаусса и Петерсона-Кодацци
G.115), G.116), и мы доказали следующую теорему.
§ 7.2. Поверхности в евклидовом пространстве 465
Теорема 7.4. Необходимыми и достаточными условиями интег-
интегрируемости деривационных формул G,96) относительно векторов
сопровождающего трехгранника pi, n являются уравнения G.115)
и G.116).
7.2.13. Основная теорема теории поверхностей
Зададимся теперь вопросом о возможности определения самой по-
поверхности по известным функциям первой и второй квадратичных
форм. На этот вопрос положительно отвечает следующая основная
теорема теории поверхностей.
Теорема 7.5. Пусть заданы дважды непрерывно дифференцируе-
дифференцируемые функции
9и=9и{Х1,Х2) G.121)
и один раз непрерывно дифференцируемые функции:
\Х2), G.122)
для которых выполнены условия интегрируемости Петерсона-Ко-
дацци G.116) и Гаусса G.115), а также условие положительной
определенности:
0, tf + ?22?H G.123)
для всякого ненулевого вектора ?/, тогда существует поверхность
3
3
G.124)
трижды непрерывно дифференцируемая, для которой gjj и bjj явля-
являются коэффициентами первой и второй квадратичной форм.
Эта поверхность определена с точностью до перемещения в про-
пространстве как жесткого целого.
Т Для доказательства теоремы воспользуемся результатами п.7.2.12,
из которых следует, что если выполнены условия интегрируемости
G.115) и G.116), то деривационные уравнения G.96) имеют решение
относительно функций р/ и п, причем р/ обладает симметричной про-
производной:
dpi dpj Ga
= GЛ
Если теперь на G.43) посмотреть как на систему уравнений относи-
относительно функций х(Х1,-Х), то опять получим переопределенную сис-
систему первого порядка. Ее решение существует, если функции р/,
считающиеся известными, удовлетворяют условию G.125). Но это
условие действительно выполнено, как было отмечено выше, таким
образом, существует вектор-функция G.124), определяющая поверх-
поверхность в трехмерном евклидовом пространстве. ^
Глава 7. Геометрия кривых и поверхностей
Упражнения к § 7.2.
Упражнение 7.2.1. Используя формулы G.46), G.45) и A.50), доказать
соотношение G.56а).
Упражнение 7.2.2. Используя формулу G.67), показать, что координатные
линии на поверхности 2 пересекаются под углом )(:
9 / 9
cos х = / ? sin X = \ / ~ ~
V ^^
Упражнение 7.2.3. Доказать формулы Риччи G.100) в двумерном случае,
используя определения G.98) и G.89).
Упражнение 7.2.4. Обозначим компоненты объекта pjj в декартовом ба-
базисе как
PiJ = P/je»> P*IJ =
Показать, что из G.77) следует формула для коэффициентов второй квадратичной
формы:
b
-pzti
V9
Упражнение 7.2.5. Показать, что формулу, приведенную в упр.7.2.4 можно
представить также в виде:
рп рЬ рЬ
р\ р\ р\
р\ р\ р\
Упражнение 7.2.6. Явным способом задания поверхности называется
случай,когда
X2 = х2,
х3 = х3(х\х2).
Показать, что при этом векторы локального базиса pj имеют вид:
_ дх3_
а метрическая матрица вычисляется следующим образом:
, {дх3\2 „ дх3дх3 „ , Гдх3\2 (дхг\
_____ § 7.2. Поверхности в евклидовом пространстве 467
Упражнение 7.2.7. Показать, что для поверхности эллипсоида вращения,
заданной в неявной форме
параметрическая форма имеет следующий вид:
х1 = acosX1sinX2, х2 = a sin X1 sin X2, x3 = ccosX2.
Упражнение 7.2.8. Показать, что для эллипсоида вращения (см.упр.7.2.7)
матрицы коэффициентов локальных базисов p*j имеют следующий вид:
(Л) = (
—asin-X sin-X a cos X1 sin X2 0
-csinX2 ) '
Упражнение 7.2.9. Показать, что коэффициенты первой квадратичной фор-
формы для эллипсоида вращения имеют вид:
a2sin2Jf2 О
О a2 cos2 X2 + с2 sin2 X
а обратная метрическая матрица имеет вид:
„ /(a'sm2^)-1 0 \
^ > ~ \ 0 (a2 cos2 X2 + с2sin2 X2)-1) •
Упражнение 7.2.10. Показать, что коэффициенты второй квадратичной
формы для эллипсоида вращения имеют вид:
Упражнение 7.2.11. Поверхностью вращения называется поверхность,
явное задание которой имеет вид:
(Z2J + (*3J = /V),
где f(x) - некоторая неотрицательная функция, ось Ох является осью враще-
вращения. Показать, что в параметрической форме поверхность вращения можно задать
следующим образом:
x2 = f{X1)cosX2,
x3 = f{X1)smX2.
468 Глава 7. Геометрия кривых и поверхностей
Упражнение 7.2.12. Показать, что матрица коэффициентов Pj локального
базиса для поверхности вращения имеет вид:
M_fl fcosX2 f'smX2\
-fsinX2 fcosX2)'
Упражнение 7.2.13. Показать, что метрические матрицы для поверхности
вращения имеют вид:
- )_(i + /'2 о\ (i/(i +Г2) о \
fl = (i + /'2)/2-
Упражнение 7.2.14. Показать, что для поверхности вращения коэффици-
коэффициенты pjj имеют вид:
0
\ 2 _{f"cosX2 -/'sinX2\
y1 PlJ-\-fsmX2 -fcosX2)'
з _ (fsinX2 fcosX2 \
PlJ~\fcosX2 -fsmX2)-
Упражнение 7.2.15. Используя результаты упражнений 7.2.5, 7.2.12 -
7.2.14, показать, что коэффициенты второй квадратичной формы для поверхности
вращения имеют вид:
h = b = 6 = 0
Упражнение 7.2.16. Используя формулу G.113), показать, что компоненты
R действительно являются компонентами тензора четвертого ранга.
§ 7.3. Кривые на поверхности
7.3.1. Векторы нормальной и геодезической кривизны
Пусть имеется некоторая кривая С на поверхности Е, заданная па-
параметрически как функция длины дуги:
x = x(X1{s),X2{s)). G.126)
Используем аппарат, разработанный в § 7.1 для описания кривых
в пространстве. Дифференцируя G.126) по з, получим вектор каса-
касательной к кривой С:
дифференцируя еще раз, получим вектор кривизны кривой С:
Л dXJdXJ d2XJ /fy100.
к = — = ри— — + Л-тт-. G.128
as as as as2
Здесь мы учли G.43) и G.74).
§ 7.3. Кривые на поверхности
.469
Теорема 7.6. Вектор кривизны к кривой на поверхности всегда
молено однозначно представить в виде суммы двух ортогональных
векторов, называемых вектором нормальной кривизны кп и век-
вектором геодезической кривизны кд (рис.7.11):
К, К,П 4"
где
Кп =
Kg = kgll X t,
G.129)
G.130)
а кп и kg - некоторые коэффициенты.
nxt
Рис. 7.11. К теореме 7.6
Т Для доказательства утверж-
утверждения G.129) достаточно пока-
показать, что все три вектора гс,
п и п х t лежат в одной плос-
плоскости, тогда они являются ли-
линейно зависимыми, и один из
них действительно можно вы-
выразить через два другие. Но
все эти векторы ортогональны
вектору касательной t: вектор
нормали п - по определению
ортогонален любому вектору
из касательной плоскости Е*,
в том числе к t; вектор к =
dt/ds ортогонален t согласно
G.14); а п х t ортогонален t в
силу свойств векторного про-
произведения.
Тем самым, действительно, векторы п, к и (n x t) лежат в одной
плоскости, а значит разложение G.129) имеет место. ^
Определение 7.12. Плоскость, содержащую вектор нормали п
it вектор касательной t к кривой С, называют плоскостью нор-
нормального сечения поверхности.
Заметим, что поскольку кривая С на поверхности была выбрана
произвольно, то через фиксированную точку М поверхности можно
провести сколько угодно таких кривых. Следовательно, в одной и той
же точке М. существует бесконечное множество плоскостей нормаль-
нормального сечения, каждая из которых проходит через один и тот же вектор
нормали п и различные векторы касательной t.
7.3.2. Нормальная и геодезическая кривизна
кривой на поверхности
Выражая к через вектор нормали и к кривой ?, запишем G.129) в
виде:
kv = knn+ kgii x t. G.130)
470 Глава 7. Геометрия кривых и поверхностей
Умножая G.130) скалярно на вектор п или (n x t), получим связь
кривизны к с кп и кд:
9 G.131)
kg = к sine, G.132)
cos0 = (i/-n), sin0 = i/« (n x t), G.133)
где в - угол между соприкасающейся плоскостью кривой С в данной
точке и плоскостью нормального сечения.
Таким образом, из G.131) и G.132) проясняется смысл коэффици-
коэффициентов кп и кд: они характеризуют кривизну кривых, являющихся про-
проекциями кривой С на плоскость нормального сечения и соприкасаю-
соприкасающуюся плоскость в данной точке М.
Определение 7.13. Коэффициенты в представлении G.130) на-
называют кп -кривизной нормального сечения или нормаль-
нормальной кривизной, a kg - геодезической кривизной кривой С на
поверхности G.131).
Радиусом нормальной кривизны гп и геодезической кривизны rg
называют обратные к кп и кд величины:
»•« = Г". Г9 = Т- G-134)
Кп Кд
Из формул G.131) и G.132) следует, что кп и кд) а также гп и гд)
могут иметь как положительные, так и отрицательные значения, в
зависимости от знака cos в и sin в. Напомним, что кривизна к кривой
всегда неотрицательна.
Если проекция нормали кривой и на нормаль п к поверхности отри-
отрицательна, то cos в < 0 и радиус нормальной кривизны гп отрицателен.
Формула G.131) составляет содержание следующей теоремы.
Теорема 7.7 (Менье). Нормальная кривизна кп поверхности, ко-,
торую имеет кривая С на плоскости нормального сечения равна кри-
кривизне к этой кривой, умноженной на косинус угла в.
Из этой теоремы также следует, что если провести через данную
точку М кривой С плоскость наклонного сечения, проходящую через
вектор касательной t и составляющую некоторый угол cos в' с плос-
плоскостью нормального сечения, то кривизна к' наклонного сечения будет
связана с кп формулой:
fcn = fc'cos0'. G.135)
Получим еще одну формулу для нормальной кривизны кп. Под-
Подставляя G.133) и G.128) в G.131):
и 1 dt dXIdXJ . 10ft.
кп = kv • n = — • n = pu • n— —, G.136)
ds ds ds
§ 7.3. Кривые на поверхности 471
а затем выражая pjj -n согласно G.75) через 6/j, a ds2 согласно G.61)
через ди, получим:
_ budX'dX'
k- GЛ37)
Таким образом, пришли к следующему утверждению.
Теорема 7.8. Кривизна кп нормального сечения поверхности Е
в точке (Х1^2), плоскость которого проходит через бесконечно
близкую точку этой поверхности с координатами (X1 + dX^^X2 +
dX2), равна отношению второй и первой квадратичной форм, по-
построенных на приращениях координат dX1.
Очевидно, что меняя направление касательной в данной точке
2 (т.е. меняя значение dX1), получаем различные значения
Обозначая вторую квадратичную форму как
d2<p = bIJdXIdXJ, G.138)
формулу G.137) можно записать в виде:
кп = d2ip/ds2. G.139)
Можно также представить G.137) следующим образом:
{Ьи - kngIJ)dXIdXJ = 0. G.140)
7.3.3. Главные кривизны поверхности
Таким образом, в каждой точке поверхности М существует беско-
бесконечно много нормальных кривизн fcn, но оказывается среди них су-
существуют две преимущественные кривизны. Для их установления
рассмотрим тензор второй квадратичной формы В G.80) с коэффи-
коэффициентами 6/jr. Так как В является симметричным тензором второго
ранга и определен на поверхности (т.е. в двумерном пространстве), то
согласно § 1.6 у него имеется два действительных собственных значе-
значения к\ и &2 и собственный базис из двух взаимно-ортонормированных
о
векторов р/, т.е. В можно представить в диагональном виде:
2
В = bjjp <8> р —/^kQpQ®pQ, G.141)
1° I л
причем \pi\ = 1.
а=1
472 Глава 7. Геометрия кривых и поверхностей
Определение 7.14. Направления, касательными к которым яв-
0
ляются векторы pj, называют главными.
Если известны коэффициенты квадратичных форм bjj и Iju в ка-
каком-либо базисе р7, то собственные значения kQ тензора В находим
из характеристического уравнения:
det (В - kQE) = 0, G.142)
или
det (Ъи - кади) = 0, а =1,2;
или в матричной записи
Ь12-кад12 =0 G142,}
Выберем теперь в точке М новую локальную систему координат
X1' = XIf(XJ), G.143)
локальный базис которой р\ совпадает с р7. В этом локальном базисе
о „,
в силу ортонормированности pj метрическая матрица д13 оказывается
единичной:
ь = 9 и Pi ® Pj->
~1 ° ° X (П 1 ЛЛ\
9и = Pi' Pj = Pi' Pi — ^/J? G.144J
базис р7 также совпадает с р7, а вторая квадратичная форма b'jj со-
согласно G.141) является диагональной:
b'jj^k^ 6'12 = 0. G.145)
Выберем также в качестве бесконечно близкой к М точку Mi с ко-
координатами (X1' + dXv,X2f). Тогда подставляя G.142) и G.145) в
G.137), получаем, что кривизна нормального сечения, проходящего
через точки М и A4i, вычисляется по формуле:
) _
Выбирая нормальное сечение, проходящее через точки М и Мг с ко-
координатами (X1', X2' + dX2'), совершенно аналогично получим, что
fci2' = k2. G.147)
Таким образом, доказана теорема.
§ 7.3. Кривые на поверхности
.473
Теорема 7.9. Два собственных значения ki тензора второй
квадратичной формы В представляют собой кривизны двух нор-
нормальных сечений, плоскости которых проходят через бесконечно
близкие точки М.\ и М.2, лежащие на собственных направлениях рТ
тензора В (или, иначе говоря, через векторы касательной t, совпа-
совпадающие с
Определение 7.15. Собственные значения kj тензора В fci и fc2
называют главными кривизнами поверхности.
Плоскости нормальных сече-
сечений, соответствующие глав-
главным кривизнам fc/, т.е. прохо-
проходящим через точки
М., ЛЛ\ и .М, Л^2?
называют главными нормаль-
нормальными сечениями Е/.
Выберем теперь нормальное
сечение Е', проходящее через
бесконечно близкую к М. точ-
точку М! с координатами
Рис. 7.12. Нормальные сечения поверх-
поверхности
+ dX ,X + dX ),
тогда кривизна к*п этого нормального сечения согласно G.137) будет
иметь вид:
11
Так как метрическая матрица д'г1 - единична, то вводя угол а между
главным нормальным сечением Si и сечением ?' (рис.7.12), формулу
G.148) можно записать в виде:
кп = fci cos2 a + к2 sin2 а,
где
cos о: =
dX1
dX2f
sin а =
Г1'J + {dX2'J
Таким образом, мы пришли к следующей теореме.
G.149)
. G.150)
474 Глава 7. Геометрия кривых и поверхностей
Теорема 7.10. Кривизна кп произвольного нормального сечения
поверхности связана с главными кривизнами поверхности по форму-
формуле G.149), которую называют формулой Эйлера»
Теорема 7.11. В направлениях главных кривизн кривизна нор-
нормального сечения поверхности кп принимает экстремальные (мак-
(максимальное и минимальное) значения, равные fci it &2-
Ў В самом деле, пусть для определенности fci ^ &2- Рассмотрим кп
как функцию угла а, тогда из формулы Эйлера следует:
М«) = (fci - k2)cos2a + к2. G.151)
Отсюда следует, что
Va fc2 = *n (J) ^ М"К МО) = *1,
это и доказывает утверждение. А
7.3.4. Гауссова и средняя кривизны
Тензор второй квадратичной формы В, как всякий двумерный сим-
симметричный тензор второго ранга, имеет два независимых инвари-
инварианта относительно группы преобразований координат, порождаемой
G.143). В качестве этих инвариантов могут быть выбраны главные
кривизны fc/. Важную роль играют два других инварианта тензора
В:
Лв..Ё, G.152)
lf(B)=det (B) = det (b/).
Записывая эти инварианты в собственном базисе р7 тензора В, по-
получим из G.141), G.144):
«Ср« ® к) • • Е (К ® h) = fci + *2, GЛ53)
a=l /3=1
Таким образом, доказано следующее утверждение.
7.3. Кривые на поверхности 475
Теорема 7.12. Инвариант Н тензора второй квадратичной
формы В есть полусумма главных кривизн, и поэтому называется
средней кривизной поверхности, а инвариант К (В) - есть про-
зведение главных кривизн, и называется полной или гауссовой
кривизной.
Записывая эти инварианты через компоненты тензоров в произ-
произвольной системе координат X1, получаем:
К = det (bIKgKJ) = * det (bIK) = *, G.154)
где
Ь = det (bIK) = bnb22 - Ъ\2. G.155)
Вспомним теперь, что согласно уравнению Гаусса G.115) Ь выража-
выражается через компоненту тензора кривизны Дтг» тогда G.154) можно
записать в виде:
К = -Д1212/0. G.156)
Из формулы G.156) следует теорема.
Теорема 7.13 (основная теорема Гаусса (Theorema Egr-
egium)). Гауссова кривизна поверхности К зависит только от ко-
коэффициентов первой квадратичной формы поверхности Tjjj и их пер-
первых и вторых производных.
Т Действительно, так как Л1212 согласно G.111) выражается только
через Tjj и их производные, а символы Кристоффеля, в свою очередь,
только через ?}н и их производные, то из G.156) вытекает утвержде-
утверждение теоремы. ^
Из основной теоремы Гаусса следует, что кривизна К поверхнос-
поверхности может быть определена только по измерениям на поверхности без
выхода в окружающее пространство IR3.
7.3.5. Классификация точек поверхности
Зафиксируем теперь какую-либо точку М с координатами
на поверхности Е и возьмем произвольную бесконечно близкую к ней
точку М! с координатами (-Х + AХг,Х2 + dX2), соединенную с М
некоторой кривой С. Кривизна нормального сечения fcn, плоскость
которого проходит через нормаль к поверхности в точке М и точку
М', вычисляется по формуле G.137). Нас будет интересовать вопрос
о значениях fcn, если кривую С выпускать из точки М. во всех воз-
возможных направлениях.
476 Глава 7. Геометрия кривых и поверхностей
Поскольку в знаменателе G.137) стоит квадрат длины дуги кри-
кривой ds2, то он всегда положителен, и знак кп определяется знаком
числителя. В числителе же стоит вторая квадратичная форма:
dV = bIJ(X1,X2)dXIdX\ G.157)
которая при фиксированных значениях X1 и переменных dX1 пред-
представляет собой алгебраическую поверхность второго порядка (тензор-
(тензорную поверхность Коши) в пространстве (dX1, dX2). Вид этой поверх-
поверхности зависит от детерминанта:
det (bu) = b = ЬцЬ22 - Ъ\2. G.158)
Если b > О, то знак этой формы при любых значениях dX1 всегда
одинаков, следовательно, кривизна кп любого нормального сечения
имеет один и тот же знак. Такая точка М поверхности называется
эллиптической.
Если b < О, то знак формы G.157) меняется при произвольных зна-
значениях dX1', следовательно, в данной точке М имеются нормальные
сечения с противоположными значениями кривизны кп. Такая точка
М. называется гиперболической.
Если b = 0, то форма G.157) представляет собой полный квадрат
и, следовательно, кп не меняет знака для всех dX1', т.е. при произ-
произвольных нормальных сечениях. Однако имеется одно положение нор-
нормального сечения, при котором кп обращается в нуль. Такая точка
М. поверхности называется параболической.
Если Ьи = 0, то кривизна кп для всех dX1 равна нулю, и поверх-
поверхность в окрестности точки /Л представляет собой плоскость. Такая
точка М называется точкой уплощения.
Точка поверхности, в которой нормальные кривизны fcn одинаковы
для всех нормальных сечений, называется омбилической (или точкой
закругления). Для омбилической точки главные кривизны совпадают
кг = к2.
Поскольку 7j > 0, то согласно G.154) знак 6 полностью определяет
знак гауссовой кривизны if, следовательно:
¦ в эллиптической точке: К > 0;
¦ в гиперболической точке: К < 0;
¦ в параболической точке: К = 0.
7.3.6. Индикатриса Дюпена
Рассмотрим произвольную точку М поверхности Е и построим ка-
касательную плоскость Е* в этой точке. В касательной плоскости Е* в
малой окрестности точки М построим вспомогательную кривую ?р
(рис.7.13) следующим образом: расстояние от точки М до любой точ-
точки М! на кривой Cd равно у/±гп, где гп - радиус кривизны нормаль-
нормального сечения, плоскость которого проходит через точку М и точку
§ 7.3. Кривые на поверхности
.477
М!. Знак (±) выбираем так, чтобы под радикалом была положитель-
положительная величина.
Кривая ?р, построенная таким образом, называется индикатрисой
Дюпена. Получим ее уравнение.
Обозначим координаты
точки М. на поверхности
П
как (Л*,Л*), а координа-
координаты точки М! как
(X1+dX1,X2 + dX2).
Расстояние между этими
точками ds вычисляем
как длину радиуса-векто-
радиуса-вектора dx, связывающего точ-
точки М и М!\
Рис. 7.13. К уравнению индикатрисы Дюпе- dx = pjdX1, G.159)
тогда
d2s = dx-dx = g
IXJ. G.160)
Согласно определению индикатрисы Дюпена это расстояние равно
ds = <y/±rn. Тогда имеем:
J = ±гп.
G.161)
Причем при г„ > 0 следует брать знак " + ", а при гп < 0 - знак " — ".
Или, переходя к нормальной кривизне fcn, получаем
kngIJdXIdXJ = ±1.
G.162)
Это и есть искомое уравнение индикатрисы Дюпена.
Поскольку всегда в малой окрестности точки М поверхности вы-
выполнено кроме того уравнение G.140), то из G.162) получаем еще одну
форму записи индикатрисы Дюпена:
bIJdXIdXJ = ±1.
G.163)
В главных осях (Хп,Х'2) тензора В это уравнение будет иметь
вид:
J + k2(dX'2J = ±1. G.164)
Отсюда следует, что если точка М является эллиптической, то ин-
индикатриса Дюпена есть эллипс, и в правой части следует брать опре-
определенный знак (" +" или " — " в зависимости от знака Jti). Если точка
478 Глава 7. Геометрия кривых и поверхностей
/А является гиперболической, то индикатриса Дюпена представляет
собой две сопряженные гиперболы.
Если точка М - параболическая, то, как было показано в п.7.3.5,
для нее хотя бы одна из главных кривизн равна нулю, тогда из G.164)
получаем:
{dX1»J = ±i-, 0 ф а. G.165)
Знак в правой части G.165) в этом случае не меняется для всей кривой
и выбирается " -f ", если кр > 0, или " — ", если кр < 0. Обозначим
±к — 1/Z2, тогда из G.165) получим:
dX'P = ±1. G.166)
Это есть уравнение двух параллельных прямых в окрестности точки
М.
Во всех трех случаях точка М. является центром симметрии кривой
Дюпена.
7.3.7. Линии кривизны
Определение 7.16. Линиями кривизны называют такие
кривые
X! = х (X}(S),X}(S)) , 7 = 1,2 G.167)
на поверхности Е, направления касательных к которым в каждой
точке совпадают с одним из направлений главной кривизны.
В G.167) функции Xj(?) обозначают криволинейные координаты
XJ, изменяющиеся вдоль кривой в зависимости от некоторого пара-
параметра ? и соответствующие /-ой линии кривизны. Поскольку направ-
направления главной кривизны соответствуют направлениям собственных
о _ w
векторов pj тензора В, то будем иметь два семейства линии кривиз-
кривизны на поверхности, причем эти семейства взаимно ортогональны.
Получим дифференциальное уравнение линий кривизны. Соглас-
Согласно определению этих линий, направление касательной к ним, опре-
определяемое вектором dx/d?, пропорционально главному направлению,
о
задаваемому вектором р/, т.е.
где 7 - коэффициент пропорциональности.
Разложим векторы jpj по локальному базису
IPi
= A/pj, G.169)
§ 7.3. Кривые на поверхности 479
где А/ - некоторая матрица коэффициентов. В силу того, что и р/, и
pj лежат в касательной плоскости к поверхности, разложение G.169)
действительно имеет место.
Тогда G.168) с учетом G.169) и G.43) можно представить в виде:
^-PJ = A/pj, G.170)
ИЛИ
дХ}/д? = \{. G.171)
Это и есть дифференциальное уравнение двух линий кривизны: / =
1,2. Их также можно записать в виде:
ЛХ1 А1 -ч
Функции Аа можно выразить через коэффициенты первой и второй
квадратичных форм. В самом деле, для нахождения собственных век-
о
торов ра тензора В имеем уравнение:
(B-fcQE).pa = 0. G.173)
Или в компонентах, используя G.169):
(Ъи - kQgjj)XJQ = 0. G.174)
Независимое уравнение в G.174) только одно, например:
(bii - fca</u)Aa + (&i2 - kQg12) = 0. G.175)
Главные кривизны kQ являются собственными значениями тензора В
и определяются из G.142):
(Ьц - кадц)(Ь22 - kQg22) - F12 - kQg12J = 0. G.176)
Выражая из G.175) kQ через Aa и подставляя их в G.176), получим
квадратное уравнение для нахождения Аа:
(<711&12 - Hl2bll)\a + (<722#U — Pll^Ma + ^22^12 - ^12^22 = 0, G.177)
решая которое, находим два значения Ai и Х2 через коэффициенты
форм Tjjj и bjj.
480 Глава 7. Геометрия кривых и поверхностей
7.3.8. Геодезические линии
Определение 7.17. Геодезическими линиями (или просто
геодезическими) называют такие кривые на поверхности ?, у ко-
которых в каждой точке нормаль к кривой совпадает с нормалью к
поверхности.
Уравнение геодезической удобно задать в параметрическом виде
G.126). Получим дифференциальное уравнение геодезической линии.
Из определения геодезической следует, что для нее в каждой точке
выполняется соотношение:
или
кп = к. G.178)
Воспользуемся теперь разложением G.129) для вектора кривизны к
кривой по поверхности, тогда G.178) можно представить в виде:
&п= кпп + к,д. G.179)
Поскольку вектор кд ортогонален к п, то из уравнения G.179) следует,
что
кд = kgu = О, k = fcn, kg = 0, G.180)
т.е. вектор геодезической кривизны вдоль геодезической линии равен
нулю, а кривизна геодезической совпадает со своей нормальной кри-
кривизной. Геодезическая кривизна кд также равна нулю.
Подставим теперь в G.179) вместо к его выражение G.128):
dX1 dXJ d2XT , ,плолл
Pu-j т- + Pi-ГГ = fc"n' GЛ81)
as as dsz
и воспользуемся деривационными формулами G.81), тогда
~KdXTdXJ L dX1 dXJ d2XT , /
^ + Ь + k (
Учитывая, что для нормальной кривизны кп имеет место формула
G.137), в которой ds2 = gudX1dXJ, получаем окончательно:
#ХК ~KdX*dX' _
-^ + г"^-^7--° GЛ83)
- дифференциальное уравнение геодезической линии.
§ 7.3. Кривые на поверхности 481
7.3.9. Асимптотические линии
Определение 7.18. Асимптотической линией называют
кривую на поверхности Е, нормальная кривизна которой кп в каж-
каждой точке равна нулю.
Направления касательных к асимптотическим линиям называются
асимптотическими направлениями поверхности.
Из определения следует, что вдоль асимптотической линии соглас-
согласно G.137) вторая квадратичная форма равна нулю:
bIJdXIdXJ = 0. G.184)
Отсюда, в частности, получаем дифференциальное уравнение асимп-
асимптотической линии:
dX1
+Ьи = 0- GЛ85)
Из определения эллиптических точек поверхности (п.7.3.5, Ь > 0)
следует, что в них не может быть действительных решений уравнения
G.185), т.е. асимптотические линии - только мнимые.
В гиперболической точке знак квадратичной формы G.185) меняет-
меняется, поэтому имеются два различных действительных асимптотичес-
асимптотических направления.
В параболической точке одно направление, в котором кп = 0 и
имеется единственное решение уравнения G.185). Следовательно, в
параболической точке есть одно асимптотическое направление, кото-
которое совпадает с направлением касательной к главному нормальному
сечению, имеющему нулевую кривизну.
7.3.10. Примеры поверхностей
До сих пор мы говорили о свойствах поверхностей в окрестности
локальной точки. Рассмотрим теперь с помощью введенных харак-
характеристик - инвариантов К и Н - примеры описания поверхностей в
целом.
Если в каждой точке поверхности инвариант Н = 0, то такая по-
поверхность называется минимальной. Для нее, очевидно, главные кри-
кривизны равны и имеют разный знак. Свое название минимальная по-
поверхность получила из-за следующего свойства. Пусть имеется не-
некоторая замкнутая кривая в прострайстве (контур). Можно беско-
бесконечным числом способов построить поверхность в виде односвязной
области, край которой был бы ограничен данной кривой, но наимень-
наименьшей площадью будет обладать именно минимальная поверхность.
Поверхность, для которой инвариант К одинаков во всех точках
К = const, называется поверхностью постоянной кривизны.
16 Тензорное исчисление
482 Глава 7. Геометрия кривых и поверхностей
Упражнения к § 7.3.
Упражнение 7.3.1. Используя G.142) и G.154), G.155), показать, что глав-
главные кривизны kQ являются корнями следующего квадратного уравнения:
к2а - 2Нка + К = 0.
Упражнение 7.3.2. Показать, что матрица коэффициентов Aj ортонорми-
о
рованных собственных векторов pj может быть вычислена с помощью следующей
системы уравнений:
Ai/A? = AQ) gIJ\IQ\Ja = l, a = 1,2,
где Ла определяется из уравнения G.177).
Упражнение 7.3.3. Показать, что каждая точка минимальной поверхности
является либо точкой уплощения, либо гиперболической точкой.
Упражнение 7.3.4. Показать, что для минимальной поверхности и только
для нее асимптотические линии образуют ортогональную сетку.
Упражнение 7.3.5. Показать, что для сферы и только для нее все точки
поверхности являются омбилическими.
Упражнение 7.3.6. Доказать, что координатные линии X = const явля-
являются линиями кривизны тогда и только тогда, когда
&12 = 0, 012 = 0
вдоль этих линий.
Упражнение 7.3.7. Доказать, что координатные линии тогда и только
тогда являются асимптотическими линиями, когда вдоль них
&12 = 0, 012 = 0.
Упражнение 7.3.8. Показать, что если координатные линии X — const
являются линиями кривизны, то главные кривизны вычисляются по формуле:
ка = Ъаа/даа, а = 1,2.
Упражнение 7.3.0. Показать, что для эллипсоида вращения (см. упр.7.2.7-
7.2.10) главные кривизны вычисляются по формулам:
ау/а* cos2 X2+ с2 sin2 X2
ас
Упражнение 7.3.10. Показать, что для эллипсоида вращения (см.упр.7.2.7-
7.2.10) меридианы (кривые X = const) и параллели (кривые X "=¦ const) яв-
являются линиями кривизны, главные направления совпадают с касательными к
меридиану и параллели, гауссова кривизна вычисляется следующим образом:
К = с2/(а2 cos2 X2 + с2 sinX2J,
§ 7.4. Геометрия в окрестности поверхности 483
и все точки поверхности - эллиптические.
Упражнение 7.3.11. Показать, что для поверхности вращения (см.
упр.7.2.11-7.2.14) главные кривизны вычисляются следующим образом:
/" 1
а гауссова кривизна - по формуле:
к = —
Упражнение 7.3.12. Показать, что для каждой точки (X , X ) поверхнос-
поверхности вращения справедливы следующие утверждения:
• если f"(x) < 0, то это эллиптическая точка;
• если f"(x) > 0, то это гиперболическая точка;
• если / (ж) = 0, то это параболическая точка.
Упражнение 7.3.13. Показать, что если для поверхности вращения / =0
(конус или цилиндр) в каждой точке, то у нее имеется единственное семейство
асимптотических линий: X — const.
Упражнение 7»3.14. Доказать, что у эллипсоида вращения нет асимптоти-
асимптотических линий.
§ 7.4. Геометрия в окрестности поверхности
7.4.1. Определение окрестности поверхности
Во многих задачах механики требуется описание физических
свойств трехмерного объекта, у которого один из характерных разме-
размеров много меньше двух других. Такие трехмерные тела называются
оболочками, а математически их удобно рассматривать как окрест-
окрестность некоторой фиксированной поверхности S, задаваемой парамет-
параметрически как и ранее некоторой вектор-функцией, но для которой будем
в этом параграфе использовать специальное обозначение:
р = р(Х\Х2), G.186)
где р - трехмерный радиус-вектор точки М, принадлежащей поверх-
поверхности Е, X1 - криволинейные координаты на поверхности.
В компонентной записи G.186) имеет вид:
р{ = р'{Х\Х2). G.186')
484.
Глава 7. Геометрия кривых и поверхностей
Определение 7.19. Окрестностью по в ерхности Е
G.186) называют трехмерную область в евклидовом пространст-
пространстве Ш3, каждая точка М! в которой имеет радиус-вектор вида:
1Х2) + Х3п(Х1,Х2). G.187)
Здесь п - вектор нормали
к поверхности S (рис.7.14),
проходящей через точку
М!, р - радиус-вектор точ-
точки М на поверхности, из
которой выпущена эта нор-
нормаль, а X3 - третья коор-
координата, отсчитываемая по
нормали к поверхности и
изменяющаяся в некоторой
области:
±. G.188)
Значение h может быть
константой (h = const),
тогда говорят об окрестнос-
окрестности (оболочке) постоянной
толщины; если h - перемен-
переменная: h = h(X1^X2)) тогда
говорят, что окрестность (оболочка) имеет переменную толщину.
Термин "окрестность" подразумевает, что максимальное значение
h мало по сравнению с характерным размером dim S поверхности S:
Рис. 7.Ц.
поверхности
К определению окрестности
max h <? dim E,
G.189)
где под dim E понимается, например, наибольшее расстояние между
любыми точками поверхности S.
Таким образом, если радиус-вектор р(Х11Х2) точек поверхности
Е зависит только от двух координат, то радиус-вектор х(Х'), г =
1,2,3, определяемый по G.187), зависит уже от трех координат, но
специальным образом.
7.4.2. Векторы локальных базисов и метрические
матрицы в окрестности поверхности
Применим теперь к соотношению G.187) аппарат гл.1. Дифферен-
Дифференцируя G.187) по X1 (г = 1,2,3), получаем с учетом определения G.43)
и G.70):
дх
дХ1
= pi + Х3щ.
G.190)
^^___ § 7.4. Геометрия в окрестности поверхности 485
Используя деривационные формулы G.96), преобразуем G.190) к
виду:
R7 = Pl - X3bJlPj = Fj - X4j)pj. G.191)
Дифференцируя G.187) по -X, имеем
R3 = n. G.192)
Формулы G.191), G.192) определяют векторы основного локально-
локального базиса в окрестности поверхности.
Перемножая R/ и Кз скалярно, получаем:
ди = R/ • Kj = {6? - X4f){6Lj - X3bLj)gKL =
= ди - 2Х3Ь„ + (X3LfbKJ, G.193)
дп = R/ • R3 = {5j - X3bj)PJ • n = 0,
033 = R3 • R3 = П • П = 1.
- компоненты трехмерной метрической матрицы в окрестности по-
поверхности gij. Здесь мы воспользовались формулой G.73).
Формулы G.193) показывают, что д^ выражаются через коэффи-
коэффициенты первой и второй квадратичной форм поверхности Е.
Свойство G.189) "малости" окрестности поверхности является ос-
основанием для использования здесь и далее линейного приближения по
координате -X, при котором слагаемые при (-ХJ и выше отбрасы-
отбрасываются. Так метрическая матрица в линейном приближении имеет
вид:
ди = ди ~ 2ХЧи, д13 = 0, д33 = 1. G.194)
Определитель д метрической матрицы д^ вычислим, используя
свойство A.55):
V? = (Ri х R2) • n = (8{ - Х3Ь[)F} - X3bJ2)(Pl x PJ) • п.
Учитывая, что ра х pQ = 0, а также определение G.56) вектора нор-
нормали р\ х р2 = \/рп> получим:
< + (ХЭJ(Ь\Ъ1 - ВД).
Переходя согласно G.154) к инвариантам Н и if, имеем окончательно:
3H+{X3JK). G.195)
Глава 7. Геометрия кривых и поверхностей
Компоненты обратной метрической матрицы д%* в окрестности
поверхности при сохранении только линейных по -X слагаемых опре-
определяются по формулам:
gIJ=fJ + 2X3bIJ, /3 = 0, </33 = 1, G.196)
которые проверяются непосредственным вычислением:
9U9JK = (9IJ ~ 2X4u)(gJK + 2X4JK) =
= 6? + 2X3(gubJK - gJKbu) = 8?. G.196')
Векторы взаимного базиса R* в окрестности поверхности, ис-
используя линейное приближение по X3, вычисляем следующим обра-
образом:
R' = g"Rj = (д» + 2ХЧ")F« - ХЧ«)РК =
= № + Х%)р'. G.197)
Трехмерный метрический тензор Е в окрестности поверхности,
имеющий компоненты </,j, в локальном базисе R1 <8> RJ записывает-
записывается в линейном приближении следующим образом:
Е =Rt- <g> R1' = ptiRf" <g> Rj = R/ ® R7 + n ® n =
= [Sj - X3bj)pj ® {5!к + X3bTK)pK +n0n =
= Pi®P* + X3(-bJKpj ®pK + bJKpj <8> pK) + n <g> n,
или, используя определение двумерного метрического тензора Е из
п.7.2.3, получим
. G.198)
7.4.3. Деривационные формулы в окрестности
поверхности
Рассмотрим вторые производные от радиуса-вектора х точек из
окрестности поверхности:
Подставляя вместо х его выражение G.187), получим с учетом G.191)
и деривационных формул G.81) на поверхности:
= P/J -
G.200)
_ § 7.4. Геометрия в окрестности поверхности 487
а также при других комбинациях индексов:
х/з = -^(pi - Х3Ъ?рк) = -bfpK,
х33 = 0. G.201)
Формулы G.200) и G.201) представляют собой деривационные форму-
формулы в окрестности поверхности. Из них при -X = 0, очевидно, следу-
следуют деривационные формулы Гаусса-Вейнгартена G.96), если учесть,
что
L G>202)
7.4.4. Линии кривизны в качестве криволинейных
координат
Часто в механике используют частный случай криволинейных ко-
координат X1 поверхности, у которых координатные линии X1 = const
совпадают с линиями кривизны этой поверхности. Запишем основные
соотношения в окрестности поверхности для этого случая.
Как было отмечено в п.7.3.7, линии кривизны взаимно ортогональ-
ортогональны, поэтому координатные линии X1 также будут ортогональными.
Тогда метрические матрицы gu, gIJ и вторая квадратичная форма
bjj являются диагональными:
д12 = 0, д12 = 0, Ь12 = 0, G.203)
и собственные направления тензора В совпадают с направлениями
координатных линий.
Главные кривизны поверхности kQ находим из уравнения G.142),
которое в данном случае имеет вид:
о О G204)
Из G.204) получаем:
9аа
Введенные по G.205) величины RQ называют главными радиусами
кривизны поверхности.
Гауссова и средняя кривизны в данном случае имеют вид:
488
Глава 7. Геометрия кривых и поверхностей
Введем параметры Ламе На в окрестности поверхности и Аа на
поверхности:
/-^)
G.207)
Тогда коэффициенты второй квадратичной формы поверхности
можно представить в виде:
Ьаа = Al/Ra. G.208)
Согласно G.194) в линейном приближении На будут иметь вид:
На =
G.209)
Используя G.207), G.208), получаем:
На =
G.210)
Используя свойство G.203), из G.90) получаем выражение для не-
ненулевых символов Кристоффеля:
pa = 1 dgQQ _ 1 ОАд
OX* " AQ дХ°'
дА2
G.211)
Г?! = ~
2^2
А\ дХ2 '
Г?2=г^
Запишем уравнение Петерсона-Кодацци, используя форму G.108):
iB ~ Ш + ^
" ^Ьп = 0) а = lf 2
G*212)
§ 7.4. Геометрия в окрестности поверхности 489
и уравнение Гаусса в форме G.107):
дтм ~ ~ ~ ~ \
Ш ~ ~5х* + TuTli " ГпГь2 9М2 = ~зК- G'213)
Учитывая G.203) и заменяя Ьаа согласно G.208), a Tfj согласно
G.211), получаем уравнение Петерсона-Кодацци в виде:
д
Id / 1? Л*У' Л v2 Id / d я v2'
\ it2 / -Tti О Л О Л \ iti / it2 с/А
дХ1
Уравнение Гаусса G.213) после аналогичных преобразований при-
принимает вид:
д
( 1 дАЛ ,_д_(±дАЛ_
U19X1) + дХ* U2 дХ*) -
ЗХ1
Уравнения G.214) и G.215) находят широкое применение в механике.
Упражнения к § 7.4.
Упражнение 7.4.1. Убедиться непосредственно, что из G.212) следует
G.214), а из G.213) следует G.215).
Упражнение 7.4.2. Показать, что для поверхности вращения ненулевые
символы Кристоффеля имеют вид:
?1 ?11
11 - i _|_ х/2'
ь"--Т+7*' Г12 = 7'
Упражнение 7.4.3. Используя результат упр.7.4.2 и G.183), показать, что
если поверхность вращения - цилиндр (/ = const), то геодезическими линиями
являются винтовые линии (см. упр.7.1.9):
490 Глава 7. Геометрия кривых и поверхностей _____
§ 7.5. Уплощенные поверхности в Ш3
Для произвольной поверхности Е в М3, вообще говоря, нельзя ввес-
ввести единые прямоугольные декартовы координаты Х;/, с помощью ко-
которых можно было бы измерить расстояние между точками поверх-
поверхности по прямолинейным отрезкам, не выходя при этом с поверхности
Е.
В частном случае, однако, такие поверхности S существуют - это
плоскости в М3. _
На всякой плоскости тензор кривизны 4R тождественно равен ну-
нулю, поскольку на ней всегда можно ввести прямоугольные декартовы
координаты Х;/, в которых T^j = 0. Обратное же утверждение, во-
вообще говоря, не верно, так как тензор Римана-Кристоффеля 4R обра-
обращается тождественно в нуль не только для плоскостей, но и для более
широкого класса поверхностей, которые обычно называют уплощен-
уплощенными.
о
Определение 7.20. Поверхность Е в Ш называют уплощен-
уплощенной, если в окрестности каждой ее точки X1 существует прямо-
прямоугольная декартова система координат X'1', в которой метричес-
метрическая матрица единичная: g'u = 6jj, а расстояние ds между беско-
бесконечно близкими точками определяется формой:
ds2 = tfjjdX'tdX11 = {dX11J + {dX'2J. G.216)
Кроме плоскостей уплощенными являются, например, цилиндри-
цилиндрические поверхности: если взять за dX'a = sQ длины дуг вдоль оси
цилиндра и в окружном направлении, то действительно получим:
ds2 = ds\ + ds\
в каждой точке цилиндра.
Теорема 7.14. Тензор Римана-Кристоффеля 4R тождественно
о
равен нулю на уплощенных поверхностях S и только на них:
4R = 0 VIJGE. G.217)
о
Т Пусть поверхность Е - уплощенная, тогда можно ввести единую
систему координат X1', в каждой точке поверхности совпадающую с
локальной декартовой системой X'1. В этой системе X1: 'g'jj — J/j,
и, следовательно, по G.90) все символы Кристоффеля тождественно
равны нулю: TjjK = 0. Тогда из G.111) получаем, что действительно
§ 7.5. Уплощенные поверхности в R3 491
о
= 0 в каждой точке поверхности Е. В одну сторону теорема
доказана.
о
В обратную сторону. Пусть теперь в каждой точке поверхности S
имеет место Rjcij* = 0 в некоторой системе координат X1. Тогда из
о о
соотношения G.156) следует, что К = 0 в каждой точке Е, т.е. Е явля-
является поверхностью нулевой гауссовой кривизны. Из G.153) получаем,
что jK" = fciA:2 = 0, т.е. хотя бы одна из главных кривизн должна быть
равна нулю в каждой точке поверхности; пусть для определенности:
*i = 0, к2 ф 0.
Выберем теперь в качестве координат X1 линии кривизны поверх-
0
ности Е, тогда в каждой точке поверхности имеют место соотношения
G.203), G.205), т.е.
&12 = 0, 6ц = кгдц = 0, Ь22 = к2д22 ф 0, G.218)
9п ф 0, д22 ф 0, Q12 = 0. G.219)
Кроме того, для данных координат X1 уравнения G.214) Петерсо-
на-Кодацци имеют вид:
^ ^ = 0, к3^± = ^y(*iAi) = 0, G.220)
интегрируя которые, получаем, что к2А2 = ^(-Х^2) ~ функция от ко-
координаты X2, a Ai = А^Х1) - функция только X1.
Выражения G.211) для символов Кристоффеля Т\г и Г2Х с учетом
этих результатов записываем следующим образом:
11 "
Воспользуемся еще одним имеющимся в нашем распоряжении урав-
уравнением - деривационным уравнением G.96) при I = J = 1, которое
принимает вид:
Это уравнение можно преобразовать к виду
1 = о
и проинтегрировать: pi/Ai = a(X2). Учитывая, что pi = dx/dX1,
проинтегрируем еще раз, в результате получим выражение для ради-
радиуса-вектора поверхности:
х1
AxdX\ G.222)
Глава 7. Геометрия кривых и поверхностей
где а/(-Х) - некоторые функции, появившиеся при интегрировании.
Эти функции удовлетворяют определенным ограничениям, покажем
их. Из G.222) находим векторы базиса:
a22, G.223)
здесь
а/2 = дЕц/дХ2.
Тогда, вспоминая, что </п = А2, получаем:
откуда следует, что вектор ai имеет единичную длину: |ai| =¦ 1. Но
для такого вектора имеют место соотношения G.13), G.14), поэтому
ai • ai2 = 0.
Воспользуемся теперь соотношениями G.219) и G.218):
и
912 = Pi' Р2 = Ai*i • (фвц2 + а22) = Aai • а22 = 0,
= Pi2 • (pi x p2) = -Aiai2 • (Aiai x (фа12 + а22)) = 0.
Используя свойство векторного произведения ai2 • (ai х ахг) = 0, по-
получаем в итоге систему соотношений ортогональности:
Г ai2 • (ai x a22) = 0, ^ Г а22 • (ai x а22) = 0,
I ai2 • ai = 0, 1 а22 • ах = 0.
Отсюда следует, что возможны три ситуации:
а) ai2 = 0, а22 ф 0;
б) а12^0, а22 = 0; G.225)
в) ai2 и а22 не равны нулю и коллинеарны, т.е.
где в(Х2) - некоторая ненулевая функция.
Случай в) следует из того, что ai2 и а22 одновременно ортогональ-
ортогональны паре ортогональных векторов ai и (ai x а22). Рассмотрим вначале
этот случай, тогда
где /i= |a22|.
__ § 7.5. Уплощенные поверхности в R3 493
Составим квадратичную форму:
ds2 = gIJdXIdXJ = gnidX1J + g22(dX2J =
2 G.226)
и введем новые координаты:
X'1 = ф cos с - Г*' h sin ccUT2, of**
^ J c(X2) /
hcoscdX2,
= / 0/idX2. G.227)
J
Несложно проверить, что с помощью замены координат G.227) форма
G.226) может быть приведена к виду G.216), причем это возможно в
о
каждой точке поверхности Е.
Рассмотрим теперь случай а), тогда ai = const, p2 = а22 и #22 =
/i2(X2), следовательно:
ds1 = AUdX1J + h2(dX2J.
Делая замену координат:
х2
х2
X'1 = ф, X12 = / hdX2,
снова приводим квадратичную форму ds2 к виду G.216) в каждой
о
точке Е.
В случае в) имеем:
р2 = фа12, 5/22 -Ф2!2,
где /2 = |ai2|2, тогда
ds2 = A2(dX1J + ф2f2(dX2J.
Осуществляя замену координат:
Д2
с= / /dX2, G.228)
квадратичная форма ds2 также может быть приведена к виду G.216).
494 Глава 7. Геометрия кривых и поверхностей
о
Следовательно, во всех трех случаях а), б) и в) поверхность Е будет
уплощенной. ^
Три типа поверхностей G.222) с условиями а), б) и в), а также плос-
плоскости (для которых &i = 0, &2 = 0) представляют собой все возможные
виды уплощенных поверхностей.
В случае произвольной, вообще говоря, не уплощенной поверхнос-
поверхности, тензор Римана-Кристоффеля не обращается тождественно в нуль,
поэтому поверхности Е в IR3 представляют собой пример двумерных
римановых пространств, более общих, чем евклидовы. Эти простран-
пространства рассмотрим далее в главе 8.
Упражнения к § 7.5.
Упражнение 7.5.1. Поверхность G.40), имеющую вид
где ai, а2 - произвольные вектор-функции, такие, что |ai| = 1 и ai, (X &12 +
а22) ~ независимы, называют линейчатой, где
а/2 = двц/дХ2.
Доказать, что всякая уплощенная поверхность является линейчатой.
Упражнение 7.5.2. Доказать, что вектор-функция G.222) с условием G.225,
а) описывает цилиндрическую поверхность с направляющей &о(Х ).
Упражнение 7.5.3. Доказать, что вектор-функция G.222) с условием G.225,
б) описывает коническую поверхность с направляющей Q.i(X ).
ГЛАВА 8
ТЕНЗОРЫ В РИМАНОВЫХ ПРОСТРАНСТВАХ И
ПРОСТРАНСТВАХ АФФИННОЙ СВЯЗНОСТИ
§ 8.1. Римановы пространства
В механике и особенно в релятивистской физике тензоры широко
применяют в n-мерных римановых пространствах, являющихся бо-
более общими, чем евклидовы. Дадим определение этих пространств,
а затем покажем, как конструируются тензоры в них. Начнем с ос-
основополагающего понятия римановых пространств - элементарного
многообразия.
8.1.1. Элементарное многообразие
Определение 8.1. Элементарным п-мерным многооб-
многообразием называют такое множество Мп, каждой точке которого
взаимнооднозначно поставлен в соответствие упорядоченный на-
набор чисел (X1.. .Хп) из некоторой связной области V С Шп, т.е.
задано биективное отображение <р: Мп —> V С Шп.
Координатами точки М Е Мп в системе координат V называют
координаты Xх Е Шп ее образа ^(Л1), изменяющиеся в области V С
Если для множества Мп имеется другое биективное отображение
<р': Мп —> V С Мп, то координаты точки М в системах координат
V и V связаны соотношениями:
ХЫ=Х"{Х*), i,j = l...n, (8.1)
которые предполагают достаточное число раз дифференцируемыми и
невырожденными, т.е. det (dX/%'/dXj) ф О, VX' е V.
Введем как и ранее обозначения для якобиевых матриц преобразо-
преобразования, а также для их производных:
& _ (дх'>\ . _ / ах* \ • _ д*х<
и кроме того в этой главе будем использовать обозначения для част-
частных производных:
Ь ^M = 'U (83)
Глава 8. Тензоры в римановых пространствах
Примером двумерного (п = 2) элементарного многообразия М2 яв-
являются поверхности в М3, на которых определены криволинейные ко-
координаты Х11 X2 и которые заданы тремя функциями G.41).
8.1.2. Касательное пространство
Определение 8.2. Кривой С в многообразии Мп называют
отображение С: [Сь^г] ? ^ —> Мп, которое записывают в ви-
виде функции:
*•¦ = **@ v^eKbfc], rer. (8.4)
Здесь Xх - координаты точки М Е Mn, [?i, ?2] " некоторый отрезок
из R1, (?i < ^2)? & функции (8.4) предполагаем непрерывно дифферен-
дифференцируемыми, по крайней мере, два раза.
Зафиксировав значение параметра ? ? [Сьбг], получим некоторую
точку М Е ?, в ней можно вычислить производные от функций
(8.4):
а? = dXx'/d^ (8.5)
Определение 8.3. Упорядоченный набор (а}...ап) производных
(8.5) называют компонентами касательного вектора ах
в точке /Л кривой С в Мп.
Если перейти к координатам Х/г той же точки М. ? ?, то соглас-
согласно (8.1) получаем, что компоненты касательного вектора ап в этой
системе координат будут иметь вид: а'х = dX'x /d? и связаны с аг
тензорным законом:
afi = Q*y. (8.6)
Поскольку через фиксированную точку М ? Мп можно провести
различные кривые ?, то, вообще говоря, в каждой точке М имеется
множество упорядоченных наборов (а1.. .ап). Определим операции с
этими наборами.
Пусть имеется две кривые С\ и ?2? заданные в виде функций -Х|(?),
-^2@? проходящие через точку М, тогда можно построить два набора
компонент касательных векторов а\ = dX[/d? иа'2 = dX^/d^.
Суммой компонент двух касательных векторов назовем набор
который представляет собой компоненты касательного вектора к кри-
кривой (Х[ + -ХзНО в Данной точке М.
Аналогично определяем произведение компонент аг на веществен-
вещественное число А:
\а* = \dXx'/di = d(\X{)ldi.
Поскольку набор чисел (а1... ап) является элементом пространства
Кп, то, выбрав базис е,- в этом пространстве, можно построить сам
касательный вектор а в точке М кривой С: а = axet: = a/lej, где
е(- = Р\ ej - новый базис.
8.1. Римановы пространства 497
Определение 8.4. Касательным пространств ом в
данной точке М элементарного многообразия Мп называют мно-
множество касательных векторов а = а*е,-, построенных ко всевоз-
всевозможным кривым С, проходящим через данную точку.
Теорема 8.1. Касательное пространство в любой точке М Е
Мп является п-мерным линейным пространством, которое обозна-
обозначают как ТмМп, а векторы е, образуют базис в нем.
Т Первое утверждение теоремы очевидно, так как операцию сложе-
сложения и умножения на число касательных векторов ai = а\е{ и аз = а^е,
можно определить с помощью соответствующих операций с компонен-
компонентами ai и а*2. Векторы е,-, г = 1.. .п, являются линейно независимыми
и действительно образуют базис. Нам нужно только доказать, что они
все принадлежат касательному пространству в данной точке М.
Пусть Xх - координаты точки М. Рассмотрим п кривых Са в Мп,
заданных следующими функциями:
4»)@ = *'¦ + ?«. «=!•••» V*€[0,fc], (8.7)
где ?i - некоторое положительное вещественное число. Эти функции
проходят через точку М при значении параметра ? = 0, а произ-
производные dXiQ\/d? = 5га образуют компоненты некоторых касательных
векторов и совпадают с компонентами векторов ea = S^ej. Очевид-
Очевидно также, что при переходе к новым координатам Х1х (X7) кривые Са
преобразуются к виду
при этом компоненты касательных векторов преобразуются действи-
действительно по тензорному закону:
= (дх«/дх*)б>а.
Таким образом, мы нашли такие кривые Са в Мп, которые прохо-
проходят через точку М и компоненты касательных векторов к которым
совпадают с компонентами векторов еа в своем же базисе, следова-
следовательно, е,- еТмМп. А
8.1.3. Определение риманова пространства
Определение 8.5. Элементарное п-мерное многообразие Мп на-
называют римановым пространств ом Vn, если в каждой точ-
точке /A G Мп с координатами Xх задана матрица gij п-го порядка,
которая является
1° симметричной,
2? невырожденной: det (gij) ф О, V-X,
498 Глава 8. Тензоры в римановых пространствах
3° компоненты ее являются непрерывно-дифференцируемыми функ-
функциями,
4° при переходе к другим координатам X'1 преобразуется по тензор-
тензорному закону:
Двумерные поверхности, рассмотренные нами ранее в Е?3, очевидно,
можно рассматривать как двумерные римановы пространства V2 с
метрической матрицей gjj.
Расстояние в римановом пространстве вводят для бесконечно близ-
близких точек М и М!, имеющих кординаты Xх и Xх -\-dXx, и определяют
его как
ds2 = xgijdXx'dXj) (8.9)
где >с - знаковое число, которое выбирают так, чтобы форма (8.9)
была положительной.
Риманово пространство называют собственно римановым, если
метрическая матрица #,j, VX1 Е V, является положительно-опреде-
положительно-определенной, в противном случае говорят о псевдоримановых пространст-
пространствах.
8.1.4. Скалярное произведение в Vn
Поскольку у нас теперь в каждой точке М. Е Мп определена мет-
метрическая матрица </,j, то в касательном пространстве ТмМп можно
ввести скалярное произведение.
Определение 8.6. Скалярным произведением каса-
касательных векторов aitb из касательного пространства ТмМп
называют отображение (р: Tj^Mn х ТмМп —> Ш1, построенное
следующим образом:
Vfc, (8.10)
где а* и№ - компоненты касательных векторов в точке М Е V" с
координатами Xk, a gij (Xk) - метрическая матрица в данной точ-
точке.
Если V" - собственно риманово, то скалярное произведение (8.10)
обладает всеми свойствами, приведенными в определении 2.8, и, сле-
следовательно, пространство ТмМп с введенной на нем операцией (8.10)
является евклидовым пространством. Его обозначают как ТмУп-
Если же V" - псевдориманово, то соответствующие пространства
Уп называют псевдоевклидовыми.
Пусть е,- - базис в T^iVn, в котором касательные векторы а и b
имеют компоненты а1, Ь1, соответствующие системе координат Xх.
Тогда из (8.10) следует, что
а • b = a*Vei • ej = ax\Pgij,
§ 8.1. Римановы пространства 499
откуда получаем
е.'-е,- =gij. (8.11)
Поскольку gij{Xk) не вырождена, то можно определить обратную
метрическую матрицу д%*(Хк):
gijgjk = Si, (8.12)
а с ее помощью - векторы взаимного базиса е1:
е1" = <?'Ч-, (8-13)
которые в соответствии с соглашением о совпадении евклидовых и
сопряженных к ним пространств (см. п.2.4.4) можно рассматривать
как элементы из 7\<Vn. To же самое относится и к псевдоевклидовым
пространствам.
8.1.5. Определение тензора в элементарном
многообразии
После того как мы ввели векторы а в касательном пространстве
Тл<Мп, можно воспользоваться формализмом, изложенным в §2.5, и
построить в каждой точке М Е Мп множество наборов касательных
векторов
где a,- Е ?мМп, Ы') Е Tjj^Mn, и ввести на этом множестве операции
B.112) сложения и умножения на вещественное число.
Определение 8.7. Тензорным касательным прост-
пространством Тп (ТмМп) типа (pq), где р -f q = 2, в точке М
элементарного многообразия Мп называют тензорное произведение
касательного пространства ТмМп на себя:
ТЛРЯ)(ТММП) = ТмМп ® ТмМп VM E Mn, p + q = 2. (8.14)
Как и ранее, тензорное произведение вводим как фактор-простран-
фактор-пространство n-ой степени декартова квадрата
ТмМп®ТмМп = [(ТмМп х ТмМп)п]
по отношению к той же самой эквивалентности, введенной определени-
определением 2.24. Теорема 2.29 тоже имеет место, и с ее помощью устанавли-
устанавливаем, что 7л\ (ТмМп) является линейным пространством, причем
pq
Базисные диады в Тп (ТмМп) введем по формулам B.118):
е;Ъек = ЫЦек)], (8.15)
где [ ] - классы эквивалентности соответствующих наборов касатель-
касательных векторов. Очевидно, что если рассматриваемое многообразие М2
является поверхностью Е в IR3, то ТмМ2 совпадает с ?*(*)> введен-
введенном в п.7.2.3, а базисные диады (8.15) с соответствующими диадами
Pi® Рк.
Глава 8. Тензоры в римановых пространствах
Определение 8.8. Тензором второго ранга А(М) типа
(pq) в точке ЛЛ Е Мп называют элемент тензорного касательного
пространства TnPq)(TMMn), p + q = 2.
Подобно тому, как это проделано в §2.5, можно ввести тензоры выс-
высших рангов кА в Мп.
Всякий тензор fc-ro ранга кА(Л4) согласно теореме 2.28а можно
представить разложением по диадному базису в Тп :
кА = A(i ipjl-'jqeil 0 ... 0 е1' 0 eh 0 ... 0 eig, p + q = fc. (8.16)
Поскольку тензор кА введен как инвариантный объект, то, пере-
переходя от координат Xх точки М Е Мп к координатам X", согласно
формулам B.158), получаем
- формулу преобразования его компонент.
8.1.6. Определение тензора в римановом пространстве
Если в многообразии Мп введена метрическая матрица gij, то оно
становится римановым пространством V", а касательное простран-
пространство в каждой точке М Е V" - евклидовым (или псевдоевклидовым)
2м Vn. Тогда используя соглашение о совпадении пространств Tj^Vn
и ТмУп (см. п.2.4.4), можно говорить о тензорном касательном про-
пространстве Тп (TxVn), заданном на римановом пространстве Vn.
8.1.7. Алгебраические операции с тензорами в Мп и Vn
Поскольку касательные тензорные пространства Тп\ (ТмМп) яв-
являются линейными пространствами, то для них определены операции
сложения и скалярного умножения тензоров на число, операции транс-
транспонирования, симметрирования, альтернирования, а также тензорное
произведение тензоров. Формальная запись этих операций для тензо-
тензоров из Тп{р9){ТмМп) совпадает с формулами B.159) - B.165).
Для тензоров из Тп (ТмУп) кроме того определены операции опус-
опускания и поднятия индексов B.166) и скалярное умножение тензоров
(см. определение 2.29).
8.1.8. Коэффициенты связности в V"
В евклидовом пространстве (см. §6.1) была определена операция
ковариантного дифференцирования тензорных полей. Эта же опера-
операция может быть введена и для риманова пространства Vn. Дадим ее
определение.
§ 8.1. Римановы пространства 501
Поскольку в каждой точке М(Хг) ? Vn введена метрическая мат-
матрица^-(А"'), компоненты которой, согласно 3°, являются непрерывно-
дифференцируемыми функциями, то можно вычислить производные
dgij/dXk и образовать из них следующие объекты:
Г;;* = 5(9itJ + 9jk9i - 9ij,k). (8.18)
Определение 8.9. Функции Г,^-*, определенные по формулам
(8.18), называют коэффициентами связности первого
рода в Vn. Коэффициенты связности второго рода вводим с
помощью обратной матрицы дг^:
Г^=5трГОр. (8.19)
Заметим, что в евклидовом пространстве Шп аналогичная формула
F.13) является следствием соотношения F.1), с помощью которого
вводились символы Кристоффеля.
В римановом же пространстве две основополагающие формулы
F.1) и F.2) имеют место только в некоторых частных случаях и за-
записываются следующим образом:
r?j=Smk(S-1)kiJ, (8.20)
E-1)fe<)i-(S-1)fcj),- =0, (8.21)
где S™ - матрица коэффициентов, связывающая два базиса е? и ет
в Vn: e? = S™ в*, которые являются аналогом базисов ё* и R* в про-
пространстве К3 соответственно. Эти частные случаи мы рассмотрим
далее, в общем же случае риманова пространства Vn формулы (8.20)
и (8.21) не имеют места.
Теорема 8.2. Коэффициенты связности Г^т и Г™, введенные в
Vn no формуле (8.18), не являются компонентами тензоров.
Т В самом деле, если определить коэффициенты связности в системе
координат X", а затем воспользоваться формулами перехода (8.8) и
обозначениями (8.2), (8.3), то получим:
\{PljPmk 9,т)ц-\(Р\Р'] 9,т)\к =
ip',- PT P». (glm,q + gqm,, - g,q,m) +
',. Ртк Pij Tlqm + glmP% P'k. (8.22)
502 Глава 8. Тензоры в римановых пространствах
Используя формулу (8.19), устанавливаем закон преобразования ко-
коэффициентов Г^-:
Г$ = 9'kmT'ijm = Q\Qmp дгр{Р\Р«тРч5 Г/д„+
% Plm) = P'iP) Q\Vq + Q\pth ¦ (8.23)
Оба закона преобразования (8.22) и (8.23) отличаются от тензорного
(8.17), что и доказывает теорему. А
Теорема 8.3. Коэффициенты связности Tijm uT^j в Vn симмет-
симметричны по паре индексов:
lira = Ijim, U T{j = Tji. (8.24)
Т Переставляя индексы i «-> j в (8.18) и (8.19), легко убедиться в
истинности этого утверждения. А
8.1.9. Ковариантное дифференцирование тензоров в Vn
Рассмотрим теперь в Vn произвольное поле тензора fc-ro ранга:
причем его компоненты Q'1' "%Pjl,,%j (Xх) будем считать непрерывно-
дифференцируемыми функциями координат X1 точки М Е Vn.
Определение 8.10. Ковариантной производной от
компонент тензора &1'%Pjl...j k-го ранга кП, определенного
в Vn, называют следующий объект:
я
«—¦ /\f I ...In U /ч| 1...t«
(8.26)
Теорема 8.4. Ковариантная производная cm компонент тензо-
тензора в римановом пространстве, определенная по формуле (8.26), сама
образует компоненты тензора (к + \)-го ранга.
Т Докажем теорему для случая к = 2, для тензоров высших рангов
доказательство аналогично. Записывая ковариантную производную
§ 8.1. Римановы пространства
.503
от тензора П\ в новых координатах X'* и используя (8.23), получаем:
= (Q'>T n'»)u + QmP W (p«- PwmQ\Kw + Q\Prjm)-
- Q'>'m<F, (p«- p-j; Q"? rU + QmT Prjk) =
= Q\Pmk РГ (fi'ra,r + r^fi^ - T?mu'w) =
= Q'/PT-PriVrfi'm. (8.27)
Здесь учтено, что
ГI - - 0
4 v - дх*дхч -и
дХ'т д2Х' д2Хг
4 р >т дХР дХ'эдХ1™
Соотношение (8.27) действительно представляет собой тензорный за-
закон преобразования компонент тензора (к + 1)-го ранга (в данном слу-
случае - третьего). А
С помощью понятия ковариантной производной можно определить
градиент тензора к-то ранга kfl в Vn:
V ® кП = V.n11-1^^.^1' ® е,-, ® ... ® е,р в е1"^1 ® ... ® elfe, (8.28)
который, согласно формуле (8.26), представляет собой тензор (к -f 1)-
го ранга; а также дивергенцию тензора
V . кп = Vl-nWa-i>p+I...|.fce<a ® ... ® etp ® е^1 ® ... ® elfc, (8.29)
представляющую собой тензор (к — 1)-го ранга, и ротор тензора
Vxfcn= -L60^ Vin;2-tp . ..^е,,®.. .®etp®el'p+1 ®.. .®eifc, (8.30)
представляющий собой тензор fc-ro ранга.
Заметим, что в евклидовом пространстве Ш3 (и вообще Шп) анало-
аналогичные формулы F.47), F.48) и F.52) были установлены как следст-
следствие, а определения градиента, дивергенции и ротора тензоров были
даны в виде первых формул в F.47), F.58) и F.51). Аналогичные
формулы в Vn, вообще говоря, не имеют места, также как и (8.20) и
(8.21):
V®fen#eI®^7fcfl, V-^e'.^bn, (8.31)
504 Глава 8. Тензоры в римановых пространствах
Теорема 8.5 (теорема Риччи). Ковариантная производная
(8.26) метрической матрицы gij в Vn тождественно равна нулю:
Vkgij=0 в Vn. (8.32)
Т Для доказательства теоремы следует проделать те же самые вы-
выкладки, которые приведены для теоремы 6.4. А
8.1.10. Абсолютная производная тензора
Пусть в Vn задано поле тензора кП(Хг). Выберем некоторую кри-
кривую С (8.4), проходящую через точку Л4(Хг) с касательным вектором
а = а'е,', где а1' = дХ*/д?.
Определение 8.11. Абсолютной производной (илипроиз-
водной по направлению вектора &) тензора k?l, заданного в Vn,
называют следующий объект:
Vkft
—— = a.V®*ft. (8.33)
of
Теорема 8.6. Абсолютная производная (8.33) от тензора к-го
ранга представляет собой тензор к-го ранга и имеет следующие
компоненты:
Vkft ЯП, i
^^^1^ = k, (8.34)
где
—Ф~л*. . =—Ц{1"Лр. . +—('Ут*'.П*1"Лв=т'.'Л'. -
d? Jl~'3<> d? Jl'q d? \" mt J1-^
(8-35)
T Тензорный характер абсолютной производной, очевидно, следует из
определения 8.11, так как а и V®*ffc являются тензорами. Подставляя
в (8.33) выражение для а и формулы (8.26), (8.28), получаем
-Ц- = -Щ-Ъ (v,0''1-4|)+1...,fcei ® e4l ® ... ® е,-р ® е''+' ® ... ® в'*) =
dX*
= -jTViUH-\+i ikeh ® ... ® е,р ® е*»+1 ®... ® eik. (8.36)
Учитывая, что
d? ЭХ* •p+i-u-^" ••,+!.«
из формулы (8.36) действительно следует (8.35). А
8.1. Римановы пространства 505
Определение 8.12. Говорят, что тензорк$1 в Vй параллель-
параллельно переносится вдоль кривой С (8.4) из точки Х%м = Хг(?м) в
точку Xjj = Хг(?м), если его абсолютная производная вдоль этой
кривой равна нулю:
Vktl/dt = О, Ы^?^ ?лЛ (8.37)
Если записать уравнение параллельного переноса (8.37) с учетом
(8.35), например, для вектора:
1
щЯ{ + Т)к?±-а = 0, (8.38)
то из (8.38) получим систему обыкновенных линейных дифференци-
дифференциальных уравнений первого порядка относительно функций ft1 (X*). Ее
решение с начальным условием ? = ?n: ft* = fl'(.M), как известно [35],
существует, единственно и продолжаемо от точки М. до Jsf. Приме-
Применяя аналогичное рассуждение для тензора кП, приходим к следующей
теореме.
Теорема 8.7. Для любой гладкой кривой С, соединяющей точки
М и Jsf в Мп, результат параллельного переноса всякого тензора
кП, заданного в Мп, существует, однозначно определяется тензо-
тензором кп(М) и линейно зависит от к?1(М).
Параллельный перенос играет важнейшую роль в римановых про-
пространствах: он позволяет сравнивать тензоры, заданные в различных
пространствах тАря){ТмМп) и Tn(pg)(T^Afn). Напомним, что тен-
тензорные пространства на Мп определялись у нас локально в каждой
точке М Е Мп и, вообще говоря, например, раскладывать тензор
кА е ТпРЯ\ТмМп) по базису пространства ТпМ\т^Мп), определен-
определенному для другой точки Jsf, так как это мы проделывали для евклидова
пространства М3 (см. гл.1), у нас нет никаких оснований. Однако с
помощью параллельного переноса вдоль некоторой кривой для каж-
каждого тензора к А(м) € Тп (ТмМп) мы можем однозначно построить
его "двойник" fcA(jV) в пространстве Тп (Т//Мп) и реализовать та-
такое разложение.
Тензор *А(д/*), построенный с помощью параллельного переноса,
называют параллельным тензору кА^у Заметим однако, что кА^
зависит от кривой ?, соединяющей точки М. и Jsf,
В заключение этого параграфа приведем еще одну важную теорему.
Теорема 8.8. При параллельном переносе из точки ЛЛ в точ-
точку Jsf вдоль любой кривой С в Мп линейная комбинация векторов
506 Глава 8. Тензоры в римановых пространствах
из касательного пространства ТмМп сохраняется в касательном
пространстве Т//Мп.
Т Пусть в ТмМп определены векторы Ъм, Ъ($)м, s = !»•••» ПРИ"
чем: Ъм = J2$=i ^*а(*)М) гДе ^' ~ вещественные не все нулевые чис-
числа. Разложим эти векторы по базису e,vw в ТмМп: Ъм = Ьгме(м,
&(*)М = a$eiM> тогда имеем в
В касательном пространстве Tj^Mn векторам Ъм и bl(s)m соответ-
соответствуют векторы Ь(?) = 6*@е« и а(*)(?) = а(,)@еи где е,- - базис в
Т//Мп, причем а},\@» ^@ удовлетворяют уравнению параллельного
переноса (8.38):
da) v . . wr
^f+ri»aU-dt = 0) при е=ы: а'(<) = a>(<w' (8'4Оа)
— + Г)кЬ> — = 0, при ? = Ы : Ь1 = 6^. (8.406)
Рассмотрим задачу (8.406) и обозначим ее решение для частного
случая начального условия ? = ?м • Ми = а\л\ как Ь/Л\(?)«
уз j уз ) уз)
Легко проверить, что тогда функция Ь'(?) = 2*=i ^*^ы(О УД°В"
летворяет уравнению (8.406) с начальным условием ? = ?м '- Ъхм —
^A'flj,)• Но в силу теоремы 8.7 решение задачи (8.406) единственно,
значит Ь1{() = 2A'K4j({) и есть ее решение.
По той же теореме 8.7 получаем, что решение задачи (8.40а) а{,ч(?)
вдоль той же самой кривой С также единственно, а поскольку задача
(8.40а) отличается от задачи (8.406) при условии ? = ?м : W5\ =
а1/* только обозначением неизвестных, то решения их совпадают, т.е.
В итоге получаем:
~ ' Ы^?^?лг- (8.41)
3 = 1
Сравнивая (8.39) и (8.41), получаем, что линейная комбинация векто-
векторов при параллельном переносе действительно сохраняется (т.е. Л5
не меняются). А
jj 8.2. Пространства аффинной связности _____507
Упражнения к § 8.1.
Упражнение 8.1.1* Аналогично определению B.29), дать определение опе-
операции скалярного умножения тензоров второго ранга из тензорного касательного
пространства 7п (^М^п).
Упражнение 8*1.2* Показать, что в собственно римановом пространстве
Vn для символов Кристоффеля имеют место соотношения, аналогичные F.11).
§ 8.2. Пространства аффинной связности
8.2.1. Определение аффинной связности
Обратим внимание, что в формулу (8.26) ковариантного дифферен-
дифференцирования явным образом не входит метрическая матрица gij, а толь-
только коэффициенты связности Г[^. На этом факте основано построение
пространств, еще более общих, чем римановы - пространств аффин-
аффинной связности, в которых разделены понятия метрики д^ (т.е. скаляр-
скалярного произведения) и связности Г^ (т.е. ковариантного дифференци-
дифференцирования и параллельного переноса) в элементарном многообразии Мп.
Математически это означает, что в таком пространстве мы, вообще
говоря, не требуем связи Г[^ с векторами базиса е,- (т.е. отказываем-
отказываемся от соотношений (8.20) и (8.21)) и с метрической матрицей д^ (в
общем случае отказываемся от (8.18)). Более того, понятие метрики
в Мп может вообще не вводиться, а коэффициенты связности, тем не
менее, используются.
Определение 8.13. Элементарное п-мерное многообразие Мп
называют пространств ом аффинной связности Ln, ес-
если в каждой точке М Е Мп с координатами Xх задана система
*
функций Г^, которые
1° являются непрерывно-дифференцируемыми функциями,
2° при переходе к другим координатам Х1% преобразуются следую-
следующим образом:
Г;? = Р\ Р«. QmT T\q + Qmr Pr{j . (8.42)
*
Функции Г?-, заданные в Ln, называют коэффициентами аффин-
аффинной связности (или просто аффинной связностью). (Мы перешли от
*
обозначений Г^ к FJJ с той целью, чтобы сохранить Г^ для случая,
когда соотношение (8.18) все же имеет место, см. об этом далее).
Так же, как и для многообразия Мп, для Ln можно определить
тензорное касательное пространство Тп[ (TmLu), построенное с по-
508 Глава 8. Тензоры в римановых пространствах
мощью, касательного пространства 7мLn:
^. (8.43)
Для тензоров fcA из Тп (TmU1) определены все те же алгебраи-
алгебраические операции, что и для тензоров из Тп\ (Мп) (см. п.8.1.7).
8.2.2. Ковариантное дифференцирование в Ln
Наличие связности Г[^ в Ln означает, что в этом пространстве
определена операция ковариантного дифференцирования.
Определение 8.14. Ков ариантной про из в одной от
компонент тензора кА Е Тп; (ТлД/1), fc = р -f q, (или иначе
ковариантной производной относительно связности Т1^) называют
следующий объект:
* «i..p И i-p А*," И i.=m гр
8 = 1
-J2hiAil'"irh..^m...i9' (8-44)
Аналогично теореме 8.4, несложно показать, что ковариантная про-
производная (8.44) от компонент тензора fc-ro ранга является компонен-
компонентами тензора (fc + 1)-го ранга V ® k А в Ln, называемого градиентом
тензора:
V ® fcА = У.-А11"*1^^ igef* ® etl ® ... ® elp ® e7'1 ® ... (8) е7'9, р + g = к.
(8.45)
Поскольку скалярное произведение в Ln у нас не определено, то, в
отличие от (8.33), абсолютной производной тензора *П, заданного в
Ln, назовем тензор fc-ro ранга
,
= fc, (8.46)
где
§ 8.2. Пространства аффинной связности 509
Тогда уравнение параллельного переноса относительно связности
FJy для тензора кП вдоль кривой С имеет вид:
Vkn/d? = 0, (8.47)
где а = (dXl/d?)ei - касательный вектор к ?.
В частности, уравнение параллельного переноса вектора вдоль С
имеет вид, подобный (8.38):
> = 0. (8.48)
Из (8.47) следует, что для одного и того же многообразия Мпу вводя
различные связности FJJ, получаем различные способы параллельного
переноса тензоров.
8.2.3. Геодезические линии в Ln
Определение 8.15. Кривая С в пространстве Ln называется
геодезической линией, если любой ненулевой вектор а, каса-
касательный к С в некоторой точке М., является касательным при па-
параллельном переносе вдоль ?.
Найдем уравнение геодезической линии в Ln.
ТЕОРЕМА 8.9. Дифференциальное уравнение геодезической линии
в Ln имеет вид:
Т Действительно, всякую кривую в Ln можно задать в параметри-
параметрическом виде (8.4): X* = -Х"'(^), ? ? [?i,6]- Но по определению 8.15
любой касательный вектор аг = dXx /d? к С в точке М параллельно
переносится вдоль нее, т.е. удовлетворяет уравнению (8.48):
= 0. (8.50)
Поскольку a* является касательным в каждой точке кривой ?, то урав-
уравнение (8.50) имеет место для всех ? Е Къ^г]» чт° и доказывает фор-
формулу (8.49). А
8.2.4. Тензор кручения
Поскольку в определение 8.13 аффинной связности Г[^ не входило
требование ее симметричности, то, вообще говоря, Г^ следует по-
полагать несимметричной. В этом случае целесообразно рассмотреть
объект Tg - rjj.
510 Глава 8. Тензоры в римановых пространствах
Определение 8.16. Тензором кручения3^ в пространстве
Ln называют следующий элемент пространства Тп {Тм^):
fitim = -(Г? - Г?-). (8-52)
Теорема 8.10. Тензор 3?1, введенный по формуле (8.51), дейст-
действительно является тензором третьего ранга.
Т Для доказательства достаточно записать компоненты п'{™ в новой
системе координат и воспользоваться формулами (8.42):
/ т 1 *т *т * / т *r *r * m
= Р^Р% Qmr Пут, (8.53)
так как Рг- согласно (8.2) симметричен по нижним индексам. А
8.2.5. Пространство Lg аффинной связности
без кручения
Рассмотрим теперь частные случаи пространств аффинной связ-
связности Ln.
Важный случай представляет пространство Lg аффинной связ-
связности без кручения, когда
Пут = О, VA-* € Lg. (8.54)
Для такого пространства в силу определения (8.52) связность Г^ сим-
симметрична:
¦ртп Tini
Теорема 8.11. В каждой точке М пространства LJ} существу-
существует такая система координат Х%, в которой коэффициенты аффин-
аффинной связности обращаются в нуль: T^(Ai) = 0.
Ў Пусть Хп - некоторая система координат. Выберем произвольную
точку М с координатами X'J^ из LJ} и определим в окрестности этой
точки следующие преобразования координат:
Г = А'ДХ'* - Х'Ь) + и*тТ$(хЧ - X'l^X'1 - Xb), (8-55)
jj 8.2. Пространства аффинной связности 511
где Ах j - некоторая неособенная матрица с постоянными коэффици-
ентами, a F^J1 - коэффициенты связности в системе координат Х/г.
Вычислим якобиевы матрицы для такого преобразования координат
в фиксированной точке Ххм: PXj = Ах ^ Q3{ = (Л),-, а также опре-
определим Рх)к = д2Хг'/дХ'здХ1к = Ах'тТ']?{М).
Коэффициенты связности Г^ в новой системе координат Xх удов-
удовлетворяют соотношениям (8.42), т.е. имеют место соотношения:
Откуда, очевидно, следует, что Т]AM) = 0 в точке М.
Заметим, что условие отсутствия кручения пространства Lq ис-
использовано нами существенным образом при составлении квадратич-
квадратичной формы (8.55). А
8.2.6. Пространство абсолютного параллелизма
Рассмотрим еще один важный частный случай пространства Ln,
в котором связность FJJ выбирается специальным образом, а именно
предполагаем справедливой для Г^ только одну формулу (8.20), отка-
отказываясь от двух других (8.18) и (8.21) по сравнению с пространством
JK •
Определение 8.17. Пространство аффинной связности Ln на-
называют пространством абсолютного параллелизма Ап, ес-
если в каждой точке Xх из Ап существует п линейно независимых
непрерывно-дифференцируемых касательных векторов е^Х7), та-
ких, что связность Г^ имеет вид:
h?j=Smk(S-1)kiJ, (8.56)
где Smk - матрица коэффициентов разложения векторов
е,- = 5TO,-eTO, a (S)*,- - обратная к ней матрица.
Обратная матрица, очевидно, существует в силу линейной незави-
симости векторов е,-.
Теорема 8.12. Коэффициенты связности (8.56) при переходе в
новую систему координат Х1х преобразуются по закону (8.42).
Глава 8. Тензоры в римановых пространствах
Т Поскольку по определению е, при каждом фиксированном г являют-
являются векторами, то коэффициенты 5Jt- с фиксированным нижним индек-
индексом г при переходе в Х'х преобразуются как компоненты вектора:
#'г = Q\Ski > (S'-Vi = (S-l№ ¦ (8-57)
тогда производные {S)^ при переходе в систему координат Х'х
преобразуются следующим образом:
(S'-1)*,,,. =((S-1)ktPti)\u = (S-1)\uPtiP«t +(S-1)ktPtij. (8.58)
Записывая связность (8.56) в новой системе координат, получаем
Г* = S'l E'-1)fc,.|i = Qmr 5rfc(E-1)fc()ttPt,P«- + (S-^P^) =
= Qmr P\ P«. 5rfcE)fctiU + Qmt P%. (8.59)
С учетом (8.56) действительно получаем правило преобразования
связности (8.42). А
Рассмотрим некоторые свойства пространства Ап.
Теорема 8.13. Векторы е,- в Ап являются ковариантно-посто-
янными, т.е. ковариантная производная их компонент тождест-
тождественно равна нулю:
V®e,- = 0, ViSmj=O, i7i{S-1)mj = 0 eA\ (8.60)
Т В самом деле, используя определение (8.45) ковариантной производ-
производной относительно связности (8.56), для векторов е,- = S^-ej (нижний
индекс у 5Jt- фиксирован), получаем:
Здесь мы использовали результат упражнения 8.2.1. А
Теорема 8.14. В пространстве Ап и только в нем параллельный
перенос из точки М в точку Af, определяемый с помощью уравнения
(8.4V> не зависит от выбора кривой С, соединяющей эти точки.
Т Рассмотрим пространство Ап и некоторый вектор b E ТмМп, па-
параллельно переносимый из точки М. в точку Af этого пространства.
Разложим вектор b по некоторому базису в точке М, в качестве ко-
которого выберем систему векторов е,-: Ъ(М) = 61е,(.М), тогда в ре-
результате параллельного переноса в точку Л/ вдоль некоторой кривой
§ 8.2. Пространства аффинной связности 513
* •* * •
С получим вектор Ь{М) = Ь1е,(Л/'), причем компоненты Ьх в силу тео-
теоремы 8.8 не зависят ни от точки Л/, ни от кривой ?. Но параллельный
перенос векторов e{(J\f) не зависит от кривой ?, так как в силу тео-
* * *
ремы 8.13: Vei/d? = а • V ® е, = 0 для любого а. Следовательно, и
перенос вектора b не зависит от кривой С.
В одну сторону теорема доказана.
В обратную сторону. Рассмотрим снова произвольный вектор b
в точке М G Ln. Выберем некоторую линейно независимую сис-
* *.*
тему п векторов е,-(.М) и построим разложение Ь(ЛЛ) = b*ei(M).
При параллельном переносе в точку J\f E Ln, получим новый вектор
h(Af) = blei(Af), причем е^ЛА) является значением параллельного пе-
* * *
реноса е,-(Л4) в точку Л/*, т.е. удовлетворяет уравнению: Uei/d? = 0.
Записывая е,- = S^ ej в некотором базисе ej, получаем:
dS"p + f* 5' dXJ - 0 (8 61)
—+ Г05р—-0. (8.61)
Поскольку Skp есть функция от XJ, то преобразуем это соотноше-
соотношение следующим образом:
(8-62)
Так как е,- и S3i, по условию теоремы, не зависят от кривой (т.е. от
касательного вектора dX* /d?), соединяющей точки М и Л/\ то соот-
соотношение (8.62) выполняется тогда и только тогда, когда обращается
в нуль выражение в скобке. Откуда получаем
г^-^-УЛ;- (8-63)
Учитывая результат упражнения 8.2.1, это выражение эквивалентно
выражению (8.56), что и завершает доказательство теоремы. ^
Вычислим компоненты тензора кручения 3П (8.52) для связности
Г$ в А". Согласно (8.56) имеем:
<У" = idS-'Ai - (S-1)^ )Smk. (8.64)
Заметим, что если бы матрица (S)^- удовлетворяла соотношени-
соотношениям (8.21), то кручение обращалось бы в нуль, и наоборот.
17 Тензорное исчисление
514 Глава 8. Тензоры в римановых пространствах
Но условие (8.21) является необходимым и достаточным для того,
чтобы дифференциальная форма (S~1)kj dX* имела полный дифферен-
дифференте
циал, который, умножая форму на е&, можно записать как
dxz=:ejdXj. (8.65)
Таким образом, тождественное равенство flj^ E 0 в А" эквива-
эквивалентно существованию "потенциала" для векторов базиса е^ в Ап.
Такой потенциал существует в евклидовом пространстве Шп (см. фор-
формулу F.23)), однако в Ап, вообще говоря, условия fltJm = 0 не выпол-
выполняются, и, следовательно, дифференциальная форма (8.65) не интег-
интегрируема. Поэтому компоненты тензора кручения п^т в Ап называют
еще объектом неголономностщ а векторы базиса е^ - неголономным
базисом.
8.2.7. Локально-аффинное пространство
Определение 8.18. Пространство Ln называют локально -
аффинным пространством LJ, если для всякой его точки М Е Ln
существует такая система координат Хп, в которой коэффициен-
ты связности Г[^ обращаются тождественно в нуль в некоторой
окрестности точки М.
*
Если же система координат Х'\ в которой Г[^ = 0, является единой
для всех точек М Е П-?, то пространство L^ является, очевидно, ли-
линейным (аффинным) пространством, изоморфным пространству Мп.
Примером локально-аффинного пространства L^ является круговой
цилиндр в пространстве М3, а примером аффинного пространства яв-
является любая плоскость в М3.
Теорема 8.15. Пространство Ап без кручения (т.е. 3$1 = 0^
является локально-аффинным.
Т Поскольку в каждой точке М. пространства Ап существует п линей-
но независимых векторов е,-, то можно попытаться построить такую
систему координат Хг\ для которой касательные векторы дХк /дХГг
к координатным линиям Хп совпадают с е,- в некоторой окрестности
точки М. Для этого рассмотрим систему дифференциальных уравне-
уравнений:
flvk
5*РП (8-66)
относительно функций Хк = Хк(Хп), где S\ {Xm) - заданные функ-
функции от Хт. Дифференцируя соотношение (8.66) по .X"'-7, получаем
д2Хк
ЕРШ •*»*'¦ (М7)
§8.3. Риманово пространство с аффинной связностью 515
Поскольку левая часть этого выражения симметрична относитель-
относительно замены i f> j, то и правая часть также должна быть симмет-
симметрична. Чтобы проверить это, умножим выражение для связности
Г* = -(S-l)mtSkmil (см. упражнение 8.2.1) на S^S^:
S^S'^-f^S',, (8.68)
Поскольку по условию теоремы Г*, = Г^, то выражение в правой
части (8.68) симметрично по i,j, и, тем самым, симметрична правая
часть (8.67): S*., Slj = 5feJ}/ Sl{. Это условие является условием ин-
интегрируемости системы (8.66), которое обеспечивает существование
ее решения с начальными условиями: Xlm = -X^J, Х'к = X'J^ в неко-
некоторой окрестности точки М. Следовательно, существует и обратная
функция Хы = Х*{Хк).
Воспользуемся теперь тем, что система координат Xх, в которой за-
записано выражение (8.56) для связности, была выбрана произвольно,
а система Х/г определяется по Xх указанным выше способом. Тогда
выберем в качестве векторов базиса е,- касательные векторы к коор-
координатным линиям X1, а сами координаты всегда можно выбрать сов-
совпадающими с Х'х. В этом случае получим, что е, = е,, т.е. 5Jt- = 5*{,
и, следовательно, Г^ = — {S~l)mtSkm t = 0. Поскольку существование
системы координат Х/г нами показано в некоторой окрестности точки
*
М, то и тождество Tkt = 0 будет выполнено в этой окрестности, что
и означает локальную аффинность пространства Ап без кручения. А
Упражнения к § 8.2.
Упражнение 8.2.1. Показать, что связность пространства Ап (8.56) можно
представить в виде:
§ 8.3. Риманово пространство с аффинной связностью
8.3.1. Определение пространства
В римановом пространстве Vn у нас была определена метрика gij
(ей соответствовала вполне определенная связность Г^), в простран-
стве же Ln - только связность F"j. Можно однако построить такое
пространство, в котором будет одновременно определена и метрика
Глава 8. Тензоры в римановых пространствах
<7,j, и некоторая "самостоятельная" связность Г^, для которой уже не
*
имеют места соотношения (8.18), согласующие Г[у и gij.
Определение 8.19. Элементарное п-мерное многообразие Мп
называют риманов ым пространствам с аффинной связ-
связностью W", если в каждой точке М Е Мп с координатами хг
заданы две системы функций gij и 1\™, вообще говоря, не связанные
никакими соотношениями и удовлетворяющие свойствам 1° - 4° из
определения 8.5 и 1°, 2° из определения 8.13, соответственно.
*
Ни одно из соотношений (8.18), (8.20) и (8.21) для Г?-, вообще гово-
говоря, не имеет места. Однако поскольку в W" определена метрическая
матрица д^, то ничто не мешает нам образовать из нее символы 1\™
по формуле (8.19):
Г? = \gmk (9ikj + 9jk,i - 9ij,k). (8.69)
Символы Г,™ уже не являются связностью: FJJ ф Г^, т.е. парал-
параллельный перенос в W" осуществляется с помощью операции ковари-
*
антного дифференцирования V (8.44), но не операции V, выражаемой
формулой (8.26) (хотя сама операция V (8.26) также определена в W7*).
Этим пространство W" отличается от Vn.
Но W1 отличается и от Ln, так как в W" с помощью д^ можно уже
ввести скалярное произведение по формуле (8.10).
Тензорное касательное пространство на W* определяем также, как
и на римановом Vn:
Причем с тензорами *А Е 7n (TmW1) определены не только алгеб-
алгебраические операции сложения, умножения на число, транспонирова-
транспонирования, симметрирования, альтернирования и тензорного произведения,
но и скалярного умножения, и поднятия - опускания индексов, подобно
тензорам на Vn.
8.3.2. Риманова связность
Риманово пространство Vn является частным случаем простран-
пространства W7*, о чем свидетельствует следующая теорема.
Теорема 8.16. Пространство W1 является римановым^ тог-
тогда и только тогда, когда оно обладает свойствами:
§ 8.3. Риманово пространстве* с аффинной связностью 517
1° его кручение тождественно равно нулю: П^-То ЕЕ О,
2° скалярное произведение любых векторов Ь, с Е ТмМп, параллель-
параллельно переносимых вдоль всякой кривой С, не меняется.
Т Необходимость. Условие 1° для пространства Vn всегда выполне-
выполнено в силу теоремы 8.3. Для доказательства 2° рассмотрим два ка-
касательных вектора b,c G ТмМп, параллельно переносимых вдоль
произвольной кривой ?, проходящей через точку Л4, т.е. эти векторы
удовлетворяют уравнениям (8.36), (8.37):
dX* dXi
__V,y = 0, —ViC> = О, Ы < ^ Ы-
Образуем скалярное произведение этих векторов в каждой точке кри-
кривой С: Ь • с = gijb%c? и вычислим его абсолютную производную (8.33):
|(Ь • с) = *?.Чы{пМ) = 9ii (e^V»tf + If^*!) = О-
(8.70)
Здесь мы воспользовались теоремой 8.5 Риччи о ковариантной посто-
постоянности gij относительно римановой связности. Таким образом, усло-
условие 2° доказано.
Достаточность. Пусть выполнены условия 1° и 2° в W", тогда в
произвольной точке М Е W* рассмотрим уравнение параллельного
переноса двух векторов b и с:
Поскольку (Ь • с) - скаляр, то по определению его абсолютная произ-
производная (8.46) совпадает с полной производной по ?:
,8.71)
Поскольку векторы b и с параллельно переносятся, то они удовлетво-
удовлетворяют уравнению (8.48):
dc? _ i, dXk db< _ *• dXk
Подставим эти выражения в (8.71) и учтем, что
dgu/dt = (dg{j/dXk)(dXk/dt),
518 Глава 8. Тензоры в римановых пространствах
тогда получим:
(ш " ^Tk9mi" ^k9m%) bicJw = °- (8J2)
Поскольку это уравнение должно выполняться при любых б1, с7 и
(dXk/d?) (т.е. ohq представляет собой тождество), то это возмож-
возможно только, когда скобка обращается в нуль:
г)п ¦ * *
-J lik9j +lfeflf
В силу симметрии связности Г^, это уравнение можно разрешить
относительно Г^ так же, как это было проделано при доказательстве
теоремы 6.1, в результате получим
рт __ гт __ 1 fcm (^Як^ %^ _ З^Л
1« -Lа - 2^ Vзх« + дх* dxk) ' [ ]
т.е. связность в рассматриваемом пространстве является римановой,
следовательно, в данном случае Wn совпадает с Vn. A
Теорема 8.17. Пространство Wn является римановымУп тог-
тогда и только тогда, когда
1° его кручение равно нулю: П^-То = 0, (8.75)
2° ковариантная производная от метрической матрицы gij в Wn
тождественно равна нулю: Vk9ij = 0. (8.76)
Т Если Wn - риманово пространство Vn, то в силу теорем 8.4 и 8.5
условия 1° и 2° выполнены.
Для доказательства достаточности рассмотрим абсолютную произ-
производную от скалярного произведения двух векторов b и с, параллельно
переносимых вдоль некоторой кривой ?:
*
V dXk
(Ь)
(8.77)
*
но так как Vk9ij = 0, a b и с параллельно переносятся, т.е.
f
то выражение в правой части (8.77) обращается в нуль. Следователь-
Следовательно,
§ 8.3. Риманово пространство с аффинной связностью 519
для любой кривой ?, т.е. выполнены условия теоремы 8.16, а значит
W71 - риманово пространство Vn. A
8.3.3. Риманово пространство абсолютного параллелизма
Пространство Wn с римановой связностью нам уже было по сути
известно, в п.8.3.2 мы лишь показали его место среди пространств с
аффинной связностью. Рассмотрим теперь важный пример простран-
пространства Wn с неримановой связностью.
Определение 8.20. Пространство Wn называют римановым
пространством абсолютного параллелизма Ау, если
его связность Г^ обладает свойством (8.56), т.е. в каждой точке
ЛЛ Е Wn существует п линейно независимых касательных векторов
е,- = Ski
таких, что
Г* = STdS-ifij . (8.78)
Здесь, как и в п.8.2.6, S* - матрица компонентов векторов е, в
базисе е,- пространства ТмМп, a (S")*,- - обратная к ней матрица.
Сравнивая определения 8.17 и 8.20, заключаем, что Ау - это про-
пространство Ап с введенной в нем метрикой, поэтому теоремы 8.12 -
8.14 имеют место и в Ау. Установим теперь свойства, присущие про-
пространству Ау.
Введем кроме gij в пространстве Ау матрицы
5у=^-ё,- и 9%к = 6\. (8.79)
Теорема 8.18. В пространстве Ау метрические матрицы д^,
g%i и д^, g%i - ковариантно-постоянны, т.е. тождественно равны
нулю их ковариантные производные:
VtfW = 0, V.-sr*1 = 0, V,-5w = 0, V,-5w = 0. (8.80)
Т Используя формулу (8.45), вычислим V</fc/, рассматривая его как
градиент от скаляра при фиксированных к и Z:
= V(efc . е,) = (V ® ек) • е/ + (V ® е,) . ек = 0. (8.81)
Здесь мы воспользовались теоремой 8.13. Тогда по определению (8.45)
* * *
получаем: Vgki = V.-flffc/e1 = 0, откуда следует V,-</fc/ = 0. Дифферен-
Дифференцируя второе соотношение в (8.79), находим:
520 Глава 8. Тензоры в римановых пространствах
* *..
поэтому VigtJ = 0.
Для доказательства первого соотношения в (8.80), используем связь
векторов е, и е, из определения 8.17, тогда
9ij = е, • ej = (Я)*,- (S-'Yje, ¦ е, = (S)*,- (Я)',**!-
Поскольку матрицы (S")*,- и дк1 - ковариантно-постоянны (см. (8.58)
и (8.80)), то и gijy а вместе с ней и g%j также ковариантно-постоянны.
А
Заметим, что хотя gij - ковариантно-постоянна, но кручение ft,jm
связности (8.78) не равно нулю, поэтому пространство Ау не является
римановым Vn.
Установим теперь соотношение между связностью Г[^ и символами
Кристоффеля Г?-, которые определены в А^ формулой (8.19). Будем,
как и в пространстве Vn, обозначать ковариантную относительно сим-
символов T?j производную как Vj, и введем новый объект:
T% = SmkVj(S-1)ki, (8.82)
называемый коэффициентами вращения Риччи (если бы в этой фор-
муле стояла производная Vj, то все выражение обратилось бы в нуль),
здесь V^S)*,. = (Я)*,,; -Г^*)*,.
Теорема 8.19. Связность в пространстве Ау может быть
представлена в виде:
Т% = Т% + Т%. (8.83)
Т Для доказательства воспользуемся третьей формулой в (8.60), ко-
которую умножим на матрицу Smk:
= 5m,E-1)*l-_,• - г?; + г^ + г;;;. (8.84)
Здесь мы добавили и вычли символы Кристоффеля Г[^, тогда, срав-
сравнивая с (8.82), получаем
Г$ = T?j+ STbUS-1)^ - r^S)* ) = Г? + Т*. А (8.85)
§ 8.3. Риманово пространство с аффинной связностью 521
Теорема 8.20. Коэффициенты вращения Риччи являются ком-
компонентами тензора третьего ранга и могут быть выражены через
тензор кручения следующим образом:
3Т = 3П + 3ПA32) - 3ПC12>. (8.86)
Т Вначале установим вспомогательную формулу, имеющую и само-
стоятельный интерес. Из теоремы 8.18 следует, что У,#ы = #*/,,• —
гь0™' - гк 9тк = 0, откуда получаем:
0Н,< = ГЙ0га,+Г;?0т*. (8.87)
Подставим эти производные в выражение (8.69) для символов Крис-
тоффеля Г^:
Г? = \gmp(hj9tp + hiVrni + T)i9ip + T^gtj - T\pgtj - Т)р9и). (8.88)
Введем обозначение
для симметризованной связности и используем определение (8.52) тен-
тензора кручения, тогда получим
- искомое соотношение между связностями Г{^» Г^ и метрической мат-
матрицей дц.
Подставим теперь формулу (8.90) в (8.83) и выразим из нее Т}™, в
результате получим
Поскольку в правой части этого выражения стоят компоненты тензо-
тензоров, то и коэффициенты вращения Риччи Тт^ являются компонента-
компонентами тензора третьего ранга:
%®е''. (8.92)
Подставляя соотношение (8.91) в (8.92), получаем соотношение
3Т = (-nyTO+nm,.i+nray)em®eIW = 3П+3П<132)-31гC12), (8.93)
522 Глава 8. Тензоры в римановых пространствах
которое и доказывает теорему. А
Поскольку 3Т - тензор, то для негб в пространстве А" определе-
определена операция поднятия - опускания индексов, поэтому коэффициенты
Т-? следует писать как Тт^ . Условимся однако для этой конкретной
комбинации индексов использовать оба обозначения: Т& = Т™^ .
§ 8.4. Тензор Римана-Кристоффеля
8.4.1. Тензор кривизны пространства Ln
В §7.2 мы ввели понятие тензора кривизны 4R - Римана-Кристоф-
Римана-Кристоффеля для поверхностей в М3. Покажем теперь как можно ввести этот
тензор в пространстве аффинной связности Ln.
Рассмотрим в точке М Е Ln произвольный вектор b = 6*е& из
TmLu и вычислим его ковариантную производную относительно связ-
связности fg (8.42):
V.-^ = |^ + r*b'. (8.94)
Вычислим вторую ковариантную производную:
* * и д * и *ь* * * I. д2Ьк дТк
Поменяем теперь индексы i и j и образуем разность:
* *i
* * * * /ЯГк дТ • * * * * \
VVhk VV -hk — si У. i Tfc Гт — Vk Vm\h8
-(rt^-r^)Vm6fc. (8.96)
Коэффициенты, стоящие в первой скобке, обозначим следующим
образом:
fffc
д.. к _ pfc . _ г*. . i f"»ffc . - гт.гк . (8 97}
Здесь, как и ранее, Fj— = dTk8i/dX*. Выражение во второй скобке в
(8.96) представляет собой компоненты тензора кручения (8.52). Тогда
получим
* bk = Rjit b' - 2fi^Vra6fc. (8.98)
__ jj 8.4. Тензор Римана-Кристоффеля 523
Теорема 8.21. Система коэффициентов Rjis , образованная по
формуле (8.97), представляет собой компоненты тензора 4R чет-
четвертого ранга из пространства Тп BмLn):
4R = Rji8 е3 ® е1 ® е' ® еь (8.99)
Т Доказательство следует из формулы (8.98), поскольку в левой части
этой формулы стоят компоненты тензора третьего ранга (см. п.8.2.2),
a Vm6fc, ft™, 6* также являются компонентами тензоров (см. теорему
8.10). А
Тензор (8.99) называют тензором кривизны пространства Ln от-
*
носительно связности Г^ (или тензором Римана-Кристоффеля).
Вместо ковариантной производной в (8.98) можно рассмотреть аб-
абсолютную производную вектора. Пусть имеются две кривые Хг(?) и
Xх (rj), проходящие через точку Л4. Вычислим абсолютные производ-
производные некоторого вектора b вдоль этих кривых:
а затем вычислим вторую абсолютную производную
Здесь мы учли, что ^ (^) = ?§? = ^ = 0, и поэтому
rm
-f'
Если теперь вычислить абсолютную производную в обратном по-
порядке, то получим
Вычитая (8.101) из (8.100), находим
(8.102)
Левую часть выражения (8.102) называют альтернированным вторым
абсолютным дифференциалом. Учитывая (8.98), приходим к следую-
следующей теореме.
524 Глава 8. Тензоры в римановых пространствах
Теорема 8.22. Альтернированный второй абсолютный диффе-
дифференциал всякого касательного вектора из Ln дпределяется тензо-
ром кривизны пространства 4R:
Wbk VVbk • k dXidXi
Щ-dJ - *}~Ф = Ri" b Ibflif (8Л03)
Иначе говоря, вторая абсолютная производная зависит от порядка
вычисления первых абсолютных производных.
8.4.2. Тензор кривизны пространства Ап
Покажем, что кривизна пространства Ln непосредственно связана
с независимостью параллельного переноса тензоров от пути.
Теорема 8.23. В пространстве Ап (в случае односвязного U1)
¦
и только в нем тензор кривизны 4R тождественно обращается в
нуль:
4R=0 в Ап. (8.104)
Т Необходимость. Рассмотрим пространство Ап. Разумеется, можно
непосредственно подставить связность (8.56) в (8.97) и убедиться, что
выполняется (8.101). Однако мы поступим по-другому.
Выберем произвольный касательный вектор b в точке М Е Ап и
параллельно перенесем его в точку J\f Е Ап, тогда b будет удовлетво-
удовлетворять уравнению (8.47), т.е. ^-Vifr7 = 0.
Поскольку мы находимся в пространстве Ап, то результат парал-
параллельного переноса не зависит от кривой, соединяющей точки М и Af,
т.е. от вектора (dXl/d?), касательного к кривой, и, следовательно,
имеет место соотношение У,-У = 0. Тогда, подставляя этот резуль-
тат в (8.98), получим, что должно иметь место тождество Rjiskb3 = 0
для любого вектора Ь8,. Следовательно, действительно имеет место
тождество (8.101).
Достаточность. Пусть в пространстве Ln тензор 4R тождествен-
тождественно равен нулю. Рассмотрим в этом пространстве некоторую кри-
кривую Х%(?), ?м ^ ? ^ ?//. Для нее всегда можно ввести семейство
кривых Xх (?,77), Vi ^ V ^ V2 с совпадающими крайними точками
X%(?miV) = Х%м> ХЧЫу1!) = X\f для любого 7/, причем для опреде-
определенности положим, что X%(?,r)i) = Хг(?).
Рассмотрим семейство векторов b(?,7j) E ТмМп, параллельно пе-
переносимых вдоль соответствующей кривой из семейства Xх (?, п). Тог-
Тогда Ь(?, л) удовлетворяет уравнению Vh/d? = 0 для любого п. Обра-
Образуем альтернированный второй дифференциал касательного вектора
§ 8.4. Тензор Римана-Кристоффеля 525
b, в силу отсутствия кривизны пространства Ln получаем
********* = 0. (8.105)
*
Здесь Vbk/dr) = (dbk/d7j) + Г*„-Ьга (dX* /drj). Поскольку по построе-
построению все кривые семейства Хг(?,т)) совпадают в крайних точках, то
dXx jdt] = 0 для ? = ?м и ? — ?лЛ Поэтому в точках М и Я имеем
Vbk jdf] = [dbk jdr\) для любого г/. Но в силу того же построения в точ-
точке ЛЛ все векторы b совпадают, поэтому dbk jdi) = Vbk /drj = 0 в точке
М. Если теперь мы обратимся к уравнению (8.105), то его можно
рассматривать как параллельный перенос вектора Vbk/dr] вдоль кри-
кривой *•'(?, ч), Ы^?^ Ы> т-е- {dX{/<%)$№&/dri) = 0. Однако мы
установили, что вектор Vbk /dr) = 0 в точке М для любого 77, тогда
результат параллельного переноса вдоль Хг(?,г]) также даст вектор-
нуль, т.е. в частности Vbk/dr) = 0 и в точке ЛГ для любого 77. Это,
в свою очередь, означает, что результат параллельного переноса из
точки М в ЛГ не зависит от той кривой семейства, по которой осу-
осуществляется перенос.
Если Ln - односвязное, то любые две кривые, соединяющие точки
М и Af этого пространства могут быть объединены в одно семейство
-Х"а(?,77) непрерывным переходом. Следовательно, полученный выше
результат о независимости параллельного переноса от пути справед-
справедлив для любых кривых. Тогда согласно теореме 8.14, рассматривае-
рассматриваемое пространство Ln является пространством абсолютного паралле-
параллелизма An. A
8.4.3. Тензор кривизны пространства Lg
Покажем теперь, что при отсутствии кручения кривизна простран-
пространства Ln связана со свойством его локальной аффинности (см. п.8.2.7).
Теорема 8.24. Для того, чтобы пространство Ln было локаль-
локально-аффинным L^ необходимо и достаточно, чтобы оно обладало ну-
нулевой кривизной и нулевым кручением:
3п = 0 и 4R=0 в Ln. (8.106)
Т Необходимость условий (8.106) очевидна, так как если Ln - локаль-
локально-аффинное, то в окрестности любой точки существует система ко-
ординат, в которой Г^ == 0, а, следовательно, по (8.97) R^jj E 0 и
*
по (8.52) ilkj = 0. Но поскольку R^jj и Ctkj являются компонентами
тензоров, то они будут нулевыми в любой системе координат во всем
Ln.
526 Глава 8. Тензоры в римановых пространствах
Покажем достаточность. Разобьем Ln на односвязные области, тог-
тогда каждая из этих областей имеет нулевую кривизну и по теореме
8.23 должна обладать абсолютным параллелизмом. Но в этих облас-
областях нет и кручения, тогда по теореме 8.15 они представляют собой
локально-аффинное пространство. А
8.4.4. Тождества Бианки в пространстве Lg
Теорема 8.25. В пространстве h^ тензор кривизны 4R удовле-
удовлетворяет следующим тождествам:
VqRnjik + VjRqnik + VnRjqik = 0, (8.107)
которые называют тождествами Бианки.
*
Т Поскольку Rnjik являются компонентами тензора, и ковариантные
производные от компонент тензора снова образуют компоненты тен-
тензора, то уравнения (8.107) имеют тензорный характер. Это означает,
что если мы покажем обращение левой части F.169) в нуль в какой-
либо системе координат X", то в любой другой системе координат X1
оно также обращается в нуль.
Согласно теореме 8.11, в каждой точке пространства Lg можно вы-
выбрать такую систему координат Xх, в которой символы Кристоффеля
обращаются в нуль: Г™ = 0 (и Tijk = 0), такие координаты называют
геодезическими. Заметим, что производные 6Tijk/dXn в этих точ-
точках уже, вообще говоря, отличны от нуля, тогда на основании (8.97)
имеем:
Меняя в этом выражении циклическим образом первые три индекса,
а затем складывая полученные результаты, находим
dvi4k drijk ( .
dxidxn дхядхп ' { >
дхпдх>
откуда действительно следует тождество Бианки. ^
8.4.5. Тензор кривизны пространства V"
В римановом пространстве Vn связность Г^ является римановой,
т.е. Г^ = Г?-, где Г^ определяется формулой (8.19). Для тензора
§ 8.4. Тензор Римана-Кристоффеля 527
Римана-Кристоффеля, порожденного этой связностью, будем исполь-
зовать специальное обозначение -Rnj™ = RnjF» гДе
Rnji - JxZ ~ JxJ + r.jr*n - VinYkj. (8.110)
Поскольку Г™ связаны с метрической матрицей, то и Яп^ можно
выразить через метрическую матрицу:
_ dgik I fdgkj dg{j dg{j dgkj\ __ dgik (R
Чисто ковариантные компоненты тензора Римана-Кристоффеля
определяют следующим образом:
iinj.fc - Дп;,- ffmfc - ffmfc ^ дХп ^ J +
+ g"(^j^>nk-rin,T,jk). (8.112)
Используя соотношение
9mk(dgml/dXn) = -gml(dgmk/dXn) = -gml(Tmnk + Tknm),
приводим Rnjik к виду
- dr0fc gr'»fc Г ,/г . ,Гь \„т'-1-
— .уп — .„^. 1 t]l(L mnk T 1 knmlil T
rroifc) + </''(Г,-,-,Г,пЛ - Г,-„|Г.д) =
'(r«r*i- - r.iTfc«m). (8.113)
Подставляя теперь вместо производных от Г,-^ их выражения (8.18)
через метрическую матрицу, находим
1 / d2gik d2gkj d2gij d2gik
tk 2\dX'dXn dX'dX» dXkdXn dXndXJ
d gkn , d gjn \ i m;/T1 г г _ >_
i dXkdXi) 9 K '"' kjm ijl knm) ~
1 / d2gkj d2gkn d2gin d2gkn \
2 4 dXi dXn dX* dXi dXk dXi dXi dXi)
+ gm'(TinlTkjm - Тц,Ткпт), (8.114)
таким образом, получаем следующую теорему.
528 Глава 8. Тензоры в римановых пространствах
Теорема 8.26. В романов ом пространстве Vn тензор кривиз-
кривизны Римана-Кристоффеля можно выразить с помощью метрической
матрицы gij:
1 / d2gkj _ d2gkn d2gin _ d29ij \
3%h 2\дХ'дХп дХ<дХ* dXkdXi dXkdXnj
+ 9ml (Tin,Tkjm - Гу,Гкпга). (8.115)
Определение 8.21. Локально - евклидовым (или упло-
уплощенным) Vjc; называют пространство Vn, для каждой точки М. Е
Vn которого существует такая система координат X'1, что мет-
метрическая матрица gij(M) является постоянной в некоторой ок-
окрестности точки М.
Очевидно, что уплощенное пространство представляет собой ло-
локально-аффинное пространство с римановой связностью (8.18)
Теорема 8.27. Риманово пространство Vn является уплощен-
уплощенным тогда и только тогда, когда тензор кривизны 4R в нем тож-
тождественно обращается в нуль: 4R = 0.
Т Необходимость очевидна, так как если Vn - локально-евклидово,
то в каждой точке М. Е Vn можно найти такую систему координат
Х'\ что Qij = const в некоторой окрестности точки .М, поэтому все
частные производные от gij обращаются в нуль. Следовательно, Г^ =
0 в этой системе координат, и по (8.110) получаем, что iJnj*fc = 0 в
системе Х/%, а значит и в любой другой.
Покажем достаточность. Пусть 4R = 0 в Vn. Так как Vn можно
рассматривать как пространство Ln со специальной связностью Г^ и
без кручения (см. теорему 8.3), то согласно теореме 8.24 оно является
локально-аффинным. Тогда в каждой точке М этого пространства
Vn существует такая система координат Х'\ в которой Г^ = 0. Но
тогда, используя формулу (8.111), получаем gikj = r,j& + Г^,- = 0
в окрестности точки М. Откуда получаем, что дц~ = const в этой
окрестности, что и доказывает локальную евклидовость данного про-
пространства Vn. A
Теорема 8.27 обобщает доказанную ранее теорему 7.14, имеющую
место для пространства V2, т.е. для двумерных поверхностей в про-
пространстве М3.
8.4.6. Свойства тензора Римана-Кристоффеля
Теорема 8.28. В пространстве Vй компоненты тензора кривиз-
кривизны Rnjik имеют симметрию по парам индексов n,j и i,k, а также
кососимметрию по индексам n,j и г, к:
Rnjik = Riknj, (8.116)
§ 8.4. Тензор Римана-Кристоффеля 529
"Rnjik = Rnjkii Rnjik = — Rjnkit (8.117)
а также имеет место следующее тождество Риччи:
Rnjik + Rjink + Rinjk = 0. (8.118)
T Доказательство очевидно следует из формулы (8.115), например,
поскольку в тождестве Риччи четвертый индекс к стоит на месте, а
три другие меняются круговой перестановкой, то из индексов nji один
равен к. Тогда положив, например, п — а и к = а, получаем сумму:
Rajia + Rjiaa + Riajoe Несложно проверить, что второе слагаемое и
сумма первого и третьего действительно обращаются в нуль. А
8.4.7. Тензор кривизны пространства Ау
Рассмотрим теперь риманово пространство абсолютного паралле-
параллелизма Ау.
*
Теорема 8.29. Тензор Римана-Кристоффеля 4R относительно
связности Г^ (8.56) в пространстве Ау тождественно равен нулю.
Т Поскольку пространство А" является одновременно пространством
абсолютного параллелизма Ап, то утверждение данной теоремы яв-
является следствием доказанной выше теоремы 8.23. Проверим однако
теорему непосредственным вычислением, которое представляет и са-
самостоятельный интерес.
Из формулы (8.56) находим, что (S")*^ = T^E")fcm. Диффе-
Дифференцируя это соотношение по индексу п, получаем
()\jn ^n()m + Tii)^ (?п + Tj^i)^
(8.119)
Поменяем здесь индексы jf+iiH получившийся результат вычтем
из (8.119), тогда получим
(s-')kiJn - (s-1)^- = (г?. „ - rfnj. + r^f^,n - irar*mj)(s-l)kp =
= Л|,.я1'E-1)*р. (8.120)
Поскольку левая часть этого выражения тождественно обращается в
нуль (так как там стоят обычные частные производные), то и выра-
выражение в правой части должно быть нулем. Но E""x)fcp не может быть
тождественным нулем, поэтому получаем, что R^^ = 0 для любого
м е ап . а
530 Глава 8. Тензоры в римановых пространствах
Поскольку в пространстве W" кроме связности Г[^ определены сим-
символы Г^ (см. (8.69)), то с их помощью по формуле, аналогичной (8.97),
можно образовать тензор четвертого ранга 4R с компонентами
=
(8.121)
который однако уже не является тензором кривизны пространства Wn
(т.е. RjiJ6 Ф Rji8k)- Для этого тензора имеет место следующая тео-
теорема.
Теорема 8.30. Тензор 4R (8J21) в пространстве Ау, вообще
говоря, отличен от нуля и определяется коэффициентами вращения
Риччи:
Л к ___ V7 гТ*к Т fTik I ггхПХ ггхк ггхТ1\ ггхк I о 1 О О \
ijs = Vi±sj - Vji,,- + lsjlmi - l8i lmy {b.IZZ)
¦
T Так как тензор 4R в Ау тождественно равен нулю, то, используя
его определение (8.97), получаем
Rjisk = ^sij - ^j.i + ^Ti^mj - ^Tj^mi = 0- (8.123)
Согласно теореме 8.19, связность Г^ можно выразить через Г^ и ко-
*
эффициенты вращения Риччи: FJJ = Г^ +^7# Подставим эти соот-
соотношения в формулу (8.123) и выделим в ней компоненты тензора Rji8k
(8.121):
k п к , /гпк гпк . -птпгрк . гртптлк тчпгрк
~ nji +\1ij ~ 1sjii+lsi1mj+1silmj ~ l 3J1mi
+ T,7T^- - 2^1*. = 0. (8.124)
Поскольку символы Кристоффеля Г[^ симметричны по г, j (см. (8.69)),
то в формуле (8.124) добавлено тождество Т%Т*т - Т*р{Т?т = 0. За-
Заметим теперь, что выражение в скобках в (8.124) представляет собой
ковариантную производную V (8.26) относительно символов TJJ\ т.е.
V;T,*. = 2*ifi + Г^.Т,7 - Г™-Т*,. - Т%Т?т. (8.125)
Подставляя эту и альтернированную по г, j формулу в (8.124), убеж-
убеждаемся в справедливости соотношения (8.122). А
§ 8.4. Тензор Римана-Кристоффеля 531
Теорема 8.31. Тензор 4R в пространстве Ау можно выразить
с помощью матрицы Skp:
Щи = 5*P(V,-ViE)pl - V^V^S)^). (8.126)
T Для доказательства вычислим ковариантные производные VtT^ от
коэффициентов вращения Риччи (8.82):
tj—OpVj(b ) i — — (? ) fVjb р, (O.LZi)
а также их произведения Т^Т^. Получим следующие выражения:
Vrpk V7 С^ V7 /С~*ЛР | С^' U П / С"-1\Р (Q 10Q\
Подставляя эти и альтернированные по i,j выражения в формулу
(8.122), действительно приходим к соотнбшению (8.126). А
8.4.8. Тензор Риччи
В пространстве Wn из тензора Римана-Кристоффеля можно обра-
образовать несколько тензоров второго ранга. Свертка транспонированно-
транспонированного тензора Римана-Кристоффеля 4R с метрическим тензором образует
тензор второго ранга:
П = 4rB314) . .Е, (8.129)
называемый тензором Риччи. Компоненты этого тензора имеют сле-
следующий вид:
е11 ® е14 •' ек ® ек =
т.е.
Rji = kkj?-=Raj№. (8.130)
Подставляя в (8.130) выражение (8.97) для компонент тензора Ри-
Римана-Кристоффеля, получаем:
4
Jxt
532 Глава 8. Тензоры в римановых пространствах
Аналогичным образом, если вместо 4R использовать тензор 4R,
определенный по формуле (8.121), то можно ввести тензор Риччи от-
относительно символов Г^-, т.е.
Rji = Rkjt = Rnji sk> (8.132)
Rji = rfi|]b - r?fc>i + Г*1** - ГЙГ^. (8.133)
Выражение для компонент тензора Риччи Rji в пространстве А" на-
находим, подставляя формулу (8.122) в (8.132):
Rji = V.-ТД - V*T? + TpA - Т]?Т^. (8.134)
Тензор R в пространстве А^ тождественно обращается в нуль: R = 0.
Так как Rnjik = Rnjik = 0 в локально-евклидовом пространстве
Vjg», то и тензор Риччи тождественно равен нулю в этом пространстве:
Rji = Rji = 0.
8.4.9. Тензор Эйнштейна
Тензоры Эйнштейна G и G образуются из тензоров Риччи 7? и TL
следующим образом:
G = *k- \iZE, G = K- ЬгЕ, (8.135)
где
^ = R.-E и 7l=:R.-E (8.136)
- свертки тензоров Риччи с метрическим тензором.
В локально-евклидовом пространстве V^ тензоры Эйнштейна тож-
дественно равны нулю: G = G = 0. В римановом пространстве Vn
* *
тензоры G и G совпадают: G = G, но, вообще говоря, отличны от
тождественного нуля.
Теорема 8,32. В римановом пространстве Vn тензор Эйнштей-
Эйнштейна G удовлетворяет следующему уравнению:
ViG'j = 0, где G1; = Rj - i&JV,. (8.137)
Т Поскольку риманово пространство Vn обладает нулевым кручени-
кручением, то его можно рассматривать как пространство Lq, в котором вве-
введена специальным образом связность FJJ по формуле (8.74). Тогда
для Vn справедливы тождества Бианки (8.107).
§ 8.4. Тензор Римана-Кристоффеля 533
Используем эти тождества Бианки, домножив их на дпкдг^ а так-
также-используем кососимметричность тензора Римана-Кристоффеля и
определение тензора Риччи:
9ijVqRij - 9ijVjRiq - 9nkVnRkq = 0. (8.138)
Внося обратную метрическую матрицу на основании теоремы Риччи
(8.32) под знак ковариантной производной, получаем:
VqR-2Vjffq = 0. (8.139)
Это уравнение можно привести к виду:
(8.140)
Откуда, очевидно, следует (8.137). ^
В тензорном виде уравнение (8.137) имеет вид:
(8.140)
*
В пространстве Wn тензоры G и G, вообще говоря, уже различны.
Теорема 8.33. В пространстве Ау тензор Эйнштейна G тож-
тождественно равен нулю, a G, вообще говоря, отличен от нуля и мо-
может быть выражен с помощью матрицы Skp:
G = 0, G = <?,te'®e(, (8.140)
G,t = ^„(V.-Vt^-1)^ - VfcV.CS-yjiT'V (8.141)
где
ii\i. (8.142)
T Первое утверждение теоремы очевидно, так как в Ау тензор кри-
*
визны тождественно равен нулю: 4R == 0.
Для доказательства второго утверждения рассмотрим ковариант-
ные компоненты G\t тензора G:
G,t = R,t - \пдн = Rim{S\8? - gimglt) = RimBimlt, (8.143)
где Btmlt определяется формулой (8.142).
534 Глава 8. Тензоры в римановых пространствах
Выразим теперь компоненты тензора вращения Риччи jRtm через
матрицу Sfcp, подставив для этого формулу (8.126) в (8.132):
Rim = ^(V.-V^S-1)^ - VfcV,(S-yro). (8.144)
Подставляя (8.144) в (8.143), действительно приходим к соотношению
(8.141). А
Тензор Эйнштейна играет важную роль в общей теории относи-
относительности (см., например, [32], [35], [45]).
Упражнения к § 8.4.
Упражнение 8.4.1. Показать, что в пространстве ILn компоненты тензора
кривизны обладают следующей симметрией: Rj{8 =~ ~R{js » а в пространстве
ILq имеют место тождества Риччи:
* к * * к
Rjis + Risj + Rsji = О-
Упражнение 8.4.2. Используя соотношения (8.116) и (8.117), показать, что
в римановом пространстве V из общего числа 81 компоненты тензора Rnjik не-
независимых - только 6, в качестве которых можно выбрать: -Ri212» ^2323» -^3131»
i?1223> -Ri231> -^2331» тогда остальные либо равны нулю, либо выражаются через
них.
Упражнение 8.4.3. Используя результат упр. 8.1.2, показать, что в собст-
собственно римановом пространстве Vn из формулы (8.133) следует соотношение
_ аг&. э2.п yg a, yg
3t~dxk дх'дх* + •' эхп iknj'
Переставляя в этом выражении индексы 2, J, убедиться, что правая часть остается
без изменений, откуда следует, что тензор Риччи TL является симметричным.
Упражнение 8.4.4. В собственно-римановом пространстве V еще один
тензор второго ранга, называемый тензором несовместности S, образуется
из 1Z сверткой с двумя тензорами Леви-Чивиты:
S = SP'Ri ® R, = A/4)е • -4R • е.
Доказать, что компоненты этого тензора имеют вид:
S*> = (l/4g)eikleimnRklmn.
Упражнение 8.4.5. Показать, что тензор несовместности, введенный в упр.
8.4.4, является симметричным.
Упражнение 8.4.6. Показать, что тензор несовместности, введенный в упр.
8.4.4, удовлетворяет соотношению Rprst = 9€ipr€jstStJ, или И = € • S • €.
Упражнение 8.4.7. Используя свойства тензора Римана-Кристоффеля
(8.116), (8.117), показать, что явное выражение для компонент тензора несовмест-
несовместности имеет вид:
511 = -Д2323, 512 = -Д2ззь 513 = ~
9 9 9
С22 __ 1 р С23 _ ^ ^
9 9
ГЛАВА 9
ИНТЕГРИРОВАНИЕ ТЕНЗОРОВ
Важную роль в механике и физике играет операция интегрирова-
интегрирования тензоров пП(ж'), заданных в некоторой области V трехмерного
евклидова пространства М3, либо либо на двумерной поверхности ?,
либо на некоторой кривой С в М3. Введем эту операцию для тензоров с
помощью операций интегрирования обычных скалярных функций ска-
скалярного аргумента, более детальное изложение которых можно найти,
например, в [39].
§ 9.1. Криволинейные интегралы от тензоров
9.1.1. Определение интеграла от тензора,
заданного вдоль кривой
Пусть имеется некоторая кривая ?, заданная в трехмерном евклидо-
евклидовом пространстве, например, параметрическим способом G.1). Точки
х(?о) и x(?/v) назовем началом и концом этой кривой. Предполагаем,
что вдоль этой кривой задан тензор пП(хг) n-ого ранга, имеющий в
декартовом базисе следующий вид:
пЩх{) = ni'i---*»(a.f")el-l ® ... ® ё,-п. (9.1)
Компоненты этого тензора п%1"Лп являются функциями декартовых
координат х\ которые изменяются вдоль кривой С:
х = х@ или х* = х'"@, ?о ^ ^ 6v- (9.2)
Разобьем отрезок [?o,6v] на N частей: [?о, 6]» •••Ка-ь &»],...
... ,[?n-i>?/v]« Этим отрезкам соответствуют N частей кривой С
(см. рис.9.1), началом и концом которых являются пары точек:
Х(о),Х(!);... ;x(a_!),X(Q);... ;x(j\r_i),X(jv); (9.3)
где
X(a) = X(?a) ИЛИ x\q) = Х*(?а), а = 0, . . . , N,
- их координаты в пространстве.
536.
Глава 9. Интегрирование тензоров
Длины дуг этих частей кривой обозначим как
ASQ = I ds, a- 1...ЛГ,
(9.4)
и введем максимальное значение
среди А5,-:
А/= шах {Два},
a=l...N
называемое максимальным ша-
шагом разбиения кривой.
На каждом отрезке [?co?a+i]
возьмем еще по одной точке ?а с
координатами:
*(«)=*•"(?«) a=l...JV, (9.5)
Рис. 9.1. Разбиение кривой на N
частей
и образуем следующий тензор интегральных сумм:
N
(9.6)
a=l
который, очевидно, является тензором того же ранга, что и ПП.
Компоненты этого тензора Sll'"tn в декартовой системе координат
связаны с П*1
1>ln следующим образом:
N
а=1
где
(9.7)
(9.8)
Поскольку каждая компонента П|1>Лп является обычной классичес-
классической функцией координат хг, то для нее можно положить, что сущест-
существуют пределы сумм (9.7) при N —у оо и стремлении к нулю макси-
максимального шага разбиения кривой А1 —у 0:
(9.9)
a=l
§ 9.1. Криволинейные интегралы от тензоров 537
Определение 9.1. Предел (9.9) называют интегралом от
компонент тензора вдоль крив ой С (или кр иволинейным ин-
интегралом от компонент тензора) и обозначают как
{1"Лп{х{)A8 = S1'1-1". (9.10)
Определение 9.2. Криволинейным интегралом первого рода
от тензора пП, заданного вдоль кривой С называют следующий объ-
объект:
nS = 5l"*-i"»el-1 ®...®efn= [ nu{x)ds. (9.11)
Jc
Теорема 9.1. Введенный по формулам (9.9), (9.11) объект nS
является тензором п-го ранга.
Т В самом деле, так как пП(х(а)), а = 1...JV, представляют собой
N различных тензоров, то их компоненты преобразуются при пере-
переходе из декартова базиса в какой-либо базис R* = Q'fcej следующим
образом:
Здесь fl^V'fcn - компоненты тензора nft(x(a)) в базисе Щ.
Поскольку якобиева матрица Q% k одинакова для всех членов сум-
суммы (9.9) и не зависит от числа разбиений iV, то используя известные
свойства пределов, можно вынести произведение якобиевых матриц за
знак предела, тогда получим:
где
а=1
так как длины дуг Asa не зависят от выбора базиса, то из (9.13) и
(9.14) следует, что S%1"An являются компонентами тензора. А
Если кривую С задать в параметрическом виде G.8) как функцию
длины дуги:
ж'=± »•(«), 0^5^/, (9.15)
где I - длина всей кривой С:
l = J*Nds, (9.16)
538 Глава 9. Интегрирование тензоров
то тензор ПП (его компоненты П*1—1п) также можно рассматривать
как функцию от s: nft(x(s)) = nft(s). Интеграл (9.11) в этом случае
будет обычным одномерным определенным интегралом с переменной
интегрирования s, изменяющейся от 0 до /:
nS= f nU{s)ds, (9.17)
Jo
причем компоненты S%1'"tn этого тензора имеют вид:
Г1
5»1..-«п = / n«i...«n^)dee (9Л8)
Jo
9.1.2. Криволинейные интегралы второго рода
от тензора
Криволинейный интеграл от тензора можно образовать иным спо-
способом.
Пусть имеется разбиение (9.3) кривой С точками Х(а), а = 0...N.
Векторы, соединяющие эти точки, обозначим как
Дх(а)=Х(а)-х(а_1) или Дя{а) = я|а)-»!„_!),
х(а)=х(?(а)), a = l...N. (9.19)
Им соответствуют приращения параметра ?:
среди которых имеется максимальное Д? = max {Д?а}-
Тензор интегральных сумм составим, в отличие от (9.8), путем
скалярного умножения векторов Дх(а) на транспонированные тензоры
(яП(х(в)))<те1-те»> (см. гл.1):
n"lTw = Е Дх(«) • "%))(Ш1"<тщ|. (9-2°)
а=1
где (mi...mn) означает некоторую подстановку индексов, одинако-
одинаковую для всех тензоров пП(х(а)) (каждое из mi... тп принимает какое-
то из значений индексов i\ ...in (см. §1.8)).
Тензор п"Т(дг) имеет ранг на единицу меньше, чем ПП (т.е.
(п — 1)), и его компоненты в декартовой системе координат имеют
следующий вид:
, (9.21)
§9.1. Криволинейные интегралы от тензоров 539
N
а=1
Здесь и далее запись Q^1'" Wn означает, что (тг — 1) компонента iWl ...
.. .iWn принимают значения i2 .. .гп, а по i\ идет суммирование.
Заметим, что хотя формально в (9.21) свободные индексы слева и
справа не совпадают, тем не менее формула (9.21) записана по обыч-
обычным правилам расстановки индексов, и ее следует расшифровывать
так. При конкретных значениях подстановки (mi...mn), например
(п, п — 1, п — 2,... ,1), индексы iWl,...iWn всегда принимают значения
из набора {i±.. . гп}. Для нашего примера это {гп^п-ъ • • • ih}- При
этом по индексу i\ в (9.21) идет суммирование, для нашего примера
это Axtlutn%n'"t^i . Такая запись будет использоваться и в дальней-
дальнейшем.
Устремляя максимальное приращение параметра Д? к нулю:
Д? —> 0, а N —> оо, предполагаем, что при этом существуют следу-
следующие пределы для каждого набора индексов i\... in-ii
? ;Г ((в)){^ (9.22)
Определение 9.3. Пределы (9.22) называют скалярными криво-
криволинейными интегралами второго рода от компонент тензора и
обозначают следующим образом:
(9.23)
Определение 9.4. Скалярным криволинейным интегралом вто-
второго рода от тензора ПП, заданного вдоль кривой С, называют
тензор (п — 1)-го ранга П~1Т с компонентами Т*1'*-1, определяе-
определяемыми по формуле (9.23).
Для этого тензора также используют интегральное обозначение:
n-iT = ра...«пё.а ® ... ® ё,-п = [ dx • "ft(™i-™») (x)# (924)
Jc
Обозначение для элементарного радиуса-вектора dx = cte'e,- ис-
использовано в (9.23) и (9.24) на том основании, что при Д? —У 0 малые
векторы Дх(а), как было отмечено в п.7.1.2, стремятся к элементар-
элементарному вектору dx вдоль кривой С.
540 Глава 9, Интегрирование тензоров
Если в формулах (9.20) - (9.24) мы поменяем знак скалярного умно-
умножения (•) на знак векторного умножения (х), то получим векторные
криволинейные интегралы второго рода:
пТ = Г1~**ё{1 ® ... ® ё.-я = [ dxx »п<го*-те»>(х), (9.25)
Jc
fki,...in = €kjh5ij Г д»'^ »¦•'.-» (x«)dxit (9.26)
v С
Здесь €к** - символ Леви-Чивиты (см.п. 1.4.1).
Если в формулах (9.20) - (9.24) также поменять знак (•) на знак
0 тензорного умножения, то получим тензорный криволинейный ин-
интеграл второго рода:
n+iT = уи....-n+i^ в в _ 0 ё = [ dx® пП(х), (9.27)
где
Wi / <««' (9.28)
Jc
9.1.3.' Связь между криволинейными интегралами
первого и второго рода
Тем же cnocoGoMj что и в п.9.1.1, можно показать, что компонен-
компоненты f1'»-1'», T1'1-1^, Tl'i-I'n+1, определяемые по формулам (9.23), (9.26)
и (9.28) преобразуются по тензорному закону при переходе в новую
систему координат, и, следовательно, криволинейные интегралы вто-
второго рода (9.24), (9.25) и (9.27) являются тензорами (п — 1)-го, n-го и
(п + 1)-го рангов, соответственно.
Установим теперь связь между криволинейными интегралами пер-
первого и второго рода.
Пусть кривая С задана в параметрическом виде (9.15). Используя
формулы G.9) и G.10), от элементарного вектора dx можно перейти
к элементарной длине дуги:
dx-tds, t = ?'§,-. (9.29)
Тогда интеграл (9.24) можно представить в виде обычного определен-
определенного интеграла:
= /
Jo
(9.30)
здесь длина дуги выступает в роли переменной интегрирования, из-
изменяющейся от 0 до /.
§9.1. Криволинейные интегралы от тензоров 541
В компонентной записи формула (9.30) имеет вид:
Г1 -•
Jo
(9.31)
Здесь Iх (s) - компоненты единичного вектора касательной к кривой С
(т.е. косинусы углов, которые имеет касательная к кривой с осями
декартовой системы координат).
Аналогичным образом можно преобразовать векторный криволи-
криволинейный интеграл (9.25):
Г1 - Г1 - -
пТ= t{s)xnn(mi'"mn){s)ds, Tki*'~in = ekiil / ii(s)Utwi';'twn(s)ds;
Jo Jo 1
(9.32)
и тензорный криволинейный интеграл (9.27):
Г1 Г1
п+1Т= / t{s)®nu{s)ds, Г*~л*+1= / ii'(s)ui^in
Jo Jo
s. (9.33)
Формулы (9.17) и (9.30), (9.32), (9.33) устанавливают связь между
криволинейными интегралами первого и второго рода.
Если кривая С задана в параметрическом виде (9.2), то криволи-
криволинейные интегралы первого и второго рода (9.17) и (9.30) можно пред-
представить следующим образом:
ft
а также
n"lT=/ ^
J
Jtio
(9.35)
То же самое представление можно получить и для векторного и
тензорного криволинейных интегралов.
Если направление интегрирования по ? или по s меняется, то ме-
меняются местами точки Х@) = х(?о) и Х(дг) = х(?дг), а у интегралов
(9.17), (9.30), (9.32), (9.33) - пределы интегрирования и знак " + " на
" — " перед интегралом.
542 Глава 9. Интегрирование тензоров
9Д.4. Независимость скалярного криволинейного интеграла
от пути интегрирования
Пусть теперь тензор ПП является не произвольным, а потенциаль-
потенциальным (см. §6.2):
nft = V ® "^Ф = V.^^-^R1'1 ® Rt2 ® ... ® Rtn, (9.36)
где ПФ - тензор-потенциал (п — 1)-го ранга.
Вычислим для него подынтегральное выражение в скалярном кри-
криволинейном интеграле (9.24), выбирая подстановку транспонирования
специальным образом:
(mi.. .тп) = A,т2,. • • , "in), (9.37)
т.е. на первом месте обязательно стоит индекс ii, а все остальные
индексы произвольны.
Тогда подынтегральное выражение
dx • »n(i">-"»n) = (dx'Rf) • V.^'^-'-nRH ® Rl2 ® ... 0 Rtn =
= _»-1
Шп-1 (9.38)
представляет собой полный дифференциал от тензора потенциала.
Записывая формулу (9.38) в декартовой системе координат (Хг =
ж1), подставим ее в (9.24), в результате получим:
Jc
1тп_1(х(о)^ (д 39)
где использована формула Ньютона-Лейбница интегрирования диф-
дифференциала от обычных функций.
Таким образом, доказана следующая теорема.
Теорема 9.2. Если тензор ПП - потенциален, т.е. удовлетво-
удовлетворяет (9.36), то скалярный криволинейный интеграл второго рода
от него не зависит от кривой С, по которой происходит интегри-
интегрирование (т.е. от "пути интегрирования ), и определяется только
разностью значений тензора потенциала П"Ф в конечной и началь-
начальной точках.
§ 9.1. Криволинейные интегралы от тензоров 543
9.1.5. Криволинейные интегралы по замкнутому
контуру
Если у кривой С начальная и конечная точки совпадают:
Х(о) = X(jv), то такая кривая называется замкнутой или замкнутым
контуром.
Криволинейные интегралы первого и второго рода (9.11), (9.24),
(9.25) и (9.27) в этом случае обозначаются следующим образом:
nS= lnSl(x)ds, n~lT= ^x-nft(mi-m»>(x), (9.40)
xxnn(mi-m^(x), n+1T=
Определение 9.5. Скалярный криволинейный интеграл в (9.40)
по замкнутому контуру называют циркуляцией тензора ПП.
Если тензор пП потенциален, то для него имеет место формула
(9.39), но если скалярный криволинейный интеграл берется по замк-
замкнутому контуру, то начальная и конечная точки кривой совпадают, а
значит и значения тензора потенциала П~1Ф в них также совпадают.
Таким образом, имеет место следующая теорема.
Теорема 9.3 (о циркуляции потенциального тензора). Если
тензор пП потенциален
mo циркуляция любого его транспонированного тензора n
равна нулю:
/лс.пПAт2-Шл) =0. (9.41)
Упражнения к § 9.1.
Упражнение 9.1.1. Показать, что для вектора а при П — 1 криволинейные
интегралы второго рода (9.24), (9.25) и (9.27) могут быть представлены в виде:
?=/Жс«а=/а« Же, t=/dxxa=-/ax Же,
Jc Jc Jc Jc
T= I dx®a= ( I a®dxj .
Упражнение 9.1.2. Показать, что если П = 2, то криволинейные интегралы
второго рода (9.24), (9.25) и (9.27) могут быть представлены следующим образом:
гр
t = / dx • П = / Пт • Же, Т = / dx х П = - ( f ПТ х Же J ,
544 Глава 9. Интегрирование тензоров
= I dx ® П = [ I П ® dx j
\ B31)
Упражнение 9.1.3. Показать, что для двусвязной области V в трехмерном
евклидовом пространстве циркуляция потенциального тензора является постоян-
постоянным тензором (не зависящим от координат):
I
dx • пЦК1т*-т*) - n~lr? = const,
С
если интеграл берется по любому, лежащему в области V контуру, несводимому
непрерывным преобразованием в точку, причем тензор n"~ T одинаков для всех
таких контуров.
§ 9.2. Поверхностные интегралы от тензора
9.2.1. Поверхностный интеграл первого рода
Рассмотрим теперь некоторую ограниченную поверхность Е в трех-
трехмерном евклидовом пространстве, заданную параметрическим обра-
образом G.40):
х{ = х*(Х\Х2), г =1,2,3, (9.42)
где X1 - криволинейные координаты на поверхности.
Предполагаем известными (см. например [39]) сведения о том, как
определяется поверхностный интеграл
L
f(x{)dS
от классической функции /(ж1), заданной на поверхности Е. Здесь
dE - площадь элементарной площадки поверхности, определяемая по
формуле G.63).
Пусть на этой поверхности Е задан тензор n-го ранга пЩхг) с де-
декартовыми компонентами ?1%1'"%п(хг(X1, X2)) (этот трехмерный тен-
тензор, вообще говоря, не совпадает с двумерным тензором на поверхнос-
поверхности, введенным в п.7.2.3).
Определение 9.6. Ловерхностным интегралом первого
рода от тензора пП называют тензор п-го ранга nS, компонен-
компонентами которого в декартовой системе кординат S%1'"Xn являются
поверхностные интегралы от компонент U%1'"ln, т.е.
(9.43)
§ 9.2. Поверхностные интегралы от тензора 545
где
Sh~'in = [ &*•••** (Х*)<1Е. (9.44)
Так же как это было проделано в п.9.1.1, можно показать, что
S%1'"tn преобразуются по тензорному закону:
5н....п = pi^ ...р«^5*1...*» (9.45)
при переходе в другую систему координат: R* = Q'^e,.
Заметим, что здесь якобиевы матрицы Q%k и Р\ не зависят от
координат х*.
Формула (9.45) позволяет получить компоненты тензора nS поверх-
поверхностного интеграла в любой системе координат.
Испбльзуя формулу G.63) для dE можно записать поверхностный
интеграл (9.43) в виде:
nS= [[ nU(XI)^7jdXldX2, (9.46)
JJzx
где тензор пП(хг(Х1)) = пП(Хт) рассматривается как функция кри-
криволинейных координат, a Ejv представляет собой двумерную область
значений этих координат X1', соответствующую поверхности Е в
трехмерном пространстве. В этом случае для поверхностного интег-
интеграла используется обозначение в виде двойного интеграла.
Формула (9.46) называется формулой замены переменных в поверх-
поверхностном интеграле.
9.2.2. Поверхностные интегралы второго рода
Если для определения криволинейных интегралов второго рода ис-
использовался элементарный радиус-вектор кривой dx, то для анало-
аналогичных поверхностных интегралов второго рода применяется вектор
ориентированной площадки G.63): ndS, который согласно G.62) мож-
можно представить в виде:
ndS = pi x p2dX1dX2, (9.47)
здесь n - вектор нормали к поверхности S.
В декартовом базисе этот вектор на основании G.44) имеет вид:
а=1
3
= ^Tdxadx%) афРфчфа, а,/3,7 = 1,2,3, (9.48)
а=1
18 Тензорное исчисление
546 Глава 9» Интегрирование тензоров
где рх j - якобиева матрица поверхности G.44), а Р*к - обратная яко-
биева матрица на поверхности:
г дХ1 { дх{ /Л .ЛЧ
Определение 9.7. Скалярным поверхностным интегра-
интегралом второго рода от тензора nft(mi•••"**) называют следующий
тензор (п — 1)-го ранга:
n-iT = fi*...ineh ® ... ® ё,-п = / n . nn(mi-m-)(x)dE. (9.50)
Здесь
3 ГГ
^ // (9.51)
- двойной интеграл, определяемый как" для обычных классических
функций. Областью интегрирования здесь является двумерная об-
область Еа: изменения координат жа, а = 1,2, соответствующая поверх-
поверхности Е.
Определение 9.8. Векторным поверхностным интегралом
второго рода от тензора пП(т1'"тп) называют тензор п-горан-
п-горанга пТ, определяемый по формуле:
пТ = f {1"Лп
... ® ё,-п = (nx nn(mi-mn)(x)dE. (9.52)
Тензор ПТ имеет следующие компоненты в декартовом базисе:
^b Л i^^P (9.53)
Q=l
Определение 9.9. Тензорные поверхностным интегралом
второго рода от тензора пП называют тензор (п -f \)-го ранга
1
(9.54)
Компоненты этого тензора в декартовом базисе имеют вид:
II Uiii^ (9.55)
§9.2. Поверхностные интегралы от тензора 547
9.2.3. Формула Стокса
Эти формулы позволяют от поверхностных интегралов переходить
к криволинейным.
Предполагаем известной (см. например [39]) формулу Стокса для
классической, непрерывной вместе со своими производными скаляр-
скалярной функции f(x%), заданной на некоторой кусочно-гладкой незамкну-
незамкнутой поверхности S, ограниченной кусочно-гладким замкнутым конту-
контуром С:
I f{xi)dxj = €jkl f nk^jdZ. (9.56)
Jc Jz °x
Формула записана в декартовой системе координат, где п* - компонен-
компоненты вектора нормали п к поверхности Е, направление которого выби-
выбирается согласованно с направлением обхода контура С от начальной
точки к конечной: из конца вектора п, проведенного в любой точке
поверхности, обход контура С виден осуществляемым против часовой
стрелки.
Умножая (9.56) на вектор базиса ej, получим инвариантную форму
записи формулы Стокса:
или
I f{x)dx = [ n x V/dE. (9.57)
Jc Jz
Здесь использованы определения векторного произведения A.33) и
градиента скаляра F.15').
Обообщением формулы Стокса (9.57) на случай тензора произволь-
произвольного п-го ранга является следующая формула:
{ dx ® пП(х) = / п х V ® nH(x)dE. (9.58)
Jc Jz
В декартовых компонентах эта формула имеет вид:
/ Q«V..«-n+1/ *Wi = 6ii*i f njb^7nl'a-i"»+l(»l")dE. (9.59)
Jc Jz °x
Справедливость формулы (9.59) непосредственно следует из (9.56),
поскольку при каждом фиксированном наборе индексов %2 ... in+i фор-
формула (9.59) в точности совпадает с (9.56).
Эта формула (9.56) называется тензорной формулой Стокса.
Для тензоров имеет место также скалярная формула Стокса:
f dx • nfl(x) = / (n x V) • nft(x)dE. (9.60)
548 Глава 9. Интегрирование тензоров
В декартовом базисе эта формула имеет вид:
t^7n{j"-<"(*<)dS. (9.61)
Перепишем формулу (9.61) следующим образом:
J2 U <ЬаП\*"л*{х{) - eaklI пк^П\*"л*<П}\ = 0.
Фиксируя какой-либо набор индексов %2 ... гп, для каждого из зна-
значений а = 1,2,3 в скобках мы снова получим формулу Стокса (9.56),
где роль / играет функция fij*"**n. Таким образом, из (9.56) следует
истинность скалярной формулы Стокса (9.60). Очевидно, что любая
перестановка индексов i\... гп не изменит сути доказательства, поэ-
поэтому имеет место скалярная формула Стокса, обобщающая (9.60):
/ dx.nn(Wl-m*> = [ (п х V) .яп(го1~те»><Е. (9.62)
Наконец, имеет место векторная формула Стокса:
I dx х пп = / (п х V) х ПШЕ, (9.63)
которая в декартовой системе координат выглядит следующим обра-
образом:
б,*и f <ЬкП"*"Л*{х*) - Ъг^*1 J nfc^ni'^'"S*lVs. (9.64)
Преобразуем это выражение к виду:
( х>п"*"л*{х*) - б^'ы / nfe^ft^-'-dE^ = 0. (9.65)
Сравнивая (9.56) с выражением в скобках при каждом фиксирован-
фиксированном наборе индексов i\.. ,гп, убеждаемся в том, что из (9.56), очевид-
очевидно, вытекает (9.65), что и доказывает истинность векторной формулы
Стокса (9.62).
§ 9.2. Поверхностные интегралы от тензора
.549
Упражнения к § 9.2.
Упражнение 9.2.1. Используя F.29), F.31), показать, что при П = 1 из
(9.63) следует:
Ф dx х а = / (п • (V ® а)т - n ® V • a) dE,
где а есть вектор п П при 71 = 1.
Упражнение 9.2.2. Используя результат упр.9.2.1 и п.6.1.6, показать, что
если в качестве а выбрать радиус-вектор X, то
i dx х х = -2 / ndE.
Jc Jz
Упражнение 9.2.3. Показать, что из (9.58) и (9.60) при 71=1 следует:
Ф dx • а = Ф а • dx = / (n x V) • adE = / п - (V х a)dS,
Jc Jc Jz Jz
ф dx ® a = / (n x V) ® adS.
Jc Jz
Упражнение 9.2.4. Показать, что из (9.60) и (9.65) при 71 = 2 следует:
Ф dx • П = Ф Пт • dx = / (п х V) • ШЕ,
Ф dxxft= / (п х V) х HdE.
n
PtiC. 9.J8. К упр. 9.2.5.
Упражнение 9.2.5. Используя ска-
скалярную формулу Стокса для вектора
(см.упр.9.2.3) и теорему о среднем для
поверхностного интеграла, показать, что
(V х а)„ = п • (V х а) =
= lim -— Ф а • tds,
az—>o AS JAC
т.е. проекция ротора вектора а на произ-
произвольное направление с вектором П в точ-
точке М. (с вектором х) есть предел отно-
отношения циркуляции этого вектора а вдоль
малого контура А?, ограничивающего
малую плоскую площадку АЕ, которая
содержит точку Л4, к площади этой пло-
площадки АЕ (см. рис.9.2).
550 Глава 9. Интегрирование тензоров
§ 9.3. Объемные интегралы от тензора
9.3.1. Элементарный объем
Как и в случае поверхностного интеграла, предполагаем известным
определение объемного интеграла (см.например [39])
/ f{x{)dV (9.66)
v
от функции /(ж1), заданной в области V трехмерного евклидова про-
пространства. В формуле (9.66) dV - это элементарный объем, который
определим следующим образом. Возьмем прозвольную точку М и
выпустим из нее три элементарных радиуса-вектора dxa вдоль коор-
координатных линий XQ. Эти три вектора всегда будут линейно неза-
независимы, поэтому можно получить некоторый объем dV, вычислив по
A.58) смешанное произведение этих трех векторов:
Так как
то получаем
dV =
dV = d>
die
с учетом A.58):
Ri • (R2 x RaJdX1
ci • (dx2
Z dXQ
dX2dX:
x dx3).
R dXa
J = J^dX4X2dX3
(9.67)
(9.68)
(9.69)
- выражение для элементарного объема параллелепипеда, построен-
построенного на векторах dxa.
9.3.2. Определение объемного интеграла
от тензора
Пусть имеется тензор пП(х), заданный в некоторой области V ев-
евклидова трехмерного пространства. Объемным интегралом от компо-
компонент тензора назовем интеграл вида:
= fil-i"»l (9.70)
где при каждом фиксированном наборе индексов %\... гп имеем обыч-
обычный объемный интеграл (9.66) от классической функции.
Определение 9.10. Объемным интегралом от тензора пП
называют тензор п-го ранга ПТ, имеющий компоненты в декарто-
декартовом базисе, вычисляемые по (9.70). Для этого интеграла используем
обозначение:
пТ = Т1"Лпё{1 ® ... ® ё,-п = [ nil{x)dV. (9.71)
J
§ 9.3. Объемные интегралы от тензора 551
Используя формулу (9.69), объемный интеграл (9.71) можно пред-
представить в виде тройного интеграла:
пТ= /ТУ nSl{Xi)y/gdX1dX2dX3i (9-72)
здесь тензор ПП рассматривается как функция криволинейных коор-
координат, a Vx представляет собой трехмерную область значений этих
координат -X, соответствующую области V в трехмерном простран-
пространстве. Формула (9.72) называется также формулой замены переменных
в объемном интеграле.
9.3.3. Формула Гаусса-Остроградского
Формула Гаусса-Остроградского является аналогом формулы
Стокса и позволяет переходить от объемных интегралов к поверх-
поверхностным и наоборот.
Полагаем известной (см. например [39]) формулу Гаусса-Остро-
Гаусса-Остроградского для классических функций /(ж1), заданных в некоторой за-
замкнутой трехмерной области V', ограниченной кусочно-гладкой по-
поверхностью S:
/я/(,^сЕ = /у^ (9.73)
где функция f(x%) предполагается непрерывной вместе со своими про-
производными вплоть до границы S области V.
Формула (9.73) записана в декартовой системе координат, где щ -
компоненты вектора нормали к поверхности Е, направленной во внеш-
внешнюю сторону по отношению к области V.
Умножая (9.73) на векторы базиса, приходим к инвариантной запи-
записи:
или
/ /(x)ndE = / VfdV. (9.74)
Js Jv
9.3.4. Формулы Гаусса-Остроградского для тензоров
Обобщением формулы (9.74) на случай тензора n-го ранга является
тензорная формула Гаусса-Остроградского:
[ п 0 nH(x)dE = / V ® "SldV. (9.75)
Js Jv
В декартовых координатах она имеет вид:
552 Глава 9. Интегрирование тензоров
Формула (9.76) является очевидным следствием (9.73), т.к. фикси-
фиксируя какой-либо набор значений индексов %2 ... гп+1, мы сразу получаем
формулу Гаусса-Остроградского (9.73) для классических функций.
Скалярной формулой Гаусса-Остроградского называется следую-
следующее обобщение формулы (9.73) для тензоров:
/ п • ПШЕ = / V • nudV. (9.77)
Jz Jv
В компонентах эта формула имеет вид:
{Л* (9.78)
Для доказательства этой формулы перепишем ее в декартовом ба-
базисе:
? (J^^ds -1 ^-^v) = о.
Зафиксировав какой-либо набор индексов %2 ... гп > для каждого из зна-
значений а = 1,2,3 в скобках вновь получим формулу Гаусса-Остроград-
Гаусса-Остроградского (9.73), где роль / играет функция Па*2—*л. Следовательно, из
(9.73) немедленно вытекает истинность (9.78) и (9.77).
Очевидно, что для любой перестановки индексов z'i... in ход доказа-
доказательства будет таким же, поэтому имеет место формула, обобщающая
(9.77):
(9.79)
Jv
Векторной формулой Гаусса-Остроградского называют следую-
следующее обобщение формулы (9.73):
/ п х ПШ? = / V х nUdV, (9.80)
Jz Jv
которое в декартовой системе координат имеет вид:
eijil [ пД.1'2-'" d? = eijil I -^тП/а"л"" dV. (9.81)
7s 1 Jv ox3 J
Доказательство того, что (9.81) является следствием (9.73) прово-
проводится так же, как и для скалярной формулы Гаусса-Остроградского.
Формулу (9.80) можно также применить и для транспонированного
тензора:
/ п х nn(mi-mn)dE = / V х nn(mi-m^d7, (9.82)
Jz Jv
§ 9.3. Объемные интегралы от тензора 553
или в базисе ё,:
$? [ ?-rUiwi'?WndV. (9.83)
[ ? [
s Jv
Упражнения к § 9,3.
Упражнение 9.3.1. Показать, что в цилиндрической системе координат
элементарный объем (9.69) имеет вид:
dV = rdrd(pdz.
Упражнение 9.3.2. Показать, что в сферической системе координат элемен-
элементарный объем (9.69) имеет вид:
dV = г2 smfldrdtidp.
Упражнение 9.3.3. Показать, что из (9.75), (9.77), (9.80) для вектора при
71 = 1 следует:
/n ® adE = / V ® adV, [ а ® ndE = / (V ® a)TdV,
is Jv is Jv
[ n • adE = / V • adV, [ n x adS = / V x adV.
7s 7v is Jv
Упражнение 9.З.4. Показать, что из (9.75), (9.77) и (9.80) для тензора
второго ранга при 71 = 2 следует:
/ n . HdE = / ilT • ndS = / V • ШУ.
is is iv
Упражнение 9.3.5. Используя результаты упр.9.3.4 и соотношение F.73),
показать справедливость формулы:
/ п • П • adS = / V • (П • a)dV = / ((V • П) • а + П • -(V ® а)т) dV.
is Jv Jv
Упражнение 9.3.6. Доказать справедливость формулы:
= - / (п • П) х xdS = / (х х V • H)dV - 2 / a;dF,
is iv iv
/ х х п • / /
s is iv
где UJ - вектор, сопутствующий кососимметричной части тензора П.
Упражнение 9.3.7. Используя скалярную формулу Гаусса-Остроградского
для вектора (см. упр.9.3.3) и теорему о среднем, показать, что
V • а = lim -—7 / n • adS,
av->o AV iAS
т.е. дивергенция вектора в точке X области есть предел отношения потока вектора
через малую замкнутую поверхность АЕ, окружающую точку X, к объему А V,
ограниченному этой поверхностью.
Приложение
ЭНЕРГЕТИЧЕСКИЕ И КВАЗИЭНЕРГЕТИЧЕСКИЕ
ПАРЫ ТЕНЗОРОВ
В механике сплошных сред очень важную роль играют определен-
определенные пары тензоров второго ранга, связанных через так называемую
работу внешних поверхностных сил. Существование этих пар тен-
тензоров при условии потенциальности (см. гл.5) позволяет получить
альтернативные тензорные функции для описания различных физико-
математических процессов. Рассмотрим эти пары, начав с некоторого
важного свойства невырожденных тензоров в пространстве М3.
Теорема Ш (о полярном разложении). Всякий невырожден-
невырожденный тензор второго ранга F можно представить в виде скалярного
произведения двух тензоров второго ранга:
F=OU или F = VO, (ЯЛ)
где U и V - симметричные, положительно определенные тензоры, а
О - ортогональный тензор, причем каждое из представлений (ПЛ)
единственно.
Т Доказательство существования разложения (ПЛ) приведем конст-
конструктивно, т.е. построив тензоры U, V и О. Для этого рассмотрим
свертки тензора F со своим транспонированным: FT • F и F • FT. Оба
эти тензора являются симметричными, так как
(рт . р)т _ ft . (ft)T = Рт . F и (F . ft)T _ (ft)T . ft = F . FT(
а также положительно определенными (см. определение 1.25):
F.a)=(F.a).(F.a) = b.b=|b|2>0 (Я.2)
для любого ненулевого вектора а, где b = F • а. Тогда, согласно
теоремам 1.13 и 1.14, у тензоров FT • F и F • FT все три собственные
°2
значения вещественны и положительны, обозначим их как Аа и А^,
причем согласно A.187)
ft • f = Е ^р« ® р«. F •рТ = Е А-р« ® р«. (я-3)
а=1 а=1
где ра - собственные векторы тензора FT • F, а ра - тензора F • FT,
являющиеся согласно A.185) ортонормированными:
Ра'Р/З =<W, Ра'Р/* = ?а/3, (ПА)
Приложение. Энергетические и квазиэнергетические пары 555
Правые части в (П.З) представляют собой квадраты некоторых тен-
тензоров U и V, определенных как
3 о л л о Л
«Ра ® Ра? ^а > U; V = у ^ ЛаРа ® Ра» ^а > U, (ii .0)
а=1 а=1
где знаки у Аа выбираем положительными. При этом имеют место
соотношения:
FT-F = U2, F-FT=V2. (Я.б)
Построенные тензоры V и U являются симметричными, что следует
из формулы (П.5), а также положительно определенными, так как для
любого ненулевого вектора а выполнено:
3 о 3
а - U • а = ]? Ааа - рв ® рв - а = ]? Аа(а • РаJ > О, (Я.7)
а=1 а=1
о
ввиду того, что Аа > 0. Аналогично доказываем положительную опре-
определенность тензора V.
Оба тензора V и U невырождены, так как по условию теоремы F
- невырожден, и из (П.б) следует (det UJ = det U2 = det (FT • F) =
= (det FJ ф 0. Тогда существуют обратные тензоры U" и V", с
помощью которых можно построить еще два новых тензора
O = V-1-F) (Я.8)
являющихся ортогональными. В самом деле, От • О =
= (F • и^1O • (F • U) = (U-1 • FT • F • и^1 = U • U2 • LT1 = Е,
о
что согласно A.209) означает ортогональность тензора О, аналогично
показываем ортогональность тензора О.
Таким образом, мы действительно построили тензоры U и О, а
также V и О, произведение которых согласно (П.8) образует исходный
тензор F:
F = О • U = V • О, (Я"-9)
причем U и V - симметричные, положительно определенные, а О и
о
О - ортогональные.
Покажем единственность каждого из разложений (П.9). Пусть про-
0
тивное, т.е. существует еще одно разложение, например, F = О • IL
Но тогда FT • F = U2 = U2, откуда следует, что U = U, так как раз-
разложение тензора FT • F по собственному базису единственно, а знаки
556 ¦ Приложение. Энергетические и квазиэнергетические пары
о ?
у Аа и Аа по условию выбираем положительными. Совпадение U и U
I о t о
влечет за собой совпадение О и О, так как О = F-U" = F-U" = О,
что и доказывает единственность разложения (П.9). Единственность
разложения F = V • О доказывается аналогично.
о
Нам осталось только показать, что ортогональные тензоры О и
О совпадают, т.е. что из (П.9) следует (П.1). Для этого образуем
тензор F • О = О • U • О . В силу (П.9) для этого тензора выполнено
соотношение:
6 U 6T=V О 6Т. (Я.10)
О 0 0
Тензор О • От является ортогональным, так как (О • От)т • (О • От) =
0 т ° т ° ° т
О • От • О • От = О • От = Е, тогда на соотношение (П. 10) можно
0 ° т
смотреть как на полярное разложение тензора О • U • О . Но этот
о о оо о о
тензор симметричен, так как (O-U-OT)T = (OT)T-(O-U)T = OUOT.
0 0 0 0
Тогда формальное равенство O-U-OT = O-U-OT также представляет
собой еще одно его полярное разложение. Однако выше мы показали
единственность полярного разложения, значит должны иметь место
соотношения:
V = OU 6Т и О 6Т=Е, (JT.11)
о
откуда и вытекает совпадение ортогональных тензоров О = О. А
Теорема П2. Собственные значения тензоров U и V, опреде-
0
ленных по (П.5), совпадают: Аа = Аа, а = 1,2,3.
Т Для доказательства воспользуемся определением (П.5) и первой
формулой в (П.И):
з з о з о
V = 2 А«Ра®Р« = O.U.OT = Y, АаО-ра®(О.ра) = 53 А«Ра®Ра.
а=1 а=1 а=1
где р^ = О • ра. Согласно этому соотношению мы получили два раз-
различных собственных базиса тензора V и два набора собственных зна-
значений, что невозможно, следовательно, р^ = О • ра = ра и Аа = Аа,
что и требовалось доказать. А
Для всякого тензора F, согласно определению E.89), можно ввести
дифференциал dF, тогда имеет место следующая основная теорема.
Теорема ПЗ. Пусть имеется два тензора второго ранга F и Р,
причем
1° F невырожден)
Приложение. Энергетические и квазиэнергетические пары
.557
Таблица П1. Энергетические пары тензоров
Номер
пары 71
I
П
Ш
IV
V
Энергетические
тензоры Т
FT • Т • F
|(FT • Т • О + От . Т • F)
от-т¦о
F" • Т • F~1T
Энергетические
(п)
тензоры С
Л=|(Е-и-2)
Е-U-1
В
U-E
С = f (U2 - Е)
#° скалярное произведение Р и F образует симметричный тензор
T = F-P,
тогда двойное скалярное произведение тензоров
в!А = Р . -dp
(Я.12)
можно представить в виде свертки одной из следующих пяти пар
тензоров:
в!А = Т • -dC, п = 1, II, III, IV, 7, (Я.13)
(») (п)
где Т и С - симметричные тензоры второго ранга, представлен-
представленные в табл.Ш.
Тензор В определяется с помощью своего дифференциала:
dB = -(dU • LT1 + LT1 • dU). (П.14)
В механике сплошной среды всем величинам, входящим в (П. 12),
(П. 13), придается определенный физический смысл: тензор Р характе-
характеризует условные напряжения в элементарном объеме сплошной среды
и называется тензором Пиола-Кирхгофа, тензор F называется гради-
градиентом деформаций, U и V - соответственно правым и левым тен-
тензорами искажений, а О - тензором ротации. Скаляр в!А в механи-
механике представляет собой элементарную работу внешних поверхностных
сил. Именно поэтому тензорные пары Т и С называют связанными
через работу или иначе энергетическими парами тензоров.
Т Доказательство теоремы проведем отдельно для каждой энергети-
энергетической пары.
(I)
Пара Л ~ Т
Подставим в выражение (П. 12) вместо тензора Р тензор Т и вос-
воспользуемся правилами A.137) перемены мест множителей в тройном
скалярном произведении:
d'A = P- -dP = (F-1 • Т) • -dP = Т • -dP - F. (Я.15)
558 Приложение. Энергетические и квазиэнергетические пары
Продифференцируем теперь тождество F • F = Е, в результате
получим: dF-F" + F-dF~1 = 0. Тогда скаляр в!А можно представить
в виде:
Разобьем правую часть этого выражения на два слагаемых:
iT..F.dF-1 + iT..F.dF"=iT-.dF"
Lt Lt Ju Zi
(Я.17)
Здесь мы воспользовались свойством скалярного произведения тензо-
тензоров по двум индексам А • -В = Ат • -Вт, а также симметрией тензора
Т.
Представим теперь в этом выражении тензоры dF и dF как тен-
тензорное произведение самих себя на метрический тензор Е:
dF~1T = Е • dF~1T = (F • F-1) ¦ dFT,
dF" = dF" • E = dF" • (FT • FT). (Я.18)
Подставляя эти выражения в (П. 17), получим
-d'A=iT.-(P-P-1-dP-1T)-PT + -T.-(P-dP-1-P-1T).PT. BГ.19)
Воспользуемся еще раз правилом A.137) перестановки скалярного ум-
умножения трех произвольных тензоров:
- d'A= \{FT • Т • F) • -F • dF-1T + \(?т • Т • F) • -dF • F~1T =
- FT . Т • F • -\ (F-1 • dF~1T + dF'1 • F~1T) = -FT • T • F • -dA.
Zi
(Я.20)
Здесь мы использовали выражение для дифференциала тензора
Л = |(Е - F • F~1T) = |(Е - U-2), тогда
-rfA = i (dF • F~1T + F • dFT). (Я.21)
Zi
Тогда, вводя новый тензор
(I)
Т = FT • Т • F, (JT.22)
получим из (П.20):
(I)
d'A=T • -dA, (Я.23)
Приложение. Энергетические и квазиэнергетические пары 559
т.е. представление (П. 13) действительно существует, а в качестве
первой энергетической пары тензоров выступает пара
(V)
Пара: Т
Введем
- С
новый
тензор:
(V)
Т
(I)
т
Л =
1.Т.
(I)
с.
р-1Т
(JT.24)
и преобразуем выражение (П. 12) следующим образом:
в!А = Р • -dF = F-1 • Т • -dF = F • Т • F~1T • FT ¦ -dF =
(V) (V) 1
= Т • FT • -dF = T • •- (FT - dF + FT • dP) =
L
(V) 1 (V)
= T ¦•-(FT -dF + dF7 -F) = T ¦-dC, (Я.25)
Здесь мы использовали свойство (см. упр. 1.6.1) скалярного произве-
(V)
дения тензоров А • «В = А • «В и учли симметрию тензора Т :
(V) (V)
Т т = (Т • F~1T)T ¦ (F-1O* = F • Т • F^1T = Т , (Я.26)
а также учли выражение для дифференциала энергетического тензора
С:
C = ^(FT.F-E) = i(U2-E), dC=^(FT.dF + dFT.F). (Я.27)
L L L
Таким образом, существует вторая энергетическая пара тензоров
(V) (V)
Т - С= С.
(IV)
Пара: Т ~ U
Для вывода третьей энергетической пары преобразуем выражение
(V)
(П.25), перейдя от Т к Т (П.24) и от С к тензору U (П.27). Тогда из
(П.26) получим
(IV) 1
Л А = Т • -<Ю = -(F-1 • Т • FT) . .(U • dU + dU • U). (Я.28)
560 Приложение. Энергетические и квазиэнергетические пары
Раскроем скобки и воспользуемся правилами A.137) перестановки по-
порядка скалярного умножения трех тензоров:
d'A = ^F-1 • Т • F~1T • U • -<Ш + Ьи • F-1 • Т • FT • -dU. (Я.29)
Учитывая полярное разложение (П.1):
F = О . U, F-1 = U. От, FT = О . U-1, (JT.30)
получаем окончательно
1 (IV)
d'A = - (F-1 • Т • О + От • Т • F~1T) • -dU = Т • -dU. (Я.31)
z
(IV)
Здесь введен четвертый энергетический тензор Т :
(IV) 1
Т = - (F • Т • О + От • Т • FT) , (Я.32)
и
(IV)
парным к которому является тензор U: С = U.
(И)
Пара: Т ~ -U
Преобразуем теперь первую энергетическую пару (П.23), заменив
тензор Л тензором U:
A=^(E-F-1.F-1T) = i(E-U-2), (Я.ЗЗ)
Z Z
где U~2 = U • U. Тогда из (П.23) получаем:
d'A = -]-FT • Т • F • • (U-1 • dV'1 + dV'1 • U) =
z
= —FT • T • F • LT1 - -dTJ-1 - itT1 . FT • T • F • -dU. (Я.34)
Используя свойства (П.30) полярного разложения, получим выраже-
выражение для d'A в виде:
(И)
d'A= T ..dJ-U), (Я.35)
где введен второй энергетический тензор:
Т = ^ (FT • Т • О + От . Т • F) , (Я.Зб)
Приложение. Энергетические и квазиэнергетические пары 561
-1 ()
парным к которому является тензор — U = С .
(Ш)
Пара: Т ~ В
Еще одну энергетическую пару можно получить из уравнения
(П.29), если вместо F и F~1T подставить их полярное разложение
(П.ЗО):
d'A= -и-^о^^.т-о.и-^и.^и + ^и.и-^о^^.т.о.и-^^и.
(Я.37)
Меняя порядок скалярного умножения, получаем
в!А = 1от . Т • О . .<ГО • 1Г1 + ^От -Т-О. -IT1 • <Ш. (Я.38)
Отсюда следует существование пятой энергетической пары:
(Ш)
d'A= T -<Ш, (Я.39)
(Ш)
где Т - третий энергетический тензор:
()
Т = ОТ Т О, (Я.40)
(Ш)
а В = С - тензор Био, который вводят с помощью выражения
(П.14).
На этом доказательство теоремы завершено. А
(п)
Обратим внимание на то, что все энергетические тензоры С обра-
образованы некоторой степенью правого тензора U и могут быть выраже-
выражены общей формулой:
ип~ш~2)> п = 1> п> IV> v- (я-41)
Здесь при каждом п следует сначала вычислить (п — III) в римских
цифрах, а затем перейти к соответствующим арабским цифрам. Вы-
(Ш)
ражение для тензора С = В представляет собой некоторый аналог
"нулевой степени" от U.
С помощью левого тензора V также можно ввести пары тензоров
(п) (п)
S и А, однако при этом скаляр в!А будет зависеть еще и от диффе-
ренциала тензора ротации dO1, поэтому такие пары ( S , А) назовем
квазиэнергетическими.
562
Приложение. Энергетические и квазиэнергетические пары
Таблица П2. Квазиэнергетические пары тензоров
Номер
пары 71
I
II
Ш
IV
V
Квазиэнергетические
(п)
тензоры S
VTV
|(V-T + T-V)
т
Kv-^t + t-v-1)
V-i-T-V
Квазиэнергетические
(п)
тензоры А
A = |(E-V2)
E-V-1
Y
V-E
J = ±(V2 - E)
Теорема П4. Пусть выполнены условия теоремы ПЗ, тогда ска-
скаляр d'A = Р • -dF можно выразить с помощью одной из следующих
пяти квазиэнергетических пар тензоров:
(п) (п) о
d'A = S . -d А + S • -<ЮТ, п = /,..., V, (JT.42)
(п) (п)
где S , А - симметричные тензоры второго ранга, выражения для
о
которых представлены в табл.П2, a S - некоторый дополнительный
тензор.
Т Доказательство также проведем отдельно для каждой пары.
(I)
Пара: S - А
Рассмотрим первую энергетическую пару (П.23) и перейдем от тен-
тензора U~2 к V с помощью соотношений (П.11) U = От • V" • О:
d'A = -^FT ¦ Т ¦ F ¦ .<Ш~2 = -^FT ¦ Т ¦ F - • (dOT . V~2 . O+
+ OT • dV~2 • О + OT • V~2 • do). (Я.43)
Раскрывая скобки и используя полярное разложение (П.1) и правила
A.137) перемены порядка скалярного умножения тензоров, получим
Т • V • -О • dOT + V • Т • V • -dV~2+
d'A = - i
Учитывая, что О • От = Е и, следовательно,
dO ¦ ОТ = -О dOT,
(Я.44)
(Я.45)
Приложение. Энергетические и квазиэнергетические пары 563
получим окончательное выражение вида (П.42):
(I) /1 \ о
в:а = s . .<* (V) + s • 'd°T' (я-46)
(I) (I)
где первые квазиэнергетические тензоры S, А и вспомогательный
о
тензор S можно выразить следующим образом:
(I) о 1
S = V • Т • V, S = J(V • Т . V" - V . Т . V). О, (Я.47)
А = А = Ье - V) = 1(Е - F~1T • F). (Я.48)
Таким образом, доказано существование первой квазиэнергетической
(I) I
пары S ~ А.
(И)
Пара: S - (-V")
Если в (П.46) от дифференциала dV~2 перейти к dV, то получим
d!A = S • -dOT - Iv • Т • V • • (V" • dV-1 + dV" • V") =
= S • -dOT - I(V - T + T • V) • -dV-1. (Я.49)
Здесь вновь использовано правило A.137). В результате приходим ко
второй квазиэнергетической паре:
(И) о
d!A = S • -d(E - V") + S . -<ЮТ, (JT.50)
(И)
где обозначен второй квазиэнергетический тензор S :
(И) 1
S =-(V.T + T-V), (Я.51)
(И) (II)
а в качестве А , очевидно, выступает тензор А = Е — V .
564 Приложение. Энергетические и квазиэнергетические пары
Пара: Т ~ Y
Воспользуемся третьей энергетической парой (П.39) и перейдем от
дифференциала еШ к dV:
d'A = loT Т О • .(dU • U + U-1 • dU) = ^От • Т • О • •
(dOT ¦ V • О + От • dV • О + От • V • dO) • От • V • О + ^От ТО
• -От • V • О(<ЮТ -V-O + OT-dV-O + OT-V. dO). (Я.52)
Меняя порядок скалярного умножения тензоров в каждом из этих сла-
слагаемых, получим
d'A = i(T • -О • <ЮТ + V1 • Т • -dV + У1 • Т • V • <to ¦ От+
+ V . Т • V". OdOT + Т . V". -dV + Т . dO . От). (Я.53)
Используя соотношение (П.45), получаем, что первое и последнее сла-
слагаемые взаимно сокращаются, и выражение (П.53) можно привести к
виду:
d'A = Т • -dY + S • -dOTy (JT.54)
где введен новый тензор Y, подобный тензору Био В, определенный
своим дифференциалом:
dY = hdV • V" + V". dV), (JT.55)
который является третьим квазиэнергетическим тензором:
(Ш) (Ш)
A =Y, S =Т. (Я.56)
(IV)
Пара: S ^ V
Выражение (П.54) с учетом (П.55) можно легко преобразовать к
виду:
d'A = hv1. T + Т . У1) • .dV + S • -dOT,
(Я.57)
что доказывает существование четвертой квазиэнергетической пары:
(IV) о
d'A= S -.dV-f S-.dOT, (Я.58)
Приложение. Энергетические и квазиэнергетические пары 565
где определены четвертые квазиэнергетические тензоры:
(IV) i (IV)
S ^-(V-^T + T.V-1), A = E + V. (JT.59)
(V)
Пара: S ~ J
Преобразуем выражение (П.57) следующим образом:
d'A = -(У1 • Т • -V • V • dV + Т • V • -dV • V • V) + S • -dOT =
- V • Т • V • .-(V • dV + dV • V) + S • -dOT. (Я.60)
Отсюда следует существование пятой квазиэнергетической пары:
(V) о
d'A = S • -dJ + S - -dOT, (JT.61)
где пятый квазиэнергетический тензор определим следующим обра-
образом:
(V)
S rV^.T-V. (Я.62)
Парным к нему является тензор
(V) 1 1
А = J = -(V2 - Е) = -(Р . FT - Е). (Я.бЗ)
Доказательство теоремы П4 закончено. А
(п)
Заметим, что все квазиэнергетические тензоры А образованы (п —
III) степенью левого тензора V:
А = —1— (Vя-111-Е), п = 1, II, IV, V, (Я.64)
п —111
(Ш)
а выражение для тензора А = Y представляет собой аналог "нуле-
вой" степени от V.
В заключение приведем еще две теоремы, поясняющие смысл вве-
введения энергетических и квазиэнергетических пар тензоров.
Теорема П5. Пусть выполнены условия теоремы ПЗ, и кроме
того скаляр d'A является полным дифференциалом скалярной тен-
(п)
зорной функции ф от С, т.е.
d'A^d-ф, ф-ф(С) Vn G {/,... V}, (Я.65)
5gg Приложение. Энергетические и квазиэнергетические пары
(п)
тогда энергетические тензоры Т являются потенциальными
(п)
тензорными функциями от энергетических тензоров С.
Т Доказательство очевидно, так как из (П.13) и (П.65) dip =
(п) (п) (п) (п) (п)
= (дф/дС) • 'dC = Т • «dC, откуда в силу независимости dC по-
получаем:
(п) (п)
Т=дф/дС. А (Я.бб)
Теорема Пб. Пусть выполнены условия теоремы ПЗ, и кроме
того скаляр d'A является полным дифференциалом скалярной тен-
(п)
зорной функции ф от двух тензорных аргументов А и О, т.е.
О)) (Я.67)
(п) (п)
тогда квазиэнергетические тензоры S и А связаны псевдопотен-
псевдопотенциальными тензорными функциями.
Т Доказательство легко следует из (П.42) и (П.67), так как
(п) (п) (п) (п) о
dф = (дф/дА) • -dA + {дф/дО) • -От = d'A = S • • А + S • -dOT.
(п) (п)
В силу независимости дифференциалов d А и <Ю (тензор А - симмет-
симметричный и имеет шесть независимых компонент, а О - ортогональный
и содержит три независимые компоненты), получаем:
(п) (п)
S = дф/дА, (JT.68)
S = дф/дО. (Я.69)
Соотношения (П.68) и (П.67) представляют собой согласно опреде-
определению 5.18 псевдопотенциальную тензорную функцию, а уравнение
(П.69) накладывает определенное ограничение на вид функции ф
(П.67). А
Энергетические пары при п = I, III, IV и V в систематическом
виде были получены Хиллом [50], пара при п = II была установлена
К.Ф.Черных [43], а квазиэнергетические пары - автором данной книги
[14].
Список литературы
1. Акивис М.А., Гольдберг В.В. Тензорное исчисление. М.:
Наука, 1972, 352 с.
2. Анчиков A.M. Основы векторного и тензорного анализа. Ка-
Казань, 1988.
3. Багавантам С, Венкатарайуду Т. Теория групп и ее при-
применение к физическим проблемам. М.: ИЛ, 1959.
4. Беклемишев Д.В. Курс аналитической геометрии и линейной
алгебры. М.: Физматгиз, 1980, 336 с.
5. Борисенко А.И., Тарапов И.Б. Векторный анализ и начала
тензорного исчисления. М.: Высшая школа, 1966.
6. Вакуленко А.А. Полилинейная алгебра и тензорный анализ в
механике. Л.: Изд-во ЛГУ, 1972.
7. Вейль Г. Классические группы, их инварианты и представле-
представления. М.: ИЛ, 1948.
8. Векуа И.Н. Основы тензорного анализа и теории ковариантов.
М.: Наука, 1978, 296 с.
9. Вустер У. Применение тензоров и теории групп для описания
физических свойств кристаллов. М.: Мир, 1977, 384 с.
10. Горшков А.Г., Рабинский Л.Н., Тарлаковский Д.В. Осно-
Основы тензорного анализа и механика сплошной среды. М.: Наука,
2000.
11. Грин А., Адкинс Дж. Большие упругие деформации и нели-
нелинейная механика сплошной среды. М.: Мир, 1965, 455 с.
12. Гуревич Г.Б. Основы теории алгебраических инвариантов.
М.-Л.: ГТТИ, 1948.
13. Димитриенко Ю.И. Механика композиционных материалов
при высоких температурах. М.: Машиностроение, 1997, 368 с.
14. Димитриенко Ю.И., Даштиев И.З. Модели вязкоупруго-
го поведения эластомеров при конечных деформациях // Вестник
МГТУ им.Н.Э.Баумана, сер. Естественные науки, 2001, N 1.
15. Дубровин Б.А., Новиков СП., Фоменко А.Т. Современная
геометрия: методы и приложения. М.: Наука, 1986, 760 с.
16. Бфимов Н.В. Введение в теорию внешних форм. М.: Наука,
1977.
17. ЭКелобенко Д.П., Штерн А.И. Представления групп Ли. М.:
Наука, 1983.
18. Канатников А.Н., Крищенко А.П. Линейная алгебра/ Под
ред. В.С.Зарубина, А.П.Крищенко. М.: Изд-во МГТУ им.Н.Э.Ба-
умана, 1998, 336 с. (Сер. Математика в техническом университе-
университете, вып. IV).
19. Кильчевский Н.А. Основы тензорного исчисления с прило-
приложениями к механике. Киев: Наукова думка, 1972.
20. Коренев Г.В. Тензорное исчисление. М.: Изд-во МФТИ, 1996.
21. Кострикин А.И. Введение в алгебру. М.: Наука, 1977, 496 с.
22. Кочин Н.Е. Векторное исчисление и начало тензорного исчис-
исчисления. М.: Наука, 1965, 436 с.
23. Курош А.Г. Теория групп. М.: Наука, 1967, 648 с.
24. Лохин В.В., Седов Л.И. Нелинейные тензорные функции от
нескольких тензорных аргументов // ПММ, 1963, 27, N3, с.393.
568 Список литературы
25. Лурье А.И. Нелинейная теория упругости. М.: Наука, 1980,
512 с.
26. Любарский Г.Я. Теория групп и ее применение в физике. М.:
Физматгиз, 1958.
27. Мак-Конел А.Дж. Введение в тензорный анализ. М.: Физ-
Физматгиз, 1963, 412 с.
28. Малолеткин Г.Н., Фомин В.Л. Тензорные базисы в кристал-
кристаллофизике. П.: Изд-во ЛГУ, 1972.
29. Мантуров О.В. Элементы тензорного исчисления. М.: Про-
Просвещение, 1991, 256 с.
30. Мурнаган Ф. Теория представлений групп. М., 1950.
31. Най Дж. Физические свойства кристаллов. М.: ИЛ, I960, 386
с.
32. Петров А.З. Пространства Эйнштейна. М.: Физматгиз, 1961,
464 с.
33. Победря Б.Е. Лекции по тензорному анализу. М.: Изд-во
МГУ, 1986, 286 с.
34. Постников М.М. Лекции по геометрии. Семестр II: Линейная
алгебра. М.: Наука, 1986, 400 с.
35. Рашевский П.К. Риманова геометрия и тензорный анализ.
М.: Наука, 1967, 664 с.
36. Седов Л.И. Механика сплошной среды. Т.1, 2. М.: Наука, 1976,
536 с, 574 с.
37. Сиротин Ю.И. Целые рациональные базисы тензорных инва-
инвариантов кристаллографических групп // ДАН СССР, 1963, 51.
38. Сиротин Ю.И., Шаскольская Н.П. Основы кристаллофизи-
кристаллофизики. М.: Наука, 1979, 640 с.
39. Смирнов В.И. Курс высшей математики. Т.2. М.: Наука,
1974, 656 с.
40. Сокольников И.С. Тензорный анализ. М.: Наука, 1971, 376 с.
41. Спенсер Э. Теория инвариантов. М.: Мир, 1974, 156 с.
42. Схоутен Я.А. Тензорный анализ для физиков. М.: Наука, 1965,
456 с.
43. Хамермеш М. Теория групп и ее применение к физическим
проблемам. М.: Мир, 1966, 588 с.
44. Черных К.Ф., Литвиненкова З.Н. Теория больших упругих
деформаций. Изд-во ЛГУ, 1988.
45. Шипов Г.И. Теория физического вакуума. НТ-Центр, 1993,
362с.
46. Широков П.А., Широков А.П. Аффинная дифференциальная
геометрия. М.: Физматгиз, 1959, 320 с.
47. Шубников А.В. Симметрия и антисимметрия конечных фи-
фигур. М., 1951.
48. Шубников А.В., Флинт Е.Е., Бокий Г.Г. Основы кристал-
кристаллографии. М., 1940.
49. Яковенко М.Г., Феоктистов В.В., Граник И.С. / под ред.
Яковенко М.Г. Применение тензорного исчисления в задачах
механики сплошных сред. М.: Изд-во МГТУ, 1982.
50. Hill R. Constitutive inequalities for isotropic elastic solids under
finite strain // Proc. Roy. Soc, London, 1970, A314, 1519.
предметный указатель
Алгебра Грассмана 156
Алгебраическое дополнение 56
Альтернирование 137
Анизотропия 201
Аффинная связность 507
Базис 89
- взаимный 121
- декартов 17
- диадный 50, 130
- кристаллофизический 174, 193
- локальный
- взаимный 20
в окрестности поверхности 486
поверхности 451
основной в окрестности поверх-
поверхности 485
- минимальный целый рациональ-
рациональный 246
- неголономный 514
- ортонормированный 14, 71, 95
- полиадный 74
- тензорный 205
- тетрадный 74
- триадный 74
- функциональный 245
совместных инвариантов 381
Вектор 13
- аксиальный 65, 83
- базиса локальный 18
- бинормали единичный 442
- вихря 406
- главной нормали 442
-Дарбу 446
- закрепленный 16
- индифферентный 71-ого уровня 216
- касательный 496
единичный 441
- кривизны 442
нормальной 469
геодезической 469
- кручения 443
- нормали единичный 454
- нулевой 13
- ортогональный 14, 94
- полярный 82
- свободный 16
- скользящий 16
- скорости движения по кривой 440
- сопутствующий кососимметрич-
ному тензору 65
Вектор-функция 439
Геодезическая линия 480, 509
Градиент
- вектора 405
- - правый 408
- от градиента скаляра 419
- от дивергенции
вектора 422
тензора 423
- от ротора вектора 422
- скаляра 404
- тензора 503
Группа 171
- изомерная 204
- коммутативная 171, 179
- максимальная 173
- непрерывная 171
- преобразований 174
- ортогональных 175
- собственно-ортогональных 175
- симметрии
тензора 202
тензорной функции 268
- симметрическая 174
- унимодулярная
собственная 175
- полная 175
- точечная 171
Девиатор обобщенный 330
Детерминант 19
- матрицы 100
- тензора 55
Диада 51
- базисная 128
сопряженная 132
Дивергенция
- вектора 407
- правая 408
- от градиента
вектора 422
- скаляра 420
тензора 423
- от дивергенции тензора 424
- от ротора
- вектора 422
тензора 423
- тензора 412, 503
Дифференциал
- тензора 411
- частичный 390
Длина
- вектора 94
- дуги 441
элементарная 440
Знак перестановки 100
570-
Предметный указатель
Изотропия 172, 208, 248
- трансверсальная 159
Инвариант
- главный 253
- квадратичный 251
- спектральный 331
- кубический 251
- линейный 251
спектральный 331
- неприводимый 246
- полиномиальный 245
- приводимый 246
- скалярный 238
- совместный 380
- неприводимый 381
- функционально независимый 239,
380
Инверсия 162
Индексы
- немые 22
- свободные 22
Индикатриса Дюпена 477
Интеграл
- криволинейный
- от компонент тензора 537
- второго рода 539
векторный 539
скалярный 539
от тензора 539
тензорный 540
первого рода 537
- от компонент тензора вдоль
кривой 537
- поверхностный
- первого рода 544
- второго рода 545
векторный 546
скалярный 545
тензорный 546
- тройной 551
- объемный от тензора 550
Интенсивность 333
Квадрат тензора 55
Класс 171
- (Л)-ромбоэдрический 256, 276,
283, 291, 315
- (В)-ромбоэдрический 256, 276,
283, 316
- гексагональный 257, 276, 284,
292, 316
- изотропии 257, 276, 294, 316
- квазиизотропный 257, 276, 316, 334
- квазитрансверсально-изотропный
256, 276, 282, 290, 315, 339
- кубический 285, 294, 334
- моноклинный 255, 275, 288, 314
- ортотропии 255, 276, 288, 314, 342
- тетрагональный 256, 276, 289, 314
- трансверсально-изотропный 257,
276, 285, 292, 316, 336
- триклинный 255, 275, 287, 313, 343
- сопряженных элементов 179, 181
- эквивалентности 124
Ковектор 121
Компоненты
- вектора 89
- касательного 496
- ковариантные
вектора 25
- тензора 53
- контравариантные
вектора 25
тензора 39, 52
- независимые 138
- полилинейной формы 141
- тензора 39, 49
в диадном базисе 131
- в полиадном базисе 132
- физические 72, 262
- функционала 118
Контур замкнутый 542
Координатные
- столбцы 89, 120
- строки 89, 119
Координаты
- вектора 15
- геодезические 526
- кристаллографические 190
- точки 495
Коэффициенты
- аффинной связности 507
- вращения Риччи 520
- второй квадратичной формы 457
- первой квадратичной формы 455
- связности 401
второго рода 501
- первого рода 501
Кривая 439
- в многообразии 496
- замкнутая 542
- плоская 443
Кривизна
- геодезическая 470
- кривой 442
- нормальная 470
- нормального сечения 470
- поверхности
- гауссова 475
главная 473
- полная 475
- средняя 475
Кристалл
- с примитивной решеткой 190
Кручение кривой 444
Куб тензора 55
Предметный указатель
.571
Лапласиан 420
- вектора 422
- тензора 423
Линейная зависимость 88
Линейная комбинация векторов 88
- тривиальная 88
Линия
- асимптотическая 481
- винтовая 448
- геодезическая 480, 509
- действия вектора 13
- кривизны 478
Максимальный шаг разбиения
кривой 536
Массив перегородок 102
Матрица 18, 97
- блочная 101
- Грама 95
- квадратная 97
- квазидиагональная 104
- кососимметричная 98
- линейного преобразования 110
- метрическая 20
в окрестности поверхности 485
обратная 486
поверхности 450
- обратная 101
метрическая 20
- ортогональная 98,158
- положительно определенная 100
- порождающая 196
- порожденная 196
- равная 97
- симметризованная 71-ого уровня 227
- симметричная 98
- треугольная 105
верхняя 105
нижняя 105
- фундаментальная 95
- якобиева 19
обратная 19
на поверхности 545
Мгновенное положение 446
Метод
- компонентный 388
- ортогонализации Грама-Шмидта 95
Минор 100
Модель
- простейшая нелинейная 364, 356,357
Набла-оператор 404, 405
Набор векторный 126
- однотипный 126
Н вправление
- главное 472
- поверхности асимптотическое 481
Неравенство Коши-Буняковского
94
Несовместность тензора 423
Нормаль к поверхности 453
Оболочка 483
- линейная 92
Образ 109
Объект неголономности 514
Окрестность поверхности 484
Оператор 109
- линейный 109
Операция
- нелинейная дифференциальная 408
- свертки 54
- скалярного умножения 14, 94
- сложения векторов 13, 87
- умножения вектора на число 13,87
Определитель 19, 100
- Вандермонда 375
- метрической матрицы 20
Ортогональная система 94
- ортонормированная 94
Ось
- анизотропии 174
- бесконечного порядка 178
- зеркально-поворотная 179
- кристаллографическая 158
- 71-ого порядка
зеркально-поворотная ??9
- инверсионно-поворотная 179
- симметрии
главная 178
- 71-ого порядка 177
Отношение
- эквивалентности 124
Отображение 109
- биективное 109
- взаимнооднозначное 109
- инъективное109
- линейное 109
- сюръективное 109
Параллельный перенос тен-
тензора 505
Параметры Ламе 70
Пары тензоров
- квазиэнергетические 561
- энергетические 557
Пересечение линейных под-
подпространств 70
Периодическая структура 189
- криволинейная 190
Плоское состояние 357
Плоскость
- касательная к поверхности 451
- кристаллографическая 158
- наклонного сечения 470
- нормальная 443
- нормального сечения 469
572.
Предметный указатель
- симметрии 178
- соприкасающаяся 443
- спрямляющая 443
Поверхность 449
- вращения 467
- линейчатая 494
- минимальная 481
- постоянной кривизны 481
- уплощенная 490
Подгруппа 173
Подпространство
- инвариантное 112
- индифферентное 216
- линейное 92
- несобственное 92
- собственное 92
Подстановка
- обратная 76
- ортогональная 77
Поле векторное 24
Полиада базисная 74, 132
Поливектор 146
Полином 96, 246
- характеристический 253
Потенциал 308
Потенциальность по fc-ому аргу-
аргументу 396
Представитель класса 124
Представление
- задающего тензора
- второе 273
- первое 273
- третье 274
- индифферентной линейной тензор-
тензорной функции
- второе 273
- матричное 274
- первое 273
- компонентное функции 267
- матричное 277, 286
группы 198
- изомерное 198
неприводимое 199
- преобразований 157
приведенное 199
- приводимое 199
- эквивалентное 198
- непотенциальной функции в тензор-
тензорном базисе 360
- потенциальной тензорной функции
в тензорном базисе 310
- спектральное 330
- квазилинейной тензорной функ-
функции 349
полное 349
приращения потенциала 347
- укороченное 349
Преобразование
- аффинное 157
- зеркального отражения 160
- зеркально-поворотное 179
- инверсии 162
- линейное 157
- ортогональное 158
собственное 159
- тождественное 159
- трансверсальной изотропии 159
- трансляционное 189
- унимодулярное 158
- центральное 157
Принцип Неймана 201
Произведение
- вектора на число 87
- векторное 29
вектора на тензор справа и
слева 54
двойное 31
- внешнее
векторов 145
кососимметричных тензоров 154
- декартово 124
- подстановок 77
- прямое 195
- скалярное 15
- двойное двух тензоров 44,49
- касательных векторов 498
- fc-кратное 138
двух базисных полиад 74
- матриц 98
- матрицы на координатный стол-
столбец 99
- смешанное 31
- тензорное 136
- базисных полиад 75
- линейных пространств 49, 50, 127
матриц 195
- функционала на число 119
Производная
- абсолютная тензора 504
- ковариантная
- ковариантных компонент
вектора 404
тензора 411
- компонент тензора 411, 502
- контравариантных компонент
вектора 404
тензора 411
на поверхности 461
- относительно связности 508
- скаляра 404
тензора второго ранга 410
- контравариантная 411
- от ковариантных компонент
вектора 404
Предметный указатель
.573
от контравариантных компонент
вектора 404
- по направлению вектора 504
Прообраз 109
Пространство
- абсолютного параллелизма 511
- арифметическое 96
- аффинное 87
- аффинной связности 507
- без кручения 510
- бесконечномерное 91
- векторное 87
- евклидово 16, 94
трехмерное 17
- изоморфное 117
- касательное 497
тензорное 451, 499
- линейное 87
- действительное 87
евклидово 94
- комплексное 87
- 71-мерное 91
- локально-аффинное 514
- локально-евклидово 528
- псевдоевклидово 498
- псевдориманово 498
- риманово 497
абсолютного параллелизма 519
с аффинной связностью 516
- собственно риманово 498
- сопряженное 120
- уплощенное 528
Псевдовектор 83
Псевдопотенциальность 396
Псевдотензор 80
- 71-ого ранга 85
относительный веса W 85
Радиус
- кривизны 442
- поверхности главный 487
- кручения 444
Радиус-вектор 17
Разбиение тензора на шаровую
и девиаторную части 333
Разложение вектора по декартову
базису 15
Размерность пространства 91
Разность векторов 88
Решетка 190
- базоцентрированная 191
- Бравэ 191
- гранецентрированная 191
- моноклинная 191
- объемноцентрированная 191
- триклинная191
Ротор
- вектора 406
правый 408
- от градиента
вектора 422
- скаляра 421
- от дивергенции тензора 424
- от ротора
- вектора 422
- тензора 423
- тензора 412, 503
Свертка 54
Свойство ортогональности мат-
матричных представлений 222
Сечение нормальное главное 473
Сизигия 246, 386
Символ
- Кристоффеля 401
двумерный 460
первого рода 403
второго рода 403
- Кронекера
- ковариантный 19
контравариантный 19
обобщенный 147
смешанный 19
- Леви-Чивиты 30, 83
71-мерный 152
Сингония 171
- гексагональная 172, 248, 274
- кубическая 172, 208, 248, 274
- моноклинная 172, 207, 247, 274
- ромбическая 172, 208, 247, 274
- ромбоэдрическая 172, 208, 248, 274
- тетрагональная 172, 208, 247, 274
- триклинная 172, 207, 247, 274
Сложение двух векторов 13
Система
- скалярных инвариантов
- функционально зависимая 240
- функционально независимая 240
- совместных инвариантов
функционально зависимая 381
- функционально независимая 381
Собственные
- векторы 59, 113
- значения 59, 113
- координаты 64
Соотношения полиномиаль-
полиномиальные 246
Сопровождающий трехгранник
- поверхности 459
- пространственной кривой 443
574.
Предметный указатель
Способ задания
- кривой
естественный 445
неявный 440
параметрический 439
- поверхности
- неявный 449
явный 466
Степень 71-ая
- декартова 124
- тензора 55
Сумма
- векторов 13
- компонент двух касательных век-
векторов 496
- линейных подпространств 93
- прямая 93
- прямая ортогональных подпрост-
подпространств 329
- тензоров 37
- функционалов линейных 119
Текстуры 173
Тело 175
- конечное 175
- кусочно-однородное 175
- неоднородное 175
- однородное 175
- симметричное 176
относительно группы Gs 177
- центрально-симметричное 179
Тензор
- вихря 407
- второго ранга 36, 48, 131, 500
- деформации
левый
отрицательный 408
положительный 408
- линейный 407
- правый
отрицательный 409
положительный 409
- единичный (метрический) 43, 49,75
- задающий линейную функцию 269
- изомерный 165
- индифферентный 202
относительно группы 202
- интегральных сумм 536
- истинный 85
- ковариантный 132
- кососимметричный 65, 144
- по группе индексов 137
- кривизны
- поверхности 463
- пространства 523
- кручения 510
- линейных преобразований 164
- на линейных пространствах 128
- на поверхности 452
метрический 453
- направляющий 206, 245
- неособенный 57
- несовместности 534
- нулевой 53
- 71-ого ранга 73
- образующий 206
- обратный 46
- ортогональный 47, 66
- относительный 71-ого ранга 84
веса W 85
- параллельный тензору 505
- положительно определенный 62
- производной 297
скаляра по тензорному аргу-
аргументу 297
тензорной функции по тензор-
тензорному аргументу 376
- ранга к 132
- Римана-Кристоффеля 523
-Риччи 531
- симметрированный по группе
индексов 136
- симметричный 45, 62
- по группе индексов 136
- четвертого ранга 77
шестого ранга 78
- смешанный 133
- соосный 64
- типа (р, q) 133
- транспонированный 45, 54
- третьего ранга 131
- частной производной скалярной
функции 390
- Эйнштейна 532
Тензорная поверхность 64
Тензорная функция 267
Тензорный закон 41
Тензорный признак
- обратный 58
- прямой 57
Теорема
- Гамильтона-Кэли 255
- Гаусса основная 475
- Менье 470
- о полярном разложении 554
- о циркуляции потенциального
тензора 543
- Рисса 122
- Риччи 413, 504
- теории поверхностей основная 465
- Холецкого 105
Тождество
- Бианки 526
- Риччи 529
Предметный указатель
.575
Точка
- гиперболическая 476
- омбилическая 476
- параболическая 476
- уплощения 476
- эллиптическая 476
Триада базисная 131
Умножение
- скалярное
тензора на вектор 38, 49
двух тензоров 43, 49
- тензора на скаляр 39, 48
Уравнение
-Гаусса 464
- параллельного переноса 505
- Петерсона-Кодацци 464
Условия интегрируемости 462
Фактор-пространство 126
Форма
- билинейная 99
- внешняя 146
- базисная 150
- квадратичная 100
- поверхности
первая квадратичная 455
- вторая квадратичная 457
- полилинейная 141
Формула
- Гаусса-Вейнгартена 461
- Гаусса-Остроградского
векторная 552
скалярная 552
- тензорная 551
- Гельмгольца 407
- деривационная 461
- в окрестности поверхности 487
- замены переменных
- в объемном интеграле 551
в поверхностном интеграле 545
- Стокса 547
- векторная 548
- скалярная 547
тензорная 547
- Френе 445
- Эйлера 474
Функционал 109
-линейный 118
Функция
- нелинейная 354
- нетривиальная 239
- полиномиальная 372
- потенциальная
квазилинейная 318
- скалярная
индифферентная 380
индифферентная относительно
группы линейных преобразова-
преобразований 295
- нескольких тензорных аргу-
аргументов 380
тензорного аргумента 295
- тензорная 267
индифферентная 268, 395
относительно группы 268
- линейная 269
нескольких тензорных аргумен-
аргументов 395
- потенциальная 308
- потенциальная по fc-ому тензор-
тензорному аргументу 369
псевдопотенциальная 369
центрированная 269
- тривиальная 239
- целая рациональная 96
Характер
- матрицы 200
- матричного представления 200
Характеристическое уравнение 60
Циркуляция тензора 543
Число независимых компонент
тензора 139
Эквивалентные элементы 124
Элементарная длина дуги 440
Элементарное n-мерное много-
многообразие 495
Элементы
- матрицы 97
- симметрии 179
- эквивалентные 124, 127
Ячейка периодичности 190
Учебное издание
Димитрненко Юрий Иванович
ТЕНЗОРНОЕ ИСЧИСЛЕНИЕ
Редактор В. А. Козлов
Художник К. Э. Семенков
Художественный редактор Ю. Э. Иванова
ЛР № 010146 от 25.12.96. Изд. № ФМ-222. Сдано в набор 16.05.2001
Подп. в печать 20.07.2001. Формат 60x90 Vi6. Бум. газетная. Гарнитура Тайме
Печать офсетная. Объем 36,0 усл. печ. л., 36,0 усл. кр.-отт.
Тираж 6000 экз. Заказ № 1592
ГУП «Издательство «Высшая школа», 127994, Москва, ГСП-4,
Неглинная ул., д. 29/14
Факс: 200-03-01, 200-06-87
E-mail: V-Shkola@g23.relcom.ru http: // www.v-shkola.ru
Отпечатано с готовых диапозитивов
во ФГУП ИПК «Ульяновский Дом печати»
432980, г. Ульяновск, ул. Гончарова, 14