С.Н. Бернштейн. Собрание сочинений Т.2. Конструктивная теория функции - Колмогоров А.Н., Петровский И.Г., Ахизер А.И., Гончарова В.Л.

Автор: Колмогоров А.Н. Петровский И.Г. Ахизер А.И. Гончарова В.Л.
Теги: математика статистика собрание сочинений академия наук ссср конструктивная теория функции
Год: 1954
Похожие
С.Н. Бернштейн. Собрание сочинений Т.1. Конструктивная теория функции
Конструктивная теория функций
Целые функции.
Собрание сочинений Т.1 Метрическая теория функций и теория функций комплексного переменного
Текст
                    АКАДЕМИЯ НАуК СССР
С.Н.БЕРНШТЕЙН
СОБРАНИЕ
СОЧИНЕНИЙ
ТОМ
КОНСТРУКТИВНАЯ
ТЕОРИЯ ФУНКЦИЙ
[1931 - 1953]
ИЗДАТЕ ЛЬСТВО
АКАДЕМИИ НАуК СССР

ИЗДАНИЕ ПОДГОТОВЛЕНО АВТОРОМ
ПРИ РЕДАКЦИОННОМ УЧАСТИИ
Н. И. АХИЕЗЕРА, В. Л. ГОНЧАРОВА, А. Н. КОЛМОГОРОВА,,
и И. Г. ПЕТРОВСКОГО

ОТ АВТОРА
Настоящий, второй том собрания моих сочинений, содержащий шесть-
шестьдесят две статьи (№ 50—111) по конструктивной теории функций, является
более или менее полным завершением моих исследований в этой области,
первая половина которых вошла в первый том (статьи № 1—49).
Для облегчения понимания отдельных статей данного тома, а также
для освещения последовательного развития рассмотренных в них вопро-
вопросов, в конце второго тома, как и в первом томе, имеются авторские ком-
комментарии, и, в частности, два небольших отрывка из моей монографии
«Экстремальные свойства полиномов» A937 г.).
В соответствии с их назначением комментарии и новые подстрочные
примечания содержат также дополнительные литературные ссылки, ко-
которые, однако, не могут претендовать на полноту.
Считаю приятным долгом выразить здесь моим уважаемым товари-
товарищам и ученикам профессорам Н. И. Ахиезеру и В. Л. Гончарову и канд.
ф.-м. наук В. С. Виденскому искреннюю признательность за помощь,
оказанную мне при подготовке к печати второго тома.
С. Бернштейн

50
ПРИМЕР НЕПРЕРЫВНОЙ ФУНКЦИИ, ДЛЯ КОТОРОЙ
ФОРМУЛА ТРИГОНОМЕТРИЧЕСКОГО
ИНТЕРПОЛИРОВАНИЯ ЛАГРАНЖА РАСХОДИТСЯ»
Пусть / F) — непрерывная периодическая функция. Полагая
6
имеем интерполяционную формулу Лагранжа
Если
k
S ! /(в*).
/(в*) = (—!)* (±* = 0, 1, 2,..., л),
то
•* 71 \ / ~~~" 71 \ /
А=—п COS
С другой стороны, строя тригонометрический полином R2n F) порядка
2п9 для которого
Л2П F*) = (—1)*, i?2n FЛ) = 0 (±Л = 0, 1, 2,. .. , л),
найдем по интерполяционной формуле Джексона
B)
v ' 1 к=-п
и в силу известного свойства
* «Exemple d'une fonction continue pour laquelle la formule d'interpolation trigo-
nometrique de Lagrange diverge». Докл. АН СССР A931), стр. 365—366 A50*).

Поэтому на основании A) при б = 4-тс
С помощью этого замечания легко построить непрерывную функцию / (б)
так, что Рп{к\ /) неограниченно растет для некоторой бесконечной по-
последовательности значений п.
Действительно, положим 2rit + 1 = 5, так что nt — четное число при
любом натуральном t.
Рассмотрим затем функцию
где 0<<а<1 и Qt (б) = R2nt(Q)- Так как ряд C) сходится равномерно,
то функция /F) непрерывна. Построим для функции /(б) интерполя-
интерполяционный полином Лагранжа порядка nto = р— . Полагая
где
?«. (°) = 2] -д+^г' Pi. (е) = 2j ^г
t=i l t=t, l
будем иметь:
Ч F; р^ = ь.F) + ^- S
где в* - ^ (±Л = 0, 1,2,..., П(.
Но для любого t^-t0
и значит,
Следовательно, в силу A)
откуда
(log ПО1"

51
О МНОГОЧЛЕНАХ, ОРТОГОНАЛЬНЫХ НА КОНЕЧНОМ
ОТРЕЗКЕ *
СОДЕРЖАНИЕ
Часть I
Введение .,....- 7
Глава I. Алгебраические основы 16
Глава II. Распространение асимптотических выражений для ортогональных
многочленов 24
Часть II
Глава III. Многочлены Якоби 52
Глава IV. Ортогональные многочлены, приводящиеся к многочленам Якоби. . 79
Частъ I
ВВЕДЕНИЕ
1. Следуя по указанному П. Л. Чебышевым пути, теорию ортогональ-
ортогональных многочленов/соответствующих данному весу на определенном отрезке,
связывают обычно с теорией непрерывных дробей.
Однако этим путем не удается решить некоторые важные задачи,
например задачу об асимптотическом представлении ортогонального много-
многочлена на всем рассматриваемом отрезке.
Метод, который я тут развиваю, состоит из соединения элементарного
алгебраического приема с переходом к пределу, основанным на теореме
Вейерштрасса о приближении непрерывных функций посредством много-
многочленов.
Исходная точка этого метода, который я также применил в моих лек-
лекциях «L. S.» для изучения минимального уклонения в конечном или
бесконечном интервале многочлена, умноженного на данную положитель-
положительную функцию, находится в моей старой заметке [13] (том I).
* «Sur les polynomes orthogonaux relatifs a im segment fini». Premiere partie.
Journ. Math, pures et appl., 9 A930), стр. 127—177 A49*); Seconde partie, там же,
10 A931), стр. 219—286 A54*). Русский перевод: «О многочленах, ортогональных
в конечном интервале», Харьков, 1937 A89*).

Таким образом устанавливается, что при очень общих условиях орто-
ортогональные многочлены асимптотически равны многочленам, наименее укло-
уклоняющимся от нуля относительно надлежаще выбранного веса. Однако
есть важные случаи, когда это равенство уже невозможно. Мы прове-
проведем специальное исследование некоторых из этих более трудных случаев,
что побудит нас пополнить в некоторых отношениях классическую тео-
теорию многочленов Нкоби.
2. Асимптотическое равенство, о котором идет речь, является обобщени-
обобщением соответствующего свойства тригонометрических многочленов Чебышева.
В самом деле, известно, что тригонометрические многочлены Чебышева
cos nQ
где х =¦ cos 6, обладают двумя свойствами:
1. Эти многочлены наименее уклоняются от нуля на отрезке [—1, + 1]
среди всех многочленов вида
Pn(x) = xn + b1zn-i+ ...+bn = ^—+c1cosn — lb+---+cn) B)
причем минимальное уклонение равно
?п = ^-. C)
2. Из всех рассматриваемых многочленов эти многочлены имеют также
наименьшее квадратичное интегральное уклонение относительно веса
Я(х) = ,гл :>
которое оказывается равным
1 п
/B) _ f Т2 (<г\ dX — С COs2 n® d®
уг 2 ^
—1 О
Следовательно, многочлены Тп(х) ортогональны относительно веса
и мы имеем
J Ы
<? = -J- Ы. E)
3. Нетрудно также показать, что многочлены Чебышева Тп(х) мини-
минимизируют интеграл
/«= \П\Рп(х)\]^==, F)
какова бы ни была неубывающая выпуклая функция f(x).

Действительно, функция f(z) обладает, по предположению, тем свой-
свойством, что
причем последний знак равенства может быть отброшен, если допустить
сначала, что выпуклость имеет место в узком смысле. Отсюда следует
при этом дополнительном условии, что многочлен Рп(х), обращающий
в минимум интеграл /п, должен быть единственным, так как если два
многочлена Рп (х) и Qn (х) дают одно и то же значение этому интегралу,.
рп (*) + Qn И
то многочлен 2 приведет к меньшему значению.
С другой стороны, при всяком ср
7Т+ф
7" = Т S f[\Pn(cosb)\]db;
2п
следовательно, в частности, взяв ср = — и замечая, что
Рп cosF Н—- j = п_г cos пЬ + с'г cosп — 1 6 + . . . + с'п,
мы должны иметь тождественно (так как многочлен, дающий минимум,,
единственен)
Pn[cos (б + ^)] = Рп (cos 6). G)
Это равенство выражает, что Pn(cos6) имеет период —. Таким
образом, ^(cosG) сводится к единственному члену
Действительно *, из равенства G) следует, что Рп (cos 6) = ¦ п_ ¦ cos nb +
+ Сп. Но Сп = 0, так как, полагая ср = — , мы получаем также, что
Рп (cos (б +-?-)) = — ф^ cos пЪ+ С'п= — Рп (cos 6)= - ^ cos nb - 6V
Доказательство окончено для случая, когда / (z) выпукла в узком
смысле. Для тогЪ чтобы перейти к общему случаю, достаточно заметить,
что всякая функция, выпуклая в широком смысле, может быть рассмат-
рассматриваема как предельная для функций выпуклых в узком смысле. Следо-
Следовательно, в этом случае также никакой многочлен Рп (х) не может дать
интегралу 1п величину, меньшую
* Этот абзац, который отсутствовал в первоначальном тексте, воспроизводит
дополнительное примечание [П к A89*). (Автор.)
9

Примечание. Можно доказать при помощи такого же рассуждения,
"ЧТО
а0 cos nb + b0 sin пб
дает наименьшую величину интегралу
27Г
я
\f(\a0 cos гсб + b0 sin гсб + аг cos тг — 16 + ... + 6n_! sin 6 + an |) o?6,
0
какова бы ни была неубывающая выпуклая функция f(z).
В частности, полагая
получаем непосредственно, на основании сказанного, что минимум
интеграла
—1
равен
4. Основным вопросом, направляющим все наше настоящее исследо-
исследование, является задача об определении того, как и в какой мере дока-
доказанное выше общее свойство многочленов Чебыгиева Тп (х) распростра-
распространяется на ортогональные многочлены, соответствующие произвольному
•весу.
Мы изучим наиболее детально ортогональные многочлены Rn (#), соот-
соответствующие весу
где функция t (x), которую мы назовем тригонометрическим весом, непре-
непрерывна и удовлетворяет на отрезке [—1, +1] условию
0<Х <*(*)<?, A0)
(X и L—определенные постоянные). Мы увидим затем, что многие наши
заключения останутся справедливыми и при более общих условиях, тогда
как другие уже не будут иметь места. Таким образом, представляется
более удобным не утомлять с самого начала внимания этими обобще-
обобщениями, которые найдут свое место в дальнейшем систематическом изло-
изложении, и сохранить на время предположение о непрерывности t (x) и
условие A0).
Обозначим через Ln [t (x)] минимум уклонения произведения
t{x)Pn{x) (И)
10

на отрезке [—1, + 1] и через Н$ [?(#)] — минимум интеграла
+1
t(x)\Pn(x)\]l-=t=Ti A2)
щ) V А. ОС
где Рп (#)—произвольный многочлен B) степени п, коэффициент при
наивысшей степени которого равен единице. Будет показано, что равен-
ство (8) обобщается асимптотически и что
V2 Д
Т()Г()
И! V2 Д ? ' {Ln [t (*)]}', A3)
по крайней мере для /^>2, причем ортогональные многочлены Rn(x),
минимизирующие интеграл A2) при 1 = 2 (соответствующие тригоно-
тригонометрическому весу t2(x)), минимизируют асимптотически интеграл A2)
при 1^>2, а также уклонение произведения A1).
Этот результат является следствием такой теоремы:
Ортогональные и нормированные многочлены Rn(x) относительно три-
тригонометрического веса t(x), т. е. определяемые условиями
1
f Rn (x) Rm (x) * ^ = 0, если п^т A4)
—1
$2г*(*)^| = 1, A5)
—1
имеют асимптотическое выражение
Rn (X) ~ У ^~ COS (Лб + ф) , A6)
где 6 = arc cos x и
' 27Г J Z X Г 1
справедливое равномерно на всем отрезке [—1, +1]> вс/ггг функция t(x)
[удовлетворяющая A0)] удовлетворяет еще условию
|*(s + 8)-*(s)||ln8ji+«<& (8>о, Л>0). A8)
5. Доказательство этой теоремы займет центральное место в первой
части нашей работы; но, допуская справедливость формулы A6), мы
выведем из нее теперь же равенство A3). Для случая 1 = 2 это утвер-
утверждение очевидно, так как многочлен Rn(x), умноженный на Y4X) > Д°~
стигает в п + 1 точках с последовательно противоположными зна-
знаками максимума модуля, асимптотически равного 1/ — , так как ф об-
обращается в нуль на двух концах +1. Следовательно, Rn(x)Yt(x)
11

осуществляет асимптотически минимальное уклонение произведения
Pn(x)Yt(x), где Рп (х) — произвольный многочлен степени п, имеющий
тот же член наивысшей степени, что и Rn (x). Следовательно, равенство
A3) для I = 2, соответствующее равенству E) для многочленов Тп(х),
вытекает из того, что
ш {х) = я(п2) [ утщт (х), A9>
где Rn (x) — ортогональный многочлен, соответствующий тому же три-
тригонометрическому весу, не нормированный, но у которого коэффициент
при хп равен единице.
Для того чтобы получить равенство A3), когда ?^>2, заметим сна-
сначала, что (ф — непрерывно)
lim \) cos
B0)
= С1 cos е [1 с/е =
г(у.
Действительно, взяв произвольно малое положительное число 8, раз-
разделим отрезок [0, тг] на достаточно малые части точками: 0, bl9 b2, . . . r
bh-i, к так, чтобы колебание ty в каждой части было меньше ^--. Тогдау
если фл некоторое значение <Ь в А-й части, получим, что
С другой стороны, можно взять п достаточно большим для того,
чтобы разность между
cos
[ cos лгб |
Ч
была по абсолютной величине меньше, чем ~-г . Следовательно,
Ait
| cos
— J | cos /гб
о
8 .
Итак, равенство A3) будет доказано, если мы покажем, что для вся-
всякого многочлена Рп(%) достаточно высокой степени п, начинающегося
12

тем же членом, что и Rn(x), имеет место
-$ \Нп(х)\ЧУ*(х)Iт4=>-*> B1)
как бы ни было мало данное положительное число е.
Но каковы бы ни были у^О, z^>0, т = у>1, имеем
у — z ^ mz [у — z) .
Следовательно,
-И
-1
Поэтому достаточно доказать, что для п достаточно большого
$ (Pl(x) -Rl(x)}t(x)\ cos(nb + -V)|'-»ей> - s . B2)
О
Для этого, разлагая |cos(n6 + ty) |г~2 в тригонометрический ряд
| cos (лб + фI~21 = Ло + А2 cos 2 (лб + Ф) + • • • +
+ Аи cos А (пЬ + ф) + еЛ ,
где А0>»0, мы можем взять к (независимо от п) достаточно большим,
чтобы иметь |ел|<С"Т" Далее> применяя формулы A6) и A7), где t(x)
заменено на tp(x), будем иметь
1р «=
о
тс
Т 5
тс р
Здесь jRprlj p (х) обозначает ортогональный многочлен степени рп, соот-
соответствующий тригонометрическому весу №(х). Следовательно, при за-
зафиксированном р^ 2, /р стремится к нулю вместе с —. Это очевидно
при р = 2 вследствие уравнений ортогональности для Я2п, 2 и того фак-
факта, что Рп(х) — Rn{%) есть многочлен степени не выше 2п — 1; точно
так же, если Qh(%) есть многочлен степени h<^n, достаточно высокой,
13

чтобы Qh (x) отличался сколь угодно мало от [t (x)] 2 , мы получим дли
тс
\ [t (х)]РДрп, р (х) Qh (х) [Р2п (х) - Ж (х)} -?=- = 0 . B3)
о V 1—х
Отсюда следует, что Iv стремится к нулю, так что для достаточно боль-
большого п
и неравенство B2) доказано.
6. Примечание. Мы доказали выше асимптотическое равенство A3)
только при условии A8), но соображения, которые нам позволят
в дальнейшем избавиться от этого ограничения в случае 1 = 2, примени-
применимы при всяком I; таким образом, все обобщения равенства A3), соот-
соответствующие I = 2, будут справедливы для 1^>2.
Рассуждение, которое мы провели, непригодно для /<^2; между темг
без сомнения, равенство A3) верно* для всех значений 1^1. Для раз-
разрешения вопроса достаточно было бы изучить интересный частный слу-
случай I = 1.
Изучение этого последнего случая позволит обобщить (асимптотиче-
(асимптотически) еще другие свойства многочленов Тп(х); не останавливаясь на этом
вопросе, ограничимся несколькими общими замечаниями.
Определение многочленов Qn-i (^) степени п — 1, минимизирующих
интеграл
-1
где вес q(x)^>0 и функция / (х) заданы, приводит к системе п урав-
уравнений г
Н «2 1
\ xvq (x) dx— \xvq (x) dx + . . . ± \ x*>q (x) dx = 0 , B4)
-1 Ч ад.
где OLi —- точки, числом не менее п, в которых / (х) — Qn-i (#) изменяет
знак. Мы будем получать, в частности, к = п всякий раз, когда /(п> (х)
не изменяет знака на отрезке [—1, +1]. Тогда для всякой функции / (я)
рассматриваемого класса искомые многочлены Qn-i (я) будут интерпо-
интерполяционными многочленами Лагранжа, соответствующими вполне опреде-
* В дополнении к статье [42] (том I) это доказано для случая, когда формула
A6) верна для всех достаточно больших п. (Автор.)
1 Для случая q (х) = 1 решение системы B4) было дано впервые Коркиным и
Золотаревым в статье «Sur un certain minimum». Nouvelles Annales de Mathema-
tiques, XII A873).
14

ленной системе узлов х, которые являются корнями многочлена B) сте-
степени п, минимизирующего интеграл
— 1
В частности, основываясь на результатах, полученных в § 3, имеем
когда qhc) = Следовательно, в этом случае
11 — х2
ah =
n
Легко также показать, что при q (х) = 1
= cos
будет тогда многочленом, произведение которого на ]/Ч —х2 наименее
уклоняется от нуля на отрезке [—1, +1]. В этом последнем случае,
1 Единственность системы решений уравнений B'±) в этом случае доказывается
следующим образом. Допустим, что существует еще одна система р1? . . . , (Зп, удо-
удовлетворяющая B4). Отрезок [—1, +1] разделится тогда точками at, Cj на 2п -j- 1
отрезков (из которых не больше, чем л — 1, могут иметь длину, равную нулю).
Обозначим через yt (? = 1, 2, ...) точки at, p?., взятые в возрастающем порядке.
Тогда система уравнений B4) примет вид
Аналогично
Среди интегралов \ xv q (x) dx найдется s таких, которые входят в B4') и B4") с
одинаковыми знаками и 5Х — с противоположными. По крайней мере одно из чисел s
или sx не превышает п. Пусть, например, s^n. Интеграл от произвольного много-
многочлена i?n_1 (х) степени п — 1, взятый по этим s отрезкам [yf, Yf-j-il co знаками, на-
налагаемыми уравнениями B4'), должен был бы равняться нулю, что невозможно,
потому что можно расположить корни Лп_1 (а:) так, чтобы сделать положительной
часть интеграла, соответствующую каждому из этих s отрезков. [Эта сноска по срав-
сравнению с первоначальным текстом несколько расширена. (Автор.)]
15

когда все формулы являются не только асимптотическими, но и точными,
лмеем также, в согласии с A3),
" п \У •*• — •? / — *-'*-/п V г "~~~ / *
Доказательство этого можно найти в моей статье [28] (том I), в которой
я получил как следствие, что из всех многочленов рп{х) вида B) много-
многочлен Тп(х) имеет минимальную полную вариацию на отрезке [—1, +1].
Эта минимальная вариация равна, следовательно, п_ .
Замечу, наконец, что две системы узлов, которые мы отметили, как
соответствующие минимумам интегралов от модулей, приводят к форму-
формулам интерполирования, которые применяли различные авторы. Первая
формула играла существенную роль в моем исследовании о наилучшем
приближении \х\, где я ее применил к функции /(#), равной -|-1 или
— 1, в зависимости от того, будет ли х^>0 или х<^0. В общем виде
эта интерполяционная формула была предметом важного исследования
М. Рисса, который, в частности, получил при ее помощи изящное доказа-
доказательство теоремы о максимуме модуля производной конечной тригономет-
тригонометрической суммы1.
Вторая формула, принадлежащая Лагранжу, тесно связана с разло-
разложением в тригонометрический ряд Фурье, и ее сходимость существенно
такого же порядка, как и сходимость последнего.
Глава I
АЛГЕБРАИЧЕСКИЕ ОСНОВЫ
1. Пусть Рп(%) — ортогональные многочлены, соответствующие весу
Построим ортогональные многочлены Rn,h{x), соответствующие весу
Qh (#) = лг- =" th{%)у B6)
где
B7)
многочлен степени h, удовлетворяющий на отрезке [—1, +1] условию
0<X<*h(s)<L. A0')
Коэффициент при наивысшей степени в Рп (х) и Rnh (x) всегда берется
равным единице.
Легко проверить, что2
n,n\ / n\ / a±ata9...ah An (alf a2, ..., ah) v f
1 M. Riesz. Comptes rendus A914).
2 Частный случай этой формулы был указан G. Szego в его работе «Entwicke-
iimg einer analytischen Pijinktion nach den Polynomen eines Orthogonalsystems* (Math.
Ann., 82, 1921, стр. 188—212).
16

где
А„(а1( а2,.. .,ал) =
Pn(ah)
B9)
А„(а1;.. .,
(«l)
n+h
B9')
так как, в силу B8), ЛПг^(х) есть действительно многочлен степени тг,
у которого член с наивысшей степенью равен хп и вторая часть равен-
равенства B8) линейна и однородна относительно многочленов Рп(х), ...,Pn+h(x).
Следовательно, применяя обозначения, принятые во введении, имеем
™ [V Ш
-И
—1
—I
_ 1 V K+i ("!• °* Ч) р .. /о («) dr .
- An+1
C0)
Само собой понятно, что в случае, когда несколько корней равны
друг другу, а± = а2 = . . . = аи, соответствующие колонны наших опре-
определителей будут содержать вместо значений многочленов значения их
последовательных производных до порядка к — 1.
2. Мы займемся в этой главе только случаем /0(#) = 1. Имеем
Далее, так как все корни аи функции th(x) находятся вне отрезка
[—1, +1], то мы имеем асимптотическую формулу
C1)
где модуль выражения
равен полусумме осей эллипса, проходящего через аи и имеющего
фокусами — 1 и +1.
2 С. Н. Бернштейн
17

Следовательно,
Ап(аъ а2, . . ., i
и, по C0),
— P1P3 — Pi
я-ОЙ-¦•(?)*•"- ?«(?)•••(¦?
<32>
Легко проверить благодаря сделанному выше замечанию, что фор-
формула C2) остается в силе и в том случае, когда корни ак не являются
различными.
3. Из формулы B8) мы можем точно так же получить асимптотиче-
асимптотическую формулу для Rn}h(x). Мы имеем, каково бы ни было х,
Rn,h(z)h(x)
C3)
2) --\г)
В случае, когда х находится вне отрезка [—I, +1], Тп(х) можно за-
заменить его асимптотическим выражением
. Следовательно,
{х—Ч) • •• (^~ аь)
C4)
где последняя формула делает очевидным, что множитель при (х +
+ Yx2 — l)n остается конечным, так как его знаменатель никогда ,не обра-
обращается: в нуль.
4. В случае, когда —1<;#<;1, полагая # = cos6 и замечая, что
числитель второй части равенства C3) в силу тождества Тп(х) =
*
есть сумма двух определителей Вандермонда, мы получим асимптотиче-
асимптотическую -формулу
th (x)
« - рА)
C5)
18

Но так как величины р& или действительны, или попарно сопряжены г
то оба произведения сопряжены, и мы имеем
— X2] . . . [(х —
(_ 1)/, (e-ie _ pi) _ . (e-ie _ р/г) =
C6)
где а^ — аргумент р& — eiQ, когда р& действительно, и а^ + а^+i — аргумент
произведения (eie — p&)(eie — pfc+i), когда р& и рд+1 сопряжены, если по-
полагать во всех случаях (поскольку р| + 1 =
cos aft — =., sin спи = — . C7)
Когда x изменяется от —1 до +1, сумма
Ф = ax + о2 + . . . + ah C8)
принимает свое первоначальное значение, которое без ограничения
общности может быть принято равным нулю или тс, так как
не обращается в бесконечность на рассматриваемом отрезке *.
Из C5), C6) и C8) выводим, что
Rn,h (x) Yth (х) ^ yWh cos (nb + ф), C9)
где
^л~ 2аг 2а2'" 2ah '
Следовательно, минимальное уклонение произведения
где Рп(х) — многочлен вида B), асимптотически осуществляется орто-
ортогональным многочленом Rn,h(x), причем
D1)
1 В случае, когда рк и 9&-\-1 сопряжены,
Vl —х* Bх — ?к —
tg ( + )
может стать бесконечным, но между его полюсами нет корня, так как знаменатель
положителен для х =*= — 5±1 , как и для х — + 1.
19 2*

Принимая во внимание соотношение C2), которое пишется в виде
имеем также
при всяком многочлене th{x).
Замечание, сделанное выше, позволяет отбросить в предыдущих асимп-
асимптотических формулах ограничение, что корни th (x) простые. Так, в
частности, когда th(x) = рЦх) есть полный квадрат, формула D1) совпа-
совпадает (в других обозначениях) с той, которая дана в моей заметке х [13]
(том I), где я указал впервые асимптотическое выражение C9).
5. Мы распространим теперь формулы D1) и C2') и, следовательно,
формулу D2), которая из них вытекает, на случай, когда th равномерно
стремится к любой непрерывной функции 2.
Для этого заметим, что неравенство
1 с < t (х)
влечет за собой
каково бы ни было п. Следовательно, ввиду C2'), можно взять п доста-
достаточно большим, чтобы иметь
7Г
Mh A - 2е) <НУ [Vt (x)] <~~Mh A + 2s). D4)
Следовательно, если t^ (x) есть другой многочлен, близкий к t (x)
и также удовлетворяющий D3), то, так как соответствующая ему вели-
величина Mh должна также удовлетворять D4), мы будем иметь
hl +2
откуда следует, что существует вполне определенное число
М = lim Mh = lim ii-. .. Р- , D5)
не зависящее от способа выбора последощтелъности многочленов t^ {x)9
стремящихся равномерно к функции t(x). В силу D4) и D1) имеем
^ ^ D6)
1 См. также «L. S.», стр. 15—19.
2 См. § 6 первой главы «L. S.».
20

Итак, соотношение D2) существует, если функцию th(x) заменить
произвольной непрерывной функцией t (x)} удовлетворяющей A0), и его
можно переписать также в виде
Из формулы D5) получается немедленно функциональное соотношение
(см. [36] (том I))
М [t (x) s (x)] = M[t (x)] M [s (х)]. D7)
Что касается других следствий из формулы D5), то я отсылаю
к моей статье [41] (том I).
6. Соотношение D7) дает возможность предвидеть, что 1пМ является
линейным функционалом функции lnt(x), от которой он зависит.
Вид этого функционала легко найти.
Будем исходить из формулы D0). Имеем:
h п ¦ . iA-4-
ln Mh = У\ In p- = У*
Применяя метод вычетов Коши к этой сумме, симметричной относительно
корней th(x), получаем
Injf^^^j 1П^ '_ -)dz,
с h
где контур интегрирования С образован: 1) отрезком [si, ei + 1]; 2) полу-
полуокружностью очень маленького радиуса е, имеющей центр в точке 1;
3) отрезком [—si + 1,—ei — 1]; 4) полуокружностью радиуса е, имею-
имеющей центр в точке —1; 5) отрезком [ei — 1, si].
Интегрируя по частям, найдем
х 1 dz
"^ lnth(x)
__ 1 Г , , , Г 1 1 -] , _ 1 Г ш h \х) ?
2tci J L2 1A-2 \\ тс J у 4 х2
С -1
Так как интеграл взят между вещественными пределами, он будет
иметь смысл, когда th(x)—>t(x), и следовательно, имеем для всякой
положительной непрерывной функции t (x) формулу
?Ш,&. D8)
—1
По D6) имеем также
JL f Inf(x)
JL f Inf(x
D9)
21

и
E0)
Формула E0) была установлена Г. Сегё х, который даже доказал ее
справедливость и при общем предположении, что ограниченная функция
lnt(x) интегрируема в смысле Лебега.
7. Формулы D9), которая существенно вытекает из равномерной при-
применимости асимптотической формулы C9) на всем отрезке [—1, +1],
у Сегё не было. Кроме того, распространение формулы D9) на разрыв-
разрывные функции более ограничено, в частности, интегрируемости в смысле
Лебега безусловно недостаточно.
Действительно, рассмотрим функцию t (х) = 1 во всех точках, где
— arc cos х рационально, и t(x) =-г во всех других точках. Формула D9)
приведет к той же величине — для Ln[]/?(#)], как и в случае, если бы
было тождественно t (х) •-= -т-. Но многочлен рп(я), который наименее
уклоняется от нуля в п + 1 точках cos -— , где по предположению t (х) = 1,
обращается в многочлен Чебышева Тп(х). Следовательно, точная вели-
величина Ln[]/t (x)] равна -^—^ при всяком /г, что противоречит формуле D9).
Для того чтобы формула D9) [а значит, и формула D2)] была верна,
достаточно, чтобы функция lnt(x) была ограничена и интегрируема
в смысле Римана.
Действительно, это условие эквивалентно утверждению, что суще-
существуют две системы непрерывных функций zh(x) и oh(x) таких, что
и что
,. С1 1пгп(х) , ,. rXbiaft(a?) C^ \nt (x) dx /К4Ч
lim \ _ v ; dx = hm \ _ dx= \ - - v ; E1)
Но для достаточно большого п имеем, как бы ни было мало е,
i=i М К (х)) < Ln
Так как
in Ы {*)] > Ln [t fx)] > Ln [аЛ
ТО,
откуда вытекает, ввиду E1), что формула D9) справедлива для нашей
функции t (х).
1 Loc. cit.
22

8. В предыдущих формулах рассматривается постоянный отрезок
[—1, +1]; при этих условиях М [t (х)] есть постоянная. Но если произ-
произвести линейную замену переменных z = ^-к— и, то отрезок [—1, +1]
перейдет в [0, и] и минимальное уклонение Ln[t(z), и] произведения
t (z) (zn + а^™-1 + ... + ап)
на отрезке [0, и] будет асимптотически дано формулой
Ln [t (z), и] ~ 2 (jj1 M (и), E2)
где
'ЩйМ,. E3)
Следовательно, функция O(z) = lnt(z) связана с F(z) интегральным
уравнением Абеля
тг
К J * J Vx A — х)
Стало быть, имеем
E3')
по крайней мере в случае, если F (и) имеет производную,
9. Тот же прием, который нам послужил для представления 1пМ
в виде определенного интеграла, может быть применен для преобразо-
преобразования выражения C4) и суммы ф, которая входит в C9) и представ-
представляется формулой C8). Займемся сначала этой последней. Имеем по C7')
i Сiw ins + y-girr-^ + i^j d E4)
4n ^ 'ft (z) z + Kz2 — 1 — x — Vx2 — 1
где контур интегрирования С тот же, что и в § 6.
Отсюда, интегрируя по частям,
==— ±-[lnth(z
= -\lnth(z)y j—f — . E5)
23

Так как <J> = 0, когда th(z) постоянна, то E5) можно представить
в виде
^ ! Clnth(z)-lnth (x) ^ /Г^П
Стягивая контур в двойной отрезок [—1, +1], находим окончательно
—г az. [рк>)
—l
Выражение C4), имеющее место для точек х, внешних по отношению
к отрезку [—1, +1], преобрааованное тем же методом, дает
Г1
Rn,
E7)
По предыдущему, формулы C9), E6) и E7) обоснованы только
в случае, если th(x) — некоторый многочлен. Распространение этих фор-
формул является менее простым, чем формул C2) и D1). Следующая глава
посвящена этому исследованию.
Глава II
РАСПРОСТРАНЕНИЕ АСИМПТОТИЧЕСКИХ ВЫРАЖЕНИЙ
ДЛЯ ОРТОГОНАЛЬНЫХ МНОГОЧЛЕНОВ
1, Начнем с вычисления ошибки наших асимптотических формул в
алгебраическом случае. Для этого мы докажем следующее предложение.
Основная лемма. Пусть
1 +Ч,х
Pi +S2,1
elfh
pa, ..., ph) =
1
Pi
1
Если для всех значений к и i имеем | рд — pi | > 81 р^ |, где | р^ |
1 и
когда 2й
Ш*<1.
24

Действительно *, S — D состоит из суммы определителей вида
82Д
число которых для каждого значения
общих множителей имеем
равно С\. После сокращения
D
где
полагая
P2,
Г = (?2—Pi) (P3—P2) (Рз—Pi) • • • (PA—Pft-i) / (pi) • • ./(P*) ,
Что касается J?^, то
где М 1г... {h_A (pfc+i,..., рл) — минор определителя 7^, составленный из /г — к
последних столбцов со строками, номера которых il9 . . . , ^_^, а сумми-
суммирование распространяется на все такие миноры. Отношение
^t, — ife-jfe (P*+i Рл)
D (P*+i Рл)
есть однородная симметрическая функция от p^+i, . .. , р/i, все коэффициенты
которой положительны **. Следовательно, его абсолютное значение не-
неуменьшится, если мы заменим p^+i» . . . , рп соответственно их модулями»
* В изложение доказательства этой леммы внесено несколько пояснений, кото-
которых не было в первоначальном тексте. (Ред.)
** Приведем доказательство этого предложения. Обозначим
1 1 ... 1
х,
'2
... X.
п
. . . X,
n—i-
Очевидно, An(#J, . . . , a;nn~1) делится на D(xv . . . , хп). Покажем, что
отношение
•Л (т° ^п—Л
является однородной симметрической функцией xv . . . , хп с положительными
25

Поэтому
м2
D
1, ... , Rh)
С другой стороны, из легко проверяемой формулы
10 0 ...0 1 ...1
Х1 С\ О ... О Х/е+х . . . ХЬ
х\ С\хх С\ ... О
х\ С\х\ С%хх ... О
h—\
находим, полагая в ней хг = — 1, что определитель
1 0 0 ... 0 1
-1 CJ 0 ... 0 i?*+
= [A
причем алгебраические дополнения его миноров
имеющие вид
Л_Л (Яа+i,
являются целыми положительными числами (т. е.!>1).
коэффициентами. Предположим по индукции, что утверждение справедливо для
определителя п — 1 порядка.
... 1
• ••*•»
0
О
п—\ тКп—\
г!—1
хъх\ - • 2лхпхг
m=o m=o
— ш—1
8=0
8=0
2 4
1=0
26

Следовательно,
zi7...
1
-1
(-1)'
0
0
0
... 1
• • • Rk+1
T>h—1
.. . 1
h
ffc-l
Rh)
Таким образом,
k\
? _|_ \)]k ,
к D-1) I 9. / ^<-
поскольку 8<2.
Итак, сумма всех частных одного индекса к меньше, чем
и окончательно
s_
D
-1
Вычтем теперь из v-й (v = 2, . . . , n — 1) строки (v — 1)-ю строку, умноженную на
a?1v v", тогда определитель в правой части, представленный в виде
т=о
т=0
2л xnxi
и—1
(I)
разлагается на сумму определителей вида

-xNt
(И)
где т1 < т2 < . . . < mn__v так как наименьшая степень xi в v-й строке определи-
определителя (I) больше наибольшей степени #. в (v — 1)-й строке. И так как по предполо-
предположению для определителя (п — 1)-го порядка в правой части (II) утверждение
справедливо, то оно справедливо и для определителя порядка п. (Ред.)
27

Следствие. Если
2_
то
D
2. Подобно предыдущему, положим
Е1Д
E9)
F0)
и через Ai обозначим определитель, который получается из Si, когда
все е^ = 0. При условиях предыдущей леммы имеем тогда
F1)
D
так как, пользуясь вычислениями, сделанными для доказательства этой
леммы, получаем немедленно
h г/ р |_ л \
D
к (fc-1)
.../(РЛ)|8 2
к=1
откуда следует F1).
Давая 8 частное значение *, определяемое равенством E9), мы выводим
из F1) неравенства, которые получаются из F0) умножением на
Заметим, что в случае /0 (х) = 1 равенство B8) получает вид
rth(xJn+h~1Rn,h(x)
— ... 1 + ±
Р '
Jl+2n-l ' ' ' I
1 + 4fT • • • cos nG
* В изложение вывода неравенства F2) внесены небольшие редакционные изме-
изменения. (Ред.)
28

Следовательно, принимая во внимание F0) и F1) и предполагая, что
корни многочленов th {х) удовлетворяют условиям основной леммы, выводим
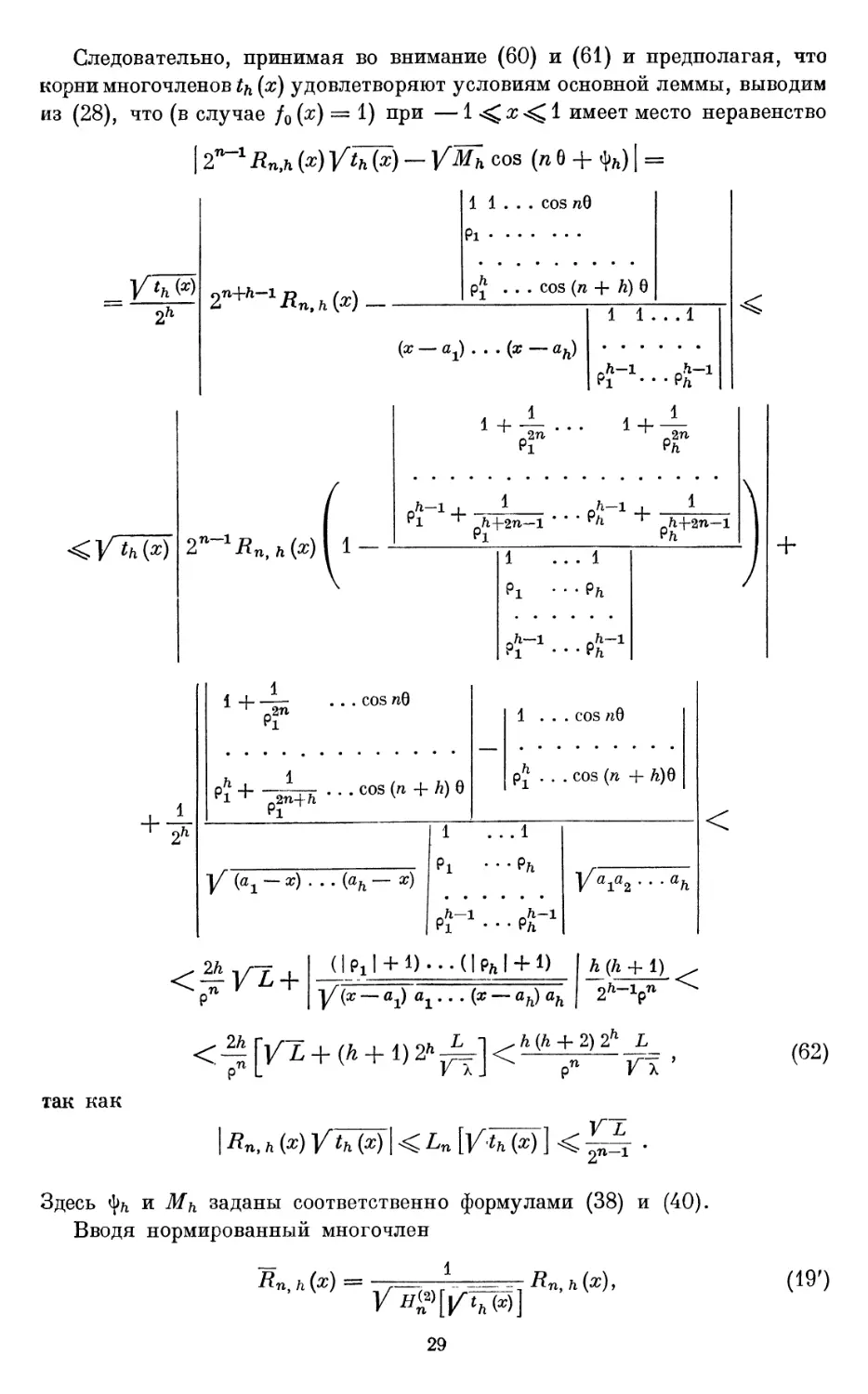
из B8), что (в случае /0 (х) = 1) при — 1 ^ х •< 1 имеет место неравенство
так как
Ч (*)
RnA (x) Vth (x) — VMh cos (n 6 + <J>ft) I =
1 1 ... COS /10
Pi
pj - - . cos (л + /г) 0
(я? — flj) ... (я? — ah)
1 1 . . .1
1-
Pl-1 +
1
plH
1
1
-2П-1
1
Px -..
P?-1 • ¦ •
1
1
h-1
+^
P/i П~1
!+__ ...cosnO
У (в1 - х) . .. (ah — х)
1
Pi
—
1 . .
. cos лб
pj - . . cos (« + Л)в
.1
•Рл
•рГ1
Vaia2'"uh
2ft-lpn
-th (x) ]
Здесь tyh и il//! заданы соответственно формулами C8) и D0).
Вводя нормированный многочлен
Rn,h(x) = -
F2)
A9')
29

мы получим сначала из C2') асимптотическое выражение
Rn, н (х) Vi^?) ~ j/^- cos (иб + фЛ), F3)
где tyh дано формулой E6). Приняв во внимание F2) и величину ошибки*
в C2'), находим затем
И
¦ л/ — — —
р
3)-2h
F4)
cos («6 + Cfh) < l/ А ±. ^J_?L?1 . F4')
F -xv. Pn
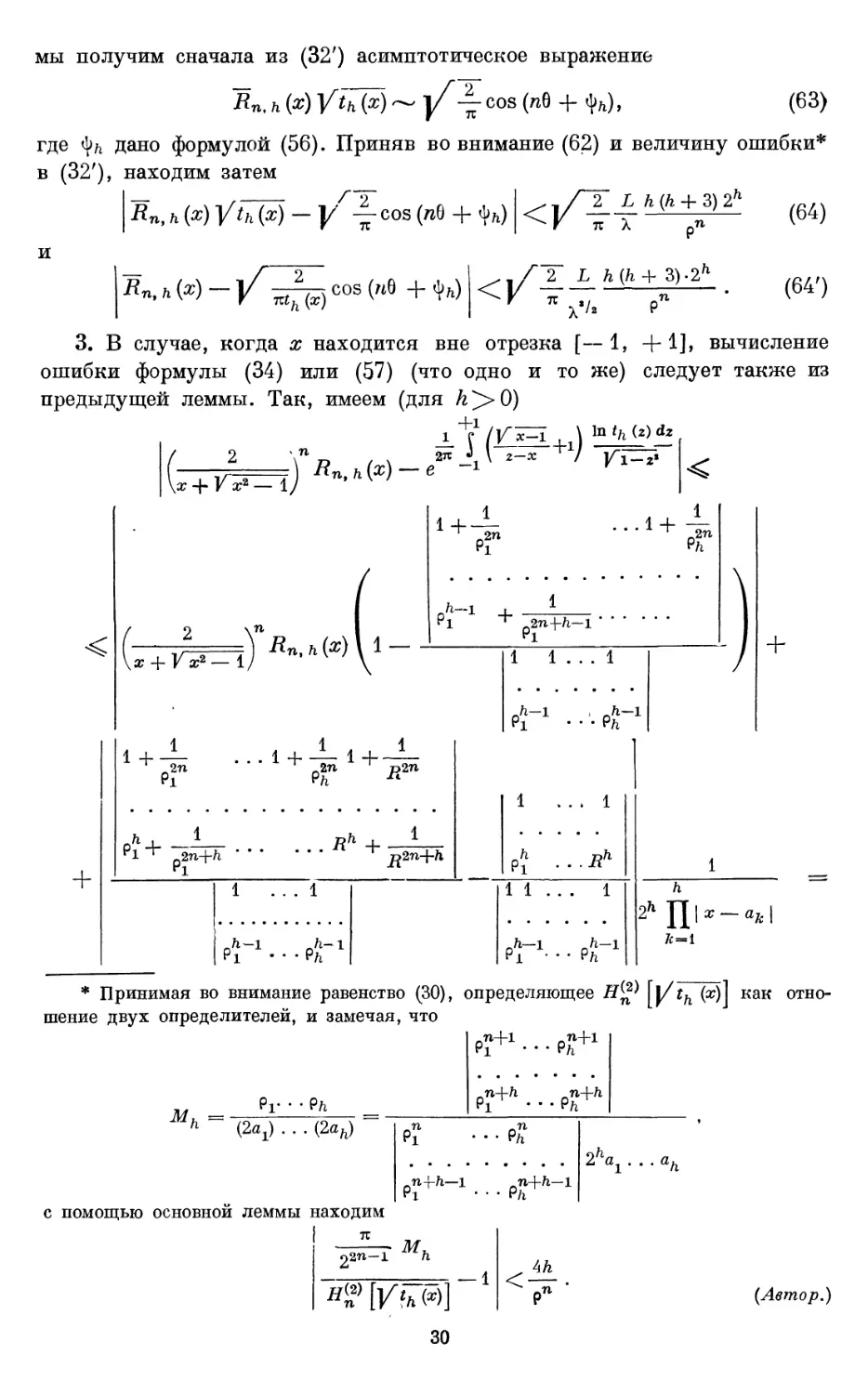
3. В случае, когда ж находится вне отрезка [—1, + 1], вычисление
ошибки формулы C4) или E7) (что одно и то же) следует также из
предыдущей леммы. Так, имеем (для
2 \
г -Ь F а?2 — 1/
i^ (V^=i , \ mini*)**
<
1
+
p2n+ft-l
1 1 . . . 1
1+-
Rh +
R2n+h
1 ... 1
Р?
..i?"
1 ... 1
11
* Принимая во внимание равенство C0), определяющее H
шение двух определителей, и замечая, что
Pr • •
(x)]
как отно-
отноа!) . . . Bah)
2\..
.ah
с помощью основной леммы находим
I я
22П~
(Автор.)
30

x 4- V~x* — 1
О
\rn)
2|Д|
F5)
где г — наименьшее из двух чисел р и | jR | = | х + Vх* — 11 > если также
Таким образом, если |i?|>p, то относительная ошибка асимптоти-
асимптотического выражения Rn, к{х) [или Rnt h (#)] во всех внешних точках (без исклю-
исключения) имеет равномерно порядок —, так как разность F5) регулярна
вне отрезка [—1, + 1].
4. В предыдущем исследовании мы должны были рассматривать мно-
многочлены th(x), имеющие различные и достаточно удаленные корни.
Неравенства F4), F4') и F5) доказаны только при условии, что
2
n
E9)
принимают все
где 8 является нижней границей 1 , причем
значения от 1 до А.
Для того чтобы иметь возможность воспользоваться этими неравен-
неравенствами, мы должны показать, что без значительного изменения значения
многочленов Sh(x), близких к данной непрерывной функции, их можно-
заменить другими, корни которых будут удовлетворять E9).
С этой целью мы докажем такое предложение.
Лемма. Пусть
*«-(«- f
— многочлен степени /г, где Ъ^ + V б| — 1 = /•&, удовлетворяет единствен-
ному условию |г#|^>р>1. Возможно построить такой многочлен
W \ aj" -\ aJ >
что
1р*1 = 1** + к*!-1|>р>1. 1р*-р,1>*1р*1.
который на [— 1, + 1] удовлетворяет условию
F6)
31

гое
Действительно, пусть
— данная положительная величина; опишем вокруг всех точек гх, г2,
. .. , r^-i., rh как центров круги радиусов соответственно
Сохраним последовательно только те из этих кругов, которые, будучи
взяты в указанном порядке, не имеют центров в кругах, сохраненных
ранее, и которые содержат, по крайней мере, одну точку с большим
индексом, не содержащуюся в предыдущих кругах. Точки г и, принадле-
принадлежащие более чем одному кругу, будут отнесены к кругу меньшего
индекса.
Пусть число точек, отнесенных к кругу с центром rki равно тк^2.
Перенесем тк — 1 из этих точек гх (I > к) на концентрическую окружность
радиуса -о-|г&| так, чтобы их взаимные расстояния стали ^ -~-| r# |, если
тк ^ 3, и не превышали —°^ к ' sin ^-—-—тг- для тк^>3, и чтобы при
атом соответствующие модули |рг| были не меньше\гк\.
Преобразованный многочлен th (x) получится, если мы заменим в sh (x)
корни bi, соответствующие точкам г?, значениями
соответствующими точкам
Так как
то
Следовательно, для х = cos 6 имеем
b
32

где
^ 880P
^-3@ 1
8Sq
3\bl\
. 16
rl
(hi' -
SoP*
1
J- 2
J
880pa
4 f
так как
la,— ж =
1-
лг9
1 (|Pl|-l)a
Поэтому
и наконец
1 —•
In
In
•(P-1K'
Следовательно, полагая 8 = ~-, мы видим, что корни а^ будут удовле-
удовлетворять требуемым условиям, и что действительно
In
«*(*)
-I)»'
(P —1);
F6)
Это неравенство, очевидно, тем более выгодно, чем больше р, но
в дальнейшем мы должны будем, напротив, предполагать р близким
к единице. Таким образом, для упрощения письма мы можем считать
р<|/2 и использовать вместо F6) формулу
In
¦(p-1K'
F7)
которая несомненно верна при предположении, что 4Тз стремится
к нулю.
Пусть, в частности,
где с — постоянная, и будем неограниченно увеличивать /г. Тогда
, In Л
Следовательно, при условии F8), имеем, по F7),
F8)
F8')
F9)
3 С. Н. Бернштейн
33

Если прибавим условие E9), которое напишется в виде
8- 2п_ . G0)
то получим
7М
__ J.
Наконец, предполагая
п>/г2, G1)
будем иметь
iG-jrK')i
Lj G2)
5, С другой стороны, мы должны найти порядок величины разности
между ортогональными многочленами Rn(x), соответствующими тригоно-
тригонометрическому весу t(x), и ортогональными многочленами Rn,h{x), со-
соответствующими многочленам th(x), к которым, по предыдущему, приме-
применимы формула F3) и неравенства F4) и F5).
Мы имеем следующую теорему:
Теорема. Если на [— 1, +1]
\t(x)-th(x)\<e, G3)
где tu (х) —многочлен степени h, удовлетворяющий A0) и условию рк
то имеем равномерно
\Rn(x)-Rn,h(x)\ = O(slnn) G4)
на [—1, +1]» когда elnn и
Pi
1
Действительно, положим
— 1
E9)
стремятся к нулю вместе с
где
"t15П (х) RK h (x) th (x) i1 e' (ж) Sn («) SA> h (or)
ax = \
ax = \
ввиду G3) и ортогональности 7?та (о;) по отношению к t (x), и
йп = 1/ „,»> ,. (х)] = 1 + «• W Я e °(S>- <76>
34

Имеем
n-l
—1
= 1/ "FT
G7)
'-1|>И8'(»)Дп(г)&
-1
Рассмотрим интеграл
Rn, н (*) Дп-1, л W - К, к (^) Дп-1, л И
(яг — z) Vl — z*
dz.
G8)
При условии E9) выражение Кп в числителе этого интеграла будет
бесконечно мало отличаться от
Сп =
[cos («9 + <Ы cos (п - 16„ + <К) —
— cos (п0о + 4»л) cos (л— 16 + фЛ)] =
где б0 и tyh — значения 0 и фь, соответствующие z.
Нужно вычислить порядок величины разности Кп — Сп. С этой целью
положим
1 1 ... 1 cos п 0
(n + 1H
. . . СО8(Л —1)в0
Pi ... cos /г 0О
(n + /i —1)
ahf
1 1 . . . cos п 0О
Pi
cos (n
1 ... 1
Pi • • • Pf
1 1 ... cos (п —1H
рх cos /г 0
cos (n + h — 1H
1 . . . 1
тгак что
35

С другой стороны, полагая
Тп(аг) ...cosnO
кп=
тп+г Ы • • • cos (п + 1) в
. ..соз(п-1)в0
• • • cos n9o
Tn(ah)
Тп-г{аг) -Тп-гЫ
**(*)*»(*)
Тп(ах)
n+i
(°i)
cos ив0
-cos (и+ 1N0
п+Н
{аг)
Tn-i(ai)
соз(п-1)в
. cos пб
соз(п + Л —
и приняв во внимание величину ошибки в C2'), будем иметь, по B8),
К'п = 22П [Rn, h (х) Rn_lf h (z) - Rn, ft (z) /J,_lt h (x)] =
= 2—з
Вычисляя определители числителя при помощи разложения по эле-
элементам последней колонны, имеем
=0 i=o
— cos (n + k -— 1) 0 cos (n -f i) 0O] =
Q ^2+1 (°o - °) sin 2n + f + ^-l (e +
j" /f -[- 1
• sin r @O + 0) sin -
-Fo-6)],
где Р| (которые равны соответствующим минорам, деленным на корень
квадратный из знаменателя) являются коэффициентами многочлена
PQy +...+рд = __ r.
Вычисляя таким же образом Кп и принимая во внимание F1), мы
видим, что
36

1=0
, . i — к
+ sin
sin i=*±i F0-6)sin *. + ' +
(в. + 6) +
2
Замечая, что при m целом
jsinmcp
получаем
sin
sin
¦и-
0
'h*2h\ Г I .
vr) I lsm
6-0П
^0 ¦+¦ e0
sm
а также
, , fh2h\h h . .0 0
i=o ft=o
Следовательно *,
j COS 0 — COS 0O
., 6-6o
sm
Так что,
cos 0 — cos 0O
|sm[Bn — 1) ?-±A + ф^ + фЛ + О (Л4 \
sinl @ + 0О)
in|"Bn —1) iz^L + ф^-фо] +о(^\,
sin—(в —60)
sm
По C7) и C8),
. — рЛ cos 0
й=1 Х + Рл — 2Рл cos 0
2 2 ZJ ak — cos0
Следовательно,
так как максимум
р
G9)
(80)
, равный р_ , достигается для х = +1,
* Формулы G9) изменены в соответствии с дополнительным примечанием
которое было сделано к A89*). (Автор.)
37

если аи, вещественная часть ак, больше единицы; если же ак, веществен-
вещественная часть ак, не больше единицы, то максимум, который достигается
при х = ак, обратится в
1
где cpft обозначает аргумент рк; он будет соответствовать также ак = 1 и
будет, таким образом, меньше ——т-. Следовательно,
и ввиду того, что по предположению
h ^ h
¦о,
п In р -^ п (р — 1)
когда л неограниченно растет, возможно найти такую постоянную J5, что
(81)
Следовательно, благодаря G9), применяя (81) в промежутке |6 — во!<С
< —и] 6+60—2т:|<<— и заменяя единицей числители правой части (80)
для оставшейся части отрезка [—1, + 1]> мы видим, вследствие G8), что
/n = 0(lnn). (82)
Так что, по G7),
G7)
где Мп — максимум \Rn{x)\ на [—1, + 1]. Следовательно, в силу G5),
G6) и G7'), можно найти такую постоянную С, что
\Rn(x)—Rnyh(x)\<C(elnn)Mn
на всем отрезке [—1, +1]- Таким образом, ввиду того, что Мп огра-
ограничено и sin л—>0, имеем окончательно
\Rn{x)-Rnth(x)\ = O(zlan). G4)
6. Сохраняя обозначения предыдущего параграфа, имеем для точек ху
лежащих вне отрезка [—1, + 1], более простое и более общее предло-
предложение, доказательство которого не требует предварительного знания
38

асимптотической формулы E7), и следовательно, мы можем даже допу-
допустить, что th (x), вместо того чтобы быть многочленом, есть некоторая
ограниченная и интегрируемая по Лебегу функция.
Лемма. Пусть t(x) и th(x) две интегрируемые функции, удовлетво-
удовлетворяющие A0) и неравенству
\t{x)-th{x)\<e G3)
на [— 1, +1]. При этих условиях имеем
\Rn{x)-Rn,h{x) \ = O(^+ Me) , (83)
где М — наибольшая из двух величин \Rnjh(x)\ и \Rn-lth(%) \ и 8 — ми-
минимальное расстояние х от отрезка [—1, + 1].
Действительно,
/ Ч 7"» / Ч ГЬ i
n, h \ ' 71-1, ч х / ^, (гЛ D /яЧ ^^ ^
—1
Следовательно, принимая во внимание G6) и G7), получим:
i
I •
(») -- Л», h (х) | = (9 (^ + Ms) . (83)
7. Для того чтобы использовать предыдущие результаты, мы должны
остановиться на некотором способе приближения данной положительной
функции t (х) многочленами th(%)- С этой целью изберем для lnt(x) ка-
какие-нибудь многочлены Gk{%) степени k, дающие на [—1, +1] прибли-
приближение наилучшего порядка. Пусть
\Gk(x)-lnt(x)\ = O(ak). (84)
Следовательно, мы имеем также
Положим затем
так что степень h многочлена Sh(x) равна к2 и мы имеем
Gk(x) о i ч I
?
где Р — определенное число (равное для достаточно большого h наиболь-
шему из чисел lnL и |1пХ|). Тогда, исключая случай, когда ^
который может представиться только, если lnZ(a;) будет целой функцией
ве выше 1-го рода и конечной степени, мы можем написать
[ Sh (x) -t(x)\ = O (а*) = О (<yF), (85)
39

Отметим только, что для применения дальнейших формул в исключен-
исключений
ном случае достаточно заменить всюду ак на -р-.
Но уравнение
*(z)-i + z + Y + --- + jr — V
к -4- 1
не может иметь корней, меньших по модулю, чем —-—, так как такой
корень удовлетворял бы неравенству
т. е.
2 ^ (* + 1)!
что невозможно.
Следовательно, если Ъ — корень Sh(x) = 0, то
С другой стороны, обозначив через Р максимум \О^(х)\ на [—1, + 1],
будем иметь
откуда
1 1
Таким образом, построенные нами многочлены ?/г(#) удовлетворяют
условию F8), в котором выбрано с = -ттг™ > и вытекающему из него усло-
условию F8').
Мы будем иметь, следовательно,
hVh,
(87>
и, предполагая попрежнему
*>*», G1)
получим
- ^щз, J • (88)
Заметим, что в случае, когда 1п?(#) не есть целая функция конеч-
конечной степени, имеем
'"JtT ' (89>
40

и тогда можно представить (89) в виде
\t(x)-th(x)\=O(airK)
(89')
В противном случае [принимая во внимание примечание, сделанное по
поводу (85)], будем иметь
11 (x) - th(x)\=O\(y=fh] > (89")
где А — постоянная.
8. Теперь легко показать справедливость асимптотической формулы
Rn{x)<
1 У (Vjc*-l_ \ In Uz)
E7)
в каждой определенной точке, лежащей вне отрезка [—1, + 1], какова
бы ни была данная непрерывная функция t(x), положительная на от-
отрезке [— 1, + 1].
Действительно, в силу F5), если положим
n = h\ G1')
увидим, что относительная ошибка формулы E7), порядок которой есть
— = — , стремится к нулю. Другими словами, имеем
(ch) Wh
.н (x) =
„
A+ %),
где
¦ -i
(90)
(91)
Умножая (90) на
l(ch) 2
- и принимая во внимание E0), полу-
получим соответствующую формулу для нормированных многочленов RUy h (x):
+1
— ^ dz (92)
где р'Л порядка %.
В силу (89х), мы получим из (92):
(X
n t (z)
:dz
(92')
41

тле
V7T
так что, при условии (88),
и в противном предположении
(eh)
(93)
С другой стороны, формулу (83) можно представить, в силу (92),
в виде
Вп(х)=Ип,н(х)[1 + О(в)],
где 8 теперь должно быть заменено через а = сс4 _ ш
Следовательно, в силу (92'), имеем окончательно
+1
V хг-~1 [ In t (z) dz
i?n (ж) = l7-4~ e ~1 Z t1 + Tn] ,
(94)
«где Чп — О/а*— \—>0 равномерно вне любой области, содержащей отре-
отрезок [—1, +1].
Имеем, очевидно, также
]п
г
(95)
Примечание. Мы можем положить
4-1
), (96)
где Рп(х) — многочлен степени п. Тогда (95) напишется в виде
где 7п = О /а4. \ — разложение по отрицательным степеням х, сходящее-
сходящееся для|#|>1. Так как /?П(^)A+Тп) н^ содержит положительных сте-
степеней х, "то можно написать
Вп(х) = Рп(х)A + ъ) + К, (97)
где 8П содержит только отрицательные степени х, что доказывает, что
многочлен Рп (х) является асимптотическим выражением Rn (x) на бес-
бесконечности, и их коэффициенты вообще асимптотически равны. Мы еще
вернемся к этому вопросу.
42

Заметим только, что без изменения формул можно заменить выше
многочленом Чебышева Тп(х). В частности, из (95) следует,
(
что когда t (х)— четная функция, Рп(%) будет [одновременно с Rn{x)]
четной или нечетной функцией в зависимости от четности п.
9. Займемся теперь сходимостью асимптотического выражения на
отрезке [—1, +1]. Применим формулу G4) и используем многочлены
th(%) (§ 7), предполагая п = /г2.
Условия, требуемые в § 5, будут выполнены по (89), если
anlnn->Q.
(98)
По известной теореме1 необходимое и достаточное условие для атого
заключается в том, чтобы функция t (х) удовлетворяла условию Дини—
Липшица. При этом последнем условии мы имеем
где А — постоянная.
В то же время, полагая
ф (Х) = ± Г In */>(*)-Ь «ftfc) / 1 - «*
^л ^ ' 2тт Д г _ х J/ 1 — za
мы имеем, в силу F4), и принимая во внимание F8),
|Дп. h (X) V th (X) — )/ 4" C0S И + Фл) | =
¦"*"¦]¦
E6')
где В — положительная постоянная.
Следовательно, при условии Дини—Липшица для тригонометриче-
тригонометрического веса t(x) имеем на [—1, +1] асимптотическую формулу
(99)
Vt (x) Rn (х) ~ / A cos (пЬ + ^у--),
гг ошибка этой формулы равномерно порядка
1 *
. / Л \
О
Выражение (99) содержит п довольно сложным образом благодаря
тому, что tyif— также зависит от п. Но в большинстве случаев фл(^)
равномерно стремится к непрерывной функции
1 Я. Lebesgue. «Sur les integrates singulieres». Ann. de Toulouse, I A909).
См. также [З] (том I).
43

A7)
когда th(x) равномерно стремится к t(x). Ясно, что тогда формула (99)
превращается в формулу A6). Следовательно, для доказательства основ-
основной теоремы § 4 введения достаточно показать, что при условии A8)
интеграл E6') равномерно стремится на отрезке [—1, +1] к выраже-
выражению A7).
Заметим сначала, что выражение A7) при условии A8) имеет смысл.
Действительно, пусть для определенности х^-0. Разбивая интеграл A7)
на две части tyi(x) + ty2(x)—первую от—1 до х и вторую — от х до 1,
мы видим, что первая часть имеет смысл, так как выражение под зна-
знаком интеграла по модулю меньше
М
2тс | (я — я?) [In (z— x)
где М — постоянная.
Точно так же
(я) | < 2^) \z—x
-l+x
. МУ~1— х
dz
I Т 'Г I I 1П ( T
\z — x i i m {z —
dz
l— z
l+x \z — x\ | in {z — x) \^~V 1 — z
2
Следовательно, замечая, что в последнем интеграле
/—-.
z —~
имеем
М
In
1-х
м
dz
ЪМ
In
1— X
Это показывает одновременно, что ф (х) стремится к нулю,
гтремится к единице. Непрерывность ф (х) на всем отрезке [
следует из дальнейшего рассуждения.
Определяя многочлены th{x), как и ранее, положим /^ =
Тогда ряд
когда х
1, +1]
In t (x) = In th (x) + 2j [In thl+l (x) - In thl (x)] ,
1=1
44

так же, как и ряд
t (х) = th (х) -
будет абсолютно и равномерно сходящимся. Кроме того, полагая
Qi (х) = In thl+l (x) — In thl (х),
мы имеем по известной теореме1, в силу условия A8),
In Л,
и но теореме А. А. Маркова2 о максимуме производной многочлена
имеем на всем отрезке [—1, + 1]
Следовательно, полагая
<1> (х) — фЛ (х) = 2 ^ (х) »
z=i
A00)
где
имеем
Полагая 8Х = -4—, мы, видим, что первый из этих интегралов8 будет
порядка ^iihl+l\rY1 =Ть тогда как два другие будут порядка In8^
так как, например (для
О <Г \ , _ = — In ox -f- In {1 — х (х + ох) +
Следовательно,
I ^,(») i = О (Т, In А,+1) = О [Tl (Z + 1)е In /г] = (
1 Jackson. «Uber die Genauigkeit der Annaherung stetiger Funktionen...» (Diss.
Gottingen, 1911), стр. 40.
2 [3] (том I), стр. 18.v
3 Функцию под знаком интеграла для | z | > 1 считаем равной нулю.
45

откуда по A00)
2
(х) - ф. (х) | = О\2е —^—1 = О Г—^—1 • A02)
Следовательно, формулы A6) гг A7) имеют место при условии A8)у
гг порядок ошибки равен О\ равномерно на отрезке [—1, +1].
Вообще из A01) следует, что порядок приближения формулы A6)
будет О Га 4 In п\ , если функция t (x) допускает приближение порядка ап
L Vn J
многочленами степени тг при
где
10. Предполагая, что условие A8) выполнено, составим тригоно-
тригонометрическое разложение
In*(cos6) = Л + ^icos6 +. . .+ 4ncos^6 +• . . , (ЮЗ)
которое вследствие A8) будет равномерно сходящимся. В этом случае
формула A7) может быть написана в виде
» / п\ 1 Г In г (cos ф) — In t (cos 0) . Л ,
ф (cos 6) = — \ —^ ^ ^ '- sin б dcp =
' V ' 7Г J COS ф — COS 0 т
- • .+ ^nsin^6+. . . , A04)
и это разложение, сопряженное с предыдущим, будет также равномерно
сходящимся. Для доказательства последнего утверждения достаточно
заметить, что
к
. 7С 1С COS/Сф— COS/С0 . Л , /лг\с\
sin kb = — \ ^— sin б d(D. A05)
7Г J COS ф COS 0 4 V '
о
Примечание. Тождество A05), которое легко проверить, является
следствием того факта, что разложение в непрерывную дробь интеграла
dz S
k_1 (х) g
Sk (x)
имеет подходящими дробями , где Тк (х) — многочлены Чебышева
степени к, и Sk-1(x) — многочлены, определяемые соотношением
г Тк (х) — Тк
1 С J к\х) —Tk\z)
- - \ uZ = Sb 1 (х).
* J (x-z)rT^zZ U ^
Но так как
? J
ATk+1 (x) + Tk^ (x) = AxTk (x),
то будет также
iSk+1 (x) + St-i (x) = kxSk (x).
40

Стало быть,
2
и ввиду того, что So (x) = 1, $! (#) = х, имеем
Отсюда
Следовательно,
т. е.
Обратно, если задаться функцией
ф (cos0) = у (^sine +. . .+ 4nsinne +• . .)>
то всякий раз, когда сопряженный ряд
In t(x) = f (cos 6) = Аг cos б +. . . + Ak cos Аб +. . .
сходится равномерно и f(x) удовлетворяет условию A8), выражения*,
l/— cos(^6+^) будут асимптотически представлять ортогональные
_ /Jx)
многочлены Rn(x), умноженные на yrt(x)=e2 , соответствующие
тригонометрическому весу 2 (#).
Из предыдущего вытекает также, что если через #fc = cos6fc обозначить
А-й корень Rn(x), то
где ел равномерно порядка а4 Inn для всех корней (к = 1, . . . , я).
Поэтому
—
где Cfc стремится равномерно к нулю вместе с — , и cos а& = Ъъ — корни
многочлена Чебышева Тп(х). Таким образом, корни хн многочлена Rn(x)
можно представить в виде
^), (*-!,...,») A06)
где р^. равномерно стремится к нулю вместе с —.
47

Следовательно, если задать сдвиг порядка —, характеризуемый не-
непрерывной функцией ф (х), корней ортогонального многочлена Rn (x) по
отношению к корням Тп{х), то тригонометрический вес t (x) будет
асимптотически определен (с точностью до постоянного множителя)
интегральным уравнением A04), решение которого может быть представ-
представлено в виде *
п cos 0
In t(x) = f (x) = 2xty± (х) — [ [ ^i M — ФаМ_ cos Qdudb, A07)
7U J J
о о
где <K(ff) = . 1 . Формула A07) имеет смысл, если tyi(x) удовлетво-
удовлетворяет A8). Не вдаваясь в исследование необходимых и достаточных усло-
условий для существования функции t(x) = е* (*\ соответствующей функ-
функции ф [х), удовлетворяющей условию A8), заметим, что во всяком случае
ф (х) должна быть непрерывна, и ф (-h 1) = 0. Достаточно, кроме того,
чтобы ^г(х) при этом удовлетворяла условию A8) с s)>l.
11. В частности, если
где th(x) — многочлен, то функции ф (х) и фл^), соответствующие этим
двум тригонометрическим весам, будут удовлетворять соотношению
*
Другое выражение для / (х) в виде
2те
(cos 0) = / (а?) = — \
ф (cos 0) sin 0 — ф (cos ф) sin ф
cos 0 — cos ф
о
выведено мною непосредственно в статье [52] [формула A1)].
Можно заметить, что поскольку 2ф (cos 0) выражается сопряженным тригоно-
тригонометрическим рядом к ряду In г (cos 0), зависимость между этими функциями выра-
выражается обратимой формулой
Ft @) = ~
о
взаимно связывающей сопряженные ряды
оо оо
F @) = 2 ак cos *0 + Ък sin *0' Fi @) = 2 аЛ Sin ^0 ~" ЪЪ C0S Л6*
Когда функция F @) четная, эта формула тождественна с A04), так как
8Шф[^(ф) — F (Q)] нечетная относительно ф функция, и соответствующая часть
интеграла тождественно равна нулю; когда функция F @) нечетная, общая формула
обращается в формулу
1 Г ^ (ф) sin Ф — /^@)sine ,
Fi @) = oZT \ ппа ^ п <*?>
COS ф — COS 0
о
тождественную приведенной выше, которая была также указана в § 2 главы III
первоначального текста: [Эта сноска с небольшими стилистическими изменениями
воспроизводит дополнительное примечание ^ к A89*). (Автор.)]
43

Следовательно,
h
1
где
cos a' = 9к~Х , sin а' = / х ~'"' . A09)
Следовательно, в данном случае
th (x) cos f nb + ytа') = A10)
1
Г (х + W — l)n(pi — х4-У^^Т) +. . .4-(ж~>г^ГГГ)^(р1^ж^_>/"^еЛ')...
где Ж"Л дано формулой D0).
Таким образом, в соответствии с результатами первой главы, имеем
Ln
но теперь асимптотическое выражение Нп{х) для Rn{x) само есть много-
многочлен степени п при всех 2/г^-Уг.
Отсюда следует, что многочлен Нп(х) среди всех многочленов B)
является многочленом, дающим минимальное уклонение произведения
Р (г) 1 = cos
и равенство
будет не только асимптотически справедливо*, но вполне точно для
2п > h.
Следует отметить связь этого результата, который в частном случае,
цогда th{x) есть полный квадрат, находится уже у Чебышева **, с исследо-
* В этом случае вполне точными, а не только асимптотическими для
являются все равенства A3) при любом Z>.1, как это показано в моей статье [42]
(том I) и в добавлении к ней. Эта сноска воспроизводит дополнительное примечание t5]
к A89*). (Автор.)
** Вывод того, что Нп (х) осуществляет наименьшее уклонение для общего слу-
случая, когда th (#)>0 — любой многочлен степени Д<2/г, имеется в «Лекциях о функ-
функциях, наименее уклоняющихся от нуля» А. А. Маркова («Избранные труды по тео-
теории непрерывных дробей. . .», стр. 244—291, М.— Л., 1948). Однако ни один из
упомянутых ученых не отметил тождественности многочленов Нп(х) с соответствую-
соответствующими ортогональными многочленами. (Автор.)
4 С. Н. Бернштейн 49

ваниями Фейера1 и его учеников о тригонометрических положитель-
положительных суммах.
Мы докажем, что случай, когда тригонометрический вес представ-
ляется в виде t(x) = — ; / '—-—, где th(x) — неотрицательный на
отрезке [— 1, +1] многочлен и а и $ равны нулю или единице, является
единственным, при котором асимптотическое выражение
есть многочлен 2.
Действительно, Fn(x) удовлетворяет разностному уравнению
Fn+1 (х) + Fn^ (х) = 2xFn (х). (ИЗ)
Следовательно, Fn(x) должно иметь вид
Fn(x) = А (х) (х + )/^=1)п + В (х) (х - yW=X)n,
и нужно, чтобы F\{x) и Fi^.1(x) были многочленами в равенстве
А (,) _ |
W + '"'^''" ] (¦
A14)
Таким образом, полагая Р (о:) = Ft (x), Q (х) = Fz+i (ж) — #^i (#), заклю-
заключаем, что произведение
должно быть неотрицательным на [—1, + 1] многочленом3 или таким
многочленом, деленным на 1 — х2 или на lHh^ B зависимости от того,
обращается Q (х) в нуль или нет для х = +1.
Имеем, следовательно, при всех п^>>1
)/•§(* -V^Tr] - cos (вв + Н A15)
так что
1 Fejer. «t)ber trigonometrische Polynome». Journal fur reine und angew.
Mathem., 146 A916). Szego. «Ober die Entwickelung einer willkurlichen Funktion
etc.», Math. Ztschr., 12.
2 Cm. [42] (том I).
8 Для этого необходимо и достаточно, чтобы Fj^ A) = JP'j A), FiJrl(—1) —
-_/¦,(-.!).
50

Ф = arctg 9W — Z6.
Случай, когда АВ будет многочленом, имеющим корни четной кратности
внутри отрезка [— 1, +1], сводится непосредственно к случаю, когда
АВ = th(x) не имеет корней, так как тогда Fi(x) и Fi^.1(x) имеют эти
корни общими, что справедливо и для всех Fn(x) при я>/, так что
формула A15) не изменится в силу сокращения общих множителей в
числителе и знаменателе первого члена.
Вообще, для того чтобы
Улв
из всех многочленов с тем же старшим коэффициентом давал минималь-
минимальное уклонение для всех степеней п^>1, необходимо и достаточно, чтобы
это выполнялось при I = п.
Действительно, если АВ не обращается ни в нуль, ни в бесконеч-
бесконечность в точках Hhl, то для того чтобы многочлен Fn(x) определенной
степени п давал минимальное уклонение, необходимо и достаточно,
чтобы максимум A15) достигался в п + 1 точках с противоположными
знаками, а это означает, что <]> должна возвращаться к своему перво-
первоначальному значению, равному нулю, когда х изменяется от — 1 до + 1.
Если АВ обращается в бесконечность в этих двух точках, то <]> должна
уменьшиться от + у до -^ , для того чтобы cos (/гб + ф) обратился в
нуль на обоих концах и имел п + 1 экстремумов с противоположными
знаками внутри. Если АВ обращается в бесконечность в одной из этих
точек (например, в — 1), то, оставаясь конечным в точке + 1, ф должна
изменяться от -^ до 0. Случай, когда АВ обращается в нуль в одной
из этих точек, сводится, очевидно, к случаю, когда в рассматриваемой
точке АВ обращается в бесконечность.
Таким образом, если Fi (x) — произвольный многочлен степени Z, все
корни которого находятся внутри отрезка [—1, + 1], можно бесчислен-
бесчисленным множеством способов сопоставить ему неотрицательную функцию
t(x), такую, что Fi (x) ]// (х) наименее уклоняется от нуля на этом
отрезке среди всех произведений Рг(х) ]//(#), где многочлен Pi(x) имеет
такой же старший член, как и Fi (x). Для этого достаточно выбрать
произвольный многочлен Рг^1(х) степени 1 + 1 такой, что корни F\ (x) и
Q (х) = Fi+! (х) — xFi(x) чередуются. Тогда будем иметь
(х) В (х) = 1 [Л (х) + ?М]. A16)
При этих условиях многочлены Fn(x) степени п^>1, определенные
формулой A15) или, что сводится к тому же, уравнением (ИЗ), будут
обладать желаемым свойством.
61) 4*

Часть II
Глава III
МНОГОЧЛЕНЫ ЯКОБИ
1. Перейдем теперь к исследованию случая, когда тригонометриче-
тригонометрический вес t{x) может обращаться на отрезке [—1, +1] в нуль или
бесконечность.
Мы ограничимся, однако, предположением, что функция t (х) может
быть представлена в виде
t(x) = to(x)\x-b1\'*...\x- Ък |Ч A17)
где bl9, . . , Ъъ — точки рассматриваемого отрезка (число к конечно),
§!,..., 8& вещественны, a to(x) удовлетворяет условию
X<*0(*)<L A0')
и интегрируема в смысле Римана.
Мы покажем сначала, что при этих условиях формулы главы I оста-
остаются справедливыми и что1
Ln [УЩ] ~^rVM, Н% [Уф)] ~ ^ М, D6')
где
+1
In t (x) dx
V
М = е -1 . D8')
Очевидно, достаточно исследовать случай, когда к = 1. Предположим
сначала, что 8Х — число целое и четное*, 8Х = 2р. Рассмотрим для опре-
определенности Ln[Yt(x)\. В силу формул D6') и D8'), которые, как мы
видели, применимы, если t(x) не обращается в нуль на отрезке [—1, + 1],
имеем
где а стремится к нулю вместе с е. Но с другой стороны, если t (х)
= to(x)(x — b)*v, то
1 См. стр. 20. Вторая из этих формул D6') находится у G. S z ego «Entwickelung
nach Polynomen eines Orthogonalsystems» (Math. Ann., 82, стр. 199).
* См. «L. S.», стр. 18. (Автор.)
S2

следовательно,
_i_ [ ln fo (*>
dx
что доказывает справедливость* D6'), когда Ьх = 2р — четное число.
Заметим, что если бы р было целым отрицательным числом, то
формулы D6') были бы непосредственным следствием того факта, что
многочлены степени п, ортогональные относительно тригонометрического
веса t (х), так же как и соответственные многочлены, наименее укло-
уклоняющиеся от нуля, тождественны соответственно ортогональным относи-
относительно t0 (х) многочленам степени п + /?, умноженным на (х — &)~~р, так
что мы имели бы в этом случае тождественно
Ln [УФ)] = Ln
+P
= Н(%
п%р
Доказав таким образом формулы D6') в случае четного положитель-
положительного или отрицательного 81? рассмотрим общий случай, когда Ьх есть
некоторое действительное число
Пусть для определенности 0<81<^2. Введем две функции tx(x) и
t2(x), интегрируемые в смысле Римана, такие, что
t± (х) = t2 (х) = t (х) для | х — b±\ ;>s
и
к (х) = (х — biJ to (х)> h (х) = fo (х) Для I х — W |< s
(е — положительное очень малое число).
Формулы D6') и D8'), по предыдущему, будут применимы к 1г(х)
и t2(x). Таким образом, в силу
имеем
In 11 (x) dx
1 f In 11 (x)
2K J V*=&
+i
1 Г ln t2 (де) dx
A18)
где an^>0 стремится к нулю вместе с —.
Следовательно, при s достаточно малом, для того чтобы иметь
С In t (x) dx С In t1 (x) d.
* Так как
: — In 2 при —:
. (Автор.)
—l
53

+1 +1
In t (x) dx С In t2 (x) dx
Г In t (x) dx
—l —1
можно будет выбрать достаточно большое п, чтобы выполнялось
_1_ p In t (x) dx i_ p In t (x) dx
"~"an e " < Ln \Vt (x)] < ^— е ~~х • A19)
Z Z
Это показывает справедливость нашего утверждения. Подобное рассуж-
рассуждение применимо к Н(п \\ft (x)].
Таким образом, имеем теперь также
и асимптотическое равенство A3) введения
У [t (х)] К /i : ' Lln [t (x)] A 3
распространяется при по^мощи аналогичных рассуждений.
2. Распространение асимптотических формул для самих ортогональ-
ортогональных многочленов является более трудным и, в частности, основная
формула
/СО8И + ф), A6)
где
—1
перестает быть верной на всем замкнутом отрезке [—1, +1]. Отсюда
вытекает, что ортогональный многочлен Rn (x) вообще не будет больше
минимизировать асимптотически уклонение произведения Рп{х) V& (х)>
где Рп{х)—произвольный многочлен степени п, имеющий „такой же
старший член, как и Rn(x), и, следовательно, необходимо дополнитель-
дополнительное исследование для разрешения основной проблемы определения мак-
максимума Rn{x)Yt(x) на отрезке [—1. +1].
В дальнейшем мы займемся единственно случаем, когда t (x) может
обращаться в нуль или бесконечность только на концах +1 отрезка.
Мы должны будем для полного исследования этого случая воспользо-
воспользоваться общими многочленами Якоби, ортогональными относительно три-
тригонометрического веса
t (х) = A - #Jр A + zJps A20)
так же, как в первой части мы пользовались многочленами Чебышева.
54

Мы должны, следовательно, начать с изучения многочленов Якоби?
для которых основная указанная нами проблема также еще не была
решена. Обозначив через q (х) обычный вес, получим
д(х)
t(x)
B50
и, следовательно, когда функция t(x) представлена формулой A20),
имеем
q /дЛ __ U дЛа //[ 1 ^\3 A21)
где
сс=2р— 4"» Р = 2Pi 5-- A22)
Можно, очевидно, ограничиться изучением того случая, когда
а>-1, Р> —1, т. е.
1 1
" — » Pi> 4"i
A23)
так как, если а = — 2s + &i, где s — целое положительное число и
—l^ocj^l, то ортогональные многочлены степени п, соответствующие
параметрам аир, будут равны произведениям на A — x)s ортогональ-
ортогональных многочленов степени п — s, соответствующих параметрам ах и рх.
Такое же соотношение будет существовать, очевидно, между соответ-
соответствующими многочленами минимального уклонения.
Согласно последнему параграфу главы II, асимптотическое выраже-
выражение A6) может быть многочленом1 только тогда, когда р = 0 или
11 к
— и рх = 0 или — (по примечанию, сделанному выше, случай р = ^-,
к
р!=-^- , где к и кг — целые положительные числа, приводится к этому).
Непосредственно проверяется, что нормированные многочлены Якоби,
^ /^
соответствующие тогда параметрам ос = н-у> C = + -о->по A22) сводятся
соответственно к
I. l/ACOsn6
/--г- cos(w + -^-
И. I/- ^—г
1
cosye
(—p—i
III. /1
IV.
т- sm|i. + T
A24)
sini-6
sine
g_ П
1 См. также мою заметку «Sur une classe de polynomes d'ecart minimum»,
Comptes rendus, 190 A930), стр. 237—240 A45*) и статью [42] (том I).
55

Однако даже в этих простых случаях [кроме первого, где t (х) = 1]
формула A6) со значением A7) для ф не является точной на всем
отрезке [— 1, + 1]. Действительно, пусть, например, t(x) = 1 + х, где
мы имеем
_ cos^ + — ^6
Rn {x) = j/^- ^ ^' . A25)
COS у 0
Следовательно, точная величина ф должна быть Ф = ~2~* и> конечно, эта
величина не может получиться из A7), обладающей свойством обращаться'
в нуль на концах. К тому же простое вычисление дает
In t {x) = In (I + cos 0) = — 1п2 + 2 [cos 6 -у cos 26+. . .1 ,
так что по A7) мы имели бы
I
ф = sin 0 —к- sin 20 + • • • у
что равно у только для х^> — 1. Но для х = — 1 имеем ф = 0, и схо-
сходимость, очевидно, не является равномерной вблизи этой точки.
То же обстоятельство представляется в общем случае многочленов
Якоби.
3. Классические многочлены Якоби Рп'®(х), ортогональные относи-
относительно веса A21), не нормированы. Таким образом, обозначая через
Rn'®(%) соответствующие нормированные многочлены, имеем
J1 (л+ 1I (л+ сс + р + 1) р(а, Э) ( ч га r,fi4
ь _j. а _j. 1) г (п + р + 1)
Точно также, если /?^' Р) (х) представляет ортогональный многочлен
степени п со старшим членом, равным хп, то
г»(ос 3) / \ / л \п Г (п + а + S + 1) /у| ч _а /^ , ч—В
Лп \Х) - V- ^ г Bл + а + plhlj- I1 ^ I1 + ^ Х
X —п [A — Л:)а4п A + xf+n]. A27)
Непосредственно проверяем, что
#<?> [A _ Ж)Р A + Ж)р.] = Y [/?(?•«(ж)]2 A — я:)" A + xf dx =
_ „гп+а+З-Ц Г (re + а + р + 1) Г (re + 1) Г(/г + а + 1) Г (я + Р 4- 1)
где
Р = у« + Т' Pi=4? + 4-- A22)
56

Следовательно, в согласии со второй из формул D6'),
(п + «)"+« (п + ft)n+3 (п + а + ft)++^ ^ ,, д>
Bл + а
Величина Ln[(l — ж)рA + #)р1] дается асимптотически, по предыдущему,
первой из формул D6'), и мы получаем
Ln [A - ху A + х)Ч ~ —L-- = Д^ . A30)
2 2
Покажем, что для
0<Р<у. 0<Pl<4- A31)
максимум | A — ж)р A + x)QlR%' P) (^) | асимптотически равен A30), и
напротив, в случае, когда условия A31) не выполняются, т. е. если
Л Л
имеем по крайней мере одно из неравенств | а | ^> —, |р|^>у, рас-
рассматриваемый максимум превышает A30).
Для этого положим
/»,,,р. (*) = A - *Т A+ *Г № 3) (*)¦ A32)
В случае, когда это не приведет к неясности, мы будем опускать
некоторые индексы и будем писать /п,р(#)> если р = рх, или просто fn{x)>
если параметры р и рх останутся постоянными на протяжении всего
рассуждения.
Полагая х = cos 6, получим, принимая во внимание известное диф-
дифференциальное уравнениег, которому удовлетворяют многочлены
Якоби, что
d2f (x) \
П'У + ± f р. * (*) = °» A33>
r
где
Хп(ж) = A - **) (п + р + PlJ + A + *) р A - 2р) + A - х) ?1 A - 2Pl) •
1 '
Так как Хп асимптотически равно ^ -9 во всякой данной об-
(п + р + piL
ласти, не содержащей точек ±1, то общий интеграл A33) асимптоти-
асимптотически равен A cos [(п + р + pi) 6 + <у] в0 всяком данном интервале,
внутреннем по отношению к отрезку [— 1, +1], где А и ср — две произ-
произвольные постоянные.
Таким образом, каково бы ни было 0<^е<^1, будем иметь на
[- 1 + е, 1 - 8]
/п, р. р, (ж) ~ A cos [(n + р + Pl) 6 + <?], A35)
1 A -x*)Rn{x) + [р - а - (а + Э + 2) *] Дп (*) + n (n + се + р + 1) Дп (ж) = 0.
57

где постоянные не представляют в настоящий момент особого инте-
интереса х.
Для определения А достаточно заметить, что
Y ?|LJ. = Hf [(I -*)pA + рН A-8),
где 8 стремится к нулю вместе с е. Следовательно, в силу A29) и A35)
получим
77 А 2 тс
откуда
P+p,-i ~ Ln [A - *>» A + я)*]. A36)
Таким образом, по A30), асимптотическая величина максимума
/n, p, Pi (#)| внутри отрезка [—1, +1] равна
л о мы должны еще исследовать величину этого максимума вблизи концов.
Полошим с этой целью
[^J A37)
Тогда, принимая во внимание A33), найдем
•откуда
dun(x)
__ ^ Г«*/п(*IЖ
- xY Pl A - 2Pl) - A + x)*9 A - 2p)
^ a?) Pl(l-2Pl)]
Следовательно, знак —г— тот же, что и:—т— . В частности, ип(а?) [так же,
•как и Х^ (ж)] будет постоянна^ если имеем одновременно р = 0 клй
1 1
р = —- ц р1 = 0 или рх = y • ^то — четыре ранее указанных случая,
когда нормированные многочлены Якоби сводятся к виду A24).
Вообще числитель A38') обращается в нуль для
(Pi — Р) A — 2р — 2Pl)
1 Формула A35) есть, впрочем, классическая асимптотическая формула
многочленов Якоби для внутренности промежутка (—1, + 1) и хорошо известно,
что 9 s=s — ?п* *
58

Следовательно, ип(х) достигнет экстремума внутри отрезка [—1, + 1]
s случае, если
pp1(l-2p)(l-2Pl)>0, A39)
т. е. если мы имеем одновременно оба неравенства A31), или если ни
одно из этих неравенств не выполняется] этот экстремум будет, следо-
следовательно, достигнут в точке
0
При предположении A31) экстремум функции ип(х) будет максиму-
максимумом: кривая тогда поднимается от — 1 до х0, а затем идет вниз, когда х
изменяется от х0 до 1. Но по A37) максимумы f^{x) равны соответст-
соответствующим значениям ип (х).
Следовательно, в случае
| <i- A31')
«абсолютный максимум Мп функции
| U (х) | = A - х)" A + хГ | i# S) (x)\ A32)
будет достигнут или для х = х0 или, по крайней мере, для одного из
последовательных корней /' (х) = 0, между которыми находится xQ.
В силу A36), асимптотическая величина этого абсолютного максимума
•есть
ДЬп [A - х)> A + *)Ч A41)
Первая часть предложения, высказанного нами в начале этого па-
параграфа, следовательно, доказана.
4. В случае, когда ни одно из Неравенств A31) не выполняется,
.экстремум ип(х) есть минимум, так что максимумы A32') идут, увели-
увеличиваясь от х0 к концам. Наконец, в случае, когда выполняется только
одно из неравенств A31), например, если 0^рх^^> Р^Т' то ФУНК~
ция Y = ип (х) изменяется все время монотонно. Точно так же и макси-
максимумы A32') в данном случае возрастают слева направо.
Мы должны показать, что теперь абсолютный максимум Мп A32'),
который равен, следовательно, по крайней мере, одному из максимумов,
наиболее близких к концам, будет и асимптотически превосходить
величину |Л|= п, i __г 9 представляющую асимптотическое выражение
для внутренних максимумов.
Положим для определенности р>у • Тогда знаменатель Х^ (х) обра-
обращается в нуль для х, близкого к +1, но нам незачем рассматривать
маленький интервал, в котором Х^ (х) будет отрицательна, так как в
.этом интервале вследствие A33) fn (x) не может иметь экстремум и тем
более не может в нем обращаться в нуль.
59

Следовательно, для достаточно большого п наиболее близкий к еди-
единице экстремум а удовлетворяет асимптотическому неравенству
sin6 = 1/Г=
п _j_ p + Pl '
где
8 = 2рBр —1)
(это неравенство, очевидно, точно для всех п, когда р^р^.
С другой стороны, на основании теории линейных дифференциальных
уравнений второго порядка, /n (x) = fn (cos 6) обязательно имеет экстре-
экстремум в интервале длины 7г?, где L — наибольшая величина Хп в этом
интервале. Стало быть, если мы положим для достаточно большого п
п + р + Pl '
то будет существовать такой экстремум а = cos 60 что
п + р + Pi ^ 6° ^п + р + Pl + п + р + Pl y-^-nf '
Минимизируя второй член A41а), получаем z2 = 5 + (тс8)*. Следова-
Следовательно,
6~ * + P + Pl <0о< /г + р + Р1 • A42>
Мы будем сравнивать максимум М^> А функции | /n | в данном ин-
интервале с внутренними максимумами А. С этой целью заметим, что при
O^cos cp^^^coscp^, соответствующих двум последовательным экстрему-
экстремумам Mjc, Mu+i функции fn(%), будем иметь, по A33) и A37), интегрируя
по частям,
фй ФЛ ФА
Следовательно, в силу A38), мы имеем
\ -js- -ж") db = fl (cos cp ) — /2 (cos cp-) =
J aO V ax) J n k±i n к
un^^db, A44)
причем положительное число /У заключено между наибольшим и наи-
наименьшим из значений дроби
d\\ (cos ф0)
at)
60

где
?ft < Ф1
Таким образом, последовательные максимумы Mjc^>Mjc+1 будут удов-
удовлетворять неравенству
Мы получим нижний предел Н, взяв для &0 и фх два крайних зна-
значения A42), что дает для достаточно большого п
[ти 3 + Зти3 S 3 + 3S 3 ]2
Следовательно, складывая неравенства A45) и взяв для 60 его наи-
наибольшее значение A42), окончательно получим
2[ти3+3tu3S3 +3S3]2
_! )}
JL ± ± 1.) У
с3 ^ 3 -1-Зте 3 S 3 / J
A46)
Примечание. Такие же рассуждения [если воспользоваться, в ча-
частности, неравенством A45) в его наиболее сильной форме и заметив,
что Хп~———зц— во внутренних точках] позволяют немного увеличить
нижний предел М, но мы не будем этим заниматься. Заметим только,
что из предыдущего не следует, что 60, определенное из неравенства
A42), является наименьшим значением 6, соответствующим экстремуму.
Во всяком случае будет не более одного экстремума при 6<^6О, так как
легко видеть, что /n(cos6) и, следовательно, соответствующий многочлен
Якоби не может иметь корня 6 <& (кроме нуля). Достаточно проверить,
что
!Ц-) < 8±, A47)
2(ти$K/
каково бы ни было 8^>0, так как интервал длины -у/, где /<^^п, не
может содержать одновременно корень и экстремум.
Следовательно, если через cos^o обозначим корень многочлена Якоби
с параметрами а — 2р — у , C = 2рх — у , где р у> у , наиболее близкий
к + 1, то 7о Для Достаточно большого п удовлетворяет A42), т. е.
Если cos cp0 = х есть наиболее близкое к единице значение х, при
котором fn{x) достигает экстремума, то <Ро<СТо и> значит,
61

так как в интервале (b, b-\-L~\ должен быть корень или экстремум
5. В случае, когда ни одно из неравенств A31) не имеет места,
экстремум Мп функции fn(x) в точке A40) дает, по обобщенной теореме
Балле Пуссена1, нижний предел выражения
каково бы ни было /г; но, по предыдущему, функция fn(x) не миними-
минимизирует уклонение соответствующего произведения даже при п—»оо„
Напротив, если неравенства A31) удовлетворяются, максимумы fn (х)
вблизи концов меньше Мп, так что в силу фундаментальной теоремы
Чебышева для конечного п имеем.
Таким образом, нижний предел Ln, который нам дает теорема Балле
Пуссена, не превзойдет величины относительного максимума \fn(x)\
вблизи концов, и с первого взгляда кажется неожиданным, что fn{x)>
не имея п -)- 1 асимптотически равных при /г—>оо экстремумов2, тем не
менее, осуществляет асимптотически наименьшее уклонение соответствую-
соответствующего произведения.
Поэтому мне кажется полезным непосредственно доказать, что fn{x)
реализует асимптотически минимальное уклонение, так как такое же
рассуждение может быть применимо в аналогичных случаях3.
Для упрощения письма мы ограничимся случаем, когда либо р1==рг
либо pi + р = у • Тогда
Х" ^ = A — ^2) (/г 4- р 4- PlJ 4- 2р A — 2р)
— четная функция.
Из A37) и A38') мы заключим, полагая х^>0, что
Следовательно, принимая во внимание, что теперь х0 = 0, имеем
1 См. «L. S.»y стр. 5; «Э. П.», стр. 20.
2 Тот факт, что указанное неравенство существует также асимптотически, может
быть установлен теми же рассуждениями, которые нас привели в § 4 к тому же за-
заключению в случае, когда A31) не имеет места.
3 В частности, если задаться коэффициентом при хк, где lim — = 1 или
Um — = 0, полагая кип одной четности и р = рх.
п
62

откуда
Ш '7P*-2ij-- A49>
(n + P + PlJ
Поэтому, обозначая через Х{ абсциссы тех точек, где f^(x) достигает
максимума, имеем
Ип@)>Вп(я)>М0)
откуда
1 + _ ^.*-2р)
A50>
так как для п четного ип @) = М^ = абсолютному максимуму \fv{x)\*, a
для /г нечетного цп @) = , + ^ ^ +У2р (i — 2р) и ^п<ггп@). К тому
же в этом случае также —т~- быстро стремится к единице, когда п—>оо.
Нам, следовательно, достаточно показать, что при всяком постоянном
а A^>а^>0) можно будет утверждать, взяв п достаточно большим, что
ни один многочлен Рп{%) степени п, имеющий старшим членом старший
член соответствующего многочлена Якоби Вп' ®\ вставленный вместо»
этого последнего в fn(x), не сделает это произведение по абсолютной
величине меньшим |1 — а\Мп на отрезке [—1, +1].
Действительно, если бы подобный многочлен существовал, то должен
был бы существовать такой многочлен Q (х) степени меньше п (полу-
(полученный при помощи вычитания), при котором
ф (х) = A - х)* A + x)*Q (x) A51)
обладала бы свойством
^==-ЛГпA-а)>^? A52)
V
для всех Xi, для которых 1—х\^>е2, где е — постоянное произвольна
малое число, а п удовлетворяет неравенству е (п + р + pi) ^ у ~~ t
причем на всем отрезке
|К)|ЛГ A53)
Но положив
F (х) = A - х*) —^ + [(Рг - р) - (р + Pi) х] Д%- 0) (ж), A54>
получим, пользуясь интерполяционной формулой Лагранжа,
С/ (ЖI == Г \Х) >, . { 100F
/ I / 4/4 \Р /4 I \Pi с" / \
63

Напишем, что коэффициент при хп в Q(x) есть нуль, таким образом,
% р*™ V (-1){^ fc;;
X ", rfi?<,,ej ' = 0, A56)
S [(p+Pi-1)*4+p-Pi] " , - [я2 +Bb + 1)(P + Pl)] Rfr ® (*j) }
принимая во внимание дифференциальное уравнение, которому удовле-
удовлетворяют многочлены Якоби Rn'^fa).
Следовательно, так как F(Xi) = 0, формула A56) преобразуется в
X
[(Р + Pi — l)*i + Р— Pi] [(р + Pi)»i + Р — PiJ г 9 /о
__ [П2 + Bл + 1) (р + Pl)]
гGг
р + PiJ
Но равенство A57), очевидно, невозможно, так как часть этой суммы,
соответствующая точкам Xi, удовлетворяющим A52), число которых
асимптотически равно пA — 2г), составлена из положительных членов и
больше, чем
п A — 2е)_а
тогда как каждый из остальных членов, число которых асимптотически
равно 2тге, не превышает по абсолютной величине, в силу A50) и A53),
I/
"г
2
Равенство A57) привело бы к неравенству
A~2:)fl <4в, A58)
¦
(И + р
64

невозможному для достаточно больших п, если выбрать
Примечание. При помощи совершенно аналогичного рассуждения
можно показать, что произведение
где Qn (х) — многочлен степени/?, достигает асимптотически минималь-
минимального уклонения
на отрезке [—1, + 1]> если в точке %^> 1
1H (?+1)'. = 1.
1 1
В случае, когда 0 ^р <С-тг » 0 <^ рх <^ -гг, smo минимальное уклонение
асимптотически реализуется соответствующими многочленами Якоби
(умноженными на постоянную).
6. Остановимся на случае многочленов Лежандра (р = рх = —J. Теперь
абсолютный максимум | fn (х) | будет достигнут для х = 0, если w = 2т
четно, и когда п — 2т + 1 нечетно, для х, равного наименьшему корню
Ш = о-
Следовательно, обозначая через Рп(%) классические многочлены Ле-
Лежандра [т. е. предполагая, что Рп A) = 1], имеем для всякого п = 2т
A - *¦)-!-( />2т (Ж) | < 123;;;2?;~1 (ieo)
на всем отрезке [—1, -f~ 1], и равенство действительно имеет место
в начале координат.
Для п = 2т + 1 максимум ип (х) будет равен
1 8m2 + 8m + 2
так как
p' few _ _l_ 1 • 3 ¦ ¦ . 2m + 1
¦^2m+i (UJ - ± 2 . 4 ... 2m '
для нечетного п, величина второй части A61) будет достигаться только
асимптотически. Таким образом, каково бы ни было п, имеем (на от-
отрезке [—1, +1]) по формуле Валлиса
ус> A62)
5 С. Н. Бернштейн 65

где т = у (величина второго члена не может быть асимптотически
понижена).
Стильтьес первый заметил, что можно указать такую постоянную А,
что
Фейер, который недавно вернулся к этому вопросу1, указывает, что
лучшее значение для А, равное 2J/ —, было получено Гронваллем2.
По предыдущему, нижний предел для А, который зависит от /г, прибли-
приблизительно в 2 раза меньше и его асимптотическая величина для /г->оо
ровно в 2 раза меньше найденной Гронваллем.
В том же месте Фейер получает неравенство для производной мно-
многочлена Лежандра
Это неравенство может быть также уточнено.
С этой целью возьмем снова ортогональные многочлены R(*> 3) (х),
имеющие хп старшим членом, так что
и рассмотрим
A63)
A62')
где мы полагаем 0 <^ р <С -^ •
Исходя из сделанного выше замечания (§ 4), заключаем, что все
экстремумы /п р+_1_(я) удовлетворяют неравенству
(l_,2)>(iL^±|_. A64)
Следовательно, в этих точках имеем
т ' KW" (я + 1 +2p)F2pBp
Но в силу A37), имеем
I ('А
2р A — 2р)
1
где Мп>р~ -^ обозначает максимум Уип(х). Стало быть,
A - *2)Р • ^ _? [jR(JVO (а;)] _2Р A — х*) 2
1 Fejer. Math. Ztschr., 22 A925), стр. 267—298.
2 Gr on wall. Math. Ann., 72 A913), стр. 213—270.

откуда
dx L ^l/y + pJ
<-—!—^->n ——Mn+lt9. A65)
Следовательно,
В частности, в случае многочленов Лежандра
р /г\ _ 1-3... Bл —1) „(о,о) / ч
гп \Х) —\ tln [X),
благодаря A65),
|A- х*)ТР'п (х) |< (п + 1)
"'7
В этом неравенстве не только коэффициент при }/Vi во втором члене
меньше коэффициента Фейера, но наиболее существенным является то,
что множитель при Рп{%) есть A — ж2L вместо A — х2) и показатель
A — х2) не может быть еще уменьшен без увеличения порядка величины
второго члена.
Если сохранить показатель 1 при 1 — х2, то при помощи такого же
рассуждения получим, заметив, что для р = р1<^-^- [в точках, где
(х) имеет экстремум]
что для достаточно большого w
\A-*)Р'п(х)\<У^, A68)
и как в A62), величина второго члена формулы A68) не может быть
асимптотически уменьшена.
7. Важно иметь верхний предел | /n (x) | для всех многочленов Якоби
(р>0, Р1>0).
Случай pSpi не требует существенных изменений в вычислениях.
Так, пользуясь формулой A63), можно перейти последовательно к про-
произвольным значениям а, р, удовлетворяющим одновременно неравенствам
где А; — некоторое целое число.
67 5*

Для этого положим
где / = /„,р,Р1, /' = d(n'^ {X) ¦ Тогда,
[р A -2р) A + х) +Pl A -2р) A - *)] =
A70)
Следовательно, 1>п(#) достигает экстремума одновременно с /^ и /^.
В частности, когда
> >4
максимумы vn соответствуют максимумам /?. Таким образом, при
условии A71) абсолютный максимум Afn>p>Pl функции J/^p.p» (#) | совпада-
совпадает с таковым функции Y^n, так что абсолютный максимум М'п р Р1 моду-
rf/n,p,Pl (*)
ЛЯ
удовлетворяет неравенству
A72)
Значит, ограничиваясь, для упрощения письма, слз^чаем р = рх, имеем,
принимая во внимание A64),
7 + р
откуда
fn+i.P. A73)
Следовательно, считая уже известным существование такойг постоян-
постоянной Ар} что
¦Vх ^ / J 2п+2р-1'
получим также для достаточно большого п
где
* ' 2
68

Будем иметь, тем более, каково бы ни было р>у,
Мп.р < 22>Ln [A - х)>] ~ Л^, A74)
что означает, что многочлены Якоби степени п, умноженные на соответ-
соответствующие множители A—х*)р, уклоняются от нуля на отрезке [—1,
+1] не более, чем многочлены Чебышева степени п, имеющие тот же
старший член.
Чтобы ограничить Д/П,Р>Р1, когда р>у, pi^y произвольны, нужно
использовать таким же образом вместо A63) формулу
|
) = —~- {A - х) A [1#'е) (х)] + »д?-« (х)}, A75)
которая следует из того, что коэффициент при хп~1 в /?п'3)(^) равен
2 х'а + В ' так чт0 многочлен степени п — 1, таким образом построен-
построенный, ортогональный на [ — 1, +1] относительно веса A — х)* A + я)Р+1>
имеет старшим членом хп~1.
Применяя A75), найдем таким образом последовательно неравенство,
аналогичное A74).
Единственный случай, который еще остается исследовать, это тот,
когда выполнено только одно из неравенств A71), пусть
? < у 7 Pi >
у •
В этом случае, по A38), абсолютный максимум | /п,р,Р1 (#) | достигает-
достигается вблизи конца —1, а ее относительные максимумы идут, убывая слева
направо. Но, с другой стороны, по A70), максимумы vn будут соответ-
соответствовать таковым /^ (#), как только
р A - 2Р) A + х) + Pl A - 2Pl) (I - х)< 0,
т. е. когда
Следовательно, неравенство A72) существует, если обозначить через
df
MnfPt9l абсолютный максимум
ке A76).
Таким образом,
для х, расположенного в промежут-
^f- A77>
Учитывая, что абсолютный максимум // 2 (х)\ достигается вбли-
•зи х= — 1, и применяя A64) (где р должно быть заменено на рх), имеем
69

по A75) для достаточно больших п
Таким образом, можно во всех случаях найти такую постоянную APl,
зависящую от рх, что
MnMl < APiLn [A - xf (I + хГ] (Pl > i) . A78)
Заметим, наконец, что в предположении
Р<у> Pi>y
ни одна из функций ип и vn не остается конечной на всем отрезке [—1,
+ 1]. Для этого случая удобно построить функцию
где
^ = (i-*)(» + P + Pi)« + p(l-2p) • A80)
Имеем на всем отрезке jj? <^ т—————\а • Применяя это неравенство
в промежутке A76), мы заключаем, что
Wn(x)<Ml,p,Pl A81)
в этом промежутке. Но когда Х^>0, что имеет место на всем отрезке
[—1, +1], за исключением весьма малого промежутка вблизи —1 и, сле-
следовательно, в частности, на части отрезка [—1, +1], внешней по отно-
отношению к промежутку A76), то i4<On- Следовательно, в этой послед-
последней части имеем
lP,Pl9 A82)
так как ип(х) убывает слева направо. Таким образом, неравенство A81)
справедливо на всем отрезке, и мы имеем тем более на всем отрезке
V-n
1 1
При р^>-р- и pi<C"o- мы получим, очевидно, аналогичный результат.
1 1
8. Таким образом, в случае p<^-7f» Pi^y нужно рассматривать
функцию ип(х) A37); в случае р^--^-, pi^ v вводится в рассмотрение
11 11
функция vn{x) A69); в случаях р<у, Pi^-y юли Р-^Т» Р1<:^Т Рас~
сматривается функция wn{%) A79) или соответственно функция wn(x),
где
70

Можно положить, следовательно,
/„ = V^cos Ф„, >,„ -~- — = Vun sin Фп
(о<Р<у, 0
> у > Pi > у
A84)
Sn @<p<y, Pi>y
где
tg Фп = — ^-n
d\nfn
И + Р +
tgSn = —I
Таким образом, так как
A85)
то Фп возрастает х от — arc tg у __Р2 до wit + arc tg |/ 1_p^ ; ^п воз-
возрастает от — у до rnz + у ; Sn возрастает от — arc tg у i_^2 до гстс +
+ y , когда 6 изменяется от 0 до тт.
Мы покажем теперь, что в каждом рассматриваемом случае имеем
для последовательных функций fn (x) одного индекса асимптотические
соотношения:
(Фп + Щ, K-
l^nSin (Фп + Щ
:т, о<Р<1),
1 dTn+a
¦ -Vvnsm(W»+kb)
(Р>У>
yncosCn + A6),
^Wn sin C» + kb)
^ A86)
1 1
1 Нужно заметить, что, за исключением случая а = + — , Р= + -^~, когда
асимптотическая формула A35) справедлива тождественно (для всех значений х и
/г), только при а = 0, р = 0 крайние значения угла (— рте, пк -f Pi^r), формально опре-
определенные этой классической формулой, соответствуют точным значениям Фп,
71

Эти соотношения имеют место равномерно на всем отрезке [—1,
если >0, с ошибкой порядка (?( — ). В формулах A86) функции Jn+kr
так же как и функции ип, vn, wn, ограничены сверху и отличаются от
рассматривавшихся до сих пор функций соответствующими множите-
множителями, которые появляются при замене Rn (x) и Лп+а (х) соответствую-
соответствующими нормированными многочленами Rn{x) и Rn+7c(x).
В силу A28), имеем, таким образом,
~2 г Bп + а + Р + 1) Г Bп + а + р -|- 2) f\ (x)
т. е.
^/n(a;). A87')
Легко проверяется реккурентное соотношение
с„Дп+1 (х) = (х + а„) Л„ (ж) + w + f47a1+p Я„ (ж), A88)
где
-/;
¦=1+От,
2(ге + 1 + а+C)т
A89)
^4n — коэффициент при хп в /?п(ж).
Остановимся сначала на первом предположении, когда ja|<ly,
| р | <Су» и положим (для упрощения письма) a = р.
Уравнение A88) принимает тогда после умножения на A — х2)р вид
откуда A90)
где
72

Но
<max Vun = max /„ (ж) =0A)
и
L — я2) -f- 2p A — 2p) ,/i „
л + 4р к
.У 2рA — 2р) , 2р
так что
A92>
Следовательно, в силу A91), A92) и первой группы формул A84),
/n+i = V ггп cos (Фя + б) + О (^J . A93)
С другой стороны, дифференцируя A88) и принимая во внимание-
дифференциальное уравнение многочленов Якоби, имеем
cnR'n+1 = Ип
х + ап ) R'n+
A94)
Предполагая снова, что а = р, и умножая на A—#2)р, найдем
Сп A _ Х2)Р Г _A±i]' = (л +1) /n + -^±i>^ A - х^)р Г_1п— Т =
A95)
^Ц
Вычитая из A95) уравнение A90), умноженное на -—-—-2 , получим
откуда
^ + 1 +
2р A — 2р)
(п +4р) A — х2)
A97)
Следовательно,
где равномерно на всем от,резке [—1, +1]
е -
.-*2)
73

Поэтому
= - ^ sin (ф« +е)
A98)
Переходя последовательно к л + 2,. . . , п + к, мы получим 2, таким
образом, первую группу асимптотических формул A86), имеющих место
равномерно на [•—1, +1] с приближением порядка —.
В частности, полагая
•будем иметь
Jn+k ~ fn COS -
Следовательно, замечая, что множитель пропорциональности, кото-
который нужно ввести для нормирования классических многочленов Лежан-
/Г2п + 1
дра Рп(х), есть 1/ —х—, мы заключаем также, что
j/sin 0 Рп+к =
= / sm i
Pncoskb
— Рп cos 6 — Рп sin2 0
. sin кЬ
Ш <199>
равномерно на всем отрезке [—1,
Для р^>у можно будет записать A90) в виде
и A96) после умножения на — 2 представится в виде
п +1 +
7? А,
га + 2р
B01;
1 Достаточно заметить, что вследствие A93), A98) и A84)
Следовательно, считая уже доказанным, что
[fn+k-i
и замечая, что | х + Т^я2 — 11 = 1, видим, что
74

где
2P(l-2p) "IT
так
как по A72) для P^>y
имеем
1 #2 sin 6
Вторая группа формул A86), следовательно, также доказана.
л л
Перейдем, наконец, к случаю р<^^> Pi!>y*
Умножая A88) на A—х)р A + я)р' > получаем
или
^+oi
B02)
Но в силу A83)
Стало быть,
так как
Р
*) р A - 2Р)
A—*)[2(р
+ pO-
n + Zp + Zpx I
(p+PlJ 1 p(l— 2p)
rt + 2р
2p + 2Pl
я + 2p + 2
a -
L—2p)
(я+2р+2р0а
1 1
Следовательно, для p <^ у , Pi > -^
/~n+i= «/» + ^nl/1^^2§ + О (I) = J/"^; cos (En + 6) + О (I) . B03)
Подобным образом, вычитая из A94), умноженного на A — х)рA + #)PS
_ -^— , находим
1 9A+ху 9х
уравнение A88), умноженное на p pl ^
—хI
(ж + ап; I /п +
' 7 (Pi-P) — g(Pi+p)l
n — /n i.^ J-
75

Умножая еще на — рп+1 У\ — х2 и приняв во внимание A89)„
получим
Р) + Р-— рг а?(р!+ р —1) + Р — Pi] ,
i=~x* л + 2о + 2Pl J +
^ + ° ^J B04>
Замечая затем, что максимумы \Jn\, так же как и j%, убывают сдева
направо, и что для отрицательных значений х
fn = 1 ^/п
где значение производной должно быть взято для значения ?<^х, так:
что \in (^) ]> V-n (^) и, таким образом,
11 dQ I '
откуда мы заключаем, что
N+i -ж11 = - (и + 1) VI - ж» !%+,/„
следовательно,
а
Ж
, (п + ^ + Р 4- Pi) х + pi— p
"*" /г + 2р+2Р1
Таким образом, окончательно
d т d f
где
так как, полагая 1 — х = /—тттчг » можно написать выражение в скобках
в виде
1 г
А —
т+ту
Все формулы A86), следовательно, доказаны.
76

9. В случае, когда р <С0, Pi<C^> нужно отказаться от рассмотрения
функции fn{x), которая обрагцается в бесконечность в точках х = 4-1.
Тогда можно рассматривать функцию
Zn (х) = Rl{x) + -^щ B06)
.(полагая для определенности р =pi). Имеем вообще
Zn = 2Rn [Rn + и(в
4p) J л(л + 4р) '
так что Zn достигает максимума в начале и минимумов на концах при
'р<0. Следовательно, теперь1 абсолютный максимум \Rn(x)\ равен
YZn@); так что асимптотически
\ А
B08)
/для четного п нужно взять вместо нуля максимум Rn , наиболее близкий
к нулю).
Таким образом, теперь уклонение Rn(x) само асимптотически равно
минимальному уклонению A—х2)°Рп(х) вместо того, чтобы давать
минимальное уклонение этого произведения, которое Rn{x) необходимо
обратит в бесконечность, если заменить им Рп(х) (здесь Рп{х) как
и Rn{x) имеют старшими членами хп).
Умножад Rn (х) на ——, для того чтобы перейти к нормирован-
ному многочлену Rn (x), мы имеем
Мах | Rn (х) | = Мах ]/ХЙ ~ |/1" • B09)
Вообще для р<СО> Pi<^0 положим
Следовательно, теперь нужно положить
Rn(x) =VZ^}cosAn, Vn{n+l + 2pi) --Kin^nAn- BЮ)
1 Напротив, для p > 0 абсолютный максимум | Rn (x) | равен | i?n (±1) |, и, есте-
естественно, мы имеем то же для соответственных многочленов Якоб и.
77

Из A88) и A94) легко получаем формулы
Rn+k (x) — У Zn (x) cos (Дп + Щ,
1 a^
Кга (га + 2р
справедливые равномерно на [— 1,+1] для >0.
В случае, когда только одна из величин р или рг отрицательна
(пусть, например, р<0), введем функцию
Fn = (l+x)*Rn(x), B12)
которая удовлетворяет дифференциальному уравнению
+ Pl> (n + 2Р + Pl) + Р1?^] i^n = 0. A33')
Пусть для определенности О^рх^у. Тогда, полагая
где } B13)
r2= l±f J
П (» + Pi) (л +2р + Pi) A+ х) + Pl (I— 2Pl),
будем иметь
Г 2
Значит, Yn достигает максимума внутри в точке х0, определяемой
уравнением
4р (п + Pl) (л + 2Р + Pl) (I + xf + Pl A - 2Pl) [4p A + *) + 1 - ж] = О,
откуда
х0 1 + —I
и максимумы Fn(x) идут, убывая для х^>х0. Но максимумы соответст-
соответствующей функции /п(#) = A — xyFn(x) идут, возрастая слева направо
по A38'), так что | /п (а?) | < п4.2^+Рг-1 для ж<0- Следовательно, имеем
тем более на всем отрезке [— 1, + 1]
\Fn{x)\<
78

Далее, замечая, что для значения х0
2 }2
~ + Р A - *о)-р
откуда мы заключаем, что для достаточно больших п на всем отрезке-
л/у~ <? 1
и для нормированных многочленов
2i->yr±. B14)
/j
7Л может, таким образом, теперь для р<^0, 0 <^ рх <^ -г- играть ту же
роль, что и функции Ид, адп, г/п, Zn в предыдущих случаях.
Также, еслир!^-^- (при р<^0), положив
B15>
можно проверить, что в этом случае Хп остается ограниченным на
[— 1, + !]• Достаточно заметить, что Хп = О (Max Fl), так как затем
максимум \Fn\ определяется шаг за шагом (последовательным прибав-
прибавлением — к рх) благодаря соотношению A75).
Глава IV
ОРТОГОНАЛЬНЫЕ МНОГОЧЛЕНЫ, ПРИВОДЯЩИЕСЯ
К МНОГОЧЛЕНАМ ЯКОБИ
1. Мы займемся теперь ортогональными многочленами, соответствую-
соответствующими весу
Я (*) = ^Ш= = ^ М ^-^ + ^ - М») A ~ ^ A + *)» B16)
где to(x) на отрезке [—1, + 1] удовлетворяет условию
Для упрощения письма мы будем всегда предполагать, что 20@) = 1»
79

По D6') и D8') главы III мы имеем
Щ] = и [A -
где
^Ш^. B18)
Предполагая сначала, что to(x) заменено положительным многочле-
•ном степени h
(^){?) B7)
мы имеем для соответствующего ортогонального многочлена Нп,ь, (х)
-формулу 1
где в определители B9) и B9') главы I нужно ввести многочлены
Якоби В^п' ^ (ж) (имеющие старшим членом хп), соответствующие весу
< ){
Как мы заметили выше, можно ограничиться рассмотрением случая,
когда а^> — 1, р> —1, ибо в противном случае Rn,h{%) обратится
в нуль для х = + 1, так что после деления на A — я)^ A + хI~® мно-
многочлен ЛП} п (х) сведется к ортогональному многочлену степени
п — [ — а] — [ — р], соответствующему весу
th (х) A - я)а+Ь°0 A + ж)&+[-И .
Уравнение A33) главы III [приводит к известным асимптотическим
выражениям многочленов Якоби вне отрезка [— 1, -f-1].
1 Формула B8') эквивалентна формуле
h
где
О2П+2& + 2Р+2РХ—1г , Лч
Ак _ Z —, ^ Л^;3) И ^^ h {х) th {х) A _ *)« A + ^K dx.
— 1
Таким образом, как только будет доказано, что
Д»,Л(*)A-*)РA + *)pl
.можно будет утверждать, что Ah = О Bк)-
80

Имеем, таким образом,
(х — 1)р A
B19)
где \х + }/х2 — 11>1. Дифференцируя, получаем такого же рода фор-
формулы для производных R^ p) (х), которые сами являются с точностью
до постоянного множителя многочленами Якоби.
, Таким образом, применяя B19) к формуле B8), мы получим асимп-
асимптотическую формулу
, h (X) th (x)
B20)
где вместо pi, фигурировавшего в формуле C3), мы пишем г{ = щ-\-
-\-Va\ — 1 (чтобы избегнуть смешения с показателями р и рх).
Предполагая х находящимся вне отрезка [—1, +1], мы имеем,
следовательно,
(*+|Т Т"*а[х+}Гх\А ri].-..
' + Vx* — 1
^]
Л (х-аг) . . . (x-ah)
. . . (rh— x + Vx1 —
-&=i \\nth(z)d2
2—x I Y\^
B21)
Таким образом, мы замечаем, что число, на которое нужно умно-
умножить многочлен Якоби Rn' 0) (х) для получения асимптотического выра-
выражения Rn,h(x) во внешней точке, зависит только от th(x) (и не зависит
от а и р).
К тому же, для конечного h порядок приближения B21) тот же,
что и порядок приближения B19).
6 С. Н. Бернштейн 81

Пользуясь классическими асимптотическими выражениями A35) мно.
гочленов Rn' &) (х) внутри (—1 + 8, 1-е), где © — данное произвольна
малое положительное число, найдем асимптотические выражения Лп? ^ (x)f
справедливые в том же промежутке.
Действительно, как и в главе II, мы получим из B20)
Дп, h (x) th (х) (~1} хР„ , ЧР1 X
ага2 . . . ah <1 — я)р A + х)р*
|У [(n+p+л) fr-ртс] (ei0 _ ri) . . . (е*_ rh) + е
и затем, полагая, как в указанном месте,
и
h
а - ^ (i + ф cos [(n + p + pl) e + ^ -pTC]' B22)
где
In th (x) dx
2. Но формула B22) имеет тот же недостаток, что и соответствующие
формулы для многочленов Якоби, поэтому мы заменим ее асимптота-
ческими выражениями, справедливыми равномерно на всем отрезке
[—1, + 1], пользуясь формулами A86) предыдущей главы.
Нам будет достаточно исследовать один из случаев, соответствующих
различным формулам A86).
Для определенности остановимся на случае 0^р^ O^^
(стало быть, | a | -^ у , | p | ^J-y), что, в частности, включает и м'ногочлены
Лежандра.
Наши заключения сами собой распространяются на все случаи, ког-
когда р>-0, pi>-0, при помощи замены функции ип(х) через vn(x)9wn(x);
введение функций Zn(x), Yn(x), Xn(x) из § 9 главы III, когда показа-
показатели р и р2 (или только один из них) отрицательны, позволит исследо-
Бать и этот последний случай.
Мы имеем, следовательно,
_ A86')
2* A - ху A + Ж)Р. R^ (Х) _ yUn cos (фп + ; '

Подставляя эти выражения в B20), находим, таким образом,
A - xf A + xf h (х) Я», h (х) ~ (~1/1ЛИяа(*) X
аа ah
• • ah
X ^^ ^S^ : B23)
1
j
или после деления на \fth(x) получаем
Rn, h (ос) A - хУ A + ж)* ]/«Л (ж) ~ YMhun (x) cos (Ф„ + ф„). B24)
Если мы заметим, что теперь (для |aj'<; —, |3|<; —), при достаточ-
но большом п (глава III, § 3),
V^? 1 > B25)
то получим асимптотически на [—1, + 1]
j Rn. h (x) A - xY A + а')"' /4 (а:) | < -^
2?
~ Ln [A - ,г)р A + ж)р. /^ (ж)] . B26)
Следовательно, ортогональные многочлены ДП) /t(#) (для |а|^
дают асимптотически минимальное уклонение произведению
где
Рп(х) = хп + Plxn~i + . . . + рп .
3. Перейдем теперь к вычислению порядка ошибки наших асимпто-
асимптотических формул в предположении, что h может также бесконечно воз-
h r
растать, но при условии, что — настолько быстро стремится к нулю,
что
) B2/>
Мы предположим еще, что все корни th(x) удовлетворяют неравенству
тогда по B19) относительная ошибка этой асимптотической формулы бу-
будет порядка . Кроме того, введем временное ограничение, требуемое
леммой § 1 главы II:
\П - /ч|>о !;-,,!. B29)
83 6"

Стало быть, в силу этой леммы и при сохранении тех ше обозначе-
обозначений (за исключением замены рЛ на гк) имеем
D
— 1
B30)
D
Таким образом, воспроизводя рассуждения § 3 указанной главы, мы
видим, что для точек я, лежащих вне [—1, + 1] и удовлетворяющих
(как ajc) условию
\х+ Vx* — 11 > 1 + -^-, B28')
относительная ошибка формулы B21) порядка * O\h\/ —^-?).
Перейдем теперь к асимптотической формуле B24), где мы должны
принять во внимание то, что формулы A86') имеют ошибку О(
Мы можем начать с введения в последнюю колонну определителя
An(di, а2, . . . , ah, x) выражений A86') вместо R%\$ (х); тогда, обозначая
измененный таким образом определитель через An (аг, а2 , . . . , ah , х)>
мы заключаем из B8'), что
ahyx\ Г Л» ]
+ 0—г" Ь B31)
аи ... fli д ( cl d ... Лг. |
Итак, остается только вычислить ошибку, проистекающую вследствие
формулы B19).
Имеем благодаря B30) (см. § 1 главы II)
(-1)"
(«1 - а
г . • • •
ah)
¦ (е-» - rh) ]\
Следовательно, замечая, что эта последняя ошибка превышает ошибку
B31), мы имеем
| Лп, h (х) A - xf A + х)р>
— VMhun (х) cos (Фп + %) | =
ft -щ / 111 ть \ / о о о \
-—т|/ , B33)
1 Эта оценка может быть улучшена (так же, как и оценка B30)), но для даль-
цейшего в этом нет надобности.
84

и для нормированных многочленов Rn> ^ (х)
1 Д«. н (х) A - xf ( УТ^
+ х)»
= О (
^-У^ф) cos (Фп
B33')
Применяя лемму § 4 главы II, мы можем избавиться от ограничения
B29). В силу этой леммы, если корни Sh(x) удовлетворяют B28), можно
построить такой многочлен th(x), удовлетворяющий B27) — B29), что
In
= О (Ш In3 n),
т. е. что
B34)
4. Нам нужно будет только распространить теорему § 5 главы II.
Если
ио(я)-*Л(ж) | = 0(в) B35)
отрезке [— 1, + 1], то на том же отрезке
B36)
где Rn{x) и Rnth(x) —нормированные ортогональные многочлены, соответ-
соответственно относительно весов
to (х) A - xf A + xf и th (х) A - xf A + xf ,
где th{x) есть многочлен степени k, удовлетворяющий условиям B27) —
B29), и eln/i->0.
С этой целью положим
Яп(х)=
B37)
где
ак = $ Rl (х) Л*, н (х) A — хI A +x)*th (x) dx =
— 1
= J е' (х) Rl (x) Rk> h (x) A - xf (I + z)e dx , B38)
Следовательно,
A - x)* A
)* [R°n (x) - Rn,h (x)] = О (e) + S,
B39)
85

где
+ 1 n—1
x)» ]s'(z)R°Jz)%Rr,;h(z
— 1
= ¦—— A — xY A + х)ъ x B40)
( )
4n — коэффициент при jn многочлена Rn>h(z), iaE> что
Положим
л:п = (l - .0" (l -t~ j)p« (i -2)p(i + z)*[Rn,h U) д„_1А B) -
-й„,Л СОД „_,,»> (я)]. B41)
Заметим сначала, что ио B33'), каково бы ни было
Стало быть,
П-1 - -2
2 A —rJp (I -f ^Jр1Лй''|(Л)=°[Л +^22л/й1пи -гЛ422Л1п2л] =О(л),
в силу B27). Следовательно,
A _ х)р A + хуг A _ 2)р A + z)Pl ^ jikJi {x) Rkh {z) = о (л). B42)
fc=o
С другой стороны, мы получаем из A86') и B33') асимптотическое
значение Сп для Кп
Кп~Сп = уГ-и^$""$ [cos (Ф„ + фЛ) cos (Ф« - 60
— cos (Ф? + фХ) cos (Ф„ - 0 + %)) =
^0 -F + ^"jsin^J . B43)
где Фп и '1>П соответствуют значению переменной z = cos6a и
86

Вычислим теперь непосредственно ошибку последнего асимптотиче-
асимптотического выражения (применяя тот же прием, что и в § 5 главы II).
С этой целью заметим *, что введение в B41) промежуточной асимп-
асимптотической формулы B31), соответствующей нормированным много-
многому
членам, приведет к ошибке порядка 01 — ) для величины Кп. Пусть
таким образом полученное выражение. Будем иметь
К' =
<й ы *,
?'В) К) • • • Л^'« К) с,
П j
?'3) («,) • • • л?>3) К)
1 1 . . . тх
rh т
11..
a!
h
—
1 1 ...<*!
rj ал+а
1 1 ... 1
Л-1
ri
)
1 1 ...т0
ri • • • тл
'л (-)
B44)
где мы положили (А = —1, 0, 1, . . . , К)
= Vun(x)cos(Фл + *6), afc+1= У вп(z)cos(Ф^ + А60). B45)
Нам остается вычислить порядок разности Кп — Сп*
Л!ы можем написать
h h
Сп =
г=0
1 В силу замечания, сделанного в сноске в начале главы IV (стр. 80), по поводу
формулы B8').
87

где числа Pi являются коэффициентами многочлена по у
оУ +¦•¦+ *=2\а%... ahVMhth(x) th{T)
K(z) {sinL=J~F0 - 6)sin[ф° + Фп + ' + *~* F0 + 8)] +
in ^p-1 (8e + 6)sin[Ф» -Фп + ^Ц^-1 (в0 - 6)]}. B46)
Следовательно, вычисляя таким же образом Кп и принимая во вни-
внимание B30), имеем
Кп — Сп =
1 (в„-в)япГф»+Ф.+ Ll±=i_(eo+e)J+
sin'-^-1 (е0 + 6)sinI ф? - Фп -J-'" + k~
^(бо —в)]| =
B47)
Итак, окончательно по B43) и B47) получаем
О (*'2»/ip
Формулы B42) и B48) дают возможность оценить
jdz el
— 22 J I
COS 0 — COS 0n
^). B48)
B49)
при условии, 2hh*l/ -^—»0, очевидно, выполняющемся в силу B27).
Действительно, мы мошем предположить для определенности О <С 6 <; -у.
Тогда в интервалах (б ,6), (б, 6-^ \ из которых первый нужно
будет заменить на @,6), когда 6<—, мы применим формулу B42).
Таким образом часть Н, соответствующая этим двум интервалам, имеет
порядок 0A). Нам остается, следовательно, оценить оба интеграла
cos 0О — cos 0
cos 0О — cos 0
88

Достаточно рассмотреть второй интеграл, который по B48) будет норядка»
sin
1
в-в0
2
+
sin
1
6-
f в0
2
/г2
гг
1
COS 6 — COS 60
Следовательно,
B50).
Пользуясь этим, приходим к заключению, что в формуле B40)
S = O(slnn) max \Rl{x)(l — xf(i + з)*]-
Так как благодаря B33') максимум Rnfh(x)(l — x)p(i + x) » ограничен,
то из B39) следует, что и максимум /?п(х)A — #)рA + #)Pl ограничен
и, следовательно,
A~ж)рA +
I —Лгцл(*)] = О(в1пя)
B36).
равномерно на ^сем отрезке [—1, + 1].
Для того чтобы е\пп->0 в случае, когда to(x) = Sh(x), достаточно
согласно B34) взять
1пл = 4Л1пй, B51)
где А^>12. Действительно, принимая во внимание B27), должно быть
2h
8/г2 In4 п = 2/г2 In4
или
— 21п/г->оо.
Но, подставляя B51), получаем
¦ оо.
5. Мы воспользуемся снова для произвольной непрерывной функции
to(x) приближёнными многочленами Sh(x), аналогичными многочленам
§ 7 главы II.
В дальнейшем мы будем всегда считать, что функция t0 (x) имеет
непрерывную первую производную to(x) на отрезке [— 1,+ 1]> удовле-
удовлетворяющую условию
t0 (х + р) - t0 (х) = О (-JL-) . B52>
89

При этих условиях, как известно, возможно построить такие многочлены
*Gk (х) степени к, что
! Gic (х) - In t0 (x) I = О (—у . B53)
Следовательно, полагая
Sh(z) = l + Gk(z) + ...+ 'У , B54)
где
k = k?, А« = |Л B55)
будем иметь
и так как из B55) следует, что
, h In In h
k
то получим также
(\) B57)
Заметим, что многочлены Sh(x) удовлетворяют условию B28), ибо в
силу сделанного в указанном выше месте (§ 7, глава II) замечания
, . .ч 1 , 2 In к 2lnh
Но, по B51),
7 Inn
Л In In n
и подавно
Строя затем многочлены th (ж), удовлетворяющие B34), получим также
B58)
предполагая, что в B51) А ограничено сверху.
Мы приходим, следовательно, к такому результату:
Если положительная функция tQ (x) удовлетворяет условию B52), то
ортогональные многочлены Д^(#), соответствующие весу B16) при
1 1
О^р^у, O^Pi^y, допускают равномерно на отрезке [— 1, + 1]
асимптотическое представление
Rl{x) Vtjx) = R°n (x) A - xf(l + xf> Vh?) ~ У^ГЙ cos (Фп + фЛ), B59)
где
90

Многочлены th (х) — указанные выше многочлены, приближающие фун-
функцию t0 (х).
Но по § 9 главы II условий, наложенных на to(x), вполне достаточно
для утверждения, что равномерно на [—1,+1]
где
1 2-к
I — z2
B60)
Имеем, следовательно, также (при прежних условиях)
#Ua)(l-a!)p(l + »)PiyrMs)~'/M*)cos(<Dn + «lO. B61)
Принимая во внимание формулы A84), можно еще написать, что
B62)
R°n (х) У1 (х) ~ /п, р, Pi cos ф + Xn dtntdl'*x sinф.
Из B61) мы заключаем, что для очень больших п
— • B63)
Таким образом, ортогональные многочлены R%,{x) асимптотически
минимизируют уклонение на отрезке [—1,+1] произведения
Рп (X)
где Рп(%) — произвольный многочлен степени п, имеющий старший член
тот же, что и Rn (x).
6. Для других значений р > 0 и рх ^> 0 рассуждения при доказательстве
аналогичных асимптотических формул совершенно не изменяются. Таким
образом, будем иметь
Яп (х) A — ху A + ж)р, Yt0 (х) ~ Vvn (х) cos (Wn +tj>) =
-/ 1 dA>,p,p. . ./^ 1 ^ 1
— /n, p, px COS Ф+ •
T П + P + Px
Rl (x)(l— x)* A + х)'г yt0 (x) ~Vwn (x) cos (Sn + Ф) =
= /n,Pl Pl cos
njP
B64)
обоих этих случаях Rn (x) A — ^)рA +
|/^0 (x) также ограни-
ограничены (по § 7 предыдущей главы) «а [—1,+1], но даже асимптоти-
91

чески они не обращают в минимум уклонение соответствующего произ-
произведения.
Как мы видели, нет надобности рассматривать случай, когда неравенства
не удовлетворяются. Предполагая, что они имеют место, мы получим,,
пользуясь тем же методом и вводя функции Хп, Yn, Zn, данные формулами
B15), B13), B06), асимптотические формулы, соответствующие случаям,
когда по крайней мере одно из чисел р и рх отрицательно. Таким образом*.
для р<0, pi<CO будем иметь (при тех же условиях относительно to(x)}
n cos (Дп + ф) =
' COS ф +
- sin
B65)
где R%' ® (х) — нормированные многочлены Якоби, соответствующие по-
показателям а = 2р — у , Р = 2рх — у .
Имеем на [—1,+ 1] в этом случае, по B09), для достаточного боль-
большого п
Имеем также
Лп(«)A + -
(х) ~ Fn cos ф + - -^- sin ф
р<0,
(х)
cos
гп -^- sin 6
B66>
(р<0, 0<Pl<y),
где
остаются ограничен-
ограниченВ силу B14), произведения | i?0 (х) A + xyt yt0 |
н&ши ка [—1,+1].
Асимптотические формулы B61 — 266), ошибка которых , равномерно
стремится к нулю на всем отрезке [— 1,+ 1], могут служить для изучения*
сходимости разложений в ряд по ортогональным многочленам.
7. Заметим, что когда t0 (x) — данный многочлен и тем более, если
t0 (х) = 1, т. е. если просто рассматриваются многочлены Якоби, равенство
Д=- = 0Aпл) B50')
92

непосредственно дает условия равномерной сходимости соответствующих
рядов.
Достаточно будет опять исследовать один случай. Рассмотрим, напри-
например, тот случай, когда р ^ 0, pi ^> О (содержащий, в частности, много-
многочлены Лежандра).
Рассмотрим разложение по соответствующим ортогональным много-
яленам
оо
f(x)= ^аЛЦх), B67)
где
+ 1
ak=\f{x)q(x)Rl(x)dx.
|
Положим
п -И п
fn (Х) = 2 "*Я°* (x)=\f (z) 9 (z) S ^* (х) ^2 (z) rfZ. B68)
Пусть <рп(ж) — какой-нибудь многочлен степени п, близкий к f{x).
Имеем тогда
/п (Х) - ?п И = S t/ (Z) - ?» BI ^ (Z> S Й* (Ж) Й* № dZ> B69)
откуда
Г/ (х) — ф (^I A — х)? A + ic)p» =
L/тг * ' тп \ /J \ / \ ' /
+ 1
= л^TГ/W-TnWl (i
[Д^+1 («) Rl (z) - R"n+1 (r) Д° (х)] rf8
А 1
ЛГ А «2
= О {[/ (z) - ?n (z)] A _ z)p A + z)p. In n}, B70)
где Ап — коэффициент при хп в многочлене Rn(x).
Следовательно, если существуют такие многочлены ®п{х), что
- ?n (z) | A - z)p A + z)p« = о (^) , B71)
то разложение B67), умноженное на A — ж)р A-}-я)р1, делается равно-
равномерно сходящимся на всем отрезке [—1, + 1].
Для того чтобы это имело место, достаточно, чтобы
f (Х\ = ЬМ , B72)
7 V ; A—*)рA+а0р»
^де Д (х) удовлетворяет условию Дини—Липшица и /х D-1) = 0. Действи-
93

тельног тогда можно построить такие многочлены ср^ (х) степени пу
что*
B73)
Поэтому тем более достаточно для обеспечения равномерной сходимости
A — х)? A + хУ* 2 anRn {%)> чтобы функция f (x) сама удовлетворяла
условию Дини—Липшица.
В случае, когда хотя бы одно из чисел р и рх будет отрицательным^
получим аналогичный результат. Достаточно формулировать его для
/1 1
Тогда само разложение
п=0
будет равномерно сходящимся, если функция
f1(x) = f(x)(l-x)*(l + x)^ B74>
удовлетворяет условию Дини— Липшица, и /7 D-1) = 0.
Я не буду заниматься другими условиями сходимости и нахождением
приближений, получающихся при этих разложениях. Ограничусь только
одним примером, который показывает, что само разложение B67) дли
о^>0, Pi>0 может вообще не быть сходящимся, когда функция удов-
удовлетворяет условию Дини — Липшица или даже условию Липшица доста-
достаточно низкой степени.
* Предполагая, например, p=Pi<!-p-i можем построить тригонометрический поли-
полином Рт (cos 0) sin 0, где Рт {z) — многочлен (z = cos0) степени т, так что
Тогда Рт {z) ~О(т). С другой стороны, A—z2)^ p допускает приближение <поряд-
<порядка 129~~г посредством многочлена Qt (z) степени Z. Следовательно, можно построить
многочлен Ql (z) Pm (z) степени п = I + m такой, что
| Рт (z) A - z2) *"Р - Рт (z) Ql (z)\ = O (mZ^-1).
Полагая Рт (z) Qj (z) = фп (г.), после умножения последнего равенства на
A — z2)p, и сложив его с предыдущим, получим
| /, (z) - ?п (z) A - ,2) р | = О (Ы*-1) +
если возьмем т = п1~2C'~г1 где 0<е<1 — 2р. [Эта сноска воспроизводит дополни-
дополнительное примечание [6] к A89*)]. (Автор.)
94

Мы положим р = р1==у, tQ(x) — l. Тогда ортогональный многочлен
будет
Рассмотрим функцию
со оо
±г \ V cos7z*0 v cos я4 arc cos # /отсч
/(*) = 2j —л-г-= 2а 7л • B;5>
n=i
Легко проверить, что эта функция переменной х удовлетворяет на
всем отрезке [— 1^ + 1] условию Липшица степени а = -^ (рассматри-
(рассматриваемая как функция от 6, она удовлетворяет даже условию Липшица
степени -т-J.
Между тем, разложение
, B68')
где
+ 1 ^_ + 1 оо
—1
расходится для х = + 1. Действительно,
= ^-2|/ Y ДЛЯ К = П*,
у для к = п* — 2,
®>к — 0 для всех остальных целых значений к, так что члены разложе-
разложения /(±1) бесконечно растут, ибо
(Согласно предыдущему, разложение B68') делается равномерно сходя-
сходящимся после умножения на sin 6 = ]/l — х2.)
Таким образом, разложения в ряд многочленов Якоби с параметрами
1 1
а = 2р—-у, р = 2рх — у, а также разложения по ортогональным много-
многочленам, приводящимся к якобиевым, следует применять предпочтительно,.
если хотят приблизить данную функцию /х (я) при помощи многочленов,,
умноженных на A — х)9 A + х)р». Тогда можно разложить
гг, умножая это разложение на A — х)р A + ^)р1> получим вообще хорошо
сходящийся ряд для f1{x). To, что порядок получающегося при этом-
95

приближения не более чем в In/г раз превосходит порядок наилучшего,
-следует из B71). Это обобщает классический результат Лебега, относя-
относящийся к тригонометрическим рядам.
Я укажу еще на такое следствие из предыдущего.
Пусть р ;> 0, Pi ^ 0. Если
f (~\ ЦгЛ(А t\p (A -4- '/Л?! /979'\
где/г(х) удовлетворяет условию Липшица степени а^-^- и /х (Ч— 1) = О,
то разложение f{x) no ортогональным многочленам Rn(x), соответствую-
соответствующим весу q (х) = A — хJC~~ Т A + #JPl~~ T ^0 (#)> делается абсолютно и рав-
равномерно сходящимся после умножения на A—х)? (\ + х)9к Доказатель-
Доказательство подобно тому, которое было мною дано для тригонометрических
рядов * [16] (том I).
8. В общем случае, когда t0 (x) удовлетворяет только условию B52)
(а не является многочленом), так что мы знаем лишь, что ошибка асимпто-
асимптотической формулы B61) равномерно стремится к нулю на [— 1, 4-1].
достаточное условие для равномерной сходимости разложения в ряд по
соответствующим многочленам должно быть немного изменено2.
Действительно, рассуждения, которые привели нас к B50), здесь
«непосредственно неприменимы.
Но во всяком случае легко видеть, что
^ dz = O(lnn). B76)
— 1
Действительно, имеем всегда
A _ ху A + Ж)Р. A_ zf A + Z)P» [д0+1 {х) д о {z) _ ^o+i B)до (х)] =
B77)
m, с другой стороны, обращаясь к доказательству формулы B36), видим,
что тем более
\Щ(х) — Лк, л (ж) |A — *)рA + а:)* = О (в Inn),
¦если к<^п, откуда следует, что
= 2 R* п (х) A — х)ъ A + ж)». + пО (е 1пп) = О (п), B42')
гак что
-?=Т = 0{п). B78)
1 См., например, L. Tonelli «Serie trigonometric he», стр. 268.
2 В случае р = pi = 0 и более общем, если
р A — 2р) = Pl A — 2Pl) = 0
условие B52) относительно t0 (#) может быть заменено условием A8) первой частж.
96

Применяя оценку B78) в промежутке ух , х ~\ ) я равен-
равенство B77) на остальной части отрезка [—1, +1], получаем немедленно
формулу B76).
Таким образом, возвращаясь к формуле B70), мы можем только
утверждать, что
Итак, для утверждения равномерной сходимости разложения / (х),
умноженного на A — ?)p(l + #)pi, на всем отрезке1 мы должны потре-
потребовать, чтобы
!/B)-?nB)lA-2)p-^(l + ^'-f = oA^r)- B79)
Другими словами, достаточно, чтобы функция
удовлетворяла условию Дини—Липшица, и /i(+:l) — 0.
Условие, которое мы здесь формулируем, менее общее, чем B72), не
является, вероятно, существенным, но для того чтобы от него избавиться,
налагая возможно меньше ограничений на to(x), нужно непосредственно
исследовать ошибку асимптотического значения величины КПу которая
во всех случаях может быть представлена в виде B43).
9. Перейдем теперь к значительно более легкой задаче распростране-
распространения асимптотической формулы B21) на внешние точки, предполагая t0 (x)
произвольным. Нам не придется добавить ничего существенного к соот-
соответствующим рассуждениям главы II.
Так, лемма § 6 указанной главы справедлива без изменения и
|Ж(х)-Rn, h(x)\=O [Me (l + {)] , (83')
где о — наименьшее расстояние х от отрезка [—1, + 1] и И — наиболь-
наибольшее из двух значений Bn>h(x) и Rn-it (#)> предполагая, что
Следовательно, при условии, что to(x)^>O непрерывна на [—1, +1],'
имеем асимптотическую формулу:
+ i
х*-1 .-Л to *о (г) dg
2-Х / l/~i__*i
A )
+ 1
(х —
B80)
1 Очевидно, что формула B76) достаточна для утверждения равномерной схо-
сходимости внутри промежутка (—1, +1) при условии B71).
7 С. Н. Бернштейн 97

где Yn равномерно стремится к нулю во всякой определенной области,
внешней по отношению к отрезку [— 1, + 1], и для нормированных
многочленов имеем
У~х*-1 [ In П (г) dz
2-т
+1
m f0 B) dt
^^. B80')
Укажем на некоторые приложения этих формул.
1. Определим минимум Nn интеграла
+ i
— 1
если задано значение Рп(х) во внешней точке х = ?.
Будем иметь
где
л? E)
ui ~~ a° ~~~W
¦"о
стало быть
+1
ш г0
П==^\ S2 /a°~ E + ve^i)^^+»e ' B81)
если предполагать Рп(%) = 1.
2. Эти формулы могут быть применены для определения минимального
колебания монотонных многочленов (и кратно монотонных), подчиненных
различным условиям.
Так, поставим себе задачу определить минимальное колебание М
монотонного многочлена Qm(x) степени т на отрезке [—1, + 1], если
его производная обращается в нуль в h внешних точках а1у а2, .. . , ah
и равна единице во внешней точке S.
Предположим, что т — h = 2п + 1 нечетно. Тогда без труда
проверяется, что многочлен, осуществляющий экстремум, может быть

представлен в виде1
X
Qm(x)= \ P2n(x)th(x)dx,
-1
Решение следует, таким образом, из формулы B81), и искомое мини-
минимальное колебание асимптотически равно
+ i
In th (z) dz
M ~ 4M52-l) Д
'-*) IMS + П2-1)-1] ¦ ¦ ¦ Ун(г + П2-1)-1] ,.ft9.
- т,ч Г- г- J у&Об)
где rt = a. + Уй? — 1 (знак перед радикалом всегда выбирается так, что
3. Асимптотическая формула B80) позволяет определить во всех слу-
случаях асимптотические значения коэффициентов ортогонального много-
многочлена
Д» (х) = хп + Агхп-г + ... + Аьхп-Ь + ... + Ап B83)
для конечного к.
Действительно, полагая |ж|^>1, имеем
^_ Г lnto(z)dz = N 1 1Г i _^i i i J[* i 1
2тг J (i -i.Vi-28 L 2a:2 JL ° я? а:л J*
где
1 [ zkInt0(z)dz ,9Я,ч
J rr=F B84)
остается ограниченным, так что в разложении
F 2 =е * ^ " =1 - -J + ... B85)
коэффициенты также ограничены.
G другой стороны, в силу B19) коэффициенты многочлена Якоби
асимптотически равны коэффициентам
[^ 22 Ж + . . . ( ) ^22l Ж + . • .J
X fl+ ^- + ...1 [l_-^ + ...l, B86)
1 См. статью [31] (том I).
99

1 к к.
где Тп(х) = -^^ cos и, arc cos ж, когда >0. Следовательно, для
коэффициенты произведения B85) на B86) асимптотически равны соот-
соответствующим коэффициентам
*° + (е - pi - »J *—' - i *—2 + ¦ ¦ ¦ + [-
+
<28?>
если только р — px— ax=^=0; в случае же, если р — рх — аг = 0, порядок
величины коэффициентов, соответствующих А = 2/ + 1 нечетному, пони-
понижается и их асимптотические значения получаются введением следую-
следующих членов B85).
Очевидно, что для конечного к коэффициенты А^ асимптотически
равны коэффициентам разложения B87), так как в разложении ^п по
степеням - в B80) коэффициенты будут порядка ^nR при всяком i?^>l.
Если к бесконечно растет, коэффициенты Аи будут асимптотически
равны Bk в
t1 1п *°
B88)
только при условии, что ^п стремится к нулю не очень медленно.
Действительно, будем иметь
где С—эллипс с фокусами —1, + 1> сумма полуосей которого есть
1 + 8 (8>0).
Таким образом, при условии lim — < 1 имеем
где 14-8 = 1/ ——т . Следовательно,
L 2nk 2 (n + 1 — к)п+1~к J
B90)
Если обозначить через Ск коэффициенты при хп~к многочлена Тп(х)9
где к = 21 четно, то формула B90) примет вид
B91)
100

так как
/ к \ ( к \ 2 2
IСГ* 1 ^ ^т2- ^ т
B/сJ
_ я Bл — <: — 2)
n 7 ГтсЛ(ЯА:)
Следовательно, для того чтобы
lim^=l, B93)
достаточно, чтобы
ЧпСкУ~к = о(Вк). B94)
к
В частности, если >0, то, согласно B86), В]с~Ск для четного А.
Стало быть, для осуществления B93) достаточно, чтобы
TnV?->0. B95)
Имеем аналогичный результат, но при более ограничительном усло-
условии, для нечетного к. Тогда для того чтобы B93) выполнялось, доста-
достаточно, чтобы ^пУп—>0.
Замечая, что коэффициенты Си возрастают быстрее членов гео-
к 1
метрической прогрессии с знаменателем г]>1, пока lim — <1 у= ,
можно распространить предыдущие заключения на случай, когда
<i_
V2
Вследствие B19) и B21) это представится, в частности, при лю-
любых р и р1( когда t0 (x) — многочлен. Заметим, что в этом случае
B96)
В случае, когда функция t0 (х) четная, и р = рх очевидно, что в силу
симметрии соответствующие ортогональные многочлены будут содержать
только члены одной четности.
В случае р = рх = 0, в силу формулы A6), Rn(z)Vto(%) достигает
асимптотически своего абсолютного максимума с противоположными
знаками в п -\- 1 точках отрезка [— 1, + 1]» м> следовательно, Rn(x) дает
(асимптотически) минимальное уклонение произведению
если Рп(х) имеет тот же коэффициент Ак при хп~к, что и
101

Следовательно, в частности, при >0, ввиду того, что 5а~Сл,
отношение этого минимального уклонения к уклонению, соответствую-
+i
In U B) dz
2п )
г 12
щему to(x) =1, асимптотически равно е , так же как и
в случае, когда к = 0, какова бы ни была непрерывная положительная
функция to(x).
к
Асимптотическое значение Аи для lim — = 1 не может быть получено
из B80); но его можно получить из B8), считая tn(x) многочленом,
а затем перейти к пределу и получить общий случай.
Не входя в детали доказательства, я ограничусь указанием резуль-
результата в случае, если р = рх и to(x)— четная функция. Тогда
+1
jL^ С In U (г) dz
lim ^ = е -1 (если lim * = 1). B97)
Тс \ J
Следовательно, формулы В. А. Маркова асимптотически справедливы,
когда -——>1 (но они неверны, по предыдущему, для lim —=0), какова
бы ни была непрерывная положительная функция to(x).
Таким образом, в частности, минимальное уклонение
Ро + X Y
на [—1, +1] асимптотически равно
Этот последний результат, впрочем, верен также и тогда, когда
to(x) будет содержать множителем A—хJ9 A + xJPl при ррх^О, и мо-
может быть получен с помощью того же рассуждения, что и следующее
общее предложение, которое мы докажем:
Если функция ср (х) обладает свойством, что, каково бы ни было
целое число Х>0,
En[x^(x)] = o{En[v(x)]}, B98)
где Еп [ср (х)] обозначает наилучшее приближение ср (х) многочленами сте-
степени п на [— 1, +1], то какова бы ни была непрерывная положитель-
положительная функция р(х), удовлетворяющая условию р@) = 1, имеем
En,vix)[<?(x)]~En[<t(x)], B99)
где Епр (Х) [у (х)]—минимальное уклонение произведения
\<t(x) — Pn(x)\p(x) C00)
на том же отрезке) Рп (х) многочлен степени п.
Действительно, пусть ph (x) [ph @) = 1] многочлен степени /г, близкий
102

к р(х), и qk (x) (q @) = 1) — многочлен степени к, близкий к —!— ,
Р \х)
так что, при произвольно данном положительном е
?5 х)р (*)<*¦+*> C01)
откуда
еJ. C02)
Полагая
ph(x) = l + xR(x),
мы заключаем из B98), что
En[ph(z)v(x)]~En[?(x)l C03)
и, следовательно, так как, очевидно,
мы можем выбрать п достаточно большим для того, чтобы было
Еп, п (ж) [? (*)] > Еп+н [? (*)] A - ?)- C04)
Таким л^е образом
Еп, Vh („ 9, (х) [? (*)] > ^n+J> рь (х, [?ft И ? (*)] ~ ^n+А-, р, (х) [? (*)]• C05)
Стало быть, в силу C02) и C05), имеем
^п [с? (х)] > ?п+,, РЛ (х) [ср (ж)] A - е)з. C06)
Принимая во внимание C01), C04) и C06), мы имеем, следовательно,
двойное неравенство
A^SL Еп-Ъ [? (X)] > En, v (х) [? («)] > -Sn+h [? (X)] A - 8J, C07)
что доказывает наше утверждение.
Теорема применима, в частности, к |#|а, каково бы ни было а]
Очевидно, также, что введение в функцию р{х) множителя вида
1 1. . . 1 — — , обращающегося в нуль на [—1, +1], не изме-
изменяет асимптотической величины ЕП} р (Х) [ср (х)], когда ср (#) подчиняется
условию B98).
10. В заключение покажем, как можно будет вычислить асимптоти-
асимптотическое значение Еп уу—г^ [? (#)], когда ср (х) является аналитической
«функцией. Мы ограничимся случаем положительной и непрерывной
на [—1, +1] функции to(x), присовокупляя временно условие A8), от
которого затем мы сможем избавиться.
103

Предположим для определенности, что ср (х) имеет единственный дей-
действительный положительный полюс а^>1 на эллипсе сходимости.
Начнем с замечания, что если тригонометрический вес to(x) удовле-
удовлетворяет условию
(^wJ+', A8)
где ?>0, то имеем не только формулу
Rl (x) ~ У~щ cos (nb + «]>), A6)
но и, пользуясь тем же методом, получаем асимптотическую формулу
для производной
\ [Rn (х)]' УГ=& = "/—щ sin («в + ф) + е„, C08)
где еп равномерно стремится к нулю на всем отрезке [—1, + 1].
Действительно, предположив сначала, что t0 (x) есть многочлен th (x), и за-
заменяя в последней колонке определителя B8) многочлен Чебышева Тп (х) че-
рез — Тп(х)У\ — х2, убеждаемся что формула C08) справедлива, с тем же
порядком ошибки, что и соответствующая формула F4). Затем, применяя
хорошо известную теорему, мы констатируем, что
R°n{x)-Rn,h(z)
= 0(&lnri),
если известно, что
\R°n(x)-Rn,h(x)\ =
Установив это, составим многочлен
= R°n (х) (ах - 1) + ^~^ (х* - 1) R°n (x), C09)
где
COS О
х — а
так что, по A6) и C08), имеем
ах — 1 У(а2 — 1) A—-х2)
= , Sin О = — '- .
х — а х — а '
SC0S^e + *+^ <310>
Так как 8 возрастает от — тг до 0, когда 6 изменяется от 0 до тс,
то функция
104

где Рп (х) — многочлен степени п, достигает п + 1 раз своего макси-
,/"
мального уклонения, асимптотически равного I/ —.
Следовательно, ~= т-т- дает асимптотически наилучшее приближение
Для нахождения асимптотического значения ?п+1(а), замечаем, что,
по A6) и C10), Sn+1 (х) + aRn+i, а (я) = о A) равномерно на всем отрезке
[— 1? + 1], где Rn+i,a {%) —нормированный, ортогональный относительно-
( % \2
тригонометрического веса to(x)ll j многочлен. Так что в силу
известной теоремы имеем в точке а
Sn+1 (a) = —a Дп+1, а(а) + о [(а + |/^ГТ)п],
т. е.
lim _ n+1 . ч = — а.
Яп+1, а (а)
Но
¦dz
V~2n
+1
__ 1 ^ Va^l [ Ш *о (z) dz
(a + \/a*-
Следовательно,
+i
* a2 1 \ —
^ 2n _i(.-*)Kl_* ^ Ci^
что также может быть записано в виде
+i
In U B) dz
Из формулы C09) можно получить и асимптотическую величину
?n+i(a).
Достаточно заметить, что асимптотические формулы для производ-
производных, которые получаются дифференцированием B80), тоже справедливы
во всех внешних точках, так как доказательство этого следует непо-
непосредственно из метода, развитого в этом мемуаре.
К тому же, достаточно доказать формулу C12) для произвольного
положительного многочлена1 th(x), чтобы иметь возможность утвер-
1 Я получил эту формулу впервые в эквивалентной форме (как произведение
множителей, что делает очевидной и алгебраическую природу рассматриваемого
интеграла) в заметке [36] (том J).
105

-ждать ее справедливость для любой непрерывной положительной
функции.
Дифференцируя по а тождество
и замечая, что, по C09), последовательные производные Sn+1(x) по а
-будут на отрезке [—1, +1] порядка 0A) для п —>оо, мы заключаем,
что правая часть равенства, которая после к дифференцирований
делается равной
где Qn^ (x) — многочлен степени п, асимптотически равняется
n+i (
Следовательно, в силу выше сделанного замечания, имеем
Ш t0 (z)'dz
0 C13)
Итак, если аналитическая функция ср (ж) имеет единственный веще-
вещественный полюс некоторого порядка на эллипсе сходимости, имеем
всегда
4-1
У~ Г ы
Я».М*>[<Р(*)]~Я»[?И]е  C14)
какова бы ни была положительная и непрерывная на [—1, +1]
функция t0 (х).
Очень вероятно, что это асимптотическое равенство справедливо
в случае, когда ср (а?) имеет логарифмические или алгебраические
особенности.

52
ОБ ОГРАНИЧЕНИИ ЗНАЧЕНИЙ МНОГОЧЛЕНА JPn(x)
СТЕПЕНИ п НА ВСЕМ ОТРЕЗКЕ ПО ЕГО ЗНАЧЕНИЯМ
В п + 1 ТОЧКАХ ОТРЕЗКА *
1. В статье «Quelques remarques sur l'mterpolation»1 я поставил следую-
следующий, вопрос:
Определить многочлен
Лг+i (ж) = {х — а0) ... (х — ап),
имеющий все корни на отрезке [—1, +1] так, чтобы максимум
A)
был возможно мал,
Я указал в том же месте, что этот минимум М порядка log гг и,
кроме того, что максимум Fn(x) действительно порядка log гг на отрезке
[— 1, + 1]» если
An+i (#) = С cos (п + 1) arc cos x.
Почти в то же время (и независимо от меня) Фабер доказал первую
часть моего утверждения 2. Что касается второй части этого утверждения,
то Гронваль3 и Гранжот4 доказали впоследствии эквивалентное предло-
предложение, в котором отрезок [—1, +1] заменен окружностью радиуса еди-
единица и
* «Sur la limitation des valeurs d'un polynome Pn (x) de degre n sur tout un se-
segment par ses valeurs епл + l points du segment». Изв. АН СССР, ОМЕН A931),
стр. 1025—1050 A51*).
1 Сообщ. Харьк. матем. общ., 15 A916), стр. 49—61 ([20], том I).
2 Faber. «tfber die interpolator ische Darstellung stetiger Funktionen». Jahresber.
D.Math. Ver., 23 A914).
3 Gronwall. «Asequence of polynomials connected with the roots of unity». Bull;
Amer. Math. Soc, 27 A920—1921).
4 Grandjot. «Uber Polynome die in Einheitskreis beschrankt sind». Jahresber.
D. Math. Ver., 34 A925).
107

Я возвращаюсь теперь к этому вопросу, чтобы вычислить асимптотиче-
асимптотическое значение М, которое оказывается равным
М~ A log я, B)
откуда следует, что никакое распределение узлов а-х не позволяет асимп-
асимптотически снизить максимум A), соответствующий
-4n+i (#) = С cos (п + 1) arc cos x.
Я напомню сначала, что функция Fn{x) представляет в каждом из
п + 2 промежутков (—1, а0), (а0, ах), ..., (ап, 1) соответственно много-
многочлен степени п, который является наибольшим по абсолютному значению
в этом промежутке среди всех многочленов, модуль которых не превы-
превышает единицы в точках а0, аъ . . . , ап. Действительно, вследствие формулы
Рп (х) = Ап+1 2 (х-аг)А'п (а) > С1 blS)
если |/>n(ai)| = l при i = 0, 1,2,..., п, и Pn(ak)Pn(a>k+i)>0,
Рп (di) Pn (ai+1) <^0, при i^k, то многочлен Рп (х) осуществит абсолютный
максимум в промежутке (а#, a^+i)« Кажется вероятным, что наибольший
из п + 2 максимумов Fn(x), соответствующих всем этим промежуткам,
будет минимизирован, если все максимумы будут равны между собой1.
Но мне удалось доказать это утверждение только в предположении, что
п бесконечно возрастает; этим случаем мы и займемся в дальнейшем.
2. Рассмотрим сначала довольно широкий класс многочленов Ап+1 (х),
для которого все п + 2 максимума A) асимптотически равны
2 ,
-log п.
Предположим, что п + 1 корней (ц многочлена Ап+1(х) имеют значе-
значения
C)
i + у) , л > а Ф* (ж) — непрерывная функция х, которую
в каждом промежутке {bi^x^bi+1) мы можем, например, интерполи-
интерполировать линейно, полагая
Ф (х) = ^~Д
1 При тг = 2, например, многочлен An+i (х) = х ( х2 — -д-1 приводит к миниму-
5 i/~2~
му М = -? максимума F2(x), достигнутому в четырех точках -f 1, +_. ; заметим,
о
что многочлен Чебышева х\ х2— -jA , который дает М = -о-, не реализует мини-
минимума при п = 2.
108

Кроме того, положим ф (+
такие постоянные Л^>0 и
= 0 и предположим, что существуют две
, что
(х) — ф (у) |
| log (ж —
при — 1<ж<1,
В таком случае
-м U
Ф/ \ лГ'л 9 ! /г. \ лГл 1.2
\Х) V 1 — X —* ф \U') V 1—О-
i=0
/»„(*)
cos (re+l)arccos x,
D)
E)
где
Ф (^)
Ф (&г) ГГ-fef
F)
если положить
А (ж)=
-*« -ф
г=0
T^J (п + 1)(х-Ьг)
(V)
Но каково бы ни было положительное е, можно выбрать п столь
большим, чтобы иметь
ф (X) V 1-Х2 — ф (Ьг) V~l
Действительно, пусть, например, Ьг^>х^>0. Тогда
(8)
i' 1 / А А2
(п+1)(х-Ьг)
(л + 1) | ж — 641 | log (Ь- — яг) |в
2ф(«)
где первый член правой части может быть заменен через
ф (&^+1) — Ф F^)
(п
109

если
Итак,
A sin -
и + 1
+
+ ¦
2 (n + 1) sb
2A
sin ~~т: | log (Ъг-Ъ1+1)\ь
(n + 1)^1 — a;a|log(l—:
2A
2 | log F, —
sin
log A -cos
log-^
Следовательно, fn (x) можно представить в виде
Ф (*) ^i — «¦ —
г=0
где
3i = O 7
Таким образом, при п~>оо будем иметь (х = cos б)
lim Jn \х) = / (ж) =—
COS 6 — COS ф
если только будет доказано, что интеграл
7Т
С I
7Т
С I ф (cos 0) sin 0 — ф (cos ф) sin ф
I COS 0 — COS ф
4
+ (9)
A0)
A1)
A2)
имеет смысл. [В этих двух формулах ty (x) представляет предел, к ко-
которому стремится функция Ф (ж), соответствующая многочлену Ап+1 (ж)
при тг->оо; она, очевидно, также удовлетворяет условию D), если в нем
постоянная А не зависит от п.] Итак, имеем
где
г Г I ф (cos 0) — ф (cos ф) . л 7л г С I, / ч sin 0 — sin ф 7
/х = \ — ^———— sin-0 db, /2 = \ Ф (cos <р) —й — аср.
1 J | COS 0 — COS ф ' . г J\ Т/ COS 0 — COS ф т
о о
Доказательство сходимости первого интеграла при условии D) имеет-
имеется в моем мемуаре «Polynomes orthogonaux relatifs a un segment fini»**
* См. [51], гл. II, § 9, стр. 46. (Автор.)
ПО

Что касается второго интеграла, то
(в —6))Etg-J
du\
достаточно заметить, что подинтегральное выражение становится беско-
бесконечным] только при 6=Ои6=тг;нов окрестности 0, например, имеем
| ф (cos и) ctg -?
i
Следовательно, имеем равномерно на [—1,+ 1]
7Г
lim fn (Х) = / (х) =1 ССФ (сое8) sin8-ф (соеФ) sin У d {Щ
п->оо ^ J cos 6— cos ф. » • v 7
о
о
откуда
1 С ф(со& 8)sin в—ф(соз ф)з1пф ^
ТС
ф( ) ф(
J COS0—СОБф
ТС J COSСОБф
lim pn(x)=p(x)=e « A3)
Замечу еще, что при указанных условиях ф(совб) разлагается в.
равномерно сходящийся ряд по синусам
ф (cos 6) = сг s-in 6 + с2 sin 26 + . . . + ск sin kb + . . . .
Из A1) следует поэтому, что
— / (cos 6) = —¦ logp (x) = сг cos 6 + с2 cos 2 б + . . . + сл cos к 6 + . . . ,
который также равномерно сходится1.
С помощью тех же рассуждений заключаем, что р (х) — непрерывная
функция x.
Итак, при бесконечном возрастании п имеем
cos (, + 1) arc cos,
Производя замену переменной
= ^ (*)• A4>
где z — монотонная функция х, находим
1 В цитированном выше мемуаре (стр. 48), напротив, дано выражение ф (я) через
/ (х) в интегральной форме
т / \ 1 [ / (COS 0) — / (COS ф) . . .
ф (х) = — —V LA L L1 XL sm 0 dcp .
Y V ' 7U J COS 0 — COS ф ' Y
о
111

причем, вследствие (9),
а = «]> (z)Vl=?- ф (ж) УГ=& = С>[(я + 1)(ж~2I =
L (log иN J
= 0 Гф (х) \ГГ=*Л = ^ г ф B) ГТ=1^ I.
L (logn)'8 J L (lognf Г
иными словами,
удовлетворяет также D), и выражение р (х) не изменится, если заме-
заменить 6 (х) на ^х(^).
Таким образом, соотношение E) может быть представлено в виде
п+1 (z) - ^n Pn (z - ** ^^ ) cos (п + 1) arc cos (z -
(
м формула A4) приводит к
lim ~n+1 x~' —=- =p{z). A7)
л-»оо Г ф, lz)V 1 — z2 I ^ W V '
cos (n + 1) arc cos z — т—л
L n ~\- l j
Формула A7), очевидно, дает асимптотическое выражение1 An+i (z)
гна [—-1, + 1]
р (z) Г Ф (z) V~l z2l
An+i (z) — cos (n + 1) arc cos z — l±±2 ^
2 L n +1 J
м г , л, , A7 bis)
'^ cos in + 1) arc cos z — 1-LJ- .
Первое асимптотическое выражение имеет то преимущество перед вто-
вторым выражением, которое из него выводится заменой фх (z) через ф (z)
(или заменой их общим пределом при п—>оо), что его корни точно
-совпадают с корнями многочлена Ап+\ (z).
Вычислим значение
— ап+\) . . . (ап — ап).
1 С помощью аналогичных вычислений определяется асимптотическое выраже-
р (z) / \n+i
ние вне отрезка [—1, + 1] Лп+1 (z) ~ ~^п+\ \z + ^*2 — ^ ) » г^е ^°ЕР (z) =
тг J 2—и , причем условия, наложенные на ф (х), могут быть гораздо мейее
ограничительны: достаточно, чтобы выражение L в формуле C) равно-
п + 1
мерно стремилось к нулю и чтобы предельная функция ф (х) была абсолютно
интегрируемой.
112

Получим
К
= (&ь — b0)... (bh - bh-i) (bh — bh+l) . . .
'^ 1
J • • •=
n + 1 sin (л + 1) arc cos bf
так как хмножитель 1 + ph (bh), который отсутствует в нашем произведении,
является пределом 1 -f- p^ (а:) при ж, стремящемся к 6^.
Итак, имеем равномерно
Шп
и, наконец,
A9)
так как, с одной стороны, имеем, вследствие непрерывности
lim
¦ Р (*л)
а с другой стороны,
3. После изложенного выше асимптотическое значение функции A),
соответствующее An+i(x), легко вычисляется.
Действительно, мы имеем
Х
Положим ^ = coscp, а^^ cos Oh, и пусть
будем иметь
Л=0
г B0)
;. Очевидно,
» B1)
'rc + l)|cos0^—coS9| ч '
8 С. Н. Бернштейн
113

если только Fn(x) бесконечно возрастает вместе с п, так как при сколь
угодно малом положительном е можно фиксировать о, не зависящее от
/г, так, что р К — 1 <Ге при \х — ак <С°- В то же время совокупность
p(ah) \ r I \ r j
членов, соответствующих корням ah, внешним по отношению к этому
промежутку, подвергается изменению при переходе от B0) к B1) мень-
меньшему, чем "Т~ , где L — максимум р при — 1 <^ у <; 1, — 1 <<; z ^ J.
Но благодаря соотношениям
— х -л , X = V +
п + 1 и '
где
мы заключаем из
что
arc cos у — arc cos x = J-~V - (у < $ < ж),
К 1 — ^2
а? — у х — у ф (у)
~ <" arc cos 2/ — arc cos x <" , = - Y-vy/
Итак, '
arc cos x = arc cos ?/ —
Таким образом, в частности, при
h, yh = cos —~ г,
имеем
(я + 1) 6Л = (/г + 1) тг - 6 (У/|) + О С—1—г) B3)
Точно так же, если
соответствует
у = cos т- тс,
ТО
(п + 1) ср? = (А: + 1) тс — 6 (cos - — | тт") + О (—-—Л , B4)
114

так что
т* 2
Следовательно, сумма, которая фигурирует в B1), примет для значения срЛ
асимптотический вид
^ s]n°k *" * sin0ri0 , JL ? sine^е .
' тг \ rnsm, —г.п.ч А V. '
.Zj (Л + 1 ) | COS дк COS фд. | 7С JCOS0—СОЭф^ ! 7Г J COS фй —COS6
к=о ' 1)
и так как в точках х = cos ojc, которые мы рассматриваем, имеет место
равенство
cos (п + 1) arc cos х — п , ,i~ ^ == ± 1 >
то получаем, наконец,
Г Ч- 7Г 1
¦р . ч ^^ 1 р sin 0 г/0 ! Г sm 0 ^0
П ^ 7Г J COS 0 СО8фд. J COS ф^ COS 0 I
"К Фг- — "z». От, _|_ ^ — Qjt.
4 sm п— sm —х-^
^ sin2 ф7. 2
- log —a ^—Т-Й ~ log Л- B6)
sm
Точно так же, полагая х—1 (или х = — 1), выводим из B1)
I
2j 1 —cos0?~^-J l-cose —
l 4 Io ^
sin —
is)
Итак, доказано, что все п + 2 максимума функции Fn(x) асимпто-
2 .
тически равны —log/г.
4. Мы покажем теперь* простейшим образом, что невозможно указать
такое распределение узлов а0, а1у а2, • • •, ап, 5^гл которого все максимумы
Fn(x) в произвольно фиксированном промежутке отрезка [— 1, + 1] бьг^гг
1
бьг асимптотически меньше, чем -y-logft. С этой целью докажем прежде
всего следующую лемму:
Если все корни многочлена Л(х) а0 <; аг <; а2 <; • • • <^ ап веществен-
вещественны, то
V\A'(ak)A'{ak+l)\-, B7)
* Независимо от предыдущего. (Автор).
115

(причем знак равенства имеет место лишь тогда, когда \А (х)^второй
степени).
Действительно, полагая
ak+i — ак =
i+i — «ft+i = Pi, ak — ak-i =
имеем
I A' K) [= 8 (8 + л) • • . (8;+ рп-
| Л' (аь+l) | = 8 (8 + ?i) - • • (o
Следовательно, замечая, что
-Г) Qv
4 + Pi
(o+ Pi), (j + Чг
получим
что и требовалось доказать.
С другой стороны, заметим, что многочлен степени п = 2т
= cosm arc cos
2а-2—
> (b>a)
который в двух промежутках (а, 6) и (—Ь,—а) не превышает единицы
по абсолютному значению, при х\= 0 приводится к
а2 4-
Следовательно, полагая
имеем
Тем более, если многочлен степени п = 2#г подчинен требованию не
превышать по абсолютному значению единицу в промежутках (а, Ь)
и (—а, —с), где 0<^с<^Ь, то это не помешает ему асимптотически до-
'1 -1
стигать значения -тг е s при х^ш0. Следовательно, функция Fn(xO сов-
совпадающая \в промежутке (ак, a^+i) -|c многочленом степени п, который
среди^ всех многочленов, не превосходящих единицу в точках a0, al9...
...,ап, имеет наибольшее абсолютное значение в промежутке (a^, aA+1)
116

длины 2а = о = ак+1—ак, должна будет достигать значения
4 «»
в этом промежутке, так как по крайней мере одна из двух величин
ajc +1 или 1 — ajc+1 асимптотически не меньше 5 = 1. Следовательно,
2
если мы хотим, чтобы это значение не было больше — log и, то необхо-
необходимо должно быть
4
— log л,
т. е.
—
или (для очень больших п)
2 log log ^
B8)
Итак, мы можем теперь рассматривать лишь такие распределения уз-
узлов aiy которые удовлетворяют неравенству B8).
Приняв это во внимание, воспользуемся неравенством B7), чтобы
оценить снизу
1
(х — ч) л
п+1
+
г]-
B9)
где х является внешней точкой по отношению к отрезку [#&, Яй+i]- Пусть
для определенности х<^ак<^а^и тогда
акА-1 У
Л+з («*)
C0)
Но каково бы ни было z>0, имеем
:> l0g A+2).
Таким образом, при х
Точно так же, при ж ]>
, имеем
получим
— X
C1)
C1 bis)
117

Следовательно, если ? и '#.находятся в фиксированном промежутке (а, В)
отрезка [— 1, + Ц и
то, полагая
, получим
где
Fn (?) = | An+! (I) | J]
h-1
*'
Таким образом,
~ "л) "+i (flfc
А ,
V 2 )
2 ^J
>
или, в случае, когда одна из сумм отсутствует, что произойдет, если
максимум будет достигнут в конце промежутка (а, C), то
C2 bis)
Итак, принимая во внимание B8), для очень больших п имеем
рп (?) > -у- log п — О (log log log п),
C3)
если максимум Ап±г (х) на [а, [3] достигается внутри отрезка [а, р] и, при
всех обстоятельствах,
n E) > 4- log л - О (log log log n).
C4)
Это неравенство сохраняет силу и тогда, когда C — а стремится к нулю
при условии, что ф—a) log log д не стремится к нулю; если предполо-
118

жить только, что (C — а) пг, где е <^ 1 — фиксированное число, не стре-
стремится к нулю, то можно было бы определить, благодаря C2) и C2 bis),
такую постоянную к, что Fn(?)^>klogn, т. е. даже на произвольном
промежутке длины —^ многочлен степени п, ограниченный в п +1
точках отрезка [—1, +1], может возрастать, как logn. Напротив, если
предположить, что п($ — а) не возрастает бесконечно, то можно рас-
распределить узлы at на отрезке [—1, +1] так, чтобы Fn(x) была огра-
ограниченной на [а, р]. Можно выразить последнее утверждение иным обра-
образом: можно выбрать лг -f- 1 точку на отрезке длины Id, в которых
многочлен степени п остается меньше единицы, таким образом, чтобы
он оставался ограниченным на всем отрезке [— 1, +1] при условии, что
n = O{d).
Действительно, среди всех многочленов степени <; 2п -f- 1, которые в
точках, где
Р2п (х) = cos n arc cos — _ (b > 1),
принимает значения +1, не превышают единицы, многочлен Р2п (х) будет
наибольшим на отрезке [—1, + 1]. Но он не превосходит на этом
отрезке значения
1 ГТ , Х-1
если d = Ъ + 1 = 2)л, где л^> 0 — фиксированное число.
5. В дальнейшем, чтобы придать вычислениям более симметричный
характер, мы заменим интерполяционную формулу Лагранжа соответст-
соответствующей тригонометрической формулой интерполирования; тогда теорема
относительно многочленов будет вытекать как следствие. Итак, мы
докажем следующую теорему:
Теорема. Каковы бы ни были 2/г + 1 точек отрезка [—тс, тт], в кото-
которых тригонометрическая сумма порядка п с действительными или ком-
комплексными коэффициентами
Sn F) = Ао + Аг cos 6 + Вг sin 6 + . . . + Ап cos пЬ + Вп sin nb
не превосходит по модулю единицы, наибольшее возможное значение Sn{ti)
2
не может асимптотически быть меньше — log п.
Гранжот1 показал, что Sn{fy не может превзойти асимптотически
-— log n в случае равноудаленных узлов; это же имеет место и при
более общих условиях, которые мы рассмотрели в § 3 в случае много-
многочлена. Заметим тут же, что, предположив формулированную теорему уже
доказанной, можно утверждать, что если
|?«Fг)!<1 A = 0,1,-..,Л)
1 Цит. выше.
119

при i = 1, 2, . . . , га, то имеем
Но в этом случае Sn(Q) = AQ + A1cosb + . . . + Ап cos габ, так как
разность Sn F) — Sn (— 6), кроме 2га корней + 6Ь имеет еще корень 6=0,
и, следовательно, тождественно равна нулю. Итак, полагая # = cos6
и замечая, что Sn (в) = Рп (#)— многочлен степени га, констатируем, что
при произвольном выборе га + 1 точек ai = cos Gi (z = 0, 1, . . ., га), есдгг
| Рп (#г) |^1> то наибольшее возможное значение \Рп (х) \ на отрезке
2
[—1, 1] не может асимптотически оставаться меньше—log га.
Итак, рассмотрим общий случай, когда 60, 6Х, . . . , G2n — произвольные
точки отрезка [0, 2тс]. Без ограничения общности можем положить
б0 = 0. Тогда тригонометрическая формула интерполирования будет
иметь вид
s m ^ Qn+1 @) V
0
0 — е,-
C5)
где
. 6 .6 — 6,
6-6.,
(?n + i (б) = sin— sin —2"-1 • • • sin 2
Таким образом,
/46) =
Q* 11 @)
2п
2-
4 А
sin -
1
э~ 0i
2
<?n+l
(9)
C6)
C7)
представит в каждой точке 0 наибольший модуль, которого действительно
может достигнуть тригонометрическая сумма ?п F) порядка га, подчи-
подчиненная условию не превосходить по модулю 1 в точках 64.
Заметим, что тригонометрические суммы, осуществляющие максимум,
имеют действительные коэффициенты (или все одного аргумента), так
как они соответствуют случаю, когда все слагаемые в C5) одного знака.
Рассмотрим выражение
n+l
3i4i
8,-
sin Sj у sin 84_|_х sin Si_1 sin (8t + 8i+1) sin (8{
120
C8)

где положено
при 0^к<^2п и 8^B7i-hi) = °&, так что ^ 8i+A = тс. Таким образом,,
имвем
2 6 2 -|/3т^+18т(^ + ^+1)
sin
X K ' V 2 У . . . C9>
j/sin Vl Sin (§i + §i-l) V Sln (§i-Ll + Si) Sin (Si + ^i+1 + S>
Можем принять, что
тогда будем иметь
sin (-J- + $i+1 + . . . + *i+h
sin (Si+1 + . .. +8i+h) sin (*. + Si+1 + . . . +
sin
у _ [cos ^ — cos (S4 + 2§i+1 + .
Zi
-—— >
D0)
так как
sin x . x
>
при >0 6>0 + 6<
sin (a; -f ^) ^^ a; +
Следовательно, имеем
D1 >
где
-« x
41/ f ^
X
[/ 1-;
i + 2Si+i
121

Заметим, что /j, рассматриваемая как функция ог,' является возрастаю-
возрастающей, а относительно 8^, напротив, — убывающей, если h^i.
Действительно, имеем
1 vi 1 2Т
"8, h 2* *з (8.- -
as,
где
С другой стороны, каждый из сомножителей, зависящих от oh, оче-
очевидно, убывает при возрастании oh. Докажем, кроме того, что /{ является
д21
выпуклой функцией относительно каждого 8, т. е. что —^ > О,
dh
каково бы ни было к. Пусть сначала к = г. Вследствие D3), имеем
таким образом,
38?" 41 58
38?" 41 58{ ;+ aS2 J 7i(L8i I 2 А
S [2 (8t + 6,.J ~ («T+^J
[2 (8t + 6,J ~ («T+^J5"]} = 7i [?М84
, 1 XJV1 ^i 1 ^> 0
"*? (8 + b] (§ + 26) (8 + *> (8 + ^^ J
Непосредственно проверяется, что вторая производная по 8^ каждого
сомножителя /,, содержащего Ьк (где k^i), также положительна.
дЧ.
Следовательно, имеем также —^^0, откуда следует, что
Таким образом, всякая симметрическая неотрицательная функций от
/0, 119 . . ., 12п будет достигать своего минимума при
так как если бы различные между собой значения о0, о1? . . .} о2п давали
минимум, то он реализовывался бы также значениями о1? 82, . . ., о2п, §о» и
2 » • • • » 2
давали бы, в силу D5), меньшее значение, что приводит к противоречию.
Замечу, что можно также проверить справедливость неравенства
122

D6)
каковы бы ни были i и к, но вычисления в этом случае более длинные
и нет надобности их приводить здесь, так как рассмотрение 1\ вместо
Hi достаточно при п—>оо. К тому же
miri Ii ~ miri Hi = -——- ,
так как при
имеем
Мы можем заметить только, например, не используя в дальнейшем
этого результата, что сумма
Qn
не может быть меньше единицы ни для какого полинома
Qn+i (в) = sin —х- sin :—-—-. . . sin ——— ,
каково бы ни было п.
В дальнейшем мы всегда будем предполагать, что п—> оо .
Рассмотрим сумму
<?n. (ej±!i±i
которая распространена только на значения 6Ь лежащие в некотором
промежутке а длины a = —^ , где е <^ 1 — данное произвольно малое по-
положительное число. Вследствие D1), имеем
где сумма распространена на тот же промежуток а. И подавно, будем
иметь
где через Д)Р обозначены выражения, которые получаются из /$, если
оставить только 2р + 1 множителей, так как отброшенные множители
больше единицы.
Пусть / + 1 будет число корней 6$, содержащихся в промежутке а,
и пусть 2 8А, 2 82, . . . , 28j — их последовательные расстояния. Предполо-
123

жим, что 1^>2р и условимся те из слагаемых /ijP (соседние с концами
промежутка а), которые содержат 8^, 8i+2> • • • , &i+p или 80, 8__i, . . . , Ь±^Р9
заменять через 1\ таким образом:
80 = 8Ь 8_х = 81_ь . . ., 8_р_ц = Sf-p-^i, |
D9)
Сумма 2 A,p будет, таким образом, преобразована в сумму
т. = \ л;р - E0)
последовательные члены которой получаются посредством циклической
перестановки индексов, и, следовательно, будет симметричной- относи-
относительно о\, 82, . . . , 8j. Поэтому, благодаря D5), минимум Та будет дости-
достигаться при
= о2 = . . . = ог =
ос
—,
так как, вследствие B8), имеем
Итак, полагая 8 = 8Х = 82 = . . . = 8р получаем
j, _ Ь C-5 ... 2 /7 + IV2 ^ 2/? + 1 S
i.P "~~ 4 B-4. . . 2рJ (р + 1) ^ /> + 1 2тг
Следовательно,
лл ^ 2» + 1 Z8 ос Гл , ^/logloa:^ . 1
s [' + о С^и+7
<52>
так как Z возрастает вместе с п, а потому можно также выбрать и
сколь угодно большим. Остается еще оценить порядок разности
которая содержит 2р не равных нулю члена, каждый из которых мень-
меньше, чем
_Г 1
I.1 Vp-b2tA
если 8Л<^р/ 8л;>|а. Мы знаем уже, что можно принять р = 0 ( og og^ j.
Но, с другой стороны, если тригонометрический полином ^п F) прини-
принимает значения +1 и ¦—1 в двух точках, лежащих на расстоянии \,
то для некоторого значения б
124

и, значит, найдутся такие значения 6, где
2
Итак, мы должны рассматривать только такое распределение 6i7 при
котором
следовательно, можно положить
l=-0(nlogn).
E3)
Таким образом, полагая //=loglogft, находим наконец
т. - д, /.,:< f [l+4]" =.о [?^*- а + о dog »)•)»] =
•откуда, благодаря E2) и D8), вытекает основное асимптотическое нера-
неравенство
^ E5)
F) | достигает
Пусть теперь ср — такое значение G, при котором
своего абсолютного максимума. Рассмотрим
<?n4-l(*)
i j
C7 bis)
Начиная от точки ср, возьмем направо и налево —- последовательных
промежутков длины
1 2тг
а = = — ;
ni—? пь
часть Fn(®), соответствующая значениям Gi промежутка (А а, (&+1)а),
будет больше, при A"J>0, чем
Ч
a я
27r sin
- E6)
I Qn+1 WO
Применяя те же неравенства в промежутках (— (к-\-1)а, — ко), имеем
— lOff Ctg -r
Tt:bo4
'2
2 A — e)
log П,
E7)
.125

и так как з может быть взято произвольно малым, то получаем наконец
n (?) > -- log /г,
E8)
что и требовалось доказать.
Следствие. Если модуль многочлена Р2п (z) степени 2п принимает
значение 1 в 2 п + 1 точках zo,z3,.. . , z2n ^# окружности С радиуса 1,
2
он может асимптотически достигать значения — logrc //а этой окруж-
окружности, каковы бы ни были данные точки z0, zlt . . . , z2n. Действиаельно^
пусть
) = (Z — Z0). . . (Z — Z2n).
1
Многочлен P2n(z), реализующий максимум модуля в точке z, будет в
этой точке иметь значение
2п
А=0
Следовательно, полагая z^ = eiefr, z = ei?p, имеем
sin^-Ty-^sm^—1 . . .
... sin
ф-1
2
sm sin ——— ... sin _—
2 2 2
что тождественно с выражением C7 bis).

53
ОБ АБСОЛЮТНОМ МАКСИМУМЕ
ТРИГОНОМЕТРИЧЕСКОЙ СУММЫ*
Пусть дана тригонометрическая сумма порядка не выше п
Sn F) = ао + ах cos 6 + b± sin 6 + . . . -f ancos n 6 + bnsin n 6. A)
Применяя обычные приемы теории наилучшего приближения, можно
получить следующий результат:
fiсли
где а <^ — , причем известно, что абсолютный максимум модуля \Sn(b)\
достигается на отрезке [О, а], то
C)
Иными словами, полагая а = — , где >О>1> имеем
Л72
причем раиенство фактически осуществляется для
D)
C0S2X
Следовательно, тем более, если \ Sn F^) | ^ 1 в 2),п раеноотстоягцих точках
6fc, mo значение
C0SX
* «Sur le maximum absolu d'une somme trigonometrique». Comptes rendus»
193 A931), стр. 433—436 A53*).
** Полное доказательство утверждений этой заметки дано в статье [56]. (Автор.),
127

X = ^> 1, будет верхнею гранью \Sn(b)\, не зависящей от п.
Кроме того, если X целое число, то [согласно D)] значение А^ фактически
достигается ^например, еслиХ = 3, то AN = -— ). Но если X не целое*
число, то более ограничительное условие, которому мы только что
подчинили Sn(Q), вообще говоря, понижает величину М, и имеет место
следующая теорема:
Если \Sn(Qk)\^l- б 2Ы = дг^-j Раен°ошстоящих точках 6#, причем
N — любое целое число*, то при всех значениях 6
sm
2N
еде значение Ln фактически может быть достигнуто.
Например: L2 = А2 = ]/2; L3 = -^ <С А3 = 2;
sin -Q- + cos -r-
о о
14 = —— = L4 /2 = У4 + 2
21 2iV
Если iV—>оо (Х-> 1), то Ljv ~ — logiV, ^iv^' — •
В зависимости от того, будет ли число точек 6# нечетным: -^—т- = 2т ~\- 1
2iV^ О Г Y
или четным: ^—7=^^> значение L^ фактически достигается одной из
следующих сумм
л
JV-1
sn F) = -j— ^ sinM6_6/) (ve^ = —Jf G)
7 ( Л- 2W + 1 Л7 m\
где h = 7n — п (так что в первом случае Л = , , а во втором 1\=-~\ .
Доказательство того факта, что значение в правой части F) не может
быть превзойдено, вытекает из конструкции интерполяционных формул
(8)
* В случае N нецелого имеем L[JV] <! Min Max | Sn @) KI^^, как видно из
Sn F) 9
статьи [96], стр. 453. (Автор.)
128

<?m+ft_! F) = -^ 2j в^ё^ / (9*) (9* = 7Г
где h <^ m, которые определяют тригонометрические суммы порядка
m + h и m +/г — 1 соответственно, совпадающие с /F) в точках 6#.
Одним из основных свойств этих сумм является то, что они тождест-
тождественны с /F)
если / F) = Sn F) — тригонометрическая сумма порядка п (п^т — /*)•
Таким образом, достаточно проверить, что
F =
Bт+ 1) BЛ + 1)
sm
N (Щ
sin2
е-еь
в предположении, что N = о?~тгт Делое х» и аналогичное неравенство для
формулы (8').
Неравенство (9) играет, очевидно, важную роль с точки зрения
сходимости интерполяционной формулы (8) в случае, когда/F)—произ-
когда/F)—произвольная непрерывная функция. Принимая во внимание замечание, сделан-
сделанное выше, легко выводим, что эта формула [равно как и (8')] сходится
равномерно, какова бы ни была непрерывная функция /F) при условии^
* h
что — не стремится к нулю.
Действительно, пусть Еп[/(Ь)] означает наилучшее приближение /F)
посредством тригонометрической суммы порядка п и пусть
Тогда из (9) следует, что
Рт U F)] < (F + 1) En_h [f F)} < B + A log -J) Ет„н [f F)], A0)
где А — постоянная, не зависящая от т и от h.
Полагая, например, m = 3fe+l, имеем
1 Без этого ограничения значение LN не имеет смысла, но легко видеть, что во
всяком случае F <; V~N, где знак равенства может иметь место только при N = 1 и
N = 2 [соответственно формуле (8')].
9 С. Н. Бернштейн

54
ОБ ОДНОМ ВИДОИЗМЕНЕНИИ ИНТЕРПОЛЯЦИОННОЙ
ФОРМУЛЫ ЛАГРАНЖА*
1. В моем докладе [47] (том I) на Всесоюзном математическом съезде
в Харькове я поставил следующий вопрос: нельзя ли построить интер-
интерполяционные многочлены степени М < Ш для произвольной непрерывной
функции /(#), совпадающие с нею в 'N определенных точках и равно-
равномерно сходящиеся к рассматриваемой функции, когда N стремится к бес-
бесконечности, если фиксированное число X меньше1, чем 2?
Я дам здесь положительный ответ на этот вопрос и, кроме того,
покажу, что число X должно быть подчинено единственному требованию
Х>1 (см. также [48] (том I)).
Можно было бы расширить класс интерполяционных многочленов,
обладающих требуемым свойством, но для определенности мы рассмотрим
класс многочленов, которые соответствуют корням многочлена Чебышева
Тп {%) = cos n arc cos z,
принимая, что рассматриваемый отрезок приведен к отрезку [—1, 1].
Известно, что интерполяционные многочлены Лагранжа
A \ тс
к y) Г ' во°бще говоря, не сходятся к- функции
/(#). Достаточные условия для сходимости в существенном те же, что и
для сходимости соответствующих рядов Фурье: так, известно, что для
сходимости достаточно, чтобы f{x) удовлетворяла условию Дини—Лип-
* «Sur une modification de la formule ^'interpolation de Lagrange». Зап. Харк.
матем. тов., 5 A931), стр. 49—57 A59*).
1 При X = 2 требуемым свойством обладает интерполяционная формула Джексона
(Jackson. A formula of trigonometric interpolation. Rend, del Gircolo Mat. di Pa-
Palermo, 37 A914)). См. также мои заметки [16] (tomIJ и F6*) и недавнюю работу
Фейера, которая также относится к случаю X = 2.
130

шица, и легко показать, например, что многочлены Рп(%) стремятся к
f(x) в каждом промежутке отрезка [—1, 1], в котором f{x) имеет огра-
ограниченную вариацию. Мы покажем, что небольшого видоизменения фор-
формулы A) достаточно, чтобы обеспечить сходимость к функции f(x) во
всяком промежутке, где f(x) непрерывна, если только на дополнитель-
дополнительной к этому промежутку части отрезка [—1,1] функция f(x) ограничена.
С этой целью возьмем фиксированное четное число 21 и разделим все
узлы х1^>х2'^>- • *^>хп на группы соседних узлов по 21 в каждой за
исключением последней группы, которая будет содержать меньшее число
узлов, если п не делится на 21. В каждой группе оставим неизменными
21 — 1 значений f(xk) = Aky отвечающих 21—1 первым узлам группы, а
вместо значения f{xk), если k = 2ls делится на 21, возьмем число A2is,
определяемое формулой
A (s—1) 1 + 1 + A (S-1) НЗ +• • •+ Alls— 1 = -42(8—1)
+ A (s-1) Z+4 + • • • + Mis- B)
Так, например, при 21 = 6 число ^16S определяется равенством
^6s—5 + ^6S— 3 + As— 1 = As—4 + As—2 + As-
Интерполяционная формула, которую мы введем, такова
и надлежит доказать, что разность
f(x)-Qn(x)
равномерно стремится к нулю, когда п неограниченно' растет, во всяком
промежутке, где f(x) непрерывна.
Переходя к доказательству, заметим прежде всего, что формула C)
дает интерполяционные многочлены Qn{x) степени М — п — 1, которые
совпадают с f(x) в N^> 77 п точках, так что
М ^ 21 __ ,
и, беря I достаточно большим, можно сделать X сколь угодно близким
к единице.
Так как
ж . ч п sin n arc cos x
то формула C) может быть переписана в виде
=i
131

Следовательно,
Но при фиксированном х
4 * X Z
есть возрастающая функция от z, так как
1 — XZ
E)
u'(z) =
(x — zJVl—z*'
Следовательно, если хко, xkl,. . . образуют монотонно убывающую после-
последовательность и | ui \ <^ а, то
I «о [и (#fto) — и Ы] + «1 № (xkl) — ^ {Хк2)\ + ... |< а | и {хко) | . F)
С другой стороны, если х = cos б, то
cos nb — cos f к Yi
Н
п(х — хк)
п cos 0 — cos ( к —) —
sin к —
1 \ те
2 У я
sine'
где 6' заключено между 6 и [к о~)—• Максимум //' для заданного х
достигается при хк, ближайшем к х, и, значит, при
Следовательно,
если 1 <С к <С п, и
2 ) п
Я<3,
п
G)
если й;=1 или к = г}, так как | rn(^) |<!n2. Таким образом, G) имеет
место всегда.
Нам достаточно рассмотреть часть суммы D), для которой Xi^>x, так
как последующие рассуждения остаются без изменения и для Xi<^x.
Пусть ш (о) означает максимальное колебание функции / (х) на отрезке
длины 8. Тогда h узлов, ближайших к х, образуют часть S1 нашей
суммы, для которой
(l±l) (8)
так как \Ai—f {
если -Try- — целое число.
я) , если — не целое число и, в силу B),
132

Остальные узлы (если таковые найдутся), соединенные в группы до
21 членов, дадут сумму S2, в которой каждая группа порядка t сможет
быть представлена в виде
г—1
cos n arc cos x
п
Принимая, что \f{x)\<^L на всем отрезке [—1, 1], мы, следовательно,
найдем в силу F), что
\S,\<~\u{xio)\,
где #г0 — узел суммы S%, ближайший к х. Но
. /. . h —1\ ти
значргт,
откуда
sm г0 —
п V 2 } п ^ п
2Л "~Л А —1
(9)
Применяя те же рассуждения к части суммы D), для которой хг<^хг
заключаем, что
h '
A0)
Следовательно, при любом е^>0, полагая h = —:r~ и беря п столь боль-
большим, что
8JL
г
9fe IL fSlL
О)
мы получим вследствие A0)
что и требовалось доказать.
Например, при 1 = 1 мы получаем следующую формулу:
X
\ 2 ) 2п
X — COS •
2к
2тг
1
7Г X COS
In
133

Легко видеть, кроме того, что сходимость и свойство принимать значения
в точках
cos
сохраняется, если второй член выражения в квадратных скобках умно-
умножить на 1 + ©л, где s^log тг->0.
¦*-4-
Заметим также, что если задана функция / (х) в п точках cos тс,
то мы получим, вообще говоря, интерполяционную формулу, лучше схо-
сходящуюся, если вместо использования всех известных значений мы изменим
в каждой группе из 21 значений одно из них так, чтобы сумма значений
с четными индексами равнялась сумме значений с нечетными индексами.
Но a priori, естественно, нет никакого основания предпочесть одно зна-
значение другому. Следовательно, целесообразнее строить интерполяционные
многочлены, использующие все значения. Для этого заметим, что на
основании предшествующего мы получим формулу (при /=1)," сходя-
сходящуюся не хуже, чем формула C), если положим
о
где f(xn+1) = f(xn).
Мы получим формулу, еще более симметричную и сходящуюся так же
хорошо, если мы построим Qn(%) по формуле Лагранжа, полагая
Таким образом, в каждое значение, даваемое наблюдением, целесооб-
целесообразно вносить поправку, учитывая соседние значения. Я замечу еще, что
для интерполирования при узлах равноотстоящих подобное внесение по-
поправок (с помощью значений в непосредственно близких точках) уже не
является достаточным. Корректирование более глубокое, которое в этом
случае должно быть произведено, вытекает из моей старой формулы для
отрезка [0, 1]
134

на основании которой
2. Укажем другое видоизменение интерполяционной формулы Ла-
гранжа, которое также приводит к многочлену Р (х) степени п + 2/г — 1,
совпадающему с непрерывной функцией / (х) в п точках, где отношение
— =8 может быть выбрано сколь угодно малым. С этой целью поло-
положим
2 cos п arc cos х ъ i—1)**11 O^lA — х\ . . ^-*ft //1ОЧ
i,Bfc + l) ? F=^P sinBA+l)arcem-2-. A2)
Очевидно, имеем
sin BA + 1) arcsina; , ,.,/icos BЙ+1) arccosa;
в BA +1) * (—^ BA+1)* ~ A3)
Значит,
и, следовательно,
Далее, в силу тождеств'а
которое верно для любого неотрицательного целого р<Сп—1, имеем
х — х
к
2j,j-i I/ l — x" I / 2sinB/i + 1) arc sin—=—-
2 COS n arc COS X Хч/"""^ ^ ^— ^ • /o; i л\ • X — Xk л
(Oh . \ 2a Г~Ц—\2 sm l^^ + 4 arc sm —о— =
A=l
Поэтому
f{x) — P(x)=
О Г* f\C2 to OT»P Г*ГЛО /Y» % "Л \ / L/ \ 7C/ * V / J I' JL ~*~ *~ *Jx7 С
= — J>j ^—__ 2 sin (z/г + 1) arc sm -
Но в силу A3) при — 1 <; x ^ 1

Таким образом, если мы выделим р узлов, ближайших к точке х по обе
стороны от нее, то часть суммы, соответствующая им, будет по модулю
меньше, чем
Остаток суммы содержит две части, из которых нам достаточно рассмо-
рассмотреть одну, например, ту, для которойхи^>х. Эта часть остатка меньше,
чем
где ;?#« — наиболее близкий к х узел рассматриваемой части. Таким
образом,
Следова тел ьно,
Число а^>0 можно взять сколь угодно малым за счет выбора столь
большого р, чтобы
4L ^ <х
tzSp ^ 2 '
и затем выбора такого большого п, чтобы
Равномерная сходимость Р (х) гарантируется в данном случае лишь во
всяком отрезке, лежащем внутри промежутка (— 1,1), и только после
умножения остатка на }/Ч — х2 мы получаем равномерную сходимость
на всем отрезке [—1, 1].
3. Указанные формулы применимы, очевидно, к тригонометрическому
интерполированию при равноотстоящих узлах. Так, формула C) дает
. 2т + 1 о
Sin ц 6 2т
2m+ 1 1L
fc«=o sin
A4)
где 0ft = 2—77т и 4 = / Ffc) для всех значений к, за исключением тех,
которые делятся на заданное число 21; значение А к для к, делящихся
на 21, определяются формулой B). Таким образом, можно также утверж-
136

дать, например, равномерную сходимость к /F) выражения
. 2т 4-1 а
sm9 g kh
4 sin
Подобным образом формуле A2) соответствует формула
. 2т + 1 А
fc=o sin2—=—
где — = 8<^i. Замечу, что при h = m эта формула сводится к фор-
формуле Джексона, которая, как я показал в цитированной заметке, опре-
определяет интерполяционный полином по условиям
Покажем, что выражение A6) равномерно сходится к периодической
функции /(б), если эта последняя непрерывна. Действительно,
. 2т + 1
S1H ^ О 2Ш / ^кг, @)__/ @ )] <)hx\
1! (^sm^F6)
sin2
Рассмотрим, с одной стороны, часть суммы (назовем ее HJ, соответствую-
соответствующую 2р значениям В&, наиболее близким к б. Имеем
С другой стороны, модуль каждого оставшегося члена меньше, чем
2JL 1
Bто + 1)BЛ+1) . в-6Л'
sm2 — —
и, значит, их сумма меньше, чем
О.члтт. птг
27Г—
г 2Ш+1
2ртс
2Ш+1
2
2m
Следовательно,
4L 7Tjt? 4mL AL 1
где а можно взять сколь угодно малым.
4. Решенная нами задача тесно связана со следующим вопросом: можно
ли указать независящую от п верхнюю грань для модуля произвольного
137

многочлена Рп{%) степени п на отрезке [—1, 1], когда известно, что
|^п(#)|<^1 в т надлежащим образом выбранных заранее точках, если
— > X, где X — число фиксированное?
Я покажу, что это возможно, каково бы ни былоХ^>1. С этой целью
построим многочлен Рп(х) степени п—1 так, что
\Рп(хк)\<1 (А = 1,2,..., л)
и, кроме того,
|*-(~т)|<» (-0.1.-.[f]).
где I — целое число, выбранное наперед. Следовательно,
Пусть х = cos 6 — какая-нибудь точка и y = cosb±, где Q1
что
^
таково,
Пусть для определенности 6 }> бх. Тогда
1 Л 7Г
ft-1
2) п АЪ*1п[к
- М 7Г
±Tn{x)Pn(cosb1),
где |^4й|^1. Значит, в силу G), выделяя 21 узлов, для которых
к = I (*!— 1) + 1» • • • > I (*i + l)i получаем
i («х-1) sin (& S-) —
у —*
п
п sin (к —
(я: — хк) (у — я:л)
Рассмотрим, например, вторую из этих сумм, для которой
Имеем
п
~ 2
sin (А — — ) —
2 J п
i+i)+i [cos е -cos (* —У) -^-] [cos ei —
cos (А —
± 3
cos 0 —
L
cos Ik
(COS0 — COS7T2J
A7)
COS 6 — COS I (t± + 1)
138

Отношение
cos ~ cos 0
n
cos 6 —cos l(tx + 1) —
n
где
будет наибольшим, если
Значит, оно не превосходит
Следовательно,
sin
4ЙГ
sm -7—
4я
A8)
Эта грань для \Рп(х)\ несомненно может быть снижена, но неравенство
A8) уже доказывает наше утверждение.
В заключение я хочу указать еще один! процесс гдля получения
верхней грани | Рп (х) | , который применим лишь при
Пусть Рп(х) — многочлен степени п, для которого
?1 (*=0, 1,2, ...,]
и пусть il/ максимум его модуля на [—1, 1], каковой достигается,
скажем, в точке #0 = cos60.
Существует значение к, для которого
т
Но вообще
Значит,
d*Pn (cos 6)
*Рп(совв)
139

поскольку ^п (х0) = 0. Следовательно,
| Рп (cos 6) — Рп (cos в0) |
откуда
и мы видим, что при
имеет место неравенство

55
ОБ ОДНОЙ ИНТЕРПОЛЯЦИОННОЙ ФОРМУЛЕ
БАЛЛЕ ПУССЕНА*
Пусть / (х) — функция, непрерывная на отрезке [—тс, тс]. Предположим,
что заданы значения / (х) в п равноотстоящих точках. Пусть, для опреде-
определенности, п = 2гп + 1. Исходя из формулы
у
т jLJ
к——т
где ак = — , Балле Пуссен1 строит многочлен Рг(х) степени 12т, т. е.
в 6 раз более высокой, чем многочлен Ньютона, который сходится,
так же как и F(x), к рассматриваемой функции f(x), принимая те же
значения, что и f(x), в точках а&, лишь бы f{x) была функцией огра-
ограниченной вариации.
Чтобы получить многочлен F1(x), Балле Пуссен поступает следую-
следующим образом. Имеем
sin rnx
полагая
k=m+i
Аппроксимируя затем Q (х) посредством многочлена S (х) степени р так,
чтобы
* «Sur une fonnule d'interpolation de M. de la Vallee Poussin». Зап. Харк. матем.
тов., 5 A931), стр. 61—64 A61*).
1 «Sur la convergence des formules d'inlerpolation entre coordonnees equidistantes».
Bull. Acad. Belgique, 1908.
Ш

легко видеть, что многочлен
Fx(x) = P{x)S(x) у (~1)Ь/К; *1**> D)
к——т
степени 2т + р, который совпадает с / (х) в точках ак, стремится к F(x),
гак как
к=—т
Степень р = 9,92 т многочлена^ (х), которую находит знаменитый автор,
можно значительно понизить: достаточно сделать р =[2,8 т. Таким обра-
образом, отношение степени многочлена F± (x) к f степени соответствующего
многочлена Ньютона может быть понижено до
?+?--2,4.3
Чтобы прийти к этому, мы используем верхний предел наилучшего
приближения Ep[(f[(x)] на отрезке [—1,1] при помощи многочленов
степени р, доставляемый известным неравенством1
где 6 — меньшая полуось эллипса, имеющего —1, 1 в качестве фокусов,
внутри которого ср (х) голоморфна и на котором |ср(#)|^ЛТ.
Применим эту формулу к функции
)]= П ^-т
Начнем с замечания, что на каждом из рассматриваемых эллипсов
максимум | ср0 (х) | достигается для чисто мнимых значений х.
Достаточно убедиться, что каждый множитель ср0 (х) обладает этим
свойством, т. е. что
| а — (]/62 + 1 cos 6 + ib sin 6J[| <А + б2,
если |Л> 1.
Но это неравенство эквивалентно такому:
[А - (б2 + 1) cos26 + б2 sin26]2 + 462 (ьа + 1) COs2 6 sin2 0 < А2 + 2АЬ2+ б4,
которое сводится к следующему
cos2 6 (cos2 6 — 2А) + 262 cos2 6 A — 2А) < О,
где знак равенства может иметь место лишь при cos 6 = 0-
1 См. «L. S.», стр. 111.
142

Следовательно, значение М, которое надо взять в формуле E)г
равно
Легкое вычисление дает асимптотическое значение М для весьма
большого т. Действительно,
Jm+1
= пЬ — 2logb — 2barctg-|- —
Значит, при
если т->оо.
Заметив вместе с Балле Пуссеном, что
на [—1, 1], мы заключаем, что можно выбрать многочлен S (х) степени р
так, чтобы иметь на [—тг, 7г]
<?(*)
Ь*
где л = -^-
Возьмем Ь = -г- . Тогда
о
/Т'
' +
~гс-2
" 4-Зл
и, следовательно, достаточно, чтобы было
откуда
Х>2,73. (9)
Это значение, должно быть, весьма близко к тому, которое минимизи-
минимизирует (8). Как бы то ни было, неравенство (9) доказывает справедливость
нашего утверждения.
Формула A) Балле Пуссена, так же как и ее преобразование, схо-
сходится к функциям той же природы, что и формула тригонометрического
интерполирования с равноотстоящими координатами. Видоизменяя фор-
формулу A) так, как мы это сделали для соответствующей формулы
143

Лагранжа, мы можем освободиться от всякого ограничения относительно
природы непрерывной функции /(#).
Применяя наш первый способ, мы должны заменить значение /(а&)
в точках, где к =? 2ls является кратным данного числа 21, таким значе-
значением Ак, чтобы
Аш = f («2ia-:i) — f (a2Zs-2) + -••+/ («218-ai+i)-
Полученный после этого видоизменения многочлена Fx(z) многочлен
той же степени 2р + т, обеспечивающий сходимость, будет совпадать
2ls
с f(x) во всех равноотстоящих точках ак, исключая спи = it, где Z —
данное число.
Второй способ позволяет сохранить все узлы без исключения ценой
некоторого увеличения степени многочлена.
С этой целью заменим формулу A) формулой
sin тх т (— 1)А/ («*) sin h (х — а*.)
v ' hm ZJ {x — cckJ 9 v '
U =—m
где — =о<1.
Заметим сначала, что равномерно в каждом отрезке промежутка
sin mx
так как имеет место тождество (при
sinmx
поскольку, каково бы ни было ?,
sin /тга?
sin/г (а? — g) _ ~ (— 1)й sin /г (aft —
Значит, в каждой точке внутри (—it, -тг),
lim ГФ (х) — (х)] = lim sinmx V (-l)fe[/К)-/W]
к=—га
Разложим сумму на две части: первую 2i» Для которой \х — а& |
я вторую 2г> Для которой \х — аи\^е. Тогда IV
<о (s) — максимальное колебание f(x) на отрезке длины г, и
оо
х 41/ С dx 4L 4L
), где
е
144

Но мы можем увеличить т так, чтобы 7nsco(s)-»0 в то время, как
гаг->оо. Отсюда следует, что
lim [Ф (х) - f (x)] = 0.
т->оо
•г, sin hx ^
Выполнив над -—т— то же преобразование, которое привело нас
sin тпх т\ / \ п / \
к замене многочленом Р ух) о (х), мы получим интерполяционный
многочлен степени (р + 2т) A + 8). Так как о можно взять произвольно
малым, то сходимость для всякой непрерывной функции может быть
также осуществлена интерполяционным многочленом, степень которого
не более чем в 2,4 раза более степени многочлена Ньютона.
Чтобы гарантировать равномерную сходимость на всем отрезке
[—7г, it], достаточно в A0) распространить суммирование до Ч- A + а) т,
при сколь угодно малом а>0, полагая /(afe)— /(тг) для а^^тс
и / Ы = / (— «) Для ак < — те.
10 С. Н. Бернштейн

56
OB ОДНОМ КЛАССЕ ИНТЕРПОЛЯЦИОННЫХ
ФОРМУЛ*
1. Никакое распределение узлов в интерполяционном многочлене Ла-
г'ранжа не может, как известно, гарантировать сходимости этих много-
многочленов, если непрерывная функция совершенно произвольна.
Я дал последовательно1 два различных метода для устранения этого
недостатка, заменяя многочлены Лагранжа многочленами, отвечающими
тем же узлам, ни имеющими степени несколько большие. Я хочу раз-
развить здесь некоторые замечания, касающиеся этих методов.
Проблема интерполирования посредством многочленов эквивалентна
проблеме тригонометрического интерполирования; рассмотрим для опре-
определенности эту последнюю.
Пусть /@) — непрерывная функция с периодом 2тг, заданная в 2т + 1
равноотстоящих точках
Образуем тригонометрическую сумму
• 2Ш + i /А А \ • 2k
sn F 0) Sin
2m
• 2Ш + i /А А \ • 2k + 1 /A AN
sin F — 0Л) Sin 7j (в — 0Л)
Bft+ 1J
о sin2
порядка m + h = n (h^.m), которая, очевидно, удовлетворяет условиям
i>n(e*) = /(9.s) (A = 0, 1, 2,..., 2т).
Полагая
п
pn (fj^ = _° -f- У] Ai cos ?6 + B{ sin ?8 B)
z i
* «Sur une classe de formules d'interpolation». Изв. АН СССР, ОМЕН, №9A931),
стр. 1151—1161 A52*).
1 См. [54] и [55].
146

и принимая во внимание тождество
^ 0 sin —^— 0
- g - = 2й + 1 + 2 {[2/г + 1] [cos б +
sin
2hcos(m — h + 1N + . . . + 2 cos (/и + /г —1N
+ cos (m—h) 6J +
3os(w + h) 6},
находим
2m
л—о
2m
..>..,.,)
i^C m — //,
= 2h
Л-0
C)
J
Заметим, что крайним случаям, когда h = 0 и h = т, отвечают соответ-
соответственно классическая формула Лагранжа и формула Джексона1. Все
промежуточные формулы, для которых 0<^h<^m, характеризуются тем,
что коэффициенты Рп(Ь) при i^m — h совпадают с соответствующими
коэффициентами формулы Лагранжа, тогда как остальные попарно удов-
удовлетворяют соотношениям
= — (n + l — i)Bh D)
если
. Можно также отметить, что при т —
E)
где Л?, В? означают соответствующие коэффициенты классической фор-
формулы Лагранжа. Отсюда коэффициенты при т <^ i ^ n выводятся по фор-
формулам D).
Существенно подчеркнуть, что в силу сказанного тригонометрическая
интерполяционная сумма Pm+h F) в случае, когда /F) — тригонометри-
тригонометрическая сумма порядка не выше т — /г, совпадает с этой последней:
Покажем теперь, что
если
|/F*)!<Af.
F)
(V)
1 Jackson. «A formula of trigonometric interpolation». Rend, del Gircolo Mat-
di Palermo A914); С Н. Берн штейн, [16] (том I).
147 10*

С этой целью заметим, что
1
Bm + 1) BЛ + 1)
= 1,
(8)
так как рассматриваемая тригонометрическая сумма, имея порядок не
выше h и не изменяясь при замене 6 на 6 + ———г , должна сводиться
к константе. Эта константа является суммой постоянных членов отдельных
слагаемых суммы (8). Так как каждый из этих постоянных членов равен
1
то указанная константа есть
2т+1 '
2m + 1
JB силу неравенства
2т
2т + 1
2m + 1
F-0*)sm:
sin2
у
— 6,
= Bm + l)Y{2m
получаем, таким образом, что
Знак равенства может иметь место лишь при h = m. Но в случае, когда
дг __ 2т + 1
iV ~" 2Л + 1
— число целое, мы дадим верхнюю грань для |Рт+л(в)|, которая может
достигаться.
Если
|/(е*)|<1 G'}
к если
дг 2т + 1
ес/иъ «fe^oe число, то
J_r_L_
LSm2iV
2iV TC J
(9)
J48

Действительно, положим к = IN + р, где X и
тельные числа, и пусть zk = 6 — 6&. Тогда
— целые неотрица-
неотрица1
sm
Bm + 1) BЛ + 1)
. 2m + 1
sm
sm
z0
JV-1
. гн
2h
2т+ 1
. 2т
sm —-с
N—i
2
. 2Л + 1
sm — 9
2ртг
2ртг
jv—i
N—1
р=о sm
причем абсолютный максимум этой суммы действительно достигается при
Ч -о - W •
Весьма замечательно, что тригонометрическая сумма Pm+/i W> которая
реализует экстремум, имеет порядок т — h, так что наше предложение
можно уточнить следующим образом:
Если тригонометрическая сумма Sm—h(fy порядка т — h численно
не превосходит 1 в 2т + 1 равноотстоящих точках
то для любого вещественного б
2т + 1 '
N-1
(9';
р=о sm
при условии, что
N =
2т + 1
— число целое*. Кроме того, значение L действительно достигается
* Очевидно, что при фиксированном т верхняя грань | Sm__h F) | монотонно убы-
убывает с возрастанием h. Поэтому, если N — нецелое число, то
шг ^J
[ЛГ]
^
. 2р + 1
fell! ^г ¦ т~г 7t
(Автор.)
149

тригонометрической суммой
дЪж-ь (V) = ^ 2j 2/1 + 1 •
p=osin—^— @ — 6р)
Достаточно заметить, что
S*m-h (в*) = (-1)"+х = (- 1)р (где к = Ш + р)
И ЧТО
'2N — 1
Неравенство F) позволяет доказать сходимость интерполяционной
формулы A), какова бы ни была непрерывная функция /F), если только
отношение
2т + 1
2/г + 1
we растет до бесконечности.
Действительно, пусть
Pn = maX|/>n@)-/F)|,
где Рп($) дается формулой A); пусть, с другой стороны, Qm__h\b) есть
тригонометрическая сумма наилучшего приближения для /F) порядка
т — h и Ет—ъ, [/F)] — соответствующее наилучшее приближение. На осно-
основании предшествующего, если мы в формуле A) заменим /F&) на Qm~.h (M,
то в левой части получим (?m-7iF)- Следовательно,
2т
. 2т-
sm
откуда, в силу F),
| Рп (Ь) - Qm-П F) ! <
Значит,
[/(в)]
что и доказывает наше утверждение.
Используя (9) вместо F), можно, конечно, улучшить оценку погреш-
погрешности рп, даваемой формулой A), так как легко видеть, что
п
2
— С 4^-~—logA7 A3)
7Г J SinZ 7Г & Я ;
2N
150

при iV->oo. В частности, мы видим, что даже при iV->oo формула A)
сходится, если /F) удовлетворяет условию Дини—Липшица.
Я замечу еще, что все заключения сохраняются в силе, если фор-
формулу A) заменить формулой
1 2m-1 sin™ F — 6.)sin/i@ — 6*)
р^) = шн 2 —¦—<Ь>г—- ><e*>' <4')
о smz
где
п = т + h — 1.
2. Добавлю еще одно предложение, которое относится к тому же кругу
идей:
Если тригонометрическая сумма* Sn(Q) [порядка п достигает абсо-
абсолютного максимума М в промежутке @, а), где а<^-т-, то имеет место
неравенство
М < ^п @) + Sl («) ~ 2Sn @) «?п(«) CQS »«
sm па.
равенства достигается при
Sn (a) sin nQ -f ^n @) sin n (a — 0)
n ^ ' sin na
Покажем прежде всего, что значение М ограничено сверху. С этой
целью образуем сумму Q*n F) порядка п, которая наименее уклоняется от
еуля среди всех сумм порядка п, удовлетворяющих условиям
где
Очевидно,
л*
и наименьшее уклонение равно
Действительно, если бы существовала тригонометрическая сумма <pn(G)
порядка п, для которой
(<p«@) = 0, ?„(во) = 1),
то тригонометрическая сумма
?!-?" (в)
* В дальнейшем ^п @) и Sn (a) предполагаются вещественными. (Ред.)
151

порядка /г, обращающаяся в нуль в точках 0 и 60<Су~> имела бы еще
л л тс о 2к 4-1 ^* /ЛЧ
2/г — 1 нулей, превосходящих ^-, между 2гс точками —^—тс, где (/пF)
имеют чередующиеся знаки.
Таким образом*, расстояние от корня уравнения Qn(b) =0 до точкиу
где Qn F) имеет абсолютный максимум, не меньше, чем -^—.
Отсюда следует, что точки, где
|?«F)-?«@)| и \Sn{%)~Sn{a)\
имеют максимум, лежат соответственно вне промежутков
Значит, на основании A5), предполагая, что
получаем
откуда
1 + sin
1 — sin —
Поскольку величина il/ ограничена, существует тригонометрическая
сумма б'п(б), для которой М достигает своего максимума М*.
Я утверждаю, что число к точек 6Х, 62, . . ., 6^ максимального уклоне-
уклонения (с чередующимися знаками) этой суммы ?пF), внешних для @, а)>
равно по меньшей мере 2/г—1.
Действительно, пусть 60<^а есть внутренняя точка промежутка @, а)>
где
и пусть, для определенности, AS'nFi)>0. Исследуем вначале предположен
ние, что число к<^2п — 1 четное. Тогда тригонометрическая сумма
. е . в— ро.е — а.е—рх .
срF) = sinysin 2MOsin——sin—2""-i. . . sin
где
к 4- 2
порядка <1и, имеет в точках Ьг (i^>0) знзки, противоположные-
знакам функции Sn(Q), и можно так распорядиться величиной C0, чтобы
* Это утверждение остается в силе и тогда, когда коэффициенты Qn @) комп-
комплексны, так как случай | Qn {%) \ = 1 умножением Qn @) на ега можно привести к-
рассмотренному выше случаю Qn(%) = 1. (Автор.)
152

Значит, при Х^>0 достаточно малом сумма
имела бы абсолютный максимум в промежутке @, а), превосходящийМ*.
Подобным образом, если к<^2п — 1 — число нечетное, достаточш>
образовать сумму
где рл>6Л, порядок которой не превышает п Iтак как —к—^п), чтобы
убедиться в невозможности этого предположения.
Следовательно, абсолютный максимум |*SnF)| достигается по крайней
мере в 2п точках. На основании сделанного выше замечания расстояние
между двумя соседними из этих точек равно —, и поэтому обязательно
где постоянные М*, с определяются при помощи данных значений Sn@),
Таким образом,
М* cos пс = Sn @), М* cos п (а + с) = ?п (а),
откуда
„ Sn (a) — iSV @) cos /га
n F) = Sn @) cos nb + sinwg sin /гб. A7)
Значит,
М- = ^Sn (°) + ^п («) - ^п @) -Уп («) «OB «а / -_ч
sin /га \ п) \ г
И
Л/<ЛГ, A4')
чти и требовалось доказать.
В частности, если
5Л@) = 5я(а) = 1,
то
a
cos^?-
2
причем равенство имеет место для
cos п (8 ^-
В этом случае абсолютный максимум действительно достигается при
6 = у между 0 и а.
Но предыдущее рассуждение вовсе не показывает, что должна суще-
твовать тригонометрическая сумма Sn(b), принимающая произвольно
заданные значения Sn@), Sn(a) и достигающая своего абсолютного.
153

максимума М в промежутке @, а). Мы доказали только, что если такая
сумма порядка п существует, то сумма, имеющая наибольшее значение
М* этого абсолютного максимума М, дается формулой A7).
Следовательно, условие, необходимое и достаточное, чтобы абсолют-
абсолютный максимум достигался в промежутке @, а), состоит в [достижении
максимума суммой A7) в этом промежутке.
Значит, чтобы абсолютный максимум Sn @) мог достигаться в про-
промежутке @, а), необходимо и достаточно, чтобы имели место оба не-
неравенства
сп,п, >cos ш, -А^Г >cosш' B0)
если
и по крайней мере одно из неравенств B0), если
Например, если Sn (а) = 1, Sn @) = — р, где 0 < р <^ 1, абсолютный макси-
максимум *?п(8) может] достигаться в промежутке @, а) лишь при а^>—arccos(- p).
Следствие. Если
|?п@)|<1, |5Л(а)|<1, B1)
где а<—, и если абсолютный максимум М выражения \Sn(b)\ дости-
достигается в промежутке @, а), то
М<-^-- A9)
cos —
2
Это очевидно при а ^> ^- , так как максимум A8) при условиях B1)
реализуется при Sn@) = Sn(a) =- 1. Но благодаря неравенствам B0) при
а<^— заключение также остается в силе.
Из A9) можно вывести следующее заключение:
Если | Sn @&) | <^ 1 в 2).п равноотстоящих точках
•где ),^>1, то для любого вещественного 0
—Ц-. B2)
При этом знак равенства действительно реализуется для К целого сум-
суммой
C0S
~~ 2Г")
COS——
2Х

57
ДОБАВЛЕНИЕ К СТАТЬЕ Е. В. ВОРОНОВСКОЙ
«ОПРЕДЕЛЕНИЕ АСИМПТОТИЧЕСКОГО ВИДА
ПРИБЛИЖЕНИЯ ФУНКЦИЙ ПОЛИНОМАМИ
С. Н. БЕРНШТЕЙНА»*
Полученный Е. В. Вороновской (*) интересный результат, что для вся-
всякой функции f (х), имеющей непрерывную вторую производную f (х)
на отрезке [0,1], справедливо предельное равенство
[п / \ "|
i (v\ "V пт f i ) т™ М т\п—т\ ~ (\ v\ f" (v\
7 \х) — ZJ Сп ' \ п J х V1 d) — 2~ X [1— X) J (X),
0 J
может быть получен несколько иным способом и в более общем виде.
Обозначим через Sjctn(x) многочлены1 степени к относительно х
п
?*, п (ж) = Мат. ож. (^ — х\ =2 (~- — х)к С™хт A— х)п-т .
* Докл. АН СССР, A932), стр. 86—92 A56*).
1 В частности, имеем
ж) A—2а:)
У L
A - »)» » A - ,) [1 - 6х A - х)]
жJ [5— 26а; A— х)\
а: A — х) [1 — 30* A — х) + 120x2 A _
Вообще, имеем рекуррентную формулу
1, n
155

В таком случае, для всякой функции, имеющей непрерывную про-
производную порядка к — 2?, справедливо асимптотическое равенство
О
1 п
где s стремится к нулю с возрастанием п, а потому
27!—lim Л' S^ № = — [ T~ \
Для доказательства A) достаточно заметить, что
2i
где а стремится* к нулю вместе с х, и кроме того, что
^ 2
если о j/ /г -> сх).
Из формулы B) заключаем, что для всякой бесконечно дифференциру-
дифференцируемой функции справедливо на отрезке [0, 1] асимптотическое выражение
которая вытекает из того, что
n '
971=0
а потому
Можно дользоваться также формулой
Sk+U п (х) = X(i~X) [ ^*, п
которая является непосредственным следствием определения S^ n (х).
* Применяя формулу Якоби для остаточного члена, получаем (при наличии про-
производной порядка 2* + 1)
1
) $ ( (ir- X))du'
(Автор.)
156

Кроме того, если функция f(x) аналитическая на отрезке [0,1]
и имеет в точках 0 и 1 радиус сходимости не менее единицы, то, оче-
очевидно,
является точным равенством для всякого целого п, причем вторая его
часть будет сходящейся для всех значений х @<ix<^i), так как
при
*>2, ?>4- .
Z
При этом сходимость распространяется также и на комплексную об-
область, ограниченную четырьмя дугами парабол, имеющих соответствен-
соответственно прямые у = Чг1 своими директриссами, а точки 0 и 1 — фокусами
и
так как внутри этого контура
\Sk,n(x)\<An&,
где Ап — постоянная, не зависящая от к, а 8 — большее из двух рассто-
расстояний от а; до 0 и до 1, и, следовательно,
при данном п.
Нетрудно убедиться, что для пригодности формулы C) на всей пло-
плоскости достаточно, чтобы /(Л) (х) возрастали при возрастании к не быстрее,
чем в геометрической прогрессии [т. е. чтобы функция / (х) была транс-
трансцендентной целой функцией не выше 1-го рода и конечной степени].
Действительно, вследствие тождества
со о /дЛ ъ _ta Г t ~\n
2 "V =е 1+*(е^-1)
Л=0 L J
имеем
мп
п 2
157

где М — максимум модуля на окружности С радиуса V п функции
Таким образом,
оо
М ^ \ Л- \хA~х)\ У/^-1 _ л , I ^ A — *) I
если | х | <^ КдГ, 11 — х | <; К^Г- Следовательно, каковы бы ни были А и п,
<-^e^-^ E)
/г 2
при |ж|<Т7^, |1 —ж|
Неравенство E) полностью доказывает наше утверждение.
Сходимость формулы D) во всей плоскости при фиксированном п
имеет место при более широких условиях: необходимо и достаточно,
чтобы f(x) была целой, так- как при фиксированном п и данном х
Sic,n(%) возрастает вместе с h не быстрее, чем в геометрической про-
прогрессии.
Заметим, что равенство B) может также быть использовано для за-
замены многочлена Рп(%) многочленом аналогичной формы, быстрее схо-
сходящимся к функции, если последняя имеет высшие производные.
Например, полагая
<ы w - 2 [г (т-) - ^ г (¦=¦)] С *¦¦ A - *>--.
О
находим
limл2 КМ*)-/(*)] =
- щ,
если функция /(ж) имеет непрерывную производную 4-го порядка.
ЦИТИРОВАННАЯ ЛИТЕРАТУРА
г. Е. В. Воронове к а я. Докл. АН СССР, А, A932), стр. 79—85.

58
ЗАМЕЧАНИЕ ПО ПОВОДУ ЗАМЕТКИ Р. САЛЕМА*
Р. Салем * рассматривает функцию
f(x,al9 ...,an)=
p=i
где коэффициенты rv^0 заданы, и исследует наименьшее значение ма-
максимума М ее модуля на действительной оси. Он получает интересный
результат:
где
п
вп = 2 гр>
р=1
и одновременно ставит вопрос: существует ли такая постоянная .D, не за-
зависящая от Гр и и, что М всегда меньше D ]ЛВП.
Я покажу, что такой постоянной D не существует и что порядок
величины М именно тот, который дает неравенство Салема.
Действительно, положим п== 4т и гр = 1 при р = 4k (k<^im) и
гр = 0 для остальных значений р. Тогда будем иметь
f(x) = e W1 *+«m> + е i^m~1 x+«m-i). . . + eiD:"+ai)- A)
Каковы бы ни были ах, а2, . . ., ат, можно взять
где целые числа bl9 b2, . . . последовательно определятся из неравенств^
2
* «Remarque a propos d'une Note de M. R. Salem». Comptes rendus, 197 A933)^
стр. 213—214 A64*).
1 Gomptes rendus, 196, 12 июня 1933 г., стр. 1776 (см. также стр. 1951, 26,
июня).
159

и т. д. В таком случае первый член / (х0) будет равен единице, а все
остальные члены будут иметь действительные части, не меньшие,
чем -71=.
V2
Следовательно,
I W 1 >. 171
n log Я
и так как Вп = гп, а т = —~ , то видим, что
Заменяя 4fc на 6fe в выражении A), можно несколько улучшить резуль-
результат и получить
Кроме того, беря Ък (вместо 4й), замечаем, что при Ъ-^оо макси-
максимум модуля функции f(x), данный равенством A), стремится к тому же
самому пределу т = ВПу каковы бы ни были а&.

59
О ТРИГОНОМЕТРИЧЕСКОМ ИНТЕРПОЛИРОВАНИИ
ПО СПОСОБУ НАИМЕНЬШИХ КВАДРАТОВ»
Интерполирование по способу наименьших квадратов периодической
2/
функции f(x), значения которой даны в равноотстоящих точках
{к == 0, 1, ...,/? — 1), приводит к суммам
h
п=0
коэффициенты которых определяются формулами
р-1 р-1
_ 2 VI ,/2/сттЛ 2/с/?
при всяком h <^ —- • Таким образом,
р-1 Г &
2 XI ^ /2*ти Л 1 , VI / 2/сти
/>_\/?/^ V р
21г +
- р 2*f[—)—i
2/сти
sin -y I х —
При /? = 2m + 1 нечетном последняя формула обращается в формулу
точного интерполирования Лагранжа, когда h = m = —— . В случае
р = 2т, точная интерполяционная формула порядка т, все коэффициенты
которой для п<^т. попрежнему даны формулами B), получает форму
2т
С //у\ k у ( \ \ "к ¦(¦ ( I о\ п* — i т —— —— I f h С1 Т\ ТУ) Т (•) )
m ^^ \ m J \ m j
где b — произвольная постоянная.
* Докл. АН СССР, 4 A934), стр. 1—8 A68*).
11 С. Н. Бернштейн 161

Из C) легко вывести, что при условии
/2/стс
D)
соблюдается неравенство
р-1
&=0
sm
2кп
sm
2/стг
2Л + 1
sin —г; тс
E)
где n0 — \ », p ¦¦; , т. e. порядок возрастания,5/, (ж) при всяком а; не выше log А.
Из E), применяя известные рассуждения, находим, что (при всяком х)
I / (*) — Sh (х) | < [log Bh + 1) + 3] Ebf (x),
F)
где Ehf(x) означает наилучшее приближение f{x) посредством сумм по-
порядка h.
Еще более удовлетворительный результат получается, если взять
среднюю из сумм Sh по образцу Фейера.
Действительно, полагая а^ =
ствие C),
находим, вслед-
sin
2кп
"• Р
к=о
2/стг
—
Р J
sm 2" i а; —
sm -я- 1 х — -
2/стг
G)
Но, замечая, что ah = lf если /f j = 1, заключаем, что из усло-
условия D) следует
Ы<1 (8)
при любых х и /г ^ -~- .
Отсюда, применяя обычные рассуждения, легко вывести, что при
неограниченном возрастании h разность ah (х) — f (x) равномерно стре-
стремится к нулю, какова бы ни была непрерывная периодическая функция'/ (х).
Можно также рассматривать более общий случай, когда
{К)
V — 1
sin [I +
¦т)(-
2Атг \ Л
—j sin -у
1Ы
—
(9)
Г . 1 / 2/стс \1
[sm — ^-—)\
В данном случае Иг также ограничена, если ограничено —. Дли
этого достаточно заметить, что
162

p-1
s
sin
h \/ 2for\ . _Л_/ 2кп\
2kn \f
sin U +
AW 2&7Г \n
sin
Поэтому, при условии D) имеет место неравенство
Е
A0)
Замечая, что Е =*Уь если /( j являются точными значениями
суммы порядка не выше Z, из A0) выводим неравенство
/(*)-s
(И)
которое показывает, что Е (представляющая собой сумму порядка
I-\-h—1) дает для любой функции f{x) приближение порядка не нижеу
чем наилучшее приближение Е\ [/ (х)] посредством сумм порядка I (если
полагать —г- ограниченным).
Отметим еще другое свойство сумм Sh(x), аналогичное свойству частич-
частичных сумм Фурье, доказанному мною в заметке [49] (том I). При условии D),
Sn(x) + Sh(x + 2h ^ А остается ограниченной, каковы бы ни были
х и Л^-^-.
Для определенности и* краткости я ограничусь изложением вывода
лишь при условии, что h = т и р = 2т + 1 [следовательно, Sm (x) есть
произвольная тригонометрическая сумма, определенная значениями
которые она принимает в точках .
Из равенства
Нт (х) = 2 ian cos nx + Ъп sin nx) cos
-и*
п=0
X
2т + 1
2m + 1
2т
COS
2т
2Bт
sin
A2)
. 1 / 2A-1 \
in~[X-2m-TTn)
~T7 2k+ 1 \\ >
mT[X-2m^fT7Z)\
предполагая (как мы вправе это сделать без нарушения общности), что
—т-, заключаем, что
sin ¦
163
11"

cos ¦
2m + 1
2m
2m + 1
cos n x
sin
2k — 1
2m + 1 :
us 2 л Г 1 1
2 Bm + 1) I 1 / л: \ + . 1 / тс
LsmT V2^+l ~x) sm Tl2"^
sm -7Г
1 /2m — 1
\2
Г
1
1
1 Bm
sm -^
2m — 1
sinTl*+2m-
1
sm -
_
cos
~2
2 \ 2m + 1
1
-fa;
sin
Зти
2 \2w+l
1
2m
1
sm
— x siti
1
¦-ч\.
cos " I
2 \2m + l "J ^ 2 \2m +
причем знак равенства соответствует случаю, когда /(- т) ~ (—ч »
где 0<^А:^га, и/(-—-^г-) — (—1)^, если к === 0 и к^>т. Тогда сумма
2к + 1
Нт(х) порядка га, обращаясь в нуль в точках -—цтт71» ПРИ 2га — 2 зна-
значениях #, не делящихся на га, достигает абсолютного максимума при х =0.
Откуда следует неравенство
A3)
Lsin
Аналогичным образом, при р = 2га, из условия D) при помощи фрр-
мулы C') получаем неравенство
4-
2
A3')
в котором знак равенства осуществляется для х =0, если
/стс
Применим в качестве примера полученные результаты к оценкам
некоторых сумм, связанных с суммами Гаусса. Пользуясь символом
Якоби (—], где р — нечетное число без квадратных множителей, пола-
164

гаем /( ) = (— )• Согласно формулам B) и известным свойствам сим-
символа Якоби, интерполяционная формула Лагранжа дает (р = 2т + 1)
Sm (х) = -р= 2 (—) cos пх или Sm (х) = ¦— ^ (— J sin пх, A4)
р 1 р 1
в зависимости от того, четное или нечетное число т.
Таким образом, вследствие E), все частичные суммы Sh{%), где h^.m9
при всяком х будут порядка не выше log h. С другой стороны, вследствие
(8), соблюдаются неравенства1
~~~) (^ —п)cos nx
S/ /г \
sinnx
A5)
Аналогичные неравенства получим, применяя A0). Применение A3) дает,
при любом х, неравенства
р-1
2
Е/ /г \ /гтс
COS — COS ПХ
г \Р J P
Кроме того, суммы
h
р-1
2( п \ rnz .
— cos— sm nx
г \ Р J P
COS;
lh + 1
cosnx или ——
также ограничены.
Vp
- A6)
1 Эти неравенства являются обобщением тех, которые были даны мною в статьях
[16] и [17] (том I).

60
OB АБСОЛЮТНОЙ СХОДИМОСТИ
ТРИГОНОМЕТРИЧЕСКИХ РЯДОВ*
1. Пусть
J со
f(x)~ 2 (ап cos nx + bn sin nx) A)
непрерывная периодическая функция с периодом 2я, и пусть En[f{x)]
означает ее наилучшее приближение тригонометрическими суммами по-
порядка п.
Если ряд
сходится**, то ряд A) сходится абсолютно. Напротив, если монотон-
монотонная последовательность {Е'п}, стремящаяся к нулю, такова, что ряд
расходится, то можно построить функцию f(x), для которой
En[f{x)]<E'n
и разложение A) которой не сходится абсолютно1.
C)
* «Sur la convergence absolue des series trigonometrique». Gomptes rendus, 199
A934), стр. 397—400A70*).
** Из сходимости ряда B), члены которого убывают, вытекает lim V"n En[f (x)] = 0;
отсюда следует равномерная сходимость тригонометрического ряда A). (Автор).
1 Будет уместно отметить здесь полную аналогию этого предложения с теоремой,
доказанной в моем мемуаре «Sur l'ordre de la meilleure approximation des fonctions
continues par des polynomes de degre donne», Memoires Gl. de Science de PAcad.
Belg. 4 A912) D6*), стр. 23—29 (см. также [3] (том I)), где существование не-
оо
прерывной производной связано таким же образом со сходимостью ряда ^ En[f(x)].
71 = 1
166

Для доказательства * первого утверждения заметим, чтох (неравенство
(9)), благодаря сходимости B),
2j cos 2m i 1 [ak cos кх + Ък sin кх] | =
— 2 cos 2т + 1 ^ C0S ^Х + 6* sin *Ж1
Отсюда при помощи равенства Парсеваля выводим
[т]+1
и, применяя неравенство D) статьи [16] (том I), полагая последовательно
m=2h(h = l, 2, ...), получаем
Г8т-}
. е.
А;=4
Следовательно, учитывая, что
так что
2h-l ^
2
заключаем
Чтобы построить функцию с не абсолютно сходящимся тригонометриче-
тригонометрическим рядом, удовлетворяющую C), я полагаю
* Мы даем здесь несколько более развернутое доказательство, чем в первона-
первоначальном тексте. (Автор.)
1 Gomptes rendus, 191 A930), стр. 976, [49] (том I).
167

где
рк — простые числа, удовлетворяющие неравенствам Зрк<С.Рк+1<^$Рк>
S 77 ^ ~ ^ cos lx
2 р" / / \
= р S V7")(/?"Z) sinlx (при ^ =
—) = + 1 обозначает символ Лежандра1.
Р J
Таким образом, будем иметь
где рк ^п<С.Р]{оЛ.1- Но, с другой стороны, сумма модулей коэффициен-
коэффициентов* F (х) должна быть больше, чем
5 V
7 7
=р2 п=р2
так как
Рк
2. Принимая во внимание общую теорему Джексона, согласно которой
1
1 Gomptes rendus, 158 A914), стр. 1661 F6*).
* Преобразование G) было бы незаконно, если бы мы имели Jim Vn 2^>o-
п->оо
Но в этом случае в примере E) можно заменить Е* через —— < е' (с > 0 постоян-
V п
ная), т. е.
так что
и в то же время ^V ^p = oo. {Автор.)
k=l
168

где со (8) — модуль непрерывности f(x), непосредственно получаем и»
первой части нашей теоремы: для абсолютной сходимости разложения
A) достаточно, чтобы ряд
был сходящимся.
Предположим, с другой стороны, что можно выбрать а
так, чтобы
была убывающей функцией переменной 8 [60.1]. Если ряд
расходится, то можно построить функцию f(x), модуль непрерывности
которой о (о) <^ о'(о) и тригонометрическое разложение которой не схо-
сходится абсолютно.
Достаточно построить функцию E), полагая
Е' = Ы (-) ,
где L — произвольная достаточно малая положительная постоянная.
Таким образом, в частности, для абсолютной сходимости A) доста-
достаточно, чтобы
Напротив, сходимость может не быть абсолютной при
Разумеется, в этом последнем случае будут также существовать
функции с абсолютно сходящимися рядами. Легко даже построить такую
функцию с модулем непрерывности о>(8), стемящимся к нулю медленнее
произвольной монотонной функции о/(о). Действительно, достаточно об-
образовать функцию
? (я) = 2 lEsh—^s
cos
где Е'п = 6 о)Ч — V разложение которой сходится абсолютно и которая
обладает свойством Еп [<р (х)] J> E'n (так как Еп [ср (х)] = Е'ф при
З ). Следовательно,
каково бы ни было п [60.2].

61
О НЕКОТОРЫХ ЭКСТРЕМАЛЬНЫХ СВОЙСТВАХ
ПОСЛЕДОВАТЕЛЬНЫХ ИНТЕГРАЛОВ*
Г. Бор1 дал (без доказательства) предложение, эквивалентное сле-
следующему:
Если функция f (x) удовлетворяет условиям
\f{x)dx = 0, /B«) = /@) A)
О
и |/'(жI^1 при'0-^х^2тс, то на том же отрезке [/(?)|<Г-тг.
Мы обобщим это предложение, принимая, что
2п
S/(a;)dx = O, у(«B«) = /»)@) (к = 0, 1,... , п - 1) B)
О
и |/(")(х)|<1.
Рассмотрим сначала случай, когда п = 2s -j-1 — число нечетное.
В этом случае
и функция
О
Г^+^в °° • j / ч 27Г+ХО со 1
, _ ,_ ,,s+1 4 "
( } Й
дает искомый максимум
* «Sur quelques proprietes extremales des integrales successives». Gomptes rendus,
200 A935), стр. 1900—1902 A73*).
1 H. Bohr, Gomptes rendus, 200 A935), стр. 1276.
170

{B2k — числа Бернулли). Этот максимум достигается при х = х0, так как
y(w) (х) = + 1 (в соответствующих интервалах) дает максимальное значение
интегралу C). Таким образом, if1 = -^-, if 3 =-^ , Мъ — ^ и M2s+i
^стремится, убывая, к —, когда s->oo.
Заметим, что при О^ж^тг (n = 2s-\-l)
/0.2S+X (*) = ^2S+1 (X) = -^ - ^уу Х-1 +
E)
так как производные четного порядка функции/0f2s+i (%) также реализу-
реализуют соответствующий максимум при х = 0.
Следует напомнить1 здесь другое экстремальное свойство, характе-
характеризующее функцию F2s+i(%) и F2s+i (-ГГ- — #)L а также ее производ-
производную
. F)
77/?гг любом п^>0 многочлен Fn(x) наиболее уклоняется от нуля
на отрезке 0>-|г среди всех функций f(x), абсолютное значение п-й
производной которых на отрезке 0,-^ не превышает значения 1 и
которые вместе со всеми производными первых п — 1 порядков обраща-
обращаются в,нуль, по крайней мере один раз на этом отрезке. При этом
максимальное уклонение Ln = МП9 если п = 2s + 1 — число нечетное, и
(где ^s — числа Эйлера), если п = 2s — число четное. Кроме того,
Ит?п = 4~ и -Г = Li> L*> • • ->1?> • • ->L*> L*>1T •
Переходя теперь к случаю п = 2s^>0, имеем вместо C) формулу*
>(a)
0 fe=l
или, учитывая, что /^""^(О) = /С"-1) Bтс), имеем также при любом с
I Л \S 27Т
7Г J
О
G bis)
1 См. [45] (том I), стр. 494.
* В настоящем издании исправлено ошибочное исследование случая п = 2s пер-
первоначального текста этой статьи. См. мою заметку в Comptes rendus, 203 A936),
стр. 147 A80*). (Автор.)
171

где
Покажем, что и в этом случае M2s = L2s. В частности, полагая в A bis)
с_ — гр ( \ 9 замечаем (вследствие убывания ср (а) в промежутке @,7с)),
что
ф (а — х) — ср (~) > 0 при | а — х \ < -?¦
9 (а — ж) — ?(-7г)< 0 при -^
, 2
так что
sign Гер (а ~ а:) — ?(-?)] rfa = 0т
Следовательно, если положить Д28^ (а) = sign ср (а — х0) — ?("?")» то
Ц1 »(а) [? (а - х) - • (т
принадлежит классу функций, удовлетворяющих условиям B) (т. е. вы-
выражаемых формулой G bis) и подчиненных требованию \ftn)(x) |<; 1); при
этом, какова бы ни была функция f (х) этого класса, отличная от +/xo,2s(^)>
имеем при любом х0
Полагая для определенности хо = —, имеем
-x)] da =
, 4 , ,., ^ sin (lh + 1) х
' nK ' 2j Bfc
B + l)
0 л.=0
Таким образом, при п = 2s имеем
M2s - f2»\T) —5Г С— i) А
/1=0 Х
При этом функция /те (ж), осуществляющая наибольшее значение
M2S при л: — — , равна F'2s+i (ж) = ^s (^) [т. е. определяется на @,гс)
.формулой F)].

62
ОБ ОДНОЙ ТЕОРЕМЕ СЕГЕ*
В своем мемуаре1 «Uber einen Satz des Herrn Serge Bernstein» Г. Cere
установил следующее общее предложение:
Если для каждого вещественного значения б
п—1
о @) = Хп + 2 У av cos vG > 0 A)
/ (G) = a0 + % cos G + Ъг sin G + • • • + ^n cos nb + bnsin тгб, B)
каждого вещественного значения б будет также
2 ^n-v («v cos vG + bv sin v6) + y\ ln-v (bv cos vO — av sin vG) < llA2. C)
l J L i J
Заметим, что неравенство C) эквивалентно неравенству
?-«-v [«v cos (vO + a) + b4 sin (vO + a)]
< 1OA = Л/ D)
при любом вещественном а. Заметим также, что знак равенства в C)
или D) имеет место, если ак = bk = 0 при к<^п и а^ + Ьп = ^42. Таким
образом, теорема Сегё эквивалентна следующей: среди функций /(G),
коэффициенты которых для всякого вещественного значения 6 и а удовле-
удовлетворяют неравенству D), где числа л удовлетворяют A), функция2
^cos(nG + Р), которая {при любом р) достигает своего абсолютного экстре-
экстремума в 2п точкаху является наименее уклоняющейся от нуля при всех
М
значениях G. Таким образом, наименьшее уклонение равно А = - .
Я намерен несколько обобщить эту прекрасную теорему и привести
новое ее доказательство, основанное на классической теории наилуч-
наилучшего приближения.
* «Sur un theoreme de M. Szego». Prace mat.-fiz., 44 A935), стр. 9—14 A74*)-
1 Schriften des Konigsberger Gelehrten Geselschaft, 1928.
2 Без утверждения, конечно, что это единственно возможная форма.
173

Предположив, что для данной пары значений а и б0
п
2 {>*n-v К cos (v60 + а) + К sin (v0o + а)] +
v—О
+ pn_v [К cos (v0o + а) — av sin (v60 + а)]} = M, E)
где jjbQ = pn = О, я прежде всего установлю необходимые и достаточные
условия, которым должны быть подчинены постоянные XQ, X ,...
• •• Дп, ^, ^2> "• > ^n-i> чтобы функция /0(б), коэффициенты котярой
удовлетворяют E) и которая наименее уклоняется от нуля среди
всех функций /(Q), удовлетворяющих E), достигала своего абсолютного
экстремума в 2п точках.
С этой целью начнем с замечания, что если коэффициенты ад, 6д
функции /@) удовлетворяют условию E), то коэффициенты
ak = ajc cos Zd0o -f ^д sin A0O, 6д = ^д cos kb0 — ад sin kbo
функции / @ + 60) удовлетворяют условию
п
S ^X«-v К cos а + ftv sin *! + ^n-v Pv cos а — av sin a]} = A/". E')
Достаточно поэтому рассмотреть случай, когда б0 = 0. Но если абсо-
абсолютный экстремум функции /0 F) достигается в 2п точках, то, поскольку
тогда av = 6V = 0 при v <^ п, функция /0 @) = ап cos nb + ^n sin тгб удовле •
творяет условию
Хо [ап cos a + bn sin a] = M,
так что (добавляя условие, что a^ + 6^ должно быть минимумом) имеем
/0F)=^cos(ne-a). F)
Следовательно, 2п точками уклонения функции /0 F) будут
Таким образом, необходимое и достаточное условие того, чтобы функ-
функция /о@) наименее уклонялась от нуля, состоит в том, что невозможно
сконструировать функцию
-FF) = 4ncos(rc6 — a)+Bnsm(nb — a) + . . . +
+ Ах cos @ — a) + Вх sin @ — a) + ^o
так, чтобы (— 1)* F(cpft) > 0 и в то же время
п
V {Xn_v [(Av cos a — Bv sin a) cos a + (^v sin a + Sv cos a) sin a] +
+ jjLn_v [(Av sin a-f 5V cos a) cos a + (Д> sin a — 4V cos a) sin a]} +
174

+ AnA0cosa^= у
+ Pn-v Bv] + XnA0 cos a = 0.
Иными словами, необходимо и достаточно, чтобы каковы бы ни были
числа Mfc>0, система уравнений
^ncos (щк — а)
n-i Pi + . . . +
-i + Aoln cos a = 0,
cos (n — l<p& — a) + . . . + B± sin (срЛ — a) +
G)
где k = 0, 1, 2, . . . , 2/г — 1 (#n не фигурирует, так как ц0 = 0 и
sm(nyk — a) == sin kit = 0), ббгуга несовместной. Но для этого необходимо и
достаточно, чтобы, каковы бы ни были величины Мк^>0, определитель
порядка 2п -\- I
Д =
cos (тг<р0 — a) cos (п — lrf 0 —- а)
cos (щг — a) cos (n — 1срх — а)
cos a
1
1
0
cos (ftcp2n-i — a) cos (n — l?2n-i — а) •
^
был отличен от нуля, т. е. чтобы все миноры, соответствующие элемен-
элементам (не равным нулю) последнего столбца имели один и тот же знак.
Обозначая через Д& минор, соответствующий элементу (— l)kMk,
имеем
rvo .
cos a
cos (Aicp^i — a)
cos (щк+1 — a)
cos (n —1<
cos (n — 1<
... sin (<pjs
. . . Sin (CB;
fc+1 — a)
1
1
cos (n<p2n-i — a) cos (n — l<p2n-i — a) ... sin (<p2n—1 — a) 1
cos a. (8)
Чтобы вычислить коэффициенты l[k\ m{k), заметим, что, если заменить
элементы Xn_i, jjLn_i (г ^> 0) первой строки в Д& соответственно на cos (г'ср — а)
и sin(icp — a), a Xncosa на 1, то он сводится к
Рк (ср) == l(ok) cos {щ — а) + 1{к) cos (п — 1ср — а) +
тг^)8т(гг-1ср-а) + . • . + m^sin (ср -а) + 1{
(9)
175

где Рк(®н) = 0, при h^k. Следовательно,
sin лг (ф — q>k) cos ^ ^к
Рк (ср) = С/,
sin —г—-
+ ДА. sin n (ср - срА),
A0)
где СкжВк — постоянные. Кроме того, так как (— 1) Рк(фк) не зависит
от к, то Cjc = {—1)кС, где С не зависит от к.
Заметив, что
sin/гб cos
sin
= cos тгб + 2 cos (/г — 1) 6 + . . . + 2 cos 6
и отождествляя оба выражения A0) и (9), мы видим, что
l^C) cos (/гср — а) = Си cos п (ср — срЛ) + 2?Л sin тг (ср — cpfe) =
= С cos (ncp — а) + (— 1)к Вь sin (тгер — а).
Значит, Z?& = 0 и /qA) = С. Точно так же при ? = 1,2,..., тг — 1
4*^1 cos (?ф — а) + т{п-г sin (icp — а) = 2Ск cos i (ср — ср*),
значит,
откуда
1%—i cos а — m{n—i sin а = 2С# cos ?срд-,
Z^li sin а + /raS^-icos а = 2Сл sin ?©д.,
^._i = 2Сд; (cos a cos i^k + sin а sin /срЛ) =
== 2Сд; cos (а — ?©л) = 2С cos (л — ?) <рЛ,
fli = 2Cfc (cos а sin ?срЛ — sin а cos i®h) =
= 2Ck sin (герд. — а) = — 2C sin (n — г) cpft
иг наконец,
4A) = с* = (-
в (8), мы приходим оконча-
окончаПодставив найденные значения 4Л),
тельно к такому заключению:
Для того, чтобы функция /F), которая среди всех функций, удовле-
удовлетворяющих E), наименее уклоняется от нуля, имела вид /0 F) = ancosn6 +
+ 6nsin/20 (уклонение которой равно —) необходимо и достаточно,
чтобы сумма (где Хо > 0)
l
Хо + 2 ^ (>ч cos ?срл — jjLt sin ?фл) + (— if ln cos a > 0
A1)
)
неотрицательной для всех значений срд. = -) (А = 0, 1, 2, ...
. . . , 2л —1).
г76

Мы можем поэтому формулировать, приняв во внимание сделанное
в начале статьи замечание, следующую теорему:
Если
| / (б) | = | Ч + «1 cos б + Ьх sin 6 + . . . + ancos nb + bnsin 6 |< А B')
для каждого вещественного значения 6, то функция
Fa F) « ^ (X*-v К cos (v6 + a) + &v sin (v6 + a)] +
v=*o
+ ^n-v [K cos (v6 + a) — avsin (v6 + a)]}, A2)
еде ^o = ^n = 0, ни при каком действительном значении 6 не может
прееыситъ {но может достигнуть) по абсолютному значению величины
М = \0А, если
П—1
>Ч) + *n COS ПОк + 2 2 (*i C0S l"?ft ~ ^i sin *'?fc) > 0
Пусть, например, а = 0. Тогда при условии B) функция
п
Fo F) = ^ {^i-v [«v cos v6 + 6V sin v6] + [xn_v [6V cos v6 — av sin v6J}
может достичь, но не превысить, значение М = \0А, лишь бы величина
R (срд.) =з Хо + 2 V (X| cos ?срд. -
была неотрицательной при ерь = — , где А: = 0, 1, 2, . . ., 2п — 1.
В случае, когда функция R (ср) неотрицательна для всех значений ср,
можно утверждать, что |Fa(e)|^X04 5лл каждого значения а. Теорема
Сегё является, таким образом, частным случаем нашего последнего
утверждения, соответствующим предположению, что [х{ = 0, каково бы
ни было i.
12 с. Н. Бернштейн

63
О ПЕРИОДИЧЕСКИХ ФУНКЦИЯХ,
ДЛЯ КОТОРЫХ НАИЛУЧШЕ СХОДЯЩИМСЯ РЯДОМ
ЯВЛЯЕТСЯ РЯД ФУРЬЕ*
1. Как известно, всякую непрерывную периодическую функцию f(x)
с периодом 2тс можно^ единственным образом разложить в ряд
(*)= 2-м*),
A)
где
fc=0
таким образом, чтобы при всяком т максимум остатка
был возможно мал. В таком случае тригонометрический полином
т
р (~\ ^ С (т\
±^Ш\Х) — /1 Оп \х)
является полиномом порядка т, наименее уклоняющимся от периодической
функции /(#), а ряд A) называется наилучше сходящимся тригоцомет-
рическим разложением или рядом функции f(x). Построение полинома,
наименее уклоняющегося от произвольно заданной непрерывной функ-
функции, представляет весьма большие трудности. Естественно поэтому по-
поставить задачу об отыскании возможно широких классов функций,
наилучше сходящийся ряд которых был бы просто связан с их тригоно-
тригонометрическим рядом Фурье. В частности, здесь мы займемся исследова-
исследованием класса функций, для которых ряд Фурье является наилучше
* Труды Ленингр. индустр. ин-та, № 10, разд. физ.-матем. наук, вып. 3 A936),
стр. 3—8 A78 *). При редактировании этой статьи принято во внимание ее изложе-
изложение, содержащееся в § 8 гл. I монографии «Э. П.» A937).
178

сходящимся рядом; назовем, для краткости, классом (А) этот последний
класс функций. Следовательно, по условию, в данном случае
Sn (х) = Ап cos nx + Вп sin nx.
Прежде всего, легко доказывается следующая
Теорема I. Условие, необходимое и достаточное бля того, чтобы
ряд Фурье
со
f{x) = ^An^osnx, B)
о
где Ап ^ О, был наилучше сходящимся тригонометрическим рядом для
функции f(x), состоит в том, что, если щ^>0 означают те значения
пг 4- 1
, для которых Ап^>0, отношение —=¦=— = 2рг + 1 должно 1бытъ
целым нечетным числом при всех
В таком случае для всякого п (щ-\-^п<С щ) тригонометрическим
полиномом порядка п, наименее уклоняющимся от f(x), будет (если по-
полагать п0 = 0)
г—1
Рп (X) = 2 Anh COS ПКХ, C>
h=0
а наилучшее приближение
со со
?„/(*)= 2 ^*= li^n,, D>
Jc=n-{-l h=l
Достаточность указанного условия, установленная мною * еще-
в 1912 году, вытекает из замечания, что
достигает своего экстремума D) с последовательно противоположными
знаками в 2щ точках — (А = 0,... 2щ — 1) периода 2тс, т. е. не менее, чем в
2тг + 2 точках, из чего следует по известной теореме, что Рп(х) есть
тригонометрический полином порядка п, наименее уклоняющийся от,
f(x). Для доказательства необходимости высказанного условия замечаем,
что максимум f(x) — Рп(х) достигается при х = 0. Но в силу только
что упомянутой теоремы, если полином Рп{х) есть наименее уклоняю-
уклоняющийся, то этот экстремум должен достигаться не менее, чем в 2п -(- 2
точках, поэтому должно быть не менее 2п + 2 точек, где
2 -4л cos Аж =
* См. [7], стр. 125, и [8], стр. 133, том I. (Автор.)
179 12*

а это будет возможно лишь при условии, что Ajc^>0 только для тех
значений к, которые делятся нацело на наименьшее из значений к = Ао,
при котором Ajco^>0, причем т число нечетное.
Следствие. Для того чтобы функция
f(x) = J\ Ak?osn(x — a)= V ai cos щ(х — а),
n =0 i=0
где fli^>0, принадлежала классу (А), необходимо и достаточно, чтобы
для всех щ^>0 число было целым и нечетным.
Если, например, f(x) есть функция Вейерштрасса без производных
i=0
где h^> — ^> 1, го
где /гх~1<тг</гх, т. е.
Теорема II. Функция
оо
f(x) = V (ai C0S nix + ^i S^rl ni#)> E)
где l+i = 2/?i + 1, является функцией класса (А).
Для доказательства заметим сначала, что сумма
ah cos cp + bh sin cp + ah+1 cos Bрг + 1) cp + 6h+1 sin B/?! + 1) cp 4- ...
достигает своего абсолютного экстремума по крайней мере в двух точках
периода 2п с противоположными знаками, так как она изменяет свой
знак при замене ср на ср -}- и. Следовательно, сумма
оо
Д (х) = ^ (а^ cos fti# + bi sin fti#)
имеет по крайней мере 2що экстремумов с противоположными знаками
в промежутке @,2ти), откуда вытекает высказанное утверждение*.
* Если все а{ = 0, то / (х) принадлежит классу (А) каковы бы ни были целые
оо
числа -ii? аи Nif так как в этом случае функция
имеющая периодом — , достигает экстремума с чередующимися 'знаками
точках отр:зка 2п. (Автор.)
180

Однако доказать, подобно теореме I, что формула E) является един-
единственной возможной формой функций класса (А), не делая никаких
дополнительных допущений, мне не удалось.
Здесь я ограничусь только доказательством одной частной теоремы.
Заметим сначала, что функции класса (А) можно также охарактери-
охарактеризовать следующим свойством.
Тригонометрический полином Рп(%) порядка тг, наименее уклоняю-
уклоняющийся от функции f(x), является в то же время полиномом, наименее
уклоняющимся от полинома Pn+i (#)• Действительно, если Рп (х) есть
тригонометрический полином порядка п, наименее уклоняющийся
от Рп+Х(х), то
Рп+1 (х) — Рп (х) = Ап+1 cos (п + 1) х + Вп+1 sin (n + l)x,
так как эта разность должна достигать экстремума в 2п + 2 точках. При
этом, конечно, не исключается возможность, что для некоторых значе-
значений п полиномы Рп+1(х) и Рп[я) тождественны, т. е. Ап+1 = Bn+i = 0.
Мы назовем классом (А*) частный класс функций класса (А)
[который, может быть, и совпадает с классом (А)], характеризую-
характеризующийся тем, что функции, к нему принадлежащие, обладают свойством,
что, если Pni__1{^)y Рпг(х), Pn^iz) представляют три отличных между
собою смежных полинома, наименее уклоняющихся от функции f(x), то
не только Pni^ix) является полиномом порядка щ — 1, наименее укло-
уклоняющимся от Pni{%)> как Рпг{%) — наименее уклоняющимся от Рн. (х)
[что характеризует, как сказано выше, все функции класса (А)], но, кроме
того, Pni_{{%) является также тригонометрическим полиномом порядка
наименее уклоняющимся от полинома Pni_^.1 (#)•
Теорема III. Все четные функции класса (А*) имеют форму
где Ani^0 отличны от нуля только для значений щ таких,
что —-— = 2pt + 1> еде pi — целое число.
Согласно определению функции класса (А*),
имеет полиномом наименьшего уклонения порядка nh — 1
*V-i(*)= 2^iCOS72i^
Следовательно, полином
/>«л+1 (*) — Pnh-i (х) = А\ cos п& + A"h+i cos Лл+1Ж-
должен иметь, по крайней мере, 2% точек максимального отклонения.
181

Теорема наша будет поэтому, очевидно, доказана, если покажем, что
тригонометрический полином
Ъ cos nhx + cos n^x (b ^ 0)
может иметь 2/г^ абсолютных экстремумов с противоположными знаками
лишь в том случае, когда —— целое нечетное число. Обозначая через р
общий наибольший делитель пи и /г^х, можем положить пи == тр,
птц_1 = т^р, где т1^>т — числа взаимно простые, и нам достаточно будет
доказать, что функция
R(Q)=b cos mb + cos m±b
не может иметь 2т экстремумов в периоде 2тг, если т^>1 или
тх число четное. Правильность нашего утверждения для 6^>0 вы-
вытекает из доказательства теоремы I (так как экстремум Ь + 1 может
достигаться в 2т точках лишь тогда, когда все экстремумы cosmO со-
сопровождаются экстремумами cosm^ с одинаковым знаком). Поэтому можем
положить Ь——а, где а>0, и рассматривать
R F) = — a cos m6 + cos mxb.
Точно так же, очевидно, что т± — т не может быть нечетным, так как,
заменяя 6 на тг + 6, мы пришли бы к предыдущему случаю, когда
оба коэффициента одинакового знака. Отсюда (помня, что числа т и тх
взаимно простые) заключаем, что оба числа т и тх должны быть нечет-
нечетными.
В таком случае, вследствие того, что R F) не может оставаться
всегда менее единицы по абсолютному значению, так что
лнак абсолютного экстремума R F) должен совпадать со знаком —acosmb.
Следовательно, положительные экстремумы могут быть лишь в проме-
промежутках
/4M-J 4М-3
причем отрицательных экстремумов в этих т промежутках не может
быть. Поэтому в каждом из этих промежутков действительно должен
быть положительный экстремум, так же, как во всех лежащих между
ними промежутках должно быть по отрицательному экстремуму; в част-
частности, отрицательный экстремум будет и в промежутке @, +о~)>'
т. е. вследствие четности функция /?F) в промежутке @, «т--]-
Но так как числа 2тх и т взаимно простые, то существуют такие
целые числа к и $, что
2тхк - т B$ + 1) = ± 1. F)
182

Поэтому, полагая 6 = — , получим
Rib) = — a -f- cos—-— = — a + cos 2s + 1 4 тс = — a — cos— .
m V — гл) т
Следовательно, если бы т^З, то L^>a. Поэтому отрицательный экстре-
экстремум R F) был бы возможен только в точках, где cosm-fi^O. Таким
образом, в частности, значение 80, где достигается первый отрицательный
экстремум, лежащий в интервале (О, Д-), должно было бы удовлетворять
неравенству
2wj ^^ "^ 2т
а потому мы имели бы
L= | Л @о) |< a cos/га60 + I<^'cos2^-+ 1. G)
л г » г 25 + 1
Между тем, с другой стороны, полагая 6= к, мы находим, бла-
благодаря F), что
r I те\ _ — a cos-
тте) C0S ^ COSB6 + 1) с
= — acosBA ч W — 1 = — a cos— — 1.
Но при т^>1 это противоречит неравенству G). Таким образом, теорема
доказана *.
* Теорема III может быть непосредственно распространена на нечетные функции
г—1
«ри условии, что все ni числа нечетные. Действительно, в этом случае
г-1
является четной функцией. См. сноску на стр. 178. (Автор.)

ОБ ОБЛАСТИ СХОДИМОСТИ МНОГОЧЛЕНОВ
1. Известно, что многочлены
п
D / (~Л "S^ / I Ш. 1 Г т^П М <r\n-~m /4\
Лп / W — 2л ' \п J n X v1 ~ X) W
сходятся равномерно к / (х) на всем отрезке [0,1], какова бы ни была
непрерывная на этом отрезке функция /(#).
Л. В. Канторович1, которому впервые пришла мысль изучить область D
сходимости многочленов Bnf (x) в случае, когда функция / (х) аналитиче-
аналитическая, доказал, что эта область D содержит, по крайней мере, эллипс схо-
сходимости Е разложения / (х) в ряд по тригонометрическим многочленам
Чебышева. Исследуя различные новые представления многочленов Bnf (x),
я получил ряд аналогичных результатов, некоторые из которых я хотел
бы здесь указать •*.
2. Пусть С произвольный контур, окружающий отрезок [0,1], внутри
которого f(x) голоморфна. Легко видеть, что (при х, отличном от 0 и 1)
_ л! V / KZAX —l) x Jr, /o\
* «Sur le domaine de convergence des polynomes
Bnf (x) = 2 / ("f) С™*™ A _ *)»—»,
Gomptesrendus, 202 A936), стр. 1356—1358 A79*).
1 Изв. АН СССР, ОМЕН, 7 A931), стр. 1103—1115.
** Впоследствии (в 1946 г.) я узнал, что еще в 1930 г. появилась весьма инте-
интересная работа Райта [Е. М. Wright, «Bernstein approximation polynomials in the
complex plane». Journal of the London Mathematical Society, 5, Part 4, A930)], в ко-
которой получены некоторые из результатов моих работ [64], [65] и [81] и, в частности,
теорема В настоящей заметки [64] доказана иначе, чем в моей большой статье [81].
(Автор.)
184

Следовательно, применяя формулу Стирлинга и воспользовавшись асимп-
асимптотическим представлением
1
z{z—
справедливым вне отрезка [0,1], получим (при п—>оо)
Из C) можно вывести несколько важных следствий.
3. Рассмотрим выпуклую петлю Ех, соответствующую данной точке
x = a-{-$i (не лежащей на отрезке [0,1]), удовлетворяющую уравнению
которая в точке z = х имеет две взаимно перпендикулярные касатель-
касательные и содержит внутри себя весь отрезок [0,1], если \х\^>\ и|1 — х\^\,
а в противном случае содержит часть этого отрезка *.
Из равенства C) выводится
Теорема А. Если функция / (z) регулярна на петле Fx, соответству-
соответствующей точке х, и внутри нее [равно как и на части отрезка [0,1] вне
петли, если таковая имеется), то точка х лежит внутри области D
сходимости многочленов Bnf[x). В противном случае точка х окажется
вне области D или на ее границе.
Из C) следует также
Теорема В. Если z0 — a + bi является единственной особой точкой
функции f[z), то область D имеет своей границей внешнюю петлю Ри,
удовлетворяющую уравнению
окружающую отрезок [0,1] и образующую в точке z0 входящий угол,
„ Зти
равный у.
Так, например, при z0 = 2 петля Р2о имеет в прямоугольных коорди-
координатах [х, у) уравнение
х* "J" У2 о ! 1/5 Г>у CV\
в котором для х << 2 нужно сохранить только ** знак плюс
* В последнем случае петля Fx [т. е. замкнутый контур, удовлетворяющий D)
может не быть выпуклой (см. [81], § 3). (Автор).
** Значению х = 2 соответствует у — 0 (т. е. особенной точке z0 = 2). В этой двой-
двойной точке кривой E) внешняя петля Р2о соединяется с внутренней петлей (которая
не играет никакой роли), удовлетворяющей тому же уравнению E) и уравнению E')
только при ж<2и при знаке минус перед корнем (см. [81], стр. 329—330). (Автор.)
185

4, В принципе, согласно формуле C), можно определить область схо-
сходимости D для произвольной функции f(z)> строя наибольшую область,
лежащую внутри петель P2q, соответствующих всем особым точкам z0
функции f(z). He буду останавливаться здесь на более или менее общих
результатах, которые я получил в этом направлении, видоизменяя на-
надлежащим образом выражение B); отмечу только, что можно построить
бесчисленное множество контуров, обладающих тем же свойством, фор-
формулированным вначале, что эллипс Чебышева Е. Например,
Теорема С2. Если функция f(z) регулярна на выпуклом замкнутом
контуре С (и внутри его), симметричном относительно действительной
ори и проходящем через точки 0 и 1 внутри окружности, диаметром
которой является отрезок [0,1], то контур принадлежит области сходи-
сходимости D.
Теорема С2. Если функция f (z) регулярна на выпуклом контуре Гд
(и внутри его), образованном окружностью радиуса R <^ 1 с центром
в 0 и касательными к ней, проведенными из точки 1, то Гд принадле-
принадлежит области D.
Теорема С3. Круг сходимости Са с центром в произвольной точке
@<^а<^1) отрезка [0,1] принадлежит области D всякий раз, как Са со-
держит отрезок [0,1].
Комбинируя эти теоремы, получаем не выпуклые контуры, обла-
обладающие тем же свойством и могущие даже образовывать входящие уг-
. 37Г
ЛЫ <Су.

65
О СХОДИМОСТИ НЕКОТОРЫХ
ПОСЛЕДОВАТЕЛЬНОСТЕЙ МНОГОЧЛЕНОВ *
1. Известно, что для произвольной непрерывной функции f(x) на
отрезке [0,1] многочлены
Вп [/ (х)] =
m=0
где С"^ = —f w-—r-f- сходятся равномерно к функции / (х) на всем от-
отрезке [0, 1].
Скорость сходимости этих многочленов на [0, 1] зависит глишь сравни
тельно мало от природы функции /(#), так как
lim п {Вп [/ (х)] - / (х)} = \ х A - х) /" И
те—>оо
©о всех точках х отрезка, в которых вторая производная ограничена и
непрерывна1. Тем более замечательно**, что, как показал Л. В. Канто-
Канторович2, последовательность многочленов Bn[f{x)] сходится равномерно
к функции f{x), когда она является аналитической, по крайней мере
в той же комплексной области, в которой имеет место сходимость раз-
разложения f(x) в ряд по многочленам Чебышева, т. е. внутри эллипса
регулярности Е функции f(x)9 имеющего фокусы в точках 0 и 1. Чтобы
получить этот результат, Канторович использует, с одной стороны,
* «Sur la convergence de certaines suites de polynomes». Journal de mathematiques
pires et appliquees, 15 A936), стр. 345—358 A82*).
1 E. В. Вороновская. «Определение асимптотического вида приближения
•функций полиномами С Н. Бернштейна». Докл. АН СССР A932), стр. 79—85.
О. Н. Бернштейн. «Добавление к статье Е. В. Вороновской», там же, стр. 86—92
157].
** См. также И. Н. Хлодовский, «О некоторых свойствах полиномов
«С. Н. Бернштейна», Труды Всесоюз. матем. съезда. Харьков, 1934. (Аатор.)
2 Л. В. Канторович. «О сходимости последовательности полиномов
>С. Н. Бернштейна за пределами основного интервала». Изв. АН СССР, ОМЕН A931),
стр. 1103—1115.
187

упомянутое разложение f(x) в ряд по многочленам Чебышева, и, с другой
стороны, замечает, что на основании одной классической теоремы (Стиль-
тьеса) сходимость многочленов Bn[f(%)] к f{x) обеспечена во всякой
области D (содержащей конечную часть отрезка [0,1]), в которой мно-
многочлены Bn[f{x)] ограничены. Он сам, кроме того, указал пример, когда
область D еще больше, чем эллипс Е.
Я хочу здесь несколько дополнить изучение области сходимости Dr
используя для этого представление Bn[f(x)] в виде степенных рядов1-
Это приведет нас в дальнейшем к рассмотрению многочленов вида
которые позволяют осуществить аналитическое продолжение функции f(x),
данной рядом Тейлора, за пределы ее круга сходимости во всех точках
регулярности функции f(x), лежащих на окружности сходимости.
2г Докажем прежде всего следующую теорему:
Теорема А. Если функция
имеет в некоторой точке с отрезка [0, 1] круг сходимости С радиуса
со
R, охватывающий отрезок [0,1], и если ^\аь\ Rk ^ М, то имеем также
о
на С (и внутри С) \Bn\f(x)]\<^M для всех целых п^-0. (Круг С при-
принадлежит, таким образом, к области D сходимости Bn[f(x)]).
Очевидно, достаточно показать, что
\Вп их — c)s]\ <J Rs, B)
каково бы ни было целое число s^>0 при \х — с\=П, предполагая.
с <Я и 1 — с <Л. Но
п
т> \(„ ^\sl "V nm(m r\vm(\ ^\n—m
•E>n[[% — С) \ — /j Is n \ ~ C\X \L —X) ,
\ ft I
следовательно, полагая
[Ъ(\—с) be In n (m—nc)b
~p nix—c) _i_ i\ v\ p n(x—c) XI ГтГП p nix—c) /ym (A ~\п—т
m=0
ВИДИМ, ЧТО
(а;_с)И 5^1 =2C(^-c)V(l-x)n-m = 5n[(^-c)S].
1 Моя заметка [64] из Gomptes rendus «Sur ledomaine de convergence des polynomes
n
Bn[j(x)]= 2 / (— Vm хШ (^ — ^)n~m», в которой применяется другой метод,
резюмирует часть результатов этой работы, а также содержит еще некоторые более
общие результаты.
188

Итак, неравенство B) будет установлено, если будет доказано, что
6s Ф
dbs
Но
C)
*!«*l
Кроме того, я утверждаю, что
\х A - с)* + A — х) ( — cf\ < | а; — с|* == Д*, D)
когда | ж — с\^-с и |а; — с | ^> 1 — с. Действительно, предполагая для
определенности, что с -^тг, и полагая а; — с= в, мы можем представить
D) в виде
1A_с)*(ц+с)+(_С)*A_с__ЦI<|Ц|*)
т. е.
| [и A — с)к - (— с)к] -A-е) с [A - с)*-* — (— c)*-i] | < |и|*. E)
Но так как коэффициент при и и свободный член в левой части E) не-
неотрицательны, то максимум модуля левой части при данном \и\ = R до-
достигается, когда и действительно и положительно. Достаточно, таким
образом, проверить, что при R ^> 1 — с
Вк - R [A - с)к — (- с)к] — A — с) с [A - с)* — (— с)*-*] > 0.
Для этого замечаем, что производная
АД*-1 _ [A _ с)к — (-с)к] > к A - с)*-* — A — с)* + (— с)* =
= (А — 1 + с) A — с)*-* + (— с)к > с [A — с)*-* — (— c)*-i] > 0
неотрицательна, а при R = 1 — с имеем
A - с)к — A — с) [A — с)* - (- с)к] — A —с) с [A - с)*-* — (— c)*-i] = 0.
Следовательно, функция ФF, ^), рассматриваемая как ряд по степеням
Ь, .имеет в качестве майорантного ряда
Ъ Ъг ък 1П Г 1П
последовательные производные которого при 6 = 0 равны единице, от-
откуда следует неравенство C)
Из этой теоремы, в частности, следует, что если функция f(x), име-
имеющая в точке у круг сходимости радиуса R ^> у , обладает только
одной особой точкой А = х -\-iy (у SO), то А является входящей угло-
угловой точкой границы L областиг D.
1 Это следствие уточнено и обобщено в цитированной заметке [64].
189

Действительно, область D необходимо будет содержать два круга
С2 и С2, проходящих через А и имеющих соответственно центры в неко-
1 1
торых точках сг < у ис2>у отрезка [0,1]. На том же основании, ка-
какова бы ни была функция f(x), никакая регулярная точка М на эллипсе
Е Чебышева — Канторовича не может принадлежать границе L области
D, если
MN^a и
где N (а,0) — точка пересечения нормали в точке М к эллипсу Е с дей-
действительной осью. Тогда круг С с центром в N и радиуса несколько
большего, чем NM, будучи внутренним по отношению к эллипсу, за
исключением окрестности точки М (и ее сопряженной), будет удовле-
удовлетворять условиям теоремы А. Этот случай представится, в частности,
для всех точек эллипса, если его большая ось по крайней мере равна 3.
3/ Теорема В. Если функция f(x) регулярна и ограничена внутри
бициялической выпуклой области SPPl, ограниченной дугой окружности
С с центром в точке 0 и радиусом р, дугой окружности с центром
в точке 1 и радиусом рх и их общими внешними касательными, то эта
область принадлежит D при условии г, что 2р }> рх >- -|-.
Для доказательства нам придется сделать новое преобразование мно-
многочленов Вп [/ (х)] и рассмотреть многочлены
(fr\ F)
соответствующие произвольному отрезку [О, Ь], так что
Bn[f{x);i]=Bn[f{x)].
Кроме того, полагая
Д [/(*),*] = Л*+ *)-/(*),
А2 [/(ж), й] = /{х + Щ — 2f{x + h) + f (x),
для краткости будем писать
когда h = —.
п
Приняв это, получим
« [/(*)] = 2 [/@)
0
1 Применяя метод, указанный в заметке [64], можно избавиться от этого огра-
ограничения; см. также статью [81].
190

Допустим теперь, что функция / (х) является аналитической и регуляр-
регулярной внутри бициклической области SPPl9 где pi^-|- и \f(x)\<^M на ее
контуре (для определенности полагаем p^-pj. При этих условиях в точке
с отрезка [0, 1] будем иметь
Л\
|Д*/@)|< max
Тогда
Следовательно [благодаря G)],
/<*><*)
к\м
где"
\Bn[f(x)\<M
bk =
n (n—1) ... (n — k + 1) I x
к=0
(8)
(9)
Группируя попарно равноотстоящие от концов множители числителя в
(9), находим (к<^п)
-
2п
1 *
1 2^
(Ю)
Следовательно, по формуле (8),
\Bn\f(x)]\<M 2 -
где r=—<^1, если Ja;|<^p'. Откуда по теореме Стильтьеса Bn\f(x)
сходится к f{x) внутри круга С радиуса р.
4. С другой стороны, осуществляя то же преобразование над много-
многочленом Bn[f(x); b], мы получим
/@), -
— 1) ... {п —
к\
(И)
* Оценка Ь% здесь сделана проще, чем в первоначальном тексте. (Автор.)
191

В частности, если 6 =—, где 1<^п целое число, мы получим
Таким образом, используя сокращенные обозначения Д^ If (х), —) =*= Akf(x),
будем иметь также при Ъ = —
Bi [Akf(c); b] = Д*/@) + /Д*+1 /@)? + ... + С? Ak+h f @)(|)" + ... .
Полагая с# = с ""¦ , получим
= Д*/@) + (и - А) Д*+1/@)с + ..'. + Cl^ Ak+hf(O)ch + .... A1 bis)
Следовательно, каково бы ни было с, имеем [из G) и (И bis)]
Вп [/(*)] = /@) + лД/@) [х - с + с] +
+ п(п~^ Д,/@)[а-с + е]« + - = gw 1/@1+
+ ("~1J,("~2) Дз/@) с2 + .
= ^п U (с)] + п(х - og«
+ & (х - cf Вп-ъ [Д* / (с*); ^] + .... A2)
Предположим теперь, что 0<с<1; тогда, принимая во внимание, что
m=0
МЫ ВИДИМ, ЧТО
так как
Таким образом,
П/Г1 п—к jm (л \п—к—т
<
yjH «-о
192

Так как при к конечном и п—» ос коэффициент при (х— с)к в A2) стре-
стремится к -^-тр-^ > то мы можем предположить, что к—>оо. В таком
случае легко показать, что
A3)
Это прежде всего очевидно в случае, когда п — к ограничено, так как
тогда 1—т~(~—т\ стремится к единице при п->оо.
Полагая m = (п — к) (с + в) и к = an, имеем, вообще
1 — — /И—А\ — 1 _ (c + s) (/г —А:J __
2л Аг /гB/г —
i - 2
где
/ з
еA—а)«— ас -—а
V2
Таким образом, при е^О имеем о<^0 и соответствующими членами
подкоренной суммы A3) нам нет надобности заниматься. С другой сто-
стороны, мы видим (вычисляя отношение последующего члена к предыду-
предыдущему), что члены в этой сумме A3) идут убывая, если е!>аA — а)сA —с).
Следовательно, остается лишь рассмотреть значения т, для которых
0<s<cA4~c). Но тогда
^ 1 1 ./ 7 \-1 1 ^ 5 е2 (п — к)
Кроме того,
1 -.
С 1 — С
_&log(l-8) = Л(8+ -!-+...j<^-
где
8 _ A — аJ с A-е) — 2дс C — 2д)
1~ 2B-с)B-а)
так что
13 с. Н. Бернштейн 193

Таким образом, чтобы доказать A3), достаточно проверить неравенство
5.2 1-е .,._ a*c{Y-a)-sa(l-ab _^
1—Z.)B-a)+ac(-5— а]_и-*)\°и-о)
которое вытекает из неравенства
'3
которое в свою очередь благодаря сA — С)^Т является следствием
Итак, каково бы ни было к,
lim
п->оо
V
п—к
к
к\ ^
Pi1— "о"
Таким образом, из A0) и A2) видим, что Bn[f (x)] остается ограничен-
ограниченным при
и, следовательно, бициклическая область *УРР1, которая при P
содержит все круги радиуса рA ^-)с центром в с @ < с<1), принад-
принадлежит к области /) многочленов Bn[f(x)].
Теорема В*. Если f (х) регулярна в пересечении HPPl двух бицикли-
ческих областей S29ltp1 и SPf 2P (¦^-<Cpi<C2p), ^o Z) содержит их пересе-
,2
чение.
Чтобы в этом убедиться, достаточно заметить, что можно представить
f(x) в виде суммы двух функций:
где /2 (я) обладает особенностями только вне S?i 2P и /2 (х) обладает осо-
особенностями только вне *У2Р1> Pl .
Заметим, что область EPPl ограничена выпуклым контуром, состав-
составленным внешней дугой радиуса р с центром в 0, внешней дугой окруж-
окружности радиуса рх с центром в 1, двумя касательными, идущими из точки
на оси абсцисс —1 к первой окружности и двумя касательными ко вто-
второй окружности, идущими из точки B, 0).
Таким образом, для того чтобы некоторая точка М (х, у) (и ее сопря-
сопряженная Мг) принадлежала области D, достаточно (при 0<^х<^1), чтобы*
194

функция f(z) была регулярной в области SPPl (и на ее контуре), имея
угловые точки в М и в М'. В случае, когда #<;0, достаточно, чтобы
/(z) была регулярной в области*? х , где р = У х2-\-у2; в случае #^-1
Р» — Р
достаточно, чтобы f(z) была регулярна в области ? i , где р = У (х—1J+ у2*
1Р» р
Отсюда следует, в частности, что если одна из действительных вер-
вершин эллипса Чебышева является регулярной точкой/(ж), то она является
внутренней точкой области D.
5. Рассмотрим теперь наши многочлены Вп [/(#); Ь], устремляя Ъ к
нулю. Положим
= /@) + xf @) + ... + Cknf\0) f^f + ... A4)
Так как коэффициенты многочлена Ап [/ (х)] меньше коэффициентов ряда
Тейлора, то область сходимости Во этих многочленов содержит, очевидно,
круг сходимости. Чтобы изучить эту область, полезно представить An[f(x)]
в виде интеграла, используя теорему Коши. Предполагая, что f (х) голо-
голоморфна в некоторой области, ограниченной контуром С, окружающим
начало, мы получим
Таким образом,
(
A«VW=%mS\& -^rdz^
Q k=*0
k
*l Г fx\n ^ ^ (n \kf
2m ) \ n j 2a k\ \x )
k0
(z)dz
G
f nz
__ n\ ( x\nCex f(z) ,
~~ 2m V n ) J 2j k\
Применяя формулу Стирлинга, выводим асимптотическое равецство
при п—> оо
Положим — = и = a + Ы и рассмотрим кривую i^j, определяемую урав-
х
нением
13*

которая имеет петлю F, окружающую начало, с двойной точкой A, 0),
где касательные образуют углы ±-т~ с осью х, так как, полагая
а — 1 = а, можно представить A6) в виде
A6 bis)
Очевидно,
при
внешнем к петле F, если a = a —
Заменой и — — фор-
ос
мула A5) преобразуется в
где Сх — контур, преобразованный из С. Таким образом, если контур Сг
является внешним по отношению к петле F при а<0и, имея с F
общей лишь ее двойную точку, преобразуется в окрестности этой точки
в маленький отрезок, перпендикулярный к действительной оси, то
где е>0 — данное число. Теперь уже легко показать, что Ап [/(#)]~/(#),
так как это следует из того факта, что An[f(x)] ограничен, то доста-
достаточно заметить, что при \f(z)\<^M на С правая часть по модулю будет
меньше, чем
п
dt
1-3... Bm — 1)
-2-4...2m
где т =
Итак, замечая, что расстояние ]/а2 + Ъг точки петли от начала воз-
возрастает слева направо, получаем следующую теорему:
Теорема С. Если радиус круга сходимости с центром в начале равен R
и если действительная точка R является регулярной для f (z), то мно-
многочлены An[f(x)} сходятся равномерно к f(x) во всех точках x^>R, для
которых петля Fx, гомотетичная F с отношением гомотетии х, не
содержит особенностей f(z).
В частности, если f(z) содержит особенности только на своем круге
сходимости и f{z) регулярна при z = ReiQ, где —60 <^ 6 <^ 60, то действи-
196

тельная точка xo^>R, наиболее удаленная, определяется уравнением
R cos 80
хое х° = Re.
Например, при 0О = -^- имеем х0 = Re. Найдем наибольшее значение х0
при б0 = тс; в этом случае имеем
xQe x° = Re,
откуда #ож3,6/?. Очевидно, тот же вывод справедлив во всех направ-
направлениях.

66
О ФОРМУЛЕ КВАДРАТУР ЧЕБЫ1ПЕВА
Чебышев вывел формулу приближенных квадратур
1 п
\f(x)dx= 1 2/(*«)•
i
i==l
где значения #г определяются условием, чтобы формула A) была верна
для любого многочлена степени п. Я показал1 в 1932 году, что при п
достаточно большом не все значения Х\ могут быть вещественными.
Таким образом, формула Чебышева неприменима для больших зна-
значений2 п. Естественно поставить вопрос: каково максимальное значение
Мп степеней многочленов, для которых формула A) была бы верна при
соответствующем выборе точек на отрезке [0,1]? Я хотел бы указать
здесь неравенство
B)
справедливое при любом п^>0, и резюмировать вкратце основные пункты
его доказательства.
Теорема 1. Пусть ^<С52<С • • • <С5т — корни многочлена Лежандра
Рт(х) степени т, отнесенного к отрезку [О, 1]. Если Мп^2т — 1, то
где S (?) — число значений x-t <^ ?.
Теорема 2. Если формула вида
1 п
\f{x)dx= 2g«/(xi),
* «Sur la formule de quadrature approchee de Tchebycheff». Comptes rendus, 203
A936), стр. 1305—1306 A81*).
1 «О формуле приближенного интегрирования Чебышева». Изв. АН СССР, ОМЕН
A932), стр. 1219—1227 A57*).
2 Укажу также на недавнюю заметку Р. О. Кузьмина, Comptes rendus, 202 A936),
стр. 272.
198

где q-i^O, верна для всех многочленов степени 2т — 1, то каждый из
отрезков [О, SJ, [?i,?2]>... , [?m> 1] содержит по крайней мере одну из то-
точек X't.
Комбинируя эти два предложения, легко убедиться, что
1<2^sin2^l<^R) (^>2m-l), D)
откуда следует, что
если Мп нечетное.
Заметим, что условие Чебышева требует, чтобы Мп^-п, так что
неравенство B) приводится к
Ж>]/2п, B')
откуда следует, что формула, предложенная Чебышевым, неприменима
при и^20. Кроме того, используя неравенство D) в его более точной
форме и учитывая, что в данном случае Мп всегда должно быть не-
нечетным (так как в случае п четного Мп=-п-\-1), видим, что все зна-
значения /г>15 также непригодны. Но, вычисляя непосредственно абсциссы
Чебышева для тг<;15, можно проверить, что они не все вещественны
уже при п > 9 (и при п = 8).
В следующей заметке * мы займемся определением нижней границы
для Мп и рассмотрим аналогичную задачу для равноотстоящих абсцисс.
* «Modifications de la formule de quadrature de Tchebycheff», Gomptes rendus,
204 A937), стр. 1526—1529 A91*). См. также [68]. (Автор.)

67
О ФОРМУЛАХ КВАДРАТУР КОТЕСА И ЧЕБЫШЕВА*
В формуле квадратур Чебышева,
^ A)
как известно, значения х-г определяются требованием, чтобы формула A)
была верна для всех многочленов степени не выше щ эта формула
применяется для п = 9. Как мною было показано (х), формула Чебышева
непригодна для очень больших значений п [67.1], так как значения xt
не могут тогда оставаться на отрезке [0,1]. Весьма существенное допол-
дополнение к моему исследованию, имевшему предварительный ориентировоч-
ориентировочный характер, сделал недавно Р. О. Кузьмин B), который нашел асимп-
асимптотическое распределение величин x-t в комплексной плоскости при
я->оо. Таким образом, требование Чебышева является слишком жест-
жестким, и необходимо значительно снизить степень Мп многочленов, для
которых формула A) должна быть верна; после этого задача определения
п неизвестных x-t из соответствующих Мп<^п уравнений становится не-
неопределенной, и несомненный интерес представляет установление макси-
максимального значения Мп, при котором все x-t могут быть вещественными.
Аналогичная задача может быть поставлена и для формулы квад-
квадратур
\
) B)
2=0 Ч '
в случае равно отстоящих абсцисс, если потребовать, чтобы все С\
были одинакового знака, так как известно, что при п весьма большом
коэффициенты Котеса, однозначно определяемые условием, чтобы формула
B) была верна для всех многочленов степени п, имеют различные
знаки [67.1].
* Докл. АН СССР, 14 A937), стр. 323—327 A83*).
200

Обозначая через Nn максимальную степень многочленов, для которых
формула B) верна, где С\ ^ 0, мы докажем, что
C)
т. е. что формула A) ни при каком подборе вещественных Xi, а формула
B) ни при каких C-t >- 0 не могут быть верны для всех многочленов
степени p^i]/n.
Для этого напомним формулу механических квадратур Гаусса
1 т
/(*)<** = 2 Р&>/(Т,) (Р?>О), D)
гДе Ti < 72 <С ••• <Лт корни многочлена Лежандра Рт(х) степени т на
отрезке [0,1], которая верна для всех многочленов степени 2т— 1.
В таком случае имеет место следующая
Теорема 1. Если формула
\f(x)dx = 2^/(yf) (п>т), E)
О i=i
где р.^>0 и числа у. вещественны, верна для всех многочленов степени
2т — 1, то существует по крайней мере одно значение yi<C^A-
Действительно, из того, что формулы D) и E) применимы к много-
многочлену
П2т-1 (X) —
следует, что
Но R2m—i (^) ^> 0 при х <^ 7i» ^2m—1 {%) < 0 при х ^> f xj поэтому, замечая,
что вследствие п^>т все члены суммы F) не могут быть нулями, заклю-
заключаем, что есть по крайней мере одно значение «у* <Л1-
Аналогичным образом доказывается
Теорема 2. Если формула
п
]? (n>m), E')
где Pi^>0, ух <; 1 (i = 1, . . . , п), верна для всех многочленов степени
2т — 1, /т?о существует по крайней мере одно значение у. в промежутке
0< Vi^^i г®е ?! наименьший из корней Р'т(х).
В самом деле, нетрудно видеть, что для всех многочленов степени
2т — 1 верна формула квадратур
1 т—1
\ / (х) dx = Яо/ @) + 2 **/ ih) + W A) > G)
0 i=l
201

тДе ^l^lPa^' * '^^m—i— корни многочлена Рт(х) (производной много-
многочлена Лежандра). Поэтому, применяя к многочлену
Р'Д (х) х A - х)
формулы E') и G), находим
откуда заключаем, подобно предыдущему, что существует по крайней
мере одно значение yi внутри промежутка (О, Вх). Разумеется, анало-
аналогичные предложения справедливы и для других промежутков между
корнями Рт{х) или Р'т(х), но мы не станем на этом останавливаться,
так как они нам не нужны в настоящий момент. Из теоремы 2 непо-
непосредственно вытекает
Следствие 1. Если формула B), где С^^О, верна для любых много-
многочленов степени 2т — 1, то
^№\ (8)
?де [l^ — наименьший корень многочлена Р'т{х).
С другой стороны,
AГ ^(*) , (т + 2)(т-1)
т(т + 1) ~ 2 "i h
(т + ^ + 1) . . . (т + 2) (т — 1) .. . (т— /с) , ,л
-1 (А + 1)! A! l"" j H
Подставляя (при т^>1) во вторую часть равенства A0) значение
4
х =т ггт—Т~о\ » нетрудно проверить, что она становится отрицатель-
ной. Поэтому
- 4
Таким образом, вследствие (8) имеем:
Следовательно, если Nn = 2т — 1 — нечетное число, то
1 < 16 .
«если же Nn— четное число, то
1 ^ 16
(if)
2)(Nn + 6) • l l}
202

Таким образом, второе из неравенств C) доказано.
Заметим, что, в случае неотрицательных коэффициентов Котеса,
Nn всегда нечетно, так как Nn = п + 1 при п четном. Поэтому в случае
п четного неравенство A1) получает вид
1 . 16
откуда n<^8, т. е. для всякого п четного среди коэффициентов Котеса
должны быть отрицательные числа, начиная от п ^ 8. При п нечетном
неравенство A1) дает
(л
т. е.
п2 — Юл — 7<0,
откуда* ?г<^11. Следовательно, для всех тг^>10 среди коэффициентов
Котеса должны быть отрицательные числа.
Для получения первого из неравенств C) нам понадобится еще
Теорема 3. Если формула A) верна для всех многочленов степени
2т — 2, то
где Yi—наименьший из корней многочлена Лежандра Рт(х), pW — соот-
соответствующий ему коэффициент в формуле D), a S (х) представляет число
значений x-t <^x.
В самом деле, применяя к многочлену
степени 2т — 2 формулы A) и D), получим
2
Но так как многочлен F2m—2(^)> представляя точный квадрат, не от-
отрицателен и производная его не имеет корней вне отрезка (^х, Tw)>-T0
^2m-2 И > 1 При Ж < fi,
поэтому из A3) вытекает A2).
Сопоставляя теорему 1 и теорему 3, получаем
Следствие 2. Если формула A) верна для всех многочленов степени
2т — 1, то имеет место неравенство
* Как известно, для п = 9 все коэффициенты Котеса положительны. (Ред.)
203

Применяя оценки многочленов Лежандра и их производных, данные
в другом месте C), имеем *
pS^-S^Tifl-Ti)- A5)
С другой стороны, подставляя х = ^—-——т- в правую часть равенства
(9), видим, что
поэтому
2 (w2 + /?гJ ^m Bm + 1) *
Таким образом, из A4) следует при il/n нечетном
1 2тг]/Т 15,4
и в случае 71/п четного
откуда для всех п вытекает первое из неравенств C).
В частности, условие Чебышева требует, чтобы Мп = п при п нечет-
нечетном и Мп = п + 1 при ?г четном. Поэтому в последнем случае (?г четное)
имеем
1 ^ 15,4 i с I 6 . .г ,
Т<(в + 2I» + 3) ' т е- " + 5 + -<15,4,
откуда ?г << 10. При п нечетном
1< т ° » + 3 + |<154
поэтому п <С 13. Таким образом, формула Чебышева во всяком случае не-
непригодна для п^>11 (и 7г = 10). Кроме того, если вместо A7) мы вос-
воспользуемся неравенством A4) и вычислим непосредственно (с точностью
до 0,0001) pW <С0,0857 < jj , то увидим, что формула Чебышева непри-
неприменима и для п = И. Заметим также, что вследствие того же неравен-
неравенства A4) она должна привести к комплексным значениям Xi и при п='8>
так как P<D < 0,1185 <-|- [67.2].
ЦИТИРОВАННАЯ ЛИТЕРАТУРА
1 С. Н. Берн штейн. Изв. АН CCCPJOMEH A932) A57*). 2 R. Kuzmin**.
Comptes rendus, 201 A935), стр. 1094; 202 A936), стр. 272. 3S. Bernstein. Journ.
de Math., X, стр. 219—286 [51].
* Это неравенство доказано в статье [71]. (Автор.)
** См. также Р. О. Кузьмин. «О распределении корней полиномов, связанных
с квадратурами Чебышева». Изв. АН СССР, серия матем. A938), стр. 427—444. {Автор.)

68
О ФОРМУЛАХ КВАДРАТУР
С ПОЛОЖИТЕЛЬНЫМИ КОЭФФИЦИЕНТАМИ*
Настоящая статья устанавливает условия необходимые и условия достаточные
для того, чтобы формулы квадратур, пригодные для многочленов данной степени,
имели положительные коэффициенты. Благодаря этому получается общий метод для
построения возможно простых формул квадратур, в которых все коэффициенты
выражаются положительными рациональными числами с возможно малым общим
знаменателем, либо таких, в которых абсциссы имеют возможно малые знаменатели
§ 1. Пусть Рг (х) будет многочленом Лежандра степени I на отрезке
[— 1, +1], ?1> Т2» • - - » Ti ег0 корни, plf р2, . . . , ^г1 корни его производной
Р\ (х). Положим
F (х, а) = Рг (х) +а(х + 1) Р\ (х), \
Ф (х, а) = (_ l)lF (- х, а) = Рг (х) + а (х - 1) Р\ (х). J
Обозначая через ii<Z%2 ^ • • • <С^ корни F(х, а) и через
— корни Ф(?, а), имеем, при а^> О
B)
так как
-Р(-1,в)-.Р(Т1,а) = о(Т1+1)Л(-1)-Р'|(т1)<0,
О,
Очевидно также, что ?л, 4 + т]г_л = 0.
Кроме того, имеет место
Теорема 1. Корни ?к (а), рассматриваемые как функции параметра
а, убывают от ^к до рл_1 при всех значениях к = 1, 2, . . . , Z
полагать C0 = — 1) ?г/ш возрастании а от 0 до оо; в то же время
возрастает от ^к до $к (если полагать $г = 1).
* Изв. АН СССР, серия матем., № 4 A937), стр. 479—503 A85*).
205

Действительно,
da A + а) Р\ (lk) +аAк + \) Р\
а)
= A_g + g r/(V+"lVg + 11 A Г)<0' №
Точно так же
Ida
С другой стороны, легко проверить, что формулы квадратур
+\f{x)dx= 2 9(h)f(h)+?af(l), )
(-1), J
-1
соответствующие корням многочлена (Z + 1)-й степени (ж — 1) i? (д;, а) или
(ж + 1) Ф(#> ^)> верны для любых многочленов R2i-\{x) степени 2Z — 1,
так как
Л () ф 1) F (, а) (?г_2 (ж) + /?z (ж),
где Qi—2 (х) степени I — 2, а потому
"j1 (* - 1) F (х, a) Q^2 (x) dx=a J (^ - 1) />', (х) ф_2 (ж) cfa = 0.
-1 -1
Очевидно, что рК_и) = р(^).
Заметим далее, что
F (х, a) dx _ V Pt(*) +a(x + i) Р\ (х) ^ _ 2а
) (,) I aZ(Z + l)+l ЙЖ " aZ (Z + l) + 1 # W
-l -1
Таким образом, при возрастании а от 0 до оо коэффициент ра растет
2
от 0 до роо — ГГГГТ)' Условимся писать Роо = р(Чг:1), имея в виду, что
когда Si (с возрастанием а до оо) стремится к пределу — 1, р^) как
2
непрерывная функция ?х стремится к значению р (— 1) = .., .. , которое
является коэффициентом р (^0) формулы квадратур, соответствующей
абсциссам % = - 1<рх< . .. < рг—i <Pi = 1.
206

Вообще, коэффициенты р (^) определим из равенств
+1 (x-l)F(x, a)P\{x)dx
Л Efc-l) К E*. «) ^ «*) (*-5*) A - Ф ^ E*. а) P'j «Л)
2
A - Ф ^ «*) [A + «) ^, E*) + « E* + 1) ^ E*)] '
Отсюда, пользуясь уравнением
A - ж2) Р"х (х) - 2х Р\ (х) + l(l + l)Pl (x) = О,
находим
"„ ч = 2
р I к> ~ A _ ф A + а) р\2 (ад + а EЛ +1) Р'г (ад №кР\ (ад -г (г +i)
2^
~~ A - Ф ^2 E^) + «[A + гьJр? «*) - г (г +1) A + ад р, (^) p'i (ад]
2 A + ^) a»
-5Л + а [1 + al(l + 1)] A
A - ф р (?ft) _ A + 5fc) рг (ад рг (ад + г (l + t) p2
Принимая во внимание, что Pift^P^i^^O, имеем, вообще, при
0<а<оо
0<pfe) < 5—то 5 J (8)
*У &-%) Р?(У + Чг +1) ^fE*) V ;
при а = 0 и а — оо получаем
Точно так же вследствие равенств ^ =—(¦ , р (т^, ) = р (il_mk
находим
р [у],) = 2 ;
Таким образом можем определить непрерывную функцию р (х) = р (— х
на промежутке (— 1, + 1) по условию, что
р (X) = 1-х2 р'2 х __ t х р
во всех промежутках (^_1? ^л) и
2
р (:г) = ТЕ т о (И bis)
(l-^^^ + ll-^PjH^^ + Z^ + l)^^) v
во всех промежутках (ffe, р^.) при значениях к = 1, . . . , Z, где, как и выше,
мы полагаем [30 = — 1, $г = 1.
§ 2. Роль функции р(#) в исследовании формул квадратур с поло-
положительными коэффициентами вытекает из следующей теоремы [68.1]:
Теорема II. Если формула квадратур
+ 1 п
[ / (х) dx = ^? p. f (х.), р ^> 0 ( 1 <^ х <С х <С <Сх <1) A2)
207

верна для всех многочленов степени 21—1, то
Pi<P(xi)> A3)
причем знак ривенства в A3) имеет место лишь при условии, что фор-
формула A2) совпадает с той единственной из формул E), в которой есть
абсцисса ?& или т]&, равная x\=f=-- — 1 {если owe xi = Ч- 1, то знак равенства
соответствует формуле квадратур с абсциссами—1 = р0, C1? . . . , $г = 1).
В самом деле, пусть #* ф ± 1 — одна из абсцисс формулы A2), лежащая
в промежутке (^_1? 7k)> совпадающая, следовательно, с корнем ?Л многочлена
F (х, а) для некоторого а ^ 0. Строим многочлен / (х) степени 2Z — 1
=
который, обращаясь в нуль в точках ?;• (/Ег= к) и 1, равен 1 при х = ?& = #*,
положителен во всех прочих точках отрезка [—1, + 1].
В таком случае
4-1 п
-1 3=1
если только все точки Xj не совпадают с корнями f(x), т. е. если формула
A2) не совпадает с E).
При хг = I, полагая
Рр (х) A + х)
2/f A)
мы получаем также, что
если только все прочие абсциссы Xj не совпадают с корнями Рг (х) A + х).
Аналогичным образом можем указать монотонно возрастающую не-
непрерывную функцию к(х), представляющую максимум суммы коэффи-
циентов ^ pi = Т (х), распространенной на все абсциссы х{^х любой
формулы квадратур A2), пригодной для всех многочленов степени 21— 1.
А именно, имеет место следующая
Теорема III. Пусть —1<^х^^г В таком случае, если, при соответ-
соответствующем выборе а, х =%к (т. е. $к_г<Сх<^ Т&)> то максимум тг (х) суммы
Т(х) осуществляется только формулой E), т. е.
х{<х k
2 рг = Т(х)^«(х) = ^ Р(У @<А<0; A4)
г—1
208

если же х = г\к (т. е. ^к<^х<С $к), то максимум iz(x) суммы Т (х) также
осуществляется только соответствующей формулой E), т. е.
A4 bis)
9
х = — 1, тс (ж) = p (— 1) = -^ (г^ 1} , а лри Yj < ж < 1, * И = 2.
Так как равенство тг(— 1) = р (— 1) вытекает из теоремы II, а равенство
тг (х) = 2 очевидно для ^ <^ ^? то доказательства требуют лишь неравен-
неравенства A4) и A4 bis). Начнем с первого: пусть х = %к.
Построим многочлен f{x) степени 2Z — 1, определяемый 21 — (I + 1) +
+ (I — 1) условиями
/' (Si) =.-.=/ (h-г) = f (Ejh-i) = •••=/' (Hi) = 0.
Так как /'(х)> кроме данных Z—1 корней, имеет еще по крайней мере
по одному корню во всех промежутках (Si, ii+i) и (?ь 1), кроме промежутка
{?&, ?&-{-i)> т° f(x) иных корней не имеет, а потому f(x) в промежутке
(?Л, ?ft+i) убывает от 1 до 0, и, кроме того, / (х) ^> 1 при ^^$л: и/(ж)^-0
при а:<^1. Следовательно, из формул E) и A2) находим
+1 к п
причем знак равенства имеет место лишь тогда, когда формулы E) и A2)
совпадают. Таким образом, A4) доказано.
Положим теперь, что х = г\к. В таком случае строим многочлен f(x)
степени 21 — 1, определенный 21 условиями
/' К) =•••=/' К.,) = /' (%+1) =...=/' G),) = 0.
Подобно предыдущему замечаем, что / (х) убывает от 1 до 0 в промежутке
(%>%+!)> и> кР°ме того^ /(ж)^>1 при — I^^^tj^. Следовательно,
применяя формулы E) и A2), получаем
+1 Тс п Х1<Щ
причем знак равенства осуществляется лишь при совпадении формул E)
и A2), откуда следует A4bis).
Заметим, что неравенство A4 bis) справедливо и при к = 1, так как
правая его часть тогда равна 2.
14 с. Н. Бернштейн 209

Принимая во внимание, что то же рассуждение может быть сделана,
переставляя точки —1 и + 1> получаем также
l
< 2р B0 + Ра - 2 - тг F^),
откуда заключаем, что
причем, за исключением случая 0<4i<CTi (К0Гда правая часть равна
нулю), существует только одна формула квадратур E), где равенство
имеет место.
Из этих неравенств вместе с неравенствами A4) и A4 bis) можно было
бы также получить теорему II.
Тем более имеет место неравенство
ТН= 2iPi>«(*)-pn, A6)
где знак равенства цри х ^> Ti невозможен, так что правая часть пред-
представляет недостигаемый минимум для сумм Т (х) [к которому Т(х),
конечно, может сколько угодно приблизиться, так как к{х) — р(х) яв-
ляется достигаемым минимумом для ^ Pi •
Следствие I. Если одна из абсцисс х\ в формуле квадратур A2) яв^
ляется корнем уравнения F(x, а)A — х) = 0 или Ф (х, а) A + х) = 0 и
х?^>.г. есть соседний корень того же самого из этих уравнений, то
%i+i^x<l> причем знак равенства имеет место лишь тогда, когда все
абсциссы являются корнями того же самого уравнения.
Действительно, если хг<^х1 два смежных корня одного из уравнений
A — x)F(x, а) = 0 или A +х)Ф(х, а) =-0, то
причем знаки равенства осуществляются лишь тогда, когда все абсциссы
Xj являются корнями одного и того же уравнения A—x)F(x, а) = 0
или A+х)Ф(х, а) = 0. Следовательно, за исключением этого случая,
xi+l <C ^г-
§ 3. Если вместо отрезка [— 1, + 1] взять любой отрезок АВ и рас-
рассматривать формулы квадратур с положительными коэффициентами Ci
^ <...<2/п<5), A7)
210

пригодные для всех многочленов степени 2/ — 1, то все они, очевидно
получаются из A2), если полагать
г В— А В —А . А + В
W = —2 Pi, Ух = ~2— хг Л §—
Поэтому
Отсюда можем вывести некоторые существенные свойства функции тс (х)
пл тхт л ТГ (ж) 2 — 7U (а?) ^
1еорема 1Y. Функции _. и — — являются монотонно убываю-
гцими в промежутке (—1, +1) {вторая из них равна нулю при x^-^i)-
Для доказательства замечаем, что если формулы
h l + i 1 Z+l
\ i A9)
где С|>0, C->0? —1^2/i^^^2/i<Cl? верны для всех многочленов
степени 21 — 1, то верна также формула
+i z+i z+i
j / (х) dx = 2 ci / ы + 2 ^ / (у*')- A7 bis>
-1 г-1 i=i
Поэтому, полагая —1<^а<^/г<^1? можем выбрать первую из формул
A9) так, чтобы
U Г _ /г + 1 /2а + 1 - /Л
2j °г ~ 2 TC vi + /г ; •
Следовательно, из теоремы III заключаем, что
Откуда, определяя h при всяком &>а из равенства
, _ 2а + 1 — h
получаем
" Т 1 /7_\ ^ / \
1 + 2а — Ъ
и так как /г = — ^— , то
Аналогичным образом выберем теперь вторую из формул A9) так
чтобы при — 1 <С
у g, _
1 — Л /26 — 1 — Л
» 2 "V 1 —i
211

г-i-i
Поэтому, замечая, что VCi = 1 + ^> имеем
г=1
Следовательно, определяя /г при всяком а<СЬ из равенства
— .— — а, т. е. h = —: ,
1 — /г ' 1 — а '
находим
откуда
2F — а) . 1 — 6
1 — а 1 — а
Т. с.
я (а) <
1—6 ^ 1-й ^Х /(Z + l)
Следствие II. Я/?гг любых значениях —1<Са<С^^Тг имеют
место неравенства
Аналогичным образом из A5) следует, что коэффициенты С$>>0 фор-
формулы A7) удовлетворяют также неравенству
>
а потому, применяя тот же прием, что при доказательстве теоремы IV,
находим
с^ ттт W4 "К (х) — р (х) 2 — -К (х) + Р (ж)
Следствие 111. Функции - м 7^—5~^—- являются мо-
монотонно возрастающими при —1<^х<С1 (первая из них равна нулю
при ж ^ yi) -
В частности, из B1) вытекает
и так как р(ж) = 1г(ж) при х<Съ> то Р(х)> 1 + х +777Т~Г\ ПРИ —
"К (х) — р (х) ~. 1 , . .
а из того, что у+ х ~ < 1 ~ z (l + 1)?слеДУет>что (~1 <
Из следствия III при — 1<><<6<1 получаем также
2 - 7Г (Д) + Р (Д) ^ 7Г F) — Р F) — 71 (Д) + Р (Д) ^ 71 F) — р F)
1-я ^ V=~a >—Г+6~~
212

Сопоставляя эти неравенства с B2), получим
Ь — а
откуда следует также, что (—
1 + Ъ
Р(Ь)
-р (а)
1 + а -р (я) -""I — я '
B5)
B6)
Р (х)
Р (?) л s- л Р (х) л
т. е. -— функция убывающая, а функция j-^-f- функция возрастаю-
возрастающая, В этом можно было бы также убедиться непосредственно из рас-
рассмотрения выражений A1) и (И bis), так как легко проверить, полагая
р(ж) = 7й' что при Р*-1<
1 — x
B7)
откуда
1—ж.
dx
ТЦГХ
(х)
^
dx A + x) A —a;2)
[Вследствие четности функции р (ж) те же неравенства верны при
<СХ<^$к]- Что же касается самой функции о(х), то, замечая, что левая
часть равенства (при Рл—1<С^<Л?)
A - х) х' (х) = I (I + 1) Р2г (х) - />, (ж) Р'г (х) A + х)-A- xf Р'г (х)
— многочлен B1 — 1)-й степени, получающий противоположные знаки в
21 — 1 точках рь Yi и имеющий корнем х = 1, заключаем, что в проме-
промежутке (— 1, Yi) ъ' (х)<С.0> а в прочих промежутках (р&_i, Y*) имеет один
и только один корень. Поэтому р (х) возрастает при изменении х от — 1
do Yi> а внутри каждого из промежутков ($к—ъ 7&)> кай: и Gft» P#)>
имеет по одному относительному минимуму. Таким образом, с другой
стороны, в точках pi, Yi кривая у = р (х) имеет относительные максимумы
с угловыми, точками. Пря этом, вследствие уравнения B7) и соответ-
соответствующего ему ^р- + z (х) = 2Р'2 (х) в промежутках (y&, pft) находим -
I2 (I 4- IJ , , ,ч л 1
"/ ч Т (Yfe)
т G*) = Y=Yk ""
7/ Ч P
Р G*) = f
¦—Tft
P (W =
P (Р*) = -Г3
B7 bis)
213

С другой стороны, эти относительные максимумы кривой ?/ = р(#) в по-
последовательных точках Ti^CPi^- • • идут, возрастая при #<^0, так что
имеют место неравенства
Действительно, из (8) следует, что
i —х*)РГ(х) +i(l+l) Р*(х) *(х)
причем знак равенства имеет место в точках Hnl, Ть &• В таком
случае знак
Z' (х) = 2Р\ (х) [I (I + 1) Рг (х) - хР\ (х) + A - х*) Р\ (х)] - ЪхР? (х)
совпадает со знаком х; поэтому Z(x) достигает минимума Z@) = Р\2{0) +
+ 1A + 1)Р* @) при х = 0.
Таким образом, абсолютный максимум р (х) достигается при ж = 0и
равен
^ 2 2 Г 2»4 . . . Z 12 Гтт
Р' ^ "~ z (z + 1) ^2(°) ~~ НМ-Т) L1-3 . . . A~ 1) J ^* Т
при / четном и
при Z нечетном.
Заметим, что, применяя асимптотические формулы для многочленов
Pi(x) и Р\{х) к выражениям A1) и (И bis), получаем, вообще
1ё B9)
при /->оодля любого данного х внутри отрезка [—1, + 1]. Как мною
показано в другой статье [71] (стр. 240), при всех конечных значениях /
Прежде чем перейти к приложениям полученных здесь результатов,
укажем еще, что в любой формуле квадратур A2)
i + x + TjrriT-^x)< 2^< 2*<1 + ж-щ+Т) + р(а;)- C0)
Таким образом, во всякой формуле квадратур A2), справедливой для
многочленов степени 21 — 1, каждая иг сумм ^.pi и У) Pi равна 1 + х
с погрешностью меньшей, чем р(х).
% 4. Теорема V. Для того чтобы формула квадратур
\f (х) dx = ^Vi [/to) + /(- ач)] +
214

соответствующая корням многочлена
R(x) = x(x*-xl)...(x* — x*_1), C2)
верная для всех многочленов f (х) степени 21—1, имела положительные
_ коэффициенты ри достаточно, чтобы
2 2
(где для определенности I предположено четным) и чтобы, кроме того,
а? < *,5 хо < х4; . . . ; *»_3 < х^ C4)
(если полагать попрежнему, что xnt^>Xi есть соседний корень того же
уравнения F (х, а) = О или Ф (х, а) = О, которому удовлетворяет х$.
В самом деле, коэффициенты ръ определяются однозначно из системы
1 уравнений
'-1 , ! ч
Г,1 А C5)
1=1
Рассмотрим, в частности, формулу квадратур, соответствующую мно-
многочлену
ЛИ- ^.^.w^-tn-.» _ C6)
где 0<< ?<Ti + 1- Легко убедиться, что коэффициенты p{$k)s р (т^)
«соответствующие абсциссам (В&, ^л (кроме ^i), т^к же, как и коэффициент
Л(Т1~~8) ПРИ абсциссе Ti"~8» будут положительны.
Действительно,
(х) [х*- (Yl-e)«] (р| - у?) <fe
+1
откуда
=
[ (Yi - гJ - Щ\ A - Y?) Pt №*) Pj
+ 1) [(Yi - еI - Э|] A -
215

Аналогично находим
P Gl S) === " 2 x " ' ^ ^'
Можем положить, например, ^i — s — xi-
После этого осуществим непрерывный переход от абсцисс х1г
Pi» 7г» • • • » 7 1 к данным абсциссам х19... , з^-! следующим образом.
Положим
— >0 72,
и заставим X возрастать от 0 до 1; функции Ai(\) последовательно опре-
определяем требованием, чтобы
C7)
Так как с возрастанием X от 0 до 1 х2 (X) = X (ж2 — Pi) + ^ убывает
от Зх до ж2, то ^з(Х) в то же время убывает от C2 до х\, т. е.
х\ (X) = Л4 (X) (xl - ря) +Р2 = 44 (X) ^ + A - А, (X)) р2,
где .Л4 (X) — некоторая монотонно возрастающая от 0 до 1 непрерывная
функция. Таким образом, убеждаемся, что все функции ^4{(Х), последо-
последовательно определяемые равенствами C7), монотонно возрастают от 0 до 1.
Отсюда следует, благодаря неравенствам C4), что при всех X @<^Х-^1)
соблюдаются также неравенства
х\ (X) = А, (X) х°2 + A- А, (X)) ^2 < А, (л) я4 + A - А, (X)) р2 - х, (X)'
и вообще при всех i (I <^ i ^ Z — 3)
4(X)<xi+2(X). C4 bis>
Для i = l неравенство х\ (X) = х\ <^ х3 (X) очевидно, так как ж3(Х)^-ж3.
Но в таком случае, так как числа pv определенные из уравнений C5),
при X = 0 положительны, они могли бы при изменении X стать отрица-
отрицательными только получив значение 0 при некотором Хо @ < Хо <; 1).
Но это невозможно для коэффициентов р . .. , рг_2, так как, благодаря
C4 bis), между х{ (X) и ж9(Х) A-^/^Z — 3) имеется лишь одно значение
216

хгл-\ (^)- Поэтому, если бы pi+1 обратился в нуль (в то время как про-
прочие коэффициенты не отрицательны), то между х{ (Хо) и х°г(Х0) не оказа-
оказалось бы ни одной абсциссы, что противоречит следствию I. Точно также
не может быть рг = О, так как тогда не осталось бы абсциссы между
О и 7Х; Pi—i ~ 0 невозможно, так как не было бы абсциссы между $i—2 и
2
Зг = 0; рх — 0 невозможно, так как не было бы абсциссы между ^ г и
2 ~2~ ~2~
Теорема, очевидно, останется в силе и в том случае, если некоторые
из неравенств C3) или C4) заменить равенствами, и в частности, если
хг = — 1.
§ 5. Эту теорему применим для построения формул квадратур с по-
положительными коэффициентами и рациональными абсциссами с возможно
малым общим знаменателем N [68.1].
Положим жх =— 1, тогда х\ = рх; поэтому, если N должен быть об-
щим знаменателем абсцисс, возможно взять х3 = ^ + -~, где О-^б-^l;
A ft
затем возьмем хъ = х\ + -& , где О<;63<<1 и т. д., х^г = ж?_3 ~\—^г
полагая для определенности I четным; нужно только, чтобы все эти хи
с нечетными значками к ^ I — 1 остались в соответствующих промежут-
промежутках, а именно ^.^ < ^2Л_1<Тл.
A ft
Аналогично полоя^им х2 = fi + "^ » гДе 0<:б0<1, ж4 = Хз + -~
@<е2<1) и т. д., Я1_2 = я?_4 + -^@<б1_4<1), причем 7л
Абсциссы .т2г—1 и ^2г—1 с нечетными значками совпадают соответственно
с корнями некоторой функции F {х, а^ = 0 и переход от xj^-i к ж2г+1 влечет
за собой (по теореме I) уменьшение параметра а\ (ai+i <Ca0- Наоборот,
#2г и ^2г являются корнями Ф (х, ui) , и переход от x^i к #2г+2 соответ-
ствует увеличению ai (ai+1^>a?).
Рассмотрим сначала четные абсциссы. На основании сказанного,
для того чтобы последовательные замены абсцисс х%, абсциссами
aj2i+2 = xli + ~^r были приемлемы, необходимо и достаточно, чтобы они
соответствовали некоторой возрастающей последовательности значений
2
Но в промежутках (f>, pft) зависимость между йпх определяется урав-
уравнением D), т. е.
dx 1 ,, . .
da ~ ~1~ а[Ц1 + 1) дТТ] ' ^ S^
1 — х 1 -f х
Поэтому
ai+l
217

ii7 принимая во внимание, что 4i+1^xli<C
аг+1
da
fl[fl/ (/ + !) + Ц
а* 1+ i+ri+1
Но, как известно1,
in
Следовательно,
о ^ V da
2г+2
IJ
>Тг7~1
2 (г + IJ
>
l!
IJ
da (i + 1) 1^2 Г 1
(Z-ИJ у (/ + 1Jа. + (г-+4)^2 (Z + 1J fl.+i + (г
2 (* + 1) V J
C9)
Таким образом, для того чтобы требуемые сдвиги были возможны, доста-
достаточно, чтобы Лт было настолько велико, что при всех i = 0,1, 2, ... , ¦ ,
исходя из значения а0 = 0, соответствующего 7]> уравнение в конечных
разностях
D0)
последовательно удовлетворяется положительными величинами ai+1, ка-
каково бы ни было 6i @<^6i<Cl)-
Полагая (Z + IJ at = bi)/*2, запишем уравнение D0) в виде
Очевидно, что если уравнение
для данного Bi^- bt^0 приводит к положительному значению /??+ъ то
тем более будем иметь Bi+1 ^> bi+1 ^> bi ^ 0. Положим
TV |^Z = a (Z -f- IJ; D3)
1 А. А. Марков. «О корнях некоторых уравнений». Избранные труды по
теории непрерывных дробей и теории функций, наименее уклоняющихся от нуля.
М.— Л., 1948.
218

тогда уравнение D2) примет вид
1 11
—т = L ~—_ D4)
или
п , . , л а(г' + 1J(Б. + г- + 1)
Так как Во = О, то нам достаточно будет установить, для каких зна-
значений а из O^Bi^i следует, что и O^Bi^ <; i + 1, чтобы утверждать,
что соответствующие им из формулы D3) значения iV приемлемы.
Но из ?ч>0 следует Bi+1^>Bi (и тем более 5i+1>>0), если
так что при условии Bi <C г достаточно, чтобы
т, е. чтобы а^>1.
С другой стороны, при этом будем иметь
Г, , ?D-а)+2-а ] .
[ а (* + 1J—B* + Ш
а (г + IJ — Bг + 1)
если а ^> 4.
Аналогичным образом для абсцисс с нечетными индексами имеем
дифференциальное уравнение
dx __ 1
1 + X 1 + X
откуда
О
*так как
Принимая во внимание, что
имеем
> v ~—^=^[—Ц Ц-1- (^
па
219

В данном случае нужно, чтобы положительные числа ai с возрастанием i
шли убывая от ал = оо. Полагая попрежнему
D3)
покажем, что, каковы бы ни были числа
чисел пг, определяемых уравнением
1 1
последовательность
положительна. Очевидно, что это будет доказано, если мы убедимся, что
значения #i^>0, если заменить в уравнении D7) с^ некоторыми опреде-
определенными числами (н<;4, так как с увеличением at при неизменном или
увеличенном аг увеличивается также а^. Но заменяя в D7) а. через
видим, что уравнению
1 1 , i
у
2B? —
2B?—
удовлетворяет
Следовательно,
(i— 1)
Таким образом, при всяком целом
=>0.
lJ D8)
возможно построить симметричную формулу квадратур для отрезка
[— 1, +1] C1) с положительными коэффициентами и с рациональными
абсциссами xi, имеющими общий знаменатель N, точную для всех много-
многочленов степени 21— 1.
Напротив, как показано в моей статье [67], такая формула невоз-
невозможна, если наибольший знаменатель п абсцисс, который может и не
быть общим знаменателем, удовлетворяет неравенству *
(/ — 1) (/ -f- 3)
П ^
Для дальнейшего полезно будет заметить, что вместо того чтобы
брать в качестве исходного значения хг = — 1, можно также положить
х1 = — 1 + -^ , где попрежнему N > 2 У2A + IJ @ < 6 < 1). В таком
случае уже не будет аг = оо, но из уравнения
Рг («О + аг (Xl + 1) Р\ (х,) = О
* Таким образом, I2 есть порядок наименьшего возможного значения N.
(Автор.)
220

имеем Pi (a?i) 2 — 1A + 1) (хг + 1)
1 P (т \ (т 4- 1 \ I (I + 1) (x± + 1)
2 —Л __
Таким образом, нужно лишь проверить, что если попрежнему в урав-
уравнении D7) а* >- 4 (i > 1), то значение а* > 0 при всех i > 1, если ах >3 "|/2
при / = 1. Для этого замечаем, что г/i |/ = г- (где 2/х = 31^2) удо-
влетворяет
поэтому
уравнению
1
Уг+i ^ +
1
1
4 /
('¦
1
У'г ^2"-
1 + ±
1
-1)
f _L A2i ч"
i
г^ прИ
36i2
-1)A2?-5)
!
4 '
§ 6. Теорема VI. Если положительные числа р17 р2,..., p2i—x удовле-
21-1 Л
творлют условию V /^ = 2, причем pi = p^i—i, и, полагая J\ pi = тс
г=1
, имеем
О < % < fi < х2 < . .. < рл_
C3)
2 t 2
{5^л определенности предполагаем I четным)] если, кроме того,
x°i < xi+2> C4 bis)
то существует формула квадратур
/ (х) dx = 2 />i t/ № + f (- 2/i)] + Рг f @), D9)
i=l
точная для всех многочленов степени 21 — 1; при этом
%<2/i<Ti> ^<^<4-x A</г</). E0)
Заметим сначала, что если формула D9) возможна, то неравенства
^50) должны быть соблюдены, так как вследствие A4) и A4 bis) имеем
221

откуда Xh-^yh, и, с другой стороны, вследствие A6), должно быть
x<Vh i=/i—l
x<xh—l x<Vh
а поэтому невозможно, чтобы
При этом знаки равенства в E0) невозможны, если их нет в условиях
C3) и C4 bis).
Для доказательства поступим так же, как в теореме V. Величины
уг (i = 1, . . . , I — 1) должны удовлетворять уравнениям
i-i
Вводя вспомогательный параметр X в коэффициенты pi, положим pi (l)—pir
хг A) = xi, и допустив, что нам известна некоторая формула D9) с коэф-
коэффициентами/??>0, которым соответствуют значения яч(О), удовлетворяю-
удовлетворяющие условиям теоремы (с неравенствами в широком смысле слова, если
для Xi не исключаются также и соответствующие равенства), положим
Как было показано, параметр X можно ввести так, чтобы точки xi (к)
при всех значениях 0<С,Х<^1 удовлетворяли (в узком смысле) условиям
C3) и C4 bis). Но в таком случае из уравнений E1) гц (X) определятся
как однозначные вещественные аналитические функций X, лишь бы только
пи при каком значении X = Хо некоторые из значений yi (X) не станови-
становились равными между собой. Однако благодаря неравенствам
yh (X) < 4-i (X) < xhH (X) < yh+1 (X)
соседние значения у^ (X) и yn+i (л) не могут совпасть.
Таким образом, остается лишь сконструировать какую-нибудь опреде-
определенную формулу квадратур, удовлетворяющую условиям теоремы. Воз-
Возможно, что путь, который мы предлагаем для этого, может быть упро-
упрощен, но не совсем бесполезно проделать его, чтобы одновременно выявить,
в чем заключается принципиальная трудность построения формул квадра-
квадратур по заданным коэффициентам.
Для этого положим
хъ = р!, х3 = 72, . . . , ^г-2 _?_
2 2
Соответствующие им значения абсцисс
Уг = Ti — Ai> 2/2 = 72 — А2> Уг = 7г + Дг, . • . , ]
2/i_2 = 7J_ — AJ_, yz_! = 7_L + AJ_ I
2 2 2 2 J
должны удовлетворять I — 1 уравнениям (/г = 1, 2, . . . , I — 1)
[P (Ti) - e] [Ti - AJ* + (Pa + s) (Та - Д^ + [р Ы ~ РЛ (Ъ + К)* +
¦¦¦+Р±[Ц_- Aj,]2" + [р (Ti.) - Pi] hl_ + A'jJ2" = пТТ '
2 2 2 2 2 2 2
222

где
? = Р Ы — Р (xi)> Р* = те (Pi) — л Ы»
Рз = * (Ра) - те (Та)» • • ¦ , /?_!_ = я (Pi—a_) — те (тг_2).
2 2 ~Y~
При этом, если % = fi, то s =± А± = Д2 = А2 = . ¦ . = A i =Ai =0. Если
же ^1<СТи т* е* ?^>0> то, так как в случае вещественности решений
системы E3), согласно E0),
2
необходимо, чтобы Aj>>0, Ai>0.
Таким образом, нам нужно лишь показать, что при достаточно малом
s^>0 система E3) имеет вещественные решения. Ввиду того, что функ-
функциональный определитель системы E3) функций Д$ и Д| переменной е
равен 0 при е = 0, мы должны положить: e~t2, A1 = t2z(t)J Ai = tVi(t),
А- = г г — и рассматривать Z—1 функций z(t), Vi(t)9 m(t)
i = 2, 3, . . . , -тр) переменной t при t^-0. В таком случае, вычитая из
2 ,
уравнений E3) уравнения, соответствующие 7 = 0, получим
* [(Та - А2J" -(Ti- АхJ'] + р (Tl) [(Tl - AxJ" - Tf J
ы «т. + a;J" - Tf] + ^2 [(T2 - a2J" - (Ta + A;f]
+ P (T ,) Kl± + A X - T* ] + P± t(Tj_ - A^J" - (T± + A^Jh] = 0. E4)
2 2 2 2 2 2 2 2 2
Замечая, что
р (Ti) а;2 - Pi (д;2 - д|) = [Pl ;(^_P;U) + ^ «j @
содержат множитель t2, видим, что все уравнения E4) по разделении на
t2 могут быть записаны в виде
Tf - Tf - 2Лр (Ti) Tf-1 z + 2ATf-*«a + h BA - 1) /^p2 tf^l + • • •
^-i u±+h BA - l)p(^ }Д Tf-^j= «?ft(«, z, в2,... , г»^), E5)
— — 2 2
2 2
где срЛ — многочлен относительно входящих в него переменных. Поэтому,
так как определитель (I — 1)-го порядка, составленный из коэффициентов
при z, и2, 1ф .. . }<у| , отличен от нуля, то полагая
223

где I — 1 постоянных z0, ац, cf удовлетворяют Z — 1 линейным уравнениям
Tf' -
Tf-1
l + hBh — '
Pi Р (Y i )
E6)
T 2
получим 2 2 решений системы E5), разлагающихся по степеням t = |/ ?
при 2 достаточно близком к нулю. Однако соответствующие значения Дь
Ai должны быть, кроме того, вещественны и положительны: для этого
достаточно убедиться, что значения с\, получаемые из уравнений E6);
положительны, и тогда, для того чтобы Дг^>0, Д|^>0 при ?^>0,
нужно будет взять все С{^>0, после чего искомое решение определится
однозначно. С этой целью заметим, что определитель, составленный из
коэффициентов при неизвестных системы E6), равен произведению мно-
множителя
(р Ы —
(р
Pi)
на определитель Н, приведенный на~стр. 225.
Для получения с? нужно составить определитель Hi, заменив элементы
B? — 1)-й колонны через ^f1 — if1* Вместо этого заменим в определителе
Н соответствующие элементы через 2hx2h~1. Полученный определитель
Hi (x) представит многочлен B1 — 3)-й степени относительно х9 который
будет иметь простыми корнями 0, Hhii'i' iTi и остальные/ — 4 значения
±Т2> • • • * ±Ti-i» ±Ti+i» • • • > ±Т_г_ будет иметь двойными корнями.
2
Таким образом,
X
2Ti "-К 2Ti+1 ...2T±
2
4т» ...4т» 4Tf+i ...4T|_
2
B/ — 4)T2'-5 (/ — 2) B/ — 5)
21— 6
V 2
V 2 ^2 /Y2
И / V *2
т
2 Г2\4
т~ т Ti (т? -
224
2Т72 27

CO
. со
CNI
ю
I ,
5*4
~1„
i
CD
CM
CM
CN1
см
CM
CM
см
I
-^*
CM
15 с. Н. Бернштейн
225

Следовательно,
Нг(х)
TJ "9/9 9ч
?2. <у& (>уА , «у<3\
J i V I i J l'
(Y? - Y?J - (Y? — Y ? J (^2 ~ Yi)(*2 - Yi)
"a"
-4*P?(*)(Y«—r?>
откуда
я } я
Следовательно,
Поело того как построена формула квадратур D9), соответствующая
значениям хх << тх, х2 = р1? • • •, ж^х = т i и приводящая к /-1 различным
значениям уг-, мы можем, как было указано в начале доказательства,
построить любую формулу D9), где х\ удовлетворяют неравенствам в
узком смысле, а затем, исходя из последней, построить также формулы,
где неравенства C3) и C4 bis) соблюдены в широком смысле (т. е. с
возможностью знаков равенства).
§ 7. Используем теперь доказанную теорему для формул квадратур,
точных для многочленов B1 — 1)-й степени
где целые числа
и я связаны равенством
Полагаем
достаточно, чтобы
при условии, что х9__г<^хг1 ^ Следовательно, после того как хг_г дано,
xi+\ можно определить из равенства
226

где -0<^6{<^1'. Но принимая во внимание, что все рассматриваемые здесь.
значения яч<ГО, из неравенства B2) заключаем, что
Но тг @) = 2 — тг @) + р @), поэтому
•"t-fi i—i ^- i
l-yp(O)
Таким образом, применяя результаты § 5, вследствие D8) требуемое
построение будет возможно выполнить, если
n(l--i-p@))>2/2(J + l)«.
Но принимая во внимание формулы B8), имеем для I нечетного
[2-4- • •(/ j) "|2 6
1 - 3 - - • Z J / -{- 4
Z четного
так как —-.— <С7 . /'» и ПРИ ^ == ° неравенство (i>8) соблюдается, а для
]"?*—Г<Г+Т« и Ш ^ = 4 неравенство
E8 bis) соблюдается.
Следовательно, для построения формулы E7) достаточно, чтобы
i). E9)
С другой стороны, как было показано в статье [67] [неравенство A7)]>
для того чтобы формула E7) была возможна, необходимо, чтобы
В действительности величина знаменателя п в формуле E7) может
быть еще уменьшена; для этого необходимо было бы для каждого опре-
определенного значения I заменить общие неравенства непосредственными вы-
вычислениями. Таким образом, можно, например, убедиться, что для мно-
многочленов 13-й степени (I — 7) возможна формула
где
А±=1, Л = 2, Л = 3, Л = 3, А5 -4, Ае -4.
16

69
ПРИМЕРЫ ФОРМУЛ КВАДРАТУР
С ПОЛОЖИТЕЛЬНЫМИ КОЭФФИЦИЕНТАМИ
И РАЦИОНАЛЬНЫМИ АБСЦИССАМИ*
1. Целью настоящей заметки является конкретное приложение одной
пз общих теорем моего исследования о формулах квадратур с положи-
положительными коэффициентами к некоторым численным примерам.
Пусть Pi (х) — многочлен Лежандра степени / на отрезке [— 1, + 1]
я Pi (х) — его производная. Пусть Ti<T2<C" ' • <Г Т^ и Pi<p2<" "<$i-i
будут, соответственно, корнями Рг (х) = 0 и Р{ (х) = 0. Нетрудно видеть,
что
причем в промежутках (— 1, ^О» (Ра, Та-ы) имеем
Pi (я)
п в промежутках (тл-^л-), (тг *
В таком случае мною доказана следующая
Теорема. Для того, чтобы все коэффициенты формулы квадратур
Котеса pi, точной для всех многочленов степени 21 — 1,
-rl 1-1
J / (X) dx = 2 Pi [/ (Xi) + f (- Xi)} + po/(O), A)
—1 1
где
бм.ггг положительны, достаточно, чтобы для всех хг<^0 соблюдались не-
неравенства
•'•- Труды Лешшгр. индустр. иы-та, № 4, раздел физ.-матем. наук, вып. 2 A937)
стр. 19—21 A86*).
228

а (жх) > a(xs) > • • • > a (a^-i) > «
> • • • > 0,
B)
2. В качестве первого примера поставим себе целью немного видо-
видоизменить классическую формулу Котееа с 21 — 1 = 11 равностоящим!}
абсциссами
которая, как известно, имеет коэффициенты различных знаков, так, чтобы
все коэффициенты стали положительны. Покажем, что этого можно дос-
достигнуть, если упразднить две ближайшие к нулю абсциссы ±т~> введя
вместо них абсциссы ± Тп fT# е* середины крайних промежутков 4--^-( 1 + -г-)>
. ,-. I X» \_/ • KJ\s LS^/X,.KJXXXM, Х\КУ1А-КХ-1-1.ЖЛ Л 11K/<J1UV<XI* 1AIU1J | ^ J. | —
1U ' di \ О j
так что общий знаменатель всех абсцисс равен 10]. Итак, в данном
случае
_ \ — 1 _ __А — 3 _ А —п
Xi — 1, х2 — ^q, %з — 5 у ^4 — ^ у Х5 — 5 ' х° — у
16 P6 (x) = 231 x« — 315 z4 + 105 x1 — 5,
с) = 198 ж5 — 180х3 + 30т.
16
7 -
Имеем
= — 1 — 0,9 = ж2
— 12,69702
- 4,758629
X
16 п'
7 6
16 Р,
{х) =
— 1
-48
16
— 0,8 = т3
3,27936
- 0,6 =
5,48352
6,268736 2,753542 4,682176
- 0,4 = х5
- 2,50752 i
Таким образом, условия
ч . 7 , х 6,268736 . А 21
г])^оо>та(.х3)--з^93^>0' У(
4,758629 ^ „
, _ 4,682176
5' ~~ 2,507о2
2,753542
выражающие, что ж^ находится в соответствующих промежутках, соблю-
соблюдены. Кроме того, соблюдается и условие B), так как
5 4,682176
Т * 7,о22об
6^8736
3,27936
47,58629 ^ 1 27,53542
_1_
133 " 12,69702
5,48352
3. Аналогичным образом покажем, что формула квадратур для мно-
многочленов 13-й степени с 2 / — 1 = 13 абсциссами
-j— Xi = 1, -t- X^= 7q > zt
i *^4 == ~o" ? IZI X5 === ~2
= 4-» ^0 = 0
229

также должна иметь положительные коэффициенты.
Действительно,
16 Р7 (х) = 429 х* — 693 х5 + 315 х3 - 35 х,
16
^ р'7 (х) = 429 х* — 495 х4 + 135 я2 — 5,
— 1
64
-16
9
"To
7,568689
6,8851999
___4_ _
о
-8,892224
3,8344192
2 _
1243
243
2836
729
4,515625
— 3,5703125
л" — ^6
6589
73433
Поэтому условия теоремы
/ \ — { 19,172096 . 1 7,140625
а\хз) — У 8,892224 ^ У '4,515625
А 7 , ч J 1 68,851999 ^ 7 , ч 1 709
1 73433
v/\-V-2; — 7 19 7,568689
соблюдены.
Таким образом, пользуясь указанными выше абсциссами, выражаю-
выражающимися дробями с знаменателями не больше 10, мы получаем симмет-
симметричную формулу квадратур (на отрезке [— 1, +1]) с положительными
коэффициентами, пригодную для всех многочленов 13-й степени. Из не-
неравенства
1 8
Гб^ ~(Г^ТУ(г + 3) '
которое необходимо (г) для того, чтобы знаменатели абсцисс не пре-
превышали 10, следует, что (сколько бы ни брали абсцисс с знаменателями
не более 10) подобная формула квадратур была бы невозможна для мно-
многочленов 17-й степени (/ = 9).
Вопрос о том, существует ли такая формула для / = 8, т. е. для
многочленов 15-й степени, остается открытым.
В наших формулах коэффициенты р\, очевидно, также рациональны,
и вычисление их не представляет труда.
ЦИТИРОВАННАЯ ЛИТЕРАТУРА
1 С. II. Берн ш тейп. О формулах квадратур Котеса и Чебышева. Докл.
АН СССР, 14 A937), стр. 323 [67].

70
ПРИМЕРЫ ФОРМУЛ КВАДРАТУР, АНАЛОГИЧНЫХ
ФОРМУЛЕ ЧЕБЫШЕВА*
1. Формула квадратур Чебышева
ь п
\f{x)dx= А=^2/Ю, (а<^<х2...<хп<Ь), A)
a i
которая должна быть верна для всех многочленов степени пу как из-
известно1, невозможна для я>9. Однако для каждого я>9 можно ука-
указать такое число пх = ф (п)<С п, что существует бесчисленное множество фор-
формул вида A), верных для всех многочленов степени пг. Для определен-
определенности можем положить а = — 1, 6 = 1, и, кроме того, для сохранения
одного из преимуществ формулы Чебышева потребуем, чтобы х-х + хк = 0,
когда i + к = п'+ 1; в таком случае наивысшая степень пх многочленов,
для которых формула верна, всегда будет нечетным числом пх = 21 — 1.
Нетрудно заметить (непрерывно перемещая абсциссы #4), что если су-
существует формула A) с знаменателем п, пригодная для многочленов
степени 21 — 1, то существует такая же формула, в которой фигури-
фигурируют не более 21—1 различных абсцисс. Поэтому задача сводится к на-
нахождению формул
4-1 1-1
^ /(x)dx = 2n [%Ai(/(Xi) + f (- a,)) + S/@) ] , B)
где Ai^O, В ^0 —целые числа, верных для всех многочленов степени
21—1. В случае 1 = 5 можно положить п = 9, .4i = J5=l, и тогда мы
получим указанную выше формулу Чебышева.
Здесь мы рассмотрим случаи I = 6 и Z = 7 (когда формула Чебышева
уже непригодна для многочленов степени 21—1).
* Труды Ленингр. индустр. ин-та, № 5, раздел физ.-матем. наук, вып. 1 A938)
стр. 3-7 A98*).
1 «О формулах квадратур Котеса и Чебышева», Докл. АН СССР, 14 A937) [67].
231

Напомним сначала обозначения моей статьи «Примеры формул ква-
квадратур с положительными коэффициентами и рациональными абсциссами >
[69]. Полагаем
Р (х)
*(«) = — {х + ^ pt> {х) (Р* < * < T*+i). C)
где 7ft и (^ — соответственно корни многочлена Pi (х) Лежандра степени
/ и его производной Р{ (х) (кроме того, ро = —1, рг = 1).
С другой стороны, обозначим через ъг{х) максимум суммы коэффи-
циентов V Ci для совокупности всех формул квадратур
верных для любых многочленов степени 21—1. В таком случае имеет
место г
Теорема. Для того чтобы при данных значениях Pi^>>0 (i = 0, 1, ...
...,Z — 1) существовала формула квадратур
+1 i-i
% f (- Xi)] + pQf @), E >
l—l
1
верная для всех многочленов степени 21 — 1, достаточно, чтобы числа
, определяемые из равенств
ъ
удовлетворяли неравенствам
a {y2k-i) > a (y2ft+i), b (y2k) < 6 (г/2й+2), (Рл-i < y2ft-i < Tfc < 2/27,- < Рл). F ^
Ниже даются таблицы функций тс6 (^) и 7и7 (ж) (вычисленные по моим
указаниям тов. Непомнящим).
2. Построим формулы, годные для многочленов 11-й степени A — Q).
Положим
п = 20, Ах = Л2 = 1, Л3 - Л4 = Б = 2, Аъ - 3. (I)
Таким образом, мы хотим убедиться в возможности формулы E), если
1 «О формулах квадратур с положительными коэффициентами». Изв. АН СССР»
ОМЕН A937) [68].
232

Таблица 1
— X
1
0,99
0,98
0,97
0,96
0,95
0,94
0,93
0,92
0,91 ¦
0,90
0,88
0,86
0,84
0,82
0,0476
0,0588
0,0718
0,0952
0,1067
0,1284
0,1523
0,1738
0,1841
0,1951
0,2075
0,236
0,269
0,306
0,334
ФуНКЦиЯ 7
X
0,8
0,78
0,76
0,74
0,72
0,70
0,68
0,66
0,64
0,62
0,60
0,58
0,56
0,54
0,52
с6 (х) A = 6)
ти(х)
0,360
0,378
0,396
0,418
0,445
0,473
0,502
0,532
0,551
0,570
0,590
0,612
0,634
0,658
0,683
— х
0,5
0,48
0,46
0,44
0,42
0,40
0,38
0,36
0,34
0,32
0,30
0,28
0,26
0,24
0,22
0,711
0,739
0,765
0,787
0,802
0,818
0,835
0,856
0,877
0,899
0,922
0,946
0,971
0,997
1,015
Из табл. 1 находим
_ Уг = 0,965; - уз = О»756'» — Уъ = 0,321; - у2 = 0,906; -у4 = 0,591.
Из формулы C) получаем
0,9>а(уг)>0,7; 0,48>а(г/3)>0,40; 0,15>аЫ>0,12.
Из формулы D) получаем
0,014 < Ъ (у2) < 0,022; 0,045 < Ъ (у,) <0,055.
Следовательно, условия теоремы соблюдены, и формула E) с коэф-
коэффициентами (I) возможна.
Положим
л = 18, А1 = А2 = 11 AS^=A^ = A5 = B=2. (И)
Теперь
ic(yi) = 0,111; «Ы = 0,444; тг(Ув) = 0,889; те(уа) = 0,222; *(у4) = 0,667.
Из табл. 1 получаем
-у1 = 0,958; -уз = 0,721; -уь = 0,329; - у2 = 0,895; —г/4 = 0,527.
Поэтому из формулы C) и D) находим
0,58>a(yi)>0,5; 0,26> а (у3) >0,21; 0,16>a(y5)>0,13;
0,023<Ъ(уа)<0,033; 0,17<6(г/4)<0,21.
Положим еще
^г = 16, Лг = Л2 = 1, Л3 = ^4 = А5 = 2, 5 = 0.
Тогда
ic(yi) = 0,125; 7г(г/з) = 0,5; те(у5) = 1; ^B/2) = 0,25; тг(г/4) = 0,75.
233

Из табл. 1 получаем
-2/1 = 0,952; -2/з = 0,
— у2 = 0,871; -?/4 = 0,472,
откуда
0,4>а(й)>0,31; 0,09>а(г/3)>0,05, а(у5) = 0;
0,05<6(г/2)<0,07; 2<6(г/4)<10.
Заметим, что из указанной общей теоремы следует, что, если форму-
формула возможна при В^>0, то возможна также формула при тех же
ТО
Alt..., Аг-2 и ^4 + -у-
с заменой коэффициента В нулем. Таким образом, в формуле (I) можно за-
заменить Аъ = 3 и В = 2 значениями А5 = 4, J? = 0, а в формуле (II)
можно А$ = В = 2 заменить на ^45 = 3, ? = 0.
Наиболее практичной мне представляется последняя формула (III),
которая имеет вид
—1
+ I [/ Ы + / Ы + / Ы + / (- ^з) + / (- ^4) + /(- О], (Ш)
верная для многочленов 11-й степени.
На приближенном вычислении абсцисс останавливаться не будем.
3. Для построения формул, верных для многочленов 13-й степени,
пользуемся таблицей для функции тс? (х), соответствующей 1 = 1.
Положим
п = 22; Аг = А2 = 1; Л3 = Л4 = А5 = 2; 4в = 3, В = 0. (IV)
*Ы = А = 0,0909; тс (у8) = Д = 0,3636; тс (у5) = ^ = 0,7273;
«Ы = д = 0Д818; «Ы^^ 0,5454; *(ув) = 1,
Из табл. 2 получаем
— yi = cosbi;
я7(ж) для 1 = 1; —ж = cos 6 F выражено в градусах).
Таким образом
0й = 15°,7; 63 = 39°,5; 6S = 62°,9;
0,4>а(У1)>0,3; 0,16>аB/3)>0I2; 0,11 > а (у,) > 0,09;
е2 = 24°,8;е4 = 51°,7;
0,03<6(у2)<0,05; 0,18<Ъ{у,)<0,28.
Следовательно, формула с коэффициентами (IV) существует:
234

f(-xs) + f (x4) + / (- *4) + / M + /(- *,)] +
+ 3 [/(*.) + /(-*,)]}. (IV)
Точно так же можно проверить существование формул, пригодных для
многочленов 13-й степени при п = 24, 26, 28 и т. д. (а также при
соответствующих нечетных я).
Таблица 2
Функция тт7 (х) (I = 7)
0
0
1
2
3
4
5
6
7
8
9
10
И
12
13
14
15
16
17
18
19
20
21
22
23
24
25
7Т (— COS 0)
0,0357
0,0359
0,0363
0,0371
0,0382
0,0397
0,0415
0,0438
0,0467
0,0501
0,0542
0,0591
0,0648
0,0717
0,0796
0,0888
0,0995
0,1114
0,1244
0,1330
0,139
0,146
0,154
0,163
0,173
0,184
0
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
7Т (—- COS 0)
0,196
0,210
0,225
0,241
0,252
0,260
0,269
0,279
0,289
0,300
0,312
0,325
0,340
0,355
0,372
0,389
0/06
0,419
0,430
0,442
0,455
0,469
0,483
0,499
0,515
0,533
0
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77,93
7Г (— COS 0)
0,550
0,571
0,592
0,604
0,617
0,631
0,645
0,660
0,676
0,693
0,711
0,729
0,749
0,769
0,790
0,804
0,818
0,833
0,847
0,864
0,881
0,898
0,918
0,937
0,955
1,000
Таким образом, при п^>16 существуют формулы, пригодные для
многочленов 11-й степени A = 6); при тг^>22 существуют формулы E),
пригодные для многочленов 13-й степени (I = 7). Не исключена возмож-
возможность, что найденные значения для п могут быть еще снижены (но при
помощи изложенного метода этого, повидимому, сделать нельзя). Во вся-
всяком случае можпо утверждать, что для I = 6 не может быть формулы B)
при /г <с^ 13, а для I = 7 не может быть формулы с тг<^16.
Из формул, годных для многочленов 13-й степени, отметим еще
(п = 24) формулу
*) dx = l2 {lf(Xl) +f(x2) + f(-Xl) + f(- x2)]
(V)
—1
+ 2 lf(x3) + f(xt) + /(- x3) + f(- xt)] + 3
+ /(-*e)+ /(-*•)]}.
возможность которой доказывается тем же способом.

Tl
ОБ ОДНОЙ СИСТЕМЕ
НЕОПРЕДЕЛЕННЫХ УРАВНЕНИЙ *
В статье «О формуле приближенного интегрирования Чебышева»ъ
мною показано, что формула, предложенная Чебышевым,
1 п
\f{x)dx = -L 2/Ы @<я4<1), A)
о *=г
не может ни при каком выборе действительных xi быть точной для всех
многочленов степени п, когда п достаточно велико. Это означает, иными
словами, что все п величин Х{, удовлетворяющих п уравнениям
t=i
не могут быть действительными. Кроме того, в двух недавних замотках -
Р. О. Кузьмин определил асимптотическое распределение величин xt,
удовлетворяющих B) при п->ое, изучая непосредственно многочлены
Но интересно исследовать, каково наибольшее число Мп ^ п уравнений (Z}
(к^Мп), которым могут удовлетворить п действительных величин х\.
Мы ограничимся здесь установлением верхней границы3 числа Мп
как функции п. Отсюда, в частности, будет следоватьу что степень Мп
* «Sur un systeme d'equations indeterminees». Jo urn. de math, pures et appliquees,
17 A938), стр. 179—186 B02*). Эта статья фактически была паштсала раньше статьи [67].
{Ред.)
1 Изв. АН СССР, ОМЕН A932), стр. 1219—1227 A57*).
2 Comptes rendus, 201, стр. 1094: 202, стр. 272. [См. также Изв. АН СССР, серия
матем. A938), сгр. 427— Ж. (Автор)].
3 Много дана нижняя граница Мп в заметке «Modifications de la formule de quad-
quadrature de Tchebycheff», Comptes rendus, 204, стр. 1526—1529 A91*).
236

^многочленов, для которых формула A) точна, не может достигать п
при /г^>9. С этой целью я докажу сначала две теоремы, которые являются
лишь применением или более или менее очевидным видоизменением одного
предложения Чебышева.
Теорема I. Пусть 7i<C72<^ - • • <Слт сУгпь т корней многочлена Ле-
жандра Рт(х), соответствующего отрезку [0, 1], а р^>, р^), . . . , р(^0 —
коэффициенты формулы механических квадратур Гаусса
{f(x)dx = fifWT,)' C)
которая точна для всех многочленов степени 2т — 1. Если формула A)
точна для всех многочленов стелена 2т — 2, то
где S (yi) — число величии xi <^ fi-
Действительно, построим многочлен степени 2т — 2
который оиределяеася условиями
Уравнение Р'От_2 (х) = 0 будет иметь, кроме т — 1 корней ^2, • • • , 7т> ещ-е
т — 2 корней, разделяющих величины ^? которые являются также кор-
корнями F2m—2(х) — 0- Итак, при х^'Хг функция /^2т-2(ж) убывает, так как
Бее 2т — 3 корней многочлеиа Р'9т_„(эс) исчерпываются корнями, указан-
указанными выше. Следовательно, имеем
<7i, \
Р2т-2{Х)>О 1фИ ?>7i- j
Так как, по условию теоремы, формулы A) и C) применимы к много-
многочлену F2m—2 ix), то имеем
F (or) dx = — S F (^) =
и, принимая во внимание неравенства E), получаем
г=1
Перейдем теперь к доказательству следующей теоремы:
Теорема II. Если формула
237

еде р^>0, точна для всех многочленов степени 2т — 1, то по крайней
мере одна точка 2/?<Лг
В самом деле, построим многочлен
Очевидно, по формуле F) получим
1 п
\R2m^(x)dx = 0= ^рЯ2т^(уг)- G)
о i=i
Но
(^) > 0 При
#2m-l («) < 0 При X > If 1,
причем знак равенства /?2m—i (ж) = 0 имеет место только для m значений
.х = у{ (? = 1, 2, . . . , т). Но вследствие условия п^>т все слагаемые
суммы G) не могут одновременно быть равными нулю, а потому суще-
существует по крайней мере одно значение Уг<^\-
Из теоремы II мы заключаем, что если формула A) применима ко всем
многочленам степени 2т — 1, то существует по крайней мере одно значе-
значение o?i <CTi- Таким образом, вследствие неравенства D) имеем
Откуда вытекает
Теорема III. Если формула A) справедлива для всех многочленов сте-
степени 2т — 1, то
Применим нашу теорему для значений т = 5, 6, 7, 8. Имеем*
4
4? 4 ^ = 0,08566225<^-,
-L < p(D = 0,06474248 < ± , ± < рСО = 0,05061427 < -^ .
Из неравенства Р^1)<:С~о- мы заключаем, что квадратурная формула Чебы-
шева при п = 8 не может быть применима к многочленам 9-й степени;
следовательно, она не применима также и к многочленам 8-й степени,
так как благодаря симметричному расположению точек х\, определяемых
уравнениями B), уравнение
V
* А. Н. Крылов. Лекции о приближенных вычислениях. М.— Л., 1950, § 31,
стр. 86. (Автор.)
238

является их следствием при п четном. Вцрочем, давно известно из не-
непосредственных вычислений, что при п = 8 абсциссы Чебышева стано-
становятся комплексными. При п = 9 неравенство p^^>-q~ показывает, что
предположение М9 = 9 непротиворечиво (вычисление показывает, что дей-
действительно М% = 9).
Неравенство pW < — доказывает, что
неравенство р^1) <^ -т^- доказывает, что
М12<12; М13<13, Ми<13, М15<13;
неравенство pW <С~тп" доказывает, что
^le^10? ^17\^> ^^IS^^^j MlQ^LD.
Чтобы доказать, что
начиная с п^>9, нам достаточно теперь доказать, что при всех п^>0
справедливо неравенство
Яп <^ кп sin , A0)
так как
2тт 2л:2
7TSin-^ —г <С"^ J-^l»
мп -ы ^ мп + 1 ^- '
если Мп ^-19, а для значений п <С 19 неравенство (9) непосредственно
проверено выше.
Неравенство A0) является следствием соответствующего неравенства
для величины р^>, стоящей в левой части неравенства (8'). С этой целью
заметим, что
где рт — коэффициент, соответствующий наибольшему корню ^ много-
многочлена Лежандра Rm (ж) в формуле механических квадратур, соответствую-
соответствующей отрезку [—1, 4-1]. Известно, что
следовательно,
где Rrm(x) — производная многочлена Лежандра Rm(x), соответствующая
отрезку [—1, + 1].
Положим
{i~x^Rm{x)=r.fm{x). A2)
239

Легко проверить, что fm (x) = fm (cos 6) удовлетворяют дифференциальному
уравнению
flu + Xf =0, A3)
7 ГУ 9. t * ' 771 ^ '
где
.2 1 — Ж2
Чтобы получить верхнюю границу р?0, мы воспроизведем в частном виде
соответствующие результаты моего мемуара «О многочленах, ортогональ-
ортогональных на конечном отрезке» [51], стр. 57 — 63. Рассмотрим функцию
A5)
Принимая во внимание A3), будем иметь
du __ 9 , dfm , 9,2 *tm d%n ^ d\
откуда
Итак, и(х), как и Х^, достигает своего максимума при х = 0, а при
-т—<JJ0. Следовательно, предполагая, что х^>0, имеем
откуда
dx
о о
Таким образом,
'1Г@)>1о?(те2 + т
т. е.
В частности, в точке ?х, где i?m (x) = 0, имеем*
BEi)=>4(S1)(l-5!)Vii?™aE1);
следовательно,
A - Й)'^ ($х) > (т* + т + 4 ) и @).
* Это же равенство справедливо для всех ?t; поэтому неравенство A7) для ?т =
= р m EХ) распространяется па все 5i? т. е. ?т(гг) < — ]/" 1 — Z% .
240

При т четном
при т нечетном
lib ~T III, ~p ~y— I/O -p IIL -J —
Отсюда, благодаря формуле Валлиса
Г1-3. . . Bg —1)]а i
L 2-4. . .2s J ~~ ^Js~-
имеем, каково бы ни было т,
Таким образом, из A1) получаем *
Кроме того, вследствие неравенства
расстояние между двумя корнями /w(9) [которое является решением урав-
уравнения A3)] меньше, чем т- . Таким образом, полагая
имеем
откуда
+ —
— \\ = sin 6X < sin
m+
и наконец, благодаря A7), получаем
Следовательно, согласно теореме III, если формула A) точна для всех
многочленов степени Мп = 2т— 1, то должно осуществляться неравенство
* Неравенство A7) равнозначно неравенству A5) статьи [67], так как 1—^\ =
— ^Yi A —Ti)* Окончательная оценка р^,которая здесь выражается неравенством A8),
хуже, чем неравенство A6) упомянутой статьи [67], где улучшена оценка ух. (Автор.)
16 С. Н. Бернштейн 241

В случае, когда Мп — четно, формула A), будучи по предположению
точной для всех многочленов степени меньшей, чем Мп, будет также
точной для многочленов нечетной степени Мп — 1. Таким -образом, не-
неравенство
Мп
справедливо, каково бы ни было число Мп.
Итак, для того чтобы система уравнений B) обладала действитель-
действительными решениями, во всяком случае необходимо, чтобы выполнялось не-
неравенство

72
НЕКОТОРЫЕ ПРИЛОЖЕНИЯ ПАРАМЕТРИЧЕСКОГО
МЕТОДА К ИЗУЧЕНИЮ КВАДРАТУРНЫХ ФОРМУЛ*
1. Пусть q (ж) (—оо<^ж^оо) — неубывающая функция, для которой
q(-oo) = 0, tf(oo) = 1
и которая обладает моментами
x4q(x) (A=l, 2,...,2я + 1).
Рассмотрим какую-нибудь формулу
оо ' т' . 771 m' m
^ р (х) dq (х) == ^ С^ (*о - 2 с^р ш> 2 с4 = 2 с; +1,
_^оэ г=1 г=1 г=1 г=1
гдеСг>0, C:>0; «i<^2<... <xm-; ух<у2<- --<Ут, верную для
всех многочленов Р(#) степени 2л. Очевидно, что т'^>п, если по край-
крайней мере одна из абсцисс у^ отлична от х-г. Действительно, в противном
случае, беря
Р (Х) = {Х — ХгУ ...(X — >т'J,
мы получили бьц справа отрицательное число, а слева число неотрица-
неотрицательное.
В дальнейшем мы будем предполагать, что т' = тг + 1, и следова-
следовательно, будем рассматривать квадратурные формулы
оо n-\-i m
Р (х) dq (*)= 2 °ip fa) ~ 2 C'ip {У С (т > 0) > 1A)
верные для многочленов степени 2п.
* «Деяш застосування параметричного методу до вивчевня квадратурных
формул», стр. 3—16. «Quelques applications de la methode parametrique a kTetude
des formules de quadrature», стр. 16—29. Зап. н.-д. шст. матем. й мех., серия 4,
15, вип. 1 A938) A97*).
243 16*

Квадратурная формула A) может превратиться в тождество только
в том случае, когда число h точек роста функции q(x), сложенное
с числом h± отличных от них абсцисс у^ равняется л + 1.
С другой стороны, как известно, существует формула, верная для
сех мюгочпз 1эв степени ^ 2п + 1
со N
; Л>0), B)
где* N — наименьшее из чисел h и п + 1. Следовательно, общее изуче-
изучение формул A), верных для всех многочленов степени 2п (или 2п + 1),
эквивалентно изучению формул
N n+1 m
2 2 2 ^ , A bis)
где ^ii > 0, ^i <C ?2 <! • • • <C ^iv — какие-нибудь заданные числа.
2. Представляя формулу (Ibis), верную для всех многочленов Р (х)
степени 2п, в виде
N т п+1
i=i г=1 г=1
и принимая, что формула A bis) не является тождеством, с помощью
известных рассуждений получаем неравенства
2 Ai+ 2 ci<^ici< 2 Ai+ 2 ?(* = i,2,...,n). C)
Заметим, что если формула A bis) справедлива также для многочленов
степени 2п + 1, то
о< 2 Ai+ 2 ^;.
Действительно, беря
Р (ж) = (х — хг) (х — х2J ...(х — Xn+J2,
находим, что левая часть A ter) должна иметь по крайней мере один
отрицательный член, что возможно лишь при справедливости по крайней
мере одного из неравенств
По той же причине должно иметь место по крайней мере одно из не-
неравенств
* В частности, если q (х) = 0 при х <; а, то ?i > а, а если, кроме того, ^ (^) = 1
при х^Ь, то ^ < Ъ. (Автор.)
244

Если формула A bis) верна только для многочленов степени 2п, то
рассмотрение многочлена
(х — хг) (х — х2J ...(х — xnf (х — хп+г)
показывает, что по крайней мере одно из указанных {четырех) об-
обстоятельств должно иметь место.
Если те же рассуждения применить к формуле A) вместо A bis), то
получатся аналогичные неравенства
к
2 C'i
+ 2 С\ {к = 1,2,..., п). C bis)
Vi<xk+i
Попутно заметим (хотя это замечание не найдет применения в дальней-
дальнейшем), что в силу C bis)
2 ' — °) ~ Я (хь-1 + 0)
С\ < Си + Ск+1 - {q (xk+1 + Q)-q{xk- 0)} < Ск + СЛ+1.
Последнее неравенство показывает, что абсолютное значение суммы
отрицательных коэффициентов, соответствующих группе всех узлов г/i, лежа-
лежащих между двумя последовательными узлами х&, хк+1, принадлежащими
положительным коэффициентам, не превосходит суммы этих последних.
В дальнейшем нам понадобится
Лемма 1. Если квадратурная формула [q(— оо) = 0,
Р (х) dq (х) = ^Сг{Р (хг) - Р (уг)} + Р (хп+1) D)
верная для всех многочленов степени 2/г, не есть тождество и если
— 0),
то обязательно
xi < Уг < ^2 < • • • < Уп < Xn+v E)
Действительно, принимая, что формула D) не есть тождество и СУ = Си
применим неравенства C bis). В частности, из
к
Vi<xk г—1
следует, что хк<^ук, так как в противном случае мы имели бы
245

Подобным образом, нз неравенства
к
2^<<7(х,+1-0)+ 2 d
i=i Vi<xk+i
вытекает, что yk<i%k+i, так как в противном случае мы получили бы
противоречащее условию леммы неравенство
Си < q (ж*+1 — 0).
Следствие 1. Если формула D) верна для всех многочленов степени
2п + 1, то
E bis)
где ?х и ?п+1 ограничены, согласно формуле B).
Примечание. Если функция q(x) имеет более одной точки роста
и если существует по крайней мере одно значение г0, для которого
0Jrl — 0), то формула D) не может быть тождеством*. Кроме
того, очевидно, что формула D) не будет тождеством, если h^>n-\-l
и, тем более, если функция q (х) непрерывна в каком-нибудь промежутке).
Следствие 2 **. Если формула
2П
Р (х) dq (х) - 2 Ыр Ы (*o<Zi<-'< Ъп), F)
где е{ = 4=1, верна для всех многочленов степени 2п^>0, то обязательно
Действительно, так как формула F) верна для Р (х) = 1, и |ei| =
= i^>q(xi) (i<^2n), то применима лемма 1, непосредственным следствием
которой и является наше утверждение.
3. Теорема I. Какова бы ни была неубывающая функция q(x)
[q (— оо) = 0, q (ос) = 1], имеющая конечные моменты порядка к <С 2п Ц- 1,
можно построить квадратурную формулу
(xo<x1<...<x2n), F bis)
i=0
верную для всех многочленов Р(х) степени 2п -\- 1 [72.1].
Сначала построим такую формулу для функции q0 (ж), определенной
равенствами
qo(x) = O (*< —1),
G)
* Доказательства этого утверждения мы не воспроизводим. (Автор.)
** В первоначальной формулировке этого предложения фигурировало условие
явно излишнеелпри гс>0, так как формула F) не может быть тождеством.
Утверждение следствия 2 означает, что формула всегда F) имеет вид F bis). (Автор.)
246

С этой целью возьмем формулу
—1
которая, как известно, справедлива для всех многочленов степени 2п -f- 1.
Для этих же многочленов тем более справедлива формула
п+1
1 С P(x)dx 1 ^п nf 2г + 1 \ /о l- \
— \ —±J— = г, Ул Р cos о Т / тс - (8 bis)
"Д/!-^2 " + 2г""~о V ^л + 4 У v '
Значит, квадратурная формула
] п+1 п
С Р (x)dx уг\ п / 2г + 1 \ \\ nf 2г + 1 \ /п
\ , = >| Р cos о Т / те — У/* cos о Т о те , (9)
1 С
— \
i=0
которая получается из (8 bis) и (8) вычитанием, будет также верна для
всех многочленов степени 2п + 1. Замечая, что числа
2лг
_
2л + 4 ' 2я + 2 ' 2д + 4 ' " ' ' ' 2я + 4 ' 2л + 2 ' In + 4
образуют возрастающую последовательность, заключаем, что узлы
хь (к = 0, 1,.. . , Ai + 1), соответствующие положительным коэффициентам
в формуле (9), перемежаются с узлами ук (к = 0, 1,... , п), которые со-
соответствуют отрицательным коэффициентам. Значит формула (9) отли-
отличается от формулы F bis) лишь тем, что в ней число узлов равно 2тг + 3,
а не 2/г + 1. Эти узлы удовлетворяют уравнениям
п-41 п °°
2 ^1—2 Ук = \ *rdq0 (х) (г = 1, 2,.. . , 2и + 1).
г=0 Л=о _io
Зафиксируем наименьшую из абсцисс формулы (9) и будем непрерывно
уменьшать наибольшую абсциссу хп+1. Мы все время будем иметь систему
2/г + 1 уравнений относительно 2п + 1 неизвестных
2/о < я2 < г/х < • •. < ?П < уп.
Решения этой системы будут непрерывными функциями от a;n_j_i, пока
один из движущихся узлов не совпадет с соседним. Но неограниченное
приближение всех движущихся узлов к наименьшему очевидно невоз-
невозможно. Поэтому совпадение пары соседних узлов неизбежно. Оно приводит к
уничтожению двух узлов в квадратурной формуле, так как соответству-
соответствующие им коэффициенты имеют одинаковые численные значения и противопо-
противоположные знаки. Таким образом, это преобразование формулы (9) переведет ее
в формулу F bis).
Итак, формула F bis) построена для функции qo(x), определенной
условиями G). Обозначим ее узлы
247

Возьмем теперь произвольную неубывающую функцию qx (х) и положим
qx (х) = lqi (х) + A — X) q0 (x),
так что q\(x) изменяется от qo(x) до q1(x)J когда X растет от 0 до 1.
Какова бы ни была функция q1(x), функция qx (x) при Х<1 будет
возрастающей функцией в промежутке (—1, 1) и потому формула F bis)
для qx (x) при Х<<4 тождеством быть не может. Узлы #г(Х), отвечающие
функции q\{x), должны удовлетворять 2п + 1 уравнениям
(х) = 2 (-1L (Х) (г = 1, 2, . .., 2л + 1). A0)
Функциональный определитель этой системы при X == 0 отличен от нуля.
Поэтому неизвестные Х{ (X) будут аналитическими функциями, определен-
определенными для достаточно малых Х^>0, и в силу неравенства E bis) они не
могут ни выйти из фиксированного промежутка, ни сливаться. Следова-
Следовательно, имея действительные решения при Х<^Х0, система A0) обяза-
обязательно имеет их также при X = Хо, и абсциссы Х{ (Хо) будут различными
и ограниченными. Поэтому невозможно, чтобы существовало такое зна-
значение Хо<;1, что система A0) имеет действительные решения для всех
Х<^Х0 и не имеет таковых при некоторых значениях iX<^X0 + г, как бы
мало ни было s>0 (так как функциональный определитель остается
отличным от нуля). Значит, система A0) имеет действительные решения
при Х= 1, что и доказывает существование формулы F bis), соответствую-
соответствующей любому весу q± (х). При этом абсциссы х\ A) могут быть вычислены
указанным приемом с помощью разложения величин Х{ (X) по степеням X
и аналитического продолжения этих разложений до Х = 1 [72.1].
4. Теорема II. Можно построить квадратурную формулу D), точную*
для всех многочленов степени 2п -+- 1, абсциссы которой удовлетворяют
E bis), каковы бы ни были данные коэффициенты Сг ^ С2 ^ .. . ^ Сп ;> 1
со
(при этом предполагается, что \ xrdq(x) имеет смысл при г<^2п-\- 1).
—оо
Действительно, исходя из формулы F), являющейся частным случаем
формулы D), удовлетворяющей условиям теоремы, будем непрерывно
увеличивать общий коэффициент С, соответствующий хг и уг от 1 до,^.
Все абсциссы будут тогда аналитическими функциями от С, пока их
функциональный определитель будет оставаться отличным от нуля,,
т. е. пока две соседние абсциссы не совпадут. Но это совпадение невоз-
невозможно, так как это сводилось бы к исчезновению абсциссы с положи-
положительным коэффициентом. После того, как первый коэффициент достигнет
значения С19 мы станем увеличивать второй коэффициент от 1 до С2^С1
и так далее. Все эти операции выполнимы без препятствий, так как
каждая абсцисса х\ (l<^i^.n) с положительным коэффициентом всегда
сопровождается с двух сторон соседними абсциссами 2/i_x и ух, коэффи-
коэффициенты которых отрицательны и имеют не меньшие абсолютные значения Т
248

так что совпадение х\ с одной из них приведет к исчезновению положи-
положительного коэффициента, что не может произойти согласно с замечаниемг
сделанным вначале; с другой стороны, абсциссы хг и хп+1 не могут уда-
удалиться на бесконечность ввиду E bis).
Было бы интересно найти необходимые и достаточные условия, кото-
которым должны удовлетворять коэффициенты Cj, чтобы была возможной
формула D).
Не останавливаясь на этом вопросе, я перейду к близкому вопросу.
5. Пусть t (х) = р (х) — q (x) — функция ограниченной вариации, где
р (х) и q (х) — монотонны [р (— оо) = q (— оо) = 0, р (оо) — q (ос) = 1].
Чтобы не останавливаться на деталях, я ограничусь пока случаемг
когда t(x) непрерывна1, так что квадратурные формулы, которые рас-
рассматриваются в наших доказательствах, не могут быть тождествами.
Первое замечание. Всегда можно построить формулу
со т
\ Р (х) dt (x) = 2 si P (xi) (si = ± 1; хх < х2 < . . . < хт; т < 4га), A1)
—со г = 1
точную для всех многочленов степени 2п, где 2 8г = 0> каково бы ни
было к <; ~ .
Действительно, имеют место формулы
со 2п со 2п
\ Р [х) dp(x)= 2 (~ 1)J Р (*i), \ Р{х) dq (х) = 2 (— 1У Р (x'i)
—со i=0 —°° г=0
(точные для всех многочленов [степени 2п -f- 1). Непрерывно приближая
Х2п к х2п, можно сохранить справедливость второй формулы для всех
многочленов степени 2/г, без того, чтобы абсциссы х\ встретились, так
как такая встреча привела бы к исчезновению положительного коэффи-
коэффициента. Вычтя затем вторую формулу из первой, прийдем к (И), где
2к
2 ег = 0, так как, каково бы ни было /<^2А:, имеем
Второе замечание. Можно построить формулу
СО 771
J P (x) dt (х) = 2 Si P (xi) (е1 = ±1,±2;а;1<жа<...<жт; 1и<2и)„
—со i=l
A1 bis)
1 Достаточно было бы допустить, что р (х) и q (x) имеют бесконечное число то-
точек роста.
249

точную для всех многочленов степени 2п, где
i
каково бы ни было I <^т
Действительно, можно произвольно передвигать т — 2п абсцисс в
формуле (И), пока т^>2п, оставляя ее точной для всех многочленов
степени 2п. Совпадения соседних абсцисс (не могут нарушить свойства
i
— 1^2?г^1 коэффициентов этой формулы, благодаря чему новые
коэффициенты не могут по абсолютному значению превысить 2.
6. Можно без ограничения общности предположить, что функция
t (с) имеет лишь конечное число максимумов и минимумов, так как ее
всегда можно заменить функцией, обладающей этим свойством и имею-
имеющей те же моменты до порядка 2п-\-1. В таком случае справедлива
Теорема III [72.1]. Если все минимумы (непрерывной) функции t(x)
[г(=Ьоо) = 0] равны нулю и если ее абсолютный максимум равен М,
то возможно построить формулу1
оо 2т—1
P(^\rlt(^r\ С "V ( /|\г П/ТЛ (т <^ п- г -"""т ^ г ^ ^ v \ (\*)\
справедливую для всех многочленов степени 2тг, какова бы ни была дан-
данная постоянная С^-М.
Действительно, пусть — оо <^ ах <^ $г <^. . . <^ад <^ оо — точки, где
последовательно достигаются экстремумы t(x); таким образом, t ($i) = 0,
Рассмотрим такие функции tx (x), t2 (x), . . . , th (x), что t± (x) = t (x)
при x ^ ^ , ti(x) = 0 при x;> $г; t2 (x) — t (x) при ^<^x <Q ^2 > h(x) — ^
h
при а;^^ и при х~^>$2 и т. д.; значит, t (x) = 2 h{pc).
г=1
Полагая tl(x) = pl(x) — qx{x), где pl(x) = tl(x) при х<^ач ирх(х) =
= t% (az) при х ^ ах, так что qx (х) = 0 при х <; ах и qt (х) = tx (аг) — tx (x)
при х^>аг, мы можем, согласно теореме II, образовать формулы
оо 2п—1
гп (С>М)
l(x) = t(al)P(x'0)+C^(-iyP(xi),
гДе Pi-i<3o<#i<---<32n<ai<#o<. -<4n<^, точные для всех
многочленов степени 2w + 1. Однако если мы пожелаем, чтобы вторая
1 Эта теорема является частным случаем теоремы VI, доказанной ниже.
250

формула была справедлива лишь для многочленов степени 2п, то мы
сможем непрерывно перемещать xQ' до х2п (соответствующее перемещение
остальных абсцисс х( будет тогда происходить слева от $\ в силу сде-
сделанного выше замечания). Следовательно, после вычитания мы получим
формулу, точную для всех многочленов степени 2п, вида
J P (х) dti (х) = С %(-iyP (Xi) (р,_! < х0 < хг < ... < х2т^ < р.)
i=o
Изменяя абсциссы х-х до тех пор, пока число различных абсцисс не ста-
станет меньше 2п + 1, мы получим для всех индексов I формулы
2т i—1
A3)
справедливые для всех многочленов степени 2п. Я утверждаю, что все
абсциссы остаются внутри промежутка (fti—i, $i)- Действительно, пока
шг ^> п + 1> оставляем фиксированными крайние абсциссы, а когда остается
лишь 2п + 2 абсцисс, фиксируем абсциссу х0 и будем перемещать вто-
вторую крайнюю абсциссу х2п+1 во внутрь, пока две абсциссы не совпаду!.
Складывая формулы A3), получаем формулу
со 2s—-1
J Р (х) dt A)=C2 (- if P B/i) B/o < 2/i < • • • < 2/2s-i), A2 bis)
—оо г—0
h
где число абсцисс 2s =•- Jj <^mi • Но существенным является то, что ее
коэффициенты имеют чередующиеся знаки, так что можно, перемещая
абсциссы, свести их число к 2т<^2/г, не меняя коэффициентов, а это
приводит к формуле A2).
Возьмем в качестве примера t (х) = 1 — | х | при — 1 -< # <; 1 и t(x) = 0
при |#];>1. Теорема III показывает нам, что в этом случае существует
формула
1 п—1
Э (т\ clт С* 7 ( \\^ Т^ (т-\ (\ ~~^ т ^">> т "~^*>> ^"*> т ^"">>. С\\ *¦
2п—1 \^7 ""^ — ^ / ] \ ±) *2п—1 у^г) \* ^ ^0 ^ 1 -^ * * * -^ ^—1 ^^" ^/>
точная для всех нечетных многочленов степени 2п—1, какова бы ни
была данная постоянная С ^ 1. Полагая х2 — г/, получим формулу
1 п—1
J />„_! (у) dy - -^ 2 (- l^n-ifot I/^Г A > У» > 2/1 > • • • Уп-г > 0),
о г=^о
которая справедлива для всех многочленов степени п—1.
В случае, когда, минимумы непрерывной функции t(x) отрицательны,
получение нижней границы для постоянной С менее просто.
251

Я ограничусь указанием следующего частного утверждения, которое-
доказывается тем же методом.
Если t (х) имеет единственный максимум, за которым следует отри-
отрицательный минимум [ | / (х) | <J М, t (+ оо) = 0], то можно построить
формулу
оо , 2&—2 2т
P(x)dt(z) = C\
где т^п, х0 < хг < ... << x2k—i <С • • • <С Х2т , справедливую для всех много-
многочленов Р(х) степени 2п + 1 (какова бы ни была данная постоянная
7. Вернемся еще к формуле A2), чтобы изучить одну проблему, рас-
рассмотренную Чебышевым1. Полагая
dt(x) = O, \ x^dt (x) = ak ,
—oo —oo
мы видим, что формула A2) эквивалентна системе 2п уравнений
2т—1
п П S^ ( 1\г rfli (I. . /JO On\
допускающей вещественные решения х0 <^ хг <^ . .. <^ x2m-i •
Предположим, что для некоторого данного значения С^>0 система
A4), где тг—7Vj>l, допускает решения при достаточно большом т. Из
приведенных выше рассуждений следует, что можно всегда взять т<С п>
каково бы пи было n^N, сохраняя то же самое значение С.
Мы будем говорить, что система A4) нормальна в случае, когда
т = п, каково бы ни было С. Наоборот, если существует хотя бы одно
значение С, для которого т<^п, то система A4) будет анормальной.
В последнем случае, моменты а19 сс2, ... , a2n—i > а2п будут связаны впол-
вполне определенной алгебраической [зависимостью, так что достаточно бес-
бесконечно-малого изменения а2п , чтобы сделать систему нормальной, С дру-
другой стороны, мы будем говорить, что С = Ст является исключительным
значением С, соответствующим 2т абсциссам (т. е. значению т), если си-
система A4) удовлетворяется при всех значениях & = 1, 2,. #. , 2т, 2т + 1
(если система анормальна и только в этом случае возможно, чтобы она
удовлетворялась также при к^>2т -\- 1). Я утверждаю, что если систе-
система A4) допускает вещественные решения хо<^х1<^ ... <^ х2^—1, то по-
постоянная С не может быть исключительной ни для какого значения
Действительно, предположим, что т — наибольшее число, при котором
можно удовлетворить 2т + h <^ 2N (h > 0) уравнениям
2т—1
г=0
1 «О квадратурах». Поли. собр. соч., т. III, 1947, стр. 49—62.
252

В зависимости от того, четно h или нечетно, можно было бы также,
по предположению, удовлетворить этим 2т + h уравнениям 2т + h + 2
или 2т + h + 1 абсциссами zi. Соединив члены одного знака, мы пришли
бы, таким образом, к 2т + h равенствам вида
т—1
2
h
m+1-f-—-
Z2i
=
2i-i
-2 J
четно)
ИЛИ
h—l
2
г=1
что невозможно, потому что 2т + 1 + -у <С 2^г + /г в первом случае и
2т-\ т—<; 2т + h во втором, так что эти равенства должны были бы
сводиться к тождествам.
Лемма II. Если в системе A4) т — п, то абсциссы х-% суть регуляр-
регулярные функции переменной С и, кроме того, х0 есть возрастающая функ-
функция С, a x2m—i есть убывающая функция С.
Действительно, первое утверждение следует из того, что функцио-
функциональный определитель системы отличен от пуля. Далее, чтобы опреде-
лить производные
2т—1
-, имеем систему
2т—1
i=0
определитель которой равен
1 1 ... 1
i=0
2m—1
2m—1
= (- 1)
-i (х0) =
поэтому
где
0
¦^ViW '
2m—l
2m—l
2 (-1L
r2m—l r2m—
г=0
2m-i
253

= J R2m-l
R2m-l
2m—1
(—1)* X1
2m-2 2j \ l> 2
i=0
2m—1
2 m—1
r2m—1
2m—2
2m
X2m—]
— \[ Q2m-l (x) dx + [ Q2m-i (x) dx + • • • + [ Q2m-i
dx
Следовательно, замечая, что R2m—\ (
жутках интегрирования, мы заключаем, что
8. Теорема IV [72.1]. Если система
2N—1
во всех проме-
промеdx.
2т—1
dC
A5 bis)
С = Со допускает вещественные решения хо<^хг <^ • • • <C^2;v—1> mo"
допускает также вещественные решения при каждом значении С ^> СOi
и никакое из значений С^>С0 не будет исключительным при m<^N*
Предположим сначала систему нормальной; дюгда, согласно лемме IIТ
при неограниченном увеличении С крайние абсциссы х0 и x2n—i будут сбли-
сближаться, причем никакие две соседние абсциссы совпасть не могут, поскольку
система нормальна. Кроме того, согласно со сделанным выше замечанием,,
никакое из значений С^>С0 не может быть исключительным при m <^ iV;
следовательно, невозможно, в частности, удовлетворить всем уравнениям
A5 bis) без последнего (к = 2N) при числе абсцисс 2m <^ 2N.
Если система анормальна, достаточно будет, сведя ее к нормальной
изменением a2iv> рассмотреть любое значение С ^> Со (которое не является
исключительны м).
Таким образом, каково бы ни было достаточно малое s^>0, система
A5 bis), в которой a2N заменяется на ct2ivit:?> допускает решения
^o^^i^ •••<CX2N—1> регулярные относительно е. Когда е стремится к
нулю, абсциссы стремятся к различным, конечным значениям. Действи-
Действительно1, если #2Jv-i->°o, то и ?2iv__2->oo, а разность |$$
должна оставаться конечной. Следовательно, oo^N_2—x\n
миться к нулю при k<^2N и, значит, все уравнения, за исключением,
—2
—\ Д°лнша стре-
стре1 Заметим, чго все абсциссы л:. = ar.(ot2/v-) возрастающие функции переменной u2
так что не может быть одновременно %2N—i -> °° и а?0 -> — оо.
254

быть может, последнего, удовлетворялись бы при 2m<^2N абсциссах,
что противоречит сделанному выше замечанию.
Лемма III. Чтобы система A4), где п^2, допускала веществен-
вещественные решения хо<Сх1<С - - • <Сх2гп~ъ необходимо выполнение неравенства
A6)
-За»
Действительно, должно быть возможным удовлетворить уравнениям
аг = С {х0 — хх + х2 — я8), а2 = СD — х\ + х\ — а|), ,
а3 = СD —^ +^-я5), а4 = С D -
Согласно лемме II, х0 убывает, a х3 возрастает при уменьшении С.
A priori возможны три случая: 1) С стремится к нулю; 2) когда С стре-
стремится к некоторому ^>0, две из абсцисс х% стремятся к совпадению!
3) когда С стремится к ^>0, хотя бы одна из абсцисс х% стремится
к ± °°* Рассмотрим первую возможность: j когда хотя бы одна из раз-
разностей х0 — хъ х2 — xs стремится к —оо. Пусть, например, | х0 — хх \ ^
>^ | х2 — х3 | -> оо. Положим С (х0 — хг) = и, С (х2 — х3) = v. Тогда
и + v =
Но третье из равенств A7) можно привести к виду
и (х20 + хохг + х\) + v (х\ + х2х3
= а
3,
откуда
3 / , \2 , 1 / \2 2 ¦ , 2 ^ I К,
try _]_ /у \л _]_ //у» /у \л /-у»* _!_ /у /у. . /у^1-1 <'^ ?_
4 1 tA^Q I ьч^О I 1 / 1 «ДуО tA/Q I «ДуО 1 tA/OiA/Q I iA/Q *\>^ ,
\ & * О/ * Л \ л О/ -ы * ? О I О ^-> i -.
тс I V
и следовательно, (ж2 — х3J < — , а это противоречит тому, что |ж2 —х3|-^сх?.
Таким образом, первое предположение недопустимо.
Второе предположение приводит к равенствам
значит
Е — — fa 4-1/ 4a — 3 2] 5 — — [
= ^ [а2 —
Наконец, третье предположение требует, чтобы ^g"-^00 вместе с
ж2 -> оо или ^о "^ — °° вместе с хх -> —оо при С -» ^ ^> 0. Эти два обстоятель-
обстоятельства не могут иметь место одновременно. Действительно, так как раз-
разности #о—#i, х\—х\ должны оставаться конечными, то разности х0 — х1г
255

.x2 — x3 должны одновременно стремиться к нулю, что невозможно, так
как cti<CO. Следовательно, если предположить, например, что xQ, хг
остаются конечными, то разность х\ — х% тоже останется конечной, так
что х\ — х\ стремится к нулю. Отсюда следует, что первые три урав-
уравнения A8) удовлетворятся при С = jj-, что' приводит нас к той же
формуле A9). Второе предположение соответствует случаю, когда сис-
система анормальна, а третье предположение — тому случаю, когда сис-
система нормальна, и лемма доказана во всех случаях.
9. Теорема V. Если система (допускающая вещественные решения
при достаточно больших С)
2т—1
ак = С %(-1Ух1 B0)
^нормальна, каково бы ни было т <^ Л7", то для каждого значения т <^ N
существует единственная исклюуителъная постоянная Ст, такая, что
при С = Ст система B0) удовлетворяется при к = 1, 2 , . . ., 2т, 2т 4- 1-
При этом
и Ст—! является точной нижней гранью значений С, для которых си-
система B0) удовлетворяется при k^2m.
Действительно, если уравнения B0) удовлетворяются при k^2m, то
можно уменьшить С, что приводит к уменьшению х0 и увеличению x2m—i-
Уменьшение величины С, которая должна оставаться более, чем Съ
сопровождается тем, что хотя бы одна из абсцисс стремится к +00. Если
ж2т-1-><х>, то же будет для х2т-2> потому что разность x%?z\—xlm-l
должна оставаться конечной. Значит, х%т_2—^m—i""^ при к<^2т — 1.
Так как система нормальна, то никакая другая пара абсцисс не будет
возрастать бесконечно. Следовательно, разность %1™_о —xlm—i тоже оста-
останется конечной, так что при С->Ст_1 будет ^т—I ~~ Х1т—1 и ^т — ^ оста-
остающиеся абсциссы удовлетворяют системе 2т — 1 уравнений (к = 1, 2, .. .
. .. , 2т - 1).
Согласно теореме IV, система 2т — 1 уравнений не может удовлетво-
удовлетворяться ни при каком значении С<^Ст—х. Но при C<^Cm—i и достаточно
близком к Ст_! можно удовлетворить системе 2т —2 уравнений
(&<2га — 2). Значит, Ст~2<Ст-1.
В случае, когда система B0) анормальна при некоторых значениях
т, теорему V можно дополнить следующим образом:
Теорема Vbis. Нижний предел pm-}-i значений С, для которых си-
система 2т + 2 уравнений
2m+l
U = С 2 (- 1)г а* (Л = 1, 2,... , 2т + 2) B1)
i=o
256

допускает вещественные решения хо<^хг<^ • • •<^х2т}-1> равен исклю-
исключительному значению Ст, соответствующему системе
2т—1
«л = Ст 2 (- IL а* (к = 1, 2, . . . , 2гп + 1). B2)
Ото значение Ст может не существовать только в том случае, когда
система
2т—3
~ Г* Х^ / а\\ ггЪ /9*}\
**А —^ /I ^ л.) Ж • \ /
анормальна и допускает в качестве исключительной постоянной величину
Ст—ъ для которой удовлетворяется система 2т уравнений
2т—3
ak = C*.-i ^ (- 1Ухкг (* = 1, 2, ... , 2т). B3 bis)
i=0
В этом случае jJWf-i = Y-m — Cm_x. Таким образом, исключительная по-
постоянная Ст, соответствующая некоторому определенному числу т,
может не существовать, если она существует для т — 1 (Ст_х = Ст_а
соответствует тогда числу уравнений, превышающему число абсцисс на
две единицы).
Действительно, применяя прежнее рассуждение, мы видим, что умень-
уменьшение С приведет нас к системе B2), если только две пары абсцисс не
исчезнут на конечном расстоянии или на бесконечности, в первом случае
теорема верна; во втором — мы заметим, как и раньше, что так как
1—^2m+i и #om+1—^m+1 Должны оставаться конечными, то х%т —
l2m+i и х\—х\ стремятся к нулю при Ж<2тга + 1- Значит, система
сводится к 2т уравнениям B3).
10. Важная анормальная система встречается при предположении,
что функция t (х) формулы A2) четная. В этом случае все абсциссы х\
попарно отличаются только знаком, так что исключительные постоянные
Ст необходимо соответствуют анормальным системам (Cm := Cm*)- Таким
образом, обозначая через \tm нижний предел [значений С, для которых
формулы
оо 2т—1
SD (пЛ fit lnr\ Р \^ / 1U Р //уЛ (<г *^ т* ^ ^ 'У \ /9/i\
мг \Х) CLI уХ) — О У \ \ — •*•/ ¦* v"i) \^0 "^v *^1 *^\ * * * ^-^ ^2т,—1/ \"^/
—оо i=0
точны для всех многочленов степени 2т, имеем
__ 1 | / а1 и<Га<Г <Га<Га ^
г2 — ~о~ I/ у 12 "^ гЗ ^5- * * * "^ гт <^ rm-j-l ^^ *
Знак равенства jim = рт+г будет иметь место лишь в том случае, когда
существует значение постоянной С = С^_х, для которого формула B4),
применимая к многочленам степени 2т, содержала бы меньше, чем 2т
абсцисс, в то время как ни для какого иного значения С формула B4)
17 С. Н. Бернштейн 257

с 2т абсциссами неприменима к многочленам степени выше 2т: тогда
|лт = jim+1 = Cm—i- В случае, когда Cm_i не существует, всегда найдется
значение С = Сто =v-m-\-i^> V-m, [для которого формула B4) (с 2т абсцис-
абсциссами) применима к многочленам степени выше 2т.
Предположим, в частности, что функция t (х) (четная) имеет один
только максимум, как в примерах, рассмотренных Чебышевым [t (х) =
= — A — х2) и t (х) = j/l — х2 при — 1 <; х <; 1] и в нашем примере
[t (х) = 1 — j#l], § 6. Легко видеть, что формулу B4) нельзя применять
к многочленам степени выше 2 т, если т = 2s четно.
Действительно, Xi = — %ь при i + к = 2т — 1. Образуем многочлен
степени 2т + 1
/> (я) = а (х2 - х2J (я2 - х22J • • • (^2 - ^_2J.
Тогда
оо О
J Р(ж)Л(а;)=2 J P(a;)cft(a;)<0,
ОО —ОО
в то время как
2т—1 т.—1
2 (-1I
i=0
i=o 'ft=i
Напротив, для каждого нечетного значения т = 2s + 1 будет существо-
существовать постоянная Cm, при ?которой в этом случае формула B4) будет
применима ко всем многочленам степени 2т + 2.
Метод, основанный на Применении непрерывных дробей, указанный
Чебышевым, можйо^ применить для эффективного построения соответст-
соответствующих; квадратурных формул. При m нечетном, таким образом, всегда
найдется вполне определенное значение для Ст, дающее квадратурную
формулу с 2т вещественными абсциссами х0 <^ х1 <^ • • • <С х2т—ъ справед-
справедливую для многочленов степени 2т + 2.
Наоборот, при т четном, согласно сделанному выше замечанию, не
может существовать формула B4) с абсциссами х0 <] хг <_ • • • < х2т—ъ
справедлива^ для многочленов степени 2т + 1. Однако не исключено,
что такая формула возможна при другом расположении абсцисс, и соот-
соответствующая постоянная необходимо будет меньше, чем \*-т = Cm—i- Эта
то, что действительно [происходит в примерах Чебышева при m = 2, где
x2<Cxi- Но при достаточно большом т во всяком случае невозможнох,
чтобы все абсциссы с положительными коэффициентами были меньше
(как это имеет место при т = 2) всех абсцисс с отрицательными коэф-
коэффициентами. Не останавливаясь на полном рассмотрении этого интересного
1 Доказательство можно провести методом, примененным в моей заметке «О фор-
формулах квадратзф Котеса и Чебышева» [67].
258

вопроса, которое, несомненно, можно провести тем же параметрическим
методом, я закончу доказательством следующего предложения.
Теорема VI. Необходимое и достаточное условие того, чтобы суще-
существовали постоянные С>>0, для которых система уравнений
2т—1
= C У. {-ifx\ (A=l, 2, ..., 2т)
A4}
допускает вещественные решения х0 <^ хг << • • • << х2т—i [т. е. чтобы фор-
формула A2) была верна для всех многочленов степени 2т], состоит в толь,
что уравнения
(A=l,2,...,2m)
B5)
должны иметь различные вещественные решения
эффициентами рг<СО; иными словами, должно быть
<С*
а2
«1 "о"
а,- а
г4-1
J-1
2i— 1
>0 (i = 1,2, ..., т).
c ко-
коB6)
Действительно, согласно теореме IV, если система A4) допускает ре-
решения для некоторого С > 0, то это имеет место для всех достаточно
больших С, а х0 стремится, возрастая, к некоторой величине ?1э в то
время как я2т—i,. убывая, стремится к ?т. Кроме того, все разности
И1 = С (x2i-2 ~ х21-г) < О
остаются конечными, так что lim (x2i—2 — ^2г—i) = 0. Следовательно, при
С-»оо, ж2г_1 имеет по крайней мере одну предельную точку i-L. А так
как система A4) эквивалентна следующей
* Х\) "Т" * * * i ^
~Г ^2m—l) == а2
B7)
то величины Ui стремятся к пределам pi, удовлетворяющим уравнениям
B5 bis)
259
17*

Необходимость, таким образом, будет доказана, если показать,
'что pi не может быть нулем и что все ii различны. По противоположное
;иривело бы к тому, что Дт = 0, так что уравнения B5), где а19 а2,..., си2т-\
фиксированы, имели бы вещественные решения Si и pi <^ 0 лишь для
вполне определенного значения а™, что невозможно, так как система A4)
продолжает иметь вещественные решения, если изменить (достаточно
мало) сст.
Чтобы доказать достаточность, допустим, что уравнения B5) имеют
различные решения ^ (?2 < S2 <С* * * <СSm) и pi<0. Положим
При этих условиях система B7), эквивалентная системе A4), принимает
вид
(Л =1,2, ...,2m).
Следовательно, для определения ]2т переменных Oj, и Xj, как функций
переменной е, имеем 2т уравнений, которые дают 8{ = )ч = О, когда
г = 0. Но при г = О функцжшальный определитель
1 0 1 ... и
Si 1 S2 ••• 1
?2 *>? л2 • • • 2?
Bm — 1) S2m~2 S?771 • • • Bm —
po...Pm П E4-У4
отличен от нуля. Значит, при достаточно малом s = -^ абсциссы хо<^ хх
—1 суть регулярные аналитические функции от е.
Заметим, наконец, что условия B6) выражают существование таких
функций tm (х) > 0 ( lim x2mtm (x) = 0), что
оо со
= — А Г ж*-^т (ж) rfa; = ( хк dtm (x) (к < 2т).
Следовательно, условившись называть эквивалентными порядка N две
функции, у которых тождественны первые N моментов, мы можем сбли-
сблизить теорему VI с теоремой III, формулируя ее так: условием, необзсо-
260

димым и достаточным для существования квадратурной формулы
2N—1
P(x) dt{x) = C ^ (-1)'^). A2)
точной при достаточно больших С для многочленов степени 2N>
является эквивалентность порядка 2N—1 функции t (x) такой функ-
функции* In (х) ^ 0, для которой
lim x2NtN(x) = 0.
* Согласно теореме Ш, если известно, кроме того, что tN (x) -<Ж, формула A2)
Берна для всех многочленов степени 2N при любом С ;> М [72.1]. (Автор.)

73
О НАИЛУЧШЕМ ПРИБЛИЖЕНИИ \х\* ПРИ ПОМОЩИ
МНОГОЧЛЕНОВ ВЕСЬМА ВЫСОКОЙ СТЕПЕНИ*
В статье дается асимптотическое значение наилучшего приближения Еп \x\v на
отрезке [—1, +1] при помощи многочленов весьма высокой степени.
1. В настоящей статье дается доказательство того факта, что наилучшее
приближение Еп\х\р на отрезке [—- 1, +1] при помощи многочленов
весьма высокой степени п удовлетворяет асимптотическому равенству1
En\xf~^- («->*>), A)
где \*< (р) не зависит от п.
Исходным пунктом нашего исследования будет формула
оо
^i ф 4 . izp .Г ир~~1 du . о / \ . /о\
л?3 х\ = — sin ~~ cos n arc sin х \ —- + Нп\х) + еп, (А)
1 тс \^и^-и^ + ^)
где, при данном />^>0, многочлен Яп(х) четной степени п возрастает
не быстрее nv на отрезке [—1, + 1], а вп равномерно стремится к нулю
на этом отрезке, когда /г->оо. Вывод этой формулы дан в дооей моно-
монографии «Э. П.» [глава II, § 6].
Таким образом, полагая
4 . тер С
= —smT"
2 J
ир г du
J
о
мы имеем
прЕп j х \v = Еп (Hv (nx) cos n arc sin x + гп). C)
* Изв. АН СССР, ОМЕН A938), стр. 169—180 A95*).
1 Для случая р = 1 это было мною доказано в статье «Sur la valeur asymptoti-
que de la meilleure approximation de |#|», Acta Mathematica A913) [12] (том I),
а также в докторской диссертации «О наилучшем приближении непрерывных
функций посредством многочленов данной степени», Сообщ. Харьк. матем. об-ва,
1912 [3] (том I).
262

Следовательно, требуется доказать, что Еп (Hv (nx) cos п arc sin x) стре-
стремится к определенному конечному пределу р(р), когда п -» ос. Очевидно,
кроме того, что
Еп [cos n arc sin хНр (nx)] = En [cos я arc sin xGv (nx)],
где
С другой стороны, так как
(^ E)
| cos л arc sin x — cos яя ] < п | arc sin x — х | = 0 (гаж3), F)
следовательно, при — 1 ^ х ^ 1
(cos /гж — cos n arc sin з;) Gv (nx) = 6> (-y^-) = О (— 1.
Поэтому
^1р — ?п[/р(лх)]|<а, G)
«г^в fv(nx) = cos nxGp(nx), причем а стремится к нулю, когда п-^оо.
1 2. Итак* обозначим через
п
PnH = 2aft^ (8)
многочлен степени /г, наименее уклоняющийся от f(nx) на отрезке
[—1, +1] [для упрощения письма мы опускаем индекс р и пишем
f(nx) = fp(nx)]. Так как функция f(nx) ограничена, следовательно,
и многочлен PZ(%) ограничен на отрезке [—1, + 1]: пусть Рп(х)-^М.
В таком случае, вследствие известных неравенств В. А. Маркова
(«Э. П.», стр. 57] (к — четное число, коэффициенты при нечетных степенях х
равны нулю)
Следовательно, полагая nx = t, имеем
к=о
\cjc\<^-rf. Таким образом, Рп(—j принадлежит к классу целых
со
функций1 cp(?) = Vcfc?fe первой степени, коэффициенты которых
1 Целая функция 9 (*) называется функцией степени р, если она удовлетворяет
п
условию ШгГ V\ ?(n) @) | = /?.
263

удовлетворяют неравенству
*ПГГ (И)
при всех значениях А, каково бы ни было данное число МХ^М.
Вместе с тем En[f{nx)] является также наилучшим приближением
f(t) на отрезке [—п, п] при помощи многочленов степени л. Следо-
Следовательно,
En[f(nx))>An[f(t)}, A2)
где Ап [/ (t)] означает наилучшее приближение функции / (t) на отрезке
[—и, п] посредством целых функций первой степени, удовлетворяющих
неравенству A1).
Так как, при возрастании п, Ап [/ (t)] не может убывать, следова-
следовательно, An[f{t)] стремится к вполне определенному пределу A[f(t)),
Принимая во внимание, что предел целых функций рассматриваемого
класса принадлежит к тому же классу, заключаем, что существует
целая функция ФB) первой степени, которая наименее уклоняется от
f (t) на всей вещественной оси7 и соответствующее наилучшее прибли-
приближение (наименьшее уклонение) равно A[f(t)]. (Заметим, что то же рас-
рассуждение справедливо по отношению ко всякой данной функции, ограни-
ограниченной на всей вещественной оси.) Следует 'лишь заметить, что целая
функция Ф (t) первой степени, наименее уклоняющаяся на всей веще-
вещественной оси от данной ограниченной функции / (t), всегда удовлетворяет
неравенствам вида A1), так как максимум модуля последовательных
производных целой функции первой степени на всей вещественной оси
не превышает максимума модуля самой функции.
Следовательно, как бы мало ни было а^>0, при п достаточно боль-
большом имеем неравенство
En[f(nx)]>A[f(t)}~a, A3)
откуда вследствие G) получаем
n*>En\x\»>A\f(t)]—2a. A4)
3. Итак, пусть Ф (t) будет целой функцией первой степени, наименее
уклоняющейся от f(t) на всей вещественной оси; ввиду ее ограничен-
ограниченности можем разложить ее в ряд
сходящийся для всех конечных значений t. Кроме того, можно указать
такие две постоянные А^>0, Ь>0, чтобы при всех вещественных t
соблюдалось неравенство
264

и, с другой стороны, если
, то
« — I'D
A7)
где s -> 0, когда -—> 0.
л
Полагая Тп(х) = cos /г arc sin ж, построим многочлен степени п
n) (_ !)i ф /Л М те
\ 2 j L n л
—г1*
Прежде всего заметим, что при —1<1;г<^1
Qn (пх) = Qn (t) = О (л2 log п),
так как
cos n arc sin x
х — sin
-4-.-
A9)
Покажем, кроме того, что, как бы мало ни было а]>0, при ^У*
V п
1О2Г П
5 имеет место неравенство
V п
B0)
только п достаточно велико.
Вследствие неравенства A7) для этого достаточно будет убедиться,
что
- 2
г=— [log2n |
_ 1_
\ ""
1
cos wo:
cos n arc sin
X
TZ X Sill
стремится к нулю, когда х находится в рассматриваемом промежутке..
Пусть, для определенности, ж^>0, и положим
1
10 ~Т
1
sin тг ^^<^sin тс (г'о^-0).
265

Рассмотрим сначала член суммы B1), соответствующий i = i0; в таком
-случае
1 . 1 ,.1
х = ¦
- тс Н = sin
rc + ~- = sin
где 0<о2<7г,
U 1 i 1 1
ох — 5 = /г I 7т — sin тт =
L n n j
6/г2
8Х = §2 cos
Таким образом,
cos ля
cos /г arc sm x
и а? — sm
п п
-п
sin 5 sin $2
sin 8
(так как из неравенства
* I sin 8 si
ных значениях о, вытекает —^
B2)
1, имеющего место при всех веществен-
Sin §! ^|л 5S |\
ч8 — 8llj-
Поэтому член с индексом i0 в сумме B1) будет порядка •— il^
Так как то же замечание применимо к индексу г = го + 1, мы можем
ограничиться рассмотрением только тех значений /, для которых
В таком случае
х — sm ¦
Следовательно, соответствующие члены суммы B1) могут быть пред-
представлены в виде
Ф( (i —] п \х (cosпх — cosnarc sin x)
(— I)'
где числа аг ограничены. При этом
|i|<log2n|/"n
TV^=O(logn),
266

li|<log2nj/~n
s
^T +
cos ra# — cos n arc sin ж = О (nxs).
Поэтому вся сумма B1) будет порядка
°{x3fllogn) + °l
и таким образом неравенство B0) установлено.
Отсюда следует, что многочлен Qn (nx) степени п на отрезке
^lZL y °jj_f- приближает функцию f (nx) с точностью Л [/ (t)] + a>
| Qn (nx) - / (ns) \<A[f (t)] + a. B3)
4. Обозначим через i?n|#|p наилучшее приближение \x\v на отрезке
~^-, -^?^- п/?гг помощи многочленов Рп (х) степени п, подчиненных
L у п У п J
условию, что | Рп (х) \ <^ ns+p на всем отрезке [—1, +1]. В таком слу-
случае, принимая] во внимание A9) и B3), имеем при п достаточно
большом
nvE*n\x\v<A[f{t)]+2*y B4)
так как согласно замечанию, сделанному вначале, разность |/(nx) — nv\x\v\
при добавлении к ней некоторого многочлена степени п, возрастающего
на отрезке [— 1, + 1] не быстрее, чем пр, остается по модулю меньше a
на этом отрезке.
Рассмотрим далее многочлен Sn степени п, дающий наилучшее взве-
взвешенное приближение En(\x\v; A — x2)h) при весе A — x2)h функции | х |р
на отрезке [—1, +1], т. е. обращающий в минимум уклонение
произведения A — x2)h [| х |р — Sn (х)] на отрезке [—1, +1]. Положим
h = -= (выбирая постоянную с так, чтобы h было целым числом).
Очевидно,
Еп (| х |р; A - *»)*) > Ет (| х |р; A - ^
где m = n + 2/г.
Но, как установлено в моей цитированной выше книге «Э. П.» (стр. 100),
при всяком р > 0 имеют место неравенства
х |р > —|- (^-^.)Р —^= , B6)
267

где
^РгЧ^- B7>
Следовательно, можно указать такую постоянную ар, что при вся-
всяком целом
а потому существует такая постоянная Ьр = 21/2
¦тг / 4 -1- тс \Р
Таким образом,
так как ——>0, а потому
Следовательно,
h
- Ьр 2 /
ifh + p +
2т
+1) (h + -f-
, ЧТО
B9).
^lp(l-sn)>-f , C0).
где sn —> 0 при п—> эо, Ару>0 некоторая не зависящая от п постоянная.
5, Покажем, что если h =
, где с = 2р + 3 + ^ (^ ^> 0), то
p; (l-x*)h)<E*n\x
(Щ
при достаточно большом п.
В самом деле, допустим, что наше утверждение C1) ложно, и пусть
Рп (х) будет многочлен степени п, осуществляющий наименьшее уклоне-
т-г* i !г> Г log n log п 1
ние/б^ \х\ на отрезке ~=г, —р=^и так что, по условию,
I V п У п j
! I т ip Р* ('А \ <^ Н* \ <г ]Р
I I х \ 1 п \л) | <ь^ Ги п j х t
на этом отрезке. В таком случае мы тем более должны были бы иметь
Г log n log n "|
на отрезке -~=г-, ~Д^-
- ж»)" 11 ж |р - /^ (.г) | < iBJ |
268
C2),

и, кроме того, так как ] Р%. (ж) |-*$ я3+р, мы имели бы и в остальной части
отрезка [—1, +1]
Г2\Л||Г|Р„ р* (т\\ <r I i^MI
благодаря неравенству C0).
Следовательно, если бы C1) было неверно, Еп (j х |р; A — x2)h) не
было бы наименьшим уклонением произведения A — х2I1 \\x\p — Sn(x)\
на отрезке [— 1, + 1].
Но из неравенства C1) вытекает, благодаря B4), что
п»Еп (| х |р; A - х*У) < A [f @J + 2а. C4)
Поэтому вследствие C0) имеем также
J' [Л [/ (/)] + 2а].
Таким образом, как бы мало ни было данное а > 0, при всяком доста-
достаточно большом п
m*Em\x\v<A[f(t)]+3oL, C5)
и, принимая во внимание A4), мы получаем требуемым результат,
а именно, что
C6)
«каков бы ни был закон бесконечного возрастания w.
6. Следовательно, \j< (p) = A[f (t)] есть наилучшее приближение
функции
4 sin ~-
?й вещественной оси при помощи целых функций первой степени.
Ввиду того, что функция /р (t) равномерно непрерывна и имеет огра-
еиченную производную по р при всяком /, функция |х (р) также непре-
непрерывна и удовлетворяет условию Липшица, так как
14 [/р, @1 - A \fp (*)] | < max |/р,@ —/р@|-
, — oo<f<oo
Отметим еще, что справедлива также формула
{*(/?) = A [Fp(t)O C7)
где
7ZD
r/>>-^)°^+2Bt8int-jrfB. C8)
269

Действительно, полагая
тэ /+ \ (t2 — и2) cos г
R (t, и) = ^-
имеем для любого данного и
C9)
причем целой функцией первой степени, наименее уклоняющейся oi
R (t, и), является нуль, так как, в силу теоремы 1 § 11 главы III цити-
цитированной выше книги «Э. П.», не существует такой ограниченной на всей ве-
вещественной оси целой функции первой степени <р(?)> что ®(t)-R(t, гг)>>0
во всех точках, где \R (t, и) | = 1.
Поэтому для получения целой функции первой степени, наименее
cos t r .
уклоняющейся от -у——$ , нужно лишь подобрать постоянную л так.,
чтобы функция
cos^ , у '(t2 — и2) cos t + 2ut sin t
оказалась целой. Следовательно*,
А\
о—2tt
Отсюда следует, что Fp (^) — /р (^) есть целая функция первой степени,
кроме того, из C8) заключаем, что
= А [Fp (t)]
sm -~
Г (р).
D0)
Прежде чем вывести из C8) также и нижнюю границу для ц (/?), укажем
еще, что
V- (Р) = AVp Wl ^ A I**/*-** @1 = ^ IU П >
каково бы ни было целое положительное число к <^ ~- , так как
оо
vP+Чи
(eu + е~и) (и2 + г2)
цР-1
*2к Л>—27с+1
При этом для О < р <С 2 имеем
оо
х п\ 4 • ™р С
fv (t) — sin -77- COS t \
(eu + e~u) (u2 + г2)
= cos
D2)
См. также [84], стр. 377. (Автор.)
270

где [Cv дано формулой B7). Таким образом, функция fv(t) является
разностью между j t \p и ее интерполяционной целой функцией пер-
первой степени, определенной значениями в точках ЧЬ(^+-о~)тс и усло-
условием быть асимптотически равной \t\v при t ~ Ч- оо.
7. Для получения из C8) нижней границы jj. (p) напишем тождество
С ~ »'
О
где
<?p(') = tT
t -f U
e-uuV-l
- & со» + 2pt sin
i -jr р
( +
~ t2) Sln t] dU'
Поэтому вследствие C8) и C9)
[Fv (О] >
Г (р) - max | ?р @ |.
D3)
Но
= 2t[2pteO*t+V-*)*int] С ^UnV_x {p _ и) du
2»)-
+ [up2 — t2(u + 2p)] sin t) du. D4)
Следовательно, замечая, что первый из интегралов в правой части ра-
равенства D4) равен нулю, и, с другой стороны,
\t[p(p + 2и) — t2] cos t + [up2 — t2(u + 2p)] sin *
находим, что при р>1
оо оо
'»)' , ^ 1
2) V*2 + u2>
оо
;_ 1)] =_±_
Поэтому вследствие D3) (при /? > 1)
sin
jx (р) = Л [Fv (t)] > —^- Г (р) [1 - ^ j.
Таким образом, из D0) и D5) вытекает, что при р -» оо
D5)
D6)
271

так как при р ^> 2
. тер
sm ~-
sm •
Г(Р)>!
Примечание. Нетрудно видеть, что при t =
fC другой стороны, каково бы ни было данное t >-0, имеем
со
С ^p-! e-. ig^u») сов. + 2^ Blni du
sin НЕ
sm - -
С цР _! \e-u
1 du[e
Поэтому при р —> 0 (^ > 0)
2ut sin г
D7)
Следовательно, замечая, что lim Fv@) — «-, заключаем, что
lim ja (/?) = — , так что асимптотическое равенство D6) справедливо также
р-И)
«[ при /> —> 0.
Поступило
4.II. 1938 г.

n
О НАИЛУЧШЕМ ПРИБЛИЖЕНИИ \х—с
§ 1. В работе [73] мною доказано, что наилучшее приближение при
помощи многочленов степени п на отрезке [—1, + 1] \х\р (где р любое
положительное число) удовлетворяет асимптотическому равенству
L{P) _ ц (р)
A)
где L (р) — некоторая определенная непрерывная функция. Здесь я хочу
показать, что при любом с (—1<с<1) имеет место равенство
lim пРЕп | х — с \v = A — с2O ц (p). B)
П—*оо
Для этого докажем сначала следующие предложения.
Теорема I. Пусть Еп^Х)[/(х)\ (а,Ь)] означает наилучшее взвешенное
приближение f (х) на отрезке [а,Ъ] при весе q{x) посредством многочле-
многочленов степени п. В таком случае
Еп,п*% [\x\v\ (а,Ь)]<ЯЯр1[|з|Р; (а, Ь)] A + ая), C)
где сс^-^О при п->оо (— 1<;а< 0<<й-< 1).
В дальнейшем для краткости будем полагать Еп>1[/(х)\ (а,Ъ)] =
= En[f(z); (а,Ь)], EnMx)[f(x); (- 1, + 1)] = En,q(x)[f(x)].
В самом деле, полагая h = logn, имеем на отрезке [а,Ь]
hk x2k
где к =[log2n], а потому** |eft|<[j—-,¦ I ,|?И<гзЛ ПРИ
* Докл. АН СССР, 18A938), стр. 379—384 A93*).
** Так как из к + 1 > log2/г и из равенства h = log я следует, что (при п > е2)
ZJ (Л+i)! ^J log я
г=1 г=0 \
(Автор).
18 С. Н. Бернштейн 273

Из равенства
заключаем, что
I Rzk {х) Q2k (х)
<^
Поэтому (т = п +
-11
2 4
2А)
= \еке
he УН
i + lj
Г' \а>
'1<2п{-]
Ь)]>Еп
R2U(X)\<
е \logen
.Me
- pn-
Г 1 г
-hx-+
-*о.
1р; (в.
> Em,R2k(x) [\х\р Q2k (x); (a, b)} > Em,R2k(x) [ | x |p; (a, 6)] -
Но мною ранее были установлены неравенства («Э. П.», гл. II, § 6)
Следовательно, вследствие | i?2ft (ж) | -^ п при | х \ <^ 1 имеем тем более
mv+2i-iEm,R2n(x) [ | х |р*>«; (a, 6)] < А Г (р + 20,
а потому из D) выводим, что при достаточно больших п
ЕпЛ21с{х) [ | х |р; (а, 6)] < A + рп) ^п [ | ж |р, (а, Ь)) +
А*
где С не зависящая от п постоянная, лишь бы > 0. Таким образом^
Q
принимая во внимание, что Еп I х |р ^>-~, где Сх не зависит от п, имеем
при /i весьма большом
Ят,н2к(Х) [\х\*>; (а, Ь)] < A + >) ^п [ | х \р; (а, 6)], D')
где тп -> 0 вместе с — .
С другой стороны, легко проверить [74.1], что при всяком 8m>Q
Em-i[\x\p; {a,b)]<Em[\x\P;(a,b)] f^I.^^
откуда, полагая A + 8m)m—p = 2/тг, получаем (при — ^-1 + 2 log 2г?г)
m
[ | ж |Р; (а, Ь)] < Bwj^ + 1 ¦ Дт [ | я JP; (а, Ь)] <
274

Следовательно,
Еп [ 1 х \v; (a, 6)] < 2-i^f±l Д 1 + ^ ^ ^)еп[\х \», (а, Ъ)} <
г=1 /
*п)Ет[\х\*](а,Ь)], E)
где еп стремится к нулю, так как —^—->0. Для окончания доказа-
доказательства достаточно перемножить E) и D'), учитывая, что Km —2к^ ¦ = 1.
Следствие 1. Как бы малы ни были числа а^>0, ^>0, возможно
указать такое число п0, что для всякого целого числа п^>щ существу-
существует многочлен Рп{%) степени пу удовлетворяющий неравенству
\Рп(х)-\х — с\Р\<A + $)Еп\х-с\Р F)
на всем отрезке [—1, + 1] и неравенству
\Рп(х)-\х~с\р\<$Еп\х — с\* (&)
в промежутках (— 1, с — а), (с + а> 1)-
Действительно, вследствие C) существует многочлен Sn (x) степени п,
удовлетворяющий неравенству
на всем отрезке [—1,6] и неравенству
в промежутках (—1,-3) и (8,6), где, если полагать для определенности
с>0,
1Н
7 1-е <n a
U At 1 lJ
1 -f с ' J~ 1+c"
37-, С
В таком случае после подстановки х = -^ многочлен
1 + с
удовлетворяет на всем отрезке [—1, + 1] неравенству
\р — Рп (хг) |< A + <*п) Еп \х1—с
11 х± - с
и неравенству
| j Xl - с \р - Рп(хг) К-^-^5- ^n |«i - с \v
в промежутках (— 1, с — а) и (с -f- а, 1). Следовательно, для осуществления
неравенств F) и F') достаточно положить щ настолько большим, чтобы
СJ
§ 2. Будем обозначать через Еп [/ (х); (a, b); L], где (— 1 < а < Ь < 1),
наилучшее приближение f (x) на отрезке [а,Ь] при помощи многочленов
Рп(х) степени п, подчиненных в промежутках (— 1, а) и F,1) условию
275 18*

Теорема И. Каковы бы ни были данные числа р > О, /г > 0, — 1 <С с < 1,
«г #ая бы ни было мало s^>0, при п достаточно большом имеет место
неравенство
Еп[\х-с [р; (а, 6); лл] >A - г) Еп \ х - с|р, G)
11 1
бьг только с — а ^>—, 6 — с ^>—> где 0<Са<-т-.
В самом деле, положим т = /? + 2/, где Z = п9 — целое число Bа <^
* В таком слУчае
ж — с |Р > ?m [ q (x) | ж — с
Известно [«Э. П.», гл. II, § 6], что можно указать такую постоянную
;.р, что
каково бы пи было целое число г^>0. Следовательно [74. 1],
-clP, (8)
где 8^->0, en—>0 при w->oo. Кроме того, из (8) следует, что существует
такая постоянная Лр, что
Пусть |-Р^ (ж) [ <^ w/l на всем отрезке [—1, + 1J. В таком случае при
1 1
с и при с -] <J:r<;i имеем вследствие (9)
п п
когда дг достаточно велико. Поэтому, принимая во внимание, что
заключаем, что из неравенства (8) вытекает * G)
* В самом деле, пусть Р*п(я) — многочлен степени /г, удовлетворяющий нера-
неравенству | Р^] (ж) | < nh (— 1 < з? < «, 6 < а? < 1), для [которого достигается наилуч-
наилучшее приближение Еп[\х — с \р; (а, Ъ)\ nh]. Тогда, в силу (8) и последнего неравенства,
A-еп)Еп\*-с\»<Е {х)\х-с\»<, тах| | х - с |Р- Р\ (х) | q (x) -
max 1 \ х-с\»-Р*п(х)\ =
= max ||*-с|Р-
276

Следствие II. Пусть *
h
f и = 2 Ai 'x"ai I
i==l
(-l<Oi<l),
A0)
* Следствие II в дальнейшем получило обобщение в работе С. М. Никольского,
Докл. АН СССР, 55 A947), стр. 99—102. Кроме того, в заметке в Докл. АН СССР
55 A947), стр. 195—198, и в статье в Изв. АН СССР, сер. матем., И A947),
стр. 139—180 С. М. Никольским произведено аналогичное исследование наилучшего
приближения | х — a f в ере днем для любых s > — 1.
Приведу один из основных результатов, доказанных в последней статье (§ 3)
(с исправлением опечаток):
«Если | а | < 1, s > — 1 (исключая s четное), то
s+l
м.
S + 1
A - а»)
(En[f (x)]L означает наилучшее приближение в среднем функции f(x) на отрезке
[—1,1] при помощи многочленов степени /г), где
7ZS
us+1du
-*mr—=Zr-dt; (II)
4
кроме того, при всех целых нечетных s ^> О
8 s! V4
1V1 =
s
;—»
:3
(III)
В действительности преобразование (II) к виду, аналогичному (III), может быть
сделано при любых вещественных s >- 0. Для этого замечаем, что при и^>0
dt
+ ^2
cos f r , .. . . .Ч1 7 si"ii2mi
^T~ [ctg (^ "" Ш) ~~ g (? H IUI dt = ~^~
f cos г <i?
j cos 2мг — cos 2t
2
Полагая а = cos 2мг > 1, имеем \ — — = — 1/ _ , arctg л/ " .
о
eu -L p~m
Поэто.му G (u) = ——! arctg
M =
. 7ZS
SJI1 -—
. Откуда (вследствие (If))
8
s
и arct^r
du =
sm
(s
u8+1du
8
sin
2
(Автор,)
277

(p j> 0 не равно целому четному числу) функция <? (х) имеет ограни-
ограниченную производную порядка [р + 1]. Пусть Мп есть наибольшее из зна-
значений Еп [А{ | % — ^4 |р] для данного п. В таком случае, как бы мало ни
было Р^>0, можно указать такое число /г0, что при всяком п^щ
l-K*$P<i + t. (И)
В самом деле, применяя следствие I к каждому слагаемому А{ \ х — а\ \р,
получим
En[f(x)]<Mn(l + $).
С другой стороны, если бы было возможно построить многочлены Рп(х)
сколь угодно высокой степени п, для которых | Рп (х) — / (х) \ ^ Мп A — 8),
мы пришли бы к противоречию с теоремой II, так как для каждого
i = 1, 2,..., h можно было бы, введя согласно следствию I многочлены
Qn,i (#) степени /г, приближающие / (х) — Аг\х — аг \р на (at — a, ai + а)
с погрешностью меньшей, чем -^- $Мп, построить ограниченные на
отрезке [— 1, + 1] многочлены Rn^ (х) — Рп (х) — Qn,i (ж), для которых
в промежутке (а* — а, ai + а).
§ 3. Пусть, в частности (—1<^а<^1),
/ (х) = | х2 — а2 \р = | х — а |р [ х + а |р = | 2а |р [ | х — а |р + | х + а |р] + ? (ж)>
где
очевидно, удовлетворяет условию следствия II, поэтому при п достаточно
большом
1 — « < "J1 ¦ п .г» < 1 + а> A2)
как бы мало ни было а
Предположим теперь, что при данном р для некоторого значения а
предельная формула
lim n* En \ x — а |р = Я (а) A3)
П->оо
верна (согласно сказанному вначале, это справедливо для а — О).
Очевидно, Н (а) = Н (— а). Положим а = 2а\ — 1. Делая подстановку
ос = 2z — 1, замечаем, что
поэтому из A3) следует также, что
lim {2п)РЕп[\z-al\p; @,1)] = Н{а).
278

Но так как
En[\z-a*\*; @>l)] = ?an[|^-aJ|P;
то при всяком п -» оо имеем
lim пР Еп | #2 — ^2 |р = Н (а),
П->оо
а потому вследствие A2) из A3) вытекает также существование предель-
предельного равенства
lim пР Еп\х — аг \р = —Щ- = Н (ах), A4)
где аг — Чг: I/ —^~" • Аналогичным образом убеждаемся последовательно
в существовании предельных равенств
lim n* En\x — ak+1 [p = ^Ч) v= H (ак+1), A4')
—г—. Полагая а — cos ср, аЛ = cos срл, Н (а) = Н (cos ср)—
== ^ (?)> ВИДИМ? что при а = 0, ср = —, поэтому срх = — или —, и вообще
ъъ = -у 9л—1 = —^п> гДе ^ — произвольное нечетное число. Таким образом,
предельная формула A3) доказана для всех a — cos 9, где угол ср =—
соответствует вершинам любого правильного многоугольника с последо-
последовательно удваивающимся числом сторон. Для определения Н (a&) = F (срЛ)
имеем уравнение
причем F f-^-j = Н @) = р. (/?), поэтому
=^{р) sin
2 cos —
\ 4
sin М" = ,Л (/?) (sin ?i)P.
Но если ^(срл) = FB 9fe+i) = V-(P) \^П(?к |р> то из (Щ следует, что
sin 2 фЛФ1
2 cos
sin
Таким образом, для всех значений a = cos-^ (при любых целых к и
?<12к) справедливо равенство
lining | х — а |р = ц (/?) A — а2) 2 . A6)
П-»оо
Но, каково бы ни было с @<<с<С1), полагая
О <С ^о = cos ^-<^ с <; cos —j:—тс = ult
279

имеем при всяком п
и так как, по доказанному,
lim п*> Еп \ I x — с |р; (——, —)] =
= lim пр ({-У Еп\х-щ\р = (^)Р у. (р) A - В*)Т\
lim „ ^„[1 х- с |р; (- ^, А)] =
следовательно, равенство B) справедливо при всяком с (— 1<^с<^1) [74 2].
Поступило
5. II. 1938 г.

=45*?=
О ТЕОРЕМЕ В. А. МАРКОВА*
В работе1 «О функциях, наименее уклоняющихся от нуля», В. А. Мар-
Марков доказал весьма важную теорему:
Если многочлен Рп(%) на отрезке [—1, -+- 1] не превышает А по-
абсолютному значению, то максимум модуля Мъ его производной порядка
к удовлетворяет на том же отрезке неравенству
М, < ЛТ^ A) = AV *lnt-$+g-2l*-m. A)
где Тп (х) = cos n arc cos х (случаю к = п соответствует теорема Чебы-
шева).
Доказательство В. А. Маркова весьма сложно. Поэтому я считаю
не бесполезным указать другое, более простое, доказательство. Уста-
повление того, что максимум | Рп (+1) i B концах отрезка равен второй
части неравенства A), вытекает из основных свойств многочленов, наи-
наименее уклоняющихся от нуля2. Таким образом, основная трудность за-
заключается в доказательстве того, что ни в какой внутренней точке
% отрезка [—1, + 1] | Рп (?) j не может превысить того же значения
АТп^ A). Этой задачей мы и займемся.
Вместо того, чтобы искать наибольшее возможное значение М^ при
данном А, можем решить равнозначную задачу нахождения наименьшего
возможного значения А при данном Mk. Таким образом, задача сводится
к определи нию многочлена степени п
Р (х) = Рг + р2 (х — ?)+•••+ рп (х - S)*-1 + Vic (x -W +
---+Рп(х—е)п, B)
наименее уклоняющегося от нуля на отрезке [— 1, + 1], если коэффициент
м
—
= —- дан, а точка ? на данном отрезке и параметры р19 . . .,рп могут
* Труды Леыингр. пндустр. ин-та, № 5, раздел физ.-матем. наук, вып. 1 A938),
стр. 8—13 A99*).
1 С.-Петербург, 1892; немецкий перевод в Math. Ann. A916).
2 «Э. П.», стр. 27—28.
281

быть выбраны произвольно. Очевидно, что если с — внутренняя точка, то
в искомом многочлене рк+1 = 0, так как иначе вблизи ? была бы точка,
где \РЮ(х)\>Мк.
Прежде всего легко видеть, что число h точек, где максимум [^(#)|
достигается с последовательно противоположными знаками, должно быть
не менее п. В самом деле, многочлен <р(ж), у которого отсутствуют
члены (х — ?)к и (ж — S)^1, не может иметь более п — 2 вещественных
корней. Поэтому, если бы k<^n—1, то, располагая по одному корню
многочлена ср (х) между двумя точками, где Р (х) достигает максималь-
максимального модуля с противоположными знаками, можно было бы построить
многочлен
Р{х)-*(х),
который принадлежал бы к классу B), но уклонялся бы от нуля меньше,
чем Р(х). Следовательно, h^>n. Заметим сейчас же, что оба конца про-
промежутка ^hl должны быть точками максимального уклонения Р(х),
так как в противном случае последний имел бы тот же самый макси-
максимальный модуль А на большем отрезке [— 1, 1 + а] или [—1 —а, 1] при
некотором а^>0. Поэтому, делая соответствующую линейную замену
переменных, при том же \^ можно было бы А уменьшить в отношении
Нужно показать, что при h — n многочлен Р (х) также не будет
давать наименьшее значение максимума \Р(х)\.
Пусть хг = — 1 << х2 < . . . <С ^п—1 <С 1 = хп будут последовательные
точки, где Р (xi) = + максимум | Р (х) | — 4k L с последовательно противо-
противоположными знаками.
Замечая, что Pf (xi) = 0 в п — 2 точках х2, . . ., хп_г, заключаем, что
Р' (х) должен иметь еще один вещественный корень, но этот последний
ее может находиться на отрезке [— 1, + 1], так как по условию
P'(xi+e)P'(xi+1-s)>0
при достаточно малом е, а потому между xi и х^г не может быть не-
нечетного числа корней Р' (х). Невозможность предположения Рг A) = 0 или
Рг (— 1) = 0 вытекает из ранее сказанного, так как тогда максимум
j P (х) | сохранял бы то же значение L внутри отрезка большей длины.
Очевидно также, что
Р (xi) Р" (xi) <0 (i = 2, 3, . . .,я-1).
При h = n снижение максимума \Р {х)\ будет возможно, как и при h<" n,
если существует многочлен
п
<?(х)= 2 «¦ (ж — ?)*, C)
удовлетворяющий п условиям
282

Таким образом, единственный случай, вызывающий сомнение, пред-
представится тогда, когда
х± - с . . . (xL - ?)*-i {х± - S)H-i . . . (х± — S)n
= 0,
так как при D^O уравнениям ср (х{) = At можно удовлетворить при
любых значениях A%.
Полагая определитель D равным нулю, заменяем многочлен Р (х)
многочленом
г (х) =
Д?2,
где
E)
имеет ту же форму, что и ср (#). Поэтому ^Л)F — Д6) = */>?Л) F) = д/А
и Pjl (^) принадлежит к тому же классу, что ж Р (х). Величину А? полагаем
достаточно малой, чтобы —1 < ? — AS <^ 1.
Разлагая /^ (х) по степеням AS, имеем
(х) = Р(х)
х) - ср
>" (ж) - ф (х)
D')
где при заданных ср (#), ф (ж) величина 6 ограничепа. Многочлен
Р' (х) — ср (ж) - и (х)
не содержит члена (х ¦— ЕO^; поэтому он определится с точностью до по-
постоянного множителя из условий
и (xi) = Р' (хг) - ср (Xi) = 0 (?-1, 2,..., л-1). F)
Таким образом,
где С — постоянная, a D (х) получается из определителя D заменой хп
через х в его последней строчке. Таким образом, хп также будет корнем
и (х) — 0, постоянную же С определим требованием, чтобы ср (х) не содер-
содержал также члена (х — Ь)к+1, откуда CD&+V (S) = Р^+2) (?).
После того, как функция ср (х) зафиксирована, нам нужно показать,
что функцию ф (х) можно выбрать так, чтобы при достаточно малом AS
на всем отрезке [— 1, + 1]
\Рг(х)\<Ь. G)
Для этого, во-первых, необходимо, чтобы
\P1(xi)\<\P(xi)\=L (i = l, 2,..., н),
283

т. е. нужно подобрать функцию ф (х) так, чтобы в указанных точках х-г
Р (Xi) [ф (Xi) + О (Xi) - у Р" (Хг)] > 0. (8)
Кроме этого, достаточно, чтобы указанное неравенство G) имело
место в точках х\, где Рг (х) — 0, так как экстремум | Рг (х) | достигается
только в этих точках и в точках хх = — 1, хп = 1. Но вследствие D'),
при достаточно малом А? точки хх = х-х + Дяч, где /\ (:г) = 0 определяются
из уравнений
р[ {х{) = Р" (Xi) Axt + [Р" (Xi) - i (хд] Д5 + ex дж? + e2 Дхг д? + е3 д?2 = о,
где 6Ь 62, б3 — ограниченные величины (l<^i<^n).
Следовательно,
где б0 ограничено.
Поэтому, благодаря D') и F),
Рг (х[) = Р (х[) + А% [Р' (х\) - с? «)] + Д
= Р (х-) + у Ах] Р" {хг) + Д| Ахг [Р" (х^ - т' (Xi)\
е; Джз + е; д
^ + ф Ы + ^i]. (9)
где 6^, 6^, 6^ ограничены, а потому s^ стремится к нулю вместе с А?.
Следовательно, при достаточно малом Д$
1Л(О К I** (*¦•)! = ? (* = 2, 3 ,« — 1), A0)
если
[^Щ] (« = 2,3,...,п-1). (И)
Таким образом, неравенство G) будет соблюдено, если функцию
п
Ф(з)= S *i (я: — 6>* E)
выбрать так, чтобы соблюдались неравенства (И) и неравенства (8),
которые при L = 2, 3,..., п — 1 являются (как и следовало ожидать)
следствиями (И), так как в точках х2, х3) . . ., хп—г
P (x-)\v'(x-) P"(x\ l - v^; \v'(x-) — P"(r-)}2^>0
г \хг) |^ср \jlx) 2 1 \^г) 2Р" (x-) I — 2P" Ы-) l * ^ ^ ^ l^ ^
284

Поэтому, кроме неравенств A1), достаточно осуществить лишь неравен-
неравенства
р (_ 1) [?' (_ 1) _ 1 р" (._ 1) + ф (- 1)] > 0, |
Но все неравенства A1) и (8') будут соблюдены, если
ф (*) = 1?' (*
Y Vi/ — 2
т. е. если положим
-1-?' (*i) (i = 1, 2, . . ., /г), A2)
1 t
_у?
[требуемая форма ^ (ат) соблюдена, так как ср^-Ы) (|) — 0].
Действительно, Р'A) Р A) >0 и, вследствие F),
? A) = р' A).
Но, замечая, что ср (х) не имеет иных вещественных корней, кроме
х2,.., 3V-! [вследствие того, что ср(А:) (?) = cp^-rD (?) = 0], имеем ср' A) <р A) > 0,
так как ср (#) ср' (#) (и все последующие производные) имеют при х ^> хп^.г
знак старшего члена ср (х), поэтому
A3)
Следовательно,
^{хг)Р(Хг)<0 (? = 2, 3 /г —1), A4)
так как при переходе от хп^г к хп = 1 знак Р (я) изменяется, а знак
ср' (х) сохраняется. При дальнейших же переходах от Х{ к хч^ (кроме
i = l) знак ср (ж) изменяется вместе со знаком Р(х).
С другой стороны, из того, что ср (х) — Р (х) =0 не имеет иных кор-
корней, кроме хъ х2, . .., хп> следует, что срг A) — р" (I) имеет знак старшего
члена ср (л:), который совпадает со знаком ср'A), а потому, благодаря A3),
и так как при всех переходах от Х{ к Xi^ одновременно изменяются
знаки обоих множителей, то
Р (xt) [?' (Xi) - Р" (Xi)] > 0 (i = 1, 2, ..., п). A5)
Таким образом, вследствие Р (хг) Р" (х{) <^ 0, [при i = 2, 3, ..., п — 1
имеем, благодаря A4) и A5),
Р ^ [Ь*г?) - ~^J = ^РЧ^Г ^ {Xi) "" ^ (:Г°] > 0 (i = 2,. .., и - 1),
так что неравенства A1) соблюдены.
285

Также будут соблюдены и неравенства (8'), так как они приобре-
приобретают вид
1Р (- 1) [ср' (- 1) - Р' (_ 1)] > О, 1Р A) [?' A) ~ ^" A)] > О
и осуществляются благодаря A5).
После того как мы доказали, что число точек максимального откло-
отклонения h^>n, остается лишь заметить, что единственный многочлен B),
который достигает абсолютного максимума L на отрезке [—1, + 1] в
п + 1 точках, есть многочлен Чебышева ±LTn(x), где значения L и ?
определяются условиями
™(Ь) = Мк, Г<?+1) E) = 0.
Следовательно, если бы при данном Мк многочлен B), наименее
уклоняющийся от нуля на [— 1, + 1], соответствовал какой-то внутренней
точке 5, то наименьшее уклонение А было бы равно наименьшему из
й
значений
где ?i (i = 1, 2, .. ., п — к — 1) — один из корней уравнения JW-D (?) = 0.
Однако нетрудно видеть, что все эти значения больше, чем
Действительно, полагая х = cos 6, имеем Тп (х) = cos n 6 и
Г'» (л) = ^ет = 2л [cos (/г - 1) 6 + cos (/г - 3) 6 + ...].
Поэтому и при всех дальнейших дифференцированиях будем получать
п
Т{п)(рс)= 2 аы cos гб,
i=0
где аи ^ 0, откуда следует, что абсолютный максимум | TW (х) | дости-
достигается при 6 = 0, т. е. при х = 1.
Таким образом, неравенство A) доказано.

76
О ВАЗЕ СИСТЕМЫ ЧЕБЫШЕВА*
В статье дается общий метод построения базы произвольно заданной системы
функций Чебышева.
Пусть /о(#), /i(#)>---> /п(я) будет какая-нибудь система Т Чебышева
на отрезке [а, Ъ]. Мы называем базой1 этой системы такую систему
полиномов
п
M*) = S^W»(*) (i=0,l,...,n), A)
которая удовлетворяет условиям
Из B) вытекает, что функции tyi (#) линейно независимы и, след о.
вательно, образуют также систему Т Чебышева (эквивалентную данной).
Условимся называть систему функций Ф* (ж) нормированной, если абсо-
абсолютный максимум Фг (я) на [а, Ъ] равен единице.
Нетрудно видеть, что система Т функций Д (х) не может иметь
более одной нормированной базы на отрезке [а, Ь], так как полиномы этой
системы, которые всегда можно представить в виде
только тогда могут удовлетворить условиям B), когда
В указанном месте мною было замечено, что в случае существования
производных первых п порядков у данных функций fi (x) функции ф$ (х)
определяются (с точностью до постоянного множителя) условиями
-1). C)
*Изв. АН СССР, ОМЕН A938), стр. 499—504 A96*).
1 «Э. П.», стр. 64—71.
287

Здесь я хочу доказать существование базы у всякой системы Т и дать
прием для ее построения в общем случае. Для этого поступаем следую-
следующим образом.
Строим сначала некоторую систему полиномов по условию
Для этого, допуская (без ущерба для общности), что /0 (я) > О, пола-
полагаем ср00 (х) = /0 (.г) и рассматриваем все полиномы вида
E)
где постоянные Ь{ определяются требованием, чтобы
/i(fl) + bi/o(a) = O (i=l,...,/г).
Среди значков г будет по крайней мере один /0 такой [для упрощения
письма можем считать функции ft (х) расположенными в таком порядке
что i0 = 1], что
lim
/o И
<оо.
F)
Тогда система функций <?00(х), ®ц(х), с?21 (я), ... , срП1 (х) удовлетво'ряет
условиям
Um^-O. G)
Кроме того, вследствие F) можем определить постоянные С{ по условию,
что
Ф•-. (а?) + с-©-, (х)
При этом, располагая функции cpuO^) B соответствующем порядке и
обозначая cpi2 (^) = cpix (x) + Ci<pn (^), будем, кроме того, иметь
lim
Ф22
<оо (i
(9)
Следовательно, сроо (ж), ?п (ж) > ?22 (ж), ?32 GT) > • • • > ?п2 (х) удовлетворяют
условиям
lim 7-т- = 0 , lim , ч =0 (i > 2) A0)
и, кроме того, благодаря (9) можно так выбрать постоянные dt, что
,. Фг2(^) +^гФ22(^) , QN
lim— —г = 0 (г>3).
Продолжая таким же образом, получим носледовательные полиномы
?оо (х) у ?п (х) у ?22 (*) > • • • > ?пп (ат), удовлетворяющие всем условиям D).
Заметим, что последовательность полиномов ®i(x), удовлетворяющих
288

условиям D), обладает свойством, что срл {х), срл+i (х) » • • • » ?т» (ж) также
представляет систему Т (порядка п — к) при всяком к^п. В самом
деле, если а < х0<^ ... < хп.<^ Ь, то определитель
Д =
(#0) ... ©о
сохраняет постоянный знак.
Положим (без ущерба для общности), что ?
точно малом. Тогда знак Д совпадает с знаком
при х — а доста-
достакоторый поэтому также знака не изменяет. Повторяя то же рассуждение,
замечаем, что при всяком к
сохраняет постоянный знак Дп=срп(^п), т. е. положителен [в частности,
?п (х) ^> 0 при а <^ х <С Ь].
Следовательно, полином
п
г ух) — ^/j агсрг W v11;
не может иметь более п — к корней при а<^х<^.Ь. Будем говорить, что
х = а является корнем кратности k-^п заданной системы Т для поли-
полинома Р (х) вида A1). Очевидно, что кратность корня х = а полинома Р (х)
не зависит от выбора полиномов ср$ (х) данной системы, удовлетворяющих
условиям D).
Аналогичным образом определим корень кратности кх (данной системы Т)
в точке х = Ь, имея в виду, что всякий полином Р (х) данной системы
может быть также представлен при помощи некоторых полиномов 6* (х),
удовлетворяющих условиям lim-
(X)
= 0, в форме
Р(х)=
причем кг >> 0, если Р (Ь) =0.
Покажем, что
A2)
19 С. Н. Бернштейн
289

Это неравенство очевидно для к± = 1, так как тогда к<^п вследствие
того, что если бы к — п, то Р (х) = апоп (х), но срп(&)}>0. Вообще при
увеличении кх максимальная кратность к корня а полинома Р{х) не
может возрастать (так как число произвольных параметров убывает);
необходимо лишь убедиться, что к при этом действительно убывает. Для
этого заметим, что если бы мы имели также
где
0, то соответствующая линейная комбинация
^
i=0
имела бы в а корень кратности Лс + 1, что противно допущению.
Но если мы для всякого к построим полиномы
ф* (х) =
= 0,1, .. . , л),
то фоС^)? ^i (ж)> • • • > фп (ж) и будут служить базой для данной системы.
Полагая
П(х) (/ = 0,1,.., л),
г=0
мы имеем при каждом данном к систему из к линейных однородных
уравнений
к
3=0
для определения Cju (/ = 0,1, .. . , к). После этого получим
к
з=о
Кроме того, так как согласно сказанному выше Сии 3:0, все главные
миноры определителя
ап1
должны быть отличны от нуля.
Замечу также, что'условия B), совместно с условиями, что Фо (х), .. .,<!>п (х)
образуют систему Т, влекут за собой, что любая часть их также
290

представляет систему Т, т. е. систему Декарта D* как справа, так и
слева. Действительно, как было показано выше, все миноры определителя
% (х0)
составленные из элементов смежных строк, положительны, если
... <^хп<^Ь. Бо в цитированном месте доказано, что отсюда вытекает
положительность всех миноров.
Поступило
20.Х. 1938 г.

77
ОБ ОБРАТНОЙ ЗАДАЧЕ ТЕОРИИ НАИЛУЧШЕГО
ПРИБЛИЖЕНИЯ НЕПРЕРЫВНЫХ ФУНКЦИЙ*
Пусть Ео ;> Ег ^ . . . ^ Еп ^> . . . — произвольная монотонная после-
последовательность чисел, стремящихся к нулю. Требуется установить, суще-
существует ли такая непрерывная на отрезке [0,1] функция f (х), нормирован-
нормированная условием
Мах / (х) = — Min f{x) = Ео A)
на отрезке [0,1], что для всех п^О
En[f(x)] = En, B)
где Еп[/(х)] обозначает наилучшее приближение f(x) многочленами
•степени п на этом отрезке. Мы увидим, что ответ утвердителен1: если
все значения Еп положительны, то существует несчетное множество не-
неприводимых функций (т. е. таких, что разность между двумя из них не
является многочленом), удовлетворяющих условиям A) и B), и, кроме
того, каждой из этих функций соответствует счетное множество функций,
удовлетворяющих условиям A) и B), которые выводятся • [посредством
добавления определенных многочленов.
С этой целью заметим сначала, что, каковы бы ни были непрерывные
функции f (х) и у(х), функция
выпуклая. Действительно, благодаря тому, что наилучшее приближение
суммы двух функций не превосходит суммы их наилучших приближений,
получаем
при всех значениях \ и /г.
* «Sur le probleme inverse de la theorie de la meilleure approximation des fonc-
tions continues». Gomptes rendus, 206 A938), стр. 1520—1523 B01*).
1 Рассуждения, которые следуют далее, остаются в силе и в том случае, когда
отрезок [0,1] заменен произвольным замкнутым ограниченным множеством, а также
в случае, если алгебраические многочлены заменить полиномами произвольной сис-
системы Чебышева.
292

Пусть Rn+i (x) — многочлен степени п -\- 1, наименее уклоняющийся
от f (х). Тогда из сказанного выше вытекает, что уравнение
F (л) = Еп [/ (х) - Rn+1 (х) + ). х «Н 1] = Яп C>
необходимо будет иметь единственное положительное решение X = Хо ^>
>0 и единственное отрицательное решение \ = \1<^0, при условии?
что EnA-i[f{%)]<^En, так как минимум F(l), равный En^1[f(x)], дости-
достигается при X = 0. Таким образом, для этих двух значений X, все функ-
функции
Ф (х) = f (х) - Rn_H (х) + л я»-Н + рп ф9
где Рп (х) — произвольный многочлен степени п, удовлетворяя C), рас-
распадаются на два различных класса, которые отличаются знаком коэффи-
коэффициента X при наивысшей степени х в многочленах степени п -\- 1, найме-
менее от них уклоняющихся.
Продолжая рассуждать таким же образом, мы можем, исходя из про-
извольной функции /(#), для которой Еп^ [f{x)\<iEn, построить 2sраз-
2sразличных функций, получающихся из / (х) прибавлением некоторых опре-
определенных многочленов степени п -\- 1, обладающих свойством
Ет[Ф(х)] = Ет G?z = 0,l, • • ./г)
и нормированных условием A), где s — число различных значений Еш
при т^п. В частности, в случае, когда Еп+г =0, существуют точно
2s многочленов степени п + 1, удовлетворяющих условиям A) и B), кото-
которые отличаются друг от друга совокупностью знаков старших коэффи-
коэффициентов многочленов степени т <; п + 1, наименее от них уклоняющихся.
После сказанного выше естественно приписывать знак наилучшему
приближению функции Еп [/ (х)] посредством многочленов Rn (x) степени
<^тг, а именно: знак3 коэффициента (не равного нулю) при старшем
члене многочлена Rm{x), отличного от Rn(x), наименьшей степени т^>п,
наименее уклоняющегося от /' (х). Приняв это, мы можем уточнить вы-
высказанное выше утверждение.
Теорема. Какова бы ни была последовательность действительных
чисел а0, а1? . . . . ап, . . , не возрастающих по абсолютной величине*
и стремящихся к нулю, существует такая функция fv(x) (нормирован-
(нормированная), что
En[f(x)] = an (л = 0, 1, 2,...)- • 'D)
Действительно, применяя указанный метод, можно построить для
всякого значения п многочлен fn{x) степени п, для которого
1 Это также знак разности / (а?) — i?n (x) а последней точке, где она достигает
своего максимального модуля ** E^[f (a?)].
* Причем, если | ап^_1 | = | <хп |, то осп+1 = ап. (Автор.)
** Действительно, согласно определению числа т существует т + 1>я + 2 точек
li < 52 < • • •< 5m+ii гДе / E*) - Rn &k) = ± En I/ Ml c последовательно противопо-
противоположными знаками. При этом вследствие En[f^x)]^>'Er^i[f(x)] во всех точках ?к
293

Em [fn {x)\ = am (m < n).
Пусть Rm)U {x) будут наименее уклоняющиеся от fn (х) многочлены сте-
степени т. Многочлены Rm,n{x) ограничены (| Дт,п(#) |<С21 ао|), поэтому
существует возрастающая подпоследовательность {щ} чисел /г, для ко-
которой
lim Rn% (x) = Rm (x)
при всяком данном значении т, где Rm(x) — многочлен степени т. Кроме
того, можно определить такое достаточно большое число Nm, что
для всех щ^ N. Таким образом, каково бы ни было s^>0, существует
такое достаточно большое число Лг, что
\fnl(T)-fnk(x)\<s
при fii^N, njc^-N. Это означает*, что fni{x) равномерно сходятся к
некоторой функции f(x), которая обладает требуемым свойством
Ет [f(x)] = lim Em [fnx{x)]= ccm,
11} —>СХЭ
причем многочлены Rm (х) являются наименее уклоняющимися от f(x).
Весьма вероятно, что функция f(x) (нормированная), онределенная
последовательностью чисел ап, единственна (как в случае, когда ап = О
для п достаточно большого). Но я не обладаю общим доказательством
этого предложения, не налагающим значительных ограничений на поря-
порядок убывания [ ап |.
имеем [/ (?А) — Rn (%к)] [Rm (?ft) — Rn (Е,к)] >0. Следовательно, во-первых, многочлен
Ит (х) — Rn (x) степени т (старший член которого совпадает со старшим членом
Rm(x)) имеет все свои т корней внутри промежутка (%lf ^т_^г) и, во-вторых, знак
разности /EW+1)—-ДгДт-Н.) тот же' что зиак ^m^m+i)—¦ДиКт+з.)» который должен
€овпадать со знаком Rm (oo). (Автор.)
* Здесь применяется известный диагональный процесс (см. подробнее И. П. На-
Натансон. «Конструктивная теория функций», стр. 145—154). Поэтому доказательство
существования / (х) является неэффективным. Лишь при некоторых ограничениях,
наложенных на закон убывания | an|, мне удалось дать конструктивный метод постро-
построения искомой функции /(ж). (Автор.)

78
КОНСТРУКТИВНАЯ ТЕОРИЯ ФУНКЦИЙ
ВЕЩЕСТВЕННОЙ ПЕРЕМЕННОЙ *
Конструктивная теория функций вещественной переменной,-возникшая
на основе синтеза идей двух великих математиков прошлого % столетия
Вейерштрасса и Чебышева, — представителей двух глубоко различных
направлений математической мысли, — получила самостоятельное суще-
существование примерно 25 лет тому назад, причем ведущая роль в этой новой
области анализа принадлежала и принадлежит математикам нашей страны.
Поэтому в очерке, посвященном достижениям советской науки после
1917 года, не выходя, по существу, из намеченных рамок, необходимо
для ясности картины вкратце изложить основы нашей теории, заложенные
не более чем за пять лет до Великой Октябрьской социалистической
революции.
Элементарной базой всей теории служит обыкновенный алгебраический
многочлен, так как все функции, встречающиеся на практике, значение
которых для каждого данного значения переменной могут быть вычислены
с заданною точностью посредством конечного числа ' арифметических
действий, являются в том или ином смысле пределом некоторой совокуп-
совокупности, многочленов, подобно тому, как всякое вещественное число является
пределом рациональных дробей.
Вследствие этого все свойства функции потенциально заложены в про-
производящих ее многочленах, и стержневой проблемой конструктивной
теории функций является исследование общих свойств многочленов (или
конечных сумм других элементарных функций, как показательные
и тригонометрические), имеющих пределом рассматриваемую функцию.
Первый, ныне завершающийся 25-летний период развития нашей теории
был, по преимуществу, посвящен непрерывным функциям, которые явля-
являются эквивалентом последовательностей многочленов, равномерно сходя-
сходящихся на данном отрезке. Каждая непрерывная функция / (х) имеет среди
всех многочленов данной степени один и только один наименее от нее
* Математика и естествознание в СССР. Изд. АН СССР, 1938, стр. 36—41 B00*)
295

уклоняющийся в данном промежутке, то есть выражающий (приближаю-
(приближающий) рассматриваемую функцию f (х) на всем промежутке с наименьшей
погрешностью Enf (х). Согласно классической теореме Вейерштрасса у
признаком непрерывности функции f(x) служит то, что Enf(x) стремится
к нулю с возрастанием п. Естественно было взять за основу классифи-
классификации непрерывных функций эту последовательность монотонно убываю-
убывающих чисел Enf(x) и в первую очередь скорость этого убывания с возра-
возрастанием степени п приближенного многочлена.
За несколько лет до революции был найден ряд замечательных но
своей простоте зависимостей между дифференциальными свойствами функ-
функции / (х) и законом убывания Enf{x). В частности, тогда же было пока-
показано, что класс аналитических функций (комплексной переменной) характе-
характеризуется тем, что последовательность чисел Enf (x) убывает быстрей, чем
в некоторой геометрической прогрессии. Это свойство впоследствии было
положено в основу систематической теории аналитических функций веще-
вещественной переменной, построенной независимо от понятия о комплексном
числе.
Эта теория исходит из того, что функция, являющаяся пределом по-
последовательности многочленов, заданных на данном отрезке, в случае
столь быстрой сходимости оказывается вполне определенной и вне данного
отрезка, т. е. однозначно (аналитически) продолжаемой. В этом случае
отсюда вытекает также законность экстраполирования соответствующих
интерполяционных формул.
В настоящее время советскими математиками связь между законом
убывания чисел Enf(x) и комплексными особенностями аналитической
функции / (х) изучена с исчерпывающей полнотой, по крайней мере для'
случая изолированных особых точек, и в общем случае непрерывных
функций еще более уточнены зависимости между ее дифференциальными
свойствами и Enf(x). В это же время исследование всех законов убыва-
убывания последовательностей Enf(x), допускающих однозначное продолжение
функции, пролило новый свет на задачу обобщения аналитических ф^нк-,
ций и привело к открытию и построению так называемых квазиаяали-
тических классов функций, причем и в этой области советские математики^
с успехом соревновались с западноевропейскими.
Дальнейшее изучение вещественных свойств аналитических функций г
представляющее весьма важную как теоретическую, так и практическую,
проблему, развилось у нас и в другом направлении, связанном с рабт
смотрением частоты корней последовательных производных рассматривае-
рассматриваемой функции. Оказалось, что функции, у которых конечные разности
любого порядка не обращаются в нуль на данном отрезке, не только,
должны быть непрерывны и иметь производные всех порядков, обладаю-
обладающие тем же свойством, но должны быть аналитическими функциями; эти
функции называются регулярно монотонными и, в частности, абсолютна
монотонными, если все производные положительны.
Всякая аналитическая функция, и только аналитическая функция,,
является на достаточно малом отрезке разностью двух абсолютно моно-
296

тонных функций. При этом радиус сходимости строки Тейлора данной
функции / (х) в каждой точке а равен наибольшему отрезку аЪ F>а),
где такое представление функции f (х) в виде разности двух абсолютно
монотонных функций возможно. Существенную роль играет характер
чередования знаков последовательных производных регулярно монотонной
функции на данном отрезке, и любопытно отметить, например, что цикли-
циклическое чередование знаков производных, подобное чередованию знаков*
последовательных производных cosx (—,—, + , + ,—, — ,-..)> на сколь
угодно малом отрезке возможно лишь у аналитических функций,
и притом целых, т. е. не имеющих особенностей во всей комплексной
плоскости.
Значительная часть этих и подобных им результатов опиралась на
полное или асимптотическое решение соответствующих экстремальных
задач о многочленах или полиномах, составленных из других элемен-
элементарных функций, подчиненных тем или иным условиям. Первые фунда-
фундаментальные задачи такого рода были разрешены еще Чебышевым, который,
поставив их в связь с своей теорией механизмов, по справедливости
должен считаться основоположником этой новой отрасли алгебры, изучаю-
щей многочлены и другие функции, наименее уклоняющиеся от нуля
среди всех функций, подчиненных одинаковым условиям.
О том, что значение указанных проблем выходит далеко за пределы
чистой математики, можно судить и потому, что, например, задача о наи-
наименьшем уклонении многочлена данной степени в промежутке, где про-
производная его достигает известного значения, решенная покойным акаде-
академиком Марковым и играющая вместе с позднейшими своими видоизмене-
видоизменениями существенную роль в современной теории функций, была поставлена
нашим великим химиком Менделеевым.
Я не могу распространяться здесь обо всем комплексе задач этой
новой алгебры многочленов, достигшей больших успехов, в особенности
в нашей стране. Замечу только, что, в отличие от классической алгебры,,
формальное решение задачи, осуществимое лишь в редких случаях, не
является целью; важны, по преимуществу неравенства и асимптотические
оценки, соответствующие бесконечному возрастанию степени рассматри-
рассматриваемых многочленов.
В качестве образца я возьму проблемы, связанные с интерполирова-
интерполированием. Всем известно, что многочлен степени п вполне определяется своими
значениями в п -f- 1 точках; если он равен нулю в п + 1 точках, то он
тождественно равен нулю. Однако, как бы малы ни были данные значе-
значения многочлена степени п в этих п -f- 1 точках и как бы их ни выбирать
в данном промежутке, этот многочлен, при п достаточно большом, может
все-таки получать в других точках промежутка сколь угодно большое
значение.
Из этого существенного свойства многочленов, которое было открыто*
почти одновременно в начале мировой войны в Германии и у нас, озна-
означающего, что никакая решетка из п + 1 точек не может при увеличении п
лишить многочлен свободы неограниченного роста, вытекает возможность
297

построения непрерывных функций, для которых никакие обычные интер-
интерполяционные многочлены (Лагранжа) не являются сходящимися, то есть
производящими многочленами в смысле, указанном в начале этой статьи.
За последние годы у нас появился ряд работ, уточняющих и обоб-
обобщающих это свойство многочленов. Во-первых, удалось указать асимпто-
асимптотическое расположение на данном отрезке решетки из п + 1 точек, наи-
наиболее стесняющее рост многочлена во всех прочих точках отрезка, и найти
асимптотический максимум ( — log и) всех многочленов степени п, на всем
отрезке не превышающих единицы по абсолютному значению в рассматри-
рассматриваемых п -{• 1 точках. Во-вторых, было показано, что, как бы мало ни
было данное число а ^> 0, возможно так сгустить решетку, выбрав A + а) п
точек, чтобы совокупность многочленов степени п, ограниченных в этих
точках, была ограничена на всем отрезке, т. е. не превышала некоторой
конечной величины, не зависящей от п. Благодаря этому были найдены
простые видоизменения интерполяционной формулы Лагранжа как для
многочленов, так и для тригонометрических сумм, сходимость которых
обеспечена для любых непрерывных функций.
Следует отметить, что вопросы сходимости интерполяционных формул
специально для аналитических функций советские математики изучали
также и другими методами, непосредственно примыкающими к теории
функций комплексной переменной. Несмотря на ценность некоторых
результатов, полученных в этом направлении, я вынужден отказаться
здесь от их изложения, так как это потребовало бы введения некоторых
новых понятий и определений, относящихся к целым функциям, к кото-
которым главным образом относятся соответствующие работы. По той же при-
причине я не буду останавливаться на экстремальных проблемах о целых
функциях, аналогичных рассмотренным выше для многочленов, хотя резуль-
результаты, полученные в этой области, по своему значению не уступают тем,
о которых говорилось до сих пор.
Недостаток места не позволяет мне также остановиться на недавних
крупных достижениях, касающихся теории приближенных квадратур,
связанных с интерполированием и основанных на той же алгебре веще-
вещественных многочленов.
Сюда же примыкает и ряд интересных работ, посвященных одной чиз
кардинальных проблем анализа — классической проблеме моментов. В эт*йх
работах проблема моментов получила новое разностороннее освещение.
В частности, следует отметить метод решения этой проблемы, связыЬаю-
щий ее с построением абсолютно монотонной функции по заданным, зна-
значениям ее последовательных производных, а также применение к решению
проблемы моментов на конечном отрезке совокупности многочленов
п
тп=1
важное значение которых и свойства были выявлены советскими матема-
математиками в ряде исследований последнего десятилетия.
298

Многочлены Bnf (z), построение которых носит чисто арифметический
характер, с одной стороны, не только служат для выражения всех непре-
непрерывных функций (и весьма широких классов разрывных функций) на
отрезке [0,1], но в случае дифференцируемости функции / (х) последова-
последовательные производные многочленов Bnf (x) сходятся к ее производным
соответствующих порядков. С другой стороны, если функция / (х) анали-
аналитическая (в точке х отрезка [0,1]), то Bnf (x) стремится к / (х) также
и в некоторой комплексной области вблизи рассматриваемой точки.
Совершенно иного характера конструкция приближающих данную
функцию многочленов, которые получаются при разложении функции
в ряды типа Фурье (тригонометрические ряды). Их вычисление и выра-
выражение существенно связаны с понятием интеграла, так как обычно опре-
определяются они по условию, чтобы средняя (так или иначе взвешенная)
квадратичная погрешность была минимальна. Всем известно центральное
место, которое занимает в анализе теория рядов ортогональных функций
и, в частности, теория тригонометрических рядов, возникшая еще
в XVIII столетии в связи с задачей о колебании струны. Естественней
было бы отнести эту теорию к конструктивной теории функции; однако
в данном очерке я остановлюсь ненадолго на весьма значительных успехах
советской математики в этой области, так как у нас принято относить ее
к метрической теории функции.
Действительно, объем конструктивной теории функций, согласно ска-
сказанному вначале, принципиально почти полностью совпадает с общей
теорией функций, исключая из рассмотрения лишь трансфинитные про-
процессы. Таким образом, различие между обеими теориями преимущественно
методологическое: первая восходит от частного к более общему, посред-
посредством построений, связанных с той или иной группой конкретных проблем,
вторая идет обратным путем. Принимая во внимание бесконечность мира
математических функций, пути эти не обязаны встретиться. Поэтому
мой очерк посвящен, главным образом, тем вопросам, которые наиболее
далеки от современного направления метрической теории функций; между
тем, в теории тригонометрических рядов оба направления встречаются,
взаимно дополняя друг друга.
Этой области исследований советских математиков уделено соответ-
соответствующее место в статье, посвященной теории функций вещественной
переменной.
Здесь я хочу лишь упомянуть о существенных достижениях, относя-
относящихся к представимости произвольной функции в виде сходящегося три-
тригонометрического ряда, приближающих нас к разрешению принципиально
важного вопроса о том, возможно ли построить непрерывную функцию,
для которой тригонометрический ряд Фурье был бы везде (или почти
везде) расходящимся.
Как давно известно, несмотря на присущее ряду Фурье свойство, -что
средняя квадратичная погрешность, даваемая конечными суммами его
членов, стремится к нулю, в некоторых точках эти суммы могут не-
неограниченно возрастать, т. е. не сходиться к соответствующему значению
299

данной функции. За последние двадцать лет были значительно дополнены
наши знания о связи между приближением, даваемым конечными сум-
суммами ряда Фурье, и наилучшим приближением, а также поставлен вопрос,
еще не получивший полного решения, для каких функций / (х) эти суммы
дают наилучшее приближение Enf(x). Также был указан ряд более или
менее простых способов преобразования указанных сумм, с тем чтобы
превратить их в сходящиеся для любой непрерывной функции, или такие,
которые в соответствующих случаях дают приближение того же порядка,
что Enf (x).
В этом далеко не полном очерке я пытался дать в возможно доступ-
доступном изложении представление об основных идеях и методах конструктив-
конструктивной теории функций, и поэтому упоминание в отдельных случаях имен
тех математиков, которым наука обязана тем или иным из приведенных
здесь результатов, мне казалось нецелесообразным.
В заключение скажу лишь, что в первые годы после революции мои
работы по конструктивной теории фупкций в узком смысле слова стояли
еще одиноко. Но в последующие годы, в связи с общим расцветом
науки и расширением научных кадров в нашей стране, дальнейшему раз-
развитию этой теории в большой мере способствовали исследования це-
целого "ряда выдающихся более молодых математиков,' из которых в пер-
первую очередь следует назвать Н. И. Ахиезера, А. О. 1;ельфонда, В. Л. Гон-
Гончарова, Л. В. Канторовича, Р. О. Кузьмина, а также М. Г. Крейна,
И. Н. Хлодовского, Я. Л. Геронимуса, Е. В. Вороновскую и др.
Если бы мы присоединили к конструктивной теории функций также
и теорию рядов типа Фурье, еще раньше достигшую в Москве большого
развития, то необходимо было бы перечислить ряд других ученых», которые,
как А. Н. Колмогоров, Д. Е. Меньшов и другие, за рассматриваемый
период обогатили науку результатами первоклассного значения.

79
ОПРЕДЕЛЕНИЕ РЯДА ФУНКЦИЙ ПО ЭКСТРЕМУМАМ
ЕГО ПОСЛЕДОВАТЕЛЬНЫХ ОСТАТКОВ *
Рассмотрим последовательность непрерывных1 функций ®п{х), не от-
отрицательных в точках х замкнутого множества Е, Достигающих максиму-
максимума 1 в одной и той же точке а С Е множества" Е и удовлетворяющих
условию
?пИ>?п-ыИ>0 A)
во всех точках х € Е.
Пусть / (х) будет какая-нибудь функция, выраженная рядом
сходящимся при х = а, так что по теореме Абеля ряд B) равномерно
сходится во всех точках х 6 Е. Пусть enNn будет (абсолютный) экстремум
на множестве Е остатка
n+i
где 7Vn>0, sn = 4:l [т. е. существуют точки, где епВп (х) = Л;п, но
нет точек, где | Rn (х) \ > Nn].
В таком случае имеет место
Теорема I. Не может быть более одной функции вида B), у которой
экстремумы всех остатков (п ^ 0) имели бы данные значения snNn на
множестве Е.
В самом деле, составляя7 разность между двумя функциями, соответ-
соответствующими равным экстремумам sn7Vn всех последовательных остатков,
получим функцию
* Докл. АН СССР, 22 A939), стр. 3—6 B04 *).
1 Условие непрерывности, как и условие замкнутости множества Е, вводится
лишь для упрощения изложения.
301

которая будет обладать свойством, что для каждого п либо будут точки
сп и ?'п множества Е, где
оо
Р*(&П)= 2 «Л?*(?п)^'О, р„F'п)<0,
либо будет по крайней мере одна точка хп, где оп (#п) = 0 при * cpn+1 (xn) ^ 0.
Но, с другой стороны, так как limpn(a) =0, можем указать [если только
п—>оо
F (ж) не равна тождественно нулю] такое значение п, что
?п {а) | > | pn+л (а) !
нри любых /г>0. Кроме того, имеем вообще
on (х) = рп (а) ?п+1 (ж) + pn+i (а) [?п+2 (ж) — ?n+i И] +
+ рп+2 (а) [срп+з И — ?п+2 (*)] + • • • [так как ап+1 = рп (а) — рп+1 (а)]. C)
Следовательно, благодаря A), при таком значении п будет
| рп (х) — рп (а) срп+1 (х) ]< | рп (а)) срп+1 (я)
для всех х(:Е, где 9r?+i(^)^>0, a потому во всех этих точках мы име-
имели бы
Рп(я)рп(а)>0,
что исключает существование точек хп, где рп (хп) = 0 [при <рп+1 (хп) >0]^
как и точек ?п и ?п, где pn(?n)pn(?n)<0.
Эта теорема единственности должна быть дополнена теоремой суще-
существования. В данном случае (в отличие от соответствующей теоремы
теории наилучших приближений, данной мною в другом месте *) нельзя
указать простого необходимого и достаточного условия, которому должна
удовлетворять последовательность экстремумов enNn для того, чтобы
существовала функция вида B), соответствующая ей. Однако, применяя
рассуждение, аналогичное указанному в упомянутой выше заметке, легко
доказывается следующая
Теорема II. Какова бы ни была монотонно стремящаяся к нулю
бесконечная последовательность чисел No ^ N± ;> ... ^ ЛТп ^ 7Vnj_i !J>...^> 0,
существует (единственная) функция
* Если бы для какого-нибудь п не было точек ни одной из этих двух катего-
категорий, то это означало бы, что Фп+1 (#) = 0 для всех п ^> 0 во всех точках х ? Е, что
противоречит условию срп , ± (а) == 1. (Автор.)
1 «Sur le probleme inverse de la theorje de la meilleure approximation», Comptes
rendus, 206 A938) [77J.
3D2

у которой последовательные остатки
n (X) = 2 Ьи ?
п+1
имеют экстремумы, равные snNn, каковы бы ни были данные sn = Ч- 1
[из доказательства будет видно, что при этом ни один из остатков Rn(x)
не может иметь одновременно экстремумом 4- N л — N].
Действительно, если
/l (X)
=.2 (&» + >Х) ?„ (X)
Fn (X) = максимум
п+1
то Fn(k) является выпуклой функцией параметра а. Положим, в част-
частности, что функция fx{x) такова, что ъ'ъ = 0 при k^n -f I, Fn+1 @)<;7Vn
и /2(ж) = срп+1(ж). В таком случае
поэтому уравнение
Fa (X) = максимум
Fn@) = Fn+1@),
оо
CD (X) -J- V Й' СО I
= Л
D)
будет иметь для всякого Л ^> Fn+! @) одно положительное решение
0 и одно отрицательное решение Хп_|_г <; 0, причем вследствие
)°
экстремум (ли+1 ?п+1 (ж) + 2 ^?* («) ) = ^,
экстремум (x;+1?nfl (х) +
п+2
= " А'
В случае Л = Z<Vh @) уравнение D) имело бы решение Х = 0 и еще
одно решение знака, противоположного экстремуму
п+2
если последний достигается только с одним знаком.
Таким образом, всегда найдется одно такое значение с .
, что
экстремум Uncn+1 ?я+1 (х) + 2&*?*(^) = ?n
303

При этом сп+1 могло бы быть равно нулю только при Nn = Fn+1(Q).
Повторяя то же рассуждение, получим функцию
п со
/"' (*) = 2 eiCi+1?i+1 (х) + 2 Ъ'к'Н (х), '
О п+2
у которой первые п -\- 1 остатков R{ (x) имеют экстремумы, соответственно
равные &iNi [так как в силу сказанного выше сг-+1 = 0 только при
вгЛ^г = 8i-hi^i+i и ПРИ сг+1 > 0 экстремум Щ (х) достигается лишь с одним
знаком, следовательно экстремумы всех остатков, отличных от
со
достигаются лишь с одним знаком].
Пусть, в частности, Д (х) ^ 0, тогда
п
fn) (x) = 2 SiCi+i?i+l («)
будет полиномом, и нам остается доказать, что fn) (x) равномерно при-
приближается к определенному пределу / (х) при п—>оо. Действительно,
положим
п+к+1
(х) - fn) (х) = 2 «i?i («). (*>0),
1
п+Л+1
В таком случае | рт (х) \ <;iVm < Л^п при т^>п. Поэтому на основании
рассуждения, сделанного при доказательстве теоремы I, при всех т <; п
должно соблюдаться неравенство •
| Рт (а) | < Nm
откуда вследствие C)
при любом х. В частности, полагая т — 0, получаем неравенство
из которого заключаем, что ^ (х) равномерно [стремится к некоторой
функции / (х) вида B), удовлетворяющей условиям теоремы.
Имея в виду один из важнейших случаев применения доказанных тео-
теорем, когда срп (х) = хп, усилим условие A) условием
?п (Я) — ?п+1 (Я) > ?п+1 (Я) — ?п+2 И > 0. E)
В таком случае имеет место
304

Теорема III. Функция f (х) вида B), у которой последовательные
остатки имеют экстремумы, равные (—l)n+Wn, где Nn^Nn+b равна
[при условии E)]
71=0
При этом все экстремумы достигаются при х = а.
Действительно, в точке а все остатки Rn (x) получают значения
(—1)n+ Wn. Поэтому нужно лишь проверить, что при всех х б Е
\Rn(x)\<Nn.
Для этого замечаем, что вследствие E),
(х) < (—1)"+1Дя (Х) = Nnyn+1 (х) + Nn+1 (cpn+1 (х) — срп+2 (ж)) -
Nn+2 (срп+2 (ж) — срп+3 (ж)) + ... = iVncpn (х) — Nn (<рп (ж) — cpn+i («)) +
+ ЛГп+1 (срп+1 (ж) - срп+2 (х)) +... + ...< 7Vn?n (ж).
Поступило
27. XI. 1938 г.

80
E ВОПРОСУ О ЛОКАЛЬНОМ НАИЛУЧШЕМ
ПРИБЛИЖЕНИИ ФУНКЦИЙ*
Докажем следующую теорему:
Теорема. Условие, необходимое и достаточное для того, чтобы функ-
функция / (х) имела непрерывную производную порядка п -\- I во всех точках
отрезка [а, Ь], заключается в том, что
о<6) A)
равномерно при $->х0, а->х0 (а <Схо<С$)9 где непрерывная функция Цх)
определяется равенством
{п + 1)! 22п+1 X (х) = | /("-bD (ж) |. B)
Для этого докажем сначала лемму:
Лемма I. Если функция f (х) имеет в точке х0 производную (п + 1)~го
порядка справа f(n^{x0), то
где р —> ж0 гг/?м р ^> а:0. Аналогичное свойство справедливо для производной
слева /(п+1)(х0). jE'cyja в точке х0 существуют производные до (п + 1)-го
порядка включительно, т. е. /(*) (ж0) = /(^ (ж0) = /(i)(^o) wi°M /^ л ~h 1> mo>
кроме того,
(Л + 1)!22п+1 '
если <х->х0, Р~>^0
Действителыю,
* Докл. АН СССР, 26 A940), стр. 839—842 B08*).
306

где s->0, если х->х0 справа. Поэтому
Аналогичным образом доказывается и вторая часть леммы.
Для доказательства необходимости условия, высказанного в теореме,
следует еще заметить, что в случае непрерывности /(n+D (x) на отрезке
[а, Ь] в равенстве
/ (х) = / (а) + /' (а) (я - а) + ... + ^ (х - а)» + (/(«+«(«) +е) (*„~У
8 стремится равномерно к нулю вместе с [3 — а при а ^ # <<^ [3 и /fa+D (а) —
— y(n+i) (?0) равномерно стремится к нулю вместе с х0 — а.
Доказательство достаточности условия нашей теоремы менее просто,
так как лемма I необратима. Для этого нам понадобятся еще три леммы.
Лемма II. Пусть f (z, X) есть непрерывная функция относительно
х, X при a^x^b, Xo^X^Xi и Рп{х, X) — многочлен степени п отно-
относительно х, наименее уклоняющийся от. f(x, X) на [а, Ь]. Если в крайних
справа точках максимального отклонения ?х0 и ixlf соответствующих Х=Х0
и X = X-l, знаки разностей / (gv Хо) — Pn (gXe, Хо) и f (EXl, Хх) — Pn EXl, Xx)
противоположны, то существует значение X = Х2 между Хо м Хх, для
которого число точек максимального отклонения f (х, Х2) — Рп [х, Х2) про-
противоположного знака не менее, чем п + 3.
В самом деле, пусть Рп^.1(х, X) = ^х^71^ + ••• будет многочленом сте-
степени п + 1, наименее уклоняющимся от / (ж, X). Как известно, коэффи-
коэффициенты его и, в частности Ах, будут непрерывными функциями X. С другой
стороны,
Рп+1 (х, X) — Рп (х, X) = / (х, I) - Рп (х, X) - [/ (х, X) — РпП (х, X)]
получает знак разности / [х, X)—Рп{%, X) во всех точках максимального
отклонения последней, если только многочлены Рп{%, X) и Ai-ы (#, Х).не
тождественны между собой (т. е. А\ = 0). Таким образом, если уравнение
Рп+1 {х> X) — Рп (ж, X) = 0 не удовлетворено тождественно для некоторого
X, то все его корни вещественны и менее ?х, а потому знак /(?х, X) —
— Рп(%х, ^) совпадает с знаком ^1х« Следовательно, AXoAXl ^0, откуда
заключаем, что Ах = 0 для некоторого X = Х2 между Хо и Хх, т. е. при
X = Х2 многочлены Рп+г {х, X) и Рп (ж, X) тождественны.
Лемма III (Д. А. Райкова1). Если при любых <х<^$ на отрезке [а,Ь]
Еп If (х); (о, Р)] < С ф - а)"+1, C)
1 В своей статье B) Д. А. Райков приводит некоторые из результатов моей моно-
монографии «L. S.» B) и отмечает, между прочим, недостаточность данного там доказа-
доказательства следующего вспомогательного предложения: если непрерывная функция
/ (х) имеет п + 1 корней на отрезке [а, Ь], то существует такое 80>0, что при вся-
всяком положительном 8 < 80 уравнение AnS = / (# + гй) —nf(x + п ^18) + ... =0
имеет не менее одного корня. В действительности, дополнительное замечание, необхо-
необходимое для строгости вывода, имеется в моей статье C) 1914 г., где это предложение
было дано впервые (стр. 452). См. также [18] (том I, стр. 234).
$07 20*

zQe Q — постоянная {не зависящая от а, C), то функция f (x) имеет про-
производные до п-го порядка включительно во всех точках [а, Ъ] и сущест-
существует такая постоянная Сг {не зависящая от а, [3), что
I/<">№)-/<">(«) К Ci(P-«)- ¦ D)
Лемма IV. Если соблюдено D) и
Со (Р - «)n+1 < En [f (х); (а, р)] (Со > 0), E)
то расстояние между точками наибольшего отклонения противополож-
противоположного знака многочлена Рп (х) степени п, наименее уклоняющегося от f (я)
на отрезке [а, [3], удовлетворяет неравенству
a), F)
2?7
Для /1 = 0, очевидно, можно положить1 А = -^-; поэтому предполо-
предположим п^>0; тогда вследствие D)
при
где
/»(*) = /(«) + Г («) (« —«) + ••• +
В таком случае
и вследствие теоремы Маркова
откуда
п An + 1 л тт
где С2— , _/i;|- ^i« Поэтому из
|/(яч+1)-Рп(а:4+1)-[/(а:0-Рп(ач)]| = 2Еп[/(а:); (а, р)]
следует, что
С2 (р - а)« | a;i+1 - хг \ > 2?'„ [/ {х); (а, р)] > 2С0 (р - а)»+1,
а потому
|*i+1-*i|>757°(P-«)- (В)
Допустим теперь, что A) имеет место равномерно на всем отрезке [а, Ъ].
Согласно известной теореме Лебега, из леммы III следует, что функция
1 Вообще для п = 0 доказательство высказанной вначале теоремы (которая в этом
случае дает условие, необходимое и достаточное для существования непрерывной
производной) может быть проведено гораздо проще.
308

(x) имеет производную /(n+i) (#) почти всюду на [а, Ь] и по лемме I в
этих точках
(х0) = (п + 1)! 2™+* 8 (х0) X (х0), G)
где 8 (х0) = ±1, причем (в случае Х(жо)*>О) знак /(п+х) (х0) совпадает со
знаком / (х) — Рп (х) в крайней правой точке максимального отклонения
на достаточно малом отрезке [а, [3], включающем х0. Пусть X (х) ^> 0 во всех
точках отрезка [а!, Ъ']. Согласно лемме IV, число точек максимального
отклонения, соответствующих достаточно малым промежуткам (ос, C) внутри
[а', U], равно п + 2 [так как в противном случае мы имели бы
En[f{x)]{oL, $)]=En[f(z); (а, РОЬгдер^р-Лф-а), причем к > Ао > О
ограничено снизу, поскольку минимум X (х) на [а', &'] отличен от нуля и
для C — а указана некоторая общая для всего отрезка верхняя граница].
Поэтому вследствие леммы II знак максимального крайне правого откло-
отклонения для всех этих промежутков (а, C) одинаков, откуда заключаем, что
во всех точках [а',Ь']9 где производная /(n+i) (x0) существует, знак ее,
т. е. о (х0) остается постоянным. Таким образом, на всем отрезке [а, Ь]
fin) (я) = рп) (я0) + J (л + 1)! 22^+18 (я) X (ж) cte, (8)
где 8 (ж) может иметь разрывы лишь при X (х) = 0, а потому подинте-
гральная функция в правой части равенства (8) непрерывна и предста-
представляет производную левой его части во всех точках [а, Ь], т. е. формула G)
или эквивалентная ей формула B) справедлива на всем отрезке [а,Ъ\*
Из доказательства видно, что теорема остается в силе, если рассмат-
рассматривать одни лишь интервалы (ос, [3), где хо = ^-~ у а также и тогда,
когда условие A) равномерно выполняется только для некоторого исчис-
исчислимого множества стремящихся к нулю значений C — а. Что касается
концов [а, Ъ], то само собой понятно, что при дополнительном предполо-
предположении, что а^а<^$-^Ь, в точках Ъ и а следует соответственно иметь
в виду лишь производную слева /(n+1) (&) и производную справа /(п+х) (а).
Поступило
19.1.1940 г.
ЦИТИРОВАННАЯ ЛИТЕРАТУРА
1 Д. А. Райков. Докл. АН СССР, 24, № 7 A939).
2 S. Bernstein. Legons sur les proprietes extremales des fonctions analytiques,
Paris, Gauthier-Villars, 1926. [«L. S.»]
3 S. Bernstein. Math. Ann., 75 A914); [18] (том I).

81
О СХОДИМОСТИ МНОГОЧЛЕНОВ jjf(~)cCxm(l-xf~т
В КОМПЛЕКСНОЙ ОБЛАСТИ*
Предлагаемая работа содержит систематическое исследование областей сходимо-
сходимости многочленов Вп [/ (х)] для аналитических функций / (х)> регулярных в данной
области комплексной плоскости.
Содержание. §1. Основное преобразование многочленов Вп[/ (х)] в комп-
комплексной области (стр. 310). § 2. Узловая линия и петля (стр. 312). § 3. Важнейшие
свойства петли Fx (стр.315). §4. Автономные области (стр. 318). § 5. Узловые окруж-
окружности (стр. 319). § 6. Общие свойства точек сходимости многочленов Вп [f (х)] (стр. 323).
§ 7. Генеральная область сходимости многочленов Вп [/ (#)] в случае одной особой
точки (стр. 329). § 8. Нахождение генеральной области сходимости DR в случае лю-
любой области R регулярности (стр. 331). § 9. Случай, когда границей области регуляр-
регулярности R является прямая, параллельная оси ординат (стр. 333). § 10. Случай, когда
функция / (х) имеет особенности на отрезке 01 (стр. 340). § И. Области сходимости
многочленов An [/ (x)] и асимптотическая форма областей сходимости многочленов
Bn[f (%)] при бесконечном удалении особых точек функции f (х) (стр., 342).
§ 1. Основное преобразование многочленов JBn[f(x)]
в комплексной области
Вопрос о сходимости в комплексной области многочленов
п
Вп[/(*)] = Bn\f{z); х, 1] = 2/(-^Km^(l - хГ~« .A)
впервые был рассмотрен Л. В. Канторовичем в прекрасной работе
«О сходимости последовательности полиномов С. Бернштейна вне основного
промежутка» г. После этого я посвятил тому же вопросу две статьи2.
*Изв. АН СССР, йерия матем., 7 A943), стр. 49—88 B24*).
^зв. АН СССР, ОМЕН A931), стр. 1103 — 1115.
2 «Sur la convergence de certaines suites de polynomes», Journ. de Math., 15 A936),
стр. 345—358 [65], «Sur le domaine de convergence des polynomes Bn [/ (x)] =
n .
= 2jf [— J C™xm A — ar)n~m», Comptes Rendus, 202 A936), стр. 1356—1358 [64].
о
310

Настоящая статья имеет целью развить идею, лежащую в основе статьи
из «Comptes rendus», и дать полное доказательство указанных в ней
теорем.
Исходной формулой является преобразование A) к виду
B)
п\ Cf (z){x — l)xdz
п [f (#)] = 2tti J z (nz — 1) . . . (nz — п) ,
С
в которой С — любой контур, ограничивающий область, где f(z), по
предположению, регулярна, включающую отрезок 01. При этом х пред-
предполагается отличным от 0 и 1.
Действительно, подинтегральная функция имеет полюсами точки
z = — (т = 0,1, . . , я) с вычетами
хтA - *)n
— 1) . . . (— 1)( — 2) . . . (т — п)
т\ (п - т)\
Покажем, что
(t)J
В самом деле,
= J log (z — t)dt + en,
где w2sn остается конечным, если z находится вне отрезка 01. Но
1 1
поэтому
= п [- 1 + A -z) log (z - 1) + zlogz + en],
т. е.
311

где щп остается конечным при тг-»оо. Следовательно, принимая во
внимание формулу Стирлинга, получаем из B)
где пр^ остается конечным, откуда вытекает C).
§ 2. Узловая линия и петля
Из C) или C bis) видно, что сходимость Вп [/ (х)] в точке х сущест-
существенным образом зависит от расположения линии
= 1, D)
которую назовем узловой линией точки (узла) х.
Полагая z = а + ib, х = а + ф и рассматривая функцию
F (z, ж) = A — z) log j?j + z log у = P* (а, 6) + f^ (а, Ъ) E)
в плоскости переменной z с купюрой по отрезку 01, где F(z,x) является
однозначной функцией, замечаем, что узловая линия определяется урав-
уравнением Рх (а, Ь) = 0 и имеет одну двойную точку (узел) а = а9 Ъ = р.
В самом деле,
J^ B #) = 0, ¦— z== — loo* • -4- I02 — :=r 0 F)
только при 2 — х, все же прочие линии уровня Рх (а, Ь) = С особых то-
точек не имеют (если не считать точек отрезка 01, которые являются точ-
точками излома). Кроме того,
1 1 dk+1F , A<ktl л
(z-l)k
поэтому вблизи точки х
)
причем радиус сходимости равен наименьшему из чисел | х \ и | х — 11
[однако в случае 0 <а<1 равенство G) неприменимо при C 6<О].
В дальнейшем, не нарушая общности выводов, будем считать C^0.
Из G) и E) находим уравнение пучка ортогональных касательных
к узловой линии в узле (а, [3):
(а2 _ а _ р2)(а _ вJ + 2р Bа - 1)(а _ а) F - р) -
— (а2 — а — Р2)F— ?J = 0. (8)
312

Лемма 1. Узловая линия состоит из петли {замкнутого контура) Fx
и ее продолжения в виде двух ветвей, исходящих под прямым углом из
узла х и удаляющихся в бесконечность; петля Fx включает в себя весь
отрезок 01, если \ х\^> 1, \х — 1J ^> 1, или часть отрезка 01, если хотя
бы одно из этих двух неравенств нарушено {если, при 0<а<1, Р~»0>
то петля Fx превращается в тючку х).
В самом деле, ординаты Ъ точек пересечения уздовой линии
^T-arg^I] = 0 (9)
с прямой а = h, параллельной оси ординат, удовлетворяют уравнению
Px{h,b) = 0. Но уравнение
дРх
—
z
=arg —T-
левая часть которого непрерывна в случае
h — у
(Ю)
^ 1
J>-o-, а в случае
1 i
h—— <С-к- имеет разрыв, равный —2ти, при 6=0 имеет не более
двух корней в первом случае и не более одного корня во втором слу-
случае, так как ему удовлетворяют только точки верхней части окружности,
проходящей через точки 0,1, х. Поэтому уравнение Рх{к.,Ь)~О не
может иметь более трех корней. В частности, если узловая линия со-
содержит замкнутый контур (петлю) Fx, то число точек пересечения Fx с
прямой, параллельной оси ординат, должно быть не более двух. С дру-
другой стороны, функция
достигает максимума при
в-1
а
log
X —
а —
X —
X
-1
-1
1
+ я
log
X
а
A1)
A2)
в той из двух гармонических точек al9 a2, определяемых уравнением A2),
которая лежит внутри отрезка 01, так как
и
дРх (а, Ъ)
да
х(а, Ъ) _
=illos!
а —1
а2 + б2
A3)
да2
(а__1J + Ь2 сР + Ъ* [(а — 1J + 62] [а2+ 6
da<l. Положим, для определенности,
, Л
отрицательна при 0<С#
т. е а ^>-^-. Тогда максимум М = Px(alt0) функции Рх(а,0) достигает-
ся в точке ах ^- -^ отрезка 01, и так как ах — '
1*1
2
М =
то
313

Кроме того, в точке (#1,0) достигается также максимум Рх(а,Ь), рас-
рассматриваемый как функция двух переменных (а,Ь), так как во всех точ-
точках 01
Поэтому линия уровня вблизи (ах, 0)
Рх(а,Ь) = С
для С<^М, достаточно близких к М, представляет замкнутый контур,
и вследствие сказанного выше это будет иметь место, когда С^>0. Рас-
Расщепление линии уровня произойдет лишь при С = 0, соответствующем
дРх дРх Л ~
узловой линии с узлом в точке х, где -=— = —zr- = 0. Следовательно, в
узле х петля Fx замкнется под прямым углом и продолжение ее пойдет
по двум ветвям, удаляющимся в бесконечность.
дР
Согласно A3), уравнение —^ = 0 представляет окружность, поэтому
уравнение Рх(а,Ъ) = 0 при данном Ъ также имеет не более трех корней,
вследствие чего прямая, параллельная оси абсцисс, пересекает петлю Fx
не более, чем в двух точках; в частности, при 6 = 0 уравнение (9)
имеет два корня, из которых один меньше а1} а другой заключен меж-
между аг и а2. Для определения положения этих двух корней, являющих-
являющихся точками пересечения петли Fx с осью абсцисс, рассмотрим три случая:
1) 1<|я—1|<|я|; 2) [ж—1|<1<|ж|; 3) js —1|<|
В первом случае
поэтому петля Fx включает весь отрезок 01. Во втором случае
Рх@,0) = log\х — 11 <;0; РхA,0) = log] х| >0,
и петля Fx включает часть отрезка 01 с концом 1, но без точки 0.
В третьем случае
рх @,0) =log\x~- l|<0; Px(l,0) = log\z\<0,
и петля Fx включает часть отрезка 01, не содержащую ни одног,о из
его концов1.
Кроме того, за исключением случая |#| = |а;—1| т. е. при ос =-^- ,
когда а2 = оо, узловая линия имеет еще одну точку я^>а2 на оси
абсцисс, так как
Рх (а,0) = a log ^j — log | a - 11 + a log 1 — - +
+ log | a: — 11 A1 bis)
становится положительным при а->+оо.
1 Если1 | х | = 1, то Fx проходит через точку 1; если \х — 1 | = 1, то Fx проходит
через 0.
314

§ 3. Важнейшие свойства петли Fx
Лемма 2. Прямые, не пересекающие отрезка 01, а также все прямые,
образующие угол не более 45° с осью абсцисс, имеют не более двух то-
точек на петле Fx (при любом узле х).
Пусть
b = т (а — а0)
— уравнение рассматриваемой прямой. Положим сначала, что она не пе-
пересекает отрезка 01, т. е. ао(ао — 1)>0. Абсцисса а точки ее пересечения
€ узловой линией удовлетворяет уравнению
Рх (а, т{а— а0)) = 0.
Для исследования числа корней этого уравнения берем первую и вторую
производные
> Л Г / Л \9 i 9 / \9 / Л \9 i
х 1 1 {а — \Y + т* (а — аог , (а — 1L-
r=2Ll0g а»+ «•(«-в.)» 10^ а? + р»
da
- 2а0) а + m2 (а — 2а0)
A7)
с?а2 (а — IJ + т2 (а — а0J а + ^2 (я — «оJ |
_ (т2 +'1Jа2— (//г2 + 1) [2бг0т2 4-1] а + т2а0 [а0 (т2 — 1) -f 2]
[(а —1J4-т2 (а—а0J] [а2 4-т2 (а—а0J] ' '
d2Px dP
Замечая, что -=-?- имеет не более двух корней, заключаем, что —-? имеет
аа da
dPx
ле более трех корней. Но при а = + оо значения —i— равны между со-
собой, поэтому число корней —^ четное, т. е. не более двух, а следова-
следовательно, число корней уравнения A6) не более трех, и петля Fx имеет не
•более двух точек пересечения с прямой A5).
В случае а0 (а0 — 1) <; 0, к которому мы теперь переходим, предыдущее
dPx
рассуждение неприменимо, так как —тг- имеет скачок, равный — 2жъ
dP ! dPx
в точке а0 отрезка 01. Заметим, что -тг-= -з—, если вместо перемен-
dP
ной а будем рассматривать Ъ — m (а — а0), так что скачок -~- при пере-
переходе в верхнюю полуплоскость отрицателен (равен — 2тт); поэтому, если
Рх достигает при этом экстремума, то это может быть только максимум.
d2Px
Таким образом, обозначая через а', а" оба корня -j-^ и учитывая, что
d2Px
знак -1-2- вне промежутка (а , а") тот же, что при а = Ц- оо, т. е. поло-
положителен, видим, что Рх не может иметь минимума между аг и а". Сле-
Следовательно, при т2 <; 1 @ << а << 1), когда
W
\ da2 Ja=a0 а0 (а0 — .
315

Рх не может иметь двух максимумов, а поэтому прямая A5) пересекает
петлю Fx не более, чем в двух точках.
Следствие 1. Если петля Fx включает отрезок [0,1], т. е. |з;|;>1,
х — 1| ^> 1, то она выпукла.
В самом деле, если, непрерывно передвигая точку на петле Fx вместе
с ее касательной, начиная от точки (а0, 0) на оси абсцисс (вне отрезка
01), мы дошли бы до точки перегиба ранее, чем до узла ху то касательная
к Fx в точке перегиба также пересекла бы ось абсцисс вне отрезка 01.
Но это противоречит лемме 2.
Замечание. Если петля Fx не включает всего отрезка 01, то она
может и не быть выпуклой. Вообще угловой коэффициент т касатель-
касательной к узловой линии определяется равенством
д1*.
т = - -—- , A8)
зь
и для того, чтобы петля Fx была выпуклой, необходимо и достаточно,
чтобы
д2Р\ дРх (д*Рх д*Р\ дРх
i т ± _ _ 4- т
"*" дадЪ) дЬ ХдасЪ^
dm \ да2 да до/ дЬ \да со бЬ1 ) da
da fdPx*
A9)
дЬ
было отрицательно в верхней части Fx и положительно в нижней ее час-
части. Полагая, попрежнему, для определенности, Р>0, а^-у, заключаем,,
как и выше, что при а0 ^> 1 правая часть петли FX) прилегающая к ее
точке пересечения а0 с осью абсцисс, заключенная между узлом х и ниж-
нижней точкой петли FX) во всяком» случае выпукла. Я утверждаю, что
если петля Fx пересекает отрезок 01 в точке а0 @<^а0<^1), то для на-
нарушения выпуклости необходимо и достаточно, чтобы по крайней мере
в одной из точек пересечения Fx с отрезком 01 угловой коэффициент ка-
касательной т0 к верхней дуге Fx удовлетворял неравенству
т2>1. B0)
Действительно, по формуле A9) в точке (а0, 0)
fdm\ i~ml т1-1
m=m0 -^ A - Ч) «о ( « + arg ^—- Д1 - о0) а0
B1)
Поэтому при условии B0) \-т-\ ^>0, и выпуклость в верхней полу-
\аа Ja=a,
316

плоскости (или в точке х0) нарушается. Напротив, в случае ml <^ 1 уг-
угловой коэффициент тг касательной в точке а0 к Fx в нижней полупло-
полуплоскости a fortiori1 удовлетворяет неравенству ml < 1, поэтому как верх-
верхняя, так и нижняя дуга Fx выпукла вблизи а0, и так как касательная
к Fx при следовании по этим дугам до узла х или до нижней точки Fx
все время образует с осью абсцисс угол меньше 45°, то выпуклость,
согласно лемме 2, не может нарушиться.
Отсюда следует, в частности, что в случае | ж К 1, | # -— 11 <С 1 (когда
Fx должна пересекать отрезок 01 в двух точках) петля Fx не может
быть выпуклой. Действительно, по крайней мере одна из касательных
в узле х имеет угловой коэффициент не менее единицы по абсолютному
значению. Поэтому, если бы соответствующая ей дуга была выпукла,
то при пересечении • с отрезком 01 она образовывала бы угол больше 45°,
т. е. неравенство B0) было бы соблюдено.
В случае \х — 1 К 1, | ж |> 1 петли Fx (имея только одну точку на
01) могут быть выпуклыми или невыпуклыми: в зависимости от нару-
нарушения или соблюдения неравенства B0) в единственной точке а0 пересе-
пересечения Fx с отрезком 01. Рассмотрим, например, петлю Fx> соответствую,
щую узлу (а, 0), где 1<а<2(# —1<1, |#|>1). Для определения а0
имеем уравнение
A - а0) log ?=± + а0 log -?- = 0. B2)
Угловой коэффициент т0 в точке а0 определяется равенством
1 Г, 1 — а0 ¦. ос —11 1 , 1 — а0 /л г т- \
тп = — 1о? — loff = — log г*. A5- bis)
Таким образом, петля Fx будет выпуклой при а, близком к 1, и будет
оставаться выпуклой пока
1-ао
а-1
где а0 удовлетворяет B2), т. е. пока
- аох A - а0) + а0 log
<***-
Иначе говоря, Fx остается выпуклой, если точка а0 пересечения петли
Fx с отрезком 01 (где а0 растет от 0 до 1, когда а убывает от 2 до 1)
удовлетворяет неравенству
т. е. при Л^ао^1, где А <[ 1 — корень уравнения ^— = еп + 1.
1 Значения т0 и т1 из A8) отличаются лишь знаменателем, который в нижней
f х \
полуплоскости по абсолютному значению (те —arg j-\ больше, чем в верхней
V х *¦ 1
317

§ 4. Автономные области
Лемма 3. Если точка х1 есть некоторая точка выпуклости на пет-
петле Fx (т. е. касательная в точке хг не пересекает Fx), то петля FXl
с узлом хг находится целиком внутри Fx.
В самом деле, если Рх (а, Ъ) = 0, РХг (а, Ъ) = 0 — уравнения двух:
узловых линий соответственно с узлами х и хъ то
PXl (а, Ъ) = Рх (а, Ъ) + Аа + ВЪ + С,
где
IО О* I 1 1ОП* —¦ ПТ»п> cwtr* Ш I r\ гч» 1 *-
1ж 1 х—{
Поэтому все точки пересечения данных узловых линий лежат на одной
и той же прямой
Аа + ВЪ + С = 0. B3)
В частности, если узел х1 петли FXl находится на петле Fx, то каса-
касательная к Fx в точке хг имеет в хг двойную точку пересечения как с FXt
так и с FXl. Поэтому B3) есть уравнение рассматриваемой касательной. Сле-
Следовательно, в случае выпуклости Fx в точке хъ т. е. при отсутствии
других точек пересечения Fx с прямой B3), Fx также не имеет других
общих точек с FXl.
Определение. Будем называть область^, включающую отрезок 01^
автономной, если петля любой точки контура С, ограничивающего эту
область, находится целиком внутри1 С (напомним, что петля точки х на
отрезке 01 приводится к единственной точке х).
Из определения непосредственно следует, что две автономные области S
и Sx всегда имеют общую часть, и сумма двух автономных областей S и
S1 также представляет автономную область.
В дальнейшем (следствие 10) будет показано фундаментальное значе-
значение автономных областей в теории сходимости многочленов Bn[f (#)]„
Поэтому мы укажем здесь важнейшие примеры автономных областей.
Следствие 2. Область S, ограниченная выпуклой петлей Fx {допол-
{дополненная в случае надобности частью отрезка 01, не попавшего внутрь Fx)t
автономна.
Следствие 3. Если дано множество Е точек х, для которых
\х\^>1, \х — 11 ^ 1, то наименьшей автономной областью S, включаю-
включающей все точки множества Еу является сумма областей, ограниченных
петлями Fx всех точек х множества Е.
Для выявления некоторых других полезных примеров автономных
областей необходимо обратить внимание еще на несколько простых свойств
петель Fx.
1 Из дальнейшего (§ 6—7) будет следовать, что петли точек, лежащих внутри
автономной области S, также находятся целиком внутри i9.
318

§ 5. Узловые окружности
Определение. Назовем первой узловой окружностью петли Fx
(или узла х) окружность Сх с центром на оси абсцисс, имеющую урав-
уравнение
B4)
на [которой находятся точки Fx с горизонтальной касательной. Назовем
второй узловой окружностью Сх петли Fx (или узла х) дугу ортогональ-
ортогональной к Сх окружности, заданную уравнением
Z 1 X — 1 /псгч
arg —— = arg—— , B5)
где находятся точки Fx с вертикальной касательной.
Легко проверить, что радиус R и абсцисса а центра окружности Сх
при любом х связаны соотношением R2 = а {а — 1). Поэтому геометриче-
геометрическим местом концов А и Аг вертикальных диаметров окружностей Сх
является равнобочная гипербола Г, имеющая уравнение
Ь2-а2 + а = 0. B6)
Вследствие (8) Г является также геометрическим местом узлов х, обла-
обладающих свойством, что пара касательных в них к петле Fx параллельна
осям координат. В силу ортогональности семейств окружностей Сх и Сх,
гипербола Г является также геометрическим местом концов В и В± гори-
горизонтальных диаметров окружностей Сх.
В общем случае, когда точка х не совпадает с А (мы считаем попреж-
нему а^--^, р^-0), для построения касательных к петле Fx в узле х
можно предложить следующее построение.
Обе касательные в точке х совпадают с прямыми хА и хАъ соединяю-
соединяющими х с концами вертикального диаметра Сх. При этом правая дуга
петли Fx направлена по хорде хА1 первой узловой окружности С'х, а левая
дуга, касаясь хорды хА, направляется вдоль нее, т. е. вверх, когда х
находится правее диаметра ААЪ и направляется по продолжению хорды х,
т. е. вниз, когда х находится на левой половине окружности Сх. Ввиду
ортогональности обеих узловых окружностей, эти касательные могут быть
также получены соединением точки х с концами В и В± горизонтального
диаметра второй узловой окружности Сх. В самом деле, если
/ (а, Ь) = (Ъ — та) (а + тЬ) = mb2 + A — т2) аЪ — та2 = 0
есть уравнение пары ортогональных прямых, то
/а = A — т2) Ъ — 2та = 0, /ъ = 2mb + A — т2) а = 0
представляют дару ортогональных прямых, образующих соответственно
вдвое большие углы с осями координат. Поэтому из уравнения пары
319

касательных в узле х
следует, что эти прямые образуют с осями координат вдвое меньшие
углы, чем прямые
являющиеся касательной и нормалью к окружности —^— = 0, т. е. B4).
Кроме того, для нахождения автономных областей с двумя осями сим-
симметрии, полезна следующая
Лемма 4. Если произвести зеркальное отображение правой верхней
/ /[ 1 \
четверти петли Fx C^0, а^--^, 6^-0, а^>— относительно оси
абсцисс и прямой а = -у, то Fx будет находиться внутри полученного
таким образом симметричного контура.
В самом деле,
Рх (а, ~Ь)=РХ (а, b) + 2b arg -^ < Рх (а, 6) B7)
дри 6>>0, Р>0. С другой стороны,
Рх A _ а, Ъ) = Рх (а, 6) - {2а - 1) log
— 1
<Рх(а,Ь). B7 bis)
Следствие 4. 1) ?с^а 2/зе.я # (Р^>0, а^- —) находится внутри ветви
\ ^ J
гиперболы Г (а2 — а — Р2>0), гао петля Fx находится внутри шести-
шестиугольника, симметричного относительно прямой а — -х- с горизонтальны-
горизонтальными сторонами, проходящими через А и Аь и боковыми сторонами хА и
хАг (координаты точек А и Ах равны -Л тт и Ч-i и, гдек= );
1 — /с ' 1 — п X \ J
2) если узел х находится между ветвями гиперболы Г (а2 — а — (З2 ^ 0),
но вне окружности а2 — а + (З2 = 0, имеющей диаметром отрезок 01,
то петля Fx находится внутри симметричного относительно оси
абсцисс шестиугольника, образованного хордами второй узловой окруж-
окружности, соединяющими х с концами ее горизонтального диаметра, и вер-
вертикальными касательными к ней; 3) если же узел находится внутри
окружности а2 — а + р2 = 0, то петля Fx находится внутри симметрич-
симметричного относительно оси абсцисс четырехугольника, имеющего сторонами
Ох и xl.
В самом деле, в первом случае, т. е. при а2 — а + C2;>0, замечаем,
что петля Fx находится внутри прямого угла АхА1 и между горизонталь-
горизонтальными прямыми, проходящими через А и Аь так как нижняя и верхняя
точки петли Fx лежат на первой узловой окружности Сх, и внутри нее
петля Fx выпукла.* Во втором случае, т. е. при а2 — а — (З2 < 0, а2 — а +
320

+ (З2 ^ 0, замечаем, что крайние правые и левые точки петли Fx нахо-
находятся на второй узловой окружности или внутри отрезка 01. В третьем
случае, т. е. при а2 — а + (З2 <^ 0, крайние правые и левые точки петли Fx
находятся на отрезке- 01, а прямые, выходящие из узла х и пересекаю-
пересекающие ось абсцисс вне отрезка 01, не могут иметь других точек на петле Fx
(лемма 2).
Лемма 5. Пусть A^^qA^ будет прямоугольник с вершинами на ги-
гиперболе Г; пусть CAl — САг будет первой узловой окружностью точек
Аг и А2 (АгА2 — вертикальный диаметр CAl), и пусть CAi = CAi будет
первой узловой окружностью точек А3 и Л4; пусть CAl = С"А^ будет вто-
второй узловой окружностью точек Аг и Л4, и САг = C"Ai — симметричная
ей вторая узловая окружность точек А2 и А3. Если область S ограни-
ограничена четырьмя выпуклыми дугами A^H12A2, A2H23A3y A3H3iA^ AJi^A^
иаходягцимися соответственно внутри внешних полукругов CAl, САг, С'Аг,
С"ао причем дуга АгН3±А± симметрична дуге А1Н12А2 относительно пря-
мой а = -^, а дуга A^H4l1A1 симметрична А2Н23А3 относительно оси
абсцисс, то область S автономна.
В самом доле, если точка х находится на дуге AtH12A2, т. е. внутри
внешнего полукруга CAl с диаметром АгА2, то радиус ее первой узловой
окружности Сх меньше -у АгА2, поэтому прямой угол между обеими ка-
касательными к петле Fx в узле х находится внутри угла АгхА2 и, сле-
следовательно, петля Fx проходит левее дуги A1Hi2A2 и правее симметрич-
симметричной ей дуги А3НМА^, оставаясь в то же время между горизонталями
А2А3 и АгА^. Если же х находится на верхней дуге -4^41^1, т- е- между
ветвями гиперболы Г, то прямой угол между касательными к петле Fx
в узле х, опирающийся на концы горизонтального диаметра второй узло-
узловой окружности Сх, находящейся внутри C?Al, лежит внутри угла А±хАъ
а потому и петля Fx проходит внутри угла А^хА1 и между вертикалями
АгА2 и А3А±.
Рассмотрим некоторые примеры автономных областей, получаемых
посредством применения леммы 5.
Следствие 5. Область S, ограниченная эллипсом
1\2
автономна, если р ;> --, р ^>q^>> р I/ -г&~г—т» а также если
Z ? xZp ~\~ 1
у тч~1—т • В частности, первый случай имеет место для
эллипсов Чебышева с фокусами 0 и 1 (q2 = p2
ч
В самом деле, в первом случае, когда р^> q — большая полуось
эллипса B8), дуга, лежащая выше стороны АХА± прямоугольника
А±А2А3А4, образованного точками пересечения эллипса B8) с гиперболой
B6), всегда удовлетворяет условию леммы 5. Для того чтобы боковые
21 С. Н. Бернштеин 321

дуги эллипса B8) также находились внутри боковых полуокружностев
с вертикальными диаметрами АгА2 и А3А^} необходимо и достаточно^
чтобы координаты хъ уг точки Аг удовлетворяли неравенству
B9)
я
которое после определения ух = —. —, х± —~ = — ^ из урав-
уравнений B8) и B6) принимает вид
> р. B9 bis)
Возведя B9 bis) в квадрат, находим эквивалентное наравенство
V 1
р2 — -т- и вторичного возведения в квадрат, по-
получаем неравенство
\ (р* + <?2J > Р2 [(Р* - <72J - 4д4] = р2 (р2 + д°) (р2 - З?2),
которое равноценно
Аналогичным образом в случае q^>p замечаем, что для применимости
леммы 5 необходимо и достаточно, чтобы удовлетворялось неравенство
которое, подобно предыдущему, приводим сначала к неравенству
- {) (<72 + ~)> (V + \
а затем к неравенству
Любопытно отметить, что в обоих случаях неравенства, связывающие
большую и малую полуоси эллипса асимптотически (при бесконечном
возрастании эллипса), равноценны и сводятся к тому, что отношение
между ними не должно превышать )/3.
Следствие 6. Всякая симметричная относительно оси абсцисс об-
область S, ограниченная выпуклым контуром, лежащим внутри круга
с диаметром 01, автономна.
Практически интересным примером такой области S может служить
область, ограниченная двумя дугами окружности с центром в некоторой
322

точке а отрезка 01 радиуса р (р<^а, р<С1 — °) и касательными к ней,
проведенными из точек 0 и 1.
Укажем еще один пример области S, не симметричной относительно
оси а = y • Это — выпуклые области Гд0, играющие большую роль в
теории нормальных рядов, которые ограничены внешней частью окруж-
окружности С радиуса R <^ 1 с центром в точке 1 и касательными к этой
окружности, проведенными из точки 0.
Следствие 7. Область Г#о автономна.
В самом деле, если х лежит на касательной к окружности С, то
петля Fx находится внутри Г до в силу следствия 6. Если же х нахо-
находится на окружности С, то слева от х петля Fx проходит ниже прямой Ох,
а с правой стороны от х петля Fx вовсе не проходит, если а2 — а — (З2 ^ 0;
в случае же а2 — а — ^2 <С 0, справа от х петля Fx не достигает (следствие 4)
ни вертикальной касательной ко второй узловой окружности Сх, ни
верхней полуокружности Сх, т. е. остается внутри С. Таким образом,
лежащая в верхней полуплоскости часть петли Fx всегда находится
внутри Г#о> а потому (лемма 4) нижняя часть Fx также находится
внутри Гд0.
Аналогично можно проверить, что если имеем две окружности ради-
радиусов R и Rx соответственно с центрами в точках 0 и 1 (R + R1^i)9
то выпуклая область, образованная ими и их общими касательными,
автономнах.
§ 6. Общие свойства точек сходимости многочленов J5™ [/(ас)]
Перейдем теперь к исследованию связи между областями сходимости
многочленов Bn[f (х)] и расположением особенностей функции f(x).
Теорема А. Если функция f (z) регулярна внутри некоторой области,
включающей петлю Fx и отрезок 01, то точка х находится внутри
области сходимости многочленов Bn[f (z); x, 1] = Bn[f (x)]. Напротив,
если f (z) имеет один или несколько полюсов внутри или на петле Fx
{будучи регулярной в остальных точках), то точка х не может быть
точкой сходимости.
В самом деле, положим, что функция / (z) регулярна внутри круга
радиуса р с центром х. Возьмем в качестве контура интегрирования
в формуле B) петлю Fx, дополненную в случае надобности бесконечно
узкими контурами, замыкающими выходящие из нее части отрезка 01;
в таком случае, вследствие D) на петле Fx условие применимости пре-
предельной формулы C) соблюдено. Петлю Fx можем затем заменить малым
отрезком D с серединой в точке х, целиком лежащим в области, где
Рх{а,Ь)<^0, который дополним контуром Сг, окружающим петлю FX,
где Рх (а, Ь) — Х<0, причем постоянную |Х| возьмем настолько малой,
1 Отметим также, что всякий круг с центром на отрезке 01, включающий этот
отрезок, является автономной областью. Доказательство этого дано в моей упомяну-
упомянутой выше статье из Journ. de Math. [65].
323 21*

чтобы контур Сх не выходил из области регулярности: функции f (z).
Для этого положим z = х + tYx A-х); тогда по формуле G)
а потому при —
грал C) примет вид
е, где е достаточно мало,
, и инте-
инте2O
C0)
где Л ограничено, а [ enF(z> x) | = enX на контуре Сх убывает в геометриче-
геометрической прогрессии с возрастанием п. Таким образом, второй из интегралов
в правой части C0) стремится к нулю с возрастанием п, между тем как
первый интеграл после замены t Yn = и преобразуется в
z]Fn
—гУп
и2/ Аи \
du-\~
Поэтому, фиксировав s достаточно малым для того, чтобы | As \ <^ у- и
чтобы на отрезке D иметь
х(\ —х)
f(x)
<fa, где a>0 задан-
пая произвольно малая величина, можем после этого взять п0 достаточна
большим, чтобы при всех п^>> п0 осуществлялось неравенство
/и
п/ du
е/п
<2a.
Но, так как при | Аг \ <^ —
lim r \ е
п-+оо V 2п \ J
L-eVrn
nl du-
со иг
du <^Az,
то, учитывая, что е произвольно Мало, заключаем, что
lim Вп [/ (х)] = lim /
324

Для доказательства второй части высказанной теоремы предположим
сначала, что функция / (z) имеет один простой полюс с внутри петли Fx
или на петле Fx (с отлично от ж), и пусть R^O будет его вычет.
В таком случае формула B) заменится формулой
Р. \ит\Л I Д "Ч*-1
Принимая во внимание, что правая часть равенства C1), согласно пре-
предыдущему, имеет пределом f(z), видим, что
Г п\ („ л\п{1—с) пс "|
lim Вп U (х)] + R -.'к ']—j-^ г = / (х), C2)
и так как точка с находится внутри петли Fx или на ней, вследствие
чего
заключаем, что
г>\ (г Л\ПA — Х) ПС
бесконечно растет вместе с /г, а потому бесконечно растет и Bn[f(x)]9
а именно:
) Ь) = -7^4• C3)
Аналогичный результат получим, если полюс с — любой кратности I,
причем Ri — коэффициент при г—: в разложении Лорана функции
(z — c)l+1
f (z) {i — 0, 1, ..., I—1). Тогда формула C2) заменится формулой
lim [вп [/ (х)] + л! V, Ji ~\ (*-уA~'}-*п* 1 1 = / (ж). C2 bis)
v г=0 J
Но учитывая, что порядок возрастания последовательных членов суммы
увеличивается с увеличением г, заключаем, что Вп [/ (х)] асимптотически
равен и противоположен по знаку главному члену суммы, соответствую-
соответствующему i = I— 1, т. е.
я г/Лги [
п U К П (I - 1)! 0*1-1 U (л* - 1) . . . (л* - "
Иначе говоря, принимая во внимание асимптотическое значение произ-
производных, находим
Y
C3 bis)
Отсюда видим, что |.Вп [/(#)][ бесконечно растет при п->оо.
325

В случае нескольких полюсов в предельном равенстве, соответствую-
соответствующем C3 bis), будет только один член, порядок возрастания которого
выше всех прочих, если среди полюсов, для которых вещественная часть
F (с, х) достигает наибольшего значения, не будет двух полюсов одина-
одинаковой кратности; тогда Вп [/ (х)] попрежнему будет бесконечно расти при
любых достаточно больших п. В противном случае, сохраняя только
полюса с1у с2, . . . , cjc наивысшей кратности /г, для которых jeF(ci>*)| =
. . . = | eF(Cfc> х) | = М ;> 1 максимальны, представим сумму асимптотиче-
асимптотических значений соответствующих им членов в виде
2 тигП ХЧ р mzs тт
s=i
где Ps равен, с точностью до отличного от нуля множителя (зависящего
от х и cs, но не зависящего от п), старшему коэффициенту разложения
Лорана близ полюса cs, между тем как izs есть мнимая часть F (cs, x).
Принимая во внимание, что все к значений elZs различны, видим, что
л-!
порядок возрастания Нп будет тот же, что п 2 Мп, по крайней мере для
одного из к последовательных значений п0, п0 + 1, . . . , п0 + к — 1 при
любом п0. В самом /деле, допустим, что существует бесконечное множе-
множество значений, для которых это утверждение ложно. Тогда к неизвестных
хПо> s = Psein°Zs удовлетворяют системе к уравнений
к нп +<
2 e%t4xn0, S = j^T = ^0, t (t = 0, 1, . . . , к - 1),
главный определитель которой (не зависящий от /г0) есть определитель
Вандермонда. При этом, так как правые части уравнений sno+f могут
стать произвольно малы, хПо> s должны были бы быть сколь угодно ма-
малыми, что невозможно, потому что j хПо> s | ¦= | Ps \ имеют определенные,
отличные от нуля значения. Следовательно, по крайней мере для одного
из последовательных значений п многочлены Вп [/ (х)] бесконечно возра-
возрастают.
Замечание. Вторая часть теоремы А, которая для мероморфной
функции дает асимптотическое значение многочленов Вп [/ (х)] в любой
точке плоскости, без сомнения, могла бы быть распространена и на
другие виды особенностей, и было бы интересно знать, верна ли она
при любых особенностях. Во всяком случае, весьма правдоподобно, что
если для некоторых функций / (z) существуют точки сходимости х0
многочленов Bn[f(x)], не удовлетворяющие условию первой части теоре-
теоремы А или не являющиеся по крайней мере предельными для точек,
удовлетворяющих этому условию, то такие точки сходимости х0 должны
были бы быть изолированными. Не останавливаясь здесь на исследова-
исследовании этого вопроса, назовем генеральной областью сходимости Dr функ-
функций / (z), регулярных внутри области Д, включающей отрезок 01, наиболь-
наибольшую область D (являющуюся частью R), в которой сходятся многочлены
326

Bn[f(x)] всех функций f(z), регулярных в области В. Таким образом,
из теоремы А вытекает
Следствие 8. Условием, необходимым и достаточным [предполагая,
что функция f (z) регулярна на отрезке 01] для того, чтобы точка х
принадлежала границе Dr' генеральной области Dr сходимости мно-
многочленов Вп [/ (х)] функции f(z)t является регулярность f (z) внутри
петли Fx и присутствие на Fx хотя бы одной особой точки, т. е.
точки, принадлежащей границе R области регулярности R.
Это следствие, которое в некотором роде аналогично теореме Коши
о круге сходимости, вместе с тем существенно отличается от последней
тем, что семейство концентрических окружностей в случае строки Тей-
Тейлора зависит только от одного параметра, тогда как совокупность петель Fx
зависит от двух параметров. Вследствие этого совокупность контуров Dr',
которые могут быть границами генеральной области сходимости, зависят
от бесконечного множества параметров (т. е. от произвольной функции).
Принимая во внимание результаты § 5, получаем
Следствие 9. Если \х\^1, \х — lj^l и точка х принадлежит гене-
ральной области сходимости Dr, то и вся область, ограниченная петлей Fx,
принадлежит Dr.
Следствие 10. Если некоторая автономная область S является частью
области регулярности R функции f{z), то она является также частью
генеральной области сходимости DR; в частности, если R = $, то
Таким образом, область сходимости многочленов Вп [/ (х)] совпадает
с областью регулярности функции f (z) тогда и только тогда, когда
последняя является автономной. Кроме того, согласно следствию 3, если
во всех точках границы генеральной области сходимости Dr \x\^>1,
\х — 11 ;> 1, то область Dr автономна.
Все результаты § 4—5 преобразуются благодаря теореме А и ее след-
следствиям в соответствующие теоремы об областях сходимости многочленов
Bn[f(x)]. Например, первая часть следствия 5 приводит к предложению:
Если функция f (x) регулярна внутри эллипса
то многочлены Bn[f(x)] сходятся внутри этого эллипса1.
Известная теорема Канторовича соответствует частному случаю эллипса
Чебышева, когда р2 = q2 -f -r •
Следует заметить, что весьма простое рассуждение, посредством кото-
которого Канторович получил свою теорему, применимо к весьма широкому
классу многочленов Рп [/ (х)], являющихся значениями линейных операто-
операторов, аппроксимирующими функцию / (х) на данном отрезке и обладающими
1 При этом, если / (z) регулярна также на некоторой дуге С этого эллипса, то
все точки дуги С лежат внутри генеральной области сходимости.
327

лишь следующими двумя элементарными свойствами многочленов Bn[f (x)]:
1) если / (х) — многочлен степени h, то Рп [/ (х)] — также многочлен
степени <; /г; 2) если \ f (х)) <; L на отрезке 01, то | Рп [/ (х)] (<JcL на
этом отрезке, где с — не зависящая от / (х) и от п постоянная.
Обобщенная теорема Канторовича. Если линейные операторы
Рп [/ (х)], удовлетворяющие двум указанным выше условиям1, равно-
равномерно сходятся к f (x) на отрезке 01, причем f (x) регулярна внутри
некоторого эллипса Е Чебышева {имеющего фокусами точки 0 и 1), то
Pn[f(x)] сходятся к f(x) внутри эллипса Е.
Следуя Канторовичу, разлагаем / (х) по многочленам Чебышева Тп{х)
для отрезка 01
Обозначая через R > 1 сумму осей эллипса Е, имеем
н
WmV\Ah\ <4~-
h—>oo
С другой стороны, так как | Т^ (х) \ ^ 1 на отрезке 01, то, в силу второго
из условий, характеризующих операторы Pn[f{x)], имеем также
на отрезке 01, причем степень многочленов Рп [Th (x)] не выше h, вслед-
вследствие первого из упомянутых выше условий. Поэтому, согласно извест-
известному свойству многочленов степени h во всякой точке z внутри эллипса Е
имеем
\Pn[Th{z)}\<co\
где 1 < р <С R — сумма осей эллипса, софокусного с Е, проходящего
через z. Итак, последовательность
h=o
ограничена во всем эллипсе с суммой осей р <^ R
и по теореме Стильтьеса сходится в нем равномерно к функции f(z).
1 Второе из этих условий можно еще обобщить, заменив постоянную С через
п
Сп, где lim l/Cn = 1.
п—>оо
328

§ 7. Генеральная область сходимости многочленов
JBn [/(<#)], в случае одной особой точки.
Перейдем теперь к решению общей задачи об определении генераль-
генеральной области сходимости /)#, соответствующей данной области регуляр-
регулярности R.
Положим сначала, что / (z) имеет только одну особую точку (вне
отрезка 01), так что R' = с — единственная граничная точка области R,
лежащая на конечном расстоянии. Если петля Fx содержит внутри себя
точку с, то х находится вне генеральной области сходимости D, Напро-
Напротив, х находится внутри области Z), если с лежит вне петли Fx\ поэтому
границей Вс области сходимости D в данном случае .будет совокупность
узлов х9 петли которых Fx проходят через точку с. При этом следует
заметить, что узлы х, обладающие свойством, что точка с находится на
внешней ветви их узловой линии, лежат внутри/). Следовательно, имеет
место
Теорема В. Если с = а0 + ib0 (вне отрезка 01) есть единственная
особая точка / (z), то область сходимости многочленов Вп [/ (х)] ограни-
ограничена наружным контуром Dc (который назовем антипетлей точки с)
линии
1 / Л \1—С / \С
dr) (f) =1' C4>
3
образующим внутренний угол -~-ъ в точке х = с, являющейся двойной
точкой линии C4), и окружающим отрезок 01.
Действительно, линия C4), которую мы можем назвать антиузловой
линией точки с, является геометрическим местом точек х = а + ф, узло-
узловая линия которых проходит через с, поэтому все точки линии C4)
находятся либо внутри области сходимости D, либо на ее границе ,DC.
Нетрудно проверить, что антиузловая линия C4), уравнение которой
может быть записано в виде
Фс (а, р) = Рх (а0, Ьо) - A - а0) log
х—1
«о" Х
+ bo [arg ~ - arg ^] = 0, C4 bis)
ограничена, так как при |#|->оо, Рх(а0, b0) ~log| х \ -> оо. Кроме того,
антиузловая линия имеет (вне отрезка 01) лишь одну особую (двойную)
точку х = с, вблизи которой Фс (а, [3) представляется как вещественная
часть разложения
F (с, х) = A - с) log(l - i=f) + clog (l - iZLf.) =
oo
= ,2 т^^л^-гМ (*-*)*•
329

Уравнением пучка касательных в точке с будет поэтому
{а% — а0 — bl) (а - а0J + 2Ь0 Bа0 — 1) (о — а0) (Р — &о) -
C5)
Сравнивая это уравнение с уравнением (8), видим, что пучок касатель-
касательных к антиузловой линии совпадает с пучком касательных к узловой
.линии с тем же узлом, но внутренний угол между касательными к на-
наружному контуру области, ограниченной линией C4), составляет в дан-
данном случае у тт.
Рассмотрим для примера частный случай, когда особая точка с = ао + ib0
находится на вещественной оси (Ьо = 0). Положим для определенности1
с = aQ ^> 1 /если а0 <С 0, то достаточно произвести зеркальное отображение
•около прямой а = —) . Уравнение C4) можем представить в виде
[(a - IJ + p] 2 (a* + o2J = (a0 - l)^a"a^.
Вводя полярные координаты a = p cos G, C = p sin 6, имеем
l-ao a
[p2 — 2pccs 0 + 1] 2 == (a0 — lI-"»^^ °
и, разрешая это уравнение относительно cos 6, находим
cos G = ± [l + р» - (До - l)^ (^-)' 'J = ? (р). C6)
Таким образом, антипетля Duo получается, если в формуле C6) брать
только наибольшее из значений р, приводящих к тому же самому значе-
значению ср (р) = cos 6. Из C6) видно, что ср (а0) = 1, т. е. 6 = 0 при р = а0;
другой же корень р0 уравнения ср (р) = 1 меньше а0 (и соответствующая
ему точка не может лежать на Azo)> так как
2?'<Р) =
имеет два корня: ао<^ао и а0, между которыми ср' (р) ^> 0, причем rf'(
вне промежутка аоао; таким образом, po<CaQ<Caoi и значения р <^ р0, для
которых ср (р) ^> 1, невозможны на антиузловой линии; при росте о от р0
угол 0 растет от нуля до максимума, соответствующего р = а0, убывая
снова до нуля при р = а0. Вся эта часть антиузловой линии вместе с ее
симметричным относительно оси абсцисс отображением остается внутри
антипетли Duo. При дальнейшем росте р ^ а0 мы уже находимся на анти-
антипетле Впо: полярный угол G на ней все время растет от 0 до тг вместе
1 Когда с—»1, то уравнение C4) стремится к |а?| = 1, т. е. пределом антипетли
является окружность радиуса 1 с центром в 0.
330

¦с р, достигая значения ти в точке оси абсцисс с отрицательной абсцис-
абсциссой — #0, которая определяется из уравнения
i0—1
C7)
Например, при а0 = 2 уравнение C6) приводится к
а уравнение C7) дает хо = 2(l-\~Y^)- Ординаты у0 точек пересечения
аптипетли i)ao с осью ординат, определяемые, вообще, из уравнения
2а0
/ о \а°—¦"• '
ф (р) — 0 или [см. C6)] 1 + р2 — (а0 — IJ ( —) , в случае В2 удовле-
\ао/
творяют уравнению 1 -\- р2 = -ттг , откуда у* = 8 + ]/80. Ординаты у1 то-
точек пересечения /)'2 с прямой a — 2 определяются из уравнения
D + y\f
1 -\- уъ = -———— 9 дающего у* = 8 для двух точек, отличных от узла
<а = 2, Ух = О).
§ 8. Нахождение генеральной области сходимости JJM
в случае любой области jR регулярности
В общем случае, когда границей области R регулярности функция
/ (z) (включающей промежуток 01) является любое замкнутое множество
Я'', применение теоремы В ко всем точкам границы R приводит к сле-
следующему общему результату:
Теорема С, Если R — граница области Я регулярности функции f(z)
(не содержащая внутренних точек отрезка 01), то генеральной обла-
областью Dr сходимости многочленов Вп [/ (х)] является область, заключен-
заключенная внутри антипетель всех точек множества Я'.
В частности, если / (z) имеет только две сопряженные особые точки
ao±ibo (bo^>O)f то границей DUQ+ibo области сходимости будет верхняя
часть антипетли Dao+ibo точки а0 + ib0 и ее зеркальное отображение, так
как из C4 bis) видно, что
Рх (а0, — Ьо) = Рх (а0, Ьо) 4- 2b0 arg ^-^ .
Поэтому обе антипетли Dao±ibo и Впо-1ъо пересекаются лишь на оси абс-
абсцисс, причем Рх(а0,—60) <0 в точке х = а0 + ib0, откуда следует, что
вся верхняя часть антипетли DaQ+ib0 точки а0 -f ib0 находится внутри анти-
антипетли Dao-ibo сопряженной точки.
Пусть, например, а0 = 1; тогда уравнение C4 bis) для точки с =
превратится в
1 \Х\ , т Г ТГ Х ~] П
s VTT? ' arg с ~ т"""arg ^ =
331

или, обозначая через <1> положительный угол, под которым отрезок 01
виден из точки х,
-*\ C8)
При 'Ъ = 0 получаем точки пересечения с осью абсцисс: х0 —
= + Vl + Ъ\е ° ьо. При возрастании ty каждому его значению соответ-
соответствуют две точки антипетли D'1+ibo , лежащие на пересечении окружности
С", из точек которой отрезок 01 виден под углом <1>, с окружностью с
центром в 0, радиус которой, определяемый уравнением C8), убывает, до-
достигая наименьшего значения ]/1 + Ь*у когда1 ф — arctg r- , тогда обе
точки антипетли Dx+ib0, постепенно сближаясь, совмещаются вг узле
с = l-\-ib0, образуя таким образом всю верхнюю часть антипетли D1+ibo,
Присоединяя к ней ее зеркальное отображение, получим границу
0[л1Ъо генеральной области сходимости, соответствующей паре особых
точек 1НЬ По-
Последует также заметить, что если &i>&0> область D1±ibo сходимости,
соответствующая паре особых точек 1 + ^о> находится целиком внутри
контура D1±ibl, так как
1 1
при & <; arctg-т— <С arctg -т—. Поэтому D1^ibo будет границей генеральной
области сходимости, когда множество особых точек R функции / (z) будет
состоять из любых точек с абсциссой 1, среди которых ближайшими к
отрезку 01 являются точки \ ±: ib0. Последнее замечание, значительно
облегчающее практическое применение теоремы С, может быть обобщено.
Назовем лучами отрезка 01 лучи, выходящие перпендикулярно к отрезку
01 из любой его точки или выходящие под тупым углом к 01 из концов
0 и 1 отрезка. Множеством Rf ближайших к отрезку 01 особенностей
функции / (z) назовем множество, состоящее из всех точек границы /Г
области регулярности функции f{z), в которых каждый из рассматри-
рассматриваемых лучей впервые достигает R.
Следствие 11. Если Rf есть множество ближайших к отрезку 01
особенностей функции f{z), то Dr* = Dr».
Для доказательства достаточно убедиться, что антипетли, узлы кото-
которых лежат на одном и том же луче, не могут пересекаться, т. е. что
петля с любым узлом х не может иметь двух точек а0 -\- ib0, ах + ^i на
одном и том же луче. Рассмотрим сначала перпендикулярный луч: 0<С #о=
= ai^l> O^^o^^i- Если бы обе точки а0 + ?60, а0-\-ib± находились
на петле Fx, мы имели бы Рх (а0, Ьо) = Рх (а0, Ьх) = 0 и Рх (а0, Ь) ^> 0 при
1 Дальнейшее увеличение ф ]> arctg соответствует «паразитной» части антиуз-
ловой линии, находящейся внутри ее наружного контура D1+ib^,
332

Следовательно, Рх(а», b) достигало бы максимума для неко-
некоторого Ъ = b2 ^> 0, и в этой точке мы должны были бы иметь
д*Рх а0 ¦ а0 -1
662 «2 + *5 к^ + ь? '
что невозможно при 0<^а0<^1. Рассмотрим также случай неперпендику-
неперпендикулярного луча, когда Ь() = т(а0 — 1), Ь1 = т(а1—1), т^О, аг^> ао^> I.
Из Рх (а0, т (а0 — 1)) == Рх (а19 т (а± — 1)) мы, подобно предыдущему,
должны были бы заключить, пользуясь второй из формул A7), что для
екоторого а (а<^а<^ а)
некоторого а (ао<^а<^ аг)
(а— 2) fl + m8(a —1) / а
__
da? ~~а — 1 а*+т*(а— IJ (а — 1) [а2 + т2 (а - IJ]
что невозможно, так как а^>ао^>1.
Отсюда же вытекает
Следствие 12. Граница автономной области S имеет одну и только
одну точку на каждом луче отрезка 01.
Из предыдущего вытекает также следующее свойство автономных об-
областей, которое можно было бы принять за их определение.
Следствие 13. Для того чтобы область S была автономна, необхо-
необходимо и достаточно, чтобы антипетля всякой точки ее границы охва-
охватывала целиком область S.
Кроме того, докажем
Следствие 14. Если \х\^?-1, \х —• 1 [ ^> 1, то область, ограниченная
антипетлей Dx, автономна.
В самом деле, в силу следствия 7, из |#'|^1 вытекает, что все
точки х петли Fx* удовлетворяют тому же неравенству |#|<;1. Точно
так же из \х' — 1 j <C 1 следует, что все точки петли Fx> удовлетворяют
неравенству \х— 1|<^1. Поэтому все точки хг антипетли Dx удовлетво-
удовлетворяют неравенству | х \ ^ 1, | х — 11 ^> 1. Но если бы область, ограниченная
антипетле!! Dx, не была автономна, то на Dx существовала бы такая
точка ?, что ее петля F% пересекла бы Dx в некоторой точке хг, петля
которой Fxt проходила бы также через точку х; но это противоречит
следствию 1 и лемме 3.
§ 9. Случай, когда границей области регулярности JK
является прямая, параллельная оси ординат
Рассмотрим более подробно случай, когда область R регулярности
функции / (z) ограничена прямой а = с^>1. Согласно предыдущему, гене-
генеральная область сходимости D включает в себя все точки х, петли кото-
которых Fx не имеют точек на прямой а = с, причем точки х, петли которых
пересекают эту прямую, лежат вне области D; поэтому границей П об-
области сходимости D будет служить геометрическое место точек x=a.-\-i$,
находящихся на прямой а = с или являющихся узлами петель, касатель-
касательных к этой прямой. Обозначая через Ьо ординату единственной точки
333

петли Fx, находящейся на црямод а = с, мы должны иметь, таким обра-
зом,
«М^-. = Jl±|zl-, C9>
так как точка с + /60 петли Fx с вертикальной касательной лежит на
второй узловой окружности, и
R2 \к-
*2
= 4
Напомним, что при р2 ^ а2 — а (внутри правой ветви гиперболы Г) край-
крайней правой точкой петли Fx является ее узел: а — с, [В = Ьо; поэтому
отрезок прямой а = с, где | Ьо \ ^ ]/с2 — с , служащий хордой гиперболы
Г, принадлежит границе D1 области D. Если [З2 <^ а2— а<^с2 — с, т. е.
если узел х находится внутри сегмента гиперболы, образованного прямой
а = с или внутри симметричного ему левого сегмента гиперболы Г, то>
соответствующая ему петля Fx не достигает этой прямой. Таким образом,
всякая другая точка х = а + ф контура D1 либо удовлетворяет неравен-
неравенству р2>а2 — а, т. е. (если полагать для определенности [3 >0) находится
на верхней половине своей второй узловой окружности C9), либо
а2 — а >с2 — с. Во всяком случае, точка кэсания с + ib0 должна нахо-
находиться на нижней половине той же окружности, так как при возрастании b
дРх
Рх (с) Щ достигает максимума при b = 60, а потому • переходит от по-
яожительных значений к отрицательным, т. е. прямая а — с входит здесь
внутрь окружности C9). Следовательно, из двух значений Ьо, удовле-
удовлетворяющих уравнению C9), всегда нужно брать меньшее по модулю, т. е„
l^o I V<C Кс2 — с и вместе с тем | Ьо | <; | р |, так как в случае (В2>а2 — а
узел х находится выше, а точка с -\- ib0 находится ниже горизонтального»
диаметра соответствующей окружности; в случае же а2 — а>с2 — с один
из корней уравнения C9) менее | р j ло модулю.
Таким образом, полагая b0 = t$ (O^t <^ 1), имеем для определения
криволинейной части контура Df:
а2 + Р2 — а _ Ji_
откуда
р» = с>-с^(«1-«), D1)
И
I с2 (t — *2) + г2 [с2 — с — * (ос* — a)] J Х
(с—IJ (t — t2)-\-t2[c2 — с — t (а2 — а
Дроби, находящиеся в первой части D0 bis), сокращаются соответственно
на at — с и (а—1) t + A — с). После этого сокращения уравнение D0 bis)
334

приводится к виду
\t[(l—а)« —с]/ \« [1 _с_ ос*]/ -1'
т. е.
Гаг+с_П2С-1_
L(a —l)f + cj -'• <*->
Полагая
< = 7ГЗ^' м>0' D3>
выводим из D2)
и из D1), D3) и D4) находим
?2 = (±±^~ и - A + «Jе-2 [1 - (с -1) «и • D5)
Таким образом, уравнения D4) и D5) определяют координаты а, 3 точек
криволинейной части (а<^с) контура D' в виде функций параметра гг^>0
(при гг —> 0 находим а = с, [З2 — с2 — с, что соответствует точке, где кри-
криволинейная часть контура смыкается с его прямолинейным отрезком
прямой a = с).
К тому же результату можно прийти и другим путем, ограничиваясь
только рассмотрением функций вида
со
f(z)=[ еК*-<*ФЪ{Ъ), D6)
о
где ф (Ь) — функция с ограниченной вариацией, так что / (z) (представляю-
(представляющая разность между двумя абсолютно монотонными функциями при
Z<CC) регулярна в левой полуплоскости а<^с. Из предыдущего следует,
что сходимость многочленов Вп [/ (х)] для всех функций D6) обеспечена
внутри контура D', определяемого уравнениями D4) и D5) и дополненного-
соответствующим отрезком прямой а = с. Докажем это другим способом,
из которого видно будет, что в данном случае точки на контуре Цг также
являются точками сходимости. Для этого заметим, что
оо п . /т \
S^_, VYi hi с )
0 0
oo h
= [ \x<f + 1 — x]n e~hc rfd) (h). D7)
j
о
В силу теоремы Стильтьеса — Витали, достаточно доказать ограниченность
Bn[f (х)] во всех точках рассматриваемого контура. Но
о
335

во всех точках х = а -\- ф, где
| ??п + A — х) К еп
при всех h ^ 0, или, если полагать еп = 1 -J- гг (гг ^- 0),
j хгг + 112 = A + аиJ + ?2гг2 < A + и)*с. D8)
Поэтому для сходимости достаточно, чтобы точка х находилась внутри
всех окружностей
(и>0). D8 bis)
Область, определяемая этим свойством, должна, очевидно, находиться
между горизонтальными прямыми
"±^L = С1— D9)
л / _ л \ С —1 ' v '
причем это значение соответствует верхней и нижней точке области схо-
димости, где а = = 1 — с. С другой стороны,
и так как правая часть минимальна при гг = 0, то а <^с; левая же часть
максимальна, когда
A + m)c-i [(с — 1) и ~ 1] = 1. E0)
Удовлетворяющее этому уравнению значение и = м0, которое является
наибольшим приемлемым значением щ при всяком с ^> 1 заключено между
1 2
—т и т. Поэтому, обозначая через —х0 абсциссу крайней слева точки
сходимости, имеем
откуда г^0 = г-, и, следовательно, х0 удовлетворяет уравнению
Вообще, из D8) получаем, что сходимость имеет место при
где а — любое число между —х0 и с. Значение и, соответствующее мини-
минимуму правой части E1), определяется из уравнения
2си A + и)**-1 — 2аи (аи + 1) — 2 A + и)*с + 2 [аи + IJ = 0,
336

или, после упрощения,
A + и)*-1 [(с — 1) и — 1] + ш + 1 = 0. E2)
Решая уравнение E2) относительно а, получаем уравнение D4) и, под-
подставляя найденное значение в E1), находим второе параметрическое урав-
уравнение D5) граничного контура D' (вместе с $2<^с2— с, при а = с, соот-
соответствующим прямолинейному отрезку контура D').
Формулы D4) и D5) могут быть также использованы для нахождения
генеральной области сходимости, когда областью регулярности является
прямоугольник Rb с вершинами (с, +6) и A — с, +&), где с2— с^Ь2.
Мы уже видели, что в случае с2 — с = Ъ2 область сходимости Db совпа-
совпадает с областью Rb, так как она автономна. Если же Ъ = оо, то, поскольку
область сходимости В^ симметрична относительно прямой а = -^-, она
заключена между прямыми <х = с и а = 1 — с и ограничена сверху и
снизу контуром, который при а^>— определяется формулами D4) и D5),
а при a-^Y — формулами, получающимися из D4) и D5) заменой a
через 1 — а. Эта область Db = D^ сохраняется неизменной при уменьше-
уменьшении Ь, пока Ь^у0, где у0 — ордината наивысшей точки области Д^. При
дальнейшем уменьшении высоты Ь2^с2 — с прямоугольника регулярности
Rb область сходимости Db сокращается за счет участка D^, выходящего
из Rb, именно при значениях а, близких к -у, для которых формула D5)
дает р2>62, нужно полагать (З2 = б2, т. е. срезать область Вл горизон-
горизонтальными сторонами прямоугольника Rb.
Заметим еще, что формулы D4) и D5) становятся иллюзорными при
с = 1. Но если составить из них
а2 + Р2 = -?г A + A + ^JC~1 [Bс - 1) и - 1]},
то для с -> 1 находим уравнение
совпадающее с уравнением антипетли точки с = 1 [согласно уравнению
C4)], так что в этом случае область сходимости D представляет круг
радиуса \х\ с центром в 0. Таким образом, если, например, областью
регулярности R является прямоугольник с вершинами @, Чг h) и A, Ч-/г),
где /г<^-тт-, то областью сходимости служит часть прямоугольника, нахо-
дящаяся внутри кругов радиуса 1 с центрами в концах отрезка 01.
Примеры. 1) Пусть с = -~; тогда уравнение C7) обращается в
откуда х0 = 3. Следовательно, абсциссы а точек области сходимости D
заключены между — и — 3. Согласно D9), ординаты этих точек заключены
22 С. Н. Б ернштейн 337

3 V^ 3 V 
между +l-kJl и y~ . Уравнения D4) и D5) обращаются в
( >
где гг изменяется от 0 до 3 на замыкающем отрезке контура а = -)Г,
Исключая и из уравнений E3), получим алгебраическое уравнение
четвертой степени
4C2 = C — |ЛЗ — 2а) A + УЪ — 2аK = 12 — 4а2 + 8 |/3^^2а^
или
При этом область сходимости D ограничена внешней частью циклау
образуемого кривой E4), которая касается прямой а = — в точках
р = Ч—^—, внутренняя же дуга кривой E4), имеющая точку возврата
при а = 1, Р == 0, должна быть заменена отрезком этой прямой между
указанными точками касания.
Интересно сопоставить уравнение E4) с уравнением C6) антиузловой
линии точки с = -у , которое приводится к виду
16 f—-~-j = (a — IJ + [З2, C6 bis)
g
где антипетле соотвеаствуют только значения а2 -\- р2 ^ — . Как всегда?
лежащие на оси абсцисс точки — х0 и с = а0 границы Z)' области сходи-
сходимости, соответствующей области регулярности а<^с, находятся на анти-
антипетле DU9 точки а0, все же прочие точки D лежат внутри DUQ.
Замечание. Значение с = -~- является единственным рациональным
числом (с>1), при котором решение xQ^>0 уравнения C7 bis) [или C7)
а0 = с] также рационально.
В самом деле, положим
С р ' С — 1 />! '
где q, р в. ql9 рг — две пары взаимно простых положительных чисел.
Отсюда
с --
так что уравнение C7 bis) принимает вид
(viY1 (Q+~P) _ fjY(9i+Pi)
338

Следовательно, необходимо, чтобы
где т^О, т1'^>0 — целые числа, A^i, В^>Л —целые взаимно простые
числа, причем
т. е.
тАтВт> + (т - mO Am+Wl - miAmiBm = 0.
Вследствие QiP — QPi^>0 имеем Ь = т — ^i>0, и так как необходимо,
чтобы о = уВт\ где у — целое положительное число, то после сокращения
на (А В)™1 получаем
?пА8 + уАт — т1Ва = 0.
Поэтому В > 1 и тх = t/i.4s, где г/х }> 0 — целое число; в таком случае из
8 = уВ^Ад
следует, что 4=1, т. е. тп1=у1 и
^ + г/i + г/ = 2/iSs; 3 = yfiUl B? Г -1). - E5)
Следовательно, о^> у + т/1? причем знак равенства имеет место лишь при
^1==2/ = 1, J5 = 8 = 2, и оба равенства E5) тогда соблюдены. Но если
о "> у -{- у±, то первое из равенств E5) влечет за собой
28 > 5* (8>2),
которое при В^>2 невозможно. Таким образом, необходимо, чтобы
В = о = 2, у = ух = А = 1, откуда /? = /?х = 1, дх = 2, G = 23 = 8, поэтому
5±- = 2, ——г- — 8, и, следовательно, с = -^- , х0 = 3.
с с — 1 ^
2) Пусть с = 2; тогда уравнение C7 bis) обратится в
откуда х0 = 2 A + ]/2) и — 2 (l + "/2) < а < 2; согласно D9), | р | < 4.
Уравнения D4) и D5) получают вид
а = 2 — 2«а - гг3? $* = A + ггL B - и2) @ < и < j/2). E6)
Для исключения и возведем в квадрат первое уравнение и сложим со
3 (р2>6).
вторым; полагая р2 = а2 + р2, получим
4 + F Зр2 2
Беря положительный корень и = ^- и подставляя его в первое
из уравнений E6), находим
339 22*

(а убывает с возрастанием р). Симметричная относительно оси абсцисс
часть этой кривой 6-го порядка, соответствующая значениям р при
в<Ср2^ 12 + 8 |/2, образует криволинейную часть контура D', замы-
замыкаемую отрезком р2 >^ 2 прямой a = 2, которой она касается в точках
B, ±1/2).
Этих двух примеров достаточно для получения ясного представления
о форме и размерах области сходимости D соответствующей области R
регулярности а <^ с (с ^> 1).
§ 10. Случай, когда функция f(x) имеет особенности на отрезке 01
При выводе основных формул B) и C) мы предполагали функцию
f (z) регулярной на всем отрезке 01, а поэтому это предположение сохра-
сохранялось и в дальнейших выводах. Однако, вводя соответствующие дополне-
дополнения в формулировки теорем, можно распространить их и на тот случай,
когда f (z) имеет особенности на отрезке 01.
Для этого заметим прежде всего, что если контур интегрирования С
в формуле B) пересекает отрезок 01 в одной или двух точках ao<^alf
то эта формула заменится формулой
rim r f т\ т /л \п—га п !
m=[aon]+l х„, ..... с z{nz-l)...(nz-n)>
B bis)
лишь бы аоп и агп не были целыми числами 1. Асимптотическое пре-
преобразование, приводящее формулу B) к формуле C), может быть сделано
и здесь при условии, что
dm. Л 1 П.л П..
;i. E7)
Действительно, в таком случае в точке а0 (или ах), где асимптотическое
преобразование неприменимо, мы имеем
2 | (па0— 1) (па0 — 2). . . (па0 — п) \ > (па0— [па0]) ([па0] — 1)! (л — [пао]—1] !,
поэтому 2
х~
1 —
1
20
1-в.
X
а0
о»
/- 1
"¦-. 1у
х —
1 —
- 1
а,
X
а,
lim у * ==
т »/ ^
= lim I/ r jtt-7 р : тт-| =
п^оо^ [пао-1]\ (п-[пао]-1)\ ({__а
и, следовательно, на контуре С вблизи а0 (и аг) подинтегральная функция
стремится к нулю. Таким образом, при условии E7) формула B bis)
1 Очевидно, что при любых а0 <[ аг это осуществляется для бесчисленного мно-
множества целых значений п. Точно так же всегда существует бесчисленное множество
значений, для которых аоп — [аоп] > A — г)п7 агп — [агп] > A — е)п, как бы ни было
мало данное е > 0.
2 См. предыдущую сноск}'.
340

преобразуется в асимптотическую формулу
\ f & [(т^тI" (т)Т *' E8>
Из E8) вытекает следующий вариант теоремы А:
Теорема A bis. Если функция f (z) регулярна на петле Fx точки х
и внутри FXi причем петля Fx пересекает отрезок 01 в одной или двух
точках а"<^а , и если f (z) ограничена на всем отрезке 01, то
]imBn[f(x)] = f(x) E9)
91—>ОО
на петле Fx и внутри ее.
Действительно, выбирая контур С достаточно близко к FX9 чтобы
формула E8) была применима, найдем, как при доказательстве теоре-
теоремы А, что
lim ?„,«,«, [/(а)] =/(*), E9 bis)
П-*эо
где #0<С а0> а1У> а\- Но благодаря условию E7) ,каждый из членов Вп [f{x)]f
не входящих в Вп,аоах [/ (^)]> менее п-ю члена некоторой убывающей
геометрической прогрессии, поэтому
lim | Вп [/ (X)] - Вп, а0о, [/ (X)] j = 0.
Из нашего рассуждения следует также, что формула E9) остается в силе
и в том случае, когда / (z) безгранично растет на отрезке 01 вне петли FX9
если только при построении многочленов Вп [/ (х)] берутся вместо значений
/(—) вне промежутка а^ любые ограниченные числа.
Отсюда вытекает любопытный факт, замеченный Л. В. Канторовичем,
что если функция / (z) на отрезке 01 склеена из нескольких различных
аналитических функций, то многочлены Вп [/ (#)] сходятся в соответст-
соответствующих областях плоскости комплексной переменной к каждой из них.
Распространяя данное ранее определение антинетли точки с на случай,
когда с находится на отрезке 01 @<^с<^1), находим, что антипетля
точки с, т. е. геометрическое место точек, петли которых проходят
через с, имеет уравнение
\х-1\1-"\х\с = A-сI-ссс @<с<1). F0)
Уравнение F0) [являющееся пределом уравнения C4) при Ь0->0] пред-
представляет лемнискату с двойной точкой с; при этом левая часть лемнискаты
соответствует узлам петель Fx, для которых с является правой точкой
пересечения с осью абсцисс, а правая ее часть соответствует петлям, для
которых с служит левой точкой пересечения с осью абсцисс.
Таким образом, из предыдущего вытекает также полное решение во-
вопроса о генеральных областях сходимости многочленов Вп Г/ {х)] к каждой из
аналитических функций, из которых составлена на отрезке 01 функция / (х).
341

Следствие 15. Пусть функчия f (х) обладает следующими свой-
свойствами: f (x) ограничена па всем отрезке 01; в каждом из промежутков
0аг, ага2, . . . , aki отрезка 01 она совпадает соответственно с аналити-
аналитическими функциями /0 (х), Д (х), . . . , fk (x)} регулярными г внутри соответ-
соответствующего промежутка. Тогда, еслиВ0, Dl9 . . . , Dj€ — генеральные области
сходимости, определяемые соответственно лежащими вне отрезка 01
особенностями функций /0 (х), fx (х), . . . , /& (х), то многочлены Вп [/ (#)]
сходятся к fo(x) внутри области, общей Do и левому овалу лемнискаты
l^-ir^laj^^a-a^-V1; F1)
внутри области, общей Z)l5 правому овалу лемнискаты F1) и левому
овалу лемнискаты
1— «2
сходятся к f± (x)9 и т. д.] наконец, внутри области, общей Dk и правому
овалу лемнискаты
х - 111-** | х |в* = A - я*I-^* ,
многочлены Bn\f(x)] сходятся к fk{x).
Например, многочлены
стремятся к нулю внутри левого овала лемнискаты
| х A х) I = -?-
и стремятся к единице внутри правого овала этой лемнискаты.
§ 11. Области сходимости многочленов Ап[/(хI
и асимптотическая форма областей сходимости многочленов Bn[f{x)
при бесконечном удалении особых точек функции f(x)
Как нетрудно видеть, все изложенное выше применяется к много-
многочленам
соответствующим при данном /г>0 отрезку 0/г. Область сходимости
многочленов J5n [/ (z); re, /г] подобна, таким образом, области сходимости
многочленов Bn\f (hz); x, 1].
а В частности, они могут быть ветвями одной и той же многозначной функции,
342

Если / (х) —¦ аналитическая функция, регулярная в точке 0, то
h-M)
=lim
/г
где конечные разности соответствуют приращениям — переменной х.
Поэтому
Лп [/ (х)] = lim [/ @) + „Д/ @) -f- + »-^ Д2/ @) (-^J
Вообще, при всяком /г^>0 формула F2), подобно формуле A), преобра-
преобразуется к виду
Bn[f{z)\x,h]= ^Г
z {nz — h). . . (nz — nh)
где Ch — любой контур, окружающий отрезок 0/г, внутри которого / (z)
регулярна. При /г->0 получаем
F4)
иш- "! \rm{f^^\(i M1 *hTdz- пУП
где контур С ограничивает область, включающую 0, внутри которой / (z)
регулярна х. Применяя формулу Стирлинга, выводим отсюда асимптоти-
асимптотическую формулу для п-^оо
(z)dz
F5)
Уравнением узловой линии при любом h^>0 будет
Рх (а, 6, А) = log
х — h
1 h 'x_h
z
= 1—г log
b
и области сходимости многочленов Bn[f (z); x, h] подобны областям схо-
сходимости Bn[f (hz)\ x} 1]. С уменьшением h области регулярности функции
/ (hz) расширяются, и при h -> 0 предельные узловые линии имеют урав-
уравнения
lim Рх (а, 6, h) =
1 Формулу F4) легко также проверить непосредственным интегрированиед! (см.
упомянутую выше статью из Journ. de Math. [65]).
343

= log
Поэтому все предельные петли Fx, соответствующие многочленам Ап [/ (х)]?
подобны петле F^ точки х = а + ф = 1, имеющей уравнение
Благодаря следствию 1 мы знаем, что предельные петли F°x выпуклы
и в силу следствия 2 область, ограниченная петлей F^, всегда автономна.
Различные виды автономных областей, соответствующих многочленам
Ап [/ (х)], которые совпадают со всеми возможными областями сходимости
этих многочленов, легко получаются непосредственно. Но их можно также
вывести как асимптотические формы бесконечно возрастающих автоном-
автономных областей многочленов Bn[f(x)]. Так, например, из леммы 5 выте-
вытекает:
Всякий квадрат с центром в О, дополненный четырьмя выпуклыми
попарно симметричными областями, окаймляющими его стороны, но не
выходящими соответственно из кругов, имеющих эти стороны диаметрами,
образует автономную область многочленов Ап [/ (х)].
В частности, из следствия 6 следует, что всякий эллипс, у которого
отношение между осями не превышает ]f'3> является автономной об-
областью.
Антипетли для многочленов Ап [/ (х)], соответствующие любой точке
с, также всь подобны антипетле с узлом 1, предстаеляюу\ей наружную
часть кривой, заданной уравнением
и получаются из последней посредством умножения на с.
Согласно следствию 14, все антипетли многочленов Ап [/ (х)] являются
автономными областями. Вследствие этого, генеральная область сходи-
сходимости многочленов Ап [/ (х)], представляющая на основании теоремы С и
следствия 11 область, лежащую внутри антипетель всех ближайших к О
особых точек функции / (z), практически получается проще, чем для
многочленов Bn[f (х)]. А именно, нужно сначала взять область, ограни-
ограниченную антипетлями всех особых точек, лежащих на окружности сходи-
сходимости1 функции f (z); если внутри полученной таким образом области
1 В случае многочленов Вп [/ (х)] вместо этого приходилось брать все ближайшие
к отрезку 01 особые точки с, расстояния которых хотя бы до одного из концов от-
отрезка 01 менее единицы.
344

Dq функция / (z) регулярна, то это и будет генеральная область D схо-
сходимости мноючленов An[f (x)]\ если же внутри Во будут еще особые
точки с, то следует учесть только антииетли этих точек, тук как Do
лежит внутри антипетель всех прочих особых точек.
Принимая во внимание, что петли F°x при удалении х по лучу по-
подобны и подобно расположены, так что F°x лежит внутри F^x, при X > 1
получаем
Следствие 16. Граница генеральной области сходимости многочленов
Ап [/ (х)] имеет всегда одну и только одну точку на каждом луче точки 0.
Например, если единственными особыми точками / (z) на окружности
радиуса 1 являются точки -f-1, а расстояние от 0 до остальных особых
точек не менее е, то границей генеральной области сходимости многочленов
An[f{x)] будет линия
и ее симметричное относительно оси ординат отображение.
Свойство генеральных областей сходимости многочленов Ап [/ (#)],
которые всегда автономны, заключающееся в следствии 16, вытекает также
из соответствующего общего свойства областей сходимости многочленов
Bn[f(x)], частным случаем которого является следствие 12. Но, так как
в § 8 это свойство не было доказано в общем виде, то мы выведем его
здесь.
Следствие 17. Граница генеральной области сходимости многочленов
Bn[f(x)] имеет одну и только одну точку на каждом луче отрезка 01.
Для доказательства нашего утверждения достаточно показать, что
если точки х0 = а0 + i C0, х1 = а1~\- 1$г лежат на одном и том же луче
отрезка 01, то их петли FXo и FXl не могут иметь общих точек; иначе
говоря, две точки антипетли не могут находиться на одном и том же
луче.
Рассмотрим сначала вертикальный луч ах = а0, рх > ро ^> 0, причем
0 <Са <С 1 • Принимая во внимание, что в данном случае все точки петель
FXq и Fx% находятся соответственно ниже их узлов х0 и хь заключаем,
что если они пересекаются в точке с = а0 + ib0, то | Ьо \ < [30 <^ р1# Беря
производную no p первой части равенства C4 bis), находим
дФс = flop — boa | A — а0) р — Ъо A — а)
^ а2 + Р2'" ' (а— 1J + р2
_ (а2 + Р2) (Р ~ Ьо) + A - 2а) Kft - &оа)
Не нарушая общности, можем считать,что aQ^~. В таком случае при
1 ^фс
а ^ у имеем -т^- > 0, а поэтому Фс (а, р) = 0 имеет не более одного
корня [3>&о- Если жеа>-г, то производная числителя равна а2 + (З2 -f-
+ 2,3 ф — 60) + а0 A — 2а) и в случае а0 < 1 при р > 60, р > 0 она
345

положительна, так что уравнение Фс (а, гр) = 0 имеет не более двух корней;
поэтому, принимая во внимание, что число точек антипетли на луче
должно быть нечетным, заключаем, что оно равно единице. В случае же
дФс
а0 ]> 1 замечаем, что —^- < 0 при $ = Ь0^>0 и C = 0, вследствие чего
дФс
—— — 0 имеет лишь один корень больший Ьо, а потому уравнение Фс (а, C) = 0
снова не может иметь более двух корней и, следовательно, имеет лишь
один корень на этом луче. Наконец, при Ь0<^0, пользуясь следствием
6ФС
4, видим, что -gg- > 0, так как $* + а* — а0 > 0 и
откуда следует, что а0 + Р§ + ао A ~~ 2а0) > 0.
Рассмотрим теперь луч, проходящий через 0 и через точку х0 = а0 + ф0,
где а0 < 0, Ро > 0- В любой точке х = а + ф этого луча имеем ж = X х0, где
X > 0. Полагая, что #0 находится на антипетле C4 bis), из
px (a
получаем
/л лп \ IA
X ' (:
+ p2) X2 — [A +
~~a0
ao)a
X [(Xa0 - IJ
a0 — a0 X) A — a0X) 4
)log
1J +
Xx0 — 1
— xp2j _ 60p0
,P0] X + o0
-6o)M
.Таким образом, при бесконечно малом изменении Х^-1, во всех точках
петли /^с0, находящихся ниже прямой
(a-ao)(l-ao) = %(b-$o), F8)
будем иметь Фс (Ха, Хро) > Фс (а0, ^0) = 0. Но прямая F8) проходит через
узел х0 петли Fx и пересекает ось абсцисс в точке
дше отрезка 01, проходя выше петли Fx вблизи ж0. Поэтому вся петля
Fx находится ниже прямой F8), и, следовательно, во всех ее точках
Ус = а0 + ibQ имеем
^хх0 (а0> Ьо)|= Фс (Ха0, Щ > 0 (X > 1),
а потому петля Fx находится][внутри петли FxXo- Аналогичным образом
346

наше утверждение доказывается для лучей, проходящих через конец
1 отрезка 01.
Возвращаясь снова к многочленам Ап [/ (х)], заметим, что они дают
простой критерий для определения, является ли данная точка на окруж-
окружности сходимости строки Тейлора особенной или нет.
Критерий регулярности функции
/ (х) = а0 -t- ахх 4- а2х2 -4- . . . + ап х11 + . . . F9)
в точке х0 на ее окружности сходимости: для того чтобы f (x) была
регулярна в точке х0 окружности сходимости, необходимо и достаточно,
чтобы существовало такое число 8>0, что для всех в, модуль которых
равен 8, многочлены
An [f (X)) = 2] (! - т ¦ • Ч1 -V fl^ G°)
0
где x — x0 (I + s), остаются ограниченными для некоторой бесконечно
возрастающей последовательности значений п (в таком случае они будут
ограничены для всех п),
В самом деле, если функция / (х) регулярна во всех точках круга С
достаточно малого радиуса 2о с центром в точке х0, то петля F°x любой
точки х = х0 A + s) находится внутри области регулярности / (х), вклю-
включающей круг С и круг сходимости ряда F9). Поэтому во всех этих
точках (все) многочлены Ап [/ (х)] равномерно сходятся к f (х), т. е. огра-
ограничены. Наоборот, если некоторая бесконечная последовательность много-
многочленов Ап [/ (х)] ограничена для всех х = х0 A -}- е) при j s | = о, то по
геореме Стшгьтьеса они сходятся к регулярной функции, являющейся
аналитическим продолжением ряда F9).
Из указанного выше критерия вытекает сразу, например, известная
теорема, что если все коэффициенты строки Тейлора ап ^> 0, то точка
хо^>О на окружности сходимости должна быть особенной.
Укажем еще аналог формул D4) и D5) для области сходимости D
многочленов Ап \f (x)], когда областью регулярности служит полуплоскость,
включающая 0. Пусть границей области регулярности будет прямая а = с.
Тогда область сходимости D будет ограничена частью кривой, имеющей
уравнение
соответствующей и ^ 0, которая касается прямой а = с в точках (с, + с)
и отрезком этой прямой, заключенным между точками касания. Формулы
G1) могут быть получены переходом к пределу из формул D4) и D5)
347

при замене основного отрезка 01 отрезком Oh, с любым h<^c в пред-
предположении, что й->0. Имеем сначала
a = — \ —
2C
Мы заменили в D4) и D5) а, ^ с соответственно через -^-, у, у и
параметр м обозначили через — ; после этого, устремляя h к нулю, на-
с
ходим G1). Наибольшее значение и0 параметра и в формулах G1) соот-
соответствует р = 0 i определяется из уравнения еи° A — и0) + 1=0; при
этом а получает наименьшее значение а = , удовлетворяющее урав-
1 Wq
нению а + се =0.

82
КОНСТРУКТИВНАЯ ТЕОРИЯ ФУНКЦИЙ
КАК РАЗВИТИЕ ИДЕЙ ЧЕБЫШЕВА*
§ 1. Конструктивной теорией фупкций мы называем направление тео-
теории функций, которое ставит себе целью дать возможно более простую
и удобную основу для качественного изучения и вычисления как эмпи-
эмпирических функций, так и всяких функций, являющихся решениями
естественно поставленных задач математического анализа (например, реше-
решений дифференциальных или функциональных уравнений). Это направле-
направление весьма близко по духу математическому творчеству Чебышева; не
удивительно поэтому, что современная конструктивная теория функций
в большой степени использует и развивает идеи нашего покойного вели-
великого сочлена.
Исследования Чебышева в области математического анализа, связан-
связанные с важными конкретными задачами, группируются в основном около
трех проблем.
1. Проблема определения выражения, зависящего от данного конеч-
конечного числа параметров, например многочлена Рп (х) степени п, из всех
многочленов степени п наименее уклоняющегося от рассматриваемой
функции / (х) в том смысле, что уклонение, т. е. максимум модуля раз-
разности
Enf{x)=mbx\f(x)-Pn{x)\
в данном промежутке, должно быть наименьшим.
2. Задача интерполирования по способу наименьших квадратов.
3. Проблема моментов.
Первая проблема, как известно, была поставлена Чебышевым в связи
€ его теорией механизмов. Вторая имела целью усовершенствование
способа наименьших квадратов Лежандра при построении эмпирических
формул, соответствующих большому числу наблюдений, и послужила
* Изв. АН СССР, серия матем., 9 A945), стр. 145—158 B28*). Эта статья опуб-
опубликована также в томе II трудов Юбилейной сессии АН СССР 1945 года,
стр. 94—108.
349

исходным пунктом для создания Чебышевым теории разложения фупкцип
по ортогональным полиномам.
Третья проблема — проблема моментов, поставленная Чебышевым для
возможно общего доказательства предельной теоремы теории вероятностей,
имела целью установить, в каких пределах должна быть заключена
вероятность нахождения случайной величины х в конечном промежутке
(а, 6), если известны математические ожидания ее последовательных
степеней.
§ 2. В мою задачу не входит подробное рассмотрение отдельных
результатов, нолучепных Чебышевым и после него другими авторами.
Я хотел бы лишь вкратце обрисовать обширную область конструктивной
теории функций, примыкающую к указанным выше трем проблемам.
В настоящее время известны вычислительные приемы, позволяющие
разрешить с любой степенью точности задачу нахождения многочлена
степени п, наименее уклоняющегося от произвольно заданной функции,
непрерывной в данном конечном промежутке. Однако с увеличением
степени п практически вычисления чрезвычайно усложняются, и тогда
важное значение получают теоретические асимптотические методы, соот-
соответствующие бесконечному возрастанию степени п и нахождению много-
многочленов R (х) степени п, дающих приближения того же порядка, что и наи-
наилучшие приближения Enf(x).
Как известно, пользуясь интегралом, связанным с уравнением тепло-
теплопроводности, Веыерштрасс показал в конце прошлого столетия, что функ-
функции / (х)—непрерывные в данном конечном промежутке — характери-
характеризуются тем, что они могут быть равномерно приближены при помощи
многочленов возрастающих степеней, т. е. тем, что Enf(x) ->0при п—>оо.
Таким образом, многочлены являются естественным конструктивным эле-
элементом для изучения непрерывных функций на конечном интервале,
и многочлены, наименее уклоняющиеся от данной функции, потенциально
содержат все ее свойства. В связи с этим особо важное значение имеет
исследование качественных или экстремальных свойств многочленов,
подчиненных определенным условиям. В частности, фундаментальным
является классический результат Чебышева, согласно которому многочлен
степени п вида
хп + PiXn~l + ашш+рп9
старший коэффициент которого равен 1, в промежутке (—1, +1) не
может оставаться по абсолютному значению менее, чем —^ ; при этом
единственным многочленом этого вида, для которого уклонение от нуля-
He превышает —^zi\ > является многочлен Чебышева
~-^zrx cos (n arc cos x).
Другим весьма важным для конструктивной теории функций результатом
оказалась теорема Маркова, дающая ответ на вопрос, поставленный
350

ему Менделеевым: каково наибольшее возможное абсолютное значение
производной многочлена степени п в заданном промежутке, где сам
многочлен не превышает по абсолютной величине единицы?
Эта новая алгебра многочленов, основанная Чебышевым, обогатилась
впоследствии открытием ряда аналогичных теорем, играющих важную
роль в конструктивной теории функций. На них опирается возможность
установления прямой связи между наилучшими приближениями функции
и ее дифференциальной природой, которая открывает общий подход
к последовательному решению первой проблемы Чебышева и позволяет
дать единый принцип для классификации всех непрерывных функций по
степени их близости к многочленам. В частности, этим была положена
основа новой теории аналитических функций вещественной переменной,
в которой аналитическая функция / (х) характеризуется особо быстрым
стремлением к нулю Enf(x), а именно тем, что при возрастании п ее
наилучшие приближения Enf (x) в данном промежутке убывают быстрее,
чем в геометрической прогрессии со знаменателем р<1. Точнее говоря,
для того чтобы непрерывная функция /(#), заданная, например, в про-
промежутке ( — 1, +1), была регулярной функцией комплексной перемен-
переменной внутри эллипса D с фокусами в точках —1, +1, сумма полуосей
которого равна г, необходимо и достаточно выполнение соотношения
П А
lim sup ]/?n/(?)==-. A)
П->оо Г
Замечательное свойство аналитической функции, выделяющее ее из
общей совокупности непрерывных функций, как известно, состоит в том,
что она представляет собою органическое целое, вполне определенное во
всей области существования, если она задана в любом произвольно малом
промежутке.
С точки зрения предложенной выше классификации естественным
продолжением непрерывной функции /(х), заданной в интервале (а, Ъ),
на большую область (а, Ь -f- г) следует считать такое ее продолжение,
при котором ее близость к соответствующим многочленам на расширен-
расширенном промежутке была бы возможно тесной. Иными словами, наилучшие
приближения En[f (x); a, b + s], относящиеся к расширенному промежутку
(a, ft + s), должны при п—> оо возможно быстрее стремиться к нулю.
Благодаря одному свойству многочленов, открытому Чебышевым, было
нетрудно показать, что в случае A), когда Еп [/ (х); а, Ъ] не провосходят
членов некоторой геометрической прогрессии со знаменателем р<^1, такое
наилучшее продолжение функции / (х) на несколько больший промежу-
промежуток всегда возможно и притом единственным образом. Это и есть анали-
аналитическое продолжение.
Если убывание En[f (х)\ а, Ь] не столь значительно, т. е. если
lim sup "j/jKn [/(#); #> b] = 1, то задача вообще не имеет единственного
П->ОО
решения, и лишь для некоторых классов функций возможно поставить
351

ее так, чтобы в случае существования решения оно было единственным,
например, если lim inf ]/2?п [/ (х); а, 6]<^1. Такие классы функций назы-
п—>оо
вают квазианалитическими; они были предметом многих тонких иссле-
исследований последнего времени, имеющих большую теоретическую ценность.
Однако вряд ли можно ожидать, что роль квазианалитических функций
в анализе будет столь же значительной, как и аналитических функций.
§ 3. Напомним теперь вкратце основные результаты, относящиеся
к нахождению порядка убывания и точного асимптотического значения
наилучших приближений конкретно заданной функции.
Из равенства A) легко видеть, что порядок убывания Enf (х) для
аналитических функций в основном определяется полусуммой осей
эллипса D, проходящего через ближайшую особую точку функции/(я),
а асимптотическое значение Еп зависит только от свойств особых точек
функции, находящихся на периферии этого эллипса, подобно тому, как
порядок убывания и асимптотическое значение коэффициентов строки
Тейлора зависит от особенностей функции, лежащих на круге схо-
сходимости.
Многие оценки, относящиеся к наилучшим приближениям, получают-
получаются благодаря использованию разложения функций по многочленам Чебы-
Чебышева
Тп (х) = cos n arc cos x;
здесь и далее для определенности мы будем рассматривать отрезок
[—1, +1J. Эти разложения, связанные со второй проблемой Чебышева,
получаются при рассмотрении задачи обращения в минимум
!L—. (]х
— взвешенного квадратичного уклонения функции / (х) на ' указанном
отрезке, решением которой является
Rn{x)= 2
Если обозначить через Inf{x) приближение функции f(x), даваемое
многочленом Rn(x), то, очевидно, Enf (x) <; Inf (x). С другой стороны,
благодаря неравенству Лебега, для любой функции
F { (v\ ^> Т {(т\ (с ,^ п
Таким образом, порядок наилучшего приближения почти совпадает
с порядком приближения, осуществляемого разложением по многочленам
Чебышева, и обычно совпадает с последним.
352

Асимптотическое значение приближения
п
Inf (#) = max I / (х) — 2 акТк (#)
вычисляется без особых затруднений, и во многих случаях удалось уста-
установить простую зависимость между асимптотическими значениями Enf (x)
nlnf(x). Отметим, например, случай, когда ближайшая особенность функ-
функции / (х) есть алгебраическая или логарифмическая особая точка с, [ с | ^> 1,
находящаяся на вещественной оси. В этом случае известны асимптоти-
асимптотические значения Еп и 1Пу и связь между ними определяется соотноше-
соотношением
F i 1т\ r^> T i (о
Из этого равенства видно, между прочим, что при бесконечном уда-
удалении ближайшей особой точки, т. е. при соответствующем превращении
функции / (х) в целую функцию, приближения Еп и 1п асимптотически
совпадают, и, напротив, отношение ~- убывает по мере приближения
точки с к краю отрезка [—1, +1]. Можно было бы ожидать, что при
Е л
|с| —1 отношение -~~—-. В действительности это не так, и исследо-
вание случая, когда особенности функции / (х) находятся на самом
отрезке, на котором мы приближаем функцию, значительно труднее.
Однако решение этой задачи за последние годы удалось продвинуть
значительно вперед.
§ 4. Первый этап на пути к решению этой задачи был осуществлен
более 30 лет назад, когда было установлено, что существует предел
lim пЕп | # | = Н-1
71—>ОО
(приближенное значение р.х равно 0,28). Недавно этот результат был
дополнен следующим образом. Установлено, что
c2 (|с|<1). B)
п->оо
Отметим следующее любопытное следствие из соотношения B): если
•вершина с угла находится на отрезке [—1, +1], а стороны проходят
через точки (—1, а) и ( + 1, Ъ), где а и Ъ — данные положительные
числа, то минимум асимптотического значения его наилучшего прибли-
приближения на отрезке [—1, -j-1] достигается, когда точка с расположена
так, что угол падения равен углу отражения.
Далее, аналогичный результат получен для Еп\х — с|р, где р~ лю-
любое положительное число, а именно, существует
lim п?Еп | х — с |р = \хр A — с2J ,
п->оо
где jj-p — определенные константы.
Как видно из этих асимптотических равенств, порядок убывания наи-
наилучшего приближения \х — с|р тем медленнее, чем меньше р. Поэтому,
23 с- Н. Бернштейн 353

если на отрезке [—1, +1] имеется несколько особых точек с различ-
ными показателями р, то асимптотическое значение наилучшего прибли-
приближения будет определяться лишь теми точками, для которых показатель р
имеет наименьшее значение.
Определение асимптотического значения наилучшего приближения
в случае, когда на отрезке [—1, +1] расположено несколько особых
точек указанного типа с одним и тем же показателем р, получается
просто, хотя и несколько неожиданно, следующим образом. Положим
для определенности /? = 1, так что
s
/(*)= 2 Ак\х-ск\ (-1<с*< + 1)
представляет собой произвольно заданную ломаную линию с абсцис-
абсциссами cjc вершин внутри или на концах отрезка [—1, +1]. В таком
случае
где
так как возможно приблизить асимптотически наилучшим образом каж-
каждый из членов
Ак\х — ск\
при помощи многочлена п-ж степени Rnk (х) (к = 1, .. . , s) так, чтобы
вне сколь угодно малого промежутка, заключающего точку c&, разность
Rnh (я) — Аи | х — ск |
оставалась во всех остальных точках отрезка [—1, +1J сколь угодно
малой по сравнению с Еп [Ак \ х — ск |]. Поэтому, складывая все эти мно-
многочлены, мы получаем многочлен степени п, з^клонение которого от / (х)
асимптотически не превышает значения —М.
Отсюда, между прочим, видно, что существует бесконечное множество
продолжений ломаной линии, обеспечивающих то же самое быстрейшее
асимптотическое убывание наилучшего приближения, что и прямолиней-
прямолинейное продолжение ее крайних сторон. В соответствии со сказанным ранее
о продолжении непрерывных функций, ломаная линия не имеет един-
единственного наилучшего продолжения.
§ 5. Благодаря замене переменной х — cos б, многочлен степени п пре-
превращается в тригонометрическую сумму п-то порядка относительно cos 6.
Поэтому все результаты, относящиеся к наилучшему приближению произ-
произвольной непрерывной функции, заданной на отрезке [—1, +1], посред-
посредством многочленов, приводят к соответствующим предложениям о наилуч-
наилучшем приближении любых непрерывных периодических функций с периодом
2-ir посредством конечных тригонометрических сумм.
Несмотря на фактическую эквивалентность задачи приближения непре-
непрерывных периодических функций посредством конечных тригонометриче-
354

ских сумм задаче приближения непрерывных функций на конечном отрезке
при помощи многочленов, принципиально эти задачи отличаются тем, что»
в первой задаче рассматриваемая область приближения бесконечна. В общем!
случае вопрос о приближении непрерывной функции на всей бесконечной,
оси вызывает особые трудности, так как элементарная функция — многочлен,
как и в случае периодических функций, не может служить для этой
цели. Возможно, правда, следуя примеру Чебышева, рассматривавшего*
задачу взвешенного наилучшего приближения, ввести соответствующие
неотрицательные веса т (#), с тем чтобы для тех или иных функций / (х)
возможно было подобрать многочлены Рп (х), для которых взвешенные
уклонения
Jnf (х) = max | [/ (х) - Рп (х)] т (х) \
стремились бы к нулю при возрастании п для всех значений х от — оо
до + оо. Обозначив произведение
мы видим, что задача обращения в минимум Jnf (х) равнозначна задаче
нахождения многочлена Рп (х) степени п по условию, чтобы произведение
Рп (х) х (х) наименее уклонялось от F (х) на всей оси. В предположении,
что .F(а;) — непрерывная функция, стремящаяся к нулю при х—>-\-оо7
установлены некоторые весьма близкие между собой необходимые и доста-
достаточные условия скорости убывания т (х) на бесконечности для того, чтобы
рассматриваемые наилучшие приближения стремились к нулю при возра-
возрастании п. Для этого достаточно, чтобы
где —т~- — четная целая функция выше нулевого рода с неотрицатель-
ними коэффициентами*. Напротив, если
т (х) > т0 (з),
где —7-^- — целая функция рода нуль, то наилучшие приближения не
могут стремиться к нулю.
Возможно также в качестве элементарных функций, приближающих
непрерывную функцию на всей оси, ввести рациональные дроби. Этот
вопрос также был предметом исследований последних лет, но, несмотря
на ряд полученных важных результатов, еще не исчерпан.
Заметим только, что наилучшее приближение функции посредством
рациональных дробей требует во всяком случае, чтобы приближаемая
функция стремилась к определенному пределу при х —> + оо и, в частно-
частности, невозможно для периодических функций.
§ 6. Рассмотренная выше задача о наилучшем асимптотическом при-
приближении | х |р на отрезке [—1, +1], естественно, привела к рассмотрению
приближения функций на всей оси при помощи специального класса
* См. «Э. П.», стр. 145—150; 163—165. {Автор.)
355 23 s8

целых трансцендентных функций, обобщающего элементарные тригономет-
тригонометрические функции sin px и cospx. Это функции
S (х) — 2л ~тт х
к
так называемого экспоненциального типа или конечной степени, обла-
обладающие свойством: k
lim sup |/j а^ | = р.
к->со
Число р называется степенью функции S (х). Таким образом, evx, cospx-
sin px являются функциями экспоненциального типа степени /?.
Оказалось, что указанное выше асимптотическое значение
равно в точности наилучшему приближению \х\р на всей оси при помощи
функций экспоненциального типа первой степени.
Наиболее глубоким основанием необходимости введения функций конеч-
конечной степени в качестве конструктивного элемента изучения непрерывных
функций на всей оси является следующее обстоятельство. Как известно,
всякая непрерывная на конечном отрезке функция является в то же вре-
время ограниченной и равномерно непрерывной на всем отрезке. Напротив,
непрерывность функций на всей оси не влечет за собой этих двух свойств.
Однако при изучении непрерывных ограниченных функций на всей оси
естественно выделить в первую очередь те из них, которые, подобно перио-
периодическим, почти периодическим и алгебраическим функциям, являются
также равномерно непрерывными на всей оси. Условие же, необходимое
и достаточное для равномерной непрерывности функции, непрерывной
и ограниченной на всей оси, состоит в том, что ее наилучшие при-
приближения на всей оси при помощи функций экспоненциального типа
степени р стремятся к нулю при неограниченном возрастании степени р.
Эта теорема тесно связана с одним из важнейших экстремальных
свойств функций конечной степени, широко обобщающим соответствующие
ранее известные свойства многочленов и конечных тригонометрических
сумм, а именно, если функция Sv (x) конечной степени р такова, что
при всех значениях х, \ Sv (х) \ <; 1, то при любом целом п для п-й произ-
производной имеем | S^ (x) | <; рп> причем знак равенства в последнем нера-
неравенстве достигается только тогда, когда
Sp (x) = cos p (х — а),
где а — произвольная постоянная.
Отметим еще, что в случае периодических функций задача о наилуч-
наилучшем приближении посредством функций конечной степени совпадает
с соответствующей задачей приближения посредством конечных тригоно-
тригонометрических сумм, так что, например, функция ниже первой степени,
наилучше приближающая на всей оси периодическую функцию с перио-
периодом, не превосходящим 2тс, есть постоянная.
356

Из указанной теоремы о максимуме производной функции конечной
степени вытекает другое важное экстремальное свойство этих функций:
если функция Sp (х) степени р при есех вещественных х удовлетворяет
условию \Sp{x)\^i, то \ Sv {x ^ric) | <^.ерс при всяком с^>0. С другой
стороны, обозначая через Avf {x) наилучшее приближение функции / (х)
на всей оси при помощи функций степени р, можно доказать, что
лр
Из этих двух свойств заключаем, что условие, необходимое и доста-
достаточное для того, чтобы ограниченная вещественная функция / (х) была
аналитической, регулярной и ограниченной внутри бесконечной полосы
— с <С У <С + с> переставая быть регулярной вне этой полосы, состоит в том,
что
V
lim sup УApf (x) = е-с<С 1. A bis)
р—>оо
Таким образом, подобно тому, как функции, аналитические на конеч-
конечном отрезке, выделяются среди других непрерывных функций наиболее
быстрым убыванием наилучших приближений посредством многочленов
возрастающих степеней, аналитические функции на всей вещественной
оси характеризуются той же самой наибольшей близостью к функциям
конечной степени.
Существует также полная аналогия между соответствующими асимпто-
асимптотическими значениями наилучших приближений указанных двух категорий
для функций, обладающих заданными особенностями. В частности, воз-
возможность аналитического продолжения (с сохранением ограниченности)
функции / (х), заданной в конечном промежутке, на всю вещественную
ось зависит от того, возможно ли такое продолжение функции / (х), для
которой Enf (x) убывает в геометрической прогрессии [см. A)] так, чтобы
и Apf (х) убывала в геометрической прогрессии [см. (Ibis)]. Очевидно,
что если такое продолжение возможно, то оно единственно.
Существуют широкие классы задач анализа, которые естественно
приводят к рассмотрению функций, аналитических и ограниченных для
всех вещественных значений переменной. В то же время изучение свойств
и особенностей этих функций в комплексной области представляет непрео-
непреодолимые трудности. Таковы, например, функции, определяемые дифферен-
дифференциальными уравнениями небесной механики. В силу сказанного, при
интегрировании таких уравнений целесообразно использовать в качество
конструктивного элемента, приближающего неизвестную функцию, ограни-
ограниченные функции конечной степени так же и в случаях, когда нет период
дичности. или почти периодичности.
Известно также, что существуют классы дифференциальных уравнений
в частных производных, все решения которых являются аналитическими
функцидми независимых .переменных.
§ 7; Этих примеров достаточно для того, чтобы признать, что проб-
проблема исследования свойств аналитических функций в вещественной области
357

приобретает особый интерес. Одним из подходов к ней является изучение
тех простых конструктивных элементов — многочленов и функций конеч-
нбй степени, о которых только что была речь, и свойств приближений
при их посредстве.
Но существует и другой путь, который связан с непосредственной
характеристикой функций посредством соответствующих неравенств. На-
Например, из известной формулы Коши — Адамара о радиусе сходимости
строки Тейлора вытекает без труда предложение: для аналитичности на
некотором конечном промежутке (а, Ъ) функции / (х) вещественной пере-
переменной х необходимо и достаточно, чтобы
limsup 1/ max
п—>оо
п\
<00.
Это условие можно заменить другим, из которого исключается непо-
непосредственное рассмотрение быстроты возрастания последовательных произ-
производных и даже самое предположение о их существовании.
Назовем функцию / (х) абсолютно монотонной в промежутке @, г),
если все ее последовательные конечные разности в этом промежутке не
отрицательны. Оказывается, что в этом случае она бесконечно дифферен-
дифференцируема и представима в виде строки Тейлора с неотрицательными коэф-
коэффициентами, сходящейся внутри круга с центром в точке 0 радиуса г.
Таким образом, условие, необходимое и достаточное для того, чтобы
функция f (х) была аналитической в промежутке @, г) и регулярной
внутри круга радиуса г, состоит в том, что в промежутке @, г) f(x)
есть разность двух абсолютно монотонных функций.
Из сказанного видно, что аналитические функции вещественной пере-
переменной представляют собой весьма частный класс функций с ограничен-
ограниченной вариацией, логически естественно возникающий из требования огра-
ограниченности вариации для каждой из последовательных производных.
С этой новой точки зрения абсолютно монотонные функции являются
простейшим объектом исследования теорий аналитических функций в дей-
действительной области, причем возможность продолжения абсолютно моно-
монотонной функции в положительном направлении определяется требованием
неотрицательности всех ее производных. Дальнейшее продолжение для
х^>г становится невозможным либо тогда, когда сама функция / (х)
или одна из ее производных становится бесконечной, либо если радиус
сходимости строки Тейлора в точке г равен нулю. В последнем случае
абсолютно монотопная функция / (х) осуществляет суммирование расходя-
расходящегося ряда Тейлора, соответствующего особой точке г, на некотором
промежутке слева. Эта задача весьма близка к упомянутой вначале
проблеме моментов, занимавшей Чебышева.
По существу она эквивалентна последней, когда промежуток абсолют-
абсолютной монотонности простирается влево до — оо. Действительно, можно
показать, что всякая функция f (х), абсолютно монотонная до — оо, выра-
выражается интегралом
358

f(x) = \et*dW(Q,
О
где W (С) — произвольная монотонная функция. Таким образом, например,
в точке х = 0 функция / (х) и ее последовательные производные совпа-
совпадают с соответствующими моментами:
о
и задача моментов, состоящая в определении монотонной функции
равнозначна определению абсолютно монотонной функции / (х). Неравенствам
Чебышева при условии, что заданы первые п -\- 1 моментов (к = 0, ... > п),
устанавливающим пределы, между которыми должна находиться раз-
разность W (b)—W (а) (Ь^>а^>0), соответствуют неравенства, которым под-
подчиняется абсолютно монотонная функция / (х) при всех значениях х,
если заданы ее значение и значения п ее последовательных производных
в некоторой точке. Экстремальные значения абсолютно монотонной функ-
функции осуществляются при этом соответствующими конечными экспоненци-
экспоненциальными полиномами
Например, функция ех из всех абсолютно монотонных от — оо до + ^
функций f(x), удовлетворяющих условию / @) = /' @) = 1, при всех х
получает наименьшее значение, m. e. f (x) ^> ех, так что абсолютно моно-
монотонная функция, совпадающая с е* еще в одной точке, тождественно
равна вх.
Весьма важным является вопрос единственности в проблеме моментов,
который в нашей трактовке соответствует вопросу об однозначной опре-
определенности абсолютно монотонной функции по ее значениям и значениям
всех ее производных в заданной точке. Не останавливаясь на формулировке
относящихся сюда общих результатов, упомянем о связи этого вопроса с
теорией квазианалитических функций. При этом следует, однако, обратить
внимание на то, что, в то время как при суммировании расходящихся
степенных рядов квазианалитическими функциями квазианалитичность
имеет место во всем промежутке суммирования, здесь, на всем проме-
промежутке суммирования, за исключением единственной особой точки 0, функ-
функция должна быть аналитической и вдобавок абсолютно монотонной, но
рост последовательных производных в этой особой точке, в противопо-
противоположность условию квазианалитичности, ничем не ограничен. Условия,
налагаемые на последовательные производные /<п> @) и вытекающие из
абсолютной монотонности до —оо функции f(x), весьма ограничительны;
они естественно ослабляются, если промежуток конечен, и тем слабее,
чем меньше промежуток абсолютной монотонности. Решениями соответ-
соответствующих экстремальных задач для функций, абсолютно монотонных
в конечном промежутке и удовлетворяющих конечному числу условий
359

(например, если заданы в определенной точке значения функции и п се
последовательных производных), являются в данном случае вместо упо-
упомянутых экспоненциальных полиномов соответствующие обыкновенные
алгебраические многочлены с положительными коэффициентами. ¦
§ 8. Упомянем еще о следующем обобщении абсолютной монотонности
функций, которое приводит к интересному классу аналитических функ-
функций, а именно классу регулярно монотонных функций. Если вместо то-
того, чтобы требовать неотрицательности всех производных в данном
интервале, мы потребуем лишь, чтобы ни одна из производных не меня-
меняла знак (заметим, что здесь также нет надобности предполагать суще-
существование производных и достаточно подчинить тому же условию после-
последовательные конечные разности), то такая функция также оказывается
аналитической в рассматриваемом промежутке и регулярной по меньшей
мере внутри круга, имеющего данный отрезок своим диаметром. Такие
функции мы называем регулярно монотонными, и здесь я хотел бы
остановиться лишь на одном типе регулярно монотонных функций, в
котором чередование знаков последовательных производных в некотором
промежутке совпадает с чередованием знаков последовательных произ-
производных sin я на отрезке 10, -^-1 , т. о. положительные и отрицательные
производные чередуются группами по две. Этот специальный класс ре-
регулярно монотонных функций, который назовем циклически монотоннымиу
замечателен тем, что все эти функции оказываются целыми трансцен-
трансцендентными функциями экспоненциального типа конечной степени, о кото-
которых мы говорили раньше. В частности, циклическая монотонность в
промежутке длины у влечет за собой следствие, что функция — не вы-
выше первой степени. И, с другой стороны, всякая функция первой степе-
степени пред ставима в виде разности между двумя циклически монотонными
функциями в любом промежутке длины <С у > но не может быть пред-
представлена с таком виде в промежутке, большем 4г .
Область мыслимых математических функций неизмеримо обширнее
конкретных функций, встречающихся в действительности, и одной из
труднейших и важнейших задач теории функций является .выбор путеГ
водной нити, обеспечивающей прочную связь между абстрактным миром
математики и естествознанием. Все изложенные выше исследования про-
проникнуты этим стремлением, и то обстоятельство, что рассмотренные
выше классы функций являются естественным обобщением важнейших
элементарных функций, служит, как мне кажется, залогом плодотвор-
плодотворности их изучения.
В заключение считаю не лишним указать, что все идеи и основные
результаты, о которых шла" речь, являются почти целиком достижениям^
рурской, и советской математической мысли*.
См. также мою статью B46*) (Автор.)

83
О НАИЛУЧШЕМ ПРИБЛИЖЕНИИ ФУНКЦИЙ \ | у \€№ (а)
НА ОТРЕЗКЕ [-1, +1]*
Автор применяет свой метод определения асимптотического значения наилучшего
приближения функций, имеющих данную особенность на рассматриваемом отрезке,
оо
к функциям вида \ | у |s с?ф (s).
о
!• В настоящей статье метод исследования наилучшего приближения
| у js на отрезке [ —1, +1] при помощи многочленов высокой степени п,
изложенный в монографии «Э. П.», распространяется на функции вида
y\sdb{s), A)
где ф ($) — данная функция ограниченной вариации.
При этом нужно, чтобы существовала такая определенная постоянная
А ^> 0, что
А. У а (у)]
Е [f (у)] •' 4» (А)
где
А
?). (Ibis)
Таким образом, в дальнейшем, при выводе асимптотических формул для
наилучшего приближения мы- можек ограничиться рассмотрением "функ-
"функций вида (Ibis).
Этому условию удовлетворяет, например, функция
* Изв. АН СССР, серия матем., 10 A946), стр. 185—196 B31*).
36!

эгде а>>0, Ь>0, когда \п\у\<^Ь (что, в частности, выполнено на отрез-
отрезке — 1<у< + 1).
Действительно,
2 [\ у |2s e2b(a-s) «fc = '^"'.^Г , C)
J ' ^ Ъ — In I/ '
a
где Л>а; но из классических теорем следует, что порядок наилучшего
Ы2А г \у\2а
приближения , _ .—г выше порядка наилучшего приближения _^tг i •
Ниже приближение функции B) будет подробно исследовано.
Кроме того, функцию ^ (s) подчиним условиям:
при м>0 близком к нулю, где a > 0 — какое-нибудь определенное число;
•существует такое значение р^-о"» чт0
En[f(y)]>e-»e (С)
для достаточно больших значений п.
Воспользуемся соотношением [«Э. П.», стр. 98, формула D8)]
-*)• - Рп,s&=^Т
где Тп (х) — многочлен Чебышева степени п, а Рп> s (х) — соответствующий
интерполяционный многочлен.
Делая замену
1 _ х = 2у2
и полагая пг = 2п, преобразуем формулу D) [учитывая, что Тп A — 2у2) =
= (— 1)пТт (у)] к виду
где ^,3 B/) = ^«,3 A — 2у2) — четный многочлен степени т относительно у.
Умножая обе части равенства Df) на dty (s) и интегрируя ло $ от О
до Л, получаем
ТС
362
E)

ТУ* i \
где Qm {у) = \ т'* dty ($) — многочлен степени т по у, a G (у) обо-
J 2
о
значает соответствующий двойной интеграл.
При достаточно больших значениях п G (у) имеет смысл в силу
условия (В).
Для вычисления асимптотического значения G (у) произведехМ замену
переменных
z + }Л2 — 1 = а;
тогда
откуда
^ 2/2 sin та (а + 1)
^ 2/ sin та (а + 1) f^y^ (,)rfc
=4 ^-^ ту- , F)
и применим формулу [«Э. П.», стр. 92, формула C7)] (см. также [8]г
том J, стр. 141)
F (z) Г {z) dz~2-&\ e «"> J? (а + -J-) d», G)
О
которая имеет место при условиях:
1) j | F (z) cph (z)| dz имеет смысл при достаточно большом А;
а
2) существует некоторый определенный произвольно малый интервал
(а, а + а), где <р (z) и ее производные первых двух порядков ограни-
ограничены и, кроме того, ?(z)>0, cp'(z)<0;
3) вне промежутка (а, а + а)
4) существует значение р<С"зг такое, что
оо ф'(в)
прж п достаточно большом.
В данном случае ср (а) = —, и первые три условия всегда выполня-
\, так как
363

Тогда (т = 2п)
оо оо _Ф'A)
G(j,) = $<p»(a)F(a)da~-?^
1
1 т*у-
при условиях (В) и (G).
Отсюда, обозначая, вообще, через рт (/(?/)) разность между функцией
/ (у) и ее интерполяционным многочленом степени т, соответствующим
2к 4- 1
узлам xjc = cos ~2 те (А = 0, ... , т — 1) ихт = 0, получаем при сделан-
сделанных выше предположениях (А), (В) и (С) асимптотическое выражение для E):
о
оо
[\\У № (*)) =
о о
JLT-(у)
9 _ / U
У ф —
где
А
Ф (в) =
О
2. Приложим полученный результат к функции B). Как уже указы-
указывалось, условие (А) здесь выполнено и^ следовательно, достаточно найти
асимптотическое значение наилучшего приближения для функции C).
В этом случае
а
Ф (^) = -4FT^T [(IJ" ' (« cqs ъа + 2k sin .га) -
_ (?УА~1 (те cos тг^ + 2Л sin тгЛ) в2>ь(«-
причем последнее равенство справедливо, когда к = Ъ — lnf—)
оо
Разобьем ^ в формуле (9) на два слагаемых
о
оо 2 Ы m
-S + 5 •
О 2 In m
364

и
Подставляя значение Ф ( — ] из формулы A0) и полагая т достаточно
и
2
большим, чтобы и2"-1 <е 2 при гг>21пт, находим для второго сла-
слагаемого оценку
1 ? и \м—х. 1
-г- \ — e~udu
It
oo — -—
2
л п р 2 л7/ о
<_L V е м_Дц = _?_. (И)
2 In m
2 in m
Пользуясь для вычисления первого слагаемого j формулой A0')
о
1
и учитывая, что, как сейчас увидим, порядок его ниже ——, получаем
/ 7 \ (-1)"8
Рт 12 J I У 1* б2Ь(а"° d5 ) ~ тгт ^m Ы X
2 In m(
^ т
4 a
J
+ 2к sin тга) — ( — ) Gт cos 7тЛ + 2к sin 7т^
X
^ т22/2
2 In m / и \2o-i
1
i-i С77 cos 7ra
DА2
Предположим сначала, что а — нецелое число: a>[a]^0. Тогда имеем
2 lnm
7т cos 7щ -{- 2к sin 7ra 7
2 1П 771 / ^ , \
С „2a-i sin тта --- ctg тта + Л
= ) J, ^^ ^ зт—^dB.
2 In тп 2 lnm
С ц а~~ sin 7га с?ц sin7ia у ц20" ^ц
^ /pw_l ^—и\Л л_ и2 \ ^ ~ 2 lnm *3 /_м , о—п\(а , ц2 "\ '
о Vе -г е ] ut -3-2" о Vе "г в Л х "г _2..2
так как >1 за исключением промежутка @, (-, ) j, при любом
с>1, в котором
In w
e-i йи =
2а (In mJac
365

Таким образом,
Сравнивая эту формулу с соответствующей формулой для р (| у \ы)
[«Э. П.», стр. 100, формула E5)], заключаем, что асимптотическое значение
I v\2a
наилучшего приближения для функции ¦, —, отличается от асимпто-
тического значения наилучшего приближения функции ] у \2а только чис-
1
ленным множителем ¦ :
Inm
A3)
Если а^>0 — целое число: а = [а]^>0, то, применяя то же вычисле-
вычисление, находим
оо
1у12° У , 2 т (Л f ига~1 du
так как re cos na -f- 2k sin тга = Ч- ти.
Таким образом, в этом случае порядок наилучшего приближения
3. В случае а = 0 условие (В) соблюдено, и, так как попрежнему
оо 2 Inm
выше порядка j , находим (га = 2п)
2 1П 77? О
2 In m
2 Inm
Разбивая \ на два слагаемых
In m- с
5 -S+ S ¦
2 In m • а 2 In m
0 0 а
замечаем, что
2 In m
если а ^ — , где г ->0 при m -> ос.
366

В самом деле,
2 in m 2 In m
du 1 1
2w (In m—In uJ 2 In m — In и
ос
11 11
2 In m
2 lnm— lnlnm—In2 2 lnm — In a
— In a + In In m + In 2 ^ — In a + In In m + In 2 __ / 1 \
2(lnm— lnlnm — In2)(lnm— lna) v 2lnw(lnw — lnlnm—In2) \lnm)r
так как In — = о (In m).
Таким образом, полагая &~т\ zr, имеем
_ ln| у
Г ^~ +-??, A4)
J (^+ O(l + 7^-) и dnm-l
где вт(т/)^гт при | г/1 <; 1 равномерно стремится к нулю при ш—>оо.
Обозначая через Ёт [f (у)] наилучшее приближение функции / (у) в
промежутке (—1, +1) при помощи многочленов степени т, обращаю-
обращающихся в нуль при у = 0, заключаем непосредственно из формулы A4)г
что
1
4L !,
|_& — ln| у
(in m)a
du
In m
L.
(nmJ lnm *
G другой стороны, применяя обобщенную теорему Балле Пуссена, легко
проверить, что
где г' —>0 при т->ос. Действительно,
m'y*
l
(In m)'
du
367

где 0 <; щ <С Пп ^2 . Таким образом, множитель при Тт (у) равняется
1 , *т(У)
In т ~ ]п т '
1
т In m
где от (?/)-> О, когда j у \ > —= ¦. Следовательно, по формуле A4)
( 1 \ 1
разность рт(г—г-j—г) получает асимптотически значение с после-
т . , кп
довательно чередующимися знаками в -^ + 1 точках ук = cos — , где
Tm(cos—^-) = (—l)fe, к = 0, 1, . . . , -^ 1, и в точке у _ = —= , так
п\ т j x J ' 2 ' ^ J^_ m In m '
2
как в последней точке
( 1 \ __
тт: —
cos m arc cos —-л = cos m[-^ arc sin
m\mlnmy m\nm \2 mlnm
m m m
= (— 1) 2 cos m arc sin—p— ~ (— 1) 2 cos-^^— ~ (— 1) 2 .
4 7 m In m ч ; In /тг v y
Отсюда следует A6), а из A5) и A6) заключаем, что
Формулу A4) можно также использовать для определения асимптоти-
т—-,—j—г . Для этого заметим сначала, что вслед-
о — m | у I j
ствие легко проверяемого неравенства [«Э. П.», стр. 61]
Мы покажем, что в данном случае асимптотически справедливо и обрат-
обратное неравенство, так что
Для этого, делая подстановку у2 = —^—, замечаем, что (т = 2п)
[11 Г 1 Л
1 __ 2 JJ =
__ ? = ^ цд\
[A + 2а2J — 1] . [1 + 2а2 + УA+ 2а2J—1]п 2а2 (а2 + 1) [а + У"а2+ 1]т ' К '
Но наилучшее приближение т—j—j—г асимптотически равно, вследствие
формулы A4), наилучшему приближению
а
2Тт(у)\. г-**
0
368

которое не больше, чем 'интеграл от наилучшего приближения подинтег-
ральной функции; но вследствие формулы A9)
Em
—Т —i
так как | и \ <^ тт ^—>0. Окончательно получаем, что интеграл от наи-
наилучшего приближения подинтегральной функции асимптотически равен
Г du
J (e« 4- e~u) (In m — In иJ
Следовательно, асимптотически
Ет \Ъ — In | у | J
2\пт '
Таким образом, равенство A8) доказано.
Делая замену переменных у = ~ , мы получим приближенный много-
многочлен степени т относительно х на отрезке [— X, + X] для функции
, подставляя -^- вместо у в соответствующий приближенный
Ь— In —
А
многочлен для функции г———j—- на отрезке [—1, +1]. Отсюда сле-
следует, что наилучшее приближение на любом отрезке [— X, + X] для
функции г—-—j—- , где \<^еъ, также асимптотически равно -^ .
И вообще Ет г—=—j—г-; а, [3 — наилучшее приближение функции
la — in | у | J
r^Ti—j—г на отрезке [а, р], где р^>О>а и Ъ — 1п|г/|>>0 — асимптоти-
1
чески равняется -=-. .
г 2 In m
Полагая у2 = х, находим, что наилучшее приближение Еп 2Ь—-Ых
в промежутке @, 1) равняется m , откуда
Длина промежутка, так же как и в предыдущем случае, не играет роли
(лишь бы он не включал других особых точек рассматриваемой функции).
Переходя к периодическим функциям и обозначая через En[f(®)\
24 С. Н. Бернштейн 369

наилучшее приближение / F) при помощи тригонометрической суммы по-
порядка п, выводим отсюда, что [Ь^>Ы(а + 1)]
?п\ т ;—; е г ~гп—» если !af<<l
[_ Ъ — In | cos 0 — а | J 2 In n ' ¦ ' ^
и
Е*\ 1 1 L.
?ju [Ъ - In | cos 0 — 1 | J 4 In n '
Напротив, как известно, Еп убывает в геометрической прогрессии при
а^>1, так как In | cos б — а\ регулярна тогда при всех вещественных 6.
Поступило
13. II 1946 г.

84
О НАИЛУЧШЕМ ПРИБЛИЖЕНИИ НЕПРЕРЫВНЫХ
ФУНКЦИЙ НА ВСЕЙ ВЕЩЕСТВЕННОЙ ОСИ ПРИ
ПОМОЩИ ЦЕЛЫХ ФУНКЦИЙ ДАННОЙ СТЕПЕНИ*
1. Целые функции
называются функциями конечной степени р (или не выше р), если
к
lim х' | ак | <; р.
В работе (х) я показал, что для всякой ограниченной на всей оси
функции f(x) существует функция Sp(x), наименее уклоняющаяся от
/ (х) на всей оси, определяемая свойством, что из множества всех функ-
функций степени р она осуществляет минимум
sup \f(x)-Sp (x)\=Apf(x).
Из этой работы видно также, что теория наилучшего приближения
при помощи функций конечной степени является необходимым дополне-
дополнением и развитием теории наилучшего приближения посредством много-
многочленов. Предлагаемые заметки имеют целью установить некоторые новые
результаты в [этом направлении, которые отчасти были изложены мною
в ноябре 1944 г. в семинаре по конструктивной теории функций в МГУ.
Докажем прежде всего следующую теорему.
Теорема I. Для того чтобы ограниченная функция f (x) была равно-
равномерно непрерывна на всей вещественной оси, достаточно и необходимо,
чтобы Apf (х) стремилось к нулю при возрастании р.
* Настоящая статья [84] представляет собой соединение пяти заметок, опублико-
опубликованных в Докл. АН СССР за 1946 год: I. 51, № 5, стр. 327—330 B32*); II. 51, № 7,
стр. 485-488 B33*); III. 52, № 7, стр. 565-568 B34*); IV. 54, № 2, стр. 103-108
B37*); V. 54, № 6, стр. 479—482 B39*).
371 24

В самом деле, из |Sp (х) |<М, |/ (ж) — ?р (ж) | < Ар следует, благо-
благодаря основной теореме [22] (том I) о максимуме производной функций
степени /?, что
\f(x + h)—f(x) \<2АР + \SP (x + h)~Sp (х) \<2АР + pMh.
Таким образом, максимум колебания со (8) функции / (х) на любом
промежутке длины 8 удовлетворяет неравенству
о) (8) < 2АР + г, A)
если 8 < —щг , а потому из Ар -> 0 следует, что <о (8) равномерно стре-
стремится к нулю вместе с о.
Напротив, допустим теперь, что ш (8) стремится к нулю вместе с о.
Рассмотрим отрезок [— X, X] и [многочлен Rn (x, X) степени п, наименее
уклоняющийся от / (х) на отрезке [—X, X]. В таком случае /?п(Хг/;Х)
будет многочленом степени п, наименее уклоняющимся от / (Хг/) на от-
отрезке [— 1, 1]. Но, так как, по предположению, \/(х)\<^М,то\ Rn(ky,l)\^2M
при j?/|<;i, и, благодаря неравенствам В. А. Маркова [«Э. П.», стр. 57],
имеем
, , . 2Мпк
где | акл | < ~jp
Полагая р = л/Х, заключаем отсюда, что
ak }
где bktx = —?- удовлетворяет неравенствам
А
ик,\ | ^ y~j у* —и, ¦»-, Z., . . .;. F)
Поэтому многочлены Rn(x;l) при фиксированном р принадлежат к
классу Ср целых функций (степени р), подчиненных неравенствам B).
Обозначая соответственно через Еп [/ (х); X] и Ар [/ (х); X] наилучднее
приближение / (х) на отрезке [— X, X] при помощи многочленов степени
п и посредством функций класса Ср, имеем поэтому
En[f(x)-l]>Ap[f(x);l]. C)
Но Ap[f{x)\\\ при неограниченном возрастании X не может убывать;
следовательно, существует
lim Ар [/ (х); X] = Ар [/ (х); оо],
который не может быть отличен от Ар f (x), так как функция Sp (x),
наименее уклоняющаяся от / (х) на всей оси, также должна принадле-
372

жать к классу Ср (согласно упомянутой выше основной теореме [22]
(том I)). Поэтому из C) следует
En\f(*Y,b]>Apf(x)-*n, D)
где еп -> 0, когда п = \р -> оо.
Остается заметить, что, как известнох, можно указать не зависящую
от со (Ь) постоянную с, при которой
Еп [/ (х); Ц = Еп [/ {Щ; 1] < c<,h (Ц = со) Ш,
где о)х (о) = со (Х8) — максимум колебания функции / (ку), когда у полу-
получает приращение не более о; следовательно, имеем при том же значении
постоянной с
Л/(*)<<
Теорема доказана. Кроме того, особо важное значение имеет неравен-
неравенство D), которое приводит не только к оценке E), но и к соответству-
соответствующей оценке Avf (x) в случае, когда ограниченная функция / (х) диф-
дифференцируема к раз и ее к-я производная f^ (x) имеет на всей оси модуль
непрерывности о)& (8); а именно: так как существует постоянная cjc, при
которой
то имеем также
Для многих функций, как это показано в работе (х), знак неравен-
неравенства в D) может быть в пределе (п -» оо) упразднен, так что, например
E^>0~ любое данное вещественное число),
lim lsEn (\x\s; 1) = lim En (| x \s; X) = Av \ x \s.
n->oo X->oo
Однако в общем случае знак неравенства в D) возможен.
Оставляя общее исследование этого вопроса до другого раза, не-
нетрудно во всяком случае убедиться, что более слабое обратное неравенство
Еп [/ (х); X] < APJ (х) +еп (еп -> 0, п -* оо) (8)
имеет место для любой функции / (х), если рг <^ п/Хе.
* а хк
В самом деле, пусть SVl (х) = V -^ функция степени рь наименее
о
уклоняющаяся от / (х). Тогда, отбрасывая остаток
1 Можно
положить (г
'),
например,
00 a
С = 27Т.
373

мы получим многочлен Рп(%) степени п, и при |#j^X имеем
сг / \ п / \ I | / \ ] ^*- >гд ^ ^у ^ 'S? 1 \.
йрг \х) — ^п\Х)\— \ 9п\-\ [?>) I <. 2л Tj ^ Vfrm 2л\ к )
где />i //?i > 1 сколь угодно близко к 1 при а достаточно большом. По-
Поэтому рп 1_х (х) -> 0, если lep^n = G << 1.
С другой стороны, полезно напомнить, что при помощи другого вари-
варианта рассуждения, которое было применено при доказательстве первой
части теоремы I, я установил еще 20 лет тому назад в монографии B)
«L. S.» (стр. 105—106), что условие сходимости ряда
где рь р2, . . ., ps, • • • — какая-нибудь последовательность бесконечно
возрастающих чисел, является достаточным для того, чтобы функция
f (x) имела непрерывную на всей оси производную k-го порядка /(*) (х) [при
том k-я. производная разности / (&•) — SPl (x) ограничена и равномерно
непрерывна на всей оси].
Таким образом, между Avf (x) и дифференциальными свойствами огра-
ограниченной функции / (х) на всей оси существуют зависимости, совершенно
аналогичные соответствующим зависимостям [между Enf (x) на данном
конечном отрезке и дифференциальными свойствами f (x) на этом
отрезке.
2. Докажем еще другую теорему, устанавливающую, что задача при-
приближения функций посредством функций конечной степени является
естественным обобщением задачи приближения периодической функции
посредством конечных тригонометрических сумм.
Теорема II. Если / (х) имеет период 2тг, то
Apf(x) = E*J(x), (9)
где Еро / (х) означает наилучшее приближение функции f (x) при помощи
конечной тригонометрической суммы р0~го порядка, где р0 — [р] — целая
часть числа р.
Покажем [сначала, что среди функций Sv{x) степени не выше р,
дающих наилучшее приближение Avf (x)} есть по крайней мере одна
периодическая с периодом 2тг. В самом деле, разность
./ (х) —Sv(x + 2/гтг) = / (х + 2/гтг) — Sp (x + 2/гтг)
при любом целом h также не превышает Apf(x). Поэтому при всяком
N целая функция степени р
h=—N
обладает тем же свойством. Но функции Ир># (х) ПРИ соответствующем
подборе возрастающих чисел Лу стремятся к предельной функции Ер (х)
374

степени не выше р, которая также отличается от / (х) не более, чем на
Apf(x), и которая в то же время должна быть периодической с периодом
2тс, так как
Zv,n (х + 2тг) - ZP>N (х) = ш-~ {Sp (х +2 (N +1) те) - Sp (х —2Niz)}
равномерно [вследствие ограниченности |5р(ж)|^1#] стремится к нулю
при iV->oo, а потому при всяком данном х
?р (х + 2тг) - ?р (x) = 0.
Таким образом,
со р0
Ер (х) = "V a* cos Ая -f bk sin Аж = V ak cos Аж + ЬА sin кх + Ь (х), A0)
где, как легко видеть, 8 (ж) = V а/.cosAa: + й/.sin Аж = 0, если р0 = [/?].
Действительно, если бы для какого-нибудь к^>р мы имели а^^О, то
после n-кратного дифференцирования равенства A0) мы получили бы^
о
что невозможно, если п достаточно велико.
Поступило
17. XII 1945 г.
ЦИТИРОВАННАЯ ЛИТЕРАТУРА
1 С. Н. Бернгатейн. Изв. АН СССР, сер. матем., 169—180 A938) [73].
2S. Bernstein. Legons sur les proprietes extremales et la meilleure approxi-
approximation. Paris, 1926 [«L. S.»].
3 H. И. Ахиезер. Лекции по теории аппроксимации. Харьков, 1940; 2-е изд.,
М. — Л., 1947. — Ред.
II
Одной из важнейших теорем теории наилучшего приближения функций
посредством многочленов данной степени является открытое Чебышевым
условие, необходимое и достаточное для того, чтобы многочлен наименее
уклонялся от данной функции в рассматриваемом промежутке. Выведем
здесь аналогичное условие, необходимое и достаточное для того, чтобы
целая функция Sv (x) степени р наименее уклонялась от. данной непре-
непрерывной функции на всей вещественной оси.
Теорема III. Для того чтобы функция Sp (x) была наименее уклоняю-
уклоняющейся от данной непрерывной функции F (х) и L = sup | F (х) — Sp (x) \
представляла наилучшее приближение L= AP[F (x)] функции F (х) при
помощи целых функций конечной степени р, необходимо и достаточно,
375

чтобы для сколь угодно малого s^>0 функция ®р(х) степени р, удов-
удовлетворяющая неравенствам
|<Р„E)|>1, <?v®[*®-Sr®]>0 A)
во всех точках S, где
L-S<[^(?)-JP(S)|<L, B>
не могла быть ограниченной на всей вещественной оси.
В самом деле, если бы существовало такое ег ^ е, что j F (ж) —
— Гр (ж) | <; L' = L — 2е1 << L на всей вещественной оси, где Tv (x) —
целая функция степени р, то функция степени р срр (х) = — (Гр (ж) —
¦— $р (#)) была бы ограничена на всей оси, причем во всех точках 5, где
соблюдается неравенство B), мы имели бы
|?р®|>1, [71p(?)-^p(?)][F(i)-.Sp(?)]>0. (Ibis)
Таким образом доказана достаточность.
С другой стороны, если ограниченная функция ор (х) (] срр (х) \ <Г /Г,
где Н^>1), удовлетворяющая требуемым условиям A), существует, та
1^(9 —[-Ы5) + Ь?р(Е)]|<Ь —X во всех точках 5 при 0<Х<^", а в-
прочих точках | F (х) — [Sp (х) + Хсрр (ж)] |<L — s + X//. Полагая X = от5
получим, что на всей оси | F (х) — [Sv (х) + Хсрр (х)] \ < L — п^—т • Следо-
Следовательно, *УР (л:) — Хсрр (а;) дает меньшее уклонение, чем ^р (а;).
Следствие. Если функция срр (ж) степени /?, удовлетворяющая
нераеенстеам A) <?о всеа; точках ?, г^е достигается абсолютный максимум
F E) — аУр (?) | = L, ке может быть ограничена, то Sv (x) есть функция
степени р, наименее уклоняющаяся от F (х) на всей вещественной оси1
и Av [F (х)] = L.
Аналогичным образом доказывается обобщение теоремы Балле Пуссена
позволяющее ограничивать снизу Av[F(x)].
Будем называть множество точек Sx, S2, . . ., ?n, . . . полным множест-
множеством степени р, если неравенства
невозможны во всех точках ^ Для целой функции срр (х) степени р,
ограниченной на всей вещественной оси.
Теорема IV. Если во всех точках Ik полного множества степени р-
осуществляются неравенства
где F (х) — Тр (х) ограничена на всей оси и Тр (х) — некоторая функция
степени р, то AV[F(x)]^>L.
1 Легко видеть, что в данном случае для единственности наименее уклоняющейся»
функции Sp (х) достаточно, чтобы функция ур (х) не могла быть ограниченной при*
более широком условии: что <рр E) (F (E) —S (%)) >0.
376

В самом деле, если бы Ар [F (х)] = L—е, где s>0, то существовала
бы такая функция Sp (х) степени р, что | F (х) — Sv (х) | <; L — s и, следо-
следовательно, [F(Zk)-Tp(tk)][Sp(h)-Tp(tk)]>O, т. е.
( - if[Sp (h) - Тр (&)] > 0 и | Sp {Ь) - Тр Aк) | > е.
При этом срр (х) — — [Sp (х) —- Тр (х)] является функцией степени р, огра-
ограниченной на всей оси, что противоречит предположению, что множества
точек ?fe является полным степени р.
Из теоремы II (заметка I, стр. 374) заключаем, например, что мно-
множество точек 0, Ч=7С>г±г2тс, . . . является полным любой степени /?<С1,
так как, согласно этой теореме, функцией степени p<Ci, наименее
уклоняющейся от cosx, служит нуль.
Укажем еще другой пример полного множества степени р, вытекающий
из теоремы I, § И гл. III монографии «Э. П.».
Если s (x) + it (sc) есть произвольный многочлен степени выше первой,
все корни которого лежат в нижней полуплоскости, то точки oft, опреде-
определяемые равенствами Ф (ок) — ро^ = Атг — X, где Ф (х) = arg [s (x) -f it (x)]
и X — данная постоянная, а к принимает все целые положительные и
отрицательные значения и нуль, образуют полное множество степени р.
Действительно, если бы /р (ок) (— l)fe^>0, где /р (х) — ограниченная на
всей оси функция степени р, то, вопреки упомянутой выше теореме,
дробь ¦ также была бы ограниченной на всей оси. Отсюда
r ^s2 (х) + г* (х) *
следует, благодаря теореме IV, что для функции
cos(Ф(х) -
V s2 (х) + t2 (х)
которая равна (— 1)к в точках о^ и не превышает единицы по абсолютной
величине на всей оси, функцией степени р; наименее уклоняющейся от нее,
является нуль.
Применим только что полученный результат к определению функции
степени р, наименее уклоняющейся от рациональной дроби
где 6^>0, В и С — произвольные вещественные числа.
Докажем, что
/Т> I Г*™\ о "РЪ
1 I D ~\~ V/ •*> \ О -а /" ТГЛП , ТОЛП /Г*\
uflp I — п j Y~n I — ,-. t o~ f "^ —I— * l л
Положим для этого
2bx
cos Ф = 2-, sin Ф =
Выбирая соответствующим образом постоянные А и л в дроби
Л cos (Ф — рх -+- к) = А 9 , 19-
377

числитель которой — функция степени р, можем приравнять ее рацио-
рациональную дробную часть данной дроби f{x). Тогда
f(x) = A cos (Ф - рх + X) + Sp (х), G)
где Sp (х) — целая функция степени р, которая и будет наименее укло-
уклоняющейся от f(x) вследствие того, что максимум разности f(x)—Sp (x),
равный по модулю А, достигается с соответствующими знаками в точках
8Л полного множества степени р. Для определения постоянных А и X
достаточно приравнять нулю
В + Сх — А [(х2 — Ъ2) cos (рх — X) + 2Ъх sin (рх — Щ при х = ±Ы,
откуда
В = — 2АЪ2е^ъ cos X, СЪ = — 2АЬ*е*>ь sin X.
7 ГЧ
Следовательно, Г^Х= — и
. Fbis)
Дифференцируя равенство G) по 6, получим
-2\* + ъ*г -s*(x) = ^ с05(ф - ^+Х)
Отсюда, применяя теорему IV, получим асимптотическое значение при
р -^ оо наилучшего приближения дроби 2 2 , если учтем, что в точках
Ьк полного множества степени р правая часть равенства (8) обращается в
^ [фь + хь1
и отношение , >0 при р-^оо. Таким образом,
Аъ
Аналогичным образом последовательным дифференцированием получим для
любого целого h > 1
1 ~ f
b*)h\ 2hT (h)
ЬЮ-. (9)
Формула (9) справедлива также для любых вещественных значений
/г, так что, например*,
л ^ Г)Ь
(р->оо).
См. [84.1] и [87]. (Автор.)
378

Из формулы F) заключаем, что если функция / (z) регулярна внутри
оо
полосы z = -±^Ы и J \ f (x ±bi) \ dx -^ M существует, то Ар [/ (х)] <
-.у—-,—, и, следовательно, lim J/Olp [/(#)] <^ е~b.
/-7г6> р-»оо
В самом деле,
1 Т (Ц - *) [/ (и - К) - / (и + Ы)] + Ы [/ (и - &Q + / (и + Ы)]
Л
Поэтому, вследствие F),
. оо
< g С ^^2 1 / (и - Ы) - f {и + fcQ la + &2 1 / (и — 6Q 4- / (м + Ы) |2
^ 1
2n J 262
—oo
С другой стороны, из того, что | аУр (#) | <^ Л/ имеет следствием при
всяком |А>0 \Sp^ (x) \<^Mpk(— oo<^x <i ex?), заключаем также, что
при этом
| Sp {х ± Ы) \ < М 2
Отсюда вытекает следующая теорема*:
р
Если lim ]Л4Р (/ (х)) *= е~ъ, то функция / (х) — аналитическая и
равномерно приближаема посредством функций конечной степени внутри
полосы z = -\-Ы.
В самом деле, по условию / (х) = "У срр (х), где при р^> Ро достаточно
большом | срр (х)! < е~ь', Ь' <С.Ъ ж b'fb сколь угодно близко к единице.
Поэтому, в силу только что сказанного, при любых значениях z — х + Ь"г,
где Ь" << 6', ряд / (z) = V срр (z) равномерно сходится, так как
Поступило
24. I 1946 г.
III
Целые функции вида [s (x) + it (х)] е~1Рх степени /?, где s (x) + it (x) —
целая функция рода нуль (или многочлен), не имеющая корней в верхней
полуплоскости, частный случай которых был нами использован в преды-
предыдущей заметке II для определения наилучшего приближения данной
рациональной функции при помощи функций конечной степени, были
* См. [82], стр. 357, и [89]. (Автор.)
379

введены в моей монографии «L. S.» при доказательстве следующей
теоремы1:
Если функция Fp (х) степени р удоелетеоряет при всех вещественных
значениях х неравенству
+t*(x) , A)
то при всех х имеет место также неравенство
I F{k) И |< | [[* (х) + И И] *-***]<*> |. B)
Эта теорема, которая для случая s (x) + it (x) = L сводится к известной
теореме о максимуме модуля последовательных производных для огра-
ограниченных функций конечной степени, а при р -- 0 содержит, как частный
случай, соответствующую алгебраическую теорему, допускает некоторые
другие приложения.
Следствием из указанной теоремы является следующая
Лемма. Из всякой бесконечной последовательности функций Fv (x)
степени р, удоелетворяюи^их A), можно извлечь бесконечную подпо-
подпоследовательность, которая сходится {равномерно в каждом конечном
отрезке) к некоторой функции F (х). Последняя, по необходимости,
должна также быть целой функцией степени р, удовлетворяющей
неравенствам A) и B) (всякая последовательность Fv(x), сходящаяся
к F (х) на некотором конечном отрезке, сходится к F (х) на всей
плоскости).
Положим
s (х) + it (х) = (х + bi)m F >0, т целое число >0).
В таком случае, полагая, что целая функция F (х) = V -^- степени
о
р удовлетворяет неравенству
т
| F (х) |< (х2 + 6V, C)
заключаем из B), что
I F{k) И К I [(
откуда
| аи |< \Ак | = pkbm
+ к {к - 1) ... (к — т + 1) рк~т, D)
если
( bi)^ J
1 Доказательство в «L. S.» проведено при предположении, что вещественные-
части корней s (x) + it (^) ограничены; кроме того, рассуждение «Э. П.» (стр. 185),
которое при р = 0 распространяло теорему на случай любой четной функции
s2 (х) +*2(#), применимо и при />>0. Н. И. Ахиезер сообщил мне, что ему удалось
доказать эту теорему без всяких ограничений. [См. статью Н. И. Ахиезера «О неко-
некоторых свойствах целых трансцендентных функций экспоненциального типа». Изв..
АН СССР, сер. матем. A946), стр. 411—428].
380

Отметим также вытекающее из D)
Следствие 1. Если для всех вещественных х имеет место C), то для
всех комплексных z = rei(? = x + iy справедливо неравенство
< 2 !^- = (Ь + г)"*". E)
В случае, когда F (х) и s2 (x) + t2 (x) многочлены, из формулированной
выше теоремы выводятся аналогичные B) неравенства для конечного
отрезка. Не останавливаясь здесь на их выводе в общей форме, огра-
ограничимся тем же частным случаем, который мы рассмотрели выше, когда
771
s2 (х) + t2 (х) = (Ь2 + х2J. В этом случае из неравенства
т
I ?п {у) \<(У2 + Ъ*У>
на отрезке [— 1, + 1], где Рп (у) — многочлен степени п, вытекает [84. 2]
I № @) | < | [Тп^т (У) Мт {у) - i^- T'n,_m (у) Nm_, (у)^к) \у=о, F)
где Тп (у) = cos n arc cos г/, л' равно п или и — 1 в зависимости от чет-
четности или нечетности числа п — к, а Мш (у) и Nm—i (у) определяются
тождеством
Мт (у) + iNm^ (у) VT^y^ = {у VT^b* + ib УТ^у~*)т. G)
Из последних неравенств можем получить точные верхние границы
коэффициентов многочлена
Л=0
если известно, что Rn (x) удовлетворяет неравенству
m
" (п>т) (9)
на отрезке [— X, X]. Не производя этих вычислений, заметим только, чтб
вследствие F), каково бы ни было п^> т,
) (Ю)
где Нт (t) — многочлен степени т с ограниченными, зависящими только
от т и b коэффициентами. Таким образом, неравенства A0) совершенно
аналогичны полученным выше неравенствам D). Это обстоятельство
позволяет нам распространить неравенство D) заметки I (стр. 373)
En[f{x); l]^Apf(x)-Sn, A1)
381

где sn—->0, когда п = Хр—>оо9 выведенные там для ограниченных функ-
функций /(#), на случай, когда существует такая постоянная q, что
при х->оо. В самом деле, рассуждая, как в указанном месте, мы видим,
что многочлен Rn(x), наименее уклоняющийся на отрезке [—X, X] от
функции / (я), подчиненной условию A2), должен удовлетворять нера-
неравенству вида (9), а потому коэффициенты его удовлетворяют соответ-
соответствующим неравенствам A0), так что Rn (x) принадлежит классу CVt m
функций степени р с коэффициентами, удовлетворяющими этим неравен-
неравенствам A0), правьте части которых, в случае надобности, мы могли бы
увеличить так, чтобы они превышали правые части неравенств D) (соот-
(соответствующих тем же т, Ь, р). Поэтому, обозначая через Ар, m[f (х); X]
наилучшее приближение функции / (х) на [— X, X] при помощи функций
степени р, принадлежащих классу CVtm, получаем
En[f(x); *\>Ap,m[f(x); X]. A3)
Благодаря указанной выше лемме, из A3) вытекает (И). Из (И)
следует также, что и неравенства E) и F) заметки I (стр. 373) остаются
в силе без предположения об ограниченности функции f(x).
Кроме того, из тех же соображений убеждаемся в правильности сле-
следующего обобщения неравенства A1). Полагая, что / (х) удовлетворяет A2),
обозначим через En[f(x); L', (ах2 + h)q; X] наилучшее приближение функ-
функции f(x) на отрезке [—L, L] при помощи многочленов Rn(x) степени п,
удовлетворяющих на отрезке [— X, X] условию: j Rn (х) | -< {ах2 -f h)q (X ^ L).
В таком случае, каковы бы ни были данные числа <7^>0, а^>0, /г^>0,
имеем
Еп [/ (х)\ L; (ax2 -j- h)q; X] > Apf (x) - sL, A4)
где sL -> 0 при X = п/р >> L -> ос.
Это неравенство замечательно тем, что s^ -»0 независимо от того, как
быстро растет X/L. Благодаря этому справедлива следующая
Теорема V. Если f (х) удовлетворяет условию A2), то
lim Еп [/ Or); L; (ах2 + h)q; X] = Apf (x) (X = 4 ) ' A5>
при условии, что L->oo и L/п достаточно быстро стремится к т/лю.
Замечу, что достаточно рассмотреть случай, когда р= 1, так как / (рх)
удовлетворяет тому же условию A2) и A±[f(x)] = Ар [f (рх)].
Для доказательства теоремы V [после того как установлено нера-
неравенство A4)] достаточно проверить неравенство, обратное A4), где г^-^0
при L—>оо и L/n-^0 (sl<CO).
Иэ теоремы V вытекает условие обратимости неравенства A1), а именно
382

Следствие 2. Если f (x) удовлетворяет условию A2), то условием,
необходимым и достаточным для того, чтобы
lim?n [/(*); п] = А^(х), A6).
п—>оо
является требование, чтобы
En[f(x); L; (ах* + h)q; n]~En[f(x)y n]
при любых п > L -> оо.
Остающуюся часть доказательства теоремы с соответствующим уточ-
уточнением мы выведем в следующей заметке из интерполяционных формул
(указанных в «Э. П.», стр. 195): существует одна и только одна
целая функция F (х) степени <[/?, принимающая в точках (к -\—тг
\ A J
\ J p
произвольно заданные значения А1{, где \А1{ j<; L(k -f 1/2)а> обладающая
свойством, что
lim —— —0 (а << w, m ^? О целое число)
= 0.
Функция, определенная этими условиями, выражается абсолютно схог-
дящимся рядом
А
F (х) = (рх)т cos рх У (— lf+1 . A7)
Эти формулы, полный вывод которых дан при а = 0 в указанном
месте, в общем случае вытекают из следующей леммы, являющейся
следствием из доказанного выше неравенства (о):
Если функция Fv (x) степени не выше р равна нулю в точках
к-\—тг)-~г и Fp(x)/xm->0 при х-^+оо, то Fp(x) = R (x)cospx, где
R (х) — многочлен степени ниже т [в частности, если т = 0, то Fv (x) = 0].
Имея в виду также и другие приложения этих формул, мы отложим,
их рассмотрение до следующей заметки.
Поступило
16. IV 1946 г.
IV
1. Возвращаясь к интерполяционным формулам A7) заметки III, от-
отметим также их вариант, соответствующий случаю, когда значения целой
функцииF(х) степени не выше р заданы в точкахkiz/p (к = 0,4^1,+2, . . .)..
В таком случае, полагая | F (kn/p) U< М (| к |а -f 1),
X
383
A)

и целое число т>сс, имеем
F(x) =F@)^^- + (рх)т sinpx
A) +
ii (кп)т(рх — кк)
+ (F'@) + xR(x))^, B)
где Л (х) = 0 в случае т<^2, а в случае т^2 R (х) — многочлен сте-
степени не выше т — 2, коэффициенты которого являются вполне определен-
определенными линейными однородными функциями значений F @), F' @), . . ., F @).
Формулы A7) заметки III, как и формулы B), могут быть использованы
для построения различных последовательностей тригонометрических сумм
порядка п (степени р)
п
о / \ Х^ кпх , , крх
Sn, v (Х) = 2л аЬ cos -^- + Ьк SID. ~^-
к=0
периода 2nr:Jpy которые при возрастании X = п/р имеют во всей комплекс-
комплексной плоскости пределом заданную функцию F (х) степени р, удовлетво-
удовлетворяющую условию A).
Предположим сначала т = 1 и для определенности будем исходить из
формулы B). Для получения1 соответствующей тригонометрической суммы
Snt p (х) определим ее, пользуясь формулой B), как функцию степени р9
заданную значениями в точках kiz/p, так что
при k=k0(mod2n), где к0 = — (п —-1), . . ., 0, 1, . . ., п и S'n, р@) = F'@).
Следовательно,
1 Интерполяционные тригонометрические полиномы Sn p (х), соответствующие
формуле A7) заметки III, определяемые при а < т = 1 значениями F @) и
F(lh0 1—1—j (—п <^ко^.п), получаются аналогичным образом и выражаются
формулой:
так что SUt р (х — -?-) = 2 а* cos "^" + &^ sin "^ , где az (Z = 0, . . . , и) и
&1 (/ = 1, . . ., п —1) выражаются формулами E) при замене в них F(kn/p) через
—n+1
384

n oo
где
= ± 2 *(¦*), «<=^ 2 *(?
+1 ч ^ y N ^
-n+i
Как нетрудно видеть, разность (— п + 1 <С к0 <J n\ s = + 1, 4-2, . . .)
рх
является величиной порядка ——л— при
— кп)
1, и, следовательно,
стремится равномерно к нулю в промежутке \х\>^ Ln, если —^ >0.
^
Кроме того, при возрастании х возрастание Sn,p (x) (как и F (х)) не выше
Cx*log\x\ (где С не зависит от п). В случае а<<0, ^п.р (х) ограничены.
2. Как известно, Б. М. Левитан (х) построил весьма замечательные
приближенные тригонометрические полиномы SUt v (x), обладающие свой-
свойством, что | Snj р (х) | <; L, если | F (х) \ ^ L на всей оси х [используя
для этого интеграл Фурье, т. е. все значения функции F (х)]. Укажем,
как можно видоизменить применение наших интерполяционных формул
[ценой соответствующего увеличения множества используемых значений
данной функции F (х)], чтобы при любом ос^>0 возрастание приближен-
приближенных тригонометрических сумм было то же, что и данной функции F (х).
При предположении, что2
<max (TV, M\x\*), G)
введем в рассмотрение функцию степени р
F(x(i- тгп)) (теп < 1), (8)
где целое число т = а ~\-о (о > 0).
1 В то время, как эта заметка подготовлялась к печати, Н. И. Ахиезер B) изящ-
изящным образом распространил метод Левитана на случай функций F (х) порядка воз-
возрастания О (хш) для любого целого m^>0.
2 Для упрощения письма при последующих выкладках мы полагаем N = М.
25 С. Н. Бернштейн 385

Ясно, что в таком случае имеем также
| Фп (х) |< max (N, М\х\а). (9)
Построим для функции Фп (х) тригонометрические суммы п-го порядка
Sn, p (х) степени р по значениям
S'n, р @) = Ф'„ @) = A - теп) F' @),
(к = к0 (mod 2л); — ft
и покажем, что в данном случае Sn, р (ж) —> Фп (ж) равномерно внутри все-
всего центрального периода (— niz/p ^ x^ rnz/p), если еп —> 0, a e™ns/log тг —> оо
и s^+1 л -> оо.
В самом деле, вследствие F) находим [первые три суммы соответствуют
членам *УП> р (ж), четвертая —Фп (ж)], что
п—1 оо
4М у 1 4Л/
ОО П—1 / т ^
______ у 1 Л/ у / J__ ^о
pa7is+1em &S+1 (Л п) 2»х7г8~1?тл \ &s w — Л
м Мп2~8 гм A + log л)
где Сх и С2 — не зависящие от п и е„ постоянные. С другой стороны,
\Фп(х)-Р(х)\ ^\H>n(x)—F(x(l-msn))\+ \F(x{l—msn)) - F (х)
^ l). A1)
Поэтому, принимая во внимание («Э. П.», стр. 171), что
заключаем из A0) и (И), что SUt v(x) — F (х) стремится равномерно к нулю
при \x\<^Ln, если вп L1nhcc->0. Таким образом, полагая, например,
log п _
?™ = ^=5"'» где Тп~^0, прячем в случае а>>0 т = [а] + 1, а в случае
a = 0 целое число т ^> 0 произвольно, видим, что равномерная сходи-
сходимость соответствующих полиномов *Sn, р (ж) к F (ж) обеспечена при | х К ЬПт
если L™ = о (ftm~a/log ft).
386

Сз^щественно также заметить, что при т четном F (х) ^ 0 влечет за
собой Фп(^)^0, поэтому полиномы Sn р(х) =—^^—к-п—— >0.
*+^
Следовательно, имеет место
Лемма 1. Конструированные указанным выше методом интерполя-
интерполяционные тригонометрические суммы порядка п периода 2mz/p S*nj p (х) схо-
сходятся к функции F (х) степени р, удовлетворяющей условию
| F (г) |< max (iV, M\x\a), G)
равномерно при \ х | <С Ln —> со, удовлетворяя на всей оси тому же усло-
условию G); при этом, если F(x)^0, то Sni р (х) ^>0.
3. Обозначим через EnjV[f(x); L\ R (х)] наилучшее приближение / (х)
на отрезке [— L, L] npw помощи тригонометрических полиномов ^п> р (х)
периода 2Ьг/ ^> 2L ()* = ^г//?) порядка лг (степени р), подчиненных при всех
х условию
|Sn, р (х) |<Л (ж)<sa (я) + ^ (г), A2)
где s2 (x) -\-12 (x) — четная монотонно возрастающая целая функция нуле-
нулевого рода. Очевидно, что
Emn\f{x)\ L; R(x)]^Ap\f(x); L; R (x)], A3)
где Av [f (л); L\ R(x)] означает наилучшее приближение f (x) на том же
отрезке [— L, L] при помощи целых функций Fp (x) степени /?, подчи-
подчиненных тому же условию A2).
Положим, что
R(x)>\f(x)\ + Apf(x). A4)
В таком случае
Av\f{x); L; R (х)] < Apf (x),
так как целая функция F (х) степени р, для которой \ F (х) ¦— / {х) | <С Avf (x)
на всей оси, удовлетворяет требуемому условию A2) и Ap\f (x)\ L\ R (х)]9
не убывая с возрастанием L, имеет, благодаря лемме заметки III (стр. 380),
пределом Avf (x). Поэтому из A3) следует
Ent Р [/ (х); L; R (х)] > Avf (x) - sL, A5)
где sL->0 при mzjp^> L-> oo.
Полагая, что данная функция / (х) подчиняется условию
1/И
г<оо, A6)
мы можем применить к функции Fv (x) степени р, осуществляющей ее
наилучшее приближение на всей оси Apf (х), выше установленную лемму 1.
Следовательно, имеем также
< р [/ (х); L; R (х)] < Avf (х) + $п, A7)
387 25*

где [Зп^0, если L/n достаточно быстро стремится к нулю. Из A5) и A7)
вытекает
Теорема Vbis. Если f (x) удовлетворяет условию A6) и
| / (х) | + Apf (x) <R(x)< s2 (x) + t* (z), A8)
s2 (x) + t2 (x) — данная четная неубывающая функция нулевого рода, то
Urn ЕтПш р [/ И; U R (х)] - Avf (x) A9)
L->oo
л/ш L/тг, достаточно быстро стремящемся к нулю (например, Ьш =
= о (nm~a/log п), где т=[а] + 1).
В случае а = 0 получаем (вследствие теоремы I заметки I)
Следствие. Для того чтобы функция f (x) была ограничена и равно-
равномерно непрерывна на всей оси, необходимо и достаточно, чтобы суще-
существовали такие ограниченные в совокупности тригонометрические суммы
+ Ь Sln
Sn, Vn (Х) == 2 а*, Рп C0S
а именно: как бы мало ни было данное число е ^> 0 и каково бы ни
было L>0, существуют Р(е) и п, удовлетворяющие условию, что
|/ (х) — Sn, vn (х) \<^г на отрезке [— L, L], причем рп<^Р (е). Кроме
того, если существует Р = lim рп> то f (x) — целая функция степени
не выше Р.
Из теоремы Vbis, являющейся несколько обобщенным аналогом тео-
теоремы V заметки III, мы получим последнюю благодаря следующей лемме.
Лемма 2. Какова бы ни была четная монотонная функция * R (х) и
данное число 0 @ < G <^ 1), имеют место неравенства
К, v U (*); 8?; R (*)] < Еп Г/ (х); и R (х)9 -^-1 + eLf п,
/N91 B0)
/ (х); GL; 2Л (-^- ^) ; у ] < < р [/ (^); ^; R (х)] + eLf n,
где еь, п-^0, если L/^г достаточно быстро стремится к нулю. (В част-
частности, если R (х) = О (| х |а + 1), то еЬ}П = О (L2+a/n).)
В самом деле, полагая для краткости р = 1, обозначим через Рп (х)
многочлен степени п, осуществляющий приближение
\f(x)-Pn(x)\t?En[f(x); L\ R (x); n] (-
и | Рп (х) | <;R (х) при —п^х^п. В таком случае тригонометрический
полином SUf х (х) = Рп I n sin —) удовлетворяет неравенству
Snti(x)\KR(nsin —) <R (x) B1)
В этой лемме никаких иных ограничений на JR (х) не налагается. (Автор.)
388

при всех х. Кроме того, при \х\
х — п sin
max
откуда следует первое из неравенств B0).
Для доказательства второго неравенства B0) положим, что Sn,i(x)
п
Si/чу* JfY*
аи cos \- bu sin— осуществляет неравенство
U(x); L; R(x)] (
и | $п, l ix) I ^ -R (x) • Строим многочлен степени не выше 2п
П П
ajc cos 2A; arc sin ——h I/ 1 — т—a ^j *л sin 2& arc sin -^ =
о п о
= 5ft, i B/г arc sin ^ + -|- |/ 1 — ^ — 1J [ 5n, x ^2/г arc sin -^ j —
n, i
2лг arc sin
Следовательно, при | x \
[2—|/ 1— |^Ji?Brcarcsm-|^)<2i? (^ х).
Кроме того, при | х | < GZ,
2п sin -?-
— cos -^
2 cos -
2» sin -^J - P2n+l\- In sin
'In
R[-T-L) =
Из неравенств B0) и теоремы V bis следует
Теорема V (новая формулировка). Если f (x) удовлетворяет A6) и
R(x) удовлетворяет A8), то при L—> оо м L/n—>0, убывающем доста-
достаточно быстро,
lim
; L; 2Л (-|- ж) ; у] = Лр
B2)
Заметим, что данное в A8) ограничение сверху функции R (х) не
может быть существенно ослаблено, так как из общих теорем о взвешенном
389

приближении вытекает, что при L—> о© и достаточно быстром убы-
убывании Ь/п
limEn\f(x); L) ср (х); ос] = О,
если о (х) — четная целая функция первого рода с неотрицательными коэф-
коэффициентами (?@)^>0). Действительно, мы знаем («Э. П.», стр. 147), что
при любом вп >> 0 существует многочлен Рп (х), для которого
\f(x) — Рп (х) | < en? (х) (— оо < х < ос).
Поэтому для каждого Ln можно еп взять достаточно малым, чтобы
?n? (Ln) -> 0, причем | Рп (х) \<i\f(x)\ + enrf (х) < ^р (ж) для всех х.
Поступило
28. V11I 1946 г.
ЦИТИРОВАННАЯ ЛИТЕРАТУРА
1 Б. М. Левитан, Докл. АН СССР, 15, № 4 A937).
2 Н. И. Ахиезер, Докл. АН СССР, 53, № 1 A946).
1. В настоящем сообщении речь будет итти только о функциях
класса
\f(x)\<H(x), A)
где II (х) — некоторая четная целая функция нулевого рода с неотрица-
неотрицательными коэффициентами (Н@)^>0).
Теорема VI. Если целая функция Fv(x) степени р удовлетворяет A),
то можно построить последовательность таких многочленов Рп (х) сте-
степени п, что, каково бы ни было с^>0, при Nc достаточно большом для
всех п^> Nc соблюдается неравенство
\ F (г\ — Р (г\\ <^ р 2 ('— — (\ с\ < г ><Г — (\ —- с\\ (*>\
\rv\Jb) ^n \X) \<^e i - ^i с;-^х<^ ii см. ^;
Заметим сначала, что при любом данном s^>0 имеем1 для
г = | х + iy | достаточно большого
Fv (x ± iy) I < ev (J/-+ ег) (у > о). C)
1 Неравенство C) можно, например, получить из представления (вывод которого
аналогичен рассуждению на стр. 197—198 монографии «Э. П.») всякой целой функции
F (х) степени р, удовлетворяющей A), в виде
^р W = A + **) Н И Uv (х) + Яо (х) cos />*,
где Up(x) — ограниченная на вещественной оси функция степени р, а Яо (х) — функ-
функция нулевой степени, которые однозначно определяются значениями F' (а?) в точ-
ках 0, Ik+A— ив корнях ci уравнения Я (х) = 0.
390

Положим далее, что
ОО
l
v (х) = 2 а, Тк (-1), ah=l\FpQ, cos 6) cos Ав dt, D)
есть разложение Фурье по многочленам Чебышева Т^ ( - )= cos к arc cos -i-
на отрезке [—X, X]. Пользуясь оценкой коэффициентов и остатка, произ-
произведенной в монографии «Э. П.» (стр. 74), находим, полагая
п
Рп (х) = ^ «* ^ (у) , j»X = n(l —с), E)
О ^
что при — /г A — с) <^ /?ж ^ п A — с)
I Л, (ж) - JPn (я) |< ^ , F)
где М = max | ^р (z) | на эллипсе с фокусами Н- X и малой полуосью 8Х.
Принимая во внимание C), можем считать Nc достаточно большим,
чтобы, взяв для определенности 6s = с8''2, иметь при всех n^>Nc.
8
и так как o-f ]/"l + o2>e 3 при всех о>0, то заключаем из F),
полагая о2 = с, что
S8
"• = Г: а . B)
-ncSj-n Г +гA-с)У~Н&\ _^Lc/2 nc /2
Из неравенства B) следует, что
для любых фиксированных q^>p, откуда
lim ?J^(.T); « 1 = 0,
lim tfJ/V-oH^Uo
B bis)
для любых целых функций Fv(x) степени р и Fp__0 (x) степени
класса A).
Следовательно, если / (х) — какая-нибудь функция класса A) и
\f{x) — Fp{z)\^Apf(z), то*
ШЕп\/{х); -^]= Ш En\f{x)-Fv{x)', -^]<Apf(x). G)
По определениго (г ;> 0)
391

Примечание. Если Avf (х) < оо при р^>р0 для некоторой функ-
функции A), то APJ (х)^оо и Apf (x) является не возрастающей функцией р,
которая всегда непрерывна справа [Ap+Of (x) = Apf (x)], так как функ-
функции FVJrZ{x) класса A) при s—>0 имеют пределом функции стенени не
выше /?. Напротив, пределом функций Fp—Z(x) может быть целая функ-
функция степени рг<СР- Поэтому Ap-0 = APl, где рх^р, причем Avf(x)
в случае рх<Ср разрывна слева, сохраняя постоянное значение APlf(x) =
~AP—Of(x) в некотором промежутке. Например, если / (х) = хт cos x -{-
+ cosa;r, где ос>1 и целое число т^>0, то Apf (х) = оо при /?<1,
Apf (х) = 1 при 1 <; р << a, Apf (х) = 0 при р >- а. Таким образом,
из B bis) следует также *
Ш. Еп [/ (х); i] < "П^ ?„ Г/ (х); " 1 < Лр_0 / (ж). G bis)
Лемма. Если существует бесконечная последовательность значений п,
для которой многочлены Rn (х) степени и удовлетворяют A) на отрезке
[— ^n> M» причем lim r^ = р<^ оо, то существует бесконечная подпо-
следовательность значений п, для которой Rn (x) ~> F (х) на всей оси, и
всякая такая предельная функция F (х) есть целая функция степени
не выше /?.
Действительно, i?n(Xn sm~ ), будучи тригонометрическими суммами
порядка п, являются целыми функциями степени рп = — , удовлетворя-
удовлетворяющими A) на всей оси, так как
¦V . X
К sm --
<] xI ; но \Н„ ( К sinr- —
\Rn (ln
i \
— Rn{%) —>0 равномерно на любом данном конечном отрезке (см. за-
заметку IV, стр. 388—389), поэтому наше утверждение вытекает из леммы
заметки III (стр. 380).
2. Теорема VII. Если /(х) удовлетворяет** A), то существуют
limEn\f(x); -?-1 = Apf(x), lim Еп Г/ (х); -^J = A^f(x). (8)
Аналогичным образом определяются lim En /(#); А и lim E \f(x); ~
n->oo L Р—UJ п"^со L -P— -•
mo/?.)
* Для этого достаточно заметить, что при любых ?х > е ]> О
n-^oo L ^ UJ n->oo L ^ — ?J ^ 1
поэтому
lim Еп Г/ (ж); -?- 1 < lim Л / (*) = A f (x). (Автор.)
n-^oo L P UJ ?!->0
** Теорема VII и ее доказательство остаются в силе при более общем предположе-
предположении, что Н (х) > 0 в A) есть четная неубывающая майоранта конечного роста
392

Вследствие G) для доказательства первого из равенств (8) достаточно
проверить*, что при условии A)
] Av f (*) = Л+о f (x). (9)
В случае функций / (x) = О (| x \m -f- 1) это следует из (И) заметки III
(стр. 381). При более общем условии A), применяя только что доказан-
доказанную лемму, где Rn (x) представляют последовательность многочленовт
наименее уклоняющихся от / (х) в промежутках — = Хп (р = lim /?n<j?n) ?
для которой** Еп / (х); — -> lim En \f{x)\ "~Xo|i получаем неравен-
неравенство (9), так как предельная функция F (х) этих многочленов Вп(х)
дает на всей оси \f(x) — F (х) \ <; lim Еп \/(х); —^ 1.
Для доказательства*** второго равенства (8), заметив, что
lim En \f (х); -JL.1 > lim Еп Г/ (ж); ~^
> lim Jim .?„ [/ (x); ^J = lim ?„ [/ (x); ^
(Я (cc) 6^)» так как ПРИ этом справедливы и теорема VI, и только что доказанная
лемма. (Автор.)
* По определению, существование lim En \f(x); ——^ означает равенства
** Существование такой последовательности /г вытекает из следующего: согласна
определению lim En\f(x); ^ , разность
а («) = lim ?„ Г/ (х); -^1 - lim i?n \f (*); -J^l > О
монотонно стремится к нулю вместе с е, так как lim E\f(x)\ монотонно воз-
растает с убыванием е. Поэтому, как бы мало ни было 8>0, можем выбрать г на-
настолько малым, что а (г) <С 8. После этого найдется такое достаточно большое п, чта
Следовательно, полагая рп — р + е, получим
(Автор.)
*** Второе равенство (8) дается и доказывается здесь в той уточненной формег
которая была принята мною в заметке [89]. (Автор.)
393

при s1>e>0, находим, благодаря той же лемме, что
1™ Еп Г/ (х); -^1 > Ига Еп [/ (ж); j]>Apf (х).
Отсюда, вследствие G bis), получаем сначала второе из равенств (8) для
значений р = pi, соответствующих точкам непрерывности, где APlf(x) =
= -4Pl_o / (х), а именно:
lim Еп Г/ (х); -И-.1 = lim ?„ [/ (ж); f 1 = APl f (x) = ^Pl_0 / (x)
n_>oo L Pi u J n~>oo L A J
(Pi — точка непрерывности).
Но всякое значение р является пределом последовательностей точек
непрерывности pi<^P2> • • -^Р^- • • » Р1с~>Р^ Для которых, таким обра-
образом, верны равенства
lim
Следовательно, предельное равенство
верно для всех р.
Следствие 1. Для того чтобы значение р {для данной функции
j (х) € A)) было точкой непрерывности Avf(x), необходимо и доста-
достаточно, чтобы lim Еп / (х); ^_0 | = lim^ / (ж); ^_0 ; в этом случае и
только в этом случае
hm En\f(x); l\=Avf(x). A0)
Действительно, из (8) вытекает, что
> lim i?n [/(*); ^-]>Л/(^)- A0 bis)
Следствие 2. .Ес^гг р—>оо и п-> оо достаточно быстро по сравне-
сравнению с р> то
lim "^'(.f) =1 [/(*NA)]. (И)
Теорема VII существенным образом дополняет * теорему V заметки IV,
а именно:
Следствие 3. Если / (х) и R (х) удовлетворяют A) и |/(#)[ +
+ ^р-о f (%) ^С R (х), я?
Avf (x) < lim ?n Г/ (а;); L; R (х); —1 < Ар_.о / (ж) A2)
L->oo L ^ J
[в точках непрерывности Ap^of(x) = Apf(x)].
* Однако утверждение A2) не равноценно равенству B2) из заметки IV в точ-
точках разрыва Ар f (x). (Автор.)
394

Следствие 4 (обобщение леммы М. Г. Крейна B)). Если функция
степени р класса A), то Fv{x) допускает представление
где s (x) + it (x) степени р/2 не имеет корней в верхней полуплоскости.
В самом деле, многочлены P7i(x)^>0 степени п, которые прибли-
приближают равномерно Fp (х) на отрезке [— л, Ц, где л = —^ , по известной тео-
теореме Маркова — Люкача, допускают представление*
1 n \L) — ll n yb) \ I J- v2 )Y n \ /'
" " ~2~
причем Д2?г (,т) <^ // (x) на этом отрезке [все корни R п (х) + i 1/ 1 — -^ (? я (г)
2 "г" ~2~
лежат в нижней полуплоскости]. Следовательно, согласно выше установлен-
установленной лемме, последовательность многочленов Rn (x) имеет предельную функ-
функцию s (х) степени не выше р/2.
Тригонометрические суммы порядка п, получающиеся из разложения
Фурье D) целой функции Fv(x) класса A) (\=—- при любом q^> p\
\ с\гл Х \ — V ( ^S \п phq 2SX _L л qhl 2S + i I . . оч
также имеют пределом Fv (x) и обладают теми же свойствами, что три-
тригонометрические полиномы Левитана — Ахиезера (х) и интерполяционные
суммы, рассмотренные в моей предыдущей заметке IV. Кроме того, сле-
следует отметить
Следствие 5. Тригонометрические суммы A3) сходятся к Fp(x)
равномерно на всяком отрезке —X (тг — а) ^ х <С X (тг — а) внутри цен-
центрального периода, если Fp (Ч^ оо) == С.
В самом деле, можем принять, не нарушая общности, С = 0. В таком
случае при L достаточно большом и L2/n—>0, как бы мало ни было
s>0, имеем: |/^ (ж) | <^s, \S7liP^()(x)\<^e для любого ж [L<^#<^ (тс-—с)
ittttt \ (*тш +и\ ^^ ПП ^* / 1 ел -1-гГчтг Т л-^~ /v» .-^^* / I О { пп\ Z) I /V» 1 I
ИЛИ — Л ^7Г — О») ^j. X <^. J^\ > d При — JU <^ X <^ L | On, р-|-0 ^/ ^^i \^) \ —
= 0(V/n)<s.
Поступило
З.ХШбг.
ЦИТИРОВАННАЯ ЛИТЕРАТУРА
1 Н. И. Ахиезер. Докл. АН СССР, 54, № 1 A946).
2 М. Г. Крейн. Уч. зап. Куйбышевск. гос. пед. ин-та, 7, 123 A943).
* Эта формула, приписываемая Люкачу (см., например, [42] (том I)), впервые
была выведена А. А. Марковым в литографированном курсе лекций в 1906 г. См.
А. А. Маркова Избранные труды по теории непрерывных дробей и теории функ-
функций, наименее уклоняющихся от нуля. ОГИЗ, 1948, стр. 268—273. Доказательство
Лгокача совершенно отлично и независимо от доказательства А. А. Маркова.
(Автор.)

85
О ВЕРХНЕЙ ГРАНИЦЕ МАКСИМУМА МОДУЛЯ
ПРОИЗВОДНОЙ МОНОТОННОЙ ФУНКЦИИ
КОНЕЧНОЙ СТЕПЕНИ *
1. Пусть ®v(x)— монотонная целая функция степени р. В таком
случае производная ср'р(я)>0 также степени р, и, следовательно, все ее
действительные корня — двойные, а комплексные — попарно сопряженные.
Поэтому 1
гДе /р/2 (х) — целая функция, степень которой равна р/2.
Решим следующую задачу: определить наименьшее уклонение от нуля
на всей действительной оси Ev монотонных функций срр (х), подчиненных
условию, что срр(#0) = 1, где х0 — заданная точка.
Не нарушая общности, можем положить х0 = 0, так как если срр (х)
дает решение задачи в последнем случае, то срр (х + х0) будет соответ-
соответствовать общему случаю. Очевидно, что одновременно с срр (х) тому же
требованию наименьшего уклонения будет удовлетворять и — ?р (— х) и,
тем более, нечетная функция — ^ , которая также будет мо-
нотонна. Следовательно, можем принять, что функция срр (х) — нечетная,
а ее производная ср' (х) есть функция четная, причем, благодаря A),
5/р/2И1а^ B)
* Докл. АН СССР, 51 A946), стр. 567—568 B35*).
1 Представление неотрицательной целой функции <р (х) конечной степени р (как
и многочлена) для всех значений действительной переменной в виде квадрата модуля
некоторой комплексной целой функции (или, что то же самое, в виде суммы
квадратов двух действительных целых функций) лежит в основе моих исследований
об экстремальных свойствах функций на всей оси («L. S.» и «Э. П.»). В весьма
содержательной статье (*) М. Г. Крейн доказал, что достаточным условием такой
представимости (где степень каждого из квадратов конечна и равна р) является
ограниченность функции <р (х) на всей действительной оси [85.1].
396

и, по условию задачи, | /р/2 @) | = 1. Так как ограниченная на всей оси
четная функция /р/2 (х) принадлежит классу L2 и
оо
х)\ ах— срр \оо)у [6)
то, но теореме Палей — Винера ((*), стр. 124), /р/2(#) допускает пред-
представление
+Р/2
/р/2 ix) = \ F (t) cos tx dt, D)
-р/2
где F (t) — функция класса L2 и
+Р/2
—р/2 О
Таким образом, нужно обратить в минимум интеграл
+Р/2
Е
? \ \F()\*d E)
-Р/2
+Р/2
при условии, что /р/2 @) — [ F (t) dt = 1. Принимая, следовательно, во
—Р/2
внимание, что
+Р/2 Г-+Р/2 _,2
р
1
-р/2 -Р/2
и что знак равенства в F) имеет место лишь при F (t) постоянном,
находим
?р=~ G)
и F (t) = 1 / р. Формула G) дает искомое наименьшее уклонение. Кроме
того, из D) получаем
+Р/2
/ (х) — L f cos txdt — ~ sin ^
/Р/2 \X) — p ^ C0S X — px Sm ~2 >
—p/2
а из B) получаем
Если известно, что монотонная функция степени р удовлетворяет на
всей оси условию | срр (х) | <^ М', то из предыдущего следует, что
397

(так как | срр (х) | <^ М означает, что | срр D- ос) | ^ М), и знак равенства
осуществляется при
х
Мр г ( 2 . рх\2 у
о Поступило
24.11946 г.
ЦИТИРОВАННАЯ ЛИТЕРАТУРА
1 М. Г. Крейн. Уч. зап. Куйбышевск. гос. пед. ин-та им. В. В. Куйбышева^
вып. 7, 123 A943).

86
ОБОБЩЕНИЕ ОДНОГО РЕЗУЛЬТАТА
С. М. НИКОЛЬСКОГО*
С. М. Никольский (х) установил при помощи весьма искусных вычи-
вычислений следующий интересный факт: если функция f (х) удовлетворяет
условию Липшица
|/(я + й)-/(*)|<й, (I)
то наилучшее приближение Enf(x) функции / \х) посредством многочлена
степени п на отрезке [— 1, + 1] удовлетворяет неравенству Enf (х) ^ —~ у
причем lim сп = ~ .
п->оэ Z
Так как, благодаря известному результату Ахиезера, Крейна и Фавара,
наилучшее приближение Ё*п f (x) периодических функций класса (I) с пе-
периодом 2тс посредством тригонометрических сумм порядка п удовлетворяет
для любого целого п ^ 0 неравенству Enf (х) ^ —^— , где сп = —, то не-
равенство сп ^ -г- очевидно; поэтому С. М. Никольскому оставалось уста-
новить при помощи построения соответствующих функций класса (I)
невозможность неравенства lim cn<^-x- -
n-^oo Z
Я хочу показать, что результат С. М. Никольского является частным
случаем некоторой общей теоремы, вытекающей из свойс!в наилучшего
приближения Apf(x) посредством целых функций конечной степени р B'3).
Будем говорить, что / (х) принадлежит классу (а), если она удовле-
удовлетворяет условию
i/(* + /*)-/(*)|</*a;
если, кроме того, / (х) — периодическая функция с периодом 2Ьг, то
f(x) класса (ос)* [когда X = 1, пишем (а)* вместо (а)^].
Обозначаем через Еп [/ (х); X] наилучшее приближение / (х) посредством
многочленов степени п на отрезке [—X, X] и через En[f {х)\ 2Хтг] —
Докл. АН СССР, 53, № 7 A946), стр. 587 — 589 B36*)
399

наилучшее приближение периодической функции / (х) с периодом 2>лг
посредством тригонометрических сумм порядка п [когда X = 1, пишем,
соответственно, Еп f (х) и Е*п / (х)].
Заметим сначала, что1
sup Apf(z)=e-&, A)
где с (а) — не зависящая от р постоянная *. Действительно, если / (х) 6 (а),
. f(Px) _A1f(.v)
то tiEp б (а), но
поэтому
sup Ар/(х)=—л sup A±(f).
(х)?(а) /> /(x)ga)
Теорема. Пусть для каждого целого п
sup ?n / (х) = -^-, sup j? / (ж) = -^-a; B)
)^() (Л + If /()g()* (Л + l)a
в таком случае
сп («) < < («) <lim сп («) = lim с; (а) = с (а), C)
П>ОО П>ОО
с (о) = sup Axf (x).
В самом деле, Еп [/ (х), X] = Еп [/(Х#)], поэтому, учитывая, что
— /(Х^N(а), видим, вследствие B), что
А
/(х)^(ог)
Но, согласно неравенству A1) заметки C), при п + 1 =
Яп[/(*), Х]>^р/(^)-8п,
1 Функции / (х), для которой Аг f (х) = sup Аг / (х) = с (а), вообще"может не сущест-
существовать, поскольку последовательности функций класса (а) на всей оси могут не иметь
подпоследовательности, которая равномерно стремится к своей предельной функции
[в отличие от функций класса (а)*].
Утверждение, что с(а)<оо, следует из того, что lim А / (х) — 0 для всякой
р->оо Р
равномерно непрерывной функции (см. B> 3)).
* Применяя A), в случае a = 1 можем получить неравенство
(которое не может быть улучшено). См. [3.6] (том I), стр. 528—529. (Автор )
400

где ^„->0. Следовательно,
V СП (°°) ^ л г / \ С (<Х)
hm —^г~> SUP -4р/И = -1г
т. е. Hm сп(а)^с(а). Принимая во внимание очевидное [вследствие того,
*]то из /(х)б(а) вытекает / (cos x) 6 (а)*] неравенство сп (а) <^с* (а), имеем
тем более
lime» > с (а). E)
С другой стороны, при всяком целом п0 = [X/?] ^ 0 имеем
sup Apf(x)> sup ^;of/(x); 2X^] = f-^-Yc; (а), F)
так как
E*n[f(x); 2Щ=Е*п;(кх).
Поэтому
выбирая кр (при заданном /г0 ^ 0) так, чтобы X/? — п0 было сколь угодно
близко к единице, находим, что (п = 0, 1, 2, ...)
с(а)>с». G)
Сопоставляя E) и G), получаем C).
В частном случае а = 1 мы получаем результат С. М. Никольского,
причем с A) = у, так как известно, что сп A) = у при всяком це-
целом тго;>О.
Интересно было бы определить значение с (а) при всяком а <^ 1: легко
1 1
видеть, что с* (а) = у тга, поэтому с (а) >- у тга.
Поступило
6. VII 1946 г.
ЦИТИРОВАННАЯ ЛИТЕРАТУРА
1 С. М. Никольский Докл. АН СССР, 52, № 1 A946).
2 С. Н. Бернштейн. Докл. АН СССР, 51, № 5 A946) [84], заметка I.
3 С. Н. Бернштейн. Докл. АН СССР, 52, № 7 A946) [84], заметка III.
26 С- н- Бернштейн

87
НОВЫЙ ВЫВОД И ОБОБЩЕНИЕ НЕКОТОРЫХ ФОРМУЛ
НАИЛУЧШЕГО ПРИБЛИЖЕНИЯ*
Укажу несколько примеров приложения теоремы VII моей последней
заметки (х).
1. Как известно B) ([83], стр. 368, формула A9)),
1 \ 1
Е*п\ х2 + а2 ) 2а* (а2 + 1) (а + Уа^ТТJп '
поэтому
откуда (х) получаем одну из формул, непосредственно установленных
в заметке C) ([84], стр. 377, формула F)):
= 2а2 '
2. Чтобы получить асимптотическое значение при р—>оо величины**
для произвольных вещественных чисел Ъ и s, положим X = — и еде-
х2 ^
лаем замену ж2 = у A — ?/), в силу которой
?2П [(аг2 + 6»)»; X] = (|)s ?
С другой стороны, для любого а^>1 имеет место формула (см. D), стр.
95, а также [9], (том I), стр. 143)
*
**
Докл. АН СССР, 54 A946), стр. 667—668 B40*).
Вывод асимптотического равенства; (р-^оэ) для Ap(x2+b2)s при любом веще-
вещественном s изложен здесь подробнее, чем в первоначальном тексте (см. также [84. 1]).
(Автор.)
402

где sn(a)->0 при тг->оо, если а зафиксировано. В интересующем нас
л , 2Ь2 , . Ъ2р2 . г
здесь случае а = 1+^ = 1-{- -—%- стремится к 1 при п -> оо и любом!
фиксированном р и поэтому для проведения предельного перехода тре-
требуется некоторое дополнительное исследование величины вп(а) = г (рг п),
Так как ищется асимптотическое значение величины Ар (х2 + Ь2)8 при*
р—>оо, то достаточно доказать, что е(р, п)—>0 при /?->оо равномерно
относительно всех достаточно больших п. Это доказательство приведено
в [87.1], где для простоты рассмотрен случай —1<^5<;0. Если ука-
указанная равномерность доказана, то при фиксированном р для всех
s—1
}2S (п2__л\ 2
2 V1 1 +
S—1
2 '
и аналогично
,
где s(p)—>0 при /?->оо. Делая в написанных неравенствах предельный
переход д->оо и используя формулу (г) A0 bis) статьи [84] (стр. 394)>
находим
откуда и следует асимптотическое при /?->оо равенство
oshs-l -bV
Ар {х* + Ъ2У ~ ** е . (II)
Теорема. Если непрерывная на всей оси функция / (х) имеет при
х^>Ь равномерно непрерывную производную порядкаk^>0, а при х<^а-^ Ь
— равномерно непрерывную производную порядка 1^0, то Avf (x) <^ ос
при всяком р^>0 и Avf(x)->0 при /?->оо.
В самом деле, замечая, что Ар [/ (х) — R (х)] = Avf (х), гдэ R (х) —
многочлен степени к +1 + 1, определенный условиями, что R^(a)=^'
= /(i) (a) A = 0, ... , I); RW (b) = /@ (b) (i = 0, ..., А), можем принять, что
/ (а) =/' (а) = ... = /^) (а) = / (Ь) = ... = р) (Ь) = 0.
Полагая в таком случае / (х) = /0 (х) + /х (х) + /2 (ж), где /0 (о:) = О
при х<Гб, /х (х) = 0 приа^^; и при х^Ь, /2 (х) = 0 при х^>>а, заклкь
403 26^

чаем, что fo}(x), f±(x) и 1^{х) равномерно непрерывны на всей оси.
Поэтому, согласно E>6), теорема верна для каждой из функций /0 (х),
f1{x), f2(x); следовательно, она справедлива и для их суммы f(x).
3. Будем обозначать через (f(x), cp (х)) непрерывную функцию, равную
f (х) и ср (х), соответственно при х<^0 и х^О. Рассмотрим, в частности,
функцию (а | х ]s, Ъх1). Полошим А± [(а | х |s, bxs)] = ps (a, b) = р8 (b, a) < оо
вследствие E> 6). В таком случае (х)
lim п*Еп (а \ х |я, bx8) = limEn [(a \ x \8, bxs); п] = ^8 (а, Ъ) , A)
п—»оо П—>оо
что представляет некоторое обобщение * и более простой вывод основного
результата [соответствующего jxs A,1) = \is] моей статьи G). Находим так-
также при t^>s^-0
lim п*Еп (а | х |s, Ьж') = lim En [(a \ x ff, Ьп*-*х*); п] = а[г8 A,0) . B)
4. Вследствие выше доказанной теоремы, для любых s>0 и
целых т>0 -4Х (| ж | * (log | ж |)т) = A (s, m)<oo. Таким образом (х),
lim Еп [| х |s (log | х |)m; n] ~ A (s, т). Положим сначала, что s = 2к — чет-
нов целое число. Тогда при
Еп [х* (log | х Н = Еп [(!J*(log | х | - log /i)-; n] =
I
m—1
1=0
поэтому (х)
lim -—г Еп [х2к (log | х | )m] — тА1 [х2к (log Ixl)] — mA BА, 1). C)
n_*oo (log П)
В случае s=f=2k
Поступило
3. X 1946 г.
ЦИТИРОВАННАЯ ЛИТЕРАТУРА
1 С- Н. Бернштейн. Докл. АН СССР, 54, № 6 A946) [84], заметка V.
2 С. Н. Бернштейн. Изв. АН СССР, серия матем., 10, 185 A946) [83].
3 С. Н. Бернштейн. Докл. АН СССР, 51, № 7 A946) [84], заметка II.
4 С. Н. Бери штейн. Экстремальные свойства полиномов A937) [«Э. П.»].
6 С. Н. Бернштейн. Докл. АН СССР, 51, № 5 A946) [84], заметка I.
* С. Н. Бернштейн. Докл. АН СССР, 52, № 7 A946) [84], заметка III.
7 С. Н. Бери штейн. Изв. АН СССР, серия матем. A938), стр. 169—180 [73].
* См. также статью II. И.Ибрагимова в Изв. АН СССР, серия матем., 14 A950),
стр. 405—412. (Автор.)

ДОБАВЛЕНИЕ К РАБОТЕ И. И. ИБРАГИМОВА
«ОБ АСИМПТОТИЧЕСКОМ ЗНАЧЕНИИ НАИЛУЧШЕГО
ПРИБЛИЖЕНИЯ ФУНКЦИИ, ИМЕЮЩЕЙ
ВЕЩЕСТВЕННУЮ ОСОБУЮ ТОЧКУ» *
Применяя соответствующий вычислительный аппарат, И. П. Ибрагимов
получил ** в выше названной работе теорему III:
Если т >>0 — нецелое число и^>0, то
m-l
Как известно, вторая часть равенства (I) представляет Еп [(с — х)т],
где с — а — 1 > 1.
Целью этого добавления является установление вытекающего из общей
теории наилучшего приближения асимптотического равенства
Еп [(с - X)" Ф (х)] ~ | Ф (с) [ Еп [(с - х)т] (Ф (с) =h 0) (И)
при т нецелом (т^О), справедливого для всякой функции Ф (х), регу-
регулярной внутри какого-нибудь эллипса Чебышева, включающего точку с.
Очевидно, что равенство (I) независимо от знака т и s есть частный
случай равенства (II), так как функция
(а — x)s In™ (а — а) =- (а — x)s In™ (I -f с — х) = (с — х)ш Ф (х),
где
, , ч , ч г 1п
ф (х) = (а- ху [
регулярна внутри эллипса, проходящего через точку а = с + 1 и Ф (с) = 1.
* Изв. АН СССР, серия матем., 10 A946), стр. 461—462 B38*).
** И. И. Ибрагимов. Изв. АН СССР, серия матем., 10 A946), стр. 438. (Ред.)
405

Для доказательства асимптотического равенства (II) полагаем
Ф (х) = Ф (с) + (с — х) Фг (ж),
где | Фх (х) | <^ М в эллипсе Dr с погтусуммой осей R ^> р = с -J- ]/с2 — 1.
В таком случае
I #п [(С - х)т Ф (ж)] — | Ф (С) | ?п [(С - Ж) ™] |< Еп [(С - Х)т+1фг (X)] . (III)
Но, при сделанных предположениях, справедливо неравенство
Еп [(с - х)^Ф1 (х)] < (^ + гп) ?п [(с - а)"**], (IV)
где sn -> 0 при гг -> ос.
В самом деле, разлагая Фх (ж) в ряд по многочленам Чебышева,
получаем
где, как известно («Э. П»., стр. 74), \Ак\<^—^ и | оп (х) | <^ д^ .
при — 1 <; х <; 1. Таким образом,
м
Еп [(с - sJ-h-kD, (.г)] < Еп [2^ЛП (х) (с -
Но, принимая во внимание, что | Тк (х) | <^ 1 при —1<^ж<^1, имеем
Еп [(с - ^^П Ml < ?n~7, (с - ж)^1 - : ?\Еп [(с -
гДе ?i^>? может быть взято сколь угодно близким к р (независимо от
n) при п достаточно большом.
Отсюда следует неравенство
Еп [(с - х)т+гф1 {х)] < 2М 2 ^к Еп [(с - х)™) + ~
7с=0
М
еоторое равнозначно (IV).
Таким образом, вследствие (III) и (IV), получаем
Еп [(с - х)" Ф (х)] = | Ф (с) | Еп [{с - х)*\ + О {Еп [{с - х)™+*\),
откуда вытекает (II), благодаря тому, что
Еп [{с — ж)«+1] ~ ^-1 (с2 - iyi*En [(с — х)™} = О ^ Е*1
406

Неравенство (IV), как нетрудно видеть, остается в силе, если заменить
(с — х)т+1 любой функцией Фо (х), для которой
Вообще, каковы бы ни были особенности функции Фо (х) на эллипсе
D9 с суммой полуосей p<^R, существует последовательность возрастаю-
возрастающих значений п, для которых еп—>0 в неравенстве [88.1]
п [Фо (х) Фх (х)] < (^~ + sn) Еп [Фо (х)]. (IV bis)
Поступило
4. III 1946 г.

89
О НАИЛУЧШЕМ ПРИБЛИЖЕНИИ АНАЛИТИЧЕСКИХ
ФУНКЦИЙ ПРИ ПОМОЩИ ЦЕЛЫХ ФУНКЦИЙ
КОНЕЧНОЙ СТЕПЕНИ*
1. В моей заметке (*) доказана следующая основная теорема VII:
Если f(x) удовлетворяет условию
(-оо<><оо), A)
где Н (х) — некоторая четная целая функция нулевого рода, то
\ B)
Я хочу указать еще одно интересное простое следствие этой теоремы.
Напомню известный результат EL И. Ахиезера B):
Если вещественная часть Re / (z) функции комплексной переменной
f (z), регулярной внутри эллипса С с фокусами -\- 1 и — 1 и малой полу-
полуосью Ь, удовлетворяет на С неравенству
C)
то
^ ПП D)
где
т=0
причем неравенство D) не может быть улучшено.
Предположим теперь, полагая 2 = #ЧЬгг/, что регулярность f (z) имеет
место при 0<^у<^Ь и условие C) соблюдается при у = Ь. В таком слу-
случае из неравенства D) следует
О 71/
En [f (х) )Ц=Еп [/ (Щ] < -2fi cp (qn> x), D bis)
* Докл. АН СССР, 56 A947), стр. 891—894 B43*).
408

где дп> х — (-г- + 1/ 1 + тг ) • Таким образом, если X = п / /?, то
)
lim gr} x = epb. Поэтому
Неравенство E) не может быть улучшено.
Для сокращения дальнейших формулировок удобнее будет предполагать
рассматриваемую функцию f(x) ограниченной (—оо<^х<^оо); соответ-
соответствующее изменение формулировок без этого предположения очевидно.
Вследствие E) и результата, установленного в конце моей заметки C),
заключаем, что
Если функция f(x) ограничена, то условие D)
v
lim i/^4 / (х) <С е~ь F)
р—>оо
необходимо и достаточно, чтобы f (z) была ограниченной аналитической
функцией внутри бесконечной полосы z = x Hh ib.
2. Интересно придать этой теореме форму, не зависимую от комплекс-
комплексной переменной.
Теорема 1. Условие F) необходимо и достаточно для того, чтобы
ограниченная (— оо <^ х <^ оо) функция f (x) была бесконечно дифферен-
дифференцируема и чтобы
п
lim max у п\ <х (—оо<ж<оо). G)
Ввиду того, что из F) вытекает равномерная ограниченность | / (х 4h iy) \
при O^y<^bf<^b, для получения G) достаточно воспользоватьсяг клас-
классической формулой Коши.
Для доказательства обратного утверждения мы воспользуемся неравен-
неравенством F)
^> "9~ k ' V°/
которое имеет место при любых к > 0, р^>0 для всякой функции, удов-
удовлетворяющей условию
|/(*> (х) | <Ж* (- оо О < оо). (9>
Но G) означает, что при любом е>0
)" o) (9 bis)
для всех п ^ пг. Поэтому, вследствие (8),
1 Дальше дано чисто вещественное доказательство более общей теоремы 3.
409

и, в частности, полагая pb = п A -f- s), находим, что (для достаточно
больших р) Avf(x)-^e 1+6, откуда следует F).
Следствие. Если f (x) ограничена, то условие
У^Щ A0)
необходимо и достаточно: 1) для того чтобы f (z) было целой функцией,
обладающей свойством, что sup | / (х + iy) | = F (Ь) <^ оо >г/ш — Ь<^у <<
о (—оо<^?<оо), а также 2) для того чтобы
lim max
п—>оо
\/~]f{n)JX)] =0 (-оо<я<оо).
Теорема 2. Для того чтобы /го>1 бьгло верхним пределом значений h,
для которых
l\m[Apf(x)]Wv)h=0, (И)
необходимо и достаточно, чтобы ограниченная функция f (х) была целой1
и чтобы р0 = -т——г- > 1 было нижним пределом значений р, <9лл которых
_ . . =0. A2)
Ь—»-оо
В самом деле, полагая | / (ж) — Gp (ж) | *< Avf (х) = sPAt, из (И) заклю-
заключаем, что (при | / (ж) | <С М)
\f(x± ib) | < 2МёР.ь + 2 2 ej* ep*+*b A < /г < /г0).
Как бы мало ни было 8>0, можем для любого данного Ъ выбрать
н-ь
Ро ^ Ък~х достаточно большим, чтобы р^~гlogеРо + 26 = — сс0<^0. В та-
ь -
ком случае, полагая pjc+1 = 2ръ, видим, что | / (х Hh ib) \ < 2Ме
+ 2Ve ° k; следовательно, lim b~~p log F (b) = 0, если p =s _ .
Наоборот, из A2), где р>ро>1, следует, благодаря E), что при
достаточно больших b ^р/(ж)<ГрЬ+ьР для любого /?>0. Поэтому,
полагая р = 2Ьр~г, имеем, при любых данных N и h<d ^_* , Apf (x)<i
<С е~ = е р—1 <; е р, если только р достаточно велико. Таким обра-
образом, [Apf (x)](llP) <ie~N, откуда следует (И).
1 Таким образом, необходимо, чтобы порядок целой функции / (z) был не выше
410

Этот результат является соответствующим видоизменением и обобще-
обобщением одной теоремы Балле Пуссена (E), стр. 150), относящейся к пе-
периодическим функциям.
Теорема 3. Для того чтобы существовало такое число1 /г^>0, что
\im[Apf (х)]^п = е~п @<ЛГ<оо), A3)
необходимо и достаточно, чтобы ограниченная функция / (х) было беско-
бесконечно дифференцируема и чтобы
Применяя то же рассуждение, что при доказатедьстве теоремы 1, заме-
заметем, что из A4) при произвольно малом s>0 вытекает
для достаточно больших т. Поэтому, полагая т = phN, заключаем, что
откуда lim (Avf (x))Mvr < e~N.
p—*oo
С другой стороны, из A3) следует, что, каково бы ни было число
h
A'<N, полагая pk+1 = A + a) pk, а>0, /„, * = $ e~N'v *,
| /С") (х) |< 2 Мрпй + 2 A + а)п 2 7". *
при достаточно большом р0. Замечая (п = m/г), что все In,k ^[-^т-).
h
г
m
обозначим через р^ = 1/ -^т* величину /?, при которой максимум /n>
достигается, и положим ръ9 = р0 A + а)^ = /?oe1//l. Тогда при к — ко =
/„.< А A + «К""+"' -1,. b(i + О-
1 В отличие от теоремы 2, здесь случай h < 1 также допускается (/г = 1 соответ-
соответствует теореме 1).
411

Поэтому, полагая, при п достаточно больших, па2 — 2, так что
видим, что
при любом N"<^N'. Отсюда следует A4).
Поступило
20. IV 1947 г.
ЦИТИРОВАННАЯ ЛИТЕРАТУРА
1 С Н. Берн штейн. Докл. АН СССР, 54, № 6 A946) [84], заметка V.
2 Н. И. Ахиезер. Лекции по теории аппроксимации функций, 1947.
3 С. Н. Берн штейн. Докл. АН СССР, 51, № 7 A946) [84], заметка II.
4 С. Н. Бернштейн. Изв. АН СССР, серия матем., 4 A945) [82].
5 Gli. de la Vallee Poussin. Lemons sur Г approximation des fonctions conti-
continues, Paris, 1918.
6 С. Н. Бернштсйя. Докл. АН СССР, 57, № 1 A947) [90].

90
О ПРЕДЕЛЬНЫХ ЗАВИСИМОСТЯХ
МЕЖДУ КОНСТАНТАМИ ТЕОРИИ
НАИЛУЧШЕГО ПРИБЛИЖЕНИЯ*
Обозначим через Skja(M) класс функций /(х) действительной перемен-
переменной (—оо <[х<^оо), дифференцируемых к^О раз, причем
| /(*) (x + h) — f] (х) | < Mh* @ < а < 1).
Очевидно, что если/(я)<ЕЗм A)=«?*,«, то Mf{x) GSM (М) и /(Xa5N*Sftf«(X*+«).
Отсюда следует, что fr. / (Хж) 6^>а> т. е. принадлежит тому же классу,
что f(x).
Известно [87] и легко проверить, что если f(x)?Skf(Xi то наилучшее
приближение A1f(x) посредством целых функций первой степени ограни-
ограничено, т. е. существует такая постоянная ск^ что
Из сделанного выше замечания заключаем, что при любом
^ [f(x) GSM {M)]9 A)
так как f[—\ ?SjcJ к^_а ) • Таким образом, в неравенстве (l)cftja не за-
зависит от р. В аналогичных неравенствах (которые можно написать
а priori)
[/()€5(АГ)] (Ibis)
дли наилучшего приближения / (х) многочленами степени п на отрезке
I- 1, 1] и
периодической функции с периодом 2тс тригонометрическими суммами
порядка п(п^>0 целое число) постоянные ск)«)П и с1куЛ}П, напротив, зависят
* Докл. АН СССР, 57 A947), стр. 3-5 B44*).
413

от п. Напомню, что в случае а = 1 AкЛ}П = с*д Г-^—jJ \ где C)
* _ 4
СМ~ тг (
1 = 0
так что limdk)lfn = с*к г. Кроме того, известно A>2), что при к— О
lim rf0HC>n = lim с^^п = сс>а.
n—»oo п—юо
Я хочу показать, что предельное равенство
lim 4}a,n = Hm скHС)П = c^ja B)
справедливо также при любых k^O, 0<^a-^l. Действительно, замечая,
что Enf (х) = ^ / (— ] ; Д и принимая во внимание, что утверждение
/ (^) 6^^^ равноценно (~) /(—) б^,а, из (Ibis) заключаем, что для
всякой функции f(x)dSjc}a имеем при любом п
так что
Л/(«) = I™ #п 1 / («); —Jq- 1 < -^г Птс».,я,„
и, вследствие A),
?fc,a ^Jim сЛ>а>п.
Кроме того, отсюда следует также, что
lim Еп \f(x); -fo-1 < -1*? [/ (») 65fc,J.
Поэтому, как бы мало ни было s>0, для всякой функции f(x)
можем взять п0 достаточно большим, чтобы при всех п^п0 иметь
откуда ск}а)П<(Ск,* + а) A + е)*+*, т. е
Из D) и E) следует второе из равенств B).
Принимая во внимание, что для периодических функций с периодом
2пк/ р
при любом целом п и 0<С8<^1, заключаем, что
п
* Это вытекает из [84] (теорема VI, стр. 390). См. также [91], стр. 417. (Ред.)
414

[полагая du^n = ( , , ) c^an имеем при всяком п даже более сильное
неравенство С?ап<^л,а, которое, однако, нам здесь не понадобится]. Нам
остается показать, что ни при каком данном s^>0 неравенство
— 8 (8).
не возможно для достаточно больших п. В самом деле, пусть для неко-
некоторой фуНКЦИИ / (х)
В таком случае, принимая во внимание, согласно теореме V bis D), что
Km ЕГ [/ (х); L; R (х)] = AJ (х), A0)
если n/L достаточно быстро растет1, подберем периодическую функцию
/i (x) ?>$к,а с периодом 2 пк, которая равна / (х) (с точностью до многочлена
степени к) при — L^x<^L и удовлетворяет, как и / (х), неравенству
(Л (#) I + ^i/ (x) <CR(z)< Если Еп>1 (^) есть тригонометрическая сумма п-го
порядка (первой степени), наименее уклоняющаяся от f1(x), так что
I к (х) - Sn,i (*) | < El [U (x); 2 mr] = ?;/1 (ш
то в промежутке (— L, L) имеем также
причем | Епд (^) | <] J? (д;) при всех х. Поэтому, вследствие A0) и (9), при
достаточно больших п имеем
что было бы невозможно, если бы допущение (8) было справедливо.
В частности, в силу упомянутых выше значений констант с?&д,п, имеем*
1=0 ч
Поступило
24. IV 1947 г.
ЦИТИРОВАННАЯ ЛИТЕРАТУРА
1 С. М. Никольский. Докл. АН СССР, 52, № 1 A946).
2 С. Н. Берн штейн. Докл. АН СССР, 53, № 7 A946) [86].
3Н. И. Ахиезер. Лекции по теории аппроксимации, 1947.
4 С. Н. Бернштейн. Докл. АН СССР, 54, № 2 A946) [84], заметка IV,
1 Напоминаю, что Е*п г [/ (х); L; 1\ (х)] есть наилучшее приближение f (х) в про-
промежутке (—I», 4-L) при помощи тригонометрических полиномов тг-го порядка
п
2 (а:) == ^ «ft cos Л + Ък sin _ периода 2 гт > 2 L, которые при всех х удовлетво-
Л /2-
ряют условию | 2 j (а:) | <; J? (х), где i? (а?) — любая данная четная функция нулевого
рода (или многочлен) с неотрицательными коэффициентами ([84], стр. 387).
* См. статью [100], формула C7). {Автор.)

91
ПРЕДЕЛЬНЫЕ ЗАКОНЫ
ТЕОРИИ НАИЛУЧШИХ ПРИБЛИЖЕНИЙ*
Мы говорим, что к функции f (х) (~оо<^х<^оо) применим пре-
предельный закон (В) (или предельная формула (В)), если при всех
имеет место предельное равенство
limEn [/ (х); _^] = Ap±of(x). (В)
В заметке (*) [84] (теорема VII, стр. 392) я доказал, что закон (В) приме-
применим ко всякой функции / (х), удовлетворяющей условию
(-оо<Ж<оо), A)
оо
где Н (х) = Va^2fc — целая функция1 нулевого рода.
о
Напомню, что, как показано в той же заметке, при еоблюдении
условия A) целая функция gv (x) степени /?, осуществляющая наилучшее
приближение Avf (х), существует и Ар+0/ (х) = Avf (x) (если Apf (x) < оо).
Кроме того, из теоремы VI заметки (]) следует, что для всех функций
/ (х) с Ар f (ж) <С С при р >. pOj удовлетворяющих тому же самому усло-
условию A) [т. е. при одной и той же функции Я (х) в правой части A)],
* Докл. АН СССР, 58 A947), стр. 525—528 B47*).
1 Нетрудно видеть, что условие A) выполняется, если, например,
с I ее I
log I / (*) I < при ± % -> оо, где a > 1, с > 0. Для этого достаточно за-
заметить, что, если рА = (к 4- 1) [log (Л + 1)]а, то функция нулевого рода
при любых х и п. и полагая п + 3 =
(|#[>е), получим
[logic: |f '^ ^ *
logH(x)> 2nlog2= ~"ws* _61og2.
[log I x |]a
416

предельная формула (В) имеет место равномерно, а именно, при любом
данном г>0 для всех этих функций может быть указано одно и то же
значение N (зависящее только от Н (х) и С), так что
?3/2
- Avf (х) | < е"п ~ (р> Ро) B)
при всех п^ N.
Применимость к функции / (х) закона (В), в частности, при усло-
условии A) (благодаря лемме (х), стр. 480), не исключает случая, когда
Apf (х) — оо для р<СРо^°° и Apf (х) <С °о для р^>р0: если р0 = оо, то
lim Еп / (х); — — сю при любом /? > 0, и наоборот. Случай р0 <^ оо
тг->оо I Р J
эквивалентен lim En\f(x); — = сю при р<^р0 ж lim Еп / (х); — <^ со при
П->оо L Р Л П->оо L Т7 J
/?>/?0- При отсутствии условия, аналогичного A), закон (В) может
нарушаться, но справедлива всегда
Теорема. Если существует такое р0 <^ оо, что Avf (x) <С оо для
всех р >> р0, то
lim Еп \f (х); -iU = Лр+0/ (а:) (В)
? ^> YjD0, ^<5^ T определяется из уравнения
| у^чп = log (Т + Vf+1). C)
Значение *[ не может, в общем случае, быть снижено (^ да 1,51).
Доказательство. Пусть gp(x) будет функция степени/?. Рас-
Рассмотрим ее разложение (х) по многочленам Чебышева на отрезке [— X, л]
gP (х) = 2 ^А-П (у), Лк = \ С gp (X cos G) cos A6 d6, D)
о ' о
и приближенный многочлен степени п
рп (х)=
о
Как известно, каково бы ни было р >- р, можно указать такое
число R, что при всех | z | ^ R
и, так как
где Л/^л,р — максимум | gv (z) \ на любом эллипсе с фокусами (— X, X) и
полусуммой осей р; следовательно, если X^-R, то, обозначая
через )Ъ малую полуось, получим
2 ср/Л ^^^
Л
27 С. Н. Бернштейн 417

Таким образом, для п
= 2е~пд
и, если с настолько велико, что при соответствующем выборе Ъ
+l- log (b + УРТТ) = - 8 < О,
о
ТО
lgp(»)-Pn(»)|< .2*~".!8 (-*<*< X).
Но если Ь = ч определяется уравнением C), то при с =j~— (a>>0)
о = — "|/^2 + 1. Следовательно,
при любом
Положим теперь, что / (х) — любая данная функция, для которой
(x) имеет определенное конечное значение при всяком данном
о- Следовательно, существует функция gy (х) такая, что / (х) — gpr{%)
ограничена (—сх><^х<^оо), а потому подчиняется закону (В). Таким
образом,
Л±о/ (х) = АР±о [/ (х) — gy (х)] = lim En f/ (х) ~ gpr (x); -?—]
при всяком р^>рг. Но, с другой стороны, если рг^>рг^, то по доказан-
доказанному выше
limtfj^fr);-^] =0
n-»oo L A±^J
и, следовательно,
UmEn\f(x)-gl/(x); ^-]= HraEn\f(x);-^-l
откуда следует (В) при всяком /?i
Остается показать, что указанное выше значение ^ не может быть
уменьшено. Для этого достаточно указать функцию, для которой равен-
равенство (В) нарушается при Px<ip^>
Примером такой функции может служить / (х) = е?** (для упрощения
письма положим р0 = 1), а именно, проверим, что
lim Еп\е^\ —= оо
n_»oo L Р 1
при всяком /?<Л- Действительно B),
1
418

где .Лп-ы — коэффициент при Тп+1 (х / X) в рассмотренном выше разложе-
разложении / (х) D). Выражая Ап при помощи коэффициентов строки Тейлора (B),
стр. 78), находим для f(x) = ех:
Y ( еХ
,2/1A + .
каково бы ни было число с = к / /г << оо. Полагая Х = п / р, имеем поэтому
^"^ 71 (С + 1) п'
где
с V2/W
и замечаем, что максимум /с, который достигается при 4/?2с A + с) = 1,
будет равен 1, если р = ^ определяется из уравнения C). Поэтому,
если р = г^—, то
Условимся говорить, что к функции /(ж) применим закон (В'), если
предельное равенство (В) осуществляется для всех достаточно больших
/?>0. Из только что доказанной теоремы следует, что закон (В') при-
применим к функции f(x), если Apf (х)<^оо для достаточно больших р.
Законы (В) и (В') соответствующим образом распространяются, если
за норму функции f(x) (—оо<^х<^оо) вместо sup|/(#)| принять
оо
[ \f(x)\*dx (?>1).
—оо
Посредством аналогичных рассуждений доказывается следующая тео
рема, которая представляет аналог упомянутой выше теоремы VII (х).
Теорема VII bis. Если существует такая целая функция Но (х) нуле-
нулевого рода, что
\\f(x)\*dx<\H0(x)\, E)-
— X
то
n_>oo \ P±U/
oo
где Apq) f (x) = min \ \f(x) — gp (x) |« dx, gp (x) — любая функция сте-
—оо
X
s
-X
пени р\ С^Р (/ (х); X) = min [ |/ (х) — Рп(х) \q dx, Pn (x) — многочлен сте-
степени п.
419 27*

Особого внимания заслуживает случай q = 2, на котором мы остано-
остановимся подробнее в другой статье. Заметим, что для соблюдения условия
E) достаточно выполнение условия A).
Поступило
9. IX. 1947 г.
ЦИТИРОВАННАЯ ЛИТЕРАТУРА
1 С. Н. Берн штейн. Докл. АН СССР, 54? № 6 A946) [84], заметка V.
2 С. Н. Бернштейд. Экстремальные свойства полиномов, 1937. [«Э. П.»]

92
О СВОЙСТВАХ ОДНОРОДНЫХ
ФУНКЦИОНАЛЬНЫХ КЛАССОВ*
ПЕРВАЯ ЗАМЕТКА
Определение. Назовем основным однородным функциональным
телом Qq (R) порядка q радиуса R совокупность всех функций / (х) дейст-
действительной переменной (—оо<;г<;оо), удовлетворяющих условию
A)
при любом р^>0.
Совокупность функций, принадлежащих хоть одному однородному
телу Qq (R) порядка д, называется основным однородным классом Qq по-
порядка q.
Лемма 1. Условие f (х) 6 Qq (R) эквивалентно )Я f (-j- x/l) 6 Oq (R) при
любом \^>0.
Определение. Назовем специальным однородным телом непрерыв-
непрерывности Sq (pl9 . . . , р%; «!,..., ал; М) порядка q радиуса М типа (plt . . .
. . . , pk; «!,..., a*) совокупность всех функций / (х) (— оо << х < оо)
алгебраического роста [т. е. таких, что для достаточно больших п
lim f (х) I хп = 0], удовлетворяющих при любом h условию г
tM\h\*. B)*
Совокупность функций, принадлежащих телу Sq {ръ ...,/?&;
хх,. . . , а^; М) хотя бы при одном М<^оо, образует соответствующий
* Настоящая статья [92] является соединением двух заметок, опубликованных
в Докл. АН СССР, 57 A947), стр. 111 — 114 B45*) и 59 A948), стр". 1379 — 1384
B50 *).
1 Можно показать, что если существует какой-нибудь отрезок (ж0, х0 + 8) данной
длины 8, где sup | / (х) \ < оо, то из B) следует, что / (х) обладает тем же свойством
в любом конечном промежутке и существует такое определенное число п (зависящее
лишь от типа Sq), что lim / (х) / хп = 0 (см. следствие 3) [92.1].
421

специальный однородный класс непрерывности Sq(pl9 . . . , /?&;! al9 . . ., аЛ)
порядка д. Лемма 1 имеет место также в случае любых специальных
однородных тел. В дальнейшем, для определенности, мы считаем сово-
совокупности чисел {pi, cci} нормированными требованиями:
k
1J^=1; 2) ах = 1<а2<...<а,.
к
Сумму V | pi | = Р назовем весом рассматриваемого специального
г=1
класса; назовем характеристикой т0 специального класса (тела)
Sq (pi, . . . , рп\ «и • • • , аи) данного типа наименьшее из целых чисел т >0,
к
для которых \J Pi a? SO (очевидно, то^к). Легко проверить, что в слу-
г=1
чае существования производной /(т°) (х) порядка т0 в точке * х
Поэтому sup
/ ° (х) <^с<^оо [означает, [что f (х) принадлежит
—оо<ж<оо
всем специальным однородным классам порядка т0.
Теорема 1. Если /](х) принадлежит хоть одному специальному
однородному 'классу Sq порядка q [f{x)jxn-^O при п^>>п0], то она
принадлежит также основному однородному классу Qq порядка q.
Доказательство. Пусть Gx (x) ^> 0 будет некоторой целой функ-
функцией первой степени, удовлетворяющей условиям'
1(«)|«|n»A<ooV rC)
Предполагая, по условию, что f (x) удовлетворяет B), положим **
* Так как
* ' ' ' ' ' % * ' 'Гто) (X) + ?{J
hm0 ' —
где ?|->0, когда /г->0. (Автор.)
** Если / (ж) — периодическая функция с периодом со, то gn (x) при любом п
имеет также периодом о, так как
г=1
Вследствие этого совершенно очевидного факта излагаемая здесь теория включает,
как частный случай, приближение периодических функций тригонометрическими
полиномами. (Автор.)
422

oo k .
(x) = \ G±(t) ^pif^x + ^-j dt =
' —oo Ъ=:1
D)
Принимая во внимание, что осг^1, gn (x) есть целая функция степени
ее выше п. Таким образом, из B) и D), вследствие C), заключаем, что
-)-f(x)]
П J J
dt
M
С„М
E)
Следствие 1. Если f (x) принадлежит хоть одному специальному од-
однородному классу Sq порядка q, то f (x) непрерывна и имеет непрерыв-
непрерывную производную fm) (x) любого порядка m<^q.
Благодаря E) это вытекает из теоремы 12 (B), стр. 105, глава II).
Напомню, что из доказательства упомянутой теоремы, воспроизводящего
доказательство аналогичных теорем, данное мною еще в 1912 г. (х), сле-
следует также, что если /(#)€?2a, где q^>l, \то /(тЦх) (: Qq-m (q^>m) *.
Следствие 2. Целая функция gn (%), определенная формулой D), при-
принадлежит тому же специальному классу Sq, что и f(x).
Действительно, вследствие B),
Pi (gn (^ + <*jh) —gn (х))
3=1
h k
k
IiIi PiPi\f (*Л~ + 4h) -f(x + ^
i=lj=l L X J Ч
dt
Лемма 2. Если целая функция g (x) конечной степени принадлежит
некоторому специальному однородному классу Sq (pi\ &{) порядка q с ха-
характеристикой т0, то ее производная g(m^ (x) порядка т0 ограничена
на всей оси, и g (x) (:Sq> (pi\ сц) при любом qr (q<; q' <; т0).
* Очевидно, что и наоборот, если fm\x) ? Пд_т, где^ — m>-0 (знак равенства
в данном случае не исключается), то / (х) g Clq. Пусть, например, | /' (х) — Gn (x) | ^
п
-< —— (д>1), тогда, согласно [86],
Аналогичный результат при любом целом т следует из [90]. {Автор.)
423

В самом деле *, согласно з^словию B), функция конечной степени
Fx (h) =
g(x+a.h)-g{x)
относительно h (—оо<^/г<^оо) удовлетворяет при всяком данном х не-
неравенству
Pi
g(x + «.ft) — g (x)
hm°
h к
В случае q = m0 отсюда непосредственно следует
В общем же случае q<^mQ, применяя указанное выше неравенство, при
| /г | ^ 1 имеем
откуда, благодаря следствию 5 статьи [99], получаем
Тс
•w
m\
(— оо<><оо),
где 5 — степень функции g (х), а с == \а^\ (так как степень функции
Fx(h) не превышает sc).
Из леммы 2 заключаем, что lim 'g ^ <C °°> откуда вследствие E)
при помощи следствия 2 вытекает
Следствие 3. Если f (x) (: Sq с характеристикой т0, то
Tim | / (х) I х
оо.
Теорема 2. Если порядок q однородности специального класса Sq (pu аг)
больше его характеристики (q^>m0), то всякая функция этого класса
есть многочлен степени ниже т0. Такой класс (q^>mQ) называем вы-
вырожденным.
Действительно, согласно теореме 1, Anf {x)<^R j п^. Поэтому / (х) (на
основании следствия 1) имеет непрерывную производную /(ш°) (х) порядка
mo<^q и, согласно сделанному выше замечанию,
7с ~к
при всяком х (вследствие B)); следовательно, fm°\x) = 0.
* В первоначальном тексте доказательство было опущено из-за недостатка
места. (Автор.)
424

Теорема 3. Если f (x)€Qq(R) и q<imo> где т0 — характеристика
некоторого однородного специального класса Sq(ply . . . , ри\ ах, . . . , а*)
порядка q, то при всяком произвольно малом п0 /По (х) = f (х) — Gno (x)
принадлежит этому классу, где Gno (x) — произвольная целая функция
степени п0, удовлетворяющая неравенству \f(x) — Gn<t (x)\ <^R / п%.
В частности, когда q не целое число, /По (х) принадлежит всем
(не вырожденным) специальным классам Sq (так как характеристика
т0 целое число).
к
Доказательство. Пусть то = q + v (v^>0) и пусть Р = 2 I P
г=1
— вес рассматриваемого класса Sq. Обозначая через Gn (x) функции степе-
степени п, наименее уклоняющиеся от / (ж), имеем
При произвольно данном h можем выбрать п по условию n\h\
PR
F)
В таком случае
Pi U (ж + <*ih) — Gn(x
2 Pi [f (x + aih) - / (x)] -
— , поэтому
ih) - Gn (x)}
(V)
С другой стороны, полагая 6>1, no = n j bl° и, вообще, ni =
где lо ^ I ^> 0 — любые цельте числа, представим Gn (x) в виде
Gn (х) = Gno (х) +
(х) (п =
где
7? 7? \
причем | Нп (х) I <;¦ 1 . В таком случае, полагая iV= —г
если к = то, или 7V =
0' К0ГДа
о, имеем C)
2 Pi [#nm (ж + «4А) — Яп.
(be+
425
sup

Поэтому
1=0 i=i
NR
откуда, полагая /„, (x) = / (ж) — GMo (я), вследствие G), находим
Следствие 4. jEc/ш / (ж) б ?lq и Aof (х) <С °о, то f (х) — Go (х) = /0 (х) б Sq,
каков бы ни был специальный класс Sq порядка q <^ то, где Go (x) означает
функцию нулевой степени, наименее уклоняющуюся от f(x).
Ограничимся пока предположением, что функция f{x) ограничена. Тогда
GQ (х) = Go будет постоянной, и из теорем 1 и 3 получаем
Следствие 5. Если функция f (x) ограничена (в частности, если
она периодична), то утверждение f (x) б Q.q эквивалентно утверждению
f(x) (:S (рх, . . ., pk\ ax, . . ., aft), какого бы типа ни был специальный одно*
родный класс Sq порядка q с любой характеристикой т0 ^> q.
Последнее следствие в частном случае, соответствующем периодическим
функциям и типу р{ = (— II C\, a. = i (i <; k = то^> q) (т. е. конечным
разностям), было установлено Зигмундом D). Таким образом, для огра-
ограниченных функций все специальные однородные классы Sq порядка q<^m
эквивалентны.
Поступило
22. V 1947 г.
ЦИТИРОВАННАЯ ЛИТЕРАТУРА
1 С. Н. Б е р н ш т е й н [3] (том I).
* S. Bernstein. Legons sur les proprietes extremales etc., Paris, 1926. [«L. S.»]
3 С. Н. Берн штейн. Экстремальные свойства полиномов, 1937. [«Э. П.»]
4 A. Zygmund. Duke Math. J., 12 A945).
ВТОРАЯ ЗАМЕТКА
1. Дополним некоторые результаты первой заметки для неограниченных
функций одной переменной и приступим затем к приложению того же
метода к функциям нескольких переменных.
Добавление к теореме 1. Все функции f (x), принадлежащие некоторому
данному специальному однородному телу непрерывности f (x)^S (pv . . ., pk;
1 Полагая в данном выше доказательстве n\h\ = c произвольным, можно несколько
снизить оценку (8) наилучшим выбором с иЬ (в первом и втором слагаемых появляются,
соответственно, множители cv и c~q). Например, в случае q = 1, т0 = 2 наивыгодней-
наивыгоднейшее Ь = 1 + 1^2 и, в частности, получим | / (х -f 2h) — 2/ (х + h) + / (я?) |< AR A+1^2) h
{полагая с = 2/Ь).
426

al9 . . ., oc&; M) порядка q радиуса М, принадлежат основному однородному
классу Qq порядка q, причем
sup n*Aj (x) = Me [S ; (p.; a.)], A)
(Pa;M) П q г г
где постоянная с [Sq (p{; а.)] не зависит от п.
Это дополнение к теореме 1 вытекает из того, что лемма 1 применима
к специальным однородным телам так же, как и к основному однород-
однородному телу Qq(R).
2. Первое добавление к следствию 5. Всякий специальный
класс S (р{; ос.) порядка q с характеристикой m^>q включает все спе-
специальные однородные классы ?Чт') (//; оф с характеристикой т'<^т.
[Это утверждение содержится в следствии 5 при дополнительном пред-
предположении ограниченности функций /(#)].
В самом деле, если / (х) 6 ?Чт') {р\\ ol; М), то целая функция степени тг0,
определенная формулой D) первой заметки
СО I
Р (т\ ¦ \ fr I/\ 7 Л f T I I rjf (А'\
—оо г
осуществляющая неравенство г
принадлежит, согласно следствию 2, телу того же специального класса
S (т'> {р\\ а!) (с радиусом М 2 \р \ \)? и ПРИ помощи леммы 2 и леммы (х) ([84],
г
заметка III) нетрудно показать, что g^ m (ж) = gn^ (x) — \gn%@) + ...+
xm—l 1
7—zrrn "^ О ПРИ соответствующем подборе последовательности
7
•го->О, каково бы ни было т^т'. С другой стороны, вследствие тео-
теоремы 3, каков бы ни был специальный класс S^ (pr, а.) с характерис-
характеристикой т^> q, из E') следует
1 При применении на практике формулы D') полезно напомнить, что оценка
погрешности E') справедлива при соблюдении лишь двух условий: Е/^= + 1,
| о^ | !> 1 • Легко проверить, что при любых р'г тело Sq (р\\ си\\ М) = Sq (р[\ ъ[\ М / /?^),
каково бы ни было г'о A << iQ <! k), если положить a4 = a^ — а^ ,— pi = pi / рг при
i^i, и а'|о = а^, Е ^' = 1. Таким образом, если можно выбрать г*0 так, чтобы все
| а" | ;> 1, заменяя в формуле D') р[ и у.[ через ^ и а"г, мы получим в правой части
неравенства E') MCq/ p[onq вместо MCq/nq. Например, если
то, полагая iQ = 5, после соответствующей замены gn (x), получим
МСп MCnV~~s
427

2 Pi и (
где постоянная L не зависит от /г0. Поэтому вследствие
2 р4 к. (* + vo - sno <*)i = 2 л re m (* + vo - с
i i
при /г0 -> 0 для всех т ^ т\ неравенство B) приводится к
C)
Следствие 6. Все однородные специальные классы *S(mo) (/у, а.) порядка qy
имеющие ту же характеристику т0, эквивалентны.
Это утверждение (очевидное для вырожденных классов т0 << q, так
как по теореме 2 последние состоят лишь из многочленов степени <Ст0
вытекает непосредственно из предыдущего в случае mo^>q. Остается
рассмотреть случай mo=q (критический класс), когда теорема 3 неприменима.
Полагая тогда т' = т = q в предыдущем рассуждении, введем соответствен-
соответственные характеристические указатели N = —} 2PiaT' ^' = —f 2Рр™^^
г " i
классов б1^1) (/?1? а.), ^^^ (/?!, а^). Пусть {iTV = iV; в таком случае для всех
целых s<^m, \*< 2jp\^ — ^Рга\~^- Обозначив через тх^>т наименьшее
г г
целое число, для которого ^ 2 Рр'™1 — 2 ^гаГ1 ^ ^ (применяя рассужде-
г i
ние, посредством которого была доказана теорема 3, где теперь роль
характеристики т0 будет исполнять тг ^> q), мы получим тогда вместо B)
неравенство вида
IipI и с* + «;*) - / и] - 2 л [/(•« + *ife) - / wi -
no (х)]
. [§щ (х + аЛ) - gno (x)]
<Lhi. B bis)
Так как функция gr4 (х) та же, что и раньше, то из B bis) вытекает
также неравенство
i г
которое и выражает эквивалентность обоих классов.
Таким образом, если нам не нужно рассматривать радиусы различных
специальных однородных тел непрерывности, к которым принадлежит
данная функция / (х), мы можем коротко обозначить через / (х) 6 S^
факт принадлежности / (х) к специальным классам S (m> (pt; a{) (q— порядок,
т — характеристика). Кроме того, выражая через / (х) 6 <?* (M) условие
Липшица порядка q = к -\- о, где к ^> 0 — целое число и 0 <^ 8 <J[ 1, данного
радиуса М
428

I f) (я _|_ /г) __ fV (x) | < M h8 ( — oo < x < oo) D)
и через / (x) ? Sq — это же условие с произвольным М", при помощи анало-
аналогичных рассуждений устанавливаем
Следствие 7. Бее специальные классы Sqm) порядка q с характеристи-
характеристикой т, где q^m<^q -\~ 1, эквивалентны1 классу Липшица Sq порядка
2 = #4-Л еде целое число к = т — 1>0, т. е. *Sr*+b1) = *S*-j-8 @ < о < 1).
Аналогично доказывается
Следствие 8. iJc/ш / (л) 6 .У^Ч ^е ?<А + 1, mo f{i) (x) ^ S^ при
всяком целом i<^q.
3. В формулировке предыдущих следствий (в которых, в отличие от
следствия 5, на функцию / (х) не накладывается никаких ограничений)
мы не можем утверждать эквивалентность классов Sq и Qq, хотя при
доказательстве мы существенно пользовались теоремами 1 и 3. Действи-
Действительно, если / (х) 6 Sqm\ то, какова бы ни была функция Fo (x) нулевой
степени, / (х) + Fo (х) = /0 (х) 6 Пф а между тем /0 (х) 6 S^ лишь тогда,
когда целая функция нулевой степени Fo (x) есть многочлен степени не
выше т. Из этого замечания вытекает
Второе добавление к следствию 5. Для функций f (x), подчи-
подчиненных двум дополнительным условиям Aof (х) - ^ oo, lim (/ (х) / хт) <^ оо
я—>+оо
(которые независимы за исключением случая т = 0), классы Sqm и Clq
эквивалентны при всех q<^m.
Для получения соответствующей эквивалентности без наложения каких
бы то ни было дополнительных ограничений на функцию / (х) следует
расширить классы Qq и ?^т), сообразуясь с теоремой 3. Введем следующие
определения: назовем основным однородным теломQq\R) порядка q радиу-
радиуса R свободным (или расширенным) до степени t совокупность всех
функций f(x), для которых
Иными словами, / (х) ? ?lq' (/?), если существует целая функция gt (зс)
степени не выше t такая, что функция ft (х) = / (х) — gt (x) ограничена и при-
принадлежит основному телу Qq (R) [ft (x) 6 Qg (R)]- Точно так же специальным
однородным телом а (/?*; а{; M)W порядка q радиуса М свободным до степени
t назовем совокупность всех функций/ (х), которые могут быть представлены
в виде суммы / (х) = gt (x) + ff (x), где gt(x) — целая функция степени не
выше t, а функция ft(x)^Sq(pi;ai; M) ограничена. Классами QW и
oq (рг\ а.)^ называем, соответственно, совокупность тел Qf') (R) и а (р.; а.;./?)(')
при любых R<^oo. Из следствия 5 непосредственно вытекает
1 Рассмотрение Ап f (x) существенно лишь для доказательства утверждения
^u+s^ СИ ^к+8- Доказательство того, что S^8 с ^^+§4 получается известным элемен-
элементарным способом дифференцирования равенства ? pi [f (x -{- ос^Д) —/ (х)]= Hhk~^8, при-
приводящего к неравенству A +&)... (к + $) я< М 2 | pt\ a^s (которое можно еще
улучшить) [92.2].
429

Третье добавление к следствию 5. Свободный до степени t
основной класс Q$ эквивалентен всем специальным однородным классам
agm) (Pv ai)(f)> свободным до той же степени t с характеристикой m^>q.
4. Переходя к однородным классам функций нескольких переменных,
ограничимся, для краткости, функциями / (х, у) двух переменных, причем из
хода рассуждений будет ясно, что выводы не зависят от числа перемен,
ных. Мы говорим, что / (х, у) 6 xS^) (p.; a.; MJ . ySgA (q.; $.; MJ,
если при всех (х, у), \ hr \ <; h
2 Pi U (* + а,А\ у) - f (х, у)] < M±hi )
E)
т. е. если / (х, у) б Sfr) (р.; а.; М±) похи/ (х, у) б ?<"«> (?/, ^.; MJ по у.
Точно так же мы пишем / (х, у) 6 xS\x (Мг) • yS\2 (М2), если / (ж, у) 6 6^ (il/1)
по х и / (ж, у) 6 5хя (Л/"а) п0 У•
Аналогичным образом определяются специальные однородные классы
функций двух переменных: / (х, y)dx S^™^ {pv a{) • yS^1^ {q.; p.), если
/ (x, У) 6 -S^> (^; a.) no x и / (ж, у) б ^) (?5; ^) по у.
Теорема 4. ?с/ш / (х, у) 6 я>5^) (р.; а.;Мг) • у^> (^; Р,-; -^2) и ^nij ^ (я, у)
означает наилучшее приближение функции f (х, у) (— оо <^ х <^ оо,
оо) пргг помощи целых функций г степени пх по х и степени п2
по у, то [полагая y^pi = ^}q. = 1, |ос{|>-1, | ^. | >- lj
AninJ (х, у) ±±
W
где Р = ^j\Pi\, Q = 2lffil' a сл м сх определяются формулами* (8).
Для построения целой функции, осуществляющей F), положим
оо оо
—оо —оо г, э
* 2) S Щ *г (^Zfi) ^ (=^) *, ^, G)
1 Мы говорим, что gnit7l2 {х, у) есть целая функция степени п1 по х и степени л2
по у, если она регулярна при всех комплексных значениях (а;, г/), причем, как бы мало
ни было s > 0, существует такое значение R, что | gn^ щ (х, у) |< е' x ' (ni+e)+l " I (na+s),
каковы бы ни были | x\^>R, \y\^R. (См. [94]). '
* Согласно сноске на стр. 422, теорема 4 и формула F) применимы к любым
периодическим функциям, / (а?, у), так как в этом случае функция gni Па (xt у),
определяемая формулой G), также периодична. (Автор.)
430

обозначая через gUl (х, у) целую функцию степени щ по х (содержащую у
в качестве параметра), введенную в первой заметке,
со
= 5
где (Зх (г) ;> О, G (?) ^> 0 (— оо <t< сю) любые целые функции первой
степени, подчиненные условиям г
со со оо
Gi (t) dt= \G (t) dt=l, \ G1 (t)! * \Kdt = cXl,
CO
Действительно, учитывая (см. первую заметку, стр. 422), что 2Р{= 2 ffj = ^
и |/(а:, ?/)—gn (^, y)Kil/ся /п^, и замечая, что вследствие G) и E)
со
[ G (t) 2 ?, [gni (x, У + ^)~ gni {х, у))
+ 2L, y)]dh
" t"l I - \ ' П.^ ' ~ ' 77... / \ /7.- ~ / I ¦"" ^^
CO CO
—CO —CO
получаем
Мл с, М-Рс
Таким же образом, изменяя последовательность преобразований, получаем
В частности, полагая п^ = п2 = и, Хх = Х2, получим
Л»,nf(x,y)<A/п\ где Л - supсЛ1 (Mi + М2Р, MXQ + М2). A0)
Из различных следствий, которые вытекают из A0), отметим, что ряд
со
f fc У) = Sn.y п. (Ж, 2/) + 2 [$Щ+1, ni+1 fe 2/) — gnif tii (Ж, У)],
i
i=0
1 Так как из E) вытекает lim (/ (х, у) / хШгутг) <оо, то в общем случае
х—>db°°
(следствие 3 и теорема 2) необходимо (и достаточно), кроме того, чтобы
со со
\ Gx (г) | г |mi ^ < оо, \ G (t) \ г |™2 dt < со,
—со —со
431

где П{+1 = Ъщ (Ь > 1), может быть почленно дифференцирован к @
раз по х и I раз по г/, лишь бы к -4- I = V << лх и
Л, п97 (ж, 2/) / Эа*^1 < Л^ / nK~v [Rv = min FXl + 1) ^+1 / (fe - 1)] A1)
[в случае ограниченности / (х, у), ограничены и dvf (x, у) / дхкду1].
При помощи следствия 8 получаем г отсюда (<v + 3 = kL = Х2)
Следствие 9. Если* f(x, y)?xS{^8m)^.г/5(г;+т)G7г>8>0), то dvf (x, у)/дх*ду1?
€ xS{8v+m) -yS{8^m) (e случае ограниченности f (x, у), dvf (x, у) / дх*ду1 6
ZxS^-yS^'* при всяком** ттг'>о) [92.3].
Поступило
21. I 1948 г.
ЦИТИРОВАННАЯ ЛИТЕРАТУРА
1 С. Н. Берн штейн. Докл. АН СССР, 52, № 7 A946) [84], заметка III.
2 С. Н. Бернштейн. О наилучшем приближении непрерывных функций посред-
посредством многочленов данной степени, Харьков, 1912, [3] (том I).
1 Следствие 9 является обоощениелг и усилением теоремы 8 (стр. 142) моей доктор-
докторской диссертации B); [3] (том I), стр. 98.
* Этот класс включает класс or*S"* + s- 2/*S"* , s и эквивалентен последнему при т =1.
(Автор.)
dvf (х у) * *
** Таким образом, если $ < 1, то можно положить /п'= 1, т. е. — .* ? xS8 ¦ yS8. Но
дхк ду1
в случае 8 = 1 необходимо, чтобы т! > 1. При этом неравенства F) остаются в силе,
хотя обычное условие Липшица для смешанных производных, как и для производных
порядка \х — 1 по одному только х (или по одному у), может нарушаться. {Автор.)

О НЕКОТОРЫХ ЭЛЕМЕНТАРНЫХ
ЭКСТРЕМАЛЬНЫХ СВОЙСТВАХ МНОГОЧЛЕНОВ
НЕСКОЛЬКИХ ПЕРЕМЕННЫХ*
Будем обозначать через
мпогочлен степени не выше n/t по каждой из к переменных Xh A<C h ^k.)
Теорема 1. (Распространение неравенств В. А. Маркова). Если мно-
многочлен
Рпх...пК {Xl, • • .,ЖЛ)|<Д/ A)
в к-мерном кубе — 1 <^ xh ^ I (l^C h ^ к), то
полагая
Т(п) (х) = cos (л) arc cos ж =
>(п) х
B)
C)
0<г<(п)
гйе (/г) = п в случае п — i четного и (/г) = п — 1, если п — i нечетно.
Ввиду того, что доказательство не зависит от числа переменных к,
ограничимся предположением, что к = 2, и положим х± = х, х2 = у.
В таком случае, полагая
где
Q\l2)(y)= V ^iijx "-" многочлепь1 степени <^ п2, и применяя к
0
* Докл. АН СССР, 59 A948), стр. 833—836 B49*).
28 с. Н. Бернштейн 433

РП1п2 (х, у), рассматриваемому как многочлен степени пг по х, неравенства
В. А Маркова, находим
Поэтому, применяя вторично неравенства В. А. Маркова к каждому
из многочленов Q^ (у), получаем
B^M. B bis)
При этом правые части неравенств B bis) [как и B)] не могут быть
снижены, так как при любых значениях i, / @^i<^.nl7 0<^
они достигаются для одного из четырех многочленов
Аналогичным образом распространяются теоремы В. А. Маркова о
максимуме производпых, а именно1: при A)
Теорема 2. Если многочлен РПг^т^Пк(х1, х2, . . .,#&) удовлетворяет не-
неравенству A) в к-мерном кубе — 1<Сяч<С 1 (i = 1, 2, ...,&), то при
любых действительных2 ?х, ?2, . . ., ?& (Si ^> 1, . . ., ?л ^> 1)
_pn n (_j_ g 9 _|_? , . . ., ?лI ^С Тп (% )Тп (S ). .. 7'n (S^) M (L\
В самом деле, ограничиваясь, как и раньше, случаем к = 2 (ввиду
аналогичности рассуждения), замечаем, что для РП1п2{х, у)=МТПг(х)Тщ(у}
неравенство D) обращается в равенство. Таким образом, требуется лишь
показать, что равенство
РП1Щ (х, у) = МгТП1 (х) Тщ (у) + <?п1Щ (х, у), E)
где Qnin2 (S, ^i) = 0 (?>1, ^>1), несовместимо с неравенством A) при
М<МХ.
Для этого замечаем, что
Vnxn2 COS —, COS^—• 1 =Pnin2 COS , COS— 1 + ( —
\ nl n2 J \ П1 П2 J
Следовательно, при условии M<^MX многочлен QUxn2 (%, cos — j сте-*
)
пени пг по х имеет последовательно чередующиеся знаки (— l)H-i+i
точках rci = cos — (i = 0, 1, . . ., %), а потому при всех ?^>1 сохраняет
постоянный знак (— 1K'+г, т. е. (— 1)з' ^ПхП8 fs, cos •^)<0 (/ = 0,1, ..., п2).
1 См. также (х), гл. VII.
2 Для любых комплексных ?i» . . ., ?л правая часть неравенства заменяется
I 5i + У 5i — 1 ... \%k + V^^l — 1 nkMlt но это значение, вообще, не достигается*
Точное значение асимптотически равно I 71 E) ... Тп (gA) lilf (см. (х» 2)).
434

Таким образом, при любом фиксированном ? ^> 1 многочлен Qn^jfe, у)
степени /г0 по у имеет все свои п2 корней в промежутке — 1 < у < 1 и
Qnxn2 (?, ^) <С 0 при всех т] у> 1, что противоречит предположению (?(?, т])=0.
Теорема 2 может быть обобщена и дополнена при любом числе пере-
переменных так же, как это было сделано мною для случая одной переменной
C). Для упрощения письма положим к = 2.
Теорема 3. Если неравенство A) соблюдено лишь в N — {пх + 1) (п2 + 1)
точках (xi = cos —, j/j- = cos—), mo во всех точках (+?, ЧЬ^), где
V ni n2 J
^^l* имеет место неравенство
! Лчп, (±6, ±^) |< Л/ГП1 (?) ГП2 (т]). D bis)
данные N интерполяционных узлов (аг , Ьг) (а^<^ 1, Щ^. 1),
1^/^Л^ = (^i + 1) («2 + 1), в которых соблюдено A), не все совпадают
с указанными узлами Чебышева (cos —, cos —), то неравенство D bis)
может нарушиться1.
Первое утверждение вытекает непосредственно из данного выше дока-
доказательства теоремы 2. Для доказательства второго утверждения из интер-
интерполяционной формулы
Рп1Пг (X, У) - ^ Р^ (**' 6*) Дп?п, (X, У) F)
замечаем, что максимальное значение РПгпг (^> ^) достигается тогда и
только тогда, когда РПгпг {av bt) = e^il/, где е^ = + 1, причем
г1^п)п (^^)^>0 для всех значений I, для которых Л^п (?, Y])gO. В част-
частности, при узлах Чебышева этот максимум, равный МTnJ$) ТПг (т]), дости-
достигается многочленом МТПх (х) ТПг (у), так что | МТПх {а{) ТПг (b{) \ <^M во
всех данных точках {al,bl), отличных от (cos —, cos— ]. Следовательно,
максимум Pnxnz(fc,*rf)> соответствующий узлам {al9bz)9 не превысил бы
МТПг (?) ТПг (-/]) лишь в том случае, когда Я{п\пг (S, ч) = О Для всех УЗЛОВ
(ai> Ьг), отличных от (cos —, cos-— ), но это невозможно, так как из
формулы F) вытекало бы тогда ложное утверждение, что всякий много-
многочлен Рщп2{%, у), равный нулю только в узлах {al,bl)9 совпадающих с
узлами Чебышева, должен быть равен также нулю при х = ?, у = "*].
Следствие. Многочлены
(х19 х2, . . ., хк) = ±МТЩ (хг) ...ТПк (хк)
1 Мы называем N точек (аг, Ьг) интерполяционными узлами порядка N, если из
равенств Рщп% (av 6^=0 (I = 1, . . ., N = (пг + 1) (п2 + 1)) следует, что Рщщ (х,у)=0
тождественно. В таком случае существует один и только один многочлен R^n%(х,У),
удовлетворяющий условиям R^n (а-, Ь{) = 1, i?^j)n (ak,bk) = O при А ^ г. Ввиду
того, что всякая система iV точек (а[, &|) является пределом интерполяционных узлов
(аг, bj), можно доказать, что теорема остается в силе для любых iV точек (av Ъг)
435 28*

являются единственными, для которых при условии A) неравенства D)
обращаются в равенства.
Заметим также, что если не все %%^ 1, то в правой части неравен-
неравенства D) фигурируют только тс множители Tni(%i), для которых ?7>1.
Например, в случае двух переменных х, у, если ?^>1, ^ <^ 1, то
1\п2 (±5, ±^I <^Упх F). В числе многочленов Рп1ПЛх>У)> осущест-
осуществляющих знак равенства, будет тогда не только гпЛ/ТП1 (;г), но также,
например, и многочлены MTUl(x) НП2(у), удовлетворяющие лишь усло-
условиям R7l2 (т,) = ± 1 и |Д?1а(у)|<1 при — 1<у<1.
Укажем еще аналогичные экстремальные свойства многочлена
* п \л 1 > •*2' • • •' хл; — ^ ^j >
*2' ^
г=0
где qL (хг, . . .,осъ) — однородные многочлены степени /, а п — порядок
многочлена Рп (хг, х2, . . ., xjj, т. е. наибольшее значение суммы показа-
показателей При Х±,Х2, . . ., .Тд-.
Теорема 4. Если
внутри сферы V х\ = R% то: 1) на сфере радиуса R"^>R0
2) на любой сфере радиуса р ( ^xt = Р2 1
(9)
Правая часть неравенства (9) достигается, когда Рп(хь х2, ..., хк) =
— МГ1\П){ * j Ba?=V' правая часть неравенства (8) достигается во
всех точках сферы Sr радиуса R многочленом МТп\—-— ) при п чет-
ном, и при любых п в точке (^, с2, . . ., ск) сферы Sr — многочленом
Полученные результаты легко обобщаются, если заменить кубы лдобыми
параллелепипедами и сферы эллипсоидами.
Поступило
25. XII. 1947 г.
ЦИТИРОВАННАЯ ЛИТЕРАТУРА
г. С. Н. Бернштейн. Сообщ. Харьк. матем. об-ва, 13 A913) [3] (том J).
2. С. Н. Бернштейп. Экстремальные свойства полиномов, М.-Л., 1937. [«Э. П.»]
3. С. Н. Бернште и п. Сообщ. Харьк. матем. об-ва, 14 A915); [20] (том I), стр. 259.

О ЦЕЛЫХ ФУНКЦИЯХ КОНЕЧНОЙ СТЕПЕНИ МНОГИХ
ВЕЩЕСТВЕННЫХ ПЕРЕМЕННЫХ*
1. Для большей наглядности и упрощения формул мы будем обыч-
обычно предполагать число переменных п = 2. Как легко видеть, все наши
рассуждения применимы также при любом п^>2, и видоизменение фор-
формул очевидно.
Функцию двух переменных (х, у)
называют г целой функцией степени (p,q) двух комплексных переменных
(х, у), если при любых а ^ О, [5 ^ 0 (а + 8 = 1)
Д/^, B)
когда lim (к/ (к + I)) = a, lim (// (к + I)) = $.
к {-Z—>оо Ъ-{-1—>оо
В этом определении участвуют верхние границы значений всех част-
частных производных рассматриваемой функции. Подчиняя функцию / (х, у)
некоторым ограничениям роста, мы определим соответствующий класс
*Докл. АН СССР, 60 (J948), стр. 949-—952 B51*).
1 Условие B) равнозначно
при любых данных а?0, у0 (действительных или комплексных), так как из B) следует,
что при любом г ;> 0 имеем для к + I >- ^V? достаточно большого
со
lGp:(l (х0, улIдх*ду1 \<(р + гI (q + s)« ^[(p + e)\xo\ f [(g + е) | у0 | ]*/П]\ =
^{р + г)" (q + е)« е(р+«) I *
437

функций конечной степени, используя лишь свойства (чистых) последо-
последовательных производных dkf (х,у)/дхк и dlf(x, у) /ду1 при действительных
значениях обеих переменных.
2. Мы будем говорить, что функция одной действительной переменной
/ (х) есть функция конечного роста с майорантой Н (х)^-0, если она
удовлетворяет неравенству
) (-оо<а;<оо), C)
и при дополнительном условии, что / (х) =Gp(x)—целая функция сте-
степени р, из C) следуют для всех ее последовательных производных не-
неравенства вида
| G<*> (х) | < #,,р (х) (- оо < х < оо), D)
где при каждом данном х
h
limyHkp{x)<p. E)
Простейшим примером функций конечного роста являются ограни-
ограниченные функции, имеющие майорантой постоянную Н(х)=М; тогда
Известно A-3) также *, что модуль всякой целой функции sx (x) -\- it1 (x)
нулевого рода* является майорантой конечного роста; в этом случае
Н (х) = \fs^ (х) + ^ (х) всегда возможно представить в виде Н (х) =
= \s(x) + it (х) | , где s (x) + it (x) не имеет корней в верхней полуплос-
полуплоскости. Тогда в неравенствах D)
Hk,p(x) = \{[S(x) + it(x)]e-iP*}W\.
Лемма 1. Для того чтобы Н (х) была майорантой конечного роста,
необходимо и достаточно, чтобы неравенство [Gv (x) конечной степени р]
\Gp(x)\^H(x) (— оо < х < оо) C bis)
влекло за собой во всей комплексной плоскости z
|Gp(Z)K|tfp(Z)|, F)
где Hv{z) зависит только от Н (х) и р, и
Ш Tjrlog \Hp(z)\^p (z=a + bi).
Лемма 2. Для того чтобы Н (х) была майорантой конечного роста,
необходимо и достаточно, чтобы из всякой бесконечной совокупности
1 Отметим также, что Н (х) = Me* есть функция конечного роста; в этом случае
Нк р (х) = Мркех при р >. 1, Нк (х) = 0 при р < 1. Исследованию различных клас-
классов функций конечного роста будет посвящена особая статья.
* В дальнейших работах (см. [96], [97], [98], [100], [110] и [111]) этот класс
майорант обозначается 5tR0 или 35 C0to = S). (Автор.)
438

Целых функций Gv{x), удовлетворяющих C bis), можно было извлечь по-
последовательность, имеющую lim Gp (x) = Gp (x) во всех точках х любого
отрезка [а, Ъ]. При этом всякая такая предельная функция G*v (x) есть
функция степени не выше р и, кроме того, последовательность Gv(x),
стремящихся к Gv (x), может быть выбрана так, что и производные
G{p)(x)~>G*{p^(x) для всех к<^п, где п — произвольно данное число.
3. Аналогично, функцию f(x,y) двух действительных переменных
называем функцией конечного роста, если
\f(x,y)\^H(x)L(y) (- оо < х < ос , - ос < у < ос), G)
где Н (х) и L{x)—некоторые майоранты конечного роста.
Например, благодаря следствию 1 B) (стр. 164), f{x,y) будет функ-
функцией конечного роста, если
между тем как f{x,y) не может быть конечного роста (по х), если
log (| / (ж, 2/) | + 1) > М/[log (И + 1)],
и, тем более, если / (х, у) ^> ес^ (с>0).
Теорема, Если f{x,y) конечного роста [т. е. удовлетворяет G)] и,
при любом действительном у, / (х, у) есть функция, степени р относитель-
относительно х, а при любом действительном x,*f (x, у) есть функция степени q относи-
относительно у, то при всех действительных х, у существуют все смешан-
к+Ч()
ные частные производные —"q и е i— ' удовлетворяющие неравенствам
Kv (х)Ь1Л{у) (В0.р (х) = H(x),L0,q(y)=L(у)) (8)
uf{x,y) есть целая функция степени (p,q) комплексных переменных
Неравенства (8) в случае /с=0 или/=0вытекают непосредственно из опре-,
деления*.Кроме того, каждая из чистых (взятых только по одной переменной)
последовательных частных производных dk f (х, у)[дхк и д1 f (х,у)/ду1, рас-
рассматриваемая, соответственно, как функция одной переменной х и од-
одной переменной у, являются: первая — целой функцией степени р по х
и вторая — степени q по у. Покажем, что д f(x,y)jdx также должна
(при любом действительном х) быть целой функцией степени q по у.
i
: При этом Hjc,p(х) должно удовлетворять E) и аналогично lim l^Lj Q(y)^C q.
(Автор.)
439

Действительно,
AGh f (*> У) = / (x + kh, y) - kf (x -f "F=^ /;, y) + . . . + (— 1 )*/ (*, у) = dhf (x', y)
(;г<^'<Сж + ^) является при любых li,x и т/ целой функцией степени
q по у, причем
где
М= sup Я*,р(ж'). (9)
Следовательно, согласно лемме 2, д7ь/ (х, у)/дхх = lim (A^f (x, y)/hk)
h l
есть целая функция степени ^ по //. Поэтому, принимая во внимание,
что, как замечено, для 1 = 0
\d*f(.r,y)ldjr*\*?Hk,p{3)L{y),
имеем также при любых
! <?+lf (.r, ?/)/fe^y I <ЯЛ,Р (х) ил (у). (8)
При этом, если Gp (x) — функция, которая для рассматриваемого к
осуществляет в точке х экстремум G^?) (х) = Hyv {г) среди всех | Gv (x) | <^
^Н(х), a Gq(y) осуществляет экстремум GW (у) = Li,q(y) среди всех
функций степени q, удовлетворяющих \Gq(y)\^L(y), видим, что верх-
верхняя грань (8) достигается, когда / (х, у) = Gv (x) Ga (у) (есть произведе-
произведение обеих экстремальных функций). Например, если II (х) L (у) = С (по-
(постоянная) , то / (х, у) = С cos р (х — a) cos q (у — b), где a, b — постоянные,
которые для каждой точки и для любых к, 1 можно определить так, что
dk+lf (х,у) I дхкду1 = Cpkql. Из неравенств (8) и E) ясно, что
fr-И
lim
где а = lim (к / (к + /)), 3 = lim (I / (к + /)), т. е. / (х, у) удовлетворяет
обычному определению целой функции степени (p,q) двух комплексных
переменных1 х,у.
Следствие 1. Если функция f\(x1, . . . ,хЛ) действительных переменных
ограничена (— ос <^xi <^ ос , 0 <^ i ^ к), т. р. I / (х±, . . . , xj{) I ^ М, и если
для всех i
П^ V\dmf(x1,...,rk)ldx?\<pi,
т-+оэ
то при любых h± ^ 0 , . . . , Лл ^> О (ЛХ + . . . 4- Л а- = ^)
I a m/ (^,..., *¦*) / ax/ч ... дхкч I < Mp*i... />,^. (И)
1 Кроме того, из лелшы 1 тгетрудно вывести, что \ f (х, у) \^Нр (х) Lg(y)
при всех комплексных х, у.
440

Обозначим через dmf (xl9 . . . , х^) f (dn)m векториальную производную
порядка т (т. е. производную по вектору, образующему углы аь . . . , а
с осями Охх, . . . , Ох к). Тогда
(dn )m
Поэтому, в силу A1), получаем
_ —11 I ^ M V -7—i j—.- I /7] COS Ол Г1 ... /?Л. COS 7.j. I fr =
= M [px I cos ai I + . . . + pk i cos aA ! ]w,
причем знак равенства возможен (аналогичное неравенство получим, если
/ конечного роста). Таким образом:
Следствие 2. Если /(%,..., ?&) ограничена или конечного роста
и является функцией степени не выше pi no каждой из переменных xv
то после линейного преобразования с действительными коэффициентами
1=1
f (xlt . . . , ееь) = F (tl9 . . . , t\) преобразуется в целую функцию конечной'
степени (Р19 . . . , Pi) переменных (tl9 . . . , t{), причем
2 ni
i=i Поступило
6. IV. 1948 г.
ЦИТИРОВАННАЯ ЛИТЕРАТУРА
1 S. Bernstein. Comptcs rendus, 176, 1782, A923) [23] (том I).
2 С. Н. Вер it штейн. Экстремальные свойства полиномов, М.—Л., 1937. [«Э. П.»|
3 Н. II. Ахиезер. Изв. АИ СССР, серия матем., 10, 411 A946).

95
РАСПРОСТРАНЕНИЕ НЕРАВЕНСТВА С. Б. СТЕЧКИНА
НА ЦЕЛЫЕ ФУНКЦИИ КОНЕЧНОЙ СТЕПЕНИ*
1.С. Б. Стечкин установил (г) следующее неравенство для тригоно-
тригонометрических полиномов Sn (ж) порядка п с периодом 2те
KlnSn{x + h)-Sn{x)\, A)
где к<^2т:/п — произвольно фиксированное положительное числ®.
Посредством замены переменной получаем для любого тригонометриче-
тригонометрического полинома Тп> х (#) = Sn (х / X) порядка п с периодом 2\ъ неравенство
^x^ + PJ-rn.xHI, B)
где р = пI л, 0<л/г =
Таким образом, если в последнем неравенстве считать фиксированным /?,
то при всяком целом п^>р {т. \е. га//? = Х^>1) неравенство B) спра-
справедливо при любом данном значении р <^2тс /р.
Покажем, что неравенство B) остается в силе, если заменить в нем
Тп> х (я) любой целой функцией Gv (x) степени р, т. е. каково бы ни было
данное число р <^ 2тс / /?, справедливо неравенство
(-оо<х<ос). C)
2sin^- x
[Неравенство C) в случае $ = к / р доказано С. М. Никольским B) непо-
непосредственно.]
Действительно, будем искать среди функций Gv (x) степени р, удов-
удовлетворяющих условию \GV (х0) I = М, где ж0 и 1>0 фиксированы, функ-
цию с наименьшим уклонением от нуля Gp(x + -§-) — Gp[x — тг) • При
* Докл. АН СССР, 60 A948), стр. 1487—1490 B52*)
442

этом мы можем произвольно зафиксировать значение Gp (х) в точке х0:
пусть х0 = О, Gp @) = 0, Gp @) = М. На основании известной леммы F),
среди этих функций существует функция Gp (x), степени не выше р,
ep(z+?)-Gp(x-l)\=*L>0.
которая осуществляет минимум sup
X N. " / N — / |
В случае р < 2ъ / р равенство L = О невозможно х, так как функция Gp (x)
имеющая период C < 2тс / р, была бы постоянной C).
Итак, пусть Gp (x) [Gp @) = 0, Gp @) = М] некоторая функция сте-
степени р, обращающая sup \GP (х + -jjr) — Gp (х ~) в минимум L >> 0.
X ' N */ V */ '
Ввиду того, что — Gp (— ^) обладает тем же свойством, можем принять,
что Gp (x) — нечетная функция, а потому
D)
есть ограниченная (| Gp (x) | <; L) четная функция степени р. В таком
случае, как известно, можно построить такие тригонометрические поли-
полиномы D»5) (прием [84] стр. 385—386 позволяет положить а0 = 0)
К, х (х) = ао,х + 2 ак>х cos -^, | Т^ (x)\^L E)
порядков п = рХ—> оо, что lira Г^, х (ж) — G*v (х) при всяком а; (— оо<;о;<;оо).
п-^оо
Определяя теперь тригонометрические полиномы ТП) х (х) из уравнений
/ТТ / . В \ /TI / м Р \ /Т7* / \ /^\
/ . т1 . ' I / « I *у ' I / л I О1* 1 [hi
¦*¦ nt х 1 «^ ч 9/ п» ^ I о / — ¦* w, a V1^/» \ /
при дополнительном условии ао,х = О, получим
2Х
Но вследствие E), F) и неравенства B)
1уп,х(ж)|<-^-5- (-сх><^<оо), B bis)
поэтому последовательность ограниченных функций ТПу \ (х) степени р
(где п = \р->оо) может быть выбрана так F), чтобы Тп> х (#) -> ^р (^)
1 Напротив, при всяком Р>2тс//? функция G^ (х) = -—- sin ^- степени 2тс/р</>
V /ТС р
давала бы L = 0. Таким образом, ограничение р<2тс//> в неравенстве C)
является необходимым для существования верхней грани | Gv (x) | при данном
sup с
2
443

равномерно в любом данном промежутке, причем Hv (x) должна быть
целой функцией степени р. Следовательно, имеем также, благодаря F),
z) dz =
Таким образом, функция &у(эг) = Gp(x)—Hj>(x) степени^/?, кото-
которая, вследствие D), удовлетворяет уравнению ^(х+~)-—ъ[х—-|М=0,
оказывается периодической с периодом ^<"тг//?, т. е. должна быть
постоянной. Следовательно, G\> (х) =_ Нр (х), откуда М =- G'p @) = Hv @) =
= lim Tltf x @). Поэтому из B bis) заключаем, что
Hv (х -%) = \ Нр (x+z) dz = lim \ Т*. х (x+
= lirn^ \Tn(x + у) - Tn (x - -|] j = lim Kt x (г) - G; (ж).
2 sin
что и требовалось доказать
2. Дополним неравенство C) неравенством
2sin
-|) ~GV (л- - |
(- оо ^
со),
G)
дающим точную верхнюю грань Gv (х + -^) — Gp (я — -L) при 3 <;тг//?
(в случае $ = к/р неравенство очевидноI.
Докажем сначала более общее предложение:
Среди функций Gv(x) степени р, получающих значения Gv(x0) = а,
Gv(x-))=b б двух данных точках ,70, х± где* 0<С^х1—хо = [3 <^ ти / р,
причем значения а, Ь таковы, что
(Ь — a cos //:>) (b cos pr$ — a) ^> 0,
{единственной) функцией, наименее уклоняющейся от нуля (—
является
(8)
sup ! Gp (.г) | > Л/о = max | ,VP (.г) | = ^
,
- 2afecos ^ •
Принимая во внимание, что при сдвиге промежутка (х0,
nsup|Gp(j)] сохраняются, можем считать, что —к / 2<
(9)
1 При р >¦ тс / /> имеем вообще Gp f х + — j — Gp [x о") ¦< 2 sup j Gp (x) [, и
это неравенство не может бь[ть улучшено, так как равенство осуществляется, если
Gp (х) = sin ргх, где рх ==• ти / [3 С J».
2 Нетрудно видеть, что при $~^>tz/ р, как и в случае нарушения (8), наимень-
наименьшее значение sup | Gp (x) j= inax (| Z> |, I a D» так как? полагая, для определенности,
& | >-1 а |, видим, что функция Gp (х) = 6 cos 7^1 (^ — а;х) степени рг < ^ удовлетво-
удовлетворяет условиям G (^х) = &, Ср (х'о) = «, если Ь cos px P = а •
444

<^?z j 2, и так как условие (8) выражает, что Sp (xQ) Sv (хг) "> 0, зафи-
зафиксируем точки х0, хг так, чтобы s'v (к / 2р) = 0 [т. е. Sp@)=0]. Тогда
Sp (х) = Mosinpr [полагая для определенности Sp (х^ ; -0).
Докажем теперь невозможность существования такой функции
Gp (x) ^Sp (x) степени р, что sup | Gp (a) \ <^ Мо. Действительно, в таком
случае, полагая ур(л) = MQsin px—Gp(x), мы имели бы F)
(.г) = C(,sy>.r (Л -
7,=-с
\'
А п Ai- = (-— 1)' о у к -\- -ту-) — U> 0 — некоторые постоянные.
Но так как каждое слагаемое суммы, вычитаемой из Л, убывает
с возрастанием х па (-— тс/2/?, тс/2/;), то <?р (.г) имела бы не более одного корня
в этом промежутке, а между тем rsp Cro) == ?р (xi) "^ 0, следовательно,
необходимо, чтобы все AJ{ = А = 0.
Рассмотрим теперь совокупность всех функции Gp (.т), удовлетворяю-
удовлетворяющих только одному условию | Gp (.rj — Gp (:r0) j = ! 6 ¦—¦ a \ = L. Если
iV = min sup j Gp (x) j соответствует значениям (а, й), удовлетворяющим (8),
то, вследствие (9),
у IJ + \Ъ (b — I) sin2 -^ /. cos i^-
L
= mi п .—7
SID
^
и осуществляется функцией Sv (х) = ———^т- при Z> = — a = L / 2. Но зна-
Л
2 sin Лу-
Лучение ^Дг не может получиться без (8), так как тогда мы имели бы1
sup J Gp (x) |^>max(j b |,' a \)^> —-. Таким образом, G) доказано.
Из G) следует, что модуль непрерывности (р^^тс)
со C, Gp (т)) = sup | Gp (x + ^-) — Gp (я — -^-) ^2 sin ~-sup IGp (х) \ .
Попу пило
ЗОЛУ.4948 г.
ЦИТИРОВЛ IIII А Я Л 11 Т Е Р А Т У Р А
1 С. Б. Сточки п. Докл. АН СССР, 60, До 9 A948).
2 С. М. Никольский. Докл. АН СССР, 60, ДЬ 9 A948).
3 С. Н. Бе ришт ей и. Докл. АН СССР, 51, № 5 A946) [84], заметка I.
4 Б. М. Левитан. Докл. АН СССР, 15, № 4 A937).
5 С. Н. Берн штейн. Докл. АН СССР, 54, Д« 2 A946) [84], заметка IV.
6 С. Н. Бериштейн. Докл. АН СССР, 52, До 7 A946) [84], заметка III.
1 См. предыдущую сноску.

96
ПЕРЕНЕСЕНИЕ СВОЙСТВ ТРИГОНОМЕТРИЧЕСКИХ
ПОЛИНОМОВ НА ЦЕЛЫЕ ФУНКЦИИ КОНЕЧНОЙ
СТЕПЕНИ *
В настоящей статье дается применение общей теории, изложенной в заметках
автора (*—4), к установлению свойств целых функций конечной степени, аналогичных
тем, которые были выведены автором для тригонометрических полиномов в
статьях E>6).
1. Лемма 1. Если абсолютный максимум** ограниченной функции
Gp(x) степени ^.р достигается на отрезке (х0, хг), где хг — хо = $<^~,
то
max | Gp (х) j < М = ^^ У G% (х0) + G% (хг) - 2GP (x0) Gp (Xl) cos p$ A)
и знак равенства осуществляется, когда Gv (x) есть тригонометриче-
тригонометрический полином
П i \ GP ^i) sin Р (Х ~~ хо) — Gp (х<>) sin Р (х — xi) /оч
Схр (х) g— B)
порядка 1 с периодом 2Ьг = —.
Де11ствительно, среди ограниченных функций Gv (x), принимающих
заданные значения Gv (x0) и Gp (хг) и достигающих абсолютного макси-
максимума на (х0, х-^), есть такая Gp (x), для которой этот максимум получает
наибольшее значение N. Но мы знаем, что, с одной стороны B»3),
где Sn,x(x) i\Snt\{x)\^N) — тригонометрические полиномы порядка п
с периодом 2,mz = , равномерно в каждом данном промежутке, и с дру-
* Изв. АН СССР, серия матем., 12 A948), стр. 421—444 B53*).
** Т. е.] max I G (х) I . Значения G (xo)9 G (х^ вещественны; max I G (х) I
—оо<я:<оо ' р ' У V I P I
будет наименьшим, когда функция Gp {x) вещественна. (Автор.)
446

гой стороны F), утверждение нашей леммы доказано для случая, когда
Gp(x) — любой тригонометрический полином. Следовательно, N = M.
Следствие 1. Расстояние от точки х0, где достигается абсолютный
максимум М целой функции Gv (x) степени р, до корня Gv (x) =0 не
менее — .
Р
Доказательство аналогично: среди тригонометрических полиномов.
Sn, \ (х) —> Gp (x) имеются, в частности, такие, для которых абсолютный
максимум также достигается в точке х0 и Sn, x (#i) = Gv (xx) = 0 в бли-
ближайшем корне Gp (х) = 0, но требуемое свойство | х± — хо\^- — (р= —
Р \ 4
установлено для тригонометрических полиномов [см. F), стр. 1159].
Следствие 2. Если абсолютный максимум М вещественной функции
Gp(x) достигается на отрезке (х0, хг), причем
( ? ) C)
то
I ^р (х) \ ^ — (— оо < х < оо). D)
При этом знак равенства осуществляется, когда
GP(x) = n
008 2jT
Для доказательства нужно определить максимум М правой части A)
при условиях C), который соответствует1
Следовательно, максимум
и B) превращается в E).
Теорема 1. Если целая вещественная функция Gv (x) степени р удо-
удовлетворяет условиям:
1) \GP (а^) |^1 в бесконечной последовательности точек а-и (± к~0, 1,...),
где ^
2) существует такое число m^>0, что lim — = 0 (т. е. функция
1 Так как при 1 < [л < 2 (cos р$ < 0) коэффициент при Gp (x0) Gp (хг) в подко-
подкоренном количестве A) > 0, а в случае \i > 2 (cos /?p > 0) неравенство Gp (x0) Gp (^iXO1
недопустимо (следствие 1) и подкоренное количество A), представляя тогда квадрат
стороны, противолежащей острому углу /?р с прилегающими сторонами Gp (xo)r
Gp (ajj), также достигает наибольшего значения при Gp (х0) = Gp (хг) = 1.
447

Gv (x) алгебраического роста) [96.1], mo Gp (х) ограничена на всей дей-
действительной оси, а именно
sup |GP(/)| = ^< —. Dbis)
—оо<л:<оо cos
Наше утверждение в случае т = О, т. е. при lira Gp (х) = О, негю-
J х->оо
средственно вытекает из следствия 2, так как тогда абсолютный макси-
максимум \Gp(x)\ достигается в точке некоторого отрезка [а^, #a-+i]- Но при
всяком данном т ^> 0 (которое можем считать целым) введем функцию
Gp+?m (х) =
степени р + гт — сгр, где s возьмем достаточно малым, чтобы с?<лг-
В таком случае
lim Gp+&m (x) = 0, | Gp+em (ak) \ < 1
и, согласно D),
Gp+zm(x)
COS тг^-
1
Полагая г->0 (се—>1), получаем D bis), так как Gp^zm(x) -> Gv (x) при
всяком фиксированном х.
2. Я^елая полностью освободиться от второго условия теоремы и
получить возможно простые результаты, уточняющие неравенство D bis),
мы остановимся теперь на случае, когда узлы а^ расположены равномерно:
Лемма 2. Если целая функция Gp (x) степени р удовлетворяет во
х х-^ = (к + у)——
1, rrw (Pi = \1Р > р)
всех точках х^ = Ik + у)—— (\х^> 1» Л = 0, + 1, ±2, . . .) неравенствам
*^„ (*+-|-)«[Л*-(*+-|-)»]
следовательно,
Действительно, п|>авая часть F) есть целая функция Нр (х) степени не
выше рь поэтому
Gp (х) = HPl (х) + F (x) cos px х,
где F (х) — целая функция конечной степени q ^> 0. Но предположение
следует отбросить, так как тогда степень F (x) cos рг х была бы
446

Vp\ + Q2^>Pi1- Принимая же во внимание, что
между тем как
если функция F (х) нулевой степени не приводится к постоянной, заклю-
заключаем, что F (х) — постоянная (т. е. F (х) = 0), ибо в противном случае
мы имели бы
lim
•о,
что невозможно (р < рг).
Из леммы 2 и теоремы 1 следует
Теорема 2. Какова бы ни была вещественная функция Gp (х), удов-
удовлетворяющая условиям леммы 2, при всех х (— оо <^ х <^ оо) соблюдается
неравенство D bis); кроме того, если р — целое число (р- == 2, 3, . . .), то
верхняя грань g^ = 1/cosk— , данная неравенством D\bis), не может
быть снижена2 [разумеется, точки хи могут быть сдвигаемы: (жЛ + а),
где а — любая постоянная].
Последнее утверждение вытекает из того, что верхняя грань D)
достигается функцией
^ , ч cos рх
COS ;
которая в случае целого
2 удовлетворяет неравенствам
1
I* \
1,
\хр
Cbis)
так как тогда
cos
*+ш
cos^- при всех целых к.
3. Для перенесения результатов § 1 статьи F) построим прежде всего
интерполяционные формулы, аналогичные тем, которые были там даны.
1 См. «Добавление», следствие 4. __
2 Очевидно, g^ является невозрастающей функцией; например, g2 — У2, g3 ¦¦
2
= —77= • Для нецелого ^ > 2 вообще
COS 7
2 Ы+2
COS'
и g —> 1 так, что lim
^м — 1] =-д-. Для {х<2 далее будут даны более точные
.
оценки g^ (в частности, будут указаны точные значения LN — #* для
при любом целом N > 1), не исключающие предположения, что Gp (x) может полу-
получать комплексные значения при — оо < х < оо (см. стр. 460).
29 С. Н. Бернштейн
449

Пусть / (х) будет какая-нибудь функция, заданная своими значе-
ниями / (ajc) в равноотстоящих точках а& = — .
Pi
Полагая — = N > 1, построим функцию
f(ak)smPl(x-ak)sinq(x-ak)
степени ^ рг + q = рг A + -*г) по значениям / (ак) = GPl+a (а&), которая
выражается абсолютно и равномерно сходящимся рядом, если значения
\/(ак)\^М ограничены. Ценные свойства этой интерполяционной фор-
формулы связаны с простым тождеством (ajc = —, Pi = qN, iV^>
ч Л.
qx
Для доказательства заметимтсначала, что, каково бы ни было iV0 > 1,
ряд G) при любом фиксированном х равномерно сходился в промежутке
l^N ^.No и, следовательно, ср (N, qx) непрерывна относительно N.
С другой стороны, функция ср (/V, qx) не зависит от х, так как она
является целой периодической функцией степени 2 переменной z — qt
с периодом — относительно этой переменной z и, следовательно A), в слу-
случае N ^> 1 обращается в постоянную ср (iV). Таким образом, равенство
? (N, qx) = ср (N) (8 bis)
имеет место при любом N > 1, а также при N = 1, полагая ср A) = lira cp (iV)r
но, подставляя в функцию ср (TV, qx) N = 1, qx = 0, находим ср A, 0) =
= ср A) = 1.
Остается вычислить значение постоянной ср (TV) при любом 7V>L
Пусть N = ^ рациональная дробь, где A^B^l. Тогда
sin2
сг> (—) =
' \ D )
со
= S
кВ у
)
"Г ZJ / тс кВ у +•••+
/c?_V "г ... -г ^j f B_i kB
450

Принимая во внимание, что каждая из В сумм, стоящих в правой
части равенства, равна ?(-тг)> получаем таким образом о (А) = Во
и, в частности, ср (А) = Ао A). Следовательно,
и, вследствие непрерывности, это равенство, соответствующее (8), спра-
справедливо для любого Лг^> 1.
Из (8) легко получить простую верхнюю границу для \GVl+q (л) I,
данного формулой G) при условии \/(а^)\-^Л1:
И
Ряд G), очевидно, сходится абсолютно и равномерно при более общем
условии
/ ы
1М {т^{).
Но в случае еще более быстрого роста / (ак) формулу G) следует заме-
заменить другой аналогичной формулой. Для этого заметим, что при помо-
помощи того же рассуждения тождество (8) обобщается следующим образом.
Если целая функция Н (х) степени 2т такова, что ряд
(?) (Ю)
к=—со
абсолютно сходится, равномерно при т <^ N <^ No <^ оо, то
ср (.х, N) =CN (— оо < х < оо; т < 7V), (И)
где
C S 1
— постоянная. Таким образом, в частности, для всякого целого s >> 0 фор-
формула G) принимает вид
/ kiz \ . ч / kiz\
00 Sin рл\х siir q[x
г t~\ _ V V Pi) *\ Pi)
де GPl+bQ(x) степени <А + ^<2/?! абсолютно сходится при
I , 1
\~-!—^M, если m<^s, а в случае /( —
= M Yc8N, (9 bis)
Pi )
451 29*

где
с —
4. Теорема З1. Если Gp(x) есть функция степени р ^ рх~ q, прини-
принимающая е точках а^ = — ограниченные значения (| Gv (а&) j = |/ (ад-)|<^Л/,
Pi
>а также е более общем случае, когда —~р^— <3/ для некоторого т<Л),
то Gfl (x) выражается формулой
r (\ ^ sm л (* - «л) sin ? (*--«*)
G() ^^Ы
(т. е. интерполяционная формула G), приближенно выражающая произ*
вольную функцию / (х) посредством целой функции GPl+q (x) степени
-T-q, которая совпадает с / (х) в узлах а*, дает точно / (х), если
— целая функция степени р <С Pi~ (I:B частности, справедлива формула
Действительно, рассмотрим функцию двух переменных (х, у)
1< (х, у) = G» (ж) т"^—~~
степени p + q^Pi относительно х, которая при всяком фиксированном
у, очевидно, удовлетворяет условию
lim x*F (x, у) = О
-1-Х -> оо
при 0<^а<^1 — т. Этого достаточно для того, чтобы, согласно формуле
B) моей заметки C),
Вследствие равномерной сходимости A4), во всякой ограниченной области
переменной х, не содержащей а^у переходя к пределу при у —> ху полу-
получаем
00 sin рг (х — uj.) sin q (x — аЛ
СИ= 2 6
1 Эта теорема распространяется аналогичным образом на интерполяционную фор-
формулу A2), а также на всякую формулу (в случае абсолютной сходимости)
оо .
2 sin рг (х — аь)
где Н (х) — любая целая функция степени q ^ р1у подчиненная условию Я @)=1.
452

Лемма 3. Если GVl+q (х) представлена выражением G), где — = X
>1 — целое число*, и GPl+q(—) <С 1, то
sm27v sin27v
причем значение Ln достигается при qx— -^, когда
Действительно, в каждой точке х
оо SllK/IX —
A6)
Положим k — IN + p (I, 0 ^ p < iV — целые числа) ir применим G),
полагая
Тогда
Г fkn\ (
го дг_! (__1)^ sin (qx - АТС - -??-
2 S ^^
Х=-о
ЛГ—1
т. е., полагая qx = z,
N -1
z \
sinNz
Сопоставляя A6) и A7), мы видим, что наибольшие значения
l4-g (x) | осуществляются построенной нами функцией A8) в точках х,
* Если N — нецелое число, то Ьгдг] <С ^дг ^ ^глп+i' но ПРИ этом точное значение
LN неизвестно. (Автор.)
453

где sin \qx — ~Л имеет одинаковые знаки при р = 0, 1, ,. ., N — 1, т. е.
когда 1гъ — -^ <J z ^ Ы (h — любое целое число). Тригонометрический по-
полином GVl j_Q (— ] порядка Лг — 1 имеет период тг при N нечетном и,
принимая значение 1 = (—l)^ в точках ~ ¦ тс и тс, достигает абсо-
лютного максимума Ljy (со знаком +) в точке тс| 1 — -^\ — середине этого
промежутка1. В случае Ат четного GPl-\.q(—) имеет период 2тс и достигает
абсолютного минимума —L^ в точке тс 1 — ^ j и максимума + L2y в точ-
точке —2~Ь • Таким образом, функция GPl+q (x)} осуществляющая абсолютпый
.максимум Ljv при любом целом N, оказывается функцией степени
р = р± — q. Отсюда следует
Теорема 4. Если функция * Gp (х) степени р <С р±( 1— — i= — удовле-
удовлетворяет неравенствам \ Gp (а^) | ^ 1 во всех точках бесконечной последо-
последовательности а^ (— ос < к - ос), где ак+г — а л = —— , то
Gp (x) j < LN (— сю ^^ х -\ сю; Т " > 1). A5 bis)
Кроме того, имеет место
Теорема 5. Какова бы ни была функция GPl^q(x) степени ^/^i + ^=
= Pi A + ~лГ' ' принимающая в точках а^ = —-'Значения
^ /ктс\ / л\А ;
G-p 4<з —) = (— Ч пРи л четном
\Pi J
и
Gpiq(—) = (— 1) тг/ш А нечетном,
\Pi J
где X = -у- , найдутся точки х (— сю ^ х <"' сю), г^е 2
i GPl+q (.г) | > LN --— (Л7;.- 1 — целое).
Действительно, если GPi^q (x) дана интерполяционной формулой G),
т. е. формулой A7), то
1 При ^V четном (—1)р = (—1)*-*л = (—1)Л; при N ыечепюм (— t)p = (—l)fc"x
* Теорема 4, как и лемма 3, с соответствующими формулами A5) и A5 bis) при-
применимы также к функциям G (х) с комплексными коэффициентами. (Автор.)
1 г 2 VT+ У~2
—— , 1.4 =» у Z -f- ^ Z, i^5
454

i^=^±LN (к — целые *).
Самая общая ограниченная функция степени рх -\- д, принимающая
кп
те же значения в точках аи = — , равна
Pi
где .4д (а;) — ограниченная функция степени
Но если ]GPl+g (ж) |^ Af, то при всяком
2 л,(*+^
Таким образом, полагая т—>оо, мы превращаем ^4д (#) в периодиче-
периодическую функцию с периодом — (не повышая sup | GPl+g (x) |), т. е.
Aq (х) = а0 + аг cos
наименее уклоняющаяся от нуля функция
g^ = z) в виде
iV—1
2j
sin дж,
z \ sin
Г ) =
Полагая z = т/ -| ^— тг, имеем
iV-l
siniVz
1
p=o
—
при N — 2^ + 1 нечетном и
представляется
. A9)
siniVy
/ tub
*=—s sin I/ +-—
р=о sm z —
ft—8+1 sin ^ + -gJv" " J
при N = 2s четном. В обоих случаях функция под знаком 2 нечетная
по у, поэтому должна быть нечетной и функция
а0 + ах cos (у + ^^ ^ + 6Х sin (у + ^^ тс) = ъ si« 2/-
Следовательно, наименьшее значение М = sup| Ср1+д (х) | получим, вы-
бирая й так, чтобы при N = 2^ + 1 уклонение ух=
1 В случае iV = — нечетного всегда +, в случае N четного — со знаком (—1)\
455

B2)
а при Лг = 2s уклонение
" " 2 - , 2.-1 ,+ь^у\ B3)
k=*—H-i si
было наименьшим.
Функции B0) и B1) принимают в точках у = -|- и ^^ T"*""iV"
абсолютные значения
ЛГ-1
2
—2*4-1 '
sin
yv > 0 при N ^> 2) с противоположными знаками. Поэтому
и для того, чтобы | Gpt+q (x) | в этих двух точках был наименьшим, нужно
определить Ь по условию
= М n —¦ Z//V.
Следовательно, -^ = и, тем более,
iV . 7U
Sm2iV
= sup | <?;1+в (ж) j > ?,w ^-~. B4)
Примечание. Неравенство B4) тем точнее, чем больше N. Только
при N^>3 оно дает нижнюю границу > 1 для Му между тем, как, оче-
оче> у у , ,
GPi+qf—j == 1. Таким образом, из
iV } 3 Л
видно, М^>>\, так как, по условию,
неравенства B4) видно, что М = 1 невозможно при iV }> 3. Легко про-
проверить непосредственным построением, что М = 1 при iV = 2 и при iV = 3.
Для упрощения письма мы можем положить q = 1, р± = N. В случае
= 3 тригонометрический полином B2) 4-го порядка G\ (x) имеет вид
4 @) - G40p) = - 1, G4(-f ) = ]
sin
smy ' . / тс
sin (?/-}--g
456

Полагая 6 = q- Для того, чтобы производные Gl'(-?) = 0, получаем
6 \ б j
B5>
Аналогично для N = 2 из B3) имеем
у + sin3y], |G3 (у) | ^ 1. B6)
Таким образом, тригонометрический полином 2-го порядка
S2 (x) = -Q- [3—8 cos х — 4 cos 2x] B5 bis)
достигает абсолютного экстремума 1 в точках: 0, -^, -Д, Bте) с после-
последовательными знаками —, +, —, (—) (в точке ~ есть относительный
7 \
максимум -Q-J , а
«У3 (х) = — [3 (sin х— cos x) — (sin Зх + cos 3x)\ B6 bis)
достигает экстремума 1 в точках: 0, -^-, те, -^ , Bте) с последователь-
последовательными знаками: —, +, +, —, (—Ив точках —г- и -у- имеются соответ-
1 1 \
ственно относительные минимум —= и максимум ¦==. .
5. Теорема 6. Какова бы ни была функция f (х), заданная своими зна-
значениями f (-—) (к = 0, rfc I, ± 2, •. •)> погрешность
\Pi/
PPl+q (/ И) = SUPI / (х) — GPl-q (x) I
ее приближении интерполяционной функцией GPl+q (x) степени
+ Я> определяемой формулой G), удовлетворяет (в случае сходимо-
сходимости х) неравенству
?Vl+a(f(x)X(LN + l)Api_qf(x), B7)
acteiV = |— и Avf(x) означает наилучшее приближение f (x) при помощи
функций степени р.
В самом деле, пусть
1 Для абсолютной сходимости G) достаточно, чтобы существовало такое число-
а>1, что
/кк\\ М [\ к \-\-1] ^ г
( — 1 <^ —-—¦ — . В случае более быстрого алгебраического воз-
возрастания /(— 1 формулу G) следует заменить формулой A2). Соответствующая
функция Hq (х) в интерполяционной формуле, указанной в сноске на стр.452, может
быть подобрана также и в том случае, когда / (— ] растет не быстрее функции
нулевого рода.
457

так что, в частности,
Тогда, вследствие теоремы 3 и леммы 3,
\f(x)- GPl+q (х) | < | / (x) - GPl_Q (x) | + | GPl_e (x)
—oo<A;<oo
- Ljv sup
< [LN + 1] APi_q f (x). B7 bis)
Следствие 3. Существуют функции f (x), для которых $ B7) имеет
место равенство.
Действительно, полагая для определенности N нечетным и q = 1
(р± = N), построим периодическую функцию / (х), принимающую значе-
значения / (—) = 0, для которой наименее уклоняющейся функцией степени
N — 1 является
N— 1
_ • Л Т
р=0 S1H X — -
так что А^— if{%) = 1. Для этого достаточно, чтобы \f{x) — G;v—i (^)l^
и, например, внутри промежутка f —^— тс, tcj была точка
где / (?) = Giv—1 (?) — 1, так как тогда в последовательности 2N точек
Ж ' * * ' ' iv l7r> ^ тс» " * *' 2тг) пеРи°Да 2тг разность / (х) — Gn-x (x) дости-
достигает +1 с последовательно противоположными знаками. Если мы поло-
положим еще
.{Ж— 1 \ тг /2iV— 1
I J ^
то в этой точке все неравенства в B7 bis) превращаются в равенства, так
как GN+1 (х) = 0 [вследствие / (аЛ) = 0, ак = — = -^1
Следствие 4. Если рост значений / (—) я/ж 4hA;~>oo произволен
\Pi 1
[так что формула G) и ее обобщения неприменимы], все же существуют
интерполяционные функции GVl+q (х) степени рг + #, удовлетворяющие
условиям
для которых неравенство B7) остается в силе [таким образом,
9 a- f (х) = °° лишь тогда, когда А _ f (х) = оо ].
Действительно, определим по формуле G) функцию FVl+q (x) степени
. кп
рг + q, принимающую в точках — значения
458

где GPl-q(x)—функция степени р1 — д, наименее уклоняющаяся от f(x).
Тогда, полагая
имеем
/Ъс
и приведенное выше рассуждение полностью применимо к / (х) — G* , (х).
6. Из формулы
/ Tctz \
B8)
которая соответствует ./V = 1 [т. е. q = /?х в G)], видно, что б этом слу-
случае из ]/(— )|<1 следует1 \G2Vi(x) |<1 (— ос<я;< оо ).
I YPi/ [
I YPi/ [
Примечание на стр. 456 может навести на предположение о существова-
^-J таких интерполяционных
р
нии при любых значениях /( —) ( /(—
( ) ( /()
функций G3pi (x) (N = 2) [и даже G4Pl (х) степени -~ (N= 3I что
\G (х) | ^ 1 и | G4 (ж) | <; 1. Однако нетрудно показать, что это неверно.
~Т~ ~з~
А именно, имеет место следующая
Лемма 4. Если — = N > 1, GPl+g f —) =ъъ и вк = ei} i = k (mod
| | д 9
причем | Sfc | = 1, mo существуют такие чередования знака s#, 9ля которых
все функции GPl+q (x) степени рг + д таковы, что
sup | GVl+q (х) | > 1.
Действительно, по предположению, можно указать такое целое число
w, что N > ~1ГТ * Применяя замечание, сделанное при доказательстве
теоремы 5, мы видим, что из существования функции GPl+q (x) степени
р± -\- q, для которой sup j GVl+q (x) \ <^ 1, вытекало бы, что тем же свойством
обладает и периодическая функция SVl+q (x), принимающая те же значения
"") = еь с периодом 2тг. Поэтому достаточно показать, что существуют
= НЬ 1, для которых невозможен тригонометрический полином Sn+q (x)
n — 1) порядка п + q, достигающий абсолютного максимума 1 в 2fi
точках — (к = 0, 1, ..., 2п—1). Но из этого требования следует, что
«производная S'. (х) = 0 при х = — , так что
S'n+q(x)=smnxTq(x) =
= asinnx + 5jfyfc [sin (n + k-x -\- cp^) -(- sin (n — k-x
1 Функция G2p (x) степени 2рг определяется однозначно дополнительным уело-
459

где Tq (х) — тригонометрический полином порядка q и а, Ь,
рые постоянные.
Интегрируя, находим
— некото-
некоток=г
C0S(W
+ фг.)
— к -X
п + к
Требуя, чтобы Sn+q(—) = е&, мы получим 2га линейных уравнений
с 2 (# + 1) неизвестными С, а, 6& cos cpft, by, sin cp&, которые не могут быть со-
совместны при всевозможных значениях е# = + 1, если1 д<Сп — 1, что и тре-
требовалось доказать.
Значения g^ = sup j Gp (x) |, полученные раньше при условии, что»
Gp(~ j ^ 1, были связаны с предположением (теорема 2), что Gp (x) — ве-
вещественная функция. Предположим* теперь, что
— любая комплексная функция степени р, и обозначим
полагая, что
(—
G
1. В таком случае имеем также
(—
) U
<1, откуда sup l
—оо<д:<оо
sup
— oo<x<oo
Следова-
тельно, во всяком случае имеем неравенство
,»/27
B9)
на уточнении которого мы здесь останавливаться не будем (заметим
лишь, что g2 = g^= У2). Отметим еще вытекающее отсюда принципиально'
важное следствие для вещественных неотрицательных функций Gp (x) ^> О,
удовлетворяющих условию
где Н (х) — целая четная функция нулевого рода.
Как показано в моей заметке D), при соблюдении условия B5) функ-
функция Gp (х) ;> 0 степени р допускает представление 2
1 В случае q — п — 1 соответствующие уравнения всегда совместны и приводят к из-
Р\х
вестной формуле Джексона, которая соответствует B8) при замене х на —^ и w->oo.
* Н. И. Ахиезер обратил мое внимание на то, что в силу теоремы 4 имеем
LN =s g^ (а не LN = g[l, как стояло в первоначальном тексте). В связи с этим не-
несколько изменено изложение конца §6, ив частности, изменены неравенства B9) и C1)
(последнее из них содержало явную опечатку). (Автор.)
2 В упомянутой заметке D) на Н (х) было наложено дополнительное ограничение,,
го Н (х) — четная функция с неотрицательными коэффициентами. Однако последнее
460

Gp (x) = *? (x) + t*_ (x) = | s^ (x) + it^ (x) p, C0)
2 2 2 2
где * s (x) я t (x) — целые функции степени -~ .
Теорема 7. Если G2P (х) ^> 0 степени 2р удовлетворяет C3) и
C1)
)С, mo
j + ^2 (—-
Действительно, из s2 —) + t2 {— <С 1 следует
кп
откуда, в силу B9), получаем C1).
Таким образом, функция G2P (x) 6 B5) в случае ограниченности ее
снизу оказывается ограниченной и сверху при решетке из тех же равно-
равноотстоящих узлов, когда степень ее вдвое выше Bр вместо /?).
Вопрос о достижимости правой части неравенства C1) в общем случае
мы рассматривать не будем, отметим лишь случай, когда \i = 2. В этом
случае, как было показано, L2 = g2 ~ V% и> следовательно, согласно тео-
теореме 7 при G2P(— )-<l [G2p(#)>-0] неравенство C1) дает
или, что то же самое, если Gp (x) 6 B5) степени р (Gp (x) ^>0) и Gp (
ограничение не является существенным, так как, если существует четная функция
нулевого рода Я (х), такая, что | Gp (х) \ < | Н (х) |, то
n==l
такя^е будет нулевого рода (так как сумма двух четных функций нулевого рода
должна быть нулевого рода [97]); но, полагая
имеем
2
Следовательно,
причем все коэффициенты Яо (х) положительны.
Таким образом, при исследовании свойств функций, удовлетворяющих условию
B3), которому посвящено нижеследующее «добавление», мы могли бы в случае
надобности ввести без ущерба для общности выводов даже более специальное пред-
предположение, что все корни Н (х) лежат на мнимой оси. (Первоначальная формули-
формулировка этой сноски была не вполне корректна.—Автор.)
* Условие, необходимое и достаточное для представимости G_(#) формулой C0),
установлено Н. И. Ахиезером (см. Докл. АН СССР, 63 A948), стр. 475—478). (Автор.)
461

то Gp(x)-^2. (Значение 2 достигается для Gv (х) = 1 + sin px). Без огра-
ограничения Gp (x) > 0 верхняя граница \Gp(x)\ была бы бесконечна.
7. Отмеченное только что свойство функций Gp (х) ;> 0 тесно связано си
свойством <<интерференции» любых функций конечной степени, подчинен-
подчиненных условию lim —— = 0.
Лемма «интерференции». Если — > 0 при х—> Ч- ос м Gp(— ) I ^1
х
Р
\ Р J \
при всех целых к = 0, -Ь 1, 4-2, . .., то при любом х (— оо <•" х << сю)
знак равенства осуществляется для
Gp (x) = Sp (x) = t^±p - cos px, C3)
i к550, 5p@) = l),
4
достигает верхней грани — /г/?гг х = 0.
Действительно, мы знаем C), что благодаря условию lim р = 0Т
CO
где ^ распространяется на все целые А^О. В таком случае
S' ("
Поэтому, складывая почленно и включая первое слагаемое в сумму V,
имеем
= cos,
г \ 1 п
^Т\ / И"" '
рх — [к — -^ ) те /?ж — U + -о- 1 я J
462

Пусть (к0 — -тг) те < рх0 < (к0 + -^) те, т. е. /?х0 = Аоте + 8, | 8 |< -?¦ . Тогда
<jcos/*r0j
1
pxo—lk —
\
{A 0—1 с- ^
2 l^1^ ?—rr
\ z /
Г 1
+ 2 I ^fc I 7 1~\
<
I cos
— ( Л 4-у ) те
fc=*o+i L [k — ~
Л + у]*-.
i
1
. 1
= | COS
+ r 1 + !
I C0S PX0 \
причем знак равенства осуществим, когде Аъ0 = 1 и Ак = (— 1)л"~А;°+1
(A^A0). Утверждение леммы, таким образом, доказано1, так как макси-
максимум функции ^cos достигается при 8 = 0.
Следствие 5. При тех же условиях
Достаточно заметить, что
1 Для тригонометрических полиномов эта лемма была доказана в статье E).
463

Применяя тот же прием, можно было бы получить точную верхнюю грань
Gv (х + —) — Gp (х) , которая во всяком случае < — .
Нетрудно видеть, что из леммы «интерференции» вытекает (при более
узком условии — >0) отмеченное выше свойство неотрицательных
функций Gp (х) б (S3). Действительно, если Gp (х) ^> 0 и Gp (— j <; 1, то,
применяя неравенство C2) к 2GP (х) — 1, получим
откуда
Gp (х) ^ 1 -| (— со <^х <^ оо),
которое, однако, не дает указанной выше точной грани 2.
Теорема 8. Если значения /(—:] произвольной функции f (x) ограничены
и Ар — ее наилучшее приближение при помощи функции степени р, то
¦р, C6)
Gp Ы = / @) S-^^- + sin /?д; V(~ 1)* / (- ) Г 1 + ~ . C7)
PW ' ^ ' рх ' r ZJV ' ' \pj IPX — кк *tcJ
В самом деле, применяя C2) к Gp (^) — Gp (x), где функция Gp (x)
степени /?, наименее уклоняющаяся от / (я), может быть представлена в виде
11, 77' /ГЛ sin
получим
я, соединяя это неравенство с неравенством
2
находим требуемое.
Замечая, что
— ^ft — — J я
/ м 1. C8)
464

мы видим, что замена интерполяционной формулы C7) интерполяционной
формулой C8) дает равномерное приближение на всей оси для всякой
равномерно непрерывной функции f (x), а именно: полагая
<op = ysup| /(*+^) + /(*-?)-2/(я)| (-°о<*<оо),
имеем, вследствие C6),
рр = sup | / (ж) - Нр (х) |< Яр + о>р < (l + i. j Av + cop, C9)
причем, в частности, очевидно,
i j
; ?) = sup
Не останавливаясь подробнее на неравенстве C9), отмечу лишь, что
всегда рр = О (сор) и что рр = О (Ар) (при /? -> оо), если — = О (Ар) для
Р
некоторого т<С2.
Добавление [96.2]
Приводимые ниже свойства функций Gp (x) б C5) вытекают из общих
теорем классической теории целых функций, но поскольку некоторые из
них, повидямому, не были до сих пор формулированы, я счел полезным
вывести нужные для данного исследования предложения.
Лемма 1. Если Gp(x) есть вещественная целая функция степени р
(т. е. lim j z I log | Gp (z) | = /?), удовлетворяющая условию
|2|-0O
| Gp (z)|<tf(z) (-oo<z<oo), (SB)
где H (x) — какая-нибудь целая функция нулевого рода, то
lim г log | Gp {ге^)\ = р | sin ср [. м\
(Иначе говоря, индикаторной диаграммой Полна функции Gp (x) является
двойной отрезок мнимой оси [— pi, + pi]).
Действительно, индикаторная диаграмма Gp (z) приводится к двойному
отрезку мнимой оси вследствие условия B5), из которого следует, что
lim х'1 log | Gp (x) | = 0.
И так как Gv (z) — степени р, то необходимо, чтобы наиболее удаленный
от 0 конец этого отрезка был на расстоянии р. Принимая же во внима-
внимание вещественность Gp (x) (при вещественном х), заключаем, что диаграм-
диаграммой служит отрезок [—pi, pi], т. е. при всех ср имеет место A).
Следствие 1. Если Gp(x) — любая комплексная функция степени
р, удовлетворяющая B5), то всегда найдется (одно) вещественное число а,
для которого степень Gp (x) eiax, равная ро = р — | а |, будет наименьшей.
30 с- н- Бернштейн 465

Действительно, индикаторной диаграммой Gp (х) служит отрезок мни-
мнимой оси, длина которого 2ро^2р, причем наиболее удаленный от 0 из
его концов находится на расстоянии р от 0; при умножении Gv (x) на
етх диаграмма смещается на величину —ос, поэтому наименьшая возмож-
возможная степень Gv (x) ei(XX есть pQ и достигается она смещением отрезка вниз
или вверх на величину | а | = р — р0, при котором середина отрезка
окажется в 0.
Функцию Gp (x) G B5) называем канонической, если отрезок, являющийся
ее диаграммой, есть [— ip, ip]. В дальнейшем мы будем иметь дело с
каноническими комплексными функциями [вещественная функция Gp (x)
всегда является канонической], поэтому мы обычно будем опускать этот
термин, особо отмечая, если встретятся случаи рассмотрения неканони-
неканонических функций.
Следствие 2. Всякая функция Gp (x) б B3) конечной степени
оо
имеет бесконечное множество корней ап и ряд "V -.—г = оо (в то время
^ \ап\ \
оо
как ряд V г— сходится при любом s
Следствие * 3. Если Gv (х) 6 B5) — степени р и Ga (х) ? B3) — степени
q, то Gv (х) • Gq (х) = ?р+д (ос) — степени р + q.
Лемма** 2. Если Gv (x) и Gq (x) — любые (не канонические) целые
функции, соответственно степени р и q, причем а = срх — ср0 угол между
направлениями, еде
lim г log | Gv (re**) | = p, lim log | Gq (re**) \ = q, A)
Г->оо Г->оо
mo G (x) = Gp(x) Gq(x) — степени h, где
h > ]//>2 + q* + 2pq cos a = | pe^ + qe{** |, B)
при дополнительном условии, что
lim r-1 log | Gp (re1^-*)) j
Г->оо
существует в направлении срх — ф вектора ре{** + qe**:
Действительно, благодаря дополнительному условию, имеем в направ-
направлении срх — & = сро-)-а — ф
lim r'1 log | G (ге{<*1-Ф>) | = lim r'1 log | Gv (rel^-W) \ +
lim r log 1 Gq (rei^i~^) | ^ p cos ty -{- q cos (a — &) =
Г->оо
* См. заметку [98], где доказана теорема 3, включающая это следствие как
частный случай. (Автор.)
** Лемма 2 воспроизводится здесь в том виде, в каком она была дана в B53 *а),
а следствие '4 формулируется в частной форме, в какой оно используется в настоя-
настоящей статье [96] на стр. 449. (Автор.)
466

Следствие 4. Если Gq (х) — любая целая функция степени q, то сте-
степень h произведения G (х) = cos px Gq (x) удовлетворяет неравенству
i-q2. B bis)
В самом деле,
limг log| cospre^\ = p J sincp |, если sin 95О,
но, каково бы ни было ср0, по крайней мере один из двух углов
а =
-у, и мнимая часть соответствующего вектора ре
отлична от нуля. Поэтому, применяя B), где cos a ;> 0, получаем B bis).
Поступило
12. VI 1948 г.
ЦИТИРОВАННАЯ ЛИТЕРАТУРА
1 С. Н. Бернштейн. О наилучшем приближении функций на всей вещест-
вещественной оси при помощи целых функций данной степени. Докл. АН СССР, 51, № 5
A946), 327—330 [84], заметка I.
2 С. Н. Бернштейн. О наилучшвхМ приближении функций на всей вещественной
оси при помощи целых функций конечной степени. Докл. АН СССР, 52, № 7 A946),
565—568 [84), заметка IIL
3 С. Н. Бернштейн. О наилучшем приближении функций на всей вещественной
оси при помощи целых функций конечной степени. Докл. АН СССР, 54, № 2 A946),
103—108 [84], заметка IV.
4 С. Н. Бернштейн. О приближении функции на всей вещественной оси при
помощи целых функций данной степени. Докл. АН СССР, 54, № 6 A946), 479—482
[84], заметка V.
5 С. Н. Бернштейн. О тригонометрическом интерполировании по способу наи-
наименьших квадратов. Докл. АН СССР, 4, № 1 A934), 1—5 [59].
6 S. Bernstein. Sur une classe de formules d'interpolation. Изв. АН СССР,
OMEH A931), 1151—1161 [56].
30*

07
О МАИОРАНТАХ КОНЕЧНОГО
ИЛИ КВАЗИКОНЕЧНОГО РОСТА*
Напомню (г) общее определение майоранты (и функции) конечного
роста: функция Н(х)^0 (—оо<^<оо) называется майорантой конеч-
конечного роста (Н (х) E Щ, если неравенство
| Gp (х) |< Н (х) (— оо < х < оо) A)
для всякой целой функции Gp (x) степени р влечет за собой для всех ее
производных
| Gf (x) \^HktP(x) (- оо О< оо), B)
причем для любого фиксированного х
к
Мы называем / (х) функцией конечного роста **, если | / (ж) | € ЯИ. В ука-
указанном месте (*) даны также две леммы, позволяющие заменить приве-
приведенное выше, определение двумя различными эквивалентными определе-
определениями: первая из них констатирует, что требование B), C) равнозначно
существованию для каждого р^>0 такой целой функции Нр (z) степени р,
что A) имеет следствием
\Gp(z)\^\Hp(z)\ D)
*нри всех комплексных z = х + iy (у >> 0) (и аналогичное неравенство
для ?/<0).
Назовем функцию Н (х) майорантой квазиконечного (или конечного)
роста (#(#) ?9Й*), если неравенство A), где Gp (x) — функция степени р,
влечет для каждого данного х (— оо
х) | < Hkt р* (х), ТшГ /iW < p*, E)
* Докл. АН СССР, 65 A949), стр. 117—120 B54*).
** Принимая во внимание это определение, мы также пишем / (х) ? Ш вместо
(х) | ? Ш (когда это не может вызвать недоразумений). (Автор.)
468

или, что то же самое, имеет следствием для всех комплексных z=x-\-iy
(У>0)
\Gp(z)\<\Hp.(z)\, F)
где Нр* (z) — целая функция конечной степени /?*, зависящая только
от Н (х) и р, причем /?* = ср (р) — некоторая конечная монотонная функ-
функция переменной р. Аналогично изменяется формулировка второй
леммы.
Прежде чем перейти к рассмотрению свойств, характеризующих весь
класс 9Й* майорант квазиконечного роста, отметим класс ЭЯ0 (a) d ffi
майорант конечного роста Н (х), который состоит из функций Н (х) =
= е*х \ Но (х) 169ЙО (а)> гДе ^о (х) — функция нулевого рода, включающий
класс ®10 @) = 5ШО=53 (см. также сноску в статье [94] на стр. 438).
Теорема 1. Если Но (х) — любая целая функция нулевого рода, то
неравенство
| Gv (х) | < е« | #0 (х)\ = Н (х) [Н (х) 6 Жо (а)], A bis)
где без ущерба для общности можно ограничиться предположением, что
Но (х) = s (x) -f- it (x) не имеет корней в верхней полуплоскости (полагая
для определенности1 а>0, А^-0, —оо<^а;<^оо, z = x-\-iy, z = x—iy,
?/>0), имеет следствием
\G^(x)\^\H{pk)(x)\, B bis)
1|ЯРB)|, Cbis)
где Нр (х) = [s (x) + it (x)] е^~1 У Р2~а23* для всех р^>а; в случае р < а
имеем тождественно Gp (х) = 0.
Перейдем теперь к формулировке общей теоремы, характеризующей
весь класс Ш* (включающий, в частности, класс WI майорант конечного
роста).
Теорема 2. Если граничащая функция Н (х) в A) есть модуль целой
функции конечной степени, то условие, необходимое и достаточное для
того, чтобы Н (х) была майорантной квазиконечного роста (Н(х)(:Ш*),
заключается в том, чтобы ее (отличные от нуля) корни ак -\- Шд. удов-
удовлетворяли требованию
При соблюдении G) неравенство A) влечет за собой для всех
в верхней полуплоскости (если представить Н (х) в виде Н (х) = \s(x) +
1 Полагая а = а + iC комплексным, мы можем представить Н (х) = | еах Н0(х)\ =
гах\ Яо (х) | и класс Шо (а) = Шо (а). Напротив, при вещественных а ^ ах SQ^0(ос)
#0 (а2) не содержат ни одной общей майоранты (кроме нуля).
469

+ it (x) |,; где s (z) + it (z) наименьшей возможной степени о и не имеет
корней в верхней полуплоскости)
и аналогичное неравенство в нижней полуплоскости; поэтому1 р* <С р-\-°-
Следствие 1. Для того чтобы Н (х)^>0 была майорантой конечного
роста класса 9Л0(а), необходимо и достаточно, чтобы вместе с Н (х)
майорантой квазиконечного [или конечного) роста была и \ Н (хег*) \ при
некотором * О (О <С б < тг).
Следствие 2. Все целые функции конечной степени s(x) + it(x), не
имеющие корней в верхней полуплоскости, являются функциями квази-
квазиконечного роста (| s (х) + it (х) | 6 2Ю*).
Действительно, по известной теореме Линделефа, в этом случае
s (x) + it (x) должна удовлетворять условию G).
С другой стороны, благодаря недавно доказанной теореме Н. И. Ахи-
сзсра C), из теоремы 2 вытекает также
Следствие 3. Для того чтобы целая функция конечной степени
Р Gp(x)^0 была майорантой квазиконечного роста (Gp (х) 6 90Г), необ-
необходимо и достаточно, чтобы она могла быть представлена в виде
Gp (x) = \s (х) + it (х) |2 = 52 (х) + Р (х),
где s(x)-\-it(x) — целая функция степени -ё-, не имеющая корней
в верхней полуплоскости.
Кроме того, принимая во внимание эквивалентность C) условия G)
условию
R
С log\H(x)H(—х) I 7 ^ /оч
sup \ —2-!—^— иах<^оо (8)
R->oo J Х
(когда // (х) конечной степени), получаем
Следствие 4. Любая2 функция конечной степени Н(х)^0, удовле-
удовлетворяющая (8), является майорантой квазиконечного роста. (См. [111].)
1 Для р — 0 [Gp (x) — многочлены] неравенство F bis) доказано впервые в моей
монографии*B) (стр. 74). (См. также [102. 1], стр. 619). Кроме того, более сильное
неравенство, установленное Н. И. Ахиезером D) при некотором дополнительном
ограничении, обеспечивает /?*=/? для р ;> а и р* <1 а для р <; а. Не исключена
возможность, что аналогичное уточнение неравенства F bis) возможно и в общем
случае, так что квазикоиечный характер роста майорант Н (х) конечной степени ст
мог бы обнаружиться, как и в случае Ахиезера, лишь для /><ст.
::' Так как в таком случае вместе с G) соблюдается и условие
-afcsm <oQ^
1
, V. — _- <оо. (Автор.)
а следовательно
2 Если Н (х) — модуль целой функции конечной степени, то условие (8) является
также и необходимым.
470

Следствие 5. Если Н{х)?Ш* и Hx(x)(:Wl*— модули функций конеч-
конечной степени, то и произведение Н (х) Н1 (х) 6 ЭЙ*, и наоборот.
Следствие* 6. Если \Н(х)\(:$Я0 и \Н1 (х) | 6 ЭЙ0 модули четных функ-
функций нулевого рода, то сумма G (х) = Н (х) + Нг (х) также является чет-
четной функцией нулевого рода1 (| G (х) | G 5ГО0).
В самом деле, пусть (т^О)
Тогда
Н* (х) - с A + х2)т Л П + -г^-г2)>\Н (х)
Аналогично строим четную функцию нулевого рода Я* (х), удовлетворяю-
удовлетворяющую условиям
Н[ (х)>\Н (х) |, III (х) >сг>0, Н\ (х) >! #! Aж) |.
В таком случае
где G (х) = Н (х) + Л\ (^) является майорантой, так как она удовле-
удовлетворяет условию (8). Поэтому, благодаря следствию 1, G (х) G 5Ш0> т- е-
четная функция G (х) — нулевого рода.
Будем называть функцию Н (х) > 0 (— со <^х<^ оо) позитивной,
если inf Н (х) = с >> 0.
Следствие** 7. Если модули функций конечной степени квазиконечного
роста Н (х) G 9JT, Яг (^) G SK* — позитивны, то и сумма [Н (х) + Нг (х)] б 27Г.
* Первоначальная общая формулировка следствия 6, утверждавшая, что сумма
любых четных майорант также является майорантой, была исправлена в следующей
заметке [98]. Здесь мы даем следствие 6 в частной формулировке сноски1 и воспро-
воспроизводим его доказательство из сноски, бывшей в заметке [98]. (Как известно [27] (том
I), если отбросить требование четности, то сумма функций нулевого рода может
не только не быть нулевого рода, но и не быть майорантой квазиконечного роста).
(Автор.)
1 Не исключена a priori возможность, что сумма майорант конечного роста ока-
окажется майорантой, квазиконечного роста. Но если четные майоранты Н (х) ? Шо и
Нг(х) ?Ш0 — нулевого рода, то и сумма их — нулевого рода, т. е. конечного роста.
** Формулировка следствия 7 воспроизводится без изменений, причем дается
доказательство этого следствия, которое в первоначальном тексте по недостатку места
было опущено. Из следствия 7 видно, что позитивная майоранта Я (х) всегда имеет
четную майоранту Н (х) -\-Н (—х). Обобщение этого следствия дано в [111]. (Автор.)
471

Действительно, пусть, для определенности, | Н (х) \ ^ 1,
тогда вследствие (8) получаем
Г \og\H (х) + Нг(х)\\Н (-х) + Нг (-х)\
1 dx<
Г log 11 + Я (х) 111 + Нг (ж) 111 + Я (- х) 111 + Я, (
1
^Г 1ой2|Я(»)|-
й Д R
J #2 ' J Ж2
11 1
Будем называть позитивную функцию Н (х) почти возрастающей
(при +#—>оо), если можно указать такую (не зависящую от х) постоян-
постоянную &^>1, что Н(х)<^кН(кх) при любом Х^-1. [В таком случае
Н (х -\- а) также будет почти возрастающей функцией для всякого дан-
данного а^О].
Теорема 3. Если модуль функции конечной степени Н (х) есть почти
возрастающая майоранта квазиконечного роста, то lim е~а 1*1 // (х) — О
ас—>±оо
при всяком а>0, т. е. индикаторной диаграммой Н (х) служит отре-
отрезок мнимой оси.
Для * доказательства нужно заметить, что в случае позитивных
\Н (х)\ условие (8) приводится к двум условиям
j[10«'g<*»d«<oo, jj toglgj.-«>l dx<oo. (8 bis)
1 1
Кроме того, если \Н(х)\ почти возрастающая функция и для некоторого
а^>0 существует такая бесконечная последовательность {хп}> что
log | Н (хп) [> ахп, то при всяком х^>хп (и данном &!>1) имеем
log IШ (х) | >- ахп. Поэтому мы имели бы (А — постоянная)
(так как мы можем принять, что -^-^> 2). Следовательно, из (8 bis)
\ хп J
мы должны заключить, что lim е~а 1^1 Н (х) = 0 при всяком а^>0-
Следствие 8. При условии теоремы 3 [как и всегда, когда
lim е-а\х\Н{х) = 0], предельная функция G (х) всякой последователь-
±
": В первоначальном тексте доказательство было опущено. {Автор.)
472

кости функций GViU(x) данной степени ?>0, для которых Н (х) слу-
служит майорантой, имеет индикаторной диаграммой отрезок мнимой оси.
Назовем функцию Н(х)^>0 антимайорантой, если неравенство A)
совместимо для совокупности функций Gp (x) данной конечной степени
р ^> 0 со свойством sup \Gv(x)\ = оо в любом промежутке действительной
оси.
Из следствия 4 видно, что, какова бы ни была почти возрастающая
функция // (х) ^> 0, условие *
R
С log I Я (х) Я (— а?) I ,
sup \ —^—2 ~ dx = oo
необходимо для того, чтобы Н (х) могла быть антимайорантой. Кроме
того, справедлива
Теорема 4. Если целая функция Н (х) конечной степени есть почти
возрастающая функция, то нарушение условия G) необходимо ** и до-
достаточно, как для того, чтобы Н (х) была антимайорантой, так и для
того, чтобы всякая непрерывная функция / (х) = о(Н (х)) могла быть
равномерно приближена при помощи функций Gv (x) некоторой фиксиро-
фиксированной степени р с весом Н (х) [т. е. чтобы при всяком данном s>0
для всех х (— оо <^ х << оо) было осуществимо неравенство \f(x) — Gv (x) | <
<*Н(х)}.
Например, Н(х)=ех + 1 есть антимайоранта, хотя ех (как и 1)
является майорантой конечного роста.
Поступило
20. I 1949 г.
ЦИТИРОВАННАЯ ЛИТЕРАТУРА
1 С. Н. Бернштейп. Докл. АН СССР, 60, № 6 A948) [94].
2 S. Bernstein. Legons sur les proprietes extremales etc. Paris, 1926. [«L. S.»].
3 H. И. А хиезер. Докл. АН СССР, 63, № 5 A948).
4 Н. И. Ахиезер. Изв. АН СССР, серия матем., 10, 411 A946).
* Доказательство этого утверждения без предположения, что Я (х) функция ко-
конечной степени (т. е. без применения следствия 4), дано в [111]. (Автор.)
** Необходимость вытекает из следствия 4; достаточность доказана в статье [108]»
(Автор.)

98
ОБ АДДИТИВНЫХ МАЙОР АНТАХ
КОНЕЧНОГО РОСТА*
1. Будем называть майораыту Н(х)^0 конечного роста (Л(х)вЩ
аддитивной и будем обозначать этот частный класс майорант через 81
[Л (х) € 21], если для некоторого с> 0 функция ** [Н (х) + с] G 5W; в даль-
дальнейшем все рассматриваемые нами майоранты предполагаются целыми
функциями конечной степени1 (или их модулями).
* Докл. АН СССР, 66 A949), стр. 545-548 B55*).
** Из этого определения видно, что условие необходимое и достаточное для
того, чтобы функция Я (х) ;> 0 конечного роста была аддитивной майорантой, заклю-
заключается в том, чтобы она имела позитивную майоранту. (Автор.)
1 В моей заметке (*) рассматривается более общий, по видимости, класс майорант
«квазиконечного» роста. Однако, для случая, которым мы ограничиваемся здесь,
когда майоранта Я (х) = | s (x) + it (x) | есть модуль целой функции конечной степе-
степени, Б. Я. Левиным B) установлен принципиально существенный факт, что все функ-
функции конечной степени квазиконечиого роста являются функциями конечного роста.
А именно, мое условие (х) майорантное™ гласит: «Условие
V |Р*' / m
2л о. . ^-<с°. (!)
где oifc + ifijc (отличные от нуля) корни функции s (z) + it B), необходимо и достаточ-
достаточно для того, чтобы Я (х) = | s (x) + it (x) | было майорантой квазиконечного' роста;
при этом, если s (z) + it (z) наименьшей возможной степени и не имеет корней
б верхней полуплоскости, то, при условии (I), неравенство
(-аэ<х<оэ), (И)
где G (х) — целая функция степени р, влечет за собой
(z) + it(z))e-ikz\ (III)
для всех z = х + iy (у >• 0) при некотором к <!р». В то же время Б. Я. Левин, неза-
независимо от меня, показал не только, что условие (I) достаточно для того, чтобы из
(II) следовало (III), но существенно уточнил этот результат, обнаружив, что число к
удовлетворяет равенству
474

Теорема 1. Если Н (х) G И, Нг (х) € % то [Н (х) + Нг (х)] 6 2Г.
Действительно, согласно следствию 4 заметки (х), утверждение Н (х)
эквивалентно условию
__f log (Я (х) + 1) (Н (— х) + 1)
1 + я2
(А)
Но*
[Я (х) + Ях (ж) + 1] [#(- х) + Нг (- ж) + 1] < [1 + Н (х)] [1 + Я(- ж)] [1+
поэтому
ah+Hi =
dx<AH
hG (в)
P
lim i- log | G (z) | = lim 1 log | (s (z) + гг (а)),
Г->оо /* ^ Г->оо Г
(IV)
ори всех значениях z = rei0 @ <C 6 <[ 71;).
Пользуюсь случаем, чтобы привести здесь доказательство моего формулирован-
формулированного вььпе утверждения касательно необходимости условия (I). Для этого нужно лишь
показать, что в случае нарушения (I) всегда возможно построить такую последо-
последовательность функций [Gv n (х)) степени /?, удовлетворяющих (II), что limG (x) =
— G(x) при всех х, причем, однако, функция G (х) не есть функция конечной степени.
Итак, пусть в правой части (II)
Я (х) = ebx
1 —
, «/с -
a?2 —:
"
?)
любая функция конечной степени [без ущерба для общности, принимаем Н @) = 1];
нарушение (I) не препятствует тому, чтобы Н (х) была конечной степени, так как,
по критерию Линделефа, для этого необходимо и достаточно лишь существование
постоянных сх > 0, с2 }> 0, для которых при любом п
r n ^n k==1 »— - Лищ1
Напротив, при нарушении (I) условие Линделефа для функции
не выполнено; поэтому F (х) не может быть конечной степени, в то время как все
ФУНКЦИИ 2х ъгп.п*
той же самой конечной степени, что Н (х) (от которой они отличаются лишь конеч-
конечным числом множителей). А между тем,
\Gp,n (*I = я(*) при-оо<х<оо, и limGptn(x)=*F{x).
п—>оо
* Настоящее доказательство теоремы представляет технически упрощенный ва-
вариант первоначального доказательства. (Автор.)
475

Благодаря (А) из теоремы 1 вытекают следствия:
1. Если Н{х)?% и |/(з)|<Я(з), то |/(з)|€Я.
2. Если майоранта Н (х) б 2К позитивна A), то Д" (ж) 6 91.
3. Если Н(х)^0 целая функция конечной степени, то условие*
необходимо и достаточно для того, чтобы Н {х)?%. См. [111].
Первые два следствия очевидны; третье получается из неравенства
2. Нетрудно видеть (см., например, Н. И. АхиезерC)), что условие A),
характеризующее функции конечного роста (конечной степени) Н (z) 6 Ж,
является необходимым и достаточным для того, чтобы функция Н (z) ко-
конечной степени допускала представление
Н (z) = ae^zm Д (l - ~^~ ) е 4 + & . (М)
В согласии с определением, данным в моей статье D) (стр. 441), на-
назовем функцию Н (z) канонической, если Ь — число вещественное, так как
в этом случае из той же заметки C) Н. И. Ахиезера следует, что степень
H(z)eiJcz при всяком к^О больше степени Н (z). Отсюда видно, что и
произведение канонических функций есть каноническая функция.
Лемма11. Две канонические функции Д (z) и f2{z) одинаковой степени р,
имеющие одну и ту же майоранту \Н(х)\ конечной степени, имеют
одну и ту же индикаторную диаграмму.
Действительно, без ущерба для общности, можно считать функцию
Н (z) канонической, так что ее индикаторная диаграмма, так же как диа-
диаграммы /х (z) и /2 (z), симметрична относительно вещественной оси. По-
Поэтому, так как равенства (IV) Б. Я. Левина
К F) = йн (в) + *i | sin б |, hf2 (б) = hH (б) + к2 | sin б | (IV bis)
справедливы при 0<С6<^> они верны также при 0^>6^ — тт. Следова-
Следовательно, hjx (б) — й/2 (б) = (кх — к2) | sin б | при всех б, и если степени fx и /2
равны, то кх — к2 = 0.
Теорема 2 (об индикаторной диаграмме2). Если Е(х)^Ж есть кано-
каноническая функция степени р (в частности, вещественная), то ее инди-
индикаторной диаграммой служит отрезок мнимой оси [—pi, pi].
* Для того, чтобы майоранта была аддитивной, необходимо, чтобы она имела
четную майоранту, но этого недостаточно. (Текст этой сноски сокращен в связи с
соответствующим изменением в заметке [97], стр. 471). (Автор.)
1 Эта важная лемма, являющаяся следствием равенства (IV), принадлежит, по
существу, Б. Я. Левину (см. первую сноску).
2 Эта теорема включает как частный случай теорему 3 заметки (А), которая может
быть доказана более элементарно ([97], стр. 472).
476

В самом деле, предположим сначала, что майоранта | F (х) | позитивна,
т. е. | F2 (х) | = F (x) F (х) >> с2 > 0. Тогда в числе вещественных функций
степени р, имеющих | F (х) | майорантой, будет функция с cos px и отре- *
зок [—pi, pi], служащий ей индикаторной диаграммой, по лемме 1, бу-
будет также индикаторной диаграммой для F(x). В общем случае, учиты-
учитывая аддитивность, видим, что F (х) F (x) -f- 1 является общей майорантой
для F2 (х) и cos2 px, и, следовательно, индикаторные диаграммы F (х)
и cos px совпадают по той же лемме.
Предположим, что, каково бы ни было г ^> 0, функция F (z), имеющая
индикаторной диаграммой отрезок, параллельный мнимой оси (или лежа-
лежащий на ней), может быть представлена в виде такого произведения F (z) =
= F± (z) II0 (z), где HQ (z) — функция нулевой степени, что существует
предел
lim ~ log | Fx (re*) \ = bFl (G) = hF (G)
Г->оо Г
при всех б (| sin G | > e); обозначим его через bF (G) = lim0 — log | F (re*) \ =
Г—*оэ
= hF (G) и назовем показателем степени F (z) в направлении 6.
Из определения непосредственно следует
Лемма 2. Произведение F (z) = Д (z) /2 (z) двух функций Д (z), /2 (z), име-
имеющих показатели степени во всех направлениях, обладает тем же свой-
свойством, и bF (G) = 8А (G) + 8/f (G) - htx (G) + hh (G).
Будем называть майоранту F (x) ^ 0 почти позитивной, если сущест-
существует отличная от нуля функция Go (x) нулевой степени, удовлетворяющая
(II), где Н (х) =F(x). Все позитивные майоранты F (х) ;> с > 0 почти по-
позитивны (как мы видели, в этом случае1 F (х) б (91)).
Лемма 3. Всякая почти позитивная майоранта Н (х) является моду-
модулем канонической функции f (z) конечной степени ру имеющей показате-
показатели степени 8/ (G) = р | sin G | во всех направлениях.
В самом деле, по определению,
\f(z)\>\G0(x)\ (-ооО<оо). (П bis)
Поэтому, полагая, что / (z), как и функция нулевой степени GQ (z), не име-
имеет корней в верхней полуплоскости, имеем, вследствие (III) и (IV bis)
Go
1
> psin G = lim — log | / (re*) \ = lim0 — log | / (re*) \ = o/ (G)
1 Нетрудно видеть, что функция F (x) ? Щ. может вообще не быть почти пози-
позитивна, и наоборот: например, | cos x \ (< Ж не почти позитивна, так как, кроме нуля,
нет функции | G (х) | <; | cos х\ (— оо < х < оо) степени ниже первой (при этом, од-
однако, | cos х | имеет позитивную майоранту 1), а почти позитивная функция (E),
«тр. 198; [27] (том I))
-не принадлежит классу 9L
477

при О^б-^п:. Но если в каноническом произведении / (z) любые из кор-
корней 0С& + i$k заменить через ос& — i$k9 то для всех полученных таким об-
образом функций /* (z) (причем |/* (х) | = | /(х) | при — оо <х< оо) имеем
8;* (б) = 8/F) = р\ sin б |. Из лемм 2 и 3 вытекает1 также
Следствие 4. Степень произведения F(z) = /p(z)fq(z) двух почти
позитивных канонических функций степени pug, соответственно г
равна р + q.
Теорема 3. Степень произведения Ф (z) = Gp(z)Gq(z), где р и q —
степени канонических функций Gv (z) 6 91, Gq (z) б 91, равна р + q.
Так как степень функции 6 91 не изменяется при переменах знака
мнимой части ее корней, положим, что G* (z) и Gq(z) не имеют корней в
верхней полуплоскости, и введем канонические функции G* (z), G*q(z),
определенные равенствами
g; (z)~g; (z) = gv (z) Ц, (Z) +1 = h2P (z)
C; (z) G\ (z) = Ga (z) Gq B) + 1 = Язд (z)
и условием, что корни Gp (z) и G*q (z) лежат в верхней полуплоскости.
На основании следствия 4, степень произведения позитивных функций
Я2Р (z) H2q (z) = Gp (z) Gq (z) Gv (z) Gq (z) + Gv (z) Gp (z) + Gq (z) Gq (z) + 1 рав-
равна 2p + 2q, а потому необходимо, чтобы степень Ф (z) = Gv (z) Gq (z), ко-
которая равна степени Ф (z), была равна р + q-
Поступило
8. IV 1949 г.
ЦИТИРОВАННАЯ ЛИТЕРАТУРА*
1 С. Н. Берн штейн. Докл. АН СССР, 65, № 2 A949) [97].
2 Б. Я. Левин. Докл. АН СССР, 65, № 5 A949).
3 Н. И. Ахиезер. Докл. АН СССР, 63, № 5 A948).
4 С. Н. Берн штейн. Изв. АН СССР, серия математ., 12, 421 A948) [96].
5 S. Bernstein. Legons sur les proprietes extremales etc. Paris, 1926. [«L. S.»].
1 Как сообщил мне Б. Я. Левин, им получены некоторые аналогичные результаты**.
* К списку литературы следует добавить статьи М. L. Cartwright (Proc.
Lond. Math. Soc, 38 A935)), которые в то время не были мне известны. (Автор.)
** Важные исследования Б. Я. Левина изложены в развернутом виде в статье
«Об одном специальном классе целых функций конечной степени» (Изв. АН СССР,
серия матем., 14, 1950). (Автор.)

99
ФУНКЦИИ КОНЕЧНОЙ СТЕПЕНИ
И ФУНКЦИИ КОНЕЧНОЙ ПОЛУСТЕПЕНИ*
Вводится класс целых трансцендентных функций Нр (х), называемых функциями
конечной полустепени р, определяемых свойством, что Hp(t2)=Gv(t) есть целая
функция степени р. Устанавливаются свойства наилучшего приближения Apf (x) по-
посредством функции Нр (х) на положительной полуоси и разрешаются некоторые
экстремальные проблемы, являющиеся предельным распространением соответствую-
соответствующих классических свойств многочленов при бесконечном возрастании их степени.
1. Проблема приближения функции f(x) на положительной полуоси
) естественно приводится к приближению на всей оси путем замены
переменной x = t2. Таким образом, поскольку для приближения произ-
произвольной непрерывной функции F (t) (— оо <С*<С °°) целесообразно поль-
пользоваться в качестве приближающих функций целыми функциями Gp (t)
конечной степени р, приближение функции f (х) = f (t2) = F (t) при по-
помощи Gp (t) (которые в данном случае оказываются четными) приводит
нас к эквивалентной проблеме приближения f (х) для х^О при помощи
целых функций Hv (x) (нулевого рода) порядка —
подчиненных, по определению, условию, что
27с
lim У\ ак | <; р. B)
Функцию Нр (х), удовлетворяющую B), мы будем называть функцией
конечной полустепени; конечную постоянную р [которая является сте-
степенью целой функции Gv (t)] будем также называть полустепенью
функции Нр (х) [степень которой, как всякой функции нулевого рода,
равна нулю].
*Изв. АН СССР, серия матем., 13 A949), стр. 111—124 B56*).
479

Теорема 1. Если целая функция Нр(х) полустепени р удовлетво-
удовлетворяет при х ^ а неравенству
(х>а), C)
то при всех х^а для последовательных производных Hvk) (х) имеют
место неравенства
Знак равенства осугцествлпется только в точке х = а и притом
лишь для
Нр (х) = М cos p Yx — а •
Действительно, принимая во внимание, что при любом постоянном а
функция Hv (х + а) имеет ту же самую конечную полустепень р, что и
Нр(х), мы можем положить а = 0. Тогда каждой из функций Нр(х),
удовлетворяющих C), соответствует четная функция Gv (t) степени р,
определенная равенством A), которая удовлетворяет условию
|СР(О|<Л/ (-оо<г<оо). C bis)
Следовательно, по известному экстремальному свойству целых
функций степени /?,
{G™ @)\ = \ak\=*g-\H™ @)\<Мр*\ E)
причем знак равенства осуществляется только для Gv (t) =M cos pt, т.е.
для Нр (х) = М cos p Yx • Таким образом, наше утверждение D) доказа-
доказано для х = а. Остается лишь заметить, что
Ми (xOi a) = sup [ Я<*> (х0) |< sup | Hf (a) \=Mk(a,a) = M ~ P*
при условии C) для всякого х0 >* а, так как Мk (х0, а) = Ми (х0 — а)
зависит только от х0 — а, причем увеличение a<jr0 в C) соответствует
расширению класса допускаемых функций Hv (x), так что функция
Ми (и) при уменьшении и = х0 — а не может убывать и, в частности,
Ми @) >- Mjc (и), если и >* 0.
Теорема 2. При условии C) [сохраняя принятые выше обозначения
(а = 0)]
МР
]
II. M^Xt + d^M^u)'^^: (Жй<М<Хй+1, Л>0), I F)
III. jrl(B)e
Для получения I и II замечаем, что при а = 0, вследствие A),
V (f«) | = | Gp' @ \<Mp (- oo <f <oo),
480

поэтому
При этом равенство осуществляется для Gp (t) = М cos pt при Yx = l =
Для получения III напомню (*) ([95], стр. 444), что если Gpr (t) есть
любая целая функция степени v, удовлетворяющая условиям
то
Поэтому при условиях G)
М — sup | Gp (t) | ^
и равенство осуществляется, когда
>а /Л — b cos pt
Следовательно, если имеет место C bis) и 6" @) = 0, то при любом
|С'р (/о) | = | Ь i < ЛГр sin^0. (8)
После замены t^ = и из (8) получаем III.
2. Обозначим через Apf(x) наилучшее приближение функции / (х)
для х^>0 посредством целой функции Hv(x) полустепени р. Ввиду то-
того, что после подстановки х = 1*
где HP(t2) =GP (t), по формуле A), есть целая функция степени р,
причем наилучшее приближение четной функции / (t2) посредством функ-
функции Gp (t) конечной степени р на всей оси осуществляется четной функ-
функцией Gp (t), заключаем, что
Alf(x) = Apf(x*). (9)
Таким образом, в частности, если / (х) ограничена при х^-0, то условие,
необходимое и достаточное для того, чтобы наилучшее приближение
Лр / (х) на положительной полуоси посредством целых функций конечной
полустепени р стремилось к 0 при р->оо, заключается в том, что
f(x2) есть функция равномерно непрерывная. В данном случае, как мы
видим, равномерная непрерывность / (х) [необходимая при*ограниченное! и
/(х)] недостаточна для limApf(x)=0.
31 С. Н. Бернштейн 481

Отметим еще тождество
AUf(x);a] = A*p[f(x + a)], A0)
где а — некоторая действительная постоянная и Al [f (х); а] означает
наилучшее приближение / (х) при х ^ а [в частности, Ар [/ (х); 0] = A*v f (x)\
посредством функций иолустепени р, так как последнее совпадает
с соответствующим приближением / (х + а) при х ^ 0. Очевидно, что
A*v\f {х)\ а] монотонно убывает при увеличении параметра а, поэтому
A1)
Теорема 3. Пусть функция f (х) удовлетворяет условию
1 +
n=l
где an — любые комплексные числа, для которых
(*>0), A2)
n=i¦ п'
В таком случаег при всяком q^>0
lim Ет Г/ (ж); О, (-^-У1 = Л^о / (ж). A3)
771—> ТО L \ i HI J J
Для доказательства, замечая, что вследствие (9)
-4*4- / (х\ = A f (х2) f9 bis)
применяем к функции / (t2) = .F (^) теорему VII B), которая к ней приме-
применима, так как / (t2) удовлетворяет условию (— оо <С t << оо)
1/(<8I<с
Следовательно,
limE2
m-*oo
\f (t*); -^L.1 = .W (*•) = ^±0/ (x). A4)
Но, так как / (t2) есть функция четная, то многочлен Р2т (t) степени
2т, наименее уклоняющийся от нее в некотором промежутке (— 6, 6),
есть четный многочлен Р2т (t) = Qm (t2) и
1 Мы обозначаем через En[f (x); а, 5] наилучшее приближение / (х) посредством
многочленов степени п на отрезке [а, Ь]. В случае а = — ?<0 мы пишем для
краткости
EnU(x);-b,b] = Enlf(x);b]
и, если 6=1, пишем
En[f(x);-i,l] = Enf(x).
482

так что
а потому
j-fU = lim Em \f(x); О, (^Y\ A5)
и, вследствие A4) и A5), получаем A3).
Напомню, что при условии A2 bis) формула A4) верна для всех
р^>0, и, кроме того, предел, стоящий в левой части ее, <^ о© тогда
и только тогда, когда правая часть <Г сю. Следовательно, тем же свой-
свойством [при условии A2)] обладает и формула A3).
Следствие 1. Если f (х) удовлетворяет A2), то условие, необходимое
и достаточное для того, чтобы f (x) была целой функцией полустепени
р, состоит в том, что, каково бы ни было е > О,
lim Ет I / {х); 0, (-^f 1 = 0, lim Ет Г/ (х); О, (-^Y1 > 0, A6)
т. е. я/ж всяком а>0 существуют многочлены Рт(х) достаточно
высокой степени т такие, что при любом г ^> О
|/(я)-/>„(*) |<а
0^x^.1—^—) , но д.я.я O^^^f ) зто неравенство невоз-
Действительно, вследствие B) -4Р+о/ (х) = A*vf (х) и A3), условия A6)
означают, что Ар f (х) = 0 и APl f (x) >- 0 при всяком рг < /?, т. е. / (х) —
целая функция полустепени р.
Следствие 2. Если Рп (х) — последовательность многочленов степени
Аг-»оо, которые в промежутках @,^) удовлетворяют одному и тому
же неравенству вида
оо
/ V-: p<^ooj, причем lim—Д^- —/?, то существует такая подпосле-
подпоследовательность РПк(х),. что hm Pnjc(x) — Hv(x), причем Нр(х) должна
быть целой функцией конечной полу степени не выше р.
Следствие 3. Если f (x) удовлетворяет A2), то
п [/ (х); a, [y^J] = A*v±o \f И, «],
каково бы ни было данное конечное действительное число а.
Действительно,
En[f(x); a,b] = En[f(x + a);O, b — a],
483 31

поэтому при всяком
En [f (x); a, -??-]=?„[/ (х + а); 0, -^ -а] =
где при п достаточно большом гех>0 и гх-^0 вместе с s~»0. Следова-
Следовательно, согласно A0),
limEn\f(x); а, *4^]
= A*p±0 [f (x + a)] = A*v±0 [f (x), a]. A7 bis)
3. Примеры. Известно C), что при любых
Следовательно (Ь = а2), согласно (9),
Последнее равенство означает, что если функция F (х) имеет вид
л w- х ZJ 2Л!
к ~
где lim"|/|^A| =Л то
Обозначая через Ap[f (t); (a,b)] наилучшее приближение / (t) на всей оси
вне отрезка [а, Ь] посредством целых функций степени р, заключаем из
/ 1 \
A8) (учитывая, что -^—четная функция], что
jT 5 ( а> а)\ — Ар (^Г+Т2) ~" ~
Точно так же получаем вообще, что, какова бы ни была четная функ-
функция / (|* |),
Avf (Vt*+ a2) = Ар [/ (|*|); F7^)]. A9)
Таким образом, например согласно D), при любых действительных s^O
Ар [j t p; (_ а, а)] = / 2^f B0)
где
?g(M)=e-"MT A + е(в)) @<?s@)<oo), B1)
484

причем cps (и) монотонно убывает, когда и растет от 0 до оо, и е (и) -» О
при и —> оо.
4. Теорема 4. Если целая функция Нр (х) полустепени р удовлетво-
удовлетворяет неравенству
\Hv(x)\<^M (я>0), Cter)
то для всякого х = — b <C О
]й)= 44 B2)
причем значение L^ достигается, когда х
Нр (х) = Л/ cos p 1/1= ^ [> ^+ e~iv ^] . B3)
Доказательство. Пусть Lv ^> 0 будет данное значение Lp =
= Hvk) (— Ъ) производной к-то порядка функции Нр (х) полустепени р,
где А: ^> О — фиксированное целое число. Среди этих функций существует
функция Нр (х) полустепени р, которая наименее уклоняется от нуля
при х J> 0; пусть М = sup | Hv (x) |. Функция Hv (x), как и все рассматри-
рассматриваемые ограниченные функции Hv (x) полустепени р, обладает (согласно
следствию 2) свойством
Яр (х) = lim Рп (.х), Яр (х) = Hm Pn (х),
Т7—>ОО 71—>0О
где Р^ (— Ь) = Р{п^ (— b) = L{p^ и многочлены Рп (х) степени п остаются
г, ^ ~ 4/г2 Л -^ гч ^
ограниченными при 0 <; х •<. ( ,2 = /^ для всякого данного s > 0. Сле-
Следовательно, если Л/п> е есть наименьшее уклонение многочленов Рп (х) на
отрезке [0, Хп], то М = ПтЛ/П)?. Но, как известно D), многочлен наимень-
глего уклонения
/
Рп (х) = -h Mn e cos 2д arc sin I / ^ ,
Таким образом, если L^ фиксировано и lim -—^= = р + е, то, полагая
?г-*оо "Г/ Хп
lini-/l/n е = Же, имеем
1 Аналогичные неравенства получаем для любых комплексных z — регф. Например,
\Hv{z)\<CMe 2.
485

и при s = О
L№> = Ц. [e»V^+ е-рГъ-^ = м [cos/, l/x]^_b • B2 bis)
Следствие 4. Среди всех функций Нр (х) полустепени р, удовлетво-
удовлетворяющих условию
\Нр(х)\^М (*>а>0), C)
наибольший модуль производной i}^ любого порядка к при х = 0 имеет
Нр (х) = М cos р Ух — а,
где Lp и наименьшее уклонение М связаны равенством B2).
5. С этими свойствами функций конечной полустепени можно связать
решение некоторых экстремальных проблем нового типа для функций
конечной степени.
Проблема 1. Пусть функции Gv(x) степени р принимают в не-
некоторой точке х = 5 значение *
Gv(i) = M (a<i<b). B4)
Требуется определить функцию Gv (x), наименее уклоняющуюся от
нуля на всей внешней части действительной оси вне промежутка (а, Ь),
и соответствующее наименьшее уклонение
Очевидно, что сдвиг промежутка (a, b) вместе с точкой ? не меняет
значения Lp; поэтому, не ограничивая общности задачи, мы можем
положить а — — Ь, а также принять, что Gp(?) = М >0. Решим сначала
соответствующую алгебраическую задачу определения многочлена степени
2п, наименее уклоняющегося от нуля при данном Х^>6>0 на двух
отрезках [—X, —6], [6, X], среди многочленов Р2п(х) той же степени 2п,
подчиненных условию Р2п (?) = М, где —b<^?<^b. Для этого построим
многочлен
гр /ч , х\ъ т ( \\ 2х2~- (X2 + б2)
T2nt\ (х) = (— l)n L (n, I) cos n arc cos х* — Ъ* =
/Х2 fr2
где L(n, X) — не зависящая от х постоянная. На каждом из рассматри
ваемых отрезков
при этом значения 4=L(^? X) с чередующимися знаками принимаются на
них в 2 (лг + 1) точках ±Ь, ±хъ • • • > ±хп-ъ ±^- Поэтому, если по-
* Не нарушая общности, можно считать величину М вещественной (положи-
(положительной). Тоже замечание относится и к проблеме 2. (Летор.)
486

стоянную L(n, X) подберем так, чтобы
М = L {n, I) cos 2n arc cos j/g—^-, B5)
то ^2п,л (^) будет искомым, наименее уклоняющимся из многочленов
^2п(я), удовлетворяющих условию P2n(?)=j|/. Действительно, если бы
существовал \Р2п (х) \<iL (п, а) на [—л, —Ь] и [6, л], то на каждом
из этих отрезков многочлен
имел бы не менее, чем по п корней, т. е. вместе с корнем $ имел бы
2п + 1 корней, что невозможно.
Но если М фиксировано, а а-^оо вместе с (целым) п—>оо так, что
2п .
— = р постоянно, то при всяком конечном х (если полагать для опреде-
определенности п четным)
_^Г = lim cos 2я arc sin 1/ 2__ а —
__р- = cosjoj/x2— б2.
Отсюда, в частности, следует, что если в равенстве B5) М фиксиро-
фиксировано, то
B6)
Таким образом, полагая
G* (х) = Lv cosp У^^Р,
мы видим, что
FT- ^г B6 bis)
представляет наименьшее уклонение целых функций Gp (x) степени р вне
промежутка (—Ь, 6), удовлетворяющих B4), так как мы знаем, что все
ограниченные функции Gp (x) степени р являются пределом многочленов
Рп (х) степени п -> оо, ограниченных при — X <; х <; X, где у <Г р + е при
произвольно малом е. Следовательно, по доказанному, \GV (х) \ ^.Lp+e
невозможно ни для какого г^>0 при всех х2^62; поэтому Gv(x) осу-
осуществляет наименьшее уклонение.
Следствие 5. Если вне отрезка [— 6, Ь]
I ^р (х)! < Д (^')
то на всей оси
РРЪ , р—рЪ
*- У ? B8)
487

и знак равенства осуществляется лишь для функции
в точке х = 0.
Проблема 2. Определить функцию Gp (t) степени р, наименее
уклоняющуюся от нуля вне отрезка [— 6, 6], если задана ее производная
Gpm) @) — ат какого-нибудь порядка т при t = 0.
Положим сначала т = 2kQ. Тогда искомая функция Gp (t), которую мы
можем считать четной, так как у [Gp (t) + Gp (— t)] также удовлетворяет
требованию задачи при заданном а2д0, имеет вид
k0—I Лк n t2k0 оо лк
Ь"р\Ч— 2a Bk)\ "f" Bko)\ "r Zl BЛ)! '
Полагая ^2 = x, получаем функцию полустепени р
ру+ -(щг-r 2i BЛ)! '
у которой задана k-я. производная Hpl<>) @) = /9Г\» fl2A:0> наименее уклоняю-
щуюся от нуля при х^-b2. Поэтому, в силу следствия 4,
Вр (х) = М cos р /х — б2, Gp (t) = M cos pYt2 — 62, C0)
где наименьшее уклонение М определяется из равенства
а*% = М [cosPyi^?]f™ = {-^f
Если задана производная a2fc0-i — G^' ^ @) какого-нибудь нечетного по-
порядка, то соответствующая задача разрешается элементарно лишь в слу-
случае b <Co-, а именно, функцией Gp (t), наименее уклоняющейся от нуля,
будет М sin pt, где Mp2je _г = a2k _±9 так как G (t) =M sin pt наименее
уклоняется от нуля даже на всей оси.
Напротив, при 6 ^> к~ наименьшее уклонение вне отрезка [— 6, Ъ]
меньшее, чем значение 2^Z\» которое соответствует функции Мsmpt,
выражается при помощи эллиптических функций. Не останавливаясь
на подробном вычислении,, покажем, что искомая функция Gp(x)y наи-
наименее уклоняющаяся от нуля вне [— b, b], имеет тогда вид
Gp (t) = M cos cp (t),
где cp (t) представляет эллиптический интеграл *
* См. статью Н. И. Ахиезера «Об одном семействе целых функций конечной
степени и одной чебышелской задаче», Изв. АН СССР, серия матем., 16 A952),
стр. 459—468. (Автор.)
488

в котором (при данном Ь^>~) оба параметра ^<^Ь<^Ь определяются из
условия Gp @) = 0, т. е. ср @) = -f- у -
Для этого нужно принять во внимание, что искомая функция Gv (t),
которая должна быть нечетной, является пределом многочленов P2n+i(t)
степени 2п + 1, наименее уклоняющихся от нуля на отрезках [— X, — Ь]
и [Ьу X] при условии Р{2п+11) @)= <*&.-!, когда п-> оо, так что —^— = р.
Согласно теории Чебышева (за исключением случая, когда число точек
отклонения на каждом отрезке максимально, т. е. равно п + 1), искомый
нечетный многочлен R2n+i @ должен иметь 2п точек отклонения, вклю-
включая + 6, + X. Следовательно, если М — наименьшее уклонение, то P2n+i @
определяется уравнением
где Ц- 8П — два дополнительных корня (| 8n | <С ^) многочлена
соответствующие абсолютному максимуму | P2n+i @ | на [— 6, 6], кото-
который больше М, а потому есть еще два значения 4h T^ fe ^ ^п)> гДе
Переходя в C2) к пределу (п->оо, nJ~ ¦ = р), получаем дифферен-
циальное уравнение
ьр (г) + 212 — &'
интегрирование которого приводит к C1), причем вследствие Gp @) = 0,
Y и 8 @ <^ х <С 8 <С ^) определяются однозначно из уравнений
J К"Fа __ t2) (?2 _ у2) ' J VQp _ t2) (ta __ у2) 2р <^
6. Наряду с функциями 7I/cos/>]/(^ — аJ — Ъг степени /?, наименее
уклоняющимися от нуля вне произвольно данного отрезка [а — b, a + 6],'
полезно также ввести функции
Gp (t) = MGl (t — a)=M cos p Y(t — aJ + Ь2\ C4)
которые являются наименее уклоняющимися на всей действительной оси
среди целых функций степени р, зависящих от трех данных параметров.
Как нетрудно видеть, получающаяся в случае 6 = 0 функция
MGV (t — a)=M cos p{t — o)
является наименее уклоняющейся среди функций степени /?, подчинен-
489

ных двум соответствующим условиям, например \ если заданы Gv @) = а0,
Ор @) = аь то функция Gp (t) степени р, наименее уклоняющаяся от нуля
на всей оси, равна
Gp (t) == М cos р (t — а) — а0 cos pt + — sin рг C5)
при а0 = М cos /?а, аг = — рМ sin /?а, откуда наименьшее уклонение
Проблема 3. Определить функцию Gp(t) степени не выше р, наи-
наименее уклоняющуюся от нуля на всей оси, если *
Gp (а) - а0, Gp (а) - 0, Gp (а) = а2 C6)
¦в некоторой точке а.
Заменяя Gv (t) через Gp (t + а), приводим общую задачу к случаю
а — 0. Следовательно, -g- [Gp (^) + Gp (— ^)] также является решением
задачи, и мы можем ограничиться лишь четными функциями Gp (t).
В таком случае, условиям C6) удовлетворит функция степени
GVl (t) = а0cospxt (b = 0),
если 0< — ~ = pl<CP2- Но если
то искомой функцией будет
Gp (t) = M cos Ур'Ч2+ с2 , M cos с = a0, — Ж -^- sin с = а2, C8)
где с<С^ является корнем уравнения р2tgс -)——с = 0. Первое утвер-
утверждение не нуждается в доказательстве, так как sup | Gv (t) \ ^
1 Аналогичное утверждение остается в силе, когда заданы
Gf@)=ak, G{*+« @) = ан+1.
Вследствие C5), находим тогда, что
откуда
причем знак равенства имеет место, когда Gp (г) вида C5).
* Отношение — предполагается вещественным. См. также статью Н. И. Ахие-
зера «О целых функциях конечной степени, наименее уклоняющихся от нуля».
Матем. сборник, 31 G3), 2 A952), стр. 415—438. (Автор.)
490

очевидно. С другой стороны, для доказательства C8) положим
рН% = рЧ% + с2. Тогда
= cos pz = ^ + sin /*
&=1
где с| — А27г2 — с2 при Aj>0, если 0<Сс<^тг. Вообще аналогичным обра-
образом всякую ограниченную четную функцию Fv (t) степени р можно
представить интерполяционной формулой
рУ"У '. C9)
Поэтому, если бы существовала функция степени не выше р, кото-
которая уклонялась бы от нуля меньше, чем C8), то существовала бы
функция Fp (t) вида C9), у которой
(а г, f™
но это невозможно, так как ( А = /^р ( —
Пусть, например, а0 = 0, а2 = 1. Тогда с =-^- п среди функций
степени /? наименее уклоняется от нуля при — ос <^t <^оо функция
Gv (t) = — Мо cos 1/ z>2^2 + -—-, Мо = о-» • C8 bis)
Если при том же а2 = 1 данный относительный минимумх а0 >> О
мы будем увеличивать, то абсолютный экстремум М^>а0 функции Gp (x),
наименее уклоняющейся от нуля, также будет возрастать от Мо до оо,
1 Так как аг =0,
491

гак как с будет расти от -^- до тт. Если же относительный минимум
~и<0, то М> —а0, причем ^ = -^- > 1 лишь при 0< с< у,
г. е. пока ао<^—; после этого М ——а0.
Отметим еще, что функции C8) при любых с ^ 0 обладают свой-
свойством, что
sup i
пслько в отличие от случая с = 0 указанное значение не достигается
ви при каком конечном t.
Поступило
31. XII 1948 г.
ЦИТИРОВАННАЯ ЛИТЕРАТУРА'
1 С. Ы. Бернштейн. Распространение неравенства С. Б. Стечкина на целые
функции конечной степени. Докл. АН СССР, 60 A948), 1487—1490 [95].
2 С. Н. Бернштейн. О приближении функций на всей вещественной оси при
помощи целых функций данной степени. Докл. АН СССР, 54 A946), 479—482
[84], заметка V.
3 С. Н. Бернштейн. Новый вывод и обобщение некоторых формул наилучшего
приближения. Докл. АН СССР, 54 A946), 667—668 [87].
4 С.Н. Бернштейн. Экстремальные свойства полиномов и наилучшее приближе-
приближение непрерывных функций одной вещественной переменной, ч. 1. ОНТИГ
Л.— М., 1937, стр. 55." [«Э.П.»].

100
О НЕКОТОРЫХ СВОЙСТВАХ ЦИКЛИЧЕСКИ
МОНОТОННЫХ ФУНКЦИЙ*
В статье излагается теория экстремальных свойств циклически монотонных
функций, основные результаты которой были опубликованы автором без доказа-
доказательств в 1928 г.
Введение. Согласно определению, данному мною в статье (х), непре-
непрерывная функция / (х) (имеющая непрерывные производные всех порядков)
называется циклически монотонной [/ (х) 6 Ц (а, Ь)] на данном отрезке
[a, Ь], если / (х) и ни одна из ее производных fW(x) не меняет знака на
всем отрезке [а, Ъ], причем для всех i ^ 0
/<*> (х) /<i+*> (*)< 0 (а < х < Ь). (А)
Геометрически это означает, что все производные fW (x) представляются
монотонными линиями, вогнутыми в сторону отрезка [а, Ь]. Если а = 0,
6=1, то мы обычно будем писать просто f (х)€ Ц вместо f (х) 6 Ц @, 1).
В статье (х) для функций / (х) 6 Д (а, &) доказано (как следствие из
соответствующего общего свойства регулярно-монотонных функций) нера-
неравенство
откуда следует, что всякая функция / (х) 6 Ц (а, Ь) есть целая функци-я
конечной степени /?, где
В моем докладе B), сделанном в 1928 г. на Международном конгрессе
математиков в Болонье, сформулировано несколько теорем, из которых
между прочим вытекает (не допускающее усовершенствования) уточнение
неравенства A), а именно,
Изв. АН СССР, серия матем., 14 A950), стр. 381—404 B57*).
493

Целью настоящей статьи является доказательство, уточнение и неко-
некоторое развитие этих результатов моего доклада, а также тех связанных
с ними, высказанных там же теорем, которые относятся к функциям
класса 5>i (a, b), обладающего свойством, что / (х) G -К (а, Ь), если она бес-
бесконечно дифференцируема на отрезке [а, Ъ] и обращается в нуль по край-
крайней мере в одной точке этого отрезка, как и все ее производные.
1. Из определения функций / (х) 6: Ц (а, Ь) видно, что если для неко-
некоторого i = п — 1 существует внутренняя точка х = х0 (а<^хо<^Ь), где
неравенство (А) обращается в равенство [/(ть~~х) (х0) /(n+D (х0) = 0], то
/<n-K) (х) = 0 тождественно, т. е. / (х) является многочленом степени <^и
(на отрезке [а, Ь]). Действительно, если /(n-D (x) >- 0, то функция у (х) =
= f{n-\) (х^ для которой у" (х) — знакопостоянна и монотонна, не может
обращаться в нуль во внутренней точке, не будучи тождественно равной
нулю.
Образцом циклически монотонных функций [/ (х) € Ц], отличных от
многочленов, являются тригонометрические функции х / (х) = sin -к-х
и ср (#) = cos-7j- х. Для первой из них
/ @) = /B*) @) = / (**+1) A) - 0,
для второй
ср A) = ?<а*> A) = cpB*+D @) = 0
при всех целых к ^ 0. Докажем, что и, наоборот, справедлива
Лемма 1. Если функция f (x) 6 Ц и, так же как и все ее производные,
имеет корень на отрезке [0, 1], то она совпадает {на отрезке [0, 1])
с одной из функций: В sin ~ х или В cos— х (В — произвольная посто-
постоянная) .
Действительно, учитывая, что / (х) не может быть многочленом (так
как всякий многочлен характеризуется тем, что одна из его последо-
последовательных производных есть отличная от нуля постоянная), заключаем,
что уравнение /(пЦх) = 0 для каждого п^0 имеет только один корень,
который равен 0 или 1. Предположим сначала, что f(x)f(x)^>0 (при
<^1). В таком случае, вследствие (А),
f(x)f"(x)<0, f'(x)f"'(x)>0
и вообще
(х) /<2*+i> (х) > 0 и /»*+« (х) /(*-Ю (х) < 0
1 Все циклически монотонные функции принадлежат одному из четырех типов
регулярной монотонности B), которые вполне определяются знаками / (х), f (x)
на отрезке [0,1]:
sin у х ( + ,+); — sin у х (—,—); cos у х (+,-—): — cos у х (—>+).
494

при 0 < ж < 1 и agA = О, a2fe+1 = 1, где ап — корень /(п> (ж). Пусть
/ A) = В; я говорю, что
ж) = Bsin~x.
В самом деле, из того, что f^k>> @) = 0 (О^А), следует, что целая функ-
функция конечной степени /*(#), с котором / (х) совпадает на отрезке [0,1],
есть нечетная функция, т. е.
/*(-*) = -/*(*), B)
а вследствие /(^Н-1) A) = 0 имеем также
.*•). C)
Из B) и C) заключаем, что /* (х) есть периодическая функция с перио-
периодом 4, так как
Г [х - 2) = - /* B — х) = — Г (х) = Г (- х) = f (х + 2).
Следовательно,
ОО 7
J* / \ ХП . КТС . 7Z
Т I 'Т* 1 ¦ -¦-- ^.» >тг , о 1 Т1 'Т1 — vTF 01 Tl sy*
J \^) 7 г Ufa Olll ~Ту «л/ ttj Olll 7" ,//5
так как степень /* (х)} вследствие A), не выше 2<Стг. Поэтому
/ (х) = /* (х) =Bsin~x @<я< 1). D)
Аналогичным образом в случае / (х) f (х) <Г 0 найдем, что / (х) —
= В cos у ж, где 5 = / @).
Следствие 1. Целая функция f (х) степени р<^ъ, обращающаяся в нуль
вместе со всеми производными четного порядка при х = 0, между
тем как ее производные всех нечетных порядков имеют корнем х = 1,
равна В sin у ж.
Примечание. Если функция (бесконечно непрерывно дифференци-
дифференцируемая) удовлетворяет в промежутке (а, Ъ) условию (А), не принадлежа
на всем отрезке [а, Ь] к Ц {а, Ъ), т. е. если существует точка х = %
(а<<жо<;б), где хоть одна производная /(i)(#), обращаясь в нуль, меняет
знак, то, в силу (А), тем же свойством будут обладать производные
f® (х) для всех неотрицательных /==г (mod 2). Поэтому если есть еще
одна точка хг (а<^х1<С Ь), где fW (хг) (пусть хг— такая ближайшая
точка справа от х0) меняет знак, то непременно k — i = 1 (mod 2) для
всех к^-0. Следовательно, / (х) С Ц (х0 хг) и удовлетворяет условиям
леммы 1, так что
1 ( \ г» • ^ (х — xi) г> тс
/ (х) == В sin -тгу Ц- или В cos
и имеет период Т = 4 (х1 — х0). При этом на всем отрезке [а, Ь] функция
495

f {ос) сохраняет тот же вид (отсюда следует, в частности, что, кроме ж0,
второй точки хх не может быть, если / (х) — многочлен).
Принимая во внимание, что на полуоси функция / (х) не может быть
циклически монотонной (если не считать линейной функции ах + Ъ, для
которой условие (А) вырождается в тривиальное равенство), заключаем,
что функция f{x)y удовлетворяющая на полуоси условию (А), имеет по
крайней мере два нуля, откуда вытекает любопытное
Следствие. Единственной х функцией, удовлетворяющей условию (А)
на полуоси (тем более на всей оси), является тригонометрическая функ-
функция Bsin(cx-\-a) при любых значениях постоянных В, с, а.
Например, функция / (х) = sin x однозначно определена условием (А)
на (— оо, + °°) тем, что в промежутке @, тг) она не меняет знака,
обращаясь в нуль в его концах, и тем, что максимум ее в этом про-
промежутке равен единице.
2. Среди многочленов Рт (х) 6 Ц степени т особо важную роль
играют многочлены, которые характеризуются тем свойством, что их
последовательные производные обращаются в нуль в концах промежутка
@,1). В таком случае, как легко видеть, из условия (А) вытекает, что
если Р(т (ак) = 0 для всех k<^m, то возможны только два случая:
1) ак = 0 при к = 0 (mod 2); <хк = 1 при А = 1 (mod 2), либо
2) ак = 1 при к = 0 (mod 2); ад = 0 при к = 1 (mod 2).
Эти многочлены с точностью до линейного преобразования переменной
¦совпадают с классическими многочленами, которые по другому поводу
были введены Эйлером. Мы будем обозначать указанные выше много-
многочлены через Sm (х) в первом случае, т. е. при а2к = 0, и через Сш (х),
когда a2fe-j-i = 0, и будем называть их для краткости2, соответственно,
циклически монотонными ^-многочленами и С-многочленами. При этом
нормируем их дополнительным условием, что
S™ {х) = <?Г (х) = 1, E)
т. е. вообще они относятся к классу многочленов Рт (х) (:Ц вида
Рт (X) - ^ + РгХ^~1 + . . . + Рт.
Таким образом, коэффициенты рь . . ., рм в случае ?т (х) и Ст (х) опре-
определяются соответственно требованиями
1 Функция ах + Ъ при всяком данном х (и фиксированных а и Ь) есть предел
N sin —-jy— при N —> оо.
2 ^-многочлены соответствуют тем же типам регулярной монотонности, что и
^fsin-^-^» а С-многочлены соответствуют +cos-k-# на @,1)-
496

для производных всех порядков, меньших т. Следовательно,
х хх хт—1 ,
Sm (х) = \ dxA dx2 • • • f dxm (
{О, при т нечетном\
1, при т четном /
хт—1
0 ! «m-l
Из G) следует, что
S'm (x) = <:,„_! (ж), С'т (х) = ^.x (ж). (8)
Поэтому вообще
™ (x) = Sm_2k (x), C™ (x) = Cm^k (x),
(9)
x) = Cm_2,_x (rc), ^fc+1) S (
Отсюда видно, что в случае нечетного т = 2А;
будет нечетной функцией от х, которую можем записать в виде
т Ыт) т— 2 Ыт) з
С ГГ\ - L 2 L L ^-3^
°mW- ^f"+!(m —2)! +* +3!(m — 3)!
а так как
х Ех Е х
Sm-2 (х) = Sm (х) = ~(т_2I + 2\\т-4)\ ^ !" (m^-З)!'
то отсюда заключаем, что числа Effi при всех 2h<^m не зависят от
верхнего индекса т. Поэтому, отбрасывая верхний индекс, имеем для
всех нечетных т = 2к + 1
^
2! B/с—1)! "^
и, вследствие (8),
х2к Е х2к~2 Е
Полагая JE28+i = 0 Для всех нечетных индексов, можно записать симво-'
лически равенства A0) и A1) в виде
заменяя везде в формуле бинома Ньютона степени i?s числами i?s. При-
Принимая во внимание, что С2и A) = 0, получаем символические равенства
A + ЕJ1 = 0 A2)
32 с. Н. Бернштейн 497

для последовательного определения целых чисел E2s (все числа Е28-^1 = 0)~
В частности,
1 + Е2 = 0, 1 + 6Е2 + Е± = О, 1 + 1ЪЕ2 + 15?4 + Е6 = О, . . .,
откуда
Яа = -1, ^4=5, Яв = -61, ... .
Для дальнейшего особый интерес представляют величины
Lm = max \Sm (x)) = 1Sm A) | = max | Cm (ж) | = \Ст @) |. A3)
0<я<1 0<эс<1
Из равенства (И) и из того (см. G)), что С2к(х) ==S2k(l — ж), получаем
так что
I я_, I
A5)
Кроме того, учитывая, что С22^(ж) = 1, из условия (А) заключаем, что
С*к (ж) (— lO^ ^- 0, поэтому вообще
{-i?E2k>0. A6)
Из G) и A0 bis) получаем
\ _ Г (С\\ — ^ +
) - — С2^+1 @) - BЛ
Л + 1I - Bft+1)! *
Целые числа Ет = A + ^)т назовем коэффициентами Эйлера второго
рода1. Так как S1{x) = x^>0, то вообще, вследствие (А),
A8)
с другой стороны, так как С2ъ A) = 0, то
Е\к = A + ^)^=0 (Л>0, ?о = 1). A9)
Учитывая A9), символическое равенство A7), определяющее Е2ъ+Ъ можно,
также записать в несколько более простой для вычислений форме:
tflfc+i = A + Е) A + ЕJк = ? A + ?J?fc. A7 bis)
Отсюда
#; = 1, ?3* = 2?2 = —2, ^ = 4?2 + 4?4 = 16,
Е* == 6^2 + 20?:4 + 6EQ = — 272,
Из A7) получаем значение
, 1 Эти числа, как видно из формул C2), связаны простыми равенствами с числа-
числами 2?2? Берну л ли:
_ВЛ (#*-&*)
498

Из A1) следует также
S2k (х) = С2к A — х) == 2^1 = 2^! = Ш~
— 2/с! B/с—1I 3!B* — 3)! B* — 1)! *
Дифференцируя, получаем
^2*-iw — B/с —1)! BА—1)! BЛ — 2)! 3! BЛ — 4)! BЛ — 1)! *
Таким образом,
^я-ц-у— BЛ —1)! '
Замечая, что при любом
так как С^ (х) есть функция, нечетная для h нечетного и четная для h
четного, и в последнем случае С$} A) = 0, согласно F), заключаем, что
i ~2fc
i [C2ft (a; + 1) + C2fc (* — 1I = йи • B2)
Дифференцируя B2), получим
| -x (x - 1)] = щ^х • B3)
Вспоминая далее, что С2к (х) = S27c A — х), из B2) получим
у №* (- х) + S2k B - х)] = 4 [5rt (ж) + S2k (x + 2)] = ^ B4)
и, дифференцируя B4), найдем
1 [Сй-i (х) + С2,_х (« + 2)] = ^щ. B5)
3. Представим многочлены Sm (x) и Ст (х) в промежутке @, 1) рядами
Фурье с периодом Т = 4 вида
оо
sro(z)= 26".«81птB/г + 1)а;>
Л=о B6)
Cm (*) = (- I)"* 5m A - Ж) = (- l)m |j (- 1)Л йй. m COS ^- BЛ + 1) X
499 32*

Принимая во внимание, что первая из периодических функций
оо
S*m(x)= ^ bKmsm^Bk + l)x,
/1=0
Cm(x) = (-:
(—
(- i)h cos
Л-0
B7}
нечетная относительно х = 0 и четная относительно х = 1, а вторая,
С^ (х), наоборот, является четной относительно ж = Ои нечетной отно-
относительно х = 1, отметим, что равенства B6) применимы к многочленам
^ (х) и Ст (ж) в несколько больших промежутках, а именно:
k^ (х) = 5^ (ж), С2к (х) = С\ъ (х) (— 1 < х < 1),
S2J? (х) = 5й (х), См-х (х) = C2Vi (ж) @ < х < 2).
B8)
Таким образом,
в частности,
так что
Ьн. т = 2 ^m (x) sin у B/г + 1) х dx,
1
ЪК0 = 2 ^siix у B/г + 1) xdx = ^ • —jj
. 7Г
B9)
h=o
Последовательно интегрируя B9) и учитывая, что C2fc—i A) = S*k @) = О,
получим
Сл-i (х) = 2 (- 1)*
C0)
и аналогично
(—
^ C1)
500

Таким образом, наибольшие по модулю значения Ст (х) и Sm (x)
равны (&>-0)
A) = -Сл+1@) =
В частности,
2,
= 2 (- 1)»
4 V ^
h=o
BЛ
\ C2)
32
/г=о
И Т. Д.
Полагая
о
имеем для всех т >- 0
т+1
Ят.
C4)
Следовательно, учитывая, что limZTm = l, получаем для всех т—>оо
т-*оо
/ О \7П+1
Lm= max |5т (ж) |~ 2 (-) . C5)
0<л:<1 \ п J
При этом для нечетного т = 2А + 1 (Л ^> 0)
так как1
1 Левая часть неравенства C6) очевидна для всех нечетных т\ правая часть рав-
равнозначна неравенству
\
которое справедливо для всех А >• 1, если оно верно для к = 1. Но для Л = 1 непо-
непосредственным вычислением проверяем, что
501

Для четных т = 2к ^ О имеем
\т+1
C6 bis)
\ •- / \ О ' ~ У \" У
так как
Из равенств C3) видим также1, что
Следствие 2. /Три всяком данном значении числа х
hm ^^-^ = sin х ж, hm ~g- - cos x ж. C8)
Высказанное утверждение непосредственно вытекает из равенств C1)
и C0), соответственно, для промежзтков (— 1, + 1) и @, 2). Но легко
убедиться, что указанные предельные равенства справедливы при любом
конечном действительном или комплексном значении х. Оба равенства C8)
между собой равнозначны. Для определенности рассмотрим второе для
четного т = 2k. Тогда из (И bis) находим
fc-*oo С2к(°) к-»оо Е2к ?->оо Е2к ^B*—2*)!
Поэтому из C2) следует, что
т. е. предельное равенство C8) справедливо для всех х.
4. Переходим к выводу основных экстремальных свойств функций
/ (х) 6 Ц. Для этого нам полезно будет немного расширить этот класс,
назвав функцию / (х) 6 Цп циклически монотонной порядка п ^> 1, если
1 Неравенства C7) для Н2к+1 очевидны; что касается неравенств для #2fc> где
я ei_[7-i——М+ | ( 1 * U 1
то достаточно заметить, что при h >¦ 1 и х >-1 есть убываю-
BЛ + 1)* Bй+3)ж
щая функция от х, так как ее производная по х равна
IgB& + 1) lgBfr + 3)
B/г + 1)л: B^ + 3)^
/ lgiV r
I вследствие того, что ¦ ° убывает с возрастанием
502

/ (х) имеет на отрезке 01 знакопостоянные производные всех порядков ^ п,
удовлетворяющие неравенству (А) (при О^г ^п— 2).
Лемма 2. Если1
f(m)(x) = F(x) (m>l, 0<я<1), C9)
еде F (х) — данная знакопостоянная функция, то функция f{x), наименее
уклоняющаяся от нуля на отрезке 01 среди функций f (x) б Z(m, обра-
обращается в нуль, так же как и ее производные fk\x) @^k<^m), в одном
из концов ock отрезка 01 (при этом, вследствие циклической монотонности,
концы ад; последовательно чередуются).
Положим для определенности, что / (х) ^> 0 и что наибольшее значе-
значение / (х) достигается при х = 1, т. е. /' (х)^0. Тогда, вследствие усло-
условий (А), имеем вообще
/(i) (х) < 0 для i = in + 2 или i = in + 3
/(г) (х) > 0 Для i = in или г = 4лг + 1
при всех i^m, возможно малым нужно сделать /A).
Очевидно, что / @) = 0, так как если / @) = с > 0, то функция
/ (х) — а 6 Цт, где 0 < а < с, удовлетворяя тому же требованию C9), укло-
уклоняется от нуля меньше, чем f(x). Остается доказать невозможность пред-
предположения, что fk) (x) будет первой из последовательных производных
(k<^m), которая не равна нулю в конце ак, так что для всех i<^k
имеем, вследствие сказанного выше, /<{) @) = 0 (а{ = 0 при i четном) и
fit) A) = 0 (cti = 1 при i нечетном). Для этого строим циклически моно_
тонный многочлен Pjc (x) = ЧЬ Sjc (x) степени А, который вполне опреде-
определяется условиями, что Рк @) = Ръ} (аг) = 0 при всех г<Аи Р^ (х) =±1,
где +1 берется при к = 0 или 1, a —1 соответствует к = 2, к = 3 по
mod 4. Таким образом, Р^ (х) > 0 при 0 < х <^ 1, и функция
удовлетворяющая C9), будет при достаточно малом а>0 циклически
монотонной порядка т, так как
/(*>(я)/(*)(я)> 0 @<i<m),
причем
так что, вопреки предположению, мы получили бы, что функция / (х) не
является наименее уклоняющейся от нуля.
Из леммы 2 непосредственно вытекает (если положить F (х) = ± 1)
алгебраическая экстремальная
1 Т. е. f{m~1) {x)=\f (x) dx.
503

Теорема 1. Из всех многочленов степени т, циклически монотонных
на отрезке 01, вида
Р{х) = ±-^r + PiZm~1 + -- + Pm D0)
наименее уклоняются от нуля на 01 многочлены ±Sm(x) и ±Ст(х)г
причем это наименьшее уклонение равно величине
Lm = \Sm(l)\ = \Cm@)\ C2 bis)
[определенной формулами C2)].
Следствие 3. Среди циклически монотонных многочленов D0) много-
многочлены Hh Sm (%) и + Ст (х) обладают также наименее уклоняющимися от
нуля производными любого порядка i<^m и это наименьшее уклонение
равно Lm-.i.
5. Из леммы 2 получаем также
Следствие 4. Если f(x) 6 Цп, /i(#) 6 Цп и для некоторого т<^п
то наименьшее уклонение функций f (х) не превышает наименьшего
уклонения функций Д(ж).
Действительно, не нарушая общности, можем положить /<т) (х) ^ 0,
, так что
где ср(т)(ж)^О. Но если f(x) есть наименее уклоняющаяся функция, то
х хт_1 х
/(*:)=$(**!... J /<*» (Я^) dxm = J /(-) (Ж) (Же)"
а0 ат—1 ао,...,ат_1
х
и так как знак ср (х) = f cp(m) (ж) {dx)m (как и ее производных) тог
же, что и знак / (х) (и ее соответственных производных), то
А (х) =
Поэтому справедливо также
Следствие 5. ifs eceo; функций f (х) 6 If, удовлетворяющих для неко-
некоторых т^>0 условию
|>1 @<ж<1), D1)
504

наименее уклоняются от нуля на 01 многочлены Эйлера •±:Sm{x) w
•~\-Ст(х)9 так что для всех этих функций
max | / (х) | > Llu = -LffJ при m = 2k,
/*+Д при m =
Отсюда получим важное
Следствие 6. Если f (x) 6 Ц и
max |
mo
В самом деле, учитывая, что максимум | ftm) (x) | достигается в конце-
отрезка 01, положим для определенности, что N = ft™) (l)>0. Тогда во-
вогнутость линии Y = /(т) (х) направлена книзу и, каково бы ни было*
^(™-ы) ^ ^ о, по лемме 2 максимум \f(x)\ будет наименьшим, если
f(m) @) = 0. Отсюда следует, что линия Y = /<т) (ж) лежит не ниже пря-
прямой Y = Nx, проходящей через начало координат и точку A, N), совпа-
совпадая с этой прямой, если /(^H-i) (x) = Л^ постоянна, так что, благодаря
следствию 4, максимум | / (х) | будет наименьшим, если f(m+V (x) = N,.
т. е. для f(x) = NSn+1(x).
Утверждение следствия 6 можно записать в виде неравенства
И = max | / (х) | > Lm+1 max
0<эс<1 0<<
которое равнозначно неравенству
Nm = max | /с») (ж) | < -^- . D3>
Из неравенства D3) следует общая экстремальная
Теорема 2. Всякая функция f (х) 6 Ц является на отрезке 01 целой
функцией конечной степени р <; ~; тг/ж этом, если
любого нечетного т = 2k + 1
max I /("» (х) I < V^— = MxKV~rT D4>
й для любого четного т = 2к
max | /("> (л) |< -j?— = ^^^V1 D4 bis>
505

и знак равенства фактически осуществляют функции
г) МС
Действительно, неравенства D4) и D4 bis) являются воспроизведением
неравенства D3) с выделением случаев т четного и т нечетного. Таким обра-
образом, принимая во внимание неравенства C6) и C6 bis), имеем для всех т
j ^(j -g- @<^<l), D5)
Зт+2
откуда следует, что / (х) — целая функция степени р ^ ~.
Следствие 7. Всякая функция f (х) ? Ц (а, Ъ) есть целая функция ко-
конечной степени р <С -?f (на отрезке [О, Ь]). В частности, f (х) € Ц К), у
есть целая функция степени р<^.1, и в этом случае при условии
имеем также для любого т^>0
+ 4-М. D6)
В последнем случае верхняя грань |/<т) (ж) | > ЛГ для всех
2
и, согласно C7), приближается к своему пределу М -g- по недостатку для
четных т и по избытку для нечетных т. Максимальные значения {/^ (х
л/ш каждом т осуществляются различными функциями М
пределом же этих функций, на основании следствия 2, является три-
тригонометрическая функция Msinx. При этом модули всех производных
имеют один и тот же максимум, равный М.
6. Из теоремы 2 без труда получается
Теорема 3. Условие, необходимое и достаточное для того, чтобы
функция f (x) была целой функцией степени р, состоит в том, чтобы
она могла быть представлена на любом отрезке длины d <^ у- в виде
разности двух циклически монотонных функций одинакового типа, но не
могла быть представлена в виде такой разности на отрезке длины
Действительно, последнее утверждение вытекает непосредственно из
следствия 7, согласно которому функция, циклически монотонная на
отрезке длины db должна быть степени Рг^-т^-г- Для доказательства
506

первого утверждения достаточно принять, что степень нашей функции / (х)
равна р = 1 — s, где е >> 0 — некоторое фиксированное произвольно ма-
малое число, и представить ее как разность двух функций G1(x) и G2 (x),
циклически монотонных на отрезке ^ , —~—' • Согласно определению
степени, возможно указать такое число Мо, что при любых к ^ О
После этого определим постоянную А так, чтобы иметь A sin у J> Mo, и
положим
G\ (%) = A sin х.
В таком случае Gx (x) будет циклически монотонной на отрезке
[е ти el
тг, —о—' и при любом к ^> О
min | Gf} (ж) | = Л sin -|- > Д/о-
Поэтому
будет циклически монотонной того же типа, что и G1(x) на отрезке
[^г> 7—тг- L так как G^ (ж) Go7^ (х) ^> О ПРИ всех к^О, и, следовательно,
j (х\ __ g /ж\ q (у\ /47)
представлена в требуемом виде.
Отсюда, в частности, вытекает
Следствие 8. Для того чтобы функция f (x) была пред ставима при
любых данных а, Ъ в виде D7), где С1{х)^Ц(а, Ъ), G2(x)(:L((a, b), необ-
необходимо и достаточно, чтобы f (x) была целой функцией нулевой степени.
Среди требуемых представлений D7) целой функции / (х) степени р
особого внимания заслуживает то, которое вполне определяется значе-
значениями производных fW(x) всех порядков k^-О, взятых в концах отрез-
отрезка [а, Ь] так, что производные четных порядков даны в одном конце, а
нечетные — в другом. Для определенности положим а = О, Ъ = 1 и пусть,
следовательно, f < |.
Составим формально бесконечный ряд по ^-многочленам
F{x) = f @) + /' A) S1(x)+ ... + /W @) S2k (x) +
oo
+ /(*+« A) S2JC+1 (x) + ¦ ¦ ¦ = 2 /(m) M Sm (x), D8)
0
где a2k =0, a2kH= 1.
507

Вследствие условия /?<^у, найдется такое значение 6<^1 и соот-
соответствующая ему постоянная Мо, что
|/(«)(z)|<Jfo(^j @<з<1), D9)
откуда, принимая во внимание C5), заключаем, что ряд D8) абсолютно
и равномерно сходится на отрезке 01. Поэтому, учитывая ранее установ-
установленные свойства ^-многочленов, абсолютно и равномерно сходящимися
будут также и ряды, получаемые при последовательном почленном диф-
дифференцировании ряда D8), и FW @) = /(а*) @), F<2*+D A) = /BЛ+1) A). Вспо-
Вспоминая далее, что все ^-многочлены принадлежат к типу регулярности
4zsin;E (S'm (x) Sm (ж)^-О), мы можем, каковы бы ни были знаки fBk)@)
и /B*+D A)? перегруппировать так члены ряда D8), чтобы представить
его в виде
F(x)=G1(x)-G2(x), D7 bis)
где функции Gx (x) 6 Ц и G2 (x) 6 Ц включают только положительные
члены и, следовательно, принадлежат к типу регулярности +sinx.
Для того, чтобы убедиться в том, что при
нужно заметить еще, что
п
Rn+1 (X) = / (X) - 2 /('П) Ы Sm (X) =
хп
= \dx1\dx2...\ /(M-D (Xn+1) dxn+1,
О 1 an
и следовательно, в силу D9),
Rn+1 (х) | < Mjfe 6]n+1 | S^ A) | < ^ 6«+i @
стремится к нулю при п~>оо.^
Теорема 3, как и теоремы 1 и 2, была высказана мною в докладе B)г
упомянутом во введении. Вопрос об условиях, каким должна удовлетво-
удовлетворять функция / (х) степени р для того, чтобы она была представима
в виде D7), где Gx (х) 6 Ц @, ~), G2 (х) 6 @, тДЛ там не быя рас-
смотрен. Укажем здесь, полагая для определенности р = 1, вытекающее-
из предыдущего
Следствие 9. Если функция f (x) удовлетворяет условиям:
1) ряд
2 I /(m) Ы I («2* = 0, а2к+1 = -=-) E0)
1 Или, если сходимость E0) имеет место для а2й. = —, а2й.^1 = 0.
508

2) Hm max | /<™> (x) \ = 0,
mo f (x) = F (x) должна быть целой функцией степени не выше первой и
может быть представлена в виде D7), где G± (х) € Ц @, •?•) ,С2(я) 6 Д @, -^-)
получаются, как и выше, из абсолютно сходящегося ряда D8) (т. е. D8 bis)),
соответствующего промежутку 0, -«- .
Первое условие [сходимость ряда E0)] необходимо и достаточно для
того, чтобы существовала функция F (х), данная абсолютно сходящимся
рядом D8 bis) [так как для F (х) второе условие вытекает из первого].
Однако соблюдение обоих условий не необходимо для D7), как это
видно из примера функции
•" 2
которая не удовлетворяет второму условию [так как max (/(m) (х) \ = 1
2
при всех /п ^ 0, а соответствующий ряд D8 bis) дает F (х) = 0].
Также можно получить
Следствие 10. Если целая функция f (x) степени р <^2 удовлетворя-
удовлетворяет только условию E0), то р <; 1, и
где
Ы Sm(^X) (а* = °- а2^+1 = -J) • D8 bis)
Действительно, / (ж) — F (х) = ср (.т) удовлетворяет условию cpBfc) @) =
= cpBfc+i) | ^.j __ q и так как степень ее /?<^2, то, в силу следствия 1,
tp (a;) = Л sin x.
Следствие 11. Для того чтобы /<m) (am) могли быть значениями про-
производных /<т> (ж) в точках а2& = 0,a2^+i =у функции f (х) (: Ц Ш, ~j типа
^bsinx, необходимо1 и достаточно, чтобы ряд E0) бьгд сходящимся; в
таком случае f (x) имеет, форму E1).
Достаточность вытекает из следствия 10. Чтобы убедиться в необходи-
необходимости сходимости ряда E0), замечаем, что во всяком случае мы должны
иметь при любом п
п
1 Кроме явно необходимого (по определению) условия одинакового знака членов
ряда D8 bis) при 0 <*< "* [т. е. / @) /' (*\ > 0, /<2*>@) /B*+2) @)<0,
509

где слагаемые в правой части одинакового знака. Поэтому при расходи-
расходимости E0) | / (х) | был бы бесконечен.
Отсюда следует, что условие E0) является также необходимым для
того, чтобы функция степени р = 1 допускала представление E1).
Отметим вытекающее из следствия 11
Добавление к следствию 7. Если f (х) 6 Ц[0, у) и |/ (х) | ^ М
0 <#< — ), то
lim|/<™> (ж) |<Л/,
причем знак равенства осуществляется лишь тогда, когда
f (x) — rt M sin ж гг./ш / (х) = Ч: Af cos #.
Обобщая несколько представление функций конечной степени в виде
D7), нетрудно показать, что представление в виде абсолютно сходящегося
ряда
f(x) = ^Gk(x) (а<я<й), E2)
где Gic(x) (:Ц (a,b), после соответствующей группировки членов приводит-
приводится к виду
/ (х) = Gx (х) - G2 (х) + G3 (х) - G4 (x),
где Gi(x) и G2 (x) типа sina;, а Сг(х) и G4 (ж) типа cos x.
Поэтому из следствия 11 заключаем, что условием, необходимым и до-
достаточным для того, чтобы f (х) степени р = 1 допускала представле-
представление E2) (а = 0, Ъ = ~), служит возможность такого представления
f (х) = срх (х) + ср2 (ж), чтобы ряд
2 [ I '-рГ @) I +1 фГ+1) (у) I +1 <рГ (f) I + I ?f+1) @)! ]
был сходящимся.
Более удобную для приложений формулировку имеет
Следствие 12. Для того чтобы функция f (х) степени р = 1 допус-
допускала представление ^E2), необходимо, чтобы f (х) была равна ср (х) +
+ Л sin я + J3 cos ж, где lim | cp(m> (х) \ = 0; тел* более, необходимо, чтобы
"Шп|/<т>(а:)|<оо
7. Перейдем к рассмотрению бесконечно дифференциру емых функций
}(х)(:У1(а, b), удовлетворяющих условию, что f (x), как и все ее производ-
производные, имеют по крайней мере один корень на отрезке [a, b]. Если а = 0,
6 = 1, то мы будем писать коротко 9? = Щ0, 1). Кроме того, будем рас-
510

сматривать вспомогательные классы функций 9tm (a, b), имеющих произ-
производные до порядка т включительно, с корнем на отрезке [а, Ь].
Лемма 3. Если f (x) 6 9?m_i и
/(т) (я) = F (х) > 0 @ < х < 1), C9 bis)
то наибольшее значение
в любой данной точке х0 @ ^ х0 <J 1) достигается функцией
х хг хт—1
f(x;aQ9...,amr-1) = {dxl[dx2. .. С F (xm) dxm =
«о «1 «
где «i = 0 гг^ггг 1 — концы1 отрезка, знакопостоянной, как и ее т произ-
производных на отрезке 01, гг
^ (Ют-1, ^ (*)) = max | / (я0) | = | / A - а0; а0> . . ., а^О |.
0<л:0<1
В самом деле, если / (х) не знакопостоянна, то / (х) + е при е ^> 0 до-
достаточно малом удовлетворяет тем же требованиям, причем одно из двух
значений
Если / (х) не меняет знака во внутреннем нуле x = i, то при т > 1 то
же замечание применимо к знакопостоянной функции / (х) + е (ж — ?), а
при /гг = 1 знакопостоянство / (х) возможно лишь при /(ао) = О. Итак,
примем, что наше утверждение верно для / (х) и для всех ее производ-
производных порядков г < k < m, так что А есть наименьшее целое число, для
которого? /W (?) = 0 @ < Е <] 1), причем ни на одном из отрезков [0, ?] и
[5, 1] не имеем тождественно/^) (х)= 0. Построим многочлен Р (х; <х0,.. .,a^!)
степени к, который со своими производными порядков i<^k обращается
в нуль в тех же концах а% отрезка, что / (х) и ее производные, но
(х; а0» • • • i ак-\) = 1, так что
Р (х; а0, . . ., aft_i) =
В таком случае, если fW (x) не знакопостоянна, то
х
к («) =/(*)+ ^ («; «о, • • •. «*-а) = ^ [/(*} (ic) ±e] {dx)k
также удовлетворяет C9 bis), и при 8 ^> 0 достаточно малом и при над-
1 Концы а^ вообще могут зависеть от х0.
511

лежащем выборе знака мы имели бы | /х (х0) | > | / (х0) I • Если /<ft) (x) зна-
знакопостоянна и fW (х) — 0 в некоторой внутренней точке х = ?, то рассмот-
рассмотрения требует лишь случай, когда к<^т—1. В этом случае
также удовлетворяет условиям леммы и | /х (х0) | ^ | / (#0) I ПРИ соответст-
соответствующем знаке е, между тем как /М (о:) не знакопостоянна.
Следствие 13. Если ® (х) 6 3lm—i и
?(«0 (ж) = Ф (Ж) >F (x) >0 @<ж< 1),
/no л/ш всяком х0 @ <; #0 <; 1)
М (Я™-!, Ф (ж); а0) > М (Ят_ъ F (х); х0)
и тем более
М (Шт-ъ Ф (х)) > М (%^l9 F (х)). E3)
Действительно, пусть
х
f (ж; а0, . . ., am_j) = ^ F (ж) (dx)m
а» «m-i
-осуществляет М C1т—ь F (х); х0) при некоторой последовательности нулей
в концах OLi отрезка 01; при этом
(_ 1) e.+.-+«m-i/ (x; a0> . . ., am_i) > 0,
какою бы функцией F1 (х) = Ф (х) — F (х) ^ 0 мы ни заменили F (х).
¦Следовательно,
Л/ ERm_1, Ф (ж); ж0) > I ? Ы | = ^ Ф ^ (^)m >
>М(^т_1, F(x);x0).
Первое дополнение к лемме 3. Если f (x) 6 9?т—i удовлетво-
удовлетворяет всем условиям леммы 3, кроме ограничения F (х) ^ 0, то
max | / (х0) | = М (%^ъ F (х); х0)
в любой точке х^ {O^x^^l) достигается, когда f (x) и все ее производ-
производные /(i) (х) порядков i <^т знакопостоянны, причем в случае т ^ 2
/ (х), . . ., /(т-2) (х) обращаются в нуль в концах а0, . . ., ат_2 отрезка 01.
В самом деле, свойство нулей / (х) и ее производных до порядка
т — 2 было доказано независимо от условия F(x)^-0; доказательство
необходимости знакопостоянства /(m~D (х) также независимо от условия
F(x)>0.
512

Второе дополнение к лемме 3. При соблюдении всех условий
леммы 3
достигается, когда все концы о^ @ ^i^m — 1) последовательно чере-
чередуются; в случае нарушения требования F (х) ^> 0 то же чередование кон-
концов OL{ должно иметь место для всех i<Cm — 2.
В самом деле, мы можем ограничиться первым случаем, когда /<т> (х) =
= F(x)^0, так как во втором случае тем же свойством знакопостоянства
обладает /(т—а) (ж). Положим, далее, для определенности, ат__1 =0, т. е.
В таком случае, вследствие монотонного возрастания fi™—1) (x), имеем
при у = 1 — х
1 У
- /im~2) (х) = $ /(m-J) (t) dt > J /("^-i) (г) Л = fT~%) (У) > С
х 0
где /х (ж) соответствует ат_2 = 1 ф ат—1> a /о (ж) соответствует ат_2 =
=:0 = ат_1.
Замечая, что, вообще,
71/ (Яп, F (^)) = Л/ (ЮП| F A - ж)) E4)
и принимая во внимание следствие 13, заключаем, что
М
причем знак равенства исключается при 7
Таким образом, если, в частности, положить F (х) = 1, то получается
Теорема 4. Если многочлен степени т^>0
Рт(х)==±х— + а±s"-i + • • • + от б Km_lf E5)
т. е. если Рт (х) имеет по крайней мере один корень на отрезке 01, как
а все его производные Р^ (х) порядков i <^ т, то
причем значения Ьт достигаются только для многочленов Эйлера ±Sm (x),
±Ст(х) (при т>2).
Отсюда следует
Теорема 5. Если для некоторого т
| /("> (х) |< 1 E7)
и f(x)€9ln (m<^n+ 1), то
|/(^)|<Lm. E6 bis)
33 с. Н. Бернштейн 513

Действительно, в случае /^ш) (х) знакопостоянного наше утверждение
прямо вытекает из следствия 13, если же /(т) (х) имеет внутренний
корень, то для получения наибольшего максимума | / (х) | нужно, чтобы
f(m—D(x) была знакопостоянна. В таком случае, если /(т—^(^)=0
@<?<1), то
| /(т-1} (х) |< | х — $ .
Но так как максимум | / (х) | будет наибольшим, если /(т—2> (х) = О при
х = 0 или 1, то, полагая, например, f(m—2) @) = 0, имеем
так что соответствующее значение
1 - *) * = * - ¦? > /(т) («) • E8)
Другая формулировка1 теоремы 5. Если f(x)^3tn (в част-
частности, если / (х) € 9?оо = 9?) и
max | / (ж)! = 1, E9)
0<<1
то
max
F0)
для всех т^п + 1. При этом, когда т = п + 1, то знак равенства в F0)
осуществляется для соответствующих многочленов Эйлера степени т.
Примечание. Теорема 4 может быть дополнена следующим образом:
max | Рт (х0) | в данной точке х0 (О <J х0 <; 1), где Рт (х) 6 У1т—1 вида E5),
осуществляется либо многочленом Эйлера Sm (x), либо многочленом Ст (т)
[при х0 = -к- этот максимум равен Sm[-^\ = Ст[ — )\ .
Из теоремы 4, которая впервые была указана в докладе B), вытекает
Следствие 14. Если целая функция конечной степени / (х) и ее про-
производные /<п> (х) всех порядков имеют по крайней мере по одному корню ап
на некотором отрезке [а, Ь] длины d и степень ее р < ^, то имеем
тождественно f(x)=O; напротив, функция / (х) степени р = -^ может
^ ( . пх\
быть при этом отлична от нуля (например, sm^-rj.
Таким образом, в отличие от случая, когда корни ап могут быть
комплексны, если корни ап вещественны и \ап\^~, то соответствующая
этим корням функция / (х) степени р ^ 1 тождественно равна нулю2.
8. В заключение я хочу обратить внимание на некоторые обобщения
изложенных выше результатов. Прежде всего отметим, что лемма 2 при
1 В докладе B) теорема 5 высказана не вполне точно.
2 Соответствующая постоянная w (Уиттекера) в случае комплексных корней ап
известна C) лишь приближенно @,7199 < w <C 0,7338).
514

помощи аналогичных рассуждений распространяется на все типы регу-
регулярно монотонных функций с той лишь разницей, что нули он последо-
последовательных производных, которые для осуществления экстремума всегда
должны совпадать с одним из концов соответствующего отрезка, вместо
того чтобы последовательно чередоваться, должны для каждого типа
чередоваться так, чтобы обеспечить принадлежность функции к тре-
требуемому типу регулярной монотонности. Отсюда вытекает также соответ-
соответствующее обобщение теоремы 1:
Среди всех многочленов Рп (х) степепи п = Хх -j- . . . -f- Xky где \ь . . ., Х& —
типовые числа, определяющие тип регулярной монотонности
Рп(х) = ±~ + рхх^ + . . . + Рп , D0 bis)
на отрезке 01 наименее уклоняется от нуля тот из многочленов Рп(х)>
который обращается в нуль при х = 0, как и все его производные по-
порядков i<^n (a2h <С г; < ^2/i+i)? где °т = ^i + ^2 + • • • + ^m, я производные
порядков /<^п (d2h+i ^ 7 <С a2/i+2) имеют корень х = 1.
Например, если все Х2Л; = 1, X2^+1 = X, то мы получим тип монотон-
монотонности 1, првсводящийся к циклической при X = 1. В этом случае наименее
уклоняющиеся от пуля многочлены Рп (х) выражаются символически
в виде (если полагать для определенности п-\~1^0 по модулю X -[- 1)
ЛМ-'-Ч,^. F1)
где Gi^O только при 1ее=0 (mod (k -\- 1)). Например, в случае Х = 2
(л = Зк + 2), при i = 3т и i = Зт + 1 Р™ @) = 0 и Pf A) = 0 при
/ = 3m + 2, а последовательные значения G3it50 определяются из
уравнений
A
1 + G3 = 0, 1 + ~ G3 + G6 = 0, 1 + Jjij (G, + Ge) + G, = 0 и т. д., F2)
т. е.
G = 0 1 + ~
откуда
G3 = — 1, GQ = 19, G9 = — 84-18—1 = —1513 и т. д.
Наименьшее уклонение, соответствующее этому типу монотонности (для
п = Зк + 2), достигается многочленом F1) при х — 1, и, следовательно, равно
G W2
Для вычисления асимптотического значения R3k+2 положим G3& =
= (ЗАI ел, так что для определения сЛ из F2) получим уравнения
сЛ + ~ск„г + ^у^-2 + • • • + з^[ = 0, F2 bis)
1 Условие (А) заменяется теперь условием /(г 1} (x)f^ x)(a?)<0 (i>0), которое-
дополняется начальным требованием / (а;) /(г) (ж) >0 для всех г<Х (при Х=1 соот-
соответствующему типу Hhsina?).
515 33*

откуда, полагая
заключаем, что (с0 = 1)
1 -?
Обозначая через р ^> 0 модуль наименьшего корня уравнения F (х) = О
находим асимптотические значения для
где Л — конечная, не зависящая от р постоянная. Отсюда следует, что
а потому функция рассматриваемого типа регулярной монотонности
(X = 2) на отрезке [ОД] должна быть конечной степени р-^р. Кроме
того, функция F (рх) степени р фактически принадлежит этому типу
па [0,1].
Напомню, что в статье К1) показано, что регулярно монотонные
функции, все типовые числа которых Xi ограничены, должны быть целы-
целыми функциями конечной степени. Там же и в докладе B) было выска-
высказано утверждение, что из всех типов регулярной монотонности, цикличе-
циклическая монотонность обеспечивает наиболее медленный рост модулей
последовательных производных, т. е. наиболее ограничивает степень
соответствующей функции (в рассмотренном выше примере мы имеем,
действительно, р>у)- Общее доказательство этого утверждения осно-
основано на лемме 3 (с ее добавлениями), откуда следует, что наименьшее
уклонение регулярно монотонных многочленов вида D0 bis) имеет наи-
наибольшее значение, если корни соответствующего многочлена, наименее
уклоняющегося от нуля, и его последовательных производных последова-
последовательно чередуются в концах отрезка, что характеризует циклическую
монотонность.
ЦИТИРОВАННАЯ ЛИТЕРАТУРА
1 С. Н. Бернштейн. О некоторых свойствах регулярно монотонных функций.
Сообщ. Харьк. матем. об-ва, серия 4, 2 A928), 1—11; [32] (том I).
2 S. Bernstein. Sur les fonctions regulierement monotones, Atti Congresso Intern.
Mat. Bologna, 2 A930), 267—275 [45] (том 1).
3 R. Boas. An upper bound for the Gontcharoff constant. Duke. Math. Journal, 15
A948), 953—954.

101
О НЕКОТОРЫХ НОВЫХ ДОСТИЖЕНИЯХ
ТЕОРИИ ПРИБЛИЖЕНИЯ ФУНКЦИЙ
ДЕЙСТВИТЕЛЬНОЙ ПЕРЕМЕННОЙ*
1. Когда в 1912 году мною впервые было установлено (lj2) сущест-
существование пределаг
р. = Пт пЕп\ х |, A)
П-+СО
из глубины технически сложного доказательства лишь неясно вырисовы-
вырисовывалась какая-то связь решенной задачи с теорией целых трансцендент-
трансцендентных функций. Казалось также правдоподобным, что и при всяком s>0
должен существовать предел
[х (s) = lim ns En j x Is = lim En \ nx js = lim En(\x |s; n). B)
n—»co n—>co n—*co
Однако прошло еще 25 лет прежде, чем мне удалось доказать C) общее
равенство B) и выяснить его истинный смысл, а именно: в работе D)
1938 г. я показал, что \i (s) есть наилучшее приближение | х \s на всей
действительной оси посредством целых функций первой степени^
* Acta Scient. Math., 12, Szeged A950), стр. 161—169 B58*).
1 ^n (/ (x)i ^) означает наилучшее приближение функции / (х) при помощи
многочленов степени п на отрезке [—А, А] при данном Х^>0. В случае Х = 1 пи-'
шем просто Еп f (x).
2 Функцию действительной переменной Gp (а?) мы называем целой функцией ко-
конечной степени />, если она бесконечно дифференцируема и регулярна на всей оси
и в какой-нибудь точке (например, х = 0)
п
:~~' г -р- а)
Эти функции совпадают с целыми трансцендентными функциями первого порядка
экспоненциального типа с показателем р, так как равенство (I) равноценно равенству
lim r г log | Gp (re1*) \ — р
Г-*оо
во всей комплексной плоскости z — relQ.
517

= Ax I x |s]. Вообще
при любом данном /?, где Avf (x) означает наилучшее приближений
функции f (х) при помощи целых функций данной степени р на всей
действительной оси. Тогда же было установлено C'5), что
s
lim ns En \x — c\8= A — с2)"з" ji (<?) (— 1 < с < 1) D)
п—>оо
и было также найдено точное значение предела
т
lim ns En F (х), где F (х) = V «л | ж — cfc |s,
которое оказалось равным jx E) max | ajc A — ел-2) 2 | при любых данных
ak и cfr (— 1<с^<1).
Хотя моя работа D) 1938 года связана со старым мемуаром F) из
«Acta Mathematica» 1913 года, содержавшим первое доказательство ра-
равенства A), но связь эта, по преимуществу, формальная. Теперь руково-
руководящим принципом исследования становится углубление и уточнение ана-
аналогий между свойствами алгебраических многочленов и целых функций
конечной степени; в частности, доказательство равенства C) свелось
к установлению того факта, что последовательность многочленов степени п,
наименее уклоняющихся от \x\s на отрезке — п- , п- , стремится при
п—>оо(р^>0) к целой функции Gv{x) степени р, наименее уклоняющейся
от \x\s на всей действительной оси.
Существование целой функции Gp (x), которая среди всех функций
степени р наименее уклоняется от | х \s, следовало из моей теоремы G)
1923 года о максимуме модуля производной целой функции Gv (x) сте-
степени р, ограниченной на всей оси (использование формул мемуара из
«Acta Mathematica)), обобщенных в русской монографии (8), нужно было
здесь, в сущности, лишь как способ построения целой функции первой
степени, уклонение которой от \x\s ограничено на всей оси). .Упомяну-
.Упомянутая выше теорема о максимуме модуля производной, которая для перио-
периодических функций была доказана (х) еще в 1912 году, утверждает, как
известно, что неравенство
Gv{x)\^L (— ос<><ос) E)
влечет для всех функций степени р
\ Grp (x) \*CLp (—00 < х < 00), F)
представляла собой первый простейший пример аналогии целых функций
конечной степени р с многочленами Рп(х) степени п, относительно кото
518

рых в 1912 году было установлено (х), что неравенство
| Рп (х) |< L {— л < х < л) E bis)
F bis)
Поэтому, если для некоторой последовательности многочленов п—> ое,
л -„- = р фиксировано, то в каждой данной точке х
lim\P'n(z)\<L?=Lp, G)
П->со Л
что совпадает с неравенством F). При этом замечательно, что в то время
как знак равенства в F bis) осуществляется для многочленов Чебышева
{ X \ ( X
LTn I = L cos n arc sin -
VА \ А
(п четпое), последние имеют пределом целую функцию степени /;
hm LTn I- ) = Lcospx [p=
\ Л / V
п->оо
для которой осуществляется знак равенства в F).
2. Соответствующим образом развивая последнее замечание, можно
прийти к исчерпывающему обобщению предельного равенства B), кото-
которое доказано в статье (9) в следующем виде:
Теорема I. Если существует такое число ро<^&э, что Avj (х) << оо,
то для всех р ^> ^р0 имеют место предельные равенстваг
YimEn (f{x); *\ = Apf{z), llmEn(f(x); ^j = Av^f (x), (8)
где ^?^1,51 определяется из уравнения
Vf+r= log G + VfTi) ¦ (9)
При этом нижняя грань ^р0 значений р, для которых (8) справедливо,
в общем случае не может быть снижена.
Отсюда следует, в частности, что равенства (8) справедливы для всех
/?>0, если Л/М<°° Ддя всех Р^>0.
Таким образом, благодаря лемме A0), утверждающей, что Ар/(х)<^ос
при всяком р^>0, если / (х) имеет равномерно непрерывную производ-
1 Нетрудно показать, что A j (х), расехматриваемая как функция р, есть функ-
функция монотонно убывающая, непрерывная справа. Согласно общему свойству монотон-
монотонных функций, множество ее точек разрыва исчислимо; из равенств (8) видно, что
в точках непрерывности Ар равенства (8) приводятся к единственному равенству
\imEn(f(x); ") = Л f(x). (8 bis)
519

ную порядка к^О при х<^а <; 6 и порядка 1^-0 при х^>Ь, из тео-
теоремы I сразу получается не только формула B), но и различные ее
обобщения A0). Например, если s>0 и т^>0 целые числа, то суще-
существует предел
lim ^ГТ Еп [* (bg | х I )w] = lim Еп\х5 flog -- Y"; nl =
>(logn
1 Г m
k
x V (- if Cl (log n)* (\oa\\ x I )m~k ; n =
fc=o J
'„[xs (log] ж I); n]=m41(»»log|a:|)
n—>oo
между тем как (если s^>0 любое вещественное число, т^>0 целое
число)
= lim En (| х \s; n) = Аг\х f = p (s).
Вместо того, чтобы ограничивать a priori класс рассматриваемых функция
/ (х) условием APJ (х) <^ оо (т. е. возможностью грубого приближения
функции / (х) при помощи целой функции GP(t некоторой данной конеч-
конечной степени р0), фактически более интересно рассматривать классы функ-
функций, характеризуемые быстротой их возрастания на действительной оси*
Этот подход связан с обобщением упомянутой выше теоремы о макси-
максимуме модуля производной, опубликованным (п) также в 1923 г.:
Если целая функция Gp (x) степени р удовлетворяет условию
GP (х) |< | Н (х) | = Vsz (х) + t* (х) (- оо О< оо),
где Н (х) = s (x) + it (x) — целая функция нулевого рода, корни которой
Як — i$k Ф&>0) лежат в нижней полуплоскости1, то производные лю-
любого порядка п^>0 удовлетворяют неравенствам
\G{? (x)\<\ {(s (х) + it (х)) е-**}™ |. A0)
В связи с этим в заметке A2) мною доказана соответствующая
Теорема II. Если
) (-оо<я<оо), (И)
где Н (х) четная функция нулевого рода, то предельные равенства (8)
1 Общее доказательство этой теоремы, которая мною была доказана в (8>13)
лишь при некоторых дополнительных ограничениях, дано впервые Н. И. Ахиезером
в A4), где он, кроме того, неожиданно для меня распространил мою теорему на не-
некоторые случаи, когда s (x) -f- it (#) является функцией конечной степени, т. е. пер-
первого, а не нулевого рода.
520

справедливы при всяком р^>Ог. (В частности, теорема II остается в силеу
если Apf (х) = оо при р<^р0<^.ос: в этом случае имеем также
lim En(f(x); —) = оо при тех же p<ZPo-)
п->оо V Р/
3. Из предыдущего следует, в частности, что к функции / (х) ? Sk,* {Щ>
дифференцируемой к раз и удовлетворяющей при всех х pi h (— оо <^
<^ х <^ оо, /г ^ 0) условию
| /(А:) (ж + А) — /(^} (ж) | < МАа @ < а < 1), A2)
предельные равенства (8) применимы при всех /?>0. Очевидно также,
что утверждения: 1) / (х) б Sk,<* A)> 2) Mf (x) 6 ?&,« (Л/), 3) / (рх) 6
€ *Sye (pfe+a) попарно равнозначны, и с другой стороны, для всякой
функции / (х) справедливо равенство
Avf(x) = AJ (~y A3)
Поэтому справедливость неравенства
А 4 (пг\ ^ Г (\ГЛ
для всех функций f (x) 6 6&,a(l), где C^ja — некоторая зависящая от к
и а постоянная (которая не может быть снижена), равнозначна справед-
справедливости для всех / (х) 6 Sfr,* A) неравенств
при любом р^>0.
Прием фактического построения функции Gp (x) данной степени р, при-
приближающей любую функцию / (х) 6 Sjc,a A), указанный, например, в замет-
заметке A7), дает некоторые конечные верхние границы для постоянных C^>a.
Как мы видим, неравенства A5), аналогичные классическим неравен-
неравенствам Джексона A8) для наилучшего приближения 2тг-периодической
функции En f (x) посредством тригонометрических полиномов порядка п,
вытекают без всяких вычислений из определения класса SjctX и из оче-
очевидного равенства A3). При этом сами упомянутые неравенства Джек-
Джексона являются прямым следствием из A5), так как во всяком случае
существуют неравенства
'El f (x) < -^~т& {п > 0 целое число) A6);
1 Полагая, в частности,
видим, например, что теорема II применима к функции / (х), если
log !/(*)[< nC|,g|,-^ (c>0, -co<a:<TO).
[log ! х | f
Благодаря указанной выше работе Н. И. Ахиезера (и) и последним исследованиям
Б. Я. Левина A8), дающим исчерпывающее распространение теоремы о модуле*
производной, условие теоремы II может быть несколько расширено.
521

для всех 2тт-периодических функций / (#) 6 ?&,а A), где постоянные С?)(Х)Г
(зависящие от к, а, п) не могут быть снижены. Но учитывая A9)
что функцией Gn+8 (х) степени не выше п + о @ ^ о <^1), наименее укло-
уклоняющейся от 2^-периодичсской функции f(x), служит тригонометрический
полином Sn (ос) порядка п, имеем вследствие A5) и A6)
Как известно, Фавар B0) и, независимо от него, Н. И. Ахиезер и
М. Г. Крейн B1) нашли точное значение постоянной С1>(ХуП для случая
а = 1, которая также оказалась независимой от п, а именно
1. n- С,д - -
BZ
1=0
Недавно [благодаря предельным равенствам, аналогичным (8)], я дока-
доказал A6), что при всех а<;1
lim С?в|П = С*,а. A9)
Отсюда следует, в частности, что1
С*,1 = См. B0)
Принципиальный интерес представляет существование другого пре-
предельного равенства, аналогичного A9):
Нт ?*,«,« = <?*,« A9 bis)
71-нЮО
[получающегося из предельных равенств (8)], где С^%а>п — наименьшая
постоянная в неравенствах
^ A6 bis)
Таким образом, из A9) и (J9 bis) заключаем A6), что
п->оо п-^-оо
при всех2 целых к^О и 0<[а<С 1.
4. Приняв в 1912 году за основу классификации всех непрерывных
на отрезке [—1, 1] функций закон убывания их наилучших приближений
Enf (x), я имел в виду главным образом создание единообразного метода
для выявления того, обладает ли заданная так или иначе функция
определенными дифференциальными или структурными свойствами
1 Справедливость равенства B0) М. Г. Крсйном B2) была установлена непосред-
непосредственно.
2 Равенство lim CQ л п = С* г впервые было доказано С. М. Никольским B3).
п—*эо ' ' '
522

[например, принадлежит ли / (х) к классу Липшица Sд-, а с данными к, а,
является ли f (х) аналитической функцией, регулярной на (—1, 1) и т. д.].
Не останавливаясь подробно на новых достижениях в этом направлении,
укажу, что, как видно из предыдущего, при классификации и прибли-
приближении функций / (х), непрерывных на всей оси, вместо многочленов следует
применять целые функции Gv (x) конечной степени, причем закон убы-
убывания Apf (х) характеризует, подобно Enf (х) на (— 1, + 1) соответ-
соответствующие структурные свойства f (x) на всей действительной оси.
В качестве достойного внимания обобщения классов Липшица рассмотрим
совокупность функций/ (х) 6 Sq (рь . . ., р^', аь . . ., ау\ М), характеризуемую
свойством A7)
(-°oO<oo), B2)
где, для определенности, полагаем: 1) ах = 1 <1 а2 << ... <^ a1t, 2)^Pi = l.
Посредством тех же соображепий, которые в § 3 привели нас к неравен-
неравенству A5), заключаем, что из B2) следуют неравенства для всех функций
f(x)<cSq{pb . . .,;?/,; аь . . . ,аъ; М)
С М
ЛР/(х)<-^, B3)
где постоянная Cs зависит только от q, pi, ai, но не зависит от р. Полагая
значение М <^ оо произвольным в неравенстве B2), мы будем говорить,
что / (х) (: Sq (pi, аг) = Sq (рь . . ., ръ\ аь . . ., а^) принадлежит специальному
однородному классу Sg(pi, аг) порядка q. Из B3) видно, что для всякой
данной функции f (x) d S (р{, а.) справедливы при всех р >> 0 неравен-
неравенства вида
А>/(*)<-^ B3 bis)
€ одной и той же постоянной R [зависящей от f (х)]. Класс Оф где
R <' оо, называем основным однородным классом порядка q. Таким обра-
образом, согласно сказанному выше из / (х) 6 Sq (pv g.) следует / (х) 6 Q . Давно
известно, что в случае A2) класса Липшица f(x)(:Sk>0L обратное утверж-
утверждение верно только при а<^1.
Полное решение3 вопроса об условии эквивалентности между счб^и
двух различныv- специальных классов S (рг, а^) и S (p*v &*), а также об
эквивалентноеги S (pv а{) основному классу О дано мною в заметках
A7'25). Для этого необходимо ввести в рассмотрение целое число т0,
которое я пазываю характеристикой класса S (рг, аг), определяемое как
п
наименьшее из целых т"-0, для которых ^/^лТ^^О. В таком случае
1 Важный шаг в исследовании этого вопроса (решающую роль играет применение
теоремы о максимуме модуля производной) для периодических функций сделан
Зигмундом B4) в 1915 году.
523

все специальные классы порядка q эквивалентны между собой, когда их
характеристики равны. Поэтому все специальные однородные классы
можем, для краткости, обозначать через Sqm°\ указывая явно лишь по.
рядок q и характеристику т0. Если, кроме того, g<^ m0 <^ q + 1? то все эти
специальные классы Sqm<>) эквивалентны классу Липшица Sk)^ где к = то—1^
О < а = q — к = q -\- i — то<^1, т- е- (пользуясь для обозначения экви-
эквивалентности классов знаком равенства) S$*? = Л, а при любых целых
к^О и 0<^а<^1. Хотя эти результаты существенным образом опираются
на рассмотрение основного однородного класса Qq, однако при исследо-
исследовании вопроса об эквивалентности основого класса Q,q соответствующим
специальным классам S™ следует иметь в виду, что первый, ?lq, вообще
шире последних, так как из B2) следует, что / (х) алгебраического роста
т. е. существует /?г<Гоо, для которого ^-^->0, при #->оо), между
V хт J
тем как это не обязательно при B3).
Поэтому для получения простых условий эквивалентности надо вводить
те или иные ограничения A7>25). Если, например, мы предположим,
для простоты, функции / (х) ограниченными A7) (в частности, периоди-
периодическими), то Sqmo) — Qq при всех q<^m0. Что касается распространения
изложенных здесь результатов на функции нескольких переменных, ко-
которое является одной из важных целей теории наилучшего приближения,
то не останавливаясь на этом вопросе, отмечу лишь заметки B5>26»27).
ЦИТИРОВАННАЯ ЛИТЕРАТУРА1
1 О наилучшем приближении непрерывных функций посредством многочленов данной
степени. Сообщ. Харьк. мат. об-ва, 13 A912), стр. 49—194; [3] (том I).
2 Sur les recherches recentes relatives a la meilleure approximation des fonctions
continues par des polynomes. Proceedings 5 International Math. Congress, Camb-
. ridge. 1 A912), стр. 256—266 [6] (том I).
3 Sur la meilleure approximation des fonctions non regulieres. Comptes Rendus Acad.
Sci. Paris, 205 A937), стр. 825—827 A92*).
4 О наилучшем приближении | х |р при помощи многочленов весьма высокой степени.
Изв. АН СССР, серия матем., № 2 A938), стр. 169—190 [73].
5 О наилучшем приближении | х — с |р. Докл. АН СССР, 18 A938), стр. 358—388 [74]
6 Sur la meilleure approximation de | x \ par des polynomes de degres donnes. Acts
math., 37 A913), стр. 1—57 [12] (tomJ).
7 Sur une propriete des fonctions entieres. Comptes Rendus Acad. Sci. Paris, 176 A923)»
стр. 1603—1605 [22] (том I).
8 Экстремальные свойства полиномов в наилучшее приближение непрерывных функ-
функций одной вещественной переменной, ч. 1 A937) [«Э. П.»].
9 Предельные законы теории наилучших приближений. Докл. АН СССР, 58 A947),
стр. 525—528 [91].
10 Новый вывод и обобщение некоторых формул наилучшего приближения. Докл.
АН СССР, 54 A946), стр. 667—678 [87].
1 Работы, приведенные без указания имени автора, принадлежат С. Н. Бернштейну»
[В статье Н. И. Ахиезера «Работы академика С. Н. Бернштейна по конст.руктивной
теории функций» (Успехи матем. наук, VI, 1951) дан более полный в некоторых от-
отношениях обзор работ С. Н. Бернштейна (Ред.)].
524

11 Sur les proprietes extremales des polynomes et de fonctions entieres sur Гахе reel.
Comptes Rendus Acad. Sci. Paris, 176 A923), стр. 1782—1785 [23] (том I).
12 О приближении функций на всей вещественной оси при помощи целых функций
данной степени. Докл. АН СССР, 54 A946), стр. 479—482 [84], заметка V.
13 Legons sur les proprietes extremales et la meilleure approximation des fonctions ana-
lytiques d'une variable rcelle. Paris 1926 [«L. S.»].
14 H. И. Ахиезер. О некоторых свойствах целых трансцендентных функций экспо-
экспоненциального типа. Изв. АН СССР, серия матем. 10 A946), стр. 411—428.
15 Б. Я. Левин. О некоторых экстремальных свойствах целых функций конечной
степени. Докл. АН СССР, 65 A949), стр. 605—608.
16 О предельных зависимостях между константами теории наилучшего приближения.
Докл. АН СССР, 57 A947), стр. 3—5 [90].
17 О свойствах однородных функциональных классов. Докл. АН СССР, 57 A947),
111—114 [92].
18 D. Jackson. Tiber die Genauigkeit der Annaherung stetiger Funktionen durch
ganze rationale Funktionen. Dissertation. Gottingen. 1911.
19 Конструктивная теория функций, как развитие идей Чебышева. Изв. АН СССР,
серия матем. 9 A945), стр. 145—157 [82].
20 J. Favard. Sur les meilleurs procedes d'approximation de certaines classes de
fonctions par des polynomes trigonometriques. Bulletin des Sciences Math., 61
A937), стр. 209-224, 243—256.
21 H. И. Ахиезер и М, Г. К р е й н. О наилучшем приближении периодических
функций. Докл. АН СССР, 15 A937), стр. 107—111.
22 Н. И. Ахиезер. Лекции по теории аппроксимации A947).
23 С. М. Н и к о л ь с к и й. Наилучшие приближения функций, удовлетворяющих
условию Липшица. Докл. АН СССР, 52 A946), стр. 7—9.
24 A. Zygmund. Smooth functions. Duke Math. Journal, 12 A945), стр. 47—76.
25 Вторая заметка об однородных функциональных классах. Докл. АН СССР, 59
A918), стр. 1379—1384 [92].
26 О целых функциях конечной степени многих вещественных переменных. Докл.
АН СССР, 60 A948), стр. 949—952 [94].
27 С. М. Никольский. Обобщение одного предложения С. Н. Бернштейна о диф-
дифференцируемых функциях многих переменных. Докл. АН СССР, 59 A948), стр.
1533—1536.
Поступило
9. XI 1949 г.

102
О ВЕСОВЫХ ФУНКЦИЯХ *
Назовем функцию Ф(ж)^0 весовой функцией [Ф (х) 6 W], если всякая
непрерывная (—-оо<^х<^оо) функция / (х), удовлетворяющая единствен-
единственному условию lim [/ (х) / Ф (х)] = 0, равномерно приближаема многочле-
X->J-ao
нами на всей оси при весе 1 / Ф (х), т. е. если при любом г ^> 0 можно
построить такие многочлены Р (х), что
\f(x)—P (х)\ < еФ (х) (— оо < х < ос). A)
В монографиях C»2) показано (см. [102.1]), что целая функция
оо
F (х) - 2 "* ^2"' К > 0, «л > 0) B)
в том и только в том случае является весовой функцией, если род ее
выше нуля1. Отсюда следует, что всякая функция Ф (х) будет весовой,
если существует такая четная целая функция B) рода выше нуля, что
F (х)< Ф (х) (— оо < х < оо).
Благодаря этому простому замечанию из цитированной теоремы может
быть выведена следующая весьма общая теорема.
Теорема 1. Если для данной функции Ф (х) ^> 0 ряд
где
, . Уф (х)
К^ mm -r-rr2
—оо<х<оо
расходится, то Ф (х) 6 W.
* Докл. АН СССР, 77 A951), стр. 549—552 B61*).
1Там же доказана теорема, означающая, по принятой мною позднее D) термино-
терминологии, что в случае, когда F (х) нулевого рода, она является майорантой конечного
роста (F(x) 6Ш1).
526

Для доказательства строим целуюх функцию
°° 1
Fx (х) = а0 + 2 ~№ Р***J* К =
которая, согласно теореме, установленной мною во втором добавлении к
монографии (]) (см. также статью C), не может быть нулевого рода,
если ряд SQ расходится. Но, с другой стороны, из определения чисел
лп следует, что (Х2йжJ7(С ^ Ф (ж) при всех х (—ос -^х<^оо) и любых
к^>0. Поэтому из D) получаем 2
Fi (*) < «о + Ф (х) 2 4? < 2Ф W • E)
Л = 1
Следствие 1. Если Ф0(х)—майоранта D>5) конечного или квази-
конечного роста, Ф0(жN 9Л*, то она не может быть весовой функцией и
соответствующий ей ряд So сходится.
Действительно, на основании леммы 2 заметки D) и ее распростра-
распространения на майоранты квазиконечного роста E), всякая предельная функ-
функция последовательности многочленов | Р (х) | ^ Фо (х) должна быть функ-
функцией нулевой (или конечной) степени, вследствие чего осуществление
неравенства A) невозможно для произвольной функции f(x). Поэтому по
теореме 1 расходимость ?0 невозможна для Фо (х) б Ш*.
Лемма 1. Если целая функция F (х) вида B), то интеграл
-** F)
сходится а том и только в том случае, когда F (х) нулевого рода.
Что интеграл Н сходится, когда F (х) нулевого рода, доказано в мо-
монографии B) и еще раньше в статье F). С другой стороны, если Н схо-
сходится, то 3 lim ——— = 0 и, следовательно, функция F (х) — нулевой
;х]->оо х
степени, а поэтому E) F(x)(z$R*. Отсюда, благодаря цитированной выше
теореме A? 2), следует, что F (х) нулевого рода.
Теорема 2. Какова бы ни была четная функция Ф(х) = ер^^>0
если интеграл F), соответствующий этой функции, сходится, илиг
1 Функция F^x) не была бы целой лишь при условии, что последовательность
монотонно убывающих чисел {Хп} имеет предел Ъ > 0. Но в этом случае Ф(х)>|^6|п,
так что Ф (х) = оо для всех | х \ ^> 1 / Ъ\ поэтому неравенство A) (— оо << х < оо) осу-
осуществляется вследствие классической теоремы Вейерштрасса для конечного отрезка
[—ijb, ljb]. Заметим, что ряд So сходится и расходится одновременно с интегралом
оо
/0 = \ l(n)dn, если формулу C) для Х = X (/г) распространить на все значения и>1.
1
2 Отсюда видно, что теорема 1 не шире моей старой упомянутой выше теоремы.
3 Учитывая, что F(a?)>l, F' (х) > 0, из сходимости Я и из равенства
log F (Л) С log F (х) , (• F' (х)
р—- + \ •—Е~т^— dx — log F A) + \ -7Г-7-Г- dx заключаем, чю обе его части
1 1
при i?->oo стрехмятся к конечному пределу, а потому lim—-~п-— =0.
527

даже, если только
is)
ограничен сверху нри R —> оо, то ряд S0 =
где лп определяется
1
формулой C), сходится.
Действительно, допустим, напротив, что ряд So расходится при огра-
ограниченном Hr. Тогда, построив целую функцию F1{x) выше нулевого
рода по формуле D), мы получили бы, вследствие E),
log 2,
что противоречит лемме 1.
Для обращения теоремы 2 нам придется внести некоторые ограниче-
ограничения. Мы предположим функцию Ф(^)>0 монотонно возрастающей до
бесконечности (при \х\-^оо). Кроме того, фиксируем лишь какую-нибудь
определенную последовательность значений {Ф (ап)}, где ап = а + Ъп и
п ^>0 — любое целое число (для простоты письма примем а = О, Ъ — 1).
Назовем последовательность {Ф (ап)} 6 iV нормально возрастающей, если
ее можно интерполировать при помощи такой непрерывно дифференцируе-
дифференцируемой функции Ф (х) = ertx\ что
$
также монотонно возрастает к бесконечности при \х\—>оо. В таком слу-
случае функцию O(x)(:N также будем называть нормально возрастающей.
Теорема, обратная теореме 2, справедлива для функций Ф (х) 6 N.
Действительно, при всех п ^> п0 достаточно больших величина
хп — х (л), для которой осуществляется G), однозначно определяется из
уравнения G), причем [так как можно принять, что Ф (х) > 1] имеем
а потому из сходимости ряда So = 2 >т тем более следует сходимость ряда
п=п0
эквивалентная ограниченности при R -> оо интеграла
11
Следовательно, интеграл
hr=
p> (i)
1 1
также ограничен (имеет предел) при R —> оо.
528

Следствие 2. Если четная функция Ф (х) = е&№ б N, то ряды 6г и
So сходятся (и расходятся) одновременно с интегралом Н.
[Напомним, что, вследствие теоремы 2, из сходимости интеграла Н выте-
вытекает сходимость So и, тем более, S± даже и без ограничения Ф (х) 6 N.].
Теорема 3. Если F(х)—целая функция вида B), то условие, необхо-
необходимое и достаточное для того, чтобы она была нулевого рода, состоит
в том, чтобы соответствующий ей ряд So (и S±) был сходящимся.
Действительно, F (х) 6 iV, так как в данном случае п (х) возрастает
при всех х^>0 вследствие
F%x) n'{x) = \xF"{x) + F'(x)]F(x)— x [F\x)f=^ 2 4 (k ~ lf акагаР+*1-1> 0.
k>i
Поэтому наше утверждение вытекает из леммы 1 и следствия 2.
Из следствия 2 получаем
Следствие 3. Если \G(x)\GN (есть модуль целой четной функции конеч-
конечной степени)*, то она является либо весовой функцией (| G (z)\(zW), либо
майорантой конечного роста (| G (x) | t Щ. При этом \G(x)\ (:W, когда
соответствующий ряд So расходится, и | G (х) | 6 9Й, когда So сходится.
Первое утверждение вытекает из теоремы 1, второе г— из следствия 2
и известного результата (8>9) Б. Я. Левина, согласно которому 2М*=9Й,
если G (х) — целая функция конечной степени.
Поступило
9. II 1951 г.
ЦИТИРОВАННАЯ ЛИТЕРАТУРА
XS. Bernstein. Lemons sur les proprietes extremales etc. Paris, 1926. [«L. S.»].
2 С. Н. Берн штейн. Экстремальные свойства полиномов, 1937. [«Э. П.»].
3 С. Н. Берн штейн. Сообщ. Харьк. матем. об-ва A924) [27] (том I).
4 С. Н. Бернштейн. Докл. АН СССР, 60 A948), стр. 949 [94].
6 С. Н. Бернштейн. Докл. АН СССР, 65, A949), стр. 117 [97].
6 S. Bernstein. Bull, de la Soc. Math, de France A924) [25] (том 1).
7 С. Н. Бернштейн. Докл. АН СССР, 66 A949), стр. 545 [98].
8 Б. Я. Левин. Докл. АН СССР, 65 A949).
9 Б. Я. Левин. Изв. АН СССР, сер. матем., 14 A950), стр. 45.
* Ограничение, указанное в скобках, излишне. См. [107]. (Автор).
1 В заметке E) мною введено понятие антимайоранты, которое определено сле-
следующим образом: Н (х) >. 0 называется антимайорантой, если неравенство
\Gp(x)\^H(x) (-сюО<сю)
совместимо для совокупности функций Gp (x) данной конечной степени р со
свойством производной sup | G (х) | = сю. Как нетрудно видеть, всякая весовая функ-
ция Ф (я?) ? W является антимайорантой. Действительно, если в неравенстве A) функция
f (х) не удовлетворяет никакому условию Липшица в промежутке (а, &), то после-
последовательность многочленов Р (х) = Go (х), для которой lim Р (х) = / (х), удовле-
—ос<зс<оо
творяет условию | Р (х)\ < с Ф (х) (с — постоянная), причем sup | Р' (х)\ = оо.
а<х<Ъ
Из следствия 3 следует, что если четная функция |6?(я?)| ? N, то | G (х)\ только
тогда будет антимайорантой, когда | G (x)\ ?W. Однако на не четную функцию G (х\
конечной степени это утверждение не распространяется, а именно: при сходимости
kS'q функция | G (х)\ может быть антимайорантой, не будучи весовой (например E),
в случае G (х) = ех + 1, см. [25.3] (том I)).
34 С. Н. Бернштейн

103
О СВЯЗИ КВАЗИАНАЛИТИЧЕСКИХ ФУНКЦИЙ
С ВЕСОВЫМИ ФУНКЦИЯМИ*
В первом добавлении** к монографии (х) мною установлены следующие
две теоремы.
Теорема В. Если наилучшее приближение Enf (x) на данном отрезке
функции f(x) при помощи многочленов степени п удовлетворяет при
всех п^>0 неравенствам
где F (x) = 2 а& ^2/fc (а& ^> 0) — целая функция выше нулевого рода, то
/ (х) = 0 яа всеж отрезке, когда f (х0) = /М (я0) = 0 /гри всех ft >0
в какой-нибудь его точке.
Теорема D'. Пусть
!$<Ап (п = 1, 2, ...). A)
Р>0
монотонно убывающих чисел
расходится, то равенство / (ж0) = /(А:) (х0) =0 б одной точке х0 при всех
&>О возможны лишь при /(#)=0 на всем отрезке.
Теорема В была выведена в (х) на основании того факта, что F(x) —
весовая функция [F (х) 6 W], а теорема D' была получена как следствие
теоремы В при помощи рассуждения \ аналогичного тому, посредством
которого в моей последней заметке B) установлена теорема 1.
* Докл. АН СССР, 77 A951), стр. 773—776 B62*).
** Воспроизведенном в томе 1 в виде статьи [26]. (Ред.)
1 Тем же способом в монографии (*) из теоремы В (см. том 1,'стр. 307) была выве-
выведена также известная теорема Данжуа—Карлемана, утверждающая, что расходимости
ряда V. -дт— ,где Мп = max l/| /(п)(а?)|, достаточно для квазианалитичности f (x)
(в том же смысле, что и выше).
У 530

Покажем, что теоремы В и D' эквивалентны, т. е. обратно, если
Enf (х) удовлетворяет условию (В), то соответствг/ющий ряд So = V ~г~
расходится. Для этого замечаем, что вследствие (В)
"= min (—^ ) > min (т
причем целая функция F (х) — ^>] аьх2к (а^ ^> 0) выше нулевого рода,
(Следовательно, согласно теореме 3 заметки B), получаем условие D'
2
Неравенства A) при условии (D') определяют, таким образом, квази-
аналитическии класс Л (Ап), аналогичны!! квазианалитическим классам
Карлемана C). При этом можно показать3, что здесь также верна и
обратная в смысле Карлемана теорема.
Теорема, обратная D'. Если ряд монотонно убывающих чисел
2 h
сгодится, то среди функции f(x), удовлетворяющих условиям
рп = max р уrEpf (х) <C кЛп (к — постоянная), A bis)
найдется функция. /0(i)^0 up квазианалитическая, т. е. удовлетво-
удовлетворяющая равенствам /0 (.r0) = f^ (х0) — 0 при всех / ^> 0.
При помощи того же рассуждения, каким была получена B) теоре-
теорема В, доказывается более общая теорема.
Теорема В\ Какова бы ни была четная монотонная (при х^>{)}
весовая функция Ф (a:) f W, если Enf (х) <^ 1 / Ф (п) (п ^ 1), то f (x) есть
квазианалитическая функция.
Заметим, что аеорема В* оказалась бы более общей, чем теорема В,
если бы существовала монотонно возрастающая четная функция Ф(?NИ\
оо п ' '
для которой ряд So = 2 Ln = 2 т*п ~т Y® (;/) ^ыл бы сходящимся 2~
=1
1 Доказательство этой теоремы дано в комментарии [26. 4] (том I) к вышеупомяну то-
толп добавлению к монографии (х), которое включено в том I собрания моих сочинений.
2 В связи с квазианалитическими функциями мы ограничиваемся здесь рассмот-
рассмотрением лишь симметричных (четных) функций. Заметим только, что для несиммет-
несимметричных функций Ф {л) g W расходимость ряда о0 не является вообще необходимой.
Действительно, назовем Фо (у) полувесовой функцией [Фо (?/) 6 ^oL если при любом
? > 0 для всякой непрерывной функции ф (у) (ф (у)/ Фо (у) ~> 0 при гу->оо), можно
построить такие многочлены Ро (у), что
I 9 (У) ~ Ро (У)\ < еФо (У) @ < г/ < со). (А)
Полагая у = х2, Ф {у) = / (+ х), Р0(у) = Р (а?), Фо (У) = Ф (± »), получаем
равнозначное (А) неравенство | / (о?) — Р (а?)| < еФ (х) (— оо < х < оо). Таким обра-
531 34*

Из формулированной выше теоремы, обратной D', вытекает1
Лемма 1. Пусть дан сходящийся ряд B). Всегда существует четнй
монотонная функция Ф0(х), не являющаяся весовой, для которой2
. п
л* = min г— ]/Ф0 (я) > -г- , (С
причем Ф0{х) определяется раеенствами
где fo(x)—не квазианалитическая функция теорельы, обратной D'.
Действительно, функция Фо (х) не может быть весовой, так каг
вследствие теоремы В*? функция /0 (х) не могла бы удовлетворять D).
Теорема 4. Пусть Ф (х) 6 N (нормально B) возрастающая функция)
Для того чтобы все функции, удовлетворяющие условию
Яр/(я)<1/Ф(р) (Р>1), E1
квазианалитическими, необходимо и достаточно, чтобы ряд
min
^о = 2j лп = 2j
был расходящимся. Это же условие необходимо и достаточно для того9
чтобы функция Ф (х) была весовой.
Достаточность условия F) уже доказана3 [даже без ограничения
зом, применяя теорему 1 B) к функции Ф (х) ? W, находим, что расходимость ряда
^ п | п
У!х = J) min -—г Уф (х) = У\ min -—- Уф0 (у) достаточна для того, чтобы Ф0A/N^о-
п \х\ У у ,
Но если, сохраняя значение Фо (у) для у^ 0, мы положим Фо (у) = оо при ?/<0,
то функция Фо (х) окажется при том же условии весовой функцией Фо (х) ? W ш
всей оси (—оо<^#<;оо), так как неравенство (А) будет автоматически удовлетво-
удовлетворено для у < 0. Между тем непосредственное применение той же теоремы 1 B) к
определенной указанным способом несимметричной функции Фо (х) привело бы к
жюраздо более ограничительному условию расходимости ряда S* = *S\ X^, где
1 Легко видеть, кроме того, что ни одна функция Ф (х) не может быть весовой,
если Хп = 0 для некоторого п = п0. В самом деле, в этом случае lim Ф (х)/хп° =0.
Поэтому, полагая произвольную функцию / (х) ограниченной, чтобы приблизить ее
чз весом 1/Ф(:г), нужно было бы пользоваться только многочленами степени <и0)
имея в своем распоряжении лишь ограниченное число тг0 параметров.
2 Следует заметить, что в правой части неравенства C) можно в случае ыадоб-
иосги заменить Ап через кАп (к — постоянная), так как ап = тт-^УФ0(кх) . По-
1 п
этому, полагая Фх (х) = Фо (кх), имеем а^ = min — УФх (х) = к7^п , причем Фо (a?) i
<!>! (х) одновременно будут (или нет) весовыми функциями. *
3 Теорема D' (х) и теорема 1 заметки B).
532

Ф (х) 6 N]. Для доказательства необходимости условия F) положим, что
оно нарушено, т. е. S0<^oc. В таком случае, согласно лемме 1, берем
не квазианалитическую функцию /0 (х), удовлетворяющую D), причем
1
=Хп= min -
pn 1<*<оо x
>п= min -]/Ф (х). G)
По определению B) функций Ф (z) 6 N, они характеризуются тем,
что функция
х Ф' (.г) / Ф (х) = п(х) = п (8)
также монотонно возрастает до оо. Поэтому1 для каждого
уравнение (8) имеет одно и только одно решение х = хп = х (п), соответ-
ствующее минимуму Xn = min — УФ (х), причем всем значениям ?%>1
х>1 х
соответствует какое-нибудь п = п(х)<^ос. Таким образом, из G) заклю-
заключаем, что для каждого х^1 имеем при соответствующем и \^=^—Ф(х) ^
хп
< (Х*)п<; —Фо (ж), откуда ФA)<Ф0(а;), т. е. для всех х>1 должно
X
осуществляться неравенство
(9)
Следовательно, ввиду того, что Фо (х) — не весовая функция, Ф (х)
также не может быть весовой функцией. С другой стороны, вследствие
равенства D), имеем (при сходимости ряда ?0)
Следствие 1. (Дополнение к теореме В). Если F* (х) есть модуль чет-
четной целой функции нулевого рода, то существует не квазианалитиче-
квазианалитическая функция fo(x), удовлетворяющая неравенству Enf0(x) ^l/F*(n).
Действительно, если Fl(x) —F0(x) = ^а^х2 (а^^-0), то это утвержде-
утверждение есть частный B) случай теоремы 4, так как Fo (x) б N. Но модуль
четной функции нулевого рода не превосходит
Следствие 2. i?c./zw [Ф (^г)} f ЛГ w
-о), (Ю)
1 Напоминаю B), что все монотонные' функции Ф (х), определяемые последова-
последовательностью {Ф (/г)} ? N, эквивалентны.
533

то функции f (x), удовлетворяющие A0), образуют квазиаиалитический
класс. 1) при том и только при том условии1, что
2) а также при том и только при том эквивалентном условии, что
ряд
^ 1 ~~ / I х > ( J
у п
п -=п0
где хп^ 1 — единственные решения уравнения (8), соответствующие
каждому целому значению п^п0, так как условие A1), как и условие A2),
равнозначно B) F).
Следствие 3. Если Ф (х) d Лт, то для того, чтобы Ф (х) б W, необхо-
необходимо и достаточно, чтобы все функции f(x), удовлетворяющие усло-
условию A0), были квазианалитичными (в определенном выше смысле).
Таким образом, если Ф (х) б N, то условие теоремы В* фактически
оказывается не более общим, чем условие теоремы В.
Поступило
1Г). И 1951 г.
ЦИТИРОВАЛИ А Я Л II Т Е Р А Т У Р А
1 S. Bernstein. Logoiib ьиг les proprietes extremales etc. Paris, 1926. [«L. S.i].
2 С. Н. Беряштейн. Докл. АН СССР, 77, № 4 A951) [102].
3 Т. Carl em аи. Fonctions quasi analytiques, Paris, 1926.
4 С Мандельбро й т. Квазианалитические классы функций. М. — Л., 1937.
Диалогичный результат доказан С. Мандельбройтом D).

104
ОПРЕДЕЛЕНИЕ И ОСНОВНЫЕ СВОЙСТВА
КВАЗИАЛГЕБРОИДНЫХ И АЛГЕБРОЯДНЫХ
ФУНКЦИЙ*
1. Будем называть функцию / (х) квазиалгеброидной на данном отрезке
(f (х) 6 А), если существует такой многочлен Р (х), что1
Enf(x)P(x)
lim nlV ; ^0. (А)
п
Нетрудно видеть, что если (А) выполняется при некотором Р (х), то
существует один и только один многочлен Dk (х) = хк + аххи~х + ... + ак
наинизшей степени &>0, удовлетворяющий (А). Этот многочлен Dk(x)
назовем характеристическим многочленом функции / {х)у а корни его
(где бы они ни находились) назовем характеристическими точками/(х).
Теорема 1. Если R^Ri = \xi + \/'х\ — 11 > г, где х{ — характери-
характеристические точки функции f (x), то
F)<i<i. A)
Следствие 1. Если R = г = 1, т. е. все характеристические точки на-
находятся на [— I, + 1], то функция f (x) не может быть аналитической
(регулярной) на этом отрезке (lim YEnf (x) = 1).
п->оо
Следствие 2. Если все характеристические точки находятся вне
отрезка [—1, + 1], т. е. г>1, то / (х) — аналитическая функция, регу-
регулярная внутри эллипса с полусуммой осей г.
* Докл. АН СССР, 79 A951), стр. 377—380 B63*).
1 Если Enf (x) означает здесь наилучшее приближение / (а?) на основном отрезке
[а, Ь], то f (x) QA на атом отрезке [а, Ь]. В конкретных формулах (при отсутствии
особых указаний) мы будем полагать Ъ = — а = 1. Обычно будем считать/ (х) непре*
рывной, т. е. Enf (x) ->0; но условие (А) применимо ж к функции с конечным числом
точек разрыва, если она становится непрерывной после умножения на соответствующий
многочлен.
535

Следствие 3. Квазиалгеброидная функция не может быть целой
функцией.
Вывод правой части неравенств A) основан на следующем общем
предложении, формулированном в моей заметке (х), общее доказательства
которого (см. [88. 1]) аналогично данному мною там же в частном случае.
Лемма 1. Пусть функция Фг (z) регулярна и ограничена (| Ф2 (z) \<^Щ
п ,
внутри эллипса С с полусуммой осейгх. ЕслиИт}/^Еп{Фо(%)) ~ — (
п—>со 9
то lim sn = 0 б неравенстве
Еп (Фо (х) Фх (х)) < [~^ + s»] E" (фо (*))• B)
Применяя лемму 1, положим Фо (х) — / (х) Dk (х), Фг (х) Dk (x) = 1;
таким образом, если взять гг<^г сколь угодно близким к г, то при
иррегулярности Фо (z) в какой-нибудь точке внутри эллипса С мы имели
бы для бесконечного множества значений п
Enf (%) <С hEn (/ (x) Dk (x)) (h — постоянная),
что противоречит условию квазиалгеброидности (А). Но если / (х) Dk (x)
должна быть регулярной внутри эллипса С, то / (х) также регулярна
в этой области.
Метод доказательства левой части неравенств A) при любом R ^ 1
тот же, что при R = 1; поэтому для определенности остановимся лишь
на случае R = 1 (соответствующем следствию 1). Нужно, следовательно,
показать недопустимость при R = 1 предположения, что / (х) и, тем более,
f{x)Dk{x) регулярны на отрезке [—1, + 1]. Для этого, учитывая, что
из предположения регулярности следует сходимость рядов по многочленам
Чебышева
оо со
/ (х) = 2 ап Тп (х), f (x) Dk (х) =^ЬпТп (х), C)
71=0 П=0
имеем для всех п>0 на основании известных B) оценок наилучших
приближений неравенства вида
VI
При этом lim ]/|fonj=—<1. Поэтому при заданном г>0, достаточно
малом для того, чтобы было рх = р — s ^> 1, существует бесконечная по-
последовательность таких значений п = щ (/ = 1, 2, .. .), что для всех
— к верны неравенства
536

С другой стороны, из уравнений в конечных разностях
к
жолучаем для всех ап+к (я S> 0) абсолютно сходящиеся ряды
со
Яп-Н-= 2Xifen+i' F>
где коэффициенты X* ограничены (\li\<^L), если все корни многочлена
к
Вк{х)— T>piTi{x) находятся на отрезке [—1, +1]. Таким образом, для
всех I — щ -f- /г имеем, вследствие E) и F),
Следовательно, благодаря D), для всех п = щ имеем сп ^> с, что проти-
противоречит условию (А).
2. Если функция / (х) Dk (x) 6 Л и имеет характеристический много-
многочлен D^l (x), то, умножая / (х) на /)& (ж) i)^ (x), мы еще более снизим
наилучшее приближение. Предположим, что, повторяя ту же операцию
конечное число раз, мы получим многочлен R (х), для которого суще-
существует такое а @ < а <^ 1), что при всех достаточно больших п имеем
Еп f (x) R (яг)
fg fix) Onfo->°°)- (Ar)
В таком случае, в соответствии с данным в сноске1 определением асимп-
асимптотичности, функцию / (х) назовем асимптотически рациональной
f (x) €Ад. Оправданием последнего термина служит теорема 2.
Теорема 2. Все функции f(x)?AR и только они являются ана-
аналитическими функциями вида
/w-Ш-Ш+'¦<*»• G)
где R (х) — многочлен, не имеющий корней вне эллипса С с суммой
полуосей /?>J, Q (х)—многочлен, а Рг(х) и F (х) регулярны внутри
эллипса Сх с суммой полуосей R1^>R.
Действительно, если / (х) вида G), то условие (AR) соблюдено при
всяком а ^> RjR\. Наоборот, из (Ar,) следует, что функция F (х) = f (x) R (х)
1 Мы будем называть две функции / (х) и fx (x) [fx (х) —/ (х)] асимптотичнымш
(на соответствующем отрезке), если Еп (/ (х) — fx (x)) — о [Enf (x)].
537

[регулярна внутри большего эллипса, чем функция / (х). Заметим еще,
что условие, необходимое и достаточное для того, чтобы при повторении
указанной операции иметь в неравенстве (Ar) a-> 0, когда степень
$ многочлена R (х) неограниченно возрастает, состоит в том, что функция
f (x) должна быть мероморфной.
3, Сейчас мы дополним условие (А) другим гораздо менее ограни-
ограничительным условием г, чем (Ar), и определим класс A* d А алгеброидных
функций f(x)dA*, обладающих свойством (А*), которое состоит в том, что
для всякого многочлена Р (х) при п->оо
либо Еп f (x) Р(х) = о [En f {х)Ъ либо Enf {x) - О [Enf \x) P (х)] (А*)
(причем существуют многочлены первой категории, так как A* d A)ti
Из условия (А*) вытекает для функций f(x)?A* следующее
Дополнение к теореме 1. Функции f(x)?A* могут быть
только двух родов: 1) функция f (x) ?А* алгеброидная первого рода
[/ (х)^А1]7 если все ее характеристические точки Х{ находятся вне основ-
основного отрезка [а, Ь]\ в этом случае все точки х\ находятся на одном
и том же эллипсе2" [с фокусами а, Щ; 2) функция f (ос) 6А* — второго
рода (/ (х) €^42)> когда все ее характеристические точки на отрезке
К Ь].
Докажем сначала невозможность предположения, что Z>& (x) = А (х) В (х),
где все корни А (х) на [а, Ь]% в то время как корни В (х) вне [а, 6].
Действительно, отсюда вытекало бы [вследствие (А*)], что
Ej(x)Dk(x) Enf{x)Dk{x)
lim г, ,, ч А , ч — Лип —„ ., ч р . ч = С).
Поэтому, в силу теоремы 1, функция /х (х) = / (х) А (х) регулярна ла
[а, Ь], между тем как /2 (х) = / (х) В (х) нерегулярна на этом отрезке.
Но это означало бы, что f (х) — аналитическая функция, имеющая, как
и / (х) В (х), полюсами корни А (х), т. е. Enf (х) — оо и Z>& (х) = А (х).
Итак, остается рассмотреть случай /(#)(: Л*, когда все характе-
характеристические, точки— вне отрезка [а, Ь]. Если бы корни А (х) находились
на эллипсе С, а корни В (х) — вне этого эллипса, то, вследствие (А*),
мы имели бы Enf1 (х) В (х) = о [Enfx (х)], т. е. Д (х) = f(x) А (х) была бы
регулярна внутри эллипса регулярности функции 1/В (х), большего, чем'
эллипс регулярности С рациональной дроби IIА (х). Следовательно, либо
/ (х) = f1(x)jA(x) регулярна на С, как и /2 (х) = f (x) В (х), но в этом
•случае, по теореме 1 [см. левую часть неравенств A)], характеристи-
характеристическим многочленом функции /2 (х) не мог бы быть многочлен А(х):
либо / (х) не имеет на С иных особенностей кроме полюсов [корней
А (х)], но тогда D^ (х) = А (х).
1 Из теоремы 2 следует, что AR ci A*.
2 Т. е. неравенства A) превращаются в равенства -р — lim >V~'En f (x) = — .
538

Следствие 4. Если f(x)?A*, то условие, необходимое и доста-
достаточное для того, чтобы многочлен Р (х) принадлежал к числу теху
для которых осуществляется (А), состоит в том1, что Р{х) должен
делиться на характеристический многочлен Вь(х) функции f(x).
Отсюда следует, в частности, что если / (х) 6 А и En+Sf(x) > с8Е„/ (х)
(где cs>0 — постоянные, не зависящие от п), то f (х) 6 А*.
Несмотря на существенное различие природы функций Л* и .4*
(причем, однако2, функции первого рода Л* на одних отрезках могут
становиться функциями А* на других отрезках), их сближает еще одно
общее формальное свойство. Назовем алгеброидную функцию элементарной,
ос ли она имеет лишь одну характеристическую точку3; исследование
функций Av как и А^ приводится к исследованию элементарных функций
благодаря следующему предложению:
Теорема 3. Всякая функция f(x)?A\ имеющая характеристический
многочлен Du (x) степени к, является суммой не более к элементарных
функций.
Поступило
29. V 1951 г.
ЦИТИРОВАННАЯ ЛИТЕРАТУРА
1 G. Н. Берн штейн. Изв. АН СССР, серия матем., 10, 461 A946) [88].
2 С. Н. Бернштейн. Экстремальные свойства полиномов, 1937, стр. 73. [«Э. n.»J.
1 Иначе говоря, / (х) ?А* тогда w только тогда, когда условие (А) осуществляется
всеми многочленами Р (х), делящимися на Dk(x)9
2 Например, \а — x\8^A*v если а вне основного отрезка, и \а — х |s ? Л* в про-
противном случае.
8 В следующей заметке будет показано, что в случае А2 корни Dk (x) всегде про-
простые. Вероятно, это же свойство обязательно и для / (а?)?Л*. [Продолжение начатого
здесь исследования мною еще не опубликовано. (Автор)].

105
О НАИЛУЧШЕМ ПРИБЛИЖЕНИИ ФУНКЦИЙ
НЕСКОЛЬКИХ ПЕРЕМЕННЫХ ПОСРЕДСТВОМ
МНОГОЧЛЕНОВ ИЛИ ТРИГОНОМЕТРИЧЕСКИХ СУММ *
1. Для определенности и сокращения письма мы ограничимся рас-
рассмотрением функций двух переменных.
Пусть F (х, у) будет непрерывной функцией в данном прямоуголь-
прямоугольнике S (а -^ х <^ Ь, а' <С у ^Ь'). Исследование наилучшего приближения
Еп*т F (х, у) в прямоугольнике S посредством многочленов Рп> т (х, у)
степени п относительно х и степени т относительно у может быть све-
сведено, в основном, к вопросу о наилучшем приближении посредством
функций, являющихся многочленами, только относительно одной из пере-
т
менных х или у. Многочлен вида 2 аъ (х) Ук> гДе а& (х)—любая непре-
рывная функция переменной ху будем обозначать через ^оо^ т ((х), у) иг
п
аналогично, (?п> т (х, (у)) = 2 Ъъ. (у) xk, где bk (у) — любая функция пе-
fe=0
ременной у. Наилучшее приближение F (х, у) в прямоугольнике S посред-
посредством многочленов QUf '^ (х, (у)) степени не выше п относительно х будем
обозначать через ЕщооР(х, (у)). Таким образом,
Ещ ooF (х , (у)) - Ent ooF (х, у) = max EnF (ж, (у)), A)
где EnF (х, (у)) — наилучшее приближение F (х, у) на (а ^ х ^ Ъ) много-
многочленами степени п по х при фиксированном у. Точно так же
¦Я*,, mF (х} у) = гаах EmF ((ж), у). Aа)
<<5
По предположению,
lim Ещ ooF (x, у) - lim Eoo, mF (з, у) = 0. "B>
* Труды Матем. ин-та им. В. А. Стеклова, 38 A951), стр. 24—29 B64*).
540

Пусть теперь (?<*>, m((#)> у)— многочлен степени т по у} наименее
уклоняющийся от F (х, у), т. е.
! F {X, У) - <?оо, т (И, У) | < Яоо, ж^ (И, у), C)
м обозначим через /*П| m (х, у) многочлен степени п по х и степени m по
г/, наименее уклоняющийся от Qoo,m((%), у), так что
I <?oo, m (И, 2/) ~ Рп, т (а, У) | < Еп, т Q^m ((*), У)- (*)
Из определения следует, что
En, m F (X, У) > ?оо, mF ((Ж), У). E)
Обозначая через /O7j ш (х, г/) многочлен, наименее уклоняющийся от F (х} у),
заключаем из D), что
max | Qoo> т ((х); у) — Рщ т (х, у) \ >?'n,m <?oo, m (И, у)- F)
Следовательно, складывая C) и F), получаем
Еп, mF {х, у) = max | F (ж, ?/) — РП( т {х, у) \ >
> ^п, m (<?оо, tn (И, г/)) - ^оо, w (F (ж, 2/)). (V)
Складывая E) и G), находим
2 Еп, mF (ж, у) > Яп> m (^oo, m ((ж), г/)). (8)
С Д})угой стороны, из C) и D) получим
En, mF (X, У) < Ясс, ж (F ((Л), у)) + Ent m (Qao, m ((х), у)). (9)
Из неравенств E), (8) и (9) видно, что порядок ЕП) mF (x, у) вполне
определяется порядками EOOtmF(x, у) и EUi m^oo, m ((^)> у)- Кроме того,
также можно получить
En, m (F (х, у)) > En, ™F (x, (у)), Eа)
2 Еп, т (F (X, у)) > Еп, т (<?«, со (X, (у))), (8а)
Еп, ш (F (х, у)) < Еп, о, (F {х, (у))) + Еп, т (Qn, о, (х, (у))), (9а)
где функция двух переменных Qn^ ^ (х, (у)), являющаяся многочленом
степени п относительно .г, наименее уклоняется от F (х, у) в прямо-
прямоугольнике S.
2. Для нахождения некоторой верхней границы ЕП} т {Q00i w((#), у))
в неравенстве (9) представим Q^, m((^), у) в виде
га
Qoo, т (И, У) = Ц Rh (У) ?* (X), (Ю)
где Rjc (yjc) — 1 и Ri (yk) = 0 при i§/ в произвольно заданных w + 1
точках Ук(а' <СУк<СЬ')- Таким образом,
541

где
Am+i(y) =
Всякий многочлен Qn, т (х, у) степени п по х и степени т по у можно
представить в виде
т
Qn, т (X, y) = ^Rk (У) Як, п (X),
fc=o
И
т
Qoo, rn ((X), У) - Qn, т (X, V) - 2 Rk (У) [?* (X) ~ Як, п (ХI (И)
к=0
откуда заключаем, что
Еп, т (Qoo, т ((%), Ук)) = Еп<?к (х) = Sk < ^п, оо (^оо? m ((ж), у)) A2)
D=0, . . ., га).
Следовательно,
m
А< If) I(т\ 9/11 <^" ттпя"V ^ с-» I /?т /^^ <Г^
л^п, т, \х со, ттг \\^/> У// ^^ -WiciA / j ^А* •''•А; \У) "^^
CLf^y^br к—q
m
< ,БП, „ (<?*,, m ((ж), у)) max Д] IЛЛ (у)). A3)
Пусть для определенности Ь' = —а! — 1. Для того чтобы, по воз-
возможности A), снизить асимптотически правую часть неравенства A3),
полагаем
А т+1 {у) = ТтЛх(у)= cos (га +1) arc cos у,
так что j/ft = cos I» / , 4 Г (к «= 0, . . . , га) и, пользуясь известной оцен,-
кой (х), выводим таким образом из A3):
Еп, т (Qoo, m ((ОС), у)) < f-| + 8m) ?n, «>Qoo, m ((x), lj) log m, A4)
где Sm -> 0 при m -> oo.
Из A4) и (9) следует поэтому, что вообще
Еп, т (F (х, у)) <?от, п (F ((х), у)) + (^ + 8т) Еп> «,<?«,, га ((ж), >v) log то, A5)
и, так как, вследствие C),
| #„, oo F (х, у) - ?„, „<?„, m ((ж), у
то
Еп> т (F (х, у)) < A + 8m) [i?n, mF (х, у) + Б*,, mF (x, у)] log т. A7)
Аналогичным образом получаем неравенство
En, m (F (х, у)) < (~ 4- 8n J [Еп, оо (/• (г, у)) + Ет, т (F (х, у))] log n, A7а)
542

более сильное, чем A7), если п<^т, и ^соответствующие промежуточные-
неравенства, из которых отметим
Еп, т (F (х, у)) < Еп, м (F (х, у)) + (А + 8n) Д», m (?n>co (х, (у))) log п. A5а).
Неравенства A5) и A5а), повидимому, не могут быть существенно улуч-
улучшены, и, если возможно, было бы интересно построить функции F(x, у),
для которых при соответствующем возрастании (п, т) порядок Еп^т F(x, у}
достигает порядка наименьшей из величин, стоящих в их правой части1.
Неравенства A7), как и A7а), выведенные из A5) или A5а) при помощи
A6), без достаточно полного использования связи между Q<x>,m {{%)-> у) и
F (х, у), вероятно, могли бы быть заменены более точными альтернатив-
альтернативными 'неравенствами. Во всяком случае, если ни одна из величин
Еп, ao(F(x, y))logn и Eootm(F(x, y))\ogm не стремится к нулю, неравен-
неравенства A7) и^A7а) становятся бессодержательными, так как из них нельзя'
заключить,> что lim 2?n> m(F(x, у)) = 0, между тем как Это предельное
п-*оо
равенство всегда соблюдается при lim EUj «, F (х, у) = lim 2?^ m F (х, у) =0.
П->оо 7П->оо
Тем не менее неравенства A7) и A7а) могут быть практически полезны,
в особенности, когда порядки убывания Еп>оо и Е^>п различны. Напри-
Например, если ЕП} оо F (х, у) = о [^ОО)п F (х, у)], то целесообразно выбрать п<^т7
чтобы сравнять порядок EnfCOF(x, у) и Еоэ^тЕ(х, у) [и пользоваться не-
неравенством A7а).
Ввиду этого я считаю не лишним привести еще другой, более кон-
конструктивный вариант вывода этих неравенств. Вместо многочленов
Qoo,m (#, У) построим интерполяционные многочлены
(У) ( _..BЛ-М)те\ A8,
В таком случае, погрешность
/oo,m (F (х, у)) - max | F (х, у) - R^m ((x), у) \
F (т iA . С) ~* ((х\ чЛ -Х- ^Ф оо> '.
< (I + 8т) Е^ ш (F (х, у)) log m. A9)
Но, принимая во внимание, что jRoo, m ((х), уъ) = F (х, ук), видим, что мно-
многочлен Rn,m(%, у) степени п по х и степени m по у, наименее уклоня-
1 При произвольно малом а>0 можно в неравенстве A5) взять m настолько»
большим, что Eoom(F(x1y))<^—f и после этого настолько увеличить п, что»
А
543

аощийся от Roo, m ({х), у), является также наименее уклоняющимся от
F (х, у) при у = Ук (к = 0, ..., т). Следовательно,
Еп, ш (Я«, m ((х), ук)) = Еп, т (F {х, у к)) < Еп, „ (F (х, у))
B0)
Еп,
т (Rco, т
(Х), у)) < ШЭХ | R^, т ((х), у) — R*f m (х, у) |
<?„.«,(*>, у)) 2 -rz
'ra-fl
(У)
„, „ (F(x, у)) (| + Зт) log да,
откуда
| F (х, у) — R-, m (а:, г/) |
B1)
,, m (F (ж, г/)) + ?„. „ (F (х, у)) (| + om) log ir,
B2)
F (x, у) - R*n, m(x, y) |< (^ +
> m
(x, y) + En, „ /?(я, г/)] log m. B3)
Вряд ли нужно отмечать, что все приведенные выше рассуждения и
оценки полностью применимы к приближению периодических функций,
^сли вместо приближения EUj m многочленами рассматривать наилучшее
приближение En, m (F (%, у)) посредством тригонометрических сумм порядка
п и т относительно х и у соответственно.
3. В связи с изложенным выше следует напомнить о результатах,
относящихся к верхней грани приближения функций данного класса
посредством функций конечной степени B»3), которая, как известно, со-
совпадает для периодических функций с соответствующей гранью прибли-
приближений тригонометрическими суммами. В частности, из теоремы 4, дока-
доказанной в заметке C) ([92], стр. 430), вытекает следующее предложение:
Если 2тс - периодическая функция F (х, у) переменных х, у удовле-
удовлетворяет условиям
dk F (х + h, у) дк F (х, у)
I
д' F(x,y +h)
ду1
* дх«
dlF(xy у)
ду1
(i)
•Щ)
то
еде
El, ш (F (х9 у)) < С sup El oo (F {х, у)) + С± sup ?•, т (F (ж, у)), B4)
(О (Н)
B5)
A)~ "" }Г \ "> J (ii) m* V"> J
(С, С1 и ^4, ^4Х — постоянные, не зависящие от л и /п). Неравенство B4)
для класса функций (I, II) точнее полученных выше [A7) и A7а)] для
функции с произвольно заданными ЕПъ со и Д», т- Однако открытым
остается вопрос о существовании такой одной и той же для всех непре-
544

рывных функций (универсальной) постоянной С, что (при всех п
Еп. т (F (ж, у)) < С {Еп, оо (F (X, у)) + #оо, m (F (X, у))} .
Между тем при помощи равенства Парсеваля легко проверить, что для
всех функций F (х, у) 6 L2 справедливо неравенство
Е™т (F (ж, у)) < ^2)оо (F (ж, г/)) + Eg? w (F (х, у)),
где ?n, m (F (Xj у)) означает соответствующее среднее квадратическое при-
приближение.
ЦИТИРОВАННАЯ ЛИТЕРАТУРА
2S. Bernstein. Sur la limitation des valeurs d'un polynome. Изв. АН СССР,
OMEH A931) [52].
2 С. Н. Бернштейн. Об однородных функциональных классах. Докл. АН СССР,
57A947) [92].
8 С. Н. Бернштейн. Вторая заметка об однородных функциональных классах.
Докл. АН СССР, 59 A949) [92].
35 С Л Бернштейн

106
ПРИМЕЧАНИЯ К ТЕОРИИ РЕГУЛЯРНО МОНОТОННЫХ
ФУНКЦИЙ*
Автор прилагает результаты и методы теории регулярно монотонных функций
к исследованию экстремальных свойств регулярно выпуклых функций.
1. В моем докладе (х) на международном конгрессе математиков в
1928 г. в Болонье, как и в статье B), я рассматривал регулярно моно-
монотонные функции, которые определяются тем свойством, что на данном
отрезке все их производные знакопостоянны. Еще ранее в добавлении к
моей монографии C), где впервые введены эти функции и установлен их
аналитический характер, я коротко остановился (стр. 196) также и на
более общем случае, когда существует только некоторая бесконечная
последовательность знакопостоянных производных fUk) (x) (или конечных
разностей порядков щ), и наметил доказательство того факта, что ана-
аналитический характер fix) при этом сохраняется, если lim—-<i <x> [между
тем как при lim -^ = ос функция / (х) принадлежит квазианалитиче-
&--ОО пк
скому классу Р].
Упомяну также, что в начале доклада (х) и в мемуаре D) (§ 15) я
ввел, в частности, класс абсолютно выпуклых функций / (х) 6 АВ(а, Ь)
на [а, Ь], который определяется условием
/B*)(я)>0 (А>0, а<ж<6). - A)
Применяя тот же прием, посредством которого в монографии C) (стр. 193)
доказано, что абсолютно монотонная на отрезке [а, Ь] функция / (х) есть
аналитическая функция, имеющая в точке а радиус сходимости ^R = b — ar
можно доказать следующее аналогичное предложение:
Если функция f (х) 6 АВ (— Л, R), то f (x) есть аналитическая функция,
имеющая в точке О радиус сходимости ^>R (причем знак равенства
фактически осуществим).
* Изв. АН СССР, серия матем., 16 A952), стр. 3—16 B65*).
546

Действительно, пусть т = 2s > 0 — любое четное число и пусть
М = max / (х) [который равен / (R) или /(—/?)]. В таком случае при
всех х (—R^x^R) имеем
/ (X) = Pm_i (я) + Рт (X),
где
/>„_! (х) = / @) + */' @) + ... + (-^1 /(»-« @),
л
х
|
B)
о о
Замечая, что рт (х) ^> 0 при — /? ^ х <! i? и /<2А:) @) ^> 0, заключаем из B)
(-R <ж<Л) C)
/>т_1(о;)+/>т_1(-ж)>0,
так что имеем также
Рт_! (ж) > — />„_! (— ж) > — Л/,
т. е.
Следовательно,
0<Pm(i?)<2M D)
и при 0^x<^R имеем [благодаря B) и D)]
- * г* * <
-^у-р„ (Я) <2« (?)-', E)
оо
откуда заключаем, что степенной ряд / (х) = V а^; ^ сходится внутри
круга | ^ | <; i?.
Очевидно, что существуют абсолютно выпуклые на [— R, R] функ-
функции, радиус сходимости которых равен Я, так как четные абсолютно
монотонные на OR функции являются АВ (— R, R), а радиус сходимости
абсолютно монотонной функции в .начале отрезка всегда равен длине
наибольшего отрезка, где она абсолютно монотонна. Случай, когда вместо
четных порядков тем же условиям A) подчинены производные нечетных
порядков, приводится к [предыдущему, так как тогда /' (х) 6 АВ. Если
одновременно / (х) 6 АВ (а, Ъ) и /; (х) 6 АВ (а, Ъ), то / (х) абсолютно моно-
монотонна на том же отрезке, и минимальная область регулярности f{x)
расширяется, обращаясь в круг, имеющий отрезок [а, Ь] радиусом, а не
диаметром.
2. Вообще, если мы будем рассматривать только те функции f{x) 6 АВ7
у которых производные нечетных порядков также знакопостоянны, но
могут иметь произвольно данный знак [т. е. если f(x) регулярно
547 35

выпукла], то мы получим регулярно монотонные функции весьма разнооб-
разнообразных типов. В частности, на основании одного из предложений, дока-
доказанных в статье B), мы выделим из класса функций / (х) 6 АВ (а, 6)
различные подклассы регулярно монотонных функций, которые обяза-
обязательно будут целыми функциями конечной степени, если потребуем,
чтобы разность между соседними значениями s, для которых выпол-
выполняется неравенство
f(**-V(x)f<fi*+V(x)^O, F)
была ограничена. Вместе с тем, из соображений, высказанных в конце
статьи G), следует, что подкласс регулярно монотонных функций наи-
наинизшей степени получится, если неравенство F) соблюдается для всех
целых s, т. е. если f (х) циклически выпукла [f (x) d ЦВ (а, Ь)]; в этом
случае, когда / (х) 6 АВ (а, Ъ) и /; (х) 6 ЦВ (а, Ь), все типовые числа равны1
двум, и мы будем коротко писать / (х) 6 Ц%(а, Ь).
При помощи приема, указанного в G), получим регулярно монотонные
многочлены любой данной стенени п вида
± Рп (X) = ^ + Pi*"-1 +...+Рп,
наименее уклоняющиеся от нуля, класса Ц2 (а, Ь) , если производные
%^ (х) всех порядков О <; т < п подчиним условиям
рМ (а) = P<f+1) (а) = i><**+* (Ъ) = Р^+3) (Ь) = О,
т. е. если PW (а) = 0 при т = kk или m = 4А + 1, а при т = 4А + 2
или т = kk + 3 |имеем Р^ (Ь) = 0.
Не останавливаясь на вычислении этих многочленов, заметим только,
что на основании тех же соображений наивысушя возможная степень
с (R) функций f (х) 6 Ц2 @, R) на отрезке длины R достигается функцией
S (х), удовлетворяющей уравнению
SW (х) = c*S (x) G)
и предельным условиям: S @) = S' @) = S" (R) = Sf" (R) = 0. Очевидно,
с (R) == -~, где постоянная р = с A) определится как наибольшая длина
R = R A) = [а отрезка, на котором функция S (х) первой степени, удовле-
удовлетворяющая дифференциальному уравнению G) при с = 1 и условиям
S @) = S' @) = 0, может оставаться положительной вместе со своей первой
и второй производными [S (x)^0, S' (x)^0, S" (х)^>>0], между тем как
Для определенности положим iS//@) = l. В таком случае решение
уравнения G) (где с = 1), соответствующее начальным условиям
1 Чередование знаков последовательных производных будет + + Н
если полагать, для определенности, /(гг)^-О, /'(
548

S (С) - S' @) = 0, S" @) = 1, будет равно
S (x, oi) = ~ [ех + е~х — 2 cos x — ol (ех — е~х — 2 sin ж)] =
5 а^
ZJ DЛ + 2)! a 2л (Ak + 3)!
k=0 k=Q
где параметр a = — S"r @, a) ^> 0, и
DA
откуда видно, что во всяком случае S" (x, a)>Q при 0<;^<^— и
з
S'" (х, а) << 0 пря 0<^х <J |/6a. Таким образом, при любом af>0 *У (х, а)
в некотором промежутке Оха, где хл — наименьший из корней уравнения
S" (x, a) = 0 или У" (ж, а) - 0.
Если ха — корень S"' (х, а) = 0, что представится при достаточно
малых а, то при х^>ха производные S (х, а) всех порядков станут поло-
положительными, и функция S (х, а) при ха<^х <^оо будет абсолютно моно-
монотонной1. При непрерывном увеличении а корень ха уравнения Sm (х, а)—О
будет возрастать и, вследствие одновременного убывания S" (х, а), наста-
настанет момент (а = а0), когда хао = R окажется совместным корнем
iSr" (R, a0) = S" (R, a0) = 0, причем это значение R будет наибольшей
длиной отрезка [0, /?], где S (х, а) может быть класса Ц2, так как при
дальнейшем возрастании a
S"(R, а)<?"(Я, ао) = О.
Таким образом, наивысшая степень ji целых функций / (х) 6 Zf2 @, 1)
равна наименьшему общему корню уравнений
S" (х, а) = Sw (x, a) = ~ [ех + е~х + 2 cos х — а (е* — е~х + 2 sin ж)] =
= ~ [ех — е~х — 2 sin ж — а (ех + ?-* + 2 cos ж)] = 0, (9)
т. е. [I есть наименьший корень уравнения
***2е~* cos х + 1 - 0. (9 bis)
Это уравнение встречается у Рэлея E) (т. I, стр. 292), откуда я за-
заимствую приближенное значение наименьшего корня уравнения (9):
fi ж 1,875104 A0)
как и следовало ожидать, р<>
V
1 Например, при a<^—, iS""(l, ос) ^> 0, и iS"'(l, a) > 0, следовательно, в этом
случае ни одна из производных не обратится в нуль при а?>-1.
549

3. Общее исследование регулярно выпуклых функций может быть
проведено методом, изложенным в B), но для функций f (х) б ЦБ (а, Ь)у
которые с точностью до множителя + 1 определяются неравенством
{-lffm{x)>0 (а<я<6), (И
более совершенные результаты получаются непосредственным примене-
применением элементарно алгебраических соображений теории циклически моно-
монотонных функций [/ (х) 6 Ц (а, &)], которые определяются дополнительным
условием [f (х)(:Ц (а, Ь)], или, с точностью до знака и до замены х на
— х, могут быть охарактеризованы неравенствами A1), дополненными
неравенствами
(-l)Y2ft)(a;)>0. A2)
Очевидно, кроме того, что синусоидный тип циклически монотонных
функций, определенный совокупностью неравенств (И) и A2), может
быть (подобно всем регулярно монотонным типам) охарактеризован явной
формулировкой любого бесконечного множества неравенств A1) или A2)
с тем, чтобы каждое из них для прочих /(п) (х) было заменено требуемым
неравенством лишь для /(п> (а), когда знаки /(пЦх) и /fa-HO (х) (а^х^Ь)
должны быть одинаковы (пермананс), и для /(п) F), когда требуется, что-
чтобы /W (x) /(n+D (я)< 0 (альтернанс).
Следует заметить, что неравенства A1), характеризующие ЦБ (а, Ь),
также могут быть заменены (за исключением некоторого бесконечного
множества значений п, для которых A1) сохраняется) соответствующей
парой неравенств1
(_ i)ft/Bft) (fl) ^ о, (— 1)*/(аЛ) (Ь) > О, (И bis)
так как после того, как известно, что
(- l)*+i/^+2> (х) > 0 (а < ж < Ь),
т. е. что кривая (—iyf№) (x) вогнута по отношению к (a, b), из нера-
неравенств (И bis) следует, что (—- i)kf^k) (х) ^-0 при всех х (а <^, х <<^ Ь).
Все функции/ (х) 6 /|Б @,1), как показали D. Widder и R. P. Boas F),
являются функциями конечной степени /?-<тг. Нетрудно показать, что
этот результат и притом в уточненной форме является простым след-
следствием моей старой теоремы относительно функций Ц, формулированной
и вкратце доказанной в докладе (х) (подробное доказательство в статье G)).
Если f (х) — циклически монотонная функция f (х) 6 Ц @, 1), не пре-
превышающая 1 на отрезке [0, 1], то ее производные порядка т = 2к—1
удовлетворяют неравенствам
^ = шах | /(»> (х) j < -J— = ^- ~ (|-Г | A3)
0<х<1 Lm+1 И°2й; \z / °
"m-fl
1 В случае других регулярно выпуклых функций соответствующие неравен-
неравенства ?Л/2Л* (я) > 0, ZjJ^ (Ь) >¦ О с данными гк ~ + 1 должны быть дополнены
неравенством efc/B^ (^4-1^ -^ ^' когда ?A;efc+i^> ^> и существ^^ет точка » = ^+i»
где /B&+1) (гг) = 0.
550

и производные порядка т — 2к удовлетворяют неравенствам1
N2k = шах | /(«О (*) |< j±- = »|±М ~ ( « Г f A3 bis)
/7/щ этом верхние грани у фактически достигаются, когда
т+1
.где т >>О,
СтA) =
Для этого достаточно заметить, что четная функция / (х) 6 ЦВ (—1, 1)
является функцией Ц @, 1) [так как нечетные производные, обращаясь
в нуль при х = 0, монотонны и, следовательно, также удовлетворяют
неравенствам f& (x) /<s+2) (ж) •< 0 при 0 *< я *< 1].
Таким образом, для четных f(x)^U1B (—1, 1) справедливы неравен-
неравенства A3) и A3bis), откуда следует, что степень их р-^-тг, а степень
f Bх) € Ц (- у , у
( )
Но если / (я) — любая циклически выпуклая функция на отрезк
длины 2, который можем привести к [—1, + 1], то, полагая, что
max |/(я)|<1, A4)
-3<х<1
имеем также
max | ср (ж) | ^ 1, A4 bis)
1<<1
где ср (х) = *-±Q—? ^ Д" @, 1) — четная функция, и, применяя к <р (ж)
неравенство A3 bis), находим
N2k= max /<№(х) <2 max ?№) (х) <у^ ffJ*^ = (fJk^ A5)
<<1 << ЬА+ V ^ У ^ \ / J
[так как /№ (ж) /<2*) (— ж) > 0].
С другой стороны, вследствие (И), имеем при всех х (—
где Nm = max |/Гт)(ж)| tTaK как /BА:~2)(Ж) знакопостоянна], откуда
1 Замечу, что в статье F) R. Boas установил для тех же функций f (х) ? Ц @, 1)
значительно менее точные неравенства, чем A3) и A3 bis), из которых он. впрочем,
т
также получил, что lim у\ /^ (х) | -< -«-.
551

Поэтому, учитывая, что Ь2к+1<С^2к-1У вследствие A5), получаем
2 У т \ (~Т ~ . A5 bis)
Таким образом, из моих старых неравенств A3), A3 bis) вытекает не
только результат R. Boas для функций ЦВ, т. е. удовлетворяющих
условию (И), но получается точный порядок верхней грани модулей
производных любых функций / (х) 6 ЦВ (a, b), a именно:
A6)
причем пример функции sin (:ЦВ@, Ъ — а) показывает, что поря-
порядок A6) не может быть снижен.
4. Для более полного исследования экстремальных свойств функций ЦВ
нужно доказать следующую общую лемму (аналогичную лемме 2 статьи
G) [100], стр. 503) для функций Ц).
Лемма. Если данная функция F (х) подчинена условию (— i)koF (x) ^-0,
то среди всех функций f (х), удовлетворяющих равенству
/B*.) (х) = F (х) A7)
и подчиненных для всех k^k0 неравенствам1 A1), функция S (х), опре-
определенная требованием
{а) - SW (Ь) - 0 (А = 0, 1, - - • , *0 — 1), A8)
получит наименьшее значение во всякой точке ? (
Действительно, совокупность функций f(x), удовлетворяющих равен-
равенству A7), определена с точностью до многочлена степени 2к0 — 1, содер-
содержащего 2к0 произвольных коэффициентов; следовательно, функция S (х)
существует и определена однозначно. Кроме того, на основании сделан-
сделанного выше замечания, S (х) удовлетворяет неравенству A1) при всех
к<^к0. Предположим сначала, что ко=1, тогда ,F(^)^0, и если
f(x)^O удовлетворяет A7), причем хотя бы одно из значений / (а) или
/ (Ь) отлично от нуля, то
Отсюда следует также, что если /<2Й:> (х)—/<2^ (х) = <р (х), где
(—l)fecp (x) ;> 0 для некоторого к<^к0, то наименьшее возможное значе-
значение (—l)fc-i/Bfc-2) (х) в любой точке (а^х^Ь) не может быть меньше
наименьшего возможного значения (—l)fc-ijfBfc—2) (xy Таким образом, при-
применяя математическою] индукцию, убеждаемся в правильности утвер-
утверждения леммы при всяком данном &
1 Если F {х) ? ЦВ(а, Ъ), то и / (х) ? ЦВ(а, Ъ), и наоборот.
552

Следствие 1. Если
|/«*«>(ж)|>1 (-1<я<1), A9)
то среди функций f (х) € ЦВ (— 1, 1) многочлен Эйлера
будет функцией, наименее уклоняющейся от нуля на [—1, 1].
Следовательно, уклонение от нуля функций f(oc), удовлетворяю-
удовлетворяющих A9), не может быть меньше, чем
(-if
^к* Bft0)I ( + )
Напротив, ес/ш 5 (х) удовлетворяет равенствам A8) гг равенству A7),
1 (F (^) знакопостоянна), B0)
функции S (x) G ЦВ21с0+2 (а> Щ удовлетворяют неравенству
Мы ввели здесь обобщающий ZE класс циклически выпуклых функ-
функций f (х) в ЦВ2{{а, Ъ) порядка 2t, определяемый условиями
(_ i)ft [/Bft) (я + Л) — 2/<2*> (ж) + /<**> (ж — Л)] < 0 (а^х
A1 ter)
при всехх Л-^^-^оо (^ = оо соответствует ЦВ).
Таким образом, если F (х) = fBt~^ (х), то f (x) dljB2t(a, b) тогда и
только тогда, когда f (х) удовлетворяет A1) при k<^t и [(—l)f F(,r) <;0]
(- 1)< [F (х + К) - 2F (х) + F(x~ h)] > 0. B2)
Следствие 2. Если f (х) 6 ЦВ.2г {a, b), t^>k0, удовлетворяет A7),
причем максимум | F (х) \ достигается в точке а (а <; а ^Ь) и
|F(a)|= max |F(*)|>1, B3)
то из всех функций f (x) наименьший абсолютный экстремум будет, иметь
наименее уклоняющаяся функция S (x, a) [SW> (а, a)=SW> (b, а)=0, k<^.k0],
^лл которой F (х) = SBk°) (x, а) представляет собой угол с вершиной
(а, (— 1)^°), опирающийся на ось абсцисс в обоих концах а и b отрезка [а, Ь].
[За исключением случая, когда а = а или b, S (х, а) 6 LfB2t (я, Ь) не при-
принадлежит классу ЦВ].
1 Как известно C), в этом случае / (х) имеет непрерывные производные всех
+B? 1) B/ 1)
порядков n<C.2t — 1, и существуют конечные производные числа /" (х), / (х)
во всех внутренних точках (и по крайней мере одно из них в каждом из концов
а и Ъ).
553

Действительно, все функции F (х), удовлетворяющие B2) и B3)
(вместе с условием (—l)k°F (х)*^>0], будучи линиями, вогнутыми по на-
направлению к [а, Ь], будут отделены от отрезка [а, Ь] сторонами указан-
указанного выше угла с вершиной в точке (а, (— 1)й°).
Весьма вероятно, что, каков бы ни был порядок 2к0 заданной про-
производной, max | S (х, а) | будет наименьшим при а = а (и при а = 6).
Во избежание дополнительных вычислений я ограничусь доказатель-
доказательством этого утверждения в предположении, что к0 весьма велико. Для
этого нам понадобится еще одно соотношение.
Пусть A2jc0 [F (х)] означает наименьшее уклонение функций
f (х) 6 ЦВ2ко+2 (—1, 1), удовлетворяющих A7) [причем Р(х)?ЦВ2 (—1, 1)
и для определенности (—l)k°F (x) ^>0]. В таком случае
Агн. [F (*)] = f 1 + il ЛЛ. [Фо (х)} (О < 6< ?) , B4)
где Фо (х) = у [F (х) + F (— х)] — четная функция (ограничиваясь для крат-
краткости предположением, что нечетная функция Ф± (х) = у [F (х) — F {—х)]
знакопостоянна при 0 <^ х <; 1).
В самом деле, функция S (х), дающая наименьшее уклонение среди
всех f{x), удовлетворяющих1 A7), обращаясь в нуль при ж = 4-1 со
всеми производными четных порядков, может быть представлена суммой
S(x)=S0{x)+S1(x)i
где
SW'\x) = <!>0(x), ??*•> (*) = <Di (я) и 42
Тогда So (x) есть функция, наименее уклоняющаяся от нуля 'на
[— 1, + 1] среди функций / (х) 6 ЦВ2ко+2 (— 1, 1), у которых f^) (Х)=ФО (я),
между тем как нечетная функция ^ (х), у которой, кроме того, ^12тп)@) = О,
будет циклически выпуклой порядка 2к0 + 2 на одном из отрезков [0, 1]
или [—1, 0] и притом наименее уклоняющейся среди f(x) 6 ЦВ27с0+2 на
этом отрезке. Учитывая, что max |Oi(^)|^ max \фо(х)\ = М, заключаем
0<х<1 0<л:<1
из A3 bis), что [так как Фо (х) — четная функция]
С другой стороны, применяя к функции Sx(x) неравенство B1),
видим, что
М
max ^(аОК^^й.,
откуда следует [так как S0@)= max |?0(ж)|, 6'1@) = 0], что
1 Нетрудно проверить, что линейный оператор, переводящий F (х) в S (х),
представляет /со-кратную итерацию оператора
х г
у [(* - 1) J (« + 1) ^ (z) dz+(x + l)^(z-l)F (z) dz
—1 X
554

Ал. [Фо (*)] < Ал, [F (х)] < А2ко [Фо (х)] [ 1 + ф--^
¦^ 11 + -^-1 ^2fc. [Фо (ж)]. B4 bis)
тде
Таким образом, благодаря1 B4) (полагая для краткости М = 1), при
доказательстве высказанного выше утверждения вместо функций S (х, а)
достаточно рассмотреть их четные части
s2s = а2й;о (х, а) = у [б1 (ж, а) + S (х,— а)],
соответствующие
Фо (ж, а) = -^ а2_1
т. е.
фо (х, а) = TXT ПРИ \х\<
1-1x
фо К а) = 1_'а2
в частности, Фо (х, 1) = — при — 1 <; х ^ \ .
Разлагая Фо (х, а) = Фо (—х} а) в ряд Фурье на [— 1, + 1], причем
для этого мы вправе принять, что вне этого отрезка
ФоB — ж, а)= — Ф0(ж, а)
откуда следует, что Фо (х, а) имеет периодом 4], получим
2А + 1 2А + 1
^ °° cos —-— тга cos —-— to
Фо («, «) = д2A_а2) Д ^nys . B6)
Поэтому @-<а<Ч)
2А + 1 2Л + 1
, а) - 1_а2 ^-j 2, BА + 1Js+2
(— l)hCOS
При этом @<><;1)
. ,, 2/2
°2S (x' a) I= r1^' ^
/ C°S 2 / 2 \2s
max a2s (ж; lj = ^ ._ _
"=0 B8)
1 В последующих формулах буква к0 везде заменена буквой 5.
555

Итак, из B8) следует
Теорема А. Если max j /<**) (х)\ = М и f (x) 6 ЦВ2т (— 1, 1) (т > к,
б частности, т=оо),то из всех этих функций при достаточно больших
к наименее уклоняются от нуля на [—1,1] многочлены ±:МР2к+1(-±-х)
степени 2& + 1, где
-ir + ... B9)
определяется условием, что 2P(^+i (х) = х — 1 ггч Р2л+1 (zb 1) = 0 для <?с&г
/г (О -^ /г <^ Л:). Наименьшее уклонение, равное максимуму этих много-
многочленов, асимптотически равно
Следствие 3. Если -}(х)(:ЦВ(—1,1) и \ f (x) |< 1 при—
то при весьма больших к имеем асимптотическое неравенство
которое не может быть улучшено.
Это значение несколько больше, чем значение (-тН -т-, которое,
согласно формуле A3 bis), соответствует дополнительному требованию,
чтобы / (х) б ЦВ (— 1, 1) была четной. Напротив, мы видим, что верхняя
граница j/Bfe) (ж) ], которую мы получили выше [им. A5)] без всяких новых
вычислений для всех к ^>0, отличается лишь множителем -х- от асимп-
тотически точного значения верхней грани C0).
5. В заключение обратим внимание на экстремальные свойства элемен-
элементарных тригонометрических функций как среди функций Ц9 так и среди
функций ЦВ, которые вытекают соответственно из леммы 2 статьи G)
и из доказанной выше основной леммы для функций ЦВ.
Для этого напоминаю сначала два предложения, доказанные в моей
заметке (8), которые позднее были получены и некоторыми другими
авторами:
I. Если на отрезке 0, —- все четные производные функции <х> (х) обра-
обращаются в нуль только при х — 0, а нечетные производные имеют един-
единственным корнем х = -^-, то ®(х)=А&шх {на этом отрезке).
II. Если четные производные удовлетворяют условиям
<р @) = cpW @) = ср (тс) = cpBw) (тс) = °
всех /г ^> 0 гг we имеют иных корней на отрезке [0, тт], /по ср (х) =
= Asmx на [0, тс].
Из формул A5) и A5 bis) следует, что производные FGc\x) функции
F (x) G ЦВ @, тс), удовлетворяющей условию
И1<1, C2)
556

должны удовлетворять неравенствам
max | Fw (x) \ < B,
C<X<7T
где J9 "> 1 —не зависящая от к постоянная, которые аналогичны соответ-
/ тс \
ствующим неравенствам для производных fW (х) функций / (х) G Ц ( 0, -^-1,
циклически монотонных на 0,у .
Поэтому, если F (х) б ЦВ (О, тг) Гили / (х) G Z( (О, -у ] удовлетворяют,
соответственно, условиям
max | F{kn) (х) | ^ М /или max | fkn) (x) \ ^>>М\ , C3)
2
где {кп} — некоторая данная последовательность бесконечно растущих
чисел, то можно указать такое 8 (тг<^8<^ lj, что
L {М) = max | F (х) \ > МЬ C4)
[или, соответственно, аналогичное неравенство для f{%)], причем суще-
существует функция F (х) 6 ЦВ @, тс), для которой L (М) = Л/о, т. е,
limL(M) — МЬ достигается. Действительно, существует бесконечное мно-
множество функций F (х) б ЦВ @, т:), удовлетворяющих C3) [такими будут
например, F (х) — A sin х + Р (х), где Р (х) 6 ЦВ @, тс) — многочлен степени
ниже кг], для которых L(M)^> МЬ сколь угодно близко к МЬ. Принимая
во внимание равномерную ограниченность всех производных этих функ-
функций F (х), можем составить из них последовательность функций, имеющих
предельную функцию Fo (х) 6 ЦВ @, тс), удовлетворяющую условиям C3),
для которой 'L (М) = МЬ. Но вследствие того, что это значение МЬ не
может быть снижено, производные всех четных порядков функции
FQ (х) G ЦВ @, тс) обращаются в нуль при х = 0, х = тс, так как Fo (x)
является наименее уклоняющейся при любой заданной своей производной
Следовательно [благодаря C1)], Fo (х) = + М sinx, 8 = 1. Таким образом,
доказана
Теорема В. Из функций F (х) 6 ЦВ @, тс), удовлетворяющих C3),
наименее уклоняется от нуля F (х) = 4z M sinх. [Из функций f (х) (:Ц ( 0, -^
наименее уклоняется от нуля f(x) = ^nMsinx или Ч- М cos,т.]
Эта теорема равнозначна следующей:
Если F (х) 6 ЦВ @, тс) удовлетворяет C2), то
lim max | F{k) (х) \ <; 1, C5)
причем знак равенства имеет место лишь в случае F (х) = -h sin x.
Действительно, неравенство C5) необходимо и достаточно для того,
чтобы 8 = 1 в неравенстве C4), причем оба эти неравенства обращаются
в равенства в силу упомянутого выше предложения (8) только в случае
F (х) = _+: A sin x.
557

Для циклически монотонных функций теорема В доказана в моей
статье G) в последней форме ([100], стр. 510).
Возвращаясь к функциям / (х) ? Ц [0, -J-J, я хочу привести еще третье
доказательство (являющееся конструктивным развитием изложенного
выше) теоремы В, основанное на решении следующей задачи:
Требуется определить наименьшее уклонение М от нуля на 0, —
функций /(х)(:Ц (О, -^-J, удовлетворяющих п условиям
max | fki) (x) \ = Mk. (i = 1, . . . л), C3 bis)
где ki+1 — ki^2, kx^>l, и соответствующую наименее уклоняющуюся
функцию /0 (х) 6 Ц (О, -^j .
Для того чтобы однозначно определить fo{x), нужно указать, к ко-
которому из 4 типов (+sin я, rbc°s^) она должна принадлежать (значение
М от этого не зависит); положим для определенности, что /(х)—типа
sin х. Тогда / 1' (х) достигает экстремума ±М^г в нуле при #i = 2s + l
нечетном, а в случае ki — 2s в конце х = -к- со знаком (— l)s.
Значения М^ должны быть связаны неравенствами
где х
оо . оо
¦ 2 \sr 8 ТГ
TZ*
Положим, например, п = 3. Тогда функция /0 (я), осуществляющая
наименьшее уклонение, будет вида
/0 (х) - аД (ж) + a2Rk2 (х) + a3Rkl {x), C7)
где Rm (х) — многочлен ^требуемого типа степени m + 1, который является
функцией / (х) б Z( @, -у L наименее уклоняющейся от нуля на 0, -у L
при условии, что (стр. 551)
max |
тс
~2~
причем коэффициенты а*, которые определяются равенствами C3 bis),
должны быть неотрицательными. Таким образом,
откуда а2 = Мк — Мк дка_к ^> 0 [первое из неравенств C6)], и для того
чтобы иметь также
% = Мь> - (Мь, - MkS*.-*t) ^,_Й1 - ^.?*._*, > 0- ¦ C8)
о Я Я ЯЧ
1 — <?1<?з<.-.<7^<.-.<?2<1^--8| [см. ('), [100],стр. 502].
558

необходимо, чтобы М^ удовлетворяло также неравенству1 C8): в таком
случае формула C7) дает искомую функцию2, и наименьшее уклонение
равно
М - max| /о (х) | = аДз + a%q^ + а^. C9)
Тот же процесс при любом п приведет последовательно к установле-
установлению всех п — 1 необходимых (и достаточных) условий для совместности
значений М^. в C3 bis), и в случае их совместности дает решение задачи.
В частности, значения М^—1 совместны при любых данных kiy как
видно из существования функции sin x. Найдем в этом случае асимпто-
асимптотическое наименьшее значение М(п) ~ М при данном конечном числе п
условий C3 bis), когда кг и ki+1— ]ц неограниченно возрастают, так что
о
при любых 1<С/^п имеем lim qkя_кш = -^ = с. Таким образом, при /г = 3,
согласно C9)" получим тогда
МC) - с {аг + а2 + а3) = с [1 + A - с) + A - сJ] = 1 - A - cf C9 bis)
и вообще Л1^п) = 1 — A — с)п; следовательно, lim M(n) = 1. Отсюда, как
П~>оо
и раньше, получаем теорему В. Укажем еще вытекающее из теоремы В
Следствие. Если f (х) 6 Ц[0, 4н, то на отрезке 0, -|- всегда сущест-
существует
()
f (ж) — dr ^ sin х + ср (ж) или f (х) = ±М cos х + ср (х),
lim cp(n)(^)=O [аналогичное утверждение справедливо для F (х) 6 ЦВ @,
п->оо
соответствующем отрезке. Поступило 31. X 1951 г.
ЦИТИРОВАННАЯ ЛИТЕРАТУРА
1 S. Bernstein. Sur les fonctions regulierement monotones. Atti del Congresso-
Internaz. dei Matem. Bologna, 1928, t. II A930), 267—272 [45] (том I).
С. Н. Бернштейн. О некоторых свойствах регулярно монотонных функций.
Сообщ. Харьк. матем. об-ва, серия 4, 2 A928), 1—И [32] (том I).
3 S. Bernstein. Legons sur les proprietes» extremales etc. Paris, 1926. [«L. S.»].
4 S. Bernstein. Sur les fonctions absolument monotones. Ac ta math., 52 A928),
1—66 [35] (том I).
5 Стрэтт (лорд Рэлей). Теория звука, т. 1. М.—Л., 1946.
6 R. Boas. A note on functions of exponential type. Bull, of the Amer. Mathem.
Soc, 47 A941), 750—754.
7 С. Н. Бернштейн. О некоторых свойствах циклически монотонных функций.
Изв. АН СССР, сер. матем., 14 A950), 381—404 [100].
8 S. Bernstein. Sur un theoreme de M. Gontcharoff Сообщ. Харьк. матем. об-ва
серия 4, 2 A928), 73—74 [33] (том I).
1 Из первого неравенства C6) вместе с C8) вытекают оба остающиеся (при /г=3)
неравенства C6).
2 Следует заметить, что наименьшим будет не только max |/0(#)!, но и значение-
j/0(#)| в любой данной точке х @><

107
О НОРМАЛЬНО ВОЗРАСТАЮЩИХ ВЕСОВЫХ
ФУНКЦИЯХ И МАИОРАНТАХ КОНЕЧНОГО РОСТА*
1. В заметке (х) (теорема 1) я показал, что, какова бы ни была дан-
данная функция Ф (х) > с >- 0, при условии
2 К = ос, где ln = min Y^^L , A)
71=1 -00<Х<00 I Х \
всегда можно построить такую функцию выше нулевого рода Ft (x), что
оо
F, (х) = а0 + 2 ак а** < 2Ф (х) {а0 > 0, ак > 0), B)
так что условие A), в смлг/ -ноем известной старой теоремы B>3), я^-
ляется достаточным для того, чтобы Ф (х) была весовой функцией
С другой стороны, в той же заметке A) установлено, что если четная
функция Ф (х) нормально возрастает [Ф (х) 6 N], то условие A) равно-
равнозначно условию
Таким образом, условие C) также достаточно для построения целой функ-
функции F± (x), удовлетворяющей B) (выше нулевого рода).
Кроме того, в заметке D) показано (теорема 4), что при отсутствии A)
[т. е. при нарушении C)], иначе говоря, при условии, что
o, D)
функция Ф (х) б N не может быть весовой, т. е. не может удовлетво-
удовлетворять B).
Докл. АН СССР, 85 A952), стр. 257—260.
560

Итак, из теоремы 1 заметки (*) вместе с теоремой 4 заметки D) следует,
что в случае четных функций Ф (х) 6 N существование неравенства вида B)
необходимо и достаточно для того, чтобы Ф (х) была весовой функцией*.
2. Принципиально интересным дополнением к этому утверждению
является недавний результат В. С. Виденского E): если четная функция
Ф (х) 6 N не является весовой [т. е. не удовлетворяет B)], то всегда
можно построить такую функцию
оо
*¦„(*)= 2 **** F*>0) E)
нулевого рода, что [107.1]
Ф(х)<Р0(х). F)
Таким образом, все четные функции Ф (х) G N распадаются на два
класса: 1) Ф(х)?Мъ удовлетворяющие неравенству вида B) [эквивалент-
[эквивалентному условию C)], которые являются весовыми функциями [Ф (х) б W],
и 2) Ф(x)?N0, удовлетворяющие неравенству вида F) [т. е. условию D)],
являющиеся майорантами конечного роста нулевого рода [согласно терми-
терминологии, введенной мною в заметке F)] в силу одной из моих старых
теорем G) 1923 г.
Очевидно, что разделение функций Ф (х) 6 N на указанные два класса
распространяется также и на несимметрические функции, лишь бы только
правая и левая ветви Ф (х) принадлежали к тому же самому классу
[т. е. обе удовлетворяли либо условию C), либо условию D)].
Как мы видим, все функции Ф (х) 6 N, удовлетворяющие D), т. е.
Ф (х) 6 No, мажорируются (— оо < х < оо) четными майорантами нулевого
рода Fo (х) 625 = 9Л0 с: 9Й, а в силу аддитивности четных майорант нулевого
рода (8) тем же свойством обладают также все целые алгебраические ком-
комбинации функций Ф (х) (i No и их производных. Последняя часть этого
утверждения вытекает из следующей леммы:
Если }(х)(:$Я есть майоранта конечного роста, причем xf (x)^>0,
то \f'(x)\ также является майорантой.
Действительно, пусть на всей оси
\GP(x)\<\f'(x)\, G)
где Gp (х) — целая функция степени р. В таком случае
Gp (x) dx
(8)
X
поэтому производные всех порядков Gp*"* (х) = —^ \ Gp (x) dx должны
о
быть соответствующим образом ограничены вследствие того, что / (х)
является майорантой.
То обстоятельство, что функции, имеющие четную майоранту Фо (х) 6 NQ,
принадлежат классу функций с майорантой нулевого рода F0
* См. также комментарий [26. 6], том I, стр. 557. (Автор.)
36 С. Н. Бернштейн 561

позволяет при помощи соответствующего неравенства F) вывести немед-
немедленно для всякой целой функции Gp (x) степени р^О, удовлетворяющей
данному неравенству
I Gp (х) I < Фо (х) (Фо (х) е AV, - оо < х < оо), (9)
верхние границы C) для \G^(x)\ при любых данных &>0 и х, а также
утверждать, что к функциям Gp (x) применима лемма (замкнутости) замет-
заметки (9) [из этой леммы следует, между прочим, что если функция Фо (х)
конкретно задана, то всегда среди функций Gv(x) не выше данной сте-
степени р0 >- 0 существует функция Gv (х, х0, к), производная которой дан-
данного порядка к достигает в данной точке х0 наибольшего значения1].
3. В заключение я хочу остановиться на случае таких несимметрич-
несимметричных функций Ф (х) 6 N, что в одном направлении Ф (х) 6 N& а в другом
Ф (х) 6 Ni- Класс таких функций мы будем обозначать через N* и будем
предполагать для определенности, что Ф* (х) ? N*o при х^>0 и Ф*(х) dN[
при х<С,0 [т. е. при х^>0 имеет место D), а при х<^0 имеем C)].
Я отметил в заметке D) ([103], сноска на стр. 531), что при этом Ф* (х) ? N*
может быть весовой функцией [Ф* (х) 6 W], а именно: если положить
ф* (х) = оо для всех х<^0, то для этого необходимо и достаточно, чтобы
^^=oo, A0)
J x2
1
т. е. чтобы Ф* (х2) 6 Nt.
Рассмотрим теперь противоположное предположение, т. е. допустим,
что имеет место сходимость интеграла
1
равнозначная [вследствие F)] неравенству вида,
A2)
П«1
при 0 <; х <^ оо. В таком случае справедлива
Теорема 1. Если целая функция
1 Как известно, для случая, когда Фо (х) ?Ш — модуль целой функции конеч-
конечной степени, эта задача давно решена (независимо от ее четности и принадлежности
классу No). В заметке A0) М. М. Джрбашян рассмотрел непосредственно случай Фо (x)(<N0
и установил существование верхней грани для первой производной | G'p {x)\ при
х = х0 (— оо <С х < ооO если G (х) — многочлен любой степени.
562

{т. е. полустепени (п) р^>0) удовлетворяет неравенству
|#р(я)|<Ф'(я) (~оо<х<оо), A3)
где Ф* (х) удовлетворяет условию A2) при х^>0, то, какова бы ни была
Ф* (х) при х<СО, имеем г
оо
( + ^г) (-<*>< *<«>)• A4)
n=l
В самом деле, неравенство A3) означает, что
оо оо
} X I2
+ Ж7| '
где Gp(x) = Hv(x2)—целая функция конечной степени р. Поэтому, при-
применяя известные неравенства A2), находим, что
п=1 '
Следовательно, при всех действительных х имеем
Нр (- |х \) |< сП A + Ч^Ц ер^^< 2сеР^" Д
п=1 ^ ' '" / п=1
Из полученного таким образом неравенства A4) видно, что для функ-
функции конечной полустепени Нр (х) функция Ф* (х) является майорантой
конечного роста (нулевого рода).
Однако очевидно, что если вместо функции конечной полустепени Нр (х)
(которая всегда нулевого рода, а следовательно, и нулевой степени) взять
в неравенстве A3) функцию степени ^>0 (или, вообще, бесконечно уве-
увеличивать полустепень /?), то правая часть неравенства A4) обратится в
бесконечность при всяком х<^0. Кроме того, из известного (8) необхо-
необходимого условия, чтобы функция | Gq (x) |, где Gq (x) — целая функция
конечной степени q ^ 0, была майорантой, следует, что если | Gq (x) \ ^>
^> с > 0 при х^>0, то | Gq (x) \ не может быть майорантой при условии
~ \og\G (х)\
jr dx=oo. A5)
Таким образом, в частности, если Ф* (х) = \ Gq (x) \ 6 N\ при
[т. е. соблюдается A5)], а при х^>0 соблюдается A1), то функция
Ф*(#), обладая всеми свойствами майоранты для функций Hv{x) конеч-
конечной полустепени р, не является, однако, майорантой для всех прочих
функций любой конечной степени
1 Т. е. даже если Ф* {х) = оо при х < 0, так что фактически неравенство A3) не
налагало бы непосредственно никаких ограничений на Нр (х) при х < 0.
563 36*

Такого рода сильно несимметричные функции Ф* (ж), которые, не бу-
будучи майорантами, играют роль майорант* для тех функций (а именно,
для всех функций конечной полустепени, в частности, для многочленов),
для которых они служат майорантами даже только на одной соответству-
соответствующей полуоси, я предлагаю называть полу майорантами.
В качестве примера полумайоранты укажем функцию
Ф* (х) = е~х + eWa, где a < 1j2.
Ввиду того, что, как показано выше, для многочленов полумайоранты
обладают на всей оси свойствами майоранты, справедливо
Следствие. Полумайоранта не может быть весовой функцией (и на-
наоборот) .
Однако вследствие теоремы 4 моей заметки [97], если приближать
произвольную непрерывную функцию f (х) = о [Ф*(#)] целыми функциями
Gq<) (х) фиксированной степени д0 ^>0, то при любом данном е^>0 можно
осуществить неравенство
\f(x)-Gqo(x) \<вФ*(х) (-оо<х<оо)
какова бы ни была данная полумайоранта Ф*(х).
ЦИТИРОВАННАЯ ЛИТЕРАТУРА
Поступило
22. V 1952 г.
1 С. Н. Бернштейн. Докл. АН СССР, 77, 549 A951) [102].
2 S. Bernstein. Legons sur les proprietes extremales etc. Paris, 1926. [«L. S.»].
3 С. Н. Бернштейн. Экстремальные свойства полиномов, 1937. [«Э. П.»].
4 С. Н. Бернштейн. Докл. АН СССР, 77, 773 A951) [103].
5 В. С. Виденский. Докл. АН СССР, 84, № 3 A952).
6 С. Н. Бернштейн. Докл. АН СССР, 60, 949 A948) [94].
7 S.-Bernstein. С. R., 176, 1782 A923) [23] (том I).
8 С. Н. Бернштейн. Докл. АН СССР, 66, 545 A949) [98].
9 С. Н. Бернштейн. Докл. АН СССР, 52, 565 A946) [84], заметка III.
10 М. М. Джрбашян. Докл. АН СССР, 84, №1 A952).
11 С. Н. Бернштейн. Изв. АН СССР, серия матем., 13, 111 A949) [99].
12 Н. И. Ахиезер. Изв. АН СССР, серия матем., 10, 411 A946).
13 С. Н. Бернштейн. Докл. АН СССР, 65, 117 A949) [97].
* Отсюда видно, что Ф*(х) не может быть весовой функцией, так что ответ на
вопрос, поставленный в заметке Н. И. Ахиезера и К. И. Бабенко (Докл. АН СССР,
хп
57 {1947)), являются ли условия ф(ж)>1 (—ооО<со), lim —- = 0 совместно О
±х>оо ф(х)
оо
условием I ]2? ^dx = оо достаточными для того, чтобы <р (х) ?W, оказывается
J 1+я2
отрицательным. (Автор.)

108
ОБ АНТИМАЙОРАНТАХ *
Статья содержит доказательство и обобщения одной теоремы об антимайорантах,
ранее формулированной автором.
1. В заметке (*) я назвал антимайорантой всякую функцию Н(х)^-0
(_ оо<<а;<;оо), обладающую свойством, что неравенство вида
|Gp(s)|<#(x) (-оо<ж<ос), A)
где Gp (х) — целая функция данной конечной степени р > 0, совместимо
на любом отрезке [а, Ъ] действительной оси с неравенством
sup| G'p{x)\>N, B)
как бы ни было велико N. ¦
Очевидно, что антимайоранта не может быть майорантой конечного
(или квазиконечного) роста. Однако класс рассматриваемых веществен-
вещественных функций нужно, повидимому, подчинить некоторым ограничениям
для того, чтобы можно было утверждать, что если функция F ft)
этого класса не является антимайорантой, то она непременно должна
быть майорантой конечного (или квазиконечного) роста. В упомянутой
заметке (*) я сформулировал без доказательства утверждение такого
рода (теорема 4), вводя ограничение, что F (х) > 0 - почти возра-
возрастающая1 функция, равная модулю целой функции конечной степени.
Основной целью настоящей статьи является доказательство этой теоремы
с соответствующим ее обобщением и уточнением **.
* изв АН СССР, серия матем., 16 A952), стр. 497—502.
1 Функция Я (х) > а > 0 называется (см. О) почти возрастающей (при ± *-*»>•
когда существует такая постоянная (не зависящая от х и y)c>i, что Н(у)<сН (х)
при 0<JL<i для всех достаточно больших \у\. В дальнейшем, не нарушая общ-
общности рассуждений, для упрощения письма положим Я (*) > 1 и примем с = 1 [т. е.
Н(х) будет просто монотонно возрастающей функцией в обоих направлениях].
** Статья 1108] в основном была написана уже в 1948 году одновременно с упо-
упомянутой заметкой [97] (которую я тогда также несколько откладывав>" ™«*
получить более законченные результаты). В частности, я предполагал что теорема 4
[97] может быть существенно улучшена. Не продвинув этого вопроса в течение
565

Введем еще одно определение, которое соответствует понятию, вклю-
включенному в формулировку упомянутой теоремы. Назовем функцию Н (х)^>0
слабо весовой (Н (х) 6F, VzdW), если всякая непрерывная функция
/ (х) (—оо<^х<^оо), стремящаяся к нулю* при х ~> 4^ оо, может быть
равномерно на всей оси приближена с весом Н (х) при помощи целых
функций Gp(x) любой данной (произвольно малой) степени р^>0, т. е.
если для сколь угодно малого е ^> О можно построить целую функцию
Gp (х, е) степени р, удовлетворяющую условию
\f(x)-Gp(z9*)\<*H(x) (-оо<я<оо). C)
Легко видеть,что конечная слабо весовая функция Н (х) dV (так же как и
всякая весовая функция) является антимайорантой.
Действительно, пусть функция / (х) в неравенстве C) с г -»0 при
данном р^>0 имеет в данном промежутке (а, Ь)
sup
D)
В таком случае все Gv (х, г) удовлетворяют на всей оси неравенству
|Gp(s,e)|<c#(s), (Ibis)
где с^>0 — фиксированная постоянная; между тем, из условия D) сле-
следует, что, как бы велико ни было N^>0, неравенство
невозможно для всех х внутри (а, 6),
2. Общая лемма. Пусть почти возрастающая функция Н\
обладает свойством, что на некоторой последовательности отрезков
[—7U|in, tcjiJ бесконечно возрастающей длины существуют многочлены
ie(n)
Яп(#) степени п<^ррп9 корни которых pj^e k (k = 1, 2,. . . ,п) для
п —> оо удовлетворяют условию
' п |sin0inM
причем, как бы мало ни было е
\H(t)-RJt)\<*H(t) (-«itn<*<«|ij. F)-
В таком случае Н (х) есть слабо весовая функция
четырех лет, я опубликовал доказательство этой теоремы лишь в настоящей статье.
Однако теперь, через год после опубликования этой статьи, вопрос в основном раз-
разрешен полностью. Читатель найдет в заметках [109—111] последовательные этапы его
решения; здесь я формулирую только следующее предложение:
Всякая почти возрастающая функция Ф (х) > с > 0 (— оо <^ х < оо) является либо
майорантой, либо антимайорантой. (Автор.)
* Если Н (х) — почти возрастающая функция, то, как очевидно из доказатель-
доказательства общей леммы, достаточно потребовать, чтобы / (сх) =о (Я (#)) ПРИ любом фикси-
фиксированном с > 0 (+ х -> оо). (Автор.)
566

Для доказательства замечаем, что, какова бы ни была данная непре-
непрерывная функция ср (х) [lim ср (х) = 0], вследствие теоремы II монографии
B) (стр. 156) можно при любом s!>0 удовлетворить неравенству
9@
Лп@
<s (-^<г<оо), G)
где Рп @ — многочлен степени не выше п.
Положим
(8)
Нечетная функция tn(x), которая является целой функцией степени
— , возрастает от —п\ъп до тсрп, когда х растет от —оо до + оо, при-
причем всегда | tn (х) | <; [ х |. Поэтому, если Рп (t) — многочлен степени п
относительно t, то
будет целой функцией степени р = —, и неравенство G) можно за-
записать в виде
о (-
H(tn(x)) H(tn(x))(l +
где. | s' | <^ е, согласно F). Следовательно,
| ? («п («)) A + е') -^р>п(х)\<еН (tn (х)) A + в),
и так как ср (гп (х)) -»0 при |?п(ж) [->оо, то имеем также
| ср [tn (х)) -Sv.„ (х) |< 2еЯ (<п (х)) < 2еЯ (х) (- оо <ж< оо). A0)
Остается доказать, что при п достаточно большом будем иметь
|?М*))-?(*)!<*#(*) (-оо<*<оо). (И).
Для этого фиксируем L настолько большим, что ср {t)<^-^-H (t) для всех
\t\^> -о- • Как бы мало ни было данное а > 0, бу
ветствующие достаточно большие л, чтобы иметь
-о- • Как бы мало ни было данное а > 0, будем рассматривать соот-
соотПоложим сначала, что
?<*<-^-?. A2)
567

Тогда
X
, ,_л о.. ^Ы . „ Sin2
Следовательно, если ж удовлетворяет A2), то
\tn(x)\>±-L, A3)
но, учитывая, что |^п(ж)| растет вместе с \х\, заключаем, что неравен-
неравенство A3) будет всегда вытекать из неравенства
|s|>L. A4)
Поэтому при соблюдении A4) осуществляется и (И).
Предположим, напротив, что | х |< L. В таком случае имеем
V"n . L1» Г1 . I2
- sin «-— > —sin a ,
откуда (учитывая, что | *n (#) | <С|ж I)
Поэтому, взяв а достаточно малым, чтобы иметь
jcp (%) — ср (ж2)|<е,
когда ] #! — ^21 <С Р и | Ж11 <С ^» ! ^21 <С ^> получим
•! ?(«)-? (*« И) |< s < еЯ @)< аЯ (ж).
Следовательно, неравенство (И) осуществляется при всех х, и мы полу-
получаем [складывая A0) и (И)]
[6 {t)—Sv, п (х) | < ЗеЯ (х) (- оо <ж < оо). C bis)
3. Теорема1. Если \Н (х)\ — почти возрастающий модуль целой функ-
функции Н (х) конечной степени /?0, корни которой ak -j- фЛ удовлетворяют
условию
00 I A I
т?ш ,| // (х) | есть слабо весовая функция и тем более Н (х) является
антимайорантой* [108.1].
1 Эта теорема, по существу, эквивалентна теореме 4 заметки (х), так как необ-
необходимость условия A5) для того, чтобы | .fiT (cc) | была антимайорантой, доказана
мною в той же самой заметке.
* В статье [110] доказано, что, какова бы ни была почти возрастающая (при ж>0)
чвщная функция | Н( х) |, условием, необходимым и достаточным для того, чтобы она
была слабо весовой, является требование, чтобы она была антимайорантой. (Автор.)
568

Пусть
со
\ «Л/1 ¦ / | lA/yyitAs m
m=0
Тогда из условия A5) следует, что корни многочлена
п
¦Tin [ft) — /1 umX
m==0
ak,n + i$k,n при п достаточно большом будут удовлетворять неравенству
как бы велико ни было данное число М, так что многочлены Rn (x)
удовлетворяют условию доказанной выше леммы на любых бесконечно-
возрастающих промежутках (— iz^n, ^г), где ^П<С—•
Особый интерес представляет применение нашей теоремы к сильно1
асимметричным функциям, когда условие
равнозначное условию A5), имеет место, хотя не только
но и
оо
С log! Я
\ — 1/
оо.
Примером такой функции может служить функция
Эта функция будет, по доказанному выше, слабо весовой функцией (т. е
антимайорантой), тем не менее, как показано в моей заметке C), она
обладает свойствами майоранты по отношению к многочленам и вообще
по отношению ко всем функциям конечной полустепени.
Таким образом, в общем определении майоранты (как и антимай-
оранты) существенно, чтобы степень р рассматриваемых функций конеч-
конечной степени была положительна (р > 0) (эта оговорка отпадает в случае
четных функций).
569

Примечание. Заметим, что условию леммы могут удовлетворять
и целые функции выше 1-го рода (т. е. бесконечной степени). Пусть,
например,
Н (х) = 2j аЪхк = 2j пкхк + 9п (%),
где
Тогда, если
(z)dz
lim max я
|2 |= К
то рп (#) —> 0, при п = pR и | х | <С е^, для соответствующей бесконечно
возрастающей последовательности значений R.
Таким образом, доказанная выше теорема распространяется также на
такие целые функции бесконечной степени.
4. Следствие 1. Если Н (х) — антимайоранта, a G* (х) — любая данная
функция конечной степени, то произведение \ G* (х) \ Н (х) также будет
антимайор антой.
Действительно, пусть при неравенстве
верхняя грань производной С'р>п(ж) для некоторой последовательности
•функций GVtn(x) конечной (ограниченной) степени р^>0 бесконечна
в промежутке (а, Ь). Тогда целые функции GVt n (х) и G* (х) конечной
(ограниченной) степени будут удовлетворять неравенствам
\Gp.n(x)Gm(z)\<^\(?(x)\H(z),
причем в гом же промежутке верхняя грань производной [GPt n (x) G* (х)]
также бесконечна, так как G* (х) имеет лишь конечное число нулей на от-
отрезке [а, Ь] и производная G* (х) ограничена на [а, Ь].
Следствие 2. Пусть целая функция конечной степени Н (х)^>0 не
является функцией конечного роста [т. е. удовлетворяет условию A6)].
В таком случае, каковы бы ни были функция р (х) > с > 0 и действи-
действительная постоянная а, функция
F{x) =
I G?^
A7)
будет антимайорантой.
Достаточно рассмотреть случай, когда р (х) = 1, а = 0. Замечаем
тогда, что функция F (х) =
I ИХ
возрастает при х —> ^Ь оо, причем
\ Н (х) dx есть функция конечной степени. Таким образом, если мы под-
о
570

чиним непрерывную функцию ср (х), фигурирующую в доказательстве
общей леммы, дополнительному требованию, чтобы отношение 2_W было
ограничено на всей оси, то для таких функций будет осуществимо не-
неравенство C bis) [т. е. C)], если в его правой части стоит функция
F(x) =
t dx
A7 bis)
[которая удовлетворяет условиям определения почти возрастающей функ-
функции, кроме требования F (х) > Ъ >> 0]. Можно сказать, что F (х) является
слабо весовой функцией с точностью до множителя х и, при помощи
рассуждения, сделанного на стр. 566, заключаем также, что F (х) —
антимайоранта [108.1].
Поступило
22. VIII 1952 г.
ЦИТИРОВАННАЯ ЛИТЕРАТУРА
1 С. Н. Бернштейн. О майорантах конечного или квази-конечного роста.
Докл. АН СССР, 65 A949), 117—120 [97].
2 С. Н. Бернштейн. Экстремальные свойства полиномов и наилучшее прибли-
приближение непрерывных функций одной вещественной переменной. М.— Л., 1937. [«Э. П.»].
3 С. Н. Бернштейн. О нормально возрастающих весовых функциях и майо-
майорантах конечного роста. Докл. АН СССР, 85 A952), 257—260 [107].

109
УСЛОВИЕ, НЕОБХОДИМОЕ И ДОСТАТОЧНОЕ ДЛЯ ТОГО,
ЧТОБИ ЧЕТНАЯ НЕУБЫВАЮЩАЯ ФУНКЦИЯ
БЫЛА ВЕСОВОЙ*
1. В настоящей заметке доказывается следующая теорема**:
Теорема А. Условие, необходимое и достаточное для того, чтобы
четная функция Ф (х) > 1 (— оо < х < оо), неубывающая при #>0, были
весовой, состоит в том, что бесконечна верхняя грань сумм
A)
г ал n -f- ifJfc, n — ко/?«гг произвольно взятых четных (или имеющих чет-
четный модуль) многочленов Rn{x) любой степени п, удовлетворяющих
условию
|Яп(*)|<Ф(*) (|Дп@)|>0) B>
(нормированных каким-нибудь условием вида \ Rn @) | = сФ @), 0<с<1).
Докажем сначала, что наше условие необходимо, т. е. что функция
Ф (х) не может быть весовой, если
<° C>
Можем принять, для сокращения письма, что
Ф (х) = 1 D>
на некотором данном отрезке [—а, а].
Итак, допустим, что существует функция F (х) ( lim ф , * =0], для
которой при всяком 8 > 0 найдутся многочлены Р (х, е), удовлетворяющие
неравенству
| JF (о?) — Р(х, е)|<еФ(ж) (— ос<х<сх)). E)
* Докл. АН СССР, 88 A953), стр. 589—592.
** Эта теорема существенн- j дополнена в моих двух последующих заметках
[110, НИ]; см. также [109.1] и [111.1]. {Автор.)
572

Пусть F (х) удовлетворяет также условию
B<:F(x)^AO(x) (-оо<ж<оо),
где 11ъ<СВ<С.А<^1. Тогда для достаточно малых е
| Р (х, е) |< Ф (х) (-оо<ж<оо)
и (вследствие D))
Пусть теперь — а
X ±Х0
. Вследствие G)
(— оо<><оо),
F)
имеем
(?)
(8)
(9)
так как
<С\х\ при | х | >> а ;> х0, а при | х \ <^ а имеем [благо-
[благодаря D)] Ф у -^ Х° ) = Ф (ж) = 1. Следовательно, полагая
A0)
находим, что многочлен RUy Жо (х), степень которого п (зависящая от s)
достаточно велика, удовлетворяет неравенству
A1)
при любом х0 (—а
также
2 ' 7 ' * V 2
(— оо <^х<^ ос)
а). Но, с другой стороны, вследствие A0) имеем
s (х) + it(x)
; A2)
разлагая на сопряженные множители четный многочлен
и {х)] [s {х) _ и
так, чтобы все корни а.к -\- i$k (которые являются функциями е, х0, п)
многочлена s (x) -\- it (x) степени п лежали в верхней полуплоскости.
Кроме того, вследствие (И), имеем, согласно условию C),
C bis)
причем [для краткости пишем Р (х) вместо Р {х, г)]
к=1
573
A3)

Таким образом, применяя мою теорему (х) (стр. 139) о максимуме
производной* к неравенству A2), находим, полагая х = О,
1
(учитывая, что всякому корню а^ + i$% при а# ^ О соответствует другой
корень аг + фг, где оц = -*- ай, pi = pft). Принимая во внимание (8), заклю-
заключаем из A4) и C bis), что
|P'(^?)K2 2-Air<A A5)
при всех значениях х на отрезке [—а / 2, а/2]. Поэтому функция F(x),
удовлетворяющая E), удовлетворяет условию Липшица
A6)
т. е. не может быть произвольной непрерывной функцией на [— а / 2, а / 2]
и, следовательно, Ф (х) не является весовой функцией.
Что касается достаточности высказанного в теореме условия, то она
доказана, по существу, в моей монографии (х) (стр. 145—146), только
там на (опорные) многочлены Rn(x), удовлетворяющие B), наложено
ограничение, что их коэффициенты вещественны. Однако легко видеть,
что доказательство остается в силе и без этого ограничения, если восполь-
воспользоваться вместо неравенства B3) (х) [?д!^(х) j х j < х/2 М, где R п (х) > О
(стр. 145)], основным неравенством A6) (х) (стр. 141) (частным случаем
которого является упомянутое неравенство B3) (х) (см. [102. 1]):
"=|ДпИ|).
2. Доказанной нами теореме эквивалентна
Теорема А*. Для того чтобы четная неубывающая при х^>0 функ-
функция Ф(^)>0 (—оо<^<ос) была весовой (Ф(х)(:\?), необходимо и до-
достаточно, чтобы учетных многочленов Rn{%) [\Rn @))=сФ @)], удовле-
удовлетворяющих B), была, бесконечна верхняя грань значений
? 1од|Дя(*)/Дп@)|
Ьп=\ 5 Я^'
Для доказательства достаточно показать, что, каков бы ни был чет-
четный (действительный) многочлен R (х) ^ 0 (R @) = 1), имеем тождественно
* См. также [23] (том I). В первоначальном тексте ссылка на литературу содер-
содержала опечатку, подавшую, повод к недоразумениям. (Автор.)
574

где
R (х) = ер(х) = П[1-\—^Л если полагать, как в (х) (стр. 148)г
= $к — ioifa причем, если ак ^ 0, то будет также сопряженное bjc= f3fc
Интегрируя по частям левую часть A7), получим
о
X
Но \ ——-— = -=— arc tg -=— , так что, полагая сначала а# = 0, имеем
J х2 + Ь% ** & h
ОО
Г dx 7Z
2 \ —2 = т—, причем, учитывая, что обе части последнего равенств»
о к
являются аналитическими функциями комплексной переменной Ьк=^к — 1ак
(регулярными при $к > 0), заключаем, что оно остается в силе для любых
afcSO. Таким образом, соединяя попарно сопряженные члены, соответ-
соответствующие Ьк и bjc, получим из A8) формулу A7).
Следствие 1, Для того чтобы четная неубывающая функция Ф (#)>(>
была весовой (Ф(^)бИ7), необходимо и достаточно, чтобы неравенство
\Р(х)\<Ф(х) (— оо < х<С оо), G bis)
где Р (х)—многочлен (сколь угодно высокой степени), было совместимо^
в любом данном промежутке (а, Ь) с неравенством
sup | Р' (х) | > N,
как бы велико ни было N.
В самом деле, необходимость очевидна. (См. [102], стр. 529.) Достаюч-
ность вытекает из доказательства [неравенство A5)] теоремы А.
Следствие 2 (Н. И. Ахиезера и К. И. Бабенко B)). Если четная
неубывающая при х-^оо функция Ф (х) ^ 1 удовлетворяет условию х
'пЩМ^.<ООг A9>
то функция Ф (х) не может быть весовой. (См. [111], стр. 589.)
1 Следствие 2 было впервые доказано в 1947 г. в заметке B) Н. И. Ахиезера
и К. И. Бабенко без ограничения монотонности и четности Ф(х). Аналогичный ре-
результат вновь получен в недавней статье Л. Карлесона D). В письме ко мне (от-
(отправленном из Еревана 28. VIII 1952 г.) М. М. Джрбашян сообщил, что ему удалось
установить теорему р максимуме производной многочлена Р (х) при неравенстве-
| Р (х) I < Ф (х) (— °° < х < оо), где Ф (х) > 0 — любая неубывающая четная функ-
функция, удовлетворяющая A9) (ранее в заметке C) он вводил дополнительное предполо-
предположение, что Ф(х) возрастает нормально). Прибавлю, наконец, что теорем, эквивалент-
эквивалентных моим теоремам А, А* и следствию 1, нет ни у одного из названных авторов.
575

Действительно, полагая, например, Ф (х) = 1 -f- х2 при — 1 <^ х<^ 1,
видим, что все четные многочлены, удовлетворяющие условию
|Д(х)|<Ф(я) (|Д @)| = 1), (-оо <*<«>), B0)
подчиняются условию
оо
Г log| Д («) |<fa ^
так что по теореме А* функция Ф (х) не будет весовой.
Легко видеть, что вытекающее из следствия 2 необходимое условие
= оо B1)
для того, чтобы четная неубывающая функция Ф (#) ^> 0 была весовой,
«е является вообще достаточным.
Действительно, пусть неубывающая четная функция Ф(ж)>0, удовле-
удовлетворяющая B1), обладает свойством, что существует целое число т^>0,
для которого
т
^^ = 0. B2)
ш
1<*<оо Х
В таком случае ясно, что все многочлены Rn (x), удовлетворяющие B),
должны быть степени п<^т. Но*, с другой стороны [вследствие B)],
1 R п {ос) |< Ф A) = С (— 1 < х < 1).
Поэтому при | х | ;> 1
Следовательно,
-г—dx<logC+\ —-ф—cfa= log С+ /11A +log 2).
1 1
Таким образом, согласно теореме А* функция Ф (я), пример которой
приведен ниже, удовлетворяющая условиям B1) и B2), не может быть
весовой.
Положим (к ^ 1)
Ф (Х) = ех" = Xn+i (хп + 1 < х < хп+1), B3)
* Из-за недостатка места окончание первоначального текста было сокращено.
(Автор.)
576

так что монотонная функция Ф (х) растет от x% до Хп+i в промежутке
(хт хп+1). Тогда Хт = 0 при всяком т>&. Но, с другой стороны,
если 3<%<Tin±1. Следовательно, условие B1) также выполняется.
Условие B1) также выполняется, если, полагая xn+i = е* Хп, определить
монотонную функцию Ф*(х) (вместо B3)) равенствами
Ф*(я?) = ех" = х1п0**^ (хп + 1 <х <xn+i). B3 bis)
В таком случае все Хт^>0, но можно показать, что-бесконечный ряд
Напомню, что, как показано в статье [102], условие
|^т=оо B4)
достаточно для того, чтобы функция Ф(#)>0 была весовой. Таким об-
образом, из B4) всегда следует B1). Как видно из примеров B3) и B3 bis),
обратное утверждение, вообще, неверно (вопрос о том, будет ли функция
B3 bis) весовой, остается открытым). Но в той же статье [102] показано,
что для функций <D(x)(:N условия B1) и B4) эквивалентны.
Поступило
10. XII 1952 г.
ЦИТИРОВАННАЯ ЛИТЕРАТУРА
1 С. Н. Бернштейн. Экстремальные свойства полиномов A937). [«Э. П.»].
2 Н. И. Ахиезер, К. И. Бабенко, Докл. АН СССР, 57, № 4 A947).
3 М. М. Джрбашян. Докл. АН СССР, 84, № 1 A952).
4 Lennart Carleson. Proc. Am. Math. Soc, 2, December A951).
37 с. Н. Бернштейн 577

110
УСЛОВИЕ, НЕОБХОДИМОЕ И ДОСТАТОЧНОЕ
ДЛЯ ТОГО, ЧТОБЫ ПОЧТИ ВОЗРАСТАЮЩАЯ (х)
ЧЕТНАЯ ФУНКЦИЯ БЫЛА СЛАБО ВЕСОВОЙ*
1. Для краткости письма мы ограничимся здесь, как и в заметке B)?
рассмотрением четных монотонно возрастающих (при х^>0) (ч. м. в.)
функций Ф (х) ^> 1 и прибавим, кроме того, допущение, что lim -=-r-r = 0.
Теорема В, Пусть Нр (х) будут любые целые функции с четным мо-
модулем \Нр(х)\ той же фиксированной степени р^>0 (| #р @) | > 0), удов-
удовлетворяющие неравенству
|Яр(ж)|<Ф(ж) (-оо <*<«>). A)
Для того чтобы ч. м. в. Ф (х) была слабо весовой х функцией, необходимо и
достаточно, чтобы была бесконечна верхняя грань Lp функционала
S[Hp(x)]=Hp@) S'4tT2 <2>
a + Р
для всех рассматриваемых функций Нр(х), где а* + ??л — корни Нр(х)*.
Сделаем два предварительных замечания. 1) Если
sup S[Hp(x)]=Lp, C)
|Яр ()|<Ф()
* Докл. АН СССР, 90 A953), стр. 487—490.
1 Функция Ф (а?) > 0 (— оо < х < оо) называется слабо весовой (г) (Ф (х) ? V),
если, каково бы ни было данное число р > 0 и какова бы ни была непрерывная
функция / (х) (lim / (х) = 0), можно построить такую последовательность целых функ-
ций Gp^ n {х) степени -< р, что равномерно на всей вещественной оси
lim =0,
п-»со Ф (X)
(Требование lim f(x) = 0 можно заменить менее ограничительным условием
f (х) — о [Ф (сх)] при х -» + оо, каково бы ни было с > 0).
578

то при всяком с>0
sup S [Яр(а)] = cLp. C bis)
|Яр (х)|<()
2) Каково бы ни было 6 @< 6 < 1),
D)
Первое утверждение следует из того, что неравенство A) равнозначно
неравенству с | Нр (х) | ^ сФ (х). Для получения второго утверждения доста-
достаточно заметить, что, благодаря монотонности Ф (х),
j Нр (Щ | = |Яер (х) | < Ф (Щ < Ф (х),
но
оо
2 2 р^. I 0
Докажем сначала достаточность. Беря Л/>1 произвольно большим,
можем подобрать функцию Нр (х), для которой
S[Hp(x)]>2M,
и затем, взяв п0 достаточно большим, построим (пользуясь строкой
Тэйлора) последовательность четных многочленов Вп (х) степеней
Яп @) = Нр @)], корни которых (Xjctn+iPft,n удовлетворяют условию
2
k=i aft, п
причем, полагая Хп = -^-, получаем
о/?
-^ =е<1 (-ап<^<Хп). F)
Вследствие 'E), согласно неравенству A6) стр. 141 монографии C),
можно построить (см. также [102.1]) такие четные многочлены Рп(х) сте-
степени не выше щ что
\\x\-Рп(х)\<г\Пп(х)\ (-оо<><оо); G)
при этом, благодаря F), имеем, в частности,
1|*!-*»('I<е(|Яр@Н-1) (-*»<*<**)• (8)
Положим теперь
t = tn (x) = ),n sin -^- . (9)
А
В таком случае при —оо<^х<;оо имеем | tn (х) | ^Хп и j tn (x) \ ^| ж |.
3 другой стороны, полагая
С^(х) = />„(гп(ж)), A0)
579 37*

видим, что G*p<t (x) будет целой четной функцией переменной х степени
р0.^ — = Зр. Поэтому из неравенства (8) после подстановки (9) вслед-
ствие A) получим
sm
< г [Ф (tn (х)) + 1] < е [Ф (х) + 1] < 2вФ (х). A1)
Заметим еще, что, каково бы ни было е>0, при Хп достаточно большом
I — х
Sin * 1I <2еФ (ж) (— оо <х<С оо). A2)
Складывая A1) и A2), получаем
; оо^. A3)
Применяя то же самое рассуждение, что в монографии C) (стр. 145—146)
(см. также [102.1]), получим из A3) аналогичное неравенство
|/(х)-СРв(а01<еФ(я) (—оо<я<оо) A4)
для любой непрерывной функции f(x) = o{i) при ж->Ч=оо# где<7Рв(#)—
целая функция степени <^ р0.
2. Доказательство необходимости, т. е. доказательство того,, что при
условии
sup S [Нр (x)] =Lp<oo A5)
|Яр(х)|<Ф(зс)
Ф (х) не может быть слабо весовой, аналогично тому, которое было
дано для случая весовых функций B). Однако для дальнейшего полезно
записать соответствующие неравенства в общем виде.
Лемма. Если функция Hv (х) с четным модулем той же степени р
(в частности, если Нр(х) имеет вещественные коэффициенты) удовлетво-
удовлетворяет A), то имеет место неравенство*
В самом деле, если представить \Нр(х)\ в виде
| Нр (х) | = | sv (х) + it, (х) | (| Яр @)! > 0),
1 Для этого фиксируем L так, чтобы иметь |#|<еФ(#) при \x\^>L\ для этих
значений х неравенство A2) соблюдено при любых Хп. После этого берем \п на-
настолько большим, чтобы при | х | < L неравенство A2) также осуществлялось.
* В первоначальной редакции доказательство неравенства A§) (и примечание)
были опущены. Если степень р ^ р0, где 2pQ степень |#р(#)|2, то /?>/>0 и при
Яр(ж) = Лр(ж) + iBp(x) по крайней мере одна кз вещественных функций А (х),
Bv(x) бУДет степени р (хотя | Нр(х) \2=А^(х) -f B^(x) — степени 2р0); поэтому нера-
неравенство A6) применимо к обеим функциям Ар(х) и Вр(х), так как каждая из них
(степени <jd) удовлетворяет A). (Автор.)
580

где
то вследствие теоремы Б. Я. Левина D) имеем [на основании A5)]
1 1
\н'р @) |< | hv @) 11 *; @) + и'р @) | = | hv @) |
A6 bis)
Примечание. В сущности применение теоремы Б. Я. Левина не
является принципиально необходимым, так как при предположении, что
| Hv (x) |2 является четной функцией конечной степени 2р, из A5) следует, что
нр
нР @) (о, (») + «, (,)) = яр @)
где ек и е^. равны +1, выражается сходящимся произведением.
Таким образом, во всяком случае,
оо
//; @) i = i jyp (о) i
Из A6) следует, что если Rv (x) — любая вещественная функция сте-
степени^/?, удовлетворяющая A), то
Для доказательства1 A7) замечаем, что
| Лр (ж) |< |#р (*) | = | Л, (х) +
(- я) |
(х),
и применяем C bis) к Нр (х).
Учитывая далее, что вследствие четности и монотонности Ф (х) имеет
место неравенство
(_00<Жо<00)_00<ж<оо)
получим
+
4- Н*
2 1 1^ Р \ 9
A bis)
Следовательно, вроизвольно фиксируя постоянную х0 (— оо <^ х0 <^ оо),
1 В случае JRp @) = 0 можно положить Нр s (а?) = | i?p (яг) + г + * (¦Rp(— *) + ?I
с произвольно малым е > 0.
531

для производной функции i?p/2 (^ xo)=Rp(—2~~^) степени j°/2 B точке
х = О имеем
т. е. [полагая Ф @) = 1] получаем
I Rv (x) \< 2 V%~ Ьр!2ФBх) (— оо <z < oo). A8)
Следовательно, осуществление A4) невозможно, если функция / (х) на
каком-нибудь данном конечном отрезке не удовлетворяет условию Липшица.
Из A8) вытекает
Следствие 1. Для того чтобы ч. м. в. функция Ф(х)^>с^>0 была
слабо весовой, необходимо и достаточно, чтобы она была антимайоран-
той (х).
Повторяя предыдущий прием, получаем
| R"p (х) |< 2 B 1/2J LPl2 Lp/4 Ф Dз) = 16 Ц>12 Ф Dж) A9)
и аналогичные неравенства для всех последующих производных1.
Теорема С. Если ч. м. в. Ф(ж)>0 не является весовой функцией
(Ф(х)^\?), но для некоторой функции f (x) при любом е>>0 возможны
неравенства
\f{x)-P{x)\< еФ (х) (- оо < х < оо), B0)
где Р(х) — многочлены, то f (х) должна быть функцией вида f (х) = ekx*S (x)t
причем S (х) есть целая функция первого рода, корни которой a& + фл
подчинены условиям
т. е. S (х) —конечной степени и конечного роста.
Теорема D. Если ч. м. в. функция Ф(#)^>0 не является слабо весо-
весовой (Ф (х) 6 V), то свойством, указанным в теореме С, обладает всякая
функция f (x), удовлетворяющая A4).
Ввиду полной аналогии теорем С и D ограничимся доказательством
последней. Для краткости примем, кроме того, что / (х) — четная веще-
вещественная функция и |/ @) | = | Gp @) | >0. На основании условия A5) и
вытекающих из него неравенств A6) и A9) для всего множества рас-
рассматриваемых функций Gv (x) степени р можно указать верхние границы
sup
sp@)
< М', sup
<М\ B2)
При этом, беря среди функций Gv (x), имеющих тот же модуль | Gv (x) |
на действительной оси, ту из них, корни которой ± aA — i$k лежат в ниж-
нижней полуплоскости, получим
1 Верхние границы, которые получаются последовательным применением этого
приема для производных высоких порядков, чрезмерно велики, чтобы останавли-
останавливаться на их вычислении. Если отбросить требование вещественности, то верхние
582

?& —"ft
«откуда
u=iD + PDa '
B2 bis)
„2 , o2\2
¦22^
fe=i
Следовательно, благодаря B2) и B2 bis), имеем
G'P @)
Г + М'* + 2М' = 2М. B3)
Принимая во внимание, что при всех вещественных и комплексных z
заключаем, что все рассматриваемые функции Gv (z), для которых соблю-
соблюдается A4), имеющие вид
во всей плоскости удовлетворяют [вследствие B3)] неравенству
2 / i 2 2 2
|Ср(а)|<|С,@)|в a*+0*<|Gp(O)|e . B4)
Для окончания доказательства достаточно учесть B2 bis) и применить
классическую теорему Стильтьеса или рассуждение, приведенное в «Э. П.»
{см. [102. 1], стр. 618).
В следующей заметке (см. [111]) даны некоторые дополнения к полу-
полученным здесь результатам.
Поступило
7.IV. 1953 г.
ЦИТИРОВАННАЯ ЛИТЕРАТУРА
1 С. Н. Бернштейн. Изв. АН СССР, 16 A952), стр. 497-502 [108].
2 С. Н. Бернштейн. Докл. АН СССР, 88, № 4 A953) [109].*
3 С. Н. Бернгатейн. Экстремальные свойства полиномов A937) [«Э. П.»].
4 Б. Я. Левин. Изв. АН СССР, 14 A950), стр: 45—84.
траницы производных G^4 (х) любого порядка всякой функции Gp (х) = Лр (х)
+ iQp(x)> удовлетворяющейA), получатся умножением на V~2 границ, соответствую-
тцих

111
СЛАБО ВЕСОВЫЕ ФУНКЦИИ И МАЙОРАНТЫ*
Установим сначала новую форму теоремы В заметки B), соответствую-
соответствующую теореме А* заметки (*).
Теорема В*. Для того чтобы ч. м. в. функция Ф(#)>0 была слабо
весовой (Ф(х)бК), необходимо и достаточно, чтобы для всех функций
Gp (x) данной степени р с четным модулем, удовлетворяющим неравен-
неравенству | Gp (x) | >< Ф (х), была бесконечна верхняя грань значений
f log\Gp(x)/Gp@)\ dx
о
Для доказательства нужно проверить, что это условие и условие тео-
теоремы В эквивалентны. Для этого достаточно заменить равенство A7) мо-
моей заметки (х) соответствующим неравенством, а именно: при помощи
интегрирования по контуру, образованному диаметром (— Я, R) и полу-
полуокружностью бесконечно возрастающего радиуса R, можно убедиться,
что при Gv @) — 1 Для четных | Gv (x) | справедливо неравенство
-dx-2^Y |P*
к =
+
A)
Применение теорем А* и В* вместо теорем А и В заметок (х» 2) по-
позволит нам другим способом доказать и усилить теоремы B) С и D.
А именно, имеют место
Теорема I. Всякая четная монотонно возрастающая при х^>0 функ-
функция Ф (х) >> 0 является либо слабо весовой (Ф (х) (: F), либо майорантной
квазиконечного роста C) (Ф (х) 6 5Ш*).
Теорема II. Всякая четная монотонно возрастающая при #>0
функция Ф (х) >>0 является либо весовой функцией (Ф(ж)бИ^), либо
майорантой квазиконечного роста для многочленов (Ф (х) (: ЗЙ^) (т. е.
из возможности при любом е>>0 неравенства**
* Докл. АН СССР, 90 A953), стр. 703—706.
** Это определение класса Шм пригодно в рассматриваемом здесь частном случае
((?(#) — Чф м. в>), в общем случае следует пользоваться определением, соответствую-
584

\/(х)-Р(х)\<еФ{х) (—оо<><оо), B)
где Р (х) — многочлены, следует, что f (x) есть целая функция конечной
степени).
Действительно, согласно теореме (г) А* (соответственно В*), если
(&(x)(:W (соответственно, Ф (х) €V), то, каков бы ни был имеющий чет-
четный модуль многочлен Р (х) (| Р @) | = с > 0) (соответственно, Р (х) —
целая четная функция данной степени р), неравенство
|/>(л)|<Ф(я) (_ооО<оо) C)
влечет за собой*
\ loglf2(a;)l dx^Mp<oc (|P@)| = l), D)
—СО
где постоянная Мр зависит только от Ф (х) (и соответственно, также от
р). Без ущерба для общности заключения ограничимся предположением1,
что log\P (х)\^>— а^> — оо. Тогда из D) следует
Dbis>
Напомню далее, что на окружности радиуса Ь верхняя грань модуля много-
многочленов | Р (beib) | (или канонических F) функций конечной степени р, для кор-
корней ak + i$k которых ряд ^ -*, k* 2 сходится), имеющих данный четный
к=\ Ч + h
модуль [ Р (х) | на всей вещественной оси, достигается в точке ib
тем из рассматриваемых многочленов Р (z), который имеет все кор-
корни в нижней полуплоскости (см. D), стр. 164 — 165, или [102.1],.
стр. 618).
Ввиду этого замечания, применяя известное неравенство Карлемана E)>
мы запишем это неравенство только для z = Ы @ <С Ь < R):
flog, P(X)\ {^ГГР— Д*
^ flog, P(X)\ {^ГГР— Д* + *^ Ц+Р, E)
R у >
щим данному в статьях [94] и [97], т. е. говорить, что Ф(х) ? Ш% тогда и только-
тогда, когда для всех многочленов, удовлетворяющих C), справедливо одно и та
же неравенство вида G). (Автор.)
* Из неравенства A) следует, что каждый раз, когда соблюдается D), то имеег
место и неравенство A5) статьи [110] (и наоборот) независимо от предположения
монотонности Ф(х). (Автор.)
1 Полагая, например, многочлен Р (х) вещественным (Р @) = 1, Ф @) > 1), мо-
можем ввести Р± (х) = Р^|+*' f тогда j/_L ^ | рх (х) | = y^HS^LtL <ф(,х),
J0! @) J = 1. Но теоремы I и II, верные для Р± (х), верны также для Р (х).
585

где
7 (JR2 — Ъ2) sin 9
< n (д» _ 62) \ log ( Р (Re1*) | sin cp dcp. E bis)
о
Рассмотрим сначала- случай, когда Р (х) многочлен (или любая функ-
функция нулевой степени). Полагая Д-» оо (при фиксированном Ь^>1), видим,
. log | Р (Де*Ф ) I
что р->0, так как lim = ^-=0. Поэтому для всех много
членов, удовлетворяющих C) и D bis) при Ь ^ 1 имеем одну и ту же оценку:
т \o^\P(x)\^^Ml ^
Таким образом, из сделанного выше замечания следует, что в круге лю-
любого данного радиуса Ъ > 1 (| z\ = b) имеем
\Р(г)\<е* ". G)
Следовательно, применяя теорему Стильтьеса (или рассуждение, приведен-
приведенное на стр. 619 [102.1]), так же, как в B), мы убеждаемся, что если имеет
м*
место A), то / (х) должна быть целой функцией конечной степени /?<;—'-.
Теорема II доказана1.
Аналогично доказывается теорема I с той только разницей, что в
случае, когда Р (я) = Gv (x) есть (каноническая) целая функция конечной
степени р^>0, являющаяся, благодаря D bis), аддитивной майорантой F),
мы используем для оценки р в неравенстве E bis) то обстоятельство, что она
имеет индикаторной диаграммой отрезок мнимой оси [—pi, pi] (см., на-
лример, теорему II заметки F)). Поэтому из E bis) получим
Z- 6')
0
(8)
где а—>0 при jR—>оо. Следовательно, при всяком фиксированном
мы получим вместо F)
log Gv (Ы) ! ? log+| Gv (x)\
! ? log+| Gv (x)\ Mp
—оо л
Следствие 1. Ч. м. в. функции Ф* (х) при любом а^>0 принадлежат
к тому же классу V, W, V или W, что и Ф (х)
1 Если вещественная функция / (х) не является четной, то рассматриваем функ-
функцию / (а?) + if (— х) с четным модулем К72 (х) + /2 (—х)-
586

Для всякого целого четного а это вытекает непосредственно из А*
(или В*), откуда то же заключение получаем сначала для любого рацио-
рационального ос, а затем переходом к пределу для всякого а>0.
Дальнейшие предложения уже не будут предполагать монотонности
и четности Ф (х) при +а;->оо и при своей большей общности они, как
правило, могут не быть обратимы*.
Следствие 2. Какова бы ни была функция F (х)^>с^>0, если для
функций конечной степени Hv(x) данной степени р, удовлетворяющих
неравенству
\Hp(x)\-^F(x) (-oc<x<oo), A0)
соблюдается D bis) с определенным конечным Мр, зависящим* только от
F (х) и р, то F (х) будет майорантой квазиконечного роста [F (х) 6 5Ш*].
Аналогичное утверждение справедливо E31% вместо 90?*), если в A0) стоят
многочлены Р (х) вместо Hv(x) [111.1] (см. также [109.1]).
Следствие 3. Если при тех же условиях из неравенства A0) следует,
что | Яр@) |><ср<< оо, то F(x)QW (соответственно, если только для
многочленов | Р' @) | -< с < ос, то F (х) 6 $Шм).
Однако, обратимость следствий 2 и 3 вытекает из предыдущего толь-
только при условии четности и монотонности F(x) (см. [111.1]).
Следствие 4. Пусть F (х) > 0 — любая функция. Если F (х) 6 F, то
11
•с + \ F (x) dx = ф (х) 6 V при с > 0 (то же самое справедливо при заме-
о
не V на W).
Теорема Ш. Если четная функция Ф (х) > 1 (независимо от предпо-
предположения монотонности для х^>0) удовлетворяет условию
o, A1)
то Ф (х) должна быть майорантой конечного роста G) (Ф (х) 6 9Я) (так
Ф()€7 и ФЙ
. * Условие A0) не исключает вообще, что Мр ограничено в то время как бес-
бесконечное множество Е точек, где функция F(x) конечна, не имеет предельной точки
на конечном расстоянии. Таким образом, если в неравенстве B) заменить монотонно
возрастающую функцию Ф(х) функцией F{x) такого рода, то a priori не исключена
возможность, что F(x) является одновременно майорантой и слабо весовой функцией,
т. е. альтернатива, выражаемая теоремами 1 и 2 для ч. м. в. функций, в общем
случае могла бы не иметь места. Кроме того, как следует из предыдущего, 1в случае
монотонности F(x) при + #-хх> М^ конечно при всех />>0, если ж конечно хо-
хотя бы при одном значении р — р0 > 0. Но в общем случае конечность М*^ (очевид-
(очевидно, сопровождающаяся конечностью М* при р < р0) совместима с М* = оо при /?>/?0;
поэтому понятие слабо весовой функции и майоранты соответствующим образом
следует дополнить введением понятия слабо весовой функции класса V(p) относительно
данной степени р и соответственно обозначать через Ш*(р) класс майорант для функ-
дий степени р (см. статью Н. И. Лхиезера, Докл. АН СССР 93, № 6 A953)). (Автор).
587

Согласно сноске на стр. 585, без ущерба для общности вывода можем
положить \Gp(x)\^l. Тогда из неравенства
| Gp (ж) |<Ф (х) (-оо<я<оо) A2)
следует
и для любого данного >
+|GH>l 7 log
6*
По теоремам I, II из A3) следует, что Ф(хN5Ш*, т. е. не может быть
ни весовой, ни слабо весовой функцией. Но при произвольно малом s
можем взять L настолько большим, что
i
Z/2 -4- 1
Тогда, полагая Ь2 ]> L\ из A1), A4) и A5) получим
)
—L
l + lf) = a, A6)
J
откуда, вследствие (9), для всех четных канонических функций Gv (x),
удовлетворяющих A2), получаем при том же самом Ь
log\Gp(be^)\ a
1 <р +-, A7)
и, следовательно, если в неравенствах B) Р (х) = Gp (x) есть функция
степени р ^> 0, то предельная функция / (х) также есть функция той же
степени р.
Как видим,' условие A1) теоремы III позволяет усилить и обобщить
теоремы I и II, но только в одну сторону. Из теоремы III вытекает
Следствие 5. Пусть F(x)^>c^>0 любая измеримая функция. Для
того чтобы F (х) была майорантой конечного роста (F (х) 6 Щ, доста-
достаточно, чтобы
]*?Ш A8)
Действительно, если Нр (х) удовлетворяет A0), то она удовлетворяет
и неравенству | Hv (x) |< F (х) + F (— х) = Ф (х), где Ф (х) > с > 0 — чет-
588

мая функция, удовлетворяющая A1), к которой применима поэтому тео-
теорема III.
Заметим, что F (х) есть аддитивная F) майоранта, так как если
F\ (х) ^> ci ^> 0 также удовлетворяет условию A8), то и F (х) + F± (x)
удовлетворяет F) A8).
Следствие 6. (Обобщение теоремы Ахиезера—Бабенко). Для того чтобы
любая функция F (х) > 0 была слабо весовой (или весовой), необходимо,
чтобы
-oo
A9)
Действительно, если F (х) (: V (или W), то этим же свойством обла-
обладает F (х) 4- 1.
ЦИТИРОВАННАЯ ЛИТЕРАТУРА
Поступило
27. IV 1953 г.
1 С. Н. Бернштейн.
2 С. Н. Бернштейн.
3 С. Н. Бернштейн.
4 С. Н. Бернштейн.
ъ N. Levinson. Gap
6 С. Н. Бернштейн.
7 С. Н. Бернштейн.
8 С. Н. Бернштейн.
9 Н. И. Ахиезер, К.
Докл. АН СССР, 88, № 4 A953) [109].
Докл. АН СССР, 89, № 4 A953) [НО].
Докл. АН СССР. 65, № 2 A949) [97].
Экстремальные свойства полиномов A937). [«Э. П.»].
and Density theorems, 1940.
Докл. АН СССР, 66, № 4 A949) [98].
Докл. АН СССР, 60, № 6 A948) [95].
Докл. АН СССР, 85, № 2 A952) [107].
И. Бабенко. Докл. АН СССР, 57, № 4 A947).

АВТОРСКИЕ КОММЕНТАРИИ
60. ОБ АБСОЛЮТНОЙ СХОДИМОСТИ ТРИГОНОМЕТРИЧЕСКИХ РЯДОВ
60.1 В первоначальном тексте здесь вводилось еще второе предположение, что
при соответствующем (х.г (О < а.г < 1) функция фх (8) = ** ^ ' становится возрастающей.
В действительности, для правильности последующего утверждения достаточно усло-
условие (А), а это дополнительное ограничение излишне.
В самом деле, если F (х) задана формулой E), где Е'п = Ьыг (—}, то, вслед-
вследствие F), ко__г ^nJ
к=о
-9Pkn™s2pkx\+2L<*' (h)
^ 1
при рк^___1<С -^ == n^Pfc0 • "° сУмма> стоящая в правой части, меньше, чем
ft,—1 л,—1
^J Jpk Г К ^J Г
ft=0 fts=0
так как, по условию (А), р^ со' ( ^)>/?та>/( 1 ПРИ всех т < ко - Следователь-
V Рк% J \ Рщ J
Рк%
но, принимая во внимание, что
где
^-J | 3a—1 '
ВИДИМ, ЧТО
I F {x + h) - F {x) |< —L (лРа.) w/ [ ) + 2L<o' (/г) < со' (/г),
если L выбрано так, что Lf2-f—=)<!.
590

60.2 После того как комментарий [60.1] был написан, появилась статья *
С. Б. Стечкина «Об абсолютной сходимости ортогональных рядов», которая среди
других результатов содержит общее ^доказательство следующей важной теоремы:
°° 1 /1\
Условием, необходимым и достаточным для того, чтобы ряд 2 = ^ ¦——со ( — ]
^Уп \п)Т
71=1
соответствующий данной функции / (#), был сходящимся, является сходимость ряда
п=1
Необходимость, выведенная в статье [60], [вытекает из [известного неравенства
Джексона. В упомянутой выше статье С. Б. Стечкина остроумным применением моих
общих методов оценки дифференциальных свойств при помощи наилучших прибли-
приближений выводится неравенство
71=1
где С — не зависящая,от / (х) постоянная,, откуда следует достаточность сходимости
ряда S для сходимости ряда 2.
Кроме того, я хочу отметить, что С. Б. Стечкин там же дает следующее обобще-
обобщение первой части основной теоремы настоящей статьи i[60], а именно:
Если
71=1
еде Е® [/ (х)] — наилучшее приближение функции f (x) посредством тригонометри-
тригонометрических сумм Sn(x) порядка п в метрике L2 , т. е.
/Vs
Е& [/ (х)] = min у -g- J [/ (х) - Sn (x)f dx,
о
то ряд A) сходится абсолютно.
Доказательство этого утверждения вытекает из неравенства
оо
Dbis>
Особое преимущество этой теоремы гСтечкина я вижу в том, 4tfo члены ряда jS2
явно выражаются посредством коэффициентов тригонометрического ряда A), поэтомуг
с одной стороны, теорему Стечкина на практике обычно удобнее применять, чем
мою, и с другой стороны, сохраняя идею вывода неравенства D), можно получить
D bis) без лишних ухищрений моего [доказательства (связанных с неравенствами
статьи [49], том I).
* Матем. сборник, 29 G1) A951), стр. 225—232. Содержание [60.1] С. Б. Стеч-
кину не было известно. Упомяну еще о недавно появившейся интересной статье
С. Б. Стечкина «Об абсолютной сходимости рядов Фурье» (Изв. АН СССР, серия
матем., 17 A953)), с которой я познакомился после составления комментария [60.2]^
591

Действительно, по определению,
2 (а*
поэтому получаем сразу неравенство
2т
2 («Е
соответствующее неравенству (В) настоящей статьи [60].
Применяя затем к (В*) (вместо (В)) лемму моей статьи [16], имеем
4п
После этого, замечая, что !
Й
Н
(при л = 1 имеет место знак равенства), получаем, полагая в (В*) т = 2
оо 4 8 оо j?B)
У (\alp\ + \'ЬЬ \) = У Л-У + . . . < 4 У ^n+1 . D bis)
ft =-5 n=l
67. О ФОРМУЛАХ КВАДРАТУР КОТЕСА И ЧЕБЫШЕВА
67.1 Предварительное исследование, о котором здесь говорится, опубликованное
пятью годами раньше A932 г.) в «Известиях АН СССР» A57*), в настоящее издание
не вошло, поэтому я приведу вкратце его содержание. Начинается эта заметка сле-
следующими словами:
«Настоящая заметка имеет целью обосновать утверждение, высказанное мною
в беседе с А. Н. Крыловым, что формула приближенного интегрирования Чебышева
ни при каких значениях х^ на отрезке [0,1] не может быть точной для произвольно
заданного многочлена степени п, если только п достаточно велико.
Как известно, указанная формула практически полезна для малых значений п\
но то обстоятельство, что при п = 8 формула A) не пригодна благодаря тому, что
точки xi оказываются комплексными (хотя при п = 9 они снова становятся действи-
действительными), для больших значений п является общим правилом. Косвенный прием,
посредством которого это будет доказано, не имеет целью установления возможно
низкой границы значений п, для которых формула Чебышева перестает быть пригод-
пригодной на вещественном отрезке».
* Подобного рода неравенства с соответствующей группировкой членов, которые
впервые использованы в [3] (том I, стр. 28—33) для оценки дифференциальных
свойств функция при помощи наилучших приближений, впоследствии применялись
во многих различных случаях как мною, так и другими авторами.
592

Моя уверенность в невозможности формулы A) для очень больших значений п
была тогда основана на неравенстве
ф(д) fl
где 9 (а)—число точек а^<я, выведенном на второй странице статьи A57*), кото-
которое легко было получить из известной оценки наилучшего приближения Еп \ х |.
С другой стороны, благодаря исследованиям Р. О. Кузьмина*, было известно^
что при равномерном распределении узлов (формула Котеса) соответствующие коэф-
коэффициенты должны быть для больших п разных знаков и бесконечно возрастать,
поэтому естественно было предположить, что то же самое свойство коэффициентов
должно сопутствовать неравенству B), выражающему асимптотическую равномер-
равномерность распределения точек xi на отрезке [0,1]. Но так как результат Р. О. Кузьмина
не мог быть использован непосредственно без дополнительных вычислений, то на
следующих двух страницах заметки пришлось построить (без помощи формул Кузь-
Кузьмина) многочлены, применение к которым формулы A) при наличии неравенств B)
приводит к противоречию.
Полезно будет для выявления той роли, которую сыграла в свое время заметка
A57*), добавить из нее еще следующий отрывок:
«Тот же прием приводит к заключению, что, как бы мало ни было определенное
число р < 1, формула A) не может быть точной для всех полиномов степени рл,
если п становится весьма большим.
Кроме того, наше заключение остается в силе, если в формуле A) вторую часть
заменить через
где все Ai удовлетворяют неравенствам
М > Аг > т > 0.
Полученный результат, представляющий только теоретический интерес, приводит
к постановке двух вопросов: 1) каково наибольшее значение я, при котором формула
Чебышева применима на вещественном отрезке? 2) Каково асимптотическое распре-
деление точек xi в комплексной области, когда п бесконечно возрастает?»
Ответ на первый из поставленных здесь вопросов дан в статье [67], на второй
вопрос ответил Р. О. Кузьмин. [См. [67], стр. 204].
67.2. В статье «О теореме академика С. Н. Бернштейна относительно квадратурной
формулы П. Л. Чебышева» (Журнал Института математики Академии наук УССР,
1937, № 3) Н. И. Ахиезер рассматривает вопрос о существовании квадратурных
формул вида
1 ~ п
о й=1
где
1
о
a Fn (х)—произвольный многочлен степени п. Доказана следующая теорема:
* Р. О. К у зьм ин. «К теории механических квадратур», Изв. Ленжнгр. поли-
технич. ин-та, 33 A931), стр. 5—14.
38 С. Н. Бернштейн 593

Для функции
» (JL) B)
квадратурная формула A) не сущестшует, если
где 8» шах {а, ?}, a Nx ^ — определенное число, которое не зависит от п и для ко-
которого дается некоторая оценка сверху.
Доказательство этой теоремы основано на следующей идее С. Н. Бернштейна:
если формула A) существует, то
^ « sup {am E + 0)-am ($-0)} ЕЕ Pm(?),
где т — произвольное целое число <; —~— , Z, — любой из крайних корней орто-
ортогонального многочлена Рт(х) степени т при весе р(х), а ат (х) пробегает совокуп-
совокупность всех неубывающих функций, для которых
1 1
xkda (х) = J х*
xkdam (х) = J х*р (х) dx (k = 0, 1, . . . , 2т - 1).
о
Далее, в отличие от С. Н. Бернштейна, который для оценки величины рт (?)
пользуется [при р (х) = 1] некоторыми оценками для многочленов Лежандра,
Н. И. Ахиезер доказывает, что
—оо
где
= cos2
/ А \ ft A
-5., / (в) = р (cos2 -тг-) sin — cos ~ .
В случае B) из C) получается, что
где
X = l + 2a, tx = l + 2p.
После этого используются оценки для крайних корней многочленов Якоби, получаемые'
при помощи явного выражения этих многочленов*.
68. О ФОРМУЛАХ КВАДРАТУР С ПОЛОЖИТЕЛЬНЫМИ КОЭФФИЦИЕНТАМИ
68. 1. Для а = 0 каждая из формул E) является известной формулой Гаусса.
Для а ^> 0 формулы типа E) и притом для произвольного веса впервые строил
и изучал А. А. Марков.
Функция р(х), как это отражает теорема II, представляет максимальную массу,
которая может быть сосредоточена в точке х при распределении массы по отрезку
[—1, -f 1], обладающему заданными моментами
* Этот комментарий написан по моей просьбе Н. И. Ахиезером.
594

+ 1
X
tkdp @ (к = О, 1, . . . , 2/ — 1)
(в настоящем случае />(«)=«). Подобным образом, тс (#) представляет при тех же
условиях максимальную массу, которая может быть сосредоточена на отрезке
— 1, х].
Впервые такие функции при любых Sk рассматривали П. Л. Чебышев и А. А. Марков.
Теоремы II и III являются частным случаем или непосредственным следствием
известных теорем А. А. Маркова.
См.: А. А. Марков. О некоторых приложениях алгебраических непрерывных
дробей (СПб., 1884).
К. Поссе. Sur quelques applications des fractions continues algebriques (СПб.,
1886).
А. А. Марков. Доказательство некоторых неравенств П. Л. Чебышева.
«Избранные труды по теории непрерывных дробей и теории функций, наименее
уклоняющихся от нуля». ОГИЗ A948), стр. 15—24.
К. А. Поссе. К вопросу о предельных значениях интегралов или сумм.
Приложение к цитированным выше «Избранным трудам. . . » А. А. Маркова,
стр. 391—410.
Главным, существенно новым результатом работы [68] я считаю вывод достаточных
условий для существования квадратурных формул, точных для многочленов степени
21 — 1 вида (§ 4—5)
"г1 ^ fmi\ ( i \
\f) [P>0 l<y<lj (A)
где j-j- — данные рациональные дроби с общим знаменателем iV, а также формул
вида (§ 6—7)
V п С
(В)
где -jjj- —данные рациональные дроби.
Такими достаточными условиями, установленными при помощи параметрического
метода, являются, соответственно, неравенства D8) и E9):
iy>2VT(Z + 1J, М>2^2"(/+ 1) (/ + 4). (I)
Сопоставление этих нижних границ для N и М с верхними границами, получен-
полученными в статье [67] [неравенства A1) и A7), соответственно, для N и М], показывает,
что наименьшие возможные значения N и М при любых данных достаточно больших
I всегда порядка I2.
Отметим еще, что практическое применение приема, вытекающего из теорем
У и VI, который позволяет строить конкретные квадратурные формулы, соответст-
соответственно, вида (А) и (В), иллюстрируется в заметках [69] и [70], где в рассмотренных
там частных случаях нижние границы для N и М удается значительно снизить.
Так, в числе других примеров в [69] для / = 6 BZ — 1 = 11) имеется формула (А),
в которой N — 10, и в [70] — формула (В) для I — 7, в которой М = И (вместо
М = 20 в формуле, приведенной без доказательства в конце настоящей статьи [68]),
39 С. Н. Бернштейн 595

72. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ ПАРАМЕТРИЧЕСКОГО МЕТОДА
К ИЗУЧЕНИЮ КВАДРАТУР
72. 1. После П. Л. Чебышева, который указал алгорифм для вычисления формулы
A2) (не занимаясь вопросом об ее возможности), формулы этого типа, как и типа
F bis), рассматривал А. А. Марков, давший некоторые достаточные условия их
существования*.
Позднее, почти одновременно с моей статьей [72] (и независимо от нее) появились
исследования** Н. И. Ахиезера и М. Г. Крейна, примыкающие к упомянутым
работам А. А. Маркова. В частности, следуя А. А. Маркову, они рассматривают
формулу F bis), верную для многочленов степени 2т +1 в виде
+1
[ \^ F(xt)~ ^ Г(Уг)\, (I)
Д t=l i=l >
где
и устанавливают («О некоторых вопросах теории моментов», Харьков, 1938,
стр. 115—118) условия, необходимые и достаточные для их существования, не
налагая никаких ограничений на знак g (х). Напомню, что при g (х) !>0 возможность
формулы (I) вытекает из моей теоремы I, причем чередование корней xt, которое
А. А. Марков вводит как дополнительное ограничение, осуществляется само собой
[в случае g(x)^>0] благодаря моему следствию 2.
Не останавливаясь на всех результатах Н. И. Ахиезера и М. Г. Крейна, допол-
дополняющих в некотором отношении настоящую статью, отмечу еще, что они исследуют
также формулы типа A2) и устанавливают необходимые и достаточные условия*** для
существования квадратурных формул (там же, стр. 109—110)
(И)
точных для многочленов степени 2m. При этом устанавливается алгебраическое
уравнение для определения inf | L \.
Практическое значение рассмотрения формул вида A) с заданными коэффициен-
коэффициентами, особо важные частные случаи которых рассматривали Чебышев и Марков
[(I) и (II)], заключается в получении формул приближенных квадратур,' пригодных
для функций / (х), встречающихся на практике.
Нетрудно проверить, что, например, формулы Маркова (J), как и формулы
Чебышева, в которых заранее не требуется последовательного чередования узлов xif
Ур позволяют вычислить интеграл
* А. А. Марков, а) Новые приложения непрерывных дробей. «Избранные
труды по теории непрерывных дробей. . .». М.—Л. A948), стр. 120—145; б) О пре-
предельных величинах интегралов в связи с интерполированием. Там же, стр. 146—230.
** Н. И. Ахиезер и М. Г. Крейн. 1) Заметка в «Gomptes rendus» 11 марта
1935 г.; 2) О некоторых вопросах теории моментов, Харьков, ГОНТИ A938),
стр. 106—120; 3) О некоторых формулах квадратур П. Л. Чебышева и А. А. Маркова,
Сборник, посвященный памяти академика Д. А. Граве, стр. 15—28.
*** сЗти условия, го существу, близки к моей теореме VI, в которой, однако, нет
эффективного определения |infzj.
596

+1 г^И-1 rn _,
С f{x)g{x)dx~L\ ^ f(*i)-% /(Уг)\ (Ibis)
Д L i-i i=i J
с точностью порядка
О
если формула (I bis) точна для многочленов степени 2т + 1. Таким образом, учитывая
классическую теорему Джексона (см. [6], том I, стр. 113), видим, что при т достаточно
большом погрешность формул (I bis) будет сколь угодно мала, если функция f (x)
имеет непрерывную производную. Замечу, что поскольку предложенные мною
видоизменения [68] формулы Чебышева, в которых все коэффициенты положительны
(и равны между собой), верны для всех многочленов степени га, когда число узлов
порядка п2 (или равно п при рациональных коэффициентах с знаменателями порядка
га2), соответствующие формулы применимы с точностью порядка О (Еп [/ (х)]) —>0 ко
всякой непрерывной функции. К сожалению, до сих пор мы не имеем достаточно
удобного общего приема для фактического построения таких формул.
74. О НАИЛУЧШЕМ ПРИБЛИЖЕНИИ | ос — с |р.
74.1. Доказательство неравенства
(\ -4- & \™ -4- 1
E^Uxf, (а,Ъ)]<Ет[\х\*; {а,Ъ)] К т> (_ 1<а <0 < &< 1),
I1 + °т) — 1
играющего существенную роль при выводе E) и (8), основано на идее, которая впервые
была использована мною в докторской диссертации [3] (том I) в случае р — 1. Если
Рт (х) = Ао 4- • • • + Ат хт — многочлен наименьшего уклонения от | х |р на [а, Ь], то
и, тем более,
X
1+8
при любом 8 > 0; поэтому
(а<Х<Ь)
| х |Р; (а, Ь)], (а^х
откуда вычитанием получаем многочлен Qm_1 (х) степени не выше m — 1, для ко-
которого
Ц х |Р [A + 8)т-Р- 1] - Qm_i {х)\ < [A + Ь)Ш + 1] Еш [| х |Р; (Д, 6)] (<*<*<*). (I) ^
Д^ля последнее неравенство на A + 8)т~р — 1, получаем требуемый результат.
При помощи соответствующего сдвига это неравенство преобразуем (полагая, в
частности, Ь — а = 2) в неравенство
Таким образом,^ полагая, как при выводе E), A+Sm)m~"p= 2m и воспроизводя
буквально то же вычисление, находим
Еп 1\*-с\р]<A + еп) Ет[\х-с\%
597 39»

_ m n + 21 I log n
где e^-^0, если — = >1 так, что >Q: последнее требование в не-
равенстве (8) выполнено, так как, по условию, I = яр, где р<^1.
74.2. Последняя часть (§ 3) доказательства предельного равенства B) может быть
значительно упрощена заменой переменной х = cos 0.
Положим
= cos0o 0<8о<- .
Имеем
Я I х—сР = Е* I cos 0 - cos 0O |р = 2V El
sin
sin
Очевидно, вообще, справедливо равенство
0 —а
Е"
sin
sin
(I)
(И)
при любом а.
С другой стороны, замечая, что
sin
= | Sin 0О |Р Sin
sin
Р] +9F), (Ш)
где функция
9@) =
sin
- |smeo|p] [| sin
- |sineo|P] - |sin0
|2р
имеет при всех 0 конечную производную порядка [/? + 1], выводим из (I) и (III)
асимптотическое равенство
Е*п | cos 0 — cos 0О |р ~ 2р | sin 0О |р Е*п\\ sin
sin ¦
> — 0п
Принимая же во внимание, что следствие II применимо к наилучшему приближению
периодической функции тригонометрическими полиномами, заключаем, на основа-
основании (II), что
Е*п | cos 0 —cos 0О |р — 2Р | sin 0О |р ?*
Применяя (IV) к частному случаю 0О = -=- , получаем
0
(IV)
sm у
Поэтому для любого 0О (IV) представимо в виде
Ё*п | cos 0 — cos 0O |p — |sin 0О|Р Е*п | cos 0 |р ,
откуда получаем требуемое равенство
Еп\х-с\»~A~ <*)*'* Еп\х\*
«ря любом с (— 1 < с < 1).
598
(IV)

84. О НАИЛУЧШЕМ ПРИБЛИЖЕНИИ НЕПРЕРЫВНЫХ ФУНКЦИЙ НА ВСЕЙ
ВЕЩЕСТВЕННОЙ ОСИ ПРИ ПОМОЩИ ЦЕЛЫХ ФУНКЦИЙ ДАННОЙ СТЕПЕНИ
84.1. Доказательство формулы (9) (стр. 378)
В + Сх \ ph~1e~vb
)
b*)hJ (лкГ(п) bh+1
Ср-»со)
для любого вещественного h может быть получено на основании теорем настоящей
статьи при помощи того же метода, который был применен для вывода формулы B5)
в статье [9] (том I).
Достаточно предположить, что
В качестве отправного пункта берем формулу G), которую перепишем в виде
р—ра
~ ^ al - Sp (x) =_ ^- К Б2 + <72я2 cos (Ф - px + X), Gbis)
где
2a;r aC
Умножая формулу G bis) на
(я2 —
и интегрируя по а от Ь до со, получаем
! r- — i?p (x) = V —-— cos (Ф —px + X) da.
Вычисляя асимптотическое значение правой части при р->оо, мы и получаем тре-
требуемую формулу (9)*.
84.2. Неравенство F) является следствием общей теоремы, которую мы здесь
приведем. Напомним прежде всего (см. том I, [42], § 2), что всякий положительный на
отрезке [—1, + 1] многочлен tm(x) степени т может быть однозначно представлен
в следующей форме:
при любом целом п ;>—, где Мп{х) и Nn_1(x)—многочлены степени п и п — 1,
все нули которых лежат в промежутке (—1, + 1) и взаимно разделены, Mn(l)^>0,t
^n—i A) > 0- Причем, как показано в § 5 только что упомянутой работы, много-
многочлены Мп(х) и Nn_1 (х) связаны с многочленами М^ (х) nN^_1(x) In >> l^> — 1 соот-
соотношением
Mn (i) + i Vl^* iVn_1 (x) - [Mx (x) + iVi=~x~* N^ (x)] (x + i КГ=Т
= 1Мг{х) +iVr=^Nl_1{x)} [Tn_l(x)-f-iSn_l(x)]f
где Tn_x (x) = cos (n — /) arc cos x, ^n_z {%) = sin (n — I) arc cos x, так что
Mn (x) = Г„_( (х) Мх (х) - L=^ г;_( (х) iV,_x (x),
Настоящий комментарий [84.1] составлен по моей просьбе Н. И. Ахиезером.
599

Очевидно, что среди функций
% ~Ь а>п лх + . . . + а,п
наименее уклоняется от нуля на [— 1, + 1 ] функция
так как она достигает своего абсолютного максимума \L\ с последовательно проти-
противоположными знаками в п + 1 точках отрезка, в которых Vi — х2 Nn_x (х) обра-
обращается в нуль.
Пусть теперь tm (x) — четный многочлен. В этом случае, как легко видеть,
многочлен Мп (х) содержит степени х только одной и той же четности. Так как,
1 х2 xzs х
с одной стороны, функции -, — , . . . , ' . — , равно как и ,...,
1 'т И Ytm (*) У *т (х) У*т ^
образуют систему Декарта (см. определение в «Э. П.», стр. 50) порядка s на
1Мп
отрезке [0,1], а с другой стороны /0 (х) = -— (п = 2s или п = 2s + 1) имеет
s -f 1 точек максимального отклонения на [0,1], то на этом отрезке /0 (х) является
полиномом-осциллятором («Э. П.», стр. 52) соответствующей системы Декарта. Тогда
из следствия I, § 12, гл. I монографии «Э. П.» вытекает
Теорема. Если многочлен Рп (х) степени ^п (п^-т) удовлетворяет неравенству
^.2\ Л7-2 („\ ( \ ^
где t^m{x)—четный положительный на отрезке [—1, + 1] многочлен, то
И*)
п, ., . Ц n'-m W Мп (х) - ^ Тп1__ш (х) Nn
(А = 1,2,..., я),
гЭе wf = и, ес/ш /г — к = 0 (mod 2), и nf ~ п — 1, ес/ш /г — к = 1 (mod).
Тождество G) вытекает из тождества *
85. О ВЕРХНЕЙ ГРАНИЦЕ МАКСИМУМА МОДУЛЯ ПРОИЗВОДНОЙ
МОНОТОННОЙ ФУНКЦИИ КОНЕЧНОЙ СТЕПЕНИ
85.1. Этот результат М. Г. Крейна распространен в моей работе [84] (заметка V)
на случай, когда | q> (х) | < Я (х) на всей действительной оси, где Я (х) — целая
функция нулевого рода.
В 1948 г. (Докл. АН СССР, 63, № 5) Н. И. Ахиезер доказал следующее общее
предложение: для того чтобы имело место равенство
* Настоящий комментарий составлен но моей просьбе В. С. Виденским на осно-
основании моих давнишних черновиков.
600

еде ф (z) — некоторая целая функция степени 2. , есе нули которой лежат в области
Im z !> 0, необходимо и достаточно, чтобы целая функция <р (z) степени р была
на действительной оси и чтобы
R
In 1 9 (х) © (-— х) | .
J ^ < °°
т. е. чтобы функция ф (х) была конечного роста.
87. НОВЫЙ ВЫВОД И ОБОБЩЕНИЕ НЕКОТОРЫХ ФОРМУЛ
НАИЛУЧШЕГО ПРИБЛИЖЕНИЯ
37.1 Напишем формулу (I) в эквивалентном ей виде
EJa-^=- Tins + Dja*-!)-1
\Г(-8)\.Г(п+2)(а+Га*-1)пУ пКИ'
так как
Г(п-8+1) _ 1 .,,_,
^ {1 +
Г (и + 2) ~ ^+Г {1 + w.
где т)п-»0 при п-г-оо, и докажем,'ограничиваясь для простоты случаем —1<\
что величина 8П (а) при любом а ^> 1 удовлетворяет в этом случае неравенству
5 A + s)
I *„(*>!<¦
2 (л + 2) Va* — 1 '
если правая его часть <1. Так как в тексте а — 1 + 9 g , то, следовательно,
R2 + 4/г4
если /? > —- , и значит, действительно, 8 (р, п) -» 0 равномерно относительно п
при
Для доказательства возьмем многочлен Рп (х, t) степени п от х, наименее укло-
уклоняющийся от на отрезке [—1, 1] при ?^>1, так что
где
1/ = а; — Vх* — 1, # = -jr- f гМ );
2 V ^У
<v пробегает окружность |^| = 1, а х — отрезок [—1, 1]. Умножая обе части A) на
V 2S+X asT2+s
601

1 / 1 \
где 0 < a < 1, a = -г- ( a H ) , и интегрируя по t от оо до а, получим *
г V «У
sin га J as A — t2)
где Qn (ж) снова многочлен степени я, а правую часть, полагая
можно с помощью интегрирования по частям представить в виде
a
/ (г,) = 21"8 оГ8 С
о
_ 2l_s a_s+1 Г(|»
(ос — t)s ЧГ (v, т) dT =
т ( a) _
Г (л+ 2)
- 21
Дифференцируя B) по т и учитывая, что | Ф (v, т)| <; 1, если | v \ — 1, находим не-
неравенство
W (v, т)
^ A _ a2J-s »
верное при | г> | = 1 и 0 < т <; ос. Следовательно,
| /2
а т
(v)\ < 5-2l"S a"S С dx С
(l_a2J-s 3 }
«j • <-* ос
dT:
5-2х~8 tt"~s+2 Г (я — s + 1) Г (s + 2)
A _ a2
С другой стороны, в точках уклонения разности
^ГТ" — Рп (*» а) = м (а) ф (^» а)
величина /х (t;) принимает с чередующимися знаками значение
Г (я + 3)
max
Поэтому
¦ /± G,)| - 21-5 ап-5+1 Г (п - s + 1) Г (s 4- 1) _
¦1=1 A - а2I"8 Г (п + 2)
S—1
= Г (п — .9 + 1) Г (s + 1) (а2 — 1) 2 _ 7
~ Г (п + 2) (а + Г^=Т)П ~ 'п
^п (й) ~~ Хп (а) < —г^- Еп (а — ^)S < Ln (а) + ^п (а)
* См. статью Н. А. Сапогова в Изв. АН СССР, серия матем., 10 A946),
стр. 463—468.
602

и значит
„ . ч«, sin ти .9
Еп (а - xf = —— Ln (a) {1 + 8п (а)},
где
IS /дч| ->"(а) = 5«A+>) _ 5A+.)
а») 2 (в + 2) У^Л '
если эта последняя величина * < 1.
88. ДОБАВЛЕНИЕ К РАБОТЕ И. И. ИБРАГИМОВА «ОБ АСИМПТОТИЧЕСКОМ
ЗНАЧЕНИИ НАИЛУЧШЕГО ПРИБЛИЖЕНИЯ ФУНКЦИИ, ИМЕЮЩЕЙ
ВЕЩЕСТВЕННУЮ ОСОБУЮ ТОЧКУ»
88.1. 1) Действительно, из условия (А) следует, что при любых данных ро> р> 1
возможно установить такое число N, что при всех m^N, h > 0
Но после того, как фиксировано N, можно указать такое число cN, что
Следовательно, при любых п — к^- N имеем
—^— < р*
Е ГФ (х)] °
Если же п — к < N, то
каково бы ни было данное рх > р0, лишь бы п > 7V было достаточно велико.
2) Для доказательства утверждения (IV bis), соответствующего единственному
предположению, что
— *> а Л
lim Ъ/ГЕп[Ф (х)] = —>-«¦ i A)
достаточно установить, что при любом данном рх > р >¦ 1 найдутся сколь угодна
большие значения л, для которых будут соблюдаться неравенства
каковы бы пи были & < п. В самом деле, положим, что это утверждение ошибочног
т. е. существует определенное р, > р, для которого при всяком гс > N найдется
такое к, что справедливо будет обратное неравенство
pi
Можем взять п^> N произвольно большим по сравнению с iV, при этом, если п — к^> N,
всегда нашлось бы и такое к, что п — к < N в неравенстве B), так как в случае
n-L — n — & ;> N мы могли бы, по предположению, применить к пг соответствующее
неравенство B), повторяя то же самое рассуждение до тех пор, пока в правой части
* Этот комментарий написан по моей просьбе Н. И. Ахиезером.
603

не окажется Ет[Ф0 (х)], где /n<iV. Тогда, перемножив все полученные таким
образом неравенства, мы придем к неравенству B), где п — к <^N. Таким образом,
для всех n^N
М
откуда следовало бы противоречащее условию A) неравенство
92. О СВОЙСТВАХ ОДНОРОДНЫХ ФУНКЦИОНАЛЬНЫХ КЛАССОВ
92.1. Для доказательства утверждения, высказанного в сноске на стр. 421 (которое
очевидно для к = 1), без ущерба для общности можно принять: а{ > 0, / @) = 0 и М = 1
в неравенстве B). Пусть дано, что sup | / (х) | = N8^ = МQ на отрезке [—$0> &0]«
Рассмотрим последовательно возрастающие отрезки [—§п, 8П], где 8П,, = A -f- p)8n,
полагая, что в условии B) — >¦ 1 + р > 1 (р > 0, i < к). В таком случае, если для
ai
какого-нибудь п установлено значение sup | / (х) |= N8 = Мп, то из неравен-
| х | -^5П п
ства B), записанного при ж = 0в виде
к—1
заключаем, что
^nS \Pi\- (I)
к
Для этого достаточно заметить, что при
*п<Ч\Ь\<К+1 (II)
значения ^Щ^-г—^— = ^п ^ля г^^ — ^ попадают на отрезок [—8П, 8П]. Полагая
затем —j j— = с и (—) j г- = d, перепишем (I) в виде
откуда следует, что
- ,0 + . 2 [Ч^1
Mn
где (in= ——. Следовательно, наконец,
С
k + rf(
604

Таким образом, в зависимости от того, будет ли с < A -j- p)q или нет, первый или
второй член будет возрастать при я->оо бесконечно медленней другого. В первом
Мп
случае sup < оо; в противном случае всегда можно будет указать такое q± ^> q,
Мп \МпЛ Мп
что с < A + Р) I т- е. = О < оо и, следовательно, sup < оо. Таким
8?l L cn J п^оо 8*1
образом, всякая функция / (ж), ограниченная на произвольно малом отрезке и удовле-
удовлетворяющая B) при всех х (—оо<#<оо), должна быть алгебраического роста. (Это
свойство используется при доказательстве теоремы I). Точное значение максимального
показателя алгебраического роста функции / (х) ? Sq (pt, at), как будет показано
в следствии 3, зависит исключительно от порядка q и характеристики т0.
92.2. Докажем утверждение сноски на стр. 429. Если
|/(А:) (а? + h)— f{k) (х)\ <МЛ5 @<8<1, к > 0 — целое) D)
то
где
p + q.Vq
Для этого замечаем, что если при данных г, йс, Я
то соответствующее уравнение (относительно h) имеет корни h = 0 и Л = &0 }> 0;
следовательно, при т > 1 уравнение
2 ^а* [/г (х + а^ - /' <ж>'= н {к + 8)лЛ+в-1
имеет корни h => 0 и Л = &х @ < h± < Ло). Повторяя дифференцирование А: < m раз,
видим, что уравнение
2 ^а? 1/(/° (* + *ih) - /(/С)(^I = Я (А + 8). . . A + 8) h8
имеет корни h = 0, h = hk @ < /ifc < hQ). Вследствие D), получаем отсюда, что
Я (к + 8).. . A + 8)< М 2| ^ | | ос{ l^8.
i
92.3. С. М. Никольский * рассмотрел случай, когда в формуле F) (стр. 430)
^i 2; Х2. Предполагая функцию / (х, у) ограниченной, он получил при помощи моего
метода интересное обобщение следствия 9.
Приводя здесь главный результат С. М. Никольского беэ предположения ограни-
ограниченности, я буду пользоваться обозначениями настоящей статьи [92]. Полагая вместе
* С. М. Никольский. «Обобщение одного предложения С. Н. Бернштейна
о дифференцируемых функциях многих переменных». Докл. АН СССР, 59, № 9.
. 605

с С. М. Никольским п*1 = /г*2 Aг < Х2) в неравенстве F) и дифференцируя последова-
последовательно к @</:<Х!) раз по х и I раз по у ряд, представляющий / (х, у), получаем (как на
d^lf (х, у)
стр. 432) равномерно сходящийся ряд для т—-, до тех пор, пока соблюдается
дхК ду
неравенство
При этом соответствующая A1) (стр. 432) оценка остатка дает
п<п* дх"ду1 \ni
Таким образом, главный результат упомянутой заметки С. М. Никольского-
включается в следующее обобщение следствия 9:
Если
dk+l f (x у)
то при соблюдении (I) :¦ ? непрерывна по обеим, переменным, причем
дхк ду1
8" 8г
дхкду1
где 81 = Х1 — к — ^1, 82 = 2^81 = Х2— I — к^.
Из того обстоятельства, что82>81 (при A2>Ar) заключаем, что также как и функ-
функция / (х, у), все ее частные производные более гладки по у, чем оо х\ в частности,
dklf
если кх есть наибольшее целое число <ХХ, то производная —тг (которая по х бо-
дх
лее не дифференцируема) будет дифференцируема по у, если Хх — кг > -^ . Таким
а2
образом, наименьшее значение порядка Л +1 непрерывной частной производной
(которая более не дифференцируема) может быть выше кх.
Пусть, например, / (х, у) 6 я^+а'ЗЛ^+е (а < !» ? < 4)» т- е- gji не существует^
тем не менее существует непрерывная - - ?xS * ^ *2/^*з ' если тольк0>
2+1 1+а
Заметим еще, что если производная 1 i более не ч дифференцируема
дх ду1
(§!<!1, 82<; 1), то она должна удовлетворять обыкновенному условию Липшица
дробного порядка по х (8Х < 1); если же она дифференцируема только по у, то после
этого дифференцирования окажетдя 8Х < 1.
Здесь уместно будет также упомянуть о новых исследованиях С. М. Никольского*,
посвященных аналогичному изучению свойств последовательных производных функций
многих переменных в разных метриках и интересным приложениям его резуль-
результатов к проблемам теории дифференциальных уравнений в частных производных.
Труды Математического института им. В. А. Оеклова АН СССР, 38 A951).
606

96. ПЕРЕНЕСЕНИЕ СВОЙСТВ ТРИГОНОМЕТРИЧЕСКИХ ПОЛИНОМОВ
НА ЦЕЛЫЕ ФУНКЦИИ КОНЕЧНОЙ СТЕПЕНИ
96.1. В теореме I второе условие [алгебраический рост функции Gp (x)] можно
отбросить. Это вытекает из следующей теоремы Б. Я. Левина (Докл. ЛН СССР,
65, № 3 A949):
«Если целая функция G (z) с шириной индикаторной диаграммы 2v = hG l~) +
+ hJ— -^-) < 2ти ограничена в точках (не обязательно вещественных) {^}~оо» пРичем
|ft-Xft|<L (± Л = 0,1,2,...)
и
mf|Xn_Xm|>28>0,
то G (z) ограничена на всей вещественной оси».
Из последовательности [ак], фигурирующей в теореме I, можно выбрать под-
подпоследовательность, удовлетворяющую условиям теоремы Б. Я. Левина.
Случай равноотстоящих узлов был ранее рассмотрен в работе М. Картрайт («Quart.
J. of Math.», Oxf. Ser., 7, A936), стр. 46).
Точные оценки впервые даны в настоящей статье [96].
96.2. В настоящем издании в тексте статьи [96] сохранена лишь та часть
«Добавления», которая непосредственно связана с основной темой статьи. Предлагаемый
комментарий воспроизводит в основном остальную часть «Добавления», объединенную
с примечанием к моей работе [96] B53 а)„ (Автор не претендует на новизну элемен-
элементарно изложенных здесь результатов.)
Лемма 3. Если ап (\ап !<| ап+11)—корни целой функции Gp (x) ?33 степени
р, то*
lim
lim
"•%
Из рассмотрения функции видно, что правые части (I) и (II) являются
точными верхними гранями левых частей.
Для доказательства (I) применим формулу Иенсена [полагая для определен-
определенности Gp @) = 1]:
RU а *Г
l0g Га а~\ = 2^ J l0g I Gv (Ле1бI dQ dan К Л
Га
I Л \ n I Q
Как заметил Линделеф**, отсюда следует, что при любом R^\a1\ справедливо
неравенство
* Неравенство (II), которое очевидно, следует из (I), было непосредственно
доказано в первоначальной редакции «Добавления» [96].
** Неравенство (I) было дано без доказательства в B53*а). Здесь мы даем это
доказательство, в котором используется один результат работы Линделефа «Memoire sur
la theorie des fonctions de genre fini», Acta Societatis Scientiarmn Fennicae, 31 A),
1901 (стр. 10—11).
607

27*
log | Gp(Reib) |o?0. Cbis)
1 * " ' о
Вследствие Gp (x) ? 93, благодаря известным неравенствам Н. И. Ахиезера, имеем,
каково бы ни было s >• О,
при i? достаточно большом. Поэтому, фиксируя произвольно малое е, выводим
C bis) для всех R (i?,>i?e) неравенство
Следовательно,
т. е.
| аг. . .an|>i?ne ^n '. Dbis)
Замечая, что для данного п максимум Мп правой части Dbis), который достигается
Bр \
при п — R ( -^ + е 1 = 0, равен
заключаем, что при всех достаточно больших я
Следовательно,
или, что то же самое,
<^L. (I)
Из (I) можно вывести также, что
п
lim 1 г<—»
откуда следует
Ш ТИТ<^. (и*>
4. Четная (или нечетная) целая функция
п=1

есть функция конечной степени
Для этого замечаем, что
, если lim .——г < оо.
есть целая функция степени X > 0; так что для всех достаточно больших | z \ имеем
П
если только
X > lim
n->oo
= ти lim
и, следовательно, степень р функции G (z) конечна и не превышает ти lim —7—г .
П-»оо | Оп |
Следствие 5. Если {ап\ есть последовательность корней канонической целой
функции конечной степени Gp (x) ? 33, то ее степень р удовлетворяет неравенствам
liui
V
п~\
¦ 2P
E)
Действительно, л^евая часть неравенства E) есть повторение неравенства (I);
для доказательства правой его части достаточно построить четную функцию
G2p (x) = Gp (x) Gp (—2?), имеющую корнями + ап, степень которой равна 2/?,
согласно следствию 3 «Добавления» [96], (стр. 466), и применить к G2p (x) лемму 4.
Из E), в частности, видно, что если существует
1лп
то
В B53*а) рассматриваются функции G (г), для которых существует
lim
lim
?*
= 5 < 00 и
(I")
(последнее требование обеспечивает соблюдение условия Линделефа конечности
степени).
В этом случае (для определенности полагаем | а01 > 0)
причем степень /> функции Gp B) ? 33 (согласно (III) равна
609

При всяком s>0 можем зафиксировать &>0 и &0>0, так что при всех
к > к0 множители Gp (iy) удовлетворяют неравенствам
1 —¦
A + сJ
(IV)
крайние части которых соответствуют множителям бесконечного произведения
sin (I + s) ipy. Поэтому при условии (III) имеем
lim —log G* (iy) =p.
y—^-oo У
Отсюда следует, что, какова бы ни была функция Gq(z) степени q, для которой
lim — log | Gq (iy) | = q, степень произведения G* (z) Gq (z) равна р -f q.
Имея в виду установить при любой функции GQ (x) степени q неравенство
h >• V р2 + Q2 ([96] (следствие 4 «Добавления», стр. 467), где h— степень произведе-
произведения G (х) = G* (x) Gq (x)), которое нужно для интерполирования при помощи
G*v (x), (вместо cosjox), я наложил дополнительное ограничение на функцию G*v(x),
заменив (III) более узким условием
/гати
(—оо<т<оо),
(V)
где с — произвольно заданная постоянная.
При последнем условии в B53*а) (стр. 572) установлено существование предела
lim r log | G* {re19) | = р \ sin ? |
Г->оо Р
(VI)
для всех sincp^O, которое (как видно из доказательства, приведенного в тексте,
стр. 467, следствия 4 в случае Gp (z) = cos pz) достаточно для получения требуемого
результата.
Действительно, при условии (V) функция G (z + xQ) для любого xQ (—оо<[#0<Соо)
удовлетворяет условию (III), где d^.2c-]
Учитывая, кроме того, что
G*p(x) е~~г I х I —>0 при + х —> оо [вследствие G^ (z) ^ Щ, находим, применяя (IV),
что при любом е ^> 0 можно указать такое Ъ ]> 0, что
— оо<ж„<со,
(VI bis)
каковы бы ни были у > 6, | х0 \ > Ъ (откуда следует (VI)).
Последний класс функций [удовлетворяющих (V)] тщательно изучен в совмест-
совместной работе Н. И. Ахиезера и Б. Я. Левина «Об интерполировании целых трансцен-
трансцендентных функций конечной степени» [Записки мат. отд. физ.-мат. фак. и Харьк.
матем. об-ва, сер. 4, 23, 1952), которая, в частности, содержит подробное (более
сложное) доказательство утверждения (VI bis) jb следующей уточненной форме (для
определенности полагаем р = п):
Аепу | z |
У
2c-fi
\y\>2c+l),
где z = х + iy\ постоянные А и В зависят только от с,
610

102. О ВЕСОВЫХ ФУНКЦИЯХ
102. 1. Первый набросок доказательства достаточности этого условия был дан
в [25] (том I). В комментарии [25.2] (стр. 541—545) воспроизведен почти весь
§ 1 главы III «Э. П.», который позволял восстановить общее доказательство достаточ-
достаточности. Однако, имея в виду важность этой теоремы и принципиальное значение алгеб-
алгебраического метода ее доказательства, при помощи которого в стат*>е [109] мною
установлено условие, необходимое и достаточное для того, чтобы любая четная моно-
монотонно возрастающая (при х > 0) функция Ф (х) > 0 была весовой, я счел целесооб-
целесообразным привести здесь также отрывок (§ 2 и начало § 3, стр. 139—J 47) главы III
«Э. П.», содержащий полное доказательство достаточности (как для случая целых
функций B) статьи [102], так и для случая любых монотонных фупкций), и § 6,
стр. 163—165, в котором была доказана необходимость.
§ 2. Взвешенное наилучшее приближение | х | при помощи многочленов
на всей вещественной оси
Вернемся к следствию* I предыдущего параграфа при дополнительном условии,
что R (х) = #2п (х) = s2 (х) + t2 (х) есть функция четная, [R @) = 1]. В таком случае
все корни R (х) попарно равны и противоположны, поэтому s (x) будет функцией чет-
четной, a t (x) является функцией нечетной
Следовательно, равенство A0) получит вид:
— - V—1— - V х 1 2 V Р* и/ч
Jlf ~~ 2j а,. + «3/ ~ 2л В, ^ Z 2л „2 , О2 ' A4)
где первая сумма распространена на чисто мнимые корни, а вторая сумма относится
ко всем прочим корням, вещественная часть которых + ai ^ 0.
Обозначая через рк = "j/a^ + р| модули корней, а через 0Л. @ < 6^. < к) — их
аргументы, можем формулу A4) записать также в виде
помня, что каждому аргументу 6fe ^ — в последней сумме соответствуют два равных
слагаемых.
Заметим, кроме того, что формулы A4) и A4 bis) остаются в силе и в том случае,,
когда R (х) =* s2 (x)-\-12 (х) имеет вещественные корни + сс^ (отличные от нуля),,
являющиеся двойными корнями s (х) = t (х) = 0; в самом деле, с одной стороны, соот-
соответствующие pfc = 0 члены в выражении -=j- равны нулю и, с другой стороны, для
Р (х)
обращения в минимум максимума дроби —¦ на всей оси необходимо, чтобы
VR(x)
х
числитель также делился на 1 ~, так что после сокращения эта дробь приме i
вид, в котором знаменатель уже не имеет вещественных корней, и формулы A4) и
A4 bis) будут к ней применимы.
Таким образом, при предположении, что R (х) неотрицательный четный многочлен
степени 2л, дробь
[25.2] (том I), стр. 544. (Автор.)
611

не может по абсолютному значению оставаться менее, чем
A4 bis)
на всей вещественной оси, но не превышает этого значения, если
Mt(x) Mt(x)
Функция A5) является, очевидно, полиномом-осциллятором на всей положитель-
положительной полуоси для системы функций Декарта («Э. П.», стр. 51)
VR (x) ' VR(x) ' "" VR (x)
так как на всей оси она достигает своего экстремума п или п +1 раз, в зависимости
от того, четно или нечетно число я, и поэтому на положительной полуоси достигает
экстремума в —^— = m + 1 точках. Следовательно, благодаря тому, что система
к
функций
(к — 1, 2, . . . , п) является также системой Декарта на положитель-
V R (х)
ной полуоси, на основании следствия I («Э. П.», § 13, гл. I) получается
Лемма 1. Функция
VW(x)
может оставаться на всей вещественной оси меньше по абсолютному значению, чем
М = — ; напротив, функция
^ sin дь
должна превысить значение МЛ
Определение. Будем называть наилучшим взвешенным приближением функ-
функции f (x) посредством многочленов степени п на всей вещественной оси при весе
^> 0 наименьшее значение максимума взвешенной погрешности
а многочлен Рп(%), осуществляющий эту наименьшую взвешенную погрешность,—
многочленом взвешенного наилучшего приближения на всей оси. Обозначать это взве-
взвешенное наилучшее приближение будем через Е&) [f (х)]. Таким образом, первая
часть леммы I приводит к неравенству
612

(R@) = 1).
A6)
Заметим, что если порядок возрастания <р (х) на бесконечности не быстрее, чем хп, то
дальнейшее повышение степени приближенного многочлена не может улучшить взве-
взвешенного приближения. Поэтому
при Л > п
Вообще, будем писать для краткости
Применяя метод,который был указан в гл. 1(«Э. П.»), мы получим и нижнюю границу
для Е^р—— [\х\]. Однако для этого мы введем допущение, что В! (х) также неотри-
неотрицательно при х^> 0.
Лемма II. Если на всей вещественной оси
A7)
VR (x)
где R (x) — четный многочлен степени 2п(п^>2т), не убывающий при х^О, то
М 1
2 A + V'2 ) '
М
Действительно, неравенство A7) равнозначно
х у
-••+Рп
при всяком (х > 0. Но так как R (х) >• Л
+ • • • + Р
, то тем более
1 g 1 A + ti) + Ру*? + . . .
Поэтому
и, вычитая из этого неравенства неравенство A7), находим, по разделении на у,, не-
неравенство вида
qmx'
.2m
VR{x)
<L
A +
Следовательно, полагая \± = 1^2 и принимая во внимание вторую часть леммы I,
заключаем, что
Следствие I. Сохраняя предыдущие условия и обозначения:
39 с. Н. Бернштейн 613

(«0
Правая часть неравенства A8) есть лишь повторение A6), а левая часть его вытекает
из леммы II, если учесть неравенство L < 2Е^)—— [ \ х |] («Э. П.», стр. 61).
Заметим, что в случае, когда все корни R (х) чисто мнимые, неравенство A8)
приобретает еще более простой вид:
A8bis)
Неравенству A8 bis) можно придать аналогичную форму (немного ухудшив его)
и в значительно более общем случае, когда все коэффициенты R (х) не отрицательны.
Лемма III. Если четный многочлен Д (х) имеет неотрицательные коэффициен-
коэффициенты, то
ъ sin 6г.
В самом деле, положим
^1 И = Л« (to),
где R2(x), представляя квадрат многочлена R(x)t является, как и R(x)t многочле-
многочленом четным с неотрицательными коэффициентами. В таком случае Rx (x) имеет ве-
вещественные коэффициенты, равные по абсолютному значению соответствующим коэф-
коэффициентам R2(x). Следует заметить, кроме того, что R2 (х) будет иметь двойные
корни pke l к, Fй>0), которым будут соответствовать повернутые на угол -тг двой-
двойные корни #i(#), причем, в частности, каждому чисто мнимому корню R (х) соответ-
соответствует двойной вещественный корень Дг(х). Поэтому, принимая во внимание, что
при всех вещественных значениях
заключаем, что значение М в формуле A4 bis), соответствующее Rx (x), не может быть
менее того, которое соответствует Л2(#),'т. е.
V sin 6* ^ V cos 6* B0)
причем знак равенства будет иметь место, если Rt (х) — R2 (х), т. е. при условии, что
многочлен R (х) содержит лишь члены ж4**, где показатель при х делится на 4.
Таким образом, благодаря очевидному неравенству
(где знак равенства имеет место лишь при 0Й =^-j, получим из B0)
Отсюда вытекает
614

Следствие II. Если JR (а?) — четный многочлен с неотрицательными коэффициен-
коэффициентами, то
У" \ о
< V [| * |] < (R @) = 1). B1)
n
2 V
Примеры. 1. Пусть Л (а?) = f 1 -\ —-J . В таком случае неравенство A8 bis)
дает (р>0)
4
Замечая, что при всех значениях
заключаем, что, каково бы ни было ср (х) ;>
поэтому
2. Пусть
Тогда
1 2
Поэтому, замечая, что
имеем
и вообще при всяком ос > О
(п) тс
^аДО II * П< 2а log B/i + 1)
и стремится к нулю при п —> оо.
§ 3. Взвешенное приближение непрерывных функций
на всей вещественной оси
Лемма 1. Если вещественная функция <р (х) переменной х (— оо <^ х < оо) облд-
дает свойством, что
n |Лп@)|-1), B2)
616 39*

еде И~ (х) — четные неотрицательные многочлены степени 2п, корни которых
i0& удовлетворяют условию
Е*(х) [| * И = 0.
Действительно, вследствие A6) и B2)
[lx\]<Evk^T) ^x^<Mn- B3)
Благодаря фундаментальной роли, которую играет | х \ при аналитическом пред-
представлении произвольной ломаной линии, отсюда вытекает следующая общая
Теорема. Если четная функция ф (х) не убыва т при возрастании \х\ и удов-
удовлетворяет условию B2) предыдущей леммы, то
F Г 77* f-rM — О О/Л
ф(эс) У* \ /1 — и' \ */
какова бы ни была непрерывная функция F (х), обладающая свойством, что
F(x)
х1\™тТ(х)=0' B5)
Действительно, как бы мало ни было заданное число е > 0, можно выбрать /?>0
так, чтобы
\F(x)\<-^P- B6)
при | х | > р.
После этого в промежутке (— р, + р) в кривую у = F (х) впишем ломаную
линию, которую влево и вправо до бесконечности продолжим соответственно горизон-
горизонтальными прямыми y = F(+p). Обозначая через y = F1(x) уравнение всей этой
ломаной линии, видим, что если соседние вершины ее, лежащие между —р и /?,
достаточно близки, то в этом промежутке будем иметь
1^И-ЛИКуфИ, B7)
причем неравенство B7) будет соблюдено вследствие B6) также и для \х\ > р7
потому что
при
при #<! — р.
Но функция F± (x) может быть представлена в виде
Fx (х) = ^ Ah I * - ah I + в* + Сf
где — р <[ ah^.p — абсциссы вершин нашей ломаной линии, Ah> В, С — численные
коэффициенты. Пусть
616

и положим р = ууу—т-г • Вследствие леммы I можно при любом ah построить мно-
многочлен Р (х), удовлетворяющий неравенству
и так как при | х | < р,
Следовательно,
< р, а при | х | > р,
2
x — a
|, то
-ап)-Вх- С\ < Щ [9 (*) + Ф (р)] -
Складывая последнее неравенство с B7), находим, наконец, что существует много-
многочлен S (х), для которого
на всей вещественной оси.
Следствие I. Если * ср (х) ^> 0 (или <р2 (х)) — четная целая трансцендентная функ-
функция с неотрицательными коэффициентами у корни которой р^ е удовлетворяют
Л
условию у. = оо [т. е. ф (х) не ниже первого рода], то
всякой функции F(x), обладающей свойством
F (х)
lim —7-f = 0.
Действительно, если ф (а?) = 2 сА а?27с (cQ > 0±, ск > 0), то, полагая
о
B5)
имеем
где i?2n (а?) удовлетворяет условию леммы I. Так как при п достаточно большом #
числе его корней будут корни, [[сколь угодно близкие к корням ф (х), лежащим
внутри круга данного произвольно большого радиуса.
§ 6. Обратные теоремы о взвешенном приближении
на всей вещественной оси посредством многочленов
Лемма. Если на всей вещественной оси
VR{x)
. e.
E0)
* См. «L. S.», стр. 62. {Автор.)
617

где Р (х) — многочлен, a R (х) = &2 (х) -f- t2 (х) — целая четная функция нулевого рода,
имеющая лишь комплексные корни осл + ipfc (Р#>0), то во всякой точке z верхней
полуплоскости соблюдается неравенство
где s (z) -f- it (z) = 0 имеет все корни в нижней полуплоскости, (Аналогичное нера-
неравенство справедливо для точек нижней полуплоскости.)
В самом деле, модуль функции
u(z)
P(z)
s (z) + it (z) *
регулярной в верхней полуплоскости, достигает максимума на вещественной оси или
на верхней полуокружности бесконечного радиуса. Но нетрудно заметить, что если
| z | = р бесконечно растет, то
lim
u(p)
¦ lim
s (p) 4- it (p)
s (z) + it (z)
Для этого достаточно сгруппировать попарно множители сходящегося бесконеч-
бесконечного произведения $ (z) + it (z), где z = а + Ы
±afc — ifik, и убедиться, что
регф, соответствующие корням
! + •
(«а —Р — ВДК
(I)
так как bpfe>.0, a2<;p2.
Таким образом, максимум |и(з)| достигается на действительной оси, где, по усло-
условию, он равен L. Следовательно,
во всей верхней полуплоскости *.
Отсюда вытекает
Теорема. Если
[/(*)]-<>.
E1)
E2)
где ** ф2 (х) = s*(x) 4-12 (x) —целая четная функция нулевого рода, то функция f (x)
также должна быть целой функцией, возрастание которой на круге бесконечное0
радиуса пе превышает воз ристания \ s (z) + it (z)\.
Действительно, E2) означает, что функция / (х) разлагается в равномерно сходя-
сходящийся на всяком отрезке вещественной оси ряд многочленов
... +Рп{х)
E3)
* Из того же вычисления следует, что
* (g) + it (z)
s (ip) + it (tp
так как знаменатель подкоренного количества в правой части (I) достигает наиболь-
наибольшего значения при а = О (Ь = р). (Автор.)
*¦ См. «L. S.», стр. 74. (Автор.)
618

[значок п при Рп{?) не совпадает, вообще, со степенью многочлена Рп (я?)], причем
1*»(*I<еп1ф(*I (-со<*<со),
где числа еп могут быть заданы произвольно. Поэтому, вследствие E1), во всей верх-
верхней полуплоскости будем иметь
Следовательно, ряд E3) будет равномерно сходящимся во всякой конечной об-
области комплексной плоскости, т. е. / (z) будет целой функцией, возрастание которой
на бесконечности не быстрей, чем наибольшее из значений \s (z) + it (z)\ (т. е. будет
также, вообще говоря, нулевого рода, и лишь в виде исключения может оказаться
первого рода нулевой степени).
Следствие I. Если ф (х) = 1 + сгх2 + -f сп х2п... есть четная целая функция
•с неотрицательными коэффициентами, то условие, необходимое и достаточное для
того, чтобы всякая непрерывная функция f (х) ( lim / (х) = 0) могла быть сколь
я»±оо
угодно прцближена равномерно на всей оси полиномами вида >,—-т—г- , состоит в
-*-* ф \х)
1
том, чтобы <р (х) не была нулевого рода.
Заметим, что доказанная выше 'лемма остается в силе и в том случае, когда
четная функция s2 (x) + t2 (x) первого рода, лишь бы ряд
был сходящимся. Действительно, в этом случае бесконечное произведение
будет также абсолютно сходящимся, и все доказательство остается неизменным.
Поэтому имеем
Следствие II. Если функция ф2(#) == s2 (x) + t2(x) есть целая четная функция
не выше первого рода, нули которой настолько близко расположены к ве-
вещественной оси, что ряд ^—i 2~~ сходится, то иэ равенства
Н + h
(*)]-0 E2)
еытекает, что функция f (x) таксисе целая функция, возрастание которой на круге
бесконечного радиуса не превышает
107. О НОРМАЛЬНО ВОЗРАСТАЮЩИХ ВЕСОВЫХ ФУНКЦИЯХ И МАЙОРАНТАХ
КОНЕЧНОГО РОСТА
107.1. После того, как В. С. Виденский сообщил мне в 1952 г. свое тогда еще
не опубликованное дополнение* к неравенству F) согласно которому для всякой
Ф (х) ? N можно построить целую функцию F (х) = 2 akx2k (ao ^ ^» ak ^ ^)»
к=о
удовлетворяющую неравенствам
i F(т)
<ф (х) <F {х)
* См. недавнюкГзаметку В. С. Виденского «О взвешенном приближении на ве-
вещественной оси» (Докл. АН СССР 92, № 2 A953)), где неравенства (А) выведены
(стр. 218) в несколько более общей форме.
619

которую он получил, опираясь на одно свойство нормально возрастающих
функций, установленное G. Мандельбройтом, я заметил, что для построения функ-
функции F0(x), удовлетворяющей неравенствам F) и (А) В. С. Виденского, нет надоб-
надобности применять результаты С. Мандельбройта, а достаточно пользоваться
величинами
Xn= min Г,ф (*> , (Ibis)
—оо<х<оо | X \
при помощи которых я построил в [102] целую функцию
00 1
* () 2 ^\
2 2* х?к К « min Ф (*)], (В)
удовлетворяющую неравенству
При условии A) функция Fx (х) оказывается выше нулевого рода. Но само нера-
неравенство B), очевидно, не зависит от того, имеет ли место A) или нет, и остается
также верным и без предположения, что Ф (х) ? N.
Но для получения целой функции F0(x), удовлетворяющей неравенству Виден-
Виденского F), нам потребуется, чтобы Ф (х) была четной нормально возрастающей функ-
функцией [Ф {х) ? TV]. При этом условии [полагая для определенности Ф A)= Ф'A) = 1],
как было замечено в [102] стр. 527, если распространить определение Хп на все (не-
(нецелые) значения ri^-1, то всякое значение х^.1 будет- для некоторого определен-
п
ного п = п (х) > 1 \п (х) = х -ф-рг осуществлять минимум функции —г—у* , т. е.
при любом х = хп ;> 1 для соответствующего п > 1 будет иметь место равенство
Х^жп = Ф (х). Вследствие Ф' (а?)> 0 и Ф A) = 1, имеем Ф (#)< 1 при| х |< 1,
а так как Хп убывает с возрастанием п, то Хп<1 при л>1. Таким обра-
образом, если некоторому х > 1 соответствует гс<2, то Ф (х) = [Хп#]п< а?2, для всех же
прочих значений х >1 имеем п == 2к + 6, где&^О целое число, 0<;б<2. Следова-
Следовательно,
Таким образом, сумма
Г °°
^(^ = 1 +[1 + 2
имеет по крайней мере один член, который не менее Ф(#), а потому
<b(x)<F(x) (— co<#<oo), F bis)
откуда вместе с B) [при Ф A) = Ф' A) = 1] получаем неравенства
со со
У ф (°) + 13 ^ (\k*fk < Ф И < 1 + ^2 [1 + 2 (\ь*Jк\ (- со < х < со),
1 /1 \2fc
которые аналогичны (А), так как tis^It) пРи всех Целых &>0. В частности,
4/с \ A J
со со
2 Г logF(x)
\к ^ °°» т0 интеграл \ —^— &х сходится и, следовательно, F (х) нуле-
k=i
logF(x)
\к ^ °°» т0 интеграл \
вого рода
620

108. ОБ АНТИМАЙОРАН TAX
108.1. При помощи аналогичного рассуждения легко вывести несколько более-
общее предложение.
Теорема 1. Если Ф (х) > 1—любая функция, обладающая свойством, что для
совокупности о> всех функций J/ (a?) g о> данной степени ро^>0, (почти) возрастаю-
возрастающих при + х —> оо [Н @) = 1] и удовлетворяющих неравенству
|Яр>I<Ф(*) (-со<><со), A>
имеет место
sup У, 2 * q2 = оо, (II)
mo Ф (а?) — слабо весовая функция [Ф (a?) g F].
Действительно, при любом е ^> 0 введем вместо функции Н (х) (стр. 566) функцию
ЯрвМ (ж) б °> степени />0, для которой
удовлетворяющую (I). В таком случае при достаточно больших М и п можно по-
построить, как в доказательстве общей леммы (стр. 566), целую функцию SpnM (x)r
аналогичную ^р^п(х), которая выполнит требуемое неравенство C)..
Для случая, когда Ф(а?)^>с]>0 — четная монотонная функция, в заметке [110J
установлено условие, необходимое и достаточное, чтобы Ф (х) б V, которое заклю-
заключается в том, что
w I h I
S [я@) 11 AР>
где Q — совокупность всех (а не только почти возрастающих) целых функций дан-
данной степени р > 0, удовлетворяющих (I).
Кроме того, следствие 3 заметки [111] означает, что условие (II*) является
необходимым для того, чтобы функция Ф (а?) > с > 0 (— оо<а?<оо) была антимайо-
рантой даже без требования четности и монотонности (см. [111.1]).
Наконец, в заметке, в «Докладах [АН СССР», (93, № 6 A953))^Н. И. Ахиезер
показал, что то же условие (II*) является maKOfce и достаточным для того,
чтобы Ф (х) > с > 0 (— оо <; х <; оо) была слабо весовой (Ф (х) ? V(p)) no отношению
ко всем функциям расоматриваемой степени р (см. сноску на стр. 587.) Этот последний
результат я считаю весьма существенным вкладом в теорию слабо весовых функций.
Возвращаясь к условию (II) теоремы 1, заметим, что при нарушении его функ-
функция Ф (х) (не будучи, может быть, майорантой) обладает свойствами майоранты
по отношению ко всем функциям Н (х) ? о, удовлетворяющим условию (I). (Дока-
(Доказательство аналогично выводу следствий 2 и 3 заметки [111]).
Таким образом, условие (II) необходимо и достаточно для того, чтобы функция
Ф (х) была антимайо рантой по отношению к совокупности функций Н (х) ? о>.
109. УСЛОВИЕ, НЕОБХОДИМОЕ И ДОСТАТОЧНОЕ ДЛЯ ТОГО, ЧТОБЫ
ЧЕТНАЯ НЕУБЫВАЮЩАЯ ФУНКЦИЯ БЫЛА ВЕСОВОЙ
109. 1. После написания этой статьи [109] основные ее результаты были обоб-
обобщены и усилены в заметках [110] и [111]: с одной стороны, теоремы о весовых
функциях [F (х) (« W] соответствующим образом распространены на слабо весовые
функции [F (х) ? V]; с другой стороны, установлено [при том же предположении
четности и монотонности F (х)], что класс функций (V), дополняющий класс (V)r
621

совпадает с классом майорант (90?*), а класс (W) совпадает с классом (Wlfy) май-
орант по отношению к многочленам (теоремы I и II статьи [111]).
Одним из очередных вопросов является вопрос о возможности получения анало-
аналогичных результатов без предположения четности и монотонности. В заметке [111]
сделан первый шаг в этом направлении. Здесь мы ограничимся лишь той частью
проблемы, которая связана с приближением многочленами. Напомню сначала отно-
относящийся к многочленам частный случай следствия 2 этой заметки и приведу его
доказательство, которое не вошло в [111] из-за недостатка места и которое основано
на методе, изложенном в той же статье [111]:
Какова бы ни была функция * Ф (х) > с > 0, если
8ирГ1
х*
о
(I)
для совокупности О всех многочленов, удовлетворяющих условию
) [!* @I = 1; -«<*<•], (II)
то Ф (х) является майорантой квазиконечного'роста для многочленов [Ф ^
(т. е. если на некотором отрезке [а, Ъ] для какой-нибудь последовательности
многочленов Р (х) ? Q, существует lim Р (х) = / (х), то / (х) — целая функция
конечной степени (см. стр. 585)].
В самом деле, ^применяя к четной функции Р (х) Р (-— х) рассуждение заметки
[111] (стр. 586) и вытекающее из него неравенство G) [111], непосредственно полу-
получаем:
\P(z)P(-z)\<eM'W, (T)
где М'—одна и та же постоянная для всех многочленов Р (х) ? О. Кроме того,
фиксируя соответствующие значения а, Ь, одновременно с (I) будем иметь
sup
О
если Рг {х) « Р (х) + ах + Ь. Поэтому, применяя то же рассуждение к Рх (х) Pt (—яг),
получаем для Рх {z) PY (— z) неравенство, аналогичное G'), и, комбинируя его е G'),
находим неравенства такого же вида:
\P(z) KCe^'I'l, \Р(— 2)|«ЗС^*1Ч
ткуда следует, что если / (х) = lim P (х) (на множестве Е, имеющем предельную
точку на конечном расстоянии), то / (х) — функция конечной степени.
Что касается соответствующего следствия 3, то оно подучается из следствия 2
(в случае многочленов) при помощи общего тождества
которое выводится так же, как A7) [109] (стр. 574) и превращается в A7) для чет-
четных Р(х).
Кроме того, из следствия 2 вытекает, что для того, чтобы Ф (х) ;> 1 была весовой,
необходимо осуществление условия
ЬI 1] (III)
* Без нарушения общности вывода можем принять с = 1.
622

[при дополнительном предположении, что Ф (х) < оо по крайней мере на каком-нибудь
отрезке вещественной оси].
Что условие III без всяких ограничений является достаточным для того, чтобы
функция Ф (х) >. 1 была весовой функцией, доказано вскоре после появления [111] в со-
совместной заметке Н. И. Ахиезера и С. Н. Бернштейна «Обобщение теоремы о весовых
функциях и приложение к проблеме моментов». Докл. АН СССР 92, N° 6 A953).
111. СЛАБО ВЕСОВЫЕ ФУНКЦИИ И МАЙОРАНТЫ
111.1. Доказательство следствия 2 для любых четных (немонотонных) функций
(F @) < оо) вытекает непосредственно из предшествующего рассуждения, в частности
из неравенства (9), вывод которого остается в силе и без предположения "монотонности
F (а?). Отбросив также предположение четности F (х), применяем то же самое рас-
рассуждение, и в частности неравенство (9), к четной функции | Gp (x) Gp (—х) |. Дока-
Доказательство заканчивается так же, как для многочленов в [109.1].
Следствие 3 получается из следствия 2 при помощи неравенства!
'log\Gp(x)Gp(-x)\
(I)
где сск + ipft — корни Gp(x), которое выводится аналогично неравенству A) (стр. 584).
Таким образом, в случае неравенства
F (х) удовлетворяет условию следствия 2.
Но принимая во внимание, что все канонические функции Gp (x) конечной степе-
степени (имеющие данный | G (х) | на вещественной оси) могут быть представленьг в виде
1С@)ф0] (см. [98])
акх
G
с вещественным &, видим, что
G'
т
поэтому условие следствия 3 влечет за собой (II), т. е. F (x) ?ffi*. Поскольку при
условиях следствий 2 и 3, единственными функциями / (х), для которых возможно
на всей оси неравенство
являются функции конечной степени, нарушение этих условий необходимо для того,
чтобы функция F (х) > с > 0 была слабо весовой, если только совокупность точек
где F (х) < оо, имеет хоть одну предельную точку на конечном расстоянии.
Отметим в заключение, что условия следствий 2 и 3, которые согласно сказан-
сказанному выше эквивалентны благодаря (I), являются не только достаточными для того,
623

чтобы F (х) > с > 0 была майорантой квазиконечного роста [F (х) ? $Щ*], но и необ-
необходимыми,
В самом деле, если условие (II) нарушено, то из (III) следует, что sup | Gp @) \ = оо,
несмотря на условие A0); следовательно, F (х) не является майорантой.
Отсюда следует, в частности, что всякая функция F (х) ^> с > 0 является, либо
майорантой, либо антимайорантой по отношению к целым функциям данной степе-
степени. Таким образом, по отношению к целым функциям степени р класс антимайорант
эквивалентен классу УЯ* (р), представляющему собой дополнение к классу майорант
квазиконечного роста ffi*(p) (см. сноску на стр. 587).
Однако, только в предположении, что множество Е точек, где F (х) <оо, имеет
предельную точку на конечном расстоянии, доказано, что если функция F (х)^> с
является майорантой, то она не может быть слабо весовой по отношению к целым
функциям той же данной степени р (без этого ограничения вопрос о совместимости
F (х) ? Ш*(р) с F (х) ? V(/>) остается открытым).

ОГЛАВЛЕНИЕ
Стр.
От автора . . , 3
Сокращенные обозначения 4
50. Пример непрерывной функции, для которой формула тригонометрического
интерполирования Лагранжа расходится 5
51. О многочленах, ортогональных на конечном отрезке 7
Часть I.
Введение 7
Глава I. Алгебраические основы 16
Глава II. Распространение асимптотических выражений для ортогональных
многочленов 24
Часть П.
Глава III. Многочлены Якоби 52
Глава IV. Ортогональные многочлены, приводящиеся к многочленам Якоби 79
52. Об ограничении значений многочлена Рп (х) степени п на всем отрезке по
его значениям в п + 1 точках отрезка 107
53. Об абсолютном максимуме тригонометрической суммы 127
54. Об одном видоизменении интерполяционной формулы Лагранжа 130
55. Об одной интерполяционной формуле Балле Пуссена 141
56. Об одном классе интерполяционных формул 146
57. Добавление к статье Е. В. Вороновской «Определение асимптотического
вида приближения функций полиномами С. Н. Бернштейна» 155
58. Замечание по поводу заметки Р. Салема 159
59. О тригонометрическом интерполировании по способу наименьших квадратов 161
60. Об абсолютной сходимости тригонометрических рядов 166
61. О некоторых экстремальных свойствах последовательных интегралов . . . 170
62. Об одной теореме Сегё 173
63. О периодических функциях, для которых наилучше сходящимся рядом
является ряд Фурье 178
п
64. Об области сходимости многочленов Bnf (х) = ^ f \т ) С™ %т A—х)п~т 184
65. О сходимости некоторых последовательностей многочленов 187
66. О формуле квадратур Чебышева 198
67. О формулах квадратур Котеса и Чебышева 200
68. О формулах квадратур с положительными коэффициентами 205
69. Примеры формул квадратур с положительными коэффициентами и раци-
рациональными абсциссами 228
70. Примеры формул квадратур, аналогичных формуле Чебышева 231
71. Об одной системе неопределенных уравнений . . . . с 236
72. Некоторые приложения параметрического метода к изучению квадратур-
квадратурных формул 243
625

73. О наилучшем приближении | х |р при помощи многочленов весьма высо-
высокой степени 262
74. О наилучшем приближении \х — с\р 273
75. О теореме В. А. Маркова 281
76. О базе системы Чебышева 287
77. Об обратной задаче теории наилучшего приближения непрерывных функций 292
78. Конструктивная теория функций вещественной переменной 295
79. Определение ряда функций по экстремумам его последовательных остатков 301
80. К вопросу о локальном наилучшем приближении функций 306
п
81. О сходимости многочленов V. / (—) С™ хт A— а?)™""™ в комплексной области 310
о W
§ 1. Основное преобразование многочленов Bn[f (х)\ в комплексной области 310
§ 2. Узловая линия и петля • 312
§ 3. Важнейшие свойства петли Fx 315
§ 4. Автономные области 318
§ 5. Узловые окружности 319
§ 6. Общие свойства точек сходимости многочленов Bn[f (x)] 323
§ 7. Генеральная область сходимости многочленов Bn[f (x)] в случае одной
особой точки 329
§ 8. Нахождение генеральной области сходимости DR в случае любой об-
области 2? регулярности 331
§ 9. Случай, когда границей области регулярности R является прямая,
параллельная оси ординат • . . . . 333
§ 10. Случай, когда функция / (х) имеет особенности на отрезке 01 ... 340
§11. Области сходимости многочленов An[f (x)] и асимптотическая форма
областей сходимости многочленов Вп [/ (х)] при бесконечном удалении
особых точек функции / (х) 342
82. Конструктивная теория функций как развитие идей Чебышева 349
• • . оо
83. О наилучшем приближении функций \ |?/|sd<]; (s) на отрезке [—1,+ 1] . . 361
о
84. О наилучшем приближении непрерывных функций на всей вещественной
оси.при помощи целых функций данной степени. I (стр. 371), II (стр. 375),
III (стр. 379), IV (стр. 383), V (стр. 390) 371
85. О ^верхней границе максимума модуля производной монотонной функции
конечной степени ,. 396
86. Обобщение, одного результата С. М. Никольского 399
87. Новый вывод и обобщение некоторых формул наилучшего приближения 402
88. Добавление к работе И. И. Ибрагимова «Об асимптотическом значении наи-
наилучшего приближения функции, имеющей вещественную особую точку» . . г 405
89. О наилучшем приближении аналитических функций при ломощи целых
функций конечной степени • 408
90. О.предельных зависимостях между константами теории наилучшего при-
приближения .., 413
91. Предельные. законы теории наилучших приближений 416
92. О свойствах однородных функциональных классов. Первая заметка (стр. 421).
Вторая заметка (стр. 426) 421
93. О некоторых элементарных экстремальных свойствах многочленов несколь-
нескольких переменных 433
94. О целых функциях конечной степени многих вещественных переменных 437
95. Распространение неравенства С. Б. Стечкина на целые функции конечной
степени 442
626

96. Перенесение свойств тригонометрических полиномов на целые функции
конечной степени 446
97. О майорантах конечного или квазиконечного роста 468
98. Об аддитивных майорантах конечного роста 474
99. Функции конечной степени и функции конечной полустепени 479
100. О некоторых свойствах циклически монотонных функций 493
101. О некоторых новых достижениях теории приближения функций действи-
действительной переменной 517
102. О весовых функциях 526
103. О связи квазианалитических функций с весовыми функциями 530
104. Определение и основные свойства квазналгеороидных и алгеброидных
функций 535
105. О наилучшем приближении функций нескольких переменных посредством
многочленов или тригонометрических сумм 540
106. Примечания к теории регулярно монотонных функций 546
107. О нормально возрастающих весовых функциях и майорантах конечного
роста 560
108. Об антимайорантах 565
109. Условие, необходимое и достаточное для того, чтобы четная неубывающая
функция была весовой 572
110. Условие, необходимое и достаточное для того, чтобы почти возрастающая
четная функция была слабо весовой 578
111. Слабо весовые функции и майоранты 584
Авторские комментарии 590
60. Об абсолютной сходимости тригонометрических рядов (стр. 590). 67. О фор-
формулах квадратур Котеса и Чебышева (стр. 592). 68. О формулах квадратур
с положительными коэффициентами (стр. 594). 72. Некоторые приложения
параметрического метода к изучению квадратур (стр. 596). 74. О наилуч-
наилучшем приближении \х — с \р (стр. 597). 84. О наилучшем приближении не-
непрерывных функций на всей вещественной оси при помощи целых функ-
функций данной степени (стр. 599). 85. О верхней границе максимума модуля
производной монотонной функции конечной степени (стр. 600). 87. Новый
вывод и обобщение некоторых формул наилучшего приближения (стр. 601). 88.
Добавление к работе И. И. Ибрагимова «Об асимптотическом значении наилуч-
наилучшего приближения функции, имеющей вещественную особую точку»
(стр. 603). 92. О свойствах однородных функциональных классов (стр. 604).
96. Перенесение свойств тригонометрических полиномов на целые функции
конечной степени (стр. 607). 102. О весовых функциях (стр. 611). 107. О нор-
нормально возрастающих весовых функциях и майорантах конечного роста
(стр. 619). 108. Об антимайорантах (стр. 621). 109. Условие, необходимое и
достаточное для того, чтобы четная неубывающая функция была весовой
(стр. 621). 111. Слабо весовые функции и майоранты (стр. 623).

Печатается по постановлению
Редакционно-издательского совета
Академии Наук СССР
Редактор издательства Д. А. Васильков
Технический редактор Г. Н. Шевченко
РИСО АН СССР № 5317. Т-01643. Издат. № 177.
Тип. ваказ № 1656. Подп. к печ. 28/1 1954.
Формат бум. 70xl081/ie- Бум. л. 19,63.
Печ. л. 53,77. Уч.-издат. 46,6. Тираж 3000.
Цена по прейскуранту 1952 г. 34 руб. 60 коп.
2-я тип. Издательства Академии Наук СССР.
Москва, Шубинский пер., д. 10.

ОПЕЧАТКИ И ИСПРАВЛЕНИЯ
Стр.
41
99
120
151
160
183
188
191
194
213
225
239
246
263
263
265
267
320
389
431
438
438
450
457
465
46С
481
500
534
564
586
590
Строка
1 сн.
2 сн.
4 св.
13 св.
2 си.
1 си.
И св.
14 св.
2 св.
3 св.
j св. 2-й
столб.
5 сп.
14 св.
6 св.
И сн.
11 св.
16 СП
5 сп.
10 св.
4 св.
2 сп.
1 сн.
11 св.
15 сн.
14 сн.
12 св.
6 св.
4 св.
6 св.
16 сн.
5 си.
6 сн.
Напечатано
nt(z)
п
*»@)
данный
на стр. 178.
(i-A)
(i-a«)
6 — а
1 + a
2/1—1
A -уа
непрерывна
Pn(a;)<A/
cos /г arc sin x
(i ~~)ж
•? SI 11
|/(n*)-n»|*|P|
a2 — a + p2 > 0
1 l/ 1 *•
2 r 4w^
[100]
(9Ko = 35)
РЯД G)
GPl-q(x)
целая
целая
(— l^cos — Bh + 1) x
У —
log GpFi)
Должно быть
In t (z)
X
iuf max | jS1 @) |
а<Д
данной
па стр. 180.
?-/(n)(°>
(l~aJ
1—a
Y2/l 1
A - ф
непрерывно возрастает
eu + e"u
\Pn(*)\<M
cos и arc sin x
f (nx) — nv | x \p
Ml/i "a
oil/ A / "9
Z \ f 4п?
[107]
(9Wo ^ 35)
ряд (8)
четная целая
нечетная целая
(-1)ЛЬЛ>тесов|BЛ + 1)*
°° 1
log | Gpr(bi) |
Pu.-i
С. Н. Беришгейн, т. II