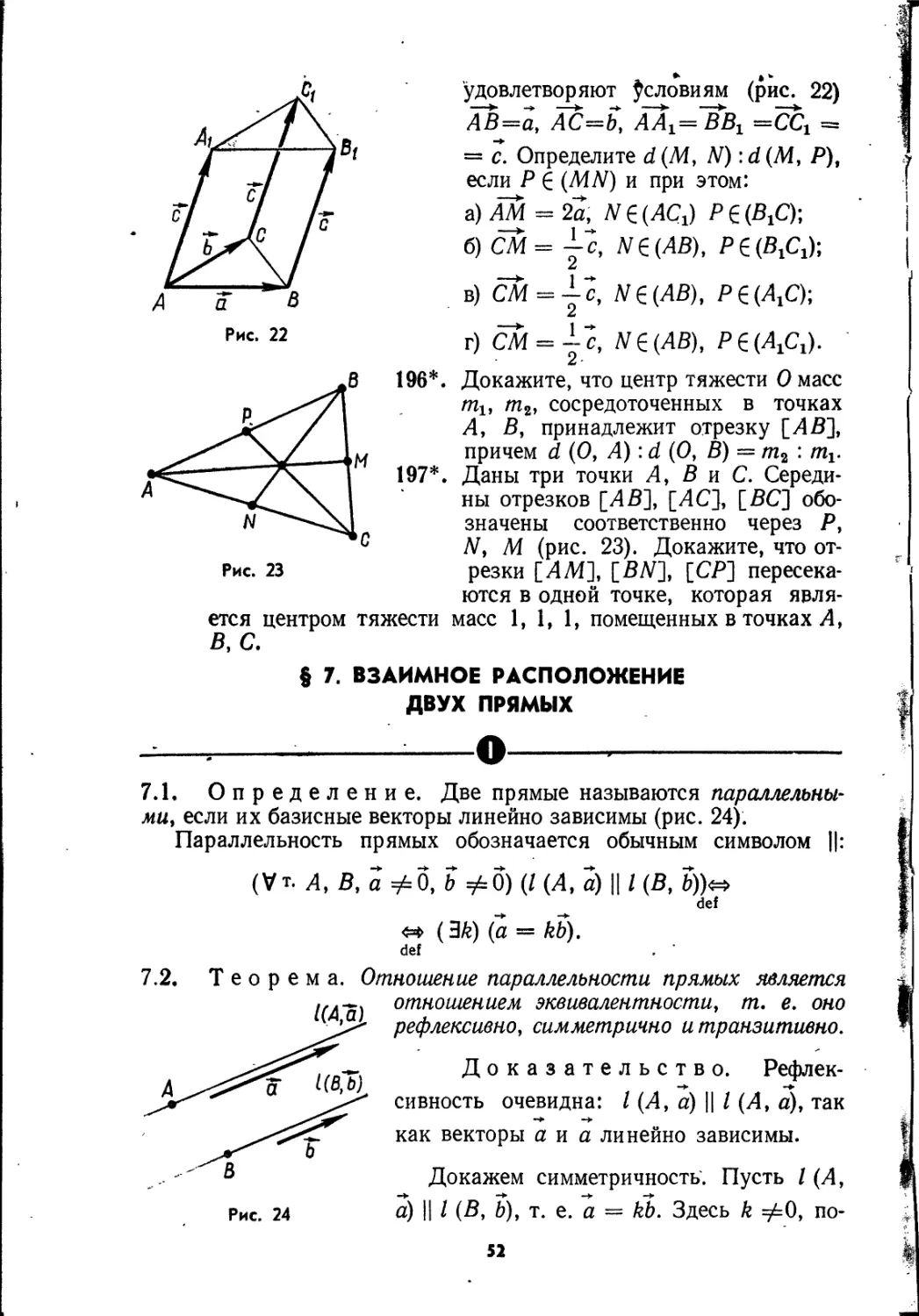
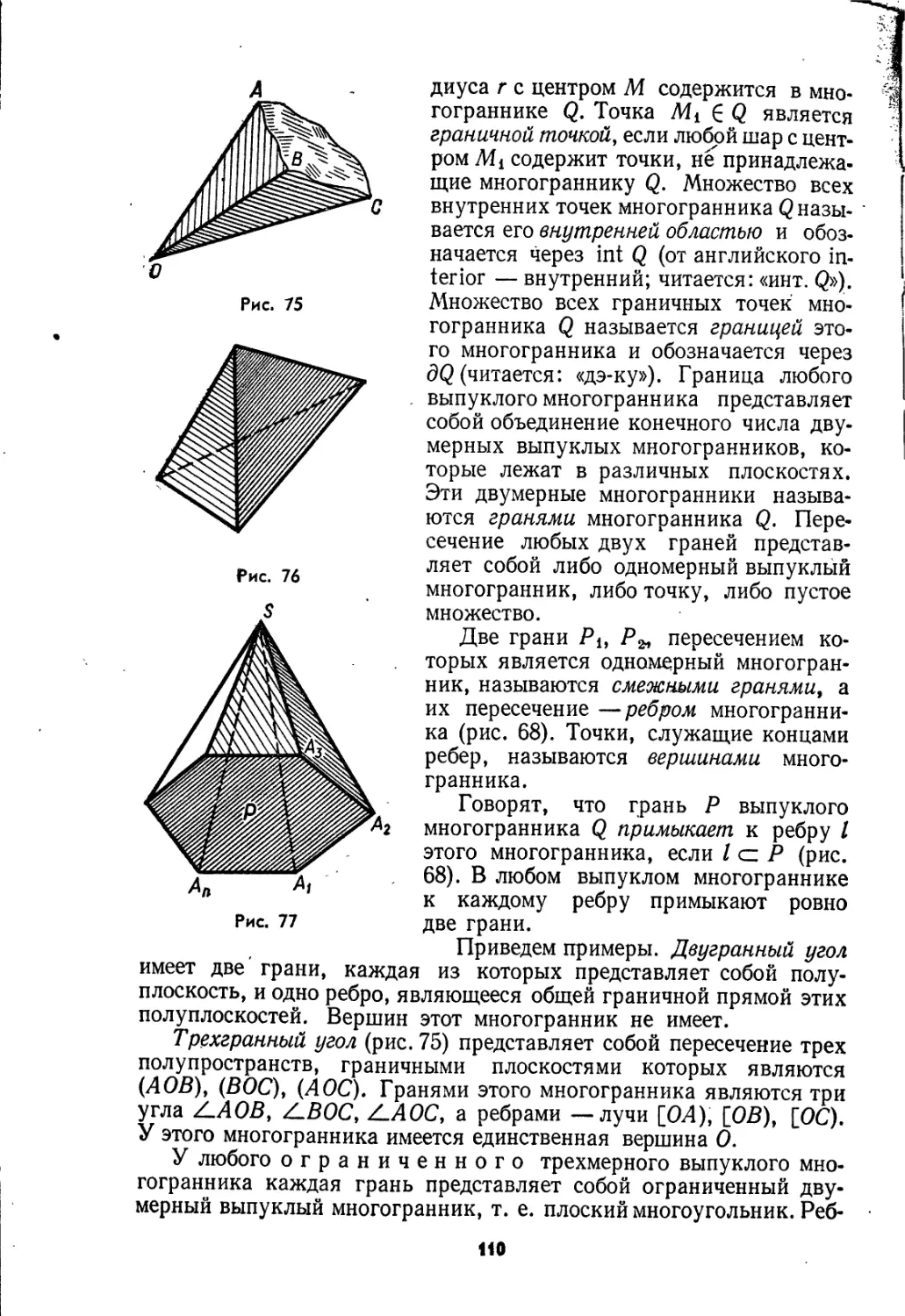
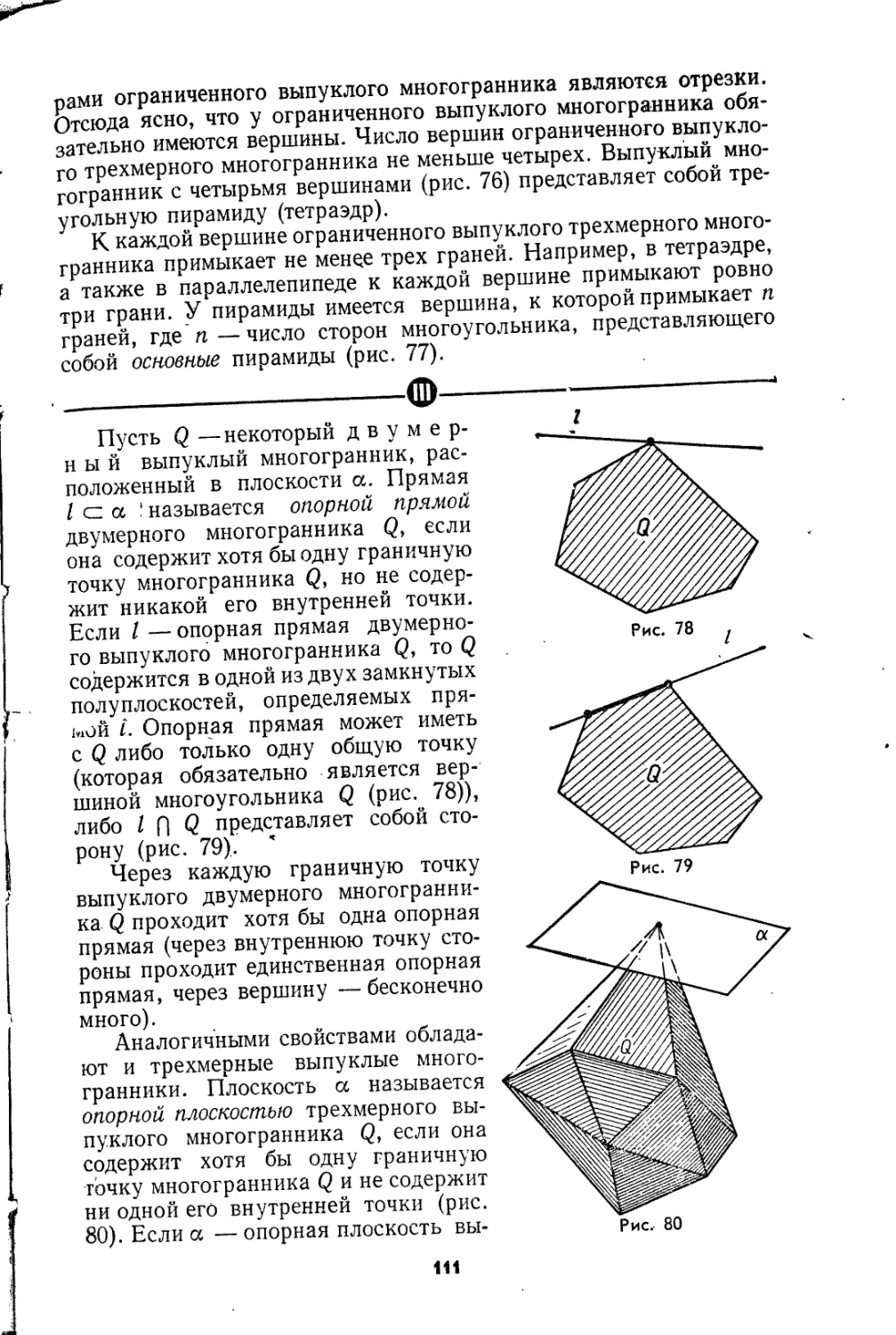
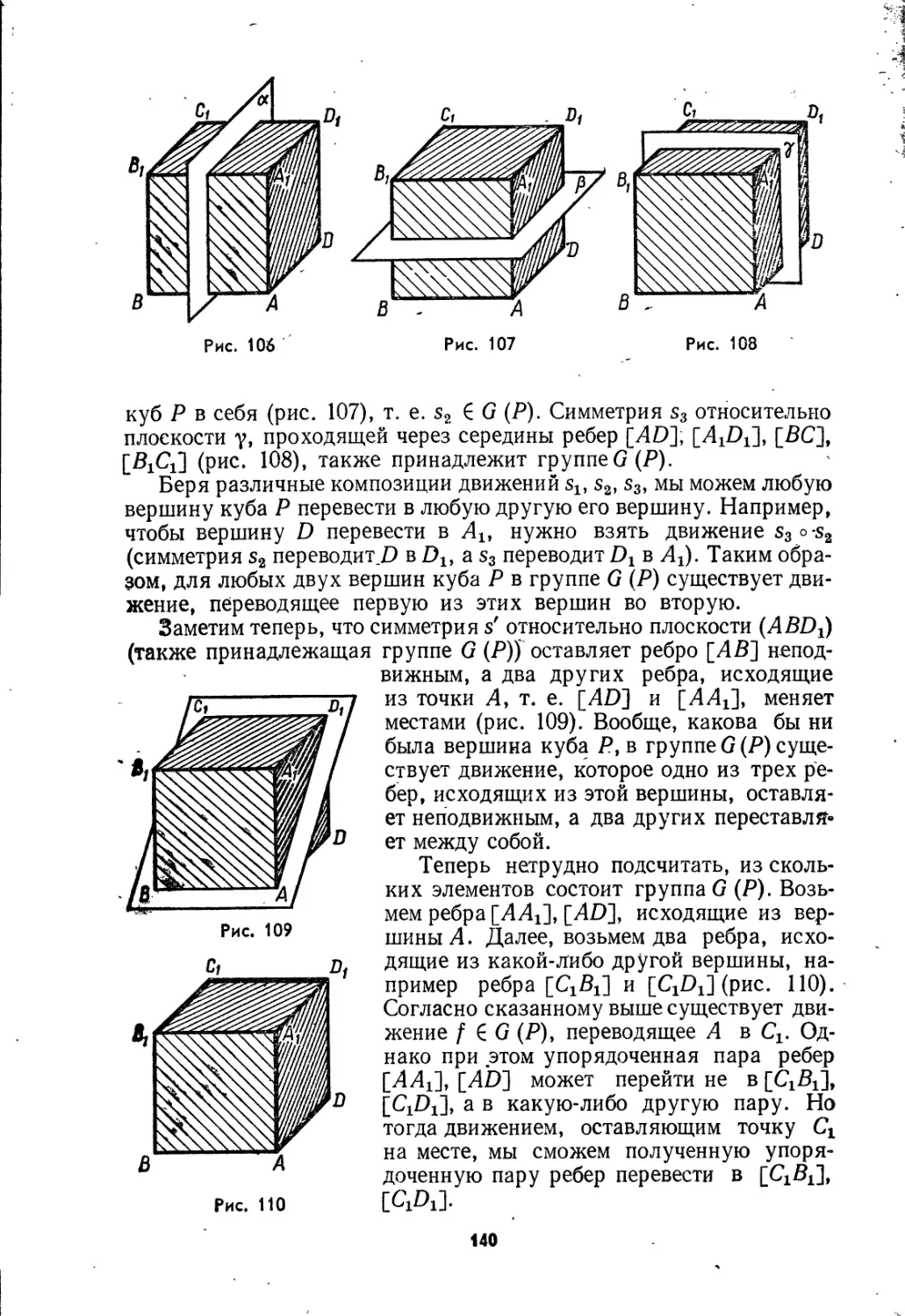
Текст
В.Г. БОЛТЯНСКИЙ, М.Б.ВОЛОВИЧ, А.Д.СЕМУШИН
ВЕКТОРНОЕ
ИЗЛОЖЕНИЕ
ГЕОМЕТРИИ
В.Г.БОЛТЯНСКИЙ, М.Б.ВОЛОВИЧ, А.Д.СЕМУШИН
ВЕКТОРНОЕ ИЗЛОЖЕНИЕ
ГЕОМЕТРИИ
(в 9 классе
средней школы)
ПОСОБИЕ ДЛЯ УЧИТЕЛЕЙ
МОСКВА
„ПРОСВЕЩЕНИЕ** 1982 г.
ББК 74.262.7
Б79
Рекомендовано
Главным управлением школ МП СССР
Болтянский В. Г. и др.
Б79 Векторное изложение геометрии (в 9 классе средней шко-
лы): Пособие для учителей / В. Г. Болтянский, М. Б. Воло-
вич, А. Д. Семушин. — М.! Просвещение, 1982. — 143 с., ил.
Пособие знакомит учителя с одним из возможных путей изложения геомегри-
ческого материала по курсу 9 класса средней школы — изложения на векторной
основе с использованием аксиоматики Вейля.
Книга содержит интересный материал для дополнительной и кружковой ра-
боты по математике.
Б 4306010400—441
103(03) — 82
122 — 82
ББК 74.262.7
513
@ Издательство «Просвещение», 1982 г.
ПРЕДИСЛОВИЕ (для преподавателя)
Эта книга представляет собой продолжение учеб-
ного пособия «Геометрия 6—8» (М., «Просвещение»,
1979) и экспериментальных учебников по геометрии для
6, 7, 8 классов (М., «Педагогика», 1972—1977), напи-
санных тем же авторским коллективом. При ее на-
писании мы стремились познакомить учителя с век-
торным аксиоматическим изложением стереометрии.'
В настоящее время известно несколько различных
путей аксиоматизации элементарной геометрии. Исто-
рически одной из первых была аксиоматика, предло-
женная на рубеже XIX и XX столетий Гильбертом.
У него к числу неопределяемых понятий относятся
«точка», «прямая», «плоскость» и др. С помощью
аксиом и неопределяемых понятий вводятся дальней-
шие (определяемые) понятия и доказываются теоре-
мы. Позднее были «сконструированы» другие аксио-
матики геометрии, отличающиеся друг от друга не
только самим списком аксиом, но также перечнем
неопределяемых понятий.
Самым коротким путем аксиоматизации геометрии
является проникнутый духом современной математи-
ки путь, предложенный в 1917 году — году величай-
ших революционных свершений — Германом Вей-
лем. Идея Вейля состояла в том, что векторные
пространства, которые все более проникают в раз-
личные разделы современной математики и ее прило-
жений, должны органично войти в курс элементарной
геометрии. Понятия «прямая», «плоскость», «конгру-
энтность» и др. Вейль исключил из числа первона-
чальных, взяв вместо них в качестве неопределяемых
другие понятия: «вектор», «сумма векторов», «произ-
ведение вектора на число», «скалярное произведение
векторов», «откладывание вектора от точки». Свойства
этих операций приняты им за аксиомы.
С формальной стороны это лишь один из возмож-
ных путей аксиоматизации геометрии, эквивалент-
ный гильбертовскому, т. е. позволяющий доказать те
же самые теоремы. Но с методологической точки
зрения вейлевский путь является неизмеримо более
ценным. Вместо скрупулезной, утомительной и длин-
ной цепочки рассуждений по гильбертовской схеме
(к тому же оторванной от других разделов математики
и от. естественных наук) вейлевская схема дает исклю-
чительно ясное и краткое изложение, насыщенное
з
современными идеями и близкое к наиболее акту-
альным разделам математики, физики, экономики и
других областей знания.
Книга может быть использована как учебное посо-
бие в классах с углубленным изучением математики,
а также для дополнительной и кружковой работы
учащихся.
В случае, если книга будет использоваться в ка-
честве учебного пособия, необходимо учитывать, что
хотя вопросам наглядности и пространственных пред-
ставлений здесь и уделено некоторое внимание, но
этого безусловно недостаточно. Поэтому необходимо
проводить специальную работу по развитию простран-
ственных представлений. В частности, целесообразно
вначале организовать знакомство с вводимыми поня-
тиями стереометрии на интуитивном уровне (как это
сделано, например, в упомянутом выше учебном посо-
бии «Геометрия 8»).
Замечания и предложения редакция просит на-
правлять по адресу: 129846, Москва, 3-й проезд
Марьиной рощи, 41, издательство «Просвещение»,
редакция математики.
Авторы
ВВЕДЕНИЕ
В курсе геометрии VI—VIII классов были рас-
смотрены основные факты, относящиеся к геометрии
на плоскости. Кроме того, в порядке первоначаль-
ного знакомства были изложены понятия простран-
ственной геометрии.
Сейчас мы приступаем к систематическому изуче-
нию стереометрии. Это изучение будет проведено на
основе аксиоматического метода.
Аксиоматическое построение’теории состоит в том,
что перечисляются первоначальные (неопределяемые)
понятия, формулируются аксиомы (т. е. первоначаль-
ные факты); дальнейшие понятия вводятся с помощью
определений, а дальнейшие факты (теоремы) доказы-
ваются на основе аксиом, а также аксиом и уже до-
казанных теорем. Доказательства теорем проводятся
с использованием логических средств, понятие о
которых было дано в курсе геометрии VI—VIII
классов.
Из курса VIII класса известно, что аксиоматиче-
ское построение одной и той же теории может быть
осуществлено различными путями. Иными словами,
существуют разные системы аксиом (аксиоматики), на
основе которых строится одна и та же теория (т. е.
могут быть доказаны одни и те же теоремы).
Это относится и к пространственной геометрии:
существуют различные системы аксиом, на Основе
которых она может быть построена. Можно было бы
при изложении пространственной геометрии перво-
начальными, неопределяемыми понятиями считать
точку, прямую, плоскость и т. д., указав с помощью
аксиом взаимоотношения между ними. Такая аксио-
матика геометрии впервые была предложена на рубе-
же XIX—XX столетий немецким математиком
Д. Гильбертом. Иные пути аксиоматического по-
строения были указаны И. Шуром, Дж. Биркгофом
и другими математиками.
При тех способах аксиоматического построения,
которые были предложены этими учеными, векторы и
операции над ними вводятся в конце курса как итог
всего построения геометрии. Представление о таком
аксиоматическом построении может дать изученный
курс геометрии VI—VIII классов. Хотя изложение
там не было аксиоматическим, можно было бы чётко
S
сформулировать те не доказывавшиеся первоначаль-
ные положения, которые заимствованы из опыта и
которые, по существу, можно было бы рассматривать
как список аксиом.
Совершенно иной путь аксиоматического построе-
ния геометрии был предложен немецким математиком
Г. Вейлем. Идея Вейля состояла в том, чтобы при-
нять в качестве основных, неопределяемых понятий
точку и вектор (включив, в частности, прямую и
плоскость в число определяемых понятий), а в каче-
стве аксиом — свойства операций над векторами (ком-
мутативность сложения векторов, дистибутивность
скалярного произведения и т. п.). Таким образом, то,
что в других изложениях появлялось в конце курса,
у Вейля принимается в качестве аксиом в начале
построения курса.
С формально-логической точки зрения вейлевский
путь аксиоматизации эквивалентен гильбертовскому,
так как позволяет доказать те же самые теоремы гео-
метрии. Но с точки зрения изложения вейлевский
путь построения геометрии имеет ряд существенных
преимуществ. Во-первых, вейлевское изложение яв-
ляется наиболее современным в научном отношении;
оно позволяет нам познакомиться с понятием вектор-
ного пространства, играющего важнейшую роль во
всей современной матежтике и в ее приложениях (к
физике, химии, экономике и т. д.). Во-вторых, вей-
левское изложение позволяет овладеть наиболее эф-
фективными (векторными) методами решения задач
пространственной геометрии. В-третьих, изложение
геометрии на основе вейлевской аксиоматики явля-
ется (по сравнению со всеми другими способами
аксиоматизации) наиболее кратким.
Вейлевская аксиоматика содержит семнадцать ак-
сиом, объединенных в пять групп. Первые пять пара-
графов курса как раз и посвящены изложению этих
пяти групп аксиом. Для удобства в каждом из этих
параграфов после рассмотрения аксиом излагаются
основные следствия, вытекающие из этих (и предше-
ствующих) аксиом. Вслед за этими пятью парагра-
фами будет излагаться материал, посвященный рас-
смотрению прямых, плоскостей, многогранников, дви-
жений.
Заметим, что аксиоматическое изложение не тре-
бует использования чертежей. Однако применение
чертежей делает изложение более наглядным и об-
легчает запоминание обозначений, взаимного рас-
положения векторов и т. д. Поэтому, хотя для дока-
6
зательств чертежи не нужны, мы будем иллюстриро-
вать изложение чертежами.
Разумеется, на геометрические понятия и факты
пространственной геометрии, интуитивно изученные
ранее (в VIII классе), мы опираться не будем; все
факты стереометрии будут заново выведены из ак-
сиом. Однако ' умение наглядно представлять себе
геометрические образы в пространстве (так же как и
обращение к чертежам) облегчит дальнейшее изучение
курса стереометрии. Иными словами, мы будем изу-
чать и те факты пространственной геометрии, с кото-
рыми учащиеся познакомились в курсе VIII класса,
но в основу изучения будет положен аксиоматический
метод.
ГЛАВА
АКСИОМАТИКА
Г.ВЕЙЛЯ
§ к ПЕРВАЯ ГРУППА: АКСИОМЫ
СЛОЖЕНИЯ ВЕКТОРОВ
——---------------------.о---------------------------
В аксиоматике Вейля вектор относится к числу первоначальных
неопределяемых понятий. К числу неопределяемых понятий отно-
сится также и сумма векторов, т. е. некоторое правило, которое
каждым двум векторам а и & однозначно сопоставляет некоторый
вектор а + Ь, называемый суммой векторов а и Ь. Свойства суммы
векторов описываются аксиомами 1.1—1.4.
1.1. (Va, b) (а + b = b 4- а);
1.2. (Vа, Ь, с) (а 4- (Ь 4- с) «= (а 4- b) -f- с);
1.3. (Э!х) (Vа) (а-{-х — а).
Прежде чем формулировать. четвертую аксиому этой группы,
сделаем замечание относительно аксиомы 1.3. Эта аксиома утверж-
дает, что существует (и при том только один) вектор х, который
для любого а удовлетворяет соотношению
- а + х = а.
Этот вектор принято обозначать через 0 и называть нулевым, векто-
ром. Таким образом, аксиома 1.3 утверждает, что существует един-
ственный вектор 0, для которого
(Va) (а 4- б = а).
1.4. (Va) (Э1у) (а 4-у = б).
8
Вектор у, существование и единственность которого утверждает-
ся в аксиоме 1.4, принято обозначать через —а и называть противо-
положным вектору а. Таким образом, в силу аксиомы 1.4
(Va)(a + (—а) = б).
V В формулировках аксиом 1.3 и 1.4 можно было бы не требовать
единственности, т. е. можно было бы сформулировать эти аксиомы в
следующем виде:
1.3 '. (Эх) (Vo) (а + х = а);
1.4 '. (Va)(3y)(a + y = б).
Единственность же при такой формулировке аксиом нужно было
бы д о к а з ы в а т ь. Мы включили в аксиомы 1.3 и 1.4 излишнее
требование единственности для простоты изложения. ▼
Перечисленные аксиомы 1.1—1.4 составляют, как вы знаете,
аксиоматику коммутативной группы. Поэтому эти аксиомы можно
охарактеризовать следующим образом: множество всех векторов
представляет собой (относительно сложения векторов) коммутатив-
ную группу.
В курсе VIII класса было показано, что из аксиом коммутатив-
ной группы вытекают две важные теоремы. Приведем формулиров-
ки этих теорем применительно к векторам. *
1.5 . Теорема. Пусть аъ а2, ..., ah — произвольные векторы.
Тогда в каком бы порядке мы их ни складывали друг с другом, ре-
зультат будет одним и тем же.
Иными словами, если мы расположим alt а2, .... ak в произ-
вольном порядке, а затем укажем порядок выполнения сложения
при помощи скобок, то результат не будет зависеть ни от порядка
расположения слагаемых, ни от способа расстановки скобок.
1.6 . Теорема. Для любых двух векторов а и b уравнение
а + х = b всегда имеет корень и притом единственный (рие. 1).
▼ Доказательство теоремы 1.6 было полностью проведено в учеб-
нике VIII класса (именно там было пока-
зано, что рассматриваемое уравнение име-
ет единственный корень х = b + (—а)).
Что же касается теоремы 1.5, то ее до-
казательство в учебнике VIII класса было
проведено лишь на частном примере (для
четырех слагаемых). Поэтому укажем
здесь полное ее доказательство.
~х
b
Рис. 1
9
Доказательство теоремы 1.5. Применим ме-
тод математической индукции: сначала проверим, что теорема вер-
на для двух слагаемых, а затем, предполагая, что теорема верна
для п слагаемых (и 2), установим ее справедливость для п + 1
слагаемых.
При сложении двух векторов аъ а2 скобки не нужны, а не-
зависимость суммы от расстановки слагаемых вытекает из аксио-
мы 1.1. Таким образом, при п = 2 теорема справедлива.
Предположим теперь, что теорема верна для некоторого п 2,
и докажем ее справедливость для п + 1 слагаемого.
Один из способов получить сумму векторов а2, ..., со-
стоит в следующем: к вектору прибавляем а2, к полученной
сумме прибавляем а3 и т. д.; в конце концов мы получим сумму п
векторов а1У ..., ап —обозначим ее через sn —и затем, последний
раз выполняя сложение, найдем сумму
р=Л + ^+1- 0)
Докажем, что при любом другом способе выполнения сложения мы
получим тот же вектор.
Пусть v — вектор, получающийся в результате сложения век-
торов alt а2, ..., ап, взятых в некотором порядке и при не-
которой расстановке скобок. Так как операция сложения опреде-
лена для двух векторов, а у нас имеется п + 1 слагаемых, то
для получения вектора v надо п раз выполнить сложение.
Рассмотрим последнее из сложений, т. е. запишем:
v = + (2)
где каждый из векторов Ьг и Ь2 есть сумма некоторых из векторов
аъ а2, ..., ап, Например, Ьг может содержать k слагаемых
(с определенной расстановкой скобок), и тогда Ь2 будет представ-
лять собой сумму остальных (и + 1) — k слагаемых.
Теперь преобразуем запись (2) таким образом, чтобы, как и в
(1), слагаемое стояло на последнем месте. Заметим, что могут
представиться две возможности: слагаемое входит либо в
сумму либо в &2. Без ограничения общности доказательства мы
можем считать, что ап^ в записи (2) входит во второе слагаемое
(если бы оказалось, что входило в blt то, применяя аксио-
му 1.1, мы записали бы v ~ Ь2 + &х).
Итак, сумма Ь2 содержит ап^ и, возможно, другие слагаемые.
10
Но во всяком случае, число слагаемых а сумме не больше «
(так как хотя бы одно слагаемое входит в
Так как сумма содержит не более п слагаемых, то по пред-
положению индукции теорема 1 для нее справедлива, т. е. при вы-
числении суммы Ь2 можно располагать-слагаемые в любом порядке.
Следовательно, сумму 62 можно записать в следующем виде:
К = с ай+1, (3)
где с — сумма всех входящих в Ь2 слагаемых, кроме а (если Ь2
содержит только одно слагаемое ап+1 , т. е. Ь2 — ап+г, то с = 0).
Сопоставляя соотношения (2) и'(3)и применяя к ним аксио-
му 1.2, находим:
V = + ^2 — lb (С + ап+1) = (fyl + С1 +
Остается заметить, что -сумма Ьх + б содержит все слагаемые
аъ й2, ап (взятые в некотором порядке и с некоторой расста-.
новкой скобок). Поэтому по предположению индукции
4- с == s„,
и, следовательно (см. (1)),
© = р. ▼
-----------------------------О--------------—---------------
1.7. Задача. Доказать, что для любого вектора b справедли-
во соотношение — (—Ъ) = Ъ.
Решение. Согласно .аксиоме 1.4 (Va) (а + (—а) .«=0).
В частности, мы можем в это соотношение подставить вместо а
вектор Ь, а также вектор (—й):
(1.)
(4)+(-Н))Л (2)
Соотношение (1) в силу аксиомы 1.1 можно переписать в виде
(-Ь) + Ь = 0. (3)
Соотношения (2) и (3) означают, что каждый из векторов — (—Ь) и
b является корнем уравнения (—Б) + х =0. Но по теореме 1.6
это уравнение имеет единственный корень, и, следовательно,
— (—Ь) =1
14
©
Из теоремы 1.5 следует, что при вычислении суммы векторов |
, сложение можно выполнять в произвольном порядке. Условимся
поэтому при записи суммы вообще не указывать порядка выполне- |
ния действий при помощи скобок, а писать векторные суммы без
скобок. Например, сумму пяти векторов a, b, с, d, е будем записы-
вать следующим образом:
а + дс + d 4-(Г
Вектор ~Ь + (—а) (являющийся решением уравнения а + х =Ь) . -•
принято, для краткости записывать в виде Ь — а и называть раз-
ностью векторов b и а. Таким образом, по определению,
b— а = Ь-]-(—а).
Аналогичным образом уславливаются записывать суммы, со-
держащие два или большее число противоположных векторов. На-
пример,
« + (—b) 4- di 4- р + (—с) = а — t>4- т-{-р — с.
Из теоремы 1.6 (как было показано в курсе VIII класса) сле-
дует* что в векторных равенствах слагаемые можно переносить
из одной части равенства в другую, изменяя при этом знак слагае-
мого.
Задачи ,
1*. Воспользовавшись аксиомами и следуя схеме доказательства
теоремы 1.5, установите равенство:
((ai + а&У + йз) + (а4 + аг) “ (((ах + а2)+ аз) + а«) + й5'
2. Докажите, что вектор х = ((—а) 4- &) + с является реше-
нием уравнения а 4- х = b + с. t
3*. Докажите единственность противоположного элемента, счи-
тая, что в аксиому 1.4 требование единственности не вклю-
чено.
4. Докажите, что —0 = 0.
5. Докажите, что —(а + Ь) == (—а) 4- (—Ь).
6. Упростите следующие выражения, указывая, какими аксио-
мами и теоремами вы при этом пользуетесь:
а) а — F 4- а 4- с 4- Ь — а — с — а\
б) (т — п)+ (а — Ь) + (п — т) 4- (& — а).
.«
7. Докажите, что
а) (а— Ь)+ (р —?4-г)= (а — Ь) — (у — р — г)>
б) (а—&)— (p — q + Ъ = (а —04- (<?—/) —г).
8.' Докажите, ’ что уравнения а + х 4- с + Ь и х 4- с — Ь
эквивалентны.
9. ’ Докажите, что —(а — b) =*Ь — а,
10*. Докажите единственность нулевого элемента, считая, что
в аксиому 1.3 требование единственности не включено.
11. Упростите следующие выражения:
а) ((а + Ь) — с) + (с — (а — 0)—Ь-\-а— Ь\
б) а — (—а) + (—а) — (а 4- (—0) — 1
12*. Прочитайте словами следующее высказывание:
(3!y)(Va)(a + y = 0).
Отличается ли оно от аксиомы 1.4? Истинно ли оно?
13*. Докажите, используя метод математической индукции, что
при любом способе расстановки скобок для обозначения сум-
мы векторов alt аг, .... ап надо использовать п — 2 пары
скобок.
§ 2. ВТОРАЯ ГРУППА: АКСИОМЫ
УМНОЖЕНИЯ ВЕКТОРА НА ЧИСЛО
-----------;-----------—О---------------------------------
К числу неопределяемых понятий в аксиоматике Вейля отно-
сится умножение вектора на число, т. е. некоторое правило, кото-
рое каждому числу k С R и каждому вектору а однозначно сопо-
ставляет некоторый вектор ka, называемый произведением вектора
а на число k. Свойства произведения вектора на число описываются
следующими четырьмя аксиомами:
2.1. (Vfe, I, a) ((k 4- Z) a — ka-\- la);
2.2. (Vft, a, b) (k (a + b) = ka-\- kb);
2.3. (V/г, I, a)(k(la) = (fe/)a);
2.4. (Va)(la = fl).
2.5. Задача. Доказать,’'что (Va)(0a = б).
о
Решение. Согласно аксиомам 2.4 и 2.1 имеем: а + 0а«
» 1а + Оа = (1 + 0)а = 1а = а. Таким образом, вектор Оа яв-
ляется корнем уравнения а 4- х « а. Вектор 0 также является
корнем этого уравнения (аксиома 1.3). Поэтому в силу единствен-
ности (теорема 1.6) Оа = 0.
2.6. Задача. Доказать, что (Vk, а)(—(ka) = (—k)a).
▼ Решение. Согласно аксиоме 2.1 мы имеем: ka + (—k)a=
«» (k + (—k))a — 0а. Поэтому на основании результата предыду-
щей задачи ka 4- (—k)a — 0. Это означает,- что вектор (_k)a яв-
ляется корнем уравнения ka + х = 0. Вектор —(ka) также явля-
ется.корнем этого уравнения (аксиома 1.4). Поэтому в силу един-
ственности (теорема 1.6) — (ka) — (—k)a.^
----------------------------ф—-----------------------------
Введем несколько важных для дальнейшего определений.
Пусть аи ..., ап — некоторые векторы, klt .... kn —действи-
тельные числа. Аксиомы второй группы позволяют рассматривать
векторы А4а?, ..., knan, Мы можем теперь рассмотреть сумму
этих векторов, т. е. вектор
4* 4*^- 4" knan (1)
(в соответствии со сказанным в § 1 мы записываем сумму векторов
без скобок).
2.7. Определение. Вектор k^ 4- ... 4- knan называется
линейной комбинацией векторов alt ..., ап с коэффициентами ku
..., ka, ~
Говорят, что вектор Ъ представляется в виде линейной комби-
нации векторов Oj, ..., ап, если существуют такие действительные
числа k^, ..., kn, что b = k^ 4- ••• 4- knan.
Линейная комбинация (1) называется нетривиальной, если
хотя бы один из коэффициентов klt ..., ktl отличен от нуля.
В противном случае (т. е. если == =» ... — kn =0) линейная
комбинация (1) тривиальна.
2.8. Определение. Векторы ах, ..., ап называются линей-
но зависимыми, если существует нетривиальная линейная комбина-
ция векторов alt ..., ап, равная нулевому вектору.
В противном случае, т. е. если никакая их нетривиальная ли-
нейная комбинация не равна нулевому вектору, векторы ..., аЛ
линейно независимы.
44
---------------------:—©------------------------—
2 9 Теорема. Пусть аъ ..., ап — линейно независимые век-
торы. Тогда, если векторы alt ..., а„, ап+1 линейно зависимы, то
а +1 представляется в виде линейной комбинации векторов а1г .... а„.
Доказательство. Так как векторы alt .... аа, а^
линейно зависимы, то существуют такие числа klt .... kn, k^,
среди которых имеется хотя бы одно отличное от нуля, что
kiai 4- ... + knan + kn+1an+1 = 0. (2)
Если бы было йл4-! = 0, то соотношение (2) приняло бы вид:
kxar + ... + kna„ — 0 (причем среди чисел klt ..., kn имелись бы
не равные нулю). Но это противоречит линейной независимости
векторов П1, .... ап. Следовательно, йл4-1т^=0.
Умножив обе части равенства (2) на число-— и произведя
^П+1
упрощения (на основе аксиом 2.2, 2.3, 2.4), получаем:
( т~*~) ai + ••• + (—т-2-) fl/t ал+1 ~
\ йл+1 / \ кп+1 /
Перенося ап^ в другую часть равенства, видим, что вектор а^
представляется в виде линейной комбинации векторов сц, .... ап.
2.10. Теорема. Если каждый из трех векторов и, v, w пред-
ставляется в виде линейной комбинации двух векторов а и Ь, то
векторы и, v, w линейно зависимы.
▼ Доказательство. Пусть и — ka + lb, v = ma+nb,
w — pa + qb.
Если k — I = 0, то и = 0, и потому векторы и, v, w (т. е. 0,
v, w) линейно зависимы.
Будем теперь считать, что хотя бы один из коэффициентов k, I
отличен от 0. Пусть для определенности k =£ 0. Тогда а = — и —
—-Ь. Подставляя это значение а в выражения для векторов v и
k
—>
получаем:
v = — и + аЬ, w = — и + рЬ, (2)
k k
ml о pl
где а = n —т, ₽ = ? — y-
k k
15
Если а = 0, то v = ~ и, т. е. —~ и + v 4- Ow = 0, и потому
векторы и, v, w линейно зависимы.
Если же а у= 0, то из первого соотношения (2) находим: b =
= Подставляя во второе соотношение (2), получаем:
a ka,
** / р Л72р\ Р •*
W = —-------- \ и +— и,
\ k ka / а
откуда видно, что и в этом случае векторы и, vy w линейно зависимы. ▼
Задачи
14. Докажите следующие соотношения:
a) (V&) (kO = б);
б) (Va) (а + а = 2а)\
в) (Va) (а 4- « + о = За);
г) (Vfe, a, b) (k (а —~b) — ka — kb)\
д) (V&, а, 6, с) (k (а 4-b + с) = ka 4- kb 4- fec|.
15. Найдите вектор, противоположный вектору (2а 4-36 — с) —
— (За — 2Ь 4- с).
16. Является ли вектор а — b + 2с линейной комбинацией век-
торов а, Ь, с?
17. Какие из следующих линейных комбинаций тривиальны:
а) 0а 4- 1 • б 4- 06; б) 0а 4- 0&; в) 0а 4- 06 4" с?
18. Рассмотрим вектор v — ka 4- lb 4- тс. Какие из следующих
высказываний истинны?
а) Если т = 0, то v представляется в виде линейной
комбинации векторов а и Ь.
б) Если v представляется в виДе линейной комбинации
векторов а и Ь, то т = 0.
19. Имеются векторы р = а 4- 2b, q = а — Ь, г — 2а 4- Ь.
Сколькими способами можно представить вектор а в виде
линейной комбинации векторов р, q, г?
20. Рассмотрим вектор и = (d — 2b 4- Зс) 4- (с 4- 26) — (За 4-
4- 4с). Какие из следующих высказываний истинны? Вектор
16
v представляется в виде линейной комбинации: а) векторов
а, Ь, с, d; б) векторов a, b, d; в) векторов а, d; г) векторов
с, d. • _ _
21. Докажите, что при любых а, b векторы а, Ь, 0 линейно за-
висимы.
22. Векторы а, Ь, с линейно независимы. При каких k, I, т
справедливо равенство
(2k + I— 3)а + (k + I + 2m)b + (3k + 21 — 5)с = б?
23. Рассмотрим векторы и = а + & + с, и = 2а —~b + 2с. Jifi-
кажите, что: а) векторы а, Ь, и, и линейно зависимы; б) век-
торы а, с, и, v линейно зависимы.
24. Докажите, что отличные от 0 векторы а, Ь линейно зависимы
в том и только в том случае, если они пропорциональны,
т. е. существует такое k 0, что а = kb.
25*. Отличные от 0 векторы а, Ъ, с линейно зависимы. Можно ли
утверждать, что каждый вектор представляется в виде ли-
нейной комбинации двух других?
26*. Докажите, что векторы Oj, ..., а„ в том и только в том случае
линейно зависимы, если какой-нибудь из них представляется
в виде линейной комбинации остальных.
27*. Какие из следующих высказываний истинны:
а) Если векторы alt ..., ап линейно зависимы, то каждый из
них представляется в виде линейной комбинации осталь-
ных.
б) Если векторы ах, ..., ап линейно зависимы, то найдется
среди них такой, который представляется в виде линей-
ной комбинации остальных.
в) Если никакой из векторов ах, ..., ап не представляется
в виде линейной комбинации остальных, то векторы ах,
..., ап линейно независимы.
г) Если каждый из векторов ах, ..., ап представляется в виде
линейной комбинации остальных, то векторы аи .... а„
линейно зависимы..
28*. В каждом из следующих- случаев найдите линейную завися-
-► -*
мость между векторами и, v, w, следуя пути доказательства
теоремы 2.10:
a) u — 0a + 0b, v = За — b, w = 2а + 5Ь;
11
б) и = la — b, о = 28а — 4b, w — 2а 4~ 56;
в) и = За-4-b, v = a----b, w = —а Qb.
3 3’ ’
<
29.* Докажите, что если векторы w, v, w линейно зависимы, то
найдутся такие векторы a n b, что каждый из векторов щ \
w представляется в виде их линейной комбинации.
30. Докажите, что:
a) (V&, /, m, a) (ka 4- la 4- та = (k +1 + т) а)\
б) (Vn, а) (а + а + ... + а = /ш);
п слагаемых
в) (У k, I, т, a, b, c)(—(ka— lb-{-тс) — —ka + lb— тс).
31. При каких значениях k линейная комбинация
(/г* 1 2 з — 3k 4- 2)а + (Л2 — 4k + 4)b 4- fe~~ 2 с тривиальна?
k +з
32. Докажите, что каждый из векторов р — а + 2b, q =я2Ь — а,
г — а — b представляется в виде линейной комбинации двух
других.
1 "* 2 * “*
33. Решите уравнение — х За----------6 — 0 и укажите, какими
з 15
аксиомами вы пользовались при решении.
34. Вектор b представляется в виде линейной комбинации век-
торов аи а3, а3. Докажите, что векторы а1( а2, а3, b линейно
зависимы.
35. Рассмотрим векторы и = 2а — 36 4- с, о= За—36 4-с.
Докажите, что векторы а, 6, и, v линейно зависимы.
36. Векторы а, 6, с линейно зависимы. Докажите, что, каким бы
ни был вектор d, векторы а, 6, с, d также линейно зависимы.
37*. Векторы а, 6, с, d связаны зависимостью 2а 4- 56 4- Ос —
— 8d — 0. Представьте каждый из векторов а, 6, d в виде
линейной комбинации остальных векторов. Можно ли ут-
верждать, что вектор с нельзя представить в виде линейной
комбинации остальных векторов?
18
§ 3. ТРЕТЬЯ ГРУППА: АКСИОМЫ
РАЗМЕРНОСТИ
Эта группа аксиом не требует введения новых неопределяемых
понятий. Она содержи^, следующие две аксиомы.
3 1. Существуют три линейно независимых вектора.
3’2 Любые четыре вектора линейно зависимы.
В дальнейшем множество всех векторов мы будем обозначать
через R3. В этом обозначении верхний индекс 3 связан с аксиомами
3.1 и 3.2; он показывает, что наибольшее число линейно независи-
мых векторов равно трем (или, как еще говорят, множество всех
векторов представляет собой трехмерное векторное пространство).
3.3. Задача. Доказать, что существует вектор а =£ 0.
Решение. Пусть а, Ь, с — три линейно независимых
вектора (аксиома 3.1). Если бы было а — 0, то мы имели бы
la + ОЬ + Ос = 0, т. е. векторы а, Ь, с были бы линейно зависимы-
ми, что, однако, противоречит их выбору. Следовательно, а #= О,
т. е. существование ненулевого вектора доказано.
----------------------------ф------------------------------.
Тройкой называют множество из трех элементов, рассматривае-
мых в определенном порядке. Обозначать тройку будем с помощью
круглых скобок. Например, (а, Ь, с) есть тройка, первым элемен-
том которой является вектор а, вторым Ь, третьим с. Аналогично .
через (а, Ь) обозначают пару, т. е. множество, элементы an b кото-
рого указываются в определенном порядке.
3.4. Определение. Базисом называется тройка (еь е^
линейно независимых векторов.
▼ Аксиома 3.1 утверждает существование базиса.
3.5. Задача. Дан базис (еь е2, е3). Доказать, что тройка
(ei. е2, е3 4- е3) также является базисом.
Решение. Нам надо доказать, что векторы et, е2, *1+*»
линейно независимы. Допустим, что при некоторых k, I, т спра-
ведливо равенство
^i+ le-i + tn (ех + е3) = б, (1)
т. е.
(k т) ех -|- 1е2 4- те3 =ь б.
е3
Уе2
Рис. 2
Так как векторы е1( е~2, е3 линейно неза-
висимы, то эта линейная комбинация
должна быть тривиальной:
k + т = О, I = 0, т = 0.
Отсюда видно, что число k также равно ну-
лю. Итак, k — 0, I = 0, т = 0, т. е. ли-
нейная комбинация (1) тривиальна. .Мы
видим, что в 0 обращается лишь три-
виальная линейная комбинация век-
торов eiy е2, + е3, и потому эти векторы
линейно независимы, т. е. составляют ба-
зис. ▼
Пусть (е1; е2, е3) — некоторый базис. Тогда
Теорема.
3.6.
любой вектор а представляется, и притом однозначно, в виде ли-
нейной комбинации векторов eit е2, е3 (рис. 2).
Доказательство. Векторы eit е2, е3 линейно не-
зависимы в силу определения базиса. Векторы elt е2, е3, а линейно
зависимы в силу аксиомы 3.2. Следовательно, по теореме 2.9 век-
тор а представляется в виде линейной комбинации векторов eit е2,
Остается доказать единственность. Допустим, что существуют
два различных представления вектора а в виде линейной комби-
нации векторов базиса:
а = xet + уе2 + ze3-,
а = x'et + у'е2 + z'e3.
Вычитая и производя упрощения, получаем:
(х — х'Х + (у — у')е2 + (г — z')e3 = б.
Отсюда следует, что
х —х' = 0, у —у' = 0, г —г' — 0,
поскольку векторы е2, е3 линейно независимы. Следовательно,
х = х', у = у', z = г', а это противоречит предположению о том,
что были взяты разные представления вектора а в виде линей-
ной комбинации векторов базиса. Этим доказана единственность.
--------------------------о-----------------------—
3.7. Определение. Пусть е^, е2, е3 — некоторый базис и
а = xel + уе2 + ге3 — (2)
20
представление вектора а в виде линейной комбинации векторов
базиса (рис. 2). Числа х, у, г называются координатами вектора а
в базисе (elt е3, es).
РавенствоД2) называется разложением вектора а по векторам
рассматриваемого базиса. Заметим, что в силу теоремы 3.6 коор-
динаты вектора а в базисе (еь е2, е3) определяются однозначно.
Координаты вектора будем записывать в виде тройки чисел (х, у, г);
для краткости будем также использовать обозначение .а (х; у, г),
которое означает, что вектор а имеет (в рассматриваемом базисе)
координаты (х; у; z).
3.8. Теорема. Пусть, даны векторы a, (х^ yf, zt), аа (ха; у2;
г2) и число k. Тогда вектор at 4- аа имеет координаты (xi + ха;
У1 + Уг! 2i + гг)> а вектор, kai имеет координаты (&хь kyit kzt). .
Все координаты рассматриваются в одном и том же базисе (et, е2, е3).
Доказательство. Имеем по определению:
Й1 - Xi6i 4- У02 4- Z0s,
а2 — х2в1 4- У2Р2 4-
Складывая, находим:
ai + а2 — (xi 4* x2)^i 4” (У1 4“ Уа)с2 4- (2i 4- z2)e3.
Это означает, что вектор1 4- а2 имеет координаты
(xi 4- Х2', У1 4~ Уг> 2i 4- 2а)-
Далее,
АЯ1 = k (,Х01 4- у02 + г1е») = (kxtiei 4- (бу 1)62 4- (kz,)e3.
Отсюда вытекает второе утверждение теоремы.
---------------------------©---------;-------------------
3.9. Теорема. Если векторы a ub линейно независимы, то их
можно дополнить до базиса, т. в. существует такой вектор с, что
(а, Ь, с) — базис.
▼ Доказательство. Пусть (et, е2, е3) — некоторый ба-
зис. Рассмотрим тройки
(a, b, ex), (а, Ь, е2), (а, Ь, е^ (3)
и докажем, что хотя бы одна из них является базйсом.
Допустим, что ни одна из этих троек не является базисом. Тогда
(так как векторы а и b линейно независимы, а векторы a, b, et ли-
нейно зависимы) по теореме 2.9
ех — ka + /б
при некоторых k и I. Аналогично с2 = та tib, е3 = ра + qb.
По теореме 2.10 векторы et, е2, е3 линейно зависимы, что, однако,
противоречит определению базиса.
Полученное противоречие показывает, что хотя бы одна из
троек (3) линейно независима, т. е. а, b можно дополнить до бази-
са. ▼
Задачи
38. Докажите, что существуют два линейно независимых век-
тора.
39*. Пусть дан некоторый базис (еь е2, е3). Каждый ли из векто-
ров а, Ь, с, d представляется в виде линейной комбинации
трех остальных векторов, если:
а) а = 2сх + Зе2 — с3, б) а = ех + 2е2,
b = 5е1 -J- е2 4- 2е3, b => 2сх — е2,
с Зс2, с ==: с2у
б=ех-|-2е2—са; d==cx4-e3?
40. Одинаковы или различны следующие тройки векторов:
а) (2Ь, а, 5с) и (а, 2Ь, 5с) при условии, что векторы а, Ь, с
линейно независимы; б) (2Ь, а, 5с) и (а, 2Ь, 5с) при условии,
что 2Ь — а — 0;
‘ в) (—а, ~Ь, с) и (а, Ь, с); г) (а, —6, с) и (1а, (—1)&, 1с)?
41. (а, Ь, с) —базис. Каковы координаты следующих векторов:
а) а; б) —5; в) б; г) 2а + 6; д) а + b + с?
42. Даны векторы а (х; у; г) и & (2х; Зу; 4г). Найдите координа-
ты векторов а + Ь, 2а —Ь, За — Ь.
43*. Дан базис (elt е2, е3). Рассмотрим векторы р — + с2+ез>
q = ех — е2 и некоторый вектор г. Докажите, что вектор г
представляется в виде линейной комбинации векторов р, q, е3.
44. . Вектор а имеет в базисе (ех, е2, е3) координаты (х; у; г).
Докажите, что вектор а в том и только в том случае представ-
22
ляется в виде линейной комбинации векторов и е2, если
? = 0.
45 Найдите координаты вектора, противоположного вектору
а (х; У!2)- ~
45. Даны векторы a (Xi; ye, z^b (х2;_у2; Z2M с (х3; у3; г3). Най-
дите координаты вектора ka + lb + тс.
47*. Докажите, что если векторы а, Ь, с составляют базис, то
каждая из следующих троек является базисом: a) (b, с, а);
б) (2а, —В, Зс); в) (а + &, 2Ь — с, с + а).
48*. Докажите, что число базисов бесконечно.
49*. Тройка (еь е2, е8) является базисом.
а) Докажете, что тройка (et + е2, Cj — е2, е3) также являет-
ся базисом.
б) Разложите вектор ei по векторам нового базиса.
в) Разложите вектор е2 по векторам нового базиса.
г) Пусть вектор а имеет координаты (х; у; г) в старом базисе.
Найдите координаты вектора а в новом базисе.
50. Даны некоторые векторы a, b, с, d. Какие из следующих вы-
сказываний истинны?
а) Векторы a, b, с, d линейно зависимы.
б) Каждый из векторов а, Ъ, с, d представляется в виде ли-
нейной комбинации остальных трех векторов.
в) Хотя бы один из векторов a, b, с, d представляется в виде
линейной комбинации трех остальных векторов.
г) Существует такая четверка векторов, что только один
из них является, линейной комбинацией трех остальных.
51. Докажите, что разность векторов а (х/, уь Zj) и b (х2; у2; z2)
имеет координаты (xt —х2; yi —у2; zt —z2).
52. Даны векторы а (1; 1; 1), b (0; 1; 2) и с (—3; 2; —1). Найдите
координаты следующих векторов:
а) р = За 2с, г = а -|- b с;
b) q = 6 — с, 7 = а — 2Ь — Зс.
53*. Дан базис (elt с2, с3) и векторы a + с2 и b — Cj —с2.
Докажите, что векторы а и b линейно независимы. Допол-
ните векторы а и д ' до базиса.
54*. Даны три вектора а, Ь, с. Докажите, что если любой вектор
представляется в виде линейной комбинации векторов а, Ь, с,
23
то векторы а, Ь, с линейно независимы. Запишите формули-
ровку этой теоремы с помощью логических символов; сфор-
мулируйте теорему, противоположную обратной.
§ 4. ЧЕТВЕРТАЯ ГРУППА: АКСИОМЫ
СКАЛЯРНОГО УМНОЖЕНИЯ
---------------------------0—--------------------------
К числу неопределяемых понятий в аксиоматике Вейля отно-
сится скалярное умножение векторов, т. е. некоторое правило, ко-
торое каждым двум векторам а, b однозначно сопоставляет некото-
рое действительное число, обозначаемое через ab и называемое
скалярным произведением векторов а, Ь.
Свойства скалярного произведения описываются следующими
четырьмя аксиомами:
4.1. (Va, b)(ab=ba)’
4.2. (V&, a, b) ((ka) b = k (ab));
4.3. (Va, b, c) (a (b + c) = ab + a c);
4.4. (Va^0)(aa>0).
В связи с четвертой аксиомой заметим, что скалярное произве-
дение аа вектора а на самого себя называется скалярным квадра-
том вектора а; таким образом, аксиома 4.4 утверждает, что ска-
лярный квадрат любого вектора a =£ О есть число положительное.
Скалярный квадрат вектора а принято обозначать через а2.-
-------------------------е—----------------------—
4.5. Определение. Векторы а и b называются ортого-
нальными, если их скалярное .произведение равно нулю.
Ортогональность векторов а и b обозначается так: a Lb.
Lq (Va, b) (a _L b) <=> (ab = 0).
T ” def
Fl 4.6. Задача. Даны векторы a =/= 0 и
г - j । b. Доказать, что существует единственное
число k, для которого вектор b + ka ор-
тогонален вектору а (р.ис. 3).
' Реше н и е. Нужно найти число k,
Р#с. з удовлетворяющее условию
24
a (b + ka) — 0,
t. e.
ab + ka2 = 0.
Так как a 0, то число а2 отлично от 0 (аксиома 4.4). Разделив
последнее равенство на это число, получаем k = ~~. Отсюда
а2
видно, что искомое число k существует, и притом, определено одно-
значно.
^4.7. Задача. Даны векторы а =£0, b '=£ 0 и с, причем а ± Ь:
Доказать, что существуют однозначно определенные числа I нт,
для которых вектор о»4- la + mb ортогонален каждому из векторов
а и Ь.
Решение. Задача состоит в том, чтобы найти числа /и
т, удовлетворяющие следующим двум условиям:
~а (с + 1а 4- mb) — 0 и b (с*+ la 4- mb) =0. .
Раскрывая скобки и учитывая, что ab—0, перепишем эти
условия в виде
ас 4- 1а2 = 0 и b с + mb2 — 0..
Отсюда (поскольку а2 0 и Ь2 =/= 0) получаем:
. ас т Ьс
1 =-----и т — — —.
a2 fe2
Таким образом, искомые числа I и т существуют, и притом опре-
делены однозначно. ▼
---------------------:—.о------------———
4.8. _ Определение. Длиной вектора а называется число
Vа2. Длина вектора а обозначается через |а|:
| а | = Va2.
Из этого определения непосредственно вытекает, что | а\ есть число
неотрицательное, прйчем |а| =0 в том и только в том случае,
если а = 0. Очевидно, что для любого вектора а справедливо со-
отношение: |а|2 = а2.
25
4.9. Теорема. Для любых векторов a, b справедливы соотно-
шения
|Л| <|а I -|b |, (1)
|а + д|<|а| + |&|. (2)
Доказательство. Если а = 0, соотношение (1)
очевидно. Поэтому в дальнейшем будем считать, что а =£ 0.
. Рассмотрим вектор ха 4- Ь, где х — произвольное действитель-
ное число. Скалярный квадрат этого вектора (как и любого век-
тора) есть число неотрицательное, т. е.
(ха + &)2 0.
Раскрыв скобки, можно это соотношение переписать в виде
х2а2 + 2х (ab) + Ь2 > 0. (3)
В! Левой части полученного неравенства (3) стоит квадратный трех-
член, у которого коэффициент при х2 положителен (так как а =£ 0).
Неравенство (3) показывает, что этот квадратный трехчлен прини-
мает неотрицательные значения при любом действительном х.
Следовательно, дискриминант этого трехчлена неположителен:
D =- 4 (ab)2 — 4а2Ь2 0; отсюда получаем:
(а Ь)2 а2 Ь2 = | а|2 • | b |2.
Извлекая из обеих частей этого неравенства квадратный корень,
получаем соотношение (1).
Докажем, теперь справедливость соотношения (2). Имеем:
|а + &|2 = (a + b)2 = а2 + 2аЬ + Ь2 <|а|2 4-2|а||&| +
+ |6|2 = (|а| + |И)2-
Извлекая из обеих частей'квадратный корень, получаем , соот-
ношение (2).
—--------------------------©-------------------:>
4.10. Определение. Базис (еъ е2, е3) называется орто-
нормированным, если векторы е2 и е3 попарно ортогональны и
длина каждого из них равна 1.
▼ Докажем, что ортонормированные базисы существуют. Возьмем
два линейно независимых вектора а и Ь. Тогда а ф 0, и потому в
силу задачи 4.6 существует такое число k, что вектор b’ = b + ka
ортогонален вектору а. Ясно, что Ь' =/= 0 (иначе векторы а и b ока-
16
зались бы линейно зависимыми). Итак, мы нашли такие^векторы
а =/= 0 b' 0, что а ± Ь'. Из этого следует, что векторы а и $ ли-
нейно независимы. ,
Дополним линейно независимые векторы а, Ъ' некоторым век-
тором с*до базиса (а, Ь', с). Согласно задаче 4.7 существуют такие
числа I и т, что вектор с' = с + la -f- mb' ортогонален каждому
из векторов а и Ь'. Ясно, что с' #= 0 (иначе векторы а, Ь* н с ока-
зались бы линейно зависимыми). Итак, мы нашли три отличных
от нуля вектора а, Ь'-, с'-, которые попарно ортогональны друг
ДРУГУ-
Возьмем, наконец, векторы
ех = —— а, е2 —— Ь', е8 = —— в',
1*1 |*Ч 1?1
Эти векторы попарно ортогональны, а длина каждого из них рав-
на 1. Из этого следует, что векторы elt et, ea линейно независимы,
т. е. (е1( е2, е3) — базис. ’ Тем самым существование ортонормиро-
ванного базиса доказано. ▼
4.11. Теорема. Пусть е1г е2, е3 — ортонормированный базис
и пусть векторы и а2 имеют в этом базисе координаты (xt; ур, г2)
и Уз! гг)- Тогда
ata2 = XiX2 4- У1у2 + zxz2. (4)
Доказательство. Имеем:
«1 = 4- ух<?2 4- гхе3, а2 = х& + у2е2 4- гД3,
и потому
«1 а2 =! (х1е1 4- ухе2 4- гхе3) (х#х+ у^+ г2е3).
Раскрывая скобки и учитывая соотношения
ехе2 = 0, е2е3 — 0, ехе3 = О, ef = 1, el — 1, ef = 1
(вытекающие из определения ортонормированного базиса), полу-
чаем равенство (4).
4.12. Следствие. Пусть вектор а имеет в ортонор мирован-
ном базисе (еь е2, е3) координаты (х; у, г). Тогда
|а\ = Кх2 4- У2 -рг2.
Действительно, в силу предыдущей теоремы
а2 = х2 4- у2 4- 22.
27
Задачи
55. Докажите, что для любых векторов а, &, с, d справедливы
соотношения:
а) а (Ь + с + d) = ab-\- а с-]-ad;
б) (а 4- Ь) (с + d) = ас + ad + be + bit.
Какие аксиомы были использованы при доказательстве этих
соотношений?
56. Докажите следующее утверждение:
(V&, a; b) (a (kb) = k (а b)).
Какие аксиомы были использованы при доказательстве?
57*. Докажите соотношения:
(—а) Ь = — (а Ь), а (—&) = — (ab), (—a) (—b) = ab.
58*. Докажите, что для любого вектора а существует вектор
Ь Ф 0, который ортогонален а.
59. . Какому условию должны удовлетворять векторы а и Ь,
чтобы векторы а + b и а —b были ортогональны (рис. 4)?
60. Векторы а у= 0 и b 0 ортогональны. Докажите, что а и b
линейно независимы.
61. Докажите, что если векторы а и b ортогональны, то скаляр-
ное произведение а (а 4- kb) не зависит от k. Сформулируйте
и докажите обратную теорему.
62*. Докажите, что утверждение задачи 4.7 справедливо и без
предложений а О, b 0, a JL Ь:
(Vа, Ьь c)(3Z, т) (с 4- 1а 4- mbi. а)/\(с + 1а 4- mb ± Ь).
Докажите также, что если векторы а, b линейно независимы,
то числа /, т определены однозначно.
63. Докажите, что если отличные от 0 векторы а, &, с попарно
ортогональны, то они линейно независимы.
64. Векторы a. b, ka + lb попарно ортогональны. Докажите,
что хотя бы один из них равен 0. -
. 65. Вектор а отличен от 0. При каком
k длина вектора ka равна 1?
^7------ 66*. Докажите, что равенство |а6|'==
= |а||Ь| имеет место в том и толь-
ко в том случае, если векторы а и &
Рис. 4 линейно зависимы.
28
67.
68.
69.
70.
71.
72*.
73*.
74*.
75.
76.
77.
Докажите, что если векторы а и
~Ь ортогональны (рис. 5), то
|д_|_ b|2= |а|2 + |b|2.Справедли-
ва ли обратная теорема?
Векторы b и с линейно независи-
мы. Найдите такие числа х и у,
что вектор а + xb + ус ортогона-
лен каждому из векторов Ь, с.
Вектор b отличен от 0. При каком
значении k вектор a+kb (рис. 6)
имеет наименьшую длину? Как
связаны между собой векторы b
и а + kb при этом значении Л?
Докажите, что для любых векто-
ров а, b справедливо соотноше-
ние
|о — &|2 = |а|2 + |£|2 — 2аЬ.
Докажите, что для любых векто*
ров а, b справедливо соотноше-
ние (рис. 7)
\а + £|2 + |а — Ь|2 = 2|а|2 + 2| £|2-
При каких условиях справедливо соотношение
|а + д| = |а| + ГЫ?
При каких условиях справедливо соотношение
|а _Ь| = |а| _ |£|?
При каких условиях справедливо соотношение
’ |а + Ь + с| = |а| + |Ь|4- |с|?
каких
условиях справедливо соотношение!ka\ *= k |а|?
При
Базис (еь ег, е3) — ортонормированный. Докажите, что век-
торы р = -L.,(ei + е2), q = y=(^i — <?2), г = et также обра-
зуют ортонормированный базис.
Даны векторы а (1; 2; —3), b (3; —1; 2). При каком k длина
вектора а + kb будет наименьшей? Вычислите при этом
значении k скалярное произведение b (а + kb).
29
78. Векторы а и b линейно независимы. Укажите среди следую- щих чисел равные: а) |а + &|, У З24-b2 — 2ab, V (З4-6)2, + —&|; • б) f3|, |ab\, УаФ, f — ab\.
79*. Векторы a, b, с имеют длину 1, причем ab = 0, ас — — —. i -» _ 2 ’ be — —. Найдите вектор, дополняющий векторы а, b до ортонормированного базиса. Сколько таких векторов су- ществует?
80*. Базис (еъ е2, е3) —ортонормированный. Дополните векторы Р =? ~ ег)> Ч = ег+ ез) До ортонормирован- ного базиса,.
81. Базис (eb е2, е3) — ортонормированный. При каком k длина вектора k + е2 + е3) равна 1? При каком k длина век- тора k (ci — е2 —е3) равна 1?
82*. Векторы а, Ь, с линейно независимы. При каком условии тройка (йа, lb,,тс) является базиерм? При каком условии каждый вектор этого базиса имеет длину 1?
83. Базис (c-l, е3, е3) — ортонормированный. При каком k век- торы р — Ci + е2 4- е3 и q = ei 4- е2 4- ke3 ортогональны? В’ задачах 84 —86 все векторы задаются своими коорди- натами в одном и том же ортонормированном базисе.
84. При каких k, 1, т векторы а(1; 3; 2), b (0; 4; k) n'etf-, rrv, 5) попарно ортогональны?
85. Даны векторы а (1; 1; 1), b (2; 0; 3), с (1; —1; 2). При каком k скалярное произведение векторов b 4- ka и b 4- kc будет наименьшим?
86. Даны векторы а (1; 0; 2), b (1; 2; 0), с (3; —1; 2). При каком
87*. k векторы а 4- kb и с ортогональны? Векторы задаются своими координатами в некотором базисе (et; е2; е3). Докажите, что если для любых векторов, a (xt; у(; Zt) и b (х2; у2; z2) справедливо соотношение ab = XtX3-{- 4- У1У2 + Zi^a, то базис (ei, е2, е3) — ортонормированный.
88. Докажите, что для любых векторов а, Ь, с справедливы
равенства
а (Ь— с) = ab— ас,
зо
(a + ЬУ = & + ~ = a* “%ab
(a 4- b) (a — b) = a'? —Is.
89 Докажите, что, каковы бы ни были векторы а, Ь, число
{ба 4" Ь)2 — (Зл 4" 2£>)2 4~
неотрицательно. В каком случае это число равно нулю?
90. Укажите среди следующих чисел равные:
(За) с, x(c + 2d), 3(са), с (За), 2dx 4- хс.
91. В каком случае вектор х ортогонален самому себе?
92. Вектор а отличен от 0. При каком k векторы а и ЗЬ — 2ka
ортогональны?
93. Векторы а и b ортогональны. При каком условии скалярное
произведение a (ka 4- Ь) отрицательно?
94. Векторы а и b отличны от 0 и ортогональны. При каком
условии вектор ka 4- lb ортогонален каждому из векторов
а, Ь?
95. Векторы а, Ь, с отличны от 0 и попарно ортогональны. При
каком условии вектор ka 4- lb 4- тс ортогонален каждому
из векторов а, Ь, с?
96* . Докажите, что для любых векторов а, Ь справедливо соотно-
шение \а —-3| > |л| — |£>|.
97. Докажите, что если векторы а и b ортогональны, то | а — Ь|2=
= 1«|2 4- I&I2. Справедлива ли обратная теорема?
98. Докажите, что | ka\ — |Aj • |a|.
99. Докажите, что для любых векторов а, Ь, с справедливо со-
отношение |а + ~Ь 4- с| |а] 4- ].Ь] 4- Id- Сформулируйте
обобщение на большее число слагаемых.
109*. При каких условиях справедливо соотношение
|a-&| = |a|4-13|?
101*. При каких условиях справедливо соотношение.
|а — Г| = |а|—- |д|?
102. При каких условиях справедливо соотношение
| ka\ = —k | a I?
«03. Базис (eit ег, e3) — ортонормированный. При каком k длина
31
вектора k + e2) равна 1? При каком k длина вектора^
k (ei — е2) равна 1?
104. Базис (еь е2, е3)—ортонормированный. Найдите значения
следующих выражений:
С^г)2» ^2(^2 ^з), (2^1 ^з)2-
В задачах 105—108 все векторы задаются своими коор- '
динатами в одном и том же ортонормированном базисе.
105. Образуют ли векторы
alL Ъ ь(0-. J=; -cl-------------------L; -U
\3 3 3/ \ /2 /Т/ \ 3/2 3/2 3/2/
ортонормированный базис?
106. Среди следующих векторов найдите пары ортогональных
векторов:
а (1; 1; 1); b (0; 1; 1); с (0; 1; —1); d(l; 1; —2); е(—2; 1; 1).
107. Даны векторы а(1;2;3) и b (3; 2; 1). Какой из векторов
а + Ь, а — b имеет меньшую длину?
108. Вычислите длины векторов
а (2;,2; —-1); b (7; —4; —4); с (8; 4; 1);
d (6; —6; 7); р (2; —6; —9); q (2; 3; 6).
§ 5. ПЯТАЯ ГРУППА: СВОЙСТВА ТОЧЕК
------------------------—О-------------------------:—-
Кроме множества 7?3 всех векторов, в аксиоматике Вейля рас-
сматривается непустое множество В3, элементы которого называ-
ются точками. Точка, как и вектор, относится к числу неопределяе-
мых понятий. К числу неопределяемых понятий относится также
некоторое правило, которое каждой упорядоченной паре точек
(Л, В) ставит в соответствие некоторый вектор (рис. 8), обозначае-
мый через АВ. Свойства точек описываются следующими тремя
аксиомами:
5.1. (VT.A, В, С) (АВ + ВС - АС);
В 5.2. (VT. А, а) (ЭВ) (АВ = а);
5.3. (VT.A, В) (АВ = 6)=>(А = В). -
дАксиома 5.2 утверждает, что, каковы
бы ни были точка А и вектор а, найдет-
Рис. 8 ся точка В, для которой АВ = а; говорят,
32
точка В, о которой идет речь в этой аксиоме, получается от-
„л^анием вектора а от точки 4- В связи с этим аксиомы пятой'
группы иногда называют аксиомами «откладывания» векторов.
2________—-----------------е-----------:--------------—
54 Задача. Доказать, что для любой точки А справедлив...
равенство АА =0.
Решение. Применим аксиому о. 1 к случаю, когда точки
А, В п С совпадают, т. е. А = В = С. Получаем:
АА + АА = АА.
Отсюда видно, что вектор АА является -корнем уравнения АА 4-
4- х = А А. Вектор 0 также является корнем этого уравнения
(аксиома 1.3). В силу единственности (теорема» 1.6) эти корни сов-
падают, т. е. АА = 0.
5.5. Задача. Доказать, что для любых двух точек А и В
справедливо равенство В А — —АВ.
Решение.' Применим аксиому 5.1 к случаю, когда точка
С совпадает с А. Получаем:
АВ 4- ВА = АА,
т. е.
АВ 4- ВА = 0
(см. задачу 5.4). Следовательно, В А = —АВ (аксиома 1.4).
5.6. Задача. Доказать, что если АВ —'DC, то ВС = AD
(рис. 9).
Решение. Согласно аксиоме 5.1
ВС = BD 4- DC.
Так как по условию DC = АВ, то
ВС = BD + АВ.
Применяя аксиому 1.1, получаем: g
ВС = АВ + BD.
Наконец, снова применяя аксиому 5.1, по-
лучаем:
D
TC = AD. Рис. 9
3 Заказ 4860
Системой координат называется четверка (О, а. Ь, с), где О £ £з '
и (а, Ь, с) — базис. Если (а, Ь, с) — ортонормированный базис '
то система координат называется прямоугольной.
Пусть (О, а, Ь, с) — система координат и А — некоторая точка.
Согласно теореме 3.6 вектор ОД однозначно представляется в виде
линейной комбинации векторов базиса:
ОА = ха + yb + гс.
Числа х, у, г называются координатами точки А в системе коор-
динат^, a, Ь, с). Тот факт, что точка А имеет координаты (х, у, z)
в * рассматриваемой системе координат, обозначают записью
А (х; у; z).
--------------------------0----------------------------
Расстоянием между точками А Н В называется длина вектора
АВ. Расстояние между точками А и В обозначается символом
d(A, В)'. ___
d(A,B) = |ДВ| = У АВ2.
5.7. Теорема. Указанное введение расстояния превращает Е3
в метрическое пространство.
▼ Доказательство. Напомним (см. «Геометрия-8»,
с. 78), что множество М называется метрическим пространством,
если для любых двух точек А, В Е М определено число d (А, В)
(расстояние между А и В) и выполнены следующие аксиомы:
1) (УД, В) (d (Д, В)> 0) Л (d (Д, В) = 0 « А = 5);
2) (УД, В) (d(A, В)'= d (В, Д));
3) (УД, В, С) (d (Д, В) + d (В, C)^d (Д, С)).
Таким образом, нам нужно проверить выполнение этих трех ак-
сиом.
В силу определения d (Д, В) 0 для любых точек А, В ЕЕ3.
Далее, равенство d (Д, В) = 0, т. е. | АВ| = 0, имеет место в том
и только в том случае, если АВ = 0, т. е. если А — В (аксиома
5.3 и задача 5.4). Таким образом, аксиома 1 выполнена.
Далее, так как ВА = —АВ = (—1)АВ, то |ВД | = |—1|- |ДВ|,
т. е. | ВА | — |ДВ|. Следовательно, d (В, Д) = |ВД| = |ДВ| =
= d (А, В), т. е. вторая аксиома также выполнена.
Наконец, для любых трех точек Д, В, С мы имеем/в силу тео-
ремы 4.9)
34
Л(А B) + d(B,C)= |АВ| + |ВС|> |АВ + ВС| =
= |АС| = d (А, С),
т е выполнена и третья аксиома. Таким образом, £’ — метриче-
СК°и Ппоказмной теоремы вытекает, в частности, что для любых
точГк Аъ Л2, Аь € £3 справедливо неравенство
d (Ai, А2) + d (A.2, A3) + ... + d (A/;-!, Ak) d (Ab Aa). ▼
_ q Теорема. В прямоугольной системе координат расстоя-
ние между точками A (xf, yt; Zi) и В (х2; у2; z2) вычисляется по
формуле ___________________________
d (А, В) = К (х8 — + (у2 — ух)2 + (z2 — Zi)2.
Доказательство. Пусть (О, elt е2, е3) — рассматри-
ваемая прямоугольная система координат. Тогда
ОА = х2е2 + ухе2 4- гхе3,
ОВ = + у2е2 + г2е3,
и потому
АВ = ОВ — ОА = (х2 — Xi)ei + (у2 — yi)e2 + (z2 — Zi)e3.
В силу следствия 4.12 имеем:
I АВ | = V(х2 — хх)2 + (у2 — ух)2 -J- (z2 — Zi)2,
откуда и вытекает справедливость доказываемой теоремы.
Этим и заканчивается изложение аксиоматики пространствен-
ной геометрии по Герману Вейлю. Все дальнейшие понятия (пря-
мая, плоскость и т. п.) вводятся при помощи определений
на основе рассмотренных выше неопределяемых понятий, все
теоремы доказываются на основе перечисленных аксиом. Это-
му будут посвящены дальнейшие параграфы.
-----:-------------о---------------------
▼ Рассмотрим теперь вопрос о непротиворечивости
аксиоматики Вейля. С этой целью мы построим модель, удовлетво-
ряющую этой аксиоматике. «Материалом» для построения модели
будут служить действительные числа. Таким образом, если мы
принимаем непротиворечивость «теории действительных чисел1, то
теоо ВСОВ₽“Й математике устанавливается, что (при использовании понятий
ральны множеств и математической логики) из непротиворечивости теории нашу-
дейст Х чисел можно вывести (построением модели) непротиворечивость теории
построением указанной модели будет установлена непротиворечи-
вость пространственной геометрии.
Идея построения модели состоит в следующем. Как мы видели,
если фиксирована некоторая прямоугольная система координат
(О, ей, е8), то каждый вектор задается тремя действительными
числами (его координатами) и каждая точка тоже задается тремя
действительными числами (ее координатами). При этом операции
над векторами и точками задаются весьма простыми формулами
(см. теоремы 3.8, 4.11 и задачу 123). Естественно для построения
модели попытаться определить вектор как упорядоченную тройку
действительных чисел, точку —также как упорядоченную тройку
действительных чисел (отличая для удобства точки и векторы
скобками разной формы) и задать операции над векторами и точ-
ками теми формулами, которые имеются в указанных теоремах.
Этот путь, в самом деле, приводит к построению требуемой модели.
Итак, условимся ‘вектором называть каждую упорядоченную
тройку <х; у; г> действительных чисел. Сумму векторов опреде-
лим формулой
<Xf, У1" *i> + <х2; у2; z2> = <хг + х2; ух + у2; гх + г2>.
Непосредственно проверяется, что в этой модели сумма векторов
удовлетворяет всем аксиомам 1.1 —1.4. Для примера покажем,
как проверяется справедливость аксиомы 1.1. Мы имеем:
У1, Zi> 4- <х2; у2; = <xt 4- х/, уг 4- у2; гх 4- z2>,
<х2; у2; г2> + <х-р, у/, гх> = <х2 4- xf, у2 + уг; г2 4- гг>.
Так как хх 4- х2 = х2+ х2 (поскольку для действительных
чисел сложение коммутативно) и аналогично уг 4- у2 =
= у2 -f- ylt Zj + z2 = г2 4- zlt то в правых частях стоит один и
тот же вектор, и потому
<Хъ уг; гг> 4- <хг; у2; z2>
<х2, у2; г2> 4- <Xi, уй Zi>,
т. е. сложение векторов коммутативно.
Аналогично проверяются остальные аксиомы 1.2—1.4; заметим
лишь, что нулевым вектором является <0;0; 0>, а вектором,
противоположным <х; у; г>, является <—х;—у;—?>.-
Далее определим произведение вектора на число формулой
Л < xj у; t > — <kx; ky; kz>.
Непосредственно проверяется, что в этой модели удовлетворяются
все аксиомы 2.1—2.4.
Проверка аксиом 3.1, 3.2 производится следующим образом.
Положим:
Oj = <1; 0; 0>, а2 = <0; 1; 0>, а3 = <0; 0; 1>.
Тогда, очевидно,
kxax 4- k2at 4- ksa3 = <k1- k2\ /г8>. (1)
36
Следовательно, вектор Ахох + k3a2 4- k3a3 только в том случае
является нулевым, если kx — k2 = k3 = 0, т. е. векторы ах, ait а3
линейно независимы. Этим установлено выполнение аксиомы 3.1.
Далее, соотношение (1) показывает, что любой вектор b — <ЛХ; й2;
k3> представляется в виде линейной комбинации векторов alt аг,
а3. Поэтому, если даны четыре произвольных вектора bt, b2,
Ь3, то, поскольку каждый из них выражается через три век-
тора ох, а3, а3, эти векторы Ь2, Ь3, Ь4 линейно зависимы (это уста-
навливается таким* же приемом, который был применен при дока-
зательстве теоремы 2.10). Таким образом, аксиома 3.2 выполняется.
Скалярное произведение определим формулой <хх;ух;гх>
<х2; у2; 2а> = *1х2 4* УхУг + 2i22' Справедливость аксиом 4.1—
4.4 проверяется непосредственным вычислением. Например, если
<х; у; г>#= <0; 0; 0>, т. е. хотя бы одно из чисел х, у, г отлично
от нуля, то мы имеем:
<х; у; г> <х; у; z> = х* 4- у2 4- г* > 0,
чем проверено выполнение аксиомы 4.4.
' . Наконец, точкой условимся называть каждую упорядоченную
тройку (а; с) действительных чисел. Каждой паре точек А =
= (ая; bi, Ci), В — (а3, &2; с2) поставим в соответствие вектор Я-
= <а2— ai, &2 — bi, с2—Ci>. Непосредственно проверяется,
что выполняются аксиомы 5.1—5.3.
Цтак, в построенной модели выполняются все аксиомы аксио-
матики Вейля, и потому эта аксиоматика непротиворечива. ▼
Задачи
109*. Докажите, что для любых точек Лх, Л2, .... ЛА справедливо
равенство
ЛХЛ2 4- Л2Л3 4- 4- =
НО. Докажите для любых точек Л, В, С, D:
АВ 4- ВС = AD 4- DC.
111*. Фиксируем некоторую точку О и для любого вектора а
обозначим через Q (а) точку, получающуюся откладыванием
вектора а от точки О. Докажите, что, сопоставляя вектору а
точку Q (а), мы получаем взаимно однозначное отображение
множества 7?3 на множество Е3.
112. Докажите, что точка В, существование которой утверж-
дается в аксиоме 5.2, определена однозначно:
(VT. А, а) (31В) (АВ) = д).
37
113. При откладывании вектора а от точ-
ки А получилась точка В, а при от-
кладывании этого же вектора а от
точки Р получилась точка Q- Дока-
жите, что АР = BQ.
114. Точки Ан В называются симметрич-
ными относительно точки О, если
ОА + ОВ = 0. Докажите, что если
точки А и В симметричны относи-
тельно О, то для любой точки Q
(рис. 10) справедливо равенство
1 (0Л + QB) = QO.
115. Точки А, В, С, D удовлетворяют ус-
ловию ВС — AD. Докажите, что ес-
ли точки А и С симметричны относи-
тельно точки О, то также точки В и
D симметричны относительно О.
116. Докажите, что если точки А и В
симметричны соответственно точкам
С и D относительно О, то d (Л, В) =
d (С, D).
117. Пусть точки А, В и С таковы, что
СА X СВ (рис. 11). Докажите, что
(d (Л, В))2= (d (В. С))2+ (d (Л, О)2-
118. Пусть Л, В, О — такие точки, что
d (Л, О) — d (В, О), а точки С и D
симметричны точкам Л и В отно-
сительно О. Докажите, что АВ X
J_ ~ВС, CD X ВС.
119. Точки Л и В симметричны относи-
тельно О. Докажите, что если точ-
ка С удовлетворяет условию ОС X
X АВ, то d(Л, С) =d(B, С).
120. Точка А симметрична точке С отно-
сительно Р, а точка В симметрична
точке С относительно Q (рис. 12).
Докажите, что PQ = АВ.
121. Точки Л, В, С, Аъ Въ Сг (рис. 13)
обладают тем свойством, что ЛХВХ =
= АВ и АгСг = АС. Докажите, что
ААг ВВг = ССХ.
38
122. При откладывании вектора р от точки А получилась точка В.
Точка А имеет в системе (О, а, Ь, с) координаты (хг; ух; zx),
а вектор р имеет в базисе (а, Ь, с) координаты х2; у2, z2. Най-
дите координаты точки В в системе (О, а, Ь, с).
123. В системе координат (О, а, Ь, с) заданы координаты двух то-
чек: А (х^, ух; zx) и В (х2; у2; z2). Найдите координаты век-
тора АВ в базисе (а, Ь, с).
124. В системе координат (О, а, Ь, с) заданы точки А (хх; ух; zx),
В (х2; у2; z2), С (х3; у3; z3). Найдите координаты векторов
АВ, ВС, АС и проверьте справедливость соотношения, ука-
занного в аксиоме 5.1.
125*. Докажите, что точки А (хх; ух; zx) и В (х2; у2; z2) в том и
только в том случае симметричны относительно точки
Р (х'; у'; г'), если хх + х2 = 2х', ух + у2 = 2у', zx 4- z2 =
= 2z' (все координаты берутся в одной и той же системе
(О, а, Ь, с)).
126. Докажите утверждение, сформулированное в задаче 5.6, с
помощью координат.
127*. Докажите утверждение, сформулированное в задаче 114,
с помощью координат, взяв систему координат (О, а, Ь, с),
где а — ОА (векторы Ь, с — произвольные, образующие с а
линейно независимую тройку).
128. Найдите расстояние между точками О и С, зная, что векторы
ОА, АВ, ВС попарно ортогональны и d (О, А) = a, d (А, В)—
= b, d (В, С) — с. Вычисление проведите в координатах,
выбрав систему координат наиболее удобным способом.
129*. Точки Лх, Вх и Сх соответственно симметричны точкам А, В
и С относительно О, причем векторы ОА, ОВ, ОС попарно
ортогональны. Докажите, что
d (А, В) = d (Л, Вх) = d (Лх, B)=d (Аи Вх);
d (Л, С) = d (Л, Сх) = d (Лх, С) = d (Лх, Сх);
d (В, С)' = d (В, Сх) = d (Вх, С) = d (В1г Сх).
Вычисление проведите в координатах, выбрав систему коор-
динат наиболее удобным способом.
130*. Докажите, что если d (Л, В) + d (В, С) = d (Л, С), то
АВ = kAC, где 0 k 1.
131. Упростите выражения:
а) ЛС -}- CD + DM + мк,
б)ХУ + ^ + У^ + УЛ + Л2;
в) ЛЛ + ДР + ЯВ;
39
г) DB + BK — DA.
132. Докажите, что для любых трех точек А, В, С справедливо
равенство АВ 4- ВС + СА = 0. Сформулируйте обобщение
этого утверждения для любого числа точек.
133. Докажите, что для любых точек А, В, С справедливы равен-
ства
АВ —АС = СВ, АС —АВ = ВС.
134. Какая точка получится, если от точки А отложить вектор
АВ + ВС?
135. Какая точка получится в результате откладывания вектора
ZY — ZX — OY — КО от точки X?
136. Упростите следующие выражения, если известно, что СА =
= ВО:
а) СВ + DK — АО;
б) ОК + AD + ВС.
137. Докажите, что если точки А и В симметричны относительно
точки О, а также С и D симметричны относительно О, то
ВС = DA.
138. Докажите, что для заданных точек А и В существует, и
притом только одна, точ^а О, относительно которой точки А
и В симметричны.
139. Точки С и D симметричны точкам Ли В относительно точки О.
Докажите, что если AC ± BD (рис. 14), то
d (Л, В) = d (В, С) — d (С, D) = d (D, Л).
140*.' Точки Л1; Въ С\ симметричны точкам Л, В, С относительно
точки О. Докажите, что AiBt • ЛХСХ == АВ • АС.
141*. Точки А и В симметричны относительно точки Р. Считая,
что точки А и В заданы в системе (О, а, Ь, с) своими коорди-
натами: Л (л^; zx), В (х2; у2; z2), найдите координаты точ-
ки Р в этой же системе.
142. Векторы А К и В К представлены в
виде линейной комбинации векто-
ров ортонормированного базиса
(^1, б2, е2).
АК — Зе2 4~ 4е2 4- 5вз, В К = —;7<?з.
Определите координаты точек Л и
В в системе (К, е1г е2, е3) и расстоя-
ние d (АВ).
40
Рис. 15
ДВ 4- ДР 4- ДХ;
В задачах 143—150 точки А, В, С,
D, Alt Blt С1( Dt выбраны таким об-
разом, что
~АВ = а, ВС = ДР = b, АА± = BBX =
= ССХ = DDr = с,
где а,1>, с — линейно независимые
векторы (рис. 15).
------------------------------->
143. Найдите сумму векторов: a) AD 4*
4-ДВ; б) DC 4- DDf,
в) ВС 4- DjXjj г) ВВ{ 4" DxDj д)
е) СХС 4- DA 4* AB.
144. Упростите векторные выражения: а) АВ 4- DtCx 4- ВгВ 4-
+ ВЛ1 + ВВх + DMi; б) А& +_&. + № +
4- ДТС; в) AJ)x + DM + В/?; г) DJ\ 4- ВА. .
145. Найдите сумму векторов: а) уДМх 4- —CD 4-ССХ;
б) -1ССХ 4- ДВ 4- СЛ; в) ВхЬ 4- ССх 4- Хвх.
146. В каждом из следующих случаев установите, являются ли
векторы линейно зависимыми: a) DC, DClt ВХДХ; ty DxD,
DCx, AD\ в) АВх, DJ), DC.
147. Можно ли вектор AD представить в виде линейной комбина-
ции векторов АхСх, АВЪ и ВХС?
148*. Точка М получена в результате откладывания вектора
— с — ~7) от точки С; точка N получена в результате откла-
дывания.вектора —а----~Ь от точки D; точка Р получена в
2 2
результате откладывания вектора —с 4- —а ет точки N.
Имеются ли среди точек М, N, Р совпадающие?
149*. Найдите сумму векторов: a) ^AxCl-\--^-BBx + —CDA-
4-1рД; б) 1аАх+±АВ + ±В£х + ^Ь-, в)|вХ>4-
4" (ВВх 4- СР) 4- РД.
150*. Представьте вектор РВХ в виде линейной комбинации век-
торов: а) АхСх, CDx и ВхС’, б) A Ax, АС и AxD; в) ВР,, ДР и
дЭ1.
41
ГЛАВА
6.1. Определение. Прямой, проходящей через точку А и
имеющей вектор а.=#0 своим базисным вектором, называется мно-
жество всех таких точек М, что векторы AM и а линейно зависимы
(рис. 16). Обозначать эту прямую будем символом I (Л, а).
Таким образом,'точка М в том и только в том случае принадле-
жит прямой I (А, а), если найдется такое действительное число k,
-что AM « ka:
I (A, а) = {М : (Эй) (Л"м = ka)}.
Одну и ту же прямую можно задавать по-разному, указывая
различные базисные векторы и различные точки, через которые
она проходит. Следующие три теоремы указывают различные спо-
собы задания одной и той же прямой.
6.2. Теорема. Если В € I (Л, а), то I (В, а) = I (Л, а).
Доказательство. Нам нужно доказать, что множе-
ства I (Л, а) и I (В, а) совпадают, т. е. что любая точка прямой
I (В, а) принадлежит прямой I (Л, а) и, на-
оборот, любая точка прямой I (Л, а) при-
надлежит прямой I (В, а).
Пусть М € I (В, а), т. е. существу-
ет такое действительное число k, что
Рис. 16 ВМ = ka. Кроме того, АВ — kta (так как
42
ПО условию В б I (А, а)). Применяя аксиомы 5.1 и 2.1, получаем:
AM — АВ 4- ВМ = kra + ka = (k{ + k) a.
Таким образом, векторы AM и а линейно зависимы, т. е.
Д4 £ I (Л, а). Аналогично доказывается, что если М С I (А, а),
то М € I (В, а).
Смысл доказанной теоремы состоит в том, что все точки прямой
равноправны, т. е. вместо А в определении Прямой I (А; а) можно
взять произвольную точку этой прямой.
6.3. Теорема. Прямые I (А, а) и I (А, Ь) совпадают в том
и только в том случае, если векторы а и b линейно зависимы.
V Доказательство. Докажем, что
(Vt. А, а=/=0, b =/= б) ((3k) (а = kb))=>(l(A, а) — 1(А, Ь)).
В самом деле, если М < I (А, а), т. е. AM = kta, то AM — ki (kb) =*
= (kkjb, и потому M С I (А, Ь).
Аналогично доказывается, что если М € I (A, b), то М € / (А, а).
Докажем теперь, что
(Vt. А, а ф б, &#=б)(/(А, а) = / (Л, Ь)) => ((3k) (а = kb)).
Возьмем такую точку М, что AM = а. Тогда М € I (А, а). Так
как I (А, а) — I (А, Ь), то имеем также М € I (А, Ь), т. е. AM =
= kb. Таким образом, а — kb.Tf
Доказанная теорема говорит о возможности замены базисного
вектора: если а — базисный вектор рассматриваемой прямой, то
любой вектор ka (где k также является ее базисным векто-
ром.
6.4. Теорема. Если В и С — две различные точки прямой
I (А, а), то I (А, а) = I (В, ВС).
Доказательство. Прежде всего заметим, что ВС=£Л,
так как В ^=С (аксиома 5.3). Поэтому мы можем рассматривать
прямую I (В, ВС). Так как В £ I (А, а), то I (А, а) = I (В, а) (тео-
рема 6.2). Остается, доказать, что прямая I (В, а)- совпадает с
I (В, ВС), для чего в силу теоремы 6.3 нужно убедиться, что векто-
ры а и ВС линейно зависимы. В самом деле, так как С € I (А, а),
т. е. С € I (В, а), то В(5 = ka.
6.5. Следствие. Через две различные точки проходит одна
и только одна прямая.
В самом деле, прямая I (В, ВС) проходит через обе точки В, С,
4]
чем устанавливается, ее существование. Единственность непосред-
ственно вытекает из теоремы 6.4. Действительно, если I (А, а) —
какая-либо прямая, которая проходит через точки В, С, al (Д', а')—
еще одна прямая, проходящая через те же точки, то в силу теоремы
6.4 I (А, а) = I (В, ВС), I (Д', а') = I (В, ВС), и потому I (A, ci) —
“ I (Д', а').
Доказанное следствие позволяет ввести удобное обозначение:
прямая, проходящая через точки В, С (где В у= С), обозначается
через (ВС).
--------------------------0----------------------------
6.6. Определение. Пусть А и В — две различные точки.
Множество
[ДВ] = {М: AM — kAB, где 0 < k < 1}
называется отрезком с концами А и В.
Ясно, что [ А В] с(ДВ). Это непосредственно.вытекает из того,
что (АВ) » I (А, АВ)— {Л4: AM = kAB), где /г — любое дей-
ствительное число}.
Y Легко видеть также, что [ДВ] = [ВД]. В самом деле, если
С t [ДВ], т. е. АС = kAB, 0 ^.k т ВС =^ВА А- АС =
=« ВА 4- kAB = (1 — k)BA. Поскольку 0 1 —k 1, соотно-
шение ВС =« (1 —k)BA означает, что С С[ВД]. Итак, если С €
С [ДВ], то С € [ВД], т. е. [ДВ] сд[ВД]. Аналогично доказывается и
обратное включение. ▼
Точки Д и В называются концевыми точками отрезка [ДВ].
Остальные точки отрезка [ДВ] — его внутренние точки. Иначе
---------------------------------------------> ——>
говоря, С — внутренняя точка отрезка[ДВ], если АС = kAB, где
О <k < 1.
6.7. Определение. Пусть Д и В — две различные точки.
Множество
[ДВ) « {М: AM = kAB, где 0 < k < оо}
называется лучом с началом в точке Д, проходящим через точку В.
'------:------------------Q----------------------------
В ряде задач требуется установить расположение трех точек
А, В, С на одной прямой (или использовать тот факт, что три точки
находятся народной прямой). Основным приёмом при решении таких
задач является применение определения прямой: чтобы установить
принадлежность точки С прямой (ДВ), достаточно доказать суще-
ствование такого действительного числа k, что АС = kAB.
44
Приведем два примера применения этого приема.
Задача 1. Даны такие четыре точки А, В, С, D, что
~дВ = DC, причем точки А, В и D не лежат на одной прямой. Точ-
ки М и N выбраны так, что AM = —АВ, AN = — АС. Доказать,
5 6
что точки D, М, N лежат на одной прямой.
Решение. Нам надо доказать, что векторы DM и DN ли-
нейно зависимы. Для этого введем векторы DM = а, АВ — b
---------------
и представим DN в виде их линейной комбинации. Мы имеем:
5м = ОА4-AM = DA4--AC; DA = DM — AM = а — -b-
1 1 6 5
ЛС = ЛО + 5с = —5л + АВ== — (a — 1ft)+ & 5= — а-г—Ь,
\ 5 J 5
и потому
DN = /а'— -b) + 1 (—а 4- -b'j = ^а,
[ 5 / ' 6 \ 5 } 6
Таким образом, DN — —DM, откуда вытекает, что точки D, М, N
лежат на одной прямой.
Задача 2. От точки О отложены векторы О А = а, 0$ =*
— Ь, ОС — ka, 0D = lb (где векторы а и Ь линейно независимы и
k =^0, 1^0). Точки М и N— середины отрезков [АВ] и [CD],
Доказать, что если точки О, М, N расположены на одной прямой,
то векторы АВ и DC линейно зависимы (рис. 17).
Решение. Мы имеем: ОМ = 4- ОА 4~ 4- ОВ = 4~ а -4 b
2 2 2 2
ON = — ОС + —00 = — а 4- — Ь. Так как точки О, М, N лежат
2 2 2 2
на одной прямой, то существует такое действительное число /п,
что ON — тОМ, т. е.
— а + — b = т(— а + 4'^'l*
22 \2 1 2 /
В силу линейной независимости векторов •
а и & отсюда следует, что k = т = I, Те-
перь имеем: /
AB = OB — OA = b — a, I
-► -» I
DC=OC — OD=ka — kb,
т. е. DC -^,kAB. Рис. 17
45
Замечание. Эту задачу можно истолковать следующим
образом. Из курса VIII класса известно, что если ABCD — трапе-
ция, О— точка пересечения ее диагоналей, а М и N— середины
оснований[АВ] и [CD], то точки О, М, N лежат на одной прямой.
В этой задаче, по существу, устанавливается справедливость об-
ратной теоремы.
. Задачи
151. Какие из следующих высказываний истинны?
а) Существует прямая, содержащая лишь конечное число
, точек.
б) Существуют три точки, не принадлежащие одной прямой.
в) Точка А принадлежит прямой I (А, а).
г) Для любой точки F, принадлежащей прямой I (А, а),
справедливо соотношение FA = ka.
д) Точка М, удовлетворяющая условию AM = —а, при-
надлежит прямой I (А, а).
152. Точка В € I (А, а); точка С такова, что ВС — qa. Докажите,
что С (: I (А, а).
153. Докажите, что если точки Р и Q принадлежат прямой / (А, а),
* ► —►
то существует такое k, что PQ = ka.
154. Докажите, что если М и ЛГ— две различные точки прямой
I (В, ЬУ, то: а) I (В, b) = l(N, MN); б) I (BJ>) = I (N, NM).
155*. Докажите, что отрезок [АВ] в том и только в том случае
совпадает с отрезком [CD], если ((А = С) Л (В = D)) V
V ((А = D) Л (В = С)).
158. Докажите, что если М, N—две различные точки отрезка
[АВ], то [MV] с: [АВ].
157*. Докажите теоремы:
a) (Vt. А, В, С, где А ф В) (С € [АВ])фф (d (А, С) +.
+ d (В, С) = d (А, В));
б) (Vt. А, В, С,_гд£ А Ф В) (CJ LAB])^ (VQ)(3k €
СО; 1J) (QC = kQA 4- (1 - k) QB).
158. Точка M называется серединой отрезка [AB], если AM =
------------
=—BM. Докажите, что следующие утверждения равно-
сильны:
а) М —середина отрезка [АВ];
б) А й В симметричны относительно точки М;
в) (VQ)(QAf =lQA+jQB).
159. Будем говорить, что точка М лежит между точками А и В
(где А Ф В), если векторы AM и ВМ имеют противополож-
46
ное направление (рис. 18),
т. е. существует такое по-
ложительное число k, что
AM = —kBM. Докажите
следующие теоремы:
а) Если точка М лежит
между А иВ, то она лежит
также между В и А.
б) Если точка М лежит между А и В, то М ( [ЛВ].
в) Точка М в том и только в том глучае принадлежит отрез-
ку [ЛВ], если она либо совпадает с одной из точек Л,
В, либо лежит между Л и В.
г) Из трех различных точек, принадлежащих одной прямой,
одна и только одна лежит между двумя другими.
160. Докажите, что если М € [ЛВ), М Л, то [ЛВ) — [AM).
161. Точка М лежит между Л и В. Докажите, что:
а) [МЛ) U [МВ) = I (М, ЛВ); б) [МЛ) [) [МВ) = {М}.
162. На отрезке ЛВ взята такая точка М, что - — а.
r d(M, В)
Выразите вектор AM через ЛВ.
163. Точки Л, М-и В удовлетворяют соотношению AM —
— а АВ. Докажите, что если а > 0, то М € [ЛВ], и
ОС -|- I
определите отношение длин отрезков [ЛМ] и [МВ].
164. Даны четыре точки Л, В, С и Д. Через /С, L, М,
N, Р, Q обозначены со-
ответственно середины от-
резков [ЛВ], [CD], [ЛД],
[ВС], [ЛС], [ВД]. Дока-
жите, что отрезки [КС],
[МАГ], [PQ] имеют общую
середину (рис. 19).
165. Пусть и /2 — две пря-
мые с одним и тем же ба-
зисным вектором. Дока-
жите, что если М, N,
Р € li, Mi, Ni, Pi С 1г,
то середины отрезков
[MMJ, [AD^], [PPJ ле-
жат на одной прямой
(рис. 20).
166*. Даны такие четыре точки
Л, В, С, D, что ЛВ =
= DC. Точки Р, N, М
расположены так, что рис. 20
47
Рис. 21
такие точки А
СР = aCD, CN = рСВ, ВМ =
= у АВ. При-каком соотношении
между а, |3, у точки М, N, Р ле-
жат на одной прямой?
167*. Дана ломаная А]А2А3 ... АгяАгя+!.
Докажите, что если середины
отрезков [Д1Л2], [Л2Д3],
[Azt-iAz.,], [Аг. A2n+il лежат на
одной прямой, то точки Д1( А3, ...,
..., Д2,_1( Л2г+1 лежат на одной
Прямой И-ТОЧКИ Д2, ^4, •••, -^21 то'
же лежат на одной прямой.
168. Даны две произвольные прямые
и /2. На прямой lL взяты
1» А2, ..., Ап, что А]А% = А2А3 =s ... —
— A„_tA„, а на прямой /2 — такие точки В1г В2, .... Вп,
что В3В2 — В2В3 = ... = В„_3Вп. Докажите, что середины
отрезков [ДзД], [Д2В2], ..., [АЯВ„] также расположены на
одной прямой (рис. 21).
169*. Из четырех точек А, В, С, D никакие три не лежат на одной
------------------------------------------------------->
прямой. Точки М, N, Q, Р, Р построены так, что AM =
= аДВ, CN = aCD, АР = ₽ЛС, = рМЛГ, ВР = QBD.
Докажите, что точки Р, Q и 7? лежат на одной прямой.
170. Векторы а, Ь, с линейно независимы. Расположены ли точки
А, В, С на одной прямой, если выполнены следующие соот-
ношения:
а) ОА — 5а — 6Ь Д- с, ОВ = а Д- с, ВС — ЗЬ— 2а;
б) ОА = а А~Ь, ОВ = а — b Д- с, ОС = а Д- 75 — Зс;
в) МВ = 5а Д- 2Ь Д- с, МС = 11а Д- 1 lb Д- 2с, АС = 8а Д-
Д-125Д-С?
171*. Векторы а, b и с линейно независимы. Точки А, В, С, Си D3
выбраны так, что АВ = а, ВС = b, CCt — с, AD3 — ЬА-с.
На прямых (BDj) и (СС3) выбраны соответственно такие точки
Р и Q, что А, Р и Q лежат на одной прямой. Определите
d (В, Р) : d (Р, DJ.
172. При обозначениях, указанных на с. 41 (рис. 15), определите
d (М, N) : d (М, Р), если следующие точки М, N, Р рас-
положены на одной прямой:
а) М = A, N £ (BDJ, Р € (ССХ);
б) AM = —с, N С (АС), Р С (C^j);
в) М = Clt N (Е (ВхС), Р € (А3В);
48
г) М = В, N € (ЛА), Р € (QD);
. д) В^М = ±&, N е (АС), Р € (BDJ.
173*. Даны три точки А, В и С, не лежащие на одной прямой, и
такие точки М, N, Р, что AM = аМВ, BN = $NC, СР =
= уРА, причем офу = —1. Докажите, что точки М, N, Р
расположены на одной прямой.
174. На прямой I (А, а) найдите точку М, находящуюся на наи-
меньшем расстоянии от точки В $ I (А, а). Докажите, что
такая точка М всегда существует, и притом только одна.
175*. Точки А и А' называются симметричными относительно
—
прямой I, если вектор А А' ортогонален базисному вектору,
прямой I и середина отрезка [ААГ] принадлежит прямой I.
Докажите, что если точки А, А' симметричны относительно
прямой I и точки В, В' также симметричны относительно
прямой I, то d (А, В) = d (Л', В').
176*. Пусть О и Л —две различные точки. Для любого действи-
тельного числа х обозначим через Мх точку, полученную
в результате откладывания вектора хОА от -точки О, т. е.
ОМХ = хОА.
а) Докажите, что, сопоставляя числу х С R точку Мх, мы
получаем взаимно-однозначное отображение множества R
' на прямую (О А).
б) Докажите, что для любых двух действительных чисел х,
у справедливо соотношение 0Мх 4- ОМУ = ОМХ+Г
в) Докажите, что для любых действительных чисел х =f= у
справедливо равенство
d (Мх, Му) = \x-y\d(O, А).
В частности, если расстояние между точками О и Л равно 1,
то d (Мх, Му) = |х — у |.
Сказанное означает, что, уславливаясь считать точку Мх
изображением действительного числа х, мы превращаем (ОЛ)
в числовую прямую.
177*. Даны точки Ль Л2, .... Ak и положительные числа тг, т2,
.... mk. Докажите, что существует, и притом только одна,
точка О, удовлетворяющая условию
т1ОА1 + /И2ОЛ2 4” ... 4" mkOAk — 0.
Эта точка называется центром тяжести масс mlt mit ..., mk,
сосредоточенных в точках Лх, Л2, ..., Ак.
178*. Пусть О — центр тяжести масс mlt ms, ..., тк, сосредоточен-
ных в точках Л1( Л2........Ак. Докажите, что для любой точки
Q справедливо соотношение
QP = -~1-~ 0Лх 4- ... -f- ——— 0ЛА.
... 4- тк mt+ ... 4- тк
49
179*. Пусть С\ — центр тяжести масс тх, ..., /пл, сосредоточенных
в точках Ль ...» Ak\ О2 — центр тяжести * масс пи nz,
сосредоточенных в точках Вх, Bz. Докажите, что центр
тяжести двух масс, т1 + ... + mk и + ... + nz, поме-
щенных в точках О2, совпадает с центром тяжести масс
/пх, mk, пг, ...» nz, помещенных в точках А19 ..., Лл,
Bi, Bz.
180*. Пусть Л, В, С — три точки, не лежащие на одной прямой.
Центр тяжести равных масс, помещенных в этих точках,
принято называть центром тяжести треугольника АВС.
Докажите, что если никакие три из точек Л, В, С, D не лежат
на одной прямой, a Alf Blf Clf — центры тяжести соот-
ветственно треугольников BCD, ACD, ABD, АВС, то отрез-
ки [ЛЛХ], [BBJ, пересекаются в одной точке О,
причем
d(O, Ax)— — d(Ot Л); d(O, В)-, d(O, =
3 3
= ±d(O, Q, d(O, D1)=ld(O, D).
3 3
181. Какие из следующих высказываний истинны?
а) Если FC — ЗЬ и b 0, то прямая 4, проходящая через
точку F и имеющая b своим базисным вектором, совпадает
с прямой I (С, Ь).
б) Прямые I (В, ВС) и I (С, ВС) совпадают.
в) Прямые I (В, ВС) и I (С, СВ) совпадают.
г) Если а — Зп. и а #= 0, то I (К, а) = I (К, п).
а) Из совпадения прямых I (М, Ь) и I (N, с) следует, что
вектор b может быть получен умножением вектора с йа не-
которое число.
е) I (D, ВС) = I (С, BD).
182. Установите, в каком случае истинны следующие высказы-
вания:
1) I (М, с) = I (К, с)-, 2) Л € / (Л, Ь)-
3) 1 (Л, р) = I (Л, с);_^4) I (Л, с) = / (В, d);
5) I (X, ХУ) = I (У, ХУ).
183*. Докажите теорему:
(Vt. Л, В, С) ((3Q) (3fe' € [0, 1]) (QC = kQA +
+ (1-^)QB))^(C С[ЛВ]).
184. Докажите, что если точки Л и В симметричны относительно
точки М, причем Л =^В, то М С [Л, В].
50
185 Докажите, что если М, N € \_АВ), М =/*N't то [МЛГ]сз
с[ЛВ).
186. Точки А, В, С и D удовлетворяют условию АВ — DC. Дока-
жите, что отрезки [ЛС] и [В£>] имеют общую середину.
187. На отрезке[ЛВ] взята такая точка Р, чтой (Л, Р) : d (Р, В)*»
>“ - ►
= т : п. Выразите вектор АР через вектор АВ.
188. Точки М, N, Р являются серединами отрезков [ЛВ], [ВС],
[СО]. Докажите, что если точки М, N, Р лежат на одной
— 1 > >
прямой, то векторы АС и BD линейно зависимы.
189. При обозначениях, указанных на с. 41 (рис. 15), докажите,
что все четыре отрезка[ЛСХ], [ЛгС], [BDJ, [BXD] имеют
общую середину.
190. Точки О, А, В а С удовлетворяют условию ОА == За, АВ
— Ь — а, ОС = ЗЬ. Докажите, что точки Л, В и С лежат
на одной прямой.
191. Установите, какие из точек В, С, D принадлежат прямой
I (OJ>), если OB = 1b; ОС = а + b, OD = За + 2Ь — с,
где векторы а, Ь, с составляют базис.
192. Точки Л, В, С, D,P, N и М выбраны так, что АВ = DC,
CP = -CD, CN=—CB, ВМ= у АВ.
3 4
При каком значении у точки М, N, Р лежат на одной
прямой?
193. Векторы а и b линейно независимы. Точки О, А, В, С, D
удовлетворяют условиям
ОА = а, АВ = Ь, ОС = ka, CD — lb.
Докажите, что точки О, В, D в том и только в том случае
расположены на одной прямой, если k = I.
194*. Точки Л„, Вл, Сп, Dn(n — 1,2, 3, 4) расположены так, что
Л^^ ВХСХ = С^,
А^В^—— Bfi, — C^Dq,
А^А^— Л2Л3 = Л3Л4,
ВХВ2= В2В3 — В3В4,
С]С2 = C2Cg = C3C4,
D^D^— D^D^ = DaDt.
Докажите, что точки Л2, В2, С2, В>2 лежат на одной прямой
и точки А3, В3, С3, £>3 также лежат на одной прямой.
195. Векторы а, Ь, сушнейно независимы. Точки Л, В, С, Лх, Вх, Сх
$1
Рис. 23
удовлетворяют Условиям (рис. 22)
АВ=а, АС—Ь, АА1='в’В1 =СС1 =
= с. Определите d (М, N): d (М, Р),
если Р 6 (MN) и при этом:
a) AM = 2а, NttACJ Р
б) СМ = у с, ЛГ€(ЛВ), Р6(В1С1);
в) CAf = -|c, М6(ЛВ), Р£(АХСУ,
г) СМ = -‘-с, ЛГ£(ЛВ), Р£(А£^.
196*. Докажите, что центр тяжести О масс
/Их, /п2, сосредоточенных в точках
А, В, принадлежит отрезку [ЛВ],
причем d (О, Л): d (О, В) — т^ : тг.
197*. Даны три точки Л, В и С. Середи-
ны отрезков [ЛВ], [ЛС], [ВС] обо-
значены соответственно через Р,
N, М (рис. 23). Докажите, что от-
резки [ЛМ], [BAf], [СР] пересека-
ются в одной точке, которая явля-
ется центром тяжести масс 1, 1, 1, помещенных в точках Л,
В, С.
$ 7. ВЗАИМНОЕ РАСПОЛОЖЕНИЕ
ДВУХ ПРЯМЫХ
7.1. Определение. Две прямые называются параллельны-
ми, если их базисные векторы линейно зависимы (рис. 24).
Параллельность прямых обозначается обычным символом ||:
(Ут. Л, В, а =#б, Ь =/=б) (/ (Л, а) || I (В, Ь))фф
def
Ф* (36) (а = kb).
def
7.2. Теорема. Отношение параллельности прямых является
отношением эквивалентности, т. е. оно
рефлексивно, симметрично и транзитивно.
Доказательство. Рефлек-
сивность очевидна: I (Л, а) || I (Л, а), так
как векторы а и а линейно зависимы.
Докажем симметричность. Пусть I (Л,
а) || I (В, Ь), т. е. а — kb. Здесь k ^=0, по-
52
скольку векторы а и Ъ ненулевые. Следовательно, b =
— а, а
k
это
означает, что I (В, b) || I (Л, а).
Докажем транзитивность. Пусть I (Л, а) || / (В, Ь) и I (В, Ь) ||
|| I (С, с). Тогда а = kb, b = 1с, и потому а = k (lc) = (kl)c. Следо-
вательно, I (Л, а) || I (С, с).
7.3. Следствие. Две прямые, параллельные третьей, парал-
лельны между собой.
Свойство транзитивности отношения параллельности означает,
что если первая прямая параллельна второй, а вторая — третьей,
то первая прямая параллельна третьей прямой. В сформулирован-
ном следствии утверждается нечто иное: если первая прямая па-
раллельна третьей и вторая тоже параллельна третьей, то первая
и вторая прямые параллельны. Справедливость этого следствия
вытекает из симметричности и транзитивности отношения парал-
лельности прямых.
7.4. Теорема. Две параллельные прямые либо не имеют об-
щих точек, либо совпадают.
Доказательст во. Пусть I (А, а) || I (В, b), т. е.
а = kb. Могут представиться следующие случаи взаимного рас-
положения этих двух прямых: а) I (Л, a) f| I (В, Ь) =« 0 и
б) I (A, а) А 1(В,Ь) Ф0. ~
В случае а) прямые I (А, а) и I (В, Ь) не имеют общих точек.
Докажем, что в случае б) прямые / (А, а) и I (В, Ь) совпадают.
В самом деле, пусть М — общая точка этих прямых; тогда I (А, а) «
= / (М, а) (теорема 6.2); кроме того, / (В, b) = I (М, b) I (М, а)
(теоремы 6.2 и 6.3). Таким образом, I (А, а) — I (В, Ь).
7.5. Теорема. Через каждую точку проходит единственная
прямая, параллельная данной прямой.
Доказательство. Пусть I (А, а) — данная прямая,
В —данная точка. Прямая I (В, а) параллельна прямой А (Л, а) и
проходит через точку В, чем и доказано существование искомой
прямой.
Докажем единственность. Пусть /' и /" —две прямые, прохо-
дящие через точку В и параллельные прямой I (Л, а). Тогда в силу
предыдущего следствия прямые I' и Г параллельны, а так как они
имеют общую точку .В, то они совпадают (теорема 7.4).
▼7.6. Замечание. В теореме 7.4 говорится о двух воз-
можных случаях взаимного расположения параллельных пря-
мых. Однако из доказательства теоремы не следовало, что обе эти
возможности реализуются: не было установлено, что сущест-
вуют две параллельные прямые, не имеющие общих точек. Тео-
S3
рема 7.5 позволяет утверждать, что эта возможность реализуется.
В самом деле, пусть I (Д, а) — произвольная прямая и В — не при-
надлежащая ей точка. Тогда прямая, параллельная I (Д, а) и
проходящая через точку В, не совпадает с прямой I (Д, а) (и зна-
чит, не может иметь с ней общих точек). ▼
ф
7.7. Теорема. Если две прямые не параллельны, то они имеют
не более одной общей точки.
Сформулированная теорема может быть записана следующим
образом:
(V пр. /") (-| (Г || Г))=> 7 (/' и Г имеют более одной общей точки.)
Как мы знаем, любая теорема эквивалентна теореме, противо-
положной обратной. В данном случае теорема, противоположная
обратной, имеет следующий вид:
(V пр. Г) (/' и Г имеют более одной общей точки)=> (Г || /").
Эту теорему мы и докажем.
Доказательство. Пусть В и С — общие точки пря-
мых Г и Г (В =/= С). Тогда по теореме 6.4 каждая из прямых /- и г
совпадает с прямой I (В, ВС). Следовательно, прямые Г и Г сов-
падают и потому Г ||
Из доказанной теоремы следует, что имеются две возможности
взаимного расположения двух непараллельных прямых; а) две
непараллельные прямые могут иметь ровно одну общую точку;
б) две непараллельные прямые могут не иметь общих точек.
▼ Обе эти возможности действительно реализуются. В самом
деле, пусть а и b — линейно независимые векторы и Д — произ-
вольная точка. Тогда прямые I (Д, а) и
I (Д, Ь) не параллельны и имеют общую
точку А. Этим показана возможность ре-
ализации случая а). Реализуемость случая
б) вытекает из доказываемой ниже теоремы
7.9.▼
7.8. Определения. Две непарал-
. лельные прямые, имеющие общую точку,
25 называются пересекающимися (рис. 25); две
/ непараллельные прямые, не имеющие об-
/Ч щих точек, называются скрещивающимися
S (рис. 26).
—- Теорема. Прямые 1(А, а) и
I (В, Ь) в том и только в том случае явля-
S ются скрещивающимися, если векторы
Рис. 26 а, Ь, АВ линейно независимы.
54
у Доказательство. Установим прежде всего, что
(У т. Л, В; а =# О, b =# 0) (а, Ь, АВ — линейно независимые век-
торы)=> (пр. / (Л, а) и I (В, Ь) —скрещивающиеся). (1)
Из условия вытекает, в частности, что а и b линейно независимы,
и потому I (Л, a)tfl (В, Ь). В силу определения остается доказать,
что прямые I (Л, а) и I (В, Ь) не имеют общих точек.
Допустим, что эти прямые имеют общую точку М. Тогда AM —
₽ ka, ВМ = lb, и потому АВ = AM — ВМ = ka — lb, что про-
тиворечит линейной независимости векторов а, b и АВ. Таким об-
разом, прямые I (Л, а) и I (В, Ь) не могут иметь общих точек и
потому являются скрещивающимися.
Теперь надо доказать обратную теорему: (VT. Л,В; а^О,
Ь =£= 0) (пр. I (Л, а) и I (В, Ь) — скрещивающиеся) => (а, Ь, АВ —
линейно независимые векторы). (2)
Вместо нее удобно доказать эквивалентную ей теорему:
(Vt. А, В; а =/= 0, b =?= 0) (а, Ь, АВ —линейно зависимые векторы)
=> (пр. I (Л, а) и Z (В, 6) —не скрещивающиеся). (3)
(Заметим, что теорема (3) по отношению к теореме (1) является
противоположной; по отношению же к теореме (2) теорема (3) явля-
ется противоположной обратной, так что теоремы (2) и (3) эквива-
лентны.)
При доказательстве теоремы (3) могут представиться два случая,
а) Векторы а и b линейно зависимы. В этом случае I (Л, а) || 1(В,Ь),
и потому эти прямые не являются скрещивающимися.
б) Векторы а и b линейно независимы. В этом случае ЛВ = ka +
A-lb (теорема 2.9). Согласно аксиоме 5.2 существует такая точка М,
что AM = ka. Ясно, что М € I И, а). Докажем также, что М € I
(В, Ь). Действительно,
ВМ~ АМ-ЛВ = ka— (ka + lb) = — lb,
откуда и вытекает, что М £ I (В, Ь). Итак, прямые I (Л, а) и I (В, Ь)
имеют общую точку М и потому не являются скрещивающимися. ▼
--------:------------------о-----------------------------
7.10. Задача. В некоторой системе координат (О, elt et, е3\
заданы точки А (—2; 3; —1), В (—3; 6; 2) и векторы а (5; —1; 4),
b (3; —2; 1). Определите взаимное расположение прямых I (Л, а)
и I (В, 1).
Н
V Решение. Установим, являются ли рассматриваемые прямые
параллельными, т. е. являются ли их базисные векторы а и b ли-
нейно зависимыми. Если бы а = kb, то было бы 5 = k • 3, —1 =
= k • (—2), 4 = & • 1 (теорема 3.8). Однако числа k, удовлетво-
ряющего всем трем этим соотношениям, не существует. Итак, век-
'торы акЬ линейно независимы, а значит, рассматриваемые прямые
не параллельны.
Остается узнать, являются эти прямые пересекающимися или
скрещивающимися, т_е. узнать, являются ли векторы а, Ь, АВ ли-
нейно зависимыми. Если бы они были линейно зависимыми, то
(в силу линейной независимости векторов а и Ь) выполнялось бы
при некоторых х, у равенство
АВ — ха + yb.
Так как вектор АВ имеет координаты (—1; 3; 3), то это равен-
ство равносильно следующей системе:
—1 = Ьх 4- Зу,
3 = —х — 2у, (4)
. 3 — 4х + у.
Рассматривая первые два из этих уравнений как систему двух
уравнений с двумя неизвестными х, у, находим х = 1, у = —2.
Однако проверка показывает, что эти значения не удовлетворяют
третьему уравнению. Таким образом, система (4) несовместна,
т. е. векторы АВ, а, b линейно независимы, и потому рассматривае-
мые прямые являются скрещивающимися. .▼
Задачи
198. Базисными векторами прямых I и т служат векторы а и Ъ.
Какие из следующих высказываний истинны?
а) Если а — Ь, то 11| т.
б) Если 11| т, то а = Ь.
в) Если 11| т, то существует такое k, что а =» kb.
г) Если /-|| т, то существует такое k, что ka = b.
д) Если 11| пг, то векторы а и b линейно зависимы.
е) Если векторы anb линейно зависимы, то 11| т.
199. Точки А и С симметричны относительно точки О, точки В и
D также симметричны относительно точки О. Докажите,
что (АВ) II (CD) и (AD) || (ВС).
200. Сохраним обозначения, указанные на с. 41 (рис. 15).
а) Докажите, что (ЛС) || (A A), (Afi) || (CDt).
б) Через середины отрезков [ДЛ1] и [BBi] проведена пря-
56
201.
202*.
203*.
204.
205.
206.
207.
208.
мая а, через середины отрезков [CCi] и [DDj] проведена
прямая Ь; докажите, что а || Ь.
в) Перечислите все прямые, параллельные (АВ), каждая из
которых проходит через какие-либо две из точек-А, В, С, D,
Ai, Вь С1( Di.
г) Точки М и N —середины отрезков [AAJ и [CG]; дока-
жите, что (МВ) || (NDt) n.(MDi) || (BN).
Известно, что || 12 и || 13. Докажите, что /3 || /2.
Известно, что I (А, а) Ц Ц и I (А, Ь) || /4. Какие из следую-
щих высказываний истинны?
а) а — Ь.
б) h Л I (А, а) = Ц П I (А, Ь).
в) (УМ) (М в I (А,~а))=> (М £1 (А, Ь)).
г) (ЗМ) (М £1 (А, а)) Л (М £ / (А, Ь)).
Даны 5 точек, никакие 3 из. которых не лежат на одной пря-
мой. Проведены всевозможные прямые, каждая из которых
проходит через две из этих точек. Можно ли из проведенных
прямых выбрать три прямые, которые были бы попарно па-
раллельны? Тот же вопрос для 6 тойек.
Даны такие четыре точки А, В, С, D, что (АВ) || (CD). Через
М и N обозначены середины отрезков [АО] и [ВС].
а) Докажите, что если точки М и N различны, то (MN) ||
|| (АВ) и (MN) || (CD).
б) Докажите, что если М = N, то (AC) || (BD).
Точки А, В, С, D, не лежащие на одной прямой, обладают
тем свойством, что (АВ) || (CD) и (AD) || (ВС). Докажите,
что АВ = DC и AD = ВС.
На прямой I взяты точки Ai, А2, ..., Ап, а на прямой т,
не совпадающей с I, взяты точки В1; В2, ...., Вл, причем
А^А2 -'А7аз = - = А^Ап и (А^) || (А2В2) || ... || (АпВп).
Докажите, что BtB2 = В2В
На прямой I взяты точки
А, В, С, а на прямой llt
не совпадающей с I, взя-
ты точки Ai, Bi, Ср До-
кажите, что если (AAi) ||
|| (BB1)||(CC1),Tod(A,B):
: d(A, С) = d(At, В^ :
:d (Аь Ci). ~ ~
Векторы a, b, с линейно
независимы. Параллельны
ли прямые (АВ) и (СО),
если выполнены следу-
ющие соотношения:
= ... = B„_2B„ (рис. 27).
Рис. 27
57
а) 0Л = a, OB — b, ОС =c, OD=a — b + c;
6) OA=a+b, 0B-a-[-c, ОС = За— b+ c, 0D= 3a 4-
4- 6— c;
в) ЛС= a + b 4- с, BC= 3a —2b — c, AD = Ila — 146—9c?
299. При обозначениях задачи 195 (рис. 22) середины отрезков
[CCi], [С1В4], [СИ!] обозначены соответственно через М,
N, Р. Докажите следующие утверждения:
а) прямые I (С, Ь) и I (В, с) — скрещивающиеся;
б) прямые I (В, а) и I (Ль с) — пересекающиеся;
в) прямые (MN) и (ВВ4) — пересекающиеся;
г) прямые (BN) и (АР) —пересекающиеся;
д) прямые (МР) и (СВ) —скрещивающиеся.
210. При обозначениях, указанных на с. 41 (рис. 15), середины
отрезков [ДЛ1], [ЛiDi], [DA], [CCi] обозначены соответст-
венно через К, М, Р и Н. Определите взаимное расположе-
ние следующих прямых:
a) (AD) и (В^);
б) (BBt) и (AD);
в) (BD) и (ЛА);
г) (АС) и (BD);
д) (КМ) и (DDi)-,
е) (КМ) и (PH).
211. При тех же обозначениях, что и в предыдущей задаче, опре-
делите взаимное расположение каждых двух из следующих
прямых:
т = {М : (3k) (ВМ = kb)}; р = {М : (36) (В?М = kb)};
п= {М : (3k) (AM = kb)}; q = {M : (3k) (DM = ka)}.
212. Базисными векторами прямых тип служат векторы а и Ь.
Какие из следующих высказываний истинны?
а) Если прямые тип пересекаются, то векторы а и Ь ли-
нейно независимы.
б) Если векторы а и b линейно независимы, то прямые тип
пересекаются.
в) Если прямые тип скрещивающиеся, то векторы а и b
линейно независимы.
г) -Если векторы а и b линейно независимы, то прямые тип
скрещивающиеся.
д) Если векторы а и b линейно независимы, то прямые тип
пересекающиеся или скрещивающиеся.
213*. Прямые /( и /2 —скрещивающиеся. Взяты четыре различные
точки А Е Z1( В 6 Zi, М Е Z2, Р Е /2. Докажите, что прямые
58
(AM) и (BP) —скрещивающиеся и прямые (АР) и (ВМ) так-
же скрещивающиеся.
214. Прямые (АВ) и (CD) — скрещивающиеся, точки M,N,P, Q—
середины отрезков [AC], [AD], [ВС], и [ВО]. Определите
взаимное расположение следующих прямых: a) (MN) и (PQ);
б) (МР) и (NQ); в) (MQ) и (NP).
215*. Является ли отношение, определенное в множестве всех
прямых и выражаемое словами «прямые пересекаются», от-
ношением эквивалентности?
216*. Сохраним обозначения, введенные в задаче 210.
а) Перечислите прямые, которые проходят через какие-либб
две из точек А, В, D, Bit Cj, D4 и пересекаются е прямой
(А4С).
б) Взята такая точка Q, что С\ — середина отрезка [QBt],
С какими из прямых (А^Ц), (CD), (ВВ4), (CiDj) пересекается
прямая (MQ)?
в) На прямой (АВ) взята такая точка Q, что прямые (CQ) и
(КМ) пересекаются. Определите d (A, Q): d (Q, В).
217. Векторы ОА, ОВ и ОС —линейно независимые, AD = ОВ
Определите взаимное расположение прямых:
a) (AD) и (ОВ); б) (ОА) и (BD); в) (ОС) и (BD).
218. . При обозначениях, введенных в задаче 209, взята такая
--------------------->• >
точка Q, что BQ = СВ. Пересекаются ли прямые (АР) и
(SiQ)?
219*. Векторы а, Ь, с —линейно независимые. Определите взаим-
ное расположение каждых двух из прямых (АВ), (CD), (АР),
если выполнены следующие соотношения:
а) ОА= —а— 2Ь — 2с, ОВ~ За — 9& + с, ОС— 2а— 9Ь —
— 2с, 0D=2a—7b—Зс, 6Р = — а—Зс;
б) АВ= 4а— 2&4-с, АС= a—2b, AD—a-\-c, АР= 2Ь -|-с;
в) QA = а— 2Ь+ 2с, QB^ За— 3b+ 2с, QC= 4а— 3b+ Зс,
QD— 5&+ с, QP= — 46+ 2с.
220. Точки А, В, С, D заданы в системе (О, е2, е3) своими коор-
динатами. Определите взаимное расположение прямых (АВ)
и (CD) в каждом из следующих случаев:
а) А (3; 7; —1); В (2; 4; 2); С (0; 3; —2); D (2; 9; —8);
б) А (2; —1; 4); В (4; 4; 1); С (3; 1; 4); D (6; 8; 1);
в) А (3; 1; 2); В (4; 4; 1); С (5; 1; 6); D (6; 4; —3);
г) А (1; 1; 3); В (2; 3; 6); С (1; 2; 2); D (2; 6; 3).
221*. Прямые а и Ь —скрещивающиеся. Прямая I пересекает обе
прямые а, Ь\ прямая т также пересекает обе прямые а, Ь.
При каком условии прямые I и т будут а) параллельными,
б) пересекающимися,^) скрещивающимися?
222. Определите взаимное расположение прямых I (А, а) и I (В, Ь),
59
если в некоторой системе координат (О, elt е2, eg) заданы
координаты точек А, В и векторов а, Ь:
а) А (3; —2; 2), В (—1; 2,5; 4); а (6; —2; 4), b (9; —3; 6);
б) А (3; 2; 1), В (8; —3; —5); а (3; 1; —2), b (—1; 3; 2);
в) А (2; —1; 2), В (—5; 0; 1); а (1; 2; —1), b (2; —1; 3);
г) А (0; 2; —2), В (—2; —3; 0); а (3; —1; 2), b (1;—1; —5).
223. Векторы а, b линейно независимы. Укажите, какие из сле-
дующих прямых параллельны между собой:
/(А, а), l(A, b), l(B, I (В, а + b), I (С, За + 3b),
I (С, 2b).
224. Сохраним обозначения задачи 195 (см. рис. 22).
а) Докажите, что (СА) || (СИО, (СВ) || (С^), (АВ) || (А^).
б) Точки М и Р — середины отрезков [CiBj] и [СВ]; дока-
жите, что (AtM) || (АР).
в) Точки N и Q — середины отрезков [AiBt] и [АВ]; пере-
числите прямые, параллельные (NQ), каждая из которых
проходит через какие-либо две из точек А, В, С, Аь Вь Сь
г) Точки К и М — середины отрезков [CtAJ и [С1В4]; до-
. кажите, что (/<М) || (АВ).
225. Известно, что I {N, а) || I (Р, Ь) и I (Р, b) || I (Q, с). Могут ли
векторы а и с оказаться линейно независимыми?
226. Известно, ’что А С b (С, р) и I (С, р) || I (С, q). Принадле-
жит ли точка А прямой I (С, q)?
227. Точки А, В, С не лежат на одной прямой; М и N — середи-
। ны отрезков [АС] и [ВС]. Докажите, что (MN) || (АВ).
228. Векторы а и b линейно независимы. На прямой I (О, а) взяты
точки А и В, а на прямой I (О, Ь) взяты точки С и D (рис. 28).
Докажите, что если (AC) || (BD), то
d (О, А) : d (О, В) = d (О, С) : d (О, D).
Точки А, В, С, D удовлетворяют
соотношениям: DA — За — Ь,
DB — а — 7b, АС = ka — 1 \b, где
а, b — линейно независимые век-
торы. Определите число k, зная,,
что (АВ) || (CD).
При обозначениях, указанных на с.41
(см. рис., 15), докажите следующие
утверждения:
60
а) прямые (ДД^ и (DCX) — скрещивающиеся;
б) прямые (Ли (BrD) — пересекающиеся;
в) прямые (АВ) и (СГР) — скрещивающиеся.
231. Сохраним обозначения задачи 195 (см. рис. 22). Точки М. Р,
К, Т — середины отрезков [Д1В1], [Д A J, [CCi], ]•
Определите взаимное расположение каждых двух из сле-
дующих прямых:
а) I (А, с); I (Въ с); I (В, с); I (С, 5);
б) (АВ)- (AM (СА)-,
в) (МТ)-, <РК); (РМ)-, (КТ)-,
г) (СВ^^Д); (СхД^иСД);
д) I (А, с); I (Дь а — с)-, I (С, а — с).
232*. При тех же обозначениях, что и в задаче 195 (см. рис. 22),
определите взаимное расположение каждых двух из следую-
щих прямых:
- m = {М : (3k) (AM = ka)}-, р = {М : (3k) (AM=k (a-R))};
n = {M-: (3k) (B^M = ka)}-, q = {M : (3k) (CM - Ac)}.
233*. Является ли отношение, определенное в множестве всех
прямых и выражаемое словами «прямые скрещиваются», от-
ношением эквивалентности?
234*. При обозначениях, указанных на с. 41 (см. рис. 15), пере-
числите все прямые, каждая из которых проходит через
какие-либо две из точек А, В, С, D, Дп Вь С1г и кото-
рые: а) являются скрещивающимися с прямой (ВВХ); б) име-
ют с прямой (ВВХ) одну общую точку.
235. Какие из следующих высказываний истинны?
a) (Vnp. I, m) (I и tn — скрещивающиеся) => ((/ f| tri) — 0);
б) (Vnp. I, tn) (I f) m = 0)=> (I и tn— скрещивающиеся);
в) (Vnp. I, tri) (I П m = 0)=> (I II tn)-,
r) (Vnp. I, tn) (l П m = 0)=> ((I II tn) \J (l и tn — скрещи-
вающиеся)).
§ 8. ПЛОСКОСТЬ
----------------------------О-------------------------------
8.1. Определение,
точку А и имеющей пару
(а, Ь) своим базисом, называет-
ся множество всех таких точек
М, что векторы AM, а, b ли-
нейно зависимы (рис. 29). Обо-
значать эту плоскость будем
символом а (Д; а, Ь).
Плоскостью, проходящей через
линейно независимых векторов
61
Таким образом, точка М в том и только в том случае принадле-
жит плоскости а (Л; а, Ь), если найдутся такие действительные Я
числа k и I, что AM = ka 4- lb: t
a (A; a, b) = (M : (3k, I) (AM = ka + lb)}.
--------------------------ф----------------------------
Одну и ту же плоскость можно задавать по-разному, указывая
различные базисы и различные точки, через которые она прохо-
дит. Следующие теоремы указывают способы задания одной и той
же плоскости.
8.2. Теорема. Если В С а (Л; а, Ь), то а (В; а, Ь) =
— а (А: а, Ь).
Доказательство. Пусть М € а (В, а, Ь), т. е. суще-
ствуют такие действительные числа k, I, что ,г
ВМ = ka 4- lb. I
Так как, кроме того, по условию ВС а (Л; а, Ь), то Л В = k±a 4- I
4- lrb. Следовательно, я
AM = АВ + ВМ = (k 4- k±) а 4- (I + 4) 1
Таким образом, векторы AM, а, b линейно зависимы, т. е.
М € а (Л; а, Ь).
Аналогично доказывается, что если М € а (Л; а, Ь), то М €
6 а (В; а, Ь).
Эта теорема показывает, что вместо Л в определении плоскости
а (Л; а, Ь) можно взять произвольную точку этой плоскости.
8.3. Теорема. Плоскости а(Л; а, Ь) и а (Л; с, d) совпадают
в том и только в том случае, если каждый из векторов а, Ь представ-
ляется в виде линейной комбинации векторов с, d. |
▼ Доказательство. Докажем, что (VT. Л; a, b, с, d, I
где а, b — линейно независимые векторы и с, d — линейно незави- |
симые векторы) ((3k, I, т, п) ((а = kc 4- Id) A (b = тс 4- nd)))=$-'
=> (а (Л; a, b) — a (Л; c, d)).
Прежде всего докажем, что не только каждый из векторов а, b
представляется в виде линейной комбинации векторов с, d, но и,
наоборот, каждый из векторов с, d представляется в виде линейной
комбинации векторов а, Ь.
62
В самом деле, мы имеем:
а == kc "4" Id
b = тс 4- nd,
с = к + Od.
Таким образом, каждый из векторов а, Ь, с представляется в
виде линейной комбинации двух векторов с, d, и потому по теореме
2.10 векторы а, Ь, с линейно зависимы. Но так как векторы а, b по
условию теоремы линейно независимы, то в силу теоремы 2.9 век-
тор с представляется в виде линейной комбинации а и Ь.
Аналогично доказывается, что d представляется в виде линейной
комбинации векторов а, Ь.
Теперь докажем, что плоскости а (А; а, Ь) и а (А; с, 2) совпа-
дают. >
Если М € а (А; а, Ь), то AM = pa + qb = р (kc + Id) +
+ q (тс + nd) — (pk + qni) c 4- (pl 4r qn)d, и потому M £ а(А; с, d).
Аналогично доказывается, что если М € а (А; с, d), то М С
€ а (Л; а, Ь) (при этом используется, что каждый из векторов с, d
представляется в виде линейной комбинации векторов а, Ь).
Наконец, докажем, что (Vt. A; a, b, с, d, где а, b — линейно
независимые векторы и с, d — линейно независимые векторы)
(a (A; a, b) = а (А; с, d))=> (3k, I, т, п) ((а = kc 4- Й)А
А (Ь = тс 4- nd)).
Найдем такие точки М, N, что AM — a, AN = Т> (аксиома 5.2).
Ясно, что M, N £ а (А; а, Ь), а так как плоскости а (А; а, Ь) и
а (А; с, d) совпадают, то М, N С а (А; с, d). Следовательно, суще-
ствуют такие числа k, I, т, п, что AM = kc + Id, AN = тс 4- nd.
Таким образом, а = kc 4- Id, b = тс 4- nd. у
8.4. Следствие. Если (а, b) и (c,d) — два базиса одной и
той же плоскости а, то каждый из векторов а, b представляется
в виде линейной комбинации векторов с, d.
В самом деле, если А — произвольная точка плоскости а,
то плоскости а (А; а, Ь) и а (А; с, d) совпадают (обе они совпадают
с плоскостью а), и потому можно применить теорему 8.3.
8.5. Следствие. Пусть (а, Ь) и (с, d) — два базиса одной
63
и той же плоскости а. Тогда если вектор р представляется в виде
линейной комбинации векторов а, Ь, то он также представляется
в виде линейной комбинации векторов с, d. .
8.6. Следствие. Для любой плоскости а существует орто-
гональный базис (а, с), т. е. такой базис, что а А. с.
В самом деле, пусть дана плоскость а = а (Л; а, Ь). Согласно
задаче 4.6 существует такое число k, что вектор с = b + ka орто-
гонален вектору а. Векторы ан с линейно независимы. Согласно
теореме 8.3 плоскости а (Л; а, Ь) и а (Л; а, с) совпадают, т. е.
(а, с) — базис плоскости а. По построению этот базис является ор-
тогональным.
8.7. Теорема. Если В, С, D — три точки плоскости
а(А',а,Ь), не принадлежащие одной прямой, то а (А; а, Ь) =
= а (В; ВС, BD).
Доказательство. По теореме 8.2 а (А; а, Ь) =
= а (В; а, Ь). Так как обе точки С, D принадлежат этой плоскости,
то ВС = ka 4- lb, BD = та + nb. Поскольку точки В, С, D не
принадлежат одной прямой, векторы ВС и BD линейно независимы.
Из теоремы 8.3 следует, что а (В; а, Ъ)а (В; ВС, BD).
8.8. Следствие. Через три точки, не принадлежащие одной
прямой, проходит одна и только одна плоскость.
В самом деле, если В, С, D — три точки, не принадлежащие
----------------------------> "►
одной прямой, то плоскость а (В; ВС, BD) проходит через все три
точки. Единственность вытекает из теоремы 8.7. Действительно,
если а (Л; а, Ь) — какая-либо плоскость, которая проходит через
точки В, С, D, не принадлежащие одной прямой, а а (Л', а', Ь')
еще одна плоскость, проходящая через те же точки, то в силу тео-
ремы 8.7 а (Л; а, Ь) = а (В; ВС, BD), а (Л'; а', Ь')=а ВС, BD),
и потому а (Л; а, Ь) = а (Л'; а', Ь').
. Плоскость, проходящую через три точки М, N, Р, не лежащие
на одной прямой, будем в дальнейшем обозначать через (А4ЛГР).
•----------------—--------О----------------------------
8.9. Определение. Вектор р называется параллельным
плоскости а, если он представляется в виде линейной комбинации
векторов, составляющих базис этой плоскости.
8.10. Теор е м а. Любые два линейно независимых вектора, па-
раллельных плоскости, составляют базис этой плоскости.
64
Доказательство. Пусть с, d — линейно независи-
мые векторы, параллельные плоскости а (Я; а, Ь). Тогда с = ka 4-
4- lb, d = та 4- nb. По теореме 8.3 а (Л; а, Ь) = а (Я; с, d), a
это и означает, что (с, d) — базис плоскости об (А; а, Ь).
8.11. Т е о р е м а.
(Упл. а, т. А, М, где А С а) (М € а) <=> (AM || а). •
Доказательство. Пусть а — а (А; а, Ту). Соотно-
шение AM || а означает по определению, что (3k, /) (AM — ka+lb).
Таким образом, доказываемое утверждение равносильно следую-
щему: (Ут. А, М; а, Ь, где векторы а, b линейно независимы)
(М € а (А; а, Ь)) «=> (3k, Z) (AM — ka 4- lb), а это непосредственно
вытекает из определения плоскости.
Задачи
236. Запишите с помощью фигурных скобок плоскость, проходя-
щую через точку В и имеющую пару векторов (р, q) своим
базисом.
237. Векторы р, q, г линейно независимы. Точки А, В, С, К, О
удовлетворяют соотношениям КА = Зр 4- 2q, ' ВК =
— —р + ±q, ОК — %р — Зг, ОС = q — Зг. Какие из точек
А, В, С, К, О принадлежат плоскости а (К; р, q)l
238. Сохраним обозначения задачи 195 (рис. 22). Какие из точек
А, В, С, Аь Blt Сх принадлежат: а) плоскости а (А; а, 3);
б) плоскости а (А; а, с); в) плоскости а (А;Ь, с); г) плос-
кости а (В; а — Ь, с); д) плоскости а (Ах; а, Ь)?
239. При обозначениях, указанных на с. 41 (см. рис. 15), дока-
жите, что следующие четыре точки расположены в одной
плоскости: а) А, В, С, D', б) Ах, Blt Clt Di, в) А, В, Сх, £>х;
г) А, В, At, Bt-, д) А, С, Ах, Сг; е) В, D, Въ Dx.
,240*. Могут ли плоскости а (А; а, Ь) и а (А; р, q) быть не совпа-
дающими, если: а) р= 2а—b, q——а-, б) р=2а—Ь, а —
= уР 4-в> “= 3Р+ 2^> 5Р
241*. Векторы а, ~Ь линейно независимы, векторы с, ~d также ли-
нейно независимы, причем среди векторов АВ, a, b, с, d
не существует трех линейно независимых. Докажите, что
а (А; а, Ь) = а (В; с, d).
3 Заказ 4860
65
242. При обозначениях, введенных на с. 41 (рис. 15), укажите,
какие из следующих пар векторов могут служить базисом
плоскости а (А; а, Ь) : а) и DC; б) AJ) и D^; в) АВ
и CD; г) АВ и ВС; д) АВ и В^; е) АВ и AAlt
243*. При обозначениях, введенных на с. 41 (см. рис. 15), ука-
жите, сколько существует различных плоскостей, каждая
из которых проходит через точку А и какие-либо две из то-
чек В, С, D, Alt Въ С1( Dt.
244*. Какие из следующих высказываний истинны?
а) Если точки А, В, С, D не лежат в одной плоскости, то
векторы АВ, AC, AD линейно независимы.
б) Если точки А, В, С, D лежат в одной плоскости, то век-
торы АВ, AC, AD линейно зависимы.
-------------------
в) Если векторы MN и PQ линейно зависимы, то точки
М, N, Р, Q лежат на одной прямой.
г) Если векторы MW и PQ линейно зависимы, то точки
М, N, Р, Q лежат в одной плоскости.
д) Если векторы АВ, AC, AD линейно зависимы, то точки
А, В, С, D лежат в одной плоскости.
245. При обозначениях, указанных на с. 41 (см. рис. 15), запи-
шите с помощью фигурных скобок плоскость, проходящую:
а) через точки D, С, Сг; б) через точки В, Blt С; в) через точ-
ки А, С, Ct; г) через точки А, Съ D.
246*. Даны 100 точек, каждые 4 из которых принадлежат одной
плоскости. Докажите, что все 100 точек лежат в одной пло-
скости.
247*. Даны четыре точки. Сколько существует различных плос-
костей, каждая из которых содержит какие-либо три из дан-
ных точек? (Рассмотрите различные возможности расположе-
ния данных точек.)
248. При обозначениях, указанных на с. 41 (см. рис. 15), взяты
такие точки Т С [АВ] и К £ [ВВ^, чтоб/ (Т, В) = ±d (А, В),
d (КВ) — — d (В, Вг), а через М и Р обозначены сере-
4
дины отрезков [ССХ] и [DC]. Докажите, что точки М, Р,
К, Т лежат в одной плоскости.
249. Векторы а + b и 2а — 36 параллельны плоскости а. Какие
из следующих высказываний истинны?
а) Векторы а, Ь составляют базис плоскости а.
б) Векторы а + b и 2а — 36 составляют базис плоскости а.
в) Если векторы а и 6 линейно независимы, то они составляют
базис плоскости а.
66
г) Если векторы а + b и 2а — ЗЬ не составляют базис плос-
кости а, то а и b линейно зависимы.
250*. Какие из следующих высказываний истинны?
а) (Упл. а; р, q) ((р [| а) A (q || а)) => ((р, q) — базис пло-
скости а);
б) (Упл. а; р,р, г) ((р || а)Д(<? Ц а) А (г || а)) =>(р, q, г ли-
нейно зависимы);
в) (Упл.а; р, q, г) | (р || а)Д (д || а) Д(г || а)) => (3k, I) (р =
= kq 4~ Zr).
251. При обозначениях, указанных на с. 41 (см. рис. 15), через
N и Р обозначены середины отрезков [ВВХ] и [ССХ]. Какие
, из следующих высказываний истинны?
а) (УМ С [ЛЛх]) (MN || (ЛВС));
б) (ЗМ С [ЛЛх]) (MN || (ЛВС));
в) (УМ е [ЛЛХ]) (ЛВ || (MNP));
г) (УМ € [ЛЛХ]) (ВС || (MNP)).
252*. При обозначениях, указанных на с. 41 (см. рис. 15), через
М и К обозначены середины отрезков [ЛЛХ] и [ВВХ], а через
Q — точка пересечения прямых (ВСХ) и (СВХ). В качестве
базиса плоскости (ВСМ) взяты векторы а = ВМ и & = СВ.
Укажите, какие из векторов Лх/С, CXDX, QDX, DXC, ЛХОХ
параллельны плоскости (ВСМ), и представьте их в виде
линейной комбинации векторов базиса.
253*. Точки Л, В, С, D, не лежащие на одной прямой, принадле-
жат плоскости а, точка S не принадлежит плоскости а.
Докажите, что векторы АВ и CD в том и только в том слу-
чае линейно зависимы, если ЛВ || (SCD).
254. Докажите следующую теорему (рис. 30):
(Ут. Л, В, М, N; пл. а, где Л, В £ а) (ЛМ=ЯУН(МУ ||а).
Справедлива ли обратная теорема?
255. При обозначениях, указанных на с. 41 (см. рис. 15), обо-
значьте тремя буквами следу-
ющие плоскости:
а = {М : (3k, I) (BJW =
= k (b — a) + lc)},
0 = {M : (3k, I) (D^M =
= £&+ Zc)}.
3*
67
256. Векторы а, Ь, с линейно независимы. Определите, лежат ли
точки А, В, С, D в одной плоскости, если выполнены еле- Ц
дующие соотношения: у
а) ОА = За— Ь + с, ОВ = 5а — 46+ 6с,
ОС = 6а— 2Ь Н-с, OD= 11а— 66+ 6с;
б) АВ= a — 36+ 5с, AC =2b— Зс, AD= а+ 3b— 4с; ' *J
в) АВ= 4а-+-3£Н-2с" BC=a — b, CD=7b+3c-,
г) ОА= а= ЗЬ — с, ОВ= 2а+ 36+ 2с, АС= 5а— Ь
вЪ=—а+Ь+ 12^ |
257. В системе (О, еи с2, е3) заданы координаты точек А, В, С, D. |
Лежат ли точки А, В, С, D в одной плоскости, если: <
а) д (_з; 1; 7); В (—2; 2; 8); С (—1; 0; 10); D (2; 3; 13); л
б) А (7; 1; —3); В (7; 4; —3); С (9; 2; 2); D (9; —5; 2); I
В) А (-4; 2; 7); В (—Зд 3; 8); С (-2; 2; 4); D (1; 5; 7). :
• 258. Параллелен ли вектор а плоскости (ЛВС), если точки А, В, С
и вектор а имеют в системе (О, elt е2, е3) следующие коорди-
наты:
а) А (1; 2; 3); В (4; 2; 5); С (2; 1; 3); а (0; 3; 2);
б)' А (1; 1; 1); В (4; 0; 1); С (3; 1; —2); а (-1; —1; 6);
в) А (2; 0; -3); В (3; 1; 0); С (-2; -1; 5); а (1; 2; -1)?
259. Даны две плоскости а (К; а, р) и а (О; р, q). Может ли ока-
заться, что: а) а = 2р; б) р — -^q; в) а — 3q?
260. Сохраним обозначения, введенные на с. 41 (см. рис. 15).
Какие из точек А, В, С, D, Аг, В1У С1( Dx принадлежат:
а) плоскости а (Л; а, 6); б) плоскости а (Л; а, с);
в) плоскости а (Л; Ъ, с); г) плоскости а (Л; а, b + с);
д) плоскости а (Л; а + b, Ь + с)?
261. Докажите, что если'плоскости а (Л; а, Ь) и а (Л; р, q) сов-
падают, то среди векторов a, b, р, q не существует трех линей-
но независимых.
262. При обозначениях, указанных на с. 41 (рис. 15), перечисли-
те все плоскости, каждая из которых проходит только через
три из точек Л, В, С, D, Аъ Въ С1г Dt.
263. При обозначениях, введенных на с. 41 (рис. 15), укажите,
сколько существует различных плоскостей, каждая из кото-
рых проходит через точки А, какую-либо из точек В, С,
D, Blt Съ
264. При обозначениях, указанных на с. 41 (рис. 15), через М, N,
Р, Q обозначены середины отрезков [Л^], [В^], [ВС] и
68
[А£>]. Докажите, что точки М, N,
Р, Q лежат в одной плоскости.
265. При обозначениях, введенных на с.
41 (рис. 15), укажите, какие из век-
торов АВ, AD, AAlf AC, АС2 па-
раллельны ПЛОСКОСТИ (Лх^Сх)?
(CGDx)? (ВВхСх)?
266. Точки А, В, С, D, S выбраны так,
что АВ = a, AD = ВС = b, ЛЗ =
= с, где а, Ь, с — линейно незави-
симые векторы. Запишите с помощью фигурных скобок:
а) плоскость (ASD)1, б) (ЛЗС); в) (BCD).
267*. Плоскости аир проходят через точку А. Векторы р и q
параллельны плоскости а, векторы а и b параллельны пло-
скости р. Какие из следующих высказываний истинны?
а) Если.а = р, то р = а и q = b.
б) Если р = 2а 4- Ь, q = 2b — а', то а — р.
в) Если р = 2а + b, q — 2Ь — а и векторы а, b линейно
независимы, то а = р.
г) Если р = 2а + b, q — 2b — а и векторы а, р линейно
независимы, то а — р.
д) Если а = р, то а 4- b есть линейная комбинация векторов
Р и q.
268. Докажите справедливость следующего утверждения (рис. 31):
(Vt. А; а;Ь) (а и b линейно независимы) =>( 31 пл. а)
((Л (а) А (а || а) А(Ь|| а)). •
Справедлива ли обратная теорема?
269. Точки А, В, С, D и векторы р, заданы в системе (О, ех, е2, е3)
своими координатами. В каждом из следующих случаев
определите, какие из точек В, С, D принадлежат плоскости
a(A;p,q):
а) А (0; 1;.2), В (0; 4; 5), С (—1; 1; 4), D (2; 6; 3), р (1; 2; 0),
<f(—1;—1;1);
б) Л (2; 1; 3), В (2;—5; 1), С (5; 1; 10), D (1; 2; 3), р(\;-1; 2),
гГ(1; 2; 3);
в) Л (3; 7; —1), В (3; 3; 9), С (1; 2; 3), D (0; 1; —4),
р (—1; —2; 3), q (3; 2; 1).
270. Точки А, В, Си векторы р, q, г заданы в системе (О, ег, е2, е3)
двоими координатами. В каждом из следующих случаев
69
определите, какие из векторов р, q, г параллельны плоскости
(ЛВС):
а) А (0; 2; 3), В (1; 3; 4), С (1; 4; 6), р (1; 2; 3), q (2; 3; 4),
г(2;1;0);
б) А (—1; 3; 2), В (—1; 5; 3), С (—2; 5; 5), р (1; 2; —1),
9(1; 4; 0), Г(3; —1; 2);
в) Л (1; —2; 5), В (—1; 3; 2), С (3; 2; 4), р (1; 1; 0), q (6; 3; 1),
г (1; 3; 2).
271. Векторы а, b заданы в системе (О, е1г е2, е3) своими коорди-
натами: а (1; 2; 1), & (—2; —1; 5). Какие из векторов
3<% + 7е3, е1 — е3 + 2ез, —3el + 11^з, + 5е2 4- 8^з па-
раллельны плоскости а (О; а, &)?
§ 9. ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМОЙ
И ПЛОСКОСТИ
9.1. Теорема. Если две различные точки прямой I принадле-
жат плоскости а, то /с а (рис. 32).
Доказательство. Пусть две различные точки А, В
прямой I принадлежат плоскости а. Выберем в плоскости а точку
С £ I. Тогда I = I (Л, ЛВ); а = а (А; АВ, АС). Для любой точки
М € I имеем: AM — kAB. Записав это соотношение в виде AM —
— kAB + ОЛС, убеждаемся, что М € а.
Таким образом, I с: а.
9.2. Определение. Прямая назы-
вается параллельной плоскости, если ба-
зисный вектор этой прямой параллелен
плоскости.
9.3. Теорема. Прямая в том и
только в том случае не параллельна пло-
скости, если она имеет с этой плоско-
стью только одну общую точку (рис. 33).
Доказательство. Пусть
прямая I имеет с плоскостью а только одну
общую точку А. Обозначим через а базис-
ный вектор прямой I. Пусть М — такая
точка, что AM = а. Тогда М€1. Далее,
так. как МФ А, то MQ а. Следовательно,
aj(.a (теорема 8.11), т. е. /^а.
Рис. 33
70
Обратно, пусть прямая I = I (Л, а) не параллельна плоскости
а = а (В; с, d), т. е. вектор а не является линейной комбинацией
векторов с, d. Тогда векторы а, с, d линейно независимы, и потому
~ДВ = ka + pc + qd (теорема 3.6). Обозначим через М такую
точку, что AM = ka. Тогда М 6 I. Далее, так как ВМ — AM —
— АВ — —рс — qd, то М € а. Таким образом, М — общая точка
прямой I и плоскости а. Двух же общих точек I и а иметь не могут,
так как I (теорема 8.11). Итак, I и а имеют ровно одну общую
точку.
9.4. - Следствие. Прямая в том и только в том случае па-
раллельна плоскости, если она либо содержится в этой плоскости,
либо не имеет с ней общих точек.
В самом деле, в силу теоремы 9.3 прямая в том и только в том
случае параллельна плоскости, если число общих точек прямой и
плоскости не равно единице, т. е. если эта прямая либо не имеет
общих точек с плоскостью, либо же имеет с ней не менее двух об-
щих точек (и тогда целиком содержится в плоскости по теоре-
ме 9.1).
------------------------ф---------------------------
В этом пункте доказываются три теоремы, в которых в зависи-
мости от взаимного расположения двух прямых решается вопрос
о том, содержатся ли эти прямые в одной плоскости.
9.5. Теорема. Если прямые и 12 пересекаются, то суще-
ствует* единственная плоскость, содержащая обе эти прямые
(рис. 34).
Доказательство. Пусть прямые 4. имеют ровно
одну общую точку А. Выберем точки В Ц и С ( отличные от
А. Точки А, В, С не принадлежат одной прямой, и потому сущест-
вует единственная плоскость, содержащая эти три точки (следствие
8.8). Эта плоскость содержит прямые 4 и /2
(теорема 9.1).
9.6. Теорема. Если две прямые па-
раллельны и не совпадают, то существует
единственная плоскость, содержащая обе
эти прямые (рис. 35).
Доказательство. Пусть А,
В — две различные точки прямой 4 и С —
точка прямой 12. Обозначим через а пло-
скость, содержащую точки А, В и С (эта
плоскость единственна), и докажем, что
прямые 4» 4 содержатся в этой плоскости.
Прямая 4 содержится в а (теорема
9.1), и потому 4*11 « (следствие 9.4). Сле-
71
довательно, базисный вектор а прямой Zx параллелен-а. Так как
а является также базисным вектором прямой 12, то Z21| а. По-
скольку, кроме того, Z2 и а имеют общую точку С, то /2 с: а.
9.7. Теорема. Прямые и 12 являются скрещивающимися
в том и только в том случае, если не существует плоскости,
содержащей обе эти прямые.
Доказательство. Пусть lY—l (Л, а) и Z2=Z (В, Ь) —
скрещивающиеся- прямые. Допустим, что существует плоскость
а, содержащая обе эти прямые. Тогда а || а, b || а. Кроме того,
АВ || а, так как прямая (АВ) содержится в плоскости а. Следова-
тельно, каждый из векторов а, Ь представляется в виде лйнейной
комбинации 'векторов с, d, где (с, d) — базис плоскости а (опреде-
ление 8.9). Поэтому векторы а, Ь, АВ линейно зависимы (теорема
2.10). Но это противоречит тому, что рассматриваемые прямые —
скрещивающиеся. Полученное противоречие доказывает, что не
существует плоскости, содержащей обе прямые Zx, Z2.
Обратно, допустим, что не существует плоскости, содержащей -
обе прямые Zx, Z2. Тогда прямые Zx, Z2 не могут быть параллельными
и не могут иметь ровно одну общую точку (теоремы 9.5 и 9.6).
Следовательно, Zx и Z2 — скрещивающиеся прямые.
о-
Пусть а — произвольная плоскость, А и В — две ее различные
точки. В силу теоремы 9.1 прямая (АВ) целиком расположена в
плоскости а, а потому в этой плоскости содержатся отрезок [Я В]
и луч [ДВ). Таким образом, в каждой плоскости а мы можем про-
водить прямые, лучи, отрезки и рассматривать образованные ими
фигуры. При этом в каждой плоскости а справедливы все теоремы,
изученные в курсе геометрии IV—VIII классов. Подтвердим это
утверждение несколькими примерами.
V Пример!. Всякая прямая /с а разбивает плоскость а
на две области таким образом, что если две точки Р, Q принадле-
жат одной области, то отрезок [PQ] не пересекается с прямой I,
а если они принадлежат разным областям, то отрезок [PQ] пере-
секается с прямой I в единственной точке.
Это утверждение было сформу-
лировано в курсе VI класса, одна-
ко доказательства там приведено
не было.
Доказательство.
Пусть Д, В—две различные
точки прямой Z, а С € а — точка,
не ' принадлежащая прямой Z
(рис. 36). Положим: а = АВ, b =?
Рис. 36
72
АС. Тогда векторы а, b составляют базис плоскости а, т’ е> “ =
= а (Л; а, Ъ). Для любой точки М € а мы имеем: AM ~ ха 4-
4- yb, где х, у — некоторые числа. Обозначим через ГЦ. множе-
ство всех точек плоскости а, для которых у > 0, а через П_—мно-
жество всех точек, для которых у<0. Для точек самой прямой I
имеем: AM — ха = ха 4- ОЬ, т. е. у =0. Из сказанного ясно, что
множества I, ГЦ и П_ попарно не пересекаются, причем I 1_)ГЦ U
U П_ = а. Мы докажем, что ГЦ, П_ как раз являются теми об-
ластями, о которых идет речь в формулировке.
В самом деле, пусть точки Р, Q принадлежат одной области,
например П+, т. е. АР — xta + уД AQ = х2а 4* у2Ц где ух > 0,
у2 > 0. Тогда для любой точки 3 € [PQ] мц имеем: PS == kPQ, где
0 k 1, и потому ДЗ = АР 4- PS = АР 4- kPQ = АР 4-
4- k (AQ — АР) = kAQ 4- (1 — k) АР = (kx2 4- (1 — k) хх) а 4-
+ (Луа 4- (1 — &)У1) Ь. Таким образом, ДЗ = ха 4- yb, где х =
= kx2 4- (1 — k) xlty — ky2 4- (1 — k)yr. Так как& 0, 1 — к'ф 0,
а оба числа ylt y2 положительны, то ky2 4- (1 4- k)y2 >0. Это
означает, что S € П+. Итак, любая точка 3 € [PQ] принадлежит
Щ и потому не принадлежит I, т. е. отрезок [PQ] не пересекается
с I. (Если обе точки Р, Q принадлежат П_, рассуждение анало-
гично.)
Пусть теперь точки Р, Q принадлежат разным областям, на-
пример Р € П+, Q С П_. Тогда АР = хга 4- уф, AQ — х2а 4-
4- уф, где у, > 0, у2 < 0. Как и прежде, для любой точки 3 € [PQ]
* > —> —►
имеем: ДЗ = ха 4- yb, где х = kx2 4- (1 — k) xlt у — ky2 4-
4- (1 — k)yr, причем 0 k 1. Чтобы найти общую точку отрез- *
ка [PQ] и прямой I, нужно найти такое значение k, для которого
у = 0, т. е. &у2 4-(1—^)у2=0. Отсюда получаем: k————.
У1—Уа
Так как ух > 0, у2 < 0, то это значение k удовлетворяет условию
0 <_k < 1, т. е. точка S, соответствующая этому значению k,
принадлежит отрезку [PQ] (и, кроме того, принадлежит прямой /,
так как при выбранном k имеем: у = 0). Тем самым доказано, что
отрезок [PQ] в рассматриваемом случае имеет общую точку с пря-
мой I (двух общих точек отрезок [PQ] и прямая / иметь не могут,
так как иначе прямые (PQ) и I совпадали бы, что невозможно, по-
скольку Р £ I, Q i I).
Доказанное утверждение позволяет (как это и было сделано в
курсе VI класса) ввести определение полуплоскости: множества
I U П+ и I U П_ называются полуплоскостями (плоскости а),
имеющими I своей граничной прямой. Далее, используя понятие
полуплоскости, можно определить треугольники: если Д, В, С —
три точки плоскости а, не лежащие на одной прямой, то треуголь-
73
Рис. 38
ник АВС определяется как пере-
сечение Пг (] П2 (~| П3, где Пх —
полуплоскость с граничной пря-
мой (ЛВ), содержащая точку С;
далее, П2 — полуплоскость с гра-
ничной прямой (АС), содержащая
точку В, и П3 — полуплоскость с
граничной прямой (ВС), содержа-
щая точку А (рис. 37).▼
Пример 2. Равнобедрен-
ный треугольник обладает осью
симметрии.
' Доказательство.
Пусть [Л В] — основание равно-
бедренного треугольника ЛВС,
т. е. точки Л, В и С (плоскости а) не
лежат на одной прямой и d (Л,
С) — d (В, С). Обозначим через М
середину отрезка [ЛВ] (рис. 38).
Нам нужно доказать, что СМ ±
>
± АВ. В самом деле, так как
МВ = —МА, то мы имеем:
СВ=СМ-\-МВ, СА — см+м\=см — мв
и потому
CM- АВ— 2СМ- MB = ((СМ+ МВ)2— (СМ— МВ)2)^
= 1 (СВ2— СА2) = 1 (d (С, В)2 — d (С, Л)2) = 0.
Из доказанной теоремы вытекает, в частности, что углы при
основании равнобедренного треугольника конгруэнтны (конгруэнт-
ные фигуры определяются, как и в V—VI классах, с помощью
движений, т. е. отображений плоскости на себя, которые
сохраняют расстояния; осевая симметрия является движением,
откуда и вытекает справедливость сформулированного утвержде-
ния).
Пример 3. Пусть I — произвольная прямая, расположен-
ная в плоскости а. Через любую точку А € а проходит (в плоскости
а) единственная прямая, параллельная I.
Это утверждение было сформулировано в курсе V класса в виде
экспериментального факта; в VIII классе мы охарактеризовали это
утверждение как аксиому параллельности. Здесь же (в изложении,
основанном на аксиоматике Вейля) справедливость этого утверж-
дения непосредственно вытекает из теорем 7.5 и 9.6. В самом деле,
в силу теоремы 7.5 существует единственная прямая I', проходя-
74
щая через А и параллельная I. Если А € I, то /' совпадает с I, и
потому I’ сд а; если же А £ I, то согласно теореме 9.6 прямая /'
расположена в плоскости, содержащей прямую I и точку А, т. е. и
в этом случае прямая I' расположена в плоскости а.
Ряд других примеров (теорема Пифагора, свойства паралле-
лограммов, ромбов, прямоугольников, свойства средней линии
треугольника и т. д.) содержится в рассмотренных ранее задачах
(№ 117, 59, 71, 116, 139, 120 и др.). Если к этому добавить, что
основные свойства векторов (доказывавшиеся в VII—VIII клас-
сах как теоремы) приняты здесь в качестве аксиом, а вопросы из-
'мерения геометрических величин (в частности, углов, длин, пло-
щадей) будут подробно рассмотрены в X классе, то, в самом деле,
станет ясно, что в каждой плоскости справедливы все ранее изу-
чавшиеся теоремы плоской геометрии.
Задачи
В задачах 272—275 приняты обозначения задачи 195 (рис.
22).
272. Содержится ли в плоскости (ЛСВХ): а) прямая (ЛЛХ); б) пря-
мая (ЛВг)?
273. Через а обозначим плоскость (ЛВС), через р — плоскость
(Л1В1С1). Какие из следующих высказываний истинны?
а) Любые прямые а сд a, b сд р являются скрещивающимися.
б) Существуют прямые a сд а, b с р, которые являются
скрещивающимися. • '
274. Обозначим через а плоскость (ЛВС), а через у — плоскость
(ЛВВХ). Какие из следующих высказываний истинны?
а) Существуют пересекающиеся прямые аса, Ьсу.
б) Существуют скрещивающиеся прямые a сд а, b сд у.
в) Существуют параллельные прямые а <= а, b сд у.
275. Докажите, что через середину отрезка [Л1В1] проходит един-
ственная плоскость, параллельная обеим прямым (ЛЛХ) и
(ВС). Проходит ли эта плоскость через середины отрезков
[ЛВ], [ЛС], [ЛгСх]? _
276*. Точки Л, В, С, М, N, Q связаны соотношениями QA =
= а — b, QB — а — b — 5е, QC — 2а — 4Ь — 4с, QM ==
= 2а — 4Ъ + с, QN = За, где а, Ь, с — линейно независи-
мые векторы. Как расположена относительно плоскости
(ЛВС) каждая из следующих прямых: I (М, с), I (N, а—ЗЬ),
ЦА,а — b), I (В, ЗЬ + с — а), I (С, b + с)?
277. Точки Л, В, С заданы в системе (О, е1( с2> ез) своими коорди-
натами:
Л (0; 3; 1), В (2; —1; 2), С (3; 1; —1)^ ~
векторы а, Ь заданы координатами в базисе (elt е2, е3):
а (4; 0; — 5), ~b (1; —1; 3).
75
а) Докажите, что прямая I (В, а)
содержится в плоскости (АВС).
б) Установите, как расположены
прямые I (Д, а) и I (А, Ь) относи-
тельно плоскости (АВС).
в) Определите взаимное положение
прямых (АВ) и I (С, Ь).
г) Содержатся ли прямые I (А, а)
и I (В, Ь) в одной плоскости?
278*. Даны прямые а, b и плоскость а.
Какие из следующих высказываний
истинны?
а) Если асаи прямые а, b пересекающиеся, то b с а.
б) Если а сд а и 6 сд а, то прямые а и b пересекающиеся.
в) Если а с а и прямые а, b скрещивающиеся, то прямая b
не содержится в плоскости а.
г) Если а с а, а прямая b не содержится в плоскости а,
то прямые а и b скрещивающиеся.
279. На двух пересекающихся прямых-а, b взяты точки А € а,
В € Ь, причем В £ а. Докажите, что плоскость а, содержа-
щая прямую а и точку В, содержит также прямую Ь.
280. Через прямую I проведены две различные плоскости аир
(рис. 39). Взяты точки А € а и В € р, не лежащие на пря-
мой I. Могут ли прямые (АВ) и I иметь общую точку?
281. Даны четыре параллельные прямые, из которых никакие
три не лежат в одной плоскости. Сколько существует плос-
костей, каждая из которых содержит две из этих прямых?
282. Через прямую I проведены две различные плоскости аир.
В плоскости а взята прямая т, параллельная I, а в плос-
кости Р взята точка В. Через точку В проведена прямая п,
параллельная т. Докажите, что п <=. р.
283. Через прямую I проведены две различные плоскости Р и у.
В плоскости р. взята прямая т, пересекающаяся с I в одной
точке. Существует ли прямая псу, параллельная /п?
284. Докажите, что если прямые I и т параллельны на — пло-
скость, содержащая прямую /, то т || а.
285. Даны две скрещивающиеся прямые а, Ьи точка М. Докажите,
что через точку М проходит единственная плоскость, па-'
раллельная обеим прямым а, Ь.
286*. Какие из следующих высказываний истинны?
а) (Упл. а; пр. а, Ъ) ((а сд а) Д (Ь сд а))=>а || Ь;
б) (Упл. а; пр. а, Ь) ((а || а) Д (Ь || а))=>а || Ь\
в) (Упл. а; пр. а) (Зпр. Ь) ((Ь с. а) Д (Ь || а));
г) (Упл. а; пр. а) (а. || а)=> (Зпр. Ь) ((Ь сд а) Д (а || Ь)).
п
287. В плоскости а расположен четырех-
угольник ABCD, точка S не лежит /
в плоскости а. Докажите, что если /
(АВ) || (CDS), то ABCD —трапеция / » /
(рис. 40). Верно ли обратное? / Д\\ /
288. Докажите, что если прямая а па- / /I \ \ /
раллельна плоскости а, то прямая, / /~7
проходящая через точку М € а и /
параллельная прямой а, лежит в Гул
плоскости а. - / а/
289. Две различные точки А, В содержат-'1 *--------J
ся в плоскости а. Докажите, что ес- Рис 40
ли AM = BN, то (MN) || а.
290. Параллелограмм ABCD расположен в плоскости а, точка S
не лежит в плоскости а. Докажите, что плоскость, содержа-
щая прямую (ЛС) и параллельная прямой (BS), делит отре-
зок [DS] пополам.
В задачах 291—298 приняты обозначения, введенные на
с. 41 (рис. 15).
291. Существует ли плоскость, содержащая прямые:
a) (AD) и (В&)-, б) (CD) и (ВХО); в) (ВС) и (ЛЛХ)?
292. Обозначим плоскость (АВС) через а, а плоскость (ABBt)
через 0. Какие из следующих высказываний истинны?
а) Любые прямые а с a, b cz 0 являются скрещивающимися.
б) Существуют прямые аса, b с 0, которые являются
скрещивающимися.
293. Через середины отрезков [ЛЛХ] и [ВВХ] проведена прямая а,
через середины отрезков [ССХ] и [DDJ — прямая Ь. Докажи-
те, что прямые а и b лежат в одной плоскости.
294. Точка А соединена отрезком с каждой из точек В, С, D,
AltBlt Сх, Di. Какие из этих отрезков лежат в одной плоскости:
а) с отрезком [ССХ]; б) с отрезком [АХС]?
295. Точки М, N — середины отрезков [ЛЛХ] и [ССХ]. Определите
вид четырехугольника MBNDi.
296. Можно ли из Л, В, С, D, Лх, Вх, Сх, Ох выбрать такие три точ-
ки, чтобы проходящая через них плоскость была параллель-
на обеим прямым (ЛЛХ) и (ВС)?
297. Докажите, что через середину отрезка [ВХСХ] проходит един-
ственная плоскость, параллельная прямым (АВ) и (DDX).
298*. Рассматриваются всевозможные прямые, каждая из кото-
рых проходит через две из точек Л, В, С, D, Лх, Вх, Сх, Dx.
Можно ли из этих прямых выбрать: а) три, б) четыре, в) пять
таким образом, чтобы никакие две из них не лежали в одной
’ плоскости?
299*. Докажите, что точки А, В, С, D ъ том и только в том случае
лежат в одной плоскости, если либо прямые (АС) и (BD)
п
имеют общую точку, либо (АВ) и (CD) имеют общую точку,
либо (AD) и (ВС) имеют общую точку.
300. Через прямую I проведены две различные плоскости аир.
Проведены прямые т сд а и п с. р так, что т || п. Докажите,
что прямые тип параллельны I.
301. Точки А, В, С, S не лежат в одной плоскости. Докажите,
что через середину отрезка [BS] проходит единственная
плоскость, параллельная обеим прямым (АВ) и (SC). Дока-
жите также, что эта плоскость делит пополам каждый из
отрезков [ВС], [ЛС], [XS]. Определите вид четырехуголь-
ника, вершинами которого служат точки пересечения рас-
сматриваемой плоскости с отрезками [ЛС], [ЛВ], [ВС], [ВВ].
§ 10. ВЗАИМНОЕ РАСПОЛОЖЕНИЕ
ДВУХ ПЛОСКОСТЕЙ
--------------------:------о----------------------------.
10.1. Определение. Две плоскости называются параллель-
ными, если у них существует общий базис (рис. 41).
Из этого определения непосредственно вытекает, что если
ах || а2, то любой вектор, параллельный плоскости alt параллелен и
плоскости а2; точно так же любая прямая, параллельная плоско-
сти alt параллельна плоскости а2.
10.2. Теорема. Отношение параллельности плоскостей реф-
лексивно, симметрично и транзитивно.
у Рефлексивность и симметричность отношения плоскостей
непосредственно вытекают из определения 10.1.
Прежде чем установить транзитивность, докажем, что если
плоскости ах и ,а2 параллельны, то любой базис одной из этих пло-
скостей является в то же время базисом другой плоскости. В самом
деле, если (а, Ь) — общий базис плоскостей ах и а2, а (с, d) — лю-
бой другой базис плоскости ах, то векторы с, d линейно независимы
и линейно выражаются через векторы а, b (следствие 8.4). Но тогда
(по теореме 8.10) векторы с, d составляют базис плоскости а2.
Докажем теперь транзитивность. Пусть а || р и р || у, т. е. су-
.------------7 шествует общий базис (а, &) плоскостей a
/ у / и р, и, кроме того, существует общий ба-
/ у (Г I—. зис (с, d) плоскостей р и у. Так как а || р,
/ / то в силу доказанного выше базис (с, d)
/ ____-/ плоскости р является также базисом пло-
/ у а / скости а. Таким образом, плоскости а и у
*-------—------7 имеют общий базис (с, d), и потому ос || Т-▼
Рис. 41 10.3. Теорема. Через каждую точку
78
проходит единственная плоскость, параллельная данной
плоскости.
Доказательство. Пусть А — данная точка и
а (В; cf d) — данная плоскость. Плоскость а (А; с, d) по определе-
нию проходит через точку А и параллельна плоскости а (В; с, d),
чем устанавливается существование. Единственность вытекает из
того, что всякая плоскость а, проходящая через точку А и парал-
лельная плоскости а (В; с, d), имеет (с, d) своим базисом и, следо-
вательно, совпадает с плоскостью а (Л; с, d).
--------------------------©.........................-
Доказываемые в этом пункте теоремы устанавливают, что может
представлять собой пересечение двух плоскостей в зави-
симости от их взаимного расположения.
10.4. Теорема. Если две плоскости не параллельны, то их
пересечение представляет собой прямую.
Доказательство. Пусть плоскости оо — а (Л; а, Ь)
и а2 — а (В; с, d) не параллельны. Тогда базис плоскости а2 не
является базисом плоскости а,, т. е. хотя бы один из векторов с, d
не является линейной комбинацией векторов а, Ь. Пусть, например,
с не является линейной комбинацией векторов а, Ь, т. е. векторы
а, Ь, с линейно независимы.
По теореме 3.6 АВ = та 4- nb 4- kc. Обозначим через М точку,
для которой AM — та + nb- Тогда М € ах. Далее, так как ВМ =
— AM — АВ — —kc, то М С а2. Итак, плоскости cq и а2 имеют
общую точку М.
Далее, так как четыре вектора a, b, с, d линейно зависимы (ак-
сиома 3.2), то по теореме 2.9 вектор d линейно выражается через
остальные: d = ра 4- qb 4- гс. Обозначим вектор d — гс через h.
Этот вектор отличен от нуля (в противном случае было бы d = гс).
Так как h = d —- гс = ра 4- qb, то h || ах и h |) а2.
Рассмотрим прямую I — I (М, h). Она параллельна плоскости аг
(так как h || aj и имеет с ней общую точку М. Следовательно,
1 с «1 (следствие 9.4). Точно так же I с а2. Таким образом,
I <= ах П аг-
Если бы плоскости otj и а2 имели еще хотя бы одну общую точку
(не принадлежащую прямой /), то они совпали бы, что невозможно
(так как cq^ccj). Следовательно, аг П “2 = I.
79
10.5. Теорема. Если две плоскости параллельны, то они либо
совпадают, либо их пересечение пусто.
Доказательство. Пусть || а2. Могут представить-
ся следующие два случая: «х П а2 = 0 и Oj П а2 ^=0. Нам нуж-
но доказать, что во втором из этих случаев плоскости ах и а2 сов-
падают.
Итак, пусть «□. П «2 и пусть С — какая-либо общая точка
плоскостей и а2, а (а, Ь) — общий базис этих плоскостей. Тогда
плоскость аъ содержащая точку С и имеющая базис (а, Ь), записы-
вается в виде otj = а (С; а, Ь). Точно так же а2 = а (С; а, Ъ), и по-
тому = а2.
10.6. Замечание.' Для каждой из теорем 10.4 и 10.5 спра-
ведлива и соответствующая обратная теорема, т. е. каждая из этих
теорем содержит необходимое и достаточное усло-
вия:
(Упл. а1( а2) (а!$,а2)<=> (at f| а2 есть прямая); (1)
(Упл. aj, а2) (ах || а2)<=* ((оч = а2) V («х ("I а2 = 0)). (2)
В самом деле, если П а2 есть прямая, то плоскости ах и а2
не совпадают, причем их пересечение непусто; следовательно, по
теореме 10.5 ax'ft.aj, чем доказана теорема, обратная 10.4.
Далее, если (ax = а2) V (ах f| а2 — 0), то пересечение
ах П а2 не есть прямая, и потому по теореме 10.4 «х II а2, чем
доказана теорема, обратная 10.5.
'г 10.7. Замечание. Схему рассуждения, позволившую дока-
зать теоремы (1) и (2), можно описать следующим образом.
Пусть доказаны две теоремы:
(Ух)Л (х)=>В(х), (3)
(Ух)”]Л (х)=>С(х), , (4)
причем предикаты В (х) и С (х) взаимно исключают
друг друга, т. е. истинно высказывание
-|(Зх)(В(х)Л С(х)\, . (5)
тогда для обеих теорем (3) и (4) справедливы обратные.
В самом деле, возьмем некоторое х = х0 (из множества, на
котором рассматриваются предикаты) и предположим, что выска-
зывание В (х0) истинно. Если бы высказывание А (х0) было лож-
ным, то было бы истинным высказывание ~| А (х0), и потому в силу
теоремы (4) было бы истинным и высказывание С (х0), а это проти-
воречит тому, что предикаты В (х) и С (х) взаимно исключают друг
друга (см. (5)). Итак, если В (х0) истинно, то должно быть истин-
ным и А (х0), т. е. теорема, обратная (3), справедлива.
Аналогично устанавливается сйраведливость теоремы, обратной
теореме (4). у
80
10.8. Задача. Доказать, что если прямая параллельна каждой
из двух непараллельных плоскостей, то она параллельна линии их
пересечения (рис. 42).
Решение. Пусть две непараллельные плоскости ах и а2
пересекаются по прямой I = I (А, а) и пусть прямая Г = I (В, Ь)
параллельна каждой из плоскостей ах, а2. Нужно доказать, что
V || I. Допустим противное, т. е. допустим, что векторы а и b ли-
нейно независимы. Так как векторы а, b параллельны каждой из
плоскостей ах и а2, то они составляют общий базис плоскостей
ах и а2, откуда следует вопреки условию, что || а2. Полученное
противоречие доказывает, что Г || I.
▼ 10.9. Задача. Доказать следующее утверждение:
(Vnp. /х, /2) (/1'||ч/2)=> (3! пл. ах, а2) ((ах || а2) Д
Л (4 с “1) Л (4 с а2)); (6)
Решение. Пусть /х = I (А, а), 12 — 1 (В, Ь). Так как по
условию прямые /х и /2 не параллельны, то векторы а, b линейно
независимы. Нам нужно найти такие параллельные между собой
плоскости ах и а2, что прямая Zx содержится в одной из этих пло-
скостей, а прямая 12 — в другой (рис. 43).
Пусть плоскости ах, а2 — искомые. Так как с ах, то Zx || ах,
и потому а || ар Следовательно, справедливо также соотношение
а || а2. Аналогично, так как Z2 cz а2, то b || а2 и b || ах. Таким обра-
зом, линейно независимые векторы а, b параллельны плоскости ах
и потому составляют ее базис (а также базис плоскости а2). Так как,
кроме того, А € ах (поскольку А € Zx и Zx с ах), то ах должна
совпадать с плоскостью а (А; а, Ь). Аналогично плоскость а2 долж-
на совпадать с, а (В; а, Ь).
Остается проверить, что плоскости
= а (В; а, Ь) являются искомыми. В
параллельны (так как имеют общий
базис). Кроме того, Zxc ax (посколь-
ку A € ax и a || ax) и l2 c: a2. Этим и
доказана справедливость утвержде-
ния (6).
Заметим, что если прямые Zx и Z2
пересекающиеся, то плоскости ах и
а2 совпадают (см. теорему 9.5).
Если же Zx и Z2 скрещивающиеся пря-
мые, то (поскольку эти прямые не
== а (Д; а, &), а2 =
самом деле, эти плоскости
Рис. 42
4 Заказ 4860
84
,——---------j лежат в одной плоскости) плоскости и
а2 различны (рис. 43). ▼
/ /
Г ’7 Задачи
/ '''“'Х, / 302*. Докажите, что если плоскости
/ а (Л; а, Ь) и а (М; р, q) параллельны,
7Кг___________7 то существуют числа k, I, т, п, для
Рис. 43 которых а — kp + lq, b = тр +
nq. Справедлива ли обратная теоре-
ма?
303. Векторы а, b составляют базис плоскости а, векторы с, d
составляют базис плоскости 0. Докажите, что если каждый
из векторов а, b представляется в виде линейной комбина-
ции векторов с, d, то а || 0.
304. Известно, что а (Л; а,"ft)|| а(В; р, q), а (С; с, d) || а (D; г, s);
с = 2р — q,d — р — 2q. Докажите, что а (Л; а, Ь) || а (D; г, s).
,305. Докажите, что если а (Л; а, Ь) || а (В; с, d) и а (С; с, 3) ||
|| а (D; р, q), то плоскости а (2И; а, Ь) и а (Л4; р, q) совпа-
дают.
В задачах 306—311 используются обозначения, введенные на
с. 41 (см. рис. 15).
800. Какие из следующих плоскостей параллельны:
(ЛВС), (ЛСО), (ЛхВ^х), (AlBlDJ, (ABBJ?
807. Определите взаимное расположение плоскостей:
а) (ЛВС) и (BjCiDJ; б) (ЛЛ^) и (ЛВВД; в) (ЛВС) и (CCjD);
г) (ЛВСХ) и (CCXD).
308. Точки М, N и Р — середины отрезков [Л1В1], [BjCj] и
[BBt], Докажите, что плоскости (ABCJ и (MNP) параллель-
ны.
309. Докажите, что линия пересечения плоскостей (ЛВгСХ и
(ЛОХВ) параллельна прямой (Afl).
310. Докажите, что плоскости (AxC^D) и (ABjC) параллельны.
311. Докажите, что существует единственная плоскость, содер-
жащая прямую (ADJ и параллельная прямой (CrD).
312. Точки Л, В, С, М, N, Q связаны соотношениями:
СЛ= 3aJ-b — c\ QB =4а+ 2ft; QC== За-f- 4ft;
QM=—a+2b\ QN=3b-\-c,
где a, ft, c — линейно независимые векторы. Как располо-
жены: а) плоскости (QMA) и (BCN); б) плоскости (ЛВС) и
(QMN); в) плоскости (QAB) и (MNC)?
82
313*. Векторы а, b, с линейно независимы, А\
АВ = 2а — b + с. Что представля- / \
ет собой пересечение: а) плоскостей / \------7
а (Д; а 4- Ь, а — с) и а(Д;д-|- \ / /
+ с, 2а + Ь — с); б) плоскостей /\ / А е
а (Д; b + с, а + Ь) и а (Д; а — Ь, / /
ЗЬ + с); в) плоскостей а (Д; а — / \ /ь /\
— 2Ь, Зс + а) и а (В; 2Ь + Зс, ЗаД- -------у—' /
+ Зс — 45)? \ /
314. Точки Д, В, С, М, N, Р заданы \/
своими координатами в системе (0; рис 44
^1» ^2> ®з)'
Д (5; 4; 1), В (3; 4; 2), С (2; 0; 5), М (2; 4; —1),
N (1; 0; 2), Р (—1; 0; 3).
Как расположены: а) плоскости (CNP) и (АВМ)\ б) плоско-
сти (АСР) и (BMN); в) плоскости (ВСР) и (Д2ИМ); г) пло-
скости (АРМ) и (ВСМ)?
315. Плоскость 7 пересекается с плоскостью а по прямой а и
с плоскостью 0 по прямой Ь. Докажите, что если а || 0, то
а || b (рис. 44).
316. Даны две непараллельные прямые а и Ь. Докажите, что если
плоскость а параллельна каждой из прямых а, b и плос-
кость 0 параллельна каждой из прямых а, Ь, то плоскости а
. и 0 параллельны.
317*. Плоскости а и 0 не имеют общих точек. В плоскости а взята
прямая а, в плоскости 0 — прямые b, с, d, попарно не па-
раллельные между собой. Можно ли из прямых а, Ь, с и d
выбрать пару скрещивающихся прямых? Можно ли выбрать
две пары? четыре пары?
318. Что представляет собой объединение всех прямых, проходя-
щих через данную точку М и параллельных данной плоско-
сти?
319. Плоскости а и 0 не имеют общих точек. Взяты точки Д,
С € а; В, D € 0. Докажите, что если (АВ) || (CD), то
d (А, В) = d (С, D) (рис. 45).
Верно ли обратное?
320. Даны две параллельные плоскости а и 0. Две прямые а, Ь,
имеющие общую точку О, пересекают плоскость а соответ-
ственно в точках Д и В, а плоскость 0 в точках С и D
(рис. 46).
Докажите, что (ДВ) || (CD).
321. Даны три различные параллельные между собой плоскости
а, 0, у. Прямая а пересекает эти плоскости соответственно
4*
83
в течках А, В, С, а прямая b —в
точках Ль Blt Си Докажите, что
d(A, В) d(Aj, BJ
d(A, С) d(Alt CJ
322. Докажите, что если плоскость 0
проходит через прямую а, парал-
лельную плоскости а, и пересекает
а по прямой Ь, то а || Ь (рис. 47).
323. Определите взаимное расположение
каждых двух из плоскостей а (/<;
а, b), a (S; а — b, ~Ь), а (С; а, с), ес-
ли векторы а, Ь, с линейно независи-
мы, CS =а + b —си KS = (а 4-Ь).
Рис. 46
326.
Какие из следующих высказываний
истинны?
а) Если плоскости параллельны, то
они не имеют общих точек.
б) Если плоскости не имеют общих
’ точек, то они параллельны.
в) Если плоскости имеют общую точ-
ку, то они не параллельны.
г) Если плоскости не параллельны,
то они имеют общую точку.
д) Существуют две плоскости, име-
ющие только одну общую точку.
Докажите, что если а (Л; а, Ь) ||
|] а (В; р, q), то плоскости а (Л; а,
Ь) и а (Л; р, q) совпадают.
Прямая I (К', р) параллельна каж-
дой из плоскостей а и 0, причем
плоскости а и 0 не параллельны и
имеют общую точку С. Докажите,
что а П 0 = I (С; р).
Докажите, что если плоскости а, 0,
у, 6 удовлетворяют условиям а || 6,
0 II Т и у || б, то а || 0.
Даны две скрещивающиеся прямые
а и Ь. Докажите, что существует
единственная плоскость, содержа-
щая прямую а и параллельная
прямой Ь.
Верно ли, что если для плоскостей
84
a, p, 7, 6 какие-либо три из соотно-
шений
«IIP, a||Y, PUT, a||6, Pl|6, у || S
справедливы, то справедливы и ос-
тальные три? Верно ли, что из спра-
ведливости .четырех соотношений
вытекает справедливость оставших-
ся двух?
330. Даны три прямые, имеющие общую
точку А, причем ни одна из этих
прямых не пересекается с плоско-
стью а; докажите, что все три пря-
мые лежат в одной плоскости.
331. При обозначениях задачи 195 (рис. Рис. 48
22) докажите, что линия пересече-
ния плоскостей (АВСх) и (АгВгС) параллельна прямой (АВ).
332*. Три плоскости а, р, у, никакие две из которых непарал-
лельны, обладают теги: свойством, что a f| Р П у = 0
(рис. 48). Докажите, что прямые. a-Q р, a Q у и р f) у па-
раллельны.
В задачах 333—337 сформулированы по две теоремы.
Убедитесь, что эти теоремы справедливы, и сделайте на ос-
новании замечания 10.7 заключение о справедливости об-
ратных теорем.
333*. Рассмотрим уравнение ах2 + Ьх + с — 0, где а =Н=0.
а) Если дискриминант D = Ь2 — 4ас неотрицателен, то су-
ществует действительное число, являющееся корнем
уравнения ах2 + Ьх + с = 0.
б) Если дискриминант D отрицателен, то не существует дей-
ствительного числа, являющегося корнем уравнения
ах2 + Ьх + с = 0.
334*. Рассмотрим систему уравнений
(ap; + b±y + (\ = 0,
(а2х + &2у + с2 = 0.
(7)
а) Если число А = ахЬ2 — a2b± отлично от нуля, то система
(7) имеет единственное решение.
б) Если А = 0, то система (7) либо не имеет решения, либо
имеет бесконечно много решений.
’ 335*. Даны две плоскости а, р.
а) Если а^р, то существует вектор, который параллелен
плоскости а, но не параллелен плоскости р.
б) Если а || р, то любой вектор, параллельный плоскости а,
параллелен и плоскости р.
336*. а) Если хотя бы одно из пересечений (АВ) Q (CD), (AD) f]
П (ВС), (AC) f] (BD) непусто, то точки А, В, C,D лежат
в одной плоскости.
85
б) Если пересечения (ЛВ)П(СО), (AD) f) (5Q, (ЛС) fl (BD)
пусты, то точки А, В, С, D не лежат в одной плоскости.
837*. а) Если базисные векторы прямых lT tn, п линейно зависимы,
то существует плоскость а, которой все три прямые па-
раллельны.
б) Если базисные векторы прямых I, т, п линейно независи-
мы, то не существует плоскости, которой все три прямые
были бы параллельны.
§ 11. ОРТОГОНАЛЬНОСТЬ ПРЯМЫХ
И ПЛОСКОСТЕЙ
11.1. Определение. Ненулевой вектор л называется нор-
малью к плоскости а, если он ортогонален любому вектору, парал-
лельно^ плоскости а:
(V пл. а, л Ф 6) (л — нормаль к пл. а) (Ча, где а || а) (л ± а).
def
11.2. Теорема. Пусть (р, q) — базис плоскости а. Для того
чтобы вектор п был нормалью к плоскости а, необходимо и
достаточно, чтобы он был ортогонален каждому из векторов р, q
(рис. 49).
Доказательство. Пусть л — нормаль к плоско-
сти -а. Так как р || а и q || а (см. определение 8.9), то вектор л орто-
гонален каждому из векторов р, q.
Обратно, пусть вектор л =#0 ортогонален каждому из векторов
р, q, т. е. пр — 0, nq = 0. Если г — произвольный вектор, парал-
лельный плоскости а, т. е. г = kp + lq (см. определение 8,9), то
nr = k (пр) + I (nq) — 0. Таким образом, л ортогонален каждому
вектору, параллельному плоскости а, т. е. л — нормаль к плоско-
сти а.
11.3. Следствие. Для любой плоскости существует вектор,
являющийся нормалью к эщой плоскости.
_ В самом деле, пусть (р, q) — ортого-
; нальный базис плоскости а (следствие 8.6)
у------------, ил — вектор, дополняющий р, q до орто-
/ й/ тонального базиса. В силу теоремы 11.2
/ п — нормаль к а.
/ Р Ц.4. Теорема. Любые два вектора,
i' являющиеся нормалями к плоскости а, ли-
Рис. 49 нейно зависимы.
86
Доказательство. Пусть nt — нормали к пло-
скости а. Выберем ортогональный базис (р, q) плоскости а. Так как
векторы р, q, пх линейно независимы, то n2 = kp + lq + mnv
Умножая это равенство скалярно на р, получаем 0 — к (рр), от-
куда k = 0. Аналогично (умножая скалярно на q) находим I — 0.
Таким образом, п2 = тпг.
11.5. Определение. Прямые и 12 называются ортогональ-
ными X Z2), если для любых точек А, В € Zx и Р, Q € Z2 спра-
ведливо соотношение АВ • PQ = 0.
11.6. Теорема. Две прямые в том и только в том случае ор-
тогональны, если ортогональны их базисные векторы.
Доказательство. Пусть ах и Oj — базисные век-
торы прямых Zx и Z2.
Допустим, что Zx X Z2. Возьмем произвольные точки А € 1Х,
Р £ 1г, и пусть В, Q — такие точки, что АВ = ах, PQ =* аг. Тогда
В С Zx, Q С Z2. Следовательно (в силу определения 11.5),
АВ • PQ — 0, т. е. ага2 = 0. Иначе говоря, аг X а2.
Обратно, пусть аг X а2. Для любых точек А, В £ llt Р, Q С Z2
мы имеем: АВ = palt PQ = qa2, где р, q— некоторые числа. Следо-
вательно, АВ • PQ — (раг) • (<?а2) = pq (alta2) = 0. Так как это
верно для любых точек А, В € Zx и Р, Q € Z2, то Zx X Z2.
11.7. Определение. Прямая Z называется ортогональной
плоскости а, если для любых точек А, В I и Р, Q € а справедли-
во соотношение АВ • PQ = 0 (рис. 50).
11.8. Теорема. Прямая I в том и только в том случае орто-
гональна плоскости а, если базисный вектор этой прямой является
нормалью к плоскости а.
Доказательство. Пусть а — базисный вектор пря-
мой Z, а (р, q) — базис плоскости а. Допустим, что Z X а. Возьмем
произвольные точки А С Z, М С а, и пусть
В, Р, Q— такие точки, что АВ = а,
MP = р, MQ = q. Тогда В £ I; Р, QZ а.
Следовательно (в силу определения 11.7),
АВ • МР — 0 и АВ MQ = 0, т. е. ар =
= 0, aq = 0. Но тогда по теореме 11.2 а—
нормаль к плоскости а.
Обратно, пусть базисный вектор а пря-
мой Z является нормалью к а. Тогда ар —
— 0, aq = 0. Для любых точек А, В € I; рИс. 50
87
P, Q € а, мы имеем: АВ = ka, PQ — тр + nq, где k, т, п — не-
которые числа. Следовательно, АВ • PQ = ka (тр + nq) =
— km (ар) + kn (aq) = 0. Так как это верно для любых точек А,
В ( I; Р, Q £ а, то I J. а.
В этом пункте будут рассмотрены четыре следствия из доказан-
ных в предыдущем пункте теорем 11.6, 11.8.
11.9. Следствие. Если прямая I ортогональна плоскости а,
то она ортогональна любой прямой т с а.
В самом деле, пусть а, b — базисные векторы прямых I, т.
Тогда а — нормаль к плоскости а (теорема 11.8) и b || а (определе-
ние 9.2). В силу определения 11.1 имеем: а ± Ь, и потому / ± т
(теорема 11.6).
11.10. С л еде т в и е. Если прямая I ортогональна каждой из
двух непараллельных между собой прямых тг, т2, содержащихся в
плоскости а, то I ± а (рис. 51).
В самом деле, пусть a, blt b2 — базисные векторы прямых I,
mlt т2.. Тогда векторы Ь± и Ь2 линейно независимы (так как тг -И"
41 т2) и параллельны а (см. следствие 9.4), т. е. (Ьи Ь2)— базис пло-
скости а. Далее, соотношения I ± /пх; I ± т2 означают, что а X &1(
а2 ± Ь2 (теорема 11.6.). Следовательно,
а — нормаль к плоскости а (теорема 11.2)
и потому I ± а (теорема 11.8).
11.11. Следствие. Две прямые, ор-
тогональные одной плоскости, параллель-
ны (рис. 52).
Действительно, пусть ± а, /2 1 а и
пусть ах, а2 — базисные векторы прямых
llt 12. Тогда каждый из векторов alt а2
является нормалью к плоскости а (теоре-
ма 11.8), и потому по теореме 11.4 векто-
ры ау и й2 линейно зависимы. Но это озна-
чает, что /х || 12.
11.12. Следствие. Через каждую точ-
ку А проходит единственная прямая, ор-
тогональная данной плоскости а.
Действительно, пусть п — нормаль к
плоскости а. Тогда прямая I (А, и) прохо-
дит через точку А и (по теореме 11.8) орто-
88
гона льна плоскости а. Этим доказано существование. Единствен-
ность вытекает из следствия 11.11 (так как две параллельные пря-
мые, имеющие общую точку А, совпадают).
---------------------------О----------------------------
Пусть а — произвольная плоскость, А — точка. В силу след-
ствия 11.12 через точку А проходит единственная прямая /, ор-
тогональная плоскости а. Прямая I пересекается с а в единствен-
ной точке А* (теорема 9.3). Эта точка А* называется ортого-
нальной проекцией точки А на плоскость а (рис. 53).
11.13. Т е о р е м а. Пусть А*— ортогональная проекция точки А
на плоскость а. Тогда А* — ближайшая к А точка плоскости а,
т. е. d (A, A*)<d (А, В) для любой точки В € а, отличной от А*.
Доказательство. Вектор А А* является нормалью
к плоскости а (или равен 0 при А' € а), а вектор А*В параллелен
а. Следовательно, АА* • А*В = 0 (определение 11.1), и потому
ЛВ2= (ЛЛ*ф- Л*В)2 = ЛЛ*2+ Л*В2 > ЛЛ*2
(поскольку А* Я В, и, значит, Л*В2 > 0). Из полученного нера-
венства ЛВ2 > АА*2 и вытекает, что d (Л, В) > d (Л, Л*).
Доказанная теорема обосновывает’ введение следующего опре-
деления:
11.14. О п р е д е л е н и е. Пусть Л* —
ортогональная проекция точки Л на плос-
кость а; число d (Л, Л*) называется рас-
стоянием от точки А до плоскости а. Это
расстояние обозначается через d (Л, а).
Пусть теперь F—произвольная фигура
на — некоторая плоскость. Ортогональ-
ные проекции всех точек фигуры F на плос-
кость а образуют некоторую фигуру F*cza,
которая называется ортогональной проек-
цией фигуры В на плоскость а. Проекцию
фигуры F на плоскость а будем обозначать
через Пра (F) (рис. 54).
Задачи
338. Сохраним обозначения, введенные
на с. 41 (см. рис. 15).
Векторы а, Ь, с попарно ортого-
нальны.
а) Докажите, что а—нормаль к пло-
скости (ЛЛХО).
б) Докажите, что с—нормаль к пло-
скости (ЛВС).
89
в) Докажите, что если|Ь| = |с|, то b 4- с — нормаль к пло-
скости (AjCD).
г) Докажите, что если |а| = |Ь| = |с|, то а 4- b 4- с—нор-
маль к плоскости (А^ВТУ).
3$9. Дан ортонормированный базис (а, Ь, с).
а) Убедитесь, что 2а — Ъ 4* 6с — нормаль к плоскости
а (А; а 4* 2Ь, За — с).
б) При каком k вектор а — 2b + kc является нормалью к
плоскости а (В; 2а 4- Ь, с — 2Ь)?
в) Найдите нормаль к плоскости а (С; За — с, а + & + с).
340. В прямоугольной системе координат заданы точки
А (3; —1; 0), В (2; 0; —3), С (1; 1; 1), D (0; 4; —3)
и векторы а (8; 4; 1), b (1; 1; 0), с (6; 3; —1). Какой из векто-
ров а, Ь, о является нормалью: а) к плоскости (АВС); б) к
плоскости (А ВО); в) к плоскости (BCD)?
341. Вектор п — нормаль к плоскости а. Докажите, что если
ап = 0, то вектор а параллелен плоскости а.
342. Докажите, что если нормаль к плоскости а параллельна пло-
скости р, то нормаль к плоскости р параллельна а (рис. 55).
343. Вектор а является нормалью к плоскости а и нормалью к
плоскости р. Докажите, что а || р.
344. Векторы а и b являются нормалями соответственно к плоско-
стям аир. Докажите, что если векторы an b линейно зави-
симы, то а || р.
345. Векторы а, b являются нормалями соответственно к плоско-
стям а (М; Ь, с), а (N; а, с). Докажите, что а — нормаль к
плоскости а (Р; а, Ь).
346. Дан ортонормированный базис (а, Ь,
с). Какие из следующих прямых ор-
тогональны:
I (А, 2а — b), I (В, а — 2Ь 4- с),
I (А, а 4- b 4- с), I (С, а 4- 2Ь 4- Зс)?
347. Введем обозначения, указанные
на с. 91, где векторы а, Ь, с об-
разуют ортонормированный базис
(рис. 56).
Какие из следующих высказыва-
ний истинны: а) (ААХ) _L (СО);
90
б) (АВ) 1 (ВД; в) (ЛСХ) 1 (BXD);
г) (ЛРХ) ± (ВД?
348. Даны четыре точки А, В, С, D.
Докажите, что если АВ CD = О,
то прямые (АВ) и (CD) ортогональ-
ны.
349*. Является ли транзитивным отно-
шение ортогональности прямых?
350*. Какие из следующих высказываний
истинны?
a) (Vnp. I, т, п) ((I ± пг) Л (т || рис. 56
|| п))=> (I 1 п);
- б) (V пр. I, пг, п) ((/ ± т) Л (I ± п)) => (пг || п);
в) (V пр. I, т\ пл. а) ((I || а) Д (I ± т)) => (пг || а);
г) (3 пр. I, т; пл. а) ((/1| а) Д (I ± пг) Л (т || а));
д) (3 пр. I, т, п) ((I ± т) Д (I ± п) Д (пг ± п)).
351. Даны прямая I и точка А, содержащиеся в плоскости а.
Докажите, что существует единственная прямая таа,
содержащая точку А и ортогональная прямой I.
352. Каждая из прямых (АВ), (ВС), (CD) ортогональна прямой I.
Докажите, что прямые (АВ), (ВС), (CD) расположены в од-
ной плоскости.
353. Точки А, В, С, D удовлетворяют условиям d (А, В)= d (А, С),
АВ • AD — АС • AD. Докажите, что (ВС) ± (AD).
354. а) Даны четыре (не обязательно различные) точки А, В, С, О.
Докажите, что если АО • ВС — 0 и ВО- • АС = 0, то
СО • АВ = 0.
б) Докажите, что в любой плоскости высоты произвольно-
го треугольника (или их продолжения) пересекаются
в одной точке.
в) Даны четыре различные точки А, В, С, О. Докажите, что
если (АО) ± (ВС) и (ВО) 1 (ЛС), то (СО) 1 (АВ).
355. Дан ортонормированный базис (а, Ь, с). Какая из прямых
I (А, а — 2b), I (В, а + & — с), I (С, 2а + Ь + Зс) ортого-
нальна плоскости а (Р; а + с, b + с)? плоскости a (Q; а +
+ b — с, ЗЬ — с)?
356. При обозначениях задачи 347 укажите, какие из следующих
высказываний истинны: а) (АВ) ± (A^D^; б) (BDt) ±
± (ЛхСхР); в) (ЛхВх) 1 (BCxD); г) (BD) 1 (ЛЛХС). .
357. Даны плоскость а и прямые а, Ь., Докажите, что если а ± a
и b || а, то а ± Ь.
358. Докажите следующую теорему:
(V пл. а, р; пр. I) ((а || р) Д (I 1 а))=> (/ ± Р).
359. Даны вектор п у=0 и точка Л. Докажите, что множество
91
а = {М : AM - п — 0}
представляет собой пло-
скость и вектор п является
нормалью к этой плоскости
(рис. 57).
Плоскости а и р не парал-
лельны. Существует ли пря-
мая, ортогональная каждой
из плоскостей а, р?
Справедлива ли следующая
теорема:
(V пл. а, Р; пр. Z, пг, где
I 1 а, т ± Р) (а || Р) <=>
<=*(/ || т)?
Плоскости аир пересека-
ются по прямой Z. Прямые
р cz а и q с р ортогональ-
ны Z и имеют общую точ-
ку А.
а) Докажите, что плоскость,
содержащая прямые р и q,
ортогональна прямой Z.
б) Докажите, что для любых
точек Р €р, Q € q прямая
(PQ) ортогональна Z.
Докажите, что две плоскости, ортогональные одной и той же
прямой, параллельны (рис. 58).
Существуют ли такие две плоскости а, р, что для любых то-
чек А, В € а и Р,
АВ . PQ = 0?
Какие из следующих
а) (V пл. а, Р; пр. Z,
362.
Рис. 58
363.
364.
365*.
360.
361.
Q $ р справедливо соотношение
высказываний истинны?
т) ((/ ± Р) Л (I II а) Л (ffl с а)) =>-
б) (V пл. а, Р; пр. Z, т) ((т 1 ₽) Л (т || а) Л (Z 1 Р)) =J-
в) (V пл. а, р, у; пр. Z) ((/ 1 р) Л (Z II а) Л (Z II ?)) =>
г) (V пл. а, Р; пр. I, т) ((т ± Р) Л (tn || а) Л (I || а)) =>
Докажите следующую теорему:
366*.
(V пл. а, Р; пр. т, где т ± а) (т || Р) «=> (3 пр. Z с= Р) (Z ± а).
367. При обозначениях задачи 347 укажите (в каждом из следую-
щих случаев), будет ли прямая, ортогональная первой пло-
скости, параллельна второй плоскости:
а) (АД1Д) и (В^О)-, б) (AA1C)h(BB1D)-,b) (AB1C)b(BC1D1).
92
368- а) Даны пять точек А,
В, С, Оъ О2, причем точ-
ки Л, В, С не лежат на од-
ной прямой. Докажите,
что если Л0х • ВС = О,
А02-ВС = 0, ВОгАС=0,
В02 • ЛС=0, то (ОД)1
1 (АВС).
б) Даны три точки А, В,
С, не лежащие на одной
прямой. Что представ-
ляет собой множество
{О : (АО • ВС = 0) Л
Д(£Ю-ЛС = 0)}?
369. Докажите, что если плоскость а содержит прямую, ортого-
нальную плоскости Р, то и плоскость р содержит прямую,
ортогональную плоскости а.
370. Плоскости аир пересекаются по прямой а. Докажите, что
если плоскость у содержит прямую I, которая ортогональна
плоскости а, и прямую т, которая ортогональна плоскости
Р, то а ± у (рис. 59). .
371. Пусть А $ а. Докажите, что точка Л* С а в том и только в
том случае является ортогональной проекцией точки А. на
*' >
плоскость а, если А А* — нормаль к плоскости а.
372. Точка В — проекция точки А на плоскость а. Прямая I cz
сг а не проходит через точку В. Взята точка С £ I. Докажи-
те, что прямая (АС) в том и только в том случае ортогональ-
на прямой I, если (ВС) ± I (рис. 60).
373. Плоскости аир параллельны. Докажите, что для любых
точек А, В С а, С € р справедливы равенства
d (Л, р) = d (В, Р) = d (С, а).
374. Точки А, В, С, S удовлетворяют условиям АВ = р, AC— q,
ЛВ —г, причем р2 = q2 — г2 = 1, рq= рг = qr = -^.
а) При каких k и I вектор г — (kp 4- lq) ортогонален пло-
скости (АВС)?
б) Определите расстояние от точки S до плоскости (АВС).
375. Известно, что d (A, S) = a, d (В, S) = b, d (С, S) = с,
d (Л, В) = р, d (Л, С) = q, d (В, С) = г. Определите рас-
стояние от точки S до плоскости (АВС).
376. Докажите, что если прямая I не ортогональна плоскости а,
то Пра (I) есть прямая (рис. 61).
93
Рис. 60
877. Докажите, что если нормаль п к плоскости а параллельна
плоскости р, то Пра (₽) = а п Р (рис. 55).
878. Прямая I не ортогональна.плоскости а. Прямая 4 —орто-
гональная- проекция прямой I на плоскость а. Докажите,
что (рис. 62):
а) если m с аи m 1 /, то m 1 4;
б) если п cz а и п ± llt то п ± I.
879. Существуют ли такие плоскости а, р, у, что ортогональная
проекция любой из них на каждую из двух других представ-
ляет собой прямую?
886. Ортогональные проекции прямых I и т на плоскость а сов-
падают. Докажите, что прямые I и т расположены в одной
плоскости.
881. Векторы а, Ь, с образуют ортонормированный базис.
а) Докажите, что b — нормаль к плоскости а (О; а, с).
б) При каких k, I вектор а + kb 4- 1с является нормалью к
плоскости а (С; За — Ъ, 2а + с)?
в) Докажите, что если р = а + b — с, q = 2а — b + с,
г — b + с, то р — нормаль к плоскости а (A; q, f}\ далее,
q — нормаль к плоскости а (В; р, г); наконец, г — нор-
маль к плоскости а (С; р, q).
882. Векторы р, q, г заданы своими координатами в ортонормиро-
ванием базисе:
"р (2; —-1; 3), q -1; -1), 7 (4; 5; -1).^
Докажите, что р — нормаль к плоскости a (A; q, г) и q —
нормаль к плоскости а (В; р, г).
883. Докажите, что если плоскости аир параллельны и п — нор-
маль к плоскости а, то п — нормаль к плоскости р.
884. Векторы а и Ь являются нормалями соответственно к плоско-
стям, а и р. Докажите, что если а || р, то векторы а и Ь ли-
нейно зависимы.
94
885. Векторы а, b, с, d заданы в ортонормированием базисе:
а (3; —1; 2), b (1; 1; —1), с (—1; 5; 4), d (5; 1; 0). Укажите,
какие из прямых I (A, a), I (A, b), I (В, с), I (В, d) ортого-
нальны друг другу.
388. При обозначениях задачи 195 (рис. 22) выполнены условия
]а] — |Ь| = |а — &| =» 1 и а ± с, Ъ ± с. Определите |с|,
зная, что (АХВ) ± (АСХ).
887. Существуют ли три попарно ортогональные прямые? четыре
попарно ортогональные прямые?
888. Вектор п является нормалью к плоскости а. Докажите, что
прямая I (А, п) ортогональна, любой прямой /пса.
889. Векторы а, b, с, d, е заданы в ортонормированием базисе:
а (3; 1; —1), b (22; 0; —33), с (—3; 7; —2), d (5; 9; 24), в (0;
8;-3).
Какие из следующих высказываний истинны:
a) I (A, d) la (Р; с, ~е), б) I (В, b) 1 а (М; b, d),
в) I (С, а) ± а (Q; с, d)t
890. Даны плоскость а и прямые а, Ь. Докажите, что если ala
и Ь || а, то. b ± а.
891. Каждая нз прямых (АВ), (АС) ортогональна плоскости а.
Докажите, что ВС — нормаль к плоскости а.
892. Докажите следующие теоремы: '
(V пр. /, т; пл. а) ((/ ± а) Д (т 1 а)) => (I || /п);
(V пр. I, т) ((3 пл.а) ((/ ± а) Л (т ± а))) => (/1| /п).
Справедливы ли обратные теоремы?
893. Прямые I и т — скрещивающиеся. Что представляет собой
пересечение плоскостей аир, если I ± а, tn ± р?
894. Докажите, что через любую точку А проходит единственная
плоскость, ортогональная данной прямой I.
395. Докажите, что если плоскости а, р и прямые /, т удовлетво-
ряют условиям а || р, I ± а, т ± р, то 11| т.
396. При обозначениях задачи 195 (рис. 22) докажите, что если
прямая, ортогональная плоскости (АВС), параллельна каж-
дой из плоскостей (ААХВ), (ААгС), (ВВ^С), то каждая из пря- .
мых (ААХ), (BBt), (CCj ортогональна плоскости (АВС).
397. Докажите, что если А С а, то Пра (А) = А.
398. При обозначениях задачи 347 определите:
а) расстояние от точки А до плоскости (ВВХС);
б) расстояние от точки А до плоскости (ВВ^Р)\
в) расстояние от точки А до плоскости (BAXD).
399. Докажите, что если прямая I ортогональна плоскости а, то
ПРа (I) состоит из единственной точки.
400*. Докажите, что если нормаль п к плоскости а не параллельна
плоскости р, то Пра (Р) = а.
’5
ГЛАВА
ВЫПУКЛЫЕ
МНОГОГРАННИКИ
§ 12. УРАВНЕНИЕ ПЛОСКОСТИ
* В КООРДИНАТАХ
----------:-------------О-------------------------
12.4. Теорема. Пусть А—произвольная точка и п— от-
личный от О вектор. Тогда множество Р — {М : п • AM = 0}
есть плоскость, проходящая через точку А и имеющая вектор п
своей нормалью (рис. 57).
Доказательство. Выберем векторы а =/= 0 и b =/= 0,
составляющие с вектором п ортогональный базис. Докажем, что
множество Р совпадает с плоскостью а (4; а, Ь). Действительно,
пусть М С Р, т. е. 5г • AM = 0. Разложим вектор AM по базису
(п, а, Ь):
AM = хп 4- ya + zb.
Умножив это равенство скалярно на п, получим х = 0. Следова-
тельно, AM = у а + zb, а это и означает, что М С а (4; а, Ь).
Обратно, пусть М С а (4; а, Ь), т. е. 4/И = ka + lb. Умножив
скалярно это равенство на и, получаем п • AM = 0, и потому
мер.
Итак, множество Р совпадает с плоскостью а (4; а, Ь). Так как
вектор п ортогонален каждому из векторов а, Ь, составляющих ба-
зис плоскости Р, то п — нормаль к плоскости ^Р (теорема 11.2).
96
12.2. Теорема. Пусть (О, е1г е2, е3) — прямоугольная систе-
ма координат. Всякое уравнение вида
Ах + By 4- Cz + D = О, (1)
в котором хотя бы один из коэффициентов А, В, С отличен от нуля,
определяет в этой системе координат некоторую плоскость, причем
любая плоскость может быть задана таким уравнением.
Доказательство. Пусть, для определенности, Д =/= 0.
Точка Ж с координатами х0 = —j-, у о — 0. го — 0> очевидно, удо-
влетворяет уравнению (1), т. е.
Ах0 4* Ву0 4~ Czq 4* D = 0. (2)
Таким образом, множество Р всех точек, координаты которых удов-
летворяют уравнению (1), непусто. Пусть М (х, у, г) — произволь-
ная точка множества Р. Вычитая равенство (2) из (1), получаем:
ААх — х0) + В(у— Уо)4-С(г —г0) = 0. (3)
— > _
Вектор МаМ имеет координаты х — х0, у — у0, г — г0. Вектор с
координатами А, В, С обозначим через п (заметим, что п #=0,
так как по предположению А =/= 0). Тогда равенство (3) можно пере-
писать в виде п • М0М — 0-. Таким образом, Р совпадает с множе-
ством {М : п • М0М. = 0} и, следовательно, представляет собой
плоскость, проходящую через точку Л1о и имеющую вектор п своей
нормалью.
\ Докажем, что любая плоскость может быть записана уравне-
нием вида (1). Действительно, если а — произвольная плоскость,
Л40 (х0, у0, z0) — какая-либо ее точка, ап — нормаль к этой пло-
скости, то, обозначив координаты вектора п через А, В, С, мы най-
дем: а = {М. : п • М0М = 0}, т. е. а есть множество всех точек,
которые удовлетворяют уравнению (3). Остается обозначить число
— Ах0 — Ву3 — Cz0 через D, и мы получаем уравнение (1).
12.3.. Следствие. Пусть Ах 4- By 4- Cz 4- D = 0 — урав-
нение плоскости а в прямоугольной системе координат (О, eif е2,
е3). Тогда вектор п (А; В; С) является нормалью к плоскости а.
---------------------------Ф-----------------------------
12.4. Теорема. Пусть Ах + By + Cz + D = 0 — уравнение
плоскости а в прямоугольной системе координат. Через п обозна-
чим вектор с координатами А, В, С. Тогда для-любой точки Л40 (х0;
у0; z0) справедливо равенство
|n| - d(M0, а) = \Ах» + Ву» + Czt + D\. (4)
97
Шх.и.гл Доказательвтво. Пусть
’ J——^а7 (-*11 УГ> «О —ортогональная проекция
/ точки А40 на плоскость» (рис. 63). Тогда
/Ч, / М0М* «= kn (теорема 11.4). Так как М* (
/ М*(Ч>й>?у £ а, то Axi + Byt + Czt + D “ 0, и, ела-
/ / довательно,
/ Ах0 + Вуй + Cz0 + D = Ах0 + Ву9 +
+ Cz0 + D — (Axt + Byi + Czi + D) ™
Рис. 63 - Л (x0 — x^ + В (y0 — yx) + C —
— Zi) = n • M*M0 (5)
(поскольку вектор n имеет координаты А, В, С, а вектор М*М9
имеет координаты х0 — хь у0 — у4, z0 — z^. Заметим, что мы
здесь пользуемся теоремой 4.11, в связи с чем систему координат
следует предполагать прямоугольной.
Из соотношения M*M0=*kn получаем d (MQ,М*) “ |Л|Х
X | п|, и потому \п А4*Л10|= \п • kn\ • |п|2 =|и| • d (А4»,
М*). Следовательно, в силу (5)
| Ах0 + Ву0 + Cz0 + D] = | п • М*М01 = | п| • d (М0М*);
Для доказательства соотношения (4) остается заметить, что d (Mt,
М*) — d (М.а, а) (см. определение 11.14).
12.5. Задача. В прямоугольной системе координат плоскость
«1 задана уравнением 2х + 2у + z — 12 = 0, а плоскость а, —
уравнением 7х — 4у + 4г — 27 = 0. Доказать, что точка М9 (8{
1; —2) равноудалена от этих плоскостей.
Решение. Обозначим через nt вектор с координатами (2;
2; 1), а через п2 —вектор с координатами (7; —4; 4). Тогда |nt|.
=/22 + 22 + I2 = 3, | и2| = /72 + (—4)2 + 42 = 9. В силу пре-
дыдущей теоремы имеем:
\ni\ • d (MQ, cq) = |2 • 3 + 2 • 1 + 1 • (—2) — 12|, ,
|п2| • d(M0,cc2) = |7 • 3 —4 • 1 + 4 • (—2)-27|,
т. е. 3 • d (Af0, ai) = 6; 9 • d (MQ, а2) = 18. Таким образом,
d (MQ, at) == 2, d (A40, a2) = 2.
▼ 12.6. Замечание. Теорема 12.2 сохраняет силу в любой
(не обязательно прямоугольной) системе координат, т. е. плоскость
задается уравнением первой степени и любое уравнение первой
степени (у которого не все коэффициенты при переменных равны ну-
лю) определяет плоскость. Теоремы же 12.3 и 12.4 существенно
относятся к прямоугольной системе координат. Факты, выража-
емые этими теоремами, в системе координат, не являющейся прямо-
угольной, записываются более сложными формулами. ▼
98
Задачи
401. Векторы а, Ь, с образуют ортогональный базис. Что пред-
ставляет собой пересечение
{М : а • AM = 0} Q {Л4 : Ь • AM - 0}?
402. Каждый из векторов а, Ь, с ортогонален вектору п (все век-
торы ненулевые). Докажите, что прямые I (А, а), I (4, Ь),
I (4, с) расположены в одной плоскости.
403. Какому условию должны удовлетворять ненулевые векторн
п2, чтобы плоскости {Л4 : /ц • AM = 0} и {Л! :
•' >
X ВМ — 0} были параллельны?
404. При каком условии линейно независимые векторы р, q со-
—> ' ' >
ставляют базис плоскости {М : п • AM = 0}?
В задачах 405—413 система координат прямоугольная.
405. Является ли вектор а (—6; 0; 12) нормалью к плоскости я —
— 2г + 7 = 0?
406. Какие из точек Р (—3; 2; 0), Q (3; —2; —1), R (1{ 4; б) при-
надлежат плоскости Зх — у — 2z + 11 « 0?
407. Какие из векторов а (5; 1; 0), b (1; 2; 3), с (—1; 1; 2), d (1в;
5; 3) параллельны плоскости х — 5у + Зг — 7 = 0?
408. При каком k плоскость Зх —Зу + kz —7 = 0 имеет вектор
а (—10; 6; 14) своей нормалью?
409. Плоскость а проходит через точки А (2; —1; 0) и В (—3; 0j
—2) и имеет вектор а (—3; k\ 1) своей нормалью. Определите
число k и напишите уравнение плоскости а.
410. Определите расстояния от точек А (0; —1; —1), В (2; 1; 3),
С (—1; —1; 2) и D (0; 0; 7) до плоскости 5х — Зу + z —7 «
= 0.
411. Определите k и I, зная, что плоскость 5х —ky + lz —•! «= 0
проходит через точку А (—1; —1; —1) и находится на оди-
наковом расстоянии от точек Р (0; 1; 3) и Q (2; 2; 4).
412. Докажите, что все точки плоскости 5х —у + Зг —7 » 0
находятся на одинаковом расстоянии от плоскости Зх — у +
+ Зг = 0.
413. Докажите, что точка (0; 0; 0) равноудалена от плоскостей
Зх — 12г + 26 = 0, 4х —7у —4г —18 = 0, —х —2у +
+ 2г + 6 = 0.
414. Докажите, что если Р, Q — произвольные точки множества
{М : п • AM = 0), то п • PQ — 0.
415. Любая ли плоскость может быть записана в виде {Л4 : пх
X AM = 0)?
В задачах 416—420 система координат прямоугольная.
99
416. Даны точки А (0; —3; 1), В (4; —9; 3), С (3; 2;—5), D (—3;
11; —8). Какие из векторов АВ, AC, AD, ВС, BD, CD явля-
ются нормалями к плоскости 2х — Зу 4~ z — 8 = 0?
417. Запишите уравнение плоскости, проходящей через точку
А (3; —4; 6) и имеющей вектор а (2; —1; —2) своей нормалью.
418. ..При каком k вектор а (2; —3; —1) параллелен плоскости
2х — ky + 5z — 7 = 0?
419. Какая из точек А (—3; 0; 2) или В (3; 3; —7) ближе располо-
жена к плоскости х — Зу + 5г + 30 = 0?
420. Определите расстояние от точек А (—1; 9; 3), В (3; 0; —2)
' и С (2; —24; —5) до плоскости Зх —у + 7г —2 = 0. Как
, расположены прямые (АВ), (АС) и (ВС) относительно этой
’ плоскости?
§ 13. ПОЛУПРОСТРАНСТВА
о—:---------------------------------
13.1. Теорема. Пусть Р — плоскость, описываемая в системе
координат (О, eif е2, е3) уравнением Ах + By + Cz + D = 0 и
пусть Mi (xt, Zi), М2 (х2, у2, —две не принадлежащие ей точ-
ки. Отрезок [/И1/И2] в том и только в том случае пересекается с
плоскостью Р, если числа ki = Axt + Byt + Czt + D и k2 = Ax2 +
+ By2 + Cz2 +P имеют разные знаки.
▼ Доказательство. Предположим сначала, что ki
и k2 имеют одинаковые знаки (для определенности оба положитель-
ны), и пусть М' (х', у', zf) — произвольная точка отрезка
т. е.
МрИ' = t • МрИ2, 0 < t < 1. (1)
Из этого равенства вытекает, что
х’ — Xi = t (х2 — xt), у' — yi = i (у2 — У1), г' — г4 = t (г2—г^,
т. е.
х' = (1 — 0xt + /х2, у' = (1 — Oyi + 1уч, г' = (1 — {)гг + /г2,
и потому
Ax' 4~ By' 4- Cz’ 4" D = (1 — t) (Лх1 4~ 5yi -f- Czi) 4*
4- t(Ax2 + Ву2 + Сг2) +D = (1 — t)kt + tk2. (2)
Так как оба числа ki, k2 положительны, а числа 1 — t,t неотри-
цательны и хотя бы одно из них не равно нулю, то (1 — t)ki + tk2 ~>
> 0. Итак,
Ах' + By' 4- Cz' 4- D > 0.
Иначе говоря, никакая точка М' отрезка [MtA12] не принадлежит
плоскости Р, т. е. Р Q [Л41А42] = 0.
Аналогично проводятся рассуждения, если оба числа ki, k2
отрицательны.
100
Пусть теперь числа kir k2 имеют различ-
ные знаки (для определенности ki>Q, k2<
< 0). Проведя те же вычисления, мы за-
мечаем, что выражение Ах’+ Ву’+ Cz' +
D (см. (2)) будет равно нулю, если t —
корень уравнения (1 — t) ki+ tk2 = 0, т. е.
, k, | k, I ",
если t= -—L— ~ • ll, Так как это чис-
*i-*s l*il+|*2|
ло положительно и меньше 1, то получа-
ющаяся при этом значении t точка М'
принадлежит отрезку [MiM2]. В то же
время эта точка принадлежит плоскости
Р, поскольку Ax' + By' + Cz' + D = 0
при этом значении t. Итак, если Z?i > 0,
k2 < 0, то отрезок [MiM2] пересекается с
плоскостью Р.
Если ki < 0, *2 >0, рассуждения ана-
логичны. ▼
Рис. 64
Рис. 65
13.2. Определение. Пусть Р — некоторая плоскость и
Мь М2 —не принадлежащие ей точки. Точки Mi, М2 называются
лежащими по одну сторону от плоскости Р, если отрезок [MiM2]
не пересекается с этой плоскостью (рис. 64). Если же отрезок [MiM2]
пересекается с плоскостью Р, точки М(, М2 называются лежащими
по разные стороны от этой плоскости (рис. 65).
Теорема 13.1 говорит о том, что если плоскость Р задается урав-
нением Ах + By + Cz + D = 0, то точки Мь М2 в том и только
в том случае лежат по разные стороны от плоскости Р, если указан-
ные в теореме числа klt k2 имеют разные знаки.
Г-------------------—©----------------------------------------
13.3. Определение. Пусть Р—некоторая плоскость и
Мо —не принадлежащая ей точка. Множество содержащее точ-
ку Л40, а также все точки, которые лежат по ту же сторону от пло-
скости, что и точка УИ0, называется открытым полупространством,
которое определяется плоскостью Р и содержит точку А40-
Если плоскость Р задается уравнением Ах+ By + Cz + D = 0,
а при подстановке координат точки Л40 в левую часть этого уравне-
ния получается, например, положительное число, то согласно теоре-
ме 13.1 рассматриваемое открытое полупространство состоит из
всех тех точек, при подстановке координат которых в левую часть
тоже получается положительное число. Иначе говоря, это открытое
полупространство состоит из всех точек М (х; у; г), координаты ко-
торых удовлетворяют неравенству Ах + By + Cz + D >0. Если
же при подстановке координат точки Мо получается отрицательное
число, то открытое полупространство, определяемое плоскостью Р
и содержащее точку Л40, задается неравенством Ах + By 4- Cz 4-
= D < 0. Из сказанного ясно, что справедлива следующая тео-
рема.
13.4. Теорема. Любая плоскость Ах 4- By + Cz -f- D == 0
разбивает все не принадлежащие ей точки пространства на два от-
крытых полупространства'.
Wt = {М (х; у; z): Ах 4- By + Cz 4- D > 0}; (3)
= {Af (x; y, z)-.Ax + By + Cz + D < 0}. (4)
Точки M1( M2, принадлежащие одному и тому же полупростран-
ству, расположены по одну сторону от рассматриваемой плоскости,
а точки, принадлежащие разным полупространствам, — по разные
стороны от нее.
▼ 13.5. Замечание. Полупространство (3) называют иногда
«положительным полупространством», определяемым плоскостью
Ах 4- By 4- Cz 4- D = 0, a (4) — «отрицательным полупростран-
ством». Однако эти названия условные: ту же самую плоскость Р
можно задать уравнением —Ах — By — Cz — D = 0, и тогда полу-
пространство, которое раньше считалось «положительным», станет
«отрицательным» и наоборот. ▼
13.6. Определение. Точки самой плоскости Р, т. е. точки,
удовлетворяющие уравнению Ах + By 4- Cz 4- D — 0, не при-
надлежат ни одному из открытых полупространств, определяемых
этой плоскостью. Объединение открытого полупространства и пло-
скости Р называется замкнутым полупространством. Таким обра-
зом, плоскость Р определяет два замкнутых полупространства:
Ах + By + Cz + D 0 и Ах 4- By + Cz 4- D 0.
13.7. Определение. Пусть W — одно из двух открытых
полупространств, определяемых плоскостью Р, и IT = Ц7 (J Р —
соответствующее замкнутое полупространство. Вектор п- #= 0 на-
зывается внешней нормалью полупространства W, если п есть нор-
маль к плоскости Р, и, кроме того, отложив от точки Ма 6 Р век-
тор п, т. е. Л40М1 = п, мы получаем точку Mlt не принадле-
жащую полупространству W (рис. 66).
13.8. Теорема. Для полупространст-
ва Ах 4- By 4- Cz 4-D 0 вектор п (Л;
В; С) является внешней нормалью (система
координат — прямоугольная).
Доказательство. Вектор
п является нормалью к плоскости Ах 4-
+ By 4- Cz 4- D = 0 (следствие 12.3).
Далее, пусть Мо (х0; у0; z0) — произволь-
ная точка этой плоскости (т. е. Ах0 4-
4- Ву0 4- Cz0 4- D = 0), а М j (xf, yr, zt)—
точка, получающаяся в результате откла-
рис, 66 дывания вектора п от точки Af0, т. е.
102
M0Mi = П- Тогда
xi— х0 = Л, yi—y0 = B, zi—z0 = C,
и потому
Axt + Byt 4* CZj 4- D = A (x0 + Л) 4- В (y0 4- В) 4-
4- C (z0 4- С) 4- D = (Ах0 4- Ву.,4- Cz0 + D) 4-
4-Л2 4- В2 4- С2 = Л2 4- В2 4- Са > О
(поскольку хотя бы один из коэффициентов Л, В, С отличен от нуля).
Итак, число Axi 4- Byt 4- Czt 4- В положительно, т. е.
точка Mt не принадлежит полупространству Ах 4- By 4- Сг + D
0. Следовательно, п — внешняя нормаль этого полупространства.
Задачи
421. Определите, какие из следующих точек расположены по одну
сторону плоскости 7х — у 4* 5z — 20 = 0 и какие — по
другую сторону:
Л (0; 0; 3), В (7; —1; 0), С (3; —2; 1),
D (—1; 0; 2), В (1; 1; 1), F (3; 3; 3).
422. Укажите, в каких из следующих случаев отрезок [ЛВ] не
пересекается ни с одной из плоскостей 2х — у + 4z — 3 «
= 0, Зх 4- 2у — z + 5 «= 0:
а) Л (0; 0; 1), В (1; 1; 0); б) Л (—1; —1; —3), В (2; 2; 3);
в) Л (1; 5; 1), В (0; —5; 1); г) Л (—2; —1; —1), В (—4; 1; 0).
423. Какие из следующих точек принадлежат открытому полу-
пространству, которое определяется плоскостью Зх + 4у —
— 5z 4- 6 = 0 и содержит точку Р (2; 0; —1): Л (1; 1; 1),
В (0; 1; 3), С (—2; 3; 4), D (1; — 1; 1), Е (2} 0; —2), F (—3;
—3; —3)?
424. В условиях предыдущей задачи укажите, какие из точек
принадлежат соответствующему замкнутому полупростран-
ству.
В задачах 425—427 система координат — прямоугольная.
425. Плоскость а проходит через точку Л (—lj 2j —3) н имеет
вектор а (—1; 2; 5) своей нормалью. Запишите неравенства,
которые задают открытые полупространства, определяемые
плоскостью а.
426. Плоскость а задается уравнением Зх — у 4- 5z — 3=0.
От точки Л (1; —5; —1), лежащей в этой плоскости, отложили
вектор а (3; —1; 5).
а) Не производя вычислений, укажите, в положительном
или отрицательном полупространстве лежит полученная
точка В.
б) Вычислите координаты точки В и подставьте их в левую
часть уравнения плоскости.
427. Укажите векторы внешних нормалей для следующих замкну-
тых полупространств! а) Зх — 5у 4- 2 — 7 0j б) —х —
103
Рис. 67
— у—2г —6^0; в) х-|-
-фу—3z>0; г) г — Н<0;
д) Зх + у — 2 > 0;
е) 2х —у—5z + ЮО 0.
Докажите, что если замк-
нутые полупространства
W и W (определяемые
двумя различными пло-
скостями) не пересекают-
ся, то их внешние нормали
п и п' связаны соотноше-
нием п' = kn, где k < 0 (рис. 67).
429. Плоскость Р описывается уравнением Зх — 2у + г + 3 = 0.
Пересекает ли эту плоскость отрезок [/GKal если точки Ки
Ki имеют следующие координаты:
а) Ki (1; 1; 1), Ki (2; 3; 0); б) Ki (-1; 2; 1), Ki (1; 3; -2);
в) Ki (2; 1; 1), Ki (-3; -2; -1)?
430. Укажите, в каких случаях точки А и В лежат по одну сторо-
ну относительно плоскости х — 2у — г = 0:
а) А (1; 2; 3), В (3; 2; 1); б) А (2; —1; 1), В (0; —3; 5);
в) А (2; —5; 3), В (4; 3; —1).
431. а) Запишите неравенство, задающее открытое полупростран-
ство, содержащее точку А (2; —1; —5) и определяемое:
1) плоскостью 2х + у —5z —4 = 0; 2) плоскостью —Зх +
4* у + 2z — 5 = 0; 3) плоскостью 4х — 2у + г + 3 — 0.
б) Запишите (неравенствами) замкнутые полупространства,
соответствующие найденным в предыдущей задаче откры-
тым полупространствам. Для каждого из этих полупро-
странств укажите вектор внешней нормали (система ко-
ординат предполагается прямоугольной).
482*, Докажите; что если внешние нормали п, п' двух замкнутых
полупространств связаны соотношением п' — kn, где k > 0,
то одно из этих полупространств содержится в другом.
§ 14. ВЫПУКЛЫЕ ФИГУРЫ
-----------------------о------------:-------------
14 .1. Определения. Фигура Q называется выпуклой, если
месте с каждыми двумя точками она содержит целиком и соединяю-
щий их отрезок:
(VQ) (Q —выпуклая фигура) «=>
«*(Vt. Мг € Q) ([AliTWal cz Q).
def
104
Прямая, отрезок, луч являются выпуклыми фигурами. Эти вы-
пуклые фигуры называются одномерными. Если выпуклая фигура
содержится в некоторой плоскости, но не содержится ни в какой
прямой, она называется двумерной. Параллелограмм, ’круг, тре-
угольник — примеры двумерных выпуклых фигур.
Выпуклая фигура, не содержащаяся ни в какой плоскости, на-
зывается трехмерной.
14 .2- Докажем для примера, что шар с центром О и радиусом г,
т. е. множество всех точек, находящихся от О на расстоянии, не
превосходящем г, является трехмерной выпуклой фигурой.
V В самом деле, пусть и Л42 —точки, принадлежащие этому
шару, т. е.
d (О, Mt) < г, d (О, М2) < г. - (1)
Рассмотрим произвольную точку М отрезка [ЛЛЛ12]. Так как
М £ то ОМ = tOMi+ (1 — t) 0М2, где 0 t 1, и потому
рМ2==/2ОЛ4?+2/(1— tfOMl. (2)
Из (1) следует, что lOAfJ2 г2, | ОЛ12|2 г2, lOAfi • ОЛ42| ^г2
(см. теорему 4.9). Теперь из (2) получаем:
ОМ2* < t2r2 + 2t (1 — t) г2 + (1 — t)2r2 = л2.
Отсюда d (О, М) г, т. е. точка М принадлежат рассматриваемому
шару. Так как М —'п роизвольная точка отрезка [AfpW2],
то весь этот отрезок содержится в шаре. Следовательно, рассматри-
ваемый шар есть выпуклое множество. ▼
14 .3. Другой пример выпуклого множества —открытое полупро-
странство. Действительно, пусть Р —некоторая плоскость и W —
одно из открытых полупространств, определяемых этой плоскостью.
Если точки Mlf М2 принадлежат W, то они лежат по одну сторону
от плоскости Р, т. е. отрезок [Л4 fM2] не пересекается с плоскостью Р.
Это означает, что весь отрезок [THjAf содержится в полупростран-
стве W, что и Доказывает выпуклость этого множества.
14 .4. Любое замкнутое полупространство также является выпук-
лым множеством.
Пустое множество и множество, состоящее из одной точки, так-
же будем для удобства считать выпуклыми фигурами.
---------------------------ф------------------------------
14 .5. Теорема. Пусть Qlf Q2, ..., Qm— выпуклые фигуры.
Тогда их пересечение Q = Qi П Q2 П ••• П Qm также является вы-
пуклой фигурой.
Доказательство. Пусть Мг € Q, € Q. Тогда
Mi и М2 принадлежат каждому из множеств Q2, ..., Q,n.
Так как Mi € Qlt М2 € Qi, то в силу выпуклости множества Qi
имеем [AfiMj] с Точно так же [AfiM2] с: Q2, .... [MiM2] с Qm.
105
Таким образом, отрезок [Л^Ма] содержит-
ся в каждом из множеств Qb Q2, .... Qm,
и потому [AfiMal с Q.
Итак, вместе с каждыми двумя точка-
ми Mlt М2 множество Q содержит весь от-
резок [MjAla]» т. е. Q — выпуклая фигура.
14.6. Замечание. Теорема эта оста-
ется справедливой (с тем же доказательст-
вом) для пересечения не только конечного,
ноибесконечного числа выпуклых
множеств.
Так как замкнутое полупространство —
выпуклое множество, то пересечение любо-
Рис. 68 го числа замкнутых полупространств яв-
ляется выпуклой фигурой.
14 .7. Опр еделение. Фигура, которая представляет собой
пересечение конечного числа замкнутых полупространств, назы-
вается выпуклым многогранником (рис. 68).
14 .8. Определение. Фигура Q называется ограниченной,
если она содержится в некотором шаре. Если фигура Q не содержит-
ся ни в каком шаре, то она называется неограниченной. В частно-
сти, можно говорить об ограниченных и неограниченных многогран-
никах.
О
Рис. 70
Рассмотрим примеры выпуклых мно-
гогранников. Пусть Wi и W2— два зам-
кнутых полупространства,' граничные пло-
скости Рь Р2 которых не параллельны.
Пересечение Q 1F2 (рис. 69) является
выпуклым многогранником, который на-
зывается двугранным углом. Двугранный
угол является примером неограниченного
выпуклого многогранника.
Если плоскости Рь Р2 параллельны, но
не совпадают, то пересечение Wx f) IF2, ес-
ли оно не пусто, представляет собой неогра-
ниченный выпуклый многогранник, кото-
рый называется полосой, ограниченной пло-
скостями Рг и Р2 (рис. 70).
Плоскость является примером неогра-
ниченного выпуклого многогранника. Дей-
ствительно, если Wi, W2 — два замкну-
тых полупространства, определенных пло-
скостью Р, то Wi Q 1F2 == Р.
Полуплоскость также является вы-
106
пуклым многогранником, так как она может быть получена пе-
ресечением плоскости с полупространством. Поэтому и пересечение
нескольких полуплоскостей является выпуклым многогранником.
Угол, меньший развернутого, треугольник, параллелограмм —
примеры двумерных выпуклых многогранников.
Прямая также является выпуклым многогранником, поскольку
она представляется в виде пересечения двух плоскостей. Луч можно
представить как пересечение прямой и полупространства, и потому
он является выпуклым многогранником. Выпуклым многогранни-
ком является и любой отрезок.
Прямая, луч, отрезок — одномерные выпуклые многогранники.
При этом прямая и луч — неограниченные многогранники, а отре-
зок — ограниченный многогранник.
Точка является нульмерным выпуклым многогранником. Иног-
да пустому множеству приписывают размерность —1, т. е. пустое
множество рассматривается как выпуклый многогранник размер-
ности — 1.
Задачи
433. Может ли выпуклая фигура состоять из конечного числа
точек?
434. Докажите, что круг — выпуклая фигура.
435. Докажите, что замкнутое полупространство есть выпуклая
фигура.
436, Фигуры Qb Qa, ..., Qn — выпуклые. Всегда ли являются вы-
пуклой фигурой:,, а) их пересечение; б) их объединение?
437*. Докажите, что если Q — выпуклая фигура и а — произволь-
ная плоскость, то фигура Пра (Q) также является выпуклой.
438. Будет ли пересечение конечного числа выпуклых многогран-
ников также выпуклым многогранником?
439. Пересечением скольких замкнутых полупространств явля-
ется: а) треугольник; б) параллелограмм; в) отрезок?
440. Может ли пересечение неограниченных выпуклых фигур
быть ограниченной фигурой? Может ли пересечение огра-
ниченных выпуклых фигур быть неограниченной фигурой?
441. Докажите, что если выпуклая фигура содержит три точки
А, В, С, не лежащие на одной прямой, то она содержит весь
треугольник АВС.
442. Является ли выпуклой фигурой угол, больший разверну-
того?
443. Докажите, что если Q2, ...,Qn —выпуклые многогран-
ники, хотя бы один из которых является ограниченным,
то Qi f| Qa П ••• П Qn — ограниченный выпуклый мно-
гогранник.
107
§ 15. СВОЙСТВА ВЫПУКЛЫХ
МНОГОГРАННИКОВ
О
Каждый с детства хорошо представляет себе, что такое паралле-
лепипед («кирпичик») и куб. Однако при аксиоматическом изложе-
нии геометрии в пространстве полезно показать, как эти многогран-
ники могут быть построены с использованием векторного аппарата;
Это полезно еще и потому, что позволит на этом примере проиллю-
стрировать общие свойства многогранников, которые сейчас играют
очень важную роль не только в самой математике, но и в ее прило-
жениях (в технике, экономике, кристаллографии и т. д.).
Пусть Л, В, С, О, Aif Bi, Ci, Di —точки, удовлетворяющие
условиям АВ= a, AD == ВС = Ь, ААг= ВВ1= CC1=DD1 = с,
где а, Ь, с—линейно независимые векторы (см. рис. 15). Точки
А, В, С, D лежат в плоскости а = а (А; а, Ь). -Точки Аъ Въ Cb
лежат в плоскости = а (Af, а, Ь). Так как плоскости а и oci
имеют_о.бщий базис, то они параллельны (рис. 71). Обозначим че-
рез W замкнутое полупространство, определяемое плоскостью а
и содержащее плоскость cq, а через Wi замкнутое полупространство,
определяемое плоскостью и содержащее плоскость а. Рассмотрен-
ные восемь точек содержатся в каждом из полупространств Wi и
W2i а потому и в полосе Р = W f]
Такое же рассуждение показывает, что точки А, Аь В4, В лежат в
одной плоскости р, а точки С, Clt Dit D —в параллельной плоско-
сти Pi (рис. 72). Все эти восемь точек принадлежат полосе Q, гранич-
ными плоскостями которой являются р и pi.
Аналогично A, Ai, Dif D лежат в одной плоскости у, а 6, Вь
Ci, С —в параллельной ей плоскости у4 (рис. 73). Все эти восемь
Рис. 71
Рис. 72
108
Рис. 73
точек принадлежат полосе 7?, граничны- с
ми плоскостями которой являются плос-
кости у и Vi.
k Пересечение /( = Р Q Q Q R называ- /ш
ется параллелепипедом, построенным на
векторах eif е2, е3. Так как каждая из по-
лос Р, Q и 7? является пересечением двух
замкнутых полупространств, то паралле-
\ лепипёд 7< представляет собой пересечение * о
шести замкнутых полупространств. Сле- Рис 74
довательно, параллелепипед является вы-
пуклым многогранником.
Если точка М параллелепипеда 7< не лежит ни в одной из
f плоскостей а, аь |3, рь у, то расстояние от точки М до каж-
дой из этих плоскостей положительно. Поэтому существует такое
число г > 0, что шар с центром М и радиусом г целиком содер-
жится в каждом из шести полупространств, дающих в пересечении
параллелепипед /(,, а значит, содержится в параллелепипеде 7<.
Иначе говоря, все достаточно близкие к М точки принадлежат /<,
т. е. М—внутренняя точка параллелепипеда К•
г Если же точка Mi £ К лежит хотя бы в одной из плоскостей а,
cq, Р, Pi, У и 71, то как угодно близко к Mi имеются не только точки,
принадлежащие /С, но и точки, не принадлежащие /<. Это означает,
что Mi — граничная точка параллелепипеда 7G
Граница параллелепипеда 7<, т. е. множество всех его гранич-
ных точек, представляет собой объединение шести параллелограм-
’ мов ABCD, AiBiCiDi, AAiBiB, DDiCiC, AAiDiD и ВВ££ (рис. 74).
Эти параллелограммы (т. е. двумерные многогранники, объединение
которых представляет собой границу параллелепипеда 7<) назы-
ваются гранями параллелепипеда. Стороны этих параллелограммов
называются ребрами параллелепипеда 7<, а концы ребер —верши-
нами параллелепипеда /С Таким образом, параллелепипед К име-
ет двенадцать ребер ЕДД11 [BBil [CCi], [£Ю1], [Д#1 ЕД i73i], [ВС],
[SiCi], ЕСТ?], ECi£>i], Е^Д1 Г.751Д1] и восемь вершин А, В, С, D, Дй
Z?i, Ci, Di.
Если векторы а, Ь, с попарно ортогональны, то построенный на
этих векторах параллелепипед называется прямоугольным паралле-
лепипедом. Если же эти векторы не только ортогональны, но и име-
1 ют одинаковую длину, то построенный на них параллелепипед на-
зывается кубом.
----------------:-----------©-------------------------------
Рассмотрим теперь в обзорном порядке (без доказательств)
основные свойства произвольного выпуклого многогранника.
Пусть Q — произвольный трехмерный выпуклый многогранник
> (рис. 68). Как обычно, точка М 6 Q называется внутренней точкой
многогранника Q, если существует такое число г > 0, что шар ра-
109
A
Рис. 75
Рис. 76
диуса г с центром М содержится в мно-
гограннике Q. Точка Mt £ Q является
граничной точкой, если любой шар с цент-
ром Mi содержит точки, не принадлежа-
щие многограннику Q. Множество всех
внутренних точек многогранника Q назы-
вается его внутренней областью и обоз-
начается через int Q (от английского in-
terior — внутренний; читается: «инт. Q»).
Множество всех граничных точек мно-
гогранника Q называется границей это-
го многогранника и обозначается через
QQ (читается: «дэ-ку»). Граница любого
выпуклого многогранника представляет
собой объединение конечного числа дву-
мерных выпуклых многогранников, ко-
торые лежат в различных плоскостях.
Эти двумерные многогранники называ-
ются гранями многогранника Q. Пере-
сечение любых двух граней представ-
ляет собой либо одномерный выпуклый
многогранник, либо точку, либо пустое
S множество.
Две грани Pi, Р* пересечением ко-
торых является одномерный многогран-
ник, называются смежными гранями, а
их пересечение —ребром многогранни-
ка (рис. 68). Точки, служащие концами
ребер, называются вершинами много-
гранника.
Говорят, что грань Р выпуклого
многогранника Q примыкает к ребру I
этого многогранника, если 1с.Р (рис.
68). В любом выпуклом многограннике
к каждому ребру примыкают ровно
Рис. 77 две грани.
Приведем примеры. Двугранный угол
имеет две' грани, каждая из которых представляет собой полу-
плоскость, и одно ребро, являющееся общей граничной прямой этих
полуплоскостей. Вершин этот многогранник не имеет.
Трехгранный угол (рис. 75) представляет собой пересечение трех
полупространств, граничными плоскостями которых являются
(ЛОВ), (ВОС), (ДОС). Гранями этого многогранника являются три
угла Z-AOB, Z-ВОС, Л.АОС, а ребрами — лучи [ОЛ), [ОВ), [ОС).
У этого многогранника имеется единственная вершина О.
У любого ограниченного трехмерного выпуклого мно-
гогранника каждая грань представляет собой ограниченный дву-
мерный выпуклый многогранник, т. е. плоский многоугольник. Реб-
110
рами ограниченного выпуклого многогранника являются отрезки.
Отсюда ясно, что у ограниченного выпуклого многогранника обя-
зательно имеются вершины. Число вершин ограниченного выпукло-
го трехмерного многогранника не меньше четырех. Выпуклый мно-
гогранник с четырьмя вершинами (рис. 76) представляет собой тре-
угольную пирамиду (тетраэдр).
К каждой вершине ограниченного выпуклого трехмерного много-
гранника примыкает не менее трех граней. Например, в тетраэдре,
а также в параллелепипеде к каждой вершине примыкают ровно
три грани. У пирамиды имеется вершина, к которой примыкает п
граней, где п — число сторон многоугольника, представляющего
собой основные пирамиды (рис. 77).
____________________________Q—
Пусть Q —некоторый двумер-
ный выпуклый многогранник, рас-
положенный в плоскости а. Прямая
I cz а ? называется опорной прямой
двумерного многогранника Q, если
она содержит хотя бы одну граничную
точку многогранника Q, но не содер-
жит никакой его внутренней точки.
Если / — опорная прямая двумерно-
го выпуклого многогранника Q, то Q
содержится в одной из двух замкнутых
полуплоскостей, определяемых пря-
мой I. Опорная прямая может иметь
с Q либо только одну общую точку
(которая обязательно является вер-
шиной многоугольника Q (рис. 78)),
либо I П Q представляет собой сто-
рону (рис. 79).
Через каждую граничную точку
выпуклого двумерного многогранни-
ка Q проходит хотя бы одна опорная
прямая (через внутреннюю точку сто-
роны проходит единственная опорная
прямая, через вершину —бесконечно
много).
Аналогичными свойствами облада-
ют и трехмерные выпуклые много-
гранники. Плоскость а называется
опорной плоскостью трехмерного вы-
пуклого многогранника Q, если она
содержит хотя бы одну граничную
точку многогранника Q и не содержит
ни одной его внутренней точки (рис.
80). Если а — опорная плоскость вы-
111
пуклого многогранника Q, то Q содержится в одном замкнутом полу-
пространстве, определяемом плоскостью а. Через каждую граничную
точку трехмерного выпуклого многогранника Q проходит хотя бы
одна опорная плоскость.
------------©
15 .1. Задача. Найти точку М (х; у; г), в которой функция
I (М) = Ах 4- By 4- Cz, рассматриваемая на заданном ограничен-
ном выпуклом многограннике Q, достигает наибольшего значения.
Решение этой задачи можно геометрически изложить следую-
щим образом. Обозначим через п вектор с координатами А, В, С
и проведем две опорные плоскости сч и а2 многогранника Q, ортого-
нальные вектору п (рис. 81). Плоскости ocj и а2 параллельны
и многогранник Q расположен в полосе, ограниченной этими
плоскостями. Выберем точку Mt 6 Q f) «1 и точку М2 € Q f] а2.
Легко видеть, что плоскость щ определяется уравнением
Ах 4- By 4- Cz — I = 0. (1)
В самом деле, плоскость (1) ортогональна вектору п, так как коэф-
фициентами при х, у, z являются числа А, В, С, и проходит через
точку Mi. Аналогично плоскость а, записывается уравнением
Ах 4- By 4- Cz — I (М2) = 0. (2)
На рисунке 81 обозначения плоскостей выбраны таким образом,
что многогранник Q лежит в отрицательном полупространстве от-
носительно плоскости <xt, а относительно плоскости а2 он лежит в
положительном полупространстве. Отсюда следует, что функция
I (М), рассматриваемая в точках многогранника Q, достигает в точ-
ке Mt своего наибольшего значения (а в точке М2
наименьшего значе-
ния). Действительно, так
как многогранник Q лежит
в отрицательном полупро-
странстве относительно
плоскости а1( то для любой
точки М (х; у; z) 6 Q
Ах 4- By 4- Cz— I (Mi)< 0,
т. е.
Ах 4- By + Cz < I (Mi),
и потому I (М) I (Mi).
Это и означает, что в точ-
ке Mi функция I (М) при-
нимает наибольшее значе-
ние.
112
Если пересечение Q П а4 представляет собой не одну вершину
многогранника Q, а его ребро (рис. 82), то в качестве Mi можно бы-
ло взять любой из концов этого отрезка, т. е. некоторую вершину
многогранника Q. Точно так же, если Q П ai — грань, т. е. неко-
торый выпуклый многоугольник (рис. 83), то в качестве Mi можно
было взять любую его вершину, которая и в этом случае является
вершиной многогранника Q.
15 .2. Вывод. Линейная функция, рассматриваемая на выпук-
лом ограниченном многограннике Q, достигает своего наибольшего
значения либо в одной вершине многогранника Q (рис. 8Г), либо на
некоторого его ребре (рис. 82), либо на некоторой грани (рис. 83).
При этом всегда существует вершина (хотя бы одна), в которой до-
стигается наибольшее значение рассматриваемой линейной функ-
ции. Аналогичные утверждения справедливы для наимень-
шего значения линейной функции на выпуклом ограниченном
многограннике.
Выше было показано, каким образом можно геометрически
найти вершину, в которой рассматриваемая линейная функция до-
стигает наибольшего значения. Однако в практических задачах про-
водить эти геометрические построения («проводить» опорные пло-
скости; искать пересечение их с многогранником и т. д.) неудобно.
Сделанный выше вывод позволяет подойти к задаче о максимуме
линейной функции на многограннике алгебраически: надо взять все
вершины многогранника Q (т. е. найти их координаты), вычислить
значения рассматриваемой линейной функции во всех вершинах и
выбрать из этих значений наибольшее. Это и будет максимум рас-
сматриваемой линейной функции на многограннике Q.
Задачи
444. Докажите, что параллелепипед имеет три четверки ребер,
причем ребра каждой четверки параллельны и имеют оди-
наковые длины.
б Заказ 4860 113
445. Докажите, что параллелепипед является ограничен-
ным выпуклым многогранником.
446. Пусть О —одна из вершин параллелепипеда, [ОД], [ОД] и
[ОС] —ребра, выходящие из этой вершины. Положим:
et = ОД, е2 = ОБ, е3= ОС.
Докажите, что точка М в том и только в том случае принад-
лежит рассматриваемому параллелегшиеду, если ее коорди-
наты в системе (О, elre2, es) удовлетворяют условиям. О х
< 1, 0 < у < 1, 0 <z < 1.
447. Дана прямоугольная система координат. Что представляет
собой множество всех точек, координаты которых удовлетво-
ряют условиям О^у^а, O^z^a?
448. Докажите, что множество всех точек, координаты которых
удовлетворяют системе линейных неравенств
AiX + Я4у -[• CjZ 4- Di ^0,
А2х 4- Д2у 4- C^z 4- D% О,
представляет собой выпуклый многогранник. Любой ли вы-
пуклый многогранник может быть записан в таком виде?
449. Какие из следующих высказываний истинны?
а) Если А — внутренняя точка многогранника Q, то найдет-
ся такое число г > 0, что шар радиуса г с центром А со-
держит многогранник Q.
б) Если Л —внутренняя точка многогранника Q,. то найдется
такое число г > 0, что шар радиуса г с, центром А содер-
жится в многограннике Q.
в) Если А — внутренняя точка многогранника Q, то любой
шар с центром А содержит точки, не принадлежащие Q.
г) Если А — граничная точка многогранника Q, то любой
.. шар с центром А содержит точки* не принадлежащие Q<
д) Если некоторый шар с центром в точке А £ Q содержит
точки, не принадлежащие Q, то А —граничная точка
многогранника 'Q.
450. Какие из следующих высказываний истинны?
а) Любой двумерный многогранник имеет бесконечно много
опорных прямых.
б) Для любого двумерного выпуклого многогранника Q
найдется опорная прямая, имеющая с Q только одну об-
щую точку.
в) Для любого двумерного выпуклого многогранника Q
найдется опорная прямая, имеющая с Q более одной общей
точки.
г) Через любую граничную точку выпуклого многоугольни-
ка проходит только одна опорная прямая.
д) Плоскость любой грани трехмерного выпуклого много-
114
451.
452.
453.
454.
гранника является
опорной плоскостью
этого многогранника.
е) Любая плоскость, про-
ходящая через три вер-
шины трехмерного вы-
пуклого многогранни-
ка, является его опор-
ной плоскостью.
Точка Л, В, С, Cj,
указанные в задаче 195'
(рис. 22), служат верши-
нами выпуклого много-
гранника {треугольной
призмы, рис. 84), который
может быть представлен
в виде пересечения пяти
замкнутых полупрост-
ранств. Одним из них
является полупространст-
во, определяемое плоско-
стью (АВС) а содержа-
щее точку Укажите
остальные четыре полу-
пространства.
Рис. .85
Выпуклый многогранник, называемый п-угольной призмой,
строится следующим образом. Берется выпуклый «-угольник
AtA2 ... А„, лежащий в некоторой плоскости а, и вектор
а Ф О, не параллельный этой плоскости. Затем строятся та-
кие точки В2, ..., Вп, что
— А2В2 — — АпВп— и.
Точки Alt А2, ..., А„, Bi, В2, .... В„ и служат вершинами
призмы (рис. 85). Пересечением скольких замкнутых полупро-
странств является эта призма? Сколько она имеет граней,
ребер, вершин?
Выпуклый многогранник, называемый п-угольной пирамидой,
строится следующим образом. Берется выпуклый п-угольник
AiA2 ... А„, лежащий в некоторой плоскости с?, и точка
S i а. Точки At, А2, ..., Ап, S и служат вершинами пирами-
ды (рис. 77). Пересечением скольких замкнутых полупро-
странств является эта пирамида? Сколько она имеет граней,
ребер, вершин?
Убедитесь, что для каждого выпуклого многогранника, рас-
смотренного в задачах 444, 451—453, справедливо соотноше-
ние
Г—Р + В=2, (3)
5*
115
где Г — число граней, Р — число ребер, В — число вершин.
Леонард Эйлер (об этом крупнейшем математике уже шла
речь в учебнике «Геометрия-7») установил, что соотношение
(3) справедливо для любого ограниченного выпуклого трехмер-
ного многогранника. Это утверждение называют теоремой
Эйлера о многогранниках.
455. Начертите на координатной плоскости выпуклый многоуголь-
ник Q с вершинами А (0; 0), В (3; 0), С (0; 2), D (3; 1),
Е (2; 3). Проведите опорные прямые многоугольника Q,
ортогональные вектору а (3; 1). В какой точке М {х\ у)
многоугольника Q функция I (М) — Зх + у достигает наи-
большего значения? наименьшего значения?
456. Прямые х «= 0, х = 2, у = 0, у = 3, 2х + у — 5 = 0 опре-
деляют на координатной плоскости пятиугольник Q (стороны
которого лежат на этих прямых). Определите координаты вер-
шин этого пятиугольника. В какой точке М (х; у) пятиуголь-
ника Q достигает наибольшего значения функция I (М) =
— Зх + 5у 4- 4? Тот же вопрос для функции Ц (М) = 4х +
4- 2у + 3.
457*. Точка А и векторы elt е2, е3 заданы своими координатами:
А (2; —1; 3), £ (2; 1; 0), еъ (1; —1; 2), es (3; 0; 2).
Вычислите координаты остальных вершин параллелепипеда
К (см. с. 109). В какой точке М (х-, у; г) параллелепипеда /(
достигает наименьшего значения: а) функция I (М) = х 4-
4- у 4- z — 8; б) функция (М) — х —2у + г — 11;
в) функция /2 (М) — 2х — 4у — За 4- 7?
458*. а) При каком D плоскость x4-y4-z4-H=0 является
опорной плоскостью параллелепипеда К., рассмотренного в
задаче 457? Что. представляет собой пересечение параллеле-
пипеда К и этой опорной плоскости?
б) Ответьте на те же вопросы для плоскости х — 2у + z 4-
4- D = 0.
в) Те же вопросы для плоскости 2х —4у —Зг 4- D = 0.
459. Сколько существует плоскостей, каждая из которых содер-
жит четыре вершины данного параллелепипеда?
460. Докажите, что противоположные грани параллелепипеда
(т. е. грани, не имеющие общих точек) параллельны.
461. Сформулируйте утверждения, содержащиеся в задачах 189,
243, 263, 292, 298, 310, 367, используя термины, относящиеся
к параллелепипеду (грани, ребра, вершины, диагонали парал-
лелепипеда, диагонали граней).
462. Навертите треугольник и проведите две опорные прямые
этого двумерного выпуклого многогранника. Сколько общих
точек может иметь опорная прямая с треугольником?
463. Перечислите грани и ребра треугольной призмы (см. .задачу
451). Укажите параллельные грани, параллельные ребра.
464. Докажите, что параллелепипед является частным случаем
призмы (см. задачу 452).
465*. Точка А и векторы а, Ъ, с заданы своими координатами:
А (2; —1; —2), а (2; 0; 1), 1 (0; 1; 2), в (1| 1; 1).
Вычислите коордицаты остальных вершин треугольной
призмы, рассмотренной в задаче 451. В какой точке М (х;
у; г) этой призмы достигает наибольшего значения: а) функ-
ция / (М) == 2х + у — г; б) функция It (М) = 2х у —
— 3z + 2; в) функция /2 (М) = х + 4у —2z.+ 5?
§ 16. ПОНЯТИЕ О ЛИНЕЙНОМ ПРОГРАММИРОВАНИИ
------------:--------------о—--------------------------
К нахождению наибольшего значения линейной функции на
выпуклом многограннике приводят многие практические задачи,
на первый взгляд никакого отношения к многогранникам не име-
ющие. Сюда относятся задачи о нахождении наиболее выгодных спо-
собов перевозок, наиболее выгодных способов раскроя материала,
наиболее эффективных режимов работы предприятий, задачи о со-
ставлении производствейных планов и т. п/Такие задачи объеди-
няются новым научным направлением, получившим название «Ма-
тематическая экономика». Тот факт, что эти задачи решаются с по-
мощью нахождения наибольших значений линейной функции на
многогранниках, был впервые подмечен академиком Л. В. Канто-
ровичем. За эти работы советский ученый удостоен в 1975 году Но-
белевской премии. В настоящее время в математике существует
целое направление, изучающее вычислительные методы решения
задачи отыскания наибольшего значения линейной функции на вы-
пуклом многограннике. Это направление носит название «Линейное
программирование».
В этом параграфе на примере задачи о транспортировке сырья
будет рассказано о решении одной из задач линейного программи-
рования.
---------------------------е----------:----------------
16.1. Задача. На три завода 32, З3 нужно завезти, сырье
одинакового вида, которое хранится на двух складах С2 в со-
ответствии с данными, указанными в таблице 1.
Расстояния от складов до заводов указаны в таблице 2 (рис. 86).
Требуется найти наиболее выгодный вариант перевозок, т. е. ва-
117
рпант, для которого' общее ко-
личество тонно-километров бу-
дет наименьшим.
Решение. Обозначим
через, х и у количество сырья-,
которое нужно вывезти со скла-
да Ct на заводы. 31( 32. Тогда со
второго склада нужно довезти
на эти заводы 1® —х и 15 —у
тони сырья . Так как общее ко-
Рис. 86 личество имеющегося наскладах
сырья совпадает с потребностью
заводов, т. е. все сырье должно быть- вывезено, со, складов-на заво-
ды, то после обеспечения заводов 3t и 32 оставшееся на складах сы-
рье полностью вывозится на завод 38, т. е. со склада на завод 38
вывозится 20 —х —у, а со склада С2 вывозится 25 — (Ю — х) —
—(15 —у) = х 4- у тонн. Эти данные о перевозках показаны в
таблице 3.
Учитывая данные таблиц 2 и 3, находим общее число тонно-
километров:
5х + 7у + 10 (20 — х — у) + 3 (.10 —х); + 4 (15 — у). + 6 (х+у).
Складывая и упрощая, получаем» что» это» общее число тонно-кило-
метров равно
290 — 2х — у. (1)
Заметим теперь, что все величины, указанные в таблице 3 (выражаю-
щие количество перевозимого по разным дорогам сырья), неотри-
цательны:
х 0, у > 0, 20 — х — у > 0, (2)
10—х 0* 15—у>0, х 4-
+У 0-
Каждое из. неравенств (2) в сис-
теме координат х, у определяет
замкнутую полуплоскость, а
система всех этих неравенств
определяет пересечение этих по-
луплоскостей, т. е. выпуклый
многоугольнике? (выпуклый дву-
мерный многогранник). Заметим,
что последнее из неравенств (2)
можно отбросить: оно является
следствием двух первых нера-
венств.
Полуплоскости, определяе-
мые первыми пятью неравен-
ствами (2), и многоугольник Q,
«18
являющийся пересечением всех этих полуплоскостей, показаны на
рисунке 87.
Таким образом, задача о нахождении наиболее выгодного ва-
рианта перевозок сводится математически к нахождению точки
М. (%, у) многоугольника Q, в которой функция (1) достигает наи-
меньшего значения.
Вместо функции (1.) можно рассматривать функцию
/(М) - —2х—у. (3)
Действительно, если будет найдено наименьшее значение функции
(3) на многоугольнике Q, то, прибавив к этому значению 290, полу-
чим наименьшее значение функции (Г) на многоугольнике Q.
Как мы знаем из предыдущего параграфа, наименьшее значение
линейной функции, рассматриваемой на выпуклом многограннике.,^
достигается в какой-либо вершине этого многогранника. Поэтому"
достаточно вычислить значения функции '(3) в вершинах многоуголь-
ника Q и выбрать из этих значений наименьшее. Непосредственный
подсчет показывает* что в вершинах многоугольника Q (см. рис. 87)
функция (3) принимает следующие значения:
I (О) = о, I (Л) - —15, J (В) = —25,/ (С) - —30, / (D) = —20.
Таким образом, наименьшее значение функция (3) (а значит, и функ-
ция (1)) принимает в точке С. Иначе говоря, наиболее выгодный
вариант перевозок соответствует точке С (10; 10), т. е. х = 10, у =
= 10. Общее количество тонно-километров для этих значений х, у
согласно t(l) равно 290 — 2 • 10—10 =260. В таблице 4 показаны
соответствующие объемы перевозок (сравните таблицу 3).
Таблица 1
Наличие сырья Потребность в сырье
С, с2 31 32 Зз
20 т 25 т 10 т 15 т 20 т
Таблица 2
31 , 32 За
ч 5 км 7 км 10 км
с2 3 км 4 км 6 км
Таблица 3
3. За З3
С1 ( X т У т <20—х—у)т
Са ! f(10—х)т ; <(15—у)т
Таблица 4
Зх 32 Зз
ci 10 т * 10 т —
С2 — 5 т 20 т
119
Таблица 5 Таблица 7
31 32 Зз 34 1 32 Зз
Ci X т У т z т (20—х—у—г)т Ci | | 6 км 7 км 10 км
С2 (8—х)т (10—у)т (12—2) т (x+t/+z+5)T С2 | 3 км 5 км 6 км
Таблица 6 Таблица 8
Зх 32 Зз 34 Зх 32 Зз
5 км 6 км 4 км 10 км с» 5 км 7 км 10 км
Са 3 км 7 км 3 км 7 км С2 2 км 4 км 6 км
---------------------:--------©------------------------------
В рассмотренной задаче все объемы перевозок со складов на за-
воды удалось выразить через две переменные х, у (см. таблицу 3).
Это позволило дать геометрическую интерпретацию получающейся
системы неравенств (2) на координатной плоскости. В результате
мы пришли к задаче о наименьшем значении линейной функции на
выпуклом многоугольнике, которую удалось полностью решить.
Допустим теперь, что при тех же двух складах число заводов
равно четырем с потребностью в сырье соответственно 8, 10, 12 и 15
тонн. Тогда нужно будет ввести три переменные х, у, z, обозначаю-
щие количество сырья, вывозимого со склада Сх на первые три за-
вода. В результате вместо таблицы 3 мы получим другую таблицу
перевозок (таблица 5). Если задать расстояния от складов до заво-
дов (таблица 6), то можно будет составить выражение для общего-
числа тонно-километров. Можно написать и неравенства, выража-
ющие неотрицательность всех выражений, содержащихся в таб-
лице 5. Теперь эти неравенства в отличие от неравенства (2) будут
зависеть от трех переменных х, у, z. Каждое из этих неравенств
задает полупространство, а система всех неравенств
определяет пересечение полупространств, т. е. выпуклый много-
гранник. Таким образом, для четырех заводов задача о перевозке
сырья будет математически формулироваться как задача о наимень-
шем значении линейной функции на трехмерном выпуклом много-
граннике.
Для двух складов и пяти заводов (при сохранении условия о
том, что все сырье должно быть вывезено полностью) потребуются
уже четыре переменные х, у, г, t, обозначающие количество сырья,
вывозимого со склада Сх на первые четыре завода. Теперь вместо
(2) мы будем иметь неравенства с четырьмя переменными х, у, z, t
и для получения геометрической интерпретации потребуется че-
тырехмерное пространство, т. е. пространство, в котором точки
(и векторы) задаются четырьмя координатами, а при большем числе
складов и заводов—пространства еще большей размерности.
120
В математике для любого натурального п рассматривается п-
мёрное пространство, в котором точки и векторы задаются п коор-
динатами х19 х2, хп. Из сказанного выше ясно, что рассмотрение
пространств, имеющих размерность большую трех, необходи-
м о для решения задач линейного программирования и, значит, для
решения задач о перевозке сырья и других задач математической
экономики. Необходимость рассмотрения n-мерных пространств
при п > 3 диктуется также математическими задачами физики, хи-
мии, биологии и других областей знания. Таким образом, хотя
пространственные свойства окружающего мира хорошо описывают-
ся геометрическим трехмерным пространством, потребности
практической деятельности человека приводят к необходимости рас-
смотрения пространств любой размерности п.
С определением и простейшими свойствами n-мерного простран-
ства вы познакомитесь в курсе X класса.
Задачи _
466. При сохранении данных.и обозначений, указанных в табли-
цах 1 и 3, решите задачу 16.1 для случая, когда расстояния
от складов до заводов задаются: а) таблицей 7; б) таблицей 8.
В каждом случае ответьте, сколько существует наиболее вы-
годных вариантов перевозок.
467. а) Используя таблицы 5 и 6, запишите (в случае четырех за-
водов) выражение для общего числа тонно-километров и
неравенства, означающие неотрицательность выражений,
содержащихся в таблице 5.
б) Проверьте, что следующие точки удовлетворяют системе
выписанных неравенств:
Лх (0; 0; 12), Л2 (0; 0; 5), Л3 (0; 10; 0\ Л4 (0; 5; 0), Л5 (8;
0; 0), Лв (5; 0; 0), Л7 (0; 10; 10), Л8 (0; 8; 12), Л9 (8; 0; 12),
Л10 (8; 10; 0), Ли (8; 10; 2).
в) Считая доказанным, что {Лт, Л2 ..., Лп,} есть множество
всех вершин многогранника Q, определяемого выписанной си-
стемой неравенств, определите наиболее выгодный вариант
перевозок.
468*. а) Выпуклый трехмерный многогранник Q задается системой
линейных неравенств, рассмотренной в задаче 448. Докажи-
те, что в каждой вершине многогранника Q по крайней мере
в трех из этих неравенств левая часть обращается в нуль.
б) Докажите, что {Лх, Л2, ..., Ли} есть множество всех вер-
шин многогранника Q, рассмотренного в задаче 467.
469. Сколько переменных потребуется для решения задачи 16.1,
если потребности заводов в сырье те же, а количества сырья
на складах Сх и С2 соответственно равны 20 т и 38 т? Запиши-
те выражения для общего числа тонно-километров (при рас-
стояниях, указанных в таблице 2) и неравенства, задающие
выпуклый многогранник.
121
ГЛАВА
§ 17. ДВИЖЕНИЯ ПРОСТРАНСТВА
----------:-------------О---------------------------
17.1. Определение. Движением пространства Е3 называ-
ется отображение пространства Е8 в себя, сохраняющее расстояние:
(V/, где f — отображение пространства Е3 в себя)
(/ — движение) <=> ( Vt. А, В) (d (А, В) — d(f {A), f (В)),
def
Множество всех движений пространства £3 будем обозначать
через D3.
Как и в случае геометрии на плоскости, движения позволяют
определить конгруэнтность фигур.
17.2. Определение. Фигура Р называется конгруэнтной
фигуре Q, если существует такое движение f, что f (Р) = Q:
(VP, Q, где Р с R3, Qc R3) (P^Q)^(3f € D3) (f (P) = Q).
def
©
Определим теперь образ в e к т o-
р а при движении. Пусть f—некото-
рое движение пространства Е3 и а—
вектор. Выберем произвольную точку
А С Е3 и обозначим через В точку, по-
лучающуюся в результате откладыва-
ния вектора а от точки А, т. е. АВ = а.
Далее, через Лх и Вх обозначим точки,
в которые переходят А а В при рас-
122
сматриваемом движении: Л! —
= / (Л), Bj. = f(B) (рис. 88).
Вектор at = ЛХВХ называется
образом вектора а при движении
f и обозначается через f (а), т. е.
f (а) = йг
Это определение можно сфор-
мулировать и иначе, сказав,
что для любых точек Л, Е3
и любого движения/справедли-
во соотношение
•/ (АВ) = / (Л) /ТВ).
▼ Рассмотренное определение страдает одним недостатком: для
нахождения вектора / (а) нужно было не только- задать движение /
и вектор а, но еще и выбрать произвольную точку А, с помощью ко-
торой вектор / (а) определяется^ Однако в действительности этот
недостаток является несущественным, так как вектор / (а) н е за-
висит от выбора точки Л, участвующей в его построении.
Докажем это. Пусть, кроме Л, взята другая точка А', от которой
также отложен вектор а, т. е. А'В' = а. Образы точек Л' и В' при
движении / обозначим через А[ и В[. Нам нужно доказать, что если
проводить построение вектора f (а) исходя не от точки Ar а ©т А',
то получится тот же самый Вектор, т. е. нужно доказать, что
Л.1В1 = АгВг. (1)
Чтобы убедиться в этом, обозначим через О середину отрезка [Л В'],
т. е. такую точку, что ОА — —ОВ' (рис. 89). Так как АВ == А'В' =
= а, то мы имеем:
ОВ = ОЛ + ЛВ = — ОВ' А-АВ' = — €& — НА' =
=— (OB'A- WA')=—ОА',
т. е. О является также серединой отрезка [Л'В]. Иначе говоря, О
является общей серединой отрезков [ЛВ'} и [Л'В],
Заметим теперь, что середина отрезка сохраняется при движе-
нии, т. е, если Р — середина отрезка [МАГ], a Plt М1г — точки,
в которые переходят Р, М, N при движении /, то Рг — середина
отрезка [ДВД. В самом деле, так как Р — середина отрезка'[МА/],
у
то d (Р, М) = d (Р, N) = — d (М, N). Поскольку при движении /
сохраняются расстояния, мы имеем: d (Ри Mt) = d (Plt Nt) —
«з
= -Pd(M1,Nl), откуда и вытекает, что Pi—середина отрезка
[ММ.
Из сказанного вытекает, что точка — f (О) является серединой
отрезка [Лх#!] и серединой отрезка [ЛI, Вх], т. е.
ОхЛ1= и 01Л1 = OjBi.
Теперь находим:
= ад— ад= лД+сад=ЛА.
чем и завершается доказательство. ▼
-------------------------ф--------------------------
17.3. Теорема. При движениях сохраняются векторные опера-
ции, т. е. если f — произвольное движение, а и b — некоторые век-
торы и k — действительное число, то
Рис. 90
fe) = f(a) + f(6),(2)
f («) f (Р) = а b, (3)
f(ka)=kf(a). (4)
▼ Доказательство.
Выберем произвольную точку А
и обозначим через В, С такие
точки, что АВ = а, ВС = b (рис.
90). Образы точек А, В, С при
движении f обозначим через Л1(
В1; С). Тогда
f £+ b)~ f (АВ + BQ=f(AC)=
=ад= ад+ад= f(AB)+
+ /(ВС) = /(а).+Ж
чем доказана справедливость
соотношения (2).
Далее, пусть О, М, N — та-
кие точки, что ОМ = a, ON=
= b, и пусть Оь Mi, Ni — обра-
зы точек О, М, N при движении /
(рис. 91). Тогда
114
\d (M, A))2 = MV2= (ON — OM)2 = (6 — a)2=
= b2 + a2 — 2ab = (d(0, M))2±(d(O, N)y~2ab,
откуда
"ab = (d(0' M»2 + <d<Q’ Nyy-(d(M, N)y
Аналогично
f (a) f(b) = + N1))9 — (d(M1, nj>* (6)
Так как при движении сохраняются расстояния, то d (О, М) —
= d (Оь MJ, d (О, N) — d (0ъ Л\), d (М, N) = d (Мъ Л\). Из
(5), (6) теперь следует, что ab = f (a)f (b), т. е. соотношение (3) спра-
ведливо.
Наконец, обозначим вектор ka через с. Тогда с — ka = 0, и
потому
с2 —о. (7)
Так как (в силу уже доказанного соотношения (3)) ас= f (a) f (с),
а2 — f (а)2, с2 = / (с)2, то соотношение (7) можно переписать в виде
f (с)2 - 2kf Са) f (с) + к2Ца)2 = 0,
т. е. (f (с)— kf (а))2 = 0. Следовательно, f (с) — kf (а) = 0. Вспоми-
ная, что с = ka, получаем отсюда соотношение (4). ▼
17.4. Следствие. При движении сохраняется линейная зави-
симость между векторами, т. е. для любых векторов alt .... ат и
чисел k1,’^...,,km справедливо соотношение
f (k^ + ... + km(Q = V (ах) + ... + kmf (ат).
Это непосредственно вытекает из соотношений (2) и (4) теоремы 17.3.
-----------:---------------------------------------------------
Пусть (О, et, е2, е3) — прямоугольная система координат и f —
некоторое движение пространства £3. Так как базис (ег, е2, е3) —
ортонормированный, то согласно формуле (3) теоремы 17.3 векторы
f (ei)> f (ег)> f (ез) также образуют ортонормированный базис. Таким
образом, (f (О), f (et), f (е2), f (е3)) — прямоугольная система коор-
динат в £3; она называется системой, в которую переходит
прямоугольная система (О, elt е2, е3) в результате движения f
(рис. 92).
12S
Рис. 92
17.5. Теорема. Пусть (О, elt
е^,е^и(О', ei, е2, е3)—две пря-
моугольные системы координат в
Е3. Тогда существует, и притом
только одно, движение f, переводя-
щее первую систему координат во
вторую.
▼ Доказательство.
Пусть М — произвольная точка,
(х, у, z) — ее координаты в системе
(О, ех, е2, е3),_ т. е.
ОМ = хег -|- уе2 -|- ге3.
Если существует движение f,
переводящее систему (О, elt е2,
«з)
в (О', e'i, е'2, е'з), то (в силу следствия 17.4) оно должно перевести
точку М в такую точку М', что
О'М' = xe’i + уе2 4- ze'3.
Иначе говоря, точка М’ = f (М) должна в системе (О', е[, 4. е'з)
иметь те же координаты, которые имеет точка М в системе (О,
elt е2, е3). Следовательно, образ f (М) точки М определяется одно-
значно, т. е. искомое движение, если оно существует, единственно.
Докажем, что искомое движение действительно существует.
Для этого для любой точки M положим f (M) = М', где М' — точка,
которая в системе (О',в\, «з, е3) имеет те же координаты, что и точ-
ка М в системе (О, еь е2, е3). Этим определяется некоторое отобра-
жение / пространства Е3 в себя, и остается -проверить, что f — дви-
жение, переводящее систему (О, elt е2, е3) в (О’, e'i, ei, 4).
Действительно, пусть М и N — произвольные точки, а (хх; ух;
zx), (х2; у2-, z2) — их координаты в системе (О, еи е2, е3). Тогда
ОМ = Ххех+ ухе2+ гге3,
ON = x2et 4- у2е2 4- z2e3.
По определению отображения f имеем:
О'М' — х& 4- у4- zxe3\
O'N' = х2е\ 4- у24 4- z2e3.
Из этих равенств следует, что
MN= ON — дм = (х2 — хх) <?х 4- (у2— ух) е24- (z2— г,)е3,
MW = O'N' — ОЧИ' = (х2 — хх) е! 4-(у2 — ух)е 2 4- (га *з.
126
Так как системы координат прямоугольные, то
d(M, N) = V (х2 — Xj)2 4- (у2— у1)а+ (г2 — г^2,
d (М', N') = V(х2— x2)2-f- (у2 — У1)2+ (гх— z2)2.
Таким образом, d (М, N) = d (М', N’). Поскольку это справедливо
для любых точек М, N, отображение f является движением.
Наконец, проверим, что f переводит систему координат (О, еъ
ег, е3) в (О', ев 62, бз). Отложим векторы еи е2, е3 от точки О, а век-
торы бь 62, бз от точки О':
et= OAlt б2= ОА2, еэ = 0Л3;
6i — O'Ai, е2 — О*А2, бз = О'А3.
Тогда координаты точки At в системе (О, еп б2, е3) равны (I; 0; 0),
а координаты точки А[ в системе (О', б[, е2, е3) тоже равны (1; 0; 0).
Следовательно, f (Лх) = /li. Аналогично f (А 2) — А2, f (Л3) = А'3.
Это означает (поскольку / (О) = О'), что / (ej = / (0Л1) =*
^UO)f(Ai) =ОЛ1 = б! и аналогично f (е2) = е2, f (е3)—е3, т. е. сис-
тема (О, е1, е2, е3) переходит в систему (О', е[, е2, ез). ▼
17.6. Следствие. Всякое движение представляет собой вза-
имно однозначное отображение пространства Е3 на себя.
1 В самом деле, пусть (О, еъ е2, е3) — прямоугольная система ко-
ординат и (О', бь е2, е3) —система, в которую она переходит в ре-,
зультате движения f. Возьмем произвольную точку М' € £*, и
пусть (х, у, г) — ее координаты в системе (О', ei, е2, бз). Рассужде-
ния, проведенные при доказательстве теоремы 17.5, показывают, что
существует, и притом только одна, точка М, которая переходит в
т при движении f, а именно, та точка Л1, которая в системе (О,
6Ь е2, е3) имеет те же координаты х, у, г. Это и означает, что f
взаимно однозначно отображает Е3 на себя.
Задачи
471. Докажите, что симметрия относительно точки является
движением.
472. Дан вектор а. Отображение t переводит произвольную точ-
ку М С Е3 в точку М' = t (М), получающуюся в результа-
—► ----------------------------------------------►- -*
те откладывания вектора а от точки М, т. е. ММ = а. До-
кажите, что t — движение.
473. Докажите, что композиция движений представляет собой
движение.
<17
474 Точки Д, В, С, D переходят при движении f в точки Дх, Вь
Сх, Какие из следующих высказываний истинны?
а) Если АВ ~ CD, то A1B1=C1D1. •
б) Если АВ=А1В1 то CD = C1D1,
в) Если векторы АВ и CD линейно зависимы, то и CrDx
также линейно зависимы.
г) АВ • CD = А^В1 • ад.
475*. Докажите, что если d (Р, 7И) = d (Р, N) = — d (Л1, Л/), то
Р — середина отрезка [ЛШ].
476. Докажите, что если f — произвольное движение и а, Ь, с —
линейно зависимые векторы, то векторы f (a), f (b), f (с)
также линейно зависимы.
477. Докажите, что фигура, конгруэнтная прямой, представля-
ет собой прямую.
478. Докажите, что фигура, конгруэнтная плоскости, представля-
ет собой плоскость.
479*. Дана прямоугольная система (О, elf е2> ^з)« Отображение f
переводит точку М с координатами (х, у, z) в точку, имеющую
(в той же системе) координаты (г, х, у). Является ли / движе-
нием?
480. Даны три прямоугольные системы координат. Движение f
переводит первую систему во вторую, движение g переводит
вторую систему в третью, движение h переводит первую си-
стему в третью. Справедливо , ли соотношение g of = №
481. Докажите, что если f— движение, то также движение.
482. Докажите, что любые две прямые конгруэнтны.
483. Докажите, что два шара в том и только в том случае конгру-
энтны, если одинаковы их радиусы.
484. Прямые а и b параллельны. Докажите, что если f — движс
ние, то прямые f (а) и f (Ь) параллельны.
485. Докажите, что скрещивающиеся прямые переходят при дви-
жении в скрещивающиеся прямые.
486. Докажите, что тождественное отображение пространства Е3
является движением.
487. Докажите, что композиция движений обладает свойством
ассоциативности.
488. Движение f переводит векторы а, b в alf bt. Докажите, что
векторы а и b в том и только в том случае ортогональны, если
аг и Ьг ортогональны.
489. Докажите, что фигура, конгруэнтная отрезку, представляет
собой отрезок.
490. Векторы е19 е2, е3 составляют ортонормированный базис.
128
Движение f удовлетворя-
ет условиям f (вх) = еъ
f (£2) — ez- Докажите, что
справедливо одно из со-
отношений f (е3) = е3,
f Й) = — е3.
Докажите, что любые две
плоскости конгруэнтны.
Плоскости аир парал-
лельны. Докажите, что
491.
492.
493.
если f—движение, то пло-
скости f (а) й f (Р) параллельны.
Прямая I ортогональна плоскости а. Докажите, что если f —
движение, то прямая f (/) ортогональна плоскости f (а).
§ 18. ОРИЕНТАЦИЯ И ВИДЫ ДВИЖЕНИЙ
--------:-------------------0-------------------------------
В этом пункте без проведения строгих доказательств будет дано
понятие об ориентации.
Пусть (е19 е2, е3) и (elfe2, е'з)—два базиса, у которых первые
два вектора соответственно одинаковы. Отложим векторы этих
двух базисов от одной и той же точки О:
= ОАЬ е2 —OA2i е3= ОА3, е3 = ОА3.
Если при этом точки А3 и А3 расположены по одну сторону от пло-
скости (OAiA2), то условимся считать, что базисы (ех, е2, е3) и (ех,
е2, е3) имеют одинаковую ориентацию (рис. 93), а если по разные сто-
роны, то противоположную ориентацию.
Аналогично обстоит дело, если в двух базисах совпадают пер-
вые и третьи векторы (или вторые и третьи).
Пусть (еь е2> *з) и й, 4, £з)—произвольные базисы. Можно
доказать, что от одного базиса к другому возможно перейти, после-
довательно заменяя каждый раз один вектор базиса. Иначе го-
воря, существует такая последовательность базисов ^1, ^2» ^з)>
Й, Й>, 4), й, 4, 4), Й, в2, е'з), что каждые два со-
седние из них имеют два общих вектора. Следовательно, о каждых
двух соседних базисах мы можем сказать, имеют они одинаковую
или противоположную ориентацию. Если, проходя эту цепочку, мы
четное число раз переходим к базису противоположной ориен-
тации, то условимся считать, что-базисы е2, е3) и е2, е3)
129
имеют одинаковую ориентацию, а если нечетное, то противо-
положную ориентацию.
18.1. Пример. Возьмем произвольный базис (ех, е2, е3) и ба-
зис, образованный противоположными векторами: V2 =»
= 4 = Для того чтобы перейти от (ех, е2, е3) к й, е2, ^3),
можно последовательно заменить сначала первый, затем второй
и, наконец, третий вектор противоположным ему вектором:
е2> гз)> (еь е2> е3), (вь е2, е8), (ej, ei е3).
В этой цепочке каждые два соседних базиса противоположно
ориентированы. Таким образом, в этой цепочке мы три раза пере-
ходим к базису противоположной ориентации. Значит* базисы
(ех, £2, ^з) и (вь е2, е3) противоположно ориентированы.
▼ Выберем теперь некоторый базис (ех, е2, е3), который примем за
«эталон», и обозначим через Q+ множество всех базисов, имеющих
ту же ориентацию, что и (ех, е2, е3), а через £2_ множество базисов,
имеющих противоположную ориентацию. Рассмотрим два произ-
вольных базиса. Если оба они принадлежат множеству й+ (или оба
принадлежат Q_), то они имеют одинаковую ориентацию.
Если же один принадлежит Q+, а другой то они противоположно
ориентированы.
Заметим, что какое из этих двух множеств обозначить через
Q+, а какое Q_ является условностью: все зависит от того, какой
базис (ех, е2, е3) выбран за «эталон». На практике при рассмотрении
базисов в реальном пространстве удобно различать «левые» и «пра-
вые» базисы в зависимости от того, можно ли к векторам (ех, е2, е3)
«приложить» большой, средний и указательный пальцы левой
(рис. 94) или правой руки. Левые и правые базисы (или системы ко-
ординат) используются в некоторых вопросах физики. Другим спо-
собом задания ориентации в реальном пространстве является так
называемое «правило буравчика» (так-
же применяемое в физике).▼
Пусть теперь f — произвольное дви-
жение пространства Е3 и (ех, е2, е3) —
некоторый базис. Если базисы (ех, е2,
е3) и (/ (ех), f (е2), f (е3)) имеют одинако-
вую ориентацию, то f называют движе-
нием, сохраняющим ориентацию. Если
же эти базисы имеют противоположную
ориентацию, то f называют движением,
меняющим ориентацию.
Это определение в действительности
не зависит от выбора исходного базиса
130
Z, , e2, e3), т. e. каждое движение f либо любой базис пере
водит в базис, имеющий ту же ориентацию (и тогда f есть дви-
жение, сохраняющее ориентацию), либо же движение f любой
базис переводит в базис, противоположно с ним ориентированный
(f меняет ориентацию).
-----------------------—ф-------------------------------
18.2. Теорема. Пусть е1; еа — единичные ортогональные меж-
ду собой векторы и е\, е2 — другая пара единичных ортогональных
векторов. Пусть, далее, О и О' — произвольные точки. Существуют
только два движения, переводящие точку О в О', а векторы elt е2
соответственно в ё2. Одно из этих движений сохраняет ориен-
тацию, а другое меняет ориентацию.
Доказательство. Выберем такой вектор е3, что -
(elt е2, е3)—ортонормированный базис, а также такой вектор е3,
что (el, ё2, е'з)—ортонормированный базис. Вектор —е'з тоже обра-
зует с e't, ё2 ортонормированный базис (е\, е2, —ез).
Согласно теореме 17.5 существует движение Д, которое перево-
дит систему координат (О, еъ е2, е3) в (О', ё\, ё2, е'з)-, точно так же
существует движение Д, переводящее (О, ег, е2, е3) в (О', e]( е2,
—е'з). Так как базисы (e'i, ё2, ё3) и (e'i, е'2, —е'з) противоположно ориен-
тированы, то один из этих базисов имеет ту же ориентацию, что
(еи е2, е3), а другой — противоположную. Следовательно, одно из
движений Д, f2 сохраняет ориентацию, а другое меняет ориентацию.
Таким образом, установлено существование двух движений,
переводящих точку О в О', а векторы ег, е2 в e'i, е'2, причем одно из
них сохраняет ориентацию, а другое меняет ориентацию. Остается
убедиться, что, кроме Д, Д, не существует других движений, пере-
водящих О, еи е2 в О', e'i, ё2. Действительно, если f такое движение,
то оно переводит систему (О, elt е2, е3) в (О', e'i, ё2, е’), причем век-
тор е3 составляет с е\, ё2 ортонормированный базис (ei, е2, е3). Но
тогда вз совпадает с одним из векторов ё3 или —е'з, и потому f совпа-
дает с одним из движений Д, Д.
---------------------------о----------------------------
Пусть а — некоторый вектор. Параллельным переносом про-
странства Е3 на вектор а называется отображение, которое произ-
вольную точку М переводит в такую точку Mlt что ММг — а
(рис. 95).
131
18.3. Теорема. Параллельный пере-
нос является движением, сохраняющие
ориентацию.
▼ Доказательство. Пусть М,
N — две произвольные точки, а Л4Ь —
точки, в которые они переходят при парал-
лельном переносе на вектор а. Тогда
ММг = a, NNt = а (рис. 96), и потому
МП = MMr + М^П= а + М^Н=М^П +
4-а = М?П + ППг = М^. (1)
Из формулы (1) следует, что d (М,
П) = d (Mlt Nj), т. е. рассматриваемый
параллельный перенос t сохраняет рас-
стояние и потому является движением.
Из формулы (1) следует также, что
параллельный перенос t переводит любой
вектор с — МП в тот же самый
вектор: t (с) — с. Поэтому параллельный
перенос t переводит произвольный базис
(еи е2, е3) в тот же самый базис и потому со-
храняет ориентацию, у
ОГ
1(0,е)
Рис. 97
Пусть О — некоторая точка пространства и е — единичный век-
тор. Движение /, сохраняющее ориентацию и переводящее О, е
снова в О, е (рис. 97), называется поворотом вокруг прямой I (О, е).
Эта прямая называется также осью поворота.
18.4. Теорема. Сохраняющее ориента-
цию движение, которое переводит некото-
рую точку О в себя, есть поворот вокруг не-
которой прямой, проходящей через точку О.
Доказательство этой теоремы мы не при-
водим.
18.5. Следствие. Всякое движение, со-
храняющее ориентацию, можно представить
в виде композиции поворота вокруг некоторой
прямой и параллельного переноса.
В самом деле, пусть f — произвольное
сохраняющее ориентацию движение. Выбе-
рем точку О и обозначим через О' ее образ:
132
q' = .f (О). Далее, через / обозначим параллельный перенос на век-
тор 00' Тогда движение g = /-1 о f переводит точку О в себя и
сохраняет ориентацию. Следовательно, g есть поворот вокруг не-
которой прямой, проходящей через точку О. Таким образом, f =
= t о g, т. е. f есть композиция поворота g и параллельного пере-
носа t.
18.6. Замечание. Из рассуждений, показывающих спра-
ведливость следствия, видно, что f можно разными спосо-
бами представить в виде композиции поворота и параллельного
переноса (в зависимости от того, какую точку О мы выбрали Ъ ка-.
честве исходной). Можно доказать, что любое движение, сохраняю-
щее ориентацию, можно представить в виде композиции поворота
и параллельного переноса таким образом, что вектор параллель-
ного переноса будет параллелен оси поворота.
,------------:----------------0----------:----------------------
Пусть а — некоторая плоскость, О — ее точка и (еъ е2) орто-
нормированный базис этой плоскости. Меняющее, ориентацию дви-
жение, переводящее О, е1У е2 снова в О, е1У е2 (рис. 98), называется
симметрией относительно плоскости а (или зеркальной симметри-
ей): Можно доказать, что эта симметрия однозначно определяется
плоскостью а, т. е. не зависит от выбора в этой плоскости точки О
и векторов еи е2.
18.7. Пример. Пусть О — некоторая точка. Обозначим через
s отображение пространства, которое произвольную точку М пере-
водит в такую точку М', что ОМ' = —ОМ (центральная симмет-
рия). Покажем, каким образом s можно представить в виде компози-
ции трех зеркальных симметрий.
Для этого возьмем произвольный ортонормированный базис
(еь е2, е3). Обозначим через Д, f2, f3 меняющие ориентацию движе-
ния, каждое из которых переводит О в себя, причем переводит
базис (е1У е2, е?) в (— е1У е2, е3);
f переводит (-—е1У е2, е3) в (—
—е3, бз); /з переводит (—е1( —е2,
£з) в (—61, —е2, —е3). Каждое
из движений /i, /2, f3 является зер-
кальной симметрией, а их компо-
зиция f = fa ° f3 ° fi оставляет
точку О на месте и переводит ба-
зрс (е1У е2, е3) в (—е1У —е2, —е3).
Покажем, что f — симметрия отно-
сительно точки О. Действительно,
133
пусть М — произвольная точка. Тогда существуют такие числа
х, у, г, что ОМ = хех + уе2 + геа. При движении /точка М пере-
ходит в такую точку М', которая имеет в новом базисе (—еи_ег,
—е3) те же координаты х, у, г (теорема 17.5): ОМ' = х (—ех) -|-
4-у (— е2) + z (—е3) = —хех — уей — ze3. Таким образом, ОМ' =
= — ОМ, а это означает, что f совпадает с s, т. е. s = /3 о /а о /
Задачи
494. Векторы ег, е3 образуют ортонормированный базис. Опре-
делите в каждом случае, имеют ли базисы (а, Ь, с)- и (Oj, &х, сх)
одинаковую или противоположную ориентацию:
а) а —а3 — er,b = bt= е2, с = 2ех—е2+ Зе3,
сх = ех 2е2 —• 3c2j
б) а =jzx = ех — е2, Ьх = 2ех+ е2,
£= £j.—е3, сх == ех -|-
в) а=ах =ех, ft=-e2, ix=-es4-% c = e3,q.=0x 4-е24-4.
495. В прямоугольной системе координат заданы точки & (0; О; 0),
Л (1; 0; 2>, Д(3; — >; 1>, С (I; I; 3), D (2; —3; 5). Напишите
уравнение плоскости (ОЛВ) и определите, по. ©дну или по
разные стороны от нее расположены точки С и D. Одинаково
или противоположно ориентированы базисы (ОЛ, ОВ, ОС)
и (ОЛ, OB, OD)?
496. Существуют ли такие три базиса, что каждые два-из них про-
тивоположно- ориентированы?
497. Какие из следующих высказываний истинны?
а) Если движения f и g сохраняют ориентацию, то движение
g о f также сохраняет ориентацию»
б) Если движения fag меняют ориентацию, то- движение
g ° f также меняет ориентацию-.
в) Если движение f сохраняет ориентацию, то движение /~1
также сохраняет ориентацию.
г) Если движение f меняет ориентацию,, та движение /-1
также меняет ориентацию.
д) Если f о g-1 меняет ориентацию, то одно- из движений f,
g сохраняет, а другое меняет ориентацию.
498. Движение/переводитО, ех, е2 в О', е[, е2 (где ех, е2 — единич-
ные векторы, ортогональные друг другу), а движение g пере-
водит О', 4, е’гВ О, еъ е2. Какие из следующих высказываний
истинны?
а) Если оба движения /, g сохраняют ориентацию, то g —
б) Если оба движения /, g меняют ориентацию, то g = F~*'
134
в) Если go f есть тождественное отображение, то оба движе-
ния Д g сохраняют ориентацию.
499. Докажите, что е£ли каждое из движений Д g, h переводит О,
elt е2 в О', е2 (где | ej = | е2| = 1, ег ± е2), то справедливо
хотя бы одно из соотношений
g'"1 о f = с, g-1 о h == е, /-1 о h = е.
500. Докажите, что композиция параллельных переносов на век-
торы а и b представляет собой параллельный перенос на век-
тор а 4- Ь.
501. Движение f переводит любой вектор в тот же самый вектор:
(Va) (а) = а). Докажите, что f — параллельный перенос.
502. Докажите, что если f — произвольное движение, a t — па-
раллельный перенос, то о to f параллельный перенос.
503. Докажите, что при параллельном переносе каждая прямая
переходит в параллельную ей прямую.
504*. Точка TVf называется неподвижной точкой движения Д если
а) Докажите, что если параллельный перенос не является
тождественным отображением, то он не имеет неподвижных
точек.
б) Докажите, что если поворот не является тождественным
отображением, то его неподвижными точками являются
точки, принадлежащие оси поворота, и только они.
в) Докажите, что если движение f имеет четыре неподвиж-
ные точки, не лежащие в одной плоскости, то f — тожде-
ственное отображение.
505. Докажите, что если f и g — повороты, оси которых проходят
через одну точку О, то g о f также есть поворот, ось которого
проходит через точку О.
506. Докажите, что если вектор а ортогонален оси поворота Д
то вектор f (а) также ортогонален этой оси.
507. Докажите, что сохраняющее ориентацию движение, имеющее
две неподвижные точки., является поворотом.
<508. Докажите, что если центр шара принадлежит оси поворота
Д то этот шар переходит при повороте f в себя.
509. Что представляет собой множество неподвижных точек зер-
кальной симметрии?
510. Докажите, что меняющее ориентацию движение, имеющее
три неподвижные точки, не лежащие на одной прямой, пред-
ставляет собой зеркальную симметрию.
511. Докажите, что если f — симметрия относительно плоскости
а и вектор а ортогонален а, то f (а) = —а.
512*. а) Докажите, что если Д g — симметрии относительно плос-
костей аир, причем а || р, то g о f есть параллельный пере-
нос (рис. 99).
135
б) Докажите, что любой параллель-
ный перенос можно представить в
виде композиции двух зеркалы
ных симметрий.
513*. а) Докажите, что если /, g — сим-
метрии относительно плоскостей а
и р, причем а-И р, то go f есть
поворот (рис. 100).
б) Докажите, что любой поворот
можно представить в виде ком-
позиции двух зеркальных сим-
метрий.
514*. Докажите, что любое движение про-
странства представляется в виде
композиции нескольких зеркальных
симметрий.
515. Даны два базиса (ех, е2, е3) и (elt
ket + те2 4- пе3). Докажите, что они
в том и только в том случае одинако-
во ориентированы, если п > 0.
516. В каком случае композиция движе-
ний fko ... ° /2 о Д сохраняет ориен-
тацию?
517. Даны точка О, единичные ортогональные векторы а, Ъ и
ортонормированный базис (ех, е2, е3). Сколько существует
движений, оставляющих точку О на месте и переводящих
векторы а, b в какие-либо два вектора базиса (еь е2, е3)?
518. Докажите, что если t — параллельный перенос на вектор а,
то I-1 — параллельный перенос на вектор —а.
519. Докажите, что при параллельном переносе каждая плоскость
переходит в параллельную ей плоскость.
520. Докажите, что если движение / переводит каждую прямую в
параллельную ей прямую, то f — параллельный перенос.
521. Докажите, что если вектор а параллелен оси поворота г,
то г (а) = а.
522. Дана прямоугольная система координат (О, е1( е2, е3). Что
представляет собой сохраняющее ориентацию движение Д
которое удовлетворяет условиям / (О) = О, f (ех) = е2, f (е2)=*
=
523*. Докажите, что множество всех неподвижных точек сохра-
няющего ориентацию движения f представляет собой либо
пустое множество, либо прямую, либо все пространство.
136
524*. Докажите, что любое движение, меняющее ориентацию, мож-
но представить в виде композиции трех зеркальных симмет-
рий, а любое движение, сохраняющее ориентацию, — в виде
композиции четырех зеркальных симметрий.
525. Докажите, что если s — зеркальная симметрия, то s-1 = s.
526*. а) Докажите, что если меняющее ориентацию движение
имеетболееодной неподвижной точки, то оно представляет
собой зеркальную симметрию.
б) Что может представлять собой множество всех, неподвиж-
ных точек меняющего ориентацию движения?
§ 19. ГРУППЫ ДВИЖЕНИЙ
--------;-------------------О------------------:-----------
Множество D3 всех движений пространства Е3 обладает следую-
щими тремя свойствами:
а) Тождественное отображение е принадлежит D3.
б) Если f € D3 и g 6 D3, то goftD3.
в) Если f € D3, то существует обратное отображение f-1 и оно
также принадлежит D3. Иными словами, D3 представляет собой
группу движений.
Множество Do всех движений, сохраняющих ориентацию, также
является группой движений. Действительно, тождественное отобра-
жение является сохраняющим ориентацию; композиция движений,
сохраняющих ориентацию, также сохраняет ориентацию; если дви-
жение f сохраняет ориентацию, то и f-1 сохраняет ориентацию.
Так как Do с D3, то говорят, что Do — подгруппа группы движе-
ний D3.
Еще одним примером группы движений является множество Т
всех параллельных переносов. В самом деле, тождественное отобра-
жение является параллельным переносом; далее, композиция двух
параллельных переносов также является параллельным переносом;
наконец, если t — параллельный перенос, то и t-1 — параллельный
перенос. Так как параллельные переносы сохраняют ориентацию,
то Т с. Do cz D3, т. е. Т есть подгруппа группы сохраняющих ориен-
тацию движений Do (и подгруппа группы D3).
----------------------------0------------------------;-----
Пусть Р cz Е3 — произвольная фигура. Множество всех движе-
ний, переводящих фигуру Р в себя, будем обозначать через G (Р).
Иначе говоря, движение f в том и только в том случае принадлежит
множеству G (Р), если f (Р) = Р. Легко видеть, что для любой фи-
гуры Р множество G (Р) является группой движений, она называется
группой самосовмещенной фигуры Р. В самом деле, очевидно, что
137
e ZGtP'). Далее, пусть,/2 < G .(Р), т. е. /х l;P) = Pu f2 (Р) = р.
Тогда (/2-°/i)‘6P) =.£2 (Л (Р)) — Р> а это означает, что
/2 о Д € G.(P). Пусть, наконец, / £-G (Р), т. е. f(P) — :Р. Применяя
f~\ получаем Г1 (/(Р>) = /-J (Р), т. е. Р = f-1 (Р), а это .означает,
что f’1 С G (Р).
Рассмотрим несколько .примеров групп самосовмещений реаль-
ных предметов. На рисунке JO 1 изображены автомобиль, самолет,
человек. Каждое из этих тел .имеет .плоскость симметрии (мы здесь
-Рис. г101
отвлекаемся от несимметрии некоторых де-
талей внутреннего устройства; например, в
автомобиле руль смещен влево). Таким об-
разом, для каждой из фигур, изображен-
ных на рисунке 1П1, существуют два дви-
жения, переводящих эту фигуру в себя:
•тождественное отображение и зеркальная
симметрия. Других движений, обладающих
этим свойством, нет, т. ^е. в этих случаях
группа G (Р) состоит из двух элементов.
Группа самосовмещений морской звез-
ды (рис. 102, а) состоит из 10 элементов:
пять поворотов вокруг прямой Z (одним из
них является тождественное отображение)
и пять зеркальных симметрий (рис. J02, б).
Заметим, что верхняя и нижняя части те-
ла -морской звезды не симметричны, т. е.
"симметрия «относительно плоскости, про-
ходящей шерез .концы ее лучей, не принад-
лежит группе G (Р).
Для снежинки (рис. 103) группа само-
совмещений G (Р) состоит из 24 элементов:
шесть поворотов вокруг прямой Z, шесть
зеркальных .симметрий относительно пло-
скостей, содержащих Z, а также еще двенад-
цать движений, каждое из которых пред-
ставляет собой композицию одного из пе-
речисленных 12 движений и симметрии от-
носительно плоскости а, в которой ле-
жат концы лучей снежинки.
Рис. 102
Рис. 103
438
Рис. 104
Горный,
хрусталь
Поваренная- Исландской:
соль
шпат.
Полевой шпат
Рис. 105
В качестве примера фигуры, группа самоеовмещений которой
содержит бесконечное множество элементов, укажем окружность.
Действительно, обозначим через I прямую, перпендикулярную пло-
скости а, в которой лежит окружность, ипроходящую через ее центр
(рис. 104). Любой, поворот вокруг прямой I (а. также симметрия от-
носительно любой плоскости a zd I) переводит окружность Р в
себя, т. е. принадлежит группе G (Р). Кроме того, если, f— любое
из этих движений, as — симметрия относительно плоскости а, то
композиция f о s также принадлежит G (Р). Указанными.движения-
ми и исчерпывается в данном случае группа G (Р).
Группа движений играет важную роль не только, в. самой мате-
матике, но и в ее приложениях. В 1890 г. русский ученый Е. С. Фе-
доров доказал, что существует ровно 230 групп движений_простран-
ства, которые могут служить группами самоеовмещений атомных
структур различных кристаллов (рис. 105). Эта работа русского
ученого сейчас во всем мире считается основой науки о кристаллах,
а открытые им группы называются федоровскими группами.
Группа самоеовмещений находит различные приложения в хи-
мии, оптике, ядерной физике.
---------------------------е---------------------------
Пусть Р — куб с вершинами А, В, С, D, Д, Д, Dlt где
АВ— a, AD — ВС — Ь, АА^ВВ^— ССХ = Е>ВГ — с
(векторы а, Ь, с имеют одинаковую длину и попарно ортогональны).
Плоскость а, проходящая через середины ребер [Л'В], [ЛрД}, [DC],
[DjCJ, перпендикулярна этим ребрам, и потому точки А, Лх, D, Dt
симметричны точкам В, Въ С, Сг относительно плоскости а.(рис. 106).
Следовательно, при симметрии %, относительно плоскости а куб Р
переходит в себя, т. е. sx G G (Р).
Точно так же симметрия sa относительно плоскости р, проходя-
щей через середины ребер [ЛЛХ], [ВД], [СД], [DDX], переводит
«9
Рис. 109
куб Р в себя (рис. 107), т. е. s2 € G (Р). Симметрия s3 относительно
плоскости у, проходящей через середины ребер [ДО]; [ДхОх], [ВС],
[ВхСх] (рис. 108), также принадлежит группе G (Р).
Беря различные композиции движений slt s2, s3, мы можем любую
вершину куба Р перевести в любую другую его вершину. Например,
чтобы вершину D перевести в Alt нужно взять движение s3 о -s2
(симметрия s2 переводит./) в Ох, a s3 переводит Ох в Дх). Таким обра-
зом, для любых двух вершин куба Р в группе G (Р) существует дви-
жение, переводящее первую из этих вершин во вторую.
Заметим теперь, что симметрия s' относительно плоскости (ABD^
(также принадлежащая группе G (Р))' оставляет ребро [ДВ] непод-
вижным, а два других ребра, исходящие
из точки Д, т. е. [ДО] и [ДДх], меняет
местами (рис. 109). Вообще, какова бы ни
была вершина куба Р, в группе G (Р) суще-
ствует движение, которое одно из трех ре-
бер, исходящих из этой вершины, оставля-
ет неподвижным, а два других переставляв
ет между собой.
Теперь нетрудно подсчитать, из сколь-
ких элементов состоит группаG (Р). Возь-
мем ребра [ДДХ], [ДО], исходящие из вер-
шины Д. Далее, возьмем два ребра, исхо-
дящие из какой-либо другой вершины, на-
пример ребра [СхВх] и [CxDx] (рис. ПО).
Согласно сказанному выше существует дви-
жение f (; G (Р), переводящее А в Сх. Од-
нако при этом упорядоченная пара ребер
[ДДх], [ДО] может перейти не в [СхВх],
[СхОх], а в какую-либо другую пару. Но
тогда движением, оставляющим точку Сх
на месте, мы сможем полученную упоря-
доченную пару ребер перевести в [СхВх]»
[СхОх].
Рис. 110
140
Итак, в группе G (Р) имеется движение, переводящее вешни™ д
и упорядоченную пару ребер [ЛЛ^, ГЛ£>] в веош™ТгР» уЛ
[<да, [ЭД]. Это движение единственно .Действительно1, по теоУ
реме 18Д существуют ровно два движения, переводящие Л, АА. АО
в G, но при Э10м одно из них переводит вектор АВ в
СгС, а другое —в противоположный вектор, и, следовательно
только одно из этих движений переводит куб Р в себя (т. е. принад-
лежит G (Р)).
При каждом движении, принадлежащем группе G (Р), вершина
А и исходящие'из нее ребра [Л Л,], [ЛД] переходят в некоторую вер-
шину и пар$ исходящих из нее ребер. Значит, в группе G (Р) столь-
ко элементов, сколькими способами можно выбрать вершину куба
и упорядоченную пару исходящих из нее ребер. Так‘как в кубе
имеется 8 вершин и в каждой вершине можно выбрать 6 исходящих
из нее упорядоченных пар ребер, то группа G (Р) состоит из 8 • 6 =
— 48 элементов.
СОДЕРЖАНИЕ
ПРЕДИСЛОВИЕ ................. з
ВВЕДЕНИЕ..................... б
АКСИОМАТИКА Г.ВЕЙЛЯ
§ 1, Первая группа: аксиомы сложения векторов ... 8
§ 2. Вторая группа: аксиомы умножения вектора на чи-
сло ............................................... 13
§ 3. Третья группа: аксиомы размерности .............. 19
§ 4. Четвертая группа: аксиомы скалярного умноже-
ния ...................’ ............. 24
§ 5. Пятая группа: свойства точек . .................. 32
ПРЯМЫЕ и плот В ПРОСТРАНСТВЕ
§ 6. Прямая .......... 42
§ 7. Взаимное расположение двух прямых • • • • . 52
§ 8. Плоскость............................... 61
§ 9. Взаимное расположение прямой и плоскости . . 70
§ 10. Взаимное расположение двух плоскостей ... 78
§ 11. Ортогональность прямых и плоскостей .... 86
142
ВЫПУКЛЫЕ МНОГОГРАННИКИ
§ 12. Уравнение плоскости в координатах ............ 36
§ 13. Полупространства * ...... . 100
§ 14. Выпуклые фигуры ............................. 104
§ 15. Свойства выпуклых многогранников ............ 108
§ 16. Понятие о линейном программировании .... 117
ДВИЖЕНИЯ И KHEMIfflUICft
§ 17. Движения пространства . .. ............ 102
§ 18. Ориентация и виды движений ................. 120
§ 19. Группы движений . ......................... >87
Владимир Григорьевич
БОЛТЯНСКИЙ
•
Марк, Бенцианович
ВОЛОВИЧ
•
Алексей Дмитриевич
СЕМУШИН
ВЕКТОРНОЕ ИЗЛОЖЕНИЕ ГЕОМЕТРИИ
(в 9 классе средней школы)
©
Редактор
Г. С. Уманский
Художественный редактор
Е. Н. Карасик
Худож ник
Б. Л. Николаев
Технические редакторы
Т. В. Самсонова
- и М. И. Смирнова
Корректор
А. А. Гусельникова
ИБ № 6092
Сдано в набор 11.08.81. Подписано к печати 03.06.82. Формат 60 X 90’Де. Бум. типограф. № 3.
Гарнит. лит. Печать высокая. Усл. печ. л. 9. Усл. кр.-отт. 9,38. Уч.-изд. я. 7,88.
Тираж 100 000 экз. Заказ № 4860. Цена 20 коп.
Ордена Трудового Красного Знамени издательство «Просвещение» Государственного коми-
тета РСФСР по делам издательств, полиграфии и книжной торговли. Москва, 3-й проезд
Марьиной рощи, 41.
Отпечатано с матриц Саратовского ордена Трудового Красного Знамени полиграфического
комбината в областной типографии управления издательств, полиграфии и книжной тор*
говла Ивановского облисполкома, 153628, г. Иваново, ул. Типографская, 6.