Автор: Епишева О.Б.
Теги: методика преподавания учебных предметов в общеобразовательной школе геометрия педагогика
ISBN: 5-85944-129-0
Год: 2002
Текст
Специальная методика обученш
геометрии в средней школе
Курс лекции
ПРЕДИСЛОВИЕ
ББК 74.262
М 54
Печатается по решению Учебно-методического объединения высших
учебных заведений Российской Федерации по специальностям педагогического
образования на базе МИРУ (протокой № 8 от 8 окгября 2002 г.)
ISBN 5 - 85944-129 -0
О.Б. Епишева. Специальная методика обучения геометрии в средней
школе: Курс лекций: Учеб, пособие для студентов физ.-мат. спец. пед. вузов. -
Тобольск: ТГПИ им. Д.И. Менделеева. 2002. — 138 с.
В пособии на основе деятельностного подхода к обучению раскрываются
общие методические закономерности н особенности изучения материала
содержательно-методических линий школьного курса геометрии, выделенных в
федеральном компоненте Государе!венного стандарта для средней школы по
образовательной области «Математика».
Резензенты:
доктор педагогических наук, профессор В.А Гусев;
доктор педагогических наук, профессор В.А. Дадингер.
ISBN 5-85944- 129-0
© О.Б. Епишева. 2002 г.
Настоящее пособие является третьей частью авторского курса лекций по
теории и методике преподавания математики в средней школе для cry дейтон
педвуза. Общие методические закономерности обучения математике в средней
школе, рассмотренные в первой части [1], здесь специализируются по
содержательно-методическим линиям школьного курса геометрии, выделенным в
федеральном компоненте Государственного стандарта для средней школы по
образовательной области “Математика” и проходящим через весь школьный курс
математики. Отсюда название курса - специальная методика обучения, а
общепринятый термин “частная методика” мы относим к методике, изучения
конкретных тем; она получается приложением специальных закономерностей
обучения к теме урока п реализуется на семинарских занятиях.
Важное значение имеет первая лекция, в которой выделено все общее в
методике изучения материала данного курса и обращение к которой обязательно
при рассмотрении всех последующих вопросов; это помогает научить студентов
видеть и использовать общие закономерности обучения в конкретных случаях.
Иому способствует, на наш взгляд, и единый план рассмотрения методики
изучения каждой содержательно-методической линии; все это подробно
представлено в предыдущем курсе [2). Кроме того, в тексте декций есть указания на
дополнительную самостоятельную работу студентов с литературой, дополняющей
и.тн иллюстрирующей материал лекции и также помогающей конкретизировать
общие теоретические положения при подготовке к семинарским занятиям н на
педагогической практике.
В первой* части каждой лекции по методике изучения содержатся ьно-
ыешдпческой линии мы обращаем внимание на компактную характеристику его
кинематического содержания и основных математических идеи и методов, т.к. без
и ого рассмотрение методических особенностей оказывается лишенным
шиемагического фундамента. При этом в помощь студенту рекомендуется
чор.нценце к вузовским учебникам математики, пособиям для учителя математики
и абшуриентов. Вторая часть лекции традиционная для такого курса здесь мы
привлекаем студентов к использованию материалов периодической печати.
Остальная часть лекции oipawaci ангорскую позицию - необходимо учить
студентов конкретизации и дифференциации учебных целей и возможности
проектирования разливающих и воспитательных целей обучения математике;
выделять не только основные типы математических задач, по и приоритетные
обобщенные приемы их решения (формирование которых является одной из
особенностей предлагаемой методики); показывать примеры специальных учебных
задач в данной линии.
Рассмотрение основных методов обучения в конкретной содержательно-
методической линии складывается из трех частей - I) Самостоятельное обращение
студентов к закономерностям использования общепедагогических методов, форм и
средств обучения применительно к данному материалу в Кинге [)]; 2) общие
методические замечания и рекомендации по использованию специальных
(зависящих от математического содержания материала) методов и приемов
обучения, 3) их представление в виде методико-технологических цепочек.
Примерный объем первой и второй лекций - по 4 часа, остальных - по 2 часа.
Возможное распределение материала лекций по семестрам, в зависимости от
учебного плана вуза, может быть следующим: курс общей методики читается в 5-м
и 6-м семестрах, в 7-м - курс специальной методики изучения арифметики и
алгебры в основной школе; в 8-м - курс методики геометрии в основной школе;
материал остальных лекций, относящийся к старшей школе того и другого курса - в
9 семестре (в зависимости от организации обучения в этом семестре материал
может изучаться студентами самостоятельно).
Автор выражает благодарность рецензентам - доктору педагогических наук,
профессору В.А Гусеву и доктору педагогических наук, профессору
В А. Далингеру.
Замечания и предложения по содержанию пособия будут с благодарностью
приняты по адресу: 626150. Тюменская область, г. Тобольск, ул. С. Ремезова,
д. 116, кн. 38 (а/я 5). Домашний телефон 8 (3451 1) - 5 - 89 -56.
Епишева О. Б
ЛЕКЦИЯ I
Общие вопросы теории и методики обучения геометрии в школе
План;
1.1. Общие задачи курс геометрии в средней общеобразовательной школе.
1.2. Содержательно-методические Динин и структура программы школьного
курса геометрии.
1.3. Основные учебники и учебные пособия для учащихся.
1.4. Общие психолого-педагогические закономерности изучения каждой
содержательно-методической линии школьного курса математики
1.5. Общая схема логико-методического анализа каждой содержательно-
методической линии школьного курса математики.
1.1. Общие задачи курса геометрии
в средней общеобразовательной школе
I 1.1. Геометрия (от греческого - землемерие) - эго математическая
дисциплина, первоначальным предметом которой являются пространственные
ошошеиня и формы тел, отвлеченные от прочих свойств реальных предметов -
геометрические фигуры, их размеры и свойства Вопросы геометрии, наряду с
арифметикой, были первыми математическими вопросами, с которыми человек
встретился уже на ранних ступенях своего развития.
Первая стаоия развития геометрии характеризуется накоплением отдельных
фактов, имеющих- непосредственное значение для бытовых и государственных
iioipeOHocieii, прежде всего, для измерения длин, площадей, объемов, и первыми
попытками установления связей между отдельными фактами. Простейшие
1 сометрнческпе сведения и понятия были известны еще древним египтянам (начало
1 ю тысячелетня до н. э.), которые формулировали геометрические утверждения в
пиле правил с примитивным обоснованием или без нею. Свои первые шаги
тсомегрия делала как физическая наука, описывая свойства физически
и in .но.таемых объектов и величин (Вавилон, Египет, Индия и др.). Начиная с VII в
г» и » и до I в. н. з. развитое геометрии происходило в основном н Древней
л
5
Греции; накапливались сведения о метрических соотношениях в треугольнике
измерениях площадей н объемов, пропорциях и подобии фигур, конических
сечениях, задачах на построение; появились первые доказательства геометрических
утверждений.
Вторая стадия развития геометрии связана с собранием известных фактов
геометрии и их логической систематизацией в книгах «Начала» александрийского
ученого Евклида (около 300 до н. э.>, в котором «первые сложились основы
аксиоматического метода (fl, лк 11, с. 150]). Евклид последовательно и дедуктивно
по схеме Аристотеля изложил основные геометрические знания, добытые многими
поколениями ученых. Предметом евклидовой геометрии стали отношения и формы
тел пространства, свойства которого определялись сформулированными Евклидом
аксиомами. Развитие астрономии и геодезии привело к созданию плоской и
сферической тригонометрии.
Дальнейшее развитие геометрии, вплоть до XVII в., происходило не столь
интенсивно, затем ее развитию способствовало возрождение наук и искусств в
Европе. Теория перспективы, задача которой состояла в изображении тел на
плоскости, была в центре внимания художников и архитекторов, и эта потребность
привела к зарождению проективной геометрии. Совершенно новый подход к
решению геометрических вопросов предложил в 1-н половине XVII в. Р. Декарт,
который создал метод координат [I, лк II, с. 159J, позволяющий привлечь в
геометрию методы алгебры, а затем и анализа. В это время появляется
аналитическая геометрия (кривые и поверхности, задаваемые алгебраическими
уравнениями, исследуются методами алгебры) и в XV1JI в. - Л. Эйлером и
Г. Монжем закладываются основы дифференциальной геометрии (применением в
геометрии методов математического анализа). В результате взаимодействия
геометрии с алгеброй и анализом в дальнейшем возникли специальные исчисления,
удобные для использования в геометрии и других разделах математики (векторное
исчисление, тензорное исчисление, метод дифференциальных форм}. Разделы
геометрии, не опирающиеся на методы алгебры и анализа н оперирующие
непосредственно с геометрическими образами, получили название синтетической
геометрии
Третья стадия развития геометрии связана с именем российского математика
П.И. Лобачевского, усгаиовпвшего, что изучение простри нет пенных форм и
огношений реального мира приводит нс только к геометрии Евклида и связанному
и ней понятию свесщцовл пространства (так хорошо отражающего простейшие
физические наблюдения» что до XIX в. оно как бы отождествлялось с физическим
пространством)» но и к другим геометриям и другим понятиям пространства. На
основе многовекового анализа «Начал» Евклида усилиями многих ученых (Г.
Пеано. М. Паша, ЛИ. Лобачевского, Я. Больаи, К.-Ф. Гаусса, Д. 1 нльберта) удалось
сощать полный, непротиворечивый список независимых аксиом евклидовой
геометрии и. таким образом, завершить разработку аксиоматического метода
построения геометрии. В 1826 г. появляется первая логически непротиворечивая
геометрия, отличная от евклидовой - геометрия НИ. Лобачевского, затем другие
неевклидовы геометрии (Б. Риман и др.) и идея многомерного пространства. Одним
иг стимулов развития и систематизации геометрии явилась ее связь с теорией групп
(<(>. Клейн, Э. Картам. С Ли) и логический анализ основ геометрии. В XX в.
геометрия стала широко разветвленной (алгебраическая геометрия, тензорный
анализ и др.).
Так как геометрия возникла из задач практической деятельности людей, то ее
предложения отражают реальную действительность и находят многочисленные
ирныенения. Геометрические идеи и методы оказались весьма важными и
плодотворными во многих областях человеческого знания (многочисленные
физические теории, дифференциальные уравнения, номография и т.п.).
Издавна различают планиметрию - раздел геометрия, в котором изучаются
фигуры на плоскости, и стереометрию - раздел геометрии, изучающий фигуры в
пространстве. а также выделяют элементарную геометрию - геометрию,
определяемую, в основном, группой перемещений (движений, изометрий) и
группой подобия. Однако содержание элементарной геометрии не исчерпывается
ум гапными преобразованиями: Так, к ней оти.осяг преобразование инверсии,
поприсы сферической геометрии, элементы геометрических построений
(ыиктруктивная геометрия), теорию измерения геометрических величии И другие
гпигросы. Элементарная геометрия продолжает развиваться и в наше время.
1
1.1.2. Школьный курс геометрии получен путем отбора материал,
соогвстствуюшсго научною курса элементарной геометрии и его дидактическо!
обработки. Его структура в определенной степени отражает исторические стадии
развития геометрии [1. лк. I. с. 14, лк. 8, с. 10] и содержит грн этап:
пропедевтический курс (его цель в - духе первой стадии развития геометрии
накопление на основе наблюдений и измерений простейших геометрически'
фактов. приобретение представлений о важнейших геометрических образах
овладение терминологией н простейшими геометрическими инструментами)
систематический курс планиметрии (его цель - логическая обработка изучаемых
геометрических фактов; это - элементарная геометрия, которая является в своей
основе евклидовой геометрией на плоскости); систематический курс
стереометрии (аналогичный курсу планиметрии). Логическое строение
систематических курсов традиционно составляют 4 положения - 1) выделяются
основные (первоначальные) понятия, принимаемые без определения (точка, прямая
и т. д.); 2) формулируются аксиомы - предложения, принимаемые без
доказательства, в которых раскрываются свойства основных понятий и отношений
между ними и система которых должна обладать свойствами полноты,
непротиворечивости, независимости; 3) последовательно определяются другие
понятия курса, через основные и раннее определенные понятия (главным образом,
через указание родового понятия и видовых отличий); 4) последовательно
формулируются и доказываются свойства этих понятий (теоремы) с опорой на
аксиомы и раннее доказанные теоремы.
От выбора первоначальных понятий курса геометрии зависят остальные из
отмеченных выше положений - система аксиом, теоремы и построение курса в
целом (с.м. Г. Глейзер. А. Калина. «Возможности логического построения
гЛЧ
школьных курсов геометрии», газета «Математика», 2000 С. 1-4), Вам известны
имеющая огромное значение для своего времени система аксиом элементарной
геометрии Евклида; первач достаточно строгая аксиоматика Д. Гильберта (за
которую он получил первую премию имени НИ. Лобачевского): точечно-векторная
аксиоматика Г. Вейля; аксиома! ика. основанная на отношении симметрии и др
(подробнее об этом. (3. гл. )5. § E2J, |4. гл. 16]).
8
Норма швные документы [5] определяют следующие основные задачи курса
ы-ометрин в общеобразовательных учреждениях:
формирование представлений о геометрических фигурах как
идеализированных образах реальных объектов: формирование умений
использовать геометрический язык для описания предметов окружающего мира;
ризвитие представлений о некоторых областях применения геометрии в быту,
пауке, технике, искусстве;
- приобретение первоначального опыта геометрической деятельности,
пинанной с геометрическими фигурами, их распознаванием н изображением, с
использованием геометрических инструментов для выполнения чертежей, с
щмерением геометрических величин;
формирование систематизированных сведений о плоских и
пространственных геометрических фигурах и основных геометрических
"Iпошевнях: формирование умения применять свойства фигур для решения
математических и практических задач;
- формирование представлений об изучаемых понятиях и методах геометрии
гак важнейших средствах математического моделирования реальных процессов и
пилений, о геометрии как элементе человеческой культуры, о ее применении в
фактике и научном познании;
- развитие логического мышления, интеллектуальных и речевых умений и
'мсипя использовать различные языки геометрии (словесный, символический,
301 ический).
1.2. Содержательно-методические линии и структура программы
школьного курса геометрии
|,2.Г Как уже отмечалось [I. лк.4, с. 57; 2, с. 7], во время любых изменений
* илержация школьных программ в них должен оставаться некоторый “костяк" пли
ядро” (акад. А.И. Маркушевич) из таких тем, без изучения которых учащиеся не
•юиучат представления о математике и ее методах. Они концентрируют в себе
ьпемагичсские знания, которыми должен обладать каждый человек в современном
"Hiiici гое. необходимые, в повседневной жизни для решения возникающих в
Ч
ггл п с, I И Лобачевского и других геометров XIX в.. Ф. Клейна, в программах по
практике задач, а также для решения внутриматематическнх проблем и зад?' ’
. nui'-iTiiTu ппя парных средних учебных заведений XIX — нач. XX в. в России,
прикладного характера Совокупность таких тем получила назвашк11 Kipl"Д Р ' 5
.. , 11апПимео в программе и учебнике М.О. Косинского (1865 /.) «Наглядная
codcpwamwbw-MeniodmecKux пинизГ школьного курса математики. например. upoi^
, уморня» изложение начинается с рассмотрения геометрических тел. образы которых
и курсе геометрии, построенном на раздельном изучении планиметрии i ' ,
1.ШСПССЯ могут найти в окружающем их мире (куба, шестигранном призмы, цилиндра), на
стереометрии. Стандартом выделяются следующие традиционные содержательно.............фпгуры „ ||Х свойства; в программе Мниистерсгаа
методические линии: «Геометрические фигуры и щ с<!0™т». «Геомстрзтеск,^ 1|рс)ссс1,1е[111Я для мужских гнМНгП|1Й „ прогимназий (1897 г.) в 5-м классе
построения». «Геометрические величины». Содержанке этого матсриалг(1(1(.Л1|опагастся и)учсцие взаимного расположения линий и плоскостей, многогранных
незначительно менялось со времен Евклида, ф. Клейн называл просто 1W1№ и (>.м _ правильных многогранников; характерной особенностью программ 1917-
удивительным историческим обстоятельством тот факт, что выработался взгляд, Г> । । было изучение каждой плоской фигуры в пространстве.
согласно которому «Начала» Евклида является подходящим учебником для В середине XX в. идея фузноиизма в пашей стране развивалась в работах
начального преподавания. Эту же мысль в 60-х годах XX в. в несколько другой И,И Аргунова, М-Б. Балка, Л.М. Бескина, Г Д. Глейзера, В.В Кутузова, Г.Г. Масловой,
форме выразил идеолог реформы математического образования в нашей стране *'М Хабиба и ар. и получила свое практическое воплощение в программах 60-х годов.
академик АН. Колмогоров: «Сложившийся сейчас характер преподавания
геометрии в 6-8 классах настолько непоследователен в своих методических
установках, что его можно объяснить только исторически как результат
незаконного компромисса между- стремлением к упрощению курса и желанием
сохранить видимость «строгости» из ложения».
С этих позиций в процессе реформы математического образования на этом
этапе была не только упрошена структура школьного курса геометрии по
сравнению с евклидовой традицией, но и в его содержание включены такие линии
как «Декарпюеы координаты», «Геометрические преобразования», «Векторы».
В содержании школьных программ по геометрии в той или иной степени
находят отражение концепции модернизации математического образования
Известны программы по геометрии для средних общеобразовательных учрежде-
ний различных профилей, школ, классов [2. лк I. с. 8-9: с. 5J, а также
экспериментальные программы по геометрии, построенные на основе идеи
фузчонизма (от латинского fuzio - слияние) - совместном изучении плоских и
пространственных фигур, позволяющем устранить разрыв школьного курса
геометрии с жизнью и развивать восприятие прос|ранства в соответствии с
психологическими особенностями возраста учащихся Отражение идеи слияния
планиметрии и стереометрии можно найти еще в трудах Авиценны,
я ш в курс геометрии 8-летней школы ввели элементы стереометрии. На необходимость
|||||>лсчеиия пространственных фигур, распределенных по всем разделам курса
iiifniiiiML-rpiiii. указывается в объяснительной записке к программе 8-летней школы 1967г
I Ml с годы XX в интерес к идее фузнонизма возобновился. Большую роль в этом
iiipvtil работы Г.Д. Глейзера, который, в частности, предлагал следующую структуру
IlliB’Ki предмета геометрии в средней школе: I) курс «наглядной геометрии» (начальная
iiinitn.i) - основное внимание работе с пространственными фигурами для создания
> । . л ipiiui.пленных представлений; 2) курс «практической геометрии» (5-6 классы) -
ihihimi1 то с основными фактами планиметрии и стереометрии; 3) систематический курс
1 'Mi'ipiiii» (основная школа), построенный на фузионистских принципах и индуктнвно-
имикиой основе, 4) небольшой аксиоматически построенный курс (старшая школа).
Птнюлсе пзвестными.фузионистскн.ми курсами в настоящее время являются
|н и 5- Н классов В.А. Гусева в рамках Межгосударственного проекта “Экология
li ЛИ 1'1СК1Пка’' («Математика в школе». 2002. №3. С. 4-8), Н.С. Подходовой
(Мигм,пика в школе». 1997. №2. С 29-34; 2000. № 10. С. 54-58).
А Кпсковкниа, Т.Г. Ходот (газета «Математика», 2000. №9. С- 19-20). Основой
П\ нш ipneims является стратегия «Я - в пространстве», центральной
• и рк.не шно-методической линией - изучение плоских фигур и их свойств как
i-н |«-11 пространственных геометрических фигур. Учебники (и другая литература)
1и ii.iiiiHXCH 5-6 классов. содержащие геометрический материал, реализуют два
10
н
Н'бички геометрии А.Д. Александрова, А.Д. Вернера («Математика в школе»,
ччо № 5, газста «Математика». 2000. №№1.2,6,13.); Л.С. Атанасяна («Математика
iiiko.’Ic». 1996. №5. - С. 40-50 и 69-78). А.В. Погорелова, («Математика в школе».
•••Я. №5. - С.34-40 п 64-69). И.М. Смирновой («Математика в школе», 1997. № 4. -
19-22. 2000. №3). И.Ф. Шарыгина («Математика в школе». 1999. № I. С. 18-24).
Авторы реализуют в учебниках свою концепцию программы
|нп11стствующсго курса геометрии, придают им соответствующий характер
1умп11птярный, прикладной, развивающего или углубленного изучения). Особенно
цо касается пропедевтического курса геометрии к профильных учебников гю
•ОМОТрИП.
1,3,2. Геомегрический материал в учебниках математики $-6 классов
|| Я Виленкина. В.И. Жохова и др. - это «Курс наглядно-практической геометрии».
IW нь которого - подготовить учащихся к осознанному усвоению систематического
урит геометрии в 7 классе, развивать интерес учащихся к этому предмету' и
uflnci чип, его у глублецное изучение в 8 классе.
П учебниках "Математика 5-6:’ Н.Б. Истоминой специальный раздел также
н«1Ыплсгся «Практическая геометрия».
I еометрнческая составляющая в учебных комплектах для 5-6 классов
I И Дорофеева и И.Ф. Шарыгина значительно отличается от геометрического
•«орнпла пропедевтической направленности, традиционного для действующих
I пиков математики 5-6 классов, в частности, увеличением обьема материала
। ^метрического содержания. Речь идет о иоглябной геометрии. изучение
poll направлено на достижение ведущей целевую установку курса - развитие
''и и инка. Геометрия, отвечая внутренним потребностям детей 10-12 лет, может
««ibHiaiL на них развивающее воздействие; дети же готовы заниматься пластом
। м< tpiui, который связан с познанием геометрических образов путем созерцания
и 1ы трпмента («Математика и школе». 1999. №5. С. 15-22). Известна также книга
•I *1 Шарыгина п Л.Н Г-рганжиевой «Наглядная геометрия».
Учебник математики для 5-6 классов Г.В. Дорофеева и Л.Г. Петерсон
ip-. Hi мшриваег два варианта программы (первый - 4 ч. в неделю, второй - 5 ч.);
основных направления - развитие пространственных представлений учашпхо1
через наглядное (игровое, сюжетное и т.п.) знакомство с геометрическим!
фшурамп и использование курса 5-6 классов для более раннего включении
учащихся в систематическое изучение геометрии на доступном для них уровне d
тем самым, включающее данный курс в систему непрерывного геометрическог'
образования (Т.Г. Ходот. «Курс геометрии 5-6 классов в структуре непрерывное
геометрического образования», газета «Математика». 2000. №18. С. 11-12).
В данном курсе лекций рассматриваются методические закономерности
изучения содержательно-методических линий действующего курса геометрии. Kai!
и при изучении содержательно-методических линий курса арифметики, алгебры К
начал анализа, содержание выделенных линий курса невозможно изучить в одно),
месте, в пределах какой-либо одной темы программы. Это объясняется, с одно!
стороны, закономерностями истории развития геометрического знания
включающей его возникновение, углубление, расширение, обобщение с течением
времени (а школьное обучение повторяет в некоторой степени исторический путь)
с другой - психологическими закономерностями понимания и усвоеннг
математического материала [I, лк 1, с. 13|. Поэтому, отражая длительный опьп
обучения математике и в соответствии с мировой практикой, школьный курс
геометрии в настоящее время имеет следующую структуру: пропедевтический курс
(1-4, 5-6 классы), систематический курс планиметрии (7-9 классы),
систематический курс геометрии (10-1) классы).
1.3. Основные учебники и учебные пособия для учащихся
1.3.1. Перечень основных учебников федеральною комплекта и других
пособий по математике (с авторским тематическим планированием, отражающим
их особенности) можно найти в журнале ‘‘Математика в школе”, 1997, №3; 2002,
№3 (с.55-57) н 4, газете «Математика», 2000. №№ 14. 16, 17. Это - учебники
математики для 5-6 классов (по первой фамилии шпоров или редактора)
НЯ. Виленкина. Л.Н. Шеврона. ГВ. Дорофеева и В.Ф. Шарыгина («Математика в
школе». 1999. №5. С.15-22); Н.П. Зубаревой (газета «Математика». 2000. №10. С.2);
12
13
oba варианта содержат темы, связанные с логической составляющей курении шинном и наглядном уровне к изучению систематического курса leoMcrpiii
матоматки и раздел «Геометрические фигуры на плоскости и в пространство». । чи i Математика». 2000. №9. 2000. С. 19-20).
Учебники Л.Н. Шеврипа выделяют в отдельные гемы «Геометрически I ) J Теоретический материал учебника «Геометрия, 7-9» JI.С. Атанасяна и
фигуры» и «Измерение площадей и объемов» (5 класс), «Координатная плоскосты ip и пожен доступно п одновременно строго, с учетом психологических
с рассмотрением перпендикулярности и параллельности прямых (6 класс), «Учимо.... num. ieii школьников и использованием оригинальных приемов изложения,
рассуждать при решении задач». Материал организован с учетом особенносте|1-ч и Hioc иииманис уделяется формулировке задач, нередко приводится несколько
психологии учащихся, с опорой па жизненные ситуации и увлекательности iiicuiili одной задачи. Учебник «Геометрия, 10-11» является продолжением
изложения, с организацией диалога с учеником, п. рпшо сохраняет аналогичную структуру. Стиль изложения становится более
В учебнике «Математика» И.И. Зубаревой, как и в других новых учебника.»
математики для 5-6-х классов, значительно увеличен, по сравнению <
традиционным, объем материала, посвященного пространственным фигурам. II
начале курса вводится понятие расстояния, которое затем используется при
изучении некоторых понятий (серединный перпендикуляр, окружность,
биссектриса).
Альтернативные учебник геометрии Н.С Подходовой для 5-6 классов
«Геометрия в пространстве» продолжает идеи «Развивающей геометрии» для 1-3
классов: построен в концепции «личность-среда» (рассмотрение окружающего
мира с геометрических позиций на основе использования личностного опыта
детей), направлен на развитие средствами геометрии пространственного мышления
как разновидности образного. В построении содержания используются
психологические закономерности развития мышления учащихся, комплексное
изучение объемных и плоских геометрических фигур, конкретные .модели и
знакомые учащимся образы, рассмотрение объектов с разных позиций и
многовариантность решения задач (с демонстрацией п конструированием),
сказочные сюжеты и юмористические ситуации.
В учебнике «Геомегрня, 5-6» Т.Г. Ходот и др. также представлен новы!,
подход к начальному обучению геометрии, направленный на развитие ребенка
средствами геометрии на любой стадии формирования его интеллекта. Три
основные составляющие концепции курса (фигуры, логика и практическая
применимость) позволяют развивать образное и логическое мышление ребснк.1,
воспитывать у него навыки практической деятельности, подготовить учащихся и,т
| Ч'ми п.пым п строгим, с соблюдением систематичности, последовательности и
иииомпчиости изложения. К учебникам разработаны рабочие тетради я
in цинические материалы.
II учебниках А.В. Погорелова (7-9 и 10-11) ведущую роль в построении курса
И। । трин играет метод координат: координаты вводятся и используются начиная с
и при изучении его различных разделов и при решении геометрических
। жч । кобениостью нового их издания является лаконичное изложение
ukiiiiiiio (часто - на основе метода координат) построенного содержания.
Il44iibh задачи решаются в тексте, при этом уделяется внимание логике
1ИМ । Kiiufi и обоснованию решения. Каждому параграфу приданы контрольные
ц»ч11,1 содержатся рекомендации для учащихся: «Что надо делать, чтобы хорошо
iwuniii ио геометрии», «Использование аксиом для доказательства теорем», «Как
luBiiiicn по учебнику самостоятельно» и другие. К учебникам разработаны
“Ш । < (ради и дидактические материалы.
II учебниках И.Ф. Шарыгина для 7-11 классов (два варианта) уменьшена роль
। ч» ц,ш’-.10гическнх рассуждений, уделяется больше внимания методам решения
Ц(1Ы< ipii'iecKux задач (выделена тема «Виды геометрических задач и методы их
riiiiH i). причем планиметрические задачи рассматриваются не только на
*111111 пи и на пространственных объектах. Учебники включают задания
ю иг их уровней сложности и разделы, предназначенные для углубленного
|Ц1|>1П1Н
II учебниках геометрии АЛ. Вернера и др. для 7-9 классов параллельно
1М11ЧНИ ипаппметрня и стереометрия, причем знакомство со стереометрией
ведется описательно, с опорой на наглядные представления. Учебник для 7 клан >1йн. .4.ра1ователыюн программы курса геометрии 10-1) классов, поэтому он
(победитель конкурса «Новые учебники для российских школ», проводимы ,,"*и 1 использоваться и я обычных классах.
Национальным фондом подютоики кадров и МО РФ) - это «строительна Ысиеримситальныс учебники «Геометрия» В.А. Гусева реализуют его
геометрия», где прежде всего выделяется 'задача построения фигур«’"Щсншю к программу и построены па идее фузнонизма; их содержание
(последовательность - прямая, круг и шар, угол, треугольник) с требуемым ыигцшпчсно на формирование общей картины мира и мыслительной деятельности
свойствами и обоснование того, что ггостроенная фигура обладает этим
свойствами. При этом проводится аналогия между плоскими и неплоским
фигурами, внутри задач используются рубрики: «Смотря», «Рисуем*
«Представляем» «Исследуем», «Доказываем» и т.п. В учебнике 8-го класса
«вычислительная геометрия», в которой основные задачи связаны с вычисление!
основных геометрических величин. Каждая глава учебников заканчиваете
вопросами и задачами на повторение, заключительные главы - заданп
повышенной трудности.
Новый учебник «Геометрия, 7-9» И.М. Смирновой и В.А. Смирнова следуе1
традициям преподавания геометрии, заложенным в учебнике А.П. Киселева i
построен аксиоматически. Аксиомы вводятся постепенно по мере необходимости, I
том числе, и аксиома параллельности вводится нс сразу, а после изложен»»
абсолютной геометрии. Помимо классических разделов планиметрии, в учебы»
включен популярный материал - графы, теорема Эйлера, проблема трех красок
золотое сечение, задачи на разрезание, задачи на оптимизацию и др В конш
учебника - «Начала стереометрии», целью изучения которых являете»
распространение изученных понятий и свойств планиметрии на случай
пространства, пропедевтика стереометрии, развитие пространственны»
представлений учащихся.
В учебниках «Геометрия, 10-1 С» И.М. Смирновой для классов гуманитарно^
профиля геометрические знания вписываются и общий контекст человечески»
ценностей, сопоставляются с историей и перспективными направлениями развнтщ
геометрии, с геометрическими закономерностями в искусстве. Иллюстративны П
материю! учебника, органично связанный с повествованием, включает, кроме
обязательных геометрических чертежей, репродукции шедевров архитектуры
скульптуры, живописи, рисунка. В учебнике содержатся все основные темы
it
ышнхея. развитие интуиции и геометрического воображения; используется
Tiiu.iuoe количество наглядности, теоретико-множественные понятия и символы,
||||11111111И непрерывности в изложении материала.
I И (Инине психолого-педагогические закономерности изучения каждой
содержательно-методической линии школьного курса математики
I 4 I Общие психологические закономерности деятельности ученика по
киник любого материала рассмотрены нами в курсе общей методики [1, лк.1,
I' I 1| н в курсе лекций [2, лк.1, с. 14-18]. Повторяя эти закономерности,
и ikiiiiii г полный цикл учебно-познавательной деятельности (УПД) ученика и
si и 1 Босния; педагогические закономерности деятельности учителя по
||р4Н1)сип1о этой деятельностью учащихся (пять ее этапов) и соответствующие им
.till учебного процесс; задачу формирования в процессе обучения математике
" iiirinikix приемов учебной деятельности учащихся и соответствующую
it । ini ЦЧССК) ю цепочку деятельности учителя.
II Метлике обучения математике выделяются наиболее подходящие для
>*«4'<1« содержания и этапа учебного процесса общие методы и средства
Н1«>«ич । ль по рассмотрено в курсе общей методики [1, лк. 12, п. 2, с. 173-176 и
Н||<| но и лк 7-10]: там же отмечаются и другие общие условия выбора
Ли,г пе'Ы1"| нческих методов и средств обучения математике - зафиксированный в
Ф <рпчче П" математике возраст учащихся; этапы усвоения знаний и способов
!• h U lin' in учащимися н соответствующий им Тип или этап урока {I, лк 12, п. 2.
11 I 7б| 1'р/>вень учебной деятельности учащихся, определяющий уровневую
Ц ]•• finii.ni!»!>> не только содержания, но и методов обучения; достижение
i«»wu iii"U|rrf п воспитательных целей обучения математике; этапы формирования
...Лип иных приемов учебной деятельности учащихся; содержание изучаемого
|7
материала, о котором мы будем говорить в построении методики изучения каждо
содержательно-методической линии отдельно
I 4.2. Общие закономерности выбора методов обучения геометрии связаны
тремя его этапами в школьном курсе - пропедевтическим. систематическим курсон
планиметрии и систематическим курсом стереометрии.
Большую роль в обучении геометрии на первых этапах изучения отдельны
гем и, особенно, в пропедевтическом курсе, играют наглядные и практические
конструктивные, интуитивные и конкретно-индуктивные методы: наблюдение
рассмотрение готовых чертежей, рисунков н моделей: вычерчивание, вырезание i
складывание из бумаги. лепка и конструирование заданных фигур, моделиро-вание
оригами; практические работы - выполнение чертежей с помощью простсйиин
геометрических инструментов, измерения (своеобразная «геометрическая фнзиг.п
в упражнениях - опытное обоснование фактов и их индуктивное обобщение)
дидактические игры с использованием практических заданий, исторического и
занимательного материала, направленные не только на усвоение геометрическою
содержания, но и на развитие познавательных процессов (внимания, памяти,
представления, воображения, сравнения, поиска закономерностей н др.) [1, лк. (М,
с. 105-124]. Это следует из особенностей содержания и истории развития
геометрии, а также из возрастных и логико-психологических особенностей
мыслительной деятельности в области математики (в частности, преобладание у
младших школьников образного и практически-действенного мышления) [1. лк. \
с. 27].
В систематическом курсе планиметрии (при сохранении наглядности и
индукции) осуществляется постепенный переход к дедуктивным методам обученш
- методам логики н специальным математическим методам, определяемым
содержанием изучаемого материала [1, лк. 10, с. 1275—147]. Систематический ку;к
стереометрии с первых уроков изучается дедуктивными методами на основе cut
аксиоматического построения {1, лк. 11, с. 148-162).
Применение каждого метода обучения целесообразно представить в виде
называемой методико-технологической цепочки, в основе построения которы)
лежат психолого-педагогические закономерности обучения.
I |,1 Па протяжении изучения всего курса геометрии учителю необходимо
Hiiii'i я об усвоении учащимися его логического строения. Ниже прпподятоя
o/iiimmc .1 'Hi этой цели общеучебные (и общематсматичсскис) приемы учебной
hi it,я in учащихся. которые должны noctcneuiio формироваться.
Усвоение и запоминание определения понятия:
1) ипомише общую структуру определения понятия;
1 hi it oin к составные части этой структуры в определении, которое нужно
I опит..
I) vui nine и запомните отдельные составляющие части определения;
I) luiinMiiiiie определение в целом
Контроль усвоения определения понятия'
проверьте, правильно ли
11 ил in ж термин (определяемое понятие);
’) )| ,н,П1 рол (родовое понятие), является ли он ближайшим;
U умгыиы видовые отличия, являются ли они а) необходимыми, б) достаточными
I ин» IMII ПОНЯТИЯ,
1> ....... связи между признаками понятия;
I) 11| прму шроваио и построено предложение в целом.
Изучение содержания теоремы (задачи):
11 ИИ11М.11СПЫ1О прочитайте формулировку;
I г гни нужно, определите понятия и сформулируйте теоремы (задачи), входящие в
11 • лип,' .тайной как составные части;
I) ин нужно, сделайте иллюстрацию содержания (чертеж, рисунок, схему);
') iiiiiiiiiiuie содержание кратко со словами “дано" и “доказать” (“найти”,
pniiih", “вычислить"). с использованием специальных символов и обозначений на
I рипии
Усвоение и запоминание теоремы:
I) npi'4iii.iiiie формулировку теоремы (по учебнику, тетради), поймите ее смысл,
• ч iy* имеющуюся иллюстрацию;
I) г in чертежа нет, сделайте его сами, сели есть - самостоятельно воспроизведите
) и iv'in те содержание теоремы;
11 пну чи те формулировку теоремы;
h up nii.itiTc доказательство, обосновывая каждый этап, следя по чертежу' и
в и первом чтении понять его основную идею;
при июрнчном чтении уделите внимание деталям доказательства и обоснованию
> ш»|ни гч пн что-то забыто, восстановите в памяти;
1 ) в,и проц шедите доказательство устно или письменно;
II nip i.illie дрггой чертеж и краткую запись доказательства;
ЧI ши । г и те теорему самостоятельно с помощью своего чертежа;
I'll и нужно, проверьте себя, прочитав доказательство еще раз,
111 |Ц|Цр"|>\ йте найти другой способ доказательства,
II ) и in u<- псе понятно, отметьте неясное и обратитесь к учителю.
Контроль усвоения теоремы
I) про», pi те ирапильно ли усвоена формулировка теоремы;
I н intuit теорему самостоятельно;
18
19
3) проверьте, правильно ли испою. ювапы при доказательстве известные теоремы 1
определения;
4) проверьте правильность выполнения чертежа;
5| проверьте ход доказательства;
6; проверьте, удалось ли достичь цели.
1.4.4, Каждый метод обучения геометрии реализуется с номою
математических ([ 1, лк. 7, с. 98-102). (12)) и учебных задач [2. лк. 1. с. 18-2!
последние получаются переводом целей учебной деятельности в задания л
учащихся тестового типа и служат для достижения этих целей в процессе обучен!
Обобщенные типы учебных задач, обеспечивающих достижение образователыи
целей (учебных, развивающих, воспитательных) при изучении люб)
содержательно-методической линии школьного курса математики, смотрите и (
лк. 1,с. 18-25].
Математические задачи в курсе геометрии называются геометрическими (I
содержанию) и делятся на три вида (по основному способу решения): 1) задачи I
доказательство (или задачи-теоремы), для решения которых используются мето)
доказательства теорем [I, лк. 10, с. 139-140]; они позволяю: осуществить переМ
от заучивания готовых доказательств к пониманию методов доказательства к
умению их применять; 2) задачи на построение, решение которых опирается |
постулаты н основные (элементарные) построения, комбинируемые различным
методами построений, и осуществляется с помощью инструментов построен!
(циркуля, линейки и пр.); эти задачи полностью принадлежат геометрии, в тц
сочетаются наглядные образы, созданные с помощью построения, и логически
рассуждения, которые нужно проводить самостоятельно, 3) задачи на вычислен!
(арифметические [2, лк. 2, с. 33-34] или алгебраические [2, лк. 4, с. 80], для решен»
которых используются методы н приемы вычислений и решения уравнена!
неравенств и их систем [2, лк. 2, с. 39-40, лк. 4. с. 80-81]; однако роль геометрии 1
сводился только к использованию специальных формул, так как и чертеж. |
необходимые теоремы, дополнительные построения в этих задачах no.Monini
усвоению собственно геометрии; четвертым видом являются комбинировании
задачи, содержащие элементы указанных трех.
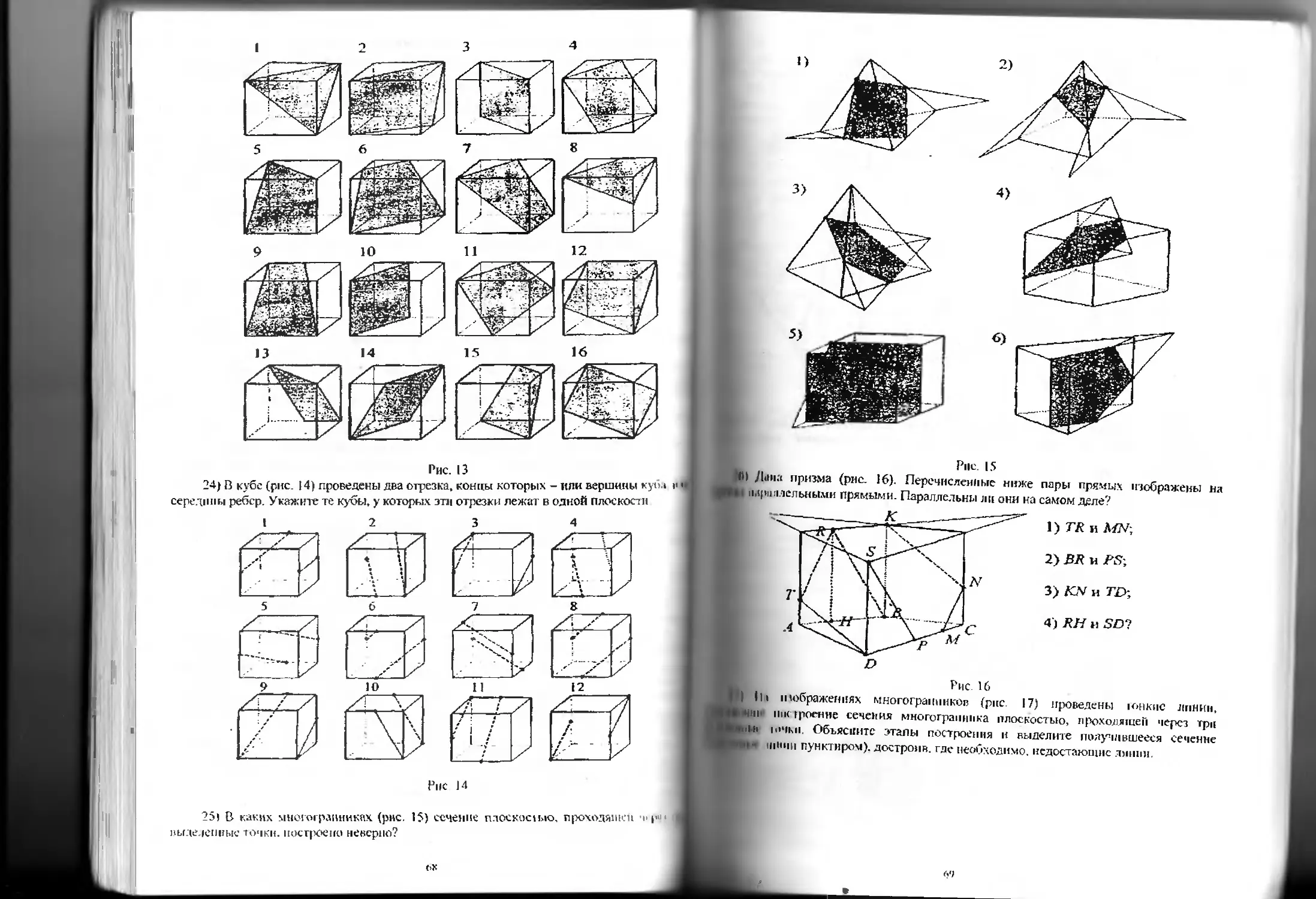
Особенностью решения всех видов геометрических задач является черте* и]
условию задачи, который при правильном выполнении помотает понят т. содерж.тпи|
ч ITI и ii.iiiin способ се решения. Полезен следующий прием.
। hlu/иЛ прием построения чертежа но условию задачи (теоремы):
11 |1Ы1и>п||яГтте чертеж от руки, не обязательно по всем правилам черчения, но
(11|»|>|||Ц| их придерживаясь (прямой усол должен выглядеть прямым углом, середина
.ни । рединой и т.п.), большим и «просторным»;
'I не перегружайте чертеж; иногда полезно изобразить лишь «функционирующие»
. hi т .юмс три1 теской фигуры (например, если нужно найти радиус окружности, то саму
I,«тип и. цепнком можно не изображать);
I) уточняйте чертеж по мере решения задачи, пытайтесь изобразить все возможные
uijiiirvp.iiliin. отвечающие условию и ходу решения задачи (лишние потом можно
ни.),
4| п< ттолыуйге дополнительные построения, облегчающие решение (вводящие
Ml Vi'iM отрезки н т.п.);
) и п> же время избегайте чрезмерного усложнения чертежа; этого можно
нттиуть in счет «выносных картинок», изображающих отдельные фрагменты всей
4* рп
I иштсито непосредственно па чертеже указывать числовые или буквенные значения
чтШ (|>||1Г)ков. углов), заданных в условии или полученных в процессе решения,
/| »т ли н задаче говорится о фигурах общего вида (например, о произвольном
Тинышкс), то нельзя изображать их как частные случаи (так, произвольный
I HHIMUIK ис должен выглядеть прямоугольным или равнобедренным);
I) п> пользуйте не только общие, ио п специальные приемы построения чертежа,
ifM» ыв и спениальных темах курса.
14) (Хнщте закономерности просматриваются и в отношении типичных
н ii>n>pvdHeHini учащихся при изучении всех содержательно-методических
ill iiimi 1I.IIOIO курса геометрии. Как отмечает В.А. Далингер [12, с. 4-12], это. в
,. hi пчередь, - формальные знания (или незнание) определений, свойств
>|»||>П'|(тК11Х фигур и их взаимного расположения, слабо развитые
. ip и |псиные представления; певладение методами решения задач, особенно,
трпческих и задач на построение. Отсюда - затруднения и ошибки в
.... ыт । формулировании суждений; в выборе метода решения задачи; в
|. |и|п птибражения фигуры, чертежа н дополнительных построений и
।...• пня к них необходимой фигуры; в обосновании чертежа по условию
11 hi и I пн’ржлсний в ее решении н других геометрических утверждений. Часто
» »и т и ошибки в построениях, приводящие к неверному результату решения
.8 1й1»,|ц Причины их возникновения могут быть систематическими
I ищи мтт in iiucTpy.McirTOB построения) и случайными, объективными и
1»« । IHIII.IMH. для их предупреждения следует выполнять определенные
I 110ими <1.1 М01 репные л лк. 3).
20
21
Li6, Д"М разнигня и поддержания интереса к геометрии на Пропслевтичсск. i| |1ф Пйтрмпша) Другие варианты, а также тематическое it примерное
•угаие проводятся кружковые занятия по истории геометрии, по решешп р «Чиче планирование И контрольные работы по различным учебникам, следует
занимашльных задач методами оригами, разрезанием и складыванием задании Ч самостоятельно там же п программе и в указанных выше журналах
фигур, лепкой и моделированием (в том числе, компьютерным): прикладных за.1.1 Uu MrtiiiMi в школе”. 1996, №5; 1997, №3; для V-V1 классов с недостаточной
с региональным содержанием в области искусства и архитектуры; практически »«ычшчсеызй подготовкой - 1997, №4, с. 3-10, поурочное планирование с
работы и юры на местности и т.п., а при изучении систематических курсов 1 и ючи шисм комплектов - там же. с 29-34; для классов с углубленным
факультативные занятия (тематика которых широко представлена в мегодическд ihiihm математики - 1997, №. с 4-22; тематическое планирование по учеб-
литературе). 1о и другое сопровождается различными соревнованиями и играми ШШ) •)" тгр1Ш1.иого комплекта всех профилей - 2002. №4, с. 20-49; № 6, с. .38-43.
математическими олимпиадами, научно-практическими конференциями и т.п.
1.5. Общая схема логико-методического анализа каждой
содержательно-методической лишит школьного курса математики
Построение специальной методики изучения каждом солержателыя
методической линии школьного курса геометрии осуществляется по гой же схеме
что и в специальной методике изучения курса арифметики, алгебры и начал аналн)
[2. лк. I, с. 25-28], которая в краткой форме воспроизводится ниже;
I) Логико-математический анализа изучаемого материала данной лини
(анализ математического содержания, математический идей, методов и логически)
организации, истории развития). В помощь самостоятельной работе студентов и
этому вопросу можно использовать вузовские учебники и лекции по геометрии. I
также методические пособия для учителя математики и абитуриентов. ’>!
материал нужно соотносить с разделом “Содержание обучения” программы
с. 17-21] и разделом “Обязательный минимум содержания образования”, а также!
Государственным образовательным стандартом.
2) Место данного математического содержания с школьной программ I
учебниках федерального комплекта (по классам и темам) в лекциях приводнця и
примере первого варианта тематического планирования по программе (5, с 2'1| !
учебникам федерального комплекта, принятых МО Г’Ф на -2002-03 vi ,.
Распределение материала линии в школьной программе показано в таблицах. । ic I
скобках отмечен одни из альтернативных вариантов в учебниках федсралы1и|1
комплекта (учебники 1-4 И.Б. Истоминой. 5-6 - Г.В. Дорофеева и И.Ф. Ubpi.nnii'|
А лтине цели изучения каждой содержательно-методической линии в
. <я| iiuiimx документах сформулированы на двух уровнях (обязательном и уровне
> uni ггН) как “Требования к математической подготовке учащихся”; лри этом
HiiiMu-ni.iioro уровня приводятся образцы задач, конкретизирующих эти
• kmui* |\ с. 66-86]. В лекциях приводится дифференциация учебных целей с
м и нормативной дифференциации, но по трем уровням усвоения (I-
ш»ы и iii.ih, >1 - обязательный, III - уровень возможностей), определяются
•<н< । ча/ тих или учебных), развивающие и воспитательные цели, связанные
I нмн*Н'« I ими содержания изучаемою материала
1i ||< ионные типы математических задач и приоритетные обобщенные
«ы их решения. В каждой содержательно-методической линии присутствуют
1мчни> ишь! математических задач, но какие-то из них являются
" nt inioiiiiiMii и им уделяется основное внимание. Основные типы учебных
• •1г1Яп1цц общими для всех содержательно-методических линий (2, лк. I,
|*| in ленту необходимо научиться конструировать их самостоятельно
I Ирм и I конкретном содержании; примеры специальных учебных задач
। .-l it» в 1СКЦИН. их можно также найти в ]5, с. 66-86]. J4, разделы “Вопросы
। англы с учащимися по теме»], и всех вариантах государственного
t «itirti- <11.ц<<|<1 стандарта как образцы задач, конкретизирующих требования к
г Hi »< <|йч 111г и.пой подготовки учащихся но геометрии.
I । 1ип1ц>||Ы1Ьгс методы ч приемы обучения (связанные с особенностями
<**«йнич uivn.ieMOro материала) и примеры их использования, нстодико-
t io ii ui line цепочки
ЛЕКЦИЯ И
Учение о геометрических фигурах
2.1. Логико-математмческиЙ анализ линии геометрических фигур
2.1.1. Геометрическая фигура (как и число) - одно из первых и основ»
понятий математики как с исторической, так и логической точки зрсн
неотъемлемый инструмент современной цивилизации и поэтому относится к чш
основных понятий образовательной области “Математика” в школе. Геоме||
возникла как наука о свойствах геометрических фигур, поэтому н учеши
геометрических фигурах традиционно является первой и основной содержатeiн
методической линией школьного курса геометрии н представляет <’<>4
последовательное изучение геометрических фигур, их свойств и простет
математических методов изучения этих свойств. Содержание материала г
линии можно условно разделить на две части - математическую и логическую
Первая часть (математическая) является сравнительно простой и состоит
каждой геометрической фигуры (плоской или пространственной) из следуюЩ
компонентов:
- определение понятия данной фигуры (содержание понятия) и всех
элементов;
- классификация фигур, подходящих под определение (объем понятия);
- формулировка аксиом, формулировка и доказательство теорем о свогкг
геометрических фигур данной классификации;
- применение свойств фигур к решению геометрических задач.
Сравнительная простота и прозрачность математической части содержа»
позволяет говорить о необходимости и возможное™ выделения в данной линии
специального изучения второй части (логической), рассмотренной в пер,
лекции данного курса, состоящей из следующих компонентов:
- логическое строение курса геометрии, каждое из составляющих <
положений имеет свое содержание и составляет, по нашему мнению, отделе и
компонент содержания второй части;
ипрецеленне и классификация понятий - их логическая структура,
ini. nit* между понятиями, логические операции с понятиями и способы их
>ц|> ihui применение к доказательству теорем и решению задач [I, як. 10,
' Н I/9|
циня । ис аксиомы и теоремы, виды теорем, их структура, способы
t • >^‘Н1|ч'пни теорем, применение к доказательству теорем и решению задач [1,
in м Illi Ъ|.
/ешокнельство теорем, общие и специальные методы доказательства,
1М»Ц| ине к доказательству теорем и решению задач [I, лк. 10, с. 137-141, лк. 11].
Ц Содержание второй части данной линии определяет
чд।>м«। ii'iccKitc (логические) методы работы с понятиями, аксиомами,
рч1»Ы|| и их доказательствами, которые используются в дальнейшем и при
шг)ч курса геометрии и математики в целом.
Методы работы с понятиями:
IIihhiiik тго мысль о предмете, отражение предмета в его существенных
Определение понятия
а) через указание ближайшего рода и видовых отличий:
П паз uni с определяемое понятие (обозначаемое А (х/);
|| т*>*ите ближайший класс объектов, элементом которого оно является (родовое
mi» ы ицпчасмое М):
р >|11сн1Пс характеристические (необходимые и достаточные) признаки,
Xi и ю in денного класса (видовые отличия, присущие только определяемому
*•••> и нцынасмые еще содержанием понятия и обозначаемые В(х};
41 цИь iiiimie п п 1-3 в наиболее краткой формулировке, запишите ее символически
«d । V » « М) (Л (х) => В (х) и используя специальную символику.
б) генетическое:
)| нншии определяемое понятие (термин);
I .inulinie способ его образования (происхождения, построения и т.п.).
в) через абстракцию:
II Miiil'iiic возможно больше разнообразных каассов объектов, подчиняемых
(•фмениму понятию;
И г I titnlui ic го общее, что имеется у всех этих классов;
и пЛ|х,|1||иг совокупность всех установленных общих признаков под одним
мяш
г) через аксиомы
II нм iNiir определяемое понятие;
0 ipMViriipyfhе отношения, связывающие это понятие с остальными изучаемыми
•|Мчи HpiHii'MiicMMC без доказательства (аксиомы);
'I i I >)*11Л11ру111с систему аксиом, определяющих названное понятие
д) конструктивное
11 Н<• IIг । нос об конструирования (построения) некоторого объекта;
25
2\ приспейте термин полученному таким образом объекту.
е) индуктивное (рекурсивное):
I) ii.tiobhic определяемое понятие:
2) определите (задайте) значение одного из его признаков для О ниц I.
3) выраяне некоторым образом его значение для и + I.
Замечание 1. Для построения другого (равносильного) определения понятия
уже известном определении нужно заменить хотя бы одно из видовых свойств и
другое, равносильное ему.
Замечание 2. Существуют также приемы, сходные с определением, но и
раскрывающие содержания понятия: описание, характеристика и демоне транш
Описание - перечисление ряда заслуживающих внимания признаков единична
предметов; характеристика - указание некоторых, важных в каком-лив
отношении признаков; демонстрация - наглядное разъяснение путем сравнспн
предметов. Такие приемы используются на ранних ступенях обучения, а сам)|
распространенным является определение понятий через указание рода и видоны
отличий.
Выведение следствий из определения понятия:
I) вспомните принятое в курсе определение данного понятия;
2) назовите все его признаки (свойства), которые включены в определение;
3) если возможно, назовите все другие существенные его свойства. котом
изучались (формулировались, доказывались) на основе определения.
Подведение под понятие:
1) вспомните (повторите, прочитайте) определение понятия;
2) проверьте принадлежность данного объекта указанному в определении родоыЦ
попят ию(х е М-2);
3) проверьте наличие у данного объекта характеристических признаков (видопи
отличий) данного понятия (х е В (х) - ?); если при этом признаки понятия сеянии
союзом “и”, то проверять их нужно все. если “пли” - то хотя бы один из них;
4) сделайте вывод о принадлежности данного объекта понятию (х е А(х) или v I
А(х)).
Построение равносильного определения:
в данном определении замените хотя бы одно из видовых отличий понятии Ы
другое, равносильное ему свойство.
Доказательство равносильности различных определений понятия:
I) сформулируйте признаки понятия первого определения как условие теоремы.
2) сформулируйте признаки понятия второго определения как заключение теорем •*
3) сформулируйте целиком построенную теорему;
4) проверьте, является ли полученная теорема известным (доказанным рапыЛ
свойством, следствием из него или отрицанием его: если "да” - и 6. если “нет" и I
данного приема;
5) докажите истинность или ложность полученной теоремы:
6) сформулируйте обратную теорему,
7) выполнить п п. 4,5 для обратной теоремы;
8) сделать вывод о равносильности определений.
Использование определения понятия:
1) каждое понятие в тексте теоремы или задачи замените его определением.
2) выведите следствия из определения каждого понятия;
3) если нужно, сформулируйте равносильные определения и следствия из них.
26 ®
I ни нужно, проверьте принадлежность какого-либо объекта данному понятию на
». и- <ч1|"Ч1слси|[я (выполните подведение под понятие).
I uulu pine in полученных предложений те. которые могут служить этапами
। II нм теоремы или решения задачи.
Лfjo.ii।>|)ы ponooibi с суждениями (аксиомами и тсоре.мамп);
• । нием называется такая форма мышления, посредством которой, сочетая
Шия 'по цибуль утверждают или отрицают о самих объектах. Суждение имеет
•ы niiii'itiyio оболочку - предложение, характерным признаком которого
1гн Hiiiiii'iiie его истинности или ложности. Приемы построения.
iiipuiiMi и записи различных видов предложений изучаются в школе на
рУ' • мио языка и являются общеучебными приемами, их специальных форм
пни и leopcM) на уроках математики (больше всего, геометрии) н являются
па ши ям iiii'iecKHMit приемами.
Приемы формулировки теорем-
Простая пряная теорема:
|| । i.iiiiiiiiirc множество объектов, о которых говорится в теореме (обозначаемое
i|"i|iMViiiipyiire известное свойство данных объектов - условие теоремы
тмыш l( J. । де т е М);
I >| "рмулируйте свойство объектов, которое нужно доказать - заключение
| < «I |иЩ|mu'iicMoe В(х))\
I •• шише обе формулировки в одно предложение, как правило, со словами
ы " (симиолическая запись (V х е М) (А(х)=э В(х) ) и используя специальные
Обратная теорема-
11 hi i.'i 'line и прямой теореме условие и заключение:
О Ним iiHilie местами условие и заключение прямой теоремы;
1| । '(•"рмулируIt it новую теорему, общий вид которой: (V х е М) (В(х) => А(х)) .
Противоположная теорема:
I Н м инг I) прямой теореме условие и заключение;
) t |»"цму<iiip> Лтс отрицание условия Л(.т);
и (ф»р n пируйте отрицание заключения В(х);
4iiipMyiiiipyi)if новую теорему, общий вид которой (V х е М) (,4(.г) В(х)).
Сложная теорема:
) и фи ге множество объектов. о которых говорится в теореме (М);
II * форму пируйте все условия теоремы, соединяя их союзом “и”;
I > ||о<|тмviinpyПтс все заключения теоремы, соединяя их союзом “и”;
1| «Ль» iiiiliiic оба предложения в одно, общий вид которого (V v е М) (А/(х) л
III « АДИ) => (Йг(х/ л Bi(x) л... л Сдх)).
Необходимое и достаточное условие
I > I р н riiijivil ге прямую теорему;
। | Мирчу пируй ie обратную теорему;
|| । • шпиц' *1ба предложения в одно с помощью слов “необходимо и достаточно”
• • |и in • 1'Пд.Г. “если и только если"); общий вид теоремы: (V х е М) (ЛМ ол-
Теорема существования:
|| »। «пн uni г множество объектов, о которых говорится |< теореме (ЛЛ.
|. pi iiipsiiic условие теоремы А(х):
1| * .»и ip iinnbiii объект. удовлетворяющий условию(У);
21
4) сформулируйте новое предложение со словами “существует... такой. что
общий вид теоремы: (V х е М) (Y) | (А(х) => Y)
Теорема-тождество:
I) установите множество объектов, о которых говорится в теореме (Л/).
_) запишите условия, которым удовлетворяют эти объекты - элементы л е Л/:
запишите аналитические отношения, в которых они находятся с использованием
специальных обозначений
Методы умозаключений:
Умозаключением называется такая форма мышления, посредством которой и
одного или нескольких суждений выводится новое знание об изучаемых объектах
Индуктивное умозаключение:
I) рассмотрите данное множество изучаемых объектов (чисел, формул, фигур и i н |
2) выделите примеры наличия у них некоторого свойства;
3) сформулируйте для каждого примера частное суждение - свойство, нрисуиа
данным конкретным объектам, используя специальные термины;
4) па основе сравнения и обобщения сформулируйте общее суждение - сво(к i м
присущее всем рассматриваемым объектам, используя специальные термины.
Дедуктивное умозаключение:
1) рассмотрите данное множество изучаемых объектов;
2) сформулируйте с использованием специальных терминов общее суждение
некоторое известное свойство всех данных объектов (называемое в данном случ
‘"большой посылкой”);
3) проверьте, истинно ли это суждение для данных (изучаемых) объектов (‘ч-Ч
посылка");
4) сформулируйте частное суждение для каждого из данных (изучаемых) объектов,
наличии или отсутствии у них общего свойства (“вывод”).
Выведение следствий из общего суждения:
1) рассмотрите изучаемый объект;
2) сформулируйте известное общее предложение об этом обз.екте (опрелелеии
теорему, правило) с использованием специальных терминов;
3) сформулируйте отдельно каждое частное свойство (частное сужлеим
включенное в общее - необходимые признаки.
Умозаключение по аналогии:
1) сравните изучаемые объекты с какими-либо известными ранее;
2) сформулируйте об известных объектах одно или несколько известных суж;ц и|
(определений, свойств, правил) с использованием специальных терминов;
3) выделите признаки, отличающие изучаемые объекты от известных;
4) сформулируйте сходное суждение (определение, свойство, правило) об изучаем,
объектах с учетом их различий с известными.
Дедуктивное доказательство теорем:
Доказать теорему - это значит, опираясь на аксиомы и ранее дока книц
теоремы, показать, что заключение теоремы является логическим следствием |
условия.
а) прямое доказательство (синтетический метод):
I) проверьте, можно ли использовать какой-либо специальный метод доказан- in и
(векторный, координатный, методы геометрических преобразований, мето; m> iit-
математической индукции и т.д); если “да”, используйте его, если “нет" - п. 2.
2) последовательно выводите следствия из условия теоремы до тех пор. и.-к i >
получится ее заключение по схеме: (А(х)о Т) => Bt(x) => 5,(г2=?.. => В(х> < ie I
определенная совокупность предложений той теории, в рамках которой док.зп и>» Я
- iifiriiiinAeiiiie (V x e KI) (A(x)-^> B(x) ). а также все составляющие
i। no. и суждения A(x) и B(x).
б) аналитический метод доказательства:
I) iHia дикиiMiiacMOro утверждения (заключения ti(x)) последовательно подбирайте
pill* основания (Z?/(x1, .. чтобы сделать вывод о его истинности;
it lifiio oiiiiv нт форм аналитического доказатепьства:
• iiu iibI'ii/h'w анализе ведущий вопрос: "что надо гнать, чтобы ответить на
11 ши in вопрос?”;
>«< । миТчин' и анализе начинайте рассуждение с предположения: “временно допустим,
hiiii’iiiie теоремы верно” и задайте вопрос: “что отсюда следует?”:
) .41. м выпадите следствия до тех пор. пока не получится истинное предложение
у. rt'iH • цис, 11|ютиворечащее одному из известных.
п) косвенное доказательство от противного — частный случай
н> чнЫид'.’о анализа (часто для доказательства обратной теоремы).
। 1111|||11ожите> что заключение теоремы ложно;
41i|imwiupyilте предложение, противоположное заключению теоремы (?(х);
1| смяидпге следствия из сформулированного предложения (по схеме, аналогичной
• ч 1 прямо! о доказательства) до тех пор, пока не получится противоречие с условием
it н । п шесгным предложением;
1) «я.nailie вывод о ложности сформулированного предложения;
it вимшйге следующий вывод об истинности заключения данной теоремы.
-) косвенное доказательство с помощью контрпримеров
(W то для доказательства ложности какого-либо предложения):
и к пример, не подходящий под заключение сформулированной теоремы или
••И1Ь 11ИНЯ111Я.
д) доказательство необходимого и достаточного условия:
II fetiili ши г из данной теоремы прямую теорему и докажите се;
I ....nine гак же обратную теорему и докажите ее;
«. iniii общий вывод об истинности дайной теоремы.
д) метод конструирования
(часто для доказательства теоремы существования):
Щщ|||> способ конструирования искомого объекта н примените его вместе с
•и Г .с и инпо доказательства.
е) метод по лной индукции (перебора)
(<) !я теорем, охватывающих конечное число объектов)
fl । с (ираничпть каким-либо способом область перебора;
*><> ।«ши |ео|>ему для каждого случая тем или иным методом;
»» ah I вывод об истинности или ложности теоремы в целом.
IkiUHI Hi iicihiuiiMX «рабочих фигур» в содержании второй части данно1~1
i«i<> м ipeyronbHUK. Установление цепочек равных треугольников -
I |н <!•' ныусмыП прием доказательства различных свойств геометрических
11 специальный метод доказательства теорем и решения задач,
М Ш чип ценным содержанием,
метод треугольников (часто для
и ц । в । ||ц|н иггпп отрезков или углов):
29
I) предстаньте данные отрезки (углы) как элементы а) двух треугольников в.
6) одною треугольника (данных или специально построенных);
2) докажите в случае а) что эти треугольники равны; в случае б) что треутолып»
равнобедренный;
3) сделайте, вывод о равенстве данных отрезков (углов).
Как при использовании этого метода, так н других, бывают необходим»
дополнительные построения', некоторые часто встречающиеся из них:
I) в трапеции бывает полезно провести через одну вершину прямую, параллелью»
противоположной стороне;
2) если в условии есть медиана треугольника, то бывает полезно продолжить ее .»
такое же расстояние («удвоить ее»), что приведет к появлению параллелограмма;
3) если в условии задачи фигурирует середина одной или нескольких сгори
четырехугольника, то стоит добавить середины каких-то других сторон или диагоналгП.
рассмотреть средние линии соответствующих треугольников (прием «средней линии»), '
4) в окружности, вписанной в треугольник или четырехугольник, всегда провор
радиусы в точки касания, которые перпендикулярны соответствующим сторонам;
5) если две окружности касаются, то обязательно проводят линию центров;
6) иногда изображают вспомогательную окружность, которая позволяет обнаружив
дополнительные соотношения между элементами фигур;
7) тетраэдр часто достраивают до параллелепипеда, диагоналями граней когорт
являются ребра данного тетраэдра;
8) для сведения стереометрической задачи к планиметрической а) изображав
отдельные элементы пространственной фигуры на плоскости без искажения, б) hih.ii
строят развертку пространственной фигуры.
Для совершенствования этого метода и развития учащихся поле г»
доказательство эквивалентности различных определений равных треугольников.
2.2. Место геометрических фигур в программе и учебниках
Таблиц»
Этап Класс Темы программы
Пропедевтический (начальная школа и курс математики 1 2 3 4 5 «Числа от 1 до 10»: точка, линии (кривая, прямая, .пр» и ломаная); многоугольник и его элементы. «Числа or 1 до 100»; утлы, прямоугольник, квадрат. «Умножение и деление»: круг, окружность, радиус ши треугольников; обозначения фигур; жуб. его элемгпц развертка куба). (Текстовые задачи: развертки геометрических тел) Т. 1 «Натуральные числа»: отрезок. прямая. нч
5-6 классов основной,школы) 6 треугольник. Т.5. «Обыкновенные дроби»: окружшн и. 1 круг. (Т.1. «Линин»: прямая, отрезок, окружной Т.5. «Многоугольники»; виды углов, многоут очмип J Т.7. «Треугольники и четырехугольники»: виды ц 1 гольников. прямоугольник. Т. 10. «Многогранники-. пр« моутольный параллелепипед, куб, пирамида, разверни) (Т.2 «Прямые и окружности»: перссскакнии » 1
1 kl!>iniin|l
|l f'liMIIIMi'IpHH
; Ч и ЦAt i <>h
•• ЙШ II IIIK(Mf.l)
параллельные прямые, взаимное расположение прямой и
окружности, двух окружностей, шар, сфера Т.Н «Фигуры
на плоскости и в пространстве»: сумма углов треугольника,
п авильные многоусольники.)
7 Т.1. «Начальные геометрические сведения»: геометричес-
кие фигуры - отрезок, угол, виды углов, равенство фигур,
свойства; перпендикулярные прямые (геометрическое тело,
поверхность, плоскость, линия. Т.2. «Основные свойства
плоскости») Т.2. «Треугольники»: элементы, виды,
признаки равенства, свойства. (Т.З. «Треугольник и
окружность Начальные сведения»: свойства хорд,
взаимное расположение, касательная) Т 3. «Параллельные
прямые»: признаки, свойства. Т.4. «Cooi ношения между
сторонами и углами треугольника»: свойства
прямоугольных треугольников; расстояние.
8 Т.1. «Четырехугольники»; виды, свойства. Т.4. «Окруж-
ность»: касательная, центральные и вписанные углы,
вписанная и описанная окружность. (Т.1. «Параллельные
прямые и углы»: признаки, свойства, виды углов, сумма
9 углов многоугольника. вписанные и описанные окружности). Т.2. «Соотношение между сторонами и углами треугольника». (В т. 2. «Длина окружности, площадь круга»: правильные многоугольники).
|Ы(|||П111П1И 10 Т.1. «Введение»: аксиомы стереометрии, следствия
1 |«|<М< IJIIIII • ► 1| МИНИН <^№<Л ШМ* 1<|| 11 («Повторение планиметрии»). Т.2 «Параллельность прямых и плоскостей» (Введение. «Прямые и плоскости в пространстве»). Т.З. «Перпендикулярность прямых и плоскостей» («Многогранники») Т.4. «Многогранники» («Круглые тела») Т.2. «Цилиндр, конус, шар» свойства, взаимное расположение. (Т.З. «Правильные многогранники»).
2JL Цели изучения геометрических фигур в школе
| 11 || lyicHiic материала линии геометрических фигур имеет общей учебной
« in 1РМПИ1ЧГСКОС изучение плоских и пространственных геометрических
lit iiinlkiu, методов их изучения и использования для решения
Ьгмк и приклндиых задач. В таблице 2 показана дифференциация этих
• >рнШ1ЧМ п()уЧСПНЯ.
31
I одержание материала позволяет проектировать цели развития у
•*•!«« |пчи.шателы1ых процессов -- внимания, восприятия, памяти,
№»|1|И1 воображения, мышления (особенно таких мыслительных операций,
I цинк классификация и конкретизация; формулировка математических
| ШИ (ям пом и теорем), индуктивные и дедуктивные умозаключения), а также
и нмнпн учиться. Характерными качествами мыслительной деятельности в
|||)час являются: образное, логическое. пространственное и
ч р »|ц|чи‘с мышление, пространственные представления и воображение, что
»•( нииюгствующие качества ума, геометрическую и графическую
Mft» «iH'MCinw творческой деятельности, конструктивные умения. Близкая
I Ии фического материала с реальной человеческой практикой и
|||.и (цнребностями математики позволяет ставить цели развития
.»•'>>» научно!о .мировоззрения; на примере развития учения о геометрических
« М *но показать, как математика развивает и совершенствует свой аппарат
11 <««11и- м ио1|>сбностей практики.
I ни I « oMd рических фигур обладает большим гуманитарным потенциалом;
। ipini геометрии, исторические, занимательные и практические задачи, что
I • *|(1ч |ь ставить цели воспитания и развития интереса к математике и
4 «••(гчыик ти в целом, обшей культуры и культуры общения, активности и
। к iMiiit in, чувства прекрасного, профессиональную ориентацию (в
!«•»•* । профессии региона).
Н i*i ионные типы математических и примеры учебных задач
» 1ИЧ1НММ типом геометрических задач в линии геометрических фигур
|1 >• I* ill ин доказательство Общие приемы (методы) решения этого типа
ним иыик
Ih •|||<ФИы<' специальные учебные задачи имеют целью усвоение
НЧ1НЧ |еомегрцческой фигуры и ее свойств, а также приемов работы
й I имiiiim.imii, теоремами и приемов доказательства теорем (приемов
^1'1 »11И1|Ы(||Л) Примеры таких учебных задач:
1) Найдите на рисунке (чертеже, картине, модели и т.п.) а) фигуры данного iu
(отрезки, углы, треугольники, квадраты, круги и т.д.) и выпишите их номера (закрж
определенным цветом); например, на модели куба - нары ребер, лежащих
скрещивающихся прямых; 6) все геометрические фигуры, использованные при созл.1ч
витража (орнамента, бордюра, картины, модели и т.п.).
2) Выделите общие и существенные свойств понятий: а) перечислите извеспи
свойства прямоугольника; б) назовите общие свойства всех четырех ун
прямоугольника; в) укажите свойства, принадлежащие всем или только некокщ
прямоугольникам; г) укажите свойства, общие у прямоугольника и ромба; сравните и
основными свойствами квадрата, параллелограмма; д) перечислите не менее 12 скиЧ
квадрата.
3) Из пяти предложенных терминов выберите два, которые наиболее и*
определяют данное математическое понятие: а) геометрия (фигура, точка. своп< И
уравнение, теорема); б) треугольник (вершина, катет, сторона, центр, перпендикуляр)
4) В приведенном определении выделите название определяемого объекта (терм»
родовое понятие, видовые признаки и характер связи между ними: а) угол, смежим
каким-нибудь углом многоугольника, называется внешним углом этого мцогоугол: пн
б) прямым (острым) углом называется угол, равный (меньший) 90°; в) треукии.
называется прямоугольным, если один из его углов прямой, г) пятиугольник
многоугольник с пятью сторонами; д) две различные прямые, лежащие в одной плоы.я
и непересекаюшиеся, называются параллельными; е) отрезок, соединяющий серели*
двух сторон треугольника, называется его средней линией; ж) два одлоимпы
многоугольника называются подобными, если углы одного соответственно равны у,
другого, а стороны, заключающие равные углы, пропорциональны.
5) Из данных понятий образуйте пары по признаку “род - вид”: а) плоскость, прм
отрезок, ломаная, замкнутая ломаная, многоугольник, четырехугольник, параллели: рэ
ромб, прямоугольник, квадрат; б) пространство, поверхность, плоскость, цилиндри'М
поверхность, многогранник, правильный многогранник, призма, цилиндр, круч я
цилиндр, прямой цилиндр, прямой круговой цилиндр.
6) Укажите ближайшие родовые понятия для понятий; а) квадрат, б) вертнты
углы, в) хорда, г) шестиугольник, д) равносторонний треугольник.
7) Назовите несколько видовых понятий для каждого изданных: а) геометрия <
фигура, б) многоугольник, в) параллелограмм, г) многогранник, д) пирамида. е> при 4
д) параллелепипед.
8) Для каждого из данных понятий подберите видовое отличие и допшнЛ
определение: а) квадрат - это четырехугольник.б) квадрат — это прямоуч о‘ц Л
9) Для каждого из данных понятий подберите родовое понятие н лоиочЛ
определение: а) прямоугольник - это _______. у которого противоположиы< I
прямые; б) прямоугольник - это_______. у которого четыре стороны и углы ир1<Л
в) треугольник - это________ с наименьшим числом сторон.
10) Сформулируйте свойства углов параллелограмма как следствие п> I
определения.
11) Выполните подведение под понятие:
а) будет ;ш выпуклым четырехугольником прямоугольник, у которого: 1) <-<. н >нЛ
симметрии; 2) противоположные углы равны; 3) каждой диагональю четырех у i i J
делится на равные части;
б) будет ли параллелограммом выпуклый четырехугольник, у которого ныне иииЛ
те же условия, что и в задании а);
в) четырехугольник, у которого противоположные стороны лежат на партии •*<Л
I 11 параллелограмм. 2) ромб или 3) прямоугольник;
II Hinn иида будет треугольник, у которого: I) один из углов больше суммы двух
II 1| 11'11111 ш углов равен сумме двух других: 3) сумма двух любых углов больше
HI И 111111Ч1ЛШ1П пирамиды лежит правильный многоугольник, можно утверждать, что
I fitzi.i правильная?
• I huh in фигур на рисунке I. каждая из которых состоит из четырех отрезков и
М ||1‘| । являются четырехугольниками?
|| hwik iHi биссектрисой угла луч. исходящий из вершины угла и образующий
•I «в л n il ни линейным углом двугранного утла а) угол, стороны которого - два
ц»1*-;1 иные п । ранях двугранного угла из одной точки ребра; б) угол между двумя
ринншкуляриыми его ребру и лежащими в его гранях?
I «it тек ли правильной призма, в основании которой лежит правильный
. I IHHIIi 1
I • mi ли назвать правильным многогранником а) правильную пирамиду
Hi iipiiiMy, б) шестигранник, составленный из двух правильных тетраэдров,
pt Hup и 01 ииипнпе:
I iipiiiirpuib, что выпиленная из куска фанеры (вырезанная из бумаги) фигура
I И нря inviniii.iiiiKoM? б) правильным треугольником?
| Мни । ин oi.iri. а) оба смежных угла прямыми? одни прямым, ругой тупым
т in 1рымн ‘(тупыми)? Какова особенность общей стороны двух равных
Hi V ь и li»। vmm.i лвух вертикальных углов быть равной 180“?
I V ммя правильного многоугольника и какой величины может быть
|bu>inl uniip.i'iMibiii угол, б) наименьший внутренний угол, в) центральный угол
Ь №1 1р> 1111 му углу?
Ill in । । imni.i между биссектрисой утла и биссектрисой утла в треугольнике?
•I HhUtiii" и исправьте ошибку в определении понятия: а) луч. выходящий из
» । я ||<|||.Ц1.1С1ся его биссектрисой; б) два угла, у которых общая сторона,
• цм IH.IMI н| диаметром круга называется наибольшая хорда, проходящая
tii| И |ыр.1л'1слог|>аммом называется многоугольник, у которого стороны
••«Hi Ihihu.i т) четырехугольник, у которого противоположные стороны равны.
Ирг iiirui ip.iMMOM; е) ромбом называется равносторонний неправильный
и 11Н1И л| прямые называются параллельными, если они не пересекаются
I ill ini iipi'ToiiKxin; з) два равных угла называются вертикальными, если
лпш:г11< я продолжением сторон другого: и) медианой треугольника
35
и равнобедреии
иеравностороиип
неравностороиии
ла разносторош
на прямоугольна
называется отрезок, делящий сторону пополам; к) касательной к окружности иазыв.»
прямая, которая касается окружности; л) угол, образованный двумя хордами, иазыи.и
вписанным; м) равнобедренный треугольник - эго когда две стороны равны; и) квалра
называется четырехугольник, у которого все стороны равны.
17) Дайте несколько разных определений а) ромба, б) параллелограмма, в) прям
угла, г) куба, д) конуса.
(8) Укажите, что объединяет между собой понятия: а) точка, прямая, плосм«
б) квадрат, прямоугольник, трапеция, ромб; в) ромб, круг, треугольник, прямоугольник
19) Установите связи .между понятиями и составьте на этой основе родослош
выделенного понятия: луч, прямая, точка, угол, смежные утлы, дополнительные лучи
20) Назовите признак, по которому разделены на группы: а) понятия (треуголы
четырехугольник, прямоугольник) и (центр, сектор, сегмент); б) отношения (//,= .<•,
21) Распределите в четыре группы, располагая в определенном порядке пои»'
биссектриса, вершина, длина, квадрат, медиана, объем, площадь, парад ле no । pi
прямоугольник, прямая, плоскость, ромб, сторона, трапеция, треугольник, точка и
четырехугольник.
22) Проведите классификацию понятий: а) треугольник (по двум основ.ипи
б) угол, в) многогранник.
23) Постройте классификацию понятий для данной темы и изобразите ее схемой
24) Проверьте правильность классификаций: а) треугольники делятся
остроугольные, прямоугольные, тупоугольные, равносторонние
б) ромбы могут быть равносторонними (квадраты) и
в) прямоугольники могут быть равносторонними (квадраты) и
г) треугольники по сравнительной длине их сторон делятся
равнобедренные и равносторонние; д) параллелограммы делятся
ромбы и квадраты; е) геометрические фигуры делятся на многоугольники и окружное И
25) Найдите среди изображенных на рисунке (рис. 3) фигур одну липни
Обоснуйте свой выбор. Какие из оставшихся фигур имеют общие свойства и какие
свойства?
Рис. 3
26) Определите, правильно пи обобщены понятия: а) ромб. параллели! |М
четырехугольник, многоугольник: б) отрезок, прямая; в) равнобедренный треуго» I
равносторонний треугольник; г) параллельные прямые, перпендикулярные иряа
д) Полукруг, круг.
27) Определите, правильно ли выполнена специализация (ограничение) |юц«(
а) равносторонний треугольник, ромб; б) трапеция, параллелограмм; в) равнобедрен^
треугольник, прямоугольный треугольник.
28) Сформулируйте определение фигуры а) семиугольник, б) «крест», обрзюпия
так: на каждой из двух пересекающихся прямых отложены по разные стороны i-i i
пересечения равные отрезки.
29) На плоскости даны лве точки. Много ли пар параллельных прямь-' >>. (
провести через эти точки?
• ь ямлинс. почему различные прямые не могут иметь двух общих точек.
П> Мня ei ни прямая а) иметь с плоскостью только общую точку? б) совсем не
I ншч кис 11.10 общих точек? в) быть параллельна только одному ребру куба, двум.
, о ич I п ci •> ребрам, только одной диагонали t рани куба?
i'l | ь шик» плоскостей можно провести через три пересекающиеся в одной точке
и 1г|. । ч<-1 ыре, через пять?
Illi 11юГ>(1,1жении куба назовите все случаи взаимного расположения прямых,
1||||1Ш<|Исж.п его ребра
141 Минни ранный угол имеет л граней. Сколько у него ребер, двугранных углов?
М । юпью трехгранных углов имеет а) тетраздр.б) параллелепипед?
Ill1 •|ц|гделн1е. верно лн сформулирована теорема, а) все точки биссектрисы угла
НИ тпапгиы от сторон этого утла; б) плоскости параллельны, если I) прямая,
и И илпои плоскости, параллельна прямой другой плоскости; 2) две прямые,
к плиой плоскости, соответственно параллельны двум прямым другой
• - til
' I i формулируйте теорему, обратную (противоположную, обратную
№ ыч11*|К1Й| какой-либо данной; истинны ли эти теоремы?
Hl Hi ирнньтков равенства треугольников выведите следствия - признаки равенства
ь»-« • чр иных треугольников, б) прямоугольных треугольников.
И1 » |соргмы-иризнака (параллельности, перпендикулярности и т.п.) ответьте на
» I» и> и я ли сформулированное в теореме условие только достаточным или также
• li.flUIM'
И| ' | пнеллино ля утверждение: прямая, пересекающая круг в его центре,
I.|Я«риа л) радиусу? б) двум радиусам? в) диаметру? г) двум диаметрам?
К' пр да?
II1К «ьяя 11|>п1м.1 не имеет диагоналей?
Ill М I пи и) основание наклонного параллелепипеда быть прямоугольником,
(ИНН ильполного параллелепипеда быть перпендикулярны плоскости основания;
|*М> tpiilib прямого параллелепипеда быть ромбом; г) всякий параллелограмм быть
>•^..*1 ир шильной пирамиды, д) правильный многоугольник быть основанием
Л и пирами лы?
fif.lil ipex отрезков - высоты, бокового ребра и апофемы правильной пирамиды
• цп щьнИ111 и илнменьший отрезки.
Н| lllliiliillb ie макеты заданных фигур (пространственных - с помощью развертки)
. H IHlItl 1П11МИ
ht ! фирму имеет сечение цилиндра плоскостью, проходящей а) через ось
11Ч«ИЦ|'1 ь) параллельно основанию; в) параллельно оси; г) наклонно к оси и
1МЬм> I hi» иПразующне?
) < IniiHiti пли in наклонены к плоскости основания конуса ei о образующие?
25. < 'пениальные методы и приемы обучения
| | l|iiiii<iriM>i- ci роение геометрии, свойства изучаемых геометрических
11 • tn Hiyi.iCMoio материала в программе, определяют такие методические
Ь ill i in мочения, как формирование запаса начальных представлений о
к 11 и ||чиур.|Х в младших классах; постепенное подведение or
37
.111
конкретнонилуктивиых выводов о свойствах фигур к необходимости аксиом
тического построения геометрии: дедуктивный характер изучения материи
систематических курсов; стремление к наглядности с помощью рисунков
моделей; постоянное возвращение в теоретических вопросах и задачах к рак
изученному материалу с целью создания опоры для нового, сравнения, аналощ
обобщения и углубления; усиленное внимание к выработке логических умении
их применению и. таким образом, к использованию методов логики при изучим
данного материала.
2.5,2. В пропедевтическом курсе 1-4 классов учащиеся знакомян»
практическом и описательном плане с простейшими геометрическими фип|и4
(точка, прямая, луч, отрезок, угол и т. д.), кубом, параллелепипедом, »I
фузнонистских курсах - с другими пространственными фигурами (пригни
пирамидой, цилиндром и др ), их названиями, обозначениями, изображением |
простейшим символическим "языком” (точки А, В. С, прямые а и др.). И ’I
классах расширяется круг изучаемых геометрических фигур, делаются некою»
обобщения свойств простейших из них. некоторым даются определенш I
формулируются простейшие выводы (пропедевтика доказательств) >
формировании понятий, применяемся, в основном, конструктивный подмм I
начале целесообразно показывать, как образуется фигура, а затем для некоторт |
них анализировать как родовое понятие, так и видовые отличия. Разном >|wi'M
геометрический материал широко используется в основном курсе 1-б юы ।
(арифметике) как наглядный счетный материал, часто в форме игры (табл. 3)
Таблица 3
л гч о □
о д □ □
□ о А
7 д о □
д о □ □
О ? А о
□ д О 1—
|В таблице изображены в npoiruiii'ii и <
[порядке геометрические фигуры. Ьпик
назван, недостающие фигуры вмени ш
? . затем называть по порядку номер ц <
и название фигуры. Подсчитать кояичи id
различных фигур, удерживая их в 1ЫЧИ1Н
If I/ /||>|1»>111ительио (17. пособие В.А. 7(a'niiiiepa|. [3, гл. 15. § 3J; [4, гл. 3(, учебники
. II и 1ч1|п.1я геометрия”).
1,1) II систематическом курсе планиметрии 7-9 классов, при сохранении
flilHi.i практических и индуктивных методов, осуществляется постепенный
Mi>. . преобладанию дедуктивных методов обучения. Важную роль (и особые
I*»* hi лпи учащихся) в этом играют так называемые первые уроки
в любом
i> Hi'n' кого курса планиметрии (как правило, это - первая тема
М MHi'K1 ком курсе геометрии), на которых
riii 1гхыгизцруются те сведения о геометрических фигурах.
которые
сознании
Ч.ИГ1 и пропедевтическом курсе, подчеркивается и закрепляется в
.«и. । Ик цжктный характер понятия геометрической фигуры;
1ым111пснный запас геометрических сведений используется для
И «iiiiiiri понятия «геометрическая фигура» и конкретных геометрических
ни » фирме так называемых подводящих задач, чаще всего, практического
। и я| построение объектов с заданными свойствами; б) измерение (длин
» lignin ут лов); в) вычисление (длин, величин углов); г) конструирование и
^HHiiiii' (разрезание и складывание, перегибание листа бумаги.
(им. ЛЯ1ПКЯ основные (первоначальные, нс определяемые, а лишь
и чписываемые), важные для дальнейшего изучения геометрии
| ' II* i|>iu)pi.( (точка, прямая), свойства которых разъясняется на
p»ltll»ii4, черюжах. предметах окружающей обстановки;
|пгим фигурам, кроме описания, даются определения, как правило,
i пн iiiijia и видовых отличий, для усвоения которых полезно
нп i.iii'ieiiuc родословной понятия» (пример на рис. 4);
ДИАМЕТР
УРДлК—. центр]
к] [точка) [окружи.
11» .m.,i|(tQ4KA(
Рис 4
ОКРУЖНОСТЬ^
[точка! |раост6яГг]
(прямая) ( точка]
19
38
- свойства тгих других геометрических фигур также рассматриваются il
только непосредственно. но и п результате некоторых рассуждений с отюроп а
свойства известных ранее фигур.
Таким образом, учащиеся постепенно подводятся к пониманию ши
логического строения курса геометрии и определению и усвоению таких попитИ
как «определение», «аксиома», «теорема», которые формулируются в ком
«первых уроков» и на основе которых со следующей темы начинается изучена
свойств геометрических фигур дедуктивными методами. Это изучение дола!
сопровождаться постепенным формированием у учащихся приемов работ и
понятиями суждениями (теоремами) различных видов, а также прием
доказательства теорем различными методами (см. первую часть данной лемм
п, 2.1.2 и [2. лк. 1,с. 14-15].
Для обучения учащиеся составляющему эти методы основному логичен >оа
умению доказывать теоремы и решать задачи на доказательство полезно '
iii 1
Г
сложное умение в явном виде разделить на составляющие:
- умения анализировать условие теоремы (задачи), выводить из |«(
следствия; выяснять условия, при которых возможно заключение теоремы (<.i । и
высказывать правдоподобную гипотезу нт. п.
- умения проводить доказательство - на основе полученной пиния
возникшей как результат поиска доказательства, выполнять последоватс'1ыв
умозаключений и обосновывать правомерность получаемых выводов.
Для формирования каждою из этих умений необходимо раскрыть ыИ
действий, лежащих в его основе, формировать частные умения, входяиць л I
состав и оформлять их в виде соответствующих частных приемов лея н и
(которые можно будет использовать при применении общих мгм
доказательства теорем) Вначале это нужно делать на примерах; так, coci.ih
находить достаточные основания можно выявить при изучении первых nj
например, о равенстве треугольников: «для того, чтобы доказать равств гни |
треугольников, достаточно доказать равенство трех соответствуюини м
элементов треугольников а) равенство двух отрезков (сторон) и равспгшп I
между ними, пли б) равенство трех сторон и г.д.» Повторяя такую рПшн I
<»|||ц| ipvntx геометрических фигур (многоугольников, многогранников и др.)
иич приученные результаты, ученик усваивает общий прием леятсльиосгп.
пни и он шве этого умения.
II ни ин важны предварительные и завершающие учебные действия по
щи нь< Hi) теорем (решению задач) - поиск решения, его оформление и
। и ni.nl (обобщающий) анализ приемов решения и другой информации,
*. и •ii.iiini.ix и полученных в ходе решения.
Поиск решения задачи (доказательства теоремы):
иыпопните одно или несколько из следующих действий:
п «ленте тип задачи (теоремы) и вспомните известный (специальный или
и 11 м се решения (доказательства);
И|и в nine общий (нисходящий или восходящий) анализ;
р. iniuiif условие или требование задачи (заключение теоремы) на части.
Ц||йи |К1псн11я (доказательства) каждой из них, затем объедините,
iiuMiiiirc задачу (теорему), аналогичную данной, прием решения
. him которой известен, сравните их и на этой основе составьте план решения
♦••Щ1И.1)
| 1.1ЩЦ н.меннте условие или требование задачи (заключение теоремы) так,
»• •и. fiu io сравнить полученную задачу (теорему) с данной; затем использовать
ЮТ ill Billin' прием аналогии;
.. । ныне условие теоремы с целью его сближения с заключением (при поиске
> > " в мтительства);
fill । ii (lie заключение теоремы с целью его сближения с условием;
и in понятия, содержащиеся в условии или заключении теоремы, их
миып-iii
ie определения понятий, которые подсказывают (или сокращают) путь
ill и in iiiMeim re определение понятия его признаком;
•| I. | идо nt пользуйте условие теоремы;
। >1 ‘ни гели можно, частные случаи задачи (теоремы) к воспользуйтесь
Bi пн приемом разделения па части.
•••• ш Д «I» Ны.|к. Поиски решения геометрической задачи И Математика в
» । W-3'l); {!?.§§ 8-11]
Оформление решения задачи:
ри uni ipnriiiiMil чертеж и (если есть) дополнительные построения;
* и. г iK'iioHiibie н дополнительные построения;
Bp! в< iiiui иигюпня для чертежа и записи решения,
Ь« I । bi Ti|iii пн ю для решения свойства и зависимости или прием решения;
•< и i.l ир11»1И1Ы1ЫМ использованием приема, символики и рациональных
Вм ip,.i ни и вычис пений.
I.I-, лнтительный (обобщающий) анализ решения задачи:
ответьте на вопросы:
Цо» i in in иная идача к какому-либо известному вам типу задач?
40
и
2) если «да», был ли известен вам какой-либо прием решения задач этого nil
Использовали лк вы его? Какие при мом встретили трудносгп. допустили ошибки11
вы их преодолели?
3) если «нет», какой другой способ решения задачи вы использовали? Являеп <
он рациональным? Сравните его с известным приемом решения и сделайте вывод:
4) какой новый прием получили при решении данной задачи? Попробуй» ,
сформулировать: в каких задачах его можно использовать в дальнейшем?
5) какие теоретические знания (определения, теоремы, методы их доказательеппь
использовали при решении задачи? Какие трудности встретили? Как вы их преодолели
6) чему вы научились при решении данной задачи?
Усвоение этих и других приемов доказательства теорем будет эффекиин
при выполнении учащимися заданий на самостоятельное а) изучение некотр!
теорем по учебнику, б) решение задач на доказательство, в) «открытие» на и
основе отдельных теорем, г) доказательство теорем с использованием обшн
специальных приемов, д) несложные учебные исследования.
Начатая на первых уроках систематического курса планиметрии рабом
определениями геометрических фигур в систематическом курсе усиливагг
вниманием к связям между изучаемыми понятиями (кроме родо-видовых), I
отношения соподчинения, обобщения, специализации (выделения части»
случаев), пересечения, противоположности н классификации (раскрываемой обм
изучаемого понятия) понятий. Например, полная класснфикащ
четырехугольников (основанная на дихотомии) может иметь следующий вид:
1} все плоские четырехугольники разделяются на простые, стороны которЦ
не имеют других общих точек, кроме вершин, и непростые, стороны котпр)
пересекаются;
2) простые четырехугольники подразделяются на выпуклые и невыпуклые
3) выпуклые четырехугольники подразделяются на трапеции и не трапеции,
4) трапеции подразделяются на равнобочные и неравнобочиые;
5) неравнобочные трапеции подразделяются на прямоугольные
непрямоугольные;
6) выпуклые четырехугольники, не являющиеся трапециями, подраздел як>||
на параллелограммы и не параллелограммы.
7) параллелограммы подразделяются, с одной стороны, на ромбы н не ром<1|
а с другой - на прямоугольники и нс прямоугольники;
8) ромбы подразделяются па квадраты и нс квадраты;
9) прямоугольники подразделяются па квадраты и не квадраты.
Широко известны схематические иллюстрации подобных классификации
11 1мг ion», необходимо постоянное обобщение и систематизация изученных
и, ।. iiMcipnaecKiix фигур, для чего удобны различные обобщающие таблицы,
Иг чш io используются и как опорные конспекты при обобщающем
, инн I Стример, обобщающие таблицы в теме «Треугольники» (табл. 4 и 5),
Таблица 4
ПI >1 СОТА, МЕДИАНА, БИССЕКТРИСА
АвВ-£_.ГЯе
* а
щади» ЛАДС
s
пгю
С
+ Ь2 + с1)
-г*— ~~
Мы OI.I h
.2
т-
I =
где р
ah€:lr>
£
b
£
с
h. ' ht:
= be : ас : ab
2
М. Ниппа т.
2
+ с2) - b2
^2(аг + Ь2) -- с2
3
+ т/ + ° 4 +
—--------
Яш । екгрнса
— ~^Jbcp(p - а)
_ * ^-сХр- ,
с- |6-сГ
2
0 — а.
= 90*
2
Р‘«
2
42
45
Таблица 5
2.5.4. Систематический курс стереометрии в 10-1 [ классах строп в |
дедуктивно па основе аксиоматического метода [1, лк. 11, с. 150-1521 I
предположении, что курс планиметрии полностью усвоен. Отсюда следуй!
некоторые особенности выбора методов обучения:
- повышение уровня строгости изложения теории и обоснования решен»
задач, и. следовательно, дальнейшее усиление внимания к развитию логически и
дедуктивного мышления;
опора на курс планиметрии. его аксиоматику и свойства плоских фигур;
hi । icJii.no. использование методов сравнения, обобщения, аналогии.
освоение методов изображения пространственных фигур па плоскости и.
в ioihiicjii.no, методов наглядности (окружающей обстановки, моделирования и
Ни) методов развития пространственного воображения, пространственных
। н i.iiHieinrri и мышления;
предполагаемый программой более быстрый темп работы обуславливает
полынсс внимание к использованию лекций, семинарских занятий (с
и пи п.юванием обобщающих таблиц-опорных конспектов, примеры которых
П|” vi.iB.'ieiibt таблицами 6-8), уроков решения задач (в частности, устно на
Мн >г'1Н\ и чертежах), самостоятельной и групповой работы, уровневой и
|1||||||>1|ц|>иой дифференциации обучения.
I ик же, как в систематическом курсе планиметрии, особую роль играют
v/wu систематического курса стереометрии, на которых с самого начала
1Н'11Н1.1с1ся его логическая организация; они включают изучение идеи логического
Iроения геометрии, основных понятий и аксиом стереометрии и доказательство
► и Ji limit из них (первых теорем).
Методико-технологическая цепочка проведения первых уроков
hi те типического курса стереометрии может быть следующей.
I; историческая справка о возникновении и развитии геометрии;
’) рассмотрение моделей пространственных фигур (в частности, моделей куба
и nip.ivipa с сечениями, предметов окружающей обстановки, изображений на
ibiikmictii. в том числе, произведений живописи, скульптуры, архитектуры),
(uiiiiiciiHC плоских и пространственных фигур;
1) повторение логического строения курса планиметрии, его основных
лишний и аксиом (с использованием обобщающей таблицы, в которой
in км,цитированы аксиомы планиметрии и сформулированы аналогичные им
Rtr ломы стереометрии; таблиц «родословных понятий» и др.);
4) подведение к основным понятиям и аксиомам стереометрии с
н>iiu'ii.TOGaiiiieM сравнительных таблице геометрической иллюстрацией и краткой
ниш 1.к> содержания аксиом планиметрии и стереометрии;
-и
5) изучение аксиом стереометрии (желательно па одном уроке) ио едини!
схеме: а) иллюстрация содержания аксиомы примерами из окружают,!
обстановки, на модели (куба, специальной модели), устное решети(
подготовительных учебных задач, б) формулировка аксиомы, в) иллюстрацш
аксиомы на рисунке, г) краткая символическая запись аксиомы; д) решен»
учебных задач на усвоение содержания аксиомы (па моделях, таблицах, рисунках
записью исходных данных, сообщаемых учи гелем, с восприятием ученики
исходных данных на слух), е) выведение следствий из аксиомы;
6) доказательство первых теорем о взаимном расположении точек, прямых!
плоскостей с использованием аксиом и следствий из них с использовании!
известных из планиметрии методов (прямое доказательство, метод доказательс । ш
от противного);
7) решение учебных и математических задач на доказательство для усвоенм
аксиом и первых теорем стереометрии;
8) контроль усвоения материала первых уроков стереометрии.
(См. дополнительно [4, гл. 12, § 43]).
Методика дальнейшего изучения пространственных геометрических фтпуч
аналогична описанной в п. 2.5.3. методике изучения фигур в систематическое
курсе планиметрии с учетом (отмеченных в данном пункте) особенностей курс]
Ill
III
стереометрии.
(Примеры методики изучения геометрических фигур в пространстве см. в [4, гл. I
14] и в журнале «Математика в школе»: С.М. Саакян и В Ф. Бутузов. Образцы решения i
оформления задач. 2000. №2. - С. 19-28: Многогранники. 2002. № 5. - С. 25- 33. Цилиндр
конус и шар).
Специально отводимые программой часы на повторение курса геометрш
нужио посвятить обобщающему и систематизирующему повторение
теоретического материала, его логической организации, методов п приемов си
изучения и применения к решению математических и прикладных зад.г
(решаемых, по существу, методом математического моделирования [1, лк II
с. 148-150]). С этой целью используются все виды обобщающих таблиц и спорны
конспектов, лекции, семинары, коллоквиумы, нестандартные и занимательны
46
( Il iii>i)i<>peiiiiH (например, кроссворд «Геометрия» на рис. 5 и криптограмма).
Таблица 6
В JAHМНОЕ РАСПОЛОЖЕНИЕ ДВУХ
ПЛОСКОСТЕЙ
—।--------------------------
Две плоскости
I |»|1г<.е'гсние
Общая прямая
НС единствен-
ная
Совпадение
Признак
нс рн ендикулярн ости:
/•р,/.!«.<
a Jp
Признак параллельности:
а' е а, <з" <= «, а' Г)<з" = А
Ь’ ер, Ъ" ер, Ь'Г\Ь" = В
а' || Ь'. а" || Ь"
а II ₽
|11Н1|н>сы кроссворда По горизонтам: 5. Инструмент для проведения прямых линии.
I rinit ii.ni.iii восьмигранник. 8. Замкнутая ломаная, состоящая из трех звеньев. II.
•г т-IN поверхность. 12. Правильный четырехугольник 14. Центр полярной системы
i-'IHimi 15- Направленный отрезок. 16. Книга по математике, написанная
•ii«t|'r'iecKHM ученым Евклидом. 20 Часть измерительного прибора. 21.
i ынисское предложение. требующее доказательства. 22. Любые зри
in пиарные вектора, взятые в определенном порядке. 25. Одна из сторон
.• iH'ii.iiiiKa 26. Тригонометрическая функция. 27. Часть прямой.
4'
Таблица
МНОГОГРАННИКИ
Пятиугольная
призма
Вопросы кроссворда. По вертика-ш: 1. Французский ученый и математик XVII иск
впервые использовавший в своих работах прямоугольную систему координат
Древнегреческий математик, хорошо известный каждому школьнику 3 Кривая вторя
порядка. 4. Единица измерения углов, луг. 7. Отрезок, соединяющий две зоч«
окружности. 9. Старинное русское название линейки. 10. Совокупность соединенных п<
углом нескольких отрезков 12. Сторона прямоугольного треугольника 13 Одно |
основных неопределяемых понятий геометрии. 17. Линия сечения шара плоскоеIH
проходящей через центр.18. Линия на плоскости или в пространстве. 19. Древнегречл к
ученый, теорема которого известна каждому школьнику. 23. Тело, полученное врашепи
прямоугольного треугольника вокруг его катета. 24 Точка круга, равноудаленная от ш
точек его границ
Таблица Я
—| ПРАВИЛЬНЫЙ МНОГОГРАННИК [
Все грани —
равные пра-
вильные мио-
|тоугольники
Все много-
гранные
углы имеют
одинаковое
I
Все ребра —
равные от-
резки
число
граней
Все
плоские
углы —
равные
— КУБ (все шесть
граней — равные
квадраты)
— ТЕТРАЭДР (все четыре грани
— равносторонние равные
треугол ья ики)
— ОКТАЭДР (все восемь гра-
ней — равносторонние
равные треугольники)
— ДОДЕКАЭДР (все
двенадцать гра-
ней —правиль-
ные равные пяти-
угольники
-ИКОСАЭДР (все
двадцать граней —
равносторонние
равные треуголь-
ники
A, ui\nhi,'/Kl\i»a
11 inn пыю решивший кроссворд без особого труда прочтет криптограмму, в которой
h 1ынп высказывание о математике великого русского поэта А С- Пушкина
«16 7 166 15 29 1628 24 |630ж1бб 15 14623428 28 12 32 12
h ‘I >> 6 33 29 2i 35 28 28
49
•• пнях
гз
25
Рис. 5
(.доказательствах» аксиомы
внимание на теоремы, в
> .1111111 теорем
доказательстве которых используем ч
параллельных, пробовать
сформулировать свойства, ocuon.iiiiiM
кружка и в качестве индивидуальных самостоятельных исследов-шши •
давать интересующимся учащимся задания на отыскание ошибок и ниц
параллельных («5-ю постулата»); оор.чш
евклидовой, можно начать еще при изучении параллельных прямых п
планиметрии. Здесь можно упомянуть о том. что вопрос об аксиоме парл/гиЛ
(аксиома это пли теорема?) был поставлен еще в 111 в. до н > и
Н.И. Лобачевский в 1824 г. показал полную безнадежность попыток док и пи
помощью других аксиом геометрии. В течение курса (возможно, in i 1
мшшюжной аксиоме. В завершение курса можно (силами тех же учащихся)
абсолютной геометрии и геометрии В.И. Лобачевского,
сути
• Миш ipuposaiL
ее интерпретации. привести примеры доказательства
и решения несложных задач, дать представление о се
L4 I IIKI.M
•1. П1Ч.Ч кис цепочки изучения геометрических фигур во всей содержатсльно-
образом, можно сформулировать основные методико-
niiiiiiii, которые определяются ее содержанием, а также
как
психологии, так и логики усвоения материала.
нпЫмн в курсе обшей методики [ ], лк. 1, с. 13. лк. 10, с. 130-147].
I апологическая цепочка изучения геометрической фигуры
И«л1>чп1и1гельный этап - рассмотрение примеров объектов, имеющих
t*lmi>ll 1гомстрической фигуры, вычерчивание, моделирование, конструи-
ыниигнпс характеристических свойств; повторение, сравнение и
Здесь же уместно рассмотреть вопрос о разных геометриях. По<т»ш
подведение учащихся к пониманию возможности разных геометрии, онигшв
.пун иными ранее фигурами и их свойствами (в частности, плоских
I Яр. । пи пц-нными). пояснения учителя.
к hi, ппеденне термина и формирование определения понятия фигуры
р пн фигуры на основе определения, ее узнавание на чертежах.
.... • ИИ'1111 II oik ПШОВКС.
. ier.iu.ix идач на усвоение определения (подведение под понятие.
• | । it । рои и i.oinpnpiiMepoB ит.л).
nib po/KK.iOBitoii и классификации (возможно, выделение других
• iiiy.it иными понятиями) введенного понятия.
»>. '► иных ыдач па усвоение классификации.
мй1«м цнчсскнх задач с использованием определения и
И itiuit
н<Н1|| и и коррекция усвоения понятия.
। ниц. та признака данной фигуры (или ее взаимною
5(|
расположения с другими) при условии, чго признаки, содержащие», ч
определении, по каким-либо причинам неудобны практически (например, ирины
параллельности)
10) Доказательство признака на основе определения понятия фшуры.
11) Решение учебных задач на применение полученного признака.
12) Выявление свойств геометрической фигуры, нс указанных в опредслси'
и признаке, или связанных с взаимным расположением фигур путем наблюден»
построения, измерений и т.п., приводящих к некоторым догадкам.
13) Проверка полученных догадок опытным путем, формудирв
соответствующих утверждений о свойствах фигуры (теорем).
14) Возбуждение потребности в доказательстве выявленных свойств н*1
доказательства, выявление метода доказательства теоремы.
15) Доказательство теоремы и его схематическая запись.
16) Рассмотрение частных случаев и выведение следствий.
17) Решение учебных задач на усвоение теоремы (в том числе, формупщ
определений понятия, равносильных введенному ранее).
18) Решение математических н прикладных задач па применение теоремы
19) Текущий контроль и коррекция усвоения теоремы.
20) Анализ, обобщение и систематизация изученного, выделение главной,
21) Итоговый контроль усвоения.
Технологическая цепочка формирования
приемов изучения геометрической фигуры
Лурс
Пропедевтический курс
Приемы изучения геометрически* ,
1. Алгоритм распознавания геометрических фин
чертеже, рисунке, модели, в окружающей сре/и
2 Частные приемы изображения геометрии нн I
на плоскости
3. Частные приемы обозначения гео.мегричсчч1 фи»
изображении и в записи.
4. Частные приемы моделирования фигур.
5. Обобщение и систематн ,ацня приемов 1 I
6 Общий прием определения понятия
Курс п-нтииетрин 7. Общие приемы работы с понятиями. 8. Прием классификации поня1ий. 9. Общий прием формулировки аксиом и теорем 10. Приемы изучения содержания теоремы. II. Общие приемы доказательства теорем: прямое доказательство и доказательство от противного. 12. Специальные приемы доказательства теорем метолом треугольников, координат и векторным. 13. Приемы выполнения чертежа (дополнительных построений) по условию теоремы (задачи). 14. Общий прием работы над геометрической задачей на доказательство. 15. Прием оформления решения задачи на доказательство.
Kvpc t m. ptitwmpuu 16. Частные приемы изображения пространственных фигур на плоскости. 17. Частные приемы обозначения пространственных фигур на изображении и в записи. 18. Частные приемы моделирования пространственных фигур и вычерчивания их разверток. 19. Повторение и обобщение приемов 6-15. 20. Специальные приемы доказательства теорем.
ЛЕКЦИЯ И1
Геометричсские построения
3.1. Логико-математический анализ линии
геометрических построений
3.1.1. Геометрические построения (или теория геометрических постросшин
раздел геометрии, где изучаются вопросы и методы построения геометричч >
фигур с использованием тех или иных инструментов построения. Эти построим
можно условно разделить на дее группы в зависимости от требования к точкой I
построения:
1) геометрические построения, не требующие особой точности, их н< и I
простота и наглядность при иллюстрации фигур и их свойств; это - изобрч*«ж
(на практике и в производстве - рабочие чертежи деталей, эскизы и схемы v М
станков и пр.; все необходимые размеры на этих чертежах проставляются с<н ча
ГОСТам);
2) геометрические построения, к точности выполнения ыи>а
предъявляются повышенные требования: в математике - для решения
графическими методами - построение фигур с заданными свойствами, графи • «
умножение, решение уравнений и неравенств, дифференциропини»
интегрирование, построение номограмм и работа с ними, в произволе । »•
выполнения чертежей, по которым затем непосредс!венпо ведется paiMiik (
обработка деталей, контрольных шаблонов. При этом точность ip.i.|ni
решения задач обуславливается двумя факторами - точностью задания и
данных (зависящей от конкретного содержания задачи) и точное н.ю rn.ni •••<
построений (зависящей от точности каждой элементарной оисрашн.......4
числа и порядка их выполнения).
Геометрические построения изучаются как в геометрии Г.вкли.ы
других геометриях (сферической, проективной, геометрии Н И ]1<>ь гн
др ), как на плоскости, так и в пространстве. В любой задаче in
(изображение) различают, кроме а) заданных элементов и их ip* г^В
(условия задачи) 61 искомой фигуры (или их совокуппостеи) <
। iiuimii (требование задачи) еще и в) инструменты, с помощью которых
I выполнить требуемое построение.
I цреиипх времен извет ны классические инструменты построений -
*и (1>1Н1Осп>ронняя. математическая) и циркуль, затем стали использовать
• шпик (чертежный), транспортир, чертежные машины (состоящие из набора
। м»н11>п) пантограф, эллипсограф, рейсмус, графопостроитель в ЭВМ. На
41И«» hi пользуются такие инструменты и приборы, как штангенциркуль (для
4- им лпиметра круга), рулетка и масштабная миллиметровая линейка (для
**•.. длин отрезков), транспортир к астролябия (дли измерения углов), экер и
• «и). । .1 ]я построения перпендикулярных прямых), рейсшина (для построения
4»<ниых прямых), малка и рейсмус (для столярных работ, например, разметка
<*!> нт in бруска прямой, параллельной краю бруска).
•I .fitll .троны, существуют построения только одним циркулем (построения
№»>р*>1Н11 одной линейкой с параллельными краями, если на плоскости
• пирз жиость н ее центр (построения Штейнера), одной линейкой с
I 1>>н краями; одним угольником (модель прямоугольного треугольника); с
I 11 HI 11 \ I Л.1 (пли только прямого угла, или с помощью двух прямых углов).
• 1|>ы премией Греции довели искусство геометрических построений до
1|1>Ф1|М сформулировали аксиомы линейки (Л) и циркуля (Ц),
Him выполняемые с их помощью построения:
* цч un-oipeiOK. соединяющий две данные (или построенные) точки;
Ь*Ц ни прнмзю проходящую через две данные (или построенные) точки;
I ||ичпь из ч in холящий из данной точки и проходящий через другую данную
»• " Ц13И1Х построений с помощью линейки выполнять нельзя
) ИН |.| in iii отрезки, даже если на ней есть деление).
i|i"ii • 1»|ч жн<к'1ь. если даны ее центр и отрезок, равный радиусу;
»lf ШЬ 1Ю1ЧЮ in 3BVX дополнительных дуг окружности, если даны центр и
I п-Иы |цг| описать из данного центра окружность данного радиуса
lull •hiinii ill oipc iok па данной прямой от данной точки.
Ц п । Hoi ipuciHie как на плоскости, так и в пространстве опираются
и н|/н1<ннч (аксиомы конструктивной геометрии), т.е. на
hn>ui ipiiM'" i.inii’iii на построение:
► •II luititni |пчкз пересечения двух данных прямых;
> nt* 111-1111111 и чьи пересечения прямой с данной окружностью,
Hi I IO4MI пересечения двух данных окружностей;
|||ф*ы 41 и Hi 11.1 окрзжности. или вне их произвольную точку.
Ilt< III II.ПК III проц шильную прямую
55
Задача считается решенной, если она сведена к конечному числу эи»
простейших задач-постулатов. Древние геометры формулировали нпгеремн»
задачи, некоторые из которых оказывались неразрешимыми с помощью циркуля I
линейки; например, гак называемые, три знаменитые классические задачи
квадратура круга (построить квадрат, равновеликий данному кругу), трнсекнн!
угла (разделить произвольный угол на три равные части.) и удвоение kv)1
(построить сторону куба, объем которого вдвое больше объема заданного куГы|
Они выделили основные элементарные построения циркулем и линеймл
а) провести прямую через две известные точки; б) определить точку пересечеим
двух известных прямых; в) провести окружность с известным центром и извести).»
радиусом: г) определить точки пересечения известной прямой и нзвестлД
окружности; д) определить точки пересечения двух известных окружное и
е) построить треугольник по трем его элементам.
Сущность задачи на построение - построение заданной геометричесы
фигуры с помощью данных чертежных инструментов (линейка н циркуль). Кажщ
такая задача представляет собой небольшое исследование и содержи) 4 лаЦ
I) анализ, 2) решение (построение), 3) доказательство, 4) исследование. Аишин
поиск решения, осуществляется с помощью классического (геометрически))
анализа древних [1, лк 9, с. 115], он заканчивается указанием способа (план
построения искомой фигуры. Решение с помощью классических инструмсни
(линейки и циркуля) сводится к последовательному выполнению перечислен)»
выше построений: (Л.1. - Л.З; Ц.1.- Ц.2.; П.1.- П.5.) соответственно выбрани»)
плану решения. На этапе доказательства последовательно обосновывается i
построенная фигура - искомая (отвечает требованию задачи). Исследован
отвечает на вопросы - всегда ли задача имеет решение, если имеет, то сколы.»
какие, возможны ли частные случаи, требующие особого рассмотрения
В практических построениях в настоящее время никто не ограничивав кмЧ
инструментов, нх набор сближается с набором инструментов чер>е*1
конструкторской практики. Рассматривают построения с «недоступными точкам!
«недоступными прямыми» и другие. При этом одну и ту же задачу на построен
можно решить нс только разными инструментами, ио и разными методами
56
1 I 1 Методы геометрических построений основаны, в конечном счете, на
। i|'»einiii отдельных точек (например, прямая определяется любыми двумя
|| rill |рсуголы1пк - вершинами, окружность - центром и радиусом).
• । и iltniiMH из них являются следующие:
Il Одним из первых является метод геометрических мест точек,
• iihwmkih еще метолом пересечений. Геометрическим местом точек (ГМТ -
(| ИШ тревних геометров) называется фигура (множество точек пространства),
>«М1 1С.МПЯ из всех точек пространства каким-либо геометрическим требованием
и, |поц). Доказательство того факта, что «некая фигура является
•Мифическим местом точек, обладающих определенным свойством»,
• •ииннпает необходимость доказательства двух теорем: I) все точки данной
М ню обладают указанным свойством; 2) этим свойством обладают только точки
нн>П фигуры, то есть если точка не принадлежит данной фигуре, то она
иным свойством не обладает. Сущность метода геометрических мест coctoikt
ММУК’Щем.
Ин и. нужно с помощью построения найти точку X, удовлетворяющую двум
иным условиям. Геометрическое место точек, удовлетворяющее первому -
«ф,1 / /, геометрнчесгое место точек, удовлетворяющее второму - фигура F?.
•» “"ti< чыю. искомая точка является точкой их пересечения (Х= Г’1 г>Л2).
'I н тбраический метод основан на алгебраических соотношениях между
• I nuiuMii фигурами как элементами бо.чес сложных фигур. Он является одним
Н ч|1иы\ методов решения задач на построения, позволяющий ответить на
V* можно ли данную задачу решить циркулем и линейкой. Так, с помощью
'•йрлпчгского метода устанавливается, что построить треугольник по трем его
'II4IH.IM биссектрисам (а по трем высотам и медианам можно); разделить
*><»» и in-iii угол на три равные част также нельзя (хотя угол, величина
•Нфн|и piiniia т. / 2". можно разделить па три равные части циркулем и линейкой).
IhupiiMcp. отрезок с. связанный с отрезками а и е соотношениями с=->/«-<з и
•* । в можно построить алгебраическим методом соответственно на основе
I* ироиоршюиальных отрезков и теоремы Пифагора.
II А/, тиды геометрических преобразований в задачах па построение (методы
I ни* нотобпя) состоят в гом. что вместо искомой фигуры первоначально
строится вспомщ тельная фигура (которую летче нострошь, временно p.n»poci
или заменив одно из условии задачи). а затем вспомогательная фигура (или и
часть) нреобразуекя в искомую с помощью какого-либо геометрическом
преобразования (параллельного переноса. поворота, симметрии, подоен»
гомогегии и т.д.). В этом смысле говоря!, чю задача решается мею.ш»
параллельного переноса («на вектор»), методом поворота, методом си.ммс|рпи
методом подобия и т.д. (подробнее об этом в лекции 5).
4) Координатный метод, основанный на определении положения точек и
плоскости (на прямой, в пространстве) с помощью чисел для решения задач п(
построение сводится к построению точек по их координатам и фигур и<> м
уравнениям (лекция 6).
5) Методы изображения и построения пространственных фигур |
плоскости. В пространстве невозможно выполнить операции аналогичные irJ
которые выполняются на плоскости циркулем и пинейкой. т к. нс cymecinyJ
инструментов для "проведения ** в пространстве прямых и плоскостей. Поэте
построения в стереометрии делятся на два вида:
а) "Воображаемые построения’ - по существу. рисунки, “изобрази ниц
цель которых - создать наглядные представления о "происходящем
пространстве, то зрительное впечатление, которое получилось бы ii|«
непосредственном рассмотрении пространственной фигуры. В этом случае обычЛ
термин ‘построить’’ заменяют термином "провести", который употребляю! I
смысле "доказать существование ” (плоскости, прямой), удовлетвори
поставленным условиям. При "воображаемых построениях’’ чертеж теряет ы,
прежнее значение: на первый план выдвигаются расеуждения-обосновываюп
существования фигуры. Изображением фигуры (оршниала) в стсреом< ipJ
называют любую фигуру. подобную параллельной проекции данной фшурыЛ
некоторую плоскость.
б) Построения на проекционном чертеже, выполняемые но праин
основанным на свойствах параллельного проектирования (нространетнепяв
фигуры на плоскость)
Свойство!. Проекция прямой есть прямая.
Свойство 2. Проекции параллельных прямых параллельны.
। иойе тво 3. Отношение длин проекций двух параллельных отрезков равно
। uiiiriiiiio длин проектируемых от резков.
Правило I 11 юбражеипем греут одышка можно считать произвольный
*1(<»1Ы1нк в плоскости проекций. При пом медианы изображаются медианами и
*'•< их пересечения делит их в том же отношении. Высота, опущенная на
ф11ь ин алы 1)Ю сторону, проводится под углом 45“ (рис. 6).
Рис. 6
Травило 2. Изображением параллелограмма (в частности, прямоугольника,
квадрата) служит параллелограмм. Длины сторон и величины углов этого
^фктецня можно выбрать произвольно (правда, угол 90° с горизонтальной
правильно изобразить углом 45“), середины сторон и другие отношения
।нипися как в оригинале (рис. 7).
Рис 7
Рис. 8
11|>лп1ию 3. Изображением трапеции служит трапеция, у которой отношение
•и нип равно отношению оснований оригинала (рис. 8).
Ilpiuuuio 4. Изображением правильного шестиугольника служит
• «rninii.miK. \ которого противоположные стороны
Цпч hi и ючке пересечения делятся пополам (рис. 9)
попарно параллельны и
Рис. 9
llpTMii.i 5. Изображением тетраэдра может служить произвольный
Ч* 1<>и ник (рис. 10). У правильного тетраэдра (как и друтих правильных
58
54
Правило б. В основе изображения параллелепипеда лежи г изображение ipd
ребер, выходящих из одной вершины, гремя произвольными отрезками
остальные ребра соответственно равны и параллельны этим трем (рис. I1).
п)
60
Vv- -
м.
п
пирамид) высота проектируется в центр основания.
Рис. I ]
Правило 7. Изображением окружности служит эллипс. i
Правило 8. При изображении сферы и шара целесообразно для болып<|
наглядности построить а) контур изображения (окружность, изображают «4
большую окружность сферы; б) одно или несколько сечений сферы (обычно «н
сечением служит так называемый экватор) (рис. 12); в) плоскость экватора браи. ii
перпендикулярной к плоскости проекций (иначе экватор изобразится в «и»
отрезка); диаметр, перпендикулярный плоскости экватора, изобразится огрсиЛ
NS. концы которого (полюсы шара) располагаются не иа контурной окружное in I
внутри нес.
Рис. 12
С
проекционном чертеже
часто выполняется построение ссчпа
। праиипкоп. Сечением многогранника плоскостью называется многоугольник.
|Ч1Усмый линиями пересечения секущей плоскости с гранями мишстранника. Из
Н|к г цепня следует метой построения сечений миоюграниика плоскостью: в
||>П ।рани многогранника построить (или найти на основе условия) линию
риечпшя секущей плоскости с этой |раныо. Эту линию можно построить двумя
||><|||1ымн способами: а) найти (или построить) в данной грани две точки.
111Н'Гп1сжапше секущей плоскости. и соединить их прямой линией;
м<11ип>)овать признаки параллслыюстп прямых п плоскостей и свойства двух
я 'iiriMibix плоскостей, пересеченных третьей.
11 in плоскость пересекает тело вращения, то, в зависимости от расположения
т<Й плоскости, сечением прямого кругового цилиндра могут быть;
••мн iniibHHK, окружность, эллипс; сечением прямого кругового конуса -
• uuMiHK, окружность, эллипс, парабола, гипербола (так называемые
ii'inkiie сечения); сферы ~ окружность, эллипс.
II некоторых случаях свойства пространственной фигуры помогает увидеть ее
-чьи - плоская фтнура, полученная с помощью ее воображаемого разрезания
В»и|||рым характерным отрезкам (ребрам многогранника, образующим конуса
НI II других случаях полезно не ограничиваться построением в одной
in проекций, а выполнить несколько чертежей при разных положениях
4i+i ‘чпосительно плоскости чертежа (особенно при таких, которые позволяют
пн и. построения без искажений).
••• построениях в стереометрии см. [4, гл. 12. §44]. а также Н.Ф. Четверухин
|k<M«i|»l4ecKlie задачи на проекционном чертеже», «Математика в школе». 1998.
I I <><> 72; статьи Г.А. Владимирского «Каким должен быть чертеж преподавателя
• - Ирин С. 72-78 и Д.Ф. Изаака «Об изображении пространственных фигур». - С. 78-
•.«ииячк Л.М. Стереометрические задачи на построение, методы решения задач на
т ЧП метод следа, метод внутреннего проектирования, образны оформления
НИЙ
*1 Криме методов геометрического построения (с помощью циркуля п
|к11мижны такие методы, как перегибание (практический) и измерение с
•I | кнннмп вычислениями (арифметический), метой оригами - один из
•»<« иишмнгельной геометрии Слово «оригами» происходит от двух японских
><|ш> - сложенный и «ками» - бумага, и может быть переведено как
• 'iiiiiH бумага». Складывание фигурок из бумаги имеет многовековую
Ч»|н и (.'коими корнями тесно связано с культурой Востока. Возможности
itepei iiohiiiih листа буматн включают и себя нс только «iеомшрию .шнспьЦ
(перегибание но прямой), по и «reoMCipuio циркуля», что «юеспетни.и
возможность решения большого разнообразия серьезных, а порой и заб.шни
задач. Некоторые задачи, решаемые методами оригами, просто не имеют pcHieitd
методами цирке ля и линейки. Как правило, решение задачи методами орш.пЩ
Проше и нагляднее. (Си. также [17, пособие С.Н. Белим]).
3.2. Место геометрических построений в программе и учебниках Габлпгы Н
Этап Класс -Г Темы программы
Пропедевтический (начальная школа и курс математики 5- 6 классов основной школы) ? 5 6 «Числа от 1 до 100»: построение прямого vuj прямоугольника, квадрата иа клетчатой бумаге. В т. 1. «Натуральные числа и шкалы»: построение от ре >*'Ч В т.8. «Инструменты для вычислений и измерешпк построение угла заданном величины. (В г.5 «Ммогоуп ники»: построение углов с помощью транспортира) В T.S. «Положительные и отрицательные чк « изображение точки на прямой. В т.9. «Координаты плоскости»: построение параллельных перпендикулярных прямых с помощью угольника 1 линейки. (В т.2 «Прямые и окружности»: построен^ параллельных и перпендику-лярных прямых В 11 «Фигуры на плоскости и в пространстве»; построим треугольников).
.... . - - Основной (курс планиметрии 7-9 классов основной школы) 7 8 о В т.2 «Треугольники»: понятие задачи иа построен^ основные задачи иа построение с помощью цирку ы 1 линейки. В т.4 «Соотношения между сторонами п yi м > треугольника»: задачи на построение. (Т.4. «Виа геометрических задач и методы их решении геометрическое место точек, обзор ГМТ, задачи ч построение методом геометрических мест. Осионии задачи на построение с помощью циркуля и thiikiim систематизация методов и приемов решения). В т.З «Подобные треугольники»: применение подпоив решению задач. Понятие о методе геометрии., U преобразований и методе координат. (В т.1. «Лара гк'И иые прямые и углы»: метод геометрических мест, м. i,i вспомогательной окружности. В г.4. «Задачи и гсор<а геометрии»: метод подобия в задачах на постро. им построение отрезка по формуле). Т.4. «Движение»: решение тадач. (В тЗ. «Координат 1 векторы»: координатный и векторный методы).
Завершающий К) В тематическом планировании не выд.-Л (В т.2. «Введение. Прямые и плоскости в прооран. IM
IO 11 классов
iiipuieli школы)
простейшие задачи на построение сечеиий тетраэдра и
куба. В 1.3 «Многогранники»: изображения многотран-
ннков на плоскости посредством проектирования;
построения на изображениях Н т.5 «Задачи и методы
стереометрии»: сечения проектирование
3.3. Цели изучения геометрических построении в школе
1 I Основной учебной целью изучения геометрических построений является
((iini'iiiH основных видов и методов построений и способов их применения к
। >но iiitio задач на построение и изображению геометрических фигур для
........ геометрических соотношений н свойств, овладение инструментами
рнЬгрпчсских построений.
II ыблине 11 показана дифференциация этой цели по уровням обучения.
1 .1 2. Содержание этого материала также позволяет продолжить развитие у
t<«iiiiixCB отмеченных в линии геометрических фигур познавательных процессов,
.-ini и умения учиться, логического, геометрического, пространственного
*ш в нпя, мировоззрения (восприятия реального пространства средствами
•г •• ipnii) конструктивных умений и элементов творческой деятельности,
• >йин11ПШ(> интереса к математике (используя богатый исторический материал и
ф».|||<тн-1|ця во мнотп.х областях гуманитарной человеческой деятельности), таких
•»*[ личности, как аккуратность, точность, эстетическое восприятие.
Я«|ы||пелытость. инициатива, воля, культура общения.
63
64
V4. Основные тнлы математических примеры учебных задач
1 'LL Основным типом математических задач в этой линии является задача
• нт троение. Ниже приведен основной обоозценный прием ес решения,
I) I Пучите содержание задачи: выделше данные в условии задачи геометрические
• 0.1 и отношения между ними; выделите искомую фигуру и свойства, которыми опа
I Ий обладать по условию задачи; дайте ей определение (уделяя внимания
ГО1ЫИМЫМ и достаточным признакам ее существования}
') Проведите геометрический анализ (поиск решения); предположив, что задача
К'Н. выполните эскиз; рассмотрите эскиз, выделите па нем данные и искомые
I ины. установите зависимости между ними, сели нужно, сделайте дополнительные
«•ритпня; выделите точки, необходимые п достаточные для построения искомой
И1|'ы (определяющие точки); выделите теоретические знания, обеспечивающие
« ||»ч'11пс искомой фигуры и установите достаточность или недостаточность для
♦ ipx'iiue данных условия задачи; проверьте, за какими знаниями могут быть «скрыты»
>н|11|>ые необходимы для построения искомой фигуры; выберите те знания, которые
«I । in пользованы для решения задачи и объясните правомерность этого выбора; исходя
I Мыто, выберите метод построения и объясните правомерность этого выбора;
•iiiiniie, какие и в каком порядке нужно выполнить элементарные геометрические
«1|«>г||ия, чтобы по данным элементам построить каждую из определяющих точек и. в
чмом счете, искомую фигуру.
1) Нмнолните выбранные построения, выполните их в определенном порядке и
1 his с использованием специальной символики
4) Дпкажите, что построенная фигура удовлетворяет условиям задачи, опираясь на
•« in iiibi построения н выбранные теоретические знания
*i Ik следуйте решение, ответив на вопросы; всегда ли возможно построение при
ВИ* '• товиях? Является ли выбранный способ решения единственным пли возможно
м»м<К1> способов решения? Единственно ли полученное решение? Если нет, то сколько
ШинII пшможно в данной задаче? Какие это решения? Возможны ли частные случаи
Si* имеет ли смысл их рассматривать? Какие из ранее известных (решенных) задач
||чн пне могут быть использованы в качестве промежуточных построений в данной
• ’ I какой из ранее известных задач на построение может быть сведена данная
fiu.ie виды п подвиды задач на построение и приемы их решения связаны с
В'нуемым методом построения и варьированием условия задачи. Так.
I ыдачтт на построение методом геометрических мест можно разделить на
ад и I) задачи, в которых дана некоторая фигура и на ней требуется найти
)< удгшлетворяющую определенным условиям (т.е. искомая точка должна
»*• (иирлть двум условиям - принадлежать данной в уловин задачи геометри-
"Й фигуре и фигуре, все точки которой обладают определенным свойством),
вичр л мпорых требуется найти точку, принадлежащую одновременно двум
л •»! обладающим каждая своим определенным свойством.
Прием решения задач первого вида методом ГМТ
11IIшорт пне геометрическую фигуру, которой принадлежит искомая точка X;
2) исходя из текста задачи, сформулируйте условие, которому уяоадегвогч11
искомая точка Л;
3) назовите ГМТ, удовлетворяющее этому условию'.
4) nocipoiiic питанное ГМТ;
5) найди те точку (точки) пересечения данной фигуры и построение! о I МI.
Прием решения задач второго вида методом ГМТ
1) на основе анализа содержания задачи сформулируйie два условия. KOiopi.uJ
удовлетворяет искомая точка А’;
2) назовите ГМТ, удовлетворяющих первому условию;
3) наторите ГМТ. удовлетворяющих второму условию;
4) построй ге названные ГМТ,
5) найдите искомую точку (точки) пересечения этих ГМТ.
Задачи на изображение тесно связаны с задачами на построение. Задач
построения изображения считается решенной, если получено любое изображены
фигуры, достаточно наглядное н удобное для проведения на нем дополнительней
линий (воображаемых построений). Например, на изображении npaBnai.iioiH
треугольника можно построить изображение высоты, проведенной к одной inn»
сторон, соединив середину этой стороны с противоположной вершшп»
треугольника; точка пересечения всех трех таких высот даст центр вписанной (•
описанной) в треугольник окружности и т.п.
Задачи на моделирование в процессе решения задач (особенно, в i......и
изучения стереометрии) играют важную роль с точки зрения подшгонки •
решению задач на построение (и других).
(См. также [17, пособие О.Б. Епишева. ВИ. Крупич. гл. 3, § 2 - специальные прщ
решения задач методом геометрических мест], М.А. Петрова. Стереометрические ха in'ifl
сечения куба плоскостью /' Математика в школе. 1998. № 5. - С 15-18).
3.4.2, Основные типы специальных учебных задач связаны с формирог-иим!
действий, составляющих общее умение решать задачи на построение: пзображм
геометрические фигуры (делать эскизы), выделять (узнавать) геометрнчл
фигуры и нх свойства на чертеже, переосмысливать элементы фигуры в и и*
другого понятия, вычленять н комбинировать отдельные элементы изобрали и <
фигуры (в частности, не указанных в условиях задачи), подводить элсмецА
изображаемой фигуры под необходимое понятие, подводить шляпную citiy.iпа
иод метол построения, выполнять элементарные и простейшие noerpoinnd
выполняп. дополнительные (вспомогательные) построения и изображения.
Примеры учебных задач:
• лью прямых (лучей) можно провести через выбранную точку?
’) Через две данные точки проведите а) прямую, б) кривую линию. Сколько прямых
piihi.ix линий можно провести через две точки? Если через них проведены две линии,
•>31 >1(1 обе эти линии быть прямыми? Почему'?
Ч Начертите при помощи чертежного треугольника четыре прямых утла в
>нн>||1ых положениях
4) Начертите два смежных угла так, чтобы их общая сторона была а) вертикальная.
1 i »||ц>1>итхтьная, в) наклонная.
JI) Начертите иа глаз а) острый угол в 60° (30", 45") и проверьте правильность
||<|>|’11пи транспортиром; б) тупой угол.
Л) Начертите треугольник АИС. измерьте а) его стороны, сравните их между собой н
• Пш нт них с суммой двух лругих; б) расстояния межцу серединами сторон, сравните
я ! к ыпшейся стороной треугольника.
I Н Лэппом треугольнике проведите а) из вершины тупого у<ла медиану, высоту и
Hkipucy, измерьте их; 6) из вершины угла С перпендикуляр к биссектрисе (медиане)
<
И) Можно ли построить треугольник со сторонами а) 15 см, 18 см, 17 см; б) Зсм,
I ч 14 см, б) равными данным на чертеже отрезками?
81 На дайной прямой I (окружности) найдите точку, удаленную отданной точки А на
! чине а (положение точки и прямой (окружности) задается).
|п) Постройте несколько точек, находящихся на одинаковом расстоянии (например,
|«1 в( а; данной прямой; б) двух параллельных прямых, в) двух параллельных
•••* ieli Сколько таких точек .можег быть построено? Где они расположены?
11) Ошуда следует, что через точку вне окружности можно провести касательную к
окружности? Сколько таких касательных можно провести?
I ?) Можно ли описать окружность около прямоугольной трапеции?
11) Вращением какой фигуры можно получить а) цилиндр, б) конус, в) шар?
14) < колько касательных плоскостей к сфере можно провести через точку, взятую
•* ||ирс,б) вне сферы9
||) Г только касательных прямых к сфере можно провести через точку, взятою а) на
В б) кис сферы?
1ь) Найдите I МТ. которые являются центрами сфер а) касающихся данной
)• in и данной точке; б) имеющих данный радиус и касающихся данной плоскости.
I ’| Верно ли утверждение: а) около всякой призмы (пирамиды) можно описать
I• нс но всякую призму (пирамиду) можно вписать сферу?
II) К № построить угол прямой с плоскостью?
1'В Изобразите развертки пространственных фигур и опишите свойства полученных
• •«о fniyp
I) какой фигурой является осевое сечение а) прямоугольника, б) пирамиды.
Niiibipn, ।) конуса, л) шара, е) полушара ?
1| Можно ,зн в сечении куба плоскостью получить а) треугольник,
И •Н)И>1Ы1ЫЙ треугольник, в) остроугольный треугольник, г) тупоугольный
• ши л) правильный треугольник, с) правильный четырехугольник, ж) правильный
• in инк. I) правильный шестиугольник, и) правильный семиугольник9 Покажите на
Hi 1.1ПНЫХ утверждений выберите верные, а) все днагонхтытые сечения прямого
Г. i'3i Пинеда - прямоугольники; б) любое сечение цн.чинлрз плоскостью есть
ь, равная окружности основания; в) плоскость, перпендикулярная осн
Во ш ргсскает его по кругу, равному основанию цилиндра
№ канте из закрашенных на рисунках фшур (рис. 13) с вершинами в вершинах
« ill | • )>г липах его ребер являются сечениями куба плоскостью?
67
1) Через произвольно взятую точку проведите а) прямую, б) исходящий >н шч
66
Рис. 13
24) В кубе (рис. ] 4) проведены два отрезка, концы которых - или вершины куба
середины ребер. Укажете те кубы, у которых эти отрезки лежат в одной плоскости
Рис 14
25) В каких многогранниках (рис. 15) сечение плоское) ыо. проходящей 'при.
вылеченные точки, построено неверно?
2)
Pile. 15
'll) Дана призма (рис. 16). Перечисленные ниже пары прямых изображены на
|В*< пари пчельными прямыми. Параллельны ли они на самом деле?
1) TR и MN -,
2 ) BR и PS-,
3) КН н Т£>-,
4) RH и 50?
Рис 16
JI I 111 и (обращениях многогранников (рис. 17) проведены юнкис линии,
* н ши ipociilie сечения многогранника плоскостью, проходящей через три
hii.ii Ц1ЧМ1. Объясните этапы построения н выделите получившееся сечение
Но - iiiHiiii пунктиром), достроив, где необходимо, недостающие линии.
1
28) На
плоскостью.
Рнс-17
рисунках Грис. )8) показаны этапы построения сечения пиртм*
пДоДяшеи через три выделенные точки. Объясните каждый -
70
29) I pcyio u.iiHK .liB/Ci является проекцией треугольника ЛВС. У треугольнике ,Ш('
|||кИ1елепы из вершины биссектриса, медиана и высота. Будут ли проекции этих отрезков
Иинп.ся биссектрисой, медианой и высотой треугольника А/ВгС/ AiB/СГ'
’О) Дано изображение равнобедренного треугольника в миле равностороннего
||«>|<1аытка. На этом изображении постройте итображенис а) биссектрисы угла при
•iKliiiiie. б) перпендикуляра к основанию, проведенного через середину боковой стороны.
Ч) Дано изображение треугольника и двух его высот. Постройте изображение
4мц|м круга, описанного около треугольника-оригинала
. ,12) Может ли изображением а) заданного четырехугольника служить произвольный
Т1.||>ехуто.п1,ник; б) трапеции - параллелограмм, и) ромба - квадрат?
J3) Какие из свойства а) ромба, б) прямоугольника останутся верными для его
*1 Гц,,! кения (проекции)? Какие могут не сохраниться?
П) Трапеция AiB/UiDf является проекцией трапеции Л BCD на плоскость,
* рдншую через АВ. Равны ли длины средних линий этих тралений, если a) ABHCD.
НИ И.иг:
,15) На изображении равнобедренного прямоугольного треугольника постройте
>М>| пжение квадрата, лежащего в плоскости треугольника, если стороной квадрата
Ц • Ит а) катет данного треугольника, б) его гипотенуза.
16) На изображении правильного шестиугольника постройте изображение
| нтпфемы шестиугольника, б) биссектрисы одного из его внешних углов,
I |Ч|г||.1ккуляра, проведенного через центр к одной из меньших диагоналей.
1) На изображении ромба постройте изображение его высоты, если угол ромба 45"
« 'ч также [17, пособие В.А. Далингера «Планиметрические задачи на построение».
•И
5,5. Специальные методы н приемы обучения
I I (Яновной специальный метод обучения в данной линии - решение задач
।роение различными методами. В пропедевтическом курсе учащиеся
। •тип я с простейшими чертежными и измерительными инструментами
Ь)*Й1н>1'| линейкой, чертежным треугольником, угольником. транспортиром) и
<»цн>1 их для построения отрезков и углов заданной величины, треугольника.
|цк\ ияра, параллельных прямых: затем - с циркулем для построения
li'i пт. выполняют наглядное изображение куба, параллелепипеда и др
B1L], В систематическом курсе танимстрии, после систематизации
в' пропедевтического курса и решения первых залам на построение (с
‘К шпем вначале только 2-х этапов - анализа и тщательного выполнения
» 11114 с применением инструментов и частных приемов построения)
»! ,ц । начинают доказывать истинность построения. Этап исследования
И нт Цо опускается (у учащихся еще отсутствуют в полном объеме нужные
тсорешческне знания), его элементы возможны лишь р. конце курса 7 класса 11|
этом в несложных задачах можно записывав только построение и доказачельсны
в бо.чсс сложных - построению должен предшествовать рабочий рисунок и пни
построения. коюрый следует из анализа. Анализ можно проводин, устно, как «
исследование; в этом случае целесообразно воспользоваться серией кодопозипниц
последовательно накладывающихся друг на друга и иллюстрирующих чат
анализа и исследования (иногда, и построения).
I (рнмеры решения задачи па построение и ее оформления.
Задача I. На плоскости даны три различные точки О. А. В; требуется посгрош
окружное гь К/, которая проходила бы через точки А и В и касалась бы в точк«
окружности К с центром О, проходящей через А.
Решение.
1. Анализ.
Если точка Л’есть центр искомой окружности (рис. 19). то эта точка Л'лежи i,
первых, на прямой ОА {в силу теоремы: если две окружности касаются, зо точка каепш
лежит на линии центров) и, во-вторых, на серединном перпендикуляре отрезка АН, )
этот серединный перпендикуляр является геометрическим местом точек. равноулалеш<||
от А и В.
2. Построение.
I) Проводим серединный перпендикуляр CD отрезка АВ (с помощью Лм
окружностей одн01 о радиуса с центрами в А и В, не показанных на чертеже).
2) Проводим радиус ОА и продолжаем его в обе стороны.
3) Берем точку пересечения А'прямых CD и ОА.
4) Проводим окружность Kt с центром в точке А', проходящую через А.
3. Доказательство.
Окружность Kt, проведенная через точку А, пройдет и через точку В, т.к. ЛА-/Н
свойству серединного перпендикуляра отрезка Окружность Kt касается окружное in 1
точке А в силу теоремы «если две окружности имеют общую точку А па липни их ueni|
то они касаются». Таким образом, окружность К/ - искомая.
4. Исследование.
Пункты I п 2 описанного выше построения выполнимы всегда, ио п 3 лини. |ц
условии, что прямая CD не параллельна прямой ОА, те. если прямая lit
перпендикулярна ОА Предполагая, что это условие выполнено, имеем только и
окружность К/, удовлетворяющую условиям задачи независимо от того, находит
данная точка В вне К (рис 19а), внутри А’(рис 196), на К (рис. 19в); г. последнем i и i
искомая окружность совпадает с данной Если АВ перпендикулярна СМ (рис 1’>1),
задача не имеет решения, т.к. негточки. которая лежала бы одновременно на прямыт I I
CD. Однако, проводя через точку А окружности с центами, расположенными па прям
ОА н неограниченно удаляющимися от А. мы будем проводить их все ближе н блин >
приближаясь к этой точке как угодно близко, и это дает основание утверждать, что к ч
особом случае гоже имеется решение, но выродившееся. окружность А'/ вырожлмп<
прямую, которую можно рассматривать как окружность бесконечно большого paaiiv я
Рис. 19
l<iwwwtic. Указание, сделанное в тексте задачи о том, что даны три различные
.«И 4, В. О. избавляет от необходимости дополнить исследование рассмотрением
к, когда две из этих точек или даже все три совпадают, что тоже имеет интерес и
••<1 Гьпь предметом дальнейшей работы. Например, при совпадении .4 и Б задача имеет
Гц. Чине число решений: окружностью Kt является любая окружность с центром на
^входящая через Л: все эти окружности составляют так называемый параболический
н.чнк
2. Построить прямоугольный треугольник по данной его гипотенузе с и
>Ы» КЛ1ГТОВ .г.
/'< шсиие.
II мшиизе прежде всего замечаем, что задачу можно решать только при условии, что
Ч I к сумма двух сторон треугольника всегда больше третьей его стороны. Затем
Врвмся, что задача сводится к построению вспомогательного треугольника по двум
ни ri ч сторонам с п 5 и углу в 45°, лежащему против стороны с.
Ilin гроенне н доказательство не представляют после этого никаких затруднений.
При исследовании, сравнивая отрезок с с катетом h равнобедренного
«><н>'1Ы10го треугольника, имеющего гипотенузой л. различаем гри случая: если <‘<Л.
• < ill ист. если c=h. существует один треугольник (равнобедренный).
• к ширяющий условиям задачи; если с>Л, существует два треугольника.
|' I «юшиеся только положением и удовлетворяющих условию «адачи. Таким образом.
*. ц|х|1-1м н достаточным условием существования решения задачи является
К '1 >11111’ неравенства Л < с < з.
||<нн ню проследить, как меняются методы решения одной и той же задачи на
•р 1П1<’ с приобретением новых знаний. Например, задача деления угла
» м решается а) в начальной школе - перегибанием листа бумаги
>|> приз ни), б) в 5-6 классах - с помощью транспортира (арифметически), в) в 7
t । помощью циркули и линейки (геометрически). К задаче 2 также полезно
k II ан рассмотреть ее решение алгебраическим методом, получая выражение
л.чя катетов искомого треугольника в виде 0.5s + -0.25.»: . Эта формула л.к|
точное :ншл1ггпчсское решение задачи, ио основанное на пей ноезроеш»
оказывайся более сложным, чем и нервом случае.
Кроме тою. наряду с циркулем и линейкой, целесообразно, в шин
приближения обучения геометрии к жизни, использовать для носгросши
чертежный треугольник и транспортир, рейсшину и пантограф, а также прием!»
построений при помощи этих инструментов, которые часто встречаются
чертежной практике и при разметке. Например, задачи па построение «I
препятствиями», построения с «недоступными точками» или построения ihl
о|ранпченном куске плоскости - различные способы построения касательно!) Я
окружности для случаев, когда центр окружное ги задан, если он находится it
чертежа и пр.; проведение высоты треугольника через недоступную вершину u ,ip I
Первым специально изучаемым методом построения является мепш
геометрических мест. Затруднения возникают у учащихся уже при изучыиЛ
понятия геометрическое место точек обычно не в связи с введением термам
«ГМТ», а в связи с тем смыслом, который в него вкладывается при peni'iM
сложных задач на построение. Термин «ГМТ» в последнее время сравни и-и.Л
редко употребляется в методической и математической литературе и замени» м
термином «множество точек»: и тот. н другой термин полезно употреблять и ><
«расширенной формулировке»: «ГМТ. обладающим данным свойс нима
«множество точек, обладающим данным свойством» и сопроно.пн
рассмотрением примеров.
Для решения задач методом геометрических мест необходимо знать осшим
геометрические места точек. Некоторые из них: 1) окружность как 111«
равноудаленных oi дайной точки. 2) серединный перпендикуляр к огрело
ГМТ. равноудаленных от ею концов: 3) биссектриса угла как ГМТ. равно» .ьЦ
ных от его сторон; 4) две прямые, параллельные данной и отстоящие <ч
данное расстояние как ГМТ. равноудаленных от данной прямой; 5) пр
параллельная двум данным прямым и одинаково отстоящая от них к.и I
равноудаленных от дпух параллельных прямых; 6) дута окружности с к<>шп<4
точках А и В как ГМТ. из которых отрезок АВ виден под данным yi mM !
которые лежаг по одну сторону от прямой АВ.
Первые три ГМТ, изучаемые в начале курса, использую гея для разъяснения
Uuiinioii выше сущности метода геометрических мест Одновременно
лхидпмо решение задач на поиск геометрических мест точек, обладающих
инн,1Ы свойством, выявление частных приемов их построения, накопление и
КМ.низация тех и других.
I'.u смотрим пример решения задачи на построение и методом оригами.
JuAiKfl. Разделить отрезок (сторону квадрата) натри равные части.
1’ис. 2|
Построение (последова1елыюс!Ь перегибаний
листа) показано на рис. 20.
Доказательство. ДАОВ - равносторонний по
построению, значит <DAB = 60".
<DAC = <СЛВ = 30" по построению.
AADC = ДЛСВ; значит. <DCA = <АСВ - 60е.
AECD = A ECO; значит, <DCE = <ЕСО = 30°.
Отсюда <ЕСВ - прямой.
GF X АВ, ЕН 1 АВ; значит.
AFCB = AFGC = AEGF = ДЕНЕ = ДАЕН как
прямоугольные треугольники, имеющие равные
либо гипотенузу, либо большой ка>ет.
Значит, и их меньшие катеты равны между собой.
Значит. All = HF = ГВ. что н требовалось
докатать.
ipniiMii методами построения учащиеся знакомятся nocieiiemio. изучая
iiMiiil теоретический материал. Например, с алгебраическим методом - при
|| морических соотношений между элементами фигур, с другими -
75
аналогично. (Си. также [17. пособие В.А. Далилiера Планиметрические ю мчи
пос гросниеи).
3.5.3. В систематическом курсе стереометрии. при изучении noci|"" »!•
как и при изучении свойств геометрических фигур, большую роль Ш|
стереометрический чертеж и методы его построения (описанные выше). Злц.гш |
построение в пространстве имеют характер, существенно отличный ог тою гй»(
имеют планиметрические задачи на построение Как уже отмечалось. 1411
решении никакого фактического построения не производится, а только и (
соответствующего рассуждения выясняется, как свести вопрос к вьпкнь-п^
конечного числа основных построений. При такой постановке вопроса pin-fl
задач на построение в пространстве становится абстрактным и поэюм) i|
требующим иллюстрации на модели и мало интересным даже лич
успевающих учащихся. В лучшем случае усваиваются приведенные и
готовые решения нескольких таких задач (яркий пример - задача на и» I
общего перпендикуляра к двум скрещивающимся прямым) как ic<ip> iii'Hfl
материал, но умения решать такие задачи учащиеся не получают По н М
использовать с привлечением моделирования как материал для нпдпы! < «
заданий (например, как темы для докладов) для закрепления теории и । * afl
пространственного воображения (см., например. [4, гл. 12, § 44, с. 2S6 Л'ЛЦ I
С этой же целью полезно рассматривать простейшие гесыстрнч*» и* fl
точек в пространстве, сравнивать, обобщать, проводить аналонт > 111мм
ГМТ на плоскости. Это ГМГ, равноудаленные отданной точки; <и /ыпн « ।
от данной плоскости; от двух данных точек; от двух прямых (пгри
параллельных, скрещивающихся); от двух плоскостей и др И
По существуют и задачи на построение в простраш ин i 4
решаемые построением на плоскости с помощью Циркулт н шп М
требующие моделирования. В таких задачах все данные сопер-м» я i
пространственной фигуры, выполненном и той или ннон пр..........Шн (
элементы (часто сечения) должны быть получены на том ж ч | •• I
таких задач на построений сечения многогроанннка приио.чнк и ни*।
Задача I Построить ееченне тетраэдра 4ВС1) плоскосп.|.. при <ит»
Л/ и Л’(внутренние точки его ребер AD и АВ) и параллельной примни и И
Решение.
Inin построшь) в данной грани две точки,
и соединил, их прямой линией; б) использовать
и плоскостей и свойства двух параллельных
В данном случае (рис. 20). линию пересечения
I Анализ.
(лк известно (и. 3.1.2. данной лекции), для построения сечения многогранника
•мктыо в каждой ею грани нужно построить (или найти на основе условия) линию
ВВМ'тепня секущей плоскости с этой гранью. Эту линию можно поароигь двумя
фчымн способами; а) найти
*>.< К'жащие секущей плоскости,
Sin uni параллельности прямых
тмей. пересеченных третьей.
♦•ни in сечения с гра,,ь|<) /ЮЛ можно получить, соединив точки Л/ и N. По условию
м н, сечения параллельна прямой АС, поэтому линии ее пересечения с гранями АСВ
W’ ||<1.1жнм быть (по теореме о линии пересечения двух плоскостей, одна из которых
i„i через прямую, параллельную другой) параллельны прямой ЯС,
2. Построение.
I) В плоскости ABD соединяем точки М
н .V.
2) В плоскости АВС проводим NPHAC п
получаем точку Р на ребре ВС.
3) В плоскости ACD проводим MQH.4C и
получаем точку Q на ребре DC.
4) Четырехугольник ЕМОР - искомое
сечение.
‘I "ИПЛЬСТВО
*ti । ВМОР параллельна прямой АС по признаку параллельности прямой и
। |>>плнпе
м iiMi'ci единственное решение, т.к. ребро ВС пересекает плоскость сечения в
41 I точке Л п по аксиоме через три точки W. Л’ Р проходит единственная
I । рп.мср - задача, составляющая часть задачи.на построение сечения
hi । плоскостью, в которой требуется
построение дополнительных
t II параллелепипеде ABCDAfBiCiDi
ц> ргпрам £>£►,, ££;, CCi, причем прямые,
ин naiioMV из ребер параллелепипеда.
М'н I/"
точки Л/, Лг, Р принадлежат
соединяющие данные точки, не
Построить линию пересечения
ВЧ1НИ искомой прямой достаточно пощронть две общие точки плоское!ей
I cioiyio in таких точек можно искать как общую точку двух
» прямых, о та из которых принадлежит плоскости Л/ЛТ. а дрхтая - АВС
2 Построение.
I) В плоскости грани CCiD/D строим
точку пересечения F прямых МР и DC (рис.
Рис. 23
2) В плоскости, определяемой
параллельными прямыми DDi и 71 В, строим
точку Е пересечения прямых ,W<V н DB.
33 Соединяем точки Fa Е.
Ifliii । pii * ii и плоскости ЛМ7’ и плоскости АВС, поэтому 17 - искомая
?7
прямая (no соотне:ствующеи аксиомеi.
4. Исследование.
Задача имеет единственное решение, т.к. точки Л(. Лг и Г определив» I <
COOTвсгствуюшсй аксиоме)единственную плоскость. Общая прямая Fh плоскостей АЛ/‘j
.4ДС существует, т.к. они имеют общую точку F. в она единственная (по cooi веге тот т«чтт- <
аксиоме).
Решение задач на построение способствует развитию и закрсилснн»
геометрических умений учащихся, по в большинстве случаев требует зиачи!сиы4
больших усилий от учащихся. Если учащиеся с ними не справляются, ну in
проверить, умеют ли они решать хотя бы более простые задачи на построепш |i
плоскости, уделить время на повторение и пополнение их знаний и умении в
этому разделу, а затем уже вернуться к задачам на построение в прострашчв
Необходимо учить тщательному выполнению чертежей, соблюдению правя
изображения видимых и невидимы линий, использовать цветной карандаш и ми
выделять главные элементы (например, сечение), обосновывать построения.
В этой работе, в целях экономии времени и достижения аккуратно! и
удобного изображения пространственных фигур в тетради, можно использони
шаблоны и трафареты, а для иллюстрации построений в пространстве
стандартными комплектами таблиц и моделей (например, сечен
многогранников), диафильмами и диапозитивами, серией кодопозитивт
иллюстрирующих динамику построения н помогающих лучше их понять, а ни
появляющимися обучающими компьгерными программами.
3.5.4,
Технологическая цепочка изучения метода геометрических построении
I) Изучение теории, иа которой основан данный метод, в курсе планиметрии
2) Рассмотрение учителем примеров задач на построение па плоски!
решаемых с помощью изученной теории.
3) Выявление .acuciBitii но применению теории к решению рассмотрсшп
задач на построение и их последовательности.
4) Обобщение выявленных действий в виде приема решения задач
построение данным метолом.
5) Применение полученного приема к решению задач па построепш
ПЛОСКОСТИ.
(?)* Примеры решения задач па построение разными методами и их сравнен
7R
7) Контроль и коррекция усвоения.
Я) Изучение теории, па которой основан данный метод, в курсе стереометрии.
>«ih'iiiie, аналогия, отличительные особенности.
ч) Гассмотрение примеров задач на построение в пространстве, решаемых с
•iiii.io изученной теории и известного приема решения планиметрических
н'1 сравнение, аналогия, отличительные особенности
10) Обобщение (на основе сравнения, аналогии н отличительных
• пиостсй) известного приема решения задачи па построение плоской или
еч ipilllCTBeHlIOH фигуры.
II) Применение полученного приема к решению задач на построение в
MipniicTBe.
I?) Итоговый контроль усвоения.
Технологическая цепочка формирования алгоритмов и приемов
геометрических построений
Таблица 12
Курс Приемы геометрических построений
шрмедеышческий курс 1. Алгоритмы н частные приемы построения прямого угла, прямоугольника, квадрата иа клетчатой бумаге 2. Алгоритм построение отрезка данной длины с помошыо математической линейки 3. Алгоритм построения угла данной величины с помощью транспортира. 4 Алгоритмы построение параллельных и перпендикулярных прямых с помощью угольника и линейки
Курс планиметрии 5. Алгоритмы решения основных задач на построение с помощью циркуля и Линейки. 6. Частные и общий приемы решения задач построение методом геометрических мест. 7. Общий прием решения задачи на построение. 8 Частные приемы решения задач на построение алгебраическим методом н их обобщение. 9. Частные приемы решения задач на построение методом движений (симметрии, поворота, параллельного переноса - вектора) и их обобщение. 10. Частные приемы решения затач на построение метолом координат и их обобщение. 11. Частные приемы решения задач на построение методом гомотетии и подобия 12. Обобщенный прием решения задач иа построение методом геометрических преобразований (обобщение
79
з Курс стереометрии
приемов 8 и 10).
13 Обобщенный прием решения задач ил нос [роешь ш
плоскости,
14. Приемы изображения прямых и илоскостсн |Д
воображаемом чертеже.
15. Частные приемы решения задач на пошроение се к пр
тетраэдра и ю. ба
16. Частные приемы
воображаемом чертеже.
17. Приемы изображения
проекционном чертеже.
18. Частные приемы
проекционном чертеже
19. Обобщенный прием решения задач на постро ши
сечений многогранников и круглых тел на ироекционн ,
чертеже.
20. Обобщенный прием решения задач на иостроеиш |1
пространстве методом координат._________
выполнения построений
Н ространст венных ф игу | >
выполнения построении
Н«
1И
ЛЕКЦИЯ IV
Геомстрические величины
4.1. Логико-мате.матпческий анализ линии геометрических величии
4 I.JL Понятие величины является одним из основных понятий. применяемых
« m п.но в математике, но и в физике, химии и других научных дисциплинах. В
। чашке определенные классы величин имеют совершенно четкое (чаще всего
помптнческое) определение. I еометрические величины - это действительные
|Па. которые характеризуют геометрическую фигуру с точки зрения се размеров
utiiii отрезков, величин углов, площади и объема. С точки зрения теории
пьсств, все геометрические величины являются примерами одного из основных
111сляемых аксиоматически общематематических понятий -меры множества.
Пусть дано некоторое семейство множеств Л, В. С,
множествами некоторого универсального множества У Говорят, что на этом
являющихся
((Пете множеств определена мера, если каждому из них поставлено в
ристствие некоторое действительное число т (А), удовлетворяющее аксиомам:
I) т{ А) г О,т(Л) = 0 тогда и только тогда, кода А - пустое множество;
) средн данных множеств существует такое множество £, что m (£) = I;
1) ранные множества А = В имеют равные меры ш (А) =чп (£’);
1) мера двух непересекающихся множеств А и В равна сумме мер данных
ivctb m (J) + m (By.
') если пт (.4) = m (В). a m (В) = m (С), то m (А) = m (С).
Легко проверить конкретный смысл этого определения для понятий длины
тм. величины угла, плошали фигуры, объема тела (как и натурального числа).
Существуют два способа измерения (определения) геометрических величин:
Ирчдственное измерение и косвенное измерение.
//< посредственное измерение - сравнение данной величины с выбранной
Вицей измерения - основано на 1-й н 2-й аксиомах меры, соответствует
имычальному наглядному представлению, например, о длине сирезка как
It показывающему, сколько раз единица длины или ее часть укладывается
|ы идея) в этом отрезке, и состоит в выполнении следующих шагов:
81
1) ныорать единицу измерения (зго можно сделать на основе 2-й аксиом1.п I
2) сравнить данное множество с единицей измерения; число (па ocnoi» |1
аксиомы), показывающее, сколько раз единица измерения содержится н длины
множестве, ecu, его мера (длина отрезка. величина угла, площадь фигуры.
тела):
3) можно убедиться, что полученное таким образом число удовлешп|м
аксиомам 3 - 5 Н дает возможное!ь выполняй, сравнение, сложение, вычш >ч
умножение it деление на число измеряемых множеств и их мер.
Для практической реализации этого способа единица измерения нанос пн»
материальные носители и получаются измерительные приборы (маеннмл
линейка, транспортир, палетка). В то же время этот способ не всегда пракгичА
удобен (например, для измерения площади палеткой) и даже не всегда осущщ1‘<
(например, для измерения объема). Поэтому используют косвенное измем
геометрических величин, которое состоит в том, что непосредственно измеряй*
только величины гех элементов геометрической фигуры - отрезков и углов, (
которых это сделать легко и практически удобно, а площадь и объем мШ
вычисляются на основе аксиом меры с помощью специально устаноил ни
зависимости между всеми геометрическими величинами данной фигуры.
4.1.2, Ниже рассматриваются методы установления такой зависнм«4
называемые методами косвенного измерения геометрических величин.
I) Метод равновеликости равносоставлснных фигур для определи
геометрических величин многоугольников и многогранников основан на 3 и и •
аксиомах (конкретизируемых как свойства площадей и объемов) и следу юпв»|
ннх теореме: равносоставленные фигуры равновелики (две фигуры назгиим
равновеликими, если их площади или объемы равны; две фигуры Haii.ini«J
равносоставлениы.мн. если каждую из них можно разбить на cootiiciciM
равные части). Для многоугольников, в частности, справедлива и обратная in । (
равновеликие многоугольники всегда равносоставлены.
Примерами использования этого метода являются доказательства ф> ( ।
площади паралле.ю! ра.мма (преобразованного в прямоугольник), греутолынци (
половины параллелограмма), трапеции (достроенного до треугольника) ф р (
объема призмы; геометрическая иллюстрация законов действий над чн> ц|.<1
82
|н|<чул тождественных ирсобратованпй [2. лк. 3. с. 63] (последние. л частноетн
i|ii\ । быть использованы для вывода формулы площади прямоугольника па основе
•ни той формулы площади квадрата).
2) Метод предельного перехода основан на определении геометрических
• Hi'iiin некоторых фигур, которые не мог у г быть определены и измерены
вНщрсдсгвенно (длина окружности или дуги) или составлены из многоуголь-
Икни (площадь круга) пли многогранников (площади боковой поверхности и
Жгч.т круглых тел) как предела последовательности соответствующих значений
•мс грнчееких величин, вписанных в данную фигуру или описанных около нее
♦тир при неограниченном увеличении числа определяющих их элементов
1«и|чыср, сторон многоугольников).
Ннсрвые этот .метод применяется для определения длины окружности и
|НП ты ее вычисления. Рассуждения выстраиваются следующим образом, так как
tiHiinn измерения длины (единичный отрезок) не совмещается с дутой
* iMuictu, можно вначале измерить длину окружности приближенно, например,
* периметр вписанного (или описанного) и нее многоугольника Чтобы
♦ ’irinrb точность приближенного вычисления, увеличивают (например,
»»"пнем) число сторон многоугольника и вычисляют его периметр; теоретически
процесс можно продолжить бесконечно. Таким .образом, получается
। чн’чная последовательность длин периметров вписанных в окружность
^питолышков Р/. Р:, Р}. .... Рп, .... которая при л->«> возрастает и ограничена
(например, периметром любого описанного многоугольника’) н.
• «.ИМ icibiio. по теореме К. Веейрштрасса имеет предел. Этот предел называется
••mil окружности и его вычисление приводит к формуле С~ 2 л г. Аналогичные
>•• • циня можно провести для определения и вывода формулы площади круга,
*т> «И поверхности к объема цилиндра, конуса, усеченного конуса
В Метол интегрального исчисления для вычисления площадей фигур,
•.•и я иных сверху и снизу графиками непрерывных неотрицательных функций
с 119] п объемов круглых тел основан на теоремах математическою
I (| имчислении плошали криволинейной трапеции н объема тела вращения
Л
Тп ым 5 = [/(т)Л и Г = J.S'(.v)tZr. Примером непосредственного применения
S3
метода интегрального исчисления яиляС1Ся вывод формулы для вы ч нелеп и я < •< ч.-
пирамиды в I I классе.
Одна и ia же фигура может имен, несколько разных формул для bipiik <г,
ее площади (Объема) для разных частных случаев (так. например, известно inn
десятка формул плошали треугольника). На формулах вычисления плопыи-И
объемов геометрических фигур основан метод пл&щаоей (и объема") 4
вычисления длин отрезков или величин углов;
1) запишите две или более формул площади (объема) данной фигуры, и «> ш
которых известны все элементы, а в другую входит неизвестный элемент (элем nii.il
2) составьте уравнение (систему уравнений) на основе того, что ни ф-чк*
выражают одну и ту же величину;
3) решите полученное уравнение (систему уравнений) и найдите искомые ив м
Разновидности метода площадей (объемов): одна фигура заменись ч ip)
J
которая ей равновелика н более удобна для решения задачи; опкннени* "ip
заменяется отношением площадей треугольников с общей вершиной (- - (I
известны), основаниями которых являются рассматриваемые отрезки.
Метод и его разновидности используются и для доказательств «I
геометрических фигур (например, таким методом доказывав и ч «и
биссектрисы угла). Как при использовании этого метода, так и дру| их и- и
дополнительные построения и общие методы доказательства теорем
4.2. Место геометрических величин в программе и учсбшч «I
Этап класс
Пропедевтический (начальная школа 3
И 4
курс математики 5-6 классов основной школы) 5
Темы программы
«Числа or I ло 10»: длина отрезка, см и им
«Числа о । I до 100»: длина ломаной
«Сложение и вычитание»; ncpiiMcip и
прямоугольника, квадрата; плснкин мм
плошадь квадрата, прямоугольники пы i И>
«Умножение и деление»: hiioiii.hu i
треугольника (объем куба, нарюглеисинн л
В т.1. «Натуральные числа»' iiim«'p-iiii |
«-Линин»: длина отрезка В i' flu
измерение углов с помощью ip.uiii>4|.iii| i I
и объемы»: площадь прямоупъ-ti.iiiiiu i-n
(В 17. Треугольники и четыре*и-« и и
единицы плошали. nmuii.vii
[В_Т.К “Инструменты ДЛИ ПЫЧИ- I 14
84
। К повнон
pi пнппнмегрнн
Чккассой
• I uiiiiili школы)
7
8
9
|Н1Ы1о|ций 10
1т|комс17>ни
I йляссоп
|| П1КШ1Ы)
11
и тмсрепис величины угла, единицы измерения углов
Т.4. «Отношения и пропорции», длина окружности и
площадь круга. (В т II «Фигуры на плоское [и и в
пространстве»: площади. объемы, объем прямоугольного
параллелепипеда).____
В т.1. «Начальные геометрические сведения»: длина
отрезка и ее свойства, величина угла и се свойства, (то же
самое в г.2. «Основные свойства плоское in».
Т.2 «Площади фигур»: понятие площади многоугольника,
площади прямоугольника, параллелограмма. треугольника,
трапеции. (В т.4. «Задачи и теоремы геометрии»:
вычислительные методы в геометрии (основанные на
метрических Соотношениях в треугольнике и окружности).
Т.З. «Длина окружности н площадь круга». (T.I. «Площади
многоугольников», Т.2. «Длина окруж-ности, площадь
круга»),______________________________________________
8. т.2. «Параллельность прямых и плоскостей»: угол между
двумя прямыми. (В т.2. «Введение. Прямые и плоскости в
пространстве»: угол между скрещивающимися прямыми,
угол между прямой и плоскостью, двугранный угол). В т.З.
«Перпендикулярность прямых и плоскостей»: угол между
прямой и плоскостью, двугранный угол. В т.4.
«Многогранники»: площадь поверхнос ти мною1ранника.
В т.2. «Цилиндр, конус, шар»: площадь поверхности
цилиндра, конуса, сферы. Т.З «Объемы тел»: всех
изученных в курсе стереометрии. (Т.1. «Объемы
многогранников», включая понятие объема. Г.2. «Объемы
и поверхности круглых тел»
щ«и> Понятие отрезков, соизмеримых и несоизмеримых с единицей
| .и i м.иривастся (в неявной форме) в курсе алгебры для более
। поеппя понятия действительного числа.
I I Цели изучения геометрических величии в школе
|| ппг материала линии геометрических величин имеет основной
| и in-line учащимися на том или ином уровне инструментами и
* I и 1НГ1ШОГ0 и косвенного измерения геометрических величии и
11 При решении математических н прикладных задач. В таблице 14
in нннлиия згой цели по уровням обучения.
Таблица 14
: № 1 Общие категории целей Примеры обобщенных типов целей 1-}Р°вень 1 II уровень | ш vnnitPlih
2. Знание Запоминание и воспроизведение изученного материала Понимание термины «геометрическая величина», ее виды и обозна- чения. процесс непосредствен- ного измерения величины, единицы измерения и из связи, формулы и алгоритмы вычисления величии с помо- щью этих формул. Ученик знает формулировки и символичес- кую запись общих свойств геометрических величии вы- вод формул для их косвенного измерения и следствия из них. специальные приемы решения текстовых прикладных задач с помощью этих формул. методы косвенного измерения величин (вывода формул), обобщенный прием решения математических и прикладных задач алгебраическим методом с использованием формул вычисления геометрических величин.
Готовность к преобразованию изученного из одной формы в другую, к его интерпретации правильно воспроизводит термины, обозначения и формулы, приводит примеры, находит в учебнике ответы на задания и вопросы но тексту Ученик приводит контрпримеры, подводит заданную ситуацию под прием решения и формулу, выражает из формул одни величины через другие. выделяет идею обобщенного метола и приема решения прикладных задач на вычисле- ние величин алгебраическим метолом, его связь с решением
3. Умения и навыки Ученик
Выполнение действий, составляющих прием учебной деятельности, под активным контролем внимания или автоматизировано Решает простейшие задачи на измерение с помощью инструментов и вычисление геометрических величии арифметически по данным формулам и алгоритмам, ио образцу или с помощью извне. решает типовые и прикладные задачи на вычисление величин в стандартных ситуациях, самостоятельно выбирая и используя формулы и специальные приемы решения и проверки. составляет простейшие задачи. решает типовые и прикладные задачи на вычисление величин в нестандартных ситуациях, самостоятельно используя обобщенные и искусственные приемы решения, проверки и переноса.
ОТ
ГО
9
g
о
Е
ГО
К
S
й
ж
tc
Sc
s
и
и
о
Хс
X
X
ж
75
X
6
о
X
ф
а
X
£Г
го
X
*с
ГО
Я
6
'ного материала также позволяем продолжить развитие у
методом опорного элемента Если в качестве опорного элемента иысгуп.ь i
площадь - метод площадей. Иногда вводят вспомогательную неимссиноч
М: 1ичнну. которую легче найти. а затем уже вычистить искомую.
Основные обобщенные приемы решения <адач этими методами приведетI
в курсе лекций но методике арифметики, алгебры и начал анализа [2. лк.2, i i'<
40, лк. 4, с. 80-811; при этом для составления уравнений и неравенств, крон
формул вычисления длин. площадей и объемов, используются мсгрпчсаш
отношения и отношения подобия в треугольниках, мпогоугалынтмз
многогранниках и т.д. Возможен и комбинированный способ - решение один
части задачи арифметически, другой - алгебраически.
Обобщенный прием решения задач
на вычисление геометрических величин
1) изучите содержание задачи, т.е. выявиie а) названия содержащихся в в »
величин, б) связи и отношения между ними, основанные на метри'юын
соотношениях, формулах вычисления геометрических величин и форч>
тригонометрии; в) количество различных ситуаций в задаче и преобладают ум
них: г) известные и неизвестные величины и связи между ними (иногда уи>Ам
полученные таким образом данные записать в таблицу): д) если нужно, слсзда»
чертеж по условию задачи и дополнительные построения.
2) в зависимости от данных, полученных в п.1, определите, каким cim<>uw
легче вычислить искомую величину - арифметическим, алгебраическим, комЛим
рованным;
3) установите величины, которые легко вычислить арифметически, зашнмм
нужные формулы и произведите вычисления;
4) выберите величину (искомую или вспомогательную, две или более) к>ин|М
естественно и удобно (наиболее выгодно для решения) принять на нештич им
обозначьте ее с использованием принятых обозначений;
5) иа основе п.1 и и 4 выразите все величины в задаче через петнип j
данные и уже вычисленные, обосновывая их ссылками иа теоремы и формулы
6) используя зависимости и связи между величипами. установите равеш m 1 I
неравенство одноименных величин и составьте на этой основе yji.iiui «4
(неравенство, систему);
7) решите полученное уравнение (неравенство, систему);
8) вычислите значения искомых величин;
9) сделайте, если нужно, проверку (исследование, особенно, если ззл.ны । 4
предварительно в общем виде, как это часто бывает при использовании ф * Д
тригонометрии) решения по условию задачи;
10) запишите ответ в терминах данной задачи.
В задачах, где требуется найти не саму величину, а отношение ucuiihhii а
величину угла, обычно поступают так: считают один из линейных нич.я
известным (обозначают буквой и называют всламогательнылт лщъши
выражают через него нужные величины, а затем составляют уравнение
. 4,4.2. Основные специальные учебные задачи имеют целью усвоение
ницимпея понятия геометрической величины; единиц измерения геометрических
ii'iiiu, их долей н отношений между ними; общих свойств геометрических
iii'iiiii п 01ЛНЧНЙ от понятий «геометрическая фигура» и «значение величины»;
шикти методов непосредственного и косвенного измерения величии (в
Ihih'iii. понятий равновеликости и равносоставленпосгп фшур) и
•HicrciByioipiix формул, а также приемов решения задач на измерение и
ни кине ।еомстрнческнх величин.
I IpiiMCpi.t учебных задач:
11 I,топните пропуски так. чтобы полученное утверждение было верным: а) если
фасиие между двумя линейными единицами равно t/m, то отношение между
•«линующими квадратными единицами равно б) одни квадратный
ip больше одного гектара в _ раз.
]| Найдите площадь (площадь поверхности, объем) модели геометрической фигуры,
•ож необходимые (доступные для измерения) ее элементы и сделав необходимые
» мшя по соответствующей формуле.
>| lli данных элементов пирамиды выберите сочетания тех, которые достаточно
»» и» вычисления ее объема: а) высота. 6) образующая, в) площадь основания,
фии и боковой поверхности, д) сторона основания.
|| Норройте отрезок (угол), равный сумме (разности) двух данных отрезков (углов)
* шины (величины) отрезка (угла) - суммы (разности)?
(I Кикие из следующих утверждений являются верными: а) равносоставленные
ЦМ равновелики; б) равносоставленные фигуры равны; в) равные фигуры
фж i дилены: г) равновеликие фигуры равносоставлены?
11 Mui у I ли быть равновелики два неравных а) прямоугольника, б) квадрата?
'I Клюю часть площади треугольника, считая от вершины, отсекает ее средняя
И I ж 1 зедуст изменить величину радиуса круга, чтобы его площадь удвоилась?
• 11 ш 1сдует изменить ребро куба, чтобы его объем увеличился в два раза?
"ЧI ,ц. шнося 1ся между собой а) поверхности двух шаров? б) их объемы?
hili колько раз объем шара радиусом I см больше объема шара радиусом J мм?
|> ll'HctaiiOBiric условие задачи, ответ которой известен: Сторона основания
а» и Гхиолыюй призмы равна 10 см. (0 -Уб см. Вычислить площадь
г юрхиосзи призмы.
II при те проводятся сечения, параллельные ее основаниям. В каком отношении
Bbl .mi, гмы дайной и вновь полученных призм?
Прньма деформируется, оставаясь призмой, так, что одно из ее оснований
В|ь ч и содержащей ее плоскости, а положение второго основания закреплено.
| иг шмы. полученные в результате такой деформации, равновелики?
||..ч1'м\ нельзя сразу решить задачу: Найти площадь полной поверхности
п uko.'ui сферы куба? Определите, каких данных будет достаточно для се
й II »|ипо< тиую стену архитектурного ансамбля Тобольского кремля встроены
ем । eiii.'c башни), форма которых напоминает комбинацию известных тел
Umi ните* для чего они были построены и почему имеют такую форму,
ыиь* измерения надо сделать и что учесть, чтобы узнать пместямосзъ
сторожевых банки Тобояьсхиго кремля.
17) Используя дополнигельпую литературу, выведите формулу объема шара
основе принципа Кавальсри.
18) Игра «Тантрам» - составление фигурок из частой квадрата.
19) Занимательные задачи «на разрезание» - задачи, в которых зрето. *«
прямолинейными разрезами разделить заданную фигуру на наименьшее возможное чп. «
частей, чтобы из них можно было сложить другую указанную плоскую фигуру.
4.5. Специальные методы к приемы обучения
4,5.1- Основной метод изучения в пропедевтическом курсе длины oip<j»|
величины угла, площади прямоугольника, квадрата, круга, обз>ема прямоуголг. ни
параллелепипеда {а также массы, температуры и з.п.) - основанное на ингуш i>uii-«1
представлении о них непосредственное измерение (взвешивание) с помощи
масштабной линейки и транспортира (весов, термометра и т.д.) и проскТНМ
вычисления (так называемых «именованных чисел») в процессе освоения >'Ы1
Для измерения площади (квадрата н прямоугольника) н объема »ку(Ц (
параллелепипеда) первоначально используется непосредственный подсчс! чм
составляющих фигуру единичных квадратов (кубов) и затем основанный нп м(
индуктивный вывод формул площадей и объемов этих фигур. Формулы М
вычисления длины окружности и площади круга сообщаются в готовом визг . I
всякого обоснования (возможны некоторые исторические сведения о числе I
связи с этим выявляются опытным путем некоторые свойства изучаемых и ни «
(отношения равенства и неравенства, сложение величин одного рода н aclk ты в
именованными числами), изучается метрическая система мер и истерю
возникновения, старинные русские единицы а .чины. веса, денег и единицы Hpifl
государств, их сравнение и использование в практических задачах, прямимым
работах (в том числе, с решением задач разрезанием ц складыванием »|м<- Д
дидактических играх, а также для иллюстрации свойств чисел (2. лк.З, с. 61|
4.5.2. В систематическом курсе планиметрии основное внимание ул» ю
переходу (на основе повторения и сие|Сматизац1Н1 приемов нзм>'|» uu(
вычисления величии) от практических методов непосредственного iiim'i
геометрических величин к изучению па основе общего их определения и « • (
методов косвенною измерения (па примере измерения площадей). Для pruning
этого перехода полезно сравнить процесс измерения длин отрезков и
90
•пни с измерением площади и познакомить учащихся с вычислением площади
luiioli плоской фшуры с помощью пачетки. Использование палетки позволяет
«'Ын. нс только aociyrnri.iM Для учащихся изучение вопроса об измерении
iii'iu.i.'iii любой плоской фигуры, но и помогает им правильно попять идею
11Ы1’рсння плошали, состоящую в подсчете числа квадратов, которые
I ынынаются на этой фигуре.
InaKOMCTBo с палеткой полезно начать с практической работы по измерению
ШиЩпдси фигур (изображений морей) на географической карте, используя
»». кчций порядок работы:
I) наложите палетку на географическую карту так, чтобы она полностью покрывала
и»н\|’ ограничивающий данную фигуру;
’) подсчитайте отдельно число квадратных единиц и их долей внутри контура
Мвиишенной фигуры.
I) вычислите площадь заданного участка поверхности земли, используя масштаб
W ।
. -I I лома сравните найденное значение площади заданного участка поверхности земли
ВК итчением. взятом из учебника географии или словаря (оценить абсолютную
W ivuitiocTb вычисления).
Можно таким же образом измерить площадь круга, сравнив результат ее
V и (синя по известной формуле. Анализируя выполнение такой работы, можно
Шины, я в сходстве свойств площади со свойствами длин отрезков и величин
Bto (выбор единицы измерения, сложение площадей и умножение на число) и
Ьши. внимание на ю обстоятельство, что до сих нор практическое измерение
ив uipe шов и величии углов с помощью масштабной линейки и транспортира нс
ю особых неудобств, а для измерения площадей такого удобного прибора
Ь ini и в принципе быть не может, т.к. измерять пяошадь. сравнивая се,
ы» р, с квадратным метром, ыа практике невозможно.
|||ц||<му важно вначале поглубже разобраться с величинами и их свойствами
• л. п потом вернуться к площадям: обеспечить полное понимание терминов
•*' 1|ч1ческая фигура». «геометрическая величина», «числовое значение
» iiii-o ' равенство», затем - «равносоставленность», «равновеликость» и их
||ч|| связи. Вывод на этой основе и на основе формулы площади
ипиышка формул площади параллелограмма, треугольника и многоугояь-
П' вызывает у учащихся затруднений. Полезны обобщающие таблицы
и Нии м^кду элементами фигур, позволяющие вычислять различные
П н-1 ними величины (например, табл 15)
91
Таблица I
где р -
2
на
геометрических величин, называемые задачами на измерение
«нелен. iv линя
расстояния
задачи решаются на основе свойств равенства и подобия геомарическпх i|hii
инструментов (см. [17, пособие О Б. Епишева. В.И. Крупич, гл.З. § 3])
между доступными точками, до недоступной
недоступными точками, которые также нельзя измерить Henocpejcnienini I
ТОЧКИ м
частности, треугольников, с последующим использованием геомсцпгц
Существуют интересные планиметрические задачи
Формула Героня:
5" = VXp - "Кр ~Ь)(.р - с) .
Если а ~ b = с, то <У = —-
4
ПРОИЗВОЛЬНЫЙ ТРЕУГОЛЬНИК
ИЗОБРАЖЕНИЕ ОСНОВНЫЕ СООТНОШЕНИЯ
в с! * 1 —Г Теорема косинусов: а' = ЬР + с2 — 2bc cos А
/У *\\Я \ \К^/ Теорема синусов: = „S = 2R sin A Sin В sin С _ abc AS
л V > ""
с /X S а л- b + с г = — • где р = Р 2
Д' с
Другой метод косвенного измерения величин (метод предельного перехода) в
тпимегрии связан с изучением длины окружности, площади круга и ее частей,
ць'чио. строгое обоснование формуя остается невозможным из-за отсутствия и
н- теории пределов, но, опираясь на теорию подобия, можно показать
1«ширц„ональностг> площадей кругов квадратам их радиусов и обратить внимание
Ц н>, что здесь мы встречаемся с тем же самым коэффициентом
фимрционяльностп л. чго в случае пропорциональности длины окружностей их
викцым Завершение этой работы возможно в курсе ачгебры в теме
Прогрессии», заключающейся понятием предела числовой последовательности.
I 5.3. Понятие объема пространственной фигуры в систематическом курсе
^цчочетрии вводится аналогично понятию площади плоской фигуры.
Фрмпчальное представление об объеме фигуры позволяет рассмотреть вопрос
I ид.еме прямоугольного параллелепипеда и вывести формулу для его
Вн< пения. Аналогично, на основе общего определения объема н его свойств, с
рнилованием аналогии с понятием площади и косвенными методами измерения
‘►миней плоских фигур (равновеликости равносоставленных фигур) изучается
lw । ризничных многогранников; новое определение понятия объема круглых тел
। шляется так же, как понятий длины окружности и площади круга.
Принципиальные трудности, возникающие при изучении.объемов, те же, что
течении площадей, ио имеют определенную специфику. Так, если при
•нин площадей непосредственное сравнение площади конкретной фигуры с
niiirif площади вызывало затруднения, но все же было возможным (палетка), то
1ц|мс|к*ш1я объемов сравнение с единичным кубом практически вообще
| 1и«но ему на смену всегда приходит измерение косвенное.
Mi 1пд предельного перехода в явном виде используется для доказательства
, “П об объеме пирамиды (г.к. .метод равновеликости равносоставленных
п|сь оказывается невозможным в принципе; пирамида - пример того, что
b> mi не многогранники не всегда являются одновременно и
1ч 1.Ц1 leifHHMH), но использовать его при изучении объемов (и поверхностей)
Н»о |с । можно для индивидуальных заданий. Изучение в курсе алгебры и
11 |нй in кг старших классов элементов интегрального исчисления (таких, как
►«•in нмошади криволинейной трапеции, объема тела вращения и объема
93
фигуры по известным площадям ее поперечных сечений) лнег возможно, и
использовать н.х как основной метод косвенного измерения объемов проецмц
с t ценных фигур (подробнее см. школьные учебники icoMcrpnii. алгебры н 1ычн
Таблица I*
анализа, (3, гл. 18]. Ниже приведены примеры обобщающих таблиц
ОБЪЕМЫ И ПЛОЩАДИ ПОВЕРХНОСТЕЙ ШАРА И ЕГО ЧАСТЕЙ
•^Лов.шар» = 4к/? _ 4жЯ* шлра ~
/Г—- к--Х 4 ? & Л'бск = -2«ЯА = tiDh = *(Rt + ft2) 5 = *(2Rh+ Rf) n{h2 + 2R?) Rt^blfR-h) = ж(я - у)й2 = 1^3^ + ft2) = = |кй2(ЗО + 2Л) V
ль г *— а 3) о ht и ft, — высоты удаленных сегмен- тов, так что 2R - ht — h3= h
л D ^елм = ^*R} - *R(h2 ft?) - ^(ftj3 + ftf) =|лл(зя,2+з/?22+й2) •S"no« - 2жЯй = -kD/t 2nR2h л ,, rc«T - 3 ~ f)D h •^пов.сект ^R^2h + <2| Л/)
91
Таблица 17
ОБЪЕМЫ ТЕЛ ВРАЩЕНИЯ
Площадь сечения тела плоскостью, проходящей
через точку Xоси ОХ перпендикулярно этой оси
ПРИМЕРЫ ВЫЧИСЛЕНИЙ ОБЪЕМОВ:
(< .<», также С.М. Саакян, В.Ф. Бутузов. Изучение темы «Объемы тел» в XI классе Н
। матика в школе. 2002. № 6. - С. 11 - 22.)
95
4.5.4,
Технологическая цепочка изучения геометрической величины
I) Повторение, систематизация и обобщение свечений о геомсгричо । >>П
величине и способов се измерения из пропедевтического курса геометрии.
2} Формулировка точного определения понятия данной геошяричч мФ
величины, уточнение терминов и обозначений.
3) Формулировка свойств геометрической величины, основанных на акиг'мм
меры множества в форме: равным фигурам соответствуют равные in.rniiHi
величины, значение величины объединения (суммы) фигур без пересечения ( -тип I
части) равно сумме значений данной величины каждой из них, рефлемнпПн. в
симметричность и транзитивность; их символическая запись, нллкк цнпм
примерами и контрпримерами.
4) Изучение алгоритма и инструментов непосредственного himi| dl
величины, если оно возможно, или обоснование его невозможности
5) Обоснование выбора метода косвенного измерения данной геоне
величины, изучение его содержания.
6) Дедуктивный вывод формул косвенного измерения величин* I
определенных программой геометрических фигур
7) Решение учебных задач на усвоение полученных теорем и м.|. 4
доказательства.
8) Текущий контроль и коррекция усвоения.
9) Рассмотрение примеров решения математических и пршоы ич! М
использованием полученных формул.
10) Выявление действий по применению теории к решению |i-i< । им
задач и их последовательности.
II) Обобщение выявленных действий в виде прием! р<ш mi 1
связанных с геометрическими величинами, алгебраическим мет тм
12) Решение геометрических задач алгебраическим менншм
13) Итоговый контроль усвоения.
96
Технологическая цепочка формирования алгоритмов и приемов
измерения (вычисления) геометрических величии
Таблица 18
Куре Приемы измерения геометрических величин
UpoiteOcemu’iecKUii Курс I. Алгоритмы измерения: длины отрезка с помощью линейки и величины угла с помощью транспортира 2 Приемы практического отыскания и вычисления площади квадрата и прямоугольника (объема куба и параллелепипеда). 3. Приемы практического отыскания н вычисления длины окружности и площади крута
Курс Hiaiiiwempuu 4. Алгоритмы отыскания длины отрезка и величины угла на основе определения и свойств величины. 5. Общий прием доказательства формул площадей многоугольников методом равновеликости равносоставленных фигур 6*. Общий прием вывода формул длины окружности н площади крута методом предельного перехода 7 Приемы вычисления площадей плоских фигур на основе определения, свойств площади и по формулам. 8. Обобщенный прием решения задачи на вычисление площади плоской фигуры.
Alpr г»г;Ч чччирии 9. Частные приемы вычисления расстояния и величины утла между скрещивающимися прямыми, угла между прямой и плоскостью, двугранного угла. 10. Частные приемы вычисления поверхностей многогранников и их обобщение. 11. Обобщение приема косвенного измерения величии методом равновеликости равносоставленных фигур для доказательства формул объема многогранников. 12 Приемы интегрального исчисления для вывода формул объема пирамиды, поверхности и объема круглых тел. 13. Обобщенный прием решения задачи на вычисление объема пространственной фигуры. 14. Обобщенный прием решения задачи на вычисление геометрической величины.
97
ЛЕКЦИЯ V
Геометрические преобразования
5.1. Логико-математический аиалиа линии ты,метрических иреобразов...
5.I.I. Выше уже отмечалось, что буквально в течение тысячелетий <ibvur.uj
геометрии в школе велось по схеме, заимствованной у знаменитых Пт'н
Евклида. Для своего времени эта книга обладала выдающимися наунн.|»н:
методическими достоинствами, таких устойчивых традиций нет в препо.'ын ншн I
одного предмета средней или высшей школы и отход от них дается < ihi iHM
трудом. Рассмотренные нами выше содержательно-методические шиши ►
геометрии (геометрические фигуры, геометрические построения, reoMiipn*Mfl
величины) называют традиционными, т.к, они присутствуют во ме< ‘м*
геометрии со времён Евклида. Геометрия Евклида считалась «школой iiuim*i.-4<
мышления», т.к. в построении курса он исходил из общих принципов п< п • п*м
построения науки, изложенных Аристотелем.
Но в конце XIX в. в связи с развитием аксиоматических ncdcjiiiiMiiifft
обнаружено, что общая схема дедуктивного построения науки не йм'Ы >ip»4H
Аристотелем до конца и что ‘•Начала”, как конкретное воплощение null >tfl
логически не безупречны, что отражается в преподавании (npeiio.i.ni н • ill fl
много времени на «строгие доказательства» почти очевидных i< o|'i м) I
сторона «груза евклидовых традиций» заключается в том. что I nm 11 < В
ним и школьное преподавание, пренебрегал движениями н ним
преобразованиями. Замечено, что он специально стремит и >
использования движений, применяя их только в том случае, мн 11 in ни • ! М
возможности (например, при доказательстве третьего при ни я
треугольников). I
Стремление Евклида к отказу от использования дни н инн м
общефилософскими, метафизическими у> гн<п
Аристотеля. Развитие математики (в частности, геометрии) и щ и « i^^^M
доказало несостоятельность стремления исключить ш i i"
преобразования; наоборот, стало ясно, что эго понятие илям i
степени связано с
М1|>«ш>ных, что оно траст в геометрии основополагающую роль я может быть
iniAetio в основу определения самого предмета геометрии. Одновременно стало
пМм пбщсмзтематнчсское значение понятия преобразования, тесно связанного с
• HIIIHMH функции и группы, которые, в свою очередь, в значительной степени
Ч»Иг ппот лицо современной математики, новые методы решения
(мыгсльных геометрических задач, чрезвычайно важные не только для самой
•»huihkh, но и для ее приложений - в первую очередь для механики и физики.
Ин ному одной из основных илей реформы математического образования [I,
| 4 и 2, с. 58] была идея внедрения в школьный курс математики
| ическнх преобразований. Она диктуется и методическими соображениями:
•<ч 1|.сгво многих геометрических теорем, связанные с преобразованиями
н *ш lynnee учащимся, чем дедуктивные выводы из аксиом; многие задачи на
» di и доказательство решаются более естественно и просто, исходя из идеи
|чй неких преобразований; использование геометрических преобразований
Rю вы расширить рамки геометрии (например, вопрос о конических
I шлипса, параболы, гиперболы - перенести из курса алгебры и черчения,
it i курса физики, где учащиеся впервые с ними знакомятся).
последовательно к этому вопросу подходил акад. А.Н. Колмогоров,
• «р» «iMRui перестройку аксиоматики школьного курса геометрии, введя в нее в
ыпнктва движений, подчинить построение курса геометрии теоретнко-
) концепции. исходя из группы движений или группы подобных
|^Г И||> Гчкой курс был осуществлен, но в силу разных причин продержался в
адшжо некоторые его идеи сохранились.
iiihiMii понятиями линии являются следующие понятия, которые
И и* понятие функции - одно из фундаментальных математических
к« р в геенно связанных с реальной действительностью.
П'Мнпш* (биекция) - взаимно однозначное отображение плоскости
иа себя. Преобразование фигуры Ф в фигуру Ф/ - взаимно
* I Hip imeiiue фигуры Ф на фигуру Фр, при этом Фу =/(Ф), Ф/ - образ
* прообраз фигуры Ф, В школьном курсе геометрии представлены,
м дпл вида геометрических преобразований движения и
«шпиня
im'/ieueu/tHue) плоскости (пространства) - преобразование.
рмкгонк Т„ St„ Se). обладает свойствами: 1) точки, лежащие
и точки, лежащие на прямой, и сохранится порядок
расположения; 2) прямая переходит в прямую; 3) луч переходит в луч; 4) фш
(отрезок, утоп и другие) переходят в равные им фигуры; 5) penin.i I
последовательного выполнения движений является движением; 6) npeobp.iкл-
ипе, обратное движению, является движением. Виды движений; ичп.ч »
центральная симметрия, поворот, параллельный перенос; виды нреобр.поицг
подобия; гомотетия, подобие.
Подобие - преобразование плоскости (пространства), изменяющее рас» i чп.
в одно и то же число раз (Но1), обладает свойствами: 1) - 3), совпадав>нп1'Ш в
свойствами движений; 4) величина утла сохраняется; 5) оаальиы'- фш fl
переходят в подобные им фигуры (их линейные элементы изменяются я * (
6) результат последовательного выполнения подобных преобразовании нн >•< |
подобным преобразованием; 7) преобразование, обратное нолк^^Н
преобразованию, является подобным преобразованием.
На этих понятиях и свойствах основаны понятия равенства и подобия ф
также соответствующие методы (доказательства теорем и решения задач) I
геометрических преобразований.
5.1.2. Метод геометрических преобразований - средство <ик«н
некоторых отношений между объектами евклидовой геометрии
равенства, параллельности, подобия). Для доказательства теорем и рсш. ш
на построение он (как частный случай математического моделировании В I
один объект заменяется другим) выглядит следующим образом [ I, ai< II I (
1) выбрать геометрическое преобразование, которое гнипоицг
наличие указанного отношения между объектами евклидовой геом< ipiiu
2) выполнить выбранное преобразование гак. чтобы один <чч.. 11 (М
часть) переходил в другой (новый, вспомогательный) объем Chui 1
исследования (или построения);
3) исследовать полученный новый (вспомогательный) обы । i н |i 'fl
4) обосновать наличие указанного отношения между ш»ь< n.miii
свойств выбранного преобразования.
Частные случаи метода геометрических преобразоп.шнИ нщичИ
центральной симметрии, поворота, параллельного перешил ч.и ш н и fl .
обоснования равенства фигур, параллельности (при пи null »llflfl J
ф|П1сндикулярносгн), отыскания кратчайшего расстояния; метод подобия - для
fu< кииия (обоснования) отношений отрезков и углов.
5 2. Место геометрических преобразований в программе и учебниках
II цеПствугошей программе отдельно эта линия не выделена, хотя и отмечено, 1Ш>|>ходимо активно использовать геометрические преобразования. Таблица 19
)птп Класс Темы программы
Н» hiпческий н»ямын школа и hr математики I мт сов • маш школы) 3 6 «Текстовые задачи»- симметрия, симметричные фигуры. (Т.6. «Симметрия»: осевая симметрия, ось симметрии фигуры, центральная симметрия, зеркальная симметрия).
• МнфпоП Р И пени метрик • < »п«И1«>П » *. И Школы) 7 8 9 (В т.2. «Основные свойства плоскости»: центральная и осевая симметрия па плоскости. Т.З. «Подобные треугольники»: применение подобия к решению задач. (Т.2. «Подобие», в т.4. «Задачи и теоремы геометрии»: метод подобия в задачах. Т.4. «Движение»: понятие движения, параллельный пере- нос и поворот. (Г 4 «Преобразования плоскости»: движе- ние плоскости, виды движений плоскости, гомотетия.
ВйМ*М11|1|11 ill • «Лton Н - •Н*И'1Ы) 10 II (В т.З «Многогранники»: изображение многогранников посредством проектирования. В т.5. «Задачи и методы стереометрии»: проектирование.) В т.1. «Метод координат в пространстве»: движения. (В т.1. «Объемы многогранников»: принцип подобия).
X I Цели изучения геометрических преобразований в школе
HiVitiiiK- материала линии геометрических преобразований имеет
рочош цепью осознание учащимися на зим или ином уровне понятия
ио преобразования пространства (плоскости, фигуры), понимание
Ipxu I еомстрических преобразований, способов их осуществления и
и геометрии и к решению прикладных задач. В таблице 20
, II Миня этой цели по уровням обучения.
101
5.3.2. Материал о геометрических преобразованиях дает возможность ставить
Исли развития всех познавательные процессов, в частности, образного.
Конструктивного и диалектического мышления, функционального стиля
мышления, диалектического мировоззрения, раскрывать общенаучную и
•цпккультурную роль математики, осуществлять эстетическое, экологическое
(испнтание, профессиональную ориентацию учащихся.
Достижение воспитательных пелен связано с воспитанием интереса к
мтематике через приложения геометрических преобразований в искусстве, в
трхигектуре, в народных промыслах н решении практических задач (например.
И'«сетных задач на местности с использованием подобия).
5.4. Основные типы математических н примеры учебных задач
I 5-4.1. Основными типами математических задач в этой линии являются
Ц|»тчн на построение и доказательство: «построить точку (фигуру) с помощью
мииого преобразования»; «доказать равенство или подобие фигур или какие-либо
кчНства фигур (в теореме или в задаче) с помощью геометрических
образований (методом движения или подобия)»; задача на построение методом
«•Имения или подобия Эти сложные задачи состоят из составляющих их более
них задач на: выделение соответствующих точек на фигурах; выделение
•••ментов, определяющих преобразование; построение образов точек и фигур в
Икрстном преобразовании.
(Наций прием решения задачи методом геометрического преобразования:
I) на этапе изучения содержания задачи уяснить взаимное расположение данных
•иных и искомых) точек пли фигур (или их частей и элементов);
.’) на этапе анализа (поиска решения) - в предположении, что задача решена, сделать
С Mi нужно) эскиз, установить связи между данными задачи и искомыми (точками,
рлми, их элементами или свойствами), выбрать геометрическое преобразование,
•| । позволит обосновать наличие того или иного отношения между объектами
^|««мн, фигурами);
I) указать (или выполнить) выбранное преобразование так, чтобы один объект
•г Копил в другой (или построить вспомогательную фигуру);
4 J и задаче на доказательство - обосновать наличие указанного отношения между
«••«шмн с помощью свойств выбранного преобразования;
') в задаче на построение - если нужно, преобразовать вспомогательную фигуру в
Miimvio и провести доказательство как в и 4 (а также исследование).
юз
3.4,2.11рпмерыучебных задач
I) Наитие на изображен к и симметричных (гомотетичных, подобных) фш ч>
соответствующие точки.
2) Назовите несколько видовых понятий для понятия "гсометричесми
преобразование”, приведите примеры названных понятий.
3) Данные понятия пронумеруйте в отношении последовательности их подчинении
по родо-видовому признаку: функция, геометрическое преобразование, симметрия
гомотетия, подобие.
4) В приведенном определении выделите термин, родовое понятие, kiibokii-
признаки н характер связи между ними: если точка О является серединой отрезка Alt ।
точки А и В называются симметричными точками относительно точки (Л
5) Найдите вокруг себя (или приведите примеры из живой природы, живоиш и
архитектуры) несколько предметов, изображение которых на бумаге а) будет иметь i»u
(центр) симметрии; б) могут быть получены один из другого поворотом (параллелын.|М
переносом, гомотетией, подобием)
6) Найдите средн заглавных букв русского алфавита симметричные фигуры, какие Н>
них имеют несколько осей симметрии?
7) Найдите несколько слов, запись которых симметрична.
8) Может ли фигура иметь бесконечно много осей симметрии?
9) Укажите оси (центры) симметрии заданных на рисунке (модели) фигур.
10) Верны ли следующее утверждения; а) произвольный параллелепипед имеет •»
симметрии; б) произвольный параллелепипед имеет плоскость симметрии; в) конус ими*
точку симметрии; г) конус имеет ось симметрии? д) всякое теле вращения имеет I) м
симметрии. 2) центр симметрии; е) следующие тела не имеют центра симметрии; шарожФ
сегмент, шаровой слой и сферический пояс?
II) Сколько осей симметрии имеет а) отрезок, фигура, образованная б) дпум!
пересекающимися прямыми, в) двумя параллельными прямыми, г) окружностью и то <к
д) окружностью и прямой, е) двумя окружностями?
12) Какое наибольшее число осей симметрии имеет а) треугольны
б) четырех угольник?
13) С помощью перегибания листа бумаги найдите осн (центры) симметрии jiiiiiiii
на чертеже фигур.
14) Изобразите в тетради произвольную геометрическую фигуру; построит <
основе соответствующего определения с помощью циркуля и линейки фшур
а) симметричную ей относительно заданной «н I; б) относительно заданной пив и I
в) поворотом около заданной точки О иа заданный угол; г) параллельным переносим
заданный вектор; д) подобную ей с заданным коэффициентом подобия к.
15) Дополните изображенные на рисунке «верхние половинки фигур» с irnri
симметрии О так. чтобы получить центрально-симметричную фигуру.
16) Покажите, что центральная симметрия есть поворот на 180°.
17) Каким преобразованием является гомотетия при к - 1, А = - 1 ?
18) Приведите примеры а) равных, б) подобных фигур; как можно в каждом i ц»'
получить одну из них из другой?
19) Нарисуйте орнамент, используя какое-либо геометрическое преобра1<иын(
Приведите еще примеры таких орнаментов (бордюров, паркетов и т.п ).
20) Будут ли подобны а) все квадраты, б) круги, в) круг и квадрат, г) равные | ии,<1
21) Может ли сумма гомотетии и движения представлять собой движение -
22) Может ли сумма двух преобразований гомотетии представлять собой линманй
23) Могут ли быть подобными неравные прямоугольные треугольники а) с p.iiiin
гипотенузами, б) с одной парой равных катетов?
24) Из признаков подобия треугольников выведите следствия - признаки iiuii'4
а) равнобедренных треугольников, б) прямоугольных треугольников; признаки p.iwii-
104
||Ч'у ельников.
25) Объясните, почему и реэультате подобия а) середина отрезка псрехолнг о
ретину отрезка; б) перпендикулярные прямые переходят в перпендикулярные прямы;
)параллельные прямые переходят в параллельные прямые, г) пересекающиеся прямые
крехолят а пересекающиеся прямые; п) окружность (.круг) переходит в окружность
(круг); касательная к окружности переходит в касательную к окружности?
26) Почему в результате подобного преобразования а) треугольник переходит в
гугольник; б) сохраняется (посторонам и углам) вид треугольника?
27) Что при подобном преобразовании треугольника является образом а) медианы,
D биссектрисы; в) высоты; г) центра вписанной (описанной) окружности?
28) Рамка картины имеет одну и ту же ширину. Подобны ли картина и картина в
Цмке?
29)Какая фигура может служить при параллельном проектировании образом
II 1реугольника. б) гранении, в) тетраэдра, г) параллелепипеда?
30) Все точки пространства проектируются на плоскость. Можно ли сказать, что эго
^обряжение является преобразованием пространства?
31) Постройте образы вершин тетраэдра ABCD при симме трии с центам Л
32) Существуют ли точки, прямые п плоскости, которые центральной симметрией
вибражаются на себя?
33) Каким преобразованием является а) преобразование, обратное центральной
фымегрии, б) композиция двух центральных симметрий?
5.5. Специальные методы и приемы обучений
, 5.5.1. В пропедевтическом курсе знакомство с геометрическими
(•о'разеваниями осуществляется на примере симметрии. Рассмотрим пример
("нации этих методов в условиях групповой работы над системой заданий.
>) После записи в тетради темы урока «Ось симметрии фигуры», учащимся
фтлагается представить образ такой фигуры и нарисовать его; рисунки
ЧИ« ншваются. 2) Затем каждой группе предлагаются рисунки (разные или
(Щипковые для разных групп) с заданиями; а) среди данных фигур выберите
Ь> имеющие оси симметрии; б) перерисуйте и.х в тетрадь и проведите осн
ю ipim (рис. 22). Одни ученик в группе выполняет задания на большом листе и
•ШИтвает на доске; по этим рисункам затем обсуждается ход выполнения
мини
L ') Следующее задание сое гонг в том, чтобы, используя перегибание листа
)К«"1 вырезать из него фигуру, имеющую а) одну ось симметрии, б) две
^ц»ид||> улярные оси симметрии, в) четыре оси симметрии. От каждой группы
г» in фигуры вывешиваются на доске, ученики объясняют, как выполняли
рсуголышков с общим основанием (рис. 23); сделайте вывод об осях симме|рип
полученных фигур. Выполнение задание снова заслушивается (обязаюлы1О кв, i
iiaii/ici четыре оси симметрии).
Рис 22 _
Рис. 23
5) Последняя серия заданий: а) начертите отрезок АВ: опредешпе i*
расположены все точки, одинаково удаленные от концов отрезка; посцднц
несколько точек, расположенных ближе к точке А, чем к точке В; где леж.п м
такие точки? б) проведите три различные окружности через данные точки К и
в) три корабля должны встретиться, пройдя при этом до места встречи рамп
расстояния, укажите место встречи кораблей; сформулируйте задачу, uciiinnil
геометрические понятия.
При обсуждении полученных результатов формулируются выяв.ппнв
свойства и кратко записываются в тетради. Задание на дом; нарисовать \ пфН
бордюры, орнаменты, раскрасить их.
(Другой пример формирования методики этого понятия см. (3. гл. 15. § i i IМ
185]).
5, 5.2. Программа систематического курса планиметрии не прсдусм-ирш I
широкого изучения свойств геометрических преобразований; основной ч< |
изучения - неполная индукция с использованием наглядности (таблицы или| i• t
табл. 21. практические работы) и примеры решения задач.
Самостоятельные практические работы связаны, в первую очер» ir I
построением образов точек, фигур и их частей в геометрическом преобр i юп.ии I
использованием а) миллиметровой бумаги, б) кальки, в) циркуля и ни •
построение подобных фигур с помощью пантографа Ниже приведены н|ч
способов выполнения таких работ.
Таблица 21
Построение симметричных относительно оси фигур
на миллиметровой бумаге:
I) с помощью линейки проведите карандашом прямую /, совпадающую с одной из
MTHi.K линий, намеченных на миллиметровой бумаге:
но одну сторону от проведенной прямой изобразите какую-либо фигуру или
• • пильную замкнутую линию;
• ) пи построенной линии отметьте ряд достаточно густо расположенных точек;
4l тля каждой точки найдите симметричную ей точку относительно прямой I.
•> н> ц " деления миллиметровой бумаги;
'Соедините между собой полученные точки.
Построение центрально симметричных фигур
с использованием циркуля и линейки:
11 in метьте на листе бумаги некоторую точку О:
107
2) изобразите на этом же какую-либо фигуру или произвольную замкнутую линию.
3) на построенной липки отметьте ряд достаточно густо расположенных точек;
4) для каждой точки найдите симметричную ец точку относительно точки О. дли
чего соедините каждую из точек с О и на продолжении полученного отрезка отложип
отрезок такой же длины;
5) соедините между собой полученные точки.
Воспроизведение центральной симметрии с помощью поворота
с использованием кальки и булавки:
I) наложите кальку на имеющийся чертеж двух симметричных относительно точки
О фигур F и Ft\
2) проткните кальку и чертеж булавкой в точке О и обведите на кальку фигуру Г;
3) оставляя чертеж неподвижным, поверните лист кальки на 180°;
4) убедитесь в том. что начерченная на кальке фигура совместится с имеющейся п.>
чертеже фигурой F/.
Построение гомотетичных фигур с использованием циркуля и линейки:
I) отметьте на листе бумаги некоторую точку' О,
2) изобразите на этом же какую-либо фигуру или произвольную замкнутую тшипч
F;
3) на построенной линии отметьте ряд достаточно густо расположенных точек;
4) каждую из отмеченных точек соедините отрезком с точкой О и раздели!'
соединяющий отрезок пополам:
5) последовательно соедините середины всех проведенных отрезков, что дает линии
F/, гомотетичную линии Fc центром гомотетии О и коэффициентом к “1/2.
Наглядными представлениями, элементарными построениями, формулируя
кой простейших определений можно ограничиться для учащихся >-го (низки»)
уровня обученности: доказательство свойств преобразования, решение несложны»
задач методом геометрических преобразований - для 2-го уровня; для 3-го уришт
возможны более сложные задачи, понятие о разных геометриях и о трунил
преобразований. Метод геометрических преобразований применяется для peuiciiui
различных типов задач - на построение (все виды преобразований), на максимум и
минимум (осевая симметрия, поворот), на нахождение кратчайшего расстояип
(параллельный перенос) (см. [4, гл. 15, § 51]) больше на факультативных занянн
внеклассной работе, гае возможно также изучать такие геометрпчеин.
преобразования, как зеркальная, поворотная и скользящая симметрии, сж.шк т
данной прямой с данным коэффициентом, проектирование на прямую и -т
плоскость.
На уроках целесообразно рассматривать такие примеры решения 33.1.1ч и
доказательство и на построение методом геометрических преобразований. ы>|п|и
показывают в определенных ситуациях его преимущества перед другими мети !
108
(например, использование движений для доказательства равенства фигур и
подобия - в задачах, связанных с отношениями и пропорциями}.
7й<Л<ч« I На высоте BD треуюльинка АВС дана точка К такая, что АК КС.
(окатать, что треугольник АВС- равнобедренный (рис. 24).
Рис. 24
Решение.
Изучение содержания задачи и анализ
показывают, что равные отрезки А К и КС могут
быть образами один другого при каком-либо
движении. Т.к. высота треугольника BD есть
серединный перпендикуляр к отрезку ,4С, то таким
движением может быть симметрия относительно
этой прямой S(i|,
При выполнении преобразования Sbd имеем:
Й-*£-’, т.к. В принадлежит оси симметрии; А-*-С,
т.к. треугольник АКС- равнобедренный и KD - его
высота (по условию).
Из свойств осевой симметрии Sbd следует.
=> АВ = СВ => АВС - равнобедренный,
что и требовалось доказать.
Задача 2. Внутри угла АВС дана точка Р Провести через точку- Р прямую, отрезок
ЙЛ'которой, заключенный между сторонами угла, делится точкой Р в отношении {:2
Решение.
I. Анализ.
Предположим, что задача решена н прямая MN - искомая (рис. 25 а). Т.к. точка Р
*жпт между точками Л/ и К и NP: РМ = 1: 2, то точка W получается из точки Л/
ймотетней с центром Р и коэффициентом -Р2. По точка Л/ принадлежит прямой ВС',
кдовательно, точка /V принадлежит прямой B,Ci, в которую переходит прямая ВС при
Усматриваемой гомотетии. Кроме того, точка /V. по условию, принадлежит прямой АВ,
ному А - точка пересечения прямых АВ и BtCu
Рис. 25
1 2. Построение.
I Построим точки В/ и < ’,. в которые переходят точка В и некоторая точка С стороны
|1 При гомотетии с центром Г к коэффициентом - Точку пересечения прямых B/C/ii
••обозначим через Л' Прямая Л'Р - искомая (рис. 25 б)
3. Доказательство правильности построения и 4 исследование, показывающее, что
и».чэ всегда имеет единственное решение, очевидны
| } 5 3. В систематическом курсе стереометрии необходимо изучение
Ь|И Iдельного проектирования и его свойств (лекция 3, и. 3.1.2.). Изучение всех
м и.ных геометрических преобразований ограничивается примерами фигур.
109
которые могут быть получены гем или иным прсооразоваинем простраш ны
обобщением их свойств (известных из курса n.iiiiiiiMcipiiu), пример imh
специальных преобразований пространства (например, симметрии относи 1е.п и ।
плоское гн) и примерами решения задач, рассмотренных в учебниках.
5.5.4.
Технологическая цепочка изучения геометрического преобразования
I) Подготовительный этап - рассмотрение примеров фигур (или нх uacieii
фотографий, макетов, узоров и т.п.), обладающих свойством быть полученными
одна из другой с помощью данного преобразования.
2) Описание, введение термина, определение данного преобразования. <т<>
элементов (и фигур, полученных данным преобразованием).
3) Построение плоских фигур данным преобразованием на оенчш
определения (перегибанием листа бумаги, с помощью миллиметровой бу Mai и,
кальки, циркуля и линейки).
4) Решение учебных задач на узнавание на чертежах, моделях, репродукциях
в окружающей обстановке определенных фигур.
5) Выявление свойств данного преобразования и нх формулировка.
6)* Примеры доказательства свойств данного преобразования.
7) Решение учебных задач на усвоение понятия данного преобразования и ein
свойств.
8) Текущий контроль и коррекция усвоения.
9) Примеры применения данного преобразования к доказательству теорем и
решению задач на доказательство и построение
10)* Выявление действий по применению теории к решению рассмотренных
задач, их последовательности и ситуаций применения.
II)* Обобщение выявленных действий и ситуаций их применения в вн.и
приема решения задач данным методом.
12)* Применение полученного приема к решению задач на плоскости.
14) Примеры геометрических преобразований пространства и фигур и
пространстве.
15)* Примеры применения полученного приема к решению задач и
1 ю
np<4 ipaiicree.
16)* Обобщение ситуаций применения метода геометрических
|||1еобразований к решению геометрических задач.
Технологическая цепочка формировании
алгоритмов и приемов геометрических преобразований
Таблица 22
К" Курс Приемы геометрических преобразований
1 Пропедсвт ическии курс 1. Алгоритмы построения геометрических фигур, имеющих ось симметрии, перегибанием листа бумаги, вырезанием. 2. Прием отыскания симметричных фигур и окружающей обстановке и на изображении. 3- Прием отыскания оси симметрии фигуры. 4. Прием рисования фигур (орнаментов и т.п.) с использованием осевой симметрии.
2 Курс планиметрии 5. Алгоритмы построения образов точек и фигур в заданном преобразовании с использованием .миллиметровой бумаги, кальки, циркуля и линейки. 6. Частные приемы выделения на чертеже соответствующих точек на фигурах в данном преобразовании. 7. Частные приемы выделения элементов, определяющих данное преобразование. 8 Обший прием доказательства равенства фигур методом движений. 9. Общий прием доказательства подобия фигур методом преобразований подобия 10. Приемы решения задач на построение методами разных геометрических преобразований. 11 *. Обобщенный прием решения задач методом геометрических преобразований
1 Курс стереометрии 12. Частные приемы построения образов точек и фигур в параллельном проектировании. 13*. Частный прием построения образов точек и фигур при симметрии относительно плоскости 14. , Обобщение приемов 5-10 для геометрических преобразований в пространстве.
ЛЕКЦИЯ VI
Координаты в школьном курсе математики
6.1. Логико-математический анализ линии координат
6.1.1. Координаты (от латинского со- - совместно и ordinatus
упорядоченный, определенный) - числа, заданием которых определяет,«
положение точки на плоскости, на поверхности или в пространстве. Прямоуголь
ные координаты употреблялись в геометрии еще математиком александрийской
школы Аполлонием Пергским (111-11 вв. до н.э.). Раздел геометрии, в котором
простейшие геометрические образы (прямые, плоскости, линии и поверхнопп
второго порядка) исследуются средствами алгебры на основе метода координат
называется аналитической геометрией. Ес возникновение в XVII в. связано <
развитием астрономии, механики и техники; первыми вошедшими л
систематическое употребление координатами являются астрономические и
географические
Исчерпывающее изложение аналитической геометрии было выполнено
Р. Декартом в его «Геометрии» (1637); Р. Декарт, размышляя над особенностям»
арифметических и алгебраических объектов (чисел и символов) и геометрически*
фигур, намеревался создать общий язык для их изучения, называя сн»
«универсальным языком» или «универсальным методом». В книге «Рассуждения <•
методе» он писал; «Видя, что хотя предметы различны, но все же они сходны
между собой в юм, что рассматривают ни что иное, как различные встречают щ < г
в предметах соотношения и пропорции, я подумал, что мне следует псслслч«,нк
эти пропорции вообще ...». Объединив язык геометрии с языком алыбрц
Р. Декарт создал общий метод для изучения свойств как фигур, так и уравненф!
построил аналитическую геометрию.
Дальнейшая разработка метода координат связана с трудами Г. ЛеГюпшн
И. Ньютона и особенно Л. Эйлера; средствами аналитической rcoMcipiui
пользовался Ж. Лагранж при построении аналитической механики и Г. Мон । и
дифференциальной геометрии. Долгое время для аналитической геометрии «•мы
принято название «декартова геометрия» (которое ввел И. Бернулли), термин
112
канали<плеская теометрия».- исходит oi Ф. Виста (1501 г. ).
Понятийный аппарат этой линии составляют понятия: координаты (абсцисса,
Ордината, аппликата), система координат (начало, координатные прямые и
кюрлипатпые плоскости), уравнение геометрической фигуры (прямой, линии,
шлоскосги, поверхности и т.д.>.
6,1.2, Координатный метод - способ определения положения точек на
плоское!и (на прямой, в пространстве) С помощью чисел [1, лк. II. с. )59). Для
решения задач и доказательства теорем он (как частный случай матсма|Ического
Моделирования. в котором в качестве формальной математической модели
(выступают уравнения и неравенства) выглядит следующим образом:
1) выбрать наиболее подходящую систему координат, т е. разместить фигуры
ва координатной плоскости (или в пространстве) гак. чтобы можно было наиболее
Ьационально выразить в координатной форме характеризующие их точки, отрезки
Ь т.д. (как данные, так и искомые) и «увидеть» возможности использования
координатного метода для нахождения искомого;
2) записать в координатной форме с учетом данных задачи необходимые для
решения точки фигуры, расстояния между ними, координаты середин отрезков,
травления линии и т.п.;
3) записать с учетом требования задачи выражения, равенства, уравнения и
। п и выполнить (если нужно) необходимые преобразования полученных
нгебраических выражений или уравнений;
4) осмыслить полученные результаты и перевести их на тот язык (в частности,
(геометрический), на котором была сформулирована задача.
Этот метод очень плодотворен, т.к. «работает» в двух противоположных
мппрлвлениях. С одной стороны, он переводит геометрические соотношения в
ниалитическне и позволяет решать геометрические задачи средствами алгебры
(находить длину отрезка, середину отрезка, координаты пересечения прямых и
I
III). с другой - осуществляет переход от аналитических соотношений к
Нвметрнческнм с целью получения наглядного представления об абстрактных
нгуациях. описанных языком уравнений и неравенств (графики уравнений,
графическое решение уравнений, неравенств и их систем, решение задач линейного
программирования и др.). В отличие от метола, основанного на непосредственном
3
©
Таблица 24
№ Общие категории целей Примеры обобщенных типов целей
I уровень II уровень 111 уровень
1. Знание Ученик знает
Запоминание и воспро из ведение изученного материала Терминологию системы коор- динат, обозначения, уравнения простейших фигур, алгоритмы построения точек, векторов' и линий по их координатам и уравнениям, правила чтения координат точки, вектора н уравнения фигуры по их изображениям в системе координат. определения основных понятий метола координат и их запись, уравнения основных фигур, свойства фигур и векторов в координатной форме, приемы расположения фигур и векторов в системе координат для решения типовых задач. метод координат, его место и роль в геометрии, изученные доказательства свойств фигур и векторов методом координат, обобщенный прием его применения к решению типовых задач в нестандартных ситуациях.
0 Понимание Ученик
Готовность к преобразованию изученного из одной формы в другую, к его интерпретации воспроизводит термины и обозначения, называет координаты точек по их изображению, читает записи, приводит примеры. переводит свойства фигур из координатной формы в геометрическую и наоборот, подводит заданную ситуацию под использование метода координат. имеет представление о методе координат как частном случае математического моделирования, выделяет идею обобщенного приема его использования в геометрии.
3. Умения а навыки Ученик
Выполнение действий, составляющих прием учебной деятельности, под активным контролем внимания или автоматизировано строит точки, векторы и фигуры по их координатам, используя алгоритмы, построения, решает обратную задачу, изображает по образцу или с помощью извне. доказывает свойства векторов н фигур в координатной форме, решает типовые и прикладные задачи в стандар- тных ситуациях, используя алгоритмы н специальные приемы их решения, доказывает свойства фигур метолом координат, решает типовые и прикладные задачи на доказательство, вычисление и построение в нестандартных ситуациях методом координат,
6.3.2. Материал о координатах дает возможность показать единство
математики, продолжить развитие всех познавательные процессов, воепшанп.
интереса к математике и ее приложениям.
6.4. Основные типы математических и примеры учебных задач
6.4.1. Основные тины математических задач - это те виды геометрически',
задач на вычисление и доказательство, для которых данные в условии задачи и
искомые фигуры удобно расположить в некоторой системе координат и при >п>м
все алгебраические выкладки будут наиболее простыми.
6.4.2. Учебные задачи связаны с приобретением необходимых умении
составляющих содержание метода координат; например:
1) Постройте точку по ее координатам (на плоскости, в пространстве).
2) Найдите координаты заданной точки (на плоскости, в пространстве).
3) По заданным геометрическим свойствам линии составить ее уравнение.
4) По данному уравнению линии выявить ее свойства.
5) Задания вида «Рисуем по координатам».
6) Какую геометрическую фигуру определяет уравнение (или неравенство): а) 2л
4у + 3 = 0; б) Ту л- 6 х - 10; в) х1 + у2 = 0; г) х2 + у2 = 6; д) ах г ву + с = 0, если х ~ 0 и у о
одновременно (если один из коэффициентов равен 0) и в зависимости от другая значений
а, в, с?
7) Окружность задана уравнением а) х2 т у2 = 21; б) (х + I)2 + (у - 2)2 = 25; в) (л ’)
+ (у + 3) - 1. Не рисуя системы координат, установите расположение относительно шт
точек а) А (-1; 3), В (4; -5), С (*3: - *2); D (0; *21); б) А (-3; 0), В (5; 0). С (4; 2); D (2. 1\
Е (—4; 6). К (3; I), L (-2; 3); в) запишите координаты какой-нибудь точки, которая лежит ты
этой окружности, и точки, которая не лежит на ней.
8) Найдите координаты центра и радиус окружности, заданной уравнением: а) х2 • i
= 5; б) л2 + (у + 5)2 4; в) (х - 2)2 + Г = 3; г) (х + 5)2 + (у- 1 )2 = 2; д) (х + З)2 4v + I)2 = ।. « I
г2 у" = а2.
6.5. Специальные методы и приемы обучения
6.5.1, 13 пропедевтическом курсе координаты можно охарактеризовать к.п>
способ представить любую точку пространства системами чисел; например. любую
точку Земли можно полностью охарактеризовать широтой, долюгой и высотой in 1
уровнем моря. Хорошей иллюстрацией этой ситуации в одномерном случат
является термометр, который помогает понять суть координатной прямой
Упражнения на построение точек на прямой по их координате и опредсленш
координаты точки, используются для иллюстрации действий с положительными и
116
отрицательными числами и их свойств. решения простейших неравенств
Аналогичный подход используются при знакомстве с коордчнапюй плоскостью-,
текстовые задачи, практические построения и шрлныс задания вида «рисуем по
координатам» точки на плоскости раскрывают идею - положение точки на
плоскости может быть определено ее расстоянием до двух фиксированных
I перпендикулярных прямых - осей координат.
6.5.2. Изучение элементов координатного метола в основной школе
I продолжается фактически вначале в курсе алгебры - исходя из формулы, задающей
I каждую изучаемую функцию, строят график этой функции по координатам
произвольных, а затем и характеристических точек. С помощью графика
исследуются свойства функции, изучается графический .метод решения уравнений,
I неравенств и их систем [2. лк. 4, с. 73-75- лк. 5, с. 95. с. 105]. В процессе решения
этих задач алгебры осуществляется знакомство с такими геометрическими
фигурами, как парабола и гипербола, не изучаемых в курсе геометрии, и понятием
I «уравнение линии» (на примере прямой и окружности)
6.5.3. В систематическом курсе планиметрии, с опорой на этот материал,
начинают решать обратную задачу - исходя из свойств некоторых кривых, вывести
। их уравнение, решение которой приводит к понятию «уравнение фигуры».
Для известных уже геометрических фигур и их свойств (отрезок, прямая,
1окружносгь, взаимное расположение прямых и окружностей и др.) выводятся
1 уравнения, с помощью которых известные задачи, раньте решаемые построением,
ггсперь решаются алгебраически (например, нахождение середины отрезка.
|||сследование взаимного расположения прямых, прямой и окружности и т.д. (4, гл.
15. § 50]). Таким образом получается новый метод исследования свойств
1||13всстных, а затем и новых геометрических фигур (табл 25)
В процессе решения задач целесообразно выделять ситуации для выбора
Iметода координат; например, вычисление длины отрезка, отыскание середин
отрезков, выяснение взаимного расположения прямых, окружностей и др.
При этом понимание преимуществ метода координат (решения
Геометрических задач средствами алгебры) достигается двумя основными
| приемами - рациональным выбором расположения осей координат и
неметрической иллюстрацией алгебраическою решения Пример решения задачи
117
на вычисление координатным мешдом нокаин ноже.
Габиипи Л>
ДЕКААТОАЫ КООРДИНАТЫ
НА ПЛОСКОСТИ
А(х: у)
х - абсцисса 1
} коорл**йты
у ордината]
А ( *.
1 Расстояние между точками: d ~ J(x, - хг)* + (й - р₽)г
2 Середина отрезка: х — *ф * *л; у - •
2 Z
УРАВНЕНИЯ ФИГУР - ...
1. Окружность
(х - о)‘ + (у - Ь)2 - Д’, (в; Ь) - центр [х* + J? - Я1]
2. Пряная
ах + by + е - О
у- kx + Ь, где k - tg а -
Й.7А
х1~хг.
ПРЕОБРАЗОВАНИЯ НА ПЛОСКОСТИ
Ф '%.: х, ~ х; У1“-₽
х, - - х; У1-У
®Z0: х. -= - х; у,-~у
@Г: xz ”= х + а; yt~ У + ъ
у
^А(х; у)
I
+—
I х
1
А/х,.-
о
Задача Hatiui расстояние между серединами днагоиалеи прячоугопьной трапеции с
основаниями « и л.
В соответствии с папами применения
координатного метода 1) выбираем расположение
осей прямоугольной системы координат так,
чтобы начало координат совпало с вершиной
прямого угла трапеции ABCD\ при этом
координатные оси проходят по сторонам этого
угла. 2) Записываем координаты всех данных в
задаче точек: А (0;0). В (<);у>. С (a.y'f, Г) (в, О).
<)i(()+u/2:(l+y/2). О: (0+ч'2: у?2*Оу, (координаты
точек <?, и (?> - по формуле координат середины
отрезка, заданного своими координатами)
3) Используя формулу расстояния между двумя
точками. заданными своими координатами,
находим ()/О> = (в - <т)/2.
В учебном курсе А.В. Погорелова координаты широко используются и при
изложении понятия «векторы»; это снимает трудности изучения операций над
векторами и их свойств, но отодвигает на второй план геометрический смысл этих
операций и, тем самым, к тому, что приложения векторов в геометрии и физике
практ ически Tie рассматриваются.
6.5.4, В систематическом курсе стереометрии - использование повторения и
обобщения изученного в пропедевтическом курсе и курсе планиметрии; аналогии
при выводе уравнений пространственных фигур (например, плоскости и сферы) и
решении задач.
(Си С.М. Саакян. В.Ф. Бутузов. Изучение темы «Метод координат в пространстве»
и 11 классе /- Математика в школе, 2001. №6. - С. 30-44; [4, гл. 15, § 50])
6.5.5
Технологическая цепочка формирования координатного метода
. 5 класс
I) Рассмотрение примеров из практической жизни, географии и т.п..
Позволяющих сформулировать основную идею метода координат
2) Изучение координатного луча и координатной прямой; координат точки па
прямой и их приложений (определения и иллюстрации операций нал числами).
3} Решение учебных задач на изображение точки по ее координате и чтение
к ч»ртннаты точки.
6 класс
4) Изучение координатной плоскости.
I |Я
5) Решение учебных задач на построение точки по ее коорпнпапо
нахождение и чтение координат точки по ос (гзображелшо на коордшишю
плоскости; «рисование» ио координатам.
6) Контроль и коррекция усвоения.
7-9-11 классы (курс алгебры и начал анализа)
7) Решение учебных задач на построение (рафиков изучаемых по программ
элементарных функций (по точкам, по характеристическим точкам), выявлешп
(чтение) по (рафику простейших свойств функции, иллюстрация свойств футн пш
на (рафике.
8) Решение задач на применение графического метода (метода интер1Ы>><>|н
решения уравнений, неравенств и их систем, связанных с изучаемой функцией
9) Изучение уравнений линии - прямой, параболы, гиперболы, окружит и'
затем - синусоиды, экспоненты.
10) Контроль и коррекция усвоения.
7-9 классы (курс планиметрии)
11) Обобщение понятийного аппарата о координатах на плоскости к мч> Л
его применения к выводу уравнений плоских фигур (прямой, окружности)
12) Применение координат к решению задач планиметрии (нахтм-н'ИН
середины отрезка, вычисление расстояния между двумя точками uiuiimiuxI
расположения прямых и окружностей и др.).
13) * Выявление действий по применению теории к решению рассм.чр inti
задач и их последовательности.
14) * Обобщение выявленных действий в виде приема решения тыпч ч« ("<
координат.
15) Решение простейших геометрических задач методом ......
16) Обобщение ситуаций применения метода координат к решению ।
17) Текущий контроль и коррекция усвоения.
18) Введение понятия координат вектора ла плоскости и нх причин в
изучению операций над векторами (сложения, вычитания, умножения и i чк
19) Решение задач векторной алгебры и их приложении и ... пш
форме (на плоскости). ♦
20) Текущий контроль и коррекция усвоения.
21) Обобщение ситуаций применения метода координат в математике
(алгебре, геометрии, математическом анализе) и ее приложениях.
22) Решение задач планиметрии координатным методом.
22) Нтоювый контроль усвоении
10-11 классы (курс стереометрии)
23) Изучение координат в пространстве. обобщение основных понятий.
24) Применение координат к выводу уравнений пространственных фигур
(плоскости, сферы).
25) Применение координат к решению задач стереометрии (например,
исследование взаимного расположения плоскостей, сфер).
26) Обобщение метода координат для решения задач в пространстве.
27) Примеры решения задач стереометрии координатным методом.
28) Текущий контроль и коррекция усвоения.
29) Координаты вектора в пространстве и их применение к изучению
итераций над векторами (скалярного и векторного произведения).
30) Решение задач векторной алгебры и нх приложений в координатной
+«>|лгс (на плоскости).
31) Текущий контроль и коррекция усвоения.
32) Обобщение ситуаций применения метода координат в стереометрии.
113) Решение задач стереометрии методом координат.
33) Итоговый контроль усвоения.
Технологическая цепочка формирования алгоритмов и приемов
g координатного метода
Таблица 26
Курс Приемы использования метода координат
11(шн€<>свтическ1ш курс 1. Алгоритмы изображения координатного луча и координатной прямой. 2. Алгоритмы изображения чисел на координатной прямой (луче) и чтения координаты точки на ней 3. Приемы иллюстрации операций над числами и их свойств на координатной прямой. 4 Алгоритм изображения прямоугольной системы координат на плоскости 5 Алгоритмы построения точки на плоскости ио ее координатам и чтения координат точки плоскости.
121
I 6. Алгоритм построения графика зависимости величии «но точкам». 7. Обобщение приемов 1-6.
; 7 Курс алгебры и начал анализа 7. Алгоритмы построения графиков элементарны- функций по точкам, по характеристическим точкам путем сдвига и деформации основного графика, на основ, исследования. Я Обобщенный прием построения графика функции 9. Приемы чтения свойств функции по графику и иллюстрации свойств на графике и их обобщение. 10. Приемы графического решения уравнений. неравен,,« н их систем соответствующего вида и их обобщение
3 Курс планиметрии 11. Приемы вывода уравнений плоских фигур. 12. Частные приемы решения геометрических задач и i плоскости методом координат. 13. Приемы разложения вектора по координатам и нахождения координат вектора. 14. Приемы выполнения операций над векторами и координатной форме. 15. Обобщенный прием решения геометрических задач и i плоскости методом координат.
4. Курс стереометрии 16 Обобщение приемов 4, 5, 11» 12. 15 иа случай трехмерного пространства.
ЛЕКЦИЯ VII
Векторы в школьном курсе геометрии
7.1. Логико-математический анализ линии векторов
7. 1.1. Понятие вектора возникло как математическая абстракция объектов,
характеризующихся величиной и направлением (например, перемещение, скорость,
напряженность электрического или магнитного поля) из нужд практики и таких
наук, как механика. Вектор (от латинского Vector - несущий, в XIX в. ввел У.
I амильтон) - направленный отрезок прямой, у которого один конец (точка Л)
Называется началом вектора, другой конец (точка В) концом вектора. Высокая
i зелень наглядности и простота привели к его использованию и в других областях
физики - кинематика, статика, динамика, гидродинамика, теория потенциала; к
<«зданию новых разделов самой математики - векторная алгебра и векторный
Ч1ПС1ИЗ, теория поля и тензорный анализ, общая теория n-мерного векторного
пространства. На векторной основе излагаются многие разделы математики от
’ 1Смептарных (комплексные числа) до более сложных (линейная алгебра,
мднтнчсская и дифференциальная геометрия, линейное программирование,
функциональный анализ), которые, в свою очередь, проникают в такие области
। нитки н техники, как биология, экономика др.
I Обзор различных подходов к определению понятия вектора дан
Д Александровым (Математика в школе 1985 №5.). С точки зрения
метрических преобразований, вектор есть параллельный перенос, т.е.
Итфажение плоскости на себя при котором, каждая точка А' -+Х' отображается
I чго 1)луч .V.V’ имеет заданное направление. 2)отрезок [А'А '] имеет заданную
• -ПНУ
I Понятийный аппарат этой линии составляют понят ия: вектор, начало и конец
модуль вектора, нулевой вектор, одинаково и противоположно
• 1|ц|||11снныс векторы, равные векторы, коллинеарные векторы, координаты
•»|ч|м Простейшие операции над векторами: сложение, вычитание, умножение
• • । pi па число, скалярное и векторное умножение векторов; преобразование
Pth'piii.ix равенств и их замена алгебраическими, разложение вектора по
123
координатам, отыскание величии, связанных с векторами - длин отрезков, углов
Раздел математики, в котором изучаются свойства операций над векторами,
называется векторным исчислением: раздел векторного исчисления, в котором
изучаются простейшие операции над (свободными) векторами, называется
векторной алгеброй.
Векторное пространство — математическое понятие, обобщающее понятие
совокупности всех (свободных) векторов обычного 3-х.мерного пространства. Его
элементами могут быть объекты самой разнообразной природы; в частности,
векторными пространствами (с обычными операциями сложения вектором i
умножения вектора на действительное число) являются: а) множество многочленов
степени не выше п с действительными коэффициентами; б) множество всех
векторов плоскости, отложенных от начала координат; в) множество «свободных»
векторов; г) множество всех параллельных переносов плоскости (или
пространства) к другие,
7. 1.2. Векторный метод решения задач и доказательства теорем [1. лк. 11, с
160], как частный случай .математического моделирования, в котором в качестпе
формальной математической модели выступают векторные соотношения, выгляди
следующим образом:
1) перевод содержания теоремы (задачи) на язык векторов: введение в нее
векторов, связанных с рассматриваемыми геометрическими фигурами; выбор
системы координат (если это необходимо) и базисных векторов; разложение всех
введенных векторов по базисным;
2) составление системы векторных равенств (равенства) или уравиент)
(уравнения):
3) преобразование векторных равенств (решение уравнении);
4) замена векторных равенств (уравнений) алгебраическими уравнениями и их
решение;
5) обратный перевод полученных результатов на геометрический я н.п
(объяснение геометрического смысла полученного решения).
Концепция векторного пространств в целом не может быть прямо переис<.сн|
в школьный курс, но понятие вектора - одно из ведущих его понятий.
124
7.2. Место векторов в программе л учебниках
Таблица 27
Этап Класс Темы программы
Основной (курс планиметрии 7-9 классов основной школы) 8 9 Т.5. «Векторы». В т.1. «Векторы. Метод координат»: понятие вектора, абсолютная величина и направление вектора, равенство векторов, сложение и вычитание, умножение на число, координаты вектора. (В т.З. «Координаты и векторы»: векторы на плоскости, скалярное произведение векторов, векторный метод).
Завершающий (курс стереометрии 10-11 классов старшей школы) 10 11 Т.5. «Векторы в пространстве»; понятие вектора в пространстве, сложение и вычитание, умножение на число, компланарные векторы. В т.1. «Метод координат в пространстве»: координаты вектора, скалярное произведение векгоров. (В т.4 «Координаты н векторы в пространстве»: векторы н пространстве, единственность разложения вектора по трем иском планарным векторам, скалярное произведение векторов.
7.3. Цели изучения векторов в школе
7,3.1. Изучение материала линии векторов имеет основной учебной целью
знакомство учащихся с понятием вектора и основами векторной алгебры (в
координатной и геометрической форме) и осознание ими' на том или ином уровне
векторного метода и идеи его применения в геометрии и к решению прикладных
задач. В таблице 28 показана дифференциация этой цели по уровням обучения.
7,3,2. Материал о векторах позволяет продолжить развития всех
познавательных процессов, в частности, логического и диалектического мышления,
мировоззрения, раскрывать прикладную роль математики, осуществлять
воспитание интереса к математике через ес приложения и решение практических
задач.
125
7.4. Основные типы математических и примеры учебных задач
7,4.1. Основные типы лм/г/елмтнческих задач - это задачи векторной алгебры
(операции над векторами в алгебраической и геометрической форме) и задачи на
I
| показаiельегво или построение векторным методом. Для их решения используются
алгоритмы векторной алгебры и общий прием решения задач векторным методом,
описанный выше.
7.4.2, Учебные задачи связаны с формированием компонентов векторного
метода. Примеры учебных задач:
1) Какие из следующих величин являются векторами: а) скорость, б) масса,
в) ускорение, г) время, д) температура, е) работа?
2) Сколько различных векторов можно образовать из сторон треугольника АБС ?
3) Можно ли утверждать, что а) АБ-ВА, если АВ ~ ненулевой вектор,
б) |7в) = |ci)j, если ЛВ = CD?
4) Как построить разность двух векторов? сумму двух векторов по правилу
а) треугольника, б) параллелограмма? произведение вектора на число?
5) Может лн равнодействующая сил Лебедя, Рака и Щуки (из басни И.А. Крылова)
быть равной нулю?
6) Какими способами можно построить вектор, равный сумме а) двух векторов;
I б) трех векторов?
7) Каким образом операцию вычитания векторов можно свести к операции
сложения?
8) Д.чя сложения всяких ли а) двух векторов применимо правило параллелограмма;
, б) Т)юх векторов - правило параллелепипеда?
9) Можно лн рассматривать умножение вектора на число как частный случай
сложения векторов?
10) Любой ли вектор можно {изложить а) по двум неколлинеарным векторам; б) по
трем некомпланарным векторам?
i I) В чем сходство и различие между свойствами скалярного произведения векторов
и свойствами умножения чисел?
7.5. Специальные методы и приемы обучения
7.5.1. В процессе реформы математического образования 60-70-х гг. в нашей
стране обсуждались два подхода к введению понятия вектора в школе, имевшие
' своих сторонников и противников: а) исторический подход: вектор как
направленный отрезок; б) научный подход- вектор как элемент векторного
пространства Вначале преобладающим оказался второй из них, автором которого
был акал А.Н. Колмогоров, проводивший в школьном курсе геометрии идею
1сометрпческих преобразований (с подробным изучением, в частности.
127
параллельного переноса как одного из движений, синонимом является вектор). В
дальнейшем ему уступил место первый подход: вектор вводится как величина,
характеризуемая нс только численным значением, но в направлением и
изображается направленным отрезком.
Таблица
ВЕКТОР - ...
а или АВ; "—►“ | а Ун - tt)» где А(х,; у,). В(хг; у9}
V
ч - у/х' +у = л1(х.-х,у+(у.-у,у
nporveooczoxHO направленные
ксилиларные
е,(1; О) и е,(0; 1) - орты (ед. | а | - 1).
Z (о, Ь) - ...
• Сравнение(«=/О«(|й| = |/;>| иП)«(координаты равны)
• Сложение а (х,; у,) + h (х.; у,) = с (х,+х:; y,+yj
• Вычитание а-Б= d (х,-х:; y,-yj
• Умножение на число ка = /й (кх,; ку,)
• Скалярное произведение db = х,х. + у,у, = iori/л cos (а. Ъ)
(3) ka — т-.1 m| - | k | а | и если * > О а н т, ТТ
* < О а и т 11
4. (а и b коллинеарны) « | Л £с
\ Кг)
5. а - ле, + уе,
6. o’-laf’
7. (ali)c(a-t - О)
7.5.2. В систематическом курсе планиметрии Л.С Атанасяна отрс ык i Н
которого указано, какой из его концов начало, а какой - конец. iuiii.iii.iri>«
направленным отрезком пли вектором. При этом сначала вектор iny*ii>nrt в
геометрической форме, затем в алгебраической (заданный в координатной <|' г '
128
В курсе А.В Погорелова вектор сразу вводится и изучается в координатной форме,
ио и здесь целесообразна геометрическая иллюстрация При таком сочетании
работают наглядные методы, позволяющие показывать приложения векторов (в
которых вектор выступает как направленный отрезок), начинают формироваться и
использоваться координатный и векторный методы (табл. 27).
Обучение решению задач векторным методом нужно осуществлять на
достаточно простых задачах, не отвлекая внимания на трудности чисто
геометрического содержания. Ниже рассмотрен пример такой задачи.
Задача. Найта угол при вершине равнобедренного треугольника, если известно, что
медианы, проведенные к его боковым сторонам, взаимно перпендикулярны.
С Решение. В треугольнике АВС: ЛС=ВС. MuN- середины сторон
/ \ А С н ВС (рис. 27). Обозначим через лив векторы СМ и CN .
а/ \ь Искомый угол С треугольника АВС есть угол .между векторами а и
/ \ s. Тогда СМ = а, СА = 2а, C.N = в. СВ~ 2в. Далее имеем:
ВМ- ВС + СМ - - 2б+а\ AN- АС + CN = - 2д+в. По условию
прямые ВМ и AN перпендикулярны, те. ВМ * AN=O, или, иначе. (-
/ \ 2в+я)(-2а+«) = 0. Раскрывая скобки, находим: 5ак - 2а2 - 2«г = 0,
или’ чт0 то жс самое> baecosa- 2а2 - 2в2 = 0, где а - угол между
В векторами ап в, т.е. искомый. Т.к. а=в. п2=в’=до, то 5с<иа- 4=0,
Рис. 27 откуда ада = 4/5 и а »36’52’.
При решении задач векторным методом (так же. как методами геометричес-
ких преобразовании и координат) необходимо, во-первых, подчеркивать его
•ффекгивность в применении к данной задаче (например, предложить решить
гзнную задачу другим методом и сравнить решения). Во-вторых, на примере
Ккдой задачи обучать учащихся системе определенных ситуаций (правил),
помогающих найти ключ к выбору метода решения. Например, этот метод хорошо
..... для доказательства параллельности или перпендикулярности двух
прямых, взяв на этих прямых отрезки и доказать для соответствующих векторов в
первом случае, что один из них может быть получен из другого умножением на
спо. во втором - что их скалярное произведение равно нулю. Для вычисления
чинны отрезка достаточно разложить соответствующий вектор по координатам и
числить его скалярный квадрат, а для вычисления величины угла - вычислить
мпппус угла между векторами на его сторонах из формулы скалярною
произведения векторов.
129
7.5.3, Методика изучения векторного метода в систематическом кур^
стереометрии аналогична. Например, доказательство тсорсмы-нризиака
перпендикулярности прямой и плоскосги (Исли прямая перпендикулярна каждой
из двух пересекающихся прямых, лежащих в плоскости, то эта прямая
перпендикулярна плоскости), которое без использования векторов в традиционном
курсе геометрии было очень громоздким.
Рис 28
Дано:
Л1 «. ole, « *;с = О,в с а,с с а
(рис. 28)
Доказать: а± а.
Доказательство.
Убедимся, что прямая а перпендикулярна любой прямой </, лежащей в плоскости >
На прямых вис выберем соответственно точки В и С. отличные от точки О; на прямые .»
и </ выберем пары несовпадающих точек А и А/, D и D/. Разложим вектор DI), ни
неколлпнеарным векторам ОН к ОС: DD,= хОВ+уОС. Обе части получение) >
равенства умножим скалярно на вектор А А.. Согласно распределительному закон)
скалярного умножения получим: £>£),* А А, - хОВ*АА,+ уОС*АА,. Но
ОС*АА1=0, т.к. ААЩЭВ н AAilOC Тогда DDI*AAI = 0, откуда АА,А (>7>,
Следовательно. о-1_</ и aLa.
(Си. также С.М. Саакян. ВФ. Кутузов. Изучение темы «Векторы в пространстве» »
курсе 10 класса// Математика в школе. 2000. № 3. - С. 11-16; [4, гл. 15, § 52]).
Вопросы построения курса элементарной геометрии на основе точечно
векторной аксиоматики Вейля могут составить содержание спецкурса в кл.к с и
математического профиля.
7,5.4.
Технологическая цепочка формирования векторного метода
I) Подготовительный этап- рассмотрение примеров физических венпчни
характеризующихся численным значением и направлением.
2) Введение геометрического изображения вектора и его элементов, к рмннк*
и обозначений.
3) Рассмотрение положения векторов на плоскости, разложение псю>>р.1 нн
базисным векторам, координаты вектора
4) Решение учебных задач па усвоение основных понятий.
во
5) Рассмотрение задач (с физическим и другим содержанием), требующих
выполнения операций над векторами.
6) Определение операции над векторами на плоскости (сложения, вычитания.
) множения на число) в геометрической и координатной форме.
7) Выявление алгоритмов и приемов выполнения операций нал векторами.
X) Решение задач векторной алгебры и ее приложений.
9) Текущий контроль и коррекция усвоения.
10) Рассмотрение примеров доказательства теорем н решения задач
планиметрии с помощью векторов.
11) Выявление действий по применению теории к решению рассмотренных
задач н их последовательности.
12) Обобщение выявленных действий в виде приема решения задач
векторным методом.
13) Понятие о векторном методе, его применении в математике и ее
приложениях (в сравнении изученными ранее методами).
14) Решение задач планиметрии векторным методом.
15) Текущий контроль усвоения.
16) Изучение векторов в пространстве, обобщение основных понятий,
17) Обобщение операций над векторами в пространстве (сложения,
вычитания, умножения на число) в геометрической и координатной форме.
18) Изучение скалярного произведения векторов
19) Решение задач векторной алгебры и ее приложений в пространстве.
20) Текущий контроль и коррекция усвоения.
21) Рассмотрение примеров доказательства теорем и решения задач
иерсометрии с помощью векторов.
22) Обобщение векторного метода и решение задач стереометрии векторным
методом.
23) Примеры решения задач стереометрии и прикладных задач векторным
Мс годом.
24) Текущий контроль и коррекция усвоения.
25)* Сравнение, систематизация и обобщение специальных методов
гометрнп - элементарных геометрических методов, алгебраического метода,
Г’.1
метода геометрических преобразований, координатною и векторного методов и их
применения к решению геометрических и прикладных задач.
26)* Сравнение, систематизация и обобщения ситуаций применения
различных методов к решению геометрических задач.
27) Итоговый контроль усвоения.
Технологическая цепочка формирования алгоритмов и приемов
векторного метода
Таблица 3<»
№ /Ггрс Приемы изучения векторного метода
I Курс планиметрии 1. Алгоритмы геометрического изображения и обозначения вектора на плоскости. 2. Алгоритмы выполнения операций сложения вычитания к умножения вектора на число п геометрической форме на плоскости. 3. Алгоритм отыскания координат вектора на плоскости 4. Алгоритмы выполнения операций сложения вычитания и умножения вектора иа число в координатной форме. 5. Общий прием применения векторов к решении» геометрических задач на плоскости.
2 Курс стереометрии 6. Обобщение алгоритмов и приемов 1-5 для пространства. 7. Приемы вычисления величии с помощью скалярного произведения векторов (в координатной форме). 8. Обобщенный прием решения задач векторн»,»м методом
7.5. Некоторые приемы заключительного повторения курса геометрии
Общий прием повторения курса геометрии заключается в том, что это должно
быть повторение с «обобщениями и дополнениями». Повторение понятий, т еорем и
формул полезно сопровождать краткой математической записью, выполненном
чертежей, приведением примеров, иллюстрациями
•<г
Повторяя определения понятий. полезно выполнить c.ne/ivu’uiih
дополнительные задания н ответить на вопросы.
1) Каким способом определяется данное понятие? Как доказать его сушесшои..
2) Каковы связи этого понятия с другими в данной теме (ращеле, курсе»'1 |..<юе и»
них служит основой для определения данного понятия?
3) Вывести следствия из определения понятия.
4) Сформулировать другие определения понятия и доказать их равносильноеть
5) HaiiTif пары аналог нчных понятий в а) данной теме; б) с другими темами, в) в
планимсгрип н стереометрии. Установил, их сходство и различие.
6) 1laiiтн к данному понятию противоположное. Как доказать его существование?
Повторяя теорему, полезно ответить на следующие дополнительные вопросы:
I) Каким видом 1 еоремы является лн данная теорема? Почему?
2) Каким методом (приемом) доказывается теорема? Почему?
3) Какие понятия используются при доказательстве теоремы? Как?
4) Какие вспомогательные построения выполняются при доказательстве? Зачем?
5) Какие предложения курса используются при доказательстве теоремы7
6) Используется ли эта теорема при доказательстве других теорем? Каких?
7) Как формулируются предложения, обратное (противоположное, противоположное
обратному, аналогичное) доказанной теореме; истинны; они или ложны?
8) Есть лн в курсе геометрии предложения, являющиеся частными случаями данной
теоремы? Ее обобщениями?
9) Можно лн найти теорему о свойствах геометрических фигур, аналогичную
данной, в а) планиметрии, б) стереометрии? Какие это фигуры и свойства?
10) Где применяется эта теорема?
Решая задачи на повторение, необходимо не только повторять используемые
общие и специальные методы и приемы решения, повторять те понятия и теоремы,
которые необходимы для решения, ио и уделить внимание обоснованию выбора
метода решения на основе анализа особенностей условия задачи Решив задачу
выбранным методом, можно решить ее другим (возможно, предложенным
учащимися) и сравнить эффективность их использования. Рассмотрим примеры.
Задача I. Окружность вписана в ромб с углом 60°, расстояние от центра окружности
зо ближайшей вершины равно 1. Докажите, что для любой точки Г окружное ги сумма
квадратов ее расстояний до вершин ромба не зависит от положения точки на окружности.
Необходимость вычисления квадратов расстояний между точками
окружное hi и вершинами ромба подсказывает целесообразность применения
формулы для вычисления расстояния между точками в координатах. Отсюда мысль
о применении для решения этой задачи метода координат и поиск рационального
выбора системы координат.
133
Задача 2. Докажите, что в треугольнике точка 6' пересечения медиан, центр О
окружности, описанной около треугольника, и точка Н пересечения высот лежат на одной
прямой (прямая Эйчера) и (Ki (ill = 1:2.
Принадлежность трек точек одной прямой и отношение образуемых ими
отрезков подсказывает целесообразность применения гомотетии. Задачу можно
решить и векторным методом.
Задача 3. Найдите объем правильной четырехугольной пирамиды, у которой
боковое ребро равно т, а диагональное сечение и основание равновелики.
Известные и неизвестные элементы пирамиды - геометрические величины и
условие равновеликости фигур говорит о целесообразности применения
алгебраического метода решения данной задачи.
Задача 4. Основанием пирамиды SABC является равносторонний треугольник АЗК
длина стороны которого равна 4*2. Боковое ребро перпендикулярно плоскости основания
и имеет длину 2. Найдите величину угла между скрещивающимися прямыми, одна и,
которых проходит через точку .У и середину К ребра ВС, а другая проходит через точку (
и середину М ребра АВ.
Для решения этой задачи могут быть использованы различные методы
координатный, векторный и традиционные элементарные средства; каждый из них
имеет определенные преимущества. При координатном методе выбор
прямоугольной системы координат не вызывает затруднений: точка С - начало
системы координат, прямые СУ, СМ и прямая СУ, параллельная АВ, - осп
координаты всех точек указанной фигуры легко определяются в выбранной
системе. В случае применения векторов выбор базисных векторов очевиден и
позволяет получить наиболее простые разложения векторов, необходимых для
вычисления угла между указанными в задаче прямыми. При применении этих двух
векторов чертеж играет вспомогательную роль. В случае применения
элементарных средств решение задачи гсометрично. чертеж п его объяспешь
играет существенную роль, в процессе решения работают многие теоремы
стереометрии и планиметрии. А если дополнить условие задачи требованием
вычислить расстояние между скрещивающимися прямыми, то решение ним
методом наиболее рационально, т.к. применение координатного п векторного
методов приводит к «ромоздким выкладкам.
13-5
Основная литература
1. Eniuucna О.Б Общая методика преподавания математики в средней школе: Курс
лекций: Учеб, пособие для иудеиюи физ -мат. спец пел. пи-топ. - Тобольск: ТГПИ
нм. Д.И. Менделеева. 1997. - 191 с.
2. Епишева О.Б. Специальная методика обучения арифметике, алгебре и началам
диализа в средней школе: Курс лекций: Учеб, пособие для студентов физ.-мат. спец. пед.
ИН-ТОВ - Тобольск: ТГГ1И им. Д.И. Менделеева. 2000. - 126 с.
3. Колягин Ю.М . Луханкин Г.Л. и др. Методика преподавания математики в средней
школе. Частные методики: Учеб, пособие для студентов физ -мат. фак. пед. ин-тов. - М.:
Просвещение, 1977. - 480 с.
4. Методика преподавания математики в средней школе: Частная методика: Учеб,
пособие для студентов пед. ин-тов по физ.-мат. спец.М.Я. Блох. В.А. Гусев, Г.В. Дорофеев
и др./ Сост. В.И, Мишин. - М.: Просвещение, 1987. - 416 с
5. Программно-методические материалы: Математика 5-11 классы. Сборник
нормативных документов / Сост. Г.М. Кузнецова. - М : Дрофа, 2000. - 320 с.
6. Программно-методические материалы: Математика 5-11 классы. Тематическое
планирование / Сост. Г.М. Кузнецова. - М.: Дрофа, 2000. - 192 с.
7. Учебники, учебные пособия и учебные комплекты по математике и геометрии для
средней школы.
Дополнительная литература
10. Оценка качества подготовки выпускников основной школы по математике /
Г.В Дорофеев, Л.В. Кузнецова. Г.М Кузнецова и др. - М.: Дрофа. 2000. - 80 с.
11 Болтянский В.Г.. Яглом И.М. Преобразования. Векторы: Пособие для учителя. -
М.: Просвещение. 1964 - 303 с.
12. Далингер В.А. Методика обучения учащихся стереометрии посредством решения
задач: Учеб, пособие - Омск: ОмГПУ, 200). - 365 с.
13. Саранцев Г.П Методика обучения математике в средней школе. - М.
Просвещение. 2002 - 224 с.
14. Методика преподавания геометрии в старших классах средней школы / Под ред.
A ll Фетисова: Пособие для учителя - М: Просвещение. 1967. - 271 с.
15 Учебники по геометрии дли педвузов
16. Статьи но вопросам методики обучения геометрии в школе в периодической
печати (ж. “Математика в школе", газета “Математика"- Еженедельное приложение к
газете “Первое сентября", газе:а “Сто друзей (методическая кухня) - приложение к
Учительской газете" и др ).
135
>7. Пособия для учшслей математики (в частности, ш серии "Библиотека учителя
математики’, Преподавание геометрии в 6-8 классах / С«С|. В. А. Гусев -
М : Просвещение, 1979, - 28) с.; Преподавание геометрии в 9-10 классах / Сост.
З.А. Скопец. Г'.Л Хабиб - М.: Просвещение, 1980. - 270 с,; В .Л. Далпшер. Пропедевтика
обучения учащихся доказательству теорем: Кн. для учителя и В.А Далингер. Методика
работы над формулировкой, доказательством и закреплением теоремы: Кн. Для учителя -
Омск: ОмГПУ. 1995. - 197 с.; В А, Далингер. Планиметрические задачи иа построение:
Учеб Пособие. - Омск: ОмГПУ. 1999. - 202 с.; О.Б Епишева, В.И. Крушит. Учить
школьников учиться математике: Формирование приемов учебкой деятельности: Кн. для
учителя. - М.: Просвещение, 1990. - 128 с.; Болтянский В.Г., Волович М.Б.. Семушиин
А.Д. Векторное изложение геометрии (в 9 классе средней школе). Пособие дчя учителей
- М.: Просвещение, 1982, Г.И. Саранцев. Решаем задачи на геометрические
преобразования. - М.: Столетие. 1997. - 191 с.; Г.И. Саранцев. Обучение математическим
доказательствам в школе - М.: Просвещение. 2002: ПК. Жннеренко. О.В. Мальцева
Наглядность на уроках геометрии (7-9-е классы): Учеб.-метод пособие. - Омск: ОмГУ
1995. - 106 с; В.М. Паповский. Углубленное изучение геометрии в 10-11 классах: Кн для
учителя, - М.: Просвещение, 1993. - 223 с.; А.Я. Цукарь. Развитие пространственною
воображения: Задания для учащихся. - СПб: «Союз», 2000. - 144 с.; Повышение
эффективности обучения математике в школе: Кн. для учителя: Из опыта работы / Сост.
Г.Д. Глейзер. - М.: Просвещение, 1989; С.Н. Белим. Задачи по геометрии, решаемые
методами складывания (оригами). - М : «Аким», 1998; и др.).
18. Пособия для учащихся и абитуриентов (например. Крамор В С. Повторяем и
систематизируем школьный курс геометрии. - М : Просвещение, 1992. - 320с.; Епишев.!
О.Б, Волкова Е.Е Повторим математику: Учеб, пособие для поступающих в вузы.
Тобольск: ГГПИ им. Д.И. Менделеева, 1995. - 462 с . Далингер В.А. Все для обеспечения
успеха на выпускных и вступительных экзаменах по математике: Выл. 1 -6’ Учеб
пособие. - Омск ОмПГУ, 1995 - 1996 г.г.; Брагин В.Г.. Грабовский А.И. Вес предметы
школьной программы в схемах и таблицах Алгебра. Геометрия. - М Олимп, ООО "Из л
во АС Г-ЛТД”, 1998. - 240 с. и др.).
136
СОДЕРЖАНИЕ
ПРЕДИСЛОВИЕ 3
ЛЕКЦИЯ I. 5
Общие вопросы теории и методики обучения геометрии в школе 5
1.1. Общие задачи курса геометрии в средней общеобразовательной 5
школе
1.2. Содержательно-методические линии и структура программы 9
школьного курса геометрии
1.3. Основные учебники и учебные пособия для учащихся 12
1.4. Общие психолого-педагогические закономерности изучения [7
каждой содержательно-методической линии школьного курса
геометрии
1.5. Общая схема логико-методического анализа каждой 22
содержательно-методической линии школьного курса математики
ЛЕКЦИЯ II. Учение о геометрических фигурах 24
2.1. Логико-математический анализ линии геометрических фигур 24
2.2. Место геометрических фигур в программе и учебниках 30
2.3. Целя изучения геометрических фигур в школе 3 i
2.4. С>сковные типы математических и примеры учебных задач 33
2.5. Специальные методы и приемы обучения . 37
ЛЕКЦИЯ III. Геометрические построения 54
3.1. Логико-математический анализ линии геометрических 54
построений
3.2. Место геометрических построений в программе и учебниках 62
3.3. Цели изучения геометрических построений в школе 63
3.4. Основные типы математических и примеры учебных задач 65
г. 3.5. Специальные методы н приемы обучения 71
ЛЕКЦИЯ IV. Геометрические величины 81
4.1. Логико-математический анализ линии геометрических величин 81
4.2. Место геометрических величин в пренрамме и учебниках 84
4.3. Цели изучения геометрических величин в школе 85
137
4.4. Основные типы математических и примеры учебных задач 87
4.5, Специальные методы и приемы обучения 90
ЛЕКЦИЯ V. Геометрические преобразования 98
5,1. Логико-математический анализ линии геометрических 98
преобразований
5.2. Место геометрических преобразований н программе и учебниках 101
53. Цели изучения геометрических преобразований в школе 101
5.4. Основные типы математических и примеры учебных задач 103
5.5. Специальные методы и приемы обучения 105
ЛЕКЦИЯ VI. Координаты в школьном курсе математики 112
6.1. Логико-математический анализ линии координат 112
6.2. Место координат в программе и учебниках 114
6.3. Цели изучения координат в школе 114
6.4. Основные типы математических и примеры учебных задач 116
6.5. Специальные методы и приемы обучения 116
ЛЕКЦИЯ VII. Векторы в школьном курсе геометрии 123
7.1. Логико-математический анализ линии векторов 123
7.2. Место векторов в профам.ме и учебниках 125
7.3. Цели изучения векторов в школе 125
7.4. Основные типы математических и примеры учебных задач 127
7.5. Специальные методы и приемы обучения 127
7.6. Некоторые приемы заключительного повторения курса геометрии В1
Рекомендуемая литература 135
138
Епишева Ольга Борисовна
СПЕЦИАЛЬНАЯ МЕТОДИКА ОБУЧЕНИЯ
ГЕОМЕТРИИ В СРЕДНЕЙ ШКОЛЕ
Куре лекций
Издано в авторской редакции
Рисунки Р.Е. Волков
Технический редактор В.В. Клюсова
Подписано в печать с готовых диапозитивов 31. 10. 2002.
Формат 42x60/16. Печать офсетная. Бумага офсетная.
Усл. п. л. 8,6 Уч. изд. л. 8,6
Тираж 1000. Заказ № 670
Издательство ТГПИ им. Д.И. Менделеева
ЛР № 040287 от 25. 06. 1997.
676150. г Тобольск, ул Знаменского, 58.
Отпечатано с готовых диапозитивов в типографии
ООО «Тобольск -Мефтехим»
г ТОйольсь