СПРАВОЧНАЯ
МАТЕМАТИЧЕСКАЯ
БИБЛИОТЕКА
ПОД ОБЩЕЙ РЕДАКЦИЕЙ
Л. А. ЛЮСТЕРНИКА
и
А. Р. ЯНПОЛЬСКОГО

С. Г. МИХЛИН и X. Л. СМОЛИЦКИЙ
ПРИБЛИЖЕННЫЕ
МЕТОДЫ
РЕШЕНИЯ
ДИФФЕРЕНЦИАЛЬНЫХ
И ИНТЕГРАЛЬНЫХ
УРАВНЕНИЙ
ИЗДАТЕЛЬСТВО «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
МОСКВ А 1 965

618 @3)
М 69
УДК 518.61 @83)
АННОТАЦИЯ
В справочнике изложены важнейшие
аналитические и приближенные численные
методы решения основных задач для
дифференциальных и интегральных уравнений.
Приведены основные результаты,
относящиеся к устойчивости и погрешности этих
методов.
Книга рассчитана на инженеров,
физиков и математиков, которым по роду их
практической деятельности приходится
сталкиваться с вопросами приближенного
решения дифференциальных и интегральных
уравнений, а также на аспирантов и
студентов старших курсов соответствующих
специальностей.

ОГЛАВЛЕНИЕ
Предисловие 10
Глава I
Приближенное решение задачи Кош и
для обыкновенных дифференциальных уравнений
§ 1. Аналитические методы " 14
1. Разложение решения в ряд Тейлора 14
2. Метод последовательных приближений 19
3. Метод Чаплыгина 22
4. Метод Ньютона — Канторовича 27
5. Метод малого параметра 31
6. Оценка погрешности через невязку 34
§ 2. Численные методы 34
1. Метод Эйлера 35
2. Метод трапеций 35
3. Метод Рунге — Кутта 36
4. Разностные методы. Экстраполяционная формула Адамса 41
5. Интерполяционная формула Адамса 47
6. Другие разностные методы 50
7. Разностные методы для систем и для уравнений высших
порядков 54
8. Построение начала таблицы 57
9. Об устойчивости разностных методов 64
10. Погрешность формул Адамса 66
И. Сравнение численных методов 68
Некоторые литературные указания 69
Глава II
Метод сеток
§ 1. Уравнения эллиптического типа . 70
1. Сеточные уравнения 70
2. Аппроксимация точной задачи сеточной 79
3. Вопросы разрешимости, сходимости и оценки погрешности 92
4. Сходимость и оценка погрешности для задачи Дирихле 109

6
ОГЛАВЛЕНИЕ
б. Итерационные способы решения сеточной задачи Дирихле 113
6. Численные примеры 118
7. Сеточная задача Неймана 126
8. Задача о собственных значениях эллиптического
оператора 136
§ 2. Уравнения гиперболического и параболического типов. . . 143
1. Задача Коши. Выбор решетки и сходимость сеточных
решений 143
2. Смешанная задача. Явные и неявные схемы 150
3. Устойчивость разностной схемы. Признаки устойчивости 156
4. Примеры устойчивых разностных схем 172
§ 3. Нелинейные задачи 175
1. Квазилинейные гиперболические системы 175
2. Параболическое уравнение; задача с подвижной границей
(модифицированная однослойная задача Стефана) . . . .181
3. Задача Дирихле для слабо нелинейного эллиптического
уравнения 183
Некоторые литературные указания 187
Глава III
Вариационные методы
§ 1. Положительные операторы и энергия 188
1. Оператор краевой задачи 188
2. Положительные и положительно определенные операторы 189
3. Энергетическое пространство 191
4. Обобщенные производные 193
5. Теоремы вложения . . 196
§ 2. Энергетический метод 199
1. Функционал энергетического метода 199
2. Построение решения вариационной задачи 200
3. Метод Ритца 202
4. Методы решения системы Ритца 203
5. Естественные краевые условия 206
6. Неоднородные краевые условия 208
7. Энергетический метод в случае положительного
оператора 210
§ 3. Приложения к задачам математической физики 211
1. Обыкновенные дифференциальные уравнения второго
порядка 211
2. Обыкновенные дифференциальные уравнения высших
порядков 215
3. Системы обыкновенных дифференциальных уравнений 218
4. Основные задачи для уравнений эллиптического типа.
Уравнения Лапласа и Пуассона 221

ОГЛАВЛЕНИЕ 7
5. Вырождающиеся эллиптические уравнения 227
6. Уравнения высших порядков 228
7. Изгиб пластин 230
8. Изгиб сжатой пластины 233
9. Принцип минимума потенциальной энергии в
статической теории упругости 234
10. Краевые задачи для бесконечных областей 241
§ 4. Проблема собственных чисел 243
1. Основные понятия и теоремы 243
2. Метод Релея — Ритца 246
3. Уравнения вида Аи — ХВи — 0 248
4. Спектр обыкновенного дифференциального оператора . . 250
5. Спектр эллиптического оператора 253
6. Устойчивость сжатой пластины 258
7. Спектр вырождающегося эллиптического уравнения . . 258
8. Собственные колебания упругих тел 259
9. Более общие условия положительной определенности
дифференциальных операторов ' 262
10. Минимаксимальный принцип 263
§ 5. Другие вариационные методы и оценка погрешности . . . 264
1. Оценка погрешности приближенного решения 264
2. Метод ортогональных проекций 266
3. Приложения к частным задачам 268
4. Метод Трефтца ; 271
5. Двусторонние оценки функционалов 278
6. Двусторонние оценки собственных чисел 279
7. Ошибка в решении, проистекающая от ошибки в
уравнении 282
§ 6. Метод наименьших квадратов 283
1. Общие замечания * 283
2. Связь с энергетическим методом . . . 285
3. Применение к задачам теории потенциала на плоскости 286
4. Применение к плоской задаче теории упругости . , , . 289
§ 7. Об устойчивости метода Ритца . 290
1. Общие замечания 290
2. Минимальные и сильно минимальные системы 291
3. Предельные свойства коэффициентов Ритца 293
4. Устойчивость метода Ритца 294
5. О числе обусловленности матрицы Ритца 299
6. Сходимость невязки к нулю 299
§ 8. Подбор координатных функций 300
1. Построение полной координатной системы 300
2. Требования к рациональному выбору координатной
системы 302
3. Одномерные краевые задачи 303
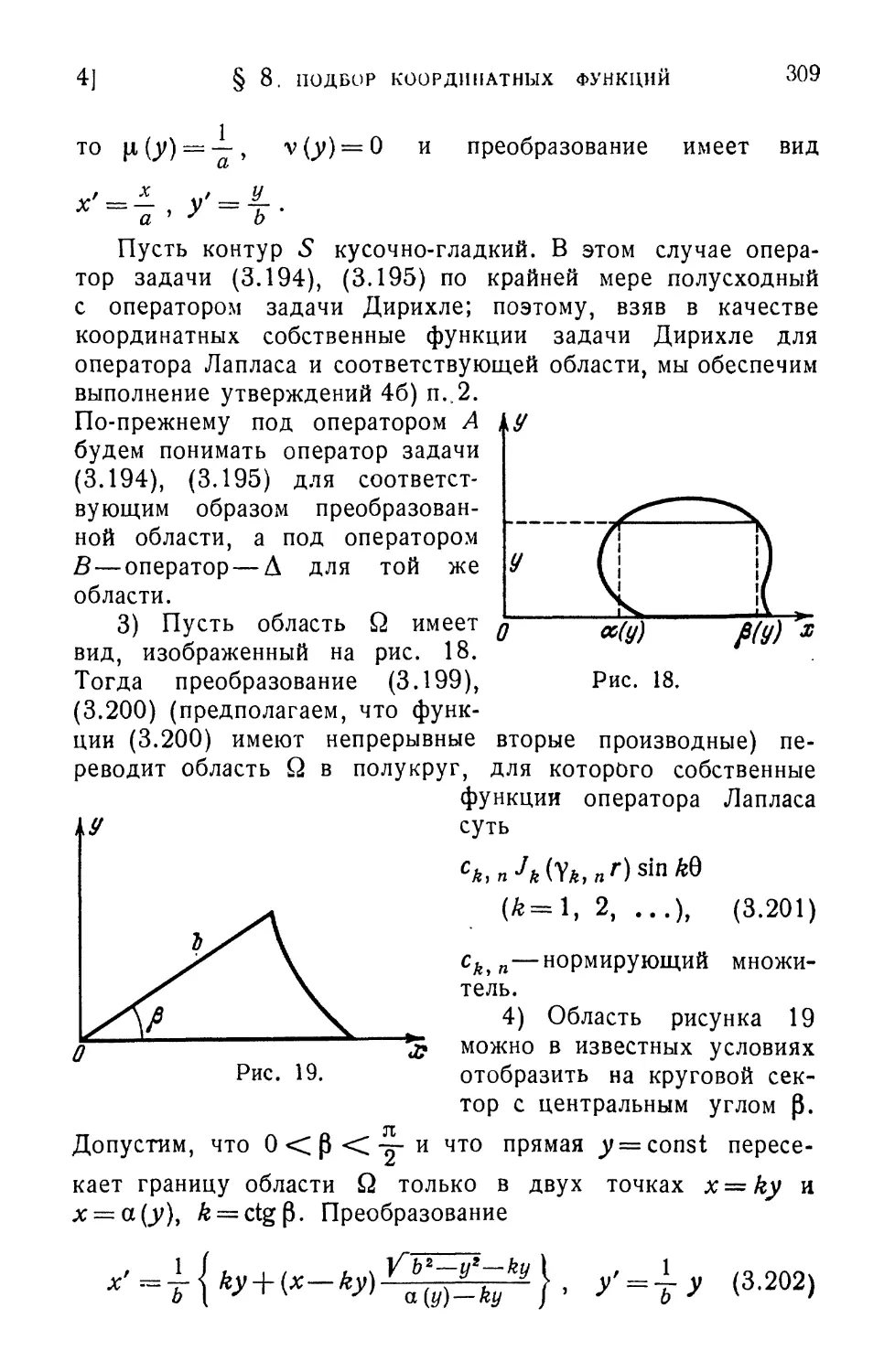
4. Двумерные краевые задачи 307

8 ОГЛАВЛЕНИЕ
§ 9. Метод Бубнова — Галёркина 314
1. Основы метода 314
2. Достаточный признак сходимости 315
3. Применение к задачам математической физики 315
4. Видоизменение метода в случае естественных краевых
условий 316
5. Обобщение метода Бубнова—Галёркина (проекционный
метод) 317
§ 10. Вариационные методы в некоторых нелинейных задачах 319
1. Общие теоремы 319
2. Метод Ритца 320
3. Нелинейная теория пологих оболочек . 322
4. Функционалы теории пластичности и их обобщение . . 323
5. Решение нелинейных систем Ритца. Метод Качанова . . 324
6. Сведение к задаче Коши 326
§11. Метод прямых 329
1. Основы метода 329
2. Метод прямых для уравнений Лапласа и Пуассона . . 331
3. Бигармоническое уравнение 333
4. Метод прямых для параболического уравнения .... 334
Некоторые литературные указания 335
Глава IV
Приближенное решение интегральных уравнений
§ 1. Приближенное вычисление характеристических чисел и
собственных функций симметричного ядра 337
1. Общие замечания 337
2. Метод Ритца 340
3. Метод моментов . . . 343
4. Метод Келлога 344
5. Метод следов 346
6. Замена ядра вырожденным 348
7. Применение определителя Фредгольма 349
§ 2. Метод итераций 349
1. Простая.итерация 349
2. Условия сходимости 350
3. Видоизменения метода итераций 352
4. Интегральное уравнение первого рода с симметричным
ядром 354
§ 3. Применение квадратурных формул 354
1. Уравнения Вольтерра второго рода 354
2. Уравнения Вольтерра первого рода 355
3. Уравнения Фредгольма 356

ОГЛАВЛЕНИЕ
9
§ 4. Замена ядра вырожденным 358
§5. Методы Бубнова — Галёркина и наименьших квадратов . . 364
1. Метод Бубнова — Галёркина 364
2. Метод наименьших квадратов 365
§ 6. Приближенное решение сингулярных интегральных
уравнений 367
1. Постановка задачи 367
2. Решение сингулярного уравнения с вырожденным ядром 368
Некоторые литературные указания 372
Библиография 373
Алфавитный указатель 380

ПРЕДИСЛОВИЕ
Цель настоящего выпуска «Справочной математической
библиотеки» — ознакомить читателя с важнейшими и наиболее
употребительными методами приближенного решения краевых
задач (включая и задачу Коши) для дифференциальных
уравнений, как обыкновенных, так и в частных производных,
а также с приближенными методами решения
интегральных уравнений наиболее часто встречающихся типов: Фред-
гольма, Вольтерра и сингулярных одномерных. Этим
охватывается вся классическая область приложений
математического анализа к механике, технике и математической
физике.
Методы приближенного решения дифференциальных и
интегральных уравнений распадаются на две большие группы:
численные и аналитические методы. Наиболее важную и
разработанную часть первой группы составляют различные
разновидности сеточных методов; в свою очередь в группе
аналитических методов наиболее важными являются
вариационные методы. Промежуточное место занимает так называемый
«метод прямых». Этот метод в последнее время привлекает
все большее внимание как теоретиков, так и прикладников;
однако он еще не настолько разработан, чтобы выделить
его особо, и авторы отнесли его к группе аналитических
методов.

ПРЕДИСЛОВИЕ
11
Построение книги в основном соответствует разделению
приближенных методов на численные и аналитические.
Основные главы книги, а именно главы 11 и III, соответствуют
основным группам приближенных методов — сеточным и
вариационным (к последним присоединен метод прямых)—и не
связаны сколько-нибудь тесно с видом того уравнения, к
которому данный метод применяется. Методы каждой из
названных глав в равной мере могут относиться к
обыкновенным дифференциальным уравнениям, к дифференциальным
уравнениям в частных производных, к интегральным
уравнениям; эти методы можно применять и к линейным, и к
нелинейным задачам. Авторы сочли, однако, целесообразным
выделить два вопроса, в силу их специфичности, в особые
главы.
Так появились две сравнительно небольшие главы: о
задаче Коши для обыкновенных дифференциальных
уравнений (глава I) и о приближенном решении интегральных
уравнений (глава IV). Дело в том, что для упомянутых здесь
проблем разработаны методы, как численные, так и
аналитические, которые трудно, а часто и невозможно отнести
к сеточным, соответственно к вариационным. Правда, часть
материала глав I и IV могла бы быть отнесена к главам II
и III; так, разностные методы для обыкновенных
дифференциальных уравнений, а также методы решения интегральных
уравнений, основанные на применении квадратурных формул,
можно было бы отнести к главе II, а методы Ритца,
Бубнова— Галёркина и наименьших квадратов в интегральных
уравнениях—к главе III. Однако этим была бы нарушена
цельность и связность изложения.
В главе I сохранено разделение методов по двум
основным группам: в § 1 этой главы излагаются аналитические
методы решения задачи Коши, в § 2 — численные методы
решения той же задачи. От расположения материала
строго по группам методов пришлось отступить в главе об

12
ПРЕДИСЛОВИЕ
интегральных уравнениях, где такое расположение было бы
недостаточно оправданным; в этой главе материал
распределен по основным задачам: вычисление собственных чисел
и собственных функций симметричного ядра (§ 1), решение
уравнений Фредгольма и Вольтерра (§§ 2—5) и решение
сингулярных уравнений (§ 6).
Глава I написана авторами совместно. Глава II написана
X. Л. Смолицким, главы III и IV — С. Г. Михлиным.

ГЛАВА I
ПРИБЛИЖЕННОЕ РЕШЕНИЕ ЗАДАЧИ КОШИ
ДЛЯ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ
УРАВНЕНИЙ
В этой главе рассматривается задача Коши как для одного
обыкновенного дифференциального уравнения, так и для
системы таких уравнений. Краевые задачи для обыкновенных
дифференциальных уравнений мало отличаются по методам
приближенного решения от аналогичных задач для уравнений
в частных производных: и те и другие решаются, как
правило, либо сеточными, либо вариационными методами. Поэтому
краевые задачи для обыкновенных дифференциальных
уравнений отнесены нами к главам II и III.
В § 1 настоящей главы рассмотрены аналитические
приближенные методы решения задачи Коши, дающие
приближенное решение в виде некоторого аналитического выражения;
§ 2 посвящен численным методам решения задачи Коши,
которые в качестве окончательного результата дают таблицу
приближенных значений искомой функции.
Задача Коши для дифференциального уравнения первого
порядка
/=/(*, У) AЛ)
состоит в нахождении интеграла этого уравнения в
некотором промежутке х0^х^х0 + а по начальному условию
У\х=н = Уо- A-2)
Пусть область О плоскости (я, у) содержит точку (л:0, у0),
и пусть в этой области функция /(я, у) непрерывна и,
df ™
скажем, имеет непрерывную частную производную ^ . В этих

14 ГЛ. I. ПРИБЛИЖЕННОЕ РЕШЕНИЕ ЗАДАЧИ КОШИ [1
условиях можно гарантировать существование и
единственность решения задачи Коши A.1), A.2) в некотором
промежутке д:0—Л<л;<С#0 + ;4, и мы будем считать, что Лесть
наибольшее из чисел, для которых в промежутке х0—А<
<Zx<.x0 + A существует решение задачи A.1), A.2). Если
окажется, что а<.Ау то поставленная первоначально задача
Коши также имеет решение, и притом единственное; если
же а>Л, то поставленная задача не имеет решения —
решение существует не в желательном для нас
промежутке х0—а^х^х0-\-а1 а только в меньшем промежутке
х0— А' ^х^х0 + А\ где А' — любое число, меньшее,
чем А. Так, например, задача Коши
имеет единственное решение ^у =tg л;, которое определено и
непрерывно только в промежутке —к-<Сх <-§-, хотя
функция 1+У непрерывна и дифференцируема на всей плоскости
(ху у). Задача о разыскании решения только что
поставленной задачи Коши на промежутке —а^х^а, где я^-тг ,
не имеет решения.
В последующем при рассмотрении приближенных методов
решения задачи Коши предполагается, что точное решение
существует на всем промежутке, на котором разыскивается
приближенное решение.
§ 1. Аналитические методы
1. Разложение решения в ряд Тейлора. Пусть функция
/(л;, у) из правой части уравнения A.1) аналитическая в
окрестности точки (л:0, у0); это значит, что указанная функция
разлагается в двойной степенной ряд
f{x,y)= S «*»(*--*.)*0'-Л)". 0-3)
сходящийся в окрестности точки (л:0, у0), т. е. при
значениях х и у, достаточно близких соответственно к х0 и у0.
Тогда, как известно (см. [18], стр. 324—326, а также [120],
§ 32), для значений х, достаточно близких к xQl решение

1] § 1. АНАЛИТИЧЕСКИЕ МЕТОДЫ
задачи Коши A.1), A.2) существует, единственной
представляет собой аналитическую функцию от х, которая,
следовательно, в окрестности точки х разлагается в ряд Тейлора
J (*) = 2^ (*-*.)*• A-4)
fe=o
Можно указать круг комплексной плоскости х (а
следовательно, и интервал вещественной оси л;), в котором
наверняка сходится ряд A.4). Именно, пусть функция /(л:, у)
аналитична, когда комплексные переменные х и у
удовлетворяют неравенствам
|*-*,|«х, |.У-Л1<Р. A-5)
где а и р—некоторые постоянные. В замкнутой области
A.5) изменения переменных х и у функция f(x, у) во всяком
случае непрерывна и потому ограничена; пусть в этой области
\f(x> jOI^H" Тогда ряд A.4) сходится в круге
I*—*J<q, Q = Min(a, £-). A.6)
Зададимся натуральным числом N и сохраним в ряде
A.4) только члены порядка ^ЛЛ Приближенная формула
У{х)ъу„{х)=-£9^{х-х,)Л A.7)
доставит нам приближенное же решение задачи A.1), A.2),
если мы сумеем вычислить величины y(k)(x0) (& = 0, 1, 2,...
..., N). Но это легко сделать, исходя из уравнений A.1)
и A.2). Действительно, начальное условие A.2) дает нам
непосредственно
У(**) = У*-
Положив теперь в уравнении A.1) х — х0> получим
/(*.) = /(*.. Л)-
Дифференцируя A.1), найдем:
/=Л(*. y)+fyi*> у)у'*
У'"=*/хЛ*> У) + 2/ху{*> У)У'+/уу(х\ y)y"+fy(*< У)У\

16 ГЛ. I. ПРИБЛИЖЕННОЕ РЕШЕНИЕ ЗАДАЧИ КОШИ [1
Полагая здесь опять д: = д:0, мы последовательно вычислим
значения /(*,), /"(х0), ... , /">(*•)•
Заметим, что приближенная формула A.7) применима в
круге A.6) комплексной плоскости, а следовательно, и в
промежутке \х—atJ^q вещественной оси х.
Пример 1. Найдем приближенное решение задачи Коши
У' = * + У\ */1*=о = 0, A.8)
соответствующее значению N =7 в формуле A.7).
Из данных задачи сразу следует:
0@)-0, */'@) = 0.
Дифференцируя уравнение A.8), находим:
у" = 2х + 2уу', у'"=2 + 2уу" + 2у'\
Уш = 2уу'" + Ьу'у\ у™ = 2ууМ + 8у'у"' + б*/,
уМ = 2уу™+ 0у'уш + 20у"у"\
ую = 2уф* + \2у'у{ь) + 30*/У4> + 20у'"\
Полагая здесь *=0 и используя уже известные значения */@)=
= ^/' @) = 0, найдем последовательно:
у" @) = 0, у'" @) = 2, Ум @) = уЫ @) = */<«> @) = 0, г/<7> @) = 80.
Искомое приближенное решение равно
*W-T+g- A.9)
В данном случае нетрудно оценить радиус сходимости ряда A.4)
и, следовательно, область применимости приближенного решения
A.9). Функция х2 + у2 аналитична при всех значениях х и г/, поэтому
числа аир в формуле A.5) можно взять какими угодно. Возьмем
Р = &а, где k — некоторая постоянная, а величина а какая угодно.
Тогда | х2-\-у* |^а*A + k2) и можно положить [i = a*(l +k2). Теперь
по формуле A.6)
e=min(a,57TTF))-
Если k фиксировано, то наибольшее значение q, равное
1/ 1 , ьа» получится при а= |/ , 2. Меняя k, убедимся, что
при fc = l получится наибольшее значение Q=--p=:. Таким образом,
решение задачи A.8) существует по крайней мере в промежутке
Y2

1] § 1. АНАЛИТИЧЕСКИЕ МЕТОДЫ
17
Рассмотрим теперь уравнение порядка п>\:
Ут = /(х, /,..., /"-"), A.10)
и поставим для этого уравнения задачу Коши: найти
интеграл, удовлетворяющий начальным условиям
Я*=*0=л> /U=*0=X.---> /n-"U*0=.vri,-(i.n)
Если правая часть уравнения A.10) есть
аналитическая функция своих аргументов в окрестности точки
(*о> JV /0> ••• »Х/г*))» т0 Рвение задачи Коши A.10),
A.11) при значениях х, достаточно близких к лс0, существует,
единственно и разлагается в ряд Тейлора A.4). По-прежнему
можно строить приближенное решение в виде A.7); величины
y(k) (хь) при k^n—1 непосредственно даны начальными
условиями A.11), а при k^n рекуррентно определяются
дифференцированием уравнения A.10) и последующей
подстановкой х = х0.
Пример 2. Найти решение задачи Коши
У° = х + у\ у]х=0 = 0, 0'U«O = 1.
Приближенное решение будем искать по формуле A.7) при
N — 8% Из данных задачи сразу находим:
#@) = 0, *'@) = 1, /@) = 0.
Дифференцируя уравнение у" — х + у2у имеем:
у'ш=\+2уу', yw = 2yy" + 2y'\
у™ = 2уу"' + 6у'у",
yW = 2yyW + 8y'y'" + by"\
уы = 2ууЫ + 1 Оу'уМ + 20у(,у"\
ую = 2yyW 4. \2y'tjw + т/'у^ + 20у'"\
При #=0 получаем, принимая во внимание значения у@), у' @),
у" @), найденные выше:
у" @) = 1, у™ @) = 2, у« @) = 0, yW @) = 8,
#<7>@) = 20, */<8)@) = 20.
Теперь формула A.7) дает приближенное решение нашей задачи:
(yS у4 ув у7 у8
*Je* + l" + 12 + 90 + ^ + 20l6e
Обратимся теперь к системам обыкновенных
дифференциальных уравнений. Будем рассматривать только системы

18 ГЛ. I. ПРИБЛИЖЕННОЕ РЕШЕНИЕ ЗАДАЧИ КОШИ [1
первого порядка; общий случай, как известно, к этому легко
сводится.
Будем искать решение системы уравнений
y)=fj(x> Уг> Л» ••• >Ут) U=l* 2, ... ,т), A.12)
удовлетворяющее начальным условиям
yj\x=xt=yJt- (ЫЗ)
Если в окрестности точки (л:0, у10, у20, ... ,уто) правые
части уравнений A.12) суть аналитические функции своих
аргументов, то при значениях х> близких к л;0, решение
задачи Коши A.12), A.13) существует, единственно и может
быть представлено разложениями в ряды Тейлора
JVM = £-\r-(*-*o)* U=h 2 да). A.14)
/г=о
Сохраняя в этих рядах только члены порядка ^N,
получаем приближенное решение
^(*) = Е-Т^*-*.>" (/=!> 2,...,/»). A.15)
/г=о
Значения величин у^ (х0) получаются из начальных
условий A.13), из уравнений A.12) и из соотношений,
получаемых дифференцированием этих уравнений и
последующей подстановкой х = х0.
Пример 3. Построим приближенное решение задачи Коши
для системы
y'=x + z2, z'=y2 A.16)
при начальных условиях
у\х=0=1, *|*яв = 0. A.17)
В целях экономии места ограничимся грубым приближением и
положим в A.15) N = 2, так что
У М =* У2 М = У @) + ху' @) + £ уГ @),
z(x)^z2(x) = z@)+xz'@) + ~z"@).
Начальные условия A.17) и уравнения A.16) дают:
У@)=1, у'@) = 0. 2@) = 0, 2'@) = 1.

2] § 1. АНАЛИТИЧЕСКИЕ МЕТОДЫ 19
Дифференцируя уравнения A.16), найдем:
г/"=1+2гг', z" = 2yy\
Отсюда
*/"@) = 1, 2"@) = 0
и окончательно
х2
^W^I+y» z2 (*)=*.
Можно указать область сходимости (вообще говоря, не
наиболее широкую) рядов A.14). Пусть fj(x,yvyv...,ym)
(/= 1,2,...,/») аналитичны в области
|*—*0|<а, |j\—Ло1<Р.
1Л~Ло1<Р> •••»1^Л—УтоКР
изменения комплексных переменных л;, д^, ^8>...,^mi и
пусть в этой области
Тогда ряды A.14) сходятся [120] в круге \х—xjsgg, где
Q = min(oc,£).
2. Метод последовательных приближений, а)
Уравнение первого порядка. Рассмотрим задачу Коши
для уравнения A.1) при начальном условии A.2). Мы не
будем больше предполагать, что функция /(х, дг), стоящая
в правой части уравнения A.1), аналитическая, и
ограничимся более общим предположением: в замкнутом
прямоугольнике плоскости (х, у), определяемом неравенствами
|х-х0|<а, 1У-ЛК*> О-18)
где а и Ь—некоторые положительные постоянные, функция
/(х, у) непрерывна и удовлетворяет условию Липшица по у:
1/(*> Уг)—/(*> ЛI<*1Л-Л1. K=const. A.19)
ли
К.
Известно, что условие Липшица A.19) выполняется, если
ч df \df\
функция /(х, у) имеет производную ~- такую, что ~
Будучи непрерывной в замкнутой области A.18),
функция /(х, у) в ней ограничена: существует такая постоянная

20 гл. I. ПРИБЛИЖЕННОЕ РЕШЕНИЕ ЗАДАЧИ КОШИ [2
Му что если х и у удовлетворяют неравенствам A.18), то
|/(*. У)\<М.
Известно (см. [93], п. 51 или [99]), что если f(x, у)
удовлетворяет перечисленным только что требованиям, то
решение задачи Коши A.1), A.2) существует и единственно
в промежутке
\х—х0\^с, c = min(a,^J; A.20)
это решение можно найти как предел последовательных
приближений, которые строятся по рекуррентной формуле
х
ЛД*)=.У. + $/('. Л-1 (<))<«. A.21)
х0
Выбор начального приближения безразличен; проще всего за
начальное приближение взять число у0.
Остановимся на каком-нибудь числе п и примем за
приближенное решение правую часть формулы A.21); мы придем
тогда к приближенному равенству
х
y{x)*yn(x)=y0+lf(t, yn-x{t))dt. A.22)
Его погрешность можно оценивать неравенством
Ы*)-л(*I<|т- t1-23*
Следует, однако, иметь в виду, что оценка A.23) часто
оказывается чрезмерно завышенной; применяя метод
последовательных приближений, следует остановиться на таком п,
для которого уп_г и уп совпадают в пределах допустимой
погрешности.
Недостатком метода последовательных приближений
является необходимость вычисления интегралов, зависящих
от параметра.
Пример 4. Применим метод последовательных приближений
к задаче A.8). Как мы видели в п. 1, решение этой задачи
определено во всяком случае в замкнутом промежутке |*|^-^=:. При
У 2
этом решение также заключено в промежутке \у\<л—^.

2] § 1. АНАЛИТИЧЕСКИЕ МЕТОДЫ 21
Оценим теперь в прямоугольнике | х | <:~-ргг , \у\^ —^
постоянную /С, входящую в условие Липшица (короче: постоянную
Липшица), для функции / (х, у) — хг-\-у2\
\ду\
К= шах
1
|*1<-^. КМ
У 2 У 2
Применяя метод последовательных приближений к задаче A.8),
выберем в качестве начального приближения #0 = г/@) = 0. Тогда
о
X
о
х
О
112 1
— у8 I л:7 1 а:11 1 -"
3 '63 г2079 ' 59535 '
При | х | ^—=. разность между уг (х) и уг {х) достаточно мала —»
V ^
она не превосходит величины
249Gf)n + 59kGfIS<0,0°0022'
и можно приближенно положить .
У (*) ^ У % W = -J х* + §з *?'
что совпадает с приближенным решением, полученным по формуле
Тейлора.
Формула A.23) дает
I у w—у. w I < 5TTT=0i118,
что, как мы увидим ниже, значительно превосходит истинную
погрешность.
б) Дифференциальное уравнение порядка
выше первого. Этот случай легко приводится к случаю
системы дифференциальных уравнений первого порядка.

22 ГЛ. I. ПРИБЛИЖЕННОЕ РЕШЕНИЕ ЗАДАЧИ КОШИ [3
в) Системы дифференциальных уравнений
первого порядка. Для задачи Коши A.12), A.13)
последовательные приближения вычисляются по формуле
х
A.24)
С?=1, 2,...,т).
При этом предполагается, что функции Л непрерывны и
удовлетворяют по переменным yk условию Липшица в
параллелепипеде
I*—*01<я> \у.—у^\^Ь (/=1, 2, ...,/»).
Если Ж—такая постоянная, что в этом параллелепипеде
то решение задачи A.12), A.13) существует в промежутке
A.20); в этом промежутке последовательные приближения
равномерно сходятся к решению.
Остановившись на каком-нибудь я, получим
приближенное решение
yj(x)&y/n{x) =
х
= У;о+иЛ*>У^п-Л^У2,п-Л*)>''^Угп,п-Л*))М A-25)
(У=1, 2, ...,т);
погрешность этого приближения оценивается неравенством
\У/(х)~У;пМ I < /С ~^! * A'26)
3. Метод Чаплыгина. Мы ограничимся здесь случаем
уравнения первого порядка. Рассмотрим задачу Коши A.1),
A.2) и будем считать, что правая часть уравнения, f{x, у),
удовлетворяет условиям п. 2. Пусть у=у (х) есть решение
нашей задачи Коши; на плоскости (jc, у) это кривая,
проходящая через точку M0(xQ1 у0). В основе метода лежит
следующая

3] § 1. АНАЛИТИЧЕСКИЕ МЕТОДЫ 23
Теорема Чаплыгина. Если кривые у = и(х) и
y = v(x) обе проходят через точку М0 и если верны
дифференциальные неравенства
u'(x)—f(x, «(*))<<>,
v'{x)—f(x,v(x))>0, x>x0, A.27)
то при х>х0 справедливо неравенство
u{x)<y(x)<v{x). A.28)
Таким образом, если бы удалось найти функции и(х) и
v (л;), удовлетворяющие неравенствам A.27) и равенствам
u(x0) = v(x0)~y0, то для искомой функции у(х) была бы
получена двусторонняя оценка. Дальнейшее состоит в том,
чтобы улучшить эту оценку, коль скоро она уже получена.
дЧ
Допустим, что вторая производная -~2 сохраняет знак в
области прямоугольника A.18). В пространстве координат
(х, У> z) рассмотрим поверхность z = f(x, у) и кривые, по
которым она пересекается с плоскостями х = const; эти кри-
d2f
вые всегда направлены либо выпуклостью вниз, если^ >> О,
d2f
либо выпуклостью вверх, если ч-2<[0, и, следовательно,
любая дуга такой кривой заключена между своей хордой и
касательной, проведенной в произвольной точке дуги.
На кривой z~f(x, у), х-= const возьмем дугу, отвечающую
значениям у из промежутка и(х)^у ^v(x), и напишем
уравнения хорды и касательной, проведенной в точке
у=--и(х):
« = /(*, и{х)) + "х> ^Zl%U{X))(y-»W) =
= M(x)y + N(x)y
* = /(*, u{x))+fy{x, u(x))(y-u(x)) = M(x)y + N(x).
Кривая расположена между касательной и хордой; это
значит, что функция f(x,y) заключена между функциями
d2f
M(x)y + N{x) и M(x)y + N(x). Пусть, например, ^->0,
тогда кривая лежит ниже хорды и выше касательной, т. е.
M(x)y + N(x)<f(x)<:M(x)y + N(x).

ГЛ. I. ПРИБЛИЖЕННОЕ РЕШЕНИЕ ЗАДАЧИ КОШИ [3
Составим линейные дифференциальные уравнения первого
порядка:
y' = M(x)y + N{x)% y' = M(x)y + N{x),
и найдем их интегралы (это задача нетрудная),
удовлетворяющие начальному условию A.2); пусть эти интегралы
будут у^=и1{х) и y = vl(x). Доказывается, что имеют место
неравенства
и(*)<»Л*)<Я*)<М*) <*(*). О-29)
которые показывают, что новые функции ил (х) и vx (x) дают
более точные приближения к неизвестной функции у(х).
Теперь, исходя из приближений их (х) и vx (x), можно
построить новые, еще более точные приближения и2 (х) и v2 {x)
и т. д. Процесс очень быстро сходится — справедлива оценка
Vn(X) — ttniX)^wrt С1'30)
где С не зависит ни от л;, ни от п.
Можно указать (см. [2]) другой прием уточнения
приближений и (х) и v (х)} при котором нет необходимости пред-
полагать, что вторая производная j~ сохраняет знак. Пусть
К— постоянная Липшица функции/(лг, у) (см. формулу A.19)).
Тогда функции
х \
ul(x) = u(x)+le-«<*-t>[f(t)u(t))--u'(t)}dt,\
\ A.31)
vt[x) = v{x)-l $-*<*-*> [v9 (t)-f(t,v(t))]dt \
удовлетворяют неравенствам A.29). Как и выше, можно
построить последовательность уточняющихся приближений
ип(х), vn[x)y повторно применяя формулы A.31);
по-прежнему ип (х) и vn (х) равномерно стремятся к у (х) при п —> оо,
но скорость сходимости меньше, чем в формуле A.30).
Основная трудность в применении метода Чаплыгина
заключается в построении исходной пары приближений и(х)
и v{x)\ сколько-нибудь общие приемы такого построения
р литературе не описаны.

3] § 1. АНАЛИТИЧЕСКИЕ МЕТОДЫ 25
Пример 5. Решим по методу Чаплыгина задачу A.8). Будем
считать, что решение ищется в промежутке 0 < х <: —j=i.
Нетрудно видеть, что можно положить
Действительно,
и{х) = — х\ v{x) = — x\
и' (х) —х2 — и2 (х) = — ~х9< О,
ш-Ш-т)*2>°-06*г>а
Вычисление функций М (х), N (х), М (х), N (х) не составляет
труда:
М(х)^х\ N(x)=x*-^Qx\
М (х) = jxs, N (х) = х2- -jх9.
■ d2f
В нашем случае j-j = 2 > 0 и, следовательно, их (х) и vt(x) суть
интегралы уравнений
2 1
u^jx^y + x2-—g- х\
' 7 3 ■ , 2 И в
10 v ' 90'
обращающиеся в нуль при * = 0. Эти интегралы суть
1
*4 Г Г 1
- ze e e dz,
7 *
40 dz.
Разлагая показательные функции в степенные ряды и сохраняя
степени х и z только до 11-й, получим:
3 г63+2079*1>
^W^iW = T + S + 9§0^

26 ГЛ. I. ПРИБЛИЖЕННОЕ РЕШЕНИЕ ЗАДАЧИ КОШИ [3
-*2-^-9
значение их (х) совпадает со значением уь(х), построенным по методу
последовательных приближений, с точностью до членов степени
выше 11-й.
Функции их (х) и v1 (x) также образуют границы Чаплыгина
для искомого решения, так как при 0<х^ —т=
их-х*-и\ = - ^gp- + 3T2079J xU + бз. 2079 *" + 2079* ** J < °'
"» -~х2~~°*=Т \2Т0— L^ + l65j^ + 7^90x8 + 330« * J / * •
Производная выражения, стоящего в фигурных скобках,
отрицательна при 0 < х ^ -у=г, и указанное выражение минимально
при наибольшем я = ——:, поэтому
Г J /J_ Ml L- 1 L I]
[210 \441M65; 4 7-990*8 3302 * 64J >
Отсюда вытекает, что
j+u+mxU<yix)<T+&+mxU' 0<x<jh'
если любую из функций их(х) или щ(х) принять за приближенное
решение задачи A.8), то погрешность этого приближения не
превосходит величины
{ш-ш) *" < Wmyw^°-mm>
что значительно меньше оценки, полученной в п. 2 по формуле A.23).
хг 11
Исходя из начальных приближений а (х) = —, и (*) = — я8, можно
о oU
построить более точные приближения и по формулам A.31).
Вспоминая, что в данном случае постоянная Липшица равна К= V %>
имеем:
м*>=т+Ил"УГс*"'>л'
о
V,(X> 30* J [10 900l )' at'
О
интегралы здесь вычисляются элементарно; мы на этом
останавливаться не будем.

4]
§ 1. АНАЛИТИЧЕСКИЕ МЕТОДЫ
27
4. Метод Ньютона — Канторовича. Под этим названием
известен разработанный Л. В. Канторовичем метод решения
весьма общих нелинейных задач. Этот метод восходит к
данному Ньютоном методу касательных для решения
алгебраических уравнений. Особенность метода состоит в том,
что если дано некоторое не слишком грубое начальное
приближение к решению данной задачи, то оказывается
возможным строить все более и более точные приближения, каждое
из которых получается как решение некоторого линейного
уравнения.
Метод Ньютона— Канторовича подробно изложен в [23]
и [24]; мы не будем здесь останавливаться на основах метода
и ограничимся только техникой его применения и условиями
сходимости в задаче Коши для одного дифференциального
уравнения первого порядка (задача A.1), A.2)) или для
системы таких уравнений (задача A.12), A.13)).
а) Одно дифференциальное уравнение
первого порядка. Пусть некоторая функцияу0(х)
удовлетворяет начальному условию A.2), так что у0(х0)=у0. Будем
рассматривать эту функцию как начальное приближение к
решению у (х) задачи A.1), A.2). Следующее приближение
уг (х) строится как интеграл линейного уравнения
у\ —fy (*, Л (*)) У1=/(х,Уо(*))—/у (*> Л (*)) Л (*)>
удовлетворяющий начальному условию A.2); вообще, если
построено приближение уп(х), то следующее приближение
Уп+1(х) строится как удовлетворяющий условию A.2) интеграл
линейного уравнения
Уп+1 — fy (*, Уп (*))Л + 1 =/{Х, Уп (X)) —
-fy{x,yn(*))yn(x). A.32)
Такой интеграл строится очень просто: если обозначить
/у(х, Уп(х))-=Рп(х)>
f{x, yn (x))—fy (х, уп (х))уп (х) = qn (х)9
то
х z
$Pn(t)dt( * -j'pnMdt \
ЛпМ = ^ \У*+)Яп(*)е х° dzj. A.33)
Х0

28 ГЛ. I. ПРИБЛИЖЕННОЕ РЕШЕНИЕ ЗАДАЧИ КОШИ [4
Приведем условие сходимости метода и оценку
погрешности приближенного решения уп(х). Допустим, что в
прямоугольнике A.18) функция f(x, у) и ее производные /у(х9у),
/у*(х,у) непрерывны и, следовательно, ограничены; пусть
\/у{х, У)\^М„ \fr(x, у)\*£Мш.
Примем также, что начальное приближение у0 (х) определено
при \х—х0\^а и что \у0{х)—у0\^Ь: Обозначим
х
6= max \y9(X)-y0-lf(t9 y0(t))dt\; A.34)
если начальное приближение близко к точному решению,
то величина Q мала. Далее положим
A.35)
A.36)
, **„. A.37)
l + /l-2Y
Тогда последовательные приближения A.33), построенные
по методу Ньютона — Канторовича, удовлетворяют
неравенству |.Уп(аг)—Уо1^^ и СХ°ДЯТСЯ к точному решению задачи
равномерно на промежутке \х—х0\^а; быстрота
сходимости оценивается неравенством
\уп(х)-у(х)\^~гBуГ-% A.38)
Метод Ньютона — Канторовича позволяет также оценить,
насколько далеко от начального приближения отстоит точное
решение: имеет место неравенство
\у(х)-у,{х)\<1+*—. A.39)
Пример 6. Применим метод Ньютона —Канторовича к
задаче A.8). Решение будем строить на отрезке |*К-у=.
Пусть
и
выполнены
у = а$М2е2М1а.
неравенства
2К ,-»

4]
§ 1. АНАЛИТИЧЕСКИЕ МЕТОДЫ
29
За начальное приближение примем
Тогда
q= max
lxl<YT
?
x - —
Mx= max \2y\=V2 =1,4142, M2 = 2.
Отсюда
v =-4= 0,0014-2-е2 = 0,015.
Y%
Вычислим первое приближение по методу
Ньютона—Канторовича. Имеем:
Ро W = Т х%* 4о(х) = х2
1
и, по формуле A.33),
01 М =
>V'K'-t-
<fe.
В силу формулы A.38) погрешность этого приближения не
превосходит величины
0,03-0,0014 = 0,000042.
Построенное нами приближение ух (х) совпадает с выражением
и1 (х), полученным выше по методу Чаплыгина. Напомним, что
х* х1
с точностью до членов степени не ниже 11-й «i(#)—-т + ?о и что
О Оо
последнее выражение совпадает со вторым приближением,
полученным выше по методу последовательных приближений.
Метод Ньютона — Канторовича иногда позволяет увеличить, по
сравнению с тем, что дает метод последовательных приближений,
длину промежутка, на котором определено решение задачи Коши.
Так, в приведенном выше примере будем рассматривать
функцию f(x, y) = x2 + y2 в квадрате |х|^1, |#|<1. Тогда М1==2,
х* х1
М2 = 2. За начальное приближение возьмем функцию -q- + ™. Это
о Оо
дает нам
max
X
х* х1 С ( tQ 2t10 t1* \ I 2 1
3" + 63 J [*2+Т + №+Ш)й1ГШ + ^5&<0>т'

30 ГЛ. I. ПРИБЛИЖЕННОЕ РЕШЕНИЕ ЗАДАЧИ КОШИ [4
и можно положить q =0,001. Теперь
у = 0,00Ы.2.е*< 0,110;
отсюда
2;^_<^^Щ=< 0,00107.
1 + Y\ -2у 1 + /1 -0,220
Теперь ясно, что решение нашей задачи существует при | х \ <; 1 и
заключено в пределах
/ ч Х Х
уМ—3—63
; о,оою7.
б) Система уравнений первого порядка.
Рассмотрим ' задачу A.12), A.13). Выберем систему функций
yi,o(x), У2,о(х), •••, Ут,о{х), удовлетворяющих начальным
условиям A.13), и будем рассматривать эту систему как
начальное приближение к точному решению задачи. Тогда
первое приближение по методу Ньютона—Канторовича
строится как интеграл системы линейных дифференциальных
уравнений
*..-£ ®.». * - </д-£ ® .*. • A-40)
k=i
G=1, 2, ..., т),
удовлетворяющий начальным условиям A.13); символ ( H
означает, что ух (х), у2(*), ..., ут(х) заменяются на
Л,о(*)» Л,оD .. ., Уа«(х). Если yJtn(x) G= 1,2, ..., т)
уже построены, то (п-\-\)-ъ приближение yjtn+l(x)
строится как удовлетворяющий условиям A.13) интеграл
линейной системы
G=1, 2, ..., т);
здесь символ ( )п означает, по аналогии с предыдущим, что
у;(х) заменяется на yjiTl(x).
Коэффициенты системы A.41), вообще говоря,
переменные, и интегрирование этой системы — задача довольно
трудоемкая. Реализация метода Ньютона—Канторовича для
системы дифференциальных уравнений A.12) может оказаться
затруднительной, тем более, что матрица элементов (^-М

5]
§ 1. АНАЛИТИЧЕСКИЕ МЕТОДЫ
31
меняется на каждом шаге. Правда, последней трудности
можно избежать, если воспользоваться модифицированным
методом Ньютона—Канторовича. Поэтому методу (#-fl)-e
приближение к решению задачи A.12), A.13) строится как
удовлетворяющее начальным условиям решение линейной
системы
^--|®.Л.- = (/Л--2;®.Л..: A-42)
при изменении п в системе A.42) меняются только
свободные члены.
Мы не приводим здесь условий сходимости и оценки
погрешности для системы ввиду их некоторой громоздкости.
б. Метод малого параметра. Этот метод имеет довольно
многообразные формы применения; мы укажем здесь только
две из них, причем вторую—на примере.
Пусть дано уравнение
/=/(*, уЛ\ A.43)
правая часть которого зависит, кроме х и у, еще от
некоторого параметра Ку и пусть требуется найти интеграл этого
уравнения, удовлетворяющий<начальному условию у \ х=х —у0.
Допустим, что при Х=^Х0 решение у = ц(х) этой задачи
нам известно. Заменой
можно свести дело к тому случаю, когда х0=у0 — к0 = 0 и
ф(л;) = 0; поэтому сразу будем считать, что уравнение
A.43) надо решать при начальном условии
>М*=о = ° A-44)
и что при Х = 0 искомое решение есть у = 0. Отсюда, между
прочим, следует, что необходимо /(а:, 0; 0) = 0.
Предположим теперь, что функция /(#, у; X) разлагается
в ряд по степеням у и X, сходящийся вблизи значений
^ = 0 и Я = 0:
00

32 ГЛ. I. ПРИБЛИЖЕННОЕ РЕШЕНИЕ ЗАДАЧИ КОШИ [5
Решение задачи A.43), A.44) будем искать в виде ряда
00
у{х)=2к*ук(х);
ft £=1
этот ряд начинается с первой степени X, так как y(x)^zQ
при А, = 0; из условия A.44) вытекают начальные условия
**!*-.•= О (А-1, 2, ...)• A-44')
Подставив последний ряд в уравнение A.43) и приравняв
коэффициенты при одинаковых степенях К слева и справа,
получим:
* = *io(*)Ji+floi(*).
У 2 = а10 (х) у2 + а20у* + а11у1 + я02
и т. д. Вообще, &-е уравнение имеет вид
yk = al0(x)yk + uk(xI
где uk(x) зависит, кроме х} еще от у1(хI ..., ^м(д;).
Решая первое уравнение при начальном условии ух \ д;=0 =•- О,
найдем у1(х)\ подставив его во второе уравнение и
проинтегрировав его при начальном условии у2\х=о==:®> найдем
у2{х) и т. д.
Изложенный здесь прием легко распространяется на
системы дифференциальных уравнений и на уравнения высших
порядков, а также на тот случай, когда уравнение (или
система уравнений) содержит не один, а несколько
параметров.
Пример 7 [31]. Рассмотрим уравнение второго порядка
/ + A+O,l-*)J'+O,l-/, = 0 A.45)
при начальных условиях
•Данное дифференциальное уравнение заменим более
общим, содержащим два параметра аир:
/ + У + аху + $у'г = 0; A.46)
данное уравнение получается из уравнения A.46) при
а~|} = 0,1. Первое приближение найдем из уравнения,

5] § 1. АНАЛИТИЧЕСКИЕ МЕТОДЫ 33
получающегося при а— C = 0:
Его интеграл, удовлетворяющий начальным условиям, есть
ух — cos х + 2 sin x. Следующее приближение возьмем в виде
«Уг — Л + Лр где ^i есть линейная функция параметров а и |5:
i\t = — ap(x) — $q(x).
Подставим у2 вместо у в уравнение A.46) и сохраним
только члены, содержащие первые степени параметров.
Приравняв нулю множители при а и Р, получим линейные
уравнения для р(х) и q(x):
р" ~\~р^х cos х + 2х sin х,
5 3
</' + q = ^ + y CDS 2л:-— 2sin 2л:.
Эти уравнения следует проинтегрировать при следующих
начальных условиях:
* = 0, р = // = ? = ?' = 0,
что дает:
р (х) = — -тг л:2 cos л: -f — * cos * + ~г *2 sin л: +
+ -н- л: sin л:—-j- sin л:,
4 1 2 5
q (х) — — 2 cos л:—у sin х— у cos 2х + у sin 2л: + у .
Чтобы построить следующее приближение, представим
его в виде уг~у2-\-ц2, где тJ есть функция второй
степени от параметров:
ц2 = а2Р(х) +a$Q(x) + $2R(x).
Подставив уг вместо у в уравнение A.46) и приравняв
нулю коэффициенты при а2, ар, р2, получим для Р{х),
Q(x), R(x) линейные уравнения, которые следует
проинтегрировать при начальных условиях
дг=0, P=P'==Q=Q' = # = #'==0.
Процесс этот может быть продолжен.
2 6. Г. Михлин и X. Л. Смолицкий

34 ГЛ. I. ПРИБЛИЖЕННОЕ РЕШЕНИЕ ЗАДАЧИ КОШИ [6
6, Оценка погрешности через невязку. Пусть У(х)—
функция, которую мы по тем или иным основаниям
рассматриваем как приближенное решение задачи Коши A.1),
A.2). Разность A{x)=r-Y(x)—y(x) будем называть
погрешностью приближенного решения Y(x), разность х{х)~
= Y' (х)—/(л:, Y(x))—его невязкой; через у(х) обозначено
точное решение задачи. Оказывается, что при некоторых
условиях можно оценить погрешность приближенного
решения через его невязку, которая, очевидно, представляет
собой известную функцию от х.
Допустим, что нам удалось найти функцию Л (х),
непрерывную на отрезке х0 ^х^х0-\-а, такую, что на этом
отрезке выполняется неравенство
\/у(х, у(х))\^А(х), A.47)
где, как уже было отмечено, у(х) означает точное решение
нашей задачи. Составим линейное уравнение
£=*A(x)z + \t(x)\
и найдем его интеграл z(x)y принимающий при х~х0
значение |К(лг0)—у0\. Тогда на отрезке лг0 ^ х ^лг0 -\-а верна
оценка
|Д(*)| <*(*). A.48)
Применение оценки A.48) в общем случае затруднено
тем, что функция Л(х)} через которую выражается z(x),
должна удовлетворять неравенству A.47), в котором левая
часть неизвестна.
§ 2. Численные методы
В § 1 были рассмотрены аналитические приближенные
методы решения задачи Коши. В настоящем параграфе
рассматриваются численные методы, предлагающие искать
решение в виде таблицы приближенных значений искомой
функции у(х) для ряда значений независимой переменной
х из промежутка х0 <; л: <; лг0 + #• Эти значения
переменной х либо назначаются заранее, либо выбираются
последовательно в процессе отыскания приближенного решения.
Эти значения переменной х назовем узлами и обозначим

2] § 2. численные методы 35
через лгв, л;,, лга, ...,%, считая, что л?п<л;я+1. Через .у„
обозначим приближенное значение для у(хп), где ^(л:) —
точное решение задачи Коши.
Для у(х) имеет место равенство
3>(*0) = Л> }(W = >W+ Г /С' ^0)Л 0-49)
(« = 0,1, ...,N-1).
Описываемые ниже численные методы решения задачи Коши
в основном отличаются друг от друга подходом к
приближенному вычислению интеграла в формуле A.49).
1. Метод Эйлера. Обычно величина hn = xn+1—хп,
называемая шагом интегрирования, выбирается достаточно
малой. Метод Эйлера состоит в том, что в коротком
промежутке хп ^ t ^ xn -f- hn функцию /(/, y{t)) приближенно
заменяют постоянной величиной /(лгп, уп), которая известна,
если хп выбрана, а уп уже определена. Тогда вместо
равенства A.49) получается равенство
Уп+г = У« +*»/(*«, У«) (я = 0. l W-1). A-50)
позволяющее последовательно определять величины
yv Уг> • • •' У& если заданы xQ, yQ и выбраны узлы.
2. Метод трапеций. Метод Эйлера можно было бы
назвать методом прямоугольника, так как замена интеграла
в равенстве A.49) произведением hnf(xn, yn) равносильна
замене криволинейной трапеции под графиком функции
/(*> УA)) прямоугольником. Более точной представляется
замена криволинейной трапеции прямолинейной, что
приводит к равенству
Л+,=Л + т^„. Л)+/(*»+!. Уп+Л 0.51)
(/2 = 0, 1, ..., N-1).
Если известны хпУ упУ xn+v то равенство A.51) можно
рассматривать как уравнение для определения уп+1. Это
уравнение для достаточно малых значений hn имеет корни,
среди которых наиболее близкий к уп обозначим через yn+J.
Этот корень может быть найден методом простой итерации.
2*

36
ГЛ. I. ПРИБЛИЖЕННОЕ РЕШЕНИЕ ЗАДАЧИ КОШИ
[3
Предложены различные способы выбора начального
приближения y^nli [60]. Проще всего для этого использовать
формулу A.50) метода Эйлера. Последующие приближения
находятся по формуле
уТ^=Уп + ^[/(хп, уа)+/(хп+1, уТ+'г")} A-52)
(m=l, 2, ...)•
Обычно в силу малости hn оказывается достаточно
небольшого числа итераций для вычисления уп+1 с принятой
точностью вычислений.
3. Метод Рунге — Кутта. Для простоты записи вместо
хп) уп, hn будем писать х, у, h. Пусть г ^2 — целое
положительное число и ах, а2, ..., аг_х — положительные числа.
Пусть числа $sm (s=\, 2, ..., г—1; /я=1, 2, . ..,5) и
Yi» Y2> •••» Yr удовлетворяют условиям
SP« = a, (s=\, 2, .... r-1), A.53)
2vy=i.
A.54)
/=1
Один этап метода Рунге — Кутта (переход от хп к хп+1)
таков.
1) Вычисляются одно за другим следующие г чисел:
К -А/С*. 7)»
ft, =A/(f+alA, У+Mi).
ft, =A/(* + atft, J^ + Mi + Mi).
fty+! = A/ (* + ayA, .y + Py A + pyiftt + ... + Py7fty),
*г =А/(^+аг-Л J' + Pr-i.A + Pr-i.A +•• • •
• • • +Pr-,, r-A-l)'
2) Вычисляется сумма произведений
г
k = 2 y A-
A.55)
A.56)

3] § 2. численные методы 37
3) Вычисляется уп+1 по формуле
Уп+г=Уп + Ь- (Ь57)
Числа asy Р5/л, у. при заданном г выбираются так, чтобы
разность
x+h
^(f(t,y(t))dt-k
X
(у (х) — решение уравнения A.1), удовлетворяющее условию
у(х)=у)) рассматриваемая как функция переменного /г, была
бесконечно малой возможно более высокого порядка /
относительно h при h—>-0. Вообще говоря, этим требованием
числа Оу, pJm, уj не определяются однозначно и при
выборе этих чисел принимаются во внимание также
соображения о простоте формул A.55) и A.56). Приведем примеры
некоторых систем таких чисел и отвечающих им значений /:
1) r = 2, a1 = pn = l, y, = Y2 = -2-> /==3;
2) г = 2, аг = рп = 1, Yl = 0, Yl=l, '=3;
3) r = 3, а1 = р11 = 1, а2=1, р„ 1,"РМ = 2Э
1 2 / л ■
Y» = Y, = -6 . Y. = T' /==4;
4) r = 3, al=spn = jf ot2^y, Рп = °э Р22 = -з"»
Yi = T' Y. = °. Y3 = t> '=*;
5) г = 4, а1 = Р11 = -5-, а2 = р22 = у, р21=0, а3 = р88=1,
Рп = Рз2 = °> Yi = Y4 = -g". Y2 = Y3 = y> ^ = 5;
6) г = 4, а1 = р11 = у, a,-—, р21 = — у, Plt=l,
Yi = Y4 = y ' Y2 = Y3 = y, ' = 5;

38 ГЛ. I. ПРИБЛИЖЕННОЕ РЕШЕНИЕ ЗАДАЧИ КОШИ [3
7) Г = 6, а1 = Р„ = -з , СЬа = у, Р21 = 25> Ргг^й»
_1 ft == 6_ о _90 R ___50 ft _8_
а4 з ' ^41 81 ' ^42 81 ' ^43 81 ' ^44 18 '
п -1 R -A ft -^ ft -12 ft - i R -0
s~ 5 » Psi~75' P52 75' r5«~5 ' ^54 75' ^55
Yl ~ 192 ' Y2~" ' Y» ~~ 192 ' Y4~"u' Ys— 192' Y6— 192 »
1=7.
Здесь приведены не все известные системы чисел.
Подробное изложение формул Рунге — Кутта можно
найти в книгах [2], [41].
Система чисел 7) приведена в книге [60]. Наиболее
употребительной является система чисел 5). Соответствующий
прием будем называть основным приемом Рунге—Кутта.
Приведем порядок вычислений в этом случае.
1) Вычисляется k[n) = hnf(xn, уп).
( h k{n)\
2) Вычисляется ft£n) = йя Д *л + Т' Уп + ~г) •
3) Вычисляется kf = hnf[xn+ nf, уп + -%-) .
4) Вычисляется АDЯ) = *„/(*„ + **> Л+*«П))' .
5) Вычисляется k{n) = 1 (Mn) + 2k[n) + 2k[n) + kf).
6) Вычисляется yn+J = yn-\-k{n).
Отметим также случай 2), который называют иногда
усовершенствованным методом Эйлера; здесь вычисления
ведутся так:
В заключение укажем на схему вычислений по методу
Эйлера и Рунге — Кутта при решении задачи Коши для
системы дифференциальных уравнений первого порядка. Для
простоты записи ограничимся случаем системы двух уравнений.

3] § 2. численные методы 39
Пусть
<-'***} (..58,
— система, для которой требуется найти решение у (х)у z(x),
удовлетворяющее условию
У\х=х0=у0, г\х=х0 = г0. A.59)
а) Метод Эйлера. Вычисления проводятся по
формулам:
Уп + г^Уп+К/^п* Уп* Zn)> \
*п+1 = *п + Ьп8{*п, У» zn) \ A.60)
(л = 0, 1, 2, ..., N--1). ]
б) Основной прием Рунге—Кутта. Вычисления
проводятся по формулам:
1) А<п) = й„/(х„, у„, га),
m(^-=hng(xn, у„, га)\
м ( h *in) m\n)
2) k™ = hj{xa + &, ya + -j-, *„+-у-
k\n) m\n)
mln) = hng(xn+hf,yn-
3) k[n) = hj{xn + ^y yn+-r> *n + -
2
4) k{n)^hn/(xn + hn, yH-\-k\T\ zn + mi\
m,
(n)
= hng(x„ + h„, yn-Ykf\ zn + mf)\
5) *<«> = -i- (k\n) + 2k[n) f 2кГ + АГ),
*»+i = *» + "*ln)-

ГЛ. I. ПРИБЛИЖЕННОЕ РЕШЕНИЕ ЗАДАЧИ КОШИ [3
В книгах [2], [30] рассмотрены другие возможные схемы
вычислений по методу Рунге — Кутта для решения систем
уравнений первого порядка и одного уравнения порядка
выше первого.
Пример 8. Для задачи Коши A.8) найдем приближенное
решение, используя основной прием Рунге—Кутта для шага & = 0, 1.
Результаты вычислений сведены в таблицу 1. Вычисления велись
с шестью цифрами после запятой. Можно убедиться, что все цифры
результата верны.
Таблица 1
хп
0,0
0,1
0,2
0,3
0,4
0,5
0,6
Уп
0,000000
0,000333
0,002667
0,009003
0,021359
0,041791
0,072448
*<">
0,000000
0,001000
0,004001
0,009008
0,016046
0,025175
4Я)
0,000250
0,002250
0,006252
0,012268
0,020336
0,030546
k(n)
0,000250
0,002250
0,006253
0,012273
0,020349
0,030576
*4
0,001000
0,004001
0,009008
0,016045
0,025174
0,036524
*(«>
0,000333
0,002334
0,006336
0,012356
0,020432
0,030657
О погрешности методов Эйлера и Рунге —
Кутта. Пусть уп— приближенное значение для У(хп)
(у (х) — точное решение задачи A.1) — A.2)). Обозначим через
уп(х) точное решение уравнения A.1), обращающееся при
х = хп в уп, т. е. удовлетворяющее условию Уп{хп) = уп.
Тогда разность
\Уп+ S f(t,y»(t))dt
Хп
Уп + 1-Уп(Хп + 1) = Уп + 1-
= (У«+1—Уп)-
ХП+1
- U((,yn(t))dt
называется погрешностью л-го шага метода численного
интегрирования. Для этой погрешности здесь приводятся
оценки в простейшей форме [30].
В последующем С1} С2, . .. будут обозначать
положительные постоянные, определяемые f(x,y) и ее
производными в некоторой окрестности точки (хю у ).

4]
§ 2. ЧИСЛЕННЫЕ МЕТОДЫ
41
Для-метода Эйлера
Для основной формулы метода Рунге—Кутта
\Уп+г-уп{ха+1)\^сХ.
Из сравнения этих оценок следует, что для достаточно
малых hn формула Рунге — Кутта, вообще говоря, дает
более точные результаты, чем формула Эйлера. .
При численном решении задачи Коши происходит
накопление ошибки от шага к шагу: если у0 задано точно, то
уже уг получается с некоторой ошибкой, оцениваемой как
погрешность одного шага; отклонение уг—у(х2) является
наложением ошибки в определении у1 и ошибки в
определении уг по у1 (ошибка одного шага); отклонение уп—у(хп)
является результатом наложения большого числа ошибок.
Для метода Эйлера (в предположении й/ = й = const)
имеет место оценка
\yn-y^n)\^C5h(e^n-xo)_l)i
из которой следует равномерное стремление уп—>у(х) при
h—*0 (nh—>х). Эта оценка предполагает, что все
вычисления для определения уп проводятся точно (без округлений).
Для метода Рунге — Кутта такой простой оценки нет. В статье
[113] приведены некоторые оценки для метода Рунге—Кутта,
из которых также следует сходимость уп к у(х) при h—>0.
Там же приводятся формулы для оценки погрешности в
предположении, что вычисления проводятся с округлением.
4. Разностные методы. Экстраполяционная формула
Адамса. В основе разностных методов решения задачи Коши
A.1) — A.2) лежит следующее простое соображение. Пусть
каким-нибудь способом уже вычислены приближенные
значениям,^, ... ууп искомой функции у(х), соответствующие
значениям xv х2> ... , хп независимой переменной. Будем
считать эти значения равноотстоящими, так что х;.+ 1—Xj=h,
где h—постоянная. Приближенное значение уп+1 величины
У(хп+1) можно вычислить по формуле
хп+г
Уп+г=Уп+ \f{X,y{x))dX. A.61)

42 ГЛ. 1. ПРИБЛИЖЕННОЕ РЕШЕНИЕ ЗАДАЧИ КОШИ [4
Заменим под интегралом функцию f{x,y{x)) ее дахр-
поляционным многочленом, который в точках х~х, (/=
= п — &, п — k+\t ... ,п) принимает значения
Этот многочлен имеет вид
WW=2/„./^D A.63)
/=о
где Pkj(x) суть многочлены степени к. Заметим, что Lntk(x)
только приближенно совпадает с интерполяционным
многочленом функции f{xyy (л:)), так как в общем случае У;фу(х})
И ПОТОМУ fj*frf(Xj,y(Xj)).
Допустим, что многочлен A.63) достаточно точно
экстраполирует функцию f(x,y(x)) на промежуток хп^х^хп+1.
В интеграле A.61) заменим функцию f(x,y(x)) многочленом
Ln,k (х) и положим х = хп -f th. Мы придем тогда к
приближенной формуле
k
yn+i=yn + hljbkjf(xn-pyn-j)> л 0-64)
где постоянные bkj определяются формулой
h l~l)J Г'(* + 1)...(*+*Ь,
о
Формула A.64) называется жстраполяционной, формулой
Адамса. Приведем значения нескольких первых
коэффициентов bkj (см. таблицу 2).
Придавая k различные значения, мы получим различные
формулы Адамса; при k = 0 получается формула A.50)
метода Эйлера, но при h постоянном.
Формуле A.64) можно придать более удобную форму,
если ввести разности функции f{x,y(x)):
A// =f(Xj+vyj+x)—f(xfiyj)>
Д7у=А(А/у)=/(л:у+2,^/+2)-2/(^у+1,з;у+1) + /(л:у,#уу),
Asfj=Mb2fj) = f(xJ+i,y/+t)-3f(xJ+vyJ+t) +

4J § 2. численные методы
Таблица 2
Значения коэффициентов bkj
0
1
2
3
4
0
1
3
2
23
12
55
24
1721
720
1
1
2
4
3
59
24
1967
360
2
5
12
37
24
109
30
3
3
8
637
360
4
251
720
и т. д. Мы получаем тогда
3Vh =Л + * (/» + *, Д/я-, + *,А1/я-1+ • • • +**А*/„-*).
A.65)
где
i
*,= у p(* + l)...(/+/)<?/. A-66)
О
Приведем значения нескольких первых коэффициентов bl
Таблица 3
Значения коэффициентов bk
к
ьк
1
1
2
2
5
12
3
3
8
4
251
720
5
95
288
6
19 087
60 480
7
5 275
17 280
8
1070 017
3 628 800
'9
1 082 753
7 257 600 \
Приведем схему расположения вычислений по формуле
Адамса A.65); для определенности положим & = 3- так что

ГЛ. 1. ПРИБЛИЖЕННОЕ РЕШЕНИЕ ЗАДАЧИ КОШИ [4
формула Адамса принимает вид
Д^« = 1„ + "^ Дт|„_t + ^ Д«т,в_, + -| Д«г!я_,; A.67)
здесь положено
Чтобы начать вычисления по формуле A.67), надо знать,
кроме j/0, еще значения yx,y2,yv соответствующие
значениям xl = x0Jrh} x2 — x0-\-2h) х3 = х0 + ЗН. По этим данным
можно вычислить величины, содержащиеся в следующей
таблице.
Таблица 4
X
1 хо
х1
Ч
Ч
ч
хп
У
Уо
Ух
Уг
*У
Аг/Э
ЬУг
j Д^2
Уг
Л
Ло
Л1
42
Лз
Ат]
ДЛо
Аг],
АЛ*
i
1
А2Л
дч
ДЧ
Д8л
Д3Ло
Зная числа, расположенные в нижней косой строке,
найдем по формуле A.67) величину Ду , а с нею и вели-

4 J *§ 2. численные методы 45
чину Л—Л + ^Л- Зная Л> вычислим Л4 = ^/(^4>Л)' Теперь
можно написать следующую косую строку:
ДтЬ = rl4—Л3» АЧ = Ar|s —Аг|2, Д\ = А2г|2 — Д1^;
записав вычисленные величины на соответствующих местах,
получим новую таблицу.
Таблица 5
X
Ч
ч
Ч
Ч
Ч
Ч
\ хп
У
Уо
Ух
Уг
Уг
Ух
АУ
АУо
&Уг
Ауг
&Уз
ч
1 ч>
Ml
42
Чз
44
Ач
АПэ
АЧ1
АЧ2
Ачз
А2ч
А2Ло
A2rii
А2ч2
А3П
А3Чо
А3Л1
Новая косая строка позволяет вычислить по формуле
A.67) значение Ду4. Теперь ^s— Л+АУ^ и пР°Десс
повторяется.

46
ГЛ. I. ПРИБЛИЖЕННОЕ РЕШЕНИЕ ЗАДАЧИ КОШИ
[4
Если пользоваться не формулой A.67), а общей
формулой A.65), то, чтобы начать процесс, необходимо иметь
значения yv Л» • • • > .Уа» соответствующие значениям л:1 =
= лг0 -f- h, х2 = xQ + 2А, ... ,xk = x9-\-kh переменной х. Один
из возможных способов вычисления величин у,.(/ = 1, 2 ..., k)
будет указан в следующем ниже примере; более подробно
вопрос о построении начала таблицы Адамса будет рассмотрен
в п. 8 настоящего параграфа.
Пример 9. Вернемся к задаче Коши A.8) и будем решать
ее по формуле A.67).
Положим А = 0,1. Для вычисления значений yv yv уг восполь-
X3
зуемся приближенным решением у =^г -^ , полученным в качестве
о
первого приближения по методу последовательных приближений.
Начальная таблица имеет такой вид:
Таблица 6
к
0,0
0,1
0,2
0,3
У
0,00000
0,00033
0,00267
0,00900
Ду
0,00033
0,00234
0,00633
л
0,00000
0,00100
0,00400
0,00901
Дт1
0,00100
0,00300
0,00501
Д2Л
0,00200
0,00201
Д3т|
0,00001
По данным этой таблицы находим:
Д</8 = 0,00901 +~ . 0,00501 +~ . 0,00201 + -| • 0,00001 =0,01236,
У^Уг + ЬУг^ 0,02136,
и можно заполнять следующую косую строку. Для значений х
между 0,0 и 0,6 результаты вычислений записаны в таблице 7.
Сравним это с результатами, полученными выше другими
методами. Различные аналитические методы привели нас в § 1 к при-
Xх X1
ближенному решению у (х) ^ ~ + ?о> погрешность которого, как
мы видели, мала. При х = 0,6 имеем -^-+—=0,07244, что дает

5]
§ 2. ЧИСЛЕННЫЕ МЕТОДЫ
47
X
0,0
0,1 '
0,2
0,3
0,4
0,5
0,6
У
0,00000
0,00033
0,00267
0,00900
0,02136
0,04179
0,07241
ьу
0,00033
0,00234
0,00633
0,01236
0,02043
0,03062
ц
0,00000
0,00100
0,00400
0,00901
0,01605
0,02517
Лт]
0,00100
0,00300
0,00501
0,00704
0,00912
Таблица 7
Л2л
0,00200
0,00201
0,00203
0,00208
Д3Т)
0,00001
0,00002
0,00005
расхождение с результатом таблицы 7 в 3-10~5. Формула
Рунге — Кутта, как мы видели (п. 3), дает значение 0,072448, в
котором все знаки верны.
5. Интерполяционная формула Адамса. Обратимся к
формуле A.61) и заменим в ней функцию f(xyy(x))
многочленом, который ее интерполирует на отрезке xn_k^x^x„
Это приведет нас к приближенной формуле
+k
л+1=л+а .2 Ч]}{*п-рУп-^ О-69)
vn + i*
/^1
где
Си,=
(-1)/
+1
k/ (; + !)!(*_,)
J
V-l)t(t + i)...(t + k)
t + i
dt. A.70)
Формула A.69) называется интерполяционной формулой
Адамса. Она, в отличие от формулы A.64), не дает сразу
значения yn+v так как оно содержится и в правой части,
а именно в слагаемом с номером / = —1. Формула A.69)
дает уравнение относительно неизвестной уп+1\ это
уравнение можно решать итерациями, если
1
Af1 = sup
12П
\ду\
A.71)

48
ГЛ. I. ПРИБЛИЖЕННОЕ РЕШЕНИЕ ЗАДАЧИ КОШИ
[5
Таким образом, интерполяционная формула Адамса
оказывается более трудоемкой, чем экстраполяционная, но зато
она точнее.
Приведем значения некоторых, коэффициентов ck,.
Таблица 8
Значения коэффициента ckj
к ^\^
0
1
2
-1
1
2
5
12
3
8
0
1
2
2
3
19
24
1
1
12
5
24
2
1 1
24
Если ввести разности функции /(#, у(х)), то формулу
A.69) можно привести к виду
где . , °
cj=j\ t(t + l)...(t+J-l)dt A.73)
G=1, 2,. ..,ft+l);
все коэффициенты Cj отрицательны. Приведем значения
нескольких первых коэффициентов с,.
Таблица 9
/
-ч
Значения коэ<
1
1
2
2
1
12
3
1
24
[)фициентов Cj
4
19
720
5
3
160
6
863
60 480
7
275
2016

5] § 2. численные методы 49
Опишем схему вычислений по интерполяционной формуле
Адамса. Для упрощения письма положим в формуле A.72)
k = 2, что приводит к частной форме интерполяционной
формулы Адамса
A^ = 4»+1—g-Дл»—^ДЧ-1—йаЧ-1-- О-74)
Допустим, что нам известны значения yl,yi1yz', в общем
случае, если используется формула A.72) с некоторым
значением 6, то заранее должны быть известны yvy2, ... ,yk, yk+1*
По данным yvy2,y5 можно составить таблицу,
совпадающую с таблицей 4 п. 4. Задача состоит в том, чтобы
вычислить следующую нижнюю косую строку элементов
г]4, Дт13, A2rj2, Д*^; тогда, положив в формуле A.74) п=^3,
мы вычислим Ду3, а затем найдем y^ = ys~\- Ауг Упомянутукг
.косую строку будем строить по методу итераций. Для
начального приближения возьмем Д3г)[0) = Д3гH. Тогда мы
найдем последовательно
дЧ0) = дч+дУ0>, Дг1<0,=ДгJ+дЧ0>, г^гы-дг^,
затем по формуле A.74) вычисляем
ДЛ°> = ^ -1 Дг,<*> -\-2 ДУ°> -1 Д°п<0)
и, наконец,
^-Л + Ду?1.
Имея у^\ вычисляем следующее приближение для той
же косой строки по формулам:
ДтЙж> = т|1ж> — -п.. ДЧ^Л^-Дг,,, ДУ^АЧ^-Д'^,
и вычисляем Ау[1) по формуле A.74); теперь у{1) =у ^Ау^К По
известному теперь значению у[1] находим т]12) ==/г/(х4,<у!1)) и
т. д. Процесс повторяем до совпадения величин r|im_1) и
например 10. Рассмотрим пример 9 предшествующего п. 4.
Исходной для нас является таблица б (см. стр. 46).

50 ГЛ. I. ПРИБЛИЖЕННОЕ РЕШЕНИЕ ЗАДАЧИ КОШИ [6
Полагаем Д%<0) = 0,00001, тогда
Д*П<0) = 0,00202; Arj<°> -= 0,00703; rj<0) = 0,01604;
Д^(о) =0,01604—^-0,00703 — — . 0,00202 —~ . 0,00001 =0,01235;
0<°> = 0,00900 + 0,01235 = 0,02135.
Вычислим первое приближение. Имеем:
П^>=0Д (x| + £/i0J) = 0.01605,
Ац[1) =0,01605—0,00901 =0,00704,
д2г,A) =,0,00704-0,00501 =0,00203,
Ь*т[1) = 0,00203-0,00201 = 0,00002.
Теперь
д^> = 0,01605-у . 0,00704—^ . 0,00203—— . 0,00002 = 0,01236,
у™ = 0,00900 + 0,01236 = 0,02136.
Вычисляя т)^ = 0,1 {042 + у[^2)> получим прежнее значение
0,01605; можно, следовательно, положить t/4 = */41) =0,02136. Теперь
можно дополнить нашу таблицу значениями */4, AySf т]4, . .. , Д5т]1 и
перейти к вычислению значения уъ. Отметим, что полученное нами
значение уг совпадает с тем, которое дает довольно точная формула
#(#)=5г-^-+£о • Метод Рунге—Кутта дает (см. п. 3) значение
#4 = 0,021359.
6. Другие разностные методы. Можно получать экстра-
поляционные формулы, отличные от формулы Адамса, если
исходить, например, из формулы
xn+i
Уп+1=Уп-*+ I f(x,y{x))dx, A.61')
xn-s
в которой s — какое-либо натуральное число, и затем
заменить интеграл в A.6Г) его приближенным значением по
какой-нибудь квадратурной формуле с узлами в точках
хп-з> xn-s+i> • • •> хп> *л+1* можно, в частности, заменить
функцию f{x>y(x)) ее интерполяционным многочленом
на отрезке xn^k^x^xn+1. При s=l получается так

6] § 2. ЧИСЛЕННЫЕ МЕТОДЫ 51
называемая экстраполяциояная формула Нистрема [30]:
1 1 29
Уп+i = Уп-г + 2т]„ + J V4 +т VsЛ„ + go V4. +
где у — разность, взятая назад, так что, например,
УЧя = Ля —Лл-1. V4, = 4„ — 2Ля-,+Лп-,
и т. д.
Можно так же строить интерполяционные формулы,
зачастую более точные, чем интерполяционная формула
Адамса, хотя и требующие более сложных итераций. Для
этого достаточно в формуле A.61) или A.6Г) заменить
функцию f{xyy(x)) многочленом, интерполирующим ее на
отрезке [xn_k, хп+р]> где р>1. Употребительны так
называемые формулы типа Коуэлла:
А., _Ч«-Н-Ик , п A2Y]^ + A2Y);2.1 A4z-i + A4i-2 |
ЧУи — 2 ' l 2 ' 2 2 ' *'*
...+aftA24-*+12+A24-*, A-76)
aj^-^-^(t + j-\)(t+j-2)...t(t-\)...(t-J)dt.
0
Значения первых коэффициентов а, таковы:
— _1 — Л _ 191
ai— 12> ^ — 720' а*"~ 60480'
При /г = 2 формула A.76) принимает вид
Ли -'Пп-н-Ип 1 A4» + A4»-i , П АЧ»-1 + А«ля-« м .
a^"~ 2 12 2 ^ 720 2 " 1 '
Изложим кратко ход вычислений по формуле A.77); в
общем случае формулы A.76) вычисления протекают
аналогично. Пусть мы как-нибудь нашли значения yv уг, уг, j>4
(в общем случае формулы A.76)—значения ух, у2, . . ., ytk).
Наша ближайшая цель—вычислить уь. Составим следующую
таблицу:

52 ГЛ. I. ПРИБЛИЖЕННОЕ РЕШЕНИЕ ЗАДАЧИ КОШИ [6
Т а б л и ц а 10
X
Ч
Ч
Ч
ч
ч
1
ч
ч
ч
У
Уо
Уг
| Уг
Уз
Ау
А//о
Ai/i
Aj/2
Д#з
-1
Л
Ло
Mi
Дт]
ЛЛо
Д^1
1
ъ
Лз
Л4 j
% J
Лв
Л7
Дъ
А^з
ДТL
А^5
A*U
Д2т]
А2Ло
ДЧ
А2г]2
А2г]3
ДЧ
Д2т]5
Д3г]
А'Ло
ДЧ
АЧ
ДЧ
ДЧ
Д4т)
дч !
ДЧ
АЧ
ДЧ-
Величины, расположенные в таблице 10 под ступенчатой
линией, неизвестны—они зависят- от еще не вычисленных
величин уъ, у9} у,. Положим в формуле A.77) п = 4:
Av _*)s + ru 1 АЧ + ДЧ , И АЧ + ДЧ.
аЛ — 2 12 2 ~*~720 2
некоторые величины, входящие в правую часть последнего
уравнения, неизвестны, и мы будем решать это уравнение
итерациями.

6] § 2. численные методы 53
Чтобы построить начальное приближение, выберем как-
нибудь начальные значения четвертых разностей. Проще
всего положить
ду ? - ду20) = ду 0з> - ду.
Теперь легко вычисляются ДУг\ ДУ? и все
остальные неизвестные величины в таблице 10. Полагаем"
д (о) _ Л(,0) + *U 1 А2ЛD0) + А2У80) , 11 АУ,0) + А4Ч(а0)
A^4 ~ 2 12 2 +720 2
и у{1] =Уь + Ay{i. Вычисляем величину
и? = */(*., У?).
Если т^—чй* т0 полагаем уь — у^°$, вставляем известные
уже числа в таблицу 10 в косую строку под ступенчатой
линией, и переходим к вычислению у6. Если же у)(^ Ф
Фч{1\ то строим следующее приближение у*\\ Для этого
вычисляем элементы первой косой строки под ступенчатой
линией:
А8т1<;> = ду;>—ду, ду1^ = ду;)—ду.
Выбираем приближения для Д4т]^ и Д4т)(^; можно,
например, принять
Д^^ДУ^ДУ1^.
Теперь можно вычислить все элементы таблицы 10,
расположенные под ступенчатой линией, и определить величины
д (р.УУ + ти 1 А2л(р + А2чA8> 11 аУ.'ЧаУУ
У 4 ~~ 2 12 2 W20 2
и у*) =^4 + ДуD}' Теперь вычисляем
если т]E} = T|(V, то полагаем ys=y{\] и переходим к
вычислению уЬУ в противном случае повторяем процесс.

ГЛ. I. ПРИБЛИЖЕННОЕ РЕШЕНИЕ ЗАДАЧИ КОШИ [7
7. Разностные методы для систем и для уравнений
высших порядков, В случае системы уравнений первого
порядка разностные методы приводят, по существу, к тем
же формулам, что и для одного уравнения. Так, если мы
остановимся на задаче Коши A.12), A.13) и введем
обозначения
ц.^Н/{Х;, ур zj), £у = Лф(*у, ур Zj), A.78)
то мы придем к следующим приближенным формулам.
Экстраполяционная формула Адамса:
tyn = л, +1 %,-i + г^дЧ-2 +1ДЧ-* + • • .
1 5 о } A.79)
Интерполяционная формула Адамса:
ДУ» = П„+, - J Ат1п —il АЧ -г —й АЧ-2 - • • ♦
Д*„= ^п+.-т А£«-Г2 д,£»-»-й АЧ-г~- • •
A.80)
Интерполяционная формула типаКоуэлла:
&Уп-
.Чп + г+Чп 1 А2Т1/г + ^п-1
12
2 +
11 А4Лп-. + Д4Пп-г
1 720 2
А, С+1 + е» * A*Sn + A'S„-i |
а*»— 5 12 9, >
11 А*Ь,-,+Д«Ея-«
"^720 2
A.81)
Проводя вычисления по той или иной-формуле A.79) —
A.81), мы должны каждый раз заполнять две таблицы,
аналогичные таблицам методов Адамса или Коуэлла для
одного уравнения; в общем случае системы т уравнений
первого порядка надо будет заполнять т таких таблиц.
Уравнение или система уравнений порядка выше первого
легко сводится к системе уравнений первого порядка, к
которой уже можно применить формулы A.79) — A.81). Мы

7] § 2. численные методы 55
остановимся здесь только на задаче Коши для односо
дифференциального уравнения вида
/=/(*, J), У\х=Ха=*У» У'\х=Ха=у1 A-82)
В этом случае можно указать разностные формулы, так
называемые экстраполяционную и интерполяционную
формулы Штёрмера, которые позволяют заполнять только
одну таблицу. Положим
lj = h*f(Xj, yj). A.83)
Экстраполяционная формула Штёрмера имеет вид
1
—1
Приводим значения первых коэффициентов а,.
Таблица 11
Значения коэффициентов о^
У
а/
2
1
12
3
1
12
4
19
240
5
3
40
б
863
12 096 |
Ограничиваясь, например, значением & = 3, имеем
^yn-l = ln + r2^%-i+kA3^->- A-85)
Чтобы воспользоваться формулой A.85), следует
предварительно каким-либо способом вычислить yl9 y2,ys. Тогда
можно составить таблицу (см. таблицу 12, стр. 56), все
элементы которой известны.
A.84)

56 ГЛ. I. ПРИБЛИЖЕННОЕ РЕШЕНИЕ ЗАДАЧИ КОШИ [7
Таблица 12
X
хо
*1
ч
Ч
Ч
- У
Уо
Ух
Уг
Уз
Д</
А^о
Аг/,
Ду»
l •
*п
Д2{/
дч
Д2л
s
6о
6.
6,
ь .
Д|
Д1о
Д1,
А|2
|
■
• -| ■ -.
д2|
Д21о
Д21,
Д81
дч.
Полагая в формуле A.85) я=3, вычисляем величину
Теперь можно найти у^:
Заполняем в таблице 12 нижние косые строки числами
у„ Ау3> А2у2; £4, Д£3, A2g2, А8^. Тем же способом вычи-
дляем у^ и т. д.

8] § 2, численные методы 57
Интерполяционная формула Штёрмера имеет вид
О
первые значения р. приведены в таблице 13.-
Таблица 13
Значения коэффициентов C,
/
Р/
2
1
2
3
0
4
1
240
5
1
240
6
221
60 480
Если ограничиться значением & = 4, то получится
следующая формула:
Д2 t i J_A2? L Л4£ —Л5?
** Уп-i «л"» 2 я~1 240 л~* 240 *«"*•
Вычисления по интерполяционной формуле Штёрмера
проводятся так же, как и по интерполяционной формуле
Адамса.
Для задачи A.82) можно строить и интерполяционные
формулы' типа Коуэлла.
8. Построение начала таблицы. Из изложенного в п. 4
следует, что для решения задачи Коши разностным
методом необходимо иметь начало таблицы, содержащее, кроме
у0 (известного из начального условия), также несколько
первых значений уг, у27 ♦ . • , yk.
Для построения начала таблицы предлагаются способы,
которые в основном можно разбить на две группы: явные и
итерационные.
Примеры явных способов.
а) Находя отрезок ряда Тейлора решения у(х) (см. § 1,
п. 1) и полагая в нем x=-h, лг=2Л, ... , x = kk, найдем
Л» Л. • • • » У к-

58 ГЛ. I. ПРИБЛИЖЕННОЕ РЕШЕНИЕ ЗАДАЧИ КОШИ [8
б) Исходя из х0, у0 методом Рунге—Кутта одно за
другим определяются к значений у19 уг, ... , yk для х =
= #lf х„ ... , xk, где Xj = x^jh.
Итерационные методы предлагают систему к уравнений
для определения уг, у21 ... , yk, которая для достаточно
малых значений h допускает решение методом итераций.
Способы этой группы отличаются друг от друга, по
существу, лишь формой записи этой системы,
последовательностью вычислений для проведения итерации и
определением начального приближения для итерации.
Основания для получения системы уравнений таковы.
Для любого целого числа г и любого целого
положительного числа ft 1^1 можно указать такие числа Af5, г) (/ =
= 0, 1,2, ... , ft), что для любого многочлена Р(х) степени
не выше ft-f1 относительно х при произвольном Л>0 имеет
место равенство
P(rh) — Я@) = А2^' r) P'(ih).
Если бы решение у(х) задачи Коши было многочленом
степени не выше ft+1, то в силу уравнения A.1) имели
бы, заменяя у(х() на у( и ^'(лг^-на f(xh yt),
Л~Л = * S4*'*/(**. Л>- A.86)
а) Полагая в A.86) г = 1, 2, ... , ft, получим систему
k уравнений [60]
Уг=Уо + ^л?'Г)/(хи Л) (г-1, 2, ..., ft). A.87)
Система A.87) для достаточно малых h имеет
единственное решение, для которого yv y21 ... , yk мало
отличаются от у0У и это решение может быть получено методом
итерации.
Начальное приближение у(\\ у^у ••• , y{k можно
получить, например, методом Эйлера.
Выпишем значения A\k' r) для ft=l, 2, 3, 4;(Xr«^ft.

§ 2. ЧИСЛЕННЫЕ МЕТОДЫ
Т а б л и
Значения коэффициентов А^
69
Таблица 14
<*. г)
1 Li- -L
2 2
* = 2
Г N.
1
2
0
5
12
1
3
1
8
12
4
3
2
1
12
1
3
6 = 3
1
2
3
0
3
8
1
3
3
8
1
19
24
4
3"
9
8
2
5
24
1
3
9
8
3
1
24
0
3
8

ГЛ. 1. ПРИБЛИЖЕННОЕ РЕШЕНИЕ ЗАДАЧИ КОШИ [8
' 1
2
3
4
0
251
720
29
90
27
80
14
45
1
323
360
62
45
51
40
64
45
2
И
30
12
45
9
10
24
45 :
3
53
360
2
45
21 |
40 !
64
45
4
19
720
1
90
3
80
14
45
В простейшем случае (k—Л) система превращается в
одно уравнение
л=л+-| [/К, л)+/(*!. л)] .
совпадающее с уравнением метода трапеций.
В случае k = 2 система имеет вид
Л=Л + Г5 [5Я*о> Л) + 8/(*1. Л)— /К» Л)] f
Л=Л +4{/<*•' Л) + 4/К, J\)+/(*„ Л)] •
Последовательные приближения вычисляются по формулам *)
^т+1)=Л+ у [/(*., У.) +4/(*„ У,т+1,)+/(*.,^ж))] •
!) Если ожидается, что число итераций будет невелико A —2
итерации), то в целях экономии вычислений допустимо заменить в
правой части второй формулы f(xlt у^т+1^) на f(xvy£m))>

8] § 2. численные методы 61
б) Система A.87) записывается в разностной форме.
Для этого вводятся разности Ayr=yr+l—уг (г = 0, 1, 2,
... , ft—1), а также x\j = hf(xp yj (; = 0, 1, 2, ... , ft)
и их разности до порядка ft. Введем величины
Bf r) = 4*- r+1)—A}k- r) (считая Af 0) = 0).
Тогда система A.87) вычитанием двух соседних
уравнений легко преобразуется в такую:
АУг=2Я?'Г) Ч ir = 0, 1, 2, ... , к-1).
* = о
Каждое уравнение этой системы преобразуется следующим
образом:
а) Если /<г, то т); заменяется линейной комбинацией
величин т)„ Дт^, ДЧ-*> ... , Дг-'т1£..
Р) Если £>г, то ify заменяется линейной комбинацией
величин
г\п Дт]^, ... ,Агт]0, Аг+1тH, ... , А\.
В результате такой замены приходят к уравнению
A^ = ^+S^°A4-(-+ £ МГ,ДЧ- A-88)
Оказывается, что числа Z)jr) не зависят от выбора ft.
Приведем таблицу чисел DJ-r) для 1^/<;5, 0^г^4 (см.
таблицу 15 на стр. 62).
Уравнения в форме A.88) предложены А. Н.
Крыловым [31].
Например, для ft = 3 система A.88) примет вид
ДУж = 4t + i Ало+й ДЧ - gj ДЧ>

62 ГЛ. I. ПРИБЛИЖЕННОЕ РЕШЕНИЕ ЗАДАЧИ КОШИ
Таблица 15
Значения коэффициентов D^
[8
0
1
2
■3
4
1
1
2
1
2
1
2
1
2
1
2
2
1
12
5
12
5
12
5
12
5
12
3
1
24
1
24
3
8
. 3
8
3
8
4
19
720
11
720
19
720
251
720
251
720
5
3 i
160
11
1440
11
1440
3
160
95
288.
Если после т шагов итерации получены значения у[т\ у{2т) ,
у 1т\ то для получения следующего приближения у[т+1) ,
УГ+1\ ylm+l) предлагается поступать так: по известным
у[т\ у[т\ ylm) вычисляются tiSw), r]!m), riim); используя эти
значения и известное значение г|0, находят значения
разностей, входящих в формулу A.88). Это позволяет
вычислить Ду*т+1) (г = 0, 1, 2) и затем последовательно
величины:
Я
<т+1ил+д^т+1),
Уг —У\
+ Ау
(m + i)
1
/?+1) = у[т+" + Ау.
(Ш + 1)
2
чем и заканчивается один шаг итерации. Процесс итерации

8] § 2. ЧИСЛЕННЫЕ МЕТОДЫ 63
повторяется до тех пор, пока величины \у(гт+1)—у[т)\ не
сделаются достаточно малыми.
Начальное приближение у[°\ у[*\ у^] для итерации
можно получить по методу Эйлера.
Для получения более точного начального приближения
можно рекомендовать прием, предложенный А. Н.
Крыловым [311.
1) Полагают Ay(J} = тH.
2) Находят у^ —у0 + Ц0 (формула Эйлера).
3) Вычисляют v^) = hf{xl, у*?).
4) Определяют разность Аг)^ = tj^ — г|0.
5) Находят приращения Ау[2) и ДУ,2) по формулам
6) Находят У,г) и у?: у[ш)=у9+А/:\ у?=у? + Ду|г).
7) Вычисляют r\[!) = hf(xv y\z)) и ц[г) = к/(х„ yiz)).
8) По величинам т]0, г\[2) и г\^ находят разности:
Дг,(:» = г^-г],, Дт)B) = Ti?>—nJ*>, Дгт,<2) = Дг,<2>-Дг)Г>.
9) Находят приращения Ду£8), Ау[*\ Ау[9) по формулам:
А^,)-Л. + 7Ач?>-нА,Л.(,).
Ау\г) = Ч<и±Аг\12) + ^АЧ*\
А^,-Ч^*, + уАч(,,) + йАЧ'>.
10) Находят У,0, У", У8):
Величины y*f\ yf\ у^ принимаются в качестве
начального приближения для итерации системы уравнений A.88)
(ft = 3).
Замечание. Если /(х, у) задается сложным аналитическим
выражением, то естественно объем работы для численного решения
задачи Коши оценивать числом вычисляемых (в процессе-решения)

ГЛ. I. ПРИБЛИЖЕННОЕ РЕШЕНИЕ ЗАДАЧИ К01ИИ [9
значений f (х, у) и как бы пренебрегая другими вспомогательными
вычислениями (образование разностей, умножение на коэффициенты
D^p и др.). Определение начального приближения по методу Эйлера
требует (в случае k = 3) трех вычислений f (х, у), по методу
Крылова—четырех вычислений. Так как более точное начальное
приближение, как правило, сокращает число необходимых (для
достижения предписанной точности) итераций, и каждый шаг
итерации системы A.88) требует четырехкратного вычисления f (х, у),
то, видимо, выгоднее начальное приближение находить по методу
А. Н. Крылова.
9. Об устойчивости разностных методов. Будем
рассматривать задачу Коши A.1), A.2). Применение любого
разностного метода связано с погрешностью, вызываемой
очевидными причинами: неточностью допущений, лежащих
в основе вывода приближенной формулы; неточностью
промежуточных действий и вызванными этим погрешностями
округления; неточностью определения исходных значений
У и Уы ••• » Ук> погрешностями итераций в случае
применения интерполяционных формул. Так как значения уп
определяются рекуррентно, то не исключено, что с ростом
п погрешность в определении уп может накапливаться и
превзойти допустимые пределы.
Отвлечемся от ошибок округления и будем считать, что
как погрешность приближенной разностной формулы, так и
погрешности исходных величин j/,, у2, ... , yk достаточно
малы. Если при возрастании п погрешность в определении
уп остается ограниченной, то разностная формула называется
устойчивой; если же упомянутая погрешность может
возрастать бесконечно при п—>оо, то разностная формула
называется неустойчивой.
Приведем критерий устойчивости разностной формулы.
Будем считать, что эта формула имеет вид
2«/Л+;-2РЯ„+у=0. A-89)
где ау и р.— вещественные числа, акф0. Отметим, что
все приведенные выше разностные формулы имеют вид A.89).
Построим многочлены
Q(z) = akzk + ak_lzk-l+...+a„ 1

9]
§ 2. ЧИСЛЕННЫЕ МЕТОДЫ
65
Будем считать, что многочлены q(z) и o(z) не имеют
общих корней—в противном случае можно было бы
упростить формулу A.89), уменьшив в ней число к. Требование,
чтобы при /г->0 приближенное решение (в предположении,
что оно вычислено без погрешности) равномерно сходилось
к точному решению, налагает на многочлены A.89) еще два
условия:
Q(l)=£cx=0, q'A) = oA). A.91)
/ = 0
К равенствам A.91) можно прийти также, исходя из
требования, чтобы формула A.89) была точна, когда ^(л:) есть
полином первой степени и, следовательно, f(x, у) — const.
При указанных условиях разностная формула A.89)
устойчива тогда и только тогда, когда все корни
многочлена q(z) расположены внутри или на окружности круга
|я|г^1 комплексной z-плоскости, причем корни,
расположенные на границе, т. е. равные единице по модулю,
должны быть простыми.
Все приведенные в пп. 4— 7 разностные формулы
устойчивы.
Приведем пример неустойчивой разностной формулы; такова
формула
Уп+ж + *Уп + 1—%« = 4Чл+1 + 2ч*- A-92)
В данном случае
q B) = 22 + 4-г—5, а (г) = 4г + 2;
многочлены q(z) и g(z) не имеют общих корней, и q A) = 0, р/A) =
= а A) =6. Корни многочлена q (z) суть 1 и —5; второй корень больше
единицы по модулю, и формула A.92) неустойчива. Чтобы
удостовериться в этом, будем по формуле A.92) решать задачу Коши
</' = </> У\х=о = 1>
точное решение которой есть у—ех. Положим h = 0,1. Чтобы
привести вычисления по формуле A.92), надо знать значение Уг=у @,1).
Примем за уг значение # @,1)=е0,1, вычисленное с шестью верными
десятичными знаками: у1 = 1,105171. Проведя вычисления, найдем
yl(i — y A) = —0,284254; погрешность, которая при п= 1 была меньше
чем 10"в, теперь имеет значение
IУ @ — г/10 | = е + 0,284254 = 3,002536.
3 С. Г. Михлин и X. Л. Смолицкий

66 ГЛ. I. ПРИБЛИЖЕННОЕ РЕШЕНИЕ ЗАДАЧИ КОШИ [10
Для уравнения второго порядка вида у"~/(х, у) при
начальных условиях
исследована устойчивость разностных формул вида
Л+1-|//Л-у-Лг.21 В,Пхя.р Л-у) = <>- A-93)
На коэффициенты формулы A.93) накладывается
требование, чтобы она была точной для дифференциального
уравнения /' = 0; отсюда вытекают соотношения
Разностная формула A.93) устойчива тогда и только
тогда, когда корни многочлена
^+1_2ЛУ=0 A.95)
; = о
удовлетворяют тому же условию, которое было выше
сформулировано для многочлена q(z): либо корни меньше
единицы по модулю, либо они равны единице по модулю, но
тогда они простые.
10. Погрешность формул Адамса. Мы ограничимся в
этом пункте формулами Адамса, как наиболее
употребительными; о погрешности других разностных формул см. [2]
и [73].
Обе формулы Адамса, как экстраполяционная, так и
интерполяционная, могут быть записаны в виде одной формулы:
Л+,=Л + АДР/(*»-/. Уп-jY' 0-96)
для экстраполяционной формулы Адамса р„1 = 0, для
интерполяционной формулы fLx>>0. Будем считать, что исходные
величины yv y2, ...yyk заданы каждая с погрешностью,
не превосходящей некоторого заданного числа е. Величины
Ук+v Укл-v ••• определяются из уравнения A.96) с
некоторой погрешностью, вызванной ошибками округления, по-

10]
§ 2. ЧИСЛЕННЫЕ МЕТОДЫ
67
грешностью исходных величин yv yv ..., yk и, наконец,
погрешностью самой формулы Адамса. Пусть мы фактически
вычислили некоторые величины уп\ они, очевидно,
удовлетворяют уравнению вида
Я.+1=Я. + * 2 Р/(*-/. Л-у) + Гй, A.97)
/=-1
где Гп — ошибка округления в уравнении A.96) и у,~
= yJ(j=01 1, 2, ..., k). С другой стороны, если у(х)
есть точное решение задачи Коши, то у(хп) не
удовлетворяет точно приближенному уравнению A.96); введя
соответствующую поправку, которую мы обозначим через /?п,
мы можем считать, что у(хп) точно удовлетворяет
уравнению
y(xn+l)=y(xn) + k2j>jf(Xn-r yiXn-fi + Rn- A-98)
Обозначим , v ,« лл,
8„ = У(ж»)-Л- A-99)
Задача состоит в оценке величины |ей|.
Обозначим через К постоянную Липшица функции f{x,y)]
можно положить . _.,
\df\
К= max
ду\
Пусть нам известны верхние границы величин | Гй | и \Rn\,
т. е. такие постоянные Г и /?, что | Гп | ^ Г и \Rn\^R.
Известно, что если решение у(х) задачи A.1), A.2) имеет
необходимое число непрерывных производных, то можно
положить я=сА'-мШах|У'+'>(*)|,
где с—постоянная, a r = k для экстраполяционной формулы
и г = &+1 для интерполяционной формулы Адамса.
Положим еще
а= 2IP/I (i.ioo)
/=-1
и выберем h столь малым, чтобы было h$„1K<Zl> для
экстраполяционной формулы Адамса последнее условие,
очевидно, выполняется при любом h. Составим уравнение
A—Ар.,/0^1 —A+АР0^^—*^21Ру1^"/==0- AЛ01)
3*

68 ГЛ. I. ПРИБЛИЖЕННОЕ РЕШЕНИЕ ЗАДАЧИ КОШИ [11
Доказывается, что оно имеет корень ^^l; через этот
корень и выражается искомая оценка:
Kl^^ + w**"-1)- (Ы02)
Можно доказать (см. [73]), что при малых h верно
приближенное равенство
zn^^eKo (xn-xQ)
i
и, следовательно, гп остается ограниченным при возрастании п.
Оценка A.102) обычно оказывается довольно грубой.
Более точна рекуррентная формула для оценки погрешности.
Пусть Ьп—верхняя граница величины | гп |, и пусть значения
6,, б2, ..., bk нам известны. Тогда бй, я > &, можно найти
из рекуррентного соотношения
A—Ар_1/СNя+1 = A+Лр0/СN„+А/С211Р/|вя -,+Я+Г.A.103)
11. Сравнение численных методов. Основное
достоинство метода Рунге — Кутта по сравнению с разностным
методом состоит в том, что шаг hn можно назначать произвольно
в любом месте вычислений. Это обстоятельство используется
для организации контроля вычислений и подбора шага,
обеспечивающего назначенную точность вычислений [41]. Для
начала вычислений по методу Рунге—Кутта не нужно строить
начальную таблицу, что также является достоинством этого
метода.
Для перехода от хп к хп+г по методу Рунге — Кутта
требуется четырехкратное вычисление/(jc)#yj>(для основного
приема); в то же время для любого экстраполяционного разностного
метода для этой же цели требуется однократное вычисление
/(я, у)у и это сравнение не в пользу метода Рунге—Кутта.
Этот недостаток метода Рунге—Кутта становится менее
заметным при сравнении с интерполяционными разностными
методами, требующими, как правило, не менее двухкратного
вычисления при переходе от хп к хп+1.
По-видимому, достоинства метода Рунге — Кутта с
появлением быстродействующих цифровых вычислительных машин
стали оцениваться выше, и в настоящее время наблюдается
тенденция более широкого использования метода
Рунге—Кутта в работе вычислительных центров.

НЕКОТОРЫЕ ЛИТЕРАТУРНЫЕ УКАЗАНИЯ
69
НЕКОТОРЫЕ ЛИТЕРАТУРНЫЕ УКАЗАНИЯ
Как аналитические, так и численные приближенные методы
решения задачи Коши для обыкновенных дифференциальных
уравнений изложены в книгах [2], [31] и [89]; численные методы
изложены еще в [30], [57], [73], [84]; см. также [22].
К п. 3 § 1. Некоторые сведения о применении метода Чаплыгина
к различным задачам теории дифференциальных и интегральных
уравнений, а также некоторые библиографические указания см. в
статье [52].. Более подробно о методе Чаплыгина см. [2], [16], [31], [106].
К п. 5 § 1. Ряд интересных сведений о методе малого параметра
можно найти в книге [31].
К п. 6 § 1. В этом пункте изложены некоторые результаты
статьи С. М. Лозинского [50], упрощенные применительно к случаю
одного уравнения первого порядка. Дальнейшее развитие идей того
же автора см. [47] —[49], [51].
К п. 1 § 2. В статье [5] дано обоснование метода ломаных
Эйлера для случая, когда функция f(x, у) в дифференциальном
уравнении A.1) терпит конечный скачок на некоторых линиях в
плоскости (х, у), но между этими линиями удовлетворяет условию
Липшица. Аналогичные результаты получены в [5] и для системы
уравнений первого порядка.
К п. 6 § 2. Большое количество разностных формул ^приведено
в книгах [59] и [60]; в ряде случаев приводятся дополнительные
формулы, служащие для контроля или для уточнения результатов,
даваемых основными формулами.
К п. 9 § 2. Понятие устойчивости разностных методов
разработано в статье Г. Дальквиста [114], в которой даны также
приведенные в тексте критерий устойчивости и пример неустойчивой
разностной формулы; в статье [114] содержатся и другие результаты,
связанные с понятием устойчивости. Основные результаты статьи [114]
подробно изложены в [2] и более кратко в [73].
Устойчивость разностных формул для уравнения вида y" = f(x> у)
исследована В. И. Крыловым в статье [32].
К п. 10 § 2. Погрешность метода Адамса была исследована
в статье [124]; оценка погрешности более общих разностных
формул вида
к k
/So /=о
дана в [107]. В статье [1] дана оценка погрешности формул того же
вида в предположении, что известны функции Yl(x) и Y2(x),
удовлетворяющие неравенствам Y1(x)^y(x)^Y2(x)) Y1(x)^~ym(x)^tY2(x)t
где у(х)—точное решение задачи Коши A.1), A.2), а ~ут(х)~-точное
решение задачи Коши для уравнения A.1) при начальном условии
У\х~х —уту а Ут есть величина, даваемая разностной формулой.
В статье [51] исследуется погрешность экстраполяционных формул.

ГЛАВА II
МЕТОД СЕТОК
§ 1. Уравнения эллиптического типа
1. Сеточные уравнения. В этой главе рассмотрены
сеточные методы приближенного решения основных задач
математической физики.
Пусть Q — конечная или бесконечная область я-мерного
евклидова пространства Еп и Г — граница области Q. Пусть
Lu — некоторый дифференциальный оператор (как правило,
линейный) над функцией и (X) = и (xv . . ., хп), где Х==
~ (х1У ..., хп)—точка Еп. Ставится задача о разыскании
функции и(Х)у удовлетворяющей в каждой точке области Q
дифференциальному уравнению
Lu=f(X) B.1)
и одному или нескольким условиям на границе
1{и\п = у{(Х) A=1, 2, ...,*), B.2)
где Г,. — части границы Г, 1{и—дифференциальные
операторы. В уравнениях B.1) и B.2) f(X) и <d(X) — функции,
заданные соответственно в Q и на Т{. Если заданы область Q,
операторы L и lh то этим задается целый класс задач, для
каждой из которых данными являются функции f(X) и
ф/ (X). По этим данным требуется определить функцию и (X).
Для приближенного решения задачи B.1), B.2)
предложены различные методы, часть из которых называют
сеточными.
К сеточным методам относятся те, в которых
разыскивается таблица приближенных значений искомого решения
в некоторой совокупности точек Xk£Q-\-T (&=1, 2, ...),
называемой сеткой; отдельные точки Xk называются узлами

1] § 1. УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА 71
сетки. Иногда кроме узлов Xk£Q-\- Г выбираются и
вспомогательные узлы вне области Q. Узлы ^6^ + Г будем
называть основными. Уравнения, которые служат для
определения искомых значений приближенного решения,
называются сеточными. Основания для выбора сетки и получения
сеточных уравнений отличают один сеточный метод от другого.
Мы будем предполагать, что каждый сеточный метод
рекомендует бесконечную совокупность сеток QA, зависящих
от одного или нескольких положительных параметров,
характеризующих плотность расположения узлов сетки. В
дальнейшем этот параметр или группу параметров будем
обозначать буквой К. Чем меньше h (параметры, составляющие А),
тем гуще сетка Qh. Предполагается, что в совокупности
{Rh} сеток можно выделить такую последовательность, что
h~+0. Те значения й, для которых существует
соответствующая сетка Qh, назозем допустимыми.
Для примера рассмотрим часто употребляемую прямо-
угольную сетку. Пусть Q — область плоскости Оху. На этой
плоскости проведем два семейства прямых, параллельных
координатным осям: #= ihv y — jh2, где hx и
h2—произвольные положительные числа, /, у = 0, ±1, +2, . .. Эти прямые
разбивают всю плоскость на прямоугольники со сторонами hx
и h2\ вершины этих прямоугольников называются узлами
прямоугольной сетки. Через Q^ обозначим совокупность
узлов прямоугольной сетки, лежащих внутри или на границе
области Q. Может случиться, что никаких ограничений на
hl и h2 накладывать не надо; тогда допустимыми h(hv h2)
будут любые положительные •А1 и Л2. Может случиться, что
область Q ограничена, а предлагаемый сеточный метод
требует наличия не менее определенного числа узлов в Q;
тогда допустимыми будут все h(hv h2), где hx и h2
ограничены сверху. Может случиться, что допустимыми будут
только такие h(hv h2), что А1 = тг-, ^^лГ» где а> ^ —
положительные числа, N1 и N2 — произвольные
положительные целые числа; так поступают, если Q — прямоугольник
со сторонами а и Ьу и желают, чтобы Q была покрыта без
остатка элементарными прямоугольниками сетки.
В этом параграфе будем предполагать, что область Q
конечна и для каждого допустимого h сетка Qfy состоит из
конечного числа Nh узлов.

72
ГЛ. II. МЕТОД СЕТОК
[1
В последующем ин будет означать таблицу
приближенных значений искомого решения. Эту таблицу будем
называть сеточной функцией, а отдельные числа этой таблицы —
значениями сеточной функции в узлах.
Для определения сеточной функции сеточный метод
рекомендует систему сеточных уравнений, решением которой
являются числа, образующие uh. Эту систему в общем виде
будем записывать так:
ЯЛиЛ=/А, B-3)
'«л»а = Ф«л (/=1, 2,..., *), B.4)
считая, что уравнения B.3) являются сеточной заменой
дифференциального уравнения B.1), а уравнения B.4)
являются сеточной заменой граничных условий B.2). Систему
B.3), B.4) будем называть сеточными уравнениями для
задачи B.1), B.2).
В случае применения прямоугольных сеток для
составления сеточных уравнений B.3) часто употребляется прием
замены производных конечно-разностными отношениями.
В последующем будут приведены примеры применения
этого приема.
Естественно предъявить следующие требования к системе
B.3), B.4).
1) Разрешимость системы B.3), B.4).
Предположим, что задача B.1), B.2) имеет, и притом
единственное, решение в некотором функциональном классе U. Для
каждого допустимого h система B.3), B.4) должна иметь
единственное решение { uh(Xk)}, где Xk— узел с номером k
в сетке QH.
2) Сходимость к точному решению задачи.
Сеточное решение uh(Xk) при h-+Q должно в каком-то
смысле стремиться к точному решению и(Х). Для описания
этого требования введем следующие пространства и нормы
(см. [13] и [104]):
а) пространство U функций, которому принадлежит
точное решение и (X) задачи B.1), B.2); в этом пространстве
введена некоторая норма ||и||с/;
б) под Uh будем понимать пространство, элементами
которого являются совокупности Nh чисел и одним из
элементов является сеточное решение системы B.3), B.4);

1] § 1. УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА 73
в пространстве Uh введена норма || uh \\цн (какая-либо норма
Л^-мерного векторного пространства Uh).
Согласование норм. Нормы \\и\\ц и ||иЛ||с/Л
предполагаются согласованными в следующем смысле: каждую
функцию u(X)£Uy поскольку ее значения известны также
в основных узлах сетки Qh, можно рассматривать как
элемент пространства Uh; для любой функции u(X)£U должно
иметь место следующее равенство:
lim\\u{X)\\Uh = \\tt(X)\\u. B.5)
Величину ||uh—u(X)\\uh назовем погрешностью
приближенного решения ин по отношению к точному решению и(Х).
Будем говорить, что uh сходится к точному решению
а (А), если
lim||eA-tf(J0||^ = 0. B.6)
Оценка погрешности. Представляется интересным
получить формулы, позволяющие оценить сверху погрешность
|| uh—u(X)\\uh. Дело обычно сводится к тому, что находят
положительную функцию со (h) от h и параметров,
характеризующих точное решение (параметры области £3, параметры
краевых условий, модули производных точного решения и
т. д.), стремящуюся к нулю при /г-^0, такую, что
\\uh-u(X)\\uh<<i>(h). B.7)
Формула B.7) позволяет судить не только о сходимости
B.6), но и о скорости убывания погрешности при h-+0.
В тех случаях, когда удается найти функцию со (/г), будем
говорить, что найдена оценка погрешности.
В заключение этих общих рассуждений приведем пример
составления сеточных уравнений для случая, когда задача
B.1), B.2) есть задача Дирихле для эллиптического
уравнения с двумя независимыми переменными.
При составлении этих уравнений будет употреблен уже
упоминавшийся прием замены производных
конечно-разностными отношениями.
Пусть Q—конечная область плоскости Оху, ограниченная
простым, достаточно кусочно-гладким контуром Г. Пусть а,
Ь> с, d) g> f—достаточно гладкие функции в_й, причем

74
ГЛ. II. МЕТОД СЕТОК
A
а>0, £>0. Рассмотрим уравнение
Lu = att + b^ + cv£+dXg—gu = f..
B.8)
Пусть на контуре Г задана функция ср. Задача Дирихле
ставится так: найти решение и(х, у) уравнения B.8),
обращающееся в ф на Г, т. е. удовлетворяющее условию
1ь\т = и(х, у)\г =ф.
B.9)
Введем обозначения: (/, у)—узел с координатами (ihv jh2)>
где i и у— целые числа; (и)Л/-—значение функции в узле
(*'» J)> uLi—значение сеточной функции uh в узле (/, у).
Положим
(ди
[дх
00 Л/
(«)/,/+!—(«)£,/-! >t
2Л2
/сРи\ (ц)/+1>г-2(ц)£|У + (ц)/-1>/
'дЧЛ ^ Wi,/+i—2(*Q/,y+"i, y-i
kWJU^ hi
B.10)
Совокупность пяти узлов (/, у), (/+1, у), (/, у+1)>
(/—1, у), (/, у—1) назовем пятиточечной звездой с
центром в (/, у) (слою
«пятиточечная» часто будем
опускать). Примем
следующую нумерацию
узлов в звезде (рис. 1).
Через ЙЛ обозначим
совокупность всех узлов,
лежащих в Q или на Г.
х Узел (/, у) назовем внут-
_ ренним, если все узлы
звезды с центром в (г, у)
также принадлежат Qh и
отрезки прямых,
соединяющих центр с остальными узлами звезды, принадлежат
Q. Заменяя в B.8) я, Ъ, ... на (а)и /, (b)it /, ... и
производные от и(х, у) на выражения, полученные из правых
частей B.10) заменой (u)ith (w)/+i,/, ...на e/f/, ui+ltJt ... ,
Рис.

1] § 1. УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА 75
получим для каждого внутреннего узла соотношение
ЯлиА = (а)/.Г
Ut /4-1 2а. ; + «,- ; . «,., ; «. - ;
+ (*)/. / ^^ J'7 "' ' + (с)л ,.^1'i—'-•-'
2А,
+ ^/^
-(*)/./«л/= (Лл/, B-Й)
которое будем считать сеточной заменой уравнения B.8)
во внутреннем узле (/, у). Таких уравнений столько, сколько
внутренних узлов в Qh.
Узел (/, у) назовем граничным, если хотя бы один узел
звезды с центром в (/, у) не принадлежит Qh или хотя бы
один отрезок, соединяющий центр с узлом звезды,
пересекает Г. Мы изложим несколько приемов замены
уравнения B.9) сеточными уравнениями.
1) Простой снос. Пусть узел (/, у) граничный, и пусть
Qiy f£Y—ближайшая к•(/, у) точка границы либо ближайшая
в направлении координатных
осей точка границы. Положим
'*«* = «/, у = Ф«М. B-12)
и, таким образом, значения uh
в граничных узлах известны
сразу.
2) Учет граничного
условия линейной
интерполяцией (Коллатц
[30]). Пусть (/, у) — граничный
узел. Тогда хотя бы один из
отрезков, соединяющих (/, у)
с остальными узлами звезды с
центром в (/, у), пересекает Г.
Пусть для определенности это будет отрезок к узлу (/+ 1, у)
(рис. 2), и пусть С?£Г—ближайшая к (/, у) точка
пересечения. Предполагается, что весь отрезок, соединяющий Q
с (/—1, у), принадлежит Q. Если бы искомая функция и(ху у)

76
ГЛ. И.. МЕТОД СЕТОК
[1
была линейной на этом отрезке, мы имели бы
где б—расстояние от Q до (/, у). Считая u(Q) = q>(Q),
получим уравнение для сеточной функции uh:
A+T1)"b/-J1"-b/=(P(Q)>
вместо которого в общем виде будем писать
WH=(l + T)u:,j-Trttr-r="f{Q), B-13)
понимая под h либо hv либо h2 в зависимости от того,
какой оси параллелен отрезок, соединяющий Q с (/, у), и
считая (/', у") узлом звезды, лежащим на продолжении
упомянутого отрезка. Каждому граничному узлу ставится в
соответствие одно уравнение B.13). Поэтому в системе,
полученной объединением всех уравнений B.11) и B.13),
число уравнений равно числу всех узлов в Qh и совпадает
с числом неизвестных.
3) Запись уравнения в граничном узле (Ми-
к е л а д з е [58]). Для простоты будем считать, что а = Ъ = 1,
£ = d =£• = (), т. е. что оператор L есть оператор Лапласа,
а уравнение B.8) есть уравнение Пуассона:
г А д2и . д2и j, /о -I л\
Lu==Au^^ + Wi = f. B.14)
Тогда соотношение B.11) принимает вид
^ ЛЙЛ = £i Г
= (/),,, B-15)

1]
§ 1. УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА
77
и для квадратной сетки (h1 = h2 — h) превращается в
A^s '*'"^ ''/+'^ У'^ '" lJ={f)i,r B.16)
Рассмотрим звезду с центром в некотором граничном
узле, не лежащем на Г. Граница Г пересекает хотя бы один
из лучей, идущих из центра к другим узлам звезды. Пусть
Sj, 82, 83, б4 — расстояния от центра звезды в направлении
лучей либо до ближайшего узла, либо до точки границы;
например, 62 может оказаться равным h2 либо меньше, чем h2.
Пусть Qv Q2, Q3, Q4 — соответствующие точки на лучах;
например, Q2 может оказаться вторым узлом звезды либо
точкой границы Г. По значениям ^(QJ, (и)/, у, tt{Qs)
составим интерполяционный многочлен и его вторую производную
примем за приближенное значение (g-s). . • Так получаем
[дх2
и i
иШ
+
u(Qs)
(и){
6i(fii + W ' б3F1 + 63) б
А/
Найдя аналогично приближенное значение для
сложив его эти приближенные значения и приравняв сумму зна
чению (f)in p получим сеточное
уравнение, заменяющее B.14)
в граничном узле. Полученное
уравнение преобразуем так:
некоторые из точек Q,, Q2, Q3, Q4
лежат на Г, и поэтому значения
и (X) в этих точках известны и
совпадают с ср(Х);
соответствующие этим точкам слагаемые
перенесем в правую часть и
полученное уравнение разделим
на сумму коэффициентов при
перенесенных значениях.
Считая для простоты сетку
квадратной и предполагая, что для
узла на Г лежат точки Q2 и
Рис. 3.
некоторого граничного
Q, (рис. 3). получим,

78
ГЛ. И. МЕТОД СЕТОК
п
6г — X' £»
обозначая -^- = б2, -£ = 63,
(в;+в;)A+в;)A+*;> e&u+e;)
д «/,/-!- д <P(Q,H д 9(QS)~
6'6l(l + Sl)(l + 6l) .
2Л й ^'./' <2Л7>
где
л=б;A + б;)+б;A+б;).
Если граничный узел лежит на Г и совпадает с точкой Q £ Г,
то полагаем
'a«a = «/,/ = <P(Q)- I2-1**)
В системе B.11), B.17), B.18) число уравнений
совпадает с числом всех узлов в Q^.
Предположим, что Qh такова, что каждый внутренний
узел можно соединить хотя бы с одним граничным узлом
ломаной, вершинами которой (кроме конца ломаной) являются
внутренние узлы и каждый последующий узел которой
принадлежит к звезде с центром в предыдущем узле.
Теорема 1. Пусть функции а, Ь, с, d, g
удовлетворяют следующим условиям:
1) существует такое число АТ;>0, что для всех
(*> y)£Q
\с\<Ма, \d\<Mb\ B.19)
2) £53*0. B.20)
Тогда системы линейных уравнений B.11), B.12) и
B.11), B.13) однозначно разрешимы для любых \ и h2,
удовлетворяющих неравенствам
K<W h*<lA- B-21>
Замечание 1. Для уравнения B.8) можно также написать
в граничном узле уравнение—аналог B.17). В условиях теоремы 1
система линейных уравнений B.11) — аналог B.17)—однозначно
разрешима.

2]
§ 1. УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА
79
Замечание 2. Вместо введенной выше пятиточечной звезды
рассмотрим девятиточечную (рис. 4). Если в левой части уравне-
ния B.8) добавить слагаемое 2е(х, у) --'- (считая е2 <
аЬ—эллиптичность измененного уравнения), то соответствующее сеточное
уравнение получится из BЛ1) добавлением в левой части слагаемого
2(^2£д 2й; и; /~
ui+it J+i — ui-i, 7+1 + цг-1, /~1 ~~ui + h 7-1
= (*)/,/-
2/1^2
дг«
£
J
7
r/
0
4
5
I
8
Рис. 4.
являющегося сеточной заменой для 2 ( в ^ " ) . Для граничных
узлов (в смысле нового понятия звезды) примем уравнение B.12)
(простой снос). Разрешимость так
полученной новой линейной системы B.11),
B.12) еще не доказана.
2. Аппроксимация точной
задачи сеточной, а)
Определения. Пусть U есть класс функций,
к которому принадлежит точное
решение и(Х) задачи B.1), B.2).
Левая часть уравнения B.1) есть
оператор Lit, переводящий класс U
в некоторый класс F. Например, если L — оператор Лапласа
и U—класс функций, т раз (т^2) непрерывно
дифференцируемых в Q, то F есть класс функций, т—2 раз
непрерывно дифференцируемых в Q. Левая часть какого-либо из
граничных условий B.2), например /^ |г., есть оператор,
переводящий U в некоторый класс Ф1 функций, определенных
на части Г,- границы Г. Например, если U—класс функций,
непрерывно дифференцируемых т раз (т^\) в замкнутой
области Q + Г и 1\— достаточно гладкий кусок границы,
нормальная производная функции и(Х)
а / и] =5-
1 г, dv
г*
в точках Гх, то 1хи \rt переводит U в класс функций, т—1 раз
непрерывно дифференцируемых и определенных на 1\. Таким
образом, операторы Lu, Iyu\y^ ••♦, lsu>\vs переводят U
в классы Г, Ф1У Ф2, ..., Ф8 функций, определенных
соответственно в Q, 1\, Г2, ..., Г3.
Пусть в каждом из этих классов введена норма. Эти нормы
обозначим ||/||л Нф^, ..., \\%\]фу Классы Г, Фг, ..., Ф^

80
ГЛ. II. МЕТОД СЕТОК
[2
не предполагаются замкнутыми по вводимым нормам;
предполагается лишь, что задача B.1), B.2) корректна (имеет
место непрерывная зависимость решения и (X) от данных
/. <Pi> Ф*> •••> Ф,) 177], [98].
Введем сеточные аналоги классов Z7, Ф1? ..., Ф^ и
соответствующих норм. Каждое уравнение системы B.3), B.4)
будем считать записанным так, что левая часть является
функцией значений искомого решения uh в некоторых узлах
и не зависит от /, ф1? ..., ф^, а правая зависит только от
функций /, <Pj, ..., qs, т. е. является некоторым
функционалом над группой функций /, ф1? ..., ф^.
Пусть Nh— число уравнений в системе B.3), a Nlh—число
уравнений в j'-й группе системы B.4) (/=1, 2, ..., s).
Сеточную функцию uh можно рассматривать как вектор
Л^-мерного пространства Uл, где Nh — число всех узлов в Qh.
Тогда совокупность всех левых частей системы B.3) можно
Рассматривать как оператор, переводящий Uh в Л^-мерное
пространство Fh, а совокупность всех левых частей /-й группы
системы B.4) можно рассматривать как оператор,
переводящий Uh в Л^-мерное пространство Фш. Совокупность
функционалов над группой /, фр ..., ф^ в правых частях системы B.3)
можно рассматривать как оператор, переводящий
произведение классов ^хФ, X ... хФ^ в Fh. Этот оператор обозначим
через П/). Аналогично через Щ обозначим оператор,
переводящий /7хФ1 X . . . хФ5 в ф.д и образованный
функционалами в правых частях /-й группы системы B.4).
Тогда система B.3), B.4) принимает вид
ЯАиЛ = Щ(/, Ф1, ..., <р,), B.22)
г/лнл = Щ(/, Ф,, ..., Ф,) (/=1, 2, .... s). B.23)
В векторных пространствах Fh, Ф1Л, ..., Ф8?1 введем
нормы, которые обозначим \\fh\\Fh, Нф1ЛИф1Л, ••♦, 11Ф*л11ф,л.
Будем говорить, что нормы ||/л||^, 11ф1Л1км ♦••> Иф*л11ф,л
согласованы с функциональными нормами \\f\\F, ИфЛф^ . . .
• • •> Иф.у11фЛ> если Для всякого набора функций {/", ф1? . . ., ф^) £
£ Fx Ф, X ... хФ,у имеют место равенства
шпнпЛлф,, ...,.Ф,Iк=11/1и
пт||Щ(/, ФР ...,Ф,)Ифл=11ф,-||ф1 (*=1, 2, ...,*).
B.24)

2] § 1. уравнения эллиптического типа 81
Замечание 1. Обычно П^ не зависит от фх, ..., ф/, пример
уравнения B.17) показывает, что П^ зависит не только от ф,
а также и от f.
Замечание 2. Если под нормой во всех вводимых
функциональных классах и векторных пространствах понимать максимум
модуля (функции, составляющих вектора), то уравнения B.11), B.12),
B.13), B.17), B.18) записаны так, что выполнены условия B.24)
согласования норм.
Определение. Будем говорить, что уравнения B.22),
B.23) аппроксимируют уравнения B.1), B.2) в классе f),
если для каждой функции и £ U имеют место равенства
m\\Rhu-K\(Lu, 1,и, ..., /,и)||,л=0, B.25)
ft-*o
lim\\rihu-Ili(Lu, /,и, ...,/,и)][Фл = 0 B.26)
(«=1,2, „.,4
Пусть а (А) [а£ (/г)] — некоторая положительная функция
параметров, составляющих Л, стремящаяся к нулю при А—► ().
Будем говорить, что аппроксимация уравнения B.1) [B.2)]
уравнением B.22) [B.23)] оценивается функцией a (A) [ctf- (A)],
если для всякой функции и £ U можно указать положительное
число М[уИ/| такое, что для каждого допустимого А имеет
место неравенство
\\Rhu-Ul(Lu, /,«, ..., lsu)\\n^Ma(h) B.27)
[\\rihu-Ulh(Lu, l,u, .... //01|Фл<УИ,а,.(АI. B.28)
Замечание. Если А — единственный параметр и а (А) = Л?
(q—положительное число), то говорят, что порядок
аппроксимации уравнения B.1) уравнением B.22) равен Q.
В последующих примерах норму в функциональных
пространствах будем понимать как максимум модуля значений
функции (равномерная норма), и в векторных пространствах
как максимум модуля составляющих вектора.
Пример 1. Для системы уравнений B.11)
составляющими вектора Rhuh являются значения левой части B.11)
для каждого внутреннего узла, а составляющими вектора Пд—
значения /(X) в этих узлах.
В последующем Ck будет означать класс функций,
производные которых до порядка k включительно непрерывны

82
ГЛ. II. МЕТОД СЕТОК
[2
в замкнутой области Q-j-Г. Пусть U—C* и (z,
j)—внутренний узел (в смысле пятиточечной звезды) прямоугольной
сетки Qh. Пользуясь формулой Тейлора, запишем значения
функции и (х, у) в узлах звезды через значения и (х, у) и ее
производных в центре звезды. Имеем, например,
(«),*,.; = ««1'+1)*„ А> = («),.j+(%), *,+
+l(S),/:+i(&)*:=H,/+(bI/,+
+^(S)„/:+i(e),/:+i(i)«-
/dhi\ /dhi\
где 1 3i ), ( jw J — значения производных в некоторых точках
отрезка, соединяющего узлы (/, j) и (/ + 1, у). Аналогичные
выражения получаются для (и) ._ь , заменой hx на —Лх и
^- на «.
Отсюда следует
"^
л J \dx2;i}/
' 24 |_U*V^~ U*V_T
(")i + i, j—(a)i-hj__fdu\ К [fdhi\ . /д»и
,+ 12 LU*V + U*3/J
2/i, \d*/f, /
и аналогичные выражения для /Tj [(w)^ y+1— 2 (и)^ y+ (и)/, y-J
и B/^2)" [{u)iJ+1 — (u)itj^x] (с очевидной заменой hx на /г2
и дифференцирования по х на дифференцирование по у).
Полученные таким образом четыре равенства помножим
соответственно на (a),-t у, (c)f> у, (#)/, у, (<*)/, у, сложим и к обеим
частям прибавим еще —(S")/,/(**)/,/• ^ результате мы слева
получим левую часть уравненияB.11), т. е. {Rhii)^ у, справа же—
сумму значения (Lu){ ,= (Щ(/,и))^ у и слагаемых,
содержащих множители hx и Д2.
Обозначая через M(k) максимальную из норм производных
порядка k функции и(х} у), через Л — максимальную из норм
коэффициентов а, Ь, с, d уравнения B.8), легко получим
|(«^)|./-(П»A««,,/|-|(«Л./-№«)|,/1<

2] § 1. уравнения эллиптического типа 83
т. е.
\\Rhu-K(Lu)\\^M{h\ + hl\ B.29)
где
м=АЫ+—)•
Неравенство B.29) означает, что аппроксимация
уравнения B.8) уравнением B.11) оценивается функцией a(h) =
= h] + h\.
Замечание 1. Если U есть класс С2, то можно лишь
утверждать, что
lim |(Дли-П£Aи)|| = 0, B.30)
т. е. лишь наличие аппроксимации.
Замечание 2. Рассмотрим краевую задачу для
обыкновенного дифференциального уравнения второго порядка: на отрезке
0<;л:<;1 найти функцию и (х), удовлетворяющую уравнению
Lu ess и" (х) + с (х) и' —g (x)u = [ (х) B.31)
и граничным условиям
а@) = а, аA)=р B.32)
tc(x\ g(x), /(х)—заданные функции, а, Р —заданные числа).
Для приближенного решения этой задачи методом сеток введем
на отрезке [0, 1] узлы xk с шагом h: xk = xQ-{-kh. В частном
случае, когда х0 = 0, h — — (N—целое положительное число), два из
узлов х0 и xpj совпадают с концами отрезка [0, 1]. В общем случае
этого не будет. Узел хк назовем внутренним, если узлы *£_, и xk+l
принадлежат отрезку [0, 1]. Для внутренних узлов составим
уравнение
+ с(xk)и^-»ь-*-g(Xk) Uk = f (хк). B.33)
Как и в примере 1, имеет место утверждение: если и(#)£С4, то
уравнение B.33) аппроксимирует уравнение B.31) и аппроксимация
оценивается функцией Я2, т. е. порядок аппроксимации равен 2.
Пример 2. Для простоты будем считать сетку
квадратной. Если узел (/, у) граничный, то ближайшая точка Q{, ,£Г
удалена от узла (i, j) на расстояние 8</г. Поэтому для
и (*> у) € С1 имеем
|(tt),f j-и (Q,f j) | <И4(,N<И4<1>А. B.34)

84
ГЛ. И. МЕТОД СЕТОК
[2
Это означает, что порядок аппроксимации уравнения B.9)
уравнением B.12) равен 1. Этот вывод верен для Ск, где
&^1, так как Ск есть часть класса С1 при &>/.
Пусть (/, у)— граничный узел. Считая и£С2 и записывая
по формуле Тейлора значения u((i—1)й, jh) и и (/Л+ 6, у/г)
через значения и(х, у) и производных .в (/, у), найдем для
уравнения B.13)
|('*«)<, /-№(/, ")]/,/| = |[A+т)^-./—Т^'-ь/]-
-в(/А + б, уй^^й^ + б^^Л^А1, B.35)
т. е. порядок аппроксимации уравнения B.9) уравнением B.13)
равен 2. Легко убедиться, что порядок аппроксимации
уравнения B.9) (для уравнения B.15)) уравнением B.17) равен 3.
Замечание. Если для задачи B.31), B.32) выбрана сетка
так, что *0 = 0, #дг=1, то сеточная замена краевых условий B.32)
такова:
«о = а. "ЛГ=Р, B.36)
и порядок аппроксимации уравнений B.32) уравнениями B.36) равен
оо (отсутствие ошибки). Если же по каким-либо соображениям
сетка выбрана так, что хотя бы один из концов л: = 0 и х=1 не
является узлом, то сеточные замены для B.32) можно строить простым
сносом, линейной интерполяцией и способом Микеладзе. Выводы
о порядке аппроксимации таковы же, как и для двумерной задачи.
б) Выбор сеточного уравнения,
аппроксимирующего линейное дифференциальное
уравнение. Пусть Lu— линейный дифференциальный оператор
порядка р, коэффициенты которого определены в некоторой
области Q плоскости Оху. Пусть в этой области выбрана
некоторая сетка Qh. Совокупность нескольких узлов Х1У . . ., Хк
и некоторую точку Х0 £ Q назовем звездой с центром в Х0
(Х0 может совпадать с одним из узлов звезды). Пусть числа
Cj, ..., ck подобраны так, что выражение
Cla(^)+...+^(^)
совпадает с значением Lu (X) в Х0 для всех целых
рациональных функций некоторой степени q>p относительно х, у.
Тогда естественно считать, что уравнение
ЯАвд==с1«д(*1) + . .. + с*ид (**) = /(*.) B.37)

2] § 1 • уравнения эллиптического типа 85
является сеточной заменой дифференциального уравнения B.1)
в Х0> Для функции и(Х), не являющейся целой
рациональной функцией степени qy разность
Rhu-(Lu)Xo = clu(Xl)+ ... +cku(Xk)-(Lu)Xo,
вообще говоря, отлична от нуля.
Обозначим через h наименьшее расстояние между узлами
звезды. Можно доказать (в предположении, что числа сг, ..., ck
определяются однозначно), что для и(Х)£Сд+1
\Rhu—[Lu)Xo\<;AM(q+l)hq-p+\ B.38)
где А—положительное число, зависящее только от
коэффициентов оператора L и формы звезды (но не от размеров
звезды).
Пусть теперь сетка Qn мельчает так, что звезда
преобразованием подобия стягивается к центру. Тогда, если под
П£ понимать f(X0), то неравенство B.38) означает, что
порядок аппроксимации уравнения B.1) уравнением B.37)
равен q—р+ !•
Пусть ааи(Х2(х, у) есть коэффициент при - а ^ в записи
оператора Lu. Тогда для определения коэффициентов cv ..., ck
служит система линейных уравнений
k
<V <*.! «.„«.(^ Л). О^а. + а.^р,
-{
где (Xj, у J)—координаты точки Xf G=0, 1, ..., k).
Не для всякого выбора звезды, оператора L и числа q
полученная система имеет решение. Если звезда и
оператор L выбраны, то целесообразно ставить вопрос о
наибольшем значении q, для которого система B.39) имеет решение.
В случае одномерных операторов (например, оператор
B.31)) система B.39) всегда разрешима [30].
Как уже указывалось, в случае прямоугольных сеток для
образования сеточных уравнений часто пользуются методом
замены производных конечно-разностными отношениями. Если

86
ГЛ. II. МЕТОД СЕТОК
[2
сетка не прямоугольная, то можно воспользоваться
описанным приемом «подбора коэффициентов» для получения
уравнения B.37).
В приводимых ниже примерах в качестве линейного
оператора L выбран оператор Лапласа Ди^-^4 + ^4.
ох2 ' оу2
Пример 3. 1) Построим на плоскости правильную
треугольную сетку. Для этого через точки (//г, 0) оси Ох (/ = 0, ±1, ± 2, ...)
проведем два семейства пря-
}^У мых, образующих с осью Ох
углы в 60° и 120°, и
семейство прямых, параллельных
оси Ох и проходящих через
точки пересечения прямых
первых двух семейств. При
этом плоскость покроется
множеством неналегающих
равносторонних
треугольников, вершины которых
являются узлами так
называемой треугольной сетки.
Звездой назовем
совокупность семи узлов,
являющихся центром и
вершинами правильного шестиугольника, составленного из шести
элементарных треугольников сетки (рис. 5). Присвоим узлам номера
О, 1, 2, 3, 4, <5, 6 @—центр) и обозначим
7 "i + и2 + иг + Uj + us + иъ—6ий
2
Рис. 5.
где и у—значение функции и(х, у) в узле с номером /.
Имеет место формула
|Ал"-(Д")о1<4^D)^
B.40)
и, следовательно, порядок аппроксимации уравнения Au = f
уравнением Ahuh = if)o B классе С4 равен двум [25], [30].
2) Покроем плоскость неналегающими правильными
шестиугольниками со стороной h и вершины будем считать узлами шестиугольной
сетки. Звездой назовем совокупность четырех узлов, указанных на
рис. 6 (на рис. 6 указаны две звезды с различным расположением
узлов относительно осей координат). Обозначим
Дл"^
4(tti + «2 + "a —Зи0)
3/i2

2]
§ 1. УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА
87
Доказано, что
|ДА*--(Ди)о1<1.36Л<!<|>Л|
т. е. порядок аппроксимации уравнения А« = / уравнением Khuh —
= (/H в классе С3 равен единице [25], [30].
Пример 4. Улучшение аппроксимации за
счет расширения звезды. Для квадратной сетки и
пятиточечной звезды порядок аппроксимации в классе С4
7
3
]6
]2
0
4
8
/
5
Рис. 6.
Рис. 7.
уравнения B.14) уравнением B.16) равен двум и q = 3.
Если взять девятиточечную звезду вида, изображенного
выше на рис. 4, то оказывается, что коэффициенты с0,
сх, ..., с8 нельзя подобрать так, чтобы #^4. Если взять
девятиточечную звезду вида, изображенного на рис. 7, то,
полагая
Л' _ l6(ul + u2j-u3 + Ui)~-(us + Ub + u7 + u%)~-60u0
адил = 12Д2 ,
будем иметь
|Дли —(ДиH
\~M^h\
т. е. теперь порядок аппроксимации в классе С6 уравнения
B.14) уравнением ДлИЛ=(/H равен 4 (теперь # = 5).
О сеточных аппроксимациях оператора Лапласа см. [21,
[25], [30],. [54], [75], [116].
в) Улучшение аппроксимации за счет
выбора оператора П£. Многоточечные
уравнения. В приведенных выше примерах оператор ПЪ, ставил в

88
ГЛ. II. МЕТОД СЕТОК
[2
соответствие каждой звезде значение правой части /(X)
в центре звезды. Можно попытаться улучшить
аппроксимацию за счет того, что П£ определяется как линейная
комбинация значений /(X) в узлах звезды. Пусть Lu, Q, Qh
и звезда определены так же как в б). Пусть числа с[, . .., c'k,
dx, . . ., dk подобраны так, что
с\и(Х1)+-*. + ски(Хк)-
- [dx (Lu)Xl +...+dk (Lu)Xk] = О B.41)
для всех, целых рациональных функций некоторой степени
#i>p относительно (х, у). Тогда естественно считать, что
уравнение
R,huh = c'1uh(Xl)+ ...+ckuh(Xh) =
= dJ{Xx)+...+dkf(Xk) B.42)
является сеточной заменой дифференциального уравнения
B.1). Считая центром звезды узел Хг и предполагая, что
удалось подобрать числа cv ..., ск так, что Rhuh в B.37)
совпадает с (Lu)xt для всех целых рациональных
функций степени #, и положив с| = сх,- ..., c'k = ckJ rf1 = l, d2 =
= d9=... = dk = 0, убедимся, что равенство B.41) имеет место
для всех целых рациональных функций степени q. Поэтому
не исключена возможность и такого выбора с[у . .., dki что
то же равенство B.41) будет иметь место для всех целых
рациональных функций степени д1>д* Для определения
коэффициентов cv ..., dk служит система линейных
однородных уравнений
X {Xj—x^-btyj—^)«а-Ь J = 0, B.43)
0<а, 0<а2> а, +а ^qv

2] § 1. уравнения эллиптического типа 89
от решения которой следует потребовать выполнения условия
21^1=1. B.44)
Если система B.43), B.44) однозначно разрешима, то
для любой и (#, у) £№ + 1 имеет место неравенство
| RhU — Ul {Lu) | < CAf«?'+1) A*-'+1. B.45)
Уравнения вида B.42) называются многоточечными
сеточными уравнениями. Как следует из неравенства B.45),
порядок аппроксимации такими уравнениями уравнения B.1)
равен qY—p-f l.
Замечание. Пусть {Йл} —последовательность сеток с h —>0.
Пусть для каждого допустимого h образовано №h звезд и для
каждой звезды записано уравнение вида B.42). Тогда П^ есть
оператор, переводящий функцию / £ Fb №л-мерный вектор. Если:
a) F есть класс С0, б) выполняется соотношение B.44) и для каждой
звезды числа dj имеют один и тот же знак, то нормы \\ffy\\Fh и || / \\р
согласованы.
Пример 5. Уже отмечалось (пример 4), что для звезды рис. 4
нельзя подобрать коэффициенты с0, cv ..., с8, дающие лучшую
аппроксимацию по сравнению с пятиточечной звездой. Числа
'____ 40 ' __ '_ '— ' — 2
С°~ 12/i2' cl~c2-c8-c4-з/l2,
'- '_ '- '-_!_ л -А
Сь~~сь'—С7~съ~ 5/г2' °~ 3 '
удовлетворяют системе B.43), B.44) для L = Д (а00 = а10—а01 = ап = 0,
а10 = а02=1, р = 2, <?! = 5), и поэтому сеточное уравнение
Длц^ _
= 4 (Па + й ( (/)l + ^* + ^8 + tf>*> B'46)

90
ГЛ. It. МЕТОД СЕТОК
[2
аппроксимирует уравнение B.14); можно доказать, что для и (х, у)£ С9
имеет место неравенство
|дл" —||-(A")o + ^[(A«)i+(A«)i + (A«)8 + (Aw)j|
<йм(в)-
В книге [30] приведена таблица многоточечных формул
для операторов Лапласа и бигармонического для квадратной
и треугольной сеток, а также для одномерных операторов
W, а", д'", uIV
Пример 6. Улучшение аппроксимации за
счет выбора ГЦ, зависящих также от
производных функций /(X). Для девятиточечной звезды
(см. рис. 4) и и£С* легко получить на основании формулы
Тейлора следующие формулы:
«1 + «1 + и1 + «4 —*«о
/А ч , 2/г2 (д*и . д*и\ ,
+ 6 ! V дх*+ %V0 + 8 ! \дх*+ дх*+ ду*+ %VJ
И5 + д6 + а7 + а8~4а0 = /г2[2(ДаH+^(-^4-
+ дх2ду2 + dy*)Q ~i~ G\[dx* + Dдх*ду2 ~1~ ° дх2ду* + ду*H"+"
где невыписанные слагаемые содержат производные восьмого
порядка функции и (х, у) в некоторых промежуточных
точках лучей, соединяющих центр с точками 5, 6, 7, 8 звезды.
Если первое из этих равенств умножить на 4 и сложить со
вторым, то после деления на 6/г2 получим
■т 4(ц1+ц, + ц, + ц4) + (ц, + цб + ц7 + ц8)----20ц0 __
= (Д«>. + £ D-«). + J* [(ДЧ + 2 (^)J +
+£,[«(£+ ■••)+(£+•••)

2] § 1. уравнения эллиптического типа 91
где
Д2а = Д(Да)^4 + 2
д*и
д*и
дх*
дх2ду2
д*и
ДЪ==Д(ДЪ) = ™+3
д«и
дх*
дхЮу2
1 ду*>
д*и д9и
дх2ду* + ар'
Если положить
(nU/)H-(/H+f>/)„+#0 [(д.д + г^)] ,
шпроксимации
Vft=n°ft(/)
то в классе С8 порядок аппроксимации уравнения B.14)
уравнением
B.47)
520/ie
равен шести и оценивается величиной ^-~-М(Ц) [30].
Замечание 1. Левые части уравнений B.46) и B.47)
совпадают.
Замечание 2. Если в примере 3 (треугольная сетка)
положить (П£(/)H = (/H + -(Д/H, то для ы£С6 вместо оценки B.40)
справедлива оценка [25]:
]ДЛ"-П°(Д«)|^М<в>.
Пример 7. Биг армонич ее кое
Пуассона. Так называется
дифференциальное уравнение
уравнение
д*и
д*и
//
0
8
д2 д*и ~
А Uz==~dx~*+ дх2ду2 ' ду*~~
= /(х,у). B.48)
Для получения сеточного
уравнения, аппроксимирующего
уравнение B.48), можно
поступить следующим образом.
Каждый узел (i, j) квадратной
сетки будем считать центром
тринадцатиточечной звезды, которая является объединением
всех узлов пятиточечных звезд, имеющих центры во всех
Узлах пятиточечной звезды с центром в (/, j) (нумерацию
узлов см. на рис. 8).
10
12
Рис. 8.

92 гл. и. метод сеток [3
Если положить Ан = АЛ (ДЛ), то получим
аи»*- дй(дЛ)=4 ["9++V"8~4Ui +
I ^5 + ^10 + ^6 + ^0 —4ц2 Ир + Ив + Цц + Цт—4ц, ,
I" ^2 I" /р " "*-
, а8 + Ц0+Ц7 + Ц12 —4ц4 ^ ц1 + ^2 + гг3 + ^4—4ц0] __
"*" Л2 /i2 J "~
= *i[20u0-S(u1 + u2 + us + uJ + 2(u5 + ui + u1+u&) +
+ к+«1.+«1,+«1«)]-
Пусть QA—совокупность всех узлов квадратной сетки,
попавших внутрь или на границу Г области Q, для
которой решается уравнение B.48). Для каждого внутреннего
(в смысле тринадцатиточечной звезды) узла (i,j)€Qh
запишем уравнение
(Mu)it / = (/k/. B.49)
В классе С8 порядок аппроксимации уравнения B.48)
уравнением B.49) равен двум (оценивается величиной
^Л*М<6)) [25].
3. Вопросы разрешимости, сходимости и оценки
погрешности, а) Разрешимость сеточных
уравнений. А. Сеточный аналог принципа максимума. Известно
следующее свойство (принцип максимума) некоторых
эллиптических операторов [61]: если функция v(X) такова,
что L^^O в Й, то ^(^0 не может достигать в Q
положительного относительного максимума.
Для ряда сеточных операторов, возникающих при
аппроксимации эллиптического дифференциального уравнения, имеет
место свойство, которое можно назвать сеточным аналогом
принципа максимума.
Занумеруем все узлы сетки Qh номерами от 1 до Nh;
эту нумерацию назовем общей. Каждый узел X.£Qh (с
общим номером j) будем считать центром некоторой звезды
и принадлежащим этой звезде; не исключено, что звезда
состоит из одного узла—центра. Всякий узел звезды, от-

3]
§ 1. УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА
93
личный от центра, назовем соседним для центра. Пусть
kj—число соседних узлов для X/, занумеруем соседние для
Xj узлы числами от 1 до k- и эту нумерацию назовем
внутренней. Через j(i) обозначим общий номер узла,
имеющего внутренний номер i в звезде с центром в Xj.
Пусть каждое уравнение сеточной системы имеет вид
(/Vft)y= А?>цй(Xj A)) + ... + А^иДХ, ,*,,)-
-A^u^X^Fj B.50)
(у=1,2, ...,Nh),
где коэффициенты А^ удовлетворяют условиям
Af>0 (i = 0, l kj), \
ki ... ... {
24" < 4" (y=i,2, ...,лд. |
Если узел Х;. таков, что 2$А(/} ==А^\ то Х^
B.51)
назовем
узлом 1 рода; если ^A\f)<zAf\ то—узлом II ро<^а.
;=i
Предположим: I) имеется хотя бы один узел II рода;
2) если имеются узлы I рода, то каждый из них можно
соединить ломаной хотя бы с одним узлом II рода так, что
все вершины ломаной (кроме конца) суть узлы 1 рода и
каждый последующий узел является соседом предыдущего
(принадлежит звезде с центром в предыдущем узле).
Лемма 1. Если сеточная функция vh такова, что
(**«*)/> 0 (У=1. 2 Nh),
то
vh(X,)*zO (у-1,2, ...,Nk).
Лемма Г. Если сеточная функция vh такова, что
(#М<° v=1'2 N^
то
vh{Xj)^0 (;'=1,2, ...,Nh).
Из лемм 1 и Г получаем
Следствие. Если (Rhvh)j = 0 (/=1,2,.,., Nh), то
Wy) = 0 (/=1,2, ...,Nh).

94 ГЛ. И. МЕТОД СЕТОК [3
Последнее означает, что однородная система,
соответствующая системе B.50) линейных уравнений, имеет лишь
нулевое решение; как известно, отсюда следует отличие от
нуля определителя системы и ее однозначная разрешимость.
Отсюда
Теорема 2. Система B.50) разрешима и имеет
единственное решение {если выполнены указанные выше
предположения о коэффициентах и узлах 1 и II рода).
Пример 8. Система B.11), B.12) однозначно разрешима.
Действительно, каждое уравнение системы B.11) можно
записать в виде
(Rhuh)L i = A^fui+lt f+Af,W /+i + 4!><-i. / +
+ Atfa, ,., -A\4)ui9 j = (Д., р B.52)
причем коэффициенты A\,\ (k — 0, 1, 2, 3, 4) в силу условий
B.19), B.20) и B.21) теоремы 1 (предполагаем эти условия
выполненными) удовлетворяют неравенствам
^/>0 (k = 0, 1,2,3,4), 2 4*}<4?/-
k = l
Уравнения B.12) можно переписать так:—#/,/ =— 4>(Qi,/)>
и, следовательно, здесь Л/,/ = —1, а звезда состоит из
одного центра. Граничные узлы являются узлами II рода.
Кроме того, из предположений о сетке Q^ для теоремы 1
следует наличие ломаной, соединяющей узлы I рода (если
таковые есть) с узлами II рода.
Пример 9. Система B.11), B.13) однозначно
разрешима. Уравнение B.13) переписывается в виде
4^,/'-(l+4)^,/=-9(Q/>/),
и если 6^0, то звезда с центром в (/, J) состоит из двух
узлов: (/',/) и (/, j). Так как г^^+тг» т0 граничный
узел является узлом II рода. Остальное, как в примере 8.
Пример 10. Сеточные уравнения B.16), B.17), B.18) однозначно
разрешимы.
Замечание. Пусть в уравнении B.31) коэффициенты с(х)
и g (*) удовлетворяют условиям: \с(х)\<М, g(x)^0. Тогда для

3] § 1 . УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО Т1ША
95
2
h < -тт система сеточных уравнений B.33) для внутренних узлов и
B.36) для граничных узлов удовлетворяет принципу максимума и
однозначно разрешима. То же можно утверждать, если граничные
условия B.32) учтены линейной интерполяцией или по способу
Микеладзе.
Пример 11. Пусть для приближенного решения задачи
Дирихле для уравнения ku—gu — f(g^0 в Q) применяют
треугольную сетку (см. п. 2, пример 3, 1)) со стороной К, Для внутреннего
узла (в смысле семиточечной звезды, рис. 5) имеем
2 / 4 \
3^2 (ui + "а + «• +  + «s + «в) — ( ,-i + te)„ ) "о = (/)о. B-53)
и, следовательно, внутренний узел является узлом I рода, если
(Я)о = 0» и Узлом II рода, если (gH > 0.
В каждом граничном узле значения «^ назначаются простым
сносом. Так полученная система линейных уравнений однозначно
разрешима.
Аналогичное заключение можно сделать для системы,
полученной употреблением шестиугольной сетки (см. п. 2, пример 3, 2)).
Замечание. Также однозначно разрешима система уравнений
2 4 / h2 \
и B.12), аппроксимирующих задачу Дирихле для Аы = / (см. п. 2,
замечание 2 к примеру 6).
Пример 12. Для приближенного решения задачи Дирихле
для уравнения Д«—gu = f (g^O) применим прямоугольную сетку
и девятиточечную звезду (см. рис. 4). Для каждой звезды, все узлы
которой принадлежат Qh (для каждого внутреннего узла в смысле
этой звезды), напишем многоточечное уравнение (см. п. 2, пример 5):
4(Ux + ut + u9 + uJ + {ug + u% + u7 + uB)—20а0_
6>h2 ~
= | ((По + feH "о)+15 Mi+te>i «i + • • • Ь
получающееся из B.46) заменой f на f + gu. Итак,
3/i2
i—^fe)i)«i + ( i—^te).)«« + (i—^te).)««+
+ [i-?feL
+ ^2( + «6 + «7 + «8)~
/ 10 2 \ 9 1
-{^+ji8)o)u0^j(f)<>+12W)i + (fk + (f)i + m- B.54)
О
Для ft2 < коэффициенты при uv u2, ... , u8 положительны,
и в силу неотрицательности g их сумма не больше коэффициента

96
ГЛ. II. МЕТОД СЕТОК
[3
при и^ так как
3/i2
[4 —j №г+(й,+й),+te)j] + -^ -
:ЗЙ«—12((g)l + (g)z + (^)з + (ё)*> ^ 3/?'
J0_ 2
3/t2+ 3
fe)e.
Поэтому всякий внутренний узел является узлом I рода, если g==0,
и может оказаться узлом II рода, если g^O. Если в граничных
узлах назначить uh простым сносом, то система всех уравнений
однозначно разрешима.
Замечание 1. Для решения уравнения Пуассона можно
воспользоваться уравнением B.47). Система B.47), B.12) однозначно
разрешима, так как левые части B.46) и B.47) совпадают.
Замечание 2. Если в примерах 11 и 12записать граничные
уравнения по типу B.13), то полученные системы будут также
однозначно разрешимы.
Пример 13. Пусть поставлена смешанная задача: найти
решение и (х, у) уравнения B.8) при условии, что задано
значение и (х, у) на некоторой части 1\ границы Г, а в
каждой точке Q£T—Г1 = Г2 задано значение i|>(Q)
производной от и(х, у) по направлению /(Q), образующему острый
угол a(Q) с внутренней нормалью, не превышающий
некоторой величины а0.
Для составления сеточных уравнений для квадратной
сетки запишем во внутренних узлах (в смысле иятиточеч-
ной звезды) уравнение B.11); в
граничных узлах, для которых
ближайшие точки границы лежат на
Г17 запишем уравнение B.12)
(простой снос). Пусть (/, j)—
граничный узел, для которого ближайшая
Щь,]) точка Q^ у границы принадлежит
Г2. Рассмотрим пятиточечную
звезду с центром в (/, }).
Предположим, что среди узлов звезды,
принадлежащих Qh, имеются два таких,
что лучи из (/, j) к этим узлам образуют острые углы \i
и К с l{Qi,j)', для определенности пусть это будут узлы
(*'+!» Л и (h J—1) (Рис- 9)- Тогда для этого граничного
узла запишем
да ui+h~uuj , uUj-i — uU] л , ,r\ \
___« Lh Lcos^ + ^__ *cosX = !>(Q,,y)
МЛ

3] § 1. УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА 97
или
cos \i
Ui + u/~
cos A,
ИГ"*'/-*'
COS Ц-fCOS X
««,/=*(Q/,y)> <2-55)
Пусть луч,
т. е. имеем уравнение вида B.50), причем (/, j)— узел
I рода.
Если все граничные узлы, для которых ближайшие точки
границы принадлежат Г2, обладают описанным свойством
(острые углы между /(Q) и лучами из узла), то для
каждого такого узла может быть записано уравнение B.55).
Совокупность уравнений B.11), B.12), B.55) однозначно
разрешима, если имеется хотя бы один узел, для которого
записано уравнение B.12), или если среди внутренних узлов
имеется хотя бы один узел II рода (что возможно, лишь
если g^z 0).
Укажем другую сеточную замену для ^-.
проходящий через граничный узел
(/, у) в направлении l(Qii ;),
входит внутрь одного из квадратов
сетки, имеющего вершиной узел
(/, Д и пересекает
противоположную для узла (/, j) сторону
квадрата в некоторой точке Q,
лежащей между ближайшими к
ней узлами (i'y /) и (/", /).
Если и (х, у) была бы линейной
на отрезке между узлами (i\ /) и (/", /), то имели бы
«(Q) = (l-f)(«V.r+f(«)r.r,
где К — расстояние от Q до (*'', /) (рис. 10).
Обозначая через oh A<а<]/2) расстояние от (/, у)
до Q, будем считать выражение
Ю'
1-т)иг-г+1Гиг.г-Ч1
ah
B.56)
ди
сеточной заменой для -^ [ПО]. Граничный узел, уравнение
для которого получается заменой левой части
уравнения B.55) на выражение B.56), будет также узлом I рода.
С. Г. Михлин и X. Л. Смолицкий

98 ГЛ. II. МЕТОД СЕТОК [3
Замечание 1. Для эллиптического уравнения B.8) способ
замены производных конечно-разностными отношениями приводит
к сеточной системе B.11), аппроксимирующей уравнение B.8) и
образующей вместе с B.12) или B.13) однозначно разрешимую систему
(как удовлетворяющую принципу максимума).
Если рассмотреть эллиптическое уравнение более общего вида
д2и , 0 д2и , ,д2и , да , ,ди , ,0 с~
aW>+2e^+bW+c^+d<ry-eu=f> B-57)
{г2 < аЬ)
то в случае ефО замена производных конечно-разностными
отношениями приводит к системе, вообще говоря не удовлетворяющей
принципу • максимума. В статье [125] доказано, что для каждого
эллиптического уравнения B.57) (при некоторых общих
предположениях о коэффициентах а, Ь, ё) можно указать звезду (для
квадратной сетки) и уравнение вида B.50) (с коэффициентами,
удовлетворяющими условию B.51)), аппроксимирующее уравнение B.57).
Замечание 2. Для уравнения B.57) в случае выполнения
условий:
а) \е(х, у)\< min (а (х, у), Ъ (х, у)),
р) \c(xt y)\<M(a{x> y)-\e(xt «/)(),
\d(x, y)\<M(b(x, y)-\e(xfy)\),
Y) g(*> У)^0,
можно указать сеточное уравнение, звезда которого является частью
девятиточечной, удовлетворяющее условию B.51) и порядок
аппроксимации которого равен 2. Это уравнение таково:
Ц)—2ц0 + ц8 , /м и,—2и0 + и4 ,
(а)о ^ г Wo jp г
+ 2(е)
u5 + u1 + 2u0—(al + u2 + us + ai)
> 2/i2
и2—и*
+ (с)о^2JT + W» ^ШГ-№м = №о, B.58)
если (еH5>0;
их— 2и0 + и3 и2—2ц0 + ц4
(а)о ^5 гF)о дг г
, 9/<л Ц1 + Ц2 + Ц3 + Ц4 — (Цв + Ц8 + 2ц0) ,
+ /(^° 2Л5 +
+ (с)о ^^ + №о ^-4-(^o = (f)o, B.59)
если (еH<0.
2
Для /i < -т-r в силу условий а), C), у) коэффициенты при их, ...
. .., и8 неотрицательны, а коэффициент при ий отрицателен и его
модуль не меньше суммы всех других коэффициентов. В случае

3] § 1. УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА 99
(еH > 0 звезда состоит из узлов 0, 1, 2, 3, 4, 5, 7; в случае
(еH<0—из узлов 0, 1, 2, 3, 4, б, 8; в случае (еH = 0—из узлов
О, 1, 2, 3, 4.
Б. Сеточный аналог самосопряженного эллиптического
дифференциального уравнения. Известно ([63], см. также
гл. III, § 3, п. 4 настоящей книги), что решение задачи
Дирихле для самосопряженного дифференциального
эллиптического уравнения
i =1 /=1 \ //
(a{j(X) — коэффициенты положительно определенной
квадратичной формы, g{X)^0) доставляет минимум функционалу
F[U]ES
в классе функций, обращающихся в заданную на Г функцию
ф(А'); наоборот, всякая функция и(Х), доставляющая
функционалу B.61) минимальное значение среди функций,
обращающихся в ф на Г, оказывается решением задачи Дирихле
для уравнения B.60). Этот факт может быть положен
в основу вывода сеточных уравнений, заменяющих задачу
Дирихле для уравнений B.60). Для построения системы
таких уравнений строят аналог функционала B.61), заменяя
д— разностными отношениями и интеграл — интегральной
суммой.
Этот сеточный аналог Fh[uh] является квадратичной
функцией (сумма квадратичной и линейной форм) от
значений uh, квадратичная форма которой положительна.
Эта квадратичная функция ограничена снизу для
сеточных функций, принимающих фиксированные заданные
значения в некоторых узлах (например, в граничных узлах
приписываются значения простым сносом). Тогда уравнения,
которым удовлетворяют остальные значения сеточной
функции, получаются приравниванием нулю производной от Fh [uh]
по каждому uh(X), где Xj—узлы с незакрепленными
значениями uh. Так полученная система сеточных уравнений
будет однозначно разрешимой.
да да
2/и
dQ B.61)
/ = 1 1
4*

100 гл. и. метод сеток [3
Пример 14. Рассмотрим задачу
д ( да , да \ . д { да . , да \ , \
Ш[аШ + еГу)+Гу[е^ + Ь^)-^==^\ B.62)
и |г = ф, '
где функции а(х, у), Ь(х, у), е(ху у) таковы, что я>0,
ft>0, ab—£2;>0. Для определенности в качестве сеточного
аналога Fh[uh] возьмем
+ (g)i,/u + 2(fkj4/\> B-63)
причем подразумевается, что заменены нулями конечно-
разностные отношения ^ — или ' , — для тех
(/, у), для которых узел (/+1, у) или (/, у+1) не
принадлежит Qh. Все узлы Qfy делим на внутренние и граничные
в смысле пятиточечной звезды. Для граничных узлов
записываем B.12) (простой снос), а для каждого внутреннего
узла (г, у) получаем уравнение вида
^.)iUi+l,J + Af,)uh/+l+A(;,}ui_1>J + At)iuiiJ_1 +
. +^к-1)у+1 + ^)"-+1.у-1-^)/«/,у = (Д,у, B-64)
где коэффициенты A\t \ определяются формулами:
,(i) _(*)»-,/+(*)ь/ -(,) __F)/,у+(*)/,у
.C) _ (g)j-l, /+(*)/-!,/ .D) Wl, /-! + (*)/, /~1
,F) __ (g)t-l, У -(8) _ ^h /-1
Л/. / Д2 » л*. / — Аа i
причем л[* /И1 /1 заменяется нулем, если узел (/—1,у+1)
[(/+1, у—1)] не принадлежит Qh.

3] § 1. УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА Ю1
Система сеточных уравнений B.64), B.12) однозначно
разрешима (если ab — е2>0). Матрица этой системы
симметрична и отрицательно определенна.
Введем обозначения:
Uh*~ h y Uhx— k
Uhy~ h ' Uhy-~~ h
Тогда уравнение B.64) примет вид
{auhx + euhyU + (euhx + Ц>,)-=/. B.65)
Уравнение B.65) можно рассматривать как полученное
из B.62) заменой производных разностными отношениями.
Если a=:b=\, e = g = 0 (уравнение Пуассона), то
B.64) совпадает с B.16).
Пример 15. Уравнения, близкие к
самосопряженным. Общее эллиптическое-уравнение вида
• д2и , 0 д2и . , д2и , * ди , .~ ди х
при достаточно гладких коэффициентах a, b, e можно
записать в виде
ди . ди\ , д ( ди , , ди\ . ди .
адх + еГу)+Уу[еГх + ЬГу) + Сд-х +
д_
дх
, ди
+ d^-gu=ft B.66)
где
* да де , ,.» де дЬ
дх ду ' дх ду
Предположим, что коэффициенты a, b, e удовлетворяют
условию: существует такое положительное число а>0,
что для всех (х уу) £ Q наименьшее собственное значение
матрицы , не меньше а (из этого предположения
следует, что а>0, Ь>0У аЬ—е2>0 для (х, у)£&). Будем

102
ГЛ. П. МЕТОД СЕТОК
[3
говорить, что уравнение B.66) близко к самосопряженному,
гели для всякого положительного достаточно малого числа е
справедливо неравенство
Пусть для уравнения B.66) поставлена задача Дирихле.
Для квадратной сетки Qh в граничных узлах (в смысле
пятиточечной звезды) запишем уравнение B.12), а для каждого
внутреннего узла (i, J) напишем уравнение, получающееся
из B.65) добавлением в левой части слагаемых
[c)t> J h "т (d)i> J h '
du . , du , ^
аппроксимирующих £-_--[--a-r- (эти уравнения обозначим
B.65')). Если уравнение B.66) близко к самосопряженному,
то полученная сеточная система уравнений B.12), B.65')
однозначно разрешима [35].
х
Пример 16. Умножением на р(х) = е° уравнение
B.31) приводится к так называемой самосопряженной форме:
г d
L^Tx
p(x)
-*(*)«=/,(*) , B>67)
dx
(q(x)=p(x)g(x), f1{x)^p(x)f{x))>
являющейся частным случаем уравнения B.60) для л=1,
если заменить а1г на р{х), g(x) на q(x) и f(x) на /г{х).
При этом функционал B.61) принимает вид
1
Ft [и] == J [р (х) (иТ+ Я (*) и2 + 2/, (х) и] dx, B.68)
и остается напомнить об эквивалентности задачи на минимум
функционала F1[u] и задачи B.67), B.32) (одномерной
задачи Дирихле).

3j § 1. УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА
Для сетки xk=kh (fe-=0, 1, ..., W; Ь = ^) введем
сеточный аналог функционала B.68) в виде
FuW^»sMx»+i)(V),+
£=о
+ ?(х,L + 2/(х,)к,].
Как и в примере 14, придем к следующей системе N—1
линейных уравнений относительно иг, ..., ttN^x (обозначая
р(** +
/,(**)=
4)=
=/,*)=
Р*+
Z
«А + 1-
1. /Г
2
iff*.
р(хк-
2
/г
2
ц*-
)-
-"л
/г
Л-
-1
2
Я -<7А=Л* B.69)
(*=1, 2, ..., N-1; и0 = а, и^=Р).
Система B.69) однозначно разрешима, а ее матрица
симметрична и отрицательно определенна. Сеточная
система B.69) удовлетворяет принципу максимума.
Пример 17. Пусть Qh—квадратная сетка в области Q
и Ql — совокупность внутренних (в смысле пятиточечной
звезды) узлов. Положим
(/. 1)^1
!<Л,у»„/]
Пусть известны значения uh в узлах, не являющихся
внутренними в смысле тринадцатиточечной звезды (см, п. 2,
пример 7). Тогда Eh[uh] является квадратичной функцией
(сумма квадратичной и линейных форм) от значений
функции uh во внутренних (в смысле тринадцатиточечной звезды)
узлах, квадратичная форма которой положительна
определенно. Eh [tift\ ограничена снизу и для некоторых
значений uh во внутренних узлах достигает минимума. Эти
значения ui% p доставляющие минимум для Eh, удовлетворяют

104 ГЛ. II. МЕТОД СЕТОК [3
уравнениям (см. B.49))
(А*"й)/,/=р120в'./-8^+«,У+а'./+. + «/-.,/ + "/,/-.) +
+ ("*+., /+«/, /+. + «,■-„ , + «,, у_»>1 = </)г, у. B-49)
число которых совпадает с числом внутренних узлов.
Предполагается, что в этих уравнениях ui+^ J+J] (| 11 -|~| т) | <;2)
заменены их известными значениями, если узел (i-\~ £, у'+Л)
не является внутренним. Полученная система уравнений
однозначно разрешима [34].
Если ставится краевая задача для бигармонического
уравнения Пуассона B.48) и сеточные краевые условия
составлены так, что позволяют указать значения и£ , в
граничных узлах (для тринадцатиточечной звезды), то система
B.49), аппроксимирующая уравнение B.48), однозначно
разрешима.
б) Корректность сеточных уравнений. Пусть
для приближенного решения задачи B.1), B.2) некоторый
сеточный метод указывает совокупность сеток {Q}hy h—*0,
и для каждой сетки йл—уравнения B.22), B.23). Пусть
в образовавшихся векторных пространствах введены нормы.
Определение. Сеточная задача B.22), B.23)
называется корректной, если по любому е>0 можно указать
6>0 такое, что для каждого допустимого h и любых двух
сеточных функций uh и uh из выполнения неравенств
1|ЯА-я***1к<«. B-7°)
lk/A«ft-^"/,lk<« (/=1, 2, ...,.*) B.71)
следует
K-«*lk<*. B-72)
Замечание 1. Если сеточная задача корректна, то для
каждого набора (Д, ф1Л, ..., ф,л) может существовать
не более одного решения uh£Uh задачи B.22), B.23).
Замечание 2. Пусть Rh и rih — линейные операторы
(этого естественно ожидать, если L и 1{ — линейные
операторы). Если сеточная задача B.22), B.23) однозначно
разрешима для каждого допустимого h, то для каждого такого h
существуют такие положительные числа Nh и NiHi что для'

3] § 1. УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА 105
любой сеточной функции uh имеет место неравенство
IIЧ Ik < Nh || Rhuh \\Fh + 2 N,ft || rihuh ||Фг.л. B.73)
г = 1
Для того чтобы сеточная задача была корректной,
необходимо и достаточно, чтобы Nh и Nih были ограниченными,
т. е. необходимо и достаточно существование таких
положительных чисел N и Ni (не зависящих от h)> чтобы для
любой сеточной функции имело место неравенство
Klk<* №*lk+ 2^-lkAlk, B-74)
i = \
А. Корректность сеточных уравнений,
удовлетворяющих принципу максимума. Пусть для каждого
допустимого h совокупность Nh сеточных уравнений,
удовлетворяющих принципу максимума, разбивается на £+1 групп
соответственно по Л^, N\y ..., Nl уравнений (Nh + Nh+ ...
Совокупность левых частей /-й группы будем
рассматривать как операторы /%, переводящие Л^-мерные векторы в
Л^-мерные векторы.
Отдельную произвольную составляющую вектора будем
обозначать скобками [ ], помещая между скобками вектор.
Под нормой будем понимать максимум модуля составляющих
вектора.
Лемма 2. Если существует s -\-1 функций
vQ(X), vx(X), ..., vs(X)
таких, что
[/?^yW]<{_J; ffi (i,j=0,\,...,s),B.75)
то для любой сеточной функции uh имеет место
неравенство
Kii<i)tyK"*ii. B-76)
i-o
где
N:=^ max г;, (X).

106
ГЛ. II. МЕТОД СЕТОК
[3
Лемма 2 позволяет доказать корректность сеточных
уравнений примеров 8—12. В каждом из этих примеров
система разбивается на две группы уравнений: для
внутренних узлов и для граничных узлов. Уравнение для каждого
граничного узла X, таково, что
4o)-i] ^=1.
1=1
Поэтому vt(X)^\ удовлетворяет условиям (/?д<У1)у = — 1
для каждого граничного узла X, и {Rhvx)j^Q Для каждого
внутреннего узла X,. Пусть функция v0 (X) положительна
в Q и такова, что для каждого допустимого h и каждого
внутреннего узла X, имеем (/?дт>0).г^—1. Для граничного
узла X. имеем
< 2 4<Ч (*,«>)< max t,0(*) ±A(p = maxt-0 (X)(A?}- 1).
Если граничное условие учитывается простым сносом, то
А(р =^1 и поэтому имеем (/?/г*>0)у<0, т. е. две функции v0 (X)
и vx {X)^ 1 удовлетворяют всем условиям леммы 2 для 5—1.
Для сеточных граничных условий B.13) имеем Л/0)— 1 =
= -7-<1; нетрудно видеть, что функция v0 (X) = v0 (X) -f-
+ maxv0(X) такова, что две функции v0(X) и vx{X)=l
удовлетворяют условиям леммы 2 для 5=1. Аналогичное
заключение верно и для уравнения B.17).
Поэтому, если существует положительная в Q функция
v0(X) такая, что {Rhv0).^—1 для всякого внутреннего
узла, то для примеров 8—12 имеем на основании леммы 2
1|"Л||<^1|ЛАиА|| + ||гА«А||, B.77)
где
а) N=maxv0(X) для граничного уравнения B.12);
б) N=2maxv0(X) для граничного уравнения B.13) и
B.17).

3] § 1 . УРАВНЕНИЯ ЭЛЛИПТИЧРХКОГО ТИПА Ю7
Укажем несколько функций v0(X) для примеров 8—12.
1) Если c = d2s0, то vQ(X) = C — [А (х—х0J + В(у —у0)% где
А, В, С — положительные постоянные и (х0, у0)—произвольная
точка.
Постоянные А и В легко выбрать так, чтобы Lv0^ — 1 для
всех точек области Q; тогда будет выполнено и [i?/^0]^— Ь так
как R/iVq — JJh(Lv0) для v0. Постоянная С выбирается настолько
большой, чтобы v0(X)^0 в Q.
Например, если область Q находится в эллипсе
то полагают
М*> У) = Ср{х, у),
где
2 min
а(х, у) Ь(х, у)\
(х, у) € Q L Р Я А
В частности, если а--~Ь^\ (оператор Лапласа) и p = q — r, то
М*» y)^j-[r2 — (x—x0J~{y-y0J].
2) Если c2 + d2^0, то предложены следующие два вида
функций v0{x, у) [30J, [83]:
а) Если область расположена в эллипсе [i (x, у)^0 и
коэффициенты а, Ь, с, d таковы, что функция
ih/v ,л — а (*' у) 1 Ь (*' У) 1 с (*» ^) 1 1 rf (*» #) 1
1>(*. </)= —-ь- + —^ - -
имеет в Q положительный минимум г|э0, то полагают [30]
v°(x* У^яуР^*' у^
р) Если p = q = r, s~ min (a+ 6) (s >0), то [83]
(a;, y)eQ
V» (*' ^ = 2^ ИГ*-*А W^ + ^^o)8]),
М2-М
где Л =—j1— , М > 0 из условия B.19).
Таким образом, сеточные уравнения примеров 8 —12 корректны.
Корректна также сеточная задача B.33), B.36).
Б. Корректность сеточных уравнений, близких к
самосопряженным. Обозначим через С/jJ множество сеточных
функций, определенных на квадратной сетке плоскости и

108
ГЛ. II. МЕТОД СЕТОК
[3
равных нулю в каждом узле, не являющемся внутренним
узлом (в смысле пятиточечной звезды) для Qh. В £/° введем норму
II "* Ну. =
h
u./)«Qh L х 7
согласованную с функциональной нормой
||a||t/e=]/'S[e, + |grada|t]dn
й
в классе U0 функций и (дг, у), непрерывных в Q вместе с
производными первого порядка. Через Fh обозначим
множество сеточных функций, определенных на множестве Qjj
внутренних узлов; в Fh введем норму
Шк=У^ X (Л, уI .
(/. У) «а£
согласованную с функциональной нормой
в классе F функций /(#, у), непрерывных в Q. Обозначим
через (Rhuh)^ , левые части уравнений B.65').
Имеет место утверждение: если уравнение B.66) близко
к самосопряженному, то существует такая положительная
постоянная N (зависящая от а, г и размеров области Q),
что для любого допустимого h и любой функции uh £ Uh
верно (см. [35]) неравенство
l|e*llt,.<^||^A||Ffc. B.78)
h
в) Теорема о сходимости и оценке
погрешности [83]. Теорема 3. Пусть выполнены условия:
а) задача B.1), B.2) имеет, и притом единственное,
решение; (J) уравнения B.22), B.23) аппроксимируют
уравнения B.1), B.2); у) сеточная задача B.22), B.23) имеет

4] § 1. УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА Ю9
решение uh £ Uh для каждого допустимого h; б) сеточная
задача B.22), B.23) корректна.
Тогда при h—>0 сеточное решение сходится к точному
решению, т. е.
l\m\\uh-u(X)\\Uh = 0. B.79)
Добавление. Если к „тому же операторы Rh и rih
линейны, то имеет место неравенство
\\uh-u(X)l\uh^N\\Rhu-Ul(Lu, /,e, ..., /,и)||^ +
S
+ ^{\\г1ни-Щ(и, 1ги, .... /,и)||ф.А, B.80)
1 = 1
и если функции a(h) и at(h) оценивают аппроксимации (см.
B.27) и B.28)), то
S
К-и W l\uh^MNa(h) +]У>1.Л/Л (ft). B.81)
i = i
Замечание 1. Правые части неравенств B.80) и B.81) могут
служить функциями со (h) в неравенстве B.7), т. е. в этом случае
найдена оценка погрешности.
Замечание 2. Может случиться, что сеточная задача B.22),
B.23) не является корректной, но числа Д/^ и Л//^ из неравенства
B.73) и функции a (h) и щ (К) таковы, что
S
(u(h)^MNha(h)+y£iMiNihai(h)—*0 при Л—*0.
/=i
В этом случае также имеет место сходимость сеточного решения к
точному и найдена оценка погрешности.
Мы сейчас используем теорему 3 для получения оценок
погрешности сеточного решения задачи Дирихле. Теорема 3
будет использована также и в других параграфах главы.
4. Сходимость и оценка погрешности для задачи
Дирихле, а) Сеточные уравнения, удовлетворя ю-
щиепринципу максимума. Задача Дирихле B.8), B.9)
при довольно общих предположениях о гладкости контура,
коэффициентов а, Ь} с, d, g и данных / и ф имеет, и притом

no
ГЛ. И. МЕТОД СЕТОК
[4
единственное, непрерывное в замкнутой области Q-f-Г
решение и (х1 у), некоторые производные которого могут
оказаться неограниченными в окрестности Г.
Если это решение и (я, у) настолько гладко, что и £ С4,
то для сеточной задачи B.11), B.12) или B.11), B.13)
имеют место оценки аппроксимации B.29), B.34), B.35) и,
следовательно, выполнены условия а) и |3) теоремы 3 для
U—C*. Кроме того, эти сеточные задачи разрешимы и
корректны, т. е. выполнены условия у) и S) теоремы 3. Поэтому
в силу линейности операторов Rh и rh в данном случае можно
пользоваться оценкой B.81). Приводим результаты, считая
для простоты сетку квадратной.
1) Система B.11), B.12) (простой снос).
Используя B.29), B.34), B.81) (/V, как в B.77), Nx = 1), получим
\\uh — u \\^NMh2+M{l)h = h(M{1) + NMh)^Ch,B.M)
т. е. порядок приближения равен 1. Это — оценка Гершго*
рина [117].
Если все граничные узлы лежат на Г, то правую часть
в B.34) можно заменить нулем и B.82) заменяется на
\\uh-u\\^NMh\ B.83)
т. е. порядок приближения равен 2.
2) Систем а B.11), B.13) (учет граничных
условий линейной интерполяцией). Используя B.29),
B.35), B.81), получим
|| Ufi _ а || < NMh2 -f ЖB)/г2 = (АГB) + NM)h2 = Ch\ B.84)
т. е. порядок приближения равен 2. Это — оценка Коллатца
[30].
Из сравнения B.82) и B.84) следует, что при одной и
той же достаточно мелкой сетке система B.11), B.13) дает
более точное решение, чем B.11), B.12).
Замечание. Для сеточной системы, учитывающей
граничное условие по Микеладзе (см. B.17)), имеет место также
оценка B.84).
3) Пусть поставлена задача Дирихле для уравнения B.8). Для
ее решения можно воспользоваться шестиугольной и треугольной
сетками, а также квадратной сеткой с уравнениями либо B.46)
(многоточечными), либо B.47) (учет производных функций f(x, #)),
учитывая граничные условия простым сносом.

4] § 1. УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА Ш
Если для каждого допустимого h некоторые из граничных
узлов не лежат на Г, то в оценке \\uh — u\\ имеется слагаемое Mwh
и порядок приближения не выше 1. Если область Q и сетка Qh
таковы, что для каждого допустимого h граничные узлы лежат на
Г, то можно надеяться на более высокий порядок приближения uh
к и. В последующем предполагается, что все граничные узлы лежат
на Г.
а) Пусть сетка шестиугольная (см. п. 2, пример 3, 2)). Если
цеС3, то
|| Uh — U ц ^ 1,36 A'MC)/i.
Р) Пусть сетка треугольная (см. п. 2, пример 3, 1)). Если аеС4,
то (см. B.40))
1|иЛ — и||<—j- h\
т. е. порядок приближения равен 2.
Если пользоваться той же сеткой и вычислять правые части
сеточных уравнений по формуле lf + —Af) , то в предположении, что
иеС6 (см. п. 2, замечание 2 к примеру б), получим оценку
7ЛШF)
у) Пусть сетка квадратная и область Q такова, что все
граничные узлы (в смысле девятиточечной звезды рис. 4) лежат на Г.
Пусть ugC6. Если воспользоваться уравнением B.46), то
ЛШF)
\\4-u\\^^~h\
Если иеС8 и пользоваться сеточными уравнениями B.47), то
,_ 520ЛШ<8>
U*fr-H||< з»8! *'
Из приведенных примеров ясно, что пользоваться «высокоточными»
уравнениями B.46) и B.47) имеет смысл только тогда, когда все
граничные узлы лежат на Г и есть уверенность в том, что иеС9 или
иеС* соответственно.
4) В 1) и 2) предполагалось, что и (х, у) еС4 Предположим
теперь, чтоэтонетак, иоиеС2. Тогда, используя B.30) вместоB.29) иB.80)
вместо B.81), убедимся в том, что \\uh—и\\—*0 при h—*0, т. е.
имеет место равномерная сходимость сеточного решения к точному.
Оценку погрешности в этом случае можно было бы выразить через
модуль непрерывности вторых производных точного решения а (л:, у).
5) Если и (х, у) не принадлежат С2, то нет уверенности в том,
что иь—у и равномерно. Если для достаточно мелкой сетки
уравнения B.11) записывать только для тех внутренних узлов, которые от

112
ГЛ. II. МЕТОД СЕТОК
[4
границы Г удалены не менее чем на некоторую величину е,
превышающую Я, а в остальных узлах Qh решение uh определять
простым сносом, то при е—>0 и h—*0 надлежащим образом (соотно-
h ™
шение — зависит от поведения вторых производных в окрестности Г)
иЛ—у и равномерно [77].
6) В работе [9] внутренним узлом квадратной сетки называется
такой, расстояние которого от Г не менее 2Л. В случае уравнения
Лапласа (B.14), / = 0) для этих узлов записывается уравнение B.16)
(/==0), а для граничных узлов указаны новые способы записи
граничных условий. В этой работе даны погрешности решения в
предположениях и (#, у) eCk (k — U 2, 3).
7) О погрешности \\u—uh\\ (и—решение задачи B.31), B.32),
uh—решение сеточной системы B.33), B.36)) можно утверждать
следующее:
\\u—uh\\^Ch2, если ыеС4,
j] u-~uh\\ ->0, если we С2
(предполагается, что \с (х)\< М, g(x)^0).
б) Сеточные уравнения, близкие к
самосопряженным. Как уже было указано (см. п. 3, пример 15),
имеет место разрешимость сеточных уравнений B.65'), если
B.66) близко к самосопряженному. Если uh£ Ul (см. п. 3, б),
Б), то имеет место корректность системы B.65') при
условии и^. , = 0 в граничных узлах (см. B.78)). На основании
теоремы 3 будет иметь место сходимость по норме U%
сеточного решения к точному, если имеет место
аппроксимация (по норме Fh (см. п. 3, б), Б) уравнения B.66)
уравнениями B.65'). Можно доказать, что такая аппроксимация
имеет место, например, для и £ С2 (если коэффициенты а,
b, e имеют ограниченные первые производные) и,
следовательно, имеет место сходимость по норме Ul сеточного
решения к точному.
Ввиду громоздкости возможных здесь оценок ограничимся
лишь сказанным выше.
в) Оценки погрешности через данные
задачи. Оценки B.82), B.84) и им аналогичные обладают
тем недостатком, что содержат в правой части величины
M{k) — нормы производных порядка k точного решения,
которые неизвестны, как и само точное решение. Это
затруднение пытаются обходить следующими путями.
а) Для принятой сетки QA решают сеточные уравнения
и определяют ип. Для найденной сеточной функции вычисляют

5] § 1. УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА ИЗ
разностные отношения, аппроксимирующие те производные,
для которых требуется определить максимум модуля.
Максимум модуля разностных отношений порядка k и принимают
за M{k). Этот путь всегда доступен, но малонадежен.
Р) Из общих теоретических соображений иногда
возможно оценить M{k) по данным задачи / и ф. Именно, для
эллиптических уравнений имеются утверждения такого вида:
если коэффициенты уравнения, контур Г, данные / и ф
достаточно гладкие, то решение задачи Дирихле принадлежит
классу Ck и M(k) не превосходит некоторой функции
величин, характеризующих гладкость коэффициентов, контура и
данных. Полученные таким путем оценки M{k\ как правило,
сильно завышены. Этот путь теоретически безупречен, но
малодоступен и навряд ли практически пригоден в силу
упомянутой завышенности оценок для M{k).
у) Пытались получить оценки погрешности
непосредственно через данные задачи. Такие попытки оказались
успешными в случае, когда область Q есть прямоугольник,
L — оператор Лапласа, сеточное уравнение имеет вид B.16)
(/=0). Приведем один результат такого рода [116].
Если Q — квадрат О^лг^а, О^у^а, то
|| uh-u || < A,4,4, + 0,43Л3а) h\ B.85)
где заданная на границе функция ф($) непрерывна на
контуре, имеет непрерывные производные до третьего порядка
на каждой стороне квадрата, Л2 — максимум |ф"| в
вершинах квадрата, Аг—максимум |ф'"| на сторонах квадрата.
Вообще говоря, при некотором выборе ф($) точное
решение не будет принадлежать С4, и тогда нельзя ожидать
оценки B.83) (можно, по-видимому, рассчитывать на оценку
типа NM{S)h). Оценка B.85) является лучшей по сравнению
с той, которая следует из B.81).
О других оценках типа B.85) см. [И6].
б. Итерационные способы решения сеточной задачи
Дирихле. Число уравнений в системе B.11), B.12) или
B.11), B.13) равно Nh—числу узлов в сетке Qh—и для
квадратной сетки примерно равно -~ , где |Q| — площадь
области Q. Помимо того, что при h—>Q число уравнений

114
ГЛ. II. МЕТОД СЕТОК
[5
в системе быстро увеличивается, мера обусловленности
системы [90], [Ю4] растет примерно так же, как и число
уравнений в системе. Поэтому применение точных методов
решения таких систем считается мало оправданным и
предпочтение отдается итерационным методам.
а) Простая итерация сеточных систем,
удовлетворяющих принципу максимума. Рассмотрим
систему B.50) в предположениях леммы 1. Если уравнение
B.50) для узла X. решить относительно uh(XX то вместо
системы B.50) получим систему уравнений вида
Ч (*/) = а?Ч (X; ы) + • • • + «J*»"* (*j <*,)) + bj B.86)
(/=1, 2, .... Nh),
где
^ = ^ ('-1' 2, ...,*,), V=-^,.
Из неравенств B.51), которым удовлетворяют А\1\
следует, что
kj
af.>0, £><<>< 1, B.87)
причем хотя бы для одного индекса j — j0 (узла II рода)
kj
£а<«<1. B.88)
Если систему B.86) записать в матричной форме
«А = Ак«А + *А> B«89)
то из свойства B.87) элементов матрицы Ah следует, что
все ее характеристические числа по модулю не превосходят 1.
Тот факт, что из каждого узла I рода (см. п. 3, а))
можно через соседние узлы добраться до узла II рода,
обеспечивает следующее: модули всех характеристических чисел
матрицы Ah меньше 1. Как известно [104], отсюда следует
сходимость процесса итерации по формуле
Bjr'> = M,W, + *A.
B.90)

5] § 1. уравнения эллиптического типл П5
где u^m) — т-я итерация, аи<0> — произвольная сеточная
функция, выбранная в качестве начального приближения.
Процесс вычисления таков: выбирают произвольную
сеточную функцию uff (Xj) и затем находят новые сеточные
функции u^(Xj), *#>(*,), u%HXj), ..., u^){Xj)9 пользу-
ясь формулами
«<-+'> (Xj) = afu^(Х/ы) +...+ а?Щ*ЦХт) + &/2.91)
(у=1, 2, .... NA).
После нескольких циклов вычисления по формулам B.91)
процесс обрывается, и результат последнего цикла
принимается за приближенное значение сеточной функции tth(X.)
(;=1, 2, ..., Nh).
Пусть проделано k циклов (k^l) и получено ufih
Далее будет указано, как по величине а^)==||а^) — к^'^Ц,
которую легко найти почти без добавочных вычислений,
можно судить о погрешности еМ== || ц^ — ин\\> где ин—т04"
ное решение сеточной системы B.86) или, что то же, B.50).
Замечание 1. Для каждого узла Ху введем величину гь==з
kj
== \^а^*. Тогда для всех узлов имеем 0<;г]у^1, а для узлов II
рода имеем т]у< 1. Пусть имеется / узлов II рода. Присвоим этим
узлам номера от 1 до / так, чтобы т]у<;г]у+1. Последующую
нумерацию узлов I рода (если такие имеются) произведем так. Каждый
последующий узел должен иметь соседом уже занумерованные узлы,
и этот процесс нумерации продолжаем до исчерпания всех узлов
сетки (этот процесс должен закончиться, так как любой узел I рода
можно через соседей соединить с узлом II рода, который уже
занумерован). При такой нумерации узлов процесс итерации Зейделя
[104] для системы B.86) будет сходящимся. По сравнению с
формулами B.91) различие в вычислениях заключается в том, что в
правой части B.91) «jjm) (Xj{i)) заменяется на ы^+1) (Ху {i))t если / (/)</.
Замечание 2. В п. 3 были приведены примеры 8—12
сеточных систем, аппроксимирующих задачу Дирихле для уравнения
Лапласа (примеры 10, 11, 12) и для общего эллиптического уравне4-
ния B.8) (примеры 8, 9). Эти сеточные .системы удовлетворяют
принципу максимума, и приближенные решения их могут быть
найдены методом итерации. Если коэффициент g (x7 у) равен
тождественно нулю, то все внутренние узлы суть узлы I рода и для того,
чтобы итерация Зейделя была сходящейся, достаточно сначала
перенумеровать граничные узлы (узлы II рода), а затем в порядке,
указанном в замечании, перенумеровать все внутренние узлы.

116 ГЛ. II. МЕТОД СЕТОК [5
Пример 18. Для приближенного решения задачи Дирихле
для уравнения Пуассона привлечем квадратную сетку. Для
внутренних узлов (в смысле пятиточечной звезды) запишем уравнение B.16),
а граничные условия учтем простым сносом. Тогда процесс
итерации протекает следующим образом. Во внутренних узлах задают
произвольно значение и^ и затем вычисление производят по
формуле
«Г/+,)-Т ( <\. /+"П+1 + 4-1 / + <4:1-,)-?tf)<W B-92)
В случае / н= 0 (уравнение Лапласа) вычисление последующих
приближений по формуле B.92) называется методом Либмана (или
методом средних арифметических). Если вместо квадратной сетки
пользоваться треугольной, то вместо B.92) будем иметь
и{т + 1)
-1 ( «<"*> + «<*> + и<"» + uiw) + aiw) + "<m)) - j (f)e.
где 0, 1, 2, 3, 4, 5, 6 — номера центра и узлов семиточечной звезды.
Для шестиугольной сетки будем иметь
«£m+I)=! («im)+«im,+«<m))-T(/)o-
Замечание 3. Для систем примеров 8—12 обозначим через
Л0 максимальный из коэффициентов Л@^ для внутренних узлов X*.
Для примеров 8 и 9 (система B.11)) А0 не превосходит ^ - +
4
+ inaxg; для примера 11 A0^-r^--\-max g (для треугольной и
шестиугольной сеток); для примера 12 Л0^^Г2" + max g (многото-
Ofl
чечное уравнение). Если граничные условия учитываются простым
сносом, то
е<*>^ || и}*>-ил || < NA0o^ B NA0\\ и^-и^'1* |[, B.93)
где N — число из неравенства B.77); если граничное условие
учитывается линейной интерполяцией, то
р.<*> ,
^ЛМ0+~)а<*>, B.94)
и, таким образом, можно судить о погрешности, которую
допускают, принимая результат k-й итерации в качестве приближенного
решения сеточной системы.
Замечание 4. Л. А. Люстерником [53] предложен метод
ускорения процесса итерации по формуле B.92), основанный на
подавлении [104] некоторых компонент ошибки и^ — и^
(компонент, отвечающих двум, отличающимся только знаком, наибольшим

5] § 1. уравнения эллиптического типа И?
по модулю собственным значениям сеточного оператора
определенного на сеточных функциях, равных нулю в граничных
узлах). Пусть получены итерации u(hm\ u[m*2\ и^п+*К Тогда:
а) по этим трем векторам вычисляется отношение
которое приравнивается величине \-{-Х2, что позволяет найти №\
Р) в качестве исправленного значения uh следует принять
ti, — u(m) ... * ( ij(m) — tAm + 2A
uh^uh \_tf I uh uh V
Приводится пример [53], [75J, где для m = 7 указанный прием
привел к значениям и^, имеющим примерно характер двадцать
шестой итерации; таким образом, этот прием позволил сэкономить
15 циклов итераций B6 — G + 4)= 15).
б) Подбор множителя. Пусть Rh означает квадратную
матрицу порядка Nh, отвечающую сеточной системе B.50),
удовлетворяющей принципу максимума; систему B.50) запи*
шем в матричной форме:
Rhuh=Fh. B.95)
Справедливо утверждение: вещественная часть каждого
собственного числа матрицы Rh отрицательна. Отсюда
следует, что существует такой положительный множитель а > 0,
для которого собственные числа матрицы E-\-aRh (Е—
единичная матрица порядка Nh) будут по модулю меньше 1.
Если такой множитель найден, то система
uh = (E + aRh)uh-aFh, B.96)
равносильная системе B.95), такова, что процесс итерации
akm+1) = (£+a#A)tf{,m> — aFh B.97)
сходится ♦
Поскольку все сеточные системы примеров 8—12
удовлетворяют принципу максимума, каждая из них может быть
преобразована к виду B.96) со сходящейся итерацией
подбором положительного множителя а. Выбор такого
множителя в общем случае системы B.11), B.12) или B.11),

118
ГЛ. II. МЕТОД СЕТОК
F
B.13) является задачей трудной, и поэтому ограничимся
случаем примеров 11, 12, а также системой B.16), B.12).
В этих примерах граничные условия учитывались простым
сносом. В каждом уравнении, написанном для внутреннего
узла, имеющего соседями граничные узлы, перенесем в
правую часть слагаемые, отвечающие граничным узлам.
Оставшаяся система уравнений также удовлетворяет принципу
максимума (так как внутренние узлы, имеющие соседями
граничные узлы, если они были узлами I рода в
первоначальной системе, стали узлами II рода в преобразованной).
Поэтому верно заключение об отрицательности
вещественных частей характеристических чисел матрицы. Так как
матрицы в этих примерах к тому же симметричны, то
характеристические числа вещественны и, следовательно,
отрицательны. Заметим, что то же можно сказать о матрице,
отвечающей системе B.64), являющейся сеточным аналогом
самосопряженного эллиптического уравнения.
Запишем эту систему в виде
где матрица Ah симметричная отрицательно определенная.
Для систем такого вида предложены [90], [116] процессы
итерации вида
«,г,,-«г,+«лмт)-^
где процесс итераций может быть значительно ускорен за
счет выбора удачной последовательности {ат}. Различные
методы (наискорейшего спуска; использующие полиномы
Чебышева; релаксации верхней и нижней и др.) предлагают
различные алгорифмы выбора последовательности {ат} ([90],
[104], [116]). В [90], [116] даны результаты испытаний
этих методов для уравнения B.16) в случае, когда
Q — прямоугольник.
Для решения сеточных систем можно воспользоваться
также так называемым методом Монте-Карло; см. выпуск
С МБ «Метод статистических испытаний (метод Монте-
Карло)».
6. Численные примеры. Изложенное выше о сеточной задаче
Дирихле заключим двумя примерами конкретного решения задач.
При решении этих задач сетка выбиралась так, чтобы число неиз-

6] § 1. уравнения эллиптического типа 119
вестных в системе уравнений не превышало 20—100, хотя
существующие быстродействующие машины позволяют в приемлемое время
решать сеточные системы с гораздо большим числом неизвестных.
Пример 19. Пусть область Q составлена из четырех
квадратов со стороной 1, центры которых расположены в точках [ 0, ~
2
0
Рис. 11.
А
2
J)
0, -^-1, (—I» у), [U -к-) плоскости Оху, а стороны парал-
11). Требуется найти решение
лельны координатным осям (рис.
и (х> У) уравнения Пуассона
Д"^ + о^-2'
обращающееся в нуль на контуре Г области Q:
и\г = 0.
Заметим, что эта задача возникает при исследовании кручения
цилиндрической балки, сечение которой совпадает с областью Q.
Пусть / — некоторая прямая плоскости Оху, Р—любая точка
плоскости, Р'—точка, симметричная с Р относительно /. Будем
говорить, что функция и (х, у) симметрична (антисимметрична)
относительно /, если и(Р) = и{Р') (и(Р) = --и(Р')) для произвольной
точки Р.
В силу симметрии области Q и данных задачи относительно
оси Оу нетрудно заключить, что точное решение и (х, у) задачи
симметрично относительно оси Оу. Поэтому достаточно определить
и(х, у) лишь в правой половине (х^0) области Q. Если выбрать
квадратную сетку с шагом /г, то область Q разобьется примерно на

120 гл. п. метод сеток [6
4
-Tg квадратиков и число неизвестных (с учетом симметрии) окажется
2
около -р- . Для того чтобы вычисления не были очень
громоздкими, потребуем, чтобы число неизвестных не превышало 20, т. е.
чтобы hz ^ у^г. Поэтому выбираем /г = — и располагаем узлы (k, /)
в точках (xk, yj), где *£ = —-—-—, y.= -Lm При этом все
граничные узлы (в смысле пятиточечной звезды) окажутся на границе Г,
а внутри правой половины области Q будет И узлов (см. рис. 11):
A, 1), A, 2), A, 3), U, 4), A, 5), B, 1), B, 2), C, 1), C, 2), D, 1),
D, 2). Через ukf j и uk • обозначим значения искомой сеточной
функции в узле (k, j) и симметричном для него относительно оси
Оу. Используя простейшую пятиточечную замену оператора
Лапласа, получим, например, для узла A, 2)
ИГ
и, учитывая wlf2=«iJ'
"i,2 = -з- ("i,i + "i,3+,2J +27 '
Аналогичные уравнения получим для узлов A, 3) и A, 4).
При составлении уравнений для узлов, не лежащих на прямой
* = -£• , учитывать симметрию решения не требуется. При
составлении уравнений для всех узлов, кроме A, 2), A, 3), A, 4),
необходимо учитывать, что значения и в граничных узлах равны 0.
Выпишем все 11 уравнений:
12 1 2
Mi,i = -3 ("i,2 + w2,i) + 27 ' Ki,i=3-(mi,i + Ki,3 + "*,2)+27 '
"i,3= у ("i,2 +,4)+ 27 » uh*=z~s (,3+ ,5)+ 27 '
1 ,2 1 , , , x , 1
"l,5 = -3 «1,4 + 27 > «2,l=-^("l,l + W2,2+"8,l) + i8 '
«2,2 = -4-("l,2 + «2,l + ,2)+ J3 » «3,l = f (W2,l + ,2+4 l) +IS »
Ч2 = -(Ц2,2 +,1 + 4 2) + 13 ' % 1= J (,1+ ,2)+J3 »
,2=4D2 + ^,1) +Jg-

6] § 1. УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА 121
Решение этой системы дает грубое приближение к точному
решению задачи. Выпишем его с четырьмя десятичными знаками:
и, ! = 0,2602, их 2=0,3265, их ,=0,2513,
и,'4 = 0,2054э к,' 5 = 0,1425, ия'1 = 0,2318,
иг* 2 = 0,2456, и,' , = 0,1992, и,', = 0,2021,
и,), = 0,1407, и^ 2 = 0,1412.
Допустим, что понадобилось получить сеточное решение для
сетки с шагом вдвое меньше: /i = —- . Если узлы выбрать в точках
k /
#ft = — , г/у=-~, то узлы новой сетки окажутся совпадающими с
центрами квадратов, срединами сторон квадратов старой сетки и
узлами старой сетки. Перенумеруем узлы так: узлам на линиях
л 1 1 1 2 5 , 7
ж = 0, , = -, * = -, * = _, *=■_, *=-, *=1, х = -£,
4
# = -q- присвоим соответственно номера 1—11, 12—22, 23—33,34—38,
39—43, 44—48, 49—53, 54—58, 59—63, причем на каждой линии
х = const номера растут с ростом у. При составлении уравнений для
узлов 1—11 следует учесть симметрию решения. Так, например,
для узла 3 уравнение запишется так:
2ц14 + Ц» + Ц4—*ц, 9 мтты „ _и2 + и4к + 2иы , 1
-р— — — z или и,— - 1~72 '
6
Не будем выписывать всю систему 63 линейных уравнений.
Она решалась методом простой итерации, причем при выборе
начального приближения ц*0) было использовано решение для старой
сетки. Узлы 13, 15, 17, 19, 21, 35, 37, 45, 47, 55, 57 совпадают с
узлами старой сетки, и значения и{0) в этих узлах примем равными
найденным ранее. Нетрудно видеть, что для ц£С4 имеет место
неравенство (см. п. 2, пример 6)
I u(x + hy y + h) + u{x + hy y—h) + u(x—hy y + h)
2/i2 ^
+ tt(x-h, y-h)-4u(x, У)__ьи(х, у)
<[m^,
из которого следует, что значение и (х, у) в центре девятиточечной
звезды можно приближенно вычислять по формуле
u(x + h, y + h) + u(x + h, y—h) + u{x—h, y + h)
u(x-h, y-h) Я2
Полагая /i = -—, (Ди)Х)У = — 2 и используя известные значения и{0)
в узлах старой сетки, найдем и{0) в узлах, являющихся центрами

122
ГЛ. II. МЕТОД СЕТОК
[б
квадратов старой сетки, т. е. во всех остальных узлах с нечетными
номерами. После этого, используя формулу B.92), найдем значения
и{0) в узлах с четными номерами. Полученная так сеточная
функция и{0) служила начальным приближением для процесса простой
итерации. Отметим, что понадобилось 80, 120, 160 итераций для
того, чтобы || и{т+1) — и{т) \j не превосходила 10"*, 10~5, 10
соответственно (и{т) — итерация с номером т, || и || — максимум модуля).
На основании формулы B.93) гарантируется, что || и{т+1) — а^|| не
превосходила 10~, 10~s, 10~4 соответственно, где uh—точное
решение сеточной системы. Результаты с четырьмя цифрами после
запятой приведены в таблице 16.
Таблица 16
Значения щ
1
2
3
4
5
6
7
9
10
11
12
13
0,1616
0,2710
0,3324
0,3517
0,3382
0,3067
0,2747
0,2443
0,2110
0,1670
0,1017
0,1599
0,2673
14
15
16
17
18
19
20
21
22
23
24
25
26
0,3257
0,3403
0,3194
0,2792
0,2462
0,2180
0,1885
0,1499
0,0920
0,1551
0,2569
0,3074
0,3087
27
28
29
30
31
32
33
34
35
36
37
38
39
0,2644
0,1891
0,1571
0,1375
0,1195
0,0965
0,0610
0,1482
0,2423
0,2827
0,2670
0,1849
0,1397
40
1 41
1 42
43
44
45
46
47
48
49
50
51
52
0,2258
0,2586
0,2363
0,1527
0,1294
0,2068
0,2343
0,2111
0,1341
0,1154
0,1824
0,2050
0,1840
53
54
55
56
57
58
59
60
61
62
63
0,1172
0,0945
0,1467
0,1637
0,1473 i
0,0951
0,0602
0,0906
0,1002
0,0909
0,0604
Нами получены сеточные функции а и и 1 . Этим обстоятельст-
~Т в
вом можно воспользоваться для построения сеточной функции и t , бо-
лее близкой к точному решению и (х, у), чем и х и и г . Для этого
~Г в
применяется способ Рунге, теоретические основы которого в случае
метода сеток изложены в книге [83], а примеры применения—в
книге [75], В нашем случае способ Рунге сводится к следующему.
Рассмотрим последовательность сеток, для которых /i = —
(N—целое положительное число, N—► оо) и все граничные (в смысле
пятиточечной звезды) узлы лежат на Г. Доказывается, что сеточная
функция к(и^—и) при h—>0 стремится к некоторой функции
v(x, у). Поэтому u^ztifi—h2v и, в частности,
1 1

6] § 1. УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА
Исключая и, найдем
123
4а.
з
функция и j определена лишь в узлах сетки Q г . Приведем спи-
~Г з
сок значений функций а х : .0,2697; 0,3449; 0,2885; 0,2222; 0,1523;
0,2458; 0,2742; 0,2094; 0,2140; 0,1487; 0,1493.
В силу гладкости данных задачи можно предполагать, что
производные любого порядка точного решения являются непрерывными
в Q, т. е. u£Ck для любого /г. Поскольку все граничные (в
смысле девятиточечной звезды) узлы лежат на Г, то имеет смысл
составить сеточные уравнения B.47) для девятиточечной звезды.
Например, для узла 3, учитывая симметрию решения, получим
4 (Ц2 + Ц4 + 2ц14) + Bц18 + 2ц15)-20ц,
или
«3 =
6(i)"
4 (и2 + и4 + 2«14) + 2 (и15 + ип) , _1
-2,
20
60
Не будем выписывать всю систему 63 уравнений. Система
решалась методом простой итерации, начальным приближением для
которой служило полученное ранее решение и i . Результаты с че-
в
тырьмя цифрами после запятой приведены в таблице 17.
Таблица 17
Значения щ
1
2
3
4
5
6
7
8
9
10
11
12
13
0,1621
0,2719i
0,3337
0,3535!
0,3417
0,3125
0,2797|
0,2480
0,2138,
0,16941
0,1032
0,1605
0,2683
14
15
16
17
18
19
20
21
22
23
24
25
26
0,3271
0,3421
0,3225
0,2856
0,2507
0,2211
0,19101
0,1521
0,0936,
0,1559
0,2585
0,3096
0,3111
27
28
29
30
31
32
33
34
35
36
37
38
39
0,2664
0,1972
0,1594
0,1390
0,1209
0,0980
0,0626
0,1492
0,2444
0,2861
0,2721
0,1926
0,1409
40
41
42
43
44
45
46
1 47
48
i 49
50
1 51
52
0,2280
0,2617
0,2395
0,1544
0,1306
0,2090j
0,2368|
0,2132
0,1351|
0,1168'
0,1845
0,2073
0,1860
53
54
55
56
57
58
59
60
61
62
63
0,1183
0,0959
0,1487
0,1658
0,1492
0,0965
0,0617
0,0922
0,1016
0,0923
0,0619

124
ГЛ. II. МЕТОД СЕТОК
[6
Обозначим эту сеточную функцию через и х . Ее значения в
в
узлах сетки Q ^ мало отличаются от значений сеточной функции
«, . Это сравнение позволяет надеяться, что их является при-
~Г Т
ближением для и (х, у) с тремя верными цифрами.
Пример 20. В области Щл:^0, г/^0, *2-{-#2<4 (рис. 12))
найти решение дифференциального уравнения
A + *2)_ + 2A-^)^ + A+^ =
= - № + У* + ху)-2(**у*)+•%(* + №], B-98)
удовлетворяющее граничному условию
 1
и
и
х=о
16
= 1
6•
B.98')
и
\х* + у*
.=о.
Так как
A+д:2)A+г/2)-A-^J = л:2 + ^ + 2^ = (А: + г/J>0
для х + у ф 0, то уравнение B.98) является эллиптическим во всех
точках области Q, за
исключением точки @, 0). Так как внутри
области Q выполняется условие
|(l-x*/)|<min((l+*2), (l+y%
то для приближенного решения
задачи можно воспользоваться
квадратной сеткой и
уравнениями B.58), B.59). В этом случае
получится система,
удовлетворяющая принципу максимума (при
удачном выборе уравнений для
граничных узлов).
Решение и (х, у) задачи B.98),
B.98') является функцией,
симметричной относительно прямой
х = у. Это следует из того, что при
замене х на у и у на х задача
переходит сама в себя, и задача
имеет только одно решение. Итак,
достаточно разыскать решение в
1 k
Мы выбираем /i = -—, xk — — ,
Рис. 12.
области Ql @ <*/<*, r> + (/2<4).
уj =-j . Тогда внутри области Qt и на границе у = х размещаются
23 узла, которые будем считать занумерованными в порядке их

6J § 1. УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА ' 125
/ 1 1\ /1 1 \ / 3 1 \
следования в следующем списке: I -т > Т Ь \ ~9~ ' Т )' ( Т ' Т г
1\ (L 1\(± iv fi iv a л fi iv
4 У V 4 ' 4/\2 4/ V4' 4/1,2' 2 у1, \ 4 ' 2)
т} ("?• Ту1' (г"' V' (т- т)' (т- т)' A( т)'
(!■!}(!■ !Ит- I-)- с * (-5-..). (!.■)•
/5 5\/3 5\„ л
■j, — j, f y , -j J. Ha границе у — О лежат 9 узлов, и
значения искомой функции в этих узлах известны. Узлы 7, 13, 18, 21,
23 являются граничными относительно пятиточечной звезды и тем
более относительно девятиточечной. В этих узлах граничные условия
учтем линейной интерполяцией (в направлении оси Ох). Например,
для узла 18 имеем
б = У 4~лт]" ^У^~7^
и поэтому уравнение примет вид
и1В —0,2938843н17 = 0.
В узлах 1, 2, 3, 4, 5, 6, 8, 9, 10, 11, 12, 14, 15, 16, 19 имеем
1—ху^О. Для этих узлов записываются уравнения типа B.58).
Например, для узла 14 уравнение примет вид (с учетом симметрии
искомой функции)
Л , 9\ци + и,-2и14 , Л 3 3 \ии + ий + 2иитBии+2и.) ,
V +iej ГТу- + {1--А-т) /Ту +
,/,, 9 \u9 + ult—2uu__
+ {1 + Гб) пу ~
- [7 9 л- 9 4- 9 ^ 2 i 9 + 3 f 9 4- 9 Y1
или, после упрощении,
7«8 + 36w9—86им + 36и15 + 7м1д = — 2,003906.
Для узлов 17, 20, 22 имеем 1 —ху < 0. Для этих узлов
записываются уравнения типа B.59). Например, для узла 20 уравнение

126
ГЛ. II. МЕТОД СЕТОК
[7
примет вид
-Иг19--2«20
(|)"
Л-Л_^_ .Л ^21 + ^19 + ^16 + "
22
+A+12)
и^ + и22 — 2и21
D)"
D)"
+'+4-)-'-5-'+t(S+'I
или, после упрощении,
28и1в + 4и17 + 37и 19 — 134и20 + 37«21 + 28«22 = — 5,612305.
Остальные уравнения системы выписывать не будем. В таблице
18 приведены (с сохранением трех цифр после запятой): в столбце
Uu — решения сеточной системы, в столбце и — значения точного ре-
<х2 4- у2J
шения и(х, у)=\—-—г^-^- в узлах сетки.
Таблица 18
Значения щ — решения сеточной системы и и — значения
точного решения
1
2
3
4
5
6
7
8
"к
0,986
0,977
0,955
0,902
0,797
0,607
0,294
0,958
и
0,999
0,994
0,976
0,929 |
0,835
0,666
0,390
0,984
9
10
И
12
13
И
15
16
"ft
0,926
0,862
0,745
0,547
0,234
0,880
0,799
0,662
и
0,959
0,902
0,795
0,609
0,314
0,921
0,847
0,718
17
18
19
20
21
22
23
"h
0,446
0,131
0,694
0,526
0,253
0,340
0,067
и
0,506
0,179
0,750
0,590
0,340
0,390
0,092
Из сопоставления uh и и следует, что uh является весьма
грубым приближением к и. Для достижения большей точности следует
брать сетку помельче.
7. Сеточная задача Неймана. Для упрощения
изложения мы рассмотрим задачу Неймана в наиболее простой

7] § 1. УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА 127
постановке: в конечной области Q плоскости Оху найти
функцию и(ху у)у удовлетворяющую в Q ^уравнению
Пуассона
д"^ё+9=/{л:'у) BЛ4)
и граничному условию
Й|Г = Ф(^^). B-99)
где -г производная функции и (х, у) в направлении
внутренней нормали к контуру Г, /(лг, .у) и ц>(х, у)—заданные
соответственно в Q и на Г функции.
Особенности этой задачи заключаются в следующем:
а) не при всяком выборе f(x, у) и ф(л;, у) существует
решение задачи; б) если для заданных / и ф существует
хотя бы одно решение и (х, у), то и (л;, у) + С, где &*—-
произвольная постоянная, также является решением (и
всякие два решения отличаются постоянным слагаемым).
Известно [94], что для существования решения задачи
B.14), B.99) необходимо и достаточно, чтобы (в
предположении достаточной гладкости /, ф и контура Г)
^fdQ+ J фйГГ = 0. B.100)
Q Г
Из условий B.100) следует, что задача весьма чувствительна
к малым изменениям / и ф: достаточно сколь угодно малых
изменений / и ф, чтобы соотношение B.100) нарушилось и
у измененной задачи не было бы решений. Аналогичное
обстоятельство будет иметь место и для сеточных
уравнений, на совместность которых приходится обращать особое
внимание.
Если выполнено равенство B.100), то решения
существуют и среди них можно выбрать одно, удовлетворяющее
какому-либо дополнительному условию, например
J u(x, y)dQ = 0 B.101)
ИЛИ
«(*., Л) = °. B-102)
где (х0, у0)—некоторая точка области £2.

128 гл. и. метод сеток [7
Рассмотрим два подхода к составлению сеточных
уравнений, заменяющих задачу B.14), B.99).
а) Замена производных конечн о-р азност-
ными отношениями. Пусть Qh—квадратная сетка.
Множество внутренних узлов (в смысле пятиточечной звезды)
обозначим через Q°h) множество граничных — через Qjj.
Каждому (/, у) £ £i°h ставится в соответствие уравнение
\^huhtitJ = JJ2 —
= (Пл(Л ф)),,у, У.ЛбОл- B.103)
Каждому (/, у) £ Qh ставится в соответствие уравнение
вида (см. п. 3, пример 13)
(rh»h)i,J =—~\ -C0S^ + \ — C0S * =
= Aй1,(/,ф))/,уЛ^Л€Ол, B.104)
где |, т)=±1 и узлы (/ + £, У) и (/, y+rj) принадлежат
£2Л, а |Л и X—углы, образуемые внутренней нормалью к Г
в точке Qtj £Г, ближайшей к (/, у) (и, следовательно,
проходящей через (/, у)), с лучами из (/, у) к (/ + £, у), (i, у + ц)
соответственно; предполагается, что O^fx^Tf, О^Я^-гг
(см. п. 3, пример 6).
В этих предположениях система B.103), B.104) такова,
что все узлы (/, у) £ Q,h являются узлами I рода и
соответствующая однородная система имеет ненулевое решение
и,-эу=1, (/, у) £ ЙЛ. Таким образом, определитель этой
системы равен нулю и ранг матрицы коэффициентов равен
Nh—1. Последнее следует из того, что если одно из
уравнений системы, соответствующее узлу (/0, у0), заменить
уравнением и£.^Л = 0, то узел (/0, у0) станет узлом II рода.
Новая система в силу теоремы 2 будет иметь единственное
решение, что и доказывает утверждение о ранге матрицы.
Поэтому существует единственная (с точностью до
множителя) система Nh коэффициентов таких, что линейная
комбинация левых частей B.103), B.104) тождественно равна
нулю. Эти множители обозначим через /г2У/>у Для (*\ У) €^л>
h&i%J для (./, у) £Q\.

7] § 1. УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА 129
Тогда система B.103), BЛ04) является совместной в том
и только том случае, если
h* S оУ/.у(ПХ(/, Ф))н/ +
+ Л S «/,,№'(/, Ф)),,у = 0. B.105)
(ь I) € ОД
Уравнение B.105) назовем сеточным аналогом
уравнения B.100). Для произвольной области Q и выбранного шага
h для определения чисел у/, / и б/, / требуется решать
систему Nh—1 линейных уравнений, что является само по себе
трудной задачей. Для областей, контур которых состоит
из отрезков прямых, параллельных координатным осям
(прямоугольник или фигура, составленная из прямоугольников),
все у.. и б£- • равны между собой и можно положить
yhj-~ б-, у=1. В этом случае уравнение B.105)
принимает вид
А2 2 (IDU/, Ф)),,у+А S (nlt/.cp)),,,^. B.106)
(/. /) е q£ </, л 6 q\
Замечание. Во второй сумме должны опускаться слагаемые,
я
отвечающие вершинам с внутренним углом -^-.
Если выполнено B.100), то область Q и контур Г можно
разбить на неперекрывающиеся части, являющиеся
окрестностями соответственно внутренних и граничных узлов. Тогда
можно положить
AК)/,/=р$/(*, y)dQ, B.107)
(ПХ)/>у = х J<prfrf B.108)
где Й- , и Г^у—выбранные окрестности соответственно для
(i, у) £й£ и ('» /') €^а* При таком выборе в силу B.100)
выполняется B.106) и система B.103), B.104) совместна.
5 С. Г. Михлин и X. Л. Смолицкий

130 гл. и. метод сеток [7
Для того чтобы задача имела единственное решение,
достаточно задать сеточный аналог либо условия B.101),
либо B.102). Таковыми, например, являются
fti S «/,у=° BЛ09)
и
»/..Л = 0, B.110)
где (/0,у0)—какой-либо узел, наиболее близкий к точке (х0,у0).
Пример 21. Пусть Q—прямоугольник со сторонами а и 6,
параллельными координатным осям, где а и Ь—соизмеримые числа,
и к выбрано так, что a = Mh и b = Nh> где М и N—целые числа.
Пусть fsO. Положим
(П£),,/=о, (/. /)€QJ.
№ (Ф»,,/= (Ф)/,/ (AI+V-2) И ф'. Г'
где сумма берется по всем граничным узлам, кроме вершин
прямоугольника. Тогда выполнено B.106) и система B.103), B.104)
совместна.
Для прямоугольника 0г^*<;1, Q^y^l гармонический
многочлен
\2
и*(х'У^{х-^У~{у-^У
имеет на контуре внутренние нормальные производные, равные +1
на горизонтальных сторонах и —1 на вертикальных. Нетрудно
убедиться, что решением сеточной задачи для • этих данных является
многочлен
М*. y) = (l-h)-lU*(x, у),
и, следовательно, погрешность сеточного решения задачи Неймана
(полученного указанным в этом примере способом) убывает не
быстрее чем h [118].
Пример 22. В работе [118] предлагается следующий способ
составления сеточных уравнений (уравнение Лапласа,
область—прямоугольник). Кроме основных узлов (i, /), (O^i^Af, O^j^N), лежащих
внутри или на границе прямоугольника, вводятся вспомогательные
узлы ( —1, /), (Аг+1, /), (i, —1), (t, N+1). Для каждого из
основных узлов (/, /') записывается сеточное уравнение B.103)
((П^);,/ —О); для узла @, /), лежащего на одной из сторон
прямоугольника, уравнение B.99) заменяется таким:
~u-hJ *

7] § 1. УРАВНЕНИЕ ЭЛЛИПТИЧЕСКОГО ТИПА 131
где суммирование ведется по всем узлам контура, включая и
вершины прямоугольника. Аналогично записываются граничные условия
для узлов на других сторонах контура.
Так полученная система совместна. Если функция <р
непрерывна и достаточно гладка на каждой стороне прямоугольника, то
погрешность сеточного решения оценивается функцией Ah2\nh (в
предположении, что как точное, так и сеточное решения в одной из
вершин прямоугольника обращаются в нуль).
Гармонический многочлен
^f. ")-(*4),-3(*-t)("-t),-t
имеет на контуре квадрата Os^x, y^l такую нормальную
производную ф, для которой решение сеточной задачи указанным в этом
примере способом приводит к функции
uh — U* (x, y)—h2x.
Следовательно, погрешность сеточного решения uh, полученного
описанным здесь способом, убывает, вообще говоря, не быстрее Я2.
Замечание 1. Уже было отмечено, что система, полученная
из B.103), B.104) заменой уравнения для некоторого узла (/0, /0)
уравнением и,- у =0, однозначно разрешима. Пусть точка Q (xQ, yQ)
является узлом для каждой сетки последовательности {Qh\ (h-+0).
Составляя систему B.103), B.104) для всех других узлов сетки Qh
и полагая uh(Q) — 0f получим для каждой сетки однозначно
разрешимую систему уравнений.
Пусть {и^—последовательность решений так полученных систем.
Можно надеяться, что и^ стремится к точному решению задачи
B.14), B.99), B.102). В статье [10] это доказано для случая, когда
область Q звездна, граница Г достаточно гладкая, а уравнение
B.104) заменено более точным сеточным уравнением; в этой же статье
получена оценка погрешности.
Замечание 2. В статье [110] рассмотрено сеточное решение
более общей задачи: найти функцию и (х, у), удовлетворяющую в Q
уравнению
д2и д2и , да , ,ди , /0 , л л.
M + W+CTx + dTy-gU=f BЛП)
и на Г граничному условию
где к — определенная на Г функция. Пусть g^0 и к^0 и либо
g^0, либо и^0. Тогда задача B.111), B.112) не может иметь
более одного решения. В статье [110] уравнение B.112) заменялось
сеточным уравнением вида (см. п. 3, B.56))
* Л я *№,/Ку=ФЮ*,/>.
5*

132
ГЛ. II. МЕТОД СЕТОК
[7
а уравнение B.111)— уравнением B.11) (а===£н=1). В силу g^O
либо к ф. О (g ^ 0, х ^ 0) для достаточно малых h система сеточных
уравнений содержит узлы II рода и удовлетворяет принципу
максимума, а также корректна. Имеет место сходимость сеточного
решения к точному решению задачи B.111), B.112).
Замечание 3. Одномерным аналогом задачи B.111), B.112)
является такая: найти решение уравнения B.31), удовлетворяющее
граничным условиям
(х0, х^О).
Если сеточные аналоги последних уравнений для сетки xk =
= khlh = —\ выбрать так:
то эти уравнения вместе с B.33) образуют систему, удовлетворяющую
принципу максимума (предполагается: либо g^O при к\+к\ — 0у
либо Xq + Xj>0). Другая сеточная замена граничных условий (см.
[25]) приводит к сеточной системе, несложно преобразующейся к
удовлетворяющей принципу максимума. В обоих случаях имеет место
корректность сеточных задач и сходимость сеточных решений к
точному.
б) Сеточный аналог вариационной задачи.
Известно ([33], [63], а также гл. 111, § 3, п. 4 настоящей
книги), что решение задачи B.14), B.99) доставляет
минимум функционалу
F[u] == J [ | grad и|2 + 2/и] rfQ + 2 J uq> dT
Q Г
в' классе достаточно гладких функций и(х, у).
Для построения сеточных уравнений следует построить
сеточные аналоги для
J | grad и |2 dQ, $ fit dQ, J q>u dT.
Сначала рассмотрим сеточные аналоги для \|grada|2dQ.
а) Пусть (/, J) £Qh. Если узлы (/+1, j) и (/, y-f-1)
оба принадлежат ЙЛ, то сеточным аналогом | grad и |8

7] § 1. УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА 133
в узле (/, у) считают
jgrad^,/^ L /J +[-^-h >-) ;
если узел (/+1, j) [(/, У+1)] не принадлежит QA, то
соответствующее слагаемое в правой части опускается. Тогда
сеточным аналогом \|gradw|2dQ считают
(/. /NQft I
где сумма в правой части распространена на все пары
соседних узлов (*', у) и (*", у") из йл.
Р) В последней сумме опускают слагаемые, отвечающие
таким парам соседних узлов (/, у) и (г', у"), когда оба эти
узла являются граничными (в смысле пятиточечной звезды).
Эту сумму обозначим
:§(«,, ,-"<■<. /-J.
Если под знаком суммы не будет стоять индекс I или
II, то будем подразумевать любой из них.
Сеточные аналоги интегралов [fudQ, \фИЯ?Г запишем
в виде й г
л2 2 «£>у(йл(/))/,у и л 2 "/,у(п1(Ф))/,у,
где (Щ (/))/,у и (щ(ф))/)У—некоторые линейные
функционалы от / и ф, зависящие от значений / и ф лишь в
некоторой окрестности узла (/, у); эти функционалы должны
быть выбраны так, чтобы указанные выше суммы было
разумно считать приближенными значениями интегралов \ fu dQ
и [<padT. Тогда сеточный аналог функционала F[u] при-
г
мет вид
+ 2h S «,|У(йл(Ф))/|у. B.113)

134
ГЛ. II. МЕТОД СЕТОК [7
Этот функционал ограничен снизу для {и{Л,
удовлетворяющих либо условию B.109), либо B.110). Для
определенности выберем условие B.109).
Для получения сеточных уравнений надо приравнять
нулю производные по каждому и1г . от суммы
где 2аЛ— множитель Лагранжа. Если (/, у) — внутренний
узел, то указанный прием приводит к уравнению (после
деления на 2h2)
/л „\ — ui+h J+Uh/+i + "/-!, f+ui,/-i—4ui,/
\ahuh)i,J= Jjz ~
= (йл(Л)/|У+ал- BЛ14)
Если (/, j)—граничный узел, то указанный прием приводит
к уравнению (после деления на 2А)
(гМ, /=т K/««4w+ ^./ц/,у+1 + Tib--1)/+
+ Л*./"«,/-, — (%./ + Л*./ + Л*./ + Л*./) в,, у] =
= (ГЦ (ф)),- ,.+ h ((III (/)),, ,+ a„). B.115)
Здесь т]^ . (&=1, 2, 3, 4) определяются различно в
зависимости от того, какая из сумм 2 или 2 подразумевается
в B.113); именно ч\к. . равен 1 для 2, если ^"й Узел звезды
с центром в (/, у) принадлежит Qhl и равен нулю в
противном случае; г)*2 . равен 1 для 2> если £-й узел звезды
с центром в (/, J) является внутренним узлом Qh, и нулю
в противном случае.
Так как сумма производных от 2(aW—ui'> i')* п0 каж"
дому из uifj тождественно равна нулю, то
для любой сеточной функции. Поэтому имеем
1
%Л2
Л2 2 Шл (/)),,; +А 2 (Йл(Ф))/,/'
.B.116)

7] § 1. УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА 135
При таком выборе ah система B.114), B.115) совместна и
при условии BЛ09) имеет единственное решение uh—
приближенное решение задачи B.14), B.99) при условии B.101).
Замечание 1. Если ah ф 0, то правые части каждого из
уравнений B.114), B.115) зависят также от значений f и ф в
далеких от (/, /) Точках, а не только от значений / и ф в
окрестности (г, /).
Для того чтобы уравнения B.114), B.115) имели «локальный»
характер и правые части граничных уравнений B.115) не зависели
от /, необходимо и достаточно, чтобы а^=0 и (Щ(/)). .=0,
(/, /)£ Q^, т. е. чтобы Щ (/) и Щ (ф) удовлетворяли условию B.106),
являющемуся сеточным аналогом для уравнения B.100). Для этого
достаточно воспользоваться B.107) и B.108).
В работах [42], [43] для случая /^0 рассмотрено несколько
примеров выбора Щ (ф) со свойствами «локальности». В этих
работах левые части B.115) записаны для 2-
Замечание 2. Предложенный здесь способ учета граничных
условий можно назвать «простым сносом». Можно было бы в
качестве сеточного' аналога \ ф« ^Г взять сумму
г
h X [A4)^гт"Лг](,ЧЧа
</. У)бй£
учитывая этим самым граничные значения линейной интерполяцией.
Этот прием не изменил бы левых частей уравнений B.114) и B.115)
и несколько усложнил бы правые части; при этом формула B.116)
осталась бы в силе.
в) Сходимость и оценка погрешности. Будем
говорить, что сеточная функция мн сходится к некоторой
непрерывной функции и (х, у) по норме L2, если
lim (h* 2 (u{fj-u{ih,jh))*) = Q.
Доказано [108], что для ф = 0 и при выборе
(П£ (/))/, у=Д/ решение системы B.109), B.114), B.115)
ui+1, /~~ % / * Щу /+1 •"" uiy /
и его разностные отношения г , т
сходятся по норме L2 к точному решению задачи B.14),
B.99), B.101) и его производным з~ и з~ соответственно.

136 гл. и. метод сеток [8
В работах [44], [45] приводятся некоторые оценки
погрешности uh— и и разделенных разностей этой погрешности.
8. Задача о собственных значениях эллиптического
оператора. Число % называется собственным значением
самосопряженного эллиптического оператора
^ttU'u&y** BЛи)
1=1 /=1
для граничного условия (Q — область я-мерного
пространства, Г — ее граница)
«|г==0, B.118)
если существует отличная от тождественного нуля функция
и(Х), удовлетворяющая на Г условию B.118) и в области Q
уравнению
Lu + Xu = 0. B.119)
Функция и (X) называется собственной функцией,
отвечающей собственному значению К. Собственная функция
называется нормированной, если
/[и, tf]==$afrfQ=l. B.120)
й
Пусть область Q конечна, функции g(X) и a^j(X)
непрерывны в замкнутой области Q и aifJ- (X) удовлетворяют
условию: существует постоянная а>0 такая, что для всех
X £ £2 имеет место неравенство
где (£г, |2, ..., £„)— произвольные п вещественных чисел.
В этих условиях множество собственных чисел счетно, и если
их занумеровать в порядке роста, то Л,—*-f-oo при k—юо,
где А/**—собственное число с номером k.
Задача о собственных значениях — задача определения
собственных чисел для заданных Q, L. Точно эта задача
решается для весьма частных случаев области Й и
оператора L.

8]
§ 1. УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА
137
Основой для приближенного вычисления X{k) служит
следующий факт: число Х{1) является точной нижней
границей функционала
г» I ..♦ _ 1 ; _ ч ■*
Lt = l / = 1
dQ B.121)
в классе функций, удовлетворяющих условиям B.118) и
B.120); если ЯA), . ..,Мк-1> уже найдены и и{1\ . ..,и{к~1) —
соответствующие им собственные функции, то %{k) является
точной нижней границей функционала B.121) в классе
функций, удовлетворяющих условиям B.118) и B.120)
и k—1 условиям ортогональности
/[и, и(,,)]= $иаA'></О = 0 (/=1, 2, ....,й—1). B.122)
Для простоты записи и рассуждений предположим, что
£2 — область плоскости Оху и L — A — оператор Лапласа.
При этом Е[и] примет вид
£^=l[®)t+(l),]dQ=l|gradB|,dQ- BЛ23)
Рассмотрим различные сеточные аналоги для B.123),
B.120), B.122).
а) Конечно-разностная замена. Рассмотрим
квадратную сетку на плоскости и будем считать и{ . = 0
для каждого узла (/, j) плоскости, который не является
внутренним узлом для Qh (в смысле пятиточечной звезды).
Тогда положим
где суммирование можно считать распространенным на все
узлы плоскости (на самом деле лишь конечное число
слагаемых суммы отлично от нуля, если ui}J^0 хотя бы для
одного внутреннего узла (/, /));
B.125)

138 гл. и. метод сеток [8
Граничное условие B.118) учтено тем, что положили
«/,/ = 0. С Л€Оа- BЛ26)
Выражения Eh [uH] и Ih [uh, uh] являются квадратичными
формами переменных uit у, (/, j) £ Q\. Требуется найти такие
uiyp для которых Eh[uh] достигала бы минимума при
условии, что /Л[«Л> йл]=1.
Как известно, эти значения uiy} образуют решение
системы Nh линейных однородных уравнений, полученных
приравниванием нулю производных от Eh[uh]—khI[uh, uh]
по каждому ui} j, (/, j)£Qh (kh—множитель Лагранжа). Это
приводит к системе уравнений вида
«/ + !,/+«/. /+! + «/-„/ +
+»/>у-»-D-М1)«/,у=0. С /NQX, BЛ27)
причем в некоторых из уравнений часть из первых четырех
слагаемых должна быть заменена нулями в силу B.126).
Для того чтобы эта система имела ненулевое решение,
необходимо и достаточно, чтобы определитель системы был
равен нулю. Определитель этой системы является
многочленом Л/л-й степени от Xh. Все. корни этого многочлена
вещественны и положительны (как собственные числа
симметричной положительно определенной матрицы). Пусть
W^W^...<b[N® B.128)
— корни этого многочлена. Доказано [38], что при h—>0
для каждого фиксированного k справедливо
ШпХГ^М*, B.129)
Л -> о
что дает основание считать К[ приближенным значением
для Х<*>.
Замечание 1. В этом способе граничное условие B.118)
учитывалось простым сносом. Можно учесть граничное условие
B.118) либо по Коллатцу, либо по Микеладзе. Один из путей
такого учета в задаче о собственных значениях описан в статье [91],
в которой кроме B.129) даны также оценки погрешности
J^-^j при А-*0.

8] § 1. УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА 139
Замечание 2. Утверждения B,129) и оценки для
\к\® — %{к) I получены в указанных работах для оператора B.117)
общего вида.
б) Полилинейная интерполяция. Под Q (А)
будем понимать область, составленную из всех квадратов
сетки, полностью принадлежащих Q; Г(А)— контур
.области Qh.
Пусть ah—произвольная сеточная функция, равная нулю
в узлах, лежащих на Г (А). В соответствие такой функции ан
поставим функцию uh(x, у), определенную и
непрерывную в й:
«а(*э JO = 0> е^ли (*, y)£Q, но (ху y)£Q(h);
ин(х, у) совпадает с uh в каждом узле (/, у), лежащем
в Q(A);
в каждом квадрате, образующем Й(А), tih(x, у)
полилинейна, т. е. линейна по каждому из аргументов в
отдельности, а именно:
М*> У) = -р№*'*>{Н-х){к-у) + и<1>'>х{к-у) +
+ u{*'l>(h—x)y + u{l>l>xy],
где и{0у 0), аA,0), ц@'1}, аA'1}— значения мн в вершинах
квадрата, одна из вершин которого принята за начало
координат, а три другие имеют координаты (А, 0), @, А),
(А, Л)-
Для функции ин(х, у) функционалы Е[ин] и I[uh, uh]
являются квадратичными формами величин а^ j ((/,/)— узлы
в Й(А)). Приравняв нулю производные от Е [ah]—khI[uhy uh]
по каждому uiy j и рассуждая далее, как в случае а), найдем
числа
где Nh—число узлов, лежащих внутри Q (А). Оказывается,
что %{hk)^X(k) и %(hk)—*%{k) при А—+0. Таким образом, при
таком способе получаются приближенные значения для
по избытку; следовательно, Я^ ^ дает верхнюю границу
для К"К

140
ГЛ. II. МЕТОД СЕТОК
[8
Каждый узел (/, J) внутри Q (h) сделаем центром
девятиточечной звезды (см. рис. 4). Тогда каждому такому узлу
ставится в соответствие уравнение
(u1 + u2 + u, + u, + u5 + u6 + u1 + us—Su0) +
+ J^[^ul + ut + ut + ttJ + {ut + tt, + u1 + ug)+l6uQ]^0i
т. е.
A+^)( +  +  + <0 +
' + A+-^){** + и. + и, + и9)-
-(8-iA%V = 0, B.130)
з rty °
где и0, uv ..., и8 — значения uh в центре и узлах звезды.
Уравнений вида B.130) столько, сколько узлов .(/, j) внутри
Q (К). Если среди узлов звезды встречаются лежащие на Г (h),
то соответствующие значения uh надо считать равными
нулю. Числа %h\ •••» М являются корнями определителя
системы уравнений B.130).
Замечание 1. Числа V£\...t If являются верхними
границами для ЯA), ..., %{к\ Для получения нижней границы первого
собственного числа к{1) можно поступить так. Пусть Q* (h) означает
область, составленную из всех квадратов сетки, каждый из которых
содержит хотя бы одну такую точку (л:, г/), что найдутся (а, Р)
@^а^/г, O^P^/i), для которых точка (л: + а, #+Р)
принадлежит Q. Область Q* (И.) содержит в себе всю область Q. Если для
области Q* (К) найти Х^ способом, указанным в пункте а)
(обозначим его через Я^*), то Х^* < М1) [129].
В работе [130] указан прием для определения нижних границ
для А,(Ч
Замечание 2. Число [х называется собственным значением
самосопряженного эллиптического оператора B.117) для граничного
условия
Р\ = 0 B.131)
(V—направление конормали [63], [94]), если существует отличная
от тождественного нуля функция и (X), удовлетворяющая на Г
условию B.131) и в Q уравнению Lu-\-\xu=^0. Существует
последовательность чисел [ilk) ([i{k) ^ jx<fe+1)), \x(k) -*■ оо при k-+QQ. He-

8]
§ 1. УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА
141
сколько изменяя рассуждения пункта а), можно получить средство
для приближенного вычисления [х(&). Так, в случае, если
L—оператор Лапласа А, достаточно в сумме B.124) оставлять только те
слагаемые [h~l (ui+lj у— щ9 у)]2 или [А" ("/,/+1~~и*,/Л2» Для
которых оба узла (/, /) и (/+'1, /') или (/, /) и (/,/+1) принадлежат £>л.
Тогда для внутренних узлов уравнение B.127) заменяется
аналогичным (kh меняется на ju,#), а для граничных узлов оно примет вид
где г|^ • таковы же, как в п. 6 для ^.
Аналогичное замечание справедливо и для собственных
значена
нии для граничного условия
+ ии =0.
dv /г
в) Замечание о нижних границах для Я().
Пусть область Q есть прямоугольник 0<;ж;а, 0^^^&,
где а и b соизмеримы. Пусть h—одна из общих мер и,
таким образом, a~Mh, b=Nh, где М и N—целые числа,
не меньшие двух. Квадратная сетка Qh такова, что
граничные узлы лежат на контуре. Внутренних узлов в сетке
(ЛГ—1)(ЛГ—1), a (M—\)(N—\) чисел
\ (т, п) 4
h2
Sin ТГГГ+Sin
A
2УИ
м-
2N
1, 1
= -тг sin
/г2
;жлг—1)
тл/i . . 2 яяЛ\
являются собственными значениями B.128) сеточной задачи
B.127). Точными собственными значениями для задачи B.119)
(L — Д) являются числа
Х(/я' п) =
выя
A<т<оо, 1<я<оо).
Нетрудно видеть, что
М1*") = №*>»>-
(т)'-ь(тЛ,.
12 П
+ 0(h% B.132)
где 0(/г4) означает бесконечно малую величину одного
порядка с А4.
Формула B.132) обобщается на широком классе областей
следующим образом.

142
ГЛ. И. МЕТОД СЕТОК [8
Пусть для каждого внутреннего узла (/, j)£Qh записано
уравнение B.127). Для каждого граничного узла (/, у), не
лежащего на Г, запишем уравнение по способу Микеладзе
(см. п. 1):
Г "(Qi)
Ц (Qi) , ** (Q,)
+ ra^-ew(^+^J]+M/,y=0, B.133)
в котором полагаются равными нулю u(Qk), если Qk£T
(k~.1, 2, 3, 4). Система уравнений, полученная объединением
уравнений B.127) и B.133), может быть записана в
матричной форме так:
где матрица Ан, вообще говоря, несимметрична в случае
наличия уравнений B.133) Пусть Лл = — (ал + а[), где
Al—транспонированная матрица для Лл. Вместо
уравнения B.134) рассмотрим уравнение
Числа Кн ) являются корнями определителя матрицы
{Ah-\-'khE), являющегося многочленом степени Nh, где Nh —
число узлов Qh, не лежащих на Г. Будем считать, что
корни занумерованы так, что
Доказывается [116], что если Q есть область, граница
Г которой состоит из конечного числа аналитических
кривых, образующих в точках стыка угловые точки с
внутренним углом меньше я, то существуют числа у{к) такие, что
Xf = ^*>—y<k)h* + o(h2),
где о (h2)— бесконечно малая порядка высшего по
сравнению с h2.
Если область Q к тому же выпуклая, то ^сЛ)>0 и,
следовательно, для каждого k существует такое h(kI что для

1] § 2. УРАВН. ГИПЕРБОЛИЧЕСКОГО И ПАРАБОЛИЧЕСКОГО ТИПОВ 143
всех h<Zh(k) имеет место неравенство
т. е. A,/f} есть нижняя граница для Xlk).
§ 2. Уравнения гиперболического и параболического типов
1. Задача Коши. Выбор решетки и сходимость
сеточных решений, а) Гиперболическое уравнение.
Простейшим гиперболическим уравнением является уравнение
колебаний струны (волновое одномерное уравнение)
n«=3^-g=/(*, t), B.135)
где f(x, t) — заданная функция.
Задача Коши для уравнения B.135) ставится так. В
полуплоскости —оо<С;е<С°о, />0 найти решение
уравнения B.135), удовлетворяющее на границе £ = 0 начальным
условиям
<=о = ФD B.136)
g\x), B Л 37)
1 I д"
* = 0
где ф(лг), g(x)—заданные функции. Решение задачи B,135),
B.136), B.137) определяется формулой {решение Далам-
бера) [98]
+ у ДО f{x>i)dxdt, B.138)
где D(jc0, /0)—треугольник плоскости (М, ограниченный
осью / = 0 и прямыми («характеристиками») x-{-t~xQ-{-tQ,
х—t = x0 —10, проходящими через (xQy tQ). Из B.138)
следует, что и (Ху t) определяется значениями ф и g в точках
основания треугольника D(xQy tQ) и значениями / внутри
и на контуре треугольника.
Рассмотрим прямоугольную сетку xk~kh, tj = jx (& = 0,
dil> ±2, .♦.; У=0, 1, 2, ...). Совокупность узлов (&, j)

144
ГЛ. II. МЕТОД СЕТОК
[1
(—оо<&<оо) назовем у-м рядом сетки. Наиболее
простая замена задачи B.135), B.136), B.137) сеточной такова:
_.,.,гЧ/+"м/в(/)<[/ BЛ39)
(* = 0, ±1, ±2, ...; /=1, 2, ...),
»*,, = Ф(*А) (й = 0, ±1, ±2, ...), B.140)
"Й'7"М = ?(Щ (* = °. ±1, ±2, ..-)• BЛ41)
Из уравнений B.140) и B.141) uh определяется в нулевом
и первом рядах сетки (uk^ 0 = ф [kh)y uky x =<p(kh) + Tg(kh)).
Уравнения B.139) таковы, что uk\+l однозначно
определяется через значения сеточной функции uh в узлах у'-го
и (у—1)-го рядов (у=1, 2,...). Отсюда следует
однозначная разрешимость системы B.139), B.140), B.141).
х
Введем обозначения: — = а, Da(x0, tQ) — треугольник,
ограниченный осью £ = 0 и прямыми oxJrt = ox0-\-t0,
ох—t = ox0 —10, проходящими через (лг0, t0). Нетрудно
видеть, что значение сеточного решения uh системы B.139),
B.140), B.141) в узле (kQ1 y0) однозначно определяется
значениями ф, g в узлах, лежащих на основании
треугольника £)о(&0/г, у0т) и значениями f в узлах внутри и на
границе Da(k0h, Лт)-
Пусть имеется последовательность сеток таких, что
h—>*0, t = aft, a= const>1, и некоторая точка (л:0, t0)
(tf0>0) является узлом каждой сетки последовательности.
Если ин(хоУ tQ) имеет предел u0(xQ1 t0) при h—^0, то
последний определяется значениями /, ф, g в Do(x0, tQ) и,
вообще говоря, отличен от u(xoi t0)— значения в (лг0, ^о)
решения задачи B.135), B.136), B.137), определяемого
значениями /, ф, g в треугольнике D(x0, tQ), содержащем
D0(xQ, ^0) как часть в случае о>1. Поэтому в случае
а>1 последовательность uh, вообще говоря, не сходится
к точному решению задачи B.135), B.136), B.137).
Пусть функции /(л:, t), ф(лг) и g(x) достаточно гладкие
соответственно в полуплоскости t^ 0 и на оси — oo<<x<;oo.

1] § 2. УРАВН. ГИПЕРБОЛИЧЕСКОГО И ПАРАБОЛИЧЕСКОГО ТИПОВ 145
Теорема 4. Если a**const<^: 1, wo при h~~*О
последовательность ин решений, задачи B.139), B.140), B.141)
сходится равномерно к точному решению и (л;, t) задачи
B.135), BЛ36), B.137) во всякой конечной области
полуплоскости t^O.
В случае о=1 имеется простая оценка погрешности.
а) Если ср' и g непрерывны и S^(/i), 6ф, (h), &g(h) — модули
непрерывности внутри (для /) и на основании (для q/, g)
треугольника D (я, t), то
\uh(x, t)-u{x, t)\<t{\\f\\-h + bf{h)+bg(h) + by. (/i)), B.142)
где
11/11= max |/|.
D (x, t)
p) Если / £ С2, g g С2, ф 6 С2, то
\uh(xft)^u(x,t)\^(\\f\\ + Mf^th+M^-h + M^)th. B.143)
у) Если ввести вспомогательные узлы (ky —1), к системе B.139)
добавить уравнение для / = 0 и B.141) заменить на
' 2т ' =g(kh), BЛ44)
то новая система будет также однозначно разрешима, и в правых
частях неравенств B.142) и B.143) надо заменить |[/||, 6 , (/i),
Мф^ нулями. Неравенства B.142) и B.143) являются примерами
оценок погрешности через данные задачи.
б) Параболическое уравнение. Простейшим
параболическим уравнением является уравнение
теплопроводности стержня {уравнение Фурье)
при наличии источников тепла (/^0). В случае, если
источники тепла отсутствуют, имеем
да д2и л /0 . с
m-w=0- BЛ46>
Задача Коши для уравнения B.145) ставится так. В
полуплоскости— оо<<л;<Соо, t^O найти решение уравнения
B.145), удовлетворяющее на границе / = 0 начальному
условию B.136).

146
ГЛ. II. МЕТОД СЕТОК
[I
Известно [98], что значение решения и(х> t) задачи
B.145), B.136) в точке (л:0, /0) определяется значениями
f(x,t) в полосе D0(xQytQ) @ <^ < /0, — оо <х< оо) и
значениями ц>(х) на всей числовой оси —оо<Сл*<оо
(«бесконечная скорость распространения тепла»).
Для прямоугольной сетки (xk = kh, tу=ут, x = oh)
уравнение B.145) естественно заменить сеточным
д5 = (/)*,У V2-147)
(* = 0, ±1, ±2, ...; /=0, 1, 2, ...),
а условие B.136) —условием B.140). Система B.147), B.140)
однозначно разрешима, так как из B.147) определяется
однозначно uh в (у+1)-м ряде, если uh известна в у-м ряде
узлов (у'^0), а из B.140) uh известна в нулевом ряде.
Нетрудно видеть, что значение сеточного решения Uh
системы B.147), B.140) в узле (/е0, /0) однозначно
определяется значениями /(лг, t) внутри и на границе
треугольника DQ(kQhy j0x) и значениями ф(лг) в узлах на
основании треугольника D0(k0h, у0т), лежащего внутри полосы
D0(kohJ0x) при любом как угодно малом а ;>0. Если
имеется последовательность сеток (й—*0, т = а/г, а = const)
и точка (л:0, /0) является узлом каждой сетки, то, вообще
говоря, uh (jc0, /0) не будет стремиться к значению и (х0У tQ)
точного решения. Для того чтобы uh(xQ> t0)—>и (л:0, tQ) при
любых данных f(x, t) и -ф(л:), необходимо, чтобы а—*0
при h—*0 (т%е. чтобы боковые стороны равнобедренного
треугольника Da(xQ, tQ) стремились слиться с полупрямыми
* = /0, л:<л:0, лг>лг0).
Положим Г — -Г*' ^Усть и (*» *) имеет в полосе 0 ^ t ^ Т
ди д2и
равномерно-непрерывные производные -^ и ^-j.
Теорема 5. Если г ^ -д-» то сеточное решение uh
системы B.147), B.140) стремится при h—►О равномерно
(в полосе 0 ^ t ^ Т) к точному решению и (л:, t) задачи
B.145), B.136).
Рассмотрим более общее уравнение параболического типа
Ш~а{-Х' ^Ш~Ь^ *)| + *(*. tL = f{x,t), B.148)

1] § 2. УРАВН. ГИПЕРБОЛИЧЕСКОГО И ПАРАБОЛИЧЕСКОГО ТИПОВ 147
где коэффициенты а(ху t\ b{x, t), g(x, t) удовлетворяют
в полосе O^t^T условиям
0<д(лг, *)<A \b{xyt)\^Ma{xJ), 0<^(лт, *)<<?>
B.149)
А М, С—числа (Л>0, М^О, О^О).
Сеточное уравнение
—^ («к/ ^
-(%, /"*+1,y^B*",,y + (gk/ «*.7 = (Л*.7 B-150)
заменяет уравнение B.148). Система B.150), B.140) также
однозначно разрешима. Если й<Сть t < А2 BЛ+GA2), то
в силу B.149) система, полученная из B.150), B.140)
умножением каждого уравнения на —1, удовлетворяет принципу
максимума (см. § 1, п. 3, а), А). Узел (&, /+1) является
внутренним со звездой из узлов (£, /+1), (&-М,Л (&> A
(/г—1,у); узел (&, 0) граничный. Функции #0 (л;, *) = / и
*\ (#, /) = 1 удовлетворяют условиям леммы 2 (§ 1, п. 3).
Уравнение B.150) аппроксимирует уравнение B.148) в классе U
функций, имеющих в полосе 0 ^ t ^ Т равномерно-непре-
ди д2и ^ 0
рывные производные gi, ^. Отсюда в силу теоремы 3
(§ 1, п. 3) имеет место равномерная сходимость сеточного
решения к точному решению и{х, t); отсюда, в частности,
следует теорема 4. Из теоремы 3 (§ 1, п. 3) получаются
также оценки погрешности. Ограничимся оценкой
погрешности для решения системы B.147), B.140) в
предположении, что и £ U и и (х, t) имеет в полосе 0 ^ t ^ Т
огранили д*и
ченные производные -^ и -=-j,
2 dt*
+А
S|] "• <2л51>
Замечание 1. Предположим, что и £ (У и а (#, f) имеет
в полосе 0^£<;Т ограниченные производные -^, ^. Пусть ыЛ
является решением системы, полученной из B.147), B.140)
т 1
для г = т^ = -£- заменой (f)k j в правых частях B.147) на

148
ГЛ. П. МЕТОД СЕТОК
[1
II «А-
И1К71
(см. § 1, п. 2, пример 6). Тогда
1
216 dt3
+
360
дх«
■Я4.
д**и
B.152)
dx2k
не п ре-
д и д2 и
Замечание 2. Если / = 0, то —- = —- и
dtk dx2k „_.. „
восходит || Ф<2*} (*) 1|« В этом случае оценки B.151) и B.152)
упрощаются и получаются оценки через данные задачи
\uh—u\\<T
\uh—u\
а
+
135
1Ф'
|ФDI|-Л2,
(в>||.Л*
соответственно.
в) Неустойчивость счета. Пусть uh—решение
системы B.147), B.140). Для сходимости uh к точному
решению и необходимо, чтобы . а—►() при h—^0, и
достаточно, чтобы г^у. Если г = const при h—► (), то а—>0
(o = rh), но при f^>-K , вообще говоря, сходимости uh—*и
может и не быть. Более того, система B.147), B.140) для г > -^
весьма чувствительна к ошибкам счета, в частности к ошибкам
округления, которые неизбежны при действительных
вычислениях.
Вычисления изведутся так: из B.140) известны значения uh
в узлах (ft, 0); по ним в силу B.147) для у'=0 вычисляются
значения в узлах (ft, 1), затем в узлах (ft, 2) и т. д.
Допустим, что при вычислении Uo, i за счет округления
возникла ошибка е, но все последующие вычисления
проводятся абсолютно точно. Приведем таблицы (табл. 19)
распространения возникшей ошибки, подсчитанные по формуле
8ft, / + 1= Zk, j + r(Ek + i,j — 2eft,/+ 8fc-i,/), во, 1=8,
e*fi = 0 (кфО).
1
Из таблицы 19 для г-
видно, что одиночная ошибка
8 в последующем оказывает все меньшее влияние на зна-
3
чения и*,/. Из таблицы 19 для г = -^видно, что в
последующих вычислениях ошибка начинает сказываться все

1] § 2. УРЛВН. ГИПЕРБОЛИЧЕСКОГО И ПАРАБОЛИЧЕСКОГО ТИПОВ 149
Таблица 19
1
1 т
з
\ k
i \
1
2
3
4
5
6
7
1
2
3
4
5
6
7
0
8
8

38
8
5s
16
35е
128
638
256
2318
1024
8
8
118
8
29ei
16
467е
128
15838
256
12 031е
1024 J
1
0
8
Т
8
т
158
^ 64
78
32
1058
512
99s
512
0
38
4
38
4
1178
64
93е
32
29558
512
53378
512
2
0
0
8
16
38
32
78
64
15е
128
495s
4096
0
0
98
16
27е
32
135е
64
495е
128
32 535е
4096 |
3
0
0
0
8
64
8
32
45е
1024
55е
1024
0
0
0
27е
64
27е
32
2295е
1024
47258
1024
4
0
0
0
0
8
256
58
512
338
2048
0
0
0
0
818
256
405е
512
4617е
2048
5
0
0
0
0
0
8
КJ4
Зе
1024
0
0
0
0
0
2438
1024
7298
1024
б
0
0
0
0
0
0
8
4096
0
0
0
0
0
0
729е
4096

150
ГЛ. И. МЕТОД СЕТОК
[2
сильней (раскачивается) и практически вычисления потеряет
всякий смысл. Поэтому использование сеточных уравнений
B.147), B.140) при г >>— для приближенного вычисления uh
неразумно даже в тех редких случаях, когда теоретически
возможна сходимость uh к точному решению и(х, t).
Аналогичное замечание можно сделать и относительно сеточной
системы B.139), B.140), B.141) в случае а>1.
2. Смешанная задача. Явные и неявные схемы. Будем
рассматривать смешанные задачи для уравнений B.135) и
B.145) в наиболее простой форме.
Пусть Q — область O^x^l, f^O плоскости Oxt, Г0—
отрезок 0^#^1, / = 0, 1\ — полупрямая х = 0, t^O,
Г2 — полупрямая лг=1, t^O; Г0, 1\, Г2 составляют части
границы Г области Q. Задача ставится так: в области Q
найти решение уравнения B.135) [B.145)], удовлетворяющее
на Г0 начальному условию B.136), B.137) [B.136)] и на Г,
и Г2 граничным условиям
/>|г,==и|Г| = *М/), BЛ53)
\u\T^u\T^%{t). B.154)
Условия согласования данных. Если решение
поставленной задачи непрерывно в замкнутой области Q, то оно
непрерывно в точках стыка частей границы 1\, Г0 и Г2, Г0
и значение и@, 0) определяется по данным задачи либо
как ф@), либо как г^ @). Поэтому для непрерывности
решения и(х, t) необходимо выполнений условий
ф@) = ^@)
и аналогично
ФA) = Ч>,@).
Для непрерывности -^ необходимы условия
г@)=ч»;@), йгA)=ч>;@)
(для задачи B.135), B.136), B.137), B.153), B.154)) и
ф'@)+/(о,о) = ф;@), Ф"A)+/A.о)=г1);@)

2] § 2. УРАВН. ГИПЕРБОЛИЧЕСКОГО И ПАРАБОЛИЧЕСКОГО ТИПОВ 151
(для задачи B.145), B.136), B.153), B.154)). Полученные
здесь необходимые условия непрерывности решения и(х, t)
и его производных в точках @, 0) и A, 0) называются
условиями согласования данных смешанной задачи.
Этот список условий можно продолжить, выписывая
необходимые условия непрерывности -^, -^, ... в @, 0)
и A,0). В последующем будем предполагать, что условия
согласования до некоторого порядка выполнены, и будем
считать, что точное решение задачи и(х, t) непрерывно
вместе с производными до некоторого порядка в замкнутой
области Q + Г.
Последующее изложение в основном будет посвящено
сеточным решениям смешанной задачи B.145), B.136),
B.153), B.154).
Для приближенного решения этой задачи воспользуемся
прямоугольной сеткой. Положим /* = т? (N—целое
положительное число), х—произвольное положительное число.
Сетка Qh (xk = khy tj = jx} 0</г<ЛГ, у = 0, 1, 2, ...)
такова, что узлы @, J) и (Л/, j) лежат на 1\ и Г2. В узлах,
лежащих на Г0, 1\, Г2, значения uh примем равными
соответствующим значениям ф, г^, г|J.
Для определения uh в остальных узлах предлагаются
различные системы сеточных уравнений, обладающих общим
свойством: значения uh в узлах (у+1)-го ряда определяются
после того, как найдены значения uh в предыдущих
(/', у—1, ...) рядах (решение «по шагам»). Для
определения иь, /+i служит некоторая совокупность уравнений,
связывающая ии, /+i с Uk'.jt (/ <:j). Эту совокупность
уравнений обозначим Aj+l.
Систему сеточных уравнений называют явной схемой,
если в каждое уравнение совокупности Aj+1 входит лишь
одно из Uk,j+i и, таким образом, каждое из Uk,j+i (&=1,
2, ..., N—1) определяется независимо от других (B.147)
является примером).
Систему сеточных уравнений называют неявной схемой,
если хотя бы в некоторые из уравнений совокупности А .+1
входит более чем одно из значений м^,/+1. В этом случае
для определения Ukj+i необходимо решать систему,
состоящую из уравнений совокупности А,+1.

152
ГЛ. II. МЕТОД СЕТОК
[2
а) Явная схема. Приведем пример простейшей явной
схемы. Узлы (&, у+1) (\^k^N—1, у^О) назовем
внутренними и каждому такому узлу поставим в
соответствие уравнение B.147); узлам на Г0 сопоставим уравнение
B.140), а узлам на 1\ и Г2 уравнения
«o./ = 4U/r), «*./ = *МА) (У=1, 2, ...). B.155)
Система B.147), B.140), B.155) однозначно разрешима, и
нетрудно видеть, что Uk0, /0 определяется значениями ф(х),
^(Z), i}J@ и /(л:, tf) в узлах, лежащих в треугольнике
£>о(&0й, у0т); точное же решение задачи u{k0h, j0x)
определяется значениями ф .на Г0, tyt и г|J на частях t^j0x
полупрямых Г, и Г2 и / в прямоугольнике 0«^л;^1,
0^t*^j0x. Отсюда, как и в задаче Коши, следует, что
для сходимости uh к точному решению при N—*оо, т—*0
необходимо, чтобы о=~г—>0 при N—>-оо.
Пусть точное решение и (х, t) задачи B.145), B.136),
ди д2ы
B.153), B.154) и его производные 37 и ^i непрерывны в
прямоугольнике Д(Г) @<лг< 1, 0 < t < 7), где Г>0 —
некоторое число. Пусть г = -р.
Теорема 6. Если r^-к, h—*0, то сеточное
решение uh системы B.147), B.140), B.155) равномерно в А (Г)
стремится к точному решению и(х, t).
Замечание 1. Теорема б имеет место для более общего
уравнения B.148) и области А (Г), где полупрямые Г\ и Г2 заменены
кривыми х = хх (t) и x = x2(t) (xx(t) <x2(t)). Предполагается, что
применяется сеточное уравнение B.150), а условия и (хх (t), t) = ^l(t)t
u(xz(t), 0=='llJ2@ учитываются простым сносом. При этом сеточная
система удовлетворяет принципу максимума и корректна (см.
теорему 5), откуда и следует утверждение.
Замечание 2. Для системы B.147), B.140), B.155) имеют
место оценки погрешности B.151) и B.152).
Замечание 3. Если /==0, то
dku _ d2ku
dtk~~dx2k '
В этом случае
d2ku

2] § 2. УРАВН. ГИПЕРБОЛИЧЕСКОГО И ПАРАБОЛИЧЕСКОГО ТИПОВ 153
удовлетворяет уравнению B.146) и условиям
0|Го = Ф(|А)М, o|ri = *i(fc)@, v\FM = yW (t).
Известно [77], что
max | v |^max < max I v I; max \v\\ ; max \ v \\ >.
A(D I r0 o</<r lri o<^<r lr2J
Поэтому в случае f^O и достаточно гладких ф, tyv г|J можно
получить оценки || Ид—и || через данные ф, tyv \f>2.
Ограничение г = -т^^-~- является весьма тяжелым, так
как число внутренних узлов в А (Т) растет при N-+oo не
медленнее, чем 2N*T. Некоторые неявные схемы для решения той же
задачи свободны от ограничения f^y
б) Неявная схема. Вместо уравнения B.147)
каждому внутреннему узлу поставим в соответствие уравнение
_ . _ —\j)k, /+i-
B.156)
Теперь сеточная система состоит из уравнений B.156),
B.140), B.155). Если значения uh в рядах @, 1, ..., у)
известны, то для определения Uk, /+1 (&=1,2, ...,iV—1)
надо решить систему уравнений
, / 1 , 2\ 1 ч
= (/k/+i + - .
(£=1,2, ...,W-1),
«o. 7+1 = ^1 ((У+ ^^ «*. /+1 = t|)t((y+ 1) t),
[ B.157)
и, таким образом, система B.156), B.140), B.155) доставляет
неявную схему. Нетрудно видеть, что система B.157)
однозначно разрешима и, таким образом, поскольку известны
значения uh в узлах на Г0, Г\, Г2, из B.157)
последовательно определяются значения в рядах: первом (/=0),
втором (У=1) и т.д., т. е. система B.156), B.140), B.155)
однозначно разрешима.

154
ГЛ. II. МЕТОД СЕТОК
[2
Сходимость и оценка погрешности. Для любого а*=
= -т- система B.156), B.140), B.155) удовлетворяет
принципу максимума, причем уравнения B.156) отвечают узлам
(k, j+\) I рода, а уравнения B.140), B.155) отвечают
граничным узлам II рода. Очевидно, каждый узел I рода
может быть соединен с узлом II рода (хотя бы
горизонтальным отрезком). На основании теоремы 2 система
однозначно разрешима (для того чтобы не рассматривать
бесконечную систему уравнений, ограничимся узлами в А (Г)).
Пусть теперь N—юо и т—>0 произвольным образом. Для
области А (Г) сеточная система B.156), B.140), B.155)
корректна в силу леммы 2, так как функции v0(x, t)^t,
vl(x, t)=\ удовлетворяют условиям леммы.
Если и(х, t) есть решение смешанной задачи,
непреда д2и а /'гч
рывное вместе с производными ^- -^ в АG), то
уравнение B.156) аппроксимирует B.145) и поэтому в силу
теоремы 2 следует
Теорема 7. Если N—-> оо, т—> 0 произвольным
образом, то uh в А(Т) сходится равномерно к и(х, t).
с Л д2и д*и
Если, кроме того, предположить, что ~ш и -^
ограничены в А (Г), то имеет место оценка погрешности
\uh—uy
д2и
dt2
12
д*и
дх*
Замечание 1. Если /==0, то в оценке B.158)
д*и
B.158)
д2и\\
dt2
дх*
могут быть заменены на
max (|| <рD) (х)
max [1^@1,
max \%(t)\)
o<t<T
(см. замечание 3 к теореме 6).
Замечание 2. Если вместо уравнения B.150) взять
уравнение
uk, j+\ — uk,j . ч uk+h J+i—2uk, j'+i + uk-i, j+\
' ^ Wk, y+i ; Y2
— (%,/+!
2/i
+ (Йл,/+1кл, 7+i== (/)*,/+!»
то для области Д (Т) (см. замечание 1 к теореме 6) при
произвольном стремлении h—►О, т—*0 справедливо утверждение теоремы 7.

(k
, + Bkvk
= 1,2, .,
*. = <*,
..,N-\),
vN=b
-Dk
2] § 2. УРАВН. ГИПЕРБОЛИЧЕСКОГО И ПАРАБОЛИЧЕСКОГО ТИПОВ 155
в) Метод прогонки (см. [2], [17], [81], [90]). Для
решения линейных систем вида
B.159)
при условии, что коэффициенты удовлетворяют условиям
Ak>0y Bk>0, Ck>0} Ak+Ck<Bk, B.160)
предложен метод, получивший название метода прогонки.
Частным случаем системы B.159) является система B.157).
Для решения системы B.159) надо
а) вычислить числа Ek, Fk (& = 0, 1, .. ., N—1):
**• = *' ^"S-w! (*=1.2,...,iV-l)
(прямой ход прогонки);
E) вычислить числа
vN=b, vk = Ekvk+1 + Fk (ft^tf-l, N-2, .... 1)
(обратный ход прогонки).
При таком способе вычислений в силу условий B.160)
числа Ek удовлетворяют неравенству 0<^Ek<\ (&=1,
2, ...,N—1), что выгодно отличает метод прогонки от
других возможных точных методов решения системы B.159).
г) Пример семейства неявных схем. Пусть
а и 8 — произвольные числа. Уравнение
uk,j+i—uk,j ( Ч+г,/+г—'%Ч, j+\ + 4-h /+i ,
+ A-а)И*+1'^2^/+Ц*"Ц=/(^, (У+9)т) B.161)
аппроксимирует уравнение B.145) в классе функций,
непрерывных вместе с производными ^ и ^ в ДG).
При а = 9 = 0 получаем уравнение B.147), при а = 6 = 1 —
уравнение B.156). Для каждого сс=£0 система B.161), B.140),

156
ГЛ. II. МЕТОД СЕТОК
[3
B.155) представляет неявную схему. Эта система однозначно
разрешима при а^О и удовлетворяет принципу максимума
и корректна в Д(Г) при выполнении условий
0<«<1, ^<w^-. BЛ62)
Поэтому при выполнении условий B.162) решение uh системы
B.162), B.140), B.155) равномерно в А (Г) стремится к
точному решению и(х, t).
3. Устойчивость разностной схемы. Признаки
устойчивости, а) Пример 23. Пусть ставится задача: в области
Q @^л:^1, t^O) найти решение уравнения B.145),
удовлетворяющее на отрезке Г0 (£ = 0, 0 s^Jt^l)
начальному условию B.136), на полупрямой ГДх^О, t^O)
граничному условию B.153) и на полупрямой Г2 (#=1, t^O)
граничному условию
sL-*.<'>• <2Л63>
Можно предложить следующие сеточные уравнения для
прямоугольной сетки Qh (xk — kh, tj = jx, h = =-, где N—
целое число). Узлы (&, J) (ls^&^/V, j^2) назовем
внутренними и для каждого такого узла напишем уравнение
(Ричардсон, 1910 г.)
ttfe,/+i— Uk% /-i uk + i,j — 2uk,j + uk-i, / _//ч /о ifivix
(ft=l, 2, ..., N; y=2, 3, ...),
аппроксимирующее уравнение B.145) с оценкой
dhi
t2+f2
Ъх*
h2
в классе функций, которые можно продолжать за
полупрямую Г2 с сохранением непрерывности производных по х до
четвертого порядка. Аппроксимация уравнения B.145)
уравнением B.164) лучше, чем уравнением B.147) или
уравнением B.156). В узлах, лежащих на Г0 и Г15 положим uh
равным соответственно ф и \|з . Для сеточной замены уело-

3] § 2. УРАВН. ГИПЕРБОЛИЧЕСКОГО И ПАРАБОЛИЧЕСКОГО ТИПОВ 157
вия B.163) введем вспомогательные узлы (Ы-\-\, у),
лежащие на расстоянии -^ от Г2. Уравнение
^+1,г^,1 = г|J(А) (/==1) 2> §§0 BЛ65)
/i
аппроксимирует уравнение B.163) с оценкой ^ L-3
h\
Уравнение B.165) позволяет находить w#+lf/-, если
известно UNtJ: Уравнение B.164) позволяет находить uh во
внутренних узлах (y-(-l)-ro ряда, если известны значения uh
в двух предыдущих рядах—у-м и (у—1)-м. Поэтому для
полного определения сеточной функции на всей сетке Qh
достаточно указать значение uh во внутренних узлах первого
ряда. Тогда
"о, 1 = ^! (т), uN+h i = uNil + hty2 (t)
и uh будет известно во всех узлах первого ряда. Из
уравнения B.164) для у= 1- определяется ин во внутренних узлах
второго ряда и затем и во всех его узлах. Таким же
образом ин определится далее на всей сетке.
Для определения uh в первом ряде предложим, например,
такой способ. Из уравнения B.145) для ^ = 0 и из B.136)
следует, что
dal = ф" (*)+/(*, 0).
dt
t= о
Поэтому в силу и(ху х)=^^(х) + Х (~ ) _ естественно
положить
Ukti=*<f{bh)+rW№+f{bh, 0)] (й=1, 2, ..., N).
и уточнить Uk 1 или
/ = 0 '
Можно было бы дифференцированием по t уравнения B.145)
д2и\
получить аналогичным путем -^
вычислить uh в нескольких последующих рядах.
Описанная здесь схема получения приближенного
решения задачи на первый взгляд кажется выгодной в смысле
хороших оценок аппроксимаций применяемых сеточных
уравнений. На самом же деле эта схема будет в последующем
забракована в силу ее неустойчивости.

158 гл. п. метод сеток [3
б) Сеточная (разностная) схема решения
смешанной задачи для уравнений гиперболическо-
го и параболического типов. Пусть La—линейный
дифференциальный оператор порядка s, содержащий
дифференцирование- только по переменной х с коэффициентами,
зависящими от х и t. Пусть р—целое положительное
число. Ставится задача: в области Й (O^at^I, t^O) найти
решение уравнения
jp-Lu = f(x, t), B.166)
удовлетворяющее р начальным условиям
0<х<1, B.167)
и линейным граничным условиям
Тхи = уг(t), Тги=^(t), ..., 7sit = tys(t), B.168)
где ltu—линейные комбинации значений и(х} t) и ее
производных по л: с коэффициентами, являющимися функциями /;
уравнение
a (t) a @,t) + р (t)px\x=9 + V V) «A,0 + « (*)% | ^=1 = ^@
является примером уравнений B.168).
Так поставленная задача B.166), B.167), B.168)
содержит как частные случаи указанные ранее (см. п.2)
смешанные задачи для уравнений гиперболических и параболических
типов.
Пусть соА означает некоторую конечную совокупность
точек отрезка —s^x^l+e (е>0):
Пусть т>0 — произвольное число. Сетку Qh будем считать
состоящей из узлов с координатами (xk, jx) (xk£ сол, у'^0).
Слоем S, назовем совокупность узлов, лежащих на прямой
t = jx. Пусть uh—некоторая сеточная функция и и]? есть
N^-мерный вектор, составляющие которого суть значения

3] § 2. УРАВН. ГИПЕРБОЛИЧЕСКОГО И ПАРАБОЛИЧЕСКОГО ТИПОВ 159
функции uh в узлах слоя S,. Совокупность сеточных
уравнений, заменяющих уравнение B.166), разобьем на группы
по следующему признаку: в группу с номером у включаются
те уравнения, в которых содержатся значения uh в S. и не
содержатся значения в Sj>, где />/. Предполагается, что
каждая такая группа уравнений в матричной записи имеет
вид
R\=±Afr<n)uU-<n)==Ilfri)(f; Фо, ....ф,.,; ^ ...,%),
B.169)
где А\1Л т) — прямоугольная матрица с Nh—s строками и
Nn столбцами, ГЦ0';) — оператор, ставящий в соответствие
группе функций/; ф0, ..., ур_г; i|>lf ..., %
(Nh—^-мерный вектор. Каждое уравнение у-й группы связывает
значения сеточной функции в q-\-\ подряд следующих слоях
sj-q> si-g+h ..., s/-v Sy, где Я^Р (в примере 23 р=1,
? = 2).
Сеточные уравнения, заменяющие граничные условия
B.168), будем считать записанными в таком виде, что
каждое уравнение содержит значение uh лишь в одном слое
и является линейным относительно этих значений; каждому
слою отвечает s уравнений, которые запишем в виде
(afrn\ и^)^и^п)(/; Фо, ..., ф^;^, .... ф,) B.170)
(л=1, 2, ..., s; j=q, q+l, ...),
где afr п) есть Л/л-мерный вектор, ((а, Ь) — знак скалярного
произведения векторов а, £), П//' п)—функционал над
группой функций (/; ф0, ..., ф^; ^, ..., %).
Предположение А. Для каждого j{j^q)
совокупность уравнений B.169), B.170) однозначно разрешима
относительно ujj\
Из предположения А следует, что если известны и^\
и^\ ..., н^-1), то ин однозначно определяется на S
Пусть ПЛ(/; ф0, ..., ф^; %, ..., г|>5) — оператор,
ставящий в соответствие группе (/; ф0, .. .,ф; tyv ..., tys)
(Л^-#)-мерный вектор, составляющие которого назначаются
значениями uh в слоях SQ1 Sv ..., Sq^_l; в примере 23

160
ГЛ. И. МЕТОД СЕТОК
[3
оператор Пн таков:
«а, о = Ф(*А)> «*,, = Ф(*А) + Т(Ф*(АА)+/(АА, 0))
(ft=l, 2, .... N)9
иол = %\ (т)> «tf+i, 1 = ttiv, i + Ai|>t (т).
Если задан оператор ПЛ и составлены сеточные
уравнения B. 169), B.170), удовлетворяющие предположению А, то
сеточная функция ah однозначно определяется.
Будем рассматривать решение задачи B.166), B.167),
B.168) в фиксированном прямоугольнике А (Г) (O^x^l,
0 ^ t ^ Т). Пусть рассматривается последовательность сеток
{ Qh }, А—*0, таких, что т->0, Л^-> оо. Через Mh
обозначим число слоев в А (Г), т. е. целое число, ближайшее к
Т
отношению — и больше его. Тогда будем иметь следующие
векторные пространства: (Л^-Ж^-мерное £/л, (Nh—s)(Mh—q)-
мерное Fh, (Mfy—#)-мерное пространство Wnh (п == 1, 2,.. ., s),
(А^'<7)-мерное пространство фл. Будем предполагать, что
в пространствах £/Л, /^, Ч^пЛ введены нормы, согласованные
с соответствующими функциональными нормами ||и||с/, ||/||f,
|| i|)n||^n (см. §1, п. 2). В ФЛ введем векторную норму,
которую будем считать согласованной сразу с несколькими
функциональными нормами ||ф0||, lltyJI, .••, Цф^-JI в том
смысле, что для всякой функции и (#, t)£U имеет место
равенство
Нш|[ПА(/;ф0, ..мф^-Г,^, ...,%) Ik =
— ^A|Фо1М]фЛ, ..-> 1|<Р,-Л), I2-171)
где/, ф0, ..., Ф^-!, tyiy ..., я|M определяются равенствами
B.166), B.167), B.168) и/Сесть некоторая однородная первой
степени положительная функция всех аргументов (например,
11Ф.П + Цф.Н + • • • + К-г\\ ИЛИ У\\%\\г + \\%\*+-.-+НР-гП
Будем говорить, что ПЛаппроксимирует и{х, t) по
введенной норме, если \\и—ПЛ||->>0 при h—'-О.
Определение 1. Говорят, что сеточная задача B.169),
B.170) устойчива по начальным условиям, если для всякой
сеточной функции uh, удовлетворяющей однородным
уравнениям, соответствующим неоднородным B.169) и B.170)
(полученным из B.169) и B.170) заменой правых частей на

3] § 2. УРЛВН. ГИПЕРБОЛИЧЕСКОГО И ПАРАБОЛИЧЕСКОГО ТИПОВ 161
нули), имеет место неравенство
11«А1К<^вI|я*||Фк, B.172)
где № — положительная постоянная, не зависящая от h.
Определение 2. Говорят, что сеточная задача B.169),
B.170) устойчива по правой части, если для всякой
сеточной функции uh, обращающейся в нуль на слоях 50,
5а, ..., S и удовлетворяющей однородным уравнениям,
соответствующим B.170), имеет место неравенство
IKIk<M'>||flA||fft,
где АЛ1* не зависит от h\ Rhuh—оператор, переводящий £/д
в FA и полученный объединением левых частей B.169).
Определение устойчивости по граничным условиям
аналогично: -
\\ и*1К<;м«> ± || rnhuh \\Vnh,
если uh равен нулю на S0, .. ., S и удовлетворяет
однородным уравнениям B.169).
Из линейности5сеточной задачи легко следует, что если
сеточная задача устойчива по начальным условиям, по
правой части и по граничным условиям, то она корректна (см.
§,1, п. 3, б)). Если u(x,t)£U, уравнения B.169) и B.170)
аппроксимируют уравнения B.166) и B.168), а ПЛ
аппроксимирует и(х, t), то uh сходится к и(х, t) при h-+0 (§ 1^
п. 3, теорема 3).
Изучению устойчивости по начальным условиям уделено
значительно больше внимания, чем изучению устойчивости
по правой части и граничным условиям. Это объясняется
тремя факторами: 1) во многих случаях ([83], [116]) из
устойчивости по начальным условиям (так называемой
равномерной устойчивости) следует устойчивость по правой
части; 2) большая часть рассматриваемых задач такова, что
граничные условия учитываются точно и в оценке
погрешности соответствующее слагаемое равно нулю; 3) изучение
влияния ошибки, допущенной при вычислении uh на
некотором слое S., на значения uh в последующих слоях 5-+1>
Sy+2, ... сводится к изучению устойчивости по начальным
6 С. Г. Михлин и X. Л. Смолицкий

162
ГЛ. II. МЕТОД СЕТОК
[3
условиям. По-видимому, последнее обстоятельство оказалось
решающим. В книге [17] дано изложение вопросов
устойчивости по правой части и граничным условиям.
В последующем изложении под устойчивостью
разностной схемы будем понимать устойчивость по начальным
условиям.
в) Устойчивость разностной схемы. Пусть Ul
означает совокупность сеточных функций uh, удовлетворяющих
однородным уравнениям B.169) и B.170).
Введем нормы: ||иЛ[|с/А для (Л^-МЛ)-мерного вектора uh\
\и{1]\\ для Л^-мерного вектора и$р; || tiff* q) || для (Nh*q)-
мерного вектора, составляющими которого являются
значения ин в q слоях Sy.f+l, Sj-q+2} ..., S.) норму \\ин\\ф^
согласованную.с функциональными нормами в смысле B.171).
Предполагается, что для любой сеточной функции uh£Uh
эти нормы связаны неравенствами:
||Ий|| 0<C0max||u(/)|| @</<Mft-l), B.173)
ft /
ll"jr,,9,ll<CJK||<x>ft) BЛ75)
где С0, Ct, C2 —положительные постоянные, не зависящие
от h. В частности, если нормы векторов понимать как
максимум модуля составляющих вектора, то эти неравенства
выполняются для С0 = Сг = С2 = 1.
Теорема 8. Если существует неотрицательная по-
стоянная С такая, что для любой uh£Uh имеет место
неравенство
\\u^^\\^(\+Cx)\\u(i^^\l ?<у<И4л-1,B.176)
то сеточная схема B.169), B.170) устойчива, т. е. для
всякой ин£Щ имеет место неравенство B:172).
Частный случай. Если p=^q=\y то норму || ufr q) \\
считают совпадающей с || и1^ [|, и тогда B.176) принимает
вид
||u</)||<(l+Ct)||^-)||, 1«Л«А-1. B.177)

3] § 2. УРАВН. ГИПЕРБОЛИЧЕСКОГО И ПАРАБОЛИЧЕСКОГО ТИПОВ 163
Пример 24. В прямоугольнике А (Г) рассмотрим
сеточное уравнение B.150) (й = ~) для (f)k, у=0 при
условиях u0i j==Um, / = 0 на полупрямых Тг и Г2. Если g(х, t)^0n
X<ih2 BЛ+ Gh2)~l, то имеет место принцип максимума и
корректность сеточной задачи и вместе с тем устойчивость по
начальным условиям. Если g{xy t) принимает и
отрицательные значения в А (Г), то сеточная система не удовлетворяет
принципу максимума, но в этом случае при условии /• = —<; —^
имеет место устойчивость, так как очевидно, что
справедливо B.177), где C=\\g(x, t)\\. Можно доказать, что
здесь имеет место и сходимость ин к и(х, t).
Замечание. В случае p = q=z=\, решая однородные
уравнения, соответствующие B.169), B.170), относительно
и^\ получим
где в]?— квадратная матрица порядка Nh. Пусть норма
матрицы выбрана согласованной [104] с нормой векторов.
Тогда достаточным условием устойчивости будет
Если коэффициенты оператора L и граничных условий
не зависят от /, то естественно коэффициенты сеточных
уравнений B.169), B.170) выбрать не зависящими от j.
В этом случае матрица 8$ н.е зависит от j и поэтому
Тогда необходимым и достаточным условием устойчивости
является ограниченность норм совокупности матриц
11E/11 (А-*0, 1</<МА-1).
г) Индекс разностной схемы ([30]). Из
предположения А о системе B.169), B.170) следует, что
значение отдельной составляющей (u^)k вектора и^р является
линейной комбинацией значений uh в слоях Sy_1? ...,Sy_^
6*

164
ГЛ. II. МЕТОД СЕТОК
[3
(предполагается ий ££/£), т. е.
где С(^;^ — коэффициенты линейной комбинации. Величина
/= max max 2 l^'v'M
7</<Af^-i xk6@ft xv 6 ©ft
называется индексом разностной схемы.
Если существует постоянная С, не зависящая от /г,
такая, что У<1+Сг> то на основании теоремы 8 разностная
схема устойчива (нормы векторов—максимумы модулей
составляющих).
д) Признаки устойчивости, полученные
методом разделения переменных. Предположим, что
коэффициенты оператора L (см. 2.166)) и линейных
комбинаций 1пи (см. B.168)) не зависят от t. Тогда матрицы AJ/* т)
и векторы atf*n) (см. B.169) и B. 170)) естественно
выбрать не зависящими от /; в этом случае будем писать
л£т) и а^К Теперь все векторы u{J)(j=Oi 1, ...) должны
удовлетворять"условиям
. К"'. «!/>H0 (Л=1, 2, ..... s) B.178)
и, следовательно, принадлежат некоторому
(Mh—^-мерному векторному подпространству Vh пространства Л/л-мерных
векторов.
Пусть Nh—5 узлов из сол считаются внутренними и
s узлов—граничными. Предполагается, что вектор vh^Vh
однозначно, определяется своими значениями во внутренних
узлах. Предположим, что строки матриц А^ отвечают
внутренним узлам сол, т. е. А^и^ — вектор, составляющие
которого суть значения некоторой сеточной функции во
внутренних узлах сол. Такой вектор в силу сделанного
предположения однозначно доопределяется до вектора из
подпространства Vh. В этом смысле прямоугольные матрицы /Цт)
можно рассматривать как переводящие всякий вектор из Vh
в вектор из Vh.

3] § 2. УРАВН. ГИПЕРБОЛИЧЕСКОГО И ПАРАБОЛИЧЕСКОГО ТИПОВ 165
Предположение Б. В Vh можно ввести скалярное
произведение так, чтобы в Vh существовал такой ортонор-
мированный базис, каждый вектор которого является
собственным вектором для каждой из матриц А^К
Это скалярное произведение обозначим через [vhy v'h]y
где vh и v'h — два вектора из Vh; векторы базиса обозначим
через v^ (/=1, 2, .. ., Nh—s)y а собственные числа
матрицы Дт> — через Qhm'l). Тогда сеточная функция uhy
значение которой в слое S, определяется равенством
«</> = ?Л/<'>,
где К—некоторое число, удовлетворяет граничным условиям
B.178); uh удовлетворяет однородному уравнению B.169)
тогда и только тогда, когда % удовлетворяет уравнению
m=o m=o
т. е. (считая кфО) уравнению
Q(o, 1)№ + 6£, /)^-*+... +Q^",f l)h + Q{hq' /} = 0. B.179)
Обозначим через A,j>» l) (fx=l, 2, ..., q) корни уравнения
B.179) и назовем их коэффициентами роста. Введем нормы
||вд|| 0= max
uh 0<i<Mh-i
"Лфн = У$Нт)\\я- B-181)
.= max || «[''Ml f BЛ8°)
и в случае р-
Теорема 9. Для того чтобы сеточная задача была
устойчива (в случае р=1) по нормам BЛЩи B.181),
необходимо и достаточно, чтобы существовала
неотрицательная постоянная С такая, чтобы для [i = 1, 2,.. ,yq
и /= 1, 2, ..., Nh—s коэффициенты роста удовлетворяли
неравенству
W' l)i<l+C%. B.182)

166 ГЛ. II. МЕТОД СЕТОК [3
Замечание 1. Для случая р>1 и специального
выбора нормы ||иЛ[|фЛ условия устойчивости изложены в [83]. В
частности, стремление к единице верхней границы модулей
коэффициентов роста является необходимым условием
устойчивости. Это значит, что если при как угодно малых h среди
коэффициентов роста найдутся такие, что \%^* 1)\ ^ 1 -(-8,
где 8 — малое фиксированное число, то сеточная задача не
является устойчивой.
Замечание 2. В случае р=\ условие
|W^'>|<1 B.183)
является достаточным условием устойчивости. При условии
B.183) ||м|^|| остается ограниченной для/—>оо.
Некоторые авторы [90], [112], определяя устойчивость как
ограниченность ll^l/MI ПРИ J—*°°> принимают B.183) как
необходимое и достаточное условие устойчивости.
е) Примеры. В последующих примерах будут рассмотрены
сеточные схемы для уравнения B.146). В качестве аппроксимации
ДЛЯ \дд)ь буА6Т пРименяться ЙГ ("*-*. /—2ak,/+uk+hJ)-
В качестве граничных условий рассмотрим такие:
а) ии=о = и|*=1 = 0»
X— 0 иЛ \х _!
дх
Р) «
да
= 0.
Х= 1
1х= о
В качестве множества сол возьмем:
a) xk=zkh, й=тг» 0<fc<N,
$)xk = kh, h==—Ц-, 0<£<tf+l,
Y) xk = (k+±) А, А=1, -1<A<JV.
Сеточными граничными условиями возьмем:
a) u0jJ=uNi/=0,
Р) Ио,/=0» "N+i,/— Ufifj=0t
Y) «0>/—«-i,y=0, «#,/—"tf-i,/=0.

3] § 2. УРАВН. ГИПЕРБОЛИЧЕСКОГО И ПАРАБОЛИЧЕСКОГО ТИПОВ 167
Сеточные функции v\^ (k):
,('),
;cos
2JV+1
fe+Mjt/
(/ = 1, 2, .
(/ = 0, 1, .
A=0, 1,
/V—1),
, ЛГ-1),
Y) «#'(*)—n -r2jN
являются собственными функциями разностного оператора
причем
(«{«^A-'lt (ft-l)-2o(*) + o(ft + l)],
аNЛ»</> =
*%£'> =
4 . ,
4 . 2
— т? Sln
А2
"^,■$0
Заметим,
,яB<+1)
Р) «а -А
случаях а)
2N> h
яB/+1)
2BiV+l)
,@
й2 sm 2#
nV)
что в
я/
Р), у) множители
. 2 я/
sin ш •
sin2 ^ д. : , sin2 — положительны (кроме случая 1 — 0 для у)) и
при изменении / в указанных для / пределах при N —*oo
принимают значения, как угодно близкие к 0 и 1. Эти множители
в последующем обозначим через qJ{\ В последующих примерах
граничные условия могут быть любые из а), C), у) и будем
выписывать только сеточное уравнение, заменяющее уравнение B.146)
для внутренних точек сетки.
Пример 25. Рассмотрим однородное уравнение B.164)
(см. а)). Подставляя в B.164) вместо u^j выражение K^vjl\k)t
найдем после сокращения на XJ'1v^ (k)
х
Я2 + 8го#> Я —1=0
/i2
Свободный член этого квадратного уравнения отрицателен, и,
следовательно, его корни вещественны, разных знаков и
отрицательный корень по модулю превосходит единицу. Обозначим его через
А^1' К Для фиксированного г для достаточно малых т и h
найдется такое /, что
>1+4г,
[41'
0|
и, следовательно
т—►(), h
•■г
разностная схема с B.164) неустойчива при
2* Г0 > 0.

168 гл. и. метод сеток [3
Пример 26. Рассмотрим семейство неявных схем B.161).
Подставляя в однородное уравнение B.161) W'v$ (k) вместо ukiJ-,
после сокращения на XJv^ (k) получим
Я —1 + 4г[аХ+ A—а)] qJ/> = 0.
Отсюда следует, что
*,= !■
1-Игд^а
и поэтому для а>0 имеем Х<1. Если выполнено неравенство
2г A — 2а) ^1, то в силу O^oj^s^l будем иметь Х^—1 и,
следовательно, |Х|«^1. Отсюда следует, что схема B.161)
устойчива, если 2г A — 2а) ^1. В частности, если а^~, то схема
устойчива для любых г > О, т. е. будет устойчивой при произвольном
стремлении т—у О, h—*0. Если а < -»-, то для устойчивости
т 1
схемы необходимо и достаточно, чтобы г — т^-^^т:—=-г.
Заметим, что из принципа максимума (см. п. 2) для O^a^l было
получено неравенство г«^сГЛ :, обеспечивающее корректность и
Z A а)
тем самым устойчивость в равномерной норме, а поэтому и в норме
B.180). Для r = fin __9 (а<-^\ получается уравнение с
хорошей аппроксимацией.
Пример 27. В случае а>0 схема B.161) является неявной
и для перехода к следующему слою требуется решать систему
линейных уравнений. Уравнение (Дюфорт и Франкел, 1953 г.)
Тх J? =0 BЛ84)
приводит к явной схеме, устойчивой для произвольного
стремления т—*-0, h—► (). Действительно,
i#> (k+ \) + vtf (Л- 1)-2 cos 4°-4° (k),
(h nl ч ч (I) яB/+1) Лч „
где Н —Jf в случаях а) и у), ^ = 2^ + 1 В слУчае Р)- По"
этому после подстановки Wvff (k) в B.184) вместо uk j и после
упрощений получим
Ь2 —1—2г[Х-2cos ^°-(X2+ 1)]=0

3] § 2, УРАВН. ГИПЕРБОЛИЧЕСКОГО И ПАРАБОЛИЧЕСКОГО ТИПОВ 169
4г cos ц<*> j _2r
Л— 1 i о =U>
1+2г 1+2г"
модули корней которого при любых значениях г>0 и р,^ меньше
единицы, и поэтому B.184) устойчиво при произвольном
стремлении т—*0, h—>0. Однако следует заметить, что уравнение
B.184) аппроксимирует уравнение B.146) только тогда, когда
т т
т *0. Если -r=G остается постоянной (а > 0), то уравнение
B.184) аппроксимирует гиперболическое уравнение
ди д2и , , д2и _
Поэтому при применении уравнения B.184) для приближенного
решения уравнения B.146) сетку следует брать с достаточно
малым а = -г- . В книгах [81], [90] приведена таблица сеточных
уравнений, аппроксимирующих уравнение B.146), и условий
устойчивости этих сеточных уравнений.
ж) Признак устойчивости для уравнений
с постоянными коэффициентами. Пусть а)
коэффициенты оператора La постоянны, б) однородные
граничные условия для д:==0 и х=\ таковы, что искомое
решение и(х, t) уравнения
pt—Lu = 0 B.185)
может быть продолжено на всю полуплоскость (—оо < #<С<х>,
t^O) так, чтобы новая функция была решением уравнения
B.185) и была периодической по л: с некоторым периодом
/я, где т—целое положительное число.
Пусть для решения этой задачи применяется
прямоугольная сетка
xk = x{0\h) + kh, t^jx
(* = 0, ±1, ±2, ...; 7=0, 1, 2, ...; bj)
и сеточное уравнение, заменяющее B.185), имеет вид
(«? = !)
v=— s v=—s

170
ГЛ. II. МЕТОД СЕТОК
[3
где s—некоторое целое положительное число, а^ и Ь^ —
коэффициенты сеточного уравнения, зависящие от выбора т
и /г, не зависящие от k и /. Граничные условия заменяются
условием периодичности сеточного решения. Сеточные
уравнения B.186) имеют решения вида
где /—произвольное целое число, Цр — постоянная,
зависящая от выбора / (и выбора h и т). Из уравнения B.186)
находим
2 #4' / ,«а\
^) = _^ [£=е if)- B.187)
v=—s
Если при h—^0, t—*0 для каждого / имеет место
неравенство
|Х^|<1+Ст, B.188)
то сеточная задача .устойчива.
В книге [81] изложена теория устойчивости разностных
уравнений для случая #^1, аппроксимирующих уравнения
вида B.185). Изложенный здесь признак B.188) является
частным результатом упомянутой теории.
Отметим, что заключения в примерах 25, 26, 27 (см. е))
могут быть получены на основании этой теории.
Следующий пример таков, что не выполняется предположение
Б, сделанное в д), и поэтому не проходит способ пункта е).
Пример 28. Асимметрическое сеточное уравнение [90]. Пусть
ставится задача: найти решение уравнения B.146) при граничных
условиях и \х-0 = и |х=1 = 0 и начальном условии w|<=0 — cp (#).
Нетрудно видеть, что если решение и (х, t) этой задачи
продолжить на ( — 1 <:* ^0, t ^0), полагая и (х, t) — —u (—x, t), и затем
продолжить периодически с периодом 2 по х на всю полуплоскость
f^rO, то полученная функция и (х, t) будет решением того же
уравнения B.146).
Пусть а —произвольное вещественное число. Для каждого
внутреннего узла сетки xk~kh, t=jx ( /i= —; fc=l, 2, . . .

3] § 2. УРАВН. ГИПЕРБОЛИЧЕСКОГО И ПАРАБОЛИЧЕСКОГО ТИПОВ 171
• . ., N—1; / = 1, 2, . . . J запишем уравнение
(l-f-га) —— — — га — ——
ft* r ' r~/z2 •
B.189)
аппроксимирующее уравнение B.146) при —
-О с оценкой
дх*\
ft2 +
dt2
т +
dt дх\\ h
Несмотря на то, что уравнение B.189) приводит к неявной схеме,
вычисление иЦ+1^ осуществляется просто. Именно, из B.189) при
A + га) фО однозначно определяется и^ у+1, если известны и$ и
и^-, ,-+1. Но и0, у+1 = 0 в силу граничного условия, и поэтому
последовательно вычисляются utjj+v н2,/+i> •••• uN-it /+i> если
известно и)/\ затем полагается «w,/+i = 0-
Из B.189) имеем
[A + ra) ukt J+1-rauk-h /+1] +
+ [Bг— 1 -га) ukt j-r A -a) uk-h /—ruk+h у] = 0
и, следовательно, на основании B.187)
. 2711
%{1)__ гA—a)£-^ + r£—Bг—1—га)
Л " A + га)—га?-1
В случае а=1, очевидно, имеем
иш., г£ + A —г) >гЁ+A-г) _ r2 + (l —rJ + 2r(l—r)cosfx _
1 Л I ~"A + г) —re-1A+r)_^-i-r2 + (l-H rJ—2r(l + r) cosp,
= 1 4r(l—cos[x) Лг^в-й^-М
г2 + A+гJ — 2r(l + r)cosp, V С У*
откуда следует 0 < | Я^^|2 < 1, и, таким образом, сеточная схема
B.189) для <х=1 устойчива при произвольном г. При применении
схемы B.189) все же следует помнить, что для наличия
аппроксимации необходимо -г —►(), и поэтому при конкретных вычислениях
следует т брать малым по сравнению с ft. Заметим, что при
а=г = 1 схема B.189) приводит к формуле
"*,/+! =
uk+i, /+Mfc-i, /+i
вычисления по которой весьма просты.

172
ГЛ. II. МЕТОД СЕТОК
[4
4. Примеры устойчивых разностных схем. а)
Перемежающаяся схема. Для приближенного решения
уравнения B.146) при граничных условиях и \ х=0 = и |х=1 = 0 и
начальном условии B.136) были рассмотрены явная B.147)
и неявная B.156) схемы. Явная схема устойчива лишь при
х ^ 1 0
г=т2^т>-, но вычисление uh на очередном слое о.
осуществляется просто; неявная схема устойчива при любых
X—уО, h—уО, но для определения uh на очередном слое Sj
требуется решение системы линейных уравнений, например,
методом прогонки, но не накладывается ограничений на
т
отношение сг = ~ (т—^0, h—*0). Оказывается, что если
вычисление и^ для четного j (нечетного j) вести по явной
схеме, а для нечетного j (четного j) — по неявной схеме, то
в целом схема получается устойчивой. Действительно,
решение сеточной задачи является суммой слагаемых вида
wtU)slnk% {1=1, 2, .... N-\).
При пользовании явной схемой при переходе от S. j
к S, имеем
wt(j — \) ^ \ /i2' ул ьш 2NJ'
а при переходе от слоя S, к слою S .+1 по неявной схеме
имеем
«М/+1) = 1
Щ (/) 1 + 4rQ</} #
Поэтому за спаренный шаг перехода от слоя 5. а к слою S.
имеем
1-4^I
щи — 0
1+44
(D
<1,
что обеспечивает устойчивость схемы при произвольном г;
устойчивость и аппроксимация имеют место при
произвольном стремлении h—^0, т—^0.
В книге [90] изучено большое число разностных схем
для решения уравнений параболического типа.

4) § 2. УРАВН. ГИПЕРБОЛИЧЕСКОГО И ПАРАБОЛИЧЕСКОГО ТИПОВ 173
б) Устойчивые разностные схемы для
р = д = 2. Рассмотрим уравнение B.166) для случая р=2ш
Если строить разностную схему B.169) для случая q — 2 и
норму в Фн выбрать равной
г-
У к°>. »п +
W-W 41>-«?)
то можно указать следующее достаточное условие
устойчивости. Если сеточная задача такова, что коэффициенты
роста (см. п. 3, д)) ^'> ((г=1, 2; /=1, 2, ..., Nh—s)
представимы в виде Л£*/)==e/Y', Ц?*1) =e~£vi, то сеточная
задача устойчива, если cosy^^ — 1+v, где v>0 —
некоторое произвольное фиксированное число [83].
Пример 29. Для решения смешанной задачи
д2и д2и _
W"dx2 y
и\х=0=и\х=1 = 0, и
=*(*>
введем сетку хА =/г/г, tj—jx \h = -^; 6 = 0, 1, ..., N; j = 0,
1,2. ...V
Рассмотрим семейство неявных схем
«*,у+,-2»*,/+ и*, /-. _[аКц(/+1)+A _а_р) а» и(/> +
4+1, j—2uk, J+ uk-i, / \
h2 )r
"о, /== UNJ= 0. м*, о = Ф (M), иА|! =■ Ф (M) + xg (kh).
nl
Выбирая v^ {k) = sinkjy (/=1, 2, ..., iV— 1), легко находим
следующее уравнение для Х$" *:
X2—2X+1 + 4q^> a2[a^2 + (l-a-P)X + p]=0
1-2е^а2A-а-р)"
т. е.
%2-2
1 + 4о^о2а
,@ а2п
1+4ора^_
Л+1 + 4о</>а2а

174 гл. п. метод сеток [4
Для а = р^0 и Q^/,a2(l-r-4a)^ 1 корни последнего
квадратного уравнения имеют вид eiyi и e~~*Yi, где
1 2Q//)q~2 , 2a2 i+a2Da-l)
cos^=1-1 + 4QJ?>o-a^1"r+lS5e--1+2 l + 4o*a '
Поэтому для a > — схема будет устойчивой при произвольном
1 т
h—5-0, х—*0. Для a = -j схема будет устойчивой при -г-^ст0,
где а0—произвольное фиксированное число. Для а = 0 схема
является устойчивой при сг< 1, т. е. при -т-^а0< 1; для а = 0 и
а=1 схема неустойчива [83].
Пример 30. Задача об упругих колебаниях стержня
ставится так: в области 0^х<;1, t^O найти решение уравнения
£+£-•• <2-1("»
удовлетворяющее начальным условиям B.136), B.137) и граничным
условиям
д2и\
ЛГ=0 ил \Х = 0
= 0. B.191)
x=i
(Можно рассматривать и другие граничные условия.)
Введем сетку xk - kh, tj= jx ( /i = —; & = — 1, 0, ..., N,
N+\; 7 = 0, 1, 2, ...).
Сеточные граничные условия запишем в виде
Ыо,/=«лг, у=0, w.i,y+Mi,y=0f uN-l9j+ujv+h/=0. B.192)
Введем оператор
К 4У) s 7? ("*+*, /~4^+i, /+ К, у—4ил.ь у+ ил-2, у).
Тогда уравнение
+ К4~1)\=0 (* = !. 2> •••> iV~1» /=Ь 2, ...)
при 0 ^ а, 0^Р, а + Р^1 аппроксимирует уравнение B.190).
Нетрудно видеть, что сеточные функции v^ (&) = sin —^-
удовлетворяют граничным условиям B.192)' и являются собственными

1] § 3. НЕЛИНЕЙНЫЕ ЗАДАЧИ 175
функциями оператора 6£ с собственными значениями T4sin49A7*
Поэтому коэффициенты роста %^'1) удовлетворяют уравнению
I2—2k+l + \6r2[aX2 + (l — а — р)Ь + 0] <#> = ()
h* 1 777 N-\ 77т = U.
l + \6ac{hl)r2 l-\-\6c^r2a
Для а = р^0, 4с^ г2A —4а)^1 корни уравнения представимы
в виде е1У1 и e~~'Yt, где
t Scjpr2 gr* t t о1 + 4г»Dа-1)
coeY/=l-1+1&i/Va^l-rpIg?i5---l+2 1 + 16r2a .
Поэтому для а > -j схема будет устойчивой при произвольном
стремлении h—>.0, т—>.0; для a=-j схема будет устойчивой при
т~9 ^Го> гДе го—произвольное фиксированное число; для a=Q
h х 1
схема является устойчивой при -гг^>го<-у •
§ 3. Нелинейные задачи
Среди нелинейных задач для уравнений гиперболического
и параболического типов имеются такие, в которых заранее
неизвестна область существования решения, а поэтому
невозможно и назначить сетку для приближенного решения
задачи.
В первых двух пунктах этого параграфа изложены
сеточные методы решения некоторых задач такого типа.
1. Квазилинейные гиперболические системы. Рассмотрим
систему двух квазилинейных дифференциальных уравнений
первого порядка относительно двух функций и (х, у) и v (х, у):
а"дх+а»дх+а"ду'}г0"ду -'I' , ( 93.
апдх~га**дх+ "ду ~*~ **ду ~~'2'

176
ГЛ. II. МЕТОД СЕТОК
[1
fy,/> // (A J==- *! ^)—функции переменных х, у, и, vy
определенные для всех значений —сю <С х, у, и, v<loo.
Вводя векторы Х(х, у), U(u, v), F(fiy /2) и матрицы А и В
с элементами а( - и b^j, систему B.193) запишем в виде
*аг+< = * <2Л94>
Определитель матрицы Ла — Z?p, где а и р— числа, является
квадратичной формой Q(a, Р) относительно а, р.
Системл B.193) называется гиперболической ark (Хоу U0),
если для Х<=Х0, U=UQ квадратичная форма Q(a, P)
разлагается на вещественные линейные множители:
Q(a, P)s(|xla-vlP)(lxIa-vip),
причем векторы (|д,г, vt) и ([i2, v2) не коллинеарны. Для
краткости будем говорить, что Q(a, P) линейно разложима.
Два направления на плоскости Оху, определяемые векторами
(|lx1, vx) и (fx2, v2), называются характеристическими для
(Ад, U0). Пусть U(x} у)—некоторая векторная функция
U{u(x,y), v(x,y)}. Тогда в каждой точке плоскости Оху
определена квадратичная форма Q(a, P), и пусть в каждой
точке некоторой области й эта форма линейно
разложима и, следовательно, с каждой точкой этой области
связаны два характеристических направления.
Характеристикой называется кривая плоскости Оху, касательная
к которой в каждой точке имеет характеристическое
направление.
Если предположить а,- ., Ь{^ достаточно гладкими
функциями от X, U, то каждая достаточно гладкая
вектор-функция U(x9 у) порождает два семейства характеристик в области
Q линей'ной разложимости квадратичной формы Q(a, P) (если
такая область существует).
Пусть теперь U(x, у) является решением системы B.193)
и Q — область линейной разложимости квадратичной формы
Q(a, P) для этого решения. Пусть для некоторого участка
какой-либо характеристики касательная не параллельна оси
Оу, т. е. для всех точек участка [х Ф 0. Тогда доказывается,
что вдоль участка
| = Q, B-195)

1]
§ 3. НЕЛИНЕЙНЫЕ ЗАДАЧИ
177
где q—один из корней квадратного уравнения
du
т и
dx
\Aq—B\ =
anQ—*« a^Q— *«
i
j = 0
dv
-г- связаны соотношением
dx
du . dv r ,
а"Тх+а^Тх-^ fl12e-*i2
du . dv ~ ,
= 0,
B.196)
которое после умножения на dx можно записать в виде
где
Ж =
Р =
^21
Ж^ + yV^ + P^JC^O,
fln ai2Q—*i.
^22 «l.Q—*«
-A anQ—*«l I/»
B.197)
— Q
Предположим, что [1^0 и |i2^=0 в Q, т. е,
характеристики нигде не параллельны оси Оу. Тогда в каждой точке
области Q оба корня уравнения B.196) конечны; будем их
нумеровать так, что Q1<CQ2- Первым семейством характеристик
будем считать то, для которого имеет место B.195) с
заменой Q на qx, вторым семейством — то, для которого g в
B.195) заменено на q2.
Пусть теперь заданы две точки Хх и Х2 плоскости Оху,
не лежащие на одной характеристике и достаточно близкие
друг к другу, и пусть известны значения иг, vx и и2, v2
функций и, v в этих точках. Пусть требуется найти точку Х3
пересечения характеристики первого семейства, проходящей через
Хх, и характеристики второго семейства, проходящей через
Х2, и значения и8, vs функций и, v в Х9.
Для приближенного решения этой задачи можно
поступить так. В точке Хг известны значения и, v и, следовательно,
известны корни qJ1 , q2 уравнения B.196). Аналогично для
С*)
Л2>
точки Х2 известны корни q\ и q2; уравнения B.196)

1>-*l) + P|>-*') = 0' } B-199)
178 гл. и. метод сеток [1
Заменяя в B.195) -j- на характеристиках через ——— и
у ц ЯХ Х3 Х1
———, получим следующие два уравнения для
приближенна Х2
ного вычисления координат точки Хг:
У,-У1 = $}(х,-*г)> Л-Л = 6*2) (*,-*,)• BЛ98)
Для приближенного вычисления значений uv vs воспользуемся
уравнениями, полученными из B.197) заменой du и dv на
из — и1> vs—vi и из — uv vs—Vz соответственно для первой
и второй характеристик, а именно:
M{z2)(us-u2) + M£
где М{/\ N{/\ F*p (/,y=l, 2) —значения функций Af, N, Р
для x = xh y=ytj u = uh v = vh q = q{ji). Таким образом,
определение х9, у9, и9, v9 требует решения двух систем
линейных уравнений с двумя неизвестными х3, у9 и uv v3
в каждой.
Так найденные xs, ys, us, vs, вообще говоря, являются грубыми
приближениями к искомым величинам. Предложены различные
способы уточнения этих значений ([2], [76], [116]); часть этих способов
является итеративными,а найденные из уравнений B.198)
иB.199)значения xs, */g, «з, v9 служат начальными приближениями процесса итераций.
Например, шаг итерации для одного из способов таков. По xz, уъ, иг, vt
находят q<3), q2s) и в B.198) заменяют qW и qB2) на Qi^y (q[1}+ q[3))
и 02 = -^- ( QJ^ + Q^) соответственно; из полученной системы
находят xv y'r
Затем в уравнениях B.199) заменяют хг—хх и хг—х2 на х9 — хх
и x\-xv а М?\ W<», ... , Р<2> на I (М^ + М<»), 1(JV{1> + W<s>),...
... , -<r (Р22^ + Р[^) соответственно (М|.у), ... означает значение М,...
для xj, yj, и/, vjt q|;)). Решая так измененную систему B.199),
получают и'3> vv на чем и кончается один шаг итерации.
Если величины \х'г— хг\ , \у3—у9\, \и'3 — и3\, \v[ — vz\ нельзя
признать малыми, то процесс уточнения продолжают и находят
*s» У** u'v vl по *з> у\> u'v v'z так же> как последние были найдены
по х8, у5) м„ и4.

1J § 3. НЕЛИНЕЙНЫЕ ЗАДАЧИ 179
Описанный здесь прием определения (л'э, yz, иь, vz) по
данным (х^ уг, и1У t\), (х2, у2, и2, v2) применяется для
приближенного решения ряда граничных задач для системы
B.193). Этот прием будем называть элементарным шагом.
Задача Кош и. Для системы B.193) задача Коши
ставится следующим образом. Пусть в плоскости Оху
задана линия С (х~х(х), у=у(х)) и в точках С заданы
значения 0 вектора U{u = u(r), v = v(x)}. Требуется найти
в некоторой окрестности линии С вектор-функцию
U{u(x, у), v(x, у)}, являющуюся решением системы B.193)
и совпадающую с О на С.
Поскольку в каждой точке линии С известны (х,у, и, v)y
то в каждой точке известна квадратичная форма Q(a, |3).
Предположение 1. Линия С и заданный на ней вектор
U таковы, что' система B.193) является гиперболической
в каждой точке линии С. (При некоторых дополнительных
предположениях это означает, что корни §г и q2 уравнения
B.196) вещественны и различны.)
Предположение 2. Линия С не является
характеристикой, т. е. в каждой точке линии
dy , dy .
Для приближенного решения задачи Коши выберем на
линии С несколько точек Х1У Х2, ... , Хъ занумерованных
в порядке следования на кривой С и таких, что соседние
точки Xt, Xi+l достаточно близки. Тогда, применяя
элементарный шаг, найдем по
(■*/> У и «I, *,-), (*/+i> Уин «/+1, */+i)
значения
D\ $\ «?\ *?>) (/=1, 2 *—1).
Применяя элементарный шаг к точкам
(/=1, 2, ...,6-2),
найдем
W2>, yf, «Г\ vf) C-l, 2,...,*-2)

180
ГЛ. И. МЕТОД СЕТОК
[1
и после к шагов таких вычислений придем к единственной
точке
W~l), y\k~l\ иГ'\ vf-%
В результате такого решения получается таблица
координат точек Х^]) (/= 1, 2, ... , к—1; /=1,2,...,А—j)
и соответствующих значений ^;)(рис. 13). Может случиться,
что этот процесс вычисле-
(г)
х
сз)
}Хм ний придется прекратить,
если корни уравнения B.196)
/ Для некоторых значений X[J\
B) U^ окажутся комплексны-
го
Рис. 13.
ми (квадратичная форма
Q(a, P) не будет линейно
разложимой).
Для того чтобы найти
аналогичную таблицу для
приближенного решения по
другую сторону линии С,
надо поменять ролями qr и
q2, т. е. через точку Xt проводить характеристику второго
семейства (q2), а через точку Xi+1 характеристику первого
семейства (qx).
Задача Гурса. Заданы две линии С, и С2, имеющие
общую точку Л, и значения Ux и 02 вектора U на Сг и С2,
совпадающие в точке Л. На каждой из линий выполнено
предположение 1 (система B.193) гиперболическая на Сх для
U, и на С2 для U2), и, кроме того, J = Q» на С1У а -£ = Q2
на С2 (т. е. линии Сг и С2 являются характеристиками
соответственно первого и второго семейства). Требуется
найти решение U(x, у) системы B.193) в окрестности точки
Л, совпадающее с Ux и U2 на Сх и С2 соответственно.
Для приближенного решения задачи Гурса выберем на
линиях Сг и С2 точки Х1У Х2У . . . , Xk и Yxy Y2, .. . , Yt
соответственно, где Хх и Yt — ближайшие к Л точки на
С, и СЁ.
Применяя элементарный шаг к Х1У Уг и данным в них
значениям U> находим точку Л1 и U(AX). Пусть Х2—бли-

2]
§ 3. НЕЛИНЕЙНЫЕ ЗАДАЧИ
181
жайшая к Хх точка на Сг. Применяя элементарный шаг к Х2
и А1У найдем Аг и U(A2) и т. д.
После Ы элементарных шагов будут найдены
приближенные значения точек At
(/= 1, 2, ... , &/) и
функции u(Ai)t v(A{) (рис. 14).
2. Параболическое
уравнение; задача с
подвижной границей
(модифицированная однослойная
задача Стефана). Задача
ставится так: ищутся
неотрицательные функции х =
*=£(*)ДО<Ш0) = а>0) Рис. 14.
и функция и(ху t)y
удовлетворяющая в области О^лгг^К^), ^^=0»
ди д2и _ п
Ж~~дх~*~
и на границе ее условиям
ди
дх
=—1.
«F@, <) = <>,
;*).
rf6
"Л1
уравнению
B.200)
B.201)
B.202)
B.203)
B.204)
\х=Ъ (О
причем относительно функции ф(лг) предполагается
Ф(*)>0 @<л:<а), ф'@) = — 1, ф(а) = 0. B.205)
Нетрудно убедиться, что если решение задачи существует,
то оно неотрицательно, и поэтому в силу B.203) тг_ =^0
и, следовательно, в силу B.204) имеем зт^О, т. е. £(/) —
неубывающая функция.
Пусть h — jT) гДе N—положительное целое число, и
в последующем будем считать xk~kh. Пусть tn означает
такое значение t9 что %(tn) = xN+n.

182
ГЛ. II. МЕТОД СЕТОК
[2
Если бы функция # = £(*) была известной, то были бы
известны значения tn1 и' тогда для определения сеточной
функции ukiU, заменяющей и(х, t), естественно написать
следующие сеточные уравнения, в которых xn==tn+l— tn\
- ^2 = U ^./UO)
(л = 0, 1, 2,...; ft=l, 2, ...,ЛЧ-л),
«о,»+1-«ы.+1 = А (л==0> !. 2, ...), B.207)
«*,о = Ф(*А)' B.208)
<Wm,*+i = °> B-209)
заменяющие соответственно уравнения B.200) — B.203)*
Если известно хп и значения uk^n(k = 0} 1, . .. , N+#)> T0
w#, n+i определяется единственным образом из B.206), B.207),
B.209). Для определения хп можно было бы воспользоваться,
например, таким уравнением:
dt
uN+n-i1n да
t = tn хп h дх
*=UtJ
заменяющим уравнение B.204). Из последнего уравнения
следует
h2
и сеточная задача однозначно разрешима (если uN+n^l w>0,
Л = 0, 1, 2,...), так как uky0 известна из B.208). Такой
способ вычисления т„, по-видимому, очень груб, и можно
предложить другой метод учета условия B.204).
Именно, для решения задачи B.200), B.201), B.202),
B.203), B.204) имеет место следующая формула:
lit) a
l(t) = t— $ и(х, t)dx+a+l<p{x)dx,
о о
которая для t=itn+l = tn + xn принимает вид
(N + n + i)h
(N+n+\)h = tn + xn- J u(x,tn+1)dx+a +
О
a
-f j ф(*) dx.

3]
§ 3. НЕЛИНЕЙНЫЕ ЗАДАЧИ
183
Положим, заменяя приближенно интеграл суммой,
N + n -| а
|л + 1 + 2Х»+. А-$<р(*) </*-/„. B.210)
Если считать, что uky n и tn уже найдены, то для
определения хп и ukin + x служит система уравнений B.206), B.207),
B.209), B.210), которую можно решать методом итераций,
один шаг которых таков: если T(n°> выбрано, то из системы
B.206), B.207), B.209) находится и^п+1; затем из формулы
B.210) находится т^.
В работе [115] доказана сходимость такого процесса
итераций и сходимость сеточного решения к точному при
А—*0.
3. Задача Дирихле для слабо нелинейного
эллиптического уравнения [111]. Пусть Q — конечная область
плоскости Оху, ограниченная контуром Г. Пусть F(x, у, z, p, q)—
функция, определенная для (л:, y)£Q, —oo<Cz, /?, q<^oo,
непрерывная, ча'стные производные первого порядка которой
по z, /?, q существуют и удовлетворяют условиям
К^0У |/>|<Л, \F'q\<A. B.211)
где А — некоторое положительное число.
Задача Дирихле для уравнения
д2и . д2и _./ ди ди\ л /nn1m
д? + ф-р[Х'У' "' К' Ту) = ° B-212)
ставится так: в области Q-f-Г найти дважды непрерывно
дифференцируемую функцию и (я, у), удовлетворяющую
уравнению B.212) и граничному условию
и(х, дО|г = Ф(*. У), B.213)
где ф(д:, у) — заданная на Г функция.
Если задача имеет решение, то в силу Fz^0 это
решение единственно.
Для приближенного решения задачи B.212), B.213)
применим квадратную сетку с шагом /г, удовлетворяющим
неравенству Ah < 2.

184
ГЛ. И. МЕТОД СЕТОК
[3
Пусть Qh—совокупность всех узлов сетки, лежащих
внутри Q или на границе Г; £>£ и Q\ — множества
внутренних и граничных (в смысле пятиточечной звезды) узлов;
Nh и Nh — число узлов в Qh и Q£. Занумеруем все
узлы в Qh числами от 1 до Nh и в Qlh числами от Л^+1
доЛГл.
Для звезды с центром во внутреннем узле X, через
уA), уB), уC), уD) обозначим номера отличных от центра
узлов звезды. Для каждого внутреннего узла X ,(х,, у Л
напишем сеточное уравнение
4
/t2 Г Vх/' -О-' И/' 2ft ' 2А /
B.214)
(/=1, 2 Л#)
и для каждого граничного узла
ttf=V(Qj) l/==Nj+l, ...,ЛГЛ), B.215)
где Q,— ближайшая к X, точка границы Г.
Доказано, что система уравнений B.214), B.215) имеет
единственное решение (при условии B.211) и Л/г<2).
Если и(х, у)£ С4, где и(х, у) — решение задачи B.212),
B.213), то имеет место оценка
|| иА—и(ху y)\\^NBM{Z) + M{*))h2 + Mil)h,
где N—некоторая положительная постоянная, зависящая от
А и диаметра области Q. Отсюда следует равномерная
сходимость сеточного решения uh к точному решению и (х, у) £ С4.
Если же и (х, у) £ С4, то относительно сходимости uh к
и(х, у) остаются в силе утверждения, сделанные для
линейной задачи Дирихле (см. утверждения 4), 5) из § 1, п. 4, а)).
Для решения сеточной задачи B.214), B.215)
предлагается следующий итерационный метод. Уравнение
*+*Fkx, у, z, p, q) = S B.216)
в силу Fz^0 имеет единственное решение относительно z

3] § 3. НЕЛИНЕЙНЫЕ ЗАДАЧИ 185
при любых фиксированных (х, у) £ Q, — oo<^p,q< oo.
Пусть
z = Yh{x, yy 5, py q)
— это решение.
Уравнение B.214) перепишем в виде
T2*ttJ{ky~UJ+ 4 Г \ ХР УР UP 2/i 2/i )'
откуда следует, что сеточная функция ил удовлетворяет
в каждом внутреннем узле (л:,, j>.) уравнению B.214) тогда
и только тогда, когда в этом узле имеет место равенство
4
tt]—*h\xp -Уу 4 2/i 2/i /'
которое перепишем в виде
И/=ФА(*/> У у. ";(i)> «yd» «yd» «УD))« B«2^7)
Пусть ц^ — какая-либо сеточная функция,
удовлетворяющая условию B.215). Тогда строится последовательность
сеточных функций и^\ значения которых в граничных узлах
определяются из B.215), а во внутренних узлах
определяются так:
Ву>=ФА(Ху, У;, «М "И*I'' и{Ш1)< "ft*") <2-218)
(/=1, 2, ..., N1).
Этот процесс итерации сходится, если выполнено условие
Fz^rj^O (y| — как угодно малое положительное число),
более жесткое, чем предположение Fz^0. Процесс итерации
по формуле B.218) есть аналог простой итерации для
системы линейных уравнений.
Обозначим через uflk)l) величину и^)» если j(k)<Zj\ и
через wfcx) Для /(&)>./• Тогда процесс итерации
W/ =ФЛ(Л7> -У/> И/A) 1 И/B) > «/(в) 1 «У D) ) B.21У)
(у=1, 2, .... i\tf)

186
ГЛ. II. МЕТОД СЕТОК
[3
является аналогом итерации Зейделя для линейных систем.
Процесс B.219) также сходящийся (при условии Fz ^ г\ *> 0).
После нескольких циклов вычислений по формулам B.218)
(или B.219)) процесс обрывается, и результат последнего
цикла принимается в качестве приближенного решения
системы B.217), B.215), равносильной системе B.214),
B.215).
Рассмотрим один шаг вычисления по формуле B.218).
Пусть (Xj, у j)— некоторый внутренний узел, и пусть заданы
значения и ,A), и .B), tfy.(8), ujU) сеточной функции в
соседних для (лгу, yj) узлах. Тогда известны значения
— uJb)~~uJM п ___ *УB) —*УD) с _ 1 ^
и остается решить уравнение B.216). Для этого,
по-видимому, целесообразно воспользоваться методом итерации по
формуле
& = Sj-£f(xp yp *1-х\ Рр 4j) B.220)
(/-1, 2, ...; 2@) = <Sy).
Этот процесс итерации будет сходящимся, если Fz огра-
h2
ничена сверху величиной В и -^В<^\. При этом, точное
решение уравнения B.216) лежит между двумя
последовательными приближениями z{l~l), z{l). После нескольких
шагов вычислений по формуле B.220) процесс обрывают
и результат последнего вычисления принимают в
качестве приближенного значения правой части B.218)
(или B.220)).
Эти результаты переносятся на случай уравнений,
получающихся из B.212) заменой g-g+g-g на
1и = а(х, у)д^2+2е(х, У)^у + Ь{х, у)^ (ab—e2>0)
при условии, что уравнение Lu=f можно аппроксимировать
уравнениями вида B.50), образующими вместе с граничными
сеточными уравнениями систему, удовлетворяющую принципу
максимума.

НЕКОТОРЫЕ ЛИТЕРАТУРНЫЕ УКАЗАНИЯ
187
НЕКОТОРЫЕ ЛИТЕРАТУРНЫЕ УКАЗАНИЯ
Систематическое изложение метода сеток в целом или его
разделов содержится в книгах: [2], [25], [30], [75], [81], [83], [90],
[116], а также в статьях [34] и [35]. В книге [75] приведено много
численных примеров применения метода сеток для решения
основных задач математической физики.
Основные понятия (нормы в функциональных и векторных
пространствах, согласование этих норм, корректность и устойчивость
сеточной задачи и т. д.) впервые систематически изложены в книге
[83]. Некоторые из этих понятий, относящиеся к применению метода
сеток к основным уравнениям математической физики, изложены
в книге [77].
Вопросы аппроксимации, разрешимости, оценки погрешности
для эллиптических сеточных задач Дирихле, удовлетворяющих
принципу максимума, изложены в [2], [25], [30], [54], [75], [116].
Для сеточных уравнений, заменяющих задачу Дирихле в
случае самосопряженных (и близких к ним) эллиптических уравнений,
вопросы разрешимости, корректности и сходимости изложены в [35]
(см. также в [34], [38]).
Обсуждение достоинств и недостатков отдельных методов
решения линейных эллиптических сеточных систем уравнений содержится
в книгах [90] и [116].
В методе сеточных уравнений, заменяющих смешанные задачи
для гиперболических и параболических уравнений, большое
внимание в последнее время уделяется вопросам устойчивости
соответствующих разностных схем. Изложение этих вопросов содержится в
книгах [17], [81], [83], [90], [116] (см. также [25], [30]). Изложенные
в книге [17] новые признаки устойчивости не нашли отражения
в главе II этого сборника СМБ.
Весьма полное изложение различных сторон метода сеток и
обширная библиография содержатся в книге [116].
Отметим цикл работ [85] — [88], [101] — [103] по вопросам
устойчивости, сходимости и оценки погрешности разностных схем,
аппроксимирующих уравнения параболического типа с разрывными
коэффициентами и соответствующие эллиптические уравнения.
В главе II настоящей книги такие вопросы не освещены.

ГЛАВА HI
ВАРИАЦИОННЫЕ МЕТОДЫ
§ I. Положительные операторы и энергия
1. Оператор краевой задачи. Всякая краевая задача
математической физики может быть сведена к уравнению
вида
А*=/. C.1)
где и—искомый элемент некоторого функционального
пространства1), Л — данный оператор и /—данный элемент того
же или иного функционального пространства. Оператор А
будем называть оператором данной краевой задачи.
Пример 1. Поставим задачу Дирихле. Пусть требуется
в некоторой области Q, ограниченной поверхностью 5,
определить функцию и (х) (х—переменная точка), которая внутри
области удовлетворяет уравнению Пуассона —Да=/(лг), где
Д — оператор Лапласа, а на границе 5—краевому условию
ц|5 = 0.
Допустим, как это часто бывает, что f(x) непрерывна
в области Q и квадратично суммируема в ней, и потребуем,
чтобы искомая функция и(х) была непрерывна в замкнутой
области Q=Q + 5, а ее первые и вторые производные были
непрерывны и квадратично суммируемы в открытой области2) Q.
Тогда и и / можно рассматривать как элементы—искомый
и данный — гильбертова пространства функций, квадратично
1) Необходимые сведения о функциональных пространствах,
в частности о гильбертовом пространстве, можно найти, например,
в книгах [13], [24], [63], [95].
2) Мы оставляем здесь в стороне вопрос о том, можно ли всегда
удовлетворить сформулированным в тексте требованиям.

2] § 1. ПОЛОЖИТЕЛЬНЫЕ ОПЕРАТОРЫ II ЭНЕРГИЯ
суммируемых в области Q; оператор А можно в данном
случае определить как взятый с обратным знаком оператор
Лапласа, заданный на функциях, которые непрерывны в
замкнутой области Q = Q -f- 5, в открытой области Q дважды
непрерывно дифференцируемы, имеют, квадратично
суммируемый в Q лапласиан и обращаются в нуль на границе S.
Пример 2. Поставим ту же задачу, что и в примере 1.
Введем новую неизвестную v — gxadu. Тогда искомую
вектор-функцию v можно рассматривать как элемент гильбертова
пространства, образованного градиентами функций,
обращающихся в нуль на границе S; данную функцию f(x) можно
по-прежнему рассматривать как элемент гильбертова
пространства функций, квадратично суммируемых в Q. Так как
Att = divgradtf = divi>, то уравнение
— Ди=/(х)
принимает вид
— divv = f(x).
Под оператором А следует в данном случае понимать
оператор дивергенции, взятый с обратным знаком.
В задачах теории упругости или гидродинамики искомый
элемент и может представлять собой ту или иную
совокупность функций (вектор смещений или скоростей, тензор
напряжений, деформаций, скоростей деформаций и т. д.).
То же относится и к данному элементу /.
Краевая задача может быть линейной или нелинейной;
соответственно будет линейным или нелинейным оператор А.
Во всей главе, за исключением § 10, будут рассмотрены
только линейные задачи и линейные операторы. Это
обстоятельство особо оговариваться не будет.
Будем также считать (если не будет оговорено
противное), что данный элемент / и искомый элемент и принадлежат
одному и тому же вещественному гильбертову пространству.
2. Положительные и положительно определенные
операторы. Симметричный оператор Л, действующий в
некотором гильбертовом пространстве, называется положительным,
если для любого элемента из области определения оператора
справедливо неравенство
(Ли, «)>0,

190
ГЛ. III. ВАРИАЦИОННЫЕ МЕТОДЫ
[2
причем знак равенства имеет место только тогда, когда
и = 0, т. е. когда и—нулевой элемент пространства.
Если А — положительный оператор, то скалярное
произведение (Аи> и) называется энергией элемента и по
отношению к оператору А. Эта терминология оправдана тем, что
во всех случаях, когда элемент и можно трактовать как
смещение некоторой системы, величина (Аи, и) совпадает,
при подходящем выборе единиц измерения, с потенциальной
энергией деформации этой системы.
Теорема 1. Если оператор А положителен, то у рае-
нение C.1) имеет не более одного решения.
Симметричный оператор А называется положительно
определенным, если существует такая положительная
постоянная у2» чт° Для любого элемента и из области
определения оператора А справедливо неравенство
(Аи, a) ^y2 II "II2- C-2)
Пример 3. Рассмотрим весьма элементарную краевую задачу
об определении функции и (х), которая удовлетворяет внутри отрезка
0<;л:^1 дифференциальному уравнению —u"=f(x), а на концах
этого отрезка—краевым условиям и @) = и(\) — 0.
В гильбертовом пространстве L2 @, 1) функций, квадратично
суммируемых на отрезке 0<;л:г^1, наша задача порождает опера-
тор А = —-т—2, за область определения которого здесь естественно
принять множество функций, непрерывных вместе со своими
первыми и вторыми производными на отрезке 0<:x<:l и обращающихся
в нуль на концах этого отрезка. Интегрирование по частям с учетом
краевых условий дает (и и v—функции из области определения
оператора А)
1 1 1
{Аи, и)= — С vu"dx= — vu' Г + \ u'v'dx = \ u'v'dx;
О 0 0
в частности, при v = u
1
(Ли, и)= С и'2 dx.
о
Из первой формулы вытекает симметричность, из
второй—положительность оператора Л. Далее имеем
и{х) = и(х) — и@)=[ и' (t)
dt

3]
§ 1. ПОЛОЖИТЕЛЬНЫЕ ОПЕРАТОРЫ И ЭНЕРГИЯ
191
и, по неравенству Буняковского,
х 1
и*(х)<х\ и'2 (t) dt^\ и'2 @ dt.
о о
Интегрируя это по х в пределах от нуля до единицы, легко найдем,
что (Аи, и)^\\ и |[2; оператор А положительно определенный,
и можно в нашем примере принять y2 = 1-
Существуют операторы положительные, но не положительно
определенные. В этом можно убедиться на следующем примере.
d2
Обозначим через В оператор —-7-5, но определенный на функциях,
заданных на бесконечном промежутке @, оо). Примем, что эти
функции непрерывны и имеют непрерывные первые и вторые
производные при #^0, отличны от нуля только на некотором конечном
промежутке (своем для каждой функции) и обращаются в нуль при
# = 0. Из легко доказываемых формул
(Ви, v) = С u'v' dx, (Ви, и) = С и'2
dx
вытекает симметричность и положительность оператора В, который,
однако, не является положительно определенным. Последнее
вытекает из того, что для функции
/ \ - / х (П
—л:K, О^Жп,
0 х> л,
удовлетворяющей всем перечисленным выше условиям, отношение
\n2J
может быть сделано сколь угодно малым при достаточно большом п.
Понятия положительного и положительно определенного
операторов допускают следующую физическую трактовку.
Будем рассматривать и как смещение некоторой системы. Тогда
положительность оператора означает, что невозможно сообщить
системе смещение, не затратив на это некоторой энергии. Если
оценивать величину смещения его нормой, то положительная
определенность оператора означает, что системе можно сообщить
большое смещение, только затратив достаточно большую энергию. Если
же оператор положительный, но не положительно определенный,
то системе можно сообщить сколь угодно большое по норме
смещение, затратив на. это сколь угодно малую энергию.
3. Энергетическое пространство. Со всяким
положительным (в частности, со всяким положительно определенным)
оператором можно связать особое гильбертово пространство,

192
ГЛ. Ш. ВАРИАЦИОННЫЕ МЕТОДЫ
[3
которое мы будем называть энергетическим пространством,-
Пусть А— положительный оператор, действующий в некото-
тором гильбертовом пространстве Я, и пусть M — D(A) —
область определения этого оператора. Введем на М новое
скалярное произведение (которое будем обозначать
квадратными скобками): если и и v элементы Ж, то положим
[u,v] = (Au,v). C.3)
Величину [и, v] назовем энергетическим произведением
элементов и к v. Доказывается, что энергетическое
произведение удовлетворяет всем аксиомам скалярного
произведения.
Раз на множестве М введено новое скалярное
произведение, это множество стало гильбертовым пространством.
В общем случае оно неполное — пополним его. Построенное
таким образом новое гильбертово пространство назовем
энергетическим пространством и обозначим через НА.
Норму в энергетическом пространстве назовем
энергетической нормой и будем обозначать символом \и\. Для
элементов области М определения оператора А энергетическая
норма определяется формулой
|и| = т/и5Г5). C.4)
Сходимость в энергетическом пространстве называется
сходимостью по энергии.
Важную роль играет вопрос о природе тех элементов,
которые служат для пополнения энергетического
пространства. Если оператор А положительно определенный, то
имеет место теорема, в силу которой все элементы
пространства НА принадлежат также исходному гильбертову
пространству Я; если и—элемент пространства Ял, то имеет
место неравенство
1М1<|М. C-5)
где символ || || означает норму в исходном пространстве Я,
а у — постоянная, входящая в неравенство C.2).
Если А — положительно определенный оператор, то из
сходимости некоторой последовательности по энергии
вытекает также ее сходимость в норме исходного пространства:
если ип 6 НАУ и € НА и К—и|-*0, то и ||ц„ —ц||—>0.

41 § 1. ПОЛОЖИТЕЛЬНЫЕ ОПЕРАТОРЫ И ЭНЕРГИЙ 193
4. Обобщенные производные. Пусть Q — некоторая
конечная область m-мерного пространства и S—ее граница.
Пограничной полосой области Q называется совокупность
тех ее точек, расстояния которых до границы S не
превосходят некоторого заданного числа б; это число называется
шириной пограничной полосы.
Область Q' называется подобластью Q, если все точки Q'
принадлежат Q, и внутренней подобластью, если Й
содержит не только все точки области Q', но и все точки ее
границы, иначе говоря, если существует пограничная полоса
области Q, не содержащая точек подобласти Q'.
Обозначим через Фк множество функций, k раз
непрерывно дифференцируемых в Q и обращающихся в нуль
в пограничной полосе (своей для каждой функции) этой
области.
Допустим сперва, что функция и(х) имеет в замкнутой
области Q = Q + S непрерывную производную
dku
дх. дх. ...дх. '
одновременно она имеет и все предшествующие этой
производные, также непрерывные в Q. Пусть ф(лг) — любая
функция множества Фк. На поверхности S функция ф(лг)
и все ее производные обращаются в нуль, поэтому
интегрирование по частям приводит к формуле
Гц **Ф dx=(—\)k$<D — dx
J дх. дх. . ..дх. v ' J Y дх. дх. ... дх.
Q lx H 1к Q h 1з 1к
Пусть теперь и(х) — некоторая функция, суммируемая
в любой внутренней подобласти Q, и пусть существует
такая функция w(x), также суммируемая в любой
внутренней подобласти й, что для любой функции у(х)£Фк
справедливо тождество
Q ll l2 lk Q
Тогда w (x) называется обобщенной производной порядка к
по переменным xix, лг/а, ..., xt от функции и(х) в
области Q. Обозначается обобщенная производная обычным
7 С. Г. Михлин н X. Л. Смолицкий

194
ГЛ. III. ВАРИАЦИОННЫЕ МЕТОДЫ
[4
символом
w(x) = a Jku я . C.6)
v ' дхи dxh ...dxt
Пример 4. Пусть f(t) и g(t)— две суммируемые, но недиффе-
ренцируемые функции переменной /, скажем, в промежутке
О ^ t ^ 1. Тогда функция
u(xvx2) = f{xx) + g(x2)t
суммируемая в квадрате Q плоскости (х19 х2), определяемом
неравенствами O^^^l, 0<:*2^1, имеет в этом квадрате вторую
д2и
обобщенную производную ^—^— и эта производная тождественно
* UXt ОХ»
равна нулю.
Действительно, пусть Ф(*)£Ф2. Тогда
I-
дхх дх2
11 11
0 0 0 0
It 11
=§nxJdx^dB?/Xi+U(x*)dXi$^dxi=0:=§o''fdx-
0 0 0 0 Й
Из только что разобранного примера видно, что функция,
имеющая обобщенную производную порядка к > 1, может не иметь
предшествующих обобщенных производных; в нашем примере
функция и (*!, хг) не имеет обобщенных первых производных.
Теорема 2. Если в области Q функции иг(х) (г=1,
2, ..., п) имеют обобщенные производные одного и того
же вида
i \ dkur
гУ ' дх1хдхи...дх^
и если сг (г = 1, 2, ..., п)—постоянные, то функция
п
2 сгиг(х) имеет обобщенную производную того же вида,
Г=1
причем
dxltdxu...dxi S 'А (*) = X W (*)•

4] § 1. ПОЛОЖИТЕЛЬНЫЕ ОПЕРАТОРЫ И ЭНЕРГИЯ ^5
Теорема 3. Пусть Q'—подобласть Q. Если w(x)
есть некоторая обобщенная производная от и(х) в Q,
то w(x) есть такая же обобщенная производная от
и(х) в Q'.
Теорема 4. Если в области Q функция v(x) есть
обобщенная производная от и (х) порядка k no xi ,
xi
к
, ,_ dku
* '~~dxildx;7...dx. '
ъ
а функция w(x) есть производная от v(x) порядка I no
xj\> xjs
dlv
W^X> дхАдх/2...дхп
mo w (x) есть обобщенная производная от и (х) вида
dk+lu
W (Х):
дХц дхB. ,.dxi dXjxdxj2.. .дх^
в той же области Q?
Теорема 5. Пусть ип(х) (л=1, 2,
...)—последовательность функций, определенных почти всюду в
области Q и суммируемых в этой области с некоторой
степенью р>1, и пусть существуют обобщенные
производные
W^X)-dX:dxi2.,.dXL '
if.
суммируемые в Q с некоторой степенью q>\. Если при
этом в любой подобласти Q'cQ функции ип(х) слабо
сходятся к некоторой функции и(х) в Z, (Q'), а функции
wn (х) слабо сходятся в Lq (Q') к некоторой функции w (x),
то предельная функция и (х) имеет в Q обобщенную
производную
dku
dxildxi2...dx[
и эта производная равна w(x).
Можно дать другое определение обобщенной
производной, равносильное приведенному выше. Пусть и(х) и w(x)
суммируемы в любой внутренней подобласти Q' области Q.

196 ГЛ. Ш. ВАРИАЦИОННЫЕ МЕТОДЫ [5
Функция w (х) называется обобщенной, производной вида
C.6) от и(х), если существует последовательность k раз
непрерывно дифференцируемых внутри Q функций ип(х)
таких, что ип—► и и
dkun
дхидхи...дх^
»w
в смысле метрики пространства L (й'), иначе говоря, если
lim ^ \un(x)—u(x)\dx~Q
и
lim \ h—д "п д w(x)
d* = 0;
через Q' обозначена любая внутренняя подобласть
области Й.
5. Теоремы вложения. Область называется звездной
относительно данной точки, если любой луч, исходящий из
этой точки, только один раз пересекается с границей
области. Так, например, всякая выпуклая область звездна
относительно любой своей точки.
Здесь и ниже будут рассматриваться только конечные
области, которые можно представить в виде суммы
конечного числа взаимно налегающих подобластей, каждая из
которых — звездная относительно любой точки некоторого
шара.
Теорема 6. Пусть функция и(х) суммируема в
области Q и имеет всевозможные обобщенные производные
некоторого порядка k > 1, также суммируемые в Q.
Тогда и (х) имеет суммируемые в Q всевозможные
обобщенные производные порядков, меньших k.
Пространство W{pl) (Q) С. Л. Соболева, где р>1,
состоит из функций, которые имеют в Q всевозможные
обобщенные производные порядка /, причем как сами функции,
так и их производные порядка / суммируемы в Й со
степенью р\ норма в этом пространстве задается формулой
II«Су (й)-ф"Г**+ШК4." .а,,Г"■ C-7>
^ о о *

5] § 1. ПОЛОЖИТЕЛЬНЫЕ ОПЕРАТОРЫ И ЭНЕРГИЯ 197
где сумма распространена на всевозможные наборы равных
или не равных между собой чисел iiy i2, ..., it, каждое из
которых не превосходит числа т—размерности области Q.
Теорема 7. Если u(x)£Wpl) (Q) и pl> т, то и(х)
эквивалентна функции, непрерывной в замкнутой
области Q. Имеет место неравенство
|| и ||с (в) <А11| «|| у, , C.8)
Р
где C(Q) обозначает пространство функций, непрерывных
в замкнутой области Q, а М—постоянная, которая не
зависит от функции и(х). Всякое множество,
ограниченное в Wpl) (Q), компактно в C(Q).
Следствие. Если u(x)£Wpl)(Q) и натуральное
число k таково, что рA—k)*>m, то u(x)£C{k) (QI),
при этом
\\tt\\cik)(Q)^M\\u\\w(l)
р
и всякое множество, ограниченное в Wp■ (Q), компактно
в C(k) (Q).
Теорема 8. Пусть Ts, s^m,— достаточно гладкое
многообразие, все точки которого принадлежат £1. Если
рК^т и s> т—pi, то всякая функция и {х) € Wpl) (Q)
эквивалентна функции, которая определена почти всюду
на Ts и суммируема на Ts с любой степенью q,
удовлетворяющей неравенству
жчёя'' C-9)
при этом имеет место неравенство
II и Ik (г.) ОИ, || и Н^, @)| (ЗЛО)
где постоянная Мг не зависит от функции и (х). Если q
удовлетворяет строгому неравенству
1) То есть производные порядка k от и (х) непрерывны в Q«

198 ГЛ. 111. ВАРИАЦИОННЫЕ МЕТОДЫ
то мш
то множество, ограниченное в Wp) (Q), компактно в
■(О,
Следствие. Если u^Wy{Q) и &</, то
где
а^_ тР
Ч— m_p(/_^) i
и справедливо неравенство
Wu\\wV-k)^Mt\\u\\ {th
Я Р
(ЗЛ2)
C.13)
где постоянная М2 не зависит от функции и(х).
Теорема 9. Пусть N—число линейно независимых
полиномов степени ^ /— 1 от т переменных хх,х2, ... 1хт.
Пусть линейные ограниченные в Wpl) (Q) функционалы
ljU (j= 1, 2, .. ., п) таковы, что они не обращаются
одновременно в нуль ни на одном полиноме степени ^ /— 1.
Тогда норма, определяемая формулой
/ = i Q lx l2 4
эквивалентна норме C.7).
Отметим два наиболее простых и важных неравенства,
вытекающих из теорем вложения.
Г. Неравенство Пуанкаре. Если и (х) £ W{21) (Q),
то
^иЫх^Л ^ (gvsid иJ dx + Aff^ и dx\\ C.15)
2°. Если и (х) £ №2A)(Q) и « = 0 на части границы 5, то
$ и2 dx^B J (grad иJ dx. C.16)
Если н = 0 на всей границе S, то неравенство C.16)
называют неравенством Фридрихса. В неравенствах C.15)
и C.16) Л, А', В — постоянные, которые не зависят от
выбора функций и{х), но зависят от выбора области Q,

1]
§ 2. ЭНЕРГЕТИЧЕСКИЙ МЕТОД
199
§ 2. Энергетический метод
1. Функционал энергетического метода. Если
оператор А положителен, то решение уравнения C.1) можно
свести к решению некоторой вариационной задачи, как это
вытекает из следующей теоремы.
Теорема 10. Пусть А— положительный оператор.
Если уравнение Au=f имеет решение, то это решение
сообщает функционалу
Fiu) = (Au,u)-2(a,f) C.17)
наименьшее значение. Обратно, если существует эле-
мент, реализующий минимум функционала C.17), то этот
элемент удовлетворяет уравнению Au=f.
Метод решения краевых задач, состоящий в замене
уравнения C.1) задачей о минимуме функционала C.17),
носит в литературе название энергетического метода.
Функционал C.17) будем называть функционалом
энергетического метода.
Теорема 10 не дает указаний ни на условия
существования решения вариационной задачи, ни на то, как такое
решение можно строить. Такие указания могут быть даны,
если оператор краевой задачи положительно определенный.
В этом случае введем в рассмотрение энергетическое
пространство НА. По формуле C.4) (Аи, и) = \и\2. Далее, по
неравенству Коши—Буняковского и неравенству C.5)
\(и> /)\ ^ 11/111] я II 5^^-|и|. Это означает, что линейный
функционал (и, /) ограничен в ИА; по теореме Риса
существует элемент и0 £ НА такой, что (и-, /)= [и, и0], если только
и£НА. Теперь функционал C.17) приводится к виду
Z7 («) = I« Р — 2 (а, /) = | а |2 — 2 [а, и0] =
= |« —а0|» —|авр. C.18)
Из формулы C.18) вытекают два простых и важных
следствия: 1) эта формула позволяет определить функционал
F(u) не только на элементах области определения
оператора Л, но и на всех элементах энергетического
пространства НА; 2) в пространстве НА функционал F(u) достигает
минимума при u = u(i.

200
ГЛ. III. ВАРИАЦИОННЫЕ МЕТОДЫ
B
Если u0£D(A), то по теореме 10 и0 есть решение
уравнения Au—f\ однако энергетическое пространство НА,
вообще говоря, шире, чем D(A), и может случиться, что
элемент и0, построенный по теореме Риса и реализующий
в энергетическом пространстве минимум функционала F(uI
не попадет в D(A). В этом случае можно рассматривать и0
как обобщенное решение уравнения Аи=/.
В связи с понятием обобщенного решения находится
возможность расширения положительно определенного оператора. Пусть
А—такой оператор. Каждому элементу / данного гильбертова
пространства Н приведем в соответствие тот элемент и0£Нд, который
реализует минимум функционала F (и) в энергетическом
пространстве; это соответствие порождает некоторый оператор G такой, что
Gf = u0. Доказывается, что существует обратный оператор A — G~l,
который является самосопряженным расширением оператора А\
обобщенное решение уравнения Au — f есть обычное решение
уравнения Au — f.
2. Построение решения вариационной задачи. Здесь
мы укажем два общих приема построения элемента н0,
реализующего минимум функционала F(u); весьма важный
метод Ритца, являющийся конкретизацией каждого из
упомянутых выше методов, будет изложен в п. 3.
1) Допустим, что в пространстве Ил существует полная
ортонормированная (в смысле метрики этого пространства)
счетная система1) сол (#=1,2, . ..)> так что
( 1 n — ky
к- ®*]={0; л**:
Тогда
П =1
Ряд C.19) представляет собой ряд Фурье (в энергетическом
пространстве) элемента и0 по ортонормированной системе
{со„}; этот ряд сходится как в метрике пространства На
(т. е. по энергии), так и в метрике пространства Н.
Пример 5. Рассмотрим упругий стержень прямоугольного
сечения, ограниченного прямыми * = 0, х — а, t/ = 0, y = b. Задача
!) Иначе говоря, мы допускаем, что пространство Ид сепара-
бельно; для этого достаточно, чтобы исходное пространство Н было
сепарабельным.

2]
§ 2. ЭНЕРГЕТИЧЕСКИЙ МЕТОД
201
о кручении такого стержня легко сводится к интегрированию
уравнения
— Ди = 1
при краевых условиях
и@, у) = и(а, у) = и{х, 0) = и(х, 6) = 0,
C.20)
C.21)
выражающих, что искомая функция обращается в нуль на контуре
сечения. В нашем случае оператор А краевой задачи можно
определить как оператор —Д, заданный на функциях, которые дважды,
скажем, непрерывно дифференцируемы в области сечения, а на его
границе обращаются в нуль1); исходным гильбертовым
пространством И здесь является пространство функций, квадратично
суммируемых в области сечения. Можно доказать, что этот оператор
положительно определенный; энергетическое произведение в нашем
случае выражается формулой
а Ъ
[и, и] = — ^ v (х, у) Ди (*, у) dx dy\
о о
интегрированием по частям можно этой формуле придать
симметричный вид:
а Ь
о о
Пространство Н& состоит из функций, которые имеют
квадратично суммируемые в прямоугольнике сечения, обобщенные первые
производные и обращаются в нуль на контуре сечения; из теоремы.,
упомянутой в п. 3 § 1, а также из теоремы 8 вытекает, что
функции, входящие в Нау квадратично суммируемы в области сечения.
Полную ортонормированную систему в На образуют, например,
функции
2 т/" ab . knx . ппу
ЩпМ = - У W + flWan —*«» —
(к, /х=1, 2, ...);
формула C.19) дает решение задачи о кручении стержня
прямоугольного сечения:
. knx . ппи
1С ... „ sin sin—~
16 a2b2 1П а Ь
и (х, у)
k, П = 1,3, 5 . .
kn{b2k2 + a2n2)
I} Требование непрерывности вторых производных можно
заменить более слабым требованием, чтобы эти производные
существовали как обобщенные и были квадратично суммируемы в
прямоугольнике сечения.

202
ГЛ. III. ВАРИАЦИОННЫЕ МЕТОДЫ
[3
2) Пусть ип—какая угодно минимизирующая
последовательность для функционала F(u). Тогда ип-+и0 по энергии,
а также, следовательно, и в метрике исходного пространства.
Любой достаточно далекий член минимизирующей
последовательности можно рассматривать как приближенное решение
задачи о минимуме функционала C.18).
3. Метод Ритца. В пространстве НА выберем
последовательность элементов
Фц Ф .фв»-м C-22)
удовлетворяющих двум условиям: 1) при любом я элементы
ф1? Ф2, . .. , Ф„ линейно независимы, 2) последовательность
C.22) полна по энергии; под этим мы понимаем следующее:
каковы бы ни были элемент и£НАп число е^>0, можно
найти такое натуральное число N и такие постоянные аг,
а2> • • • > алг> чтобы выполнялось неравенство
N
I»—2«*Ф*Ке-
Элементы C.22) называются координатными.
По методу Ритца задаются натуральным числом п и
строят приближенное решение ип вариационной задачи в виде
«п=2Хф* (з-23)
где ak—постоянные, которые выбираются так, чтобы
величина F(un) была минимальной) для определения этих
постоянных получается линейная алгебраическая система
1фц Ф1К+[ф2> Ф1]а2+...+[ф„, Ф,] *„ = (/, ФЛ
[Фх> Ф,К + [фц Ф2К+••• + №*> Ф2К = (/> Ф2)>
1Фр Ф»К + [ф« Фя1а1+---+[фя. Ф«] *« = (/. Ф«).
называемая системой Ритца.
В силу линейной независимости элементов фп ф2, . . . , cprt
определитель системы Ритца отличен от нуля и эта система
единственным образом разрешима.
Метод Ритца находится в тесной связи с представлением
решения в виде ряда C.19). Последовательность C.22) коор-
>C.24)

4]
§ 2. ЭНЕРГЕТИЧЕСКИЙ МЕТОД
203
динатных элементов подвергнем процессу ортогонализации в
метрике пространства НА, что приведет нас к некоторой
полной ортонормированной в Ил системе {соп}. Теперь
искомый элемент и0 можно представить в виде ряда C.19).
Оказывается, что приближенное решение ип, построенное
по методу Ритца с помощью формул C.23) и C.24), есть
п-я частичная сумма ряда C.19).
Последовательность приближенных решений, построенных
по методу Ритца, есть также минимизирующая
последовательность для функционала C.18).
С возрастанием п энергетические нормы приближенных
решений по Ритцу возрастают (точнее, не убывают) и
стремятся к энергетической норме точного решения
К1<К1> £<", Ит|кв| = К|.
Далее, имеет место тождество
C.25)
Условимся погрешность приближенного решения ип
оценивать величиной \и0 — ип\. Из формулы C.25) следует,
что погрешность приближенного решения по Ритцу
убывает (точнее, не возрастает) при добавлении новых
координатных элементов.
Если координатные элементы принадлежат не только
пространству НА% но также и области определения данного
оператора Д .то [ф,, Ф^] = (^ф;, Фл) и систему Ритца можно
представить в виде
(Aplf ФХК +
+ Иф2, %) а2 + .. . + Ифп1 ф,) ап = (/, ф,),
(АФп Ф«К +
+ И<Р„ Ф2) а2 4- . . . + (Иф„, ф2) ап - (/, ф2),
(АФи ФпК +
+ Иф», Ф„) а% + .. . + Ифя, ф„) ап = (/, ф„).
C.24')
4. Методы решения системы Ритца. Матрица системы
Ритца C.24) положительно определенная, и для решения

204 ГЛ. III. ВАРИАЦИОННЫЕ МЕТОДЫ [4
этой системы пригодны все методы, применяемые для
решения систем линейных алгебраических уравнений с
положительно определенной матрицей. Методы эти подробно
изложены в книге [104]; здесь мы остановимся только на методе
итераций. ч
Матрицу системы C.24) обозначим через Rn, вектор,
составленный из неизвестных а1У а2, . . . , ап, — через а,
вектор, составленный из свободных членов (/, фг), (/, ф2), . ..
•••> (/> Фя)> — через Ь. Систему C.24) можно записать как
одно векторное уравнение:
Rna = b. C.26)
Уравнение C.26), очевидно, равносильно следующему:
a = (I—aRn)a + aby C.27)
где /—единичная матрица п-то порядка и а—любое не
равное нулю число. Собственные числа Х[ \ Я/2 \ .. . , Ai ^
матрицы Rn все положительны; расположим их в порядке
возрастания:
0<A,ln)<Mn,<...<^rt).
Собственные числа матрицы /—aRn равны 1—сщ
(А=1, 2, ... , /г); если взять
а= (пJ ,я1 , C.28)
то все собственные числа матрицы /—aRn будут заключены
между числами
и
и, следовательно, будут все меньше единицы по абсолютной
величине; итерации, выполняемые по формуле

4] § 2. ЭНЕРГЕТИЧЕСКИЙ МЕТОД 20§
сходятся к решению системы Ритца со скоростью
геометрической прогрессии, знаменатель которой равен
#>+*<"> Тп + \'
C.30)
где Тп~—~ есть число обусловленности Тодта матрицы Rn.
Если п возрастает, то Х[п) не возрастает, а Х^ не
убывает. Может случиться, что имеет место хотя бы одно из
соотношений
%\v _ о, Х{пп) -+ оо;
П->сс /1-х»
тогда величина C.30) стремится к единице при п-+оо.
В таком случае при больших л, нужных для того, чтобы
приближение по Ритцу было достаточно точным, итерации
будут сходиться очень медленно. Поэтому практически
особенно интересен тот случай, когда все собственные числа
матрицы Rn заключены между двумя положительными
постоянными, которые не зависят от п:
0<с1<4/г)<с2,<оо; C.31)
в пп. 2 — 4 § 8 настоящей главы будет указано, как
следует выбирать координатную систему, чтобы соотношение
C.31) имело место. В этом случае можно взять
a=cTR- C-32)
Собственные числа матрицы /—aRn заключены тогда между
числами
Со ^1 — i ^2 Сл ш
c* + ci Съ + сх*
итерации, выполняемые по формуле
^'^'-d^K+d^- <3-зз)
сходятся при любом nt как прогрессия с знаменателем
Ш- C-34)

206 ГЛ. 111. ВАРИАЦИОННЫЕ МЕТОДЫ [5
5. Естественные краевые условия. Во многих
практически интересных случаях оператор А краевой задачи
представляет собой дифференциальный оператор, а его область
определения есть множество функций, имеющих производные
необходимого порядка и, что в данный момент для нас более
существенно, удовлетворяющих некоторым однородным
краевым условиям. Соответствующее пространство НА получается
из области D(A) определения оператора А присоединением
к ней новых функций, которые могут и не подчиняться всем
тем требованиям, которые были наложены на функции из
области D(A). В частности, функции из ИА могут не
удовлетворять тем или иным краевым условиям задачи. Краевое
условие, которому удовлетворяют все функции, входящие в
область задания положительного оператора Л, называется
естественным для этого оператора (или для
соответствующей краевой задачи), если в энергетическом пространстве
НА существуют функции, этому условию не удовлетворяющие.
Краевые условия, которым обязательно удовлетворяют
элементы энергетического пространства, называются главными.
В теории упругости главные краевые условия принято
называть геометрическими или кинематическими, естественные
краевые условия — динамическими.
Координатные функции в методе Ритца нет
необходимости брать из области определения оператора, достаточно,
чтобы они были элементами энергетического пространства.
Отсюда вытекает, что нет необходимости подчинять
координатные функции естественным краевым условиям; это
существенно облегчает подбор координатных функций.
Можно указать простое правило, позволяющее отличать
естественные краевые условия от главных и пригодное для
весьма широкого класса краевых задач. Пусть оператор А
дифференциальный, порядка 2s, положительный на множестве
функций, удовлетворяющих некоторым однородным краевым
условиям вида Gku — 0. Такое краевое условие будет
естественным, если Gku содержит производные от и порядка s
и выше, и главным, если Gku не содержит производных от
и порядка выше s—1.
Пример 6. Для оператора Лапласа s~\; краевое
условие задачи Дирихле и |$= 0 главное, а краевое условие
смешанной задачи U- + ow =0, а ^0, естественное.

5] § 2. энергетический метод 207
Пример 7. Для бигармонического оператора
дх*^'дх*ду*^ду*>
входящего в уравнение изгиба тонких пластин, 5 = 2.
Условия жесткого закрепления края (v — внешняя нормаль к краю)
= 0
5
для этого оператора главные, а из условий свободного опи-
рания края (о—постоянная Пуассона, q — радиус кривизны
края)
«u-o. h-^s?],-»
первое главное, а второе естественное.
Пример 8. Уравнения статической теории упругости в
самом общем случае неоднородной и неизотропной среды
можно записать в виде
Au^-Y* 4:(cikimZim{u) х[0)) = К. C.35)
Lk.l.m=\ l
Здесь и—вектор упругих смещений, К—вектор объемных
сил, л40) — вектор координатной оси лгА,
коэффициенты упругости сцащ удовлетворяют известным
условиям симметрии
Cikltn —cimik~ ckilm*
Для уравнения C.35) s = \. Условие жесткого закрепления
границы тела а|5 = 0 главное; условие, что граница тела
свободна от действия внешних сил, может быть
представлено в виде
s
Е eiki»*i» (*) cos (v> **)**в> = 0,
i, k, /, т~\
и очевидно, что оно естественное.

208
ГЛ. III. ВАРИАЦИОННЫЕ МЕТОДЫ
[6
6. Неоднородные краевые условия. Энергетический метод
можно часто использовать и в том случае, когда краевые
условия данной задачи неоднородные. Поясним это на двух
конкретных краевых задачах.
1) Рассмотрим уравнение Пуассона —Аи=/(х) при
краевом условии и \s ~g{x); ограниченную поверхностью *S область,
внутри которой мы ищем функцию и(х), обозначим через Q.
Примем пока следующее допущение: существует функция
i|)(.x:)£ W[2) (Q) такая, что г|> \s = g(x). Положим v = u—г|).
Функция v(x) удовлетворяет дифференциальному уравнению
— Av—f(x)— Дг|) и краевому условию v\$ =0. В качестве
исходного гильбертова пространства возьмем пространство
L2(Q) функций, квадратично суммируемых в Q. В этом
пространстве оператор —Д положительно определен на
множестве функций, которые обращаются в нуль на границе 5,
и функцию v [х) можно строить как решение задачи о
минимуме функционала
F(tf)=—(Av, v)—2(v, f— Ai|>) =
= — \ [vAv + 2v (/— АЩ dx =
Q
= 5[(grad^J~2^(/— by)]dx\ C.36)
й
упомянутый минимум можно искать на множестве функций,
которые принадлежат пространству W± (S) и обращаются
в нуль на S.
Полагая в C.36) опять v = u — я|), найдем после
некоторых несложных преобразований, что F (и) только постоянным
слагаемым отличается от функционала
$[(gradaJ — 2uf\dx. C.37)
Отсюда следует, что решение поставленной нами задачи
можно строить как решение задачи о минимуме функционала
C.37) на множестве тех функций из Wi1] (Q), которые на
границе S принимают заданное значение g(x).
Мы пришли к этому выводу, потребовав, чтобы
существовала функция ty(x) £ W{22) (Q), удовлетворяющая условию
\|)|5 = ^(лг). Это требование можно несколько ослабить: д<?-

6]
§ 2. ЭНЕРГЕТИЧЕСКИЙ МЕТОД
209
статочно, чтобы ty(x)£WBl) (£1). Последнее требование и
необходимо: если не существует функции из WW (Q),
принимающей на S значение g(x), то задача о минимуме
функционала C.37) лишена смысла.
Применяя к функционалу C.37) метод Ритца, можно
выбрать систему координатных функций ц>1 (х)у ф2 (х), ... ,
удовлетворяющих условиям п. 3; в частности, эти функции
должны обращаться в нуль на границе. Приближенное
решение по Ритцу следует искать тогда в виде
п
»» = ♦(*) + 2 <*№(*)•
2) В качестве второго примера рассмотрим задачу об
интегрировании того же уравнения —Аи=/(х) при краевом
условии т- + <*и =h(x), где а—положительная и, скажем,
непрерывная функция, заданная на границе S. Чтобы свести
нашу задачу к вариационной, допустим, как и выше, что
существует функция i|)(x) £ Wl2) (й), удовлетворяющая
краевому условию ^+°Г'Ф =й, и положим и — ty = v. Тогда
— Av=f(x)—Ая|) и 3"- + ^^ =0« Последняя задача
сводится к задаче о минимуме функционала
(_дФ> v)—2(v, /-Дф),
который в данном случае приводится с помощью
элементарных преобразований к виду
J [(grad vJ — 2v (/— Дф)] dx + \ ov*dS. C.38)
Для этого функционала краевое условие "д- + <тсч =0
естественное, и минимум функционала следует искать на
функциях пространства WBl) (Q), не подчиненных никаким
краевым условиям. Полагая в C.38) v = u—ф, мы, как и
выше, убедимся, что функционал C.38) только постоянным
слагаемым отличается от функционала
J [(grad aJ — 2uf] dx+l {ou2 — 2uh)dS. C.39)

210
ГЛ. III. ВАРИАЦИОННЫЕ МЕТОДЫ
[7
Тем самым неоднородная смешанная задача приведена к
задаче о минимуме функционала C.39); минимум следует
искать в пространстве W^ (&)•
В данном случае допущение о существовании функции
i|)(x) на самом деле не необходимо.
7. Энергетический метод в случае положительного
оператора. Рассмотрим уравнение Аи=/У предполагая, что
в выбранном гильбертовом пространстве оператор А
положительный, но не положительно определенный. По теореме
10 наше уравнение по-прежнему равносильно задаче о
минимуме функционала C.17), однако в данном случае эта
вариационная задача, вообще говоря, неразрешима даже в
обобщенном смысле. Укажем необходимое и достаточное .условие
разрешимости этой задачи.
Как и в случае положительно определенного оператора,
можно построить энергетическое пространство НА\ на этот
раз оно содержит не только элементы исходного
пространства, но и некоторые новые элементы.
Имеем (Ли, ц) = |ц|2, так что
F(u)H"l2-2(a, /).
Для того чтобы задача о минимуме функционала F(u) имела
решение в НА, необходимо и достаточно, чтобы в этом
пространстве был ограничен линейный функционал (и, /).
В этом случае по теореме Риса существует такой
элемент и0£НА, что (и, /) = [и, н0], если и£НА;
элемент и0 реализует минимум функционала F(u) в
пространстве НА.
К положительным операторам часто приводят краевые
задачи для бесконечных областей; подробнее об этом будет
сказано в § 3, п. 10.
То обстоятельство, что и0 £ НА, можно интерпретировать
физически так, что этот элемент имеет конечную энергию;
если выполнено условие ограниченности функционала (и, /)
в НА, то соответствующий элемент uQ будем называть
решением с конечной энергией для уравнения Au—f.
Заметим, что в случае положительно определенного
оператора также можно трактовать элемент, реализующий
минимум F(u), как решение с конечной энергией.

1] § 3. ПРИЛОЖЕНИЯ К ЗАДАЧАМ МАТЕМАТИЧЕСКОЙ ФИЗИКИ 211
§ 3. Приложения к задачам математической физики
1. Обыкновенные дифференциальные уравнения
второго порядка. Многие важные задачи математической физики
сводятся к обыкновенному дифференциальному уравнению
второго порядка вида
Lu==~±(p{x)g)+q(x)a=f(x), C.40)
которое надлежит проинтегрировать в промежутке а^х^Ь
при краевых условиях
ш {а)—$и (а) = 0, уи (Ь) + 8и (Ь) = 0, C.41)
где a, (J, у, б—некоторые постоянные. Простейшая из задач
такого рода—это задача о статическом прогибе струны,
которая в состоянии равновесия занимает отрезок а^х^Ь
оси х и элемент (х} x-\-dx) которой находится под
воздействием восстанавливающей силы q (x) udx и внешней силы
f(x)dx, причем к концам х к x-\-dx элемента приложены
силы натяжения р(х) и p(x-\-dx) соответственно. Краевые
условия C.41) в общем случае соответствуют упругому
закреплению концов струны.
В частном случае, если, например, а Ф 0, E = 0, то конец
х~а струны свободен; если же а = 0, р Ф 0, то этот конец
жестко закреплен.
Для того чтобы оператор L, определенный левой частью
уравнения C.40) и краевыми условиями C.41), был
положительно определенным, достаточно, чтобы были выполнены
следующие условия:
1) При а^х^Ь функции р(х) и q{x)
кусочно-непрерывны и неотрицательны.
2) Функция р(х) может обращаться в нуль в некоторых
точках интервала а<х<С.Ь> но так, чтобы интеграл
а
сходился. Мы предполагаем еще, что р(а) Ф 0, р(Ь) Ф 0.
Простейший случай, при котором условие 2) выполняется,
это случай р(х)^р0> где р0—положительная постоянная.

212 гл. ш. вариационные методы [1
3) Постоянные а, |3, у, б неотрицательны, причем хотя
бы одна из постоянных Р и б положительна.
При выполнении перечисленных условий, а также
дополнительного условия а Ф О, у Ф 0 интегрирование уравнения
C.40) при условиях C.41) сводится к задаче о минимуме
функционала
ь
J [P(x)u'2(x) + q(x) и* (х)-2/(х) и (х)] dx +
а
+ Lp(a)u*(a) + ±p(b)u*(b); C.43)
краевые условия C.41) в этом случае естественные, и им
заранее удовлетворять нет нужды. Если какая-либо из
постоянных а или у равна нулю, то соответствующий внеин-
тегральный член в C.43) следует вычеркнуть, а
соответствующее условие C.41) становится главным. В частности,
если a = Y~0> так ЧТ0 краевые условия принимают вид
!i(a) = a(fc) = 0, C.44)
дело сводится к нахождению минимума интеграла
ь
\[p{x)u\x) + q{x)u2{x) — 2f(x)u(x)]dx C.45)
a
на множестве функций, удовлетворяющих краевым условиям
C.44).
Если ип(х) (л=1, 2, ...)—минимизирующая
последовательность для функционала C.43), то сама эта
последовательность сходится к точному решению равномерно, а
последовательность производных и'п (х) сходится к
производной от точного решения в среднем с весом р (х); это значит,
что если и0(х)—точное решение, то
ь
Urn [p(x)[u'n(x)-u'0(x)]2dx = 0.
а
В частном случае, когда р (х) ограничена снизу
положительным числом: р (х) ^ pQ > 0, то и'п (х) сходится к и'9 (х)

1] § 3. ПРИЛОЖЕНИЯ К ЗАДАЧАМ МАТЕМАТИЧЕСКОЙ ФИЗИКИ 213
в среднем:
ь
lim \K(x)-uf0(x)]2dx = 0.
a
Рассмотрим теперь исключенный ранее случай j} = 6 — 0;
краевые условия принимают вид
и'(а) = и'(й) = 0. C.46)
Если при этом неотрицательная по условию 1) функция
q(x) отлична от тождественного нуля, то оператор L остается
и в этом случае положительно определенным; интегрирование
уравнения C.40) при краевых условиях C.46) сводится к
задаче о минимуме интеграла C.45) на множестве функций,
которые не обязаны удовлетворять каким бы то ни было
краевым условиям. Если же q(x) = 0 и jj = 8 = 0, то
оператор L, который в данном случае принимает вид
*»=-£('<*>£)' <3-47>
при краевых условиях C.46) не будет даже положительным.
В этом случае задача Lu=^f(x)) и' (а) = и' (Ь) = 0,
неразрешима, если не выполнено равенство
ь
(/, 1)=$/(*)</* = 0, C.48)
а
поэтому будем считать упомянутое условие выполненным.
Условие C.48) означает, что f(x) принадлежит
подпространству Н пространства L2(a, b)y ортогональному к единице.
В этом подпространстве оператор C.47) при краевых
условиях C.46) оказывается положительно определенным, и задача
об интегрировании уравнения
при условиях C.46) имеет решение, которое можно получить,
отыскивая минимум интеграла
ь
[p(x)u,2{x)dx
а

214
ГЛ. III. ВАРИАЦИОННЫЕ МЕТОДЫ
[1
на множестве функций, удовлетворяющих условию (и, 1) = 0.
Следует, впрочем, заметить, что уравнение C.49)
интегрируется элементарно.
Представляет интерес и тот случай, когда функция р{х)
обращается в нуль на одном из концов а, Ь (или на обоих
сразу). Такой случай, например, имеет место, если изучается
смещение под действием внешней силы тяжелой струны,
подвешенной за верхний конец; в этом случае функция
р(х), пропорциональная весу участка струны от нижнего ее
конца до точки ху обращается в нуль на нижнем конце.
Для простоты ограничимся случаем, когда р(а) = 0,
р[Ь)фО и краевое условие на конце b имеет вид и(Ь) = 0.
Может случиться, что интеграл C.42) сходится; тогда, чтобы
задача имела определенное решение, следует поставить
некоторое краевое условие при х — а. Можно поставить условие
и(а) = 0; тогда оператор L положительно определенный и
дело сводится к задаче о минимуме функционала C.45) при
краевых условиях C.44). Если интеграл C.42) расходится,
то на конце х — а краевое условие задавать нельзя: в общем
случае не существует решения, удовлетворяющего такому
условию. В случае расходимости интеграла C.42) условие
на конце х = а заменяется требованием, чтобы искомая
функция и (х) была квадратично суммируема в промежутке
а<Сх<Ь. При перечисленных условиях оператор! будет
положительно определенным, если интеграл
ь
[^=4dx C.42')
а
сходится; это будет иметь место, например, если при
некоторой постоянной а < 2 выполняется неравенство р(х)^
^С(х—а)ау C=const>0. Если интеграл C.42') сходится,
то отыскание решения уравнения C.40), удовлетворяющего
условию и(Ь) = 0 и квадратично суммируемого в промежутке
a<Zx<Cby сводится к отысканию минимума функционала
C.45) на множестве функций, которые обращаются в нуль
при х =Ь. Тот же результат имеет место и тогда, когда
интеграл C.42') расходится, но функция р(х)
удовлетворяет неравенству р(х)^С(х—аJ, С= const >0.
Если р(х) удовлетворяет неравенству р(х)^С(х—а)а,
где а>2, то на множестве функций, обращающихся в нуль

2] § 3. ПРИЛОЖЕНИЯ К ЗАДАЧАМ МАТЕМАТИЧЕСКОЙ ФИЗИКИ 215
при х = Ь, оператор L будет положительным, но не
положительно определенным; сформулированная выше краевая
задача по-прежнему сводится к задаче о минимуме
функционала C.45) на том же множестве функций, которые при
х = Ь обращаются в нуль; однако эта вариационная задача
может не иметь решения.
2. Обыкновенные дифференциальные уравнения высших
порядков. Рассмотрим уравнение порядка 2т:
L^b-^UPk(x)d^)^m' C-50)
и будем искать решение этого уравнения, определенное
в промежутке а^х^Ь и удовлетворяющее простейшим
краевым условиям
и(а) = и'(а)= ...=и{т~1){а) = 0} C.5Г)
и {Ь) = и (Ь) = ... = и{т~1) (Ь) = 0. C.5Г)
Допустим, что все коэффициенты pk(x) неотрицательны, а
старший коэффициент рт (х) удовлетворяет еще и более
жесткому условию Рт(х)^с, где с — положительная
постоянная. Тогда оператор L положительно определенный на
множестве функций, удовлетворяющих условиям C.51);
краевая задача C,50), C.51) равносильна задаче о минимуме
функционала
т \
I*Pk(x)(^ky-2f{x)u(x)\dх C.52)
на множестве функций, удовлетворяющих условиям C.51).
Эти условия главные.
Если ип(х) (л=1, 2, ...) — последовательность
приближенных по Ритцу решений нашей задачи, a uq(x) — ее
точное решение, то ц^т) (х)—>и[т)(х) в среднем; производные
низших порядков от приближенных решений сходятся к
соответствующим производным точного решения равномерно.
Пусть теперь старший коэффициент рт (х), будучи
положительным при a<.x<Zb, обращается в нуль при х^=а.

216
ГЛ. III. ВАРИАЦИОННЫЕ МЕТОДЫ
[2
Допустим, что при этом
сх (*_<*)« ^Рт (Х) < с2 {х-а)\ C.53)
где cv с2, a — положительные постоянные. Если а^2т,
то оператор L оказывается положительно определенным на
множестве функций, удовлетворяющих условиям C.51") и,
кроме того, условиям
и(а) = и'(а)= ...=M(OT"Jl-I)(a) = 0, C.54)
где [X— целая часть показателя а. В частности, если а<1,
то следует удовлетворить всем условиям C.5Г); в другом
крайнем случае, когда 2т—1<Са<^2/#, никаких условий
на конце х — а задавать не следует. Если выполняется
неравенство C.53), то задача об интегрировании уравнения
C.50) при краевых условиях C.51") и C.54) равносильна
задаче о минимуме функционала C.52) на множестве
функций, удовлетворяющих краевым условиям C.51") и C.54).
Обозначая по-прежнему через и0(х) точное решение
задачи, а через ип(х) приближенное решение по Ритцу,
можно доказать, что и^ (х) т^ (х) в среднем свесом
П -> 00
(л:—а)а; это значит, что
ь
lim \(x — a)a[uT)(x)—uT){x)]2dx=0\
П-+ 00 а
отсюда следует, что производные порядка ниже т от
приближенных решений сходятся к соответствующим
производным точного решения равномерно на отрезке а-\- е^ж; Ь,
где е—любое положительное число.
Если в неравенстве C.53) а>2т, то можно задавать
только краевые условия C.51"); при этих условиях
оператор L положительный, но не положительно определенный.
Краевая задача равносильна задаче о минимуме функционала
C.52) на множестве функций, удовлетворяющих условиям
C.51"), но эта последняя задача может оказаться
неразрешимой.
Краевые условия могут иметь вид, отличный от C.51);
некоторое, хотя и далеко не полное представление о других
возможных типах краевых условий можно получить из
следующего примера.

2] § 3. ПРИЛОЖЕНИЯ К ЗАДАЧАМ МАТЕМАТИЧЕСКОЙ ФИЗИКИ 217
Пример 9. Изгиб балки, лежащей на упругом основании.
Пусть ось балки занимает отрезок @, /) оси х. Сечение
балки будем считать, вообще говоря, переменным.
Обозначим через и (х) прогиб балки в сечении с абсциссой х, через
1(х) — момент инерции этого сечения, через К(х) и f(x)—
коэффициент податливости основания и интенсивность
действующей на балку нормальной нагрузки в том же сечении.
Наконец, через Е обозначим модуль Юнга материала балки.
Уравнение изгиба балки имеет вид
Ia==^(f/(*)g)+ *(*)«==/(*). C.55)
Рассмотрим сперва случай, когда ни одно из сечений
балки не вырождается в точку или линию, так что момент
инерции 1(х) всегда остается больше некоторой
положительной постоянной. Если концы балки жестко закреплены, то
и @) = и' @) = 0, и (/) = и' (/) = 0 C.56)
и мы приходим к частному случаю задачи C.50), C.51).
Прогиб и (х) можно найти как решение задачи о минимуме
функционала
J {eI(x) @L К{х)и* (*)-2/(*)и(*)| dx C.57)
о
на множестве функций, удовлетворяющих условиям C.56).
Если ип(х) — приближенное решение по Ритцу, а и0(х)—*
точное решение, то ип(х)—>и0(х) в среднем, а ип(х) -+u'Q (x)
и ип(х)—>ио(х) равномерно.
Если один из концов балки, например конец х = /,
свободен, а другой жестко закреплен, то вторая пара условий
C.56) заменяется следующей:
«"(/) = 0, ±[ЕЦх)а'(х)]х=, = 0. C.58)
Оператор L остается положительно определенным и в этом
случае. Условия C.58) естественные.
Допустим теперь, что в каком-либо сечении 1(х)
обращается в нуль. Остановимся на частном случае, когда
стержень имеет вид конуса произвольной формы с вершиной

218
ГЛ. III. ВАРИАЦИОННЫЕ МЕТОДЫ [3
в точке л; = 0. В этом случае 1(х) = -^1A) и мы приходим
к неравенству C.53), которое в данном случае переходит
в равенство при с1 = е2 = -~ и a—2w = 4. Краевых
условий на конце л; = 0 задавать нельзя; если конец х = 1
жестко закреплен, то следует положить иA) = и' (/) = 0.
Оператор Z, и в этом случае положительно определенный;
задача сводится к вариационной задаче о минимуме
интеграла
I {^V (£?)' + *(*)«■ (*)-2/(*)e(*) } dx
О
на множестве функций, удовлетворяющих условиям u(l) =
= и' (/) = 0. Эта вариационная задача разрешима; если
и0{х)—ее точное решение, аип(х)— приближенные решения
по Ритцу, то ип(х)—>uQ(x) в среднем с весом х4, а
Un(x)—>uQ(x) и ип(х)—>и0(х) равномерно на отрезке
г^х^1, где е — любое положительное число.
3. Системы обыкновенных дифференциальных
уравнений. Рассмотрим простейший случай, когда система имеет
вид
-S{5('/*W^) + */*W«*] -/,(*> C.59)
(у=1, 2, ..., s; a<x<b),
а краевые условия принимают простейшую форму
Uj(a) = Uj(b) = 0 (/=1,2,...,*). C.60)
Коэффициенты pJk{x) и q,k(x) считаем вещественными,
ограниченными и измеримыми; практически интересен тот
случай, когда эти коэффициенты непрерывны или
кусочно-непрерывны.
Совокупности данных функций fx (х), /2 (х)} ..., /s(x)
и искомых функций иг(х)у и2(х), ..., tis(x) можно
трактовать как векторы/(лг) и tt(x) с s компонентами. Левые
части уравнений C.59) вместе с краевыми условиями C.60)
порождают некоторый оператор в пространстве ^-компонент-

3] § 3. ПРИЛОЖЕНИЯ К ЗАДАЧАМ МАТЕМАТИЧЕСКОЙ ФИЗИКИ 219
ных вектор-функций, суммируемых с квадратом в
промежутке (а, Ь). Этот оператор симметричен, ес/ш р k(x)==pk .(x)
и QjkW — Qkj^*)) и положительно определен, если матрица
коэффициентов p.k (x) положительно определенная, а матрица
коэффициентов qjk(x) неотрицательная, точнее говоря, если
для любых вещественных чисел tXJ t2, ..., ts справедливы
неравенства
S S S
где |Д-0 — некоторая положительная постоянная. При
выполнении этих условий задача интегрирования системы C.59)
при краевых условиях C.60) равносильна задаче об
отыскании вектор-функции, удовлетворяющей тем же краевым
условиям C.60) и реализующей минимум функционала
I \ £ Ipjk (*) d£?d-S+и*/ м и* (*)] - Ел (•*>"• w idx-
В качестве координатных функций здесь следует
выбирать вектор-функции
Ф, (■*) = {фи (*)> Ф«(*). •••> Ф„(*)},
Ф1МНФ11С*). фи(*) Фи (■*)}.
Фв W = {фщ W» Ф.Л*)» •••- Ф»,(*)},
краевые условия главные, поэтому необходимо, чтобы
Ограничиваясь я координатными функциями, получаем
следующее выражение #-го приближенного по Ритцу
решения:
«»(*) = 2 **<М*)
/г = 1
ИЛИ
■И/„(*)=2 <**ф/*(*) (;'=1. 2. • ••, «).

220
ГЛ. III. ВАРИАЦИОННЫЕ МЕТОДЫ
[3
dx.
Коэффициенты ak определяются из системы C.24); в данном;
случае
р Г * ^ф7/^Фзл
a La. P=i
Если координатные функции принадлежат области
определения оператора данной задачи2), то можно
воспользоваться также формой C.24') системы Ритца; в нашем случае
a L ct, P = i
^ЛГ.
О сходимости приближенного решения к точному можно
повторить все, что было сказано об одном уравнении
второго порядка (см. п. 1 настоящего параграфа).
Если через р (х) и q (л:) обозначить матрицы с
составляющими Pjk(x) и qjk(x), то уравнения C.59) и C.60)
можно записать в виде
U(a) = U (b):
:0,
C.59')
C.60')
что по форме совпадает с уравнениями C.40) и C.44).
Можно указать и более сложные краевые условия, при
которых оператор в левой части уравнения C.59) будет
положительно определенным. Так будет, например, если краевые
условия имеют вид
a'(a) —p»(a) = 0, U' F) + 6tt(fc) = 0,
где р и б — неотрицательные матрицы, из которых хотя бы
одна положительно определенная.
Можно рассмотреть и систему уравнений порядка выше
второго
£<-i>*£(>*w£)-/<*>. C.50')
1) В простейшем случае, когда коэффициенты Pjk (х) непрерывно
дифференцируемы, а коэффициенты qjk\x) непрерывны, для этого
достаточно, чтобы функции фу„ (х) имели непрерывные вторые
производные и обращались в нуль при х = а и х — Ь<

4] § 3. ПРИЛОЖЕНИЯ К ЗАДАЧАМ МАТЕМАТИЧЕСКОЙ ФИЗИКИ 221
где и (х) и f(x)— 5-компонентные вектор-функции, a pk{x) —
симметричные матрицы порядка s. Будем решать эту
систему при краевых условиях C.51), разумеется, полагая,
что входящая в эти условия функция и (х) векторная, так
что эту функцию лучше обозначить через U (х).
Порожденный такой задачей оператор будет положительно
определенным, если матрицы pk (х) (& = 0, 1, 2, ...,
т—^неотрицательны при всех х, а^х^Ь, а матрица рт(х) при
этих же х положительно определенная; точнее говоря,
о матрице рт (х) мы предполагаем, что все ее собственные
числа (которые, вообще говоря, зависят от х) ограничены
снизу некоторой положительной постоянной.
4. Основные задачи для уравнений эллиптического
типа. Уравнения Лапласа и Пуассона. Будем рассматривать
самосопряженное уравнение эллиптического типа второго
порядка
т
ли=- х 4K^)+CWtt=/w- {3-61)
Коэффициенты A(j и С в общем случае суть функции
координат xt1 х2У . .., хт переменной точки х; в частных
случаях эти коэффициенты могут быть и постоянными. Будем
считать, что искомая функция должна быть определена
в некоторой конечной области Q.
Уравнение C.61) мы считаем эллиптическим в области
Q; это значит, что, каковы бы ни были точка x£Q и
вещественные числа tlt t2, ..., tmi найдется такая
положительная величина \л{х), что
т т
i, / = i i = i
Приходится различать два случая:
1) Нижняя грань чисел \i(x) положительна. Тогда
существует такая положительная постоянная pi0, что для любой
точки x£Q выполняется неравенство \i(x)^\i0. В этом
случае эллиптическое уравнение называется невырождаю-
щился, Для невырождающегося уравнения справедлива

222
ГЛ. 111. ВАРИАЦИОННЫЕ МЕТОДЫ
[4
неравенство
т т
2 AvW/^oS О, fx0 = const >0.
i, / = i / = i
2) Нижняя грань чисел (Л (х) равна нулю. В этом случае
эллиптическое уравнение называется вырождающимся. Если
коэффициенты Л-j непрерывны в замкнутой области Q -+- S,
то на некотором множестве точек поверхности *S величина
jli (л:) = 0. Это множество в зависимости от его структуры
называют линией, поверхностью и т. д. вырождения.
Для .невырождающихся эллиптических уравнений чаще
всего ставятся следующие задачи, различающиеся по типу
краевых условий, которые пока будем считать однородными.
Задача Дирихле или первая краевая задача:
а|5 = 0. C.62)
Задача Неймана или вторая краевая задача:
ди
cos (vyx{)
L t.y=i
= 0.
Третья краевая задача:
ди
X AU дЧ~>
L i.i=i J
COS (v,Xi) + GU
= 0.
C.63)
C.64)
Здесь v—внешняя нормаль к поверхности 5,
о—неотрицательная и отличная от тождественного нуля функция,
определенная на поверхности 5.
Если коэффициент С(х)^0, то при краевых условиях
C.62) и C.64) оператор Л, входящий в левую часть невы-
рождающегося уравнения C.59), положительно определенный.
Задача Дирихле сводится к задаче о минимуме
функционала
lit^w+^-^Y C'65)
(dx — элемент объема) на множестве функций,
удовлетворяющих условию C.62); третья краевая задача сводится

4] § 3. ПРИЛОЖЕНИЯ К ЗАДАЧАМ МАТЕМАТИЧЕСКОЙ ФИЗИКИ 223
к задаче о минимуме несколько иного функционала:
в классе функций, на которых этот функционал имеет
конечное значение, т. е. в классе W^ (Я) (см. § 1, п. 4).
Краевому условию C.64) подчинять эти функции нет
необходимости, так как это условие естественное.
Если коэффициент С(х) не только неотрицателен, но и
отличен от тождественного нуля, то оператор А
положительно определенный и на множестве функций,
удовлетворяющих условию C.63); задача Неймана равносильна
вариационной задаче о минимуме интеграла C.65) на функциях
класса ^^(Я). Краевое условие C.63) естественное.
Особо остановимся на задаче Неймана в случае, когда
С = 0. Уравнение C.61) принимает вид
т
Задача Неймана для этого уравнения в общем случае
неразрешима; необходимым и достаточным условием ее
разрешимости является равенство
(/, l)=$/(*)rf* = 0. C.68)
Q
С другой стороны, если задача Неймана разрешима, то она
имеет бесчисленное множество решений, которые
различаются на постоянное слагаемое. Можно это слагаемое
подобрать так, чтобы (и, 1) = 0. Теперь можно в уравнении
C.67) рассматривать данную функцию/(х) и искомую и(х)
как элементы подпространства, ортогонального к единице.
В этом подпространстве оператор А0 положительно
определенный на множестве функций, удовлетворяющих условию
C.63). Задача Неймана равносильна задаче о минимуме
интеграла

224 гл. ш. вариационные методы [4
на множестве функций из W^ (Q), удовлетворяющих
условию
(и,\)= ^u(x)dx = 0; C.69)
эта вариационная задача разрешима и имеет единственное
решение.
Иногда рассматриваются краевые условия смешанного
типа: граница S разбивается на две части S' и S", искомое
решение подчиняется условиям
1
и |^ = 0,
Ё A7^.C0S(v>*y) + ™
L/. /=i
= 0. C.70)
5"
Оператор А в уравнении C.61) при этом положительно
определенный, и «смешанная» краевая задача равносильна
задаче о минимуме функционала
т
на множестве функций, удовлетворяющих первому из
условий C.70); второе из этих условий естественное.
Все сказанное об эллиптических уравнениях в полной
мере относится к уравнению Пуассона
-Ди =*/(*), C.61')
где А—оператор Лапласа. Краевые условия второй и
третьей краевых задач для этого уравнения упрощаются и
принимают вид
f-l =0 C.63')
и
[£+Н,-°- <з-б4'>
Для определенности будем писать последующие формулы
в предположении, что и зависит от трех координат (л:, j/, z).
Задачи Дирихле и Неймана для уравнения Пуассона равно-

4] § 3. ПРИЛОЖЕНИЯ К ЗАДАЧАМ МАТЕМАТИЧЕСКОЙ ФИЗИКИ 225
сильны задачам о минимуме интеграла
на множествах функций из класса W^ (Q), подчиненных в
случае задачи Дирихле условию C.62), а в случае задачи
Неймана условию C.69); в этом случае необходимо, чтобы
функция f(x) удовлетворяла условию C.68).
В п. 6 § 2 указаны вариационные задачи, к которым
сводятся основные краевые задачи для уравнения Пуассона
(или Лапласа) в случае неоднородных краевых условий. Для
общего уравнения эллиптического типа результаты
аналогичны, а именно:
1) Пусть требуется проинтегрировать уравнение C.61) при
краевом условии
u\s = g(x). C.62')
Допустим (это допущение необходимо), что существует
некоторая функция \|) (х) £ W{12 (Q), удовлетворяющая этому
краевому условию, так что ty\s = g{x). Тогда наша задача
сводится к нахождению функции, реализующей минимум
функционала C.65) на множестве тех функций из W^ (Q),
которые удовлетворяют краевому условию C.62').
Применяя здесь метод Ритца, следует представить
приближенное решение в виде
п
где ty{x)—упомянутая выше функция, удовлетворяющая
условию C.62'), и <pk(x)—функции из P7A2>(Q),
обращающиеся в нуль на границе S и удовлетворяющие условиям
п. 3 § 2 для координатных функций.
2) Пусть то же уравнение C.61) требуется
проинтегрировать при краевом условии
т
[EAvJ!cos(v> *,) + <ra]s~A(*). C.64")
8 с. Г. Михлин и X. Л. Смолицкий

226 ГЛ. III. ВАРИАЦИОННЫЕ МЕТОДЫ [4
Эта задача приводится к задаче о минимуме функционала
т
a i> i-1 J s
минимум следует искать на множестве функций W^J (Q);
условие C.64") естественное.
Пример 10. Для иллюстрации метода рассмотрим задачу о
нахождении интеграла уравнения
-*—(S+3)-1 <"■>
в области квадрата —l«^*,t/<;l при условии, что на контуре
квадрата искомый интеграл обращается в нуль:
и(*, ±1) = и(±1, У) = 0. C.72)
Искомая функция и(х, у) только постоянным множителем
отличается от функции напряжений задачи о кручении стержня
квадратного сечения.
Условия C.72) главные, и координатные функции необходимо
должны им удовлетворять. Возьмем в качестве координатных
функций полиномы вида
(я*—1)(у*—1)хтуп (т, /1 = 0, 1, 2, ...).
Из постановки задачи видно, что функция и (х, у) четная как
относительно х, так и относительно у\ кроме того, она не . изменится,
если х и у поменять местами. Отсюда легко следует, что в качестве
координатных достаточно использовать такие функции:
(*2—1)(«/2 — \)(хшу2П + х2Пу2т) (т, л = 0, 1, 2, ...).
Ограничимся двумя первыми координатными функциями;
приближенное по Ритцу решение имеет вид
М*. #Ж*2-1)(^-1)К+М*2 + </')].
В данном случае энергетическое произведение определяется
формулой
— 1 —1
и мы получаем следующую систему Ритца (ср. формулу C.24)):
256 1024 __16
45 °1+525 в«—9 •
1024 11264 __32
525 ai+4725 a*~45 '

5] § 3. ПРИЛОЖЕНИЯ К ЗАДАЧАМ МАТЕМАТИЧЕСКОЙ ФИЗИКИ 227
или
16
64
15а1 + 175а2~~ 3 '
32
352
Отсюда
1295,
= 4432'
35 01+325^-
: 0,292,
3 *
525 ,
= 8864 :
: 0,0592
и, следовательно,
а2 = (хг—1) (г/2 — 1) [0,292 + 0,0592 (х2 + у2)].
C.73)
Ниже (см. п. 3 § 5) мы сможем составить некоторое суждение
о точности построенного приближения.
5. Вырождающиеся эллиптические уравнения.
Ограничимся здесь рассмотрением задачи Дирихле для наиболее
простого уравнения с двумя независимыми переменными
где непрерывные функции ф(лг, у) и со (л:, у) положительны
при j/>0, но одна из них обращается в нуль при у = 0.
Уравнение C.74)
эллиптическое в верхней полуплоскости \У
и вырождается на оси х.
Пусть область Q имеет
вид, изображенный на рис. 15;
граница S состоит из двух
частей: £', представляющей
собой отрезок оси х, и S'\
расположенной в верхней
полуплоскости. ™
Пусть ф (х, у)>0 при у >
> 0, ф (лг, 0) = 0 и со (*, у) ^ А,
где к—положительная постоянная. Тогда для уравнения
C.71) можно ставить обычное условие C.62) задачи
Дирихле; на множестве функций, удовлетворяющих этому
условию, оператор—^^ф (л:, y)£j— jy [® (*, у)щ)
оказывается положительно определенным, и наша задача сводится
8*

228
ГЛ. III. ВАРИАЦИОННЫЕ МЕТОДЫ
[6
к задаче о минимуме интеграла
И[ф(л;' у)[^У + (*{х' у){д£У~2/(х' у)и] tedytf.TS)
на множестве функций, удовлетворяющих условию C.62).
Рассмотрим теперь случай, когда ф (л:, у) остается
положительной при у^О, но со (л:, 0) = 0. В этом случае
разрешимость задачи зависит от скорости убывания функции со
при у—>0.
Допустим, что (o(jc, у)—у*(й1 (х, у), где ш1 (л:, y)^kx,
а и kx — положительные постоянные. Если сс< 1, то можно
ставить обычное условие C.62). Задача Дирихле
равносильна только что сформулированной задаче о минимуме
функционала C.75). Если 1^а^2, то на линии вырождения
S' ничего задавать нельзя: оператор в левой части уравнения
C.74) положительно определенный на множестве функций,
удовлетворяющих единственному условию
«Is*-0, C.76)
и уравнение C.74) при краевом условии C.76) имеет
единственное решение, которое можно получить, решая задачу
о минимуме интеграла C.75) при условии C.76). Если
а>2, то при условии C.76) оператор в C.74)
положительный, но не положительно определенный; по-прежнему
краевая задача равносильна задаче о минимуме интеграла C.75)
при условии C.76), но эта последняя в общем случае
неразрешима.
6. Уравнения высших порядков. Уравнения
эллиптического типа четвертого порядка встречаются в теории изгиба
пластин, в плоской задаче теории упругости, в теории
кручения анизотропных стержней; в некоторых задачах
теории упругости анизотропных сред встречаются уравнения
шестого порядка; уравнения восьмого порядка играют роль
в теории оболочек. Уравнения высших порядков
встречаются и в некоторых других задачах.
Самосопряженное уравнение в частных производных
порядка 2л в пространстве т независимых переменных хх,
X2i • • • » хт в самом общем случае можно записать в

6] § 3. ПРИЛОЖЕНИЯ К ЗАДАЧАМ МАТЕМАТИЧЕСКОЙ ФИЗИКИ 229
виде
Ak«-Zdx.idx.2 ... dXik [Ап> /,. ... . М*)Щ^^Щ-) •
C.77)
В выражении Л^# суммирование производится по
всевозможным наборам индексов iv iz, ... , ik и д, у2, ..., ул,
каждый из которых независимо от других пробегает
значения 1,2,...,/»; коэффициенты Л}}; £ ;;; ; fa не меняются
ни при какой перестановке верхних и нижних индексов, а
также при замене верхних индексов нижними и наоборот.
Уравнение C.77) называется эллиптическим не
вырождающимся в данной области &, если выполнено следующее
условие. Пусть tiu ,2, ... , in—вещественные переменные, не
меняющиеся ни при какой перестановке значков /г, /Ё, ...
... , in\ существует такая положительная постоянная \хп,
что при любом х £ Q и при любых значениях переменных
ttu i2, ..♦ . in выполняется неравенство
2^/1! h> ..- .' /IW^t. ta. .•♦ » itJhr /a /n ^ И"*! 2 *'i» *a 'n'
C.78)
Общее уравнение C.77) будем рассматривать при
простейших краевых условиях
дга I дп-г а
s
dxudxtJs ' ' * "' dxildxi2...dxin_1
-0,
C.79)
где значки iv iv ... , in-Y независимо друг от друга
пробегают все значения от 1 до т; условия C.79) означают,
что функция и и все ее производные до порядка п—1
включительно обращаются в нуль на границе S.
На функциях, удовлетворяющих условиям C.79),
оператор Lin будет положительно определенным, если для каждого
оператора Ak найдется такая постоянная \ik} что
выполняется неравенство
2^*1» h, .." ! ik^iu hi ... . ik^lu /V ... > /k ^ №k 2j **i» ia &>
C.78')

230
ГЛ. 111. ВАРИАЦИОННЫЕ МЕТОДЫ
[7
причем Ц„>0 и \ik^0 при O^k^n—1.
Соответствующая уравнению C.78) и краевым условиям C.79)
вариационная задача состоит в нахождении минимума интеграла
2u2* Ah> h. •••'. &дхидх1г ... dxik dxjxdxJZ ... dxjh~~ 2fU
dx
C.80)
на множестве функций, удовлетворяющих условиям C.79).
С помощью формул C.77) можно записать и систему
уравнений в- частных производных, если под и(х) и f(x)
понимать s-компонентные вектор-функции, а под
А)\\ /*; ;;; ; fk(x)— матрицы порядка s. Все сказанное в
настоящем пункте об одном уравнении распространяется без
изменений и на системы уравнений; при этом надо только в
неравенстве C.78) понимать под tiu ,-2 in произвольный
s-компонентный вектор с вещественными компонентами.
7. Изгиб пластин. Уравнение изгиба тонких упругих
пластин имеет вид
A«w = 5igJ4 C.81)
или, в более подробной записи,
d*w , 9 d*w d^w_ __ q(x, у)
дхг "Г Z dx2 dy2 + ~di*~ ~D '
Здесь w(x, у)— нормальный прогиб пластины в точке с
координатами х, у; q(x, у) — интенсивность нормальной на-
Ehz
грузки, D— ion— ч1 где ^и а—М°ДУЛЬ Юнга и
постоянная Пуассона материала пластины, 2/г—ее толщина. Область,
которую пластина вырезает из плоскости (х, у), обозначим
через Q, контур этой области — через S. В зависимости от
характера закрепления края пластины имеем следующие
наиболее часто встречающиеся краевые условия.
1) Край пластины жестко закреплен:
w
5 ' д\
= 0. C.82)

7] § 3. ПРИЛОЖЕНИЯ К ЗАДАЧАМ МАТЕМАТИЧЕСКОЙ ФИЗИКИ 231
2) Край пластины свободно оперт:
о, Гд«,_1=£^'
Is L Q dv.
w
= 0.
C.83)
3) Край пластины упруго закреплен:
w
-о,
'*"-(¥-к№,-°- C-841
4) Край пластины свободен:
[*—"->(S-7S).
рд^ ,« п\(~ * ^ ?!?!
-о,
:0.
C.85)
В формулах C.82) — C.85) v означает внешнюю
нормаль к 5, 5—направление касательной к контуру, k —
положительную постоянную, q—радиус кривизны контура S.
Разные части края «S могут быть закреплены по-разному; в
соответствии с этим 5 может распадаться на несколько
частей, на каждой из которых выполняются те или другие из
условий C.82) —C.85).
Если хотя бы на части контура 5 выполняется одно из
условий C.82) — C.84), то бигармонический оператор А*
оказывается положительно определенным. Задача об изгибе
пластины равносильна вариационной задаче о минимуме
функционала
CC[fd2wY , п d2wd*w , fd2w\2 , 0 м ч / d2w у
*-«]dxdy + k§(d^ds.
D
dv J
C.86)
где 5,—упруго закрепленная часть края S; если никакая
часть края не находится в состоянии упругого закрепления,
то контурный интеграл в выражении C.86) отсутствует.
Минимум надлежит искать на множестве функций из класса
Wl(Q), которые удовлетворяют условиям C.82) на жестко
закрепленной части края и условию w\s=^Q на свободно
опертой и упруго закрепленной частях края. Остальные
краевые условия C.83)—C.85) естественные, и нет нужды
удовлетворять им заранее.

232
гл. ш. вариационные методы
[7
Если весь край пластины жестко закреплен, то
функционал C.86) можно представить в любой из двух более
простых форм:
ИТ(Д^J—%w\dxdy =
"-pS),+»(&),+C),M-}**-<8-'7>
Пусть w0(x, у)— точное решение задачи об изгибе
пластины, a wn(x, у) — приближенное решение задачи о
минимуме функционала C.86), построенное, например, по методу
Рйтца. Тогда вторые производные от wn сходятся к
соответствующим производным от wQ в среднем с показателем 2.
Из теорем вложения (§ 1, п. 5) вытекает, что -^—► ~-°
и -г-2—►-г-2 в среднем с любым сколь угодно большим
показателем, a wn—*w0 равномерно в Q + 5.
Если пластина имеет переменную толщину, то уравнение
C.81) заменяется таким:
+$-(*,$)+><'-*>ет»(*,Й}Ь*. <«•»>
Р*д Е
12A — о*)*
Краевые условия на закрепленной или свободно опертой
части края имеют тот же вид, что и для пластины постоянной
толщины. Если.толщина 2й пластины нигде не равна нулю,
то .на множестве функций, удовлетворяющих условиям C.82)
и C.83) соответственно на закрепленной и свободно опертой
частях края, оператор C.88) положительно определенный;
соответствующая вариационная задача состоит в отыскании
минимума интеграла
и

$] § 3. ПРИЛОЖЕНИЯ К ЗАДАЧАМ МАТЕМАТИЧЕСКОЙ ФИЗИКИ 233
при условиях C.82) на жестко закрепленной части края
и «/|5 = 0 на его свободно опертой части.
Особо рассмотрим случай, когда часть края пластины
острая, т. е. когда на некоторой части края толщина 2h
обращается в нуль. Ограничимся случаем, когда пластина
в плане имеет вид, изображенный на рис. 15, и пусть
толщина удовлетворяет неравенству
cy^h(xt y)^c2y\ C.90)
где ct, с2, a — положительные постоянные, так что острый
край пластины совпадает с S'. Для простоты ограничимся
случаем, когда край S" жестко закреплен.
Если 0<а<;—, то на S' можно задавать обычные
о
условия жесткого закрепления
, л dw
s'
12
Если у^скс-х-, то на S' можно задать только одно
условие. Можно потребовать в этом случае, чтобы на S'
было w — 0.
2
Если а^г-^-, то условий на S" задавать нельзя. Во всех
перечисленных случаях оператор в уравнении C.88)
положителен, поставленная здесь краевая задача имеет не более
одного решения; если такое решение существует, то оно
будет и решением также вариационной задачи о минимуме
функционала C.89) при тех же краевых условиях.
Если а^-^-, то при упомянутых выше краевых условиях
о
оператор C.88) положительно определенный и
соответствующая вариационная задача имеет решение.
8. Изгиб сжатой пластины. Пусть пластина постоянной
толщины 2/г находится под действием нормальной нагрузки
интенсивности q(x} у) и напряжений Тхх, Тхуу Ту,
действующих в серединной плоскости пластины, причем объемные
силы отсутствуют. Соответствующие главные напряжения
в серединной плоскости обозначим через Тг и Тг- Уравнение

234
ГЛ. III. ВАРИАЦИОННЫЕ МЕТОДЫ
[9
равновесия такой пластины имеет вид
Л*™ k (т Л Л ОТ ^L\T d*W\ Я. /QQ1\
краевые условия имеют по-прежнему вид C.82) — C.85)
в зависимости от характера закрепления края. Как и выше,
будем считать, что хотя бы на некоторой части края
выполняется какое-либо из условий C.82) — C.83). Тогда можно
указать два случая, когда оператор в левой части
уравнения C.91) положительно определенный: либо Тг^0 и Г2^0,
либо Тг и ,Г2 достаточно малы по абсолютной величине.
Оба случая можно объединить. Обозначим через Т меньший
из минимумов величин Тг и Т2 в области Q. Пусть А и
В—постоянные, входящие в неравенства Пуанкаре и Фрид-
рихса (§ 1, п. 5), и пусть С = В'1, если имеется жестко
закрепленный участок края, и С=A—сг)Л-1, если такого
участка нет, но имеется, следовательно, участок края,
который либо свободно оперт, либо упруго закреплен. Оператор
CD
C.91) положительно определенный, если Т> т-. Краевая
задача для уравнения C.91) в этом случае равносильна
задаче о минимуме функционала
+ ~о[т**[~д1г) +2ТхУ~дГ~ЩГ + Туу(~дЦ)\~
— 2qw\dxdy + k[(^Vds C.92)
при краевых условиях, сформулированных в п. 7 для
функционала C.86).
9. Принцип минимума потенциальной энергии в
статической теории упругости. Статическое упругое состояние
тела описывается системой уравнений в частных производных,
которая не подходит под тип, рассмотренный в п. 6: эта
система не удовлетворяет неравенству C.78). Тем не менее
задачи теории упругости допускают, применение
вариационного метода'..

9] § 3. ПРИЛОЖЕНИЯ К ЗАДАЧАМ МАТЕМАТИЧЕСКОЙ ФИЗИКИ 235
Приводимые ниже соотношения верны для любой
неоднородной и неизотропной упругой среды, если деформации
и повороты малы, а напряжения подчинены линейному
закону Гука.
Обозначим через и(и1, и2, иг) вектор упругих смещений.
Составляющие тензоров напряжений и деформаций обозначим
через xik~xki и 2e/ft = 2eAl. соответственно; при этом
Линейный закон Гука задается формулами
3
*,-*= 2 сШтъ1т; C.94)
/, m = i
коэффициенты ciklm удовлетворяют соотношениям симметрии
Ciktm~ clmik = Ckilmi
так что различных коэффициентов не более 21.
Если К(К1У К2, Кг) — вектор.объемных сил, то
напряжения удовлетворяют известным уравнениям равновесия
3
Щг + *< = 0 ('=1, 2, 3).
Исключая напряжения с помощью соотношений C.94),
получаем уравнения равновесия в смещениях; их можно записать
в виде одного векторного уравнения
S
I, k, I, m = i l
C.95)
где х^ — орт оси xk, a A—дифференциальный оператор,
который преобразует вектор упругих смещений в вектор
объемных сил.
Основные краевые задачи теории упругости определяются
следующими краевыми условиями, которые пока предполагаем
однородными; как обычно, через S обозначена поверхность
области Q, занятой упругой средой.
I. Задача с заданными смещениями (первая задача):
a|s = 0. C.96)

236
ГЛ. III. ВАРИАЦИОННЫЕ МЕТОДЫ
[9
II. Задача с заданными напряжениями (вторая задача):
*Ь=0; C.97)
здесь t—вектор напряжений, действующий на элементарную
площадку поверхности 5. Если v — внешняя нормаль к S,
то по известной формуле Коши
s
'= 2 tf*cos(v, *,Le>.
i, k = i
III. Задача о жестком контакте (третья задача):
"ы|5 = 0. ^,U = 0. C.98)
Значки (v) и (s) означают проектирование на нормаль и
касательную плоскость к S.
IV. Смешанная (четвертая) задача: поверхность 5 разбита
на части Si, Sn, Sin, на каждой из которых выполнено
соответствующее краевое условие задач I, II, III. Может
случиться, что одна из частей Si, Sn, Sm отсутствует.
Введем в рассмотрение вещественное гильбертово
пространство L2(Q) векторных функций, абсолютные величины
которых квадратично суммируемы в Q. Если и (и19 и2, иь)
и v(v19 v2, v3) — две такие функции, то по определению
(», «) = $ 2 аъ dx' IIиИ2=S 2 a)dXsa SIaI2dx-
Оператор Л, входящий в левую часть уравнения C.95),
будем трактовать как оператор в £2(Q); допустим также,
что K£L2(Q)y т. е. что существует интеграл
\\К\2 dx.
В условиях любой из задач I — IV оператор А
симметричен и имеет место тождество
{Аи, u) = 2\wdx, C.99)
Q
где
3 3
i, k = i i, k, /, w = i

9] § 3. ПРИЛОЖЕНИЯ К ЗАДАЧАМ МАТЕМАТИЧЕСКОЙ ФИЗИКИ 237
есть плотность потенциальной энергии деформации.
Известно, что W—положительно определенная квадратичная форма
от составляющих деформации, так что F^O и (Аи, и)^0;
можно, если угодно, сказать, что в условиях задач I — IV
оператор А неотрицателен.
Укажем несколько наиболее важных случаев
положительной определенности оператора А.
1) В случае задачи I оператор А положительно
определенный в пространстве L2(Q).
2) В случае задачи II оператор А в L2 (Q) не
положительно определенный и даже не положительный. Однако его
можно рассматривать в некотором подпространстве, в котором
он будет положительно определенным. При отсутствии
поверхностных сил (условие C.97)) главный вектор и главный
момент объемных сил должны обращаться в нуль:
$ #</*=:0, \RxKdx = 0, C.100)
где /?— радиус-вектор точки х. С другой стороны, в условиях
задачи II вектор смещений определяется только с точностью
до произвольного малого жесткого смещения. Этот произвол
можно устранить, потребовав, чтобы
\udx = 0, ^Rxudx^O. C.100')
Q Q
Равенства C.100') и выделяют из пространства L2 (Q)
подпространство, в котором оператор А в условиях задачи II
оказывается положительно определенным.
Ниже, при анализе задач III и IV, нам также придется
иногда выделять подпространства положительной
определенности оператора Д. Каждый раз окажется, что К необходимо
принадлежит такому подпространству, а и можно, подчинив
его подходящим условиям, сделать элементом этого
подпространства.
3) В задаче III оператор А положительно определенный
в I2(Q), если 5 не есть поверхность вращения.
Если 5 имеет одну ось вращения, скажем ось xs, то
А положительно определен в подпространстве, которое

238
ГЛ. III. ВАРИАЦИОННЫЕ МЕТОДЫ
[9
определяется неравенством
$(*!«,—xtux)dx = 0. C.101)
Если 5 имеет две оси вращения, то S есть сфера или
совокупность двух концентрических сфер; поместим начало
координат в центр этих сфер. В этом случае оператор А
положительно определен в подпространстве, в котором
$/?X«tf* = 0. C.102)
4) В задаче IV оператор А положительно определен
в L2 (Q), если имеется часть границы Si, на которой и — О.
Если часть Sx отсутствует, то этот оператор также
положительно определен в L2 (Q), за исключением следующих
случаев:
а) Поверхность 5щ состоит из кусков цилиндрических
поверхностей с параллельными образующими. Направим ось хг
параллельно этим образующим; тогда оператор А будет
положительно определенным в подпространстве, в котором
\uxdx = 0. C.103)
Может случиться, что цилиндрические куски, из которых
состоит 5ш, вырождаются в куски параллельных между собой
плоскостей. Направим плоскость xz = 0 параллельно
указанным плоскостям; оператор А положительно определенный
в подпространстве L2(Q)> в котором
\uYdx^\u2dx = 0. C.104)
б) Sui есть поверхность вращения (или состоит из
нескольких кусков таких поверхностей) с одной осью х9
или с двумя осями. В этом случае оператор А положительно
определен в подпространстве, определяемом равенством
C.101) или C.102) соответственно.
в) 5цi состоит из одного или нескольких кусков
винтовых поверхностей
Arl = ecosco, Ar£ = Qsino), Xa =/(q) + Лео,

9] § 3. ПРИЛОЖЕНИЯ К ЗАДАЧАМ МАТЕМАТИЧЕСКОЙ ФИЗИКИ '<&У
где q и «— параметры, определяющие положение точки
на поверхности, h—постоянная. Оператор А положительно
определен в подпространстве, в котором
\(xxu%—xjix+hu%)dx = 0. C.105)
Итак, во всех случаях оператор А положительно
определен либо в самом пространстве L2 (Q), либо в некотором
его подпространстве. Сформулированные выше четыре задачи
теории упругости сводятся к задаче о минимуме одного
и того же интеграла
^BW—2Ku)dx
Q
на множестве вектор-функций, принадлежащих
соответствующему подпространству и удовлетворяющих главным краевым
условиям соответствующей задачи.
Во всех перечисленных здесь задачах теории упругости
энергетическая норма выражается формулой
|я|2 = 2 $ Wdx=) 2 ciklmeihelndx;
Q Q i, k, I, m=i
если векторы и! и и!' оба принадлежат соответствующему
пространству #л, то их энергетическое произведение таково:
[и\ »"] = } 2 ciklefitifiimdx;
й и k, I, m-\
здесь e'ik и е# — деформации, соответствующие смещениям
и' и и".
В практически наиболее интересном случае изотропной
среды коэффициенты сШт выражаются через так называемые
постоянные Ламе К и (х по формулам
ст = К + 2|г, ciikk = %, cikik = 2|i, / ф k%
остальные коэффициенты cikim = 0. В этом случае

240 ГЛ. III. ВАРИАЦИОННЫЕ МЕТОДЫ [9
выражения энергетической нормы и энергетического
произведения принимают вид
й \ a=i /
Q \ i, k-i I
В более употребительных обозначениях координат х} у, z
+ 2eJ„ + 2eL + 2е^)} tf* tfy dz,
[и', и"] = Ш {кг'г" + 2|х (е'ххь'хх + г'уУг"уу + гггггг +
+ 2гхугху + 2гхггхг + 2e^Q} dx dy dz.
Укажем также вариационную задачу, соответствующую
неоднородным краевым условиям. Ограничимся случаем
смешанной задачи в предположении, что Бщ отсутствует; как
частные случаи получатся отсюда задачи I и II.
Пусть краевые условия имеют вид
«!*,=/> *\su=e- C-Ю6)
Соответствующая вариационная задача заключается в
нахождении минимума функционала
[{2W—2Ku)dx— J ugdS C.107)
й sn
на множестве векторных функций, удовлетворяющих условию
предполагается, что существует хотя бы одна такая
функция, сообщающая интегралу
J Wdx
и
конечное значение.

10] § 3. ПРИЛОЖЕНИЯ К ЗАДАЧАМ МАТЕМАТИЧЕСКОЙ ФИЗИКИ 241
10. Краевые задачи для бесконечных областей, В случае
бесконечной области Q обычно встречающиеся
дифференциальные операторы, такие, как взятый со знаком минус
оператор Лапласа или оператор теории упругости C.95), при
обычных краевых условиях чаще всего оказываются
положительными, но не положительно определенными. Если Л —
положительный оператор, действующий в гильбертовом
пространстве Я, и /—данный элемент этого пространства, то
уравнение Аи=/> вообще говоря, неразрешимо, т. е. не имеет
решения, принадлежащего пространству Я. В частности,
если А—дифференциальный оператор, Я—пространство
^2(^) функций, квадратично суммируемых в Q, и
f(x) £Z,2 (Q), то уравнение Аи=/{х) далеко не всегда имеет
решение, квадратично суммируемое в й. С другой стороны,
требование существования такого решения нельзя считать
оправданным. Так, если ищутся смещения в бесконечной
области с закрепленной границей, то нет оснований ожидать,
что на бесконечности смещения обращаются в нуль; тем
более нет оснований ожидать, что они квадратично
суммируемы. В то же время естественно выделить те случаи этой
задачи, когда потенциальная энергия деформации,
соответствующая искомому решению, остается конечной.
Обобщение приведенных для этой частной задачи
соображений приводит в случае положительного оператора
к тому, что в качестве обобщенного решения уравнения
Au—f рассматривается элемент и0 (если он существует),
принадлежащий энергетическому пространству НА и
реализующий минимум функционала
F{u) = \u\*-2(u, /).
В п. 6 § 2 было указано необходимое и достаточное
условие существования такого «решения с конечной
энергией»; это условие состоит в том, чтобы скалярное
произведение (#, /) было функционалом, ограниченным в
энергетическом пространстве Яд. Здесь мы конкретизируем
указанное условие для некоторых простых задач математической
физики.
Будем говорить, что некоторый вектор 0(х) имеет
обобщенную дивергенцию divG(x) = g(x)y если для любой
непрерывно дифференцируемой в области Q функции ф(лг),
равной нулю вблизи границы S области Q, а также во всех

242 гл. ш. вариационные методы [10
точках этой области, достаточно удаленных от начала
координат, имеет место тождество
] ф (*) g(*) dx=* — J grad ф- G {x) dx.
q я
Уравнение Пуассона
— Au=f(x)
при краевом условии u\s = 0 имеет решение с конечной
энергией тогда и только тогда, когда f(x) есть обобщенная
дивергенция вектора, абсолютная величина которого
квадратично суммируема. Если F(x)—такой вектор, а и0—решение
с конечной энергией, то
| и J2 == $ (grad и0J rf* < S | F(*) |2 <**,
где |jF| — абсолютная величина вектора F.
Тот же результат остается в силе и для более общего
эллиптического уравнения
т
i, / = i J
если его коэффициенты удовлетворяют неравенству
m ч m m
где |х0 и \ix—некоторые положительные числа, t\ — любые
вещественные числа и х—любая точка области Q.
Существование решения с конечной энергией в случае краевых
условий второй или третьей задачи можно доказать,
предполагая, что f(x) = dlvF(x)9 где F(x)£Lt(Q) и, кроме
того, M±<zL2(Q).
Обратимся к уравнениям теории упругости. Пусть
область Q бесконечна. Допустим, что существуют такие
положительные числа |Л0 и \11У что для любых eik верно
неравенство
3 3
i, k-\ i, k = i

1] § 4. ПРОБЛЕМА СОБСТВЕННЫХ ЧИСЕЛ 243
где W определяется формулой C.99); это неравенство во
всяком случае имеет место, если упругая среда однородна.
Тогда уравнение C,95) имеет, при краевом условии C.96),
решение с конечной энергией тогда и только тогда, когда
существует симметричный тензор с квадратично
суммируемыми в Q составляющими s(j такой, что вектор объемных
сил К есть обобщенная дивергенция этого тензора, так что
А д${1 @)
где л;/0) есть орт /-й координатной оси.
§ 4. Проблема собственных чисел
1. Основные понятия и теоремы. Уравнение
Аи — КВи = 0, C.108)
в котором Л и В—линейные операторы и К—численный
параметр, имеет очевидное решение и = 0, называемое
тривиальным. Может, однако, случиться, что при некоторых
значениях X уравнение C.108) имеет нетривиальное (т. е.
отличное от тождественного нуля) решение. Такое решение
называется собственным элементом (собственной
функцией, если и — функция одной или нескольких численных
переменных) уравнения C.108), а соответствующее
значение %—собственным числом этого уравнения. Если
В—тождественный оператор, так что уравнение имеет вид
Ли—Хи=0у C.109)
то говорят также о собственных элементах и собственных
числах оператора А. Совокупность собственных чисел
уравнения или оператора называется его собственным спектром.
Если собственному числу К соответствуют собственные
элементы их, и2, ..., ип уравнения C.108), то их любая
отличная от нулевого элемента линейная комбинация схих-\~
+ с2иг+ .. :+спип, где с„ с2, ...., ^ — произвольные
постоянные, также есть собственный элемент того же
уравнения, соответствующий тому же собственному числу Я.
Таким образом, дополненное нулевым элементом множество

244
ГЛ. Ш. ВАРИАЦИОННЫЕ МЕТОДЫ
И
собственных элементов данного, уравнения, соответствующих
данному собственному числу, есть множество линейное.
В весьма широких условиях1) это множество есть
подпространство, называемое собственным подпространством
уравнения C.108), соответствующим собственному числу %\
размерность этого подпространства называется кратностью
собственного числа.
К отысканию собственных чисел и собственных
элементов обычно приводит разделение переменных в методе Фурье.
Например, если уравнение имеет вид
где А и В—линейные операторы, не зависящие от времени,
то, отыскивая решения вида £/(лг, t) = u{x)f(t)y приходим
к уравнению C.108) для неизвестной и{х). К той же задаче
о собственных числах и собственных функциях приводят и
задачи устойчивости.
В прикладных вопросах наиболее 'важным является
исследование собственного спектра симметричных и, особенно,
положительно определенных операторов.
Перечислим основные свойства собственных чисел и
собственных элементов таких операторов.
1) Собственные числа симметричного оператора
вещественны.
2) Собственные элементы симметричного оператора,
соответствующие различным собственным числам, ортогональны.
3) Если данному собственному числу соответствует
несколько линейно независимых собственных элементов, то
можно, применив к этим элементам процесс ортогонализации,
сделать их ортогональными. Имея это в виду, будем впредь
считать, что совокупность всех собственных элементов
симметричного оператора образует ортогональную систему.
4) Симметричный оператор может иметь либо конечное,
либо счетное множество собственных чисел, которые можно
поэтому записать в виде конечной или счетной
последовательности Х1У Xt, ..., ХПУ ... Разумеется, возможен и такой
случай, когда симметричный оператор вовсе не имеет
собственных чисел.
J) Если оператор А—\В замкнут.

1] § 4. ПРОБЛЕМА СОБСТВЕННЫХ ЧИСЕЛ 245
5) Собственные элементы положительно определенного
оператора ортогональны по энергии.
6) Собственные числа положительно определенного
оператора положительны.
Если система собственных элементов самосопряженного
оператора полна в гильбертовом пространстве, в котором
действует данный оператор, а его собственные числа Хп—юо,
П-> 00
то говорят, что данный оператор имеет дискретный спектр.
Условимся в последовательности %1У Я2, ... собственных
чисел оператора выписывать каждое собственное число
столько раз, какова его кратность. При этом каждому
собственному числу будет соответствовать только один линейно
независимый собственный элемент, но среди собственных
чисел могут встречаться равные.
Ниже на всем протяжении настоящего параграфа
рассматриваются только положительно определенные операторы.
Это обстоятельство оговариваться не будет.
Если А—положительно определенный оператор, то
£#>* <3»°>
где у* — положительная постоянная. В таком случае левая
часть последнего неравенства имеет положительную точную
нижнюю границу, которую мы обозначим через Хг
Теорема И. Если существует элемент ux£D(A)
такой, что
(Аии и1)_»
^ и,) -л1»
то %J — наименьшее собственное число оператора А,
а их— соответствующий этому числу собственный элемент.
Теорема 12. Пусть Xl^Xi^:. . .^Хп суть п
непосредственно следующих друг за другом первых
собственных чисел оператора А и и1У и21 ..., ип—соответствую-
щие им ортонормированные собственные элементы. Пусть
Хп+1 есть точная нижняя граница тех значений,
которые отношение C.110) принимает на множестве
элементов из D(A), ортогональных к uv ut, ..., ип. Если в этом
множестве существует такой элемент ип+1} что
{Аип+1, un+i) л
(un+1, ип+1) Л»+1'

246 ГЛ. III. ВАРИАЦИОННЫЕ МЕТОДЫ [2
то ип+1 есть собственный элемент оператора Л,
соответствующий собственному числу Хп+1. Это собственное
число — ближайшее, следующее за Хп.
Теорема 13, Пусть оператор таков, что всякое
множество элементов, энергетические нормы которых
ограничены в совокупности, компактно в метрике
данного гильбертова пространства. Тогда спектр данного
оператора дискретен и совокупность его собственных
элементов полна по энергии {т. е. в соответствующем
энергетическом пространстве).
Наименьшее собственное число оператора А равно
минимуму величины \и\\ при условии \\и ||2 = 1. Если первые/г—1
собственных чисел Х1У Я2, ..., %п_г и соответствующие им
собственные элементы и„ и2У . .., ип_г известны, то
ближайшее следующее собственное число Хп можно определить
как минимум величины \и\2А при условиях
Н«||'=1, («,«*) = 0 (£-1,2, ...,л-1).
2. Метод Релея—Ритца. Пусть оператор Л имеет
дискретный спектр. Для определения собственных чисел
этого оператора можно поступить так. Зададим
последовательность координатных элементов фп£#л (п= 1, 2, ...),
где НА—соответствующее энергетическое пространство;
координатные элементы подчиним тем же требованиям, что
и в п. 3 § 2 настоящей главы. Составим уравнение
1 fat. <Pil-M<Pi. <Pi) Гфа. <Pil-M<Pa. <Pt) ••• [<Pn»<Pil-M<Pn. <Pi)
ГФ1. <P*]-M<Pi»<P2) [фа. фа]-Мф2. Фа) ... [Фп. ФаЗ-^(Фп. Фа)
I [ф1,Фп]-Мф1»Фп) Гф2»Фл]-^(ф2»Ф«) ... [Фп.Фп1-^(Фп. Фп)
Это уравнение степени п\ его корни все положительны.
Расположим их в порядке возрастания: Х[п) ^ Х[п) ^ ...
... ^ Х^\ Каждый из этих корней является приближенным
значением сверху для соответствующего собственного числа
данного оператора, так что Хр ^Х и lim Хрп^=Х . Сле-
дует иметь в виду, что с возрастанием р точность
приближенного равенства X » Хр ухудшается.
=о. C.111)

2] § 4. ПРОБЛЕМА СОБСТВЕННЫХ ЧИСЕЛ 247
Приближенные значения нормированных собственных
элементов имеют вид
f=S«A! (ЗЛ12)
коэффициенты aik определяются из уравнений
п
2**{[фу.Ф*]-4П)(Ф/,Ф*)} = ° 1/=1,2,...,я), C.113)
2 (фу.ф*)в/**=1« (ЗЛ14)
Определитель системы C.113) равен нулю, и решение этой
системы находится с точностью до произвольного
множителя, значение которого определяется уравнением C.114).
Вид уравнения C.111) несколько упрощается, если
координатные элементы ортонормированы либо в метрике данного
гильбертова пространства, либо в метрике энергетического
пространства. В первом случае
, ■ ( 0, ]фк,
ЪрчА-Х 1, /=*,
и уравнение C.111) принимает вид
[фг, %\ — К [<р„ q>J ... [<р„, Ф,]
к. Ф*1 [ф,. Фг]~*- ••• [ф». Ф,1
[ф, Ф»] 1Ф». Ф«]
во втором случае
[ф«. Ф«] — Ь
= 0;
[фу.Ф*1 = | lf
1ФЬ
и уравнение C.114) приводится к виду
1 — Мф,. ф.) — Чфг. ф.) ••• — ^(Фя. Фг)
— Мф„ ф,) 1 — Мф„ ф,) ••• — Мф„. ф.)
— Мф„Ф„)
"Мф.-Фв)
1 —МФя.Фя)
= 0.

248 гл. ш. вариационные методы [3
Если координатные элементы принадлежат не только
энергетическому пространству, но еще и области
определения данного оператора1), то уравнение C.111) можно
представить также и в следующем виде:
D<Pi, <Pi)-A, (<Pi. Фх) (Лфа, ФО-А, (ф2, Ф,) ... (Aq>n, ф^-Л, (фп, фО
(Лфр ф2)-Я (ф!, фа) (Лф2, ф2)-Я (ф2, ф2) . .. (ЛфЛ, ф2)-Я (фп, ф2)
(A<Pi> Фп)-^ (Ф1» Фп) Иф2, Фп)-* (Ф2> Фп) • • • (^Фп. Фп)-Ь (Фп. Фп)
3. Уравнения вида Аи—кВи = 0. Будем предполагать,
что оба оператора А и В положительно определенные и что
область определения оператора В шире соответствующей
области оператора Л, так что D(A)cD(B). Для всякого
элемента из области D(А) можно тогда двояко определять
энергию, связывая ее либо с оператором А, либо с
оператором В. Соответственно этому будем говорить об «энергии
оператора Л» или «энергии оператора В».
Теорема 14. Собственные числа уравнения C.108)
положительны.
Теорема 15. Собственные элементы уравнения C.108)
можно сделать ортонормированными по энергии
оператора В; при этом они также ортогональны по энергии
оператора А.
Теорема 16. Если существует элемент иг такой,
что
(Аи1У и1)_
где
(Buv иг)
-К
1 (Ви, и)'
то Х1 есть наименьшее собственное число уравнения
C.108), а их — соответствующий этому числу собствен-
ный элемент.
Теорема 17. Пусть Kv Я8, ..., %п суть следующие
в порядке возрастания п первых собственных чисел
уравнения C.108), a uv и2, ..., ип—соответствующие им
собственные элементы. Пусть Хп+1 есть точная нижняя
*) Если оператор дифференциальный, то это означает, что
координатные функции имеют производные тех порядков, которые
входят в уравнение, и что эти координатные функции удовлетворяют
всем, в том числе и естественным, краевым условиям задачи.

3] § 4. ПРОБЛЕМА СОБСТВЕННЫХ ЧИСЕЛ 249
граница функционала
(Аи, и)
(а, и)
при условиях
(Bu,uk) = 0 (£=1, 2, ..., п).
Если существует удовлетворяющий этим условиям
элемент ип+1 такой, что
(Аип+г, ип+1)_*
то Хп+1 есть собственное число уравнения C.108),
ближайшее следующее за Хп, а ип+1 есть соответствующий
собственный элемент.
Теорема 18. Пусть операторы Л и В таковы, что
всякое множество элементов, у которых нормы энергии
по оператору А ограничены в совокупности, компактно
в норме энергии оператора В. Тогда уравнение C.108)
имеет бесконечное множество собственных чисел 0 < Xt ^
^ К2 ^..., причем Хп —► оо при п —> оо, а
соответствующие собственные элементы образуют систему, полную
как по энергии оператора А, так и по энергии
оператора В.
Наименьшее собственное число уравнения C.108) равно
минимуму величины | и \2А при дополнительном условии ]и|^=1;
через |и\А и \и\в мы обозначаем энергетические нормы
элемента и в пространствах НА и Нв соответственно. Точно
так же символы [и, v]A и [и, v]B будут обозначать
энергетические произведения элементов и и v в соответствующих
пространствах. Если известны первые п — 1 собственных
чисел и соответствующие им собственные элементы и1У
иг, ..., ии-1, то /z-е собственное число есть минимум той
же величины \и\*А при дополнительных условиях |а|^=1,
[".«*Ъ = 0 (*=1, 2, .... л-1).
Приближенные значения первых п собственных чисел
уравнения C.108) можно найти как корни уравнения
I ГФ1. Ф^-ЯГф», ф,]в [ф2, фЛд-Мфа. Ф1]Я...[ФП, Ф^^-Л, [Фп. Ф^д |
[Фь Фа1Л-^[ф1» фа]в [ф2, ф2]л-Я[ф2, ф2]в...[фп» ф2]Л-^[фп» Фа]д I 0,
| [Фх. Фп]д-^ [Ф1. Фп1д [Фа. Ч>П]А~Ь [Фа. Фп1д • • • [Фп. Фп]д ' * 1Фп» Фп]д |
C.115)

250
ГЛ. III. ВАРИАЦИОННЫЕ МЕТОДЫ
[4
координатные элементы <р,, ф2, ... должны удовлетворять
следующим условиям: 1) ц>п£Нл; 2) взятые в любом
конечном числе элементы фп линейно независимы; 3) совокупность
координатных элементов полна в НА.
Если <f)n£D(A), то уравнению C.115) можно придать вид
I (APii <Pi)-M£<Pi» <Pi) (Aq>2, Ф1>-^(Вфа, ф,) ... (Лфп, Ф»)-Я,(Вфп> ф,) I
(Аф» фаЭ-МВф!, ф2) (Лф2, ф2)-Л(Вф2, ф2) ... (ЛфЛ, ф2)-Я(Вфп. ф2) I
I (Aq>t, фп)-Х (Вф!, фп) (Лф2, фп)-Я (Вф2, фп) ... (Лфп, фп)-Я (Бфп, фп) |
4. Спектр обыкновенного дифференциального оператора.
Оператор •
-й(р(*>£)+«<*>в (ЗЛ16)
при краевых условиях
ш' {а)—р«(а) = 0, ун'(&)+би(*) = 0 C.117)
имеет дискретный спектр, причем все собственные числа
положительны, если выполнены следующие условия:
1) р(х)^р0,тлер0 — положительная постоянная; 2) q(x)^0;
3) постоянные а, |3, у, б неотрицательны, и хотя бы одна
из постоянных р и б не равна нулю.
Спектр оператора C.116) остается дискретным и тогда,
когда числа а, Р, y» 6 какие угодно, a q(x)> не будучи
обязательно неотрицательным, удовлетворяет неравенству
q(x)^—N, где N—неотрицательная постоянная. При этом
может случиться, что среди собственных чисел окажется
конечное число отрицательных или равных нулю.
Наименьшее собственное число оператора C.116) при
краевых условиях C.117) равно минимуму функционала
ь
1[р М (ёJ+ч <*> "8 (Ar)]dx+irp (а)"'(а)+
а
+±p(l>)u*(l>) C.118)
при дополнительном условии
ь
\u2{x)dx=\. C.119)
а

4] § 4. ПРОБЛЕМА СОБСТВЕННЫХ ЧИСЕЛ 251
При этом, если а Ф О и у Ф О, то условия C.117)
естественные. Если же, например, а = 0, то в функционале C.118)
следует опустить член, содержащий а, а функции и(х)
в этом функционале следует подчинить не только условию
C.119), но еще и главному условию и(а) = 0. Если а = у = 0,
наименьшее собственное число равно минимуму функционала
ь
а
при дополнительных условиях C.119) и C.117); последние
при этом имеют вид и(а)—-и(Ь) = 0.
Аналогичные заключения справедливы и для собственных
чисел уравнения
~Тх {р W й) +1W и ~Хг М и = О-
если г (х) заключено между некоторыми положительными
числами г0 и гх. На этот раз наименьшее собственное число
равно минимуму функционала C.118) при дополнительном
условии
ь
\ г (х) и2 (х) dx = 1
а
и при главных условиях C.117), если таковые имеются.
Теперь рассмотрим случай, когда р (х) может обращаться
в нуль. Допустим, что р(а) = 0 и р(х)^>0 при х>а.
Примем, что функция и (я) удовлетворяет краевым условиям,
упомянутым в п. 1 § 3. Оператор C.116) при этих
краевых условиях имеет дискретный спектр, если сходится
интеграл
ь
С (х—а) dx
а
В частности, если С, (л:—а)а<:р(х) < С2 (х —-af, где Сх и
С2 — положительные постоянные, то спектр оператора C.116)
дискретен при а<2 и недискретен при а^2.
Рассмотрим уравнение порядка выше второго:
IIna-UMH = 0. C.120)

252
ГЛ. III. ВАРИАЦИОННЫЕ МЕТОДЫ
[4
где n^>s и
L2SU
а функция и (х) удовлетворяет краевым условиям
и(а) = ц/(а)=...=и("-,)(а) = 0, |
в (ft) = и'(ft) ==...= в*"-1) (ft) = 0. / (ЗЛ2!)
Допустим, что рп(х)^С, где С—положительная
постоянная. Допустим также, что при краевых условиях C.121) оба
оператора L2n и L2S положительно определенные; для этого
достаточно (но не необходимо), чтобы
pk(x)^0 (/е=1,2, ...,л —1)
и
qk(x)^0 (Л=1, 2 «)t
причем хотя бы одна из функций qk(x)^*C', где С—
положительная постоянная. При этих условиях спектр
уравнения C.120) дискретный и все его собственные числа
положительны. Наименьшее собственное число есть минимум
функционала
!£'*<*> (£)'** (ЗЛ22)
а /г=о
при дополнительном условии
fe«.<*>(S0'«*
а & = о
и краевых условиях C.121).
Пусть теперь рт(а) = 0, но рт(х)>0 при д:>а. Более
определенно, допустим, что Сг(х — а)а ^ рт (х) ^ С2 (х—а)а,
Сх и С2 — положительные постоянные. Рассмотрим уравнение
L2na—Ки = 0 при краевых условиях C.51) и C.54). Спектр
этого уравнения дискретен при а<2/г и недискретен при
А:=о

5] §4. ПРОБЛЕМА СОБСТВЕННЫХ ЧИСЕЛ 253
а^2п. Если а < 2л, то наименьшее собственное число
равно минимуму функционала C.122) при дополнительном
условии C.119) и при краевых условиях C.51) и C.54).
Пример 11. По методу Релея—Ритца найдем приближенное
значение наименьшего собственного числа оператора
В качестве координатных возьмем функции
Фа(*) = (!-*)** (*=1,2, ...).
Ограничимся тремя первыми координатными функциями. Уравнение
C.115) в данном случае имеет вид
0,404757774-1 X 0,216156130-^ X 0,135002282- JL X
о\) ои lUo
0,216156130-1*, 0,510789821--4Я 0,675363337-4о *I = 0
oU lUo loo '
0,135002282-^ X 0,675363337-у^ X 1,023822057-~ X
Это уравнение решалось по методу Ньютона; для наименьшего
собственного числа оператора C.123) было получено значение с
избытком
Я<8)= 12,12255. C.124)
5. Спектр эллиптического оператора. Рассмотрим
самосопряженное уравнение второго порядка
т
- Е ^-(AJk{x)^-) + C(x)u-Kr(x)u = 0 C.125)
при каком-либо из краевых условий C.62)—C.64). Примем
следующие допущения: 1) в рассматриваемой конечной
области й оператор
т
— JL дГЛА/кдГк)
j, k=\ J ч R
эллиптический невырождающийся, так что имеет место
неравенство
т т
X ЛУД^^Е'/' ^о = const >0;

254
ГЛ. III. ВАРИАЦИОННЫЕ МЕТОДЫ
[5
2) С(х) ^ а, где а — постоянная какого угодно знака; 3) г0 ^
^г(х)^гх, где г0 и гх — положительные постоянные;
4) в случае условия C.63) или C.64) область Q
удовлетворяет условиям п. 5 § 1. При перечисленных условиях
оператор C.125) имеет дискретный спектр. При этом все
собственные числа будут положительными, если выполнены
следующие требования:
а) В случае краевых условий C.62) или C.64) достаточно,
чтобы С(х)^0.
Это требование можно сразу же ослабить следующим
образом. Пусть к1 — наименьшее собственное число
уравнения
т
при соответствующем одном краевом условии C.62) или
C.64); как только что было сказано, Х1^>0. Собственные
числа уравнения C.123) при том же краевом условии
положительны, если С(х)> — Я1#
б) В случае краевого условия C.63) собственные числа
уравнения C.123) положительны, если коэффициент С(х)
неотрицателен и отличен от тождественного нуля.
Наименьшее собственное число уравнения C.125) при
краевом условии C.62) равно минимуму функционала
на множестве функций, удовлетворяющих условию C.62)
и дополнительному условию
\ru2dx=A. C.126)
В случае условия C.64) (его" частным случаем при а = 0
является условие C.63)) наименьшее собственное число
уравнения C.125) равно минимуму функционала
Q Ч, * = i J * ' S
при дополнительном условии C.126).

5]
§ 4. ПРОБЛЕМА СОБСТВЕННЫХ ЧИСЕЛ
255
Для задачи Неймана (условие C.63)) в случае, когда
С(х) = Оу наименьшее собственное число равно нулю; ему
соответствует одна линейно независимая собственная функция
и = const. Наименьшее положительное собственное число
задачи Неймана в этом случае равно минимуму интеграла
5
V л d——dx
при дополнительных условиях C.126) и
(a, l)=$adx = 0.
Рассмотрим теперь уравнение более высокого порядка:
Z,2nw—U2,u = 0, n>s, C.127)
где L2n определяется формулами C.77), a
L2S—аналогичными формулами
^ = Х^н,
bkU "* ** дхидхи ... дхь \ '» " '* W dx,tdxU...dxJ
Уравнение C.127) будем рассматривать при краевых
условиях C.79). Примем следующие допущения:
1) выполнено неравенство C.78), так что оператор L2rl
эллиптический невырождающийся;
2) коэффициенты оператора Lln ограничены;
3) оператор L2S положительно определен.
Тогда уравнение C.127) имеет дискретный спектр; если,
кроме того, при условиях C.79) оператор Lzn положительно
определен, то собственные числа уравнения C.127)
положительны. Наименьшее собственное число равно минимуму
функционала
п а и)-[УУА'-и* » **" д*и dx

256
ГЛ. III. ВАРИАЦИОННЫЕ МЕТОДЫ
[5
на множестве функций, удовлетворяющих краевым условиям
C.79) и дополнительному условию
aHj ь''2"-; dxixdxh...dxik dx,\dxj2...dx}k
Особо рассмотрим задачу о частотах собственных изгиб-
ных колебаний тонкой упругой пластины. Если толщина
пластинки постоянная, то эти частоты пропорциональны
собственным числам бигармонического оператора
а 2 d*w , 0 d*w . d*w
при одном из краевых условий, рассмотренных в п. 6 § 3.
Допустим, что имеет место общий случай, когда край
пластины разбит на четыре части, Siy 52, 58, 54, на каждой
из которых выполнено соответственно условие C.82), C.83),
C.84), C.85). Спектр бигармонического оператора в этих
условиях дискретен.
Наименьшее собственное число бигармонического
оператора в этом случае равно минимуму функционала
+ k§(d^Jds; C.128)
этот минимум ищется на множестве функций,
удовлетворяющих равенству
\\w%dxdy=\ C.129)
и краевым условиям
я,, г
= 0. C.130)
, да
W|s1+sa+s3=o, ^
St
Если весь край пластины жестко закреплен, то наименьшее
собственное число бигармонического оператора равно также

5]
§ 4. ПРОБЛЕМА СОБСТВЕННЫХ ЧИСЕЛ
257
минимуму интеграла
JJ (Awfdxdy,
где функции w(x) удовлетворяют равенству C.129) и крае-
вым условиям w\s = 0} -д- =0.
/z-e собственное число Кп бигармонического оператора
связано с #-й собственной частотой сод колеблющейся
пластины соотношением
где у—плотность материала пластины и D — Eh2j\2(\ —а2)—
коэффициент жесткости пластины на изгиб.
Если толщина 2h пластины переменная, то уравнение
собственных колебаний пластины имеет вид
£(*-S)+4=(^)+4(*'5)+
+S(*,i?)+j<,-«>s5f(*,I55)-»* <3131>
где на этот раз параметр X связан с частотой со
собственных колебаний пластины соотношением
Е
Наименьшее собственное значение Х1 равно минимуму
функционала
РГгз \{d2w\2 , 0 d2wd2w , (d2w\2 ,
+ 2<1-ff)(^),]<te*' + *I*,E)i<" <злз2>
при дополнительном условии
J$ Wrf*dy=l C.133)
и краевых условиях C.130).
9 С. Г. Михлин и X. Л. Смолицкий

258 ГЛ. III. ВАРИАЦИОННЫЕ МЕТОДЫ [6
6. Устойчивость сжатой пластины. Пусть напряжения
в пластине пропорциональны некоторому параметру К и,
следовательно, имеют вид кТхх, kTxv, ХТуу. Допустим еще,
что отсутствует участок границы, свободный от напряжений.
Для простоты примем также, что толщина пластины
постоянная. Если хотя бы в одной точке пластины по крайней
мере одно из главных напряжений, определяемых полем
напряжений Тхх, Тх Т сжимающее, то при некоторых
положительных значениях К пластина потеряет устойчивость.
Эти значения Я («критические значения») и соответствующие
им прогибы w связаны уравнением
А2 M/~ d2w , 0~ d2w , _ d2w\ Л
&w—^iKTxx^-r2TxyW^+TyyWj = 0;
кроме того, w удовлетворяет соответствующим условиям
закрепления. Наименьшее критическое значение равно
минимуму функционала C.128) при краевых условиях C.130) и
дополнительном условии
7. Спектр вырождающегося эллиптического уравнения.
Ограничимся здесь в существенном уравнениями второго порядка; кроме
того, рассмотрим спектр собственных частот пластины с острым
краем. В обоих случаях мы предполагаем выполненными те
краевые условия, которые указаны в п. 4 и п. 6 § 3.
Рассмотрим уравнение
s(»<*'")|)+^(e<*'*)^)+x"=° (ЗЛ34>
при только что упомянутых краевых условиях.
Спектр уравнения C.134) при этих условиях дискретен, если
ф(*, */)>0 при г/>0, со (л:, у)=у*щ(х9 у), щ(х,у)^к, где к —
положительная постоянная, и 0<а<2. Наименьшее собственное
число уравнения C.134) равно, как и в случае невырожденного
уравнения, минимуму интеграла
^[^^^{^J+@(x'y)i^J]dxdy

8] § 4. ПРОБЛЕМА СОБСТВЕННЫХ ЧИСЕЛ 259
на множестве функций, удовлетворяющих краевым условиям задачи
и, кроме того, равенству
\ \ u2dxdy=\,
Q
Если а ^2, то спектр уравнения (ЗЛ34) недискретен.
Спектр собственных частот пластины переменной толщины
определяется уравнением C.131) и соответствующими краевыми
условиями. Допустим, что САу* < h (х, */)<С2г/а, где Clf C2,
а—положительные постоянные. Тогда спектр собственных частот пластины
дискретен, если а < 2, и недискретен в противном случае. Как и
выше, наименьшее собственное число есть минимум функционала
C.132) на множестве функций, удовлетворяющих краевым условиям
задачи и дополнительному условию C.133).
Заметим еще, что спектр оператора в левой части уравнения
C.131), т. е. спектр уравнения
д2 f,3d2w\ , д2 (ubd2w\ , д2 f,3d2w\ ,
, д* I uzd*w\ .ом ^ д* (us d'W \ 1
4
дискретен только при значениях а < -^-.
8. Собственные колебания упругих тел. При краевых
условиях, перечисленных в п. 8 § 3, оператор
з
I, k, I, m = \ 1
имеет дискретный спектр. Собственные числа оператора А
положительны в тех случаях (см. п. 8 § 3), когда этот
оператор положительно определенный; в остальных случаях
несколько первых собственных чисел равны нулю.
Наименьшее собственное число оператора А равно минимуму
удвоенной потенциальной энергии деформации упругого тела
з
2$Wtf* = $ J! Ctklm*tlPlmax
Q Q L k, I, m-\
при главных краевых условиях задачи и дополнительном
условии
з
9*

260 гл. ш. вариационные методы [8
Собственные числа Хп оператора А связаны с собственными
частотами соп упругого тела соотношением Хп = у&2п, где
Y— плотность упругой среды, которую мы считаем постоянной.
Пример 12. Найдем наименьшую собственную частоту
колебаний однородного и изотропного упругого круглого цилиндра со
свободной границей; ограничимся случаем радиально-симметричных
колебаний. Пусть X и \i — постоянные Ламе, R — радиус, h — высота
цилиндра. Введем цилиндрические координаты q, Ф, г и обозначим
через и и uz составляющие вектора смещений и по направлениям
Q и z соответственно; составляющая щ в направлении Ф равна
нулю в силу радиальной симметрии смещений. В нашем случае
Rh
'ди, _ .
+
й оо
. /дип
+ 2|х
Наименьшая собственная частота (ох колебаний цилиндра
связана с наименьшим положительным собственным числом задачи их
соотношением к1 = уы21', однако хх не есть наименьшее собственное
число задачи—это последнее равно нулю, и соответствующие ему
собственные элементы суть малые жесткие смещения. Поэтому к1
можно построить как минимум написанного выше интеграла при
условиях
R h
2п\ С (u*Q + ul)QdQdz = l
R h
V a dx = 2я \ \ и Q dq dz = 0,
Q 0 0
Rh
\ rxudx=^2n \ \ rxUQdQdz = 0,
из которых последние два равносильны условиям ортогональности
вектора и к вектору произвольного жесткого смещения.
Краевые условия задачи естественные, и вектор и можно им
не подчинять.
Из соображений симметрии ясно, что и0 = 0 при q —0.
Примело
няя метод Релея — Ритца, возьмем —— и uz в виде полиномов,
расположенных по степеням q2 и z\ ограничиваясь выписанными ниже

8] § 4. ПРОБЛЕМА СОБСТВЕННЫХ ЧИСЕЛ 261
членами, будем иметь:
"? = Q (<*о + <V + <x2q2 + a8z2),
"z=Po + PiZ + P2Q2 + P8z2.
Упомянутые выше условия ортогональности приводят к
соотношениям:
п _ q f^h a2R2 a3h2\
a0 3{ — + — + — ],
о _ /Pi^P**2 , Рз^2 \ "_ 6 /М2 «з^\
Исключив коэффициенты а0, ро, ах, убедимся, что и и иг суть
составляющие следующего вектора:
5
/г = 1
где
«1 = Pl> «2 = «2» «3 = Р2» «4^а3» «5 = Рв
и
/6#2 ЗЯ2 2 £2\
Ф4 = (-gQ — hQZ + *2Q> °J» Фз = (о; 22—-g-J.
Основное гильбертово пространство задачи в нашем случае
есть пространство квадратично суммируемых по области цилиндра
радиально-симметричных векторных функций; в этом пространстве
скалярное произведение элементов ф и г|) определяется формулой
R h
(q>, 1|>) = 2я J ^(<vfl?+Vz%)QdQdz;
о о
энергетическое произведение в нашем случае имеет вид
о о v
Теперь можно составить уравнение C.115); мы только заменим
в нем обозначение X на х, так как у нас X уже означает одну из

262
ГЛ. III. ВАРИАЦИОННЫЕ МЕТОДЫ
[9
постоянных Ламе. В данном случае уравнение C.115) 5-й степени;
оно распадается на следующие три:
(X + \i)R2h5 p^/i3 R*h*
90 + 12 720 Х =
= 0,
(X + 2\i)R2h R2h3
2 24
2XR*h
2XRlh
b(X + \i)R5 nR*h
25/i + 4
■ XR4h
G4*,+124ц) R*h 2>R*h
75
200
= 0,
6R2
bh2
(X + 2\i) R2h* R2h5
360 X
-0.
Чтобы сделать вычисления определенными, возьмем случай
X = 2fx, что соответствует значению постоянной Пуассона а = — .
о
Далее положим /? = 2, h = 4, так что осевое сечение цилиндра —
квадрат. Наименьший из всех корней написанных выше уравнений
равен х,== 2,722808ц, откуда
со! = 0,1650051
/f
9. Более общие условия положительной определенности
дифференциальных операторов. Ограничимся одним примером
—распространение на другие случаи не вызовет затруднений. В п. 3 § 3
было указано, что при краевом условии и|5 = 0 невырождающийся
эллиптический оператор
т
/, k=\ J
будет положительно определенным, если С(х)^0. Это условие,
однако, не необходимо. При краевом условии u\s = Q наименьшее
собственное число Я, оператора
*'£)
положительно. Но
(и, и) || и ||2
и для любой функции u^D(Aj)t т. е. для функции u^W\(Q)t
равной нулю на S,

10] § 4. ПРОБЛЕМА СОБСТВЕННЫХ ЧИСЕЛ 263
Теперь очевидно, что оператор А будет положительно
определенным, если С (х) >—jLi, где постоянная р < Kv Действительно,
(Аи, и) = (А,иу и) + (Си, и)>к1(и, и) — ii (и, u) = (Xl— \i) || и ||2.
Пример 13. Пусть
Аи = -Ьи-а(х2 + у2)и = - ^2+^-а(х2+у*)и, и|5 = 0,
где а—положительная постоянная и область Q есть квадрат
0-^л:, (/^1; как всегда, S означает границу этого квадрата.
В данном случае Л1а = —Дм, и\$ — 0. Собственные числа первой
краевой задачи для оператора Лапласа в единичном квадрате
определяются хорошо известной формулой kmn = n2 (т2 + /г2) (т, п=\,
2, ...); наименьшее из них Х1 = ки = 2л2. В квадрате Q, очевидно,
— а (х2-\-у2)^ — 2а, и оператор А будет положительно
определенным, если — 2а >—2я2, или а < к2.
10. Минимаксимальный принцип. Пусть А—положительно
определенный оператор с дискретным спектром, и пусть
\ ^^2 ^- • .^^п^. . .—его собственные числа. Для
вычисления я-го собственного числа Яп можно указать способ,
не требующий знания собственных элементов иу, а2У ...
..., un_v соответствующих предшествующим собственным
числам %v Х2, ..., Яп_,; заключается этот способ в
следующем. Возьмем в энергетическом пространстве НА
произвольные элементы vl7 v2, ..., vn_t и найдем минимум
величины \и\2д при дополнительных условиях
||и|Г=1, (и, vk) = 0 (ft=l, 2, ..., л-1);
этот минимум обозначим через k(vx, v2, ..., vn_l).
Оказывается, что
Яя = МахМг\, vt, ..., vn^); C.135)
максимум берется по всевозможным наборам элементов
*\» V2, •••> ^n-i» принадлежащих энергетическому
пространству НА. Равенство C.135) носит название минимакси-
мального принципа.
Минимаксимальный принцип позволяет в известных
условиях сравнивать собственные числа различных операторов.
Пусть А и В—два положительных оператора. Будем
говорить, что оператор А не меньше оператора В, А^В, если
пространство Нв содержит все элементы пространства НА
и для каждого элемента и£НА имеет место неравенство

264
ГЛ. III. ВАРИАЦИОННЫЕ МЕТОДЫ
[1
\и\А^? \и\в. Доказывается, что если А^В и В имеет
дискретный спектр, то А тоже имеет дискретный спектр; если
^п и V'n (п~^у 2, ...) — собственные числа операторов А
и В соответственно, то kn^z\in при любом п.
Отметим некоторые простые случаи. 1) Пусть две
мембраны (или пластины) с жестко закрепленными краями
изготовлены из одного материала и одна мембрана
полностью укладывается в другой. Тогда собственные частоты
колебаний меньшей мембраны больше соответствующих
собственных частот большей мембраны. 2) Пластина с жестко
закрепленным краем имеет большие частоты собственных
колебаний, чем та же пластина, край которой упруго
закреплен; в свою очередь в этом последнем случае частота
больше, чем в случае свободно опертого или тем более
свободного края.
§ 5. Другие вариационные методы и оценка погрешности
1. Оценка погрешности приближенного решения. Пусть
и0 и ап—соответственно точное и приближенное решения
уравнения
Au=f, C.136)
где оператор А предполагается положительно определенным
(Аи, u)^y*\\u\\\ Y2 = const>0. C.137)
Задача заключается в оценке погрешности и0 — ап в
предположении, что приближенное решение известно, а точное
неизвестно. Эту погрешность удобно характеризовать ее
нормой в том или ином пространстве; проще всего
воспользоваться нормой ||и0—ип\\ гильбертова пространства Я, в
котором действует оператор Л, или нормой \и0—ип\л
энергетического пространства НА.
Если un£D{A), то верна простая формула для оценки
погрешности
IK-"JI<^IM"n-/ll- C.138)
Формулу C.138) можно использовать, например, если ап
построено по методу Ритца, причем в качестве координатных
использованы элементы из области D(A). Если оператор А

1] § 5. ВАРИАЦИОННЫЕ МЕТОДЫ И ОЦЕНКА ПОГРЕШНОСТИ 265
дифференциальный, то это означает, что координатные
функции удовлетворяют всем краевым условиям задачи.
Следует иметь" в виду, что оценка C.138) грубая.
Другой, практически более важный способ оценки
погрешности таков. Обозначим через F(u) функционал
энергетического метода:
F(u) = (Au, и)-2(и, /) = |а|2-2(и, Л,
и через d—его минимум. Если б — любое число, меньшее,
чем dy то
К-«„К ]/>(«„)-6; C.139)
как следствие отсюда получается еще одна оценка:
К-М^уТ^Ю-б- C.140)
Применение формул C.139) и C.140) не предполагает,
что un£D(A)) достаточно, чтобы ип£НА (в частности, ип
может не удовлетворять естественным краевым условиям);
это всегда имеет место, если ип построено по методу Ритца.
В этом случае можно указать удобную формулу для
вычисления величины F(un). Именно, если
п
«й=2Хф»
k=l
где фА—координатные элементы, a ak — решение
соответствующей системы Ритца, то
F(un) = -iak(/, Фа). C.141)
fe = l
Общий прием построения чисел 8<Cd таков. Известно,
что
d = min F{u) = — | и012.
Допустим теперь, что нам удалось найти функционал
Ф (v), обладающий тем свойством, что
min Ф (г/) = — d = — min F{и). C.142)

266
ГЛ. III. ВАРИАЦИОННЫЕ МЕТОДЫ
[2
Если v —любой элемент из области определения
функционала Ф, то (&(v)~^ — d или —<&(v)^d и,
следовательно, можно положить 6 = — Q)(v). Построим для
функционала <&(v) минимизирующую последовательность, т. е.
такую последовательность vm (m=\, 2, ...), что
lira Q>(vn) = — d,
и, положив в формуле C.139) 6 = — Ф(ят), мы получим
оценку погрешности, сколь угодно близкую к ее
действительной величине, если только т достаточно велико.
Заметим, что последовательность vm можно строить по методу
Ритца. Дело сводится к построению функционала Ф,
удовлетворяющего условию C.142). Наиболее важными методами
такого построения являются метод ортогональных проекций
и метод Трефтца. Заметим тут же, что каждый из этих
методов позволяет строить приближенные решения
уравнения C.136).
2. Метод ортогональных проекций. Обратимся к
уравнению C.136). Пусть входящий в это уравнение
положительно определенный оператор А можно представить в виде
произведения двух сопряженных операторов 7* и 7, так что
А =7*7. При этом необязательно, чтобы операторы 7* и 7
действовали в том же пространстве Я, что и оператор А;
можно допустить, что 7 переводит элементы пространства И
в элементы некоторого гильбертова пространства «!р, тогда,
наоборот, 7* переводит элементы пространства «<р в элементы
пространства И.
Положим в уравнении C.136) Tu = v, тогда
7*г> = /. C.143)
Для дальнейшего интересен только тот случай, когда
уравнение T*w = 0 имеет решения, отличные от нулевого.
Их совокупность образует в пространстве ф некоторое
подпространство, которое мы обозначим через <§2.
Ортогональное дополнение к <!р2 обозначим через tQv так что
§ = &Ф&' Легко доказывается, что искомый элемент
^о=7Ч)€|>1 и что IKIk=KL'' здесь ио~Решение
уравнения C.136).

2] § 5. ВАРИАЦИОННЫЕ МЕТОДЫ И ОЦЕНКА ПОГРЕШНОСТИ 267
Найдем какой-либо элемент V£&, удовлетворяющий
уравнению C.143); предполагается, что это нетрудно
осуществить. Тогда искомый элемент v0 есть проекция
элемента V в подпространство ^х; разность V—v0 есть,
следовательно, проекция того же элемента V в
подпространство §2.
Как известно из свойств проекции,
IKII« = Min||V-w|U,
где минимум берется по всем элементам w, принадлежащим
подпространству «£J. Отсюда видно, что в качестве
функционала Ф можно взять
<[>[w) = \\V—w\\l C.144)
Будем решать задачу о минимуме функционала C.144),
например, по методу Ритца, и пусть wm — приближенное
решение этой задачи. Положим vm= V—wm. По формуле
C.139) имеем теперь
K-"„l<V^W + IKIll. C-145)
Элемент vm можно рассматривать как приближенное значение
элемента v0=Tu0; справедлива оценка
\\v0-vm\\l^-/.F(un) + \\vm\\l. C.146)
В формулах C.145) и C.146) ип означает приближенное
решение уравнения C.136), построенное по энергетическому
методу.
Если за приближенное значение v0 принять среднее
арифметическое Y^un~^vm)i T0 получается точная формула
для погрешности
\-^(Tun+vm)\s=\-\/rF(un) + \\vm\\%- C-147)
Эта формула была получена Дж. Синджем [126].

268
ГЛ. Ш. ВАРИАЦИОННЫЕ МЕТОДЫ
[3
3. Приложения к частным задачам. Для уравнения
Пуассона в трехмерном пространстве
А [д2и . д2и , д2и\ х. ч /Q Г/40ч
-Au==-(w + W* + d?)=f{x' у' z) (ЗЛ48)
поставим задачу Дирихле: найти интеграл этого уравнения,
удовлетворяющий краевому условию C.62):
Как известно, Ди = div gradtf, и мы положим Та = — gradtf,
причем буде.м считать, что оператор Т определен только
на функциях, удовлетворяющих условию C.62). В нашем
случае H=L2{Q); в качестве пространства ,!р можно взять
пространство L2(Q) векторов, абсолютные величины которых
квадратично суммируемы в Q. Сопряженный к Т оператор
jT*0 = div0, так что —Д=Г*7\ В рассматриваемом случае
подпространство <!р2 состоит из векторов с нулевой
расходимостью (соленоидальных векторов), а подпространство^ —
из градиентов скалярных функций, которые обращаются
в нуль на границе S. В качестве V можно взять любое
решение уравнения
divV = /(*, у, z),
можно, например, положить
г
V=@, 0, -$/(*, у, z)dz),
а
где а — любое фиксированное число, для которого последний
интеграл имеет смысл. По методу ортогональных проекций
следует найти минимум интеграла
о
где VXi V' Vz и wx, w wz суть проекции векторов V и
w на оси координат; минимум ищется на множестве
векторов w, удовлетворяющих уравнению div до = 0. Если к этой
задаче применить метод Ритца, то следует построить
полную в «!р2 систему векторов <р„ (п=\, 2, ...) и положить
m

3] § 5. ВАРИАЦИОННЫЕ МЕТОДЫ И ОЦЕНКА ПОГРЕШНОСТИ 269
для определения коэффициентов а^ мы получаем систему
уравнений *)
(Фп 4>i) ах + (Ф«. %) а2 + • • • + (Ф«1 <Pj ит = (V, ф,),
(Фр Ф«К + (Ф., Ф2К+ • • • +(ФЛ> Фа)«« = (^ Ф2)>
(Фг>ф^)а1 + (ф2,ф^)а2+-.--Мф^>ф^)^==(^ф«);
здесь скалярное произведение (ф, \J?) двух векторов ф и \|)
определяется формулой
(Ф, Ч>) = J J J (ф А + %% + Ф А) ^ 4У dz.
Если для уравнения C.147) ставится задача Неймана с
краевым условием
si.-*
то в качестве 7 берется оператор Ти = grad и,
определенный на этот раз на всех скалярных функциях и (х, у, z),
для которых grada£L2(Q), т. е. на всех функциях, для
которых
(grad иJ dx dy dz < оо;
никаким краевым условиям эти функции не подчинены. При
этом оказывается, что T*v = — divtf, где теперь вектор v
должен быть подчинен условию, что на границе S его
нормальная составляющая равна нулю: ^1^=0. Дальнейшее
протекает, как в задаче Дирихле, с той лишь разницей, что
координатные векторы ф^, должны удовлетворять краевому
условию ф^|5 = 0; эт0 обстоятельств несколько затрудняет
применение метода ортогональных проекций к задаче
Неймана. То обстоятельство, что уравнение C.147) содержит
три независимые переменные, несущественно.
В применении к основным задачам теории упругости
метод ортогональных проекций приводит к известному
принципу Кастильяно.
г) Заметим, что система C.149) применима всегда, когда
используется метод ортогональных проекций, а не только для задачи
C.148), C.62).
U3.149)

270 гл. ш. вариационные методы C
Пример 14. Применим метод ортогональных проекций к
задаче C.71), C.72). Положим —gradw = tf, где v—двумерный вектор;
ди да Л/ /0 „оч
его составляющие суть vx =— -^- , vy — — — . Уравнение C.72)
переходит в следующее:
divtf = 1.
Легко построить вектор V, удовлетворяющий последнему
уравнению; достаточно, например, положить Vx = x, Vу — О. Выберем
теперь полную систему векторов фп, удовлетворяющих уравнению
div Ц>п = 0. Такую систему можно построить, выбирая
составляющие векторов фп в виде произведений степеней х и у\ следует при
этом иметь в виду, что понадобятся не все такие векторы. Дело
в том, что функция и (х, у), решающая задачу C.71), C.72), четная
как относительно х, так и относительно у\ поэтому составляющая
ди
vx — ^- должна быть нечетной по л: и четной по у, а
составляюсь „ _
щая vy = ^ нечетной по у и четной по х. Такими же должны
быть и составляющие вектора w= V—v\ так как векторы wn
нужны только для аппроксимации вектора wf то их можно
подчинить тем же условиям четности и нечетности и можно положить
<Pi = (*> —У), ф2=Ф3> —3**0). ф8 = C^2, — у3), ...
Ограничиваясь выписанными членами, положим
w ^ wz = с^ф! + а2ф2 + а3ф,
или, более подробно,
wx ^ w3x = а^х + а2х3 + Zazxy2,
wy ^= w3y = — су/—За2х2у — а8#3.
Коэффициенты av а2, а8 следует определить из системы C.149),
которая в данном случае имеет следующий вид:
8 , 32 , 32 4
3-а1 + 1Ба2 + -а3 = т,
32 , 104 , 8 4
32 , 8 , 104 4
а1 + Та2 + -оГа8=-
15^-г 5  ' Ж"8~~Т'
^0,1944, «. = ^
7 7
Отсюда а, = 0,5000, а2 = — ^^~0,1944, а8 = ^^0,1944 и,
следовательно,
о>8=0,5000ф1--0,1944ф2 + 0,1944ф3.
Приближенное решение по методуортогональных проекций имеет вид
и8х = а:—@,5000л:—0,1944x3 + 0,5832;q/2),
v3y = — @,5000£/—0,5832хг/2 + 0,1944*/3).

4] § 5. ВАРИАЦИОННЫЕ МЕТОДЫ И ОЦЕНКА ПОГРЕШНОСТИ 271
Имея это решение, можно оценить погрешность приближенного
решения C.73), построенного по энергетическому методу. В формуле
C.145), дающей оценку погрешности, величину F(w3) можно
вычислить по формуле C.141); для величины || vz |j2 можно тем же
способом получить аналогичную формулу
1К112нт12-2м^<ы.
Произведя необходимые вычисления, получим:
F(u2) = — 0,5616, ||vs ||2 = 0,5630
и, следовательно,
|и — и«|< ^0,5630—0,5616= уНрбП = 0,0374,
что дает относительную погрешность по энергии порядка 6°/0.
В силу формулы (ЗЛ46) та же величина 0,0374 дает верхнюю
границу погрешности приближенного решения^, построенного по методу
ортогональных проекций.
Если за приближенное значение вектора V — — grad и принять
v= — ( —gradw8 + *«),
то по формуле C.147) имеем точное равенство
\\v—5|| = у У0Щ4 = 0,0187.
4. Метод Трефтца. Пусть в области Q требуется
проинтегрировать линейное дифференциальное уравнение
Lu=f.(x) C.150)
при некоторых, скажем однородных, краевых условиях
Gku\s=--0 (A=l,2 г),
и пусть оператор Л, совпадающий с L на множестве
функций, удовлетворяющих этим краевым условиям, положительно
определенный.
Чтобы сформулировать метод Трефтца, введем сперва
понятия билинейного и однородного квадратичного
функционалов. Функционал Ф(иу v), зависящий от двух переменных
элементов и и v, называется билинейным, если он линеен
по отношению к каждому из элементов и и v в отдельности,

272
ГЛ. III. ВАРИАЦИОННЫЕ МЕТОДЫ
[4
т. е. если для любых постоянных ах и а2 верны равенства
Ф (axttx + а2и2, v) = ахФ (uv v) + а2Ф (av v),
Ф (и, axvx + a2v2) = агФ (и, vx) + а2Ф (и, vt).
Однородный квадратичный функционал получается из
билинейного, если в последнем положить u = v: Ф(?;) — Ф(г>, v).
Обозначим через и0 решение задачи, сформулированной
в начале настоящего пункта. Метод Трефтца заключается
в том, что строится какой-нибудь неотрицательный
однородный квадратичный функционал Ф, определенный на
решениях уравнения C.150) и удовлетворяющий на этих
решениях неравенству Ф(^)^Ф(и0) и равенству ф(#0) =
= /и0|2. Коль скоро этот функционал построен, ставится
задача о нахождении такого решения уравнения C.150),
которое реализует минимум этого функционала на множестве
всевозможных решений упомянутого уравнения. Если в
нашем распоряжении имеется какое-либо частное решение
уравнения C.150) и полная система линейно независимых
решений однородного уравнения Lp — О, то задачу о
минимуме функционала 0(v) можно решать по методу Ритца;
координатными функциями при этом служат упомянутые
решения однородного уравнения.
Можно указать общий прием для построения
«функционалов Трефтца» (см. литературные указания в конце главы);
здесь мы ограничимся тем, что приведем эти функционалы
для некоторых простейших задач.
1) Для задачи об интегрировании уравнения Пуассона
— Аи=/(х) при краевых условиях
"lsi=°> [£ + ra]s2 = 0> a^oro==const) 5i + 5, = 5.
можно взять
ф (V) = J (grad vJ dx+\ av2 dS +
Q S
s2
где a — любая функция, подчиненная неравенству 0^<t<;g.

4] § 5. ВАРИАЦИОННЫЕ МЕТОДЫ И ОЦЕНКА ПОГРЕШНОСТИ 273
В случае задачи Дирихле поверхность S2 отсутствует
и можно взять
ф (v) = J (grad vJ dx + ^ av2 ds? C.151")
где а—любая неотрицательная функция; можно, в
частности, положить а = 0.
В случае задачи Неймана можно принять
ф(гг)= Ugm&vJdx—a (V<fc-f ~ f (|? — агЛ\/$,C.15Г')
где а—достаточно малая постоянная. Минимумы
функционалов C.151) следует искать на решениях уравнения
Пуассона — Av = f(x).
2) Рассмотрим уравнение изгиба пластины
А™=^+21>Ш?+^=/{х'у) (ЗЛ52)
при краевых условиях w\ = 0, ^- =0. В данном случае
функционал Ф имеет очень простой вид:
Ф (v) == J J (Аг;J rfjt dy, C.153')
где Q — область пластины, v(x, у)— любое решение
уравнения C.152). Этот функционал можно еще упростить,
положив Av — q(x, у). Тогда дело сводится к нахождению
минимума функционала
Ol(q) = ^qtdxdy C.153")
на множестве решений уравнения &q~f(x, у).
3) В случае свободно опертой пластины функционал
метода Трефтца имеет различный вид в зависимости от того,
будет ли контур S пластины выпуклым или он содержит
невыпуклые участки. Если контур выпуклый, то можно

274
ГЛ. III. ВАРИАЦИОННЫЕ МЕТОДЫ
14
положить
+iHMS+i£)F <3|53'">
S
Здесь 0—постоянная Пуассона, q—радиус кривизны
контура, s—длина его дуги. Если контур содержит
невыпуклые участки,, то можно положить
C.153IV)
Здесь а и |3— положительные постоянные, причем
постоянная а достаточно мала.
Минимумы функционалов C.153) следует искать на
множестве решений уравнения C.152).
Скажем подробнее о нахождении минимума функционала
<D(v) Трефтца. Пусть я|>— какое-нибудь частное решение
уравнения C.150), р — произвольное решение однородного
уравнения Lp = 0. Любое решение уравнения C.150) можно
представить в виде v = ty-\-p. Как известно, при весьма
широких условиях решения уравнения Lp = 0, квадратично
суммируемые в данной конечной области £2, образуют в
пространстве L2 (Q) некоторое подпространство. Пусть
последовательность {рп (х)} элементов этого подпространства (иначе
говоря, решений однородного уравнения, квадратично
суммируемых в Q) полная в нем, и пусть функции рп (х)
таковы, что ни на какой их конечной линейной комбинации
функционал Ф не обращается в нуль, если только
коэффициенты такой комбинации не все равны нулю. Примем
функции рп (х) за координатные; приближенное решение задачи

4] § 5. ВАРИАЦИОННЫЕ МЕТОДЫ И ОЦЕНКА ПОГРЕШНОСТИ 275
о минимуме функционала Ф (v) будем искать в виде
т
*°т (*) =>1> (*) + Д ал (*);
коэффициенты ад определяются из линейной системы
2Ф(рЛ,Ру)аЛ=-Ф(ф,ру) (/=1,2, ;..,;»), C.154)
которая разрешима и имеет единственное решение. Очевидно,
0(vm) ^Ф(ц0), поэтому можно в формуле C.62) положить
б — — Ф(?^),и мы получаем новую оценку погрешности
приближенного решения, построенного энергетическим методом:
\u0-uj ^VFiuJ+ФК). (ЗЛ55)
Если функционал Ф определен также и на решениях
однородного уравнения Lp—Q, то формула
/ф(«,-«,)<^A(„) + Ф(в.) C.155')
дает некоторое представление о погрешности приближенного
решения vm, построенного по методу Трефтца.
О сходимости метода Трефтца см. [63].
Пример 15. Рассмотрим задачу о кручении стержня
квадратного сечения, которой мы уже занимались в п. 4
§ 3 и в п. 3 настоящего параграфа. Решения уравнения
х2
— Д?/=1 имеют вид1/ = — -к- + р(-*г, у), где
р—гармоническая функция. Функционал Трефтца возьмем в виде C.151"),
положив при этом а = 0; дело сводится к построению
функции р (х, у), гармонической в квадрате —1 ^х, у^\
и реализующей минимум интеграла
1 1
Ф(«)= j J(grad(p(*,.y)-if-)),d*'0' =
-И [(£-*)■+(&
dxdy.
Можно доказать, что система гармонических функций
cos Bm — 1) пх ch Bm — 1) пу {п1_л 9 v
sin 2 sh 2 lm- lj 2- ' •>

2 ГЛ. III. ВАРИАЦИОННЫЕ МЕТОДЫ [4
удовлетворяет перечисленным выше требованиям. В силу
свойств симметрии искомого решения достаточно взять в
качестве координатных функций
. ч B/л — \)пх иBт—1)лх , л л '
Рт(х> У)***™- 2"^Ch 2" (m=1» 2' ••■)•
Нетрудно проверить, что функции рт удовлетворяют такому
соотношению «ортогональности»:
-1-1
Поэтому в у-м уравнении системы C.154) слева останется
только член, содержащий ал эта величина, следовательно,
легко вычисляется, она равна
(-ЦМ6
B/ — I)8 я8 ch о
Пользуясь тем же соотношением «ортогональности», легко
найдем, что
Л/ >-4 256 "Ш^2~Я
ф^|я'~ 3 я5 1л Bk — 1M '
/г = 1
Слагаемые в последней сумме довольно быстро убывают, и
можно ограничиться небольшим значением т. Взяв т — 3,
получим Ф(?>8) = 0,5620. Выше (см. п. 3) было приведено
значение F(u2)=—0,5616; формула C.154) дает теперь
\и0 — и21 < |/0,5620—0,5616 = 0,02.
Таким образом, решение C.73) точнее, чем это следует из
оценки п. 3.
Пример 16. Рассмотрим задачу об изгибе упругой
квадратной пластинки, заполняющей область —1<;*, t/^1, жестко
закрепленной по краю и находящейся под действием равномерно
распределенной нормальной нагрузки. При подходящем выборе
единиц измерения задача сводится к интегрированию уравнения

4] § 5. ВАРИАЦИОННЫЕ МЕТОДЫ И ОЦЕНКА ПОГРЕШНОСТИ 277
при краевых условиях
w(x, ± \) = w(± 1, y) = wx(± 1, y) = wy{xt ± 1) = 0.
Решая эту задачу энергетическим методом, следует приближенно
вычислить функцию, удовлетворяющую только что
сформулированным краевым условиям и реализующую минимум интеграла
1 1
Р И = \ \ [(kwJ—2w'\ dx dy.
Координатные функции возьмем в виде
(x2 — lJ(y2—\J(x2ky2m + x2my2k) (k, m = 0, 1, 2, ...);
такие координатные функции учитывают симметрию задачи.
Ограничиваясь двумя первыми функциями, можно так записать
приближенное решение:
i»« = (xI-l)t(yi-l)tlfl,+fl«(*, + yf)].
В нашем случае система C.24) имеет вид
7 а>+77 а2~~ 128 '
36 96 __1_
77«i + 91 «2-64
Решив эту систему, найдем
ш2 = (х2—lJ(i/2—IJ [0,02067 + 0,0038 (х2 + у2)].
Соответствующее значение функционала F равно F (w2)= —0,02486.
Найдем теперь приближенное решение по методу Трефтца, для
чего нам понадобятся решения уравнения Д<?= 1; эти решения можно
х2 4- и2
представить в виде q (x, #) =—т~^ + Р (х> У)> где Ар = 0. В качестве
координатных функций возьмем гармонические полиномы,
учитывающие симметрию задачи и ортонормированные по области квадрата.
Первые три из них равны:
рл*. y)=Y> Pi{x> y)==i Yyz [-5+j(x*-Qx2y2+y^]>
Pi(x, y) = 0,356359^,- у ~4,76724p2-l,40625yV8J ,
где
Ns = x*—28x«y2 + 70л:4 у*—28x2y* + у9.
Приближенное решение задачи о минимуме функционала C.153")
будем искать в виде
х24- и2
Яг = —-j~ + а,р, (х, у) + а2р2 (*, у) + а3л3 (*, у).

2?8 гл. ш. вариационные методы [5
Благодаря тому, что полиномы pk ортонормированы, система C.154),
в которой следует заменить Ф на Ф2, принимает особенно простую
форму:
с, = |, а2=—0,1397, а3 = 0,0014.
Не определяя соответствующую функцию v3 (это было бы связано
с трудными вычислениями), можно все же утверждать, что Ф(^8) =
Sr=d>1(q9)=z0,02491. Теперь по формуле C.155)
I w0—wt1 < jA) ,02491 —0,02486 = 0,0071;
здесь w0—точное решение задачи. Имея оценку энергетической
нормы, можно оценить абсолютную величину разности wQ — w2
см. [63]); эта оценка имеет вид \w0—^;21 < 0,005.
5. Двусторонние оценки функционалов. Часто бывает важно
найти не само решение уравнения Au0 = f, а некоторый функционал
от этого решения вида (и0, g), где g—данный элемент
рассматриваемого гильбертова пространства. Простейший и самый грубый прием
для этого состоит в том, что находят приближенное решение ип
данного уравнения и полагают приближенно
("о, ё)^(иПУ g). C.156)
Погрешность этого приближенного равенства оценивается формулой
1К> £)-("*> g)\<llg\\\\Uo-fn\\.
Если А — положительно определенный оператор и ип£НА, то ве*
личину \\и0 — ип\\ можно оценить, используя метод ортогональных
проекций или метод Трефтца. Можно строить приближенные
формулы, вообще говоря, более точные, чем формула C.156). Можно
положить приближенно
(«о. g)^bn = (un, g) + (f-fn, vn), C.156')
где fn = Aun и vn — приближенные решения уравнения Av0 — g.
Погрешность формулы C.156') определяется неравенством
IK> g)-bnl<\Uo-Un\-\Vo-Onl C.156")
Правую часть формулы C.156") можно оценить, привлекая для
этой цели метод ортогональных проекций или метод Трефтца.
Еще одну приближенную формулу можно построить следующим
образом. Пусть, как в п. 2 настоящего параграфа, А=Т*Т. Пусть
и и v — произвольные элементы из области определения оператора
Т, а и' и V1 — произвольные решения уравнений T*u' = f и T*v'=g.
Положим
<* = («. g) + (v, f)-{Tu, Tv)9 P = («*', v').
Погрешность приближенного равенства

6] § 5. ВАРИАЦИОННЫЕ МЕТОДЫ И ОЦЕНКА ПОГРЕШНОСТИ 279
не превосходит величины
^\\Tu-u'\\\\Tv-v'\\.
6. Двусторонние оценки собственных чисел.
Энергетический метод дает приближенные значения собственных чисел
положительно определенного оператора с избытком. Важная
задача об определении приближенных значений с
недостатком не может считаться в настоящее время решенной
полностью. Здесь мы укажем два приема решения этой задачи;
каждый из них имеет довольно ограниченную область
применения.
1) Пусть данный положительно определенный оператор
дифференциальный. Если известна его функция Грина G(x, у),
то его собственные числа совпадают с характеристическими
числами интегрального уравнения
и(х) — % J Q(x, y)u(y)dy = 0. C.157)
Будучи функцией Грина положительно определенного
оператора, функция G(x, у) симметрична. Допустим еще, что
«двойной» интеграл
\\\0{х,у)\*йхAу
йй
конечен. Обозначим через Gm (x, у) т-е итерированное ядро
уравнения C.157) и через ат так называемый след этого
ядра:
Q
Если наименьшее характеристическое число 'к1 имеет
кратность р, то справедливо приближенное равенство *)
%^*Vr-> C.158)
дающее значение X с недостатком.
') Подробнее об этом см. гл. IV настоящего справочника, § 1, п. 5.

280 гл. ш. вариационные методы [6
При т—»-оо получается точное равенство
Кл =\\т
1 2ГП
тчюо
п/ •
V агт
Поэтому при достаточно большом т погрешность формулы
C.158) сколь угодно мала. Если характеристические числа
уравнения C.157) Я, и Х2 оба простые и значение Х1
известно точно или с избытком, то формула
I2m/~Z
^К У «■
дает значение %2 с недостатком. Можно построить
аналогичные формулы и для случая кратных характеристических
чисел Хг и А,2, а также для последующих характеристических
чисел.
Изложенный здесь прием дает удовлетворительный
результат для некоторых типов обыкновенных дифференциальных
уравнений, когда построение функции Грина и ее итераций
выполняется сравнительно просто.
Пример 17. Обратимся к примеру 11. Легко построить
функцию Грина оператора C.123); при х^у она равна
G(,,,)=inAT^iHO->AH^) .
]/*2—1
значение ее при х > у получается перестановкой аргументов х и у.
Значение второго итерированного ядра при х^у таково:
°'<* У)=^7% { <^-^> [ (^-1)(_2-,-|2-
-YlLyYTTy)-^{fT+-y-\)\\ ;
для х > у значение Gz (x, у) опять получается перестановкой
аргументов х и у. По общему правилу вычисления итерированных ядер

6) § 5. ВАРИАЦИОННЫЕ МЕТОДЫ И ОЦЕНКА ПОГРЕШНОСТИ
имеем
1 1
С4 (х, У)=\ог (х, s) G2 (s, у) ds = Г G2 (x, s) G2 (у, s) ds.
Отсюда
1 11 IS
fl4=V Gt(x,x)dxz=[^Gl (x, s)dxds = 2 \ ds ^ 022(x)s)dx^
О 0 0 0 0
= 0,50092905.10-*.
Как хорошо известно, собственные числа первой краевой задачи
для обыкновенного дифференциального уравнения второго порядка—
простые, поэтому р = 1, и по формуле C.158) мы получаем
Л, ^т-£=== 11,88655.
V ал
Воспользовавшись формулой C.124), найдем
11,88655 <ЛХ< 12,12255.
Среднее арифметическое обоих приближенных значений дает нам
новое приближенное значение
Xl ^ 12,00455,
с относительной погрешностью, меньшей 1%.
2) Еще один прием был разработан на частном примере
А. Вайнштейном и в общем случае Н. Ароншайном. Другое
изложение того же по существу приема было позднее дано
И. В. Свирским; здесь мы следуем последнему изложению,
как более простому.
Пусть кроме данного оператора Л нам известен также
меньший оператор Л0, область определения которого D (Л0) z>D (Л),
и пусть все собственные числа оператора Л0 нам известны.
Если %п и V£) — собственные числа операторов А и А0
соответственно, то кп^№\ и мы сразу получаем значения
чисел %п с недостатком, однако эти значения будут, вообще
говоря, весьма грубыми. Для их уточнения строится
последовательность операторов Ak (А=1, 2, ...) таких, что
А0 <: Ах <Л2г=^ ... ^Л. Тогда при любом k будет Wn°> ^
^Х^)^ЯЛ, где ^ — собственные числа оператора Ak%

282
ГЛ. III. ВАРИАЦИОННЫЕ МЕТОДЫ
[7
Операторы Ak строятся следующим образом. Полагаем
А—А0 — С; оператор С неотрицательный. Выбираем к
элементов fr£D(A)y удовлетворяющих соотношениям
Теперь можно положить
k
Aku = A0u+%(Cu, fr)Cfr.
Г = 1
Целесообразно строить оператор Ak так, чтобы имело место
строгое неравенство № <z№kK Это будет иметь место, если,
каков бы ни был собственный элемент ф оператора Л0,
соответствующий собственному числу %Qi найдется такой
элемент /г, что (С/п ф) ф 0. Для этого в свою очередь
достаточно, чтобы число k было больше или равно кратности
собственного числа Х[0).
Некоторые оценки снизу для наименьшего собственного
числа можно получить из следующих соображений. Пусть Л —
положительно определенный оператор с дискретным
спектром. Пусть, далее, и — произвольный элемент из области
определения оператора Л, такой, что ||и|| = 1. Положим
(Аи, и) = г[ и \\Аа — ци\\2 = \\Аи\\2—т|2 = ва. Известно, что
тогда в промежутке г\ — е^А^т]-{-е есть хотя бы одно
собственное число оператора А. Допустим теперь, что нам
известна хотя бы грубая оценка для второго собственного
числа: А,2>р, и при этом оказалось, что г] + е<р. Тогда
первое собственное число Х1 заключено в пределах
т] — бг^А^г^т] и, следовательно, г) — 8 есть приближенное
значение Хг с недостатком.
Если собственное число %х простое (однократное), то
можно указать, вообще говоря, более точное значение К1
с недостатком:
7. Ошибка в решении, проистекающая от ошибки в
уравнении. С целью упрощения задачи часто заменяют данное уравнение
Au = f другим уравнением Bu — f, содержащим более простой
оператор В. Это приводит к некоторой ошибке в решении, которую можно
оценить следующим образом.

1] § 6. МЕТОД НАИМЕНЬШИХ КВАДРАТОВ
283
Пусть оба оператора Л и В положительно определенные, и
пусть соответствующие энергетические пространства Ид и Нв состоят
из одних и тех же элементов. Тогда существуют такие
положительные постоянные ах и <х2, что
<h\u\%<\u\ Д<а2|и||.
Пусть uQ и а, удовлетворяют уравнениям Au0 = f и Bul = f. Имеет
место неравенство
где
1"о— 1В<Л1МЛ>
., /К — 11 |а2 —1|\
Ti = MaxM— L, — L .
1 V <*, «2 /
М. Г. Слободянский [92] заметил, что константу т) можно
уменьшить, если заменить ах на а2 = -~-( 1 \av Тогда
а9—а,.
§ 6. Метод наименьших квадратов
1. Общие замечания. Пусть Л—линейный оператор,
действующий в некотором гильбертовом пространстве; ни
симметричности, ни тем более положительности оператора А
мы не предполагаем. Пусть уравнение
Au=f C.159)
разрешимо. Тогда элемент и0, удовлетворяющий этому
уравнению, очевидным образом реализует минимум функционала
\\Аи—/\\*. C.160)
Метод наименьших квадратов и состоит в замене
уравнения C.159) вариационной задачей о минимуме
функционала C.160). Эту задачу можно решать по методу Ритца.
Выберем последовательность координатных элементов
фл (л=1, 2, ...), принадлежащих области определения
оператора Л, положим
п
«П=2«АФ„ (ЗЛ61)
k=l

284 гл. in. вариационные методы [1
и подберем постоянные ak так, чтобы величина \\Аип—/||2
получила наименьшее значение. Это приводит к системе
линейных алгебраических уравнений
ИФр ApiK + Иф,, Лф1)а2+...
•••+Ифя. 4q>i) *« = (/. Лф1),
Ифц ^Ф«)«1+Иф„ ^ф2)Я2+...
...+ИФЯ, ^Ф.)ая = (/| лФ2)> > C.162)
ИФр ^ф„К + (Лф2, Лфп)а2+...
... + Ифи, ^ф*К = (/, лч>п)- ,
Теорема 19. Пусть выполнены следующие условия:
1) последовательность элементов Лфп (п= 1, 2, . . .) полна
в рассматриваемом гильбертовом пространстве; 2)
уравнение C.159) разрешимо; 3) существует и ограничен обрат-
ный оператор А'1, иначе говоря, существует такая
положительная постоянная К, что для любого элемента
u£D(A) имеет место неравенство
|| а || </ГЦ Ли ||. C.163)
Тогда при любом п система C.162) имеет одно и только
одно решение; если ип—элементы, построенные по
формуле C.161), а и0 — точное решение уравнения C.159), то
к-«.н-.°. и*..-/!!„т.0-
Справедливо неравенство
lk-"JI<Kll-4,-/11. C-164)
дающее оценку погрешности метода наименьших квадратов.
Если оператор А положительно определенный, то имеет
место неравенство
К-"п1л<1//?1М"„-/Н; C.165)
в этом случае приближенные решения, построенные по
методу наименьших квадратов, сходятся также и по энергии,
но эта сходимость более медленная, чем для приближенных
решений, построенных по энергетическому методу с помощью
тех же координатных элементов фА. Преимущество метода
наименьших, квадратов в атом случае состоит в том, что

2] § 6. МЕТОД НАИМЕНЬШИХ КВАДРАТОВ 285
Аап—*/, так что приближенное решение приближенно
удовлетворяет данному уравнению] как известно, в общем
случае это соотношение не имеет места, если ип построено
по энергетическому методу.
На практике метод наименьших квадратов удобно
применять в следующей форме» Пусть задача состоит в
отыскании одной или нескольких функций и^\ и<2>, ..., w<m>,
которые удовлетворяют двум системам линейных уравнений:
однородной
£у(иA), иB), ..., «<">) = 0 (/=1, 2, ..., т) C.166)
и неоднородной
Oj(ub\ tf<2\ ..., цС«>) = /(/) (/=1, 2, ..., w). C.167)
Совокупности (а*1*, н<2>, ..., н(т)) и (/(О, /(*>, ..., /("*))
будем трактовать как элементы некоторого гильбертова
пространства И; в выборе этого пространства остается
значительный произвол, который можно использовать для
упрощения и уточнения вычислений. Координатные элементы
фЛ={ф(л1), Ф^2), ..., Ф(лт)} (л=1, 2, ...) выбираются так,
чтобы они удовлетворяли однородной системе C.166). Далее
полагаем
п
k = i
или, подробнее,
/г
и коэффициенты ak определяем из условия || Gun—/||2 = min;
через G обозначен оператор, порожденный в пространстве Н
совокупностью операторов G..
2. Связь с энергетическим методом. Пусть Л*—
оператор, сопряженный с А. Если уравнение C.159) разрешимо и
f£D(A*), то уравнение C.159) равносильно уравнению
Л*Ли = Л*/. C.168)
Далее, если выполнено неравенство C.163), то оператор А*А
положительно определенный:
(А*Аи)^К-ж\\и\\\

286
ГЛ. III. ВАРИАЦИОННЫЕ МЕТОДЫ
[3
Решение уравнения C.168) реализует минимум функционала
(А*Аи, и)-2(А*/, а) = |МЦ-/||г-||/||2,
который только постоянным членом — II/H2 отличается
от функционала [| Ли—/||2. Таким образом, при
перечисленных здесь условиях метод наименьших квадратов для
уравнения C.159) совпадает с энергетическим методом для
уравнения C.168).
С другой стороны, если оператор А положительно
определенный, то энергетический метод для уравнения C.159)
совпадает с методом наименьших квадратов для уравнения
АЧ^и^А-1''2/,
равносильного уравнению C.159).
3. Применение к задачам теории потенциала на
плоскости. Пусть D — конечная односвязная область комплексной
плоскости z~x-\-iy и S—граница этой области. Границу 5
будем считать достаточно гладкой; точнее говоря, будем
считать, что угол между нормалью к 5 и осью х имеет по
крайней мере г -f- 2 непрерывных производных по дуге;
г — вводимое ниже число. Через L2(S) обозначим
комплексное гильбертово пространство функций, квадратично
суммируемых вдоль 5, а через ISp E), г>0,—также
комплексное гильбертово пространство, элементы которого суть
функции, непрерывные на S вместе со своими производными
порядка до г—1 по комплексной координате переменной
точки контура S, тогда как их (обобщенные) г-е
производные квадратично суммируемы вдоль 5. Скалярное произведение
и норму в Dr) (S) зададим формулами:
(ф> Ф)г = J [ф (*) W) + Ф(г) (*) ¥7Г&) ds%
s
Здесь z — комплексная координата (аффикс) переменной точки
контура L и ds = \dz\. Скалярное произведение и норма
в L% (S) определяются обычными формулами:
(ф, ф)=S ф (*) W) <**. ii ф о2=S i ф с*) i2 <ts.
s s

3]
§ 6. МЕТОД НАИМЕНЬШИХ КВАДРАТОВ
287
Задачу Дирихле для области D поставим так: требуется
найти гармоническую в D функцию и (х, у), которая на
контуре S совпадает с заданной вещественной функцией f(z),
определенной на S. Как известно, и (х, у) = Re {со (z) }> где
со (z) есть голоморфная в D функция переменной z = x + iy.
Функция со (z) определена с точностью до чисто мнимого
постоянного слагаемого, которое мы нормируем, поместив
начало координат внутри D и потребовав, чтобы
Im{co@)}-0. C.169)
В качестве координатных функций возьмем целые
неотрицательные степени z\ в соответствии с этим приближенное
решение задачи Дирихле будем искать в виде полинома
п
<*п (*) = и„ {х, у) + ivn (х, у) = 2 <V*
с комплексными коэффициентами ak = ak -f- /Eft. Чтобы
удовлетворить условию C.169), положим р„ = 0. Коэффициенты
а0,а„ ...,<хп, р„ ..., Рге определим из условия ||и„—/|| 2 = min.
Система C.162) имеет в данном случае следующий вид
(Фо = 1- <Pft = Re(A ifA=Im (**)):
(фо> Фо) «о + (Фи Фо) а. + • • • + (Ф«. Фо) ап~ )
(Фо. Ф.) ао + (Ф,- Ф,) а, + • • • + (фя. Ф.) а« —
-(Ф„Ф,) Р,- (Ъ.ф.) Р,- • . • - (ф„,ф.) Рп = (/,Ф,),
(Фо- Ф„) а, + (ф„ Ф„) а, + • • • + (ф„, ф„) аи —
-(Ф..Ф„) Р, -(Ф,Ф„) Р.- • • • -<Ф„,Ф») Р» = (/,фя).
(Фо. Ф1)а. + (Ф„ Ф.К +•••+№„, Ф,К —
-(Ъ.Ф,) Р,-(Ф„*,) Р,- • • • - (ФпЖ) Р„ = Ш),
(Фо. Ф») «о + (Ф,. Ф») а, + • • • + (Ф„, Ф„) а„— |
-(Ф..Ф») Р1-(Ф„Ф„) Р,-. • .-(ФВ,ФЯ) Р„ = (/,ФЯ). J
C.170)

288 гл. ш. вариационные методы [3
Если коэффициенты удовлетворяют системе C.170), то
\\ип—/||—*0, a (un(z)—>(u(z) равномерно в любой
внутренней подобласти D; отсюда, как известно, вытекает, что
в любой внутренней подобласти производные со^} (z)
равномерно стремятся к (D(fe> (z) при любом k.
Коэффициенты ak можно определять также из условия
\\ап—/|j* = min. Это приведет к системе вида C.170), в
которой все скалярные произведения следует снабдить
индексом г. Если ak удовлетворяют такой системе, то при
O^k^r—1 (&№ (z)—>(d{k)(z) равномерно в замкнутой
области D — D + S.
Задачу Неймана поставим как задачу о построении
гармонической в D функции, нормальная производная которой
на 5 совпадает с заданной вещественной функцией h (z);
для разрешимости задачи необходимо и достаточно, чтобы
^h(z)ds = 0.
s
В данном случае голоморфная в D функция со (z)
определяется с точностью до постоянного слагаемого, которое мы
нормируем условием со@)==0. Приближенное решение ищем
в виде
со„ (z) = ип (х, у) + ivn {x, y)=% akz\ ak = ak + i$k.
Положим
Q* (*) = £*>(**),
v—внешняя нормаль к S. Если коэффициенты ак оп-
-~—h{z)\\ =min, то получится
ределять из условия

4) § 6. МЕТОД НАИМЕНЬШИХ КВАДРАТОВ
система
(&. Q,)r«. + (в„ e,)ra*+ • • • 4- (Q„, 0,)л,—
— К. Q.),P, —(*», в.)Л—•••—(o«, Q,)rP» =
= (*. Qi)r.
(Gi» Q»)r «i + (Qt.Q»)r a, + • • • + (Q„, Qn)r an —
— (<*vQn)r$i — (°*>Qn)'r$*—'--—(an>Qn)rh=s |
= (*> Q„)„ I
(Ci. <*,)/• a,+ (Q2> ^i)r«i+ •••+(C. ffi)ra«— |
— (°i> аЛ P,—K, a,),p,— ... —(<r„, a,), p„ =
(Qlt ff„)ra1 + (y2, a„)ra2+...+(Q„, an)ran—
— (<*,. 0»)rPi — K' ff«)rP2— • • • —K- 0«)r P« =
/
Можно, в частности, положить г = 0, тогда скалярное
произведение (,)г переходит в обычное скалярное
произведение (,).
Если коэффициенты ak, $k получены из системы C.171)
иО<^< г— 1, то со^ {z) —► со<Л) (г) равномерно в замкнутой
области.
4. Применение к плоской задаче теории упругости.
Рассмотрим случай заданных на границе смещений; в случае
заданных напряжений применяется, с незначительными
изменениями, та же схема. Предполагаем, что объемные силы
отсутствуют. Область D считаем конечной односвязной, ее
контур S—достаточно гладким. Как известно, задача
сводится к нахождению голоморфных в области D функций
<р(г) и ф(#), удовлетворяющих на S соотношению
C_4а)ф(*)-^7~^)—Wz) = g(*)>
где а—постоянная Пуассона, а g(z)— функция, заданная
на контуре. Функция ap\z) определяется с точностью до
постоянного слагаемого, которое мы нормируем условием
ф@) = 0; как и в л. 3, мы помещаем начало координат
внутри области D. Приближенные значения функций ф(г) и
289
C.171)
10 Q. Г. Михлин и X. Л. Смолицкий

290 гл. ш. вариационные методы [1
фB) будем искать в виде полиномов
и потребуем, чтобы
|| C—4а)Ф (z)-z^)^№)-g(z) ||; = min. C.172)
Отсюда получается система уравнений для неизвестных
коэффициентов. Укажем ее построение. Обозначим
ak = ak+ *<*„+*. bk = а2п + к+г+ /a3»+ft+2.
ф2*-, (*) = *'*>- Ф2* («) = *'**, 1 < Л < я,
Ф^зеО, да>2л,
¥ro(z)==0, да<2л,
^ (*) = C - 4<х) Ф, (г)-^(z)-¥,(*).
Из условия C.172) получается следующая система для
коэффициентов ak:
4П + 2
2 Re^eyJa^Re^gy) G=1,2, ...,4л + 2),
которая разрешима и имеет единственное решение. Если г ^2
то
фя(*)—*ф(*). Фп(^)—*ф'(*) и *,»(*)—*Ч>(*)
равномерно в замкнутой области. Если г<2, то
равномерная сходимость имеет место в любой замкнутой подобласти.
§ 7. Об устойчивости метода Ритца
1. Общие замечания. Если координатная система
удовлетворяет требованиям, перечисленным в п. 3 § 2, то
приближенное по Ритцу решение стремится, при возрастании его
номера до бесконечности, к точному решению. Это
утверждение верно, если само приближенное решение вычислено
без погрешности. На практике, как правило, дело обстоит
не так: обычно можно считать точно заданными только
координатные элементы, коэффициенты же приближенного

2] § 7. ОБ УСТОЙЧИВОСТИ МЕТОДА РИТЦА 291
решения определяются из системы Ритца, которая и строится,
и решается не точно, а с некоторой погрешностью. Эти
погрешности, которые мы предполагаем малыми, не очень
существенны, если порядок системы Ритца невелик, иначе
говоря, если по методу Ритца ищется грубое приближение;
в этом случае практически пригодна любая координатная
система, удовлетворяющая упомянутым выше условиям. Если
же желательно построить более точное приближение, то
необходимо прибегнуть к системам Ритца более высоких
порядков, а при этом погрешности, допущенные при
вычислении матрицы системы Ритца и столбца ее свободных
членов, а также при решении этой системы, могут приобрести
существенное значение, коль скоро координатная система
взята произвольно. Возникает вопрос об устойчивости метода
Ритца по отношению к такого рода малым погрешностям.
Относящиеся к этому вопросу основные результаты изложены
в последующих пунктах настоящего параграфа.
2. Минимальные и сильно минимальные системы. Будем
рассматривать некоторое гильбертово пространство «§.
Последовательность элементов ФА£<!р (конечная или бесконечная,
безразлично) называется минимальной в §, если вычеркивание
любого элемента этой последовательности сужает натянутое
на нее подпространство1). Вместо термина «минимальная
последовательность» употребляют также термин
«минимальная система».
Пример 18. Конечная система линейно независимых
элементов минимальна: то обстоятельство, что элемент фх
не выражается линейно через ф2, <р8, ..., ф„, означает, что
фх не принадлежит подпространству, натянутому на элементы
ф2> Ф«> • • •» 4V мы> следовательно, сузили подпространство,
натянутое на данные элементы, когда вычеркнули элемент ф1$
Пример 19. Конечная система линейно зависимых
элементов неминимальна: если фх линейно выражается через
ф2> Фз> • • •» Фя> т0 Ф1 принадлежит подпространству элементов
ф21 Фз> • • ч Фл и вычеркивание элемента ф1 не сужает
подпространства.
*) Определение минимальной последовательности сохраняет силу
и тогда, когда гильбертово пространство заменено любым банаховым
пространством.
10*

292
ГЛ. Ш. ВАРИАЦИОННЫЕ МЕТОДЫ
[2
Пример 20. Всякая ортонормированная система
минимальна.
Пример 21. В пространстве «§ = L2 @, 1) система
х, sinKX, sin2jtA:, ..., sinnnx, ...
неминимальна. Действительно, вычеркнув элемент л;, мы
получим полную в £2@, я) систему
sin nXy sin 2ялг, .. ♦, sin плх, ...;
натянутое на нее подпространство в силу полноты системы
совпадает с Z,2@, я), и потому вычеркивание элемента х не
сузило подпространства.
Пример 22. Последовательность {xk} (& = 0, 1, 2, ...)
неминимальна в L2 @, 1). Это вытекает из известной теоремы
Г. Мюнца, в силу которой любая система функций вида
#м* (& = 0, 1, 2, ...), [х = 0, полна в Z,2@, 1), если
расходится ряд
00
Для того чтобы система элементов {ф^} была минимальной
в данном пространстве «!р, необходимо и достаточно, чтобы
в этом пространстве существовала система {ч^}, биортого-
нальная к системе {ф^}, так что
(ф/>^Ь=| lf Jsskm C.173)
Всякий базис в пространстве § есть система, в этом
пространстве минимальная.
Бесконечная система {ф^}, Ф鈫!р, называется сильно
минимальной в §, если наименьшее собственное число матрицы
Я.ЧКФу.Ф*)!*!^? C-174)
ограничено снизу положительным числом, которое не зависит
от /г. Всякая сильно минимальная в некотором пространстве
система минимальна в этом пространстве.
Всякая ортонормированная в S& система сильно минимальна
в $: в этом случае все собственные числа матрицы Rn равны
единице при любом п.

3]
§ 7. ОБ УСТОЙЧИВОСТИ МЕТОДА РИТЦА
293
Теорема 20. Пусть А и В— операторы,
самосопряженные и положительно определенные в некотором
гильбертовом пространстве Н, и пусть все элементы
пространства НА принадлежат также и пространству Нв.
Если yk£HA(k—\y 2,...) и система {ф^} минимальна
{соответственно сильно минимальна) в Нв, то она
минимальна (соответственно сильно минимальна) и в НА.
Следствие 1. В условиях теоремы 20 система,
ортонормированная в Нв, сильно минимальна в НА.
Следствие 2. Если Л—положительно определенный
оператор, то система, минимальная (соответственно
сильно минимальная) в Н, будет также минимальной
(соответственно сильно минимальной) и в НА. В
частности, система, ортонормированная в И, сильно
минимальна в НА.
3. Предельные свойства коэффициентов Ритца. В
формуле (см. п. 3 § 2)
п
и» = 2 «аФл.
дающей выражение я-го приближенного по Ритцу решения,
коэффициенты ak на самом деле зависят еще и от л; в
соответствии с этим будем обозначать эти коэффициенты через
а^ и писать
"« = 2 «£%• C-175)
Теорема 21. Если координатная система минимальна
в Яд, то существуют пределы
а^ПтарК C.176)
П -» со
Если, кроме того, система, биортогональная в НАк
координатной, ограничена в метрике НА, то стремление к
пределу в формуле C.176) равномерное относительно k.
Теорема 22. Пусть координатная система сильно
минимальна в НА, и пусть ak F= 1, 2, . ..) суть пределы
C.176). Ряд
со
2Ы2

294 гл. ш. вариационные методы [4
сходится, тан: что последовательность
а = (а„ аа> ..., аю ап+1У ...)
есть элемент пространства /2; если положить
а<и> = (а<»>, а<»>, ...,<>, О, 0, ...),
то
цт ||a(w>—а||/2=0.
Последнее неравенство означает, что
ltmB|4n)-a*|4 2 |e*r} = 0.
4. Устойчивость метода Ритца. Допустим, что при
составлении системы Ритца C.124) каждое энергетическое
произведение [q>ki фу] вычислено с некоторой малой
погрешностью y£/ = Y/a» а свободные члены (/, ф.) той же системы
вычислены также с малыми погрешностями Оу. Вместо системы
C. 124) мы на самом деле получим следующую систему:
2 {fo*,<P/] + Y*Mn>'= (/,<!>,) + */ (У=1,2, ...,«). C.177)
k = l
Введем следующие обозначения: а^п\ а^п)\ 6<п>— векторы,
составляющие которых соответственно равны
а<»\ а(«>, ...,<л);
Гп—матрица с элементами ykJ (у, & = 1, 2, ♦.., п). В /z-мер-
ном унитарном пространстве матрица Г„ порождает
оператор, норму которого обозначим через ||ГП||; как известно1),
l|rj2< 2 ukj\\
Будем говорить, что система Ритца устойчива по
отношению к малым изменениям ее матрицы и столбца ее сво-
1) По терминологии, принятой в книге [94], величина || Г„ || есть
«третья норма» матрицы Гл.

4]
§ 7. ОБ УСТОЙЧИВОСТИ МЕТОДА РИТЦА
295
бодных членов, если существуют такие не зависящие от п
постоянные р и q, что при достаточно малых ||ГЛ|| и j|6(n)|
верна оценка
\\aW-a<*>\\*Zp\\Tn\\ + q\\6™\\;
напомним, что норма любого вектора t — {tx,t2, ...,tn) в
унитарном пространстве п измерений определяется формулой
Пусть координатная система сильно минимальна в НА,
и пусть А,>0— нижняя граница собственных чисел матриц
Ритца.
Если погрешности ykj настолько малы, что ||Гп||^А,р,
Р<1, то
\\а«У-а™\\<> ^%КП1ГЛ+У'11У">11 . (ЗЛ78)
Оценка C.178) означает, что верна следующая теорема.
Теорема 23. Если координатная система сильно
минимальна в ИА> то решение системы Ритца устойчиво
по отношению к малым изменениям ее матрицы и столбца
ее свободных членов.
Теорема 24 [109]. Если координатная система сильно
минимальна в НА, то приближенное решение по Ритцу
устойчиво по отношению к малым изменениям матрицы
системы Ритца и столбца свободных членов этой системы.
Поясним утверждение этой теоремы. Пусть
где коэффициенты а^У удовлетворяют системе C.177). Если
координатная система сильно минимальна в НА, а || Гп || и
|| б(Л) || достаточно малы, то существуют такие постоянные р1
и q„ не зависящие от п, что\ип— ип | <ра || Г„ ||+^ || 6{П) ||.
П р и м е р 23 [62]. Рассмотрим упругую пластинку в форме
кольцевого сектора; величины, характеризующие размеры
пластинки, обозначены на рис. 16. Пластинка подвержена
действию равномерного давления q; внутренний дуговой край
пластинки жестко закреплен, остальная часть края свободна.

296 гл. ш. вариационные методы [4
Через гиб обозначим полярные координаты и положим
1
0-
еп
0:
0 =
** а
еп
Обозначим еще через w прогиб пластинки, через D ее
жесткость и через w безразмерную величину
w =
Dw
qa2
функция w реализует минимум функционала
Ш(
S)'+(ff)'+2<'-
J d*w V .
9 d2w d2w
2 ~
a
dx dy
на множестве функций, обращающихся в нуль при Q = 0;
эта функция определялась по
методу Ритца, причем вычисления
производились дважды, с двумя
системами координатных функций.
Функции первой системы имели
вид
w£/=Q/+Itf> (/,/=0, 1,2, ...);
вторая система была получена из
первой следующим приемом орто-
гонализации: отдельно были
подвергнуты ортогонализации в
промежутке 0 ^ q <; q0 функции
ф. (р) = q1+2 и в промежутке
1 1
— Y^®^~2—ФУНКЦ«ИИ 'фу('д) = '&2/. Полученные таким
образом ортонормированные функции от одной переменной
обозначим через ф. (q) и 'фДФ); функции второй
координатной системы имеют вид
W// = 9l-@)*/(*)
Рис. 16.
(/,7=0,1,2,...).

4] § 7. ов устойчивости метода ритца 297
Можно доказать, что функции первой координатной
системы не сильно минимальны в энергетическом
пространстве нашей задачи; функции второй системы сильно
минимальны в том же пространстве.
Вычисления были проведены для пластинки, у которой
Q0 = 1,82; 0о = 48°. Было использовано 12 координатных
функций каждой координатной системы, именно были
использованы функции w(j с индексами i — 0, 1, 2, 3 и у= 0,1,2
из первой координатной системы и полученные из них
упомянутым выше процессом ортогонализации функции w{ -
второй координатной системы. Приведем значения
соответствующих функций (ft (q) и я|); ('&):
Ф„(д) = }/"92, %(q) = QV7(q'—|q2),
Ф2(е) = 84(е1-|е3+^е2),
t(*)=l, ^(^ = 6/5(^-1),
Вычисления производились на ЭВМ «Стрела»; эта
машина считает с девятью десятичными разрядами. В программе
были предусмотрены команды, позволяющие заменить в
элементах матрицы Ритца 1, 3 или 5 последних десятичных
разрядов нулями и тем самым внести определенную
погрешность в матрицу Ритца. При фактическом производстве
вычислений нулем заменялся только девятый десятичный
разряд. При этом самое решение системы Ритца, как точной,
так и содержащей погрешность, проводилось с достаточной
точностью, так что ошибками округления, по всей
видимости, здесь можно было пренебречь.
Приведем некоторые результаты вычислений. Обозначим
через 6д, бш, 8м соответственно относительные погрешности
в коэффициентах Ритца, прогибах, моментах в случае
применения первой координатной системы; для второй
координатной системы мы обозначим аналогичные величины через
бд, 8W> 8л*. Приведем табличку отношений ба/б0 и бл/б0,

298
ГЛ. Ш. ВАРИАЦИОННЫЕ МЕТОДЫ
[4
где 60=*10~7 есть верхняя граница относительной
погрешности элементов матрицы Ритца, в которых девятый
десятичный разряд заменен нулем.
/, 1
6<А
fyz/^o
0,0
875
0,195
1,0
3930
0,692
0,1
54 400
0,550
l.l
126 800
0,314
2,0
10 900
0,521
0,2
13 000
2,82
/, /
ба/б0
бЛ
2,1
34 700
0,67
1,2
16 900
0,47
2,2
20 200
0,595
3,0
23 600
39,7
3,1
58 000
2,13
3,2
22 900 j
0,957
Таким образом, при использовании первой, не сильно
минимальной координатной системы погрешности
коэффициентов Ритца чрезвычайно велики по отношению к
погрешности элементов матрицы Ритца—отношение этих
погрешностей есть величина порядка 10*—105. При
использовании второй, сильно минимальной координатной системы
названное отношение резко падает — оно меньше единицы,
за исключением двух случаев, когда 2<6fl/60<C3, и одного
случая, когда \j8Q = 39,7.
Из приведенных в статье [62] результатов видно, что,
например, на внешнем дуговом крае пластинки отношение
6о,/60 колеблется в пределах от 35,9 до 82,4, отношение
SmI&q — в пределах от 272 до 1520; отношения же 8wj80
и бм/60 изменяются в пределах от 0,10 до 0,23 и от 1,37
до 2,95 соответственно.
Приведенные здесь результаты показывают бесспорное
преимущество сильно минимальных координатных систем
перед не сильно минимальными.

6] § 7. ОБ УСТОЙЧИВОСТИ МЕТОДА РИТЦА 299
б. О числе обусловленности матрицы Ритца. В
предшествующих пунктах настоящего параграфа предполагалось,
что система Ритца решается точно, так что погрешности
возникают только при составлении этой системы. Однако
при решении системы неизбежны ошибки округления. Если
координатная система только сильно минимальна в HAl то
число обусловленности матрицы Ритца, равное отношению
ее наибольшего и наименьшего собственных чисел, может
возрастать до бесконечности вместе с п и решение системы
Ритца может оказаться неустойчивым по отношению к
ошибкам округления. Очевидно, число обусловленности матрицы
Ритца будет ограничено независимо от я, если ее
собственные числа будут ограничены сверху и снизу
положительными числами.
Укажем условие, при котором только что
сформулированное свойство имеет место. Наряду с данным оператором А
рассмотрим еще один положительно определенный
оператор В, Пусть оба оператора таковы, что пространства НА
и Нв состоят из одних и тех же элементов; для этого
необходимо и достаточно, чтобы существовали такие
постоянные с1>0 и с2<Соо, что
Если при решении уравнения A\i—f принять за
координатную любую ортонормированную и полную в Нв систему, то
собственные числа матрицы Ритца будут ограничены сверху
и снизу теми же положительными числами сх и с2; число
обусловленности матрицы Ритца ограничено величиной cjc^
6. Сходимость невязки к нулю. Если уравнение
Аи=/У где А—положительно определенный оператор,
действующий в данном гильбертовом пространстве Я,
решается по методу Ритца и ип есть приближенное по Ритцу
решение этого уравнения, то в общем случае Аип не стремится
к / при п—юо. Это ясно хотя бы потому, что
координатные элементы, а с ними и приближенное решение ип не
обязаны входить в область определения оператора Л, а тогда
выражение Аип может просто оказаться лишенным смысла.
Но и в том случае, когда координатные элементы cpft G £> (^)i
равенство \imAun = f, вообще говоря, не имеет места.

300
ГЛ. III. ВАРИАЦИОННЫЕ МЕТОДЫ
[1
Можно доказать, что если при любом выборе координатной
системы, элементы которой принадлежат области
определения D (А) оператора Л, имеет место упомянутое выше
равенство, так что «невязка» Аип—/ стремится к нулю при
п—*оо, то оператор А необходимо ограничен.
Однако при специальном выборе координатной системы
невязка может стремиться к нулю и тогда, когда оператор А
не ограничен.
Один такой способ выбора дает следующая
Теорема 25 [69], [98а]. Пусть А и
В—положительно определенные самосопряженные операторы такие, что
D(A) = D(B) и имеет место неравенство
\{Аи, Ви)\^т\\ Аи\\2, т = const>0;
пусть последовательность собственных элементов
оператора В полна в исходном пространстве И. Если
собственные элементы оператора В принять за координатные
при построении приближенного решения уравнения Аи=/,
то невязка Аип—/ стремится к нулю при я—>оо.
§ 8. Подбор координатных функций
1. Построение полной координатной системы. При
выборе координатной системы следует прежде всего
позаботиться о ее полноте в энергетическом пространстве. В этом
смысле оказывается полезной следующая
Теорема 26. Пусть q>n£D(A) (п= 1, 2, ...), где А —
положительно определенный оператор, и пусть
последовательность {Ацп} полна в данном гильбертовом
пространстве Н. Тогда последовательность {фл} полна в
энергетическом пространстве НА.
При установлении полноты системы координатных функций
полезно и такое замечание: если А и В—положительно
определенные операторы и пространства ИА и Нв состоят
из одних и тех же элементов, то любая система, полная
в Нв, полна в #л, и наоборот.
Пример 24. Рассмотрим уравнение
Л« = -^(р(*)|-:)+?(*)« =/(*), и@) = иA) = 0,
где р {х) ^ р0 = const ;> 0, q (х) ^ 0.

1] § 8. ПОДБОР КООРДИНАТНЫХ ФУНКЦИЙ
Положим
Ва==~ё> «@) = «A) = о.
Пространства ИА и Нв состоят из одних и тех же
элементов, а именно из функций, для которых и @) = и A) = 0 и
1
С u'2(x)dx<. oo;
о
поэтому полноту достаточно проверять в Нв. Но полнота
системы функций {фл(*)} в Ив есть полнота системы
производных {фп (х)} в подпространстве функций,
ортогональных к единице, пространства L2@, 1). Отсюда легко
заключить, что функции
Фя(*)«*лA-*) (л = 1,2, ...)
образуют систему, полную в НА.
Пример 25. Рассмотрим задачу
и @) = и' @) = ... = «<*-*) @) = 0,
a(l) = w' A)= . _ =u(s-J) A) = 0.
Пусть ps(x) ^p0 = const >>0, а остальные коэффициенты
jdx (л:) таковы, что оператор Л при краевых условиях
задачи положительно определенный.
Система координатных функций
фяМ = *и+'A-*)8 (л=0,-1,2| ...)
полна в НА.
Пример 26. Пусть со (д^, хг) ... , хт) = 0— уравнение
границы S области Q. Допустим, что со>0 внутри Q и что
эта функция и ее первые производные непрерывны в Q + 5.
Система координатных функций
w (*i> хг> • • • >xm)xi х*~ • • • хт

302 гл. ш. вариационные методы [2
в которых nl,n2f . . . , пт пробегают независимо все целые
значения от нуля до бесконечности, полна в НА, где
есть невырождающийся положительно определенный
эллиптический оператор.
Пример 27. В примере 24 можно в качестве
координатных выбрать собственные функции оператора Ви = — j-g ,
и @) = и A)==0. Это суть функции slnnnx (/2=1,2,...).
В примере 26 можно за координатные выбрать
собственные функции оператора Лапласа для области Q.
2. Требования к рациональному выбору координатной
системы. Утверждения настоящего пункта основаны на
результатах § 7.
Если дело идет о построении грубого приближения по
Ритцу, с использованием небольшого числа координатных
элементов, то достаточно подчинить координатную систему
следующим требованиям:
1) Все элементы координатной системы принадлежат
энергетическому пространству данной задачи. В частности,
если дело идет о краевой задаче для дифференциального
уравнения или системы дифференциальных уравнений, то
координатные функции должны: а) иметь всевозможные
обобщенные производные порядка =^&, где k—наивысший
порядок производных, входящих в интеграл энергии (или,
что то же, в выражение квадрата энергетической нормы);
б) сообщать интегралу энергии конечное значение; в)
удовлетворять всем главным краевым условиям данной задачи.
2) Взятые в любом конечном числе, координатные
элементы линейно независимы.
3) Координатная система полна в энергетическом
пространстве данной задачи.
Перечисленных требований недостаточно, если
желательно построить приближенное по Ритцу решение с малой
погрешностью. Для этого необходимо использовать большое
число координатных элементов, а тогда следует позаботиться
об устойчивости как процесса решения системы Ритца, так
и самого приближенного решения. Желательно также, если

3] § 8. ПОДБОР КООРДИНАТНЫХ ФУНКЦИЙ
это возможно, добиться улучшения сходимости
приближенного решения к точному; так, например, желательно
добиться того, чтобы невязка приближенного решения
стремилась к нулю. Целесообразно поэтому по возможности
добиваться того, чтобы координатные элементы обладали
следующими свойствами:
4а) Координатная система сильно минимальна в
энергетическом пространстве Нл; в этом случае решение системы
Ритца для уравнения Аи=/У а также само приближенное
решение устойчивы.
46) Два положительно определенных оператора А и В
назовем полусходными, если их энергетические пространства
НА и Нв состоят из одних и тех же элементов. Пусть
последовательность {yk} полна и ортонормирована в Ив\ если
эту последовательность принять за координатную для
уравнения Au=fy то устойчивы и решение системы Ритца,
и приближенное по Ритцу решение этого уравнения, а число
обусловленности матрицы Ритца ограничено независимо от л.
4в) Два самосопряженных положительно определенных
оператора А и В назовем сходными, если их области
определения совпадают, так что D(A)—D(B). Допустим, что
имеет место неравенство
| (Ли, Ви)\^т || Ли ||2, т = const > О,
и система собственных элементов оператора Ву которую мы
будем считать нормированной в Яв, полна в Нв. Тогда
эта система полна и в НА; если ее принять за
координатную для уравнения Ли—/, то как решение системы Ритца,
так и приближенное по Ритцу решение устойчивы, число
обусловленности матрицы Ритца ограничено независимо от
п и при п—► оо невязка Аип—/ стремится к нулю.
3. Одномерные краевые задачи. В этом пункте
приводится несколько примеров выбора координатных систем
для решения краевых задач, связанных с обыкновенными
дифференциальными уравнениями; эти примеры, разумеется,
не исчерпывают всех возможных случаев. Во всех примерах
настоящего пункта исходным гильбертовым пространством
является пространство L @,1).

304 гл. т. вариационные методы [3
Пример 28. Рассмотрим дифференциальное уравнение
второго порядка
-^(pW^) + ?W« = /(x) C.179)
при краевых условиях
и@) = мA) = 0. C.180)
Мы допускаем, что функции р(х), р' (л:), q{x) непрерывны
на отрезке [0,1], р(х) ^р — const >0, q(x)>—A,t, где
^ — наименьшее собственное число оператора C.179), C.180)
при #(л;)=0. Сходным с оператором данной задачи являет-
d2
ся оператор В= — -г-^ при тех же краевых условиях C.180);
его собственные функции, нормированные в Нв, суть
VnM = ^sinnnx (//-1,2, ...); C.181)
если эти функции принять за координатные для задачи
C.179), C.180), то справедливы утверждения 4в) п. 2.
Пример 29. Рассмотрим теперь уравнение C.179) при
краевых условиях
и@) = 0, «'A-) = 0. C.182)
Для оператора задачи C.179), C.182) сходным является
дифференциальный оператор — j-^ при краевых условиях
C.182); его собственные функции, нормированные в метрике
соответствующего этому оператору энергетического
пространства, суть
. ч 2]^2 . Bп — \)пх . 1 п ч /о ioov
Уп(*)~ B„-i)jtsin T~ (^=1,2,...); C.183)
применение этих функций в качестве координатных
гарантирует справедливость, утверждений 4в) п. 2.
Пример 30. Рассмотрим уравнение C.179) при краевых
условиях
в'@) = и'A) = 0; C.184)
коэффициент ^(л:) будем считать таким, чтобы оператор
задачи C.179), C.184) был положительно определенным;
для этого достаточно, например, чтобы q(x) было строго

3] §8. ПОДБОР КООРДИНАТНЫХ ФУНКЦИЙ 305
положительным. Для упомянутого оператора сходным будет
d2
положительно определенный оператор — -r-2-\ I
{I—тождественный оператор) при краевых условиях C.184).
Нормированные в соответствующем энергетическом пространстве
собственные функции этого оператора суть
Фо(л:)==1>Ф«М= V n2J* + \cosnjlx (л==1'2» ...); C.185)
их применение в задаче C.179), C.185) гарантирует
справедливость утверждений 4в) п. 2.
Пример 31. Пусть дифференциальное уравнение C.179)
решается при краевых условиях
а'@) — сш@) = 0, e'O) + Ptf(l) = 0, а>о, р>0. C.186)
Сходным в этом случае является оператор —-г-2 ПРИ тех же
условиях C.186). Однако построение собственных функций
сходного оператора связано с решением некоторого
трансцендентного уравнения и потому затруднительно. Если это
затруднение преодолеть не удастся, то нетрудно построить
все же оператор, полусходный с оператором C.179), C.186).
Таков, например, рассмотренный в примере 30 оператор
d2
— -7-5 + / при краевых условиях C.184); если систему C.185)
его собственных функций принять за координатную при
решении задачи C.179), C.186), то будут верны
утверждения 46) п. 2. Полусходным с оператором C.179), C.186)
является также оператор
Ви = -ё> "'@)-«@) = 0, «'(!) = 0, C.187)
которому соответствуют энергетические производные и норма
1
[и, v]B = u @) v @) + J и' (х) v' (х) dx,
0
1
C.188)
Нетрудно построить последовательность функций, ортонор-
мированную и полную в метрике C.188); такова, например,

306
ГЛ. III. ВАРИАЦИОННЫЕ МЕТОДЫ
[3
система
1 У2 sin ях У2 sin 2nx |/*2 sin плх /Q 1 QQV
1,*, JJ . 2S '••'» м '••• ^Л8у)
Если функции C.189) использовать как координатные при
решении задачи C.179), C.186), то будут справедливы
утверждения 46) п. 2.
Пример 32. На практике представляет интерес и тот
случай, когда функция р(х) разрывна (чаще всего, кусочно-
непрерывна). Допустим, что функция р(х), будучи
разрывной, удовлетворяет неравенствам р*^р(х)^рг> где р и
рх — положительные постоянные. Применение координатных
функций, указанных в примерах 23 — 31, гарантирует
справедливость утверждений 46) п. 2.
Пример 33. Рассмотрим случай вырожденного
уравнения. Пусть в уравнении C.179)
p(x) = x*Pl(x), C.190)
где 0<С<х<2, а функция рх(х) ограничена сверху и снизу
положительными числами. Уравнение C.179) будем решать
при следующих краевых условиях:
e@)-«(lH0f 0<а<1, \
иA) = 0, 1<а<2. / (<ЗЛ91)
Сходным с оператором C.179), C.191) будет в данном
случае оператор, определяемый дифференциальным выражением
Ви — — Т~\Х*1Г) ПРИ тех же Условиях C.191);
собственные функции этого оператора суть
1-а , а х
1—а
V J lZ а| C.192)
здесь Yv,« — я-й положительный корень функции Бесселя
7v(x), a постоянная сп должна быть выбрана так, чтобы
|фл|5=1. Приведем значение этой постоянной:
с" - /£ { |^ [ж^ Vv(Y.. .*>] '*}-*;
знак плюс берется при а<1, знак минус — при а>1.

4] § 8. ПОДБОР КООРДИНАТНЫХ ФУНКЦИЙ 307
4. Двумерные краевые задачи. Собственные функции
оператора В = — А (Д— оператор Лапласа) для единичного
круга при условии, что на окружности круга упомянутые
функции обращаются в нуль, имеют вид
Ф*.„(*. y) = cktnJk(yktnr)^kB
(* = 0, 1, 2, .. . ; л= 1, 2, 3,.. .) л; = г cos 9, y = rs\nQ;
C.193)
коэффициент ckyn таков, что |фл> п\в=\.
Рассмотрим задачу
- X щ{А^щ)+Са^^х^ *i = *. ^,=^C.194)
и |s =0. C.195)
Здесь 5—граница конечной области Q; мы примем, что эта
граница достаточно гладкая, так что угол между нормалью
и осью х имеет по крайней мере две непрерывные
производные. Далее, примем, что A,k и С суть функции от л: и
у такие, что дифференциальный оператор C.194)
эллиптический невырожденный, а оператор задачи C.194), C.195)
положительно определенный; примем также, что функция С
непрерывна, а функции Ajk непрерывно дифференцируемы
в замкнутой области Q = Q -f- S.
Допустим, что преобразование
* = Ф(*\ /), y = W,f) C.196)
взаимно однозначно преобразует единичный круг К
плоскости (х'Ушу') в область Q плоскости (лг, у), причем
функции C.196) дважды непрерывно дифференцируемы,
а их якобиан
г Р(*. У)
D(x', у')
ограничен сверху и снизу положительными постоянными.
Преобразование C.196) переводит задачу C.194),
C.195) в следующую:
- Ё £r(A'ikdir)+CJtt=Jf' Xi==x'> х>=у'> (зл97)
и|г = 0. C.198)

308
ГЛ. III. ВАРИАЦИОННЫЕ МЕТОДЫ
D
Здесь Г—единичная окружность в плоскости (#', у') и
чгч дх- dxk
Aik = J Zu Ar*lhrihr:
r, s = i
dxr dxs
Оператор задачи C.197), C.198) сходный с оператором
В = — Д} упомянутым в начале настоящего пункта;
применение функций C.193) в качестве координатных
гарантирует справедливость утверждений 4в)
п. 2.
Можно указать некоторые случаи,
когда преобразование C.196)
строится просто.
1) Известно конформное
преобразование круга на область Q.
2) Пусть область Q такова, что
прямые, параллельные оси х,
пересекают границу S не более чем в двух
точках. Расположим ось х посередине
между параллельными ей опорными
прямыми (рис. 17), расстояние между
которыми обозначим через 2с. Прямая
у = у0У |^0|<<с, пересекает контур S в точках, абсциссы
которых обозначим через а (у) и $(у). Положим
Рис. 17.
x'=*xp{y)—v(y),
, 1
У =7*
где
u(v)= 2/*-уЯ у(у) = ^у) + а{у) V'c2-y\
C.199)
C.200)
Пусть контур 5 таков, что функции C.200) имеют
непрерывные вторые производные при \у\^с; тогда функции
C.199) осуществляют взаимно однозначное и дважды
непрерывно дифференцируемое отображение области Q на
единичный круг.
Пример 34. Если Q — внутренность эллипса
г~ГЬг Ч

4] § 8. ПОДБОР КООРДИНАТНЫХ ФУНКЦИЙ 309
ТО \1(у):
v(y) — 0 и преобразование имеет вид
X
а
У_
b
Пусть контур 6* кусочно-гладкий. В этом случае
оператор задачи C.194), C.195) по крайней мере полусходный
с оператором задачи Дирихле; поэтому, взяв в качестве
координатных собственные функции задачи Дирихле для
оператора Лапласа и соответствующей области, мы обеспечим
выполнение утверждений 46) п.,2.
По-прежнему под оператором A j^y
будем понимать оператор задачи
C.194), C.195) для
соответствующим образом
преобразованной области, а под оператором
В—оператор—Д для той же
области.
3) Пусть область Q имеет д"
вид, изображенный на рис. 18.
Тогда преобразование C.199), Рис. 18.
C.200) (предполагаем, что
функции C.200) имеют непрерывные вторые производные)
переводит область Q в полукруг, для которЬго собственные
функции оператора Лапласа
суть
Ск,п'к{Ук,пГ)йпМ
(*=1, 2, ...), C.201)
с^ п—нормирующий
множитель.
4) Область рисунка 19
^ можно в известных условиях
отобразить на круговой
сектор с центральным углом |3.
Допустим, что 0<р<^-и что прямая у = const
пересекает границу области Q только в двух точках x = ky и
х — а(у), & = ctgp. Преобразование
X'^{ky + (x-ky)^l=^}, у^у C.202)
Рис. 19.

310
ГЛ. III. ВАРИАЦИОННЫЕ МЕТОДЫ
[4
переводит Q в круговой сектор рис. 20; мы допустим при
этом, что отношение
C.203)
непрерывно дифференцируемо
при 0 ^y^b sin p.
Собственные функции оператора
Лапласа для сектора рис. 20 суть
chyn Jknl Укп г) sin
Р
Рис. 20.
(А=1, 2,... ; п-
C.204)
1, 2,...).
Пример 35. Для прямолинейного треугольника (рис. 21)
с острым углом р
, ч , Ь cos P — а
а(у) = аА ;—г-о— Ы\
Ki" ^ 6 sin Э у*
дробь C.203) принимает вид
Ь sin Р УЬ2—у2—у ctg p
а Ъ sin p—у
и бесконечно дифференцируема
при 0 <;t/«^ b sin p.
5) Иногда целесообразно
отобразить область Q на
прямоугольник, для которого
собственные функции оператора Лапласа хорошо известны: если
прямоугольник задан неравенствами О^лг'^а, 0 ^у' ^Ь,
то упомянутые собственные функции, нормированные в
метрике интеграла Дирихле, имеют вид
1
п ifk2 . п2
V ai + F*
. knx . nny ,. 1 п
Sin Sin—77" \k, /Z=l, 2,.
a b v ' ' '
.). C.205)
Так, пусть Q имеет вид трапеции (рис. 22), каждая из
«боковых сторон» которой пересекается с прямой у = const
только в одной точке; пусть а (у) и р (у) — абсциссы точек
пересечения. Примем, что эти две функции дважды непре-

4] § 8. ПОДБОР КООРДИНАТНЫХ ФУНКЦИЙ 311
рывно дифференцируемы. Преобразование
X =;
-а (У)
-<*(*)'
У=тУ
C.206)
22 на квадрат 0 ^х,у^\.
1 с
ц.
1
ь
_1_
2?
Рис. 22.
отображает область рис.
Область рис. 23
можно сперва отобразить на
область рис. 22, введя
координаты xltyv где
У г = arctg -| .
Пример 36. В
квадрате 0<;лг, г/^1
рассмотрим уравнение
— &и—9(х2 + у2)и =
~~ \дх* + ду2)
-9(x2 + y2)u=f(xt </)
при краевом условии и|5 = 0, где 5—контур квадрата. Оператор
этой задачи положительно определенный (см. п. 9 § 4) и сходный
с оператором —Да, и\$ — 0. Неравенство теоремы 25 в данном
случае выполняется. В качестве
координатных функций целесообразно
взять собственные функции
последнего оператора, нормированные
в его энергетической метрике; по
формуле C.205) это будут функции
2
— - sin knx sin пли
nVk2-\-n*
(k} я = 1, 2, . . .).
Число обусловленности
матрицы Ритца при таком выборе
координатных функций ограничено
независимо от ее порядка (см, п. 5
§ 7); оценим границу этих чисел,
для чего оценим постоянные сх и cv входящие в неравенство п. 5 §7.
Обозначим через А оператор нашей задачи, через
В—оператор — Д при краевом условии ц|5 = 0. Имеем:
Рис. 23.

312 гл. ш. вариационные методы [4
Отсюда |«и^1я и» следовательно, можно положить с2=1.
Далее, наименьшее собственнное число оператора В, как хорошо
i2
\и
В
известно, равно 2я2, поэтому, если «£//#> то у—^^2я2, или
и **1'2
1 1
я
u*dxdy^=-tlu\*B.
2я
о о
Теперь
о о
поэтому
11 11
9 И {x'+yl) utdxdy<1* fI иЫхс1у<2-г\и\гв ,
О О
l«fia-(i-5)l»6
и можно взять с« = — ]Лгс2—9. Число обусловленности матрицы
я
Ритца не превосходит величины
с, я
]/~я2-9
<4,5.
Если систему Ритца подвергнуть преобразованию C.33), то ее
можно решать итерациями, которые при любом порядке системы
сходятся, как прогрессия с знаменателем
я + У я2 —9
Для матриц Ритца конкретных порядков результаты могут
оказаться и лучшими. Возьмем, например, матрицу б-го порядка,
которая получится, если мы ограничимся координатными функциями:
2 2
ф! = 7== s*n пх s*n пУ> Фг — 7= sin пх sm 2я#,
яУ 2 як 5
2 2
Ф, = —y=- sin 2ял: sin я#» Ф4 = —7= sin nx sin Зл#,
яУ 5 яУ 10
1 2
ф! = —jr=_ sin 2я* sin 2я#, ' ф6 = —7= sin ^я* sin л#»
яУ 2 яУ 10
для которых /г + п^4. Матрица Ритца тогда имеет следующий
вид (см. стр. 313):

41
§ 8. ПОДБОР КООРДИНАТНЫХ ФУНКЦИЙ
313
V
к
1ю
СО
|СО
+
Е
1°
V
сп
00
К
1°
V
СП
ICN
СО
I—I О
+
г*
со
к
1*
СО
со
,~~'
1°
£
en
i
<о
*
К
1°
О)
1**
w|e
s" Г*
- К
l^f
1
Н<о
-
1-
00
СО
*-'
«*
К
|<N
V
Ю
(N
О
|ю
1 К
ICO
1
-1^
"+"
ч*
к
|о
1—1
V
СП
о
1ю
1Л
^
32я:
СО
^
О
СО
•~"'
е
1°
V
СП
(N К
1Ю
10 СО
|С0 С
1
^
"+f
оо
о
00
<*
£
|<N
ю
см
со
ТГ
£
|ю
СО
5
41
1°
V
СП
"к
1°
СП
:>
||ю

314 ГЛ. Ш. ВАРИАЦИОННЫЕ МЕТОДЫ [1
Нетрудно видеть, что в этом случае итерации сходятся и для непре-
образованной системы Ритца, и притом довольно быстро.
Действительно, диагональные элементы матрицы Ритца все больше единицы, а
сумма модулей остальных элементов любой строки не превышает величины
1 22
^= < 0,0127.
я*
§ 9. Метод Бубнова — Галёркина
1. Основы метода. Пусть дано уравнение Ли—/=0,
где Л — линейный оператор, действующий в некотором
гильбертовом пространстве Н; мы не предполагаем об операторе Л
ничего, кроме его линейности.
По методу Бубнова — Галёркина выбираем
последовательность элементов фп £ D (А) и ищем приближенное решение
в виде п
»B=Sw C-207)
коэффициенты ak определяем из условия, чтобы левая часть
данного уравнения после подстановки в нее ип вместо и
оказалась ортогональной к элементам ф1? ф2, ... , ф„. Это
приводит к системе уравнений
Иф„ <Pl) а1 + Иф.» Фх) а2 + ' ' • + Мфя» %) ап = (/, Фх),
Ифц Ф«) ai + Иф2, ф2) аш + ... + (Лф„, ф2) ап = (/, ф2),
Ифц Фя) ^l + Иф«» Фя) а2 + • . • + (ЛФл> Фя) «Я = (/, Фя)>
C.208)
по форме совпадающей с системой C.24'). Отсюда сразу
следует, что метод Бубнова — Галёркина совпадает с
методом Ритца, если Л — положительно определенный оператор.
Метод Бубнова—Галёркина можно применять и в задаче
0 собственных числах. Так, если требуется найти
собственные числа уравнения Ли—Хи = 0, то по методу Бубнова —
Галёркина их приближенные значения находятся как корни
уравнения
(Aq>lt <Pi)-M<Pi. <Pi) <Лф2, <Pi)-& (Ф2, <Pi) ... (Лфп. Ф^-^ (Фп. <Pi) I
(Ауи ф2)~Мф1. Ф2) (^Фа. ф2)-Я(ф2> ф2) . . . (Ац>п, ф2)~Мфп. фз) __0
1 (Лф!, Фп)-^ (Ф1. Фп) Ифя, Фп)-^ (ф2. Фп) • • • Ифп, фп)-Я (Фп. Фп) I
C.209)

3] § 9. МЕТОД БУБНОВА—ГАЛЁРКИНА 315
Приближенные значения собственных чисел более общего
уравнения Ли—ХВи = 0 находятся как корни уравнения
I (Aq>lt фО-МВчч фО (Лф2, Ф^-МВфа. ц>г) , . . (Лф„, ф^-Я (Вфп. фО I
ИФ1, Фа)-*< \^Ф1, Фа) (Лф2> Фа)-Я Шф2, фа) . . . (Лфт ф2)-Я (Вфп, ф2) I Q
I (Лфр Фп)-^(Вф1» Фп) ИФа. Фп)-Ь (Вфа. Фп) • • • ИФп. Фп)-Ь (Вфп, фп) |
C.210)
2. Достаточный признак сходимости. Предположим,
что оператор А имеет вид Л = Л0 + В, где Л0 —
положительно определенный в данном гильбертовом пространстве Н
оператор, и D(B)zdD(A). Допустим еще, что оператор А~1В
вполне непрерывен в энергетическом пространстве
Покоординатные элементы ф„ выберем так, чтобы: 1) они
входили в D(A0); 2) взятые в любом конечном числе, они
были линейно независимы; 3) их совокупность была полна
в Яд,. В перечисленных условиях верны следующие теоремы.
Теорема 27. Приближенные решения уравнения,
построенные по методу Бубнова—Галёркина, существуют
при достаточно больших п и сходятся в норме
пространства Нд0 к точному решению данного уравнения, если
это последнее разрешимо и имеет только одно решение.
Теорема 28. Приближенные собственные числа
уравнения А0и—ХВи = 0, построенные по методу Бубнова —
Галёркина, сходятся к соответствующим точным
значениям этих чисел.
3. Применение к задачам математической физики. Мы
перечислим здесь некоторые задачи, к которым применимы
теоремы 27 и 28.
Уравнение
при краевых условиях
u{a) = u'{a)=:...=u{s-1){a)^0i |
u(b) = u'(b)=...=u<s-l>(b) = 0 f C,212)
допускает применение метода Бубнова — Галёркина, если
р(х)^р0, где р0 — положительная постоянная и
В—дифференциальный оператор порядка ^2s—1 с ограниченными
коэффициентами.

316
ГЛ. III. ВАРИАЦИОННЫЕ МЕТОДЫ
[4
Метод Бубнова — Галёркина применим к невырождаю-
щемуся уравнению эллиптического типа
-ZAJ>l>tt + ZBj& + Cu=№ C-213)
при краевых условиях задачи Дирихле
u\s=Q C.214)
или смешанной
т
2 Ajk£™s\y> xk) + au
j.k=i S
= 0; C.215)
задача Неймана (a = 0) не представляет исключения.
Приближенные собственные числа, построенные по методу
Галёркина, для уравнения
(-^&(р(^)-Ш = о
при краевых условиях C.212) сходятся к соответствующим
точным собственным числам, если р(х) и В удовлетворяют
тем же условиям, что и в уравнении C.211). То же верно
для собственных чисел уравнения
при краевых условиях C.214) или C.215).
4. Видоизменение метода в случае естественных
краевых условий. Пусть по-прежнему А = А0-{-В, где Л0 и В
удовлетворяют условиям п. 2. Предположим дополнительно,
что D(B)z)HAo, так что оператор В определен на всех
элементах пространства НЛо. В этом случае необязательно брать
координатные элементы из области D (AQ) определения
оператора А достаточно, чтобы они принадлежали
пространству НАо. В применении к задачам математической физики
это означает прежде всего, что координатные элементы
могут не удовлетворять естественным краевым условиям.
Система уравнений для коэффициентов ak, входящих в

5] § 9. МЕТОД БУБНОВА—ТАЛЁРКИНА 317
формулу C.207), теперь пишется следующим образом:
{[Фп <Pi] + (APi. ФЛК + КФг ФгЖ^ фОК+т-
{[Ф1. Ф.ЖДфп Ф2)К + {[ф2> Ф»]+(Яф„ Ф.Ж+---
•••+{[ф»> Ф,]+(ДФя. Ф2Ж=(/, Ф2)>
{[Фх> фя] + («Р1, ф„Ж + {[ф«. Ф„]+(Яф2, Ф„Ж+ —
- + {[ф«> ФиЖ^Ф*' ФпЖ=(/> Фп)-
Точно так же для собственных чисел уравнения Л0и—кВи = 0
вместо C.210) получается следующее уравнение:
[<Pt. Ф1] -^ (Bq>v Ф0 [ф2, фЛ-fc (Вф2, ф4) ... [фя, ф!] -Я (Вфл. Ф1> I
[ф1. фЯ] -Я,(Вф!, фа) [фя. ф2]-Я(Бф2, ф2) ... [фл, ф2] -А, Eф№, фа) _Q.
[ф|. ФиЬМВфо ф„) [фа, Фм]-А.(Вф2, фп) ... [ф№, ф»]-Д.(Вфп, фп) I
квадратные скобки означают энергетическое
произведение в НАо.
5. Обобщение метода Бубнова — Галёркина
(проекционный метод). Пусть дано линейное уравнение
Лв=/, C.216)
где и£Ех, f£E2, E1 и Е2 — некоторые банаховы
пространства и Л — оператор, действующий из Ех в Ег. Зададим
последовательность подпространств Ln размерности п, где
п=\, 2, ..., причем LncD (Л)с:Е1 при любом п. Зададим,
далее, последовательность /z-мерных подпространств МпаЕ2,
и пусть Рп — оператор проектирования из пространства Е2
в подпространство Мп. Проекционный метод состоит в том,
что точное уравнение C.216) заменяется приближенным
уравнением
PnAun^PJ, un£Ln. C.217)
Очевидно, проектор Рп имеет вид
k = i
где ifj, а|?2, ..., я|)„—базис подпространства Мп, a lk{u) —
линейные ограниченные в Е2 функционалы. Если ф1} ф2, . . ., фп
есть базис для подпространства Lm то ип имеет вид C.207)

318 гл. ш. вариационные методы [5
и уравнение C.217) сводится к линейной алгебраической
системе
3'уИф*К = '/(/) С/=1, 2 л); C.218)
k=i J J
при такой записи нет необходимости явно указывать
подпространство Мю достаточно указать функционалы /,.
Пример 37. Обычный метод Бубн ова— Г а
лерки на. Пусть Е1 = Е2=.Н, где Н—сепарабельное
гильбертово пространство. Выберем в нем бесконечную систему линейно
независимых координатных элементов ф1? ф2, ..., и пусть
Mn — Ln есть подпространство, натянутое на фх, ф2, ..., фл.
Тогда система C.218) совпадает с системой C.208).
Пример 38. Обобщение Г.И.Петрова.
По-прежнему пусть Е1=Е2 — Н. Введем в рассмотрение две
последовательности {фп} и {г|)п} элементов пространства Я такие, что
элементы фх, ф2, . .., фл, так же как и элементы tyv г|;2, . . . ,af)n,
линейно независимы при любом п. Пусть Ln и
Мп—подпространства, натянутые соответственно на элементы фи ф2, ..., ф^
и я^, я|;2, ..., \j)„. В этом случае система C.218)
принимает вид
(Ар,, г|\К + Иф2, Уг)аш+...+{А<рп, г|I)ая = (/, я|\),
Ифр ФйК + Иф„ *„)«,+ ••. +Иф„, W *„ = (/, *„).
C.219)
Иногда полагают tyn = Byni где Б—подходящим образом
выбранный оператор; в этом случае говорят о методе
моментов. При В= А мы приходим к методу наименьших
квадратов.
Пример 39. Метод разделения области. Пусть
El = E2=L2 (Я), где Q — область /я-мерного евклидова
пространства. Подпространства Ln построим так же, как в
примерах 37 и 38. Разобьем теперь область Я на п
подобластей Я1? Q2, ..., Я„ и обозначим через \рл (л:)
характеристическую функцию области Qk1 т. е. функцию, равную единице при
л;£Ял и нулю при x£Qk. За Мп примем подпространство,
натянутое на г^, я|э2, . ..,г|эп. В этом случае система C.218)

1] § 10. ВАРИАЦИОННЫЕ МЕТОДЫ В НЕЛИНЕЙНЫХ ЗАДАЧАХ 319
сводится к следующей:
п
£Х $A<tkdx= [fdx (y=l, 2, ..., п). C.220)
Пример 40. Метод коллокации. Пусть Л —
дифференциальный оператор порядка s, Ех = Os) (Q), E2 = C {Q). Выберем
последовательность функций ф1? ф2, ..., удовлетворяющих
всем краевым условиям задачи; как обычно, потребуем, чтобы
при любом п функции ф1? ф2, . . ., фи были линейно
независимы. Натянутое на ф15 ф2, ..., фп подпространство примем
за Ln, тогда ип имеет вид C.207). В области Q выберем
теперь п точек glf g2, ..., %п и положим lj(u)-=u (£у).
Система C.218) в данном случае имеет вид
2«*Иф*)~*,=/F/) (/=1, 2, .... п). C.221)
§ 10. Вариационные методы в некоторых
нелинейных задачах
1. Общие теоремы. Приводимая ниже теорема 29
выделяет класс нелинейных уравнений, решение которых можно
заменить решением некоторой вариационной задачи.
Теорема 29. Пусть Р—нелинейный, вообще, говоря,
оператор, действующий в вещественном гильбертовом
пространстве Н и определенный на линейном множестве М,
плотном в И, и пусть ищется решение уравнения
Ри=/, /б Я. C.222)
Пусть оператор Р удовлетворяет следующим условиям:
1) РО=0; 2) дифференциал Гато P'{u)h существует для
любых ut h£M, линеен относительно h и, как элемент И,
непрерывен при фиксированном h в любой плоскости двух
измерений, содержащей точку и; 3) при любом и£М one-
ратор Р' (и) симметричен и положителен, так что при
(P'(u)hxi h%) = {h„ Pf(u)h,)y
[P'{u)hy ft)>0, h^0.

320
ГЛ. III. ВАРИАЦИОННЫЕ МЕТОДЫ
[2
Если при перечисленных условиях существует решение
уравнения C.222), то это решение единственно и
реализует минимум функционала
Ф (и) == J (Р/в, в)Л —(/, и). C.223)
О
Обратно, если существует элемент множества М,
реализующий минимум функционала C.223), то этот
элемент удовлетворяет уравнению C.222).
Теорема 29 устанавливает эквивалентность двух задач
о разрешимости уравнения C.222) и о минимизации
функционала C.223), но не утверждает существования решения
ни той, ни другой задачи. Условия существования решения
вариационной задачи и некоторые свойства решения вытекают
из следующих теорем.
Теорема 30. Пусть выполнены условия 1)—3)
теоремы 29, и пусть, кроме того, существует такая
постоянная Y>0> что
[P'{u)h, A)>YfP||\ и, h£M. C.224)
Тогда: а) функционал C.223) ограничен снизу\ б) любая
минимизирующая для этого функционала
последовательность сходится в метрике пространства Н к некоторому
пределу.
Предел, существование (и единственность) которого
вытекает из теоремы 30, называется обобщенным решением
задачи о минимуме функционала C.223).
Теорема 31. Пусть выполнены условия 1)—3)
теоремы 29, и пусть существуют такие положительные
постоянные |3 и у, что для любых и, h£M
(Р' (и) A, А) ^ р2 (Р' @) A, Л) ^ y2PH2. C.225)
Тогда обобщенное решение задачи о минимуме
функционала C.223) принадлежит пространству НА, где А = Р' @).
2. Метод Ритца. Для приближенного решения
нелинейных вариационных задач, точнее говоря, для построения
минимизирующей последовательности, обычно используется
метод Ритца. Допустим, что ищется минимум некоторого
функционала Ф(и), область определения которого линейна.

2] § 10. ВАРИАЦИОННЫЕ МЕТОДЫ В НЕЛИНЕЙНЫХ ЗАДАЧАХ- 321
Выбираем координатную систему {уп} (л=1, 2, ...),
подчинив ее обычным условиям: 1) все элементы координатной
системы принадлежат области определения данного
функционала; 2) координатные элементы, взятые в любом конечном
числе, линейно независимы; 3) координатная система полна
в некоторой метрике, определенной на области определения
данного функционала. Расстояние между элементами и и v
в этой метрике будем обозначать через q(#, v); если в
упомянутой метрике D (Ф) окажется банаховым пространством,
то будем писать q(u, v)=\\u— v\\0.
Множество О(Ф) линейно, поэтому при любых значениях
постоянных а1? а2, ..., ап
п
и„=2в*Ф*€Я(Ф) C.226)
и выражение Ф (ип) имеет смысл. Это выражение есть
функция конечного числа переменных а1У а2, . . ., ап. Найдем те
их значения, при которых Ф (ип) достигает минимума; для
этого надо решить систему уравнений
^1 = 0 (j=\, 2, .... я) C.227)
и проверить, что найденные значения постоянных ak
действительно реализуют минимум величины Ф(ип). Подставив
эти значения в выражение C.226), получим элемент ип,
который назовем п-м приближенным по Ритцу решением
данной вариационной задачи.
Функционал Ф называется возрастающим в данной
метрике q, если
lim ф(и)= + оо. C.228)
0 (и, о)-*оо
Функционал Ф (и) называется полунепрерывным сверху в точке и
и в метрике Q, если по любому данному числу е>0 можно
найти такое 6>0, что Ф (и) — Ф (v) > — 8, если q(u}v)<:8;
этот функционал просто называется полунепрерывным сверху
(в метрике q), если он полунепрерывен сверху в любой
точке u£D (Ф).
Теорема 32. Пусть функционал, Ф (и)
полунепрерывный сверху и возрастающий в некоторой ^метрике q;
допустим еще, что этот функционал непрерывно
дифференцируем в любом конечномерном линеале из области своего
11 С. Г. Михлин и X. Л. Смолицкий

322
ГЛ. Ш. ВАРИАЦИОННЫЕ МЕТОДЫ
[3
определения. Тогда: 1) функционал Ф (и) ограничен снизу;
2) приближенное по Ритцу решение можно построить при
любом п\ 3) последовательность приближенных по Ритцу
решений — минимизирующая для функционала Ф(и).
3. Нелинейная теория пологих оболочек. Задача о
равновесии пологой оболочки под действием нормальной
нагрузки q (л;, у) приводится к задаче о минимуме потенциальной
энергии этой оболочки:
+ -§■0— |i)ej,j — qw\dxdy. C.229)
Здесь приняты следующие обозначения: Е—модуль
упругости, [А—постоянная Пуассона, h—толщина оболочки,
Eh3
В = 12 ,« 2,—жесткость оболочки при изгибе,
5—срединная поверхность оболочки,
ди . , .1 fdw\2
дх^ l ^ 2 \дх) '
dv . , , 1 fdw\2
*> = Ty + k'W+2[Ty) '
ди . dv ydw dw
г^~д^^~дх^~дхдГу '
и, v—тангенциальные смещения, w—нормальное смещение,
kx и k2—начальные кривизны в сечениях, параллельных
соответственно плоскостям zx и zy. Оболочка предполагается
жестко закрепленной по краю.
Пользуясь уравнениями равновесия оболочки, можно
выразить и и v через w, для чего достаточно решить некоторую
линейную задачу; теперь можно считать, что функционал
C.229) зависит только от w. Об этом функционале
доказывается, что: 1) он ограничен снизу; 2) приближенные по
Ритцу решения можно строить при любом п\ 3) множество
этих приближенных решений компактно в метрике
\\w\\2 = Ц (AwJ dx dy;

4] § 10. ВАРИАЦИОННЫЕ МЕТОДЫ В НЕЛИНЕЙНЫХ ЗАДАЧАХ 323
4) каждая предельная точка названного множества реализует
некоторый относительный минимум функционала C.229).
4. Функционалы теории пластичности и их обобщение.
Некоторые задачи теории пластичности можно свести к
задаче о минимуме функционала вида
Ф(«) = ( Е S Q/(&)*6 \dx-\fudx, f£LM{Q). C.230)
Здесь q. — неотрицательные функции от |, заданные в
промежутке 0^£<Соо, Q — конечная область в пространстве
координат, х) (и) — неотрицательные квадратичные формы
относительно функции а и ее производных до некоторого
порядка; предполагается, что для функций,, удовлетворяющих
однородным краевым условиям данной задачи, по крайней
мере при одном значении /=у выполняются неравенства
Qy(^)^Qo=:Const>0 и
J т/ (и) dx ^ y2 S u* dx> У = const > °. C.231)
Приведем два примера.
Пример 41. Для задачи упруго-пластического кручения
г" Т2 п
dx dy, C.232)
Q L о
где Т2 = (ч~) +(g-) , & — область сечения стержня,
со — постоянная; функция и (х, у) должна обращаться в нуль на
границе области Q, которая предполагается односвязной.
Наконец, функция g(^) удовлетворяет неравенствам g' (£) >»0,
g-(^)^-^» гДе О—модуль сдвига материала в упругом
состоянии.
Пример 42. Ползучесть пластинки, закрепленной по
краю. В этом случае
dxdy, C.233)
фИ = ^Ц- J g(l)*l-l*»
ltH

324
ГЛ. III. ВАРИАЦИОННЫЕ МЕТОДЫ
[5
где w—нормальный прогиб, р — интенсивность нормальной
нагрузки,
я2 /д2оЛ2 fd2w\2 d2wd2w ( d2w У .
W~-\dx*J ~т~[ду2) ~т~дх* ду*+[дхду) *
на границе области Q функция ^ и ее нормальная
производная обращаются в нуль. Наконец, g(%) — некоторая
функция, ограниченная сверху и снизу положительными числами.
При выполнении перечисленных выше условий
доказывается, что функционал C.230) достигает минимума и что
процесс Ритца для этого функционала сходится.
5. Решение нелинейных систем Ритца. Метод Качанова.
Л. М. Качанов изложил свой метод применительно к одной
задаче теории пластичности, С. Н. Розе распространил его
на некоторые более общие функционалы1).
Пусть данный функционал имеет вид
ф(")Ч|£ S ftF)rf6 \dx-{f, «), C.234)
a [i=i о J
где функции Q; (I) и формы х] (и) удовлетворяют условиям
п. 4 h/£Z,2(Q). Задачу о минимуме функционала C.234)
будем решать по методу Ритца, для чего выберем
координатную систему {ф^}, удовлетворяющую условиям п. 2,
положим п
J k = l
и составим уравнения
^-^О (/=1, 2, .... п). C.235)
Чтобы решить эту систему, поступим следующим
образом. В интеграле C.234) заменим q. (£) некоторыми
постоянными Q(.0)^0, причем постоянная q(.0) должна быть
положительной; полученный таким образом квадратичный
функционал обозначим через Ф#1 (и):
1) См. литературные указания в конце главы.

5] § 10. ВАРИАЦИОННЫЕ МЕТОДЫ В НЕЛИНЕЙНЫХ ЗАДАЧАХ 325
Положим
п
k =i
и подберем коэффициенты akl так, чтобы Ф1 (ип1) было
минимальным; как легко видеть, для этого достаточно
решить линейную относительно коэффициентов akl систему.
Определив эти коэффициенты, заменим в функционале
C.234) Q;(l) на Q; (т*(иЯ1)), что приведет к новому
квадратичному функционалу:
Фг(М)=$2 Qi(T°(uni))T)(u)dx-(f, и).
Положим п
И*2=2Я*2<Ь
/e = i
и подберем коэффициенты акг так, чтобы Ф2 (аП2) было
минимальным. Этот процесс продолжаем. Если
последовательность решений
(aw> a2Si ..., ans) E=1, 2, ...)
стремится при s—*оо к некоторому пределу, то этот
предел есть решение системы C.235).
Пример 43 ([29], [82]). Функция напряжений и (х, у) упруго-
пластического кручения стержня квадратного сечения со
стороной 2 реализует минимум функционала
1 1 Т
[ С [[f{K)\dh--2<i>u\dxdy
—1 —1 0
на множестве функций, которые обращаются в нуль на контуре
квадрата. Здесь со — угол кручения на единицу длины,
— интенсивность касательных напряжений, связанная с
интенсивностью деформаций сдвига Г соотношением Г — }(Т)Т.
Выполнив под знаком внутреннего интеграла подстановку
№ = 1, мы приведем наш функционал к виду
1 1 Г2
S ШQ (|)^-2Нdxdy> «(б> =*■§• /(vi).
— 1 —i 0

326 ГЛ. III. ВАРИАЦИОННЫЕ МЕТОДЫ [6
Вычисления проведены для случая, когда со = 0,015, а соотношение
между Г и Г имеет вид
т f 8-105Г, Г < 0,0025,
'~"\ 1940 + 24-108Г, Г^0,0025.
Отсюда легко найти, что
| й-10-«, |<4.10в,
Q (£) = \ i / тип \
Были использованы две координатные функции:
<Pi = (*"-!) Of-1), ф2 = (^2—1)A/2—О (^2 + г/2),
так что
и. = (^-1)(У1-1)[в1 + в.(х1 + У1)].
По методу Л. М. Качанова проведены 32 итерации; счет
проводился на ЭВМ «Урал». Первое приближение соответствует
упругому состоянию и резко отличается от всех последующих
приближений, которые сравнительно близки между собой; после 30
итераций первые 5 знаков стабилизируются (см. таблицу).
S
1
2
3
4
1 5
6
| 7
9
10
|П
12
13
14
15
16
al6-10-5
0,0701256598
0,0180226718
0,0178718986
0,0177279558
0,0175541842
0,0175513918
0,0175429202
0,0174617178
0,0174521578
0,0174036396
0,0174005660
0,0174035498
0,0174068752
0,0174099386
0,0174126626
0,0174150636
a2S.10-5
0,0142167558
-0,0033820822
-0,0037645918
—0,0038018398
—0,0036417728
—0,0037422022
—0,0038871818
—0,0037578672
—0,0037292512
—0,0036996034
—0,0036923128
—0,0036916262
—0,0036924296
—0,0036936516
—0,0036950292
—0,0036964422
S
1
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
ац-10-*
0,0174171448
0,0174189902
0,0174205806
0,0174219636
0,0174231448
0,0174241668
0,0174250498
0,0174258064
0,0174264580
0,0174270162
0,0174274962
0,0174279068
0,0174282610
0,0174285608
0,0174288402
0,0174290410
а2гЮ-5
—0,0036978272
—0,0036991472
-0,0037003790
—0,0037015066
-0,0037025316
—0,0037034506
-0,0037042658
-0,0037049904
—0,0037056288
—0,0037061862
—0,0037066732
—0,0037070980
—0,0037074664
—0,0037077868
—0,0037080636
—0,0037082982
6. Сведение к задаче Кош и. Другой прием решения
нелинейной системы Ритца основан на следующей идее (см.,

6] § 10. ВАРИАЦИОННЫЕ МЕТОДЫ В НЕЛИНЕЙНЫХ ЗАДАЧАХ 327
например, [19]). Пусть требуется решить систему уравнений
А(*г> а» •••• ап) = ° ('=1, 2> .-м *)• C-236)
Построим функции Ft(al7 а2, ..., ая, А,) так, чтобы
и чтобы выражение Ft(a^ а2, ..., а„, 0) было достаточно
простым; для определенности пусть
Ft(a„ а2, ..., аПУ 0) = *,. C.237)
Уравнения
7^, я2, .... апУ Я) = 0 (/-1, 2, ...,л)C.238)
определяют ах, а2, ..., ап как функции от X; для наших
целей достаточно знать значения этих функций при Я=1.
Дифференцируя уравнения C.238) по Я, получим систему
обыкновенных дифференциальных уравнений первого порядка
^-ч dFtdak . dF; A
Ц^Ж + Ж=0 (/=1, 2, ...,«), C.239)
для которой соотношения C.237) дают начальные условия
a,|;t=o = 0. C.240)
Если задача Коши C.239), C.240) имеет решение на
промежутке 0^А<;1, то, построив каким-нибудь
приближенным методом это решение и положив в нем А,= 1, мы
решим систему C.236).
При некоторых условиях, о которых сказано ниже, такая
задача Коши действительно имеет решение.
Рассмотрим функционал Ф(а), заданный на линеале,
плотном в некотором вещественном гильбертовом
пространстве Я, и являющийся потенциалом некоторого оператора
Р(и); это означает, что
Я<Ъ{* + щ\Ыо = {Р{и)9 К)
для всех и, h£D (Ф).
Будем предполагать, что дифференциал Гато DP (и, И) —
= P'(u)h оператора Р(и) есть равномерно положительно
ограниченный снизу оператор. Это значит, что существует
такая положительная постоянная у, не зависящая ни от и,

328 ГЛ. III. ВАРИАЦИОННЫЕ МЕТОДЫ [6
ни от h, что справедливо неравенство
(P'(u)h, й)^7г||А||2. -
Поставим задачу о минимуме функционала Ф (и) и будем
решать ее по методу Ритца, для чего зададимся
последовательностью, координатных элементов, удовлетворяющих
обычным условиям, и будем искать приближенное решение
в виде
п
Л = 1
Метод Ритца' приводит к следующей системе уравнений для
коэффициентов ak:
(РЮ, Фу) = 0 (У=1, 2, ..., п). C.241)
Заметим, что к этой же системе приводит применение
метода Бубнова—Галёркина к уравнению Р(и) = 0, которое
является уравнением Эйлера—Лагранжа для вариационной
задачи о минимуме функционала Ф (и).
Применяя метод сведения к задаче Коши, возьмем
систему C.238) в виде
а;+ЩР{ип), Ф/)-ау]=0 (у=1, 2, ..., л), C.242)
что приводит к следующей задаче Коши:
р+{Р(ип), <Pj)-af +
+ ^[(P'(un)<pk, Фу)-*/А]з?} = 0 C.243)
a j k=o = 0. C.244)
Определитель Д„ матрицы коэффициентов при
производных в системе C.243) отличен от нуля при всех Я£[0, 1],
и эту систему можно решить относительно производных
-pi-, которые по формулам Крамера могут быть
представлены в виде
da, A</}
Ж=Т^ = е№"а" •••>а*'Я) U=h2, ...,л). C.245)

1]
§11. МЕТОД ПРЯМЫХ
329
Предполагаем следующее:
1) Функции коэффициентов алл а2,
(/>(«„), ф,.) И (/*(«„)<?*, фу),
непрерывны при всех значениях аргументов и имеют
полиномиальный порядок роста на бесконечности, так что
\(РЮ, ФУ)|<Л,(К1, KI, •••» К|), C-246)
К^("»)Ф*. Фу) К Р»-,(|в,1, KI, ••-, |вя|); C.247)
здесь рт и рт_т обозначают полиномы степеней т и /»—1
соответственно; т — некоторое натуральное число.
2) Имеет место оценка
т —1
(P'(un)h, A)>ivfs ej) 2 № W= const >0. C.248)
Тогда решение задачи Коши C.243), C.244) существует
в промежутке 0^Х^\.
Можно доказать, что для функционала C.230) при
некоторых дополнительных предположениях относительно
функций Qi(l) условия C.246), C.248) выполняются при т=\.
§ 11. Метод прямых
1, Основы метода. Метод прямых является
промежуточным между аналитическими и сеточными методами.
Сущность его состоит в том, что производные по одним
независимым переменным заменяются их приближенными
выражениями через конечные разности, тогда как производные
по остальным переменным оставляются без изменения. Тем
самым данное дифференциальное уравнение заменяется
системой дифференциальных уравнений, но с меньшим
числом независимых переменных.
Поясним сказанное на примере уравнения второго порядка
с двумя независимыми переменными.
Пусть требуется найти интеграл уравнения
А(х, у)ш + 2В(х, у) — + С(х, y)W2 + D(x, y)Tx +
+ Е(х, у) | + F(x, у) u=G{x, у) C.249)

330 ГЛ. III. ВАРИАЦИОННЫЕ МЕТОДЫ [1
в некоторой области Q. Для определенности допустим, что
данное уравнение эллиптическое, а область Q конечная.
На границе 5 этой области должно быть задано некоторое
краевое условие. Допустим, хотя это и необязательно, что
каждая прямая, параллельная оси х> либо вовсе не
пересекается с границей S, либо имеет с этой границей общий
отрезок, либо пересекает ее не более чем в двух точках.
Проведем прямые, параллельные оси х, и пусть
расстояние между соседними прямыми постоянно и равно h. Пусть
при этом область й пересекает прямые
У=У0 + кЬ=ук (А = 0, 1, 2, ..., л). C.250)
В уравнении C.249) положим y~yk и заменим производные
по у разностными отношениями. Можно, например, положить
где ик(х)~и(х, ук). Аналогично
д2и | 1 , , , . , , ч1
ду2
= -h2[Uk + *{X)-2ak(X) + Uk-^X)}-
У=Ук
Подставим это в уравнение C.249), в котором уже
положено у~Уъ> мы получим систему п обыкновенных линейных
уравнений с п-\-2 неизвестными функциями и0{х)у иг(х),...
..., ип{х), ип+1(х).
Если область Q имеет вид, изображенный на рис. 22
(см. стр. 311), то недостающие два уравнения можно
получить из краевых условий на прямолинейных участках АВ и
CD границы. Краевые условия для неизвестных функций
ик (х) естественным образом получаются из краевых условий
для функции а (х, у) на участках границы АС и BD.
Аналогично можно свести к системе обыкновенных
дифференциальных уравнений линейное (а также и нелинейное)
уравнение более высокого порядка или систему
дифференциальных уравнений в частных производных; тип уравнения
(или системы) при этом особой роли не играет. Нетрудно
распространить метод прямых и на случай большего числа
независимых переменных,

2] § 11. МЕТОД ПРЯМЫХ 331
Применение метода прямых, скажем, к уравнению
C.249) целесообразно, если его коэффициенты постоянны
или зависят только от у: в этом случае мы приходим
к системе линейных обыкновенных уравнений с постоянными
коэффициентами.
2. Метод прямых для уравнений Лапласа и Пуассона.
Для уравнения Лапласа
дги . д*и_~
дх*+ду~2~~
система метода прямых имеет вид
т ч м+тй К+. w+в* -1(*I +
+ jp[«*+,(*)-2«*(*)+«*-l(*)]=0 (ft=l,2, ...,л). C.251)
Аналогично для уравнения Пуассона
получаем систему
+ ^ ["*+■! W-2«ik (*) + «*.» Wl-^W^O C.252)
(*=1, 2, ..., /2),
где Fft (x) = |-Д (*) + ~ [fk+l (x) +/kmml (x)].
Подробнее рассмотрим тот случай, когда область имеет
вид, изображенный на рис. 22, а уравнению Пуассона
сопутствует краевое условие и \$ = 0. В этом случае
и0{х)=*ип+1(х) = 0 и система C.252) содержит п уравнений
с п неизвестными функциями ul{xI uz(x), ..., ип(х).
Введем векторы
и матрицу / _ 2 1 0 ... 0 О
0*0 0 '..'.' 1 —2/

332 ГЛ. III. ВАРИАЦИОННЫЕ МЕТОДЫ [2
Тогда систему C.252) можно записать в виде
(e+±m}u" + ^U-F=0, C.253)
где Е— единичная матрица порядка п.
Нетрудно найти такую матрицу В, чтобы матрица В~1МВ
была диагональной. Именно, если обозначить элементы
матрицы В через bks9 то
**-<-1>*+'/;т8,пят1-
+ 1 я + 1
Матрица В одновременно ортогональна и симметрична, так
что В = В* = В-\ Теперь BMB=(kv Xt, ..., Кп) и,
следовательно,
М = Я(А„ Я,,, .... Х„)В,
где, как легко подсчитать,
ЯЛ = -2(Ц-С05-*Я
Введя теперь обозначения:
BU=V=(vvvt,...,va),
BF=Q=*{glt gv..:,g„),
А"A+Й) l+}t
мы сведем систему C.252) к п независимым уравнениям
v"k(x)-a2vk(x) = <pk(x) (А=1, 2, ...,л). C.254)
Интегрируя эти уравнения и возвращаясь затем к неизвестным
uk(x), найдем, например, для задачи, симметричной
относительно оси у,
п
«*W = E(-1).*+'C,sin7^cha,* +
S=l
* „ , ,ч*_1.* ^?Г.., ^S
■J2
v S=l
О
я (— 1)*+^ V2
sin -
+ \£ у==-^±± shas {х-t)ys(t)dt. C.255)

3]
§11. МЕТОД ПРЯМЫХ
333
Произвольные постоянные Cs определяются из алгебраической
системы, которая получается из C.255) после подстановки
краевых условий.
Интегралы в формулах C.255) определяют частное
решение системы C.252). Разумеется, в частных случаях частное
решение можно строить и в более простой форме. Так, если
в уравнении Пуассона f(x, у) = —1, то таким частным
решением является совокупность постоянных
_k{n + \—k) и2
ak- ^ п •
3. Бигармоническое уравнение. Будем рассматривать
бигармоническое уравнение на плоскости в предположении,
что на границе области заданы сама искомая функция и ее
нормальная производная; допустим, что область имеет вид,
изображенный на рис. 22 (см. стр. 311). Уравнения метода
прямых в этом случае имеют вид
символы в левой части уравнения C.256) имеют те же
значения, что и выше, a F означает вектор, определенным
образом зависящий от данных на границе и от неизвестных еще
значений иг(х) и ип(х). Систему C.256) можно приближенно
заменить распадающейся системой, в которой каждое
уравнение содержит только одну неизвестную. Для этого в
выражении вектора F положим
аг (х) - gn (х) + *£« (*)> ия (х) = g12(x) + hg22 (x),
где glx и glz означают данные значения искомой бигармони-
ческой функции и(х, у) на прямолинейных отрезках АВ и
CD (см. рис. 22), a g21u g22 — значения нормальной
производной искомой функции на тех же отрезках. Теперь вектор
F становится известным. Полагая
BU= V=(vlt vtt... ,v„), BF= G=(gv gi>... ,gn),
получим п независимых уравнений
44) + P*v* + Y*«* = —T— (A.= 1, 2, ... , я),

334
ГЛ. III. ВАРИАЦИОННЫЕ МЕТОДЫ
14
где введены обозначения
kk + Tn*l ! %\
3*~ h2 л , 1 Л ' Yk— я4, . j_
6
l+~kh 1 + «Хл
4. Метод прямых для параболического уравнения.
Рассмотрим уравнение
т
^-La+/(x, у)= X ±(A/k(x)^-)+/(x,y).(S.257)
Пусть точка х меняется в конечной области Q пространства
координат х1, х2У ... ,хт, а переменная t — в промежутке
0г^<оо. Пусть на границе 5 области Q задано краевое
условие
и U = 0, C-258)
а при £ = 0—начальное условие
<=, = ФМ. C-259)
Будем считать, что оператор L положительно определенный
при краевом условии C.258). Рассмотрим последовательность
моментов времени tk = kh (/5=1, 2,...) и положим
u(tk, x) = uk(x). Функция и0(х) известна в силу начального
условия C.259), а именно: и0{х) = ц>(х). Для определения
функций uk(x) при &>0 заменим производную по времени
разностным отношением по формуле
да
Ж
t=tk h
Это приводит нас к последовательности уравнений
Luk+±uk(x)=f(x, <*) + !«*-,(*). C-260)
которые надлежит решать при краевом условии
uk\s = 0. C.261)
Оператор задачи C.260), C.261)положительно определенный,
и эту задачу можно решить, например, энергетическим
методом. Таким образом, зная функцию и0{х) и положив в

некоторый литературные указания
335
последних уравнениях k=ly мы найдем функцию и1 (х);
теперь те же уравнения при к — 2 позволяют найти функцию
и2{х) и т. д.
Относительно метода прямых для уравнений
параболического типа сделаем следующие замечания:
1) Заменив производную -^ \ по формуле
да
дГ
*=** h
мы могли бы на каждом шагу непосредственно определять
функцию uk+1 по уже известной функции uk1 не решая при
этом никакой краевой задачи, однако такой процесс был бы
неустойчив.
2) Метод прямых применим и к общему уравнению вида
щ=Аи+/г C-262)
где А — оператор, положительно определенный в некотором
гильбертовом пространстве. В частности, можно
рассматривать уравнения более высоких порядков с граничными
условиями, обеспечивающими положительную определенность
оператора задачи.
3) Если оператор Л в уравнении C.262) неположительно
определен, а только ограничен снизу, то метод прямых
можно применять, выбрав достаточно малое А, так, чтобы
был положительно определенным оператор Л + -тгАгДе / —
тождественный оператор.
НЕКОТОРЫЕ ЛИТЕРАТУРНЫЕ УКАЗАНИЯ
Основные результаты, относящиеся к теории и приложениям
вариационных методов для линейных задач и полученные до 1956 г.,
изложены в книге [63]. На цитированную в этой книге литературу
в настоящей главе, как правило, ссылок не делалось.
Ряд сведений о вариационных методах можно найти в
следующих трудах: [25], [46], [70], [97], [119], [122], [131].
К пп. 4 и 5 § 1. Понятие обобщенных производных было введено
С. Л. Соболевым; ему же принадлежат основные результаты,
относящиеся к этому понятию и к теоремам вложения. См. книгу этого
автора [97], а также книгу [95]. Теорема 6 вытекает из результатов
Е. П. Калугиной; см. [20], [21].

336
ГЛ. III. ВАРИАЦИОННЫЕ МЕТОДЫ
[4
К п. 3 § 3. Составление системы Ритца обычно связано с большим
количеством аналитических выкладок. Проведению их на ЭВМ
посвящена статья [96].
К пп. 7 и 8 § 3. Об изгибе пластин с острым краем и о
спектрах соответствующих задач см. [55], [56].
К п. 2 § 5. Подробный вывод формулы C.147) см. в [126].
К п. 4 § 5. О методе Трефтца в его наиболее общей
формулировке и о полученных здесь результатах см. [3].
К п. 6 § 5. Соображения Вайнштейна и Ароншайна подробно
развиты в работах [119] и [131]. Относительно последующих
соображений см. статьи [121], [127], [128], [132].
К § 7. Определение сильно минимальных систем см. в [100].
Вопросам, связанным с устойчивостью метода Ритца, посвящены
работы [65], [68], [109].
К п. 1 § 8. Ряд интересных соображений о построении
координатных систем содержится в книге [25].
К пп. 2—4 § 8. Подробнее о рациональном выборе координатных
систем для конкретных классов задач см. [67].
К п. 5 § 9. Общее понятие о проекционном методе и ряд теорем
о его сходимости даны в статье [80].
К § 10. Многие важные вопросы, касающиеся применения
вариационных методов к нелинейным задачам, трактуются в следующих
работах: [7], [12], [14], [15], [19], [27], [28], [39], [40], [66], [82],
[123]. Этот перечень ни в коем случае не претендует на полноту.
К § П. О методе прямых для уравнений Лапласа и Пуассона
и для бигармонического уравнения подробнее см. [63]; там же
приведена библиография. О применении метода к простейшему
параболическому уравнению см. [94]; общий случай рассмотрен в [37].
В статье [36] метод прямых применен к более сложному уравнению
вида
л д2и , _ ди , _ ,
AW+Bdt+Cu=f-

ГЛАВА IV
ПРИБЛИЖЕННОЕ РЕШЕНИЕ
ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ
§ 1. Приближенное вычисление характеристических чисел
и собственных функций симметричного ядра
I. Общие замечания. В настоящем параграфе через
K(x,s) будет обозначаться симметричное ядро, так что
#($,#) = /e(*,s). Принимается, что х и s суть
вещественные переменные, пробегающие один и тот же промежуток
(а, 6), который может быть и бесконечным; все последующее
верно, впрочем, и тогда, когда х я s суть точки одной и
той же области пространства любого числа измерений или,
в более общем случае, одного и того же измеримого
множества. Ядро считается таким, что интегральный оператор
ь
Ky=lK(x1s)<p(s)ds D.1)
а
вполне непрерывен в пространстве L2 (а, Ь)\ для этого
достаточно например, чтобы двойной интеграл
ь ь
В2 = $ \\K{x,s)\2dxds D.2)
а а
был конечным — в ряде случаев будем принимать это
допущение. Другой важный класс ядер, делающий оператор D.1)
вполне непрерывным; это ядра со слабой особенностью (их
называют также ядрами со слабой полярностью); они имеют
вид

338 ГЛ. IV. ПРИБЛКЖ. РЕШЕНИЕ ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ [1
где постоянная а заключена в пределах О <С а < 1, а
функция А (л;, s) ограничена и в случае симметричного ядра сама
симметрична. Если х и s не вещественные числа, а точки
/^-мерного многообразия, то показатель а может быть
заключен в пределах 0 <^а<С.пг. Если ядро имеет слабую
особенность, то промежуток (а, Ь) (в общем случае — область или
многообразие, которое пробегают точки х и s) следует
считать конечным — тогда оператор D.1) будет вполне
непрерывным в пространстве I2 (a, b).
Характеристическим числом ядра К(х, s) называется такое
значение численного параметра Я, при котором однородное
интегральное уравнение
<р(*)—МГ<р = 0 D.4)
имеет нетривиальное (отличное от тождественного нуля)
решение; это решение называется собственной функцией ядра,
соответствующей характеристическому числу Я. Если оператор
D.1) вполне непрерывен, то каждому его характеристическому
числу соответствует только конечное число линейно
независимых собственных функций; множество характеристических
чисел конечно или счетно, в последнем случае оно имеет
единственную предельную точку на бесконечности.
Характеристическое число называется простым, если ему
соответствует лишь одна линейно * независимая функция, и
кратным в противном случае. Число линейно независимых
собственных функций, соответствующих данному
характеристическому числу, называется его кратностью.
Характеристические числа данного ядра можно выписать
в виде последовательности, расположенной в порядке
возрастания модулей. Принято при этом повторять каждое
характеристическое число столько .раз, какова его кратность. При
такой записи среди характеристических чисел могут
встречаться равные, но каждому характеристическому числу
соответствует только одна линейно независимая собственная
функция.
Числа, обратные к характеристическим числам ядра,
называются собственными числами этого ядра.
Характеристические числа симметричного ядра
вещественны; соответствующие собственные функции можно считать
ортогональными и нормированными (как мы будем говорить
короче, ортонормированными).

1] § 1. СОБСТВЕННЫЕ ФУНКЦИИ СИММЕТРИЧНОГО ЯДРА %2>9
С симметричным ядром К(х, s) можно связать так
называемую квадратичную форму этого ядра
ь ь
<ЛГф,ф)=$ ^K(x}s)(f{x)(f(s)dxds\ D.5)
а а
ее значения вещественны.
Теорема 1. Собственные числа симметричного ядра
совпадают со стационарными значениями его
квадратичной формы, которые она принимает на множестве
нормированных функций <р(х); соответствующие собственные
функции суть те функции, на которых эти стационарные
значения достигаются.
На практике часто бывает удобно пользоваться
следующими теоремами.
Теорема 2. Наибольшее по модулю собственное
число а, симметричного ядра К{х, s) равно по
абсолютной величине максимуму выражения | (Аср, ф) | при условии
||ф||2=1; соответствующая собственная функция (fl(x)
совпадает с функцией, на которой указанный максимум
достигается.
Теорема 3. Пусть о\, сг2, ... , ап—первые п
собственных чисел симметричного ядра К(х, s),
расположенные в порядке убывания их модулей, и пусть ф1 (х),
Ф2 (л:), ... , ф„ (х) — соответствующие им ортонормирован-
ные собственные функции. Абсолютная величина
ближайшего по модулю к данным числам а19 а2, ... ,ап
собственного числа оп+1 равна максимуму выражения |(/(ф, <р)|
при условиях
!1ФИ2 = 1, (Ф, ФЛ = (Ф, Ф2) = •. • - (ф, Фя) = 0; D.6)
соответствующая собственная функция фп+1 (х) совпадает
с функцией, которая удовлетворяет условиям D.6) и на
которой упомянутый максимум достигается.
Симметричное ядро называется положительно
определенным, если его квадратичная форма принимает при ф (л:) ф 0
только положительные значения; эти ядра представляют
наибольший интерес, и ниже в этом параграфе мы главным
образом такие ядра и будем иметь в виду. Для
положительно определенных ядер теоремы 2 и 3 упрощаются и
приводятся к следующим.

340 ГЛ. IV. ПРИБЛИЖ. РЕШЕНИЕ ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ [2
Теорема 2а. Наибольшее собственное число at no-
ложительно определенного ядра равно максимуму его
квадратичной формы при условии ||ф||2= 1;
соответствующая собственная функция совпадает с функцией, на ко-
торой этот максимум достигается.
Теорема За. Пусть ах, сг2, ... , ап—первые п
собственных чисел положительно определенного ядра К(х, s),
следующие в порядке убывания, и (р1 (х), Ф2 (#)> ... , ц>п (х) —
соответствующие им ортонормированные собственные
функции. Ближайшее к данным собственное число ап+1
равно максимуму квадратичной формы (АГф, ф) при
условиях D.6); соответствующая собственная функция
совпадает с функцией, которая удовлетворяет условиям D.6)
и на которой указанный максимум достигается.
2. Метод Ритца. Выберем последовательность функций
{i|)n(x)|, называемых координатными. Эти функции должны
удовлетворять следующим трем условиям: 1) tyn (x) £Z,2 (a, b);
2) каково бы ни было число п, функции ур1 (х), ^2 (л;), ... ,tyn(x)
линейно независимы; 3) последовательность координатных
функций полна в L2 (a, b); это означает, что по данной
функции f(x) £ L2 (a, b) и данному числу е > 0 можно
подобрать натуральное число N и коэффициенты ар а2, ... , aN
так, чтобы
N
П/-2МУ<е.
Заметим, что всем перечисленным условиям можно
удовлетворить, взяв в качестве координатной любую полную в
Lz (а, Ь) ортонормированную систему.
По методу Ритца полагаем
п
Ф»=2в*Ч>*; D.7)
k = i
коэффициенты дА подчиняем условию ||фя||2=1, что дает
2 (% %)a~ak=\, D.8)
и ищем при этом условии стационарные значения квадра-

2] § 1. СОБСТВЕННЫЕ ФУНКЦИИ СИММЕТРИЧНОГО ЯДРА 341
тичной формы
п
(*Фя. Ф„)= 2 (Щ, ф»)а1. D.9)
У, /г=1
По методу Лагранжа это приводит к однородной линейной
системе относительно коэффициентов ak (a—множитель
Лагранжа):
2 {(Щ, %)-oWj, %)}ак = 0 D.10)
k =1
G=1, 2, .... л),
определитель которой должен быть равен нулю:
(/OI>2, "Ф^-аСФа, ti>t) (*Фа. Ф2)-СГ(Ч12> ^a)...(/Cl|)a» Фп) ~ <* СФ2. Фц =0
)
I (/СФп. W ~ су (Фп. *Ы (КФп> Фа) - а (фп, а|>2). .. (*ФП. 4>п) - or Ofo. Фп) I
D.11)
Корни уравнения D.11) дают приближенные значения
собственных чисел ядра К{х, s). Наибольший из корней
уравнения D.11) дает приближенное значение наибольшего
собственного числа с недостатком, поэтому наименьшее
характеристическое число получается с избытком. При
стремлении п к бесконечности первые k корней уравнения D.11),
где k—любое фиксированное натуральное число, стремятся
к первым k собственным числам ядра К(ху s).
Найдя а из уравнения D.11), можно подставить его
в систему D.10); ее нетривиальное решение, подставленное
в выражение D.7), приводит к приближенному выражению
собственной функции, соответствующей найденному
собственному числу.
Пример 1. Найдем по методу Ритца приближенное значение
наименьшего характеристического числа положительно
определенного симметричного ядра
*<*■•>={*.*<'« <4л2>
конец промежутка интегрирования а = 0, Ь=\,
За координатные функции возьмем полиномы урп (х) — РпBх—1)
(п = 0, 1,2, ...), где Рп есть n-Pi полином Лежандра. Полиномы tyn(x)
ортогональны в промежутке @, 1), так что (я|?у, tyk) = Qt j Ф k\ легко

342 ГЛ. IV. ПРИБЛИЖ. РЕШЕНИЕ. ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ [2
1
видеть также, что (г|)^, %) =
. В формуле D.7) ограничимся
2k+\'
двумя слагаемыми, так что
Имеем:
(Р., Р0)=1, (Рв, /\) = 0, (Plf Р,) = 1.
Для вычисления значений (КРт, Рп) заметим, что
(W*. Р„)= J Лс | J sPm (s) Р„ (х) ds + J *Рга (s) Pn (х) ds\ ■
о V о х )
применив ко второму из двойных интегралов справа преобразование
Дирихле, получим
1 X
(КРт, Рп)= J dx J а [Рт (s) Рп (х) + Рт (х) Рп (s)} ds.
о о
Отсюда найдем:
Уравнение D.11) принимает вид
1 п 1
3™а П
I ±_1
12 30 З0
или
Отсюда
13
°1-30а + 80 = 0-
0^ = 1A3+/124), сг2 = ~ A3- 1^124).
Это дает приближенные значения первых двух характеристических
чисел ядра D.12):
^ = 1=^2,4859,
о*,
v
: 32,226.

3] § 1. СОБСТВЕННЫЕ ФУНКЦИИ СИММЕТРИЧНОГО ЯДРА 343
Точные значения характеристических чисел ядра D.12) суть
_Bft~l)*n*
Л*= 4 (л-=1, А ...)>
это легко установить, если заметить, что интегральное уравнение
1
Ф (х) — Х ^ К (х, s) ф (s) ds = 0,
о
где К(х, s) —ядро D.12), равносильно дифференциальному
уравнению ф'У4-А,ф = 0 и краевым условиям ф @) = 0, <р' A) = 0. Точные
значения первых двух характеристических чисел суть
тт2 Чтг2
A^j = 2,4674, Л2 = ^ = 22,2066.
Таким образом, использовав в методе Ритца две координатные
функции, мы получили сравнительно точное значение Ях и грубо
неточное значение Я2. Последнее не случайно: чтобы получить
достаточно точное значение &-го характеристического числа, надо
использовать больше (и даже существенно больше) чем k
координатных функций.
3. Метод моментов [11]. Метод моментов является одной
из реализаций метода Ритца. Пусть ярх, г|J, ... , \|)n — первые
п координатных функций, Rn — натянутое на них
подпространство и Рп— оператор проектирования из L2(a, b) в Rn.
Применение метода Ритца (формулы D.7) — D.11))
равносильно отысканию характеристических чисел не оператора Ку
а конечномерного оператора РпКРп. Метод моментов состоит
в том, что за координатные берутся функции <фот = /С/я"о)
(/я=1, 2, ...), где функция со(лг) выбирается произвольно;
предполагается только, что при выбранном п функции
со, /Ссо, ... , Кп~1<& линейно независимы. Вычисления по
методу моментов производятся так: собственные числа
оператора РпКРп получаются как корни уравнения
оя + ая_1аЛ-1+...+ав«0> D.13)
коэффициенты которого в свою очередь находятся из системы
2(*/> »*K-i + M>/. *»+i) = 0 (/=■!. 2> ...1 я). D.14)
Метод моментов применим и к несимметричным ядрам.

344 Гл, IV. ПРИБЛИЖ. РЕШЕНИЕ ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ [4
Пример 2. Найдем приближенные значения
характеристических чисел ядра
f-g" B — s)xt *<s,
I
— B—x) s, x^s.
Положим (д (х) = sin nx и я = 3. Имеем:
ojjj (x) = со = sin яд;,
■ / ч /31 ,1,1V *" Л , з \ , *• , l ,
Для постоянных аЛ получаем систему
0,5000000а0+ 0,1013212а, + ю-«. 2,384240а2+ 10"»- 5,761453 = 0,
О,Ю13212ао + 10-2.2,384240а1 + 10-8.5,761453а2+Ю-»-1,398529 = 0,
10-2.2,384240а0+Ю-3-5,761453а, + Ю-8-1,398529а2 +
+ 10-3,397373=0,
которая дает:
а0= —10-4-1,249, а, = 10~2.1,35979, а2 =—0,296814.
Уравнение D.13) имеет вид
а' —0,296814а2 + КГ8-1,35979а— Ю"*. 1,249 = 0,
его корни:
а, = 0,242963, а2= 10~2-4Д45, а,= 10-*-1>2,
откуда
Я, = 4,11585, Я2 = 24,20, Я3 = 80.
Значения характеристических чисел, верные с точностью до
выписанных знаков, суть
Я, = 4,11585, Л2 = 24,14, Л, = 63,61.
4. Метод Келлога. Пусть К{ху s) — симметричное ядро,
которое для простоты будем считать положительно
определенным, и со (л;) — произвольная функция класса L2(a, b).
По методу Келлога строятся последовательность функций
со^(х) = Кпсо (а = 1, 2, 3, ...) и последовательность чисел

4] § 1. СОБСТВЕННЫЕ ФУНКЦИИ СИММЕТРИЧНОГО ЯДРА 345
Пусть фх (х)> ф2 (х), . .. суть ортонормированные
собственные функции ядра К(х, s), a
X1^Ji2^...—соответствующие характеристические числа. Пусть функция ф(х)
ортогональна к собственным функциям ух(х), ... , ^к-г(х),
но не ортогональна к собственной функции <f>k(x). Тогда
последовательность D.15) имеет пределом &-е
характеристическое число Kk, а последовательность функций
@П(Х)
имеет пределом некоторую линейную комбинацию
собственных функций, принадлежащих характеристическому числу Xk.
В частности, если функция (й(х) не ортогональна к собственной
функции ф1 (х\ то предел последовательности D.15) равен %1Ш
К тому же пределу, что и последовательность D.15),
стремится последовательность
У\\?п\\'
В предположении, что (со, cpj Ф О, получаем две
приближенные формулы для наименьшего характеристического
числа:
к-№- <4Л6>
^-тЬ- DЛ7)
и приближенную формулу для первой собственной функции:
^{х)~Ш' DЛ8)
Формула D.16) дает значение KY с избытком. Заметим
еще, что формулой D.17) можно пользоваться при
достаточно больших /г.
Если данное ядро симметричное, но не положительно
определенное, то формулы D.16) и D.17) дают
приближенные значения наименьшей абсолютной величины
характеристических чисел данного ядра.
Пример 3. Вычислим по методу Келлога наименьшее
характеристическое число ядра D.12). Возьмем со(х)=* и я = 3. Заметим,

346 ГЛ. IV. ПРИБЛИЖ. РЕШЕНИЕ ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ [5
С 1 / Хп+2
о
отсюда легко получается
^i М = /Ссо = -g- *—^ х*,
/ ч rs 61 5 а , 1 s 1 .
«>м=к^=тх-тх+2йх-шьх-
Отсюда
|| о)! || = 0,23238, ||со2 || = 0,0939б, ||©, || = 0,03792.
Полагая в формуле D.16) последовательно гг = 2 и /г = 3, получим
два приближенных значения Ях с избытком:
Я, ^г 2,475, ^2,477.
б. Метод следов, т-ы следом ядра К(х, s) называется
число
ь
а
где Кт{х, s) означает /#-е итерированное ядро. Если ядро
симметрично и удовлетворяет условию D.2), то его следы,
начиная со второго, конечны. Следы ядра связаны с его
характеристическими числами соотношением
00 1
2^ хт
= 1 Л
П =1
отсюда вытекают приближенные формулы для наименьшего
характеристического числа, пригодные, если число т
достаточно велико;
■ 1М*= гЛг2-, D-19)

5] § 1. СОБСТВЕННЫЕ ФУНКЦИИ СИММЕТРИЧНОГО ЯДРА
В формуле D.20) г есть кратность характеристического
числа кх. Если наряду с Х1 число—Хх также является
характеристическим для данного ядра, то под г следует понимать
сумму кратностей характеристических чисел %г и —К .
Формула D.19) дает значение |^J с избытком, формула
D.20) — с недостатком.
Можно получить приближенные формулы того же типа
и для следующих характеристических чисел, но формулы
эти оказываются довольно громоздкими. Так, если
характеристические числа Х1 и Х2 простые, причем числа —\ и —Х2
не суть характеристические числа данного ядра (это будет,
например., если данное ядро положительно определенное),
то верны приближенные формулы
где
4/Л
^гт — А*™> — Аш» D.23)
формула D.21) дает значение \%г\ с избытком, формула
D.22) — с недостатком.
При аналогичных предположениях имеем
^Л^-т- Л/ -г-1 • D-24)
* I l 12 1 f I/ п* OD V '
Заметим еще, что следы четного порядка для
симметричного ядра можно вычислять по формуле
ЬЬ Ьх
Л.«= $$!*•(*. s)\2dxds = 2^\Km(x, s)\'dsdxiD.25)
а а аа
требующей вдвое меньшего числа итераций.
Пример 4. Найдем по методу следов первое
характеристическое число ядра D.12). Легко найти, что
К2{х, s) = xs — y~-4p> s<*.
и по формуле D.25)
А*-6' Л* —5040'

348 ГЛ. IV. ПРИБЛИЖ. РеШЕНИЕ ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ [6
Характеристические числа ядра D.12) все положительны,
поэтому, полагая в формуле D.19) ш=1, получим
Я,^ "l/-2^ 2,532.
Далее, характеристические числа ядра D.12) также и простые,
поэтому в формуле D.20) надо принять г=1; полагая в этой
формуле т = 2, получим
Л1^т4= = 2,460.
Рассмотрим еще один пример.
П р и м е.р 5. Квадраты корней функции Бесселя JQ (х) суть
характеристические числа симметричного ядра
1 —Vxslnx, x^ss, a — 0, b=l.
Найдем по методу следов первые два корня функции J0 (x).
Для второго итерированного ядра легко находим
1г (Х> s) = i-^5 [(л:2 + s2)\nx+\—x2l x^s.
Теперь по формуле D.25)
. 1 A- U ■ " 1
Полагая
получим:
1 32' 4 12288' 2 12288*
Х^ 5,7813, А,2^ 27,117.
Отсюда для первых двух корней функции JQ (x) получаем
приближенные значения с недостатком:
аг ^ 2,4044, а2 ^ 5,2702;
более точные значения этих корней суть
0^ = 2,4048, а2 = 5,5200.
6. Замена ядра вырожденным. Если ядро вырожденное:
п
К (х, s) = 2 "«(*)f«(*),

1] § 2. МЕТОД ИТЕРАЦИЙ 349
то его собственные числа совпадают с собственными числами
матрицы ||Лв?||2;|!=?, где
ь
Лс?= [**{*) fy(x)dx.
Определение этих собственных чисел есть задача
алгебраическая, решаемая хорошо известными методами. Поэтому,
если каким-нибудь способом (см. ниже, § 4)
аппроксимировать данное ядро вырожденным, то отыскание собственных
чисел данного ядра приближенно сводится к алгебраической
задаче об отыскании собственных чисел соответствующей
матрицы.
7. Применение определителя Фредгольма. Характеристические
числа ядра К (х, s) (необязательно симметричного) можно найти как
корни его определителя Фредгольма
00
В(Х)=^(-^"С"*А D.26)
п=о
Коэффициенты сп можно вычислять, пользуясь следующими
соотношениями:
с0 = 1, BQ(x, s) = /((*, s)
ь
сп + х = \ Вп(х, x)dx,
а
Ъ
Вп(*> s)=cnK(x, s)—n ^K(x, t) Bn-X(t, s)dt.
D.27)
Вычислив по формулам D,27) несколько первых коэффициентов
ст заменяем затем ряд D.26) его отрезком, который представляет
собой полином относительно Я; корни этого полинома и дают
приближенные значения характеристических чисел данного ядра. Способ
этот на практике мало употребляется.
§ 2. Метод итераций
1. Простая итерация. Рассмотрим уравнение
Ф(*) — Я/Г<р = /(*), D.28)
где
#Ф= \к(х% s)y(s)ds;

350 ГЛ. IV. ПРИБЛИЖ. РЕШЕНИЕ ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ [2
ядро К(х, s) здесь и всюду ниже не предполагается
обязательно симметричным. По методу простой итерации,
называемому также методом последовательных приближений,
с помощью рекуррентной формулы
ь
Фп+i (х) =/(*) + К $ K{x, s) Фя (s) ds =/ (х) + Щр„ D.29)
а
строится последовательность функций {уп (х)}, которые
рассматриваются как приближения к искомому решению
уравнения D.28); начальное приближение ср0 (л:) может быть
выбрано произвольно.
Если в качестве начального приближения выбрать
свободный член уравнения, так что Ф0(лО =/(#), то
ф„(*)= S w/.
т=о
2. Условия сходимости. Будем считать,
ь ь
£2=$ \\К{х, s)\* dxds <оо,
а а
Ь
l\f(x)\2dx<oo;
а
эти требования не необходимы, но в случае их выполнения
условия сходимости метода простой итерации формулируются
проще.
Теорема 4. Пусть выполнены условия D.30).
Последовательность D.29) сходится в метрике L2 (а, Ь) к решению
уравнения D.28), если |^|<|^J, где Хх есть наименьшее
по модулю характеристическое число ядра К(х, s). Если
ядро удовлетворяет еще дополнительному условию
ь
J | К(х, s) |2 ds < А = const, D.31)
а
то последовательность D.29) сходится к решению
уравнения D.28) равномерно в замкнутом промежутке [а, ft].
Справедлива теорема, в некотором смысле обратная
теореме 4: если при некотором % процесс простой итерации
что
\ D.30)

2] § 2. МЕТОД ИТЕРАЦИЙ 351
сходится, каков бы ни был свободный член уравнения, то
IM<IU
Условие |Л|<|^1| не всегда легко проверяемо, и мы
укажем некоторые более простые достаточные условия
сходимости простой итерации.
Процесс простой итерации сходится в метрике L2 (a, &),
если
|^|<£-1. D.32)
Если ядро удовлетворяет условию D.31), то сходимость
равномерна в [а, Ь].
Если промежуток (а, Ь) конечен, а ядро ограничено:
| К {х, s) | ^ М = const,
то процесс простой итерации сходится равномерно при
условии
При этом необязательно, чтобы свободный член /(х)
удовлетворял условию D.30); достаточно, чтобы был конечным
интеграл
ь
\\f{x)\dx.
а
Для ядра со слабой особенностью
K(x,s)= ^'/jl, \A{x,s)\*ZM= const, 0<а<1,
процесс простой итерации сходится, если
I '^2аЛ1(& —аI~а#
Если промежуток (а, £) конечен, а ядро вольтерровское,
то процесс простой итерации сходится при любом значении А,.
Если, кроме того, ядро ограничено, то процесс сходится
равномерно, если только свободный член суммируем, т. е.
существует упомянутый выше интеграл
ь
[\f{x)\dx.
а

352 ГЛ. IV. ПРИБЛИЖ. РЕШЕНИЕ ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ [3
Формула D.29) содержит зависящую от параметра х
квадратуру
ъ
а
для ее вычисления можно использовать известные
квадратурные формулы. Пусть квадратурная формула имеет вид
) F(x)dx = SV7!*/)-
a *=1
Тогда значения функции К<рп в точках xt можно вычислить
по формуле
т
(*Ф„)* = 2 AtK(xh Xj)<pn(xj);
удобное расположение вычислений приведено в монографии
Л. В. Канторовича и В. И. Крылова ([25], гл. III, стр. 127).
3. Видоизменения метода итераций. Такие
видоизменения могут быть указаны, например, для положительно
определенного симметричного ядра [23].
а) Метод наискорейшего спуска [23].
Рассмотрим интегральное уравнение
ь
Лф = ср(л;)+$ К{х, s)y{s)ds = f(x) D.34)
а
с симметричным положительно определенным ядром К(х, s)t
Уравнение D.34) можно заменить равносильной вариационной
задачей о минимуме функционала
/7(Ф)-(Ф, ф) + (*ф, ф)-(/, ф)-(ф, /) =
ь ь ь
= ) |ф(*I*^*+ 5 j ^'(*> s)q(x)y(s)dxds —
а а а
Ь
— 2^e^(f(x)f{x)dx.

3]
§ 2. МЕТОД ИТЕРАЦИЙ
353
По методу наискорейшего спуска выбираем произвольное
нулевое приближение ф0 (х). Далее подбираем такой элемент
ф' с фиксированной нормой, чтобы
й^(Фо + еф')| ;=тах*
Построив элемент ф', выбираем число е так, чтобы
/7(фв+еф/) = тш.
Элемент Ф1 = Ф0+еф' принимаем за первое приближение
и повторяем процесс. Вычисления ведутся до того момента,
когда два соседних приближения практически совпадают.
Элемент ф' и число е определяются по формулам
Ф -^Ф„ h 8-(Лф',ф/) •
Процесс сходится со скоростью прогрессии с знаменателем
,2 + а,
где о1 — наибольшее собственное число ядра К{х, s).
6) Применение простой итерации к
преобразованному уравнению [74]. Пусть в уравнении
D.34) ядро по-прежнему симметричное и положительно
определенное. Перепишем уравнение D.34) в виде
y^y-d+Jb+g.) ^+A+^2+0,)/» <4-35>
где at — наибольшее собственное число ядра К{х> s), и
применим к уравнению D.35) метод простой итерации. Это
приводит к рекуррентному соотношению
Ф1.+1-Ф11—(l+al)B + al) Аф» + A+<г1)B + *1)/*
Процесс сходится, как прогрессия с знаменателем
/ 2 2 + 2о1 + о*Л
а = max =-;— , - ;
так как ядро К(х> s) по предположению положительно
определенное, то а1>0 и #<1.
12 С. Г. Михлин и X. Л. Смолицкий

354 ГЛ. IV. ПРИБЛИЖ. РЕШЕНИЕ ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ [4
4. Интегральное уравнение первого рода с
симметричным ядром [105]. Пусть К(ху s) — симметричное положительно
определенное ядро, и пусть уравнение
ь
#<р= J К(Х, s) ф (s) ds =/ (*) D.36)
а
разрешимо. Выберем произвольную функцию ф0 (х) £L2 (a, b)
и число X из промежутка '0<Л,<2Я1, где Кх — наименьшее
характеристическое число ядра К(х, s). Последовательность
функций, определяемых рекуррентным соотношением
фя + 1(*) = Фя (*)+*[/(*) — Кф«].
сходится в метрике L2(a} b) к решению уравнения D.36).
§ 3. Применение квадратурных формул
1. Уравнения Вольтерра второго рода. Пусть в
уравнении Вольтерра
X
<?(x) — \K(x,s)<p{s)ds=f(x) D.37)
а
х меняется в конечном промежутке [а, Ь]у свободный член
непрерывен в этом промежутке, а ядро непрерывно в
треугольнике a^x^b, a^s^x. Интеграл в уравнении D.37)
заменим по какой-нибудь квадратурной формуле, не
содержащей значения подынтегральной функции в правом конце
промежутка интегрирования. Если квадратурная формула
имеет вид
^F(x)dx = n^A^(xm)9
а т~°
то, полагая в уравнении D.37) х = хп, мы заменим это
уравнение следующим:
«PW-S^^ *.)Ф (*«>=/(*»)• D-38)
т = о
Уравнение D.38) есть рекуррентное соотношение,
позволяющее определить значения ф(хл), начиная с ф (#)=/(#).

2J § 3. ПРИМЕНЕНИЕ КВАДРАТУРНЫХ ФОРМУЛ 355
Может случиться, что ядро К[х, $) не непрерывно;
тогда целесообразно предварительно так преобразовать
уравнение D.37), чтобы подынтегральная функция стала
непрерывной, и тогда уже применять квадратурную формулу.
Пусть, например, ядро имеет слабую особенность прид; = 5,
так что уравнение имеет вид
X
Ф(*)-$£=^Ф(*) **=/(*). D-39)
■ а
В этом случае целесообразно перейти к итерированному
ядру, взяв число итераций настолько большим, чтобы новое
ядро оказалось непрерывным.
2. Уравнения Вольтерра первого рода. Уравнение
X
^K(x,s)y(s)ds=f(x), f(a) = 0, D.40)
а
сводится к уравнению второго рода, если ядро К(х, s) и
свободный член f(x) непрерывно дифференцируемы и К(х, х) ф 0.
Применение квадратурных формул позволяет избежать такого
сведения. Пусть квадратурная формула содержит значение
подынтегральной функции в конце промежутка
интегрирования, так что
хп п
\ F (х) dx = 2 ^ F (*«.), АпП) Ф 0.
Уравнение D.40) заменяется системой
^А^К(хп, *„)ф (*„)=/(*„),
из которой рекуррентно определяются значения ф (хт) во
всех узлах квадратурной формулы, кроме xQ = a; для этого
значения имеем
__ Г (а)
^а)-Ша^У
12*

356 гл. IV. ПРИБЛИЖ. РЕШЕНИЕ ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ [3
3. Уравнения Фредгольма. В уравнении
ь
Ф (*)- S K(x, s) Ф (s) ds=f(x) D.41)
а
заменим интеграл по какой-нибудь квадратурной формуле.
Пусть эта формула имеет вид
]F(x)dx= %AMF{xJ.
a m = 1
Уравнение D/41) приближенно заменяется следующим:
п
Ф (*)- 2 Ат К{х, хт) Ф (хт) =/(*). D.42)
Положив здесь x = Xj (у=1, 2, ... , я), получим
алгебраическую систему для неизвестных значений ф(лг,):
п
Ф (*у)~ S Лт K{Xj, хт) <p (*J = /(*,) D.43)
m = i
(/=1, 2, ...,/z).
Решив ее и подставив полученные значения в формулу
D.42), получим приближенное решение данного
интегрального уравнения. Можно также восстановить неизвестную
функцию ф(л:), не прибегая к формуле D.42), а
воспользовавшись какой-нибудь интерполяционной формулой.
Можно рекомендовать как наиболее точные квадратурные
формулы Гаусса и Чебышёва; если ядро и свободный член
периодичны с периодом Ъ — а, то можно воспользоваться
формулой прямоугольников, которая в этом случае также
дает достаточно высокую точность.
Пример 6. Решение плоской внутренней задачи Дирихле
для области, лежащей внутри достаточно гладкого замкнутого
контура L, можно свести к решению интегрального уравнения
... 1 Г cos (у, г) . . , , ,„ ,, ллх
МО--] —^-^Mt)da==/@. D-44)
L
Здес t и т — значения параметра, определяющего положение точки
на кривой L; г — расстояние между точками, отвечающими этим
значениям параметра; v —внешняя нормаль к [в точке т; do—эле-

3J § 3. ПРИМЕНЕНИЕ КВАДРАТУРНЫХ ФОРМУЛ 357
мент длины дуги; pi (t)— искомая и / @—данная функции.
Интегральное уравнение D.44) получается, если гармоническую функцию
искать в виде потенциала двойного слоя с плотностью jut(t).
Решим приближенно уравнение D.44) в случае, когда L есть
эллипс
х = a cos t, x — bsint;
для определенности вычислений положим а = 5, 6 = 3. Зададимся
также определенным видом функции f(t); пусть
/ (t) = х2 + у2 = 25 —16 sin2*.
Интеграл в уравнении D.44) легко приводится к виду
у ЧП— e2cos2 —^г—
L —л 2
где 8—эксцентриситет эллипса; при выбранных выше значениях
a, b и /@ уравнение D.44) принимает вид
я
J 1—0,64 cos2 '
точное решение этого уравнения известно и равно
17 128
ц @ = ^- + -f2 cos 2* = 8,50 + 7,53 cos 2t.
3 ^
Коэффициент перед интегралом в уравнении D.45) -—— =0,0958;
для упрощения вычислений округлим его до 0,1 и будем,
следовательно, решать уравнение
я
»*<*>+ J I'M 6,8-з/соз(; + т) -М-"»**'*. D.46)
-я
Нетрудно видеть, что
Интеграл в D.46) заменим по формуле прямоугольников, взяв число
ординат л =12. Обозначим

358 ГЛ. IV. ПРИБЛИЖ. РЕШЕНИЕ ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ
Система D.43) в данном случае приводится к следующей;
1,19^ + 0,35^ + 0,31^ + 0,15^ = 25,
0,18^ + 1,34^ + 0,32^ + 0,16^ = 21,
0,16^+0,32^+1,34^ + 0,18^=13,
0,15^+0,31^ + 0,35^+1,19^ = 9.
Отсюда
1701 ICAQfi 13Ш 10 07У1
*3==i06^4'726' ^=io6=fe0'953-
D.48)
Функцию 'fi (/) восстановим с помощью ее ряда Фурье, который,
в силу соотношений D.47), имеет вид
00
и-(о=2 anc°s2rt^
rt=0
Величины D.48) позволяют приближенно вычислить коэффициенты
первых четырех членов этого ряда:
a0 = ^ = 8,500, at = ^ ^7,547, a2 = a8 = 0.
Отбросив остальные члены ряда Фурье, получим
ц @ = 8,50+ 7,55 cos 2*.
что мало отличается от точного значения.
§ 4. Замена ядра вырожденным
Пусть уравнение
ь
<Р(*) —S*(*. s)<f{s)ds = f{x) D.49)
a
разрешимо при любом свободном члене /£L2(a, b). Пусть
ядро К (х, s) разбито на сумму
К(х, s) = L {x, s) + R {ху s)9 D.50)
причем ядро R(x, s) имеет малую норму в метрике
Lz(a, b\ a, b):
bb
S Sl#(*. s)\2dxds<:z\ D.51)

§ 4. ЗАМЕНА ЯДРА ВЫРОЖДЕННЫМ
359
где 8—достаточно малое число. Тогда решение уравнения
ь
if (*) — ^L(xt s)ty{s)ds=f(x) D.52)
а
существует при любом свободном члене f£L2{a, b) и
|| ф—-ф || = 0(e). Если разбиение D.50) выполнить так, чтобы
ядро L (х, s) было вырожденным, то уравнение D.52)
сводится к линейной алгебраической системе. Если ядро К{х, s)
удовлетворяет неравенству D.31), а разбиение выполнено
так, что R(x, s) удовлетворяет не только неравенству D.51),
но еще и неравенству
ь
\\R{x, s)\2ds<ce21 с = const, D.53)
а
то верна не только приведенная выше оценка в среднем, но
и равномерная оценка |ср(#)—^ (*) [ = О (е), которую, если
угодно, можно представить в виде ||<р—я|) || с = О (б).
Оценку величины ||ф—г|)|| можно уточнить. Обозначим
через Тк(х, s) и TL(x, s) резольвенты ядер К(х, s) и
L(xy s), через ||/?||, ||Г#||, || rj| — нормы операторов с
соответствующими ядрами. Тогда
IIФ—Ч»II «= II/?II A+11 Г*||)A+||ГЛ) Ц/Ц. D.54)
Норма в формуле D.54) может быть взята в любом
функциональном пространстве. Если эта норма взята в
пространстве L2(a, b), то в силу неравенства D.51) ||/?||<;в
и, следовательно,
|| ф-о|) ||< е A+1| Тк || )A+ IHYU) Ц/Ц. D.54')
Разбиение D.50) можно выполнить многими способами,
притом так, что ядро L (лг, s) будет вырожденным. Укажем
некоторые из этих способов.
1°. Пусть последовательность^*) (а=1, 2, ♦..) орто-
нормирована и полна в 1г (я, Ь). Тогда ядро К(х, s)
разлагается в двойной ряд Фурье, сходящийся в среднем:
00
К{х, s)= 2 Алгиа{х)иЛв),
a, p = i

360 ГЛ. IV. ПРИБЛИЖ. РЕШЕНИЕ ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ
где
ъ ь
Л«3= И Ki<x* 5) "«W ЬМ) dx ds>
а а
взяв достаточно большое я, можно положить
п
L(x, s)= 2 Ад«« (■*)«? (*)•
a, 0=i '
2°. Можно также построить разложение
00
' К(х, s)= 2 B^ua{x)u*(s),
a, p=i р
где
& ь
В«? = И К^ 5) В« (*) U$ (S) dx ds>
а а
и положить
п
L{x, s)= 2 V«W"?(S)-
а, 3=i
3°. Пусть последовательность функций аа (х) (а = 1, 2, ...)
полна, но не ортонормирована в 12 (а, Ь). Тогда
последовательность функций иа (х) Ua (s) полна, но не ортонормирована в
L2(a, b\ a, b). Можно положить
п
L(xt s)= 2 V«WM5)'
а, p = i Р Р
выбрав коэффициенты Ла3 так, чтобы
6 Ь
\\\К{х, s)—L(x, s)\'dxds = mln; D.55)
а а
для этого достаточно определить упомянутые коэффициенты
из системы
ь ь
2 А«? ) и« М Ма' М d* $ й? (s) и& И d5 =
a, p=i а а
= $$#(*, 5)^7^Г%И^^ («', Р' = 1, 2, ..., П).
а а

§ 4. ЗАМЕНА ЯДРА ВЫРОЖДЕННЫМ 361
Можно также положить
п
L{x, s)= 2 В^иа (х) и, (s)
a, p=i
и определить коэффициенты £?а3 из системы
ь *
2 Ва3 \ иа (х) »0' (х) dx \ «а {s) щ- (s) ds =
а. P=i ' i a
ь ъ
= \\к{х, s) ца< (х) % E) dx ds (а',р' = 1, 2, ..., я).
а а
4°. Оба способа п. 3° являются частными случаями
следующего более общего способа. Пусть две
последовательности {иа(х)} и {va(x)}> l^a<oo, полны, но, вообще
говоря, не ортонормированы в L2(a, b). Можно положить
п
a, p = i
выбрав коэффициенты А^ так, чтобы выполнялось
требование D.55); для коэффициентов Ла^ получается система
* b
2 К А "<* М и* (х) dA Ч (s) Ч' (s) ds =
a, 3=i ^ Z
ь ь
= \ \ К U, s) иа (х) v$> (s) dx ds.
a a
5°. Если промежуток (а, b) конечный и ядро непрерывно
в квадрате а^лг, s^b, то ядро можно равномерно
аппроксимировать полиномом от х и s и принять этот полином
за L (л:, s) .
6°. Метод Бубнова — Галёркина и метод наименьших
квадратов, о которых будет сказано в следующем параграфе,
представляют собой применительно к интегральным
уравнениям некоторые специальные способы замены данного ядра
на вырожденное.
Пример 7. Рассмотрим уравнение
1
Ф (*) — [ sin xs ф (s) ds= f (x). D.56)
о

362 Гл. IV. ПРИБЛИЖ. РЕШЕНИЕ ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ
Положим
тогда
X S
L{x, s) = xs g-,
г»/ ч г ^s8 X*S*
R(xt s) = sinxs —;ts+~6"==720"~ ••«
Приближенное уравнение
i i
*(*)—* Cs\|5(s)ds + ^3 f s4>(s)ds = /(*)
о о
дает
^W = /W + ^ + V5, D.57)
где
i i
с, = \ s-ф (s) ds, c2 = — -g- \ ssty (s) ds.
о о
Xs
Умножая равенство D.57) на х, соответственно на —^ и ин-
о
тегрируя, получаем:
_2 I _f 1 ,43 __
где
Fi = \ */ W dx> /i=-g] *V (*) dx\
о о
решив эту систему, найдем приближенное решение i|)(a:).
Оценим разность ф—г|э по формуле D.54). Примем сперва, что
норма берется в метрике пространства С функций, непрерывных
на отрезке [0, 1]. Тогда, например,
1
|| R || = Мах [ | R (х, s) | ds;
о
аналогично определяются нормы и других интегральных операторов.
Имеем \R(x, s)\< -^; отсюда
|/г»<м-/1шл = 72о-

§ 4. ЗАМЕНА ЯДРА ВЫРОЖДЕННЫМ 363
Далее,
lir*n--MJI.-
■1-11*1
Но
К\\ — Мах \ sin xsds— Max
1 —cos л:
О < * < 1 J 0 < Af < 1 Х
о
Отсюда
ЦГИ<1.
Точно так же
»1 —cos 1 < 1 —cos -5- = y
,|L||e,.Sx<J(x—?)ЛТЙх<.(т-яL-я-я
П
13*
Теперь по формуле D.54)
1 24 1
ф^,|<7^-2,Т51|/||==1?5[1/,|==0'0051311/||==
= 0,00513 Max ]f(x)\.
О < X < 1
Оценим теперь разность ф—ур в метрике L2@, 1). Как известно,
в пространстве L2(a, b) норма интегрального оператора с ядром
/£(*, s) не превосходит величины В, определяемой формулой D.2).
Отсюда, так как
"Л"<12оШ*,,1М<ЬЛ}1-1
о о
1 1 111
|| /С II <| JJsinljtsdA:ds|T<| Г r^V^rfs|T = -l,
0 0 0 0

364 ГЛ. IV. ПРИБЛИЖ. РЕШЕНИЕ ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ [1
Отсюда
IIIVIKy. II Г£ || < -i-
и
Нф—•ф||<Т^5--|-||/» = 0,00170||/||.
§ 5. Методы Бубнова — Галёркина и наименьших
квадратов
1. Метод Бубнова — Галёркина. Чтобы решить уравнение
ь
<р(*) —к\К(х, s)y(s)ds = f{x) D.58)
а
по методу Бубнова—Галёркина, выбирают полную в L2 (я, Ь)
последовательность функций ил(х) (а= 1, 2, .. .) такую, что
при любом п функции иг(х), и2(х), ..., ип(х) линейно
независимы, и ищут приближенное решение в виде
Ф-(*)= 2 «««.(*); D-59)
коэффициенты аа определяют из условия, чтобы невязка
уравнения D.58) была ортогональна к функциям и1 (х),
и2(х), ..., ип(х); это дает линейную систему
г Г г
53 М "«(*)-*} K(xis)ua(s)ds
a=i a L a
b
= 5 /(*) ^(x)dx (P = 1, 2, ..., n). D.60)
a
Если значение К не характеристическое, то при
достаточно больших п система D.60) разрешима единственным
образом; при п—► сю приближенное решение D.59) стремится
в метрике L2 (a, b) к точному решению ф (х) уравнения D.58).
Имеет место оценка
||ф_фп||<A+еп)||ф-Рпф||, D.61)
где Рп—оператор проектирования в подпространство,
натянутое на функции их, ц2, ..., ип, а гп >0.
Ир (a:) dx =

2] § 5. МЕТОДЫ БУБНОВА—ГАЛЁРКИНА И НАИМЕНЫ11. КВАДРАТОВ 365
Иногда применяется следующее обобщение метода
Бубнова— Галёркина. Вводятся две полные в L2(a, b) системы
{ип{х)} и {vn (х)} такие, что при любом п как функции и19
и2, ...,ип, так и функции vJtv29 -..yvn линейно
независимы; решение ищется в форме D.59), но коэффициенты
аа определяются из условия ортогональности невязки к
функциям Uj, v2, ..., vn. Это приводит к системе для
определения коэффициентов аа:
п 6 г * 1
2 fl«J "aW"*' )К(ХУ S)U0i(s)dS Vf{x)dX =
b
= J/W^ (p = l, 2, ...,/*). D.62)
a
Сформулируем условие сходимости обобщенного метода
Бубнова—Галёркина. Допустим прежде всего, что
последовательности {ип} и {vn} суть базисы в L2 (a, b). Обозначим
через Unn l/n подпространства, натянутые на их, н2, . ..,ил
и vx, v2J ..., vn соответственно, и пусть Рп—оператор
проектирования в подпространство Un. Допустим, далее, что
существует такая постоянная С>0, что для любого элемента
v £ Vn справедливо неравенство \\v\\ ^C\\Pnv\\. Тогда: 1) при
достаточно больших п система D.62) разрешима
единственным образом; 2) уп—^ф в метрике Li(a1 b); 3) верна оценка
D.61).
2. Метод наименьших квадратов. Выберем
последовательность координатных функций {иа(х)}} удовлетворяющую
тем же условиям, что и в п. 1, зададим приближенное
решение в виде D.59) и будем определять коэффициенты аа
из условия, чтобы невязка уравнения D.58) имела
минимальную в L2 (a, b) норму:
b\ b |2
||фя—Шр„1|2=$ Ф„(*) — ^$ К(х> s)ffn{s)ds\ dx = m\n.
а \ a J
Это приводит к линейной алгебраической системе
2 ал (АиаУ Аир) = (/, Аи# ф = 1, 2, . .., п)у D.63)

366 ГЛ. IV. ПРИБЛИЖ. РЕШЕНИЕ ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ [2
в которой положено
ъ
Аи = и (х)—ККи = и (х) — Х J К (*, s) и (s) ds.
а
Более подробно коэффициенты и свободные члены
системы D.63) можно записать так:
ь
(A*., Au^)=^u<l(x)u^(x)dx—
а
i Ь Ь .
— 2Rem ^K(x,s)tta{s)a^(x)dxds \ +
\ а а '
ЬЬЬ
+I *• I2 ffi к(*>s) к(х>f) U^S) н wdx ds dt>
a a a
b b b
(/, Лщ)= ^f(x)tifi(x)dx—k [[K(x> s)f(x)Up(s)dxds.
a a a
Если данное значение X не является характеристическим
для ядра К(х, $), то система D.63) разрешима при любом
п и фп—>ц> в метрике L2(af Ь)у где ф—решение уравнения
D.58); если приближенное решение фп построено, то его
погрешность можно оценить по формуле
||фи-ф||<М||Ф„-Шр„-/||;
здесь М—постоянная, равная норме оператора Л.
Может случиться, что К есть характеристическое число
ядра К(х, s); тогда однородное уравнение
Au = u(x) — %^K(x,y)u(y)dy=0 D.64)
имеет нетривиальные решения, среди которых, как известно,
только конечное число линейно независимых; эти последние
обозначим через ®1 (дг), со2(л:), ..., (ор{х). Столько же
линейно независимых решений имеет и сопряженное
однородное уравнение А*и—0. Для разрешимости уравнения D.58)
необходимо и достаточно, чтобы функция f(x) была
ортогональна ко всем решениям уравнения А*и = 0. Примем,
что это требование выполнено, тогда уравнение D.58) имеет

1] § 6. РЕШЕНИЕ СИНГУЛЯРНЫХ ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ 367
бесчисленное множество решений. Среди них есть одно и
только одно решение, ортогональное ко всем функциям
(х)г(х)у сог(х), ..., со^л:). Если эти функции известны, то
упомянутое решение можно построить по методу
наименьших квадратов. Для этого выберем координатные функции
uk(x), как указано выше, возьмем л>р и положим
п
ф»(*)= 2 йаМ«
£=1
Потребуем, чтобы
п
(Фш ©у) = 2 ч («*. ©у) = ° и = и,..., р).
С помощью этих соотношений выразим р коэффициентов
ak через остальные и затем потребуем, чтобы \\Аип—/||* =
= min. Это приведет нас к линейной алгебраической системе,
из которой мы и найдем оставшиеся п—р коэффициентов ak.
§ 6. Приближенное решение сингулярных
интегральных уравнений
1. Постановка задачи. Будем рассматривать уравнение
ЛФ = a (t) ф (t) — b{t) &р + [ K{t, т) ф (т) dx=f(t), D.65)
т ш J т—t
г
Для простоты примем, что данные функции в уравнении
D.65) удовлетворяют условию Липшица с положительным
показателем по тем переменным, от которых эти функции
зависят. Примем также, что контур интегрирования Г
представляет собой простую замкнутую кривую, обладающую
непрерывной кривизной; кривая Г делит плоскость комплексной
переменной на две области: внутреннюю D+ и внешнюю D".
Коэффициенты a (t) и Ь (t) подчиним условию
min| а2 @ — b*(t)\>0, D.66)
t е г
играющему основную роль в теории сингулярных
интегральных уравнений.

368 ГЛ. IV. ПРИБЛИЖ. РЕШЕНИЕ ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ [2
В перечисленных условиях любое решение (если оно
существует) уравнения D.65), суммируемое со степенью,
большей единицы, удовлетворяет условию Липшица с
положительным показателем.
Через а (А) обозначим число линейно независимых
решений однородного уравнения Лф = 0; соответственно а (А*)
будет обозначать число таких же решений сопряженного
однородного уравнения Л*г|) = 0. Числа а (А) и а (Л*)
конечны. Разность т — а(А) — а (Л*), называемая индексом
оператора А или уравнения D.65), не зависит от ядра
K(t, т); она.вычисляется по формуле
1 Г , a(t) + b(t) /л с-ч
Д = 5ГаГ'а<Н0' D'67)
г
Уравнение D.65) разрешимо тогда и только тогда, когда
его свободный член f(t) ортогонален ко всем
решениям уравнения Л*г|) = 0. Если это условие выполнено и
если, кроме того, решения однородного уравнения Лф = 0
известны, то уравнение D.65) можно приближенно решить
по методу наименьших квадратов точно так же, как это
делается в случае уравнения Фредгольма (см. конец
предшествующего параграфа) *). Другой метод приближенного решения
уравнения D.65) может быть основан на том, что если
K(t, т) = 0, то это уравнение решается в замкнутой форме
в квадратурах; если же K(t, x) есть вырожденное ядро,
то к вычислению квадратур добавляется нахождение
решения некоторой линейной алгебраической системы. Способы
приближенной замены фредгольмова ядра вырожденным
изложены в § 4; здесь мы ограничимся поэтому только тем,
что покажем, как решается уравнение D.65) в случае, когда
ядро K(t, т) вырожденное.
2. Решение сингулярного уравнения с вырожденным
ядром. Пусть
(Х = 1
*) Подробно об этом см. статью автора «Метод наименьших
квадратов в задачах математической физики», Уч. зап. ЛГУ, № 111, сер.
матем. наук, вып. 16 A949), 167—206. Специально о сингулярных
уравнениях см. в этой статье стр. 174—176.

2] § 6. РЕШЕНИЕ СИНГУЛЯРНЫХ ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ 369
Уравнение D.65) принимает вид
a(t)y(t)-b(t)S<p=f(t)-j? caua(t), D.68)
a=i
где
с. = ^«(т)Ф(т)Л. D.69)
г
Рассматривая правую часть уравнения D.68) как
известную, применим к этому уравнению метод Карлемана. Вкратце
напомним этот метод. Правую часть уравнения D.68)
обозначим через / (t) и положим Ф (z) = к—. \ dxy где z— лю-
Г
бая не лежащая на контуре Г точка комплексной плоскости.
Поместим начало координат внутри Г, тогда
где функция 0 (t)_ однозначна на Г; эта функция
удовлетворяет условию Липшица с положительным показателем.
Уравнение D.68) приводится к виду
Ф+ С)-tme* <" Ф- (*) = я(/).% . D-70)
где Ф+(t) и Ф~ (t) суть пределы функции Ф(г), когда
z-+t, /еГ, изнутри, соответственно, извне Г. Положим
г
и введем новую неизвестную функцию F(z), полагая Ф(г) =
= F(z)e^{Z). Обозначим через со (t) сингулярный интеграл
г
Тогда уравнение D.70) принимает следующий вид:
т
F* (t) — F- (t) {т = Ше-Ш^Л D,71)

370 ГЛ. IV. ПРИБЛИЖ. РЕШЕНИЕ ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ [2
Дальнейшее зависит от значения индекса т.
Если т = 0, то уравнение D.68) имеет единственное
решение, которое можно представить в виде
Ф@ = ф0(')-5]свфв(а D.72)
a=i
где
■a*(t)-b4t) ■
Va2 {t)—b2 (t) ni J Y& (x)-b2 (x) (x-t)
a фа(/) определяется по той же формуле D.73), если
заменить в ней f(t) на ua{t).
Из формулы D.72) и D.69) получаем систему для
неизвестных са:
CP + -S e«?ce=ftp (p=l,2, .... л). D.74)
a=i
Здесь
0«р = £ф.(ОМ')<", *p = J/(')^@«- D.75)
г г
Если определитель системы D.74) отличен от нуля, то
уравнение D.65) разрешимо и имеет единственное решение;
если же этот определитель равен нулю, то уравнение D.65)
разрешимо тогда и только тогда, когда столбец свободных членов
системы D.74) удовлетворяет соответствующим условиям
ортогональности; это равносильно тому, что некоторым условиям
ортогональности удовлетворяет свободный член уравнения
D.65). В этом случае решение уравнения D.65), если оно
существует, не единственно.
Если /и>0, то решение уравнения D.68) имеет вид
Ф @ = %(()- 2 сафв(/) + £ gft (t). D.76)
a=i Y=1
Здесь g—произвольные постоянные, а Ф (t) суть решения
однородного уравнения

2] § 6. РЕШЕНИЕ СИНГУЛЯРНЫХ ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ 371
функция ф0 (t) на этот раз определяется формулой
т
b(t)e»<b l_C тУ^>/(т) dx
' V'tm[a*(t)-P(t)} ™J Vaz{x)—b2(x) t —* ' ' '
а фа(/) получаются, если в формуле D.77) заменить f(t)
на иа(/). Для постоянных са и g получается система
п т
«3 + 2 «в3с.-2 Vt = *3 (Р = 1, 2; .... л), D.78)
a=i y=1
где аа? и Ь^ имеют прежние значения D.75), а
Если ранг матрицы коэффициентов при неизвестных в
системе D.78) равен я, то уравнение D.68) всегда разрешимо,
а соответствующее однородное уравнение имеет т линейно
независимых решений. Если же ранг этой матрицы г<Сп,
то уравнение D.68) разрешимо тогда и только тогда, когда
/(/) удовлетворяет некоторым п — г условиям
ортогональности; число линейно независимых решений
соответствующего однородного уравнения, равно т-\-п—г.
Пусть теперь т<;0, т~ — [i. Если решение уравнения
D.65) существует, то оно необходимо имеет вид
ф(*)=ф.(')-2с.ф.@.
где ф0 (/) по-прежнему определяется формулой D.77), а
ф« @ получается по той же формуле D.77) заменой /(/)
на ua{t). Функция

372 ГЛ. IV. ПРИБЛИЖ. РЕШЕНИЕ ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ [2
необходимо должна удовлетворять следующим условиям
ортогональности:
a=i
(ft = 0, 1,2, —, fx—1).
к г
СО (Т) - 2
J /а" (т)-**(*)
flfr = 0 D.79)
Коэффициенты са должны удовлетворять еще условиям D.74).
Решение уравнения D.65) существует, если система
уравнений D.74) и D.79) совместна, и не существует в
противном случае; решение единственно, если ранг матрицы
системы D.74) и D.79) г = [х, и не единственно, если r<Z\i;
в этом случае однородное уравнение D.65) имеет \х — г
линейно независимых решений.
НЕКОТОРЫЕ ЛИТЕРАТУРНЫЕ УКАЗАНИЯ
Вопросы приближенного решения интегральных уравнений
подробно трактуются в книгах [30], [64], а также [25].
Метод простой итерации для преобразованного уравнения
(см. п. 3 § 2) разработан в статье [74] И. П. Натансоном,
рассматривавшим уравнения более широкого класса. Более общее
преобразование уравнения дано в статье [4]. .
Подробное изложение метода Бубнова — Галёркина см. в
главе III настоящего справочника, а также в [63].
О решении сингулярных интегральных уравнений с одной
независимой переменной см. [8], [71], [72].

БИБЛИОГРАФИЯ
1. Бахвалов И. С, К оценке ошибок при численном
интегрировании дифференциальных уравнений экстраполяционным методом
Адамса, ДАН 104, №5A955).
2. Бе резин И. С. и Жидков Н. П., Методы вычислений,
т. II, М., Физматгиз, 1960.
3. Б и р м а н М. Ш., Вариационные методы решения краевых
задач, аналогичные методу Трефтца, Вестн. ЛГУ, № 13, сер.
матем., мех. и астр., вып. 3 A956).
4. Бирман М. Ш., Об одном варианте метода последовательных
приближений, Вестн. ЛГУ, № 9 A952), 69—76.
5. БудакБ. М. и Горбунов А. Д., О разностном методе
решения задачи Коши для уравне'ния у" — / (л:, у) и для системы
уравнений х. = Х( (t, xv ..., хп) (i = 1,..., п) с разрывными
правыми частями, Вестн. МГУ, сер. матем., № 5 A958), 7—11.
6. Бут Э. Д., Численные методы, М., Физматгиз, 1959.
7. В а й н б е р г М. М., Вариационные методы исследования
нелинейных операторов, М., Гостехиздат, 1956.
8. Век у а Н. П., Системы сингулярных интегральных уравнений,
М. — Л., Гостехиздат, 1950.
9. Волков Е. А., К вопросу о решении методом сеток
внутренней задачи Дирихле для уравнения Лапласа, Вычислит, матем.,
сб. 1 A957).
10. Волков Е. А., О методе сеток для краевой задачи с косой и
нормальной производной, Журн. выч. матем. и матем. физ. 1,
№ 4 A961), 607—621.
11. Воробьев Ю. В., Метод моментов в прикладной математике,
М., Физматгиз, 1958.
12. Во ров и ч И. И., О существовании решений в нелинейной
теории оболочек, Изв. АН, сер. матем., 19 A955), 173—186.
13. В у лих Б. 3., Введение в функциональный анализ, М.,
Физматгиз, 1958.
14. Га ген-Торн Л. Н., О разрешимости систем Ритца для
функционалов теории пластичности, Труды Матем. ин-та им.
В. А. Стеклова 66 A962), 190—195.
15. Г а ген-Top н Л. Н. и Ми х ли н С. Г., О разрешимости
нелинейных систем Ритца, ДАН 138, № 2 A961).
16. Гельфанд А. В., Приближенное интегрирование системы
обыкновенных дифференциальных уравнений первого порядка,
Изв. АН, сер. матем. A938), 583—594.

374
БИБЛИОГРАФИЯ
17. Годунов С. К., Рябенький В. С, Введение в теорию
разностных схем, М., Физматгиз, 1962.
18. Г у р с а Э., Курс математического анализа, т. II, М. — Л., ОНТИ,
1936.
19. Д а в и д ен к о Д. Ф., Об одном новом методе численного
решения систем нелинейных уравнений, ДАН 88, № 4 A953).
20. Калугина Е. П., Класс Аф как выпуклое многообразие,
ДАН 98 A954), 13—16.
21. Калугина Е. П., О классах Нф (г„ г2, ...,ги), ДАН 96
A954), 13-15.
22. Камке Э., Справочник по обыкновенным дифференциальным
уравнениям, М., ИЛ, 1950.
23. Канторович Л. В., Функциональный анализ и прикладная
математика, УМН 3, вып. 6 B8) A948).
24. Канторович Л. В; и А к и л о в Г. П., Функциональный
анализ в нормированных пространствах, М., Физматгиз, 1959.
25. К а нто р ови ч Л. В. и Крылов В. И., Приближенные
методы высшего анализа, М.—Л., Гостехиздат, 1949.
26. Канторович Л. В. и Крылов В. И., Численные методы,
в сб. «Математика в СССР за 30 лет», М. —Л., 1948.
27. К а ч а н о в Л. М., О вариационных методах решения задач
теории пластичности, Прикл. матем. и мех. 23, вып. 3 A959).
28. К а чанов Л. М., Основы теории пластичности, М.,
Гостехиздат, 1956.
29. К а чанов Л. М., Пример решения вариационным методом
задачи упруго-пластического кручения, Исслед. по упруг, и
пластичн., сб. 1, Изд. ЛГУ A961), 157—161.
30. К о л л а т ц Л., Численные методы решения дифференциальных
"уравнений, М., ИЛ, 1953.
31. Крылов А. Н., Лекции о приближенных вычислениях, М.,
Изд. АН СССР, 1949.
32. Крылов В. И., Сходимость и устойчивость численного
решения дифференциального уравнения второго порядка, ДАН
БССР 4, № 5 A960), 187—189.
33. Курант Р., Гильберт Д., Методы математической физики,
т. I, M. — Л., ГТТИ, 1933.
34. Ку р а нт Р., Ф р и д р и х с К., Л ев и Г., О разностных
уравнениях математической физики, УМН, вып. VIII A941).
35. Л а д ы ж е н с к а я О. А., Метод конечных разностей в теории
уравнений с частными производными, УМН 12, вып. 5 G7)
A957), 123—148.
36. Ладыженская О. А., О нестационарных однородных
уравнениях и их приложениях к линейным задачам математической
физики, Матем. сб. 45 (87): 2 A958), 123—158.
37. Ладыженская О. А., О решении нестационарных
операторных уравнений, Матем. сб. 39 (81): 4 A956), 491—524.
38. Ладыженская О. А., Смешанная задача для
гиперболического уравнения, М., Гостехиздат, 1953.
39. Лангенбах А., О некоторых нелинейных операторах
теории упругости в гильбертовом пространстве, Вестн. ЛГУ, № 1,
сер. матем., мех. и астр., вып. 1 A961).

БИБЛИОГРАФИЯ
375
40. Лангенбах А., О применении вариационного метода к
некоторым нелинейным дифференциальным уравнениям, ДАН
121, № 2 A958).
41. Л а не Дж. Н., Численные методы для быстродействующих
вычислительных машин, М., ИЛ, 1962.
42. Лебедев В. И., Метод сеток при второй краевой задаче для
уравнения Пуассона, ДАН 127, № 4 A959).
43. Лебедев В. И., О конечно-разностном аналоге задачи
Неймана, ДАН 126, № 3 A959), 494—497.
44. Лебедев В. И., Об оценке погрешности метода сеток для
задач Дирихле и Неймана, ДАН 128, № 4 A959).
45. Лебедев В. И., Оценка погрешности метода сеток для
двумерной задачи Неймана, ДАН 132, № 5 (I960).
46. Лейбензон Л. С, Вариационные методы в теории
упругости, М.—Л., Гостехиздат, 1943 (см. также: Собрание трудов
акад. Л. С. Лейбензона, т. 1, Изд. АН СССР, 1951).
47. Лозинский СМ., О приближенном решении систем
обыкновенных дифференциальных уравнений, ДАН 97, № 1 A954),
29—32.
48. Лозинский С. М., Об интервале существования решения
системы обыкновенных дифференциальных уравнений, ДАН 94,
№ 1 A954), 17—19.
49. Лозинский СМ., Об уравнениях в вариациях, ДАН 93,
№ 4 A953).
50. Л о з и н с к и й СМ., Оценка погрешности приближенного
решения системы обыкновенных дифференциальных уравнений,
ДАН 92, № 2 A953), 225-228.
51. Лозинский С М., Оценка погрешности численного
интегрирования обыкновенных дифференциальных уравнений, Изв.
вузов, Математика, 5 A958).
52. Лузин Н. Н., О методе приближенного интегрирования
акад. С А. Чаплыгина, УМН 6, вып. 6 D6) A951), 3—27.
53. Л юстер ник Л. А., Замечания к численному решению
краевых задач уравнения Лапласа и вычислению собственных
значений методом сеток, Труды Матем. ин-та им. В. А. Стек лова
20 A947), 49—64.
54. Лю стерни к Л. А., О разностных аппроксимациях оператора
Лапласа, УМН 9, вып. 2 F0) A954).
55. Маховер Е. В., Изгиб пластинки переменной толщины с
острым краем, Уч. зап. Ленингр. пед. ин-та, физ.-матем. ф-т,
17, № 2 A957), 28-39.
56. Маховер Е. В.,О спектре собственных частот пластинки с
острым краем, Уч. зап. Ленингр. пед. ин-та 197 A958), 113—118.
57. М и к е л а д з е Ш. Е., Новые методы интегрирования
дифференциальных уравнений, М.—Л., Гостехиздат, 1951.
58. Микеладзе Ш. Е., О численном интегрировании уравнений
эллиптического и параболического типа, Изв. АН, сер. матем.,
5, № 1 A941), 57—73.
59. Милн В. Э., Численный анализ, М., ИЛ, 1951.
60. Милн В. Э., Численное решение дифференциальных уравнений,
М., ИЛ, 1955.

376
БИБЛИОГРАФИЯ
61. Миранда К., Уравнения с частными производными
эллиптического типа, М., ИЛ, 1957.
62. Миткевич В.М., Применение метода Ритца к задаче об изгибе
консольной плиты, Сб. тр. Лаб. гидравл. машин АН УССР,
вып. 9 A961), 48—57.
63. Ми х лин С. Г., Вариационные методы в математической
физике, М., Гостехиздат, 1957.
64. Ми х лин С. Г., Интегральные уравнения и их приложения,
М.—Л., Гостехиздат, 1949.
65. М и х л и н С. Г., Некоторые условия устойчивости метода Ритца,
Вестн. ЛГУ, № 13, сер. матем., мех. и астр., вып. 3 A961).
66. М и х л и н С. Г., О методе Ритца в нелинейных задачах, ДАН
142, № 4 A962).
67. Михлин С. Г., О рациональном выборе координатных
функций в методе Ритца, Журн. выч. матем. и матем. физ. 2, № 3
A962).
68. Михлин С. Г., Об устойчивости метода Ритца, ДАН 135,
№ 1 A961).
69. М и х л и н С. Г., По поводу метода Ритца, ДАН 106, № 3 A956).,
70. Михлин С. Г., Проблема минимума квадратичного
функционала, М.— Л., Гостехиздат, 1952.
71. Михлин С. Г., Сингулярные интегральные уравнения, УМН '3,
вып. 3 B5) A948).
72. М у с х е л и ш в и л и Н. И., Сингулярные интегральные
уравнения, М., Физматгиз, 1962.
73. Мы со век их И. П., Лекции по методам вычислений, М.,
Физматгиз, 1962.
74. Натансон И. П., К теории приближенного решения
уравнений, Уч. зап. Ленингр. пед. ин-та 64 A948), 3—8.
75. Панов Д. Ю., Справочник по численному решению
дифференциальных уравнений в частных производных, М.—Л.,
Гостехиздат, 1951.
76. Панов Д. Ю., Численное решение квазилинейных
гиперболических систем дифференциальных уравнений в частных
производных, М., Гостехиздат, 1957.
77. Петровский И. Г., Лекции об уравнениях с частными
производными, М., Гостехиздат, 1953.
78. Польский Н. И., Некоторые обобщения метода Галёркина,
ДАН 86, № 3 A952).
79. Польский Н. И., Про зб1жн'1сть методу Б. Г. Гальоркша,
ДАН УРСР, В'щ. ф1з.-матем. та xiM наук, № 6 A949), 7—12.
80. Польский Н. И., Об одной общей схеме применения
приближенных методов, ДАН 111, № 6 A956).
81. Рихтмайер Р. Д., Разностные методы решения краевых задач,
М., ИЛ, 1956.
82. Розе С. Н., О сходимости метода Л. М. Качанова, Вестн.
ЛГУ, № 19 A961).
83. Рябенький В. С, Филиппов А. Ф., Об устойчивости
разностных уравнений, М., Гостехиздат, 1956.
84. С а л ь в а до р и AL Дж., Численные методы в технике, М.,
ИЛ, 1955.

БИБЛИОГРАФИИ
377
85. Самарский А. А., Априорные оценки для разностных
уравнений, Журн. выч. матем. и матем. физ. 1, № б A961).
86. С а м а р с к и й А. А., Априорные оценки для решения
разностного аналога дифференциального уравнения параболического
типа, Журн. выч. матем. и матем. физ. 1, № 3 A961).
87. Самарский А. А., Однородные разностные схемы для
нелинейных уравнений параболического типа, Журн. выч. матем.
и матем. физ. 2, № 1 A962).
88. Самарский А. А., Фрязинов И. В., О сходимости
однородных разностных схем для уравнения теплопроводности
с разрывными коэффициентами, Журн, выч. матем. и матем.
физ. 1, № 5 A961).
89. С а неоне Дж., Обыкновенные дифференциальные уравнения,
т. И, М., ИЛ, 1954.
90. Саульев В. К., Интегрирование уравнений параболического
типа методом сеток, М., Гостехиздат, 1960.
91. Саульев В. К., К вопросу решения задачи о собственных
значениях методом конечных разностей, Выч. матем. и выч.
техн., сб. II, 1955.
92. Слободянский М. Г., Оценки погрешности приближенных
решений линейных задач, Прикл. матем. и мех. 17, вып. 2
A953).
93. Смирнов В. И., Курс высшей математики, т. II, М., Физ-
матгиз, 1958.
94. Смирнов В. И., Курс высшей математики, т. IV, М., Физ-
матгиз, 1958.
95. С м и р н о в В. И., Курс высшей математики, т. V, М., Физ-
матгиз, 1959.
96. Смирнова Т. Н., Полиномиальный прораб и проведение
аналитических выкладок на ЭВМ, Труды матем. ин-та
им. В. А. Стеклова 66 A962), 77—112.
97. Соболев С. Л., Некоторые применения функционального
анализа в математической физике, Изд. ЛГУ, 1950.
98. Соболев С. Л., Уравнения математической физики, М.,
Гостехиздат, 1954.
98а. Соболевский П. Е., Об уравнениях с операторами,
образующими острый угол, ДАН 116, № 5, 1957.
99. Степанов В. В., Курс обыкновенных дифференциальных
уравнений, М., Гостехиздат, 1953.
100. Талдыкин А. Т., Системы элементов гильбертова
пространства и ряды по ним, Матем. сб. 29 G1): 1 A951).
101. Тихонов А. Н., Самарский А. А., Об однородных
разностных схемах, Журн. выч. матем. и матем. физ. 1, № 1 A961).
102. ТихоновА. Н., С а м а р с к и й А. А., Однородные
разностные схемы высокого порядка точности на неравномерных
сетках, Журн. выч. матем. и матем. физ. 1, № 3 A961).
103. Тихонов А. Н., Самарский А. А., Разностная задача
Штурма—-Лиувилля, Журн. выч. матем. и матем. физ. 1, № 5
A961).
104. Фаддеев Д. К., ФаддееваВ. Н., Вычислительные
методы линейной алгебры, М., Физматгиз, 1963.

378
БИБЛИОГРАФИЯ
105. Фридман В. М., Метод последовательных приближений
для интегральных уравнений первого рода, УМН 11, вып. 1F7),
A956).
106. Чаплыгин С. А., Новый метод приближенного
интегрирования дифференциальных уравнений, М.—Л., Гостехиздат, 1950.
107. Шура-Бура М. Р., Оценки ошибок численного
интегрирования обыкновенных дифференциальных уравнений, ПММ 16,
вып. 5 A952).
108. Эйду с Д. М., О решении краевых задач методом конечных
разностей, ДАН 83, № 2 A952), 191 — 194.
109. Я с к о в а Г. Н. и Яковлев М. Н., Некоторые условия
устойчивости метода Петрова—Галёркина, Труды Матем. ин-та
им. В. А. Стеклова 66 A962), 182—189.
110. Batschelet E., Uber die numerische Auflosung von Rand-
wertproblemen bei elliptischen partiellen Differentialgleichungen,
Zeifs. angew. Math, und Phys., Bd. Ill, № 3 A952), 165—193.
lib Bers L., On mildly nonlinear partial difference equations of
elliptic type, Journ. Res. Nat. Bur. Standards 51, № 5 A953),
229 236.
112. Brien G. G., Ну man M. A., Kaplan S., A study of the
numerical solution of partial differential equations, Journ. Math,
and Phys. 29, J\fe 4 A951), 223—251.
113. Garr J. W., Error bounds for the Runge—Kutfa single-step
integration process, Journ, Assoc. Comput. Mach. 5, № 39
A958).
114. Dahlquisf G., Convergence and stability in the numerical
integration of ordinary differential equations, Math. Scand. 4,
№ 1 A956), 33-53.
115. Douglas Jim, G a 11 i e Т. М., On the numerical Integration
of a parabolic differential equation subject to a moving boundary
condition, Duke Math. Journ. 22, № 4 A955), 557—571.
116. ForsytheG. E., W a s о w W. R., Finite-difference methods for
partial differential equations, New York—London, 1960.
(Имеется русский перевод: В. В азов, Дж. Форсайт,
Разностные методы решения дифференциальных уравнений в
частных производных, М., ИЛ, 1963.)
117. Gerschgorin S., Fehlerabschatzungen fur Dif ferenzenverf ah-
ren bei Losung partiellen Differentialgleichungen, Zeits. angew.
Math, und Mech. 10 A930), 373—382.
118. Giese J. H., On the truncation error in a numerical solution
of the Neumann problem for a rectangle, Journ. Math, and Phys.
37, № 2 A958), 169-177.
119. Gould S. H., Variational methods for eigenvalue problems,
University of Toronto Press, 1957.
120. Horn J., Gewonliche Differentialgleichungen, Berlin und
Leipzig, 1937.
121. К a to Т., On the upper and lower bounds of eigenvalues, Journ.
Phys. Soc. Japan 4, № 1 A949), 334—339.
122. Kryloff N., Les methodes de solution approchee des proble-
mes de la physique mathematique, Memor. Sci. Math. 49
" A931).

БИБЛИОГРАФИЯ
379
123. Langenbach A., Variationsmethoden in der nichtlinearen
Elastizitat- und Plastizitatstheorie, Wiss. Z. Humboldt-Univ.
Berlin, Math-Nath. R., IX, 1959/60, 145—164.
124. Mises R., v., Zur numerischen Integration von Differential-
gleichungen, Zeits. angew. Math, und Mech. 10 A930), 81—92.
125. Motzkin T. S., Wasow W , .On the approximation of linear
elliptic differential equations by difference equations with
positive coefficients, Journ. of Math, and Phys. 31, № 4 A953),
253—259.
126. Synge L. E., The method of the hypercircle in functionspace
for boundary value problems, Proc. Royal Soc, ser. A, № 1027,
191 A947), 447—466.
127. Temple G., The computation of caracteristic numbers and
caracteristic functions, Proc. London Math. Soc. 29 A928).
128. Temple G., The theory of Rayleigh's principle as applied to
continuous systems, Proc. Royal Soc. 119 A928).
129. Weinberger H. F., Upper and lower bounds for eigenvalues
by finite difference methods, Comm. Pure and Appl. Math. 9
A956).
130. Weinberger H. F., Lower bounds for higher eigenvalues by
finite difference methods, Pacific. Journ. Math. 8, 339—368.
131. Weinstein A., Etude des spectres des equations aux de-
rivees partielles de la theorie des plaques elastiques, Memor.
Sci. Math. 88 A937).
132. Weinstein D. H., Modified Ritz method, Proc. Nat. Acad.
Sci. USA 20 A934), 529—532.

АЛФАВИТНЫЙ УКАЗАТЕЛЬ
Аппроксимация точной задачи
сеточной 79.
Ароншайн Н. 281
Бигармоническое уравнение
Пуассона 91
Вайнштейн А. 281
Выбор координатной системы
рациональный 302
— решетки и сходимость сеточных
решений 143
— сеточного уравнения,
аппроксимирующего линейное
дифференциальное уравнение 84
Дальквист Г. 69
Дифференциальные уравнения
второго порядка обыкновенные 211
— — высших порядков
обыкновенные 215
Достаточный признак сходимости
метода Бубнова—Галёркина 315
Дюфорт 168
Задача Гурса для квазилинейной
гиперболической системы
дифференциальных уравнений 180
— Дирихле для невырождающихся
эллиптических уравнений 222
— — — слабо нелинейного
эллиптического уравнения 183
— Коши для дифференциального
уравнения первого порядка 13
— — — квазилинейной
гиперболической системы
дифференциальных уравнений 179
— краевая вторая 222
— — двумерная 307
— — для бесконечных областей 241
— — одномерная 303
— — первая 222
— — третья 222
— Неймана для невырождающихся
эллиптических уравнений 222
— — сеточная 126
— о жестком контакте 236
— — собственных значениях
эллиптического оператора 136
— с заданными напряжениями 236
— — — смещениями 235
Задача с подвижной границей для
параболического уравнения 181
— смешанная 150, 236
— Стефана модифицированная
однослойная для параболического
уравнения 181
Замена конечно-разностная 137
— производных
конечно-разностными отношениями 128
— ядра вырожденным 358
Запись уравнения в граничном узле
76
Звезда 84
— девятиточечная 79
— пятиточечная 74
Значения сеточной функции в узлах
72
— собственные самосопряженного
эллиптического оператора 136, 140
Изгиб пластин 230
— сжатой пластины 233
Индекс оператора 368
— разностной схемы 164
Интегральное уравнение первого рода
с симметричным ядром 354
Интерполяционная формула Штёр-
мера 57
Интерполяция полилинейная 139
Итерационные способы решения
сеточной задачи Дирихле 113
Итерация сеточных систем,
удовлетворяющих принципу максимума
114
Калугина Е. П. 335
Канторович Л. В. 352
Качанов Л. М. 324
Квазилинейные гиперболические
системы дифференциальных
уравнений 175
Колебания упругих тел собственные
259
Коллатц 75
Корректность сеточных уравнений
104
— — —, близких к
самосопряженным 107
— — —, удовлетворяющих
принципу максимума 105
Коэффициент роста 165

АЛФАВИТНЫЙ УКАЗАТЕЛЬ
381
Краевая задача вторая 222
— — двумерная 307
— — для бесконечных областей 241
— — одномерная 303
— — первая 222
— — третья 222
Кратность собственного числа 244
— характеристического числа 338
Крылов Л. Н. 61, 63
Крылов В. И. 69, 352
Лозинский С. М. 69
Люстерник Л. А. 116
Метод Бубнова — Галёркина 314
— — — решения интегрального
уравнения 364
— итераций 349 — 354
— Качанова 324
— Либмана 116
— малого параметра 31
— наименьших квадратов 283
— — — в применении к
интегральному уравнению 365
— наискорейшего спуска 352
— Ньютона— Канторовича для
дифференциального уравнения
первого порядка 27
— — — — системы
дифференциальных уравнений 30
— ортогональных проекций 266
— последовательных приближений
для дифференциального уравнения
первого порядка 19
— — — — — __ порядка выше
первого 21
— — — — системы
дифференциальных уравнений 22
— прогонки 155
— проекционный 317
— простой итерации 349
— прямых 329
— — для бигармонического
уравнения 333
— — — параболического уравнения
334
— уравнения Лапласа 331
— — — — Пуассона 331
— Релея — Ритца 246
— Ритца 202, 320
— Рунге — Кутта 36
— сеточный 70
— средних арифметических 116
— трапеций 35
— Трефтца 271
— Чаплыгина 22
— Эйлера интегрирования
дифференциальных уравнений 35
— энергетический 199
— — в случае положительного
оператора 210
Методы решения системы Ритца 203
Микеладзе Ш. Е. 76
Направление характеристическое 176
Натансон И. П. 372
Невязка приближенного решения 34
Неравенство Пуанкаре 198
—- Фридрихса 198
Норма 105
— энергетическая 192
Область звездная 196
Обобщенные производные 193 196
Обыкновенные дифференциальные
уравнения второго порядка 211
— — — высших порядков 215
Оператор краевой задачи 188
— положительный 189
— положительно определенный 190
Определитель Фредгольма 349
Основной прием Рунге — Кутта 38
Оценка Гершгорина ПО
— Коллатца ПО
— погрешности 73
— — для задачи Дирихле 109
_____ Неймана 135
— — — смещенной задачи 154
— — приближенного решения 264
— — — —, полученного методом
Ньютона — Канторовича 28
— — через данные задачи 112
— — — невязку 34
— собственных чисел двусторонняя
279
— функционала двусторонняя 278
Пограничная полоса области 193
Погрешность вариационного метода
264, 265
— метода Рунге — Кутта 40
— — Эйлера 40
— приближенного решения 34, 73
— формул Адамса 66
Подобласть 193
— внутренняя 193
Подпространство собственное 244
Полилинейная интерполяция 139
Полоса пограничная 193
Постоянная Липшица 21
Построение начала таблицы при
разностных методах 57 — 64
— полной координатной системы
300
— решения вариационной задачи 200
Приближенное вычисление
собственных функций методом Келлога 344
— — — — — моментов 343
— — — — — Ритца 341
— — — — — следов 346
— — _ чисел методом Келлога 344
— — — — — моментов 343
— — — Ритца 340
— — — — — следов 346
— — характеристических чисел с
помощью определителя
Фредгольма 349
— решение задачи Коши для
дифференциального уравнения
первого порядка 15
— _ — — — — — п-то
порядка 17
— — — — — системы
дифференциальных уравнений IS

382
АЛФАВИТНЫЙ УКАЗАТЕЛЬ
Признак устойчивости для
уравнений с постоянными
коэффициентами 169
Признаки устойчивости 156
— — сеточной задачи 164
Применение квадратурных формул
354—358
— метода Бубнова — Галёркина к
задачам математической физики
315
— — наименьших квадратов к
задачам теории потенциала на
плоскости 286
— — — — — — — упругости 289
Принцип максимума 92
— —, сеточный аналог 92
— минимаксимальный 263
— минимума потенциальной энергии
в статической теории упругости
234
Произведение энергетическое 192
Производные обобщенные 193, 196
Простая итерация сеточных систем,
удовлетворяющих принципу
максимума 114
Пространства С. Л. Соболева 196
Пространство энергетическое 192
Разложение решения
дифференциального уравнения в ряд Тейлора
14-19
Разностные методы для систем
дифференциальных уравнений .54
— схемы устойчивости 173
Разрешимость сеточных уравнений 92
Рациональный выбор координатной
системы 302
Решение Даламбера 143
— нелинейной системы Ритца 324
— — — — сведением к задаче
Коши 326
— обобщенное 320
— с конечной энергией 210
— сингулярных уравнений с
вырожденным ядром 368
— тривиальное 243
Ричардсон 156
Розе С. Н. 324
Ряд сетки 144
Самосопряженное эллиптическое
дифференциальное уравнение 99
Свирский И. В. 281
Свойства предельные коэффициентов
Ритца 293
— собственных чисел 244 — 245, 339,
340
Сетка 70
— правильная треугольная 86
— прямоугольная 71
— шестиугольная 86
Сеточная задача Неймана 126
— (разностная) схема решения
смешанной задачи для уравнений
гиперболического и
параболического типов 158
Сеточные уравнения, близкие к
самосопряженным 112
Сеточные уравнения,
удовлетворяющие принципу максимума 109
Сеточный аналог вариационной
задачи 132
— — принципа максимума 92
— — самосопряженного
эллиптического дифференциального
уравнения 99
Сингулярное интегральное уравнение,
приближенное решение 367
Система минимальная 291
— Ритца 202
— сильно минимальная 292
— обыкновенных дифференциальных
уравнений 218
След ядра 346
Слободянский М. Г. 283
Слой 158
Смешанная задача 150, 236
Снос простой 75
Соболев С. Л. 335
Собственная функция 136
— —, нормированная 136
Собственное значение
самосопряженного эллиптического оператора
136, 140
— число 243
Собственные колебания упругих тел
259
— функции, приближенное
вычисление методом Келлога 344
— —, — — — моментов 343
— —, — — — Ритца 341
— —, — — — следов 346
— — ядра 338
— числа, приближенное вычисление
методом Келлога 344
— —, — — — моментов 343
— —, — — — Ритца 340
— —, — — — следов 346
— — ядра 338
Собственный элемент 243
Согласование норм 73
Спектр вырождающегося
эллиптического уравнения 258
— дискретный 245
— обыкновенного
дифференциального оператора 250
— собственный 243
— эллиптического оператора 253
Сравнение численных методов 18
Схема неявная 151, 153
— перемежающаяся 172
— явная • 151, 152
Сходимость невязки к нулю 299
— по энергии 192
— приближенного решения для
задачи Дирихле 109
— — — — — Неймана 135
— — — — смешанной задачи 154
— сеточных решений 143
Теорема о сходимости и оценка
погрешности 108
— Чаплыгина 23
Теоремы вложения 196
Теория пологих оболочек
нелинейная 322

АЛ
Узел внутренний 74
— второго рода 93
— граничный 75
— первого рода 93
Узлы сетки 70
— — основные 71
Улучшение аппроксимации за счет
выбора оператора 87, 90
— — -— — расширения звезды 87
Уравнение, близкое к
самосопряженному 101
— волновое одномерное 143
— Вольтер ра второго рода 354
— — первого рода 355
-— гиперболическое 143
— параболическое 145
—* Пуассона бигармоническое 91
— Фредгольма 356
— Фурье 145
— эллиптическое 101
— — вырождающееся 222, 227
— — высшего порядка 228
— — невырождающееся 221
Уравнения сеточные 71, 72
— — многоточечные 89
— эллиптического типа 221
Условия геометрические 206
— динамические 206
— кинематические 206
— краевые главные 206
__ _ естественные 206
— — неоднородные 208
— положительной определенности
дифференциальных операторов 262
— согласования данных смешанной
задачи 150
— сходимости метода Ньютона —
Канторовича 28
— — — простой итерации 350
Усовершенствованный" метод Эйлера
38
Устойчивость метода Ритца 290, 294
— равномерная 161
— разностной схемы 156, 162
— разностных методов 64
— сеточной задачи по граничным
условиям 161
— — — — начальным условиям 160
— — — — правой части 161
— сжатой пластины 258
Учет граничного условия линейной
интерполяцией 75
УКАЗАТЕЛЬ 383
Формула Адамса интерполяционная
47
— — экстраполяционная 42
— Нистрема экстраполяционная 51
— Синджа 267
— типа Коуэлла 51
— Штёрмера интерполяционная 57
— — экстраполяционная 55
Франке л 168
Функционал возрастающий 321
— полунепрерывный сверху 321
— теории пластичности 323
—- энергетического метода 199
Функция сеточная 72
— собственная 136, 243
— — нормированная 136
Характеристическое направление 176
— число кратное 338
— — простое 338
— — ядра 338
Характеристические числа,
приближенное вычисление с помощью
определителя Фредгольма 349
Ход прогонки обратный 155
— — прямой 155
Число собственное 243
— характеристическое кратное 338
— — простое 338
— — ядра 338
Шаг интегрирования 35
Ширина пограничной полосы 193
Экстраполяционная формула Адамса
42
— — Нистрема 51
— — Штёрмера 55
Элемент собственный 243
Элементы координатные 202
Эллиптическое уравнение 101
Энергетическое произведение 192
— пространство 192
Энергия элемента 190
Ядро симметричное 337
— — положительно определенное
339
— со слабой особенностью 337
—- — — полярностью 337

Справочная математическая библиотека
Приближенные методы решения
дифференциальных и интегральных уравнений
М., 1965. г., 384 стр. с илл.
Редактор А. Ф. Лапко.
Техн. редактор К. Ф. Брудно.
Корректор Т. С. Плетнева.
Сдано в набор 4/VI 1964 г. Подписано к
печати 26/IX 1964 г. Бумага 84x108/32. Физ. печ.
л. 12. Условн. печ. л. 19,68. Уч.-изд. л. 18,07.
Тираж 20750 экз. Т-14811. Цена книги 1 р. 05 к.
Заказ 1633.
Издательство «Наука».
Главная редакция
физико-математической литературы.
Москва, В-71, Ленинский проспект, 15.
Первая Образцовая типография
имени А. А. Жданова
Главполиграфпрома
Государственного комитета
Совета Министров СССР по печати.
Москва, Ж-54, Валовая, 28.