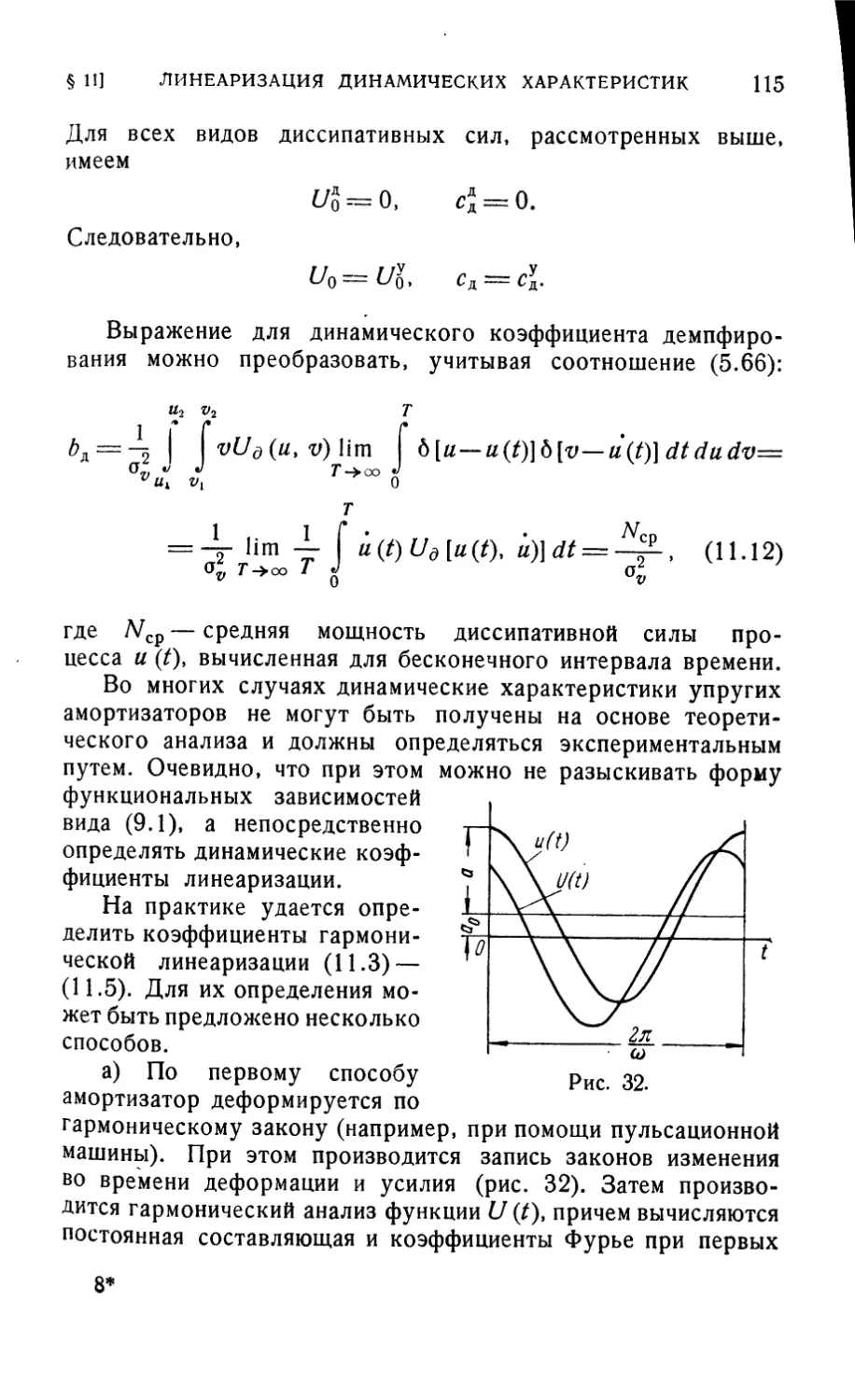
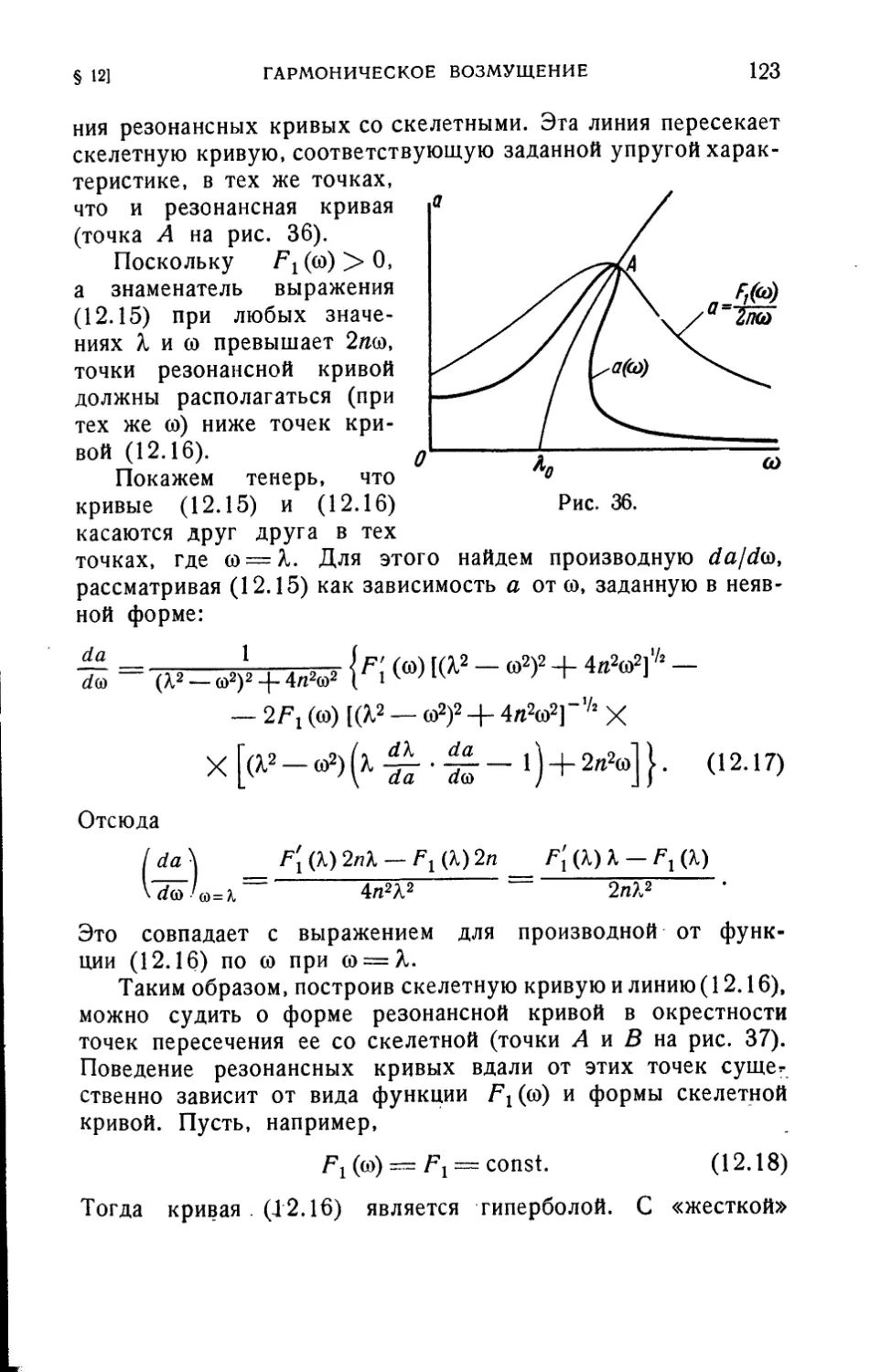
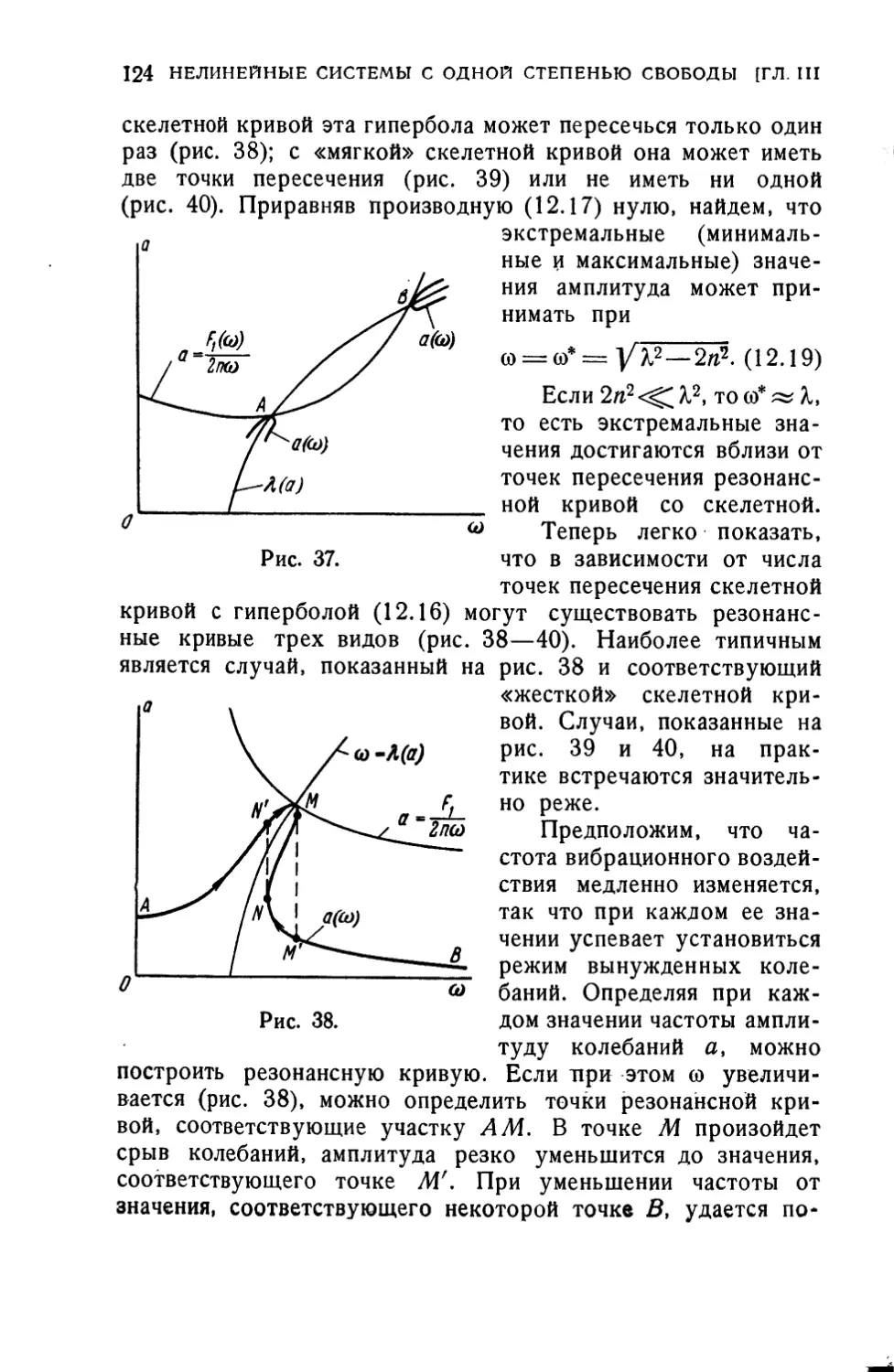
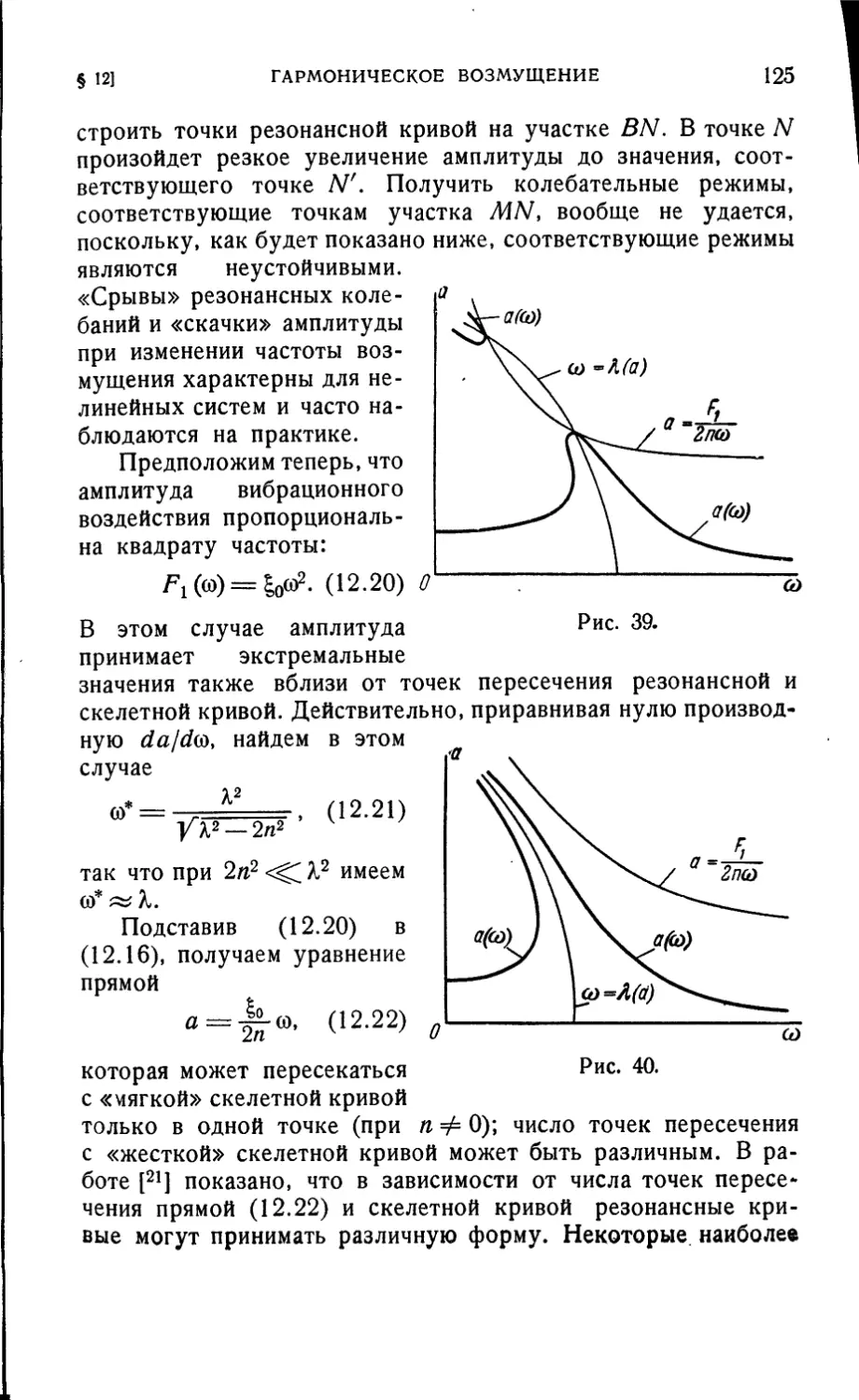
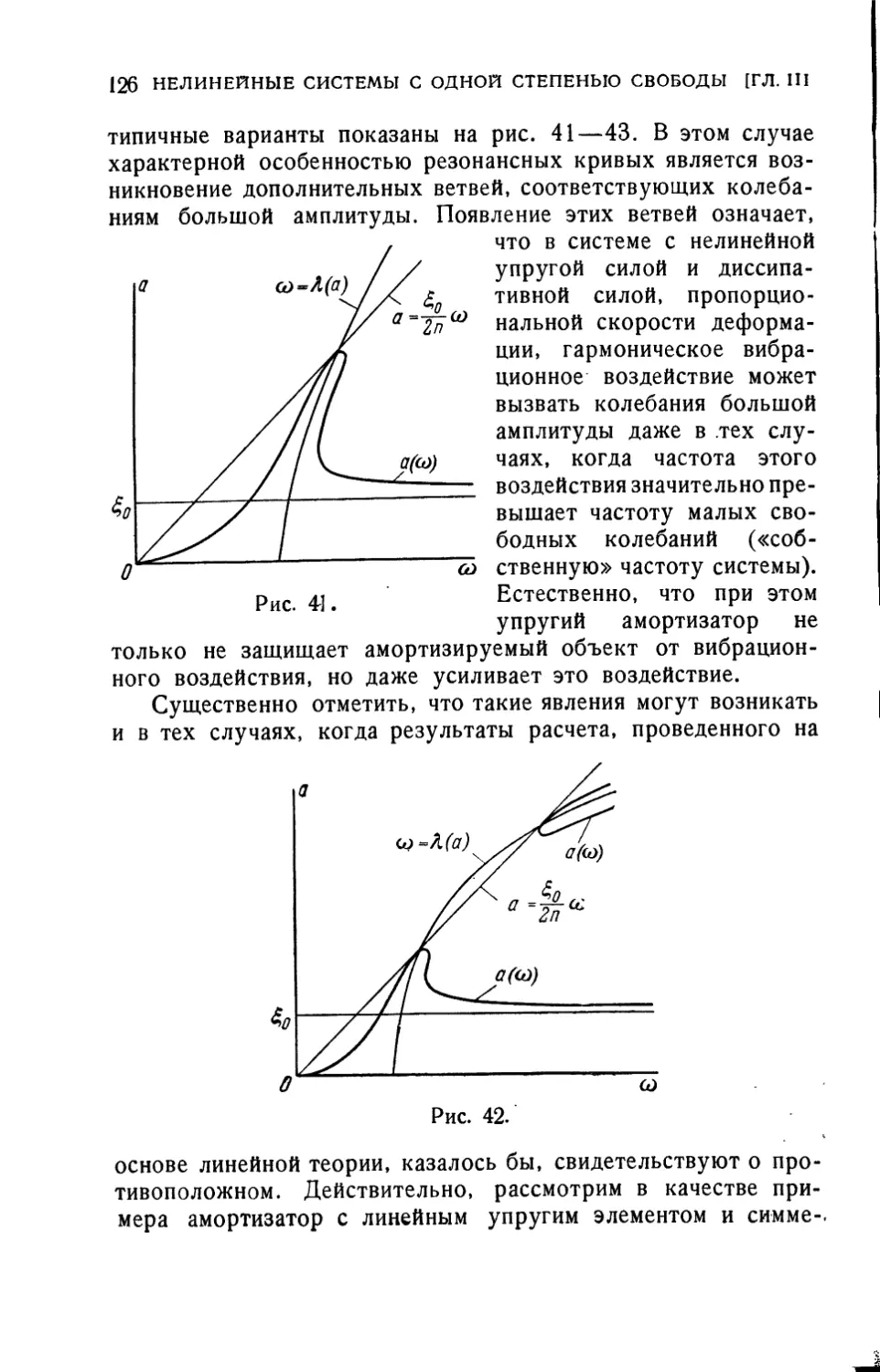
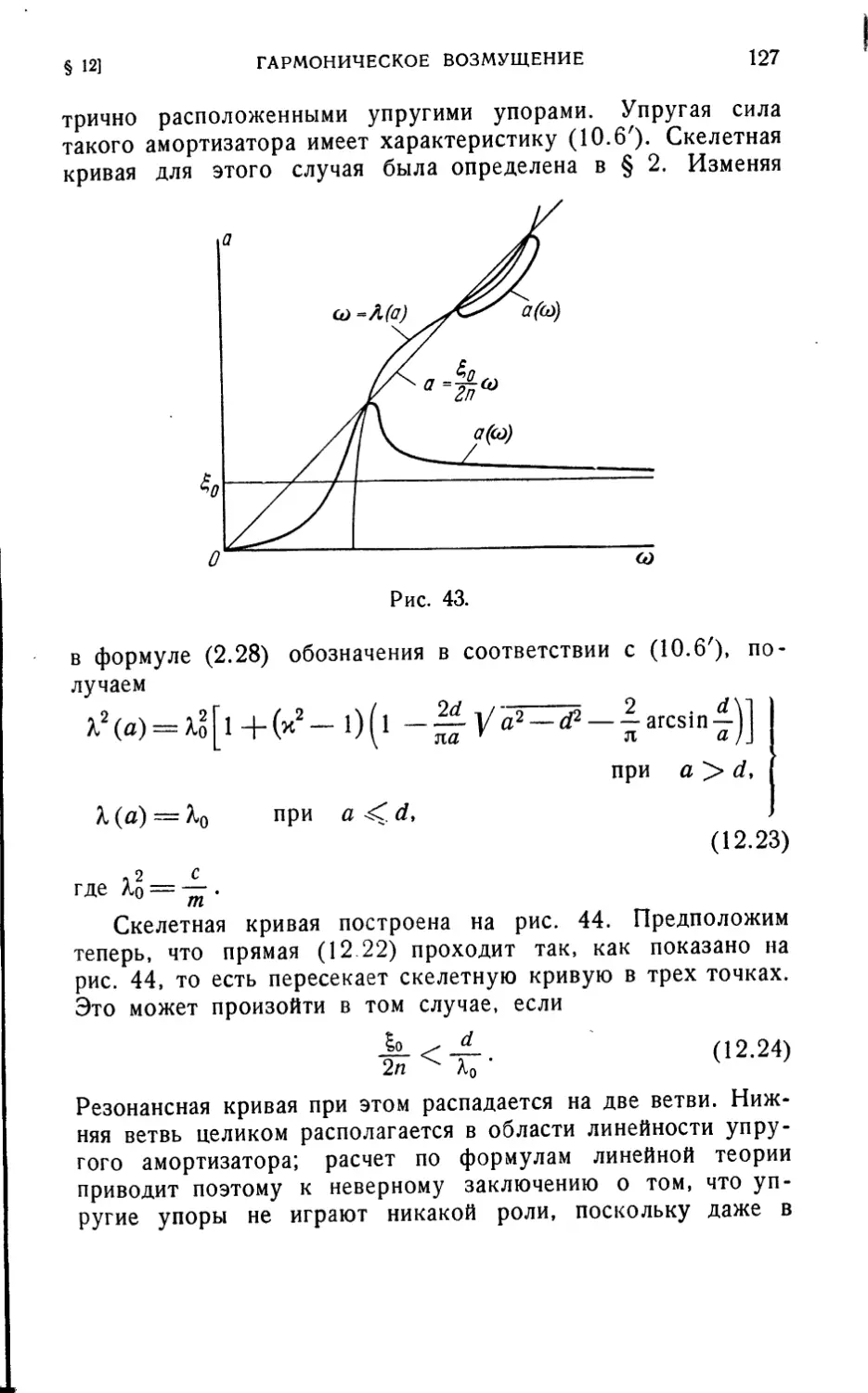
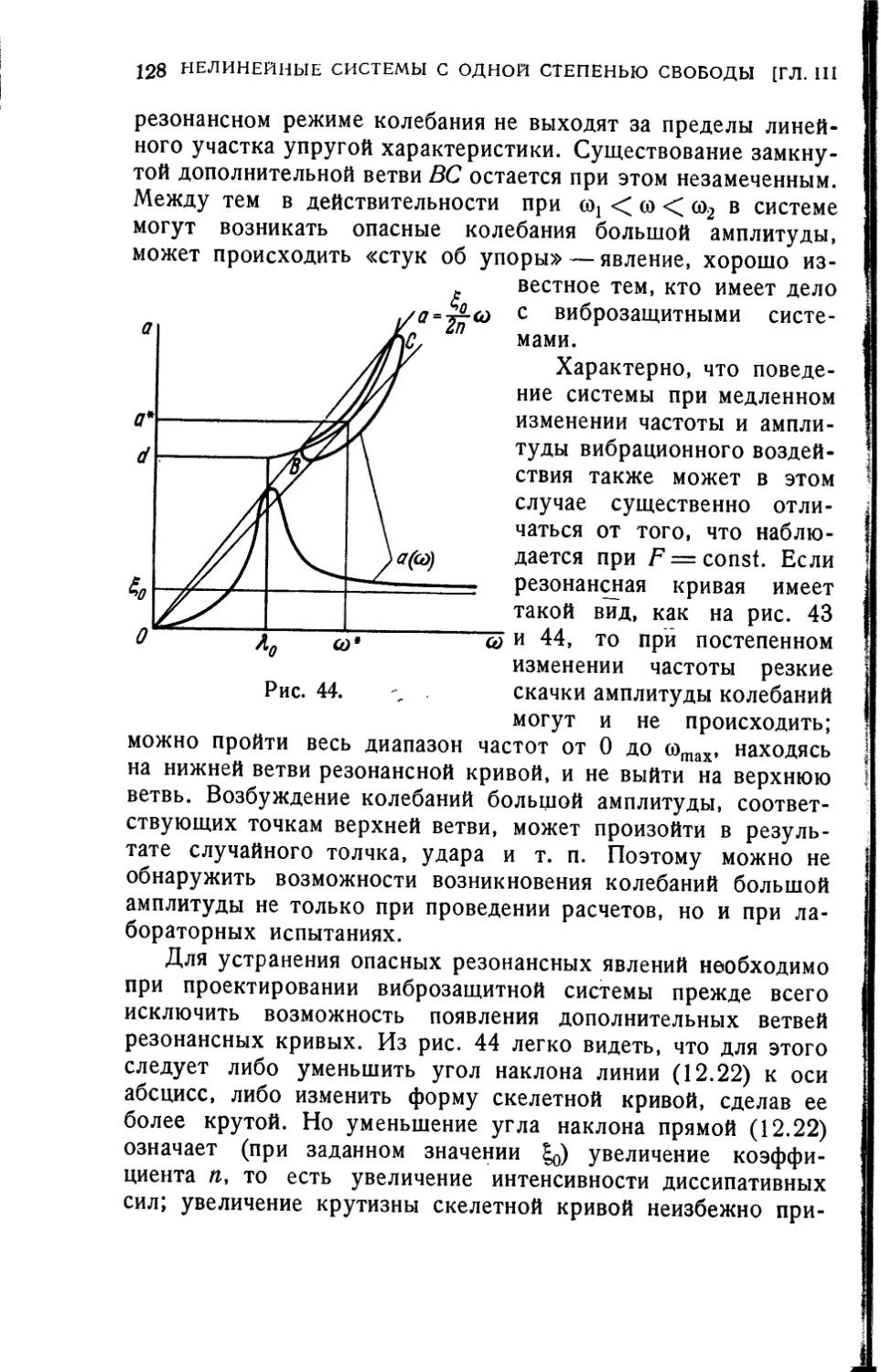
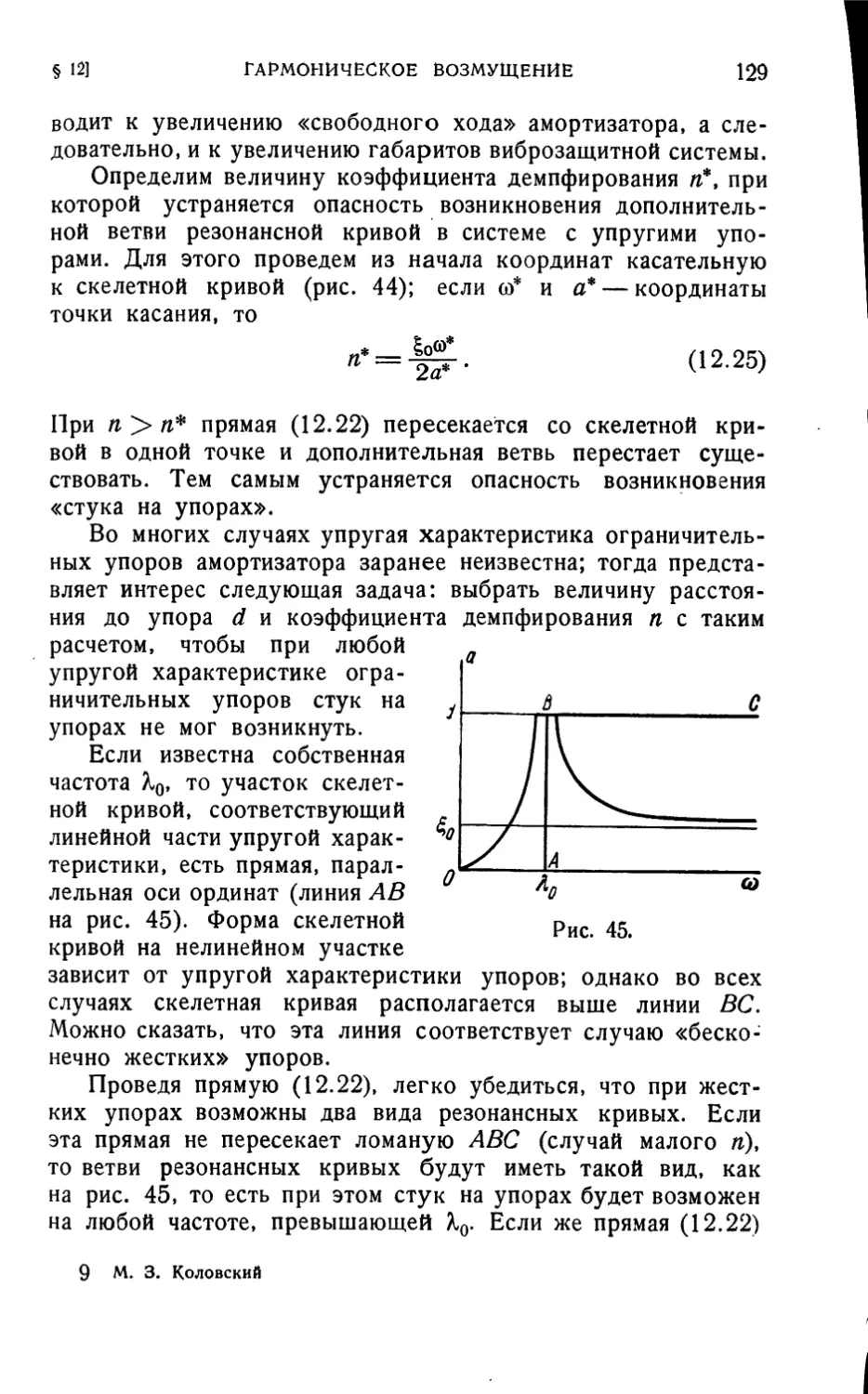
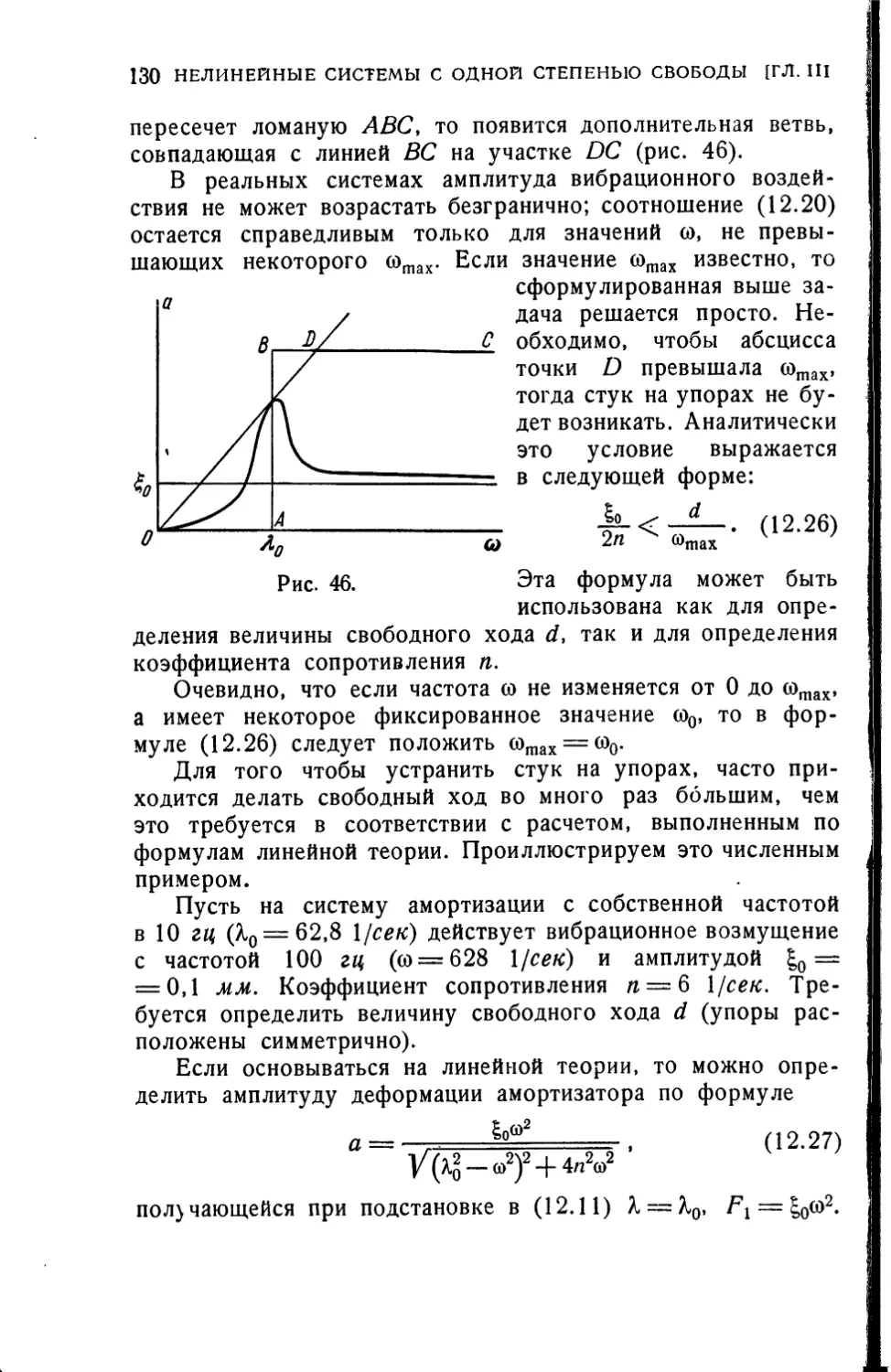
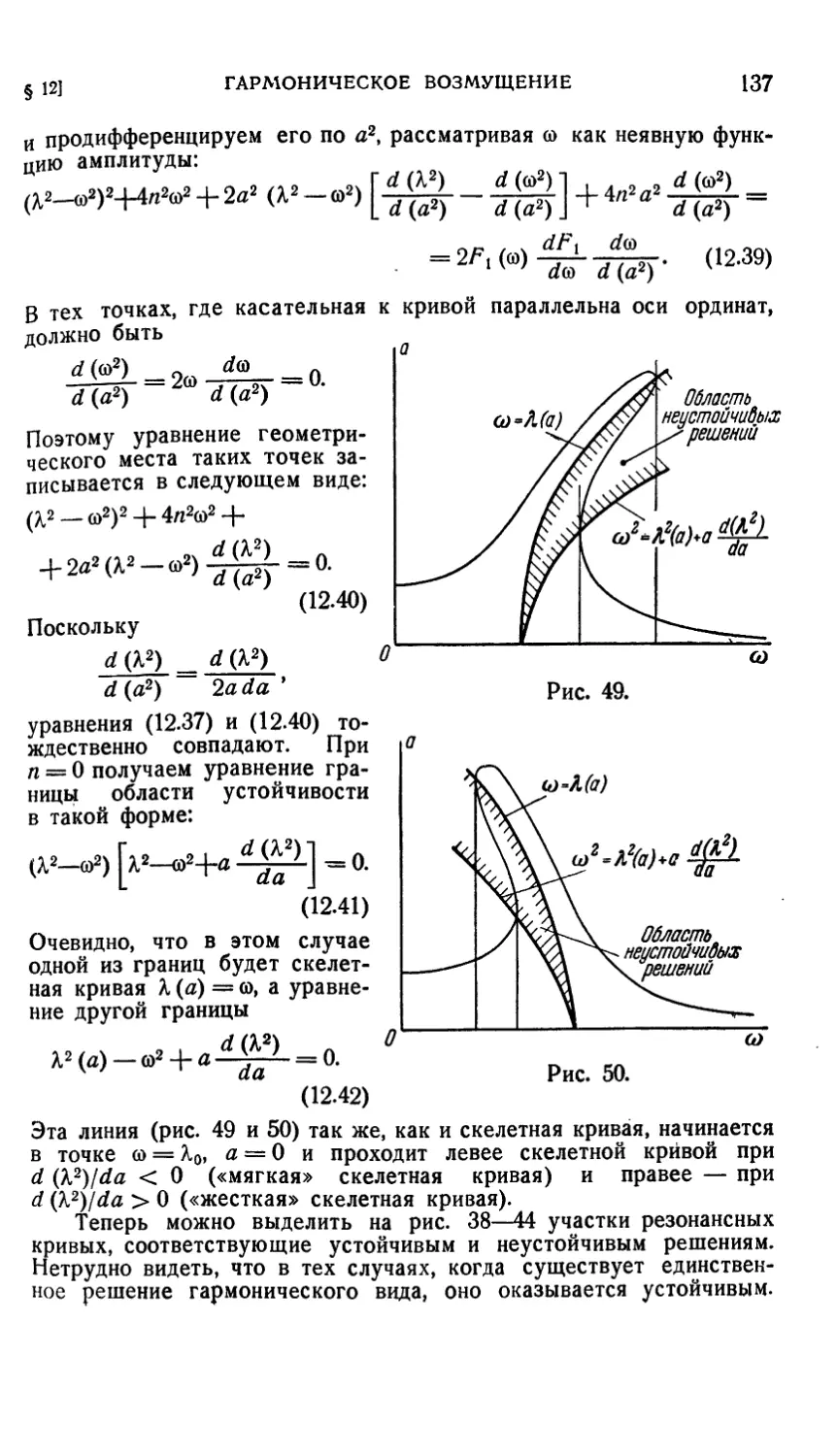
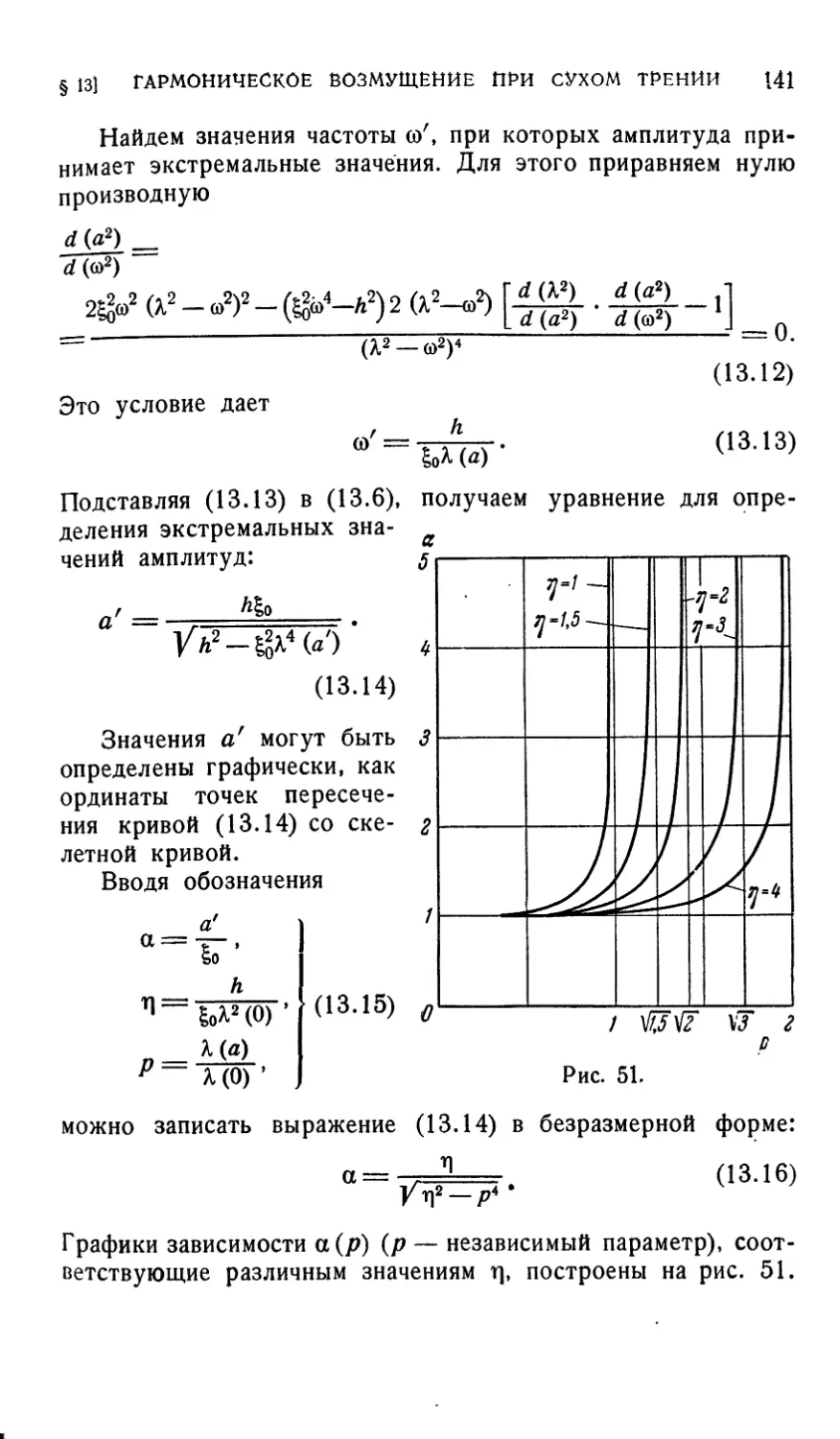
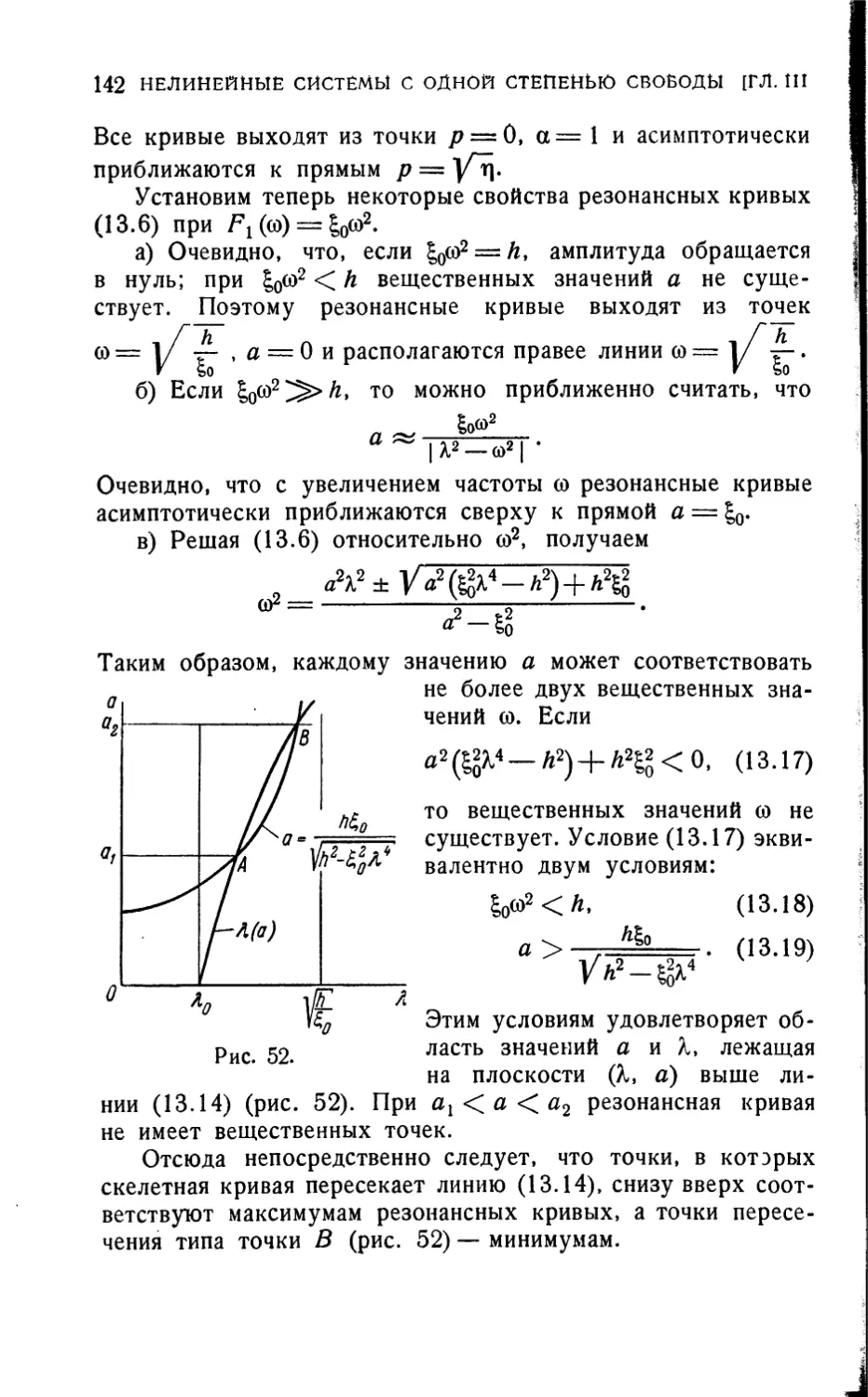
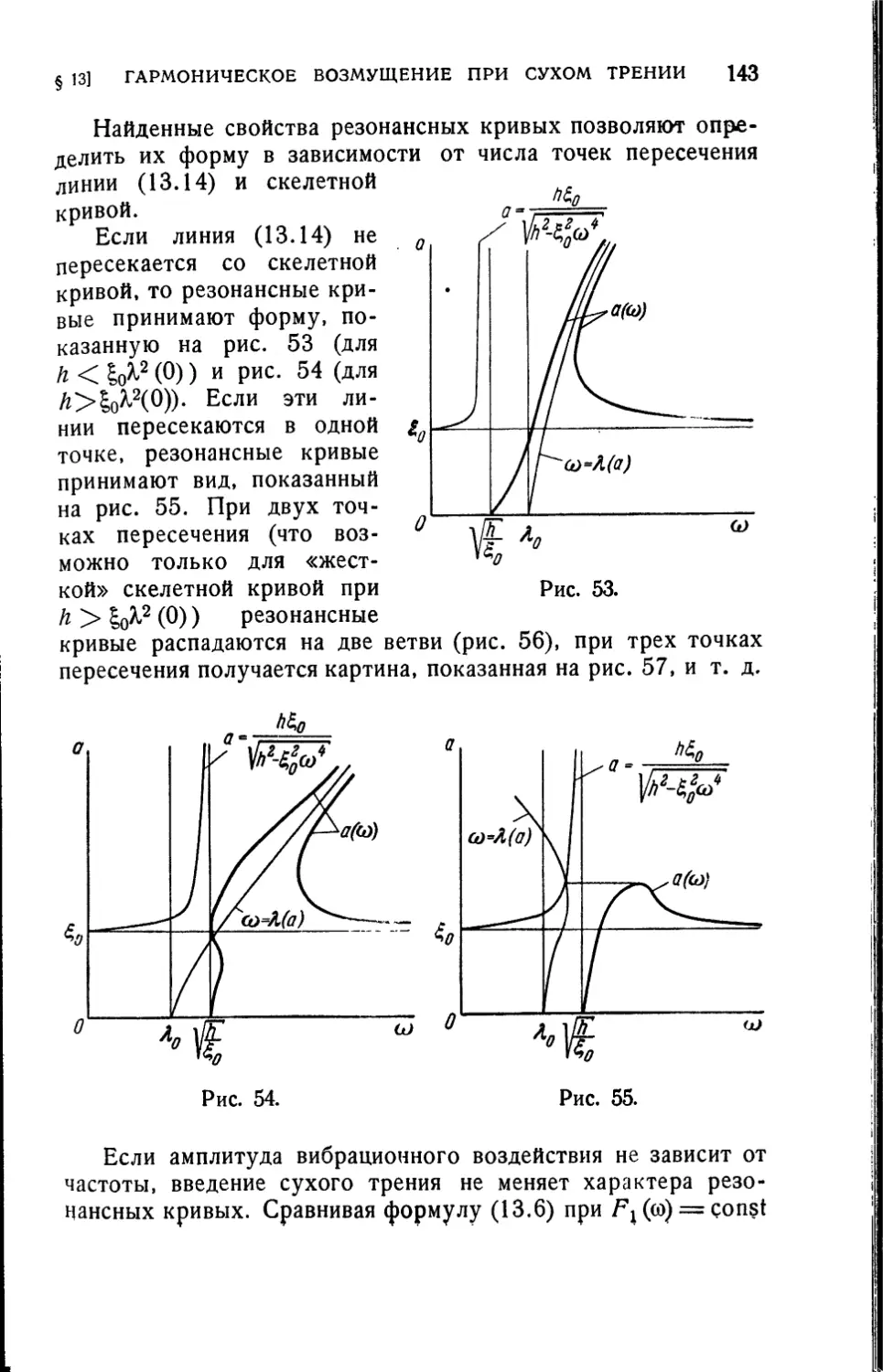
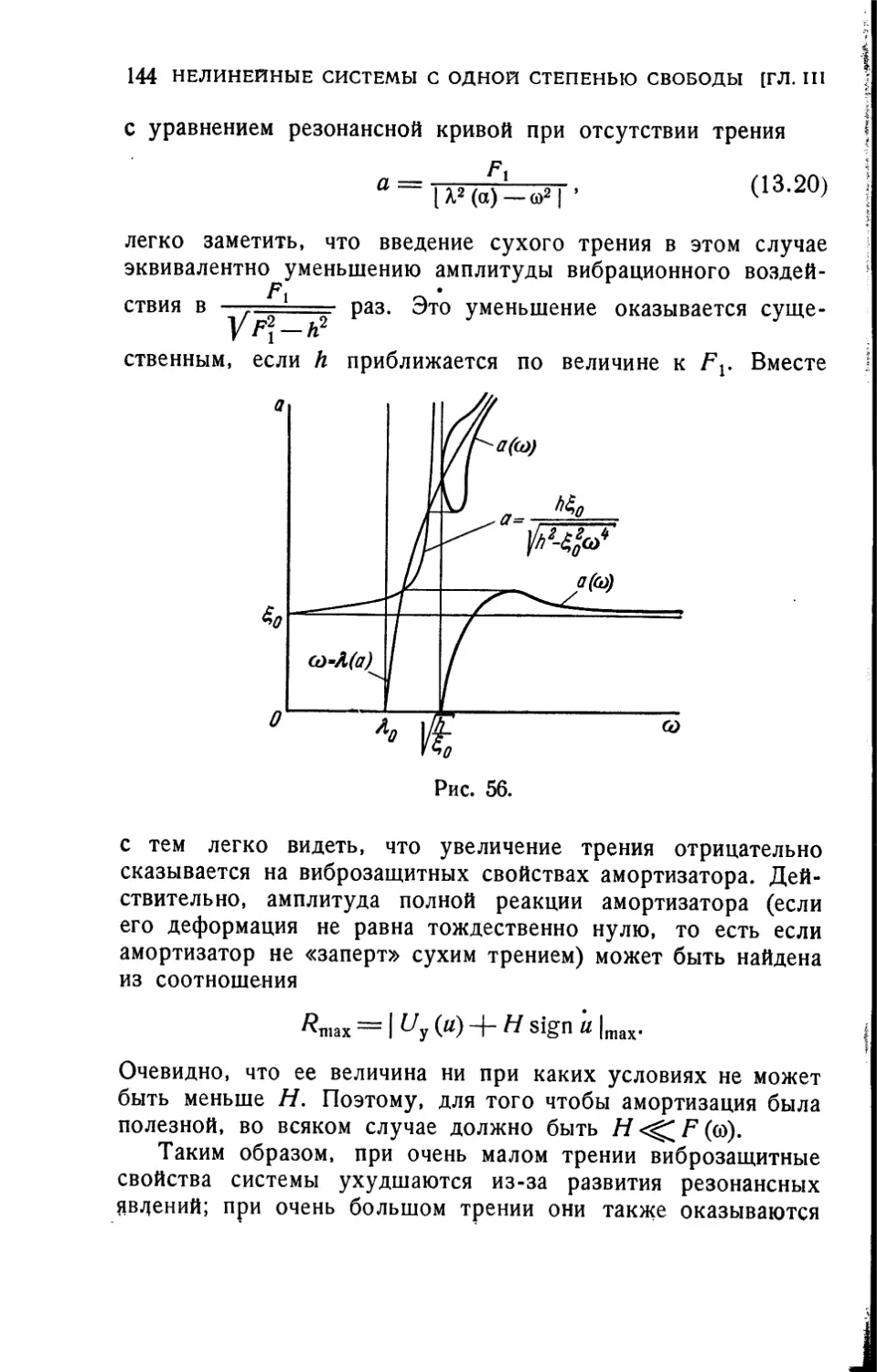
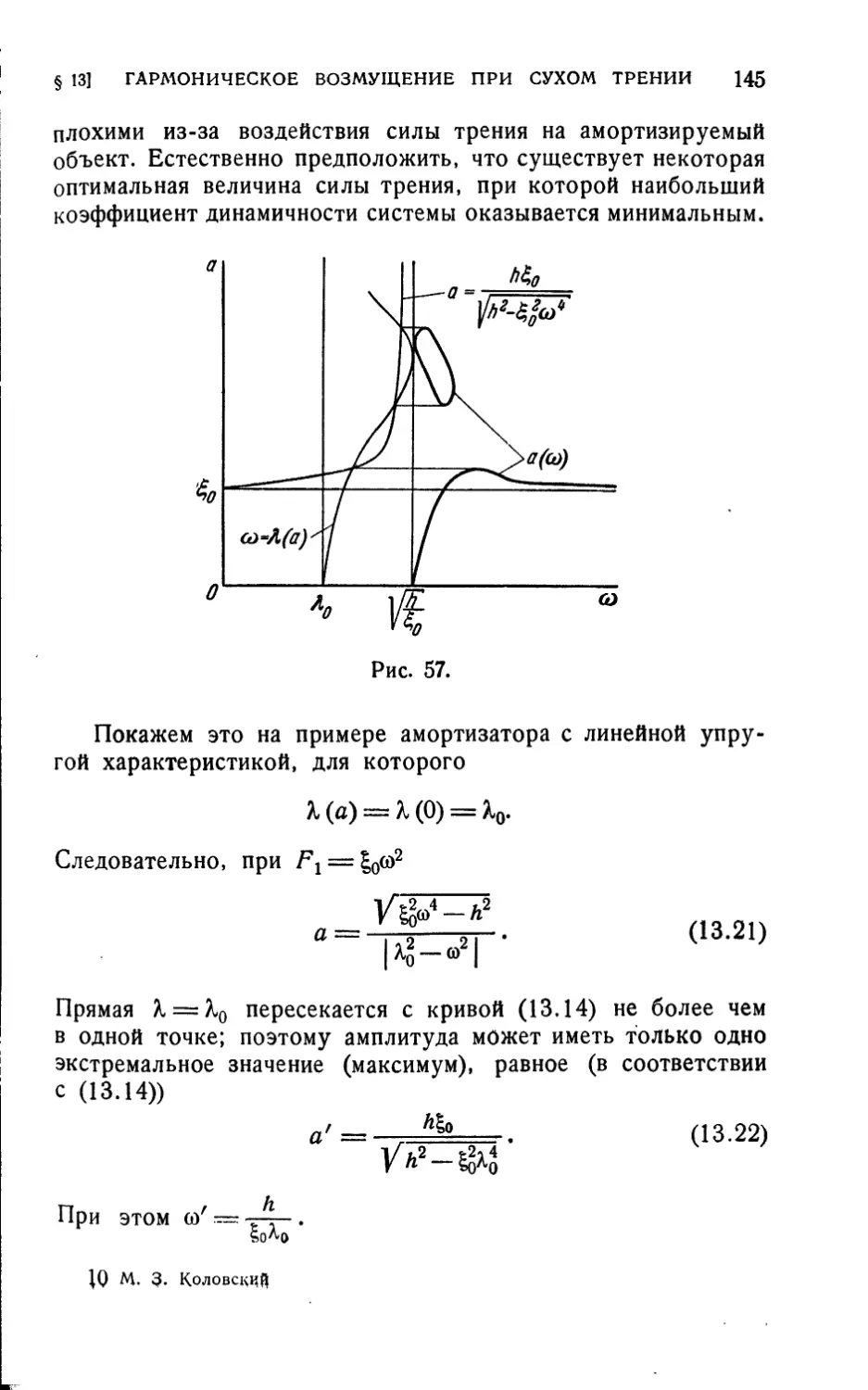
Текст
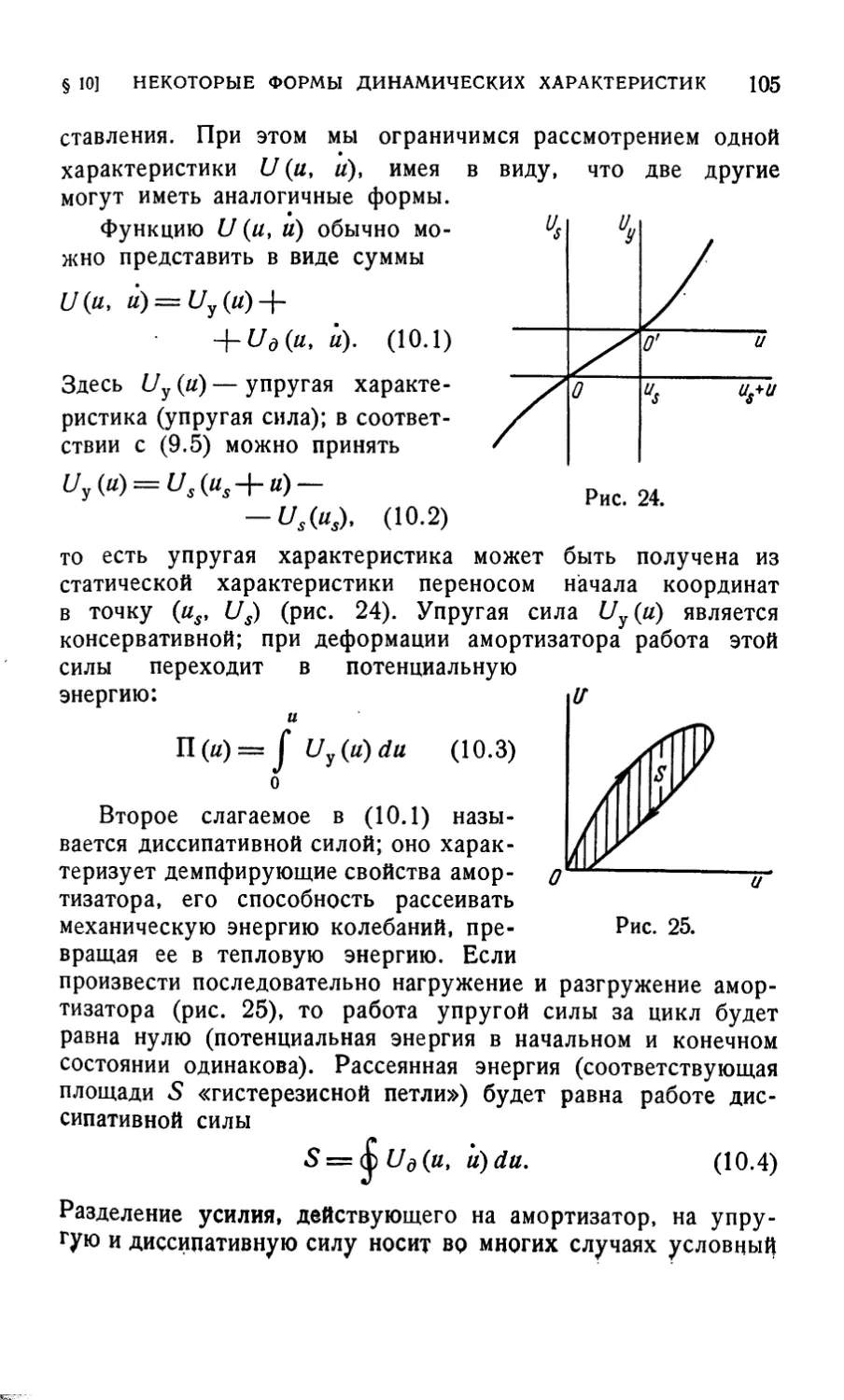
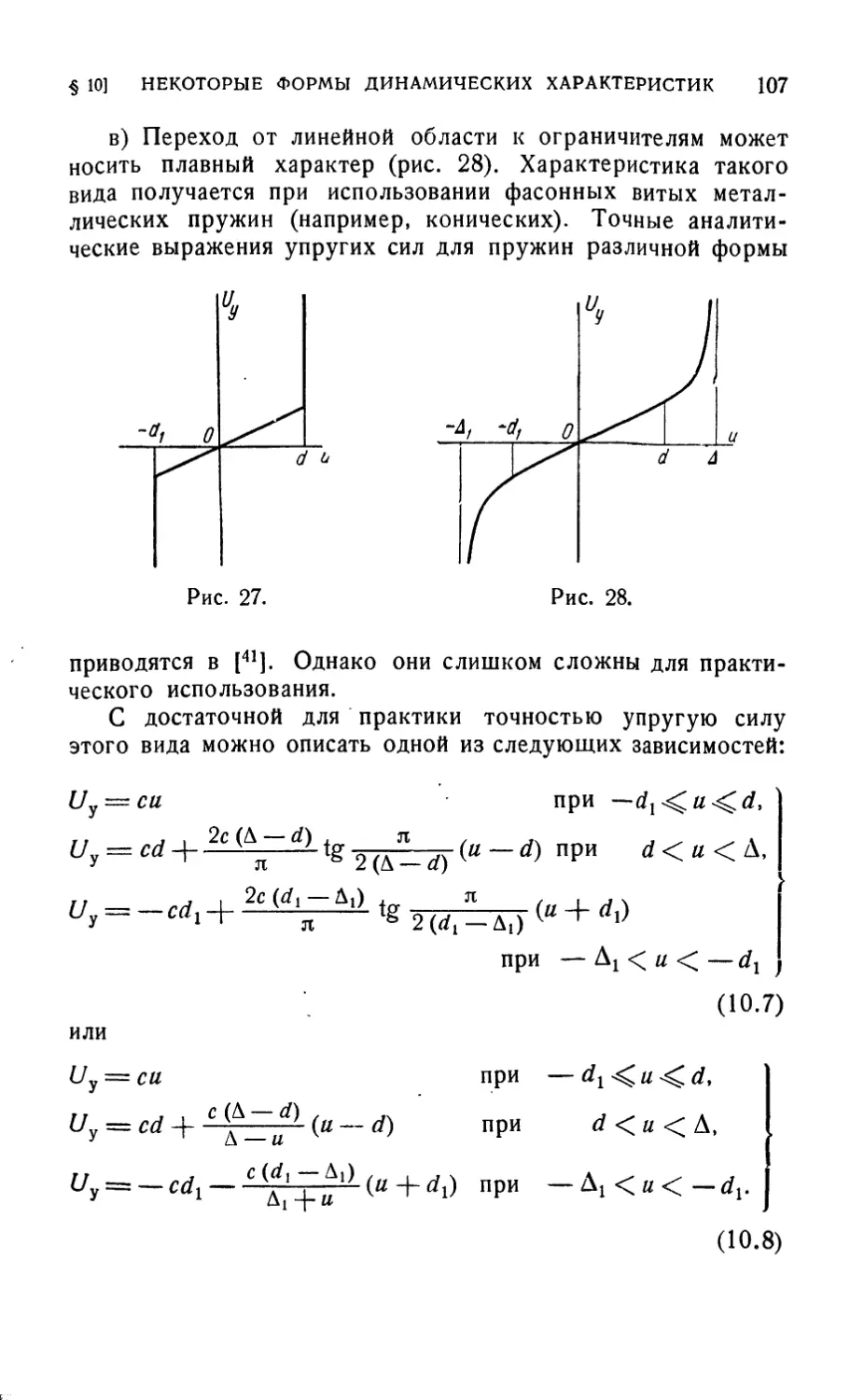
M. 3. КОЛОВСКИЙ
НЕЛИНЕЙНАЯ
ТЕОРИЯ
ВИБРОЗАЩИТНЫХ
СИСТЕМ
ж
ИЗДАТЕЛЬСТВО «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
МОСКВА 1966
531
К 61
УДК 534.1
2-4-2
162-66
ОГЛАВЛЕНИЕ
Предисловие 5
Введение 9
Глава I. Некоторые приближенные методы анализа
нелинейных систем 23
§ 1. Метод гармонического баланса 23
§ 2. Свободные колебания массы на нелинейной пружине 31
§ 3. Гармоническая линеаризация 41
§ 4. Линеаризация по критерию минимума
среднеквадратичного отклонения 46
§ 5. Линеаризация по функции распределения 50
§ 6. Метод Галеркина 72
§ 7. Метод статистической линеаризации 78
§ 8. Устойчивость стационарных решений 90
Глава II. Упругие амортизаторы и их динамические
характеристики 99
§ 9. Динамические характеристики упругих амортизаторов 99
§ 10. Некоторые формы динамических характеристик ... 104
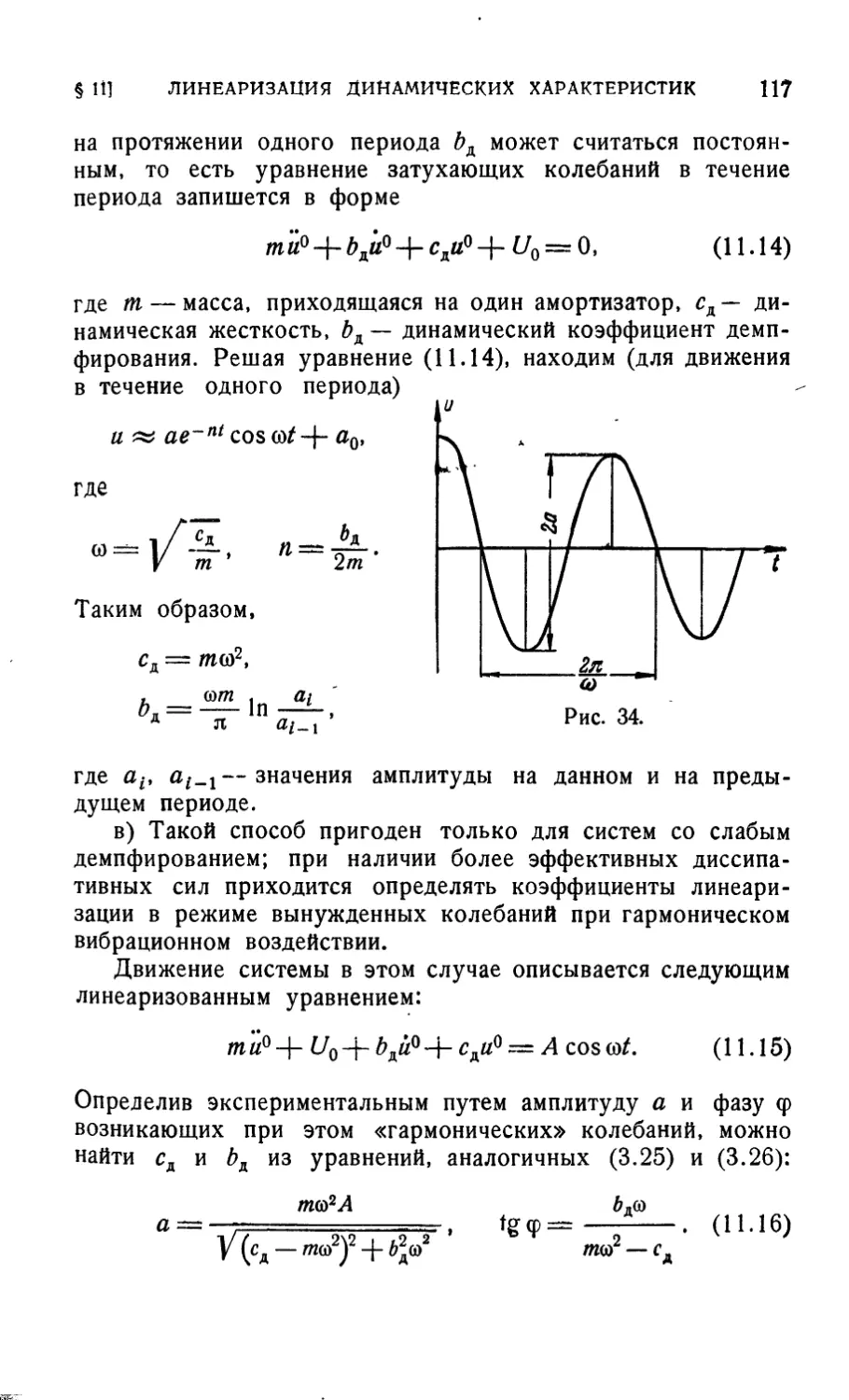
§ 11. Линеаризация и экспериментальное исследование
динамических характеристик 112
Глава III. Нелинейные системы с одной степенью
свободы 119
§ 12. Вынужденные колебания при гармоническом
вибрационном воздействии и силе сопротивления,
пропорциональной скорости 119
§ 13. Вынужденные колебания при гармоническом
вибрационном воздействии и силе сухого трения 138
§ 14. Вынужденные колебания в системе с внутренним
трением. Сравнение различных форм демпфирования 148
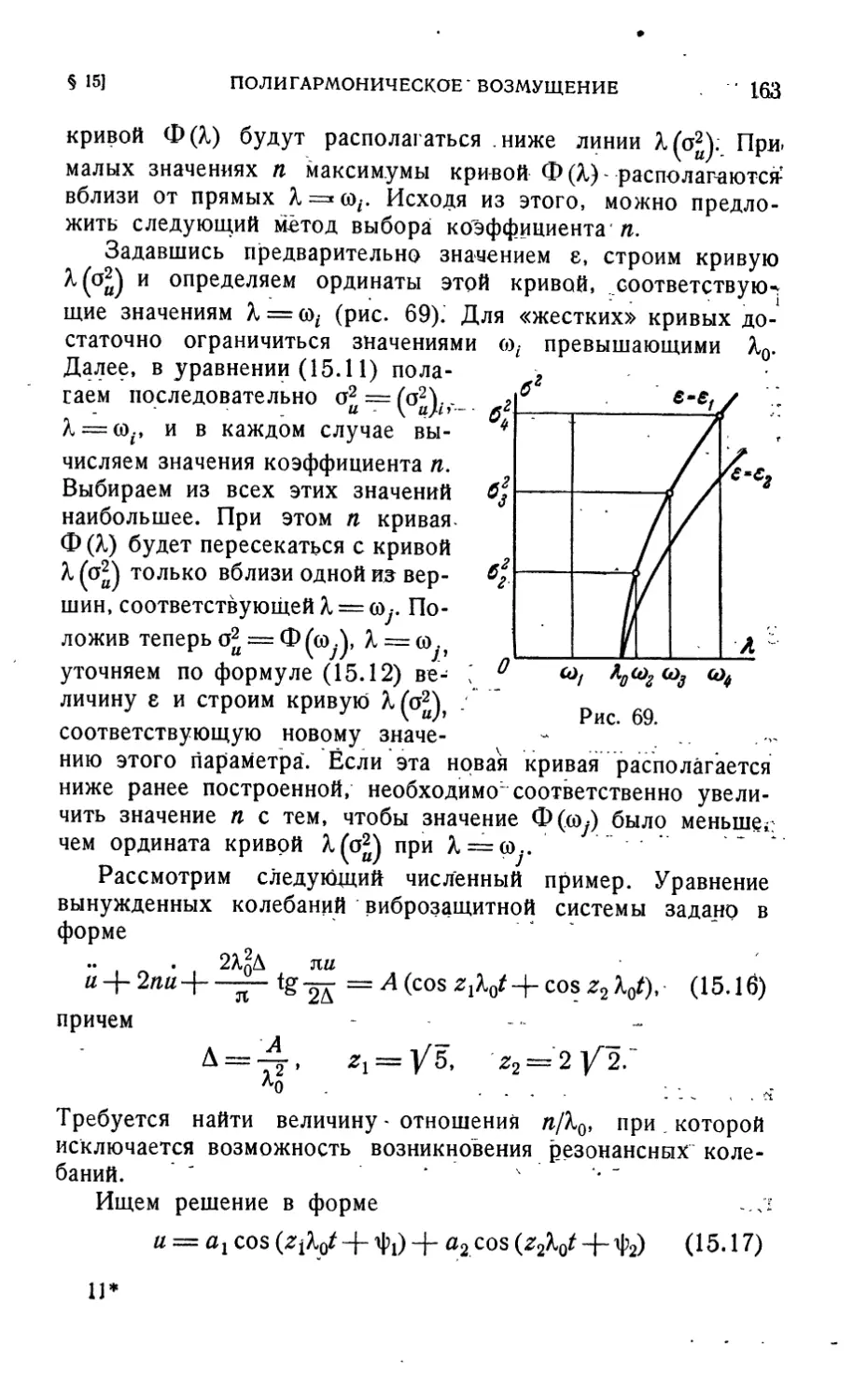
§ 15. Вынужденные колебания при полигармоническом
возмущении 158
§ 16. Резонансы дробного порядка в виброзащитных
системах 172
§ 17. Субгармонический резонанс в системе с жесткими
упорами 187
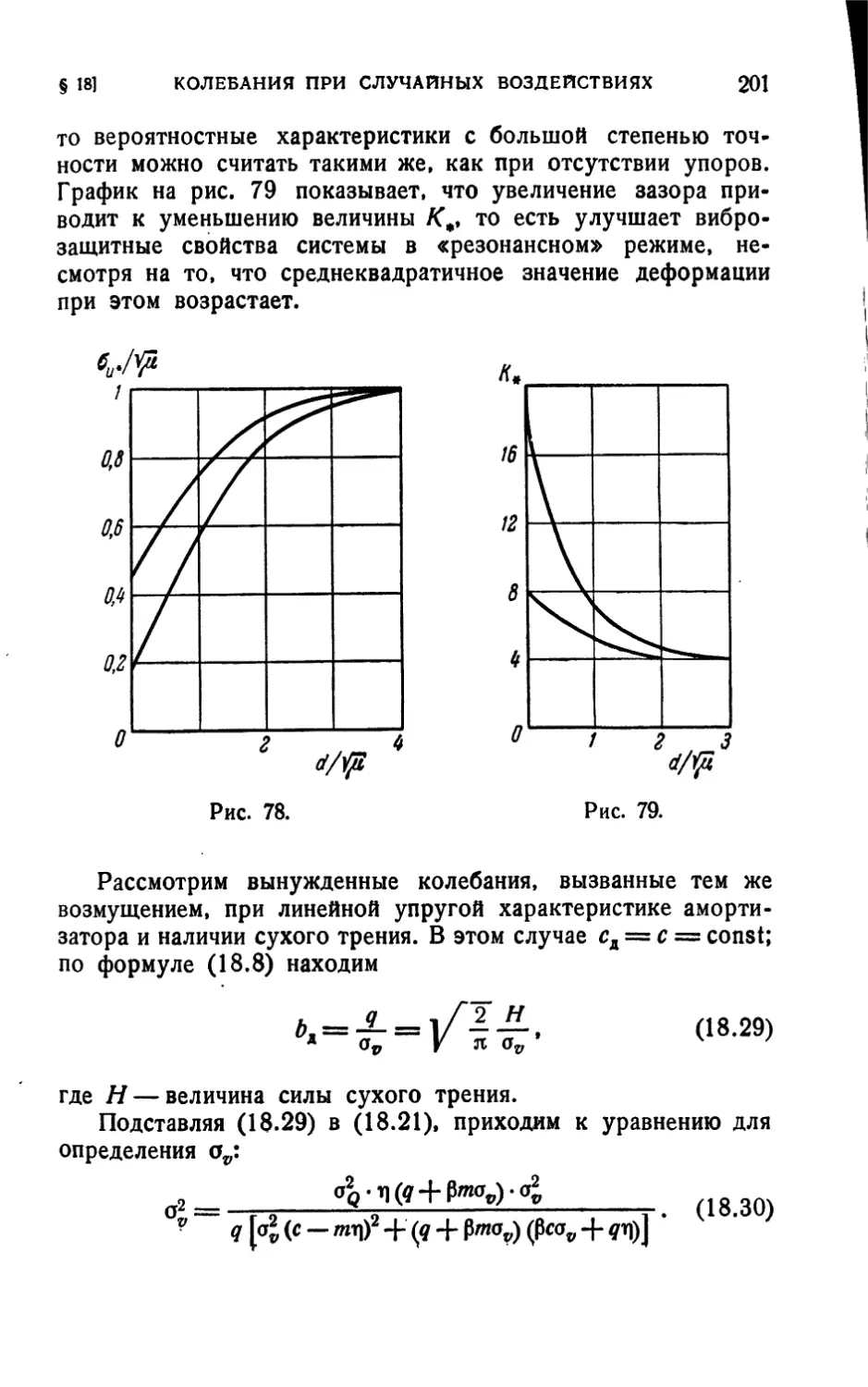
§ 18. Вынужденные колебания при случайных воздействиях 195
1*
4 ОГЛАВЛЕНИЕ
Глава IV. Нелинейные системы с несколькими
степенями свободы 204
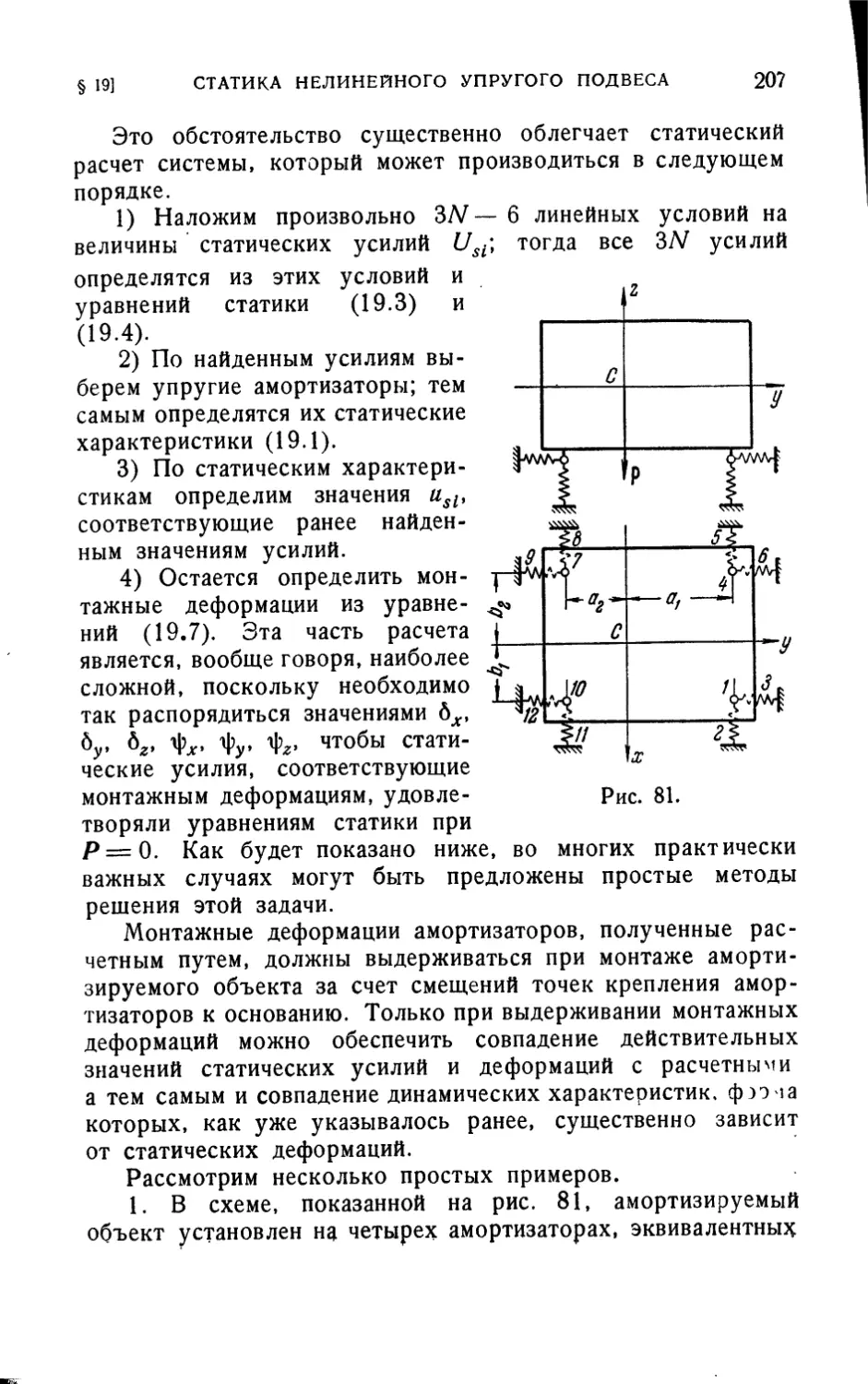
§ 19. Статика нелинейного упругого подвеса 204
§ 20. Малые колебания твердого тела на упругом подвесе 211
§ 21. Колебания амортизируемого объекта на нелинейных
упругих амортизаторах 221
§ 22. Свободные колебания нелинейной виброзащитной
системы 232
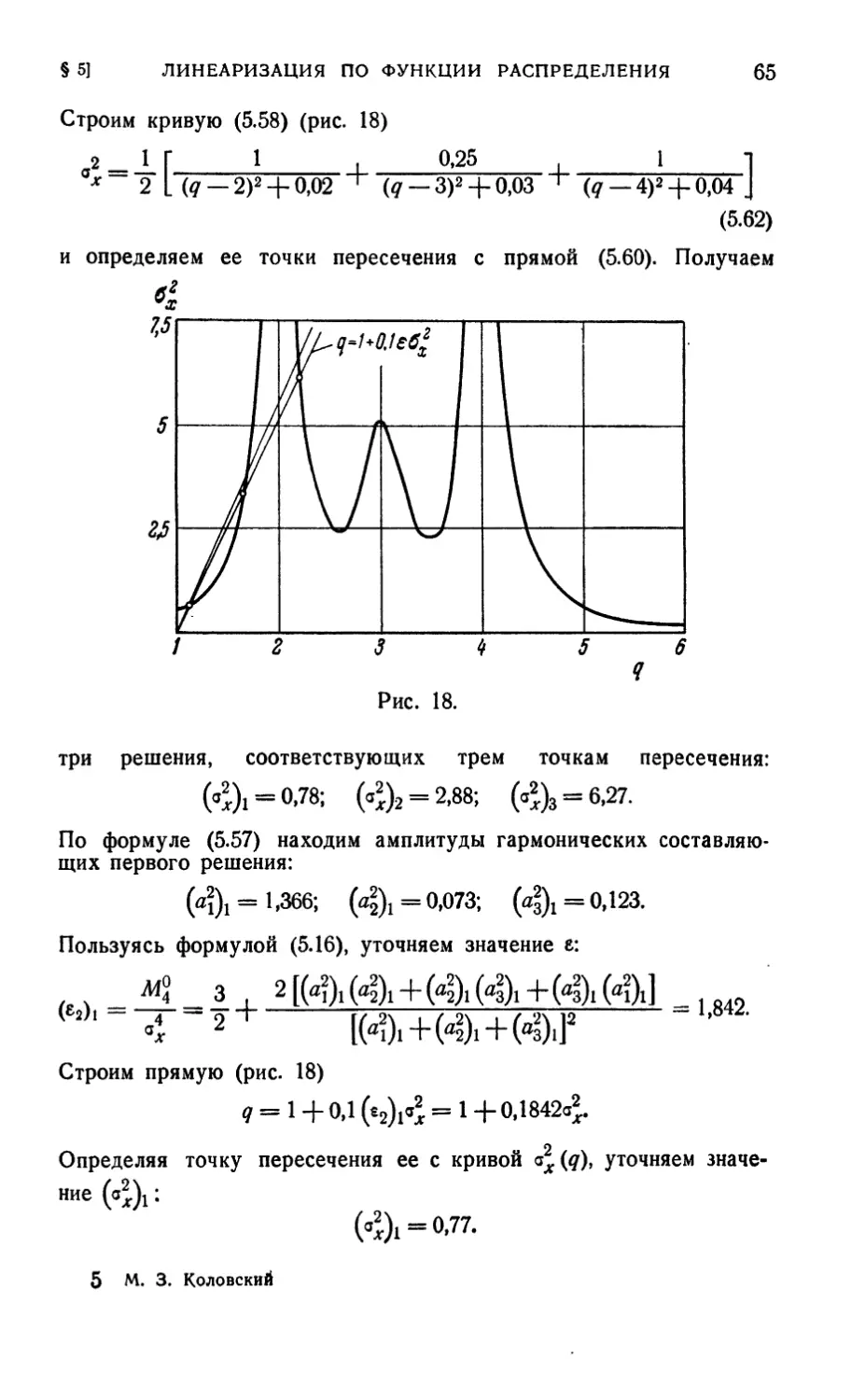
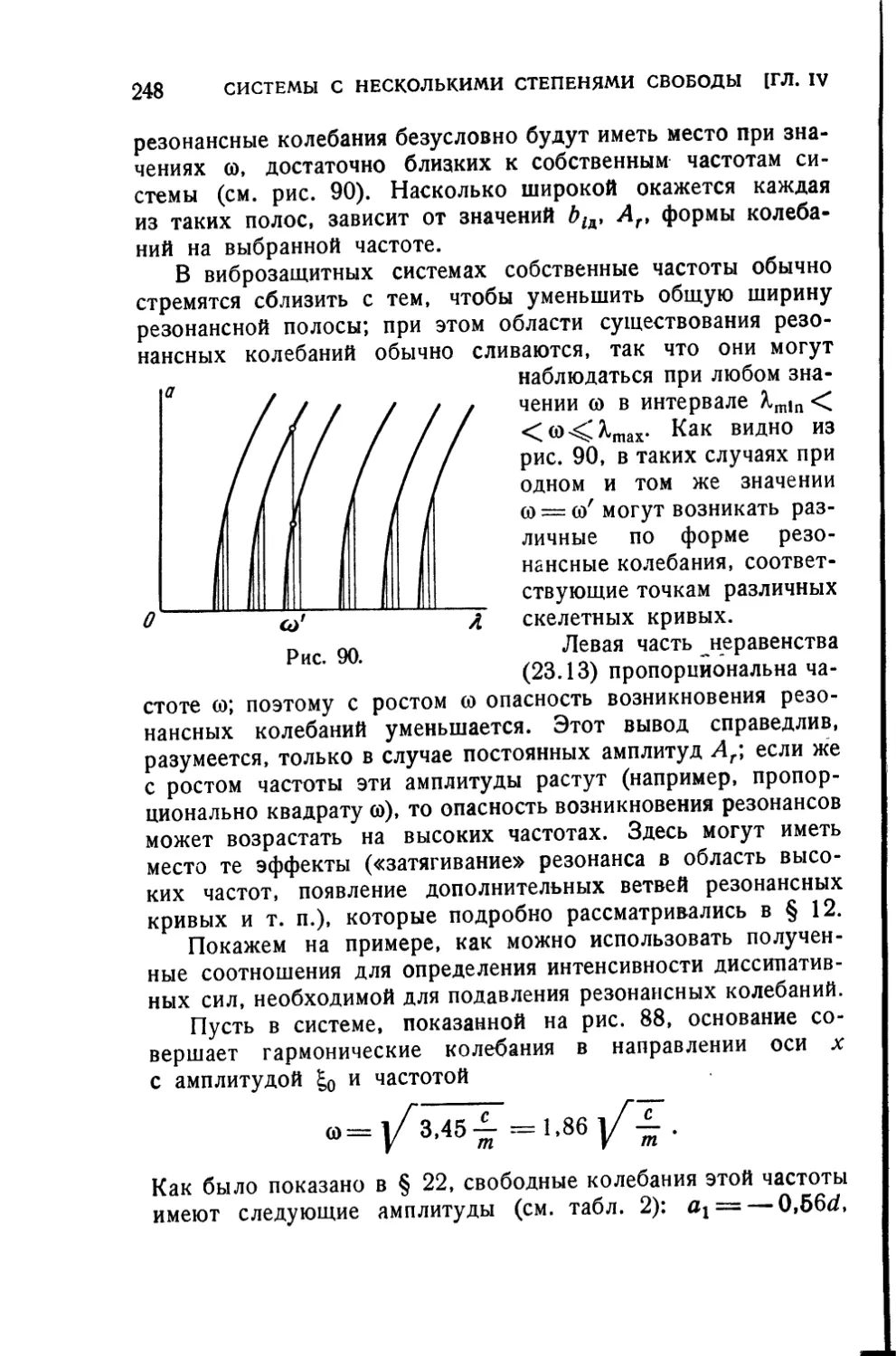
§ 23. Резонансные колебания 243
§ 24. Вынужденные колебания в системах с сухим трением 251
§ 25. Вынужденные колебания упругих тел 258
Глава V. Колебания виброзащитных систем при
ударных воздействиях 271
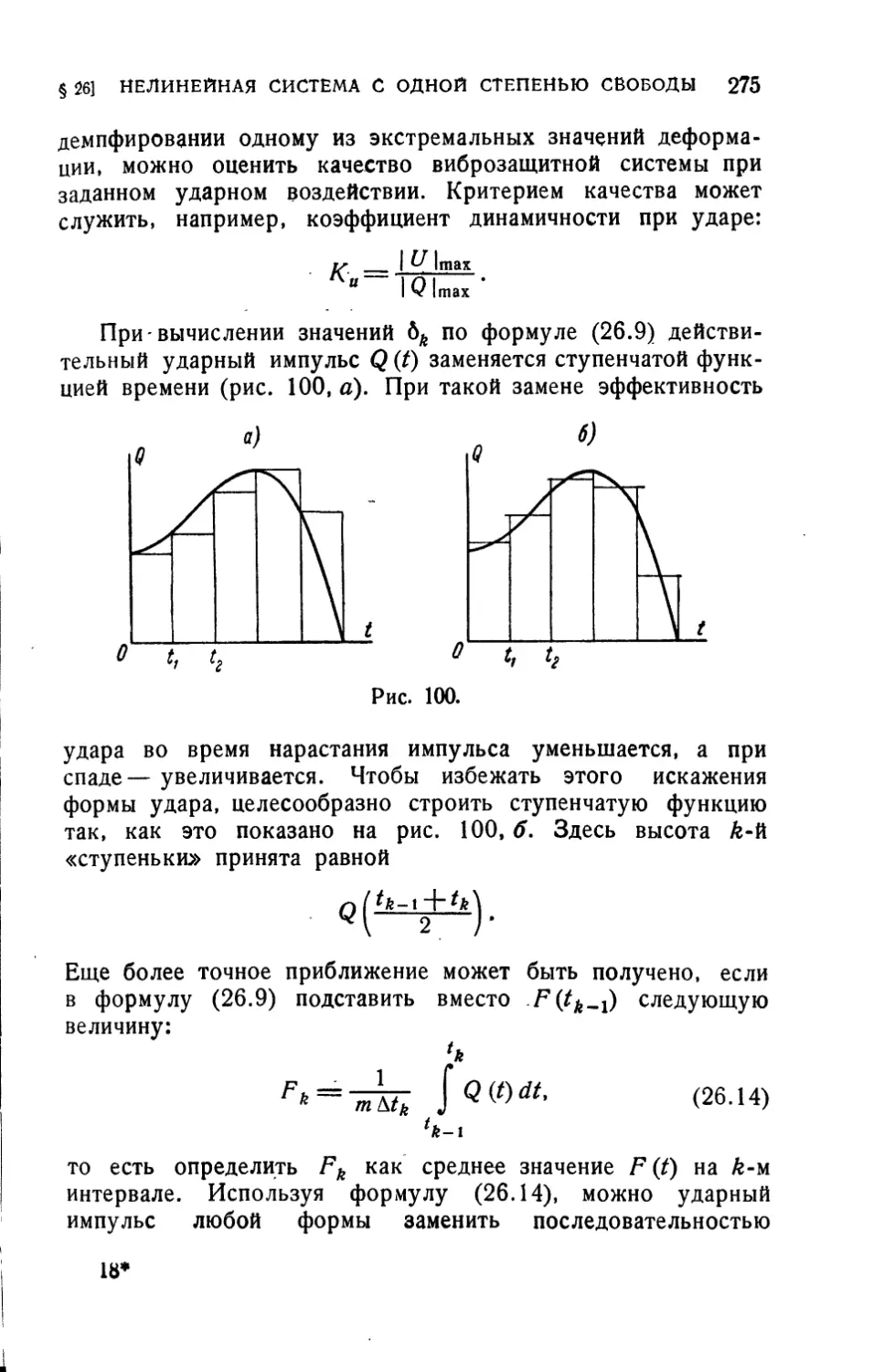
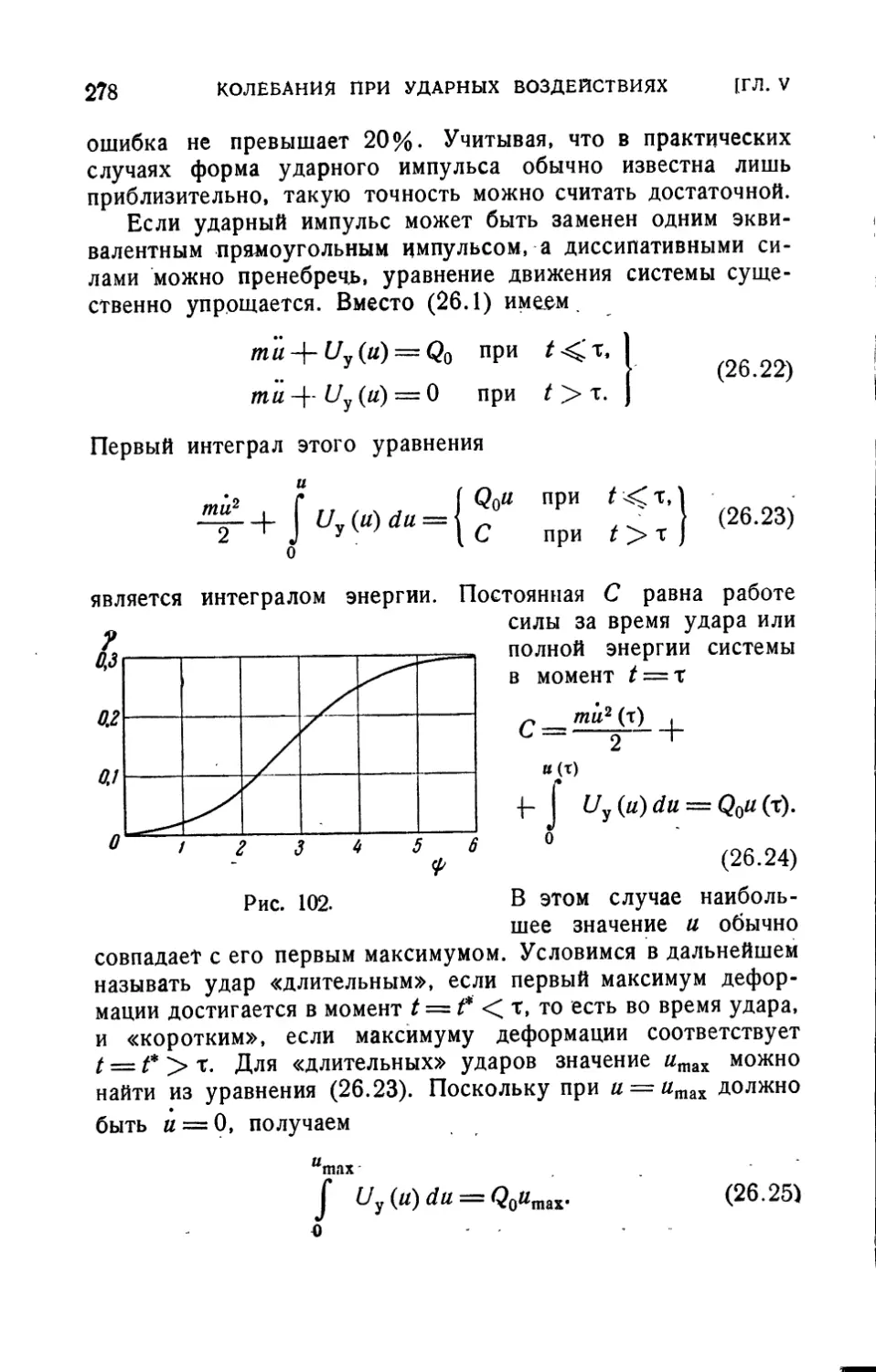
§ 26. Удар в нелинейной системе с одной степенью
свободы 271
§ 27. Примеры расчета систем с одной степенью свободы 286
§ 28. Системы с несколькими степенями свободы 295
§ 29. Некоторые вопросы синтеза противоударных устройств 306
Литературные указания 312
Литература 314
ПРЕДИСЛОВИЕ
Создание эффективных средств защиты от вибраций и
ударов является одной из важных проблем современной
техники. Особенно большое значение приобретают вопросы
виброзащиты в современных транспортных объектах:
летательных аппаратах, автомобилях, морских судах. Поскольку
интенсивность вибраций и ударов обычно возрастает с
увеличением скорости, движения, развитие транспортных средств
сопровождается непрерывным повышением требований к
виброзащитным устройствам.
Применение упругих амортизаторов является одним из
наиболее распространенных способов виброзащиты. В
настоящее время существует большое число конструктивных
разновидностей амортизаторов, предназначенных как для
защиты приборов и оборудования, устанавливаемых на
колеблющихся Основаниях, так и для защиты оснований и
фундаментов от динамических воздействий. Создание амортизи-:
рующих устройств, способных защитить объекты от вибраций
и ударов и, вместе с тем, обладающих ограниченными
размерами, является сложной технической проблемой,
правильное решение которой возможно только при всестороннем
учете характера возмущений и конструктивных свойств
амортизаторов. В связи с этим первостепенное значение
приобретают вопросы теории и расчета виброзащитных
систем.
Теории виброзащитных систем посвящено большое число
работ. В первую очередь следует отметить моногоа^ин
6
ПРЕДИСЛОВИЕ
Ю. И. Иориша [9] и Ч. Е. Крида [56], а также книги
В. С. Ильинского [8] и У. Кер Вильсона [4]. В этих работах
наибольшее внимание уделяется развитию линейной теории,
основанной на приложении методов классической теории
малых колебаний к исследованию виброзащитных устройств.
Линейная теория, разработанная как для простейших систем
с одной степенью свободы, так и для общего случая
колебаний твердого тела на упругом подвесе, рассматривает
упругий амортизатор как фильтр низких частот; задача
виброзащиты сводится при этом к выбору таких параметров
системы амортизации, при которых ее собственные частоты
оказались бы значительно ниже частот, содержащихся
в спектре внешнего воздействия. В настоящее время методы
линейной теории широко применяются при исследовании и
проектировании виброзащитных устройств.
Вместе с тем в последнее время все в большей степени
стала проявляться ограниченность линейной теории, ее
непригодность для объяснения ряда явлений, возникающих
в виброзащитных системах. Ю. И. Иориш, по-видимому,
впервые обратил внимание на это обстоятельство и
исследовал одно из таких явлений — субгармонический резонанс
в системе с упругими упорами. Дальнейшие исследования
показали, что возникновение нелинейных эффектов, часто
приводящее к резкому ухудшению качества виброзащиты,
является не случайным конструктивным недостатком
отдельных систем, а неизбежным следствием увеличения
интенсивности вибрационных и ударных воздействий. С другой
стороны, применение амортизаторов с нелинейными
характеристиками в ряде случаев может оказаться полезным.
Указанные обстоятельства привели к развитию
нелинейной теории виброзащитных систем, составляющей содержание
настоящей книги.
Стремясь сделать эту теорию доступной широкому кругу
специалистов, автор предпочел излагать ее, основываясь не
ПРЕДИСЛОВИЕ
7
на классических методах теории нелинейных колебаний, а на
некоторых приближенных методах, широко использовавшихся
в последние годы главным образом для анализа нелинейных
систем автоматического управления. Не являясь математически
строго обоснованными, эти методы отличаются вместе с тем
исключительной ясностью физических концепций, лежащих
в их основе, и сравнительной простотой математического
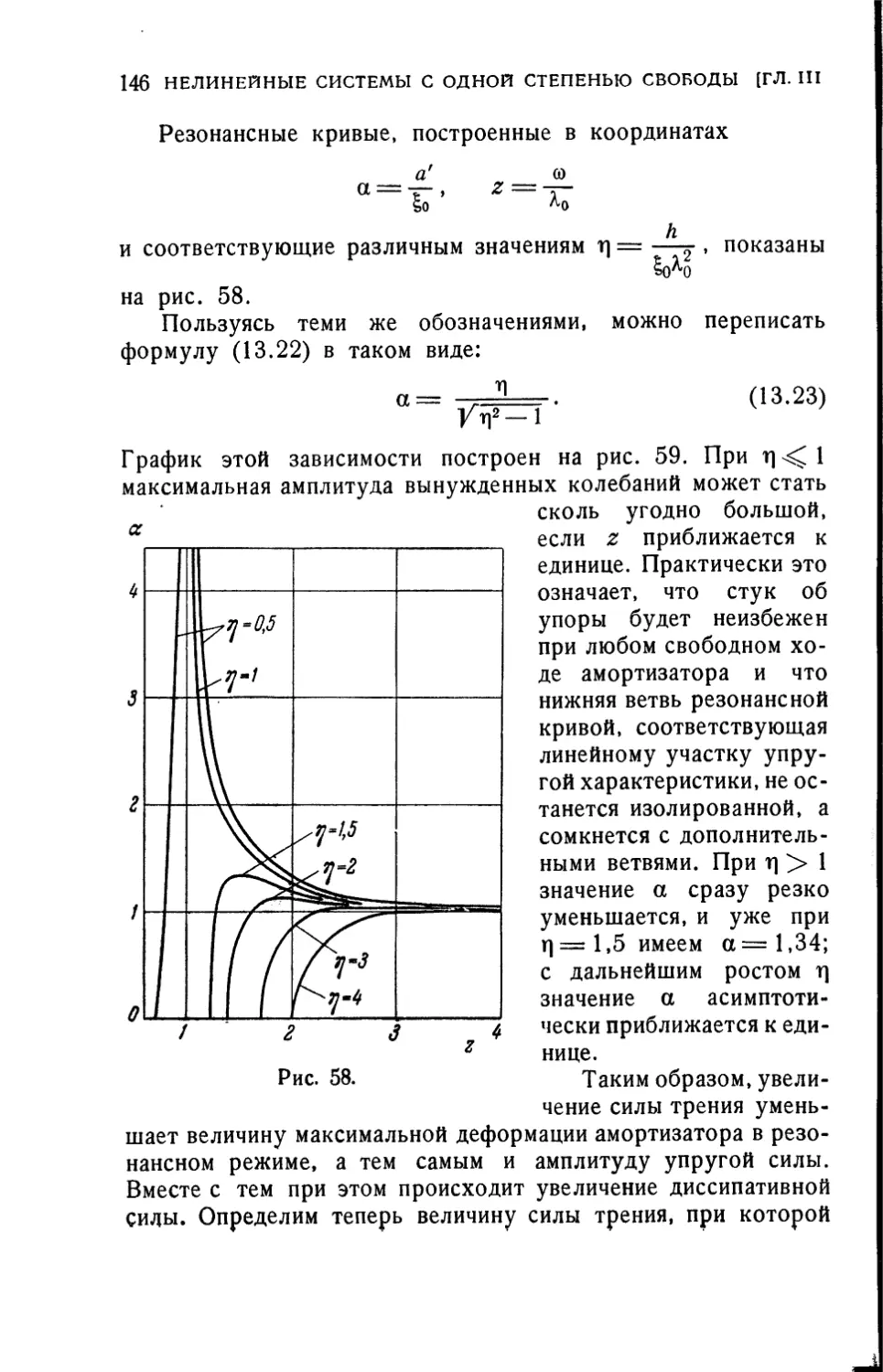
аппарата. Эти два преимущества делают их незаменимыми
при проведении инженерных расчетов, не претендующих на
высокую точность и предназначенных главным образом для
качественной оценки поведения системы.
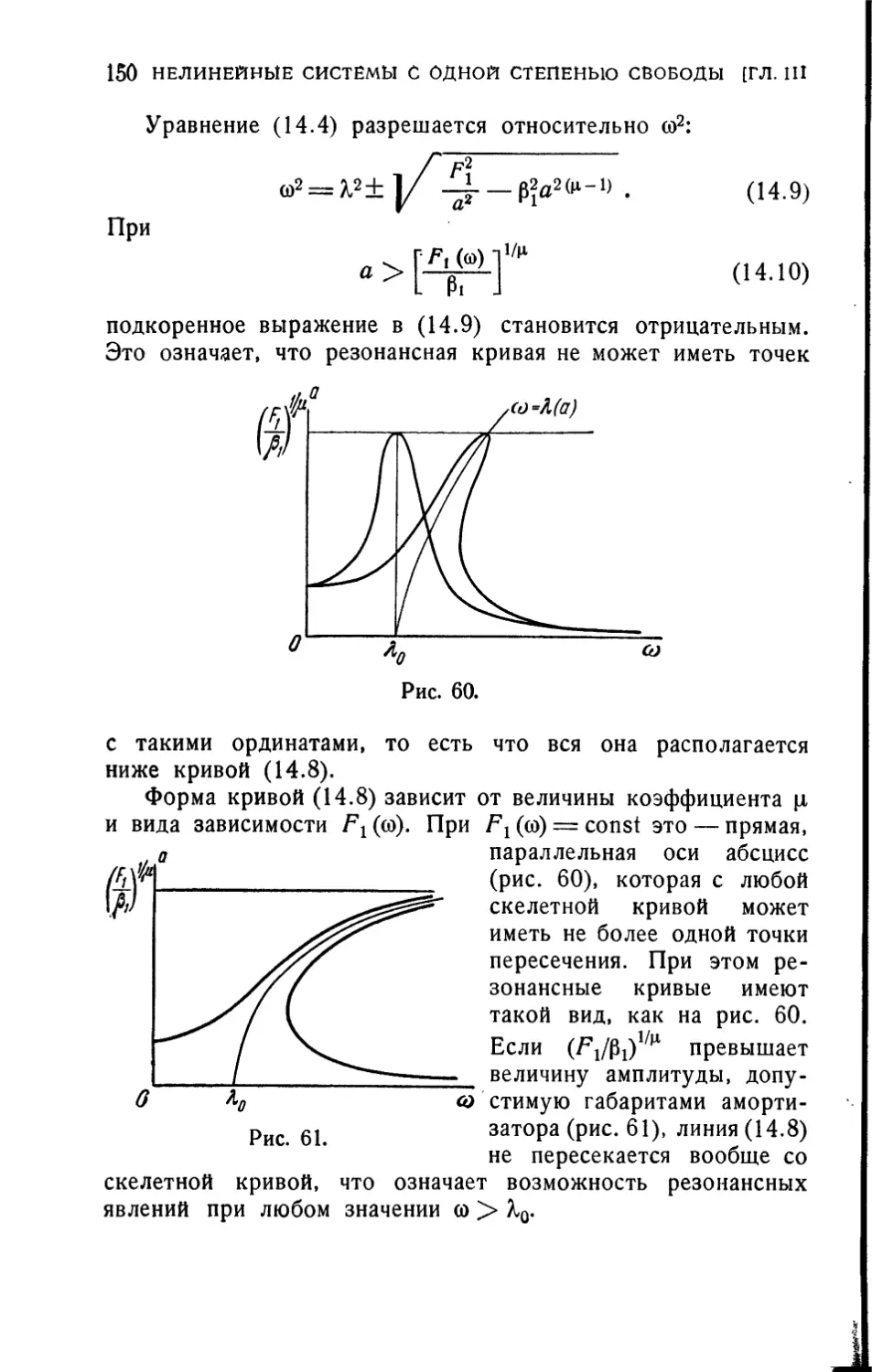
Изложению приближенных методов посвящена первая
глава книги. Наряду с широко известными методами
гармонического баланса, гармонической линеаризации,
вариационным методом Галеркина, в ней излагается сравнительно
новый метод линеаризации по функции распределения,
применение которого оказывается особенно полезным при
анализе полигармонических колебаний, характерных для
современных виброзащитных систем. Изложен также метод
статистической линеаризации, позволяющий исследовать поведение
нелинейных систем при случайных воздействиях.
Применение приближенных методов к исследованию
виброзащитных систем оказывается возможным в тех
случаях, когда динамические характеристики упругих
амортизаторов удовлетворяют определенным условиям,
сформулированным в главе второй. Здесь рассмотрены также «типовые»
формы статических и динамических характеристик и методы
их экспериментального определения.
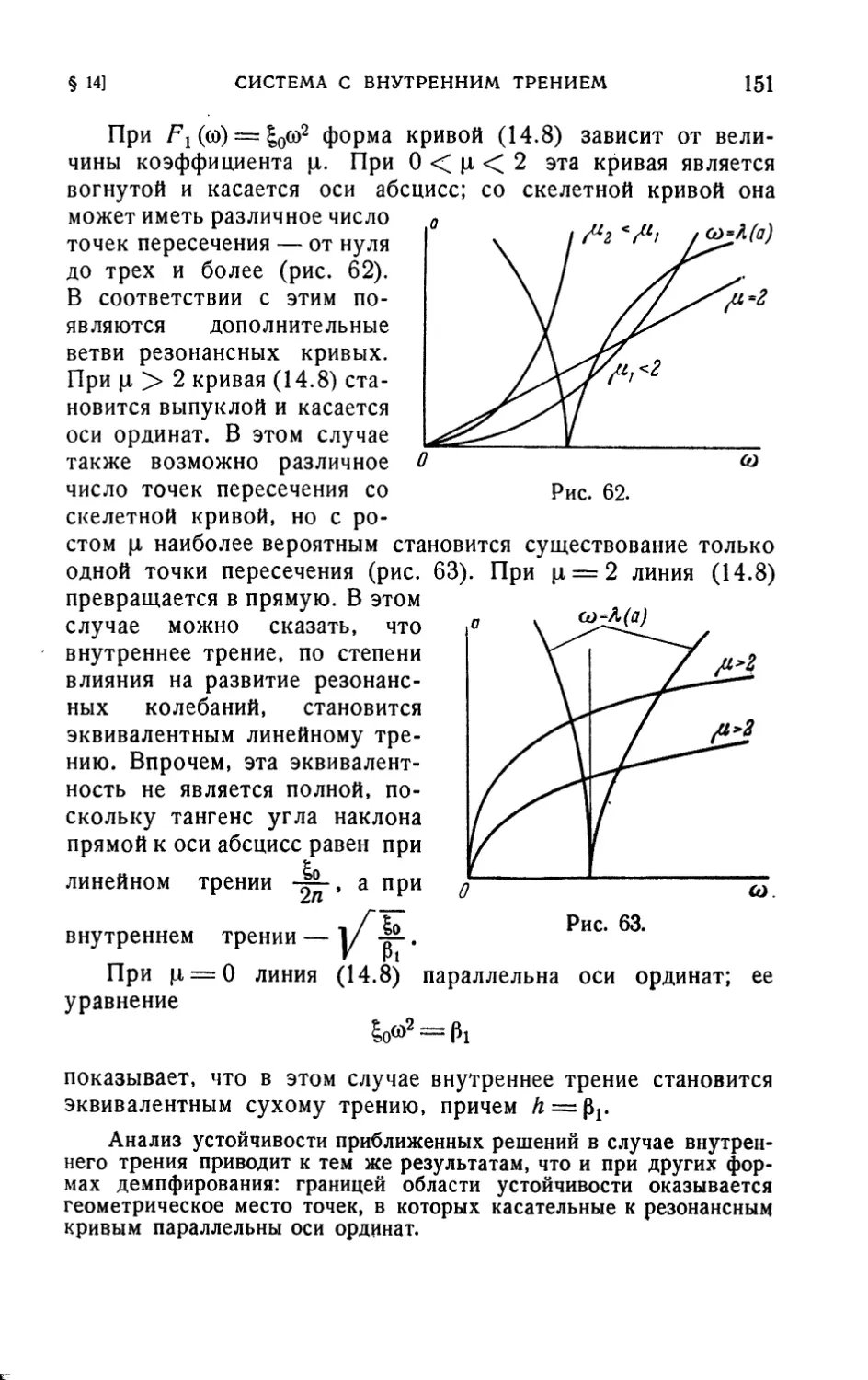
В третьей и четвертой главах методы теории нелинейных
колебаний применяются для исследования виброзащитных
систем. В третьей главе исследуются системы с одной
степенью свободы; при этом особое внимание уделяется
выявлению физической природы нелинейных явлений, анализу
условий их возникновения и подавления. В четвертой главе
в
ПРЕДИСЛОВИЕ
рассматриваются системы с несколькими степенями свободы.
Здесь исследована задача о колебаниях твердого тела на
упругом подвесе и, в простейшей постановке, рассмотрена
задача об амортизации упругого объекта.
Особые методы анализа необходимы для исследования
нестационарных процессов в нелинейных системах. В пятой
главе изложены методы исследования одного важного класса
нестационарных процессов — колебаний виброзащитных
систем при ударных воздействиях. Рассмотрены также
некоторые вопросы синтеза противоударных устройств.
Книга предназначается для инженеров и научных
работников, занимающихся исследованием и проектированием
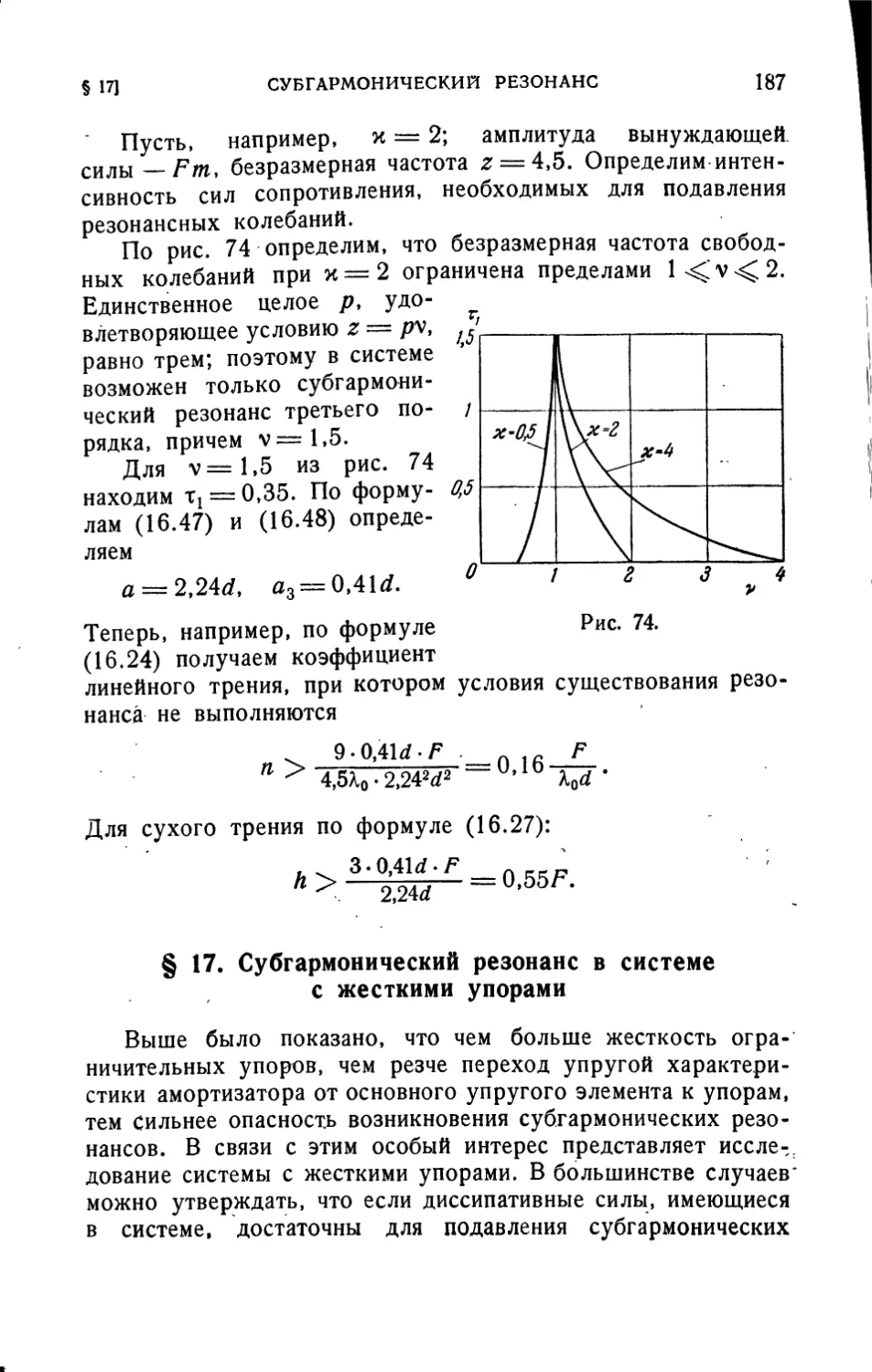
виброзащитных систем. Предполагается, что читатель знаком
с теорией обыкновенных дифференциальных уравнений и
рядов Фурье в объеме обычного вузовского курса, с основами
линейной теории колебаний в объеме курса Л. Г. Лойцян-
ского и А. И. Лурье I30], или И. М. Бабакова [2], а также
с основами теории вероятностей. Необходимые сведения
из теории случайных процессов приведены в § 7, впрочем,
изложены они весьма кратко, и для лучшего понимания
материала, содержащегося в этом параграфе и § 18,
читателю полезно более подробно ознакомиться с теорией
случайных процессов, например, по книге А. А.
Свешникова [47]- В ряде случаев для сокращения письма
использованы матричные обозначения; для чтения соответствующих
разделов вполне достаточно сведений, содержащихся,
например, в приложении I к книге А. И. Лурье [31].
Автор выражает глубокую благодарность И. Б. Баргеру,
с которым он неоднократно советовался при написании этой
книги, А. Е. Кобринскому, ознакомившемуся с рукописью
и сделавшему ряд важных замечаний, и В. И. Бабицкому,
проделавшему большую работу по ее редактированию.
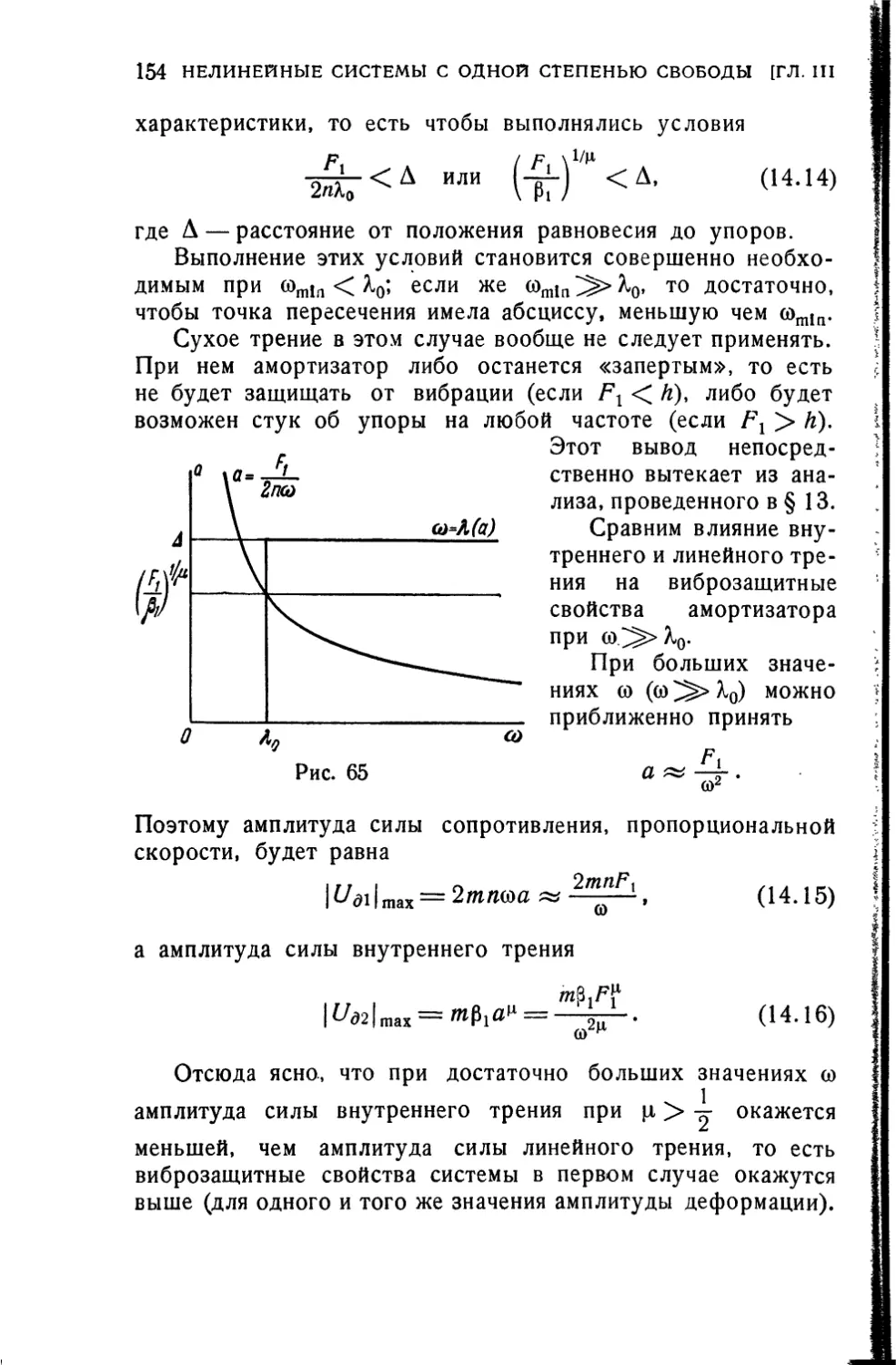
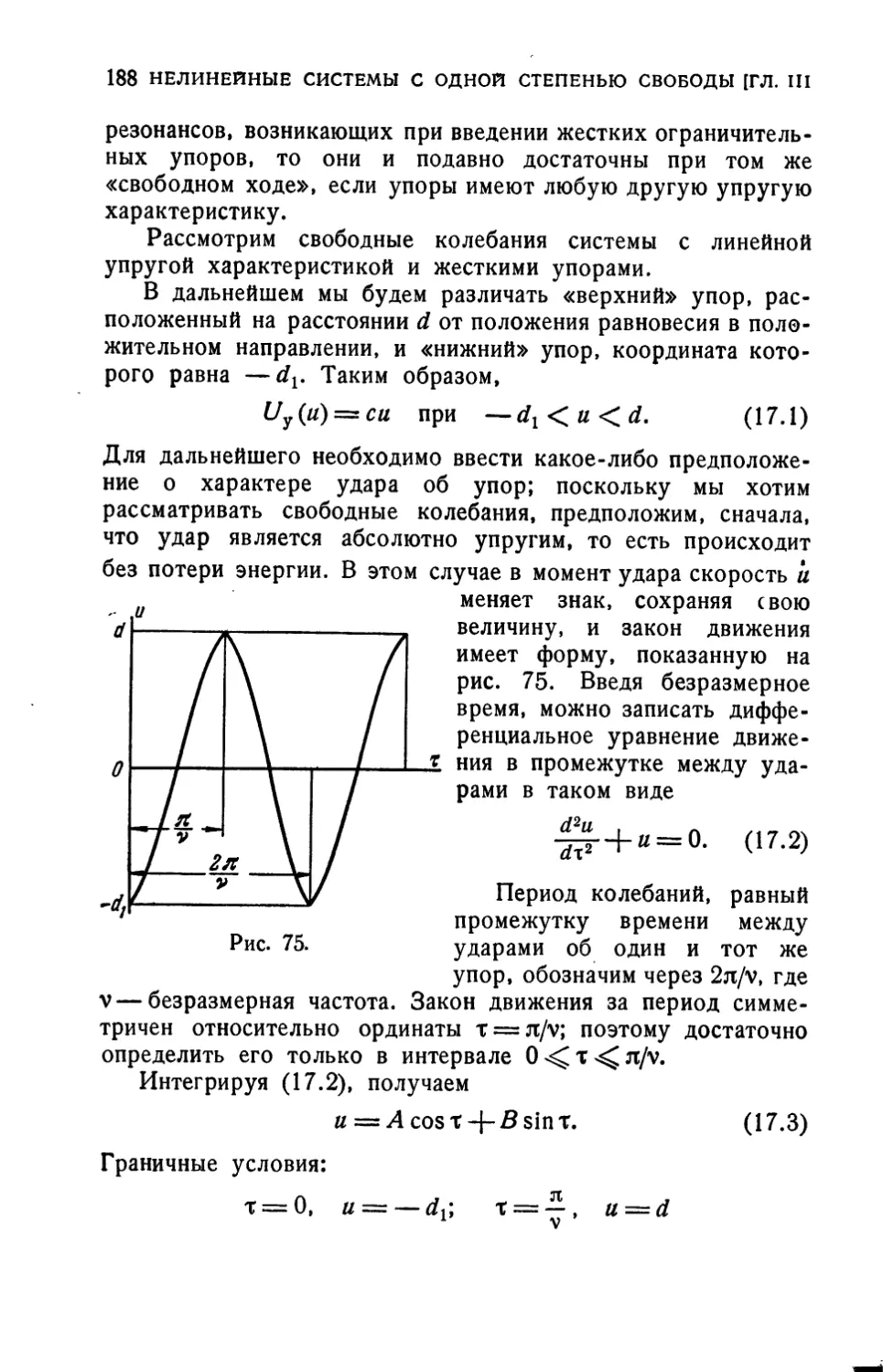
ВВЕДЕНИЕ
В этой книге будут рассматриваться виброзащитные
системы, основными элементами которых являются упругие
амортизаторы (3 на рис. 1), устанавливаемые между
основанием 1 и
амортизируемым объектом 2.
Виброзащитные системы такого рода могут
быть разделены на две группы.
К первой группе относятся
активные системы, в которых
внешние, переменные во времени силы,
приложены к амортизируемому
объекту, а задачей упругих
амортизаторов является защита основа- Рис. 1.
ния от действия этих сил. В
пассивных системах, составляющих вторую группу,
динамические воздействия вызываются движением основания с
переменным ускорением. Задачей амортизаторов в таких системах
является защита амортизируемого объекта от этих
динамических воздействий.
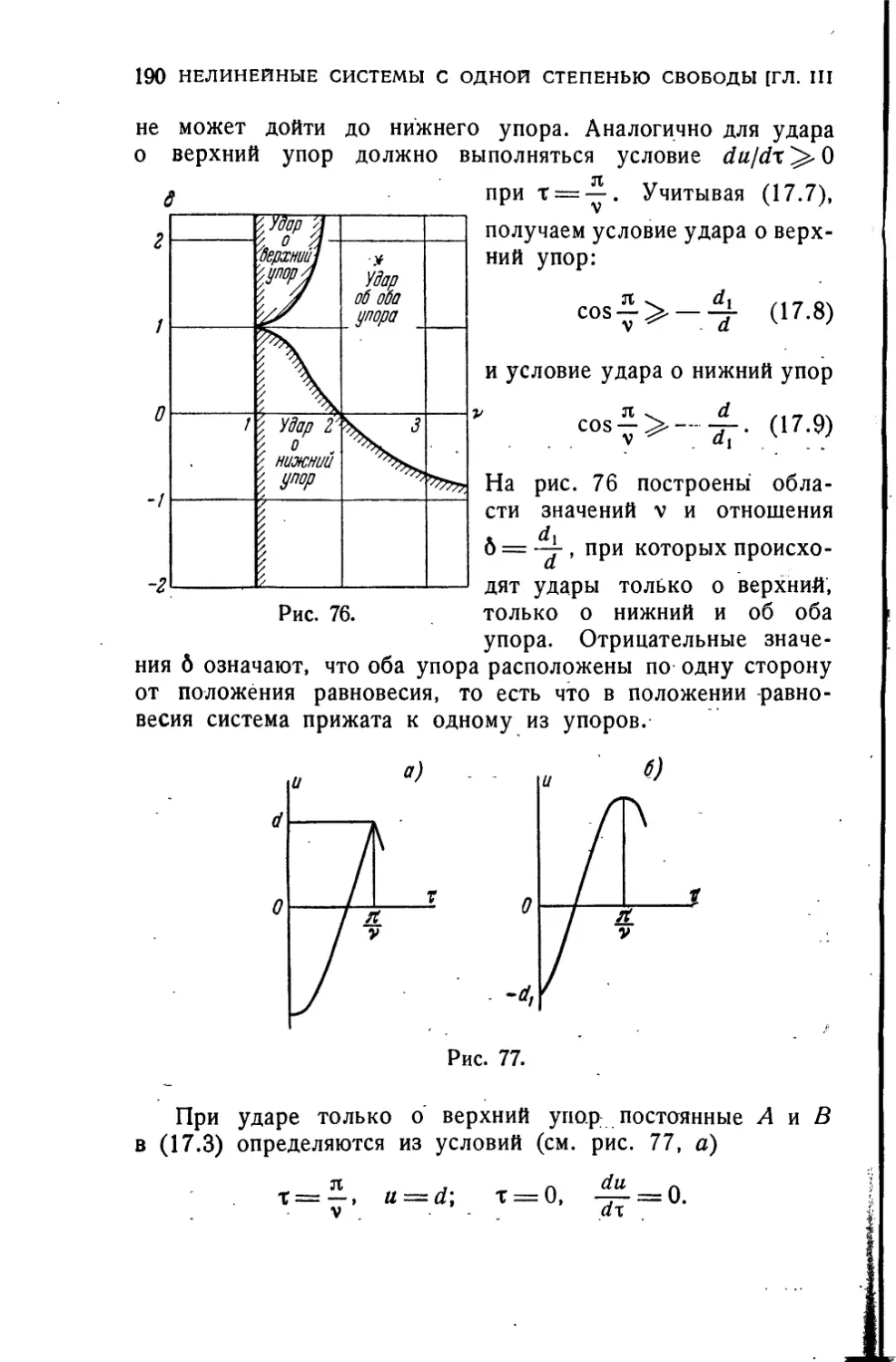
На рис. 2 приведены принципиальные схемы простейших
виброзащитных систем с одной степенью свободы, активной
(рис. 2, а) и пассивной (рис. 2, б). В обоих случаях
положение амортизируемого объекта относительно основания
определяется координатой и. Начало отсчета выбирается
таким образом, чтобы в положении статического
равновесия и равнялось нулю. Используя второй закон Ньютона,
составим уравнения движения амортизируемого объекта,
имеющего массу т. Для активной системы получим
mu = Q(,t) — U, (1)
10
ВВЕДЕНИЕ
где и— ускорение объекта, —U — реакция упругого
амортизатора, Q(t) — внешняя сила, приложенная к объекту.
Для пассивной системы
mlu + l(f)] = — U.
(2)
Здесь |(Y) — закон движения основания, а и— относительное
ускорение объекта.
В активной системе на основание передается сила U\
уменьшение динамической (переменной) составляющей этой
б)
МШ/МЖ/ША
Ж
Ш/ШШ///Ш Ш
Рис. 2.
силы — основная задача виброзащитной системы. В пассивной
системе, как это видно из уравнения (2), реакция
амортизатора — U представляет собой силу, приложенную к
амортизируемому объекту; поэтому и здесь виброзащитная система
должна уменьшать динамическую составляющую этой силы.
Реакция идеально упругого амортизатора является
функцией его деформации и\ в реальных амортизаторах
деформация всегда сопровождается рассеянием энергии, вызванным
либо внутренним трением в деформируемом материале, либо
применением специальных демпфирующих устройств, о
назначении которых речь будет идти ниже. Если учитывать
демпфирование, то оказывается, что величина реакции
зависит не только от деформации, но и от ее производных
по времени. В большинстве случаев при проведении
практических расчетов достаточно ограничиться учетом только
первой производной, то есть принять, что
y = U(ut и).
(3)
ВВЕДЕНИЕ
11
При этом уравнения (1) и (2) могут быть записаны в
следующей общей форме:
mu-\-U{u, e) = Q(0, (4)
причем в случае пассивной системы
Q(t) = -ml(t). (5)
Поведение системы (4) определяется характером
внешнего воздействия («вынуждающей силы») Q(0- В теории
виброзащитных систем рассматриваются два класса внешних
воздействий. К первому классу относятся вибрационные
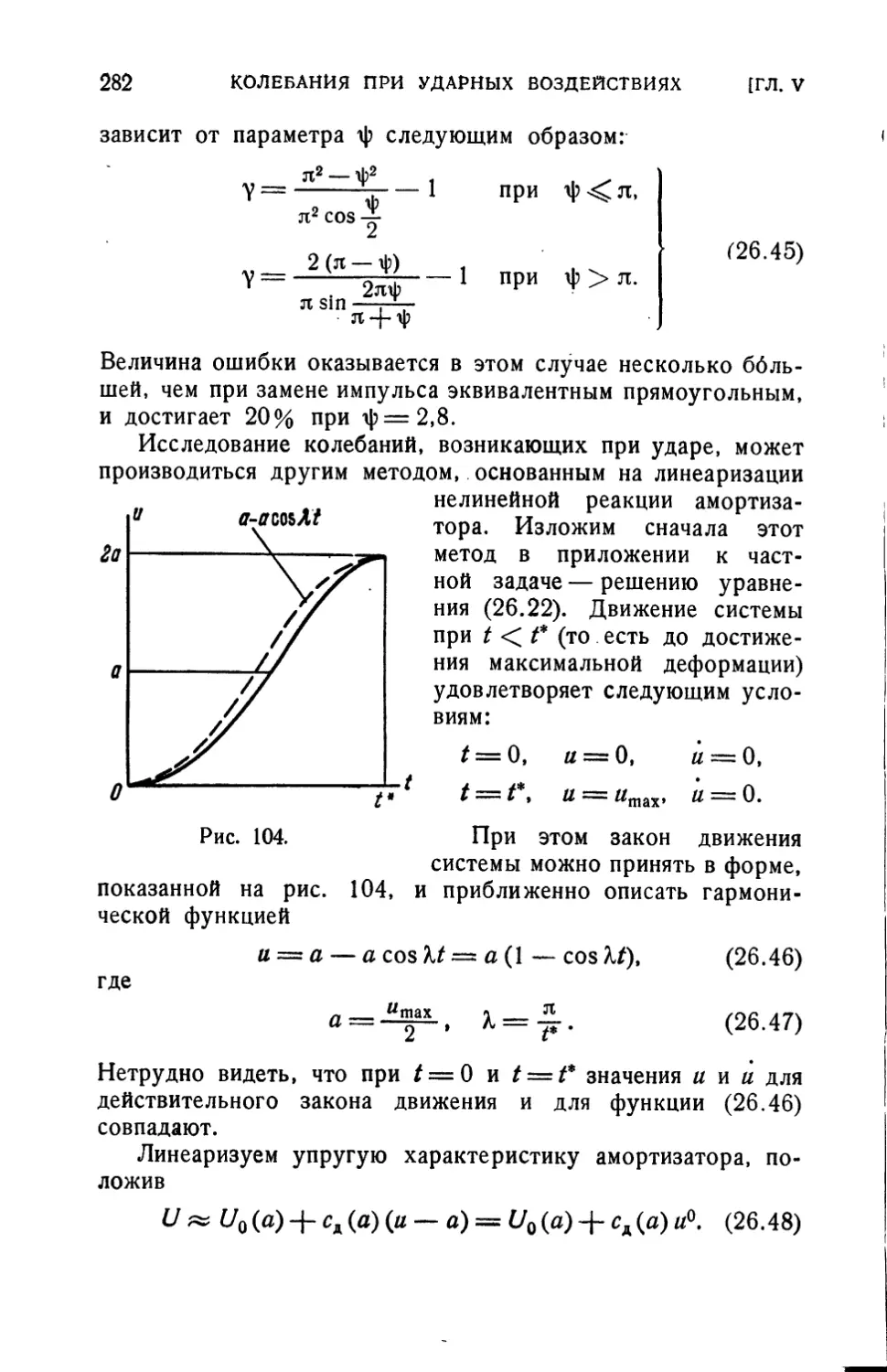
воздействия, классическим примером которых может
служить гармоническая вынуждающая сила
Q(f) = Q0cos©f. (6)
Вибрационные воздействия, с которыми приходится иметь
дело при исследовании современных виброзащитных систем,
обычно являются полигармоническими, то есть могут быть
представлены в виде суммы конечного или бесконечного
числа гармонических компонент
N
Q (0 = 2 Q/cos (©,*+!>,). (7)
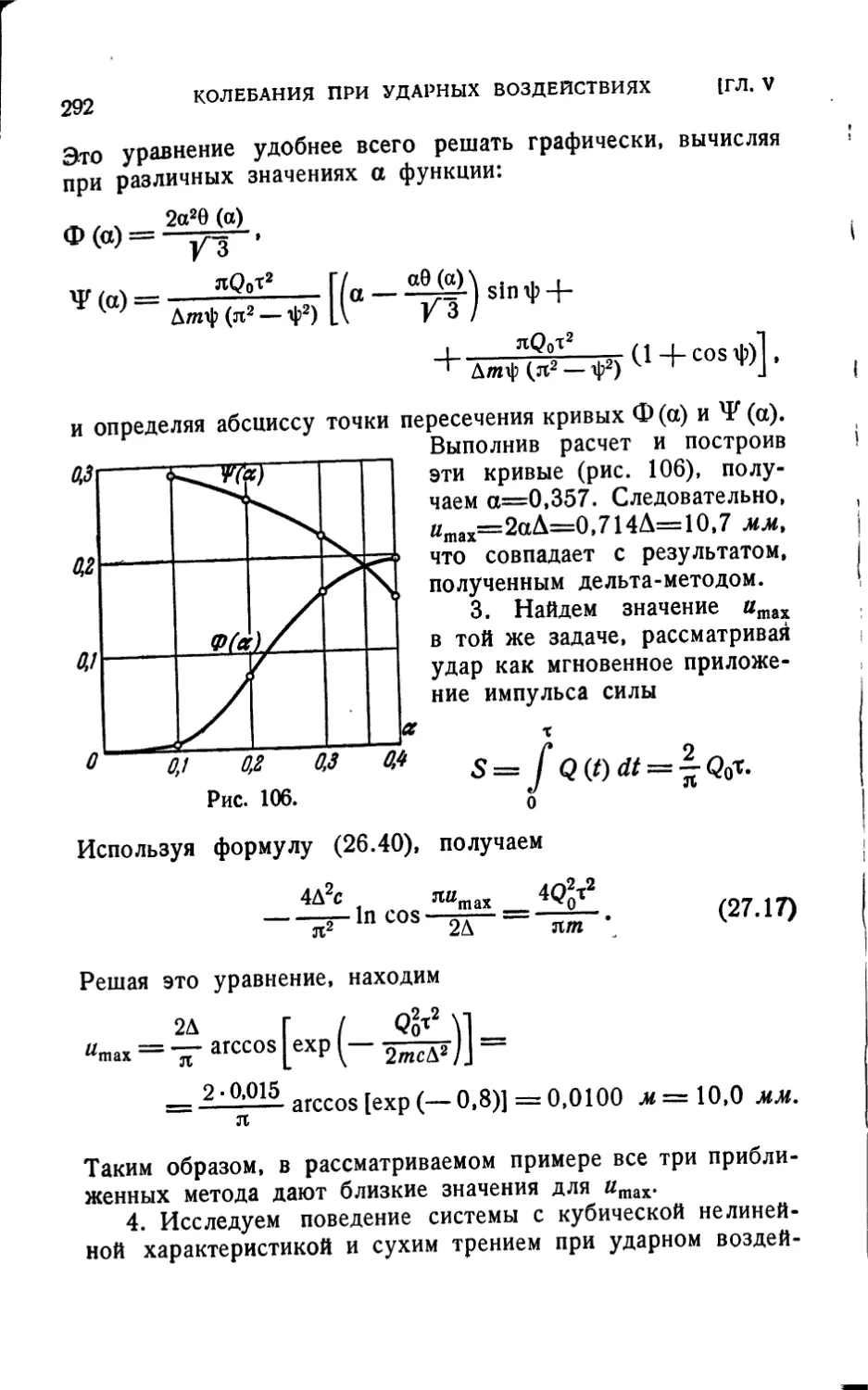
i = l
Второй класс вынуждающих сил, рассматриваемых в
теории виброзащитных систем, образуют ударные воздействия.
Классическим примером ударного воздействия может служить
силовой импульс — воздействие бесконечно большой силы
в течение бесконечно малого интервала времени, вызывающее
изменение количества движения системы на конечную
величину. Такой «мгновенный» удар является, разумеется,
идеализацией, которая далеко не всегда пригодна для описания
реальных ударных воздействий. В теории виброзащитных
систем термин «удар» имеет более широкий смысл: ударом
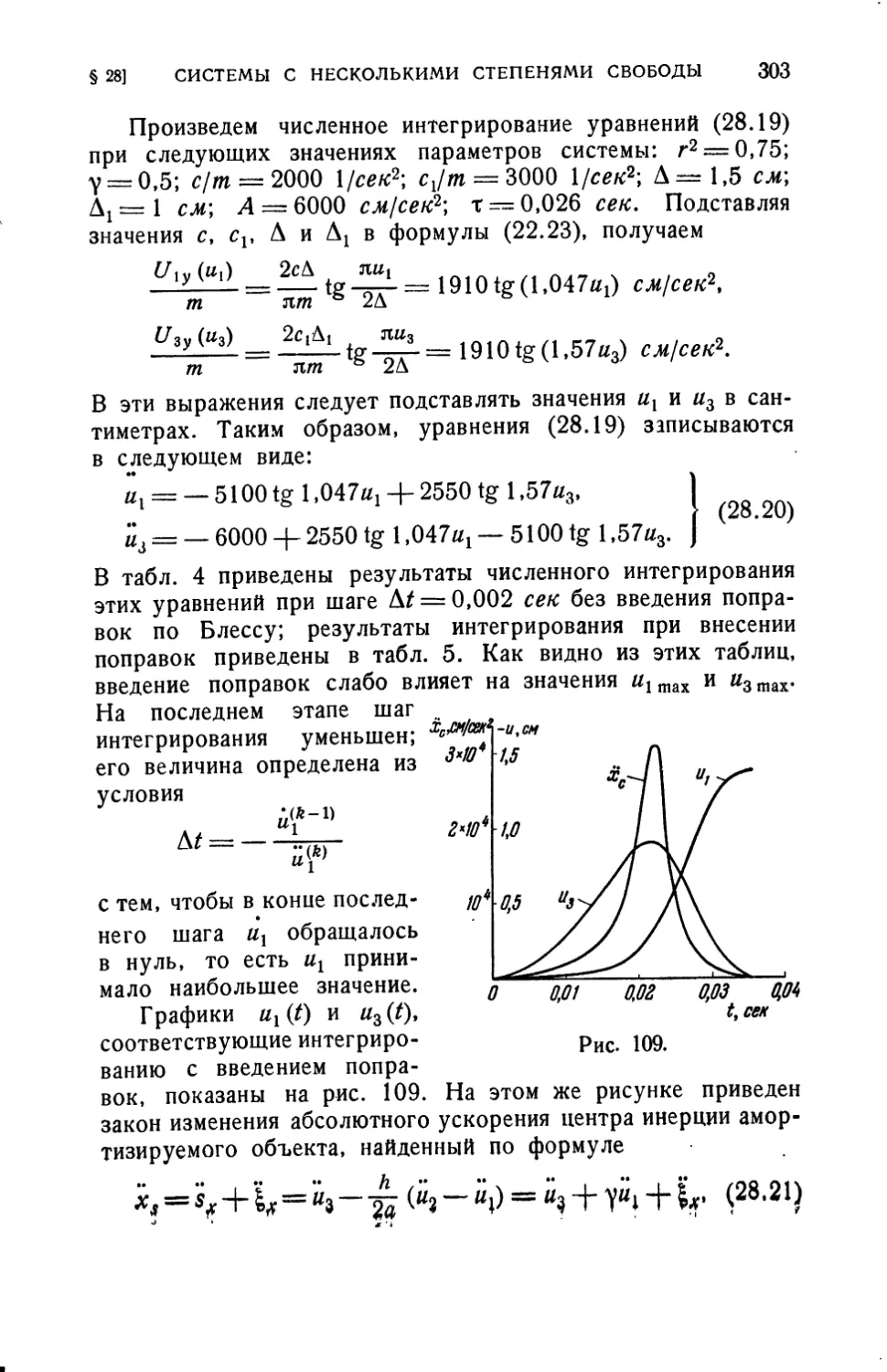
называется обычно кратковременное воздействие на систему
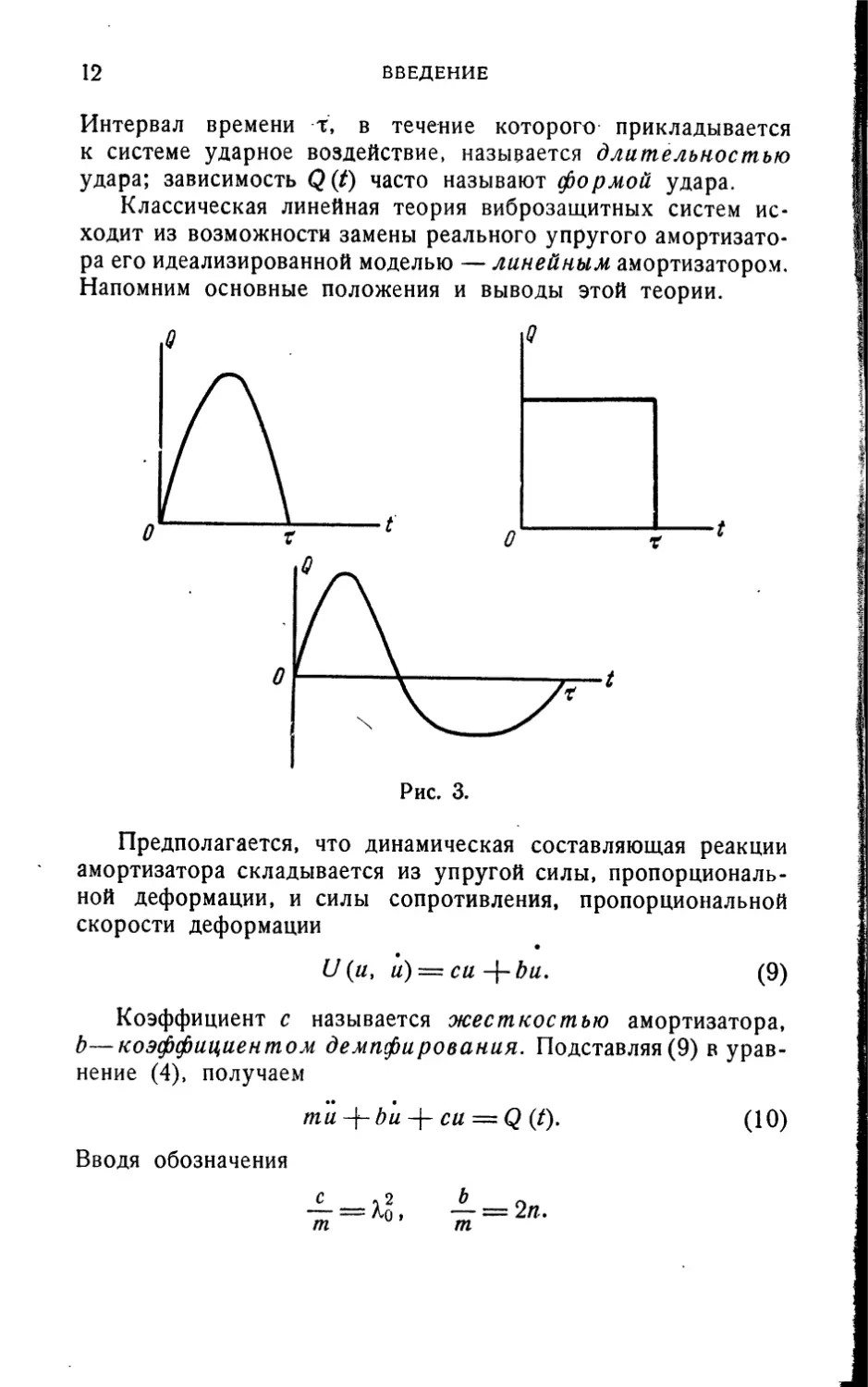
сравнительно больших внешних сил. Ударное воздействие
характеризуется законом изменения Q(t)\ некоторые
возможные формы этой зависимости показаны на рис. 3. Во всех
случаях
Q(t) ФО при * <т, 1
Q{t) = 0 при *>т. I ( ^
12 ВВЕДЕНИЕ
Интервал времени т, в течение которого прикладывается
к системе ударное воздействие, называется длительностью
удара; зависимость Q(t) часто называют формой удара.
Классическая линейная теория виброзащитных систем
исходит из возможности замены реального упругого
амортизатора его идеализированной моделью — линейным амортизатором.
Напомним основные положения и выводы этой теории.
Рис. 3.
Предполагается, что динамическая составляющая реакции
амортизатора складывается из упругой силы,
пропорциональной деформации, и силы сопротивления, пропорциональной
скорости деформации
U {и, и) = си -\-Ьи.
(9)
Коэффициент с называется жесткостью амортизатора,
b—коэффициентом демпфирования. Подставляя (9) в
уравнение (4), получаем
ти -\-bu-\- cu = Q (t).
(Ю)
Вводя обозначения
ВВЕДЕНИЕ
13
приводим уравнение (10) ;к следующей- форме: - ■ ■
u + 2nu + ^u = ^Q(t). (И)
Общее решение этого уравнения, как известно, складывается
из общего решения соответствующего однородного
уравнения и частного решения неоднородного уравнения. При
начальных условиях
t = 0, и — и0, u= uq
общее решение уравнения (11) имеет такой вид [30]:
и = e-nt U0 cos lxt + ц° + ш° sin kxt) +
t
-f-^- \ e-nV-nsinl^t-nQindt', (12)
где
Vkl — fi
2
Исследуя поведение виброзащитной системы при
вибрационном воздействии, обычно ограничиваются определением
установившегося движения, соответствующего достаточно
большим значениям t. Поскольку при наличии
демпфирования (п > 0) свободные колебания, соответствующие первому
слагаемому в выражении (12), затухают, установившееся
движение оказывается не зависящим от начальных условий
и полностью определяется видом вибрационного воздействия.
При гармоническом вибрационном воздействии (6)
установившиеся вынужденные колебания также оказываются
гармоническими. При этом
и== Qo =г- cos (erf —6). (13)
ml/(^-cD2)2 + 4nV
где В г— сдвиг по фазе между колебаниями и вибрационным
воздействием, определяющийся по -формуле:
tge = ^. (И)
Aq — (0
Подставляя (13) в формулу (9), можно определить усилие,
14
ВВЕДЕНИЕ
передаваемое амортизатором при вибрационном воздействии:
£/ = 0,
где
У(Х1- со2)2 + 4«V
2лгсо
COS (Gtf — В + 8), (15)
tge = -
i2 *
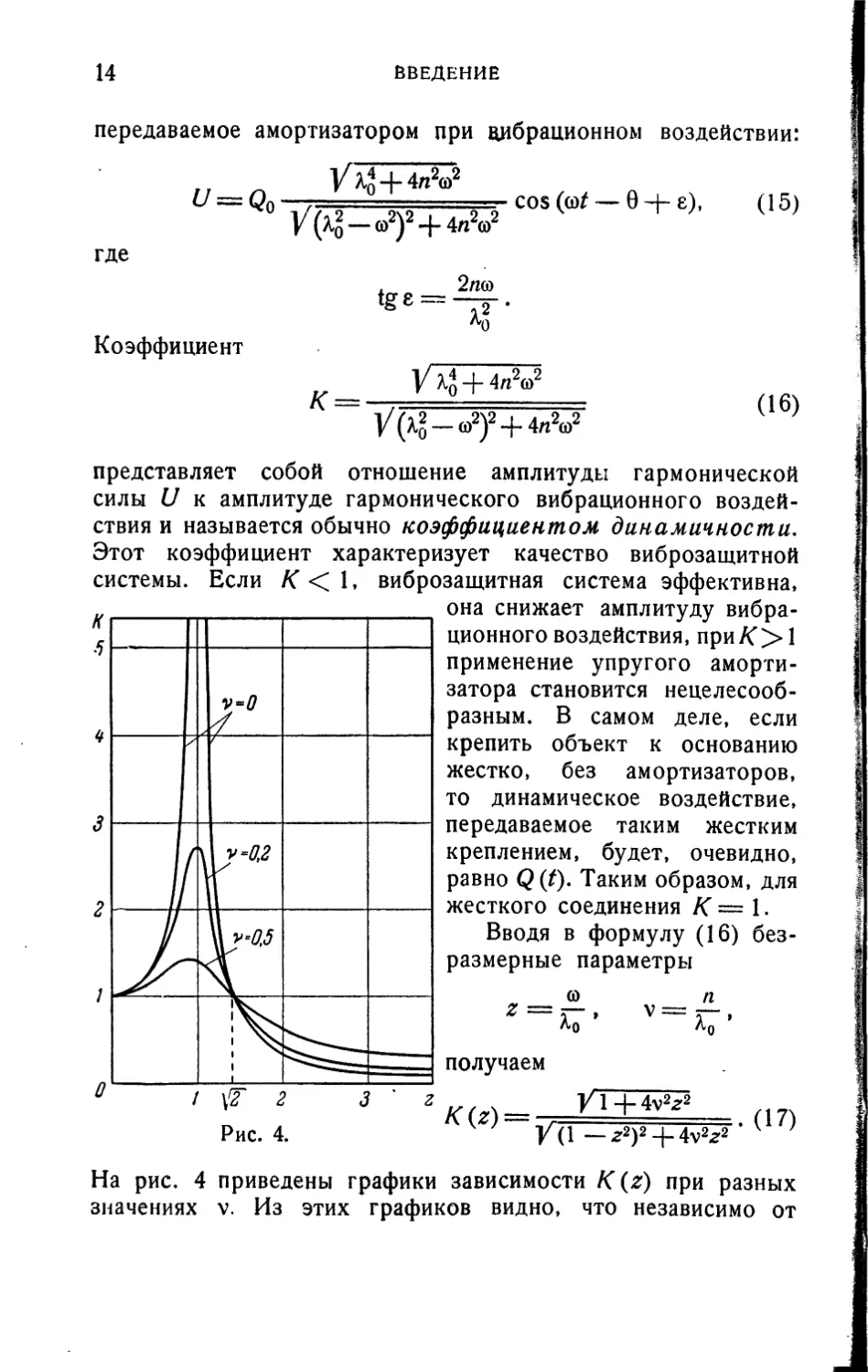
Коэффициент
К = -
VxS + 4/iV
V(xg — со2)2 + 4л2а>2
(16)
представляет собой отношение амплитуды гармонической
силы £/ к амплитуде гармонического вибрационного
воздействия и называется обычно коэффициентом динамичности.
Этот коэффициент характеризует качество виброзащитной
системы. Если /С<1, виброзащитная система эффективна,
она снижает амплитуду вибра-
•5
г
v-0
V
у
vJ=0,2
\y-oj
ционного воздействия, при/С> 1
применение упругого
амортизатора становится
нецелесообразным. В самом деле, если
крепить объект к основанию
жестко, без амортизаторов,
то динамическое воздействие,
передаваемое таким жестким
креплением, будет, очевидно,
равно Q(t). Таким образом, для
жесткого соединения К = 1.
Вводя в формулу (16)
безразмерные параметры
Z 7 у
Ад
v =
получаем
/ \Т
Рис. 4.
К{г)-.
У1+4у2г2
V(l — *2)2 + 4v2*2
.(17)
На рис. 4 приведены графики зависимости K(z) при разных
значениях v. Из этих графиков видно, что независимо от
ВВЕДЕНИЕ 15
значения v, при z > \ 2 коэффициент динамичности меньше
единицы, причем его величина тем меньше, чем меньше v4
При полигармоническом вибрационном воздействии вида (7)
вынужденные колебания являются полигармоническими.
Используя принцип суперпозиции, получаем
N
где
= £ Т/Л2 QL^,22COS(^-e')' ^18)
Аналогично, для силы U имеем
U=ZiQ>47KT=242 , 2 aCoK^-e^ + ei). (20)
причем
Очевидно, что если для всех / выполняется условие сог > ]/2А,0,
то амплитуда каждой из гармонических составляющих силы U
меньше, чем амплитуда соответствующей гармоники
вибрационного воздействия, и виброзащитная система окажется
эффективной.
При ударном воздействии обычно исследуется движение,
соответствующее нулевым начальным условиям
t
а = -L Г е-п <'-''> sin кг (t — tf) Q {tr) df. (22)
о
Подставляя это выражение в формулу (9), получаем
t
и=Т;1 е-п«-п[(%\ — n2)sinM* — *') +
о
-+ 2лА.г cos ^ (f — /')] Q (О ^'. (23)
16
ВВЕДЕНИЕ
Качество виброзащитной системы при заданном ударном
воздействии может быть оценено коэффициентом
динамичности при ударе Ку, равным отношению
максимального значения усилия U к максимальному значению Q
K'~w£- <24>
В линейной теории рассматриваются обычно
виброзащитные системы со слабым демпфированием; в таких системах
при исследовании удара можно с достаточной степенью
точности принять п = 0. При этом формулы (22) и (23)
принимают такой вид:
t
и = J- j sinX0(^ — t') Q (f') dt\ (25)
d
U = k0fs'mX0(t — t') Q (O df. (26)
о
Найдем значение Ку для удара «прямоугольной» формы
Q (t) = Qm = const при t <; т
Q(t) = 0 при *>т, j (27)
предполагая, что п = 0. Из выражения (26), произведя
интегрирование, получим
U = Qm(\ — cos V) при *<т, (28)
U = Qm [cos k0 (t — т) — cos VI ПРИ' t>x. (29)
Первое из этих выражений достигает максимума при / = /j=
= я/А,0. Этот максимум, равный 2Qm, может быть достигнут
только в том случае, если
Х0т > jx. (30)
Если же
Л0т<Л' (31)
то максимальное значение U определяется по формуле (29):
tf«« = 2<?msin-^. (32)
ВВЕДЕНИЕ 17
Оно достигается при
Таким образом,
/Cy = 2sin-~- при т<^,
° I (34)
/Су = 2 при т > у .
Для того чтобы амортизатор уменьшал ударное воздействие,
должно быть /Су < 1, что обеспечивается при
Я„<£. (35)
Этот вывод остается справедливым для ударного воздействия
любой формы. В самом деле, определим значения и (т) и
и{х) для удара произвольной формы. Дифференцируя
выражение (25), находим
t
ii (*) = --L Г cos А,0 (* — f) Q (Г) Л'.
о
Таким образом,
т
а (т) = -jL J sin lQ (т - О Q (О Л'. (36)
о
т
и (т) = -1 Г cos Я^ (т — f) Q (tf) dt'. (37)
о
При t > т в системе происходят свободные колебания,
амплитуда которых, равная максимальной деформации
амортизатора, определяется, как известно, следующим образом:
«max = у ^
Aq
При отсутствии демпфирования максимальное усилие
соответствует максимальной деформации. Поэтому
£Anax = Cj/a2(T)-f--^. (38)
2 М. 3. Колоеский
18 ВВЕДЕНИЕ
При выполнении условия (35) ядра интегралов (36) и
'(37) положительны при всех значениях t'. Поэтому, если
|Q(0|max = Qm.
ТО
ъ0
й(т)<^-(1—cosV).
"W<-^rsinV-
Учитывая эти неравенства, получаем
Уш = с j/""2 (т) + ■£$*■ < Qm Vr(l-cosA0T)2-(-sin2X0T=
Таким образом, при заданных значениях Qm и т величина
максимального усилия, передаваемого амортизатором,
оказывается наибольшей, если удар имеет прямоугольную форму.
Отсюда, в частности, следует, что при выполнении
условия (35) Ку окажется меньше единицы, какова бы ни была
форма удара.
Учет демпфирования не изменяет сколько-нибудь
существенно полученных результатов. При ударе прямоугольной
формы для усилия U(u, и) получаем
U = Qm\l—e'ni(zosKlt—^sinllt\\ при /<т, (39)
U = Qme^nt ^cos^tle^UosX^ + ^sinl^] — ll +
+sinA,1qe/lt(sinX1t — Т" C0S^iT) + "r"|f ПРИ t > т- (40)
Если отношение п/Х0 является малым, то, пренебрегая членами
порядка я2До. можно получить следующие выражения для
коэффициента динамичности при ударе:
^у-2!1-^) при х>^г .
Ky~2\l-2x;)sm-t при Т<-1Г
ВВЕДЕНИЕ 19
Исследование поведения линейной системы с одной
степенью свободы при вибрационном и ударном воздействии
позволяет сделать следующие выводы:
1) Уменьшение жесткости амортизатора, а следовательно,
и собственной частоты системы приводит к улучшению ее
виброзащитных и ударозащитных свойств. Для того чтобы
линейная система защищала от вибрационных воздействий,
должно выполняться условие
K<yf> , (42)
где o)min — наименьшая из частот гармонических компонент,
имеющихся в вибрационном воздействии. Для защиты от
ударных воздействий достаточно, чтобы выполнялось
условие (35).
2) Если выполнено условие (42), то увеличение
демпфирования может только ухудшить виброзащитные свойства
системы. С этой точки зрения введение сильного
демпфирования является нежелательным; слабое демпфирование,
обеспечивающее затухание свободных колебаний, возникающих
в системе при ударных воздействиях, оказывается вполне
достаточным для виброзащитных систем.
Эти выводы, составляющие основу линейной теории
виброзащитных систем, могут быть распространены и на системы
с несколькими степенями свободы. В гл. IV будет показано,
что основные рекомендации (желательность снижения
собственных частот системы и нецелесообразность введения в
систему сильного демпфирования) сохраняют силу и в этом
случае.
Казалось бы линейная теория предлагает универсальный
метод эффективного решения задач, связанных с защитой от
вибраций и ударов: необходимо создавать достаточно мягкие
линейные системы со слабым демпфированием. Однако опыт
проектирования и эксплуатации реальных виброзащитных
систем показал, что в большинстве случаев этот метод не
приводит к желаемым результатам. Более того, в последние
годы развитие конструкций виброзащитных систем пошло
в направлении, противоречащем рекомендациям линейной
теории. Появились и получили широкое применение жесткие
и сильно демпфированные системы. Причиной такого
несоответствия является ограниченность линейной теории, ее
2*
20
ВВЕДЕНИЕ
непригодность для описания ряда явлений, происходящих
в виброзащитных системах.
Ограниченность линейной теории связана в первую
очередь с ограниченностью размеров виброзащитных устройств.
Любой реальный амортизатор может иметь линейную
упругую характеристику лишь в некоторой области значений
деформации, называемой обычно областью линейности;
в любой реальной виброзащитной системе должны
существовать «ограничители хода», устанавливающие предельно
возможные размеры области линейности. Естественно, что
использование линейной 'теории для анализа виброзащитной
системы возможно лишь в том случае, если при заданных
воздействиях деформации амортизаторов не выходят за пределы
области линейности. Однако во многих задачах выполнение
этого условия оказывается практически невозможным.
Рассмотрим следующий пример. Пусть мы желаем защитить объект
от удара, вызванного движением основания с ускорением
£=150 м/сек2 в течение времени т = 0,05 сек.
Максимальное ускорение объекта, равное, очевидно, отношению UmaJm,
не должно превышать 50 м/сек2. Попытаемся применить для
защиты линейную систему без демпфирования. Поскольку
в рассматриваемом случае Qm=mt>, получаем
is ^max ^max *
У Qm ml 3
Отсюда из выражения (34) находим
2 Ку 2
^0 = — arcsin-y ==jr-~-arcsin0,167 = 6,6 \/сек.
Найдем величину наибольшей деформации такого
амортизатора при заданном ударном воздействии. Используя
формулу (32), получаем
Такая величина «свободного хода», разумеется,
практически неприемлема; поставленная задача оказалась
невыполнимой, во всяком случае при использовании амортизаторов
с линейной характеристикой.
ВВЕДЕНИЕ
21
Не менее существенными оказываются размерные
(«габаритные») ограничения при вибрационных воздействиях.
Наиболее четко их влияние сказывается в тгх случаях, когда
частота вибрационного воздействия оказывается настолько
низкой, что не удается избежать резонанса. При са = Х.0
формула (13) дает
Qo Qo
т2пХ0 2cv
(43)
Для того чтобы ограничить максимальную амплитуду при
резонансе, не допустить выхода системы за пределы
линейной области, приходится увеличивать коэффициент v, то есть
вводить более сильное демпфирование.
Однако влияние габаритных ограничений этим не
исчерпывается. Они приводят к возможности возникновения ряда
явлений, носящих ярко выраженный «нелинейный характер»
и не обнаруживаемых при линейном анализе. Дело в том, что
в силу ограниченности линейного участка упругой
характеристики становится уже неправомерным предположение о
независимости установившегося движения от начальных условий;
в реальных виброзащитных системах оказывается возможным
существование нескольких установившихся колебательных
режимов при одном и том же вибрационном воздействии.
При колебаниях, выходящих за пределы области
линейности, виброзащитная система уже не защищает от
вибрационных воздействий; поэтому во всякой удовлетворительно
работающей системе возможность возникновения таких
колебаний должна быть исключена. Как будет показано ниже, это
достигается в первую очередь за счет увеличения
демпфирования. Вместе с тем, как мы видели, с ростом
демпфирования ухудшаются виброзащитные свойства системы при
высокочастотных воздействиях; в связи в этим возникает
задача о выборе оптимального демпфирования, решение
которой становится одной из главных проблем теории
виброзащитных систем.
В свою очередь введение интенсивного демпфирования
является еще одной причиной нелинейности реальных
виброзащитных систем. Практически сложно осуществить
достаточно эффективные демпферы, сила трения в которых была бы
пропорциональна скорости; значительно более простыми
22
ВВЕДЕНИЕ
в конструктивном отношении оказываются нелинейные
демпферы, например, использующие сухое трение.
Чем выше уровень вибрационных и ударных воздействий,
тем сильнее сказываются перечисленные выше обстоятельства,
приводящие к ограниченности линейной теории. Именно
поэтому в последнее время с появлением новых интенсивных
источников вибраций и ударов стала особенно актуальной
необходимость исследования вибрэзащитных систем
нелинейными методами. Изложению этих методов и их приложению
к расчету виброзащитных систем посвящена эта книга.
ГЛАВА I
НЕКОТОРЫЕ ПРИБЛИЖЕННЫЕ МЕТОДЫ АНАЛИЗА
НЕЛИНЕЙНЫХ СИСТЕМ
§ 1. Метод гармонического баланса
Метод гармонического баланса служит для разыскания
приближенных периодических решений нелинейных
дифференциальных уравнений.
Рассмотрим, например, систему с одной степенью
свободы, движение которой описывается дифференциальным
уравнением
* + /(*. x) = F(Qt), (1.1)
где / (х, х) — нелинейная функция, F (Qt) — периодическая
функция времени, имеющая частоту Й. Предположим, что
уравнение (1.1) имеет периодическое решение частоты о
очевидно, что должно быть со = —, где р — целое число),
и попытаемся искать это решение в виде ряда Фурье
оо
х = а0 -f- 2 (ai cos/otf+ ^/sin "°0» (1-2)
оо
* = CD 2 U— al Sin/(0f-f-&jCOS/(Df). (1.3)
Для определения неизвестных коэффициентов а0, a-r bt
подставим (1.2) и (1.3) в (1.1) и разложим периодически^
24 НЕКОТОРЫЕ ПРИБЛИЖЕННЫЕ МЕТОДЫ [ГЛ. I
функции f(x, х) и F(Qt) в ряды Фурье
/ \ао + 2 (ai cos '©* + *jsin to*)»
со -I
со 2 /(—fl/sinto/ + fy cos /otf) =
oo
= /o + S (/*/ cos ^ + Л/sin *»*), (1.4)
i=l
oo
f(Qf) = F(p®t) = Л0+ 2 И/ c°s to* + Я, sin forf). (1.5)
Приравнивая в левой и правой частях уравнения (1.1)
постоянные составляющие и коэффициенты при costot и sin/erf,
получим систему уравнений для определения коэффициентов
ао> ai> bt. В общем случае каждый из коэффициентов /0,
fci* fsi зависит от всех коэффициентов Фурье функции х (t);
поэтому система уравнений принимает такую форму:
,/о(*0- а\ К . ..) = А>.
-№*c+-fct(a0' ai bv...) = Al (/=1, 2, ...),
-«и2*,+/,/(** *i ftlf ...) = В/.
(1.8)
Эту систему бесконечного числа трансцендентных уравнений
с бесконечным числом неизвестных в общем виде решить
невозможно. Только в том случае, когда
f(x, x) = ax-\-$x,
то есть когда уравнение (1.1) является линейным, система (1.6)
записывается в более простом виде
аа0 —Л0; — a)42ai-\-aai-\-$bli(i) = At (/=1, 2, ...), 1
— oft^ + aft, —topa^B, (f=l. 2, ...).( (L7)
Для каждого значения / получается независимая система
линейных алгебраических уравнений; это позволяет
последовательно определять коэффициенты aQ; av btf av b^ .. ,
§1]
МЕТОД ГАРМОНИЧЕСКОГО БАЛАНСА
25
Для нелинейных систем приходится ограничиться
приближенным определением коэффициентов Фурье, а следовательно,
и приближенным решением уравнения (1.1). Такое
приближенное решение можно получить, если оставить в (1.2)
конечное число гармоник, отбросив остальные. Пусть
/i, h> • • •» lm — номера оставленных гармоник; тогда
га
х « х = а0 -(- 2 (aircos 'Vе0* ~г~ bir sin ir(dt), (1.8)
га
д: « д; = со 2 *Д— Д/г sin/r(of-f-£/r cos/,.(*>*)• (1-9)
г=1
Подставив (1.8) и (1.9) в f(x, х), получим периодическую
функцию, содержащую, вообще говоря, все гармоники.
Отбросим в этом разложении все гармоники, кроме тех,
которые оставлены в х, то есть примем, что
/(*, х)ж f0+%(fcirco$ir(>>t -\-fsirsmir(i)t). (1.10)
т-\
Приравнивая коэффициенты при одних и тех же гармониках
в левой и правой части уравнения (1.1), получим в этом
случае систему конечного числа уравнений для определения
неизвестных а0, alv biv ..., alm, bim. Это, вообще говоря,
система трансцендентных уравнений, которую практически
удается решить только при оставлении в х весьма
небольшого числа гармоник. Чаще всего ограничиваются
отысканием решения в виде
х- а0-\- аг cos Ы-\-Ьх sin со/, (1-11)
то есть оставляют в (1.8) только постоянную составляющую
и первую гармонику периодического решения. Именно в такой
форме рассматриваемый метод разыскания периодических
решений и называется обычно методом гармонического
баланса.
26
РШКОТОРЫЕ ПРИБЛИЖЕННЫЕ МЕТОДЫ
[ГЛ. !
Уравнения для определения коэффициентов а0, ах и Ьг
записываются в следующем виде:
2л
/о(я0> 01. *i)= 2^ J /(a04-^icosi|) + ^isini|),
о
— ajcosin г|) -f- #icocos^) city = A0,
2Я
— a^ sin ^ -f- ^co cos ^) cos я|? tf\|) = Av
2Я
— w2#i + — /(ao+a^os^ + ^jsinij),
о
—аг(д sin i|) + ^co cos i|)) sin •tydty = Blt
где i|> = co/. Введя вместо ах и ^ амплитуду а и фазу <р
первой гармоники, то есть положив
(1.12)
где
х== а0~\~а cos (со/-f~cp),
(1.13)
(1.14)
можно упростить выражения (1.12):
2я
/o(ao> a)=2Sj /(^o+^cos^, — aa>sinф)rfi() = Л0.
— co2acos<p-f-
2я
+ — / (a0-f~a cos ф, — a©sini|))cosi|)rfi|) = Av J
2л
co2asincp-|-
Цп«
0+acosiJ?, — acosin^)sin^^ = -ei.
15)
Из этих уравнений можно определить a0, a, cp, если
известна частота периодического решения со. Частота может
считаться известной, если система (1.1) неавтономна, то есть
§ U МЕТОД ГАРМОНИЧЕСКОГО БАЛАНСА 27
если F (Ш) ф 0. В этом случае, как уже указывалось выше,
частота решения со должна быть в целое число раз меньше Q
(или равна 2); в противном случае при подстановке решения
левая и правая части уравнения (1.1) будут иметь
различный период. Если же система (1.1) автономна (F(Qt) = 0),
то частота периодического решения является неизвестной.
Однако в этом случае фаза ф может быть выбрана
произвольно, поскольку решение автономной системы вообще
определяется с. точностью до произвольной фазы. Поэтому
в случае автономной системы уравнения (1.15) позволяют
определить а0, а, со.
Применяя метод гармонического баланса, следует иметь
в виду, что он является математически нестрогим.
Приближенное решение вида (1.8) или (1.11) может иметь смысл
только в том случае, если существует точное периодическое
решение уравнения (1.1), в котором амплитуды всех
отброшенных гармонических составляющих действительно
достаточно малы.
Обратное заключение является неверным: из
существования приближенного периодического решения, найденного по
методу гармонического баланса (то есть из существования
вещественных решений системы (1.12)), не следует
существование близкого к нему точного решения той же частоты.
Предположение о существовании периодического решения
должно быть дополнительно обосновано какими-либо иными
соображениями, не связанными с методом решения.
Этот недостаток присущ всем приближенным методам,
рассматриваемым в этой главе. Во всех этих методах заранее
предопределяется форма искомого решения, то есть
выбирается некоторое семейство функций, зависящее от конечного
числа параметров, и предполагается, что решение принадлежит
этому семейству. В (1.11) такими параметрами являются
а0, alt bx. Естественно, что найденное таких путем решение
может оказаться достаточно точный только в том случае, если
форма его «угадана» правильно, то есть если среди функций
семейства существует такая, которая мало отличается от
точного решения.
Выбор формы решения чаще всего производится на основе
физических соображений, то есть на основе некоторых
априорных представлений о свойствах рассматриваемой системы.
В частности, при анализе виброзащитных систем обычно
28 НЕКОТОРЫЕ ПРИБЛИЖЕННЫЕ МЕТОДЫ [ГЛ. I
оказывается допустимым пренебрежение высшими
гармониками в периодическом решении. Это происходит потому, что
любая виброзащитная система является механическим
фильтром низких частот. Переписав уравнение (1.1) в форме
£ = —/(*, x) + F(Qt), (1.16)
нетрудно заметить, что даже если функции F(Qt) и f(x, х)
содержат существенные по величине высшие гармоники,
решение для х может оказаться мало отличающимся от
гармонического, поскольку амплитуды всех гармоник будут при
двухкратном интегрировании делиться на квадрат номера
гармоники. Записав уравнение (1.1) в форме (1.16), можно
построить систему последовательных приближений к
искомому решению на основе рекуррентного соотношения
£<*>= —/(*<*-!>, i<*-i>)+/*(Qf). (1.17)
Не рассматривая здесь вопрос о сходимости этого
итеративного процесса к точному периодическому решению,
отметим только, что, приняв в качестве первого
приближения гармоническое решение (1.11), подставив его в правую
часть соотношения (1.17) и произведя интегрирование, можно
получить так называемое «улучшенное первое
приближение», содержащее уже, вообще говоря, все гармоники
оо
*у=~2(~fwAt cosш + ~frJ~B'sinш) + а°- <*•18>
1=1
Нетрудно видеть, что коэффициенты при cosotf и sinotf
в этом выражении совпадают с ах и Ьх\ таким образом,
улучшенное первое приближение не приводит к уточнению
первой гармоники и постоянной составляющей по сравнению
с первым приближением.
Часто при разыскании улучшенного первого приближения
в функции f(x, x) выделяют линейную часть^ Пусть
/(*, x) = k?x-\-g(x> i), (1.19)
где
*2 = -й(0. 0); i£(0.0) = 0.
§ 1] МЕТОД ГАРМОНИЧЕСКОГО БАЛАНСА 29
Тогда уравнение (1.1) можно записать в таком виде
х-\-Ь?х = — g{x, x) + F(Qt). (1.20)
Если
g(aQ~\- alcosa)t-{-bls\n(ut, — ajcosin ayt-^b^cosatf) =
oo
= go + 2 tedcos ш+gstsin '«ю.
то для улучшенного первого приближения получается
следующее выражение:
оо
*, —2(7?-^»' coslarf+^gtiffslntofj+fl,. (1.21)
i = l
Подставляя (1.11) в (1.19), легко убедиться, что при />-2
fci = gd и fsi = Ssh поэтому выражения (1.21) и (1.18)
дают различные значения для коэффициентов Фурье при
высших гармониках решения. Выражение (1.21) оказывается
предпочтительнее в тех случаях, когда нелинейная часть
является заведомо малой, то есть когда мы имеем дело
со слабо нелинейной системой. Впрочем, при анализе
виброзащитных систем обычно рассматриваются такие
периодические режимы, для которых со>-&. Тогда при />-2, /2со2^>£2,
и различие между (1.18) и (1.21) становится несущественным.
Метод гармонического баланса легко обобщается на системы
более общего вида. Для произвольной динамической системы
x = X(x,t), (122)
где X и х — л-мерные векторы, а X—периодическая функция t
частоты Q, можно искать решение периода ю — — в виде ряда
Фурье
оо
х = а0 + 2 (а*cos |#а)* + bi sin Ш), (1.23)
i = \
где a0, ait bi — я-мерные векторы, составляющие которых являются
коэффициентами Фурье периодических функций хи ..., хп.
Подставляя (1.23) в (1.22) и раскладывая периодическую функцию X
в ряд Фурье, получаем бесконечную систему векторных уравнений
для определения неизвестных векторов а0, аь а2, ...» bu Ь2, ...
Ограничиваясь постоянной составляющей и первой гармоникой,
то есть разыскивая приближенное решение в виде
х = а0 + аг cos atf -f- b\ sin со*, (1-24)
30
НЕКОТОРЫЕ ПРИБЛИЖЕННЫЕ МЕТОДЫ
[ГЛ. I
получаем систему трех векторных уравнений с тремя
неизвестными. Как и в случае системы с одной степенью свободы,
допустимость пренебрежения в решении высшими гармониками
определяется фильтрующими свойствами линейной части системы,
характерными для виброзащитных систем, у которых спектр собственных
частот лежит обычно ниже спектра частот внешних воздействий.
Следует отметить, что ошибка, допускаемая при отбрасывании
высших гармоник, существенно зависит и от вида нелинейной
функции Х(х, t). Эта зависимость определяется следующей
теоремой. Пусть функция Х(х, t) непрерывна и имеет непрерывные
частные производные по х и t вплоть до s-ro порядка (это означает,
дХ; dXj д2Х; d2Xj
что непрерывны производные -щ. -^-, ^-^-, -^ и т. д.,
где Xj — составляющие вектора X). Тогда для остатка ряда Фурье,
получающегося при отбрасывании первых т гармоник в
периодическом решении уравнения (1.21), справедлива оценка
|/?ml<0K-7CT. О'25)
а для коэффициентов — оценка
]аш]<1$я- "m/l<d£*- (Ь26)
Здесь Rmi — остаток ряда Фурье для составляющей xi
периодического решения х (/); am,-t bmi — коэффициенты Фурье; Vi —
некоторая постоянная, не превышающая величины полного изменения
(5 + 1)-й производной по t от Х(. Доказательство этой теоремы
основывается на том, что оценки (1.25) и (1.26) справедливы, если
xi имеет по t непрерывные производные вплоть до (s -f- 1)-го
порядка. Это — известное положение теории рядов Фурье,
доказательство которого имеется, например, в [52].
Остается показать, что х (t) имеет непрерывные производные
вплоть до (s-f-l)-ro порядка. Действительно, подставляя решение
x(t) в уравнения (1.22), получим тождество
x{t) = X{x(t)J). (1.27)
Справа стоит непрерывная функция от t, поэтому и х (t)
непрерывна. Продифференцировав (1.27) по t, получим
*<*>-■£+ИМ ю- (Ь28)
Вследствие принятых допущений и непрерывности x(t), в правой
части (1.28) стоит непрерывная функция t. Следовательно, х
непрерывна. Продифференцировав (1.28) еще s—1 раз, легко
показать аналогичным способом, что х (t) имеет непрерывные
производные вплоть до (5-f- 1)-го порядка.
§ 2] СВОБОДНЫЕ КОЛЕБАНИЯ МАССЫ НА ПРУЖИНЕ 31
Из доказанной теоремы следует, что чем более «гладкими»
являются нелинейные функции, входящие в дифференциальные
уравнения, тем с большим основанием можно предполагать, что
метод гармонического баланса даст положительные результаты.
Более глубокие обоснования метода гармонического баланса,
основанные на рассмотрении интегральных уравнений, содержатся
в работах Е. Н. Розенвассера [45» 46].
§ 2. Свободные колебания массы на нелинейной пружине
В качестве примера применения метода гармонического
баланса рассмотрим задачу о свободных колебаниях массы,
имеющей одну степень свободы, на пружине с нелинейной
упругой характеристикой (рис. 5). Как будет показано ниже,
эта задача имеет прямое отношение к теории
виброзащитных систем.
Выберем начало координат в положении
статического равновесия; тогда уравнение свободных
колебаний массы т запишется в следующей форме:
*+/(*) = 0. (2.1)
где f(x) ——— отношение упругой реакции
пружины к массе.
Если исследуются колебания, происходящие Рис* ^
вблизи положения равновесия, и функция f(x)
имеет непрерывную первую производную в точке х = О, то
уравнение (2.1) может быть линеаризовано, то есть
функция f(x) может быть заменена на
k*x = f'(0)x.
При этом общим решением полученного линейного
уравнения будет гармоническая функция времени частоты к.
Если, однако, мы не ограничиваемся исследованием малых
колебаний или если при х = 0 f(x) не имеет непрерывной
производной, то обычная линеаризация становится
недопустимой.
Уравнение (2.1) интегрируется в квадратурах при помощи
подстановки
dv dv
32
НЕКОТОРЫЕ ПРИБЛИЖЕННЫЕ МЕТОДЫ
[ГЛ. I
Интегрируя получающееся уравнение по х> найдем
л
■£+ \f{x)dx = C,
(2.2)
где С — произвольная постоянная.
Система (2.1) консервативна, и (2.2) является интегралом
энергии. Величина С представляет собой полную энергию
колеблющейся системы,
отнесенную к единичной массе.
Уравнению (2.2) соответствует
замкнутая кривая на плоскости v — х
(рис. 6); изменяя величину С,
получим семейство кривых,
называемых фазовыми траекториями.
Изменению х и v в процессе
движения соответствует
перемещение изображающей точки по
фазовой траектории. Замкнутость
фазовых траекторий означает, что движение в
рассматриваемой системе будет периодическим. Из (2.2) получаем
Рис. 6.
— •#-/> [с-
J /w
dx
откуда
I
dx
/2[С-П(*)]
ln(x)=j f
(х) dx
(2.3)
Обратив интеграл (2.3), получим закон движения системы
при начальных условиях
„2
* = *0, х = х0. C=^-f J f{x)
dx.
(2.4)
Отметим, что если ф(£) есть решение уравнения (2.1),
то ф (t -+■ т) будет также решением этого уравнения при любом
вещественном значении т. Это следствие автономности
системы. Все решения, соответствующие различным значениям т,
изображаются одной и той же фазовой траекторией.
§ 2) СВОБОДНЫЕ КОЛЕБАНИЯ МАССЫ НА ПРУЖИНЕ 33
Точная зависимость x(t), как правило, не выражается
в элементарных функциях; это существенно усложняет
исследование закона движения. В частности, из (2.3) и (2.2) трудно
получить в явном виде зависимость частоты свободных
колебаний от амплитуды. Значительно удобнее исследовать
приближенное решение, которое может быть получено методом
гармонического баланса. Поскольку система автономна,
частота периодического решения заранее неизвестна. Обозначим
ее через А, и будем искать решение вида
х = а0 + cl cos {Xt -\- ф). (2.5)
Как уже отмечалось, в силу автономности системы фаза ф
может быть выбрана произвольно (введение фазы ф
эквивалентно сдвигу решения во времени на т = -|Ц. Поэтому
можно ограничиться разысканием частного решения,
соответствующего ф = 0:
х = а04- a cos kt. (2.6)
Подставив (2.6) в f(x), представим полученную
периодическую функцию в виде ряда Фурье. Поскольку решение
(2.6) зависит только от cos It и не содержит члена с sinW,
оно является четной функцией времени. Но тогда и f(x)
должно быть четной функцией Л то есть разложение f(x)
в ряд Фурье должно содержать только члены с косинусами
кратных гармоник:
/(*) = /<> + 2/*cos М. (2.7)
где
2л
/о = i J / (*о + * cos Ф) **. (2-8)
о
2л
/, = 1 J* / (а0 + a cos ф) cos ty <*ф. (2.9)
о
Следуя методу гармонического баланса, отбрасываем в (2.7)
все члены разложения, кроме постоянной составляющей и
первой гармоники, то есть полагаем
f{x)**f0 + fxcosU. (2.10)
3 М. 3. КоловскиЙ
34 НЕКОТОРЫЕ ПРИБЛИЖЕННЫЕ МЕТОДЫ [ГЛ. 1
Подставляя (2.10) в (2.1), получаем
— Х2а cos Xt -f- /0 + fx cos It = 0.
(2.11)
Приравнивая нулю постоянную составляющую и коэффициент
при cosXt, получаем два соотношения, связывающие
неизвестные а0, а, X:
2Л
/0 (а. а0) = ^ J/(a0+acost|j)di|j = 0. (2.12)
о
2л
Л*:
1 1
: —/t(a, a0) = — J /(а0 + асовф)со8фЛ|>. (2.13)
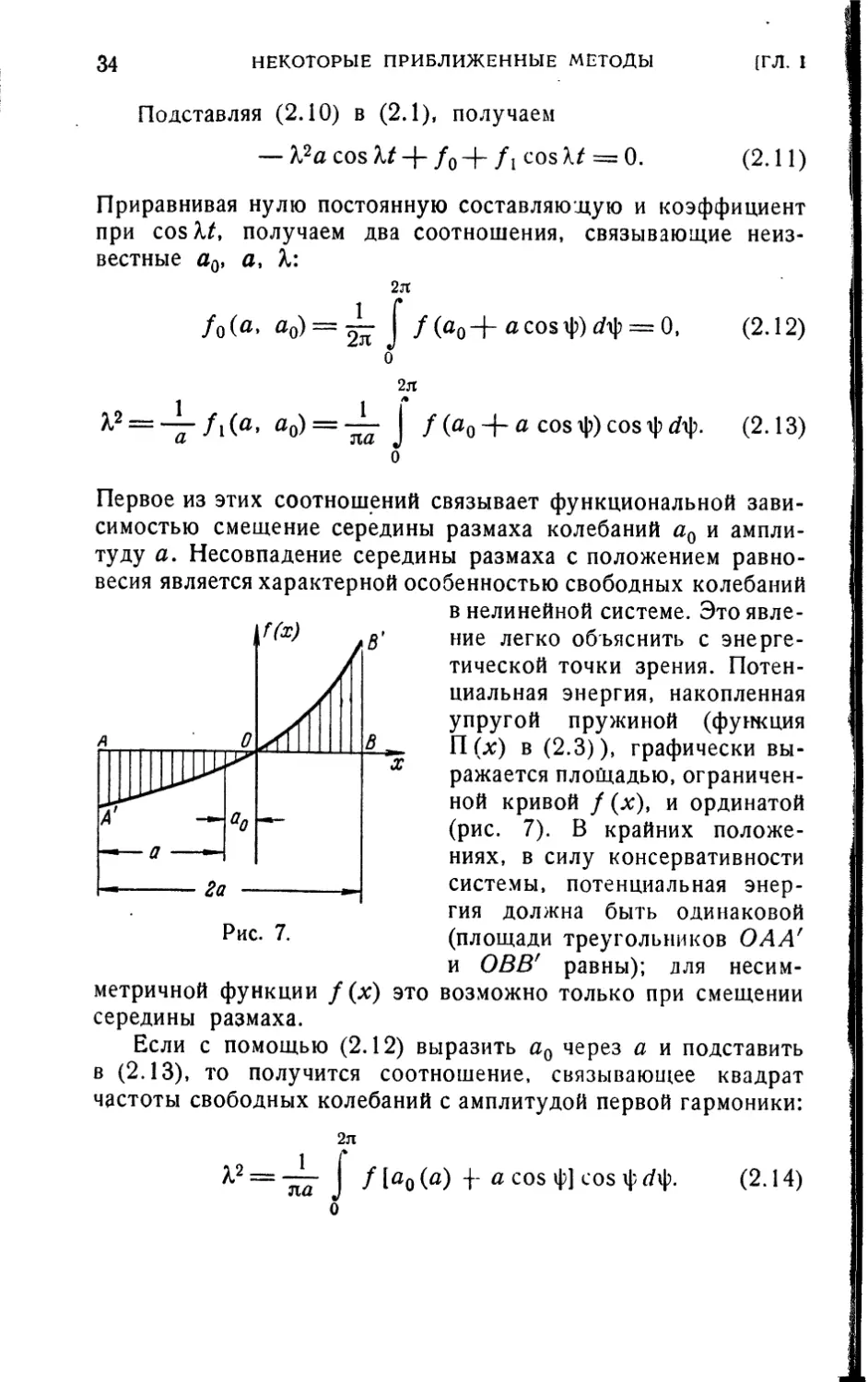
Первое из этих соотношений связывает функциональной
зависимостью смещение середины размаха колебаний а0 и
амплитуду а. Несовпадение середины размаха с положением
равновесия является характерной особенностью свободных колебаний
в нелинейной системе. Это
явление легко объяснить с
энергетической точки зрения.
Потенциальная энергия, накопленная
упругой пружиной (функция
П(д:) в (2.3)), графически
выражается площадью,
ограниченной кривой f (х), и ординатой
(рис. 7). В крайних
положениях, в силу консервативности
системы, потенциальная
энергия должна быть одинаковой
(площади треугольников ОАА'
и OBBf равны); для
несимметричной функции f (х) это возможно только при смещении
середины размаха.
Если с помощью (2.12) выразить а0 через а и подставить
в (2.13), то получится соотношение, связывающее квадрат
Рис. 7.
частоты свободных колебаний с амплитудой первой гармоники:
2л
*» = -L
па
б
/ [До (а) +" а cos Ф1 cos Ф ^Ф- (2.14)
§ 2] СВОБОДНЫЕ КОЛЕБАНИЯ МАССЫ НА ПРУЖИНЕ 35
Это соотношение выражает вторую характерную особенность
свободных колебаний в нелинейной системе — зависимость
частоты от амплитуды. Оно имеет фундаментальное значение
в теории виброзащитных систем и поэтому заслуживает более
подробного исследования.
Графическое изображение зависимости Х(а) называется
скелетной кривой. Соотношения (2.12) и (2.14)
устанавливают однозначное соответствие между функцией f (х) и
формой скелетной кривой.
Значение X при а = 0 совпадает с собственной частотой
линеаризованной системы, то есть
если только /' (х) непрерывна при х — 0. Это — частота
малых свободных колебаний нелинейной системы.
Пусть f (х) — нечетная функция, то есть f(x)= — /(—х).
Тогда решение уравнения (2.1) не должно содержать четных
гармоник; в частности, а0 = 0 (кривая f (х) симметрична
относительно положения равновесия). При этом
л
2л 2
1 Г А **
%2 — — / (a cos г|0 cos г|) dty =— | f (a cosip .osi|)tf\|).
i\iil щ) Jill' щ}
о о
Интегрируя по частям, получим
я
Т
Х2 = — /' {a cosi|))sin2^Gh|).
1 о
Следовательно,
2
d
da
(l2) = — f /" (a cos -ф) sin2 ф cos^ *l>- (2.15)
В интервале О^ф^-у, sin\|)^0, cos^^O. Следовательно,
знак производной d (№)/da совпадает со знаком f'(x) при
х >0.
3*
36 НЕКОТОРЫЕ ПРИБЛИЖЕННЫЕ МЕТОДЫ [ГЛ. I
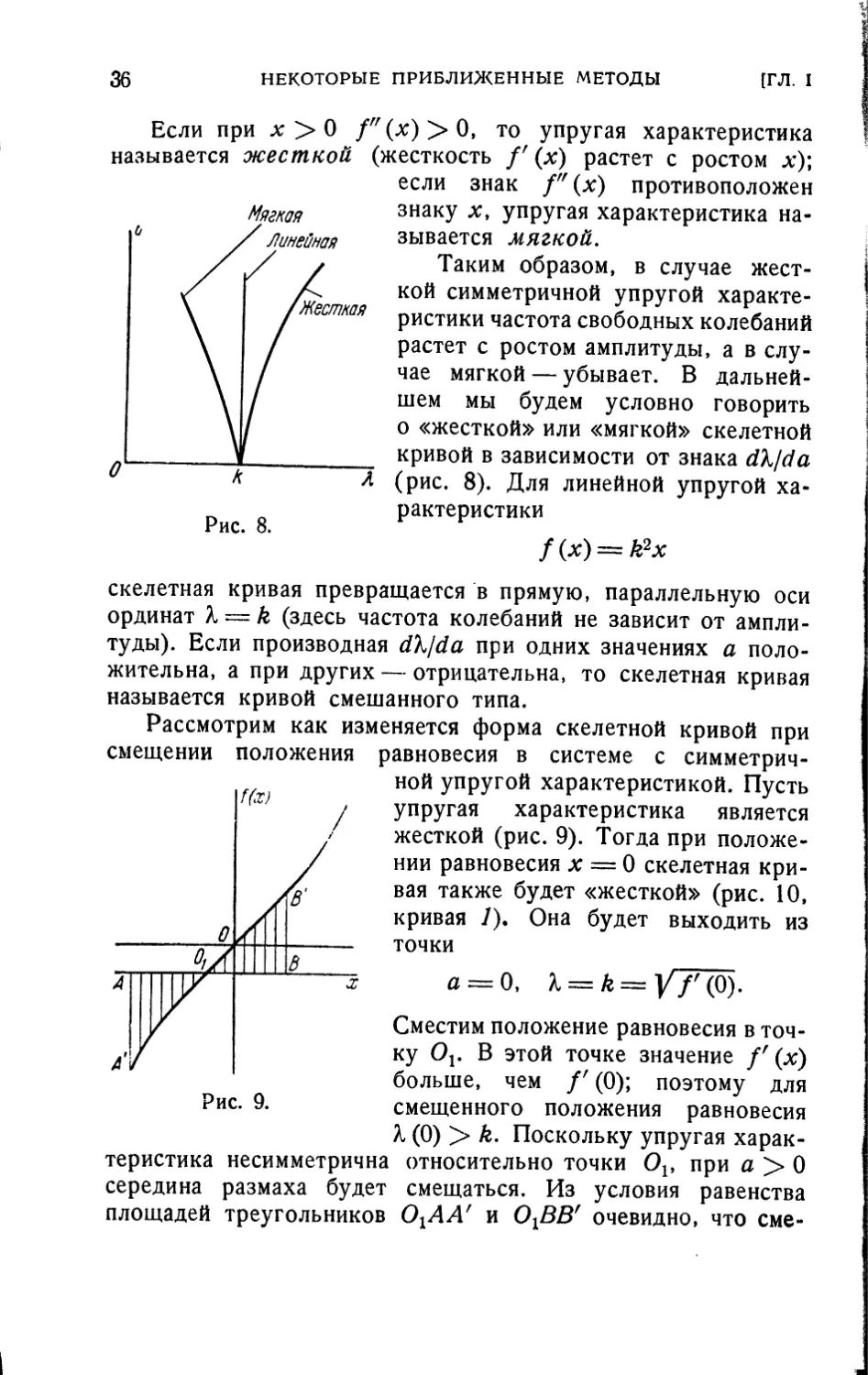
Мягкая
Линейная
Если при х > О ///(д:)>0, то упругая характеристика
называется жесткой (жесткость /' (х) растет с ростом х);
если знак /"(*) противоположен
знаку х, упругая характеристика
называется мягкой.
Таким образом, в случае
жесткой симметричной упругой
характеристики частота свободных колебаний
растет с ростом амплитуды, а в
случае мягкой — убывает. В
дальнейшем мы будем условно говорить
о «жесткой» или «мягкой» скелетной
кривой в зависимости от знака dX/da
(рис. 8). Для линейной упругой
характеристики
f(x) = k2x
Рис. 8.
скелетная кривая превращается в прямую, параллельную оси
ординат K — k (здесь частота колебаний не зависит от
амплитуды). Если производная dX/da при одних значениях а
положительна, а при других — отрицательна, то скелетная кривая
называется кривой смешанного типа.
Рассмотрим как изменяется форма скелетной кривой при
смещении положения равновесия в системе с
симметричной упругой характеристикой. Пусть
упругая характеристика является
жесткой (рис. 9). Тогда при
положении равновесия х = 0 скелетная
кривая также будет «жесткой» (рис. 10,
кривая /). Она будет выходить из
точки
0
OiA
JT1
f(X)
/
/в'
\\в
X
Сместим положение равновесия в
точку Ov В этой точке значение f'(x)
больше, чем /' (0); поэтому для
Рис. 9. смещенного положения равновесия
А, (0) > к. Поскольку упругая
характеристика несимметрична относительно точки Ог> при а > 0
середина размаха будет смещаться. Из условия равенства
площадей треугольников 01АА/ и 01BBf очевидно, что сме-
§ 2] СВОБОДНЫЕ КОЛЕБАНИЯ МАССЫ НА ПРУЖИНЕ 37
щение будет происходить в сторону прежнего положения
равновесия. Это означает, что скелетная кривая будет
приближаться к прежней; в результате она примет форму,
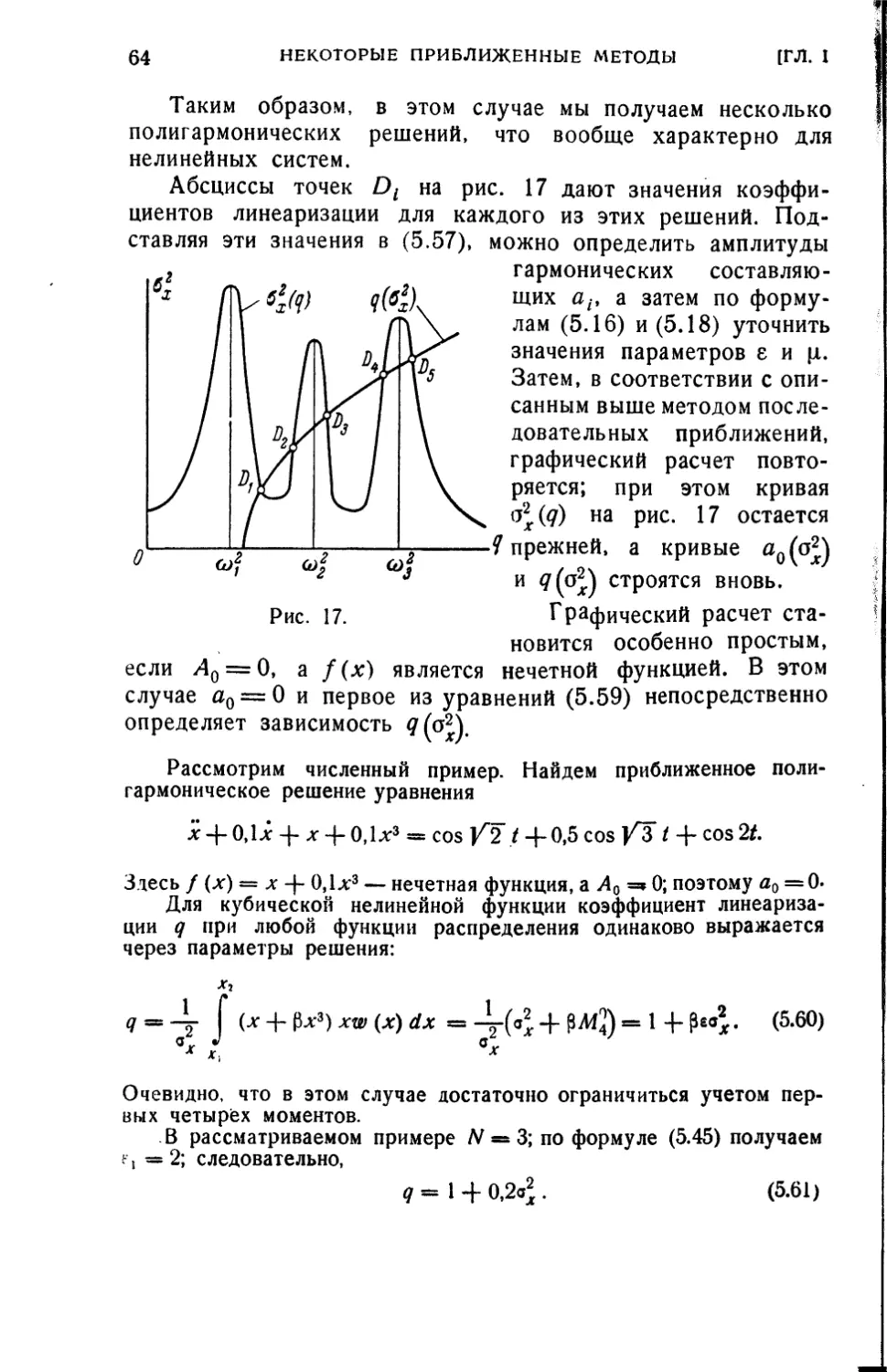
показанную на рис. 10 (кривая 2). Получилась кривая
смешанного типа. Характерная особенность систем со скелетными
кривыми смешанного типа — возможность существования двух
и более режимов свободных колебаний с различной
амплитудой и одинаковой частотой
(Я,, на рис. 10).
Найдем теперь улучшенное
первое приближение. Для этого
подставим (2.7) в (2.1)
x + fo +
оо
+ 2//Cos/Ai = 0. (2.16)
/ = 1
к - л,
Рис. 10.
Для того чтобы х было
периодической функцией
времени, должно выполняться условие (2.12); в противном
случае появляется член f0t2. Предполагая, что условие (2.12)
выполнено и интегрируя (2.16), найдем
x = ao-+-jjYdiLcosi:
at.
(2.17)
i=i
Очевидно, что выражение для коэффициента Фурье при
первой гармонике
2Я
о
совпадает с (2.13). Таким образом, значения а0 и ах = а
в улучшенном первом приближении не изменились.
Если принять, что
/ (х) = tfx~i-g (х) (tf = f (0)), (2.18)
то уравнение для определения улучшенного первого
приближения получится в следующей форме:
х -+ k?x + 2 gi cos Ш + go = 0, (2.19)
/•=1
38 НЕКОТОРЫЕ ПРИБЛИЖЕННЫЕ МЕТОДЫ [ГЛ. I
где
2я
go = i ) £(*<>+в cos 1|>)*|>.
6
2л
gi = IT J £(<>о+а cosФ)cos ^ ^-
(2.20)
0
Отсюда
* = —fi-+S г*/-*«cos /u (2-21)
Таким образом,
2Л
о
g-(a0+acos^)<% (2.22)
2л
а-а,— & = I
■щ- J «" (л0 + л cos ф) cos ф Л|>.
6
(2.23)
Рассмотрим некоторые примеры:
1. / (х) = k2x -+- yxz.
В силу симметрии характеристики коэффициенты Фурье
при четных гармониках решения обращаются в нуль
(поскольку g2p = 0). Для коэффициентов при нечетных
гармониках получаем
2л
gV*i = ^J Y(^cos\|))3cos(2/?+l)^^ =
о
= -^- | (cos 3\J? -J- 3 cos -ф) cos (2p H- l) if rf-ф.
0
§2]
СВОБОДНЫЕ КОЛЕБАНИЯ МАССЫ НА ПРУЖИНЕ
39
Если р Ф О и р Ф 1, то g2p+x
2л
gx = ^— (cos 3iJ? + 3 cos \|)) cos г|) ^i|) = — ^a3,
2Я
g-3—-|^- (cos3i|)-|-3cosi|))cos3\|?^i()==-jYa3-
0
Следовательно, по формуле (2.21)
*у = ^f" (т^^Ж C0S W + 931»-*» C0S Ш) '
Амплитуда а связана с частотой А,
(2.23):
3 уа3
соотношением
или
4 X2 — k2*
4
3Y
(X2 — k2). (2.24)
-£
Рис. 11.
Скелетная кривая, определяемая этим
уравнением, является частью гиперболы
при v>0 и частью эллипса при у < 0.
Таким образом, для кубической
характеристики улучшенное первое
приближение содержит только первую и
третью гармонику. Вообще можно
показать, что если / (х)— полином
степени т, то улучшенное первое приближение содержит
гармоники кратности не выше т.
2. / (х) — k2x + с sign х (рис. 11).
Здесь sign х — функция х, равная -f-1 при х > 0 и — 1
при х < 0. В этом случае g2p также обращаются в нуль, а
82р+х^^1 sign (cos ф) cos (2р+1)Ф^ = (-1)ря(2Д1Г
(2.25)
Следовательно,
££<-»'
cos (2/> +1) t|>
р=0
(2р + 1)[Л2(2/'+1)2-*2] *
(2.26)
40
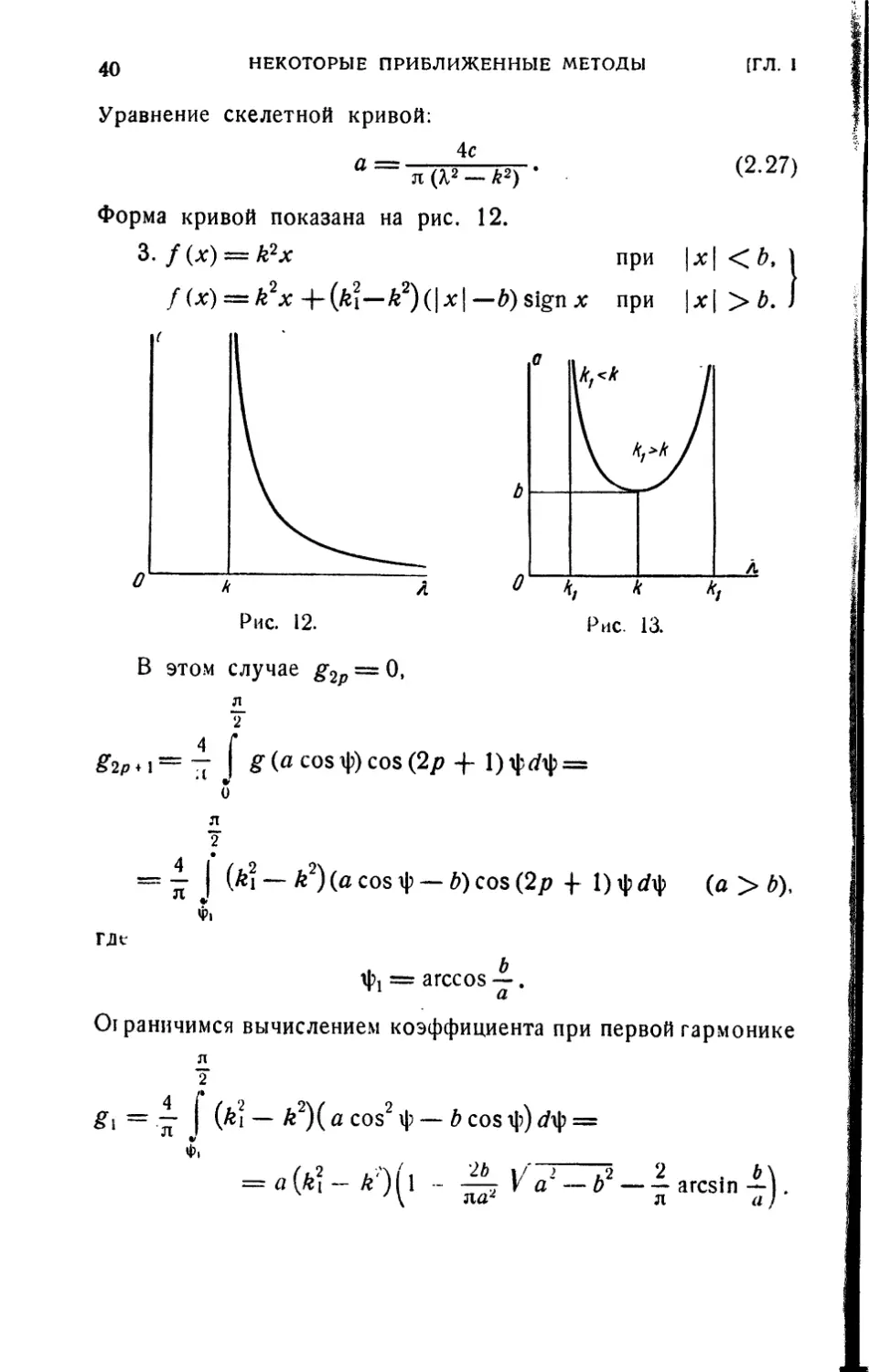
НЕКОТОРЫЕ ПРИБЛИЖЕННЫЕ МЕТОДЫ
[ГЛ. 1
Уравнение скелетной кривой:
а=-
4с
л (Я2 — k2)
Форма кривой показана на рис. 12.
3. f(x)=:k2x
(2.27)
при \х\ < #,
f(x) = k2x-h(k2i—k2){\x\— ft) sign at при \x\>b.
Рис. 12.
В этом случае g2p = 0,
Рис. 13.
gVi=~ I £ (я cos ф) cos (2/? + 1)гИф =
= 4 I (*i — ^2)(^со8ф — b)cos(2p + 1)ф</ф (a>ft),
Ф.
ГЛс
ф, = arccos —.
Ограничимся вычислением коэффициента при первой гармонике
£i = — (&i — &2)(а соБ2ф — ft cos ф) */ф =
л j
= «(*?- A"0(l - —< V'?^72-larcsini.l
§ 31 ГАРМОНИЧЕСКАЯ ЛИНЕАРИЗАЦИЯ 11
Уравнение скелетной кривой (рис. 13)
-*' + (*!- О (1 -£ /«' - ^-1 arcsin i) . (2.28)
§ 3. Гармоническая линеаризация
В гл. II будет показано, что уравнения движения
виброзащитных систем, при некоторых предположениях о
свойствах упругих амортизаторов, могут содержать нелинейные
функции, зависящие только от одного скалярного аргумента
и, может быть, еще от его производной по времени.
Нелинейности такого вида
/ = /(*. х) (3.1)
будут в дальнейшем называться простыми.
Предположим, что мы разыскиваем по методу
гармонического баланса периодическое решение частоты со системы
уравнений, содержащей простую нелинейность вида (3.1).
Подставляя в (3.1)
х = а0 ~Ь я cos со*, х =— aoosincol, (3.2)
получим периодическую функцию частоты со. По методу
гармонического баланса мы должны в разложении этой
функции в ряд Фурье отбросить все гармоники, кроме нулевой
(постоянная составляющая) и первой. Очевидно, что если
существует такая функция /*(х, х), которая при
подстановке (3.2) раскладывается в ряд Фурье, отличающийся от
разложения /(а:, х) только высшими гармоническими
составляющими, то замена в уравнениях движения функции / на
функцию /* не изменит решения, полученного по методу
гармонического баланса. Постараемся выбрать /*(*, л;) таким
образом, чтобы отыскание гармонического решения системы
дифференциальных уравнений не вызывало затруднений.
С этой целью выберем f* в виде функции, линейно
зависящей от а: и а::
/* (*, х) = qx +rx -f 5, (3.3)
где q% r, 5—некоторые коэффициенты.
42 НЕКОТОРЫЕ ПРИБЛИЖЕННЫЕ МЕТОДЫ [ГЛ. I
Подставляя (3.2) в (3.3), получим
/*(ао+ а cosoitf, — am sin Ы) =
= ?а cos otf — raco sin со/ + s -j- qa0. (3.4)
Для дальнейшего удобно ввести обозначения
х° — х — а0 — a cos(dt, х°—х, s~\-qa0 = f0.
Тогда (3.3) запишется в форме
/•(*. х)==^°+^° + /о- (3.5)
С другой стороны, подставляя (3.2) в (3.1) и отбр.асывая
высшие гармоники, получим
/ (a0 + a cos otf, — дсо sin со/) ~ /о + /^ cos to/ -f /l5 sin соЛ
(3.6)
Здесь
1 f
/0=2^ I /(^o+^cos\|), — acosin^)^, (3.7)
и
2Я
/1(? = — /(a0-f-acosij?, —acosin^)cos^flh|), (3.8)
0
2я
/ь —"S" / (я0 + a cos Ф» — acosin гр) sin гр^/гр. (3.9)
о
Для того чтобы при отыскании решения гармонического
вида можно было заменить нелинейную функцию (3.1)
линейной функцией (3.5), необходимо и достаточно выбрать
коэффициенты q, г, /0 следующим образом:
2я
/0 = /o=2S" J f(ao+acos^ — л©sinф)rf4> == /0(a0i a, со),
0 (3.10)
q —-
2я
= — / (a0 + a cos ф,—acosin\|?)cos\|)dh|) = <7(a0, a, co),
0
(ЗЛ I)
§ 3] ГАРМОНИЧЕСКАЯ ЛИНЕАРИЗАЦИЯ 43
а®
лаю
О
2л
/(#о+ acosi|), — a0sini|})sini|)^ = r(ao, а, 0).
(3.12)
Коэффициенты линейной функции оказались зависящими от
параметров искомого решения. В этом — коренное отличие
метода гармонической линеаризации от обычной линеаризации,
принятой в теории малых колебаний. Коэффициенты qt г, /0
могут считаться постоянными только при отыскании
решения вида (3.2).
Для определения параметров колебательного процесса
необходимо решить линеаризованное уравнение, полученное
при замене / на /*. Если система автономна, то в результате
решения будут получены зависимости а0, а и со от /0, q и г;
я0=Яо (U Я> г),
а = а (/0, q, r),
© = ©(/о. <7> г).
(3.13)
Подставляя сюда /0, q, г из (3.10) — (3.12), получим три
уравнения с тремя неизвестными, решение которых дает
искомые значения а0, а, со.
Если система неавтономна, то частота о должна считаться
известной. Однако в этом случае появляется новый
неизвестный параметр — сдвиг по фазе между решением и
периодической функцией времени, входящей в уравнение.
Пусть
причем
f(x. х) =/<»(*)+ /(2)(*. *). (3.14)
/(2)(*, х) = — /(2)(*. —х).
В механических системах представление нелинейной силы
в форме (3.14) соответствует обычно выделению в ней
упругой и диссипативной составляющей.
44 НЕКОТОРЫЕ ПРИБЛИЖЕННЫЕ МЕТОДЫ [ГЛ. I
Нетрудно видеть, что
2л
| /(2) (^о+ а cos г|?, —ao)sin\|))^ =
о
я
= Г/(2) (а0+acos\|;, —acosini])) ^i|)-f-
о
2я
-f- Г—/(2) («о+ acos\|), acosini|))^i|) = 0,
я
2я
Г/(2Ч^о+acos^' —a0sini|))cosi|)^i|) =
о
я
= I /(2) (#о + #cosi|), —aosin^cosi])^-!-
о
2я
-+ J —/(2) (^о+acos^» a(osini|?)cosi|?d'i|) = Ol
я
2л
Г /(1) (ао+ а cos Ф)sifl Ф dty =
о
2я
Г /(1) («о + л cos -ф) [— </ (cos ф)] = 0.
о
Поэтому для данного случая
2л
fo^-^ j f{l)(a0+acos^)d^^f0(a0t a), (3.15)
о
2л
q = ~L J /(1Ч*о+* cosф)cos*МФ = ?(<*<)• а). (3-16)
о
2л
г = /(2) (а0 + acosif, — acosini|))sin^^==
о
= /Ча0, а, со). (3.17)
§ 3] ГАРМОНИЧЕСКАЯ ЛИНЕАРИЗАЦИЯ 45
Применим метод гармонической линеаризации к некоторым
частным задачам.
Рассмотрим сначала систему (2.1). Заменяя f (х)
функцией f*(x) = fQ-jrqx°> получаем «линейное» уравнение
# + /о+?*° = 0, (3.18)
где /0 и q определяются по (3.15) и (3.16). Решая
уравнение (3.18), получаем
/0(я0. <0 = 0, (3.19)
*0=acosM. X2=zq(a0, a). (3.20)
Полученные соотношения совпадают с (2.12) и (2.13), что
и следовало ожидать, поскольку метод гармонической
линеаризации является, по существу, модификацией метода
гармонического баланса.
Рассмотрим теперь вынужденные колебания в нелинейной
системе с одной степенью свободы при вынуждающей силе,
содержащей гармоническую и постоянную составляющие
* + /(*, x) = A0 + Acos(dt. (3.21)
Решение уравнения ищем в виде
x = aQ-\- acos(atf+ <р), х = — aa)sin(Gtf-|-(p). (3.22)
Линеаризуем нелинейную силу f(x, x)\
x° + qx°-{-rxV + f0 = A0+Acos(ut. (3.23)
Подставляя (3.22) в (3.23), получаем
а (д — о2) cos (at -f- ф) — га® sin (otf -f- cp) -f- /0 =
= A0 -) A cos [(atf + <p) — ф] =
= A [cos (otf -f~ ф)cos Ф + sin (otf -j- ф) sin ф] -j- AQ.
Отсюда
/oOo» a) = A0,
a(q — (d2) = Acosq), \ (3.24)
— /-aco = А этф.
46 НЕКОТОРЫЕ ПРИБЛИЖЕННЫЕ МЕТОДЫ [ГЛ. I
Из двух последних соотношений находим
а= . А (3.25)
VW (ло.«) - «2]2 + г2 (До, а) со2
бТ со2 — # (ао,а) v '
Решая систему уравнений (3.24)—(3.26), можно найти а0, я, ср.
§ 4. Линеаризация по критерию минимума
среднеквадратичного отклонения
В виброзащитных системах часто происходят колебания
полигармонического вида
N
* = я0Ч- 2 */ cos (©,* + */) = ао+ х° (')■ (4.1)
ы\
Если частоты со,- являются целыми кратными некоторой
частоты со, то функция (4.1) будет периодической; если среди
частот а>1 имеются такие, отношение которых выражается
иррациональным числом, то (4.1) относится к классу так
называемых почти-пе риодических функций.
С решениями вида (4.1) приходится иметь дело, например,
при исследовании вынужденных колебаний, вызванных
воздействием на систему нескольких независимых периодических
возмущений. В этих случаях уже нельзя пользоваться методом
гармонической линеаризации, поскольку в x(t), а
следовательно, и в f[x(t)t х (t)] может не быть одной
превалирующей гармонической составляющей. .
Вместе с тем во многих задачах оказывается допустимой
линеаризация нелинейной функции f(x, x), основанная на
других критериях «близости» к ней линейной функции
вида (3.5). Одним из таких критериев может служить
величина среднеквадратичного отклонения f*(xt x) от f(x, x)
на бесконечном интервале времени
Ф(<7. г, /0) =
Т
== lira -L [ {/ [х (*). х (/)] - qx° (0 - гх° {() - /0ja dt. (4.2)
§ 4]
ЛИНЕАРИЗАЦИЯ
47
Линеаризация по критерию минимума среднеквадратичного
отклонения заключается в выборе таких значений q, г, /0,
при которых Ф имеет минимальную величину.
Для разыскания минимума приравниваем нулю первые
частные производные
т
дФ
dq
дФ
— lim
Г-»оо
(4.3)
[ [/(*. x)—qx*—rx*—fdxPdt = Q9
о
т
т£- = - lim J \ !/(*• x)-q*fi-rif>-f0]x*dt = 0.
т
i£- = - lim -1 Г [/(*, i)_?j:o_rio_/ j Л = 0.
Если х(^) имеет форму (4.1), то
т
lim -1 Г Jc°jc0rf^= Ilm ijilA^]2 —4[*^0)]21 = 0.
Г Т
lim 4г I *°Л = 0, lim -^ \ x°dt=:0.
Т-*со J J Г->оо / J
Учитывая эти соотношения, из (4.3) получаем
т
где
1 if
<7=-5- lim — /(*» x)x°dt,
°х т+со Т J
г
1 1 Г
г==-аг lim -ж- /(jc, x)x°dt,
К т+™ J i
т
/0 = lim -я? /(*, jc) tf/.
т т
о> = lim -1 | (х0)2*, о* = lim ~ Г (x^dt (4.7)
(4.4)
(4.5)
(4.6)
48
НЕКОТОРЫЕ ПРИБЛИЖЕННЫЕ МЕТОДЫ
(ГЛ. I
Известно (см., например, [52]), что выполнение неравенств
д2Ф
dq2
>0.
д2Ф д2Ф
dq2 dq дг
д2Ф д2Ф
Ц дг дг2
>о,
д2Ф д2Ф д2Ф
dq2 dq дг dq д/0
д2Ф д2Ф д2Ф
"дг2 дгд/о
д2Ф д2Ф
dqdr
д2Ф
dq df0 дг df0 dft
> 0 (4.8)
является достаточным условием минимума функции (4.2) при
значениях q, r, /0, найденных из (4.3). Эти условия
выполняются, поскольку
г т
г
dfl
lim
Г->оо
д2Ф
д2Ф
dq д/0 дг д/0
= 0.
Таким образом, линейная функция л: и л: с
коэффициентами q, r, /0, определяемыми выражениями (4.4)—(4.6),
является наиболее близкой к /(х, л:) в смысле
среднеквадратичного отклонения на бесконечном интервале времени.
Естественно, что близость по среднеквадратичному
отклонению не эквивалентна близости в каждый момент времени,
поэтому линеаризация по минимуму среднеквадратичного
отклонения, как и гармоническая линеаризация, является
методом, не вполне корректным в математическом отношении.
Существование полигармонического решения линеаризованного
уравнения, вообще говоря, не гарантирует существование
близкого к нему точного решения нелинейного уравнения.
Как и при применении метода гармонического баланса,
проблема существования решений, близких к полигармоническим,
решается обычно на основе физических соображений.
При применении метода линеаризации по минимуму
среднеквадратичного отклонения частоты 0/ в разыскиваемом
решении вида (4.1) обычно являются заданными. Тогда
коэффициенты (4.4)
а,, . ... ад,, ф,,
линеаризованного
(4.6) являются функциями параметров а0
. ., фдг. С другой стороны, при решении
уравнения параметры а0, ах aN,
ЛИНЕАРИЗАЦИЯ
49
ф,, . .., фдг оказываются функциями коэффициентов q, r и /0.
Подставляя эти функции в выражения (4.4) — (4.6), получим
систему трех уравнений с тремя неизвестными
q = q(a0, ax
Ь> •
где
г = г(а0, ах aN, ф,, ..
/о = /о(йо. «I Одг- Ь-
ai — at(q. r, /0) (/ = 0, 1.
Ч>« = */(?. '• /о) ('=1. ••
*дг).
... ло.
ло.
(4.9)
Из этих уравнений могут быть определены значения
коэффициентов линеаризации, а затем, из линеаризованных
уравнений, и значения параметров а{ и ifj.
Покажем, что метод гармонической линеаризации
обеспечивает минимизацию среднеквадратичного отклонения
функции (3.5) от функции (3.1) на решении гармонического вида.
Действительно, подставив (3.2) в (4.4) — (4.6), получим
т
Л о
f(a0+ a cos otf, — асо sin со/) a cos со£ rff =
о
=== 9jt 2 / (а0 + а C0S Ф» — а(д Sm Ф) C0S Ф <*♦•
* О
1 1 Г
= —S- Пт— f (a0-\-a cos a>tt—aa>sina>t)(—a(os\na>t)dt =
а; г->оо Г J
о
2я
т- Г /(#n+ac0s^» — acosin^)sini|)rfibf
v J
а®
2яо|
/о== Пт ^ f(a0-\- a cos att— aa)sinco^)^ =
Г->оо ' J
~ T~~ / (^o + а cos ^» — асо sin я])) tfh|\
4 M. 3. К,олоискиД
50
НЕКОТОРЫЕ ПРИБЛИЖЕННЫЕ МЕТОДЫ
1ГЛ. I
Поскольку в этом случае
(О
о2х = -«—- J (a cos of)2 dt — -Y>
о
(О
0г, = — (acosincttf)2^ =—о"",
о
полученные соотношения для q, r и /0 тождественно
совпадают с (ЗЛО) — (3.12). Таким образом, метод гармонической
линеаризации может считаться частным случаем метода
линеаризации по критерию минимума среднеквадратичного
отклонения.
Линеаризация по минимуму среднеквадратичного
отклонения редко применяется в приведенной форме. Зависимости
коэффициентов линеаризации от параметров
полигармонического процесса оказываются обычно весьма сложными. Во
многих случаях получение этих зависимостей в явной форме
вообще не представляется возможным . (например, при
кусочно-линейных функциях f(x, х)). Чрезвычайно
громоздкими получаются и уравнения (4.9). Для упрощения
рассматриваемого метода требуется уменьшить число параметров
полигармонического процесса, от которых существенно зависят
коэффициенты линеаризации. Один из способов уменьшения
числа параметров рассматривается в следующем параграфе.
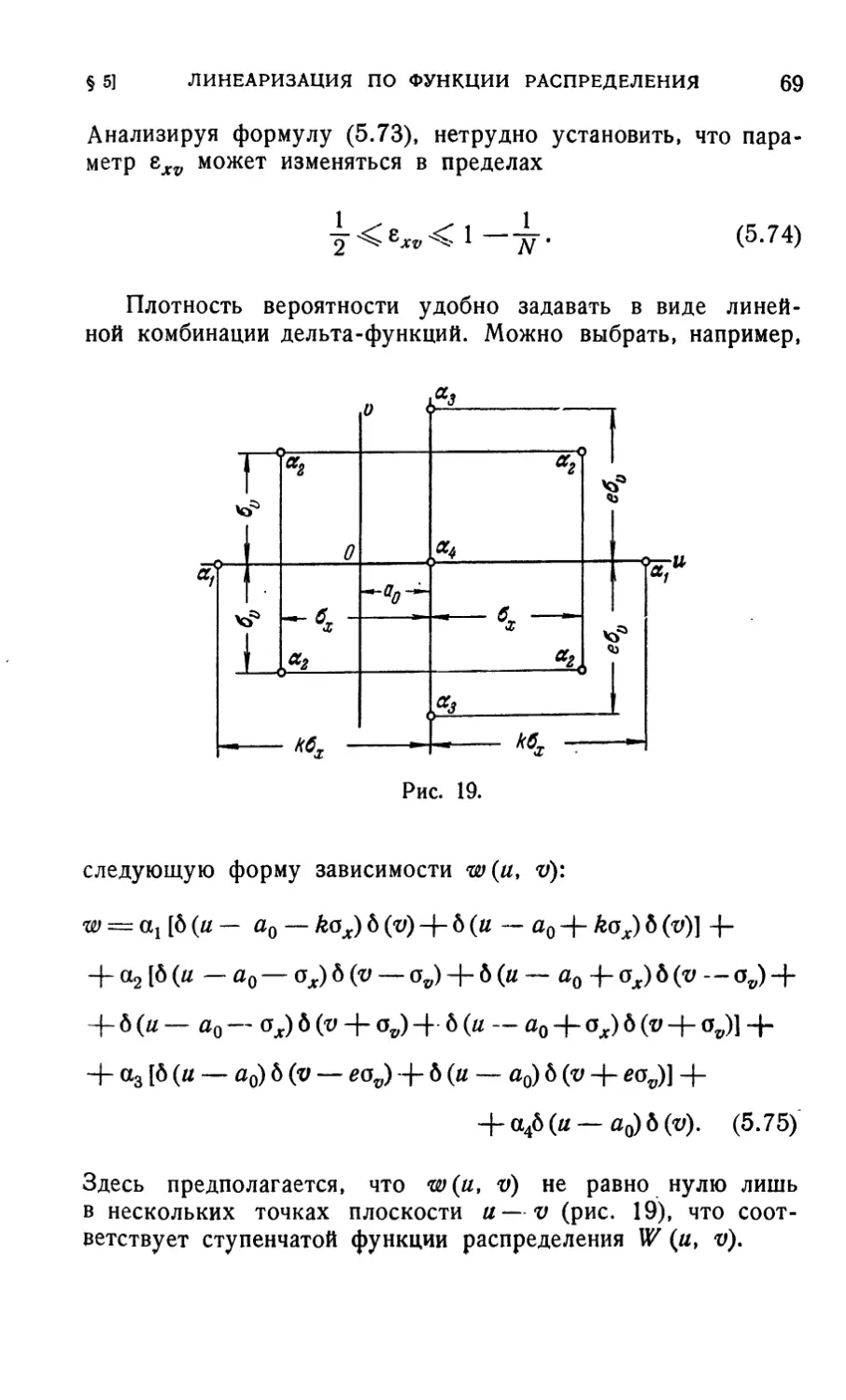
§ б. Линеаризация по функции распределения
Функцией распределения W (и) полигармонического
процесса (4.1) будем называть относительную продолжительность
интервалов времени, в течение которых выполняется
неравенство
*(<)<*■ (5-1)
Производную dW/du назовем плотностью вероятности
процесса х {t).
§5]
Линеаризация по функции распределения
51
Для аналитического представления W (и) введем в
рассмотрение «единичную» функцию г\(х)
I 1 при х > О,
ц(х) = \ I/2 при * = 0,
О при х < 0.
(5.2)
Производная dr\/dx представляет собой функцию особого
вида — дельта-функцию Ь(х). Эта функция равна нулю
всюду, кроме точки х = 0; в этой точке она обращается
в бесконечность, причем при любом сколь угодно малом е
6 (х) dx = ц (г) — т) (— е) = 1;
0 8
b(x)dx— J 6 (х) dx = -тг.
(5.3)
Свойства 6-функции подробно рассмотрены в [43]. В
дальнейшем будет использовано только одно из них,
непосредственно вытекающее из (5.3). Для любой непрерывной
функции fix) имеем
J f(x)b(x — x0) dx = f (л;0) (а<х0< b)t
а
х, b
J f(x)b(x — xQ)dx = J f(x)6(x — x0)dx = jf(x0).
Xq
(5.4)
Пользуясь определениями единичной и 6-функции, получаем
т
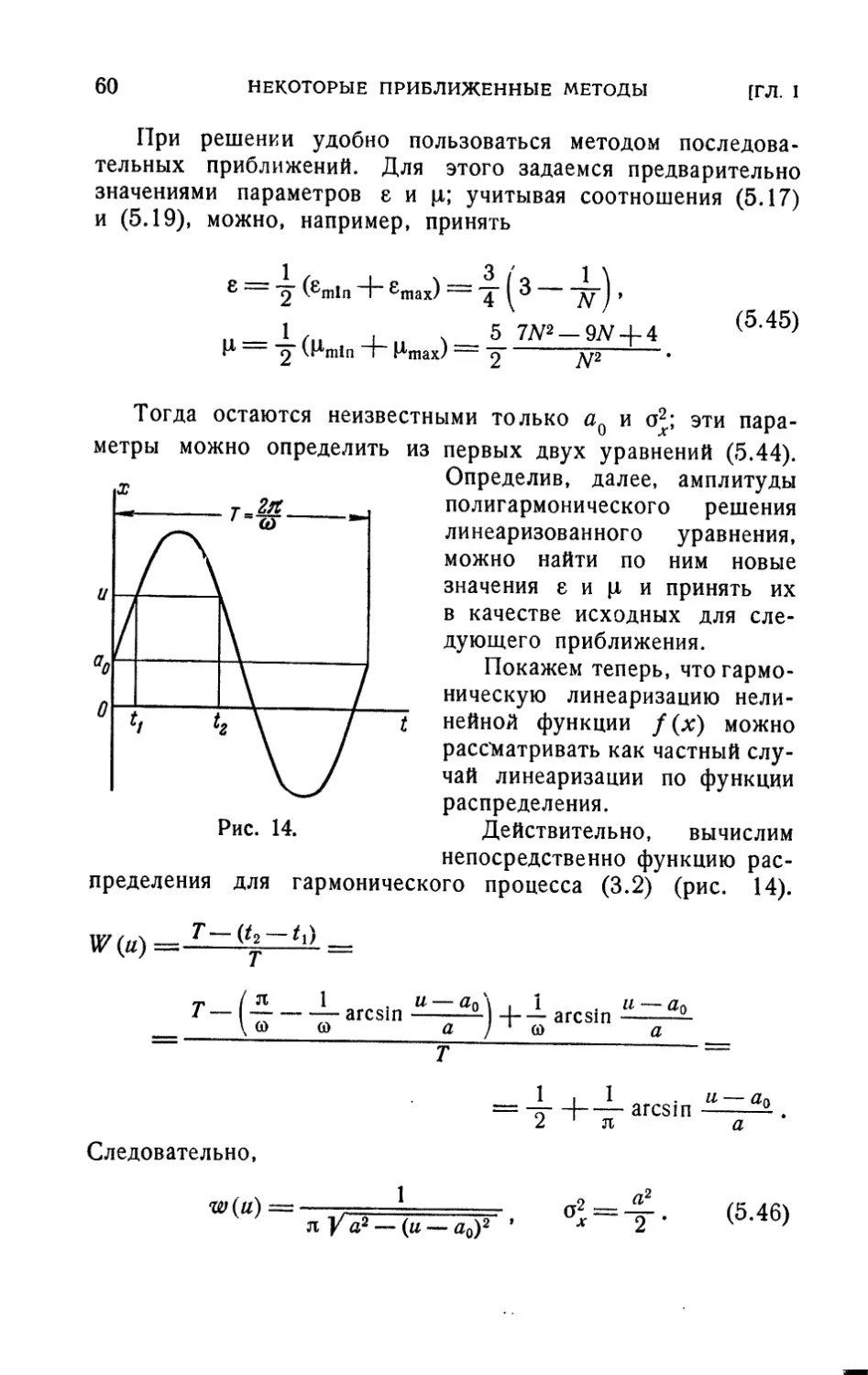
W(u)= lim 4- I i\lu — x(f)]dt, (5.5)
r
dW(u) .. \ Г
^W^—dtr-^^T) ^-x{f)\dt. (5.6)
4*
52
НЕКОТОРЫЕ ПРИБЛИЖЕННЫЕ МЕТОДЫ (ГЛ. I
Нетрудно видеть, что W (и) представляет собой вероятность
выполнения неравенства (5.1) при случайном выборе
значения t (то есть если t — случайная величина, равномерно
распределенная на бесконечном интервале). Этим и объясняется
применение «вероятностных» терминов для нее и ее
производной.
Функция w(a) обладает всеми свойствами, характерными
для плотности вероятности случайной величины. В частности,
w(u)du=\. (5.7)
Здесь л?! — наименьшее, а х2—наибольшее значение
функции х (/). Если для полигармонической функции (4.1)
N
а== 2 Я/>
то
Центральным моментом k-го порядка процесса x(t)
будем называть среднее по времени значение [x°(t)]k
т
Ml {*(*)} = lim -L Г [x°(t)]kdt. (5.8)
В силу (5.6) эти центральные моменты совпадают с
центральными моментами случайной величины, имеющей плотность
вероятности w(u)
х2
Ml [х] = J (и — mx)k w {и) du =
Х\
*2 Т
= J (и — mxf lim 4- I Ъ[и — x(t)]dt =
Xi 0
T
= lim i I [x(t)—mx]*dt. (5.9)
T + ao l £
§ 5] ЛИНЕАРИЗАЦИЯ ПО ФУНКЦИИ РАСПРЕДЕЛЕНИЯ 53
Здесь тх — среднее значение х (t), равное а0,
тх=а0. (5.10)
Перечислим некоторые свойства нескольких первых
центральных моментов полигармонического процесса.
а) Центральный момент второго порядка называется
дисперсией и обозначается
Л*2 {*}=(& (5.11)
Если в (4.1) все со,- различны (что всегда можно
предположить), то дисперсия не зависит от фаз ^ и выражается
через амплитуды следующим образом:
N
ol = j%a2r (5.12)
/=i
б) Центральный момент третьего порядка м\ обращается
в нуль, если среди частот со^ нет таких, которые
удовлетворяли бы одному из следующих соотношений:
2(0, = 0);, со,- -f- coy = g>£, со, — (x)j = соЛ. (5.13)
Если же такие частоты существуют, то зависимость Жз от
амплитуд и фаз выражается следующим образом:
Ml = ^fiaj cos (2ifo-l>yH- ^2а^аксоз(^+%—%)^
+T S3 а'а>а*cos (*' — % — **)• <5-14)
Здесь в 2г S2» 2з суммирование производится по тем
сочетаниям чисел j, i и &, для которых выполняются
соответственно первое, второе или третье из соотношений (5.13).
в) Центральный момент четвертого порядка не зависит
от фаз <p/f если среди частот со,- нет удовлетворяющих одному
из соотношений:
За); = о)у.; 2(0; - о)у ± (ок = 0; со^ ± coy — со^ ± щ = 0.
(5.15)
54 НЕКОТОРЫЕ ПРИБЛИЖЕННЫЕ МЕТОДЫ [ГЛ. t
При этом зависимость момента четвертого порядка от
амплитуд определяется выражением'.
^-4(«1+т £'аи1 (5.16)
Здесь штрих при знаке суммы означает, что суммируются
только члены с I ф j.
Легко определить, что для любого полигармонического
процесса, для которого М\ определяется соотношением (5.16),
отношение M\loAx лежит в следующих пределах:
3 М°4 3
_<^==е<3-_ (5.17)
где N — число гармоник в процессе. Наименьшее
значение е, равное 3/2, соответствует гармоническому процессу,
при котором только одна из амплитуд отлична от нуля;
наибольшее значение е принимает в том случае, когда
амплитуды всех N гармоник одинаковы.
Можно показать, что центральные моменты более
высокого порядка тоже могут зависеть от фаз только при наличии
в полигармоническом процессе частот, отношение которых
является рациональным числом. Если же все частоты со^ таковы,
что отношения любых дву^ из них выражаются
иррациональными числами, то все центральные моменты нечетного
порядка обращаются в нуль (функция w(u) симметрична
относительно ординаты а = а0), а четные центральные моменты
зависят только от амплитуд. Приведем выражение для момента
шестого порядка
N
Здесь суммирование производится по всем членам, для
которых /, j и к различны.
Отношение ji == м1/о6х лежит в пределах
у<^<5 2^2 • (5-19)
§ 5] ЛИНЕАРИЗАЦИЯ ПО ФУНКЦИИ РАСПРЕДЕЛЕНИЯ 55
Наименьшее значение \х соответствует гармоническому
процессу; наибольшее — полигармоническому процессу с равными
амплитудами гармоник.
Пусть задана нелинейная функция вида / (х). Найдем
по формулам (4.4) — (4.6) коэффициенты линеаризации qt г, /0,
используя соотношения (5.6) и (5.4)
т
q=\\\m -1 Г f(x)jfidt =
X 0
T x2
= — lim — [ dt \ f(u)(u — a0)6[« — x(t)]du =■
Oj Г->оо T J J
0 Xl
x2
T
r =-L lim — f f(x)x°dt = 0, (5.21)
о
T x2
/0 = Jlim^-i- J f(x)dt= | / («) at («)rf «. (5.22)
Таким образом, коэффициенты линеаризации, найденные из
условия минимума среднеквадратичного отклонения, могут
быть определены, если известна плотность вероятности
решения.
При линеаризации по функции распределения выбирается
семейство функций вида
«(*. л,. <#. Л& М% ...) (5.23)
и предполагается, что плотность вероятности искомого
решения принадлежит этому семейству. При подстановке (5.23)
в (5.20) и (5.22) коэффициенты линеаризации выражаются
через моментные характеристики решения
Я = я(тх. <£• М% М% ...); /0 = /<>(«,. о% М% М% .. .>
(5.24)
56 НЕКОТОРЫЕ ПРИБЛИЖЕННЫЕ МЕТОДЫ [ГЛ. I
Эффективность метода объясняется тем обстоятельством,
что значения коэффициентов линеаризации в основном
определяются несколькими первыми моментами и слабо зависят
от моментов высокого порядка. Действительно,
аппроксимируя функцию f(x) на интервале хг^.х <^с2 полиномом
степени т
т
получаем
1 г2 т 1 т
7 = -jr J 2] Cl(U ~ ao)l+1 <*(«)<*« = ^" J 'X+i •
* Jf, /=0 X /=1
г, /=0 Ы2
При такой аппроксимации замена w(x) любой другой
функцией, имеющей такие же первые т + 1 моментов, не повлияет
на значения коэффициентов линеаризации. В силу этого,
выбор вида функции (5.23) является в значительной мере
произвольным.
Число первых моментов, учитываемых в законе
распределения, зависит от желательной точности расчетов. На
практике обычно достаточно бывает ограничиться учетом первых
четырех или шести моментов. Если можно предположить,
что Мз=М5 = 0, то количество неизвестных параметров
в (5.23) уменьшается до трех или четырех: тх> о2х> г или
тх, о% е, \х.
Для упрощения расчетов удобно выбирать ступенчатую
функцию распределения W (а):
S
W {и) = 2 <¥1 (« — */). (5.25)
что соответствует выбору плотности вероятности w (а) в виде
линейной комбинации 6-функций:
5
w (и) = 2 «/* (и — */)• (5.26)
Здесь xv .... х9—некоторые значения х, лежащие между
§ 5] ЛИНЕАРИЗАЦИЯ ПО ФУНКЦИИ РАСПРЕДЕЛЕНИЯ 57
х{ и дг2, а1§ .... ал — положительные числа, связанные
соотношением
= Г w (a) du = W (х2) = 1. (5.27)
S
Определив моментные характеристики закона
распределения, по формуле (5.9) получим
m, = aft
S «/*/> (5.28)
/=i
M°k = 2 «/ U* - "**)* (ft = 2. 3, ...). (5.29)
С помощью полученных соотношений можно выразить
параметры аь и xt через моменты. Если мы хотим учесть
в законе распределения первые р моментов, то количество
уравнений оказывается равным р -f 1. При s = — (/?-}-1)
число неизвестных равно числу уравнений; в некоторых
случаях число ступеней требуется увеличить для того, чтобы
обеспечить вещественность значений х{ и положительность щ.
В дальнейшем мы будем иметь дело с такими
полигармоническими процессами, плотность вероятности которых
с точностью до моментов шестого порядка может считаться
симметричной функцией (Мз = М, = О)- Тогда плотность
вероятности (5.26) может быть выбрана в такой форме
w(u)^ax[b(u~- а0 — ${) + Ь(и — a0 + p^] +
+ a2 [6 (я - a0 — fe) + 6 (a - a0 + p2)] (p2 > P0- (5.30)
Здесь принято, что
*i = 0o+Pi. *2 = flo —Pi«
*3 = До + P2» *4 = a0 — P2'
Учет первых шести моментов приводит к следующим
уравнениям а ля определения параметров av а2, Р^ р2:
2(сц +а2)=1
2(<xifti + a2fti)= l.
2 (aiftl 4 fykt) = e»
2(aifti4 a<bft2) = |i.J
(5.31,
58 НЕКОТОРЫЕ ПРИБЛИЖЕННЫЕ МЕТОДЫ [ГЛ. I
Здесь
*i = T". *a = -J1- (5-32)
2 2
Решая систему (5.31), находим, что k\ и k<i являются корнями
уравнения
ц — е
L —£2
ы ttj и а2 выража
образом:
2 2
Параметры ctj и а2 выражаются через е, k\ и ki следующим
°-'~Щ^Щ' аа_ 2^(*]-А?) ' (5,34)
Можно показать [20], что при е и \х, лежащих в пределах
2 2
(5.17) и (5.19), k\, k<i> о>\ и а2 получаются положительными.
Если ограничиться приближением по первым четырем
моментам, то можно выбрать трехступенчатую функцию
распределения, приняв
w (и) = а06 (и — а0) + щ [6 (и — а0 — Pi) + 6 (и — а0 -f р^].
(5.35)
Значения а0, alf Pj определяются из уравнений:
а0 -+- 2ах = 1,
откуда находим
20^1=1, 1 (5.36)
2a1&i —e, j
fci = e, a, ^-^i", ao==i__. (5.37)
В дальнейшем, при линеаризации мы будем пользоваться
законами распределения в форме (5.30) или (5.35).
Подставляя w(u) в (5.20) и (5.22), получаем следующие формулы
для коэффициентов линеаризации:
а) при приближении по шести моментам
q = —[aiki[f(aQ-+klax) — f(a0—k1ax)] +
+ a2£2 [/ (a0 + k2ox) — f(a0~ k2ox)]}> (5.38)
/0 = ai I/ (ao — Ьгох) + / (a0 -f /^a,)] +
+ аз I/(*<>■- W +/(«0 + *Лг)1: (5.39)
§ 5] ЛИНЕАРИЗАЦИЯ ПО ФУНКЦИИ РАСПРЕДЕЛЕНИЯ 59
б) при приближении по четырем моментам:
g==^yfti(ao+Veox)-f(a0-Vz ох)], (5.40)
(5.41)
При нечетной /(х) и а0 = 0 получаем /0 = 0 и
соответственно
q = -|- [а А/ (*Лг) + а2/г2/ (£2<**)Ь (5.42)
или
q = —L-f(yZox). (5.43)
Уе<*х
Полученные формулы позволяют выразить коэффициенты
линеаризации через моментные характеристики искомого реше*
ния. С другой стороны, заменив в уравнениях движения f (х)
на/0-f-# (л: — тх), можно найти полигармоническое решение
линеаризованного уравнения. При этом амплитуды а{ и
фазы Vpi окажутся функциями коэффициентов линеаризации.
Далее можно, выразив моменты решения через амплитуды
и фазы, получить уравнения для определения численных
значений моментов.
При симметричном законе распределения и учете первых
шести моментов эти уравнения могут быть записаны в
следующей форме:
0о=ао(?. /о)» •
N
N
Aj3_|al = | % *]{Я. fo)*)(4. fo).
N
M°e-5ol(Ml-ox) = l 2' a*t{q.f0)a)(q.f0)al(q,f0)
(5.44)
(? = </К. <& Ж?. М§). /0 = /0(a,. <& Л& Лф).
Г
60
НЕКОТОРЫЕ ПРИБЛИЖЕННЫЕ МЕТОДЫ [ГЛ. I
При решении удобно пользоваться методом
последовательных приближений. Для этого задаемся предварительно
значениями параметров е и \i; учитывая соотношения (5.17)
и (5.19), можно, например, принять
е — 9 ^emln \ emax.
: о v^mln "Г" М-тах)
5 7N2-
-9^ + 4
N2
(5.45)
Тогда остаются неизвестными только а0 и о2х\ эти
параметры можно определить из первых двух уравнений (5.44).
Определив, далее, амплитуды
полигармонического решения
линеаризованного уравнения,
можно найти по ним новые
значения е и \х и принять их
в качестве исходных для
следующего приближения.
Покажем теперь, что
гармоническую линеаризацию
нелинейной функции f(x) можно
рассматривать как частный
случай линеаризации по функции
распределения.
Рис. 14. Действительно, вычислим
непосредственно функцию
распределения для гармонического процесса (3.2) (рис. 14).
У(в) =
T-(t2-tx)
arcsin А
\ со со а } 1 со
arcsin
-д0
1,1 . и —
~ _ .J arcsin
2 ' л а
а0
Следовательно,
§ 5] ЛИНЕАРИЗАЦИЯ ПО ФУНКЦИИ РАСПРЕДЕЛЕНИЯ 61
Подставляя (5.46) в (5.20) и (5.22), получаем
а = —т / (я) (я — Яо) =
aQ~a
СО
= !Г" / (^о + а cos ^O cos ^ ^> (5.47)
о
aQ+a
/о = J /(tf) лУа2-(и — а0)2 =
а0-а
со
= -frj f(a0 +a costal) dt. (5.48)
о
Эти выражения совпадают с (3.15) и (3.16).
Изложенные выше соображения позволяют существенно
упростить зычисление коэффициентов гармонической линеа-
3 5
ризации. Для гармонического процесса е==у, ji = -^-. Решая
уравнения (5.31), находим
kl=\/~X~4-' ^lA+HT' 01 = 08 = 1-.
Следовательно,
kpx — К-ё= « 0,383а, k2ax = fc2-^ sw 0,924o,
и формулы (5.38) и (5.39) дают для гармонического процесса:
q = Ь {0,9241/(а°+ 0,924а) — /(°о — 0,924с)! +
+ 0,383 [/(а0+ 0,383а) — / (а0 — 0,383а)], (5.49)
/о =-у [/(во-0.924а)+/(с0-0.383а) +
+ /(воН-0.383с)4-/(в0 + 0.924а)1. (5.50)
Если а0 = О, a / (л;) — нечетная функция, то /0 = 0 и
q = -i-10,924/ (0,924с) + 0,383/ (0,383а)]. (5.51)
62
НЕКОТОРЫЕ ПРИБЛИЖЕННЫЕ МЕТОДЫ
[ГЛ 1
Если ограничиться приближением по первым четырем
моментам, то формулы (5.40) и (5.41) дадут:
^7Fr[/(e»+JTe)-/(e»-1Te)]- (5'52)
/о = -д-[/(^ + /(воЧ-3т^в)+/(во-17-в)]. (5-53)
а для нечетной функции при а0 = 0
Формулы (5.49) — (5.54) будут в дальнейшем
использоваться при гармонической линеаризации нелинейностей
вида /(л:). Очевидно, что все, сказанное выше, остается
справедливым и для линеаризации нелинейных функций
вида ф(х).
В качестве примера применения метода линеаризации
по функции распределения рассмотрим задачу о
вынужденных колебаниях в нелинейной системе с одной степенью
свободы при полигармоническом внешнем воздействии.
Уравнение движения в этом случае может быть записано в
такой форме
N
x-\-2nx-\-f(x) = A0+ 2 ^cos(G>^-f (ft). (5.55)
/ = i
В первом приближении ищем решение этого уравнения в виде
х = а0+ 2 a/cos(©^ + ^) = a0 + j:0t (5.56)
то есть оставляем в решении гармонические составляющие
только тех частот, которые имеются во внешнем воздействии.
Заменим в (5.55) f(x) на fQ-f~qx0 и подставим (5.56)
в линеаризованное уравнение. Приравнивая коэффициенты
при sin((0jf+ i|)j) и cos (со^ -\- яр/) в левой и правой части,
находим
(?--w?) a£ = Л, cos (<р,--*,), ^ /=1,...,ЛГ.
2да/о>/ = Л,sin ((ft ~-i|)j),
/0 = Л0.
§5]
ЛИНЕАРИЗАЦИЯ ПО ФУНКЦИИ РАСПРЕДЕЛЕНИЯ
63
Из первых 2/V уравнений находим
At
я,- = ■
2„2
откуда
V(q—ff + **
2 1 V ■> IV
*8Г <Ч>* — Ч»*> —
2пщ
Ч — <°21
А
£ (»—У + 4»2-?
(5.57)
(5.58)
Выберем значения е и [i в соответствии с (5.45) и найдем
зависимости <7(а0, о£) и /0(ао' о^) (формулы (5.38) -(5.43)).
Теперь необходимо определить а0 и ох из (5.58) и
соотношений
* = *К«). /оК«) = ^о
(5.59)
Сначала из уравнений (5.59) исключаем а0. Для этого
строится семейство кривых /0(я0» с£). соответствующих
различным значениям а0 (рис. 15). Проводится линия /0 = Л0-
го <*& (<$,
Рис. 15.
Рис. 16.
по абсциссам точек пересечения ее с кривыми и значениям а0
строится зависимость я0(о£) (рис. 16).
Построим теперь кривую G2x(q), соответствующую
уравнению (5.58) (рис. 17), и кривую д(о2\ получающуюся при
подстановке в первое из уравнений (5.59), зависимости я0(о£).
Ординаты точек пересечения этих кривых определяют
значения д2, являющиеся решением системы уравнений (5.58)—
(5.59); соответствующие значения а0 найдутся из графика
на рис. 16.
64
НЕКОТОРЫЕ ПРИБЛИЖЕННЫЕ МЕТОДЫ
[ГЛ. I
Таким образом, в этом случае мы получаем несколько
полигармонических решений, что вообще характерно для
нелинейных систем.
Абсциссы точек Dt на рис. 17 дают значения
коэффициентов линеаризации для каждого из этих решений.
Подставляя эти значения в (5.57), можно определить амплитуды
гармонических
составляющих а(, а затем по
формулам (5.16) и (5.18) уточнить
значения параметров е и [х.
Затем, в соответствии с
описанным выше методом
последовательных приближений,
графический расчет
повторяется; при этом кривая
о2х(д) на рис. 17 остается
-Ч прежней, а кривые я0(с£)
и <7(о^) строятся вновь.
Графический расчет
становится особенно простым,
если Л0 = 0, a f (х) является нечетной функцией. В этом
случае а0 = 0и первое из уравнений (5.59) непосредственно
определяет зависимость Я(о2\
Рассмотрим численный пример. Найдем приближенное
полигармоническое решение уравнения
х + o.li + х + 0,1*3 » cos /2"/ +0,5 cos VJ t + cos 2t.
Здесь / (x) = x + 0,1л*3 — нечетная функция, аИ0=»0; поэтому а0 = 0.
Для кубической нелинейной функции коэффициент
линеаризации q при любой функции распределения одинаково выражается
через параметры решения:
Рис. 17.
1
*2
j (х + р*») xw (х) dx = -L(4 + ml) - 1 + f*e
(5.60)
Очевидно, что в этом случае достаточно ограничиться учетом
первых четырех моментов.
В рассматриваемом примере N =* 3; по формуле (5.45) получаем
ь-1 ~ 2; следовательно,
9=1 + 0,2^.
(5.61)
§ 5] ЛИНЕАРИЗАЦИЯ ПО ФУНКЦИИ РАСПРЕДЕЛЕНИЯ 65
Строим кривую (5.58) (рис. 18)
2_ 1 Г 1 . 0,25 1 ]
°х 2 |_ (<7 — 2)2 + 0,02 "^ (^ — 3)2 + 0,03 "+" (q — 4)2 + 0,04 J
(5.62)
и определяем ее точки пересечения с прямой (5.60). Получаем
*1
щ
три решения, соответствующих трем точкам пересечения:
(4)1 = 0,78; (4)2 = 2,88; (4)3 = 6,27.
По формуле (5.57) находим амплитуды гармонических
составляющих первого решения:
(а\)г = 1,366; (4)i = 0,073; (с$)г = 0,123.
Пользуясь формулой (5.16), уточняем значение е:
(е2)
М\ 3 , 2[(^)1(^)1 + (^1(^)1+(^)1(^)1]
1,842.
4 ~2" Ш+(4)г + Ш2
Строим прямую (рис. 18)
? = 1+0,1 (*2),4= 1+0.18424-
Определяя точку пересечения ее с кривой <?x{q), уточняем
значение (а^:
(а^ =0,77.
5 М. 3. КоловскиЙ
66 НЕКОТОРЫЕ ПРИБЛИЖЕННЫЕ МЕТОДЫ [ГЛ. I
Второе приближение оказалось очень близким к первому, поэтому
можно ограничиться найденным приближенным решением.
Найдем амплитуды гармонических составляющих третьего
решения:
• (а*)3 = 11,834, (4)3 = 0,426, (й|)з = 0,324.
Уточняем значение параметра е
(2)з"2 + Ш+Ш+Ш "
Строим прямую
^ = 1 +0.1 (е2)з4 = ! +0.1673а2
и уточняем значение (а^)3 и q
(а2)3 = 7,3б, ? = 2,23.
Значение (а^.)3 существенно отличается от исходного; поэтому
процесс последовательных приближений должен быть продолжен.
Находим новые значения амплитуд в третьем решении
(^)з = 13,7, (^)з = 0,402, (4)3 = 0,318,
и уточняем значение е:
(ез)з = lj639> ^ = 1+0,1 (е3)3а^ = 1 + 0,1639aJ. (5.63)
Решая совместно (5.62) и (5.63), находим
(°2)з = 7>48> Я - 2,225, (а\)3 = 14,24,
(^)3 = 0,401, (^)3 = 0,318.
Это приближение уже достаточно хорошо совпадает с предыдущим,
поэтому можно им ограничиться. Аналогичным путем можно
уточнить и второе решение.
Метод линеаризации по функции распределения легко
обобщается на нелинейные функции вида f(x, х). Назовем
совместной функцией распределения полигармонического
процесса х(£) и его производной x(t) функцию W (u> v)%
представляющую собой относительную продолжительность
интервалов времени, в течение которых одновременно
выполняются неравенства
*(*)<«. *(*)<* (5-^4)
§ 5] ЛИНЕАРИЗАЦИЯ ПО ФУНКЦИИ РАСПРЕДЕЛЕНИЯ 67
или, в аналитической форме,
т
W(u, v)= lim -±r I r\lu — x(t)]r\lv — x(t)]-dt.(5.65)
Совместной плотностью вероятности х и x назовем
частную производную
т
w^ v) = d2Vdudv^ = ГП™ 4~ J6[u — x ffll 6 [v — x (QI <*'•
(5.66)
Центральные моменты совместной функции распределения
совпадают со средними по времени значениями произведения
Ж^ = (и — mx)k vlw (u9 v) da dv =
T
= lim 1 I [x (t) — mj**1 (*) <tf, (5.67)
где vl и #2— наименьшее и наибольшее значения х (f).
При линеаризации нелинейная функция f(x, x) заменяется
функцией fo~}-qx0-\-rx0, причем коэффициенты /0, q, r
определяются по формулам (4.4) — (4.6), которые с помощью
соотношения (5.66) записываются в следующей форме:
т
q = \ lim -Jr f f(Xi *)*°Л =
QX T + co T j
x2 v2
—-T J J (<u~ mx)f(u> v)^(«. v)dudv, (5.68)
НЕКОТОРЫЕ ПРИБЛИЖЕННЫЕ МЕТОДЫ [ГЛ. I
Т
■ = \ lim 4- I / (*. *) *° Л =
о£ Г-»оо ' J
=="Г \ vf(u> v)w(ut v)dudv, (5.69)
X2 V2
аналогичной является зависимость Мм от амплитуд гармо
/0= lim ~y \ f(x* x)dt= \ J f(u, v)w(u, v)dudv.
(5.70)
Если полигармонический процесс x(t) имеет
симметричный закон распределения, то, как нетрудно видеть,
функция w(u, v) также будет симметричной относительно осей
и=а0 и г/ = 0. В этом случае среди центральных
моментов, порядок которых не превышает четыре (&-{-^<^4), не
равными нулю будут только следующие:
<hc\ ol; М% = гхоАх\ м1А = гуо\\ М22 = е^о£о£. (5.71)
Зависимость М% от амплитуд а{ дается формулой (5.16);
аналогичной является з
ник x(t)t равных а^:
К=4 к+т 2' «?®Ж) • <5-72)
Значения е^ могут лежать в тех же пределах, что и
значения е (неравенство (5.17)).
Момент М%2 для полигармонического процесса (4.1)
вычисляется по формуле (5.67):
Л4 = 1 (oyv + ± З^ а\а)<А. (5.73)
V /, ; = 1 /
При этом предполагается, что среди частот coi нет таких,
которые удовлетворяли бы одному из условий
®/ + со;. = 2сол; coi — coy = 2сол.
лг
§ 5] ЛИНЕАРИЗАЦИЯ ПО ФУНКЦИИ РАСПРЕДЕЛЕНИЯ 69
Анализируя формулу (5.73), нетрудно установить, что
параметр exv может изменяться в пределах
1<е <\ -L
2 ^ **xv ^ 1 дг •
(5.74)
Плотность вероятности удобно задавать в виде
линейной комбинации дельта-функций. Можно выбрать, например,
ч
V
1
1 *
с>
>
«г
0
.«г
,
Нбх -
1
-а0~
^
,**
*s
""*
«г
-'» —
Л
ч
q
1
1)
i
Ч>*
, 1
кб
KQX -
.
а1
Рис. 19.
следующую форму зависимости w(u, v):
-f a2[6(tt—a0 — а^)6 (г/ — оГ) + *(« —л0+-^)*(^—0 +
+ Ь(и— а0— ох)Ь (я + оГ) + 6(я — ао + о*Ж* + М +
+ a3[6(w — а0)6(г; — *о^ + 6 (в — а^ 6 (tr + вод]+
+ а46(й —а0)6(г/). (5.75)
Здесь предполагается, что ад(#, v) не равно нулю лишь
в нескольких точках плоскости а — v (рис. 19), что
соответствует ступенчатой функции распределения W {и, v).
70
НЕКОТОРЫЕ ПРИБЛИЖЕННЫЕ МЕТОДЫ
[ГЛ. I
Значения параметров av a2, а3, е, k, а4 найдутся из
следующей системы уравнений:
2ах + 4a2-f- 2а3 + а4 = 1,
2а1/г2+4а2=: 1,
2а3е2 -f- 4а2 = 1,
2а^4 + 4а2 = гх,
2а3е4-Иа2 = е„,
Решая эту систему, находим
4а2 = е^.
(5.76)
О-е*»)8
2\tx exv)
tx — е
а2 = -
ая =
О
/г2
2(tv-
1 txv
(l-e^)(eA-
1— е*
' гх "" ег> + 2е.™ ~~ елтг»)
(елг — ел-г>) (ег> £*г>)
(5.77)
Подставляя (5.75) в (5.68) — (5.70), получаем следующие
выражения для коэффициентов линеаризации:
q—~ [a.iklf(a0 + kox, 0)-
■f(a0-kax, 0)] +
(5.78)
+ a2[/(Oo+0jc. Oj — /(«0 — °Л- °г.) +
+ /(а0 + ож> — av) — /(Со — ож, — ав)]}.
/• = -^ («г [/ («о + а,- а») + / («о — о*. %) —
—/(а0 + а,, — 0О) —/(а0 —о,, — av)] +
+ a3eJ/ (ас «»e) — / (а0, — «с,)]}, (5.79)
/o^Oil/K+Ao,. 0) + /(c0-Aojr. 0)] +
4-а2[/(ао + °лг. о„)4-/(оо—о*. о„) + /(во-г-°*. — °*) +
+ f(a0 — ax, ~~av)]-\-a3[f(a0, eav) + f(a0, - eov)] +
+ а4/(а0, О). (5.80)
Пользуясь этими соотношениями, можно упростить
определение коэффициентов гармонической линеаризации для
нелинейной функции f(x, х). Если x(t) — гармоническая
функция времени, то -
3 _ 1
елг — ег> 2 '
§ 5] ЛИНЕАРИЗАЦИЯ ПО ФУНКЦИИ РАСПРЕДЕЛЕНИЯ 71
При этом уравнения (5.76) имеют следующее решение:
ai = a2 = a3 = -g-, a4 = 0, k2 = e2=:2. (5.81)
Характерно, что при этом точки, в которых w(at v)^0,
располагаются на фазовой траектории, соответствующей
процессу (3.2).
Формулы (5.78)—(5.80) при подстановке в них (5.81)
дают
V2
Sa
|/2/(a0 + a. 0)-"^2/(во-a, 0) +
+ /2/(a0. a») —V"2/(a0> —aw)l, (5.83)
/o="g-[/(«o + «. 0) + /(a0-a, 0) + /(a0+^,^ +
(5.84)
Эти соотношения могли бы быть получены и
непосредственно как формулы для приближенного вычисления
интегралов (4.4) — (4.6) при гармоническом x(f).
В дальнейшем нам придется иметь дело с функциями
/(#, л:), четными по х и нечетными по л:. Для таких функций
f(x, x) — f(—х, л:) = — f(xt — х) = — /.(— х, —х).
72 НЕКОТОРЫЕ ПРИБЛИЖЕННЫЕ МЕТОДЫ [ГЛ 1
Если при этом еще а0 = 0, то по формулам (5.78) — (5.80)
получаем
/0 = 0, q = 0, r=^-[2a2/(ax, av) + «13/(0, eav)]. (5.85)
Для гармонического процесса
/о = 0, , = 0, ^[Щ-fa. ^) + /(0, о»)].
(5.86)
§ 6. Метод Галеркина
Линеаризуя нелинейное уравнение любым из
рассмотренных выше способов, можно приближенно определить только
те его решения, которые близки к решениям
линеаризованного уравнения. Однако нелинейные уравнения могут иметь
периодические решения иного вида, для разыскания которых
удобно пользоваться вариационным методом Галеркина.
Пусть движение некоторой системы с п степенями
свободы задано уравнениями Лагранжа второго рода:
d [ dL \ dL n , • • .
(Л=1 л). (6.1)
где L—функция Лагранжа, представляющая собой разность
между кинетической и потенциальной энергией системы;
Qk—неконсервативные обобщенные силы, являющиеся
периодическими, с периодом Т, функциями явно входящего
времени t.
По методу Галеркина периодические решения системы
уравнений (6.1) ищутся среди периодических функций
периода Т, принадлежащих некоторому семейству, зависящему
от / параметров:
?а«9а==Фа(*. «1 <*/) (А=1 л). (6.2)
Для отыскания решения используется вариационный
принцип Гамильтона—Остроградского, в соответствии с которым
для любого точного периодического решения системы (6.1),
§ 6] МЕТОД ГАЛЕРКИНА 73
имеющего период 7\ должно быть справедливо соотношение:
•s-/i(^-s-^)"'*—/!«••••* -<б-з>
Здесь
т
5 = Г Ldt
о
является действием по Гамильтону, взятым вдоль замкнутой
траектории в пространстве координат qv . . ., qn,
соответствующей точному периодическому решению; bqk—вариации
координат, являющиеся периодическими непрерывными функ*
циями времени.
Используем условие (6.3) для выбора приближенного
решения среди функций семейства (6.2). Варьирование
функций сводится к варьированию параметров (Ху. При этом
У=1 7=1
где через 5 обозначено действие по Гамильтону,
получающееся при подстановке qk и qk в функцию Лагранжа L и
являющееся функцией параметров а;-. Подставляя (6.4) в (6.3)
и учитывая независимость вариаций 6(Ху, получаем систему /
уравнений для определения значений параметров,
соответствующих приближенному периодическому решению системы
(ел)
РА* «<)=£+ /2<?.-з&<«=о c/=i о-
1 О й=1 '
(6.5)
Если уравнение движения системы с одной степенью
свободы задано в форме (1.1), а приближенное решение ищется
в виде
£ = ф(*, (^ (Xj), (6.6)
74 НЕКОТОРЫЕ ПРИБЛИЖЕННЫЕ МЕТОДЫ [ГЛ. I
то условия (6.5) приводятся к такому виду:
т
Pj(av.... щ)= J {ф(*. av ..., с^ + ЯфС а1§ ..., а/),
о
Ф(*. а15 .... а/)]-/?(О0} щ^ = 0 (/=» О- (6-7)
Для того чтобы метод Галеркина оказался достаточно
эффективным, необходимо, чтобы хотя бы одна из функций,
принадлежащих семейству (6.2), была близка к точному
решению. Существует обширный класс систем, для которых
может быть указан метод выбора формы семейства (6.2),
обеспечивающий выполнение этого условия.
Рассмотрим, например, систему с малыми
неконсервативными силами
d I dL\ dl ~ , • • ,ч
TtKEQ-^r^{qi <*■*•■■••<••'>
(й=1, ..., п)> (6.8)
отличающуюся от (6.1) наличием малого параметра \х в
правой части. Пусть при jut ===== 0 имеется семейство
периодических решений периода Т
q°k = %(t, a, о,). (6.9)
Учитывая малость неконсервативных сил, можно
предположить, что периодическое решение уравнения (6.8) будет
близким к одной из функций (6.9), то есть искать
приближенное периодическое решение в форме
5* = ФлС ai> •••• <*/)• (б. 10)
Поскольку при любых значениях а;- (6.10) является
решением для консервативной системы, должно быть выполнено
условие
6S = 0,
а это означает, что производные dS/ddj тождественно
обращаются в нуль, и уравнения (6.5) принимают более простой
вид
г п
Pj(av .... а,) = J 20*-35Тл = ° V=l 0- (6Л1)
0 А = 1 ;
§6]
МЕТОД ГАЛЕРКИНА
75
При |i = 0 система (6.8) становится автономной, поэтому
если она имеет хотя бы одно периодическое решение
периода 7\ то существует и семейство решений
?* = Ф* (' + <*)•
При этом условие (6.11) сводится к следующему:
т п
(6.12)
(6.13)
О А = 1
поскольку
да —q*
Условие (6.13) имеет простой физический смысл: работа
неконсервативных сил за период на искомом решении
приравнивается нулю. Строгое математическое обоснование
необходимости выполнения условий (6.11) для существования
периодического решения системы (6.8) может быть получено
с помощью метода малого параметра (метод Пуанкаре).
Изложение этого классического метода теории нелинейных
колебаний можно найти, например, в книге И. Г. Малкина^].
С его помощью можно также доказать, что если av
ai~
изолированное решение системы уравнений (6.11), то есть
если
дРх дР{
да{ dai
dPi
дщ '
dPi
дщ
фО,
araJ
то значения а*, действительно определяют приближенное
решение системы (6.8), стремящееся к точному при jj,—>0.
Метод гармонического баланса в случае системы с одной
степенью свободы может рассматриваться как частный
случай метода Галеркина. Действительно, выражение (1.11)
определяет семейство периодических решений, в котором а0,
ах% Ьх являются параметрами. Условия (6.7) при подстановке
76 НЕКОТОРЫЕ ПРИБЛИЖЕННЫЕ МЕТОДЫ ^Л. I
в них (1.11) вместо ф(£, аР ..., at) оказываются условиями
равенства постоянных составляющих и коэффициентов при
sinotf и cosotf в левой и правой частях уравнения (1.1).
В качестве примера применения метода Галеркина
исследуем уравнение
х + 2ял; + k2x + с sign х = Л cos о/, (6.14)
описывающее вынужденные колебания в системе с
начальным натягом. Покажем, что при достаточно малых значениях
Л и п это уравнение может иметь решения, частота
которых в целое число раз меньше со. Для этого обозначим
n = rii\i, А = Ах\л и перепишем уравнение в такой форме:
х -f- k2x -f- с sign х = |i (— 2пхх ~\- Ах cos at). (6.15)
Мы получили уравнение вида (6.8). Правая часть его является
периодической функцией времени с периодом Т = 2л/со;
очевидно, что ее периодом является также и 7\ = /пТ, где
m — любое целое число.
При |i = 0 уравнение (6.15) имеет решение (2.26)
х°~ п ZiK l) (2/> + 1)[Р(2/>+1)2-*2] ' (tMb'
где а — произвольный параметр; X— частота колебаний,
которая может принимать любое значение, превышающее к
(рис. 12).
Пусть—==А,>&; тогда существует решение (6.16),
имеющее частоту —. Найдем условия существования
близкого к нему решения уравнения (6.15). Для этого
необходимо найти параметр а из условия (6.13), которое в
рассматриваемом случае принимает такую форму:
тТ
Р(а) = — Г [2nlx0(t-{-a)-{-Alcos<j)t]x0(t + a)dt — 0.
(6.17)
Первое слагаемое выражает работу силы сопротивления на
периодическом решении х0. Его величина не зависит от а,
§ 6] МЕТОД ГАЛЁРКИНА 7?
она может быть найдена подстановкой (6.16) в (6.17):
Ь
6
т\ [ оо \2
: = — j 2n1{x(pdt =
о
о 1р=о J
— ~"7^^X2^ [Я2(2/> + 1)2-*2]2- (6Л8)
р=0
Второе слагаемое в (6.17) выражает работу
вынуждающей силы на свободном колебании л:0. Подставляя в него х0,
получаем
т.1
Wb= Лj cos m%tx0(t-{-a)dt =
о
О /?=0
Учитывая, что
7-1
cos mM sin [(2р + 1) к (t +a)] dt =
!0 при 2/? + 1 Ф mt
-^~sinmA,a при 2р -\-\ = т,
получаем
Wb = (-l) 2 4СЛ11||^Г. (6.19)
Подставляя (6.18) и (6.19) в уравнение (6.17), находим
m-l
ОО г
у _ 4сХ2 п у (Х2т2 — k2)(—1) 2 _
sin юла — -jp- л ^ [Р (2/? +1)2 — *2]2 ~
га-1 °°
_ — too»/»»» у о»-*» (620)
~^ U Л -J [ю2(2/>+1)2-*2]2 ' ^^
р=0
78
НЕКОТОРЫЕ ПРИБЛИЖЕННЫЕ МЕТОДЫ [ГЛ. I
Значения а получаются вещественными только в том случае,
если модуль выражения, стоящего в правой части, не
превышает единицу.
Вынужденные колебания, частота которых в т раз
меньше, чем частота вынуждающей силы, называются
субгармоническими порядка т. Возможность возникновения
таких колебаний является одной из существенных
особенностей нелинейных систем, которая будет подробно
исследована ниже.
§ 7. Метод статистической линеаризации
Колебания, возникающие в виброзащитных системах,
часто приходится рассматривать как случайные процессы,
при которых координаты системы являются случайными
функциями времени.
Случайной функцией называется совокупность
конечного или бесконечного числа детерминированных функций
(реализаций), связанных некоторыми вероятностными
соотношениями. Основными вероятностными характеристиками
случайной функции являются функции распределения.
Функция Wl(ul, t{), равная вероятности того, что
значение случайной функции X (t) *) в момент времени tx не
превышает uv называется одномерной функцией
распределения
W(uv tl) = P{X(tl)^u1\ (7.1)
(Р — знак вероятности).
Двумерной функцией распределения W2(uv tv и2, t2)
называется вероятность совместного выполнения неравенств
*('i)<«i. X(tJ^u2. (7.2)
Аналогичным образом определяется я-мерная функция
распределения
w„("i. h йя, /„) = я {*&)<«! *(;„)<«„}.
(7.3)
*) Случайные функции (процессы) будут обозначаться
прописными буквами; их реализации — строчными.
§ 7] МЕТОД СТАТИСТИЧЕСКОЙ ЛИНЕАРИЗАЦИИ 79
Случайный процесс называется стационарным в узком
смысле, если
Wn(uv tx ип, tn)==Wn(uv Ь + т. ..., йл. tn + r)
(7.4)
для любых tx tn, т и для любого п.
Одномерная функция распределения стационарного в
узком смысле процесса не зависит от времени, а двумерная
зависит от x = t2— tx:
W1 = W1(u1)\ W2 = W2(ul9 я2, t). (7.5)
Очевидно, что каждая из реализаций стационарного
случайного процесса должна быть определена на бесконечном
интервале времени при — оо < t < +00.
Отметим, что одномерная функция распределения
стационарного случайного процесса, вообще говоря, не имеет
ничего общего с функцией распределения
детерминированного процесса, определенной в § 5. Действительно, в
одном случае речь идет о распределении значений случайной
функции на различных ее реализациях в один и тот же
момент времени; во втором случае—о распределении
значений одной детерминированной функции на бесконечном
интервале времени.
Моментами п-го порядка случайного процесса X (t)
называются математические ожидания произведений значений
случайной функции в моменты времени tv .. ., tn
*!„(*, tn) = M{X(tl).X(t2). ....*(/„)} =
ОО ОО
= J* ... J* uxu2 ... unwn (elt tv uv t2, ...
-00 -00
.... un, t^)duxdu2 ... dun, (7.6)
где функция
«»<*i.'i «»^=Д»Л <7-7>
называется я-мерной плотностью вероятности случайного
процесса.
80 НЕКОТОРЫЕ ПРИБЛИЖЕННЫЕ МЕТОДЫ [ГЛ I
В дальнейшем нас будут интересовать моменты первого
и второго порядка. Момент первого порядка
оо
mx(t) = \ uwx(u, f)du (7.8)
— со
называется математическим ожиданием случайного
процесса X (t). Если mx(t) = 0t процесс называется
центрированным. Момент второго порядка центрированного
случайного процесса
X0(t) = X(t)-mx(t),
определяющийся по формуле
Кх (*„ t2) = М {[X (/,)- тх (ЭД [A" (t2) - тх (t2)\) =
ОО СО
= J* §1и\—™х(tx)\ [и2 — тх(tz)] w2(uv tv u2, t2)dux du2,
-co —oo
(7.9)
называется корреляционной функцией случайного
процесса. Если тх не зависит от времени, а Кх зависит только
от разности t2 — tx
тх (0 ~-=тх = const; Кх (tv t2) = Кх (t2 — tx) = Кх (т),
(7.10)
то случайный процесс называется стационарным в
широком смысле. Очевидно, что всякий стационарный в узком
смысле процесс является стационарным в широком смысле,
но не наоборот.
Полагая в (7.9) t2 = tv получаем
K(tv ti)=M{[X(tJ-mx(td]*)=o*(tl). (7.11)
Эта величина называется дисперсией случайного процесса.
Для стационарного в широком смысле процесса
°i со=*, d - 'о=кх (°)=c°nst- (7-»2)
Спектральной плотностью центрированного
стационарного в широком смысле случайного процесса X°(t) на-
§ 7] МЕТОД СТАТИСТИЧЕСКОЙ ЛИНЕАРИЗАЦИИ 81
зывается функция Sx(a>)f получаемая преобразованием Фурье
корреляционной функции
оо
Sx(a>) = je~^Kx{x)dx С/ = }ГГ1). (7.13)
— ОО
С помощью обратного преобразования корреляционная"<функ-
ция может быть выражена через спектральную плотность:
оо
К^х) = ^ j eJ™Sx(e>)d®. (7.14)
— ОО
Полагая в (7.14) т = 0, получаем
ОО
Кх (0) = о2х = ± fsx (со) <to. (7.15)
— эо
Случайный процесс X (t) называется нормальным или
гауссовым, если его я-мерная плотность вероятности при
любых значениях tv . .., tn является нормальной
относительно переменных uv ..., ип. В дальнейшем нам
понадобится только выражение для одномерной плотности
вероятности нормального стационарного процесса:
Показано [43], что все вероятностные характеристики
нормального процесса полностью определяются, если известны
его математическое ожидание и корреляционная функция.
Это обстоятельство существенно упрощает анализ
нормальных случайных процессов. Как видно из формулы (7.16),
при нормальном процессе допустимы реализации, в которых
переменная величина достигает сколь угодно больших
значений. Поскольку в реальных системах все координаты
остаются ограниченными, очевидно, что нормальный процесс
должен рассматриваться как некоторая идеализация реальных
процессов. Примечательно, что сумма большого числа
статистически независимых случайных процессов всегда близка
к нормальному процессу, если только ни одна из
компонент не превалирует над остальными [43]. В силу этого,
§ М. 3. Коловс^ИЙ
82
НЕКОТОРЫЕ ПРИБЛИЖЕННЫЕ МЕТОДЫ [ГЛ. I
например, можно считать нормальным вибрационное
возмущение, вызванное совместным действием большого числа
независимых источников.
Вероятностные характеристики определяют
статистические свойства совокупности (ансамбля) детерминированных
функций, образующих случайный процесс, но ничего не
говорят о свойствах отдельных реализаций. Однако при
решении практических задач обычно имеется возможность на
основе представлений о физической природе случайного
процесса сделать некоторые заключения о свойствах его
реализаций (их непрерывности, дифференцируемости и т. п.).
Стационарные случайные колебания, возникающие в
виброзащитных системах, во многих случаях могут считаться
полигармоническими функциями времени, в которых амплитуды,
частоты и фазы являются случайными величинами
N
X (0 = 2 *i cos (©,* + tfo) + a0. (7.17)
Очевидно, что любая из реализаций этого процесса —
непрерывная и дифференцируемая любое число раз функция
времени.
Стационарный процесс, спектральная плотность которого
является постоянной при всех значениях со от — сю до -+- оо,
называется белым шумом. По формуле (7.14) находим
оо
^(т> = ё J«/etrf«> = -S06_(T). (7.18)
— ОО
то есть корреляционная функция белого шума является
дельта-функцией. Из формулы (7.15) видно, что белый шум
должен иметь бесконечно большую дисперсию, то есть
является физически нереализуемым. Подобно нормальному
процессу, белый шум — удобная идеализация
широкополосных стационарных случайных процессов, то есть таких
процессов, у которых спектральная плотность близка к
постоянному значению S0 в широком диапазоне значений со.
Особый класс стационарных случайных процессов
составляют так называемые эргодические процессы. Пусть
задана некоторая функция f(x). Вычислим математическое
ожидание случайной величины f[X(tx)] для любого момента
§ 7] МЕТОД СТАТИСТИЧЕСКОЙ ЛИНЕАРИЗАЦИИ 83
времени tv производя усреднение по всем реализациям
случайного процесса X (t), и определим среднее по времени
значение f[x(t)] для какой-либо одной реализации. Если
окажется, что
т
M[f[X(tl)])=lim^r [ f[x(t)]dt (7.19)
-Г
для любой функции f(x) и для любой из реализаций, то
стационарный случайный процесс называется эргодическим *).
Положив f (х) = ц(их — х) (т] — единичная функция (5.2))
и учитывая, что
Wl(ul)=M{x\[ul-X{t)])t (7.20)
получаем для эргодических процессов
т
У1(я1)= Hm i Г Л [«i — x(f)]dt, (7.21)
Т + со*' JT
то есть одномерная функция распределения стационарного
случайного эргодического процесса тождественна функции
распределения любой из его реализаций, найденной в
соответствии с определением, данным в § 5.
При f(x) = x получаем
т
mx=M{X (*)} = lim 4f f x (') dt> (7-22)
то есть математическое ожидание эргодической случайной
функции совпадает с ее средним по времени значением на
любой из реализаций. Очевидно, что (7.22) можно
рассматривать как следствие (7.21).
Наконец, для корреляционной функции, приняв
f[x(t)] = X(t)'X(t+T),
*) Точнее, выполнение равенства (7.19) требуется почти для
всех реализаций; могут существовать отдельные «нетипичные»
реализации (образующие «множество меры нуль»), для которых это
соотношение несправедливо.
6*
I
Ы НЕКОТОРЫЕ ПРИБЛИЖЕННЫЕ МЕТОДЫ [ГЛ. 1
находим
т
Кх(т)= lim ^ f x(t)x(t + x)dt. (7.23)
Это соотношение используется обычно для вычисления
корреляционной функции эргодического стационарного
случайного процесса по экспериментально полученной записи одной
из его реализаций. При этом усреднение производится на
конечном интервале времени, в течение которого
производилось измерение; поэтому получаемое выражение для
корреляционной функции является приближенным.
Если все реализации случайной функции X (t) k раз
дифференцируемы по t* то выражение
К(0 = М/>)*(0>
где Lk{p) — полином k-ft степени от оператора
дифференцирования р=^-гг, определяет случайную функцию Y(t).
При этом Y (t) является стационарным процессом, если
X (t) — стационарный процесс.
В теории стационарных случайных процессов выводятся
соотношения, позволяющие выразить вероятностные
характеристики У (t) через вероятностные характеристики X (t).
Нам понадобятся в дальнейшем только выражения,
связывающие математические ожидания и спектральные плотности:
my = L„(0)mx. (7.24)
Sy(<*) = \Lk(J<*)\*Sx(v>). (7.25)
Эти соотношения остаются в силе и в тех случаях, когда
оператор Lk (р) представляет собой дробно-рациональную
функцию р
где Mk(p) и Dk(p)— полиномы, степень которых не
превышает k. При этом выражение (7.25) остается
справедливым для всех значений со, при которых Dk(ja)) не
обращается в нуль.
§ 7] МЕТОД СТАТИСТИЧЕСКОЙ ЛИНЕАРИЗАЦИИ 85
В теории виброзащитных систем приходится иметь дело
с нелинейными функциями стационарных случайных
процессов вида
У (0 = /[*(01 (7.27)
или
К (0 = /[*(*), X(t)\. (7.28)
Метод статистической линеаризации [п] является
наиболее распространенным способом приближенного
исследования систем, содержащих нелинейные функции такого вида.
Этот метод сводится к замене нелинейных функций (7.27)
и (7.28) линейными
У*(0 = h + q\X(0- «,] = /о + qX<> (7.29)
ИЛИ
Y*(t)=fQ + q\X{t)-mx\ + rX(t) = U + qX<>+rX*.
(7.30)
Коэффициенты /0, #, г определяются из 'условия минимума
дисперсии случайной функции
&Y(t) = Y(t)—Y*(t). (7.31)
В силу стационарности случайного процесса (7.31) его
дисперсия не зависит от времени и может быть найдена
следующим образом:
оо
Ж{[АК(0]2}= /[/(«)-/о-?(«-»*)]'«!(«)(<*«). (7-32)
— оо
если Y* выбрана в форме (7.29);
M{[AY(t))*} =
оо оо
= / flf^'^ — fo — qi"— тх) — rv\2 wi («. <0 da dv,
—оо —оо
(7.33)
если К* выбрано в форме (7.30). В выражении (7.32)
wx (и) — плотность вероятности стационарного случайного
процесса X (t)\ в (7.33) w{(u, v) — совместная плотность
86 НЕКОТОРЫЕ ПРИБЛИЖЕННЫЕ МЕТОДЫ [ГЛ. I
вероятности процессов X (t) и X (t)
Подобно тому, как это делалось при линеаризации по
функции распределения, предполагается, что плотность
вероятности процесса wx (а) (или совместная плотность
вероятности wl(ui v)) принадлежит некоторому семейству
функций, зависящему от нескольких первых моментов. Часто,
например, принимают, что закон распределения случайного
процесса X (t) близок к нормальному, то есть что плотности
вероятности могут быть выбраны в следующей форме:
«"<">=ykj^b1^}- <7-35>
Wl(Ut <y)a_J_expr- <«-^)2—4-1. (7.36)
Здесь о?— дисперсия процесса X (t)\ учитывается, что для
стационарного процесса среднее значение скорости mv должно
равняться нулю.
Условия минимума функционала (7.32) приводят к
следующим выражениям для коэффициентов линеаризации:
оо
q = \ f /(uHu — mJWiMdu. (7.37)
•* — оо
со
/о= //(«)»!(«)</«. (7.38)
— СО
Аналогично, минимизируя функционал (7.33), получаем
со оо
q = — /(#> ^)(и— tnjw^u, v)dudv, (7.39)
CO CO
r = -i~ \ f(u, v)v-w1(u, v)dudv, (7.40)
и —со -co
CO CO
/0= Г f/(#> v)wl(u, v)dudv. (7.41)
§ 7] МЕТОД СТАТИСТИЧЕСКОЙ ЛИНЕАРИЗАЦИИ 87
Коэффициенты линеаризации оказываются функциями тх,
ох, ъ\. В тех случаях, когда выбирается нормальный закон
распределения, можно пользоваться готовыми зависимостями
q> rt /0 от тх, а^, о£, вычисленными для некоторых
наиболее часто встречающихся нелинейных функций f (х) и
/(*. х) П.
Получив линеаризованное уравнение, можно найти
математическое ожидание и спектральную плотность его
стационарного решения по математическому ожиданию и
спектральной плотности внешнего воздействия, пользуясь
соотношениями (7.24) и (7.25). Соотношение (7.25) при Ll(p) = p
определяет спектральную плотность производной
Sv(e>) = <&Sx(e>). (7.42)
Естественно, что при этом тх, Sx{<$) и Sv(со) оказываются
функциями коэффициентов линеаризации q* г, /0, а
следовательно, функциями моментов тх> ох, а2. Выражение (7.24)
и соотношения
оо
—оо
оо
°t = ir j Sv(<o)d®. (7.44)
— ОО
составляют систему уравнений, из которых можно
определить моменты.
Рассмотрим, например, следующее уравнение:
X -f 2nX'+ k2X + yX* = Z (0 = mz + Z° (f), (7.45)
где Z° (t) — нормальный белый шум
52(co) = S0 (—оо<со<оо). (7.46)
Если бы уравнение (7.45) было линейным, его
стационарное решение непременно являлось бы нормальным
процессом, поскольку всякое линейное преобразование не
нарушает нормальности процесса. Решение нелинейного
уравнения (7.45), строго говоря, не является нормальным
процессом; можно, однако, предполагать, что при малых
88 НЕКОТОРЫЕ ПРИБЛИЖЕННЫЕ МЕТОДЫ [ГЛ. I
значениях y его закон распределения будет мало отличаться
от нормального и, в первом приближении, искать плотность
вероятности процесса в форме (7.35).
Подставляя (7.35) в (7.37) и (7.38), получаем после
интегрирования следующие выражения для коэффициентов
линеаризации нелинейной функции f(X) = yXz:
* = 3y« + oJ); /0 = Y^K + 3a2). (7.47)
Линеаризованное уравнение
X«+2nlX"+(k* + q)X* + k*mx + f0==Z<>(t)+-rriz (7.48)
равносильно двум уравнениям для постоянной и
центрированной случайной составляющих:
*Чг + Л = тх [*2 + Y К + Ч)] = тг> (7«49)
х°=
По формуле (7.25) получаем
Sx (<*>) = | {j(d)2 + 2пх (уо) + k* + q I2 ' (7,51^
Следовательно, в силу (7.15)
оо
„2_ J_ Г ?«*» —
>— 2я J
x°=P>+2nJ+k>+qz0- <7-50>
1С^)* + 2я,0) + *, + *1*
—оо
00
1_ Г S0d<o
!я J
~ 2nJ [(»2 + 2я, W + k* + q) [(- /a)* + 2/1, (- уо>) + *2 +1}'
(7.52)
Интегралы вида
/ __L f Sn(M
'"— 2я J AeCA»)Ae(-/o) '
—оо
где §•„ и hn — полиномы
hn(p) = a0pn + aipn-1-\- ... +в».
gn(P) = t>oP'2n-2 + t>iP2n-i+ ••• +Vl-
§ 7] МЕТОД СТАТИСТИЧЕСКОЙ ЛИНЕАРИЗАЦИИ 89
часто встречаются в задачах теории случайных процессов.
Они выражаются в явной форме через коэффициенты
полиномов gn и hn\ соответствующие зависимости приводятся,
например, в [40] и [43]. В рассматриваемом случае п = 2;
а0=1; al = 2nl] a2 = k2-\-q; b0 = 0; bx = S0. Из таблиц
интегралов находим
г aobj — a2bQ S0
2 2айаха2 . bn{(k2-{-q) '
Таким образом,
^п^ + ЗуК + ^Г (7'53)
Решая систему уравнений (7.49) и (7.53), можно определить
значения тх и а2.
Пусть, например, /иг = 0; тогда, в силу симметрии
характеристики, имеем
тх = 0. /0 = 0.
Уравнение (7.54) приводится к виду
S,
(7.54)
* 4я1(*Чэ¥о»Г
Решая это уравнение, находим
^-W+Zw+t^y- (7'55)
Между методом статистической линеаризации и методом
линеаризации по функции распределения имеется много
общего; в обоих методах используется фактически один и
тот же формальный аппарат для определения моментных
характеристик искомого решения. Различие между этими
методами заключается в том, что в одном из них моментные
характеристики получены в результате усреднения
детерминированной функции на бесконечном интервале времени,
в другом — усреднением по множеству реализаций
случайного процесса. Кроме того, при линеаризации по функции
распределения мы ищем полигармоническое решение и имеем
возможность, определив это решение, уточнить форму закона
распределения; при статистической линеаризации мы, вообще
говоря, ничего не узнаем о форме отдельных реализаций
90
НЕКОТОРЫЕ ПРИБЛИЖЕННЫЕ МЕТОДЫ [ГЛ. I
решения и не имеем возможности уточнить выбранный закон
распределения.
Все эти различия связаны с тем обстоятельством, что
в одном случае внешнее воздействие на систему является
детерминированным, а в другом — случайным процессом.
§ 8. Устойчивость стационарных решений
Между реальной динамической системой и ее математической
моделью — системой дифференциальных уравнений — не может быть
полного соответствия. Дифференциальные уравнения могут лишь
с той или иной степенью приближения описывать поведение
реальной системы; неизбежные неточности в определении параметров
системы и внешних воздействий, наличие малых сил, не
учитываемых при составлении уравнений, неточности в задании начальных
условий и другие возмущающие факторы приводят к
расхождениям между решениями уравнений и действительными законами
изменения координат системы.
В связи с этим важное значение приобретает исследование
устойчивости решений дифференциальных уравнений. Устойчивое
решение мало изменяется при воздействии достаточно слабых
возмущающих факторов. Неустойчивое решение претерпевает с
течением времени существенные изменения даже при малых
возмущающих воздействиях, а так как такие воздействия неизбежно
существуют в реальной системе, то оно оказывается физически не
реализуемым.
Пусть дифференциальные уравнения движения системы заданы
в форме (1.22). Для исследования устойчивости какого-либо его
решения
* = М') (8.1)
сделаем замену переменных, положив
х = Ъ«) + у. (8.2)
Подставив (8.2) в (1.22), получим так называемое уравнение
возмущенного движения:
у =, Х[10 (t) + y, t] - Х[*0 (0, t). (8.3)
Исследуемому решению (8.1) уравнения (1.22) соответствует
нулевое решение уравнения (8.3).
Согласно Ляпунову [33], нулевое решение уравнения (8.3)
называется устойчивым, если для любого сколь угодно малого
положительного числа е может быть найдено такое положительное
число г] (е), что для всякого решения уравнения (8.3),
удовлетворяющего условию
\У(*о)\<Я (8-4)
в любой момент времени t > t0 выполняется, условие
|jr(*)l<e. (8-5)
§ 8] УСТОЙЧИВОСТЬ СТАЦИОНАРНЫХ РЕШЕНИИ 91
Здесь модуль (норма) вектора у определяется как корень
квадратный из суммы квадратов его составляющих.
Если для всех решений уравнения (8.3), удовлетворяющих
условию (8.4), выполняется условие
lim |^(0I = 0, (8.6)
то нулевое решение этого уравнения называется асимптотически
устойчивым.
Решение (8.1) уравнения (1.22) считается устойчивым
(асимптотически устойчивым), если устойчиво (асимптотически устойчиво)
нулевое решение уравнения (8.3).
В силу определения, устойчивое по Ляпунову решение мало
изменяется (для любого t) при малых изменениях начальных
условий. Доказано, однако, что решение, асимптотически устойчивое по
Ляпунову, остается устойчивым и по отношению к другим
возмущающим факторам [8б]. Поэтому достаточно ограничиваться
исследованием устойчивости по Ляпунову.
Пусть функция Х(х, t) имеет непрерывную производную по х;
тогда уравнение (8.3) может быть линеаризовано по у.
Получающееся при этом линейное уравнение
*e-3jto>('M]J (8.7)
называется уравнением первого приближения, или уравнением
в вариациях для решения (8.1) уравнения (1.22).
Ляпунов показал, что в большинстве случаев суждение об
устойчивости или неустойчивости решения (8.1) может быть сделано
на основе анализа устойчивости нулевого решения уравнения в
вариациях. Исключение составляют лишь так называемые
критические случаи, которые при анализе колебаний в виброзащитных
системах практического значения не имеют.
В общем случае исследование уравнения в вариациях (то есть
системы скалярных линейных уравнений с переменными
коэффициентами) связано с большими математическими трудностями.
Наиболее просто эта задача решается в тех случаях, когда
уравнение (1.22) является автономным, а исследуемое решение (8.1)
представляет собой положение равновесия
х = х0. (8.8)
Тогда уравнение (8.7) становится линейным с постоянными
коэффициентами
У = ^(*о)У „ (8.9)
и вопрос об устойчивости решается анализом корней
соответствующего характеристического уравнения
!|(*0)-£X|=0, (в.10)
где £—.единичная матрица.
92
НЕКОТОРЫЕ ПРИБЛИЖЕННЫЕ МЕТОДЫ [ГЛ. I
Уравнение (1.22) в случае автономной системы эквивалентно
системе п скалярных уравнений
xs = Xs (хх хп) (s = 1, ..., п).
(8.11)
Система уравнений в вариациях для положения равновесия xs = xs0
записывается в форме
(*ib • • м *яо) У к (5 = 1 п). (8.12)
*=1
Соответствующее характеристическое уравнение:
(дХЛ _х /дХЛ /дХЛ
\ дхх )0 \дх2)о"\ д*п /о
(дХЛ (дХЛ (дХЛ _ к
\ дхх )о \ дх2 /о ' ' \ дхп /о
= 0 (8.13)
является скалярной формой уравнения (8.10).
Если все корни уравнения (8.10) имеют отрицательные
вещественные части, то положение равновесия (8.8) является
асимптотически устойчивым.
Исследование устойчивости стационарных (периодических или
почти-периодических) решений нелинейных дифференциальных
уравнений приводит к уравнениям в вариациях с периодическими
или почти-периодическими коэффициентами. Уравнениям с
периодическими коэффициентами посвящена обширная литература, однако
эффективные методы исследования устойчивости разработаны лишь
для некоторых классов уравнений ([34], [35], [53]). Анализ
уравнений с почти-периодическими коэффициентами является еще более
сложным. Следует также иметь в виду, что для нелинейных систем
обычно удается определить лишь приближенное решение, поэтому
и уравнение в вариациях для этого решения является
приближенным, а выводы об устойчивости решения на основе анализа
приближенного уравнения в вариациях часто не являются
корректными.
Поэтому на практике часто пользуются другими методами
анализа устойчивости, которые непосредственно связаны с
рассмотренными выше методами определения приближенных решений.
Как уже отмечалось в § 1, все эти методы сводятся к
разысканию приближенного решения среди функций, принадлежащих
некоторому семейству, зависящему от конечного числа параметров.
В методе гармонического баланса такими параметрами являются
амплитуды первой гармоники и постоянные составляющие искомого
решения, в методах, связанных с линеаризацией нелинейных
функций, — коэффициенты линеаризации, в методе Галеркина —
параметры <xlf ..., щ и т. п.
§ 8] УСТОЙЧИВОСТЬ СТАЦИОНАРНЫХ РЕШЕНИЙ
93
Иными словами, приближенное решение уравнения (1.22) ищется
в форме
х«ЯР(Л Pi Р/). (8.14)
При исследовании устойчивости предполагают, что
возмущенное движение (8.2) может разыскиваться также в форме (8.14), но
параметры ру должны уже рассматриваться не как постоянные,
а как неизвестные функции времени, так что
х = 4 <*, Pi Р,) + J -щ h- (8.15)
Подставляя (8.15) в (1.22), получают дифференциальные уравнения
для неизвестных функций рь ..., Pj
/
^llk'h==Xl'Ht' Pl' "" РЛ t]^(ti Pl' ••- W" (8Л6)
Приближенному стационарному решению уравнения (1.22)
вида (8.14) соответствует «приближенное положение равновесия»
системы (8.16). Стационарное решение (8.14) считается устойчивым,
если устойчивым оказывается это «положение равновесия».
Нетрудно видеть, однако, что такой метод анализа
наталкивается на ряд затруднений, одним из которых является, например,
несоответствие порядка системы (8.16) (п) числу неизвестных
функций времени (/).
Полное преодоление всех затруднений в рамках приближенной
теории является принципиально невозможным. В каждом
конкретном случае используются различные частные приемы; некоторые
из них будут рассмотрены ниже. Поскольку метод
исследования является математически нестрогим, полученные с его
помощью результаты следует использовать с большой осторожностью.
Выведем критерии устойчивости приближенных решений
уравнения (3.21), найденных методом гармонической линеаризации. Как
было показано в § 3, при линеаризации это уравнение сводится
к системе:
/оК.«) = Л. (8.17)
х° + rx° + qx° = A cos со/. (8.18)
Уравнение (8.17) является конечным соотношением, связывающим
параметры а0 и а; уравнение (8.18) может быть записано в виде
системы двух уравнений первого порядка
х° = у,
у = — гу — qx° -f- Л cos at.
Эта система имеет решение
х° = a cos (со* + Ф), у ч= — ясо sin (со/ -|- ср). (8.20)
(8.19)
94
НЕКОТОРЫЕ ПРИБЛИЖЕННЫЕ МЕТОДЫ
[ГЛ. I
Исследуя устойчивость этого решения, предполагаем, что
параметры а и ф являются функциями времени. Поскольку в данном
случае число переменных параметров равно порядку системы,
соотношения (8.20) определяют преобразование координат, то есть
переход от переменных лг° и у к переменным а и ср.
Подставляя (8.20) в (8.19), получаем
a cos (art -f- ф) — а (0 -\- <р) sin (0/ + ф) = — aco sin (0/ -|- ф),
— ясо sin (0/ + ф) — ясо (о -(- ф) cos (со/ -\- ф) =
= га sin (0/ + ф) — qa cos (0/ -(- ф) + Л cos со/,
или, после элементарных преобразований,
a cos (0/ -f- ф) — ац> sin (0/ -(- ф) = 0,
■ a sin (0/ + ф) — яср cos (0/ + ф) =
= га sin (0/ -(- ф)
1 ^
— (# — 02) a cos (0/ + ф) -| cos 0/.
(8.21)
Из этих уравнений находим а и ф:
а = — ra sin2 (0/ + ф) -|— (q — 02) a cos (0/+Ф) sin (0/4-ф)—
cos 0/ sin (0/ -(- ф),
Ф = — г sin (©/ + ф) cos (0/ + Ф) +
1 Л
-f — (q — 02) cos2 (0/ + Ф) — — cos 0/ cos (0/ + ф).
Легко проверить, что эта система уравнений имеет решение
Л ,_ г©
(8.22)
V(Q — ю2)2 + г202
*£Ф* =
02 —?
(8.23)
которое может рассматриваться как «положение равновесия» на
плоскости параметров а, ф. Поскольку при этих значениях а и ф
производные а и <р обращаются в нуль, надо полагать, что в
некоторой достаточно малой окрестности «положения равновесия»
они остаются малыми. Это означает, что для движений, близких
к периодическому решению (8.20), параметры а и ф являются
медленно меняющимися функциями времени. Учитывая это
обстоятельство и исследуя поведение системы в достаточно малой
окрестности «положения равновесия», можно заменить правые части
уравнений (8.22) их средними за период Г = — значениями. При
этом получаем
га А .
а = j — -^ sin ф = А (я, <р),
Ф = -
20
2а©
cos ф ». Ф (я, ф).
(8.24)
§ 8]
УСТОЙЧИВОСТЬ СТАЦИОНАРНЫХ РЕШЕНИЙ
95
Формулы (8.23) определяют положение равновесия автономной
системы (8.24); при исследовании устойчивости этого положения
равновесия необходимо учесть, что коэффициенты
линеаризованного уравнения являются функциями а0 и а, или, поскольку а0
выражается через а с помощью уравнения (8.17), — функциями
амплитуды а.
Приняв
я = а% + а, ф = ф* + б,
составляем уравнения первого приближения в форме (8.7):
дА . . . дА , ч s
а = -gj (*.. Ф*)« + -RjT (а*' ф*) б'
дФ , дФ
& = -^ К> Ф*) а + "^ К> Ф*) 6.
(8.25)
(8.26)
Находим
К, Ф*) = — -j [г* + "37 ("** а*}'
(q* — (d2)a*
дА
да
дА , ч А
2оэ
2©
(8.27)
(8.28)
дФ , А . г
-з— (#*> Ф*) — ?J sin Ф* = — тг >
дф v * ™ 2я#со Y* 2
где <7* = ? (а*), г* = г (л#).
Подставляя (8.27) в (8.26), получаем
1 Г i dr / ч 1 (?* —ю2)я* *
Для устойчивости системы линейных дифференциальных
уравнений с постоянными коэффициентами (8.26) должны выполняться
следующие условия, обеспечивающие отрицательность
вещественных частей корней характеристического уравнения:
— + — <0 дА_ дФ_ _ дФ_ дА_
да ' дф ' ^ ^(р да д<р ' \ • )
Это приводит к окончательным выражениям для критериев
устойчивости решений гармонического вида уравнения (1.1):
2г.+ з£-(<*•)*•> 0,
(8.30)
(Я* - *>2) [я* ~<»2 + а*^ <«•)] + г* [г* + Цг (*.)] > a <8'31)
96 НЕКОТОРЫЕ ПРИБЛИЖЕННЫЕ МЕТОДЫ [ГЛ. I
Исследуем теперь устойчивость полигармонических решений
уравнения (5.55), найденных методом линеаризации по функции
распределения. Так же, как и в предыдущем случае,
линеаризованное уравнение распадается на два уравнения:
/о (во, Я) = Л, (8.32)
N
*о + 2пх° + Ях° = 2 Ai cos W + *')• (8'33)
Предполагая, что и в неустановившемся режиме сохраняется
зависимость а0 от q, определяемая конечным соотношением (8.32),
ограничиваемся анализом устойчивости решения уравнения (8.33)
N
*° = 2 aicos <®*'+**+е*>- (8-34)
Полагая, что в этом выражении а/ и 0/ являются функциями
времени, находим
N
Х° = 2 ^ C0S W + *' + 9<> "" ai (0/ + ^> Sin (®** + ♦* + 9')1' (8-35>
*o = 2 f^ cos W + *' + e<> ~" 2"t (^ + k/) sin (©,* + ifo + 9/) —
- a. (0, + 9 .)2 cos (0/ + ^ + Э.) - a^ sin (0/ -f ф. + 9.)]. (8.36)
Подставляя (8.34), (8.35) и (8.36) в уравнение (8.33), получаем
N
2 {Й - */ (©, + ё,)« + 2/ii, + qat\ cos (©,* + % -f в,) -
- [afii + 2a, (0/ + 6t) + 2nat (©, + в,)] sin (©,* + % + в,)} =
= 2 Л* lcos W + % + ^/) cos в, + sin (©,* + fy + в,) sin в,]. (8.37)
/ = i
Введя 2JV неизвестных функций вместо одной, мы вправе наложить
на них 2N — 1 условий. В качестве таких условий выберем
следующие:
(щ + fy)2 + 2nat + qa{ = At cos 9/
(/-1, .... АО.
afii + 2a/ (0/ + 9/) + 2n (o, + 9/) ai^ — At sin 9/
(/-1 АГ-1).
Тогда, в силу уравнения (8.37), должно удовлетворяться условие
«А + &N <?N + V + 2" (aN + V «JV —" ^V 31П V <8-39)
(8.38)
§ 8]
УСТОЙЧИВОСТЬ СТАЦИОНАРНЫХ РЕШЕНИЙ
97
Соотношения (8.38) и (8.39) образуют систему дифференциальных
уравнений, содержащую неизвестные функции времени #/ и 0/.
Эта система обладает «положением равновесия», которое может
быть найдено, если в уравнениях (8.38) и (8.39) принять а) = ai =
= 0/ = 0,- = 0. При этом для сц и 9/ получаются выражения,
совпадающие с (5.57).
Итак, полигармоническому решению линеаризованного
уравнения соответствует «положение равновесия» системы (8.38) — (8.39).
Исследуя его устойчивость, составляем уравнения возмущенного
движения, учитывая при этом, что коэффициент линеаризации q
зависит от амплитуд я/. Предполагается, что форма зависимости
коэффициента линеаризации от амплитуд сохраняется такой же, как
для полигармонического решения
*-«(о»)-«^|«?).
(8.40)
При этом уравнения возмущенного движения записываются в такой
форме:
N )
(р2 + 2np + q — со?) at + at ч V akak — 2a&ipbi = |
d™ * = i \ (8,
= — At sin 9Д-,
2co/ (p + n) щ + at (p2 + 2np) bt = — At cos 9/6/.
41)
Здесь p — оператор дифференцирования, щ и б/ — вариации
амплитуд и фаз. Коэффициенты этого уравнения вычисляются для
значений Л/, 0/ и q, соответствующих полигармоническому решению.
Учитывая, что
A, sin 9
-2/Ш/©/,
Л, cos 9, =(? — ©?) a/f
и обозначив
dq
*(<*)
-с,
можно записать систему (8.41) в ином виде:
N
(р2 + 2np + q — со?) ai -f atc 2 НЧ — 2ai®i (n + P)^i = °>
k = i
2(Di(n + p)ai + ai(p2 + 2np + q-«><?)bi = 0.
(8.42)
Нулевое решение линейной системы (8.42) устойчиво, если
отрицательны вещественные части корней ее характеристического
7 М. 3. Коловский
98 НЕКОТОРЫЕ ПРИБЛИЖЕННЫЕ МЕТОДЫ [ГЛ. I
уравнения. Как показано в [18], это характеристическое уравнение
может быть записано в следующей форме:
VI о p2-\-2np-\-q — со?
1 + 2с V а] -г-; ZJ -0 5" = °- (8-43)
В рассматриваемом случае порядок полученного
дифференциального уравнения для параметров аь и 0/ не совпадает с
порядком исходного дифференциального уравнения. Устойчивость по
Ляпунову полигармонического решения исходного уравнения
обеспечивается в том случае, если при малых возмущениях остаются
малыми вариации х и х\ устойчивость «положения равновесия»
системы (8.38)—(8.39) означает малость вариаций всех амплитуд и
фаз. Учитывая это, следует весьма осторожно использовать
полученный критерий устойчивости. Как показано в [18], на практике
полезно использовать лишь одно из необходимых условий
устойчивости системы (8.42) — условие положительности свободного
члена характеристического уравнения
N 2
VI о q — со7
1 + С L ** 7 242 ,\ 2 2 > °- <8-44)
Мы ограничимся рассмотренными здесь примерами
исследования устойчивости стационарных решений нелинейных
дифференциальных уравнений. Более подробно этот вопрос рассмотрен
в ряде работ I1, 3> 35], где использованы более строгие
математические методы.
Отметим, что в теории виброзащитных систем вопрос об
устойчивости стационарных решений не имеет такого значения, как,
например, в теории автоматического управления. Ниже будет
показано, что при исследовании резонансных явлений в виброзащитных
системах основное внимание должно уделяться анализу условий
существования, а не условий устойчивости.
ГЛАВА II
УПРУГИЕ АМОРТИЗАТОРЫ И ИХ ДИНАМИЧЕСКИЕ
ХАРАКТЕРИСТИКИ
§9. Динамические характеристики упругих амортизаторов
Основными элементами виброзащитных систем,
рассматриваемых в этой книге, являются упругие амортизаторы.
Известно большое число конструктивных разновидностей
амортизаторов. Наиболее существенной частью
виброзащитного амортизатора 'любой конструкции является упругий
элемент — деталь, обладающая большой податливостью
и способная служить механическим фильтром низких частот.
Любой амортизатор обладает также устройствами для крепления
упругого элемента к амортизируемому объекту и к
колеблющемуся основанию (рис. 20—22).
Простейшими амортизаторами могут служить обычные
цилиндрические витые пружины, или резиновые шнуры, на
Рис. 20.
которых амортизируемый объект подвешивается к
колеблющемуся основанию. Широко распространены резино-метал-
лические амортизаторы различной конструкции (рис. 20),
7*
100
УПРУГИЕ АМОРТИЗАТОРЫ
[ГЛ. II
в которых резиновый упругий элемент («резиновый массив»)
привулканизирован к металлическим деталям крепления.
Недостатком резиновых упругих элементов является
их чувствительность к температуре окружающей среды,
Рис. 21.
влажности, способность к окислению и т. п. Под влиянием
всех этих факторов резино-металлические амортизаторы
изменяют свои упругие
свойства. От этих недостатков
свободны металлические
пружинные амортизаторы.
В последние годы все
большее распространение
получают демпфированные
амортизаторы, снабженные
специальными устройствами
для рассеяния энергии
колебаний — демпферами.
В амортизаторах серии AD
(рис. 21) использован
воздушный демпфер. При
деформации амортизатора,
вызванной перемещением
штока /, происходит сжатие резинового баллона 2; воздух
выходит из него через калиброванное отверстие 3. При этом
создается сила сопротивления, обеспечивающая
демпфирование. В амортизаторах серий ЛФД и АПН (рис. 22)
установлены демпферы сухого трения. Пластмассовые сегменты /
Рис. 22.
§ 9] ДИНАМИЧЕСКИЕ ХАРАКТЕРИСТИКИ АМОРТИЗАТОРОВ 101
прижимаются к корпусу 2 кольцевой пружиной 3. При
перемещении штока 4 возникает демпфирование.
Демпфирование колебаний осуществляется и в
амортизаторах, не снабженных специальными демпферами; там оно
происходит за счет внутреннего трения в упругом элементе.
Однако такое демпфирование обычно является слабым,
особенно в амортизаторах с металлическими упругими
элементами. Стремление увеличить демпфирование в
цельнометаллических амортизаторах, нечувствительных к изменениям
внешних условий, привело к появлению амортизаторов
с демпфером из металлической сетки и амортизаторов
с упругими элементами из прессованной металлической
проволоки.
Упругий элемент соприкасается с деталью, соединяющей
амортизатор с объектом, по некоторой поверхности,
называемой площадкой крепления. При практических расчетах
можно обычно пренебречь размерами
площадки крепления и говорить
о точке крепления амортизатора
к амортизируемому объекту (рис. 23).
Перемещения точки крепления
при колебаниях и ударных
воздействиях вызывают деформацию
упругого элемента, которая определяется
вектором и — перемещением точки
крепления относительно основания.
Силовая реакция амортизатора /?,
вызванная его деформацией, вообще
говоря, не противоположна по
направлению вектору и. Однако в любом упругом
амортизаторе могут быть определены три взаимно перпендикулярных
направления, обладающие тем свойством, что перемещение
точки крепления в одном из этих направлений вызывает
реакцию только противоположного направления. Такие
направления будут называться главными.
Проекции вектора и на главные направления
амортизатора будут обозначаться через и, v и wt а проекции
вектора /?, представляющего собой силу, действующую на
амортизатор, — соответственно через £/, Vt W.
Учитывая упругие и демпфирующие свойства реальных
амортизаторов, мы будем в дальнейшем предполагать, что
102
УПРУГИЕ АМОРТИЗАТОРЫ
[ГЛ. И
составляющие силы R по главным направлениям могут
зависеть только от соответствующих составляющих
вектора а и от первых производных по времени.
Соответствующие функциональные зависимости
V = V(v, v)t
W = W(w, w)
(9.1)
называются динамическими характеристиками
амортизатора.
Зависимости (9.1) носят приближенный характер. В
действительности, деформации упругого элемента в одном
из главных направлений вызывают изменение динамических
характеристик в других направлениях. Однако в большинстве
практических задач, особенно в тех случаях, когда
статическое нагружение амортизатора происходит в одном из
главных направлений, характеристики могут приниматься
в форме (9.1).
В дальнейшем, при анализе динамики виброзащитных
систем, предполагается, что в положении равновесия
(J = V=W = 0't u = v = w = 0. (9.2)
Тем самым исключаются из рассмотрения статические
нагрузки и статические реакции амортизаторов.
Для проведения статического расчета необходимо знать
статические характеристики амортизаторов, определяющие
зависимость статической реакции амортизатора Rs от его
статической деформации us\
Проектируя вектор Rs на главные направления и
предполагая, что величины проекций зависят только от
соответствующих компонент вектора статической деформации,
получим статические характеристики в следующей форме:
Ut = Ut(uj, Vs = Vs(vs), Ws = Ws(ws), (9.4)
Динамические характеристики амортизатора (9.1)
существенно зависят от его статических характеристик; в боль-
§ 9] ДИНАМИЧЕСКИЕ ХАРАКТЕРИСТИКИ АМОРТИЗАТОРОВ ЮЗ
шинстве случаев можно принять, что
U (и, 0) = £/,(«,+ «)-!/,(в,).
V(v. 0) = Vs(vs + v)-Vs(vs),
W («, 0) = Ws (ws + w) — Ws (ws),
(9.5)
то есть что полная динамическая реакция амортизатора при
и = 0 не отличается от его статической реакции при той же
деформации.
Динамические и статические характеристики
амортизаторов являются, вообще говоря, нелинейными. Их нелинейность
может обусловливаться:
а) нелинейными упругими свойствами материала, из
которого изготовлен упругий элемент (например, резины);
б) конструктивными особенностями упругого элемента,
приводящими к нелинейности его характеристик (например,
использованием в качестве упругого элемента фасонной витой
пружины, жесткость которой зависит от деформации);
в) наличием внутреннего трения в материале упругого
элемента, которое всегда носит нелинейный характер;
г) применением нелинейных демпферов (например,
демпферов сухого трения);
д) ограниченностью габаритных размеров амортизатора,
приводящей к неизбежному появлению упругих или жестких
ограничительных упоров.
В классической линейной теории виброзащитных систем
рассматриваются малые .колебания амортизируемого объекта
вблизи положения равновесия. Предполагая, что составляющие
вектора а и их производные по времени являются малыми,
можно произвести линеаризацию динамических характеристик,
основанную на разложении функций (9.1) в ряд Маклорена
и пренебрежении членами разложения, имеющими порядок
малости выше первого
U(и, и)'-
— (0. 0)a + -^(0, 0)i:
ди ди
dV
dv
cW
(0, 0)v
dV
dv
(0, 0)V:
•■cuu + buu,
■ cvv + bvvt
(0, 0) w-\ —
uw dw
(0, 0)w = cww-\-bww.
(9.6)
104 УПРУГИЕ АМОРТИЗАТОРЫ (ГЛ. It
Коэффициенты си> cv, cw называются жесткоетями
амортизатора в главных направлениях, a bu, bv> bw —
коэффициентами демпфирования. Очевидно, что при нелинейных
динамических характеристиках жесткости и коэффициенты
демпфирования зависят от статических деформаций. Для
некоторых видов амортизаторов жесткости и коэффициенты
демпфирования остаются постоянными, если значения us, vs, ws
удовлетворяют неравенствам
«;<«,<*:• <<^«. <<«,«. о.?)
В этих случаях говорят, что условия (9.7) определяют
область линейности амортизатора.
Линеаризация динамических характеристик допустима,
dU
как известно, в том случае, если производные -?—,
dU
—г-,.. . существуют и непрерывны при нулевых значениях
ди
аргументов. Это условие в некоторых практически важных
случаях не выполняется (например, в амортизаторах с сухим
трением). В этих случаях мы будем говорить, что
амортизатор является существенно нелинейным. В системах
с существенно нелинейными амортизаторами даже малые
колебания не могут быть исследованы с помощью класси- I
ческой линейной теории. j
Учет нелинейности динамических характеристик является \
необходимым при исследовании колебаний большой ампли- \
туды. Как уже отмечалось выше, в виброзащитных системах
такие колебания являются обычно нежелательными, а
нелинейность динамических характеристик часто является
причиной их появления.
§ 10. Некоторые формы динамических характеристик
Расчет нелинейных виброзащитных систем является обычно
приближенным. Поэтому и динамические характеристики
амортизаторов могут задаваться в приближенном виде, |
аппроксимироваться простыми аналитическими зависимостями. |
Мы рассмотрим теперь некоторые, часто встречающиеся на |
практике, формы нелинейных динамических характеристик |
и укажем, какие аналитические зависимости могут быть |
использованы для их приближенного аналитического пред- я
§ Ю] НЕКОТОРЫЕ ФОРМЫ ДИНАМИЧЕСКИХ ХАРАКТЕРИСТИК 105
ставления. При этом мы ограничимся рассмотрением одной
характеристики U(и, и), имея в виду, что две другие
могут иметь аналогичные формы.
Функцию U (и, и) обычно
можно представить в виде суммы
U (и, u) = Uy(u) +
+ Ud(u, и). (10.1)
us
иу
0
[/
0'
us
/
и
V"
Рис. 24.
Здесь Uy (и) — упругая
характеристика (упругая сила); в
соответствии с (9.5) можно принять
U7(u) = Us(us+tt) —
-Us{us), (10.2)
то есть упругая характеристика может быть получена из
статической характеристики переносом начала координат
в точку (us, Us) (рис. 24). Упругая сила Uy(u) является
консервативной; при деформации амортизатора работа этой
силы переходит в потенциальную
энергию:
П(й) = f Uy(u)du (10.3)
Второе слагаемое в (10.1)
называется диссипативной силой; оно
характеризует демпфирующие свойства
амортизатора, его способность рассеивать
механическую энергию колебаний, пре- Рис. 25.
вращая ее в тепловую энергию. Если
произвести последовательно нагружение и разгружение
амортизатора (рис. 25), то работа упругой силы за цикл будет
равна нулю (потенциальная энергия в начальном и конечном
состоянии одинакова). Рассеянная энергия (соответствующая
площади 5 «гистерезисной петли») будет равна работе
диссипативной силы
(10.4)
S = &L?d (и, и) da.
Разделение усилия, действующего на амортизатор, на
упругую и диссипативную силу носит bq многих случаях условный
106
УПРУГИЕ АМОРТИЗАТОРЫ
[ГЛ. II
характер. Если, например, диссипативная сила
представляет собой силу внутреннего трения в материале упругого
элемента, отделение ее от упругой силы оказывается
физически неосуществимым. Тем не менее представление реакции
амортизатора в форме (10.1) оказывается удобным при
анализе динамических явлений.
Рассмотрим некоторые наиболее типичные формы упругих
характеристик.
а) Если в качестве упругого элемента используется
металлическая пружина (витая или плоская), зависимость
упругой силы от деформации на
некотором участке носит линейный
характер
-*/ 0
с\/
Г\с'
d и
UY{u)
■ си.
(10.5)
Область линейности всегда
ограничена, поскольку ограничены
габариты амортизатора, его
«свободный ход».
б) При применении упругих
ограничителей хода зависимость
упругой силы от деформации
изображается ломаной линией (рис. 26). Аналитическое
выражение этой зависимости:
Рис. 26.
(Jу {и) — си
Uy (и) = cf(u — d)-\- cd
Uу (и) = с"> + dx) — cdx
при
при
при
— dx < и < d
u>d,
u<—d1.
(10.6)
Жесткости ограничителей с' и с" обычно во много раз
больше жесткости основного упругого элемента с. Иногда
они настолько велики, что могут считаться бесконечно
большими (рис. 27). В этих случаях при работе амортизатора
могут происходить жесткие удары об ограничитель,
сопровождающиеся «мгновенным» изменением скорости и.
Для симметричного амортизатора с упругими упорами
(с' = с" = к2с, d = d{) имеем
Uy (и) = си
U у (и) — %2си
(и2
при |й|<;*/,
\)cds\gnu при .|«|></.
(10.60
§ 10] НЕКОТОРЫЕ ФОРМЫ ДИНАМИЧЕСКИХ ХАРАКТЕРИСТИК 107
в) Переход от линейной области к ограничителям может
носить плавный характер (рис. 28). Характеристика такого
вида получается при использовании фасонных витых
металлических пружин (например, конических). Точные
аналитические выражения упругих сил для пружин различной формы
d и
Рис. 27.
Рис. 28.
приводятся в [41]. Однако они слишком сложны для
практического использования.
С достаточной для практики точностью упругую силу
этого вида можно описать одной из следующих зависимостей:
Uy = cu
Uv = cd-
2с (Л — d)
te
2 (Л — d)
Uy — —cdx
2c (</,-*,)
tg
при —rf1<tt<^,
(u — d) при d < и < Д,
■(« + <*i)
или
Uy = cu
U, = cd + ±£=4-(*-d)
Д —и
2(d,-A,)
при — At < и < — dx
(10.7)
при —dl<^u^,d,
при d <и < A,
U, = -cdi- °(f; + ЦД1) (« + rfi) при _A1<B<_dl.
(10.8)
108
УПРУГИЕ АМОРТИЗАТОРЫ
[ГЛ. II
Нетрудно убедиться, что при этом сохраняется
непрерывность производной U' при u — d и и =— dy
Для симметричных амортизаторов (Д = Д1, d = d{)
получаем соответственно
t/v
: CU
Uy = cd sign и -
при |я|<^, )
2с (Л — d) . Г я , . . л
при d < |а| < Д
(10.70
при |«|<tf,
.JA^^(u-dsignu) при Д>М>^
(10.80
г) У амортизаторов с резиновым упругим элементом
область линейности практически отсутствует. Упругая сила
может быть аппроксимирована соотношениями вида (10.7)
или (10.8), если в них положить ^ = ^ = 0. Для
характеристики (10.7) получаем при этом:
или
U у —си
Uу = cd sign и -
Uv
2сА . пи
л g 2А
*^У Jt ^ 2А2
при Д > и > 0,
при —Дх < и < 0.
Для симметричного амортизатора
^у= —*2д- при И<Д.
Соответственно для характеристики вида (10.8)
при Д > и > 0,
У А — и
cAiW
(10.9)
(10.9')
(10.10)
"t—^fSt при -д1<и<°-
*Л, = -—",."1- .. при |«|<Д. (10.10')
и в симметричном случае
с Ди
Д — и sign и
§ 10] НЕКОТОРЫЕ ФОРМЫ ДИНАМИЧЕСКИХ ХАРАКТЕРИСТИК Ю9
д) В некоторых задачах удобно аппроксимировать
упругую силу полиномом. При этом обычно можно ограничиться
трехчленным выражением
Uy (и) = си + du2 + ей*. (10.11)
Для симметричных амортизаторов следует принять ^ = 0
Uy(u) = cu + eu* (10.110
или умножить квадратичный член на sign и
Uy (и) = си + du2 sign и + ей*. (10.11")
е) Упругая характеристика амортизатора с начальным
натягом (см. § 2):
Uy — cfu-\- f при и > 0, |
{Jy^c"a — fx при к<0. J (10Л2)
Для симметричного амортизатора (сг = с'7 = с; / = Д):
£/y = a* + /signw. (10.120
Рассмотрим некоторые виды диссипативных сил,
встречающихся в реальных амортизаторах.
а) Выражения (9.6) показывают, что для малых колебаний
можно считать диссипативную силу линейной функцией
скорости
Ud(u. u) = bu, (10.13)
если только она не является существенно нелинейной. Для
больших деформаций выражение (10.13) может считаться
справедливым только при использовании в системе демпфера
вязкого трения. Однако такие демпферы в виброзащитных
амортизаторах применяются редко: они конструктивно сложны
и слишком чувствительны к изменениям внешних условий.
Линейную характеристику вида (10.13) имеют и демпферы
индукционного типа, в которых диссипативная сила
возникает при перемещении проводника с током в магнитном поле:
такие демпферы также редко применяются в виброзащитных
системах.
б) Диссипативная сила, возникающая в демпфере сухого
трения, вследствие закона Амонтона — Кулона, имеет
следующую характеристику:
Ud(ut и) = Н sign и, (10.14)
110
УПРУГИЕ АМОРТИЗАТОРЫ
[ГЛ. И
L
о
где Н—сила сухого трения, пропорциональная силе
нормального давления на соприкасающихся поверхностях.
Многочисленными опытами установлено, что коэффициент
пропорциональности (коэффициент трения) зависит от
скорости скольжения, материала и ка-
н чества обработки соприкасающихся
поверхностей.
Примерный вид зависимости
коэффициента трения от скорости
показан на рис. 29. В первом
приближении можно считать, что при
и Ф 0 сила трения постоянна
(трение движения Нд)\ при относитель-
Рис. 29. ном покое {и = 0) сила трения может
равняться любой величине от нуля
до некоторого значения Нп (трение покоя),
соответствующего началу движения. Как известно, трение покоя обычно
больше трения движения.
В работе [28] показано, что величина трения покоя
существенно зависит от интервала времени, в течение которого
соприкасающиеся поверхности
находились в состоянии относительного
»—, покоя (время выстоя т на рис. 30).
/ Если движение происходит без оста-
» новок (например, по гармоническому
закону), то есть если время, в
течение которого скорость скольжения
близка к нулю, является достаточно
q ; ^ малым, то можно принять, что
Нп = Нд = Н. Такое предположение
Рис. 30. в дальнейшем будет принято при
исследовании колебательных
режимов без остановок. При исследовании движений с
остановками (а такие движения, как будет показано ниже, возможны
в системах с сухим трением) приходится различать трение
движения и трение покоя.
в) Исследованию диссипативных сил, возникающих за счет
внутреннего трения в материале, посвящена обширная
литература I38]. Однако аналитические зависимости, выражающие
диссипативную силу через мгновенные значения деформации
Ъ
§ IUj НЕКОТОРЫЕ ФОРМЫ ДИНАМИЧЕСКИХ ХАРАКТЕРИСТИК Ш
и ее скорости, в литературе отсутствуют. Более того, в
результате многочисленных экспериментов установлено, что
получение таких зависимостей вообще не представляется
возможным.
Действительно, эксперименты, проводившиеся при
деформации упругих элементов по гармоническому закону,
показали, что для большинства материалов величина силы
внутреннего трения практически не зависит от частоты
гармонического процесса (если только эта частота не слишком
мала). Этот факт можно было бы удовлетворительно
согласовать с динамической характеристикой вида Uгд(и, и) только
в том случае, если бы последняя имела такую форму:
Цд (#, и) = £/т (и) sign и.
(10.15)
А к
и,
Рис. 31.
При характеристике иного вида неизбежна зависимость силы
от частоты колебаний. Для характеристики вида (10.15)
гистерезисные петли будут иметь форму, показанную на
рис. 31, то есть ширина петли по
оси ординат не будет зависеть от
амплитуды деформации. Однако это
расходится с экспериментами,
которые свидетельствуют о
существенном влиянии амплитуды на ширину
гистерезисной петли.
Удовлетворительное объяснение
экспериментальных фактов,
по-видимому, возможно лишь при
предположении, что величина силы внутреннего трения зависит не
от мгновенных значений и и и, а от всего закона
изменения u(t) на протяжении некоторого интервала времени,
предшествующего рассматриваемому моменту. Такая трактовка
внутреннего трения не противоречит существующим взглядам
на его физическую природу.
Практически все это означает, что функция UT(u) в (10.15)
должна зависеть от некоторых параметров, характеризующих
процесс и (t) в среднем на некотором интервале времени.
Для гармонического процесса такого рода параметром
является амплитуда.
Различными авторами предложено большое число формул,
выражающих зависимость силы внутреннего трения от ампли'
112 УПРУГИЕ АМОРТИЗАТОРЫ [ГЛ. II
туды гармонической деформации. Многие из этих формул
приведены в работе [38]. Впрочем, при приближенном анализе
колебательных явлений, при которых деформация изменяется
по гармоническому закону, или близка к гармонической,
нас обычно интересует не сама сила, являющаяся
периодической функцией времени, а лишь ее первая гармоника.
Как было показано в гл. I, это означает, что в выборе
формы зависимости £/#(#, а) допустим некоторый произвол.
В связи с этим Е. С. Сорокин и Я. Г. Пановко предложили
такую формулу для силы внутреннего трения, которая
существенно упрощает анализ:
Ud(u9 и) = $а» j/l — ^ sign и. (10.16)
Здесь р и \х—параметры, характеризующие свойства
материала, а—амплитуда гармонических колебаний.
Следует подчеркнуть, что формула (10.16) пригодна
только для анализа колебаний, близких к гармоническим.
Учитывая, что при этом
и = a sin at, 1/1 —-т = | cos ®t |.
1 2~ si&n u>
можно записать формулу (10.16) в более простом виде
(О
Ud(u, и) = $?-—и, (10.17)
то есть произвести гармоническую линеаризацию диссипа-
тивной силы.
Вопрос о выражении силы внутреннего трения через
параметры полигармонического процесса до сих пор в
литературе не рассматривался.
§ 11. Линеаризация и экспериментальное исследование
динамических характеристик
При исследовании многих колебательных процессов,
возникающих в виброзащитных системах, динамические
характеристики амортизаторов могут быть линеаризованы с помощью
одного из методов, описанных в гл. J,
§ 11] ЛИНЕАРИЗАЦИЯ ДИНАМИЧЕСКИХ ХАРАКТЕРИСТИК ИЗ
Выбор метода линеаризации определяется характером
исследуемых колебательных явлений. При анализе малых
колебаний вблизи положения равновесия динамические
характеристики, если только они не являются существенно
нелинейными, могут быть линеаризованы в соответствии с
формулами (9.6). При исследовании установившихся колебаний,
сопровождающихся значительными деформациями,
линеаризованная характеристика может быть записана в форме:
£/(«, k) = U0+cluu* + bMu. (11.1)
Здесь и0—разность между деформацией а и ее постоянной
составляющей а0; £/0, сли, ^„--коэффициенты, зависящие
от параметров колебательного процесса.
В дальнейшем U0 будет называться динамической
постоянной составляющей; ст— динамической жесткостью; Ьда —
динамическим коэффициентом демпфирования. Пока речь идет
только о характеристике в направлении оси #, индексы „#а
при сш и Ьш могут быть опущены.
Если предполагается, что колебания, возникающие в
виброзащитной системе, близки к гармоническим (такое
предположение часто оказывается справедливым, если на систему
действует гармоническое вибрационное возмущение), то коэф-
фициеты U0, сд, Ьл являются коэффициентами гармонической
линеаризации.
Полагая в этом случае
и — а0 + a cos ayt (11.2)
и учитывая, что динамическая характеристика может быть
представлена в форме (10.1), по формулам (3.15) — (3.17)
получаем
2я
a° = i \ tfy(«o+«cosW^ = £/0(a0. a), (11.3)
о
2Я
сд = — uy(aQ + a cos ф) cos Ф d-ty = cA(a0, a), (11.4)
2л
1
А . лаю
б
^Л?(#оН~ ясоэ/ф, —acDSinij))sin,i|5d,i|5 =
= bA(aQ, а, со). (11.5)
§ М. 3. Коловский
П4 УПРУГИЕ АМОРТИЗАТОРЫ [ГЛ. II
Формула (11.5) может быть преобразована:
2Я
Ьл= t/a(a0-[- acosij), —acosin^)^ (acosi|)) =
0
= -i-a &Ud(u, ii)du = -?-T, (Ц.6)
где 5 — площадь петли гистерезиса, соответствующей на-
гружению по гармоническому закону с амплитудой а и
частотой со.
Таким образом, величина коэффициента Ьк зависит только
от площади петли гистерезиса, амплитуды и частоты
колебаний. Именно по этой причине при исследовании колебаний,
близких к гармоническим, можно не интересоваться формой
гистерезисной петли.
При исследовании полигармонических колебательных
процессов удобно пользоваться методом линеаризации по
функции распределения. Для линеаризации нелинейной упругой
силы можно воспользоваться формулами (5.20) и (5.22):
щ
иу0= f Uy(u)w(u)du, (11.7)
и,
и2
с1 = Jf { Uy (*) (« ~ ао) ™ («) du. (11.8)
и и,
При линеаризации диссипативной силы, в соответствии
с формулами (5.68) — (5.70), получаем
и2 v2
Uo= Г Г Ud(u, v)w(u, v)dudv, (11.9)
и2 v2
~~Y (и— a0)Ud(u, v)w(u, v)dudv, (11.10)
u и, vx
u2 v2
&д = -у vUd(u, v)w(u, v)dudv. (H.ll)
c\
«i vx
§ 11] ЛИНЕАРИЗАЦИЯ ДИНАМИЧЕСКИХ ХАРАКТЕРИСТИК 115
Для всех видов диссипативных сил, рассмотренных выше,
имеем
Следовательно,
£/S-o,
U0=Ub, сд = с1.
:0.
Выражение для динамического коэффициента
демпфирования можно преобразовать, учитывая соотношение (5.66):
«2 ^2
а = * I [vUd(utv)lim [ b[u—u{t)]b[v—u(t)]dtdudv=
о:. J J г->оо J
1 ,. If-
-s- lim — й
o£ Г-»оо Г J
(t)Ud[u(t), ii)]dt:
К
cp
(11.12)
где jVcp — средняя мощность диссипативной силы
процесса и (t)> вычисленная для бесконечного интервала времени.
Во многих случаях динамические характеристики упругих
амортизаторов не могут быть получены на основе
теоретического анализа и должны определяться экспериментальным
путем. Очевидно, что при этом можно не разыскивать форму
функциональных зависимостей
вида (9.1), а непосредственно
определять динамические
коэффициенты линеаризации.
На практике удается
определить коэффициенты
гармонической линеаризации (11.3)—
(11.5). Для их определения
может быть предложено несколько
способов.
а) По первому способу
амортизатор деформируется по
гармоническому закону (например, при помощи пульсационной
машины). При этом производится запись законов изменения
во времени деформации и усилия (рис. 32). Затем
производится гармонический анализ функции U (t), причем вычисляются
постоянная составляющая и коэффициенты Фурье при первых
8*
116
УПРУГИЕ АМОРТИЗАТОРЫ
[ГЛ. И
гармониках. Как было показано в § 3, имеют место
следующие соотношения:
2л
ю
СО
^о = ^- I U(t)dt,
о
со
. = — Г U (t) cos ®tdt.
2п
bR = — — Г t/(Osin<o*<tt.
д па J w
(11.13)
Коэффициенты t/0, сд, Ьл определяются для различных
значений а0, а, со. Результаты эксперимента позволяют
построить графики зависимости коэффициентов линеаризации
от параметров.
б) Второй способ основан на анализе свободных
колебаний массы, установленной на исследуемом амортизаторе.
Установив некоторую массу на
нескольких одинаковых, симметрично
расположенных амортизаторах, получим систему,
которая при колебаниях, направленных
по оси симметрии (ось и на рис. 33),
может рассматриваться как система с одной
степенью свободы.
Дадим системе начальное отклонение
и запишем возникающие при этом
свободные колебания. Если диссипативные
силы, действующие в системе, достаточно малы, то
колебания будут медленно затухать, так что в пределах одного
периода процесс может считаться близким к гармоническому
(рис. 34). Анализируя каждую волну, ,можно определить
смещение середины размаха а0> амплитуду а, частоту со,
то есть построить скелетную кривую. Сравнивая величины
двух последовательных размахов, можно определить (для
соответствующих значений амплитуды и частоты) величину
динамического коэффициента демпфирования. Действительно,
г
Рис. 33.
§ It] ЛИНЕАРИЗАЦИЯ ДИНАМИЧЕСКИХ ХАРАКТЕРИСТИК 117
на протяжении одного периода ЬА может считаться
постоянным, то есть уравнение затухающих колебаний в течение
периода запишется в форме
ти° + by + сди° -+-1/0 = 0,
(1Ы4)
где т — масса, приходящаяся на один амортизатор, сА—
динамическая жесткость, ЬА — динамический коэффициент
демпфирования. Решая уравнение (11.14), находим (для движения
в течение одного периода)
и ж ae~nt cosotf-f- aQ,
где
0):
V т ' п 2т'
Таким образом,
сд = яш2,
, com ,
Д/-1
1^
к
ГА 1
\ /
\ */.
Г
1
\
\
1
\
NJ
/7
1/
Рис. 34.
где av at^x—значения амплитуды на данном и на
предыдущем периоде.
в) Такой способ пригоден только для систем со слабым
демпфированием; при наличии более эффективных диссипа-
тивных сил приходится определять коэффициенты
линеаризации в режиме вынужденных колебаний при гармоническом
вибрационном воздействии.
Движение системы в этом случае описывается следующим
линеаризованным уравнением:
т и0 + U0 -f- Ьяй° + сАи° = Л cos ayt.
(11.15)
Определив экспериментальным путем амплитуду а и фазу <р
возникающих при этом «гармонических» колебаний, можно
найти с
и ЬА из уравнений, аналогичных (3.25) и (3.26):
т&2А
а —
V{c
-ГП(д'
У+ьу
tgqp =
6д<0
(11.16)
ш>— с.
118 УПРУГИЕ АМОРТИЗАТОРЫ [ГЛ. II
Решение этих уравнений значительно упрощается, если
найти такой режим (то есть выбрать такие значения Л и со),
чтобы сдвиг по фазе между вынужденными колебаниями и
вынуждающей силой равнялся у. При этом tgcp = oo и,
следовательно,
сА = тсо2,
. т«А (И-17)
*д = —Г- ■
ГЛАВА III
НЕЛИНЕЙНЫЕ СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ
СВОБОДЫ
§ 12. Вынужденные колебания
при гармоническом вибрационном воздействии
и силе сопротивления, пропорциональной скорости
Рассмотрим виброзащитные системы с одной степенью
свободы, принципиальные схемы которых приведены на
рис. 2, а и б. Уравнение движения каждой из этих систем
может быть записано следующим образом:
mu+U(u> u) = Q(f). (12.1)
Здесь т—масса амортизируемого объекта; и — деформация
упругого амортизатора, отсчитываемая от положения
статического равновесия; U — сила, приложенная к амортизатору
в направлении оси и\ Q{t) — вибрационное воздействие,
представляющее собой либо активную силу, либо силу инерции
объекта в его переносном движении (то есть произведение
массы на ускорение основания, взятое с обратным знаком).
В этой главе будут исследованы некоторые частные
случаи виброзащитных систем с одной степенью свободы,
движение которых описывается уравнением (12.1).
Предположим сначала, что диссипативная сила
пропорциональна скорости деформации амортизатора; тогда сила,
действующая на амортизируемый объект, может быть
представлена в следующей форме:
U(и, й) = иу(и) + Ьи, (12.2)
где b — постоянный коэффициент.
120 НЕЛИНЕЙНЫЕ СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ [ГЛ. III
Предположим также, что вибрационное воздействие
является гармонической функцией времени:
Q(t) = F cos at. (12.3)
Такое воздействие имеет место при вибрационных испытаниях
различных объектов с помощью гармонических вибраторов
и вибрационных стендов, при наличии в системе
вращающейся неуравновешенной массы и во многих других случаях.
Подставив (12.2) и (12.3) в уравнение (12.1), получим
та + Ьи + Uy (a) = F cos cot. (12.4)
Решение этого уравнения будем искать в форме
и = а0 + и0 (t) — a0-f- a cos (со/ + ф) (12.5)
с помощью метода гармонической линеаризации. Используя
формулы (11.3) и (11.4), линеаризуем нелинейную упругую
силу
Uy^U0(a0, а) + сд(а0, а) и0, (12.6)
где
2л
и^1К \ ^уК+ясозгЮ^ (12.7)
о
2я
сд = — t/y^o+acosiWcosil)^. (12.8)
о
Подставив (12.6) в (12.4), получаем линеаризованное
уравнение
ти* + bifi + U ^+с jp*==F cos ®tt (12.9)
имеющее ту же форму, что и уравнение (3.23).
В соответствии с (3.24) — (3.26), получаем следующие
уравнения для определения смещения середины размаха а0,
амплитуды колебаний а и сдвига по фазе между колебанием
и вибрационным воздействием ср:
[У0(а0, а) = 0. (12.10)
Fi (12.11)
У (Я2 — а>2)2 + 4л2со2 '
2п(д
да1 —V '
*Ф = -=Йт. (12Л2)
}
§ 12] ГАРМОНИЧЕСКОЕ ВОЗМУЩЕНИЕ 121
где
с, (я0, a) b F
А,2 = д , л = -5—. Fx= — . (12.13)
Очевидно, что связь между смещением середины размаха и
амплитудой, определяемая уравнением (12.10), остается
такой же, как и при свободных колебаниях. Сравнивая
выражения (12.8) и (2.14), легко убедиться, что Х(а0, а)—частота
свободных колебаний, имеющих амплитуду а и смещение
середины размаха а0. Если с помощью уравнения (12.10)
выразить а0 через а, можно получить в явном виде
зависимость А. (а), то есть уравнение скелетной кривой
2л
^(a) = -^=i J" U7[a0(a)+acosWcos$dy. (12.14)
о
Подставив А, (а) в уравнение (12.11), можно определить
амплитуду. Решение этого уравнения удобнее всего производить
графическим способом.
Построим для этого график
зависимости а (к), рассматривая А,
в выражении (12.11) как
независимый параметр. При малых
значениях п (что, кстати говоря,
характерно для большинства
виброзащитных систем) этот
график будет иметь форму,
показанную на рис. 35.
Нанесем на этот же
график скелетную кривую A, (a), q ^
Точки пересечения обеих кри- рис 35,
вых определяют решения
уравнения (12.11). Из рис. 35 видно, что в случае нелинейной
упругой силы уравнение (12.11) может иметь несколько
решений. Это означает, что в рассматриваемой системе возможно
установление различных колебательных режимов, близких
к гармоническому, отличающихся амплитудой и фазой. Какой
из этих режимов будет устанавливаться в действительности,
зависит от начальных условий. В практических задачах
начальные условия обычно не являются определенными, они
зависят от многих случайных факторов; поэтому приходится
122 НЕЛИНЕЙНЫЕ СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ [ГЛ. III
считаться с возможностью возникновения любого из найденных
режимов.
Множественность установившихся решений — одна из
характерных особенностей неавтономных нелинейных систем,
с которой нам в дальнейшем придется неоднократно иметь
дело.
Во многих виброзащитных системах частота
вибрационного воздействия может принимать различные значения. Так,
например, неуравновешенная масса может вращаться с
различной угловой скоростью, стол вибростенда может колебаться
с различной частотой и т. п. Если изменять величину со и
для каждого ее значения определять амплитуду а из
уравнения (12.11), можно получить амплитудно-частотную
характеристику системы а (со). Графическое изображение
этой зависимости называется обычно резонансной кривой.
Прежде чем перейти к исследованию формы резонансных
кривых, отметим, что в реальных системах амплитуда
вынуждающей силы F является обычно функцией частоты со.
Если, например, Q(t) представляет собой составляющую
центробежной силы, вызванной вращением неуравновешенной
массы со статическим моментом |ы, то F = tuo2, то есть
амплитуда вибрационного воздействия пропорциональна квадрату
частоты. Такая же зависимость имеет место и в случае
пассивной виброзащитной системы, если амплитуда колебаний
основания не зависит от частоты и равна £0. При этом
F^m^Qto2. Возможны и другие формы зависимости F от со.
Поэтому в общем случае уравнение амплитудно-частотной
характеристики должно быть записано в таком виде:
а= г FlW (12.15)
V[X2(a) — со2]2 + 4л2со2
Это уравнение и определяет резонансную кривую.
Найдем точки пересечения резонансной и скелетной кривых.
Если в уравнении (12.15) принять, что А, = со (в точке
пересечения должно, разумеется, выполняться это равенство), то
получится следующая зависимость амплитуды от частоты:
-f,W (12.16)
2п(д
Это уравнение определяет на плоскости (а, со) некоторую
кривую, являющуюся геометрическим местом точек пересече-
§ 12]
ГАРМОНИЧЕСКОЕ ВОЗМУЩЕНИЕ
123
ния резонансных кривых со скелетными. Эта линия пересекает
скелетную кривую, соответствующую заданной упругой
характеристике, в тех же точках,
что и резонансная кривая
(точка А на рис. 36).
Поскольку Fx (со) > О,
а знаменатель выражения
(12.15) при любых
значениях Я, и со превышает 2жо,
точки резонансной кривой
должны располагаться (при
тех же со) ниже точек
кривой (12.16).
Покажем теперь, что
кривые (12.15) и (12.16)
касаются друг друга в тех
точках, где cd = /L Для этого найдем производную da/da,
рассматривая (12.15) как зависимость а от со, заданную в
неявной форме:
Рис. 36.
da
d®
1
fr.-ttv+w И(co) [(^2 - <*?+4Л21,/2 -
— 2FX (со) [(I2 — со2)2 + 4я2со2Г72 X
x[<V-*)(x^-S-i)+w.]}
Отсюда
/ da \ F[ (X) 2nX — Fx (X) 2n F[ (X) X — Fx (X)
\d(d )(л=к
(12.17)
4л2Л2
2nX2
Это совпадает с выражением для производной от
функции (12.16) по со при со = Я.
Таким образом, построив скелетную кривую и линию (12.16),
можно судить о форме резонансной кривой в окрестности
точек пересечения ее со скелетной (точки А и Б на рис. 37).
Поведение резонансных кривых вдали от этих точек сущег
ственно зависит от вида функции /^(со) и формы скелетной
кривой. Пусть, например,
Fx (со) = Т7! = const.
(12.18)
Тогда кривая . (12.16) является гиперболой. С «жесткой»
124 НЕЛИНЕЙНЫЕ СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ [ГЛ. III
скелетной кривой эта гипербола может пересечься только один
раз (рис. 38); с «мягкой» скелетной кривой она может иметь
две точки пересечения (рис. 39) или не иметь ни одной
(рис. 40). Приравняв производную (12.17) нулю, найдем, что
экстремальные
(минимальные и максимальные)
значения амплитуда может
принимать при
со
Рис. 37.
©•=VV —2л*. (12.19)
Если 2п2<С ^2. то со*« А,,
то есть экстремальные
значения достигаются вблизи от
точек пересечения
резонансной кривой со скелетной.
Теперь легко показать,
что в зависимости от числа
точек пересечения скелетной
кривой с гиперболой (12.16) могут существовать
резонансные кривые трех видов (рис. 38—40). Наиболее типичным
является случай, показанный на рис. 38 и соответствующий
«жесткой» скелетной
кривой. Случаи, показанные на
рис. 39 и 40, на
практике встречаются
значительно реже.
Предположим, что
частота вибрационного
воздействия медленно изменяется,
так что при каждом ее
значении успевает установиться
режим вынужденных
колебаний. Определяя при
каждом значении частоты
амплитуду колебаний а, можно
построить резонансную кривую. Если при этом со
увеличивается (рис. 38), можно определить точки резонансной
кривой, соответствующие участку ЛМ. В точке М произойдет
срыв колебаний, амплитуда резко уменьшится до значения,
соответствующего точке Mf. При уменьшении частоты от
значения, соответствующего некоторой точке 5, удается по*
\°
к^^
\ А (о -А(а)
Я/А ^^^" 2nd)
/ 1 1
/ ^г^—■ В_
О)
Рис. 38.
§ 12]
ГАРМОНИЧЕСКОЕ ВОЗМУЩЕНИЕ
125
строить точки резонансной кривой на участке BN. В точке N
произойдет резкое увеличение амплитуды до значения,
соответствующего точке ЛГ. Получить колебательные режимы,
соответствующие точкам участка MN, вообще не удается,
поскольку, как будет показано ниже, соответствующие режимы
являются неустойчивыми.
«Срывы» резонансных
колебаний и «скачки» амплитуды
при изменении частоты
возмущения характерны для
нелинейных систем и часто
наблюдаются на практике.
Предположим теперь, что
амплитуда вибрационного
воздействия
пропорциональна квадрату частоты:
Fi(<*) = bfi?- (12.20)
В этом случае амплитуда
принимает экстремальные
значения также вблизи от точек пересечения резонансной и
скелетной кривой. Действительно, приравнивая нулю
производную da/da, найдем в этом
случае
а>
Рис. 39.
со*
X2
У~Х2 — 2п2
(12.21)
так что при 2п2 <С; к2 имеем
©•«а,.
Подставив (12.20) в
(12.16), получаем уравнение
прямой
1о
а =
2я
со, (12.22)
Рис. 40.
которая может пересекаться
с «мягкой» скелетной кривой
только в одной точке (при п ф 0); число точек пересечения
с «жесткой» скелетной кривой может быть различным. В
работе [21] показано, что в зависимости от числа точек
пересечения прямой (12.22) и скелетной кривой резонансные
кривые могут принимать различную форму. Некоторые наиболее
126 НЕЛИНЕЙНЫЕ СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ [ГЛ. III
типичные варианты показаны на рис. 41—43. В этом случае
характерной особенностью резонансных кривых является
возникновение дополнительных ветвей, соответствующих
колебаниям большой амплитуды. Появление этих ветвей означает,
что в системе с нелинейной
упругой силой и диссипа-
тивной силой,
пропорциональной скорости
деформации, гармоническое
вибрационное воздействие может
вызвать колебания большой
амплитуды даже в тех
случаях, когда частота этого
воздействия значительно
превышает частоту малых
свободных колебаний («соб-
~сй ственную» частоту системы).
Естественно, что при этом
упругий амортизатор не
только не защищает амортизируемый объект от
вибрационного воздействия, но даже усиливает это воздействие.
Существенно отметить, что такие явления могут возникать
и в тех случаях, когда результаты расчета, проведенного на
Рис. Ф1.
Рис. 42.
основе линейной теории, казалось бы, свидетельствуют о
противоположном. Действительно, рассмотрим в качестве
примера амортизатор с линейным упругим элементом и симме-
§ 12] ГАРМОНИЧЕСКОЕ ВОЗМУЩЕНИЕ 127
трично расположенными упругими упорами. Упругая сила
такого амортизатора имеет характеристику (10.б'). Скелетная
кривая для этого случая была определена в § 2. Изменяя
Рис. 43.
в формуле (2.28) обозначения в соответствии с (10.б'),
получаем
Я2(а) = ^[1+(н2-1)(1-^.Уа-^^2_1агС51п|)]
при а > а?,
о при а < d,
(12.23)
Х(а).
с
т
^2
где А0:
Скелетная кривая построена на рис. 44. Предположим
теперь, что прямая (12.22) проходит так, как показано на
рис. 44, то есть пересекает скелетную кривую в трех точках.
Это может произойти в том случае, если
d
2п ^'
(12.24)
Резонансная кривая при этом распадается на две ветви.
Нижняя ветвь целиком располагается в области линейности
упругого амортизатора; расчет по формулам линейной теории
приводит поэтому к неверному заключению о том, что
упругие упоры не играют никакой роли, поскольку даже в
128 НЕЛИНЕЙНЫЕ СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ [ГЛ. III
резонансном режиме колебания не выходят за пределы
линейного участка упругой характеристики. Существование
замкнутой дополнительной ветви ВС остается при этом незамеченным.
Между тем в действительности при (Oj < со < о>2 в системе
могут возникать опасные колебания большой амплитуды,
может происходить «стук об упоры» — явление, хорошо
известное тем, кто имеет дело
*Ж<о с виброзащитными систе-
мами.
Характерно, что
поведение системы при медленном
изменении частоты и
амплитуды вибрационного
воздействия также может в этом
случае существенно
отличаться от того, что
наблюдается при F — const. Если
резонансная кривая имеет
такой вид, как на рис. 43
со и 44, то при постепенном
изменении частоты резкие
скачки амплитуды колебаний
могут и не происходить;
можно пройти весь диапазон частот от 0 до сотах, находясь
на нижней ветви резонансной кривой, и не выйти на верхнюю
ветвь. Возбуждение колебаний большой амплитуды,
соответствующих точкам верхней ветви, может произойти в
результате случайного толчка, удара и т. п. Поэтому можно не
обнаружить возможности возникновения колебаний большой
амплитуды не только при проведении расчетов, но и при
лабораторных испытаниях.
Для устранения опасных резонансных явлений необходимо
при проектировании виброзащитной системы прежде всего
исключить возможность появления дополнительных ветвей
резонансных кривых. Из рис. 44 легко видеть, что для этого
следует либо уменьшить угол наклона линии (12.22) к оси
абсцисс, либо изменить форму скелетной кривой, сделав ее
более крутой. Но уменьшение угла наклона прямой (12.22)
означает (при заданном значении |0) увеличение
коэффициента п, то есть увеличение интенсивности диссипативных
сил; увеличение крутизны скелетной кривой неизбежно при-
Рис. 44.
§ 12]
ГАРМОНИЧЕСКОЕ ВОЗМУЩЕНИЕ
129
водит к увеличению «свободного хода» амортизатора, а
следовательно, и к увеличению габаритов виброзащитной системы.
Определим величину коэффициента демпфирования п*, при
которой устраняется опасность возникновения
дополнительной ветви резонансной кривой в системе с упругими
упорами. Для этого проведем из начала координат касательную
к скелетной кривой (рис. 44); если со* и а* — координаты
точки касания, то
loco*
п' = ■
2я*
(12.25)
При п>п* прямая (12.22) пересекается со скелетной
кривой в одной точке и дополнительная ветвь перестает
существовать. Тем самым устраняется опасность возникновения
«стука на упорах».
Во многих случаях упругая характеристика
ограничительных упоров амортизатора заранее неизвестна; тогда
представляет интерес следующая задача: выбрать величину
расстояния до упора d и коэффициента демпфирования п с таким
расчетом, чтобы при любой
упругой характеристике
ограничительных упоров стук на
упорах не мог возникнуть.
Если известна собственная
частота Х0, то участок
скелетной кривой, соответствующий
линейной части упругой
характеристики, есть прямая,
параллельная оси ординат (линия АВ
на рис. 45). Форма скелетной
кривой на нелинейном участке
зависит от упругой характеристики упоров; однако во всех
случаях скелетная кривая располагается выше линии ВС.
Можно сказать, что эта линия соответствует случаю
«бесконечно жестких» упоров.
Проведя прямую (12.22), легко убедиться, что при
жестких упорах возможны два вида резонансных кривых. Если
эта прямая не пересекает ломаную ABC (случай малого я),
то ветви резонансных кривых будут иметь такой вид, как
на рис. 45, то есть при этом стук на упорах будет возможен
на любой частоте, превышающей А,0. Если же прямая (12.22)
0
В С
1
7^
/
^_
А
Ч °
Рис. 45.
9 М. 3. КоловскиЙ
130 НЕЛИНЕЙНЫЕ СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ [ГЛ. Ill
пересечет ломаную ЛВС, то появится дополнительная ветвь,
совпадающая с линией ВС на участке DC (рис. 46).
В реальных системах амплитуда вибрационного
воздействия не может возрастать безгранично; соотношение (12.20)
остается справедливым только для значений (о, не
превышающих некоторого сотах. Если значение сотах известно, то
сформулированная выше
задача решается просто.
Необходимо, чтобы абсцисса
точки D превышала сотах,
тогда стук на упорах не
будет возникать. Аналитически
это условие выражается
в следующей форме:
i<>-<-A_. (12.26)
а
в
\ / j
в/ с
А
6>
2п
^max
Рис. 46.
Эта формула может быть
использована как для
определения величины свободного хода d, так и для определения
коэффициента сопротивления я.
Очевидно, что если частота со не изменяется от 0 до сотах,
а имеет некоторое фиксированное значение со0, то в
формуле (12.26) следует положить сотах = со0.
Для того чтобы устранить стук на упорах, часто
приходится делать свободный ход во много раз большим, чем
это требуется в соответствии с расчетом, выполненным по
формулам линейной теории. Проиллюстрируем это численным
примером.
Пусть на систему амортизации с собственной частотой
в 10 гц (Х0 = 62,8 l/сек) действует вибрационное возмущение
с частотой 100 гц (со = 628 \/сек) и амплитудой £0 =
= 0,1 мм. Коэффициент сопротивления п = 6 \/сек.
Требуется определить величину свободного хода d (упоры
расположены симметрично).
Если основываться на линейной теории, то можно
определить амплитуду деформации амортизатора по формуле
а —
So*2
V№-<*2)2 + 4n'
V
(12.27)
пол} чающейся при подстановке в (12.11) А, = А,0, Fx = 10(й2
§ 12]
ГАРМОНИЧЕСКОЕ ВОЗМУЩЕНИЕ
131
Подставляя в (12.27) значения А,0, я, со, получаем а =
= 0,101 мм. Для того чтобы при колебаниях с такой
амплитудой не происходило ударов об упоры, расстояние до
упора должно быть больше, чем амплитуда. Отсюда,
казалось бы, можно принять: d = 0A5 — 0,25 мм.
Однако этот вывод неправилен. В действительности
требуемая величина d должна определяться по формуле (12.26),
которая дает (при сотах = со0):
,>£_Wj« _„.,„.
Требуемый зазор в 50 раз превышает амплитуду
деформации, найденную по формуле (12.27)! Если же, например,
принять tf —0,25 мм, то для исключения возможности
возникновения стука об упоры необходимо в 20 раз увеличить
диссипативную силу.
При проведении практических расчетов обычно наиболее
трудной задачей является построение скелетной кривой,
особенно в тех случаях, когда упругая характеристика
амортизатора является несимметричной (а0 Ф 0). Для того чтобы
показать, каким образом могут быть преодолены
возникающие трудности, рассмотрим еще один пример.
Амортизируемый объект массой в 1 кг установлен на
линейном упругом амортизаторе, жесткость которого с =
= 40 н/см; ограничительные упоры установлены на
расстояниях:
верхний — d = 5 мм, нижний — dx = 3 мм от положения
равновесия; их жесткости соответственно равны с' = 1000 н/см
и с" = 640 н/см. Амплитуда гармонического вибрационного
воздействия зависит от частоты следующим образом:
Fi— 0,1со2 см/сек2 при со<;60я \/сек (|о=1 мм = const),
/71 = 360л2 см/сек2 = const при со > 60л \/сек.
Требуется определить величину коэффициента
сопротивления я, необходимую для исключения «стука на упорах».
В зависимости от значений а0 и а в системе с
несимметричными упорами могут возникнуть следующие
колебательные режимы:
а) колебания без ударов об упоры
a0+a<d, aQ—a>—di9 (I)
9*
132 НЕЛИНЕЙНЫЕ СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ [ГЛ. III
б) колебания с ударами только о верхний упор
aQ-{-a>d, a0 — a>—d1\ (II)
в) колебания с ударами только о нижний упор
a0-\-a<d, a^ — a^—d^ (III)
г) колебания с ударами о верхний и нижний упоры
aQ-{-a>d, a0 — a<—dv (IV)
Для дальнейшего исследования удобно в системе
координат (а0, а) построить линии a0~{-a = d и а0 — а = — dv
Рис. 47.
разделяющие полуплоскость а > 0 на четыре области, в
каждой из которых выполняется одно из условий (I) — (IV)
(рис. 47).
Далее, в тех же координатах следует построить
кривую (12.10); для этого необходимо знать в явном виде
аналитическую зависимость U0(a0, а). При этом удобно
пользоваться приближенным соотношением, полученным
с помощью формулы (5.50):
£/у(а0-0,924*0+t/y(a0— 0,383а) + £/у(а0+0,924а) +
+ £/у(а0+ 0,383а) = 0. (12.28)
§ 12] ГАРМОНИЧЕСКОЕ ВОЗМУЩЕНИЕ Ш
При выполнении условий (I), очевидно, должно быть
а0 = 0 (упругая характеристика линейная). Поэтому
в области (I) линия (12.10) совпадает с осью абсцисс
(участок О Л). Далее мы попадаем в область (III), то есть
начинаются удары о нижний упор. При а < -тгщг все че"
тыре точки упругой характеристики, в которых определяются
значения упругой силы, входящие в формулу (12.28), лежат
на линейном участке. Поэтому линия (12.10) на участке
di<a< -Щ4 (3 < а < 3,25)
по-прежнему совпадает с осью абсцисс (участок АВ). Далее
первая точка (и = а0 — 0,924а) попадает на участок упругой
характеристики, соответствующий нижнему упору; остальные
точки продолжают оставаться в области линейности.
Уравнение (12.28) принимает при этом такую форму:
с" (а0 — 0,924а + dx) — cdx + c (a0 — 0,383а) +
+ с (а0 + 0,924а) + с (а0 + 0,383а) = 0,
или
а0(3с + с") — 0,924а (с"— с)^^^" — с) = 0.
Это — прямая линия (участок ВС):
а0 = 0,73а —2,37. (12.29)
Координаты точки пересечения ее с линией a0-\-a = d — 5:
а = 4,25 мм, а0 = 0,75 мм
определяют значения амплитуды и смещения середины
размаха, при которых начинаются удары о верхний упор. С этого
момента линия (12.10) попадает в область (IV).
Построим теперь прямые
а0 — 0,924а = — йх (а), а0 + 0,924а = tf (у),
а0 — 0,383а = — dx (р), а0 + 0,383а = d (6).
При каждом пересечении линии (12.10) с одной из этих
прямых изменяется форма уравнения (12.28), поскольку при этом
одна из четырех точек, в которых определяются значения
упругой силы, переходит на другой участок упругой
характеристики.
134 НЕЛИНЕЙНЫЕ СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ [ГЛ. III
Первый излом линии (12.10) происходит в точке D:
а = 4,45 мм, а0 = 0,88 мм.
На следующем участке получаем уравнение:
с" (а0 — 0,924а + d{) — cd^c (а0 — 0,383а) +
+ с' (а0 + 0,924а — d) + cd+ с (а0 -+- 0,383а) = 0
или
а0 (2с+ с'+0 +0,924а (</ — <?") +
+ cf'dx — c'd + c (d — dx) = 0.
Подставляя численные значения параметров, получаем
уравнение участка DE:
а0 = — 0,193а+1,75; (12.30)
в точке Е
а = 8,25 мм, а0 = 0,И мм.
Дальнейшее исследование формы кривой (12.10) не
требуется, поскольку большие значения амплитуды нас не будут
интересовать. Отметим, что в точках ВУ D, Е линия (12.10)
терпит разрыв; значения а0 в этих точках изменяются
скачками. Эти небольшие скачки объясняются тем, что
уравнение (12.28) является приближенным.
Теперь, зная зависимость а0(а), вытекающую из
уравнения (12.10), можно строить скелетную кривую. Для этого
удобно использовать формулу (5.49), которая в. принятых
здесь обозначениях может быть записана следующим образом:
Х2 = ^-{0,924 [t/y(a0 + 0,924a)— Uy(a0— 0,924a)]+
+ 0,383 [^/y(a0+0,383a)—t/y(a0-0,383a)]}. (12.31)
Очевидно, что при значениях а, соответствующих участку ОВ:
0 < a < 3,25 мм%
следует принять:
Х2 = — = 4000 \/сек2, I = 63,5 \/се/с = const.
12]
ГАРМОНИЧЕСКОЕ ВОЗМУЩЕНИЕ
135
На участке BD, используя уравнение (12.29), получаем
Я2 = -2^- {0,924 [с (1,654а - 2,37) -
— с" (— 0,194а — 2,37 + 3) + Ъс\ +
+ 0,383 ИМ 13а —2,37) —*(0.347а— 2.37)]} =
т\ а )
На участке DE, учитывая (12.30), находим
Я2 = _1-{0.924 [с'(0.731 с+1.75 —5) +
+ 5с — с"{— 1,117а + 1,75 + 3) + Зс] +
+ 0.383 [с (0,19а + 1,75) — с (— 0,576а + 1.75)]} =
= .1(16,68-££).
т \ a J
Таким образом, получается скелетная кривая, построенная
на рис. 48. Проведя из начала коор- а
динат касательную к ней, находим
требуемое значение коэффициента
сопротивления п:
л> 12,5 \\сек.
До сих пор речь шла об
определении амплитуды деформации
амортизатора; в практических задачах
более важно определить реакцию
амортизатора.
Как указывалось во введении,
отношение амплитуды реакции к и 1 2 . J
амплитуде вибрационного воздейст- д
вия характеризует виброзащитные рис 48.
свойства системы.
Динамическая составляющая реакции складывается из
упругой и диссипативной силы:
R = — U(ut u) = —bu — Uy(tt). (12.32)
В первом приближении для определения амплитуды
реакции можно воспользоваться линеаризованным выражением для
z4 a=-,
4
136 НЕЛИНЕЙНЫЕ СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ [ГЛ. Ill I
упругой силы (12.6). Учитывая, что £/0 = 0, получаем I
#тах « I Ьа + cjfi |тах = a |/"ftW + ^ = т а ^ + 4«W . )
(12.33) ;
Следует иметь в виду, что значение /?тах, полученное по i
формуле (12.33), является весьма приближенным. Дело в том, |
что эта формула определяет лишь амплитуду первой гармо- t
ники силы и не учитывает высших гармоник. По соображе- 1
ниям, изложенным достаточно подробно в § 1, пренебрежение I
высшими гармониками обычно допустимо при определении \
деформации, но не при вычислении нелинейной силы.
Более точное значение /?тах может быть получено непо- #
средственным вычислением функции R(t) по формуле |
R (t) = b aco sin (t)t—Uy(a0-\-a cos at). (12.34)
. При малых диссипативных силах (baax^ Uy max) можно!
принять, что амплитудное значение реакции совпадает с ам- j
Т1литудным значением упругой силы, то есть что \
Rm*x~Uy(a0±a)t (12.35) ]
причем выбирается наибольшее из этих двух значений £/у.
В заключение исследуем устойчивость периодических решений, '
соответствующих различным точкам резонансной кривой. Для этого ,
воспользуемся критериями устойчивости решений гармонического
вида, найденными в § 8 (формулы (8.30) и (8.31)). В рассматривае- i
мом случае *
г = 2л, q (а) = Я2 (а).
Очевидно, что условие (8.30) выполняется тождественно, поскольку I
п > 0. Условие (8.31) запишется в такой форме: I
4л2 + -1- [V (а) - со2] |\2 (а) - со2 + а^£р-~\ > 0. (12.36) \
Если значения а и со, соответствующие приближенному реше- 1
нию уравнения (12.4), удовлетворяют этому условию, решение 1
является устойчивым. I
Граница области устойчивых решений на плоскости (я, со) опре- I
деляется, таким образом, уравнением I
[V (а) - со2] h2 (а) — со2 + а ^^Ц + 4л2со2 = 0. (12.37) :
Покажем, что это уравнение определяет геометрическое место точек,
в которых касательные к резонансным кривым параллельны оси
ординат. Для этого перепишем уравнение (12.15) в форме
а2 [(X2 - со2)2 + 4nV] = Р\ (со) (12.38) i
12]
ГАРМОНИЧЕСКОЕ ВОЗМУЩЕНИЕ
137
и продифференцируем его по а2, рассматривая со как неявную
функцию амплитуды:
(%2—(д2)2+4п2<д2-\-2а2 (А,2 — ©2) Г
d(K2) __ d(a>2)
d (a2) d (■
£11,
a2)J^
= 2Л(со)
<*Л
4я2#2
rf(D d (a2) '
d((o2) _
rf(a2) ~~
(12.39)
В тех точках, где касательная к кривой параллельна оси ординат,
должно быть
d (со2)
d(a2)
= 2(0
d®
d\a2)
= 0.
Поэтому уравнение
геометрического места таких точек
записывается в следующем виде:
(Я/2__(О2)2 + 4А1202 +
+ 2a2(X2-<*2)d{X2)
Область
неистойчибых
-решений
Поскольку
~сГ(а2)
dm
= 0.
(12.40)
2а da
d(a2)
уравнения (12.37) и (12.40)
тождественно совпадают. При
п = 0 получаем уравнение
границы области устойчивости
в такой форме:
(12.41)
Очевидно, что в этом случае
одной из границ будет
скелетная кривая X (а) = ю, а
уравнение другой границы
Рис. 49.
<о=Л(а)
da
= 0.
(12.42)
Рис. 50.
Эта линия (рис. 49 и 50) так же, как и скелетная кривая, начинается
в точке © = А.0, а = 0 и проходит левее скелетной кривой при
d (K2)/da < 0 («мягкая» скелетная кривая) и правее — при
d (к2)/da > 0 («жесткая» скелетная кривая).
Теперь можно выделить на рис. 38—44 участки резонансных
кривых, соответствующие устойчивым и неустойчивым решениям.
Нетрудно видеть, что в тех случаях, когда существует
единственное решение гармонического вида, оно оказывается устойчивым.
138 НЕЛИНЕЙНЫЕ СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ [ГЛ. III
Если же существует несколько решений, имеющих одинаковую
частоту, то некоторые из них оказываются неустойчивыми. При трех
решениях устойчивы режимы с наименьшей и наибольшей
амплитудой. Этот анализ показывает, что среди решений,
соответствующих дополнительным ветвям резонансных кривых, одно всегда
является устойчивым. Соответствующие режимы являются, таким
образом, физически реализуемыми и представляют реальную
опасность.
§ 13. Вынужденные колебания при гармоническом
вибрационном воздействии и силе сухого трения
Пусть диссипативной силой, действующей в амортизаторе
с нелинейной упругой характеристикой, является сила сухого
трения. Тогда уравнение вынужденных колебаний при
гармоническом вибрационном воздействии имеет следующий вид:
mil + Я sign it + Uy (и) = F cos Ы (F = F (со)), (13.1)
где Я— сила трения, которая будет считаться постоянной
(см. § 10).
Разыскивая приближенное решение в форме (12.5) и
применяя метод гармонической линеаризации, получаем
Uy(u)^U0+cAu°, Я sign и «*дй. (13.2)
Коэффициенты линеаризации определяются по формулам
(11.3)—(1L5). Для коэффициента Ьл получаем
2я
£_ = -^— Я sign (—acDsin\b)sinibtfhb = . (13.3)
д па® J ь ч т/ т т ла(д \ j
Решая линеаризованное уравнение
ти° + -jjjjj- a0 +CbU°+U0 = F cos erf, (13.4)
получаем уравнения для определения параметров решения:
U0(a0, а) = 0,
(сд — may2) a = F cos ф,
4Я
Fsincp.
(13.5)
§ 13) ГАРМОНИЧЕСКОЕ ВОЗМУЩЕНИЕ ПРИ СУХОМ ТРЕНИИ 139
Отсюда находим
У>*(со)-/*2
а— |Я2 (а) — со2| '
У F\ — h2
где
F(a) АН с л
1 ч / т пт т
Выражение (13.6) представляет собой амплитудно-частотную
характеристику системы, заданную в неявной форме.
Исследуем форму резонансных кривых, являющихся графическим
изображением зависимости амплитуды деформации от частоты.
Анализируя выражение (13.6), замечаем, что оно не всегда
дает для а вещественные значения; при
Fx{<d)<h (13.8)
вещественных значений для а не существует, то есть в этом
случае не удается, пользуясь методом гармонической
линеаризации, найти приближенное решение гармонического вида.
Нетрудно понять физический смысл этого результата. Если
сила сухого трения Н превышает амплитуду вынуждающей
силы F (со), движение объекта относительно основания не может
начаться; амортизатор, как говорят в таких случаях, остается
«запертым». Можно показать, что если дать такой системе
начальный толчок, задать ненулевые начальные условия,
система в конце концов придет в положение равновесия.
Действительно, пусть при некоторых начальных условиях
движение системы (13.1) определяется следующей функцией
времени:
u = ^(t).
Тогда работа силы трения за некоторое время от
момента tx до момента t2 определяется выражением
wtp=h f\w\dt.
(13.6)
(13.7)
140 НЕЛИНЕЙНЫЕ СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ [ГЛ. Ill
С другой стороны, работа вынуждающей силы за то же
время составит
WnuiH = F (со) J* cos юЭД (0 dt.
ВЫН "
Но
F (со) < Я, cos G)A|) (t) < |ф (01.
Таким образом, рассеиваемая энергия все время
превышает энергию, поступающую в систему; поэтому система
непременно должна прийти в состояние относительного покоя.
Условие запирания
F(<*)<H (13.9)
не совпадает с условием (13.8). Решение гармонического вида
не получается и в тех случаях, когда
Я</7((0)<-^Я. (13.10)
Анализ колебаний, возникающих в этом случае, показал, что
здесь имеют место движения с остановками, при которых
в течение некоторых периодически повторяющихся интервалов
времени система остается в состоянии относительного покоя.
В виброзащитных системах такие режимы колебаний
встречаются редко и здесь анализироваться не будут.
Предположим теперь, что
?№ = №•
Тогда система остается запертой при
0)2<^-. (13.11)
Решения гармонического вида получаются при
9 ^ h
So
При А, = со амплитуда становится бесконечно большой, поэтому
резонансные кривые, вообще говоря, не пересекаются со
скелетной кривой. Исключение возможно только на частоте
со* = ^H/Iq] при этом и числитель и знаменатель выражения
(13.6) могут одновременно обращаться в нуль.
§ 13) ГАРМОНИЧЕСКОЕ ВОЗМУЩЕНИЕ ПРИ СУХОМ ТРЕНИИ 141
Найдем значения частоты со', при которых амплитуда
принимает экстремальные значения. Для этого приравняем нулю
производную
d{a2) _
d(a2)
2|202 (,2 _ W-№^*№^[^
(А,2 —со2)4
d(a2)
d((i>2)
1
Это условие дает
(13.12)
(13.13)
— ЕоМ*> "
Подставляя (13.13) в (13.6), получаем уравнение для
определения экстремальных зна- а
чений амплитуд:
а =
(13.14)
Значения af могут быть 3
определены графически, как
ординаты точек
пересечения кривой (13.14) со ске- г
летной кривой.
Вводя обозначения
а =
ёо
ч =
р =
|0Я2(0)
К (а)
МО)'
(13.15) €
1
ъ
г
-И
\
У
г"
; VtfVJ \з г
D
Рис. 51.
можно записать выражение (13.14) в безразмерной форме:
а:
Vy\2-P4'
(13.16)
Графики зависимости а(р) (р — независимый параметр),
соответствующие различным значениям г), построены на рис. 51.
142 НЕЛИНЕЙНЫЕ СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ [ГЛ. Ш
Все кривые выходят из точки /? = 0, а= 1 и асимптотически
приближаются к прямым р = УИ\.
Установим теперь некоторые свойства резонансных кривых
(13.6) при ^((0) = ^.
а) Очевидно, что, если |0со2 = /г, амплитуда обращается
в нуль; при |0со2 < h вещественных значений а не
существует. Поэтому резонансные кривые выходят из точек
со = 1/ у- ,а = 0и располагаются правее линии (о= 1/ ■=-•
б) Если \^2^>ht то можно приближенно считать, что
" |Я2 —©2| •
Очевидно, что с увеличением частоты со резонансные кривые
асимптотически приближаются сверху к прямой а = £„.
в) Решая (13.6) относительно со2, получаем
©2:
Таким образом, каждому значению а может соответствовать
не более двух вещественных
значений со. Если
fl2(^4 —A2) + A2lg<0> (13.17)
то вещественных значений со не
существует. Условие (13.17)
эквивалентно двум условиям:
!о<о2<А, (13.18)
ЛЬ
а>
Vh2-tW'
(13.19)
Рис. 52.
Этим условиям удовлетворяет
область значений а и к, лежащая
на плоскости (к, а) выше
линии (13.14) (рис. 52). При ах < а < а2 резонансная кривая
не имеет вещественных точек.
Отсюда непосредственно следует, что точки, в котзрых
скелетная кривая пересекает линию (13.14), снизу вверх
соответствуют максимумам резонансных кривых, а точки
пересечения типа точки В (рис. 52) — минимумам.
§ 13] ГАРМОНИЧЕСКОЕ ВОЗМУЩЕНИЕ ПРИ СУХОМ ТРЕНИИ 143
Найденные свойства резонансных кривых позволяют
определить их форму в зависимости от числа точек пересечения
линии (13.14) и скелетной
кривой.
Если линия (13.14) не
пересекается со скелетной
кривой, то резонансные
кривые принимают форму,
показанную на рис. 53 (для
h < !<А2 (°)) и рис- 54 (для
#>!сЛ2(0))- Если эти ли"
нии пересекаются в одной
точке, резонансные кривые
принимают вид, показанный
на рис. 55. При двух
точках пересечения (что
возможно только для
«жесткой» скелетной кривой при
h > |0A,2 (0)) резонансные
кривые распадаются на две ветви (рис. 56), при трех точках
пересечения получается картина, показанная на рис. 57, и т. д.
J
Q =
V
IIL>aM
h~co=A(a)
№- л„
CO
Рис. 53.
Рис. 54.
Рис. 55.
Если амплитуда вибрационного воздействия не зависит от
частоты, введение сухого трения не меняет характера
резонансных кривых. Сравнивая формулу (13.6) при Fx (со) = const
144 НЕЛИНЕЙНЫЕ СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ [ГЛ. III
с уравнением резонансной кривой при отсутствии трения
а =
^2(а)-со*| ■
(13.20)
легко заметить, что введение сухого трения в этом случае
эквивалентно уменьшению амплитуды вибрационного воздей-
F
ствия в 1 - раз. Это уменьшение оказывается суще-
\ F\ — h2
ственным, если h приближается по величине к Fv Вместе
Рис. 56.
с тем легко видеть, что увеличение трения отрицательно
сказывается на виброзащитных свойствах амортизатора.
Действительно, амплитуда полной реакции амортизатора (если
его деформация не равна тождественно нулю, то есть если
амортизатор не «заперт» сухим трением) может быть найдена
из соотношения
#шах = \U7(U)+H Sign U |max.
Очевидно, что ее величина ни при каких условиях не может
быть меньше Н. Поэтому, для того чтобы амортизация была
полезной, во всяком случае должно быть Н <^F (со).
Таким образом, при очень малом трении виброзащитные
свойства системы ухудшаются из-за развития резонансных
явдений; при очень большом трении они также оказываются
§ 13] ГАРМОНИЧЕСКОЕ ВОЗМУЩЕНИЕ ПРИ СУХОМ ТРЕНИИ 145
плохими из-за воздействия силы трения на амортизируемый
объект. Естественно предположить, что существует некоторая
оптимальная величина силы трения, при которой наибольший
коэффициент динамичности системы оказывается минимальным.
Покажем это на примере амортизатора с линейной
упругой характеристикой, для которого
Следовательно, при /71 = |0со2
а = -
|^-С02|
(13.21)
Прямая 1 = Х0 пересекается с кривой (13.14) не более чем
в одной точке; поэтому амплитуда может иметь только одно
экстремальное значение (максимум), равное (в соответствии
с (13.14))
а' =
hlo
Vh2-&t
(13.22)
При ЭТОМ 0)' = -г-г-
\Q M. 3- Коловскц^
146 НЕЛИНЕЙНЫЕ СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ (ГЛ. III
Резонансные кривые, построенные в координатах
а
(1 = 1-,
50
—
и соответствующие различным значениям тр
на рис. 58.
Пользуясь теми же обозначениями,
формулу (13.22) в таком виде:
ёо^о
показаны
а =
УУ-1
можно переписать
(13.23)
График этой зависимости построен на рис. 59. При т]^1
максимальная амплитуда вынужденных колебаний может стать
сколь угодно большой,
а если z приближается к
единице. Практически это
означает, что стук об
упоры будет неизбежен
при любом свободном
ходе амортизатора и что
нижняя ветвь резонансной
кривой, соответствующая
линейному участку
упругой характеристики,не
останется изолированной, а
сомкнётся с
дополнительными ветвями. При ц > 1
значение а сразу резко
уменьшается, и уже при
ц = 1,5 имеем а =1,34;
с дальнейшим ростом ц
значение а
асимптотически приближается к
единице.
Таким образом,
увеличение силы трения
уменьшает величину максимальной деформации амортизатора в
резонансном режиме, а тем самым и амплитуду упругой силы.
Вместе с тем при этом происходит увеличение диссипативной
силы. Определим теперь величину силы трения, при которой
1
h
г
Рис. 58.
§ 13] ГАРМОНИЧЕСКОЕ ВОЗМУЩЕНИЕ ПРИ СУХОМ ТРЕНИЙ 147
достигается минимум максимальной амплитуды реакции
амортизатора
#max = I m^oa cos (со* + ф) — Н sign sin (orf + ф) |тах «
« mX^a -\- Я.
Поделив на m^olo» находим коэффициент динамичности
системы
К = -^= . Л +-Л- (13.24)
Зависимость /С (л) построена на рис. 59. Оптимальное
значение т), при котором /С минимально, найдем, приравняв
нулю dK/dr\. При этом получим
л'=1,47, ATmln = 2,52. (13.25)
Итак, оптимальное значение силы сухого трения,
обеспечивающее защиту от гармонического вибрационного воздействия
с амплитудой,
пропорциональной квадрату частоты, равно °*тах^
(13.26) 3
Это соотношение должно
приниматься во внимание при
выборе демпфирующего
устройства амортизатора.
При высокочастотном
воздействии полная реакция
амортизатора практически равна Рис. 59.
силе трения. Действительно,
амплитуда вынуждающей силы не может расти безгранично,
поэтому с ростом частоты £0 всегда убывает, приближаясь
к нулю. Вместе с £0 убывает и амплитуда деформации,
поскольку lim а = 10. В результате упругая сила амортизатора
Ю->00
также уменьшается, и полная реакция приближается по
величине к силе сухого трения.
10*
\\ffp
Лц)
148 НЕЛИНЕЙНЫЕ СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ [ГЛ. Ш
Исследуем устойчивость движений, близких к гармоническим,
в системе с сухим трением, пользуясь критериями (8.30) и (8.31).
Условие (8.30) выполняется, поскольку
dbn № Ш
2Ьл(а) + а-^- = - >0.
А ' аа лаа ла®
Условие (8.31) принимает такую форму:
Ш ( 4Я АН
а—тг-
или
(Л2 - со*) [л* - 02 + а -^рА > 0. (13.27)
Таким образом, скелетная кривая и линия (12.42) всегда
являются в этом случае границами области устойчивости (см.
рис. 49 и 50).
§ 14. Вынужденные колебания в системе
с внутренним трением.
Сравнение различных форм демпфирования
Предположим теперь, что демпфирование осуществляется
только за счет внутреннего трения в материале. Поскольку
по-прежнему речь будет идти о колебаниях гармонического
вида, можно линеаризовать силу внутреннего трения в
соответствии с формулой (10.17):
Ud(u, и) = ^~-и% (14.1)
где а — амплитуда, а со — частота гармонических колебаний.
Подставляя (14.1) и (12.6) в уравнение (12.1), получаем
линеаризованное уравнение
mu*±^^i* + cKtfi+ U0 = Fcos«>t. (14.2)
Разыскивая приближенное решение этого уравнения в форме
(12.5), получаем следующее выражение для амплитуды
колебаний:
а= , Fi(ti>) (14.3)
1/[^(а)-<о2]2 + ^2(ц~1)
где
__JL
Pi m
§ 14)
СИСТЕМА С ВНУТРЕННИМ ТРЕНИЕМ
149
Исследуем форму резонансных кривых; для этого, прежде
всего, определим экстремальные значения амплитуды а'.
Уравнение (14.3) запишем в такой форме:
а2 (к2 — со2)2 + $W* = F\ (со). (14.4)
Продифференцируем это выражение по со2, рассматривая
квадрат амплитуды (а2) как функцию квадрата частоты (со2):
Q2,,„2Gx-i) d(a2) __0 dFx
d(a>2) —*ri d((.o2)
_L_ A2.!/*2^"1' U K" } — OF
Приравнивая нулю производную d (a2)/tf (со2), получаем
(aW2_w2) = _Fl_i|!_. (145)
йРл
Если Fx (со) = const, то . 2 = 0 и, следовательно,
Х(а') = ®9 (14.6)
то есть в этом случае экстремальные значения амплитуда
принимает в точках пересечения резонансной кривой со
скелетной.
Если же Fx (со) = |0со2, то из (14.5) находим
%Ча')=*<&[\--^. (14.7)
Обычно экстремальные значения а' значительно
превышают £0. Поэтому и в этом случае можно считать, что
экстремумы достигаются вблизи от точек пересечения
резонансных кривых со скелетными (исключением является только
точка а = 0, со = 0, которая, как нетрудно убедиться, тоже
является точкой экстремума).
Для того чтобы найти точки пересечения резонансной
кривой со скелетной, следует положить в (14.3) А, = со.
Тогда получаем
«=mw- <■«>
Таким образом, достаточно определить точки пересечения
скелетной кривой и линии (14.8). Количество точек
пересечения определяет, как и в ранее рассмотренных случаях
число ветвей резонансной кривой.
150 НЕЛИНЕЙНЫЕ СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ [ГЛ. Ill
Уравнение (14.4) разрешается относительно со2:
При
:Я2±|/ -^--P^-D
■>[W
(14.9)
(14.10)
подкоренное выражение в (14.9) становится отрицательным.
Это означает, что резонансная кривая не может иметь точек
со =Л(а)
Рис. 60.
с такими ординатами, то есть что вся она располагается
ниже кривой (14.8).
Форма кривой (14.8) зависит от величины коэффициента \х
и вида зависимости /^(со). При Fx (со) = const это — прямая,
параллельная оси абсцисс
(рис. 60), которая с любой
скелетной кривой может
иметь не более одной точки
пересечения. При этом
резонансные кривые имеют
такой вид, как на рис. 60.
Если (/VPl)1^ превышает
величину амплитуды, допу-
<о стимую габаритами
амортизатора (рис. 61), линия (14.8)
не пересекается вообще со
скелетной кривой, что означает возможность резонансных
явлений при любом значении со > Х.0.
Рис. 61.
§ 14]
СИСТЕМА С ВНУТРЕННИМ ТРЕНИЕМ
151
При Fx (со) = |0со2 форма кривой (14.8) зависит от
величины коэффициента jm. При 0 < \х < 2 эта кривая является
вогнутой и касается оси абсцисс; со скелетной кривой она
ay А (а)
Рис. 62.
со=Л(а)
может иметь различное число
точек пересечения — от нуля
до трех и более (рис. 62).
В соответствии с этим
появляются дополнительные
ветви резонансных кривых.
При \х > 2 кривая (14.8)
становится выпуклой и касается
оси ординат. В этом случае
также возможно различное
число точек пересечения со
скелетной кривой, но с
ростом \х наиболее вероятным становится существование только
одной точки пересечения (рис. 63). При \х = 2 линия (14.8)
превращается в прямую. В этом
случае можно сказать, что
внутреннее трение, по степени
влияния на развитие
резонансных колебаний, становится
эквивалентным линейному
трению. Впрочем, эта
эквивалентность не является полной,
поскольку тангенс угла наклона
прямой к оси абсцисс равен при
линейном трении —-, а при
внутреннем трении — у -|^.
При |ы = 0 линия (14.8) параллельна оси ординат; ее
уравнение
!o«>2 = Pi
показывает, что в этом случае внутреннее трение становится
эквивалентным сухому трению, причем h = $v
Анализ устойчивости приближенных решений в случае
внутреннего трения приводит к тем же результатам, что и при других
формах демпфирования: границей области устойчивости оказывается
геометрическое место точек, в которых касательные к резонансным
кривым параллельны оси ординат.
Рис. 63.
152 НЕЛИНЕЙНЫЕ СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ [ГЛ. III
Условие (8.30) всегда выполняется; условие (8.31) принимает
следующий вид:
1Хр2а2(^1)+[Л2(а)~02][л2(а)^02 + а-^-]>О. (14.11)
Теперь можно сравнить различные виды демпфирования
и сделать некоторые выводы о целесообразности их
применения в виброзащитных системах. Как мы уже убедились,
влияние демпфирования на развитие вынужденных колебаний
в системе существенно зависит от формы упругой
характеристики (точнее, от формы скелетной кривой) и от вида
функции Fx (со). Здесь сравнительный анализ влияния дис-
сипативных сил будет проводиться при следующих
предположениях, наиболее характерных для большинства
виброзащитных систем.
1) Будет предполагаться, что скелетная кривая имеет вид,
показанный на рис. 64, а, б, я, г или д. Во всех этих случаях
Рис. 64.
возможная амплитуда деформации амортизатора ограничена
упорами и не может превышать величины А. Это
обстоятельство, как нетрудно понять из анализа, проводившегося
выше, имеет решающее значение. Форма скелетных кривых
на рабочем участке упругой характеристики не является
§ 14] СИСТЕМА С ВНУТРЕННИМ ТРЕНИЕМ 153
столь существенной. Скелетные кривые, показанные на рис. .64,
соответствуют упругим характеристикам следующего типа:
а) — линейная характеристика с симметричными жесткими
упорами,
б) — линейная характеристика с упругими упорами,
жесткость которых растет с ростом деформации,
в) — нелинейная симметричная характеристика типа (10.9')
и (10.10'),
г) — нелинейная несимметричная характеристика типа (10.9)
или (10.10),
д) — характеристика с начальным натягом и
ограничительными упорами.
2) Будут рассмотрены следующие формы зависимостей
а) Fx (со) = Fx == const при comln < (О < сотах, (14.12)
б) /71(©) = ^ при сот1п<со<сотах. (14.13)
В каждом из этих вариантов нам придется рассмотреть
два случая: когда comIrl меньше собственной частоты 7,0 или
имеет тот же порядок, что и Х0, и когда сопЛ11^>^0.
Как уже отмечалось ранее, демпфирование в
виброзащитной системе необходимо только для подавления резонансных
колебаний, характеризующихся большой амплитудой
деформации; при малых амплитудах оно является вредным,
увеличивая полную реакцию амортизатора и тем самым ухудшая
его виброзащитные свойства. Поэтому очевидно, что
наиболее подходящей для виброзащитных систем является такая
форма зависимости величины диссипативной силы от
амплитуды, при которой с ростом амплитуды происходило бы
быстрое увеличение силы сопротивления. Из рассмотренных
выше видов демпфирования эгому условию в наибольшей
степени удовлетворяет внутреннее трение при больших
значениях параметра \i. Наихудшими свойствами обладает сила
сухого трения, величина которой вообще не зависит от
амплитуды колебаний.
Если зависимость /^ (со) определяется формулой (14.12),
линии (12.16) или (14.8) пересекутся со скелетной кривой
рассматриваемого типа только в одной точке (рис. 65). Для
того чтобы исключить стук на упорах, необходимо, чтобы
эта точка пересечения лежала на рабочем участке упругой
154 НЕЛИНЕЙНЫЕ СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ [ГЛ. III
характеристики, то есть чтобы выполнялись условия
2пХ0
< Л или
№
<А.
(14.14)
где А — расстояние от положения равновесия до упоров.
Выполнение этих условий становится совершенно
необходимым при сот1п < V» если же сот1п^>Я0, то достаточно,
чтобы точка пересечения имела абсциссу, меньшую чем comIn.
Сухое трение в этом случае вообще не следует применять.
При нем амортизатор либо останется «запертым», то есть
не будет защищать от вибрации (если Fx < К), либо будет
возможен стук об упоры на любой частоте (если Fx > h).
Этот вывод
непосредственно вытекает из
анализа, проведенного в § 13.
Сравним влияние
внутреннего и линейного
трения на виброзащитные
свойства амортизатора
при со.^>Х.0.
При больших
значениях со ((а^>Х0) можно
приближенно принять
i*
®
2па>
сй=К(а)
со
Рис. 65
а ж
Поэтому амплитуда силы сопротивления, пропорциональной
скорости, будет равна
\Udi\an = 2mma^^^. (14.15)
а амплитуда силы внутреннего трения
|{/02|тах=|ЛМД =
л2»*
(14.16)
Отсюда ясно, что при достаточно больших значениях со
амплитуда силы внутреннего трения при \х > -^ окажется
меньшей, чем амплитуда силы линейного трения, то есть
виброзащитные свойства системы в первом случае окажутся
выше (для одного и того же значения амплитуды деформации).
14]
СИСТЕМА С ВНУТРЕННИМ ТРЕНИЕМ
155
Теперь рассмотрим тот случай, когда Fl(a)) задано
формулой (14.13). Характер резонансных кривых определяется
числом точек пересечения со скелетной кривой линий (12.22)
(для линейного трения), (14.8) (для внутреннего трения) или
прямой (о2 = — (для сухого трения). Построив эти линии
(рис. 66) и выбрав, например, скелетную кривую, соответ-
\°
\ /*>2
s' p<2
I У0"''
-№
со
to.
гп<°
Aft
ствующую линейной упругой
характеристике с жесткими
упорами, убеждаемся, что
в этом случае «стука на
упорах» можно избежать только
одним способом: добиться
того, чтобы точка
пересечения построенных линий с
линией а = А имела абсциссу,
превышающую сотах:
й>1 > Ютах-
При сухом трении это
обеспечивается только в том
случае, когда амортизатор остается «запертым» вплоть до сотах,
то есть должно быть
(И.17)
со,
Рис. 66.
h > У0:
.2
max*
Для линейного трения получаем необходимое условие
в форме (12.26). Наконец, для внутреннего трения должно
быть
.2 Ч1/|Х
(14.18)
4>(V4.y
Очевидно, что чем больше |ы и plf тем легче выполнить это
условие.
Если условия (12.26) или (14.18) выполнены, то при
А,0 <^ со < сотах амплитуды диссипативных сил определяются
по формулам (14.15) и (14.16), в которые следует
подставить Fx = |0со2.
При этом
\UdiU*= 2тпуо, (14.19)
I "*!=*№
(14.20)
156 НЕЛИНЕЙНЫЕ СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ [ГЛ. III
Здесь уже при любом значении \х виброзащитные свойства
оказываются более высокими, если в системе используется
внутреннее трение.
Подводя итоги, можно сказать, что наилучшим способом
борьбы с резонансными колебаниями в виброзащитных
системах является применение демпферов внутреннего трения.
Если на практике приходится использовать другие формы
демпфирования (в том числе и сухое трение), то это
происходит потому, что создание демпферов с интенсивным
внутренним трением является чрезвычайно трудной конструкторской
задачей. Для большинства конструкционных материалов
значение параметра р является очень малым.
Наиболее эффективным в этом отношении оказывается
использование таких материалов, как резина (в резино-метал-
лических амортизаторах) и специальным образом
спрессованная металлическая проволока, однако и в этих материалах
внутреннее трение оказывается недостаточным, например,
для подавления резонансных колебаний в виброзащитных
системах современных летательных аппаратов.
Эффективность внутреннего трения часто характеризуется
так называемым коэффициентом поглощения г|) [38], равным
отношению площади петли гистерезиса к максимальной
потенциальной энергии деформации. Для упругого элемента с
линейной характеристикой имеем
^=2фР_==2яЬ fl|l_If 2
са Х0
где с — жесткость упругого элемента. Если воспользоваться
выражением (14.21), можно формулу (14.3) представить
в виде
Fl (<D) (14.22)
/w-?+(£)V
поскольку в линейной системе А. = А,0. При со=А,0 получаем
в' = АМ. (и.23)
Л°"21Г
Для обычных конструкционных материалов величина я|э
не превышает 0,3—0,5; если Fx (») = ^ю2, то формула
§ 14] СИСТЕМА С ВНУТРЕННИМ ТРЕНИЕМ 157
(14.23) дает
то есть коэффициент динамичности при резонансе
оказывается весьма значительным. В современных системах
пассивной виброзащиты амплитуда |0 достигает 1 —1,5 мм,
поэтому, если ограничиться внутренним трением, то
потребуется «свободный ход» амортизатора увеличивать до
25—40 мм, что часто недопустимо по габаритным
соображениям.
Сочетание различных форм демпфирования часто
позволяет более успешно решить проблему борьбы с
резонансными колебаниями. Мы здесь ограничимся рассмотрением
совместного действия внутреннего и сухого трения. В этом
случае
Ud(u. w) = tf signtt' + pa»-1^ (14.24)
и, следовательно,
—(±+*Я- <-«5>
Для амплитудно-частотной характеристики получаем
следующее уравнение:
а = , 1 =. (14.26)
Легко показать, что и здесь амплитуда принимает
экстремальные значения вблизи от точек пересечения резонансной
кривой (14.23) со скелетной. Для того чтобы найти эти
точки, полагаем в (14.26) Х. = со; тогда
а' = г^г—) • (14-27)
Следовательно, достаточно найти точки пересечения линии
(14.27) со скелетной кривой ь> = Х(а). Рассмотрим тот
случай, когда скелетная кривая имеет форму, показанную на
158 НЕЛИНЕЙНЫЕ СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ [ГЛ. Ill
рис. 64, а, и /^ (со) = £0со2. При этом линии (14.27)
начинаются в точке
со
-/*• -
О
и при различных значениях ц имеют форму, показанную на
рис. 67. Если при этом h > |<До» то линии (14.27)
пересекаются со скелетной кривой в одной точке (точка В на
рис. 67) и необходимо только,
чтобы абсцисса точки
пересечения была больше, чем сотах.
Если это условие выполнено,
резонансные колебания в
системе оказываются
подавленными.
Рассматривая условия
возникновения резонансных
колебаний в системах с жесткими
60 упорами, мы считали, что эти
колебания будут сохранять
форму, близкую к
гармонической. Такое предположение,
вообще говоря, является неверным; при ударах об упоры
высшие гармоники играют очень существенную роль. Поэтому
результаты, полученные для таких систем в предыдущих
параграфах, носят лишь ориентировочный характер. Более
строгое исследование явления удара об упоры, учитывающее
также и диссипацию энергии при ударе, будет дано ниже.
Рис. 67.
§ 16. Вынужденные колебания при полигармоническом
возмущении
Во многих задачах теории виброзащитных систем
приходится иметь дело с полигармоническими вибрационными
воздействиями. При амортизации машин с поступательно
движущимися частями, двигателей внутреннего сгорания,
поршневых компрессоров, как правило, необходимо
учитывать высшие гармонические составляющие периодических
вынуждающих сил, исследовать условия возбуждения
резонансных колебаний высшими гармониками. Вибрации
автомобилей, судов, летательных аппаратов всегда являются
§ 15]
ПОЛИГАРМОНИЧЕСКОЕ ВОЗМУЩЕНИЕ
159
полигармоническими; поэтому виброзащитные системы для
приборов и аппаратов, устанавливаемых на этих объектах, также
приходится рассчитывать на полигармоническое внешнее
воздействие.
Итак, предположим, что в уравнении (12.1) правая часть
является полигармонической функцией времени:
N
Q(0=S^cos(©^ + V/). (15.1)
Эта функция может оказаться периодической, если все
гармоники возбуждаются одним источником или несколькими
кинематически связанными источниками вибрации; она будет
почти-периодической функцией, если имеется несколько
независимых источников возмущения и частоты колебаний,
возбуждаемых этими источниками, являются несоизмеримыми.
И в том, и в другом случае стационарное (периодическое
или почти-периодическое) решение уравнения (12.1) должно
быть полигармоническим.
Поскольку уравнение (12.1) является нелинейным, это
решение должно содержать, вообще говоря, не только
гармоники частот со£., но и другие гармонические
составляющие: кратных частот (рсо^, где р—целое число),
комбинационных частот (2/?/СоЛ и т. д.
В этом параграфе приближенное решение мы будем
искать в форме
N
и = Яо-ЬЕ a/Cos(cD^ + <P/). (15.2)
ы\
сохраняя в нем гармоники только тех частот, которые
имеются в вибрационном воздействии. Выбор такой формы
решения является естественным, если уравнение (12.1) близко
к линейному, поскольку решение линейного уравнения имеет
именно такую форму. Для отыскания решения вида (15.2)
воспользуемся методом линеаризации по функции
распределения, изложенным в § 5.
Рассмотрим сначала несколько конкретных примеров.
1. Исследуем поведение системы с нелинейной упругой
силой и силой сопротивления, пропорциональной скорости
160 НЕЛИНЕЙНЫЕ СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ [ГЛ. III
деформации. Для такой системы уравнение движения
записывается в следующей форме:
N
mu-\-bu-]-UY(u)~ 2 ^\-c°s (<»)/£ + ф/). (15.3)
Линеаризуем нелинейную упругую силу
U7W=U0+cAifi.
(15.4)
где и°= и — а0, а коэффициенты U0 и сл определяются по
формулам (11.7) и (11.8).
Выбираем плотность вероятности в форме (5.26) и
ограничиваемся приближением по первым четырем моментам;
тогда U0 и сд могут быть определены по формулам,
аналогичным (5.40) и (5.41):
+ (e-l)t/y(a0)]. (15.5)
ся = —^ [f/y(a0+ Угоа)- Uy(a0- V7oa)). (15.6)
2 у ZGU
Подставляя (15.4) в (15.3), получаем линеаризованное
уравнение; приравнивая постоянные составляющие и
коэффициенты при sin((o^4~^/) и cos(co^ + i|)/), приходим к
следующей системе уравнений:
U0(a0, aa>e) = 0,
[I2(a0. oB, e) - cofj a. = Л. cos(<p. - г|>.) (/ = 1. .
2nai{ni — Л;. sin (cpf- — i^) (/ = 1, .
где
cr b Ft
m m l m
Из уравнений (15.8) и (15.9) получаем
«.= 4 , 1
Л — (Of
•
(15.7)
...ло.
(15.8)
... ло.
(15.9)
(15.10)
§ 15}
ПОЛИГАРМОНИЧЕСКОЕ ВОЗМУЩЕНИЕ
161
Отсюда
2 _ J[_ Y 2 _ 1 V
°и^- 2 2jai~ 2 2d (г2 — «2\2_ци2л1?
I V о IV
л?
i = l
£ (л2_и?)Ч4«Ч
:Ф(Л). (15.11)
Л4°
лг
™4 J , d Y1' 2 2
TV
% ГГЛ2 —со?
^М5
(15.12)
Уравнения (15.7), (15.11) и (15.12) позволяют- определить
неизвестные aQ, о2и и е, после чего можно определить А,2 и
найти по формулам (15.10) амплитуды и фазы отдельных
гармоник решения. Параметры aQ% о2и и е удобно искать так,
как это делалось в § 5, то есть задаваться первоначально
величиной е, используя
первую из формул (5.45), а
затем методом
последовательных приближений искать а
и а2 и уточнять величину е.
Покажем теперь, каким
образом можно определить
величину коэффициента
сопротивления я, необходимую
для подавления резонансных
колебаний в системе.
Если задаться
величиной е, можно из
уравнения (15.7) определить aQ как
функцию ои. Подставив затем эту функцию в выражение
для Л, получим зависимость А.(о2). графическое изображение
которой на плоскости (к, оа) является своего рода аналогом
скелетной кривой. Используя формулы (15.5) и (15.6)
нетрудно построить семейство таких кривых, соответствующих
различным значениям е. Построив в соответствии с
формулой (15.11) зависимость Ф(Х) (рис. 68) и наложив на
полученный график кривую h(o2u), соответствующую выбранному
И М. 3. Коловский
162 НЕЛИНЕЙНЫЕ СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОЕ-ОДЫ [ГЛ. itt
значению е, можно получить значения ои и X,
соответствующие первому приближению. Далее можно уточнить значение е
по формуле (15.12) и, выбрав другую* кривую Х{о2\ найти
значения ои и X во" втором приближении.
Графики функций Ф(Х) при не слишком больших
значениях п имеют форму, показанную на рис. 68. Кривая
Х(о2\ может пересекать кривую Ф(^) в нескольких точках
(Dlt . .., D5), определяя тем самым несколько стационарных
решений исходного нелинейного уравнения. Одно из этих
решений может быть нерезонансным (точка Dx на рис. 68);
другие решения представляют собой резонангы на
гармониках частот со,-.
Резонансные решения располагаются попарно вблизи от
прямых A, = (fy; легко показать, что в каждой паре решений имеется,
по крайней мере, одно неустойчивое. Для этого воспользуемся
условием устойчивости в форме (8.44); в данном случае q = Х2\
ах = ои.
Вычислим, производную dO/dX
i^-^hw^w+^w (15ЛЗ)
Сравнивая (8.44) с (15.13), видим, что условие устойчивости
может быть записано в форме:
, 1 d(X2) d<b л dX аГФ л
1 7-«f = 1 т^т > °- (15.14)
2Х d(o2u) dX d(o2u) dX
Но в точках D2 и DA
dO dX d® d(o2u)
dX d (o2u) ~~ dX ' dX
поэтому в этих точках необходимое условие устойчивости не
выполняется. В точках Dh D3, D5 выражение (15.15)/меньше
единицы, поэтому эти точки могут соответствовать устойчивым
решениям. Вообще, для всех точек пересечения кривых Ф (X) и
Х(р2и)} в который ' '
.■-. ; • ' ■ • dX dX ' \ -
необходимое условие устойчивости не выполняется.
fc Для того чтобы подавить резонансные
колебания,..достаточно выбрать такую величину л, при которой вершины
>1; (15.15)
§ 15]
ПОЛИГАРМОНИЧЕСКОЕ' ВОЗМУЩЕНИЕ
' 163
кривой Ф(А,) будут располагаться ниже линии Х(о2\: При»
малых значениях п максимумы кривой Ф(А,)-располагаются-*
вблизи от прямых ^=^(0^ Исходя из этого, можно
предложить следующий метод выбора коэффициента п.
Задавшись предварительно значением е, строим кривую
Х(о2\ и определяем ординаты этой кривой, соответствую-г
щие значениям % = со^ (рис. 69). Для «жестких» кривых до
статочно ограничиться значениями со,- превышающими
Далее, в уравнении (15.11) пола
А,0.
гаем последовательно о2 = (о2).._
А==(ог и в каждом случае
вычисляем значения коэффициента п.
Выбираем из всех этих значений
наибольшее. При этом п кривая-
Ф (к) будет пересекаться с кривой
к (р2Л только вблизи одной из
вершин, соответствующей X = Юу. По-
:(0
v
г\б *-*<У
А \ . А
\—мл '
v\ \ \ л
со,
А0и>2 <од
<Ол
Рис. 69.
ложив теперь о2и = Ф((оЛ X ■•
уточняем по формуле (15.12)
величину е и строим кривую h(o2\}
соответствующую новому
значению этого параметра. Если эта новая кривая располагается
ниже ранее построенной, необходимо" соответственно
увеличить значение п с тем, чтобы значение Ф(хоу) было меньше*;
чем ордината кривой Xfo2^ при Х = со..
Рассмотрим следующий численный пример. Уравнение
вынужденных колебаний виброзащитной системы задано в
форме
и-\~2пи-\-
причем
2^Д
пи
tg— == Л (cos zxl0t-{-cos z2l0t)t (15.16)
^ = 1/5, z2 = 2 У 2.~
Требуется найти величину - отношения п/Х0, при . которой
исключается возможность возникновения резонансных
колебаний. " " " " ч
Ищем решение в форме - л
и = ах cos (z{k<jt + Ф1) + а2cos О2 V + ^2) О5-17)
11*
164 НЕЛИНЕЙНЫЕ СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ [ГЛ. III
(а0 принимаем равным нулю, поскольку нелинейная
функция является нечетной). По формуле (15.6) находим
2%1 Д /я г- \
V(e. ou) = —^tg(—Veoa). (15.18)
я у е аа \2/S. J
Поскольку N = 2, по формуле (5.45) имеем
е1= 1,875.
Подставляя гх в (15.18), получаем зависимость Х(ои).
Находим значения о2а при X = zxk0 и X = г2А,0. Для этого
решаем уравнения
_ 2А,§Д
*l 2A ^0|
2Я§Д / я ,,_ \
(15.19)
Здесь удобно обозначить
— 2Д~ — S'
Тогда уравнения (15.19) принимают такую форму
tg s = z\s> tgs = z\s.
Решая эти уравнения, находим
5Х= 1,432; s2= 1,487.
Запишем теперь уравнение (15.11):
2_ j£^__
Of.—
Я^
_±Л»Г 1_
~2 [(?-*№ + <
или, после сокращений и подстановки чисел:
'0*2.1
!=2,3lf
1
где
Г+(/-^)Ч^]' (15-20)
§ 15] ПОЛИГАРМОНИЧЕСКОЕ ВОЗМУЩЕНИЕ 165
Подставляя в (15.20) соответственно p = zv 5 = 5X и
р = z2, s = s2, находим в обоих случаях значение v:
^ = 0,248, v2 = 0,211.
Большее значение v соответствует резонансу на
частоте zxXq\ поэтому необходимо уточнить расчет именно
этого режима; для этого уточняем значение параметра е:
_3 3 пЧ\ Я*Д4 _
82 ~ I+7' ~ыЩ' 4v\4 [(4- 4f+^14] xg ~! ,637"
(15.21)
Приняв е==е2, определим новое значение vx. При этом, как
нетрудно видеть, величина sx не изменится; изменится только
коэффициент в правой части уравнения (15.20). Решив это
уравнение, найдем
v1 = 0,246.
Это значение \г настолько мало отличается от предыдущего,
что в дальнейших приближениях уже нет необходимости.
Рассмотренный пример был сравнительно простым;
поэтому нам удалось обойтись без применения графических
методов решения, которые в более сложных случаях
становятся необходимыми.
2. Рассмотрим действие полигармонического
вибрационного возмущения на систему с линейной упругой силой и
сухим трением.
В уравнении движения
N
mu + Hslgnu + cu = 2 /7/cos(oo^ + 9/) (15.22)
линеаризуем силу сухого трения.
По формуле (11.12) находим
1 Г Н Г
ьл = — yHsignyw(y)dy=:-4 \y\w(y)dy, (15.23)
V VX V Vt
где ад (у) — функция распределения полигармонического
процесса v = u(t)\ о£ — дисперсия v(jt).
166 НЕЛИНЕЙНЫЕ СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ [ГЛ. Ш
Покажем, что коэффициент линеаризации ЬА всегда
может быть представлен в форме
A=-f. (15.23')
"где ц—коэффициент, величина которого зависит только от
отношений центральных моментов четного порядка к
соответствующей степени ov. Действительно, симметричный
закон распределения w(y) всегда можно с любой степенью
приближения представить в виде линейной комбинации
6-функций
w(y) = 2Sa/6(y-y/)- (15.24)
Подставив это выражение в (15.23), получаем
2ЯТ1 I I 2Я V
где
^ = 1Ti' Л = 2//2аЛ- (15-25>
/=о
Значения а1 и kt должны определяться из уравнений
вида (5.28) и (5.29), которые в рассматриваемом случае
принимают такую форму:
2ga, = i, 2Да.^=Ж0р (/>=1,2, ...)..
Поделив все эти уравнения, кроме первого, на о2*7 и
учитывая соотношения (15.25), непосредственно приходим к
выводу, что коэффициент ц зависит только от отноше-
шй Щр\о\Р.
Линеаризуя уравнения (15.22), получаем
N
г+^*+я'вл"=2^со8(^+*/)' (15-2б>
где
-15] ПОЛИГАРМОНИЧЕСКОЕ ВОЗМУЩЕНИЕ
г. Решая линеаризованное уравнение, находим
/=1
причем
N
*=1
'■■" /с
^ = <P/ + arctg
..2\2
)2 + ^
\&1
°v№-4)
Составим выражение для о;
;2-
1 * : 1 Л
/=1 /=1
4»!
~(^-^)2+V?
167
(15.27)
(15.28)
(15.29)
. Значения о\, удовлетворяющие этому уравнению, можно
определять графическим методом. Для этого строится график
функции ,
N.
°£<*) = т21;
АА
2 £(*о-<#+->?
• . - . ■ {\ь-щ
и гипербола , ' - " .■
.<£=-£• (15.31)
Точка пересечения линий .
(15.30) и (15.31) определяет #L
значение о^, соответствую- рис ^
щее решению уравнения
(15.29) (рис. 70). Естественно, лто длялостроеция линии (15.31),
нужно знать значение коэффициента Y- Если ограничиться
приближением по первым .,шести моментам функции
распределения- процесса" v{t)\ коэффициент линеаризации можно
определять по формуле (5.42). При этом
1й ' *" " * ^
У=*—7ЩЩ + ^)- (15.32)
Коэффициенты alf %, kv k2 выражаются через
параметры е и р. с помощью уравнения,(5.33) и формул (5.34).
168 НЕЛИНЕЙНЫЕ СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ [ГЛ. Ill
Задавшись предварительно значениями е и |i, например,
в соответствии с формулами (5.45), можно затем
производить их уточнение по методу последовательных приближений.
Линия (15.30) может не иметь с гиперболой (15.31) общих
точек; это означает, что решение вида (15.27) не существует.
Здесь следует различать два случая:
а) если кривая (15.30) располагается ниже гиперболы (15.31)
(в этом случае обе линии, формально говоря, пересекаются
в точке о^ = 0, z = oo\ то это означает, что вибрационное
воздействие недостаточно для преодоления силы трения;
амортизатор «заперт», или происходят движения с остановками;
б) если кривая (15.30) располагается выше гиперболы
(15.31) (это возможно только в том случае, если А,
совпадает с одной из частот о)^ в противном случае при z = 0
q2 имеет конечное значение, и кривая (15.30) не может
лежать выше гиперболы), то это означает, что величина а^ не
является ограниченной, происходят резонансные колебания,
характерные для линейной системы с сухим трением.
Исследуем более подробно уравнение (15.29) в5 случае,
когда N=2. При этом получаем
ч=
л2 2
Л|а§
(15.33)
Преобразуя это выражение, приходим к квадратному
уравнению относительно at.
[6
(tf—ff
2\2
Нетрудно
если
J2 —
л\+4
А2
л2
У2(д\(4
w—Df
+
О. (15.34)
°J>0.
видеть, что это уравнение имеет решение
Если же
Y2<
f>
А\+4
(15.35)
Л\+А\
2 .
§ 15]
ПОЛИГАРМОНИЧЕСКОЕ ВОЗМУЩЕНИЕ
№
то тогда и подавно
то есть оба коэффициента в уравнении (15.34) являются
положительными, и положительных решений оно иметь не
может. Условие (15.35) является поэтому необходимым для
существования решения вида (15.27).
Рассмотрим особо тот случай, когда одна из частот
гармоник вынуждающей силы совпадает с собственной частотой.
Пусть, например, со1 = Х.0; тогда уравнение (15.30)
принимает такую форму
^-iIt+^-^+^J- (15-36)
Очевидно, что при
Л2
линия (15.36) будет расположена выше гиперболы (15.31),
то есть будет иметь место неограниченное увеличение а|.
Если же
4"<Y2. (15.37)
то кривая (15.36) либо целиком располагается ниже линии
(15.31), либо пересекается с ней в точке, соответствующей
конечному значению о^. Таким образом, условие (15.37)
обеспечивает отсутствие резонансных колебаний, какова бы ни
была величина амплитуды Л2. Это положение, полученное
здесь приближенными методами анализа, подтвердилось при
моделировании уравнения (15.22) на электронной машине.
3. Рассмотрим теперь в более общей форме задачу об
отыскании полигармонических решений. Пусть уравнение
движения системы задано в виде
л
mil + Ud (#, и) -f Uy (и) — 2 Fi cos (o,f + фД (15.38)
ы\
Если при отыскании совместной плотности вероятности
процессов # ц it ограничиться приближением по моментам
I7G НЕЛИНЕЙНЫЕ СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ [ГЛ. III
первого и второго порядка, то коэффициенты U0, -сд и Ь^
в линеаризованном уравнении
ти-\- &дИ + Ц> + сдй°==21 /^cos(cd^ + (P*) (15.39)
будут являться функциями а0% о2и и o2v; они могут быть
определены по формулам (11.9) — (ГГ.И).
Разыскивая решение линеаризованного уравнения в форме
(15.2), получим
«i= .гг.л>~ * ..,. :, /> о5-40)
где
Следовательно,
N
; 1
-2
» = 7 ^ № (о*\ -«?12 + 4п? Го?, o?Vtf ^ ° W' C15'41^
ЙИФ^Ч^фф*"
лг
д2,л2
1 V4 ^Ь"1
°^Т1 [^-«jp + ^jft a2)o)f =*<*>• (15.42)
Непосредственное определение о^ и а£ из этих
уравнений является обычно весьма трудоемкой задачей. ОднаЙочгри
исследовании виброзащитных систем обычно в перЬую
очередь требуется определить, могут ли в системе возйик»уть
резонансные колебания, или же имеющееся в ней
демпфирование обеспечивает -их подавление, Если ограничиться
только таким исследованием, то можно применить метод
расчета, аналогичный рассмотренному выше, в первом примере.
Уравнения (15.41) и (15.42) бпре&ёШФг в2и и о*^кШ
функции параметров К и пг При мэлых величиях пА (слабое
демпфирование) можно принять, что максимумы этих
функций соответствуют значениям параметра А., совпадающим
с:©/. Положив ^(Оу)==гй>г найдем по графику кривой Цо£)
соответствующие максимальные значения {Ф\^ Для кэддог©
§15]
ПОЛИГАРМОНИЧЕСКОЕ ВОЗМУЩЕНИЕ
из них определяем (n2^i из уравнения
171
(15.43)
Из рис. 71 ясно, что при этом значении пл кривая Ф(А,)
коснется скелетной кривой в точке с абсциссой X = (ut.
Подставим найденное значение (л*), в уравнение (15.42) и
найдем (a2Y. из соотношения
AU
(15.44)
Определим теперь значение га*,,
соответствующее (о*), и (o*)t,
«*-
2/и
(15.45)
Если оказывается, что я*;> яд/. рис 71
то это означает, что
значение 0(00/) в действительности меньше, чем (ofy, то есть
что кривая Ф(К) располагается вблизи точки 7, = со, ниже
скелетной кривой. При этом гармоника частоты со, не может
вызвать резонансных колебаний. В противном случае
(n*i<n .) опасность резонанса сохраняется.
В качестве примера рассмотрим вновь систему,
описываемую уравнением (15.16), предположив, однако, что
линейное трение заменено диссипативной силой, имеющей
следующую характеристику:
ид(и, tf) = pV*2a2 — и2sign и, (15.46)
где k — отношение йтах к ой.
Если совместную плотность вероятности и и и искать
в форме (5.75), то коэффициент линеаризации ЬД можно
определить по формуле (5.85):
(15.47)
bA = &(2a2 Vk*ol-ol + ea6kou) =
ae2 = -=== = 0.69A.
172 НЕЛИНЕЙНЫЕ СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СЬоЁОДЫ [ГЛ. ill
где С—коэффициент, зависящий от a2, a3, kt e, то есть,
в конечном счете, от ги и euv.
Найдем величину £, при которой обеспечивается
подавление резонансных колебаний.
Сначала решение производится тем же путем, что и выше,
в примере 1. Определив значения v{ и v2 из уравнения (15.20),
мы должны затем найти o2v и o2v по формуле
2 * Л' Г *1 *2 1
(/=1, 2).
Получаем
ovl = 0,99 ДЯ0, a„2= 1,51 ДА,0.
С другой стороны,
Для подавления резонансных колебаний должны
выполняться условия
ТГ - *Г > 2vAo> Т —3* > 2v^o-
Подставляя найденные значения v1§ v2. ай, а^, получаем
С>0,742Яю и £>0,92^.
Очевидно, что должно быть выполнено второе условие, как
более сильное.
В заключение напомним, что формулы для коэффициентов
линеаризации, использованные в этом параграфе, являются
справедливыми лишь в том случае, если среди частот cfy нет
таких, которые удовлетворяли бы условиям (5.13) и (5.15);
в противном случае необходимо учесть зависимость моментов
третьего и четвертого порядка от фаз i|^.
§ 16. Резонансы дробного порядка в виброзащитных
системах
В этом параграфе излагается общая теория резонансов,
которые могут возникать в системе с одной степенью
свободы при периодическом вибрационном воздействии.
* 161
РЁЗОНАНСЫ ДРОБНОГО ПОРЯДКА
173
В физике резонансами принято называть колебания
большой амплитуды, вызванные относительно слабыми внешними
воздействиями на систему. Для того чтобы глубже
разобраться в природе резонансных колебаний, напомним сначала
некоторые характерные особенности резонанса в линейной
системе с одной степенью свободы, уравнение движения
которой записывается в форме (11). Пусть
-Lq(O = F0cosV. (16.1)
то есть вибрационное воздействие является гармоническим,
а частота его совпадает с собственной частотой системы.
Разыскивая установившееся решение уравнения (11) в форме
e = acos(V + 6). (16.2)
получаем, после подстановки (16.2) в (11)
— allcos (V + G) — 2паХо sin (V + 6) +
+ aA.gcos(y + 9) = /70cosy. (16.3)
Очевидно, что упругая сила тождественно равна и
противоположна по знаку произведению массы на ускорение,
совершенно так же, как при свободных колебаниях системы
в отсутствие сил сопротивления. Отсюда следует, что внешнее
воздействие должно в любой момент времени равняться силе
сопротивления
— 2па'к0 sin (У -f- 9) = F0 cos у,
откуда сразу получаем
« = тяЬ в=—тг- О6-4)
^0 л ГС
2пХ0 * 2
Таким образом, при достаточно слабой диссипативной силе
(ж^Ио) в системе могут возникать колебания большой
амплитуды, при которых амплитуды упругой силы и силы
инерции будут значительно превышать амплитуду внешнего
воздействия. Действительно,
\и\ =\Х*и\ =aX*=s£g±*^>F0. (16.5)
1 'max I 0 |max 0 2п ^^ и . у
Все изложенное позволяет рассматривать резонанс в
линейной системе с одной степенью свободы как свободные
колебания, поддерживаемые внешним воздействием. Возможность
174 НЕЛИНЕЙНЫЕ СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СЕОЁОДЫ [ГЛ. itj
существования резонанса обусловлена здесь тем; что в
идеальной консервативной системе, при, отсутствии сил
сопротивления, могут происходить гармонические колебания сколь
угодно, большой амплитуды, если соответственно выбраны
начальные условия, В реальной системе свободные колебания
затухают из-за. рассеяния энергии силами сопротивления.
Внешнее гармоническое- воздействие способно* поддерживать
амплитуду свободных колебаний на таком уровне, при
котором влияние диссипативной силы полностью компенсируется.
Аналогичное по физической природе явление может иметь
место и в нелинейных системах. Рассмотрим вновь систему
с одной-степенью свободы (уравнение (12.1)), полагая, что
вибрационное воздействие Q (t) является периодической
функцией времени с периодом Т. Представим реакцию
амортизатора в виде суммы упругой и диссипативной силы и
перепишем уравнение (12.1) в следующей форме:
mu-\-Uy(u) = — Ud(u, u)-{-Q(t). (16.6)
Обобщая понятие «резонанс» на нелинейные системы,
будем называть резонансными такие колебания системы (16.6),
при которых амплитуды упругой силы и силы инерции
существенно превышают амплитуду вибрационного воздействия.
При резонансных колебаниях силы, стоящие в правой части
уравнения (16.6), являются малыми. Это позволяет
предположить, что периодические решения этого уравнения будут
близки к периодическим решениям уравнения
««o + {/y(«o) = 0. * (16.7)
тр есть к свободным колебаниям системы при отсутствии
сил сопротивления. Таким образом, и в этом случае речь
идет о «свободных колебаниях», поддерживаемых
вибрационным внешним воздействием.
Для определения периодических решений уравнения (16.6)
воспользуемся результатами, полученными в § 6. При малых
силах Ud и Q(t) система (16.6) «близка» к консервативной
системе (16.7) и условия существования периодических
решений могут быть записаны в форме (6.13). .
Уравнение (16.6) может иметь периодические решения
с периодом, равным или кратным Т\ в силу основных
положений метода Галеркина нас должны, интересовать
периодические решения уравнения (16.7), имеющие такие же периоды.
§ 16] РЕЗОНАНСЫ ДРОБНОГО ПОРЯДКА 175'
Пусть уравнение (16.7) имеет периодическое решение4
периода рТ, где р — некоторое целое число; тогда,
вследствие автономности, оно имеет семейство таких -решений
вида
u0 = q>(t + а, рТ), (16.8)
где а — произвольный вещественный параметр.
Легко показать, что решение (16.8) может быть
-разложено в ряд Фурье, содержащий только косинусы кратных
гармоник; это следует хотя бы из того, что уравнение (16.7)
не изменяется при замене t на —t. : > -^
• Таким образом,
Ч'-
2я
(16.9)
Значение параметра а, определяющего сдвиг по фазе
между вибрационным воздействием и вынужденными
колебаниями, должно определяться из уравнения (6.13), которое
в рассматриваемом случае может быть записано в следующей
форме:
Рт Рт
Р(о) = — j ид(цф 'u0)u0dt + f Q(t}abdt = 0. (16.10)
о * - ' о- * - * ' - "'
Первый из интегралов представляет собой работу дисси-
пативных сил на свободном колебании консервативной
системы; величина его, очевидно, не зависит от параметра а и
равна площади петли гистерезиса
рТ '■•<•'
№,= J Ud(u0, UQ)u0dt = ±Uo(u, u)du. (16.11)"
о ' .)
В случае линейного трения
рт
Wc= f bhQuQdt^ " - '
рт г
_ 4лЧ / V л
-\2
9 И*}
,ttlnjj'«+u)
dt=2^ 2 aft" (16.12)
РТ
м
176 НЕЛИНЕЙНЫЕ СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ [ГЛ. III
Для сухого трения
рТ рТ
Wc = f Hsignu0u0dt = f H\ii0\dt = 4Ha, (16.13)
о о
где а — амплитуда свободных колебаний (предполагается,
что перемена знака скорости при свободных колебаниях
происходит лишь дважды в течение одного периода).
Обычно при практических расчетах можно ограничиться
определением приближенного значения We% найденного в
предположении, что свободные колебания близки к гармоническим.
При этом для случая линейного трения имеем
Wc~^f-a\, (16.14)
где а1 — амплитуда первой гармоники.
Аналогичным образом можно определить Wс и для других
форм демпфирования.
Исследуем теперь второй интеграл в уравнении (16.10),
выражающий работу вибрационного воздействия на
свободном колебании консервативной системы. Разложим
периодическую внешнюю силу в ряд Фурье:
со
Q(0 = ^(Qcj^sj^t + Qsjsmj^-t)9 (16.15)
где Qcj и Qsj—коэффициенты Фурье. Предполагается, что
постоянная составляющая в силе Q(t) отсутствует.
Подставив выражения (16.9) и (16.15) в (16.10) и
учитывая, что
F ( 0 при /=£/>,
cos j -£tsini-£;(t-{-a) = { рТ . . 2яа
J T pTK i J ^- sin J —j- при / = у/?,
j
f f 0 при 1Ф]р,
sin / у t sin / —y (t -j- а) = j
9
■tj-cosj-y при i = Jp,
§ 16] РЕЗОНАНСЫ ДРОБНОГО ПОРЯДКА 177
получаем
рт
wb=\ Q(t)u0(t)dt =
о
оо
= —np^Japj(QcjSlnj2f-a+QsJcosj2f- а), (16.16)
; = i
где индекс pj — произведение числа р на номер у, по
которому производится суммирование. Таким образом, параметр а
должен определяться из уравнения
оо
Wc+^P^J^pj(Qcj^j^a + Qsjcosj^a)=Ot (16.17)
которое, как мы видели, имеет простой физический смысл:
работа вибрационного воздействия за один цикл колебаний
должна равняться работе диссипативной силы за тот же
период.
Анализируя выражение (16.17), нетрудно понять, в чем
состоит основное различие в условиях возникновения
резонансных колебаний между линейной и нелинейной системой.
В линейной системе с одной степенью свободы свободные
колебания являются гармоническими и всегда происходят
с собственной частотой. Здесь
и0= acosk(t-\-a),
причем а и а могут выбираться произвольно.
Выражение (16.16) не обращается в нуль только в том случае, если
/•-=- = А,, то есть если частота одной из гармоник
вибрационного воздействия совпадает с собственной частотой
системы. Только эта гармоника вибрационного воздействия
способна произвести не равную нулю работу на свободном
колебании системы и тем самым поддержать свободные
колебания, возместить рассеяние энергии, вызванное наличием
диссипативных сил.
В нелинейной системе свободные колебания не являются
гармоническими. Поэтому гармоническое вибрационное воз*
действие способно произвести не равную нулю работу и
в том случае, когда его частота кратна частоте С8О09ОД9Г9
Щ ty. з. Колоас^й
178 НЕЛИНЕЙНЫЕ СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ [ГЛ. III
колебания, то есть совпадает с частотой одной из его
высших гармоник.
Резонансные колебания, период которых в р раз
превышает период вынуждающей силы, называются
субгармоническими резонансами порядка р или дробными резонан-
сами порядка \/р. При этом рассмотренные в предыдущих
параграфах резонансные колебания, период которых
совпадает с периодом внешнего воздействия, могут быть названы
резонансами порядка 1. Часто их называют основными
резонансными колебаниями.
Вообще, при совпадении частот г-й гармоники
вибрационного воздействия с /?-й гармоникой свободных
колебаний, в выражении (16.16) появляется не равный нулю член.
Это означает, что в системе ив этом случае становится
возможным возникновение резонансных колебаний, частота
которых относится к частоте вибрационного воздействия
как г/р. Такой резонанс называется дробным резонансом
порядка r/р. Для того чтобы резонансные колебания имели
период, равный или кратный периоду вибрационного
воздействия, необходимо, чтобы отношение р/r являлось целым
числом.
Рассмотрим теперь более подробно условия
возникновения дробных резонансов при гармонической вынуждающей
силе
Q(t) = Fcos®t. . (16.18)
Очевидно, что, поскольку в этом случае возбуждение является
гармоническим, в системе возможно возникновение только
резонансов порядка \/р. Уравнение (16.17) принимает при
этом такую форму (у = 1)
P(a)==Wc + 7ipapFsivi(i)a==0. (16.19)
Чтобы значение а получилось вещественным, должно
выполняться условие )
|sincoa
или
wc
npapF\<1 (^20>
Кс\<\*Р*рП' (16.21)
Это неравенство и является условием возможности
возникновения субгармонического резонанса порядка /?. Проанзлизи?
руем его более подробна
im
РЁЗОЙАНСЫ ДРОБНОГО ПОРЯДКА
179
• • Левая часть неравенства зависит от интенсивности и вида
демпфирования. С увеличением интенсивности диссипативных
сил наступает момент, когда неравенство (16.21) нарушается;
при таком демпфировании возникновение субгармонического
резонанса становится невозможным: Правая часть неравенства
пропорциональна произведению рар, где ар — коэффициент
Фурье при /?-й гармонике свободных колебаний. Величина
этого произведения убывает с ростом р во всех случаях,
когда функция Uy (и) имеет непрерывные частные
производные первого порядка. Вообще, чем более гладкой является
ъ>=Л(а)
со-Л fa)
Рис. 72.
упругая характеристика амортизатора (то есть чем выше
порядок производных функции Uy{u), остающихся
непрерывными), тем быстрее убывают величины коэффициентов ар
и, следовательно, тем менее вероятным является
возникновение субгармонических резонансных колебаний. Поэтому такие
резонансы чаще всего возникают в виброзащитных системах
с ограничительными упорами, дающими разрыв функции U* (#).
Опасность возникновения субгармонических резонансов
усиливается с ростом амплитуды вынуждающей силы F.
Поскольку субгармонические резонансные колебания близки
к свободным, решение (16.8) может быть использовано не
только для определения условий существования этих
колебаний, но и для оценки их амплитуды. В первом приближении,
как и в случае основных резонансных колебаний, можно
считать, что амплитуда субгармонических колебаний
совпадает с амплитудой свободных колебаний, имеющих ту же
12*
180 НЕЛИНЕЙНЫЕ СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ [ГЛ. Ш
частоту. Практически для оценки амплитуды
субгармонического резонанса порядка р удобно использовать скелетную
кривую X (а) (рис. 72). Поделив частоту вынуждающей силы сох
на р, непосредственно находим величину амплитуды а.
Из рис. 72, а и б легко видеть, что в системе с «жесткой»
скелетной кривой субгармонические резонансы порядка р
возможны при ($! > рХ& а в системе с «мягкой» скелетной
кривой — при 0^ < рХ0.
А. М. Кац [15] показал, что условие устойчивости решения
уравнения (16.6), найденного описанным выше способом, может
быть представлено в следующей форме:
■£«•)•-£> а (16.22)
Здесь а* — корень уравнения (16.10), соответствующий исследуемому
решению, а значение dX/da определяется по скелетной кривой, для
значения Я, совпадающего с частотой этого же решения.
Отсюда, в частности, следует, что по крайней мере одному из
корней уравнения (16.19) всегда соответствует устойчивое решение.
В самом деле, это уравнение имеет два корня аг и а2> причем
производная
dP
-— sss прар<йг cos оа
при этих значениях а* принимает противоположные знаки, а
значение dX/da в обоих случаях одинаково. Следовательно, для одного
из решений условие (16.22) безусловно удовлетворяется.
Перейдем теперь к исследованию условий существования
субгармонических резонансов в некоторых частных случаях.
Прежде всего, запишем условие (16.21) для различных видов
демпфирования.
Для линейного трения, подставляя (16.12) в (16.21),
получаем
2я<— , (16.23)
©2^5
где
§ 16] РЕЗОНАНСЫ ДРОБНОГО ПОРЯДКА 181
Условие (1(5.23) можно упростить, если использовать
приближенное выражение для работы диссипативной силы (16.14)
2п < F ' р' . (16.24)
ш\
Отсюда можно, в частности, получить условие существования
основных резонансных колебаний, соответствующих
/7=1, ар = аг. (16.25)
При этом получаем
ак£. (16.26)
Этот результат полностью совпадает с тем, что было
получено в § 12. Формула (16.26) означает, что резонансные
колебания с амплитудой а* и частотой со могут возникнуть
в том случае, когда линия (12.16) пересекает скелетную
кривую выше точки а*.
При сухом трении получаем, используя формулу (16.13):
и<—w~
или
(16.27)
где
Для
основного
^ а
резонанса получаем
h<Flt
что соответствует условию существования решений, близких
к гармоническим, полученному в § 13.
Наконец, для внутреннего трения, при гармоническом
внешнем воздействии, можно пользоваться формулой (14.1).
При этом работа диссипативной силы за период свободных
колебаний выражается площадью петли гистерезиса,
соответствующей амплитуде а:
Н^ = ярац+1. (16.28)
182 НЕЛИНЕЙНЫЕ СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ [ГЛ. Ill
Следовательно, для существования субгармонических резо-
нансов должно быть
Ь = ^<фг- (16-29)
При исследовании конкретных виброзащитных систем
использование полученных результатов сводится к
определению таких параметров демпфирования, при которых
существование субгармонических резонансных колебаний полностью
исключается, то есть неравенство (16.21) выполняется с
обратным знаком. Наиболее трудной частью исследования
является определение коэффициента Фурье при /?-й
гармонике свободных колебаний. Каким образом он определяется,
мы покажем на конкретных примерах. В этих примерах
удобно ввести безразмерное время
t = V» (16.30)
где Х0—собственная частота упругого амортизатора, а также
безразмерную частоту свободных колебаний и вибрационного
воздействия;
В качестве первого примера рассмотрим амортизатор с
симметричной кубической характеристикой, свободные колебания
которого описываются уравнением
ти + са + еиъ = 0. (16.32)
Переходя к безразмерному времени, получаем
4J + * + Y"3 = 0, (16.33)
где
е
Y = 7-
Уравнение (16.33) интегрируется в квадратурах. Для этого
следует использовать «интеграл энергии» (см. формулу (2.3)):
тЫ +т+*т=-г+?х. (16-34)
где а — амплитуда свободных колебаний.
du
"dx
16] РЕЗОНАНСЫ ДРОБНОГО ПОРЯДКА
-Из (16.34) находим
= |Дя2-«2) + ^(я4-а4) =
183
= а }/1 + f *2У(1 - £2) (1 + г20,
где
е'=-
уа2
с=
2-[-уд2 * " л
Теперь интегрируем уравнение (16.34)
и
du
О |/(а2_„2)+Х(а4_ц4)
]Л+je2 °
Jo-
rfC
С2)(1+е2С2)
(16.35)
Решение исходного уравнения (16.32) является обращением
этого интеграла и представляет собой эллиптическую функцию
~acn[Yl +Y^(T + To)]-
(16.36)
Теперь, пользуясь известным разложением эллиптической
функции в ряд Фурье, находим
и = а
Sib^Tcos^+1)^
*КМ%1 + *
(16.37)
Здесь и—модуль эллиптического интеграла (16.35), К(н) —
значение полного эллиптического интеграла первого рода,,
соответствующее этому модулю, if^v^ + T,,), а величина ^
определяется выражением
184 НЕЛИНЕЙНЫЕ СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ [ГЛ. III
Разложение (16.37) позволяет выразить коэффициенты Фурье
через амплитуду свободных колебаний
2л
аР===а кК(х) T+F ПрИ Р~нечетном'
ар = 0 при р— четном,
(16.38)
Необходимо еще выяснить, как связана частота свободных
колебаний с их амплитудой. Для этого проинтегрируем (16.35)
по а в пределах от 0 до а, приняв т0 = 0; тогда получим
Г = _Щ=г или У=^Г+^. (16.39)
4 Яо/1+Y^2 2К(у)
Теперь можно построить скелетную кривую, выражающую
зависимость безразмерной частоты свободных колебаний от
амплитуды, а затем по формуле (16.38) найти р-ю
гармонику свободных колебаний. Разумеется, при приближенном
решении можно заменить точное выражение для скелетной
кривой (16.39) приближенным, определяемым по методу
гармонической линеаризации.
Определим величину силы сухого трения, обеспечивающую
подавление субгармонических резонансов третьего порядка.
Подставляя (16.38) в (16.27), получаем
h>wkTT¥F- <16-40>
Если частота вынуждающей силы равна со, то для третьей
субгармоники X = со/3 или v = 2/3. Определив из этого
соотношения v, можно по формуле (16.39) найти а, а затем
из (16.40) — h.
Отметим, что приближенный анализ, основанный на
определении высших гармоник свободных колебаний методом
гармонического баланса (улучшенное первое приближение;
см. § 1), в рассматриваемом случае дал бы весьма грубое
приближение. Так, например, при v— 1, z = 3, величина силы
сухого трения получается бесконечно большой, поскольку
отношение az/a1 стремится к бесконечности, если под ах
понимать амплитуду первой гармоники.
Рассмотрим теперь амортизатор с симметрично
расположенными упругими упорами (характеристика (10.6')), После
16]
РЁЗОНАНСЫ ДРОБНОГО ПОРЯДКА
185
перехода к безразмерному времени уравнение свободных
колебаний записывается в такой форме
d2u . Л
при
1) sign в при
|«|<rf.
|«|>rf.
(16.41)
d
м
и
Г2у^
\ г
Найдем свободные колебания, безразмерная частота которых
равна v. Для этого используем метод «припасовывания»,
часто применяющийся в теории нелинейных колебаний при
исследовании
кусочно-линейных систем.
Поскольку фаза свободных
колебаний может выбираться
произвольно, примем для
определенности, что при т = 0,
и = 0, -т- > 0. В силу
симметричности упругой
характеристики, свободные колебания Рис. 73.
должны иметь форму,
показанную на рис. 73, где каждая из полуволн симметрична
относительно своей максимальной ординаты. Поэтому
достаточно определить закон движения в интервале 0 ^ х <^ у-.
Пусть хх — момент времени, соответствующий u — d;
интегрирование линейных уравнений (16.41) дает
их = Агsinт-fZ?icost при 0 <т<т1, ]
и2 = Л2sin>cT-f-^2cos>ст+^/(х2— 1) при т1<т<~. [
Для определения постоянных Av Bv A2, В2 и момента
времени хх используем начальные условия и условия
«припасовывания», являющиеся в данном случае условиями
непрерывности и и du/dx при x — xv
Начальные условия: т = 0, иг — 0.
Условия припасовки: 1) x — xv u{ = d-t 2) x = xv ul = u2;
3) x = xv -j-!-===-j-£. Наконец, используем условие
максимума при r = n/2v:
л du2
т =
2v •
dx
= 0.
НЕЛИНЕЙНЫЕ СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СЁОВОДЫ [ГЛ. Ill
Определяя постоянные из этих условий, находим
1 Sin Ti
£т = 0,
sin
хя
"2^
cos
в,
27
. (16.43)
2 х2 (п \ ' . ~* к2 ( п \
COSX\27-"Tl) C0SXUr-T\)
Величина тх определяется при этом из следующего уравнения:
teVigf-g.-T,):»*. (16.44)
На рис. 74 приводится зависимость хх от v при различных
значениях х.
Подставляя (16.43) в (16.42), получаем
sint
ai=dimv
d
"2 = ТХ
cos
IK(lr-T)
-f и2
(16.45)
(16.46)
Амплитуда колебаний, очевидно, равна значению н2 при
T=n/2v; поэтому '
а = -
1
cos
*{^~х)
1
(16.47)
Теперь можно найти коэффициенты Фурье функции #(т).
Коэффициенты при четных гармониках равны нулю в силу
симметрии; для коэффициентов при нечетных гармониках
получаем
2л \ . • ;
e-p^ij"-
cos pvr dx •■
Ti
> 2v
~ ~^~ \ uicos Pvx dx-\- \ u2 cos pvt dx
4flf (к2 — 1) (cos p\xx • tg Tt — pv - sin jpvtQ
я /? (/>V — 1) (/>V — x2) tg Ti
(16.48)
§ 17] СУБГАРМОНИЧЕСКИЙ РЕЗОНАНС 187
Пусть, например, х = 2; амплитуда вынуждающей,
силы—Fw, безразмерная частота z = 4,5. Определим
интенсивность сил сопротивления, необходимых для подавления
резонансных колебаний.
По рис. 74 определим, что безразмерная частота
свободных колебаний при х=2 ограничена пределами l<v<2.
Единственное целое р,
удовлетворяющее условию г = pv,
равно трем; поэтому в системе
возможен только
субгармонический резонанс третьего
порядка, причем v= 1,5.
дЛя v=1.5 из рис. 74
находим т1 = 0,35. По
формулам (16.47) и (16.48)
определяем
а3 = 0,4Ы.
Рис. 74.
0,5
*m°£j
\\*"*
jc-4
а = 2,24rf,
/
Теперь, например, по формуле
(16.24) получаем коэффициент
линейного трения, при котором условия существования
резонанса не выполняются
п>
4,5А,0 • 2,242д?2
= 0.16
F
K0d
Для сухого трения по формуле (16.27):
h>
3.QAU.F
2,24d
= 0,55/7.
§ 17. Субгармонический резонанс в системе
с жесткими упорами
Выше было показано, что чем больше жесткость
ограничительных упоров, чем резче переход упругой
характеристики амортизатора от основного упругого элемента к упорам,
тем сильнее опасность возникновения субгармонических резо-
нансов. В связи с этим особый интерес представляет иссле-:
дование системы с жесткими упорами. В большинстве случаев*
можно утверждать, что если диссипативные силы, имеющиеся
в системе, достаточны для подавления субгармонических
188 НЕЛИНЕЙНЫЕ СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ [ГЛ. III
резонансов, возникающих при введении жестких
ограничительных упоров, то они и подавно достаточны при том же
«свободном ходе», если упоры имеют любую другую упругую
характеристику.
Рассмотрим свободные колебания системы с линейной
упругой характеристикой и жесткими упорами.
В дальнейшем мы будем различать «верхний» упор,
расположенный на расстоянии d от положения равновесия в
положительном направлении, и «нижний» упор, координата
которого равна —dv Таким образом,
Uy(u) = cu при — dl<u<d. (17.1)
Для дальнейшего необходимо ввести какое-либо
предположение о характере удара об упор; поскольку мы хотим
рассматривать свободные колебания, предположим, сначала,
что удар является абсолютно упругим, то есть происходит
без потери энергии. В этом случае в момент удара скорость и
меняет знак, сохраняя свою
величину, и закон движения
имеет форму, показанную на
рис. 75. Введя безразмерное
время, можно записать
дифференциальное уравнение
движения в промежутке между
ударами в таком виде
-g- + B = 0. (17.2)
Период колебаний, равный
промежутку времени между
Рис. 75. ударами об один и тот же
упор, обозначим через 2n/v, где
v — безразмерная частота. Закон движения за период
симметричен относительно ординаты t = ji/v; поэтому достаточно
определить его только в интервале О^т^я/v.
Интегрируя (17.2), получаем
и = A cos т + В sin т. (17.3)
Граничные условия:
т = 0, и =
— du * = -
u = d
§ 17} СУБГАРМОНИЧЕСКИЙ РЕЗОНАНС
позволяют определить постоянные А и В:
189
d-\-dx cos —
sin -
(17.4)
Отсюда
и=—L-^sinT-rfjSln^-t)] (о<т<£). (17.5)
sin —
V
Теперь можно определить коэффициент Фурье при /?-й
гармонике:
*/■
cos pvx dx =
л J
sint
. я
sin —
v
■dv
8|п(т-т)
sin —
v
cos pvxdx —
2v(d — di) ,_ jt
—тт гтсЧ-сГ ПРИ четном pt
я(1—/?V) & 2v r r
2v(d + d{) , я .
Я(1-^^у при нечетном />j
(17.6)
Если d — dv то есть если упоры расположены симметрично.
коэффициенты при четных гармониках обращаются в нуль.
Мы предполагали, что происходит удар об оба упора;
однако это имеет место не при всяких значениях d, dx и v.
Определим du/dx на участке 0 < х ^ —
du
= -i— LfcosT + rfiCosf*. — tYI. (17.7)
sin —
v
Для того чтобы при т = 0 произошел удар о нижний упор,
должно быть du/dx ^0; в противном случае система просто
190 НЕЛИНЕЙНЫЕ СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ [ГЛ. III
не может дойти до нижнего упора. Аналогично для удара
о верхний упор должно выполняться условие du/dx^Q
$ при т = —. Учитывая (17.7),
получаем условие удара о
верхний упор:
-/
/
ЬУОар'Л
'верхний]
1\
2 Удар 2-
Z ° <
> нижний
i упор
L
Удар
об оба
упора
К 3
л ^ dt
cos —> т-
v ^ d
(17.8)
и условие удара о нижний упор
(17.9)
я n. d
cos —^ -т-.
v ^ dt
На рис. 76 построены
области значений v и отношения
6 = -j , при которых
происходят удары только о верхний,
Рис. 76. только о нижний и об оба
упора. Отрицательные
значения 6 означают, что оба упора расположены по одну сторону
от положения равновесия, то есть что в положении
равновесия система прижата к одному из упоров.
Рис. 77.
При ударе только о верхний упор постоянные А и В
в (17.3) определяются из условий (см. рис. 77, а)
§ 17] СУБГАРМОНИЧЕСКИЙ РЕЗОНАНС 191
Получаем
й = </-£2!1-. . (17.10)
cos —
V
Отсюда легко определить
Л
V
2v Г , cos т _ , / 1чо 2dv , я
2V I . COST _ , / ivjp ^"V , Я
а„ =— d cos pvr- dx = (—1)p • t 9 я—rrte —.
(17.11)
cos —
V
Амплитуда колебаний в этом случае равна
1
2а = и№\ — я(0) = <* Л
я
cos —
V
(17.12)
При ударе только о нижний упор имеем (рис. 77t б)
1 v dx
Отсюда
cos
(4-)
н = — di ^ '-. (17.13)
Я
cos —
V
Соответственно,
2v Г ^ C0S\T-T . 2rf,v . я
COS —
V
(17.14)
2а = в1-£)-й(0) = -<Ы—V-A. (17-15)
= «(^)-«(0)—rfif-V
4 ' .1 cos —
V v
Теперь нетрудно определить величину диссипативной силы,
необходимой для подавления субгармонических резонансов.
Рассмотрим, например, такую задачу. На. систему действует
возмущение, безразмерная частота которого г = со/Я0 —5,
а амплитуда равна m • F. Расстояние до нижнего упора
192 НЕЛИНЕЙНЫЕ СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОГЮДЫ [ГЛ. Ill
dx = 0,5d. Определить силу сухого трения, достаточную для
подавления субгармонических резонансов.
Поскольку z = pv, a v>l, в системе возможны
субгармонические резонансы следующих порядков:
р — 2, v = 2,5;
р = 3, v=l,67;
/? = 4, v=l,25.
Обращаясь к рис. 76 и учитывая, что 6 =-1 = 0,5,
находим, что в первых двух случаях будут происходить
удары об оба упора, а в последнем случае — только о нижний
упор. Пользуясь формулой (17.6), получаем
при , = 2 v = 2.5. «. = -зщ^*т = 0'024*
при/> = 3 v=1.67. e, = 4^g-cig^ = 0.047rf.
В обоих случаях a = -^-(d-\-(1^ = 0,75(1.
По формуле (16.27) получаем
р = 3, h> *'*№ F = 0.№P.
Для jo = 4 по формуле (17.14) и (17.15):
2 • 0,5d • 1,25 , я . мм.
а4= я (25-1) tgx^ = 0.0303rf,
а = — 0,25й? ( 1— 1 \ = 0,56rf.
vcos-t5s )
Следовательно, должно быть
*>±8Г|>-ми|..
Сравниваем полученные значения h и выбираем наибольшее
из них: h = Qt2\4F. При этом значении h все
субгармонические резонансы будут подавляться. Этот пример показывает,
§ 17] СУБГАРМОНИЧЕСКИЙ РЕЗОНАНС 193
что более опасными могут оказаться субгармонические резо-
нансы более высокого порядка (в данном случае р = 4),
если один из ограничительных упоров расположен значительно
ближе к положению равновесия, чем другой.
До сих пор мы не учитывали, что удары об упоры
в реальных системах всегда сопровождаются потерями
энергии. Эти потери можно определить, пользуясь известной
теоремой Карно, которая в рассматриваемом случае удара
материальной точки о преграду приводит к следующей формуле:
ЛГ= m{i~k2) и2у. (17.16)
Здесь hW— потеря энергии при ударе; иу — скорость
движущейся точки перед ударом, к — коэффициент
восстановления, величина которого зависит от механических свойств
соударяющихся тел и может принимать значения от 0 до 1.
Возникает вопрос, можно ли в случае удара вычислять
потери энергии SW% исходя из решения уравнения (16.7),
то есть подставляя в (17.16) значения скоростей иг найденные
из интегрирования уравнения свободных колебаний. В
работе [27] показано, что это можно делать в тех случаях,
когда коэффициент восстановления близок к единице, то есть
когда удар близок по своему характеру к абсолютно
упругому. При этом величина AW должна быть прибавлена
к работе сил сопротивления за один цикл колебаний, то есть
условие существования субгармонического резонанса
порядка р в системе с упорами может быть записано в такой
форме (вместо (16.21)):
\Wc+AW\<\npapF\. (17.17)
При ударе об оба упора по формуле (17.7) находим
V
4 'т = SHI— N '
13 М. 3. Коловский
194 НЕЛИНЕЙНЫЕ СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ [ГЛ. Ill
где ин и ив—скорости при ударе о нижний и о верхний
упоры. Отсюда находим
bW = %(l-k*)(%+i*l) =
== m(l — k7)[(d2-+-dt) cos ^-^A^cos^-l • ll (17.18)
Очевидно, что если
\&W\ > \npapF\, (17.19)
то есть если потери энергии при ударе превышают работу
вынуждающей силы на свободном колебании, то
соответствующий субгармонический резонанс в системе вообще
не может возбудиться; в этом случае резонанс подавляется
ударами об упоры. Отметим, что потери энергии при ударах
пропорциональны квадратам расстояний до упоров, а правая
часть формулы (17.19) — только первым степеням. Поэтому
раздвигая упоры всегда можно добиться устранения
субгармонических резонансных колебаний.
В случае удара только о верхний упор получаем
Д№ = \tn{\ — k2)l20d2tg2^, (17.20)
при ударе только о нижний упор:
Д№ = 1|ц(1— k2)k20dbg2j. (17.21)
Определим, например, какое значение должен иметь
коэффициент восстановления, для того чтобы обеспечить
подавление субгармонического резонанса четвертого порядка в
рассмотренной выше задаче. Используя формулу (17.21), получаем
условие (17.19) в такой форме (v—1,25)
1
т{\ — k2)X20d\ • 0,7252 > я • 4 • 0№06dxF.
2 '" vA n //vo(
Отсюда получаем
/г2< 1 — 0,345
d{kl
Если принять, например, что dx = 5 мм; Х0~62,8 \/сек\
F = 4g ^ 40 м/сек2, то получаем
£2 < 0,31; /г < 0,55.
§ 18J КОЛЕБАНИЯ ПРИ СЛУЧАЙНЫХ ВОЗДЕЙСТВИЯХ 195
§ 18. Вынужденные колебания при случайных
воздействиях
Существует обширный класс задач теории виброзащитных
систем, в которых вибрационное воздействие удобно
рассматривать как стационарный случайный процесс. К этому
классу принадлежат задачи об амортизации «повозок»
(автомобилей, тракторов, танков и т. п.). движущихся по дороге
со «случайным» профилем, приборов и аппаратов,
установленных на самолетах и ракетах, где имеется большое число
независимых источников вибрации, и, в частности, такой
мощный источник, как реактивный двигатель, задачи о
виброзащите корабельных механизмов и приборов при качке
корабля и многие другие.
Во всех этих задачах факторы, определяющие характер
вибрационных воздействий (профиль дороги, физические
процессы, протекающие в двигателе, высота морской волны),
не являются детерминированными; поэтому и сами воздействия
не могут быть описаны какими-либо детерминированными
функциями времени, и дэлжны рассматриваться как
случайные процессы.
В большинстве случаев вероятностные характеристики
вибрационных воздействий не могут быть получены априорно, например,
на основе анализа физических свойств источника вибрации. Такой
анализ оказывается, как правило, практически неосуществимым,
и вероятностные характеристики случайного процесса определяются
в результате статистической обработки некоторого конечного числа
реализаций, измеренных на конечном интервале времени. Следует
отметить, что при этом можно было бы вообще отказаться от
вероятностной постановки задачи и ограничиться исследованием
поведения виброзащитной системы при детермированных воздействиях,
соответствующих каждой из известных реализаций; при этом
безусловно имеющаяся информация о вибрационном воздействии
была бы использована с наибольшей полнотой. Однако такой подход
связан обычно с большими вычислительными трудностями и в
первую очередь с необходимостью представления в аналитической
форме каждой из реализаций, полученных экспериментальным путем.
Вероятностная постановка задачи оказывается в таких случаях
удобным приемом, упрощающим решение задачи, а в тех редких
случаях, когда известны только вероятностные характеристики
вибрационного воздействия, она является единственно возможным
методом исследования.
С другой стороны, знание лишь конечного числа реализаций
случайного процесса (из возможного бесконечного множества)
оказывается, вообще говоря, недостаточным для однозначного
13*
196 НЕЛИНЕЙНЫЕ СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ [ГЛ. Ill
определения его вероятностных свойств. Неполнота информации
приводит к возможности постулирования таких свойств случайного
процесса, как эргодичность и стационарность.
Вынужденные колебания, возникающие в виброзащитных
системах при стационарных случайных вибрационных
воздействиях, также представляют собой стационарный случайный
процесс. Анализ вынужденных колебаний сводится к
определению их вероятностных характеристик по вероятностным
характеристикам вибрационного воздействия.
Займемся исследованием вынужденных колебаний
виброзащитной системы с одной степенью свободы при случайном
вибрационном воздействии. Пусть в уравнении (12.1) Q(t) —
центрированный нормальный случайный процесс. Для
определения вероятностных характеристик деформации
амортизатора и (t) воспользуемся методом статистической
линеаризации, описанным в § 7. Для статистической линеаризации
нелинейной функции U (и, и) необходимо знать законы
распределения случайных процессов a(t) и a (t). Предполагая, что
они также имеют нормальное распределение, получаем
выражения для коэффициентов линеаризации, подставляя (7.36)
в (7.39) —(7.41):
оо оо
(18.1)
сд= . \ (« -mu)U(u, v)X
Хч[-^-Й*л (18-2>
ОО СО
(18.3)
Здесь о2и и g\ — дисперсии деформации амортизатора и ее
скорости, ти—среднее значение деформации, отсчитываемой
от положения статического равновесия.
§ 18] КОЛЕБАНИЯ ПРИ СЛУЧАЙНЫХ ВОЗДЕЙСТВИЯХ 197
Уравнение (12.1) после линеаризации принимает
следующий вид:
ти*+ сдиО+Ьжи0-\-ио = Q (*), (18.4)
где и° = и — та — центрированный случайный процесс.
Выражения для коэффициентов линеаризации упрощаются
в тех случаях, когда нелинейная функция представима в виде
суммы
U(и, ii) = Uy(u)+Ud(u), (18.5)
При этом получаем
со
со
с*-vh[Iи*(й)(и-"•■>ехр[-i£tjr!]du- (187>
со
b*=v£tiUd(v)vexp(~U)dv- (18-8)
Линеаризованное уравнение позволяет определить момент-
ные характеристики деформации и ее скорости по
спектральной плотности (или корреляционной функции) вибрационного
воздействия Q(t). Сначала находим спектральные
плотности и и и:
S.W-l^-ffivjbp. 08-9)
(d2Sn (ю)
S^-T^^T^MW- (18Л0)
Теперь по формулам (7.43) и (7.44) находим дисперсии:
а2
и
а*
V
1 Г „ If 50 (®) rf®
= — 5а(со)^со = — т Q 2Ч2 , о о. (18.11)
2я _J а 2я j) (сд —т©2)2 + £2®2
1 ? 1 Г ®2Sn (о) rf©
= — Sr(©)rf©=— т Q242 , 2 2. (18.12)
2л J * 2л J (сд-т©2)2 + ^2
198 НЕЛИНЕЙНЫЕ СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ [ГЛ, III
Наконец, приравнивая нулю постоянную составляющую в левой
части уравнения (18.4), получаем
t/0 = 0. (18.13)
Выразив в уравнениях (18.11) — (18.13) коэффициенты
линеаризации UQt cR и bR через о2, а2 и ти, с помощью
соотношений (18.1) — (18.3) получим систему трех уравнений,
из которых можно определить неизвестные моменты.
Для оценки качества виброзащитной системы наиболее
интересным является получение вероятностных характеристик
силовой реакции амортизатора. Из линеаризованного
уравнения находим
U {и. u)=U0 + cAifi^bAefi. (18.14)
Отсюда получаем среднее значение и спектральную
плотность U:
ти = ио = 0.
(18.15)
ч__ l^co+-cJ2.SQ((o) _ (c2 + fr2co2)SQ(co)
Следовательно,
2 * f с , w l Г (cl + bl<»2)SQ^ A ,1Q 1ЛЧ
a2= —- Su(со) df© = — 7-^ 9\2 2 2 flf0)- (18.16)
17 2л J u 2л J (сл —mft)2)2 + ^(o2
-co —oo V A / ' A
Перейдем теперь к решению некоторых примеров. Пусть
спектральная плотность нормального вибрационного
воздействия задана следующим выражением:
5о(®) = 1 а Л- .2» (18.17)
Q N — со2 + рую |2 ч '
Спектр такого вида получается, например, в том случае,
когда широкополосный процесс, близкий к белому шуму,
пропускается через линейную систему второго порядка
(фильтр). В виброзащитных системах таким фильтром может
служить упругое основание. Такой же характер может иметь
спектр процесса и в том случае, когда среди источников
возмущения имеется один доминирующий, создающий
вибрацию, близкую к гармонической. Параметр ц в (18.17)
приблизительно равен квадрату преобладающей частоты, а
параметр р определяет ширину «полосы пропускания» фильтра.
§ 18] КОЛЕБАНИЯ ПРИ СЛУЧАЙНЫХ ВОЗДЕЙСТВИЯХ 199
Подставляя (18.17) в (18,11), получаем
„- оо
а"= 2S" J 2^°Q | т| — <в» + ру© I* | с« — «»2 + bjm |2 - (18Л8>
— ОО
Для вычисления интегралов такого вида, как уже
указывалось ранее, можно воспользоваться готовыми выражениями,
имеющимися во многих руководствах (например, в [43]).
Произведя вычисления, получим ,
д __ 2 т2№ + Ьлсл + Ь$(ЬА + т$)
u-°Q ЬжсАЦсА-тг\)' + (ЬА+т$)(ЬсА+Ьлт\)] * U }
°1
Аналогично найдем
аЪ—2п J |л^(в* + р7а|*|сд —ямв' + йдущр —
— ОО
а [Сд (Уд + "»2РЧ) + >« (>д + яР) (М + Ре,)]
_°<? *д[(ед-яп)2 + (*д + «Р)(Рсд + М)] ' ([*М)
ОО
о;=о=- 2Рло2,
2л J '••"'"Oh —<в» + р/щ|«|вд —ям»*Н-*д/»|я ~
— СО
. Л (^Д + «Р)
= 0Q М(«*-«Л)8 + (*Д+*Р)(РСд+М>] ' (18*21)
Таким образом, коэффициент динамичности К, равный
отношению среднеквадратичного знлчения силовой реакции
амортизатора к среднеквадратичному значению силового
вибрационного воздействия, определяется выражением
сА (^дсд + т'Рл) + ЪА (6Д + mP) (M + Рсд) 9
* ~ М(Сд-™л)2 + (*д + ™Р)(СдР + М)] ' u '
При малых р и £д и переменном г) максимальное значение К
сл
достигается приблизительно при ц = —. При этом
т
*8в<=1 +wis>- . , (,823)
о, (оу = д»-^+»дР)»--ж0« = . ■ (18.24)
200 НЕЛИНЕЙНЫЕ СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ [ГЛ. Ill
Исследуем теперь действие вибрационного возмущения
вида (18.17) на систему с симметрично расположенными
упругими упорами и линейным трением.
Полагая, что Wq = 0, и учитывая симметричность
упругой характеристики, находим
Кроме того, очевидно, что ЬЛ = Ь = const.
Подставляя (10.6') в (18.7), получаем после
интегрирования
где Ф(и) — функция Лапласа,
и
Ф(и) = -р==- Jexp(-i£)<*«- 08.26)
По формуле (18.24) получаем
„2.
Kl=l
«-"-тщ^щ (-■*¥*7)-<,827)
Определив ои* из этого уравнения и подставив его в (18.25),
найдем значение cv а затем из уравнения (18.23) —
значение к1
т*^{,+*[1-»(£)]}- <108)
На рис. 78 и 79 построены зависимости ou*/Y\i и ^* от
безразмерного параметра d/Y~\Si. При этом принято, что
Р = — = 0,2 l/^.
v т у т
Из графиков видно, что при достаточно большом зазоре
даже сравнительно жесткие упоры практически не влияют
на вероятностные характеристики вынужденных колебаний
амортизированного объекта. Если при проектировании
амортизатора обеспечить выполнение условия
§ 18] КОЛЕБАНИЯ ПРИ СЛУЧАЙНЫХ ВОЗДЕЙСТВИЯХ 201
то вероятностные характеристики с большой степенью
точности можно считать такими же, как при отсутствии упоров.
График на рис. 79 показывает, что увеличение зазора
приводит к уменьшению величины /(„, то есть улучшает
виброзащитные свойства системы в «резонансном» режиме,
несмотря на то, что среднеквадратичное значение деформации
при этом возрастает.
/Г*
8
Рис. 78.
/ 2 3
Рис. 79.
Рассмотрим вынужденные колебания, вызванные тем же
возмущением, при линейной упругой характеристике
амортизатора и наличии сухого трения. В этом случае сл = с = const;
по формуле (18.8) находим
(18.29)
где Н — величина силы сухого трения.
Подставляя (18.29) в (18.21), приходим к уравнению для
определения о„:
4.т)(?+р>шр).д|
q |а| (с - /ил)2 +' (? + P""V) (Р«*„ + #4)J '
гт2=.
202 НЕЛИНЕЙНЫЕ СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ [ГЛ. III
Это уравнение приводится к квадратному
<£[(« - «т»2 + стЩ + av [g ~°Q f>mr\ + ftc) +
из двух корней которого только положительный имеет смысл.
Поэтому
°v~ 2q[(c — тч\)2 + cmf>2] "+"
, V [(4 - f) Mm + М2 + Ул (a2Q - Я2) (с - шЛу
"+" 2<7[(с — mri)2 + cmp2] ' U«^)
Положительное значение ov существует, очевидно, при
oQ>q. (18.32)
В резонансе, при с = /ит], среднеквадратичное значение
остается конечным по величине; в этом — одно из отличий
рассматриваемой задачи от случая гармонического
вибрационного воздействия. Подставляя с — тц в (18.31), получаем
о2п — Я2 Я Я2
((V)2^ Q b#= — =2 2 wp. (18.33)
?/тф ov* Oq — q'
Пользуясь этими соотношениями, находим
(а y = d» (' + »> =
2 2
=^w[c(0«-^)+mpV]- (18-34)
/2 2 ч
/С?= 1 Ч -. г = 1 + —о -?- — -V • (18.35)
Если параметр т] (квадрат доминирующей частоты
вибрационного воздействия) достаточно велик, так что тц^>с, можно
получить из (18.31), пренебрегая малыми членами,
УН - Я") т\Г + 4^2Л3 (о% ~ I2) У^7
J
§ 18] КОЛЕБАНИЯ ПРИ СЛУЧАЙНЫХ ВОЗДЕЙСТВИЯХ 203
Следовательно,
ьА~ IfflfL.
Подставляя это значение Ьл в (18.20) и переходя к пределу
при т]->оо, получим
\\mo2u = q2 (при т!->оо).
Это означает, что если спектр вибрации лежит в
высокочастотной области, то среднеквадратичное значение реакции
амортизатора в т/я/2 Раз меньше силы сухого трения.
ГЛАВА IV
НЕЛИНЕЙНЫЕ СИСТЕМЫ С НЕСКОЛЬКИМИ
СТЕПЕНЯМИ СВОБОДЫ
§ 19. Статика нелинейного упругого подвеса
Рассмотрим общий случай движения амортизируемого
объекта, подвешенного на упругих элементах.
В дальнейшем всюду, кроме § 25, будет предполагаться,
что амортизируемый объект может рассматриваться как
абсолютно твердое тело; как известно, это предположение
является допустимым, если
низшая собственная частота
упругих колебаний объекта
существенно превышает
максимальную частоту вибрационного
воздействия.
Пусть объект связан с
основанием N упругими
амортизаторами. Для сокращения
записи удобно обозначить
составляющие деформаций
амортизаторов в главных направле-
Рис. 80.
ниях через av u2,
сто «lt vlt wv
w
ZN
вме-
UN* VN> W
ЛГ-
Тем самым мы как бы условно
заменяем каждый из амортизаторов тремя простыми упругими
элементами, прикрепленными к объекту в одной и той же
точке (рис. 80). Ось каждого простого элемента совпадает
с одним из главных направлений амортизатора, его реакция
всегда направлена вдоль оси и зависит только от
соответствующей составляющей деформации и ее производной по
времени. Таким образом, статические и динамические харак-
§ 19] СТАТИКА НЕЛИНЕЙНОГО УПРУГОГО ПОДВЕСА 205
теристики упругих амортизаторов (9.4) и (9.1) могут быть
записаны в такой форме:
Ust = Vsi(usi\ (19.1)
Ui = Ui(ttlt ut) (/=1 ЗЛО. (19.2)
Простые элементы будут условно изображаться в виде
пружинок (рис. 80); однако их не следует отождествлять
с обычными упругими пружинами. В частности, следует
помнить, что перемещение точки крепления в направлении,
перпендикулярном оси элемента, не влияет на величину его
реакции; между тем известно, что для обычной пружины
учет поперечных перемещений часто оказывается
необходимым.
Остановимся сначала на некоторых вопросах, связанных
со статическим расчетом упругого подвеса, то есть с
определением статических усилий Usi и статических
деформаций usi. Выберем начало системы координат xyz в центре
инерции амортизируемого объекта. Обозначим через a/f p/f yt
косинусы углов, составляемых осью /-го простого элемента
(то есть одним из главных направлений амортизатора),
соответственно с осями х, у и г. Статические нагрузки,
действующие на амортизируемый объект, складываются обычно
из сил веса и сил инерции, вызванных постоянной
составляющей ускорения основания. Равнодействующая этих сил Р
приложена в центре инерции. Пусть xt, ylt zt — координаты
точки крепления /-го элемента к объекту. Составим
уравнения статики:
W ЗЛГ 37V
%Usfli=Px, 1>и^ = Ру, %Usiyi = Pz, (19.3)
i = l / = 1 * = 1
w злг J
2 Usi (y/Yi - г fit) = 0, 2 Usl (z,a, - *м) = 0,
(19-4)
i-l J
Эти 6 уравнений содержат 3N неизвестных, что при N > 2
приводит к статически неопределимой системе.
Предположим, что в ненагруженном состоянии (в
отсутствии статических нагрузок) деформации простых элементов
206 СИСТЕМЫ С НЕСКОЛЬКИМИ СТЕПЕНЯМИ СВОБОДЫ [ГЛ. IV
равнялись u°sl. Эти предварительные деформации принято
называть монтажными. При приложении статических нагрузок
объект получит некоторое перемещение, которое может быть
представлено как сумма поступательного перемещения вместе
с центром инерции 8 и поворота на угол ф. Если
предположить, что угол поворота является малым (в реальных
виброзащитных системах это предположение допустимо,
поскольку расстояния между точками крепления амортизаторов
во много раз превышают их деформации), можно найти
перемещения точек крепления следующим образом:
8/ = 8 + *Хг£. (19.5)
где rt—радиус-вектор точки крепления. Определим
деформацию /-го элемента
Usi=U°si + *i'ni (/==1> ••- ЗД0- О9'6)
Здесь tti—единичный вектор, направленный по оси /-го
элемента. Раскрывая выражение (19.6), получаем
usi = иЪ + 6/А+V/ + 6ьЪ =
= U°si + (6* + %Zi - %Уд ai + (6y + V/ - V/) P* +
+ (^4-*xy/-V/)Y/ ('=1 ЗЛО. (19.7)
Решая совместно уравнения (19.1), (19.3), (19.4) и (19.7),
можно определить 6Л/" -f- б неизвестных — статические
усилия Usl, статические деформации usi и параметры,
определяющие перемещение объекта как твердого тела (6^., 6 6^,
^дг» Фу %)• Естественно, что, поскольку статические
характеристики (19.1) могут быть нелинейными, решение этой
системы уравнений является весьма нелегкой задачей.
Однако в действительности решать ее и не требуется.
Дело в том, что обычно выбор тех или иных упругих
амортизаторов производится на основе статического расчета.
Поэтому при проведении статического расчета характеристики
амортизаторов вообще неизвестны. Только определив
величину статической нагрузки в каждом из главных направлений,
можно выбрать упругий амортизатор, пригодный для этой
нагрузки.
§ 19] СТАТИКА НЕЛИНЕЙНОГО УПРУГОГО ПОДВЕСА 20?
Р
МзН1
\~°г
?//
ж.
-а, Л'
Л/wf
Это обстоятельство существенно облегчает статический
расчет системы, который может производиться в следующем
порядке.
1) Наложим произвольно 3N — 6 линейных условий на
величины статических усилий Usi\ тогда все ЪМ усилий
определятся из этих условий и
уравнений статики (19.3) и
(19.4).
2) По найденным усилиям
выберем упругие амортизаторы; тем
самым определятся их статические
характеристики (19.1).
3) По статическим
характеристикам определим значения usl,
соответствующие ранее
найденным значениям усилий. &. ...
4) Остается определить мон- т*г4А^
тажные деформации из
уравнений (19.7). Эта часть расчета
является, вообще говоря, наиболее
сложной, поскольку необходимо
так распорядиться значениями 6^,
6у, 62, tyx, i|)y, %, чтобы
статические усилия, соответствующие
монтажным деформациям,
удовлетворяли уравнениям статики при
Р = 0. Как будет показано ниже, во многих практически
важных случаях могут быть предложены простые методы
решения этой задачи.
Монтажные деформации амортизаторов, полученные
расчетным путем, должны выдерживаться при монтаже
амортизируемого объекта за счет смещений точек крепления
амортизаторов к основанию. Только при выдерживании монтажных
деформаций можно обеспечить совпадение действительных
значений статических усилий и деформаций с расчетными
а тем самым и совпадение динамических характеристик, фэо ia
которых, как уже указывалось ранее, существенно зависит
от статических деформаций.
Рассмотрим несколько простых примеров.
1. В схеме, показанной на рис. 81, амортизируемый
объект установлен на четырех амортизаторах, эквивалентных
'И
и
х
Ж
Рис. 81.
208 СИСТЕМЫ С НЕСКОЛЬКИМИ СТЕПЕНЯМИ СВОБОДЫ [ГЛ. 1\
12-ти простым упругим элементам. Сила Р направлена по
оси z, то есть Px = Py = Q; PZ = P. Главные направления
амортизаторов параллельны осям координат, так что
<*1 = Pi = а4 = ?4 = а7 = ?7 = аЮ = PlO = Р2 = Y2 = Рб =
= Y5 = Ps = Ys = Рп = Yii = а3 = Ys = «6 = Ye =
= a9:=rY9 = ai2==Yi2==0'
Y! = а2 = p3 = Y4 = а5 = Ре = Y? = а8 = Рэ =
= Yio = аи = Pi2 = 1-
В этом случае можно наложить на статические усилия
следующие условия, не противоречащие уравнениям статики:
Ua = U* = U« = Ua = "л = U* = Usii = ^12 = 0, (19.8)
то есть предположить, что реакции всех четырех
амортизаторов параллельны оси z.
Схема статического нагружения, в которой статические
нагрузки и статические реакции амортизаторов образуют
систему параллельных сил, называется однонаправленной.
Для однонаправленных схем число уравнений статики
сокращается до трех. В данном случае эти уравнения записываются
в такой форме:
(Usl-\-Us4)ai~(Us7-\-UsW)a2 = 0, | (19.9)
(^i + tW h ~ (t/,4 + Usi) b* = 0.
Поскольку число неизвестных превышает число уравнений,
система остается статически неопределимой.
Наложим на усилия Usl, UsAt Usl, Usl0 дополнительное
условие, например, в такой форме
ив1агЬг — UsAaxb2 + Us7a2b2 — UslQa2bx = 0. (19.10)
Решая систему линейных уравнений (19.9) и (19.10),
определим значения UsV Us4, Us7, UslQ (можно показать, что при
принятом дополнительном условии все усилия будут
положительными). Далее выберем упругие амортизаторы так,
чтобы найденные усилия лежали в пределах, допустимых
для этих амортизаторов, и определим значения u^t usA, us7,
§ 19] СТАТИКА НЕЛИНЕЙНОГО УПРУГОГО ПОДВЕСА 209
usl0. Обратимся теперь к уравнениям (19.7). В
однонаправленных схемах всегда должны выполняться условия
6, = 6у==фх==фу==ф, = 0,
(19.11)
в противном случае не будут выполняться условия (19.8).
Иными словами, в положении равновесия амортизируемый
объект должен устанавливаться без перекосов и иметь
поступательное смещение только в направлении оси z. Монтажные
деформации в этом случае могут
быть выдержаны, например, с
помощью прокладок.
Подставляя (19.11) в (19.7),
находим
*s\'
"sl-K*
и* л — и
U°s7 = Us7-bz>
*si
r/0 _
54
tt"i = ",io-6*-
p
4- 4.
С
4- +
jr
4 -4- N
X
4, = ТК+в*4+вЛ + в4|
(19.12)
Условие (19.10) можно было бы
изменить, например, следующим
образом:
^4 = 4-
Значения статических усилий по- Рис. 82.
лучились бы при этом иными;
иными могли оказаться и выбранные амортизаторы. Однако
и в этом случае можно было бы определить значения
статических деформаций, обеспечивающих выполнение
условий (19.11). Произвол в выборе дополнительных условий
позволяет в практических задачах обеспечить выполнение тех
или иных конструктивных требований.
2. Рассмотрим однонаправленную схему статического
нагружения с N амортизаторами (рис. 82). Запишем
уравнения статики:
N N N
2^/ = я 2 */,**, = о. 2*/,/У/ = о. (19.13)
i=i i=i /=i
Н М. 3, Коловски^
210
СИСТЕМЫ С НЕСКОЛЬКИМИ СТЕПЕНЯМИ СВОБОДЫ [ГЛ. IV
Здесь Usi — усилие, действующее на /-й амортизатор в главном
направлении, параллельном оси z. Выберем дополнительные
условия в форме
",i =
U
sN>
(19.14)
то есть потребуем, чтобы реакции всех амортизаторов были
одинаковыми по величине. Количество условий (N—1)
превышает число лишних неизвестных в уравнениях (19.13);
поэтому эти условия выполнимы лишь при определенных
соотношениях между координатами точек крепления.
Подставляя (19.14) в (19.13), получаем
N
Р^
N '
/=1 /=1
N
u*i= ••- =u,n = tj> S^ = 0' S^ = 0- (19Л5)
Если все выбранные амортизаторы одинаковы, то очевидно,
что их статические деформации также будут одинаковыми,
и выравнивание системы при монтаже не потребуется.
3. Рассмотрим схему нагружения, показанную на рис. 83.
Она не может быть однонаправленной, поскольку сила Р и
h —I
г»
ф
Its '
4
Is
7
Г г?
с
Ц
а:
Щ
Рис. 83.
параллельные ей реакции амортизаторов образуют момент,
который вызывает появление сил, направленных вдоль оси у.
Учитывая симметрию системы относительно плоскости ycz,
выбираем дополнительные условия следующим образом:
U,
*з-
•U,
56-
Us<* = Usn-
0, Ua = Ut
sb~
■■Ua=U,i»
usl = u
Si'
и
sT
■U
*ip*
(19.16)
§20] МАЛЫЕ КОЛЕБАНИЯ ТВЕРДОГО ТЕЛА НА ПОДВЕСЕ 211
usi=
U.i =
= Uss =
= "* =
u*=
-v«
им
= -
p
~ 4 '
-t/,io
= P
b
2Л * J
Часть уравнений статики при этом выполняется
автоматически; остальные уравнения дают
(19.17)
Очевидно, что амортизаторы 1 и 4 работают на растяжение,
а 7 и 10—на сжатие. Для компенсации перекосов
необходима установка прокладок под амортизаторы 7 и 10,
толщина которых равна разности статических деформаций
амортизаторов 1 и 7:
"°rf = «2l0= «,!-«*• О9'18)
§ 20. Малые колебания твердого тела
на упругом подвесе
Рассмотрим теперь малые колебания амортизируемого
объекта. Предполагается, что динамические характеристики
всех упругих элементов могут быть линеаризованы
Ui = citti + blai (i=l ЗЛО. (20.1)
где ut — деформации упругих элементов, отсчитываемые
от положения статического равновесия; ct и bt —
соответственно жесткость и коэффициент демпфирования /-го
элемента. При этом предположении мы приходим к системе
линейных дифференциальных уравнений движения с
постоянными коэффициентами, методы исследования которой
подробно рассматриваются в классической линейной теории
колебаний. Мы ограничимся здесь весьма кратким
изложением некоторых основных положений линейной теории,
которые будут использованы ниже; более подробное
изложение приводится в многочисленных монографиях (см.,
например, [2> 6' з0]).
Предполагается, что начало неподвижной системы
координат совпадает в положении статического равновесия с
центром инерции объекта. В качестве подвижных осей координат
выберем главные центральные оси инерции амортизируемого
твердого тела х, у, г\ неподвижные оси £, г], £ в
положении равновесия совпадают с подвижными.
14*
212 СИСТЕМЫ С НЕСКОЛЬКИМИ СТЕПЕНЯМИ СВОБОДЫ [ГЛ. IV
Рассматриваемая система обладает шестью степенями
свободы. В качестве обобщенных координат выберем
координаты, характеризующие перемещение объекта относительно
основания. В случае активной виброзащитной системы
относительные перемещения совпадают с абсолютными; при
рассмотрении пассивных систем можно, используя известное
положение динамики относительного движения, учесть
движение основания, вводя силы инерции в переносном
движении и кориолисовы силы инерции. Последние при
рассмотрении малых колебаний могут быть отброшены, как имеющие
второй порядок малости (они пропорциональны произведениям
малых переносных угловых скоростей на малые скорости
в относительном движении).
Перемещения амортизируемого объекта относительно
основания будем отсчитывать от положения статического
равновесия и характеризовать вектором смещения центра
инерции 5 и вектором малого угла поворота в.
Кинетическая энергия объекта в его движении относительно
основания определяется выражением
Т =
jm(i2+-2+-2 + p2e2 + p2e2 + p2e2)f (20.2)
где пг — масса объекта; р^, ру, р2 — его радиусы инерции
относительно осей х, у, z.
Займемся определением потенциальной энергии. С этой
целью найдем перемещение точки крепления /-го простого
элемента
*/ = * + • Х*> (20.3)
Проектируя это векторное равенство на оси координат,
находим
*/* = **+ву2, — 6,у,, |
*/у = *у + е**, — М„ (20.4)
*л = *а + 0*У/ —Оу*/- J
Найдем теперь деформацию /-го простого элемента:
«/ = SuPi + siyh + sizVi = s*ai + syf>i + 5*Y/ +
+ 0,(УМ" *fii) + by(*fli — *iyi) + bz(xfii — yfli) (20.5)
(/=1 ЗЛО-
§ 20] МАЛЫЕ КОЛЕБАНИЙ ТВЕРДОГО ТЕЛА НА ЙОДВЕСЁ 213
Подставив (20.5) в выражение для потенциальной энергии
п=т5Ь^ (20-6)
1=\
найдем
R=*(c 52 JL С s2 i c S2\_2C S S -f-2C S S +
x 2 \ x x у У z z xy x у ' yz у z '
+ 2MA + 2/^s A + 2/,ysA + 21ХЖ$ЛЪЖ + 2lyxsyQx +
+ 2/yy5yey + 2/У2*А+2/^A+и,у*2еу+2izzszQz+
+ Mxxtfx+ Myy92y + Л1„в5+ 2Л!хувхву+ 2Л1у,вув* +
+ 2MZXQXQZ). (20.7)
Здесь введены следующие обозначения:
т ЗЛГ SN Ш
Сх = 2 Ср*9 С = 2 *$. С = 2 С$,
1 = 1 J 1=1 1 = 1
3N ЗЛГ SN
Сху = 2 **<*#,. Суж = 2 Cfifli. Схг = 2 */УЛ,
/ = 1 / = 1 / = 1
W 3N
'« = 2 сfl.t (yiVi-zfii). lxy = 2 cfli tefli—xto),
i=\ i=\
ЗЛГ
lxz=^cfldxih — УМУ*
i = \
lyx= 2 *А(М*~*А). 'yy = J *А(*Л--*М).
ЗЛГ
/У, = 2'А(*А —УЛ):
3N ЗЛГ
hx=% Ciyiiyfli — Zih)» 'jy= 2 cfltizpt—xcti).
ZN
^==2^Y/(^A — У A);
ЗЛГ ЗЛГ
A«„ = 2 *, (yft + 4P?). ^yy = 2 ct (zyt + xfYf),
37V
^=2/Д^р!+уК>
(20.8)
214
СИСТЕМЫ С НЕСКОЛЬКИМИ СТЕПЕНЯМИ СВОБОДЫ [ГЛ. IV
3/V
Мху = S ct (yflt — zfii) {zfl.t — xtyt)t
ZN
Myz = S ct {ztat — xfo) (x$t — yflj).
У2 1 = 1
ZN
Mxx=^ci(xfir
УЛ)(М/—*/P/)«
(20.8)
Определим диссипативную функцию Релея [30]:
ZN
ф=тИ^?- (20-9)
Определив ut из (20.5) и подставив в (20.9), найдем
ф=\ {ьЛ+Vя,+ЬЛ+2 VA + V А+2*. А+
+ 2^s А + 2едА9у + 2е,2« А 4- 2 Vs'А + 2eyy'sjdy+
+ 2 V А + *«* А + 2 V A + *JA + °*A +
+ Gyy0y + Ог A + 2G,y9 A + 20,M + 20 J A)- (20.10)
ezV ^хх;
Gy
Формулы для bx, by, ..., bxz\ exx, .
могут быть получены соответственно из формул (19.26),
если в последних заменить с( на bt.
Для того чтобы в дальнейшем пользоваться более
компактной формой записи, введем векторные и матричные
обозначения. Координаты, определяющие положение объекта,
обозначим вектором-столбцом q, имеющим шесть составляющих:
еу, ?в = е,. (2o.li)
^1 = *лг' ?2 = V
% =
Вводя матрицы:
а) коэффициентов
А =
т.
0
0
0
0
0
= *«•
?4 =
инерции
0
т
0
0
0
0
0
0
т
0
0
0
= »*.
0
0
0
mpj
0
0
Чъ =
0
0
0
. о
«Ру
0
в». «
0
0
0
0
0
/тер
(20.12)
§ 20] МАЛЫЕ КОЛЕБАНИЯ ТВЕРДОГО ТЕЛА НА ПОДВЕСЕ
б) коэффициентов жесткости
215
С =
ху
-ху
"ху
'yz
"ух
"УУ
'yz
*гу
I
ху
ух
I
УУ
/,
/
уг
L
м
vzy
м
ху
ху
м
м
УУ
У*
I'xz
I'yz
hz
мх
м
У*
(20.13)
в) коэффициентов демпфирования
В =
'ху
"ху
'ху
'yz
"ух
"УУ
"yz
'yz
"zy
'ух
"ху
"УУ
*zy
'yz
Ox
G
о,
GVX1 Gr
'ху
ХУ
o*« о
'УУ
yz
G
yz
(20.14)
можно представить выражения для кинетической и
потенциальной энергии и функции Релея в виде квадратичных
форм
T = ±iTAq,
ГЬ
Ф:
q*Cq,
q*Bq,
(20.15)
(20.16)
(20.17)
где q*— вектор-строка. Теперь можно записать уравнения
малых колебаний системы в виде уравнений Лагранжа
второго рода:
d дТ дТ дП. дФ
dt dq dq
dq dq
+ Q>
(20.18)
где Q — вектор внешних сил, действующих на
амортизируемый объект. В случае активной виброзащитной системы-
составляющими вектора Q являются проекции на оси координат
216 СИСТЕМЫ С НЕСКОЛЬКИМИ СТЕПЕНЯМИ СВОБОДЫ [ГЛ. IV
главного вектора и главного момента приложенных
внешних сил
h h h
Qi = 2 Fkx> Q2 = 2 Fky Qz = 2 Fkz*
k=l k=l *=1
Q^^{FkiYk-FkyZk), Q5==2(^,Zft-/^*ft), }(20.19)
Здесь Fkx, Fky, Fkz — проекции &-й внешней силы на оси
координат; Xk, Yk% Zk -- координаты точки приложения этой
силы. В случае пассивной виброзащитной системы Q —
вектор сил инерции в переносном движении амортизируемого
объекта вместе с основанием. Если основание движется как
абсолютно твердое тело, его перемещения можно
характеризовать вектором смещения § той его точки, которая в
положении равновесия совпадает с центром инерции объекта, и
вектором малого угла поворота р. Тогда
Qi = — т\х9 Q2 = — т\у. Qz = — т\г,
Q4 = -mP*A- Qs^-nffiy Q* = -m9lK (20-2°)
Подставляя выражения (20.15) — (20.17) в уравнение (20.18)
и учитывая, что
—r = Aq, = Cq, —r=Bq, -— = 0, (20.21)
dq 4 dq ч dq H dq '
получаем
Aq + Bq + Cq = Q(t). (20.22)
Это уравнение эквивалентно системе шести скалярных
неоднородных линейных уравнений с постоянными коэффициентами.
Рассмотрим сначала уравнение свободных колебаний.
Полагая
В = 0. Q = 0.
ролучаем
ity + Cf = 0. (20.23)
§20] МАЛЫЕ КОЛЕБАНИЯ ТВЕРДОГО ТЕЛА НА ПОДВЕСЕ 2l7
В соответствии с общей теорией линейных
дифференциальных уравнений с постоянными коэффициентами, частное
решение этого уравнения ищем в форме:
q = q0 cos It, (20.24)
то есть предполагаем, что все координаты системы
изменяются по гармоническому закону с одной и той же
частотой и фазой.
Тогда при подстановке (20.24) в (20.23) получаем
следующее уравнение, эквивалентное системе шести
алгебраических линейных однородных уравнений:
(С — а,М)?о —0- (20.25)
Для того чтобы это уравнение имело ненулевое решение,
необходимо, чтобы его определитель обращался в нуль:
Д (*2) = | с — №А | = 0. (20.26)
Мы получили так называемое частотное уравнение системы.
Пользуясь выражениями для матриц Л и С, перепишем его
в скалярной форме:
А
=
(*■*) =
сх—т X2
сху
Cxz
1хх
*ху
>хг
сху
Су—тК2
cyz
lyx
lyy
'у*
CXZ
cyz
cz—m K2
'«
<;y
'«
'xx
h*
Izx
Mxx-mPx\2
Mxy
мхг
M
'xy
lyy
'zy
Mxy
yy—mpyk
Myz
hz
'yz
Izz
мхг
Myz
Mzz~mffi\
= 0. (20.27)
Это— уравнение шестой степени относительно АЛ В теории
колебаний [6] доказывается, что оно всегда имеет шесть
положительных корней (необходимо только, чтобы положение
статического равновесия было устойчивым). Значения Хг,
%2* •••• ^6» удовлетворяющие этому уравнению, называются
собственными частотами системы. Существуют
многочисленные способы решения уравнения (20.27), они подробно
описаны в литературе и здесь рассматриваться не будут.
218 СИСТЕМЫ С НЕСКОЛЬКИМИ СТЕПЕНЯМИ СВОБОДЫ [ГЛ. IV
Если в уравнение (20.25) подставить вместо X одну
•из собственных частот системы Xs, то оно будет иметь
бесчисленное множество решений. Показано [6], что при
некратных корнях частотного уравнения все эти решения
отличаются произвольным скалярным множителем, то есть что
q(s) ^ a(s)g(s)t (20.28)
Свободные колебания, при которых каждая из координат
системы изменяется по гармоническому закону, называются
главными колебаниями. Выражение (20.28) показывает, что
отношения между амплитудами координат при главных
колебаниях не зависят от начальных условий и определяются
только параметрами системы. Вектор q[s\ компонентами
которого являются отношения амплитуд колебаний к
некоторому произвольно выбранному числу, называется формой
главного колебания, происходящего с частотой ks, или 5-й
собственной формой.
Рассмотрим теперь вынужденные колебания системы при
отсутствии сил сопротивления. Поскольку для линейных
систем справедлив принцип суперпозиции, достаточно
рассмотреть тот случай, когда все составляющие вектора Q(t)
являются гармоническими функциями времени, имеющими
одну и ту же частоту и фазу
Q(t) = Q0cos<utt (20.29)
где Q0—некоторый постоянный вектор.
Решение дифференциального уравнения вынужденных
колебаний
Aq-\-Cq = Q0 cos ®tt (20.30)
как известно, складывается из общего решения однородного
уравнения (20.23), определяющего свободные колебания
системы, и частного решения уравнения (20.30). В реальных
системах действие диссипативных сил приводит к затуханию
свободных колебаний, в силу чего наибольший интерес
представляет частное решение, характеризующее установившиеся
колебания системы. Это частное решение ищется в форме
0=racosco/; (20.31)
где а — вектор, компонентами которого являются амплитуды
колебаний по каждой из обобщенных координат»
§ 20] МАЛЫЕ КОЛЕБАНИЯ ТВЕРДОГО ТЕЛА НА ПОДВЕСЕ 219
Подставляя (20.31) в (20.30), получаем для определения
вектора а следующее уравнение:
(С — Лео2) а == Q0. (20.32)
эквивалентное системе шести скалярных уравнений.
Решение уравнения (20.32) может быть записано в таком
виде:
а = (С — AaP)-lQQ, (20.33)
то есть для определения вектора а необходимо построить
матрицу, обратную (С — Лео2). Как известно, это возможно
сделать только в том случае, если определитель
Л (со2) = |С — Ло)2|^0,
то есть если ®фХ$ (5=1 6).
При совпадении частоты вибрационного воздействия со
с одной из собственных частот системы уравнение (20.32)
не имеет решений. Этот случай соответствует резонансу
в линейной системе. Если со близка по величине к одной из
собственных частот, амплитуды колебаний достигают больших
значений. Действительно, решение системы скалярных
алгебраических линейных уравнений, соответствующих векторному
уравнению (20.32), легко найти с помощью формул Крамера:
А (со2)
(20.34)
Здесь А (со2) — определитель (20.27), в который вместо А,2
подставлено со2; АЛ (со2) получается заменой £-го столбца
определителя А (со2) компонентами вектора Q0. Поскольку
А(х1)==0, можно сделать ak сколь угодно большим, если
разность о2 — Я,2 сделать достаточно малой.
Таким образом, в линейной системе с шестью степенями
свободы область резонансных колебаний охватывает всю
ширину спектра собственных частот. Для того чтобы по
возможности сузить эту область, следует стремиться к
сближению максимальной и минимальной собственных частот,
выбирая соответствующим образом координаты точек креп*
ления и жесткости упругих амортизаторов.
220 системы с несколькими степенями свободы [гл. iv
Для исследования вынужденных колебаний в линейной
системе удобно перейти к так называемым главным
координатам с помощью преобразования:
q = Rf, (20.35)
где /—вектор главных координат системы, R— матрица,
столбцами которой являются векторы qM q@\ При
переходе к главным координатам в выражениях для
кинетической и потенциальной энергии остаются только члены
с квадратами координат и скоростей
6 б
Г = Т2^' П=тЪл*/1> (20-36)
S=l 5=1
где
и уравнение (20.30) распадается на шесть скалярных
уравнений, каждое из которых содержит только одну из главных
координат
/, +Ч^=^в5 cos со*. (20.37)
Здесь Qs — компоненты вектора в, который определяется
следующим образом:
где R*— матрица, полученная транспонированием матрицы R.
Решая уравнения (20.37), найдем, что в линейной системе
без трения коэффициент динамичности по каждой из главных
координат
**=р^| (20-38)
становится меньше единицы, если со>А,5 У~2. Если ©>А,5тах У"2,
то коэффициенты динамичности по всем шести главным
координатам меньше единицы; в этом случае виброзащитная
система становится эффективной.
Учет демпфирования приводит к усложнению
исследования, поскольку в этом случае использование главных
координат не дает разделения переменных в уравнениях
движениях. Не проводя подробного анализа, отметим только,
что введение демпфирования дает здесь тот же эффект, что
§ 21] КОЛЕБАНИЯ НА НЕЛИНЕЙНЫХ УПРУГИХ АМОРТИЗАТОРАХ 221
и в системе с одной степенью свободы: максимальные
амплитуды колебаний в резонансной области уменьшаются, вместе
с тем несколько ухудшаются виброзащитные свойства
системы при высокочастотном вибрационном воздействии
(т. е. при со > Хтлх уТ).
§ 21. Колебания амортизируемого объекта
на нелинейных упругих амортизаторах
Выведем дифференциальные уравнения колебаний твердого
тела, подвешенного на нелинейных упругих амортизаторах,
динамические характеристики которых заданы в форме (19.2).
Выбрав те же обобщенные координаты, что и в
предыдущем параграфе, составим уравнения движения в форме
уравнений Лагранжа второго рода:
дТ .Sr (г = 1, . .., 6). (21.1)
JLIJI).
dt \ dqT I
dqr
Выражение для кинетической энергии (20.2), очевидно, не
изменится; с учетом обозначений (20.11) его можно
переписать в такой форме:
Т = \ m(q\ + kl + il+f>lql+plql + plqt)- (21.2)
Для определения обобщенных сил Sr составим выражение
для элементарной работы всех сил, действующих на
амортизируемый объект: реакций упругих элементов —U^a^u^
и внешних сил Qr. Получим
6 37V 6
bW = ^Srbqr^-^Ui{ui, ^)4 + 2Qr4- (21.3)
Г=1 1=1 Г=1
Если по-прежнему считать, что углы поворота твердого тела
являются малыми, деформации at будут выражаться через
обобщенные координаты по формулам (20.5). Определив из
этих формул but й подставив их в (21.3), получим
bW = — %Ui[ui(ql <7б)> Щ(Я\ <7б)1Х
X [Щ bqx + р; bq2 + y* ty8 + (УМ — * А) ьЯа +
6
+ {z^ — х^д bqb + (л:^ — ytat) 6?б] + 2 Qr 6?r (21-4)
r«l
222 СИСТЕМЫ С НЕСКОЛЬКИМИ СТЕПЕНЯМИ СВОБОДЫ [ГЛ. IV
Отсюда
S, = Qr
S2 = Q2 "
*->3 = Q3 '
S4 = Q4-
S5 = Q5-
Sq = Qq-
.
находим
3N
/ = 1
3/V
/ = 1
злг
i = l
злг
злг
злг
.., д6), «/(gi, .
• •. Я6). u-i (ki.
■ • • <76)> «< (<7i- •
• - <7б)- «г (<7i> • •
•. 96). «< (?i- • •
•. <76)- "/ fai- • •
... д6)]щ,
• ■. д6)] Р«>
• •. ?б)1 Yi-
•. Ч6)] (У1У1—zfii)>
•.?в)1(гЛ—*<Y/).
••^К^А—УЛ)-
(21
Исследование уравнений движения, которые получаются
при подстановке выражений (21.2) и (21.5) в (21.1)
оказывается обычно практически невозможным. Это объясняется
тем, что нелинейные функции U\ имеют чрезвычайно сложную
структуру: они зависят от всех шести обобщенных
координат и их производных. Поэтому нам придется перейти к иной,
более простой, форме дифференциальных уравнений движения.
С этой целью выберем в качестве обобщенных координат
деформации ut\ очевидно, что в общем случае число их
окажется большим, чем число степеней свободы системы.
Поэтому нам придется применить особую форму уравнений
Лагранжа второго рода— уравнения с «лишними»
координатами, которые иногда называются также уравнениями Фер-
рерса [44]. Прежние обобщенные координаты, вообще говоря,
могут быть выражены с помощью соотношений (20.5) через
деформации любых шести упругих элементов. Не нарушая
общности рассуждений, можно дать этим элементам номера
с 1 до б. Очевидно, что для разрешимости первых шести
уравнений (20.5) относительно координат qx q6
необходимо и достаточно, чтобы определитель правых частей
не обращался в нуль. Легко показать, что это эквивалентно
§ 21] КОЛЕБАНИЯ НА НЕЛИНЕЙНЫХ УПРУГИХ АМОРТИЗАТОРАХ 223
требованию фиксации объекта выбранными шестью упругими
элементами; недопустимо, чтобы объект, подвешенный на
элементах 1, ..., б, сохранял возможность перемещения без
деформации элементов. В самом деле, если определитель
первых шести соотношений (20.5) равен нулю, то при иь =
== 0 (/—1, ..., б) эта система линейных алгебраических
уравнений будет иметь ненулевые решения для коордш а г
qv . . ., <7б.
Если условие фиксации выполнено, то координаты qv ...
.... qQ однозначно выражаются через и{, ..., иб.
Соответствующие зависимости оказываются линейными:
б
</r = 2<Jrft«ft (/•=!. «... 6). (21.6)
k = i
Подставив эти выражения в остальные 3/V — 6 соотношений
(20.5), можно выразить и1% ..., и3лг чеРез uv •••» uq:
6
«/ = Sv,A (/ = 7. .... 37V). (21.7)
k=i
Это выражение удобно записать в иной форме:
6
%(ии .... я6. ul) = ul— %vlkuk = 0 (1 = 7 ЗЛО.
(21.70
А = 1
Из (21.6) находим
б
<7г = 2 °гА (г=\ 6); (21.8)
подставляя эти выражения в (21.2), получим: .
6
T = ~Y 2 И*г«а«г. (21-9)
Л,г=1
причем, если ввести обозначения
т{= т2= w3 = т, тА~р2хт, т5 = р2т, tn6 = p2zm,
(21.10)
224 системы с несколькими степенями свободы [гл. iv
то выражения для \xkr записываются в симметричной форме:
б
Vkr = 2 mflik°ir = Vrk- (2Ы1)
В выражении для элементарной работы (21.3) первое
слагаемое не изменяется; во втором слагаемом Qr — заданные
функции времени, а для вариаций 6^ имеем вследствие (21.6)
б
V = 2or>*. (21.12)
Таким образом, обобщенная сила Ui, соответствующая
координате ut, определяется следующим образом:
б
</! = — £//(«/. i|)H-2Qr°r/ (/=1. ..-.6). (21.13)
r-l
t/J = — £/,(«,, щ) (t = 7 3N). (21.14)
Уравнения Лагранжа с «лишними» координатами могут
быть записаны в такой форме:
dt dui дщ Ad дщ
/=7
где Л/ — новые неизвестные функции времени (множители
Лагранжа). Воспользовавшись выражениями (21.9), (21.7'),
(21.13) и (21.14), получаем
6 ЗЛГ 6
2 »*««* + Ut («,. «',) + 2 A|V|< = 2 QfOn (/ = 1 6),
(21.16)
Ui(*i* ul)~Al = 0 (/ = 7, ...,3iV). (21.17)
Эти соотношения и выражения (21.7') образуют систему
6N — б уравнений с 6Л/ — б неизвестными функциями
времени (uv ..., uZN, Л7, .... Лзлг). Таким образом, количество
неизвестных и число уравнений увеличилось по сравнению
с первоначальной формой (21.1). Однако нелинейные
функции, входящие в новые уравнения, имеют простую форму:
они зависят только от одной координаты и ее производной,
то есть могут быть линеаризованы одним из способов,
рассмотренных в гл. I.
§ 21] КОЛЕБАНИЯ НА НЕЛИНЕЙНЫХ УПРУГИХ АМОРТИЗАТОРАХ 225
Во многих практических задачах количество
дифференциальных уравнений может быть уменьшено. Это происходит,
прежде всего, в тех случаях, когда на движение
амортизируемого объекта заранее накладываются некоторые
ограничения, уменьшающие число степеней свободы системы. Если,
например, движение объекта является плоским, то число
степеней свободы уменьшается до трех, объект,
вращающийся вокруг неподвижной оси, имеет одну степень свободы
и т. д. Часто, даже при отсутствии дополнительных связей,
можно заранее утверждать, что при заданном направлении
вибрационного воздействия будут изменяться только
некоторые из обобщенных координат. Обычно это имеет место,
если виброзащитная система симметрична относительно тех
или иных координатных плоскостей, а вибрационное
воздействие направлено по одной из осей координат (см. табл. 1).
Во всех этих случаях мы будем условно называть объект
частично амортизируемым.
Таблица 1
Обобщенные координаты, изменяющиеся
при вынужденнных колебаниях
Плоскости симметрии
виброзащитной системы
хСу
yCz
zCx
хСу и yCz
yCz и zCx
zCx и хСу
хСу, yCz, zCx
Направление вибрационного воздействия 1
по оси х
sx> sy* "2
sx, ey> ег
sx> sz, "у
sx> %
Sx> 9y
Sx
SX
по оси у
Sx, Syi %
Sy> Sz, vx
sy, 0*, §z
Sy
Sy, §X
Sy, Qz
Sy
по оси z
sz> ®x> Gy
Sy, SZi бд.
sx, Sz, By
sz> ®x
Sz
sz, ey
Sz 1
Пусть p — число степеней свободы частично
амортизируемого объекта; qlt ..., qp — его обобщенные координаты.
В такой системе обычно некоторые из упругих элементов
не деформируются вследствие наложенных на движение
системы ограничений. Поэтому число работающих упругих
элементов в этом случае не обязательно втрое больше
числа амортизаторов, и мы обозначим его через N'.
15 М. 3. Коловский
226 СИСТЕМЫ С НЕСКОЛЬКИМИ СТЕПЕНЯМИ СВОБОДЫ [ГЛ. IV
Обобщенные координаты могут быть выражены через
деформации элементов с помощью соотношений,
аналогичных (21.6):
^г=2*гА ('«1 />)• (21-180
На деформации uk(k=\% .... ЛГ) должно быть наложено
ЛЛ— р условий связи, аналогичных (21.7'):
р
ф«(«1 V ui) = ui— Sv/A = 0. (21.19)
Выражения для кинетической энергии и коэффициентов \ikr
также могут быть получены из формул (21.9) и (21.11):
Ц2 fWr (2120)
р
1**г=2 mflik<*ir- (21-21)
Проделав все необходимые преобразования, получаем
следующие уравнения движения:
р N' р
2 !*«£* +<Л(«*. «i)+ 2 ЛЛ,= 20Л| (21-22)
* = 1 /=р+1 г=1
('=1 Л.
*/,(«,. i,)-Л, = О (/ = /> +1 Ю- (21.23)
В следующих параграфах будут рассмотрены общие методы
решения дифференциальных уравнений движения, заданных
в форме (21.16) и (21.17) или (21.22) и (21.23). Здесь мы
рассмотрим некоторые частные случаи, в которых уравнения
движения существенно упрощаются.
Пусть число упругих элементов равно числу степеней
свободы системы. В полностью амортизированной системе,
при применении обычных упругих амортизаторов,
допускающих смещения объекта относительно основания во всех
трех направлениях, этот случай практически нереализуем,
поскольку он соответствует установке объекта на двух
амортизаторах. В частично амортизируемых системах
совпадение числа упругих элементов с числом степеней свободы
§21] КОЛЕБАНИЯ НА НЕЛИНЕЙНЫХ УПРУГИХ АМОРТИЗАТОРАХ 227
не только возможно, но и целесообразно, посколько оно
соответствует наиболее простой в конструктивном
отношении схеме амортизации, использующей минимально
допустимое количество упругих элементов.
При N'= р уравнения (21.22) упрощаются, поскольку
все Aj = 0, а уравнения (21.23) пропадают. Если к тому же
точки крепления отдельных упругих элементов и
направления их осей выбраны таким образом, что обеспечивается
выполнение условий
jmftr = 0 при кфг% (21.24)
то переменные в уравнениях (21.22) разделяются. При этом
для деформации /-го элемента получаем следующее
независимое уравнение:
р
Vu»i + Ui («/. Щ)= S Qrorit (21.25)
которое может быть исследовано методами, подробно
рассмотренными в предыдущей главе.
Разделение переменных в уравнениях (21.22) означает,
что каждый из упругих элементов может рассчитываться
независимо от остальных так, как если бы он был нагружен
массой \Хц. В случае пассивной виброзащиты правые части
уравнений (21.25) могут быть представлены в более удобной
форме. Для этого введем следующие обозначения:
ЬЛГ=== Ь1» fey === Ъ2» fez===fe3» /oj OR}
Px = fe4' Py = ^5» Рг = £б-
При этом выражения (20.20) с учетом обозначений (21.10)
принимают такую форму:
Qf = —тД, (г = 1 6). (21.27)
Обозначим через ^ (/ = 1 W) проекцию перемещения
точки крепления /-го упругого элемента в переносном
движении вместе с основанием на ось этого элемента (то есть
на направление и(); очевидно, что £г могут быть выражены
через t\k (й=1 р) с помощью соотношений,
аналогичных (21.18),
6г=2*гЛ <Г=1 Л (21-28)
!*•
228 СИСТЕМЫ С НЕСКОЛЬКИМИ СТЕПЕНЯМИ СВОБОДЫ (ГЛ. IV
Тогда
р р р ъ! ..
2 Qfin = — 2 ntr\rari = — S тг°п 21 <>г№ =
r=l r=l r=l *=1
— S^A- (21.29)
При выполнении условий (21.24) имеем
2 QrCr/ — — М^Л-
г=1
(21.30)
Таким образом, вибрационное воздействие на /-й элемент
полностью определяется переносным движением точки
крепления его к объекту. Такая
«автономность» каждого из упругих
элементов во многих случаях оказывается
полезной.
Условия (21.24) носят чисто
геометрический характер; они не
зависят от динамических характеристик
амортизаторов и в одинаковой
степени пригодны как для нелинейных,
так и для линейных систем. В
последнем случае координаты ut являются
главными. Отметим, что при этом
наличие диссипативных сил не
препятствует разделению координат; это
обстоятельство, вообще говоря, не имеет места, если главными
являются обобщенные координаты qv ..., др. Поскольку
количество условий (21.24), равное -^р(р—1)» всегда
меньше числа коэффициентов ork, выполнение их обычно не
вызывает существенных затруднений. Рассмотрим, каким
образом могут быть выполнены эти условия в некоторых
частных случаях.
а) Пусть твердое тело с массой т, имеющее малые
размеры («материальная точка»), крепится к основанию тремя
упругими элементами («пружинами») (рис. 84). Очевидно,
что здесь число упругих элементов совпадает с числом
степеней свободы системы.
Рис. 84.
§ 21] КОЛЕБАНИЯ НА НЕЛИНЕЙНЫХ УПРУГИХ АМОРТИЗАТОРАХ 229
Поскольку
Я\ = $х = ttlal + й2а2 + tt3a3»
q2 = Sy = Ufa -f иф2 +■ %Р3>
?з = s* = «iYi + "2Y2 + «sYa-
(21.31)
получаем
>\k-
■a*. <hk*=h* <>а* = У* (A =1.2.3). (21.32)
'13
J23
Ф0,
Определитель
I an ai2
l0rftll=°21 °22
I °31 a32 v331
если оси всех трех упругих элементов не лежат в одной
плоскости. Условия (21.24)
выполняются, если
ft2 =i» (ал+ 0102 + 7172) = °-
*г13 = т (а^з + Рхр3 + Y1Y3) = °»
jx23 = т (а2а3 + Р2Р3 + Y2Y3) = °»
(21.33)
то есть если оси упругих элементов
взаимно перпендикулярны.
б) В схеме, показанной на рис. 85, Рис. 85.
твердое тело обладает двумя
степенями свободы (предполагается, что движение может
происходить только в плоскости yz, причем sz = 0). Положение
его определяется координатами у и 9^; при этом
Uib4-u2a А щ—Uo о
^i = У = —^+"6— • ^2 = вх = -^р/, ml = m, w2 = mp2.
(21.34)
Следовательно,
« — Ь 1 л а 1
аи — т+т> a2i = ^4T» ai2e-jqry. a22 = —-^р--
Определитель |ar^|j не обращается в нуль:
Ь
°r* li =
a+b '
a+6 '
1
a + b
1
я + &
*0.
230 СИСТЕМЫ С НЕСКОЛЬКИМИ СТЕПЕНЯМИ СВОБОДЫ [ГЛ. IV
Условие разделения координат:
Г ob ' р* "I
\х12 = тгаиа12 + ™2°2ia22 = т [ (а+Ь)* (a + b)2 J = °
выполняется, если
а& = р2. (21.35)
При этом
9 | 9 Г &2 I £ 1 «*
2 2
9i 9 \ а , Рлг 1 та
\i22= mxo\2+ m2ol2=m [(а + Ь)2 + {а + Ь)* \ = Т+Т'
(21.36)
Попутно отметим, что при произвольных нелинейных
зависимостях Ul(uv u{) и U2(u2, и2) разделение переменных
ц
{У
\ (21.37)
Рие. 86.
в уравнениях движения, записанных в координатах у и Qx:
my+Ux(y + aQxt y-f аЬх) +
+ U2(y- bQx, у - bhx) = Qx (*).
mf|L+ cVi (У + a9*« У + a9*> —
r~bU2(y—bQxt y~ bbx)=Q2(t),
не может быть достигнуто ни при каком расположении
точек крепления упругих элементов.
в) Найдем условия разделения переменных в случае
установки объекта на трех упругих элементах (рис. 86);
§ 21] КОЛЕБАНИЯ НА НЕЛИНЕЙНЫХ УПРУГИХ АМОРТИЗАТОРАХ 231
на систему наложены ограничения — не допускается поворот
объекта вокруг оси z и движение центра инерции в
направлении осей а: и у. В этом случае, обозначив
Я\ = sz> Ь === 9дг. Чг = еу
получаем, в соответствии с формулами (20.5),
«1 = ?1 + У#2 —*А ('=1. 2> 3)- (21-38)
Отсюда находим
п _ «I (*зУг—*2Уз)+"2 (^1Уз—-ЕзУО+Из (х2ух—хху2) )
4i— о '
п _ »i {*2 — *з) + Ц2 (*з — *0 + "з (*i — *2) ' /01 олч
V2— /5 » J (21.оУ)
п _ ^i(y2 — Уз) + МУа — У1) + цз(У1~ У2)
Яг— о »
где
D = *3у2 — *2Уз 4~^1Уз— *зУ 1 + -^2^1 — *1У2-
Условия разделения переменных:
(х3у2 - х2у3) (х 1Уз - *3у0 + Р* (*а - *2) (*i ^ *з) +
+ Р2у(Уз-У2)(У1--Уз) = 0'
(^ 1Уз - *зУ i) (*2У i - *1У2) + 91 (хг - *3) (*2 - *i) +
+-Ру(У1~Уз)(У2"У1) = ^
(х2ух — х,у2) (х3у2 - х2у3) + р2 (х2 - хг) (х8 - х2) +
+р2у(у2-уО(Уз-у2) = о. )
(21.40)
Если, например, точки крепления расположены симметрично
относительно центра инерции, так что
х _, х 1 х _±. v_0 v"—II" v -Я
то условия (21.40) дают
Р* = 9У = yrj '
232 СИСТЕМЫ С НЕСКОЛЬКИМИ СТЕПЕНЯМИ СВОБОДЫ [ГЛ. IV
то есть для разделения координат радиус окружности, на
которой расположены точки крепления, должен в |^2 раз
превосходить радиусы инерции рх и ру.
§ 22. Свободные колебания нелинейной виброзащитной
системы
Дифференциальные уравнения свободных колебаний
твердого тела, установленного на упругих амортизаторах и
обладающего шестью степенями свободы, могут быть
получены из уравнений (21.16) и (21.17), если принять, что
Qr = 0(r = l, .... 6), £/,(«,, и,) = £/|у(«,) (/==1 ЗЛО,
(22.1)
то есть если рассматривать движение при отсутствии сил
сопротивления и вибрационных воздействий..
При этом получаются следующие уравнения движения:
6 3W
2 Hflk + Uiy (»i) + 2 v„A£ = 0 (/ = 1 6), (22.2)
Uiy (я,) — At = 0 (1 = 7 ЗЛО, (22.3)
к которым необходимо добавить уравнения связей (21.7)
или (21.70-
Целью исследования свободных колебаний, как и
в случае нелинейной системы с одной степенью свободы,
является получение зависимостей между частотами и
амплитудами деформаций упругих элементов. Как будет показано
ниже, эти зависимости оказываются весьма полезными при
исследовании условий возникновения резонансных колебаний.
С помощью уравнений (22.3) можно исключить из
уравнений (22.2) неизвестные функции А1 и тем самым сократить
число неизвестных до 3N(ttx, ..., ит):
6 ЗЛГ
2 |i*A + Uiy (в|) + S Uiy («i> vtt = 0 (1, ..., 6) (22.4)
Мы будем разыскивать приближенные решения системы
уравнений (22.4) и (21.7) вида
ut = а01 -+- at cos Ktt (22.5)
§ 22] СВОБОДНЫЕ КОЛЕБАНИЯ ВИБРОЗАЩИТНОЙ СИСТЕМЫ 233
предполагая тем самым, что в рассматриваемой системе
могут существовать такие движения, при которых
деформации всех упругих элементов изменяются по законам, близким
к гармоническому.
Напомним, что при исследовании свободных колебаний
в системе с одной степенью свободы было сделано
аналогичное предположение, основывавшееся на существовании
точных периодических решений уравнения (2.1). В случае
системы с несколькими степенями свободы существование
периодических решений, вообще говоря, не может быть
гарантировано. Оно доказано лишь для некоторых систем
частного вида, например, для так называемых систем
Ляпунова [34], к которым рассматриваемая консервативная система
принадлежит в случае аналитичности функций Uly(ut).
Впрочем, существование периодических колебаний с
достаточно малой амплитудой может быть доказано и для
консервативных систем с неаналитическими упругими
характеристиками; существование периодических колебаний большой
амплитуды доказывается методом малого параметра лишь для
слабо нелинейных систем, в которых упругие характеристики
мало отличаются от линейных. В дальнейшем предполагается,
что периодическое решение существует и тем самым является
обоснованным применение приближенных методов для его
определения.
В выражении (22.5) отсутствует член с sinAi; это всегда
допустимо для консервативной системы, инвариантной к
изменению знака времени.
Для разыскания решений вида (22.5) применим метод
гармонической линеаризации; линеаризуя нелинейные функции,
полагаем
"„ Ы ~ uot + Ь («, - «„,) = иы + йА, (22-6)
где U0i и qt — коэффициенты гармонической линеаризации,
зависящие от параметров а01 и at.
Подставляя (22.6) в (22.4), получаем линеаризованные
уравнения
6 3N
tS^+^o+-^4-2(^o+^)v„ (/=i 6).
(22.7)
234 СИСТЕМЫ С НЕСКОЛЬКИМИ СТЕПЕНЯМИ СВОБОДЫ [ГЛ. IV
Теперь подставим (22.5) в уравнения (22.7) и (21.7).
Выделяя в полученных выражениях постзянные и гармонические
члены, придем к 6N уравнениям, сьязлвающим бЛ^-f-l
параметров (а10 я3лг,о» а\ азлг» ^):
6 W
-Ь2 2 №н«/ + ?/*| + 2 ?/«|Vw = 0 (/= 1 6), (22.8)
Л = 1 /=7
6
«/ = 2^А (' = 7 3/V), (22.9)
* = 1
злг
f//o+2^/oV« = 0 (/=1. .... 6), (22.10)
б
t//o= 2 v^0 (/=7, .... ЗЛО- (22.11)
Рассмотрим сначала систему уравнений, содержащих £//0;
подставив (22.11) в (22.10), уменьшим число уравнений
до шести:
6 ЗЛГ
^o+2f/*o2v«V|* = 0 (/=1 6). (22.12)
k = l Ы7
Покажем, что эта система линейных однородных уравнений
может иметь только нулевые решения. Действительно,
ненулевые решения возможны только в том случае, если
определитель системы (22.12) равен нулю. Но тогда эта система
будет иметь бесчисленное множество решений, причем одно
из значений Ui0 можно будет назначать произвольно. С другой
стороны, очевидно, что уравнения (22.12) совпадают с
уравнениями статического равновесия системы (22.2) — (22.3).
Таким образом, при обращении в нуль определителя
уравнений (22.12) система должна обладать бесчисленным
множеством положений статистического равновесия, что
невозможно, если выполнены условия фиксации амортизируемого
объекта.
Отсюда следует, что
Uio(aot> Я/) = 0 (/=1, ..., ЗЛО. (22.13
то есть упругие силы всех амортизаторов не имеют постоян
ной составляющей. Таким образом, зависимость смещения
середины размаха aQi от амплитуды колебаний at сохраняется
§ 221 СВОБОДНЫЕ КОЛЕБАНИЯ ВИБРОЗАЩИТНОЙ СИСТЕМЫ 235
для каждого из амортизаторов такой же» как и при
свободных колебаниях в системе с одной степенью свободы
(разумеется, при соответствующих значениях статистических
деформаций usi). Это позволяет выразить aoi через аь и
рассматривать коэффициенты линеаризации qt как функции
только от av то есть использовать при решении системы
уравнений (22.8) — (22.9) скелетные кривые, построенные
предварительно для каждого из амортизаторов.
При этом система уравнений (22.8)—(22.9) содержит
3N+1 неизвестных — амплитуды ах% . .., aZN и частоту X.
Поскольку число неизвестных превышает число уравнений,
одно из них может задаваться произвольно (разумеется,
в известных пределах, с тем, чтобы система имела
вещественные решения).
Полученные уравнения являются, вообще говоря,
трансцендентными; их решение связано обычно с вычислительными
трудностями, для преодоления которых оказывается
целесообразным использование цифровых вычислительных машин.
При этом удобно пользоваться изложенным ниже алгоритмом,
позволяющим свести решение к последовательности операций,
имеющих стандартную программу, — решению алгебраического
уравнения шестой степени и решению системы линейных
алгебраических уравнений.
Предположим, что характеристики Uiy{Ui) имеют при
й/ = 0 непрерывные производные; тогда можно при
исследовании малых колебаний принять, как обычно,
то есть в уравнениях (22.8) положить
7| = £/;,(0) = вр (22.14)
При этом получается система линейных алгебраических
уравнений:
6 3N
— ^22 ^^/ + ^+2 ^^==0 ('=1 6)> (22-15)
6
a^Sv^ (i = 7 ЗЛО. (22.16)
к-1
236 СИСТЕМЫ С НЕСКОЛЬКИМИ СТЕПЕНЯМИ СВОБОДЫ [ГЛ. IV
или, после подстановки аь (I > 6) из второго уравнения
ь первое,
6 / 37V \
2 cfikt - ХЪы + 2 <Wftv„ К = О (I = 1 6), (22.17)
где Ьм — символ» Кронекера
{1 при / = ft,
О при / Ф k.
Эта система имеет ненулевые решения при значениях X,
обращающих в нуль ее определитель. Из получающегося
при этом частотного уравнения могут быть определены
собственные частоты Xv ..., А,б, которые, разумеется, совпадают
с рассмотренными выше, в § 20.
Соответствующие гармонические решения представляют
собой главные колебания системы. Уравнения (22.17)
позволяют определить форму каждого из главных колебаний,
то есть величины амплитуд a[s), ..., a^s) с точностью до
произвольного множителя y^sh
a{s) = y(s)a(s) (/ _ i 6). (22.18)
Далее, используя выражение (22.16), можно найти амплитуды
деформаций остальных амортизаторов:
б
a<f) = yu) S v/ikaj*> (/ = 7 ЗЛО- (22.19)
Тем самым решается линейная задача: определяются
собственные частоты и формы; это решение отличается от
рассмотренного в § 20 только выбором обобщенных координат.
Зададимся теперь некоторым значением параметра y(s)=y(s).
При этом амплитудам aft\ найденным по формулам (22.18)
и (22.19)
aft> = v(5)aft>,
будут соответствовать определенные значения giv вообще
говоря, не совпадающие с (22.14). Подставим эти значения qn
вместо сх в уравнения (22.17); решив эти уравнения, найдем
новые значения «собственных» частот и новые «коэффициенты
§ 22] СВОБОДНЫЕ КОЛЕБАНИЯ ВИБРОЗАЩИТНОИ СИСТЕМЫ 237
форм» а$. которые также будут отличаться от первоначальных
Подставив эти коэффициенты в выражения (22.18) и (22.19),
найдем новые значения амплитуд а$ и по ним — значения q$.
Продолжая таким образом итеративный процесс, можно
с любой степенью точности определить решение системы
(22.8)—(22.9). Можно доказать, что при достаточно малых
значениях y(5) процесс последовательных приближений
сходится и тем быстрее, чем меньше величина ^ и чем меньше
характеристики Oiy{Ui) отличаются от линейных.
Расчет необходимо произвести для всех шести форм
(5=1 6) и для нескольких значений у(у)» лежащих
в интересующем нас диапазоне. При этом целесообразно для
каждого из последующих -,
значений y(5) выбирать в
качестве исходного
приближения значения коэффициентов
формы, найденные методом
итераций для предыдущего,
меньшего значения.
В результате опреде- ____
ляются зависимости всех ше- ° Л
сти «собственных» частот Рис. 87.
системы от параметра у,
характеризующего в некотором масштабе амплитуды
деформаций амортизаторов. Эти зависимости в определенном смысле
аналогичны скелетным кривым (рис. 87).
Все изложенное в этом параграфе является справедливым
и для частично амортизированных систем; изменяется только
число уравнений и неизвестных. В частности, если число
степеней свободы системы равно р, а число упругих
элементов N't уравнения для определения амплитуд колебаний
принимают такую форму:
р N'
— *2 SftK**+ AW+ 2 д1а1чи**0(1=\,....р). (22.20)
ft=i i=p+i
al = 1> viftaft. (22.21)
k = l
Рассмотрим простой пример.
238
СИСТЕМЫ С НЕСКОЛЬКИМИ СТЕПЕНЯМИ СВОБОДЫ [ГЛ. IV
В схеме, показанной на рис. 88, амортизируемый объект
совершает плоское движение (в плоскости хсу). Обобщенные
координаты объекта:
Координаты точек крепления упругих элементов:
х1 — д:3 =
а,
•а,
■У1 = У2 = УЗ=У4 = —*•
Деформации упругих элементов выражаем через обобщенные
координаты:
и\ = sy — a®z>
u2 = sy-{-aQ2,
Осюда находим
t
•1
L
с
-4w*hi
'Х- 0 —
Ч
i
— а —2Г
X
"ft
_ h
Рис. 88.
Qi-
q2 — Sy — 2 '
u2 — ux
2a
«i).
?8 = 8.
По формулам (21.21) определяем \ikr:
,„=fe=i(1+-+i). ,1!=i(,_|i-4).
/и/г m/г
^13 — *2^~» fe— go"» М-зз—m-
Переменная иА связана с новыми обобщенными координатами
uv и2 и «з простым соотношением иг = и4. Таким образом,
v41 = v42 = 0, v43=l. Составляем уравнения типа (22.20)
и (22.21):
— № (Н-п*! 4 Mi2a2 + !*1заз) 4- <7i<*i = 0,
— I2 (М-12^1 4 М-22^2 4 М<23аз) 4 ?2а2 = °»
— ^2 (^13*1 4 !%«2 4 М^ЗЗ^з) 4 <7з*3 4-<74а4 = °>
а4=я3-
Предположим, что
JL — L 2L — Y1
а ~ 2 * а ~ 2 '
(22.22)
§ 22] СВОБОДНЫЕ КОЛЕБАНИЯ ВИБРОЗАЩИТНОЙ СИСТЕМЫ 239
тогда
т
т
lit- л //*
т
М-23 — 5~ ' ^33 — т'
Предположим также, что все элементы имеют упругие
характеристики вида (10.9')
,, 2сД , пих
'IV
U,
2У
2сД . ли2
п g 2Д '
2clAi ки4
я й 2Aj
(22.23)
с
"2 *
а, =4.
причем
*ita-J1 "1— 2
Коэффициенты линеаризации определяем по формуле (5.54):
2 2сД . / я УЗ* \ d . (аЛ
d . I a2\ cd , (2я3 \ cd . (2a» \
ч*=ст^\-т)' *e^*m' *=Ег*Ьп'-
где
d =
4Д
я Уз •
Подставляя эти выражения в уравнения (22.22), получаем
—'(тг~*)+--£*(*)-°-
—»(*-*+«.)+:Н*(^)-«>-
(22.24)
где z = %Ymlc — безразмерная частота.
При малых амплитудах ах, а2, а3
1.
При этом уравнения (22.24) становятся линейными.
240 СИСТЕМЫ С НЕСКОЛЬКИМИ СТЕПЕНЯМИ СВОБОДЫ [ГЛ. IV
Из условия обращения в нуль определителя системы
1 2 '
0,
0,
1 — —
1 2 '
4
4
1 — Z*
= 0
находим собственные частоты:
г2^~
0,845,
г| = 3,155.
Определяем собственные формы, подставляя значения
собственных частот в линеаризованные уравнения (22.23):
('-4)»i"-4<,=°'
(.-#)
4"+
А
4 4° = °.
-т-4°+т-<+(1-*?К)==0-
Отсюда находим
eu>== —а£>==0.366а£>.
а<2) = 42>, 42> = 0,
ар = — 43) = — 1,36543).
Легко видеть, что вторая форма соответствует
поступательным колебаниям амортизируемого объекта в направлении
оси у. В рассматриваемой схеме эти колебания при любых
амплитудах являются независимыми, так что для них
скелетная кривая может быть построена как для системы с одной
степенью свободы. Поэтому в дальнейшем мы будем
интересоваться только первой и третьей формами,
определяющими связанные колебания по оси х и вокруг оси z.
Учитывая, что при этих колебаниях всегда а2 = — av
можно упростить систему (22.24), сведя ее к двум
уравнениям с двумя неизвестными
- •' >ь -.]„_* <22-25)
т«. + [£*(*)-
§ 22] СВОБОДНЫЕ КОЛЕБАНИЯ ВИБРОЗАЩИТНОЙ СИСТЕМЫ 241
Эти уравнения и будут в дальнейшем использованы для
определения зависимости частот свободных колебаний от
амплитуд деформаций упругих элементов.
Рассмотрим сначала колебания низшей частоты. Зададимся
каким-либо значением одной из амплитуд, например,
примем, что
41> = 0,25rf.
Тогда в соответствии с первой формой, полученной при
исследовании линейной системы, найдем
При этом
aU) = 0,366 • 0,25rf = 0,0915d
Hl)
tg
24J
Д)
>,0915
),0915
tgQ,5
0,5
1,
= -^-l-= 1,092.
Подставив эти выражения в уравнения (22.25), приходим
к новому частотному уравнению:
1 —II _£_
1 2 ' 4
— -у- 1,092—л:2
:0,
решая которое, находим
*2 = 0,904,
4 = 3,22.
Нас интересует, разумеется, только значение меньшей
частоты, поскольку при составлении уточненного частотного
уравнения мы исходили из первой формы колебаний.
Уточняем форму колебаний
а</>:
= а<1>.
:0,412ajf>.
Таким образом, выбранному значению а^ соответствует
а& — 0,412- 0,25d = Q,103rf.
16 М. 3. Коловский
242
СИСТЕМЫ С НЕСКОЛЬКИМИ СТЕПЕНЯМИ СВОБОДЫ [ГЛ. IV
Впрочем, это практически не влияет на частотное уравнение,
поскольку по-прежнему .
d (dp .
tg 0,103
»1.
ay \ d I- 0,103
Итак, можно принять, что при а(31) = 0,25; £2 = 0,904
af> = 0,412aW = 0.103rf.
Примем теперь, что
Выбрав в качестве первого приближения форму колебаний,
соответствующую a^ = 0t25d,
получаем
ар = 0М2.0Ай = 0ЛШ.
При этом v
tg 0,165
а?,
d ъ,
иг
V
\и
ш
Г У
/ d
d . м»\
24"
tg
2a?»
0,165
tg0.8
0,8
= 1,01;
1,29.
Решая частотное уравнение
Q2 0,4 a$>
Рис. 89.
у
1,01
2 '
2 *
1,29
= 0,
получаем z\ = 1,02. Это дает следующее уточнение формы
колебаний:
1 2 (2,02 — г\) 3
Таким образом, а(,1) = 0,51 -0,4^ = 0,204^. При этом
d (dP\ tg 0,204
0,204
= 1,014.
§23]
РЕЗОНАНСНЫЕ КОЛЕБАНИЯ
243
Изменение частоты, вызванное этой поправкой, оказывается
практически несущественным (отличие в четвертом знаке);
поэтому можно принять aM — 0,4d\ 2f=l,02; **(/> = 0,2(Ш.
Совершенно аналогично могут быть найдены значения
низшей частоты свободных колебаний, соответствующие
другим значениям амплитуды а$\ На рис. 89 построены графики
зависимостей z\\a^\ и af> [<$>].
Анализ свободных колебаний наиболее высокой частоты
(третья форма) не отличается от рассмотренного выше.
Результаты вычислений, выполненных для двух значений af\
приведены в табл. 2.
Таблица 2
п/п
1
2
а3
0,25</
OAd
4
3,32
3,45
а?) 1
—0,335йП
—0,56d
§ 23. Резонансные колебания
Разнообразные резонансные явления, подробно
исследованные в гл. III, могут иметь место и в нелинейной системе
с несколькими степенями свободы. В отличие от линейной
системы, резонансные колебания могут возникать в тех
случаях, когда частоты вибрационного воздействия существенно
превышают собственные частоты. Такие резонансы,
разумеется, являются недопустимыми; в правильно
спроектированной виброзащитной системе возможность их возникновения
должна быть исключена.
Физическая природа резонансных явлений — та же, что и
в системе с одной степенью свободы (см. § 16). Всякий
резонанс представляет собой движение, близкое к свободным
колебаниям консервативной системы, и может рассматриваться
как «свободные колебания», поддержанные вибрационным
воздействием. Именно в связи с этим обстоятельством и
приобретает важное практическое значение исследование
свободных колебаний, изложенное в предыдущем параграфе.
Рассмотрим вновь уравнения движения амортизируемого
объекта, например, в форме (21.22)—(21.23) (уравнениям
16*
244 СИСТЕМЫ С НЕСКОЛЬКИМИ СТЕПЕНЯМИ СВОБОДЫ [ГЛ. IV
вида (21.16), (21.17) соответствует /7 = 6, N'= 3N).
Исключая из уравнений (21.22) Аг, с помощью уравнений (21.23)
получим
Р N' р
2 i*w«*+<Л(«*. «*) + 2 v,,*/,^. ^) = 2 Q^ (23.1)
(/=1 р).
В дальнейшем предполагается, что вибрационное воздействие
* 2л
является периодическим с периодом Т = —.
Выделив упругую и диссипативную составляющую сил Ult
перепишем уравнение (23.1) в следующей форме:
р N*
2>*Л+^у("/) + 2 VuUiy(*d = — Uid(*i> «/) —
TV' Р
- 2 ^Л*,. ^)+2<?А* ('=1 />)• (23.2)
К этим дифференциальным уравнениям необходимо добавить
уравнения связей
«i-2viA = 0 ('=/>+! АГ). (23.3)
Положив правые части уравнений (23.2) равными нулю,
получим уравнения свободных колебаний. Поскольку
резонансные колебания близки к свободным, можно искать
периодическое решение системы (23.2) — (23.3) на семействе
периодических решений частоты со уравнений свободных колебаний,
пользуясь методом Галеркина.
Пусть
«, = Ф,(* + а) (/=1 ЛГ) (23.4)
— семейство периодических решений периода Т уравнений
свободных колебаний системы. Как уже указывалось выше,
существование семейства решений, зависящего от параметра а,
обусловлено автономностью уравнений. Тогда, в соответствии
с формулой (6.13), значение параметра а соответствующее
§ 231 РЕЗОНАНСНЫЕ КОЛЕБАНИЯ 245
приближенному решению системы (23.2) — (23.3), близкому
к свободным колебаниям, должно определяться из уравнения
Т р_ (
Г 2W№/(' + *). <М' + а>1 +
о '-и
+ S uu>W + *)- «Pi (' + <*)] v„ —
— J °г#г (О Ф, (* + а) Л =* 0. (23.5)
Если это уравнение имеет вещественные корни, то
резонансные колебания периода Т могут возникнуть в системе.
При отсутствии вещественных значений а, удовлетворяющих
уравнению (23.5), возможность возникновения резонансных
колебаний исключается.
Так же, как и для системы с одной степенью свободы,
уравнение (23.5) представляет собой условие баланса энергии:
работа диссипативных сил на свободном колебании должна
быть равна работе вибрационного воздействия.
Пусть известно приближенное гармоническое решение
уравнений свободных колебаний, имеющее частоту со:
ut = аы + сц cos со (t + a), ut = — ®at sin со (t + а). (23.6)
Предположим также, что все вынуждающие силы Qr(t)
являются гармоническими той же частоты
Qr(t) = Ar cos at. (23.7)
Подставив (23.6) и (23.7) в уравнение (23.5), получим
т р |
о ы\ I
лг
+ 2 Vut/ialfloj+ajcostttf + a), — cousin со (f + a)] —
i=p+\
— У\лгcos в* * °rt 11- (oai sin со (^ + a)] tf/ = 0. (23.8)
r=I
246 СИСТЕМЫ С НЕСКОЛЬКИМИ СТЕПЕНЯМИ СВОБОДЫ [ГЛ. IV
Учитывая, что в силу выражений (11.5)
т
— j Uid la0l + ai C0S © С + a>»
— oa/ sin со (f + a)] sin (a) (f + a)] dtf =
2я
= — — yid(aoi^aicos^* —o>a| sin *ф) sin г|? rfip =nbiAaL%
о
и поскольку
cos ayt sin [со (t -f- ex)] dt = ~ sin coa,
о
упростим выражение (23.8):
2 I nbiitocii -f- 2 nbuaiafiWu -f- 2 лЛга^ sin coa • orЛ = 0.
(23.9)
Отсюда находим
ю
/7 / AT'
2Кда/ + 2 Mrtvw
sincoa = с"х x p ppri '-. (23.10)
2 2 Arai°n
Поскольку в силу соотношений (23.3)
р N' N' p N'
2 2 buawu^ 2 *u*i2!*/vw= 2 *««*?. (23.11)
получаем окончательно
°>26/дл?
sincoa = -^— . (23.12)
2 2 Arai°n
Резонансные колебания могут возникнуть, если |sincoa|^l,
то есть если
© 2 »*д*?< 2 2 Ат*Рп- (23.13)
§23]
РЕЗОНАНСНЫЕ КОЛЕБАНИЯ
247.
Очевидно, что, обеспечив достаточно интенсивное
демпфирование в амортизаторах (то есть достаточно большие
значения #/д), можно нарушить условие (23.13) и тем самым
исключить возможность возникновения резонансных колебаний
частоты со.
Аналогичным путем могут быть выведены условия
существования резонансных колебаний и в случае периодического
вибрационного воздействия; если не учитывать наличия высших
гармоник свободных колебаний, то условия существования
в этом случае совпадают с (23.13), поскольку
дополнительной работы на гармоническом свободном колебании высшие
гармоники внешних сил не дадут. Определив высшие
гармоники свободных колебаний, можно получить условия
существования резонансов дробного порядка. При гармоническом
вибрационном воздействии это — субгармонические резонансы.
Установив возможность возникновения каких-либо
резонансов, мы в то же время получаем возможность
приближенно оценить их амплитуды, поскольку близость
резонансных колебаний к свободным означает и близость по амплитуде.
Более точные оценки обычно не требуются.
Проанализируем теперь более подробно условия (23.13),
при которых могут возникать резонансные колебания,
совпадающие по частоте с вибрационным воздействием. Очень
часто именно такие колебания оказываются наиболее опасными.
Рассмотрим сначала систему с диссипативными силами,
пропорциональными скоростям деформаций упругих
элементов, то есть предположим, что все biA — постоянные
коэффициенты. Предположим также, что амплитуды вибрационных
воздействий Ат сохраняются постоянными, а частота со может
изменяться в некотором диапазоне от ©mln до сотах,
охватывающем спектр собственных частот системы.
Для определения «опасных» значений со, при которых
могут возникать резонансные колебания, удобно использовать
«скелетные кривые» системы, выражающие зависимость частот
свободных колебаний от амплитуды деформации одного из
упругих элементов (рис. 90).
Левая часть неравенства (23.13) пропорциональна
квадратам амплитуд dj, а правая часть зависит от амплитуд линейно.
Поэтому при достаточно малых значениях ai неравенство
всегда будет выполняться. Это означает, что в системах
с силами сопротивления, пропорциональными скоростям,
248 СИСТЕМЫ С НЕСКОЛЬКИМИ СТЕПЕНЯМИ СВОБОДЫ [ГЛ. IV
резонансные колебания безусловно будут иметь место при
значениях со, достаточно близких к собственным частотам
системы (см. рис. 90). Насколько широкой окажется каждая
из таких полос, зависит от значений biJk, Ar, формы
колебаний на выбранной частоте.
В виброзащитных системах собственные частоты обычно
стремятся сблизить с тем, чтобы уменьшить общую ширину
резонансной полосы; при этом области существования
резонансных колебаний обычно сливаются, так что они могут
наблюдаться при любом
значении со в интервале кт{п <
<со<;А,1Т1ах. Как видно из
рис. 90, в таких случаях при
одном и том же значении
со = со' могут возникать
различные по форме
резонансные колебания,
соответствующие точкам различных
и со* Л скелетных кривых.
рис до Левая часть неравенства
(23.13) пропорциональна
частоте со; поэтому с ростом со опасность возникновения
резонансных колебаний уменьшается. Этот вывод справедлив,
разумеется, только в случае постоянных амплитуд Ат\ если же
с ростом частоты эти амплитуды растут (например,
пропорционально квадрату со), то опасность возникновения резонансов
может возрастать на высоких частотах. Здесь могут иметь
место те эффекты («затягивание» резонанса в область
высоких частот, появление дополнительных ветвей резонансных
кривых и т. п.), которые подробно рассматривались в § 12.
Покажем на примере, как можно использовать
полученные соотношения для определения интенсивности диссипатив-
ных сил, необходимой для подавления резонансных колебаний.
Пусть в системе, показанной на рис. 88, основание
совершает гармонические колебания в направлении оси х
с амплитудой £0 и частотой
Как было показано в § 22, свободные колебания этой частоты
имеют следующие амплитуды (см. табл. 2): ах — — 0,56d,
§ 23] РЕЗОНАНСНЫЕ КОЛЕБАНИЯ 249
as = 0Ad. По формуле (21.30) получаем
Qi°u + <2з<*з1 = — ^пЛ1 = 0,
QiOiz + <Эзазз = — ^ззЛз = — mbf& cos at.
Отсюда
А\<*п + ^3a3i = 0. А\<*\ъ + АзР& = ^1о02»
р р
Для подавления резонансных колебаний необходимо, чтобы
неравенство (23.13) выполнялось с обратным знаком:
<а(\,а1 + *2да2 +V*!+^a4) > 1.38c d^.
Поскольку аг = а2* #з = #4» то» полагая Ьи = *2д, £3д = ^д»
имеем
1
,86 ]/£ 2^ (0,31*1д+0,16$3д) > l,38*tf£0.
Примем, что коэффициенты демпфирования пропорциональны
корню квадратному из жесткости соответствующего упругого
элемента
■5^ = ^ или *1д=/2*3д. .
ус У сх
При таком предположении коэффициент поглощения при ма^
лых колебаниях у всех упругих элементов оказывается
одинаковым.
При этом
2,23rf^-^^> 1.38^0
или
^д>0,62V7^-|..,
Несколько иными оказываются условия возникновения
резонансных колебаний в системе с сухим трением. Здесь
Ьи = 4f* , . (23.14)
и условие (23.13) принимает следующий вид:
SI^kkSS^w,,. (23л5)
i=i *=1 *-=1
250 СИСТЕМЫ С НЕСКОЛЬКИМИ СТЕПЕНЯМИ СВОБОДЫ [ГЛ. IV
Обе части неравенства пропорциональны величинам
амплитуд аь\ поэтому при достаточно больших значениях Нь
колебания, близкие к свободным, не могут возникнуть, как бы
малы ни были их амплитуды. Практически это означает, что
либо система оказывается «запертой» силами сухого трения,
либо в ней возникают движения с остановками. .
Следует отметить, что в системе с несколькими степенями
свободы «запирание» может осуществляться не по всем
координатам; при этом сухое трение как бы уменьшает число
степеней свободы системы.
Если в примере, рассмотренном выше, предположить, что
в амортизаторах действуют силы сухого трения, условия
подавления резонансных колебаний
примут такую форму:
-!(#!.! а, |+Я2|а2| + Я3|я3| +
+ Я4|а4|)>1,38с<%
При #! = Я2, #3 — ^4 имеем
%м* i <°'56Я1 + °'4Яз) > 1.38*Ь,
(23.16)
При выполнении этого неравен-
Рис. 91. ства движения, близкие к
связанным свободным колебаниям по
координатам х и 9г, не могут возникнуть. Однако это не
означает, что система окажется запертой. В самом деле, пусть
Я3 = 0, //,>-^-clo = 0,97C|o.
Тогда неравенство (23.16) выполнено. Более того, система
будет заперта по координате 0г, поскольку амплитуда
вынуждающего момента, равная произведению амплитуды
вынуждающей силы т10аР на плечо /г, не превышает момента
сил трения (рис. 91)
/я|0со2/г = т|0 • 3,45 -— h = 3,45^0/г,
2Нха = 4hHx > 3,88с£0/г > /п£0со2/г.
Таким образом, в системе будут происходить поступательные
колебания по координате х. Для определения амплитуды
§24] ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ ПРИ СУХОМ ТРЕНИИ 251
этих колебаний необходимо исследовать систему с одной
степенью свободы, получающуюся при абсолютно жестких
элементах ах и и2- Уравнение свободных колебаний такой
системы
Линеаризуя нелинейную упругую силу, получаем уравнение
скелетной кривой
"-=г*(¥).
из которого при z2 = 3,45 находим
a3 = 0,68d = 0,49A.
Величина а3 оказалась близкой к предельно возможной
♦ деформации упругих элементов 3 и 4. Это означает, что
свободные колебания с такой амплитудой будут
сопровождаться сильным стуком об упоры. Естественно поэтому,
что принятые значения Нх и #3 неприемлемы.
Приняв
Я = 2Я3>0,72^0,
мы вновь удовлетворим условию (23.16), однако при этом
резонансные колебания по координате х уже не смогут
возникнуть, поскольку условие запертости по углу Q2 не будет
выполняться.
§ 24. Вынужденные колебания в системах
с сухим трением
Если установлено, что в исследуемой виброзащитной
системе при заданном вибрационном воздействии не могут
возникнуть резонансные колебания, то в принципе эта система
может считаться пригодной для использования. Для
уточнения ее виброзащитных свойств требуется исследование
вынужденных колебаний, возникающих при вибрационном
воздействии и не носящих резонансного характера. При этом
исследовании обычно можно ограничиться линеаризацией
нелинейных характеристик по формулам (9.6), поскольку
при нерезонансных колебаниях деформации амортизаторов
могут считаться малыми. Исключение составляют системы
с существенно нелинейными характеристиками, из которых
252 СИСТЕМЫ С НЕСКОЛЬКИМИ СТЕПЕНЯМИ СВОБОДЫ [ГЛ. IV
особого внимания заслуживают системы с сухим трением,
получившие в последнее время широкое распространение.
С некоторыми особенностями анализа таких систем мы
познакомимся на конкретном примере.
Рассмотрим вновь систему, показанную на рис. 88,
полагая, что в элементах /—4 имеются силы сухого трения:
Uid = Hlslgn'ui (/=1 4). (24.1)
В дальнейшем принимается, что
Н1 = #2, #3 == На*
Пусть основание совершает гармонические колебания в
направлении оси х с амплитудой £0 и частотой со.
Ограничиваясь рассмотрением нерезонансных колебаний, считаем
упругие характеристики амортизаторов линейными с жесткостями с
(элементы / и 2) и сх (элементы 3 и 4).
Составим дифференциальные уравнения движения в форме
(21.22); учитывая (21.29), получаем
Mll«l + Ml2% + M-13% + Щ + #! Sign UX = |Х13£о«>2 COS СО/,
\112иг + М%«2 + *%% + CU2 + Н\ Sigfl «2 = \hfof& C0S <*>*.
\X\Zu\+\h&*2 + V&4 + 2^ltt3 + 2#3 si£n H = 1*88^ °°S tot.
(24.2)
При составлении этих уравнений учтено уравнение связи
Подставив в (24.2) найденные ранее выражения для \х1к,
найдем
= |-|0<D2COSCD/,
4 «l H 4 a2 — у аз "+" ~2" 2 ' "m g 2
= — yio^cosorf,
у «1 — y «2 + «3 + *la3 + ~ si£n «3 = ^ C0S <**•
(24.3)
§ 24] ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ ПРИ СУХОМ ТРЕНИИ 253
Здесь
r = ^, y = -. & = — , fc? = ^-. (24.4)
а т а т г т к '
При заданном вибрационном воздействии в системе возникнут
вынужденные колебания по координатам х и 6г, при которых
У, = 0, «1 = — «2-
Учитывая это соотношение, при котором первые два
уравнения (24.3) оказываются тождественными, приходим к
системе двух дифференциальных уравнений с двумя неизвестными:
2Н
(г2 + Y2) и\ + У«з + k<2ui Ч—~ si£n u 1 = Ylo®2 cos <**.
Y«i + «з + *1«з + "jp siSn «a = bfi^ cos <**•
(24.5)
Приближенное периодическое решение полученной системы
нелинейных дифференциальных уравнений разыскиваем в
гармонической форме:
их =s a01 + a1cos(<o^-f-9), а3 = аоз + азс08(0)* + ,Ф)- (24.6)
Постоянные составляющие в рассматриваемом случае
оказываются равными нулю, в чем нетрудно убедиться, подставив
(24.6) в (24.5).
Производим гармоническую линеаризацию сил сухого
трения, по формуле (13.3) находим
2Я, . • 8Я, •
—Д-signих « — #,,
2Я3 . • 8Я3 •
—- sign йо « — «о.
(24.7)
В линеаризованных уравнениях удобно одну из неизвестных
фаз ввести в правые части, записав эти уравнения в такой
форме:
где
пт ' 1а пт
(г« Н- Y2) «1 + Y«3 + #«1 + -^ «i=Y^ cos(^ - Ф).
Y«i + «3+ *i«3 + -^ «з = ^ cos («* — ф).
8Я| 8Я3
(24.8)
254 СИСТЕМЫ С НЕСКОЛЬКИМИ СТЕПЕНЯМИ СВОБОДЫ [ГЛ. IV
а решение должно разыскиваться в форме
ul = alcos(ot9 я3= a3cos(Gtf-f-\|j). (24.9)
Подставляя (24.9) в (24.8) и приравнивая в левых и правых
частях уравнений коэффициенты при cosatf и sinatf, получим
конечные соотношения, из которых могут быть определены
неизвестные параметры аХл а3, ф. tp:
[k2 — а? (г2 -f- у2)] ах — а2уа3 cos г|> = y£o<*>2cos ф,
©2Y^3sin^|) — r|j =\£о(о28*пФ»
— у^аг + (к\ — co2)cos\|)a3 — Tfesln^^coscp, | (24Л0)
— {k\ — со2)a3 sin i|> — ri3 cos ф = ^ю2 sin ф. J
Решение этой системы в общем виде требует сравнительно
громоздких выкладок. Целесообразно в первую очередь
исключить фазы. С этой целью умножим третье и четвертое
уравнения на у и вычтем их соотретственно из первого и
второго:
yk?a2 cos t|) — у\ sin г|) = (k2 — a?r2) a. \
. I f.2 • ■ f (24Л1)
Возводя эти уравнения в квадрат и складывая их, получим
соотношение, связывающее ах и а3:
С другой стороны, решая систему (24.11) относительно sin г|)
и cosi|), получаем
cos^ = -_—§ . (24.13)
тФз + УПз
Возводя в квадрат первые два уравнения (24.10) и складывая
их, находим
[k2 — со2 (г2 + y2)]2 а\ + Y2®4a2 + Л? —
— 2yco2 [/г2 — (б2 (г2 + y2)! я^з cos г|> — 2Yco2a3T|1 sin г|> = Y2^04-
(24.14)
§24] ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ ПРИ СУХОМ ТРЕНИИ 255
Подставляя (24.13) в (24.14), получаем второе соотношение,
связывающее ах и а3:
а\чУ [Y2«>2 - 2 (ft2-co2r2)] + а\\х\\(ft2_co2)2+ft4 (ng—^§co4)] +
+ а\ (ft2 — со2)2ft4 + а*а\ [Щу2®* - 2со2 (ft2-co2) (ft2-со2г2)] ft2 +
;. +2aTa3^%<o4 + ^(n23-^) = 0. (24.15)
Исключив из (24.15) ах спомощью (24.12), получим
следующее уравнение четвертой степени относительно а2:
(a\k\ [(/г2 — со2) (ft2 — coV2) — /jfyV]2 + a2 \fh\ [y2co4 —
— 2со2 (ft2 - co2r2)] I2 + (£2 — co2r2)2 [л2 (ft? — со2)2 +
— 2co2 (ft2 — со2) (k2 — co2r2)]} -f (y2^ — Л?) [Y2»4 —
— 2<o| (ft» - co2r2)] + ц2 (ц2 — ^co4) (ft2 — co2r2)2)2 =
= 4а4л2л1»12 (ft2 — foV2)2 y2 + 4а2л2Л^8 (ft2 — ©V2)2(y2^-Л?).
\ (24.16)
Отсутствие положительных корней у этого уравнения
означает, что рассматриваемая система при
соответствующем вибрационном воздействии остается полностью или
частично запертой. Истинное значение а2 может
характеризовать только такой положительный корень, который при
подстановке в (24.12) дает для а2 также положительное
значение, то есть удовлетворяет условию
уЩа2 + у2ч2~-ц2>0. (24.17)
Определив значения амплитуд и фаз, можно оценить
качество виброзащитной системы. Для этого в случае
пассивной виброзащитной системы определяется абсолютное
ускорение какой-либо точки амортизируемого объекта, чаще
всего — центра инерции. При этом, как и в случае системы
с одной степенью свободы, не следует пользоваться
линеаризованными уравнениями, необходимо непосредственно
определять ускорение из-уравнений-движения.
256 СИСТЕМЫ С НЕСКОЛЬКИМИ СТЕПЕНЯМИ СВОБОДЫ [ГЛ. IV
В рассматриваемом примере абсолютное ускорение центра
инерции направлено по оси х:
х = и$ — Iq©2 cos at. (24.18)
Из второго уравнения (24.5) получаем
х = — уаг - k\u* — Щ± sign щ, (24.19)
Определяя и{ из первого уравнения (24.5) и подставляя
в (24.19), находим
• [ух + *Ч + Щ^~ sign я,) — k\uz — Ц± sign «з
^-r2 + Y2
или
- =^(^+^sign «x)_il±^(^3+^sign ь).
(24.20)
При высокочастотном вибрационном воздействии амплитуды ах
и аъ оказываются обычно малыми. Поэтому при определении
амплитуды х можно пренебречь в выражении (24.20) членами,
линейными относительно их и й3, и принять в первом
приближении:
В этом выражении оба слагаемых арифметически
суммируются, поскольку при \|) Ф 0 всегда найдется такой момент
времени, в который они будут иметь одинаковый знак.
Вернемся вновь к уравнению (24.16). Если коэффициент
при старшем члене этого уравнения (а|) стремится к нулю,
то один из корней стремится к оо, причем этот корень
безусловно удовлетворяет условию (24.17). Таким образом,
при частоте со, удовлетворяющей уравнению
(ft? — co2)(ft2 — coV) — ftfyW = 0. (24.22)
в рассматриваемой системе возникает резонанс, причем
амплитуды колебаний неограниченно возрастают, и в конце концов
колебания выходят за пределы области линейности упругих
характеристик. Если такие колебания недопустимы, система
§ 24] ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ ПРИ СУХОМ ТРЕНИИ 257
должна оставаться запертой на всех частотах,
удовлетворяющих уравнению (24.22), которое, как нетрудно убедиться,
совпадает с частотным уравнением линейной системы. Легко
показать, что подобными свойствами обладает любая система
с линейными упругими
характеристиками и демпферами сухого
трения: если при частоте
вибрационного воздействия,
совпадающего с одной из собственных
частот, система оказывается не
запертой, то в ней развиваются
колебания с теоретически
неограниченно возрастающей
амплитудой. Учитывая это обстоятельство,
обычно выбирают силы сухого трения с таким расчетом,
чтобы система оставалась запертой на всех собственных
частотах.
Предполагая, что в рассмотренном выше примере должно
выполняться это условие, получаем из уравнений (24.5)
Рис. 92.
Щ± > YbAi
2Я3
'О шах'
> У*.
(24.23)
Решая частотное уравнение (24.22), определяем X
Теперь условие (24.21) дает
2
max"
i^lmax >
(24.24)
(24.25)
Таким образом, как и в системе с одной степенью свободы,
сухое трение существенно ухудшает виброзащитные свойства
системы при высокочастотном вибрационном воздействии.
Улучшение виброзащитных свойств может быть достигнуто
изменением конструкции амортизатора с сухим трением.
В амортизаторах, схематически изображенных на рис. 92,
демпфер сухого трения соединяется с объектом через
дополнительный упругий элемент. Подробный анализ работы таких
амортизаторов выполнен в [25],
17 М. 3. Коловский
258 системы с несколькими Степенями Свободы (гл. tv
§ 25. Вынужденные колебания упругих тел
\£0№<ot
До сих пор амортизируемый объект рассматривался как
абсолютно твердое тело; однако в реальных виброзащитных
системах приходится иметь дело с упругими объектами.
В этом параграфе излагаются методы анализа .виброзащитных
систем, содержащих амортизируемые объекты, обладающие
линейными упругими характеристиками. Предположение о
линейности упругих свойств оказывается
в большинстве случаев приемлемым,
поскольку деформации амортизируемых
тел обычно не выходят за пределы
области линейности их характеристик.
Мы ограничимся анализом
простейшей системы, состоящей из упругого
тела, соединенного упругим
амортизатором с основанием (рис. 93).
Предполагается, что точка крепления
амортизатора к объекту может
перемещаться только в направлении оси х\
в том же направлении может
поступательно перемещаться и некоторый
малый элемент упругого тела,
примыкающий к точке крепления. Предположим также, что основание
колеблется в направлении оси х по гармоническому закону
l(0 = £ocosc^-
Если бы амортизируемый объект был абсолютно твердым
телом, мы имели бы в этом случае систему с одной степенью
свободы, подробно рассмотренную в гл. III. В случае упругого
объекта число степеней свободы системы определяется
выбором расчетной модели упругого тела, которое обычно
представляется в виде совокупности нескольких твердых тел,
соединенных упругими элементами, или в виде системы
с распределенными параметрами. Методы выбора расчетной
модели линейной упругой системы подробно изложены
в имеющейся литературе и здесь рассматриваться не будут.
Отметим только, что выбор той или иной модели упругого
тела в значительной степени определяется спектром частот
вибрационного воздействия. Если эти частоты существенно
меньше, чем собственные частоты упругого тела, можно
Рис. 93.
§25] ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ УПРУГИХ ТЕЛ 259
считать последнее абсолютно твердым: чем выше частоты
вибрационного воздействия, тем более сложной оказывается
расчетная модель амортизируемого объекта.
Уравнения движения виброзащитной системы будут в
рассматриваемом случае содержать одну нелинейность —
характеристику упругого амортизатора, так что их можно будет
решать методами, изложенными выше. Однако такой путь
решения часто оказывается слишком сложным. Это относится,
прежде всего, к таким упругим объектам, для которых
затруднительно выбрать простую расчетную модель, и, вместе
с тем, имеется возможность экспериментального анализа
частотных свойств. В таких случаях оказывается полезным
применить другой метод анализа, основанный на описании
частотных свойств линейной системы с помощью так
называемых матриц переноса. Мы ограничимся здесь изложением
лишь самых элементарных сведений об этом методе,
необходимых для решения сформулированной выше простейшей
задачи. Метод матриц переноса, получивший i 1
в последние годы широкое распростране- _^_| И
ние, подробно излагается во многих работах Ах \уХв
(см. [5i], [<»]). '■ '*
Рассмотрим некоторую сколь угодно рис# 94.
сложную линейную систему, которая связана
с другими системами в точках Л и В (рис. 94).
Предположим, что перемещение каждой из этих точек ограничено
связями и определяется одной координатой (хА или хв).
Пусть известно, что в системе происходят гармонические
колебания с частотой со. Это означает, в частности, что хА и хв
изменяются по гармоническому закону
ха = Ia cos (со* -г-фА), хв = lB cos (firf + фд). (25.1)
По гармоническому закону изменяются и усилия, возникающие
в точках А и В и представляющие собой силы
взаимодействия между рассматриваемой системой и системами,
связанными с ней:
XA = PAcos(vt-\-tyA), XB = PBcos(<ot + tyB). (25.2)
Поскольку частота со предполагается известной,
переменные хА, хв, Xд, Xв полностью определяются заданием так
17*
260 СИСТЕМЫ С НЕСКОЛЬКИМИ СТЕПЕНЯМИ СВОБОДЫ [ГЛ. IV
называемых комплексных амплитуд |д, 1В> РА, Рв>
определяемых следующим образом:
\Рл\=Рл- KgPA=^A>
\1в\ =Ъв> *т81в = (Рв'>
\рв\ =рв* *чРв = Ъв-
Метод матриц переноса основывается на том, что между
введенными таким образом комплексными амплитудами всегда
существуют следующие линейные зависимости:
(25.3)
lB = sn(<d)lA + sn{a)PA, I
Р5 = 521(0)|д + *22(ю)Яд. (
Здесь
$п> ^12» $21» $22 — некоторые комплексные числа,
значения которых для заданной линейной системы являются
функциями со. Матрица, составленная из этих чисел,
называется матрицей переноса линейной системы
« , ч 1*11 (©) *12(©)| _ .ч
S-((0) = IU2i(co) *«о)|' (25'4)
Матрицы переноса могут быть введены и в более общих
случаях, когда перемещения на «входе» (точка А) и «выходе»
(точка В) системы определяются несколькими параметрами,
так что хА и хв оказываются векторами, однако эти случаи
нам не понадобятся в дальнейшем. Определение матриц
переноса для различных линейных систем рассматривается в
упомянутых выше работах. Обычно для определения матрицы
переноса сложную систему разбивают на ряд последовательно
расположенных «участков», для каждого из которых строится
матрица переноса. Матрица переноса всей системы
определяется как произведение матриц переноса участков.
/77,
/ //
-VWWWW
с1
тг
III IV
mi
в
Рис. 95.
Рассмотрим, например, линейную систему, состоящую из
нескольких масс, соединенных упругими элементами. На
рис. 95 приведена система, состоящая из трех масс, mv m2, пгг,
соединенных упругими элементами, с жесткостями сх и с2.
, 25]
ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ УПРУГИХ ТЕЛ
261
В дальнейшем удобно будет вместо жесткостей ввести
обратные им величины — податливости Ех= 1/сх и Е2= 1/с2.
Разобьем систему сечениями /—IV на участки. Первый участок —
масса mv Если она совершает гармонические колебания
с амплитудой 1А и частотой со, то очевидно, что
Pt = PA-mlaPlA.
Таким образом, определяется матрица переноса для массы тх\
1 О
— т^2 1
sA-,=
(25.5)
(25.6)
На участке /—// получаем
ln = li+EP,
P,i = Pi
и, следовательно,
Аналогично находим
| 1
-7-Я
1
О
1
(25.7)
(25.8)
m2<s?
Sjv
О
/7I3(02 1
1 E2
0 1
(25.9)
Связь между \в, Рв и \А, РА записывается в матричной
форме следующим образом:
, \1л
(25.10)
В II \\*~А (I
Матрица SAB определяется как произведение матриц
переноса для отдельных участков:
Sab = Sjv-b-Siii-iv • S//-/// -5/-//
Sa-i =
SU 512
а21
*22
262 СИСТЕМЫ С НЕСКОЛЬКИМИ СТЕПЕНЯМИ СВОБОДЫ [ГЛ. IV
После умножения матриц получаем:
sn (со) = (1 — т^со2) (1 — m2E<f?) — Е2тг(о2%
sl2 (со) = Ех + Е2 — ЕгЕ2т2а)2,
s2l (со) = — {тх -+- w2 H~ Щ) ®2~+~ (тхт2Ех + тхтъЕ2 -f-
+ тхт3Ех + тгт2Е2) со4 — тхт2тгЕхЕ2ау6,
s22 (со) = (1 — т2Ехау2) (1 — тгЕ2а>2) — тъЕх<&2.
Все элементы матрицы переноса оказались вещественными
числами; это произошло потому, что не учитывалось
демпфирование, имеющееся в линейной системе.
Составим матрицу переноса для упругого элемента с
линейным трением. Деформация этого элемента и связана с
действующими на него силами XА и Xв следующим образом:
ХА = X в = bit + си. (25.11)
Если XA = PAeJ&t> то из (25.11) находим
С другой стороны, хв = хА-\- и, поэтому
_ _- РА
1в=1а+ bj(i> + C '
то есть матрица переноса имеет следующий вид:
Sab = \0 l\- (25.13)
где £= l/#/co-f-c называется обычно комплексной
податливостью линейного элемента с трением.
Одной из модификаций метода матриц переноса является
метод динамических податливостей. В рассматриваемом
простейшем случае динамической податливостью линейной системы
в точке Л называется отношение амплитуды перемещения этой
точки к амплитуде действующей силы
eA(©) = 4L. (25.14)
§ 251 ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ УПРУГИХ ТЕЛ 263
Разделив первое из уравнений (25.3) на второе, получаем
ев (со) = 4Д- = п -л ^ 12 . (25.15)
Таким образом, динамические податливости на входе и
выходе линейной системы связаны между собой некоторым
дробно-линейным соотношением.
Для сосредоточенной массы из (25.5) находим
7 — ^ (25.16)
1 — т.(д2е я
1 А
Для упругого элемента с трением
** = «]* + £• (25.17)
С помощью этих двух соотношений можно выразить
динамическую податливость в точке Bi для рассмотренной выше
трехмассовой системы. Выражение для динамической подат*
ливости представляет собой цепную дробь:
1 <iv - 1 1
\-m^eIV _m3(o2 + ^L -mztf-
*1V Е2 + еШ
1
— /Я30)2+
1
■ m2co2 -f- -=—
о , 1
— m302H
(25.18)
-т2®2+ l
&x +
m^2 —(— -=—.
eA
Рассмотрим теперь, каким образом метод матриц
переноса может быть использован при исследовании
виброзащитных систем.
264 СИСТЕМЫ С НЕСКОЛЬКИМИ СТЕПЕНЯМИ СВОБОДЫ [ГЛ. IV
Предположим, что вынужденные колебания, возникающие
при гармоническом вибрационном воздействии в системе
«линейное упругое тело -J- нелинейный амортизатор», близки
к гармоническим. Пусть мы желаем определить амплитуду
колебаний некоторой точки В объекта в определенном
направлении (рис. 93). Тогда связь между выходом линейной
системы хв и входом хА определяется соотношениями (25.3).
Если, как это показано на рис. 93, перемещение хв не
вызывает появления силы Xв (система имеет «свободный»
выход), то
Рв = 521 (со) ЪА + s22 (со) РА = 0.
(25.19)
Проведем гармоническую линеаризацию динамической
характеристики упругого амортизатора
где U0t £д, Ьд определяются по формулам (11.3)
(25.20)
(11.5) и
ампли-
являются функциями постоянной составляющей
туды а и частоты со деформации и.
Если на амортизируемый объект не действуют
постоянные внешние силы (это будет всегда, когда объект
полностью амортизирован и не имеет неподвижных точек), то
должно быть
UQ(a, а0) = 0,
то есть а0 выражается через а, и коэффициенты сд и Ьл
могут считаться известными функциями амплитуды а.
Составим теперь матрицу переноса для линеаризованного
элемента. Имеем
ь=ь+-?г^««о+*д<а.«)Яо.
•■р»
(25.21)
где
£'(а> (0)-сд(а) + Ма,о);о>-
Подставляя выражения (25.21) в условие (25.19), получаем
*2i (<•>) 1о -+-1*21 (<°) £д (а• ш) + «22 (*»)) Pq—°- (25.22)
§25]
Отсюда
ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ УПРУГИХ ТЕЛ
265
Р0 = -|0-=
*2l (<*>)
£д(а, ю)521(ю)4-522(й))
= -6о-
1
£д (а, ©) -
522 (0) •
s2l (о)
(25.23)
С другой стороны, из соотношения (25.12) ясно, что
л>
Cb+bJ®
1 Р („ «л п 1... г
— ъо
1
^HfSS-!<"<«>+
£д
F 1 S22 (»)
. Д+««(в)
&д (а, ш) у»]
(25.24)
Из этого выражения можно определить амплитуду
деформации амортизатора.
Поскольку, в силу условия (25.19),
599И 1А
■=—=А = —*Лю),
(25.25)
22
S21 *w' ' A
выражения (25.23) и (25.24) могут быть записаны в следую
щей форме:
So
/>о=-^
а = -
£д(а, ©)-- еА((а)
to
|1-*А(ю)[сд(а) + *д <*,©)>]!
(25.26)
(25.27)
Во всех этих формулах £0 является вещественным числом,
то есть фаза вибрационного воздействия принята равной
нулю.
Учитывая, что при свободных колебаниях системы |0 = ^»
Р0ф0, можно из (25.26) получить уравнение для
определения частот свободных колебаний системы:
£д(а, со) — 7А (со) = 0. (25.28)
Обычное частотное уравнение получается отсюда при bR = 0:
eA(p)cg{a)=l. (25.29)
266 СИСТЕМЫ С НЕСКОЛЬКИМИ СТЕПЕНЯМИ СВОБОДЫ [ГЛ. IV
Решая его, можно определить зависимость частот свободных
колебаний системы от амплитуды деформации амортизатора.
Определив амплитуду а из уравнения (25.27) и подставив
ее значение в £д, можно затем из (25.23) и (25.21) найти
Р0, 1А и Рд, а из (25.3) определить %в> решив тем самым
поставленную задачу.
Аналогичным путем можно определить амплитуду
перемещения любой «свободной» точки амортизируемого объекта;
некоторые особенности решения в случае «несвободного»
выхода будут рассмотрены ниже при решении конкретных
примеров. Мы видим, что при исследовании вынужденных
колебаний системы в первую очередь необходимо знать
динамическую податливость упругого объекта еА (со) в точке
крепления амортизатора. Эту характеристику нетрудно получить
экспериментальным путем. Для этого достаточно установить
амортизируемый объект на вибрационном стенде, закрепив
его в точке А без амортизатора, и измерить амплитуду силы
взаимодействия, возникающей между столом стенда и
объектом при гармонических колебаниях стола с частотой со и
амплитудой |д. При этом, в силу (25.19), имеем
Если при том же эксперименте замерить также амплитуду |в,
то можно будет определить, какой будет эта амплитуда при
установке объекта на амортизаторе.
Действительно,.
%в = sn (со) |д + sl2 (со) РА =
=-= [su (со) еА (со) + sl2 (со)] Яд = е' (со) РА. (25.30)
Величина ef (со) не зависит от свойств амортизатора. Поэтому,
определив при эксперименте, ее значение, можно затем,
учитывая выражение (25.26), определить \в для
амортизированной системы следующим образом:
1д = ?(со)Рд^?(со)Р0=-1о гг , е\((д)- , ч • (25.31)
ЬА(а,(д) — еА((д)
Амплитуда деформации а должна быть предварительно опре-
делена из уравнения (25.27).
§ 25J
ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ УПРУГИХ ТЕЛ
267
в
W
«Выходом» системы.не обязательно должно быть
перемещение одной из точек амортизируемого объекта. В качестве
выходной координаты может быть выбран любой
интересующий нас параметр, например,
напряжение в одном из элементов конструкции упругого
тела* или даже электрическое напряжение, если
амортизируемый объект представляет собой
электромеханическую систему. Необходимо, конечно,
чтобы выходной параметр обнаруживал линейную
зависимость от входного воздействия — вибрации
точки Л. Экспериментальная проверка линейности
объекта не вызывает обычно каких-либо
затруднений. _
Рассмотрим теперь некоторые примеры.
1. Найдем матрицу переноса для двухмассового упругого
тела (рис. 96). Разбивая систему на участки и используя
формулы (25.6) и (25.8), получим
1 0 III Е ЦП 1 Е II
/77,
Рис. 96.
^дя —
— m0w
1 О
1 ЦП — я^со2
1 — Zrm^2
1 —Emx<sP I
т№
т2®2 -f- Ет1т2(й4 1 — £т2со2 |"
Отсюда определяем динамическую податливость в точке Л:
1 — £/и2(о2 s22 (со)
*л(<») =
тх®2-\- /и2со2 — £т1/и2ю4
s2i (со) '
(25.32)
Тот же результат можно получить и иным методом;
используя выражения (25.16) и (25.17), имеем
ев((*):
1
1
— /И2С02 +
1
41
m2coJ
1
Е + е,
— т2со2 +1
(25.33)
— /и.со2 -\ .
еА
С другой стороны, £5(со) = оо, поскольку Яд = 0.
Следовательно, знаменатель выражения (25.33) должен равняться
268 СИСТЕМЫ С НЕСКОЛЬКИМИ СТЕПЕНЯМИ СВОБОДЫ [ГЛ. IV
нулю. Отсюда получаем для еА выражение, совпадающее
с (25.32).
Предположим теперь, что амортизатор имеет линейный
упругий элемент и демпфер сухого трения. Тогда
= с +— у© = с + -!у, (25.34)
£д (я, со) jwoo
где
_ 4Я
^ я
Составим уравнение (25.27):
Ь> _
а =
1-^н(с + |у)|
|о
[1-С«д(0))]2-
Решая это уравнение, получаем
/"г
4НП2
(25.35)
fl== |1-V| • <25-36>
Тем самым определяется амплитудно-частотная характеристика
системы. Из (25.36) легко получить условие запертости
амортизатора
6о<1*л(©)|'Ч- (25.37)
При £ = 0 (жесткое соединение масс) формула (25.32) дает
Подставляя это значение в (25.36) и (25.37), приходим к
выражениям, соответствующим амортизации абсолютно твердого
тела с массой w1-f-m2.
Теперь можно определить амплитуды колебаний
различных точек амортизируемого объекта. Для этого сначала
определяется Р0 по формуле (25.26):
« ь «■('+*') F
°~ 1 — 7 тГТ"~~ ^'
.25]
ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ УПРУГИХ ТЕЛ
269
Определим амплитуду 1А из (25.21):
1а = 1о + ^дЛ) = £о — ■
So
1 — е , (со)
Теперь можно определить %в\
(«+}')
!-1о
к+Ц
\—е
hi')'
= (1— ЕтУ)
Ы>)
1-е
£io(c+|y) b(' + ij)
Ы>)\
1-е
,(•+*>) '-*(«+*>)
/^-1
(Ее дМ^в? — еА — Е),
(25.38)
. (25.39)
Л*
lbl = 5ol£«^'»iffl' —«л —£1- /-—
\/0-сел)2 + 1т
Не составляет труда определить и амплитуду какого-либо
другого параметра системы. Найдем, например, амплитуду
усилия в упругом элементе Е:
Р1 = Рл-Щ<*1л =
= 1о
«+*'
•-Ч'+*')+1-Д«4')
=1»
<+*'
■-*(«+*')
(ж^вд—1). (25.40)
|^1 = У*Л- И
/"+*
/с1-^)2^!-
(25.41)
270 СИСТЕМЫ С НЕСКОЛЬКИМИ СТЕПЕНЯМИ СВОБОДЫ [ГЛ. IV
В'
2. Рассмотрим теперь трехмассовый упругий объект,
показанный на рис. 97, причем ограничимся только
определением динамической податливости в точке Л,
поскольку остальные выкладки не будут
принципиально отличаться от
рассмотренных выше.
Для определения еА (со) воспользуемся
методом динамических податливостей. При
этом учтем, что при параллельном
соединении двух ветвей их суммарная
динамическая податливость может быть
определена по формуле
1 1 ' 1 (25.42)
Ж
iv i
т
Рис. 97.
ес е1 е11
В точках В и В' динамические податливости равны оо.
Поэтому
1 1
— т02 +
1
— т(о2 +
1
■тю2 +
1
/// + £1
1
"IV
— та2 +
1
1
£i +
1
1
Е2+
1
1
•тх®2-\—— —т2ю24-'
= (1 — Ехтх&2) (1 — Е2т2&2) [тха2 (Е2т2(д2 — 1) +
+ т2(д2 (Ехтхв>2 — 1) — та2 (Ехтх(д2 — 1) (Е2т2(о2 — I]"1. (25.43)
Знак минус поставлен при еА по той причине, что при
определении податливостей мы шли от точек В и В! к точке Л,
в то время как в ранее полученных формулах было
выбрано противоположное направление.
Разумеется, что для рассмотренных простейших систем
можно было бы пользоваться и обычными методами
составления уравнений движения и их интегрирования.
Преимущества рассмотренных здесь методов проявляются при
решении более сложных задач.
ГЛАВА V
КОЛЕБАНИЯ ВИБРОЗАЩИТНЫХ СИСТЕМ
ПРИ УДАРНЫХ ВОЗДЕЙСТВИЯХ
§ 26. Удар в нелинейной системе
с одной степенью свободы
Как уже указывалось во введении, под ударом мы
понимаем кратковременное воздействие на виброзащитную систему
сравнительно больших сил. Ударные воздействия часто
встречаются в современных виброзащитных системах, причем во
многих случаях они оказываются более опасными, чем
вибрационные.
Колебания, возникающие в виброзащитной системе при
ударных воздействиях, являются нестационарными; они,
вообще говоря, не могут быть описаны с помощью
полигармонических (периодических или почти-периодических) функций
времени. Поэтому для анализа ударных явлений не могут
быть использованы приближенные методы, рассмотренные
в гл. I. Кратковременность колебаний, возникающих при
ударе, позволяет применить другие методы, основанные на
непосредственном интегрировании дифференциальных
уравнений движения.
Рассмотрим сначала методы исследования ударных
явлений в системе с одной степенью свободы, движение которой
описывается уравнением
mu+U(u> u) = Q(t). (26.1)
Это уравнение по форме не отличается от уравнения (12.1),
только функция Q(t), определяющая внешнее воздействие
на систему, носит иной характер. При ударном воздействии
272 КОЛЕБАНИЯ ПРИ УДАРНЫХ ВОЗДЕЙСТВИЯХ [ГЛ. V
принимают, что
<2У)Ф0 при О < t < т,
Q(f) = 0 при t>x,
где т — длительность удара.
Нас будет интересовать решение уравнения (26.1),
соответствующее заданным начальным условиям. Обычно
предполагается, что ударное воздействие прикладывается к
системе, находящейся в положении статического равновесия,
то есть при нулевых начальных условиях:
и = 0, я = 0 при t = 0. (26.3)
Поскольку при t > т вынуждающая сила обращается
в нуль, в системе происходят свободные колебания,
затухающие вследствие рассеяния энергии. Поэтому практически
достаточно определить движение на некотором конечном
интервале времени Г0, в течение которого деформация
амортизатора и может принимать сравнительно большие значения.
При этом особенно важно определить наибольшие значения
реакции амортизатора, определяющие в конечном счете
качество виброзащитной системы, ее способность защищать
объект, или основание, от ударных воздействий.
Наибольшее значение реакция —U (и, и) может принимать как во
время удара (то есть при t < т), так и после его окончания
(при t > т). В последнем случае наибольшими всегда являются
первые максимумы, поскольку при свободных затухающих
колебаниях амплитуда реакции уменьшается. В дальнейшем
определение наибольшего значения реакции амортизатора мы
будем считать основной задачей анализа ударных явлений и
в соответствии с этим выбирать величину интервала
времени Г0, на котором должно быть определено решение
уравнения (26.1). Если демпфирование в системе является
слабым, то наибольшее значение U(и, и) приблизительно
совпадает с £/(#Наиб> 0)» то есть вместо определения
наибольшей реакции можно определять наибольшую деформацию
амортизатора.
Решать уравнение (26.1) можно различными способами.
Наиболее универсальным приближенным методом является
численное интегрирование; этот метод будет подробно
рассмотрен в следующем параграфе применительно к исследо-
(26.2)
§ 26] НЕЛИНЕЙНАЯ СИСТЕМА С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ 273
ванию систем с несколькими степенями свободы. Для системы
с одной степенью свободы целесообразнее пользоваться
графическими методами, связанными с построением фазовых
траекторий; при этом наиболее удобным является так
называемый дельта-метод [12»39].
Уравнение движения запишем в следующей форме:
Здесь
(0^ + ф(й, U)
и-\-<х%и-\-ц(и, u) — F(t).
U (и, и)
т
Fit):
Q(t)
т
(26.4)
(26.5)
Величина со0 выбирается в известной 'степени произвольно;
она может быть принята
равной собственной частоте
системы
(Ол
v/^;(0)
\— V т '
V~mo)2Qu
V-mA20u
Рис. 98.
или несколько большей, с тем,
чтобы линейная характеристика
U = тФ*и была ближе «в
среднем» к упругой
характеристике амортизатора (рис. 98).
Введем безразмерное время 6 —(0(/; тогда уравнение (26.4)
примет такой вид;
(26.6)
d.4
М2
Обозначив
da d2u
dd — Vt dW ~~
получим
dv dv
dti ~~~du~Vt
F (t)—q> (ы, (d0v)
°>о
dv 6 (w, v, t) — и
du
b(u, v, /), (26.7)
(26.8)
При применении дельта-метода полагают, что в течение
некоторого достаточно малого интервала времени значение
J8 М. 3. Коловскнй
274
КОЛЕБАНИЯ ПРИ УДАРНЫХ ВОЗДЕЙСТВИЯХ
[ГЛ. V
функции &(#, v, t) может быть принято постоянным и
равным ее значению в начале этого интервала. Разбив
интервал [О, Г0], на котором ищется решение, на N малых
интервалов [О, /J, [tlt t2], .... [tN^v T0], принимают для £-го
интервала
6(«, v. t) = bk = ^<»-»>-<PMfr-.).<M> (<»-.)] . (26 9)
Интегрируя теперь уравнение (26.8), получаем уравнение
участка фазовой траектории,-соответствующего &-му
интервалу времени:
& + (u-btf = (?k. (26.10)
Это — дуга окружности, координаты центра которой
u = bk> v = 0, (26.11)
а радиус
** = С* = /(»*-! -**)' + *
.2
А-1 '
(«a-i = «('a-i). ^-i = ^6f*-i)). (26.12)
поскольку фазовая траектория проходит через точку к =
= йл_1, T> = i/fe_1. Угол Hyk (рис. 99), соответствующий
дуге на &-м участке, связан простой зависимостью с
интервалом времени ktk = tk — tk_v В са-
и
р4-
1-<
Ш
ъ4п
о*/
ик-1 "
\М
£±
\А"
и
вк
мом деле, из подо
ников ОлД*-А-1
имеем
бия треуголь-
и Л^Л^
Поскольку Д#л ^ со0 Д^л-1,
^л-И* ~ ДУ/Л» то отсюда
следует, что
Ду*««\)А'* =
= ДВА. (26.13)
Рис. 99. Таким образом, начав
построение в точке и0 = О, v0 — 0, можно
построить по участкам фазовую траекторию,
соответствующую искомому решению. .Точки пересечения траектории
с осью абсцисс будут соответствовать максимумам и
минимумам деформации и. Определив наибольшую по
абсолютной величине реакции),, соответствующую при слабом
§ 26] НЕЛИНЕЙНАЯ СИСТЕМА С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ 275
демпфировании одному из экстремальных значений
деформации, можно оценить качество виброзащитной системы при
заданном ударном воздействии. Критерием качества может
служить, например, коэффициент динамичности при ударе:
[/". —. I Ч Imax
При-вычислении значений bk по формуле (26.9)
действительный ударный импульс Q(t) заменяется ступенчатой
функцией времени (рис. 100, а). При такой замене эффективность
Рис. 100.
удара во время нарастания импульса уменьшается, а при
спаде— увеличивается. Чтобы избежать этого искажения
формы удара, целесообразно строить ступенчатую функцию
так, как это показано на рис. 100, б. Здесь высота £-й
«ступеньки» принята равной
q(^).
Еще более точное приближение может быть получено, если
в формулу (26.9) подставить вместо F(tk_x) следующую
величину:
1
тЬЛь
то есть определить Fk как среднее значение F (t) на k-ы
интервале. Используя формулу (26.14), можно ударный
импульс любой формы заменить последовательностью
18*
276
КОЛЕБАНИЯ ПГ>Й УДАРНЫХ ВОЗДЕЙСТВИЯ*
[ГЛ. V
прямоугольных импульсов (рис. 101), причем каждую из «полу^
волн» заменить одним прямоугольным импульсом. Такая замена
при не слишком длительных
интервалах,
соответствующих каждой «полуволне»,
мало влияет на результаты
i расчета, в чем нетрудно
убедиться на следующем
примере.
Рассмотрим линейную си-
Рис. 101. стему с одной степенью
свободы без демпфирования.
Пусть ударное воздействие имеет форму полуволны
синусоиды. Уравнения движения системы
%,
0
0 п
/
/
f
— ь
\
\
\
®ог
Ооз
..
V /
\ '
ч^/
'— гг 1
/'~~Ч
/ \
/ \
\~~h "
1
mu-\-cu — Q0s\n — t при £<".т, I
ти-\-си — 0 при £>т
(26.15)
при нулевых начальных условиях имеют следующее точное
решение:
т h
nQ0
(■"
~sinA,(/-- ^0sin— /)
xX0m {^p — Xjjj
при t <T, t,
[sin^0(£ — T) + sinA,0^]
(26.16)
при t > t,
где Аю —c/m.
Анализируя это решение, нетрудно определить
максимальное значение деформации и:
/иД|
m\i
2яф cos -
jt2 —ч|?2
2л1|)
г|? sin
л •
при i|) <C я,
при \|) > л,
(26.17)
где ф = Я,0т.
§ 26] НЕЛИНЕЙНАЯ СИСТЕМА С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ 277
Заменим теперь синусоидальный импульс эквивалентным
по площади прямоугольным:
г ]
Qi(t) = ±rJQ0sm±tdt = lQo ПрИ ,<Tt I (26i8)
Qx (t) = 0 при t > т. j
В этом случае, интегрируя уравнения движения, получим
20
и — и* = —^(1—cosA,0O при *<т,
2Q0
2Q0
и = и* = 2 [cos А,0 (f — т) — cos А,</] при t > т.
Определяя максимальную деформацию, находим
2
I
(26.19)
ft 4 , f
-^~- • — sin -J при г|? <.. я,
пгкг. л
при i|) > я.
(26.20)
Относительная ошибка в величине максимальной деформации,
вызванная заменой действительного ударного импульса
импульсом прямоугольной формы, составит:
Y =
Зависимость y(ty) определяется следующим образом:
.+
Y=l-
Y=l
2tg^.(t2-4>2)
4 (я — ф)
яф sin
2я1|?
при 1|)<!я,
при i|) > л.
(26.21)
Из графика этой зависимости, построенного на рис. 102,
видно, что при т < Ji/A.0, то есть если длительность удара
меньше, чем полупериод свободных колебаний системы,
278 КОЛЕБАНИЯ ПРИ УДАРНЫХ ВОЗДЕЙСТВИЯХ [ГЛ. V
ошибка не превышает 20%. Учитывая, что в практических
случаях форма ударного импульса обычно известна лишь
приблизительно, такую точность можно считать достаточной.
Если ударный импульс может быть заменен одним
эквивалентным прямоугольным импульсом, а диссипативными
силами можно пренебречь, уравнение движения системы
существенно упрощается. Вместо (26.1) имеем
mu-\-Uy(u) = QQ при
ти-\~ Uy (и) = 0 при
Первый интеграл этого уравнения
Ur (u)da = \
J у [С при t > т J
(26.22)
(26.23)
является интегралом энергии.
Постоянная С равна работе
силы за время удара или
полной энергии системы
в момент t = x
п ти2 (т) ,
и(т)
f J* Uy(u)du = Q0u(x).
о
(26.24)
Рис. 102.
В этом случае
наибольшее значение и обычно
совпадает с его первым максимумом. Условимся в дальнейшем
называть удар «длительным», если первый максимум
деформации достигается в момент / = **"< т, то есть во время удара,
и «коротким», если максимуму деформации соответствует
t = f > т. Для «длительных» ударов значение #тах можно
найти из уравнения (26.23). Поскольку при и-
быть и = 0, получаем
ятах должно
mux
j Uy(u)du = Q0u„
(26.25)
§ 26] НЕЛИНЕЙНАЯ СИСТЕМА С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ 279
Это уравнение для итах может решаться графическим
методом. Необходимо определить точку пересечения кривой
П(й)= Г Uy(u)du,
(26.26)
выражающей зависимость потенциальной энергии
амортизатора от его деформации, с прямой
<D(e) = Qoir. (26.27)
Для некоторых форм характеристик уравнение (26.25) легко
решается аналитически. Для линейного амортизатора имеем
и
и, следовательно,
П(#) = cudu = —1r-
о
2Q0
WmaY
(26.28)
(26.29)
Мы получили известное соотношение между величиной
динамически приложенной силы Q0 и максимальной деформацией
линейного элемента.
Для амортизатора с упругими упорами, имеющего
упругую характеристику вида (10.6'), находим
/2
Щи):
си*
при й<^,
r/i2 ~rf
n(«) = i|- + cflf(« — </)-}-L-(e — d)2 при u>d.
(26.30)
Подставив это выражение в уравнение (26.25), получим
2Q»
cd
при Q0<-o-.
(26.31)
4mM = d-\--r[Q0-cd4-
+ V(Q<fi-df + (2Q0 -cd)c'd] при Q0>£|.
Для амортизатора с упругой характеристикой (10.9')
и
П, . 2сД С . ли 4Д2с . тш ,п„ пп.
280
КОЛЕБАНИЯ ПРИ УДАРНЫХ ВОЗДЕЙСТВИЯХ
[ГЛ. V
и, следовательно, итах может быть определено как корень
трансцендентного уравнения
Q0u
O^max"
4А2с . JtWmax л
—5— In cos ™ = 0.
2Д
В случае характеристики (10.10')
и
П(и)=сА Г-гif_:=cд(дln-г-^—
(26.33)
и), (26.34)
и нтах определяется из уравнения
«-=—з^а-1»!1-^)- (26-35)
При «коротких» ударах величина #тах может быть
определена из уравнения
(l-ufL)-
ma
U у (a) da = Q0u (т),
(26.36)
если известно значение и (т). Для определения последнего
приходится строить фазовую траекторию системы с помощью
дельта-метода. В ходе
построения определяется зависимость u(t),
а следовательно, и значение и (т).
Применяя дельта-метод для
решения уравнения (26.22), можно
предварительно построить график
функции
^ —£/ (в) + са2и
* / ч т У
6 (U) =: 2 •
©0
(26.37)
Тогда построение становится
более простым (рис. 103).
Максимальную деформацию при
«коротком» ударе можно приближенно
искать, пользуясь также другим методом, известным из
классической теории удара. В этом методе полагают, что
ти2 (т) Ql%2
~2 =~2т"'
(26.38)
§ 26] НЕЛИНЕЙНАЯ СИСТЕМА С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ 281
то есть удар рассматривается как мгновенное приложение
к системе импульса силы Q0t, сообщающего системе
начальную скорость, равную Q0x/m. При этом #тах определяется
из условия равенства потенциальной энергии при и = #тах
и кинетической энергии, сообщенной объекту при ударе:
"Г QW
J U,(u)du = -±r. (26.39)
О
Этот метод пригоден для импульсов любой формы: требуется
только, чтобы знак Q(t) при ударе оставался постоянным.
Для произвольной функции Q(t) получаем уравнение (26.39)
в таком виде:
итах
J* l/,(e)Ai = |^. (26.40)
о
где
Т
S = fQ(t)dt. (26.41)
о
На примере линейной системы (26.15) оценим ошибку
рассмотренного метода. В этом случае имеем
т
5= Г Q0sin —/^ = —Q0t, (26.42)
J Т Jt
о
"та
9 л 1 9
си' mXiu:
Uy{u)du = -f?- = °2тах . (26.43)
Подставляя эти выражения в (26.40), находим
„ _ 2Q0t _ Q„ 2ф
лтК, тЯп я
(26.44)
Сравнивая эту формулу с точным значением йтах
(формула (26.17)), получаем, что ошибка приближенного решения
282 КОЛЕБАНИЯ ПРИ УДАРНЫХ ВОЗДЕЙСТВИЯХ [ГЛ. V
зависит от параметра \|) следующим образом:
я2 — \р2
Y =
л2 cos -^
2 (я — ф)
1 при г|><;л,
я sin
2я\|?
я + Ф
1 при ф > л.
(26.45)
а-аъъьМ
Величина ошибки оказывается в этом случае несколько ббль-
шей, чем при замене импульса эквивалентным прямоугольным,
и достигает 20% при г|)=2,8.
Исследование колебаний, возникающих при ударе, может
производиться другим методом, основанным на линеаризации
нелинейной реакции
амортизатора. Изложим сначала этот
метод в приложении к
частной задаче — решению
уравнения (26.22). Движение системы
при t < f (то есть до
достижения максимальной деформации)
удовлетворяет следующим
условиям:
я = 0,
к = 0.
Рис. 104.
/ = 0, й = 0,
* = *•, и — ит9Х.
При этом закон движения
системы можно принять в форме,
показанной на рис. 104, и приближенно описать
гармонической функцией
и = а — a cos Xt = a (1 — cos kf), (26.46)
где
а = -
А— -рг-
(26.47)
Нетрудно видеть, что при / = 0 и t = t* значения и и и для
действительного закона движения и для функции (26.46)
совпадают.
Линеаризуем упругую характеристику амортизатора,
положив
U « U0 (a) -f- сА (а) (и — а) = U0 (a) + cA (a) tfi. (26.48)
§ 26] НЕЛИНЕЙНАЯ СИСТЕМА С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ 283
Подставляя (26.46) в нелинейную функцию Uy(u) и в
линеаризованную характеристику (26.48) и приравнивая в
полученных выражениях постоянные составляющие и первые
гармоники, получаем
2Я
UQ(a) = _L J £/у [а (1 — cos*)] A|>. (26.49)
о
2Л
сл(а) = — -^ Г Uy[a(\— cos\|))]cos^tf\|). (26.50)
о
Эти соотношения могут быть получены непосредственно
из формул (11.3) и (11.4), если в последних заменить а0 на а
и cos^ на —cosi|).
Найдем теперь решение линеаризованного уравнения
{Q0 при t < т,
0 при *>т (26-М)
при начальных условиях
* = 0, и° = и— а = — а, и° = 0. (26.52)
Используя формулу (12), получаем
и°= — acosAi-f-
t
+ Ж J {Qol^ - Ц(^ - г)]-U0(a)} sink (t-tydt\ (26.53)
о
Здесь ri (f) — единичная функция (5.2), Я, связано с сж
обычным соотношением
Произведя интегрирование, находим
и = и°+ а = [а — Qo~^2°(а)] (1 -cosIt) при *<т, (26.54)
и—а—шг г ^p-+^jjcosW+
_Оо_
тЛ2
+ -§-2cosX(^-t) при />т. (26.55)
284 КОЛЕБАНИЯ ПРИ УДАРНЫХ ВОЗДЕЙСТВИЯХ [ГЛ. V
Если удар является «длительным», то для определения
максимальной деформации следует пользоваться
формулой (26.54). При этом, сравнивая выражения (26.54) и (26.46),
получаем
Q0-U0(a) = 0
или
2я
±- j Uy[a(\-cosЩ 4ф = Q0. (26.56)
о
Из этого уравнения можно определить амплитуду а.
Подставляя ее значение в формулу (26.50), можно найти сж, а
затем по формуле
г=х = я/? <26-57>
определить момент, при котором выражение (26.54)
достигает максимума. Если при этом окажется, что t* < т, то удар
действительно является длительным, и тогда максимальная
деформация равна удвоенной амплитуде. Если же я/А. > т,
то удар является «коротким» и для определения максимума
деформации следует пользоваться формулой (26.55).
Отметим, что в этом случае форма решения
линеаризованного уравнения уже не является гармонической; график
движения состоит из двух синусоид, сопрягающихся в точке
с абсциссой т. При этом использование метода гармонической
линеаризации носит несколько необычный характер: близость
первоначально выбранного и полученного решения
обеспечивается приравниванием максимальных значений и (t).
Представляя формулу (26.55) в виде
и = а
тК2
+ [a+^<1+cos^)-^r]cosW+
+ ^sinA,TsinM, (26.58)
находим максимум этого выражения:
т№
+
§ 26] НЕЛИНЕЙНАЯ СИСТЕМА С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ 285
Приравнивая его максимуму и, полученному из (26.46) и
равному 2а, получаем уравнение для определения а:
[ml2а — £/о (0) + Qo 0 + cos Ал;)]2 ■+■ Q20 sin21л =
= [т12а + и0(а)}2, (26.60)
которое может быть преобразовано к более удобному виду
Q0(\ + cos to) [m№a — U0 (a)-\-Q0] = 2m№aU0 (а). (26.61)
Изложенный метод может быть применен и для решения
уравнений более общего вида. Если уравнение движения
задано в форме (26.1), то, разыскивая решение вида (26.46)
и полагая
U(и, a)^U0+ cRu°+bRu°t (26.62)
можно получить следующие формулы для коэффициентов
линеаризации:
2л
U0 = ~ J U [а (1 — cos ф), Ха sin ф] dty, (26.63)
о
2л
сЛ = — -^ I t/[a(l—cos-ф), basing] cos 1ИФ» (26.64)
о
2я
**~!wrj ^1а(1— cosф), A,asin^]sini|)^- (26.65)
о
Решая линеаризованное уравнение
m в°'+ *дв°Ч- *д«° + ^о = Q (0- (26.66)
при начальных условиях
получаем
# = #04- a = a(l —cosA,^)-)-
J- J [^.О-^^^^М'-О*'- (26.67)
0
286 КОЛЕБАНИЯ ПРИ УДАРНЫХ ВОЗДЕЙСТВИЯХ [ГЛ. V
Здесь
зависят от амплитуды а. Определив максимум
выражения (26.67) и приравняв его 2а, можно получить уравнение
для определения а. В общем случае это уравнение получается
сложным, и для его решения требуется значительная
вычислительная работа. Только в наиболее простых случаях,
примеры которых будут рассмотрены в следующем
параграфе, удается получить сравнительно простые уравнения.
§ 27. Примеры расчета систем с одной степенью свободы
1. Определим максимальную деформацию и максимальную
упругую силу, возникающие при ударе в системе
. •• , 2сД .ли ^ . я . /n- f4
ти\ —tg — = Q0sinTt, (27.1)
если
т=10 кг, с = 40 000 н/м, А = 0,015 м, Q0 = 600rt,
т = 0,02 сек.
Для решения задачи воспользуемся дельта-методом.
Сначала выберем величину со0. Поскольку, как указывалось
выше, желательно, чтобы выполнялось условие
<*о > К = y-j£ = 63,5 1/сек,
принимаем
со0 = 77,5 \/сек\ cog = 6000 \/сек.
Запишем выражение для функции 6(«, t):
©5 \ т х лт 2Д ° /
Вводя обозначения
Q0 с г и г и
/wcdqA /W0q Д ' Дю0
получаем
*<|ilepgl„^_£tg-;-• + «'. (27.3)
27]
Примеры расчёта
28?
В рассматриваемом случае
60(Г
Р =
поэтому
10.77,52 - 0,015
0,68,
"40000
10.77,52
0,68,
~2х.
= 0,424",
5(% ° = 0,68 sin i * — 0,424 tg |- и! + в'. (27.4)
Построение фазовой траектории будем производить в
безразмерных координатах и! и v'. Шаг времени выбираем
равным At = 0,002 сек, то есть принимаем tk = 0,002&.
В формулу (27.4) подставляем значения sin — t при
t -4-1 ^
t = *~ з k . Радиус соответствующего участка фазовой
траектории определяем графически (рис. 105). Вычисления
ЬЬЬШ °w
°3 °8 °Л¥б
Рис. 105.
функции 6 (я, *)/Д сведены в табл. 3, столбцы которой
заполняются в ходе построения. Угол Д^, соответствующий
k-uy участку фазовой траектории, определяется по
формуле (26.12)
Д^ = со0Д/ = 0,155.
В результате построения определяется величина йтах, как
абсцисса точки пересечения фазовой траектории с осью и.
Из рис. 105 находим
«тах=0.715Д = 0,0107 л*=10,7 мм.
288 КОЛЕБАНИЯ ПРИ УДАРНЫХ ВОЗДЕЙСТВИЯХ [ГЛ. V
Таблица 3
t
0,001
0,003
0,005
0,007
0,009
0,011
0,013
0,015
0,017
0,019
0,021
0,023
0,025
0,027
0,029
sini,
т
0,155
0,454
0,707
0,891
0,988
0,988
0,891
0,707
0,454
0,156
—
—
—
—
—
3sln— /
0,106
0,309
0,481
0,606
0,673
0,673
0,606
. 0,481
0,309
0,106
—
—
_
—
и'
0
0,003
0,010
0,025
0,055
0,095
0,150
0,220
0,300
0,380
0,470
0,545
0,610
0,660
0,695
0
0,0047
0,0157
0,039
J.086
0,150
0,236
0,348
0,471
0,603
0,735
0,855
0,958
1,035
1,09
i. Л ,
0
0,0047
0,0157
0,040
0,086
0,151
0,240
0,363
0,509
0,689
0,904
1,150
1,422
1,685
1,917
я s 2
0
0,002
0,007
0,017
0,036
0,064
0,102
0,154
0,216
0,292
0,383
0,487
0,603
0,714
0,811
6 (и, /)
А
0,106
0,310
0,484
0,614
0,692
0,704
0,654
0,549
0,393
0,198
0,085
0,058
0,007
—0,054
-0,116
Определяем максимальное усилие, передаваемое
амортизатором при ударе
t/yn,ax = ^-tgi^ = i^tg(l,57.0,715) = 800«.
Таким образом, максимальная сила превышает Q0 на 33%,
то есть в данных условиях амортизатор не защищает от
удара.
Построение фазовой траектории можно было бы
производить только до точки Л10, соответствующей моменту
времени t = т. Определив из графика значение а (т) и и (т),
можно затем найти #тах из уравнения
"max # и (Т)
J Uy(a)du= т*(х) + [ Uy(u)du. (27.5)
о о
Левая часть этого уравнения представляет собой
потенциальную энергию, соответствующую и = #тах. После окончания
удара система становится консервативной, поэтому
максимальная потенциальная энергия должна равняться полной энер-
§ 27] ПРИМЕРЫ РАСЧЕТА 289
гии системы при t = x. Произведя интегрирование в (27.5),
получим
«jl,.4t-H_-[.-w)4*. (27.6)
"»(т<С,)
Из графика находим, что й'(т) = 0,47> г//(т)==0,5. Решая
уравнение (27.6), определяем величину #шах:
и = А • и' =
max max
= ^ arccos { cos [£ и' (т)] ехр [_ ^ (г/ (т) f] } =
= 0,695Д=10,4 л*л*.
Таким образом, ошибка графического построения на участке
т < £ < Г составляет приблизительно 3%.
2. Решим теперь ту же задачу, применяя метод
линеаризации. Находим решение линеаризованного уравнения
ти* ' " '-* ' - п Л ! *
(27.7)
+ t/0(a) + ^tt° = Q0sin — f при *<т
т^04-^/о(а) + сдй° = 0 ПРИ *>т J
при начальных условиях
Используя формулу (26.67) и учитывая, что в рассматри*
ваемом случае я = 0, получаем
tto_ — acoskt-{-
t
+ ±\{Qo^t'[\-4{t'-x)\-U0}s\n%(t'-%)dt'. (27.8)
о
19 М. 3. Коловский
290 КОЛЕБАНИЯ ПРИ УДАРНЫХ ВОЗДЕЙСТВИЯХ [ГЛ. V
Производя интегрирование, находим
и = и°+ а = (1 - cos It) (a - -^-) +
_| 0° г (— sin X/ — Л,sin — Л при *<т, (27.9)
« = <1--совЦа—^) +
~| -р^ r[sinX.(/ — t) + sin^] при t>x. (27.10)
тХх
£-»)■•
Из проведенного выше расчета нам известно, что удар является
«коротким», то есть, что f > т, и величину #тах следует
определять по формуле (27.10), которую можно привести
к следующей форме:
UQ . ( U0 jiQ0 sin Kx \ * . .
^,Q.(l + cos4) sjnU (J711)
mkx
(*-»)
Максимальное значение а равно сумме постоянной
составляющей и амплитуды колебаний; приравнивая его 2а, получаем
уравнение для определения а:
—ёь+
+ УГ[-ЩТ— a-C(a)sinU]2 + C2(a)(l+cos>.T)2 = 2a,
(27.12)
где
яф0
На)--
Это уравнение легко преобразуется к более простому виду
2e-S5F = t<a>[(a—^-)sin^ + S(«)(l+cosU)]. (27.13)
§ 27] ПРИМЕРЫ РАСЧЕТА 291
В этом уравнении следует представить £/0 и X как
функции а. Используя формулы (5.52) и (5.53), определяющие
коэффициенты гармонической линеаризации с точностью до
моментов четвертого порядка, и учитывая, что в
рассматриваемом случае а0 = а, получаем
»-=WM-+1?-)-<'>(—?•)]-
ята/з1ё 4Д S 4Д J
_ 2с _ Lg (2Ч-КЗ)яа tg(2-K3)rta1 (27 И)
я«а V 3 L 4 4 J *
tf0 = ± [f/Да) + t/Да + ^ а) + tfy (а - i^-a)] =
Bffi [tgf+ tg (2 + ^™ +tg Q-^>"«], (27.15)
где
Вводя обозначения
а
(2 + ^3)яа ., (2-1/~3) яа
tf аД ё 2 "^ё 4 "Г"1* 4 аЛ
Т7%-9(а)'
гоЛ2 /3 ^ (2 + Т/1)яа ^ (2 —У1)яа /3
lg 4 Cg 4
приводим уравнение (27.13) к следующему виду:
^3 Д/иф(я* —**) 1Л КЗ/ *'
19»
292 КОЛЕБАНИЯ ПРИ УДАРНЫХ ВОЗДЕЙСТВИЯХ [ГЛ. V
Это уравнение удобнее всего решать графически, вычисляя
при различных значениях а функции:
Ф(«)=2а2е(а)
а9(а)
tO(a)\ . , ,
т¥)ип*+
лО т2 т
+ Am^^^^)^ + cos^)J'
и определяя абсциссу точки пересечения кривых Ф(а)иТ (а).
Выполнив расчет и построив
эти кривые (рис. 106),
получаем <х=0,357. Следовательно,
«тах=2аД=0,714Д=10,7 мм>
что совпадает с результатом,
полученным дельта-методом.
3. Найдем значение итах
в той же задаче, рассматривая
удар как мгновенное
приложение импульса силы
t
5 = /q(0^ = |q0t.
0,1 0,2 0,3
Рис. 106.
Ofi
Используя формулу (26.40), получаем
4Д2с
•In cos-
*тах
$Л
2Л
. «Ф
ит
(27.17)
Решая это уравнение, находим
^ах = -агссо8[ехр(-^^)] =
2-0,015
arccos[exp(— 0,8)] = 0,0100 л =10.0 мм.
Таким образом, в рассматриваемом примере все три
приближенных метода дают близкие значения для итах.
4. Исследуем поведение системы с кубической
нелинейной характеристикой и сухим трением при ударном воздей-
§ 27] ПРИМЕРЫ РАСЧЕТА 293
ствии, имеющим форму полной волны синусоиды
ЯШ
+ ^ + ^3 + ^signtt = Q0sin^^Ml — Л('—*)]. (27.18)
приняв следующие значения параметров:
т = \0 кг, с = 40000 н/м, е = 2.108 я/л*3, #=150 и,
Q0 = 600 и, т = 0,03 с<ж.
Если ограничиться определением первого максимума
деформации, то учет сухого трения не вызывает затруднений.
Поскольку во всем интервале времени 0 <^ t ^ f знак и
сохраняется постоянным, сухое трение может рассматриваться
как постоянная сила, которая должна вычитаться из
внешнего воздействия. Следует только учесть, что система остается
запертой до тех пор, пока
и движение начинается в момент времени t0, который может
определяться из условия
Q(t0) = H. (27.19)
Решим задачу с помощью дельта-метода.
Из условия (27.19) находим
t0 = — arcsin-£j-=-g— arcsin 0,25 = 0,0024 сек.
С этого момента следует начинать построение фазовой
траектории, принимая при этом
Как и в предыдущем примере, принимаем:
со0 = 77,5 \/сек, g>2 = 6000 \/сек2.
Составляем выражение для функции 6 (и, t)
6(и, 0 = Л[— sin^- *-— — — «3 + К-Я,2)й1, (27.20)
щ I т т т т 4/J
где
Л5 ==-£■=-4000 1/сяА
294
КОЛЕБАНИЯ ПРИ УДАРНЫХ ВОЗДЕЙСТВИЯХ
[ГЛ. V
Введем новую переменную:
г U
U о
тогда
б (и\ t)
2л
: Sill t-
X
Н
*&?
ГП(дп
("У + 1
i2\
В рассматриваемом примере имеем:
_ <?о _
тюп
= 0,01 м,
Н
Qo
= 0,25,
etf
rm&
= 0,333, 1
cog
= 0,333.
Таким образом,
ifi^^sln 2^-0,25 +
Л т '
+ 0.333 [в' — (в')3]. (27.21)
Это выражение справедливо при
и > 0; если и < 0, то знак при Н
в (27.20) следует изменить на
противоположный; соответственно изменяется и формула (27.21):
5 <цд' ° ==Sin^^+-0,25 + 0,333 [и' — (ц')31- (27.2Г)
На рис. 107 построена фазовая траектория в координатах и'
и г/ = #/(о0Д. Из графика находим
йтах = 0,ЗЗД = 0,33 см.
Максимальная сила, передаваемая амортизатором, в этом
случае равна сумме максимальной упругой силы и силы
сухого трения
*Апах («. «) = Uy ("max) + Я =
= 4- 104 • 3,3 • 10~3-f 2- 108- 3,33. 10"9+150 = 289 н.
В этом примере амортизатор уменьшает амплитуду ударного
эоздействия приблизительно в два раза.
§ 28] СИСТЕМЫ С НЕСКОЛЬКИМИ СТЕПЕНЯМИ СВОБОДЫ 295
§ 28. Системы с несколькими степенями свободы
Перейдем теперь к исследованию ударных явлений в вибро-
защитных системах с несколькими степенями свободы. При
выводе дифференциальных уравнений движения твердого тела,
подвешенного на упругих амортизаторах, мы не делали каких-
либо предположений о характере вынуждающих сил Qs(t);
поэтому уравнения движения в форме (21.16)—(21.17) или
(21.22) — (21.23) остаются справедливыми как для
вибрационных, так и для ударных воздействий. Однако при
анализе ударных явлений нас будет интересовать не
стационарное решение, соответствующее установившемуся движению
системы, а решение задачи Коши, описывающее движение
при заданных начальных условиях, которые, как и в случае
системы с одной степенью свободы, будут предполагаться
нулевыми:
ui = 0i и1==0 при * = 0 (/= 1, .... N'). (28.1)
Здесь N' — число простых упругих элементов.
Исключив из уравнений (21.22) и (21.23) неизвестные
функции Aj и добавив к ним уравнения связей в форме (21.7),
получим следующую систему:
Sii^ + t/jto. i,)+ 2 v„t/,(«/f it)=%o8lQ3(t) (28.2)
0=1 p).
«/ = 2 Wk Q = P+l N'). (28.3)
* = i
Единственным универсальным методом .решения такой
системы дифференциальных уравнений является численное
интегрирование. Из разнообразных приемов численного
интегрирования, описанных в литературе, наиболее удобным для
решения рассматриваемой задачи является, пожалуй, метод
Блесса [54>б4^ специально приспособленный для
интегрирования систем уравнений второго порядка.
При применении метода Блесса уравнения (28.2) следует
разрешить относительно старших производных uk\ это всегда
возможно, поскольку \ikl — коэффициенты определенно
положительной квадратичной формы (кинетической энергии
296 КОЛЕБАНИЯ ПРИ УДАРНЫХ ВОЗДЕЙСТВИЯХ [ГЛ. V
системы), и определитель матрицы М, составленной из этих
коэффициентов, не может обращаться в нуль. Обозначим
через Mtj алгебраическое дополнение элемента /-й строки
и у-го столбца определителя |М|; умножая /-е уравнение
системы (28.2) на МГ} (у = 1 р) и складывая эти
уравнения, получаем
р V р N'
l.5=i /=^fi
/=i
— Mi
5=1 /=1 /=JP+1
(/=1..... p).
Здесь
p . />
/=i *=i
При составлении уравнений (28.5) иногда более удобно
пользоваться другим выражением для коэффициентов р^. Пусть S —
матрица, составленная из коэффициентов ог& Тогда правые части
уравнений (28.2) образуют вектор S*Q, где Q — вектор обобщенных сил,
а звездочка — знак транспонирования матрицы. С другой стороны,
формулы (21.21) могут быть записаны в матричной форме
следующим образом:
М = AS*S,
где А — диагональная матрица, составленная из коэффициентов т^
Отсюда, если В — матрица, составленная из коэффициентов рг-у, то
BQ = M'^Q — A"1 (S*yl S*Q = A" lS~lQ.
Таким образом,
B==A'lS'1
и, следовательно,
где sSJ- — элементы матрицы S"1.
Выберем величину «шага» интегрирования А/;
предполагается, что в течение этого интервала времени правые части
уравнений (28.4) могут быть приближенно приняты
постоянными и равными их значениям в начале интервала. Тем самым
§ 28] СИСТЕМЫ С НЕСКОЛЬКИМИ СТЕПЕНЯМИ СВОБОДЫ 297
истинное движение на интервале At заменяется движением
с постоянными вторыми производными функций Uj(t).
Пусть нам известны значения и1 и ut (/ = 1 Nr)
в начале г-го интервала, то есть при t = tr_1 — (r—\)At.
Определив значения Ut в этот момент времени
Ui Cr-i) = Ui \Щ C-i). Щ 0r-i)l С = 1 Ю
и подставив их в уравнения (28.4), получаем
р р М N'
5 = 1 / = 1 /=/? + 1
(У = 1 />)•
Поскольку в течение г-го шага значения Uj считаются
постоянными, в конце интервала имеем
uf = и j (tr) = uf i^. + ity-D A* + «y-D (28.7)
C/=l />)>
ity> = ay (g = uf At + ity-D (/=1 p). (28.8)
Далее, используя соотношения (28.3), находим
afp = 2 vuuf {i = p+ 1 ЛГ). (28.9)
^) = 2 vtJu{p Q = P + 1. • • •. AT). (28.10)
Таким образом, по значениям #£. и^ в начале г-го
интервала могут быть определены их значения в конце интервала.
Это позволяет, исходя из начальных условий (28.1),
последовательно определить значения деформаций и их
производных по времени при t = Att 2At, ЪА1 и т. д.
Естественно, что при применении такого способа
численного интегрирования может происходить постепенное
накопление ошибок, так что точность решения может уменьшаться
с ростом времени. Для того чтобы избежать этого, Блесс
црадцож?ц щ к^ждрм пятрм ш$ге интегрирования вводить.
293 КОЛЕБАНИЯ ПРИ УДАРНЫХ ВОЗДЕЙСТВИЯХ Ц'Л. V
поправки в значения Uj и #у, величины которых могут быть
получены следующим образом:
~(j>*) = ui5k) + _*_ (д^2 ^f) + 20af~3) — 2§uf ~4)), (28.11)
Й(у?л) = ^)-+.-^_А^(11«(5Л+1) _[_5«^-3>— 16tt</fe-4>). (28.12)
Здесь u$k) и и$к) — уточненные значения деформации и ее
производной в конце 5/г-го интервала.
При расчете ударных явлений промежуток времени, на
котором ищется решение, обычно оказывается небольшим и
содержит немного «шагов» интегрирования; с другой
стороны, точность расчетов требуется невысокая. Поэтому,
применяя метод Б лесса, можно в этих случаях обходиться без
введения поправок. При этом целесообразно, как и при
расчете систем с одной степенью свободы, заменить в
выражениях (28.6) значения вынуждающих сил в начале г-го
«шага» их средними значениями на г-м шаге:
Q{PcP = -£f /QsWdt. (28.13)
<r-i
Естественно, что в этом случае выражения для поправок
(28.11) и (28.12) становятся уже несправедливыми, и
пользоваться ими не следует.
Точность численного интегрирования существенно зависит
от выбора «шага» Д£. Учитывая практически достижимую
точность определения динамических характеристик
виброзащитной системы, следует выбирать его с таким расчетом,
чтобы деформация каждого из простых элементов за время Д£
не превышала 1—2 мм. Исходя из этого условия и
используя формулу (28.7), можно оценить допустимую величину Д£
по вычисленным значениям иФ и и^~1). При этом не
обязательно Д/ должно быть постоянным, его можно уменьшать
в тех случаях, когда скорость деформации увеличивается и
увеличивать при уменьшении скорости.
Целью расчета может являться определение максимальных
усилий, передаваемых амортизаторами, или максимальных
ускорений отдельных точек амортизируемого объекта. В
первом случае при слабом демпфировании достаточно огрзед*
i 28]
СИСТЕМЫ С НЕСКОЛЬКИМИ СТЕПЕНЯМИ СВОБОДЫ
299
читься определением максимальных деформаций; это может
быть сделано непосредственно в ходе численного
интегрирования уравнений движения. Для определения ускорений точек
объекта необходимо от координат ut перейти к абсолютным
ускорениям по обобщенным координатам, характеризующим
перемещения амортизируемого объекта как твердого тела.
Для этого удобнее всего воспользоваться соотношениями
(21.18). Дифференцируя их дважды, получаем
£ = 2^5,
(5=1 р).
(28.14)
Подставляя в эти выражения значения и^\ найденные по
формулам (28.6), можно определить значения q(p, то есть
найти законы изменения qs. Абсолютные ускорения
(линейные и угловые) по обобщенным координатам могут быть
получены сложением переносных
цу относительных ускорений.
В случае полностью
амортизированного объекта (р — 6) имеем
*, = tfi+L' e* = ?4 + P*»
(28.15)
Э
Рис. 108.
У* = ?2 + £у.
Яг = ?3 + £*'
Здесь хс, у,
абсолютного перемещения центра
инерции амортизированного объекта на оси координат;
ех, бу, гг — составляющие вектора углового ускорения.
В качестве примера рассмотрим виброзащитную систему,
схема которой приведена на рис. 108. Найдем движение
системы при ударе, вызванном перемещением основания с
постоянным ускорением А в направлении оси х. Длительность
удара — т. При этом будем считать, что упругие
характеристики простых элементов определяются формулами (22.23),
а диссипативными силами можно пренебречь.
Система обладает тремя степенями свободы. Единственное
уравнение связи вида (28.3)
й4 = я3 (28.16)
300 КОЛЕБАНИЯ ПРИ УДАРНЫХ ВОЗДЕЙСТВИЯХ [ГЛ. V
выражает деформацию «лишнего» элемента через
деформации остальных элементов. Таким образом,
v4i = v42 = 0, v43=l.
Выражая обобщенные координаты системы qx = sx, q2 = sy1
q^ = Qz через деформации упругих элементов их, #2, иъ%
получаем
Ч\ = "з — 2^ ("2 ~
Следовательно,
h
°11 — 1а' °12 =
ч и, 4- и2
h « *
jhZZJb.
* »» 2а
1
°22 — у>
о13=1, о31 = —^, о32 = -^, 023 = 033 = 0.
Если т —-масса объекта, р—его радиус инерции
относительно оси у, то m1 = /tt2 = /7t, /я3 = /ир2. Отсюда по
формулам (21.21) получаем следующие выражения для
коэффициентов \iik:
^11 = ^22= Т(1+у2 + Г^ 1Х12=Т(1_ у2~ Г2)»
^13= у Y» fe=-yY. ^зз=^»
где
Составив из этих коэффициентов матрицу Ж, найдем
значение ее определителя:
|А*1 = -Т-"
и алгебраических дополнений Мц\
f 28]
СИСТЕМЫ С НЕСКОЛЬКИМИ СТЕПЕНЯМИ СВОБОДЫ
301
Теперь по формулам (28.5) определяем коэффициенты р^
и е,
Рз1~
:Pl2==P23===^»
1
*41 = -
тг2а *
У
тгл
Р32 =
е42 — "
Pl3 =
1
тг2а
V
тг2 '
'■ $2\ — ?22 — 7и '
Рзз:
ь43*
тг2а '
_У2 + г2
Наконец, по формулам (20.20) находим обобщенные силы
Ql — — mA, Q2 = 0, Q3
:0.
Составим теперь уравнения движения системы (28.4):
"1= 7F l~(1 + г2> "* <*i> + 0 ~ '№у («а) +
4~Yt/3y(%)+Y^4y(tt4)]'
*2 = ^ Id - **> t/ly (*l) - (1 + '2) ^2y W> -
— У^зу(«з) — Y^4y(«4)b
«3 = — Л + -L,- [yUly (ux) — yU2y (u2) —
- (Y2 + '2) t/зу («a) - (Y2 + r2) f/4y («4)].
Решение этой системы при условии (28.16) и нулевых
начальных условиях: £ = 0, #1 = я2 = й3 = 0, й1 = м2==% = 0
(28.17)
будет удовлетворять соотношению
и2 = — иг.
(28.18)
В самом деле, поскольку упругие характеристики £/,у и £/2у
нечетны и имеют тождественную форму, имеем при
условии (28.18) t/ly(tt1) = — £/2у(%)- При этом первые два
уравнения системы (28.17) оказываются тождественными, и эта
система сводится к двум уравнениям:
«1 = "^72 I— U\y (ul) + Y^3y («a)L
% = — л 4-
mr
■ [Y^iy («i) ~ (Y2 + г2) «/зу («з)1-
(28.19)
В этих уравнениях учтено, что и3 = #4 и элементы 3 и 4
имеют одинаковые упругие характеристики.
302
КОЛЕБАНИЯ ПРИ УДАРНЫХ ВОЗДЕЙСТВИЯХ
[ГЛ. V
Хм *
<
11111111111%а
(N <N (N ^
o~ o~ o* ©*
V *
3 *
S со 4j
< 3
«о *• m m
I I I I 00
oo oooo^c^^cocoooo
0 . . . , ол o^ c\ о с\ ^ f-»_ c^
«Ob- 00 <N CfT О* О* О* О* О* O" O"
oiio
Oi О Q CO
Ю t OO
<N <N (N i-i
o-s^immmiT?
O^ C» (N C0^ 0\ CO^ 00^
of Т-Г ^* о* осГ iC т^"
7777 I i I
^1 «Я 4. °°« *° **
,-T V со* стГ tC ю~
X^ Tf 00 <N
со
I I I
< *
8 00 Ю (N О CO
CO 00 Ю CO П-
°111111
? О Ю 00 r-«
"?^2^2|28$2
I II I
1§8§1S
Ю lO uj Ю ^ CO
(N
Ь- О О Q О Q
00 W 00 О ^ Q
о о о о
Ю i-i О со
ь- со со ^
,'ТТ
1 53 й S 8 S
о17П77
n с? 5 *• Я 5
i i i 7 i i
ю с
11
• а ^
1 *
Ол с» Ож СО С* «О С0л t^ 1-»л Ь»л ^ СОж
^
co^SSScoS^
82й&£3
lesSSS
со ь- со
со f-T
77
°°?Ti I I 1777^722=77
Ю* ^ СО
I I I
,-* ю ю
(N Ю 00
Ю Ю »-н
СЪ СО -*
00 0> 00
ю со о со
8322
CN 00 S S 00 СО
Ю ■* СО СО
I I I I СО
О О О О 5
Г—I f—I Т—I f—• ^
О О • • • • °Г
СО 00 *ф О* О
? *f Y *?
00 О Ю
(N Ю 00
о о о
г—I г—I СГ>
П- Tf 1—•
О f-» СО
Ю ^-i Ю Ю Ю
(О 05 гн СО ^
tn^miii
«о. «-
^(NC0^i0{ON00№O»-«(NC0^iOc0S00
§28]
СИСТЕМЫ С НЕСКОЛЬКИМИ СТЕПЕНЯМИ СВОБОДЫ
303
Произведем численное интегрирование уравнений (28.19)
при следующих значениях параметров системы: г2 ==0,75;
Y = 0,5; с/т = 2000 \/сек2\ с1/т = Ш0 \/сек2\ А =1,5 см;
Д1=1 см\ А = 6000 см/сек2; т = 0,026 сек. Подставляя
значения с, cv 4 и ^ в формулы (22.23), получаем
lyv — ■tg-2^=1910tg(l,047e1) см/сек2,
Угу («з)
я/и
ят
jtw3
tg—r=1910tg(l,57tt3) см/сек2.
2И
В эти выражения следует подставлять значения их и и3 в
сантиметрах. Таким образом, уравнения (28.19) записываются
в следующем виде:
й. = — 5100 tg 1,047ttj + 2550 tg 1,57uv )
Г (28-20)
us = — 6000 + 2550tg 1,047»! —5100tgl,57a3. ]
В табл. 4 приведены результаты численного интегрирования
этих уравнений при шаге А^ = 0,002 сек без введения
поправок по Блессу; результаты интегрирования при внесении
поправок приведены в табл. 5. Как видно из этих таблиц,
введение поправок слабо влияет на значения tflmax и «я
На последнем этапе шаг
интегрирования уменьшен; V*Mj-*/,w
его величина определена из
условия
*3 max*
;,(*-D
te-
ii
и
(ft)
1
t,cex
с тем, чтобы в конце
последнего шага их обращалось
в нуль, то есть их
принимало наибольшее значение.
Графики ux{f) и иъ(Ь),
соответствующие интегриро- рис юд#
ванию с введением
поправок, показаны на рис. 109. На этом же рисунке приведен
закон изменения абсолютного ускорения центра инерции
амортизируемого объекта, найденный по формуле
304
КОЛЕБАНИЯ ПРИ УДАРНЫХ ВОЗДЕЙСТВИЯХ
[ГЛ. V
«« 5?
A» *»
< z
:a *$
:a ^
.a ^
• a v>
a
В
(N CO <Л О »-■
^ p5 ю oo o>
о о о о о
7 7 7 7 7
Ю ■*• СО «О
I I I I
О О О О
Ю S 00 (N
7 f 7 1
О 00 М СО О)
(N ~ t-н* О* 00*
7 7 7 7 '
Ф 00 Ю <N
О СО 00 Ю
7 7 7 7
S^s
7 7! 7
00 ^ч S О
_ "f О) (N СО
О 00 О 00
о я & £ £
I Г Г
§00
ь- со
П- со
° ° о* о" -**
77
N « S S
н * О 00
17 11
I I I
о о о
Ю 00 ^
С* Ю <N
77
н (N « t lij
(N
•a
ю
£
•a
ю
S
О
7
r-i CO © 0> -*
*-« C4 CO <N ^
7" 1 1 1 1
2 S Я Й 8
о о о о о
7 7 7 7 7
Tf тС 00 О
ю. ^ h. ч h.
s ю" ^ со со
Ь- СО (N
со сч оо со о
7 7
R
ь-
7
g
о
i
<У
1
ь- §
Ю 00
7 '
8 8
<о ^
1 1
!-• (N
0> *Ф
7 7
g
о
to
1
о
CD
7
s
00
СО
о
о
7
^
п-
7
q (N ю о ©^
со со о* ^ *—«
7 7 17 7
т-ч (N Ю Ю Tf
Ь- 00 О СО СО
(N СО Ю СО Ь-
7 7 7 7 7
00 00
о о о о о
7 7 7 7 7
Ф N 0D О О
28]
СИСТЕМЫ С НЕСКОЛЬКИМИ СТЕПЕНЯМИ СВОБОДЫ
305
Т 8
.a "*
< Z
:a ^
<4>
:a a?
i ^
•a v>
■a £
ft» 2
a
'"a
a
iq
ii
eo
• a
<o
ocT
»—1
1
II
•a*
<o
t^
о
о
1
II
со
a
<o
со"
S
1
II
a"
1С fO (N N Tt<
S 8 2 8 S
о © о4 о" о"
n со n м Tf
н 00 (N ^ W
и н N N W
7 7 7 7 1
\2
СО (N (N О
оо* о* © ю о*
СО СО СО *-*
00
iO <N 0\ СО, «О,
t** 00* СО* О* О*
777'"
о о о о о
СО О <N О <N
1—| СО О со О
о> ^ ю i^ *-■
»-н СО i-i
о о о о о
т|- О ^ •* О
N гч 4 СО W
СО О) 00 1 1С
7 7 '
СО (N О О 00
*-* СО* со* со* О*
Tf со Oi оо
оо со, ь-
П-* О* Ю (N СЧ
П- h- О <N <N
1 i 7 7 7
00 «-ч 0О СО О
Ь- (N Ю С5 00
00 О 00 СО ^
7 7 7 7 7
со о со О со
^ 0> h- О -*
1— (N rf l^ Oi
11111
*-* <М СО ^ Ю
(N
ю*
7
II
ео
•а
*ч
II
• а*
<о
S
о*
II
ео
а.
со"
g
о*
II
а*
ю
СО
о*
ю
ю
1—1
о*
1
00
п*
о
г—1
ю
1
о
о
со
|<
СО
о
1
8
7
1—1
7
2
J- ..'--■ Л ■ -
о* о*
OO Q
о о
7 7
7" 7 •
О со*
7 7
сож оо^
оо* ю
ю со
Ю* СО*
7 7
00 СО
2 S
7 7
Й 58 2М
Q 00 00 I
со w п
7 7 7
Ь- 00
»—1 »—1
gO M. 3- Кодоаскй^
306 КОЛЕБАНИЯ ПРИ УДАРНЫХ ВОЗДЕЙСТВИЯХ [ГЛ. V
причем
{Л при t^xt
0 при t > т.
Из графика видно, что при заданном ударном воздействии
введение амортизаторов приводит к увеличению максимального
абсолютного ускорения центра инерции более чем в 5 раз.
§ 29. Некоторые вопросы синтеза
противоударных устройств
В начале этой книги (стр. 20) на конкретном примере
было показано, что в ряде случаев защита от удара с
помощью линейных амортизаторов может оказаться практически
невыполнимой из-за слишком больших относительных
перемещений амортизируемого объекта. В этом параграфе мы
попытаемся выяснить, в какой степени возможности
противоударной защиты могут быть расширены за счет
использования амортизаторов с любыми нелинейными динамическими
характеристиками. При этом мы будем предполагать, что
защита от удара является единственной целью применения
амортизации и поэтому виброзащитные свойства системы
могут не приниматься во внимание.
Рассмотрим простейшую систему, в которой
амортизируемый объект обладает одной степенью свободы, а форма
удара является прямоугольной
Q (t) = Q0 при t < т,
Q (t) = 0 при t > т.
Пусть требуется, чтобы коэффициент динамичности при ударе
не превышал некоторого числа \х:
l^axK^Qo- (29.2)
Определим, каким минимальным «свободным ходом» должна
обладать рассматриваемая система, для того чтобы
условие (29.2) могло выполняться. При этом мы не будем пока
накладывать какие-либо ограничения на конструкцию
амортизирующего устройства; оно может быть сколь угодно
сложным, использующим любые технические средства. С
математической точки зрения это означает, что реакция
амортизирующего устройства — С/ ^) может быть, любой кусочно-
(29.1)
§29]
СИНТЕЗ ПРОТИВОУДАРНЫХ УСТРОЙСТВ
307
непрерывной функцией времени, удовлетворяющей
условию (29.2). Тем самым мы приходим к следующей формулировке
поставленной задачи. Задано уравнение движения объекта:
mu = Q(t) — U{f).
(29.3)
Среди всех кусочно-непрерывных функций U(t),
удовлетворяющих условию (29.2), требуется найти такую, при которой
максимальное значение абсолютной величины функции a(t)t
являющейся решением уравнения (29.3), при нулевых
начальных условиях оказалось бы наименьшим. Требуется также
определить величину этого наименьшего из максимумов
Amin = minmax | и (t) |, (29.4)
которая, очевидно, и будет равна наименьшему свободному
ходу.
Интегрируя дважды уравнение (29.3) и используя
известную формулу преобразования двойного интеграла (см.,
например, [48]), получаем
t t
и = ± \ dt [ [Q{f)~ U(t)]dt^
о о
= i \ (f -1') [Q (?) - U (t')] dt' =
о
т t
[it— /')t/(0^' = «i
где
_Qo.
m
tf)dt' =
2m l
t)2i
при
при
t')U(t')dt'.
(29.5)
(29.6)
20»
308 КОЛЕБАНИЯ ПРИ УДАРНЫХ ВОЗДЕЙСТВИЯХ [ГЛ. V
Очевидно, что при \х^1 задача имеет решение
U(t) = Q(t). (29.7)
Действительно, в этом случае функция U(t) удовлетворяет
условию (29.2), a u(t) тождественно равна нулю. Этот
результат означает, что в тех случаях, когда не требуется
уменьшить ударное воздействие, передаваемое на объект,
всегда можно создать систему амортизации со свободным
ходом, равным нулю, независимо от того, какова
длительность ударного воздействия. Выполнение условия (29.7) может
быть достигнуто самым тривиальным способом — жестким
креплением объекта к основанию. Таким образом,
относительное перемещение становится необходимым только при
|ы < 1, то есть если ударное воздействие должно быть
уменьшено амортизатором.
В этом случае |(/(0| < Qo и поэтому при £<т
относительное ускорение и является положительным, au(t) —
монотонно возрастающей функцией времени. Отсюда ясно, что
первый экстремум относительного перемещения окажется
положительным и будет достигаться при t = t* > т. Для того
чтобы этот первый максимум был наименьшим, следует
сделать наибольшим слагаемое и2. Поскольку, вследствие
условия (29.2),
/ t
й2 = А. | (,_;')t/(0<tf'<i \ (t-t')nQ0dt = ¥§*-?.
О О
следует принять
U(t)==\iQ0 при 0<*<Г.
При этом их — и2 будет принимать при любом t наименьшее
возможное значение
u^ux — u2 = 4^-t2(\ — \i) при *<т,
в = й1-й2 = ^-[/2(1-|1)-(/-Т)2] При Т <*<*'.
(29.8)
Значение t* определяется из условия обращения и в нуль:
§ 29] СИНТЕЗ ПРОТИВОУДАРНЫХ УСТРОЙСТВ 309
Отсюда
Таково наименьшее возможное значение первого максимума
относительного перемещения. Остается выбрать функцию U(t)
при t > t* таким образом, чтобы все последующие
экстремальные значения и не превосходили по абсолютной величине
первого максимума. Это можно сделать не единственным
способом. Можно, например, принять
i/(0 = 0 при t>t\
тогда при / > t* и (t) будет оставаться постоянным и равным
первому максимуму.
Таким образом, при заданных условиях свободный ход
амортизатора не может быть сделан меньшим, чем
Дт1п~ 2^1 • (29Л°)
если же удар (29.1) может быть приложен в любом
направлении, величина Amin должна быть увеличена вдвое. Однако,
определив минимально возможное значение свободного хода,
мы еще не решили задачу оптимального синтеза
противоударного устройства. Неизвестно, реализуема ли практически
система амортизации, в которой свободный ход равнялся бы
найденному минимальному значению. Задача заключается
в определении такой динамической характеристики упругого
амортизатора U(u, и), для которой решение уравнения
mu-\-U(u, u) = Q(t)
при t < t* оказалось бы тождественным выражению (29.8),
а при t > t* было по абсолютной величине не больше А.
Покажем, что в рассматриваемом случае эта задача может
быть решена по крайней мере двумя способами,
а) Пусть
U(и, u) = \iQ0signu. (29.11)
310 КОЛЕБАНИЯ ПРИ УДАРНЫХ ВОЗДЕЙСТВИЯХ [ГЛ. V
При и > 0 £/=*= \xQ0, что и требуется по условию. При t > t*
система будет совершать свободные колебания с амплитудой,
равной Ат|П; поэтому условие
l^lmax^^mln
будет выполнено.
б) Примем теперь, что
U(и, u) = \iQ0signu. (29.12)
Поскольку при t <it* и > 0, и в этом случае получаем
При £ > t* относительное перемещение останется постоянным
и равным Amln.
Для получения динамических характеристик (29.11) и (29.12)
необходимо использовать начальный натяг или сухое трение.
В обоих случаях характеристика реального амортизатора
будет несколько отличаться от требуемых. В системе с
начальным натягом реальная характеристика будет иметь такой
вид
U(a, u) = \iQ0signu + cu,
где с — жесткость пружины, создающей натяг. В систему
с сухим трением также придется ввести пружину,
возвращающую объект в исходное положение равновесия. Это
означает, что действительное значение |#|тах окажется всегда
несколько большим, чем Amm-
Найдем теперь, какой эффект дает применение любых
амортизирующих устройств по сравнению с линейными
упругими амортизаторами. Из соотношения (34) находим
значение собственной частоты линейной системы А,0, при
котором передаваемое воздействие не превышает \iQ0:
^0 = ~-arcsin^-. (29.13)
При этом
Итак
2Q,
AqT
mKQ
Qot2
2т
tfarcsin-тг j
(29.14)
§29]
СИНТЕЗ ПРОТИВОУДАРНЫХ УСТРОЙСТВ
311
Сравнивая формулы (29.10) и (29.14), определяем отношение
максимальных деформаций:
Y = i"Jmax. = ii! " (29.15)
Дт1п 2(1—|i)farcsln^.r
При [х < 1 можно принять arcsin ~ ж ~-; тогда
v«T=ir- <29Л6>
Если |i близко к единице, это отношение может быть весьма
большим, с уменьшением jm оно уменьшается, приближаясь
к двум. Таким образом, чем существеннее должно быть
уменьшено ударное воздействие, тем меньшее преимущество
может дать использование нелинейных амортизирующих
устройств.
Рассмотрим численный пример. Пусть Q0/m= 150 м/сек2.
т = 0,05 сек, |i = 0,33. Подставляя эти значения в формулу
(29.10), получаем
А 150.25-Ю-4-0,67 лотк
Лтт = 2~ЛЗЗ— — °'375 м-
Ранее, для того же случая, но при использовании
линейных амортизаторов, мы получили #тах = 1,15 м (см. стр. 20).
Уменьшение свободного хода за счет использования
нелинейных амортизаторов может на первый взгляд показаться
значительным, тем не менее и уменьшенное его значение
остается достаточно большим.
В более общем случае задача оптимального синтеза
противоударных устройств рассматривалась в работах В. В.
Турецкого [7]. В этих работах приводится методика
определения Дт1п для ударного воздействия произвольной формы.
ЛИТЕРАТУРНЫЕ УКАЗАНИЯ
Подробное изложение линейной теории виброзащитных
систем, а также некоторых вопросов нелинейной теории,
содержится в книгах, упомянутых в предисловии [4>8»9»56].
Обширный справочный материал содержится во втором
томе справочника [63]; там же имеется библиографический
указатель, охватывающий главным образом работы
американских авторов.
К главе I
С основами классических методов теории нелинейных
колебаний читатель может ознакомиться по книгам А. А.
Андронова, А. А. Витта и С. Э. Хайкина [l], Н. Н. Боголюбова
и Ю. А. Митропольского [3], И. Г. Малкина [34], Дж.
Стокера [50], Г. Каудерера [13]. Подробное изложение методов
гармонического баланса и гармонической линеаризации
содержится в книге Е. П. Попова и И. П. Пальтова [42].
В работе А. И. Лурье и А. И. Чекмарева [32] изложен
метод Галеркина в применении к задачам теории нелинейных
колебаний. Метод линеаризации по функции распределения
рассматривался в работах А. А. Первозванского и
автора [18.19,20jf а Метод статистической линеаризации — в
работах И. Е. Казакова [п], книгах В. С. Пугачева [43] и
А. А. Первозванского [40]. Некоторые основные положения
теории устойчивости стационарных решений содержатся
в книгах Дж. Стокера [50] и Т. Хаяси [53]; более подробное
изложение теории устойчивости движения можно найти,
например, в книге И. Г. Малкина [35]. Подробное изложение
приближенных методов теории нелинейных колебаний
содержится также в книге В. Каннингхэма [12].
К главе II
Имеется большое число работ, рассматривающих влияние
внутреннего трения на развитие колебаний. Цаибод^е четкие
ЛИТЕРАТУРНЫЕ УКАЗАНИЯ 313
изложение основных результатов можно найти в книге
Я. Г. Пановко I38], где имеется и обширный
библиографический указатель. Следует упомянуть также работу Е. С.
Сорокина [49]. Некоторые вопросы, связанные с физической
природой сухого трения, рассмотрены в книге И. В. Кра-
гельского и В. С. Щедрова [28].
Описания конструкций упругих амортизаторов можно
найти в книгах Ю. И. Иориша [9], В. С. Ильинского [8],
справочнике [63], а также в книге Ч. Морроу [61].
К главе III и IV
Исследованию вынужденных колебаний в системах с
одной степенью свободы посвящены работы А. М. Каца [14«15»16].
Субгармонические колебания впервые были исследованы
в работе Л. И. Мандельштама и Н. Д. Папалекси [36].
Подробный анализ субгармонических колебаний содержится
в книгах Дж. Стокера [50] и Т. Хаяси [53]. Колебания в
механических нелинейных системах при случайных воздействиях
рассмотрены в работах Р. Лайона[59»60], С. Крендалла и
У. Марка [29'55], С. Кауфмана, У. Лапинского и Р. Мак Кеа [58].
Колебания в системах с жесткими упорами рассмотрены
точными методами в работе А. Е. Кобринского [17].
Теория малых колебаний в линейной системе с многими
степенями свободы излагается в книгах И. М. Бабакова [2],
Л. Г. Лойцянского и А. И. Лурье [30], Ф. Р. Гантмахера [6].
К главе V
Удар в нелинейной системе исследуется в книге Ч. Крида [86],
работе Фына и Бэртона [57] и ряде других работ. Проблеме
оптимального синтеза противоударных устройств посвящена
работа В. В. Турецкого [7].
ЛИТЕРАТУРА
1. Андронов А. А., В и т т А. А., X а й к и н С. Э., Теория
колебаний, изд. 2-е, Физматгиз, 1959.
2. Бабаков И. М., Теория колебаний, Изд-во «Наука», 1965.
3. Боголюбов Н. Н., Митропольский Ю. А.,
Асимптотические методы в теории нелинейных колебаний, изд. 2-е,
Физматгиз, 1958.
4. Вильсон У. Кер, Вибрационная техника, Машгиз, 1963.
5. В е н т ц е л ь Е. С, Теория вероятностей, изд. 2-е, Физматгиз, 1962.
6. Г а н т м а х е р Ф. Р., Лекции по аналитической механике,
Физматгиз, 1960.
7. Г у р е ц к и й В. В., О предельных возможностях защиты
оборудования от воздействия ударов, Изв. АН СССР, ОТН, Механика,
№ 1 (1965).
8. И л ь и н с к и й В. С, Вопросы изоляции вибраций и ударов,
«Сов. радио», 1960.
9. Иориш Ю. И., Защита самолетного оборудования от вибрации,
Оборониздат, 1949.
10. Иориш Ю. И., Субгармонический резонанс в системе с
упругими ограничителями хода, ЖТФ, т. 16, № 6 (1946).
11. Казаков И. Е., Некоторые вопросы теории статистической
линеаризации и ее приложений, Труды 1 Международного
конгресса по автоматике, изд. АН СССР, т. 3, 1961.
12. К а н н и н г х э м В., Введение в теорию нелинейных систем,
Госэнергоиздат, 1962.
13. Каудерер, Нелинейная механика, ИЛ, 1961.
14. К а ц А. М., Бигармонические колебания диссипативной
нелинейной системы, вызываемые или поддерживаемые
гармонической возмущающей силой, ПММ, т. XVIII, вып. 4, 1954.
15. К а ц А. М., Вынужденные колебания нелинейных систем с одной
степенью свободы, близких к консервативным. Прикладная
математика и механика, т. XIX, вып. 1 (1955).
16. К а ц А. М., О вынужденных нелинейных колебаниях. Труды
Ленингр. индустриального ин-та, ГОНТИ, 1939.
17. К о бри некий А. Е., Механизмы с упругими связями, Изд-во
«Наука», 1964.
18. Коловский М. 3., Первозванский А. А., О
линеаризации по функции распределения в задачах теории нелинейных
колебаний. Изв. АН СССР, ОТН. Механика и машиностроение,
№ 5 (1962).
ЛИТЕРАТУРА
315
19. Коловский М. 3., Первозванский А. А., Применение
метода функций распределения для определения
полигармонических решений нелинейных уравнений. Изв. вузов.
Машиностроение, № 4 (1963).
20. К о л о в с к и й М. 3., О выборе закона распределения при
линеаризации нелинейных дифференциальных уравнений. Труды
Ленингр. политехи, ин-та, № 235, Изд-во «Машиностроение», 1964.
21. Коловский М. 3., Вынужденные колебания в нелинейных
амортизаторах при наличии силы сопротивления,
пропорциональной скорости относительного перемещения. Труды Ленингр.
политехи, ин-та им. М. И. Калинина, № 210, Машгиз, 1960.
22. Коловский М. 3., Вынужденные колебания в упругих
амортизаторах при наличии силы сухого трения. Труды Ленингр.
политехи, ин-та им. М. И. Калинина, № 210, Машгиз, 1960.
23. Коловский М. 3., О расчете нелинейных упругих
амортизаторов с одной степенью свободы. Изв. АН СССР, ОТН,
Механика и машиностроение, JSfe 4 (I960).
24. К о л о в с к и й М. 3., О колебаниях твердого тела на нелинейных
упругих амортизаторах. Изв. АН СССР, ОТН, Механика и
машиностроение, № 2 (1961).
25. К о л о в с к и й М. 3., О некоторых разновидностях
виброизолирующих амортизаторов, Научно-технич. информационный бюллетень
Ленингр. политехнического ин-та им. М. И. Калинина, № 8,
Изд-во Ленингр. политехи, ин-та, 1959.
26. Коловский М. 3., Вынужденные колебания амортизированного
объекта при случайных воздействиях, Изв. АН СССР, ОТН,
Механика и машиностроение, № 1 (1963).
27. Коловский М. 3., О применении метода малого параметра
для определения разрывных периодических решений. Труды
Международного симпозиума по нелинейным колебаниям, т. 1,
Изд-во АН УССР, 1963.
28. К р а г е л ь с к и й И. В., Щ е д р о в В. С, Развитие науки
о трении, Машгиз, 1955.
29. К р е н д а л л С, Случайные колебания нелинейной системы
с предварительно поджатой пружиной, Сб. переводов «Механика»,
№ 3, 1962.
30. Л о й ц я н с к и й Л. Г. и Лурье А. И., Курс теоретической
механики, т. II, Гостехиздат, 1938.
31. Лурье А. И., Аналитическая механика, Физматгиз, 1961.
32. Лурье А. И. и Ч е к м а р е в А. И., Вынужденные колебания
в нелинейной системе с характеристикой, составленной из двух
прямолинейных отрезков, ПММ, т. 1, вып. 3, 1937.
33. Ляпунов А. М., Общая задача об устойчивости движения,
Гостехиздат, 1950.
34. М а л к и н И. Г., Некоторые задачи теории нелинейных
колебаний, Гостехиздат, 1956.
35. М а л к и н И. Г., Теория устойчивости движения, Гостехиздат,
1952.
36. Ма нде ль шта м Л. И., Папа леке и Н.-Д., О явлениях
резонанса я-го рода, Мандельштам Л. И. Полное собрание
трудов, т. II, Изд-во АН СССР, 1947.
316
ЛИТЕРАТУРА
37. Н и к о л е н к о Г. И., Теория амортизации вибрационных машин,
Сб. «Механика и расчет машин вибрационного типа», Ин-т
машиноведения АН СССР, 1957.
38. П а н о в к о Я. Г., Внутреннее трение при колебаниях упругих
систем, Физматгиз, I960.
39. П а н о в к о Я. Г. и Г у б а н о в а И. И., Устойчивость и
колебания упругих систем, Изд-во «Наука», 1964.
40. П е р в о з в а н с к и й А. А., Случайные процессы в нелинейных
автоматических системах, Физматгиз, 1952.
41. Пономарев С. Д., Расчет и конструирование витых пружин,
ОНТИ, 1938.
42. Попов Е. П. и Пальтов И. П., Приближенные методы
исследования нелинейных автоматических систем, Физматгиз,
I960.
43. Пугачев В. С, Теория случайных функций и ее применение
к задачам автоматического управления, изд. 3-е, Физматгиз, 1962.
44. Розе Н. В., Лекции по аналитической механике, изд, ЛГУ, 1938.
45. Р о з е н в а с с е р Е. Н., Вариационный подход к оценкам
метода гармонического баланса, Изв. АН СССР, ОТН, Техническая
кибернетика, № 1 (1964).
46. РозенвассерЕ. Н., О применении интегральных уравнений
к теории нелинейных колебаний, Доклад на Втором
Всесоюзном съезде по теоретической и прикладной механике, 1964 (в
печати).
47. Свешников А. А., Прикладные методы теории случайных
функций, Судпромгиз, 1961.
48. С м и р н о в В. И., Курс высшей математики, т. II, изд. 16-е,
1958.
49. Сорокин Е. С, Метод учета неупругого сопротивления
материала при расчете конструкций на колебания, Сб.
«Исследования по динамике сооружений», Госстройиздат, 1951.
50. Стокер Дж., Нелинейные колебания в механических и
электрических системах, ИЛ, 1953.
51. Троицкий В. А., Матричные методы расчета колебаний
стержневых систем. Труды Ленингр. политехи, ин-та им. М. И.
Калинина, № 210, Машгиз, 1960.
52. Ф и х т е н г о л ь ц Г. М., Курс дифференциального и
интегрального исчисления, т. I—III, Гостехиздат, 1949.
53. X а я с и Т., Вынужденные колебания в нелинейных системах, ИЛ,
1957.
54. В I a e s s V., Zur angenaherten Losung gewohnlicher Differential-
g-leichungen, Zeits. VDI, Bd. 81, 1937.
55. С r a n d a 11 S. H., Ma г k W. D., Random vibration in mechanical
systems, N. Y. — London, 1963.
56. Crede Ch. E., Vibration and Shock Isolation, John Willey and
Sons, N. Y. — London, 1952.
57. Fung I. C, Barton M. V., Shock response of a nonlinear
system, Trans. ASME, E29, 3, 1962.
58. Kaufman S., Lapinski W. L., McCaa R. C, Response of
a single-degree of freedom isolator to a random disturbance, J. of
the Acoust. Soc of Amer., v, 33, N 8, 1961.
ЛИТЕРАТУРА
317
59. Lyon R. H., Equivalent linearisation of the hard-spring oscillar
tor, J. of the Acoust. Soc. of Amer., v. 32, N 9, 1960.
60. Lyon R. H., On the vibration statistics of a randomly excited
hard-spring oscillator, J, of the Acoust. Soc. of Amer., v 32, N 6,
1960; v. 33, N 11, 1961.
61. Morrow Ch. Т., Shock and vibration engineering, John Willey
and Sons, N. Y. —London, 1963.
62. О к u m u r a A., On a method for vibration problems of branchtype
systems, Proc. 2nd Japan Nat. Congr. Applied Mech., 1952, Tokyo,
1953.
63. Shock and vibration handbook, v. I—II, McGraw-Hill, 1961.
64. Zurmtihe R., Zur numerischen Integration gewohnlicher Diffe-
rential-gleichungen zweiter und h6herer Ordnung. Zeits. fur angew.
Math, und Mech., Bd. 20, 1940.
Михаил Захарович Коловскпй
Нелинейная теория виброзащитных систем
М., 1966 г., 320 стр. с илл.
Редактор В. И. Бабицкий
Техн. редактор И, Ш. Аксельрод
Корректор Г. Г. Желтова
Сдано в набор 21/Х 1965 г. Подписано к
печати 11/1 1966 г. Бумага 84xl087a2. Физ. печ. л. 10.
Условн. печ. л. 16,80. Уч.-изд. л. 15,55. Тираж 4500 экз.
Т-01417. Цена книги 1 р. 18 к. Заказ № 1949.
Издательство «Наука»
Главная редакция
физико-математической литературы.
Москва, В-71, Ленинский проспект, 15.
Ленинградская типография № 2
имени Евгении Соколовой Главполиграфпрома
Комитета по печати при Совете Министров СССР,
Измайловский проспект, 29.
ИЗДАТЕЛЬСТВО «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
Москва, В-71, Ленинский проспект, 15
ИМЕЮТСЯ В ПРОДАЖЕ:
Карачаров К. А. и ПилютикА. Г., Введение в
техническую теорию устойчивости, 1962, 143 стр., 73 коп.
Кирпиче в В. Л., Беседы о механике. Изд. 5-е, 1951,
360 стр., 87 коп.
Купрадзе В. Д., Методы потенциала в теории
упругости, 1963, 472 стр., 1 р. 70 к.
Лурье А. И., Аналитическая механика, 1961, 824 стр.,
2 р. 70 к.
П а н о в к о Я. Г., Внутреннее трение при колебании
упругих систем, 1960, 193 стр., 62 коп.
П а р к у с Г., Неустановившиеся температурные
напряжения. Перевод с немецкого, 1963, 252 стр., 82 коп.
Прагер В., Проблемы теории пластичности. Перевод
с немецкого, 136 стр., 63 коп.
Ройтенберг Я. Н., Некоторые задачи управления
движением, 1963, 140 стр., 10 000 экз., 38 коп.
Синг Дж. Л., Классическая динамика. Перевод с
английского, 1963, 448 стр., 1 р. 27 к.
Фрейденталь А. и Гейрингер X.,
Математические теории неупругой сплошной среды. Перевод с английского,
1962, 432 стр., 1 р. 27 к.
Требуйте вышедшие книги в магазинах Книготорга. На
печатающуюся литературу принимаются предварительные
заявки. В случае отсутствия перечисленных книг на месте и
при отказе от приема предварительного заказа следует
обращаться в областные, краевые или республиканские магазины
«Книга — почтой», высылающие литературу наложенным
платежом (без задатка).
ИЗДАТЕЛЬСТВО «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
Москва, В-71, Ленинский проспект, 15
ГОТОВЯТСЯ К ПЕЧАТИ:
А й з е р м а н М. А., Теория автоматического
регулирования.
Вольмир А. С, Устойчивость деформируемых систем.
Изд. 2-е, перераб. и дополн.
И в л е в Д. Д., Теория идеальной пластичности.
Коган М. Н., Динамика разреженных газов.
Мусхелишвили Н. И., Некоторые основные задачи
математической теории упругости. Изд. 5-е, дополн.
Р а б о т н о в Ю. Н., Ползучесть элементов конструкций.
Ройтенберг Я. Н., Гироскопы.
Запросы можно направлять отделу технической
литературы В/О «Союзкнига» по адресу: Москва, В-71, Ленинский
проспект, 15, «Союзкнига».