Автор: Соколов А. Иваненко Д.
Теги: физика математика статистика теория поля математические методы учебное пособие для университетов
Год: 1951
Текст
Д. ИВАНЕНКО и А. СОКОЛОВ
КЛАССИЧЕСКАЯ
ТЕОРИЯ ПОЛЯ
(НОВЫЕ ПРОБЛЕМЫ)
ИЗДАНИЕ ВТОРОЕ
Допущено Министерством высшего обра-
образования СССР в качестве учебного пособия
для университетов
ГОСУДАРСТВЕННОЕ ИЗДАТЕЛЬСТВО
ТЕХНИКО-ТЕОРЕТИЧЕСКОЙ ЛИТЕРАТУРЫ
МОСКВА 195 1 ЛЕНИНГРАД
Первое издание книги
удостоено Сталинской премии в 1950 г.
АННОТАЦИЯ
Книга посвящена ^классической (некванто-
(неквантовой) теории поля. Однако в ней используются
математические методы, получившие своё разви-
развитие в квантовой механике. В частности показано,
как с помощью ^-функции находить функцию
Грина и получать этими методами решения ряда
задач классической электродинамики, в том
числе имеющих большое практическое значение.
Подробно освещен целый ряд новейших ре-
результатов, до сих пор отражённых только в жур-
журнальной литературе и в значительной части являю-
являющихся оригинальными исследованиями советских
авторов. Так, изложены: проблемы теории «сверх-
«сверхсветового» электрона Черенкова, нелинейной
электродинамики, собственной массы, теория
Х-процесса и би-поля, теория светящегося элек-
электрона. Последняя глава посвящена разбору про-
проблем классической мезодиыамики и тяготения.
Во втором издании переработано несколько
параграфов, сделан ряд уточнений и добавлены
ссылки на новейшую литературу.
Книга предназначена для научных работни-
работников, аспирантов и студентов старших курсов
физических факультетов.
ОГЛАВЛЕНИЕ
Предисловие ко второму изданию 6
Предисловие к первому изданию 8
Глава I. Общая теория д-функции 11
§ 1. Определение tf-функции 11
§ 2. fl-функция и интеграл Стильтьеса • 13
§ 3, ^-функция как предельный случай непрерывкой
функции • 15
§ 4. ^функция и разложение Фурье 20
§ 5. tf-функция в пространстве п измерений 29
§ 6. Важнейшие формулы с tf-функциями 30
§ 7. Функция Грина 34
Глава II. Статические уравнения эллиптического типа . . 38
§ 8. Одномерное уравнение Лапласа 38
§ 9. Уравнение Лапласа-Пуассона на плоскости ... 41
§ 10. Трёхмерное уравнение Лапласа-Пуассона .... 45
§ 11. Простейшие задачи электростатики ....... 49
а) Заряженная плоскость 49
б) Заряженный цилиндр 52
§ 12. Краевые задачи электростатики 55
§ 13. Краевые задачи теории кароттажа ........ 60
а) Источник тока в скважине 62
б) Бесконечно тонкий пласт 64
§ 14. Обобщённое уравнение Пуассона 70
а) Теория ядерных сил и мезонов (классическая
мезодинамика) 70
б) Теория гравитации Зеелигера 70
в) Теория сильных электролитов 71
г) Теория сверхпроводимости , . . 72
Глава III. Уравнения, зависящие от времени 74
§ 15. Уравнение движения классической механики . . 74
§ 16. Уравнение теплопроводности (уравнение парабо-
параболического типа) 77
§ 17. Волновое уравнение Даламбера (уравнение гипер-
гиперболического типа) ^ 84
§ 18. Решение уравнения Даламбера в случае моно-
монохроматических колебаний 90
4 ОГЛАВЛЕНИЕ
§ 19. Нестационарные колебания 94
§ 20. Интегрирование волнового уравнения Клейна ... 99
§ 21. Интегрирование волнового уравнения в п-мерном
пространстве 107
§ 22. Распространение электромагнитных волн в прово-
проводящей среде 115
Глава IV. Классическая электродинамика 119
§ 23. Основы классической электродинамики 119
а) Значение классической электродинамики в со-
современной теории частиц и полей 119
б) Инвариантность и трансформационные свойства 122
в) Основные уравнения классической электроди-
электродинамики 135
§ 24. Интегрирование уравнений Максвелла-Лорентца . 145
§ 25. Потенциалы Лъенара-Вихерта и формула Брейта . 148
§ 26. Поле точечного заряда, движущегося равномерно
и прямолинейно 151
§ 27. «Сверхсветовой» электрон Черенкова 154
§ 28. Тензор энергии 168
§ 29. Импульс электромагнитного поля • . 171
§ 30. Теория электромагнитной массы в электродинамике
Максвелла-Лорентца 175
а) Тензор энергии максвелловского поля .... 175
б) Тензор момента количества движения поля . . 185
§ 31. Вывод классического уравнения движения электро-
электромагнитной массы по методу Лорентца 193
§ 32. Нелинейная электродинамика 199
§ 33. Электродинамика полей с высшими производными 211
§ 34. Теория неполевой массы 220
а) Теория Х-процесса • . . 224
б) Теория би-поля 230
§ 35. Интегрирование уравнения движения электрона 239
§ 36. Рассеяние света свободными электронами ... 246
§ 37. Когерентное колебание двух связанных электронов 251
§ 38. Простейшая теория бетатрона 253
§ 39. Излучение электромагнитных волн электронами,
движущимися по окружности 261
§ 40. Угловое распределение излучения 269
§ 41. Зависимость интенсивности излучения от частоты 272
§ 42. Асимптотическое приближение для бесселевых
функций высокого порядка 273
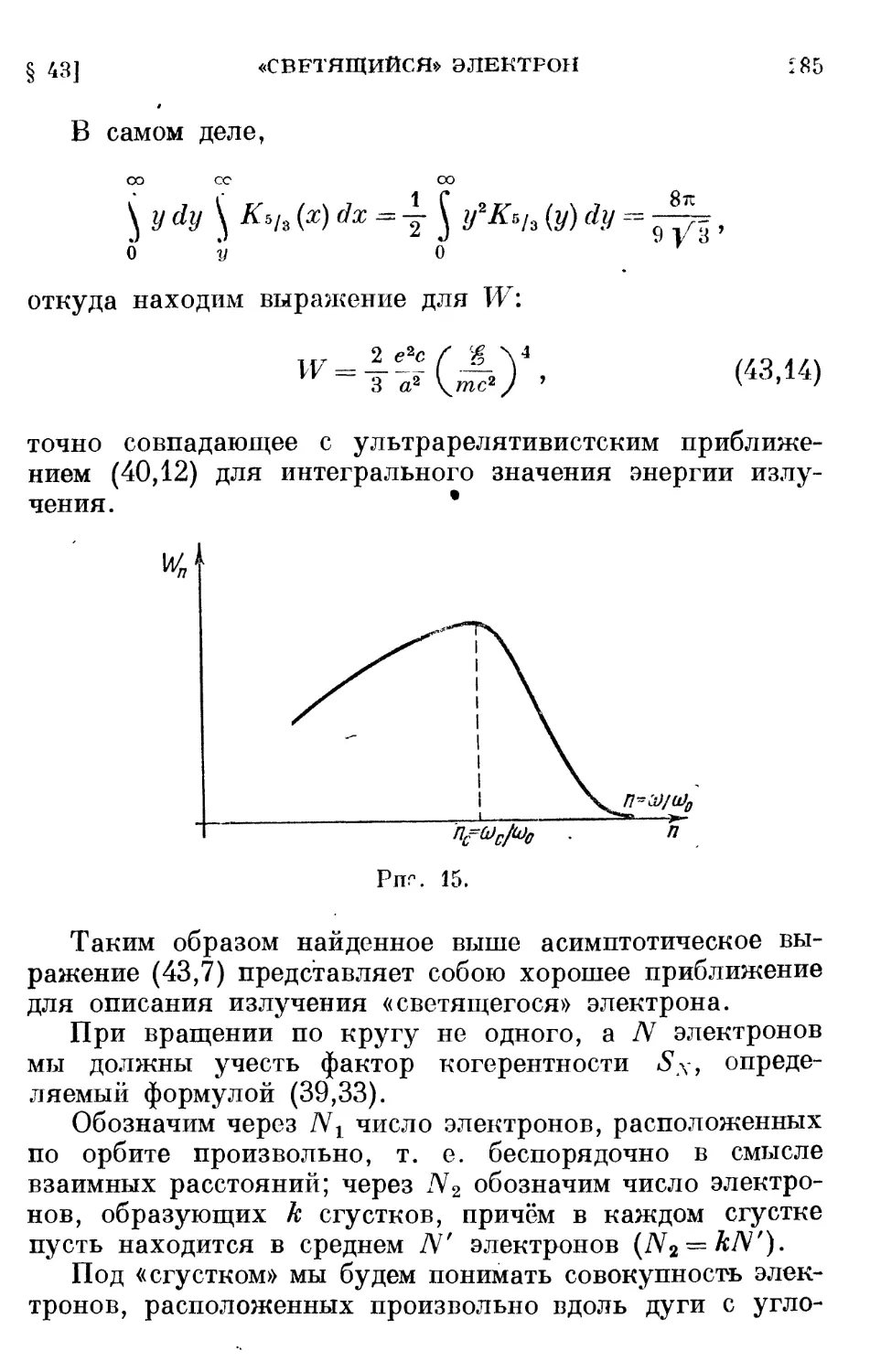
§ 43. «Светящийся» электрон 279
Глава V. Классическая мезодинамика 295
§ 44. Проблема ядерных сил 295
а) Модель атомного ядра 295
б) Свойства ядерных сил «... 300
в) Теория парных ядерных сил 315
г) Мезон 319
ОГЛАВЛЕНИЕ 5
§ 45. Скалярное мезонное поле • . . . 835
а) Скалярные ядерные силы 335
б) Общая теория скалярного поля 342
в) Комплексное скалярное поле • 352
§ 46. Псевдоскалярное мезонное поле 357
а) Псевдотензоры 357
б) Псевдоскалярное поле 365
§ 47. Векторное мезонное поле 372
а) Основные уравнения 372
б) Общая теория векторного мезонного поля . . . 375
в) Векторное мезонное поле при наличии нуклеон-
ных источников 381
г) Векторные ядерные силы 386
§ 48. Псевдовекторное поле. Дипольные трудности . . . 391
а) Псевдовекторное мезонное поле 391
б) Общая форма взаимодействия нуклеонов. . . . 395
§ 49. Распространение плоских векторных мезонных
волн в вакууме 404
§ 50. Интегрирование уравнений мезонного поля при
помощи векторов Герца 406
§ 51. Излучение векторных мезонных волн квазиэлек-
квазиэлектрическим и квазимагнитным диполем 409
§ 52. Квазиэлектрическое рассеяние векторных мезонов 413
§ 53. Квазимагнитное рассеяние векторных мезонов . . 415
§ 54. Силы реакции мезонного поля 419
§ 55. Рассеяние векторных мезонных волн с учётом
затухания 426
§ 56. Гравитация и элементарные частицы 436
Дополнение, Развитие теории вакуума 450
а) История вопроса 450
б) Сдвиг уровней 454
е) Сверхмиоговременной формализм 462
г) Полевая масса фотона . .' 464
д) Новые правила регуляризации 464
Предметный указатель 472
ПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ
Во втором издании общий план книги не подвергся
существенному изменению. Наряду с исправлением заме-
замеченных опечаток, в некоторые параграфы был внесён ряд
уточнений и добавлены ссылки на новейшую литературу.
Однако физика элементарных частиц и полей, введением
в теорию которых в значительной мере является наша
книга, продолжает быстро развиваться, что побудило нас
сделать более существенные дополнения в следующих
пунктах.
Прежде всего, теория «светящегося» электрона допол-
дополнена рассмотрением сжатия орбит. Далее мы считали не-
необходимым переработать материал, относящийся к про-
происхождению и природе космического излучения и раз-
различных мезонов в связи с рядом работ, выполненных за
последнее время в значительной мере советскими физиками.
В частности, следует подчеркнуть, что открытие нейтраль-
нейтральных мезонов A950 г.) впервые подвело реальный фунда-
фундамент под классическую мезодинамику, изложение которой
зайимает одно из центральных мест в нашей книге. Вве-,
денное прежде гипотетическое поле нейтральных мезонов
получает теперь, во всяком случае с качественной сто-
стороны, экспериментальное подтверждение.
1 В теории ядерных сил сделано добавление, касающееся
нового варианта устранения дипольной трудности в теории
псевдоскалярных сил. Кроме того, особое внимание было
обращено на недавние эксперименты по рассеянию быстрых
нуклеонов, позволяющие сделать важные выводы о харак-
характере "ядерных сил.
Мы ввели также дополнительный параграф, посвящен-
посвященный новейшему <?бъяснению сдвига энергетических уров-
ПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ 7
ней электронов в атомах, а также объяснению происхо-
происхождения дополнительного магнитного момента электрона
на основе квантовой теории вакуума, которая в некоторой
степени проясняет также вопрос о природе собственной
массы. Отметим ещё, что рассмотренное нами прежде в §34
компенсирующее би-поле используется сейчас для устра-
устранения квантовых расходимостей. Этот пример ещё раз
показывает значительную эвристическую силу предвари-
предварительного исследования проблемы собственной массы при
помощи классической теории.
В заключение авторы считают своим приятным долгом
поблагодарить всех товарищей, которые сделали свои
замечания по поводу первого издания. Авторы благодарны
также редактору книги В. А. Лешковцеву за вниматель-
внимательное отношение к её второму изданию и за помощь при
составлении указателя.
Физический факультет тт
Московского Государственного М
Университета
им. М. В. Ломоносова
Ноябрь 1950 г.
ПРЕДИСЛОВИЕ К ПЕРВОМУ ИЗДАНИЮ
Появление книги, посвященной классической, т. е.
неквантовой трактовке различных полей и элементар-
элементарных частиц, несомненно требует пояснения. Наличие
большого числа монографий и курсов, посвященных тео-
теории электромагнитного и гравитационного полей, делает,
казалось бы, излишним новое изложение классической
теории. Кроме того, рассмотрение процессов с элемен-
элементарными частицами, в частности мезонами, обычно почти
тривиальным' образом представляется требующим непре-
непременно квантовой теории.
Предлагаемая вниманию читателей книга ни в какой
мере не предполагает заменить обычный курс электро-
электродинамики.
Одна из наших задач заключается в использовании
некоторых математических методов квантовой теории
для исследования классических явлений.
В связи с этим мы систематически излагаем теорию
8-функции (гл. I), гс помощью которой можно опи-
описать различные особенности, связанные с зарядами
(точечный заряд, поверхностный заряд и т. д.), а также
дать новую трактовку функции Грина. Во второй
и третьей главах мы развиваем математический аппа-
аппарат, позволяющий использовать S-функцию при реше-
решении ряда задач математической физики и электродина-
электродинамики. Например, особенно просто с помощью теории
В-функции формулируется так называемый принцип из-
излучения .
В этих трёх главах мы показываем, в частности,
каким образом новые методы могут быть использованы
для решения многих старых проблем. При этом мы
ПРЕДИСЛОВИЕ К ПЕРВОМУ ИЗДАНИЮ 9
предоставляем в руки читателей лишь рабочий аппарат,
предлагая вниманию математиков более строгое обосно-
обоснование всего нового формализма.
Классическая теория поля и элементарных частиц
переживает за последние годы известное возрождение.
Многие явления, открытые за последнее время: «сверх-
«сверхсветовой» электрон, «светящийся» электрон, а также
другие эффекты, связанные с ускорением заряжен-
заряженных частиц, могут быть описаны в основном с по-
помощью неквантовой релятивистской теории. Наряду с
этим анализ далеко ещё не разрешённой проблемы соб-
собственной массы с классической точки зрения способ-
способствует более глубокому проникновению в физическую
сущность этого вопроса и может во всяком случае сыг-
сыграть эвристическую роль при дальнейшем развитии
теории элементарных частиц. Всем этим проблемам мы
посвящаем четвёртую главу нашей книги. Таким образом
в этой главе читатель найдёт систематическое изложе-
изложение ряда вопросов, которые были известны лишь по от-
отрывочным журнальным статьям.
Наконец, пятая, последняя глава книги посвящена
в основном проблемам, возникшим в связи с развитием
классической теории мезонного поля. Хотя нейтральные
мезоны, для которых непосредственно применима клас-
классическая трактовка, ещё с полной достоверностью не
открыты, однако многие результаты и методы клас-
классической мезодинамики сохраняют силу также в стро-
строгой квантовой теории, трактующей как нейтральные,
так и заряженные мезоны. Главное внимание мы обра-
обращаем здесь на вопрос о ядерных силах, представляющий
одну из центральных проблем всей современной физики
элементарных частиц. Сам по себе эффект взаимодействия
частиц через поле имеет классическую природу, поэтому
не удивительно, что многие результаты мезонной тео-
теории ядерных сил в основном могут быть получены уже
из классической трактовки. Проблема рассеяния мезо-
мезонов на нуклеонах (протонах и нейтронах) с учётом
затухания, которая также рассматривается в этой главе,
оказалась важной не только в теории прохождения
космических лучей через материю, но также для иссле-
Ю ПРЕДИСЛОВИЕ К ПЕРВОМУ ИЗДАНИЮ
дования общих вопросов, связанных с природой соб-
собственной массы. Проблемы гравитационного поля
затронуты лишь незначительным образом, главным обра-
образом потому, что исследования по тяготению, связанные
с выяснением его роли в теории элементарных частиц,
находятся ещё в стадии разработки.
Значительная часть всех этих вопросов впервые была
рассмотрена советскими авторами.
Хотя наше изложение посвящено классической теории
поля, но во всех главных пунктах мы даём указания
на дальнейшие результаты, полученные при квантовом
обобщении.
Таким образом наша книга, с одной стороны, может
служить дополнением к известным курсам электродина-
электродинамики и теории поля, а с другой, является введением
в современную теорию элементарных частиц, опираю-
опирающуюся при дальнейшем исследовании на квантовую
механику.
Физический факультет тт Мапирикп
Московского Государственного #4 • •" оипсппи
им. М^В^Ломоносова А. СОКОЛОВ
Сентябрь 1948 г. ,
ГЛАВА I
ОБЩАЯ ТЕОРИЯ 8-ФУНКЦИИ
§ 1. Определение о-функции
В современной классической и квантовой физике,
наряду с непрерывно распределёнными плотностями,
часто рассматриваются точечные массы, заряды, диполи
и т. п.
Если стремиться сохранить весьма удобное с физи-
физической и математической стороны понятие плотности
масс или зарядов также для точечных величин, то при-
приходится пользоваться так называемой В-функцией, кото-
которая была введена Дираком в 1926 г. Например, при
линейном распределении заряда е вдоль оси х плотность
равняется
г de
Отсюда видно, что в случае точечного заряда, рас-
расположенного, например, в начале координат, плотность
р будет равняться нулю везде, кроме точки х = 0, в кото-
которой она обращается в бесконечность.
Введём функцию Ъ(х' — х), равную нулю во всех
точках, кроме особой точки х' — х, где она обращается
в бесконечность, притом так, чтобы интеграл от этой
функции по всему промежутку оставался j* конечным
и равнялся бы единице:
(z'-z)dz' = l*). A,2)
*) Здесь и в дальнейшем интеграл, написанный без пределов,
берётся в интервале от —оо до +оо.
42 ОБЩАЯ ТЕОРИЯ 5-ФУНКЦИИ [Гд. I
Тогда о-функция будет связана с плотностью заряда р
точечного источника простым соотношением:
еЪ(х). A,3)
Учитывая, что S-функция во всех точках, кроме
особой, равняется нулю, мы можем вместо равенства
A,2) написать для участка а < Ь:
1' Ь>1>а' A,4)
0; ж>6 илиж<а v
Точно так же для непрерывной в рассматриваемой
области функции /(х) легко получить соотношение*):
8 (*'-*)«fa'-f/l*>: Ь>*>а' A,5)
Действительно, применяя теорему о среднем значе-
значении, имеем при b > х > а:
ъ х+*
^ f{х')Ь(х' — x)dx' = /(х +ае) ^ b(x' — x)dx'9 A,6)
а х—•
|а|<1, з>0,
откуда непосредственно следует равенство A,5), если
мы примем во внимание A,4) и будем стремить а
к нулю.
о-функция, определённая подобным образом, выходит
за рамки величин рассматриваемых в классическом ана-
анализе. Точно так же указанные интегралы нельзя пони-
понимать в смысле определения обычного интеграла.
Оказывается всё же, что интегралы с 8-функциями
можно связать или с интегралом Стильтьеса или рас-
рассматривать их как результат некоторого предельного
перехода от обычного интеграла.
*) Предельный случайна; = а или"ж = £/ требует дополнительного
исследования и ^зависит от конкретной конструкции ^-функции.
Более подробно см. § 4, формулу D,15).
§ 2] 8-ФУНКЦИЯ И ИНТЕГРАЛ СТИЛЬТЬеСА ДЗ
§ 2. S-функция и интеграл Стильтьеса
Интеграл Стильтьеса*) определяется как предел сле-
следующей суммы:
B,1)
К — 1
Это выражение можно наглядно трактовать как
обобщённый момент типа /(#), обязанный распределе-
распределению некоторых величин (например, масс, зарядов и т. д.),
характеризуемых функцией Ф(х). При f(x)~x имеем
момент первого порядка, при f(x) = x2, х3 и т. д.—
квадратичный момент и моменты высших порядков.
Если Ф(х) имеет интегрируемую производную
d$(x) = <p'(x)dx, B,2)
то интеграл Стильтьеса будет сводиться к обычному
интегралу:
ь
^'(х)<1х. B,3)
Однако интеграл Стильтьеса имеет смысл и в таких
случаях, когда функция распределения Ф (х) не является
непрерывной, и, вообще говоря, может быть определён
при весьма общих предположениях о характере разры-
разрывов" функции Ф(х).
Например, возьмём случай разрывной функции:
( + |; х>0,
Ф (*)-?(*)-{ ; B,4)
(-4; *<о.
В этом случае приращение функции у (х) во всех точках
равно нулю [Ду(#) = О], кроме точки # = 0, где это при-
приращение обращается в единицу: Ау@) = 1.
*) Об интеграле Стильтьеса см. В. И. Смирнов, Курс
высшей математики, т. IV, Гостехиздат, 1948.
14 ОБЩАЯ ТЕОРИЯ 8-ФУНКЦИИ [ГЛ. 1
Подставляя B,4) в B,1), получим:
\ f(x)d^(x)=lim^f(xk)^(xk)t B,5)
где хк = а+ к-^- и, кроме того, предполагается, что
точка разрыва х — 0 лежит внутри интервала а, Ь, т. е.
я<0< Ь.
Переходя к пределу в выражении B,5), получим:
а<О<Ъ. B,6)
Сравнивая B,6) с формулой A,5) и полагая в послед-
последней особую точку хг лежащей в начале координат
(х' = 0), видим, что S-функция в качестве подинтеграль-
ного фактора может быть 'определена как производная
от разрывной функции:
Ч*)=^ = Т'(*)- B,7)
Очевидно, такое определение вполне соответствует
наглядному смыслу 8-функции, исчезающей везде, кроме
точки разрыва.
Таким образом, если стремиться придерживаться
известной и строго разработанной математической „тео-
„теории, то можно было бы о-функцию вовсе не вводить,
а пользоваться интегралом Стильтьеса. Однако это было
бы в большинстве случаев чрезвычайно громоздко и при-
примерно соответствовало бы систематическому использова-
использованию теории пределов и бесконечных сумм вместо диф-
дифференциального и интегрального исчисления. Кроме того,
формализм о-функции позволяет оставаться на почве
более привычных приёмов классического анализа, допу-
допуская простые обобщения на пространство многих изме-
измерений, и даёт удобное описание, сложных разрывов
мультипольного типа, встречающихся в физике.
§ 3] «-ФУНКЦИЯ КАК ПРЕДЕЛ НЕПРЕРЫВНОЙ ФУНКЦИИ 15
§ 3. ^-функция как предельный случай
непрерывной функции
Всю теорию с-функции можно построить, применяя
предельный переход от известных непрерывных функций
путём стремления некоторого параметра к определён-
определённому пределу.
Возьмём, например, вспомогательную функцию y(xf a),
которая при а > 0 непрерывным образом зависит от х
и в пределе принимает значения: .
limy (*,«) = { J C,1)
Этому требованию удовлетворяет, в частности,
функция
а) = т \
:=Iarctgi. C,2)
Производная от у(#, а) по х, которую обозначим
через Ь (х, а), в данном случае равна
8 (х, а) = 1 [ е~*к cos kxdk = ±. _^L_ . C,3)
О
В пределе при а, стремящемся к нулю, легко пока-
показать, что
( 0; хфО,
Iim8(^a) = { n C,4)
lim \ Ь(х, a)dx=l.
а->0 J
Сравнивая C,4) с нашим определением 8-функции
(см. § 1), мы можем рассматривать ^-функцию как пре-
предельное значение вспомогательной функции 8 (х, а) при
а—>0, т. е.
8 (ж) = lim 8 (ж, а). C,5)
0
16 ОБЩАЯ ТЕОРИЯ 8-ФУНКЦИИ [гЛ. I
Однако, если мы хотим брать интегралы в обычном
понимании, то предельный переход а—»0 должен совер-
совершаться после вычисления интеграла. Иными словами,
бесконечно малый параметр а должен иметь меньший
порядок малости, чем бесконечно малое приращение
Ах, т. е. интеграл с о-функцией означает вычисление
предела суммы, когда
Дя—»0; а-» О,
причём
Подобные интегралы относятся к классу несобственных.
Аналогично в этом смысле равенство A,5) следует
трактовать как
ь
\f(x')b(x'-x)dxf =
а
Ь
= lim if (xf) 8 (xf - я, a) dx' = f(x); a < x < b. C,6)
a->0 J
a
Правильность последнего выражения легко проверить,
если подставить в C,6) конкретное значение для Ь (х, а)
из равенства C,3). Тогда мы получим известное из тео-
теории интеграла Фурье соотношение
ъ
lim \ / (хг) 8 (xf — х9 a) dx' =
o J
\
а
= I ^ dk \ f (xf) cos к (х' - х) dx' = / (х), C,7)
О а
совпадающее с результатом C,6).
Производная вспомогательной функции 8 (х, а) опре-
определится соотношением
|8(*, а)= -1 J ^sinbdb -л1^. C,8)
5 з) 8-функцин как йрёДЕЙ НёпреШ^ной фунйЦйй
Интеграл, содержащий в качестве подинтегралыюгЬ
фактора величину ^, следует понимать как предел
выражения
ь
lim
dx'.
a a
Вычисляя последний интеграл по частям и прйшг-
Рис. 1.
Рис. 2.
мая во внимание, что на границе области функция 8 (х)
обращается в нуль, получим:
а<х<Ь.
Подобным образом мы можем обобщить понятие
интеграла на случай, когда под интегралом стоят
производные высшего порядка от 5-функции.
В этом случае
ъ
^f(x')№(x'-x)dx' = {-l)"fW(x)'t a<x<b. C,11)
а
Графики вспомогательных функций у (х, а), 8 (х, а) и
—^-^ = 8'(ж, а) изображены соответственно на рис. 1, 2
и 3. Они имеют весьма наглядный смысл и помогают
1%
оёЩай теорий в-фунКЦий
л> t
6'(Х,СС)
уяснить физическое значение предельных величин у (я),
8(я)и&». '
При а, стремящемся к нулю, область крутого пере-
перехода функции y (х> а) от нижнего к верхнему значению
сужается, и в пределе мы имеем скачок в точке х — 0
от —1/2 до +х/2 (рис. 1, пунктирная линия). Одновре-
Одновременно при а—>0 график функции Ь (х, а) сжимается
возле точки х = О, стремясь по абсолютному значению
к бесконечности, соответствен-
соответственно, например, плотности то-
точечного заряда.
График Ь' (х, а) беспредель-
беспредельно возрастает, принимая в двух
соседних бесконечно близких
точках равные по величине и
противоположные по знаку
значения, что физически соот-
соответствует, например, случаю
электрического диполя. Дей-
Действительно, по определению мо-
момента диполя имеем следующее
значение для его плотности:
I
Рис. 3. г \ / ~ \ / w —
= -/й'(я), C,12)
где р является моментом диполя и равняется произ-
произведению положительного заряда е на расстояние между
зарядами I.
Вместо рассмотренных выражений для вспомога-
вспомогательных функций у (х, а) и о (х, а) за исходный пункт
можно было выбрать бесчисленное множество других
функций, удовлетворяющих предельным соотношениям
C,1), C,4) и C,10).
Таким образом конкретный вид вспомогательной
функции является несущественным, и мы можем (под-
(подразумевая каждый раз необходимость совершения пра-
правильного предельного перехода) непосредственно исполь-
использовать окончательные выражения для ч(х), 8 (я) и ■
при а, равных нулю.
8] fc-ФУШШЙЯ КАЙ ЙРЁДЕЛ НЕПРЕРЫВНОЙ ФУНКЦИЙ 19
Следовательно, вместо вспомогательных функций C,2)
C,3) и C,8) напишем
ООГ
sin kx
dk,
C,13)
C,14)
со
8' (я) = -1 ^ к - sin As dft = ^ ikeik*dk. C,15)
В качестве другого примера функции у (ж, а) при-
приведём выражение
е а +1
которое в пределе а—^0 даёт
для f(x', х, а) два значения:
+1; х'<х,
0; ^>я.§
C,17)
lim
или
f(x',z,0) = + l_Y(a;'_a-).
Рис. 4.
" Поэтому производная от
функции }{х\ х, а) по х' бу-
будет иметь «дельтообразный» характер ^х ' ?' а' =
= —8 (ж', х, а) (рис. 4). Подобного рода функция харак-
характеризует распределение частиц в статистике Ферми-Ди-
Ферми-Дирака. Предельный случай а—>0 соответствует закону
распределения частиц при абсолютном нуле (полное
вырождение).
2*
Теорий з-фунШШЙ \?л. i
Известная предельная форма для интеграла Пуас-
Пуассона
—тс
также может быть выражена через 8-функцию. В этом
случае вспомогательная функция 8 (ср, г) будет иметь
вид
Легко показать, что
0; ср ф 0,
1 C'2°>
со; 1 =
T 4"
lim \ 8 (ср, г) с?ср == 1.
г—►! *)
Таким образом мы можем положить
§ 4. 8-функция и разложение Фурье
Пусть нам дана функция /(^), удовлетворяющая усло-
условиям разложимости по некоторой замкнутой системе ор-
ортогональных и нормированных функций уп{х) в заданном
промежутке а, Ъ (а < Ь).
Тогда в случае дискретного спектра
со
/(*) = 2 *»?„(*)• D,1)
п—п0
Умножим обе части равенства на ср*/ (х) и проинте-
проинтегрируем по всей области изменения х. Тогда, учитывая
ещё условия ортонормированности
ъ
Чп»(х)Чп{х)йх = Ъпп', D,2)
I 4] 8-ФУНКЦИЯ И РАЗЛОЖЕНИЕ ФУРЬЕ
где символ Кронекера-Вейерштрасса
найдём следующее значение для обобщённых коэффи-
коэффициентов Фурье*):
ь
an=\f(x)^n{x)dx. D,4)
а
Отсюда, подставляя D,4) в D,1), имеем:
оо Ь
/И=2 $/(*')?«(*')?„(*)<**'• D,5)
п=По а
Заметим, что в равенстве D,5) существенен порядок
операций интегрирования и суммирования. Сперва необ-
необходимо произвести интегрирование по х'', а затем уже
взять сумму бесконечного числа членов.
Однако, если мы хотим представить полученный ре-
результат с помощью формализма ^-функции, мы должны
сперва ввести вспомогательную функцию, равную сумме
конечного числа членов:
N
Л=По
и представить D,5) в виде предела:
N Ъ
; /(*) = lim 2 W(*')?n(*')<Pn (*)<**'. D,7)
п»=по а
Меняя теперь порядок интегрирования и суммирова-
суммирования, получим:
b
f (x) = lim [ f (x') 8Ж (х' - x) dx'. D,8)
*) При вычислении коэффициентов Фурье ап мы переменим
порядок интегрирования и суммирования бесконечного числа чле-
членов. Законность этой операции, если угодно, можно рассматривать
как условие разложимости функции / (х) в ряд Фурье.
22 ОБЩАЯ ТЕОРИЯ 8-ФУНКЦИИ [гл. I
Выражение D,8) запишем в виде
ъ
f(x)=\f(x')b(x'-x)dx', D,9)
а
где
'-х). D,10)
N-*oo
Несобственный характер интеграла D,9) заключается
в том, что переход к пределу D,10) мы должны совер-
совершить после вычисления интеграла.
Таким образом, как явствует из D,9), 8-функция
представляет собой ядро некоторого интегрального опе-
оператора Q, превращающего в любой функции аргумент
х' в х\
j{x) = Qf{x'). D,11)
Новое определение 8-функции D,10), как предела
выражения D,6), является более общим, чем данное
в предыдущем параграфе, ибо оно имеет место также
для функций f(x), обладающих разрывами первого рода,
а также пригодно для крайних значений х'~а или
х' = Ь, если только функция f (х) допускает разложение
по ортонормированным функциям срл (х) в крайних
точках.
Разберём теперь ряд конкретных примеров предста-
представления 8-функции через различные системы ортонорми-
рованных функций, наиболее часто встречающихся в ма-
математической физике.
а) В качестве первого примера возьмём систему три-
тригонометрических функций, записанных в показательной
форме:
'*"*, D,12)
определённых в интервале периодичности — I < X < /,
где « = 0, ±1, ±2, ...
§ 4] 6-ФУНКЦИЯ И РАЗЛОЖЕНИЕ ФУРЬЕ 23
Тогда согласно D,6)
2V
21
откуда
n =—oo
Учитывая возможные разрывы функции f(x), имеем
согласно известной теореме Фурье
Чтобы проделать переход к непрерывному спектру,
т. е, к разложению f(x) в интеграл Фурье, мы должны
прежде всего положить
т = &, тДл=т=АА, К = ~- D,16)
Затем, переходя к пределу: /—>оо, N —> со, К равно
конечной величине, имеем
Л:)> D,17)
где вспомогательная функция
к
8 (», *) = !;$ е-'** <** = 1 s-^ . D,18)
Равенство D,15) переходит в этом случае в выражение
известного разрывного интеграла Дирихле:
24
ОБЩАЯ ТЕОРИЯ 8-ФУНКЦИИ
[ГЛ. 1
График вспомогательной функции D,18), изображён-
изображённый на рис. 5, ещё раз наглядно иллюстрирует несоб-
несобственный характер 8-функции. Действительно, при стрем-
стремлении К к бесконечности главный максимум в точке
х = 0 беспредельно возрастает, побочными же уменыпа-
„. ющимися максимума-
х% ми в пределе прене-
пренебрегаем.
Согласно преды-
предыдущему мы будем пи-
писать
Рис. 5.
D,20)
подразумевая, что с
точки зрения инте-
интеграла Римана пе-
переход к пределу
(К—> со) необходимо
совершать после вычисления того интеграла, где в ка-
качестве подинтегрального множителя стоит 8 (х' — х).
Условие ортонормированности для непрерывного спек-
спектра, т. е. для функций
1 ^'~ D,21)
будет цметь вид
-ft). D,22)
Таким образом о-функция, в частности, является обоб-
обобщением символа Кронекера-Вейерштрасса [см, D,3)] на
цепрерывный спектр.
В случае непрерывного спектра мы также можем со-
сохранить формулу D,6) для связи 8(# — #') С системой ор-
$qнормированных функций,
§ 4] 5-ФУНКЦИЯ И РАЗЛОЖЕНИЕ ФУРЬЕ 25
Для этой цели вместо функций D,21) мы должны
ввести
***. Г (*, *')= Vf*e~ikX'>
после чего условие ортонормированности принимает
вид:
+ (*', х) 9(*, s) ds = £ $ в'я(*"*/)dx = dkb (к-к').
Тогда
8 (*-*')= 2 ?+ (Л' ж') ? (*' ж) $ 6'*
/с
Если отказаться от метода 8-функции, то приходится
пользоваться для нормировки собственных функций в не-
непрерывном спектре гораздо более громоздким приёмом
Вейля. При этом за основу берётся так называемый «соб-
«собственный дифференциал» от ср(#, х), определяемый сле-
следующим образом:
где интеграл от рассматриваемой функции ср (к, х) рас-
распространён по малому промежутку собственных значе-
значений Ак.
Тогда условие нормировки Вейля гласит *)
Af\2dx=l. D,24)
Например, для случая D,21) имеем
Af(kyx)= j/l
X
sin-
*) В. А. Ф о к, Начала квартовой механики, Кубуч, 1932»
стр. 24-25, 36;
26 ОБЩАЯ ТЕОРИЯ 5-ФУНК1ШИ [ГЛ. I
откуда
т. е. более простой способ нормирования с помощью
8-функцяи D,22) является совершенно эквивалентным спо-
способу Вейля D,24). Приём Вейля сводится, очевидно,
к сглаживанию несобственной 8-функции.
Отметим, что равенство D,20) представляет собой
разложение о-функции в интеграл Фурье, причём все
коэффициенты Фурье оказываются постоянными и рав-
1
НЫМИ д- .
Все полученные соотношения можно установить
также для любых других систем ортонормированных
функций.
б) При разложении по бесселевым функциям Jm (x)
в интервале 0<г<Д в случае дискретного спектра ор-
тонормированными функциями являются *)
где т > — 1, a sn являются корнями уравнения
/m(sn) = 0.
Следовательно, 8-функиия в данном случае будет иметь
вид
При переходе к непрерывному спектру мы должны по-
положить: sn—>oo, R—>ос, ~ = к равное конечной вели-
*) Р. О. Кузьмин, Бесселевы функции, ОНТИ, 1935,
стр. 104.
§ 4] 8-ФУНКЦИЯ И РАЗЛОЖЕНИЕ ФУРЬЕ 27
чине. Чтобы определить корни sn, возьмём асимптоти-
асимптотическое выражение для функции Jm:
пт 7i 1
откуда sn 2 T^V^^yJ^' где w является целым
числом, причём нас интересуют лишь большие значе-
значения п.
Из последних соотношений находим
Поэтому, переходя в D,26) от суммирования к инте-
интегрированию, получим
6 (/•' - г) = /fP ^ /f/m (кг) /,„ (Лг') rfA;; 0< г, г' < оо.
D,27)
Это выражение при г > 0 эквивалентно равенству
оо оо
\kdk\r>f{r')Jm(kr)Jm(kr')dr' =
6
6 О
известному под названием интеграла Фурье-Бесселя, ко-
которое имеет место для функций /, удовлетворяющих усло-
оо
вию Дирихле и для которых \ j/V / (г) dr Ф оо.
о
Заметим, что для предельного случая г —0 (см. § 1),
равенство D,27) сохраняет силу, если т = 0, т. е.
со
8 (г') = г'\ kJ0 (krr) dk. D,28)
28 ОБЩАЯ ТЕОРИЯ 5-ФУНКЦИИ [ГЛ. I
В самом деле, с помощью равенства
оо
8 {г', а) = г' [ е-*к kJ0 (кг') dk = % г'а^
с
легко показать, что:
K/2
о *
limo(r/,a) = 0; г1 Ф 0 и lim \ 8 (г', a) dr' = 1,
о
или
в) При разложении произвольной функции по поли-
полиномам Лежандра Рп (х) в интервале —1<^<1 ортонор-
мированными функциями являются
Рп(*). D,29)
Поэтому в этом случае 8-функция примет вид
со
8 (х' - х) = 2 ^ Л («') ^п («)• D,30)
п = 0
г) Наконец, при разложении по эрмитовым функциям,
когда собственные функции имеют вид
где Нп (х) — полиномы Эрмита-Чебышева, 8-функцию
можно представить в форме
( )
N->oo
где вспомогательная функция
N
S (ж' - *, N) = 2 -р^т
1 5) ь-Ф^нйцйй в Пространстве п измерений
Последняя ^умма моЖё* быть вычислена прибли-
приближённо *):
8 (*' -x,N) = sin V*W+i)V~4 Q
При достаточно больших значениях N вспомогатель-
вспомогательные функции D,33) и D,18) будут отличаться на вели-
величину, обращающуюся в нуль в предельном случае (iV—>оо).
§ 5. о-функция в пространстве п измерений
Теория й-функции, развитая выше для случая одной
переменной, без труда обобщается на п измерений.
За основу определения и-мерной ^-функции возьмём
равенства:
\\ dx't... Ь (х[-хи х'2-х2, ...) = 1 E,1)
при ах <хг < Ьх и т. д.,
8 (х[ — хъ х'2 — х2 ...,) = О при хг Ф х[ и т. д. E,2)
Аналогично одномерному случаю на основании послед-
последних равенств можем написать
bi Ъ2
\dx[^ dx'2... о(х[-х19 х'2-х2, ...)/К. «I. •••) =
а± а2
= f(xlf х2, .. .) при аг < хх < Ь± и т. д. E,3)
В качестве примера двумерной S-функции можно при-
привести интеграл
8(в'_е, «p'-<p)=U
Х
l--2r[cos6' • cose + sin6' • sine • cos (cp' — cp)] +г2
0<ср', ср<2тг,
*) В. А. Ф о к, О несобственных функциях в квантовой меха-
механике, ЖРФХО (часть физическая), 61, 1, 1929; В. А. К р а в ц о в,
О математических обоснованиях новой квантовой механики,
ЖРФХО (часть физическая), 61, 9, 1929.
80 ОёЩай Теорий е-ФУНВДйй [гл. 1
Легко проверить, что последнее выражение удовле-
удовлетворяет равенствам E,1) и E,2).
Из E,4) мы получаем соотношение
у 1-г* Г , , Г sin6'/F',cp')d6> __
= /@.*), E>5)
известное из теории решения трёхмерного уравнения
Лапласа.
Особенно удобно произвести обобщение на я-мерный
случай, положив в основу определения 8-функции крат-
кратный интеграл Фурье.
Ввиду простых свойств аддитивности показательных
функций можно положить
= l(x1)Z(zi)... E,6)
В частности, в трёхмерном случае *)
о (г) = 8 (я) 8 (у) 8 (z) = ^
где
Л-) = dkxdk2dk3 и кг = кгх + к2у + k8z. E,8)
§ 6. Важнейшие формулы с 8-функциями
Приведём сводку основных формул с 8-функциями,
наиболее часто встречающихся в приложениях.
Как легко проверить,
8(-я) = 8(а), F,1)
т. е. 8-функция является чётной функцией.
*) В равенстве E,7) мы имеем тройной интеграл, распростра-
распространённый по всему пространству волновых чисел к(— оо < А'< оо
и т. д.). Для простоты мы будем писать при многократном инте-
интеграле один знак интеграла, [подразумевая, что всюду число инте-
интегралов должно равняться числу дифференциалов.
БАЖЙЁЙШИЁ ФОРМУЛЫ t 6-ФУН*ЩйЙМЙ 31
Для производной 8-функции имеем
Ъ'(-х)=-Ь'(х), F,2)
т. е. производная от с-функции является нечётной функ-
функцией, причём штрих означает производную по тому аргу-
аргументу, от которого зависит функция. Далее имеем ряд
важных формул:
-*), F,3)
F,4)
|7w1 1 <».)!
S S
Здесь a;s являются простыми корнями уравнения ср (ж) =
= 0, лежащими в рассматриваемом интервале.
5М = ^> F,6)
F,7)
В частности, при а—>0 находим:
\х\Ь (х2) ~1 (хO F,8)
ьп
J * J «» v » /
0; Ьп<ап.
Здесь яп является наибольшим значением из % и а2,
а 6П — наименьшим значением из Ьг и fc2 (ai <C ^i', й2 < 62).
Для функции, имеющей конечный разрыв в точке х0,
/1 \Х), X <^ Хо,
/2 (ж0) -
/'(»)=лз(*-*о)+
В частности,
F,12)
Ш Ьбщая теория s-функцйй [гл. 1
Соотношения F,1), F,3) и F,4) легко могут быть про-
проверены с помощью соотношения A,5). Так, например, вы-
выражение F,1) эквивалентно равенству
-ж) dx~ ^ f(-x)b(x)dx,
-ь
причём в нашем случае b > 0 > а, поэтому — а > 0 > — Ь.
Справедливость последнего соотношения не вызывает
сомнений, так как его левая и правая части равны /@),
а функция f(x) не должна обладать в интервале a, b
бесконечными разрывами.
Подобным же образом с помощью равенства C,10)
проверяем соотношение F,2).
Для вывода формулы F,5) разобьём весь промежуток
интегрирования на отдельные интервалы: xs— ss, xs+es
(ss>0), так, чтобы в каждом из них лежал только
один корень [в случае кратных корней равенство F,5)
теряет смысл].
Затем, сделав замену переменных
найдём для каждого интервала
/ (х) 5 (ср (х)) dx = \ f(x)-^du.
2
Здесь мы учли, что us = ср (xs) = 0 и u's --= ср' (xs) Ф 0
(нет кратных корней).
Величину ss мы всегда можем выбрать таким образом,
чтобы знаки верхнего и нижнего предела последнего инте-
интеграла определялись линейными членами относительно es.
Тогда при us > 0
Р _ / (xs) f (xs)
При Us < 0 мы должны поменять местами пределы
интегрирования, чтобы нижний предел был меньше
верхнего.
$ 6] ВАЖНЕЙШИЕ ФОРМУЛЫ С 6-ФУНКЦИЯМИ 33
В этом случае
Fs= - Т/(*) lWdB = _/fe)eZM.
Распространяя интегрирование на весь участок, по-
получим равенство
ь
$/(*) а [?(*)]«**=2 *".=2 тЯйг*
a s s
Символически записываемое в виде F,5).
Полагая в F,5) ср (х) = ах и ср (х) ~х2 — а2, находим
формулы F,6) и F,7), выведенные ещё Дираком.
Особая точка (х=^0) 6-функшш, входящей в равен-
равенство F,8), является крайней точкой интеграла, так как
+ ОО СЮ
\\х\Ь (х2) dx = 2 [ хо (х2)dx.
-оо О
Точное значение интеграла зависит от конструкции
о-функции. Рассматривая 8 (х2) как предел выражения
Ъ(х2) = о(х2- е); е~>0
и учитывая, что согласно C,3) при а > 0:
найдём
8 (ж); е>а,
||()|
Поэтому равенство F,8) имеет место, для е > О.Для
вывода формулы F,11) функцию f(x) представимв виде
Учитывая при дифференцировании последнего соот-
соотношения равенство B,7) и F,10), докажем справедливость
формулы F,11).
3 Д. Иваненко и А. Соколов
•-34 ОБЩАЯ ТЕОРИЯ 5-ФУНКЦИИ <[гл. I
Наконец, соотношение F,12) мы поткем рассматри-
рассматривать как частный случай предыдущего равенства.
В самом деле, мы имеем
пх~~\ 1п||f; х < О,
или
In х = In | х | -i- in ^y - у (
откуда, взяв производную по #, получаем соотношение
F,12).
§ 7. Функция Грина
Одним из наиболее важных применений теории
S-функции является построение функции Грина линей-
линейных дифференциальных уравнений с постоянными коэф-
коэффициентами *).
Пусть нам дано неоднородное уравнение
L<f(xlf x29...)= — \?{хг, хъ...), G,1)
в котором под аргументами xl9 хъ... можно в общем
случае подразумевать как пространственные г (х, у, z),
так и временную t координаты.
Здесь линейный оператор
£ = во + а1|- + ва^- + ...+ви^+..., G,2)
а р является плотностью источника.
Решение уравнения G,1) символически записывается
в форме
<P=-£-V G,3)
*) Вообще говоря, этим методом мы можем также воспользо-
воспользоваться, если коэффициенты, образующие оператор L, являются
переменными; существенно, чтобы нам удалось составить 5-функцию
из таких ортопормированных функций, для которых легко опреде-
определить собственные значения X оператора L (см. £§ 17, 18): Lun = —\2ип.
§ 7] ФУНКЦИЯ ГРИНА 35
Представив правую часть уравнения G,1) с помощью
^-функции в виде
[>{xlt ж21- ••)= j \>(x[f x2i...)l{x'1-xlix2—x2y...)dx'1dx2...
G,4)
и учитывая, что оператор L действует только на нештри-
хованные координаты х19 х2, ..., имеем вместо уравне-
уравнения G,3)
<Р(Ж1, Х2, . ..) =
При этом решение уравнения G,1) примет вид
); G,6)
вектор в тг-мерном пространстве имеет составляющие
хг, Хо, ..., (dxf) = dx[ dx'2..., a G по определению есть
функция Грина данного уравнения.
Следовательно, функция Грина может быть связана
с о-функцией при помощи следующего символического
равенства*):
G(x',z)= —L-4(x' — z). G,7)
Умножая на оператор L, имеем
LG= -8 (ж'-ж). G,8)
Строго говоря, деление на оператор является неодно-
неоднозначным действием, и поэтому к правой части равен-
равенства G,7) мы можем добавить несингулярную часть
функции Грина GOi которая является решением одно-
однородного уравнения LG0 = 0. Функция Go подбирается
из дополнительных условий (граничных, начальных
и т. д.).
*) Д. Иваненко и А. Соколов. Обобщённое волновое
уравнение и классическая мезодинамика, ДАН, 36, 37, 1940; см.
также А. Соколов, Дельта-функшш и её применение к решению
некоторых математических задач геофизики, Свердловск, 1946.
В*
36 ОБЩАЯ ТЕОРИЯ 8-ФУНКЦИИ [гл> I
Интегрируя G,7), найдём, что ядро интегрального
оператора, соответствующего обратному дифференциаль-
дифференциальному, является функцией Грина:
L-i = -Д G (я', я)... (dxf). G,9)
Представляя 8-функцию в виде разложения Фурье
6(«'-х) = JL \ etk*<**-**> d^dk2... G,10)
и замечая, что действие оператора L на показатель-
показательную функцию равняется
о
находим значение для функции Грина t
где
ik x
r L_ С e a dkxdk2...
Ul — B«)я 3 «о + **A + ^2«2 + ''' +(^i
Это представление для G3 соответствует известной
теореме Мерсера*), согласно которой, например, в слу-
случае дискретного спектра,
где Хп —собственные значения оператора L.
Из равенств G,7) и G,8) вытекают следующие свой-
свойства функции G:
а) Сингулярная часть Gl9 так же, как и 8-функция,
симметрична относительно аргументов хг и х.
б) Gx является решением однородного уравнения
во всех точках, кроме точки х[ = х19 и т. д. В этой
точке особенности определяются через о-функцию.
*) Р. Курант и Д. Гильберт, Методы математической
физики, т. I, стр. 124, Гостехиздат, 1951.
§ [7 ФУНКЦИЯ ГРИНА 37
Физический смысл уравнения G,1) заключается
в том, что источник [) порождает данное поле. Гринов-
ская функция даёт ту долю поля в точке х в момент
времени ty которая порождается источником единичной
интенсивности, находящимся в момент t' в точке х'.
Полное поле ср получится в результате интегрирования
по всему распределению источника и по всему проме-
промежутку времени, в течение которого он действовал.
Близкое определение гриновской функции даётся
в так называемом операционном исчислении, где вместо
разложения Фурье используется разложение Лапласа-
Мел лина *).
*) Основы операционного исчисления изложены, например,
в книге А. И. Лурье «Операционное исчисление», Гостехиздат,
1950. Там же указана основная литература по операционному исчис-
исчислению.
ГЛАВА II
СТАТИЧЕСКИЕ УРАВНЕНИЯ
ЭЛЛИПТИЧЕСКОГО ТИПА
§ 8. Одномерное уравнение Лапласа
В настоящей главе мы рассмотрим решения линей-
линейных дифференциальных уравнений, не зависящих oi
времени. К их числу в первую очередь относится уравнение
Лапласа-Пуассона
(8,1)
которое, как известно, играет весьма важную роль
в самых различных разделах теоретической и матема-
математической физики: электродинамике, гидродинамике,
теории тяготения и др.
Найдём гриновские функции уравнений Лапласа-
Пуассона для случая одного, двух и трёх измерений.
В случае одного измерения уравнение Лапласа-
Пуассона имеет вид
Ьр = ^=-4*Р<*)- (8,2)
По общему правилу [см. G,8)] гриновская функция
оператора L определяется из уравнения
LG = - 8 {х - х') - -1 ^ dk e'*(*-*'> ,. (8,3)
откуда согласно правилу деления на оператор G,11)
имеем
G = - Ь'Ч {х - х') =1 J dk ^Г + Схх + С%. (8,4)
I 8] ОДНОМЕРНОЕ УРАВНЕНИЕ ЛАПЛАСА 39
Здесь двучлен Сгх-\-С2 является решением одноР°Дного
уравнения
Ьср = О. (8,5)
Кроме того, мы добавили к сингулярной части (чтобы
сделать её конечной) постоянный бесконечный член
вида
Интегрируя по частям, в (8,4) имеем
dk *'
откуда окончательно гриновская функция уравнения
Лапласа-Пуассона в одномерном случае равняется
G= -~±\х-х'\ + Сгх + С2. (8,8)
Неизвестные коэффициенты Сг и С2 должны опреде-
определяться из дополнительных условий.
При помощи (8,8) найдём искомое решение уравне-
уравнения (8,2):
ср = 4л: ^ dx'f (xf) G{x- x'). (8,9)
В частности, если мы имеем электрический заряд е,
расположенный в начале координат, т. е.
Р(а') = е8(я'). (8 ДО)
то для ср получим .
ср - - 2-е | х | + ЬтгхСг + 4тгеС2. (8,11)
При определении потенциала постоянный член 4-еС2
можно отбросить, так как начало отсчёта не является
существенным. Кроме того, в силу симметрии потенциала
относительно знака х коэффициент С19 в данном случае
следует принять равным нулю.
Поэтому окончательное решение имеет вид
<р=. -2ice|a:|. (8,12)
40 СТАТИЧЕСКИЕ УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА [гл. Ц
С точки зрения трёхмерного случая это решение соот-
соответствует потенциалу плоскости, равномерно заряжен-
заряженной электричеством с поверхностной плотностью
с = е. (8,13)
В случае наличия граничных условий
Т @) = «Р A) = Q, % (8,14)
ИЛИ
G@-x') = G{l-x') = 0, (8,15)
найдём
Сл=\\х'\, C1 = 4|1-z'|-yI*'I- (8,16)
Поэтому выражение для функции Грина примет вид
или при
G(x, x')= -~±-(\x-x'\ — x — x'
1-х); х>х\
=|
-х'); х<х'. V '
Подставляя (8,17) в (8,9), имееА! для 0 < х < 1
X 1
<р = 4ти J ж' A - х) р (х*) dx' + 4тг ^х A - х') f (x') dxf. (8,18)
О х
Эту же задачу можно было решить также при другом
выборе собственных функций, образующих ^-функцию.
За ортонормированные функции удобно взять
(8,19)
8 (х' — х) = 2 53 sin ъпх' • sin ъпх. (8,20)
1
где л —целые числа, изменяющиеся от 1 до со.
Тогда
§ 9] УРАВНЕНИЯ ЛАПЛАСА-ПУАССОНА НА ПЛОСКОСТИ 41
Отсюда, повторяя предыдущие вычисления, найдём
00
Г1, •* су у sin теш/ . sinnnx
G(x , x) = Z 2j
Если мы введём ещё граничные условия (8,15), то
несингулярное решение Go следует положить равным
нулю и
оо
Г1„> ~\ V cos теп (ж' —ж) —cos теп (ж'-f-ж) /о оо\
Сг(Х Х) = £ \Р^£)
т. е. в данном случае нам удалось подобрать для
образования о-функции такие ортонормированные функ-
функции срп, которые удовлетворяют заданным граничным
условиям (8,15), и поэтому мы могли отбросить несин-
несингулярное решение.
Воспользовавшись известным значением для суммы
оо
Е сов ту = а у» 1 . ,g 23
71 = 1
получим выражение для G, совпадающее с (8,17).
Этот пример особенно ясно показывает, что различ
ный выбор систем ортогональных функций, применён-
применённый для конструирования 8-функции, приводит к оди-
одинаковым значениям гриновской функции. Иными сло-
словами, как уже неоднократно отмечалось в гл. I,
конкретный выбор вида S-функции является несуще-
несущественным.
§ 9. Уравнение Лапласа-Пуассона на плоскости
По общему определению гриновскую функцию дву-
двумерного уравнения Лапласа-Пуассона найдём из урав-
уравнения
(9,1)
42 СТАТИЧЕСКИЕ УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА [гл. II
где
Отсюда, проделывая вычисления, указанные в § 7, имеем
для сингулярной части гриновской функции
к[+Щ dkl d*2'
Для обеспечения конечности G, так же, как и в пре-
предыдущем случае, нами добавлен постоянный бесконеч-
бесконечный член
Переходя к полярным координатам, имеем к2 = к\ + А|;
йкг dk2 = A: dk dcp;
*i (« — х') + *2 (У — У') = fy cos Т.
где
Р = /(*-*')я +(У-У')я-
Интегрируя по переменной ср, с помощью равенства
^el*Pcos?rfc? = 27r/0(/c,), (9,5)
6
где /0—бесселева функция, получим
со
GW~^ \ л dk*
о
Отсюда видно, что
G(l) = 0. (9,6)
Дифференцируя функцию G(^) no [j и принимая во
внимание, что
7
= ^р, найдем
2™,) ^ 2т;р'
§ 9] УРАВНЕНИЕ ЛАПЛАСА-ПУАССОНА НА ПЛОСКОСТИ 43
Учитывая (9,6), имеем
G= -2^lnP= -±\пУ(х-хТ + (у-у')\ (9,1)
т. е. логарифмический потенциал удовлетворяет урав-
уравнению
(^ + ^^\^^Т? = 2кЦх)Ь(у). (9,8)
Отсюда легко получить, что в случае точечного заряда е,
когда правая часть уравнения имеет вид 4^ = АкеЬ (х) 6 (у),
потенциал ср будет определяться из равенства
cp = — 2eln ] x2~\-y2.
С точки зрения трёхмерного случая этот потенциал
соответствует потенциалу прямой линии, равномерно
заряженной электричеством с линейной плотностью х = е.
Двумерная гриновская функция позволяет найти
связь о-функции с оператором Коши из теории функций
комплексного переменного.
Для этой цели рассмотрим криволинейный интеграл
/ — r£ w (Хщ ^ Й7 (Q Q*
взятый по некоторому замкнутому контуру /. Здесь
z = x-\-iy, w-u + iv. Действительные функции и и v
не должны обладать особенностями на контуре или
внутри его.
Выражение (9,9) мы будем понимать как сумму двух
контурных интегралов, один из которых является дей-
действительным, а другой мнимым.
Применим к интегралу (9,9) известную формулу пре-
преобразования линейного интеграла в поверхностный:
(9,10)
где интегрирование проводится по площади S, заключён-
заключённой внутри контура Z. Полагая
44 СТАТИЧЕСКИЕ УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА [гл. II
найдём
Так как
1 я-— iy
то
dyj z \ дх2 ду2
При этом мы воспользовались формулой (9,8).
Подставляя последнее выражение в (9,12), получим
— dz = 2izi \ wb (x) 8 (у) dx dy
Наконец, если tv удовлетворяет условию Коши-
Римана
ИЛИ
ди dv ди
dx~ dy ' dy- ~-te\ (9'17)
то мы получаем известную формулу Коши из теории
функций комплексного переменного
= 2TC£w @, 0). (9,18)
Таким образом имеет место следующее операторное
соотношение:
§^ (9,19)
где вместо многоточия мы можем подставить любую ана-
аналитическую функцию.
^ 10] ТРЁХМЕРНОЕ УРАВНЕНИЕ ЛАПЛАСА-ПУАССОНА 45
§ 10. Трёхмерное уравнение Лапласа-Пуассона
По общему определению функцию Грина трёхмерного
уравнения Лапласа-Пуассона найдём из формулы
LG = V2G = - $ (г - г') = - ^з \е ih^-r') (dk), A0,1)
где
V2 = £-+l^+e> №) = dkidbdks, A0,2)
кг = кхх + A2J/ + ^з2*
Отсюда
В случае «естественных» граничных условий, когда
G = 0, при г—> со мы должны положить несингулярную
часть Go равной нулю.
Интегрирование выражения A0,3) легко произвести,
введя сферические координаты (А, 6, ср) в пространстве
волновых чисел к:
(dk) = к2 dk sin 6 d6 d<p. A0,4)
Направляя ось к3 по вектору R = г— г', получим
оо тс 2те
G = ^L ^ dk ^ sin 6 е1'^ cos е йб jj dcp. A0,5)
Интегрируя A0,5) по сферическим углам с помощью
равенства
\ sin beikR cos ЧЬ^ d(? = 4n ^~ , A0,6)
6 6
получим
',6 СТАТИЧЕСКИЕ УРАВНЕНИЙ ЭЛЛИПТИЧЕСКОГО ТИПА [гл. I
Отсюда решение уравнения Лапласа-Пуассона для
трёхмерного случая
V«9(r)=-4!C,(r) A0,8)
имеет вид
Различные случаи распределения зарядов, облада-
обладающие особенностями того или иного типа (точечный
заряд, поверхностный заряд и т. д.), которые без
S-функции требовали дополнительных исследований с
помощью сложных предельных переходов, теперь могут
быть весьма просто описаны с помощью формализма
с-функции.
Пусть весь заряд расположен в точке I. Тогда его
плотность равна
P(r)=e8(r-l)- A0,10)
В самом деле,
а ,> (г) всюду, кроме особой точки?* = lf обращается в нуль.
Если г, т. е. расстояние от начала координат до точки
наблюдения, много больше if— <С 1 \ то выражение A0,10)
может быть разложено в ряд:
e5(r — l) = eo(r) — еA - V) о (г) +
Плотность
Ро = в8 {г)
является плотностью точечного заряда; выражение
п-1,2,3
даёт плотность диполя; член
п, к
§ 10] ТРЁХМЕРНОЕ УРАВНЕНИЕ ЛАПЛАСА-ПУАССОНА 47
является плотностью квадруполя. Следующие члены
разложения дают плотности точечных мулътиполей
высшего порядка.
Потенциалы плотности «точечных» мультиполей
высшего порядка (точечный заряд, диполь и т. д.)
могут быть найдены или с помощью формулы A0,9)
или непосредственным образом. Представляя трёх-
трёхмерную о-функцию разложенной в интеграл Фурье
[см. A0,1)]:
имеем для потенциала заряда
-- >■ / , ' \ (г1Тс\ (\С\ \\\
для потенциала диполя
где р = е I — момент диполя; наконец, для потенциала
квадруполя мы найдём
1 vi 1
п, пг
где величины рппг = е C1п1п> — 12ЪПП') являются ком-
компонентами квадрупольного момента, образующими сим-
симметричный тензор второго ранга. Он обладает пятью
независимыми составляющими, так как между шестью
компонентами симметрического тензора Рпп' — Рп'п имеется
одно тождественное соотношение:
Pxx + PuU+Pzz^O. A0,14)
Заметим, что к потенциалу A0,13) мы добавили
член
еП v-, 1^/2 1
(п == > о г V V / — V* A0 1 Si
Т А /л Tin' у п. и' — a v «» v1-'»^/
nfn'
48 СТАТИЧЕСКИЕ УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА [гл. II
равный нулю при г Ф 0. Благодаря этому нам удалось
в наиболее простом виде написать соотношение A0,14)
между компонентами квадрупольного момента.
Для случая заряда, распределённого по поверхности,
заданной уравнением
/(г) = 0 A0,16)
с поверхностной плотностью а (г), объёмная плотность
определится выражением
P = o(r)8(/)|grad/|. A0,17)
В самом деле, р (г) будет равняться нулю везде кроме
точек, лежащих на поверхности, определяемых уравне-
уравнением A0,16). Полный же заряд равен
е = \ р (г) {dr) =Л о (г) 8 (/) | grad /1 (dr). A0,18)
Для того чтобы доказать соотношение A0,17), пред-
представим элемент объёма (dr) равным произведению dS dn,
где dS — элемент поверхности /— const, a dn—элемент
линии, направленной по нормали к этой поверхности.
Тогда
С 0 (г)-| К | g (/) dS dn = с. A0,19)
Вычисляя далее последний интеграл по формуле F,5),
получим
e^iadS. A0,20)
В последнем выражении интегрирование должно совер-
совершаться по поверхности / = 0.
Таким образом мы приходим к обычной связи между
величиной заряда е и поверхностной плоскостью а.
В частности, если заряженной плоскостью является
плоскость (х, у) f то
? = elx,y)t(z). A0,21)
В случае же заряженной цилиндрической поверхно-
поверхности радиуса а
-a). A0,22)
j 1J] ПРОСТЕЙШИЕ ЗАДАЧИ ЭЛЕКТРОСТАТИКИ 49
Здесь г, z, ср представляют собою цилиндрические коор-
координаты.
Наконец, если заряженной поверхностью является
сфера радиуса а, то
P = o(e,?)8(r-fl)f A0,23)
где б и ср являются сферическими углами.
§ 11. Простейшие задачи электростатики
Применим теперь полученные решения уравнения
Лапласа-Пуассона к различным конкретным примерам.
а) Заряженная плоскость
Рассмотрим решение уравнения Лапласа-Пуассона для
случая осевой симметрии, когда заряды, порождающие
поле, распределены на плоскости z —0.
В этом случае согласно A0,21) объёмная плотность
зарядов [j будет связана с поверхностной плотностью а
при помощи соотношения
P = o(r)8(z), A1,1)
где г= \f х* -х- у2- Тогда уравнение Пуассона примет вид
V2<p=-4*a(rM(z), A1,2)
ИЛИ
оо
V2cp= -4тг jj a (г') 8 {г' -г) S (z) dr'. A1,3)
о
Подставим в A1,3) значение для о (z) из D,20):
±\fdx, A1,4)
и используем весьма естественное для задачи с осевой
симметрией представление 8 (г' — г) через бесселевы функ-
функции [см. соотношение D,27)]:
оо
8 (г' - /•) = i/'fF jj kJ0 (кг') Jo (kr) dk =
^J0{krt)JQ(kr)dh. A1,5)
Д« Иваненко я А. Соколов
50 СТАТИЧЕСКИЕ УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА [Гл. II
При этом из соотношения F,3) следует
откуда
оо оо
V2cp= —2 J Ac ^ ftdft ^ rro(rf)eHzJ0(krr)JQ(kr)drf. A1,6)
о о
Здесь /0 является бесселевой функцией нулевого порядка»
Деление на оператор V2 даёт
eHzJ0 (кг) _ eixzJ0 (кг) (Ц 1)
которое легко проверить путём непосредственного диф-
дифференцирования, замечая, что
£ + 50 'о (кг) = (£ + ЦУ0 (кг) = - AV0 (кг).
A1,8)
Отсюда находим значение потенциала <р:
оо оо
<р = 2 \ г 'a (rr) dr' \kdkJ0 {кг') /0 (кг) \ tfx j^-t. (И ,9)
о о
Интеграл по к удобнее всего взять, применяя теорию
вычетов.
В данном случае интеграл в границах от — оо до + сю,
дополненный интегралом по кругу бесконечно большого
радиуса (рис. 6), который в пределе * = ioo даёт исчеза-
исчезающий добавок, должен равняться произведению 2тл на
единственный вычет, получающийся в результате инте-
интегрирования вокруг точки y. = ik.
i v!" 1 7м т!
причём на рис. 6 путь интегрирования *) в комплексной
*) В. И. С м и р н о в, Курс высшей математики, т. III, ч. 2,
Гостехиздат, 1949, стр. 226.
11]
ПРОСТЕЙШИЕ ЗАДАЧИ ЭЛЕКТРОСТАТИКИ
51
плоскости изображён замкнутой кривой. Тогда A1,9)
переходит в
где
A1,11)
A1,12)
i = 2*\r'8(r')/0(ftr')dr'.
•I
0
В частном случае постоянной поверхностной плотности
о = const
Подставляя A1,13) в A1,11)
и производя интегрирова-
интегрирование по к, имеем
e~k\z\
ср == 2тго lim -^—j— =
*о к
= 2тгз ( Ит-т- — \z
A1,14)
причём постоянный бесконечный член -j- может быть
отброшен.
В случае же точечного источника е, расположенного
в начале координат:
р = eb (x) S (у) = е-^, A1,15)
ибо согласно D,28)
Отсюда
и
/(*)=*
A1,16)
A1,17)
4*
52 СТАТИЧЕСКИЕ УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА [гл. II
Вычисляя интеграл A1,17) с помощью формулы Лип-
Липшица*), получим известное выражение для потенциала
точечного источника
б) Заряженный цилиндр
Найдём потенциал, вызванный зарядами, распреде-
распределёнными на поверхности кругового цилиндра радиуса а.
Направляя ось z по геометрической оси цилиндра и пред-
предполагая, что поверхностная плотность о будет зависеть
только от z, имеем
Принимая во внимание (см. также предыдущий пример),
что
с (z) = \ 8 (z' - *) о (z1) dz' =
\ zr, A1,20)
CX)
8 (r- a) = a ^ kJ0 (ha) /0 (kr) dk9
о
имеем
=: _ 1 ^ Лс J о B') e*»<*-*'> dz' J kJ0 (ka) Jo (kr) dk,
0
откуда
CO
u. A1,21)
При интегрировании по переменной к предположим,
что г> а, так как в силу симметрии интеграла относи-
относительно величин г и а в противоположном случае г < а
мы должны в окончательном результате просто переста-
*) Р. О. Кузьмин, Бесселевы функции, ОНТИ, 1935,
стр. 143.
§11] ПРОСТЕЙШИЕ ЗАДАЧИ ЭЛЕКТРОСТАТИКИ 53
вить величины г и а. Интеграл, входящий в последнее
равенство, преобразуем к виду
°° ,Л (to) Jq (fa)
1 (*
Последнее соотношение легко проверить, если написать
. значение для первой функции Ханкеля
=J0(x) + iN0(x), A1,22)
H{0i)(-x) = Hi0i)(x)-2J0(x). A1,23)
Замыкая далее путь интегрирования от — оо до + со
по кругу в комплексной плоскости бесконечно большого
радиуса и учитывая, что при k = ioo имеем исчезающий
добавок (сравни с рис. 6), а также, что знаменатель под-
интегральной функции имеет в верхней полуплоскости
"единственный вычет в точке Ы, получим
=!
Кь (| * | г) /0 (| х | а); г > а (вне цилиндра), ^
^o(Nfl)Mlxlr); /*<« (внутрицилиндра),
где цилиндрические функции от мнимого аргумента
определяются равенствами
I0(x) = J0(ix); К0{х) = ^Н[{){1х). A1,25)
Тогда для искомого потенциала <р находим
? = -1Л е'«/М^*> A1,26)
где
/ (х) = \ е-1"'с [z') dz'.
В частном случае постоянной поверхностной плотности
(о = const);
, A1,27)
54 СТАТИЧЕСКИЕ УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА [гл. Ц
и следовательно,
<р = lim 2c
или
/ о х f In г; г > я,
<р = 2з.Ит( 1п--С )-2а{ ' A1,28)
где С = 0,577 ...—постоянная Эйлера; кроме того, так
же как и в предыдущем случае, постоянный бесконечный
член 2а ( In Cj может быть отброшен.
При стремлении радиуса цилиндра а к нулю мы полу-
получим потенциал заряженной нити:
«/(x)JS:0(|x|r)dx. (Ц,29)
Наконец, рассматривая точечный заряд как предель-
предельный случай заряженной нити, когда
a{z') = el{z'), A1,30)
найдём для потенциала ср известное выражение
со
<? = | \ cos v.z ■ Ко (хг) dx = yJ== . A1,31)
Последний интеграл проще всего вычислить с помо-
помощью известного из теории цилиндрических функций соот-
соотношения*):
(а>0, 6>0,m> — 1), в котором необходимо положить
0 « 0
*) Р. О. Кузьмин, Бесселевы функции, ОНТИ» 1935,
стр. 151.
5 12] КРАЕВЫЕ ЗАДАЧИ ЭЛЕКТРОСТАТИКИ 55
§ 12. Краевые задачи электростатики
Пусть нам заданы электрические заряды, распределён-
распределённые с плотностью р в двух средах, обладающих диэлек-
диэлектрическими постоянными £х и s2> между которыми имеется
некоторая поверхность раздела. Требуется определить зна-
значение потенциалов в обеих средах. В дальнейшем все
величины, относящиеся к первой и второй средам, будут
отмечаться соответственно индексами 1 и 2.
На поверхности раздела должны иметь место обычные
граничные условия:
где п является нормальной составляющей к поверхности
раздела.
Метод решения будет заключаться в искусственном
введении некоторых фиктивных зарядов: при нахождении
потенциала срь кроме плотности зарядов plf распреде-
распределённых в первой среде, мы вводим фиктивную плотность
зарядов р*, распределённых во второй среде. Аналогично
при определении ср2 вводим фиктивную плотность р|^
Тогда для потенциалов получим:
Неопределённые пока что фиктивные плотности [>*
и р| следует находить из граничных условий A2,1).
Рассмотрим некоторые конкретные случаи:
а) Если поверхность раздела является плоскостью
z = 0, то для случая одного точечного заряда, расположен-
нбго в первой среде в точке (х = у — 0, ъ = z0 > 0) (рис. 7),
имеем
(z-z0), A2,3)
56 СТАТИЧЕСКИЕ УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА [Гл. II
Значения для фиктивных плотностей будем искать так
же, как и в классическом методе изображений, в виде
A2,4)
При этом на рис. 7,я изображено истинное расположе-
расположение заряда и диэлектрических сред. На рис. 1,6 и 7,в
мы имеем изображение зарядов и диэлектрических сред
— е
с, w
Б7 X
п)
- е
с, х
б)
Рис. 7.
д)
для нахождения потенциала соответственно в верхней
(z > 0) и нижней (z < 0) средах.
Отсюда получим
■
_L
Vх2
A2,5)
Подставляя A2,5) в A2,1), найдём для определения
неизвестных фиктивных зарядов ег и е2 следующие урав-
уравнения:
i ==~-*2,
откуда
s^'z 2«ча
1 ~~ •- -l s2 в> 2 "^ в, +6, *
A2,6;
A2,7)
12]
КРАЕВЫЕ ЗАДАЧИ ЭЛЕКТРОСТАТИКИ
57
Подставляя A2,7) в A2,5), находим искомые значения
для потенциалов:
1 . е1-з2 1
* + (z — Z
(z + zo)
-)-
б) Пусть границей раздела двух сред является
бесконечный круговой цилиндр радиуса а. Диэлектри-
Диэлектрическую постоянную внутренней части цилиндра (г < а)
обозначим через elf внешнего же пространства (/*>«) —
через г2. Найдём потенциалы, вызванные наличием
точечного заряда, помещённого на оси
цилиндра в начале координат (рис. 8).
Фиктивные вспомогательные заряды
согласно только что изложенному методу
расположим на поверхности цилиндра.
Тогда согласно формулам A1,26) и
A1,31) имеем: для внутренней части ци-
цилиндра г < а
Ъ = ^
с,ег
Рис. 8.
+ /1(x)ifo(|x|fl)/o(|x|r)]dxi A2,9)
для внешней части цилиндра
"/2(x)tfi,(|*|rO0(|x|eldx.
A2,10)
Как видно из A1,26), вместо фиктивных поверхно-
поверхностных плотностей мы ввели вспомогательные величины
//<у\ ТПГ Т | V 1
J I Л I XL #2 \Л/»
Используя граничные условия, имеем для нахожде-
нахождения /х и /2
f[Jfo(|x|fl) + /iJfo(|x|fl)/o(|x|fl)] =
(| xj a)-/,^,Ax10O,Ax10) =
/А
A2,12)
58 СТАТИЧЕСКИЕ УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА [гл. II
Определяя отсюда величины Д и /2, найдём иско-
искомые значения для потенциалов:
ос
I A2,13)
ф = *. \ cos xz go (хг) л. /12 14)
^2 s27i .) ха[аКй(ха) 11(ха)-}-10(ха) Кг(ха)] • V » /
О
При этих вычислениях мы учли следующие соотно-
соотношения:
fcosx,
J
3,
в) С помощью 8-функции можно описать также
скачки потенциала и его градиента при наличии заря-
заряженных поверхностей.
Пусть на плоскости z=0 расположены поверхност-
поверхностные заряды с плотностью с (xf y)f а также имеется двой-
двойной электрический слой интенсивности g*(x, у).
Тогда значение для потенциала <р может быть найдено
из следующего уравнения:
У2ср = — 4тгр — 4тсао (z) — 4из*о' (z). A2,16)
Плотность заряда и потенциал верхней части полу-
полуплоскости обозначим через рх и ср1э а нижней—через
Р2 и ?2t т« е- ПОЛОЖИМ
A2,17)
С помощью разрывной функции B,4) мы можем
записать:
f 1 N Г 1
§ 12] КРАЕВЫЕ ЗАДАЧИ ЭЛЕКТРОСТАТИКИ 59
Подставляя последние равенства в A2,16) и учиты-
учитывая, что
f(z) = b'(z), A2,19)
/(z)8(*) = /(O)8(*).
найдём
= -4т;с5 (z) -4toV (z), A2,20)
откуда автоматически получим искомые граничные
условия:
A2,2Г
Наконец, пусть мы имеем уравнения
div JD = 4r:p + 4тиао (z),
rot J5 = 0, A2,22)
где с является поверхностной плотностью зарядов,
а поля в верхней (с индексами 1) и нижней (с индексами 2)
части полупространства определяются из соотношений
div Dj = 4тго1,
А- ТЪ / A2>23)
div D2 = 4тср
Тогда полагая
A2,24)
60 СТАТИЧЕСКИЕ УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА [гл. II
найдём
+ div Б2 • (у - Y (г)) + S (z) (n (D, - ВД,
rot E= rot Ех ■ (д + у (z
где м — единичный вектор, направленный по оси z;
сравнивая A2,24) с A2,22), получим условие на гранич-
граничной плоскости
§ 13. Краевые задачи теории кароттажа
Интересной областью для применения краевых
задач теории электричества представляется «кароттаж»
или один из методов геологической электроразведки.
Как известно, основная задача теории кароттажа заклю-
заключается в отыскании потенциала, вызванного током, в
среде с проводимостью.
Нетрудно показать, что основные задачи кароттажа
могут быть сведены к электростатике путём определён-
определённого сопоставления величин.
Действительно, исходя из уравнения непрерывности
для плотности тока j и заряда р
| A3,1)
и закона Ома
A3,2)
получим уравнение, связывающее потенциал ср с плот-
плотностью распределения зарядов {>;
§ 13] КРАЕВЫЕ ЗАДАЧИ ТЕОРИИ КАРОТТАЖА 61
При наличии неподвижного точечного источника,
расположенного . в точке v', имеем
р = в(*)8(г—г')- A3,4)
Подставляя A3,4) в A3,3) и учитывая ещё определе-
определение тока
1=-%, A3.5)
найдём основное дифференциальное уравнение теории
электрического кароттажа:
V2cp=-^8(r-r'). A3,6)
При наличии двух сред с различными проводимо-
стями Хх и Х2, необходимо ещё учесть граничные усло-
условия, выражающие равенство потенциалов и нормальных
составляющих токов jn на поверхности раздела:
Тем самым задача кароттажа будет сведена к за-
задаче электростатики, если произвести следующее сопо-
сопоставление:
/-»4тге, Х->з A3,8)
(см. соответствующие формулы предыдущего пара-
параграфа).
Таким образом результаты предыдущего параграфа
дают готовый ответ на аналогичные задачи кароттажа:
отыскание в двух средах потенциала, вызванного током
при наличии плоской или цилиндрической поверхности
раздела.
Однако в случае электростатики соприкосновение ди-
диэлектрика с металлом приводит к граничному условию:
<Р = 0, A3,9)
т. е. к задаче Дирихле, поскольку в металле мы мо-
можем положить поле равным нулю. В то же время в тео-
теории кароттажа соприкосновение проводящей среды с
62 СТАТИЧЕСКИЕ УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА [гл. II
диэлектриком приводит к проблеме Неймана, когда на
границе
2 = 0, A3,10)
так как ток не может входить в диэлектрик.
Рассмотрим несколько типичных задач, сводящихся
к задаче Неймана.
а) Источник тока в скважине
Найдём потенциал точечного • источника тока, поме-
помещённого в начале координат в некоторой проводящей
среде и отделённого от внешнего пространства, являю-
являющегося диэлектриком, цилиндрической поверхностью
радиуса, равного единице (а = 1), с осью, направлен-
направленной по оси z (см. рис. 8, где необходимо положить
а = 1, е = -^> Ч = ^> &2 = У = 0). В данном случае при-
применим только что изложенный метод, поскольку на
границе диэлектрика с проводником
?1 =0. A3,11)
Для решения этой задачи мы будем исходить из общего
уравнения
££^iw. A3Д2)
В последнее выражение вместо 8 (z) подставим обычное
значение:
Z(z) = ±\e**d*. A3,13)
При конструировании же 8 (г) используем известное
в теории бесселевых функций равенство [ср. также
с D,26I:
1
2 Г
jtt-\ \ гJo (rsn) JQ (rsnr) dr = 8nnr, A3,14)
^o \sn) J
§ 13] КРАЕВЫЕ ЗАДАЧИ ТЕОРИИ KAPOTTAJ&A 63
где sn являются корнями уравнения
ЛЫ = 0, A3,15)
равными
so = 0, $х=3,83, ^2 = 7,02 и т. д.
Согласно равенству D,26) мы можем при 0<г<1
написать соотношение
оо
г ~ 2л J* (e )JO\rsn)JoV Sn),
п=0
сохраняющее силу также для предельного случая г' —>0:
п-0
Подставляя эти выражения для S-функции в A3,12)
и учитывая равенство A1,7), найдём значения для
потенциала
ЙЙМЙЗЬ ,17,
Вычисляя значение последнего интеграла по фор-
формуле A1,10), получим*)
\nJ*0(sn) so
n=0
Решение однородного уравнения выбирается равным
?о = — ttv » тогда потенциал ср останется во всех точ-
ках конечным. Данный выбор ортогональных функ-
S (г)
ции для конструирования —^ автоматически приводит
к выполнению граничного условия A3,11):
-^-и1 = -^^) = 0- A3'19)
*) См. В. А. Ф о к, Теория кароттажа, ГТТИ, 1933.
64
СТАТИЧЕСКИЕ УРАВНЕНИЙ ЭЛЛИПТИЧЕСКОГО ТИЙА [гл. И
Выделяя из суммы A3,18) член при w = 0, найдём
со
п=1
В частности, на больших расстояниях от источника
тока (|z|>l) можно ограничиться одним первым чле-
членом, т. е. потенциал ср будет зависеть только от z:
*=-53il*l- A3'21)
Значение же для плотности тока вдоль оси z будет
оставаться в этом случае постоянным и равным
А- <13'22)
Напомним, что радиус скважины а положен у нас
равным единице.
Коэффициент % обусловлен разветвлением тока в обе
стороны.
б) Бесконечно тонкий пл^аст
Найдём потенциал в точке В с координатами г =
= У^х2 -+- у2 = О, z, вызванный точечным источником тока /,
расположенным по оси кругового отверстия радиуса
а = 1 на расстоянии zQ > 0 от начала
координат *) (рис. 9).
Обозначая проводимость среды
.„* iff через X и считая бесконечно тон-
| кий пласт идеальным изолятором
ЛА (У = 0), мы должны решать основное
уравнение A3,6) при условии, что
" на поверхности пласта z= ±0
g = 0f A3,23)
т. *e. sb предположении, что ток не проходит через пласт.
Рис. 9.
*) Не нарушая общности задачи, мы всегда можем выбрать
такое направление оси z, при котором величина zQ будет иметь
шоложительное значение.
§ |3] КРАЕВЫЕ ЗАДАЧИ ТЕОРИИ КАРОТТАЖА 65
Разделим всё пространство на две области: z > О
(соответствующие величины будем обозначать инде-
индексом 1) и z<0 (соответствующие величины будем обо-
обозначать индексом 2).
Для решения задачи применим метод введения допол-
дополнительных фиктивных токов, определяемых затем из
граничных условий, аналогично методу фиктивных заря-
зарядов, рассмотренному выше.
Искомые потенциалы будем определять из урав-
уравнений
1
+ ^8(з) \al(r')b(r-r')dr'] , A3,24)
О
1
Здесь в правой части уравнения для cpi введён,
во-первых, фиктивный зеркальный источник тока в точке
— z0, равный
I4z + z0)^, A3,25)
и, во-вторых, фиктивные поверхностные токи
i-i(z)\ а, (г') 8 (г' - г) dr' = f L Ь & 3i И: г < 1, A326)
2Л 6^ I 0; г>1,
расположенные в отверстии пласта с поверхностной плот-
плотностью ах (г).
В правой части уравнения для ср2 достаточно огра-
ограничиться фиктивным поверхностным током в отверстии
скважины.
Граничные условия примут в нашем случае вид
5 Д. Иваненко А. Соколов
66 СТАТИЧЕСКИЕ УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА [гл. II
Подставим в A3,24) вместо 6 (г — г') значение D,27),
согласно которому
^kJQ(kr)JQ(kr')dk. A3,29)
о
Кроме того, учтём, что последнее соотношение сохра-
сохраняет силу для предельного случая [см. равенство
D,28)], т. е.
^kJQ(kr)dk. A3,30)
о
Вместо 8 (z) мы можем подставить значение A3,13).
Тогда имеем
со
—етзс S kJ°{kr) dk \eUz dx x
О
1
X [<Н**э + eix*> + \ r'J0 (уУ) gx (/•') dr'].
о
Воспользовавшись далее правилом деления на опе-
оператор V2, получим
6?X \
о
X Г
f rVofxr'Ja^r'Jrfr'] . A3,31)
о J
При интегрировании по переменной х примем во
внимание равенство A1,10):
х Г rA|t-fii + .-«^ю) + г*« Jrv0 (*r;) ^ (г1) dr' 1. A3,32)
Щ КРАЕВЫЕ ЗАДАЧИ ТЕОРИИ КАРОТТАЖА 67
Далее с помощью формулы A1,17) найдём
1 Г 1 1 д I
471Л L у/ г2 -f- B — z0J у r2 + (z + z0J
00 1
е-** /0 (Ar) rfA \ r'JQ (kr') a± (rf) drr 1. A3,33)
о о
Аналогичным путём получим
с» 1
г'7о (^') (г') di". A3,34)
Для определения плотности поверхностных токов
ах и а2 найдём значение для потенциалов и их нормаль-
нормальных составляющих при z=0.
Учитывая соотношения A3,33) и A3,34), легко пока-
показать, что
со 1
д з \ I Г г Г
6 6
= ] "~4^Xai^); r<1' A3,35)
I 0; г>1.
0; г>1.
Отсюда видно, что граничные условия A3,27) будут
выполняться автоматически.
Соотношения же A3,28) приведут нас к следующим
уравнениям для определения искомых значений поверх-
поверхностных токов аг и а2:
оо 1
^ /0 (Аг) rfA ^ r'JQ (krf) с (/•') dr' = I . A3,36)
00
Последнее уравнение при z0 = 0 (т. е. когда источ-
источник Л находится в начале координат) решается точно.
б*
68 статические Уравнений эллиптического типа [гл. II
В этом случае
в(г) = Ш, A3,37)
а для потенциалов cpi и Ъ получаем значения
<fc = <P' = iy=f <13>38>
которые также имели бы место при отсутствии диэлек-
диэлектрической прокладки.
В частности, в точке В, находящейся на оси цилиндра
(г= 0), имеем (z0 = 0)
•ь = * = та71Г- A3>39)
В дальнейшем полезно будет воспользоваться теоре-
теоремой взаимности, согласно которой значение потенциала
должно оставаться неизменным, если мы переменим-
местами точки А (источник тока) и В (точку наблю-
наблюдения) .
Поэтому, например, мы можем утверждать, что при
любом положении источника А на оси скважины потен-
потенциал в начале координат будет определяться формулой
ь = ъ = йш- A3>40)
Интегральное уравнение A3,36) решается прибли-
приближённо, но с большой точностью при | zo\ > 1, т. е. когда
источник тока находится от отверстия скважины на рас-
расстоянии, во много раз превышающем радиус скважины
(zo># = l). Полагая в этом случае
)] A3,41)
*о L
где символ О ( -у ) означает, что порядок отброшенных
членов по сравнению с единицей достигает значения
1
-j- , получим
Последнее равенство легко проверить, если учесть из-
§ 13] КРАЕВЫЕ ЗАДАЧИ ТЕОРИИ КАРОТТАЖА 69
вестные из теории цилиндрических функций соотношения:
1
sin к С sin к т /7 ч ,7 п . л /J(O /o.
^^(*г)£» ;г<1. A3,43)
Подставляя A3,42) в равенства A3,33) и A3,34), найдём сле-
следующие значения для потенциала на оси скважины (/• = 0):
A3,44)
= i/(M, zo), A3,45)
где
A3'46
Согласно теореме взаимности последнее выражение
можно представить также в виде
f(\z\, zo) = f(zo, \z\) =
4
Формулой A3,46) мы должны пользоваться при
zo>l, т. е. когда источник А находится на большом
расстоянии от границы раздела, а формулой A3,47)
при \z\ > 1, т. е. когда точвд наблюдения В удалена на
большое расстояние от границы раздела*).
Если же обе точки находятся на большом расстоя-
расстоянии от границы раздела (|z|>l) и z0 > 1), то, при-
принимая во внимание, что
.11 1
arct?— = —,
Ь Z0 I «О » 1 Ч
**) В теории кароттажа случай | z \ < 1 и z0 < 1 интереса не
представляет, так как расстояние между источником и точкой на-
наблюдения должно всегда во много раз превышать радиус скважины,
Т. е. |*-*9|>1.
70 СТАТИЧЕСКИЕ УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА . [гл. II
найдём для / в согласии с теоремой взаимности выра-
выражение, симметричное относительно \z\ и z0:
Наконец, когда одна точка А или В пересекает пласт
(например, zo = 0f a. z > 1), то
' = T7j'
откуда находим значение для потенциала, совпадающее
с точным выражением A3,39).
§ 14. Обобщённое уравнение Пуассона
Простейшим лилейным обобщением уравнения Пуас-
Пуассона является уравнение
V*<p-AjT=-4«p, A4,1)
имеющее весьма широкие применения в различных обла-
областях современной физики.
а) Теория ядерных сил и мезонов
(классическая мезодинамика)*)
В теории ядерных сил величина к0 пропорциональна
массе мезона т, т. е. массе частицы, переносящей ядер-
ядерные силы. Тогда [j является статической плотностью
ядерных зарядов (нуклеонов: протонов, нейтронов), поро-
порождающих мезонное поле. Несмотря на то, что теория
мезонных ядерных сил встретилась с рядом трудностей
и не может считаться законченной, всё же уравне-
уравнение A4,1) выражает основные фундаментальные законо-
закономерности ядерных взаимодействий.
б) Теория гравитации Зеелигера
В теории тяготения Ньютона, где потенциал подчи-
подчиняется уравнению Пуассона (к^—>0), существует извест-
*) Более подробно классическая мезодинамика будет изложена
р гл. V.
§ 14] ОБОБЩЁННОЕ УРАВНЕНИЕ ПУАССОНА 71
ная космологическая трудность: уравнение Пуассона не
имеет конечного решения при равномерном распределе-
распределении [> во всём пространстве. Для устранения этой трудно-
трудности Нейман и Зеелигер предложили дополнить уравнение
Пуассона членом —/cgcp, приведя его к виду A4,1).
Тогда при р = const потенциал будет также иметь постоян-
постоянное конечное значение, равное
При построении общей теории относительности, кото-
которая представляет собою обобщение теории тяготения
Ньютона, мы встречаемся с аналогичной трудностью.
Для её устранения Эйнштейн предполагал сначала до-
дополнить свои уравнения тяготения космологическим чле-
членом, аналогичным поправке Зеелигера. Впрочем, как
было показано А. А. Фридманом, даже без дополнитель-
дополнительного космологического члена можно устранить указан-
указанную трудность, если перейти к геометрической струк-
структуре мира, зависящей от времени, иначе говоря, к ком-
компонентам метрического тензора g^v (t). Ввиду этого
обстоятельства космологический член сейчас часто в тео-
теории не рассматривается. Здесь следует подчеркнуть
сугубо предварительный характер каких бы то ни было
космологических теорий, представляющих попытки опи-
описания известной части бесконечной вселенной в тече-
течение некоторого отрезка времени.
в) Теория сильных электролитов
Уравнение типа A4,1) лежит в основе теории сильных
электролитов, где ср является потенциалом ионной атмо-
атмосферы. Для простейшего случая бинарных электроли-
электролитов, у которых плотности положительных и отрицатель-
отрицательных ионов равны (п+ = п- = п), а сами ионы обладают оди-
одинаковыми валентностями, имеем Z+ = Z_ = Z. При опре-
определении потенциала ср будем исходить из уравнения
Пуассона:
-^(/, -A4,3)
где г — диэлектрическая постоянная раствора.
72 СТАТИЧЕСКИЕ УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА [гл. Ц
Плотность заряда р' Дебай и Хюккель задают по фор-
формуле Больцмана в виде
где p — плотность внешних зарядов.
Разлагая последнее выражение в ряд и ограничиваясь
линейными относительно е членами, получим уравнение
вида A4,1), где
hl %{eZ)\ A4,5)
г) Теория сверхпроводимости
В теории сверхпроводимости Лондона, имеющей ма-
макроскопический феноменологический характер, электро-
электромагнитные потенциалы также подчиняются уравнению
вида A4,1), причём постоянная к^ равна:
A?=S-\ A4,6)
где п — число электронов в единице объёма, г — заряд,
am — масса электрона.
Величина \ =.— определяет так называемую «глу-
* °
оину проникновения» полей в сверхпроводник.
Подставляя в A4,6) значения для заряда е и массы т
электрона, а также экспериментально найденное значение
для X ~ 10~5 см, получим для концентрации сверхпрово-
сверхпроводящих электронов значение п = 1022.
Установим теперь функцию Грина G обобщённого
уравнения Пуассона, которая может быть найдена из
уравнения
V2G-hlG= -Ъ(г-г')= -8 (Л). A4,7)
Повторяя вычисления § 10, найдём
Интегрируя A4,8) по сферическим углам [см. фор-
формулу A0,6)], получим
J 14] ОБОБЩЁННОЕ УРАВНЕНИЕ ПУАССОНА 73
где
jR= \r-r'\.
Беря последний интеграл при помощи теории выче-
вычетов [см. также A1,10)], находим для сингулярной части
p-k0R
с Ъ <1410)
Определив функцию Грина, мы можем записать реше-
решение уравнения A4,1) в виде
(r')-^(dr'). A4,11)
В частности, в случае точечного источника единичной
интенсивности, расположенного в начале координат:
Ро = 8(гЬ
для искомого потенциала находим
Отсюда видно, что поведение обобщённого потенциала
характеризуется эффективной длиной:
ro=i. A4,13)
Если г < Го, то потенциал ср с точностью до членов порядка
— совпадает с потенциалом уравнения Пуассона:
С другой стороны, на больших расстояниях от источ-
источника (г > г0) потенциал ср будет убывать с увеличением
г по экспоненциальному закону.
Таким образом взаимодействие, характеризуемое
уравнением A4,1), приводит к так называемым силам
короткого действия, которые оказываются отличными
от нуля практически лишь на расстояниях, не превы-
превышающих некоторого значения г0.
ГЛАВА III
УРАВНЕНИЯ, ЗАВИСЯЩИЕ ОТ ВРЕМЕНИ
§ 15. Уравнение движения классической механики
Как известно, уравнение классической механики при
прямолинейном движении имеет вид
s=/(*), (ад
где f(t) является внешней силой, v — скоростью движе-
движения, а масса частицы положена равной единице.
Решение последнего уравнения, вообще говоря, хоро-
хорошо известно. Однако мы хотим провести здесь анализ
его решения с помощью формализма 6-функции. Согласно
§ 7 будем искать решение в виде
v=-\G(t,t')f{t')dt'. A5,2)
Функция Грина G равна
где GQ= - С— ^= const, т. е. несингулярная часть
функции Грина является решением однородного урав-
уравнения A5,1).
Подставляя вместо b(t — tr) выражение D.20), найдём
Взяв главное значение для последнего интеграла,
имеем
1 t—t' n 1 /—1 —С; t>t'y
— С; t < t'.
§ 15] УРАВНЕНИЕ ДВИЖЕНИЯ КЛАССИЧЕСКОЙ МЕХАНИКИ 75
Общее решение для v может быть представлено в виде
где
t оо
Ъ'= ^ (l+C)f(t')dt', va=^Cf(t')dt'. A5,4)
-оо t
В первом решении (vr) мы интегрируем по всем зна-
значениям времени t\ меньшим значения t. Наоборот, во
втором решении (va) интегрирование производится по
всем значениям времени t\ превышающим t. Иными
словами, в первом случае мы учитываем «запаздывающее
действие» силы на материальную точку, а во втором —
« опережающее».
Для определения постоянной С задаём значение ско-
скорости, которую принимаем в некоторый момент вре-
времени t0 равной нулю (г;0 = 0).
Пусть скорость задана в какой-то момент, предше-
предшествующий действию €илы, например, v = О при t= — оо.
В этом случае С = 0, т. е. решение, соответствующее
опережающему действию, исчезнет, и мы будем иметь
t
v=\^ f(t')dt'. A5,5)
—оо
Точно так же, если скорость задана в какой-то момент
времени после действия всех сил, например, г; = 0 при
t = + о", получим С = — 1.
В этом случае решение, соответствующее запаздываю-
запаздывающему действию,* исчезает:
оо
\ A5,6)
Таким образом следует учитывать запаздывающее,
илл соответственно опережающее действие силы на мате-
материальную точку в зависимости от того, задаём ли мы
нулевое значение скорости в моменты времени до или
после включения силы.
76 УРАВНЕНИЯ, ЗАВИСЯЩИЕ ОТ ВРЕМЕНИ {ГЛ. III
Найдём значение для координаты в том случае, когда
начальная скорость v и координата х заданы, как обычно,
в момент, предшествующий включению силы, т. е. х = О,
v = О при to= — оо.
Как видно из A5,5), в этом случае
t
'Ь= \ (t-t')f(t')dt'. A5,7)
Правильность последнего соотношения легко прове-
проверить, так как
| = о= \ f{t')dt'
—оо
и при t = — оо, х = 0.
С помощью й-функции мы можем также задать силу,
сообщающую точке мгновенно конечную скорость v0,
или даже конечное перемещение х0, например, в момент
времени t = 0.
Для этой цели мы должны положить
/ @ = Vo% @ + Sos' It). A5,8)
Тогда согласно A5,7) имеем
Таким образом мгновенная бесконечная сила v0 8 (t)
сообщает материальной точке конечную скорость.
Две бесконечные силы xoh'(t)9 равные по величине и
противоположные по направлению и действующие одна
после другой через бесконечно малый промежуток вре-
времени [см. определение C,12), данное для производной от
S-функции], сообщают материальной точке конечное пере-
перемещение.
Решение наиболее простой задачи механики, когда
кроме действующей силы F (i) заданы ещё начальные
условия в виде значений координаты и скорости (х0 и
г;0 при t = 0), мы также можем получить при помощи
формулы A5,7).
16] УРАВЙЕНИЕ tEnjIOilPOBC^HOCtH 75
Полагая
/ (t) = *o§' (t) + vob (t) + F{t)(j + t (*)) , A5,10)
найдём следующее выражение для искомой координаты:
0; t < 0.
Аналогичным образом с помощью формализма 8-функ-
ции решается ряд других задач механики, сформулиро-
сформулированных в виде линейных дифференциальных уравнений.
§ 16. Уравнение теплопроводности
(уравнение параболического типа)
Уравнения параболического типа не менее важны
для физики, чем эллиптические и гиперболические. В
самом деле, к ним относятся уравнение теплопровод-
теплопроводности, диффузии, статистические уравнения типа Фоккера-
Планка, а также основное уравнение Шредингера нере-
нерелятивистской квантовой механики (содержащее мнимый
коэффициент при времени). Мы остановимся для простоты
на типичном примере уравнения теплопроводности.
Уравнение теплопроводности, описывающее распро-
распространение тепла в стержне, имеет вид
Lu(x,t)=-±Q(x,t), A6,1)
где
j
дхг а2 дг
т —¥- — - L
~ Яг* п* ЯГ »
и — искомая температура стержня, зависящая от коор-
координаты х и времени t, Q — внешний источник тепла, кото-
который характеризует количество тепла, сообщаемое в еди-
единицу времени единице длины стержня; х и а2 являются
соответственно коэффициентами внутренней теплопровод-
теплопроводности и температуропроводности.
78 УРАВНЕНИЙ, ЗАВИСЯЩИЕ ОТ ВРЕМЕНИ [гл. Ш
Согласно G,6) решение уравнения A6,1) следует искать
в виде
и fat) = 1 ^ G (х, х'\ t, tf) Q (х', t') dx' dt'. A6,2)
Как обычно, функцию Грина G мы находим из условия
где GQ является решением однородного уравнения A6,1).
Считая стержень простирающимся безгранично в обе
стороны, мы вместо Ь(х — х') и 6 (t — ?) можем подставить
значение D,20). Тогда получим
dkl dk + G°e
Интегрируя последнее выражение по переменной к19
получим [ср. с вычислением интеграла A1,10)]
°; *>*'' A6,4)
t<t'.
Несингулярная часть функции Грина Go может быть
представлена в виде
оо
Go = J \ е~к2«2 С-'')cos k(z-z')f (A) dk, A6,5)
где /(/.) ограничено лишь требованием, чтобы последний
интеграл имел смысл для всевозможных значений t — t'
и х - х'.
В случае запаздывающего действия мы должны по-
положить / (к) = 0. Тогда
['>cos k(x — x')dk; t>t', /ла а.
v ' Ad,d)
о
0; t<t'.
§ 16] УРАВНЕНИЕ ТЕПЛОПРОВОДНОСТИ 79
Наоборот, в случае опережающего действия мы имеем
/(*)= -1. Тогда
0; t > *',
к; t<t'. A6'7)
Последний интеграл расходится. Поэтому в задаче
теплопроводности функции Грина с одним лишь опере-
опережающим действием не существует, что связано с пара-
параболическим характером исходного уравнения*).
Вычисляя интеграл A6,6), находим окончательное
выражение для функции Грина:
(х-х'J
17Щ=ще ' t>l A6,8)
0; t<t'.
Подставляг A6,8) в равенство A6,2), найдём извест-
известное решение, которое находится обычно более громозд-
громоздким способом:
t (ar-s')a
и (х, t) = -^- \ dx' \ \*a^r)Q {х\ Г) dt'.
ZX \ ТС J —оо X t 1
A6,9)
Применим полученное решение к некоторым типичным
случаям, которые особенно просто формулируются с по-
помощью 8-функции.
а) Найдём распределение температуры в зависимости
от времени t и положения х, когда мгновенный источник
нагревает в момент t = 0 стержень до начальной темпера-
температуры /(#), которая является функцией координаты х.
*) Заметим, что для оператора L = —а + —г ^т» наоборот, не
существует решений с запаздывающим действием.
80 УРАВНЕНИЯ, ЗАВИСЯЩИЕ ОТ ВРЕМЕНИ [гл. III
Вместо начальной температуры мы можем задать внеш-
внешний источник с помощью формулы
Q{x',t') = lJ{x')l{t'). A6,10)
В самом деле, интегрируя по времени, получим из-
известное соотношение между количеством тепла и темпе-
температурой:
^(x',t')dt' = ^-J(x'). A6,11)
Формула A6,10) заменяет обычный способ задания
начального условия.
Подставляя A6,10) в равенство A6,9), найдём
^f{x')dx>. t>0, A6>12)
0; t < 0.
В частности, если внешний источник сообщает неко-
некоторое количество тепла q в момент t = 0 одной лишь точке
х = 0, то
Тогда полученное выше решение для распределения
температуры при t > 0 принимает вид
_ х2
е~Шг ш A6,13)
и ш
б) В качестве следующего примера найдём распреде-
распределение температуры в стержне, появляющейся благодаря
движению с некоторой постоянной скоростью v точечного
источника, отдающего в единицу времени количество
тепла, равное q. В этом случае
Q (x'9 t') = go (a/ - vt'). A6,14)
Подобная задача имеет, например, место при иссле-
исследовании горения угольного пласта или при исследовании
нагревания стержня при электросварке.
§ 16] УРАВНЕНИЕ ТЕПЛОПРОВОДНОСТИ 81
Подставляя A6,14) в общую формулу A6,9), получим
после интегрирования по х'
u = -^L=e^I9 A6,15)
2х у тс
где
1 = 2 \ е *»2v2 4a2 dy, A6,16)
t = x — Ы и y = \/~t — t'.
Разбивая последний интеграл на два интеграла:
и вводя новые переменные:
найдём
Здесь
а функция Гаусса ^(х) определяется известным равен-
равенством:
-*! dz. A6,18)
6 Д. Иваненко и А. Соколов
%% УРАВНЕНИЯ, ЗАВИСЯЩИЕ ОТ ВРЕМЕНИ [гл, Ш
Прежде всего определим температуру источника тепла.
Подставляя в выражение A6,15) значение / при £ = О,
имеем
A6,19)
2а
т. е. с увеличением времени температура источника
ha2
постепенно возрастает, приближаясь при t > -у- к своему
предельному значению
да2
00 xv
Найдём распределение температуры в различных
точках стержня, лежащих вблизи источника (| £ [ < vt)
/ иа2 N
при больших значениях времени t f t > — ) •
Формулы A6,15) и A6,17) дают в этом случае сле-
следующее выражение для температуры:
— е а2\ I >0 (x> vt),
v K h A6,20)
Таким образом температура тех точек стержня, через
которые прошёл источник (Е < 0, х' < г;£), оказывается
постоянной и равной температуре источника. По направле-
направлению же движения источника (х > ы или £ > 0) темпера-
температура спадает с увеличением расстояния по экспоненциаль-
экспоненциальному закону.
В качестве последнего примера укажем на случай
покоящегося источника, действующего неопределённо
долгое время, начиная с момента t = 0.
Этот пример, очевидно, является частным случаем
предыдущего, когда скорость источника стремится к нулю.
Полагая в равенствах A6,15) и A6,17) скорость
о = 0, найдём распределение температуры вдоль стержня:
A6,21)
\2a/t) J
§ 16] УРАВНЕНИЕ ТЕПЛОПРОВОДНОСТИ 83
Отсюда, полагая х = О, найдём температуру источника
tt = *^' A6,22)
которая будет возрастать пропорционально квадратному
корню из времени.
Выражение A6.22) можно рассматривать также как
предельное значение соотношения A6,19), в котором
скорость движения v -следует положить равной нулю.
При помощи последних формул мы можем найти
полное количество тепла, которое выделяет источник
в течение времени t.
Умножая A6,21) на \dx Г 4~К0ЭФФиЧиент тепло-
теплоемкости J и интегрируя по всей длине стержня, найдем
У
A6,23)
Как известно,
]dx = ±
откуда
Это выражение равняется количеству тепла, выделен-
выделенного внешним источником в течение времени t. Полагая
в A6,14) г? = 0 и интегрируя затем по времени (от 0 до t)
и по длине стержня, содержащей источник, получим
вновь аналогичное значение для Q.
Метод, развитый нами в этом параграфе, допускает
также простое обобщение на случай распространения
тепла в плоском или в пространственном случае.
6*
84 УРАВНЕНИЯ, ЗАВИСЯЩИЕ ОТ ВРЕМЕНИ [Гл. III
§ 17. Волновое уравнение Даламбера
(уравнение гиперболического типа)
Как известно, уравнение Даламбера
L<p=-4iup, A7,1)
где L = V2—о"^¥> имеет весьма большое применение
во многих областях математической и теоретической
физики, так как оно описывает распространение электро-
электромагнитных, гравитационных, звуковых волн и т. д.
С точки зрения релятивистской квантовой теории поля,
это уравнение применимо ко всем полям, не связанным
с частицами, обладающими массой покоя.
Следуя общему правилу, решение уравнения Далам-
Даламбера будем искать в виде
t'9 A7,2)
где (dvf) ~dx' dy' dz' является элементом объёма трёх-
трёхмерного пространства, а функция Грина G может быть
найдена из соотношения
G= -L~xb{r-r')b(t—tK). A7,3)
Пусть искомая функция ср удовлетворяет некоторым
заданным граничным условиям.
Постараемся подобрать систему ортонормированных
функций, удовлетворяющих уравнению
Lvn = — \2vn,
причём
\ A7,4)
а величина X2 представляет собой собственное значение
оператора L и является вещественной величиной; соб-
собственные же функции vn, зависящие от трёх параметров п
(щ, п2, п3) должны удовлетворять тем же граничным
условиям, которым подчиняется искомая функция ср,
наконец, трёхмерный символ Кронекера-Вейерштрасса
равен
W1=W1> Л2=^2> П3=Пву
во fecex остальных случаях.
'Ч
§ 17] ВОЛНОВОЕ УРАВНЕНИЕ ДАЛАМБЕРА 85
Выражение для S-функцйй, входящих в равенство
A7,3), мы представим в виде
8 С - *') = Тъ \ e-icxit-n Л. A7,5)
Здесь сумма по п является тройной и берётся по всем
значениям целых чисел п19 п2 и п3.
Подставляя найденные соотношения в A7,3) и учи-
учитывая равенство A7,4), найдём
0 = 6, +Go, A7,6)
где сингулярная часть функции Грина Gx равна*)
или, интегрируя по переменной х, найдём
^ = 4,fcf, 2 t+(r')»n(r)Sinclrn • A7,8)
n
Несингулярная часть Go может быть представлена
в форме
Со=т 2 * (О ^ (^)
A7,8а)
удовлетворяющей однородному уравнению
Если задача требует ограничения одними запаздыва-
запаздывающими потенциалами, то следует положить А = 1 и В = 0.
*) Здесь и в дальнейшем, когда полюсы лежат на вещественной
оси, мы будем вычислять главное значение интеграла. Вообще же
интеграл, у которого полюсы лежат на вещественной оси, не является
однозначным. Эта неоднозначность будет компенсироваться нами
путём прибавления к главному значению несингулярной части.
В рассматриваемом случае этой несингулярной частью явдяется
решение Gq. я '
86 УРАВНЕНИЯ, ЗАВИСЯЩИЕ ОТ ВРЕМЕНИ [ГЛ. III
В этом случае получаем
К (V) »п (г) ^ -^; t>f,
0; t<t\
т. е. для того, чтобы найти потенциал в данный момент
времени t, следует учесть влияние источников только
в предшествующие моменты времени.
Точно так же, если требуется решить задачу с опере-
опережающими потенциалами, следует положить А = — 1
п В = 0.
Тогда функция Грина будет иметь следующий вид:
0; *>*',
о2]0+(г00,(г)вДпсУ^>; t<f. ("ДО)
Заметим, что несингулярная часть функции Грина
при А = 1 и В = 0 может быть представлена также в виде
=т- 2
e"les(f-'') ft
Поэтому для функции" Грина мы найдём формулу
G = i 2 \ оJ (О у- И «-te(l"l') [ ЯСТ. ±
, A7,11)
причём для GT мы должны взять при втором слагаемом
верхний знак, а для Ga — нижний. Появление дополни-
дополнительных членов типа ± in —,Ь (X2 — х2) приводит к асим-
метрии решения относительно запаздывающих и опере-
опережающих потенциалов, иначе говоря, используя тот или
иной знак у дополнительного члена, мы получим расхо-
расходящиеся или сходящиеся волны*). Следовательно, мы
*) О принципе излучения см. А.Соколов, Дельта-функция
и её применение к решению некоторых математических задач гео-
геофизики, Свердловск, 1946; см. также А. Тихонов и А. Самар-
Самарский, ЖЭТФ, 18, 243, 194§. ♦
§ 17] ВОЛНОВОЕ УРАВНЕНИЕ ДАЛАМБЕРА 87
имеем излучение электромагнитных волн только в том
случае, когда этот дополнительный член будет отличным
от нуля (см. также § 27).
Найдём теперь функцию Грина в важном частном
примере, когда на бесконечности источники отсутствуют
и для потенциала имеют место «естественные» граничные
условия (т. е. на бесконечности ср обращается в нуль).
В этом случае для о (г —г»') целесообразно взять пред-
представление E,7):
Собственные значения оператора V2 будут равны—/с2,
т. е. X = А.
Отсюда найдём
п с Т С мъ sin ckT
где
причём у СП будет равно + у в зависимости от того,
является ли Т ^ 0. Для произвольного четырёхмерного
временного вектора с уо>0
Точно так же для несингулярной части функции
Грина Go имеем
Со=±|Д, A7,12)
где
=^ щ \
ikM~ic%T
является так называемой первой А-функцией, играющей
важную роль при вторичном квантовании электромаг-
электромагнитного поля. В формуле A7,12) мы берём верхний или
88 УРАВНЕНИЯ, ЗАВИСЯЩИЕ ОТ ВРЕМЕНИ [гл. Щ
нижний знак в зависимости от того, хотим ли мы взять
запаздывающие или опережающие потенциалы.
Вторая Д-функция имеет вид
= ~ ^ eikB'~icxTb(k2-yL2)(dk)d* A7,14)
и может быть получена из равенства A7,8а) при подста-
подстановке .4 = 0 и J5 = 1. Функции Д и Аг можно принять
за два независимых релятивистски инвариантных решения,
удовлетворяющих однородному уравнению Даламбера*).
Интегрируя последнее выражение по углам при по-
помощи следующей формулы [см. также A0,6)]:
<*«/(*) {dk) = J \ smkR • f{h)kdk A7,15)
6
6
и учитывая соотношение F,7), получим
R
с Т 1
1 = Т\Т\ ==~Sn'
A7,16)
Отсюда видно, что в согласии с основными свойствами
симметрии для функции Грина уравнения Даламбера,
как для всякого самосопряжённого выражения, сингу-
сингулярная её часть Gx является чётной функцией координат
*) Заметим, что функции Д и Дх инвариантны относительно
преобразований Лорентца, так как они состаллены из инвариант-
инвариантных комбинаций: фазы ТсЦ.—слТ% четырёхмерной длины к2 — ха
и четырёхмерного объёма (dk) йл.
Появление множителя ъ/\ х | в функции Д связано с нечётной
зависимостью Д от времени Т.
Т
Заметим, что знаковую функцию р=-7 можно также записать
в виде щ =
§ 17] ВОЛНОВОЕ УРАВНЕНИЕ ДАЛАМБЕРА 89
и времени, в то время как первая Д-функция является
лишь чётной функцией координат и нечётной функцией
времени. Нечётный характер зависимости Д от Т связан
с возможностью излучения, к которому ведёт несингу-
несингулярная часть функции Грина Со, пропорциональная Д.
Наконец, функция
является чётной функцией координат и времени. Необхо-
Необходимо ещё отметить, что особенности функций Д и Ах
лежат на световом конусе.
Для решений с запаздывающими потенциалами на-
находим
В случае же опережающих потенциалов имеем
Таким образом, функция Грина уравнения Даламбера
может быть представлена в виде
£{) A7,20)
причём в случае запаздывающих потенциалов е = 1, для
опережающих потенциалов е=—1; наконец, для полу-
полусуммы запаздывающих и опережающих потенциалов з = 0.
Ограничиваясь запаздывающими потенциалами, мы
получаем известное выражение для решения уравнения
Даламбера
-г
'-^{dV). ■ A7,21)
причём в доеледнем интеграле t' = t .
90 УРАВНЕНИЯ, ЗАВИСЯЩИЕ ОТ ВРЕМЕНИ [Гл. III
§ 18. Решение уравнения Даламбера
в случае монохроматических колебаний
Особый интерес для многих проблем математической
физики представляют исследования излучения точечного
гармонического осциллатора. В этом случае изменение
плотности заряда со временем описывается по закону
t(r', 1') = аЪ(г'-го)е-^', A8,1)
где (« — круговая частота колебаний, а г0 — координата
источника.
Ограничиваясь решениями с запаздывающими потен-
потенциалами, найдём для искомой волновой функции согласно
равенствам A7,2) и A7,9)
t
<? = 4пса^и+(то)ъпA) I \ е-*"*'sincl{t-t')dt'. A8,2)
n —оо
Интегрируя последнее выражение по f, получим
ср = 4тш ^ У+ (Го) »« 0 ) е~Ш X
X
В случае опережающих потенциалов в последней
скобке перед множителем (пропорщюнальным с-функ-
ции), определяющим излучение, следует взять знак
минус*).
*) Введём две функции:
о
с»
§ 18] СЛУЧАЙ МОНОХРОМАТИЧЕСКИХ КОЛЕБАНИЙ 91
Разберём некоторые примеры распространения моно-
монохроматических волн, которые особенно просто решаются
при помощи соотношения A8,3).
Как известно, простейшим источником электромаг-
электромагнитных волн является точечный диполь, электрический
момент которого можно задать в виде
Р =рЬ (т - Го) е~ш. A8,4)
Вектор Герца выражается через момент диполя при
помощи уравнения
Электромагнитные поля Е и Н связаны с Z при помощи
соотношений
l^graddivZ--1,^-, A8,6)
H-irotf.. A8,7)
Исследуем распространение электромагнитных волн
в простейшем волноводном канале с диэлектрической
постоянной .2 = 1, образованном двумя абсолютно прово-
проводящими плоскостями х — О и х~1.
Направляя диполь, находящийся в точке А, по оси х
(вертикально направленный источник), имеем для цилин-
цилиндрических координат (х, г = \/ у2 -\- z2, <р) (рис. 10)
Ри=Рх 0, Рх = Р = рУ£е-™Ъ(х-х0), A8,8)
(О2
Полагая в последних равенствах z=A2 , мы видим, что
функция дч (х) автоматически ведёт к расходящимся волнам,
а а_(я) — к сходящимся. Выражение A8,3) может быть получено
также из A7,11). См., например, П. A.M. Дирак, Основы
квантовой механики, изд. 2-е, ГТТИ, 1937, стр. 213.
92 УРАВНЕНИЯ, ЗАВИСЯЩИЕ ОТ ВРЕМЕНИ [гЛ. III
причём
Далее согласно A8,6) и A8,7) находим
# = # - О Я — — ——
На границах волноводного канала с абсолютным про-
проводником, т. е. на плоскостях ^ = 0 и х = 1, тангенци-
тангенциальная составляющая векто-
\х pa E должна обращаться в
нуль (i?r = 0).
Таким образом, мы имеем
два краевых условия:
Ц = 0 A8,10)
при ж = 0 и при х = /.
Для конструирования
трёхмерной о-функции соста-
составим систему ортонормиро-
ванных функций, которые в
цилиндрических координатах могут быть найдены из
условия V2v = — \2v. Поскольку в &ТОЙ задаче мы имеем
аксиальную симметрию, получаем:
Полагая далее v = r>1(r)v2(z), найдём:
&+*:».=о,
f 7F
цри условии, что Х2 =
§ 18] СЛУЧАЙ МОНОХРОМАТИЧЕСКИХ КОЛЕБАНИЙ 93
Для функций v2i удовлетворяющих граничному усло-
условию A8,10), имеем прерывный спектр
1 /ап ппх
v2n = у -f cos —
(ао = у , ап=-1, если w =£ 0^) , A8,12)
а для функции vx имеем непрерывный спектр (см. § 4):
г>1*= J/ -9^ Jo Си-
Условия ортонормирования будут иметь вид
z
^2п(*К„'(*) йя ==&„„', A8,13)
о
vlk(r)vlk, {гJкгйг = йкЪ(к-к'). A8,14)
о
Последнее равенство представляет собой условие нор-
нормирования для непрерывного спектра [см. также D,22)
и D,23)], откуда для искомой трёхмерной дельта-функ-
дельта-функции (при азимутальной симметрии) мы находим
j
п-0 0
Подставляя последние соотношения в A8,3), а также
принимая во внимание A8,8), получим для точечного
источника
Z = *-/*-*<* 2 «ncos^?cos =^Fn, A8,15)
где
1*8 (А2 + ^ я' - р) ] A dft. A8,16)
94 УРАВНЕНИЯ, ЗАВИСЯЩИЕ ОТ ВРЕМЕНИ [гл. III
Воспользуемся теперь следующими соотношениями
[см. также A1,24)]:
A8,17)
О
оо
которые легко могут быть проверены, если принять во
внимание, что
Отсюда для искомого вектора Герца находим формулу
(см., например, работу Краснушкина) *):
оо ,
г* i27ZD , . ^П КП% TZUXn mn / Т / СО2 7127I2\
7. — L. р—Ш1 \ « гг>4 ГГ>Ц - ТТС1) Г ■/
^ — i е Zj п / / о \ ^ с8 /а / '
0
п=0
которая получается автоматически, поскольку в нашей
основной формуле A8,16) учтены только запаздывающие
потенциалы, ведущие в данном случае к расходящимся
волнам.
§ 19. Нестационарные колебания
Прежде всего найдём общие формулы, с помощью
которых мы можем исследовать распространение электро-
электромагнитных, упругих и других вЪлн, исходящих от точеч-
точечного источника (помещённого в точке г0), начинающего
*) П. Е. Краснушкин, Метод нормальных волн в приме,
нении к проблеме дальних радиосвязей, Изд. МГУ, 1947, стр. 17
§ 19] НЕСТАЦИОНАРНЫЕ КОЛЕБАНИЯ 95
с момента времени t = 0 колебаться с круговой частотой со.
Внешний источник в этом простейшем нестационарном
случае можно представить в виде
(r-rQ)e~™; t>0*),
0; *<0. A9Д)
Согласно A8,2) имеем следующее выражение для иско-
искомого потенциала ср:
t
<р = Ьъса ^ v+(r0)vn(r) j ^ er™'sincu (t-f)dt\ A9,2)
п 0
откуда, интегрируя по V\ найдём
— Ш p—icXt „-Ш i
5Li^
A9,3,
а) В качестве первого примера разберём распростра-
распространение волн в одномерном безграничном пространстве
(например, в безграничной струне) при естественных
граничных условиях.
Пусть точечный источник помещён в начале коор-
координат (жо = О). Ортонормированные функции для непре-
непрерывного спектра имеют вид
а собственные значения для параметра X будут равны
С помощью A9,3) находим
е« 1*1 + е-« I * I е-Ш _e-ickt
( f)
*) Реальное значение имеет лишь вещественная часть плот-
плотности р, т. е.
— r0)cosco£; t > 0,
t<0.
\ 0;
96 УРАВНЕНИЯ, ЗАВИСЯЩИЕ ОТ ВРЕМЕНИ [гл. Ill
Вычисляя последний интеграл с помощью теории
вычетов и отбрасывая минимую часть, получим
0; t < М. ( >)
Таким образом, формула A9,3) автоматически приводит
к расходящимся волнам, причём наряду с фазовой ско-
скоростью мы находим также скорость фронта волны, харак-
характеризующую распространение начала волнового процесса.
В нашем случае обе скорости равны скорости света с.
б) Рассмотрим колебания закреплённой с обеих сторон
струны длины 2/, когда в середине её расположен точеч-
точечный источник.
Помещая источник в начале координат (хо = 0), мы
можем для решения нашей проблемы выбрать следующую
систему ортонормированных функций:
»n = yfsm™(z + l) A9,7)
(л = 1, 2, 3,...), которые удовлетворяют граничным
условиям:
е„(-0 = М0 = 0. A9,8)
Принимая во внимание, что собственные значения
параметра X равны
найдём с помощью A9,3)
со
2 8 XI • НМЛ . П(Оп(х -\- I) 1
пас* >. sin——sin— • -.— X
1 *—> С С ШиH
^ / e-i»t_e-tw*tt -шГ_е.Пш0<у
где соо = ~ представляет собою собственную круговую
частоту колебания струны.
§ Щ НЕСТАЦИОНАРНЫЕ КОЛЕБАНИЯ 9?
Из A9,10) видно, что потенциал <р будет удовлетюрять
требуемым граничным условиям, т. е.
Учитывая в дальнейшем соотношение
Sin —- Sin ov ^ ' = — [1 — ( — l)n] COS —2- , A9,11)
С С JL С
аг также отбрасывая мнимую часть, не имеющую реаль-
реального значения, находим
T = Ti + ?o, A9,12)
цричём вынужденные срх и собственные ср0 колебания струны
определяются соотношениями
<19ДЗ)
.
Форма вынужденных колебаний всегда может быть
преобразована с помощью соотношения*)
*''во • ' • /^ ^ ' I I
cos B/1-1) у тс smcx VT~ y
V cos Byi"^ ч У _ IL
n-i cos y
кьвиду
:: . . гъ & / \x\
2izca cos o>£ . sin -^ f 1 —^p-
A9,16)
так как в нашем случае:
0<-ц*1 * A9Д7)
*) См., например, И. М. Р ы ж и к, Таблицы интегралов, сумм»
рядов и произведений, Гостехиздат, 1948, стр. 277.
Д. Иваненко и А. Соколов
УРАВНЕНИЯ, ЗАВИСЯЩИЕ ОТ ВРЕМЕНИ [гл. Щ
Решение A9.16) является непригодным в случае резо-
резонанса
^-==1, 3, 5, ...*),
т. е. когда знаменатель равенства A9,16) обращается
в нуль. В этом случае, как и следовало ожидать, мы
получаем вынужденные колебания с бесконечно воз-
возрастающей амплитудой.
В случае резонанса особенно сильно должно сказаться
влияние диссипативных членов. Однако более подробно
случай резонанса мы здесь исследовать не будем.
Что касается собственных колебаний, то при наличии
диссипативных членов при г—>оо они должны, вообще
говоря, исчезнуть, и мы будем иметь одни лишь вынуж-
вынужденные колебания, которые приводят к стоячим волнам.
Кроме того, представляет интерес разобрать колеба-
колебания струны в течение времени, когда фронт волны ещё
не дошёл до границы, т. е. рассмотреть случай, при кото-
котором г < —.
При вычислении ср0 воспользуемся тождеством:
Bi)
cog Bw _
совBп-1)ш0(*-М)] . A9,18)
Так как в нашем случае t < —:
с
0<0)С
A9,19).
мы можем произвести суммирование по л с помощью
соотношения A9,15). Тогда
пас f _.„ Г ло> f л , \х\
с
) д
Г. Гтю> f \х\ \ 1 ,
{ S1I1 \ -z О) ( t + J ) +
♦) Как видно из A9,14) и A9,13), при —
л меть условия резонанса.
A9,20)
2, 4, 6,. . . мы не
§ 20] ИНТЕГРИРОВАНИЕ ВОЛНОВОГО УРАВНЕНИЯ КЛЕЙНА 99
Отсюда для искомой волновой функции <р легко получить
выражение
12пас . f \х\\ л ^ | х |
sm ш ( t — J—L ) ; t > —L,
найденное нами также дли безграничной струны. Совпа-
Совпадение обоих результатов является с физической точки
зрения вполне понятным, поскольку значение для функ-
функции ср не может зависеть от граничных условий, пока
волна не дойдёт до границы.
§ 20. Интегрирование волнового уравнения Клейна
Как будет показано ниже (см. гл. V), в современной
релятивистской квантовой механике и, в особенности,
в теории мезонов и ядерных сил особо важную роль
играет простейшее квантовое релятивистское уравнение
для де-бройлевских волн, связанных с массой покоя*):
s-i J- *•)<р = -4*,. B0,1)
•) В квантовой механике было сначала установлено О. Клейном
A926) волновое уравнение для свободной частицы с покоящейся
массой т:
(Я2—с2/?2—иг2с4)<р = О,
где операторы энергии Е и импульса р определяются равенствами:
h д h
k — постоянная Планка, с — скорость света.
§| Заменяя массу т через %—- , мы после сокращения уравнения
на тт получаем левую часть уравнения B0,1). Клейн пришёл
# своему уравнению как волновому уравнению во вспомогательном
пространстве пяти измерений. Действительно, последний член в урав-
уравнении B0,1) эквивалентен второй производной по пятой координа-
ie при условии цикличности: -^ =—Л?,, если ф=^ф (#, г/, z, t) elk°Xb.
ох&
Вскоре после этой работы уравнение B0,1) было установлено мно-
7*
100 УРАВНЕНИЯ, ЗАВИСЯЩИЕ ОТ ВРЕМЕНИ [ГЛ. III
В уравнении B0,1) величину к\ можно рассматривать
как некоторую константу, независимо от её толкования
как члена с массой покоя и вне связи с квантовой меха-
механикой, в рамках классической теории поля. Это уравне-
ние описывает поле частиц с покоящейся массой 7Г^- ,
создаваемое источником плотности р. Для определён-
определённости, имея в виду позднейшее обоснование (см. § 44),
будем говорить об этих частицах как о скалярных мезонах.
Если в бесконечно удалённых точках источники отсут-
отсутствуют, то мы можем решение уравнения B0Д) искать
в виде
ср (г, t) = 4тг ^ G {г, v\ t, t') p (r\ г') {dr') dt'. B0,2)
В полной аналогии с решением уравнения Даламбера
функция Грина G будет складываться из двух частей:
части сингулярной Gl9 по общему определению равной
€ikR-ixcT
~ 16.С* \т\)
у к*+к*)
где R = r — r', T — t — t\ и части несингулярной Go,
которая является решением однородного уравнения B0.1)
В данном случае двумя независимыми решениями
однородного уравнения оказываются релятивистски инва-
гими авторами обычным путём как результат действия релятивист-
релятивистского соотношения между энергией и импульсом, понимаемого как
оператор, на волновую функцию ср.
Далее, в дискуссии одного из авторов (Иваненко) с В. А. Амбар-
цумяном была сбсуждена возможность, по аналогии со случаем
электромагнитного поля, написать в правой части равенства B0,1)
член, характеризующий источник ср-волн.
§ 20J ИНТЕГРИРОВАНИЕ ВОЛНОВОГО УРАВНЕНИЯ КЛЕЙНА Ю1
риантные Х)-функции, по существу являющиеся «переста-
«перестановочными» функциями *):
B0,4)
Функция Gl9 как видно из B0,3), связана с D при
помощи соотношения
Решение, соответствующее запаздывающим или опе-
опережающим потенциалам, мы получим, если положим
GD
B0,6)
для запаздывающих потенциалов и
Go=-jD B0,7)
для опережающих потенциалов.
Интегрируя по углам равенство B0,4) с помощью соот-
соотношения A7,15), получим
D=z L EL n.= —dJ± BПЫ
где
B0,9)
т
Величины ft и i —^гт f являются соответственно дейст-
*) Функпии Д и А] являются частными случаями функций
B0,4), когда масса частиц (мезонов) равняется нулю, т. е. Д = Нт D
и Дх = lim Dv Релятивистская инвариантность функций Dm Dx
даказывается тем нее способом, как и для функций Д и Дг (см. § 17).
102 УРАВНЕНИЯ, ЗАВИСЯЩИЕ ОТ ВРЕМЕНИ [гл. III
вительной и мнимой частью интеграла
1T1- <20Д0)
B0,11)
Введём замену переменных
Кроме того, при с | .7^ | > R мы можем положить
с | Т | = a ch cp0, R = а sh cp0,
где ср0 — постоянная величина, a a==Y^c2T2—Л8.
Точно так же при | с \ Т < R мы имеем
где
Тогда интеграл B0,10) примет вид
Р, с|Г|>Я,
; с | Г |< Л,
B0,12)
откуда, учитывая чётность или нечётность подинтеграль-
ных функций относительно переменной ср, находим
sin ^A*°a ch
T
= 0;
-НУ, c\T\>R,
c\T\<R.
*) Значение интегралов B0,13) и B0,14) можно найти в книге:
P.O. Кузьмин, Бесселевы функции, ОНТИ, 1935, стр. 89—90.
.ЛПЕГРИРОВАНИЕ ВОЛНОВОГО УРАВНЕНИЯ КЛЕЙНА 103
Аналогичным способом для второй функции /х имеем
Г
\ cos (k0 ax ch ср) dtp
i
c*T*-R*); c\T\>R,
B0,14)
cos (k0 ъ^ sh 9) d<p =
-R*); c\T\<R.
Для вычисления D-функции, a также функции Грина
мы должны выражение B0,13) продифференцировать по R.
При этом необходимо учесть, что производная от разрыв-
разрывной функции равняется произведению 8-функции, описы-
описывающей особенность - в точке разрыва, на амплитуду раз-
разрыва. Кроме того, при с2Т2 — Д2 > 0 получаем
dJ0{k0Yc2T2—R2) _ __
dJ0(k0 Y с*Т*—
dR
hR
Поэтому
Z):
Ло у
7?2\. T\xt
ь
0;
*0
л
-т > B0>15)
104 УРАВНЕНИЯ, ЗАВИСЯЩИЕ ОТ ВРЕМЕНИ [гл. III
Как видно из формулы B0,4), функции D и D± можно
также представить в виде
ikJR—icxT
Di *= 8^5 \ eihlt-™T Ь (к2 - *2 + kl) (dk) dr..
С помощью формул
L С а
2 )
8 (А2 - *2 + к) = ± \ е'а С- +*?) da
легко преобразовать последние выражения
i г г *• п B0,15а)
= ~i )sin [а (с2Г2 - ^2) + % ]йа-
О
Отсюда, принимая во внимание соотношение
для функции D вновь получаем выражение B0,15), а для
функции Dj находим соотношение, которое также МойЫ
получить из формулы B0,8) и B0,14):
к1 яЛкрУ c*T*-R*) c2f2 R2
Д2
В частности, при ^ = 0 из формул B0,15а) легко
получить значение функций A=limZ) и ^1—-limD1 для
Здравнения Даламбе^а [см. соотношения jA7,16) hjA7,17J].
§ 20] ИНТЕГРИРОВАНИЕ ВОЛНОВОГО УРАВНЕНИЯ КЛЕЙНА Ю5
Из B0,15) находим функцию Грина уравнения Клейна
для решений с запаздывающими потенциалами:
G =-2
s . B0I6)
0; 71 < |,
и для случая опережающих потенциалов:
, с /■ Т
~ 2 \\Т\
0; T > -A
—Я»
Л (*0 /с2Г2-Л2); Г < —
R
( j
Окончательное выражение для 'потенциала ср с запазды-
запаздывающими решениями согласно B0,2) будет иметь вид
д
\
При Ао = 0, т. е. когда масса покоя частиц, сопоставленных
мезонному полю (т. е. мезонов), равна нулю, потенциал ср
переходит в решение уравнения Даламбера (т. е., в част-
частности, уравнений для потенциалов электромагнитного
цоля), из которого видно, что от источника начинают
распрострдняться волны со скоростью с. В нашем случае,
- когда волны сопоставлены частицам, обладающим массой
покоя, от источника, кроме волн, распространяющихся
со скоростью с (скорость фронта волны), будут распро-
распространяться другие волны со всевозможными скоростями
с' = =-, меньшими с. С физической точки зрения
106 УРАВНЕНИЯ, ЗАВИСЯЩИЕ ОТ ВРЕМЕНИ [гл. III
полученный результат является совершенно понятным.
В самом деле, в теории электромагнитного поля сигналы
переносятся фотонами, которые распространяются со ско-
скоростью света, так как покоящаяся масса фотонов равна
нулю. В нашем же случае сигналы переносятся мезонами,
покоящаяся масса которых не равна нулю, и поэтому
скорость их движения лежит в пределах от 0 до с.
Формула B0,18) принимает более простой вид, когда
правая часть уравнения B0,1) изменяется по гармони-
гармоническому закону, т. е.
p(i-,*) = PoWe-"of. B0Д9)
причём круговая частота ш > ск0 *).
В этом случае решение уравнения B0,1) будем искать
в виде
Принимая во внимание тождество
сведём уравнение B0,1) к уравнению Даламбера, опи-
описывающему распространение сигналов со скоростью
Со)
v = - > с:
Решение последнего уравнения с учётом запаздыва-
запаздывающих потенциалов имеет вид
{dv'). B0,22)
Фазовая скорость v распространения волн зависит
от частоты со, однако для монохроматических волн оня
должна оставаться величиной постоянной.
Решение B0,22) может быть получено также из более
общего выражения B0,18).
*) Случай о) < скк) не даёт волнового пропесса и для нас сейчас
особого интереса не представляет.
§ 21J ИНТЕГРИРОВАНИЕ n-МЕРНОГО УРАВНЕНИЯ Ю7
§ 21. Интегрирование волнового уравнения
в и-мерном пространстве*)
В и-мерном пространстве обобщённое волновое урав-
уравнение типа Клейна имеет вид
L(p=( 2 щ -?■■£ -*:)?=-4*р(*.. о, B1.1)
где р является плотностью источника, а ср —искомой
волновой функцией.
Обобщая рассуждения предыдущего параграфа, мы
найдём следующее значение для функции Грина, соот-
соответствующей запаздывающим потенциалам и естествен-
естественным граничным условиям:
+^ {dk)n. T>0, {21 2)
s=l
Прежде всего найдём функцию Грина в том случае,
когда мы имеем одно (п = 1) или два (п = 2) пространствен-
пространственных измерения.
В первом случае (п=1) мы находим
f со
| те J /*" + *8 B1,3)
0; Т < 0,
*) См. Д. Иваненко и А. Сок о л о в, ДАН, 36, 37, 1940.
108
УРАВНЕНИЯ, ЗАВИСЯЩИЕ ОТ ВРЕМЕНИ [Гл. III
или, принимая во внимание соотношения B0,9) и B0,13),
получаем
G%=\
' С
0; Т<^.
Точно так же во втором случае (п = 2) находим
с_ f kJ0(kR) о.„ ^T1/T^j7p) dk; T > 0,
B1,4;
B1.5J
0;
если примем во внимание, что
B1,6)
Интеграл B1,5) является известным разрывным инте-
гралюм Сонина*), равным
с cos (&0
0;
Г<А.
B1,7)
*) Как известно, разрывный интеграл Сонина имеет вид
(см. P.O. Кузьмин, Бесселевы функции, стр. 150)
Г
1, 7а)
0;
0< a < by
где rc > m > — 1, а число х может принимать любое комплексное
значение. Чгсбы получить наше соотнсшение B1,7), необходимо
1
I 21] ИНТЕГРИРОВАНИЕ n-МЕРНОГО УРАВНЕНИЯ дед
Для вычисления функции Грина, в случае трёх и боль-
большего числа пространственных измерений *) удобно ввести
сферические координаты, которые в и-мерном простран-
пространстве будут связаны с декартовыми при помощи соотно-
соотношений:
кх = к cos cp sin 6Х sin G2 ... sin Gn_2,
k2 = к sin со sin Gx sin G2 ... sin 6n-2,
k3 = к cos Gx sin 62 • • • sin Gn-2, B1,8)
• • • sinGn_2,
причём
а сферические координаты изменяются в пределах:
0<&<оо, 0<ср<2тг, 0<6<тг. B1,9)
Составляя якобиан, находим известное выражение
элемента объёма в сферических координатах:
(^)n=A;"-idA:dcpsinG1dG1sin2G2dG2... sinn-2Gn_2dGn_2. B1 ДО)
Телесный угол в /г-мерном пространстве равняется
2-гс тс -л ъ
®п= \ d<f\ sinЬгdbt ^ sin2G2dG2..
0 0 0
Для вывода последнего соотношения принимается во
внимание, что**)
*) Точнее говоря, полученными формулами можно пользо-
пользоваться, начиная с л =2.
**>Р. О. Кузьмин, Бесселевы функции, ОНТИ, 1935, стр. 10*
НО УРАВНЕНИЯ, ЗАВИСЯЩИЕ ОТ ВРЕМЕНИ [гл. Ill
Направляя ось п по направлению вектора Л, имеем
Rn=R, Rs = 0 (если*#гс). B1,13)
Поэтому
п
2 k8Rs = knR = kRcoabn-2. B1,14)
Интегрируя равенство B1,2) по углам ср, Gi,...,6n-3,
имеем
n = * ^ Г *-i si
П BТ1)П П Х J
о /*• + *!
70
X \ sin" 6 eikR cos ° db\ T > 0,
о
Т<0.
Учитывая далее соотношение *)
sin"-2 6 eikR cos о cW = ]/я Г Г^^) "АЛМ2)/2
можем представить функцию Gn в виде
со п
0; Г<0.
B1,17)
Разберём прежде всего обобщённый электростатиче-
электростатический случай. При этом вместо функции Грина Gn и-мер-
ного волнового уравнения удобно ввести функцию Грина
статического n-мерного уравнения Лапласа2 j^ = ~~ ^Р»
s=l
*) Е. Т. У и т т е к е р и Г. Н. Ватсон, Курс современ-
современного анализа, т. II, ГТТИ, 1934, стр. 178.
§ 21] ИНТЕГРИРОВАНИЕ л-МЕРНОГО УРАВНЕНИЯ |Ц
сингулярная часть которой равна
j mj^u B1fl8)
Последний интеграл может быть вычислен с помощью
равенства *)
00 — Л
\ к2 /iL1 (*Д)га = *г Т" * л 1 (ЛоД). B1Д9)
\ _1 (
J 2 у
В этом случае для функции Грина находим
^ = 5 (га)"*"'**-, <*>*>• B1,20)
В частности, полагая тг = 3, получаем функцию Грина
уравнения Пуассона, обобщённого на член с массой
покоя:
В этих рассуждениях речь везде идёт о сингулярной
части. При переходе к предельному случаю (/со = 0) необ-
необходимо учесть соотношение**)
xsKs(x) = 2s~1 Г (s). B1,22)
0
*) Равенство B1,19) может быть получено из формулы A1,32)
при а=0, л = 1 и т?г= — — 1.
**) Формулой B1,22) мы можем пользоваться при s > 0, шъ
этому функция Грина B1,23) относится к случаю трёх, четырёх
к
и т. д. измерений. При s==0 мы имеем Ко (k0R)= —In Л—In-~ .
к
Отбрасывая бесконечный, но постоянный множитель In — ; к0 —>> 0,
получим функцию Грина двумерного уравнения Пуассона [см. соот-
соотношение (9,7)]:
^20= "-«^ ^п^-
112 УРАВНЕНИЯ, ЗАВИСЯЩИЕ ОТ ВРЕМЕНИ [Гд. III
Тогда
ns* __ ^ 2 J /0/1 о о\
При и = 3 мы вновь находим функцию Грина трёхмер-
трёхмерного уравнения Пуассона:
а при п = 4 — функцию Грина четырёхмерного уравнения
Лапласа-Пуассона
4 B1,25)
При вычислении функции Грина в общем случае мы
должны различать случаи нечётного (лг = 2v -h I; v=l,
2, 3,...) и чётного (n = 2v; v = l, 2, 3, ...) числа
пространственных измерений.
В первом случае (п = 3, 5, 7 и т. д.) из равенства
B1,17) находим
со 1
V—2 у ft2 + ft?
Принимая во внимание соотношение
\_
* 2
2
находим
со
х С ^Sin/cfisin^j^±^^; У > 0, B1,28)
J у А2 + ft?
G2v+i = 0; Т < 0.
J 21] ИНТЕГРИРОВАНИЕ n-МЕРНОГО УРАВНЕНИЯ
В частности, при v = 1
s™^X^dk, T>0,
,29)
0; 71 < 0.
Последний интеграл был взят нами прежде и опре-
определяется равенством B0,16).
Как видно из последних соотношений, функция C2v+i
может быть выражена через функцию G3:
Л
1 (RdRy
G3. B1,30)
3 V » /
G3
1 3
Точно так же в случае чётного числа пространствен-
пространственных измерений функция Грина G2v будет равняться
причём функция Грина двухмерного пространства опре-
определяется выражением B1,5).
Наконец, разберём вопрос о выполнении принципа
Гюйгенса при распространении волн в пространстве
с различным числом измерений.
Как известно, принцип Гюйгенса сводится к следую-
следующему положению: если источник испускает волны в тече-
течение времени At, то этот поток волн должен действовать на
приёмник в течение этого же момента времени Д£, т. е.
скорость распространения волн не должна зависеть от
частоты колебаний источника и при своём распростра-
распространении волны не должны подвергаться деформации в смы-
смысле размазывания и образования «хвоста».
С точки зрения формализма 6-функции это означает,
что соответствующая функция Грина должна быть про-
порциональной или 5 ( Т J или производной от5-функ-
ции. Как видно из наших формул, для выполнения прин-
принципа Гюйгенса кроме основного требования исчезнове-
исчезновения покоящейся массы у волн или частиц, сопоставлен-
8 Д. Иваненко и А. Соколов
114 УРАВНЕНИЯ, ЗАВИСЯЩИЕ ОТ ВРЕМЕНИ [гл. III
ных волнам (й;0 = 0), необходимо также, чтобы число про-
пространственных измерений было нечётным. Согласно ра-
равенствам B0,16) и B1,30) в этом случаемы имеем
—с)
2B7l)v (RdR)
y-i R
B1>32)
Отсюда видно, что потенциал <р будет зависеть лишь от
состояния источника, взятого в предшествующий момент
времени. При этом сдвиг определяется временем, необхо-
необходимым для прохождения расстояния R между источни-
источником и точкой наблюдения со скоростью с, и никаких
«хвостов», т. е. волн, движущихся со скоростью, меньшей
чем с, и ведущих к размазыванию формы потока волн,
здесь не возникает.
Нетрудно показать, что принцип Гюйгенса не будет
выполняться в случае чётного числа пространственных
измерений, даже при исчезающей массе покоя у частиц,
сопоставленных волне.
В самом деле, из B1,7) и B1,31) следует
B.)- (дм)*-' ./^3 ; Г>Т> щ qox
V с* B1,33)
0; Т < —
с '
т. е. потенциал <р в этом случае будет зависеть от состо-
яния источника не только в момент t' = t , но также
от его состояния во все предшествующие моменты вре-
мени /' < t . Иными словами, кроме фронта волны,
распространяющегося со скоростью с, за ним будет
следовать целый «хвост» волн, движущихся со всевоз-
всевозможными скоростями, начиная от нуля и кончая с. Как
видно из формулы B0,16), аналогичный «хвост» должен по-
появиться также в случае нечётного числаизмерений, если
покоящаяся масса к0 отлична от нуля (см. также § 20).
Аналогичная проблема выполнимости принципа Гюй-
Гюйгенса для /г-мерных обобщённых волновых уравнений
§ 22] РАСПРОСТРАНЕНИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН Ц5
рассматривалась Адамаром и другими математиками *). При
этом, однако, дополнительный член (включавшийся притом
в уравнение с обратным знаком -f £§9) трактовался чисто
формально, ввиду неизвестной прежде его интерпретации
как члена с массой покоя. Поэтому, несмотря на формаль-
формальную правильность результатов Адамара, окончательного
физического толкования вопроса о выполнимости принципа
Гюйгенса он, по указанным причинам, получить не мог.
§ 22. Распространение электромагнитных волн
в проводящей среде
Уравнение, описывающее распространение электро-
электромагнитных волн в проводящей среде, имеет вид так назы-
называемого телеграфного уравнения:
4р«(*"~у1?~ж)***' 0= -*Ф(г, ')> B2,1)
где постоянный в данном случае коэффициент с является
проводимостью среды.
Для сингулярной части функции Грина при естест-
естественных граничных условиях мы имеем
где R=r — r', T = t — t'.
Применяя теорию вычетов, получим**)
$_£^L_
0; T<0.
*) См., например, Р. Курант и Д. Гильберт, Методы
математической физики, т. 2, стр. 531, Гостехиздат, 1945.
••) Отметим, что наличие в уравнении B2,1) первой производ-
производной по времени ведёт автоматически к запаздывающим потенциалам
для сингулярной части функции Грина. Поэтому, ограничиваясь
вообще одним запаздывающим решением, несингулярную часть Go
мы должны положить равной нулю. Так же, как и в параболическом
уравнении теплопроводности (см. § 16), здесь не может иметь места
решение с одними лишь опережающими потенциалами.
8*
116 УРАВНЕНИЯ, ЗАВИСЯЩИЕ ОТ ВРЕМЕНИ [гл. III
Отсюда для функции Грина находим
О; Г<0.
Во многих исследованиях можно ограничиться этой
формой для функции Грина. Однако интеграл B2,4)
допускает явное выражение через бесселевы функции.
Интегрируя далее последнее выражение по углам,
с помощью соотношения A7,15) имеем
где F является разрывным интегралом Сонина [см. также
B1,7а)]
L
с B2,6)
0; т < f,
a /0 — бесселевой функцией от мнимого аргумента.
Учитывая, что производная от разрывной функции
даёт ^-функцию, получим
О;
.-Д«); Т> А,
« B2|7)
Как видно из B2,7), в проводящей среде принцип
Гюйгенса, ввиду образования затухающего «хвоста»,
§ 22] РАСПРОСТРАНЕНИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН Ц7
не будет иметь места. Физически это связано с тем обстоя-
обстоятельством, что лишь скорость распространения фронта
электромагнитных волн в проводниках равняется с,
сам же сигнал в проводящей среде размазывается, и фазо-
фазовая скорость изменяется в пределах от 0 до с (см. ниже).
В частности, при з = 0 (диэлектрик) мы найдём преж-
прежнее значение для функции Грина уравнения Даламбера:
в которой автоматически отобраны решения лишь с за-
запаздывающими потенциалами.
В другом предельном случае
■— = а = const,
найдём функцию Грина для уравнения теплопроводности
в трёх измерениях:
8тш
При этом мы использовали следующее асимптотическое
выражение для функции 1г:
Наконец, найдём решение уравнения B1,1) в случае
наличия точечного источника, испускающего монохро-
монохроматические волны с круговой частотой со:
рКО = Р!Мв-ы'. B2,10)
Воспользовавшись значением для функции Грина
B2,4), получим
-у) Bin U Е-
dt>
B2,11)
118 УРАВНЕНИЯ, ЗАВИСЯЩИЕ ОТ ВРЕМЕНИ [гл. Ш
или после интегрирования по V
Ъ \ <22'12)
Таким образом при наличии затухающего члена,
связанного с проводимостью, простое деление на оператор
даёт запаздывающие потенциалы для монохроматических
волн без добавления какой-либо вспомогательной функции
типа Go, которая была необходима в случае уравнений
Даламбера, допускающего также решения с опережа-
опережающими потенциалами [см. равенство A8,3)].
Наконец, вычисляя интеграл B2,12), найдём
9 = -E-e-t'e-iu>{t-^). B2,13)
Отсюда видно, что фазовая скорость распространения
электромагнитных волн в проводящей среде с коэффициен-
коэффициентом проводимости о равняется
/40+
B2,14)
и зависит от частоты колебаний.
Кроме того, как и следовало ожидать, волны, распро-
распространяющиеся в проводящей среде, являются затуха-
затухающими, причём коэффициент затухания р также зависит
от частоты:
B2Д5)
! В предельном случае исчезающей проводимости а = О,
т. е. идеального диэлектрика, скорость волн становится
равной постоянной величине с, а коэффициент затухания
обращается в нуль.
ГЛАВА IV
КЛАССИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА
§ 23. Основы классической электродинамики
а) Значение классической электро-
электродинамики в современной теории
частици полей
Законы классической электродинамики, т. е. теории
электромагнитного поля и заряженных частиц, вообще
говоря, в целом неприменимы к элементарным части-
частицам, ядрам, атомам, молекулам. Например, движение
электронов в атомах и молекулах и движение протонов
в ядрах, так же как излучение света ядрами, атомами
и молекулами и т. д., должны описываться квантовой
теорией поля и частиц. Точно так же движение свободных
электронов, например, в космических лучах, также под-
подчиняется квантовой механике. Во всех этих случаях вели-
величины «действия» за период процесса сравнимы с планков-
ской постоянной h = 6,6 • 10~27 эрг-сек. Иначе говоря,
длина де-броклевской волны А = —, или при малых ско-
скоростях А = -—-, сравнима с размерами исследуемых об-
областей. В частности, при движении электронов в атомах
А будет порядка размеров орбит ~ 10~8 см. Может соз-
создаться неправильное впечатление, что вся физика эле-
элементарных частиц должна быть только квантовой в том
смысле, что классические теории представляют собой
совершенно непригодное приближение. Однако подобная
крайность не соответствует действительности.
120 КЛАССИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА [rJIt iy
В ряде случаев, например, весьма быстрых движений,
длина де-броглевской волны электрона оказывается зна-
значительно меньше размеров орбиты либо характерного
промежутка длины, или, что сводится к тому же, дей-
действие за период процесса оказывается значительно
больше /г. Таким образом при х\—>0, или h—>0, мы
вправе трактовать многие процессы с элементарными
частицами классическим путём, а точное квантовое реше-
решение, как правило, будет давать лишь незначительные
поправки. Это относится, в частности, к движению
заряженных частиц в ускорительных установках, притом
как к нерелятивистскому случаю движения протонов,
дейтеронов, а-частиц и других ядер в циклотронах, так
и к релятивистскому движению лёгких частиц — электро-
электронов в бетатронах и синхротронах. Теория движения
электронов в современных ускорителях типа бетатрона —
синхротрона является важнейшей областью применения
неквантовой релятивистской теории электрона и элек-
электромагнитного поля. В частности, оказалось возможным
предсказать и дать теорию испускаемого электронами
в этих условиях излучения нового типа, являющегося
иногда видимым и обладающего рядом других интерес-
интересных особенностей, — эффект «светящегося» электрона
(см. § 43).
Кроме того, классическая релятивистская теория поля
и электрона позволила объяснить другое новое явление —
эффект «сверхсветового», электрона (эффект Черенкова),
заключающийся в излучении света электроном, движу-
движущимся в среде равномерно со скоростью, большей фазовой
скорости света (см. § 27).
Наряду с этими конкретными новейшими примене-
применениями современная неквантовая релятивистская электро-
электродинамика оказывается необходимой также для анализа
ряда'принципиальных вопросов, прежде всего проблемы
собственной массы и вывода уравнений движения элек-
электрона.
Ни классическая, ни квантовая теории не смогли ещё
объяснить природу массы элементарных частиц и тем
более вывести численные значения масс. На базе клас-
классической теории возникла и была перенесена в кванто-
§ 23] ОСНОВЫ КЛАССИЧЕСКОЙ ЭЛЕКТРОДИНАМИКИ 121
вую механику гипотеза «полевой» массы, согласно кото-
которой собственная энергия или масса частиц обязана энер-
энергии полей. л
Возникшая при этом трудность с бесконечным значе-
значением энергии любого поля, порождаемого точечной части-
частицей, не была окончательно удовлетворительно разрешена
ни путём введения конечного радиуса частиц, ни каким-
либо другим классическим или квантовым способом.
При этом, поскольку взаимодействие частиц посредством
какого-либо поля является в своей основе эффектом клас-
классическим, лишь иначе интерпретируемым квантовой меха-
механикой, то и «самодействие» или обратное действие поля
на породившую его частицу, и связанный с этим эффект
возникновения собственной полевой массы, можно пред-
предполагать в основном также классическими. Это предпо-
предположение подкрепляется тем обстоятельством, что из кон-
константы заряда е, скорости света с и длины г0 («классиче-
(«классический радиус») можно составить, не вводя постоянно^
Планка /г, величину размерности массы
т = ~ ( или, наоборот, г0 = —
С другой стороны, не следует, конечно, забывать о нали-
наличии чисто квантовой величины с размерностью длины,
так называемой комптоновской длины волны Ло = — =
1jp
— о • о—5 , в 2тт . or1 = 2тг . 137,02 раза большей клас-
тс2 2тсе2 г
сического радиуса, которая характеризует область длин
волн, ниже которых сказываются релятивистские кван-
квантовые эффекты.
Таким образом априори классическая теория, неви-
невидимому, способна объяснить хотя бы отчасти природу
массы. Конечно, все выводы её подлежат проверке п уточ-
уточнению при помощи квантовой механики. С другой сто-
стороны, оставляя в стороне вопрос о природе массы, мы
можем, беря т просто за некоторую константу, задаться
вопросом о выводе классических релятивистских уравне-
уравнений движения на базе неквантовой теории. В последнее
время обе эти проблемы: вывод уравнений движения
122 КЛАССИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА [гл. IV
и задача о собственной массе, довольно усиленно обсуж-
обсуждались не только с квантовой, но и классической точки
зрения.
Как бы то ни было, классическая трактовка помо-
помогает глубже проанализировать физическую сущность
проблемы, расчленить классические и квантовые стороны
вопроса и тем самым, если не может дать окончательного
решения, то во всяком случае способна подготовить для
него почву.
Ввиду всех изложенных обстоятельств мы рассмот-
рассмотрим в данной части книги как ряд принципиальных
вопросов, так и ряд новейших конкретных применений
классической электродинамики. В этом кратком вступ-
вступлении мы естественно не останавливались на издавна
хорошо известных и излагаемых в курсах электронной
теории и классической электродинамики многочисленных
разнообразнейших явлениях излучения, распростране-
распространения и поглощения электромагнитных полей и движе-
движения электронов, описываемых неквантовой электроди-
электродинамикой*).
б) Инвариантность и трансфор-
трансформационные свойства
Остановимся сначала на общих трансформационных
свойствах, которым должны удовлетворять согласно
теории относительности любые уравнения полей и эле-
элементарных частиц, в том числе уравнения теории Макс-
Максвелл а-Лорентца, описывающие электромагнитное поле
заряженных частиц.
Как известно, в общем случае следует различать
законы преобразования для контравариантных и кова-
риантных компонент векторов и тензоров.
*) Я. И. Френкель, Электродинамика, ч. 1 и 2, ОНТИ,
1935 Л. Д. Л а н д а у и Е. М. Л и ф ш и п, Теория поля,
Гостехиздат, 1948; И. Е. Т а м м, Основы теории электричества,
Гостехиздат, 1949; Г. А. Л о р е н т ц, Теория электронов, ГТТИ,
1934; Р. Б е к к е р, Электронная теория, ОНТИ, 1936; А б р а-
гам-Беккер, Теория электричества, ОНТИ, 1936.
§ 23] ОСНОВЫ КЛАССИЧЕСКОЙ ЭЛЕКТРОДИНАМИКИ 123
Переход от одного вида тензоров к другому осуще-
осуществляется при помощи фундаментальных метрических
тензоров: (g^v) и (glxv), определяемых в простейшем слу-
случае отсутствия гравитации, иначе говоря, плоского (так
называемого псевдоевклидова) мира, равенствами
Соответствующие значения g^v = 0, ±1 носят название
галилеевых. Пространственные составляющие будем обо-
обозначать латинскими индексами п(п = 1, 2, 3), а времен-
временную значком 0. Переход от ковариантных А^ векторов
к контравариантным A^t и наоборот, осуществляется
с помощью формул:
где ^, v = 0, 1, 2, 3, а по значку, входящему дважды,
необходимо произвести суммирование, т. е.
v=0
Отсюда видно, что временные составляющие обоих видов
векторов равны друг другу (А0 = Ао), а пространствен-
пространственные отличаются знаком (Ап~ — Ап).
В частности, скалярное произведение двух векторов,
представляющее собою инвариант, равно:
АУ'А^. = Aq — А^ — А2 — -^-з*
Если вместо координаты времени х0 = ct ввести мни-
мнимую величину Xi~ict и положить А^ = iA0, тогда можно
ограничиться, например, только ковариантными векто-
векторами, из которых образуется скалярное произведение,
124 КЛАССИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА [гл. IV
являющееся инвариантом:
уА, А) = .Др,^!^ = А/± + А^ -f- А% 4~ А3 = Ао -f- AnAn ).
Нетрудно видеть, что в этом случае компоненты кова-
риантных и контравариантных векторов будут равны
друг другу, а компоненты метрического тензора обра-
образуют единичную матрицу:
A 0 0 0\
So? §) - <23'1а>
0 0 0 1/
Волновые функции, описывающие поля и элементар-
элементарные частицы, должны иметь определённые трансформа-
трансформационные свойства, т. е. изменяться закономерным обра-
образом при преобразованиях координат или соответствую-
соответствующих движениях систем отсчёта. При этом в релятивист-
релятивистской теории речь идёт о преобразованиях в четырёхмерном
мире (пространство — время) в приближённой же нере-
нерелятивистской теории, пригодной лишь при малых ско-
скоростях, — о преобразованиях в трёхмерном пространстве
и отдельно о преобразовании времени, сводящемся
в данном случае к переносу начала отсчёта. Наиболь-
Наибольшее значение имеют инварианты (скаляры), т. е. величины,
не изменяющиеся при переходе к различным координатным
системам. Сами уравнения, описывающие те или иные
поля и частицы, согласно теории относительности не
должны зависеть от выбора системы координат и должны
сохранять при различных допустимых преобразованиях
свою форму.
Требования инвариантности на современном этапе
развития теории поля принадлежат к числу наиболее
общих и глубоких физических законов, выражающих
основные свойства пространства и времени, движения
частиц и их взаимодействий.
Перечислим преобразования, оставляющие уравне-
уравнения полей и частиц инвариантными. За всеми подроб-
*) Здесь и в дальнейшем греческие буквы пробегают значения
от 1 до 4 (х, у, z, Ш), а латинские от 1 до 3 (х, у, z).
§ 23] ОСНОВЫ КЛАССИЧЕСКОЙ ЭЛЕКТРОДИНАМИКИ 125
ностями мы отсылаем к монографиям по теории отно-
относительности и теории групп*).
1) Отсутствие абсолютного центра в пространстве
и какого-то начала отсчёта времени, т. е. однород-
однородность пространства — времени, приводят к инвариант-
инвариантности относительно переноса начала координат («принцип
относительности начала отсчёта»). Следовательно, все
уравнения должны быть дифференциальными в четырёх
координатах. Преобразования переноса записываются
в виде линейной неоднородной трансформации:
#а = #а+Яа (а=1, 2, 3, 4),
или для бесконечно малых преобразований
Ъх'л = Ъха.
2) Отсутствие каких-либо избранных направлений или
изотропность трёхмерного пространства («принцип
относительности направлений») приводит к инвариантности
по отношению к трёхмерным пространственным вращениям.
Соответственные линейные ортогональные преобразо-
преобразования координат имеют вид
хг = o>rsxs у
или для бесконечно малых преобразований
bx'r = tarsxs,
причём тензор 8ars, характеризующий малый угол
поворота, является антисимметричным cars= —casr.
Как ясно уже из-наглядных геометрических соображе-
соображений, при этом остаётся инвариантным расстояние (или
квадрат расстояния) между двумя точками, например,
с координатами @, 0, 0) и (х1} х2, xs) в старой системе
координат, соответственно @, 0, 0) и (х'19 х'2, х'3) в новой
системе координат, т. е.
xl + xl + xl = xi* + x'* + z?,
или 2
*) См. В. Паули, Теория относительности, Гостехиздат>
1947, § 8; В. И. Смирнов, Курс высшей математики, т. III,
ч. I, Гостехстздат, 1949, § 52; В. Паули, Релятивистская теория
элементарных частиц, ИЛ, 1947; Ф. Мурнаган, Теория пред-
представлений групп, ИЛ, 1950.
126 КЛАССИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА [гл. IV
3) «Принцип относительности равномерных и прямо-
прямолинейных движений», или «специальный прин-
принцип относительности» (иногда для сокращения
говорят просто «принцип относительности»), установлен-
установленный на базе работ Лорентца Эйнштейном и Пуанкарэ
в 1905 г., утверждает эквивалентность всех так называе-
называемых инерциальных систем отсчёта, движущихся прямо-
прямолинейно и равномерно друг относительно друга. Принцип
относительности требует включения четвёртой коорди-
координаты, т. е. времени, в значительной мере на равных мате-
математических основаниях наряду с тремя пространствен-
пространственными координатами (х, yy z) и приводит к инвариант-
инвариантности всех уравнений относительно так называемых
преобразований Лорентца, которые в формальном отно-
отношении сводятся к вращениям в плоскостях (ху t)y (г/, t),
(z, t) и выражают переход от одной инерциальнои системы
отсчёта к другой. При этом инвариантным остаётся интер-
интервал или квадрат расстояния между двумя точками
в четырёхмерном мире, например, с координатами/*, #4 = i°t
(в старой системе), и соответственно г', x± = ict' (в новой
системе) и началом координат @, 0, 0, 0):
ИЛИ
Ввиду различных знаков при квадратах пространствен-
пространственных и временных координат это четырёхмерное простран-
пространство иногда называется псевдоэвклидовым.
Тем самым мы, очевидно, приходим к изотропности
всего четырёхмерного пространства — времени и к усло-
условию инвариантности уравнений относительно четырёх-
четырёхмерных вращений, включающих как обычные вращения,
так и преобразования Лорентца в собственном смысле
слова. Общая формула четырёхмерных вращений имеет
тот же вид линейных ортогональных преобразований,
что и в трёхмерном случае, если подразумевать пробе-
гание индексами координат не трёх, а четырёх значений:
1234
23]
ОСНОВЫ КЛАССИЧЕСКОЙ ЭЛЕКТРОДИНАМИКИ
(или для бесконечно малых преобразований Ъх^ —
где Ьа^ — бесконечно малый четырёхмерный антисим-
антисимметричный тензор 2-го ранга, определяющий соответству-
соответствующее вращение). В частном случае преобразований Ло-
рентца, сводящихся к вращению координатной систе-
системы в плоскости xly x±=:ict, или, иначе говоря, в случае
перехода от одной инерциальной системы к другой,
движущейся со скоростью v = $c вдоль оси хг, имеем сле-
следующие формулы:
где к = у 1 — ра.
Таким образом матрица преобразований Лорентца
в этом частном случае имеет вид
тоо£
0 10 0
0 0 10
Как известно, для малых скоростей лорентцовы пре-
преобразования переходят в галилеевы, при которых время
остаётся неизменным:
/у»' . /у» _ 1 7 W 'У* /У| —— 'У* • тт Tiтг 'У* , л* o^т^ ^ i , т^
О/- — ^2 ~j- ^po/^j о/д — ^4^ Л Jill ^ — »с/ — UV) ь — Lm
4) Произвольность выбора правой и левой систем
координат, а также симметрия по отношению к прошлому
и будущему приводят к инвариантности относительно
зеркальных отражений (инверсий), а также к инва-
инвариантности относительно обращения времени. Эти пре-
преобразования записываются в виде
?' — г т' т y* — y г' — y (tr t\
428 КЛАССИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА [гл. IV
Весьма существенно, что первичные дифференциальные
уравнения современной релятивистской квантовой меха-
механики, так же как уравнения неквантовой и нерелятивист-
нерелятивистской механики, обратимы по времени. Необратимость же,
как известно, трактуемая вообще путём статистического
рассмотрения, может также учитываться, например,
в случае задачи излучения через дополнительные усло-
условия (использование одних запаздывающих потенциалов).
В случае инверсий, очевидно, нет речи о непрерывных
преобразованиях или бесконечно малых преобразованиях.
5) Кинематике полей и элементарных частиц можно
придать так называемую оощековариантную форму, запи-
записав их согласно Эйнштейну A916) в тензорном виде при
помощи компонент метрического тензора g.j.v*)- Форму-
Формулы преобразования координат при этом будут иметь
вид (х = хи у=-х2, z = z3, ict^Xt):
(p,v = 1, 2, 3, 4),
где коэффициенты
являются теперь функциями точки, а не постоянными,
как в прежних случаях в пп. 2 и 3. При этом инвариант-
инвариантным является «интервал» или квадрат бесконечно малого
♦) Если мы имеем дело не со скалярами или векторами и, вооб-
вообще говоря, не с тензорами любого целого ранга, а со спинорами,
которыми, например, описываются согласно квантовой теории Дира-
Дирака электроны, а также все частицы полуцелого спина, то для записи
уравнения Дирака и других в общековариантной требуемой нали-
наличием гравитации форме следует применить обобщённые дираков-
окие матрицы ^А, появляющиеся в результате факторизации или
расщепления ^v, как было показано Фоком и Иваненко.
Эти матрицы удовлетворяют соотношению
Tp.Tv ~* fvYji." £p-v
См. Д. Иваненко, Изв. АН СССР, 73, 1929; V. Foe k und
D. Iwanenko, Phys. Zs., 30, 648, 1929, С. R., Paris, 1929;
V. Fock, Zs. f. Phys., 54, 798, 1929.
§ 23] ОСНОВЫ КЛАССИЧЕСКОЙ ЭЛЕКТРОДИНАМИКИ 129
расстояния между двумя точками, который теперь имеет
вид
ds2 = g^v dx» dx*.
Подобная форма интервала характерна для геометрии
кривого, в данном случае четырёхмерного мира Лоба-
чевского-Римана, а не плоского псевдоэвклидова про-
пространства.
Заметим, что в галилеевой системе координат при
x^ — ict коэффициенты g^ образуют единичную матрицу.
Коэффициенты g^v становятся отличными от единич-
единичной матрицы, во-первых, когда галилеева система коор-
координат начинает двигаться с ускорением, благодаря чему
возникают так называемые «силы инерции» и, во-вторых,
при наличии гравитационного поля. Эти обстоятельства
привели к появлению кинематического направления
в развитии общей теории относительности, сводящегося
к попыткам отождествить гравитационные силы с «силами
инерции» (принцип эквивалентности). Однако это на-
направление оказалось бесплодным.
В самом деле, в первом случае тензор Римана-Кристоф-
феля, т. е. тензор четвёртого ранга, составленный опреде-
определённым образом из первых и вторых производных коэф-
коэффициентов g^v, обращается в нуль Л^^.бД = 0, благодаря
чему путём простого преобразования координат мы можем
во всех точках пространства уничтожить «силы инерции»
й перейти к галилеевой метрике.
Во втором случае (т. е. при наличии гравитацион-
гравитационного поля) тензор Римана-Кристоффеля будет отлич-
отличным от нуля. Всё же и в этом последнем случае для
рассматриваемой точки можно найти такую систему
координат, в которой тензор g^v образует единичную
матрицу, и первые производные от него обращаются
в нуль, правда, только в малой области в окрестности
точки. Вторые же производные в общем случае будут
отличными от нуля и только в частном случае однород-
однородного в данной области гравитационного поля обращают-
обращаются в нуль.
Таким образом, путём выбора любой другой системы
координат нельзя скомпенсировать реальные гравита-
* Д. Иваненко и А. Соколов
130 КЛАССИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА . [гл# jy
ционные силы, и в этом заключается их принципиаль-
принципиальное отличие от фиктивных «сил инерции». Следователь-
Следовательно, принцип эквивалентности гравитации и поля ускоре-
ускорения имеет место лишь для малой области, в случае, когда
гравитационное поле является однородным. Попытки
распространить его на общий случай являются заведомо
ошибочными.
6) Уравнения поля, вообще говоря, не инвариантны
относительно конформных преобразований, сохраняющих
неизменным уравнение светового конуса: сЧ2 — г2 = 0, при
которых, однако, величина интервала не сохраняется, но
умножается на некоторую функцию координат. Однако,
как было показано Бэтменом и Кэннингемом, уравнения
электродинамики Максвелла конформно инвариантны,
что тесно связано с отсутствием массы покоя у электро-
электромагнитных волн (т= 0) или сопоставленных им согласно
квантовой теории частиц—фотонов, и тем самым с отсут-
отсутствием какой-либо характерной длины типа компто-
новской длины волны Ао —— '. Однако, как показал
Паули, например, квантовые дираковские уравнения для
электрона при исчезающей массе (что, вероятно, спра-
справедливо для нейтрино) всё же не будут конформно инва-
инвариантны.
Предыдущие преобразования относились непосред-
непосредственно к координатам. Рассмотрим теперь два важных
типа преобразований, которые могут испытывать сами
вещественные или комплексные волновые функции, хара-
характеризующие поле.
7) Исходя из наглядной возможности выбрать произ-
произвольно начало отсчёта электромагнитных потенциалов,
иначе говоря, возможности добавлять к потенциалам
члены, не меняющие напряжённостей поля, мы приходим
к требованию инвариантности уравнений электромагнит-
электромагнитного поля и уравнений всех других частиц, взаимодей-
взаимодействующих с этим полем, относительно «к а* л и б р о в о ч-
н ы х» преобразований потенциалов (преобразований калиб-
*) Н. Bateman, Proc. London Math. Soc. B), 8, 228, 1909:
E. Bessel-Hagen, Math. Ann., 84, 258, 1921.
§ 23] ОСНОВЫ КЛАССИЧЕСКОЙ ЭЛЕКТРОДИНАМИКИ 131
ровки 2-го рода по номенклатуре Паули), имеющих вид
* * с дЬ '
где /—скалярная функция всех четырёх координат.
Поэтому сами электромагнитные потенциалы не могут
входить явно в уравнения Максвелла, содержащие в со-
согласии с этим лишь производные от потенциалов. (Более
подробно см. § 24.)
8) Хотя электромагнитные потенциалы входят явно
в уравнения Шредингера, Дирака и в другие кванто-
квантовые уравнения полей и частиц, но изменение их калиб-
калибровки компенсируется изменением фазы у волновых
функций.
Наглядная возможность изменить фазу квантовых
волновых функций подсказывает требование инвариант-
инвариантности всех квантовых, так называемых волновых урав-
уравнений (в том числе и нерелятивистского уравнения Шре-
Шредингера) относительно фазового или «кали б-
ровочного» преобразования волновых функций (ка-
(калибровочного преобразования 1-го рода по номенклатуре
Паули);
2тие .
Действительно, непосредственно наблюдаемыми вели-
величинами являются билинейные комбинации квантовых,
вообще говоря, комплексных волновых функций типа
плотности вероятности 0*ф, которые не изменяются при
подобном преобразовании.
С другой стороны, квантовые вещественные волно-
волновые функции и напряжённости поля сами по себе явля-
являются физически измеримыми величинами. Таким образом
непосредственно измеримыми являются величины инва-
инвариантные при калибровочных преобразованиях. В клас-
классической теории поля все величины вещественны, и все
они являются, конечно, измеримыми.
9*
d32 Классическая электродинамика [Гл. IV
Квантовая теория заряженных частиц отличается
от классической теории лишь инвариантностью отно-
относительно калибровочных преобразований 1-го рода, т. е.
фазовых преобразований волновых функций (п. 8); в кван-
квантовой теории нейтральных частиц это преобразование,
очевидно, не имеет места. При пренебрежении влиянием
тяготения, т. е. вне рамок общей теории относительности,
когда можно ограничиться инерциальными системами
отсчёта, отпадают преобразования (п. 5). Особое положе-
положение конформных преобразований (п. 6) уже было отмечено.
Инвариантность, или, точнее, ковариантность уравнений
относительно всех остальных преобразований является
обязательной. В нерелятивистском приближении, при-
пригодном при описании медленных движений и процессов
с малым балансом энергии отпадает, очевидно, группа
лорентцовых преобразований (п. 3).
Заметим теперь, что преобразования Лорентца (п. 3)
так же, как трансформации переноса (п. 1) и трёхмерных
вращений (п. 2), а также преобразования координат
типов пп. 5, 6 и калибровочные преобразования (пп. 7, 8),
образуют группы непрерывных преобразований, т. е.
два последовательных преобразования могут быть за-
заменены одним преобразованием того же типа. На-
Например, два преобразования вращения эквивалентны
одному вращению и т. д. В каждой группе имеется
единичное (тождественное), а также обратное преобра-
преобразование.
С другой стороны, преобразования инверсии сами
по себе, очевидно, группы не образуют, но вместе с
собственно ортогональными преобразованиями (п. 3) или
(п. 2) образуют более общую группу вещественных ор-
ортогональных преобразований, для которых определи-
определитель, составленный из коэффициентов ars1 равен ± 1,
тогда как в случае чистых вращений определитель
равен *+1.
Весьма важно подчеркнуть, что инвариантности урав-
уравнений, описывающих какое-либо поле, и, следовательно,
инвариантности соответствующего лагранжиана или вари-
вариационного интеграла действия относительно каждой непре-
непрерывной группы преобразований соответствует свой особый
§ 23] ОСНОВЫ КЛАССИЧЕСКОЙ ЭЛЕКТРОДИНАМИКИ 133
закон сохранения (теорема Нетер)*). Например, из инва-
инвариантности всех уравнений относительно переноса начала
трёх пространственных координат и отсчёта времени
(п. 1) вытекают универсальные законы сохранения трёх
компонент количества движения и энергии (всего четыре
закона). Инвариантность всех уравнений относительно
вращений в пространстве (п. 2) приводит к универсаль-
универсальному закону сохранения момента количества движе-
движения (три закона сохранения). Инвариантность всех
уравнений относительно преобразований Лорентца, т. е.
вращений в плоскостях (zt), (yt)y (zt)y приводит к обоб-
обобщённому закону сохранения движения центра тяжести
(три закона сохранения). Указанные десять фундамен-
фундаментальных законов сохранения соответствуют универсаль-
универсальной инвариантности относительно непрерывных, в част-
частности бесконечно малых, преобразований конечной груп-
группы, обозначаемой через GlQy зависящей всего от D + 3-f
+ 3 = 10) десяти параметров.
Специальная инвариантность уравнений Максвелла
относительно конформных преобразований приводит к но-
новым соотношениям типа законов сохранения, не имею-
имеющим, впрочем, какого-либо обычного непосредственного
физического смысла, что ещё раз показывает исключи-
исключительное положение этой группы^**). Относительно дока-
*) Е. N о е t h е г, Goettingen Nachricht, 235, 1918; Е. В е s s e 1-
Н a g e n, Math. Ann., 84, 258, 1921 (применения к классической
электродинамике Максвелла); М. А. Марков, Phys. Zs. der
Sowjetunion, 10, 773, 1936 (применения к теории электрона Дирака).
♦•) Отметим, что общая группа преобразований координат G
является конечной и зависящей от 10 параметров (р= 10). С другой
стороны, например, при калибровочном преобразовании потенциа-
потенциалов (п. 7) электромагнитного поля мы имеем бесконечную группу
Goop = 6?OOl, определяемую некоторой функцией калиброгки (р=1).
Точно так же произвольные точечные преобразования общей теории
относительности (п. 5) образуют бесконечную группу, определён-
определённую четырьмя произвольными функциями: Goo4: (р = 4) (связанными
с преобразованиями четырёх координат). В случае инвариантности
относительно бесконечно малых преобразований какой-либо беско-
бесконечной группы G^ имеет место теорема Гильберта, утверждающая
наличие р тождественных соотношений между лагранжевыми вари-
вариационными производными соответствующей функции действия и их
134 КЛАССИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА [гл. IV
зательства теоремы Нетер в частных интересующих нас
случаях смещения и вращения координат см. ниже § 30.
Перечислим теперь кратко различные типы волно-
волновых функций, вообще говоря, комплексных, способных
описывать волновые свойства элементарных частиц и слу-
служить тем «строительным материалом», из которого при
помощи указанных требований инвариантности можно
конструировать теорию тех или иных полей.
1) Скалярная функция (или инвариант, т. е. тензор
ранга 0). Сжаляр ф не изменяется при всевозможных
преобразованиях.
2) Четырёхмерный вектор с четырьмя компонентами
ty^ = Alf А2, А3, А± (тензор ранга 1).
3) Тензор 2-го ранга, который, в частности, можно
получить, беря произведение двух векторов.
В теории могут играть роль как антисимметричные
тензоры 2-го ранга, имеющие шесть составляющих (ше-
стивектор):
Л [XV == ^*Vp.>
например тензор электромагнитного поля, образованный
из производных четырёхмерного векторного потенциа-
потенциала, так и симметричные тензоры, например метрический
тензор
имеющий десять различных компонент, играющих роль
гравитационных потенциалов.
Тензоры высшего ранга также можно использовать
для описания тех или иных полей, однако до сих пор
особой надобности в этом не встретилось.
4) В качестве волновых функций тех или иных полей
можно использовать также волновые функции, «дуаль-
«дуальные» к скаляру (псевдоскаляр) и к вектору (псевдовек-
(псевдовектор). Более подробно см. § 46.
производными. Например, ввиду наличия четырёх тождеств в об-
общей теории относительности из десяти гравитационных потенциа-
потенциалов g остаётся всего шесть независимых (D. H i I b е г t, Matlj.
Ann., 92, 1, 1924; Gesamm. Werke, Bd. III).
§ 23] ОСНОВЫ КЛАССИЧЕСКОЙ ЭЛЕКТРОДИНАМИКИ 135
5) Для описания волновых свойств частиц с полуце-
полуцелым спином (например, электрона, протона, нейтрона)
необходимо применить спиноры или тензоры ранга 1/2
(употребляются также термины: семивекторы, полу-
полувекторы). Обычные тензоры и спиноры можно тракто-
трактовать совместно как спинтензоры или согласно Бельин-
фанте—ундоры*). В настоящее время производится разра-
разработка теории волновых функций, являющихся тензорами
(или спинорами, см. стр. 128) высшего ранга и свя-
связанных, как выясняется, с частицами высшего **) спина.
в) Основные уравнения
классической электродинамики
Получив основные сведения об инвариантности и ха-
характере величин, из которых строится теория того или
иного поля, перейдём к анализу классической электро-
электродинамики, т. е. неквантовой релятивистской теории элек-
электромагнитного поля и заряженных частиц. Уравнения
поля можно получить из вариационного принципа, если
известна соответствующая лагранжева функция.
В данном параграфе координаты электрона будем
обозначать через
Эти координаты зависят от собственного времени s
(равного в покоящейся системе координат т), производную
по которому будем обозначать точкой, т. е. £1Х = -^. Для
координат же электромагнитного поля напишем х^ = г, ict
В согласии с многовременным формализмом теории
относительности частицы и поле будем характеризовать
своими отдельными координатами времени.
При этом мы отвлекаемся сейчас от учёта собст-
собственного магнетизма частиц, который к тому же по
*) Э. К а р т а н, Теория спиноров, ИЛ, 1947; F. В е 1 i n f а п-
t e, Theory of heavy quanta, Hague, 1940.
**) См., например, И. ГельфандиА. Яглом, ЖЭТФ,
J9, 703, 1948.
136 КЛАССИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА [гл. IV
существу имеет квантовую природу, а под зарядами для
определённости будем понимать электроны*).
Тензор электромагнитного поля Н^ связан с четырьмя
составляющими четырёхмерного вектора, являющегося
потенциалом A^ = Af гср, соотношением «вихря»
н^=='ЦГ~д^9 Cf ]
причём
23 Н21 Н12\ __ / Нх Ну Нл
4i Я42 Hj " \iEx iEy iEj ' K ' '
где Е и Н. являются векторами электрического и маг-
магнитного поля. Таким образом основными величинами клас-
классической электродинамики, на базе которых строится
вся теория поля, являются скалярный потенциал ср и век-
вектор-потенциал А.
Во главу угла всей классической электродинамики, как
и в случае других полей, целесообразнее всего поставить
вариационный принцип или принцип наименьшего дей-
действия для соответствующей функции (интеграла) дей-
действия S, или же для непосредственно связанной с ней
лагранжевой функции L. Равенство нулю вариации функ-
функции действия: об1 —0, даст искомые уравнения как эйле-
эйлеровы уравнения вариационной задачи.
Функция действия S состоит из трёх частей:
S = SX+S2 + S3. B3,4)
Часть Sj является функцией координат и определяет
уравнение свободного движения электрона; часть S2
является функцией потенциалов А1Х и приводит к урав-
уравнению свободного электромагнитного поля в отсут-
отсутствии источников; последняя же смешанная часть S3y
являющаяся функцией величин, характеризующих как
поле, так и частицу, будет описывать взаимодействие
*) См. ниже § 47, где трактуется близкий вопрос о связи
нуклеонов с векторным мезонным полем при наличии у частиц ква-
виэлектрических зарядов и квазимагнитных моментов.
§ 23] ОСНОВЫ КЛАССИЧЕСКОЙ ЭЛЕКТРОДИНАМИКИ 137
V
между электроном и электромагнитным полем. Функция
действия S, как и её три части в отдельности, должна
быть инвариантом относительно всех перечисленных выше
допустимых преобразований четырёх координат и вол-
волновых функций, т. е. потенциалов поля.
Важно подчеркнуть, что при заданных трансформа-
трансформационных свойствах величин, из которых строится Sf
при условии ограничения низшей возможной степенью
производных и при условии линейности уравнений поля,
функции действия Sl9 S2, S3, а тем самым дифференциаль-
дифференциальные уравнения поля получаются однозначно, и окон-
окончательное выражение S зависит только лишь от произ-
произвольных констант, на которые могут быть умножены
отдельные части функции действия. При этом константа,
входящая в Sl9 есть по существу масса покоя частицы
Шу значение которой берётся из опыта; константа, вхо-
входящая в S2f есть множитель нормировки, определяющий
выбор единиц, в данном случае гауссовых. Наконец,
константа в S3 есть коэффициент связи заряженной
частицы с полем или электрический заряд (в более общем
случае в Ss входит также магнитный момент, определя-
определяющий связь «магнитной» частицы с полем).
Функция действия для свободной частипы будет иметь
вид интеграла, взятого вдоль мировой линии между
какими-либо двумя точками четырёхмерного мира:
s, B3,5)
так как интервал ds есть единственный инвариант, кото-
который можно образовать из дифференциалов координат
точечной частицы. Вместо этого можно также для удоб-
удобства написать
учитывая, что инвариант (с^^), являющийся квадра-
квадратом четырёхмерной скорости, равен, как будет показано
ниже, — с2
138 КЛАССИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА [ГЛ IV
Принимая во внимание, что
где и == т— равняется трехмерной скорости движения
частицы, можем положить
Определённая подобным образом функция Лагранжа Lx
в случае свободной частицы равна известному из теории
относительности выражению
L1 = ™C2_™C2 J/ i__.L2> B3,6)
причём в последнем выражении мы добавили постоян-
постоянный член тс2, который не меняет уравнений движения.
В нерелятивистском приближении при малых скоростях
v < с лагранжиан принимает известный из классической
ньютоновской механики вид
J71V2
£l=-2-t B3>7)
что и оправдывает* выбор констант в лагранжиане.
Перейдём к смешанной части S3. Единственный допу-
допустимый инвариант, из которого можно образовать функ-
функцию действия S3, имеет вид
S4 = ±[ds
Здесь четырёхмерный объём (dx) = (dr) dt = dx dy dz dt,
A^ и А\ являются соответственно потенциалами, созда-
создаваемыми самим электроном и внешним полем. Нетрудно
усмотреть, что этот инвариант образован по правилу,
которое неоднократно будет использовано в дальнейшем:
вектор частицы (т. е. скорость Zlx) умножается на вектор
ПОЛЯ (^jx+^fx)*).
*) При учёте собственного магнетизма частицы следовало бы
добавить сюда ещё член, равный произведению тензора магнит-
магнитного и электрического момента частицы jiap на тензор поля На^
(см. § 47), т. е. i- na[Jtf ap.
§ 23] ОСНОВЫ КЛАССИЧЕСКОЙ ЭЛЕКТРОДИНАМИКИ 139
Инвариантная величина р, имеющая характер плот-
плотности, может быть представлена в виде*)
D (fc> *«) етг-1)-пЫ1-*) (dk) dkt,
где форм-фактор D должен являться инвариантной функ-
функцией компонент вектора ку = к, й:4, например функцией
четырёхмерного инварианта-квадрата длины: к2 — к\\
(dh) = (dk) dk±.
В частности, для точечного электрона следует поло-
положить D = 1. В этом случае
р = 8(г-Е)8(«—г). B3,9)
Принимая во внимание, что £4=- icif § = vz (у — трёх-
трёхмерная скорость), выражение £3 для точечного элек-
электрона можно привести к виду
], B3,8a)
из которого легко будет найти силу Лорентца.
Наконец, часть функции действия S2, относящаяся
к самому полю, будет равна
0(dx), B3,10)
где Lo является инвариантной функцией полей H^v.
В частности, к интересующим нас сейчас уравнени-
уравнениям Максвелла-Лорентца электромагнитного поля (т. е.
к уравнениям первого порядка и линейным относи-
*) Мы ввели мнимую четвёртую координату лишь для опреде-
определения полей, чтобы избавиться здесь от необходимости одновремен-
одновременного применения ко- и контравариантных составляющих, различие
между которыми несущественно при отсутствии тяготения, т. е. вне
рамок общей теории относительности. Если же время входит в эле-
элемент четырёхмерного объёма или в качестве аргумента для плотно-
плотности зарядов, его проще оставить действительным.
140 КЛАССИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА [гл. IV
тельно i/,xv) приводит только инвариант Лармора,
равный *)
^^ (^n B3,11)
Другие основные инвариантные комбинации, состав-
составленные из функций поля, приводят или к нелиней-
нелинейным уравнениям (второй основной инвариант поля:
/2 = (.Е • 2ГJ**) или к уравнениям, зависящим явно от
потенциалов, т. е. не удовлетворяющим требованию
калибровочной инвариантности (третий основной инва-
инвариант поля /3 = ср2 — А2 = — А^Ар). На этом вопросе
мы остановимся более подробно в других параграфах
(см. §§32, 33 и 47).
При варьировании функции действия по собствен-
собственному времени, что приведёт к уравнению движения ча-
частицы в электромагнитном поле, мы можем отбросить £2,
подинтегральное выражение которой не зависит от соб-
собственного времени s.
*) Так как нас сейчас не интересуют дифференциальные
уравнения, описывающие свободные внешние поля Hl,xv, то мы
не включаем в лагранжиан Lo внешних полей. В противном случае
следовало бы написать, например, вместо Lo
Внешние поля были нами введены лишь в смешанное выражение
функции действия для того, чтобы определить воздействие внешнего
поля на движение электрона.
**) Инвариант /^ можно написать в виде
A ~
~2 Za
где sapT§—единичный антисимметричный псевдотензор четвёртого
ранга* с помощью которого данному антисимметричному тензору
Яар сопоставляется дуальный тензор #т§ =-— ^а^На^. Тогда
произведение дуального тензора на основной даст псевдоскаляр:
Ят§Ят8 (произведение полярного вектора Е на аксиальный Я),
квадрат которого будет скаляром (инвариантом). Более подробно
см. § 46.
§ 23] ОСНОВЫ КЛАССИЧЕСКОЙ ЭЛЕКТРОДИНАМИКИ 141
Таким образом для этой задачи функция действия
принимает вид
S' =* ^ L'ds, B3,12)
где лагранжиан
B3,13)
Эйлеровское уравнение искомой вариационной задачи
IS' = 0 при условии исчезновения вариаций на обоих
пределах (о^)-^ (S£vJ = 0 даёт
ЯГ' ЯГ' A AT'
\jJ-j UJ-j to US-j г\ /ОО Л / \
ОС QC US л 2"
Из B3,13) следует
где
откуда
Учитывая далее равенство
а также соотношение
J ^|^/И(^)= J p(*-6)J£-(<fa), B3,15)
142 КЛАССИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА [гл. IV
получим следующее уравнение движения частицы с мас-
массой покоя т:
B3,16)
Здесь так называемая сила само действия (т. е. сила
обратного действия поля на частицу) или сила взаимо-
взаимодействия «элементов» частицы друг с другом равняется
. B3.17)
В частности, для точечного электрона имеем выражение
Р^ = ~КН^). B3,18)
Точно так же находим, что сила, действующая на частицу
со стороны внешнего поля, имеет вид, точно совпадаю-
совпадающий с известным выражением лорентцовой силы:
n—ilXvtfi). B3,19)
Поля Н^ и Н\ч являются антисимметрическими тен-
тензорами. Поэтому они ортогональны к симметрическому
произведению £jjv.
В самом деле,
СцЛ-у" P-V ==: "о" $\&уН (jlv ~Г "о" SVSjjl-" VP- == "о" ^Ц-Чv (■" Ц-V "Т" ■" V^) == ^*
Отсюда следует, что силы F^ и F^ должны быть орто-
ортогональными к вектору скорости £^:
Учитывая последние равенства, находим из B3,16) орто-
ортогональность четырёхмерных скоростей и ускорений
VA, = O. B3,20)
§ 23] ОСНОВЫ КЛАССИЧЕСКОЙ ЭЛЕКТРОДИНАМИКИ 143
Иными словами, квадрат четырёхмерной скорости дол-
должен оставаться величиной постоянной:
Кк = LL - с2т2 = const. B3,21)
Постоянная величина может быть найдена из условия,
что для неподвижного электрона %п = 0, т = 1, т. е.
const = — с2.
Поэтому трансляционное уравнение движения заряжен-
заряженной частицы принимает окончательно вид
mi^Fl + Fv*). B3,22)
Перейдём теперь к выводу уравнений электромагнитного
поля путём варьирования функции действия S по элек-
электромагнитным потенциалам. Мы можем отбросить часть
Sl9 не зависящую от потенциалов.
Тогда, очевидно, имеем
^t B3,23)
где лагранжиан
L = Lo + -с \ Р (х - Е) [^ (А» + 4I ds. B3,24)
Из уравнений Эйлера вариационного принципа 8£" = 0
при условии исчезновения вариаций (ЬА1У) на границах
получим
Здесь
Обозначая тензор моментов поля (смещений) через D^:
^v = 4«^, B3,26)
*) Более подробно вопрос о силе самодействия Fp будет рас-
рассмотрен ниже (см. §§ 31 и 34).
144 КЛАССИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА [гл. IV
находим общие дифференциальные уравнения для опре-
определения полей
В частности, согласно B3,11) для максвелловского
поля
Dw = H^. B3,28)
Поэтому уравнения электромагнитного поля Максвелла-
Лорентца окончательно принимают вид
^-Q^cfe, B3,29)
где в правой части стоит выражение плотности четырёх-
четырёхмерного тока.
Для точечного электрона имеем:
р (ж —Е) = в(г —S)8(« —-с). B3,30)
Подставляя B3,30) в B3,29) и интегрируя по £(£—-т),
с помощью соотношения F,5) получим
(первая группа уравнений Максвелла-Лорентца в четы-
четырёхмерном виде) при условии, что т = t.
Для определения тензора H^v имеем уравнение B3,2),
которое можно представить в виде
дЗ ^ + р» = 0 B3,31)
дх ' dx x ' f
дх
л
(вторая группа уравнений Максвелла, сводящая к исчез-
исчезновению «цикла» антисимметрического тензора поля) *),
*) При помощи символа еарт8 (см. § 46) уравнение B3,31)
можно записать в виде
дх^
§ 24] ИНТЕГРИРОВАНИЕ УРАВНЕНИЙ МАКСВЕЛЛА 145
откуда, переходя к векторной форме, запишем первую
группу уравнений Максвелла при наличии точечного
источника:
v s" B3>32)
i — g),
где ^ является трёхмерной скоростью движения частицы,
т. е. v = -т^ . К этим уравнениям мы должны добавить
уравнение B3,2), связывающее компоненты поля с по-
потенциалами, или эквивалентное ему уравнение B3,31).
В трёхмерных обозначениях уравнение B3,2) имеет
вид
Н = го1А, ^=-gradT-; ^. B3,33)
Вместо последних уравнений, являющихся определением
напряжённостей поля, можно написать тождественно со-
совпадающую с ними вторую группу уравнений Максвелла-
Лорентца [см. B3,31)]
1 ОН ,л
O
divjff=O. B3,34)
§ 24. Интегрирование уравнений Максвелла-Лорентца
При интегрировании уравнений Максвелла-Лорентца
мы должны прежде всего учесть так называемую калибро-
калибровочную инвариантность, которая возникает в связи с не-
неоднозначным выбором потенциалов при заданных элек-
электромагнитных полях (см. условие 7 в § 23).
В самом деле, вводя новые потенциалы
где / — произвольная скалярная функция калибровки,
мы видим, что электромагнитные поля Hav будут свя-
связаны одинаковым соотношением как с потенциалами А^,
Ю Д. Иваненко и А. Соколов
146 КЛАССИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА [гл. JV
так и с А'р\
___дА ЭА^_ЭА> ЭА'^
Уравнения Максвелла-Лорентца B3,29), а также урав-
уравнение движения электрона B3,22) не содержат в явном
виде потенциалов и поэтому, как уже указывалось вы-
выше, не должны зависеть от выбора калибровочной
функции /*).
Неопределённость выбора значений для потенциалов
приводит к тому, что мы не можем однозначно опре-
определить Ац, не наложив дополнительного условия на ка-
калибровочную функцию /. Как правило, калибровочная
функция / выбирается таким образом, чтобы потенциалы
удовлетворяли дополнительному условию Лорентца:
^ = 0] B4,3)
Г или в трёхмерном виде: div А-\— ~— 0 V Однако ка-
калибровка Лорентца не является единственной возмож-
возможной, и, в частности, для электромагнитных (световых)
волн накладывается другая калибровка, соответству-
соответствующая наличию одних лишь поперечных колебаний
= 0. B4,4)
Перейдём теперь к решению системы уравнений Макс-
Максвелла-Лорентца B3,29) при дополнительном условии
Лорентца B4,3).
*) При калибровочном преобразовании к смешанной функции
действия Sz добавляется величина
которая может быть отброшена, так как она с помощью равенства
B3,15) приводится к полному дифференциалу:
и поэтому не может влиять на уравнения движения.
§ 24] ИНТЕГРИРОВАНИЕ УРАВНЕНИЙ МАКСВЕЛЛА 147
Подставляя вместо Н^ значение B3,2), получим
уравнение:
D Л = (V» - I -g) Л = - ^ J Р (* - £) I Л. B4,5)
Решая уравнения Даламбера, находим согласно A7,20)
р (*'-£) 8 (/Р-сТ») (l+ е^) (dx')9
где
В = !•-*', T = t-t', {dx') = (dr')df, B4,6)
а величина е в зависимости от того, берём ли мы за-
запаздывающие, опережающие или полусумму тех и дру-
других потенциалов, будет соответственно равна +1, —1
или 0.
Для точечного электрона [см. соотношение B3,9)]
решение с запаздывающими потенциалами приводит
к выражению
Л =« J К cR> ds>
J cR>
где
Вводя трёхмерную скорость v = ~- , получим для ска-
лярного потенциала <р = -г-* и вектор-потенциала Л сле-
следующие выражения;
R'\
с / ,
10*
148 КЛАССИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА [гл. VI
§ 25. Потенциалы Льенара-Вихерта
и формула Брейта
При помощи соотношений B4,8) для потенциалов то-
точечного электрона весьма просто получаются выражения
для потенциалов Льенара-Вихерта, а также классиче-
классический вид формулы Брейта.
Для того чтобы получить потенциалы Льенара-Вихерта
для точечного заряда, мы должны взять интеграл B4,8)
по времени т, учитывая, что R' зависит от т без всяких
дополнительных предположений о распределении плот-
плотности заряда электронов в пространстве.
Тогда согласно равенству F,5)
При выводе последней формулы мы учли, что
Здесь Rf° = ^r является единичным вектором, а для
определения времени т служит уравнение т — t -f — =0.
Аналогичным образом для вектор-потенциала А
находим
<> B5,3)
Выражения B5,1) и B5,3), известные под названием
потенциалов Льенара-Вихерта, обычно получаются с по-
помощью предельного перехода от электрона, обладающего
плотностью, распределённой в пространстве, к точечной
частице, что в нашем выводе автоматически учитывается
при помощи формализма S-функции.
Определим теперь энергию взаимодействия между
двумя движущимися точечными зарядами, которые будем
обозначать соответственно индексами 1 и 2.
§ 25] ПОТЕНЦИАЛЫ ЛЬЕНАРА-ВИХЕРТА И ФОРМУЛА БРГПТА 149
Как известно, эта энергия взаимодействия опреде-
определяется выражением [см. B3,8а)]
ee1(vlAa), B5,4)
где ег и vx являются зарядом и скоростью первого
электрона, а <р2 и А2— электромагнитными потенциала-
потенциалами, создаваемыми вторым электроном в той точке, где
находится первый электрон.
Если мы подставим сюда вместо ср2 и А2 пйтен-
циалы Льенара-Вихерта, то увидим, что V12 будет зави-
Tit
сеть от двух различных времён t и t , где R—рас-
R—расстояние между двумя электронами. Мы будем опреде-
определять приближённое значение для энергии взаимодей-
взаимодействия V12f отнесённой к одному и тому же моменту вре-
V2
мени ty с точностью до величин порядка -2 .
Для этого разложим S-функцию по величинам — :
Ограничиваясь при вычислении ср2 тремя членами
разложения, а при вычислении Л2 одним первым членом,
получим, учитывая правила интегрирования с с-функ-
с-функцией:
R "^ 2c2 dt*
где R—расстояние между двумя электронами, отнесён-
отнесённое благодаря интегрированию по 6-функции и её про-
производным к одному и тому же моменту времени t.
150 КЛАССИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА [гл. IV
Совершим калибровочное преобразование к новым
потенциалам. Выбрав величину / равной е2—*\ найдём
JLc ot
£ gva*. B5,8)
Учитывая соотношение B5,2), имеем
dt
откуда
Подставляя B5,10) и B5,7) в равенство B5,4), полу-
получим важную формулу, определяющую взаимодействие
между двумя движущимися электронами с точностью
до величин второго порядка относительно v/c:
Это выражение было найдено впервые Брейтом. Оно
симметрично относительно обоих электронов и учитывает
запаздывающее действие, несмотря на то, что все вели-
величины, входящие в формулу, относятся к одному и тому же
моменту времени t. Соответственное обобщение формулы
Брейта было получено также в квантовой механике.
В случае взаимодействия электронов, которые описы-
описываются квантовыми спинорными уравнениями Дирака,
следует для перехода к квантовой формуле Брейта за-
заменить скорости vx и 02 соответственно на дираков-
ские матричные операторы сах и са2, а также трактовать
всё выражение как оператор, действующий на волновые
ф-функции. Нетрудно получить квантовое обобщение
*) См., например, Л. Ландау и Е. Лифшип, Теория
поля, Гостехиздат, 1948, стр. 193.
§ 26] ТОЧЕЧНЫЙ ЗАРЯД, ДВИЖУЩИЙСЯ РАВНОМЕРНО 151
формулы Брейта также для случая взаимодействия заря-
заряженных частиц, описываемых скалярным, векторным
и другими уравнениями, что должно иметь применение
в квантовой теории мезонов, повидимому, характеризуе-
характеризуемых этими уравнениями.
Формула Брейта была с успехом применена в кван-
квантовой теории атома, в частности, при рассмотрении тонкой
структуры спектра гелия и ионизированного лития,
обладающих двумя электронами, а также при рассмо-
рассмотрении рассеяния электронов. Заметим, что в квантовой
механике для приближённого учёта взаимодействия двух
зарядов наряду с формулой Брейта применяется формула
Мёллера, также учитывающая запаздывающее действие
и представляющая собою инвариантное относительно
скоростей выражение, являющееся результатом разложе-
разложения по степеням постоянной тонкой структуры*).
§ 26. Поле точечного заряда,
движущегося равномерно и прямолинейно
Пусть вдоль оси z движется точечный заряд с постоян-
постоянной скоростью v. Тогда для плотности заряда [* и тока
]г мы имеем следующие выражения:
Р = е? (а?) 8 (у) 8 (*-»*).
В этом случае волновые уравнения для определения
скалярного и векторного потенциала примут вид:
72 - ? Ю * = -
B6.2)
♦) См. Г. Бете, Квантовая механика простейших систем,
ОНТИ, 1935, стр. 145 и 305; В. Г а й т л е р, Квантовая теория
излучения, Гостехиздат, 1940, стр. 115; М. А. Марков, ЖЭТФ.
18, 510, 1948. f
152 КЛАССИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА [гл. IV
где р равняется отношению скорости заряда v к скорости
света с в пустоте, т. е. р = — , причём согласно теории
с
относительности мы всегда должны иметь р < 1.
Из последних формул видно, что
4 = Р<Р- B6,3)
Кроме того,
Для компонент электромагнитного поля имеем
JOjt= — — , Л/ц = — — ,
х дх' у ду
Здесь мы учли равенство B6,3), а также тот факт,
что все компоненты полей зависят только от разности
(z— Ы), поэтому
Чтобы определить скалярный потенциал ср, подста-
подставим в правую часть B6,2) разложение Фурье трёхмер-
трёхмерной о-функции:
= 8^5 \ dkl dk* dY- в^^+^+'С-1")], B6,6)
откуда, производя деление на оператор Даламбера и выби-
выбирая решения с запаздывающими потенциалами, получим
plj о [к\ + *» + х2 A - ря)] J ЙАХ с?Л? d*, B6,7)
§ 26] ТОЧЕЧНЫЙ ЗАРЯД, ДВИЖУЩИЙСЯ РАВНОМЕРНО 153
При выборе опережающих потенциалов в последних
квадратных скобках перед о-функцией следовало бы
взять знак минус.
В случае, когда р < 1, аргумент, от которого зависит
S-функция, не будет содержать особой точки, т. е. не
будет обращаться в нуль, поэтому 6-функцию, стоящую
в скобках, мы можем просто отбросить. Таким образом
как запаздывающие, так и опережающие потенциалы
приводят к одному и тому же значению для ср.
При интегрировании выражения B6,7) проделаем
замену переменных
^. B6,8)
Тогда для ср находим
ч+ч+ч
Последнее выражение пропорционально гриновской
функции уравнения Пуассона с решением, найденным
нами в § 10 [см. формулу A0,11)]:
ср = ~, B6,9)
где
т^у (l-p2)(^ + y2) + (z-^J-
Эквипотеи пальными поверхностями г2 = const здесь
будут сплюснутые (вдоль оси z) эллипсоиды, исследо-
исследованные впервые Хивисайдом. С помощью формул B6,4)
мы можем определить также поля Е и Ш.
Как известно, электрон, движущийся с постоянной
скоростью в вакууме, не излучает энергии, так же как
это имеет место тривиальным образом для покоящегося
электрона. Наглядно можно представить себе, что в этом
случае поле, связанное с электроном, движется равно-
равномерно вместе с ним, не «отрываясь». Это связано фор-
цально с тем обстоятельством, что при v < с уравнение
154 КЛАССИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА [гл. IV
Даламбера для потенциала, имеющее гиперболический
вид, может быть сведено к уравнению эллиптическо-
эллиптическому, соответствующему потенциалу покоящегося заряда.
Иначе говоря, с помощью преобразований Лорентца
мы всегда можем выбрать такую систему координат,
относительно которой равномерно и прямолинейно дви-
движущийся электрон будет покоиться и, следовательно,
не должен излучать.
Вообще говоря, излучение является необратимым
процессом, и поэтому оно должно быть связано с нали-
наличием членов, несимметричных относительно запаздываю-
запаздывающих и опережающих решений. Подобным несимметрич-
несимметричным членом является выражение с S-функцией, стоящее
в подинтегральном уравнении B6,7). Поэтому излучение
должно отсутствовать, когда этот несимметричный член
обращается в нуль.
§ 27. «Сверхсветовой» электрон Черенкова
Согласно теории относительности скорость движения
электрона не может превосходить скорости света в 'ва-
'вакууме Г р = — < 1 j . Однако при движении электрона
в какой-либо среде его скорость v, оставаясь меньше
скорости света в вакууме, может оказаться больше
фазовой скорости света в данной среде: с' = — < с
(л —показатель преломления среды), т. е. возможен
случай, когда — < v < с. В этом случае электрон обго-
обгоняет поле, которое, говоря наглядно, «отрывается» от
него, т. е. излучается.
Остановимся на теории этого вопроса, впервые под-
подробно разработанной для движения электрона в ди-
диэлектрике И. Е. Таммом и И. М. Франком, показавшими,
что в данном случае будет иметь место излучение *), кото-
*) И. М. Франк и И. Е. Т а м м, ДАН, 14, 107, 1937.
Подробная теория эффекта Черенкова дана в статье И. Е. Т а М М §
(Ig. ТафДО. Joiji», of Phys. USSR, 1? 439, 1939).
§ 27] «СВЕРХСВЕТОВОЙ» ЭЛЕКТРОН ЧЕРЕНКОВА 155
рое действительно было наблюдено ещё ранее в 1934 г.
П. А. Черенковым (в лаборатории С. И. Вавилова)*).
Для краткости указанное явление Черенкова разумно
назвать также согласно его физическому смыслу «эф-
«эффектом сверхсветового электрона». При этом наблюда-
наблюдалось весьма слабое видимое свечение, вызванное бы-
быстрыми электронами, двигавшимися в различных жидко-
жидкостях и твёрдых телах с высоким показателем преломле-
преломления (например, в циклогексане, где п = 1,4367). Элек-
Электроны получались как из внешнего источника, так и воз-
возникали за счёт комптон- и фотоэффекта от уизлучения
радиоактивных препаратов. Большую трудность пред-
представило отделение нового свечения от различных видов
люминесценции, а также наблюдение свечения крайне
малой интенсивности.
Перейдём к теории эффекта Черенкова. Если точеч-
точечный электрон движется в среде с показателем прелом-
преломления п = \/ е (г—диэлектрическая постоянная) по оси z
с постоянной скоростью v9 то уравнения Максвелла при-
принимают вид
4tf, B7Д)
= 4тгр,
где
H=rotA,
1 дА
s-i>0, B7,2)
Векторы D и JE связаны между собою соотношением
D = CJE) = (*2JS). B7,3)
*) С. И. В а в и л о в, ДАН, ?, 457, 1934, П. А. Ч е р е н к о в,
ДАН, 2, 451, 1934. Полная сводка экспериментальных результатов
П. А. Черенкова содержится в его докторской диссертации, опубли-
опубликованной в Трудах Физического института АН СССР им. Лебедева,
2, № 4, 1944.
156 КЛАССИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА [гл. IV
Последнее соотношение имеет место, когда показа-
показатель преломления п является величиной постоянной.
В общем же случае п зависит от частоты ш. Тогда
равенство B7,3) будет носить операторный характер *)
и будет иметь место для отдельных компонент Фурье,
т. е. для отдельных частот. Разлагая поля в интегра-
интегралы Фурье:
D= [ D(a>)e-ia>f du>, JE=[ Е-(«>) е-*0'da> и т. д., B7,4)
мы раскроем смысл равенства B7,3) в виде формулы
е~ш dm. B7,5)
Отсюда для компонент Фурье имеем
В{и) = п2Е{ы). B7,6)
Заметим, что деление на оператор, содержащий вели-
величину п2, является вполне законным действием так же,
как и деление на линейные операторы, составленные из
частных производных. В самом деле, из равенства B7,3)
имеем
E-(^D)SePe~md^ <27>7)
что находится в полном согласии с формулой B7,6).
В дальнейшем мы не будем особо оговаривать опера-
операторный характер величин, содержащих показатель пре-
преломления п.
Учитывая условие Лорентца
4,.=^ = о,
а также соотношение B7,1), найдём
С27*8)
*) Чтобы подчеркнуть операторный характер равенства B7,3),
мы заключаем величину п2Е в круглые скобки, т. е. будем пи-
писать (n2JE7).
§ 27] «СВЕРХСВЕТОВОЙ» ЭЛЕКТРОН ЧЕРЕНКОВА 157
Электромагнитные поля Е и JET будут связаны со
значением скалярного потенциала ср при помощи ра-
равенств
B79)
Я.-fta-g. Я, =-?»•£. # 0 J '
где у2 = и2?2 — 1.
Подставляя в правую часть уравнений B7,8) вместо
8-функции её значение из формулы B6,6), найдём
2тх8 J n2
X dkxdk2d^ B7,10)
В нашем случае, когда электрон движется со скоро-
скоростью *;>.— , величина у2=р27г2— 1 будет больше ну-
нуля, и поэтому мы не можем отбросить в подинтеграль-
ном выражении B7,10) член, пропорциональный 8-функ-
8-функции, обусловливающий излучение.
При интегрировании последнего выражения мы сде-
сделаем переход к цилиндрическим координатам
jj, x) .
Тогда, интегрируя по полярному углу <]>, найдём со-
согласно B1,6)
[ F^Wnn] K B7Д1)
где
158 КЛАССИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА [Гл. IV
откуда при помощи соотношений A8,17) получим
окончательно основную для всей теории формулу для
скалярного потенциала электромагнитного поля, поро-
порождённого прямолинейно и равномерно движущимся элек-
электроном:
B7,12)
Теперь мы можем найти количество энергии, кото-
которую излучает электрон в единицу времени.
Согласно теореме Умова-Пойнтинга
B7>13>
Интегрирование произведём вдоль цилиндрической
поверхности радиуса г, геометрической осью которой
является ось z.
Элемент поверхности dS равняется
dS^rdydzy, B7,14)
где *
Принимая во внимание значения компонент поля
B7,9), имеем
B7,15)
причём согласно операторному равенству B7,5)
X [| х | /0 (П | х |) + wiV0 G7 | х |
§ 2'7] «СВЕРХСВЕТОВОЙ» ЭЛЕКТРОН ЧЕРЕНКОВА 159
Подставив последние соотношения в B7,13), по-
получим
оо
-*Я=\*№СГ \ £f(*Vo-JoNo)dv., B7,17)
причём цилиндрические функции зависят от произведе-
произведения гух, а штрих означает производную по этому аргу-
аргументу.
Здесь принято во внимание, что подинтегральное выра-
выражение обладает азимутальной симметрией; далее, при
интегрировании по переменным z и х' мы учли, что
С ei-<*-*
Наконец, при интегрировании по величине х в пре-
пределах от — оо до -f оо мы отбросили нечётные подинте-
гральные функции и заменили удвоенным интегралом
в пределах от 0 до со чётные функции.
Как известно, в теории бесселевых функций имеет
место соотношение*)
JV'O (х) Jo (х) - J'o (x) No (x) = ±. B7,18)
Поэтому выражение B7,17) для энергии излучения
принимает вид **)
где вместо переменной х введена частота колебаний
o) = y.v. Заметим, что показатель преломления с увеличе-
увеличением частоты со уменьшается и для рентгеновских лучей
становится меньше единицы. Поэтому верхний предел
*) Р. О. Кузьмин, Бесселевы функции, ОНТИ, 1935,
стр. 52.
.**) См. также обзорную статью И. М. Франка в «Успехах
физических наук», 30, № 3—4, стр. 149,1946; там же имеется подроб-
подробный список литературы.
160 КЛАССИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА [гл. VI
интеграла по ш следует определить из уравнения
р»Ю = 1. B7,20)
Наконец, найдём уравнение для эквипотенциальных
поверхностей в простейшем случае, когда п — const.
Преобразуем выражение B7,12) к форме
+ cos x (z - vt) No (r{y)] d*. B7,21)
Из теории бесселевых функций известно соотно-
соотношение
сю со
\ sin х<х/0 (х[3) rfx = — \ cos xaiV0 (x^) dv. =
о 6
а>Р>°>
B7,22)
Р0
6
0 ; Р>а>,
откуда находим для искомого потенциала *
; vt — z > Y^ = 7 V %2 + У2,
0 ; ^-2<уг. B7,23)
Вычислим, далее, значение полей и направление
вектора Умова-Пойнтинга для момента времени £ = 0.
Для других значений времени t мы должны будем в най-
найденных выражениях z заменить через я — vt.
В этом случае
f С
— z > vr,
1 B7,24)
27]
«СВЕРХСВЕТОВОЙ» ЭЛЕКТРОН ЧЕРЕНКОВА
161
Эквипотенциальные поверхности могут быть найдены
из уравнения
- const,
B7,25)
г>и
которое описывает гиперболоиды вращения (рис. И),
причём, как видно из B7,24), потенциал, а значит, и поля
отличны от нуля лишь в области отрицательных значений
z (z < 0). Поля будут
заключены внутри ко-
конуса (огибающий ко-
конус), образующие ко-
которого определяются
из уравнения*)
С помощью формул
B7,9) находим знат
чение полей
тт
n2(R2 —
где радиус-вектор R имеет составляющие х, у, z, а единич-
единичный вектор скорости v° направлен по движению частицы,
т. е. вдоль оси z.
Составляющие вектора Умова-Пойнтинга
9 = ± [ЕЩ
на оси координат будут равны
*<0,
B7,27)
B7,28)
*) Рис. 11 является пространственной фигурой, обладающей
аксиальной симметрией вокруг оси z. Поэтому величина г может
иметь только положительные значения.
11 Д. Иваненко а А. Соколов
162 КЛАССИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА [гл. jy
где
Е - r F- V F2 и F2
r ~~ ~R x *~ v •
откуда
© = V& + <S2z=^n*EErf B7,29)
i B73°)
Как видно из формул B7,26), значения полей и век-
вектора Умова-Пойнтинга при
cos G = A B7,31)
обращаются в бесконечность. Поэтому всё излучение будет
происходить по направлениям, перпендикулярным к обра-
образующим конуса, огибающего поле (см. рис. 11). Физически
это связано с тем, что по направлениям, определяемым
условием B7,31), излучаемые электромагнитные волны
будут усиливать друг друга, а по всяким иным направ-
направлениям они будут взаимно 'гаситься.
Если подсчитать общую энергию, которую излучает
точечный электрон при постоянном значении показателя
преломления, то мы получим бесконечную величину.
Этот же результат следует из формулы B7,19), поскольку
в случае п— const частота шт обращается в бесконеч-
бесконечность. Однако на самом деле энергия излучения является
согласно более строгой теории конечной величиной, по-
потому что случай п — const является физически нереаль-
нереальным и, как мы уже указали, спектр обрывается на неко-
некоторой частоте, для которой п начинает резко уменьшаться
[см. соотношение B7,20)].
Теория движения частиц в различных средах со скоро-
скоростями, превышающими фазовые скорости волн, которые
они образуют, рассматривается также и в других областях
физики.
В частности, в механике давно уже были обна-
обнаружены особые звуковые волны, возникающие при
§ 27] «СВЕРХСВЕТОВОЙ» ЭЛЕКТРОН ЧЕРЕНКОВА 163
движении тел, например снарядов, в атмосфере со сверх-
сверхзвуковыми скоростями. Эффект сверхсветового элек-
электрона является по существу электродинамическим ана-
аналогом излучения подобных звуковых волн. Эксперименты
Черепкова находятся в полном согласии с теорией, раз-
разработанной на основе классической электродинамики
как в смысле спектра поляризации, так и угловой зависи-
зависимости излучения в эффекте сверхсветового электрона.
Возникает вопрос о квантовой трактовке эффекта
Черенкова.
Не останавливаясь здесь подробно на выводе кванто-
квантовых формул этого явления, укажем, что при квантовом
рассмотрении излучения фотонов прежде всего должны
выполняться одновременно в каждом элементарном акте
законы сохранения энергии и импульса.
Как известно, энергия электрона Ш связана с его
импульсом р и массой т соотношением
Ш = с \/т2с2 + р2.
Со своей стороны фотон обладает энергией hv и импуль-
импульсом hkt где v —частота света, а к = у —- волновое число.
Обозначая импульс электрона до и после излучения
соответственно через р и /У, будем иметь следующие
соотношения, получаемые из закона сохранения энергии:
с \fm2c2 -г р2 —• hv = с\гт2с2 -+- р'2
и закона сохранения импульса:
р _ hk=p'.
Возводя оба последних равенства в квадрат и вычитая
одно из другого, найдём следующее выражение для ко-
косинуса угла между первоначальным направлением дви-
движения электрона р и направлением к, по которому
И*
164 КЛАССИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА [гл#
излучается фотон:
причём здесь принято во внимание, что отношение ско-
скорости электрона к скорости света определяется через
импульс р выражением
в == — =z Ц. =
с % У
.»*» + />»
Напомним, что в вакууме у фотонов частота v связана
с волновым числом к соотношением
v = ск.
Поэтому выражение B7,32) для косинуса угла излуче-
излучения принимает вид абсурдного неравенства
cos 0=1 > 1.
Это означает, что движущийся по инерции электрон
так же, как и в классической трактовке, не может излу-
излучить свет, так как при этом не могут быть одновременно
удовлетворены законы сохранения энергии л импульса.
Рассмотрим далее вместо вакуума диэлектрик как
непрерывную среду, характеризуемую показателем пре-
преломления п, в которой свет распространяется с фазовой
скоростью с' = — . Тогда вместо прежнего выражения
получим следующее соотношение между v и к:
и ск
Поэтому формула B7,32) принимает новый вид:
§ 27] «СВЕРХСВЕТОВОЙ» ЭЛЕКТРОН ЧЕРЕНКОВА 165
где Л = длина де-броглевской волны движущегося
электрона, а Х= -г — длина волны излучаемого света.
Отсюда видно, что когда скорость движения элект-
электронов будет больше фазовой скорости распространения
света в среде, т. е. п-< 1, то становится возможным из-
излучение света, ограниченное со стороны малых длин
волн значением \min, при котором cos б обращается в
единицу.
Описывая электрон квантовым релятивистским урав-
уравнением Дирака и применяя обычные квантовые методы
подсчёта, находим следующее выражение для энергии,
излучаемой электроном в единицу времени*):
B7,33)
2нс
где круговая частота со = —у .
Согласно последней формуле даже при п = const
максимальная частота излучения, а значит, и энергия
излучения не обращаются в бесконечность»
Последние соотношения приобретают более простой
вид в нерелятивистском квантовом случае — < 1. При-
Принимая во внимание, что излучение «сверхсветового» элек-
vn л
трона возможно лишь при условии — > 1, мы должны
в нерелятивистском приближении положить п > 1. В этом
случае вместо B7,32а) и B7,33) имеем следующие более
*) А. Соколов, ДАН, 28, 415, 1940. Квантовая теория
эффекта Чсренкова для обоих предельных случаев (нерелятивист-
(нерелятивистского и ультрарелятивистского) была разработана также В. Гинз-
Гинзбургом, ЖЭТФ, 10, 589, 1940; см. также статью J. M. Jauch
and К. М. Wa t s о n, Phys. Rev., 74, 1485, 1948, где развита общая
схема квантовой феноменологической электродинамики.
166 КЛАССИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА [гл. IV
простые соотношения:
dU еЧ
О
В частности, при X > А, как это имеет место, например,
в экспериментах Черенкова, квантовыми поправками мож-
можно пренебречь fy=(n, чт0 оказывается эквивалентным
пренебрежению отдачей, получаемой электроном при излу-
излучении; при этом квантовые формулы B7,32а) и B7,33)
переходят соответственно в классические B7,31) и B7,19).
Физическая причина возможности отбрасывания кван-
квантовых поправок при реально наблюдаемом излучении
сверхсветового электрона заключается в том, что де-
броглевская длина волны электронов оказывается меньше
тех длин волн, которые излучает электрон при своём дви-
движении и диэлектрике. Квантовые эффекты, как известно,
сказываются в тех случаях, когда де-броглевские длины
волн будут порядка размеров орбит или порядка длины
световых волн, излучаемых электроном (т. е. А~Х). Эти
же квантовые поправки начинают давать о себе знать при
столь малых длинах волн излучаемого света, при ко-
которых нарушается условие -^ < 1, ввиду быстрого умень-
уменьшения показателя преломления с увеличением частоты.
Вообще говоря, рассмотренная выше макроскопическая
теория эффекта Черенкова не является строгой как при
квантовом, так и при классическом рассмотрении, потому
что излучение сверхсветовых электронов происходит
благодаря взаимодействию атомов диэлектрика с движу-
движущимися электронами, которое в нашем случае учитывается
путём формального введения некоторого среднего показа-
показателя преломления п = |/е. Однако рассмотренный метод
подсчёта излучения оказался весьма продуктивным и был
впоследствии использован Ферми *) для вычисления общей
*) Е. Fermi, Phys. Rev., 57, 485, 1940; см. также статью
П. Е. Кунина в сборнике «Мезон», Гостехиздат, 1947.
§ 27] «СВЕРХСВЕТОВОЙ» ЭЛЕКТРОН ЧЕРЕНКОВА 167
потери энергии движущимся в среде электроном как на
возбуждение атомов среды, так и на потери при излуче-
излучении сверхсветового электрона. Ферми отбросил ограни-
ограничение вещественности для показателя преломления или
диэлектрической постоянной е, а использовал обычное
в электродинамике комплексное выражение для з, меи-
мая часть которого учитывает поглощение энергии элек-*
тромагнитных волн. Таким путём было найдено хорошее
приближение к формулам для потерь энергии движу-
движущимся зарядом, полученным в классической теории
Томсоном-Бором и развитым далее в квантовой механике
Бете и Б лохом (см. цитированную книгу Гейтлера).
В дальнейшем излучение сверхсветового типа Че-
ренкова было теоретически исследовано во многих дру-
других случаях, прежде всего при прохождении заряжен-
заряженных частиц не через диэлектрик, но через ферромагнетик,
когда рассматриваемое излучение начинается при ско-
скоростях v > —£= , где ;i0 — магнитная проницаемость среды
Ун
(когда s положено равным 1)*). Излучение сверхсвето-
сверхсветового типа, очевидно, должно иметь место также при дви-
движении незаряженных, но магнитных частиц, например
нейтронов, и вообще явиться комбинацией зарядной
и магнитной частей в случае заряженных и магнитных
частиц, таких, как протоны или же электроны, если
учесть наличие у последних недавно обнаруженного соб-
собственного вакуумного магнитного момента.
Наряду с излучением в среде аналогичное излучение
должно наблюдаться также для всех заряженных и маг-
магнитных частиц при их переходе из одной среды в другую,
например из вакуума в диэлектрик или металл или при
движении частиц в узких каналах, вырезанных в диэлек-
диэлектрике или ферромагнетике с размерами, меньшими излу-
излучаемой длины волны. Интенсивности подобных излуче-
излучений весьма малы при исследовавшихся случаях не слиш-
слишком высоких энергий электронов.
*) Д. Иваненко и В. Гургенидзе, ДАН, 67, 997,
1949.
168 КЛАССИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА [гл. IV
Заметим в заключение, что излучение сверхсветового
типа должно также иметь место не только в электро-
электродинамике, но и в мезодинамике (см. ниже, гл. V) при
движении нуклеонов—протонов или нейтронов через слой
вещества достаточно высокой плотности. Тогда, например,
в случае прохождения нуклеона через атомное ядро
будут иметь место потери как при столкновениях, так
и при излучении сверхсветового типа. При этом целе-
целесообразно плотную среду характеризовать аналогично
электродинамике путём развития феноменологической
мезодинамики, вводя квазидиэлектрическую постоянную
и квазимагнитную проницаемость, задавая соответствую-
соответствующий закон дисперсии, использование которого всегда необ-
необходимо для трактовки эффекта Черенкова.
Таким образом открытый сравнительно недавно
эффект Черенкова оказался весьма важным и общим
явлением, имеющим место во многих случаях движения
электрона и других частиц*).
§ 28. Тензор энергии
Перейдём к рассмотрению новой важной величины,
характеризующей электромагнитное поле, — тензору
энергии. Тензор энергии позволяет, в частности, свести
четырёхмерный импульс силы самодействия к прира-
приращению электромагнитного количества движения.
При помощи равенств B3,17) и B3,27) находим
B8,1)
причём значения для H{Ly и 2ХЛ определяются равенствами
B3,2) и B3,26).
*) Различные стороны сверхсветового излучения анализиру-
анализируются в книге Н. Бора и О. Бора «Прохождение атомных
.частиц через вещество», ИЛ, 1950.
§ 28] ТЕНЗОР ЭНЕРГИИ 169
В случае максвелловского поля имеея
D^ = H^. B8,2)
Подинтегральное выражение правой части соотно-
соотношения B8,1) преобразуем к виду:
Пользуясь уравнением B3,31), а также свойством
антисимметричности тензоров Dvx и Н^9 имеем
В частности, для лагранжианов Lo, являющихся
функцией только 11^ = AVtV, — А1Ч^, получим
dL{) _ dL0
B8,3)
откуда следует
" F^ds= \%^{dx), B8,4)
причём компоненты тензора энергии находятся из
равенства
гр 1 тт тл л Т /OQ tr\
* p.v = г- flvi ^av — S^v Ь. (^o,5)
Точнее эту величину следовало назвать тензором плот-
плотности энергии импульса — натяжений.
Как видно из формулы B8,4), тензор энергии T^v
определён лишь с точностью до величины Т'^, четырёх-
^мерная расходимость которой равняется нулю: -^— = 0.
170 КЛАССИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА [гл. IV
Вводя тензор энергии, мы можем импульс собствен-
собственной силы B8,4) преобразовать к виду:
TvndSn+~ \dt^ 7V4 (di), B8,6)
где dS является элементом поверхности, ограничиваю-
ограничивающей рассматриваемый объём, элемент которого равен (dt).
С другой стороны, из равенства B3,22) находим
\ -—-*= \ /^ ds+ \ Fids, B8,7)
Исключая из двух последних уравнений импульс соб-
собственной силы, получим
- -^ \ Т^ (dr) \ = ^Flds + \dt§ T^n dSn. B8,8)
Величина /п;^ является механическим количеством дви-
движения. По аналогии с этим интеграл
B8,9)
получил название количества движения или импульса
электромагнитного поля. Компоненты —Т^ь являются,
очевидно, составляющими плотности количества движения
электромагнитного поля.
В правой части к импульсу внешней силы \ F1^ ds
необходимо добавить импульс поверхностных сил:
B8,10)
Отметим, что величины G^ и 7\. в отдельности в общем
случае могут и не образовывать четырёхмерных векто-
векторов, только их линейная комбинация [см. правую часть
равенства B8,6)] образует четырёхмерный вектор.
§ 29] ИМПУЛЬС ЭЛЕКТРОМАГНИТНОГО ПОЛЯ 171
§ 29. Импульс электромагнитного поля
Сравним теперь трансформационные свойства меха-
механического и электромагнитного количества движения.
Существуют два условия, при которых количество
движения электромагнитного поля G^ является четырёх-
четырёхмерным вектором и тем самым оказывается совпадающим
по трансформационным свойствам с количеством дви-
движения частиц.
1. Если мы имеем пространство без зарядов, т. е.,
как видно из равенства B8,4), расходимость от тензора
дТ
энергии обращается в нуль: ^д — (^ то величина
B9,1)
будет представлять собою четырёхмерный вектор.
В самом деле, в отсутствии зарядов электромагнит-
электромагнитное поле не будет обладать особенностями, и поэтому
импульс поверхностных сил [см. B8,10)] после удаления
поверхности интегрирования в бесконечность должен
исчезнуть.
Учитывая, что комбинация количества движения элек-
электромагнитного поля £,х и импульса поверхностных сил
всегда является вектором, а сам импульс обращается
в нуль, мы приходим к выводу, что величина G1JL должна
вести себя как четырёхмерный вектор.
Подобным условиям удовлетворяет, например, элек-
электромагнитное поле, находящееся в пространстве без
зарядов. В частности, благодаря этому в теории фотонов
(т. е. квантов света, сопоставленных согласно квантовой
теории элементарным электромагнитным волнам) Эйнштейн
смог охарактеризовать фотон не только энергией е = hv,
но также количеством движения р = —, причём в со-
совокупности эти величины образуют четырёхмерный
вектор.
2. Теорема Лауэ формулирует условие, при котором
энергия и импульс электромагнитного поля образуют
172 КЛАССИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА [гл. IV
четырёхмерный вектор при наличии зарядов. Для этой
цели найдём закон преобразования для четырёхмерного
импульса Ср., когда электромагнитное поле порождается
заряженной частицей, например электроном.
Прежде всего рассмотрим систему отсчёта, относи-
относительно которой электрон покоится, и обозначим в этой
координатной системе тензор энергии через Т^, а эле-
элементарный объём через (dr0).
В силу сферической симметрии мы можем утверждать,
что для недиагональных компонент (^ Ф v) всегда должно
выполняться равенство
% (dr0) = 0, B9,2)
в то время как интегралы от диагональных компо-
компонент
\ ТщХ (dr0) (суммирования по ^ нет) B9,3)
могут быть отличными от нуля.
Поэтому согласно B9,2) и B8,9) имеем
G«=0f GJ = ^f B9,4)
с
где Uo= \ Г44 (dr0) является энергией электростатиче
ского поля.
Для того чтобы определить релятивистскую кова-
ковариантность вектора Gu, сделаем переход к другой системе
координат, относительно которой электрон движется
с постоянной скоростью у.
Направив ось х по вектору скорости, имеем согласно
преобразованиям Лорентца-Эйнштейна
О Хл-\-1$Хх 0 0 0 Хл—i&T, /on г\
si= k - , *2 = заг> хз = хъ, xk= k . B9,5)
где
§ 29] ИМПУЛЬС ЭЛЕКТРОМАГНИТНОГО ПОЛЯ 173
При переходе к движущейся системе координат новые
значения для компонент Tv.v и объёма (dr) будут свя-
связаны со старыми при помощи соотношений
о 0 л Э
71 — л р Т°
У IJ-v — ■* ар,
5а> <Ч B9,6)
(dr) = k(dr0).
Оставляя для тензора Г°р только диагональные члены
(а — $) и учитывая, что при движении вдоль оси х необ-
необходимо оставить только составляющие, для которых
jj^ v = 1,4, имеем
ох,х дх^ rpQ ip
1
x dx\
откуда находим
= lkc \ (T^-fT^idro). B9,9)
Теория относительности требует, чтобы электромаг-
электромагнитное количество движения и энергия образовывали
вместе четырёхмерный вектор, закон преобразования
для компонент которого имеет вид
о о
или сообразно с B8,9)
B9,11)
174 КЛАССИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА [гл. IV
Сопоставляя B9,9) с B9,11), мы видим, что коли-
количество движения электромагнитного поля образует
четырёхмерный вектор в том случае, когда
B9,12)
Последнее соотношение выражает теорему Лауэ,
согласно которой электромагнитное количество дви-
движения G^ является четырёхмерным вектором только в том
случае, если в покоящейся относительно электрона
системе координат для всех компонент тензора энергии
соблюдается соотношение
i I U-f qI W, y&V jJ-O)
кроме составляющей Т^, интеграл от которой является
постоянной величиной и равняется полной энергии поля,
порождённого частицей. Эту энергию поля мы можем
приравнять собственной энергии частицы, выражая тем
самым основную идею полевой гипотезы. Согласно послед-
последней собственная энергия частицы £/0, делённая на с2, или
её масса mel равняется
B9,14)
Покажем, что равенство B9,13) формулирует не
только условие, при котором количество движения G^
образует четырёхмерный вектор, но также выражает
собою необходимое условие, при котором весь заряд
должен находиться в равновесии.
В самом деле, в статическом случае {Тп± = 0) вместе
B9,13) имеем
) = 0. B9,15)
Учитывая, далее, равенство
§ 30] ТЕОРИЯ ЭЛЕКТРОМАГНИТНОЙ МАССЫ 175
мы получаем вместо соотношения B9,15)
*0) = 0. B9,16)
ОТ0
Как видно из B8,4), величина ^ является плот-
плотей
ностью силы, а всё выражение B9,16) представляет собою
вириал сил, который,. как известно, пропорционален
средней кинетической энергии [более подробно см. соот-
соотношение D4,1)]. При обращении в нуль вириала сил
средняя кинетическая энергия также обращается в нуль
и общий заряд должен находиться в равновесии. Та-
Таким образом только что выведенные теоремы, указы-
указывающие условия возможности приравнивания вектора
энергии-импульса частицы вектору энергии-импульса
поля, являются весьма существенными при построении
полевой теории электрона.
§ 30. Теория электромагнитной массы
в электродинамике Максвелла-Лорентца
а) Тензор энергии максвелловского
поля
В электродинамике Максвелла-Лорентца функция Ла-
гранжа для поля равна [см. B3,11)]
причём для величины моментов поля [см. равенство
B3,28)] имеем
D^ = H^. C0,2)
Отсюда для компонент тензора энергии согласно B8,5)
получаем
?Vv = ^H^HAV -f ^Sp.vi/apHa.$. C0,3)
Тензор riAV содержит девять пространственных соста-
вляющих, образующих трёхмерный тензор поверхност-
176 КЛАССИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА [гл. IV
ных натяжений:
Тпк = ^ [ ЕпЕк + НпНк - 1 Ьпк (Я2 + £2) ] ; C0,4)
П, К — L, 6, О,
шесть пространственно-временных компонент:
Tnt=-icgn, Г4„ =--;©„, C0,5)
причём плотность электромагнитного количества дви-
движения gn связана с вектором потока энергии поля Умова-
Пойнтинга
соотношением
Наконец, временная составляющая 7^44 является плот-
плотностью энергии электромагнитного поля:
Г44 = и = ~ {Е2 + Я2). C0,8)
Таким образом тензор энергии имеет вид
т1а
^
23
33 " Щ
5о и
. C0,9)
У
Соотношение C0,7) между плотностью электромагнит-
электромагнитного количества движения д и потоком @ является
следствием симметричности тензора энергии в максвел-
ловской теории:
гр ^с\
JXV — -■ VP- /*
*) В общем случае , когда D^v ф Я^%1, мы имеем два тензора
поля:
I Щ) ТЕОРИЯ ЭЙЕЙТРОЙАГНЙТНОЙ ЙАССЙ Ш
Проверим tentepb шйШшкмо'сть теоремы Лауэ B9,13)
в Феерии МакЪвшша-Ло^ентца*
В системе координат, неподвижной относительно элек-
электрона, магнитное поле обращается в нуль, а электриче-
должно обладать сферической симметрией. Поэтому
Электрические составляющие носят названия напряжённости поля
(Е) и индукции (Л); магнитные называются напряжённостью (Н)
и индукцией (В).
Для векторов B?, Е) и B), Н) имеют место уравнения, совпа-
совпадающие с уравнениями Максвелла для диэлектрической среды:
В — tot A, JB7==~gradf ^-,
rot Н— — д-^- =1тг/, div D = л«р,
причём для точечной частицы [см. B3, 30)]
В случае материальной среды тензор энергии может оказаться
несимметричным. В самом деле, согласно B8,5) имеем
7 ^ п Ф Тп^
Выражение тензора энергии B8,5) совпадает с определением, дан-
данным Минковским и Далленбахом.
С другой стороны, Абрагам ошибочно считал, что тензор энер-
энергии всегда должен быть симметричным и, оставляя для компонент
Т1п значение, найденное Минковским (Т^п — Т±п), положил
Аргументация Абрагама является, очевидно, неубедительной,
и мы должны остановиться на тензоре Минковского-Далленбаха,
являющемся необходимым следствием общей теории, основанной
jia вариационных принципах. Относительно более подробную дис-
дискуссию физических следствий, связанных с обоими тензорами, мо-
можно найти в книге Тамма (см. И. Е. Т а м м, Основы теории электри-
электричества, Гостехиздат, 1949, § 116).
12 Д. Иваненко и А. Соколов
по самому смыслу равенства B9,2) нас могут интересо-
интересовать только диагональные компоненты тензора энергии,
определяемые соотношениями
^E) C0,10)
Отсюда находим:
44 (dr0) = ~ \ Е* (dt0) = f/0, C0,11)
где С/о —энергия электростатического поля.
Учитывая, далее, сферическую симметрию вектора Е,
имеем
=-luo, C0,12)
т. е. для электромагнитного поля, порождённого заря-
зарядом, теорема Лауэ не выполняется.
В соответствии с B9,9) находим следующие значения
для компонент количества движения электромагнит-
электромагнитного поля, порождённого электроном, движущимся со
скоростью v:
^;?> VV с2к'
Таким образом компоненты Gv не образуют четы-
четырёхмерного вектора в противоположность компонентам
количества движения самого электрона р = • г о/ =• ;
г У 1 — и2/с2
_ ^Й
Обратимся теперь к гипотезе полевой массы в рамках
классической электродинамики. Согласно этой гипотезе,
выдвинутой в конце XIX века Дж. Дж. Томсоном и раз-
I |5j ^ёорйЙ эЛейтромагнй'гной массы i^
витой Лорентцем, Абрагамом и Пуанкарэ, собственная
энергия электрона (или его масса) полностью обусло-
обусловлена энергией электромагнитного поля, связанного с
электроном, или, что сводится к тому же—инерция ча-
частицы обязана инерции поля. Точно так же импульс
электрона предполагается обязанным импульсу поля.
Хотя программа полевой теории и не была осуще*
ствлена вплоть до наших дней, основные её физические
идеи и методы расчётов всё время играли стимулирую-
стимулирующую роль. Для успеха полевой теории массы должны
быть осуществлены по крайней мере следующие условия.
Во-первых, следует получить конечное значение энергии
поля, порождённого частицей, которое можно было бы
точно приравнять конечной энергии частицы (т. е. массе,
умноженной на квадрат скорости света: Щ = тс2). Во-вто-
Во-вторых, значение импульса поля, порождённого частицей,
должно быть не только конечным, но и находящимся
в правильном соотношении с энергией, образуя с послед-
последней четырёхмерный вектор. В-третьих, теория должна
суметь вывести уравнения движения электрона.
При дальнейшем развитии теории следует сверх того
потребовать вывода спина, т. е. собственного момента
количества движения электрона как спина поля, что,
однако, относится к квантовому обобщению теории поле-
полевой массы, так как спин является квантовым эффектом.
Точно так же получение не просто конечного, но данного
определённого значения массы электрона и других
частиц, очевидно, также лежит в сфере действия кванто-
квантовой теории. Поэтому сейчас в рамках классической тео-
теории полевой массы мы ограничимся прежде всего про-
проблемой получения конечной массы и импульса и их
взаимным согласованием, возможность чего также не
очевидна.
Возвращаясь к максвелловской электродинамике и
оставляя пока что вопрос о конечном значении энер-
энергии поля в стороне, мы видим, что массу частицы с полевой
точки зрения возможно определить двумя способами.
Во-первых, исходя из количества движения электро-
электромагнитного поля Gl9 можно определить массу как коэффи-
коэффициент пропорциональности между количеством движе-
12*
Ш '«ЯлесйчкскАЯ эЛектроДинамийа \tn% tV
ния поля и трёхмерной скоростью частицы;
и?
Подобный закон изменения массы электрона со ско-
скоростью движения был действительно подтверждён экс-
экспериментально в начале 20-го века (Кйуфман, Гюи
и Лаванши), что казалось одно время сильным аргу-
аргументом в пользу гипотезы полевой электромагнитной
массы.
Во-вторых, однако, если рассматривать собственную
энергию электрона как равную или совпадающую с энер-
cGA
гиеи поля, а массу как отношение энергии поля -г-
(т. е. четвёртой составляющей количества движения поля)
к квадрату скорости света с2, мы получим противореча-
противоречащее предыдущему уравнению и экспериментальным данным
соотношение
Этот результат не совпадает ни с требуемой теорией относи-
относительности правильной формулой mel = ~, ни с невер-
неверным соотношением C0,14):
™ег = Т&- C0Д6)
Таким образом масса и импульс электрона не могли
быть приведены друг с другом в согласие при разработке
полевой теории в рамках классической максвелловской
электродинамики. Кроме того, следует подчеркнуть, что
согласно специальной теории относительности масса вся-
всякого тела изменяется со скоростью по закону:
/-5
§ 301 ТЕОРИЯ ЭЛЕКТРОМАГНИТНОЙ МАССЫ 181
где т0 — масса в состоянии покоя, а импульс равняется
V = —m°v . Эти соотношения имеют место совершенно
/5
независимо от какой бы то ни было модели массы, так что
экспериментальное подтверждение изменения массы со ско-
const
ростью по закону т = — ни в коей мере не является
аргументом в пользу полевой гипотезы электромагнит-
электромагнитного происхождения массы. Точно такой же закон измене-
изменения массы имеет место и для незаряженных частиц, напри-
например нейтронов.
Более того, согласно теории относительности энергия
всякого тела равняется % = °° , где 80 = w0c2
yi-tJ/c2
есть собственная энергия в состоянии покоя. Все эти фор-
формулы теории относительности прекрасно подтверждены
экспериментами. Появление дополнительного множителя
-г- в выражении количества движения C0,14) и множи-
теля A + -О-Р2) в выражении энергии C0,15), не согласо-
согласованных друг с другом и противоречащих опыту и соотно-
соотношениям теории относительности, показывает, что масса,
энергия, импульс, а следовательно, и механическое поведе-
поведение электрона не могут быть объяснены в теории Макс-
велла-Лорентца из рассмотрения его собственного электро-
электромагнитного поля. Таким образом, в частности, масса
электрона не может иметь чисто электромагнитного про-
происхождения.
Как мы видим, эта первая неудача классической поле-
полевой теории массы электрона связана с рассмотренным
выше нарушением условий выполнимости теоремы Лауэ.
Оказывается, что компоненты количества движения и энер-
энергии электромагнитного поля не образуют четырёхмер-
четырёхмерного вектора и, следовательно, не могут быть приравнены
импульсу и энергии электрона, образующих вектор.
Если всё же оставаться на почве полевой теории, то
следует ввестд какое-то вспомогательное поле, отличное
182 КЛАССИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА [гл. IV
от максвелловского, для того чтобы энергия и импульс
этого поля смогли компенсировать излишнюю долю
поля, связанную с коэффициентами 1/3 в выражении
импульса и член l/3 [32 в выражении энергии. Это добавоч-
добавочное поле приводит к так называемому давлению Пуан-
карэ, удерживающему электрон в «равновесии» (см. ниже).
Учтя подобную неудачу классической полевой теории
электрона в согласовании значений энергии и импульса
частицы и поля, обратимся всё же к анализу следующего
основного пункта, связанного с проблемой конечного
значения энергии поля, создаваемого глектроном.
Для покоящейся частицы р = 0, й = 1; поэтому масса
покоящегося электрона равнялась бы согласно тому или
другому из двух указанных определений mel = -^ -~
по C0,14) или тп = ~ по C0,15). Здесь Uo есть электро-
электростатическая энергия точечного заряда. Так как энергия
поля Uo точечного электрона равняется бесконечности,
то для устранения этой трудности предлагается пред-
представить заряд распределённым в некотором объёме,
который для простоты возьмём сферическим с радиусом г0.
Необходимо с самого начала подчеркнуть, что подобное
введение радиуса нарушает релятивистскую инвариант-
инвариантность теории и может поэтому рассматриваться лишь
как весьма предварительный приём.
В случае поверхностно заряженной сферы радиуса г0
полная энергия электрического поля равняется
Для случая заряда, равномерно распределённого по
объёму, f/0 = >- — • Во
распределении заряда
3 е2
объёму, ?70 = у- —. Вообще говоря, при том или иноад
I gO] ТЕОРИЯ ЭЛЕКТРОМАГНИТНОЙ МАССЫ Jgg
причём коэффициент а зависит от характера распределе-
распределения заряда и имеет порядок единицы.
Не придавая значения точному виду распределения
заряда «внутри» электрона в этой весьма предваритель-
предварительной неквантовой модели, которая к тому же при любом
распределении заряда нарушает релятивистскую инва-
инвариантность, попытаемся всё же оценить порядок радиуса
электрона, отвлекаясь от всех коэффициентов, имеющих
порядок единицы. Приравняем энергию электростати-
электростатического поля Uq собственной энергии электрона те1с2:
Подставляя сюда вместо е, т, с известные числен-
численные константы для электрона: масса т=9 • 10~28 г,
заряд е = 4,8-10~10 абс. эл-стат. ед., скорость света
с — 3 • 1010 см/сек, находим
("точнее —2 = 2,8 - 1(Н3 см). C0,18)
Последнее выражение даёт значение для так называ-
называемого классического радиуса электрона. Точнее говоря,
речь идёт сейчас о классическом электрическом радиусе,
так как радиус можно было бы совершенно аналогичным
путем, применяя те же идеи теории полевой массы,
вычислить для случая магнитного поля, отвлекаясь
от того обстоятельства, что магнитный момент, как и спин
электрона, обусловлен квантовыми эффектами.
Приравнивая магнитную энергию, обусловленную
дипольным моментом электрона р. и по порядку равную
gp^^g—собственной энергии электрона тс2, имеем
Гц.
mc2~t- , откуда для классического магнитного радиуса
электрона имеем
см,
тс2
1ак как согласно эмпирическим данным
184 КЛАССИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА [гл. IV
электрона равен боровскому магнетону
eh
г 4тгтс
Точно так же для классического гравитационного ра-
радиуса электрона имеем rg =-¥ ~ 10~55 см*)9 так как
тс2 ^-— (/—гравитационная постоянная).
г
Несмотря на крупные дефекты указанной гипотезы
полевой массы, всё же нельзя отрицать её известного
успеха, заключающегося в том, что полученное значение
для электрического радиуса электрона C0,18) действи-
действительно соответствует каким-то эффективным «размерам»
электрона, сказывающимся, например, при рассеянии
света на электроне, который при всех подобных расчётах
предполагается точечным. Как будет показано ниже
(§ 36), классическое томсоновское эффективное сечение
для рассеяния света на точечном электроне определяется
в согласии с опытом в основном величиной а ^ /•§, причём
квантовая теория рассеяния света на точечном элек-
электроне, необходимая для случая коротких длин волн,
когда электрон получает заметную отдачу (эффект Комп-
тона), приводит в согласии с опытом к формуле Клейна-
Нишины**) для эффективного сечения, которая также
содержит в качестве основной величины /•§. Поэтому
можно сказать, что с точки зрения полевой теории масса
или энергия электрона действительно обязана в основном
электростатическому полю. С другой стороны, поскольку
классический магнитный или гравитационный радиусы
не имеют ничего общего с эффективными размерами
электрона, проявляющимися при его взаимодействиях,
его движении в атомах ит, д., следует заключить, что
гравитационное и магнитное поля не играют существен**
ной роли в структуре элрктррна с полевой точки зрения*
*) См. Д. Иваненко и А. Соколов, Вестник МГУ,
№ 8. 1947.
**) О. Klein imd J. Nishina, Zs. f. Phys., 52, 853, 1929,
Втд формула б^ша выведена также Ц. Б, Таммом (J, Т а Щ Щ,
£s. f. Phys., 62, 545, l?30)r
§ 30] ТЕОРИЯ ЭЛЕКТРОМАГНИТНОЙ МАССЫ 185
Вспомним теперь указанный выше результат о необ-
необходимости введения немаксвелловских сил для проведе-
проведения программы полевой теории электрона. Нетрудно
усмотреть наглядную физическую причину для допуще-
допущения подобных сил.
Поскольку электрон-шарик представляется заряжен-
заряженным одноимённым электричеством, он должен неминуемо
разлететься под действием одних максвелловских (в дан-
данном случае кулоновских) сил. Следовательно, для того
чтобы сдержать «части» электрона вместе, мы должны
ввести немаксвелловские силы.
Совершенно ясно, что с точки зрения понимания элек-
электрона как элементарной частицы говорить о его «частях»
в строгом смысле слова нельзя, что ещё раз подчёркивает
сугубо предварительный характер модели электрона-
шарика.
б) Тензор момента количества
движения поля
К тензору энергии электромагнитного поля, а также
всех других полей, можно придти непосредственно,
исходя из рассмотрения функции Лагранжа L.
Ограничиваясь для простоты случаем свободного поля
без зарядов, имеем согласно B3,11) для максвелловского
случая
L=-~H^HX,. C0,19)
Найдём производную L по координате х^
dL
дх^ d^x.v dz
C0,20)
Здесь мы учли, что
dL 1
:4i
1 гг
= 7-ZlAv
- Принимая во внимание, что в пространстве без заря-
зарядов
d dL 1 дН^
186 КЛАССИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА [гл. IV
мы можем равенство C0,20) преобразовать к виду
■^р- = °> C0,21)
где компоненты так называемого канонического тензора
энергии (точнее говоря, тензора плотности энергии,
импульса и натяжений) определяются соотношением
can I dL o
Уравнение C0,21), выражающее исчезновение четы-
четырёхмерной расходимости, эквивалентно четырём обычным
законам сохранения, которые получаются при значениях
индекса {а = 1, 2, 3, 4.
Действительно, при (л = 4 получим уравнение
выражающее закон сохранения энергии, так как TAi
является плотностью энергии. Умножим последнее урав-
уравнение на элемент объёма {di) и проинтегрируем по всему
пространству. Тогда, преобразуя объёмный интеграл
\ div T4 (dv) в поверхностный по теореме Остроградского
и учитывая, что на бесконечности компоненты Т^ исче-
исчезают, получим
ддг \ Т^ (dr) - 0, т. е. ^ Г44 (dr) = const.
Точно так же доказываются три закона сохранения
для компонент импульса.
Как было указано в § 23а, согласно теореме Нетер
инвариантности лагранжиана относительно каждой дан-
данной группы непрерывных преобразований соответствует
свой закон сохранения для той или иной величины.
Кроме того, имеет место и обратная теорема, утвержда-
утверждающая наличие инвариантности при выполнении законов
сохранения. Легко показать, что общий закон сохране-
сохранения C0,21) для тензора энергии соответствует инвариант-
инвариантности уравнений Максвелла относительно группы сме-
смещений всех четырёх координат, В самом деле, при пере-
§ 30] ТЕОРИЯ ЭЛЕКТРОМАГНИТНОЙ МАССЫ 18?
носе начала координат мы имеем следующее изменение
(вариацию) для функции Лагранжа:
которое сводится к вычислению производной -— . Таким
образом независимость L от смещении координат при-
приводит к тождественному исчезновению \ bL (dx) и вместе
с тем к законам сохранения энергии и импульса поля
C0,21). В этом смысле теория поля вполне аналогична
механике точки, где инвариантность действия или лагран-
лагранжиана относительно смещений всех четырёх координат
также непосредственно приводит к четырём законам
сохранения для компонент четырёхмерного вектора
импульса, т. е. для трёх компонент количества движения
и для энергии.
Таким образом можно сказать, что группа смещений
координат индуцирует как построение канонического
тензора энергии, так и закон его сохранения в виде усло-
условия исчезновения четырёхмерной расходимости, при по-
помощи инвариантного лагранжиана или соответственного
инвариантного вариационного начала. Совершенно ана-
аналогичным образом можно придти к тензору энергии
и закону его сохранения не только в случае уравнений
Максвелла, но для всех иных полей: например, гравита-
гравитационного поля, а также скалярного, векторного, псевдо-
псевдоскалярного и- псевдовекторного полей, возможно описы-
описывающих мезоны, затем для полей дираковских спиноров
и т. д., поскольку уравнения всех этих полей инвариантны
относительно смещений ввиду однородности пространства-
времени.
Канонический тензор энергии представляет собою
по существу обобщение на случай поля выражения
функции Гамильтона
относящейся к материальной точке, причём в случае
188 КЛАССИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА [гл, IV
поля функция Гамильтона является одной из компонент
тензора плотности энергии импульса (Н — Т±$).
Наконец, возможно ещё ввести всегда симметричный
метрический тензор энергии, который согласно Гильберту
получается путём варьирования функции Лагранжа по
компонентам метрического тензора*):
C0>23)
причём в окончательном результате, переходя к плоскому
псевдоэвклидовому миру (при отсутствии тяготения),
мы должны положить компоненты gw равными, в нашем
случае (#4 = ict), единичному дельта-символу g,.v = g^v = 8^v
[см., например, соотношение B3,1)]. Точно так же опре~
делитель, составленный из компонент g^v, следует поло-
положить равным единице (g=- 1).
В случае поля Максвелла метрический тензор энергии
совпадает с полученным выше тензором C0,3) **)
который является симметричным {Т^Хт ~Т^Хг) и удо-
удовлетворяет в вакууме законам сохранения:
Канонический же тензор энергии не является сим-
симметричным и отличается от метрического на вели-
величину:
грг ™сап /yimetr 1_ д д и д ±
расходимость от которой обращается в нуль:
*) См., например, А. С. Э д д и н г т о н, Теория относитель-
относительности, ГТТИ, 1934, § 79.
**) Вывод соотношения C0,24) будет дан в § 47.
№ОРЙЙ ЭЛЕЙТРоМагНИТНОЙ MACCbt frj$
Несймметрия канонического тензора энергии непо-
непосредственно связана с наличием нескольких компонент
волновых функций у всех полей, кроме скалярного (или
псевдоскалярного). Ина**е говЬря, эта несимметрия свя-
связана с поляризационнымисйойстШми поля, или с отлич-
отличным от нуля значением спин& <с'ойоставленных полю
частиц.
Обратимся теперь к моменту количества движения
электромагнитного поля, напомнив прежде всего выраже-
выражение момента количества движения из механики точки.
jB четырёхмерной записи механический момент коли-
количества движения равен антисимметричному тензору
2-го ранга
М __ х р х р
Чисто пространственные составляющие (p., v=l, 2, 3)
этого тензора моментов имеют известный вид обычного
аксиального вектора момента количества движения
Ж = [1р]; Мх - М23 - урх — zpy,
остальные же пространственно-временные составляющие
дают вектор с компонентами
М, —ir
Как уже указывалось, изотропность пространства—вре-
пространства—времени приводит к инвариантности интеграла действия или
лагранжиана относительно вращений [см. § 23, б), п. 3],
откуда согласно теореме Нетер вытекают законы сохра-
сохранения компонент тензора М^ (^№^ = 0) .Три закона
сохранения компонент момента количества движения
Мпк хорошо известны из механики точки. Остальные же
три закона сохранения М^п — const представляют собою
релятивистское обобщение закона равномерного дви-
движения центра инерции, в чём легко убедиться, например,
при переходе в сумме 2 ^4п по всем массам системы
к приближению малых скоростей, когда %^тс2*).
*) Ср. Б. В ess el-H age n, Math. Ann., 1921; Л. Лан-
Ландау иЕ. Лифшиц, Теория поля, Гостехиздат, 1948, § 13.
i% кЙАССЙЧЁСКАЯ ЭЛЕЙТРОДЙНАМЙЙА \rfta IV
Отсылая за полным анализом момента количества
движения поля к указанной выше литературе, мы полу-
получим сейчас непосредственно выражение тензора момент
тов, точнее плотности «орбитального» момента поля
как обобщение тензора моментов из механики точки
в виде:
При этом вместо импульсов ру в механическом тензоре
сейчас необходимо подставить компоненты канониче-
ского тензора энергирх 1 vA f точно так же, как при пере-
переходе к теории поля вместо того же вектора импульса-
энергии (р —р\ iS/с) мы получали компоненты тензора
(плотности) энергии Т4 , и, в частности, вместо энергии
Ш компоненту 7^ для плотности энергии. Тогда ком-
компоненты полного, «орбитального», момента количества
движения в обычном смысле выразятся как интегралы
по объёму от антисимметричных в пространственных
координатах компонент тензора плотности моментов M[TS] ±\
например,
Мх = ^ Ml23] 4 (dr) и т. д. C0,26)
Расходимость тензора моментов
д
может быть легко найдена, если принять во внимание
законы сохранения C0,21), а также соотношение
• Эта расходимость будет исчезать, т. е. момент коли-
количества движения C0,25) будет подчиняться закону сохра-
сохранения и оставаться величиной постоянной только в том
случае, когда канонический тензор энергии T^J1 является
симметричным, т. е. только в случае скалярного (или
псевдоскалярного) поля (/^ [vA] = 0).
I 36) ^ёо^йя эЛё'ктромагиййной ЙАСеЫ 1^1
С другой стороны, отсутствие симметрии канони-
канонического тензора энергии в случае векторного (максвеллов-
ского) и всех прочих полей показывает, что для обеспече-
обеспечения сохранения тензора момента количества движения
к полученному выше «орбитальному» моменту количества
движения поля следует добавить некоторый новый тен-
тензор третьего ранга:
*■'■*■ r^vl X — Гр-vI A ™i Гр-vI Л> lOvjfaiOJ
такой, чтобы их общая сумма удовлетворяла закону
сохранения,^т. е.
:0. C0,29)
дхх
Из равенства C0,27) видно, что для этой цели мы
должны положить
f -^(A^H^-A.H^). C0,30)
Тогда расходимость C0,30) в сумме с расходимостью
C0,27) даёт нам значение нуль. Следует отметить, что
производимая во всех обычных курсах теории поля
«симметризация» тензора энергии без выяснения только
что указанных соотношений не выясняет физического
смысла отсутствия симметрии.
Величину ^[[XVjA мы можем рассматривать как тензор
плотности собственного или спинового момента количе-
количества движения поля (что соответствует для случая элек-
электромагнитного поля в корпускулярном аспекте спину
фотона). Закон сохранения полного тензора плотности
моментов поля C0,29) согласно теореме Нетер соответ-
соответствует инвариантности в данном случае уравнений Макс-
Максвелла и, следовательно, их лагранжиана относительно
четырёхмерных вращений, иначе говоря, изотропности
всего пространства-времени. Аналогичные соотношения
имеют место также в случае иных полей.
ISi кЛАССИЧЕСКАЯ ЭЛЕКТРОДИЙАМЙКА [гл. IV
По аналогии с равенством C0,26) мьг мошем найти
общее значение дли спина поля:
= )
или, подставляя вместо S^23]4 значение C0,30)-, имеем
Квантовые исследований показывают, что спин фотонов
в долях Л/2тг равен единице. Наглядно это вытекает из
того обстоятельства, что для фотонов частоты v мы имеем
1 дА 2tiv , А , г, тт
причём в случае круговой поляризации векторы JE и А
имеют взаимно перпендикулярные направления.
Учитывая, что полная энергия поля определяется
формулой
находим следующее соотношение между вектором \S \ и U:
откуда, принимая во внимание, что согласно квантовой
теории U -- Ау, получаем
За подробностями, связанными с каноническим
и метрическим тензором, а также с моментом количества
движения поля, отсылаем к соответствующей литературе*).
*) В. Паули, Релятивистская теория элементарных частиц,
ИЛ, Москва, 1947, стр. И; F. В elinf ante, Physica, 6, 887, 1939;
А. Соколов и А. Мухтаров, Вестник МГУ № 8, 1948.
Об экспериментальном определении спина, т. е. вращательного
момента электромагнитной волны, предсказанного ещё в классиче-
классической электродинамике Садовским, см. Г, Розенберг, УФН,
40, 328, 1950.
§ 31] ВЫВОД УРАВНЕНИЯ ДВИЖЕНИЯ ПО ЛОРЕНТЦУ 193
§ 31. Вывод классического уравнения движения
электромагнитной массы по методу Лорентца
Кроме определения электромагнитной массы через
компоненты тензора энергии можно получить её непо-
непосредственно через силу самодействия. Этот способ опре-
определения силы обратного воздействия поля на частицу,
его породившую, впервые был указан Лорентцом.
Ограничимся исследованием наиболее простого слу-
случая движения электрона вдоль оси х с нерелятивистской
скоростью v < с, что является несущественным ограниче-
ограничением для выяснения идеи данного метода.
В этом случае мы имеем
тх=* еЕ\ + е J EVo(r) (dr), C1,1)
где 2?*—-внешнее электрическое поле, а Е —среднее
поле, создаваемое самим электроном:
). C1,2)
Оба поля направлены вдоль оси х. Плотность
р0 (f) = ?il2 t удовлетворяющая соотношению
(г) (*•) = !, C1,3)
характеризует распределение заряда электрона внутри
некоторого объёма.
Для определения поля самодействия воспользуемся
уравнением
Е=-дЛ-±д-£. C1.4)
дх с dt v '
Согласно формулам B4, 8) для точечного источника,
движущегося со скоростью v вдоль оси х9 имеем сле-
следующие решения в запаздывающих потенциалах:
**) R'
13 Д. Иваненко и А. Соколов
') dt''
1&4 КЛАССИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА [гл. tV
где R' = г — 1' (f) — расстояние между точкой наблю-
наблюдения и источником.
Силу самодействия мы отнесём к одному и тому же
моменту времени t. Для этого разложим 8-функцию
по величине — (физический смысл этого разложения вы-
выяснится в дальнейшем)
^ ^..t C1,6)
причём точки, поставленные над S-функцией, означают
производные по времени V.
Подставляя разложения C1,6) в формулу C1,5) и вос-
воспользовавшись правилами интегрирования по 8-функции
и её производным, получим
__ е - е d2R e д3Я*
? — R ~*~ 2с2 dt2 бс3 at* + '" •'
где w — ускорение движущегося электрона, аВ = г —Т* (t).
При дифференцировании по t учтём формулы
i'(t) = v r'(t) = w и т. д., C1,8)
причём vx = v, vy = 0, vz=r0 и т. д. Тогда
dR_ (д у) __ Rx dR*_
гдо
Ограничиваясь сейчас лишь линейными членами отно-
относительно скорости и ускорений, получим
л ev
I 31] ВЫВОД УРАВНЕНИЙ ДВИЖЕНИЯ ПО ЛОРЕНТЦУ
откуда согласно C1,4) находим
Как видно из C1,1) и C1,2), сила самодействия будет
равна
[\ C1,11)
Принимая во внимание соотношение C1,3), *а также
равенства, имеющие место при сферической симметрии,
, C1,12;
найдём окончательно следующее нерелятивистское урав-
уравнение движения для электрона с учётом силы само-
самодействия:
тх=*еЕг-те1х + 1 $г'% + ••• C1,13)
Коэффициент те1у являющийся полевой электромагнит-
электромагнитной массой
Щ^фЯ C1Д4)
имеет порядок величины
где г0 является классическим радиусом электрона. Смысл
подобного радиуса, призванного обеспечить конечность
массы электрона, и трудности, к которым он в свою оче-
очередь приводит, были уже рассмотрены раньше (§ 30).
Для выяснения физического смысла величины элек-
электромагнитной массы, полученной подобным способом,
ia*
19В КЛАССИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА [гл. IV
сопоставим mel с электростатической энергией Uo покоя-
покоящегося электрона.
Как известно, электростатическую энергию заря-
заряженной частицы мы можем выразить через потенциал
поля ср и плотность заряда р:
C1,15)
Потенциал ср, создаваемый электрической плотностью еро(г)
равен
ср(г) = Д ?±Ю- (drf), C1,16)
где
откуда имеем
C1,17)
Поэтому для электромагнитной массы вместо C1,14)
можем написать
™e' = U- C1Д8)
Последняя величина для нерелятивистского случая
точно совпадает со значением электромагнитной массы
C0,14), полученной из рассмотрения компонент количе-
количества движения общего тензора энергии поля.
Если проделать указанные вычисления в реляти-
релятивистском приближении, то в знаменателе правой части
выражения C1,17) или C1,18) появится характерный
множитель к = \/1 — $2.
Таким образом метод Лорентца привёл вновь к преж-
прежним результатам.
Множитель 4/3 в формуле C1,18), который был
подробно проанализирован в § 30, снова свидетельствует
о «неустойчивости» классического лорентцева электрона
(в смысле теоремы Л§уэ) и о необходимости введения
каких-то немаксвелловых натяжений для обеспечения
его равновесия, если вообще оставаться на почве класси-
классической полевой теории.
I де] ВЫВОД УРАВНЕНИЯ ДВИЖЕНИЯ ПО ЛОРЕНТЦУ 197
В теории Лорентца полевая электромагнитная масса
появляется наряду с неполевой массой т, природа кото-
которой ближе не уточнялась. Поскольку в уравнение C1,13)
обе массы (т и mel) входят совершенно одинаково, неполе-
неполевую массу т можно положить равной нулю. Тем самым
мы становимся на точку зрения чисто электромагнитной
природы массы электрона в духе программы полевой
теории. Тогда уравнение, движения электрона примет
вид
о С
C1,19)
Это уравнение движения отличается от простой, более
привычной формы добавлением члена с третьей произ-
производной, выражающего силу лучистого трения. Важно
подчеркнуть, что этот член может быть получен совер-
совершенно независимо от предыдущих рассуждений (т. е.вполне
независимо от каких бьг то ни было гипотез и методов
расчёта, связанных с полевой теорией) из рассмотрения
баланса энергии при излучении электрона. Действи-
Действительно, приравнивая среднюю энергию, излучённую
электроном за 1 сек.
О
средней работе силы лучистого трения
получим для случая периодического движения электрона
(с периодом колебания Т) для искомой силы Означение,
найденное выше:
Метод Лорентца позволяет найти также область при-
применимости уравнения C1,19), ограниченную со стороны
больших частот колебания электрона.
198 КЛАССИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА [ГЛ. IV
Пусть электрон совершает гармонические колебания
с частотой v (соответствующая длина волны X будет
равна — j . Сравнивая между собою первый и второй чле-
члены силы самодействия, видим, что разложение, к кото-
которому приводит равенство C1,13), производится по вели-
величине
В случае гармонических колебаний
а^£. C1,20)
Следовательно, пригодность уравнения движения C1,19)
ограничена условием, что длина волны гармонического
колебания электрона много больше его радиуса. Таким
образом полученное уравнение пригодно пока что для
медленных движений (v < с) и при взаимодействии с по-
полями не слишком высоких частот (\ > г0). При взаимо-
взаимодействии с полями, обладающими длиной волны, мень-
меньшей чем радиус электрона, разложение по величине а
производить нельзя, и характер колебания электрона дол-
должен резко измениться. Это замечание относится также
к любым другим теориям полевой массы, в которых вво-
вводится длина, играющая роль радиуса электрона (см.
последующие параграфы).
Уравнение C1,19) можно уточнить в двух напра-
направлениях. Во-первых, обобщая вычисление, приведшее
к его выводу, на релятивистские скорости электрона у^с,
получим релятивистское выражение силы самодействия
F, которое будет выведено иным, не лорентцовым спосо-
способом, но с тем же результатом в § 34 [см. C4,35)]. Во-вто-
Во-вторых, можно сохранить в уравнении члены с производны-
производными от х выше третьей. Все эти члены с x^IY\ #(у) и т. д.
в противоположность члену трения, пропорциональному #,
играющие роль лишь для высоких частот, будут явно
зависеть также от радиуса или формы электрона. Согласно
предыдущему этим членам нельзя придавать непосред
23] НЕЛИНЕЙНАЯ ЭЛЕКТРОДИНАМИКА 19$
ственного физического значения, и их наличие является
недостатком полного уравнения движения электрона
Лорентца.
Заканчивая на этом изложение старой классической
теории полевой массы электрона-шарика, подчеркнём,
что её существенным недостатком являлась также невоз-
невозможность непосредственного обобщения на квантовую
теорию»
§ 32» Нелинейная электродинамика
Перейдём теперь к рассмотрению других теорий элек-
электромагнитной массы* Прежде всего рассмотрим нелиней-
нелинейные уравнения электродинамики, на возможность кото-
которых указал впервые Г. Ми A912).
Схема Ми оказалась порочной, так как в его урав-
уравнения явно входили электромагнитные потенциалы, и по-
поэтому вся теория не удовлетворяла требованию калибро-
калибровочной инвариантности. Всё же следует отметить, что
идея построения новой обобщённой электродинамики
путём использования различных инвариантов поля
оказалась весьма плодотворной и была, в частности,
использована при построении общей теории относи-
относительности. Кроме того, у Ми мы вновь находим ясную
формулировку идеи «унитарной» теории поля, в которой
характеристики заряжецной частицы должны были полу-
получаться из описания пола. Излишне говорить, насколько
преждевременной была попытка Ми добиться решения
вопроса о структуре электрона до открытия его спиновых
и магнитных свойств и установления квантовой меха-
никп.
В 1934 г. Борну удалось развить нелинейную теорию,
удовлетворяющую всем условиям инвариантности, и по-
получить на её основе конечное значение для электро-
электромагнитной массы заряженной частицы*).
Как было указано выше (см. § 23), из компонент анти»
симметрического тензора поля Н^ можно составить
*) М. Вогп,Ргос. Roy. Soc. A, 143, 410, 1934; М. Вогц and
U Infeld, ibid. 144, 425, 1934,
200 КЛАССИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА [гл. IV
только два основных инварианта, не содержащих
потенциалов и высших производных от потенциалов:
^^ C2,1)
C2,2)
Так как любая функция от инвариантов есть также
инвариант, то ясно, что одного услЪвия инвариантности
и ограничения низшими производными для построения
теории недостаточно, если мы отбрасываем условие линей-
линейности.
Для получения нелинейных уравнений поля Берн
выбрал сперва лагранжиан в виде следующей функции
от одного инварианта 1Х:
к=§ 0
где величина Ео представляет собою так называемое
максимальное поле.
В теории Борна выполняется некоторый принцип
соответствия*), а именно, когда максимальное поле Ео
стремится к бесконечности, иначе говоря, при полях,
значительно меньших максимального:
(к)*1- (л
выражение C2,3), как легко видеть, переходит в ла-
лагранжиан максвелловской электродинамики:
Некоторой аналогией для указанного выбора функции
Лагранжа Борну послужил переход от функции Ла-
*) О значении принципа соответствия см. И. В. Кузнецов,
Принцип соответствия в современной физике и его философское
значение, Гостехиздат, 1948.
J 32] НЕЛИНЕЙНАЯ ЭЛЕКТРОДИНАМИКА 201
гранжа L = тсг fl--j/l—^j, известной из механики
теории относительности для свободного электрона, к клас-
классическому пределу [см. соотношение B3,6)] L = ^y-, кото-
который получается при с2 —> оо. В дальнейшем оказалось
возможным подобрать другие комбинации инвариантов
1Х и /2, также приводящих к конечному значению для
собственной энергии электрона Uo. В частности, Борн и
Инфельд развили общую теорию поля, исходя из ла-
лагранжиана, являющегося функцией обоих инвариантов
1г и /2 вида
El
Некоторым формальным основанием для выбора подоб-
подобной, опять-таки произвольной, комбинации инвариантов
оказывается то, что этот лагранжиан является так называе-
называемым объёмом тензора H^t равным значению определи-
определителя, построенного из элементов
где gp.v — компоненты фундаментального тензора, взятого
в данном случае с галилеевыми значениями [см. соотно-
соотношение B3,1I. Шредингер использовал другую произволь-
произвольную комбинацию
, Я2 —Я8
4 Выбор лагранжиана должен обеспечить также устой-
устойчивость точечного электрона, так как только в этом слу-
случае мы получим правильное соотношение между импуль-
импульсом электромагнитного поля и его энергией, т.е. согласно
полевой гипотезе между импульсом и энергией частицы.
Лагранжиан C2,3) оказывается одной из простейших
нелинейных функций инварианта /lf при котором обеспе-
обеспечивается как конечное значение для электромагнитной
массы, так и устойчивость точечного заряда в указанном
смысле.
202 КЛАССИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА [гл. IV
Ограничимся рассмотрением наиболее важного случая
электростатического поля точечного электрона по клас-
классической нелинейной теории.
Составим общую функцию Лагранжа L из простей-
простейшего нелинейного лагранжиана C2,3) для поля Lo и по-
потенциальной энергии взаимодействия поля с электроном.
Полагая Д = 0, Е=— gradcp, \>(ж — £) = 8 (r)b(t — s),
найдём согласно B3,24)
*-§ 0-/hSJ)-•*»<*>• <з2»4>
С помощью вариационного принципа получаем
[см. соотношение B3,25)]
1 дпп dL 0
4тс дхп д?~~ '
где вектор Dn является по своему определению электро-
электростатической индукцией (смещением)
El
Отсюда находим следующее уравнение для определения
поля:
divD = 4Tce8(r). C2,6)
Подставляя сюда вместо плотности точечного заряда
его разложение в интеграл Фурье:
найдём, как обычно,
± C2,8)
Учитывая равенство A0,11), получим известное в мак-
свелловской теории решение
D-J. C2,9)
I 32J НЕЛИНЕЙНАЯ ЭЛЕКТРОДИНАМИКА 203
т. е. с точки зрения D-поля электрон следует рассматри-
рассматривать как точечный.
Из соотношения C2,5) для напряжённости поляг вы-
вызванного точечным зарядом, находим
1 + ^
C2'10>
где
Отсюда получаем
<f={Erdr = - {-M=r. C2,11)
Г Г/10
В начале координат (г=0) напряжённость достигает
своего максимального значения:
тр е г? /оо /io\
'о
а потенцдал ср остаётся конечной величиной, равной
с»
с С dx
О '
Численное значение этого эллиптического интеграла
равно
00
Поэтому
^ « 1,8541... f . C2,14)
С точки зрения анализа JEJ-поля электрон не является
точечным, и плотность распределения его заряда может
быть найдена из уравнения
, div JB7 erb Пп лё.
204 КЛАССИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА [ГЛ. IV
Иными словами, с точки зрения .2?-поля заряд можно
рассматривать распределённым в основном в объёме
радиуса г0, так как при г^>г0 плотность будет быстро
стремиться к нулю. Поэтому величину г0 можно рассма-
рассматривать как эффективный радиус заряженной частицы,
под которой в дальнейшем для определённости будем
подразумевать электрон*). Легко показать, что общий
заряд частицы равен е.
В самом деле, общий заряд определяется из равен-
равенства
~ ^ divE (dr) =±§EdSr=Umr*E(r) = е. C2,16)
Наличие двух типов полей и соответствующие им два
определения для плотности заряда, как известно, имеют
место в теории диэлектриков. В данном случае, по уста-
устарелой терминологии электростатики диэлектриков, «истин-
«истинной» плотностью зарядов является плотность [> (т. е. то-
точечный источник), а «свободной»— (/ («истинные» плюс
«связанные» заряды). Отношение величины D к Е можно
рассматривать как «диэлектрическую постоянную» ваку-
вакуума, являющуюся функцией положения:
C2,17)
На больших расстояниях от точечного заряда, когда
!±. —^ О, г принимает значение, равное единице, как в обыч-
обычной электродинамике. Можно сказать, что вместо выра-
выражения энергии — Борн берёт — , причём уменьшение г
компенсируется увеличением е, так* что полная энергия
остаётся конечной.
*) Точнее говоря, под радиусом электрона мы будем понимать
То наибольшее расстояние от центра симметрии, при котором начи-
начинает практически сказываться отклонение от обычного кулоновского
поля точечного варяда.
§ 32] НЕЛИНЕЙНАЯ ЭЛЕКТРОДИНАМИКА 205
Найдём теперь тензор энергии в борновской теории.
Согласно B8,5) имеем
? C2,18)
Г44 = 1(Ш>)--1,0>
прячем
Подставляя сюда вместо JE ги D Гих значения из
C2,10) и C2,9) и принимая во внимание сферическую сим-
симметрию, найдём
C2,20)
\ ^'«4 {di) = ~ (&i —B2).
Здесь
C2,21)
Интеграл В2 может быть преобразован посредством инте-
интегрирования по частям:
с» оо
хА dx
1 _1_ я4K/2 '
Интегрируя второй раз по частям, имеем
ЛВг, C2,22)
Ш классическая электродинамика [гл. tv
откуда н&ходим* что
Таким образом в рассмотренном варианте теории Борна
выполняется теорема устойчивости. Следовательно, бор-
новский электрон является в данном смысле устойчи-
устойчивым.
Величина полевой массы электрона, как известно,
может быть найдена из равенства
Подставляя сюда значение потенциала ср0, получим
= 1,2361... д-. C2,24)
Отсюда, зная численные значения для т, е и с, найдём
эффективный радиус электрона, практически равный
классическому радиусу электрона:
го^3,5- 10-13 см, C2,25)
а также значение для максимального поля, являющегося
полем в центре электрона (г = 0):
Ео = -4- = 4 • Ю16 абс. эл.-стат. ед.
го
Таким образом, исходя из некоторого формально
безукоризненного гипотетического нелинейного обобщения
электродинамики, удалось получить конечную собст-
собственную энергию (или массу) заряженной частицы как
величину, полностью обусловленную энергией поля этой
частицы.
Кроме того, в этой теории выполняется теорема устой-
устойчивости и достигается правильное соотношение между
энергией и импульсом частицы. Всё это бесспорно является
немалым достижением теории, в известном смысле осуще-
осуществившей программу построения «унитарной» чисто
} 321 НЕЛИНЕЙНАЯ ЭЛЕКТРОДИНАМИКА 20?
полевой теории электромагнитной массы электрона.
Однако успехи нелинейной теории этими пунктами в сущ-
сущности и ограничиваются. Точное сравнение с эксперимен-
экспериментом каких-либо дальнейших конкретных следствий
теории не имеет особого смысла обсуждать, так как неё
основание теории покоится на произвольном выборе ла-
лагранжиана и не обосновано экспериментом, что является
основным пороком данной теории.
Подчеркнём также, что, устранив так или иначе труд-
трудность, связанную с бесконечной «продольной» собствен-
собственной энергией в классической теории поля, необходимо
ещё, во-первых, подтвердить этот результат квантовым
путём и, во-вторых, как подчёркивалось выше, устранить
новую специфически квантовую «поперечную» часть бес-
бесконечной собственной энергии (см. ниже § 34). Обе эти
задачи в теории Борна не были решены.
Квантовое же обобщение самой теории Борна как в её
простейшем изложенном выше случае, так и в других
вариантах не привело к каким-либо существенным
новым физическим результатам. Самое квантование
какой-либо нелинейной теории пока что ограничивается
лишь установлением некоторых общих соотношений.
Всё же на теории Борна, являющейся простейшей
известной нелинейной схемой, оказалось нередко удоб-
удобным анализировать характерные нелинейные эффекты.
Как известно, в электродинамике Максвелла, являю-
являющейся линейной теорией, электромагнитные поля обла-
обладают свойством суперпозиции, т. е. аддитивности, сумма
решений уравнений вновь является их решением (волны,
не взаимодействуя, проходят друг сквозь друга). В не-
нелинейной теории свойство суперпозиции нарушается,
ввиду чего эта теория приводит к характерным нелиней-
нелинейным эффектам, в частности, к рассеянию света на свете,
нелинейному рассеянию света на зарядах, отражению
света от света, видоизменению планковского закона для
равновесного излучения и т. д., которые были довольно
поучительным образом рассмотрены по этой теории. Все
эти нелинейные поправки крайне малы.
Проблема нелинейной электродинамики приобрела
реальное, а не формальное значение лишь после открытия
208 КЛАССИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА [гл, IV
взаимного превращения частиц, предсказанного впервые
в квантовой релятивистской теории электрона-позитрона.
Действительно, согласно релятивистской квантовой меха-
механике два фотона (или две электромагнитные волны),
могут при столкновении друг с другом виртуально поро-
породить пару частиц (электрон-позитрон или два противо-
противоположно заряженных мезона), которая в свою очередь
может аннигилироваться и дать два новых фотона, т. е.
в конечном счёте мы получим столкновение двух фотонов,
приводящее к двум новым фотонам, иначе говоря, рас-
рассеяние света на свете. Таким образом, возможность вза-
взаимного превращения частиц приводит к нелинейным
эффектам.
Можно задаться вопросом: какому изменению теории
Максвелла в нелинейном смысле будет эквивалентно
подобное включение эффектов, связанных с парами
частиц? Символически можно сказать, что указанная
релятивистская теория вакуума Дирака плюс линейная
электродинамика Максвелла будут эквивалентны неко-
некоторой нелинейной электродинамике, характеризуемой
особым лагранжианом. Так как искомый лагранжиан
при пренебрежении высшими производными, т. е. при огра-
ограничении медленно меняющимися полями, есть функция
инвариантов 1Х и /2, то при не слишком высоких значе-
значениях полей его можно разложить в ряд по степе-
степеням 1Х и /2:
Задача сводится к определению коэффициентов а,
. . . Теория пар Дирака приводит к коэффициентам
а-7В в- д 1 еЧг
Довольно любопытно, что различные, как подчёркива-
подчёркивалось, с физической точки зрения произвольные варианты
формальной нелинейной электродинамики приводят к близ-
близким значениям коэффициентов, если учесть, что радиус
§ 32] НЕЛИНЕЙНАЯ ЭЛЕКТРОДИНАМИКА 209
электрона
_ е2 \ h
0 тс2 137 2тшгс*
Величина различных нелинейных эффектов, возни-
возникающих согласно теории пар, при указанных ограниче-
ограничениях оказывается крайне незначительной, как и по теории
Борна. Например, эффективное сечение рассеяния света
y ~ const.
на свете, выражающееся формулой j=—^—, даже
для /-лучей достигает всего лишь порядка ^10~60 см2,
что лежит далеко за пределами современных экспери-
экспериментальных возможностей.
Наряду с перечисленными выше эффектами и поправ-
поправками в теории взаимодействия нелинейные теории поля
существенно отличаются от линейных теорий тем, что,
принципиально говоря, позволяют вывести уравнения
движения частиц из уравнений порождаемого ими поля.
В самом деле, уравнения движения заряженных (или
магнитных) частиц включаются в линейную электроди-
электродинамику независимо, наряду с уравнениями поля Макс-
Максвелл а-Лорентца, а не вытекают из последних. Это осо-
особенно ясно из следующего примера. Пусть мы имеем
два покоящихся заряда ег и e2i для которых напряжён-
напряжённости полей равны ех\г\ и е2/г|. Ввиду линейности обыч-
обычных уравнений сумма этих решений является также
решением, т. е. должна соответствовать возможному
состоянию системы зарядов. На самом же деле два заряда
не могут находиться в покое, они будут двигаться оттал-
отталкиваясь, либр притягиваясь. Это движение зарядов никак
не вытекает из линейных уравнений поля, но описы-
описывается путём добавочных уравнений движений, в которые
включаются силы, действующие на заряды со стороны
других зарядов.
В теории гравитации уравнения поля согласно общей
теории относительности являются нелинейными. Это
обстоятельство в самом деле позволило вывести уравне-
уравнения движения частиц под влиянием сил тяготения из
уравнений поля, порождаемого этими частицами*).
♦) В. Ф о к, Journ. of Phys. USSR, 1, 1, 1939; см. также А. Е i n-
stein, В. Hoffmann, L. Infeld, Ann. of Math., 1938.
14 Д. Иваненко и А. Соколов
210 КЛАССИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА [гл. IV
Поэтому из рассматриваемой нелинейной теории,
принципиально говоря, также возможно вывести урав-
уравнения движения частиц из уравнений поля, порождён-
порождённого этими частицами, подобно тому как это было сделано
в теории гравитации.
Заметим, однако, что нелинейная электродинамика,
вытекающая из релятивистской квантовой механики,
которую до сих пор удалось построить лишь при неко-
некоторых ограничениях, например для случая медленно
меняющихся полей, сама по себе оказалась не в состоя-
состоянии устранить хотя бы трудность, связанную с бесконеч-
бесконечной продольной собственной энергией поля. Согласно
подсчётам Всйскопфа указанная расходимость в теории
вакуума Дирака, в известной мере эквивалентной введе-
введению нелинейностей, приобретает всё же более слабый
логарифмический характер вместо расходимости типа г,
при г—> О*).
Заметим здесь же, что аналогично обстоит дело в мезо-
динамике, где, например, принципиальная возможность
виртуального порождения пары нуклеонов или нуклеона
и аптинуклеопа двумя мезонами и последующего виртуаль-
виртуального их уничтожения с испусканием двух новых мезо-
нов# даёт типичный ыелинейньгй эффект рассеяния мезо-
мезонов* на мезонах, нарушающий суперпозицию мезонных
<]>-функций.
Нелинейная мезодинамика, на необходимость которой
мы здесь указываем, до сих пор обсуждалась лишь в виде
программы; она должна будет привести к квазидиэлек-
квазидиэлектрической постоянной и квазимагнитной цроницаемости
вакуума и к таким эффектам, как поляризация нуклеон-
ного вакуума, нелинейное рассеяние мезонов на мезо-
мезонах и т. д., а также сможет, повидимому, обусловить
ослабление взаимодействия нуклеонов на малых рас-
расстояниях, возможно содействуя устранению дипольной
трудности в теории ядерных сил (см. § 48). Мы уже имели
выше аналогичное ослабление электростатического по-
•) Н. Euler, Ann. d. Phys., 26, 398, 1936; H. Euler und
W. Hpise#iberg, Zs. f. Phys., 98, 714, 1936; V. Weisskopf,
Kgl. Danske Videnskab. Mat. *Fys., 14, 6, 1936; Zs. i. Phys., 89,
27, 1934; SO, 817, 1934; Phys. Rev., 56, 72, 1939.
§ 33] поля с высшими производными 211
тенциала в рассмотренной нелинейной теории, обязан-
обязанное поляризации вакуума.
Так как все частицы так или иначе могут при столк-
столкновениях виртуально порождать пары различных дру-
других частиц, которые после виртуальной аннигиляции
могут вновь превращаться в пары частиц первоначаль-
первоначального типа, то отсюда можно заключить об универсальной
нелинейности уравнений всех частиц, в том числе уравне-
уравнений полей электронов, позитронов, нуклеонов и т. д.
Было бы преждевременно обсуждать здесь эти новые
сложные проблемы. Укажем лишь, что для нелинейных
уравнений поля теряет смысл разложение на отдельные
компоненты типа ряда Фурье и тем самым теряет непо-
непосредственный наглядный смысл вторичное квантование,
заключающееся в сопоставлении амплитудам Фурье
чисел частиц. Таким образом, повидимому, самое поня-
понятие частиц в нелинейной теории приобретёт иной смысл.
Во всяком случае следует подчеркнуть, что новейшее
развитие теории вакуума (см. дополнение), учитывающее
превращения частиц, использует до сих пор лишь линейную
квантовую теорию, не прибегая к введению эффективных
нелинейно стей.
§ 33. Электродинамика полей с высшими
производными
В последнее время неоднократно обсуждался вопрос
о возможном обобщении уравнений электромагнитного
поля путём введения высших производных. Простейшим
вариантом подобной теории, которая в формальном отно-
отношении удовлетворяет всем условиям инвариантности,
является схема Боппа и Подольского*). Вводя высшие
производные следующего порядка в уравнения Максвелла,
этим авторам удалось в известном смысле осуществить
идеи полевой теории электрона, получив конечное зна-
значение для собственной электромагнитной массы.
*) F. В о р р, Ann. d. Phys., 38, 345, 1940; В. Р о d о 1 s k у,
Phys. Rev., 62, 68, 1941; В. Podolsky and Schwed, Rev. Mod.
Phys., 20, 40, 1948
14*
21$ КЛАССИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА [гл. IV
Оставляя в силе максвелловское соотношение между
полем и потенциалами:
а также дополнительное условие Лорентца, наклады-
накладываемое на потенциалы:
^- = 0, C3,2)
заменим волновое уравнение Даламбера B4,5) уравне-
уравнением четвёртого порядка:
C3,3)
Это уравнение является релятивистски инвариантным
и при Щ—> оо переходит в уравнение Даламбера.
Если функция Лагранжа L зависит от потенциалов А[К
и производных от потенциалов АД|а = -^- , Ал,ар —
то вариационный принцип приводит к следующему
уравнению для определения полей:
В частности, мы получим уравнения C3,3), если
положим
Отсюда, как обычно, находим тензор энергии и другие
основные величины, характеризующие поле.
Однако мы используем сейчас другой способ иссле-
исследования уравнения четвёртого порядка C3,3), а именно,
сведём новое обобщённое поле к двум полям, подчиня-
подчиняющимся уравнениям второго порядка.
§ 33] ПОЛЯ С ВЫСШИМИ ПРОИЗВОДНЫМИ 213
Для этой цели введём два потенциала А^ и А^9 со-
соответственно равные
,_ i J C3,4)
А^ — тг LJ Ар,
Отсюда видно, что потенциал нового поля А^ будет
равняться разности потенциалов обоих полей:
а„. = а\,-а;. C3,5)
Далее, как видно из C3,3), потенциал А'^ будет под-
подчиняться уравнению Даламбера:
□ А'* = ~^\ \м (х- *) ds, C3,6)
а потенциал А£ — уравнению Клейна с правой частью
(см. § 20):
(D - Ц) а;=-^\ км {х - a) ds. C3,7)
Таким образом первоначальное поле сведено к двум
полям (своеобразному би-полю), именно: к электромаг-
электромагнитному полю (т. е. с квантовой точки зрения к фото-
фотонам с массой покоя, равной нулю) и ко второму полю,
вектор-потенциал которого подчиняется уравнению
Клейна (т. е. с квантовой точки зрения к полю, свя-
связанному с частицами с отличной от нуля массой покоя
m
J
Образуя из потенциалов А'^ и А^ поля
, д< эл'а ал; за;
имеем согласно C3,5)
Функция Лагранжа L, которая приводит нас
к уравнениям C3,6) и C3,7), должна состоять из двух
частей U и L";
l = L'-L". C3 ДО)
214 КЛАССИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА [гл. IV
Z/ является лаграшкианом максвелловского поля.
Поэтому согласно B3,24) и B3,11) имеем
-£)&, C3,11)
где
Т ' ^ TJ' TJ' /QQ Л О\
L" является лагранжианом уравнений, которые спе-
специально используются также для описания векторных
мезонов (подробности см. ниже, § 47), причём
где
Ц= -1я;,я;-.^-4^. (зз,14)
Варьируя лагранжиан L по потенциалам Л^ и А^,
получим в качестве уравнений Эйлера для полей Н'^у
уравнения Максвелла:
i^efe, C3,15)
а для полей Н"v уравнения, которые используются также
для описания векторных мезонов
§Ах = — \ р (х — ^.) ^d^. C3,16)
Отсюда легко показать, что потенциалы будут удовле-
удовлетворять исходным уравнениям C3,6) и C3,7).
Как видно из C3,11) и C3,13), энергия связи нового
поля с заряженными частицами имеет вид
'^Jx^j уХ—С) CIS, (OOjl/j
совпадающий с прежним выражением B3,13). Поэтому
для силы самодействия мы должны получить выраже-
выражение B3,17):
F{l~—lv \ р (z — E) H^ (x) (d%), C3,18)
где учтено, что H[xv=sH^-~ //^v.
I 33] поля с высшими производными 215
. Для определения тензора энергии образуем импульс
силы самодействия.
Принимая во внимание соотношения C3,15), C3,16)
и C3,18), получаем
C3,19)
Отсюда видно, что тензор энергии 7\,v равняется раз-
разности двух тензоров:
-* p.v ~ •* i-iv •* p-v (оо,^0)
Тензор максвелловского поля 7\',v определяется из
равенства
или [см. также B8,5)]
C3,22)
Аналогично для нахождения тензора Т1^ имеем урав-
уравнение
^1 ^ + ii я;л^1, (зз,2з>
откуда, принимая во внимание тождество
C3*24)
а также переход от равенства C3,21) к равенству C3,22),
получаем
C?,25)
Рассмотрим теперь статический случай. Полагая
для покоящегося точечного электрона
(*-s)f C3,26)
216 КЛАССИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА [гл. IV
найдём для скалярного потенциала следующие урав-
уравнения:
). C3,27)
Подставляя вместо плотности заряда значение C2,7),
получим
И^' C3>28)
7^Г- C3'29>
Потенциал точечного заряда нового поля равен
т^?'_т* = ±(\-е ■*>*)• C3,30)
При r>Y~ формула C3,30) переходит в известный элек-
тро статиче ский потенциал:
? = ~, C3,31)
а при г —0 останется величиной конечной и равной
9=--е*0. C3.32)
Так же, как в нелинейной теории, к вопросу о плот-
плотности заряда можно подходить с двух точек зрения.
В самом деле, в случае данной теории мы также имеем
два типа полей: вектор электрической напряжённости
Е= -grad<p C3,33)
д вектор электрической индукции"
_-^v2)?- C3,34)
Поэтому наряду с «истинной» плотностью заряда
|- = -^Г- = в8A-). C3,35)
.которая является плотностью точечных зарядов, mj*t
§ 33] поля с высшими производными 217
можем ввести ещё понятие плотности «свободных»
зарядов:
_div^_=e*|^^ 33,36)
1 4те 4тс г * v > /
которая даёт «размазанный» заряд, в основном распре-
распределённый внутри сферы радиуса г0 ^ -г—. Таким обра-
зом величина г0 играет роль эффективного «радиуса»
электрона.
Из последних равенств видно, что вакуум в рассма-
рассматриваемой теории, аналогично нелинейной теории, как
бы обладает «диэлектрической постоянной», оператор-
операторное значение которой равно
Для исследования устойчивости точечного электрона
необходимо найти компоненты тензора энергии. Согласно
соотношениям C3,20), C3,22) и C3,25) имеем
Подставляя сюда вместо <р' и <р" разложения C3,28)
и C3,29), получим
U(dr) = £ ) {-^ Bks + ktJ ) (die). C3,39)
В последнем интеграле в силу сферической симметрии
мы можем положить
&? = 4*2 C3,40)
или, вводя новую переменную,
к = кох,
найдём
$ £5 £!■.<**. C3,41)
218 КЛАССИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА [гл. IV
Последний интеграл равен нулю, так как, вводя замену
1
переменных у = — , имеем
В силу равенства \ Ти (di) - О точечный электрон
будет устойчивым.
Отсюда видно, что в этой теории роль механических
натяжений, необходимых для компенсации отталкива-
отталкивания «частей» заряда, играет второе линейное поле,
энергия которого в рассматриваемом случае является
величиной отрицательной (см. § 47).
Общая электростатическая энергия поля покояще-
покоящегося электрона определяется из равенства
Uo= [ Ttl(dr) =^ \ ¥ТкГ^Г> C3,43)
О
откуда для собственной энергии (и тем самым массы)
электрона, обусловленной полной энергией поля, на-
находим
m'i = i^=_Jr-=4-. C3,44)
с2 2с2 ?с2г0 v ' '
Подставляя сюда вместо массы и заряда известные
численные значения, найдём для радиуса электрона
величину разумного порядка
го^1,4 • 1(Н3 см.
Таким образом теория полей с высшими производ-
производными, как и нелинейная теория, позволяет построить
последовательные релятивистски инвариантные модели
полевой массы, я они принадлежат в этом смысле
к лучшим классическим теориям.
Однако рассмотренная здесь теория с высшими про-
производными является всё же линейной теорией, и по-
§ 33] ПОЛЯ С ВЫСШИМИ ПРОИЗВОДНЫМИ 219
этому с помощью её мы не сможем получить в проти-
противоположность борновской теории характерные нели-
нелинейные эффекты, например рассеяние света на
свете. Не представляет особого труда дать квантовое
обобщение теории Боппа-Подольского и убедиться, что
оно приводит попрежнему к конечной (продольной)
массе частицы, порождающей поле. Следует вновь под-
подчеркнуть, что даже при конечном значении продольной
части собственной массы частицы поперечная часть
массы, обусловленная с полевой точки зрения энергией
поперечной части поля, порождённого частицей, и
имеющая чисто квантовый характер, всё равно ока-
оказывается согласно квантовой механике равной беско-
бесконечности. Нетрудно также обобщить теорию с высши-
высшими производными на случай, когда оба поля связаны
с какими-то массами покоя mlt m2. Любопытным обра-
образом взаимодействие между двумя частицами (напри-
(например, нуклеонами), переносимое подобным мезонным
полем, не будет уже страдать пороком дипольной труд-
трудности (см. § 48).
Наряду с бозевскими полями уравнения с высшими
производными можно также ввести в теорию спинорных
частиц. Ввиду произвольности выбора функции Лагранжа,
а также добавочных трудностей, появляющихся при кван-
квантовании поля, связанных с отрицательной энергией
второго поля*), теория полей с высшими производными
также является далеко не убедительной.
Следует отметить, что для развития теории полей
с высшими производными в настоящее время наиболее
существенным является физическое обоснование самой
необходимости введения высших производных, а не рас-
рассмотрение отдельных конкретных вариантов, являю-
являющихся к тому же неоднозначными.
Это обоснование следует произвести с той же
убедительностью, с какой, например, доказывается об-
общая необходимость нелинейного обобщения на осно-
основании теории превращения пар частиц. В последнее
*) См. Д. Ива"невко и] А. Соколов, ЖЭТФ, 14,
379, 1944,
220 КЛАССИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА [гл. IV
время в этом направлении первые шаги были пред-
предприняты Крамерсом, а также группой Баба, показав-
показавшими из общих формальных соображений, что уравненгя
с высшими производными получаются, естественно, в рам-
рамках общих ундорных (спин-тензорных) уравнений.
Следует отметить возрождение интереса к теории с выс-
высшими производными в связи с новой теорией вакуума
(см. дополнение) вследствие того, что при помощи подоб-
подобных уравнений, как видно, например, из C3,30) [см. также
D8,16)], можно составить обобщённые «регуляризованные»
гриновские функции и, следовательно, функции, опре-
определяющие перестановочные соотношения, которые не
будут обладать сингулярностями, и положить эти функ-
функции в основу теории. К подобному приёму в сущности
сводятся методы регуляризации Паули-Вилларса и Фейн-
мана, хотя они и были введены самими авторами как
искусственные приёмы, вне связи с теорией высших
производных. Кроме того, следует подчеркнуть, что идеи
и методы теории с высшими производными, способной
описывать различные «размазанности», возможно, будут
применены в связи с размазыванием заряда в новой
теории вакуума.
Таким образом, ввиду общей произвольности тео-
теории, ограничивающейся притом ближайшими степенями
высших производных, и ряда трудностей с отрицатель-
отрицательной энергией эта попытка, несмотря на известные
успехи, также не является окончательно убедительной
и должна рассматриваться скорее лишь как предвари-
предварительное указание на новые интересные возможности.
§ 34. Теория неполевой массы
Вопрос о природе массы электрона представляет
в современной физике одну из центральных проблем
теории элементарных частиц. В предыдущих парагра-
параграфах были разобраны различные варианты классической
теории электрона, основанные на гипотезе полевой массы.
Экспериментальное исследование* зависимости массы
от скорости не даёт возможности решить вопрос о её
природе, поскольку закон изменения массы от скоро-
I 34] ТЕОРИЯ НЕЙОЛЕВОЙ МАССЫ 22 J
сти согласно теории относительности как для полевой,
так и для неполевой массы имеет один и тот же уни-
универсальный характер:
Однако, как оказывается, поведение электрона
в быстропеременнЫх полях существенным образом зави-
зависит от той или иной трактовки его массы.
Как было указано выше (см. § 31), существующие
полевые теории при колебаниях электрона с длиной
волны, меньшей его радиуса, приводят к весьма слож-
сложным интегро-дифференциальным уравнениям, притом
с членами, зависящими от «размеров» частицы. Дирак*),
исходя из ряда гипотез, построил новый вариант клас-
классической теории точечного электрона, обладающего
только неполевой массой, дифференциальное уравнение
движения которого имеет один и тот же вид независимо
от частоты колебания электрона.
В настоящее время ещё нет окончательных аргу-
аргументов в пользу той или другой точки зрения, однако
предложенная выше теория обладает следующими
достоинствами.
Во-первых, классическая релятивистская теория Ди-
Дирака приводит к простейшему уравнению движения элек-
электрона в быстропеременных полях, совпадающему с реля-
релятивистской- формой уравнений Лорентца, при отбрасы-
отбрасывании в последнем членов с производными выше третьей*
Во-вторых, классическая (тем самым предваритель-
предварительная) теория неполевой массы частицы, в известном
смысле, ближе всего соответствует квантовой теории,
поскольку последняя в настоящем её состоянии сущест-
существенным образом пользуется представлением об электро-
электроне с неполевой массой. Отметим, однако, что при иссле*
довании взаимодействия точечного электрона с электро-
электромагнитным полем согласно квантовой теории появля-
появляются бесконечные полевые массы двух типов: 1) про-
продольная, возникающая благодаря взаимодействию заряда
с продольной частью электрического поля и имеющая
*) P. A. M. D i г а с, Ргос. Roy. Soc. A, 167, 148, 1938.
222 КЛАССИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА [гл. IV
своим классическим аналогом полевую массу Лорентца,
подробно обсуждавшуюся выше, и 2) поперечная масса,
возникающая при взаимодействии заряда с поперечной
частью поля, т. е. с фотонами в собственном смысле,
которая не имеет классического аналога (точнее говоря,
обращающаяся в классическом приближении в нуль).
Как показывается в квантовой теории*), физической
причиной, обусловливаюшей эту поперечную часть энер-
энергии, возникающую согласно квантовой механике даже
для покоящегося электрона (с которым по классической
теории никакое поперечное поле не связано), явля-
являются флуктуации электромагнитного поля. Напряжён-
Напряжённость поля не исчезает даже в том случае, если число
фотонов равно нулю (см. дополнение). Появление указан-
указанных бесконечных масс представляет собой пока что
непреодолимую трудность при построении квантовой
теории элементарных частиц. Согласно полевой гипо-
гипотезе значения для обеих масс должны быть конеч-
конечными и равными в сумме массе той или иной частицы.
Однако до настоящего момента мы не имеем реля-
релятивистски инвариантной квантовой теории конечной
полевой массы, аналогичной, например, классическим
теориям Борна или Б оппа-П о дольского. В самом деле,
как неоднократно подчёркивалось, даже при успеш-
успешном квантовом обобщении классической теории ко-
конечной продольной массы всё равно мы остались бы
лицом к лицу перед специфически квантовой труд-
трудностью бесконечной поперечной массы.
С другой стороны, согласно точке зрения неполевой
теории, обе массы—как продольную, так и поперечную,—
следует отбросить (точнее говоря, необходимо построить
теорию, в которой обе полевые массы были бы значи-
значительно меньше, чем неполевая масса)**). Конечно, тем
самым вопрос о природе массы пока что снимается
с рассмотрения и подлежит разработке в будущей тео-
теории. Таким образом основная трудность построения тео-
теории точечной частицы как при классическом, так и при
*) В. Гейтлер, Квантовая теория излучения, Гостехиздат,
1940, стр. 201. *
**) См. А. А. С о к о л о в, Journ. of Phys. USSR, 5, 231, 1941.
; 34] ТЕОРИЯ НЕПОЛЕВОЙ МАССЫ 223
квантовом рассмотрении связана с появлением беско-
бесконечных собственных масс.
Для обращения полевой массы в нуль в классиче-
классической теории было предложено несколько способов:
а) обращение бесконечной полевой массы в нуль
с помощью предельного ^-процесса (Вентцель, Дирак*);
эта идея, несмотря на неоднозначность введения пара-
параметра X, обратила на себя известное внимание, по-
поскольку теория л-процессов может быть сравнительно
просто обобщена на квантовый случай; б) исключение
бесконечной полевой массы электрона при помощи вве-
введения некоторого вспомогательного поля (теория би-по-
ля). Последний способ**) позволяет наиболее прямым
путём придти к уравнению движения точечного заряда.
В заключение заметим, что последние успехи новейшей
квантовой теория вакуума, подтверждённые рядом экс-
экспериментов (подробнее см. дополнение), помогли всё же
выяснить некоторые вопросы теории собственной массы.
Фактически удалось показать, что небольшая часть
массы электрона носит явно полевой характер. Эта поле-
вая доля оказывается примерно равной Am-^ j—r т.
Остальная часть массы, повидимому, не может быть об-
обусловлена энергией электромагнитного поля, тем более
энергией других полей. Следовательно, у электрона, как
и у других элементарных частиц, должна существовать не-
некоторая основная «затравочная» масса, к которой уже до-
добавляется пЛевая масса. Возможно, что классическая тео-
теория неполевой массы поможет со своей стороны в той или
другой степени разобраться в вопросе о природе «затра-
«затравочной» массы элементарных частиц. Появление новых
более совершенных теорий, относящихся к учению о при-
природе собственной массы элементарных частиц, а вместе
с тем и ученрте о строении материи, будет в значительной
*) См., например, Г. Вентцель, Введение в квантовую
теорию волновых полей (дополнения), Гостехиздат, 1947;
P. A. M. D i г а с, The principles of quantum Mechanics, 3-rd.
Oxford, 1947, § 78; M. А. Марков, УФН, 29, 269, 1946;
Д. И. Б л о х и н ц е в, Вестник МГУ, № 1, 1948.
**) А. А. Соколов, Вестник МГУ, № 2, 1947; см. также
ЖЭТФ, 18, 280, 1948.
224 КЛАССИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА [гл. IV
мере зависеть от новых экспериментов в области ядерной
и космической физики.
Во всяком случае, существующие как классические,
так и квантовые теории, связанные со строением элемен-
элементарных частиц, носят еще предварительный характер.
О неисчерпаемости изучения вопроса о строении мате-
материи писал ещё Ленин в 1908 г.; в частности, он указал.
„ «Материя исчезает»—это значит исчезает тот предел, до ко-
которого мы знали материю до сих пор, наше знание идёт
глубже; исчезают такие свойства материи, которые каза-
казались раньше абсолютными, неизменными, первоначаль-
первоначальными (непроницаемость, инерция, масса:т т. п.) и кото-
которые теперь обнаруживаются, как относительные, присущие
только некоторым состояниям материи. Ибо единствен-
единственное «свойство» материи, с признанием которого связан
философский материализм, есть свойство быть объек-
объективной реальностью, существовать вне нашего созна-
сознания ' *).
а) Теория Х-п р о ц е с с а
Представим трёхмерную плотность неподвижного за-
заряда при e-^Uразложенной в интеграл Фурье:
где амплитуда Фурье ;.о (к) характеризует распределение
плотности электрона в пространстве импульсов, т. е.
даёт так называемый форм-фактор. Для равномерно заря-
заряженного электрона-шарика радиуса г0 плотность р ("i) =
const при г<г0 и р (!•) ^0 при г > г0.
Для точечного электрона р0 (к) — 1, поэтому
|i(r) =е5(г).
Значение потенциала может быть найдено из уравнения
Пуассона:
причём в последнем выражении переменную к мы заменили
на —к'.
*) В. И. Ленин, Материализм и эмпириокритицизм, Госпо-
литиздат, 1949, стр. 243.
34J ТЕОРИЯ НЕПОЛЕВОЙ МАССЫ 225
Полная энергия Uo поля, связанного с зарядом, равна
Т
Подставляя сюда значения для <?(т) и [>(/*) и учи-
учитывая соотношение
получим
Интегрируя последнее выражение в случае сферической
симметрии по углам вектора к, находим
Постараемся теперь подобрать для форм-фактора
р (/с) такой вид, при котором энергия поля Uo, связан-
связанного с электроном, обратилась бы в нуль. Задача эта,
очевидно, не имеет однозначного решения.
Остановимся на одном из возможных вариантов, при
котором
\)\(к) = cos k\.
Здесь параметр \ является пока что некоторой постоян-
постоянной величиной.
Электростатическая энергия Uo поля заряженной
частицы будет при этом равняться
Uo = — \ cos k\dk.
о
Последний интеграл пропорционален 8-функции:
которая при всех конечных значениях X обращается
35 Д, Иваненко и А. Соколов
|J6 КЛАССИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА [гл. IV
в нуль*), за исключением случая Х = 0. Поэтому, оста-
оставляя параметр X конечным, но в пределе сколь угодно
малым, найдолт. что электростатическая энергия поля,
связанного с точечным электроном, а значит, и продоль-
продольная полевая электромагнитная масса не только не равны
бесконечности, но даже обращаются в нуль в классиче-
классическом неквантовом случае. Нетрудно видеть, что теорема
устойчивости будет при этом тождественно выполнена,
так как в покоящейся системе координат все компоненты
\ Т% (dr0) равняются нулю. Таким образом 8-образная
плотность в пространстве импульсов обеспечивает «устой-
«устойчивость» заряда в рассмотренном выше смысле. Очевид-
Очевидным недостатком X-процесса является добавочное требо-
требование стремления X к нулю лишь|в качестве последнего
этапа вычислений, так как в противном случае полу-
получаются прежние расходящиеся результаты.
Мы видим, что введение форм-фактора является весьма
общим методом, позволяющим с единой точки зрения
сформулировать такие разнородные модели электрона,
как частица-шарик и точечный предельный электрон.
Важным преимуществом Х-форм-фактора является
возможность его представления в релятивистски инва-
инвариантном виде. До сих пор мы ограничивались трёх-
трёхмерным случаем, пригодным для покоящегося электрона.
Введём теперь четырёхмерный вектор Х^ с компонентами
1 Г
♦) Строго говоря, д(Х) =— \ cos kXdk является величиной,
п J
о
неопределённой даже при X ф 0. Поэтому этот интеграл, следует
понимать, согласно замечаниям, сделанным, выше о ^-функции,
как предельное значение некоторого выражения, например, типа
(множитель 'е"лк обращает осциллирующую на бесконечности
функцию cos к\ в нуль). Переходя к пределу а ~* 0, получим при
ХфО
j 34j f еорий непоЛеёой МассЫ 22?
X, Xo, причём Xo> | X |» т« е- четырёхмерный вектор Xu
должен быть времени-подобным. Тогда вместо произве-
произведения АХ, которое входит в форм-фактор, мы будем иметь
инвариант \ок— Х&- Для конечного значения X теория
не инвариантна, так как вспомогательный вектор Хц
определяет некоторое избранное направление в четырёх-
четырёхмерном мире, но в пределе X—>0 теория оказывается
инвариантной.
В системе координат покоящегося электрона мы можем
положить Х0 = Х, Х~0 и Для \>1(Щ П0ЛУчим прежнее
выражение cos АХ.
Очевидно, можно ввести другие инвариантные форм-
факторы, приводящие к конечной или исчезающей поле-
полевой массе, однако в числе последних Х-форм-фактор
является, повидимому, простейшим. Мы не рассматри-
рассматриваем здесь других обрывающих множителей, приводящих
к конечной полевой массе, так как подобные теории не
привели к каким-либо убедительным или физически инте-
интересным результатам.
В Х-теории электрон остаётся точечным в смысле про-
пространственного распределения, но ему сперва припи-
приписывается некоторая протяжённость во времени, т. е. дли-
длительность, величина которой в пределе стремится к нулю.
Можно сказать, что вспомогательный вектор X своеобраз-
своеобразным путём заменяет радиус электрона.
Нетрудно показать, что введение Х-форм-фактора типа
cos(AX0 —fcX) эквивалентно следующему видоизменению
Д-функции [см. соотношение A7,13)], и 2)-функции
[см, соотношение B0,4)], определяющих пуассоновы скобки
для величин поля классической теории (а также соот-
ветствующие четырёхмерные правила перестановки кван-
квантовой теории полей):
и, соответственно,
Действительно, подставляя форм-фактор плотности
Х-теории, т. е. cos (&Х0 — &X)> B разложения Фурье А-функ-
15*
22ft КЛАССИЧЕСКАЙ ЭЛЕКТРОДИНАМИКА [гл. Jy
ции и Х)-функции и производя интеграции, получим выше-
вышеприведённые выражения.
Одним из достоинств X-теории, как всякого .реляти-
.релятивистски инвариантного формализма, является возмож-
возможность его перенесения в релятивистскую квантовую
механику. При этом четырёхмерные правила перестановки
волновых функций и других разнообразных величин,
определяющих поля, например, электромагнитных по-
потенциалов, гравитационных и мезонных потенциалов,
будут определяться не А-функцией или D-функцией, но
видоизменёнными функциями Дл и 2)я*).
Как и в классической теории, X-форм-фактор обеспе-
обеспечивает в квантовой теории исчезновение продольной по-
полевой массы или собственной энергии частицы, обра-
обращая электростатическую энергию поля точечного заряда
в нуль. Jfe
Заметим, однако, что никаких разумных способов
устранения бесконечной поперечной энергии до сих пор
не указано. Одно время Дирак придерживался мысли
о необходимости введения для этой цели отрицательных
энергий фотонов и отрицательных вероятностей, но эта
сложная и неплодотворная схема была им самим оставлена
(см. третье издание его книги).
До сих пор мы рассматривали Х-теорию с точки зрения
введения в классической и квантовой теории нового форм-
фактора, предназначенного, главным образом, для устра-
устранения расходимости в продольной энергии поля. Однако,
точно так же, как в теории классической полевой массы,
можно исходить не только из выражения энергии или
импульса, но брать за отправной пункт вывод уравнения
движения Лорентца. В этом случае теория Х-процесса
приводит к другой трактовке этих уравнений движения.
*) Как известно из релятивистской квантовой механики, четы-
четырёхмерные правила перестановки для простейшего скалярного поля
имеют вид (см. § 45)
i i
В теории же Х-процессов в правую часть последнего равенства
вместо функции D мы должны подставить функцию Dk
§34] ТЕОРИЯ НЕПОЛЕВОЙ МАССЫ 229
Первоначальная мысль Вентцеля заключалась в исполь-
использовании многовременного формализма, описывающего
электроны и поле своими отдельными координатами g и г
и значениями времени х и t. Тогда при определении дей-
действия поля на точечный электрон в данный момент времени
необходимо корректным образом совершить предельный
переход т —> t. Для уточнения этого перехода вводится
вспомогательный вектор Хр., полагаемый затем равным
нулю:
t = т -f Xo.
Наметим совсем коротко дальнейший ход этих идей.
Введя новые потенциалы, совпадающие с максвеллов-
скими в областях вне светового конуса и равные разности
запаздывающих и опережающих максвелловских потен-
потенциалов в области абсолютно прошлого, Вентцель и Дирак
получили, совершая при помощи вектора Х^ переход
х —> t, релятивистские уравнения движения для точечного
электрона без инерциальных полевых членов и без членов
с производными выше третьей, но с правильным членом
затухания. Это уравнение будет выведено нами иным
способом [см. C4,36I. Паули и Яух применили Х-процесс
в теории мезонного поля, причём выяснилось, что полевая
продольная мезонная масса нуклеона не будет уже равной
нулю, а равняется по порядку величины массе мезона*).
Других существенных результатов эти приложения Х-тео-
рии не дали.
Окончательный итог проведённого краткого анализа
Х-теории не может, очевидно, говорить в её пользу.
*) W. P a ul i, Phys. Rev., 64, 332, 1943; J.M.Jauc h, Phys.
Rev., 63, 335, 1943.
В простейшем случае потенциал скалярного мезонного поля
(созданного нуклеоном: протоном, нейтроном) определяется функ-
пией Грина обобщённого уравнения Пуассона (см. § 44). С учётом
А-форм-фактора вместо A4,9) мы будем иметь:
sin kR
230 КЛАССИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА [гл. IV
Сам вспомогательный вектор Х^ не имеет никакого физи-
физического смысла и не проявляется непосредственно в каких-
либо явлениях. В качестве форм-фактора его введение
удобно, но совершенно произвольно и не однозначно*).
Кроме того, с помощью X-процессов не удалось устра-
устранить трудностей с расходимостью поперечной энергии,
возникающей при квантовой трактовке.
б) Теория би-поля
Перейдём теперь к выводу классического релятивист-
релятивистского уравнения электрона при помощи нового мето-
метода, основанного на введении второго вспомогательно-
вспомогательного поля.
Вектор-потенциал второго (немаксвелловского) поля
будем обозначать маленькими буквами а^.
Компоненты тензора немаксвелловского поля h^ будут
равны <4
Для компонент максвелловского поля Н^ остается старое
выражение B3,2), т. е.
в частности, для потенциала самодействия (R —> 0)
1 Г *acos*X 1 ... к0 ко
о
или для малых значений X
Подсчёт магнитных моментов нуклеонов приводит согласно Х-тео-
рии к конечным значениям, но с обратными по сравнению с тре-
требуемым эмпирически знаками. Таким образом, уже самые простые
обобщения Х-теории на мезонное поле показали её несостоятель-
несостоятельность.
♦) См., например, И. Померанчук, ЖЭТФ, 17, 567, 1947,
f 34]* ТЕОРИЯ НЕПОЛЕВОЙ МАССЫ * ДО
Подберём тензор h^ таким образом, чтобы новое вспо-
вспомогательное поле действовало только на электрон, его
порождающий, и не могло быть излучённым в виде свобод-
свободных волн.
Для функции действия S (см. § 2с$) имеем
S^ + Sa + Sa. C4>4)
Для первой части функции действия St9 определяющей
свободное движение частицы, мы оставляем выраже-
выражение B3,5):
St = - тс J К-Цх ds. C4,5)
Для второй части функции действия S2, относящейся
к полю, вместо B3,10) и B3,11) напишем выражение
f C4,6)
причём в функцию Лагранжа наряду с максвелловским
if^v введено также немаксвелловское поле h^. *
Наконец, последняя часть функции действия опреде*
ляет взаимодействие поля с электроном:
- C4,7)
При этом к обычному потенциалу А^ прибавляем потен-
потенциал А1[Х9 создаваемый внешними источниками, и вычитаем
в согласии с излагаемой гипотезой особый (немаксвел-
ловский) потенциал а.^, действующий только на заряд,
его порождающий.
При варьировании функции S по координатам
электрона нас будут интересовать только части
Sx и £3:
S'^tf-^-(£'<&, C4,8)
233- КЛАССИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА [гл, IV
где
L' = -mcV — Уц +
kA -av)](dx). C4,9)
При помощи уравнений B3,14) и B3,20) находим
уравнение движения частицы
mi^Fi + F». C4,10)
Здесь
— ^
есть сила, действующая на электрон со стороны внеш-
внешнего поля [ср. B3,19); с другой стороны,
(х) - h^ (х)] (dx) C4,11)
обозначает результирующую силу самодействия со сто-
стороны максвелловского и немаксвелловского полей.
Равенство C4,10) содержит в себе четыре уравнения.
Однако вм^то четвёртого уравнения всегда можно взять
•уравнениёд23,20), которое выражает собою ортогональ-
ортогональность четырёхмерного вектора скорости по отношению
к ускорению:
6"Л = О. C4,12)
Отсюда также следует равенство, которым мы восполь-
воспользуемся в дальнейшем:
?^=-UV C4,13)
При варьировании функции действия по электро-
электромагнитным потенциалам мы можем отбросить часть Sl9
не содержащую потенциалов А^.
Тогда
§ 34J ТЕОРИЯ НЕПОЛЕВОЙ МАССЫ 233
причём
L = Lo + ± \ р (х - k) [I, D + А» - о,»)] &. C4,14)
Вариационный принцип, применённый к лагранжиану L,
даёт [см. также B3,25)]
Аналогичное уравнение получаем для второго потен-
потенциала а^.
Отсюда находим дифференциальные уравнения для
максвелловского и немаксвелловского полей:
Подчиняя потенциалы условиям Лорентца
получим
Таким образом мы приходим к частному случаю
теории полей типа Боппа-Подольского, когда покоящаяся
масса второго (немаксвелловского) поля равна нулю
(&0 = 0). Следовательно, здесь можно использовать полу-
полученные для указанной теории результаты, согласно кото-
которым наш электрон оказывается устойчивым, а его электро-
электромагнитная масса, пропорциональная к0 [см. соотноше-
соотношение C3,44)], должна обращаться в нуль.
Далее, из последних формул мы видим, что потен-
потенциалы Ар и пу. подчиняются одним и тем же дифферен-
f34 КЛАССИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА [гл* IV
циальным уравнениям. Используя произвольность выбора
решений этих линейных уравнений, при решении ура-
уравнения С обычными потенциалами А^ мы возьмём одни
запаздывающие потенциалы, которые приводят к излуче-
излучению электромагнитной энергии, а при решении уравне-
уравнений, содержащих немаксвелловские потенциалы а^ вто-
второго вспомогательного поля, возьмём полусумму запазды-
запаздывающих и опережающих потенциалов (наличие комбина-
комбинации в виде полусуммы запаздывающих и опережающих
потенциалов сделает, очевидно, невозможным излучение
немаксвелловских волн; см. выше § 17).
Релятивистски инвариантная плотность р (х — £) для
точечного электрона равна
Р (« — Е) = 8 (-г — g) 8 (* — х). C4,18)
Тогда для силы самодействия получаем
lU C4,19)
Принимая во внимание замечание, сделанное о выборе
решений для потенциалов максвелловского и немаксвел-
ловского "полей, имеем
(запаздывающие потенциалы),
а^^{А^ + А1) C4,20)
(полусумма запаздывающих и опережающих потенциа-
потенциалов), откуда
Итак, со стороны собственного поля на электрон дей-
действует сила, определяемая полу разностью запаздыва-
запаздывающих и опережающих потенциалов. Введение подобной
гипотетической комбинации, используемой также в теории
классического электрона Дирака A938 г.), может быть
§ 34J ТЕОРЮ НЕПОЛЕВОЙ МАССЫ 335
сведено простым путём, как мы сейчас показали, к гипо-
гипотезе о существовании второго немаксвелловского поля.
Как видно из A7,20), функция Грина уравнения
Даламбера с решениями, являющимися полуразностью
запаздывающих и опережающих потенциалов, будет равна
G = ±f(x,z'), C4,22)
где
1(х,х')=П(г-гУ-с*A-1Г]-£Ещ. C4,23)
Поэтому, когда в правой части уравнения Даламбера
стоит четырёхмерный ток точечного заряда, равный
то для вектора-потенциала находим
f(Z,t')ds'. C4,25)
Здесь для краткости введено обозначение
откуда с помощью C4,19) и C4,21) получим следующее
значение для силы само действия:
*V-t- $ (^^^i)/(*' £')ds'" C4'26)
Введём в дальнейшем обозначение
в = (^-?У(^-^). C4,27)
Тогда
^ = Т 5 [M'v(^-«;)-^(«v-E'v)]g&', C4,28)
причём здесь принято во внимание, что
236 КЛАССИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА [гл. IV
Учитывая наличие 8-функции под знаком интеграла
в C4,28), можно заключить, что область интегрирования
по величине s' будет лежать около точки s.
Вводя новую переменную
u = s'-s C4,29)
и разлагая подинтегральные выражения по малому пара-
параметру и, находим
5'ц = 5ц (s + и) = 5^ + юбц + \ 5|i + ...,
При помощи равенств C4,12) и C4,13) получаем
/.3..2 .. ..3 ...
Далее имеем
Подставляя последние соотношения в формулу C4,28)f
находим
ег С Г 1 •• 1 /••• i • •• " \
Интегрируя последнее выражение по частям и принимая
во внимание, что
8(со) = 0,
имеем
§ 34] ТЕОРИЯ НЕПОЛЕВОЙ МАССЫ 237
Как видно из равенств C4,27) и C4,25), о= — с2и2 пред-
представляет собою квадрат четырёхмерного расстояния между
двумя положениями электрона.
В частности, в нерелятивистском приближении (t=s)
мы можем рассматривать а как предельное значение сле-
следующего выражения:
s=-c2(s' ~sJ + г2 = — с2и2 + г2,
при г—>0, где г является уже трёхмерным расстоянием.
Рассматривая Ь(с2и2) как предел выражения о(с2и2 — г),
s > 0, форма которого не может измениться при переходе
к релятивистскому случаю, найдём согласно F,8)
\b{v*)dv = ±. C4,33)
Кроме того, мы имеем соотношение
= 0, C4,34)
которое следует из того факта, что подинтегральное
выражение является нечётной функцией.
Отсюда получаем следующее выражение для силы
самодействия:
»=т % О'11 ~ ? ^v) • C4>35)
Выражение же для собственной массы, пропорциональное
интегралу C4,34), обращается в нуль(т€' —0). Подчерк-
Подчеркнём ещё раз, что исключение бесконечной собственной
массы существенно связано с тем обстоятельством, что для
силы самодействия мы выбрали полуразность запазды-
запаздывающих и опережающих потенциалов. При любых других
комбинациях полей (одни запаздывающие или одни опе-
опережающие потенциалы, полусумма запаздывающих и опе-
опережающих потенциалов) собственная полевая масса для
точечной частицы обращается в бесконечность.
Подставляя последнее выражение в равенство C4.10)
найдём окончательно следующее классическое (не кван-
квантовое) релятивистское уравнение движения для точеч-
238 КЛАССИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА [гл. IV
ного электрона:
ml;=уъни+4 % ('€ - ? У v?v) • C4,36)
Для ясности подчеркнём снова, что это уравнение отли-
отличается от уравнения Лорентца C1,13),во-первых, отсут-
отсутствием члена с полевой массой; во-вторых, отсутствием
членов с производными выше третьей; в-третьих, урав-
уравнение C4,36) сформулировано в релятивистски инвари-
инвариантном виде. Величина
dG^=-|-Jyvi"vcb C4,37)
представляет собою четырёхмерный импульс излучения.
Проекция импульса на временную ось Gt = ~Git т. е.
энергия излучаемых световых волн, взятая со знаком
минус, является отрицательной величиной, (т > 0). Это
связано с тем обстоятельством, что электрон всегда
теряет энергию на излучение, когда он движется с уско-
ускорением.
Другой член четырёхмерного импульса самодей-
самодействия
dG;~l£\ds C4,38)
связан с электромагнитным полем движущегося элек-
электрона. Эта часть импульса не излучается, так как
равняется полному дифференциалу от электромагнит-
электромагнитного количества движения
C; = |£i C4,39)
и является поэтому обратимой величиной. В нереляти-
нерелятивистском приближении члены затухания, добавленные
к лорентцевой силе, сводятся к известному выражению
для силы лучистого трения (см., например, § 31).
Заметим, что аналогично теории регуляризации*) или
приведения к конечному виду различных расходимостей
*) W. P a u I i and. F. V i 11 а г s, Rev. Mod. Phys., 21, 434,
1949. См. также Сборник «Сдвиг уровней атомных электронов»,
ИЛ, 1950.
§ 35] ИНТЕГРИРОВАНИЕ УРАВНЕНИЯ ДВИШЕН. ЭЛЕКТРОНА 239
в новейшей теории вакуума можно назвать приём устра-
устранения бесконечностей с помощью X-процесса «формали-
«формалистическим», поскольку в конечном выводе X-вектор стре-
стремится к нулю и исчезает из конечного результата. С дру-
другой стороны, метод устранения бесконечностей при помощи
компенсирующего би-поля следует назвать «реалисти-
«реалистическим», поскольку это гипотетическое поле предпола-
предполагается реально существующим и остаётся в конечном
результате. Очевидно также, что недавние работы Пайса*)
представляют собой по существу не что иное, как даль-
дальнейшее развитие идеи компенсирующего би-поля уже
при помощи не векторного, а скалярного и других полей.
§ 35. Интегрирование уравнения движения электрона
Интегрирование уравнения движения точечного элек-
электрона вида C4,36) встретило ряд затруднений. В силу
того, что это уравнение содержит третью производную
по собственному времени, необходимо, кроме тривиаль-
тривиальных начальных условий, т. е. задания начальной коор-
координаты и начальной скорости, ввести ещё какое-то
новое третье дополнительное условие.
Для примера остановимся на исследовании прямо-
прямолинейного движения.
Как известно, электрон будет двигаться по прямой
линии в том случае, когда на него со стороны внешнего
поля действует только электрическая сила, направлен-
направленная по оси х, совпадающая с направлением начальной
скорости. Принимая во внимание, что в этом случае
отличной от нуля будет лишь одна компонента, и вводя
обозначения (Hi41 = iEI х—^г и £ = — £4> находим
£ (х- ±i(£»_cV)) , C5,1)
тсЧ = ехЕ +|^ [сЧ -t(x*- А*)]. C5,2)
*) О работах Пайса см. сборник «Сдвиг уровней атомных
алектронов», ИЛ, 1950.
240 КЛАССИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА [гл. IV
Вместо равенства C5,2) мы можем взять соотноше-
соотношение B3,21), которое в нашем случае принимает вид
^с*. C5,3)
Чтобы удовлетворить уравнению C5,3), положим
C5,4)
х — cshq.
Величина д связана с трёхмерной скоростью движе-
движения соотношением
»=ъ=г=сьъд. C5'5)
В частности, для малого значения скоростей v (нереляти-
(нерелятивистский случай) находим
* с г
Подставляя C5,4) в равенство C5,1), получим урав-
уравнение для определения величины д:
где so = -^-— , а величина ro = -?-j является классическим
«радиусом», играющим роль его эффективного размера.
При решении уравнения C5,6) примем, что внешнее
поле является функцией одного собственного времени.
Вообще же говоря, оно может зависеть как от t, так и от#.
В этом более общем случае решение нашей задачи примет
уже вид интегрального уравнения; как обычно, это
интегральное уравнение будет эквивалентно не только
исходному дифференциальному уравнению движения,
но также будет автоматически учитывать и начальные
условия.
Решение уравнения C5,6) будем искать в виде
-S')ds', C5,7)
35] ИНТЕГРИРОВАНИЕ УРАВНЕНИЯ ДВШКЕН. ЭЛЕКТРОНА 241
где функция Грина G определяется из равенства
GsG 8fc s')
- C5,8)
откуда
=:G1 + G0. (o5,9)
Здесь Gx является сингулярной частью функции Грина:
Несингулярная же её часть определяется из решения
однородного уравнения
Go-So<?o = O. C5,11)
При вычислении функции Gx разложим подинтеграль-
ное выражение на сумму двух членов:
ik s(ik)* = k + ririk- C5'12)
VlX —~~ if) I it\l l/К JL in IK
С помощью теории вычетов (см. § 11) находим
1
; s>s'f
C5,13)
Из уравнения C5,11) получаем значение для функции Go:
S-S'
\-C2es\ C5,14)
Поэтому функция Грина уравнения C5,6) равна
S-S'
)е s° ; s<s'.
C5,15)
Отсюда следует, что искомая величина q будет содер-
содержать две части:
q = qr + qa, C5,16)
16 Д. Иваненко и А. Соколов
242 КЛАССИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА [гл. IV
причём
s s—sr
£ ] *')Е (*') ds'> <35'17)
S — S'
е"^1 Е <*') ds> ■ C5'18)
В решении C5,17) мы интегрируем по всем значениям
,<?', меньшим чем s. Наоборот, в решении C5,18) мы
интегрируем по всем s\ большим чем s. Иными словами,
в первом случае (qT) мы учитываем запаздывающее воз-
воздействие внешнего поля Е (s) на точечный электрон,
а во втором (qa )— опережающее.
Прежде всего, следуя аналогии с классической меха-
механикой, оставим решение, определяемое только запазды-
запаздывающим воздействием (см. § 15).
В этом случае мы должны положить ^ = 0, С2= — 1.
Тогда равенство C5,16) принимает вид
C5>19)
Однако решение C5,19) с физической точки зрения
является абсурдным. В самом деле, полагая, например,
E = EQrj(s'), находим
Ь£-^*>0> C5,20)
0; *<0,
т. е. после окончания действия силы (s > 0) электрон
будет продолжать двигаться .с ускорением (самоуско-
(самоускоряющийся электрон)*). Попробуем избавиться от этого
решения с помощью введения опережающего воздей-
воздействия.
*) Решение уравнения движения с запаздывающими потенциа-
потенциалами исследовалось также А. П. Б е л о у с о в ы м (ЖЭТФ, 9, 658,
1939) и М. А. Марковым (ЖЭТФ, 16, 800, 1946).
§ 35] интегрирование Уравнений движен. электрона 243
В этом случае дополнительные условия необходимо
задать не только для момента времени до начала действия
силы (.9= — со), но также и для момента после окончания
её действия (см. также § 15).
В качестве подобного дополнительного условия по-
потребуем, чтобы как при s = — оо, так и при s = со уско-
ускорение электрона (т. е. величина, пропорциональная q)
равнялось бы нулю (само собой разумеется, что это требо-
требование автоматически выполняется в случае исчезновения
внешней силы при 5= i оо)*).
Заметим далее, что мы всегда можем выбрать систему
координат, относительно которой электрон при s= —оо
будет покоиться в начале координат.
Поэтому дополнительные условия примут оконча-
окончательно вид
q = 0, х = 0, t = s при .9= — оо C5,21)
(начальные условия);
д = 0 при ,9= оо C5,22)
(конечное условие).
Отсюда находим С1 = С2'= 0. Поэтому согласно C5,16)
имеем
')*'] . C5,23)
Далее, при помощи C5,4) получаем окончательное
значение для искомых величин в виде /
s s
х = с ^ sh g (sr) ds', t = s + ^ [ch q (*') -1] ds'. C5,24)
В решении C5,23) мы учитываем как запаздывающее
воздействие (sr < .9), так и опережающее (sf > s). Появле-
*) Эти условия были сформулированы одним из нас (А. С о к о-
лов, Вестник МГУ, № 2, стр. 33, 1947; ЖЭТФ, 18, 280, 1948).
16*
2U КЛАССИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА [гл. IV
ние решений с опережающим воздействием*) оправды-
оправдывается введением опережающих потенциалов при реше-
решении уравнений с собственным полем. Перейдём теперь
к выяснению физического смысла решения, связанного
с опережающим воздействием. Электрон является как бы
размазанным по оси времени и поэтому практически
за s0 секунд раньше начинает замечать появление внеш-
внешнего поля. За это время электромагнитная волна про-
проходит расстояние
soc =" ~s r° " ¥ т~& ' C5,25)
которое следует принять за радиус электрона**).
Таким образом, если в классических теориях полевой
массы мы должны каким-то образом ввести величину гОу
играющую роль радиуса электрона, с которой связы-
связывается затем электромагнитная масса, то в классической
неполевой теории точечной частицы наоборот, в основные
уравнения движения вводится масса электрона т,
а радиус г0 появляется автоматически при интегрировании
уравнений движения.
В частности, в нерелятивистском случае, когда мы
можем положить д = — и пренебречь величинами ква-
*) Вопрос о введении опережающего воздействия в других
задачах был рассмотрен также А. Власовым (Учёные записки
Московского Университета, раздел Физика, вып. 75, 1945 г.).
**) Интересно заметить, что, пренебрегая силой лучистого тре-
трения (т. е. полагая so = O), вместо C5,6) получаем уравнение
которое совпадает с уравнением A5,1), применяющимся в класси-
классической механике.
В этом случае в решении уравнения C5,6) [см. соотношение
C5,23)], как и следовало ожидать, будут отсутствовать решения
с опережающим воздействием, т. е.
—oo
Аналогичное выражение было найдено нами в § 15 при решении
уравнения A5,1).
§ 35] ИНТЕГРИРОВАНИЕ УРАВНЕНИЯ ДВИЖЕН. ЭЛЕКТРОНА 245
дратичными относительно #(<72~0), решения C5,24) при-
принимают вид
t = s,
t
х= ^ v(t')dt'. C5,26)
—со
Подставляя сюда вместо v — cq значение C5,23),
получим после ряда преобразований
t-t' + so)E(t')dt' +
C5,27)
Правильность последнего выражения может быть легко
проверена, поскольку решение C5,27) удовлетворяет
как новому начальному условию C5,26), т. е, х~0 при
t — —ос, так и дифференциальному уравнению C5,23).
Как известно, в классической механике существует
два способа трактовки вариационных проблем.
Метод Лагранжа, при котором функция действия
задаётся на всём интервале времени движения материаль-
материальной точки:
C5,28)
где s — собственное время.
В этом случае мы должны потребовать, чтобы на гра-
границах (т. е. при s = sx и s = s2) вариации от координат ох
обращались бы в нуль, т. е. мы фактически должны
задать как начальные, так и конечные условия.
Во втором способе, известном под названием метода
Гамильтона-Якоби, функция действия имеет вид
S=
=^Lds, C5,29)
246 КЛАССИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА [гл> \\
или, иными словами, функция S обрывается на некото-
некотором моменте времени s.
Метод Гамильтона-Якоби допускает решения только
с начальными условиями.
В классической механике рассматриваются такие
лагранжианы, для которых оба метода являются совер-
совершенно тождественными, т. е. когда возможно свести всю
проблему к случаю, когда заданы только начальные
условия.
К решению нашей задачи (движение точечного элек-
электрона с учётом силы трения) мы подошли с помощью
метода Лагранжа, растягивая пределы интегрирования
от s± = — оо до s2 = + оо.
Так как решение этой проблемы может быть дано
только в том случае, когда наряду с начальными задаются
ещё конечные условия, подобная задача не может тракто-
трактоваться методом Гамильтона-Якоби, допускающим, как
было указано, лишь задание начальных условий.
§ 36. Рассеяние света свободными электронами
Как было указано выше (см. § 34), определяя зависи-
зависимость массы от скорости, при равномерно-прямолиней-
равномерно-прямолинейном движении электрона мы не можем решить вопроса
о её происхождении (полевая и неполевая массы изме-
изменяются с увеличением скорости по одному и тому же
закону).
Однако уравнения движения для полевой и неполе-
вой массы будут различны в быстропеременных полях
благодаря наличию членов с 4-й, 5-й и т. д. производ-
производными в полевой теории Лорентца, и поэтому исследование
колебаний электрона с большой частотой может явиться
критерием в пользу той или другой классической предва-
предварительной модели, если мы находимся вне облаоти кван-
квантовых эффектов.
Пусть точечная частица совершает прямолинейное
гармоническое колебание с нерелятивистской скоростью.
В этом случае
t = s, z = tl9 £3=5з = 0. C6,1)
§ 36] РАССЕЯНИЕ СВЕТА СВОБОДНЫМИ ЭЛЕКТРОНАМИ 247
Уравнения движения C5,1) и C5,2) примут вид
mw = eE + — w, C6,2)
evE = *£**, C6,3)
где v = х и w = х являются соответственно скоростью
и ускорением частицы.
При получении уравнения C6,2) мы пренебрегли
величиной — по сравнению с w. Jto вытекает из того
обстоятельства, что при гармоническом колебании элек-
электрона с амплитудой а и круговой частотой to
VW2
т. е. в нерелятивистском случае последняя величина
действительно может быть отброшена.
Уравнение C6,3) выражает собою закон сохранения
энергии. В левой части равенства стоит работа, кото^
рая совершается внешней силой в единицу времени,
а в правой части количество энергии W, которую излу-
излучает электрон в одну секунду, т. е.
^ C6,4)
Уравнение C6,2) было получено также Лорентпом
для движения электрона, обладающего электромагнитной
массой [см. формулу C1.19YJ. Однако исходное уравне-
уравнение C6,2) предполагается в неквантовом приближении
пригодным для колебаний с любыми длинами волн
вто время как уравнение Лорентпа является ограниченным
и имеет место только в том случае когда длина волны
больше радиуса электрона (X > г0), т. е. когда членами
о производными выше 3-й можно пренебречь. Различие
248 КЛАССИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА [гл. IV
между обеими моделями сказывается при рассмотрении
вопроса о рассеянии света на свободных электронах.
Пусть на электрон падает электромагнитная волна
с круговой частотой ш.
Внешнее электрическое поле задаётся уравнением
Е =r Eo cos u>t, или Е = Еое~ш. C6,5)
Решение для ускорения w будем искать в виде
и> = пое-ш. C6,6)
Подставляя C6,6) и C6,5) в равенство C6,2), находим
№=L(ад
где
Как известно, эффективное сечение а при рассеянии
света свободными электронами равняется отношению
количества энергии W, которую излучает электрон
в единицу времени, к количеству энергии /, которая
падает в 1 сек. на единицу поверхности.
Для величины W согласно C6,4) имеем
где черта означает усреднение данной величины по
времени.
Значение для / определяется из соотношения
При нахождении средних значений по времени w2 и Е2
мы, отбросив мнимые части, учли, что
л
cos2 ®t = sin2 (ot = -к- •
§ 36] РАССЕЯНИЕ СВЕТА СВОБОДНЫМИ ЭЛЕКТРОНАМИ 249
Отсюда находим
°'=т-г^г* C6Д0)
где г0 = —2, а длина волны падающего света X = —- .
В частности, при больших значениях X (X > г0) мы
получаем формулу Томсона:
з = -дяг8. C6,11)
т. е. в этом случае эффективное сечение имеет порядок
площади поперечника электрона, линейные размеры
которой равны г0, хотя никаких размеров точечному
электрону заранее не приписывалось.
Таким образом при рассеянии света точечный элек-
электрон ведёт себя как шарик с радиусом г0.
В • теории точечного электрона выражение C6,10)
должно иметь место также для сколь угодно малых длин
волн Х(Х < г0).
В этом предельном случае эффективное сечение при-
принимает вид
1
C6,12)
в то время как с точки зрения теории протяжённого
электрона (например, электрона Лорентца) выражение
C6,10) имеет место лишь при X > г0 (см. § 31), когда
сила трения играет роль поправочных членов. При ма-
малых же X теория Лорентца приводит к существенно
иным выражениям.
Поэтому экспериментальная проверка формулы C6,12)
при малых X может решить вопрос в пользу гипотезы
полевой или неполевой массы.
Следует, однако, заметить, что при X < Хс ( Хс = — ) ,
ч тс/
или подавно при
н
(
250 КЛАССИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА [гл. IV
т. е. когда энергия падающего света (кванта света)
достигает порядка 137 /тгс2 *), мы должны рассматривать
всю проблему с точки зрения квантовой механики, влия-
влияние которой становится существенным уже при X ~ Хс
Хс = — ), и, в частности, наблюдать комптоновское
изменение длины волны при рассеянии.
Однако вычисления, проделанные по квантовой меха-
механике для рассеяния света на точечном электроне с учё-
учётом затухания в предположении, что электрон не обла-
обладает полевой массой, иначе говоря, при пренебрежении
продольной и поперечной энергией поля, приводят к
аналогичным результатам.
Действительно, при больших длинах волн (X > hjmc)
мы вновь получаем согласно нерелятивистской квантовой
механике формулу C6,10), или при пренебрежении зату-
затуханием, которое в этой области мало, формулу C6,11).
В области более коротких длин волн (|/ о < X < h/mc)
квантовая релятивистская теория Дирака приводит для
эффективного сечения рассеяния света на электроне к
формуле Клейна-Нипшны, имеющей в системе координат,
где покоится центр инерции системы электрон плюс фотон,
вид:
и ~ 4т; К
Затухание при этом ещё не играет заметной роли.
Наконец, в области крайне малых длин волн X < }/" о
*) Как известно из квантовой теории, энергия кванта света
определяется выражением
. he
£ = /iV = -г- ,
л
где h =6,6 • 10~27 эрг • сек — постоянная Планка.
16ti2 />oY v >. л ^Ьъ
Для случая, когда —^— ( -j- ) > 1 или а < — г0, имеем
Здесь принято во внимание, что так называемая постоянная тон»
2тге2 1
кои структуры а = -г-— численно равняется .
tlC jo/,Ua
§ 37] КОГЕРЕНТ. КОЛЕБАНИЕ СВЯЗАННЫХ ЭЛЕКТРОНОВ 251
эффективное сечение в пределе сохраняет при учёте
затухания вид C6,12) в той же избранной системе коор-
координат*). Однако при этих энергиях существенную роль
начинает играть рождение пар (электронов и позитро-
позитронов), в силу чего этот вывод проверить экспериментально
весьма затруднительно.
Нельзя не считать, что совпадение классических
и квантовых результатов является сильным аргументом
в пользу пригодности, в известных пределах, теории час-
частицы с неполевой массой и ещё раз показывает рациональ-
рациональность предварительного рассмотрения вопросов, связанных
со структурой элементарных частиц, с точки зрения клас-
классической теории, лучшим в известном смысле вариантом
которой является изложенная выше гипотеза вспомога-
вспомогательного компенсирующего поля.
§ 37. Когерентное колебание двух связанных электронов
Рассмотрим когерентное движение двух связанных
электронов, т. е. тот случай, когда оба электро-
электрона колеблются с длиной волны X = — , во много раз
превышающей расстояние между ними /?(Х>Д).
Ради простоты ограничимся исследованием нереляти-
нерелятивистского одномерного колебания вдоль оси х.
Обозначая координаты обоих электронов соответ-
соответственно через хг и х2у найдём согласно C6,2) следующие
уравнения движения:
• • О/э2 •••
тхх = Fye-™ + F12 + ~-s xx C7,1)
(для первого электрона),
тх2 = F2e-^ +- F21 + ~ *2 C7,2)
(для второго электрона).
Здесь Рге~ш и F2e~it£>t являются внешними силами,
приводящими в колебательное движение оба электрона;
*) А. С о к о л о в, Journ. of. Phys, USSR, 5, 231, 1941.
252 КЛАССИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА [гл< jy
F12 и F2l — силы взаимодействия между электронами,
которые связаны с полями Е2 и El9 создаваемыми вто-
вторым и первым электронами, соотношениями
C7,3)
C7,4)
Оба поля путём разложения по величине — могут
быть отнесены к одному времени.
Полагая в нашем случае R2 = R% — [хг (t) — x2(t)]29
найдём согласно C1,10)
C7,5)
Из последних соотношений находим уравнение коле-
колебания для центра тяжести системы х — Хг Х2 :
2mx = Fe-™ -&£z + ^&gx+..., C7,6)
где общая внешняя сила
Отсюда видно, что при когерентном движении элек-
электронов к общей массе добавляется электромагнитная
масса
которая при движении одного электрона благодаря
введению немаксвелловского поля была сведена нами
к нулю-. -
38]
ПРОСТЕЙШАЯ ТЕОРИЯ БЕТАТРОЙА
253
Для силы трения (пропорциональной х), а следова-
следовательно, также для общей энергии излучения аддитивность
не имеет места, поскольку сила трения пропорциональна
квадрату заряда. Поэтому при увеличении заряда в два
раза сила трения увеличивается в четыре раза.
§ 38. Простейшая теория бетатрона
Как известно, в постоянном магнитном поле Н элек-
электроны двигаются по окружности радиуса
cmv
а =
еН
C8,1)
с постоянной скоростью v (если их начальная скорость
направлена перпендикулярно к вектору Н).
Принцип действия бетатрона сводится к ускорению
электронов вихревым электрическим полем, возника-
возникающим благодаря изме-
изменению со временем маг-
магнитного поля. При этом
изменение магнитного
поля в пространстве та-
таково, что оно заворачи-
заворачивает обратно ускоряе-
ускоряемые электроны и заста-
заставляет их в конце концов
двигаться по некоторой
стабильной окружности.
Таким образом, бета-
бетатрон является своеобраз-
своеобразным трансформатором,
в котором ток в первич-
первичной обмотке электро-
электромагнита преобразуется
во вторичный ток уско-
ускоряемых электронов, дви-
движущихся, однако, не во вторичной обмотке, но в пустот-
пустотной тороидальной кольцевой трубке (рис. 12).
Бетатрон, построенный Керстом в 1941 г. после
теоретических работ Видерое и Терлецкого, является
Траектория
электрона
Кольцедая
трубка
Рис. 12.
254
КЛАССИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА
[ГЛ. IV
релятивистским прибором, в противоположность цикло-
циклотрону, работающему нормально лишь при энергиях,
меньших собственной энергии частиц тс2, когда изме-
изменение массы со скоростью ещё не сказывается.
Условия же работы бетатрона не ставят предела
достижимых энергий из-за изменения массы от скорости.
Однако следует указать на наличие другого фактора,
приводящего к появлению предельных значений для
энергий, которые могут быть достигнуты в бетатроне.
Действительно, в бетатроне частицы двигаются уско-
ускоренно (даже в случае v — const частицы будут обла-
обладать центростремительным ускорением), вследствие чего
согласно законам классической элек-
электродинамики электроны будут излу-
излучать электромагнитную энергию.
Пренебрегая квантовыми эффек-
эффектами (см. § 43), в основу теории
бетатрона положим классическое ре-
лятивистское уравнение движения
электрона с учётом силы трения
C4,36), полученное для точечной
частицы.
В этом параграфе мы найдём усло-
условия, определяющие положение устой-
устойчивой орбиты, а также предельное значение для энергии
движения, обусловленное влиянием силы лучистого трения.
Обозначим координаты электрона, находящегося
в точке А (рис. 13), соответственно через х, г/, z, ict.
Направим магнитное поле Н по оси z и предположим,
что оно обладает аксиальной симметрией, изменяясь
со временем по синусоидальному закону с круговой
й
Рис. 13.
частотой ш
где
= -Я-
C8,2)
г =
Тогда электрическое поле, которое ускоряет электрон,
будет направлено по касательной к окружности. Соот-
§ 38] ПРОСТЕЙШАЯ ТЕОРИЯ БЕТАТРОНА 255
ношение между Е и Н может быть найдено из второго
уравнения Максвелла, представленного в интегральной
форме:
§\±\zdS. C8,3)
Интегрирование по контуру / следует производить по
всей окружности, которая ограничивает площадь S.
Учитывая аксиальную симметрию магнитного поля
[см. соотношение C8,2)], получим
^dS, C8,4)
откуда
Здесь Н является магнитным полем, усреднённым
по площади S.
Проекции вектора Е на оси координат будут равны
ЕХ=-±Е, Е,=^Е, Ez = 0. C8,6)
Принимая во внимание соотношения B3,3), найдём
составляющие уравнения C4,36) на пространственные оси
координат
mx = etEx + -l yirz--j£(iw*-xc*). C8,7)
Аналогичное уравнение будем иметь для составляю-
составляющих на оси у и z, причём в случае плоского движения
мы можем положить z ~ 0.
Наконец, для составляющей на ось t мы получим
уравнение:
тсЧ = в (хЕх + уЕу)-£9 (*«,* -tc*). C8,8)
Здесь четырёхмерное ускорение равно:
w\ = х2 4- у2 — сЧ*.
256 КЛАССИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА [Гд. IV
Сделаем далее переход от четырёхмерных к трёхмер-
трёхмерным величинам, принимая во внимание, что
i = —^= = -^7, C8,9)
х = vj, wl = *4w2 - с2/2 A — р2),
где £? является энергией частиц, г? и w — её обычной про-
пространственной скоростью и ускорением.
Тогда, пренебрегая силой лучистого трения в уравне-
уравнении C8,7), легко свести его к известному релятивистско-
релятивистскому уравнению движения электрона в электромагнитном
поле:
Уравнение же C8,8), в котором мы в правой части отбро-
отбросим малые величины, пропорциональные t и ty будет ха-
характеризовать изменение энергии в единицу времени:
Из последнего уравнения видно, что увеличение энергии
обязано работе электрических сил:
A = e{vE), C8,12)
ускоряющих электроны. Благодаря же излучению проис-
происходит уменьшение энергии на величину:
C8,13)
о С
которая отличается от соответствующего нерелятивистского
выражения появлением множителя £4.
Рассмотрим прежде всего движение по устойчивой кру-
круговой орбите, для которой 7*"а = const.
Проекции уравнения C8,10) на радиус и касательную
к окружности равны:
vH, C8,14)
iL_^L_. = e£. C8,15)
dt VI — ji2
§ 38] ПРОСТЕЙШАЯ ТЕОРИЯ БЕТАТРОНА 257
Сокращая уравнение C8,14) на величину v и диф-
дифференцируя его затем по времени t, найдём:
4- ™==*-аЩ. C8,16)
dt y\ __ pa с dt \ » /
Сопоставляя между собою уравнения C8,15) и C8,16),
а также принимая во внимание соотношение C8,5), нахо-
находим основное условие, определяющее существование рав-
равновесной орбиты электрона:
Н = \Н. C8,17)
Это условие Видерое было подробно исследовано Тер-
лецким*) и является основой современной теории бета-
бетатрона. Отсюда видно, что магнитное поле Н в точках,
расположенных на равновесной орбите, должно быть в
два раза меньше, чем среднее значение магнитного поля
на площади круга, охватываемого этой орбитой.
Электрон будет находиться на равновесной орбите до
тех пор, пока энергия излучения W будет много меньше
работы А электрического поля, ускоряющего электроны:
W^A. C8,18)
Рассматривая ультрарелятивистский случай (v^c), когда
можно положить:
с2 • еаН /оо АГк.
и учитывая далее соотношение C8,2), а также C8,15)
и C8,16), имеем вместо неравенства C8,18):
2 e*Ht3 „ »„ 41
3 mac ^
*) Я. П. Терлецкий, ЖЭТФ, 11, 96, 1941. Вопрос об устой-
устойчивости движения электрона на равновесной орбите и другие
детали теории бетатрона мы разбирать не будем, отсылая чита-
читателей к работам Терлецкого (Journ/ of Phys. USSR,
9, 159,1945), Керста-Сербера (D. Kerst and R. Serber,
Phys. Rev., 60, 53, 1941); см. также А. П. Гринберг, Методы
ускорения заряженных частиц, Гостехиздат, 1949. Kayser и др.,
Nucleonics, февраль, 1948; см. также научно-реферативные сборни-
сборники, вып. I, Резонансные ускорители, ИЛ, 1948 и вып. II, Бетатрон,
ИЛ, 1948.
17 Д. Иваненко и А. Соколов
258 КЛАССИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА [гл. IV
Отсюда получаем основное условие, при выполнении ко-
которого электрон остаётся на равновесной орбите:
Ш < gCr, C8,20)
где
a /•0 = -^-g является радиусом электрона*).
Когда энергия электронов достигает порядка критиче-
критического значения $СТУ они начинают терять заметную долю
энергии и сходят с равновесных орбит**), становясь ис-
источниками интенсивного излучения электромагнитных волн.
* Рассмотрим прежде всего вопрос о сжимании орбит, кото-
которое проще всего исследовать с помощью уравнения C8,11).
В ультрарелятивистском случае уравнение C8,11) при-
ншЖает вид:
yt^ecE-W, C8,21)
причём энергия электрона Ш связана, согласно C8,19),
с магнитным полем Н соотношением:
электрическое поле Е определяется равенством C8,5), а
для энергии, излучаемой в единицу времени, имеем, со-
согласно C8,13) и C8,19), выражение
™=т*£г- C8'22>
Равенство C8,21) представим в виде:
w=xf-e^r- C8>21а>
Последующие преобразования сделаем с помощью соот-
соотношений:
dr Н
*) Д. Иваненко и И. Померанчук, ДАН, 44, 343, 1944.
**) Сжимание орбит было обнаружено Блюиттом (Т. В le-
levy ett, Phys. Rev., 69, 87, 1946).
§ 38] ПРОСТЕЙШАЯ ТЕОРИЯ БЕТАТРОНА 259
Далее, как известно, поля Н (среднее магнитное поле)
и Н (магнитное поле на круговой орбите) связаны между
собою формулой:
т. е.
дХ£- = 2гН. C8,23)
Отсюда находим
C8,24)
" 2г dt
или
О
Для равновесной орбиты (г —а) имеем:
Н(а, 1) = ^-^-. C8,25)
Кроме того, дифференцируя выражение C8,23) по г, на-
находим, что для равновесной орбиты производная от сред-
среднего значения магнитного поля будет равна:
Та в а ' (Ж.гЬ)
Полагая далее в левой части выражения C8,24)
найдём, учитывая соотношения C8,25) и C8,26):
(г, 0 „, ,_br
4 ' у а да
Отсюда получаем, что в течение времени I электрон
отклонится от равновесной орбиты на величину:
t
Та
17*
260 КЛАССИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА [гл IV
В частности, полагая, что вблизи равновесной орбиты маг-
магнитное поле изменяется по закону:
Н = Лг^ sin со'/,
где А — некоторый постоянный коэффициент, а ш'— кру-
круговая частота изменения магнитного поля, имеем для
величины Дт* следующее значение:
( f </) v '
где
У
F (у) = -.— \ sin4 у dy.
о
Вычисляя последний интеграл, находим:
В частности, при у = ^-, т. е. при том времени, когда
электрон получает наибольшее ускорение, величина F
становится равной:
Подставляя сюда согласно Блюитту A. с.)*) а = 83 см,
а/=377 сек, д=—т-> 4aQ = 4000 гаусс, найдём для
изменения радиуса в течение времени, равного четверти пе-
риода f Ы = ^ ),.следующее значение:
Дг - 3,2 см.
Излучение электронов, движущихся с релятивистскими
скоростями, обладает рядом особенностей по сравнению
с излучением медленно движущихся электронов.
Вопрос об интенсивности излучения в зависимости
от номера гармоники будет разобран в следующих
параграфах.
*) О работе Блюитта см. также научно-реферативный сборник,
вып. II, Бетатрон, ИЛ, 1948.
§ 39] ИЗЛУЧЕНИЕ ВОЛН ЭЛЕКТРОНАМИ 261
§ 39. Излучение электромагнитных волн электронами,
движущимися по окружности
Как было указано в предыдущем параграфе, враща-
вращающийся по окружности (например, в ускорительных
приборах типа бетатрона или синхротрона) электрон
должен явиться источником излучения электромагнит-
электромагнитных волн.
Так как при движении электрона по окружности
излучение происходит, главным образом, за счёт нор-
нормального ускорения w (см. предыдущий параграф), то
мы можем ограничиться исследованием случая равно-
равномерного вращения.
Длина волны X при дипольном излучении связана
с круговой частотой вращения ш следующим соотно-
соотношением:
где а является радиусом орбиты, а г; —скоростью дви-
движения электрона.
Вместо C9,1) мы можем написать
? = 7 = Р- <39'2>
Интенсивность излучения высших гармоник (номера п)
с длиной волны — имеет порядок интенсивности диполь-
ного излучения (п = 1), умноженной на величину
^у<-1) = р2 („-!,. C9,3)
Поэтому при нерелятивистских скоростях, когда р < 1,
мы можем ограничиться лишь дипольным излучением.
Однако в ультрарелятивистском случае, когда v
достигает порядка скорости света с(Р~1), разложе-
разложение C9,3) теряет смысл, и вопрос о распределении
интенсивности излучения в зависимости от номера гар-
гармоники п требует дополнительного исследования*).
*) Как было отмечено в предыдущем параграфе, Д. Иваненко
и И. Померанчук указали, что в ускорителях с круговыми траекто-
траекториями, по которым движутся с релятивистскими скоростями части-
262 КЛАССИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА [гл. IV
Равномерное движение электрона по окружности
(в плоскости х, у) возникает, например, под действием
постоянного магнитного поля, направленного по оси z
[см, формулу C9,2)]. В этом случае в тензоре электро-
электромагнитного поля Н^ отличной от нуля будет одна
составляющая H12 = HZ = — Н = const. Общее количество
энергии —т—, излучаемое электроном в единицу собст-
собственного времени, может быть найдено с помощью фор-
формулы C4,36). Полагая %± = icz, имеем для четвёртой
составляющей {\х = 4) указанной формулы
dU dmcH 2 е2 • 2 « ""\ /ол /\
^лГ = аГ-= г &■(*<-**)' C9'4)
где w\ является квадратом четырёхмерного ускорения,
которое при равномерном вращении электрона по окруж-
окружности согласно C8,9) равно
^ = Л¥, C9,5)
d*
где ю = -р является угловой скоростью вращения элек-
электрона, а величина
\ ^ ,1 = \ C9,6)
равняется отношению энергии электрона Щ к его соб-
собственной энергии тс2.
Из C9,6) следует, что при равномерном вращении
величина р остаётся постоянной, благодаря чему т~0.
Поэтому согласно C9,4) имеем для общего количества
энергии, излучаемой электроном в единицу времени:
dU _ 1 dU __ 2 еУсо* ,эд _.
dz "" • Г"~3 с3A~^2)а ' ( ' '
цы, необходимо учитывать наличие заметного излучения. Спектр
подобного излучения исследовался рядом авторов: Л. А р п и м о-
вич и И. Померанчук (Journ. of Phys. USSR, 9, 267, 1945)
и Л. Шифф (L. Shif f, Rev. Sci. Instr., 17, 6, 1946) и др. Замкнутые
формулы, равномерно пригодные во всей интересующей нас области
спектра, были получены в нашей работе (Д.Иваненко и А. Со-
Сокол о в, ДАН, 59, 1551, 1948), см. также G. S с h о tt, Electromag-
Electromagnetic Radiation, Cambridge, 1912, стр. 109.
§ 39] ИЗЛУЧЕНИЕ ВОЛН ЭЛЕКТРОНАМИ 263
Отсюда, принимая во внимание, что
v Вс
0) = — = -*—
а а
найдем
Ш-_^_-
3 а*A —
тт, dU 2 efB*c /on Q\
W = ^Г=^„,/4_Н.м • C9>8)
Это можно переписать также, учитывая значение уско-
ускорения, обусловленного магнитным полем согласно C8,19),
не вводя явно радиуса а:
Полученная формула определяет общую (глобаль-
(глобальную) энергию, которую излучает вращающийся элек-
электрон, но не даёт ни спектрального, ни углового распре-
распределения излучения.
Прежде чем определить спектральную и угловую зави-
зависимость интенсивности излучения, мы должны найти
поля Е и J9T, создаваемые электроном в волновой зоне.
Пусть орбита электрона (окружность радиуса а)
лежит в плоскости (ху) (рис. 14).
Определим поле в точке Р со сферическими коорди-
координатами г, G, <р в момент времени t. Обозначая поляр-
полярный угол, характеризующий положение электрона в пло-
плоскости движения через <}>, имеем:
^ = (JJT.
Согласно равенству B4,8) имеем следующее выра-
выражение для вектор-потенциала:
где
При определении поля в волновой зоне, где напря-
напряжённости Е и И будут порядка 1/г, следует, очевидно,
в выражении для вектор-потенциала А отбросить вели-
величины порядка 1/г2 и выше.
264
КЛАССИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА
[ГЛ. IV
Поэтому мы получаем следующие приближённые ра-
равенства:
(^^y/2cos/, C9,11)
,1, + ^-"*»"»*) Л, C9,12)
где х является углом между вектором а и проекцией г
на плоскость (ж, у), т. е.
х==шх_т. C9,13)
В нашем случае движение является периодическим.
Рис. 14.
Период движения Т связан с угловой частотой о соот-
соотношением
Т — —
О) *
C9,14)
Представляя 2-функцию, входящую в выражение
C9,12), в виде
C9,15)
n =—oo
и учитывая, что интегрирование должно быть ограни-
ограничено периодом Т, мы легко можем найти компоненты
Фурье векторного потенциала
C9,16)
§ 39J ИЗЛУЧЕНИЕ ВОЛН ЭЛЕКТРОНАМИ 266
где.
А (п) = — 4- [ v &«*-«*»**•*** da, C9,17)
О)Г ТС
a = z + т •
Проекции скорости в сферических координатах равны
Vy = vcosy = v sin a,
гH = ^ cos 6 sin у; = — г? cos 6 cos a, C9,18)
откуда для проекций вектор-потенциала находим
те
Af(n) = ^--^ J sin a • в' (na-">sin •sin a> da, C9,19)
Ae (n) = — — cos 6 JL ^ cos a - в1 (n*-«P si° * ** a) c/a. C9,20)
Проекция вектора ^1 на ось г нас не интересует,
так как в волновой зоне ввиду поперечности электро-
электромагнитных волн она обращается в нуль.
Как известно, в теории цилиндрических функций
имеют место соотношения
— TC
с помощью которых находим
Лр (лг) = i — J'n (/г р sin 6),
Де (л) = — -1 ctg 6 /п (л р sin 6). C9,23)
266 КЛАССИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА [гл>
Оставляя, как обычно, в волновой зоне лишь члены
Д=[Нг°], C9,24)
1
порядка — , имеем
откуда
п = — оо
оо
cos w Y»
C9,25)
Найдём теперь радиальную составляющую вектора
Умова-Пойнтинга ©г:
@г - ^ (£в#? - Е?Нв) = ^ (Н$ + Щ). C9,26)
Количество энергии, которую излучает электрон
в едицицу времени внутри телесного угла dQ, равняется
dW = ®rdQ. C9,27)
Подставляя сюда выражение C9,26) и усредняя по
периоду вращения электрона Т с помощью равенств:
т г
-уг V cos /iy cos л'у dt = -г- \ sin щ sin /г'у Л = у 8ПП',
6 о
г
-i- ^ cos щ sin л'у Л = 0, C9,28)
получим
оо
= 2 dW- C9«29)
п-1
§ 39] ИЗЛУЧЕНИЕ ВОЛН ЭЛЕКТРОНАМИ 267
где
dWn - ^g-c [ctg2 6/п (np sin 6) + $Ч'п (п$ sin 6)] dQ. C9,30)
Последнее соотношение определяет собою зависи-
зависимость интенсивности излучения от угла 6 и номера гар-
гармоники п.
При вращении по окружности не одного, а N элек-
электронов мы будем вместо равенства C9,25) иметь
оо N
' н° = "¥ 2 2n/« (ЛР sin 6)cos п (Т + Ф/). C9,31)
П=1 У=1
где у = юг — — ср + — , а фу является начальной фазой
/-го электрона. Аналогичное соотношение мы получим
также для составляющей Ну.
Воспользовавшись формулой
cos п (у + <J>/) ~ cos лгу cos /гфу — sin щ sin лг фу,
а также соотношением C9,28), найдём выражение для
энергии лг-й гармоники, излучаемой всеми N электро-
электронами:
dWn>N = SNdWn, C9,32)
где «фактор когерентности»
N N
SN = N+y% ^ сов и (фу-Ы C9,33)
показывает, во сколько раз энергия, излучаемая N элек-
электронами, увеличивается по сравнению с энергией dWn9
излучаемой одним электроном.
Если электроны расположены по орбите произвольно,
т. е. беспорядочно, то среднее значение, взятое по сумме
разностей фаз, должно равняться нулю. Тогда
SN = N9 C9,34)
и общая энергия, излучаемая N электронами, будет
268 КЛАССИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА [гл. IV
равняться сумме энергий, излучаемых каждым электро-
электроном (некогерентное движение).
Если же электроны расположены по орбите равно-
равномерно, т. е. таким образом, что угол между двумя сосед-
ними частицами равен -^-, то в этом случае мы будем
иметь для фактора SN, характеризующего равномерность
круговой концентрации электронов, выражение
iV-l
SN = N (l + 2 cos2ти/-£) . C9,35)
Вычисляя последнюю сумму, получим
C9,36)
Отсюда видно, что Sn равняется нулю, если номер
гармоники не будет кратным числу электронов /V,
• п
т. е. отношение -jt = v не равняется целому числу.
Наконец, когда v = -^- является целым числом, фак-
фактор когерентности S^ становится равным
SN = N2. C9,37)
Таким образом, при вращении нескольких электро-
электронов, равномерно распределённых по окружности (ко-
(когерентное движение), интенсивность излучения для
некоторых гармоник Г-^-=не целому числу) обра-
обращается в нуль, а для других Г-^- = целому числу j будет
возрастать пропорционально квадрату общего числа
электронов.
В дальнейшем мы ограничимся исследованием излу-
излучения, происходящего от одного вращающегося элек-
электрона, потому что переход к случаю N вращающихся
электронов можно осуществить при помощи фактора S^.
§ 40] УГЛОВОЕ РАСПРЕДЕЛЕНИЕ ИЗЛУЧЕЙИЙ 269
§ 40. Угловое распределение излучения
Для того чтобы определить зависимость интенсивности
излучения от сферического угла 6, мы должны выраже-
выражение C9,30) просуммировать по номерам всех гармоник п.
Воспользуемся следующими соотношениями, извест-
известными из теории цилиндрических функций *):
г2 • D0,2)
Л О 11—Xя) >й
Эти соотношения-могут быть проверены при помощи
разложения левых и правых частей последних равенств
по величине х, причём для квадрата бесселевой функции
и её производной удобно воспользоваться соотношениями:
D0,3)
Выражение D0,4) может быть получено путём дву-
двукратного дифференцирования равенства D0,3) и исклю-
исключения Jn(y) с помощью уравнения Бесселя:
n(y). D0,5)
Отсюда для общей энергии, излучаемой всеми гар-
гармониками в единицу времени внутри телесного угла dQ,
♦) См., например, книгу G. S с h о 11, Electromagnetic Radia-
Radiation, Cambridge, 1912, стр. 125. Заметим, что формула D0,1) приве-
приведена в книге В а т с о н, Теория бесселевых функций, ч. I, ИЛ,
1949, стр. 630, с опиской: I/2 вместо 7/2.
270 КЛАССИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА [гл. IV
имеем
со
dW = "S" (ctS2 6 2
sin
+ ?■ 2 л'-С (npsinеЛ<ZQ =
■?*} (i + cos' G - sin* 6 A +
■?} (i + cos G 1 sin 6 A + ЗрЛ ) .
D0,6)
При малых скоростях электронов, когда р < 1, прене-
пренебрегая членами порядка р2, находим обычную нереляти-
нерелятивистскую зависимость от угла
dw=-££;* (* +cos2
т. е. максимум интенсивности излучения будет лежать
в направлении, перпендикулярном к плоскости вращения
электрона (при 6=0). Интегрируя выражение D0,7)
по телесному углу, найдём для глобального излучения
Это значение для W совпадает, как и следовало ожи-
ожидать, с нерелятивистским приближением интегральной
формулы C9,8).
Далее, как видно из формулы D0,6), в ультрареляти-
ультрарелятивистском случае, когда ф~1), максимум интенсивности
излучения будет лежать вблизи плоскости движения
электрона, причём всё излучение будет сосредоточено
практически внутри угла, имеющего порядок Дер ^ |/1 — р2.
Для того чтобы получить общую энергию W, которую
излучает электрон в единицу времени, мы должны равен-
равенство D0,6) проинтегрировать по углам <р и 6.
♦) В работе Л. Арпимовича и И. Померанчука
A,- с.) аналогичная формула получена в приближённом виде.
Точная формула без вывода приводится в статье Ш и ф ф а
A. с).
§ 40] УГЛОВОЕ РАСПРЕДЕЛЕНИЕ ИЗЛУЧЕНИЯ 211
С помощью простых преобразований найдём
Т/Г/ ^ р с С Г* L ^ J I
~~ 4af j [ [A —f*2)sin20-f-cos26]7/2 "■
О
2 sin 6 cos4 8 + 3 sin3 6 cos2 0 1 ,fl „~ qv
[A — p2)sin28+cos26]7/2 J ^ ' '
Воспользовавшись значением для определённого инте-
интеграла *)
п
* * ' 1г/л ь«\ ~:„ • О 1 о cifl 4-S 9. i1 /я _1_
2 > + ) (
D0,10)
получим
Подставляя сюда вместо Г-функций Эйлера известные
значения, получим для Wпрежнее глобальное выражение:
которое, как и следовало ожидать, совпадает с точной
интегральной формулой C9,8).
При ультрарелятивистских скоростях электрона мо-
можем положить
откуда имеем удобное для приложений выражение
♦) Например, И. М. Рыжик, Таблицы интегралов, сумм,
рядов и произведений, Гостехиздат, 1948, стр. 165.
2?2 КЛАССИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА [Гд. IV
§ 41. Зависимость интенсивности излучения от частоты
Для того чтобы определить зависимость интенсив-
интенсивности излучения от частоты излучения (т. е. от номера
гармоники п), мы должны формулу C9,30), выражающую
парциальную интенсивность п-и гармоники, проинтегри-
проинтегрировать по телесному углу dQ.
Тогда найдём количество энергии с частотой п ■£- ,
которую излучает электрон в единицу времени:
^21 JJ [ctg« e/n2 (pn sin 6) +
6
+ $Ч'п2 (pit sin 6)] sin 6 db. D1,1)
С помощью равенства D0,4) последнее соотношение
легко привести к виду
Wn=-^-[2pM1-(l-p«)^]. D1,2)
Здесь
K(y)smbde, D1,3)
о
а величина у связана с углом б соотношением
j/ = jtosin6. D1,4)
Подставляя сюда вместо /*(у) разложение D0,3)
и принимая во внимание значение для определённого
интеграла *)
♦) См. Р. О. Кузьмин, Бесселевы функции, ОНТЙ, 1935,
стр. 10.
§ 42] ЛСИМПТОТИЧ£;СКОЕ ПРПБЛШЖКГ.ИЕ ФУНКЦИЙ 27'Л
§
получим
о
откуда окончательно находим
D1,7)
Последнее выражение, полученное впервые Шоттом,
даёт распределение интенсивности излучения в зависи-
зависимости от номера гармоники. Так как номгр гармоники
не только входит в аргумент, но определяв/ также по-
порядок бесселевой функции, то практически пользоваться
этой формулой весьма затруднительно. Поэтому в следу-
следующем параграфе мы выведем другое довольно точное
асимитотпческое приближение к формуле D1,7), пригод-
пригодное в интересующем нас ультрарелятивистском случае
§ 42. Асимптотическое приближение для бесселевых
функций высокого порядка
Приближённые формулы, найденные Ватсоном *), для
бесселевых функций высокого порядка (v >'l) вида /v(v^),
где 0<#<;1, определяют лишь верхнюю границу для
функции /v (v#) и только при х ~ 1 дают хорошее при-
приближение. Поэтому мы воспользуемся другим способом
нахождения асимптотического выражения для бесселевых
функций указанного вида **).
*) В а т с о н, Теория бесселевых функций,, ч. I, ИЛ, 1949,
стр. 287.
**) См., например, В. А. Ф о к, ДАН, 1, 97, 1934, R Lan-
go г, Trans. Amer. Math. Soc, 33, 23, 1931.
18 Д. Ипаненко и А. Соколов
274 КЛАССИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА [гл. IV
Как известно, функции Бесселя подчиняются уравне-
уравнению
D2,1)
Наша задача заключается в определении асимптоти-
асимптотического решения последнего уравнения, когда х изме-
изменяется в пределах от 0 до v.
Метод Вентцеля-Бриллуэна, применённый в квантовой
механике, даёт следующее приближённое решение этого
уравнения:
j/"s/v (х) = L- (Ае* + Ве~*), D2,2)
где z = \ 1/ ~~ш — ldx, а х0 является единственным
х
V* — 1/
корнем функции / (х) = ~L — 1, т. е. / (х0) = 0. При
больших значениях v мы можем принять х0 = v.
Однако решение D2,2) является хорошим приближе-
приближением лишь при больших значениях z (x < v) и непригодно
вблизи точки х = х0.
Как было показано *), решение уравнения D2,1),
равномерно пригодное во всей области изменения х,
включая особую точку х0 @ < х < v), следует искать
в форме
r^-,h{z), D2,3)
где Is является бесселевой функцией от мнимого аргу-
аргумента.
Подставляя D2,3) в исходное уравнение D2,1), полу-
получим уравнение для определения неизвестной функции z,
*) А. С о к о л о в, Вестник МГУ, № 4, стр. 77, 1947. В не-
несколько более общем виде асимптотическое представление решений
волнового уравнения с помощью разложения по малому параметру
было найдено также П. Краснушкиным (Вестник МГУ,
№6, 1948). См. также Н. A. Kramers, Zs. f. Phys., 39, 828,
1926.
§ 42] АСИМПТОТИЧЕСКОЕ ПРИБЛИЖЕНИЕ ФУНКЦИЙ 275
а также величины s, характеризующей порядок искомой
цилиндрической функции:
i ! = *'« (!_.), D2,4)
где
1 — 8
4S
в
При получении последних формул мы воспользова-
воспользовались также дифференциальным уравнением, которому
удовлетворяет функция Is(z):
причём штрих означает производную по аргументу,
от которого зависит функция.
Постараемся подобрать параметр s таким образом,
чтобы на всём интервале изменения х (О << х -< v) величина
г оставалась много меньше единицы.
Из уравнения D2,4) мы находим для искомой функ-
функции следующее хорошее приближение:
г
=\
J
Введём в случае больших значений х новую пере-
переменную величину Е:
« = v(l —£). D2,7)
При z<^>vf т. е. при 5 с 1, мы найдём
*-Т<2*>"": ■£=-7-|==-»/51ит- д- D2'8)
Подставляя D2,8) в равенство D2,5), получим
^ D2.9)
27Г> КЛАССИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА [гл. IV
откуда, полагая s— ± —, находим условие, при котором
величина е при £ —>0 становится исчезающе малой.
Поэтому для искомой функции мы можем написать
Л (х) = -±- /-^ [ЛЛГ1/8 (Z) + Z?/J/3 (z)], D2,10)
где вторая функция Бесселя от мнимого аргумента равна
Kn(z)=^cosecnn[r-n(z)-In(z)]. D2,11)
В случае малых значений х ( 0 < х < — ) находим
^; ^ 0, ш=-- и т. д. D2,12)
Величина е, имеющая при ^—>0 порядок —-, может
быть также отброшена, т. е. решение D2,10) является
пригодным на всём интересующем нас интервале изме-
изменения х*).
Наконец, нам остаётся ещё определить значения
постоянных величин А и Б.
Учитывая при этом асимптотические значения для
К и / при больших £**)
Кп (z) ^ У £ е-"; /„ (z) с* -4г е*, D2,13)
а также формулу Стирлинга:
получим
*) В пашей задаче необходимо знать асимптотическое поведение
функций Бесселя только в случае больших значений х (х <^> v; £ <^ 1).
Однако для определения постоянных А и В, а также для опре-
определения интенсивности излучения при малых скоростях v(v<^c),
мы должны воспользоваться другим крайним значением искомой
функции при х -> 0.
**) Р. О. К у з ь м и н, Босселевы функции, ОНТИ, 1935,
стр. 78.
§ 42j АСИМПТОТИЧЕСКОЕ ПРИБЛИЖЕНИЕ ФУНКЦИЙ 277
С другой стороны, принимая во внимание, что для малых
значений х
D2'15)
получим уравнение для определения постоянных А и В:
Х -Л Х _|_ R ^ * (V + ^) / А у Л l>\
2'i' (v + 1) 2'r(v + l) 2tz^z'
откуда находим, что А = ~~ , В =^ 0. Окончательно иско-
искомое асимптотическое выражение для функции Бесселя
принимает вид
т / ч 1
Л
т. у х
D2,16а)
Заметим, что при больших значениях аргумента z функ-
функция Kijz(z) не зависит от номера порядка, т. е. в данном
случае от индекса г/3 и определяется равенством D2,13).
Поэтому
lf^(x) = ^J==re-'. D2,17)
Последнее же решение совпадает с приближённым
решением D2,2), найденным методом Вентцеля-Бриллуэна
и пригодным лишь для больших значений z. С другой
стороны, изложенный в настоящем параграфе прибли-
приближённый метод, включающий как частный случай способ
Вентцеля-Бриллуэна, позволяет получать решения как
для больших, так и для малых значений z.
*) Как известно, цилиндрические функции порядка Уз непо-
непосредственно связаны с интегралом Эйри F соотношением (:г>0):
0 '
см., Р. О. К у з ь м и п, Беотлевы функции, ОНТИ, 1935, стр. 98-
278 КЛАССИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА [гл. IV
В частности, в наиболее интересующей нас области
больших значений z получаем
(*) = ± УЩ- Кщ (-J- B6)'/.) , D2,18)
где
V
Из D2,18) находим
/v (#) =—7^-^2/3 (^-B%)*^ , D2,19)
а также
X
\ /v (х) dz = ± \ y—l-KiU(z) dz. D2,20)
о о
Вместо последнего выражения можно взять
X 1
\ Jw(x)dx= -^ \ 1/2Ш,,(£BE)V.) d£. D2,21)
Формула D2,21) является менее точной, чем D2,20),
так как вместо z мы подставили значение D2,8), пригод-
пригодное лишь при £—>0. Однако, принимая во внимание,
что при £—>1(з—>оо) функции /STi/8(z) и -^i/3(y BE)8/aJ
быстро стремятся к нулю, наше новое приближение
является вполне пригодным. Наконец, вводя новую
переменную величину г/ = -^-B£K/2 и растягивая предел
о
интегрирования для больших v, практически до оо,
получим
X СО
/v (х) dz = -1=- [ Кг,ш (У) dy. D2,22)
Формулы D2,18), D2,19) и D2,22) представляют со-
собою искомые асимптотические выражения для функций
Бесселя,
§ 43] * «СВЕТЯЩИЙСЯ» ЭЛЕКТРОН 279
§ 43. «Светящийся» электрон
Как было найдено выше, зависимость энергии излу-
излучения от номера гармоники определяется равенством
D1'7>:
2$>п
Wn = ^ [ 2pVJB Bn?) - A - р*) \ /2П (х) dx ] . D3,1)
О
Рассмотрим теперь два случая: нерелятивистский
д(р < 1) и ультрарелятивистский A -—р < 1).
В нерелятивистском случае мы можем положить
в согласии с D2,15)
у 2п
о
Тогда для энергии /г-й гармоники находим
Максимальную энергию будет излучать основной тон
( 1)
Энергия излучения гармоники с частотой пъ
(п = 2, 3, 4, ...) будет иметь порядок $2(п~1)\¥1, поэтому
в нерелятивистском приближении её можно отбросить.
Формула D3,4), как и следовало ожидать, совпадает
с нерелятивистским приближением выражения C9,8),
определяющим общую энергию излучения.
Длина волны основного тона [см. также равенства
C9,1) и C9,2)] равна •
т. е. вращающийся электрон будет излучать электро-
электромагнитные волны с длиной волны X, превышающей
в несколько раз размеры орбиты.
280 КЛАССИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА [1Л. IV
Совершенно другое положение вещей мы будем иметь
в ультрарелятивйстском случае.
Вводя обозначение х = 2п$ = 2п A -- I) и принимая
во внимание соотношения D2,18) и D2,22), получим
следующее выражение при £ < 1 и больших значениях п
для энергии излучения п-и гармоники *): '
2nd-:)-
5 ]
Здесь величина
представляет собою отношение собственной энергии тс2
электрона к его общей энергии Щ. В ультрарелятиви-
ультрарелятивистском случае -это отношение является малой величи-
величиной B£ < 1).
Круговая частота излучаемой гармоники равняется
где
с
@о = ~~
является круговой частотой основного тона.
Вводя далее критическую частоту
D3,6;
и учитывая, что для больших номеров гармоник ?г>1 из-
изменение частоты излучения ш мы можем считать непре-
непрерывным:
*) Д. Иваненко и А. Соколов, ДАН, 59», 1551.
1948.
§ 43] «СВЕТЯЩИЙСЯ» ЭЛЕКТРОН 281
так как приращение номера гармоники dn = 1 по срав-
сравнению с п можно считать за малую величину, получаем
d\V - Wn dn =
n '
3 \ГЪ
, D3,7)
где величина у равняется отношению частоты излуче-
излучения со к критической частоте сос, т. е.
Прицимая во пнимание известное рекуррентное со-
соотношение
мы можем значение для dW представить также в другом
виде:
dW = Чг 7?
\ КчЛ*)йх. D3,7а)
Найдём теперь энергию излучения dW в следующих
предельных случаях.
1) В случае со < ^с величина у будет много меньше
единицы [у <t 1).
Предельное значение для dW при у < 1 значительно
проще может быть найдено из равенства D3,7), чем
вд равенства D3,7а).
Воспользовавшись формулами
кп(у) = ^р^, у-*о, п>о,
\ Kn (x) Ж2п1+1-п dx = 22™-n Г (m + 1) Г (/W + 1 ~ Л),
о
m + 1 > /г > О, D3,8)
282 КЛАССИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА [Гд. IV
получим
т. е. энергия излучения будет возрастать пропорцио-
пропорционально корню кубическому из частоты излучения <о = г/»с,
или корню кубическому из номера гармоники п, дости-
достигая своего максимального значения при @^шс.
Как видно из формулы D3,6) при очень больших
энергиях вращающегося электрона критическая частота
излучения (частота, при которой интенсивность излу-
излучения достигает своего максимального значения) может
попасть в видимую часть спектра, несмотря на то, что
основной тон обладает длиной волны порядка радиуса
орбиты.
Поэтому вращающийся электрон может стать «светя-
«светящимся» в буквальном смысле слова.
Действительно, подобное свечение, предсказанное
в указанных выше работах, было визуально обнаружено
в 1947 г.*), причём экспериментальное исследование
подтвердило характер спектрального распределения, уста-
установленного теорией [формулы D3,9) и D3,12)].
Наконец, установим связь между направлением излу-
излучения и номером гармоники. В § 40 мы нашли, что макси-
максимум интенсивности излучения лежит вблизи плоскости
орбиты электрона (б = ~+Аср j , причём всё излучение
фактически будет сосредоточено внутри угла порядка
— р2. Обратимся к формуле C9,30), устанавли-
устанавливающей зависимость энергии излучения от номера гар-
гармоники п и от угла 6.
В частности, для углов 6, лежащих вблизи плоскости
максимального излучения ( б = у j , мы находим сле-
*) Н. С. Pollock и др., Phys. Rev., 71, 829, 1947,
и 74, 52, 1948. См. также УФН, 34, 398,1948. Фотографии нового
излучения см., например, в Electronics (сентябрь, 1947).
§ 43] «СВЕТЯЩИЙСЯ» ЭЛЕКТРОН 283
дующий аргумент, от которого должна зависеть функ-
функция Бесселя, входящая в равенство C9,30):
где
тс
(X = — -
2
Учитывая равенство D3,6), будем иметь отличное
от нуля значение для интенсивности, когда
В частности, для гармоник, дающих отличную от нуля
общую интенсивность, т. е. удовлетворяющих неравенству
находим, что отличная от нуля интенсивность спек-
спектрального излучения будет сосредоточена внутри угла
пл*< 1,
откуда находим предельное значение для угла излучения
ап = п-11к D3,10)
С увеличением номера гармоники телесный угол излуче-
излучения будет всё время уменьшаться, приближаясь к пло-
плоскости движения электрона.
2) В другом предельном случае со > сос мы имеем
у > 1. Для вычисления dW воспользуемся выраже-
выражением D3,7а).
Принимая вовкнимание, что при больших значе-
значениях у (t/> 1)
284 КЛАССИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА [гл. IV
найдём
^=Ш^Ш4у[г'8{у~у)иу- D3Д1)
Здесь
z
g (г) = -4= e-(i dt
является функцией Гаусса.
В частности, для больших значений z мы имеем
g() C
V 7:2
откуда
(*=»:-:)•
Таким образом для частот выше критических со > сос
энергия излучения будет быстро, практически экспонен-
экспоненциально, уменьшаться с увеличением частоты или номера
гармоники п. Следовательно, главная часть излучения
обязана частотам, лежащим вблизи критической сос.
Примерная графическая зависимость энергии излу-
излучения Wn от номера гармоники и = — представлена
на рис. 15.
Наконец, найдём глобальную энергию излучения, ко-
которая согласно D3,7а) будет равняться
Последний интеграл может быть легко вычислен с по-
помощью соотношения D3,8).
§ 43] «СВЕТЯЩИЙСЯ» ЭЛЕКТРОН
В самом деле,
оо со
^ у dy ^ КьЫ (х) dx^~
by о
откуда находим выражение для W:
_8тс_
D3,14)
точно совпадающее с ультрарелятивистским приближе-
приближением D0,12) для интегрального значения энергии излу-
излучения. •
Таким образом найденное выше асимптотическое вы-
выражение D3,7) представляет собою хорошее приближение
для описания излучения «светящегося» электрона.
При вращении по кругу не одного, а УУ электронов
мы должны учесть фактор когерентности Ss, опреде-
определяемый формулой C9,33).
Обозначим через Nx число электронов, расположенных
по орбите произвольно, т. е. беспорядочно в смысле
взаимных расстояний; через N2 обозначим число электро-
электронов, образующих к сгустков, причём в каждом сгустке
пусть находится в среднем N' электронов (iV2 = &/V').
Под «сгустком» мы будем понимать совокупность элек-
электронов, расположенных произвольно вдоль дуги с угло-
286 КЛАССИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА [ГЛ. IV
вым раствором ср, так, что их плотность быстро убывает
по какому-либо закону, например, по гауссовой формуле
при удалении от центра сгустка.
Электроны сгустка должны когерентно излучать
гармоники с интенсивностью, пропорциональной N'2
в области длин волн X, превышающих размеры сгустка
яср(Х > аср) *). Наконец, через N3 обозначим число элек-
электронов, расположенных по орбите регулярно (т. е. на
равных расстояниях друг относительно друга).
Общая энергия излучения для п-т гармоники будет
равняться
W% = Wln + W2n + WSn. D3,15)
Энергия Wln, излучаемая электронами, расположен-
расположенными на орбите произвольно, будет равняться сумме
энергий Wn, излучаемой каждым электроном (см. § 39),
т. е.
Wln = Wn. D3,16)
Энергия W2n, излучаемая сгустками, должна быть
пропорциональной квадрату числа частиц (или квадрату
заряда), т. е.
W2n = kN'*Wn = N2N'Wn. D3,17)
Наконец, энергия W3n, излучаемая регулярно рас-
расположенными электронами, будет равняться
Wan = SNaWB, ■ D3,18)
*) Вообще под когерентным излучением мы будем понимать
такое излучение, при котором излучение двух или более электро-
электронов не будет равняться сумме интенсивностей излучения каждого
электрона в отдельности. В нашем случае мы имеем двоякого рода
когерентность: во-первых, когерентное излучение, происходящее
из-за движения равномерно распределённых по окружности элек-
электронов [фактор когерентности определяется равенством C9,36)],
и, во-вторых, когерентное излучение, связанное с тем обстоятель-
обстоятельством, что часть электронов будет расположена друг относительно
друга на расстояниях, меньших чем длина излучаемой ими волны
(см. § 37).
§ 43] «СВЕТЯЩИЙСЯ» ЭЛЕКТРОН 287
причём согласно C9,36) и C9,37) фактор когерентности
равен
(О, когда -£г будет не целым числом,
7 D3,19)
iV|, когда v^- будет целым числом.
В частности, при N3 > пс ~ ( —-2 j последняя группа
электронов практически не должна излучать. Например,
идеальный постоянный круговой ток мы можем рас-
рассматривать как движение регулярно расположенных
по орбите электронов при N3 —> оо. Этот вывод согла-
согласуется с тем известным фактом, что постоянный ток не
излучает электромагнитной энергии. Таким образом ре-
регулярность расположения электронов должна в общем
случае привести к уменьшению энергии излучения.
Рассмотрим вопрос о границах применимости класси-
классической теории «светящегося» электрона*).
Решая релятивистскую задачу в плоских полярных
координатах, когда можно пренебречь спиновыми эффек-
эффектами, находим для энергии электрона %Xs и волновой
функции tyitS следующие выражения:
D3,20)
где квантовые числа /, s = 0, 1, 2, 3, ..., CUs является
нормированным коэффициентом, радиальная функция R
связана с обобщёнными полиномами Лаггера L соотно-
соотношением
а безразмерная величина р равна
*) А. Соколов, ДАН, 67, 1013, 1949.
288 КЛАССИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА [гл. IV
В случае круговой орбиты (s= 0) квантовое число /
связано с радиусом а соотношением
сЫ
Если квантовое число s не равно нулю, то от круговой
орбиты радиуса а возможно отклонение на величину
Определим излучение электрона при переходе из со-
состояния (/, 0) в состояние (/', $'), причём номер гармо-
гармоники излучения равняется п = I — (/' + s').
Из формулы D3,20) можно найти круговую частоту
излучения:
где соо - - .
Интенсивность излучения n-ik гармоники внутри телес-
телесного угла rfQ равна:
п 2т:т*с3 /-J V ^ У/ ~*>
где
аналогичное выражение имеем для Ру.
Для интенсивности излучения находим:
= dwn s в!-,
где dl/^ — классическая интенсивность излучения, опре-
определяемая формулой C9,30), а коэффициенты В\ равны:
При вычислении суммы 2 Ь\ члены порядка и2// сокра-
§ ,43] . «СВЕТЯЩИЙСЯ» ЭЛЕКТРОН 289
щаются, и отношение квцнтовых поправок для суммарного
излучения к классическим результатам будет равно
В ультрарелятивистском случае де-броглевскую длину
волны движущегося электрона можно положить равной
Отсюда для величины а находим выражение
пА
Таким образом, при .излучении обертонов номера п
квантовые поправки для частоты и суммарной интенсив-
интенсивности излучения начинают сказываться, когда де-броглев-
ская длина волны становится сравнимой с — . Напомним,
что для дипольного излучения (п = 1) мы получим обыч-
~ное условие Д~а.
Подставляя сюда вместо п значение той гармоники,
/ % \3
которая даёт максимум излучения п^[ —^ ) , находим
условие, при котором начинают сказываться ^ квантовые
поправки для суммарной интенсивности излучения:
что значительно превосходит достигаемые в настоящее
время энергии.
Как известно, при классическом рассмотрении пло-
плоского движения электрона в постоянном магнитном поле
траектория электрона всегда должна оставаться круго-
круговой. На языке квантовой механики это означает, что
из состояния s = 0 возможны только такие переходы, для
которых s' также равняется нулю. Как видно из послед
них формул, это возможно лишь в том случае, когда
величина у = ~Т — П~— будет много меньше единицы (у<1),
в противном случае мы должны учесть эффект отдачи,
19 Д. Иваненко и А. Соколов
200 КЛАССИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА [гл. IV
который может повлиять на траекторию движения
электрона, что связано с возможностью перехода в состоя-
состояния $•' Ф 0.
Из условия y~ 1 находим значения для энергии Щ,
, при которой следует учитывать эффект отдачи:
что, повидимому, лежит на границе наблюдений.
При последнем условии, повидимому, следует пере-
пересмотреть также вопрос о когерентности излучения не-
нескольких электронов, поскольку каждый электрон полу-
получает новые степени свободы (изменение радиальных функ-
функций) при квантовых переходах.
В заключение небезынтересно остановиться на исто-
истории открытия нового эффекта «светящегося» электрона*
Предсказание нового излучения, испускаемого элек-
электронами в бетатронах, может на первый взгляд пока-
показаться в значительной мере тривиальным, так как дви-
движение по стабильной круговой орбите является уско-
ускоренным. Поэтому важно подчеркнуть, что первый суще-
существенный пункт теории светящегося электрона заклю-
заключается в доказательстве весьма значительной величины
потерь на излучение, растущих пропорционально
той степени энергии. При энергии порядка 100
потеря энергии на излучение, согласно Блюитту (см. §38),
достигает 2°/0, а радиус орбиты'с 83 см уменьшается при-
примерно на 3 см.
При некоторой критической энергии потеря энергии
оказывается равной энергии, приобретённой электроном.
Наличие потолка работы бетатрона является вторым су-
существенным выводом теории*).
Поэтому неудивительно, что первые работы с новым
бетатроном на 100 MeV были посвящены выяснению роли
предсказанного излучения. После окончательного под-
подтверждения существования нового излучения проектиро-
проектирование бетатронов сверхвысоких энергий без добавочных
*) Это обстоятельство было выяснено в первой же работе
(/. с.) по светящемуся электрону, явившейся результатом дискус-
дискуссии на одном ив семинаров в Московском университете.
§ 48] «СВЕТЯЩИЙСЯ» ЭЛЕКТРОН 291
приспособлений, очевидно, оказывается нецелесообразным.
С другой стороны, бетатрон останется весьма эффектив-
эффективным прибором для получения ускоренных до 100—200 MeV
электронов и для получения тормозных рентгеновых лу-
лучей примерно этой же энергии, возникающих при столк-
столкновении электронов с мишенью в бетатроне.
В-третьих, переход от излучения отдельного электрона
к излучению пучка вызвал возражение в связи с отсут-
отсутствием излучения кругового тока; была высказана мысль,
что благодаря взаимной интерференции реальный пучок
электронов в ускорителе типа бетатрона вообще излучать
не будет. Однако излучение возникает вследствие нали-
наличия флуктуации в пучке электронов, нарушающих равно-
равномерное распределение типа кругового тока*). В результате
флуктуации излучение пучка электронов в бетатроне в ос-
основном является суммой излучений отдельных электронов.
Далее, как было показано в § 40, это излучение
имеет особое угловое распределение, будучи направлено
при ультрарелятивистском движении электрона вперёд
по движению.
Наконец, одной из наиболее характерных и суще-
существенных сторон нового излучения является его спек-
спектральное распределение. При ультрарелятивистском дви-
движении излучается отнюдь не одна основная волна, соот-
соответствующая дипольному излучению, а имеет место интен-
интенсивнее испускание, обертонов крайне высокого порядка,
причём максимум энергии приходится как раз на высокие
обертоны порядка п ~ ( —5 J . При этом спектр является
практически непрерывным, так как разница между часто-
частотами незначительна по сравнению с критической частотой,
в области которой происходит основное излучение. Отсюда
ясно, что первоначальные предположения об излучении
микрорадиоволн и поиски, например, Блюиттом этих
волн в данных условиях были ошибочными, так как ма-
максимум излучения при энергии электронов в десятки
миллионов электрон-вольт должен приходиться на область
видимого света. В полном согласии с этими довольно
*) Вопрос о флуктуапиях был впервые обсуждён в дискуссии
с Я. П. Терлепким.
19*
292 КЛАССИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА [Гл. IV
парадоксальными выводами об излучении видимого света,
лаборатории Поллока (/. с.)~удалось наконец"в 1947 г.
визуально обнаружить в синхротроне, являющемся модер-
модернизированным видоизменением бетатрона, свечение, испу-
испускаемое движущимися электронами в виде красноватого
при 30 MeV и голубовато-белого при 70 MeV пятна, столь
яркого, что оно было видно даже при дневном свете.
В этой связи следует отметить, что в противополож-
противоположность всем прежним косвенным способам наблюдения
электрона вновь открытое свечение является наиболее
непосредственным. В самом деле, наблюдение сцинтил-
сцинтилляций или следов частиц в камере Вильсона или в фото-
фотопластинках, а также регистрация отсчётов в счётчике,—
все эти методы позволяют надёжно отметить присутствие
или прохождение частиц косвенно по их воздействию
на другие частицы. В эффекте Черенкова электрон наблю-
наблюдается более непосредственно по его излучению, которое,
однако, самым тесным образом связано с наличием среды.
Лишь в новом эффекте, который разумно назвать явле-
явлением «светящегося» электрона, наблюдается свечение,
исходящее непосредственно от электрона, движущегося в
поле, и не обусловленное частицами окружающей среды.
Термин «светящийся» подчёркивает наиболее интересное
свойство нового типа излучения при практически исполь-
используемых ускорениях до энергий в десятки миллионов
электрон-вольт.
Резюмируя эти замечания, можно сказать, что теоре-
теоретические и экспериментальные исследования показали
ряд специфических, частью неожиданных свойств пред-
предсказанного излучения и доказали его важность для работы
ускорительных установок.
Весьма интересно, что новое излучение «светящегося»
электрона, исследованное вначале как помеха при работе
ускорителей, в свою очередь оказалось интересным явле-
явлением, которое можно использовать разнообразными спосо-
способами. Более того, явление «светящегося» электрона играет
роль не только в лабораторных условиях. При движении
быстрых электронов и других частиц, входящих в состав
космического излучения, в магнитном поле Солнца и звёзд
мы будем, очевидно, иметь условия, аналогичные поло-
§ 43] «СВЕТЯЩИЙСЯ» ЭЛЕКТРОН 293
жению в ускорителях типа синхротрона и бетатрона,
ввиду чего должно иметь место излучение электромаг-
электромагнитных волн космическими заряженными частицами.
Не исключено, что подобное новое космическое излучение
будет хотя бы отчасти ответственным за открытое недавно
радиоизлучение звёзд*). Кроме того, следует отметить,
что интенсивное излучение в магнитном поле, например,
Земли ставит известный предел энергии, которой могут
обладать частицы, достигающие Земли из мирового про-
пространства (для электронов около 10l7eV)**).
Предсказание и открытие явления «светящегося» элек-
электрона ещё раз с полной наглядностью показало весьма
глубокое универсальное значение утверждения Ленина
о том, что «Электрон так же неисчерпаем, как и атом»***).
Действительно, электрон, как и другие элементарные
частицы, характеризуется теперь не только массой и элек-
электрическим зарядом, но и открытыми позднее магнитными
моментами разного типа, спином, типом статистики, волно-
волновыми свойствами, ядерными квазизарядами, проявляющи-
проявляющимися при взаимодействиях с нуклеонами и т. д. Все эти
вновь и вновь открываемые качества электрона (как и всех
других частиц) проявляются в неисчерпаемом множестве
всё новых свойств поведения, таких, например, как явле-
явления диффракции электронных волн, способности превра-
превращения в другие частицы, поглощения атомными ядрами
(К — захват), способности излучать видимый свет с особы-
особыми свойствами при движении со скоростями, близкими к
скорости света, и т. д.
Не останавливаясь сколько-нибудь подробно на вопро-
вопросах, связанных с ускорителями, укажем коротко, что
в настоящее время описаны весьма эффективные уско-
ускорительные установки, основанные на идее Векслера****)
*) См. также Н. A If v en and N. ?Н е г lof son, Phys. Rev.,
78, 616, 1950; H. 0. Kiepenheuer," Phys. Rev., 79, 738, 1950.
**) И. Я. Померанчук, ЖЭТФ, 9, 915, 1939.
***) В. И. Ленин, Материализм и эмпириокритицизм,
Госполитиздат, 1949, стр. 245.
****) В. В е к с л ер, Journ. of. Phys. USSR, 9, 153, 1945; см.
также А. П. Гринберг, Методы ускорения заряженных частиц,
Гостехиздат, 1949. Научно-реферативные сборники: вып. I, Резонан-
Резонансные ускорители, ИЛ, 1948; вып. II, Бетатрон, ИЛ, 1948; сборник
294 КЛАССИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА [гл. \\
медленного добавочного изменения частоты электриче-
электрического поля в циклотроне (синхроциклотрон или фазотрон),
или введения в циклотроне медленно изменяющегося маг-
магнитного поля. Аналогичным образом применяются бета-
бетатроны, с добавочным ускорением электронов при помощи
включения радиочастотного промежутка—так называемые
синхротроны. Эти установки оказались гораздо менее
громоздкими и более экономичными при постройке. Излу-
Излучение светящегося электрона было обнаружено впервые
именно на синхротроне (условия наблюдения в бетатроне
на 100 MeV были неблагоприятны ввиду покрытия ваку-
вакуумной трубки слоем серебра, не пропускавшим света).
В последнее время вновь обратились к различным
линейным ускорителям резонансного или волноводного
типа. Одним из преимуществ подобных приборов является
отсутствие заметных потерь на излучение, обусловленное
прямолинейностью движения частиц и незначительностью
величины ускорения в данном случае по сравнению с кру-
круговым движением.
статей «Резонансные циклические ускорители элементарных частиц»,
ИЛ, 1950; Д. К. С л е т е р, Конструкция линейных ускорителей
УФН, 37, 459, 1949.
ГЛАВА V
КЛАССИЧЕСКАЯ МЕЗОДИНАМИКА
§ 44. Проблема ядерных сил
а) Модель атомного ядра
Ввиду того, что новейшая теория взаимодействия частиц
развивалась главным образом, в связи с проблемой отыска-
отыскания ядерных сил, остановимся несколько подробнее на этом
вопросе.
Как известно, до 1932 г. атомные ядра считались
составленными из двух типов известных тогда элементарных
частиц: протонов и электронов. Однако эта модель не
могла объяснить ряда важных свойств ядер. В особен-
особенности отчётливо противоречия выступали при анализе
спина, статистики и магнитных моментов ядер. Магнитные
моменты всех ядер примерно в тысячу раз меньше элект-
электронных и по порядку равны ядерному магнетону:
рЪ
^° ^ м у где ^"~масса протона. Сам протон имеет
магнитный момент ^р= + 2,792 [х0 (Штерн, Раби, Хиппль).
Магнитный же момент электрона лишь незначительно от-
отличается от боровского магнетона ^в~ ~~"л и Равняется
Ре = Рв \* + %к) » а ^ Тс ^ 137 ' СовеРшенно непонятно,
каким образом магнитные моменты электронов могли бы
оказаться полностью скомпенсированными во всех ядрах.
Значения спинов ядер и характер статистики также
не получались по старой модели. Например, для тщательно
исследованного ядра азота xfN (предполагавшегося со-
составленным из 14 протонов и 7 электронов) получался
296 КЛАССИЧЕСКАЯ МЕЗОДИЫАМИКА [гл. V
полуцелый спин*) и фермиевская статистика, тогда как в
действительности эти ядра имеют целый спин s =^ 1 и под-
подчиняются бозевской статистике. Эта «азотная катастрофа»
и другие примеры ^заставили некоторых физиков обсу-
обсуждать даже вопрос о «потере» электронами своего спина
или о неприменимости квантовой механики к ядру.
С другой стороны, подобная ситуация побудила произ-
произвести более тщательный анализ существования различных
частиц в системах столь малых размеров, как ядра. При
этом, выяснилось, что лёгкие частицы, такие, как элек-
электроны (и позитроны), в ядрах вообще не могут существо-
существовать, сохраняя свою индивидуальность, так как их соб-
собственная энергия Ш = тс2 ^ 0,5 • 106 eV значительно мень-
меньше энергии взаимодействия в ядрах, которая достигает
нескольких миллионов электрон-вольт на частицу. Таким
образом испускание электронов или позитронов при бета-
распаде является порождением этих частиц в точной ана-
аналогии с испусканием фотонов атомами и*ли ядрами.
После открытия нейтрона Чадвиком в 1932 г. и обна-
обнаружения нейтронов в результате расщепления многих
ядер, ряд авторов предложил компромиссную модель
ядра, составленного из протонов, электронов и нейтронов
(Перрен и Ожэ), что оставляло, очевидно, неустранён-
ными указанные выше принципиальные трудности. Во-
Вопреки этому была выдвинута нуклеонная модель ядра,
составленного только из тяжёлых частиц: протонов и ней-
нейтронов**). Число протонов определяется порядковым
номером Z в периодической системе, а число нейтронов д/
разностью атомного номера А (атомного веса в круглых
числах) и порядкового номера Z, т. е. N = A — Z. Нуклеон-
Нуклеонная модель ядра указывает на то, что нейтрон является
элементарной частицей, обладающей спином 1/2 и, в согла-
согласии с полуцелым значением спина, подчиняющейся фер-
*) Как известно, спин электрона, как и позитрона и протона,
или точнее—компонента спина на данную ось, в единицах h/2iz рав-
равняется s— -^ 1/2, и эти частицы подчиняются фермиевской стати-
статистике. О более точных значениях магнитных моментов частиц см.
дополнение.
**) Д. Иваненко, Сборник «Атомное ядро», ГТТИ, 1934,
стр. 51; также Nature, 129, 798, 1932; С. R., Paris, 195, 439, 1932.
§ 44] ПРОБЛЕМА ЯДЕРНЫХ СИЛ 297
миевской статистике. Эти свойства нейтрона полностью
подтвердились опытом. В дальнейшем у нейтрона был
открыт магнитный момент, равный рп = — 1,913 р.о (Блох)*).
Теперь трудности старой модели непосредственно устра-
устраняются, так как, например, магнетизм ядер обуслов-
обусловливается собственными и орбитальными моментами нукле-
нуклеонов, которые все будут порядка ядерного магнетона.
Движение нуклеонов описывается квантовой механикой,
притом в основном оказалось достаточным нерелятивист-
нерелятивистское приближение, т. е., в частности, использование урав-
уравнения Шредингера. В дальнейшем магнитные моменты ядер
удалось вычислить не только по порядку величины, но для
лёгких ядер также с известной точностью на базе правдо-
правдоподобных представлений о конфигурациях нуклеонов.
Ядро азота ^N оказывается на самом деле состав-
составленным из 7 протонов и 7 нейтронов, всего 14 нуклеонов,
что объясняет целый спин и бозевский характер стати-
статистики. Так как общее число нуклеонов равняется атомному
весу, то нуклеонная модель в согласии с опытом непо-
непосредственно объясняет целые (или полуцелые) значения
спина и бозевский (или фермиевский) характер статисти-
статистики у ядер чётного (или нечётного) атомного веса. Действи-
Действительно, чётное число значений спина по ss = ± гЫ каждое
даёт целый спин. Нетрудно также показать, что система
из чётного (нечётного) числа фермиевских частиц подчи-
подчиняется бозевской (фермиевской) статистике. Следует под-
подчеркнуть, что согласно фундаментальной теореме Паули
A939 г.) фермиевская (бозевская) статистика с необходимо-
необходимостью следует для частиц полуцелого (целого) спина **).
Обратимся к энергии связи. На каждый нуклеон
приходится в ядре в среднем энергия 7—8 MeV, кроме
ядер легче альфа-частицы. Для дейтерона удельная энер-
энергия связи несколько больше 1 MeV. Это, по существу
отрицательное, значение энергии представляет собою раз-
разность между отрицательной потенциальной и положитель-
положительной кинетической энергией и совпадает с так называемым
*) См. таблицу ядерных моментов J. E. Mack, Rev. Mod.
Phys., 22, 64, 1950.
**) В. Паули, Релятивистская теория элементарных частиц,
ИЛ, 1947, стр. 72.
298 КЛАССИЧЕСКАЯ МЕЗОДИНАМИКА [гл. V
упаковочным коэффициентом или дефектом массы, при-
приходящимися на частицу и выраженными в энергетических
единицах. Заметим, что эта энергия гораздо меньше
собственной энергии нуклеонов % =il/c2^918 MeV. При
этом важно подчеркнуть в качестве добавочного аргу-
аргумента в пользу нуклеонной модели ядер, что длина де-бро-
глевской волны нуклеона подобной средней энергии, кото-
которую можно подсчитать по нерелятивистской механике,
равняется
А = А^2. 10-13 см,
что по порядку как раз совпадает с размерами ядер
и ядерных орбит (также, как в атоме де-броглевская
длина волны электронов по порядку совпадает с разме-
размерами орбит Л ~ а -о 10 8 см). С другой стороны, де-бро-
де-броглевская длина волны предполагавшихся внутриядерных
электронов, которую нужно подсчитывать по релятиви-
релятивистской формуле, была бы равной при тех же энергиях
Л^Л=^* 2- 1(Н2 еж,
Р (о
что превышает размеры ядер, аналогично тому как длины
волн света, фотонов, испускаемых атомами, но не суще-
существовавших в готовом виде в атомах, превышают его
размеры.
Таким образом величины энергий и длин де-броглев-
ских волн также говорят в пользу нуклеонной модели.
Следует, наконец, в ряду основных аргументов против
старой модели ядра ещё отметить, что наличие электронов
и позитронов в ядрах привело бы к их аннигиляции
и соответствующему гамма-излучению, никогда не наблю-
наблюдавшемуся. Самые основные факты ^-распада также
говорят против наличия лёгких частиц в ядрах, так как
электроны и позитроны всегда испускаются не в момент
расщепления и образования искусственно-радиоактивных
ядер, но. спустя некоторое время, в среднем весьма про-
продолжительное с точки зрения ядерных периодов (от
Т -^ 0,01 сек. вплоть до 108 сек.). Кроме того, предполо-
предположение о существовании электронов и позитронов в ядрах
§ 44] ПРОБЛЕМА ЯДЕРНЫХ СИЛ 299
заставило бы принять наличие какого-то удерживающего
их потенциального барьера, размеры которого должны
были бы, однако, оказаться абсурдно большими.
Различные попытки, возникавшие время от времени,
трактовать нейтрон как сложную частицу, сортавленную
из протона и отрицательного мезона, и свести тем самым
ядерные силы к обменным силам наподобие сил в моле-
молекуле водорода (Тамм-Ландау), так же как рассмотрение
нейтрона в виде комбинации протон плюс электрон
(Темпле), не дали какого-либо положительного результата.
Устранение противоречий старой модели, обнаруже-
обнаружение многих эмпирических закономерностей, к которым
приводило новое представление (Гапон, Гейзенберг) *),
а также последовавшее в 1932—1933 гг. открытие поро-
порождения электронов и позитронов и их трансмутации в два
фотона, — в!ё это сравнительно быстро сделало новую
нуклеонную модель ядра общепризнанной**). Никакие
последующие попытки вернуться к сложному протону
или сложному нейтрону успеха не имели.
Одним из наиболее важных приложений нуклеонной
модели, являющейся отправным пунктом всей современ-
современной ядерной физики, явилась теория р-распада, развитая
Ф. Перреном и в особенности Ферми, на базе предста-
представления о порождении пары частиц: электрона (или пози-
позитрона; и нейтрино ядрами, или, соответственно, погло-
поглощения электрона и испускания нейтрино ядрами при
if-захвате. Изложение этой теории лежит вне рамок
настоящей книги, и мы ограничимся здесь замечанием,
что теория [3-распада требует участия заряженных частиц
в ядерном поле, к рассмотрению которого мы сейчас
перейдём.
*) W. Heisenberg, Zs. f. Phys., 77, 1, 1932; Rapports
du congres Solvay, Paris A934). E. Гапон, Zs. f. Phys., 84,
509, 1933; Г. А. Бете и Р. Ф. Вечер, Физика ядра, ч. I,
Харьков, 1938; Э. В. Шпольский, Атомная физика, т. II,
Гостехиздат, 1950; Э. Разетти, Атомное ядро, Гостехиздат,
1940; В. Гейзенберг, Физика атомного ядра, Гостехиздат,
1948; Г. Бете, Лекции по теории ядра, ИЛ, 1949; Е. Fermi,
Nuclear Physics, Chicago, 1950.
**) См. М. L a u e, Geschichte der Physik, Bonn, 1949.
300 КЛАССИЧЕСКАЯ МЕЗОДИНАМИКА [гл, у
б) Свойства ядерных сил
Важнейшей проблемой, которую выдвинула нуклеон-
ная модель ядра, является фундаментальный вопрос
о силах, действующих между протоном и нейтроном.
Укажем сразу, что эта проблема до сих пор оконча-
окончательно не решена, хотя при её анализе достигнуты очень
большие успехи как в смысле выяснения природы ядерных
сил, так и в направлении построения общей теории взаимо-
взаимодействия всех частиц и полей. Наиболее существенный
прогресс связан, во-первых, с открытием возможности
взаимодействия через частицы с конечной массой покоя,
сопоставленные некоторым полям, и, во-вторых, с пред-
предсказанием и открытием новой частицы,—мезона, перенося-
переносящей ядерные силы, средней по массе между нуклеонами
и электронами.
Прежде всего легко убедиться, что никакие обычные,
до сих пор известные силовые поля непригодны для
объяснения самого наличия ядерных взаимодействий,
независимо от какого бы то ни было их более детального
описания. В самом деле, поле тяготения (или сопоста-
сопоставленные слабому полю, согласно квантовой теории ча-
частицы—гравитоны) отпадает для всех атомных и ядерных
частиц ввиду своей чрезвычайной малости, обусловлен-
обусловленной ничтожными массами частиц и незначительностью
константы тяготения. Напомним, что сила ньютонова
притяжения, например, двух протонов будет примерно
в 1036 раз меньше их кулонова отталкивания:
М2 '
г2 ' г2 ~~ хМ
где у. — гравитационная постоянная.
Электрические силы между нуклеонами отпадают
ввиду нейтральности нейтронов. Магнитные силы (возни-
(возникающие благодаря наличию магнитных моментов) также
слишком малы по своей величине. По порядку величины
магнитная энергия взаимодействия нуклеонов равна
F~p^/r3, где р-0 — ядерный магнетон, г~10~13 см, т. е.
F~105eV вместо требуемых 107eV. Кроме того, магнит-
магнитное взаимодействие не способно дать устойчивых состоя-
§ 44] ПРОБЛЕМА ЯДЕРНЫХ СИЛ 301
ний. Так как последнее обстоятельство существенно для
дальнейшего, выясним его несколько подробнее.
Как известно, в классической и квантовой механике
имеет место теорема вириала, гласящая, что в случае
периодических движений частиц, среднее по времени
значение кинетической энергии Т связано со средним
значением потенциальной энергии V соотношением
где ^—координаты частиц.
Если потенциальная энергия является однородной
функцией координат степени п, то на основании теоре-
теоремы Эйлера об однородных функциях имеем вместо D4,1)
Отсюда для среднего значения полной энергии мы
получаем
Для того чтобы было возможно устойчивое периодиче-
периодическое движение, для закона V ~ гп при п < 0 необходимо,
чтобы не только V < 0, но ввиду Т > 0 также Ё < 0 (так
как | V 1> Т), т. е. показатель однородности п должен быть
больше —2. Как известно, кулоновское или ньютоновское
притяжение (F~— г) дают устойчивые орбиты, а на-
например, при взаимодействии двух магнитных диполей
(F~ —г~3) устойчивые состояния невозможны. Критиче-
Критический случай, очевидно, имеет место при /г™ —2.
С точки зрения квантовой механики невозможность
устойчивых состояний при дипольном взаимодействии
можно показать также из следующих соображений.
Если бы частица двигалась в области с линейными раз-
размерами г, то её импульс согласно известной формуле
соотношения неточности имел бы порядок величины
h
302 КЛАССИЧЕСКАЯ МЕЗО ДИНАМИК А [гл. V
а кинетическая энергия
2т тг2 '
Следовательно, в случае, например, кулоыовского поля,
притяжение частиц друг к другу на самых малых рас-
стояниях V= компенсируется быстрым возрастанием
кинетической энергии, что приводит к возможности устой-
устойчивых состояний. Из условия F~ T немедленно получает-
получается даже правильный порядок радиуса боровской орбиты:
Го ^ те2 '
В случае же дипольной энергии взаимодействгя
jT const
V = з кинетическая энергия не в состоянии ском-
скомпенсировать рост потенциальной, и устойчивые состояния
невозможны.
Все взаимодействия в атомах, молекулах, твёрдых
и жидких телах и газах сводятся в конце концов к электри-
электрическим и, отчасти, магнитным силам. Напомним, что элек- '
трические кулоновские силы благодаря квантовой кине-
кинематике и сложности систем частиц, подчиняющихся в слу-
случае электронов статистике Ферми, пррхводят к появлению
дисперсионных ван-дер-ваальсовых, эффективных обмен-
обменных и других химических сил. Для больших скоплений
атомов начинает играть заметную рель тяготение, пре-
превалирующее в случае астрономических объектов.
Таким образом, мы стоим перед фундаментальной
задачей понять природу или построить модель ядерных
сил, обусловленных каким-то полем, или частицами,
или же комбинациями частиц нового типа. В XVIII веке
подобная проблема не вызвала бы, вероятно, особого
смущения, и в науку были бы введены чисто феноменоло-
феноменологически новые «ядерные» силы (или соответствующая
«жидкость») наряду с электрической, магнитной, тепло-
тепловой и световой (эфиром) «жидкостями». Задача заклю-
заключалась бы в подборе удачного математического выраже-
выражения новых сил (подобно ньютоновскому закону тяготения).
Не отказываясь от подбора удачных выражений для сил,
§ 44] ПРОБЛЕМА ЯДЕРНЫХ СИЛ 303
сейчас, однако, мы непременно должны связать рассма-
рассматриваемое ядерное поле с какой-либо новой комбинацией
известных частиц или допустить существование новых
частиц, сопоставленных ядерному полю.
Напомним современную модель электрических сил.
Два заряда еже' оказываются связанными друг с другом
благодаря тому, что один из них порождает вокруг себя
электрическое поле, а другой это поле поглощает, и об-
обратно, первый заряд поглощает электрическое поле,
порождённое вторым зарядом. Квантовая теория взаимо-
взаимодействия формулирует то же положение вещей несколько
иначе, говоря о виртуальном испускании фотонов, точнее
псевдофотонов,—корпускул продольного электростатиче-
электростатического поля, одной частицей и поглощении их другой
частицей. Аналогичным образом толкуются ньютоновские
силы тяготения, обязанные, согласно квантовой трактовке,
испусканию и поглощению гравитонов.
Хотя квантовый вывод в данном частном случае
покоящихся зарядов или масс не даёт ничего нового,
воспроизводя обычный закон Кулона: V — — *), или Нью-
Т7-/ mm/ - „
тона: V — —у. — , он обладает огромной эвристической
силой. Действительно, следует сделать заключение,
что всевозможные взаимодействия могут переноситься
также различными частицами конечной массы, а не
только квантами электромагнитного (или гравитаци-
гравитационного) поля с массой покоя, равной нулю. Эта идея
лежит в основе всей современной теории взаимодействия,
в частности теории ядерных сил.
Сформулируем основные эмпирические свойства новых
сил, отсылая за подробностями к специальной литера-
литературе по ядру**).
*) Обмен между зарядами, квантами света (фотонами), т. е.
корпускулами поперечного поля, ведёт к брейтовской части взаи-
взаимодействия (см. § 25).
**) Кроме литературных указаний на стр. 296 и 299 см. также
Г. Бете, Лекции по теории ядра, ИЛ, 1949; Ch. Wei z sack e г, Die
Atomkerne, Leipzig, 1937; А. Ахиезер и И. Померанчук,
Некоторые вопросы теории ядра, Гостехиздат, 1950; L. R о s e п-
f e I d, Nuclear forces, Amsterdam—New-Jork, 1948.
304 КЛАССИЧЕСКАЯ МЕЗОДИНАМИКА [гл. V
1. Силы короткого действия. Ядерные
силы в согласии с данными о размерах ядер, о ядерных
реакциях и масс-дефектах должны быть силами короткого
действия с радиусом действия порядка г ~ 10~13 см\ на боль-
больших расстояниях они быстро убывают и становятся ни-
ничтожными по сравнению с электрическими силами. Всё же
некоторое влияние ядерных сил сказывается в атомах
на ближайших электронных орбитах.
Размеры атомных ядер были определены, во-первых,
из теории альфа-распада (радиус потенциального барьера
для радиоактивных ядер), затем из рассмотрения обрат-
обратных реакций бомбардировки ядер заряженными части-
частицами, а также из анализа энерпш связи в ядрах, отли-
отличающихся заменой протона нейтроном. Кроме того, при
реакциях с быстрыми нейтронами, де-броглевская длина
волны которых мала по сравнению с ядерными размерами,
эффективное сечение будет в пределе высоких энергий
равняться геометрическому значению а = т:Д2. Все эти
данные позволяют установить эмпирическую формулу для
возрастания радиуса ядер в зависимости от числа нуклео-
нов, т. е. атомного веса А:
Я = 1,5 • Ю-18^1/» см.
Эта формула передаёт лишь основную закономерность,
не учитывая отклонений для ядер чётного и нечётного
А и Z или влияния оболочек нуклеонов.
Так как
= const,
то, следовательно, плотность ядерного вещества (или,
наглядно говоря, «нуклеонной жидкости») остаётся в ос-
основном постоянной и равняется
где М = 1,6 • 10~24 г — масса протона.
§ 44] ПРОБЛЕМА ЯДЕРНЫХ СИЛ 305
Напомним теперь, что согласно квантовой механике
каждой частице с массой покоя т сопоставляется харак-
характерная длина, так называемая комптоновская длина
волны
\ h
тс
Таким образом радиусы ядер R лежат в пределах между
комптоновской длиной волны Ап^10~14сж тяжёлых частиц
(нуклеонов) и комптоновской длиной волны Ас — 2,4.10~10 см
лёгких частиц (электронов—позитронов):
Лп < R < Ас.
Короткодействующий характер ядерных сил следует
также из сравнения масс-дефектов, т. е. энергий связи
у дейтерона fH(F =—2,19 MeV, т. е. около 1 MeV на
частицу), тритона |H(F=—8,5 MeV, т. е. около 3 MeV
на частицу) и у альфа-частицы |Не (V=—28 MeV, т. е.
около 7 MeV на частицу). У более тяжёлых ядер энергия
связи лежит в пределах 7—8 MeV на частицу, достигая
наибольшего абсолютного значения примерно в середине
периодической системы и снова понижаясь для самых
тяжёлых ядер. При этом мы отвлекаемся сейчас и в даль-
дальнейшем, как и в случае ядерных радиусов, от индиви-
индивидуальных колебаний отдельных значений в масс-дефектах
ядер чётного и нечётного А, а также от периодичностей
как в значениях масс-дефектов, так и других ядерных
свойств (эффективных сечений захвата нейтронов, рас-
распространённости, числа изотопов, квадрупольных момен-
моментов, спинов, магнитных моментов и др.), вероятно, свя-
связанных с заполнением некоторых оболочек протонами
и нейтронами и, возможно, также с образованием структур
типа а-частиц. Факт прекращения роста абсолютного
значения энергии связи в ряду ядер, начиная с дейтерона,
означает прежде всего достижение «насыщения» в ядре
гелия (|Не), а быстрый рост энергии связи в семь раз
от дейтерона к гелию при увеличении числа частиц все-
всего в 'два раза был бы невозможен при силах далёкого
действия.
20 д. Иваг.гнко и А. Соколов
306 КЛАССИЧЕСКАЯ МЕЗОДИНАМИКА [гл. V
Резюмируя, можно сказать, что ядерные силы явля-
являются короткодействующими с эффективным
радиусом действия порядка
г ^10~13 см.
Поэтому, ограничиваясь этим наиболее существенным
признаком ядерных сил, с феноменологической (описа-
(описательной) точки зрения ядерный потенциал можно было бы
представить в виде какой-либо произвольной потенциаль-
потенциальной функции, зависящей только от г, т. е. ведущей
к центральным силам, и достаточно быстро убывающей
с расстоянием. Подсчёты производились, например, с пря-
прямоугольной потенциальной ямой с параметрами: V =
= — 21 MeV при г < а, V = 0 при г у- а, а ^ 2 • 10~13 см
(в основном состоянии дейтерона). Использовались также
функции вида F— — Ае~аг; V = — Ае~$т2; F=— А + Вг2
(осциллаторный потенциал) и другие аналогичные предва-
предварительные формы с параметрами, подбиравшимися на
основании опытных данных. При этом выяснилось, что
многие ядерные проблемы и эффекты, как задача дейтерона,
рассеяние нейтронов на протонах, альфа-распад и другие,
в области относительно малых энергий, не очень сильно
зависят от уточнения вида потенциала короткодейству-
короткодействующих сил.
В частности, ограничиваясь центральными коротко-
короткодействующими силами, получаем для основного состояния
дейтерона сферически симметричное ^-состояние; на са-
самом же деле основное состояние есть смесь ^-состояния
и небольшой доли .D-состояния. Далее, рассеяние нейтро-
нейтронов на протонах при небольших энергиях, до 10 MeV
соответствует сферически симметричному ядерному потен-
потенциалу, что доказывает как короткодействующий характер
сил, так и их в основном центральный характер.
Конечно, с принципиальной точки зрения использова-
использование подобных произвольных видов взаимодействия совер-
совершенно неудовлетворительно и должно быть заменено фор-
формой однозначно определённой на основе полевой теории
ядерных сил. Важно сразу подчеркнуть, что полевая тео-
теория ядерных сил непосредственно приводит к коротко-
короткодействующим силам, что является её основным успехом.
§ 44] ПРОБЛЕМА ЯДЕРНЫХ СИЛ 30?
Здесь и в дальнейшем мы будем употреблять термин
«полевая» теория сил, имея в виду теорию ядерного
поля, связанного с теми или иными частицами («пере-
(«переносящими» взаимодействие), т. е. парами лёгких частиц
или одиночными мезонами и т. д., и противопоставляя
ей формально-феноменологическую теорию ядерных сил,
ограничивающуюся лишь подбором произвольных потен-
потенциалов, на основе ряда признаков ядерных сил с после-
последующим уточнением этих потенциалов при помощи эмпи-
эмпирических данных.
2. Спиновые силы. До сих пор мы ограничи-
ограничивались рассмотрением короткодействующего характера
ядерных сил , являющегося их наиболее специфическим
признаком. Второй класс свойств ядерных сил связан
с их существенной зависимостью от спинов. Это доказы-
доказывается прежде всего значительной разницей в энергии
основного устойчивого триплетного (SS) уровня дейте-
рона, в котором спины протона и нейтрона параллельны,
а энергия связи равна—2,19 MeV, и энергии виртуального,
сингулетного уровня A»Sr), соответствующего антипарал-
антипараллельным спинам нуклеонов, равной + 0,064 MeV. Магнит-
Магнитное взаимодействие нуклеонов само по себе слишком
незначительно, чтобы объяснить это большое расстояние
между уровнями, которое поэтому имеет другую физиче-
физическую причину, чем аналогичное дублетное расщепление
в атомных уровнях электронов. Спиновый характер ядер-
ядерных сил между протоном и нейтроном непосредственно
доказывается также разницей в эффективных сечениях
рассеяния нейтронов молекулами орто- и параводорода.
Ортоводород рассеивает нейтроны сильнее, чем параводо-
род, и отношение эффективных сечений (з0— для ортово-
дорода, ар — для параводорода), согласно последним
экспериментам равно
Наличие спиновых сил снова "можно было бы учесть фено-
феноменологически, добавляя к основной энергии взаимодей-
взаимодействия ^(г)член F2 (г) (ОаОв), характеризующий собой
в некоторой мере взаимодействие двух диполей со спинами
20*
308 КЛАССИЧЕСКАЯ МЕЗОДИНАМИКА [гл. V
О а и о в (в совпадают с матрицами Паули), где А и В —
индексы двух нуклеонов. Значение же для V2 может быть
подобрано из опыта. Очевидно, V2 (r) также должно пред-
представлять потенциал сил короткого действия. С принци-
принципиальной точки зрения эта процедура также неудовлетво-
неудовлетворительна. Поэтому важно здесь же подчеркнуть, что поле-
полевая теория ядерных сил, как мы покажем ниже, приводит
не только к короткодействующим, но также и к спиновым
силам.
3. Нецентральные силы. Следующим важ-
важным и характерным свойством ядерных сил является их
нецентральный характер. Ядерные силы подобно маг-
магнитным зависят не только от расстояния между нуклео-
нами, но и от взаимной ориентации спинов и радиус-
вектора, ведущего от одного нуклеона к другому, т. е.
являются силами квазимагнитными. Нецентральный ха-
характер сил доказывается наличием у дейтерона JH (JD)
электрического квадрупольного момента, открытого в лабо-
лаборатории Раби. В самом деле, по известному из теории
электричества определению тензор квадрупольного момен-
момента задаётся выражением
eQnm = eCxnxm-r4nm) D4,2)
(см., например, § 10), где г — радиус-вектор протона.
Диагональный элемент этого тензора определяет эф-
эффективную площадку, характеризующую квадрупольный
момент
В случае, если распределение плотности протона есть р,
среднее значение «квадрупольного момента» равняется
Q = \ р (З*2 - г2) di - C?- 7). D4,3)
При центральных силах основное состояние является
л
^-состоянием, для которого z2 = у2 = х2 = — г2, и следова-
о
тельно, ()=0. Поэтому, если бы основное состояние дейте-
дейтерона было чистым ^-состоянием, то его квадрупольный
момент равнялся бы нулю, и обратно, факт обнаружения
§ 44] ПРОБЛЕМА ЯДЕРНЫХ СИЛ 309
на опыте у дейтерона квадрупольного момента, определя-
определяемого площадкой
(Н +2,73-Ю-27 см\
доказывает, что основное состояние дейтерона не есть
чистое ^-состояние. Положительный знак Q указывает на
«сигарообразный» характер распределения плотности за-
заряда, вытянутого вдоль спиновой оси. Дальнейший кван-
товомеханический анализ показывает, что к ^-состоянию
примешана, как уже указывалось, небольшая доля ^-со-
^-состояния, причём вероятность пребывания в .©-состоянии
равна примерно 4%.
Следует подчеркнуть, что влияние нецентральных сил
оказывается, вообще говоря, незначительным не только
при расчёте основного состояния дейтерона, но также,
например, при рассеянии нейтронов на протонах, захвате
нейтронов протонами и фотоэффекте на дейтероне, и других
процессах, если они разыгрываются при малых энергиях.
Наличие нецентральных сил также можно было бы
учесть с формально-феноменологической точки зрения,
добавляя к энергии взаимодействия центральных бесспи-
бесспиновых сил Vx (г) и центральных спиновых сил F2 (г) (QaQb)
член квазимагнитного типа V3(r)SABj где
Sab - 3 (оАг°) (овг°) - (qa*b) D4,4)
и снова подбирая форму короткодействующего потен-
циала V3 из опыта. Член Sab • -т точно совпадает по
форме с выражением энергии взаимодействия двух ма-
магнитных диполей Joa и foB- Конечно, с принципиальной
точки зрения эта процедура весьма мало удовлетворитель-
удовлетворительна. Важно поэтому подчеркнуть, что полевая теория ядер-
ядерных сил естественно, без всяких добавочных предположе-
предположений приводит к нецентральным силам. Более того, нецен-
нецентральные силы были впервые введены в ядерную теорию
ещё до экспериментов Раби уже на базе первой модели
ядерных парных бета-сил. Они получаются, как мы
покажем ниже, также и в современной мезонной теории
ядерных сил.
310 КЛАССИЧЕСКАЯ МЕЗОДИНАМИКА [гл. у
Позднее, существенно используя результаты полевой
теории ядерных сил, оказалось возможным доказать, что
выражение энергии взаимодействия нуклеонов вида
У = Уг (г) + V2 (г) (олОв) + Vs (r) SAB D4,5)
является наиболее общим при соблюдении всех требова-
требований инвариантности относительно смещений, инверсий
и вращений как обычных, так и спиновых координат
и при независимости от скоростей частиц.
Как будет показано ниже, полевая теория ядерных
сил приводит к определённому виду короткодействующих
потенциалов Vx, V2 и V3 вместо их подбора из эмпирических
данных, в чём заключается одно из её коренных преиму-
преимуществ.
4. Зарядная независимость. Важное свой-
свойство ядерных сил заключается в равенстве хотя бы поряд-
порядка сил между любыми нуклеонами: протон—нейтрон, про-
протон—протон, нейтрон—нейтрон, т. е. в их независимости
от электрического заряда. Доказательство основано
на экспериментах по рассеянию протонов на протонах,
проделанных впервые Тьювом при энергиях около 1 MeV
и расширенных затем до более высоких энергий. Как извест-
известно, рассеяние заряженных частиц друг другом описывается
формулой Резерфорда, которая подтверждается квантовой
механикой. Как показал Мотт, учёт тождественности
частиц приводит ~к добавочному члену, знак которого
определяется типом статистики.
Опыты показали, в частности, значительно большее
число протонов высокой энергии, рассеянных под углом
45° по сравнению с предсказанием теории, основанной
на чисто электрическом кулоновском взаимодействии.
Например, при энергиях ~ 10 MeV рассеяние примерно в
40 раз больше; с другой стороны, при низкой энергии
0,4 MeV рассеяние под углом 45° значительно меньше чисто
кулоновского.
Анализ подобных экспериментов, проделанный Брейтом
с сотрудниками, привёл к выводу, что кроме кулоновской
силы отталкивания между двумя протонами действует
сила притяжения короткодействующего характера, кото-
которая будет превосходить кулоновскую при высоких энер-
§ 44] ПРОБЛЕМА ЯДЕРНЫХ СИЛ 311
гиях, когда протоны могут ближе подходить друг
к другу при столкновении. При умеренных энергиях
речь идёт лишь об ^-состояниях подобной системы. Ввиду
симметрии ф-функции в координатах протонов, спиновая
функция должна быть антисимметрична, что исключает
триплетное состояние SS. Положение вещей с этими
новыми силами можно с феноменологической точки зрения
охарактеризовать, например, прямоугольной потенци-
потенциальной ямой радиуса а = 2,8- 1О~13 см и величиной по-
потенциала Fpp^ll MeV.
Сравнивая это значение с данными для рассеяния
нейтронов на протонах в том же XS состоянии, когда
согласно эмпирическим данным Vpn^ 11,9 MeV, мы по-
получаем замечательное совпадение энергий взаимодействия
Vpp и Vpn, по крайней мере, в ^-состоянии. Отметим, что
для ^-состояния глубина эффективной прямоугольной
потенциальной ямы при взаимодействии нейтрона с про-
протоном на основании анализа дейтерона равна 21,3 MeV.
Из анализа масс-дефектов можно заключить, что силы
между двумя нейтронами также примерно равняются
ядерным силам между двумя протонами. Таким образом,
обобщая данные опыта (с 15 на все состояния), мы прихо-
приходим к положению о зарядной независимости ядерных
сил при не слишком высоких энергиях (подробнее см.
§ 48 б). Укажем ещё, что кулоновское отталкивание,
несмотря на наличие ядерных сил притяжения, не допу-
допускает образования стабильной системы из двух протонов.
Требование зарядной независимости ядерных сил
может быть удовлетворено простейшим вариантом поле-
полевой теории сил, полностью отвлекающимся от электри-
электрических зарядов и допускающим, что все взаимодействия
между нуклеонами, обладающими одинаковыми специ-
специфическими ядерными квазизарядами g и квазимоментами /,
обязаны их связи с полем нейтральных частиц. Если бы
ядерное поле было связано с одними заряженными части-
частицами, удовлетворение условия зарядной независимости
^казалось бы практически невозможным.
5. Обменные силы. Последним известным фун-
фундаментальным свойством ядерных сил является их обмен-
обменный характер. Доказательство основывается на известном
312 КЛАССИЧЕСКАЯ МЕЗОДИНАМИКА [гл. V
«насыщении» ядерных сил, выражающемся, как уже
упоминалось выше, в росте энергии связи (а также
объёма ядер) в основном пропорционально числу ну-
клеонов:
Е== -аА.
Все данные указывают на то, что нуклеоны взаимодей-
взаимодействуют преимущественно только с ближайшими соседями,
тогда как, например, в случае кулоновских сил каждый
протон взаимодействует с каждым, так что общая энер-
энергия отталкивания растёт не линейно, но для большого
числа частиц, примерно квадратично с числом частиц
~-Z(Z — 1) ~ Z2. После того как при построении самых лёг-
лёгких ядер *Н, JH, Ще достигнуто насыщение в альфа-части-
альфа-частице gHe, средняя энергия связи остаётся примерно постоян-
постоянной в огромном диапазоне всей периодической системы
элементов: <х~ 1 — 8 MeV. По всей видимости потенциаль-
потенциальная энергия какого-либо обычного типа не может пол-
полностью объяснить свойств ядерного поля, препятству-
препятствующих частицам взаимодействовать с числом соседей,
большим некоторого.
Гейзенберг предложил объяснить насыщение обмен-
обменным характером ядерных сил по аналогии с обменными
химическими силами, также обеспечивающими известное
насыщение, выражающееся в факте образования двух-
двухатомной молекулы водорода Н2 и в невозможности обра-
образования трёхатомяой молекулы Н3. Нетрудно указать
все возможные варианты обменных сил:
1) нуклеоны при взаимодействии могут обмениваться
зарядами или, что сводится к тому же, спинами и коорди-
координатами (гейзенберговские силы);
2) нуклеоны при взаимодействии обмениваются коор-
координатами (майорановские силы);
3) в ядерной физике обычные необменные силы принято
иногда называть вигнеровскими;
4) наконец, возможен тип взаимодействия, при кото-
котором нуклеоны обмениваются одними спинами (бартлет-
товские силы).
Поскольку описание ядерного поля, обязанного заря-
заряженным частрцам и приводящего к обмену нуклеонор
§ ;4] ПРОБЛЕМА ЯДЕРНЫХ СИЛ 313
зарядами, лежит вне рамок классической теории, огра-
ограничимся здесь лишь несколькими замечаниями.
Принимая во внимание известный успех теории обыч-
обычных необменных сил для процессов малой энергии, когда
учитывается лишь нижнее ^-состояние (/^0), следует
заключить, что основные силы должны быть вигнеров-
ского или майорановского типа; однако обычные силы не
способны обеспечить насыщения. Кроме того, бартлеттов-
ские силы, как выяснилось, приводят к разным знакам
потенциальной энергии в сингулетном и триплетном со-
состояниях дейтерона подобно гейзенберговским силам и не
могут поэтому вместе с последними играть роль основных
ядерных сил. Поэтому для объяснения насыщения при
феноменологическом подходе можно ядерные силы взять
в основном майорановскими с примесью гейзенберговских.
Действительно, чисто майорановские силы не способны
объяснить спиновый характер сил, в частности, большое
различие в энергиях связи 1S- и ^-состояний дейтерона.
С другой стороны, майорановские силы приводят в соот-
соответствие с опытом к ядру гелия (*Не) как насыщенной
конфигурации, тогда как гейзенберговские силы ошибоч-
ошибочно дали бы насыщение уже для дейтерона, энергия связи
в котором на частицу всего около 1 MeV. В этом варианте
разумной пропорцией оказывается смесь примерно 75%
майорановских сил и 25% гейзенберговских сил. При
этом, конечно, не исключается наличие необменных и
бартлеттовских сил.
Все эти феноменологические соображения об основных
свойствах ядерных сил, не были связаны с уточнением
радиальной зависимости потенциалов V от расстояния.
Гейзенберговское феноменологическое направление в
теории ядерных сил заключалось в предварительном
анализе обменного характера сил и оставляло вопрос
о виде V(r) так же, как и строгом выводе пропорции
смеси сил, открытым. При этом для конкретных под-
подсчётов, как указывалось выше, потенциал брался в про-
произвольном виде, обеспечивающем короткодействующий
характер сил (прямоугольная яма, осцилляторный потен-
потенциал, экспоненциальная форма и т. д.), а пропорция
сил подбиралась на основе эмпирических данных. Конечно,
314 КЛАССИЧЕСКАЯ МЕЗОДИНАМИКА [гл. V
подобная процедура являлась весьма неудовлетворитель-
неудовлетворительной с принципиальной точки зрения. Отметим ещё побоч-
побочный недостаток данного круга работ, связанный с отсут-
отсутствием в использованных выражениях важных нецен-
нецентральных сил. Поэтому следует подчеркнуть, что суще-
существенным успехом полевой теории ядерных сил является
естественное введение обменных сил всех типов в опреде-
определённой пропорции, притом способной удовлетворить тре-
требованиям опыта. Как мы увидим ниже, это связано с тем,
что в составе ядерного поля или частиц, переносящих
взаимодействие, оказываются заряженные частицы. Тем
самым, однако, мы вступаем, как отмечалось выше, в
некоторый конфликт с требованием зарядной независи-
независимости порядка ядерных сил, проще всего удовлетворяю-
удовлетворяющимся путём взаимодействия через нейтральные частицы.
Выходом является, как оказывается, использование смеси
тех и других частиц.
Кроме основного факта объяснения насыщения ядер-
ядерных сил, влияние обменных сил сказывается на разных
эффектах при высоких энергиях, когда в игру войдут
состояния с I Ф О (Р-, D-, .. ., состояния), в которых раз-
различные типы обменных сил будут иметь разные знаки.
В частности, рассеяние весьма быстрых нейтронов на
протонах будет согласно предсказаниям теории существен-
существенно иным в случае обменных и обычных сил. Недавние
эксперименты с рассеянием нейтронов огромной энергии
около 100 MeV на ядрах показали, что ядерные протоны
при этом выбиваются с теми же примерно значениями
энергии и летят вперёд, т. е. меняются местами с нейт-
нейтронами. Это доказывает наличие существенной доли об-
обменных сил в ядерном поле. К тому же заключению
приводит анализ рассеяния протонов на протонах в диа-
диапазоне 40—200 MeV (см. § 486).
К этому введению в проблему ядерных сил добавим,
что поскольку, как выяснилось в настоящее время, ядер-
ядерное поле, в значительной мере, если неполностью, обязано
мезонам, теория должна также выяснить вопросы
взаимодействия мезонов с нуклеонами и лёгкими ча-
частицами (порождение и поглощение мезонов нуклеона-
нуклеонами, распад мезонов на лёгкие частицы и для ряда
§ 44] ПРОБЛЕМА ЯДЕРНЫХ СИЛ 315
сортов мезонов их взаимное превращение и т. д.). Кроме
того, теория ядра должна дать объяснение основным
закономерностям ,8-распада. Поскольку при jB-распаде
ядрами испускаются заряженные частицы (электроны
или позитроны вместе с нейтрино), чисто Е1ейтральная
теория ядерного поля представляется неудовлетворитель-
неудовлетворительной. Зарядная независимость ядерного поля не позволила
бы также заключить о наблюдающейся тенденции
неустойчивых искусственно радиоактивных изотопов более
тяжёлых, чем нормальные (например, J6N, "О, 2Ц\] и т. д.),
испускать электроны, а изотопов более лёгких, чем нор-
нормальные (X73N, Xg0 и т. д.), испускать позитроны. В случае
же присутствия заряженной части в ядерном поле «отры-
«отрывание» от него каких-то порций в виде заряженных
частиц непосредственно представляется возможным. Ха-
Характер ядерного поля, как электрически заряженного,
позволяет также качественно объяснить наличие отрица-
отрицательного магнитного момента у нейтрона и определённой
доли врождённого некинематического момента у протона,
поскольку магнетизм этих нуклеонов обязан отчасти
магнетизму порождённого ими поля, если последнее
связано с электрическим зарядом, который в свою очередь
ведёт к наличию магнитного момента. Эти качественные
соображения подчёркивают невозможность оперировать
с одним нейтральным так же, как с одним заряженным
ядерным полем.
в) Теория парных ядерных сил
Перейдём к анализу полевой теории ядерных сил. Так
как согласно изложенному выше все возможности опи-
описания ядерных сил известными полями (или сопоставлен-
сопоставленными им корпускулами) т. е. гравитационным и электро-
электромагнитным полем оказались непригодными, было пред-
предложено прежде всего объяснить взаимодействие между
нуклеонами переносом сил не отдельными известными
корпускулами, а их комбинациями, именно парами частиц:
электрон—нейтрино и позитрон—нейтрино, которые ведь
могут не только виртуально испускаться и поглощаться
нуклеонами, но и реально испускаются при C-рас-
316 КЛАССИЧЕСКАЯ МЕЗОДИНАМИКА [ГЛш V
паде*). Взаимодействие нуклеонов осуществляется тогда
по схеме:
0) начальное состояние: протон—нейтрон {р, п)\
1) промежуточное состояние: протон испускает пози-
позитрон—нейтрино и превращается в нейтрон; остаётся ней-
нейтрон, пара лёгких частиц (позитрон и нейтрино) и ней-
нейтрон (пу е+, v, п)\
2) конечное состояние: нейтрон поглощает пару, испу-
испущенную протоном и превращается в протон, остаются:
нейтрон—протон (я, р).
Взаимодействие может осуществляться также через
испускание пары электрон—нейтрино или антинейтрино
нейтроном и поглощение её протоном. Символически:
0) (р, п),
1) (Р, е~, v, р),
2) (п, р).
При этом протон и нейтрон обмениваются зарядом или,
как непосредственно очевидно, своими координатами,
а также спинами.
Так как поле пар фермиевских частиц, притом свя-
связанных с зарядом, не имеет классического аналога,
теория парных электронно-нейтринных сил или, иначе
говоря, р-сил может быть только квантовой. Беря за
основу простейшую энергию связи нуклеонов с полем
пар, именно закон Ферми, использованный в теории
р-распада, получаем энергию взаимодействия между
протоном и нейтроном в виде
Здесь gF—ядерный «парный» квазизаряд нуклеонов.
Этот вид взаимодействия относится к областям г < —
/ h \
( комптоновская длина волны электронов ) ; на
V тс х J
*) И. Т а м м, Д. Иваненко, Nature, 133, 981, 1934;
Д. Иваненко и А, Соколов, ДАН, 3, 361, 1936.
§ 44] ПРОБЛЕМА ЯДЕРНЫХ СИЛ 317
больших расстояниях взаимодействие ещё быстрее убывает
[именно экспоненциально ^ e—r (mc/h)].
С принципиальной точки зрения, антинейтрино (v')
и нейтрино (v), описываемые как все частицы полуцелого
спина уравнением Дирака, различаются в обычной трак-
трактовке; например, обе частицы (ещё с достоверностью не
обнаруженные, ею несомненно участвующие в процессах
Р-распада, if-захвата и распаде мезонов) могут обладать
магнитными моментами разного знака. Майорана пред-
предложил вариант теории, в которой нейтрино и антиней-
антинейтрино тождественны. Наблюдение двойного ^-распада
принципиально позволяет сделать выбор между обоими
вариантами теории. Для дальнейшего указанная не-
неоднозначность, вообще говоря, несущественна, за ис-
исключением пунктов, где это специально оговорено.
Фермиевское выражение энергии связи нуклеонов с
полем пар имеет вид £/"=^gF«l)*^^ +комплексно сопряжён-
сопряжённый член, где () —оператор, действующий на волновые
функции нуклеонов и превращающий протон в нейтрон,
и обратно.
Первоначальное значение константы связи с полем пар
gF = 4,5 • 10~50 эрг • см3 ныне согласно эмпирическим дан-
данным оказывается увеличенным до~108 эрг • еж3;
tye> tyv~ волновые функции электронов (позитронов) и ней-
нейтрино (антинейтрино). Уже простейшие соображения раз-
размерности приводят к правильной структуре формулы
взаимодействия нуклеонов D4,6) при учёте того, что
это выражение должно быть квадратичным относительно
квазизарядов gF аналогично кулоновской формуле.
Построение теории парных ядерных сил, в которой
впервые была доказана возможность переноса взаимодей-
взаимодействия частицами конечной массы, несомненно, явилось
немалым успехом. При этом были непосредственно полу-
получены обменные гейзенберговские силы короткого действия;
в дальнейшем спиновые и нецентральные силы, а также
обменные силы всех различных^типов (гейзенберговские,
майорановские, бартлеттовские), также оказались есте-
естественно включёнными в теорию. Кроме того, на базе
первой модели ядерных сил удалось качественно объяс-
объяснить наличие магнитного момента у нейтрона и несовпа-
318 КЛАССИЧЕСКАЯ МЕЗОДИНАМИКА [гл. V
дение момента протона с ядерным магнетоном (Вик) *),
Сущность этого объяснения, так же как и общие методы
расчёта ядерных сил, были перенесены затем в современ-
современную мезонную теорию ядерных сил. Однако величина
взаимодействия нуклеонов, обязанного переносу парами
лёгких частиц, оказывается ничтожной (V ^ — 10 6eV при
г~10~13сж вместо требуемого опытом V ^ — 104 eV),
и парные силы являются лишь «копией» главных ядерных
сил. Физическим основанием подобной малости р-сил
является, очевидно, их связь с р-распадом, крайне мало-
маловероятным, так сказать, «геологически» редким в жизни
ядер явлением, характеризуемым незначительной констак-
той£^. Наглядно говоря, на месте крайне редкого «переб-
«переброса» парами лёгких частиц должен, очевидно, стоять
весьма частый обмен нуклеонов какими-то иными частица-
частицами, связь с полем которых является гораздо более сильной.
Заметим, что, кроме того закон D4,6) согласно теореме
вириала при столь сильном возрастании потенциала на
малых расстояниях (V^ —г; г—>0J не может при-
привести к устойчивому состоянию в задаче дейтерона
(протон плюс нейтрон); последняя трудность не является,
однако, специфической для парных сил и могла быть пред-
предварительно устранена обрезанием потенциала на каком-то
расстоянии г0 ~ 10~13 см. Попытки объяснить ядерные силы
полями, соответствующими переносу парами и другими
комбинациями прочих известных частиц, например, парой
позитрон и электрон, или двумя нейтрино (Тамм), успеха
также не имели. Эти последние предположения подсказы-
подсказывали, однако, возможность отрыва ядерных сил от причин,
непосредственно обусловливающих 3-распад и тем самым
подготовляли почву для введения новой, особой константы
связи нуклеонов с ядерным полем требуемой величины.
Несмотря на указанную коренную неудачу, после
появления теории В-сил начался новый период в теории
ядра и в развитии общего учения о взаимодействии,
поскольку самая возможность взаимодействия через поля
или частицы, обладающие массой покоя, а не только через
*)См. В. Гейвенбер г, УФН, 16, 1, 1936.
§ 44] ПРОБЛЕМА ЯДЕРНЫХ СИЛ 319
гравитационные или электромагнитные поля, была впервые
доказана в этой теории. Подчеркнём ещё раз, что эта
идея является весьма характерной для современного
понимания взаимодействий, которые могут осуществляться
любыми частицами, обладающими массой покоя, полями,
не связанными с массой покоя, и разнообразными ком-
комбинациями частиц.
г) Мезон
1) Теоретическое предсказание ме-
мезона. Второй этап теории ядерных сил связан с работа-
работами Юкава A935—1938 гг.)*), который, сохраняя основную
идею переноса сил частицами конечной массы, наглядно
говоря, предложил в известном смысле объединить элек-
электрон—нейтрино в одну частицу: отрицательный мезон,
а позитрон—нейтрино в положительный мезон, и тем
самым объяснить ядерные взаимодействия новым, ещё
гипотетическим в то время, мезонным полем, иначе говоря,
новыми частицами—мезонами. Несмотря на незавершён-
незавершённый ещё характер теории ядерных сил, сейчас нет сомнений,
что взаимодействия между нуклеонами действительно
в основном обусловлены какими-то мезонами, заря-
заряженными и нейтральными. Обмен нуклеонов заряжен-
заряженными мезонами можно пояснить следующим образом.
Протон, превращаясь в нейтрон, испускает положитель-
положительный мезон тг+, поглощаемый нейтроном:
0) начальное состояние р, п,
1) промежуточное состояние п, тг+, п,
2) конечное состояние п, /?,
или, наоборот, нейтрон испускает отрицательный мезон,
поглощаемый затем протоном. При переносе взаимодей-
взаимодействия нейтральными мезонами, как и в случае электромаг-
электромагнитных сил, нуклеоны, очевидно, сохраняют своё зарядное
состояние.
При этом добавочно предполагается, что мезоны имеют
целый спин и в связи с этим подчиняются бозевской
*) H.Yukawa, Proc. Phys. Math. Soc, Japan, 17, 48, 1935.
Дальнейшие работы Юкава и сотрудников см. там же, 1937—1938 гг.
320 КЛАССИЧЕСКАЯ МЕЗОДИНАМИКА [гл. у
статистике и, следовательно, могут переносить взаимо-
взаимодействие «поодиночке», как и другие «бозоны», а не па-
парами, как частицы полуцелого спина в теории [3-сил, или
другие «фермионы». Действительно, при испускании
одной частицы полуцелого спина нуклсоны должны были бы
перейти в состояние целого спина, что невозможно.
В первоначальном варианте теории рассматривались
простейшие бесспиновые заряженные мезоны, описываемые
скалярными волновыми функциями.
В дальнейшем были рассмотрены как заряженные,
так и нейтральные мезоны (нейтретто) различных масс,
притом наряду с бёсспиновыми скалярными и бесспиновые
псевдоскалярные, а также мезоны полуцелого и единич-
единичного спина. Связь нуклеонов с мезонным полем того или
иного типа обусловливается наличием у них специфиче-
специфической константы связи с этим полем, иначе говоря, некото-
некоторого квазизаряда g. Ряд простых соображений приводит
к значению g ~ 5е в долях элементарного электрического
заряда (см. ниже). Вопрос о массе мезонов будет рас-
рассмотрен ниже, сейчас ограничимся указанием на то, что
значение мезонной массы должно быть средним между
массами тяжёлых нуклеонов и лёгких частиц. В самом
деле, для того чтобы мезоны в качестве частиц ядерного
поля, не существующих реально в ядре, могли осуще-
осуществить взаимодействие, между нуклеонами, их масса долж-
должна быть в достаточное число раз меньше нуклеонной;
с другой стороны, как стало уже ясно из теории парных
сил, короткодействующий характер сил непосредственно
обусловлен наличием массы покоя у частиц, переносящих
взаимодействие. Мы будем иметь для обеспечения коротко-
г
действующего характера сил множитель типа е А ,
, h
где комптоновская длина волны частиц А = — должна
примерно совпадать с величиной радиусов лёгких ядер,
т. е. А~10~13сж, откуда масса мезона примерно должна
быть равна
где т — масса электрона.
§ 44] ПРОБЛЕМА ЯДЕРНЫХ СИЛ 321
Укажем теперь же на добавочное предположение, вы-
высказанное Юкава и непосредственно не связанное с теорией
ядерных сил, что мезоны могут быть связаны также и
с лёгкими частицами, а не только с тяжёлыми, иначе гово-
говоря, что электрон (е~), позитрон (е+) и нейтрино (v) (как и ан-
антинейтрино v') обладают некоторыми квазизарядами g', обе-
обеспечивающими их связь с каким-то мезонным полем, Это
давало бы возможность мезонам (как предполагалось, [х-ме-
зонам, см. ниже) распадаться на пары частиц по схеме
Распад заряженных мезонов, переносящих ядерное вза-
взаимодействие, будет воспринят как [3-распад. В самой
теории [3-распада ничего не изменяется благодаря подоб-
подобной модели, включающей мезон в качестве промежуточ-
промежуточного звена. Действительно,
п —> р + \tr —>р + е" + v (электронный распад),
р-~>п + р* —>п + е+ + v (позитронный распад).
Приведённая схема [В-распада могла бы иметь место
только в том случае, если бы спин мезона оказался цело-
целочисленным. Последние же данные (распад (л-мезона на 3
частицы, см. стр. 326) говорят о том, что схема Юкава
для ^-распада нуждается в дальнейшем уточнении, тем
более, что в переносе ядерных сил, повидимому, основ-
основную роль играют тг-мезоны, непосредственно но распада-
распадающиеся на электрон и нейтрино.
Далее с точки зрения современной мезонной теории, не-
независимо от всех её уточнений, качественное объяснение
«врождённого» магнетизма нуклеонов заключается в сле-
следующем: протон, будучи связан с заряженным мезонным
полем, испускает кванты этого поля (превращаясь в ней-
нейтрон плюс положительный мезон) и вновь их поглощает.
Точно так же нейтрон «диссоциируется» на протон плюс
отрицательный мезон. Доля времени пребывания нуклеона
в диссоциированном состоянии оказывается примерно
равной 20%. Магнитный момент нейтрона, следовательно,
будет примерно равняться 20% магнитного момента
21 Д. Иваненко и А. Соколов
322 КЛАССИЧЕСКАЯ МЕЗОДИНАМИКА [ГЛ. V
отрицательных мезонов, поскольку значительно меньшим
магнитным моментом более тяжёлого протона в этом
диссоциированном состоянии можно пренебречь. Точно
так же у протона возникает дополнительный положитель-
положительный магнитный момент, обязанный магнитному моменту
положительно заряженного мезонного поля.
Таким образом, исходя из теории ядерных сил, пред-
предсказывается новая частица средней массы, предполага-
предполагаемая обладающей целым спином и, следовательно, бозев-
ского типа, порождаемая нуклеонами и притом радио-
радиоактивная в свободном состоянии.
Это замечательное предсказание до некоторой степе-
степени подтвердилось после открытия заряженных мезонов
с массой около 200 масс электрона, точнее B12±4) т,
в космических лучах в 1937 г. Андерсоном и Неддермейе-
ром, названных позднее [^-мезонами и в особенности
после открытия более тяжёлых ir-мезонов.
Тщательные наблюдения над жёсткой компонентой
космических лучей показали, что подавляющее большин-
большинство проникающих частиц действительно обладает массой,
меньшей, чем у протона, но гораздо большей, чем у элек-
электрона, и, следовательно, не теряет столь много энергии на
тормозное излучение фотонов, как лёгкие частицы. Отсюда
их название: мезон (или мезотрон) от греческого «мезос»—
средний. Наряду с (--мезонами в состав проникающей
компоненты входут также некоторое число нуклеонов,
двигающихся с релятивистскими энергиями.
2. Основные свойства мезонов*)
Так как открытие и в значительной мере исследование
мезонов, а также изучение многих ядерных процессов
*) См. сборник «Мезон» под редакцией И. Е. Т а м м а, Гос-
техиздат, 1947, а также L. Janossy, Cosmic Rays, 2 ed.,
Oxford, 1950 (Сокращённый русский перевод первого издания вы
шел в 1949 г.); Е. Fermi, Nuclear Physics, Chicago, 1950;
Д. В.цСкобельцын, УФН, 41, 331, 1950; научно-рефера-
научно-реферативный сборник, серия 2, тшп. II, Космические лучи, ИЛ, 1950.
(Примечание при корректуре: см. также С. tl. Powell, Reports
Progress Phys., 13, 350, 1950.)
§ 44] ПРОБЛЕМА ЯДЕРНЫХ СИЛ 323
связаны с космическими лучами, остановимся на этом
вопросе подробнее. Исследования мезонов в космических
лучах и мезонов, порождённых в лабораторной обстановке
при помощи ускорителей, проведённые в течение послед-
последних трёх л*ет, значительно расширили и уточнили наши
прежние сведения об этих частицах. Что касается косми-
космических лучей, то в самом кратком виде современное их
понимание можно резюмировать следующим образом.
Хотя место, время и способ порождения первичных кос-
космических лучей ещё с достоверностью не выяснены, одна-
однако сейчас эта проблема вышла из тупика, в котором она
находилась ранее, когда как будто самым надёжным выво-
выводом было отрицательное заключение, что ни звёзды, ни
Солнце и никакие другие известные объекты или физиче-
физические процессы не могут быть источниками космических
лучей.
Сейчас, в частности работами Я. П. Терлецкого,
показано, что электрические поля на Солнце и звёздах,
вызванные переменными магнитными полями, обязан-
обязанными наличию магнитных моментов, непараллельных оси
вращения (космический индукционный ускоритель, близ-
близкий к бетатрону), действительно могут ускорять частицы
до огромных энергий. Ускорение также может иметь место
согласно Дэвису в случае параллельности магнитного
момента оси вращения звезды, действующей в этом случае
в качестве униполярной машины. Эти гипотезы приобре-
приобрели значительный вес после открытия Бэбкоком магнетиз-
магнетизма у ряда звёзд (Девы L78 и других), причём напряжён-
напряжённость поля достигает значений в тысячи гауссов. Далее
Ферми заметил, что при столкновении достаточно быстрых
протонов с облаками межзвёздной материи, вероятно
намагниченными, частицы могут добавочно ускоряться.
Как подчеркнули Теллер и Рихтмейер, весьма веро-
вероятно, что первичные космические частицы, прежде чем
попасть на землю, довольно долго диффундируют, притом
скорее всего внутри галактики, что обеспечивает изотроп-
изотропность потока. Таким образом, даже не прибегая к другим,
менее правдоподобным или же возможным, но играю-
играющим вспомогательную роль механизмам, например мо-
модели «небесного циклотрона», осуществляемого согласно
21*
324 КЛАССИЧЕСКАЯ МЕЗОДИНАМИКА [гл. V
Алфвену намагниченными двойными звёздами, или наличию
излучения высокой частоты при аннигиляции нуклеонов
с неоткрытыми ещё гипотетическими антинуклеонами, или
ускорению частиц при взрывах сверхновых звёзд, или уско-
ускорению частиц гипотетическими космическими полями,
или же какому-то ещё менее ясному ускорению путём по-
побочных процессов при образовании химических элементов
в предзвёздном состоянии, мы можем сейчас, так или
иначе, начать строить в общих чертах картину проис-
происхождения первичных космических лучей*). Главная доля
космических лучей обладает энергией около 1010 eV; число
частиц более высоких энергий убывает по закону
т«т const d %
Вопреки более старым представлениям 30-х годов,
современные непосредственные наблюдения на больших
высотах при помощи саморегистрирующих приборов, под-
поднятых на баллонах до 30 км или ракетами примерно до
150 км, а также анализ геомагнитных эффектов привели
к выводу, что лёгкие частицы (электроны—позитроны)
в первичном потоке отсутствуют, но что первичные лучи
в основном являются протонами (Шейн, Джонсон, Вернов).
Все известные мезоны, как и нейтроны, ввиду их неста-
нестабильности не могут входить в состав первичного потока.
Важно ещё подчеркнуть, что в первичных космических
лучах на больших высотах были непосредственно обна-
обнаружены в 1947 г. (Брадт, Петере и др.) наряду с прото-
протонами, составляющими основную часть первичного потока,
также ядра гелия (несколько процентов от числа прото-
протонов), углерода, кислорода и другие лёгкие ядра (в сумме —
десятые доли процента от числа протонов) в общем согласии
с предсказанием Терлецкого.
Попадая в атмосферу и реагируя с ядрами атомов
(кислорода и азота), протоны высоких энергий
A09 -10l0eV), во-первых, выбивают из ядер другие еди-
единичные протоны и нейтроны, которые, обладая высокой
энергией, в свою очередь могут присоединиться к первич-
*) Подробности см. в статьях Я. П. Терлецкого, ЖЭТФ,
19, 1059, 1949 и ter H a a r, Rev. Mod. Phys., 22, № 2, 119, 1950.
§ 44] ПРОБЛЕМА ЯДЕРНЫХ СИЛ 325
ному потоку и выбивать третичные и т. д. нуклеоны; во-вто-
во-вторых, протоны и вторичные нуклеоны могут «нагреть» ядро
и вызвать испарение многих нуклеонов, а также альфа-
частиц и других осколков ядер, иначе говоря, произ-
произвести расщепления типа «звёзд», открытых впервые
А. П. Ждановым при помощи метода толстослойных
фотопластинок Л. В. Мысовского; в-третьих, при столкно-
столкновении весьма быстрых нуклеонов друг с другом могут
одновременно образоваться мезоны. Иначе говоря, будет
происходить излучение мезонов, или «отрывание» мезон-
ного поля от нуклеонов при торможении, весьма анало-
аналогичное испусканию фотонов (т. е. отрыванию поля элек-
электромагнитного) при столкновении заряженных частиц.
Наиболее существенная разница между двумя последними
явлениями заключается в том, что оторвавшееся элек-
электромагнитное поле не обладает массой покоя, представляя
собой «поле» в узком смысле слова, а излучённое мезонное
поле связано с массой покоя, благодаря чему его кор-
корпускулярные свойства значительно более ярко выражены;
иначе говоря, мы имеем мезоны «частицы» в обычном
узком смысле слова. Как было доказано группой Пауэлла
в 1948 г. при анализе фотографий космических звёзд,
нуклеоны, сталкиваясь с ядрами, непосредственно порожда-
порождают заряженные тяжёлые мезоны обоих знаков заряда с
массой 276 ± 4 электронных масс, названные тг-мезонами
(тг-primary—первичный *)). Кроме того недавно выясни-
выяснилось важное обстоятельство: возможность не только еди-
единичного, но и кратного порождения нескольких тг-мезонов
при столкновении двух нуклеонов весьма высокой энергии.
Несколько позднее эти же т:-мезоны были открыты
Лэттесом и Гарднером в лабораторных условиях при бом-
бомбардировке различных мишеней нуклеонами и ядрами
гелия с энергиями в сотни миллионов вольт (вплоть до
380 MeV для альфа-частиц), полученными в фазотроне**),
а Мак-Миллан наблюдал порождение 7г_ и ^-мезонов
при бомбардировке ядер у-лучами с энергией около
335 MeV, полученными в синхротроне. В свою очередь
*) Ферми предлагает для этой частицы наименование пи-он.
**) См. УФН, 34, 450, 1948.
326 КЛАССИЧЕСКАЯ МЕЗОДИНАМИКА [гл. у
тг-мезоны интенсивно реагируют с ядрами; отрицательные
тт-мезоны, поглощаясь ядрами (скорее всего путём про-
процесса типа if-захвата с орбиты атомного типа, на которую
они сначала попадают при замедлении в течение
^ 10~12 сек. в конденсированной среде), образуют вновь
звёзды (отсюда их прежнее наименование с-мезоны, от
c-star, т. е. звёздообразующие). При этом в случае за-
захвата на водородную орбиту образуется своеобразный
атом «мезоводорода».
Весьма важным явилось открытие распада тс -мезонов
на более лёгкие, обычные ^-мезоны и нейтральную частицу,
вероятно, псйтрипо или же, возможно, лёгкий нейтраль-
нейтральный мезон v' по схеме тг± —>^± + у. По наблюдениям в
космических лучах и непосредственным лабораторным
измерениям время жизни по отношению к подобному
распаду для покоящихся тг-мезоыов оказалось порядка
Tn^ 10~8сек. *). С другой стороны, более тщательное
изучение р-мезонов показало, что они распадаются не на
две частицы, как предполагалось ранее [электрон (пози-
(позитрон) и нейтрино], а на три частицы**), из которых две
нейтральные, т. е. нейтрино, или, возможно, какие-либо
лёгкие нейтральные мезоны. Таким образом, распад
(л-мезонов идёт по схеме: р± ■—>e±+2v или \i± —»e±-fv-fv'.
Спонтанный распад [х-мезонов был изучен в космиче-
космических лучах многими способами, общая идея которых за-
заключается в сравнении числа частиц, распадающихся за
время прохождения некоторого слоя вещества, распреде-
распределённого один раз на большом пути (например, в атмосфере),
а другой раз сконцентрированного в узком участке (на-
(например, в воде). Для медленного или покоящегося мезона
время жизни 7^ = 2,15 • 10~~6 сек.; для быстрых частиц,
в согласии с теорией относительности, время жизни уве-
увеличивается в зависимости от скорости по закону
*) См. обзор А. Б. Мигдала и Я. А. Смородинско-
го, УФН, 41, 133, 1950.
**) Одними из первых к этому выьод}^ пришли Г. Б. Ж д а н о в и
А. А. X а й д а р о в (ДАН, 65, 287, 1949); подробнее см. научно-ре-
научно-реферативный сборник, серия 2, вып. II, Космические лучи,ИЛ, 1950.
§ 44] ПРОБЛЕМА ЯДЕРНЫХ СИЛ 327
Разетти, затем Ожэ и Росси смогли определить Т^
в лабораторных условиях при исследовании распада кос-
космических мезонов, заторможённых в блоке свинца.
Открытие новых, более тяжёлых тг-мезонов, значитель-
значительно более интенсивно взаимодействующих с ядрами, чем
[х-мезоны, объяснило казавшийся парадоксальным факт, об-
обнаруженный недавно группой Пиччони и заключавшийся
в слабом поглощении лёгкими ядрами обычных \i-мезонов,
составляющих главную долю жёсткой компоненты косми-
космических лучей. При этом имеет место интересная реак-
реакция: р 4-р._—> п -*- v.
Отметим, что различные авторы время от времени сооб-
сообщают о наличии некоторого числа мезонов других масс
в космических лучах, в том числе специально тяжёлых
т-мезонов с массой около 900—1000т (Лепренс-Ренге)*),
а также нейтральных т-мезонов, распадающихся
с Т^ЛО10 сек. на две заряженные частицы (Рочестер, груп-
группа Андерсона), или лёгких мезонов с массами < 200 гп. Все
эти наблюдения далеко ещё не являются достоверными**),
кроме, повидимому, недавно подтверждённых z-мезонов.
*) См. статью Lepri nc e-R inguet в сборнике «L e m е-
s о n», Paris, 1945.
**) Последнее заключение относится также к так называемым
«варитронам», т. е. мезонам разных масс и зарядов (вплоть до
20 000 т), об экспериментальном обнаружении которых сообщали
неоднократно АИ АлихановиА. И. Алиханьянс сотруд-
сотрудниками (см. ЖЭТФ, 18, 301, 1948; 19, 1021, 19>9>. Во всяком
случае, общую картину космических лучей на сегодняшний день
можно построить без варитронов (см., например, обзор Д. В. С к о-
бельцына, УФЫ, 41, 331, 1950), особенно с подобным спект-
спектром масс и в количестве нескольких процентов от всего состава
жёсткой компоненты, не говоря уже о том, что современная теория
не предсказывает «варитронов» и т. д., как, впрочем, и не запрещает
их. С другой стороны, весьма вероятно, что современная физика
далеко ещё не исчерпала всех элементарных частип как в мезон-
ном диапазоне, так и ближайших по массе к нуклеонам.
«Супрачастипы» с массами, в несколько раз превышающими
нуклеонные, могут быть с некоторым основанием предсказаны,
исходя из предположения о возможности существования частип,
взаимодействия между которыми могут переноситься нуклеонами,
аналогично тому, как мезоны реализуют поле сил между нуклеонами
(см. Д. Иваненко, УФЫ, 32, 306, 1947). Возбуждённые же состоя-
состояния нуклеонов по теории сильной связи нуклеонов с мезонным
полем (Вентпель-Гейтлер-Ма) должны иметь массы, лишь незначи-
328 КЛАССИЧЕСКАЯ МЕЗОДИНАМИКА [гл. \
Наконец, весьма важным обстоятельством явилось
недавнее открытие в космических лучах и в лаборатор-
лабораторных условиях A950 г.) относительно тяжёлых нейтраль-
нейтральных тг0-мезонов (нейтретто) с массой около 270 т, также
нестабильных, со временем жизни То ^ 10~14 сек. и рас-
распадающихся на два фотона по схеме
Г0->2Т.
При этом процесс предполагается идущим благодаря вир-
виртуальному порождению пары нуклеон-антинуклеон и её
аннигиляции с превращением в у-фотоны:
В этой связи упомянем недавнее предварительное пред-
предложение Ферми построить модель мезона как сложной
частицы, состоящей из пары тесно связанных частиц—нук-
леона и антинуклеона. тг0-мезоны образуются так же, как и
т:±-мезоны, при столкновении нуклеонов или у фотонов с ну-
клеонами(Брюкнер, Штейнбергер, Поповский). Интересно,
что малое время яшзни нейтральных тсд-мезонов делает пре-
преимущественно именно эти новейшие частицы ответствен-
ответственными за порождение более поглощаемой, мягкой электрон-
но-позитронно-фотонной компоненты в космических лучах.
Наряду с у~лУчами от ^о~мезонов мягкая компонента
ведёт своё начало также от электронов и позитронов рас-
распада fj-_j_-мезонов, от 8-электронов, т. е. атомных электро-
электронов, выбитых космическими частицами, всевозможных
фотонов, образующихся при относительно незначитель-
незначительном тсрмозном испускании протонов, тс±-мезонов, р±-мезо-
нов и, вероятно, также фотонов, возникающих при излу-
излучении перезарядки протона в нейтрон *) и т. д. В даль-
дальнейшем, как известно, у-лучи высокой энергии при стол-
столкновении с ядрами порождают пары лёгких частиц
у -\~MZ—^Mz ~\-e+ + e_, а электроны и позитроны в свою
очередь излучают тормозные у-фотоны в поле ядер, при-
тельно превышающие нуклеонные (см. также статьи И. Т а м м а,
В. Гинзбурга и др. в сборнике «Мезон», Гостехиздат, 1947).
*) На необходимость последнего указали недавно Померан-
чук и Шмушкевич, а также Хайакава.
§ 44] ПРОБЛЕМА ЯДЕРНЫХ СИЛ 329
водя к хорошо изученным мягким каскадным ливням,
открытым в 1933 г. Блэккетом *).
Следует отметить, что гипотеза порождения нуклеона-
ми нейтральных тг0-мезонов, являющихся частицами, непо-
непосредственно не наблюдаемыми, в противоположность тг±-ме-
зонам, обнаруживаемым по их следам в камере Вильсона
или фотопластинках, а также их распада на два фотона,
возникла первоначально из невозможности объяснить
какими-либо известными механизмами (тормозное испуска-
испускание и т. д.) наличие неожиданно значительного числа
электронов, позитронов и, по всей видимости, породив-
породивших их фотонов наряду с нуклеонами в ядерных «звёзд-
«звёздных» взрывах. Исследование этих смешанных «электронно-
ядерных» взрывов, индуцирующих затем дальнейшие
аналогичные электронно-ядерные ливни, успешно про-
проводилось главным образом Памирской экспедицией под
руководством Д. В. Скобельцына, В. И. Векслера, '
С. Н. Вернова и Н. А. Добротина. Кроме у-лучей и элек-
электронов-позитронов, в состав мягкой компоненты входит
также некоторое число нуклеонов и мезонов, двигаю-
двигающихся с незначительными нерелятивистскими энергиями.
На уровне моря космические лучи, интенсивность кото-
которых падает примерно до 0,1 первичной интенсивности, со-
состоят из жёсткой компоненты, т. е. в основном из [J-мезонов
(80%) и отчасти мягкой компоненты B0%).
Для ядерной физики, очевидно, весьма важны разно-
разнообразные данные физики космических лучей; особенно
существенным с точки зрения проблемы ядерных сил
является открытие того обстоятельства, что ядерное поле,
окружающее нуклеоны, в основном состоит из среднетяжё-
лых частиц: тг-мезонов как заряженных, так и нейтраль-
нейтральных. Действительно, подчеркнём ещё раз, именно тг-мезоны
*) Полная теория каскадных ливней, являющихся электро-
электромагнитными процессами, была, вслед за работами Гейтлера и Баба,
Оппенгеймера и Карлсона развита и завершена главным образом
советскими физиками Ландау и Румером, Иваненко и Соколовым,
Таммом и Беленьким. См. монографии: С. 3. Беленький.
Лавинные процессы р космических лучах, Гостехиздат, 1948;
Росси и Грейзен, Взаимодействие * космических лучей
с веществом, ИЛ, 1949 и цитированную книгу Я н о с с и о кос-
космических лучах.
330 КЛАССИЧЕСКАЯ МЕЗОДИНАМИКа [гл. у
непосредственно с наибольшей вероятностью порождают-
порождаются и поглощаются ядрами. Очевидно, 7с± и тг0-мезоны в
первую очередь являются также передатчиками внутри-
внутриядерных взаимодействий между нуклеонами. Тем самым
приобретает первостепенное значение определение всех
основных свойств тг-мезонов: в первую очередь после их
массы значение спина.
Как следует из самого факта распада тг0-мезонов на два
фотона, обладающих каждый единичным спином, спин
тг0-мезона должен, по видимому, равняться нулю. Анало-
Аналогичное положение вещей было выяснено в теории «позит-
«позитрония», т. е. атомноподобной системы, ещё непосред-
непосредственно не обнаруженной, состоящей из позитрона и элек-
электрона, обращающихся вокруг общего центра тяжести
впредь до взаимной аннигиляции с превращением в фото-
фотоны. При этом система парапозитрония с общим спином,
равным нулю, превращается в два фотона (Г~ 10~9 сек.),
тогда как ортопозитроний, обладающий спином единица,
должен превращаться, во всяком случае при подсчёте
в нерелятивистском приближении, в три фотона
(Т^10~7 сек.)*).
Вероятнее всего, что тг0-мезон является псевдоскаляр-
псевдоскалярным, а не скалярным (см. § 46), что доказывается в первую
очередь более близким совпадением экспериментальных
данных с предсказаниями псевдоскалярной теории. Кро-
Кроме того, самые общие основы теории ядерных сил указы-
указывают на существенную роль спиновых свойств нуклеонов
и ядерного поля, т. е. в основном ir-мезонного, что не
могло бы иметь места при скалярном характере тс-мезо-
нов. Судя по более удовлетворительному согласию пред-
предсказаний псевдоскалярной теории с опытом, заряженные
ти^-мезоны также являются псевдоскалярными и, следо-
следовательно, обладают спином 0.
*) См. ряд работ Иваненко- Соколова-Мухтар о-
ва б ДАН и в Весптике МГУ за 1947—1948; а также Ландау-
Померанчука в ДАН за 1948. Заметим, что при своей диф-
диффузии в веществе медленные тс+ и [х+-мезоны также могут реком-
бинировать с электронами, образуя новую кпроткгживущую
атомнопоцобиую систему «мезотроний». С яругой стороны тс__ и ц__-
частицы могут захватываться на атомные орбиты подобно элек-
электронам.
§ 44] ПРОБЛЕМА ЯДЕРНЫХ СИЛ 331
Открытие тг0-мезонов или нейтрального мезонного поля
не только подводит более реальный базис под современ-
современную теорию ядерных сил, но и оправдывает построение
чисто классической теории, «классической мезодинамики»
мезонного поля и ядерных взаимодействий. Для заряжен-
заряженных тг±-мезонов, строго говоря, необходима квантовая
трактовка, хотя многие основные результаты могут быть
получены из теории нейтральных частиц. Подчёркивая
основную роль тс-мезонов как частиц ядерного поля, мы
не должны ещё ввиду незаконченного характера как
теории ядерных сил, так и экспериментов в данной обла-
области категорически исключать возможности участия иных,
возможно, более лёгких мезонов в ядерном поле, хотя
устранение трудностей теории ядерных сил, по всей види-
видимости, не связано с введением иных мезонов. Ввиду целого
спина, статистика тс-мезонов должна быть бозевской. Так
как не исключена ещё возможность как скалярного ха-
характера этих мезонов, так и значения их спина 1, то
разумно проанализировать все варианты описания, при-
пригодные при целом спине: 1) скалярное или псевдоскалярное
уравнение (спин 0); 2) векторное или псевдовекторное
уравнение (спин 1).
Для описания ^-мезонов как частиц, повидимому,
полуцелого спина, как и для электронов, необходимо ис-
использовать спинорное уравнение Дирака. Никаких осно-
оснований предполагать у каких-либо мезонов спин больше
единицы не имеется. Тем самым нет причин привлекать
для описания мезонного поля более сложные волновые
функции, обладающие большим числом компонент, чем
четырёхмерные векторы.
Дополнительная гипотеза Юкава о связи мезонов вну-
внутриядерного поля с р-распадом привела к предска-
предсказанию факта самопроизвольного распада свободных
мезонов, действительно подтверждённому опытом. Од-
Однако теперь нам понятна неудача построения точной
количественной теории, которая позволила бы связать
р-распад и распад [^-мезонов, единственно известных
в 1937—1947 гг. Время распада покоящихся ^±-мезонов
Гц, = 2,15 • 10~6 сек. оказалось слишком большим по сравне-
сравнению с требованиями теории [В-распада, данные по которому
332 КЛАССИЧЕСКАЯ МЕЗОДИНАМИКА [гл. V
приводили к значениям Т<^>10~8 сек. Это значение сов-
совпадает по порядку со временем жизни недавно открытых
7г-мезонов. Однако последние, по крайней мере в сво-
свободном состоянии, отнюдь не распадаются на электрон
(позитрон) и нейтрино, поэтому известный распад тг-мезона
в случае, если он имеет место также для тг-мезонов,
переносящих ядерные силы, никак не может служить
объяснением для ^-распада*). Ввиду доказательства распада
|х±-мезонов на три частицы они также непосредственно
не могут быть привлечены в качестве промежуточных
звеньев при ^-распаде, даже если эти мезоны участвуют
в переносе ядерных сил парами (например, парами [х+
и |л__ или вместе с нейтрино |л+ и v и т. д.) Таким обра-
образом, пока что, несмотря на привлекательность гипотезы
о сведении ^-распада к распаду промежуточных мезонов,
переносящих ядерное взаимодействие, приходится трак-
трактовать [3-распад феноменологически в духе теории Ферми,
при помощи независимой константы gF, связывающей
нуклеоны с электронно-(позитронно)-нейтринным полем.
Вернёмся к общей теории мезона. Для понимания даль-
дальнейшего развития теории мезонов и теории ядерных сил
прежде всего необходимо подчеркнуть, что первоначаль-
первоначальное описание ядерных сил" посредством одних скалярных
мезонов, заряженных или нейтральных, оказалось слиш-
слишком упрощённым. Для того чтобы объяснить спиновые
и нецентральные ядерные силы, необходимо связать нукле-
нуклеоны с мезонным полем, обладающим какими-то спиновыми,
например дипольными, свойствами. Наилучшим способом
оказалось описание мезонов посредством псевдоскаляр-
псевдоскалярного уравнения (спин 0) (во вновь открытых тг-мезонах,
повидимому псевдоскалярных, эти теоретические требо-
требования нашли теперь реальное обоснование) или векторных
уравнений (спин 1).Таким путём удаётся придти к спино-
спиновым и нецентральным силам, в частности, истолковать
квадрупольный момент дейтерона. Одинаковый порядок сил,
*) Недавно попытки в этом направлении были сделаны
Финкельштейном и др., рассматривавшими промежуточное вир-
виртуальное порождение пары нуклеонов вместе с антинуклеонами
по схеме
§ 44] ПРОБЛЕМА ЯДЕРНЫХ СИЛ 333
действующих между протоном и нейтроном, протоном—
протоном и нейтроном—нейтроном, настойчиво требовал
введения наряду с заряженными также нейтральных ме-
мезонов (нейтретто) в качестве частиц, переносящих взаи-
взаимодействие. Открытие тг0-мезонов со своей стороны под-
подводит реальную почву под эту теорию. Обычно теория
развивается на базе использования смеси заряженных
и нейтральных мезонов, чаще всего в равной, «сим-
«симметричной» пропорции. Наконец, неоднократно обсуж-
обсуждались всевозможные иные смеси, например, векторных
и псевдоскалярных мезонов, которые одновременно дол-
должны реализовать согласно гипотезе Мёллера и Розен-
фельда ядерное поле. Другие авторы использовали только
заряженные или только нейтральные частицы и т. д.
Однако удовлетворить всем требованиям теории ядер-
ядерных сил до сих пор не удаётся. В теории ядерных сил
имеется фундаментальная трудность, связанная с эффек-
эффективной дипольностью мезонного поля (как векторного,
псевдовекторного, так и некоторых вариантов псевдоска-
псевдоскалярного), которая приводит к появлению в энергии взаимо-
взаимодействия, вычисляемой классическим путём в случае
нейтральных мезонов и квантовым путём в случае мезо-
мезонов заряженных или нейтральных, членов, имеющих
квазимагнитный вид, на относительно малом расстоя-
расстоянии: V/~^r~3.
Как уже указывалось (см. теорему вириала), при таком
быстром возрастании энергии взаимодействия на малых
расстояниях нуклеоны упали бы друг на друга и стабиль-
стабильные орбиты были бы невозможны. Подобные дипольные
члены возникают при нерелятивистском подсчёте; провести
же точный релятивистский подсчёт ещё не удалось, хотя
в псевдовекторном и псевдоскалярном случаях (см. ниже)
при релятивистском улучшении диподьные члены удалось
устранить.
Как будет подробно показано ниже, дршольность мезо-
мезонов проявляется также при разнообразных эффектах рас-
рассеяния: мезонов на нуклеонах и различных частиц, в том
числе и фотонов, на мезонах. При этом эффективные сече-
сечения этих процессов безгранично растут с ростом энергии,
что, конечно, нелепо. В векторном случае подобные •
334 КЛАССИЧЕСКАЯ МЕЗОДИНАМИКА [ГЛ. V
трудности возникают как при электромагнитных, так и при
специфически ядерных взаимодействиях, тогда как в псевдо-
псевдоскалярном случае к трудностям приводят лишь ядерные
эффекты. Из всех способов, предложенных для устране-
устранения дипольных трудностей при рассеянии, наиболее
эффективным и бесспорным оказался учёт обратного дей-
действия мезонного поля или зат хания на испускающие его
частицы, разработанный каь в классической теории ней-
нейтральных мезонов (Иваненко и Соколов, Баба), так и в кван-
квантовой теории заряженных мезонов (Соколов, Гейтлер,
Вильсон, Гора). Во всех случаях учёт затухания приво-
приводит к уменьшению эффективных сечений при высоких
энергиях. Однако учёт затухания не позволяет устранить
дипольные трудности при взаимодействии. Впрочем, в по-
последнее время ситуация с дипольнои трудностью несколько
улучшилась, так как для псевдоскалярных мезонов уда-
удалось устранить эту трудность по крайней мере во втором
приближении, при релятивистском подсчёте, учитывающем
скорости нуклеонов (см. §§ 46 и 486). Так как псевдоска-
псевдоскалярные мезоны во многих других отношениях дают наи-
наилучшее описание ядерного поля, то разумно эти частицы
взять за основу. Поскольку, однако, до сих пор не имеется
полной уверенности в возможности ограничиться одним
этим полем, основы теории ядерных сил следует проана-
проанализировать на базе всех четырёх полей спина 0 и 1.
Таким образом, несмотря на общий успех в понимании
мезонов, связанный с самим предсказанием новой части-
частицы средней массы, её роли в ядерных силах и её спонтан-
спонтанного распада, а также на удачное описание ряда эффектов,
даже несмотря на новейшее открытие заряженных и ней-
нейтральных тг-мезонов и выяснение распада тг- и и-мезоновэ
общее положение теории ядерных сил и теории мезонов
остаётся пока что неудовлетворительным. Ввиду такой
ситуации разнообразные ядерные эффекты приходится
временно вычислять с энергией взаимодействия искус-
искусственно подобранной формы, передающей указанные выше
основные признаки ядерных сил, главным образом исходя
как из данных по дейтерону, так и сведений о рассеянии
нуклеонов при высоких энергиях порядка 100—400 MeV,
или же использовать мезонный вид взаимодействия, обре-
§ 45] СКАЛЯРНОЕ МЕЗОННОЕ ПОЛЕ 335
занный на малых расстояниях. К счастью, как указыва-
указывалось выше, понимание многих важных явлений не зави-
зависит от более точного вида взаимодействия. Тем самым мы
должны в известной мере использовать результаты фено-
феноменологического направления теории ядерных сил, беря,
однако, что весьма существенно, за основу все результаты
полевой мезонной теории.
Проблема построения ядерных сил является, очевидно,
одной из важнейших во всей современной физике. Знание
точного закона взаимодействия между нуклеонами, подоб-
подобного ньютонову или кулонову, позволило бы рассчитать
любые ядерные эффекты. Сейчас ещё неясно, коренятся
ли затруднения теории ядерных сил, не позволяющие при-
придать закону взаимодействия нуклеонов окончательную
форму, главным образом в недостаточном ещё знании
свойств тг-мезонов, переносящих в основном ядерные
силы, или других мезонов, возможно участвующих в ядер-
ядерном поле, или же эти трудности связаны с общими про-
проблемами релятивистской квантовой механики элементар-
элементарных частиц, в частности с недостаточным ещё развитием
теории вакуума мезонов и нуклеонов.
Для облегчения анализа проблемы ядерных сил начнём
изложение теории с простейшего её варианта, именно ней-
нейтрального скалярного мезонного ядерного поля. Имея в ви-
виду вероятное, но всё же не обязательное применение к
любым нейтральным мезонам, в частности ^-мезонам (ней-
третто), будем называть для краткости излагаемую теорию
вещественного поля «классической мезодинамикой» *).
§ 45. Скалярное мезонное поле
а) Скалярные ядерные силы
Рассмотрим простейший вариант теории ядерных сил,
с самого начала обеспечивающий их зарядную незави-
независимость (в смысле § 44а, п. 4), который сводится к
допущению, что к силам притяжения между любыми
нуклеонами приводит нейтральное мезонное поле, опи-
описываемое однокомпонентной скалярной вещественной
•) Д. Иваненко и А. Соколов, ЖЭТФ, 10, 709, 1940.
336 КЛАССИЧЕСКАЯ МЕЗОДИНАМИКА [гл. V
функцией <р- Теорию скалярных ядерных сил будем
строить в рамках классической мезодинамики.
В этом отношении мы имеем известную аналогию с нью-
ньютоновым полем тяготения, которое как раз приводит к при-
притяжению, действующему между любыми массами.
Как известно, для определения потенциала ньютонова
поля, который будем обозначать также через ср, создавае-
создаваемого точечной массой т, находящейся в начале коорди-
координат, имеем следующее дифференциальное уравнение:
r), D5,1)
где у. — гравитационная постоянная.
Отсюда с помощью A0,11) при естественных гранич-
граничных условиях находим значение для потенциала на рас-
расстоянии г от источника
Ч=-~- D5,2)
и для потенциальной энергии взаимодействия двух оди-
одинаковых масс, расположенных друг от друга на рас-
расстоянии г:
F = iwcp. D5,3)
Переходя теперь к ядерным силам, мы не можем
ограничиться подстановкой нового специфического мезон-
ного заряда g нуклеонов, обеспечивающего их связь
с ядерным полем вместо гравитационного заряда т ]/" х.
Действительно, в этом случае мы вновь пришли бы к силам
тг 1
далекого действия V ~ — вместо треоуемых короткодей-
короткодействующих сил. Поэтому прежде всего проделаем замену выра-
выражения D5,2) и тем самым D5,3) формулами, обеспечивающи-
обеспечивающими, по крайней мере, короткодействующий характер
искомых сил. Для этой цели достаточно изменить уравне-
уравнение поля D5,1), например, в том же направлении, как это
было сделано Зеелигером и Нейманом в теории тяготения
(см. § 14). Следовательно, за основу разумно взять вместо
уравнения типа Пуассона уравнение Зеелигера или, иначе
говоря, статическое приближение к уравнению B0,1):
(v2-AJ)T=4i:g3(r), D5,4)
приводящее к потенциалу короткодействующих сил.
§ 45] СКАЛЯРНОЕ МЕЗОННОЕ ПОЛЕ 337
При этом, как было указано в § 20, постоянная к0
должна быть связана с массой частиц р,, сопоставлен-
сопоставленных полю, соотношением &$ = —£-- Вообще говоря,
учитывая корпускулярно-волновой дуализм, точная фор-
форма которого устанавливается в квантовой теории, мы всё
время имеем в виду как поля, так и частицы, им сопо-
сопоставленные, например, электромагнитное поле и фотоны,
мезонное поле и мезоны, и т. д.
С другой стороны, для*энергии связи нуклеона с мезон-
ным полем можно полностью сохранить выражение типа
D5,3), пригодное в статическом нерелятивистском при-
приближении для связи любых частиц с полем через какие-
либо «заряды». Подставляя сюда мезонный заряд, по-
получим
V = g<p. D5,5)
Таким образом классическое нерелятивистское уравнение
движения нуклеона массы М должно определяться фор-
формулой
Эти же соотношения получаются строго из функция дей-
действия S, состоящей из трёх частей (см. § 23):
аЗ = Oj -f- O2 "Т~ ^з* \ыу1)
Здесь ^ — функция действия свободной частицы (ну-
(нуклеона), которая в нерелятивистском приближении име-
имеет вид
v*dt', D5,8)
где v2 = z'2 + y'2+ z'2, а координаты нуклеона зависят
от времени V.
S2 обозначает функцию действия одного веществен-
вещественного скалярного мезонного поля, выражающуюся через
интеграл от лагранжиана L, который является единствен-
единственным инвариантом, удовлетворяющим условиям линей-
линейности уравнения и наинизшей возможной, именно второй,
22 Д. Иваненко и А. Соколов
338 КЛАССИЧЕСКАЯ МЕЗОДИНАМИКА [гл. V
степени производных от скаляра <р B уравнении поля
Sa = J L (dr) = - -^ $ (TvTv + К г) (dx), D5,9)
где (dx) = dxdydzdt, xf y, z, Z - координаты поля и
ф^=-±- . Действительно, самое ср, а следовательно, и ср2,
а также квадрат четырехмерного градиента ^vTv являются
инвариантами.
Наконец, S3 обозначает смешанный член функции дей-
действия, определяющий взаимодействие мезонного поля
с нуклеонами, причём
S3 - — { ds \v(x- x') U (x) (dx). D5,10)
Здесь величина £/, играющая в релятивистской теории
роль энергии связи, является скаляром и получается
по правилу образования смешанных инвариантов, т. е.
равняется сумме произведений скаляра поля на скаляр
частицы, вектора поля на вектор частицы и т. д.
Для скалярного поля мы имеем
где Vp является скоростью нуклеона, a g и / являются
ядерными «зарядами».
Используя особое калибровочное преобразование
(см. §§ 46, 48) или же просто ограничиваясь нереляти-
нерелятивистским приближением, последний инвариант, пропор-
пропорциональный скорости, мы можем вообще отбросить.
Тогда
U = g?. D5,10а)
В нерелятивистском приближении для точечного нукле-
нуклеона, когда можно положить собственное время б* равным
*'(* = *') и
имеем
S8 - - g J dt' \^Ь (г - У) 8 (t -1') <p (x) (dr) dt. D5,11)
I 45] СКАЛЯРНОЕ МЕЗОННОЕ ПОЛЕ 339
Для определения уравнений поля при наличии нукле-
онных источников мы берём лишь функции действия S2
(поля) и S3 (член взаимодействия):
, D5,12)
причём функция Лагранжа теперь равна
L= -^(?v«Pv + At.«P8)-g?5 dt'b{r-l')b{t-t'). D5,13)
Варьируя L по потенциалу ср, получим из эйлеровых
уравнений
уравнение скалярного мезонного поля, создаваемого точеч-
точечными нуклеонами:
В частности, в статическом случае нуклеона, помещён-
помещённого в начале координат У = 0, получаем исходное урав-
уравнение D5,4).
Точно так же уравнение движения нуклеона может
быть найдено из функций действия S2 (частицы) и £3
(взаимодействия):
/Л/. D5,16)
Здесь нерелятивистская функция Лагранжа равна
L'= Ц-№п-&(*',?), D5,17)
откуда, варьируя V по координатам нуклеона и исполь-
используя эйлеровы уравнения
получаем уравнение D5,6), описывающее трансляционное
движение нуклеона в мезонном поле.
22*
340 КЛАССИЧЕСКАЯ МЕЗОДИНАМИКА [гл. V
Потенциальная энергия V взаимодействия нуклеойа
с мезонным полем может быть найдена из равенства
£8=-$ Vdt', D5,19)
из которого для точечного покоящегося нуклеона вновь
получаем формулу D5,5).
Таким образом смешанная функция действия S3 при-
приводит в полной аналогии с максвелловской теорией как
к выражению для плотности нуклеонов, порождающих
мезонное поле [см. правую часть равенства D5,4)], так
и к силе, действующей со стороны мезонного поля на нук-
леон [см. правую часть равенства D5,6)]. В нашем случае
мы ввели в S3 лишь член, описывающий один точечный
нуклеон, поэтому правая часть уравнения D5,6) пред-
представляет собою по существу силу самодействия. Однако,
вводя в функцию действия ещё внешнее поле ср1 (см. также
§ 23), легко показать, что сила, действующая на нуклеон
со стороны внешнего поля, будет равняться
Fl= — grad gcp1'.
С помощью формулы A4,10) находим из уравнений
D5,4) и D5,5) следующее важное для всей теории ядер-
ядерных сил значение для потенциала мезонного поля на
расстоянии г от источника:
<f=-g±T-- D=5,20)
Отсюда имеем для потенциальной энергии взаимодей-
взаимодействия через вещественное скалярное поле двух точечных
нуклеонов, находящихся соответственно в начале коорди-
координат и в точке г:
F = gcp=-g2-^. D5,21)
На больших расстояниях г>-т- = -—» превышающих
. 1
комптоновгкую длину волны ло=т7, соответствующую
мезонам массы jx, полученная энергия взаимодействия
быстро убывает и практически обращается в нуль.
§ 45] СКАЛЯРНОЕ МЕЗОННОЕ ПОЛЕ 341
тт ^ 1
На малых же расстояниях при г < т- можно заменить
Экспонент через единицу:
F=—f, D5,22)
т. е. скалярная энергия связи частиц имеет вид ньютоно-
ньютоновой энергии гравитационного взаимодействия двух масс.
Для того чтобы внутри ядра (г ^ 103 см) для энергии
связи получить разумное значение F~10MeV, мы
должны положить ядерный заряд равным g~5e.
Важно подчеркнуть, что квантовая теория переноса
взаимодействия скалярным вещественным полем (так же
как и в случае электростатического и гравитационного
полей, а также для всех других вещественных бозевских
полей, описываемых не спинорными, а тензорными функ-
функциями) или сопоставленными этому полю частицами целого
спина вновь приводит к тому же выражению, которое
сейчас было нами получено классическим путём.
В случае же взаимодействия протонов и нейтронов
через заряженные бозевские поля, описываемые ком-
комплексными функциями и не имеющие столь непосредствен-
непосредственной классической аналогии как поля вещественные, кван-
квантовая механика приводит к тем же выражениям энергии
взаимодействия нуклеонов Vе, что и для нейтральных
полей, но умноженным на некоторый дополнительный
множитель, так называемый оператор обмена Р [более
подробно см. D5,47)]. Таким образом только что получен-
полученное выражение для скалярных сил следует считать окон-
окончательным для вещественного поля и передающим вели-
величину взаимодействия с точностью до знака в случае заря-
заряженного поля, для нерелятивистского приближения.
Этот простой и наглядный результат имеет фунда-
фундаментальное значение для всей современной теории ядер-
ядерных сил. В самом деле, устанавливая перенос взаимодей-
взаимодействия через поле, связанное с массой покоя jx, мы полу-
получаем силы, имеющие короткодействующий характер, что
является одним из наиболее существенных свойств ядер-
ядерного поля.
Возвращаясь к основной формуле теории короткодей-
короткодействующих сил D5,21), мы видим, что, подбирая константу
342 КЛАССИЧЕСКАЯ МЕЗОДИНАМИКА [гл. V
к0, которая по существу является массой покоя частиц
скалярного поля ( к0 = -^~ j , можно добиться исчезно-
исчезновения сил на требуемом расстоянии порядка г~10~13 см
(совпадающем примерно со значением классического ра-
радиуса электрона). Отсюда масса частиц, переносящих
взаимодействие, по порядку оказывается равной р ^ 200—
—300 массам электрона. Таким образом, сделав гипотезу
о том, что ядерное поле является скалярным, связанным
с частицами, обладающими массой покоя, мы немедленно
можем определить порядок массы частиц, переносящих
взаимодействие. Тем самым предсказывается суще-
существование новых (в данном случае нейтральных) элемен-
элементарных частиц средней массы, промежуточных между
электронами и нуклеонами. При этом, как уже указыва-
указывалось выше, теория заряженного скалярного поля приводит
к тем же результатам в отношении порядка массы и ядер-
ядерного заряда.
Как выяснилось в классической и квантовой теории
сил, взаимодействие через поле, связанное с массой покоя,
иначе говоря, перенос взаимодействия частицами конеч-
конечной массы, всегда приводит к силам короткого действия
с радиусом г0, определяемым массой покоя, именно:
1 h
причём в классических уравнениях поля к0 можно рас-
рассматривать как некоторую константу.
Таким образом с помощью скалярного поля, связан-
связанного с массой покоя, удаётся объяснить короткодейству-
короткодействующий характер ядерных сил притяжения, притом зарядно-
независимый для поля нейтрального и обменный в случае
заряженного поля.
б) Общая теория скалярного поля
Разовьём теперь в кратком виде основные соотношения
общей теории скалярного поля*).
*) W. P a u I i und V. Weisskopf, Helvetica Physica
Acta, 7, 809, 1934; Д. Иваненко и А. Соколов, Труды
СибФТИ, 5, 32, 1937.
§ 45] СКАЛЯРНОЕ МЕЗОННОЕ ПОЛЕ 343
Ограничиваясь сперва для простоты случаем OTcyis
ствия нуклеонных источников, имеем согласно D5,9)
следующее выражение для функции действия свободного
вещественного поля:
S=^L(dz)9 D5,23)
где лагранжиан
"D5,24)
Отсюда, варьируя L по волновой функции ср, получим
уравнение для скалярных мезонов в вакууме
которое является частным случаем уравнения D5,15)
в отсутствии нуклеонов (g — 0).
Пусть при решении волнового уравнения для свобод-
свободных частиц на волновую функцию ср накладывается
условие периодичности по пространственным координатам.
Обозначая через L длину куба периодичности, имеем
?(^п) = <р(^п + £)>
где п=-1, 2, 3.
Указанным условиям периодичности удовлетворяют,
например, следующие ортонормированные функции:
1 г -г- пг
z
где
a nlf n2, п3 являются целыми числами, принимающими
любые положительные и отрицательные значения, вклю-
включая значение нуль. :
Введём волновой вектор
344 КЛАССИЧЕСКАЯ МЕЗОДИНАМИКА [гл. V
Тогда условие ортонормированности примет вид
\_ [ е1 ** . е-'" *'* (dr) = Ъккг = 8„яП; 8П2п^ 5Пз^,
L*v
причём интегрирование совершается по объёму V = L3.
Волновую функцию представим разложенной в трёхкрат-
трёхкратный ряд Фурье:
где тройная сумма берётся по всевозможным значениям
вектора А".
Подставляя последнее выражение в D5,25), получим
следующее дифференциальное уравнение для определения
коэффициентов А (к, t):
A(te,t)+c2K*A(k,t) = 0,
где
откуда находим
A(k,t) = A (к) e~icKt + В (к) eic**.
Здесь А и В являются произвольными постоянными, кото-
которые могут зависеть лишь от вектора А\
Учитывая, что функция ср является вещественной, мы
должны положить
Поэтому общее решение скалярного уравнения без источ-
источников имеет вид
Ч = £h 2 И М e-fel«+«" + А* (к) е**«-*"],
к
причём в последней сумме мы заменили вектор к на—к.
Решение волнового уравнения может быть найдено
также без дополнительного условия периодичности фун^
кции «р для весьма общего вида ср.
§ 45] СКАЛЯРНОЕ МЕЗОННОЕ ПОЛЕ 345
В этом случае решение может быть записано в виде
трёхкратного интеграла Фурье:
? = 7ГЫ \ tA <*> e~icKt+ikr + ^ (*) «*«- '*"] (d*).
Подставляя последнее выражение в D5,25), легко убедить-
убедиться, что оно представляет искомое решение.
Найдём канонический тензор энергии (точнее говоря,
тензор плотности энергии—импульса—натяжений).
Для этой цели воспользуемся следующим тождествен-
тождественным соотношением:
dL dL dL д dL \ f d dL dL.
откуда, учитывая D5,25), находим закон сохранения
для некоторого тензора 2-го ранга, являющегося иско-
искомым тензором энергии (см. также § 30):
Полученный закон сохранения находится в согласии
с теоремой Нетер, поскольку образование канонического
тензора энергии обязано инвариантности лагранжиана
относительно смещения координат. Этот канонический
тензор является симметричным G\р = Т$а) и поэтому дол-
должен совпадать с метрическим тензором энергии.
Для плотности энергии имеем выражение
±
, D5,26)
которое является положительно дефинитным в согласии
с теоремой Паули о положительности плотности энер-
энергии для полей, описываемых не спинорными, а тензорными
(в данном случае скалярными) функциями и тем самым
сопоставленным бозевским частицам целого спина*).
*) В. Паул и, Релятивистская теория элементарных ча-
ртиц> ИЛ, 1947, стр. 72.
346 КЛАССИЧЕСКАЯ МЕЗОДИНАМИКА* [гл. V
Для вектора плотности количества движения скаляр-
скалярного поля имеем
(ЬЬ 27^
дхп di' К^^П
Остальные компоненты Тпк определяют «натяжения».
Плотность момента количества движения скалярного поля
(см. также § 30 б) по общему определению находится из
равенства
М[о PJ Y = i- (ха Тп - хь Ты). D5,28)
Симметрия тензора энергии Та$ обеспечивает выпол-
выполнение закона сохранения для тензора моментов:
Поэтому к тензору момента А/"[ар] т не требуется доба-
добавления спинового момента поля, с тем, чтобы полный
момент (орбитальный плюс спиновый) удовлетворял
закону сохранения. Иначе говоря, спиновый момент ска-
скалярного поля равен нулю. Это обстоятельство физически
весьма наглядно связано с тем, что при наличии одной
компоненты поляризационные свойства у поля отсутствуют
и, следовательно, согласно квантовому корпускулярно-
волновому дуализму, частицы, сойоставленные скаляр-
скалярному полю, не должны обладать спином.
Покажем, что условие обращения расходимости от
тензора Т^ в нуль
ведёт к законам сохранения энергии и импульса поля.
В самом деле, последнее равенство может быть пред-
представлено в виде
Умножая его на элемент трёхмерного объёма (dv) и
учитывая, что при интегрировании по всему проотран-
I 45] СКАЛЯРНОЕ МЕЗОННОЕ ПОЛЕ 347
ству объёма V
J дхп
имеем
. = 0,
т. е. при [3~4 мы получаем закон сохранения энергии:
U= \ Ти {dr) = const,
а при Р = 1, 2, 3—закон сохранения импульса.
Подставляя сюда вместо ср разложение в ряд Фурье
и учитывая, что
h 2 2 \м(*)eikrN (fe/) е~Шг(dr)= 2 м
найдем
Как и следовало ожидать, временные члены в выраже-
выражение для энергии U не входят.
В квантовой теории энергия частицы импульса s—
ch Tr
равна д-л, поэтому, полагая
(к) = |/^ а (*), ^+ (*) - /± а+ (к),
К
имеем
Отсюда видно, что величину а+ (к) а (к) следует рас-
рассматривать как число скалярных мезонов, обладающих
энергией ^- К.
Обобщим теперь скобки Пуассона, применяемые в меха-
механике при исследовании движения системы материальных
точек, на случай волновых функций поля.
348 КЛАССИЧЕСКАЯ МЕЗОДИНАМИКА [гл. V
Как известно, в классической механике функция дей-
действия имеет вид
«S = yj£dt, D5,29)
причём лагранжиан L зависит от обобщённых координат
» dgi
qt и скоростей qt = -~ .
Вводя понятие импульса
D5,30)
мы можем составить выражение для скобок Пуассона:
(дЛ™*А**Лш D5,31)
d*dj v }
где сумму следует брать по всем степеням свободы систе-
системы материальных точек.
В частности, полагая величины А и В равными обоб-
обобщённым координатам и их импульсам, находим
[qn> ?n'] = [Ai> /V] = O,
D5,32)
[Рп, <7n'] = 8nn'-
Отсюда ясно, что пуассонова скобка для двух величин
будет равна единице только в том случае, если эти вели-
величины являются канонически сопряжёнными, т. е. если
выбрав одну из них за координату qt^By мы получим
в качестве сопряжённой величины импульс: р = А.
Для того чтобы найти скобки Пуассона для волновых
функций поля, мы приведём выражение вариационного
принципа D5,25) к виду D5,29):
;dt, D5,33)
где
Г= [ L (dr). D5,34)
§ 451 СКАЛЯРНОЕ МЕЗОННОЕ ПОЛЕ ,, 349
Поэтому, как указывалось раньше, функция Лагран-
жа поля L является по существу плотностью функции
Лагранжа в смысле определения механики точки.
В качестве обобщённых координат следует выбрать
волновые функции ср.
Таким образом мы имеем континуум значений вол-
волновых функций ср, соответствующих каждой точке про-
пространства.
Для простоты рассуждений разобьём всё пространство
на отдельные ячейки, каждую из которых будем харак-
характеризовать тремя числами п(п1у п2, п3) или радиус-век-
радиус-вектором Тп-
Обозначая объём каждой ячейки через
можем представить лагранжиан D5,34) в виде
Х-
где плотность функции Лагранжа L зависит от обобщён-
обобщённых координат ср (тп) — ср (п) и их скоростей ср (п) = ^ .
Согласно определению D5,30) канонический импульс
равен
р (п) = 4^- - р (п) AF, D5,35)
d'i (п)
причем величину р (п) = -г можно рассматривать как
импульс поля или точнее плотность импульса.
В частности, в случае лагранжиана скалярного поля
D5,24) мы имеем для плотности импульса
Скобки Пуассона D5,31) примут в нашем случае вид
г л Bi V ! ( дА дВ дВ дА
*) Для простоты положим, что объёмы всех ячеек равны
ДРУГ ДРУГУ-
350 КЛАССИЧЕСКАЯ МЕЗОДИНАМИКА [гл. V
Подставляя вместо величин А и В значения обобщён-
обобщённой координаты ср и плотности импульса р, получаем
[ср (и), <р (п1)] = [р(п), у (п')] = 0, D5,38)
[р{п), ?(«')] = %■'; D5,39)
иными словами, скобки Пуассона для координат и плот-
плотности импульса, относящиеся к различным точкам, обра-
обращаются в нуль, а для одинаковых точек етремятся к бес-
бесконечности, т. е. просто равны 8-функции. Действи-
Действительно,
lim T.^AF=1,
кроме того \ о (т — У) (d'l') = 1. Поэтому при переходе к
пределу &V —» 0 мы получаем следующее выражение для
классических скобок Пуассона скалярного поля:
Ыт, t), <p(r', t)]=*[p(r, t), P(r', 01 = 0,
D5,40)
[Р(т, t), ф', t)]=b(i'-r).
Последние скобки Пуассона (трёхмерные) составлены
из двух волновых функций, относящихся к различным
пространственным координатам, но к одному и тому же
моменту времени.
Произведём обобщение трёхмерных скобок Пуассона
на четырёхмерный случай, при котором каждая из вол-
волновых функций должна зависеть от своей координаты и
от своего времени (релятивистски инвариантные скобки
Пуассона).
Нетрудно показать, что четырёхмерные скобки Пуассо-
Пуассона связаны с перестановочной ^-функцией B0,4):
), D5,41)
Mr, t), 9(J-', /')] = 4wZ>(!•--*', t-t'). D5,42)
§ 45] СКАЛЯРНОЕ МЕЗОННОЕ ПОЛЕ 351
В самом деле, принимая во внимание соотношение
мы можем из D5,42) получить все три равенства D5,40).
Отсюда вытекает важное заключение об инвариант-
инвариантности четырёхмерных скобок Пуассона, связанное с реля-
релятивистской инвариантностью функции D. Как известно,
с помощью скобок Пуассона можно проделать переход
от классической механики к квантовой.
В квантовой теории классические скобки Пуассона
должны быть заменены квантовыми, определяемыми равен-
равенством
[A,B]K< = ?f(AB-BA), D5,43)
т. е. в квантовом слунае величины А и В рассматриваются
как операторы, в общем случае не коммутирующие друг
с другом.
Например, в квантовой механике вместо классических
скобок Пуассона механики точки D5,32) мы имеем для
простейшего случая q = х
™(рхх-хРх) = 1. D5,44)
Для того чтобы удовлетворить последнему соотноше-
соотношению, мы должны выбрать оператор импульса в виде
рх 2™ дх '
причём справа необходимо поставить функцию ф, на кото-
которую действует оператор.
Таким образом операторное равенство D5,43) экви-
эквивалентно следующему:
Т-[Рх№-*(рА)] = Ч- D=5,45)
Точно так же, для того чтобы проделать переход от
классической теории поля к квантовой, мы должны заме-
заменить классические скобки Пуассона D5,40) квантовыми,
352 КЛАССИЧЕСКАЯ МЕЗОДИНАМИКА [гл. \
которые для скалярного поля согласно D5,43) и D5,36)
сведутся к следующим операторным равенствам:
cp(r-, t) <?(?•', *)-<?(»•', t) <?(/-, г) =
= р(г, г)р(У, t)-p(v', t)p(r, t) = 0,
p(f, t) 4{r',t)-4(ir',t)p{r,t) = b{r-4-')-!^.t D5,46)
где согласно D5,36)
В релятивистски инвариантном четырёхмерном случае
вместо последних соотношений следует положить
D5,47)
что оправдывает название D функции, как перестано-
перестановочной.
В квантовой теории доказывается, что волновые
функции ср и их производные следует теперь рассматри-
рассматривать в качестве операторов, действующих на функцию от
числа частиц, сопоставленных полям.
в) Комплексное скалярное поле
Не входя в детали, выпишем теперь некоторые основ-
основные соотношения для случая комплексного скалярного
поля, не имеющего столь непосредственного классического
аналога, как цоле вещественное, и описывающего в кор-
корпускулярном аспекте не нейтральные, а заряженные части-
частицы (скалярные заряженные мезоны спина 0). Теория ком-
комплексного поля эквивалентна теории двух действительных
полей, равных действительной и мнимой части комплекс-
комплексного поля. Лагранжиан комплексного поля имеет вид
Отсюда, варьируя L по координатам ср+:
8L дЬ д дЬ 0
§ 45] СКАЛЯРНОЕ МЕЗОННОЕ ПОЛЕ 353
мы получим уравнение для волновой функции ср:
= °- D5,49)
Точно так же варьирование по ср даёт аналогичное
волновое уравнение для <р+.
Для тензора энергии будем иметь выражение
В частности, для плотности энергии находим снова
положительно дефинитное выражение:
D5,50)
Комплексное скалярное поле (т. е. в корпускулярном аспек-
аспекте заряженные бессппновые мезоны) может взаимодейст-
взаимодействовать с электромагнитным полем. Это взаимодействие
лучше всего описать при помощи добавления к лагранжи-
лагранжианам свободного скалярного и свободного электромагнит-
электромагнитного полей смешанной части, составленной по общему
правилу. Как и в других случаях взаимодействия полей
заряженных частиц с электромагнитным полем, этот доба-
добавок сводится к членам, получающимся путём замены ком-
компоненты импульса /?v на обобщённый Pv = /?v AVy или
с
замене градиента ^— , действующего на мезонную функ-
функцию, на оператор
Vv==^_2-|-e^v D5,51)
(А^—потенциалы электромагнитного поля).
Поэтому лагранжева функция скалярного * поля вме-
вместе со смешанной частью, описывающей связь с полем
электромагнитным, будет иметь вид
23 Д. Иваненко и А. Соколов
354 КЛАССИЧЕСКАЯ МЕЗОДИНАМИКА [гл. V
Отсюда обычными методами получим как уравнения для
самих волновых скалярных функций (т. е. заряженных
мезонов) в электромагнитном поле, так и тензор энергии
и все другие основные величины, характеризующие поле.
Например, скалярное уравнение для ср будет теперь
иметь вид:
Тем самым воздействие электромагнитного поля на ска-
скалярные мезоны оказывается полностью описанным. С дру-
другой стороны, заряженное скалярное поле (т. е. сопостав-
сопоставленные ему частицы—бесспиновые заряженные мезоны)
само является источником электромагнитного поля, так
что плотность заряда—тока скалярного поля необходимо
включить в правые части уравнений Максвелла-Лорентца.
Так как уравнения Максвелла-Лорентца получаются путём
вариации лагранжевой функции по электромагнитным
потенциалам, то вариация смешанной части лагранжиана
(описывающей связь скалярного и электромагнитного по-
полей) по потенциалам должна дать четырёхмерный вектор
плотности тока. Выпишем значение плотности тока, вы-
вызванного скалярным заряженным полем (бесспиновыми
мезонами).
8L ie
или при отсутствии электромагнитного поля
* dp
Отсюда видно, что для вещественного поля (<р+ = <р) ток
обращается в нуль, и поэтому, как неоднократно под-
подчёркивалось, подобное поле описывает поведение ней-
нейтральных частиц.
Легко убедиться в том, что вектор плотности тока удо-
удовлетворяет уравнению непрерывности:
§ 45] СКАЛЯРНОЕ МЕЗОННОЕ ПОЛЕ 355
Заметим, что несмотря на явное включение электромаг-
электромагнитных потенциалов в лагранжиан, уравнения поля, как
и требуется, являются инвариантными относительно пре-
преобразований калибровки.
В самом деле, при преобразованиях калибровки
A'v = Av + — ,
новые функции будут иметь вид
2та'е . 2-rcie .
где /—произвольная скалярная функция всех четырёх
координат.
В справедливости этих преобразований легко убедить-
убедиться, воспользовавшись тождеством
дх^ he уJ т \дху he
С точки зрения теоремы Нетер закон сохранения тока
(т. е. уравнение непрерывности) соответствует инвариант-
инвариантности уравнений комплексного скалярного поля относи-
относительно преобразований калибровки.
Обратим внимание на выражение плотности заряда
D5,52) р =— /4 скалярных частиц при исчезающем электро-
электромагнитном поле (Ау = 0):
S¥O <45'53>
Это выражение индефинитно (т. е. может принимать как
положительные, так и отрицательные значения) в проти-
противоположность известному из теории Шредингера выра-
выражению
являющемуся нерелятивистским приближением к фор-
формуле D5,53).
23*
356 КЛАССИЧЕСКАЯ МЕЗОДИНАМИКА [гл. V
Поэтому, в то время как делением на заряд в нереляти-
нерелятивистском случае получается дефинитное выражение ср+ср,
которое интерпретируется как плотность вероятности,
в релятивистском случае для скалярного уравнения непо-
непосредственное истолкование величины 3L как плотности
вероятности, очевидно, невозможно. Это обстоятельство
в добавочной связи с тем, что скалярное уравнение приво-
приводит в кулоновом поле к уровням энергии соответствующей
бесспиновой частицы, не согласующимся с подтверждён-
подтверждённой опытом формулой Зоммерфельда для тонкой структуры
уровней энергии электрона, послужило Дираку поводом
первоначально считать самое скалярное уравнение пол-
полностью ошибочным. Дирак начал искать новое релятивист-
релятивистское уравнение, ставя во главу угла теории дефинитное
выражение плотности вероятности tyvtyv» гДе волновая
функция tyv была взята теперь уже с несколькими компо-
компонентами, необходимыми для описания спиновых свойств.
Впоследствии выяснилось, однако, что скалярное уравне-
уравнение, конечно, непригодно для описания электрона и дру-
других спиновых частиц, но способно вполне закономерно
описывать бесспиновые частицы, которые естественно име-
имеют другие уровни энергии в кулоновом поле, например
ядра, по сравнению с электронами.
Как показал Паули A939 г.), индефинитность плот-
плотности заряда также представляет собою закономерный
факт, общий для плотности заряда любых бозевских
частиц целого спина, описываемых не спинорными, а обыч-
обычными тензорными функциями (скалярами, псевдоскаляра-
псевдоскалярами, векторами и т. д.). С другой стороны, плотность энер-
энергии для бозевских частиц будет всегда положительно
дефинитной (например, для скалярных и векторных ме-
мезонов).
Далее выяснилось, что комплексные поля описывают
одновременно заряженные частицы обоих знаков заряда,
так что индефинитность плотности заряда в конце концов
после надлежащей интерпретации частей волновых функ-
функций Ф7 и 0^, связанных с противоположно заряженными
частицами, выражает тот тривиальный факт, что общий
заряд равняется разности зарядов.
§ 46] ПСЕВДОСКАЛЯРНОЕ МЕЗОННОЕ ПОЛЕ 357
§ 46. Псевдоскалярное мезонное поле
а) Псевдотензоры
Немаловажную роль в современной теории волновых
полей и элементарных частиц играет использование волно-
волновых функций, дуальных к скаляру, вектору и т. д.
Для построения дуальных величин рассмотрим тен-
тензор четвёртого ранга cpapY§, антисимметричный относи-
относительно любой пары значков, т. е. <р^рт5 = -—<рр<*тз и т. д.
Все составляющие этого тензора с двумя одинаковыми
значками должны равняться нулю, так как согласно опре-
определению, например, <рт§ = — ?т5- Отличными от нуля
будут только те составляющие, у которых все значки
а, р, у и 8 будут отличаться друг от друга и, следовательно,
будут составлять произвольную перестановку чисел
1, 2, 3 и 4. В каждом данном случае мы можем путём
ряда транспозиций перейти к составляющей тензора ср1234.
Обозначая для краткости основную компоненту ср1234 через
ср, мы видим, что каждая из 256 компонент антисимметрич-
антисимметричного тензора четвёртого ранга должна иметь одно из
значений:
+ ?! О, -С?.
Целесообразность особого обозначения указанной вели-
величины специальным образом через значок тильда (~) выяс-
выяснится ниже.
Поэтому мы можем положить:
срарг8==влрТ5?1 D6,1)
где
0, если среди значков а, C, у, 8 имеются
равные;
1, если значки а, C, у, о можно располо-
__ i жить в порядке 1, 2, 3, 4 посредством
— S чётного числа транспозиций;
— 1, если необходимо нечётное число
транспозиций для перевода значков
а, р, у, 8 в порядок 1, 2, 3, 4.
358 КЛАССИЧЕСКАЯ МЕЗОДИНАМИКА [гл. V
Составляющие eapYe ведут себя как компоненты
антисимметричного тензора четвёртого ранга по отно-
отношению к любым четырёхмерным вращениям системы коор-
координат; однако при изменении направления одной или
трёх координат символ £арт8 уже не совпадает с тензором
в буквальном понимании, отличаясь от него знаком.
Поэтому в дальнейшем мы будем его называть антисим-
антисимметричным псевдотензором четвёртого ранга, ставя вверху
над псевдовеличинами значок тильда ~.
В частности, поведение символа sapYs при зеркальных
преобразованиях
#п= — %п, #i = #4 D6,2)
отличается от поведения тензоров.
В самом деле, при переходе от одной системы к другой
компоненты тензора четвёртого ранга преобразуются по
закону
дх[ дх'ъ дх'ъ дх\
При зеркальных преобразованиях D6,2) имеем
где эйзенхартовы значки г^ (применяемые с пользой при
операциях в псевдоэвклидовом мире), индексы р, при ко-
которых не учитываются при правилах суммирования, равны
ех = г2 = г3 = — 1, е4 = 1,
т. е. в нашем случае
= sl522334?1234 = —
отсюда видно, что основная компонента тензора должна
менять знак, в то время как символ е1234, будучи опре-
определённым одинаково для всех систем координат, не меняет
знака.
§ 46] ПСЕВДОСКАЛЯРНОЕ МЕЗОННОЕ ПОЛЕ 359
Таким образом компоненты псевдотензоров не удо-
удовлетворяют обычным правилам, известным для тензоров
при зеркальных преобразованиях.
Скалярные произведения двух псевдотензоров будут,
очевидно, удовлетворять правилам поведения тензоров
при зеркальных преобразованиях и поэтому являются
тензорами.
В частности, произведение
^' = 24
оказывается скаляром*).
Наряду с антисимметричным тензором четвёртого ран-
ранга срарт5, полученным с помощью символа sapY8 из величины
ср, которая, как нетрудно видеть, является псевдоскаляром,
мы можем аналогичным образом получить также антисим-
антисимметричный тензор третьего ранга, исходя из псевдо-
псевдовектора. Действительно, имеем
Точно так же образуем антисимметричный тензор второго
ранга:
1 -
где срар называется антисимметричным псевдотензором
второго ранга.
Все величины, образуемые при помощи символа заРт8,
называются дуальными к исходным; таким образом псев-
псевдотензоры дуальны к обычным, и обратно.
*) В случае преобразования криволинейных координат, суще-
существенном в общей теории относительности, значения символа
в новой и старой системах связаны соотношением
360 КЛАССИЧЕСКАЯ МЕЗОДИНАМИКА [Гл. V
В самом деле, из последних равенств мы можем обратно
псевдотензоры выразить через обычные тензоры:
1
24 г*
? И Т. Д.
Если законы преобразования для тензоров при зеркаль-
зеркальных преобразованиях имеют вид
то для псевдотензоров эти правила гласят:
причём среди a, p, y, 8 не должно быть равных значков.
Приведём несколько примеров образования псевдо-
псевдотензоров, или величин, дуальных к исходным.
Как известно, антисимметричный тензор второго ранга
электромагнитного поля определяется равенством
где
Нп = Н„ Я14= —iEx и т. д.
§ 46] ПСЕВДОСКАЛЯРНОЕ МЕЗОННОЕ ПОЛЕ 361
Дуальный по отношению к нему антисимметричный
псевдотензор второго ранга равен
Яер= ■g-e.pp.v/fp.v, т. е. #12 = —iEz, HU*=HX и т. д.
Таким образом компоненты Н^ составлены из ком-
компонент Н^ путём перестановки вектора магнитного
поля Н с вектором электрического JE7, которые обладают
различной зеркальной инвариантностью. Действительно,
вектор JE при зеркальных преобразованиях всех трёх
координат меняет знак, а вектор И остаётся неизменным.
Приведём ряд других примеров псевдовеличин. В трёх-
трёхмерном пространстве объём параллелепипеда, построен-
построенного на трёх векторах А, В и С, определяется формулой
и характеризуется псевдоскаляром. С точки зрения тен-
тензорного анализа объём задаётся антисимметричным тен-
тензором третьего ранга с компонентами
Vkm=
АкАгА
Lm
Jm
причём
v=vm.
Векторное произведение двух векторов, т. е. площадь
параллелограмма, построенного на векторах А и В:
С=[АВ],
является псевдовектором, получившим название аксиаль-
аксиального вектора, в противоположность истинному, т. е.
полярному вектору. С точки зрения тензорного анализа
площадь определяется антисимметричным тензором вто-
второго ранга:
причём С1 = С23 и т. д.
362 КЛАССИЧЕСКАЯ МЕЗОДИНАМИКА [гл. V
Наконец, укажем, что с понятием псевдотензоров нам
придётся встретиться при исследовании взаимодействия
нуклеонов с полем мезонов, подчиняющихся различным
уравнениям (скалярному, псевдоскалярному, векторному
или псевдовекторному). Образуем смешанную функцию
действия по общему правилу [см., например, D5,10I
где U должно являться инвариантом, характеризующим
энергию взаимодействия.
Накладывая на энергию U требование, чтобы она
была линейна относительно функций мезонного поля
и не содержала высших производных, мы получаем одно-
однозначный ответ для образования U (х).
Особенно просто можно составить выражение для
S3 в квантовой теории, когда нуклеоны подчиняются урав-
уравнениям Дирака:
где у — волновая функциянуклеона, Е — — -к—.-к;] Р = <г~
являются соответственно оператором энергии и опе-
оператором импульса и а, р3 — матрицами Дирака, образо-
образованными из четырёхрядных матриц рп и оп(/г = 1,2, 3),
удовлетворяющих соотношениям
3n = l, pn = l, Pj|3n'=<*n,pn И Т. Д.
Как известно, из шестнадцати матриц Дирака, обра-
образующих группу*), мы можем составить следующие ве-
величины:
1) Четырёхмерный вектор:
*) Всевозможные произведения и степени матриц равны дру-
другим матрицам р тр^лостью до значения коэффициентов, равных
± i или ± 1.
§ 46] ПСЕВДОСКАЛЯРНОЕ МЕЗОННОЕ ПОЛЕ 363
Здесь I является единичной матрицей. Точнее, компо-
компонентами четырёхмерного вектора являются так назы-
называемые матричные элементы
которые равняются отношению компонент четырёхмерной
скорости электрона к скорости света.
Если мы введём матрицы сь о2, о3из4 = pxi, то матрица
скорости будет равняться
2) Антисимметричный тензор второго ранга при р. Ф v
образуется из следующих матриц:
Его составляющие будут равны
/а23 а31 а12\ _ / p8alf р3а2, РзазА //6 3)
Умножив последнюю матрицу на величину , полу-
получим значения собственного магнитного (верхняя строка)
и электрического момента электрона и других частиц
спина ~ — , описываемых уравнением Дирака.
Вместо компонент антисимметричного тензора <х^
можно ввести компоненты дуального тензора:
причём
«23— al4=
ai4— cc23 =
3) Антисимметричный тензор третьего ранга, компо-
компоненты которого при разных значениях значков р-, v и е
равны
364 КЛАССИЧЕСКАЯ МЕЗОДИНАМИКА [гл. V
Вместо антисимметричного тензора третьего ранга
можно ввести псевдовектор
причём составляющие псевдовектора
т. е. матрицы Ср., образуют псевдовектор, и в дальнейшем
мы их будем писать без значка «тильда» (~). Матрицы
о характеризуют спин электрона и других частиц полу-
целого спина. Спин s~-—~q.
4) Наконец, мы имеем ещё антисимметричный тензор
четвёртого ранга, компоненты которого при различных
значениях значков р> v, э, р равны
где псевдоскалярная матрица
Р =Р2-
Смешанная функция действия S% в квантовом случае
равна
При переходе к классическому случаю мы должны
положить трёхмерную плотность у+*£ равной
а вместо матриц Дирака поставить классическое прибли-
приближение для матричного элемента, например
D6,4)
чем в дальнейшем мы и будем пользоваться.
Энергия взаимодействия U представляет собою инва-
инвариант, образованный как сумма инвариантов по правилу:
произведение скаляра мезона на скаляр нуклеона плюс
вектор мезона на вектор нуклеона и т. д.
§ 46] ПСЕВДОСКАЛЯРНОЕ МЕЗОННОЕ ПОЛЕ 365
При переходе к нерелятивистскому случаю матрицы,
v Г
пропорциональные рх и р2, имеют порядок — ( например,
a^piC-—— j , и поэтому могут быть отброшены, а ма-
матрицы р3 и / следует положить равными единице. Трёх-
Трёхмерный же вектор а переходит в единичный вектор, харак-
характеризующий направление спина нуклеона. Отсюда,
например, в случае скалярных мезонов мы имеем для энер-
энергии взаимодействия нуклеонов со скалярным полем вы-
выражение
которое в нерелятивистском приближении совпадает с
равенством D5,10а).
б) Псевдоскалярное поле
Как было показано в предыдущем параграфе, с по-
помощью скалярного мезонного поля удаётся объяснить
короткодействующий характер ядерных сил. Однако ска-
скалярное поле не может объяснить возникновения спино-
спиновых (центральных и нецентральных) сил, играющих основ-
основную роль в ядерном взаимодействии.
К спиновым силам мы можем придти, если введём
псевдоскалярное, векторное или псевдовекторное поле
(или поле пар фермиевских спинорных частиц).
Поэтому следующий этап теории ядерных сил естест-
естественно должен быть связан с исследованием этих полей.
Прежде всего остановимся на анализе псевдоскаляр-
псевдоскалярного поля, в основу которого взята псевдоскалярная
функция ср.
Это поле в настоящее время стоит в центре внимания
по двум причинам. Во-первых, потому, что тс-мезоны,
нейтральные и заряженные, принимающие, повидимо-
му, наибольшее участие в переносе ядерных сил, явля-
являются по всей вероятности псевдоскалярными. Во-вторых,
по тому, что при помощи псевдоскалярного поля с устра-
устранённой хотя бы приближённо дипольной трудностью
366 КЛАССИЧЕСКАЯ МЕЗОДИНАМИКА [гл. V
удается дать наилучшее возможное сейчас описание
ядерных сил.
Введём антисимметричный тензор четвёртого ранга
<раМ, связанный с псевдоскаляром ср соотношением
<PapY8=SapT8<P- D6,5)
Из тензора четвёртого ранга мы можем образовать
также антисимметричный тензор третьего ранга
связанный с четырьмя компонентами псевдовектора
сра = ^- D6,5а)
соотношением
г* f
Полную теорию свободного псевдоскалярного поля,
связанного с массой покоя (мезонов), можно развить,
исходя из функции Лагранжа, построенной из обычных
тензоров и приводящей к линейным уравнениям с наи-
наинизшими производными
При этом мы, как обычно в данном изложении, огра-
ограничиваемся вещественным полем, соответствующим ней-
нейтральным частицам, которое может быть полностью
истолковано классическим путём.
Учитывая соотношения D6,5) и D6,5а), мы можем пред-
представить этот лагранжиан в более простом виде через
исходный псевдоскаляр ср и псевдовектор сра:
Таким образом лагранжиан псевдоскалярного (мезон-
ного) поля совпадает в случае отсутствия источников
(нуклеонов) с лагранжианом скалярного поля.
§ 46] ПСЕВДОСКАЛЯРНОЕ МЕЗОННОЕ ПОЛЕ 367
Поэтому как для волнового уравнения, так и для
тензора энергии, спина и т. д. свободных псевдоскаляр-
псевдоскалярных частиц оказываются непосредственно применимы
результаты, полученные выше для скалярных частиц
с соответствующей заменой скаляра <р на псевдоскаляр ср.
В частности, спин псевдоскалярных мезонов, так же как
и скалярных, оказывается равным нулю.
Различие между скалярным и псевдоскалярным поля-
полями появляется при определении энергии взаимодействия
мезонного поля с нуклеонами или же лёгкими частицами,
которые все имеют полуцелый спин и описываются спинор-
ными функциями.
Смешанная функция действия S3, определяющая вза-
взаимодействие мезонного поля с полем нуклеонов, в псевдо-
псевдоскалярном случае имеет вид [см. также D5,10)]
S3 = - [ ds J p (x-z')U(x)(dx). D6,7)
Здесь инвариантное выражение взаимодействия U должно
равняться сумме произведений псевдоскаляра поля ср на
псевдоскаляр нуклеонов р2 и псевдовектора поля сра
на псевдовектор нуклеонов са, т. е.
U = g[^ + K?^ D6,8)
где р2 и crjx представляют классические приближения матриц
Дирака [см. D6,4)]. В прежней теории псевдоскаляр-
псевдоскалярного поля сразу же совершался переход в этом выраже-
выражении к нерелятивистскому случаю. При таком переходе
псевдоскалярная величина р2 и четвёртая составляющая
псевдовектора спина о^ — гн имеют порядок — и по-
с
этому при нерелятивистском приближённом рассмотре-
рассмотрении вообще могут быть отброшены. В классическом слу-
случае единичные векторы трёх пространственных составля-
составляющих псевдовектора спина мы обозначим через ап. Значки
тильда у трёхмерного псевдовектора спина мы писать не
будем. Следовательно, в классическом нерелятивист-
нерелятивистском приближении получим
368 КЛАССИЧЕСКАЯ МЕЗОДИНАМИКА [ГЛ. V
Поэтому окончательно для точечного нуклеона [см.
также вывод формулы D5,11)] имеем
5»= -/J Л' J b(r-ir')b(t-t')onfn(dT)dt. D6,9)
Отсюда вместо D5,4) и D5,5) можно найти следующие
статические уравнения для псевдоскалярного поля, соз-
создаваемого точечным нуклеоном, находящимся в начале
координат:
Ч 1 D6 10)
F = /(*?) ср ) («МО)
Решение уравнения D6,10) может быть легко найдено
с помощью формулы A4,10). Оно имеет вид
Отсюда для потенциальной энергии взаимодействия
двух точечных нуклеонов, обозначаемых соответственно
значками А и В, в псевдоскалярной теории, находим
в статическом случае
е~ког
V)-r . D6,11)
Раскрывая последнее выражение, имеем
'~^а, D6,12)
где
D6,13)
Г
Таким образом взаимодействие через псевдоскалярное
мезонное поле, обеспечивающее так же, как и в скаляр-
скалярном случае короткодействующий характер сил, опреде-
определяемый наличием экспоненциального множителя е~к°г
(обусловленного массой покоя мезонов), приводит, сверх
§ 46] ПСЕВДОСКАЛЯРНОЕ МЕЗОННОЕ ПОЛЕ 369
того, к требуемым спиновым и нецентральным силам
между нуклеонами.
Силы эти определяются характерным фактором Sy\n,
появляющимся также в выражении энергии взаимодей-
взаимодействия двух магнитных или электрических диполей. При
исчезающей массе покоя /'0 = 0 или на относительно малых
расстояниях всё выражение D6,12) переходит в выраже-
выражение энергии взаимодействия двух диполей. Таким обра-
образом псевдоскалярные силы являются «квазимагнитными».
Однако наряду с этим известным успехом нереляти-
нерелятивистское приближение псевдоскалярно!! теории приводит
по сравнению со скалярной к так называемой диполь-
ной трудности. В самом деле на относительно близких
расстояниях г —^ 0, превышающих всё же расстояние
— ~ 10 14 см, для которых нерслятшшотское в пукле-
онах приближение имеет смысл, потенциальная энергия,
как видно из D6,12), расходится пропорционально г~3,
и поэтому согласно теореме вириала (см. § 44) нере-
нерелятивистские псевдоскалярные мезонные силы не могут
обеспечить устойчивых состояний нуклеонов хотя бы,
например, в ядре дейтерона.
В теории векторных сил возникает совершенно ана-
аналогичная дипольная трудность. Более тщательный анализ
показал, однако, что на самом деле дипольная трудность
в псевдоскалярном случае в известном приближении
устраняется*).
Рассмотрим сначала скалярное поле и покажем сразу
для квантового случая, что путём некоторого касатель-
касательного (калибровочного) преобразования с функцией S,
где о = —а"/?1 можноустранить из выражения энергии
взаимодействия (см. стр. 365):
все релятивистские члены с константой /.
*) Е. С. Nelson, Phys. Rev., 60, 830, 1941; F. J. Dyson,
Phys. Rev., 73, 929, 1948; G. Л г a k i, Phys. Rev., 75, 1101, 1262,
1949; К. М. Case, Phys, Rev., 75, 1306, 1949.
24 Д. Иваненко и А. Соколов
370 КЛАССИЧЕСКАЯ МЕЗОДИНЛМИКА [гл. V
Речь идёт ио существу о применении известного метода
перебрасывания членов взаимодействия из гамильтониа-
гамильтониана в волновую функцию. Действительно, производя над
оператором L преобразование
e-sLeJSy/, D6,14)
где у' — новая волновая функция частицы (нуклеона),
взаимодействующей со скалярным мезонным ^-полем,
учитывая, что согласно D5,46) ср коммутирует с ср, — ~
и yep n различных точках, и отбрасывая бесконечные
члены самодействия, обязанные совпадающим простран-
пространственным точкам, получим в преобразованном уравнении
Дирака лишь нерелятивистский член с константой g:
Z =
о-й'8?)/ = О, D6,15)
где
— — h д Ch а г - о Мс2
Таким образом, векторная часть связи со скалярным полем
полностью исчезает и не ведёт в любом приближении
к каким-либо процессам.
Перейдём к псевдоскалярному случаю, когда энергия
взаимодействия нуклеона с мезонным полем задана выра-
выражением D6,8) и уравнение Дирака имеет вид
|)]Z = 0. D6,16)
Полагая в этом случае
S=-?J/.'i? D6Д7)
и учитывая правила перестановки матриц (v = 2, 3) с функ-
функцией es:
^es = e-s{Jv = es{Jv.„ с$ A _ e-2S) pv> D6,18)
которые проще всего проверить, разлагая es в ряд, по-
получим
[Do -gw + A - е^ ?1/?) (Мс\3 + g^2)] •/' = 0. D6,19)
§ 46] ПСЕВДОСКАЛЯРНОЕ МЕЗОННОЕ ПОЛЕ 371
Ограничиваясь в последнем уравнении линейными отно-
относительно псевдоскалярной функции ср членами, получим
окончательно выражение энергии взаимодействия без
дипольной части. Следовательно, уравнение Дирака для
нуклеона, взаимодействующего с псевдоскалярным ср-по-
лем, в данном приближении будет иметь вид
(Л0-^O/ = 0, D6,20)
где G-g + —g-i.
Замечая, что по порядку величины, как следует из
эмпирических данных, / — |-, где масса мезона равна
^-, и что gxzg', перенормированную константу связи
можно представить в виде
= g + fV. где Jf = g. D6,21)
Так как энергия взаимодействия нуклеона с псевдоскаляр-
псевдоскалярным полем
U = Gw D6>22)
имеет по существу тот же вид, что и энергия связи с полем
скалярным
то для энергии взаимодействия частиц А и В, подстав-
подставляя вместо g величину G[j2, получим выражение типа
D5,21), не содержащее явно дипольньтх членов
Как видно, энергия взаимодействия содержит реляти-
релятивистские матрицы р2. Таким образом, мы получили выра-
выражение более точное, чем обычные нерелятивистские фор-
формулы, поскольку в некотором приближении здесь учтён
эффект скоростей нуклеонов. Вместе с тем новая форму-
формула D6,23) отнюдь не может считаться точным оконча-
окончательным выражением, как видно уже из анализа про-
'#2*
372 КЛАССИЧЕСКАЯ МЕЗО ДИНАМИК А [гл. V
деланного выше преобразования, не являющегося к тому
же однозначным. Исключение псевдовекторной части, ве-
ведущей к дипольному взаимодействию, из псевдоскалярной
теории является наиболее существенным успехом общей
теории ядерных сил в последнее время. Однако, к сожа-
сожалению, при этом способе исследования зачёркиваются
нецентральные силы, играющие огромную роль в ядерных
взаимодействиях.
§ 47. Векторное мезошюе поле
а) Основные уравнения
Как было указано выше, уравнения Максвелла время
от времени обобщались в различных направлениях.
Упомянем, например, нелинейное обобщение, предложен-
предложенное Борном, или обобщения на высшие производные Боппа-
Подольского. В годы построения релятивистской кван-
квантовой механики Я. И. Френкель выдвинул идею обобще-
обобщения максвелловских уравнений добавочными членами,
соответствующими наличию покоящейся массы частиц;,
сопоставленных полю. Последняя задача была окончатель-
окончательно разрешена Прока, установившим некоторую систему
уравнений для поля в пустоте, которая была уже исполь-
использована нами выше в качестве второго поля при рассмотре-
рассмотрении теории с высшими производными *). Естественно воз-
возникает вопрос о возможности использования векторных
уравнений для описания мезонного поля.
Для компонент вещественного векторного мезонного
поля выберем электромагнитные обозначения.
Мезонные поля Н[Х^, которые в случае нейтральных
мезонов являются вещественными, связаны с четырёх-
четырёхмерным потенциалом AiX = А, щ соотношением
Компоненты H12 ~ Н'7 и Нп — 1ЕХ будем соответственно
называть компонентами квазимагнитной и квазиэлектри-
квазиэлектрической напряжённости поля.
*) А. Ргоса, Journ. do Phys., 7, 348, 1936.
§ 47] ВЕКТОРНОЕ МЕ30НН0Е ПОЛЕ 373
При отсутствии источников уравнения Максвелла сле-
следующим образом обобщаются на случай (мезошюго) поля,
связанного с массой покоя:
^ + ^ = 0, D7,2)
где к0 связано с массой р. сопоставленных пилю мезонов
7 2TCJJLC
соотношением к0 = —,— .
Установленные таким образом векторные уравнения
для «тяжёлых» фотонов (нейтральные мезоны) прп/0—>0
переходят в обычные максвелловские. '
При переходе к трёхмерным обозначениям уравнения
D7,2) будем называть уравнениями первой группы. Они
принимают вид
rot,ff--^ + AS4 = 0,
с dt ° D7,3)
d *$ O
Точно так же вместо D7,1) мы будем иметь вторую груп-
группу векторных уравнений:
i дл
Нетрудно показать, что условие Лорентца
Jb = O D7,5)
получается для векторных мезонов совершенно автома-
автоматически. Для этого мы должны уравнение D7,2) продиф-
продифференцировать по -— и учесть, что произведение симмет-
ричного тензора -—— на антисимметричный H[IV обра-
обращается в нуль.
Напомним, что в электродинамике условие Лорентца
представляет собою дополнительное уравнение, которое
накладывается на потенциалы, чтобы избежать неопре-
37'* КЛЧССИЧЕСКЛЯ МЕЗОДИНАМИКЛ [гл. V
делённости при выборе калибровки. Для «тяжёлых фото-
фотонов» потенциалы входят явно в первую группу уравнений,
и поэтому уравнения для векторных мезонов не обладают
инвариантностью относительно калибровочных преобра-
преобразовании мезониых потенциалов.
Заметрш, что сам Прока сперва ошибочно предназна-
предназначал свои уравнения для релятивистского квантового опи-
описания электрона взамен дираковских спинорных уравне-
уравнений, ведущих к состояниям с отрицательной энергией.
Это казалось одно время трудностью, которая была раз-
разрешена при помощи гипотезы о позитронах как дырках
среди заполненных уровней отрицательной энергии.
Открытие позитрона, в согласии с предсказаниями теории,
а также взаимного превращения электрона и позитрона
в два фотона и обратно, всё более укрепляло уверенность
в правильности дйраковского уравнения для электрона.
В то же время нами в сотрудничестве с Дурандиным
и Ершовым*) было показано, что векторные уравнения
* описывают частицы бозевского, а не фермиевского типа
и поэтому совершенно непригодны для электронов. Позд-
Позднее было доказано, что кванты векторного поля, как и фото-
фотоны, имеют спин 1. Открытие в космических лучах и позд-
позднее в лабораторных условиях новых полутяжёлых элемен-
элементарных частиц—мезонов, некоторые из которых обладают,
по всей вероятности, целым спином и подчиняются бозев-
ской статистике, заставляет обратить внимание на век-
векторные уравнения как на возможный способ описа-
описания мезонов спина 1. Сейчас известно, что частицы
спина 1 могут описываться также при помощи псевдо-
псевдовекторной волновой функции, однако подобная трак-
трактовка мезонов оказалась мало пригодной для объяснения
ядерных сил. Векторные же уравнения бесспорно стоят
всё время в центре теоретической дискуссии вместе
с псевдоскалярными и являются отправным пунктом
всевозможных вариантов описания мезонов, переносящих
ядерные силы.
Теория мезона, учитывая возможность значения спина О,
применяет также уравнение для псевдоскалярной
Е. Дура н д и н н А. Е р ш о в, ЖЭТФ, 8, 5, 1938.
§ ^7J ВЕКТОРНОЕ Л1ЕЗОШЮЕ ПОЛЕ 375
волновой функции (см. предыдущий параграф) наряду
с описанием мезона при помощи скалярного уравнения,
использованного первоначально Юкава. Как было ука-
указано выше, взятое само по себе скалярное уравнение для
бесспиновых частиц непригодно, так как не позволяет
учесть важных спиновых свойств мезонного поля и поля
ядерных сил, которое, но всей вероятности, является
мезонным. Конечно, не исключается возможность суще-
существования мезонов различных спинов.
Мы остановимся здесь на изложении классической
теории нейтрального векторного поля, которая независимо
от непосредственной применимости к гипотетическим век-
векторным нейтретто (нейтральные мезоны) спина 1 обладает
значительной эвристической силой, позволяя простым
и наглядным путём проанализировать многие успехи
и трудности теории ядерных сил и получить важные
результаты, которые, как оказывается, полностью или по
порядку величины сохраняют силу и в квантовой теории
нейтральных и заряженных векторных частиц спина
единица.
б) Общая теория векторного
м с з о п н о г о поля
С точки зрения теории инвариантов и групп преобра-
преобразований уравнения для вещественного векторного поля
отличаются от максвелловских уравнений классической
электродинамики лишь в одном пункте: в теории мезонов
отбрасывается требование калибровочной инвариантно-
инвариантности (калибровка 2-го рода) потенциалов мезонного поля,
поэтому в уравнения могут явно входить сами потен-
потенциалы. Иначе говоря, теория векторных мезонов строится
при помощи двух фундаментальных инвариантов век-
векторной теории,
/i=-i#,v/V, u /,= -4А. D7,0)
а не одного первого инварианта /г, используемого в тео-
теории Максвелла. С другой стороны, в обеих теориях
сохраняется условие линейности уравнений, поэтому
376 КЛАССИЧЕСКАЯ МЕЗОДИНАМИКА [гл. V
инвариант вида /2 = (EJETJ, с помощью которого можно
составить лишь нелинейные уравнения, в нашем случае
попрежнему не используется. Точно так же в обеих
теориях учитывается условие ограничения наинизшими,
именно вторыми производными.
Во главу угла всей теории, как обычно, ставится
лагранжиан, являющийся линейной комбинацией всех
допустимых инвариантов, в данном случае [см. также
соотношение C3,14)]
L = «/1 + fc/8 = -^tf^tf^-*!^, D7,7)
к2
где для удобства нормировки взято а = 1, Ь = ^-.
Лагранжиан позволяет сконструировать все основ-
основные величины, характеризующие поле. Прежде всего
нетрудно убедиться, что вариационный принцип
t = O D7,8)
действительно-приводит к уравнениям D7,2), т. е. систе-
система векторных уравнений является эйлеровыми «уравне-
«уравнениями движения», получающимися вариацией L по потен-
потенциалам или волновым функциям Aj., играющим роль
обобщённых координат:
дь _дЬ д dL _Q (,„ q
Установив функцию Лагранжа, найдём канонический
тензор энергии.
Для этого так же, как и в теории Максвелла (см. § 30),
воспользуемся тождественным соотношением
^ JL л 4- dL л
~дА\
.дх[х " ^А, v
Учитывая далее, что A^f V<JL = A?t p.v, имеем
*'*- D7'10)
§ 47] ВЕКТОРНОЕ МЕЗОННОЕ ПОЛЕ 377
Принимая во внимание равенство D7,9), а также, что
в нашем случае
дАх, v 4* *У'
преобразуем D7,10) к виду, определяющему закон со-
сохранения тензора плотности энергии — импульса — на-
натяжений:
причём компоненты, канонического тензора энергии равны
• 7^ = 1^,^-8^. D7,12)
Отсюда видно, что канонический тензор является несим-
несимметричным:
Г сап .
Аналогичное заключение было сделано при исследо-
исследовании максвелл овского поля (см. § 30).
Это приводит к тому, что плотность тензора момента
количества движения поля
%
МI>v] Л Z=Z Т (З'Р-* VA
не удовлетворяет закону сохранения
Закону сохранения так же, как и в случае максвел-
ловского поля удовлетворяет тензор момента, равный
\] А,
причём величину
^ ) D7,13)
следует рассматривать как тензор, описывающий спин
мезонного поля (т. е. согласно квантовой теории—мезона).
378 КЛАССИЧЕСКАЯ МЕЗОДИНАМИКА [гл. у
Поэтому в полной аналогии с электромагнитным (фотон-
(фотонным) полем мы получаем для мезонного поля следующее
значение полного спина:
\ D7,14)
откуда видно, что спин векторных мезонов так же, как
и фотонов, равен единице.
Кроме канонического тензора, мы можем образовать
также метрический тензор энергии:#
D7Д5)
Для того чтобы вычислить метрический тензор, сле-
следует сперва проводить вычисления в произвольной коорди-
координатной системе и только в конечном результате (в слу-
случае z± = ict) положить: g^v — glfXV = o^v [см. соотношение
B3,1а)], а определитель, составленный из фундаменталь-
фундаментального тензора
(gll ft 2 #13
£21 #22 #23 ?24
ёз\ #32 #33 §34
#41 §42 g43 §
равным единице.
При произвольном значении метрического тензора g^v
для функции Лагранжа L векторных уравнений будем иметь
Отсюда получим
Tmet
Принимая во внимание известное для метрического
тензора соотношение
§ 47] ВЕКТОРНОЕ ME ЗОННОЕ ПОЛЕ
а также равенство D7,15), находим
r?vet=I^Mjyiv-gi4^v-8^. D7,17)
Аналогичное выражение для тензора энергии было
получено нами при исследовании второго поля уравнений
с высшими производными [см. соотношение C3,25)].
Заметим, что при hi = О мы получаем метрический тензор
C0,24), найденный для электромагнитного поля. В даль-
дальнейшем метрический тензор мы будем обозначать без
значка met вверху, т. е. Т^=Т™1.
Метрический тензор является симметричным:
Разность между каноническим и метрическим тензора-
тензорами, как и сами эти тензоры
пр* грсап гр lj тт I „ /1 4 — _L Л ТТ
удовлетворяет закону сохранения:
и поэтому в полном согласия с вариационными принципами
оба тензора отличаются на величину, четырёхмерная рас-
расходимость от которой обращается в нуль (см. также § 28).
Из D7,17) найдём плотность энергии или гамильтониан
векторного нейтрального поля
Ти = ±[Е* + Н*+ %(<? +А*)], D7,18)
который является положительно дефинитным.
Плотность потока энергии, или вектор Умова-Пойн-
тинга имеет вид
или
l D7,19)
380 КЛАССИЧЕСКАЯ МЕЗОДИНАМИКА [гл. V
Наконец, в полной аналогии со скалярным полем мы
можем написать значение для скобок Пуассона в реляти-
релятивистски инвариантном виде.
Так как мы имеем четыре обобщённые координаты
(четыре компоненты потенциалов поля), то вместо D5,42)
в данном случае получаем при помощи той же основной
перестановочной /^-функции
[АЛг.О; A,(^O] = V/^/>(r-rV--n. D7,19а)
Если бы все координаты поля А^ были независимыми
величинами, то следовало бы естественно положить
Однако потенциалы А^ связаны условием Лорентца
поэтому коэффициенты a^v следует выбрать в таком виде,
чтобы правая часть D7,19а) также удовлетворяла усло-
условию Лорентца:
ф-5£-0. D7,20,
Для этой цели коэффициенты alxv следует положить
равными:
так как, принимая во внимание, что
мы автоматически удовлетворим при этом равенству
D7,20).
Зная четырёхмерные скобки Пуассона для вектор-
потенциала, мы можем найти скобки Пуассона для полей
HlxVf а также трёхмерные скобки Пуассона (t = tr). Переход
к квантовым уравнениям поля осуществляется путём
замены классических скобок Пуассона на квантовые согла-
согласно общему правилу D5,43),
§ 47] ВЕКТОРНОЕ МЕ30НН0Е ПОЛЕ 381
Наконец, можно построить также теорию заряженного
векторного мезонного поля.
В этом случае функция Лагранжа будет связана
с комплексными полями соотношением
Г — —. * Н+ И ^о А* А
^ — g?i \LV-fi |j.v 4^ -^ц-^ц-
Комплексное векторное поле (т. е. заряженные мезоны)
может взаимодействовать с электромагнитным полем, что
лучше всего описать при помощи добавления к лагран-
лагранжиану некоторого члена, зависящего от потенциалов
электромагнитного поля А6^1. Этот добавок сводится,' как
и в случае комплексного скалярного поля, к членам,
получающимся благодаря замене четырёхмерного гради-
ента -—, действующего на мезонные функции А^, опе-
ратором
v _ д Чше Ае1
dxv~~ hc '
Дифференцируя, как обычно, лагранжиан по потен-
потенциалам электромагнитного поля, мы получим значение
для плотности электрического тока, обусловленного дви-
жением- заряженных мезонов:
,\=~1 = ^(Щ^-А;Н,,). D7,21)
Лагранжева функция, а следовательно, и вся теория будут
инвариантны относительно преобразования калибровки
электромагнитных потенциалов, несмотря на явное вклю-
включение потенциалов (емг также теорию скалярного урав-
уравнения) .
в) Векторное мезонное поле при
наличии нуклеонных источников
Перейдём к установлению полной системы векторных
уравнений со включением источников, порождающих по-
поле. Для определённости будем иметь в виду в качестве
источников нуклеоны, хотя лёгкие частицы также могут
играть эту роль.
382 КЛАССИЧЕСКАЯ ME30ДИНАМИКА [гл. V
Для этой цели, кроме функции действия поля мезонов
S2 = \j L0(dx),
где лагранжиан
Lo^ -I^A^v -|ЛЛ> D7,22)
а тензор
>-'-^—tov •
причём
/A* Аи D12\ f Вх Ву Bz ^
\А4 Аи Arf/ \-iDXf-iDv,-iDz/ '
мы должны ввести ещё смешанную функцию действия £3,
определяющую взаимодействие мезонного поля с нукле-
онами.
Как и в предыдущих случаях, значение для S3 запи-
запишем в виде .
^ ds [ р {х-х') U (x) (dx), D7,23)
где инвариантное выражение взаимодействия U (х) будет
для векторного поля равняться сумме произведений:
вектора потенциала А.х мезонного поля на вектор ско-
v
рости а^ == — нуклеонов и тензора поля D^y мезонов на
тензор GCjj,v, характеризующий квазимагнитный и квази-
квазиэлектрический моменты нуклеонов, т. е. *)
U= -gaa^~|/vAv. D7,24)
Других линейных (относительно функций мезонного
поля) комбинаций инвариантов, удовлетворяющих также
*) Связь классического приближения величин а^ и a^v с со-
соответствующими матрицами Дирака указана формулой D6,4).
§ 47] ВЕКТОРНОЕ МЕЗОННОЕ ПОЛЕ 383
условию наинизших (вторых) производных, для энергии
взаимодействия векторного поля с нуклеонами не суще-
существует.
Для того чтобы провести более глубокий анализ по-
последнего выражения, обратимся опять к выражению сме-
смешанного взаимодействия с точки зрения квантовой тео-
теории. Выражение D7,24) может быть записано через ма-
матрицы Дирака при помощи равенства
- g (? - (аА)) - / (Ря (aB) + н (oD)).
Здесь а^—матрица скорости, а <х^—матрица магнитного
й электрического моментов, связанная с матрицами
р2 и ро и матрицей спина а соотношением D6,3).
Учитывая, что при малых скоростях р3—>1, а а,
V тт
[i2 ~ — , имеем следующее выражение для и, пригодное
в нерелятивистском приближении:
причём в классическом пределе под а следует понимать
единичный вектор, характеризующий направление спина.
Поэтому в нерелятивистском приближении для точеч-
точечного нуклеона имеем
Отсюда для потенциальной энергии взаимодействия
нуклеона с мезонным полем находим
= U(r',t') = g<?-f(oB), D7,25)
где волновые функции ср и JB зависят от координат нуклео-
нуклеона г', t'.
Функция действия мезонного поля с учётом энергии
взаимодействия с нуклеонами будет
384 КЛАССИЧЕСКАЯ МЕЗОДИНАМИКА [гл
где
- х') (g*^ + A/o^A,v) . D7,26)
С помощью уравнений Эйлера
находим основную систему векторных уравнений мезон-
ного поля при наличии источников
г) FT
^1 + ЩА^, D7,27)
jjlv= ±7ГТ4 = ^v"~7roltX%, D7,1о)
причём тензор квазимагнитного момента и вектор тока
нуклеонов соответственно равны
(х х')а ds,
При переходе к трёхмерным обозначениям введём
следующие векторы:
1) вектор квазимагнитной t и квазиэлектрической на-
напряжённости
2) вектор квазимагнитной и квазиэлектрической ин-
индукции
В —D — A D — —D dp _ 1 дАх
у — 23 — х » X — 41 ^д. с dt "
3) вектор квазимагнитной и квазиэлектрической поля-
поляризации
5 47J ВЕКТОРНОЕ МЕЗОННОЕ ПОЛЕ 385
Тогда уравнения D7,27), образующие так называемую
первую группу векторных уравнений, примут вид
di v
где j, i'p образуют в совокупности четырёхмерный ток.
Точно так же для второй группы векторных уравнений
D7,28) мы имеем
H B4kS
( ' }
При исчезающей массе покоя Л:§ —> 0 мы получаем
уравнения для электромагнитного поля в более общем
виде, чем в электродинамике, поскольку магнитные мо-
моменты электронов согласно релятивистской квантовой
механике возникают благодаря своеобразному движе-
движению заряда и равны магнетону Бора уе = т—'— • В пер-
первоначальной теории Дирака дополнительные моменты
(8 и Т) просто не вводились (более подробно см. допол-
дополнение). Всё же наша теория целиком применима для
электродинамики, если положить А§ .^0, а у источников
наряду с кинематическим моментом ввести ещё вро-
врождённый момент, как это имеет место, например, у про-
тонов, магнитный момент которых больше, чем ядерный
магнетон Бора р0, т. е. равняется сумме кинематического
и врождённого моментов^ или у нейтронов, обладающих
только врождённым магнитным моментом (см. § 44).
Заметим, что врождённые магнитные моменты нуклео-
нов имеют порядок ядерного магнетона Бора
eh
так как в знаменателе стоит масса иуклеонов М. Поэтому
у частиц, обладающих зарядом и магнитным моментом
(протон), магнитные свойства особенно сильно начинают
сказываться лишь в области, релятивистской относительно
нуклеонов.
25 Д. Иваненко-и А. Соколов
386 КЛАССИЧЕСКАЯ МЕЗОДИНАМИКА [гл. V
В мезодинамике, для того чтобы квазимагнитные (т. е.
нецентральные) и квазиэлектрические силы имелиАоди-
наковый порядок в нерелятивистской относительно нукле-
она области, необходимо положить
т* е. в знаменателе поставить не массу нуклеона М, а мас-
массу мезона [х.
В случае, если векторное мезонное поле порождается
какими-то лёгкими частицами (электронами, позитронами,
нейтрино и т. д.), то в правых частях вместо членов,
описывающих нуклеоны, следует включить совершенно
аналогичные члены, характеризующие соответственные
лёгкие частицы, заменив заряды g и моменты / на новые
константы связи g' и /'.
Если всё же принять, предварительную гипотезу Юкава
в виде своеобразного феноменологического описания ^-рас-
^-распада, то согласно данным теории [З-распада мы должны
положить константы связи заряженных мезонов с элек-
электронно-нейтринным полем равными:
Не исключена возможность, что нейтральные ядерные
мезоны распадаются на пару частиц (электрон—позитрон)
или на два у-кванта (например, 7г0-мезоны). Поэтому сле-
следовало бы ожидать непосредственного испускания пар ча-
частиц или улучей некоторыми нестабильными ядрами.
г) Векторные ядерные силы
Для нахождения энергии взаимодействия между двумя
покоящимися нуклеонами следует найти величину мезон-
hqto поля, создаваемого одним нуклеоном, и подставить
её в выражение энергии связи другого нуклеона с ме-
зонным полем.
В случае точечного нуклеона, покоящегося в начале
координат, имеем согласно D7,28)
Р =
§ 47] ВЕКТОРНОЕ МЕ30НН0Е ПОЛЕ 387
где QA — единичный вектор, определяющий направление
спинового, и тем самым магнитного момента первого нукле-
она. В согласии с эмпирическими данными предположим,
что нуклеоны обладают одинаковыми квазизарядами.
Для покоящегося нуклеона ток j, а также компо-
компоненты тензора квазиэлектрического момента обращаются
в нуль (j = T=0).
Если нуклеон приходит в движение, то компоненты
четырёхмерного тока /^, а также тензоры квазимагнит-
квазимагнитного и квазиэлектрического моментов могут быть легко
выражены через покоящиеся компоненты по правилам
тензорного анализа, причём будем иметь j ~ ~ р и Г ~ — S.
В статическом случае уравнения для мезонного поля,
порождённого точечным нуклеоном, принимают вид
Е + g/ad cp = О,
H-/rotA=-
Условие Лорентца принимает вид
Исключая из последних уравнений мезонные поля
Е и JET, получим следующие дифференциальные уравне-
уравнения для определения потенциалов, которые обобщают
благодаря членам с к0 обычные соотношения электро-
и магнетостатики:
(V2
(V2 - Щ) А = - 4ic/ rot аАЬ (г) .
Решение последних уравнений согласно § 14 имеет вид
е-ког
25*
§88 КЛАССИЧЕСКАЯ МЕЗОДИНАМИКА [гл< V
Отсюда согласно D7,25) находим для энергии взаимо-
взаимодействия двух нуклеонов через вещественное векторное
поле, связанное с массой покоя (т. е. через нейтральные
векторные мезоны)
Принимая во внимание векторные тождества
[~kor I
ОА grad t-— J = _
+ V
Г*!_1 = Л81_1. (г#0), D7,31)
получаем
г г
Раскрывая последнее выражение, находим
^, D7,33)
причём множитель Sab определяется формулой D6,13).
Первый квазиэлектрический член взаимодействия, про-
пропорциональный g2, совпадает (с точностью до знака)
с энергией взаимодействия в скалярном случае.
Второй член, пропорциональный /2, даёт квазимаг-
квазимагнитную, дипольную энергию взаимодействия. На боль-
больших расстояниях г > -у- благодаря наличию множителя
е-кОг все взаимодействие быстро исчезает, так что в соот- ч
ветствии с ожиданием силы имеют короткодействую-
короткодействующий характер.
§ 47] ВЕКТОРНОЕ МЕЗОННОЕ ПОЛЕ 389
На малых расстояниях ' г<^т~ ) , что соответствует
v "о /
стремлению к0 к нулю, первый член/как и в скалярном
случае, приобретает чисто кулонову форму
а второй член (как и в псевдоскалярном нерелятивист-
нерелятивистском случае) при к0—>0 принимает вид энергии взаимо-
взаимодействия Двух магнитных диполей, обеспечивая наличие
спиновых и нецентральных сил (w^ = /Ga и w^b/)
Благодаря нейтральности поля взаимодействие вида
D7,33) имеет место между любыми двумя нуклеонами
(протон—нейтрон, протон—протон, нейтрон—нейтрон),
что ведёт к зарядной независимости сил.
Подчеркнём теперь, что квантовая механика при
переносе взаимодействия нейтральным векторным мезон-
ным полем воспроизводит при помощи подсчёта во втором
Приближении точно то же выражение энергии взаимо-
взаимодействия между любыми нуклеонами.
При переносе взаимодействия заряженными вектор-
векторными мезонами (комплексное поле), так же как для слу-
случая заряженного скалярного или псевдоскалярного поля,
добавляется лишь специфический множитель Р — опера-
оператор гейзенберговского обмена нуклеонов зарядами, кото-
который по абсолютному значению при взаимодействии протона
с нейтроном обращается в единицу, а при взаимодействии
между двумя протонами или двумя нейтронами—в нуль.
Тогда энергия взаимодействия различных нуклеонов,
обязанная заряженному векторному полю, оказывается
равной V =t=VP, где V определяется через D7,33).
Для получения же взаимодействия через заряженные
мезоны между одинаковыми нуклеонами нужно, как
и в случае скалярного, псевдоскалярного и других полей,
провести подсчёт в четвёртом приближении квантовой тео-
теории возмущения, что приводит к выражениям, существенно
отличающимся от величины энергии взаимодействия между
390 КЛАССИЧЕСКАЯ МЕЗОДИНАМИКА [гл. V
протонами и нейтронами, получающейся в результате
подсчёта во втором приближении.
Так как эмпирические факты говорят за примерную
зарядную независимость хотя бы порядка ядерных сил,
то следует заключить, что, по крайней мере, некоторая
доля взаимодействия! между нуклеонами должна осуще-
осуществляться через нейтральное мезонное поле. С другой
стороны, заряженные мезоны также несомненно уча-
участвуют в переносе взаимодействия, так как, повидимому,
только они могут обеспечить обменный характер сил
между протоном и нейтроном, требуемый опытами по рас
сеянию при высоких энергиях, и обеспечивающий насы-
насыщение.
Обычно берут смесь заряженных и нейтральных мезо-
мезонов в пропорции, которая подбирается из эмпирических
соображений и окончательно ещё не установлена (подроб-
(подробнее см. § 48).
Существенным преимуществом векторных мезонных
сил, так же как и нерелятивистских псевдоскалярных, над
скалярными является наличие* в энергии взаимодействия
нуклеонов квазимагнитного члена с фактором Sab у при-
приводящим к спиновым силам в качественном согласии
с эмпирикой ядерных сил*).
Не удивительно поэтому, что в современной теории
ядерных сил оба эти поля применяются наиболее часто.
Вместе с тем, однако, эти же квазимагнитные члены ведут
к серьёзной «дипольной» трудности для векторных сил.
Действительно, ввиду недопустимо быстрого ростд
потенциальной энергии на малых расстояниях,
устойчивые состояния согласно теореме вириала (см. § 44)
оказываются невозможными. При конкретных подсчётах
ядерных эффектов приходится поэтому обрезать потен-
*) Как было недавно показано (L. van Hove, Phys. Rev., 75,
1519, 1949), дипольные члены сохраняются для векторного поля
даже после своеобразных калибровочных преобразований ^см. § 46),
в противополояшость*исчезновению их для псевдоскалярного поля.
§ 48] ПСЕВДОВЕКТОРНОЕ ПОЛЕ. ДИПОЛЬНЫЕ ТРУДНОСТИ 391
циал векторных или псевдоскалярных мезонных сил при
некотором г0, порядка 10~13 см, определяя более точно
границу обрезания из эмпирических данных и подбора
потенциала при г < г0 (например, V = const или F = 0).
Конечно, подобное положение вещей совершенно неудо-
неудовлетворительно и является до последнего времени наибо-
наиболее серьёзной трудностью всей теории ядерных сил.
Заметим, что при рассеянии мезонов на нуклеонах,
обязанном специфическим ядерным силам, эти же ди-
польные члены приводят также к трудности — безгранич-
безграничному росту эффективного сечения.
До настоящего времени не существует универсального
способа разрешения дшюльной трудности одновременно
и в теории взаимодействия и в теории рассеяния векторных
мезонов; калибровочное преобразование, которое позво-
позволило устранить дипольные члены в псевдоскалярном
случае, в векторном и псевдовекторном случаях приво-
приводит в лучшем случае лишь к исключению продольной
части поля. Это соответствует тому обстоятельству, что
квантовый релятивистский подсчёт, учитывающий ско-
скорости нуклеонов до второго порядка, в векторном слу-
случае сохраняет члены типа г~3.
В последующих параграфах мы остановимся на неко-
некоторых попытках устранения этих трудностей как в задаче
взаимодействия, так и в задаче рассеяния.
§ 48, Псевдовекторное поле» Дипольные трудности
а) Псевдовекторное мезонное по л 4е .
Рассмотрим в заключение ещё вещественное псевдо-
псевдовекторное мезонное поле, в основу которого положен
вещественный псевдовектор Ал.
Для того чтобы описать псевдовекторное поле, введём
прежде всего антисимметричный тензор третьего ранга
А*рг> из которого мы можем образовать антисимметрич-
антисимметричный тензор второго ранга
Антисимметричный тензор Аа^ связан с псевдовектором
392 КЛАССИЧЕСКАЯ МЕЗО ДИНАМИК А [гл. V
Аъ соотношением
Точно так же вместо тензора /?ар можно ввести псев-
псевдотензор или дуальный тензор j5Yg, причём
Подставляя последние соотношения в равенство D8,1),
получаем уравнение
£ар
с решением
Функция Лагранжа, приводящая к линейным урав-
уравнениям с наинизшими производными, должна иметь вид
г __ * п п ** л л
Подставляя сюда вместо тензоров псевдотензорные
величины, получим
Отсюда видно, что функция Лагранжа при отсутствии
источников псевдовекторного поля совпадает с функцией
Лагранжа векторного поля.
Поэтому как для волнового уравнения, так и для тен-
тензора энергии, спина и т. д. полностью применимы резуль-
результаты теории векторного поля при условии, что мы должны-
заменить векторные величины соответственно на псевдо-
псевдовекторные. В частности, поэтому спин псевдовекторного
поля должен равняться единице.
Различие между обоими полями появляется при опре-
определении энергии взаимодействия между нуклеонами и
нолем, . ~
§ 48] ПСЕВДОВЕКТОРНОЕ ПОЛЕ. ДИПОЛЬНЫЕ ТРУДНОСТИ 393
Смешанная функция действия S3 будет иметь вид
S3 = - ^ds\ р (х - х') U (х) (dz), D8,3)
где инвариантный член взаимодействия U (х) должен
в общем случае равняться сумме произведений: псевдо-
вектора нуклеонов на псевдовектор поля и псевдотензора
нуклеонов на псевдотензор поля, т. е. согласно § 46а:
где D23 = Вх\ Du = — Wx и так далее.
Отсюда для псевдовекторных мезонов вместо D7,27)
и D7,28) мы получаем следующие уравнения:
первая группа уравнений:
вторая группа:
тт г dL
где
= if \ Р (#— #')
В статическом случае для поля, создаваемого точеч-
точечным нуклеоном, покоящимся в начале координат, имеем:
rot g{),
divJL + kly = O, D8^4)
Е + grad 9 = 4ти/ал8 (г),
394 КЛАССИЧЕСКАЯ МЕЗОДИНАМИКА [гл. V
Учитывая, что div rot Ы = 0, находим вместо условия
Лорентца
div А = Щ- div <зАЪ (г) = Щ вАП (г).
Исключая из последних уравнений векторы JET и Ё
и принимая во внимание модифицированное условие
Лорентца, находим дифференциальные уравнения для
определения компонент полей А и Z):
где Z)=— gradcp. Их решение мы можем представить
в виде:
Наконец, чтобы найти энергию взаимодействия двух
точечных нуклеонов, следует подставить значения полей,
создаваемых нуклеоном А, в энергию V взаимодействия
нуклеона В с этим мезонным полем.
Как видно из D8,3), энергия взаимодействия равна
т. е. в нерелятивистском случае:
V=-g(QBA)-f(QBb), D8,6;
где ов—единичный вектор, характеризующий направле-
направление спина нуклеона В.
Подставляя D8,5) в D8,6), находим значение для
искомой энергии взаимодействия двух нуклеонов через
нейтральное псевдовекторное поле^ в нерелятивистском
§ 48] ПСЕВДОВЕКТОРНОЕ ПОЛЕ. ДИПОЛЬНЫЕ ТРУДНОСТИ 395
приближении для нуклеонов, т. е. на расстояниях г > ^- :
V = U [(M) (B) g (^в)] ^
-/2(eAV)(aBV)^-r. D8,7)
При переносе сил заряженным полем энергия взаимо-
взаимодействия нуклеонов будет равна F'=F-P, где -Р—опера-
-Р—оператор обмена зарядом.
Члены, содержащие нецентральные силы~(а^7) (a#?),
приводят к тем же дипольным трудностям (V со r~s при
г—>0), о которых мы упоминали при исследовании
псевдоскалярного и векторного полей.
б) Общая форма взаимодействия нуклеонов
Резюмируя предыдущие параграфы, мы видим, что
статический закон взаимодействия между двумя нуклео-
нами (А и J5), обязанный нейтральному мезонному полю,
согласно классической и квантовой теории должен иметь
в нерелятивистском приближении вид:
1) для скалярных мезонов:
Уг=-ё1е-^, D8,8)
2) для псевдоскалярных мезонов:
^-r, D8,9)
2а) для них же при некотором релятивистском уточ-
уточнении
К 2 — 2 ^2 г 7
3) для векторных мезонов:
е^1\ D8,10)
396 КЛАССИЧЕСКАЯ МЕЗОДИНАМИКА [гл. V
4) для псевдовекторных мезонов:
«
—. D8,11)
В случае взаимодействия через заряженные «мезоны
-квантовая теория приводит к тем же выражениям, но
-умноженным ещё на оператор Р обмена нуклеоцов заря-
зарядами, иначе говоря, координатами и спинами.
Здесь для общности мы учли, что кажйый сорт
мезонов в общем случае может иметь различные массы.
Для ясности выпишем снова выражение энергии
взаимодействия двух покоящихся нуклеонов одновре-
одновременно через мезонное поле всех четырёх типов (кх = к2 =
= А;3 = ki = k0), отделяя бесспиновые и спиновые цен-
центральные и нецентральные силы: . - -
V = [Сг + С2 (о а* в) + С3 (aAV) (a*V)]e— .
С точки зрения обменного характера нейтральные
скалярные силы являются вигнеровскими, заряженные
скалярные силы — гейзенберговскими. Спиновые члены
вида (GaGb) в векторном, псевдовекторном и нерёляти-
вистском псевдоскалярном случаях приводят для нейтраль-
нейтральных полей к бартлеттовским силам, так как оператор
обмена спинами согласно Дираку равен Ро ~ —у* . •
Майорановские силы возникают лишь при обмене нуклео-
нуклеонов заряженными частицами, притом для всех полей,
кроме скалярного, так как обмен одними координатами
эквивалентен гейзецберговскому обмену координатами
и спинами, скомбинированному с бартлеттовским обме-
обменом одними спинами.
Простейший закон взаимодействия, обязанный скаляр-
скалярным мезонам, объясняя короткодействующий характер
сил, не приводит к спиновой зависимости и поэтому должен
быть оставлен.
, К спиновым и нецентральным силам приводят три
остальных типа мезонов в нерелятивистском приближе-
§48] ЙСЕВДОЁЕ&ТОРНОЕ ПОЛЕ. ДИПОЛЬНЫЕ ТРУДНОСТИ 395
нии. При релятивистском подсчёте, учитывающем скорости
нуклеонов до второго порядка, дипольные члены, как
было показано в псевдоскалярном случае, выпадают.
К сожалению, с появлением нецентральных сил воз-
возникают дипольные трудности, так как характерное вы-
выражение
<48'12>
[см. также D6,12)] содержит члены, пропорциональные
г~3, а согласно теореме вириала при этом не могут возник-
возникнуть устойчивые состояния.
Было предложено также взять нерелятивистскую
комбинацию псевдоскалярных и векторных мезонов*),
полагая
В этом случае закон взаимодействия принимает вид
в котором также выпадают нецентральные силы.
Этот приём может быть использован безразлично как
в теории нейтральных, так и заряженных полей. Однако
тщл самым устраняется возможность объяснения кваДру-
польного момента дейтерона через нецентральные силы,
Меллер и Розенфельд надеялись получить нецентральные
силы в виде небольшого добавка при учёте релятивистских
поправок. Однако, как показали дальнейшие расчёты,
релятивистские поправки дают слишком малое значение
для квадрупольного момента.
Швингер**) предложил некоторое видоизменение по-
подобной смеси, взяв векторные и псевдоскалярные мезоны
с разными массами, но попрежнему полагая /2 = /3.
*) С. М 6 1 1 е г and L. R о s e n f e I d, Kgl. Danske Vid.
Selsk. Math.-fys. Medd., 17, № 8 A940).
*♦) J.Schwinger, Phys. Rev., 61, 387, 1942.
ЗЭ8 КЛАССИЧЕСКАЯ МЕЗОДИНАМИ&А [ГЛ. V
Тогда опасные дипольные члены с^г~3 исчезают,
а знак тензорного дипольного взаимодействия опреде-
определится разностью масс.
Действительно, в этом случае мы имеем
е~кгГ~е~к2Г
-/§(oaV)(aBV) екгГ~ек2Г D8,13)
или, принимая во внимание соотношение D8,12), най-
найдём, что когда г—»О,
%№-*$ I Is -2 Омов)],
причём согласно D6,13)
Sab =
При решении задачи дейтерона с таким потенциалом ока-
оказалось лучше всего положить в случае заряженного поля
g3 = 0, а отношение масс — = т5- взять равным примерно 1,6.
Тогда для квадрупольного момента мы получаем пра-
правильный знак, но слишком малое значение, почти в три
раза меньше экспериментального.
Другой весьма предварительный способ устранения
опасных дипольных членов заключается в обрезании
Потенциала на некотором малом расстоянии г0, причём в
промежутке @ — г0) потенциальная энергия берётся либо
постоянной V ==V (r0) = const, либо равной нулю.
Совершенно очевидно, что эта процедура является
неудовлетворительной с принципиальной точки зрения:
например, она нарушает релятивистскую инвариантность.
Однако в некоторой мере обрывание потенциала соответ-
соответствует, повидимому, учёту какого-то эффективного «ради-
«радиуса» частиц и не является физически совершенно абсурд-
абсурдным. Критический радиус действия сил г0 подбирается из
сравнения выводов теории с эмпирическими данными
в применении, например, к дейтерону.
§ 48] ПСЕВДОВЕКТОРНОЕ ПОЛЕ. ДИПОЛЬНЫЕ ТРУДНОСТИ] 399
В случае векторных нейтральных сил Бете получил
значение для г0 ~ 0,32 — 0,4— , причём это значение
практически не зависит от выбора потенциала при г < г0:
F = 0 или V = V(r0) .
Заметим, что дипольные члены могут быть устранены
автоматически в теории ядерных сил путём введения
уравнений с высшими производными *), типа предложенных
в теории электромагнитного поля.
В этом случае основное статическое уравнение для
определения потенциала, создаваемого единичным точеч-
точечным зарядом
G2-*«)/ = 4*8A.) D8,15)
с решением
f=—^-r-, D8,15а)
должно быть заменено уравнением четвёртого порядка:
(V» - *J) (V« - A*) U = - 4* (** + *f) 8 (г).
Решение последнего уравнения можно представить
в виде
/п1
2 = — li
г*2
Это выражение при к2 —» оо переходит в потенциал
Юкава:
/»= —'
а при ^ = 0 даёт потенциал
/о г »
найденный Боппом и Подольским в их обобщённой элек-
электродинамике (см. § 33).
Развивая теорию высщих производных для скалярных,
псевдоскалярных и т. д. частиц, мы легко можем полу-
получить для энергии взаимодействия между нуклеонами
♦) Д. Иваненко и А. Соколов, ЖЭТФ, 14, 379, 1944.
400 КЛАССИЧЕСКАЯ МЕЗОДИНАМИКА [ГЛ. V
законы типа D8,8—48,11), в которых вместо потенциала
D8,15а) мы должны подставить потенциал D8,16).
Как видно из анализа формулы D8,13), в этом случае
дипольные члены как в псевдоскалярном, так и векторном
взаимодействии должны исчезнуть.
К сожалению, теория высших цроизводных встречает
затруднения при обобщении на квантовый случай, так как
частицы с большей массой (к2 > kj) должны обладать
отрицательной энергией (см. также § 33).
Нетрудно сообразить, что, вводя в дифференциальные
уравнения ещё более высокие производные
(Р-А») (?»-*•)... (?»-*•„)/ =
мы можем описать поведение частиц с различными мас-
массами (кг < к2 < ... < кп). Так же как и в случае двух
масс, функция Грина уравнений с высшими производ-
производными будет равняться линейной комбинации функций
Грина уравнений второго порядка вида D8,15) *).
Наряду с этим в теории ядерных сил существенно учесть
то обстоятельство, что константы связи нуклеонов с мезон-
ным полем или мезонные квазизаряды нуклеонов g вели-
велики по сравнению с зарядом е, иначе говоря, соответствен-
2и "я 1
ные мезонные постоянные тонкой структуры р = -т2- ^ -^
превышают зоммерфельдовскую постоянную тонкой струк-
2пе2 1 ^
туры а =-^г ~-j37 ' Благодаря этому связь нуклеонов с
мезонным полем является сильной, и квантовые подсчёты,
использующие метод возмущений, ведут к плохой сходи-
сходимости, причём вероятности эффектов высшего порядка не
намного меньше, чем для эффектов низшего порядка. По-
Попытка построить теорию сильной связи привела к инте-
интересному предсказанию высших возбуждённых состояний
нуклеонов, несколько отличных по массе от основ-
*) Более подробно на этом вопросе мы остановимся в до-
дополнении.
Jv8] ПСЕВДОВЕКТОРНОЕ ПОЛЕ. ДИПОЛЬНЫЕ ТРУДНОСТИ Ш
ного изобара и обладающих как высшими спинами C/2,
б/г» • • •)> так и любыми зарядами (+ 2е, + Зе ..., а также
—€, —2е, —Зе, ...). Последовательной релятивистской
теории сильной связи, использующей модель протяжён-
протяжённого нуклеона, дать ещё, однако, не удалось, и все под-
подсчёты ведутся сейчас по обычному методу возмущений,
пригодному лишь при слабой связи частиц с полем.
'. Наконец, остановимся на эмпирических формулах ядер-
ядерного взаимодействия, которые были специально подобраны
для объяснения некоторых явлений, связанных с взаимо-
взаимодействием между нуклеонами.
. Анализ эмпирических данных показывает, что при
энергиях взаимодействия, меньших чем примерно 7MeV,
точной радиальной зависимости короткодействующего ядер-
ядерного взаимодействия установить невозможно, но в то же
время удаётся установить эффективную область действия
сил и наличие нецентральных и спиновых членов.
Многие количественные результаты, связанные с взаимо-
взаимодействием протона с нейтроном в таких явлениях, как
проблема дейтерона, квадрупольный момент дейтерона,
рассеяние нейтронов протонами (с энергией, меньшей чем
7 — lOMeV), могут быть получены, если предположить, что
радиальная часть потенциальной энергии, включающей
спиновые члены, имеет вид прямоугольной ямы *)
{r), D8,17)
. Г'— 13,89 MeV при г < 2,8 • 103 см,
J (r) = ( 0 при г > 2,8 • Ю-13 см,
g — 0,0715, у = 0,775 и SAB — тензорный член, описывающий
нецентральное взаимодействие, определяемый формулой
D6,13). Формула D8,17) годится только для описания чёт-
чётных состояний (например ^-состояния) и обобщается на
другие случаи в зависимости от того или иного предпола-
предполагаемого характера обменных сил.
Для дальнейшего уточнения характера ядерных сил
весьма важными являются эксперименты по рассеянию
*) Более подробно см. Г. Бете, Лекции по теории ядра,
ИЛ, 1949, стр. 109.
26 Д. Иваненко и А. Соколов
402 КЛАССИЧЕСКАЯ МЕЗОДИНАМИКА [ГЛ. Y
быстрых (порядка 50 —300 MeV) нуклеонов на нуклеонах.
Анализ подобных опытов должен помочь установить более
точный закон взаимодействия между нуклеонами, вклю-
включая вид короткодействующей функции/(г), тип оператора
обмена и роль нецентрального члена так же, как в своё
время опыты Рёзерфорда с рассеянием а-частиц атомами
доказали применимость закона Кулона к внутриатомным
явлениям и помогли установить ядерную модель атома.
Имеющиеся в настоящий момент экспериментальные
данные по рассеянию нейтронов с энергией от 40 до 90 MeV
на протонах*) позволяют прежде всего заключить, что,
ядерные силы, хотя бы частично, носят обменный характер,
поскольку в системе центра инерции частиц эффективное
сечение растёт, когда угол рассеяния приближается к 180°.
Это означает отброс нейтрона назад или превращение пер-
первичного протона в нейтрон, так как первичный нейтрон,
превратившись в протон, стремится двигаться вперёд.
На основе подобного анализа можно придти к следующей
полуэмпирической формуле для энергии взаимодействия
нейтрон — протон: „
D8,18)
где
V^g*6-^, V^-ifSAB*-^. D8,19)
Здесь ядерная постоянная тонкой структуры имеет два
значения: —j- = 0,405 при рассеянии частиц с параллель-
ными спинами и -^ = 0,280 при рассеянии частиц с анти-
антипараллельными спинами; у = 0,16; Рх — оператор обмена
координатами.
Отсюда видно, что энергия взаимодействия V состоит
из двух частей. Часть Vl9 имеющая характер юкавского
потенциала, обладает центральной симметрией и прости-
*) В. Segrc и др., Phys. Rev., 75,351, 1949; подробный
реферат этой работы содержится в научно-реферативном сборнике,
серия 2, вып. I, Теория элементарных частиц, опыты с частицами
ы f-квантами большой энергии, ИЛ, 1950, стр. 50.
I 48)- ПСЕВДОВЕКТОРНОЕ ПОЛЕ. ДИПОЛЬ НЫЕ TPVAHOCTll 403
рается на некоторое эффективное расстояние R = -г-, кото-
"о
рое согласно этим экспериментам равно /2 = 1,2 • 1О13 см*
что соответствует массе сопоставленных полю мезонов, рав-
равной 326 электронным массам, весьма близкой к массе как
нейтральных, так и заряженных тг-мезонов. Другая, тен-
тензорная часть F2, приводящая, в частности, к квадруполь-
ному моменту дейтерона, имеет эффективное расстояние,
в три раза большее, чем первая часть, и связана поэтому с
мезонами с массой, примерно равной 100 электронным массам.
Интересно заметить, что несколько ранее мы пришли
к выводу о возможном существовании мезонов подобной
массы*), применяя метод самосогласоваш ого поля Фока»
Хартри для построения статистической теории тяжёлых ядер.
Дальнейшие эксперименты по рассеянию нейтронов
протонами (вплоть до энергии 280 MeV) и рассеянию про-
протонов протонами (вплоть до энергий 350 MeV) в основном
подтвердили как существование двух частей энергии
взаимодействия**), так и несколько большее значение для
эффективного расстояния тензорной части. Тензорная часть
взаимодействия, повидимому, должна носить мезонный ха-
fe'hQr\
рактер ( J; эмпирически еще не исключен экспонен-
экспоненциальный (е~коГ) характер. Что касается первой части, то
для неё эффективное расстояние слишком мало, и поэтому
более точный вид радиальной функции / (г) может быть
уточнён при изучении рассеяния ещё более быстрых нук-
леонов. Анализ рассеяния нуклеонов указывает на раз-
различный закон взаимодействия между двумя протонами и
протоном — нейтроном в области больших энергий. Это
-заключение, однако, не исключает возможности одинако-
одинаковой радиальной зависимости для тех и других сил, но,
.повидимому, с достаточной ясностью подчёркивает разли-
различие в обменном их характере.
Таким образом, установление эмпирических формул для
^взаимодействия между нуклеонами в последнее время также
адёт по пути, указанному полевой теорией. В этих эмпи-
*)А. Соколови Б. Керимов, ДАН, 46, 199, 1949.
**) R. Christian и др., Phys. Rev., 77, 441, 1950; 79, 85,
3950.
26*
404 КЛАССИЧЕСКАЯ МЕЗОДИЙАМИКА [Гл. V
рических формулах не только вид тензорной и спиновой
зависимости берётся из полевой теории, но, по мере опре-
определения вида функции, описывающей,короткодействующую
часть взаимодействия, мы от произвольной формы радиаль-
радиальной функции J (г) постепенно приближаемся к форме,
полученной в мезонной теории.
Различие сил между протоном — нейтроном а прото-
протоном—протоном также находит своё объяснение, хотя бы
в качественном отношении. В самом деле, взаимодействие
между протоном — протоном может переноситься во втором
приближении только нейтральными мезонами, в то время
как взаимодействие между протоном и нейтроном перено-
переносится не только нейтральными, ко и заряженными мезонами.
Во всяком случае, развитие полевой теории ядерных
сил и последние эксперименты по рассеянию быстрых
нуклеонов позволяют надеяться, что б недалёком будущем
будет установлен закон взаимодействия между двумя
любыми нуклеонами, в результате чего под многие полу-
полуэмпирические закономерности ядерной физики будет под-
подле дён единый фундамент.
§ 49. Распространение плоских векторных
мезонных волн в вакууме
Можно поставить вопрос о распространении мезонных
волн, излучаемых нуклеонами, причём в задаче рассеяния
падающую мезонную волну, приходящую с большого рас-
расстояния, можно рассматривать как плоскую.
Выбирая ось х по направлению распространения волны,
мы получаем, что наряду с поперечными векторными вол-
волнами могут распространяться также продольные. Продоль-
Продольная составляющая подчиняется уравнениям
dx7dt
D9,1)
дх ~" °^ дх с dt '
Поперечные составляющие удовлетворяют уравнениям
49} РАСПРОСТРАНЕНИЕ МЕЗОННЫХ ВОЛН В ВАКУУМЕ 405
и дх 9 z с dt
При этом уравнения D9,3) можно отдельно не иссле-
исследовать, так как они получаются из D9,2) путём замены осей
координат г/, z соответственно на оси z, —у.
Из последних соотношений видно, что каждая составля-
составляющая мезонного поля F (т. е. Е, Н, А, ср) удовлетворяет
уравнению Клейна
Беря падающую мезонную волну монохроматической
сК
с частотой v = — , можно каждую компоненту поля пред-
представить в виде
p^p^-icKt+ikx^ ' D9,5)
где К2 = k2 + /rg, ?;= с-т-— фазовая скорость, а
dK к
vv=^cdk"=cW—гРУпповая скорость мезоннои волны.
Комплексный вид D9,5) для поля F взят исключитель-
исключительно в целях удобства, так как физический смысл в случаэ
нейтрального поля имеет только вещественная часть урав-
уравнения D9,5), так что можно положить
Re** = cos a, Rieu = — sin а. D9,6)
В дальнейшем символ R, означающий, что от комплекс-
комплексной величины берётся лишь вещественная часть, мы пи-
писать не будем.
1^ Подставляя D9,5) в уравнения D9,1), D9,2) и D9,3),
найдём следующие соотношения между компонентами:
для продольной волны
cp^i-4,; Ex = ik±Ax; H, = 0, D9,7)
406 КЛАССИЧЕСКАЯ МЕЗОДИНАМИКА [Гл V
для поперечной волны
Аи=-±Ев = -±Нг. D9,8)
В дальнейшем при вычислении эффективного сечения
рассеяния мы используем выражение, связывающее интен-
интенсивность первичного излучения / (среднее значение энер-
энергии, падающей в единицу времени на единицу площади)
со средней плотностью энергии и [значок —(черта) озна-
с
чает усреднение величины по времени, т. е. u = —\udt,
о
где т — полный период]:
ji£u. D9,9)
На основании последних формул легко показать, что
интенсивность первичного излучения / связана с по-
полями Е и JET следующими соотношениями:
для продольных волн
для поперечных волн
Ц=С£гН\. D9,11)
§ 50. Интегрирование уравнений мезонного поля
при помощи векторов Герца
Если в задаче рассеяния первичная волна задаётся
плоской и свободно распространяющейся в пространстве,
то вторичное (т. е. рассеянное) поле по существу является
волной, непосредственно порождённой нуклеонами, при-
приведёнными в движение первичной волной. Поэтому для
определения вторичной мезонной волны мы должны,
прежде всего, проинтегрировать векторные уравнения в об-
общем виде, т. е. суметь выразить компоненты поля (ср, А, Е,
Ш) через произвольно заданные плотности, токи (р, р— j
ц моменты (S и Т) нуклеонор,
§ 50] ИНТЕГРИРОВАНИЕ ВЕКТОРНЫХ УРАВНЕНИЙ 407
По аналогии с интегрированием уравнений Максвец-
ла мы можем наиболее просто проинтегрировать эти
уравнения, полагая
P=-divP; IH = I^ + rotM, E0,1)
где _Р и М — векторы квазиэлектрической и квазимаг-
,нитной поляризации. Введём теперь по аналогии с элек-
электродинамикой вместо потенциалов ср и Л два вектора
типа Герца: Zx (квазиэлектрический) и Z2 (квазимаг-
(квазимагнитный), образующих в совокупности антисимметрич-
антисимметричный тензор Герца второго^ранга: ZtJLV = Z2, iZj *).
При этом, чтобы удовлетворить условию Лорентца
D7,5), необходимо положить
ср = - div Zlt A = \ Ц* + rot Z2. E0,2)
Подставляя E0,2) в равенство D7,30), найдём выраже-
выражение для полей через векторы Герца
[OV,O)
= rot -1 ™Ь + rot rotZ2 -
Подставляя затем E0,1), E0,2) и E0,3) в уравнения
D7,29), получим
= -rot [(П -к\) Z2 + 4то0-+ 4жМ], E0,4)
div [(□ - *5) Zx + 4тгТ+ 4тгР] = 0,
где оператор Даламбера
Соотношениям E0,4) можно удовлетворить, допустив,
что векторы Герца удовлетворяют следующим уравне-
*) Заметим, что близкая задача интегрирования уравнений
Максвелла при наличии магнитных диполей была решена Я. И.Френ-
И.Френкелем в его книге «Электродинамика», ч. 1, ГТТИ, 1934.
408 КЛАССИЧЕСКАЯ МЕЗОДИНАМИКА [гл, V
ниям*):
(п - ki) zx = - 4* (jp + т),
(□ - Ы) Z2 = - 4тг(М + S). E 'Ь}
В дальнейшем ограничимся нерелятивистским слу-
случаем малых скоростей движения нуклеонов. Тогда, пре-
пренебрегая величинами М и Т, имеющими по сравнению
с Р и S порядок — [см. § 47], получим
с
(n-A02)Z2=-4irtf.1 E0,7)
Определяя отсюда векторы Герца Z, и Z2 через
Р и 8 и подставляя найденные значения в выражения
E0,3), сможем окончательно найти значения мезонных
полей через произвольно заданные вектор поляризации
Р и вектор квазимагнитного момента 8 нуклеонов.
Общее решение уравнения типа E0,7), т. е. неодно-
неоднородного релятивистского уравнения Клейна, содержащего
в правой части член, характеризующий источники,
было дано в § 20.
В частном случае монохроматических колебаний век-
вектора поляризации _Р:
E0,8)
решение уравнения для Z± можно искать в виде
Zx=Z,e-™«. E0,9)
В этом случае имеем
где v = с -г , Л =
*) Уравнения E0,6) написаны в предположении, что при от-
отсутствии нуклеонов векторы Герпа Zx и Za подчиняются для пустогр
пространства уравнению:
51] ИЗЛУЧЕНИЕ ВЕКТОРНЫХ МЕЗОННЫХ ВОЛН 4 09
Поэтому в случае К > к0 вектор Zx будет подчиняться
волновому уравнению Даламбера:
EG>10)
приводящему к известному решению:
(Л-') Л'. E0,11)
В случае запаздывающих решений следует в аргу-
аргументах функции взять верхние знаки, а в случае опе-
опережающих—нижние. Общее решение является суперпози-
суперпозицией запаздывающих и опережающих решений. Совер-
Совершенно аналогичное выражение в случае монохромати-
монохроматических колебаний вектора квазимагнитной поляризации
можно получить также для вектора 2Г2.
§ 51. Излучение векторных мезонных волн
квазиэлектрическим и квазимагнитным диполем
В дальнейшем мы ограничимся случаем, когда векторы
JP и 8Л характеризующие поляризацию и момент нукле-
онов, совершают гармонические колебания с часто-
частотой v = —. Тогда интегральные выражения для век-
векторов Герца Zx и Z2 согласно результатам предыдущего
параграфа будут иметь вид:
E1,1)
410 КЛАССИЧЕСКАЯ МЕЗОДИНАМЙКА [ГЛж V
В дальнейшем разделим доезонные поля на части, зави-
зависящие от квазиэлектрического Zx (индекс 1) и квазимаг-
квазимагнитного мезонного вектора Z% (индекс 2).
На основании формул E0,2), E0,3) и E0,6) для квази-
квазиэлектрических составляющих, имеем
Zlt E1,2)
Для квазимагнитных составляющих получим
E1,3)
Для вычисления энергии излучения найдём значение
в волновой зоне мезонных полей, создаваемых точечным
нуклеоном. Тогда, полагая векторы поляризации и момен-
момента в виде
Р=р @ 8 (г) =jpoe 8 (г),
и подставляя значения E1,4) в решение E1,1), получим
E1,5)
С помощью последних формул получим для волно-
волновой зоны, в которой можно отбросить величины порядка
-j-, следующие значения для мезонных полей:
51] ИЗЛУЧЕНИЕ ВЕКТОРНЫХ МЕЗОННЫХ ВОЛН 411
а) Для продольных составляющих, зависящих от Z3 *):
E1,6)
где
а вектору является функцией t — —, т. е.
р = pbe-':cKt+ikr.
б) Для поперечных составляющих, зависящих от Zx:
, .. E1,7)
в) Для поперечных составляющих, зависящих от Z\.
vr
—Л cvr L UJ7 —z v2r •
где
rn = ^6-^= mne-icKt+ikr.
Наконец, продольными квазимагнитными составля-
составляющими в нерелятивистском приближении можно просто
пренебречь.
Подставляя найденные значения полей в выражение
D7,19), получим для частей мезонного вектора Умова-
*) Для того чтобы разбить вектор р на продольную (относи-
(относительно г°) и поперечные составляющие, воспользуемся, как обычно,
тождеством р=г°(рг°) — [[рг°]г°], из которого видно, что первый
член правой части равенства является продольной, а второй—
роперечной составляющей.
412 КЛАССИЧЕСКАЯ МЕЗОДИНАМИКА [гл. V
Пойнтинга, зависящих соответственно от продольных
и поперечных составляющих векторов ZY и 2^:
где 0 —угол между вектором т° и направлением coqt-
ветствующего диполя (р или т).
Среднее значение потока энергии, проходящего в еди-
единицу времени чере,з площадку r2dQ (dQ —- телесный
угол), связано с вектором Умова-Пойнтинга известным
соотношением
dW = (<&r°)r2 dQ. E1,9)
Подставляя вместо вектора Умова-Пойнтинга только
что найдендое значение, имеем
Интегрируя, далее, по сферическим углам, получим
окончательно общее выражение для энергии, излучен-
излученной в единицу времени.
При квазиэлектрическом излучении
W1 = W\ -\-W = — — A +— \ E1,11)
цри квазимагнитном излучении
§ 52] КВАЗИЭЛЕКТРИЧЕСКОЕ РАССЕЯНИЕ МЕЗОНОВ 413
§ 52. Квазиэлектрическое рассеяние векторных
мезонов
Для вычисления дифференциального эффективного сече*
ния da рассеяния мезонного поля (т. е. мезонов) нукле»
онамй по классической теории мы должны в точной анало*
Гйи с рассеянием света (т. е. фотонов) взять отношение
количества энергии dW, которую излучает в единицу
времени приведённый в движение первичной волной ну-
клеон [см. формулу E1,10)], к интенсивности потока энер-
энергии первичной мезонной волны [см. формулы D9,10)
и D9,11)], т. е.
dc = ~j-. E2,1)
Для вычисления dz при квазиэлектрическом рассея-
рассеянии, обусловленном квазиэлектрическим нуклеонным дипо-
диполем р, воспользуемся трансляционным уравнением дви-
движения нуклеона массы М в квазиэлектрическом поле JE:
Mp = g*JE, E2,2)
причём ограничимся здесь нерелятивистским приближе-
приближением и пренебрежём пока что силой обратной реакции
мезонного поля (влияние силы реакции на излучение
будет учтено в § 55).
••
Заменим в формулах для da угол 8 между р и направ-
направлением рассеянного мезона углом б между падающей
и рассеянной мезонной волной. При этом, если пада-
падающий мезон является продольным, то 8 = 6, а для по-
поперечного мезона
cos 8 = cos 6 cos 60 + sin 6 sin 60 cos <p, E2,3)
где 60 является углом между р и направлением падаю-
падающей мезонной волны, который в случае поперечных
мезонов является прямым 60 = ^ .
4i4 классическая мезодинамийа [*л. V
Квадрируя равенство E2,3) и усредняя по азимуту,
получим
sm2 б "^"ПГ l + cos2G
: sm2 ft =
zrrr sm2 б "^"ПГ l + cos2G /crn ,.
cos2 ft = —2~-: sm2 ft = — . E2,4)
При вычислении дифференциальных и полных эффект
тивных сечений следует различать следующие случаи.
1) Падающие и рассеянные мезонные волны являются
продольными:
тогда E2,5)
где гн = ^-y — квазиэлектрический радиус нуклеона.
2) Падающая мезонная волна является продольной,
а рассеянная—поперечной:
E2,6)
°= з ^ (г) '
3) Падающая мезонная волна —поперечная, а рас-
рассеянная — продольная:
**Л
E2,7)
it) '
4) Падающая и рассеянная мезонные волны являются
поперечными:
, 9 1 + COS20 7П
d^rN s dB9
E2,8>
5^53] ЗИМАГНИТНОЕ РАССЕЯНИЕ МЕЗОНОВ^ 415
Как видно из полученных формул, при рассеянии
вероятность образования продольного мезона в (~ j
раз меньше вероятности образования поперечного мезона.
В частности, когда энергия падающего мезона зна-
чительно превышает его собственную массу, т. е. ~ —>0,
мы можем пренебречь продольными эффектами. Попе-
Поперечные же мезонные волны будут рассеиваться в точной
аналогии с электромагнитными волнами (т. е. фотонами)
по известной формуле Томсона, в которой лишь элек-
трический радиус электрона го=—-г заменён квазиэлек-
трическим радиусом нуклеона rN = -h-% •
§ 53. Квазимагнитное рассеяние векторных мезонов
Перейдём к рассеянию мезонных волн, обязанному их
взаимодействию с квазимагнитными моментами нуклеонов.
Если бы в природе существовали изолированные маг-
магнитные (или квазимагнитные) заряды, то рассеяние на
них фотонов (или мезонов) происходило бы по тем же
законам, которые имеют место при рассеянии на электри-
электрических (или квазиэлектрических) зарядах.
Однако магнитных или квазимагнитных зарядов пока
что обнаружить не удалось*). Что касается мезонного
поля, то необходимо допустить существование в природе
лишь «жёстких» квазимагнитных («врождённых») дипо-
диполей у нуклеонов величины т, которые при воздействии
на них квазимагнитного мезонного поля ЕС испытывают
механический момент, равный
E3,1)
и wi результате приходят во вращательное движение.
*) В этой связи см. новую теорию Дирака, трактующую
о возможных магнитных полюсах: Ргос. Roy. Soc. A, 133, 60, 1931;
Phys. Pev., 74, 817, 1948.
416 КЛАССИЧЕСКАЯ МЕЗОДИНАМИКА [гл< V
Опять-таки, пренебрегая пока что реакцией излуче-
излучения, а также релятивистскими эффектами, в качестве
основного уравнения вращательного движения для квази-
квазимагнитного диполя имеем выражение
m = x[mJB], E3,2)
где величина у. равняется отношению квазимагнитного
момента частицы |/п [ ==/, т. е. в данном случае нуклеона
к механическому моменту /. .
Как показывают опытные данные, кг*азимагнитный
момент нуклеона / связан с его квазимагнитным зарядом g
соотношением
где р. —масса мезона.
Заметим, что в согласии с опытом по квантовой теории
кинематический собственный магнитный момент ре элек-
электрона также связан с зарядом е соотношением типа E3,3)
Г именно: р-е = — S, где*?== — — ) , однако в знаменате-
ле стоит не покоящаяся масса электромагнитного поля,
равная нулю, а масса электрона. Поэтому, если в электро-
электромагнитной теории магнитные эффекты достигают заметной
величины лишь в области релятивистской относительно
электрона, то в мезонной теории нуклеонов квазимагнит-
квазимагнитные эффекты должны становиться заметными по сравне-
сравнению с квазиэлектрическими уже в области релятивистской
относительно мезона, но ещё нерелятивистской относи-
относительно нуклеона. Например, при г > тс2 скорость элек-
электрона не будет слишком мала по сравнению со ско-
скоростью света, поэтому томсоновское эффективное сечение
для рассеяния света на электроне, как известно, заменяется
квантовой формулой Клейна-Нишина, вычисленной по
дираковскому уравнению, автоматически учитывающему
магнетизм электрона.
Мы не будем останавливаться здесь на обсуждении
различных попыток истолковать на основе классической
теории квантовое по существу соотношение E3,3).
§' 53] КВАЗЙМАГНИТНОЕ РАССЕЙНИЕ ЙЕЗОНОВ 4f?
Отметим, что отношение между квазимаШйтГньШ и ме-
механическим моментами нуклеона для частиц со спи-
ном j (в единицах — \ равно
E3,4),
В случае падающей монохроматической волны
H'=ITQe~icKt уравнение движения E3,2) приводит к еле-.
дующему соотношению между т и Н:
| т | о* /1 у-сКН sin а |, E3,5)
где а—-утбл мёя<ду направлениями векторбв т ш Ш.
Отсюда по формулам D9,11), E1,10) и E2Д) находим
дифференциальное эффективное сечение при квазпмаг-
нитном рассеянии:
E3,6)
Если вектор квазймагнитного момента н^клёойк fit
параллелен JBT, то а = 0, и эффективное «ечение de
обращается в нуль. Наоборот, если вектор т пер-
перпендикулярен к jET, будем иметь максимальнее значе-
значение для da у причём здесь мы должны различать два
случая.
а) Вектор Ш ориентирован по направлений) Движений
парвоначай'ьногЬ мезона (т. е. по н&пр&йлению к). Тогда
угол 8 (между ггь и направлением рассеянного мезона)
равен углу б (между направлением падающего и расее-
янного мезона), поэтому
E3,7)
б) Вектор т параллелен JE (т. е. н^йр&йлён перпен-
перпендикулярно к первоначальному направлению двийёния
мезона). В этом случае согласно равенству E2,4)
Sn^=i(l + cos*6),
27 д. Иваненко и А. Соколов
4$в КЛАССИЧЕСКАЯ МЕЗОДИНАМИКА [гл. .V
благодаря чему
Так как при т ±_ И квазимагнитная потенциальная
энергия нуклеона в мезонном поле U= —(mil) в обоих
указанных случаях равна нулю, то обе ориентации явля-
являются равновероятными, ввиду чего усреднённое дифферен-
дифференциальное эффективное сечение равно
E3,9)
Отсюда после интегрирования по углам находим выра-
выражение для полного эффективного сечения рассеяния век-
векторных вещественных мезонных волн на квазимагнитном
моменте нуклеона
(в нерелятивистском приближении для движения нуклео-
нов и при пренебрежении затуханием или обратной реак-
реакцией поля). Квантовая теория рассеяния полностью под-
подтверждает этот результат для нейтральных мезонов, а для
заряженных мезонов приводит к выражению, отличающе-
отличающемуся лцшь на числовой множитель порядка единицы.
Резюмируя полученные результаты, подчеркнем, что
эффективное сечение для квазиэлектрического рассеяния
при увеличении энергии падающих мезонов остаётся вели-
величиной постоянной или начинает быстро убывать (см.
предыдущий параграф). В случае же квазимагнитного рас-
рассеяния мезонных волн эффективное сечение, в области
релятивистской относительно скорости движения мезонов,
возрастает в ( -т- ) раз по сравнению со значением для
эффективного течения при рассеянии поперечных мезонных
волн на квазизаряде. Появление этого характерного «ди-
польного» множителя обусловливается дипольным урав-
• ••
нением движения E3,2), связывающим иг с Н{т-^сКН),
в противоположность квазйэлектрическому трансляцион-
§ 54] СИЛЫ РЕАКЦИИ МЕЗОННОГО ПОЛЯ 4Д9
ному уравнению движения E2,2), связывающему р с Е
(р~-В).
Тем самым эффективное сечение при квазимагнитном
рассеянии безгранично возрастает с увеличением частоты
падающих векторных мезонных волн (т. е. энергии мезо-
мезонов). Подобное возрастание является совершенно недо-
недопустимым, так как благодаря ему число и, следовательно,
общая энергия рассеянных мезонов стремится стать
больше числа и, следовательно, энергии падающих.
Поэтому наряду с трудностями, связанными с беско-
бесконечным значением энергии мезонного поля, порождённого
точечными частицами, и тем самым — с полевой точки зре-
зрения—расходимостью собственной массы нуклеонов, труд-
трудностями, которые свойственны также классической и кван-
квантовой электродинамике, в векторной мезонной теории
появляются ещё свои добавочные специфические труд-
трудности, связанные с дипольным характером взаимодействия
нуклеонов с мезонным полем и с эффективной диполь-
ностью векторного поля.
§ 54. Силы реакции мезонного поля
Вопрос об отыскании силы, которую оказывает мезон-
ное поле, создаваемое нуклеоном, на сам нуклеон
(сила самодействия), тесно связан с установлением уравне-
уравнения движения. Последующие рассуждения применимы для
векторного случая.
Если воспользоваться для этой цели методом Ло-
рентца, рассмотренным в § 31, то в полной аналогии
с теорией электромагнитного поля возникает трудность,
связанная с бесконечной полевой собственной массой,
обязанной энергии мезонного поля самого нуклеона. Для
её устранения прежде всего можно предположить, что
нуклеонная масса полностью обязана энергии мезонного
поля, притом порождённого частицей, обладающей каким-
то конечным радиусом а («полевая» гипотеза классической
теории протяжённой частицы).
Тогда полевая мезонная масса^нуклеона, складываю-
складывающаяся из двух частей: квазиэлектрической МР и квази-
квазимагнитной Мт будет конечной, по порядку .равной
27*
420 КЛАССИЧЕСКАЯ МЕЗОДИНАМИКА [гл. V
Ме ~ ^ —, Мт ~ -g —,з (более точные, довольно громозд-
ел с а
кие выражения содержат параметр к0 и зависят, как и в
электродинамике, от предположений о характере распре-
распределения мезонного заряда «внутри» нуклеона: например
поверхностный или объёмный случай).
Наряду с полевой массой в уравнение вращательного
движения войдут значения полевых моментов инерции.
Точно так же, как и в случае электродинамики, введение
конечного радиуса является неудовлетворительным ввиду
нарушения релятивистской инвариантности. Кроме того,
даже получив конечное значение полевой массы при помо-
помощи радиуса частицы, невозможно будет, как и в электро-
электродинамике, привести его в согласие со значением импульса
ввиду невыполнения условия Лауэ.
В дальнейшем мы ограничиваемся классической тео-
теорией. Относительно квантового обобщения заметим лишь,
что точно так же, как для электродинамики, квантовая
теория мезонного поля любого типа, вообще говоря,
вновь приводит к бесконечной энергии поля, порождён-
порождённого точечным% нуклеоном, что видно, например, из вы-
выражений энергии взаимодействия (см. § 48). Кроме того,
квантовая мезодинамика подобно квантовой электроди-
электродинамике приводит к добавочным специфическим кванто-
квантовым бесконечностям для энергии поля, порождённого
нуклеоном, связанным с флуктуациями поля (поперечная
э^ургия, см. дополнение).
Положительной стороной классического метода Лорентца
является включение весьма простым путём сил самодей-
самодействия в уравнения движения.
Однако лорентцовы уравнения движения нуклеона
в мезонном поле кроме членов, не зависящих от радиуса
нуклеона а, будут содержать бесконечное число членов,
пропорциональных радиусу, типа ГуТ(п = 1, 2, . . .),
не имеющих, очевидно, непосредственного физического
смысла и подлежащих, как обычно, отбрасыванию. Тем
самым уравнения движения нуклеонов в мезонном поле
должны быть ограничены со стороны малых частот поля
(\ — длина волны мезонного поля). Мы получим в мезо-
§ 54] СИЛЫ РЕАКЦИИ МЕЗОННОГО ПОЛЯ 421
динамике такие классические уравнения движения нук-
леонов, в которые с самого начала входили бы лишь члены,
связанные с внешним полем и силой само действия, но не
связанные с радиусом частиц подобно тому, как это было
сделано в электродинамике Дираком для трансляцион-
трансляционного случая (теория ненолевой массы). Самым простым
способом получения подобных уравнений является метод
компенсирующего поля, при котором также естественно
включается сила самодействия, а инерционные члены
с полевой массой автоматически выпадают (см. §34). Тем
самым мы можем получить уравнения, позволяющие опи-
описывать колебания нуклеонов с любыми частотами, причём
в случае колебаний с большими частотами основную роль
вновь будут играть члены с силой лучистого мезонного
трения.
В частности, метод Лорентца приводит к следующему
уравнению ротационного движения в нерелятивистском
приближении:
где а— радиус нуклеона, а г; —скорость мезонных волн.
Кроме того, мы предполагаем, что квазимагнитный заряд
распределён по поверхности нуклеона.
Третий член справа с реакцией излучения был уста-
установлен нами; полное релятивистское уравнение было затем
найдено Баба. В нём мы вычеркнем сразу инерционный
член, пропорциональный [mm], который был получен
Гейзенбергом, опустившим, однако, член с третьей про-
производной*).
Учитывая силу самодействия, имеем для определения
движения квазиэлектрического диполя и квазимагнитного
*) Д. Иваненко и А. Соколов, ЖЭТФ, 10, 709, 1940;
А. М у х т*а р о в, Вестник МГУ, № 7, 61, 1948: Н. J. В h a b h а,
Proc. Roy. Soc, A 178, 314, 1941; ibid., 172, 384, 1939; W. H e i s en-
be г g, Zs. f. Phys., 113, 61, 1939. См. также В. Гинзбург,
ДАН, 31, 319, 1941*
422 КЛАССИЧЕСКАЯ МЕЗОДИНАМИКА [гл. V
момента вместо E2,2) и E3,2) в нерелятивистском при-
приближении соответственно уравнения
gml +gF,
т = у. [mHl] + Y.JL. E4,1)
Здесь JE1 и Н1' являются внешними квазиэлектриче-
квазиэлектрическими и квазимагнитными полями. Далее, предполагая
нуклеон распределённым с некоторой пространственной
плотностью р, нормированной на единицу заряда, най-
найдём для силы самодействия Ж и момента самодействия
Ъ выражения (см. § 31)
E4,2)
причём средние поля определяются равенствами
_ р E4,3)
И = \ И (г, У) Ро (У) Ро (У) (dr) (dr'),
где Е(Т, 7-') и М(т, г') —собственные поля в точке т\
создаваемые точечным нуклеоном, находящимся в точке г,
причём в нерелятивистском случае можно считать, что
поля Е и 2Г возникают благодаря наличию моментов р и
т9 а р0 — нуклеонная плотность, нормированная на
единицу.
Вообще говоря, при определении полей ограничивают-
ограничиваются только запаздывающими потенциалами. Однако, сле-
следуя теории, развитой в § 34 для исключения полевой
массы, введём ещё второе поле, действующее только на
нуклеон, его порождающий. При этом для того чтобы
компенсирующее поле не могло быть излучённым в виде
мезонных волн, при его вычислении возьмём полусумму
запаздывающих и опережающих потенциалов, а при опре-
определении общего поля в полной аналогии с выражением
§ 54] СИЛЫ РЕАКЦИИ МЕЗОННОГО ПОЛЯ Ь%$
C4,21) мы должны взять полу разность запаздывающих
и опережающих потенциалов.
Поэтому в случае точечного нуклеона, т. е. когда
) () [см. также соотношения E1,4) и E1,3)], находим
E4,4)
S + graddiv)Z*'
причём согласно E1,5)
E4,5)
Л'.
Здесь R' = v-r'(t').
Раскладывая 8-функцию в ряд по величине -- , по-
получим
2R' ~
= ±l(t'-t) + ^V(t'-t)+ .... E4,6)
откуда с помощью формулы C,11) находим
*" ! to8 ^ +"" E4,7)
7 _ т 1 д* (Д2)
где В = г — г'(О-
КЛАССИЧЕСКАЯ МЕЗОДИНАМИКА [гл. V
Принимая во внимание равенство
а также то обстоятельство, что для точечного нуклеона
в конечном результате мы должны положить Л=0,
вдлучим
^ ■ E4,8)
j^ 2 т
Окончательно уравнения движения нуклеона E4,1) с учё-
учётом силы лучистого мезонного трения примут вид
E4,10)
Важно отметить, что в полной аналогии с электроди-
электродинамикой мы можем получить точно такие же выражения
для собственных полей также другим методом, основан-
основанным на балансу энергии.
Действительно, добавим в уравнениях движения нукле-
нуклеона E4,1) к внешним полям JE* и Н{ значения собствен-
собственных полей Е и J5T, подобранных так, чтобы нуклеон в еди-
единицу времени излучал при квазиэлектрическом взаимо-
взаимодействии количество энергии Wx [см. формулу E1,11I,
а при квазимагнитном взаимодействии количество энер-
щц W2 [см. формулу E1,12)]. Тогда, обозначая период
колебания нуклеона через т, получим, принимая во вни-
внимание, что
§ 54] СИЛЫ РЕАКЦИИ МЕЗОННОГО ПОЛЯ 425
и т. д., для определения собственных полей следующие
уравнения:
Отсюда видно, что собственные поля, которые следует
добавить в уравнениях движения, будут точно опреде-
определяться формулами E4,8).
Как и следовало ожидать, исходя из баланса реально
излучённой энергии, мы не могли получить для собствен-
собственных полей дополнительных членов, пропорциональных
• • • •
производным чётного порядка, в данном случае р или т
{см. метод Лорентца), поскольку последние связаны лишь
с собственной массой или моментом инерции нуклеона.
Таким образом, метод баланса энергии (в котором учиты-
учитывается только реально излучённая энергия) и метод Лорент-
Лорентца приводят к различным значениям для силы само действия.
Именно, укажем ещё раз для ясности, что в методе Ло-
Лорентца появляются дополнительные инерциальные члены,
•• ••
пропорциональные р и ш. В нашем методе, взяв для силы
самодействия полуразность запаздывающих и опережаю-
опережающих потенциалов, мы смогли исключить инерциальные
члены. Поэтому оба метода, т. е. метод определения силы
самодействия при помощи компенсирующего поля и метод
баланса энергии, приводят к тождественным результатам,
и их применимость не ограничена большими частотами
колебаний нуклеона. Согласно теории электромагнитного
вакуума (см. дополнение), полевая масса электрона соста-
вляет примерно ^ часть всей массы. Возможно, что часть
/ 2тг/?2\
массы нуклеона ( невидимому, составляющая долю -Hf- )
426 КЛАССИЧЕСКАЯ МЕЗОДИНАМИКА [гл. V
будет также носить полевой характер. В этом случае пО-
левые члены дадут небольшую поправку к нашим урав-
уравнениям E4,9) и E4,10). Однако более подробно этот во-
вопрос можно будет проанализировать лишь после построения
теории мезонного вакуума.
§ 55. Рассеяние векторных мезонных волн
с учётом затухания
Рассмотрим прежде всего квазиэлектрическое рассея-
рассеяние нейтральных векторных мезонов с учётом затухания.
Ограничимся здесь наиболее важным случаем больших
энергий (k^>K), когда рассеянием продольных мезонов
можно пренебречь.
Задавая квазиэлектрическуд) напряжённость поля пада-
падающей мезонкой волны в виде
E = Eoe-icKK E5,1)
найдём, используя формулу E4,9), для второй производ-
производной от квазиэлектрического дипольного момента нуклео-
на, вызванного этой волной, выражение
откуда
^- E5'3)
4 МО
Полное эффективное сечение рассеяния находится, как
обычно, по формуле E2,1)^
<*' = у. E5,4)
Здесь в согласии с равенствами D9,11) и E1,11) интен-
интенсивность падающих волн положена равной
/ = £^ E5,5)
§ 55] РАССЕЯНИЕ МЕЗОННЫХ ВОЛН С УЧЁТОМ ЗАТУХАНИЯ 427
и энергия вторичных волн, излучённых за секунду,
^ = |£. E5,6)
Из последних формул находим для квазиэлектрического
эффективного сечения рассеяния мезонов на нуклеонах
с учётом затухания следующее выражение:
где rN — r2~- — квазиэлектрическии радиус нуклеона.
Вспоминая, что эффективное сечение без учёта зату-
затухания определяется соотношением E2,8), т. е.
871 _
можно выражение E5,7) представить в виде
С точки зрения классической неполевой теории час-
частиц (в данном случае нуклеона), развиваемой в духе
классической теории Дирака, уравнение движения E4,9),
а вместе с тем и формула для эффективного сечения рас-
рассеяния E5,8) не ограничены в нерелятивистском случае
каким-либо условием.
Напомним, что в § 36 была получена аналогичная
формула для рассеяния света на электроне.
С другой стороны, с точки зрения классической тео-
теории Лорентца, допускающей полевую массу неточечных
частиц, как уравнение движения E4,9), так и величина
эффективного сечения E5,8) являются пригодными лишь
для длин волн, превышающих соответственно классиче-
классический, в данном случае квазиэлектрический радиус гж час-
частиц [ввиду необходимости отбрасывания в уравнениях
движения членов типа (rN/\)n].
Как видно из E5,8), сила лучистого трения начинает
оказывать влияние при таких частотах, когда выполняешься
428 КЛАССИЧЕСКАЯ МЕЗОДИНАМИКА [Гл. V
соотношение
ак2^1, E5,9)
или
^£ E5,10)
При более высоких энергиях эффективное сечение
становится равным
где длина падающих мезонных волн А = — .
Однако при: энергиях падающего мезона, превышающих
в несколько раз собственную энергию нуклеона Мс2, мы
вступаем в область релятивистской энергии относительно
нуклеона. Здесь с большой вероятностью при рассеянии
будут иметь место квантовые явления, в частности, ком-
птон-эффект, т. е. некогерентное рассеяние мезонов с изме
нением частот, в противоположность рассматриваемому
сейчас когерентному рассеянию без изменения частоты*).
Перейдём н квазимагнитному рассеянию мезонных
волн (мезонов) на нуклеонах.
Предположим, что вектор внешнего мезонного поля И
с сК
изменяется гармонически с частотой — и направлен по оси
z. Пусть вектор момента нуклеона т расположен в
плоскости zz. Тогда, пренебрегая центростремительным
ускорением, имеем т~ —с2К2т.
Проектируя уравнение движения E4,10) на оси коор-
координат, получим
Н — bmzmx + bmxmz, E5,12)
= —bmxmy,
*) Как было нами указано в § 36,. в системе координат, где
покоится центр тяжести мезон—нуклеон, квантовая теория рас-
рассеяния приводит к формуле, по существу совпадающей с E5,8)
вплоть до ультрарелятивистских энергий ( -^— > Мс8 J .
§ 55] РАССЕЯНИЕ МЕЗОННЫХ ВОЛН С УЧЁТОМ ЗАТУХАНИЙ 429
где
Отсюда находим
т Н '
ти — — х гт /,2~г > mx = bmzmj > W£ — — bmxm , E5,13)
где т =■■ У^гпх + ml, или
m = ■
Полагая в формуле для эффективного сечения
в согласии с равенствами D9,11) и E1,12)
найдём следующее выражение для эффективного сечения
квазимагнитного рассеяния поперечных мезонов с учё-
учётом затухания, в предположении, что угол между векто-
векторами m и 2Г равен ~:
r- E5>14)
Здесь а — полное эффективное сечение при квазимагнит-
квазимагнитном рассеянии без учёта затухания [см. соотношение
E3,10I-
0
480 КЛАССИЧЕСКАЯ М ЕЗОДИНАМИКА [гл. V
Для малых энергий падающих мезонных волн, когда
Ъ-,
E5,16)
(где [а —масса мезона; величина [32 = h ° ^ 6 есть ме-
зонная постоянная тонкой структуры), т. е. при
для эффективного сечения находим старый результат
E5,15), который был получен без учёта затухания.
Для умеренно больших энергий падающих резонных
волн
превышающих лишь в несколько раз собственную энергию
мезона (т. е. практически ещё нерелятивистская область
энергий относительно нуклеона), величина сА2 стано-
становится больше единицы. Поэтому, начиная с этих энергий,
необходимо учитывать силу лучистого мезонного трения.
При высоких энергиях эффективное сечение становится
равным
и перестаёт возрастать с увеличением энергии. Отсюда
видно, что учёт силы лучистого трения устраняет диполь-
ную трудность при квазимагнитном рассеянии векторных
мезонов.
Совершенно аналогичным образом трактуются эффек-
эффекты, связанные с классическим псевдовекторным полем,
дипольнЫе свойства которого будут точно подобны век-
векторному и, как видно непосредственно из выражения
энергии связи с этим полем, должны полностью прояв-
проявляться при взаимодействии с нуклеонами.
Таким образом классическая мезодинамика позволяет
не только выяснить вопрос о происхождении дипольной
§ 55] РАССЕЯНИЕ МЕЗОННЫХ ВОЛН С УЧЕТ.ОМ13АТУХАНИЯ 431
трудности, сказывающейся в недопустимом росте эффек-
эффективного сечения для квазимагнитного рассеяния, но
также даёт возможность устранить эту трудность путём
учёта затухания, т. е. обратного действия поля.
Квантовая теория рассеяния нейтральных и заряжен-
заряженных векторных, псевдовекторных и т. д. мезонов на нукле-
онах полностью подтверждает эти результаты, в свою оче-
очередь позволяя устранить рост вероятности или эффектив-
эффективного сечения квазимагнитного рассеяния благодаря учёту
затухания *).
Эти результаты, как выяснилось при дальнейшем
анализе, имеют фундаментальное значение во всей со-
современной теории поля, выходящее за рамки теории
рассеяния.
Другим весьма интересным g-эффектом является тор-
тормозное испускание мезонного поля (мезонов) быстрыми
нуклеонами при столкновении их друг с другом, совер-
совершенно подобное тормозному излучению электромагнит-
электромагнитных волн (фотонов), особенно интенсивному при боль-
больших энергиях сталкивающихся частиц.
Как известно, вероятность тормозного испускания
фотонов быстро возрастает с энергией, и, например, для
энергий порядка десятков и сотен миллионов электрон-
вольт потери энергии электронов в потоке мягкой компо-
компоненты космических лучей, главным образом, обусловле-
обусловлены излучением. Вероятность же их столкновения с атом-
атомными электронами и значительных потерь энергий на иони-
ионизацию в этой области энергий ничтожна.Вполне аналогично
быстрые нуклеоны при прохождении через слой вещества
с наибольшей вероятностью теряют свою энергию при
тормозном испускании мезонов. По современным пред-
представлениям благодаря столкновениям первичных прото-
протонов с ядрами может происходить порождение разнообраз-
разнообразных заряженных и нейтральных мезонов в верхних
♦) А. Соколов, Journ. of Phys. USSR, 5, 231, 941;
В. Паули, Мезонная теория ядерных сил, гл. IV, ИЛ, 1947;
Г. Вентцель, Введение в квантовую теорию волновых полей,
Гостехиздат, 1948. Там же приведена дальнейшая литература по
квантовой теории затухания.
432 КЛАССИЧЕСКАЯ МЕЗОДИНАМИКА [гл. V
слоях атмосферы, а также недавно обнаруженное порож-
порождение мезонов в лабораторных условиях.
Подобно испусканию электромагнитного (или мезон-
ного) поля частицами, приведёнными в движение падаю-
падающими волнами, тормозное испускание также является по
сути дела эффектом классическим; квантовые поправки
здесь, однако, весьма существенны. Полная теория, соот-
соответствующая действительности, должна быть квантовой,
и окончательные выражения для вероятности тормозного
излучения при е-силах и при g-силах зависят от план-
ковской константы /г, иначе говоря, от постоянной тон-
2тте / „
кои структуры а = -т— ( или соответствующей мезоннои
константы р =? -^- j . Несмотря на это как было показано
для случая электромагнитного поля *) и как можно пока-
показать также для поля мезонного**), возможно дать псшу-
квантовую приближённуй) трактовку задачи о тормозном
испускании, учитывающую суть явления.
Дело сводится к тому, что поле падающей частицы,
сталкивающейся с какой-то покоящейся, разлагается на
плоские волны, и тормозное излучение при столкновении
трактуется как результат суммы актов рассеяния отдель-
отдельных волн.
В самом грубом виде суть подобного вывода тормозното
испускания фотонов заключается в следующем. Электрон,
пролетающий в поле ядра заряда Ze на расстоянии г,
еЕ Ze2 л
испытывает ускорение w ~ — ^ —- и благодаря этому
в течение времени т ~ — испускает энергию
*) Williams, Phys. Rev., 45, 729, 1934; Rev. Mod. Phys.,
17,1945, Wei zs acker, Zs. f. Phys., 88, 612,1934; В. Гейтлер,
Квантовая теория излучения, Гостехиздат, 1940, % 17. •
♦♦) Heitler and Peng, Proc. Irish. Academy Sci. (A),
1942—1943 гг. (ряд статей).
jj 55] РАССЕЯНИЕ МЕЗОННЫХ ВОЛН С УЧЁТОМ ЗАТУХАНИЯ 433
Для получения эффективного сечения crad тормозного
испускания нужно это выражение умножить на вероят-
вероятность попадания электрона на площадку Ъкгйг, затем
разделить на начальную энергию ^ тс2 и, наконец,
проинтегрировать по г, т. е.
/*е2
Г dr
Здесь существенно сказывается квантовая механика,
утверждающая, что границу применения классической тео-
теории следует задать при rmin ~ — ; тогда
Точная квантовая теория также приводит к выражению,
содержащему в качестве основного фактора только чт<&
полученное выражение.
Для испускания мезонов нуклеонами, обусловленного
их квазиэлектрическими зарядами, мы получим аналогич-
аналогичное выражение, заменяя е на g и т на М:
f ло = -~i — квазиэлектрическии радиус нуклеона у.
Однако, как мы видели на примере задачи рассеяния,
при высоких энергиях наиболее существенную роль
играют квазимагнитные члены. Производя с ними те же
выкладки, получим значение эффективного сечения для
квазимагнитного тормозного испускания нейтральных век-
векторных (или псевдоскалярных) мезонов нуклеонами, кото-
которое снова абсурдным образом растёт с энергией нуклео-
нов Е:
Grad ^ const v2 ^ const Е1 (где положено Е = Av).
Квантовая теория тормозного испускания подтверж-
подтверждает в основном этот результат, что вновь ставит нас перед
задачей устранения дипольной трудности. Закономерным
способом устранения этой трудности и предотвращения
28 Д. Иваненко и А. Соколов
k34 КЛАССИЧЕСКАЯ МЕ-ЗОДИНАМИКА [гл. V
недопустимого роста эффективного сечения тормозного
испускания мезонов нуклеонами при росте энергии по-
последних также является более точная трактовка задачи
с учётом затухания как в классической, так и в последова-
последовательной квантовой теории. Действительно, только после
учёта затухания стало возможным развить теорию тор-
тормозного порождения мезонов нуклеонами, лежащую ныне
в основе понимания процессов в космических лучах
в высших слоях атмосферы и объясняющую образование
мезонов в лабораторной обстановке.
Дипольная трудность имеет место для векторных ме-
мезонов не только в случае эффектов, связанных с g-силами,
но также для электромагнитных процессов (е-силы). На-
Например, эффективное сечение рассеяния света на подоб-
подобных мезонах (комптон-эффект) растёт с частотой света*).
Здесь также необходимо учесть затухание, которое и устра-
устраняет недопустимый рост сечений. Кроме того, диполь-
дипольная трудность возникает также в задачах взаимодействия
при е-силах и проявляется, например, в невозможности
стационарных состояний векторных заряженных мезо-
мезонов в кулонойом поле точечного заряда**), иначе говоря,
в частности, Ь невозможности образования мезоводо-
рода и других своеобразных мезо-атомов из ядер с вра-
вращающимися вокруг них векторными мезонами. Резюмируя
эту ситуацию, можно сказать, что эффективная диполь-
ность векторного мезонного поля делает мезон при боль-
больших энергиях или на малых расстояниях не зарядом,
а скорее магнитом, магнитные же силы, как мы указы-
указывали выше (§ 45), не дают стабильных уровней. Этот при-
пример с дипольной трудностью в случае электромагнит-
электромагнитного взаимодействия мезонов весьма аналогичен проявле-
проявлению дипольнсй трудности при взаимодействии нуклео-
нов через мезшшое поле при связи с последним благо-
благодаря квазимагнитным моментам. В обоих случаях до сих
пор не указано бесспорных способов устранения диполь-
дипольной трудности при взаимодействии. Предварительный не-
нерелятивистский метод обрезания потенциальной энергии
*) Я. А. Смородинский, ЖЭТФ, 10, 840, 1940.
••) И. Е. Т а м м, ДАН, 29, 551, 1940.
§ 55] РАССЕЯНИЕ МЕЗОННЫХ ВОЛН С УЧЁТОМ ЗАТУХАНИЯ 435
при некотором весьма малом rmin, конечно, неудовлетво-
неудовлетворителен.
Как уже упоминалось, дипольная трудность отсут-
отсутствует для электромагнитных эффектов в случае псевдо-
псевдоскалярного поля, что легко усмотреть из общего вида
уравнений или смешанного лагранжиана псевдоскаляр-
псевдоскалярных частиц в электромагнитном поле, в котором отсут-
отсутствуют дипольные члены. Тем самым, например, эффек-
эффективные сечения различных электромагнитных процессов
(комптон-эффект, тормозное испускание света псевдо-
псевдоскалярными мезонами и т. д.) не дают роста с энергией
в случае псевдоскалярных частиц.
Эти обстоятельства в известной мере побуждают считать
векторную теорию менее пригодной для описания мезонов
и склониться в пользу псевдоскалярного уравнения*).
Однако этот аргумент**) относится лишь к е-силам,
т. е. к взаимодействию псевдоскалярных мезонов с электро-
электромагнитным полем.
Что касается мезонной теории g-сил, то в ней мы,
с одной стороны, не можем обойтись без тензорной или
нецентральной части ~<5л.в» которая обеспечивает квад-
рупольный момент дейтерона; в то же время в любом
варианте теории это тензорное взаимодействие содержит
дипольные члены.
Однако более подробно этих вопросов мы здесь
касаться не будем.
Выяснение большой роли, которую играет затухание
в полях, обладающих эффективной дипольностью, полу-
полученное в классической и квантовой мезодинамике, побу-
побудило развить общую теорию затухания в различных на-
направлениях.
Следует подчеркнуть, что стремление ко всё более
точному учёту обратного действия поля является весьма
характерным для развития теоретической физики самых
Последних лет. Речь идёт о построении общей теории связи
частиц с полями мезонным, электромагнитным или грави-
*) J.R. Oppenheimer, Phys. Rev., 59, 462, 1941,
R. F. Christy and S. К u s a k a, Phys. Rev., 59, 405, 1941.
**) См. обзор С. З. Беленького в сборнике «Мезон» под
ред. И. Е. Т а м м а, Гостехиздат, 1947, стр. 146.
28*
436 КЛАССИЧЕСКАЯ МЕЗОДИНАМИКА [гл. V
тационным и разделении эффектов,, приводящих к ко-
конечным результатам от бесконечностей типа членов само-
самодействия, возникающих при классических и квантовых
подсчётах и обязанных прежде всего энергии поля то-
точечных частиц. Новейшему развитию этих вопросов по-
посвящено дополнение в конце книги,
§ 56. Гравитация и элементарные частицы
Так как настоящая книга посвящена главным обра-
образом проблемам, связанным с элементарными частицами,
мы не останавливались сколько-нибудь подробно на теории
гравитационного поля, поскольку тяготение практиче-
практически не играет роли среди разнообразных взаимодействий
между частицами. Действительно, как уже указывалось
выше, потенциальная энергия тяготения, например между
двумя протонами, Vm совершенно ничтожна по сравнению
с их электростатической энергией Ve:
Vm-V. = *^:-r^iO*: E6,1)
Точно так же гравитационная энергия мала по срав-
сравнению с мезоннои потенциальной энергией между теми же
элементарными частицами на расстояниях г < —:
E6J)
Вводя тюнятие гравитационного заряда, совпадающего
по существу с массой тела: т' = |Лс • т, можно сказать,
что гравитационные заряды элементарных частиц малы
по сравнению с их электрическими или мезонными заря-
зарядами*).
Гравитация начинает играть заметную роль лишь
для макроскопических тел и превалирует над остальными
*) При 1этом, конечно, не следует всё же упускать из виду воз-
возможного влияния тяготения в таких вопросах, как собственная
энергия частиц, на важность чего недавно было вновь обращено
внимание М. Ф. Широковым (Вестник МГУ, № 4, 1947).
§ 56] ГРАВИТАЦИЯ И ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ 437
видами взаимодействия для астрономических объектов,
обладающих огромной массой.
Кроме того, изложение основ теории гравитации
тесно связано с использованием тензорного анализа,
л обычно является предметом особых монографий*),
Однако мы должны всё же дать здесь хотя бы самое
краткое изложение основ теории гравитационного поля,
для того чтобы показать, с одной стороны, наличие
у этого поля многих общих, притом не отмеченных ранее,
свойств с полями электромагнитными и мезонными, что
позволяет провести трактовку гравитации теми же метода-
методами, какие были применены к полям электромагнитному
и мезонному, а с другой стороны, чтобы отметить ряд
специфических особенностей, присущих этому полю.
Остановимся прежде всего на истории теории тяготе-
тяготения. В понимании поля тяготения следует различать три
этапа. Первый из них связан с теорией Ньютона, класси-
классической физикой и отчасти специальной теорией относитель-
относительности. Согласно этим теориям гравитационное поле оста-
осталось в стороне от известного объединения различных
разделов физической науки XIX века и начала XX века,
в результате чего . была установлена связь между свето-
световыми, электрическими и магнитными явлениями, а также
искривлением пространства и временем и т. д. Второй
этап представлен общей теорией относительности Эйн-
Эйнштейна A916 г.), согласно которой гравитационное поле
является полем метрическим, возникающим при наличии
любого типа вещества, определяющим искривление про-
пространства—времени, возможность которого впервые была
доказана в неэвклидовой геометрии Лобачевского. Можно
сказать, что общая теория относительности как будто
*) См. П. Г. Бергман, Введение в теорию относитель-
относительности, ИЛ, 1947; А. С. Эддингтон, Теория относительности,
ГТТИ, 1934; Л. Ландау и Е. Лифшиц, Теория поля,
Гостехиздат, 1948; В. Паули, Теория относительности, Гостехиз-
дат, 1947; R. Т о 1 m a n, Relativity, Thermodynamics and Cosmology,
Oxford, 1934. О связи теории гравитации и современной теории поля
ем. также: W. P a u I i and M. F i e г z, Ргос. Roy. Soc. A, 173,
211, 1939; L. de В г о g 1 i e, Theorie generaie des particules a spin,
Paris, 1943.
',38 КЛАССИЧЕСКАЯ МЕЗОДИНАМИКА [гл. V
окончательно оторвала гравитационное поле от обычного
вещества, которое, как мы знаем, состоит из элементар-
элементарных частиц д полей.
Как было недавно в этой связи подчёркнуто, физи-
физические объекты разделены на «метрическое поле» g^v
(гравитация), с одной стороны, и электромагнитное поле
H^v (т. е., точнее говоря, элементарные частицы и поля),
с другой*).
Третий этап теории тяготения связан с релятивист-
релятивистской квантовой механикой элементарных частиц и полей,
которая не только позволяет построить квантовую тео-
теорию слабого гравитационного поля, но по крайней мере
на данном этапе в " случае линейного приближения
приводит с необходимостью к заключению о возможности
взаимных превращений элементарных частиц и квантов
гравитации (гравитонов) друг в друга. Тем самым, в из-
известной мере, гравитация объединяется с системой осталь-
остальных элементарных частиц, что приводит к принципиаль-
принципиальной возможности построения объединённой теории всех
полей и частиц**).
Перейдём теперь к самой краткой математической
формулировке теории тяготения.
Согласно классической теории Ньютона поле тяготе-
тяготения является статическим и описывается однокомпонент^-
ной функцией, потенциалом ср, который подчиняется
уравнению Лапласа-Пуассона
V2cp = W?zp, E6,3)
где та — масса тела, создающего поле, р — плотность распре-
распределения этой массы. В случае точечной частицы, находя-
втцейся в точке т = 0, вместо р следует подставить Ъ(т).
Здесь можно принять электромагнитную нормировку, вве-
введя ср' = —т= и гравитационный заряд т' = V х - т; тогда
У*
*) A. Einstein, The meaning of relativity, Princeton,
1946.
**) Д. Иваненко, УФН, 32, вып. 2, 3, 1947. Д.Ива-
Д.Иваненко и А. Соколов, Вестник МГУ, № 8, 1947; ДАН, 58,
1633, 1947.
§ 56] ГРАВИТАЦИЯ И ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ 439
Энергия взаимодействия тела массы т с гравитацион-
гравитационным полем в ньютоновом приближении равна U = — /тр.
Перейдём к математической формулировке второго
этапа теории тяготения, связанного со специальной и об-
общей теорией относительности. Теория тяготения Ньютона
обобщается при этом в разнообразных направлениях. Как
заметил ещё Пуанкарэ при построении специальной тео-
теории относительности, статическое уравнение Пуассона
должно быть во всяком случае заменено волновым урав-
уравнением для гравитационного потенциала. Следовательно,
ньютонов закон также является лишь статическим при-
приближением соответС1ЧИ^йй|ей формулы, зависящей также
от скоростей 'тяготеющих масс, подобно, например, фор-
формуле Брейта в электродинамике. Дальнейшие обобщения
связаны с общей теорией относительности Эйнштейна.
Согласно последней гравитационное поле должно описы-
описываться не однокомпонентным потенциалом, но 10 компо-
компонентами волновой функции, образующими симметричный
тензор ^lxv = grvii (p-, v = l, 2, 3, 4). При этом тензор грави-
гравитационного поля оказывается совпадающим с метриче-
метрическим тензором g^v = g™vtr, характеризующим искривление
четырёхмерного пространства—времени, предуказанное
Лобачевским A826 г.). В этом пункте, очевидно, коренится
наибольшее своеобразие, вся не имеющая аналога в слу-
случае других полей специфичность эйнштейновской теории
гравитации, отождествляющей последнюю с метрическим
полем, т. е. полностью её геометризирующей. Вообще
говоря, все обычные поля тяготения являются слабыми,
соответствующими незначительному искривлению про-
пространства—времени. Поэтому можно положить для кова-
риантных составляющих: g^ — g^ + h^ и для контрава-
риантных: g:xv = g$v — hf, где g^v с индексом 0 равны
постоянным псевдоэвклидовым значениям
-1
-1
440 КЛАССИЧЕСКАЯ МЕЗОДИНАМИКА [гл. V
а квадратами h^v, как правило, пренебрегается. Ньютонов
потенциал оказывается лишь (статической) добавкой к од-
одной из компонент слабого поля: ср = —-i± . Компо-
Компоненты слабого поля h^ образуют симметричный тензор
относительно линейных преобразований. Используя знач-
значки Эйзенхарта, индексы у которых не должны учиты-
учитываться при суммирования:
имеем
81 «А*. 8,;
h =
= J J £ = vy'_ у-^£
81 = «А*. 8,;= J J £ = vy' у^£= 1 + k
Как и в случае других полей, мы имеем в гравитации
дело с двумя основными проблемами: описание воздей-
воздействия гравитационного поля на вещество и описание по-
порождения или излучения поля веществом. Отсылая за
разъяснениями по неквантовой теории к монографиям по
общей теории, относительности, укажем здесь, что реше-
решение первой задачи, в конце концов, оказывается весьма
простым, поскольку для этого достаточно лишь записать
соответствующие лагранжианы или уравнения свободных
частиц (или полей) в ковариантном виде, т. е. в общих
четырёхмерных криволинейных координатах с помощью
компонент g,^. Добавочные члены, возникающие при
этом, по сравнению с псевдоэвклидовым случаем, будут
соответствовать взаимодействию с гравитационным полем.
Подставив затем в указанные выражения приближённые
значения g[iy = g^ -f /^v, мы получим описание взаимо-
взаимодействия со слабым полем. Впрочем, поскольку слабое
гравитационное поле к^у можно рассматривать в точной
аналогии с другими полями: электромагнитным, мезон-
ным и др., сохраняя в первом приближении псевдоэвклидов
характер метрики, то энергию взаимодействия со слабым
полем любого данного поля (или частиц) возможно полу-
получить, конструируя по общему правилу лагранжиан, учи-
учитывающий связь данного поля (или частиц) со слабым
гравитационным.
5 56] ГРАВИТАЦИЯ И ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ 441
СлабоеГ гравитационное поле содержит, как было
указано, десять компонент; в плоской волне имеет смысл
назвать (Л44) продольно-продольной частью, (h±n) — про-
продольно-поперечной n(hnk) — поперечно-поперечной. Беско-
Бесконечно малым преобразованием координат можно всегда
добиться того, что отличными от нуля будут в плоской
волне лишь две поперечно-поперечные компоненты. Ана-
Аналогично случаю электромагнитного поля, реально излу-
излучаться может лишь одна поперечно-поперечная часть.
Компоненты hnk удовлетворяют уравнению Даламбера
ПЛП/С = О, причём между шестью компонентами поля
имеются четыре соотношения:
Таким образом, поперечно-поперечная часть обладает
лишь двумя независимыми составляющими.
Далее, основное уравнение релятивистской квантовой
механики (v^V^— &g)& = 0 приобретёт в гравитационном
поле вид
где {[xv, а} обозначают трёхзначковые скобки Кристоф-
феля, зависящие от первых производных компонент g^v:
Ограничиваясь слабым полем, притом его реально излу-
излучаемой поперечной частью, имеем
v = еД^- hnsVnVs;
g^ frv, а} ?а- Gshnshnk) Vk + 1 еа (vAiA..) ?а.
Отсюда основное уравнение Клейна примет вид
где
i- e.
442 КЛАССИЧЕСКАЯ МЕЗОДИНАМИКА [гл> V
Таким те образом путём введения четырёхмерных
криволинейных координат и ковариантных производных
при помощи компонент guV видоизменяются все уравнения
частиц и полей бозевского типа, т. е. целого спина,
требующие для своего описания обычных тензоров того
или иного ранга, т. е. скаляров, векторов, антисимметрич-
антисимметричных тензоров 2-го ранга и т. д. С другой стороны, частицы
и поля полуцелого спина, описываемые при помощи спи-
спиноров и не имеющие непосредственного классического
аналога, требуют добавочного исследования. Как было
ранее указано (см. § 23, стр. 128), уравнение спинора, или
семивектора (тензора ранга 1/2), в гравитационном поле
может быть записано при помощи матриц у^, являющихся
своеобразными корнями квадратными из компонент guv
в виде [у^ (vn — IV)"~~ **о] '^ = 0» гДе IV ~" коэффициенты,
характеризующие параллельный перенос спинора.
Напомним, что сам оператор дираковского уравне-
уравнения возникает в результате «линеаризации» уравнения
Клейна.
При наличии гравитации матрицы у^. уже не являются
константами, но представляют собою функции координат
и времени, удовлетворяющие соотношению
В случае слабого поля имеем
гг _}_ yvya = 2gav = 2е^ - 2е^еф^.
Можно также ввести вектор слабого гравитационного
поля, положив
где yg удовлетворяет обычному соотношению
YeYo+Y2Yox = 2eAv;
тогда получим
^ = у То*Ая-
Заметим, что тем самым решается не только принци-
принципиальная задача учёта воздействия на электрон гравита-
§ 56] . ГРАВИТАЦИЯ И ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ 443
ционного поля, представленного в данном случае компо-
компонентами у[А, но также немаловажная задача написания
уравнения Дирака в любых криволинейных координатах.
При исследовании слабого гравитационного поля
будем прежде всего исходить из общего выражения
лагранжевой функции
где
Для слабого поля получаем
{pa, P} = ер [pa, р] = -i ер (?a/vP + ?^ag
Выбирая калибровку так, чтобы А = в11Л1ХЦ. = О> и отбра-
отбрасывая продольные компоненты поля, получим для попе-
поперечно-поперечной части лагранжиана
L V?a^ [pa, p] [цр, а].
В частности, для случая распространения гравитаци-
гравитационных волн вдоль оси #! = #, замечая, что /г22 + Л33 = 0,
будем иметь отличными от нуля лишь две компоненты
hn и Л2а — h33. Тогда лагранжиан будет равняться
Выражение лагранжиана, как обычно, даёт возможность
построить всю теорию поля, в данном случае слабого
поперечного гравитационного поля.
В частности, для плотности энергии, как временной
компоненты тензора энергии, получаем
444 КЛАССИЧЕСКАЯ МЕЗОДИНАМИКА [гл у
где
Следовательно,
В согласии с общей теорией плотность энергии гравита-
гравитационного поля, описываемого тензорными, а не спинор-
ными функциями, оказывается положительно дефинит-
дефинитной. Ввиду наличия нескольких компонент у волно-
волновой функции спин гравитационного поля, очевидно,
отличен от нуля. Его выражение можно найти по общему
правилу (см. § 30).
В квантовой теории доказывается, что спин грави-
гравитона, т. е. корпускулы, сопоставленной гравитационной
волне, равен 2 — .
Напомним, что спин фотона, описываемого векторным
максвелловским полем, так же как и векторного проков-
ского мезона, равен 1 — . К тому же результату отно-
относительно спина гравитационного поля можно придти
из подсчёта числа независимых компонент поля (попе-
(поперечных и продольных), замечая, что значение спина s
связано с числом компонент п соотношением n = 2s+l.
В данном случае слабого гравитационного поля
десять компонент h^ связаны, во-первых, четырьмя
условиями калибровки и, во-вторых, условием исчез-
исчезновения следа h. Следовательно, остаётся 5 независимых
компонент, что ведёт к значению спина s—2.
Важно отметить, что излучение слабого гравитацион-
гравитационного поля имеет квадрупольный характер, в противопо-
противоположность электромагнитному полю, обладающему не-
непосредственно дипольным характером. Квадрупольный
характер гравитационного поля связан, наглядно говоря,
со следующим обстоятельством. В электродинамике про-
простейшей излучающей системой является,, как известно,
дицоль. Величина излучённой энергии определяется
§ 56] ГРАВИТАЦИЯ И ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ 445
квадратом ускорения дипольного момента. Этот же ре-
результат подтверждается квантовой механикой, которая
лишь на место плеча диполя ставит матричный элемент,
соответствующий переходу между двумя данными со-
состояниями.
Для периодического движения с круговой частотой
со имеем по классической теории
Как хорошо известно, для произвольной системы
зарядов возможно ограничиться дипольным члендм в об-
общем выражении для вектор-потенциала поля, порождён-
порождённого системой в том случае, когда размеры R малы
по сравнению с длиной волны R <С X и когда скорости
зарядов малы: v < с.
Для системы частиц, обладающих одинаковым удель-
удельным зарядом — = const, ускорение дипольного момента
равно нулю и, следовательно, дипольное излучение от-
отсутствует. В самом деле, в этом случае
V* е ХЧ е п/г
Л — z \ i i """""* /! i ■ i — • о >
где r0 — радиус-вектор центра инерции, М — общая масса
системы. Однако всегда возможно выбрать начало системы
координат в центре инерции, т. е. положить т0 = 0, сле-
следовательно, взять р = 0. Иначе говоря, излучение будет
отсутствовать, если центр инерции покоится или дви-
движется равномерно, т. е. го=О.
Представим себе теперь, что мы интересуемся следую-
следующими членами разложения вектор-потенциала поля ввиду
исчезновения дипольного излучения, или благодаря
необходимости учёта размеров системы при излучении
малых длин волн, когда г ^ X, либо, наконец, по причине
необходимости учёта релятивистских поправок по-
порядка г?/с. Тогда, как доказывается в электродинамике,
следует принять во внимание излучение, обусловлен-
обусловленное электрическим квадруцольным моментом и магнитным
дипольным моментом системы заряженных частиц. Этот
446 КЛАССИЧЕСКАЯ МЕЗОДИНАМИКА [гл. V
же результат подтверждается квантовой механикой, заме-
заменяющей соответствующие классические выражения на
матричные элементы. Наглядно положение вещей можно
пояснить весьма просто, замечая, что при дипольном излу-
излучении мы пренебрегаем членами порядка х/\ в выражении
для вектор-потенциала или для радиуса-вектора
1 -х/с)
= еШ f 1 __ Ь?Щ. V
Таким образом, второй член разложения даст в выра-
выражении для излучения поправочный множитель порядка
Действительно, величина квадрупольного излучения
равняется
где тензор квадрупольного момента распределения частиц
равняется
Следовательно, отношение величины квадрупольного
излучения к дипольному по порядку равно
4-
с2
Обратимся снова к интересующему нас случаю гра-
гравитации. Аналогично потенциалу в электростатике,
потенциал гравитационного поля, вызванного распреде-
распределением масс, можно представить в виде суммы членов
<р = ср0 + <pi + <р2 + • • • I гДе Фо есть обычный ньюто-
ньютонов потенциал, обусловленный полной массой системы
ср0 = ^- . Потенциал диполя cpi B случае гравитации
равен нулю. В самом деле, отношение гравитационного
§ 56) ГРАВИТАЦИЯ И ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ 447
заряда к массе будет во всех случаях одинаково
и равно
Потенциал ср2» обязанный квадрупольному моменту
распределения масс, будет иметь обычный вид
Поэтому, в то время как излучение электромагнит-
электромагнитных волн имеет обычно дипольный характер и приобре-
приобретает тип квадрупольного лишь в особых случаях, излу-
излучение слабого гравитационного поля является в основ-
основном квадрупольным. Не приводя здесь точного вывода
величины гравитационного излучения, ограничимся лишь
пояснением полученной по классической теории формулы
для величины гравитационной энергии, теряемой в еди-
единицу времени:
dU ша fi2
dt с6 v '
Эта формула вполне аналогична результату электро-
электродинамики, что легко усмотреть, заменяя электрический
заряд е на гравитационный \/ % • т. Квантовая теория
подтверждает этот результат, заменяя величину квадру-
квадрупольного момента на соответствующий матричный элемент.
Имея величину гравитационного излучения, мы можем,
применяя обычное сравнение баланса энергии и силы,
получить величину силы гравитационного лучистого тре-
_ния или затухания.
Подобно силе лучистого электромагнитного трения,
силу гравитационного лучистого трения следует также
ввести в уравнение движения отдельной частицы*). Эта
сила оказывается по существу равной 5-й производной
по времени от квадрупольного момента, в противополож-
*) См. также Д. Д. Иваненко и А. М. Бродский,
ДАН, 75, 519,-1950.
448 КЛАССИЧЕСКАЯ МЕЗОДИНАМИКА [гл. V
иость 3-й производной в случае дипольного излучения.
Действительно, вместо
е2 •••
сз
сейчас будем иметь
^т~ * —з- а>б#3 ~^
Как легко проверить, излучение гравитационной
энергии в случае слабого поля и нерелятивистских ско-
скоростей частиц, для которых развивается вся эта теория,
ничтожно, ибо у элементарных, частиц крайне малы их
массы, хотя частоты колебаний велики, у астрономиче-
астрономических же объектов, таких, как, например, двойные звёзды,
несмотря на значительную величину масс, весьма малы
частоты.
Подставляя для грубой ориентировки в случае звёзд
ш^Ю-3, m~1032, r~10u, получим —^~~1032, что
составляет примерно 10~2С собственной энергии.
Упомянем в заключение, что одно из наиболее интерес-
интересных и на первый взгляд парадоксальных следствий реляти-
релятивистской квантовой теории гравитационного поля заклю-
заключается в предсказании принципиальной возможности пре-
превращения гравитационного поля в обычные элементарные
частицы и обратно (например, превращения пары элек-
электрон—позитрон в два гравитона). Вероятность или эф-
эффективное сечение подобного превращения в случае сла-
слабого поля крайне мала, поскольку она определяется
квадратом гравитационного радиуса гт =■- -у , а не квадра-
том электрического радиуса ге — —-а, как в случае став-
ших привычными электромагнитных трансмутаций.
Не приводя вывода соответствующих квантовых фор-
формул, лежащих вне рамок данной книги, поясним лишь
их смысл путём сравнения с выражением для электро-
электромагнитных превращений. Как известно, в случае малых
скоростей квантовая теория даёт следующее выражение
§ 56] ГРАВИТАЦИЯ И ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ 449
для эффективного сечения превращения электрона и пози-
позитрона в два фотона:
Наши подсчёты для соответствующей гравитационной
трансмутации, т. е. превращения той же пары частиц
в два гравитона, приводят в случае малых скоростей
к выражению
Кроме замены электрического радиуса на гравита-
гравитационный, мы имеем ещё появление характерного ква-
друпольного множителя (%/тс2)* (вполне аналогично
появлению дипольного множителя (ё/тс2J в формулах
векторной мезодинамики). Очевидно, в обычных усло-
условиях (Ш ~ тс2) слабого поля вероятность подобной грави-
гравитационной трансмутации ничтожна:
Однако вероятность гравитационных превращений
весьма быстро возрастает с энергией и при значениях
Ш ~ 1021тс2 будет достигать порядка электромагнитных
эффектов.
Повидимому полученный результат имеет известное
принципиальное значение, поскольку благодаря возмож-
возможности указанных превращений стирается резкая граница
между гравитационным полем и другими полями и части-
частицами, которая имелась во всех предыдущих воззрениях на
тяготение. Этот вывод можно рассматривать как один из
первых шагов -на пути построения некоторой более общей
картины строения всего вещества, соответствующей имею-
имеющимся сведениям об элементарных частицах и сопостав-
сопоставленных им полях и их взаимных превращениях.
29 д. Иваненко и А. Соколов
ДОПОЛНЕНИЕ
РАЗВИТИЕ ТЕОРИИ ВАКУУМА
а) История вопроса
Новейшая теория полей и элементарных частиц раз-
развивается в направлении построения такой общей теории
взаимодействия частиц с электромагнитным, мезонным,
гравитационным полями, полем пар электронов — пози-
позитронов и других частиц, которая учитывала бы нулевые
флуктуации этих полей. Иначе говоря, последнее развитие
квантовой теории поля делает новый шаг в уточнении
физических свойств вакуума, влияние которого сказы-
сказывается в ряде эффектов. Новейшая квантовая теория поля
развивается, вообще говоря, в рамках существующей
релятивистской квантовой механики на базе лагранше-
вой функции и гамильтонова формализма и правил пере-
перестановок. При этом оказалось возможным придать всей
теории более законченную релятивистскую форму на
основе нового своеобразного сверхмноговременного фор-
формализма Швингера-Томонага, который, впрочем, приводит
к результатам, совпадающим с полученными обычным
путём. Наиболее существенными являются результаты
теории не в направлении улучшения формализма, но
в объяснении двух весьма важных физических явлений,
обнаруженных на опыте: во-первых, сдвига энергетиче-
энергетических уровней атомных электронов по отношению к их
положению, вычисленному на основе релятивистской
квантовой теории электрона Дирака, не учитывавшей
нулевых флуктуации, и, во-вторых, в доказательстве
наличия у электрона дополнительного к обычному спино-
спиновому, некинематического собственного магнитного мо-
РАЗВИТИЕ ТЕОРИИ ВАКУУМА 451
мента. Вместе с тем новейшая теория вакуума проли-
проливает известный свет на проблему собственной массы эле-
элементарных частиц.
Как мы подчеркнули, новейшая теория вакуума
является существенно квантовой, так что её подробное
изложение выходит за рамки настоящей книги*). Однако
ввиду важности этой теории для понимания ряда свойств
элементарных частиц, в особенности природы их массы,
иначе говоря, для вопросов, которые анализируются
в данной книге, мы дадим краткое изложение истории
основных идей и результатов новейшей теории вакуума.
Это тем более необходимо, что квантовая теория вакуума
во многих пунктах, как и в других случаях, развивает
идеи и методы, возникшие на почве классической теории.
Изложение этих новейших вопросов в конце данной
книги уместно также в качестве введения в квантовую
теорию поля.
Поскольку новая теория вакуума в значительной
мере развивалась в связи с толкованием упомянутых
выше двух эффектов, мы остановимся сначала на их
открытии. Установление сдвига уровней имеет долгую
историю. Как известно, квантовая механика весьма
успешно определяет значения энергии электронов в ато-
атомах. При этом в атоме водорода релятивистская кванто-
квантовая теория Дирака давала для энергии электрона, дви-
движущегося в электростатическом кулоновом поле точеч-
точечного протона, формулу, установленную ранее Зоммер-
фельдом, с более точными значениями квантовых чисел.
Формула эта в общем прекрасно подтверждалась опытом,
являясь одним из фундаментальных подтверждений
предпосылок теории. В частдости, согласно теории Дирака
имеет место вырождение, и термы 2Л/2 и 2А/2 должны
совпадать. Это последнее обстоятельство явилось пред-
предметом специальных экспериментальных исследований,
прдчём Хаустон и Вильяме ещё более десяти лет назад
обнаружили обычным оптическим методом с помощью
*) См. реферативный сборник, серия вторая, вып. I, ИЛ,
1950 и сборник статей и рефератов под ред. Д.Иваненко «Сдвиг
уровней атомных электронов», ИЛ, 1950.
29*
452 дополнение
приборов высокой разрешающей силы незначительное
нарушение формулы Зоммерфельда-Дирака, которое было
правильно истолковано Пастернаком как следствие
сдвига уровня Si/2 относительно Pi/2 вверх в сторону мень-
меньших по абсолютной величине энергий. Эти результаты
возбудили некоторый интерес, но не показались убеди-
убедительными. Сдвиг уровня указывает на уменьшение при-
притяжения. Причину этого прежде всего казалось есте-
естественным искать в модификации закона Кулона, напри-
например, за счёт неточечности протона, придавая ему какой-то
эффективный радиус, или относить её за счёт размазан-
размазанности заряда протона, проводящего примерно 0,2 вре-
времени в диссоциированном состоянии р—>п + тг+ (Гейтлер
и др.)- Несомненно, обе эти причины ослабления куло-
нового притяжения имеют место, однако можно пока-
показать, производя подсчёт с уточнёнными волновыми
функциями электрона, с самого начала учитывающими
объём ядра, что они ведут к слишком незначительным
сдвигам*). Указание Бора и Оппенгеймера, что причину
сдвига мояОяо искать в более точном учёте обратной
реакции поля, так же как аналогичное замечание Блохин-
цева в одном из докладов, не были разработаны подроб-
подробнее**). Неясность ситуации лучше всего характеризуется
замечанием Зоммерфельда в его работе 1941 г., что
ввиду исчерпания, как тогда казалось, всех теоретиче-
теоретических возможностей в этом направлении, следует надеяться,
что никакого сдвига на самом деле экспериментально
обнаружено не было! Окончательно сдвиг уровня в под-
подтверждение прежнего открытия был обнаружен с бес-
бесспорностью уже не оптическим, но радиочастотным мето-
методом в 1947 г. Лэмбом. и Ризерфордом, получившими для
расстояния B6*1/2—2А/2) термов значение A062 ±5) мгц,
лежащее в области тонкой структуры A мгц~
= 4,1 • 10~9 eV; основной терм водорода соответствует энер-
энергии 13,5 eV). Эти прецизионные измерения возбудили
общее внимание и повели к разработке соответствующей
*) См. Д. Иваненко и В. Р о д и ч е в, ДАН, 70, 80,
1950; Д.Иваненко и А. Цандер, ЖЭТФ, 18, 434, 1948.
**) См. обзор Я. А. Смородинского, УФН, 39, № 3, 325,
1949.
РАЗВИТИЕ ТЕОРИИ ВАКУУМА 453
теории сдвига, исходившей из учёта вакуумных флуктуа-
флуктуации электромагнитного поля, которыми ранее теория
Дирака пренебрегала. Первоначальный нерелятивистский
подсчёт Бете хотя и давал хорошее согласие с опытом,
но использовал произвольное обрезание логарифмически
расходящегося интеграла при % ъ тс2; дальнейшая реля-
релятивистская теория была более последовательной и привела
к конечному и совпадающему с опытом результату. По-
Последующий анализ подтвердил, что все другие возможные
поправки и причины сдвига играют второстепенную роль.
Сдвиг уровней предсказывается также в других атомах и
наблюдался в общем согдасии с теорией в ионизирован-
ионизированном Не*.
История установления дополнительного магнитного
момента электрона гораздо короче. После того как не-
несколько лет назад в лаборатории Раби радиочастотным
методом исследования Зееман-эффекта ряда спектров
(Na, Ga) было найдено отклонение гиромагнитного коэф-
коэффициента g для электрона, указывающего соотношение
между магнитным и механическим моментами, от обыч-
обычного значения g = 2, Брейт предложил объяснить это
расхождение наличием у ^электрона дополнительного
(«аномального») магнитного момента. Вскоре на базе
новой теории вакуума Швингер и другие получили в пре-
прекрасном согласии с опытом следующее значение маг-
магнитного момента электрона*):
eh
a
В дальнейшем новая теория вакуума была применена
к подсчёту отклонений от формулы Клейна-Нишины при
эффекте Комптона, затем к отклонениям от формулы
Резерфорда для рассеяния заряженных частиц и т. д.;
однако во всех случаях, кроме двух указанных эффек-
эффектов, поправки оказались лежащими за пределами воз-
возможностей современного эксперимента. Применение новой
теории вакуума к мезонномуполю, в частности к подсчёту
*) См., например, А. Д. Г а л а н и н, ЖЭТФ, 19, 521, 1949.
Подробные рефераты статей Швингера имеются в сборнике «Сдвиг
уровней атомных электронов», ИЛ, 1950,
\№ ДОПОЛНЕНИЕ
магнитных моментов нуклеонов, обязанных виртуальной
их диссоциации, дало качественно разумные, но далеко
не окончательные результаты. К полю гравитационному
новая теория вакуума ещё не применялась, несмотря
на очевидную естественность подобного обобщения.
б) Сдвиг уровней
Как уже указывалось выше, новая теория вакуума
является закономерным развитием предыдущего этапа
релятивистской квантовой теории частиц и полей, отнюдь
не выходящим за рамки этой теории при помощи каких-
либо добавочных гипотез, хотя бы и обрабатываемых кван-
квантовыми релятивистскими методами. Среди последних ука-
укажем, например, гипотезу квантованного пространства—вре-
пространства—времени*), или борновскую гипотезу наличия какой-то фикси-
фиксированной лагранжевой функции, или недавнее предложение
Борна симметризовать теорию в координатах и импульсах
на основе некоторого принципа «взаимности»**), или
общую теорию «слияния» де-Брогля ***), развивающую
прежние идеи нейтринной теории света ****), и т. д. Более
того, новая теория вакуума представляет собой в значи-
значительной мере реабилитацию полной системы релятивист-
релятивистской квантовой механики, приведшей в своё время с
необходимостью к предсказанию нулевых флуктуации и
других характеристик вакуума, которые, однако, описы-
описывались расходящимися интегралами и поэтому подверга-
подвергались сомнениям в смысле их физического значения.
Как известно, неоднократно предпринимались по-
попытки запретить переходы в состояния отрицатель-
отрицательной энергии, полностью удалить последние из теории,
*) Эта гипотеза была предложена В. Амбарцумяноми
Д. Иваненко (Zs. f. Phys., 64, 563, 1930) и неоднократно
в дальнейшем обсуждалась в литературе; см., например, работу
Снайдера (Snyder, Phys. Rev., 71, 38, 1947).
**) М. Born, Rev. Mod. Phys., 21, 463, 1949.
***) L. de Broglle, Theorie generale des particules a spin,
Paris, 1943.
****) Основы нейтринной теории света изложены, например, в
работах А. А. Соколова: ЖЭТФ 7, 1055, 1937; 8, ИЗ, 644, 1938,
РАЗВИТИЕ ТЕОРИИ ВАКУУМА 455
отбросить нулевые флуктуации и т. д. Новая теория
вакуума в сущности предлагает прекратить эти попытки
отхода в сторону от закономерных следствий релятивист-
релятивистской квантовой механики и принять эти следствия со
всей серьёзностью, придать наиболее непосредственный,
возможно даже наглядный, смысл нулевым флуктуациям
полей и вместе с тем добиться с минимумом произвола
хотя бы частичного устранения бесконечностей. Одну
из основных идей новой теории вакуума и вывода из неё
выражения сдвига уровня электрона наглядно, хотя далеко
не строго, пояснил Вельтон следующим полуквантовым
нерелятивистским рассуждением.
Хорошо известно, что энергию поля излучения можно
представить в виде суммы энергий осцилляторов. Послед-
Последние, однако, согласно квантовой теории обладают нулевой
энергией ё0, не исчезающей даже в нулевом состоянии
при тг = О:
( l) go = *!. E7,1)
Всё это ведёт к тому, что даже в отсутствии фотонов име-
имеются флуктуации энергии. Оставим для дальнейших рас-
рассмотрений эту нулевую энергию, несмотря на то, что
сумма нулевых энергий по всем частотам поля равна
бесконечности и попытаемся придать ей реальный смысл
энергии электромагнитного поля, под действием которого
беспрерывно находится электрон, даже в отсутствии ка-
каких-либо внешних полей. Действие этого вакуумного поля
«нерождённых» фотонов заставит электрон совершать коле-
колебания в грубом приближении согласно уравнению дви-
движения
mr = eXJBSLK. E7,2)
Таким образом смещение координаты электрона под влия-
нием вакуумного поля будет равно:
Аг= — \ —~ cos o>£ йсо,
m J о2 '
где 22Ш — амплитуда Фурье разложения электрической
456 ДОПОЛНЕНИЕ
напряжённости JE7Ba]K = JE7:
JE= \ jEJw cosw^ do.
Следовательно, для среднего по времени имеем:
До сих пор мы имеем дело с обычным классическим урав-
уравнением движения. Теперь сделаем решающий шаг и
приравняем энергию поля, как известно, равную
Е*
к энергии квантовых, притом нулевых флуктуации
1 Ы\ со2 ,
)d
где второй множитель под интегралом есть известное
выражение плотности состояний частоты ш в интервале
о, о) + с?ш. Отсюда -So, == -^^ .
Следовательно,
Расходимость этого выражения не представляет прин-
принципиальной трудности и связана с легко устранимыми
пренебрежениями. Во-первых, электрон не является
свободным, но связан в атоме, что устраняет расходимость
на нижнем пределе. Во-вторых, при нерелятивистском
рассмотрении не имеет смысла интегрировать по сколь
угодно высочим энергиям или частотам, поэтому следует
в качестве верхнего предела взять не оо, но величину
^max~wc?, о)шах'^27г-—-. Дальнейшей анализ подтверж-
подтверждает эти заключения.
Таким образом, мы приходим к важному выводу о том,
что под влиянием вакуумного поля свободный покоящийся
электрон совершает своего рода брауновское движение
РАЗВИТИЕ ТЕОРИИ ВАКУУМА 457
с определённым квадратом смещения. Тем самым вакуум-
вакуумные колебания, как подчеркнули особенно ясно Бого-
Боголюбов и Тябликов*), индуцируют у первоначально точеч-
точечного электрона некоторую размазанность или эффектив-
эффективный радиус, величина которого оказывается средним гео-
геометрическим между классическим электрическим радиу-
радиусом и квантовым радиусом, т. е. комптоновской длиной
волны
У
- h
ос
2-ктс '
Наличие подобного эффективного радиуса скажется на
ряде эффектов при анализе поведения электрона. В част-
частности для взаимодействия электрона с внешним элек-
электрическим полем вместо старого
V = — еср (г)
мы будем иметь, с учётом вакуумных членов, новое выра-
выражение:
V = -
так как
Следовательно, изменение энергии взаимодействия, с учё-
учётом влияния вакуумного поля, равно:
ибо [см. A0,8)] для атома водорода:
Наконец, чтобы получить искомый сдвиг уровня как
усреднённое по состоянию атомного электрона значение
♦)Н. Н. Боголюбов и С, В. Тябликов, Изв.
АН УССР, № 5, 10, 1946.
458 ДОПОЛНЕНИЕ
изменения энергии взаимодействия, необходимо величину
V' — V умножить на |ф(?*)|2 и проинтегрировать по всему
пространству.
Тогда для искомого сдвига уровня находим значение:
где kmin связано со средней энергией возбуждения ЬЩ соот-
соотношением
Как известно, для «S-состояния:
где а — боровский радиус, а п — главное квантовое число.
Для других состояний (Д й и т. д.)
Отсюда мы получаем формулу Бете, из которой видно,
что сдвиги уровней, обусловленные вакуумными поправками,
должны наблюдаться в нерелятивистском приближении
только для ^-состояний:
где Ry представляет собою энергию ионизации основного
состояния водорода. В частности, для 2а5-состояния (п = 2,
Д§ = 17,8 Ry) находим для сдвига термов 1040 мгц.
Величину искомого сдвига энергетических уровней мы
подучаем, вычислив один раз энергию взаимодействия
с нулевыми колебаниями электрона свободного и другой
раз электрона, связанного в атоме. Оба раза получается
бесконечный результат, расходящийся квадратично.
Однако разность двух расходящихся величин оказывается
в нерелятивистской теории лишь логарифмически расхо-
расходящейся, а в релятивистской, с учётом новых правил ре-
регуляризации (см. стр. 464) — величиной конечной и даю-
дающей в прекрасном согласии с опытом значение сдвига.
Энергия взаимодействия электрона с нулевыми колебания-
РАЗВИТИЕ ТЕОРИИ ВАКУУМА 459
ми обусловлена связью его с поперечной частью электро-
электромагнитного поля, представленного в вектор-потенциале А:
(напомним, что в неквантовой теории для покоящегося
электрона этот член взаимодействия отсутствует). На-
Наглядно говоря, взаимодействие обязано испусканию и
поглощению квантов поля. В данном случае сам электрон
испускает и поглощает поперечные фотоны, что приво-
приводит к бесконечной энергии самодействия или собственной
электромагнитной энергии и, следовательно, соответствен-
соответственной бесконечной массе частицы. Эта поперечная собствен-
собственная полевая энергия добавляется к полевой классиче-
классической продольной электростатической энергии поля, поро-
порождённого электроном. Наряду с этим играет роль другое
фундаментальное обстоятельство новой теории вакуума:
перенормировка массы. Идея перенормировки массы за-
заключается в следующем. Вместо того, чтобы отбрасывать
указанные бесконечные полевые массы или устранять
их сейчас же каким-либо гипотетическим образом, допу-
допустим, что последующее развитие теории каким-то образом
устранит бесконечности и даст конечное значение массы.
Поэтому предлагается считать указанные бесконечные
члены включёнными в конечное эмпирическое значение
массы, перенормировав последнюю. Эта перенормировка
отнюдь не является простым переименованием выраже-
выражений, так как, будучи применённой к электрону связан-
связанному, она ббязывает нас вычесть из его полной полевой
энергии значение полевой энергии свободной частицы.
При этом разность оказывается, как указывалось, ко-
конечной.
Мы отмечали выше неоднократно, что строгий реляти-
релятивистский подсчёт уменьшает степень расходимости в энер-
энергии взаимодействия электрона с его электромагнитным
полем или вакуумом. Суть дела заключается в том, что
электрон связан не только с нулевыми колебаниями поля
электромагнитного, но также с флуктуациями поля вир-
виртуальных пар электронов—позитронов. Поэтому в при-
присутствии электрона виртуальные электроны—позитроны
460 ДОПОЛНЕНИЕ
вакуума, во-первых, несколько смещаются, вакуум свое-
своеобразно «поляризуется», так что его диэлектрическая
постоянная оказывается меньше единицы примерно на
г^= в области порядка z вокруг электрона *). Отме-
Отметим, что подобные поляризационные поправки слишком
малы:
т. е. поляризационное смещение уровня для 2iS'-cocTOfl-
ний примерно равно г^ рассмотренного выше смещения
%'', обусловленного связью с нулевыми колебаниями
фотонов. Наряду с этим всякий внешний заряд инду-
индуцирует в вакууме заряд бесконечной величины, который
следует считать включённым в реальный конечный за-
заряд**), произведя перенормировку его подобно перенор-
перенормировке массы. Во-вторых, влияние вакуума пар элек-
электронов-^-позитронов сказывается в том, что ввиду прин-
принципа Паули возникает эффективное отталкивание элек-
электронов вакуума от реального внешнего электрона, и это
перераспределение заряда в вакууме сказывается в виде
размазывания заряда электрона. Как раз это обстоя-
обстоятельство делает классическую электромагнитную соб-
собственную энергию равной
т. е. расходящейся только логарифмически при стремле-
стремлении эффективного радиуса электрона к нулю, г0 —>0.
В-третьих, нулевые колебания электромагнитного поля
взаимодействуют с виртуальными парами электронов—
позитронов, благодаря чему смещение и энергия элек-
электрона, вызванные нулевыми фотонами, оказываются суще-
существенно уменьшенными. Средний квадрат смещения ока-
•) В. В е й с с к о п ф, см. сборник «Сдвиг уровней атомных
электронов», ИЛ, 1950, стр. 23.
*•) См. Дирак, Сборник «Атомное ядро», ГТТИ, 1934 и сбор-
сборник «Сдвиг уровней атомных электронов».
РАЗВИТИЕ ТЕОРИИ ВАКУУМА 461
зывается теперь сходящимся и не зависящим от радиуса
электрона (вместо логарифмической расходимости), а сред-
средняя энергия, приобретённая электроном под влиянием
толчков нулевых фотонов (полевая собственная попереч-
поперечная энергия), будет расходиться только логарифмически,
а не квадратично, т. е. будет значительно более слабо
зависеть от структуры электрона. Наконец, разность
полевых энергий для свободного и связанного электро-
электронов оказывается, как подчёркивалось выше, конечной.
Мы не будем останавливаться сейчас на пояснении
дополнительного вывода магнитного момента электрона,
который, говоря наглядно, обязан воздействию нулевых
колебаний вакуума на дрожащее движение шредингеров-
ского типа, совершаемое дираковским электроном. Как
известно, благодаря дрожанию обычный собственный
магнетизм электрона можно наглядно истолковать как
величину, обязанную круговым токам радиуса
Здесь важно лишь подчеркнуть, что значение вакуумной
добавки к магнитному моменту получается совершенно
естественно в рамках общей теории поля, учитывающей
взаимодействие с вакуумом, а весь магнитный момент
электрона будет равен
§■;)•
2ти
С принципиальной точки зрения следует подчеркнуть
не только успех теории при выводе сдвига уровней и
получения дополнительного момента, но также наличие
более общей точки зрения на природу массы. Пови-
димому, не исключено, что собственная масса частиц
имеет двойственную природу (сравни § 34). Некоторая
основная, «затравочная» масса (механическая масса по
терминологии классической теории электрона Лорентца)
ещё не может быть расшифрована, и не исключено, что
именно её объяснение потребует существенного выхода
за рамки нынешней релятивистской квантовой механи-
механики. С другой стороны, полевая доля массы, возможно,
1
окажется в конце концов конечной, порядка Тойт-
462 ДОПОЛНЕНИЕ
Аналогичным образом следует подойти к объяснению
масс других частиц, например нуклеонов, которые,
повидимому, кроме основной «затравочной» массы будут
обладать полевыми мезоиными массами, а также некото-
некоторыми полевыми электромагнитными и т. д. массами.
После перенормировки массы и заряда бесконечности ока-
оказываются удалёнными из теории, и всем выражениям можно
вновь придать в терминах эффективных потенциалов
и других величин относительно наглядный смысл. Наряду
с эффективным радиусом и дополнительным магнитным
моментом взаимодействие с вакуумом индуцирует, как
можно показать, у электрона и других частиц эффек-
эффективные мультипольные моменты высшего порядка, т. е..
квадрупольный момент и т. д., которые следует учиты-
учитывать в энергии связи уравнения Дирака для электрона.
После указания на основные физические идеи новой тео-
теории вакуума и пояснения двух важных эффектов, остано-
остановимся ещё коротко на некоторых более формальных, но
играющих принципиальную роль сторонах современной
теории поля.
в)Сверхмноговременной формализм
Наряду с развитием теории вакуума обычными методами
релятивистской.квантовой механики, позволившими выяс-
выяснить все основные физические идеи, необходимые для
объяснения сдвига уровней атомных электронов и допол-
дополнительного магнитного момента электрона, те же резуль-
результаты были получены несколько иным методом нового
«юверхмноговременного» формализма*). Этот формализм,
не выходящий за рамки релятивистской квантовой меха-
механики, представляет известное преимущество сплошной
релятивистской ковариантной формулировки теории,
тогда как обычно, несмотря на ковариантный по существу
характер теории, время, единое для поля и всех частиц,
оказывается существенно выделенным, и ковариантность
приходится доказывать дополнительно, нередко громозд-
♦) J. Schwinger, Phys. Rev., 73, 415 A948); 74, 1439
A948); 75, 651 A949); рефераты этих и других близких работ
см. в сборнике «Сдвиг уровней атбмных электронов», ИЛ, 1950.
РАЗВИТИЕ ТЕОРИИ ВАКУУМА 463
ким путём. Сверхмноговременной формализм является
обобщением многовременного формализма Дирака — Фо-
Фока—Подольского, в котором в системе частиц, взаимодей-
взаимодействующих с полем, наряду с общим для всего поля вре-
временем Т для каждой частицы вводилось своё особое
время tt*). Как было отмечено Марковым**), мно-
многовременной формализм можно применить также к клас-
классической релятивистской теории взаимодействия ча-
частиц с полем. Аналогичное замечание, очевидно, следует
сделать также относительно применимости нового сверх-
многовременного формализма к классической теории.
В новом формализме, который можно также назвать «бес-
«бесконечно временным», каждой точке поля или простран-
пространства сопоставляется своё локальное время t~a(x,y,z).
Таким образом, время выступает в качестве простран-
пространственно-подобных гиперповерхностей в четырёхмерном
пространстве, в результате чего положения в простран-
пространстве и во времени оказываются неразрывно связанными.
Место 'дифференцирования по времени от волновой функ-
функции — в новой теории занимает функциональная произ-
производная от функционала 4f(txyg)= ^*(<з), или в неквантовой
теории от функции действия S (з)
j
dt 8a '
При переходе от одной гиперповерхности к другой вол-
волновые функции преобразуются при помощи некоторого
унитарного оператора
причём для предельного случая трансформации от бес-
бесконечно удалённого в прошлом состояния к бесконечно
удалённому в будущем оператор U совпадает с 5-матри-
цей. Гейзенберга. Таким образом, квантовая электроди-
электродинамика и теория вакуума, остающиеся на почве лагран-
•) См. П. А. М. Дирак, Основы .квантовой механики,
ГТТИ, 1932; Г. Вентдель, Введение в квантовую теорию вол-
волновых, полей, Гостехиздат, 1947.
**) М. А. М а р к о в, ЖЭТФ, 10, 1311, 1940.
464 ДОПОЛНЕНИЕ
жева и гамильтонова формализма, содержат как частный
случай теорию Гейзенберга, который пытался отбросить
гамильтонов формализм, полагая невозможным опреде-
определить изменение ф-функции за бесконечно малый проме-
промежуток времени, процессы в течение которого будто бы
являются ненаблюдаемыми ввиду наличия предполагае-
предполагаемого минимального промежутка длины и времени
(несколько в духе квантования пространства и вре-
времени).
г) Полевая масса фотона
Поскольку собственная полевая масса частиц обуслов-
обусловлена взаимодействием частицы с различными полями
всех других частиц и полей, с которыми данная
частица взаимодействует, иначе говоря, с частицами и
полями, которые данная частица может порождать, то воз-
возникает проблема конечности полевой массы фотона. В са-
самом деле, фотон виртуально порождает пары электронов —
позитронов, пары заряженных мезонов и протонов — ан-
антипротонов. Подсчёты полевой массы фотона привели
различных авторов к несовпадающим результатам, в
том числе расходящемуся, конечному (Вентцель) и рав-
равному нулю. Последний результат, требуемый калибро-
калибровочной инвариантностью, был подтверждён в дальней-
дальнейшем. Эта ситуация заставила ещё раз более тщательно
проанализировать операции с различными расходящи-
расходящимися выражениями и попытаться установить более одно-
однозначные правила «регуляризации» подобных выражений.
д) Новые правила регуляризации
Как было уже показано выше (см. §§ 32—34), вопрос об
устранении бесконечной собственной полевой энергии
электрона возник ещё в классической теории Лорентца
и обсуждался затем неоднократно. Все приёмы регуля-
регуляризации удобно по терминологии Паули-Вилларса раз-
разбить на два класса.
1) «Реалистические» теории, которые предлагают
ввести, кроме электромагнитного, какие-либо иные поля,
РАЗВИТИЕ ТЕОРИИ ВАКУУМА 465
предполагаемые действительно существующими, энергия
которых могла бы скомпенсировать бесконечность в ком-
компонентах тензора энергии электромагнитного поля и обес-
обеспечила бы как конечность, полевой массы электрона (или
даже привела бы к окончательному выражению этой
массы, согласно добавочной полевой гипотезе), так и исчез-
исчезновение компонент натяжения; последнее необходимо со-
согласно Лауэ для обеспечения устойчивости электрона и для
выполнения правильного соотношения между энергией
и импульсом. К реалистическим теориям относятся: теория
давления Пуанкаре в дорелятивистской схеме, теория
компенсирующего векторного поля, образующего вместе
с максвелловским би-поле (Сгколов, см. §|84б); теория
полей с высшими производными {Бопп и др. § 33) *), а также
новая теория компенсирующего нейтрального скалярного
поля Пайса (с-мезонов). До сих пор не удалось прозёсти
реалистическую программу в любой степени приближе-
приближения квантовой теории возмущений. Ёозможно, что подоб-
подобная теория должна с самого начала использовать правила
перестановки, свободные от сингулярностей. Кроме того,
яи компенсирующее векторное поле, ни с-мезоны нигде
яе проявляются в каких-либо физических явлениях,
и вопрос об их реальном существовании остаётся от-
открытым.
2) С другой стороны, возможно стать на «формалистиче-
«формалистическую» точку зрения и вводить для компенсации беско-
бесконечностей вспомогательные поля,которые в окончатель-
окончательном результате исчезают, например, путём обращения
в нуль некоторых векторов или обращения в бесконеч-
бесконечность масс, которые связаны с полями. К формалистичег
ским теориям относится, очевидно, метод предельного
Х-процесса (см. § 34а).
,- В связи с развитием новой теории вакуума было при-
приложено несколько новых формалистических приёмов
регуляризации. Типичным является метод Паули-Вил-
*) См. также позднейшие работы Н. I. В h a b h a, Rev.
Mod. Phys., 17, 200 A945); 21,-451 A945); H. A., Rrim-ers,
F. 1. Beliafante, I. K, Lubans-ki, Physfca, fe, 598
A941).
30 д. Иваненко и А. Соколов
466 ДОПОЛНЕНИЕ
ларса*), заключающийся в замене сингулярной на свето-
световом конусе функции Грина G± уравнений Даламбера и
скалярного уравнения, а также связанных с ней функций
А и D, определяющих правила перестановок (§§ 17 и
20), на новые регуляризованные функции GR, являющиеся
суммой подобных же функций, но с рядом вспомогатель-
вспомогательных масс Мг = хЬ~, стоящих на месте старой массы w =
= 9» связанной с частицами данного поля:
где G(kt) согласно § 20 имеет вид
при этом с0 = 1, il/0 = m, а коэффициенты ct (i Ф 0) и вспо-
вспомогательные массы кг подчиняются условиям
2'*,=.о, 2'с4*?«о.
В конечном результате все kt стремятся к бесконечности.
Этот приём регуляризации связан с тем обстоятельством,
что гриновская функция скалярного уравнения вблизи
Ъветового конуса /, = с2Т2 — /?2—>0 имеет вид (см^ § 20), а
также C,1)
Вместо дискретного ряда вспомогательных масс и ком-
компенсирующих полей можно использовать непрерывное
распределение. Применение подобной регуляризации под-
подтвердило прежние результаты теории вакуума, дало тре-
требуемое значение нуль для массы фотона и внесло извест-
известную ясность также в ряд других расчётов.
Существенно отметить, что, несмотря на формалисти-
формалистический исходный пункт регуляризации через вспомога-
вспомогательные массы, можно придать этому методу более реаль-
•) W. Р а и 1 i and F. Vi liars, Rev. Mod. Phys., 21,
434, 1949; см. сборник «Сдвиг уровней атомных электронов», ИЛ,
1950.
РАЗВИТИЕ ТЕОРИИ ВАКУУМА 467
ный физический смысл. В самом деле, взяв за исходный
пункт регуляризованную функцию GRf будем рассматри-
рассматривать её как гриновскую функцию некоторого поля. Тогда
нетрудно показать, что это поле соответствует частицам
разных масс Mt и описывается уравнением с высшими
производными. От четырёхмерной гриновской функции
можно перейти к статическому закону взаимодействия,
который, очевидно, будет иметь вид (см. также § 48):
[е~~к°г e~kir ' )
|— h сг ——h ... У .
V = const
При этом характерное для теории с высшими производ-
производными различие знаков коэффициентов с{ (см. § 33) непо-
непосредственно ведёт к условию (I). Мы видим, что стремле-
стремление вспомогательных масс к бесконечности, необходимое
для устранения компенсирующих полей в окончательном
результате, с указанной только что точки зрения вовсе не
обязательно.
Другие формалистические методы заключаются в том,
что нерелятивистское обрезание расходящихся интегралов
заменяется релятивистским. Одна из попыток в этом на-
направлении была сделана путём введения инвариантного обре-
обрезания в пространстве импульсов электрона, на чём мы
сейчас не останавливаемся. Более широко сейчас исполь-
используется фейнмановское предложение релятивистского разма-
размазывания закона взаимодействия заряда с электромагнит-
электромагнитным полем*), таким образом, чтобы эффекты с частотами,
много меньшими 137-т- , давали бы старый результат,
в то время как расходящиеся интегралы стали бы конеч-
конечными.
Практически вычисления проводятся по следующей
схеме: прежде всего интеграл
*) R. P. Feynman, Phys.Rev.,74, 939, 1948; 74, 1430 1948:
подробный реферат статьи Фейнмана содержится в сборнике
«Сдвиг уровней атомных электронов», A.. с).
468 ДОПОЛНЕНИЕ
представляется в виде
а инвариантное размазывание сводится к тому, что для
устранения бесконечностей при к —> go четырёхмерная
сингулярная функция плотности 8Г--5 — к2) заменяется
выражением
где G (к) — произвольная гладкая функция, нормированная
на единицу и достигающая максимума в области X поряд-
порядка 137 —j— . Этот метод применим как ь классической, так
и квантовой теории. В результате подобного обрезания
полевая энергия электронов (или полевая масса), оказы-
оказывающаяся конечной, определяется из выражения:
где
In l0 = \ G (I) In Idl.
о
Отсюда видно, что полевая масса электрона составляет
всего примерно лишь — часть общей массы, что было
указано нами выше, а также обладает требуемыми свой-
свойствами тензорной размерности, т. е. пропорциональна ма-
матрице р3.
Для того чтобы избежать инфракрасной катастрофы,
которая появляется при вычислении того же сдвига уровней,
следует, согласно Фейнману, вместо функции 8 Г~ — A" j
ввести функцию 8 С^ — к2 — A2min)> причём лт1п подби-
РА8ВИТИВ ТЕОРИИ ВАКУУМА 469
рается из условия, чтобы релятивистское выражение пере-
переходило в нерелятивистскую формулу Бете, в которой
ограничение на нижнем пределе обязано связи электрона
в атоме (см. стр. 458).
Тогда необходимо положить: щ
In Xmin = In 2A-min — у f
где
. _2к(Щ_
KlDiD ck~
Сдвиг «У-уровней относительно /'-уровней при внутрен-
внутреннем квантовом числе /—-к- и любом значении главного
квантового числа п будет складываться из трёх частей:
Сдвиг %' (пропорциональный коэффициенту In ^J= — In2+
+ 24, где In = = 7,6876) является по существу бетевским
сдвигом. Сдвиг %" (пропорциональный коэффициенту — ^)
связан с поляризацией электронно-позитронного вакуума.
Наконец, сдвиг %'"( пропорциональный коэффициенту—J
связан с взаимодействием дополнительного момента элек-,
трона с электростатическим полем.
Для атома водорода мы находим для общего сдвига:
2&/а —2А/я«1051 мгц,
что улучшает первоначальный результат Бете A040 мгц)
и находится в хорошем согласии с опытом A062 мгц).
Заметим, что любой формальный вспомогательный ме-
метод при всём его удобстве и простоте применения (на-
(например, обрезание), даже независимо от вопросов однознач-
однозначности, может, в лучшем случае, представлять собой лишь
предварительную ступень теории, которая в дальнейшем
должна будет придать реальный физический смысл любым
470 ДОПОЛНЕНИЕ
вспомогательным полям и частицам, вводимым в рас-
рассмотрение.
Следует подчеркнуть, что все перечисленные «реа-
«реалистические» и «формалистические» способы регуля-
регуляризации представляют^ собой пока что гипотетический
выход за рамки современной физики, поскольку первые
теории предсказывают новые частицы или поля, ещё
не обнаруженные на опыте, а теории второго клас-
класса хотя и действуют, подобно реалистическим, метода-
методами релятивистской квантовой механики, но сущест-
существенно выходят за рамки теории, обобщая гриновские
функции и правила перестановки за счёт новых фик-
фиктивных полей, устраняемых в конечном результате. Во
всяком случае несомненно, что общая теория элемен-
элементарных частиц должна быть замкнутой, т. е. беско-
бесконечности во взаимодействии частиц А с частицами
В должны быть компенсированы какими-либо ины-
иными, возможно, всеми остальными реальными частица-
частицами и полями.
Хотя ввиду успехов теории, позволившей объяснить
новые явления и изолировать бесконечности, например,
в собственной массе, потребность более существенного
выхода за рамки релятивистской квантовой механики
не является сейчас слишком острой, всё же вновь отметим
возникновение ряда гипотез, пытающихся на базе новых
допущений быстрее продвинуться вперёд в понимании
элементарных частиц. Сюда относятся, в частности,
теория взаимности, различные формы пятимерной тео-
теории, возрождённая гипотеза квантования пространства
и времени, а также общая теория сведения одних полей
к другим путём особого «слияния» (например, в духе ней-
нейтринной теории света).
Заканчивая описание успехов и затруднений теории
элементарных частиц и полей, мы видим, что развитие
учения о строении вещества может быть правильно понято
только с точки зрения философии диалектического мате-
материализма, согласно которой каждый новый этап наших по-
познаний связан с нахождением (на основе плодотворного со-
содружества теории и эксперимента в тесном контакте с
практикой и новейшей техникой) более глубоких законов;
РАЗВИТИЕ ТЕОРИИ ВАКУУМА 4^i
всеобщей взаимосвязи явлений природы.
Таким образом, эволюция наших представлений о строе-
строении материи с полной убедительностью подтверждает из-
известное положение И. В. Сталина «...что нет в мире
непознаваемых вещей, а есть только вещи, ещё не познан-
познанные, которые будут раскрыты и познаны силами науки
и практики.»*).
*) И- Сталин, Вопросы ленинизма, Госполитивдат, 1939,
стр. 543.
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Алихановы, варитроны ^327
Андерсон и Неддермейер, от-
открытие ц-мезона 322
Антинейтрино 317
Бесселя функции, асимптотиче-
асимптотическое приближение 273
Р-распад 298, 299, 315, 321.
331
fi-силы ядерные 315
Бете формула сдвига атомных
уровней 458, 469
Бетатрон 120, 253, 290
—, излучение 254, 258
—, потолок работы 258, 290
—, сжатие орбиты 258
—, условие Видерое 257
Би-поле, теория 219, 223, 230,
465
Блэккет, открытие каскадных
ливней 329
Боголюбова и Тябликова ис-
исследование вакуумных коле-
колебаний 457
Боппа-Подольского электроди-
электродинамика с высшими производ-
производными 211, 233
Бора магнетон 295
Борна-Инфельда нелинейная
теория поля 201
Б рейта формула 148, 150
Вакуум, диэлектрическая по-
постоянная 204, 217, 460
—, квантовая теория 223, 450
—, поляризация 460
Варитроны 327
Вейля условие нормировки 25
Векслера ускорители 293
Вектор квазимагнитной индук-
индукции 384
напряжённости 384
поляризации 384
— квазиэлектрической индук-
индукции 384
— тока 384
— четырёхмерный 362
Векторное мезонное поле 372
Векторы ковариантные 123
— контравариантные 123
Вентцеля-Бриллуэна метод 277
Вернов, изучение первичной
компоненты космических лу-
лучей 324
Видерое условие 257
Власова исследования опере-
опережающего воздействия 244
Волны длина де-броглевская 119
комптоновская 121, 305
— мезонные, излучение квази-
квазимагнитным диполем 409
, — квазиэлектрическим
диполем 409
, распространение в ваку-
вакууме 404
, рассеяние с учётом зату-
затухания 426
~, распространение в одномер-
одномерном пространстве 95
— электромагнитные, излучение
87, 90, 293
, скорость фронта 96, 105,
114, 117
, фазовая скорость 96, 105,
114, 117, 118, 154
Время, квантование 454, 470
—, обратимость 127
—, однородность 125
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
473
Гамильтона функция 187
Гамильтона-Якоби метод 245
Гаусса функция 81
Гельфанд и Яглом, теория ча-
частиц высшего спина 135
Геометрия Лобачевского-Ри-
мана 129, 437
— псевдоэвклидова 129, 188
— вектор 91, 94
— вектор квазимагнитный 407
— вектор квазиэлектриче-
квазиэлектрический 407
Гильберта-Негер теорема 133
Гравитация 436
—, излучение 447
—, история теории тяготения
437
—, квадрупольный характер по-
поля 444
—, квантовая теория слабого
поля 441
—, теория Зеелигера 70
Грина функция 34, 39, 42, 45,
72, 74, 79, 86, 89, 100, 105,
107, 111, 412, 116
Даламбера уравнение 84, 90
d-функция, важнейшие форму-
формулы 30
— в п мерном пространстве 29
— и интеграл Стильтьеса 13
разложение в тригоно-
тригонометрический ряд 22
по полиномам Ле-
жандра 28
функциям Бесселя
26
эрмитовым функ-
функциям 28
Фурье 20
— как предельный случай 15
—, общая теория 11
—, определение И, 14, 15, 22
—, примеры представления 22,
26, 28
—, связь с оператором Коши 43
Д-функция вторая 88
— первая 87, 227
Децтерон, квадрупольный мо-
момент 308
Дейтерон, основное состояние
306
—, энергия связи 297
Дирака матрицы 128, 362
— релятивистская теория ва-
вакуума 208
— уравнение квантовое 362
классическое 221, 370
Дирихле задача 61
— интеграл 23
Диполь, плотность 46
—, потенциал 47
—, электрический момент 91
Дипольная трудность 369, 390,
397, 418, 430, 434
Дифференциал собственный 25
D- функция вторая 101, 104
— первая (перестановочная)
101, 227, 351
Дурандина-Ершова теория век-
торных уравнений 374
Жданов А. П., «звёздьи в косми-
космических лучах 325
Законы сохранения 133, 186,
345-347, 377
Заряды фиктивные 55, 65
Заряженная плоскость 49, 58
Заряженный цилиндр 52
Зеелигера теория гравитации
70, 336
Зеркальные отражения, инва-
инвариантность 127
Зоммерфельда-Дирака формула-
451
Зоммерфельда постоянная тон-
тонкой структуры 400
Иваненко модель атомного ядра
296
— и Померанчук, предсказание
«светящегося» электрона 258,
261
— и Соколова теория «светя-
«светящегося» электрона 276
— и Фока теория ковариантной
производной от спиноров 128
Излучение гармонического ос-
осциллятора 90, 198
474
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Излз'чение гравитационное 447
— когерентное 286
— «сверхсветовое» 120, 154,
167
— света электронами в ускори-
ускорителях 261, 279
, зависимость
интенсивности от частоты 272
, угловое рас-
распределение 269
— тормозное мезонов нуклео-
нами 431
фотонов 432
— электромагнитных волн 87,
90
космическими части-
частицами 293
Импульс излучения четырёх-
четырёхмерный 238
— канонический 349
— самодействия четырёхмерный
238
Инвариант, интервал 126, 129
—, плотность 139
—, скалярное произведение 123
—, форм-фактор 227
— электромагнитного поля вто-
второй 140
первый 140, 200
третий 140
Инвариантность 122, 125—129,
136, 139, 140, 199, 200, 227
— относительно зеркальных от-
отражений (инверсии) 127
• калибровочных преобра-
преобразований потенциалов 131
конформных преобразо-
преобразований 130
преобразований Лорент-
ца 126
трёхмерных вращений 125
Кароттаж, бесконечно тонкий
пласт 64
—, источник тока в скважине 62
—, краевые задачи теории 60,
62, 64
—, основное уравнение 61
Квантования пространства—
времени гипотеза 454, 470
Квантовая механика нереляти-
нерелятивистская 250, 297, 301, 433,
451
релятивистская 163, 228,
438, 448, 451, 454
— теория «сверхсветового»
электрона 163
светящегося электрона 287
Кинематика полей и частиц,
общековариантная форма 128
Клейна-Нишины формула 250,
416, 453
Клейна уравнение волновое 99
— в п -мерном 1гростран-
стве 107
Колебания нестационарные 94
— струны 96
, резонанс 98
Комптона эффект 428
Космические лучи, ливни кас-
каскадные 329
, мезоны 325
, первичная компонента
324
, происхождение 323
, процессы в атмосфере
325
, радиоизлучение 293
, электронно-ядерные взры-
взрывы 329
Коши оператор 43
— формула 44
Краснушкина метод решения
волнового уравнения 94
Кронекера-Всйерштрасса сим-
символ 21, 24, 84
Кулона закон 303
Лагранжа функция (лагранжи-
(лагранжиан) 138, 200, 349
- Лапласа-Пуассона уравнение
двумерное 41
одномерное 38
трёхмерное 30, 45
Лармора инвариант 140
Лауэ теорема 171, 177
Ленин о неисчерпаемости элек-
электрона 293
— об изучении строения мате-
j; рии 224
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
4*5
Ливни каскадные 329
Линейный ускоритель 294
Липшица формула 52
Лобачевского-Римана геомет
рия 129, 437
Лондона теория сверхпроводи-
сверхпроводимости 72
Лорентца преобразования 126,
132
— сила 142
— теория электромагнитпой
массы 175, 193
— уравнение 247
— условие для потенциалов 146
А-предельный процесс 223, 224
Льенара-Вихерта потенциалы
61, 148
Магнетон Бора 295
— ядерный 295
Максвелла-Лорентца уравне-
уравнения 144, 145, 177
, инвариантность 133
, интегрирование 145
Марков, многовременной фор-
формализм в классической теории
463
Масса, изменение со скоростью
180
— ji-мезона 326
— неполевая, теория 220, 461
— ти-мезона 325, 330
— покоя 137, 197
— полевая 121, 178, 197, 419,
461
—, природа 121, 222 •
— протона 304
— фотона полевая 464
— электромагнитная по Макс-
веллу-Лорентцу 175
, уравнение движения 193
— электрона 180
— элементарных частиц 120
Мезоводород 434
Мезодинамика квантовая 420,
431
— классическая 70, 295
, уравнения с высшими
производными 399
— нелинейная 210
Мезонная теория ядерных сил
319, 335, 357, 372, 391
Мезонное поле, силы реакции
419
Мезонные волны векторные, из-
излучение къазимагнитным ди-
диполем 409
, — квазиэлектриче-
квазиэлектрическим диполем 409
, интегрирование урав-
уравнений 406
, квазимагнитное рас-
рассеяние 415, 428
, квазиэлектрическое
рассеяние 413, 426
, распространение в ва-
вакууме 404
, рассеяние с учётом
затухания 426
Мезоны 319, 325
— векторные 372, 386
— в космических лучах 325
—, время жизни 326, 331
—, дипольность 333
— лабораторные 325
—, масса 320, 326, 327, 330
—, модель Ферми 328
— [х 326
— нейтральные 320, 328
—, основные свойства 322
— ти заряженные 325
нейтральные 328
— псевдовекторные 391
— псевдоскалярные 357, 365
—, распад 321, 326, 330
—, спин 330
—, теоретическое предсказание
319
—, тормозное испускание ну-
клеонами 431
«Мезотроний» 330
Меллера-Розенфельда смесь ме-
мезонов 397
Меллера формула 151
Мерсера теорема 36
Метод перебрасывания членов
взаимодействия 370
Минковского-Далленбаха тензор
плотности энергии 177
Момент диполя 18
476
ПРЕДМЕТНЫЙ» УКАЗАТЕЛЬ
ji-мезон 326
Мысовский и Жданов, метод тол-
толстослойных фотопластинок
325
Неймана задача 62
Нейтретто (тг0-мезон) 320, 328
Нейтрино 317
Нейтрон 296, 299
—, магнитный момент 297, 321
—, спин 296
Нейтроны быстрые, рассеяние
304, 314, 402
Нетер-Гильберта теорема 133,
186
Нуклеоя 296
—, возбуждённое состояние 327
—, общая форма взаимодей-
взаимодействия 395
—, полевая масса 419
—, тормозное испускание ме-
мезонов 431
—, уравнения движения 424
Ньютона закон 303
— теория тяготения 437
Ортонормирования условия 93
Остроградского теорема 186
Осциллятор гармонический 90,
198
Пары частиц, превращение в
гравитоны 448
, фотоны 208, 299,
449
, теория Дирака 208
Паули-Вилларса метод регуля-
регуляризации 220, 465
тс-мезоны заряженные 325
— нейтральные 328
Плотность дипольного момента
46
— заряда, индефинитность 355
поверхностная 40,' 48, 49
точечного 46, 139, 202
— квадрупольного момента 46
— объёмная 48, 49
Поле движущегося точечного за-
заряда 151
— мезонное векторное 372, 395
Поле мезонное векторное, век-,
торные ядерные силы 386
, общая теория 375
*—, основные уравнения
372
при наличии нуклеон*
ных источников 381
, интегрирование уравне*
—^ 406
, квазимагнитное рассея-
рассеяние 415, 428
, квазиэлектрическое рас-
рассеяние 413, 426
псевдовекторное 391, 39-6
псевдоскалярное 357, 365,
395
— —, силы реакции 419
скалярное 335, 395
, общая теория 342
— — — комплексное 352
— электромагнитное, излучен
ние 87, 90
, импульс 171
, распространение 84, 115
, тензор энергии 168
Померанчук, произвольность
Х-форм-фактора 230
Потенциал векторный 147, 148
— диполя 47
— заряда 39, 43, 47, 54, 73, 216
— квадруполя 47
— линии 43, 54
—, обрезание 398
— плоскости 40
— скалярный 147, 148, 158
Преобразований группы 132
Преобразования инверсии 127,
132
— калибровочные 131, 140, 145,
369, 374
— конформные 130, 132
— Лорентца 126, 132
— переноса 125, 132
— фазовые 131
Принцип вариационный 136
— относительности начала от-
отсчёта 125
общий 437
специальный 126
— соответствия 200
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
477
Прока уравнения 372
Пространство, изотропность 125
—, квантование 454, 470
—, однородность 125
Протон, магнитный момент 295,
322
—, масса 304
—, спин 296
Псевдовектор 134, 361
Псевдовекторное мезонное поле
391, 396
Псевдоскаляр 134, 361
Псевдоскалярное мезонное поле
357, 365, 395
Псевдотензоры 357
Пуассона интеграл 20
— скобки квантовые 351
Пуассона скобки обобщённые 348
, связь с д-функцией 350
, ^-функцией 350
— уравнение обобщённое 70
Рассеяние быстрых нейтронов
протонами 402
ядрами 314
протонов протонами 403
— мезонов квазимагнитное 415
квазиэлектрическое 413
— нейтронов в пара- и ортово-
дороде 307
— света на свете 207, 209
свободных электронах
207, 246
Регуляризации метод Паули-
Вилларса 220, 465
Фейнмана 220, 467
— теории «реалистические» 464
«формалистические» 465
Римана-Кристоффеля тензор 129
Сверхпроводимость, теория Лон-
Лондона 72
«Сверхсветовой» электрон 120,
154
«Светящийся» электрон 120, 279
Свойства трансформационные
122
Сдвиг уровней атомных электро-
электронов 454
Сила самодействия 121,142, 193,
419
Силы ван-дер ваальсовы 302
— инерции 129
— «квазимагнитные» 369
— магнитные 300
— нецентральные 308
— обменные 302, 311
— реакции мезонного поля 419
— спиновые 307
— электрические 303
-— ядерные 295, 300, 304, 341
Синхротрон 120, 261, 292
Скалярное мезонное поле* 335,
342, 352
— произведение 123
Скаляры 124, 134
Скобельцын, электронно-ядер-
электронно-ядерные взрывы 329
Соколова теория ватухания
431
компенсирующего поля
219, 223, 230, 465
Сонина интеграл разрывный 108,
116
Спин гравитона 444
— мезона 330
— нейтрона 296
— поля 192, 378
— протона 296
— фотонов 192
— электрона 179, 296
Спинор 135
Спинтензор 135
Сталин о познаваемости мира
471
Стильтьеса интеграл 13
Стирлйнга формула 276 •
«Супрачастицы» 327
Тамма и Франка теория «сверх-
«сверхсветового» электрона 154
Тензор 134, 135
— квазимагнитного момента
384
— момента количества движе-
движения поля 185, 189
— плотности момента количе-
количества движения поля 190, 377
— энергии 169, 205
канонический 187, 345,
377 '
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Тензор энергии максвелловско-
го поля 175
метрический 188, 378
, «симметризация» 191
Тензоры метрические фундамен-
фундаментальные 122
, галилеевы значения
123
Теорема взаимности 68
— вириала 301
— устойчивости 206
Теория относительности общая
71, 199, 437, 439
специальная 126, 173, 180,
439
Терлецкого теория бетатрона
253, 257
— гипотеза происхождения ко-
космических лучей 323
Ток фиктивный 65
Томсона формула рассеяния
света 249, 415
Тритон, энергия связи 305
Умова-Пойнтинга вектор 161,412
— теорема 158,
Уравнение волновое 84, 90, 99
в га-мерном пространстве
107
— движения в классической
механике 74
заряженной частицы 142,
143
электромагнитной массы
193
— телеграфное 115
— теплопроводности 77, 79, 80,
82
Уравнения гиперболического
типа 84
—, зависящие от времени 74
— параболического типа 77
— статические эллиптического
типа 38
Условия ортонормирования 93
Фазотрон 294
«Фактор когерентности» 267
Фейнмана метод регуляризации
220, 467
Ферми теория р-распада 316
Флуктуации нулевые 454
Фок, ассимптотическое иссле-
исследование бес селевых функций
273
Формализм многовременной 229
— сверхмноговременной 462
Фотон, масса 464
—, спин 192
Френкеля обобщение максвел-
ловских уравнений 372
— теория магнитных диполей
407
Функция действия 136
Функции перестановочные 87,
88, 101, 227, 350
Фурье-Бесселя интеграл 27
Фурье разложение 20
Циклотрон 120
Частицы, «само действие» 121,
142, 193, 419
—, собственный магнетизм 138
— элементарные 119
, конечный радиус 121
, масса 120
Чебышева-Эрмита полиномы 28
Черенкова эффект 120, 154,
163, 167
Швингера смесь мезонов 397
— формула магнитного момен-
момента электрона 453
Шредингера уравнение 131
Эйнштейна теория тяготения
71, 199, 437, 439
Эйри интеграл 277
Электрические силы 303
Электродинамика квантовая 119
132
— классическая 119 и д.
, основные уравнения 135
■ релятивистская 120
— нелинейная 199
— полей с высшими производ-
производными 211
Электролиты сильные, теория 71
Электромагнитные волны, излу-
излучение 87, 90
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
479
Электромагнитные волны, из-
излучение космическими части-
частицами 293
, импульс 171
, распространение 84, 115
Электрон атомный, сдвиг Уров-
Уровней 451
—, гиромагнитный коэффици-
коэффициент 453
—, движение в ускорителях 120
—, излучение электромагнит-
электромагнитных волн 261, 269
—, изменение массы со ско-
скоростью 180
—, классический радиус 183,
206
—, гравитационный 186
—, магнитный 185
—, магнитный момент 295
—, собственный некине-
некинематический 453
— «сверхсветовой» 120, 154, 163
— «светящийся» 120, 279
, квантовая теория 287
—, спин 179
—г уравнение движения 238,
239
—, г релятивистское 256
—-, эффективный радиус 204, 217,
244, 457
Электронно-ядерные взрывы 329
Электроны свободные, рассеяние
света 207, 246
— связанные, когерентные ко-
колебания 251
Электростатика, краевые задачи
55, 57, 58
—, метод изображений 56
—, простейшие задачи 49, 52
Элементарные частицы 119
Эффективное сечение, квазимаг-
квазимагнитного рассеяния мезонов
417, 429, 430
квазиэлектрического рас-
рассеяния мезонов 414, 427,
428
Эффективное сечение превраще-
превращения пар в гравитоны 449
фотоны 449
мезонов с учётом зату-
затухания 427
— нейтронов в пара- и
ортоводороде 307
света на свете 209
свободными элек-
электронами 249
тормозного излучения 433
Юкава"теория ядерных сил 319
Ядерные силы 295, 300, 304г
315, 332
бартлеттовские 312, 317,
396
векторные 372, 386, 395
вигнеровские 312, 396
гейзенберговские 312,
317, 396
, зарядная независимость
310
майорановские 312, 317,
396
, нецентральный харак-
характер 308
, обменный характер 311
, общая форма взаимодей-
взаимодействия нуклеонов 395
парные 315
, полевая теория 307, 315
пеевдовекторные 391
псевдоскалярные 357, 365
, радиус действия 306, 341
скалярные 335, 342, 352
, спиновый характер 307
Ядро, «врождённый» магнетизм
321
—, модель 295
—, потенциал 306
—, размеры 304
—, спин 295
—, статистика 296, 297
—, энергия связи 297Г 305
Редактор В. А* Лешковцев.
Техн. редактор Л. А. Голубкова.
Подписано к печати 23/IV | 1951 * г.
Бумага 84х108/$з. 7,5 бум.' л. 24,6
неч. л. 26,24 уч.-изд. л. 42 660 тип. зн.
в печ. л. Тираж 10 000 экз. Т-02319.
Цена 9 р. 20 к. Переплёт 2 р. Зак. № 795.
16-я типография Главполиграфиздата
при Совете Министров СССР.
Москва, Трехпрудный пер., 9.