Автор: Макаров И.М. Виноградская Т.М. Рубчинский А.А. Соколов В.Б.
Теги: вычислительная математика численный анализ математика
Год: 1982
Текст
ТЕОРИЯ
ВЫБОРА
И ПРИНЯТИЯ
РЕШЕНИЙ
ТЕОРИЯ
ВЫБОРА
И ПРИНЯТИЯ
РЕШЕНИЙ
Допущено Министерством высшего
и среднего специального образования СССР
в качестве учебного пособил
для студентов вузов, обучающихся по специальностям
«Прикладная математика» и «Экономическая кибернетика»
i
МОСКВА «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
1982
22.18
Т 33
УДК 519.6
КОЛЛЕКТИВ АВТОРОВ:
И. М. МАКАРОВ, Т. М. ВИНОГРАДСКАЯ,
А. А. РУБЧИНСКИЙ, В. Б. СОКОЛОВ
Теория выбора и принятия решений: Учебное пособие. — М.: Наука. Глав-
ная редакция физико-математической литературы, 1982.— 328 с.
Книга дает цельное представление о математическом аппарате теории вы-
бора и принятия решений. В ней обобщены основные направления исследова-
ний в рассматриваемой области и изложены методы построения алгоритмов и
процедур выбора.
Приведено большое число примеров и упражнений, направленных на вы-
работку систематических навыков применения математических методов в при-
нятии решений.
Для студентов университетов и вузов по специальностям «Прикладная
математика» и «Экономическая кибернетика», а также для экономистов, инже-
неров, разработчиков АСУ и робототехнических систем.
Рис. 84. Библ. 126 назв.
т 1502000000—162
Т 053(02)-82 14'82
g) Издательство «Наука».
Главная редакция
физико-математической
литературы, 1982
ОГЛАВЛЕНИЕ
Предисловие.......................................................... 6
Введение............................................................ 9
ЧАСТЬ I
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ВЫБОРА АЛЬТЕРНАТИВ
Глава 1. Бинарные отношения.......................................... 13
§ 1. Понятие бинарного отношения.................................... 13
§ 2. Способы задания отношений..........................*........... 15
§ 3. Операции над отношениями........................................ 19
§ 4. Свойства отношений............................................ 24
§ 5. Отношения эквивалентности, порядка, доминирования .............. 28
§ 6. Понятие /^-оптимальности........................................ 30
Глава 2. Функции выбора t • • ...............» •............... 32
§ 1. Функции выбора, порожденные бинарными отношениями........... 33
§ 2. Логические формы функций выбора............................. 38
§ 3. Операции над функциями выбора............................... 46
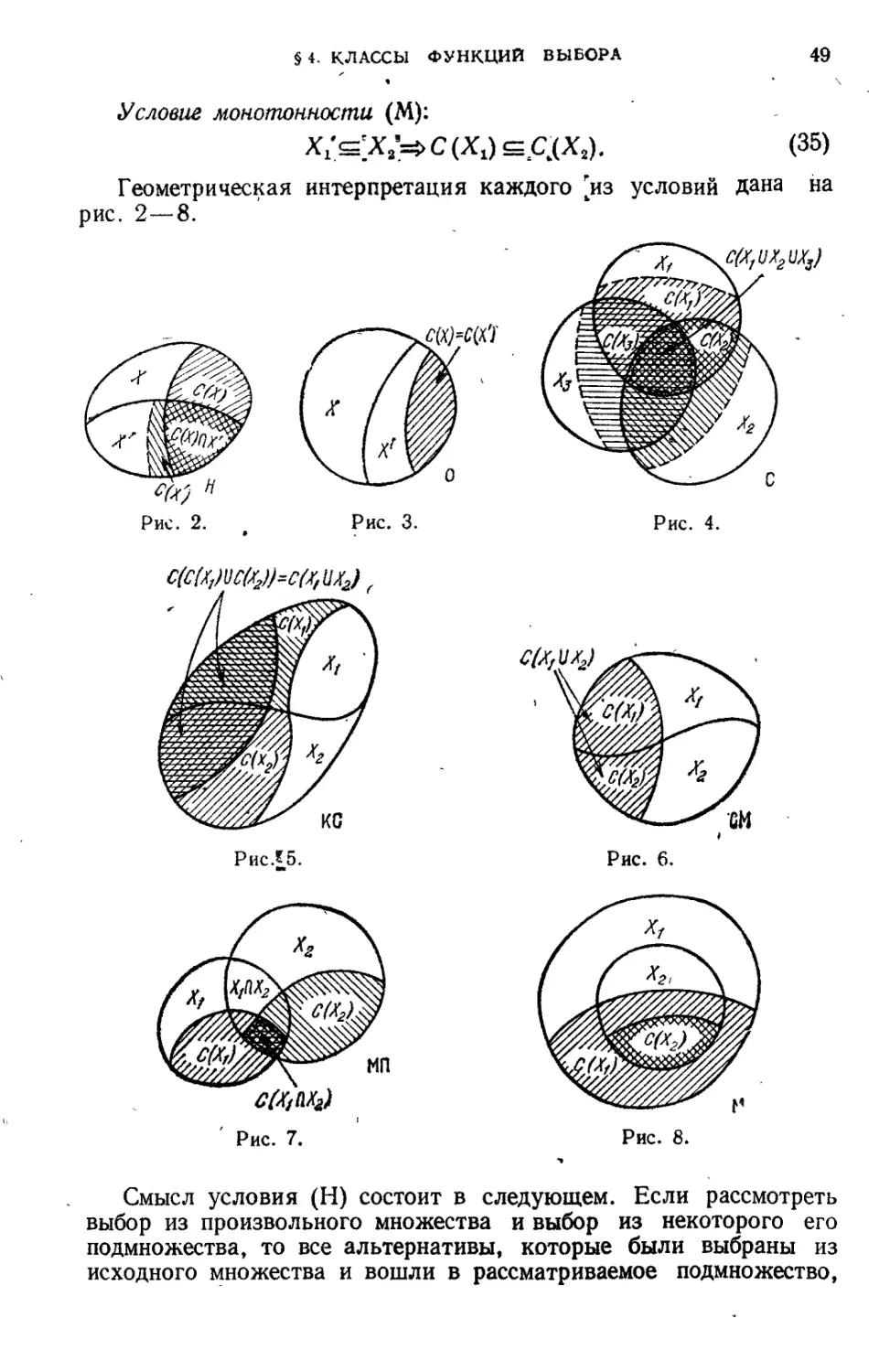
§ 4. Классы функций выбора....................................... 48
§ 5. Взаимосвязи классов функций выбора ......................... 56
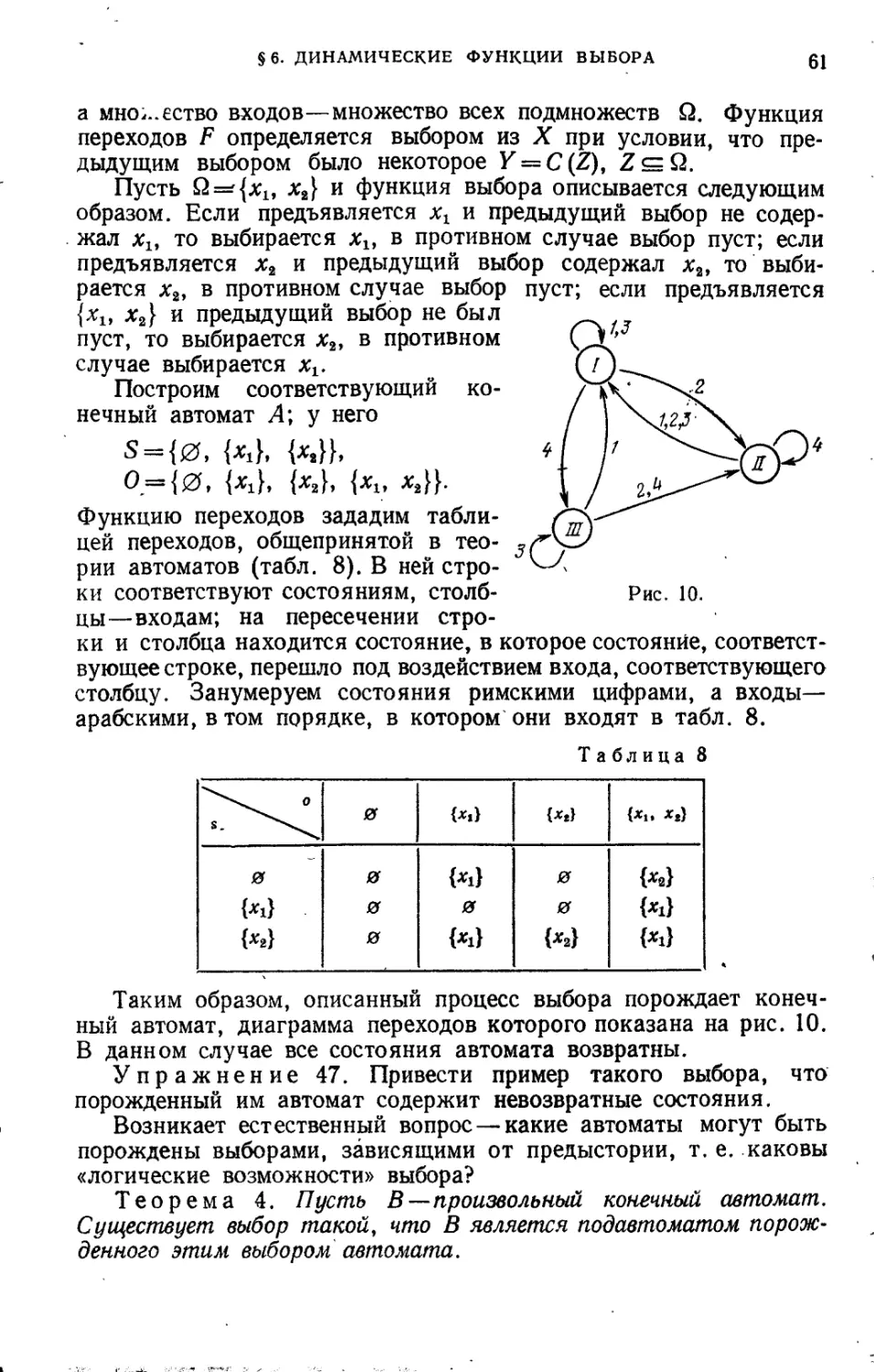
§ 6. Динамические функции выбора................................. 60
Глава 3. Бинарные отношения на Ет................................ 62
§ 1. Общие свойства инвариантных отношений..................... 63
§ 2. Условия отделимости......................................... 67
§ 3. Мажоранты по отделимым отношениям........................... 75
Глава 4. Координатные отношения .................................. 77
§ 1. Понятие координатных отношений и логических форм............. 78
§ 2. Структура множества координатных отношений .............. 83
§ 3. Необходимые и достаточные условия на ЛФО для основных свойств
бинарных отношений................................................ 89
§ 4. Свойства некоторых классов координатных отношений............ 96
§ 5. Иерархические отношения..................................... 101
§ 6. Квазикоординатные отношения................................. 104
Глава 5. Декомпозиция функций выбора............................. 109
§ 1. Общие декомпозиции.......................................... ПО
§ 2. Частные декомпозиции....................................... 114
§ 3. Декомпозиция нормальных функций выбора...................... 119
§ 4. Реализации декомпозиций нормальных фуйКций ................. 124
§ 5. Сложность декомпозиций . . ................................ 126
§ 6. Некоторые интерпретации декомпозиций и композиций........... 130
1* Зак. 515
4
ОГЛАВЛЕНИЕ
ЧАСТЬ II
ПРОЦЕДУРЫ И АЛГОРИТМЫ ПРИНЯТИЯ РЕШЕНИЙ
Глава 1. Экспертные процедуры для принятия решений................. 131
§ 1. Задача оценивания............................................. 132
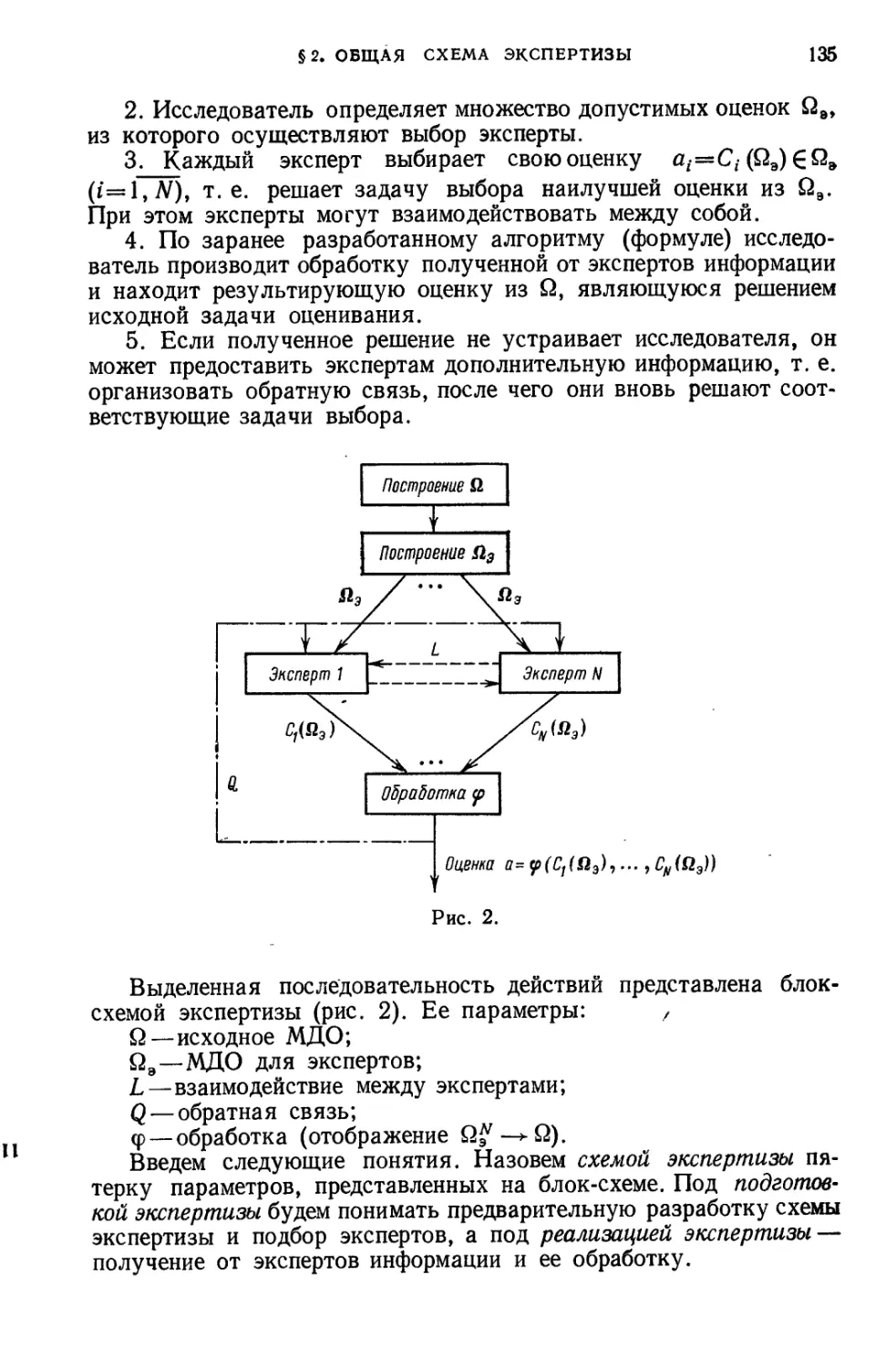
§ 2. Общая схема экспертизы...................................... 134
3. Подготовка экспертизы......................................... 136
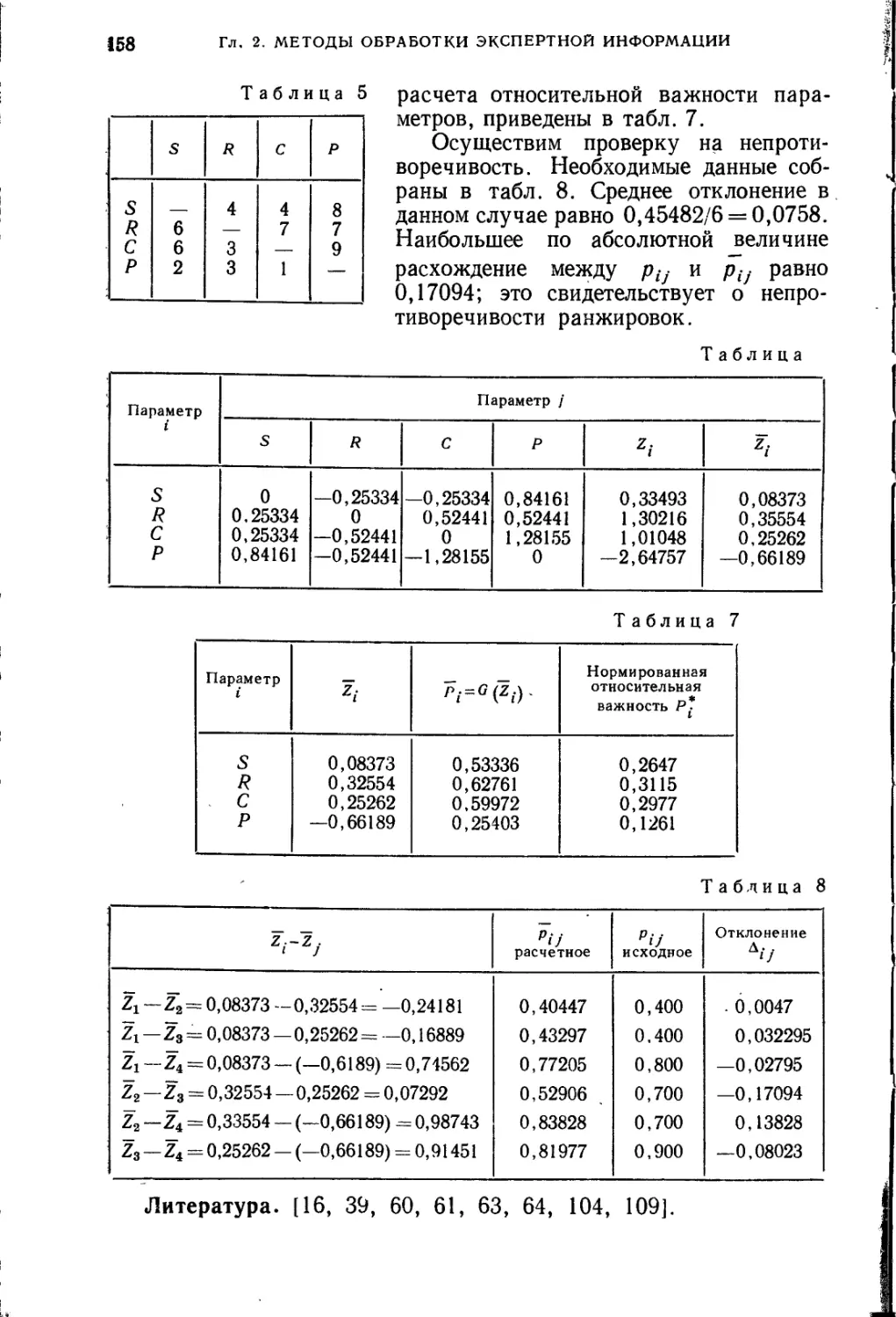
Глава 2. Методы обработки гхсп^пнэй информации.................... 141
§ 1. Статистические методы........................................ 141
§ 2. Алгебраический метод......................................... 149
§ 3. Методы шкалирования........................ ............... 152
Глава 3. Формирование исходного множества альтернатив............ 159
§ 1. Общая характеристика алгоритмов.............•................. 159
§ 2. Алгоритмы формирования ИМА.................................... 160
Г л а.в а 4. Задача выбора..................................... 164
§ 1. Математическая задача выбора.................................. 165
§ 2. Алгоритм решения общей задачи выбора.......................... 166
§ 3. Алгоритмы построения . . . ................................. 170
§ 4. Задача выбора с функцией полезности......................... 173
Г лава 5. Вероятностные характеристики мощности множества Q* . . 175
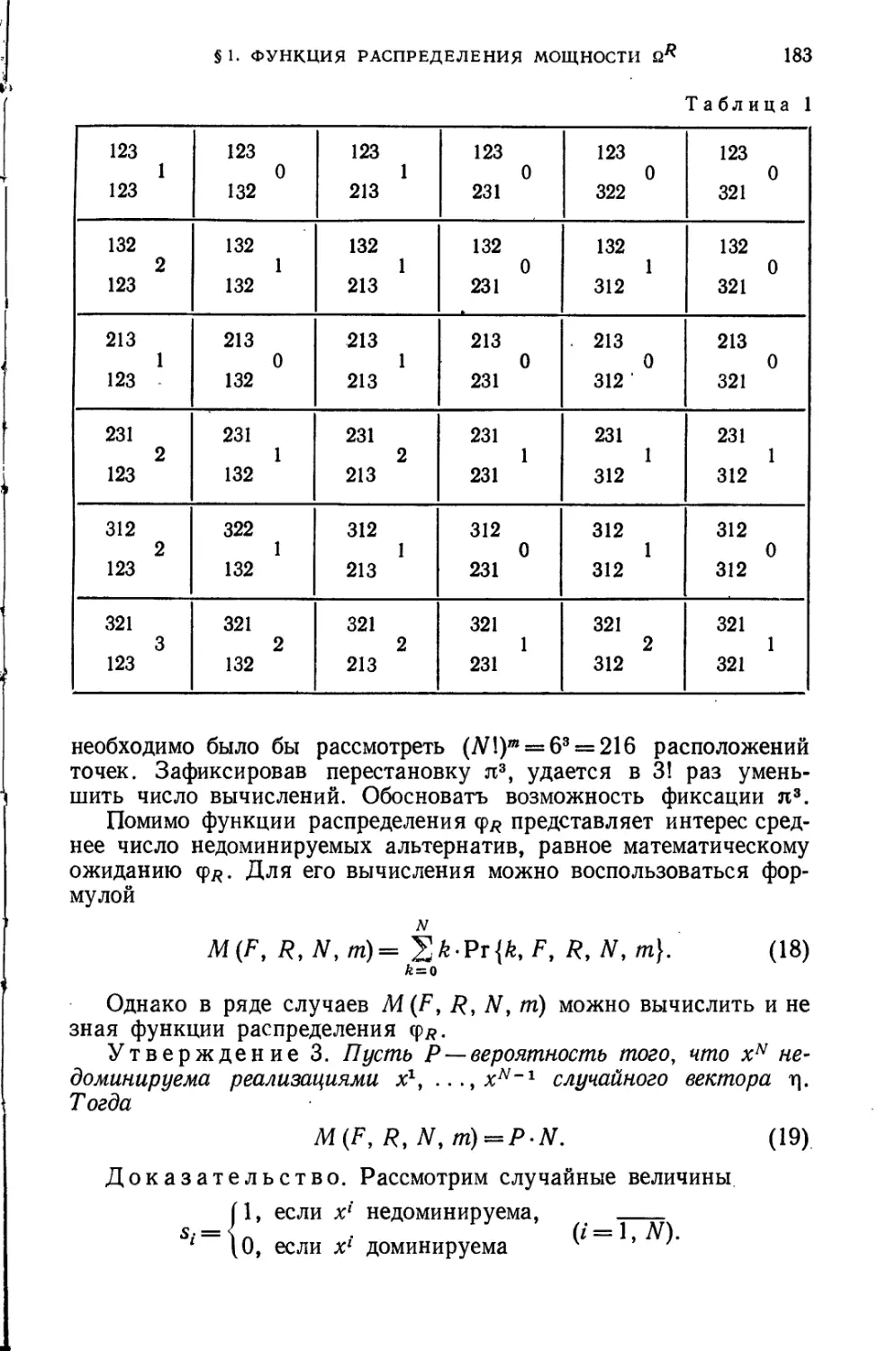
§ 1. Функция распределения числа недоминируемых альтернатив .... 176
§ 2. Среднее число недоминируемых альтернатив..................... 185
§ 3. Вероятностные характеристики мощности множества Парето .... 195
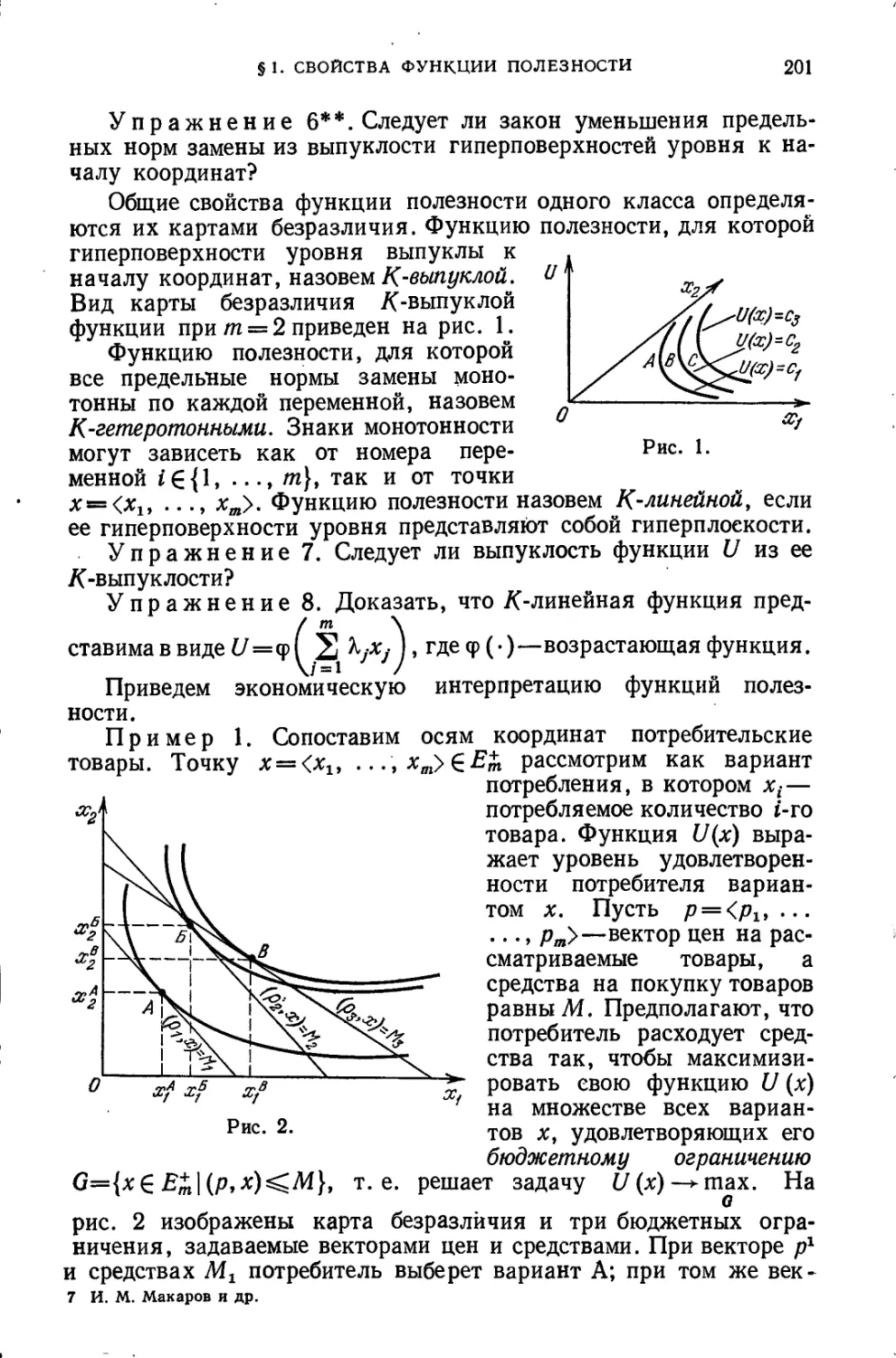
Глава 6. Функции полезности в задачах выбора..................... 198
§ 1. Общее понятие и свойства функции полезности................. 198
§ 2. Алгоритмы оптимизации функции полезности ................... 203
§ 3. Влияние ИМА на оптимизацию функции полезности............... 209
§ 4. Оптимизация при наличии помех............................... 213
Глава 7. Задачи выбора с заданным принципом оптимальности ... 215
§ 1. Задачи с упорядоченными по важности критериями.............. 215
§ 2. Метод идеальной точки ...................................... 225
§ 3. Выбор с учетом числа доминирующих критериев................. 228
ЧАСТЬ III
МНОГОКРИТЕРИАЛЬНЫЕ ЗАДАЧИ
ОПТИМАЛЬНОГО УПРАВЛЕНИЯ
Глава 1. Задача управления при многих критериях.................... 235
§ 1. Постановка задачи и ее свойства............................... 235
§ 2. Общий алгоритм решения для функции полезности................. 239
§ 3. Динамические многокритериальные задачи........................ 240
§ 4. Оптимальное управление в условиях противодействия.............. 241 4
§ 5. Многокритериальные задачи математического программирования ' 244
Глава 2. Дискретные многокритериальные задачи...................... 248
§ 1. Задача с дискретным временем................................. 249
§ 2. Многокритериальная задача с дискретным временем............... 250
§ 3. Задача независимого выбора.................................. 253
§ 4. Задача конструирования........................................ 255
ОГЛАВЛЕНИЕ
5
Глава 3. Многокритериальная задача с непрерывным временем . . . 258
§ 1. Задача с одним критерием и принцип максимума........... . . . 259
§ 2. Многокритериальная задача и ее Х-свертка..................... 263
§ 3. Необходимые условия оптимальности ........................... 265
Глава 4. Марковские^модели принятия решений....................... 267
§ 1. Общие понятия................................................ 267
§ 2. Управляемые цепи Маркова с векторными доходами............... 273
§ 3. Оптимальные стратегии управления цепью Маркова с векторными
доходами........................................................ 278
§ 4. Многокритериальная задача об оптимальной остановке........... 282
§ 5. Двухуровневая оптимизация управляемых цепей Маркова ..... 287
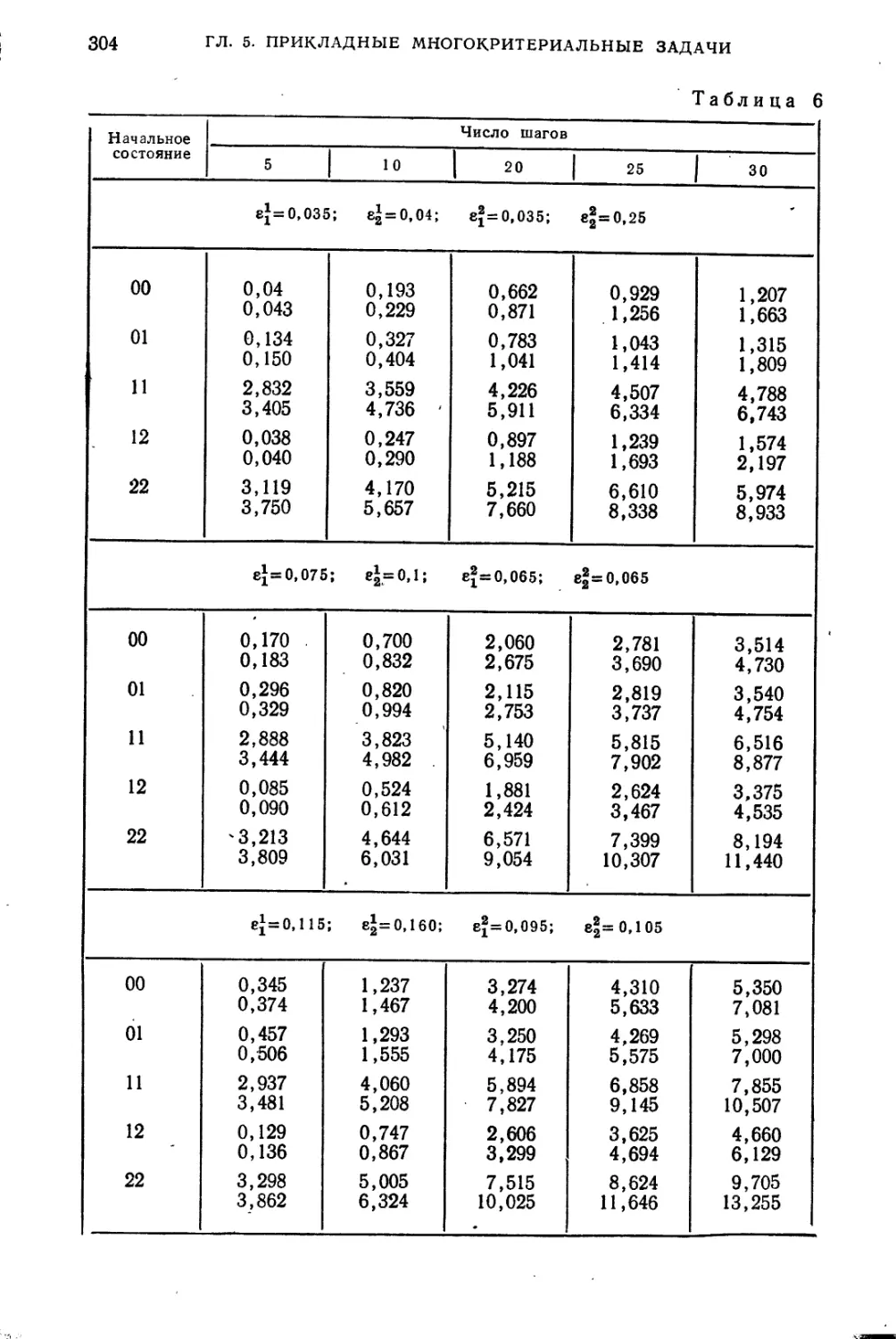
Глава 5. Прикладные многокритериальные задачи оптимального
управления . . ............................................... 288
§ 1. Проектирование оптимального программного комплекса........... 289
§ 2. Оптимальное управление трехотраслевой экономикой............. 295
§ 3. Разрешение конфликтов в многопроцессорных вычислительных
системах.......................................................... 301
§ 4. Многокритериальная задача оптимального последовательного выбора 305
§ 5. Игровая задача с векторными-доходами......................... 311
Литература...................................................... 316
Предметный указатель............................................. 321
Основные обозначения.............................................. 326
ПРЕДИСЛОВИЕ
Процессы принятия решений лежат в основе любой целенап-
равленной деятельности. В экономике они предшествуют созда-
нию производственных и хозяйственных организаций, обеспе-
чивают их оптимальное функционирование и взаимодействие-
в научных исследованиях—позволяют выделить важнейшие науч-
ные проблемы, найти способы их изучения, предопределяют раз-
витие экспериментальной базы и теоретического аппарата; при
создании новой техники—составляют важный этап в проектиро-
вании машин, устройств, приборов, комплексов, зданий, в раз-
работке технологии их построения и эксплуатации; в социальной
сфере—используются для организации функционирования и раз-
вития социальных процессов, их координации с хозяйственными
и экономическими. Оптимальные (эффективные) решения позво-
ляют достигать цели при минимальных затратах трудовых, мате-
риальных и сырьевых ресурсов. Вопросы принятия эффектив-
ных управленческих решений выделены как особо важные
в материалах XXVI съезда КПСС. Таким образом, анализу и
методам принятия эффективных решений уделяется большое вни-
мание.
Методы поиска оптимальных решений рассматривают в разделах
классической математики, связанных с изучением экстремумов
функций, в математическом программировании. Однако решение
здесь—математический объект, основным свойством которого
является то, что он доставляет экстремум заданной функции или
функционалу. Зачастую оценка решения производится по одному
аспекту или критерию. На практике решение нужно оценивать
с различных точек зрения, учитывая физические (габариты, вес),
экономические (стоимость, ресурсоемкость), технические (реали-
зуемые функции) и другие аспекты. Это требует построения моде-
лей оптимизации решений одновременно по нескольким аспектам
или критериям. Такие модели разрабатывают в теории выбора
и принятия решений. Здесь при постановке задачи уже не доста-
точно построить оптимизируемые функционалы. Требуется ввести
принцип оптимальности, который определяет понятие оптималь-
ного решения. Поскольку оптимальность решения даже в одной и
той же ситуации может пониматься по-разному, вид принципа опти-
мальности в моделях принятия решений заранее не фиксируют.
ПРЕДИСЛОВИЕ
7
Именно в этом состоят основные особенности задач принятия
решений.
Элементы теории выбора и принятия решений в той или иной
форме включаются в. учебные программы по широкому кругу спе-
циальностей: прикладной математике, технической кибернетике,
автоматизированным системам управления, экономической кибер-
нетике, автоматизации проектирования и другим.
Цель настоящего пособия состоит в изложении вопросов, кото-
рые являются общими для разных специализаций.
Во введении дана характеристика задач оптимизации, выбора,
принятия решений и установлена связь между ними. В части I
изложены общетеоретические основы для решения указанных задач;
в части II рассмотрено их решение; в части III описан класс
многокритериальных задач оптимального управления.
Части I, II раскрывают сущность теории выбора и принятия
решений и демонстрируют возможности использования ее резуль-
татов. Часть III показывает возможность объединения аппарата
теории выбора и принятия решений с классическим аппаратом
оптимизации на примере решения многокритериальных задач опти-
мального управления.
Уровень изложения материала предполагает знакомство с мате-
матическими дисциплинами в объеме программы технических вузов.
Специальные понятия и приемы поясняются там, где это необхо-
димо. Упражнения повышенной трудности отмечены звездочкой;
особо трудные упражнения—двумя звездочками. Список литературы
не является исчерпывающим, а содержит только источники на
русском языке. В конце каждой главы даны ссылки на рекомен-
дуемую литературу из общего списка. Не все приводимые факты
сопровождаются доказательствами; некоторые доказательства опу-
щены, поскольку они выходят за рамки пособия; простые доказатель-
ства предлагаются в качестве упражнений.
В каждой главе использована своя нумерация формул, рисун-
ков, утверждений, теорем, без указания номера части и главы.
При ссылках на результат из другой главы той же части приме-
няется двойная нумерация, где первая цифра указывает номер
главы. При ссылке на результаты из другой части используется
тройная нумерация. Например, формула (II.5.27) обозначает фор-
мулу (27) из главы 5 части II.
Пользоваться пособием следует по-разному, в зависимости от
цели читателя. Начинать во всех случаях нужно с введения.
Общее представление о задачах оптимизации, выбора и принятия
решений можно получить, прочитав §§ 1.1.1, 1.1.6, 1.2.1, 1.2.2,
1.3.1, 1.5.1, II.3.1, II.4.1, 11.4.2; о многокритериальных задачах
оптимального управления—прочита⧧ 1.1.1, 1.1.6, 1.3.1, III.1.1,
Ш.1.2, III.2.1, III.2.2, Ш.3.1, III.3.2, III.4.1, III.4.2; о
прикладных задачах оптимизации и оптимального управления —
прочитав §§ 1.1.1, 1.1.6, II.4.1, П.4.2, II.7.1, II.7.2, III.1.1
8
ПРЕДИСЛОВИЕ
III.4.1, III.5.1—III.5.5. При таком чтении доказательства утверж-
дений и теорем можно опустить, сосредоточив внимание на поста-
новках задач, их свойствах, идеях решения. В случае появления
понятий, не определенных в указанных параграфах, их следует
найти, воспользовавшись предметным указателем, приведенным
в конце пособия.
Для более детального знакомства с теорией выбора следует
прочесть всю часть I, а также §§ II.4.1, II.4.2 и главы II.5—II.7,
с теорией многокритериального оптимального управления—главы
1.1, 1.3, П.4 и всю часть III. Читателю, интересующемуся алго-
ритмами, достаточно прочитать по алгоритмам подготовки реше-
ний главу П.З, используя в качестве справочного материал части
I и глав II.1 и II.2; по алгоритмам выбора—главы II.4 и II.6,
используя в качестве справочного материал части I.
Для выработки систематического навыка постановки, исследо-
вания и решения рассматриваемых задач необходимо изучение
всего материала пособия и выполнение предложенных в нем упраж-
нений (кроме наиболее сложных).
Пособие рассчитано в первую очередь на студентов старших кур-
сов, аспирантов и преподавателей вузов. Теоретические разделы
полезны для специалистов по системному анализу и исследованию
операций. Прикладные разделы могут представить|’интерес для
консультантов и разработчиков алгоритмов.
Авторы глубоко благодарны члену-корреспонденту АН СССР
С. С. Шаталину, сотрудникам возглавляемой им кафедры матема-
тических методов анализа экономики МГУ и профессору Ю. П. Ива-
нилову за высказанные замечания и рекомендации, которые позво-
лили улучшить состав, структуру и методическую целостность
настоящего пособия, а также коллегам по работе С. С. Порошину
и А. В. Щербакову за помощь при подготовке рукописи.
И. М. Макаров, Т. М. Виноградская,
А. А. Рубчинский, В. Б. Соколов
ВВЕДЕНИЕ
Теория выбора и принятия решений исследует математиче-
ские модели процессов принятия решений и их свойства. Ос-
новной в ней является задача принятия решений, которая соот-
ветствует широкому кругу практических ситуаций. Приведем
примеры.
На предприятии освободилась должность главного инженера..
Задача директора—назначить главного' инженера.
Строительному тресту поручено выполнить комплекс работ.
Задача управляющего трестом—распределить работы по строи-
тельным управлениям.
Транспортному агентству необходимо перевезти заданный объем
грузов. Задача диспетчера—определить маршрут перевозок.
В рассмотренных и других сходных ситуациях общим явля-
ется следующее. Имеется множество вариантов (кандидатов на
должность, назначений работ, маршрутов); нужно выделить ив
него некоторое подмножество, в частном случае—один вариант.
Выделение требуемых вариантов производится на основе пред-
ставления директора, управляющего, диспетчера об их качестве.
Представление о качестве вариантов характеризуют принципом
оптимальности.
Указанные элементы—множество вариантов и принцип опти-
мальности—позволяют ввести следующие понятия. Задачей при-
нятия решений назовем пару <Й, ОП>, гдемножество вариан-
тов, ОП—принцип оптимальности; решением задачи <Й,ОП> —
множество Й0Л£Й, полученное с помощью [принципа оптималь-
ности ОП.
Отсутствие хотя бы одного из указанных элементов лишает
смысла задачу в целом. Если нет множества О, то выделять ре-
шение Ооп не из чего, Если нет принципа оптимальности, то
найти решение невозможно.
Математическим выражением принципа оптимальности ОП слу-
жит функция выбора Соп. Она сопоставляет любому подмножеству
X = Q его часть Con (X). Решением йоп исходной задачи является
множество Соп (Q).
Задачи принятия решений различают в зависимости от имею-
щейся информации о множестве О и принципе оптимальности ОП.
В общей задаче принятия решений как Q, так и- ОП могут быть
10
ВВЕДЕНИЕ
неизвестными. Информацию, необходимую для выделения й
получают в процессе решения. Задачу с известным й назовем
задачей выбора, задачу с известными й и ОП—общей задачей опти-
мизации. Таким образом, задача выбора и задача оптимизации
являются частными случаями общей задачи принятия решений.
Особенность развиваемого здесь подхода к решению задачи выбора
состоит в том, что он в общем случае не требует полного восста-
новления принципа оптимальности, а позволяет ограничиться только
информацией, достаточной для выделения йоп. Общая задача опти-
мизации может не предполагать максимизации одной или несколь-
ких числовых функций. Ее смысл состоит в выделении множества
лучших элементов, т. е. в вычислении значения Соп(й) при задан-
ных й и Соа. Если Соп—скалярная функция выбора на множестве
й, то получаем обычную оптимизационную задачу.
Элементы множества Й называют альтернативами или вариан
тами. Принцип оптимальности задает понятие лучших альтерна
тив: лучшими считают альтернативы, принадлежащие Соп(й).
В практических задачах альтернативы обладают многими свой-
ствами, оказывающими влияние на решение. Пусть некоторое
свойство альтернатив из й выражается числом, т. е. существует
отображение <р: й—>-Ег. Тогда такое свойство называют критерием,
а число <р(х) — оценкой альтернативы х по критерию. Одновре-
менный учет отдельных свойств может быть затруднительным.
При этом выделяют группы свойств, которые агрегируют в виде
аспектов. Аспект представляет собой сложное свойство альтерна-
тив, которое одновременно учитывает все свойства, входящие в
соответствующую группу. В частном случае аспект может являться
критерием.
Пусть все свойства ..., km, учитываемые при^решении
задачи <й, ОП>, являются критериями. Поставим в соответствие
критерию kfj-ю ось Ет (j = 1, т). Отобразим множество Й в Е
сопоставив каждой альтернативе ' х £ й точку®ф(х) = (х), . Г.’
•••> Ф» (х)> 6Ею, где фу (х)—оценка х nofкритерию = щ).
Критериальным пространством называют пространство Ет, коор-
динаты точек которого рассматриваются как оценки по соответст-
вующим’ критериям.
При'4 определении маршрута перевозок альтернативами явля-
ются различные маршруты. Диспетчер учитывает следующие свой-
ства: протяженность, загрузка, энергоемкость, безопасность/стои-
мость, техническое обслуживание и ряд других.Техническое об-
служивание на данном маршруте зависит от числа и расположе-
ния станций обслуживания, их мощности, загрузки и сроков выпол-
нения ремонтных работ. Таким образом, техническое обслуживание
является аспектом, агрегирующим указанные свойства. Стои-
мость маршрута складывается из стоимости топлива, стои-
мости обслуживания транспортных средств, зарплаты водителей
ВВЕДЕНИЕ
11
за время пути и других составляющих, т. е. стоимость также
является аспектом. Однако возможность вычисления стоимости
указывает на то, что данный аспект можно рассматривать как
критерий. Протяженность маршрута измеряется в километрах, т. е.
выражается числом и поэтому является критерием.
Процесс решения задачи <Q, ОП> организуют по следующей схе-
ме: формируют множество Q, т. е. подготавливают альтернативы, а
затем решают задачу выбора. При назначении на должность сна-
чала готовят список кандидатов, а затем назначают лицо из этого
списка. В процессе формирования множества Q используют условия
возможности и допустимости альтернатив, которые определяются
конкретными ограничениями задачи. При этом считают известным
универсальное множество всех мыслимых альтернатив. Задача
формирования Q является задачей выбора <Q^, ОПг>, где ОПХ —
принцип оптимальности, выражающий условия допустимости альтер-
натив. Множество Й^СопДЙу), полученное в результате решения
указанной задачи выбора, называют исходным множеством альтер-
натив (ИМА). При назначении на должность в качестве рас-
сматривают всех специалистов. Условия допустимости определяются
конкретными обязанностями, предусмотренными должностью,
зарплатой и другими факторами.
Итак, общая задача принятия решений сводится к решению
двух последовательных задач выбора. В процессе решения этой
задачи участвуют: лицо, принимающее решение, эксперты, кон-
сультанты.
Лицом, принимающим решения (ЛПР), называют человека, име-
ющего цель, которая служит мотивом постановки задачи и поиска
ее решения. ЛПР, являющееся компетентным специалистом в своей
области и обладающее опытом деятельности в ней, наделено необхо-
димыми полномочиями и несет ответственность за принятое решение.
В задаче принятия решений основная функция ЛПР состоит в
выделении йоп. В рассматриваемых процедурах принятия решений
ЛПР дает информацию о принципе оптимальности.
Экспертом (Э) называют специалиста, имеющего информацию
о рассматриваемой задаче, но не несущего непосредственной ответ-
ственности за результат ее решения. Эксперт дает оценки альтер-
натив, необходимые для формирования ИМА и решения задачи
выбора.
Консультантом *) (К) называют специалиста по теории выбора
и принятия решений. Консультант разрабатывает модель исходной
задачи, процедуру принятия решения, организует работу ЛПР и
экспертов при поиске решения.
В простейших случаях задачу <Q, ОП> решает непосредствен-
но ЛПР без использования специальных процедур. Однако часто
*) Консультанты называются также исследователями, аналитиками, членами,
рабочей группы и др.
12 ВВЕДЕНИЕ
требуются математические модели и методы, которые помогают
ЛПР получать обоснованные эффективные решения. Изложению
теории построения таких моделей и методов посвящено настоящее
пособие.
. Как и в других случаях, прикладные результаты, теории выбора
и принятия решений имеют вид алгоритмов решения исследуемых
задач. Часть приводимых далее алгоритмов может быть реализована
вручную. В общем случае реализация алгоритмов предусматривает
использование ЭВМ, оснащенных терминалами и соответствующим
математическим обеспечением для диалогового режима работы.
Алгоритмы, которые рассматриваются в части II настоящего
пособия, могут быть использованы для-построения диалоговых сис-
тем принятия решений широкого назначения, алгоритмы из части
III—для построения специализирован ных диалоговых систем реше-
ния задач управления.
ЧАСТЬ I
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ
ВЫБОРА АЛЬТЕРНАТИВ
В части I рассмотрен математический аппарат, который поз-
воляет формализовать понятия лучшей альтернативы и сравнения
альтернатив в задачах принятия решений. Аппарат рассчитан на
использование в условиях, когда отсутствует единое понятие луч-
шей альтернативы (которое всегда присутствует в математических
задачах оптимизации), и позволяет изменять содержание понятия
оптимальности в зависимости от условий конкретной задачи. При
этом в главах 1, 2 будут описаны общие конструкции (бинарные
отношения и функции выбора); в главах 3, 4—конструкции в
критериальном пространстве; в главе 5—взаимосвязи общих и
частных конструкций в виде соответствующих декомпозиций.
Г л а в а 1
/БИНАРНЫЕ ОТНОШЕНИЯ
Простейшая “ситуация, которая позволяет сделать обоснован-
ный выбор из нескольких объектов, возникает, когда задан один
«критерий качества», позволяющий сравнить любые два объекта,
четко указать, какой из них лучше, и выбрать тот (или те), на
котором этот критерий достигает максимального значения (подроб-
нее об этом см. § 2.5). Однако в большинстве реальных ситуаций
выделить один такой критерий не удается; более того,часто вообще
трудно выделить критерии.Тем не менее для некоторых пар объек-
тов можно указать, какой из объектов пары лучше (предпочти-
тельней) другого. В таких случаях говорят, что эти два объекта
находятся в бинарном отношении. Понятие бинарного отношения
позволяет формализовать операции попарного сравнения. Поэтому
оно широко используется в теории выбора. В § 1 даны примеры и
определение бинарных отношений; в § 2 рассмотрены методы за-
дания отношений; в § 3 введены операции над отношениями; в
§ 4 описаны свойства отношений; в § 5—основные классы отно-
шений; в § 6—понятие оптимума по отношению.
1. Понятие бинарного отношения
Что такое отношение, 'проще всего пояснить примерами. Рас
смотрим суждения, которые выражают взаимосвязи между не-
которыми объектами: «Иван—брат Петра»; «Татьяна старше Алек-
14
ГЛ. 1. БИНАРНЫЕ ОТНОШЕНИЯ
сандра»; «Киев южнее Москвы»; «Железо тяжелее воды»; «Слово
«ночь» и слово «день» содержат одинаковое число букв». Эти пять
предложений выражают отношения разного типа. Однако можно
заметить сходство в характере отношений, утверждаемых первым
и пятым предложениями. Они говорят о том, что некие два объекта
принадлежат общему классу: сыновей общих родителей, слов с
фиксированным числом букв. Второе, третье и четвертое отношения
имеют то общее, что выражают некоторый порядок объектов в
системе.
В дальнейшем эта разница между отношениями того и другого
типа будет четко определена. Первый и пятый пример—это отно-
шения эквивалентности, определяющие разбиения множества объек-
тов на классы подобных друг другу. Остальные три примера—
это отношения порядка, устанавливающие относительное расположе-
ние объектов в системе.
Важно обратить внимание на тот факт, что во всех пяти примерах
четко выделяются названия объектов (Иван, Киев и т. д.) и назва-
ния отношений (брат, старше, южнее и др.). Если вместо названия
данного объекта подставить в предложение название другого
объекта, то возможны следующие ситуации: 1) отношение опять
будет выполнено; 2) отношение перестанет выполняться; 3) отноше-
ние потеряет смысл. Так, если в четвертое предложение вместо
<уюва «железо» подставить слово «свинец», то суждение останется
справедливым. Если в третье предложение вместо слова «Москва»
подставить «Ашхабад», то оно перестанет быть верным. Если же
в третье предложение вместо слова «Москва» подставить «железо»,
то суждение потеряет смысл. В отличие от первых четырех, в пятое
предложение можно подставить любые слова, поскольку для любого
слова имеет смысл говорить о числе букв. Здесь сама форма суж-
дения ограничивает класс объектов—объектами отношения могут
быть только слова.
Итак, говорить об отношении можно только тогда, когда мы
умеем выделять множество объектов, на которых это отношение
определено. Отношение может быть определено не только для
пар объектов, но и для троек, четверок и т. д. Например, отно-
шение «составлять экипаж лодки-восьмерки» выполняется для
некоторых групп из восьми людей. Это отношение следует отли-
чать от отношения «входить в экипаж одной и той же лодки-
восьмерки», определенного для пар людей. Пример трехместных
(или тернарных) отношений дают алгебраические операции. Отно-
шение «образовывать произведение» имеет смысл для троек чисел
<х, у, z> и выполняется в том случае, когда х-у=г.
Мы будем рассматривать бинарные отношения, т. е. отноше-
ния, которые могут выполняться (или не выполняться) между
двумя объектами из одного и того же множества. Поэтому в
дальнейшем будем говорить об отношениях, имея в виду только
бинарные отношения.
§ 2. СПОСОБЫ ЗАДАНИЯ ОТНОШЕНИЙ
15
После выяснения содержательного смысла понятия отношения
можно перейти к его точному определению, способам задания,
свойствам и классификации отношений.
Отношением 7? на множестве й называется подмножество R
множества йхй, т. е. R £ЙхЙ. Содержательный смысл такого
определения состоит в том, что задание Подмножества R в мно-
жестве йхй определяет, какие пары находятся в отношении R.
Это подчеркивается следующим соглашением об обозначениях.
Если пара <х, г/> входит в R, т. е. <х, г/> С R, то пишут xRy,
что читается: «х находится в отношении R с у».
Подчеркнем, что отношение—это не просто множество соот-
ветствующих пар, а подмножество пар йхй при фиксированном
множестве й. Множество й называется областью задания отноше-
ния. В тех случаях, где существенна область задания отношения,
будем пользоваться для его обозначения парой <7?, й>.
(Пусть й*—множество студентов группы, й2—множество сту-
дентов факультета, й3—множество студентов всего института.
Естественно определяются три разных отношения: <7?ъ йх>,
<Т?2, й2>, <7?3, й3>; отношение R{—множество таких пар <х, «/>,
что «х знаком с у», но при i = 1 областью задания отношения
<7?z, Xf> является множество студентов одной группы; при i —
= 2—факультета, при i = 3—института.
цТаким образом, рассмотрение разных множеств приводит к
разным отношениям.
Упражнение 1. Описать словесно и изобразить на чер-
теже каждое из следующих множеств (отношений на множестве
действительных чисел):
1)
2) их,
3) {<х,
4) Их,
5) их,
6) Их,
7) 1<х,
8) Их,
9) {<х,
Ю) <х,
И) <х,
12) (<х,
У п р аж
У>€Е2
у>$е2
У>£Е2
У> € Е2
у>$е2
У>£Е2
у>$е2
у>$е2
у>$е2
у>еЕ2
у>^е2
У>£Е2
некие
х2+у2 = 1};
у — 2х, у=3х);
х2 —1/2 = 0);
х<у}-,
х2 + «/2>1};
x>«z};
х2 + 4г/2=1);
I * I+21//|=#};
х2+#2 > 1, х > 0};
У>0, г/<х, х+у<1};
х = у).
2. Доказать, что среди любых шести чело-
век найдутся либо трое попарно знакомых, либо трое попарно
незнакомых.
§ 2. Способы задания отношений
Для того чтобы задать отношение <7?/, й> на множестве й,
нужно указать все пары <х, #>£йхй, которые содержатся в R,
т. е. пары <х, r/> Е й2, для которых выполняется отношение R.
16
ГЛ. 1. БИНАРНЫЕ ОТНОШЕНИЯ
Кроме непосредственного указания всех пар, для которых вы-
полняется отношение R, существуют три основных способа зада-
ния отношения: задание отношения матрицей; задание отношения
графом; задание отношения сечениями.
Остановимся подробнее на каждом из них, так как они необ-
ходимы далее для пояснения способов описания задач выбора и
способов представления требуемой для их решения информации.
Задание матрицей. Рассмотрим пример. Пусть Q—мно-
жество участников шахматного турнира. Будем говорить, что «х —
победитель у», если х в! этом турнире обыграл, у (предполага-
ется, что турнир игрался в один круг). Вместо того чтобы выписы-
вать все пары <х, уу, для которых выполнено отношение «быть
победителем», можно просто выписать турнирную таблицу, заме-
нив половинки нулями (если участники х и у сыграли вничью,
то никто из них не является победителем другого; в этом случае
не выполнены оба соотношения: «х—победитель у» и «у—побе-
дитель х»), Приведем откорректированную таким образом таблицу
турнира в Тилбурге в сентябре 1980 г. (табл. 1). Она иллюстри-
рует способ задания отношения на конечном множестве, кото-
рый называется матричным.
Таблица 1
1 2 3 4 5 6 7 8 9 10 и 12
1 А. Карпов 0 1 0 1 0 0 0 1 1 1 0
2 Л. Портиш 0 0 0 0 1 0 1 0 0 0 1
3 Я. Тимман 0 0 0 0 0 0 1 0 0 1 1
4 Г. Сосонко 0 0 0 0 0 0 0 0 1 0 0
5 Б. Спасский 0 0 0 0 0 0 1 1 1 0 0
6 М. Таль 0 0 0 0 1 0 0 0 0 . 0 0
7 В. Горт 0 0 0 0 0 0 0 0 0 0 0
8 Б. Ларсен 1 0 0 0 0 0 1 0 0 1 0
9 У. Андерсен 0 0 0 0 0 0 0 0 0 0 0
10 3. Рибли 0 0 0 0 0 0 0 . 1 0 0 0
11 Р. Хюбнер 0 0 0 0 0 0 0 0 0 0 1
12 Л. Кавалек 0 0 0 0 0 0 0 0 0 0 0
Упражнение 3. Доказать утверждение о возможности в
общем случае восстановления «настоящей» турнирной таблицы
по таблице типа табл. 1.
В общем виде этот способ можно описать так. Пусть Q со-
стоит из п элементов, R есть отношение на Q. Занумеруем эле-
менты множества й целыми числами от 1 до п. Построим квад-
ратную таблицу размера пхп. Ее i-я строка соответствует t-му
элементу множества й, обозначенному через х,-, а /-й столбец —
элементу ху. На пересечении i-й строки и /-го столбца ставится
единица, если выполнено x^Xj, и нуль—в противном случае.
$2. СПОСОБЫ ЗАДАНИЯ ОТНОШЕНИЙ^
17
gBSST™ -
Обозначим элемент, стоящий на пересечении i-й строки и /-го
столбца, через а;/. Общее правило задания матрицы отношения
'R формулируется так:
, ( 1, если выполнено x{Rxt, .. . •:—. ,1Ч
%(/?) = { ' ' J' = (1)
(О, если не выполнено xtRxj
Очевидно, матрица (а^ (R)) = A (R) содержит всю информацию
о том, для каких пар элементов из £2 выполнено отношение R.
Использование матричного способа задания для доказательства
утверждений, связанных с отношениями, будет продемонстриро-
вано в следующем параграфе. 3
Итак, отношение /? на конечном множестве £2 из п элемен-
тов может быть задано матрицей A (R) = (а^ (R)). Произвол (со-
стоит только в выборе нумерации элементов £2. Ясно, что можно
выбрать п\ различных нумераций и со-
ответственно п! матриц, описывающих %
данное отношение. Если!,задана мат- sJ
рицаЛ размером пхп из нулей и еди- ?
ниц и выбрана нумерация элементов 11^ / Н TV J
множества Q, состоящего из п элемен- V \ / к
тов, то тем самым на £2 задается не-
которое отношение R = R (Л) такое, что хХ
xtRxj выполнено тогда и только тогда,
когда аи = 1. $
Задание графом. Поставим во 8 7 ,
взаимно однозначное соответствие эле- Рис [
ментам конечного множества £2 вер- ис>
шины графа хх, ..., хп (при некоторой
нумерации). Проведем дугу от xz к Xj тогда и только тогда, ког-
да выполнено XjRxj (при i = / дуга (х;, ху) превращается в пет-
лю при вершине х;).
Изобразим в виде графа (рис. 1) турнирную табл. 1. Ясно,
что петель в этом графе нет. Номера вершин соответствуют но-
мерам участников в таблице.
Если задан произвольный граф G с п вершинами и выбрана
нумерация на множестве £2, то тем самым на £2 задается некото-
рое отношение А? = R (G) такое, что XiRxj выполняется тогда и
только тогда, когда в графе G есть дуга (х,-, ху).
Граф является геометрическим представлением отношения,
аналогично тому, как график является геометрическим пред-
ставлением функции. Геометрический язык полезен, когда граф
достаточно прост (либо у него мало вершин, либо он имеет прос-
тую структуру). Наоборот, изучать и описывать сложные графы
с большим числом вершин часто удобнее в терминах отношений.
В' дальнейшем будем говорить о графе отношения R, обозначая
его G(R).
18
ГЛ. 1. БИНАРНЫЕ ОТНОШЕНИЯ
Задание сечениями. Этот способ менее распространен,
чем предыдущие. Однако, в отличие от них, он пригоден и для
задания отношений на бесконечных множествах.
Рассмотрим отношение 7? на множестве Q.
Верхним сечением R+(x) называется множество элементов
таких, что <у, x>£R: z ' '
R+(х) = {уеЩ<у, x>^R}; (2)
аналогично определяется нижнее сечениех
R- (х} = {у$Щ<х, y>£R}. (3)
Таким образом, множество R~ (х)—это множество всех эле-
ментов у € й, с которыми фиксированный элемент х С Q находится
в отношении R. Множество R+(х)—это множество всех элемен-
тов у£&, которые находятся в отношении R с фиксированным
элементом х£й.
Пусть Q—множество участников шахматного турнира, в Тил-
бурге. Запишем рядом с каждым элементом x{£Q соответствую-
щее верхнее сечение R+ (х/), т. е. множество номеров всех участ-
ников турнира, выигравших у х/.
' 1 - {8}, 5 - {1, 6}, 9 - {1. 5},
2 — 0, 6 - {2}, 10 - {1, 4, 5},
3 - оь 7 -{8}, И - {1, 3, 8},
4 — 0, 8 — {2, 3, 5, 10}, 12 — {2, 3, 11}
Приведенная запись полностью определяет отношение «у —
победитель х».
В общем случае отношение R полностью задано, если для
каждого xgQ задано множество R+(х) (или для каждого x£Q
задано множество R~(x)).
Упражнение 4. Для отношения R, заданного табл. 1 и
рис. 1, выписать все нижние сечения.
Упражнение 5. Вывести формулу, выражающую нижнее
сечение R~ (х) через все верхние сечения {7?+(х)}, x^Q.
Упражнение 6. Выписать верхние и нижние сечения для
отношений из пп. 1), 2), 4), 6), 7), 11) упр. 1.
Проиллюстрируем введенные способы задания отношений на
четырех отношениях специального вида.
Отношение называется пустым (обозначается 0), если оно
не выполняется ни для одной пары <х, у>£й2.
Для пустого отношения 0 справедливо:
1) матрица Л (0)—такая, что а;у(0) = О для всех i и /;
2) граф G (0) не имеет дуг;
3) 7?+ (x) = R~ (х) = 0 для любого xgQ.
Отношение называется полным (обозначается U), если оно
выполняется для всех пар <х, у> 6
§ 3. ОПЕРАЦИИ НАД ОТНОШЕНИЯМИ
19
Для полного отношения U справедливо:
1) матрица A (U)—такая, что a,y(t/)=l для всех i и /;
2) граф G ({/)—такой, что дуги соединяют любую пару вер-
шин;
3) £+ (x) = R~ (х) = й для любого х£Й.
Отношение называется диагональным или отношением равен-
ства (обозначается Е), если оно выполняется для всех пар
<х, #>£й2, состоящих из совпадающих элементов: хЕу, если х
и у—один и тот же элемент множества й.
Для диагонального отношения Е справедливо:
1) матрица А (£)—такая, что
1 \ 0 при 1#=/;
2) граф G (£)—такой, [что присутствуют только петли при
всех вершинах, а других дуг нет;
3) (х) — (х) = {х) для любого х£й.
Отношение называется антидиагональным (обозначается £),
если оно выполняется для всех пар <х, у>£й2, состоящих из
несовпадающих элементов. __
Для антидиагонального отношения Е справедливо:
1) матрица А (£)—такая, что
«,.,.(£) = {
О при i = /,
1 при
2) граф G (£)—такой, что присутствуют все дуги (х;, Ху) при
i j (отсутствуют только петли);
3) £+(х) = £“(х) = й\{х} для любого х£й.
Упражнение 7. Показать, что отношение £, для которого
матрица A (R) не зависит от нумерации элементов множества О,
либо пустое, либо полное, либо диагональное, либо антидиаго-
нальное отношение.
Упражнение 8. Какое из отношений упр. 1 диагональ-
ное?
§ 3. Операции над отношениями
Рассмотрим основные операции над отношениями. Всюду в
этом параграфе (если не оговорено противное) будем считать,
что все отношения заданы на одном и том же множестве Й.
Поскольку любое отношение £ есть подмножество множества
пар й2, то для отношений можно определить все те операции,
которые определены для подмножеств фиксированного множе-
ства: пересечение, объединение, дополнение и т. д.
Определим операцию вложения отношений. Отношение Ei
вложено (включено) в отношение /?2 (обозначается /?2),
20
ГЛ. 1. БИНАРНЫЕ ОТНОШЕНИЯ
если множество пар, для которых выполнено отношение со-
держится в множестве пар, для которых выполнено Т?2.
Будем писать < #2, если Rt < R2 и R^ R2.
Равенство отношений понимается в том же смысле, что и
равенство множеств. Например, отношение «меньше» вложено в
отношение «меньше или равно». В самом деле, если х < у, то
заведомо х у. Но существуют такие пары, что х у, но не
верно соотношение х<у (это будет в случае, когда х = у).
Упражнение 9. Доказать, что для любого отношения R
выполнено 0 < R < U.
Упражнение 10. В упр. 1 указать все пары вложенных
отношений.
Упражнение 11. Пусть R1 < R2. Доказать, что
1) Для всех i и /;
2) Rf (х) = Rt (х), Rt (x)'s Rt (х) для всех х
Определим операцию дополнения. Отношение R называется
дополнением отношения R, если оно выполняется для тех и
только тех пар, для которых не выполняется отношение R.
Очевидно, что 7? = й2\ R. Легко видеть, что
в матричной записи
aif (R) = 1 -ац (R) (i, / = 1~); (4)
в графе G (R) присутствуют те и только те дуги, которые
отсутствуют в графе G(R);
^+(х) = Й\Я+(х), /Г-(х) = Й\/?-(х) (Ухей). (5)
Нетрудно убедиться, что антидиагональное отношение Е явля-
ется дополнением диагонального отношения Е, a 0 = t7; ясно
также, что для любого отношения R
R = R.
(6)
Упражнение 12. В упр. 1 указать все пары взаимно до-
полнительных отношений.
Введем операции пересечения и объединения отношений. Пе-
ресечением отношений Rt и (обозначается n R2) называет-
ся отношение, определяемое пересечением соответствующих под-
множеств из Q2; объединением отношений R± и Т?2 (обознача-
ется U R2) называется отношение, определяемое объединением
соответствующих подмножеств из Q2.
Если Rt—отношение «больше» на множестве чисел, /?2 —
отношение «равно», то —это отношение «больше или
равно».
§ 3. ОПЕРАЦИИ НАД ОТНОШЕНИЯМИ
21
Упражнение 13. Доказать, что при любых У?! и R2
йц (^i 0 (^i) Л о.ц (Rz)< (7)
i, j = T"n. (8)
Здесь V и Д — знаки дизъюнкции и конъюнкции.
Упражнение 14. Доказать, что при любых 7?i и /?2
(/?1n/?2)+(x) = T?1+(x)n/?2+W, (9)
(₽1U/?2)-(x)=₽r(x)U/?2-(x). (Ю)
Введем операцию обращения отношений. Обратным к отно-
шению R называется отношение R~\ определяемое условием
xR-'yo yRx.
Так, если R—отношение «больше» на множестве действительных
чисел, то R~1—отношение «меньше». Действительно, из х < у
следует у > х и наоборот. Если R означает «быть мужем», то
7?-1 означает «быть женой».
Упражнение 15. Доказать, что
1) = I, ] = (Н)
2) граф G(R~1) получается из графа G(R) изменением нап-
равлений всех дуг;
3) (R-iy(x) = R-(x), (R~"r(x) = R+(x). (12)
Операция обращения обладает свойством, которое выража-
ется следующим утверждением.
Утверждение 1. (R~1)~1 — R.
Доказательство. По определению обратного отношения
х(/?-1)_1у равносильно yR~1x\ последнее по тому же определе-
нию равносильно xRy.
Остановимся еще на одном свойстве, касающемся ранее вве-
денных операций дополнения и обращения. Оказывается, резуль-
тат последовательного выполнения этих двух операций не зави-
сит от порядка, в котором они выполняются.
Утверждение 2. /?-1 = (7?)-1. _____
Доказательств о.| Рассмотрим а17 (А?-1). В силу (11)
% (Я-1)=«//(£)» а в силу (4)
а17 (R^) = 1 -aif (/?"’) 1 -aJt (/?).
Аналогично, в силу (4) а/;(7?)=1—aj^R) и в силу (11)
%((^)-1)=a/,W=l-o//(7?).
Таким образом, пришли к требуемому равенству а,7(/?-1) =
= ol7 ((7?)”1). Утверждение доказано.
22
ГЛ. 1. БИНАРНЫЕ ОТНОШЕНИЯ
Приведенное доказательство можно использовать только для
отношений на конечных множествах. Однако сам факт верен для
произвольных отношений.
Упражнение 16. Доказать утверждение 2 в общем случае.
(Воспользоваться свойствами сечений (5) и (12).)
На основе операций дополнения и обращения введем опера-
цию перехода от отношения А? к двойственному отношению Rd,
которое играет важную роль в теории выбора на основе бинар-
ных отношений. Двойственным к R называется отношение Rd,
определяемое формулой
Rd=R^. (13)
Иными словами, двойственным к R является отношение Rd, до-
полнительное к обратному к R (или обратное к дополнитель-
ному к R, что одно и то же в силу утверждения 2).
Утверждение 3. Отношения R и Rd связаны соотноше-
ниями двойственности
(Rd)d=R, (14)
(R1URi)tt=R(nRl, (15)
(RiOR^RfURl. (16)
-Доказательство. Имеем (Rd)d = (R~1)~1 = ((R)~l)~1 —
= R=R. Второе равенство в цепочке следует из утверждения 2;
соотношение (1-4) доказано. Имеем
(Wи T?2)rf)+ (х) = ((W*)+ (х) = Q\ (W U /?2)-1)+ (х) =
= Й\ W U RJ- (х) = (Q\ Ri (х)) n (Q\ (х)) =
= (Й\ (₽1"1)+(х)) Г) (Q\ (W)) = ((7?f)+(x)) Л ((^)+(х)).
Четвертое равенство в цепочке верно в силу правил де Моргана;
соотношение (15) доказано. Формула (16) доказывается анало-
гично.
Упражнение 17. Доказать, что для того, чтобы осущест-
вить переход от графа G (R) к графу G(Rd), необходимо:
1) удалить из G (R) все пары противоположных дуг и все
петли;
2) присоединить новые противоположные дуги (i, /) и (/, i),
соответствующие парам вершин i и /, не связанным в G (R) дугой;
3) добавить все петли (i, i), которые отсутствовали в графе
GW-
Рис. 2 иллюстрирует переход от графа G(R) к графу двой-
ственного отношения G (Rd).
У пражнение 18. Для отношений 1)—5) из упр. 1 выписать
дополнительные, обратные и двойственные отношения.
Введем операцию произведения отношений. Назовем произве-
дением Rt и R2 отношение, определяемое следующим образом:
§ 3. ОПЕРАЦИИ НАД ОТНОШЕНИЯМИ
23
xR^-R^y, если существует z£Q, для которого xRxz и zR^y, где
Rx-Ri—символ произведения отношений.
Пусть 7?х—отношение «быть братом», а Т?2—отношение «быть
з
родителем». Тогда произведение Rt- Rt есть отношение «быть бра-
том одного из родителей», т. е. «быть
дядей».
Рассмотрим отношения «меньше» (7?г)
и «больше» (Т?2) на множестве целых
чисел. Пара чисел <х, у> находится в
отношении Rt- R2, если существует чис-
ло z такое, что х < z н г>у. Таким
образом, в данном примере Rr-Re—
полное отношение, т. е. R^ R2 = U.
Упражнение 19. Какой вид имеет отношение R- R, когда
R—отношение «меньше» на множестве действительных чисел?
Когда R—произвольное отношение?
Упражнение 20. Доказать:
1) J?. 0 = 0. 7? = 0 для любого R-,
2) R-E = E- 7? = R для любого R.
Упражнение 21. Доказать, что для произведения отно-
шений выполняется ассоциативный (сочетательный) закон
J (Л.В)«С = Д.(В-С),
Ассоциативный? закон позволяет^’отказаться от [[расстановки
скобок в произведениях й писать просто А-В-С, A-B-C-D и
т. п. Вместо произведения п одинаковых отношений R будем
писать Rn.
Рассмотрим матрицу А(7?1*7?2) произведения отношений Rt
и Т?2.
Утверждение 4. A (7?r Т?2) = A (7Д)-А (Т?2).
Доказательство. Произведение матриц А1 = А (7?г) и Аг—
= А(7?2) определим формулой
а1к = . V[(a$Aa*fe)A К17)
Пусть Х/7?!-T?2xfe. Покажем, что величина aik, вычисленная
по формуле (17), равна единице. По определению произведения
отношений существует такой, что XiR^Xj и Х;Егхк. Это
значит, что a|/=ajft=l. Поэтому (fy AaJfe=l. По правилам буле-
вой алгебры получаем aik = 1.
Пусть теперь а1к—\. Тогда среди слагаемых в (17) хотя бы
одно равно единице. Пусть это будет a}j Д а*к. Но тогда а},- =
= а*к=\., а это значит, что XtRiXj и XjRzxk, т. е. xiRl-I^ixk.
Утверждение доказано.
В дальнейшем нам понадобятся следующие понятия,' устанав-
ливающие связь между отношениями, заданными на различных
множествах.
24
ГЛ. 1. БИНАРНЫЕ ОТНОШЕНИЯ В
Отношение <7?х, йх> называется сужением отношения <7?, Q>
на множество Qx, если Qx s Q и 7?х = 7? р Заметим сразу, что
граф <3 (7?j) отношения <7?х, Qx>—это подграф графа G (R), порож-
денный множеством вершин Qx s Q. Сужение отношения < 7?, Q>
на множество йх будем называть также отношением 7? на под-
множестве
Пусть Qx, Qa—два множества, на которых заданы отношения
7?! и 7?2 соответственно. Введем понятие изоморфизма отношений
<7?х, Qx> и <7?а,
Отношения <7?х, йх> и <Т?2, й2> называются изоморфными,
если, существует 'взаимно однозначное отображение <p: йх —> £2В
такое, что
<=^<р (х) 7?2<р (у).
Отображение <р при этом называется изоморфизмом <Т?2, Qx> и
Q2\
Отображение <р: йх—>й2 называется гомоморфизмом {.Rt, Qx>
в <Т?2, Q2>, если
х/?^=Ф<р;(х)57?2(р (у).
§ 4. Свойства отношений
Укажем некоторые важные свойства отношений, которые
позволят в дальнейшем выделить классы отношений, применяю-
щиеся в теории выбора и принятия решений.
Отношение 7? называется рефлексивным, если Е < 7? (напом-
ним, что Е—диагональное отношение). Иначе говоря, если xRx,
то R рефлексивно. Отношения «быть похожим на», «быть не стар-
ше» (я не старше самого себя) рефлексивны. Отношения «быть
братом», «быть старше» не рефлексивны. В матрице А (7?) реф-
лексивного отношения 7? на главной диагонали стоят единицы;
в графе G(7?) при каждой вершине имеется петля; х£7?+(х),
х£7?“(х) для любого х£Й.
Отношение R называется антирефлексивным, если 7?Г)£’ = 0-
Иначе говоря, антирефлексивное отношение 7? может выполняться
лишь для несовпадающих объектов, т. е. из xRy следует х=/=#
или R <,Е. Антирефлексивными являются приведенные выше не
рефлексивные отношения.
В матрице A (R) антирефлексивного отношения на главной
диагонали стоят нули; в графе G (7?) петли отсутствуют; x^R+ (х),
х(£7?“(х) для любого x£Q.
Двойственные 'отношения, задаваемые графами на рис. 2, не
являются ни рефлексивными, ни антирефлексивными.
Упражнение 22. Доказать, что если R рефлексивно, то R*
антирефлексивно; если R антирефлексивно, то R* рефлексивно.
Отношение R называется симметричным, если R < 7?-1. Иначе
говоря, если выполнено xRy, то выполнено и yRx. Отноше-
м
5 4. СВОЙСТВА ОТНОШЕНИЙ 25
ния «быть похожим на», «быть родственником» (но не «быть мужем»)
симметричны. Матрица А (7?) симметричного отношения 7? симмет-
рична (а// = Я/|) для всех i, j; в граф G(7?) вместе с каждой
дугой (xh xj) входит и дуга (х/г х,); 7?+(х) = 7?“ (х) для любого
х £ Q.
Утверждение 5.Отношение R симметрично тогда и только
тогда, когда R = R~\
Доказательство. По определению 7?</?-1. В силу
того, что
получаем
или
Сравнивая это включение с исходным, приходим к выводу,
что /? = 7?“1. Обратное очевидно. Утверждение доказано.
Отношение 7? называется асимметричным, если 7?Г)7?“1 = 0.
Иначе говоря, из двух выражений xRy и yRx по меньшей мере
одно несправедливо. В матрице A (R) асимметричного отношения
= O для всех i, j; граф G(R) не может содержать
одновременно дуги вида (xz, Ху) и (ху-, xj; для любых х С Q и у € R~ (х)
сечение R~ (у) не содержит х. Отношение «быть братом» не является
ни симметричным, ни асимметричным. Действительно, если Петр —
брат Федора, то Федор—брат Петра; но если Игорь—брат Ольги,
то неверно, что Ольга—брат Игоря.
^Утверждение 6. Если отношение R асимметрично, то оно
антирефлексивно.
Доказательство. Пусть для х£& выполнено xRx. По
определению обратного отношения это значит, что х/?-1х. Но
тогда х(7?П7?-1)х, т. е. -R П 7?-1 =/= 0, что противоречит асим-
метричности.
Отношение R называется антисимметричным, если 7? П R~l < Е.
Иначе говоря, выражения xRy и yRx справедливы одновременно
только тогда, когда х — у. В матрице A (R) антисимметричного
отношения ai} (R),\a/{(R)—Q, если i ф у, граф G (7?) не может
содержать одновреденно дуги вида (xz, xj) и (ху, х,) при i^j',
для любых х С Q и у £ R~ (х), х =Н= у, сечение R~ (у) не содержит х.
Упражнение 23. Привести пример антисимметричного отно-
шения, которое при этом не симметрично и не асимметрично.
Упражнение 24. Описать отношения, являющиеся одно-
временно симметричными и антисимметричными.
Отношение R называется транзитивным, если R2 < R. Раскры-
вая это включение, приходим к следующему: если xRz и zRy,
toxRy. Отсюда по индукции получаем: еслих^гь z1Rz2, ..., z^^Ry,
то xRy.
Упражнение 25. Какие из отношений упр. 1 являются тран-
зитивными?
26
ГЛ. 1. БИНАРНЫЕ ОТНОШЕНИЯ
Упражнение 26. Доказать, что для рефлексивного отноше-
ния 7? транзитивность эквивалентна равенству 7?2 = 7?.
Упражнение 27. Привести пример транзитивного отноше-
ния, для которого 7?2 < 7?.
Упражнение 28. Привести пример транзитивного антиреф-
лексивного отношения, для которого 7?2=7?.
В матрице А (7?) транзитивного отношения 7??для любых i, k
п
/=1
в графе G (7?) существует дуга (х, у), если существует путь из х
в у, для любых х£й и y£R+(x) справедливо R+ (у) = 7?+ (х).
Отношение 7? называется ацикличным, если 7?*Г)7?-1 = 0 для
любого k. Ацикличность 7? означает, что из xRzlt z±Rz2, ...
• •Ч-ЛУ следует х=£у.
Отношение «быть отцом» ациклично, но не транзитивно.
Упражнение 29. Показать, что всякое ацикличное отно-
шение асимметрично.
Упражнение 30. Показать, что всякое антирефлексивное
транзитивное отношение ациклично.
Упражнение 31. Привести пример транзитивного не ацик-
личного отношения.
Упражнение 32. Выписать условия ацикличности для мат-
рицы A (R).
Если точки х и у в графе G (R) ацикличного отношения соеди-
нены путем, то в нем нет дуги (у, х). Пусть z± С 7?+ (х), z2 С 7?+(г1),
..., i/G 7?+ тогда сечение 7?+ (у) не содержит х. Аналогич-
ное условие выписывается и для нижних сечений.
Ацикличность и транзитивность отношений особенно важны
в теории выбора и принятия решений, так как эти свойства выра-
жают некоторые естественные взаимосвязи между объектами. Дейст-
вительно, если х в каком-либо смысле лучше, чем у, а у в этом же
смысле лучше, чем z, то естественно считать, что в этом смысле
х лучше, чем z (транзитивность), и во всяком случае z не лучше х
(ацикличность).
Введем еще одно необходимое в дальнейшем понятие. Отноше-
ние R называется отрицательно транзитивным, если его допол-
нение R транзитивно.
Упражнение 33. Сформулировать условия на матрицу, граф
и сечения отрицательно транзитивного отношения.
Отношение R называется сильно транзитивным, если оно одно-
временно транзитивно и отрицательно транзитивно.
Структуру сильно транзитивных отношений (и тем самым
структуру соответствующих им графов) описывает следующая
теорема.
§4. СВОЙСТВА ОТНОШЕНИЙ
27
Теорем’а 1. Пусть <R, й>—сильно транзитивное отноше-
ние на Й, |й|<оо. Тогда существует разбиение й= и й;,
z=i
П йу= 0 при i -ф j, такое, что
1) xRy, если x^Qh y€fy « i< j;
2) сужение отношения R на любое из Q{ является либо пустым,
либо полным отношением на Q{.
Доказательство. Рассмотрим два основных случая.
I. R+(x)=£0 для любого х£й.
II. Существуют такие х^й, что R+(x)=0.
I. Так как R+(x)=£0 для всех х, то существует последова-
тельность хь х2, ..., часть элементов которой гъ ..., zt в силу
конечности множества й образует цикл, т. е. ZjRz^ (I = 2, /) и zxRzt.
Из транзитивности R непосредственно следует, что ztRzj для
любых I, /=1, /, т. е. сужение R на Z={zb ..., zt}—полное
отношение. Обозначим через Zx максимальное (по включению) под-
множество Q, содержащее Z, на котором R—полное отношение
(легко видеть, что Zx определяется однозначно). Если ZX = O, то
теорема доказана. Пусть yRz для всех y^Q\Zx и всех z£Zx.
Тогда zRy для всех у £ Q\ZX и всех z € Zx. Действительно, пусть zRy.
Тогда из yRz и сильной транзитивности R следует zRz, что про-
тиворечит полноте R на Zv В этом случае положим Q1 = Z1; легко
видеть, что сужение R на также сильно транзитивно, поэтому
все рассуждения можно проводить на й\йх.
Осталось рассмотреть случай, когда для некоторого t/^Q\Zx
и z^Z, имеет место yRz. Поскольку мы рассматриваем случай I,
то существует х такой, что xRy. Продолжая эти рассуждения,
приходим к Z2, на котором R полно; если z^Z2, то zRy. Ясно,
что Za(]Z1= 0, поскольку иначе Z2 = Z1, y£Zx, что противоречит
y£Q\Zx. Продолжая эти рассуждения, в конце концов придем к Zk
такому, что R полно на Zk и для всех у£й\/й и z£Zk справед-
ливо yRz. Но тогда, как было показано выше, можно положить
Qx = Zk и продолжить рассуждения на й\йх.
II. Положим й1 = {х|7?+’(х) = 0}. Если ЙХ = Й, то теорема
доказана. Пусть #€й\йь хх£й и xxRy. Если х, ^й^ то xtRy
(в противном случае xxRx^, x^Ry влечет ххRy). Пусть у£ й\йъ
хх € и xxRy. Поскольку R+ (у) 0, то найдется z такой, что zRy,
легко видеть, что z^Qx. Продолжая эти построения, приходим
к множеству Zx такому, что ZxnQx = 0, R полно на Zx и для
всех z^Zx выполнено xxRz. По построению zRxx, откуда zRz, что
противоречит полноте R на Zv Полученное противоречие дока-
зывает, что для всех у € й\йх и всех х £ йх имеет место xRy.
Поэтому все рассуждения можно продолжить на й\йх. Теорема
доказана.
28
ГЛ. 1. БИНАРНЫЕ ОТНОШЕНИЯ
Упражнение 34. Привести пример отношений, обладающих
в точности одним, двумя, тремя и четырьмя свойствами из числа
следующих: рефлексивность, симметричность, транзитивность, анти-
симметричность.
§ 5. Отношения эквивалентности, порядка, доминирования
Воспользуемся -рассмотренными свойствами для выделения отно-
шений, представляющих интерес для теории выбора и принятия
решений.
Отношение 7? называется отношением эквивалентности (экви-
валентностью), если оно рефлексивно, симметрично и транзитивно.
Обозначим его символом
Отношениями эквивалентности являются: отношение «быть на
одном курсе» на множестве студентов одного факультета; отношение
«иметь одинаковый остаток при делении на 3» на множестве нату-
ральных чисел; отношение подобия на множестве треугольников.
Упражнение 35. Пусть отношение эквивалентности
на множестве £2. Доказать, что
х£7?+(х);
если х ~ у, то /?+(х)= 7?+(у);
если 7?+(х)Л 7?+ (*/)=# 0, то 7?+ (х) = R + (у).
п
Пусть задано разбиение Q= 1)£2; и £2(-п£2/- = 0 при i Ф j. Вве-
I ” 1
дем на Q следующее отношение xRy тогда и только тогда,
когда существует подмножество содержащее х и у.
Упражнение 36. Доказать, что определенное выше отно-
шение R—эквивалентность.
Результаты двух последних упражнений означают, что зада-
ние эквивалентности на некотором множестве Q равносильно зада-
нию разбиения Q на классы эквивалентных друг другу элементов.
Наоборот, любое разбиение Q определяет соответствующую ему
эквивалентность.
Упражнение 37*. Сколько отношений. эквивалентности
существует на множествах из двух, трех, четырех и п элементов?
Часто требуется определить некоторый порядок расположения
элементов множества (см. § 1). Это можно сделать, введя отно-
шение порядка.
Отношением нестрогого порядка (нестрогим порядком) назы-
вается отношение, обладающее свойствами рефлексивности, анти-
симметричности и транзитивности. Отношением строгого порядка <
(строгим порядком) называется отношение, обладающее свойствами
антирефлексивности, асимметричности и транзитивности.
Пусть — нестрогий порядок на множестве Q; ему можно
сопоставить строгий порядок <, определяемый следующим обра-
зом: x<Zy тогда и только тогда, когда х^у и х=£у.
§5. ЭКВИВАЛЕНТНОСТЬ, ПОРЯДОК. ДОМИНИРОВАНИЕ
29
Наоборот, пусть <—отношение строгого порядка на мно-
жестве й; ему можно сопоставить отношение sC таким образом:
х^.у то’гда и только тогда, когда х < у или х = у.
Итак, по нестрогому порядку можно указанным образом найти
соответствующий строгий порядок и наоборот. Поэтому будем:
пользоваться термином частичный порядок, понимая под ним нестро-
гий порядок.
Определим отношение включения на множестве ®(Й) подмно-
жеств фиксированного множества й следующим образом: Z^Z^,
если Z1sZ2. Легко видеть, что отношение включения является
частичным порядком.
Утверждение 7. Произвольный частичный порядок на мно-
жестве й изоморфен сужению отношения включения на некоторое-
подмножество Зд (й), т. е. существует такое отображение 0: й —►
что из х^.у следует 0(х) S0(у) и наоборот.
Доказательство. Пусть гС—частичный порядок на мно-
жестве й. Сопоставим каждому х£й подмножество 0(х)С^(й}
(0 (х) s й) по формуле
Легко проверить, что из х=£у следует 0(х)#=0(г/) и что х^у
«огда и только тогда, когда 0(x)s0(«/).
Частичный порядок на й называется линейным порядком, если
для любых х, у выполняется одно из трех условий:
х<у, х = у, х>у.
Упражнение 38. Для каких множеств Й отношение влюче-
ния является линейным порядком?
Упражнение 39. Привести пример отношения, являющегося
одновременно частичным порядком и эквивалентностью.
Упражнение 40*. Сколько частичных порядков существует
на множествах из 2, 3, 4 и п элементов?
Отношением доминирования называется отношение, обладающее
свойствами антирефлексивности и асимметричности. Будем гово-
рить, что х доминирует у, и писать х^у, если х в каком-либо
смысле превосходит у. Так, х может быть спортсменом или коман-
дой, победившей спортсмена или команду у, лицом, пользующимся
авторитетом у лица у, свойством, которое предпочтительнее свой-
ства у.
Таким образом, отношение строгого порядка является частным
случаем отношения доминирования,^при котором дополнительна
требуется транзитивность. В общем случае для доминирования
как транзитивность, так и ацикличность могут не иметь места.
30
ГЛ. I. БИНАРНЫЕ ОТНОШЕНИЯ
§ 6. Понятие /^-оптимальности '
Приведенный ранее материал был связан с формализацией поня-
тия попарного сравнения элементов, которое необходимо для
выделения лучшего элемента (или нескольких лучших) из всего
множества й. Чтобы выделить лучшие элементы, необходимо фор-
мализовать понятие «лучший элемент». Воспользуемся для этого
аппаратом бинарных отношений.
Введем необходимые понятия. Элемент х£й называется мак-
симумом по отношению R, заданному на й, если для всех у С й
выполнено xRy. Аналогично, х£й называется минимумом по
отношению R, заданному на й, если для всех у £ й выполнено yRx.
Максимумы и минимумы по отношению R могут существовать
или не существовать. Например, множество всех действительных
чисел с отношением «больше или равно» не имеет ни максимума,
ни минимума по этому отношению. Сужение этого отношения на
множество всех неотрицательных чисел имеет минимум (нуль),
но не имеет максимума.
Упражнение 41. Имеются ли максимум и минимум по отно-
шению включения?
Упражнение 42. Доказать, что максимум по частичному
порядку единствен.
Упражнение 43. Верно ли утверждение предыдущего упраж-
нения для произвольного R?
Будем пользоваться понятием максимума по отношению для
формализации понятия «абсолютно лучший элемент».
От максимума и минимума следует отличать понятия мажо-
ранты и миноранты по отношению R. Элемент х£й называется
мажорантой по отношению R, заданному на Й, если для всех у С й
выполнено yRx. Элемент х£й называется минорантой по отно-
шению R, заданному на Q, если для всех
г/£й выполнено xRy.
Рассмотрим отношение, заданное графом
на рис. 3. Здесь — мажоранта, bt—ми-
норанты; максимумы и минимумы отсут-
ствуют.
Упражнение 44. Могут ли одновре-
менно существовать максимумы и мажоранты,
не являющиеся максимумами, по одному отношению R?
Пусть R—произвольное отношение на множестве й; й+ (R)—
множество максимумов по отношению R; й+ (R)—множество мажо-
рант; й” (R)—множество минимумов; й_(7?)—множество мино-
рант.
Упражнение 45. Доказать тождества
Й+(7?) = Й-(/?-1), Q-(R) = Q+(R"*), ....
Й+ (7?) = й_ (R-1), Й_(/?) = й+(/?-1). '
Рис. 3.
§6. ПОНЯТИЕ «-ОПТИМАЛЬНОСТИ
31
Рассмотрим" еще одну взаимосвязь между введенными подмно-
жествами Й.
Утв'ер’жде'н’ие 8.
Й+(Я) = Й+(Я“), (18>
Q~(R) = Q_(Ra). (19>
Д о к а з a Ye л ь с т в о. Пусть х £ й+ (7?). Это значит, что для
всех у выполнено xRy или yR~*x и, следовательно, не выпол-
нено yR-*x, т.е. не выполнено yRdx. Это значит, что x^Q+(7?rf);
тем самым доказано включение^+ (R) s й+ (У?4). Наоборот^ пусть
х£й+(/?*). Это значит, что для всех у£й выполнено yR*x или
x(7?rf)-1z/; в силу (14) для всех у £ й выполнено xRy, т. е. х £ й+(/?).
Формула (19) доказывается аналогично. Утверждение доказано.
Множество й+ (/?), играющее важную роль в теории выбора,
называется также множеством недоминируемых по R элементов*,
входящие в него элементы называются R-оптимальными. Для
обозначения множества всех /^-оптимальных на й элементов ис-
пользуется обозначение йл, а для множества’максимумов по от-
ношению R—обозначение QR.
Максимальной цепью по отношению R, заданному на £2 (макси-
мальной цепью), назовем последовательность элементов xlt ..., Хм
такую, что
1) XiRxi+1 (i = l, М-1);
2) не существует последовательности со свойством 1) большей
длины.
Теорема 2. Гомоморфизм <р отношения <R, й> в линейный
порядок существует для любого ацикличного R; | <p (й) | q,
где q—длина максимальной цепи в й.
Доказательство является конструктивным, т. е. состоит в непо-
средственном построении <р. Пусть Qf—множество недоминируемых
по R элементов й, т. е. Й^ = й\ Положим
Й« = (Й\Й«)*,
о*=(й\(й*иед*
й?=<й\и'й?у,
Й\/ и й^=0 .
\J=1 /
Гомоморфизм ф можно задать формулой ф(х)=$—i, если х£й^
Оценка | ф (й)| q очевидна. Теорема доказана.
Упражнение 46. Где в доказательстве теоремы 2 использу-
ется ацикличность R7
Литература. [14, 57, 66, 87, 125]
32
ГЛ. 2. ФУНКЦИИ ВЫБОРА
F л а в а 2
[ФУНКЦИИ ВЫБОРА] '
В практической ситуации выбора при некотором множестве аль-
тернатив й лицо, принимающее решение, выбирая некоторую аль-
тернативу, руководствуется своим личным представлением о лучших
альтернативах. У разных лиц в одной и той же ситуации (при
одном й) представление о лучших альтернативах может различаться,
а следовательно, они могут выбирать разное альтернативы. При
этом каждый из них может привести вполне рациональное обос-
нование сделанного выбора. Даже при выборе одних и тех же
альтернатив разными лицами обоснования могут различаться. Таким
образом, по известному выбору в конкретной ситуации вряд ли
можно сказать что-либо определенное о тех причинах, которые
побудили сделать именно данный выбор, а не другой, т. е. вос-
становить логику выбора.
Рассмотрим несколько взаимосвязанных ситуаций выбора, в
которых множества альтернатив X являются подмножеством й.
Обозначим через С (X) множество альтернатив, выделенных лицом,
принимающим решение (ЛПР), из X, и установим связи между
множествами С (X) при разных множествах X. Заметим, что выбор
при этом осуществляет одно и то же ЛПР. Далее везде термин
выбор из X будет использоваться для обозначения С(Х).
Пусть й—множество всех групп вуза; X—произвольное под-
множество й (например, множество групп 3-го курса, множество
групп механического факультета и т.д.). Пусть С(Х)—лучшая
группа из множества групп X. Отвлекаясь от того, кто и по каким
признакам выбирает лучшую группу, естественно считать, что
лучшая группа вуза будет лучшей группой своего курса, своего
-* факультета и т. д. Формально это записывается следующим об-
разом:
если Х'еХ и х € С (X) П X; то х £ С (X'). (1)
Конкурс на лучшую группу, в котором лучшая группа вуза ока-
зывается не лучшей группой своего факультета, вряд ли можно
считать объективным, независимо от того, по каким показателям
подводятся его итоги.
Итак, не всякий выбор в.конкретной ситуации может быть при-
знан логически обоснованным при известных выборах в других си-
туациях, связанных с данной, так как множества С (X) оказываются
зависимыми при разных X, например, в смысле (1). Для формали-
зации взаимной зависимости выборов С(Х) при взаимосвязанных
ситуациях пользуются понятием функции выбора. Функцией выбора
С называется отображение, сопоставляющее каждому Хей его
подмножество С (Х)еХ.
Далее в этой главе всюду будет рассмотрен «выбор в целом»,
который задается функцией выбора С. В § 1 рассмотрены функции
§ 1. НОРМАЛЬНЫЕ ФУНКЦИИ ВЫБОРА
33
выбора, порожденные бинарными отношениями; в § 2—способы
задания функций выбора; в § 3—операции над функциями выбора;
в § 4 приведена классификация функций выбора; в § 5 описаны
структуры некоторых классов функций выбора; в § 6—выбор,
зависящий от предыстории.
Упражнение 1. Что является областью задания функции
выбора и что—областью ее значений?
Будем интерпретировать С(Х) как наиболее предпочтительные
элементы из X. Отметим, что в общем определении функции вы-
бора никаких априорных ограничений на С(Х)не накладывается.
В частности, не исключается возможность пустого выбора, т. е.
С(Х) = 0.
Обычно С (X) — 0 называют «отказом от выбора» или «альтер-
нативой статус-кво».
Примером, когда возникает отказ от выбора, может быть си-
туация, в которой студент не берет ни одной из предлагаемых
ему библиотекой книг для подготовки к экзаменам, или ситуация,
в которой покупатель уходит из магазина, не купив в нем ничего.
§ 1. Функции выбора, порожденные бинарными отношениями
Сопоставим произвольному бинарному отношению функцию вы-
бора. Пусть на й задано бинарное отношение R и для x,y£Q
выполнено xRy. Будем считать теперь, что для выбора предъяв-
лено множество Х = {х,у}. Учитывая, что xRy, при описании
результата выбора из X можно считать, что у не включается в
С(Х). С другой стороны, можно полагать, что х должно быть
включено в С(Х). Рассмотрение всех пар элементов из й, для
которых выполнено х-Ry, с учетом сказанного порождает на й
две различные функции выбора:
C^(X) = {xCX|Vz/€X yRx}, (2)
CR(X) = {xeXi\yyeX xRy}. (3)
Функции выбора СЛ(Х) и С^(Х), порожденные бинарным отно*
шением R, называются блокировкой и предпочтением соответственно*
Утверждение 1. Пусть Rj— сужение отношения R, за-
данного на й, на множество X s Й; Ri—отношение, двойствен-
ное к Ri, Rd— отношение, двойственное к R', Rd—сужение Rd
на X. Тогда Rf—R$.
Упражнение 2. Доказать утверждение 1.
Пусть R—бинарное отношение на й; Rt—его сужение на
X s й. Формула (2) означает, что CR (X) состоит из всех мажо-
рант Ri, а формула (3)—что СЛ(Х) состоит из максимумов по
Rlt т. е.
С*(Х) = Х*>, С₽(Х) = ХД1. (4)
Тем самым из утверждений 1 и 1.8 следует
2 И. М. Макаров и др.
34
ГЛ. 2. ФУНКЦИИ ВЫБОРА
Утверждение [2. Функции [выбора CR и CR связаны соот-
ношениями
Cr = Cri, CR = CRi, (5)
где Т?4—отношение, двойственное к R.
В силу утверждения 2 из двух функций выбора, порожденных
бинарным отношением R, достаточно рассматривать только одну,
так как блокировка по отношению R совпадает с предпочтением
по двойственному отношению Rd и наоборот. Всюду в дальней-
шем, если не оговорено противное, будем сопоставлять бинар-
ному отношению R функцию блокировки CR, определяемую фор-
мулой (2), и называть ее функцией выбора, порожденной отно-
шением R. Такие функции называются также нормальными.
Упражнение 3. Верно ли, что R2 => CRt CRR
Упражнение 4. Сколько существует различных функций
выбора на й = {х, у}?
Упражнение 5. Сколько существует различных бинарных
отношений на Q = (x, у}?
Произвольная функция выбора С не обязательно совпадает
с некоторой CR. Рассмотрим следующую функцию выбора на
Q = {x, z/}:
С (х) = х, С (у) = 0, С|(х, у) = {х, у}. (6)
Определим, существует ли бинарное отношение R на Q такое,
что C = CR. Допустим, что R существует. Из (2) и из того, что
Сл(х) = х, сразу следует, что верно xRx, т. е. неверно xRx\
аналогично, из [CR(y) — 0 следует, что верно yRy. -Но тогда
неверно yRy и, значит, yf£CR(Q), что противоречит ^(6); значит,
предположение о существовании R неверно. В силу утвержде-
ния 2 не существует и бинарного отношения R такого, что C = CR
(иначе можно было бы перейти к двойственному отношению Rd,
для которого CR = CRd).^ \ Ж- : В : '
Приведем еше один пример, который ^показывает, что бинар-
ное отношение и «выбор в целом» на двухэлементном множестве
являются существенно различными понятиями, хотя с первого
взгляда могут показаться тождественными. Рассмотрим всевоз-
можные функции выбора С на Q = {x, у} и определим для каж-
дой из них отношения и R2 такие, что C — CRt = CR2, если
это возможно (мы видели, что это возможно не всегда). Отноше-
ния 7?! и R2 будем задавать графами, которые представлены
в двух последних столбцах табл. 1. Соответствующие этим гра-
фам функции выбора C = CRi = CRi представлены во 2-м—4-м
столбцах. Например, строки 5 и 6 табл. 1 показывают, что уже
для двухэлементных множеств не всякая функция выбора С может
быть Порождена бинарным отношением.
Приведенные примеры показывают, что даже для двухэле-
ментных множеств не все функции выбора нормальны.
§ 1. НОРМАЛЬНЫЕ ФУНКЦИИ ВЫБОРА
35
Таблица 1
№ а (х) С' (у) а (%, у)
1 X У {х, у} « у Qt 0
2 X У X »- X у
3 X У У я* У
4 X У 0 х Qc yQ .
5 X 0 {х, у} не существует не существует
6 0 У {х,У} не существует не существует
7 X 0 X , Q . .х у х у 0-^- О’ 2/
8 X 0 У не существует не Существует
9 0 У У От у От* *у х'
10 0 У X не существует не существует
И X 0 0
12 0 У 0 У х у 5-^0
13 0 0 {х,У} не существует не существует
14 0 0 X не существует не существует
15 0 0 У не существует не существует
16 0 0 0 О Ф Q ' Q & у а у
& У
* J ( _।
у х^— J у ^у
2* И. М. Макаров и др.
4
36J гл. 2. ФУНКЦИИ ВЫБОРА
Упр а’ж н е н и е 6. Какие гтроюГтабл. 1 дают ответ на вопрос
упр. 3?
Упражнение 7. Указать в табл. 1 все пары двойственных
отношений.
Упражнение 8. Привести пример функции выбора, не
являющейся нормальной, на Q таком, что |Q|=sl000.
Упражнение 9. Пусть С—произвольная функция выбора.
Всегда ли существует бинарное отношение R такое, что С(Х) =
= С/?(Х) для всех двухэлементных множеств X? Единственно
ли оно?
Заметим, что если рассматривать двух- и одноэлементное мно-
жества, то ответ заведомо будет отрицательным, как это следует
из табл. 1.
Упражнение 10. Сколько существует различных нормаль-
ных функций выбора на множестве из N элементов?
Обратимся снова к табл. 1. Из строк 7, 9, 11, 12, 16 следует,
что разные бинарные отношения могут порождать одну и ту же
функцию выбора С. Это связано с тем, что наличие петли в графе
бинарного отношения (например, в вершине у строки 7) «блоки-
рует» выбор соответствующего элемента (элемента у) из любого
подмножества X, независимо от наличия других дуг, ведущих
в эту вершину (дуга (х, у)). В результате наличие или отсутствие
дуг типа (х, у) приводит к разным бинарным отношениям R, но
не влияет .на порождаемую ими функцию выбора CR.
Выделим среди всех /?, порождающих одну и ту же функ-
цию CR, отношение /?*, не» содержащее пар вида <х, г/>. Назовем
его минимальным отношением, поскольку граф такого отношения
имеет минимальное число дуг.
Для формального описания класса нормальных функций выбора
определим для X s Q накрывающее семейство Х{ s Q (i € О
такое, что и Xz э X.
ier
Утверждение 3. Функция выбора С является нормальной
тогда и только тогда, когда для любого множества X s Q и
любого накрывающего его семейства Xt (i € I)
Х\С(Х) = Х*\ПС;(Х,.). (7)
ie /
Доказательство. В силу утверждения 2 функция С нор-
мальна, если C — CR. Покажем сначала, что для любого X = Q
функция CR удовлетворяет (7). Если x(zX\CR(X), то найдется
у^Х такой, что xRy. Пусть у содержится в некотором мно-
жестве X/ накрывающего X ’семейства. Тогда х^Сд(Х;),
так как xRy, и, следовательно, х(£ л CR(XZ), что и доказы-
1'е/
вает (7).
$ 1. НОРМАЛЬНЫЕ ФУНКЦИИ ВЫБОРА
37
Пусть теперь С—функция выбора, удовлетворяющая (7). Зада-
дим отношение R формулой
/?= U С(Х)хХ. (8)
Покажем, что C = CR. Выражение (8) означает, что <х, y>£R,
если х принадлежит С(Х) хотя бы для одного X, которое со-
держит х и у одновременно. Из него следует
C(X)s|C₽(X), (9)
так как все элементы из С (X) являются в X максимумами по
отношению /?.
Остается доказать обратное включение: из x£CR(X) следует
х£С(Х). Допустим противное, т. е. х(£С(Х). Тогда в силу (7)
заключаем, что х£Х\ П C(XZ), т. е. х(£С(Х,) хотя [бы для
одного множества из семейства Xz (/£/). С другой стороны, xRy
для всех у£Х. Это значит, что существует такое семейство X,-
(i € /), накрывающее X, что х € С (Xt) для всех i £ I. Полученное
противоречие доказывает утверждение.
Утверждение 3 означает, что всякий объект из X, не попав-
ший в число лучших, т. е. в С(Х), обязательно не входит
в C(XZ) хотя бы для одного множества Xz из накрывающего X
семейства. Как следствие, можно отметить, что если функция С
нормальна, то
* \ С (X) <= X \ С'(Х2), (10)
т. е. если элемент 'не выбран из множества X, то он не будет
выбран из любого содержащего его множества.
Упражнение 11. Эквивалентны ли формулы (1) и (10)?
Установим связь между свойством ацикличности бинарного
отношения /? и свойством соответствующей ему нормальной функ-
ции выбора CR.
Утверждение 4. Сл(Х)#=0 для любого Х^йтагдаи
только тогда, когда отношение R ациклично.
Доказательство. Пусть R ациклично, XsQ, х£Х.
Если для всех у£Х выполнено yRx, то в силу (2) х£С(Х) и
поэтому С(Х)=£0. В противном случае найдется У*£Х такой,
что y*Rx. При этом либо у*£С(Х), либо найдется z такой, что
zRy*. Продолжая этот процесс, найдем к^Х такой, что дня всех
w£X выполнено wRv, т. е. v£C(X). В противном случае в силу
конечности X получим противоречие с ацикличностью R. Таким
образом, при ацикличном R выбор СК(Х) непуст.
.Пусть R не ациклично. Это значит, что существуют xz££2
такие, что xi+1Rxi (i= 1, ..., k—1) и х^хк. Но тогда в силу (2)
С(Х)==0, где Х = {х1, .... хк}. Утверждение доказано.
38
ГЛ. 2. ФУНКЦИИ ВЫБОРА
Итак, каждому бинарному отношению 7? на й соответствует
некоторая порожденная им функция выбора CR на й; разным /?
могут соответствовать одинаковые CR\ функции выбора 4С, кото-
рые совпадают с CR для какого-нибудь бинарного отношения
</?, й>, 'называются нормальными; не все функции выбора нор-
мальны. .уЙ
$ 2. Логические формы функций выбора
-Пусть й = {х1, . .., xN}, XsQ. Сопоставим каждому эле-
менту х;£й булеву переменную Установим взаимно однознач-
ное соответствие между 2N подмножеств 2 и 2Л’ векторов длины N
с компонентами 0 и 1 по формулам
₽(Х)=<МХ).....МХ)>,
( 1, если Х:^Х,
= | q если х-ФХ
(И)
(12)
Множеству й соответствует вектор Р(Й)=а<1, 1>, а мно-
жеству 0 —вектор р(0) = <О, 0>.
Пусть на й задана функция выбора С. Рассмотрим семейство
булевых функций от Af—1 переменных
(13-
которое построено по следующему правилу:
0/(X) л ft.® (X))«1 СХХ), (14)
где
ЛФНМРи •••> Р/+„ .... Ы. i А17Ж’
/1(₽)вА(0», ...» fry), Av(PWv(f\, - • Лаг-J. и '
, Логической формой функции выбора С (ЛФ В(С)) называется
семейство функций <_flt fv> от N—1 переменных, построен-
ное по С с помощью формулы (14).
Если задано произвольное семейство булевых функций
<fi, • ••, fiv> ог N — 1 переменных, то соотношения (14), (15)
однозначно определяют функцию выбора С; ЛФВ(С) совпадает
с исходным семейством </\, ..., Следовательно, задание
функции выбора эквивалентно заданию ЛФВ(С).
Рассмотрим примеры, иллюстрирующие переход от С к ЛФВ(С)
и обратно.
Пример 1. Пусть й=я{х1, х2, х3, xt} и задана функция
выбора
C(Xi)=>Xi; 'C\(xt/xj)^xk, где 7г = min {i, /};
C(xz, Xj, xk)=a{xh Xj, xkWxr, где r=smax{t, /, k}\
С(Й) = хг.
§ 2. ЛОГИЧЕСКИЕ ФОРМЫ ФУНКЦИЙ ВЫБОРА
39
Таблица 2
X ст Р(Х) 0(С(Х))
Xi Х1 <1000> <1000>
X2 Х2 <0100> <0100>
x3 Хз <0010> . <0010>
х4 Х4 <0001> <0001>
Х1, х2 Х1 <1100> <1000>
Xlt х3 Х1 <1010> <1000>
Xlt х4 Х1 <1001> <1000>
Х2, Х3 Х2 <0110> <0100>
х2, х4 Х2 <0101> <0100>
Х3, Х4 Хз <0011> <0010>
х19 х2, х3 Х1, х2 <шо> <1100>
xlt х2, х4 Х1, Х2 <1101> <1100>
Xlt х3, х4 Х1, Хз <1011> <1010>
x2t Xg, Х4 х2, Хз <01 п> <0110>
Х1, х2, х3, х4 Х1 <1111> <1000>
Построим для нее логическую форму. Из табл. 2 с помощью
(14) получим таблицы, задающие функции fu f2, fa, ft (табл. 3).
Используя табл. 3 и разложение функций в совершенную дизъюнк-
тивную нормальную форму (СДНФ), имеемj
А(Ра, Рз, Р4)^Ь
fa (Pi, Рз> Р4) = Pi V РзР4 V РзР4,
f з (Pi» Ра» Р4) = PiPa V РаР4 V Р1Р4,
' f4(Pi> Ра» Рв)==Р1РаРз»
лфв(сх/ъ fa, fS(f4>.
Упражнение 12. Найти ЛФВ(С)'для функции выбора С11
из табл. 1.
Пример 2. Решим задачу определения функции выбора по
ее логической форме. Пусть й = х2, ха, х4} и задано семейство
булевых функций
/1(?ь Та, Тз) = Ь\/?2, ' /а(Т1» Та- Тз)=1,
fs(7i. Та. 7з)^0, f4 = (Vi. Та, Тз) = Уа»
ЛФВ ft, f„ ft>.
40
ГЛ. 2. ФУНКЦИИ ВЫБОРА
02 03 04 fl
0 0 0 0 0 0 1 1 0 1 0 1 1 1 1 1
1 1 1 1 0 0 г 1 0 1 0 1 1 1 1 1
Таблица 3
01 03 04 ft
0 0 0 0 0 0 1 1 0 ' 1 0 1 1 1 1 1
1 1 1 1 0 0 1 1 0 1 0 1 0 1 < 1 0
01 02 04 /з
0 0 0 1
0 0 1 1
0 1 0 0
0 1 1 1
1 0 0 0
1 0 1 1
1 1 0 0
1 1 1 0
0! 02 03
0 0 0 1
0 е 1 0
0 1 0 0
0 1 1 0
1 0 0 0
1 0 1 0
1 1 0 0
1 1 1 0
02 03 04 fl
0 0 0 1
0 0 1 1
0 1 0 0
0 1 1 0
1 0 0 1
1 0 1 I
1 1 0 1
1 1 1 1
Таблица 4
01 03 04 ft
0 0 0 1
0 0 1 1
0 1 0 1
0 1 i 1
1 0 0 1
1 0 1 1
1 1 0 1
1 1 1 1
S 2. ЛОГИЧЕСКИЕ ФОРМЫ ФУНКЦИЙ ВЫБОРА
41
01 0» 04 fa
0 0 0 0 0 0 1 1 0 1 0 1 0 0 0 0
1 1 1 1 0 0 1 I 0 1 0 i 0 0 0 0
01 02 03
0 0 0 0
0 0 1 0
0 1 0 1
0 1 1 1
1 0 0 0
1 0 1 0
1 1 0 1
1 1 1 1
Восстановим функцию выбора
в соответствии с (15):
С, Перенумеруем переменные
ЛСРз, Рз> Pi) — Ра V Рз, /V(Pi> Рз> P«)—
Гз(Рз, Pa, Pi) = 0, fi(Pi, Pa, Рз)~Ра;
полученные функции сведем в табл. 4. Используя данные табл. 4
и (14), получаем функцию выбора, С (табл. 5).
| Та бли ца 5
X 0! Pi 03 04 0ifi 0«f« 03fa • C(X)
0 0 0 0 0 0 0 0 0 0
Х1 1 0 0 0 1 0 0 0 X1
Х2 0 1 0 0 0 1 0 0 X2
Х3 0 0 1 0 0 0 0 , 0 0
х4 0 0 0 1 0 0 0 .0 0
хъ х2 1 1 0 0 1 1 0 0 Xl, x2
xlt х3 1 0 1 0 0 0 0 0 \ 0
хъ х4 1 0 0 1 1 0 0 0 X1
х2, х3 х2, х4 0 0 1 1 1 0 0 1 0 0 i 1 0 0 0 1 , X2 \ x2, x4
xj, х4 0 0 1 1 0 0 0 0 \ 0
xlt x2t х3 1 1 1 0 1 1 0 0 1 V x2
Xl> X2t Xi 1 1 0 1 1 1 0 x1\x2f x4
*1, X3i х4 1 0 1 1 0 0 0 0 1
х2, Х3, х4 0 1 1 1 0 1 0
*1, Х21 х3, х4 1 1 1 1 1 1 0 1 *t,y«
\
ГЛ. 2. ФУНКЦИИ ВЫБОРА
_Уп_ражнение 13._Пусть 'Q=a [хп х.г, х3, х4}; f2 =
= Т1Т2?з> /з^1. /i^YaYa- Построить функцию выбоэа С по ее
лфв(О=«<а, ft, fa, ft>.
Упражнение 14. Доказать, что функция выбора С, по-
строенная в упр. 13, нормальна; дарисовать граф отношения А?
такого, что C — CR. (Воспользоваться конструкцией из доказа-
тельства утверждения 3.;
Воспользуемся логической формой функции выбора для выяв-
ления свойств множества а4Ь всех функций выбора на Q.
Утверждение 5. Пусть |й|=яУ. Общее число различных
функций выбора на £2 равно
Доказательство. Пусть 3?—общее число различных
функций выбора на Q. Рассмотрим все различные наборы из АГ
булевых функций от У—1 переменных. Учитывая, что на каж-
дом из У мест набора может стоять любая булева функция от
У—1 переменных, а число таких функци^равно 22V~I, получим
<5’ = (22'v-1)w.
Утверждение 5 определяет Мощность множества возможных
функций выбора на Q.
Воспользуемся логическими формами функций выбора для
задания структуры на множестве всех функций выбора на Q.
Пусть задана ЛФВ(С), т. е. задано соответствующее упорядочен-
ное семейство У булевых функций от У — 1 переменных ...
..., Av>. Рассмотрим 2W*1 наборов из нулей и единиц длины У — 1.
Занумеруем их числами от 1 до 2ЛГ“1 в следующем порядке:
1^<0, 0, ..., 0,|0>,
2<->’<0, 0, .... О, 1>,
3W<0, 0, ..., 1, 0>, (16)
2"-1<-><1,’1, .... 1>.
Набор с /-м номером обозначим через ( pz=;<pi, ..., р^_4>
(/ = 1, 2V-1). Рассмотрим всевозможные пары вида <i, |3Z> (i^l, У;
/ —1, 2V-1); номер i будет соответствовать номеру функции
в ЛФВ(С). Общее число q всех таких пар равно, как легко
видеть, /У^-1. Занумеруем пары
<1/₽1>, <1, р2>, .... <1, р«л,-1>, <2,’Р'>.<У, ₽2W-1>
последовательностью чисел от 1 до q=tN •2V-1.1
Рассмотрим q-мерный единичный\ку5 Di, т. е. подмножество
Eq, определяемое формулой
/ D» = ^€£JO<^<1 (i^l“)f (17)
§2. ЛОГИЧЕСКИЕ ФОРМЫ;ФУНКЦИЙ ВЫБОРА
43
Вершины куба £)«—это ^-мерные векторы, компоненты которых —
нули и единицы.
Упражнение 15. Сколько вершин имеет куб ZW
Сопоставим функции выбора''/? вершину xc=<xf, ..., х£>
куба D4'.
= i = /=”2^), (18)
мин nr акав. ши ни । -Ъмманапгп wttib нп ми ан ммаммшнм
где г—номер пары <i, |У>; <Д.fx>—ЛФВ(С).
Пусть теперь х—произвольная вершина; она[ определяет не- '
которую функцию выбора Сх соотношениями
W)=*r (г=1,?; ' = 1-N> /~1.2 '); (19)
ЛФВ (C*) = <ft, .... й>.
Таким образом, доказано сл<
Утверждение 6. Множес.
жестве Q взаимно однозначно
соответствует множество вер-
шин N •2м~1-мерного единичного
куба.
Упражнение 16. Какие
функции выбора соответству-
ют вершинам <0, ..., 0> и
<1, ...» 1>?
ПримерЗ. Пусть # = 2.
Тогда q = N • 2л,-1 = 4. Рассмот-
рим последовательность вершин
4-мерного куба: <0, 0, 0, 0>,
<0, 0, 0, 1>, <0, 1, 0, 1>,
<0, 1, 1, 1>, <1, 1, 1, 1>
(см. рис. 1). Везде далее будем
называть последовательность
вершин путем, а число вер-
шин—длиной пути. Пользуясь
(19), определим функции выбо-
ра С1, ..., С5 на П = {хп х2),
деленного пути (табл. 6). Таки
щее' утверждение.
всех функций выбора на мно-
соответствующие вершинам вы-
образом, пример иллюстрирует
утверждение 6.
Установим частичный порядок на множестве o/fl. Функция
выбора Сх вложена в функцию С2 (обозначается С± < С2), если
Сх(Х)^С2(Х), Хей. Если Cj<C2 и неверно, что С2<СХ, то
строго вложена в Сг (Ci<C2). В^примере 3, как видно из
табл. 6, С‘ вложена’в Ci+k (i=l,4; i-^-k'^.5).
Определим бинарное отношение на множестве формулой
CxRCi^C1<C2, ! (20)
44
ГЛ. 2. ФУНКЦИИ ВЫБОРА
легко проверить, что это отношение является частичным поряд-
ком.
Упражнение 17. Пусть Cj<C2. Доказать, что Сх(Х)с
сС2(Х) для некоторого Х = Я.
Таблица 6
i /f(0) f/(l) ^(0) fl (1) d (ха d (x,) Cf (xlt xs)
1 0 0 0 0 0 0 0
2 0 0 0 1 0 0 X2
3 0 1 0 1 0 0 %1, x2
4 0 1 1 1 0 *2 xlf x2
5 1 1 / 1 1 *1 x2 X19 x2
Понятие вложенности функций выбора является естественным
обобщением соответствующего понятия для бинарных отношений.
Рассмотрим, как связаны между собой функции выбора, порож-
денные вложенными отношениями.
Утверждение 7. Пусть Ru Rt—отношения на Q такие,
что Тогда
Доказательство. Пусть Хей, х£С*«(Х). Это значит,
что yR^x для всех у£Х. Но тогда’yR^x, поскольку из < /?а
следует 7?а< Rv. В(”силу (2) х£Сл‘(Х). Тем самым доказано, что
CR*{X)^CRi{X) для любого Хей. Утверждение доказано.
Упражнение 18. Проверить, верно ли утверждение Rr<
<Ra=t>CR'<CR>.
Свяжем свойства частичного порядка (20) с относительным
расположением вершин куба' D4. Ближайшей к С сверху {снизу)
наз овем^ функцию выбора С (С) такую, что С<С (С<С) и не
существует C*(CJ такой, что С<С*<С (С_<С«<С).
в примере 3 для функции £/(i = 2, 3, 4) ближайшей сверху
является С/+х, а ближайшей снизу С'-1. Заметим, что, как пра-
вило, бывает несколько ближайших как сверху, так и снизу
функций к функции выбора С.
Упражнение 19. Какие функции являются ближайшими
сверху к функции С8 из примера 3?
Упражнение 20. Найти функцию выбора, если известно,
что она является единственной ближайшей сверху к функции С.
Пусть CiKCgK ... <Cft—цепочка строго вложенных функ-
ций выбора. Цепочка называется максимальной, если не сущест-
вует другой цепочки, в которую она входит как часть. Цепочка
СХ<С3<С4 из примера 3 не является максимальной, так как
она входит в цепочку Сх < С2 < С3 < С4 < С3.
Упражнение 21. Проверить, является ли последняя це-
почка максимальной.
§ 2.’ЛОГИЧЕСКИЕ ФОРМЫ ФУНКЦИЙ ВЫБОРА
45
Упражнение 22. Доказать, что в любой максимальной
цепочке Сложенных функций выбора любые две соседние функ-
ции являются ближайшими друг к другу.
Сужение Частичного порядка (20) на множество функций вы-
бора, образующих максимальную цепочку, является, очевидно,
линейным порядком.
Теорема 1. Любому пути по кубу Di из вершины <0, ...,0>
в вершину <1, ..., 1> минимальной длины взаимно однозначно
соответствует максимальная цепочка вложенных функций выбора.
Б лижайшим функциям Сг и С ^соответствуют ЛФ В (Cj) и ЛФВ (С2),
у которых только для одного г'€{1...N} СДНФ функций
и ft* отличаются одной элементарной конъюнкцией.
Доказательство. На любом пути минимальной длины из
<0, ..., 0> в <1, .... 1> координаты последующей вершины по-
лучаются из предыдущей заменой ровно одного нуля на единицу.
Это значит, что две соседние вершины имеют вид
X® = <Х1, • • •' J, 0, Xr+i, • • .,
X1 = • • •, 1, Xr+i, .. .,
Пусть г—-номер пары <t*, Р,‘>. .Рассмотрим функции выбора
С*" и Сх'. Из|(19) следует, что
для всех. i Ф i* ft = ft;
щиП=с и
при / = »• и/ = /• (₽/’)= 1.1
Это’ значит, что функции С^Ти Сх* являются ближайшими друг
к другу; таким образом, цепочка функций выбора, соответствую-
щая рассматриваемому пути, является максимальной. Аналогич-
ные рассуждения показывают, что максимальной цепочке соот-
ветствует минимальный путь. Вторая часть теоремы следует из
того, что СДНФ функций, отличающихся лишь на одном наборе
значений переменных, отличаются одной элементарной конъюнк-
цией, соответствующей этому набору.
Путь, рассмотренный в примере 3, является путем минималь-
ной длины, а цепочка функций С1—Св—максимальной.
Упражнен ие 23. Являются ли функции выбора из упр. 16
нормальными?
Упражнение 24. Укажите максимальную цепочку, состоя-
щую из нормальных функций выбора, при N— 2 (воспользовать-
ся табл. 1).
Упражнение 25. Существуют ли максимальные цепочки,
состоящие только из нормальных функций выбора, при N > 2?
Упражнение 26. Существуют ли максимальные цепочки,
в которых все функции, кроме первой и последней, не являются
нормальными?
Упражнение 27. Чему равна длина максимальной цепочки?
46
ГЛ. 2. ФУНКЦИИ ВЫБОРА
Доказанная теорема и утверждение 6 устанавливают связь
между вершинами единичного куба, функциями выбора и их ло-
гическими формами. Таким образом, установлена структура на
множестве всех функций выбора на Q, которую можно исследовать
методами булевой алгебры. Представления функций выбора их
логическими формами создает единую основу для исследования
всех свойств функций выбора, их классификации и декомпозиции
на более простые.
§ 3. Операции над функциями выбора
Введем следующие операции. Объединением функций выбора
С\ и С2 называется функция С, определяемая формулой
[C(X)=Ct(X)uCs(X); (21)
пересечением функций выбора Сг и С8 называется функция С,
определяемая формулой
С(Х)=Сх(Х)пСа(Х); (22)
дополнением функции Сг называется функция Сн определяемая
формулой
С1(Х) = Х\С1(Х). (23)
У пражнение 28. Проверьте, что функции, определяемые
формулами (21)—(23), являются функциями выбора.
Упражнение 29. Найти функцию С2иС4 по данным при-
мера 3. Какая вершина куба О4 ей соответствует?
Установим соответствие между введенными операциями и опе-
рациями над ЛФВ.
Теорема 2. Пусть
a) С = СхиС2; б) С = СхпСа; в) С = СХ.
Тогда для любого i=l,N
а) ff=;ff*v/F2; б) в)
Доказательство. Пусть Хей, xt,^C1(X)\jC2(X).
В силу (14)
(Р, (X) A f Ч‘ (р (X))) v (Р,- (X) A fr (Р (X))) = 1. (24)
После преобразований имеем
Р,- (X) А (tf 1 (Р (X)) V f с2 (Р (X))) = 1. (25)
С учетом условия а) получим
хг.бС(Х)=Ф₽,.(Х)/? = 1.
§3. ОПЕРАЦИИ НАД ФУНКЦИЯМИ ВЫБОРА
47
Пусть теперь Р/ (X)f^ (Р(Х)) = 1. Из (24) следует, что по край-
ней мере одно из слагаемых в (24) равно 1. Тогда в силу (14)
xt С Cr (X) и Сг (Х) = С(Х). Таким образом, PJ7 = 1 =фх(. g С(Х), и
условие а) доказано.
Условия б) и в) доказываются аналогично.
Упражнение 30. Доказать условия б) и в) теоремы 2.
Произведением функций выбора Сг и Сг называется функция
выбора С, определяемая равенством
С(Х) = С2(С1(Х)).
Содержательный смысл этой операции состоит в следующем. Сна-
чала осуществляют выбор в соответствии с функцией выбора
а затем из Сг (X) осуществляют выбор в соответствии с функцией
С2. Такие ситуации бывают, например, когда первоначальный
выбор осуществляет экспертная комиссия, а окончательный выбор
из отобранных комиссией проектов осуществляет ЛПР.
Упражнение 31. Верна ли формула С!С2 = С2С1?
Упражнение 32. Найти произведение функций выбора из
примеров 1 и 2 и логическую форму полученной функции.
Упражнение 33. Будет ли нормальной функцией произве-
дение двух нормальных функций выбора?
Связь между ЛФВ произведения и ЛФВ сомножителей слож-
нее, чем при введенных ранее операциях.
Утверждение 8. Пусть^С ==€£2. Тогда
frCt=fr р/+7г.. •, Mfr ^fr (р2, •••
• • , Р/-1,1, Р/+1, IUS • , ₽,-Д (Pi/• • •, Р/-2,1, Р,-+1,’ • , РД
/-* П ЧТЯ uiniiiwii А. ик.4*
Pi + i/h-I (Pi, •••» Pi-1» 1, P/ + 2, •••> РдО» •••
.... РлЛ*'(Рь •••, Pz-i, 1.1Р/+1. ..'.Раг-О). (26)
Доказательство. Пусть Р(Х)=,<рх(Х),| ..., Рдг(Х)>.
Рассмптпим множество Y = Ci(X). Ясно, что
PXn=<PJf'(P(X), .... РлЖР(Х)))>.
Построим ЛФВ функции выбора СХС2, подставив в (14) вместо
р(Х) выражение 0(У) = Р(С!(Х)). Получим
Xi е с (X) р£?< (р (X)) fъ (PJf ЧР (X)), ...
• Р;ОгС2/(Р(Х)), Р,.+1^Т(Р(Х))..Paz^KP (X))),
откуда и следует (26). Утверждение доказано.
Установим взаимосвязь между свойствами функций и резуль-
татов операций над ними.
Утверждение 9. Пусть Сг и С2—нормальные функции
выбора. Тогда CjClCa—также нормальная функция выбора.
48
ГЛ. 2. ФУНКЦИИ ВЫБОРА
Доказательство. Пусть С1 — Ск', С2 — Ск*. Докажем, что
Ci ПСг==Ск,ия'. Пусть XsQ, х £ С\ (X) Г) С2 (X). -Тогда в силу
(2) для всех у^Х выполнено.
yRi_x, yR2x (27)
или, что то же самое, у (2^ п 2?а) х. Последнее эквивалентно
(в силу правил де Моргана) условию
#(2?iU Ra)'x, (28)
откуда С. (X) Г| С2 (X) = (X).
Докажем обратное включение. Пусть х£ CRtUR2 (X). Тогда для
всех у(-Х выполнено (28), из которого следует (27), т. е.
х С С( (X) П С2 (X). Утверждение доказано.
Упражнение 34. Верны ли утверждения, аналогичные
приведенному, для объединения и дополнения функций выбора?
У пражнение 35. Найти пересечение и объединение функ-
ций выбора из примеров 1 и 2.
Упражнение 36. Найти функцию выбора, дополнительную,
к функции из упр. 13. Будет ли она нормальной?
§ 4. Классы функций выбора
Функции выбора удобно классифицировать по тем условиям,
которые обычно используются при их изучении. Приведем неко-
торые из них. Одновременно с введением классов будем давать
их характеристику в терминах логических форм.
Условие наследования (Н):
если X'^s X то С(Х')эС(Х)пХ'. (29)
Условие независимости от отвергнутых альтернатив (О):
если С(Х)>Х'= X, то С(Х')==С(Х). (30)
Условие согласия (С):
П C(Xz)sC(uXz). (31)
Условие /7яо/шпа—независимость выбора от пути (КС):
- С(Х1иХ2) = С(С(Х1)иС(Х2)). (32)
Функции выбора, удовлетворяющие условию Плотта, называются
квазис умматорными.
Условие сумматорности (СМ):
С(Х1иХа) = С(Х1)иС(Х2). (33)
Условие мультипликаторности (МП):
С(Х1пХ2) = С(Х1)лС(Ха). (34)
§4. КЛАССЫ ФУНКЦИЙ ВЫБОРА
49
Условие монотонности (М):
Х^'Х^> С (Хх) <= С.(Х2). (35)
Геометрическая интерпретация каждого 'из условий дана на
рис. 2—8.
Рис. 2. t Рис. 3. Рис. 4.
РисЛб. Рис. 6.
Рис. 7. Рис. 8.
Смысл условия (Н) состоит в следующем. Если рассмотреть
выбор из произвольного множества и выбор из некоторого его
подмножества, то все альтернативы, которые были выбраны из
исходного множества и вошли в рассматриваемое подмножество,
50
ГЛ. 2. ФУНКЦИИ ВЫБОРА
будут выбраны также из этого подмножества. Например, если
проводится международный конкурс проектов, то условие (Н)
означает, что если победителем стал проект из Болгарии, то он
должен быть и победителем болгарского конкурса.
Смысл условия (О) состоит в том, что если рассмотреть произ-
вольное подмножество X', содержащее все альтернативы, вы-
бранные из X, то выбор из X' будет совпадать с выбором из
исходного подмножества; в частности, С(С(Х)) = С(Х). Если про-
веден конкурс, в котором проект х не включен в число лучших,
то в конкурсе, в котором участвуют все те же проекты, что и в
первом конкурсе, за исключением х, состав победителей останет-
ся прежним.
Смысл условия согласия состоит в том, что альтернативы,
которые были выбраны из каждого множества Xz, будут также
выбраны из их объединения.
Условие Плотта требует, чтобы выбор из объединения мно-
жеств совпадал с выбором из объединения выборов, сделанных
из каждого множества в отдельности. Если проводится между-
народный конкурс, то это значит, что можно сначала отобрать
победителей национальных конкурсов, а потом проводить конкурс
среди них. —1
Условие^сумматорности предполагает, что выбор из объедине-
ния множеств равен объединению выборов из каждого множества
в отдельности. Например, на районной доске почета представле-
ны люди, выбранные в коллективах отдельных^ организаций
района.
Смысл условий (МП) и (М) очевиден; в частности, (М) озна-
чает, что выбор из более широкого множества будет шире.
Упражнение 37. Какими из перечисленных свойств обла-
дают функции выбора из примеров 2, 3 и из табл. 1?
Упражнение 38. Есть ли в табл. 1 функции выбора, не
удовлетворяющие ни одному из перечисленных свойств?
Каждое из сформулированных условий определяет некоторый
класс функций выбора, удовлетворяющих данному условию.
Сохраним за классами обозначения соответствующих условий.
Запись С£Н будет означать, что рассматривается функция,
удовлетворяющая условию наследования.
Рассмотрим теперь, каким условиям должна удовлетворять
ЛФВ(С) функции выбора С, наделенной перечисленными свойст-
вами.
Теорема 3. Функция выбора С является:
а) наследственной',
б) независимой от отвергнутых альтернатив',
в) удовлетворяющей условию согласия',
г) квазисумматорной', д) сумматорной',
е) мулътипликаторной', ж) монотонной
тогда и только тогда, когда
4 КЛАССЫ ФУНКЦИЙ ВЫБОРА
51
а) РЧ<Р2 =» ft (Р1) A ft (Р2) (i -1 Л) *);
бШ/(Р2)СР'<Р? (^l.^PtMH^MP1) (»' = 1Л);,
в) АКР1) л fi (Р2) A h (Р1 VJP2) (I = 1 Л);
г) (PflVPDMP1 VP2) = (P1A(P1) VjMP^/JPiACP^V _
V Р!А (Р2).PVa (Р1) V РШ(Р2)) G=1 Л);
д) ft (Р) о или ft (Р) I (i = 1 ,N^_
e) fi (P1 A P2) - fi (P1) A h (P2) (i =£Л);
Ж) РСР2=?>Л(Р1)<Л(Р2) (1 = 1Л).
Доказательство, а) Из определения наследования полу-
чаем ___
Рх С Р2 PV/ (Р1) А Р1А (Р2) Р) (i=Гл). (36)
При Р) = 1 в силу р1 Р2 выполнено р? = 1, поэтомуАз (36) сле-
дует а), поскольку ff(P) от Pi не зависит.
в)Шерепишем условие согласия
/А \ / k \ f / А \ / k & \
(Л РЯЛ^ЛЛСР1))^ Х1РЯЛЛ V РИ (/ = ТЛ), (37)
которое должно'выполняться для произвольных наборов Р1, ...
..., р*. Очевидно, что (37) эквивалентно условию (в силу неза-
висимости fi от р;)
A WP'Xf/v Р') (» = ТЛ), (38)
S=1 уз=1 у
которое в свою очередь эквивалентно в).
д) Перепишем условие сумматорности С^иХ^
=С (Xi) U С (Х2); получим
(К V pt) fl (PIV Р2) = PVz (Р1) V P-A (Р2) (i = r,N). (39)
Положим р; = 1, P/ = 0 ((#=/), p2 = 0. Тогда из'(39) получаем
A(P2) = A(°) Для любого p2 = <Pt, .... P2-i, 0, Pt+i, • • •," Рд?>,
откуда и следует д).
Доказательство остальных формул непосредственно получится
при записи соответствующих условий с помощью булевых функ-
ций из ЛФВ. Теорема доказана.
Хотя выделенные классы функций выбора описываются наи-
более часто используемыми условиями, они не исчерпывают всего
их многообразия.
Приведем пример выбора, который может быть описан функцией
выбора, не удовлетворяющей некоторым из приведенных условий.
*) Здесь и далее запись 'fPsCp2, где Р—векторы, понимается "покомпо-
нентно.
52
ГЛ. 2. ФУНКЦИИ ВЫБОРА
Пример 4. Турнирное правило. Пусть происходит турнир
(каждый участник один раз встречается с каждым) и в каждой
партии возможны три исхода (выигрыш, победа, ничья). Изобра-
зим всех участников точками (вершинами графа) и проведем
дугу из х в у, если х победил у. На множестве Q участников
тем самым определено бинарное отношение /?; однако в турнир-
ной практике победители определяются не на основе CR (Q), как
можно было бы ожидать, а по следующему правилу: для каж-
дой вершины определяется разность между числом выходящих
из нее и входящих в нее дуг и победителем (или победителя-
ми) объявляются те участники, у которых эта величина макси-
мальна. Ц
Упражнение 39. Доказать, что это правило совпадает с
общепринятым правилом определения победителя по сумме очков
(за проигрыш—0, за ничью—1, за победу—2).
Если X в нашем примере—любое подмножество участников, то
в соответствии со сказанным С(Х) = {х£Х| такие, у которых
сумма очков в играх с остальными участниками у£Х макси-
мальна}.
Такое правило используется, в частности, при подведении
итогов чемпионатов по футболу. В 1976 г. проводились два
чемпионата СССР по футболу в высшей лиге (весной и осенью);
в каждом происходил турнир в один круг. В табл. 7 приведены
результаты осеннего первенства. Если в качестве множества Xt рас-
смотреть только динамовские команды, то С (Хх) = {Динамо Тб.};
если взять Xj = Q\{ТорпедоU Днепр}, то С(Х2) = {Динамо К.}.
Заметим, что C(X2)sXx и С(Х1)^С(Х2). Тем самым для ука-
занного (бывшего в действительности) выбора нарушено условие
(О). Ясно также, что С(Хх) С(Х2) П Хх. Тем самым нарушено
и условие (Н).4*
Упражнение 40. Какие еще из сформулированных условий
нарушаются для описанной в примере 4 конкретной функции
выбора?
Упражнение 41. Какие из условий выполняются для лю-
бой турнирной функции выбора, т. е. функции, определяемой
турнирным правилом?
Для выделенного ранее в § 1 класса нормальных функций
выбора HP справедливо
Утверждение 10. Функция С на& — {хг, ..., xN} нормаль-
на тогда и только тогда, когда существует разбиение множества
7 = {1, ..., N} на подмножества I, 70, 7Х (любое из которых
может быть пустым) такие, что
1. (Vt € 7) [37z <= J, Jt Ф 0 | Д = A jTj.
2.
3. (Vi€!]•
54. КЛАССЫ ФУНКЦИЙ ВЫБОРА
53
Чемпионат СССР 1976 г. (осень)
54
ГЛ. 2. ФУНКЦИИ ВЫБОРА
Доказательство. Необходимость. Пусть (?€НР,
т. е. C = CR для некоторого Ясно, что для любого
x(-£Q возможна только одна из следующих трех ситуаций:
1. (Э/х, ..., ..., 2V}) (s=l,/), yRx
при y${xit, ..., Х/Д].
2. x(RXi.
3”R+(Xl) = 0.
Образуем множество / из индексов, относящихся к 1-й ситуа-
ции, множество 10—ко 2-й, множество Ц—к 3-й. Очевидно, что
е^-тих) /о’ 71 образуют требуемое разби-
—7—ение. Необходимость доказана.
Достаточность. Определим
/ следующим образом: XjRxt
[X \ для любого I и любого
I * \ xiRxi для ^любого i£/0. Очевидно,
I I что C = CR. Достаточность доказана.
\ ---7 С помощью утверждения 10 легко
/ получить ответы к упр. 8, 10, ^14,
\ х} / 23, 25, 33, 34, а также дать про-
j/ стое доказательство утверждения 9.
-------Рассмотрим ряд свойств функций
Рис- 9.-выбора, которые являются естествен-
ным обобщением рассмотренных^ ра-
нее свойств отношений. Функцию выбора назовем:
рефлексивной, если С(х) = 0;
антирефлексивной, если С(х) = х;
полной, если С(Х)#=0 для всех’’Х#= 0;
транзитивной, если
^С(Х1иХ2) = С(Х1)^0,
[ С (Х2 U хз) = С (Х2) =£ 0 => С (X. и хз) = С (Хх);
ацикличной, если
C(XftuXft+1) = C(XA)^0 (6="1, п-1)=^>Хх=#Х„.
Понятия рефлексивности и антирефлексивности функций выбора
близки к аналогичным понятиям для бинарных отношений. Не-
сколько более сложная аналогия между понятиями транзитив-
ности и ацикличности функций выбора и отношений. Транзитив-
ность можно интерпретировать так: если выбор из объединения
множеств Xj и Х2 содержится в Хх, а из Х2 и Х3 содержится
в Х2, то выбор из объединения множеств 'Хх и Х3 должен со-
держаться в Хх (рис. 9).
Проиллюстрируем свойства транзитивности и ацикличности
примером. Проводилась олимпиада в трех классах, и лучшими
среди учеников классов А и Б оказались два ученика из клас-
са А, лучшими среди учеников классов Б и В—три ученика^из
§4. КЛАССЫ ФУНКЦИЙ ВЫБОРА
55
класса Б. Ясно, что лучшими среди учеников А и В являются
упомянутые ученики из класса А; при этом они же будут побе-
дителями среди всех трех классов. Соответствующая функция
выбора транзитивна.
Пусть теперь лучшими среди учеников 'классов А и Б при-
знаны два ученика из класса А. Пусть затем взяли работы уче-
ников одного из классов А или В (обозначим этот класс через X).
Тогда, если лучшими среди учеников Б и X стали три ученика
из класса Бчто ясно, что класс X не является классом А. Соответ-
ствующая функция выбора ациклична.
Переформулируем введенные свойства в терминах свойств логи-
ческих форм выбора.,
| Утверждение 11. Функция визора С является', а) реф-
лексивной, б) антиргфгекшвной, в) полной, г) транзитивной,
д) ацикличной тогда и только тогда, когда
а) /\(0, ..., 0) = 0 (t=TjV)-.
5) /ДО, 0)«1 (f=H, У);
N
в) для всех р выполнено у /, (Р) = 1;
г) (Р1 V Р?) h (Р* V Ра) = ШУ), (У V Р?) Л- (Р2 V Р3) = Р?Л (Р2)
0 =1, Ю,
N N
vP’MPl)=* VP?A(P2)=»1 =5*(Р?УР?)Л-(Р1 vP3)=Pjf,-(P1)
i=i i=i
____ (i = T7W);
д) (p? v р'г ч rt (Pft v pft+t) =-PVz (P4) (i i, у), g
AZ ______
Vp?MPft)^l (Ы, n-l)=^.p^p».
1=1
Упражнение 42. Доказать утверждение 11.
Установим некоторые взаимосвязи между нормальными функ-
циями выбора, обладающими введенными свойствами, и порож-
дающими их бинарными отношениями с аналогичными свойствами.
Утверждение 12. 1. Если отношение R: а) транзитивно,
б) ациклично, то функция CR является: а) транзитивной, б) ацик-
личной.
2. Если R антиргргексизнэ и CR — транзитивная функция
выбора, то отношение R транзитивно.
Доказательство. 1. а) Пусть С? ( X и У) = CR (X) #= 0.
Это значит, что (Ух^С^(Х), /у^У) [v/?y]. Если Со(Уи2) =
= С^(У)^=0, то
(Уу6СЛ(У), Vz(=Z) [у₽г].
В силу транзитивности R это значит, что
(Ух € CR (X), У г е Z) [xRz], т’е. ZCR’(X) = CR (X U Z).
56
ГЛ. 2. ФУНКЦИИ ВЫБОРА
Ясно, что (VxCX\CR(X)) (x<C»(XUZ)]. Пусть z£Z\X и
z^.Cf!(X{jZ). Тогда (Ух£Х) [zRx] и, следовательно, (VyGY)
[z/fy], т. е. z£CK(YuZ). Это значит, что z£CR(Y)^Y, откуда
yRx (VxgX), что противоречит С/?(ХиУ) = Ся(Х). Полученное
противоречие доказывает а).
б) Пусть С(ХкиХй+1) = С(Х*)=/=0 (&=1, п—1) и Хп = Хх.
Это значит, что существуют x-^Xf (i— 1, и) такие, что x{Rxi+i
(i = 1, п— I) и xnRxlt что противоречит ацикличности R.
2. Пусть CR транзитивна, xRy, у Rz. Тогда С(х, у) — х,
С (у, z) — y и, значит, С(х, z) — x, т. е. xRz. Утверждение дока-
зано.
Упражнение 43. Доказать, что всякая сумматорная функ-
ция выбора транзитивна.
Отметим, что теорема 3 и утверждения 10—12 демонстрируют
возможности введенного ранее аппарата логических форм функций
выбора при изучении классов функций выбора в силу связей
между свойствами функций выбора и ‘ соответствующих булевых
функций.^
§ 5. Взаимосвязи'классов функций’выбора]
Установим связи между классами функций выбора, рассмот-
ренными в предыдущем параграфе. При этом нам по ходу рас-
суждений потребуется ввести несколько других классов функций
выбора, которые оказываются комбинациями ранее рассмотренных.
Утверждение 13. Функция выбора нормальна тогда и
только тогда, когда она принадлежит пересечению классов Н и С.
Доказательство. В силу условий а), в) теоремы 3 и
утверждения 10 достаточно доказать, что булева функция
gf(a1( ..., <хг) удовлетворяет одновременно условиям а) и в) тео-
ремы 3 тогда и только тогда, когда она удовлетворяет условию
утверждения 10.
Необходимость. Пусть g удовлетворяет условию в). Тогда
она удовлетворяет (38), что эквивалентно следующему условию
(при g^O):
g(a*) = l (s=l, k)=3>gl V'a*) = l.J (40)
\s=l '
Найдем вид функции g, для чего разложим" ее в СДНФ:
лР ~Р
g(a1( ...,a,)= Va/ ...а/,
pel
Разобьем / = {1, .... 4 на два подмножества:
/- = {/|gr(ai, .... ar)= l=»a, = 0),
/+ = {t | (Ha* = <a’b ..., at-t, 1, az’+l, ..., a,*» [tf(a*) =1]}. ’
S 5. ВЗАИМОСВЯЗИ КЛАССОВ ФУНКЦИЙ ВЫБОРА
57
Для упрощения записи будем считать (без ограничения общно-
сти), что /+ = {1, .... q}. Тогда
£(а) = ф(аъ ...,а)д( Д аД
где d
Ф(ап oQ =
Р=1
Докажем, что ф(а1( т. е. g удовлетворяет усло-
вию 1 (при /~=/=0) или 3 (при /_ = 0) утверждения 10. Пред-
положим противное. Тогда существует [набор . ...а^,
0, ..., 0> такой, что g(сс) = <р (dtj, ..., а~) = 0. Из определения
/+ следует, что для i = l, q существует набор a*(i) такой, что
- ч
g(a*(i))=l и а<(0=1. Ясно, что а— уа*(1) = <1, ..., 1,
0, .... 0>, откуда в силу (40) g(l, ..., 1, 0, 0)=1. Таким
образом, а^а, g(a) = 0, g(a)=l, что противоречит условию а)
теоремы 3; g = 0 удовлетворяет условию 2 утверждения 10. Не-
обходимость доказана.
Достаточность. Пусть g(«i, ..., а,)=Да;г Тогда
S=1
функция g отлична от нуля лишь на наборах, в которых а^ = 0
(s = 1, I). Но дизъюнкция любых двух таких наборов также обла-
дает этим свойством (0\/0=0), поэтому условие в) теоремы 3
выполнено.
Выполнение условия а) очевидно, так как функция /(a) = a(
‘ i аж
монотонно убывает и поэтому g, равная конъюнкции Д a;s, также
S=1
монотонно убывает. При g = 0 или gz==l условия а) и в) также
выполняются. Утверждение доказано.
Функция выбора С на й называется общей скалярной функ-
цией, если существует числовая функция g'. Q-^-E^ такая, что
С (X) = Argmax g (х), (42)
х
и скалярной, если g(x)=£g(tj) при х=£у. Такие функции выбора
порождаются вполне определенными бинарными отношениями.
Утверждение 14. Функция выбора С является общей ска-
лярной функцией выбора тогда и только тогда, когда она порож-
дена сильно транзитивным антирефлексивным бинарным отно-
шением.
Доказательство. Необходимость. Пусть С—общая
скалярная функция. Положим
й, = Argmax g, Q2 = Argmax g, ..., —Argmax g==Argming
£2 Я\Я, k— 1 Я
' Q\ U О-
58
ГЛ. 2, ФУНКЦИИ ВЫБОРА
Ясно, что , Qk образуют разбиение Q. Определим на £2
бинарное отношение R следующим образом: aRb &a£&i, b£&j
и i<j. В силу (42) CR = C. Сильная транзитивность построен-
ного отношения R следует из теоремы 1.1. Необходимость дока-
зана.
Достаточность. Структура сильно транзитивных графов
(и соответствующих отношений) установлена теоремой 1.1. Пусть
йь ..., ЙЛ—разбиение Q. Положим g(x) = k— i, если
Функция выбора CR, очевидно, совпадает с функцией С, по-
строенной по g по формуле (42). Достаточность доказана.
Упражнение 44. Доказать, что для всякой общей ска-
лярной функции выбора С найдутся скалярные функции С1( ..., Ск
такие, что
С= U G. (43)
t=t
Функцию выбора С, являющуюся объединением скалярных,
назовем совокупно экстремалсной. Соответствующий класс обозна-
чим через СЭ. Смысл введенного понятия состоит в следующем. На
Q задано г числовых функций (критериев) gx.gr. Из предъяв-
ляемого множества X сначала отбираются элементы, оптималь-
ные по 1-му критерию (Argmax g^, затем—по 2-му и т. д., после
чего берется объединение полученных выборов.
Установим связь класса СЭ с классами Н и О. Для этого
введем понятия характеристической функции и запретов. Пусть
функция выбора С сумматорна (С С СМ). Положим (см. теоре
му 3, д)) A = {xz|fz==l !(i=l, N)\. Из (14) непосредственно
следует, что для любого Хей имеем С (Х) = X П А. Отсюда при
X = Q получим А = С (й).
Это приводит к следующему понятию. Пусть A s й. Функ-
цию выбора, определяемую формулой
№Х) = ХПА,' (44)
назовем характеристической функцией множества А. Теорема
3, д) утверждает, что всякая сумматорная функция является ха-
рактеристической функцией некоторого Лей. Обратное очевидно.
Пусть Cj—произвольная функция выбора на й, Лей. Рас-
смотрим функцию выбора С, определяемую формулой
С=С^ПС1. (45)
Легко видеть, что
С^С^С^ЛС,. (46)
Смысл формулы (45) состоит в следующем. Сначала делается
выбор Сп а затем в выбраннсм множестве оставляют только эле-
§5. ВЗАИМОСВЯЗИ КЛАССОВ ФУНКЦИЙ ВЫБОРА
59
менты, принадлежащие А, или, что то же самое, из него удаляют
все элементы, принадлежащие В = О\Л.
Функцию входящую в формулу (46), будем называть функ-
цией выбора с запретом, так как в соответствии с (46) запре-
щается выбирать элементы из Сх(Х), входящие в В = £2\Д.
Для любого множества Л функций выбора выделим подмно-
жество Л0'.
. ^=={C€^1(VX = Q, Х#=0) [С(Х)#=0]}.
Утверждение 15. Множество совокупно экстремальных
функций выбора совпадает с (Н П О)® = Н0 Л О0.
Таким образом, всякая функция выбора из пересечения клас-
сов Н и О представима в виде объединения скалярных, если
выбор из любого непустого подмножества непуст.
Другой вид взаимосвязи классов Н и О устанавливает
Утверждение 16. НпО = КС.
Установим связь классов Н, О и С. Функция выбора С на Q
называется паретовской, если существуют числовые функции
gi, • • •» gm такие, что
С(Х) = {х[(-|Эг/€Х, у=£х) [g^yl^g^x) (i = I7mj]}. (47)
Сформулируем без доказательства несколько утверждений от-
носительно паретовских функций выбора.
Утверждение 17. Функция выбора С является паретов-
ской тогда и только тогда, когда она порождается транзитив-
ным антирефлексивным бинарным отношением.
Утверждение 18. Класс П паретовских функций выбора
совпадает с (Н П О П С)а.
Утверждение 19. Для всякой функции С£ Н Л О Л С су-
ществует BsQ такое, что С = С1ЛС^, где С^П, С^—харак-
теристическая функция множества В.
Это утверждение является частным случаем более общего
утверждения 5.3 относительно НПО.
Последние три утверждения устанавливают структуру пересе-
чения НлОлС, которое совпадает с классом нормальных функ-
ций, порожденных транзитивными антирефлексивными отношения-
ми (с учетом запретов).
Обозначим через А дополнение к множеству А функций вы-
бора на одном и том же £2.
Упражнение 45. Доказать, что все классы^
’ НлОлС, НлОлС, НЛОЛС..........НЛОЛС
непусты. «
Упражнение 46. Доказать строгое включение |
СМаНпОлС.
60
ГЛ. 2. ФУНКЦИИ ВЫБОРА
§ 6. Динамические функции выбора
Во всех предыдущих рассуждениях рассматривались функции
выбора такие, в которых выбор из предъявляемого подмножества
определялся только им самим и свойствами функции. С другой
стороны, возможны ситуации, когда на выбор С (X) оказывает
влияние также ранее сделанный выбор (выборы).
Пусть лицо W покупает продукты только в одном магазине
(поблизости нет других, а нести тяжести N не может). Пусть
й—множество всех наименований продуктов, которые могут по-
ступить в этот магазин; X—множество тех продуктов, которые
имеются в магазине в данный день. В рассматриваемой ситуации
ясно, что выбор продуктов зависит не только от имеющегося
множества X и от потребностей лица N, но и от того, какие
продукты имеются дома, т. е. уже были выбраны ранее. Ясно,
что эта ситуация не описывается ранее введенной конструкцией
функции выбора.
Будем считать, что подмножества X множества й предъяв-
ляются для выбора последовательно: Хп Х2, ...,ХП, ... Иными
словами, если i > /, то множество X,- было предъявлено после Х7.
В качестве основного предположения примем следующее. Выбор Y
зависит от предъявляемого множества X и уже осуществленного
выбора из одного предшествующего множества:
У,=С(Х,., У,..,) (*=1,2,...). (48)
В рассматриваемой модели результатом выбора является вся
последовательность (48) с заданным начальным состоянием Уо,
а процесс выбора задается совокупностью всех таких последо-
вательностей предъявлений X,-.
Адекватной математической моделью для описания процессов
с отдельными реализациями выборов типа (48) является теория
конечных автоматов. Напомним, что конечный автомат задается
двумя множествами: множеством S состояний и множеством О
входов и функцией переходов F: OxS->-S. Иначе говоря, если
на автомат, находящийся в состоянии s£S, подать входной сиг-
нал О, то он перейдет в состояние s' = F (о, s).
Пусть задано начальное состояние segS, и пусть [входные
сигналы поступают в моменты времени 1, 2, ... Тогда состояния
автомата в последовательные моменты времени выражаются [фор-
мулой
5/ = ^(о,-, S/-0 (i=l,2, ...). (49)
Легко видеть, что формулы (48) и (49) аналогичны? Можно счи-
тать, что выбор порождает конечный автомат.
Будем говорить, что кснекньм ае тема тем, порсокденньм вы-
бором, называется автомат А, у которого множество состояний S
есть множество всех возможных выборов из всех подмножеств й,
§6. ДИНАМИЧЕСКИЕ ФУНКЦИИ ВЫБОРА
61
пует; если предъявляется
а множество входов—множество всех подмножеств Q. Функция
переходов F определяется выбором из X при условии, что пре-
дыдущим выбором было некоторое Y = С (Z), Z = Q.
Пусть Q —xt} и функция выбора описывается следующим
образом. Если предъявляется и предыдущий выбор не содер-
жал хх, то выбирается хХ) в противном случае выбор пуст; если
предъявляется х2 и предыдущий выбор содержал х2, то выби-
рается хг, в противном случае выбор
{xlt х2\ и предыдущий выбор не был
пуст, то выбирается х2, в противном
случае выбирается хх.
Построим соответствующий ко-
нечный автомат А; у него
S~{0, {^i}f {я2}},
О = {0, {•*•!»
Функцию переходов зададим табли-
цей переходов, общепринятой в тео-
рии автоматов (табл. 8). В ней стро-
ки соответствуют состояниям, столб- Рис. 10.
цы—входам; на пересечении стро-
ки и столбца находится состояние, в которое состояние, соответст-
вующее строке, перешло под воздействием входа, соответствующего
столбцу. Занумеруем состояния римскими цифрами, а входы—
арабскими, в том порядке, в котором они входят в табл. 8.
Таблица 8
О 0 {Х,} {ха {•»!. *«)
0 0 К} 0 {^}
{*1} 0 0 0
{*2} 0 {*1} {*2} {*1}
Таким образом, описанный процесс выбора порождает конеч-
ный автомат, диаграмма переходов которого показана на рис. 10.
В данном случае все состояния автомата возвратны.
Упражнение 47. Привести пример такого выбора, что
порожденный им автомат содержит невозвратные состояния.
Возникает естественный вопрос — какие автоматы могут быть
порождены выборами, зависящими от предыстории, т. е. каковы
«логические возможности» выбора?
Теорема 4. Пусть В—произвольный конечный автомат.
Существует выбор такой, что В является подавтоматом порож-
денного этим выбором автомата.
62
ГЛ. 3. БИНАРНЫЕ ОТНОШЕНИЯ НА Ет
Доказательство. Пусть S—множество состояний автома-
та В; О—множество его входов; F—функция переходов. Положим
Q = SllO и определим выбор следующим образом. Если было
выбрано sgS и предъявляется множество SU{о}, то из него
выбирается s' = F(o, s). Во всех остальных случаях выбор поло-
жим пустым. Легко видеть, что В—подавтомат автомата, порож-
денного указанным выбором. Теорема доказана.
Упражнение 48. Останется ли верной теорема 4, если
потребовать, чтобы В был автоматом, порожденным выбором?
Естественным обобщением рассматриваемой ситуации является
учет не только одного предыдущего, но и нескольких предыду-
щих выборов.
Теорема 4 показывает, что с формальной точки зрения длина
учитываемой предыстории не имеет значения при оценке логиче-
ских возможностей порождаемого выбором конечного автомата.
Таким образом, для описания выбора с учетом «последействия»
возможно использовать конечно-автоматную модель выбора и
ограничиться учетом только одного шага предыстории.
Литература. [2, 5, 34, 70, 122. 123].
Г л а в а 3
БИНАРНЫЕ ОТНОШЕНИЯ НА Ет
Решение практической задачи выбора может оказаться затруд-
нительным при задании альтернатив в виде элементов абстракт-
ного множества; оно может потребовать их более подробного
описания. С этой целью каждую альтернативу представляют
описанием в критериальном пространстве. Для формального
описания критериального пространства используют евклидово
пространство Ет. Это требует некоторой модификации общей
конструкции бинарного отношения с учетом свойств Ет. Итак,
бинарное отношение на Ет есть отношение с областью задания Ет.
Далее для краткости будем называть его просто отношением.
Принято среди всех отношений выделять отношения, инва-
риантные относительно переноса, или просто инвариантные. Отно-
шением, инвариантным относительно переноса, называется отно-
шение такое, что верхнее сечение в любой точке может быть полу-
чено параллельным переносом верхнего сечения в] любой другой
точке, т. е. для^любых х1, х2£Ет выполняется
/?+;(х1)=/?+(х2)+х*—Xs. (1)
(В случае, если рассматривается^отношение ;/? не на всем Ет,
а на будем употреблять запись Rq (х) и Rq (х).)
Далее в этой главе и главе 4 будут рассматриваться именно
такие отношения.
§J. ОБЩИЕ СВОЙСТВА ИНВАРИАНТНЫХ 'ОТНОШЕНИЙ
63
§ 1. Общие свойствами вариантных отношений
У т в е’р ж д е н nje 1 .^Отношение R инвариантно тогда и толь-
ко тогда, когда
| [х1—х2 = х3—х4]]=» [х1 Rx^&'x3 7?х4]. (2)
Дока’з’а.тел'ь“ст|во. ь1. |Пусть -х1—х2 = х3—х4. ВМИЛУ1(О
Я-^(х1)—х2 = R~ (х3)—х4. (3)
Если xlRx3, то х2£ /?~£(х1) и
ОеЯМхЧ-х2. £(4)
Из |(3) и (4) получаем, что 0£R~(x3)—х4, или х4^/?“(х3) и
x3Rx*. Наоборот, если xlRx3, то 0^R~(x1)—х2=7?~(х3)—х4 и,
значит, х32?х4; формула (2) доказана.
2. Пусть х1, хг£Ет, х3^7?~1(х1). Положим
х4 = х2 + (х3—х1). (5)
Из (2) 11^(4) получаем, что х4^ 7?" (х2), но х3 = х44-х1—х2, или
х3 € (х2) + х4—х2, а поскольку х3—произвольная точка из
R~ (х1), то это доказывает включение R~ (х1) sj/?- (х2)4-х1—х2.
Обратное включение доказывается аналогично.
У^п р аж не н и"еА1. Доказать, что условие
/?-(х1) = 2?Д(х2)4-х1—х2 (6)
эквивалентно (1).
Класс отношений, инвариантных относительно переноса, обозна-
чим через 3; для указания на размерность пространства, на ко-
тором заданы отношения из 3, будем писать 3т, где это необ-
ходимо.
Утверждение 2. Пусть R^3. Тогда
1. R- (0) = - R+ (0).
2. [/? транзитивно] 4Э [a, b£R~ (0)М> (а+b) С R~ (0)]
k
• А»е₽-(0)=>2«/'^+(0)
i= 1
3. [7? ациклично] & at,
Доказательств о. |1. Пусть хС R~ (0); это значит, что QRx.
Формула (2) эквивалентна соотношение
\xRy&(x + z)R (y + z),
(7)
которое также можно принять за определение инвариантности.
Положив ,z = — х, из ORx получаем —xRQ, т. е. —х£7?+(0).
Тем самым доказано включение R~ (0) R+ (0). Обратное вклю-
чение доказывается аналогично.
2. Пусть a, b£R~(O). Тогда QRa, ORb. Из ORa в силу (7)
получаем bR(a-]-b). Так как ORb, то в силу транзитивности по-
64
ГЛ 3. БИНАРНЫЕ ОТНОШЕНИЯ *НА Ет
лучим 0/? (а 4-6), т. е. (а4-6) € (0). Наоборот, пусть aRb и bRc.
Тогда в силу (7) имеем 0R(b—a), OR (с-—6), откуда по условию 2
получаем 07? [(6—а) 4- (с—6)], т. е. 0R (с—а) или aRc. Тем са-
мым доказана транзитивность R.
3. Из а,Е7?_(0) получаем
0Roif ty7?(ty+ty), (ty+ty)R(ty4-ty4-ty), ...
(k-i \ / k \
2 ty ) # ( S «/ )•
r=i / V = i J
/ k \___ к
Ацикличность означает, что ( StyJ R0, т. е. S а/ $ Я+ (0)- Пусть
ty, • •.» ак£Ет, diRa^i (7=1, k—1). Отсюда имеем 07?(а1+,—ty),
Л-1
т.е.(а/+1—az)€ (0). Тогда по условию 3 получим 2 (а1+1—ty) =
— (ак—ty)^7?+(0), т. е. (аь—ty)/?0, и в силу (7) имеем ty7?ty.
Это значит, что R ациклично. Утверждение 2 доказано.
В силу инвариантности отношений R&3 для их задания до-
статочно описать верхнее или нижнее сечение в начале координат.
Утверждение 3.
7?Г (0) £=А" 1(0) < ^2. (8)
Доказательство. Пусть aR^b', это означает, чтв 0Rx (6—а),
или (6—а) £ 7?г (0). По условию 7?г (0) е R2 (0) получаем, что
(Ь—й)£7?Г(0), или 0Т?2(6—a), aR2b. Утверждение доказано.
Утверждение 4. Для любого .инвариантного отношения
имеет место
R+(x) = 2x—R~ (х). (9)
Упражн.ени!е |2. Доказать утверждение 4.
Упражнение >3. Верно ли для QczE, что
7?+ (х) = 2г-/?^(х)?
Конусом называется множество К точек из Ет, обладающее
свойствами:.
а) если х£К и a > 0, то ах£К’,
б) если х£К и у£.К, то (х4-!/)€#•
Конус называется телесным, если его внутренность не пуста,
т. е. есть точки, которые содержатся в нем вместе с некоторой
окрестностью. Говорят, что отношение RK порождено конусом К,
если оно задается формулой
xRKy&(x-y)eK\{0}. (10)
Утверждение 5. Отношение RK инвариантно для любого
конуса К.
§ 1. ОБЩИЕ СВОЙСТВА ИНВАРИАНТНЫХ ОТНОШЕНИЙ
65
Упражнение 4. Доказать утверждение 5.J
Упражнение 5. Доказать, что
Як (0) = К\{0},*Я^0) = -К\{0}. (И)
Приведем примеры инвариантных отношений.
Отношение Парето (Р):
(Ух, у 6Q) [хРу] ФФ {(V/= \jn)[xj > уj] и (3/о £ {1,..., ш}) [я, > у,-]}.
На рис. 1 изображены верхнее и нижнее сечения отношения Р
в точке х* е Ег:
р- (х*) = {х£Ет\х*Рх}, Р+ (х*) = {х£.Ет\хРх*}.
Упражнение 6. Доказать, что для любых точек х°, х* £ Еп
р~ (х°) = Р- (х*)4-Х°—X*, Р+ (х°) = Р+ (х*) + х° — X*,
т. е. что отношение Р инвариантно.
Рис. 1. Рис. 2.
Р'(т')
X’®
*х3
Множеством Парето на йс £я называется множество
£у={хей|(¥Уей)[1/р^]}.
Из определения множества следует, что йр содержит те и только
те элементы х*, для которых Р+ (х*) = 0.
Приведем пример множества Парето. Пусть
й = {х1, ..., х6};
х}==2, х? = 3, X® = 1, Xj=l, х? = 4, х’ = 5;
х| = 5, х1 = 3, xf = 4, xf = 3, Хг = 3, х| = 4.
Множества й и йр изображены на рис. 2. Легко видеть, что
Ро(х1) = 0, Ра (х2) = {х\ х6}, Р5(х3) = {х\ х6},
Рй(х‘) = {х1, х2, х3, Xs, Xе}, Pq(x5) = x6, Pq(x6)=0.
Альтернативы, входящие в й₽, обладают следующим свойством.
Если рассмотреть любую координату х} альтернативы х' ^й₽, то
3 И. М. Макаров и др.
66
ГЛ. 3. БИНАРНЫЕ ОТНОШЕНИЯ НА Ет
среди оставшихся альтернатив в Q₽ не найдется хк, для которой
было бы выполнено
х* > xj,
• • • > */-1, Xk+i, . . •, Хт> Р <Cxj, . . ., Xj-i, xj_lt . . ., Х^У
(здесь Р—отношение с областью задания Em_lt являющейся про-
екцией Ет вдоль /-й оси).
Бинарное отношение R на Ет называется рациональным, если
P<R.
Пусть на осях координат задан линейный порядок такой, что
> k2 > ... > km, где kt—номер координаты на i-м месте порядка.
Отношение лексикографии (Еу
(Vx, у € Е J [xLy\ о [xftt > z/J, или
[ч == У к, и xki > yki}, или ... > [х ф у].
Множество Q£ состоит из единственного элемента.
Упражнение 7. Показать, что для любых точек х°, х* С Ет
L- (x?) — L~ (х*)+х°—х*, L+ (xf>) = L+ (х*)+х°—х*.
т. е. что отношение L инвариантно.
Рис. 4.
Верхнее и нижнее сечения отношения L в точке x*g£2 изоб-
ражены на рис. 3. Здесь — первая координата, k2—вторая. На
рис. 4 показаны сечения для отношения L в случае, если в ка-
честве используется вторая координата, а в качестве k2—первая.
Упражнение 8. Доказать, что (Vx£Em) [Р“ (х) с L~ (х)].
Из упр. 8 и утверждения 3 следует, что отношение L ра-
ционально.
Отношения Р и L порождены конусами; конус К, порождаю-
щий отношение Р = Р&, совпадает с неотрицательным ортантом
§2. УСЛОВИЯ ОТДЕЛИМОСТИ
67
Ет, обозначаемым
Ет={х е £и’| (Vi=Т7^) [х,- >;о]}7
У прежней ие 9. Каким кону-
сом порождено отношение L?
Не все инвариантные отношения
порождены конусами, что иллюстри-
руется следующим примером. Рас-
смотрим отношение R £ 32, задавае-
мое верхним сечением R + (0), показан-
ным на рис. 5. Пусть a£R+(P),
b£R+(O). Легко видеть, что имеет место (a+b) СR+ (0), т. е.
/^транзитивно, но R+ (0) не является конусом.
§ 2а Условия отделимости
При решении задач выбора часто возникает следующая ситуа-
ция: в пространстве Ет задано бинарное отношение R£3', среди
элементов Qc:Em необходимо найти недоминируемые по бинарному
отношению R (точнее, по отношению, являющемуся сужением R
на Q). Для решения этой задачи способом, отличным от простого
перебора всех пар из Q2, можно воспользоваться специфическими
свойствами рассматриваемых отношений. Одним из основных и
широко используемых свойств является отделимость. Пусть ‘к£Ет\
(а, Ь)—скалярное произведение векторов а и Ь. Отношение {R
на Ет называется ^-отделимым, если
xRy =$>(%, х)>(К,'у). (12)
Упражнение 10. Доказать, что отношение Парето Х-отде-
лимо при любом векторе X с положительными компонентами.
^Упражнение И. Верно ли это высказывание для векторов
X с неотрицательными компонентами?
Упражнение 12. Указать все векторы X, при которых от-
ношение RK, заданное конусом К, Х-отделимо.
Пусть отношение R Х-отделимо и Х2-отделимо, т. е.
xRyz^t, х) > (Хх, у), (Х2, х)|> (Х2, у). (13)
Легко видеть, что при этом R будет также (Хх + Х2)-отделимо.
Если R Х-отделимо и s—положительное число, то R будет sX-ot-
делимо. Тем самым доказано
^Утверждение 6. Множество векторов к £Ет, для которых
отношение R ^-отделимо, представляет собой конус, обозначаемый
через KR.
fc* Назовем конус RR двойственным конусом отношения. Этот
термин связан с хорошо известным понятием двойственного ко-
нуса: конусом К*, двойственным к конусу К, называется конус,
3* И. М. Макаров и др.
68
ГЛ. 3. БИНАРНЫЕ ОТНОШЕНИЯ НА Ет
образованный множеством векторов X £ Ет таких, что (1, х) > О
для всех х$К.
Пусть отношение R порождено конусом К, т. е. xRy х—у £ К.
Тогда конус К*, двойственный к R, является замыканием ко-
нуса KR. Двойственные конусы К и К* показаны на рис. 6.
Утверждение 7. =
Если в (12) заменить строгое неравенство на нестрогое (>),
то придем к понятию нестрогой ^-отделимости. При этом конус,
двойственный к конусу К, совпа-
дет с конусом KR для отношения
R, порожденного К.
Многие отношения обладают
свойством нестрогой Х-отделимо-
сти и не обладают свойством /-от-
делимости. Рассмотрим отношение
лексикографии L. Легко видеть,
что L нестрого /-отделимо при
единственном векторе Х=<1, ...
..., 0> (^=1). Действительно, из
xL# следует, что х^ уг, т. е.
(/, х)>(Х, у).
Упражнение 13. Доказать,
что L не является /-отделимым
ни при каком X.
котррых отношение R нестрого
1) RZ3-
2) существует телесный конус К такой, что К (0);
3) R ациклично.
Тогда R нестрого ^-отделимо.
Доказательство. В силу условия 1) соотношение (12)
достаточно доказать для х = 0: существует /€£„ такой, что для
всех #£R~(0) выполнено (X, у)<^0.
Обозначим через К~ конус, натянутый, на R~ (0), т. е.
₽/>0, Z>(.£R-(O), n£N
I 1=1
и через К~—замыкание К~. Если К" не совпадает со всем про-
странством, то его двойственный конус К* непуст и в качестве
X можно взять любой вектор из К*.
Осталось доказать, что не совпадает со всем пространст-
вом. Предположим противное. Это значит, что для любой точки
у£Ет существует последовательность а1, а\ ..., ап, ... такая,
чтоЪ'Ч-ГД'- и limo!n=z/. Возьмем в качестве у любую внутрен-
п 00
Рис. 6..
Установим свойства, при
X-отдел имо.
Теорема 1. Пусть
§2. УСЛОВИЯ ОТДЕЛИМОСТИ
69
нюю точку конуса К.. В силу (11) и условия’ 2) #£/?+(0). Так
как последовательность а„ сходится к у, а у—внутренняя точка
К, то существует М такое, что при всех п > М ап—внутренние
точки конуса К. Возьмем любую из них и обозначим ее через z.
По построению К~ имеем
+ • • • +₽Л=z € №|Г (0),!
z—внутренняя точка К, (14)
b^R-^Q) (i=TTd),
6,->|0 (t = 171)4
Заменим в (14) на достаточно близкие к ним рациональные
числа (так, чтобы не выйти из /С). Тогда можно считать, что
в (14) pf—рациональные числа. Пусть М—наименьшее общее крат-
ное их знаменателей. Умножив 1-е из соотношений (14) на М,
получим
= Я+’(0), . «1, п2, nd€N. (15)
£ = 1|
Запишем (15) в^виде
’g
2 6,-= +|(0) (16)
i = i
(здесь tijbj представлено как^-f- ... (пх раз) и т. д.). Напом-
ним, что Z>/€/?“(0) (i = 1, g). В силу части 3 утверждения 2 по-
лучаем, с учетом (16), что R не ациклично, что противоречит
3-му условию. Полученное противоречие доказывает теорему.
Заметим, что условия теоремы 1 не являются жесткими. Во
всяком случае, опустить слово «телесный» в ее формулировке
нельзя. Следующий пример как раз и демонстрирует отсутствие
отделяющей гиперплоскости, если не предполагать телесности со-
держащегося в R+ (0) конуса.
Рассмотрим отношение /?£52, У которого верхнее сечение
в нуле задается следующим образом:
aRQ <=> [а2 = 0,*a4>J0], или [а2 = п],?
или [а2 = —2] (здесь п € N).
k
Пусть ’"а2, ..., С ^+i(0) Л Проверим, что аг ^ R~ (0). Дей-
k
ствительно. 2 а'1имеет[видлибо\Д*0>[(Ь >'0),5либо <£»,[/гг—ntp<2>,
i = 1 I
где b—любое, afn1 и n2—неотрицательные целые числа, не рав-
ные одновременно нулю. В то же время любая точка из R~ (0)
70
ГЛ. 3. БИНАРНЫЕ ОТНОШЕНИЯ НА Ет
имеет вид либо <&, 0>1Ь<0), либо <&,—п^, либо <Ь, паК2>,
где b—любое, пг, n2£N. В силу части 3 утверждения 2 это зна-
чит, что R ациклично. Заметим, что,точки из верхнего сечения
в нуле находятся по обе стороны любой прямой в плоскости Е2,
т. е. нестрогая отделимость отсутствует.
М Для конечных множеств условия отделимости удается ослабить.
Отношение R = Е^ называется отделимым на множестве X, если
существует X такой, что (12) выполняется, как только х, у^Х.
Отношение R называется отделимым, если оно отделимо на каж-
дом''конечном множестве Ха:Ет. Заметим, что А зависит от X:
Х=Х(Х).
Упражнение 14. Доказать отделимость отношения L.
Было бы желательно доказать, что для всех отношений R С 3
ситуация такая же, как и для L: из нестрогой Х-отделимости
следует отделимость. Однако близкий к желаемому результат
имеет место, если только наложить определенные требования на
множества X.
Теорема 2. Пусть
1) R&3;
2) R ациклично;
3) все координаты точек х из конечного множества Q—р зо-
нальные числа.
Тогда R отделимо на Q.
Доказательство. Рассмотрим множество
Z = {z£Em\z = x—у, х, у£&, xRy}.
Пусть для некоторого Ъ£Ет
[(X, z)]>|0]. (17)
По построению Z это значит, что из xRy следует (X, х—#)]>[0,
или (X, х) > (X, у). Поэтому достаточно доказать (17), т. е. от-
делимость Z от 0 гиперплоскостью с нормалью X. Как и в дока-
зательстве теоремы 1, рассмотрим конус К, натянутый на Z.
В силу конечности Z конус К будет замкнут.
Для завершения доказательства достаточно установить, что
конус К—острый, т. е. из а£К п—а£К следует, что а — 0
(если это так, то для некоторого X (X, z) > 0 для всех г£К).
Предположим противное. Это значит, что существуют z}, ..., zj,
г?, ..., zfgZ такие, что для некоторых положительных аъ ...
• ’ Р1» • • • » Pt
t i)P7z? = 0. . (18)
1 = 1 / = 1
Среди векторов , 4 найдется максимальная система ли-
нейно независимых: ..., 4, zf, ..., z| (fesCs, Тогда
k i d
X a,-zj + P/Zj = S Tv zv. (19)
i=l /=1 v=l
§2. УСЛОВИЯ ОТДЕЛИМОСТИ
71
Рассмотрим (19) как систему линейных уравнений относительно
ап • • •» Рп • • •, Рр Так как любой вектор zv является линей-
ной комбинацией z*, ..zf, то ранг матрицы системы
равен рангу расширенной матрицы и по теореме о ранге система
имеет единственное решение. Заменим все yv на достаточно близ-
кие к ним рациональные числа. Получшм решение системы (19)
такое, что все его компоненты ..., аъ рь ..., Р,—положи-
тельные рациональные числа (так как все коэффициенты и сво-
бодные члены системы (19)—рациональные числа в силу условия
3 теоремы). Возвращаясь к (18), видим, что аь ..., а, и • • •
. .., —близкие к исходным положительные рациональные числа.
Умножая их на наименьшее общее кратное их знаменателей, при-
ходим к равенству
s t
ntj-zj = О,
или (так как nh ntj € N)
2z/=o, z^Z. (20)
i = i
Учитывая, что zt — x—у, где х, у£&, xRy, в силу условия 1
имеем zz7?0, 07? (—z,) (t = l, г). Перепишем (20) в виде
llzr----zr, -zr£R-(Q). (21)
Выражение (21) противоречит в силу части 3 утверждения 2 ус-
ловию 3 доказываемой теоремы. Полученное противоречие завер-
шает доказательство.
Условие рациональности координат элементов й не является
ограничивающим, так как при решении практических задач ме-
ханизмы измерения объектов по критериям таковы, что в резуль-
тате измерений получают рациональные числа (например, оценки
критерия «вес» измеряются в килограммах, критерия «цена»—в
рублях и т. д.). Отказ от условия рациональности приводит
к отсутствию отделимости.
Рассмотрим отношение R £ 32, которое задается своим сече-
нием в нуле (рис. 7):
xRQ ^[х1+х2 > 0],
или [х1+х2 = 0, х2 > 0 и f х | = г—k]/2 (k—1, 2, ...)],
или [x1-f-x2 = 0, х2 < 0 и (х ] = kV2 — г (k=l, 2, ...)]
(здесь г—любое положительное рациональное число).
72
ГЛ. 3. БИНАРНЫЕ ОТНОШЕНИЯ НА Ет
Покажем, что транзитивно и ациклично. Для этого доста-
точно доказать, что
X1 € R+ (0), х2 е R+ (0) => (х14-х2) € 7?+ (0).
Действительно, если х\или х2 лежит строго выше прямой xL + х2 = 0,
то из рис. 7 видно, что (хЧ-х2)€ ₽+(0). Необходимо лишь рас-
смотреть случай, когда х1 и х2 лежат на прямой Хх4-х2 = 0. Здесь
надо учесть три возможности: х2, х2 > 0, х2, х2 < 0, х| > 0,
х| < 0, т. е. точки х1 и х2 лежат на прямой Xj-f-Xa по разные
стороны от нуля. Первые два варианта очевидны.
Рассмотрим 3-й вариант. Если | х11 > |х2|, то сумма х1 и х2
лежит на прямой по ту же сторону от нуля, что и х1. При этом
J х14-х21 = | х11 -1 х21 = (г, -k^2) -(bJ/2 - r2) =
= (o + o)-(^ + ^)l/2.
Если |хг | < |х2|, то
| х14- х2| = | х21 -1 х11 = (k.V2 - г 2) - (г2 - k^2) =
= (^ + ^)/2 -(Гх4-'а)
Покажем, что |х1|=/=|х2|. Действительно, иначе
ri—^У2 = k2V~2—г2 =Ф г г 4- rt = (&J 4- V2,
и К2 рационально.
Определим точки на прямой Хх4-х2 = 0 так, как это показано
«а рис. 8: Q = {0, z, а2}, где 1^1 = 10—У~2, |а2| = 5—У2,
^1 = 31^2—0,001. Легко видеть, что ORz (так как—zRQ), ах/?0,
а2/?0. Все точки множества Q лежат на одной прямой, причем z
.лежит между аг и а2.
Приведем условия, обеспечивающие отделимость R.
Теорема 3. Пусть
1)
§2. УСЛОВИЯ ОТДЕЛИМОСТИ
2) 7? транзитивно и антирефлексивно\
3) lirn уп = у, ynR0 (n = l, 2,j...) =>QRy,
4) xIR0=>(kx)IR0 (6=1, 2; IR = Q2\(RUR"1)).
Тогда R отделимо.
Доказательство. Проведем индукцию по размерности.
Идея состоит в том, что сужение R на любое подпространства
в Ет также удовлетворяет условиям 1)—4).
Докажем прежде всего, что теорема верна при размерности 1.
Предположим противное. Это значит, что существуют хп х2 такие,
что г, > 0, х2 > 0, х^О, 0Rx2. В силу транзитивности /nXjRfr
для всех натуральных т\ если^бы было (mlq)xlRQ при <7С(1, ...},
то получили бы (в. силу |4)) mXjRO. Тем самым доказано,что
aXjRO при всех положительных рациональных а. Но тогда
x2 = limx(-, x,-R0 и по условию 3) 0Rx2. Полученное противоречие-
1->00
"оказывает утверждение для размерности 1.
Пусть У—конечное множество в Ek, Y = У1иУ2, У1ПУ2 = 0
и существует- вектор лх такой, что
(^i, У1 У2)^0 ^/2 €^2)-
Положим Z1 = Y1n Z2 = Y2f)n1. Пусть существует jq, так|что*
гиперплоскость (гиперплоскость обозначена той же буквой,
что и определяющий ее вектор) отделяет Zr от Z2, т е-
(ль z2)>0 (Vz.CZ^ Vz2eZ2).
Тогда существует вектор л2 такой, что -
(лг, У1 — Уг),>'Р (Vyi^Yi, Уу2^Уг)- (22)-
Формула (22) следует из геометрических соображений, пред-
ставленных на рис. 9.
74 ГЛ. 3. БИНАРНЫЕ ОТНОШЕНИЯ НА Е
4 т
Пусть теорема 3 доказана для всех подпространств размерно-
сти k—1. Рассмотрим любое подпространство L размерности k
иЧюложим Xk = X A L. Пусть
^1(0)?}, т?;до)={^...................П
к к — —
Рассмотрим конусы К+ и К~, натянутые на 7?^(0) и 7?*fe(0).
Пусть К = К+ fl ТС-; легко видеть, что при положительных ра-
циональных а,-, Ру
07? (tp,-А
Поэтому К—не телесный в L конус. Тогда существует гипер-
плоскость Li в подпространстве L, отделяющая 7?~^(0) от 7?+ (0).
Если она отделяет строго, то для L теорема доказана. В против-
ном случае воспользуемся формулой (22) и предположением ин-
дукции. Теорема доказана.
Введем еще одно понятие, которое будет использовано в даль-
нейших главах. Отношение R называется положительно к-отде-
лимым, положительно отделимым на X, положительно отдели-
мым и т. д., если все, компоненты к положительны. Аналогично
определяется неотрицательная отделимость.
Вернемся к основному, исходному определению 1-отделимости.
Что же «отделяют» отделимые отношения, т. е. с чем связано
их название? Пусть Ь£Ет. Как расположены в Ет множества
7?~ (Ь) и 7?+ (&), если 7? Х-отделимо? Проведем через точку b ги-
перплоскость к: (к, х) — (к, Ь). Если у£ R+ (b), то yRb и (X, у) >
> (X, Ь). Если же y£R~(b), то bRy и (X, у) < (X, Ь). Иными
•словами, множество «лучших, чем Ь» элементов (7?+ (/>)) лежит
по другую сторону гиперплоскости X, проходящей через Ь, чем
множество «худших, чем Ь» элементов (R~ (&)). Ясно, что для
инвариантных отношений достаточно (для отделимости) доказать
отделимость верхнего сечения от нижнего только в нуле.
Упражнение 15. Доказать, что из Х-отделимости следует
ацикличность.
Условия отделимости рассматривались в ряде работ.
I- Предлагались различные системы аксиом (т. е. требований на
отношение 7?) для того, чтобы <гакие функции существовали.
Приведем одну из таких систем.
Модель Аумана. Пусть отношение 7? удовлетворяет тре-
бованиям:
1) R$3',
2) xRy, а > 0 —> (ах) 7? (аг/); _
3) из xR (ky) при всех 0 следует, что yRQ и QRy.
•Тогда .7? является Х-отдёлимым.
§3. МАЖОРАНТЫ ПО ОТДЕЛИМЫМ ОТНОШЕНИЯМ
75
Условие 2) накладывает жесткое ограничение на 7?. Однако,
как показывает рис. 5, это условие не является необходимым
для отделимости. В этом смысле условия теорем 1—3 являются
значительно более слабыми.
§ 3. Мажоранты по отделимым отношениям
^Рассмотрим теперь, каким образом свойство отделимости на Q
позволяет находить недоминируемые по отношению 7? элементы.
Утверждение 8. Пусть R—отделимое на й отношение.
Тогда Argmax (X, х) = йк.
о
Доказательство. Предположим противное. Это значит,,
что для некоторого х*^ Argmax (X, х) найдется такой, что-
о
yRx*, откуда (X, у) > (X, х*), что противоречит включению х*£
С Argmax (X, х). Утверждение доказано.
Q
Упражнение 16. Привести пример отношения R такого,
что Q^^Argmax (X, х).
й
Упражнение 17**. Сформулировать утверждение, анало-
гичное утверждению 8, для нестрого отделимых на й отношений -
Рассмотрим на Ет отношение RK, которое
определим следующим образом:
(Vx, y£Em)\xRKy<$ (X, х) > (X, у)}.
На рис. 10 изображены верхнее и ниж-
нее сечения отношения R\ в точке х*£Е2.
Легко проверить, (что (й^ = Argmax (X, х),
где й х —множество недоминируемых по от-
ношению Ri векторов. Отсюда следует, что
поиск множества йЛх недоминируемых по от-
ношению Rx векторов (точек) эквивалентен отысканию максимумов
функции у = (Х, х), которую обычно называют линейной сверткой.
Упражнение 18. Доказать, что й x = Argmax(X, х).
о
Упражнение 19. Найти множество всех Хх и Х2 таких, что-
йЛач = х1, wx« = xe, где й—множество, показанное на рис. 2.
Упражнение 20. Найти такой вектор Хо, что й^» £ йр,
где й—множество, показанное на рис. 2.
Упражнение 21. Доказать, что для любого Х€£в отно-
шение инвариантно и Х-отделимо.
Упражнение 22. Указать все ‘k^Em, для которых отно-
шение RK рационально.
76
ГЛ. 3. БИНАРНЫЕ ОТНОШЕНИЯ НА Ем
tn
Рассмотрим теперь вопрос о том, какие элементы из множе-
ства й могут быть выделены рациональными отношениями типа
т. е. какие элементы из й могут быть получены максимиза-
цией линейной свертки (X, х) с неотрицательными коэффициен-
тами. Другими словами: через какие точки г£й может прохо-
дить отделяющая гиперплоскость?
Утверждение 9 (лемма Карлина). Пусть й—выпук-
лое замкнутое множество в Ет. Для любого- х*£й₽ существует
вектор л такой, что максимум функции g (х) = (X, х) дости-
гается на х*.
Условие выпуклости множества й представляется чрезмерно
жестким. По сути дела, нужна не выпуклость й, а какой-либо
аналог выпуклости для Qp. Множество S s Ет называется К-выпук-
лым, если множество 5Ц-Л выпукло. На рис. 11, а представлен
конус Л; на рис. 11, б—Л-выпуклое множество Sf, на рис. 11, в—
не Л-выпуклое множество S2.
Рис. 11.
Утверждение 10. Пусть К—конус, й является
(—Д)-выпуклым множеством в Ет. Тогда для любой' точки
х»^йЛк существует вектор %£/(* такой, что максимум функ-
ции (X, х) достигается на х*.
Доказательство. Докажем, что для любой точки х* £ Ййл'
выполнено х* $ Int (й—К). Предположим противное. Тогда
х*£й—К вместе со своей окрестностью, в которой обязательно
имеются точки и такие, что vRKx*, т. е. v—х* = а1£К. Поскольку
ц£й—К, это значит, что для некоторой точки y£Q и некото-
рого а2$К v = y—a2, откуда
у—а2—х* — а1, (23)
где alt а2£К, у, х*£й. Из (23) получаем у—х*£К, а это про-
тиворечит тому, что х* €
Докажем теперь, что й—К—х*П^ = {0}. Предположим про-
тивное. Тогда для некоторого jgQ и о1( получим
у—аг—х* = а2, что опять противоречит тому, что
ГЛ. 4. КООРДИНАТНЫЕ ОТНОШЕНИЯ ‘ 77
Доказанные два факта означают, что конус, полученный пере-
несением вершины К из 0 в х*, и множество Q—/(, содержащее
х*, пересекаются только по одной точке х*. Теперь восполь-
зуемся выпуклостью Q—/< нА. Два выпуклых множества, пе-
ресекающиеся по одной точке, можно разделить гиперплоскостью
(к, х), проходящей через х*. Очевидно, что ясно также,
что вектор К удовлетворяет требованиям утверждения, поскольку
QgQ—/(. Утверждение доказано.
В утверждениях 9 и 10 предполагается, что Z-^О. Аналог
этих утверждений для конечных Q приведен в § II.6.3.
Литература. [58, 120].
Г л| aj в а 4 ;
КООРДИНАТНЫЕ ОТНОШЕНИЯ
Среди всех бинарных отношений, заданных на Emi особое
taecTO занимают координатные отношения, для сравнения по ко-
торым пары альтернатив достаточно иметь информацию лишь
о знаках разностей одноименных координат (с чем и связано их
название). Можно сказать, что структура любого конечного мно-
жества с точки зрения выбора по любому из отношений
такого типа полностью определяется лишь порядком располо-
жения всех его элементов по каждой оси пространства Ет. При-
мерами координатных являются рассмотренные в § 3.1 отношения
Парето и лексикографии.
В настоящей главе рассматриваются общие свойства класса
всех координатных отношений и отдельных его представителей.
При этом используется аппарат логических форм. Логические
формы отношений (ЛФО) позволяют описать структуру класса
координатных отношений и получить формализованный способ
исследования свойств любых подклассов и их отдельных пред-
ставителей, создающий предпосылки для аналитического построе-
ния координатных отношений с любььм наперед заданным набором
свойств. Изучение свойств координатных отношений позволяет
в определенном смысле стандартизировать процедуры выбора по
бинарным отношениям на конечных множествах, поскольку далее
будет установлен изоморфизм между произвольным бинарным и
координатным отношениями.
В § 1 вводится понятие координатных отношений и их логи-
ческих форм; в § 2 исследуется структура множества всех ко-
ординатных отношений; в § 3 приводятся необходимые и доста-
точные условия для ацикличности, транзитивности и других
свойств координатных отношений в терминах ЛФО; в § 4 рас-
смотрены основные подклассы координатных отношений; в § 5—
иерархические отношения, построенные с учетом информации
78 ГЛ. 4. КООРДИНАТНЫЕ’ОТНОШЕНИЯ I
V
о сравнительной важности критериев и/или их групп; в § 6 —
квазикоординатные отношения, являющиеся обобщением коорди-
натных.
§ 1. Понятие координатных отношений и логических форм
Вернемся к отношениям Парето (Р) и лексикографии (L),
рассмотренным в § 3.1. Напомним, что
xPy«=>(Y/ = l, tri) [х7>г/7] и [х#=«/];
хАг/^[х,или [xlt = ylt, х,а>^а],
ИЛИ ... Гх,- = щ, .... X.- .<=у{ ,, X: > у, ].
в иной форме. Пусть
«/(х, z/) = sgn(fy(x, у)),
Перепишем эти определения
/у(х, у) = ху—уу,
где
sgn (&) =
1,
О,
—1,
если
если
если
&>0,
&== О,
Ь<0.
Тогда
xPytt(Vj = l, tri) [/Дх, г/)>0]
и (Э/о€{1, т\) [/А(х, г/)>0];
xLy^[tit(x, у) > 0], или [^Дх, у) = Ъ, tlt(x, у)>0] . ..
... и (□/„€{!......т}) Д/о(х, у) > 0].
Приведенная запись означает, что отношения Р и L задаются
некоторыми правилами, определяемыми однозначно знаками раз-
ностей одноименных координат. Можно сказать, что эти отноше-
ния определяются вектором а(х, «/) = <аДх, у), ..., аДх, у)>,
в том смысле, что если а(хх, г/1) = а(х2, у2) для произвольных
двух пар <х\ у1) и <х2, у2>, то x'Ry1 <=> x2Ry2. Таким образом,
если у двух упорядоченных пар знаки разностей одноименных
координат совпадают, то эти пары одновременно или принадле-
жат или не принадлежат отношению R (R = P или R = L).
Пусть
х1 = <5, 4>, / = <6, 3>, х2 = <6, 7>, г/2 = <20, 6>;
Цх1, у1) = <—1, 1>, Цх2, у2) = <—14, 1>;
сДх1, у1) = <—1, 1>, а(х2, у2) = <—1, 1>, т. е. а(х\ у1) = а(х2, у2).
Ясно, что
<х\ у*>$Р, <х2,
<х2,
§ 1. ЛОГИЧЕСКИЕ ФОРМЫ КООРДИНАТНЫХ ОТНОШЕНИЙ
79
Пусть
х3 = <5, 4>, г/3 = <0, 2>, х4 = <6, 7>, #4 = <5, 6>;
Цх®, у®) = <5, 2>, г(х4, у4) = <1, 1>;
а(х®, у3) = <1, 1>, а(х4, у4) = <1, 1>, т. е. а(х3, у3) = а(х4, г/4).
Ясно, что хъРу'л, х*Ру\ х*Ьу2, xlLyl.
Отношение R называется координатным, если для любых
<х\ у1), <х2, t/2> из а(х\ г/х) = а(х2, у2) следует, что хх7?ухФФ
Ф»х2##2. Множество всех координатных отношений обозначим
через 3^, множество всех координа гных отношений на Ет—через 3£т.
Замечание. Если а(хх, ^^«(х8, у2), то это не означает,
что из xLRyi обязательно следует x2Ry2. Например, пусть
х* = <5, 4>, ух = <4, 3>, а(х\ у*) = <1, 1>;
х2 = <6, 5>, у2 = <5, 7> а(х2, «/2) = <1, —1>.
Очевидно, что а(хх, ^1)#=а(х2, у2), однако xlLyY и x2Ly\
Все пары <х, у>, у которых а(х, у) равны, находятся в одном
и том же координатном отношении. Это позволяет задать любое
координатное отношение некоторой функцией фат)
такой, что
х/?у=>ф(а(х, t/)) = l, х£у=>ф(а(х, z/)) = 0; (1)
наоборот, любой функции ф от т трехзначных переменных со-
поставим R£Wml
ф(а(х, у))= 1 =$xRy, ф(а(х, у)) = 0=>xRy. (la)
Функция ф(а) не принимает других значений, кроме 0 и 1; ко-
ординаты аргумента а,- принимают значение из {0, 1, —1}. Вве-
денная конструкция позволяет переходить от отношений R к функ-
циям ф (а) и наоборот.
Как будет ясно из дальнейшего изложения, значительно
удобнее для анализа и практического использования задавать
отношение не одной, а семейством функций, каждая из которых
является функцией от двузначных переменных, т. е. булевой
функцией. Воспользуемся следующей конструкцией.
Пусть I — {i\, .... it}. Обозначим ₽/=<₽/,, P,z>. Зако-
дируем функцию ф(ап .. , ат) семейством булевых функций по
формулам
М0/) = Ф(®1> •••. О, (2)
где 7 = {t|a(. =^0}; Pz = (a,-+l)/2
Так как az£{0, 1, —1} и функция ф определена на всех 3я
наборах длины т, каждый из которых состоит только из эле-
ментов множества {0, 1, —1), то /£{/}, где {/} — множество
всех возможных подмножеств множества У = {1, т}, вклю-
80
ГЛ. 4. КООРДИНАТНЫЕ ОТНОШЕНИЯ
чая пустое множество 0.' Равенство 1 — 0 соответствует случаю,
когда а,- =0 (7=1, т), a I — J соответствует случаю, когда
а,-0 (t = 1, т). j
Проверим, какие значения может принимать переменная
= (а< +1 )/2. Заметим, что она определена только для t £ 7,
т. е. а,-=^0. Отсюда следует, что
о _ I 1, если а,- — 1, ’
р'— Y 0, если а(= — 1.
Таким образом, формула (2) по любой функции ф (ап
однозначно определяет семейство булевых функций {ft (£,)} (7 £ {J}).
С другой стороны, семейство булевых функций {/z(Pz)j (7 £{./})
однозначно определяет некоторую функцию ф(аь ..., aa) = /:z(pz),
где
[ 0, если i 4 /,
а' \ 20( — 1, если i £ I. а)
Действительно, а,- может принимать три значения:
0, если i^I,
1, если i ё 1 и Р, — 1,
ч—1, если i С 7 и Р/ = 0.
Таким образом, установлено взаимно однозначное соответствие
между множеством всех функций ф(а1, ат) и множеством
всех семейств булевых функций {/z(₽z)} (7 ${•/}). Ранее было
установлено взаимно однозначное соответствие между всеми ко-
ординатными отношениями и всеми функциями ф(а1т ..., а,л).
Теперь установлено взаимно однозначное соответствие между мно-
жеством <ЗСт всех координатных отношений R на Ет и семейством
булевых функций при J = {1, ..., т}. Это соответствие задается
следующим образом:
xRy 1, (3)
где
) 1, если Xi > yt ,
7 — Uis}' 0, если xif < yts-
Семейство булевых функций {/z(₽z)} (7 £{./}) такое, что xRy&
= гДе / = уназывается логической формой
отношения R (ЛФО(Я)), а /Z(PZ), где J = {1, ..., т}, называется
главным членом логической формы отношения R (ГЧ Л ФО (7?)).
Итак, любое RG.W однозначно задается логической формой
отношения, следовательно, свойства функций Л ФО (7?) полностью
определяют свойства отношения R. С другой стороны, любое
семейство логических функций порождает некоторое координатное
§ 1. ЛОГИЧЕСКИЕ ФОРМЫ КООРДИНАТНЫХ ОТНОШЕНИЙ 81
отношение на Ет, т. е. существует взаимно однозначное соответ-
ствие между ЛФО и координатными бинарными отношениями
на Ет. Таким образом, свойства функций ЛФО(R) полностью
определяют свойства отношения /?, поэтому для исследования
свойств ЛФО (7?) можно воспользоваться хорошо развитым ап-
паратом булевой алгебры.
Приведем примеры координатных отношений и их ЛФО.
Пример 1. Пусть R — P. Обозначим через Р(Ет) отноше-
ние Парето на пространстве Ет. Тогда
ЛФО(Р(£3)): f,(P,) = P,(f=O), J,7(Pf, Р7) = Р,- А Р/, ‘
ГЧ ЛФО(Р(£3)): М3(01э ₽8, P3) = Pi А Р2 А Рз‘>
ЛФО(Р (£J): fz(pz) = А ₽,•;
ie I
ГЧ ЛФО(Р(Еа)У fM- А P/ = Pi А • • • А Рот-
1
. Пример 2. Пусть R = L. Обозначим через L (Ет) отношение
лексикографии на пространстве Ет. Имеем
ЛФО(£(£3)): f: (Р;)=р;(t= Г3), /,7(р;, р7) = рг> где r=min(i,/);
ГЧ ЛФО(Д(£3)): Рз, Р,)=Рг,
ЛФО(1 (Еа)У где г = mint;
ГЧ ЛФО(£(£Я)): f7(Py) = P1.
Пример 3. Определим отношение V на Ет следующим об-
разом:
x\Ry ФФ xPty (i = l, 3),
xVkytt([xk^yk] и [хь-1>Ук-1] и [уУк-^У
или ([xft = t/ft] и = и xVk_2yy
Нетрудно установить, что ЛФО(1/3) = ЛФО(Р3); при этом
ГЧ ЛФО(И) имеет вид
Ш) = РЛ-1(Р,и-з7 OT-3 V (Pm_4p„_5(...))). (4)
Упражнение 1. Доказать, что главному члену ЛФО(Г)
соответствует формула (4).
Прим.ер 4.-Определим отношение (k<tn) на простран-
стве Ет следующим образом:
xDky фф t/ij и [(3/j, ..., Ik, (s=l, k))
[xis>yis (s=O)]]
Прежде чем построить ЛФО(£Ц)Г выпишем в явном виде
определение отношения DI'.
хО2у^[х1>у1\ и [(3Z1€{2, 3}) [xz,>«//,]];
82
ГЛ. 4. КООРДИНАТНЫЕ ОТНОШЕНИЯ
перепишем это определение в эквивалентной форме:
xD13y<^[x1> z/x] и [[х2>у2] или [x8>z/8]].
Теперь выпишем ЛФО(£>1):
MPi) = Pi, А(Р/) = О (1 = 2, 3),
MPi, Pz) = Pi G = 2,3), /28(р2, р3) = 0;
ГЧ ЛФО(£>£):
/123 (Pl, Ра, Рз) = Pi Л (Ра V Рз)-
Выпишем ЛФО(От):
/ 0, если 1 £ I,
PiA (VP«,...₽»p, если s = k —1{2, ..., /п}\/| > О,
fAfii) = \ где дизъюнкция берется по всем
наборам {qlt qs}^ I\{ 1},
( Рг, если s = k — |{2, ..., zn}\Z | ^0;
(5)
ГЧ ЛФО(£)*):
/j(Pj) = Pi A (V P/,-•-Pzft),
где дизъюнкция берется по всем наборам {Zlt ...,/*} s {2, ..., tn}.
Упражнение 2. Построить ЛФО(£>|).
Упражнение 3. Доказать, что ЛФО(О^) соответствует
формула (5).
Пример 5. Определим отношение Мт на пространстве Ет
следующим образом:
xM„y^(3it, ..., ik) [xis>yis (s = O)], где & = [m/2]4-l.
ЛФО(Мз):
Д.(Р,.) = О (z = TT3), МРо Р/)=Р/АР/,
ГЧ ЛФО(М8):
/123 (Р1» Ра» Рз) = Р1Ра V PiPs V РаРз>
ЛФО(МИ):
| 0, если 111 < k,
f/(P/) = <| у Р»,-• .P»ft, если ]/| > k,
где~ дизъюнкция берется по всем наборам {1\, ..., ik} таким, что
{it, •••> —
ГЧ ЛФО(МИ):
/M)=vpG...pift,
§2. СТРУКТУРА КООРДИНАТНЫХ^ ОТ НОШЕ НИЙ
8$
где дизъюнкция берется по всем наборам Mi1( .... ik} длины
k — [т/2] 4-1.
Отношение Мт называется мажоритарным.
Упражнение]^. Доказать, <что ЛФО^д,) • соответствует
формула (6).
§ 2. Структура множества|координатных’отношений
Напомним, что любое координатное отношение"/? можно за-
дать некоторой функцией ф^о^, ..., ат) со значениями; из мно-
жества {0, 1} и аргументами из множества {—1/1, 0} при по-
мощи формулы
xRy <=> ф^(а (х, у))=1, xRy &$R(a(x, у)) = 0, (7)
где a = <«i...а,л>, a,- = sgn(xt.—у{).
По формуле (7) произвольной функции ф указанного вида
можно сопоставить некоторое координатное отношение ! на Ет.
Отсюда следует, что число элементов множества равно 23”1.
А" 4 4 4 ’"'1 л?/
Рис. 1.
Пример 6. Рассмотрим множество всех координатных отно-
шений на fj. Число разных функций ф(ах) равно 23’ = 8. Со-
ставим табл. 1, в которой укажем все функции ф^) и соответ-
ствующие им семейства функций {fz(Pz)} (/ €{/}), полученные по
формулам (2). Семейство {fz(Pz)} состоитЦиз двух функ-
ций [ф и Аф|), так как т=1. п ?
Поставим в соответствие каждой функции|фА[(а1) координат-
ное отношение на Е/.
fe=l, /?1 = 0,
k 2, xR3y 4Ф х2 У1,
k~ 3, xR3y 4-^ х^ pi,
k = 4, xR^yox^y^
k = 5, xRiy^x1<_y1,
k = 6, xRsy Xj ул
k = 7, xR^y
k = 8, RS = U.
Пусть в Ei заданы три произвольных вектора*^, a2, a3; построим
графы, соответствующие каждому из отношений Rlt ..., R3 по
следующему правилу: из а,- дуга ведет в тогда и только то-
гда, когда aiRaj. Пусть a1( а2, а3£Ег расположены так, как
показано на рис. 1. Граф Gk соответствует отношению Rk (k= 1, 8).
.84
ГЛ. 4. КООРДИНАТНЫЕ ОТНОШЕНИЯ
Таблица 1
k Значения Значения
<4(0 (о k Z* <0) f* (1)
1 0 0 0 0 0 0
2 0 0 1 1 0 0
3 0 1 0 0 0 1
4 0 1 1 1 0 1
5 1 0 0 • 0 1 0
6 1 0 1 1 1 0
7 1 1 0 0 1 1
8 1 1 1 1 1 1
На рис. 2 показано сужение всех отношений Rk (6=1,8) на
множество {aj, а2, а8}.;Сопоставим каждой функции ф6 (k=\JS)
точку х=<хъ х2, х3>€£3 следующим образом:
= 1)> ^ = ФИ1). *з = Фй(0)-
Таким образом, всем функциям фА (k = 1,8) сопоставлены все вер-
шины трехмерного куба.
На рис. 3 представлен единичный куб D3 в Ея, номера вер-
шин которого соответствуют номерам координатных отношений
в табл. 1.
СТРУКТУРА КООРДИНАТНЫХ ОТНОШЕНИЙ
85
Заметим, что 1 = 0 также принадлежит множеству {/}. Легко
видеть, что при /g=l отношение R рефлексивно, так как ^ =
= 1<^х7?х; при f£ = 0 отношение R антирефлексивно. Если рас-
смотреть класс только антирефлексивных отношений, то в рас-
сматриваемом примере их будет всего четыре: R3, R.-,
все такие отношения можно представить вершинами квадрата
в плоскости у^.
Обобщим конструкцию, рассмотренную в примере б, на случай
z/г > 1. Рассмотрим произвольную функцию ф ат). Она
на каждом наборе значений <а1( ..., ат> принимает значение 0 или
1. Обозначим через А множество всех возможных наборов а длины т\
число элементов множества А равно З1®, так как на каждом из т
мест любого набора a = <«i, ...,ада> может стоять одно из трех
чисел из множества {—1, 0, 1}. Занумеруем все наборы А в сле-
дующем порядке:
<-1, ..., -1, -1>, <-1, ..., -1, 1>, <-1, ..., -1, 0>,
<—1, 1,—1>, ...,<0, .... 0,0/.
Задание любой функции ф (а1; ..., ат) эквивалентно сопостав-
лению некоторой последовательности нулей и единиц длины 3*®
множеству наборов А, пронумерованных в указанном порядке.
При этом на каждом из 3“ мест может стоять или 0, или 1, по-
этому число всех функций вида ф(ан ..., ат) равно 23,в. Заметим,
что единичный куб D® в Q-мерном пространстве (Q = 3m) содер-
жит 23<в вершин, множество которых обозначим через VDQ. Таким
образом, вершинам единичного куба можно взаимно однозначно
сопоставить множество всех функций ф(аь ...,аи) последующему
правилу.
Пусть х—произвольная вершина единичного Q-мерного куба.
Тогда ее координаты задаются вектором х = <хп ...,х<?>, где xs
равно 1 или 0. Функции ф(а) сопоставим вершину х такую, что
J 1, если ф|(а*)=-1,
( 0, если- ф(а3) = 0,
гдез=1, 3ю. -Наоборот, вершине х = <хХ1 ..
функцию ф (а) такую, что
( 1, если х5=1,
t(a’)=) а если х _А
и, если и,
Xq> сопоставим
<8а)
где s=l, З”. В соответствии с введенным правилом вершине
<0, ..., 0> по формуле (8а) сопоставляется функция ф(а) такая,
что ф(а) = 0 для всех а£А.
Установим структуру на множестве ‘Хт всех координатных
отношений на Ет. Рассмотрим произвольное отношение Сопо-
ставим ему функцию фя*(а!, ...,ага), а функции фк« сопоставим
86 гл. 4. КООРДИНАТНЫЕ ОТНОШЕНИЯ
вершину = куба DQ, где
J 1, если ф^» (as) = 1,
Xs'~ I о, если ip7** (a*) = 0.
При этом вектору as соответствует пара </4, р^>, где
/,={М«9=/=°Ь ₽^=<(«|,-Fl)/2, ...»(а?Л+ 1)/2>,
s J 1, если (as) = 1,
о, если 1рЯ1(а®) = 0.
Вершина —вектор из нулей и единиц. Заменим теперь нуль
на единицу, например, на d-м месте и полученную так новую
вершину обозначим через xR*. Вершине xRt будет соответствовать
функция фЛ»(«!,..., am) такая, что фЛ>(а7) = ф^*(а') для всех
j^d и ф/’»(а<*)=1, а фЯ,(atf)_.о. Новое отношение /?2—такое,
что Ю= !» где P/d> соответствует a4, (Pz) = ff» (Pz) для
всех </, Pz>=/=</d, p^>.
Таким образом, все пары <х, уу £ Е2т, которым соответствует
</, pz> Ф <Jd, ^did>, принадлежат или не принадлежат одновременно
отношению 7?! и отношению Т?2 и только пары <х, уу € Ет, ко-
торым соответствует </d, $1аУ, принадлежат R2 и не принадлежат
/?х. Это значит, что и /?2 совпадают, за исключением тех пар,
которым соответствует </d,
Заметим, что было произведено минимальное изменение вер-
шины: от вершины перешли к вершине находящейся от xR*
на расстоянии 1, т. е. ближайшей к лЛ. Назовем отношения
и Т?2 ближайшими. Ясно, что вложено в /?2 (/?1<Т?2).
Далее в настоящей главе (если не оговорено специально) будем
рассматривать только антирефлексивные отношения, т. е. такие,
у которых ф(0, ..O) = f0 = O. Нетрудно убедиться, что множе-
ству всех таких отношений можно взаимно однозначно сопоставить
вершины куба Z)Q, где Q — Зт — 1.
Упражнение 5. Установить взаимно однозначное соответ-
ствие между всеми антирефлексивными отношениями и вершинами
единичного куба DV, где Q = 3m— 1.
Итак, показано, что любое координатное отношение R на про-
странстве Ет можно задать точкой xR в пространстве EQi все
координаты которой равны 1 или 0, т. е. вершиной^ единичного
куба. Подобные построения уже проводились в § 2.2 для иссле-
дования структуры множества всех возможных функций выбора,
но там число вершин куба определялось не размерностью прост-
ранства Ет, а числом элементов исходного множества альтерна-
тив Q. Здесь размерность Q от числа альтернатив не зависит,Га
зависит только от отношения R.
§2. СТРУКТУРА КООРДИНАТНЫХ ОТНОШЕНИЙ
87
Рассмотрим два произвольных отношения и R2 на Ет.
Пусть им по указанным выше правилам сопоставлены точки xR*
и xR* в Eq. Справедливо следующее утверждение.
Утверждение 1. Ri< R% О xR*PxR<, где Р—отношение
Парето на Eq.
Доказательство. 1) Докажем, что R^R.^ xR*PxR'.
Сопоставим отношениям Rx и функции ф^ (аь ..., аЛ) и
ф^оч, . ..,ат) по формуле (1):
xRty => ФЛ* (аъ ..., ат) = 1, xR2y => ф*« (ах.ат) = 1.
Так как то xR^y=^xR2y и найдется пара <х°, у°> такая,
что x^Ritf и x^Ritf, а, значит, если ф₽<(а4)=1, то ф₽»(а4) = 1 и
найдется набор ad такой, что фй> (ad) = 0, фЛ> (arf) = 1.
Теперь по формулам (8) построим xR' и xR*-.
я ( 1, если (as) = 1, R J 1, если фЛ> (a4) = 1,
Xs‘~~ | о, если г|А(а4) = 0; х$2~ | о, если ф^(а4) = 0.
Пусть sl,...,sk—номера наборов as таких, что ф/?1(а’|)=1
* (i=l, k). Следовательно, координаты вершины хЛ> с номерами
«1» ••>sk равны единице, а все остальные—нулю; координаты xR*
с номерами sn ..., sk также равны единице и известно, что хотя
бы еще одна координата тоже равна единице; отсюда xR*PxR'.
2) Докажем, что xR*PxR< => R1 < R2. Сопоставим вершинам лЛ
и xRt функции фк>(а) и фЛ1(а). Так как xR*PxR', то координаты
xRi и xR' с номерами sn ..., sk равны единице и найдется хотя
бы еще одно d такое, что х§' — 0, х^—\. Отсюда ясно, что
(as<) = ф^ (asij — 1 для всех i — 1, k и что (а) = 0 для всех
а asz (i = 1, k), ф*» (arf) = 1. Следовательно, если sgn (х—у) — а5'
(i = 1Д), то xRry и xR2y, а для всех <х, у> таких, что sgn (х—у) Ф
i ¥=as<’ (i = 1, k), имеет место хРгу\ отсюда по определению /?х< R2.
Утверждение доказано.
1 Отношение R называется ближайшим сверху к R, если R < R
1 и не существует R* такого, что R < R* < R. Отношение R назы-
вается ближайшим снизу к R, если R < R и не существует R*
такого, что 7? </?,</?.
,; [Из предыдущих рассуждений ясно, что если рассмотреть xR
1 для произвольного отношения, то xR можно получить, заменяя
в вершине xR ровно одну нулевую координату на единичную, а
х%—заменяя в вершине xR ровно одну единичную координату на
нулевую.
Исследуем вопрос о том, каким образом изменяются функции
ЛФО(7?) при переходе от вершины xR к ближайшим. Пусть /ф) —
произвольная булева функция от k переменных; p = <Pi.
88
ГЛ. 4. КООРДИНАТНЫЕ ОТНОШЕНИЯ
pz равно (Гили 1 для всех £ == 1, k. Выделим из множества всех
наборов нулей и единиц длины k те, на которых f (Р) = 1, и обо-
значим их через Pz, т. е.
| 0, если
Нетрудно проверить справедливость равенства
f Ф)= V А • • А (9)
Напомним, что Р“ = Р,-, ₽г = Р,-, а представление f (Р) в виде (9)
называется разложением f в совершенную дизъюнктивную нор-
мальную форму (СДНФ). Заметим, что/(р) на стольких наборах
равна единице, сколько элементарных конъюнкций входит
в ее СДНФ.
Пусть имеется ЛФО(7?), т. е. семейство булевых функций
{fitfii)} Построим СДНФ каждой из них, воспользовав-
шись соотношениями
v Р*‘...р(а5 .
•••.₽,•?Iff (P/)=U-
Утверждение 2. ЛФО(Д) получается из ЛФО (R) добавле-
нием ровно одной (любой из ранее не входивших) элементарной
конъюнкции в СДНФ ровно одной (любой) функции /Z(PZ); ЛФО (R)
получается из ЛФО (R) удалением ровно одной (любой) элементар-
ной конъюнкции из СДНФ ровно одной (любой) функции ff(^).
Доказательство. Функция, в СДНФ которой добавлена
одна элементарная конъюнкция, принимает значение 1 еще только
на одном наборе. Пусть R—исходное отношение, a Rt—отноше-
ние, которому соответствует ЛФО (7^), отличающаяся от ЛФО (R)
только добавленной элементарной конъюнкцией в одну из функ-
ций Пусть xR—вершина D®, соответствующая R, a xR' —
вершина Z)Q, соответствующая Rt. Заметим, что xR^ отличается
от xR только тем, что одна нулевая координата заменена единич-
ной, т. е. вершины xR* и xR—ближайшие; отсюда следует, что
R<R19 т. е. R} = R. Аналогичное рассуждение в случае удаления
одной конъюнкции завершает доказательство.
Утверждение 2 аналогично части 2 теоремы 2.1 для функций
выбора.
Пусть — произвольное отношение. Положим
' и Ш)^о},
ИхЧЛЖ-Ч и A(PZ) = 1}.
Обозначим через R~ отношение, у которого а через
7?+—отношение, у которого = Ясно, что для любого
§ 3. НЕОБХОДИМЫЕ И ДОСТАТОЧНЫЕ УСЛОВИЯ НА ЛФо
93
имеет место 7?“<7?</?+, т. е. тем‘самым доказана
справедливость следующего утверждения.
УтверждениеЗ. Единственным минимумом по отношению <
на множестве является R~. Единственным максимумом яв-
ляется R+.
Заметим, что выбор по /?+ из любого Q^Em (|Q|> 1) пуст
(QR+=0), так как в соответствии с определением R+ yR+x
для всех <//,%>€ Ет, У¥=х. Выбор по R~ из любых
совпадает с Q (Q/?_ = Q).
Назовем максимальной любую цепочку вида R~ = R° < R1 <...
.. .< Rh= R+, в которой любые два соседних по цепочке отно-
шения являются ближайшими. Из утверждений 1 и 2 следует, что
каждой максимальной цепочке можно сопоставить путь
S = <xR“, ...,гх*+> по вершинам D®, где хл- = <0, ...,'0>,
х,?+==<1, ..., 1>, и среди координат каждой последующей вер-
шины ровно на одну единицу больше, чем у предыдущей. Отсюда
непосредственно получаем следующее утверждение.
Утверждение 4. Длина' h любой максимальной цепочки
равна Q 4-1=3"".
Если вершине <0, ...,0> сопоставить отношение R~, а вер-
шине <1, ...., 1>—отношение R+ и рассмотреть путь из <0, ..., 0>
в <1, ..., 1> по вершинам куба, то пути минимальной длины со-
ответствует максимальная цепочка вложенных отношений (это
аналогично части 1 теоремы 2.1).
Рассмотрим теперь подкласс 3Cg координатных отношений (бу-
дем называть их главными), у которых при I=£J. От-
ношения R класса ^g характеризуются тем, что если у пары
точек <х, уу значения хотя бы одной координаты совпадают, то
эта пара не принадлежит R. Класс отношений используется
при решении задачи оценки мощности множества (глава II.5).
На класс 3£g переносятся все определения и утверждения на-
стоящего параграфа: устанавливается взаимно однозначное соот-
ветствие между Wg и вершинами Q-мерного единичного куба, где
Q = 2”. Каждой максимальной цепочке отношений*из (т. е.
... < 7?^) соответствует последовательность вершин xR* ,
..., xRe t т. е. путь по вершинам куба DQ. _
Упражнение 6. Построить единичный куб DQ, ^соответст-
вующий классу 3£g на Ег.
§ 3. Необходимые и достаточные условия на ЛФО >
для основных свойств бинарных отношений
В предыдущем параграфе установлено, что отношение R реф-
лексивно тогда и только тогда, когда f0 — 1; отношение R анти-
рефлексивно тогда и только тогда, когда f0 = O. Сформулируем
90
ГЛ. 4. КООРДИНАТНЫЕ ОТНОШЕНИЯ
условия симметричности, антисимметричности, асимметричности
в виде следующего утверждения.
Утверждение 5. Произвольное координатное отношение R
1) симметрично €{/}) [f7(P/) = /f (Р/)]1
2) антисимметрично Ф> [ff (0Z) = /f (0Z) = 1] => [/ = 0];
3) асимметрично Ф> (V/ £ {J}) (р,) = 1 => (0Z) = 0].
Упражнение 7. Доказать утверждение 5.
Несколько сложнее условия ацикличности и транзитивности.
Сформулируем условие ацикличности:
(A)(W£{J}) [3i€/] такое, что (V/'s_/1 i £/') [^(₽г) =
= ₽<Л£(Р/'м)] или (yr<=i\ien [MM=IW(IW].
Обозначим через множество всех ацикличных координатных
отношений.
Теорема 1. R£WA тогда и только тогда, когда ЛФ0(Я)
удовлетворяет условию (А).
Доказательство. Необходимость. Пусть R£XA.
Предположим, что условие (А) не выполнено. Это значит, что
найдется I £{J} такое, что для любого i С / найдется Г = /, для
которого i£ /' и
MM^P.Ag'OW, (10)
и найдется Г'^1, для которого i^T и
А£"(Р/"м). (Юа)
Если//-(Р/<) = 0, то очевидно, что fr (P/') = Pz Л 0, поэтому
(10) не выполнено. Аналогично,/у» (р/»)^0. Таким образом, можно
найти наборы переменных
Р' = <р;1,...,р1>, р"=<р;-,...,р;г>
(r={ilt ...,u, r=u. •••./;})
такие, что (P') = /r (Р") = 1 и рг = р'у, т. е. i-я переменная pz
входит в эти два набора с противоположными значениями. Ана-
логичные пары наборов построим для всех i £ / и выпишем их
подряд:
P1 = <P^,...,ph>,...>Pi = <P^,...,P^>.
Напомним, что по построению этих наборов
/jf(P9=i (Л = {/(, (П>
и для любого i С / переменная pz входит по крайней мере в два
набора с противоположными значениями. Пусть dz—число набо-
ров, в которых If — число наборов, в которых pz = 0. По-
§ 3. НЕОБХОДИМЫЕ И ДОСТАТОЧНЫЕ УСЛОВИЯ НА ЛФО
91
ложим ut — l/dh Vi = l/li и определим последовательность точек
из Ет:
^ = <0, ..0>;
/7^ + 1 _—
ai —
га1 + и{, еслц Р,- входит в t-й набор со значением 1,
а\—vit если pf входит в t-й набор со значением 0, (12)
a*t, если р,- не входит в t-й набор.
Таким образом, построена L-г 1 точка. Докажем, что aL+l = a1.
Действительно, к i-й координате dt раз прибавилась величина l/d(
и раз отнялась величина \/lh откуда af-+1 = а\. Заметим также,
что в силу (12)
sgn(a|+1—а^= <
0, если i-я переменная не входит
в набор р*,
1, если Р* — 1,
— 1, если р£ = 0.
(13)
Из (13), (11) ^определения координатного отношения получаем
af+W (/=I7Z);
вместе с условием aL+1 = a1 это означает, что построен цикл, что
противоречит ацикличности отношения R. Поэтому условие (А)
выполняется. ___
Достаточность. Пусть а0, а1,.. .,aL£Em, asRas~l (s= 1, L),
и пусть выполнено условие (А). Докажем, что а£#=а°. Положим
It={i /== U Is.
s= 1
Пусть (А) выполнено для i*£l и для всех Г е I таких, что
1* G справедливо fr (р/-) — р(-* Д £(Рг\;*). Если i*(£Is, то по
построению Is имеем
asi* = asi;1-, (14)
если I* б Л, то по условию (А) и в силу того, что по-
лучаем
М(Рл) = Р»* Л g(P/,\<») = 1»
откуда р,« = 1, или в силу (3)
а}, > afc1. (15)
Так как i* £ I, то по построению 1 найдется хотя бы одно s
такое, что i*£ls, для которого, следовательно, выполнено (15).
Поэтому из (14) и (15) получаем, что af» > а?«, т. е. а£#=а°.
Аналогичные рассуждения можно провести, когда в условии (А)
в качестве множителя выносится не Р,-., а р,.. Теорема доказана.
92
ГЛ. 4. КООРДИНАТНЫЕ^ОТНОШЕНИЯ
Для дальнейшего изложения введем дополнительные обозначе-
ния и понятия. Пусть заданы две конъюнкции: Р^Л-.-ЛР^ и
ч
Р-/‘ л ... Л'Р% и индекс k е {ч, .... Л {/i, ...» /т}. Будем го-
ворить, что pft входит в указанные конъюнкции с одинаковыми
(противоположными) знаками тогда и только тогда, когда суще-
ствуют sg{l, .. .,J} и t С{1, ..., т} такие, что 1) is = jt = k;
2) = %
Пусть заданы две функции:
о
К (₽/.. • • •. Рл)=Р^ л... л р.ч h (Рл, . ., P/J=Р> Л • • • Лр^
r lPd '«Г
и индекс ke{ii, • • - , iz}n{/i, • • •, jm}.
' Будем говорить, что pft входит согласованно в и f2 тогда и
только тогда, когда существуют s £ {1, ..., d} и t С {1, ..., г} та-
кие, что 1) iPs — i4j~ k\ 2) ; в противном случае бу-
дем говорить, что pft входит несогласованно.
Заметим, что в конъюнкции функций Д и /2 могут входить не
все переменные; в связи с этим pft входит несогласованно в Д и f2
в следующих двух случаях:
1 . k(£(ipt, • • • , ip^} Л {/9l, • , jqr}-
2 . k£{ipt, . . ., ip^f Л{/?,, . jqr}, HO Pfc входит в конъюнкции
с противоположными знаками.
Пусть Zn /2 G {/}; положим I — I /2, I' — Ii Л Ц, I"={k(z Г |pfc
входит в f z, (Рг,) и /z2(Pz2) несогласованно}, /4 = /\/, где ZsZ".
Сформулируем следующие условия:
(Tl) (V/<j{J}0) [fz(Pz) А • • • АРА ({ilf /)];
(Т2) (V/j, I2^{J}0, VI) [множество Zd(£{J}„, и при Г\1
ни одна из переменных pft не входит в конъюнкцию fid(-)]\
(ТЗ) (У7Ъ I9${J}0, Vf<=I", Vk£l'\I") [переменная pft либо
не входит в конъюнкцию ft , либо входит в нее с тем же знаком,
что в fz, И fzj;
(Т4а) s (VI = I",Vk^Id\k£ /х\/2, pft входит в конъюнкцию fi )
[Pft_входит в конъюнкцию fz, с тем же знаком, что и в fzd];
(Т4б) аналогично (Т4а), с заменой It на /2.
Обозначим через множество транзитивных отношений.
Теорема 2. R^'Xt тогда и только “тогда, когда ЛФО(К)
удовлетворяет условиям (Т1)—(Т4).
Доказательство. Необходимость. 1. Пусть
J^{J}0. Докажем, что для J выполнено (Т1).' Пусть аг = <а1, ...
§3. НЕОБХОДИМЫЕ И ДОСТАТОЧНЫЕ УСЛОВИЯ НА ЛФО 9$
а^>, а2 = <aj, ..., am> таковы, что fj (a1) = fj (a2) = 1 и a}^a?.
Положим a3 = <af, aj, ..., aj,>, a4 = <a}, af, ..., a^>. Докажем, чта
/>’)=М«‘)=1.
(16}
Пусть a1 g Em\ определим о2, a3:
f 1, если a| = 1,
a2—а\ = { , , n
( —1, если a*=0
( 0,1, если a2=l,
af—a2 = < . , , л
I —0,1, если a2 = 0
( 3, если al — 1,
1 1 I —3, если al — 0.
(i = 1, m);
(i = 2, tri)',
(17}
В силу (17) a2 A? a1 и a3/?a2; в силу транзитивности a3Ra1. Из (17)
ясно, что а (а3, а1) = а3, откуда f7(a3) = l. Аналогично доказы-
вается, что fj(a4)=l. Такую же конструкцию можно построить
для любого i такого, что a*#=a2. Таким образом, J разбивается
на /+ и 1~ такие, что
(Vi£/+)
(¥« = <«!, ...,az, ...,am>), либо |/,(a)= 1 =>az= 1],
либо [/j (a) = 1 => a(- = 0]^
(3a1 = <aj, ..., a1, ..., a2 = <ab ..., a^>
такие, что /J(a1) = f7(a2) = 1 и a|=#=a(|.
В СДНФ функции fy(₽) любая элементарная конъюнкция мо-
жет быть записана в виде
<18>
причем в силу (16) и определения 1~ вместе с любым членом
вида (18) присутствует член
( А А ( А ,
\ е/+ j Viet- 1 J
где o = <ctZi, ...,ог,г>—произвольный набор нулей и единиц.
— .... tj). Отсюда следует, что
7/(Р)= А 0Г‘.
iei+
Аналогично доказывается, что (Т1) выполнено для V/
2. Обозначим
Ei = {<x, у>}еЕтхЕт\х^у( (1^7), Х(=*у[ (1$/)}-
94
ГЛ. 4. КООРДИНАТНЫЕ ОТНОШЕНИЯ
Пусть 7Х, Определим а1, а2, а3£Ет так, чтобы
<а2, 4>СБ/(, <а3)а2>€Б/„ a2Ra\ a3Ra2,
I 4—4 | = | a9—4 |, sgn (a3—a2) = — sgn (a2—a}) (s £ I), (19)
I a?—af |#=|4—4I (t(£7).
В силу (19) <a3, и no условию a3Ra1, t. e.
Ясно также, что знак разности а3к—ак, где k£l"\i, может быть
выбран любым, откуда следует, что не входит в конъюнкцию
'’’Условие (Т2) доказано.
^ГЗ. Пусть входит^с отрицанием, ав/л(рл)Иу/г(р/а)—
без .отрицания. Из a2Ra2 следует, что4 > ак, иза3/?а2—что4>4-
Поэтому ак > а\, откуда в силу предположения имеем a3 Rd, что
противоречит транзитивности. (ТЗ) доказано.
4. Пусть
<a2, a1>C£'z1, <a3, a2> Е Д/2, <a3, ax>€.Eid, a^Ra1, a3Ra2, a3Ra1.
По” условию a3k — al, ak^=ak иsgn(4—*4) определена однозначно.
Легко видеть, что sgn (4—ак) = sgn (4—4) для любой пары
<а2, 4> £Zi такой, что a2Ra1, откуда и следует (Т4а); (Т4б) до-
казывается аналогично.
Достаточность. Пусть а1, а2, а3 £Ет, a2Ra1, a3Ra2. Оче-
видно, что <а3, d^y^Ei для некоторого I = В силу (Т2) !<$.
f£{7}0; (П) означает, что является конъюнкцией; если
то в силу (Т2) не|входит'в конъюнкциюhd($/d)- Для
Ук£1'\Г в случае, если входит в hd(fiid), в силу (ТЗ)’и оп-
ределения согласованности получаем
sgn (4—4) = sgnj(4—4)=sgn (4—4).
•откуда следует, что значение переменной равно 1 (так как
a3Rd и a3Ra2). В случае k^Ilf или k£/lt к^/2 также
получаем, что p£ft=l (в силу (Т4а) или (Т4б)). |Таким образом,
для^любой переменной p£ft, входящей в конъюнкцию fid(fiid), вы-
полнено Р°*=1, ^откуда следует, что f/d(₽/d)=l. т- je- a3 Rd-.
"Теорема доказана.
Пример 7. Пусть отношение R на Е3 задано следующим
образом:
.xRy^^ > у„ хг > уг, х3 > у3], или [Xj > ylt х3^у2, х3 = у3],
или [Х1 = У1, Хг>у2, х3=/=у3], или [хг =/=(/!, х2 = у2, х3 > t/3],
или [х, >у{, Xj = y}- i=l,3)].
§3. НЕОБХОДИМЫЕ И ДОСТАТОЧНЫЕ УСЛОВИЯ НА ЛФО
95*
ЛФО(7?) имеет вид
Z1W (01 > 02, 0з) = Р10203 > /12 (01 > 0г)=01> /13 (0И 0з)=03,
/23 (02, 0з) = 02, Л(0,)=0,- (i = T73).
Из теоремы 1 следует, что 7? не ациклично, так как условие (А)>
не выполняется для / = {1, 2, 3}; 7? не транзитивно, так как для
/х = {1, 2, 3} и /2 = {1, 2} не выполняется (Т2) (теорема 2).
Пример 8. Отношение 7? на Ег задано следующим образом:
xRy^lx^yr, ха>у2],
ИЛИ [%!> ylt Х2 = у2], ИЛИ [х1 = у1, х2 < у2].
ЛФО(7?) имеет вид
/12 (01, 02) =0102, /1(01)=01, /2(02) = 02-
Условие (А) выполняется для / = {1,2} и i* = 1 (для остальных /
его выполнение очевидно). Поэтому R ациклично, но в силу (Т3)<
не транзитивно.
Пример 9. Отношение R на Е3 задается следующим образом':.
xRy [Xj ~^> ylt х2 у3, х3 Уз], или [Хц уц х2 = у2, > Уз],
или [х1>у1, х2>у2, Хз = Уз], или [Х1 = У1, Х2>у2, х3<у8],
или [х1>у1, х2 = уа, х3 = у3], или [х1 = у1, х2>у2, Х3 = у3]..
ЛФО(7?) имеет вид
/123 (01, 02, 0з) = 01, /13 (01, 0з)=0103, /12 (01, 0г) = 0102,
/аз (02» 0з) = 020з, /1(01) = 01, /г (0г) = 02, /з(0з) = О.
Из теорем 1 и 2 следует, что R ациклично и транзитивно.
Упражнение 8. Установить, воспользовавшись необходи-
мыми и достаточными условиями на ЛФО, свойства отношений
Р и L.
Упражнение 9. Показать при помощи ЛФО, что отноше-
ния Dk и V ацикличны и не транзитивны, а М не транзитивно
и не ациклично.
Условия ацикличности и транзитивности значительно упро-
щаются для R £ 9Cg:
(Аг): Ш) = 0?'-АФ(0/м);
(Тг): fAM-^V
Упражнение 10. Доказать справедливость (Аг) и (Tg).
В утверждении 5 и теоремах 1 и 2 содержатся необходимые-
и достаточные условия, при которых отношения обладают пере-
численными в них свойствами. Это позволяет строить координат-
ные отношения с любым заданным набором свойств. Знание
96 ГЛ. 4. КООРДИНАТНЫЕ ОТНОШЕНИЯ
структуры множества координатных отношений позволяет построить
отношение с желаемым набором свойств, в том или ином смысле
ближайшее к заданному.
§ 4. Свойства некоторых классов координатных отношений
В главе 3 введено понятие рациональности отношения. Отно-
шение 7? названо рациональным, если в него вложено отношение
Парето, т. е. Р,<₽. Применим понятие рациональности к коор-
динатным отношениям f Р € ЭС. Обозначим класс координатных
рациональных отношений через 9^г.
Примерами рациональных координатных отношений являются
отношение лексикографии и отношение Парето.
Упражнение 11. Установить, являются ли рациональными
отношения V и Dk (см. примеры 3 и 4).
Таким образом, если рассматривать задачу выбора из мно-
жества Q как задачу выделения множества то для рацио-
нальных отношений 0й всегда содержится в множестве Q₽.
Упражнение 12. Верно ли, что для рациональных отно-
шений (Q₽)/? = Q/??
Будем говорить, что х лучше у по i-й оси Ет, и писать хЕ^у,
если fi($t(x, у)) = 1 (fi (Р()—член ЛФО, отвечающий / = {i}).
Введем класс отношений, который связан с рациональными
отношениями. Отношение R назовем уномонотонным, если xRy—>
Класс таких отношений обозначим через 3fy.
Таким образом, уномонотонное отношение R гарантирует, что
если xRy, то альтернатива х хотя бы по одной оси лучше аль-
тернативы у. Очевидно, что любое рациональное отношение яв-
ляется уномонотонным.
Упражнение 13. Привести пример координатного уномо-
нотонного, но не рационального отношения.
Отношение R назовем значимым, если {7}в = 0. Класс таких
отношений обозначим через Ws.
Напомним, что {J}0 = {/1f{(Ру) = 0}. Поэтому для значимых
отношений при любом I €(/} найдутся в Ет две альтернативы х,
у, отличающиеся только по координатам с номерами из /, такие,
что xRy. Нетрудно показать, что если координатное отношение R
транзитивно, то для значимости R достаточно, чтобы (Vi £ J)
[^ {/}.]•
Упражнение 14. Доказать, что если и (Vi t J)
[*<{/}.], то ReWs.
Введем понятие подобия отношений. Отношения Rt и У?2 по-
добны (Rx~ R2), если (37lg(J}) такое, что при замене рл на рл
Ф/x/., P/n/.) = f/2(P/Р/п'.) (20)
для всех /£{•/}.
§ 4. СВОЙСТВА КЛАССОВ КООРДИНАТНЫХ ОТНОШЕНИЙ
97
Заметим, что если R1~RS, то координаты точек ]xRi
(xR>, xR>^TD^—вершины (3“—1)-мерного куба) содержат
и XRt
оди-
наковое число единиц и, следовательно, точки находятся на оди-
наковом расстоянии от хл+ и xR~. Подобные отношения изо-
морфны.
Рассмотрим преобразование <р: Ет—>-Ет, определяемое^[сле-
дующим образом:
( X:, если i&L
Ф(х) = х,
V—xh если it?
(21)
Непосредственно из (21) получаем, что'из Ri~R2 следует, .
что xR±y ФФ <р (х) 7?2<р (у), т. е. все свойства и R2 совпадают
при преобразовании ф. Таким образом, понятие подобия отноше-
ний позволяет заменить одни отношения другими, более удобными
для исследования, с сохранением свойств исходных.
Будем обозначать = 5^,-Л (i, j = T, А, г, U, S).
Утверждение 6. Пусть R E^ts- Тогда любая переменная
входит во все конъюнкции с одним и тем же знаком.
Доказательство. Пусть 12^1г, входит в fIt и k£l2.
Тогда входит с тем же знаком в flt. Это непосредственно сле-
дует из (Т2) при 1 = 0. При l = {k}s Л, I = {k}^ I2 входит
в /Л и в fIt с тем же знаком, что и в fk=^k- Утверждение
доказано.
Следствие. Всякое значимое транзитивное отношение R
подобно значимому транзитивному [отношению R такому, что
ЛФО(К) состоит из конъюнкций без отрицаний.
Полученное следствие означает, что в данном случае для
изучения свойств всего класса отношений $?rs достаточно изу-
чить отношения R$.9€TS, в^ЛФО^которых все конъюнкции не
содержат отрицаний.
Назовем обобщенной лексикографией Е^,,'отношение,*Л ФО
которого задается формулой,
. Ж)=₽ГЛ г = min{/J i^I}. (22)
Пр.имер 10. Обобщенная лексикография опре-
деляется следующим образом:
х/. > ИЛИ fXg^Z/g, дли \x2==y2,^Xi=zyi,'^x2 > j/sj*
От обычного отношения лексикографии обобщенное отличается
тем, что понятие «лучше по Лй оси» может означать как больше,
так и меньше.
Рассмотрим сужение введенного на множестве отношения <
на классы УСц и
Утверждение ?. Любая миноранта на 3CTS по отношению
< подобна отношению Парето, а любая мажоранта на ЭСТЗ сов-
падает с некоторой обобщенной лексикографией.
4 Н. М. Макаров и др.
98
ГЛ. 4. КООРДИНАТНЫЕ ОТНОШЕНИЯ
Доказательство. 1. Пусть 7?—миноранта на 9£rs; ст,- —
тот знак, с которым переменная р,- входит во все конъюнкции
ЛФО(#) (см. утверждение 6). Положим
//*(₽/)= А И) (23)
16/
и определим # как отношение, ЛФО которого определяется фор-
мулой (23). Принадлежность R^k классу очевидна. Подо-
бие R с отношением Парето задается множеством /1 = {i|o( = l).
Докажем теперь, что R = R. Пусть xRy; пара <х, у> принадле-
жит Е[ для некоторого I. Это значит, что A Р®' (х, J/)=l. Сле-
/е/
довательно, /7(Р;) = A (х, w)=l, т. е. xRy. Тем самым
доказано, что R < R и в силу того, что R—миноранта, R = R.
2. Пусть R—мажоранта на WTS. По теореме 2 fj(PJ =
= А Выберем произвольно и положим J1 = J\i1,
S€
G1 = oii. Пусть fji(p,)= д р°\ Выберем произвольное i2fzJ*
и положим o2 — о(-з, J2 = J1\i2. Продолжая этот процесс, опре-
делим i3, о3, ..., i„„ <jm и обобщенную лексикографию R =
__т <ai> •••> От>
— ^<4, .... im> *
Докажем, что R < R. Пусть xRy. В силу транзитивности^#
имеем Р": А ••• А Р«*= 1, где {qx, ..., qs} = J. Пусть r=min {р | tp €
• ••» ?s}}. [Тогда xip = yip (p < г), поэтому xRy. В силу
того, что R— -мажоранта, имеем # = #. Утверждение доказано.
Упражнение 15. Сформулировать и доказать аналог утверж-
дения 7 для класса 3^т.
Сформулируем одно свойство ЛФО рациональных отношений.
Утверждение 8. R€%°r&(VI €{J}) р(Р/)= A^P/VfifAP/)].
Утверждение 8 является очевидным следствием утверждения 1.
Следствием же утверждения 8 является равенство =
Далее рассмотрим свойства ацикличных отношений.
Утверждение 9. 'WASU = 'XAS.
Упражнение 16. Доказать утверждение *9.
Утверждение 9 означает, что всякое значимое ацикличное
отношение уномонотонно: если R С З1^as, то для любой пары <х, у>
такой, что xRy, найдется ось Ет, по которой х лучше, чем у.
Остановимся подробнее на некоторых следствиях из теоремы 1.
Пусть R£9CA. Применим к функции />(РУ) условие (А). Одна
переменная обязательно «вынесется»:
Zj(P/) = P?Agi(P/xh). (24)
§4. СВОЙСТВА КЛАССОВ КООРДИНАТНЫХ ОТНОШЕНИЙ
99
Аналогично, положим /1==^\А и
л,(₽л)=р’.‘а^(Ра^)- •••>Ч(Ч)=р?++11Л^+1^‘>+1)’ •••
(25)
Продолжая эти построения, находим последовательность ilt сц, ...
..im, от и соответствующее отношение обобщенной лексикографии
L^’, im> • Заметим сразу, что последовательность fy, ..., г’™™ по
отношению R определяется неоднозначно.
любую последовательность <7‘, ..., построенную по фор-
мулам (24), (25), назовем"'мажорирующей последовательностью
ацикличного отношения R и обозначим через обобщен-
ную лексикографию обозначим через Л(<1^>(/?)).
Смысл определяемого термина связан со следующим свойством.
Утверждение 10. Для любого ацикличного отношения R
и любой® мажорирующей последовательности <iss>(R)
lRl<L«iass>(R))-
Док азател ь’ство. Пусть xRy. Это значит,^что [для неко-
торого / <х, y>^Ej. Положим]
.- = inin‘{p'|ip€/}. (26)
В’силу (26) xi =yi (р = 1, г— 1)Т(напомним, что <7*, ..., 1°т>\—
мажорирующая R последовательность). Ясно также, что
(здесь J0 = J). Поскольку 01г—переменная, которая «выносится»,
то в силу условия (А) из xRy следует, что pf/ (х,гр) = 1. Это
значит, что xL (<№> (/?)) у. Утверждение доказано.
Следствие. Любая мажоранта на 3£А по отношению <
совпадает с некоторой обобщенной лексикографией.
Положим
Qkp=Ix|x£Q, (3tgJ) Гх;£ fmax’x,-, minx,-
I L ) q 4 a
Множество йкр назовем множеством крайних элементов.
Утверждение И. Пусть R^.'Xa u йр = {х*}.
Тогда х*£йкр.
Доказательство. Определим мажорирующую последова-
тельность <iss>(7?). Положим fe = min{s|(3x, y^Q) [х^ =#yts]}-
Пусть х1 £й, х1 #=х*. Тогда существует последовательность х1, . . .
..., xL = x* такая, что xi+1Rx‘ (i=l, L—1). Если xjA1 #=X;ft, то
в силу выбора k имеем х^^—х^ (s < &), и поэтому из ху1 + 7?х/
следует, что
х'Д1— х£ > 0, если <yk — 0,
? к (27)
X;*1 — x’ik < 0, если 0к = 1
4 И. М. .Макаров и др.
100
ГЛ. 4. КООРДИНАТНЫЕ ОТНОШЕНИЯ
(по построению <is/>(₽))- Из (27) [получаем, ^что х\к^х^
х*й). В силу произвольности х1 это доказывает утверждение.
Отсюда ясно, что если выбор по ацикличному отношению из Q
состоит из единственного элемента, то оценка этого элемента
экстремальна хотя бы по одной оси Ет.
Остановимся еще на одном свойстве ацикличных координат-
ных отношений.
Утверждение 12. Любое R^'KA нестрого Х-отделимо.
Упражнение 17. Доказать утверждение 12.
Пример, приведенный перед доказательством теоремы 3.3, ука-
зывал на то, что из нестрогой /.-отделимости не обязательно сле-
дует отделимость. Однако для координатных отношений имеет
место .
Теорема 3. Пусть R£9CA. Вектор К£Ет, определяемый
формулой
Xb = 7,3(ra-s>(1._2CTj (s=i77n), .(28)
где <iss> = <iss>(R)—любая мажорирующая последовательность,
Т= maxmax max max ( ai~b,1-1, rn], (29)
a.beD i k : | ak-bk |#= 0 \l ak~bk I /
удовлетворяет условию отделимости (3.12) на конечном мно*
жестве Q.
Доказательство. Пусть а, & £ Q. Положим I — {i | at =/= 6,},
^=min{s|i^C !} Так как />(0Z) = P“* Л g(₽/\ife), то из aRb сле-
дует, что
Ч) = _2стй+1» ah—= O (S< k).
Поэтому
(X, a) — (X, 6) =
fc- 1 *n
= S К (ais—bis) 4- X(fe (Oik—bik) + jy; X,, (ais—blf) >
-bib!- J T“m-^\ais-bls\>
' K al s=fe+l
Приведенная цепочка соотношений доказывает теорему.
§5. ИЕРАРХИЧЕСКИЕ ОТНОШЕНИЯ
101
§ 5. Иерархические отношения
Введем необходимые формальные понятия. Пусть fV— <3^J, ...
..., —семейство вложенных разбиений множества </={ 1, ..., т}:
Xsг= , Ksls>, U 'Kf=J, Ksi п К/= 0 (< ¥= /), S=Г,7.
/=lj
Вложенность означает, что любой элемент разбиения s-ro уровня,
т. е. множество К/, является объединением нес кольких множеств
К/Г*» ••••К-"1 (s—1)'го Уровня. Введем обозначение К*<->
ip U
«-НКГ1, ..., КГг>, если Ks= U КГ1; положим /(К9) =4. Будем
i= 1
считать, что ЗТ''₽<{1, ..., т}>, т. е. разбиение верхнего уровня
состоит из одного множества J. ____
С каждым элементом разбиения К} (se=2, г) свяжем функ-
цию //(«j, ..., гДе «,€{0, 1» —1}- С каждым элемен-
том К1 1-го уровня свяжем бинарное отношение (не обяза-
тельно координатное) на подпространстве EKi пространства Ет,
порождением координатными осями с номерами & такими, что
{i[, ..., 1₽у}в=К}. Введенные понятия позволяют задать 'отноше-
ние R на Ет, зависящее от семейства разбиений X и связанных
с ним семейств функций {/)} и отношений {К,-}. Для этого пред-
лагается следующая конструкция.
Пусть К*’*-; <К}, ...» К)>. Определим отношение К; на EKi по
формулам (при />1) 1
(30)
1 1 1, если КЗ
1, если (31)
0, если хк}~Ук-
(Здесь ь далее ак&—проекция а на подпространство Еку) При
I е= 1 положим К’ == Rj. Если уже определены все отношения! Ks-J
(s—1)-го уровня, то отношения! R* s-ro уровня при /> 1 опре-
деляются следующим^ [формулами: если K®*-*<Ki-l>
Л ....а,) »= 1(32)
та. 1 11
S-1,
’ 1, если
а.₽=/ —1, если x^-iKr’^s-i,
О, если xKs-i«= yKs~i.
(33)
102
ГЛ. 4. КООРДИНАТНЫЕ ОТНОШЕНИЯ
Если то Отношение R по построению сов-
падает с Rr— единственным отношением r-го верхнего уровня.
Отношение R, определенное по семейству разбиений 3^ и по
связанным с ним семействам функций {f}} и отношений
формулами (30)—(33), назовем иерархическим отношением.
Пример 11. Пусть /п = 6. Рассмотрим семейство разбиений
g£: 3i*i = <{l, 2, 3}, {4, 5}, |6}>, g^2 = <J>. Соответствующий граф
показан на рис. 4. Положим R^P, R2 = L, RS = P,
1, если 1 (t = l, 3), /д..
0 в остальных случаях.
Зададим иерархическое отношение ^формулами (30) — (33);
легко видеть, что
xRtfc* [xt > у{ (i =# 4, 5), xt > у<\,
или (i#<4, 5), х4=у4 и х5>у6].
Л (а1( а2, а8) =
Общая формула^для ЛФО иерархических отношений будет
приведена ниже.
Заметим, что все* отношения Rs s-ro уровня (s = 2, г) также
являются иерархическими. Если функция fs(аь ...,аг) задает
12 3 « 5 з в Et отношение Парето (лек-
\ Т / \ / / сикографии, V и т. д.), то от-
\ / с\/ р/ ношение Rs будем называть
X. У иерархическим отношением Па-
рето {лексикографии, V и т. д.).
Смысл введенного понятия со-
стоит в том, что оно позволяет
Рис 4 по отношениям, заданным в не-
пересекающихся подпростран-
ствах Ek {k < т) строить резуль-
тирующее отношение на всем; пространстве Ет.
Дадим рекуррентные правила построения ЛФО(Л?). Для этого
нам понадобится
Утверждение* 13. Иерархическое отношение является коор-
динатным, если все отношения Rj нижнего уровня координатные.
Доказательство. Координатнссть отношений R} второго
уровня следует из формул (30), (31) и определения координат-
ного отношения. Координатность иерархического отношения R}
любого уровня при s > 2 следует из формул (32), (33). При s=r
получаем, что иерархическое отношение R, совпадающее с Rr,
является координатным. Утверждение доказано.
Определим ЛФ0(А?5), заданного на E«s, через ЛФО(7?;-1), за-
данных на EKs-i, где /ОПусть l^Ks. Положим
(35)
Л(Р/) = ^(а1> (36)
§ 5. ИЕРАРХИЧЕСКИЕ ОТНОШЕНИЯ
103
где
I 2<pgs-i(PBs-i)—1, если
1 0, если В*г\= 0,
(37)
и Фв?-1(₽3?-1)-членЗЛФО;(/?Г). В случае /=1 Л ФО (/?') =
=ЛФО(7?5-1); ЛФО (Я) определяется при последовательном при-
менении формул (35)—(37).
Утверждение 14. Иерархическое отношение, у которого
все определяющие его отношения, начиная со 2-го уровня, явля-
ются иерархическими отношениями Парето или лексикографии,
а отношения 1-го уровня являются отношениями частичного по-
рядка, является отношением частичного порядка.
Доказательство. Пусть s = 2, a,b,c£EKs, aRsb, bRsc.
Докажем, что aRsc. Пусть Rs—иерархическое отношение Парето.
Тогда из aRsb следует, что либо a^s-iR^b^-i, либо a„s-i=5„s-t
(1 = 1, l). Аналогично, либо либо &KS-1 = CKS-J
(i=l, l}. Но тогда, поскольку J?)-;1—отношения^частичного по-
рядка, получаем [либо a^s-iR^c^-i, либо a^s-i=cKs-i (i — 1, /)
и в силу (32) и (33) aRsc, т
рядка. Доказательство для
Rs в случае иерархического
отношения лексикографии
аналогично. Положив после-
довательно s = 2, 3....г и
повторяя проведенные рас-
суждения, получим, что R —
отношение частичного поряд-
ка. Утверждение доказано.
Пример 12. Построим
иерархическое отношение R
е. Rs—отношение частичного по-
по информации, получаемой
от ЛПР. Пусть имеются девять критериев klt ..., k3 и от ЛПР
получена информация о том, что критерий kY важнее k3, критерии
&3, k3 лексикографически упорядочены; ke важнее k4\ относи-
тельно kg и kt ничего не известно. Отсюда
ЗГ = <{1, 2}, {3, 4, 5}, {6, 7}, {8, 9}>.
Информацию^} важности критериев опишем в виде
Ri = L, R3 = L, R3 = L, Rt = P.
Пусть имеется дополнительная информация о взаимосвязи
критериев: группа критериев {klt k3} важнее группы {k3, k3, k3}-,
остальные две группы равноценны. Отсюда 9£2 = <{1, 2, 3, 4, 5},
{6, 7, 8, 9}>; RI—иерархическое отношение лексикографии; —
104 . Е ГЛ. 4. КООРДИНАТНЫЕ ОТНОШЕНИЯ
иерархическое отношение Парато. Обе группы критериев из 3£4
равноценны. На основе этой информации построим дерево иерар-
хического отношения (рис. 5). Пэ формулам (35)—(37) ]можяо
построить ЛФЭ(Я). ^Главный член его .имеет вид
(PjWiAP.APeAP*. .
J§ в. Квазикоординатные отношения^
Пусть /?ь ..., —произвольные бинарные отношения на
Q1, ..., £2Я соответственно. Любой элемент х из Q=»QLx ...
имеет вид х=а<хь ..., хет>, где Рассмотрим два элемента
х, и положим ’
Г-'.J
У) =»<<(*!. У1)’ •••» аЛ*т. Ут»Л
—1,
если XtRiyt,
если Xi=»yt и х^гу{,
если '^'у(- и X RM
(38)
£(39)
Запись xt=»yi означает, что х{ и у{ являются’одним и тем
же ’элементам множества Qz. ____
Упражнение 18. Пусть |Qz|=aNt (i=al, т). Чему равно |Q |?
т
Рассмотрим некоторое бинарное отношение R на й=» [TQZ.
i=lj
Отношение R назовем квазикоэрданатным, если
[х](хг, yx)=*z(x\ y2)]^[x1Ryci^\x2Ryi], (40)
Класс квазикоординатных отношений обозначим через 'УСУ*.
Пример 13. Пусть Пг=аЕ1 (i=»l, /п); отношения 2?z—отно-
шение «больше» на (xz/?zy{ xt > у;). При этом Q=aQrx...
... и из формул (33) —(40) следует, что квазикоорди-
натное отношение на £2. является координатным отношением.
Таким образом, введенное понятие является обобщением понятия
координатного ‘отношения.
, Пусть ^заданы бинарные отношения <_Rlt Qx>, ..., </?„,
и функция Г(аъ ...,ада) со значениями из множества {0, 1}
от т трехзначных переменных (az£{—1, 0, 1}). Им можно со-
поставить квазикоординатное отношение R^aRlR^ ..., Rm-, F)
tn
на Й = Цй( по формуле
BfixRy «Ф F (ax (xx, Pi), , <xa (xm, ym)) =□ 1, (41)
где az(xz, yt) определяются по формуле (39). Возникает вопрос —
можно ли любое квазикоординатное отношение представить в виде
R^R(Rlt Ra\ F)f
S[6.| КВАЗИКООРДИНАТ НЬ!Е; ОТНОШЕНИЯ “ ПО®
Утверждение 15. Пуеть{ задень: Синорнье сггнсиения
_ т ~
<Rit й,-> (i*= 1, tn) и кеагиксординаггнсе ыгнсшение R на Qr=ljQf.
1=1
Тогда существует функция F(alt ..., am) (а,£{0, 1, —1}) со зна-
чениями в {0, 1}, для- кстсрсй сь полнено ссстнсшение (41).
Доказательство. Пусть ав<ап ..., аи>, afg{0, 1, —1},
j wTTw. Для каждого а возможен один из двух следующих случаев:
1 .[Для любого i«=l,/n найдется пара точек’ х{, Ц-таких,
что
J(42)
где a-i (xh yt) определяется по' формуле (39).
2 . Существуют i £ {1, ..., т} такие, что 'не найдется 1 пары
точек xh у{, для которых выполнено' (42). i*'
Разделим все наборы ав=<а3, ..., аге> на два класса’Л/и
те, для которых выполняется случай 1, и те, для которых'выгсл-
няется случай’ 2. Для' всех c₽<aJ('.... o,„) гележгм’ £
{1, если 'xRy,
’ (43)
О в противном случае, '
где лв=<Х], ..., хт>, у*=<У1, ...,уту, xh у{ удовлетворяют (42)
F (a)«=F(alt ..., aj. Для всех а£«42 определим F(а) произ-
вольным образом. Из формул (40), (42) и (43) следует, что для
F(а1; ...,ав) выполнено (41). Утверждение доказано.
Из доказательства; утверждения 15 явствует, что фонкпия
F(ait ...,аи), удовлетворяющая соотношению (41), определяется,
вообще говоря, неоднозначно. Заметим, что в случае^ координат-
ных отношений задающая их функиия F (а„ ...,ато) определя-
лась однозначно. Каковы должны быть бинарные отношения
<Rh й,-> для того, чтобы функция F(«1( ...,аю), удовлетворяю-
щая (41), определялась однозначно?
Упражнение 19. Доказать, что функпияГ F (аи ..., аи),
удовлетворяющая (41), определяется однозначно тогда и только
тогда, когда для всех i «= 1, т одновременно выполнят тся следую-
щие три условия: а) Я,- не рефлексивно: б);'R,Л (Й5{\£Л ¥= 0;
в) Ftn(f 0-
Рассмотрим теперь случай ,когда й3, ..., конечные множе-
ства.; Пусть заданы бинарные отесп ения Rlt ..., Rm на й,'(7е= 1, т)
и функция F («з, ..., aw). Спределим формулой (41) бинарное
отношение R^(Rlt ..., Rm‘, F). Обозначим порожденною гм
нормальною функцию выбора через С в= С (/?n ...,Rm; F), aj функ-
ции выбора, верен денные Rj,— через! C. (R{). Пусть[ Ri, ..R„
таковы, что Cj (R{) ^=С{ (R^)’ (i'*= 1, ni). Есзникает [вопрос—будут
ли совпадать функции выбсра]С (RJt .. F) и C(Rj. ...,R^-,F)?
I
106
ГЛ. 4. КООРДИНАТНЫЕ ОТНОШЕНИЯ
Пример 14. Положим Qx={x}, Q2={x!, х2}. ТогдаЙ=й1хП2=
={<х, Xi>, <х, х2>}. Зададим бинарные отношения R2 и 7?)
графами Glt Gt и и2, показанными на рис. 6. Функцию F (аь а22
z зададим следующим образом:
* х2
Рис. 6.
бинарные отношения R2 и
функцию выбора на (см. i
бинарные отношения R и Ь
г(0, —1) = 1, г(0, 0) = 0,
Г(0, 1) = 0; (44)
на остальных наборах а = <ап а2>
пусть F(an а2) = 0. Заметим, что
R't определяют одну и ту же
абл. 2.1). Найдем по формуле (41)
' на Q. Из рис. 6 непосредственно
видно, что
«1 (х, х) = 0, а2 (хп Xi) = а2 (Xj, xj — 0,?
а2 (х2, х2) ®а2 (х2, х2) = 1, ос2 (х2, Xj)= а2 (х2, х^) == 1, (45)
<МХ1’ хз)=~1 > °£(xi > -ч) = 1 •
Положим t/i = <x, Xj>, г/2 = <х, х2>, й = {г/1, f/2). Из (44) и (45)
получим
F(a1(x, х), а2 (xn х2)) = F (а1 (х, х), а;(хь x1)) = F^(0, 0) = 0,
F (ах (х, х), а2 (х2, х2)) = F («J (х, х), а; (х2, х2)) = F (0, 1) = 0,
^(ajx, х), а2(х2, x1)) = F(a1(x, х), а2(х2, х1)) = Г(0,^—1) = I,
F (аг (х, х), a/(xn х2)) = F (0, — 1) = 1,
Л(а1(х» х), a2(Xj, х2)) = Г^(0, 1) = 0.
В соответствии с (41) имеем
У1%У1, У^Уг, У*КУ1, yiRy%, yiR’yi, УЛ’Уг, У^’Уъ уЛ'у*-
Графы G и G' отношений R и R' представлены на рис. 7. Ясно,
что С (/?)#=£(/?'). Таким обра- в ег
зом, пример 14 дает отрицатель- ____
ный ответ на поставленный выше , • •-*----•
вопрос. ---уу2 у’ Уг
Упражнение 20. Найти не- Рис 7
обходимые и достаточные условия
на функцию F для того,чтобы при любых Rt, ..., Rm и R[, ...,
Rm таких, что С(Rj) = C(R'i) C(Rlt..., Rm\ F) сов-
падало c C(Ri, . •Rm, F).
Упражнение 21. Найти необходимые'и достаточные усло-
вия на функцию F, для которой R (Rn ..., Rm-, F) транзитивно,
как только транзитивны Rt
Упражнение 22. Вопрос из упр. 21 для свойства ацик-
личности.
Итак, нормальную функцию выбора C(Rlt ..., Rm\ F), вообще
говоря, нельзя выразить через нормальные функции выбора С{ (Ri),
§6. КВАЗИКООРДИНАТНЫЕ ОТНОШЕНИЯ
107
так как она зависит от того, какие именно Rt среди всех отно-
шений с одной и той же функцией Ct(Rt) подставлены в фор-
мулы, определяющие C(Rlt ..., Rm', F). Это и показано в при-
мере 14.
Упражнен'ие223. Пусть |£2г| = ЛГ(. Чему равно общее ко-
т
личество различных квазикоординатных отношений на Й= П Q,-?
£ =:
Приведем еще один^пример квазикоординатных отношений.
? П р‘и м.е’Р 15. Пусть отношения е .
R± и Т?2 заданы графами Gx и G2, О
показанными на рис. 8. Построим ж,» •---**•
квазикоординатные отношения R*= х' 1 г
=R (Rt, R2; FJ и R* = R (Rlt R2; Ft), Рис. 8.
где Fx (ax, a2) и F2 (ax, a2) определя-
ются следующим образом:
Fx(ax, a2) =
F2 (CCX, =
I, если afb# —l для i £ {1, 2}
и <ax,ax>#=<0, 0>,
0 в остальных случаях;
l, если az=l для i С {I, 2},
0 в остальных случаях.
(46>
Пусть
И = Qx X й2 = {<Хх, УхУ, ^^х, УгУ> <.Хц> У1>1 УгУ}=
= {<ZX, Z2, zs, z4>}.
Найдем ; векторы a(zz, Zy) = <ax(z^, z}), a2(z|, zf)> для каждой
пары <z,-, zy>, имея в виду, что z} = xx, zf = yu ---,А = У^ Эти
векторы вместе со значе-
ниями функций Fx и Ft
на соответствующих набо-
рах приведены в табл. 2.
Графы G2 и G1, задающие
отношения и R1 на £2,,
приведены на рис. 9.
Отношение вида R =
=R(Ri, ..., Rm; F) назо-
вем F-произведением от-
Рис. 9.
ношений Ru ..., Rm", со-
ответствующий граф G = G(R) назовем F-произведением графов
( \ т F
G (Ri), ..., G (Rm) ( обозначается G = Ц G(-
\ i=i
В примере 14 G является F-произведением графов Gx и G2,
G'—F-произведением Gx и G2; в примере 15 G1 является Гх-произ~
ведением Gx и G2, G®—Г2-произведением Gx и G2.
108
гл.54. коэрдинатныв^отношения
Упражнение 24. Зависит ®ли F-произведение графов от
порядка сомножителей?
Упражнение 25. Найти Ft- и Fj-произведения графов Gt
и Gx из примера 15.
Т а б л'иц’а^З
*» / a, (z,, zy) а8 (Zp г.) Fi(at(«(4 Zy), a» (zz. Zy)) F»(at(zz, Zy), a«(zz. Zy))
►-* Н* 4—* 4—» 4* QO tO»— 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2, 1 2, 2 2, 3 2, 4 0 0 1 1 о о 0 0 0 1 0 0 1 1
3, 1 3, 2 3, 3 3, 4 1 1 0 0 1 1 1 1 1 1 1 1 1 1 1 1
4, 1 4, 2 4, 3 4, 4 1 1 0 0 —1 0 —1 0 0 1 0 0 1 1 0 0
Пусть Qz (i = 1, т)—конечные множества. Занумеруем их
элементы: Qz=a{xf...xfj. Рассмотрим случай, когда li=l1=sl
(i,/ = 1, т), т. е. |Qz|=a|Qy| (i, /=а1, т). Пусть заданы бинар-
ные отношения </?i, </?я, QM>; определим /?=а
= .... Rm\F).
т
Напомним, что диагональю прямого произведения Q=a ГГ Q;
t=i
называется множество . ..,Xi*>, ..., <х), . ..,х?*>.
Рассмотрим сужение отношения R(Rt, .Rm‘, F), заданного
на О, на диагональ = Пусть и, это значит, что
и=а<х), ..., х?*>, у=я<х), ..., х/1>, где i, / €{1, т}. Тогда
в силу (39) при всех s«l, т
если xs{R..xj, |
если i == / и х</?,х),
если i # / и tfRstf.
as (и, V) =а
0,
(47)
Заметим, что при и=£о в силу (47) а,(«, »)€{!> —1}.
ГЛ. 5. ДЕКОМПОЗИЦИЯ ФУНКЦИЙ ВЫБОРА'
:оэ
Зададим R на по формуле (41) с "учетом (47)Ти положим
Ж, ...,?J = F(2P1-1, ...Ж.-1).’ ”
Функцию f($lt назовем главным членом квазикоординат-
нога отношения R.
В дальнейшем нас будет интересовать случай, когда Q/=Q/=Q*
(i, /=1, т), т. е. бинарные j отношения /?,• заданы на одном и
том же множестве Q*. При этом диагональ прямого произве-
дения й = (□*)“ имеет вид {<хп х#>}, где
Q* = {Xi, ..х{}. Иными словами, ее можно отождествить с самим
множеством й*. Таким образом, приходим к следующему понятию.
Сужение отношения 7? = R(7?ъ ..., Rm-, F), где А?,- заданы
на одном й том же множестве й*, на диагональ (й*)т, отождеств-
ляемую с £2*, назовем'F-суммой отношений Rlt .... Rm ^обозна-
чается R = У Rt V; граф, соответствующий полученному отно-
1=1 ./
шению, назовем F-суммой графов,’задающих отношения 7?i, ...,
/ т F \
( обозначается .0=2 О,- ).
\ ; = 1 /
Пример 16. Рассмотрим графы и б2, показанные на
рис. 8. Будем считать, что множества их вершин совпадают, т. е.
%! = #! и xi = y.1. Сужение /^-произведения 0а и &
G2 на диагональ, состоящую из и z4 (см.
пример 15), является графом О, показанным на ----------->•
рис. 10). j uf иг
Упражнение 26. Найти F2-cyMMy графов Рис. 10.
6Ь G2, изображенных на рис. 8.
Отметим, что понятие координатного 'отношения и связанные
с ним понятия иерархического и квазикоординатных отношений
основаны на идее разложения отношений на несколько составляю-
щих, которая будет рассмотрена более подробно в следующей
главе.
Литература. [23,31,32,33].
Г л а в а 5
ДЕКОМПОЗИЦИЯ ФУНКЦИЙ ВЫБОРА
Под декомпозицией функции выбора будем понимать ее экви-
валентное представление (в смысле результатов выбора на всех
X = й) с помощью определенной совокупности других функций
выбора, композицией которых является исходная функция выбора.
Для обычных функций действительной или комплексной перемен-
по
ГЛ. 5. ДЕКОМПОЗИЦИЯ ФУНКЦИЙ ВЫБОРА
ной хорошо известны разложения в степенной ряд, в ряд Фурье
и др. Введем сходные конструкции для функций выбора.
В главах 1—4 были рассмотрены математические конструк-
ции для описания результатов выбора из конечного множества.
Наиболее общая из таких конструкций—функция выбора. Менее
общей конструкцией является бинарное отношение, и уж совсем
частной конструкцией представляется координатное отношение.
Несмотря на это,* между всеми названными конструкциями суще-
ствует взаимосвязь, которая позволяет описать результаты произ-
вольных выборов из конечного множества любой из этих конст-
рукций. Для выявления такой взаимосвязи потребуется понятие
декомпозиции (разложения) функции выбора.
Будем называть общими декомпозициями такие конструкции,
которые применимы к любой функции выбора, а частными деком-
позициями—такие, которые применимы к функциям выбора
только из некоторого класса.
Будем говорить, что отношение R на й реализуется коорди-
натным отношением R* на Ет, если найдется й* с Ет, | Й*| =| й |,
такое, что сужение R* на Й* изоморфно R. Соответствующий
изоморфизм назовем реализацией.
В § 1 рассматриваются общие декомпозиции функций выбора на
нормальные. Показана возможность получения других общих
декомпозиций. В § 2 приведено несколько частных декомпозиций.
Декомпозициям нормальных функций выбора посвящен § 3; § 4
показывает возможность реализации произвольного бинарного
отношения координатным отношением и тем самым замыкает
цепочку связей между функциями выбора, бинарными отноше-
ниями и координатными отношениями. В § 5 приводятся оценки
сложности рассмотренных декомпозиций, которые определяются
через числа элементов в соответствующих конструкциях.
В § 6*даются^интерпретации построенных композиций и деком-
позиций.
§ 1. Общие декомпозиции
Учитывая, что^в данной главе^исследуется связь между функ-
циями выбора и бинарными отношениями, установим возможность
декомпозиции произвольной функции выбора на’нормальные.
Напомним, что нормальная функция выбора C#—это функ-
ция выбора, порожденная бинарным отношением \R s й2. При
этом
[С*|(Х) = ХК
где"Хл—множество недоминируемых по R элементов.
Декомпозиция 1. Пусть"Rlt..., Rk—бинарные -отноше-
ния на й; ф(уп . ..,yft)—булева функция. Определим функцию
§ I. ОБЩИЕ ДЕКОМПОЗИЦИИ 111
выбора С = С(7?!, 7?*; 40 на
х€С(Х)«Фф(ь, ...,т»)=1, (1)
где
( 1, если х£СЯ;(Х),
— \ 0, если х^Ся'(Х). ' '
Функцию выбора С = С(7?1, . ..,7?ft; ф), определенную фор-
мулами (1) и (2), назовем ^-композицией нормальных функций
выбора, порожденных бинарными отношениями. 7?ь 7?**).
Возникает вопрос—насколько широк класс функций выбора вида
С (7?lt Rk, ф) при произвольных 7?п ..., Rk и ф? Если ока-
жется, что он совпадает с классом всех функций выбора, то
это значит, что любая функция выбора представима в виде неко-
торой комбинации нормальных, т. е. допускает декомпозицию на
нормальные функции выбора.
Теорема 1. Для любой функции выбора С HaZ Q сущест-
вуют бинарные отношения Rlt ..., Rk и булева функция ф
такие, что%
:С = С(7?1, ..., 7?ft; ф).« (3)
.«^Доказательство. Пусть ЛФВ (С) = </п • ••,/#>•! Фор-
мулы (1), (2), определяющие С(7?п ..., Rk, ф), можно запи-
сать в виде
Ж---Лу)=Ф(фЖ,
................................................... (4)
/лг(Рх» • • • ’ 0/V- 1) = Ф (флг (Р1> • • •> P/V-1), Фм (Р1 > • • • > PiV—х)> • • •
Фм(Р1, •••.Рл-1)),
где ф!,'..., <p)v, упорядоченные в виде’<ф}, <р|, ..<р}у>, обра-
зуют ЛФВ(СЛ1) и т. д., а ф?, ф£, .... ф^—ЛФВ (CRft).
Для доказательства теоремы 1 достаточно доказать, что для
любых f = <Л, ..., fN> существует'решение (ф, ф^—<ф1, ..., ф}у>,...
..ф6 = <ф^, ..., ф5/>) системы функциональных уравнений (4)
при дополнительномТтребовании
Ф?е/О, 1, ДМ (г=Г7Уф=ТД). (5)
I /е/J
Так как функции ф,- в (4) при различных i между собой не
связаны, то достаточнолнайти решение одного уравнения]
/ф) = ф(ф1ф), • ...Ф» (6)
при фиксированной функции ф, произвольной f и условии (5) на ф5.
*) Аналогично определяется ф-композиция С (Сх, Cft; ф) произвольных
функций выбора Cj, Ck.
112
ГЛ. 5. ДЕКОМПОЗИЦИЯ ФУНКЦИЙ ВЫБОРА
Зафиксируем функцию ф. Положим k*=N— 1 + и
Ф(?Н •••, ТдГ-1, Ъ/, •••, Тл7_1 + ^-1)= I
- V гж-,.,(т? • «?) . (?) |
!!
где d—номер элементарной конъюнкции в нумерации I ;
<0, ..., 0, 0>, <0, ...,'0, 1>, <0,’. 0), Г
<0,^..,Ч,|1>,»Л|.*<1....1,1>.
Построим Грешение уравнения (6)Тв7[явном! виде. Разложим f L
в СДНФ: ' /
f(0i, (8)
М=> л1 "~1
где элементарные 'конъюнкции, входящие в СДНФ (8), имеют '1
номера рх....pi. Обозначим номера элементарных конъюнкций,
полученных из них заменой о=<ох...стлг_1> на о=<с^, ..., оЛг_1>,
через qlt ..., qt.
Определим теперь <р\(₽х, .... ....<р*(р1( ..., PyV_1): (
<Ps(0i...0^i)=0, (s-17W=T), (9)
флг-i+rwoj^^s^j^ (10)
|ф"-»+*/«1 (/-1, /). g(H) ,
Из (9)—(11), (7)Л<2(8) с^учетом определения qlt ...,qt получаем I
I Р+ Р+ < _ __р4 - npt
/(01, ...,0лг-1)= V 0а1‘ •••0Х-1= V (01)*1 ••• (0ЛГ-1) "-* =
. /=1 1 Л —1 /==1
V/01) 1 ...(0Л7-1) Л'-1= V/<P1(0)) 1 ...(Фа7-1(0)) .
4 Л1
= V L<pv-i+Д<PiJ . • • q>A7-riJJ=W.(0)....fo*(0)).
Приведенная цепочка равенств’завершает доказательство теоремы. 5
Итак, произвольная функция выбора, какая бы сложная она |
ни была и каким бы классам ни принадлежала, всегда допускает !
декомпозицию на функции, порожденные бинарными отношениями. j
Упражнение 1. Единственно ли представление произволь-
ной функции С в^виде (3)? Привести примеры возможных пред- j
ставлений.
§ 1. ОБЩИЕ ДЕКОМПОЗИЦИИ
113
У п р'а ж н е н и'е 2. Рассмотрим функцию выбора С на
« {xt (i = T~T)}:
С (£2) = {х2, Х8, Х4), С(Xlt Х2, Х8) — {х2, Х8},
(С {Xj, Х2, Х4) = {х2,*Х4}, С (Хь Х8,*Х4) = {х1, Х8, х4},
С|(х2, х8, х4) = {х8, х4}, С (хь х2) — х2, С (хь х8)в{х1, х8},
= С (х2, х8)=х8, С (х2, х4) == {х2,*х4),
С(х8, х4) = х4, Cftx,)—х, (i=h4).
Проверить, что С=С(₽П Я2, ₽8; ф), ruet-w, V fs, a Rlt R2, R»
задаются графами Gn G2, G8, показанными на рис. 1.
Упражнение 3. Построить разложение функции выбора из
упр. 2 по способу, изложенному'при ^доказательстве теоремы 1.
Декомпоз]ици’я |2. Функцию выбора [С, определяемую
соотношением
( х,-, если х>, х,- € X,
С(Х) = < ‘ 17 (12)
[ 0 в остальных случаях, '
назовем функцией разрешения и обозначим через С?{. Функцию С:
xf, если х{£Х, х$Х,
0 в остальных случаях
С’(Х) =
(13)
назовем функцией запрета и обозначим через Сц.
Смысл функций разрешений и запретов очевиден. Именно,
при функции разрешения элемент х; выбирается из X тогда и
только тогда, когда в X входит и элемент xf, при функции
запрета элемент xf выбирается из X тогда и только тогда, когда
Ху не входит в X.
Упражнение 4. Нормальны ли функции Cfi, С^?
Легко видеть, что ЛФВ(С/у) = <0, ..., 0> и
Л(Р1, Р/+1, РлО = Р/- Аналогично, ЛФВ(С,7) =
=<0.....Ру......0>«
Воспользуемся введенными в § 2.3 операциями объединения и
пересечения.
Теорема 2. Произвольная функция выбора представима
в виде объединения пересечений функций разрешений и запретов.
114
ГЛ. 5. ДЕКОМПОЗИЦИЯ ФУНКЦИЙ^ВЫБОРА
Доказательство. Пусть С—произвольная 'функция вы-
бора. Положим
Cz(X) = xzAC(X). (14)
Очевидно, что
лг
С(Х) = и CZ(X). (15)
i= 1
Поэтому теорему достаточно доказать для функции Cz. Ясно, что
ЛФВ (Cz) = <0, ..., Д, ..., 0>, где компонента ЛФВ (С).
Разложим Д в СДНФ:
/, = (V (16)
и положим
= (/ = ТГ/). (17)
Очевидно, что
С,= и С\. (18)
t = 1
В силу (18) достаточно доказать, что С,- является пересечением
разрешений и запретов. Действительно, в силу (17) и теоремы
2.2, б) о соответствии между пересечением функций выбора и
конъюнкцией членов их ЛФВ
C*i = Сае! Л ... Л Cfc, Л Л ... Л CatNN,
( +, если <4 = 0,
где а, = <| е„ли Теорема доказана.
Упражнение 5. Построить разложение на разрешения и
запреты для функций выбора из примеров 2.1, 2.2 и упр. 2.
Упражнение 6. Построить декомпозиции вида (3) функ-
ций выбора из примеров 2.1, 2.2.
Упражнение 7. Единственно ли разложение функции вы-
бора в объединение пересечений разрешений и запретов? Привести
примеры возможных разложений.
§ 2. Частные декомпозиции
Декомпозиция 3. Введем следующие понятия. Булева
функция
Фм(Тп •••, Тй)=Уул...у^, (19)
где дизъюнкция берется по всем наборам длины d = [£/2]4~ 1,
называется мажоритарной или функцией голосования. Название
§2. ЧАСТНЫЕ ДЕКОМПОЗИЦИИ
115
объясняется тем, что фЛ1=1 тогда и только тогда,[ когда больше
половины переменных равны 1 (правило большинства).
Функция выбора вида С(/?1( Rk'. 4>i) называется мажо-
ритарно-нормальной. Класс всех таких функций обозначим через
МНФ. Таким образом, класс МНФ составляют все те функции
выбора, которые получаются правилом большинства из нормаль-
ных. Элемент х выбирается из X тогда и только тогда, когда он
выбирается более чем половиной из функций выбора, порожден-
ных бинарными отношениями Rt, ..., Rk.
Таким образом, правило композиции для’функций класса МНФ
то же самое, что и в § 1; отличие состоит лишь в том, что вместо
любых булевых функций рассматривается одна фиксированная
функция: мажоритарная. Возникает вопрос—сужается ли при
этом класс представимых указанным образом функций? Совпадает
ли класс МНФ с множеством всех функций выбора или с одним
из ранее рассмотренных классов?
Утверждение 1. Класс МНФ совпадает с классом Н.
Доказательство. Докажем включение Н = МНФ. Вейлу
теоремы 2.3, а) из С£Н 'следует, что антимонотонны, т. е.
Р1^р«=?>/Г1.(р1) Д. (Р2) для? всех i=l, N. Докажем, что всякую
антимонотонную функцию g(aj, ..., аг) можно представить в виде
g== •>*). (2°)
где _ ___
?/^0, 1,ДаД (i = l, k), (21)
I !
как в случае нормальных функций выбора.
Так как g антимрнотонна, то она представима в виде ДНФ,
в которую все переменные входят только с отрицаниями:
-- §(«!/.."., ar)=V ( А* аД . (22)
/=1 yS€Qy )
Положим J
у7a,) = A[a, (j=T0,
s^Qj______________________ (23)
?/(«ь (/ = / + 1, 2t — l)t
равенство (20) следует из; (22) и (23) с учетом (19). Действительно,
подставив (23) в (20), получим при p1 = j^t, p2=i-j-l, ...
..., pt = 2t— 1:
УрУр. •••?» = A a..
‘ s в Q j
Аналогично [получим и все остальные членьГДНФ (22); кроме'
них, получим их произведения вида ( Д аД ( Д аД и т. д.,
Vе J \ss<?7a J
116
ГЛ. 5. ДЕКОМПОЗИЦИЯ ФУНКЦИЙ ВЫБОРА
которые можно удалить по 'формулам поглощения (х\/ху = х).
Число k переменных в фЛ равноД2/—1 и определяется числом
членов в ДНФ (22).
Представим' теперь все функции (Р) ЛФВ (С) в виде, анало-
гичном (22):
A(0)=v ( AM (/=TTiV). (24)
С помощью известного правила булевой алгебры x\J х = х урав- '
няем число членов tt в разложениях (24), доведя его везде до
if = max/,. Получим
АФ) = V ( A (»=П)
)
и в силу (20)
ЛФ) = Фм(?Ж ••.тГ’Ф)), (25)
где у| удовлетворяют условиям нормальности (21); (25) означает,
что С = С(7?!, R2t-i, Фм)> где ЛФВ (CR*) = <yl, у|, ...,ysN>
(s=l, 2t—1). Включение Н s МНФ доказано.
Докажем обратное включение МНФеН. Действительно, под-
ставляя y,g/O, 1, А РД в (19), получаем либо функцию
I S«A I
в ДНФ которой все переменные входят с отрицаниями, либо
либо = т. е. антимонотонную функцию. В силу тео-
ремы 2.3, а) получаем, что C(Rlt ..., /?^;Фж)€Н. Утверждение
доказано.
Декомпозиция 4. Пусть снова Rlt .... Rk—бинарные
отношения на Q. Полоцким
•••/?») = ViV...VT*- (26)
Функцию вида C(Rlt ..., Rk; фД назовем суммарно-нормальной
функцией. Введем класс СНФ таких функций.
Утверждение 2. Класс СНФ совпадает с классом Н.
Упражнение 8. Доказать утверждение 2.
Декомпозиция 5. Введем понятие конечно-нормальных
функций выбора. Назовем конечно-нормальной функцию, которая
представима произведением конечного числа нормальных функций
выбора.
Множество [таких функций выбора образует класс конечно-
нормальных функций (КНФ).
Возникает тот же вопрос—как «устроен» класс КНФ? Иными
словами, какие функции выбора С представимы в виде
С = (С**-* (.. .(СА(СА))...))? (27)
। §2. ЧАСТНЫЕ ДЕКОМПОЗИЦИИ Ц7
Упражнение 9. Доказать, что не все‘функции выбора при-
надлежат КЙФ.
^Упражнение 10. Привести пример функции С на £2 = {х2}
такой, что С(£КНФ.
Упражнение 11. Верно ли, что КНФ = С?
Упражнение 12. В каких из классов функций выбора, вве-
денных ранее, содержится класс КНФ? Какие содержит он?
Упражнение 13. Содержится ли в КНФ функция выбора
из упр. 2?,
Декомпозиция .6. Из формул ~(1), (2) и (26) непосредст-
венно следует, что
* В-
Си СЧ (28)
1=1
Тем 'самым ’приходим к понятию декомпозиции функции выбора
в виде объединения нормальных.
Рассмотрим не произвольные нормальные, а скалярные функ-
ции выбора. Бинарные отношения, порождающие скалярные
функции, задаются линейными графами, т. е. представляют собой
линейные порядки. Один из видов разложения
k
С= и С{ (29)
рассмотрен в главе 2 (формула (2.43)).
Напомним, что функции выбора С вида (29), где С,-—скалярные
функции выбора, названы совокупно экстремальными. Возникает
вопрос—с каким классом ^совпадает множество всех совокупно
.экстремальных функций выбора? Ответ дает утверждение 2.15.
1 Обобщим результат этого утверждения на случай произвольных
С€НГ)О.
Утвержден иеЗ. Пусть С £ Н п О. Существуют ^скалярные
функции Clt ..., Ск и множество W = Q такие, что
(k \
*Uj С[ ] Л Си?.
Доказательство. Напомним, что С&—характеристическая
функция множества W, т. е. С^(Х) — Х Л IF. Другими словами,
нужно доказать, что любая функция из Н Л О является совокупно
экстремальной с запретом. Пусть для некоторого Хей выбор
С(Х) = 0. В силу свойства О для всех х£Х] выполняется
С (х) — 0 .’’Поэтому множество
Z = {z€Q|C(z) = 0}
непусто. Ясно, что для XsZ имеем sC’(X) = 0. Докажем, что
для всех X$CZ C(X)=«C(X\Z). Действительно, если z£Z, то
z^C(X) для любого ХеЙ (в силу! свойства Н из zgC(X)
118
ГЛ. 5. ДЕКОМПОЗИЦИЯ ФУНКЦИЙ ВЫБОРА
следует С (Z) = С (X) Г1 z — z, что противоречит C(z) = 0). Таким
образом, C(X)sX\Z, и по свойству О C(X) = C(X\Z). Рас-
смотрим теперь сужение С на Q' = Q\Z; по построению Z
С(Х)^=0 для всех XcQ'. Поэтому в силу утверждения 2.15
С—совокупно экстремальная функция на Q'. Доопределим теперь
каждую из функций Cz(i = 1, k), определенную на Q', на всей так,
чтобы значения всех числовых функций fh задающих С; (i = 1, /г), на
всех элементах из Z были меньше, чем на всех элементах из Q'.
При таком доопределении’ очевидно, что для всех X sE Z имеем
UiCz(X)= и C, (X\Z) = C(X\Z) = C(X) и для X = Z имеем
С^(Х) = 0, где № = Q\Z. Тем [самым доказано, что для W =
= Q\Z выполнено требование утверждения 2.15. Утверждение 3
доказано.
Декомпозиция 7. Пусть в (29) функция С и все функции
С(—нормальные функции выбора, порождаемые соответственно
бинарными отношениями </?, Q> и </?,-, Q>. В терминах сечений
нормальная функция выбора CR может быть описана следующим
образом: элемент х выбирается из X, содержащего х, в том и
только том случае, когда
ХлЯ+[(х) = 0 (30)
В рассматриваемом случае имеет место следующее утверждение.
Утверждение 4. Для; того чтобы набор нормальных функ-
ций выбора {С,} был разложением вида (29) нормальной функции
выбора С, необходимо и достаточно, чтобы для некоторого набора
Rlt ..., и R, порождающих С1У ...,Ck и С соответственно,
для каждого элемента х нашелся индекс i* € { 1 ,*..., k} такой,гчто
k
R+r(x)~ Л Rt(x), (31)
1=1
и чтобы при этом
Л Rf(x) — R+(x). (32)
1=1
Доказательство. [Пусть С,- (1 = 1, k) и С—нормальные
функцйи выбора, для которых выполнено (29). Рассмотрим их ЛФВ:
<Й, (1=ТД), <Л,
В силу теоремы 2.2, а) выражение (29) эквивалентно равенствам
k ____
v (s=i, jv). (зз)
1 = 1
С учетом" утверждения 2.10 из (33) получаем (если fs 0,
k _ _ ____
V А Р/= A (8=1, л/); (34)
1=1/ев| /ел*
§3. ДЕКОМПОЗИЦИЯ НОРМАЛЬНЫХ ФУНКЦИЙ ВЫБОРА Ц9
(34)2 означает, чт0 для некоторого k} выполняется
k
Bs{, = Af и для всех i справедливо А* = В}. Поэтому П Rt (xs) —
i=l
—R+[(xt)'> равенства (31), (32) получаем в силу Bst = As. Случай
^=1 рассматривается аналогично (здесь Xs = 5) = 0 (z = l,fe)).
Пусть /j = 0. Это возможно, только если xs С R+-(xs),'ir. е-
<xs, xsy € R. Выберем графы отношений /?,- так, чтобы других
дуг, кроме петли, у вершины xs не было (минимальные отноше-
ния). Тогда выполнение (31) и (32) очевидно. Необходимость
доказана. Достаточность следует из того, что условия (31) и (32)
влекут равенства (34). Утверждение доказано.
Доказанное утверждение справедливо и в случае, когда С —
паретовская функция выбора, а С(—скалярные функции выбора.
Возможность представления паретовской функции в виде объеди-
нения (29) скалярных непосредственно следует из утверждений
2.18 и 2.
Упражнение 14. Сформулировать и доказать аналог
утверждения 4 для нижних сечений R~(x)A
§ 3. Декомпозиция нормальных функций выбора
Тля развития результата общей декомпозиции 1 рассмотрим
декомпозицию нормальных функций выбора на скалярные.
Введем необходимые понятия. Пусть ^Rlt Q>, ..... <Rm, й>—
произвольные бинарные отношения на одном и том же множе-
стве Q; /(Рп ...,Pm)—-произвольная булева функция. Назовем
f-суммой отношений Rt, ...,?Rm отношение R, задаваемое фор-
мулами
xRyl&’J (Pi (х, у}, .... р,л (х, //))=!, (35)
где
f 1, если xR{u>
A D <36)
L Е 7 ( 0, если xR^.
Перенесем определение /-суммы на графы отношений; /-суммы
отношений и графов можно рассматривать как композиции отно-
шений и графов. Представление отношений и графов в виде /-сумм
можно принять за их декомпозиции. Для обозначения /-суммы
отношений и /-суммы соответствующих графов используем запись
[т т
“У % и 6=2^.'
= 1 « = !
Прим'ер 1. Пусть R*и'R2—отношения, заданные графами
Gt и С2 на рис. 4.8. Рассмотрим Д—главный член квазикоорди-
натного отношения R (Rlt R2; F,) (пример 4.15). Найдем с по-
мощью (4.46) и запишем в табл. 1, откуда с учетом (35),
120
ГЛ. 5. ДЕКОМПОЗИЦИЯ ФУНКЦИЙ ВЫБОРА
(36) получаем, что A=Pi₽2 и что /j-сумма графов GT и С2 явля-
ется графом G, показанным на рис. 2.
Таблица 1
г
> ' —>»
«t U2
Рис. 2.
31 (*! («1» а2) fl (Зо 3±)
0 0 — 1 0 0
0 1 — 1 1 0 0
1 0 1 —1 0 0
1 1 1 1 1 1
Упражнение 15. Найти /2-сумму тех же 1рафсв, где f2—
главный член квазикоординатного отноцения R (Rx, 7?»; F2) из
примера 4.15. Ответ сравнить с ответом упр. 4.26.
Упражнение 16. Чем отличается введеннсе понятие /-суммы
отношений от введенного в § 4.6 понятия F-суммы, если f—глав-
ный член квазикоординатного отношения R (Rlt ..., Rm; F)?
Упражнение 17. Найти необходимые и достаточные усло-
вия на функцию F(a1, (az^{ — 1, 0, 1}), при которых
для любых отношений Rr.....Rm их г-сумма совпадает с /-сум-
мой, где /—главный член квазикоординатного отношения.
Упражнение 18. Пусть R*—/-сумма отношений Rlt ..., Rm.
Доказать, что всегда существует функция F (аг, (az£
—1, 0, 1}) такая, что / является главным членом квазико-
ординатного отношения R (Rlt ..., Rm; F) и F-сумма Rlt ..., R„
совпадает с их /-суммой.
Результат упражнения 18 означает, что при исследовании
отношений, заданных на одном и том же множестве Й, достаточно
рассматривать только /-суммы, а не F-суммы.
Упражнение 19. Пусть RJt ..., Rm—произвольные би-
нарные отношения на й и
т т
6)/=v₽/.
Z=1 1=1
Доказать, что /-сумма Rlt .... Rm совпадает:
а) с пересечением отношений Ru ...,
б) с объединением отношений Rlt .... /?и7
У п р а ж н е’г и е j20ЛДоказать, что
т пгw т__
2Ми ^fRt=U,
z=13 i=' li=l i=l
Таким^образом, определена операция? гад сн оп сетями и гра-
фами— /-сумма отношений и графов. Далее потребуется /-сумма
линейных графов. Рассмотрим граф 1Л, задакптй лтсйтьй гс-
рядок на Й={х1( ...,
XpRXg^p^q.
§3. ДЕКОМПОЗИЦИЯ НОРМАЛЬНЫХ ФУНКЦИЙ ВЫБОРА
121
Линейным графом L% назовем граф, полученный из LN перену-
мерацией л его вершин.
-„Под перенумерацией вершин л понимается следующее: л —
произвольная перестановка <i\, ..., iN> множества {1, ..., IV};
вершина s в графе LN имеет номер is в графе L„; дуга из it ве-
дет в it в графе Ад тогда и только
тогда, когда s <11.
На рис. 3, а представлен линейный ат хз *2 >*2 >xt
граф”L<a, з, i>; на рис. 3, б представле- 4 а) . Б)
но другое изображение того же графа, Рис. 3.
которое иногда оказывается удобнее.
Теорема 3. Любой граф без петель представим в виде
f-суммы линейных.
Доказательство. Пусть граф G содержит N вершин. Рас-
смотрим 14-A/’(V—1)/2 перестановок с условными номерами
О, (1, 2), (N — I, N) (т. е. число перестановок равно С^4-1
и каждая перестановка, кроме нулевой, нумеруется парой (i, j);
для определенности считаем, что i < j). Перестановка с номером О
является тождественной, т. е. л0 = <1, ..., А/>. Перестановка л
с номером (i, /) имеет вид
<1, ..., i-1, j, i + 1, .... /-1, i, /4-1, N>, (37)
т. e. i и / поменялись местами, а все остальные индексы оста-
лись на месте.
Рассмотрим линейные графы L%t определяемые указанными
перестановками. Пусть (xs, xt) — любая упорядоченная пара вер-
шин графа G. С этой парой свяжем набор булевых переменных
длины ’1 +N(N—1)/2 (см. формулу (35)):
Р(-^4> ^t) <Ро (^з> -^t), •••» Р(/,Xf), ..., Р(ДГ-1, до (•*$»
(38)
Определим компоненты ^набора по формуле (36), имея в виду,
что в линейном графе Ln
XipR^Xi-i фф р < у. (39)
С учетом (37) и (39) получим
XsRa{s, t)Xf Ф^ Ху Rn(s,lt)Xls ФФ t s; (40)
{1, если t < s,
0, если t > s;
f 1, если s < t,
P<p, «> (*,,y(t)=» | 0) если s>/( p=£s, q^t; (41)
r (r Pu,«(^. *t), если sgn(s — 0 = sgn(<7 — t), q^t,
Pu,«)l. f. P \ PUtf)(x„ xt), если sgn(s—0#=sgn(<7—0,
r и-* P<4,t>(^, xt), если sgn(f — s) = sgn(p —s)'p^s,
p</,, f)l 4, t) | pu,ft(x„ xt), если sgn (Z —s)^=sgn(p—s), p^s.
122
ГЛ. 5.'ДЕКОМПОЗИЦИЯ ФУНКЦИЙ ВЫБОРА
В силу (41) получаем
P(Xs’, xz<)=#P(xs", хгДпри (s',?t')=£(s", Г). (42)
Действительно, при (s", — s') получаем несовпадение век-
торов в (42) на компоненте с нулевым, номером. Поэтому можно
определить булеву функцию /(уп ..., y1+N (w-D/г) такую, что
Это возможно сделать в силу (42). Из (35), (36) и (43) непосред-
ственно следует, что G = ^ L„.
z/ Теорема доказана.
1 2
Упражнение 21. Поче-
му приведенное доказательст-
во не годится для графов G,
содержащих петли?
Пример 2. Проиллюстри-
руем приведенный способ по-
g - -- Т V Jp j J V/Х’Л VAAVVVV A1V
? 2 ^~~^3 *"* 2* * строения /-сумм на двух гра-
Рис. 4.
фах Gt и G2 (рис. 4, а). Рас-
смотрим k = 1 4- N (N — 1 )/2 =
= 14-3-2/2 = 4 перестановок
вершин графов, построенных
по схеме доказательства тео-
ремы 3. Соответствующие ли-
нейные графы показаны на
рис. 4, б. Построим’,наборы Р (г, /) в соответствии с (38) и (36)
0(1/2) = <1, 0, 0, 1>,
0(2, 1) = <0, 1, 1, 0>,
0X1, 3)=<i, i,"o, i>,
0(3, 1) = <0, 0,4, 0>,
0(2, 3) = <1, 1, 0, 0>,
0(3, 2) = <О, 0, 1, 1>.
Для графаТО! получаем (см. (43) и рис. 4, а)
’/’(0(1, 2)) = 0, /’(0(2, 1))=1, fi(0(l, 3)) = 0,
f/1 (0(3, 1)) = 0, /’(0(2,3))=!, /’(0 (3,^2)) = 1;
для графа G2 —
/’(0(1, 2))=1, /’(0(2, 1)) = 0, /’(0(1, 3)) = 0,
/’(0(3,1)) = !, /’(0(2, 3)) = 0, /’(0(3, 2)) = 0.
§3. ДЕКОМПОЗИЦИЯ НОРМАЛЬНЫХ ФУНКЦИЙ ВЫ5ЭРЛ
123
Построим по (44) и- (45) СДНФ для f* и f*:
fХ (Pl» р2 > Рз» Р<) 1=5 Р1Р2Р3Р4 V P1P2Рзр4 V р 1Р2Р3Р4 >
f* (Pi, Рг> Рз> Р4) ~ Р1Р2Р3Р4 VР1Р2Р3Р4•
Граф Gx совпадает с f1-суммой четырех линейных графов, пока-
занных на рис. 3, б, а граф G2—с их /2-суммой.
Декомпозиция графа в f-сумму линейных называется паре-
товской декомпозицией, если. Р,.
1=1
Результат упражнения 19 означает, что граф G, допускающий
паретовскую декомпозицию, является пересечением линейных.
Утверждение 5. Всякий транзитивный граф допускает
паретовскую декомпозицию.
Для произвольных графов верно следующее
Утверждение 6. Пусть Gu ..., Gr—произвольные графы
без петель. Существуют т и f($lt ..., 0И) такие, что каждый
из графов G{ представим в виде f-суммы т линейных.
Доказательство. Из определения /-суммы следует, что
если G представим в виде /-суммы т линейных графов, то любой
его подграф тоже представим в виде /-суммы т линейных графов.
Рассмотрим граф G, являющийся объединением Gr, ..., Gr (т. е.
множество вершин G является объединением множеств вершин G,
и дуга соединяет две вершины, когда она входит в один из гра-
фов G,). В силу теоремы 3 граф G представим в виде /-суммы
т линейных. Следовательно, это же верно и для его подграфов
Gn ..., Gr. Утверждение 6 доказано.
Теперь можно перейти к декомпозиции нормальных функций
выбора на скалярные.
Декомпозиция 8. Пусть ...,Ст—скалярные функции
выбора, каждая из которых порождается отношением линейного
порядка /?!, ..., Rm соответственно, и /(0Ь ..., рга)—булева
функция.
Назовем /-суммой функций С1; ..., Ст нормальную функцию
выбора, порожденную /-суммой отношений ..., Rm.
Из теоремы 3 следует, что любая нормальная антирефлексив-
ная функция выбора представима в виде определенной комбинации
функций, порожденных линейными порядками, т. е. в виде ком-
бинации скалярных функций выбора.
В случае, если функция не является антирефлексивной, то
можно воспользоваться понятием запрета (§ 2.4). Именно, поло-
жим Z = {z | CR (z) = 0} и удалим петли из соответствующего
графа (оставив все вершины). Полученный граф уже допускает
декомпозицию указанного типа. После этого можно взять пере-
сечение полученной функции с характеристической функцией Сц?,
где UZ = Q\Z. В результате получим представление исходной
нормальной функции выбора в виде пересечения функции выбора,
допускающей декомпозицию 8, и характеристической функции С^,.
124
ГЛ. 5. ДЕКОМПОЗИЦИЯ ФУНКЦИЙ ВЫБОРА
§ 4. Реализации декомпозиций нормальных функций
Установим связь между произвольными бинарными и коорди-
натными отношениями. Пусть — некоторое коорди-
натное отношение на Ет и Q*<zEm. Если Й*—конечное множество,
то сужение на й* определяет некоторое отношение 7? на й*.
Будем считать, что R* антирефлексивно, т. е. 0. Пусть за-
дано произвольное антирефлексивное отношение R на конечном
множестве й. Найдутся ли конечные множества Й* и координат-
ное отношение R* в Ет такие, что сужение R* на й* изоморфно 7??
Положительный ответ на этот вопрос оказывается тесно связан-
ным с возможностью представления произвольных графов в виде
f-суммы линейных.
Теорема 4. Если граф отношения R представим в виде
f-суммы \т линейных, то отношение R изоморфно некоторому
сужению R*£Wm с ГЧ, равным f.
т
Доказательство. Пусть G— L%. Ясно, что(хк, хг) =
= 1 < л?х(г). С ’^каждой вершиной [хк графа G свяжем
точкуЗ?/* £Ет формулой
^«#4-1—л?1^) (46)
Ясно, что у* > у[ «Ф л?1 (k) < л;1 (г). В силу (35), (36) и опреде-
ления координатного отношения
ykR*yr& xkRxr,
где | R*—координатнсе отнсшение с главным членом f. Теорема
доказана.
Теорема 4 объясняет введенный выше термин паретовской де-
композиции. Действительно, в этом случае отношение R реали-
зуется отношением Парето на Ет (допускает паретовскую реали-
зацию).
Введем следующие понятия. Пусть М—дерево, все дуги кото-
рого ориентированы в направлении от корня. Назовем Т-деревом
граф, полученный из М добавлением всех дуг, ведущих из' а
в Ь, если между а и Ь в М есть ориентированный путь. Добудем
называть остовом Т-дерева (рис. 5).
Некоторые (или все) дуги (х, у) остова заменим на сильно
транзитивные графы. Для этого соединим х со всеми недомини-
руемыми вершинами сильно транзитивного графа и каждую из
его вершин 'соединим с у. В получившийся граф G добавим все
дуги вида (а, Ь), если между а и b в G есть ориентированный
путь. Полученный граф G назовем ST-дерееом. Пример ST-дерева
приведен на«рис. 6. Здесь в Т-дерево рис. 5 вместо дуги (х, у)
подставлен граф с вершинами а, Ъ, с.
$ 4. РЕАЛИЗАЦИИ ДЕКОМПОЗИЦИЙ
125
Утвер-жде'ние 7. Двумерную "паретовскую реализацию до-
пускают: а) сильно транзитивный граф', б) Т-дерево-, в) ST-дерево
(при т = 2).
Доказательство, а) Структура сильно транзитивных гра-
фов установлена теоремой 1.1. Из нее следует, что при отсут-
ствии петель множество вершин Q сильно транзитивного графа
распадается на два подмножества: Qx, состоящее из всех недоми-
нируемых вершин, и Q2 = Q\Q1 (Qt всегда непусто). Любая вер-
шина из Q2 доминируется любой вершиной из Qi. Рассмотрим
Рис. 5. Рис. 6.
подграф, порожденный множеством П2; предположим, что он
допускает двумерную паретовскую реализацию. Тогда очевидно,
что ее допускает и исходный граф G (рис. 7). Таким образом,
задача реализации сильно транзитивного графа G сводится к за-
даче реализации его подграфа G', число вершин у которого
меньше, чем у G. Утверждение 7, а) следует из того, что любой
подграф сильно транзитивного графа также сильно транзитивен.
б) Предположим, что 7, б) доказано для всех Т-деревьев с
числом вершин, меньшим k. Рассмотрим произвольное Т-дерево
G с k вершинами. Пусть в его остове из корня х9 ведут дуги
Рис. 8.
в вершины хп ..., хг. Т-дерево G является объединением Т-де-
ревьев Ох, ..., Gt с корнями ..., xt и вершины х9. Каждое
из Т-деревьев Glf ..., Gt реализуется в силу предположения
индукции, следовательно, точки, соответствующие вершинам Gt
в Е2, можно расположить внутри любого прямоугольника. Воз-
можность реализации всего Т-дерева G следует из геометрических
соображений (рис. 8). Базис индукции при 6 = 1 очевиден.
126
ГЛ. 5. ДЕКОМПОЗИЦИЯ ФУНКЦИЙ ВЫ БОРАП
в) Доказывается аналогично (с учетом а)).
Утверждение доказано.
Итак, каждая функция выбора является ф-композицией'функ-
ций выбора, порожденных бинарными отношениями (теорема 1).
Каждое бинарное отношение реализуется как координатное отно-
шение на Ет (теорема 4). Таким образом, в определенном смысле
изучение любой функции выбора сводится к изучению^ коорди-
натных отношений на Ет.
§ 5. Сложность декомпозиций]
Обычно, когда идет речь о декомпозициях, представляет интерес
число входящих в них составляющих. Вопрос о сложности общих
декомпозиций функций выбора в настоящее^время мало исследо-
ван. Далее будут рассмотрены возможные подходы к оценке слож-
ности общих декомпозиций и конкретные результаты по частным
декомпозициям функций выбора, бинарных отношений и графов.
Введем величину р(С)—расстояние между вершиной хс еди-
ничного куба D4, соответствующей функции С, и ближайшей
к ней вершиной, соответствующей нормальной функции выбора.
Эта величина характеризует то, что в литературе называют «сте-
пень зависимости выбора от контекста», и может быть принята
за меру сложности функции выбора С. Назовем ее ^-сложностью.
Положим
НР(С)-тшИЛ|КЭ^........Rk, Ф(?))[С = С(₽1, ...» Rk, ф)]}. (47)
Величину НР?(С), определенную формулой (47), назовем НР-слож-
ностью функции С.
Минимально возможное 'число разрешений и запретов в раз-
ложении С вида
с= и(ЛС?/),
где а—знак + »или J—, назовем РЗ-сложностью и обозначим
через РЗ(С).
Таким образом, для произвольной функции] выбора введены
три величины, характеризующие в том или ином смысле ее слож-
ность: р(С), HP (С), РЗ(С). Заметим сразу, что для любой нор-
мальной функции
р(С) = 0, НР(С)=1, РЗ(С)<№.
Упражнение 22. Найти р(С), НР/С) и РЗ(С) для~функ-
ции С из упр. 2.
Положим теперь
p(W) = maxp(C), HP;(7V) = maxHP(C), РЗ(АО = тахРЗ(С),
где максимум берется по всем функциям выбора на Q:|Q| = AT.
§8. СЛОЖНОСТЬ ДЕКОМПОЗИЦИЙ
127
Введенные характеристики 'позволяют поставить следующие
задачи:*
1. Найти способ вычисления или оценки р(С), HP (С) и РЗ (С)
для любой функции С.
2. Найти асимптотику p(Af), HP (TV) и РЗ (N) при N —>оо.
Зафиксируем k. Число бинарных отношений на множестве й,
состоящем из N элементов, равно 2A'S; число булевых функций
от. k переменных — 22&. Таким образом, общее число функций
выбора С, у которых- HP (C)}^k, не превосходит
в то время как общее число функций выбора равно 2N~2N~l
(утверждение 2.5). Сравнение 2kN‘+ik и 2N'2N~1 показывает, чти
при больших N «почти все» функции имеют HP-сложность по-
рядка N или выше.
Упражнение 23. Найти асимптотику РЗ(У) при N—
Обратимся к частным декомпозициям из § 2. Здесь также можно
ставить вопросы о минимальном числе составляющих, об асимп-
тотике этого числа при N —*оо и т. д. Остановимся на некото-
рых результатах.
Утверждение 8. Число слагаемых в разложении функции
выбора С£Н в объединение нормальных вида (3) при ф = ф^ (см.
(26)) равно]
max q (ft),
ie (1.N]
где q(g)—минимальное число членов ДНФ антимонотонной/функ-
ции g.
Упражнение 24. Доказать утверждение 8.
Рассмотрим класс КНФ, называемый также классом функций
последовательного выбора. Глубиной k (С) функции С € КНФ назы-
вается минимальное число бинарных отношений таких, что вы-
полнено] равенство (27).
Глубина конечно-нормальной функции выбора также может
характеризовать ее сложность. Обозначим через множество
всех С € КНФ глубины не более k. Ясно, что s Y2 =... s =...
Упражнение 25*. Доказать, что имеют место строгие вклю-
чения ... сТ^с ...
Утверждение 9. При A = const и N —>оо
lira |Тй(У)|/(Зй4-1)"<"-1)/2 = 1,
А7->ос
где |4Tfe(7V)[—мощность класса на Й:|Й| = Л/.
Обозначим через |КНФ(А)| мощность класса всех конечно-
нормальных функций на й = {х!, ..., Xjv}.
Упражнение 26**. При достаточно больших^
(0,28A/logaW)"2/‘ < | КНФХУ)|ККЗУ72)Л’2/2.
128
ГЛ. 5. ДЕКОМПОЗИЦИЯ ФУНКЦИЙ ВЫБОРА
В § 2 утверждалось, что'любая паретовская функция выбора
представима в виде объединения скалярных функций. Дадим точ-
ную оценку минимально возможного числа слагаемых. Введем
необходимые понятия.
Напомним, что цепью графа G = (Q, U) называется последо-
вательность вершин xlt ..., xt такая, что (х{, xi+1) £ U (i=l, /—1).
Антицепью называется множество несвязанных дугами вершин;
максимальной антицепью—антицепь, в которую нельзя добавить
ни одной вершины. Наибольшее число вершин, образующих анти-
цепь, называется шириной графа. Согласно теореме Дилворта
ширина графа равна минимальному числу цепей, которыми можно
покрыть все вершины графа.
Напомним также, что паретовская функция выбора—это нор-
мальная антирефлексивная функция, порожденная любым тран-
зитивным антирефлексивным отношением. Поэтому граф отно:
шения определяется однозначно.
Утверждение 10. Пусть задана паретовская функция вы-
бора С и граф G порождающего ее транзитивного отношения
имеет ширину k. Тогда существует разложение (29) функции С
в объединение k скалярных функций и не существует разложения
с меньшим числом скалярных функций.
Докажем только вторую часть утверждения. Предположим,
что число скалярных функций выбора меньше k. Рассмотрим их
сужение на V—максимальную по числу вершин антицепь G. По
условию |У|==&. Кроме того, вершины из V не связаны дугами,
поэтому C(V) = V. Так как |
d
(d;<^), (49)
' К,-(Ю|~1 - (50)
(поскольку Ci—скалярные функции), то из (49)Jh (50) получим
| С (V)] d < k. Полученное противоречие доказывает вторую часть
утверждения. Таким образом, если под сложностью паретовской
функции выбора понимать число скалярных слагаемых, то слож-
ность равна ширине соответствующего графа.
За оценку сложности бинарного отношения (антирефлексив-
ного) можно принять минимально возможное число слагаемых
в разложении его графа на линейные. Пусть G—произвольный
граф без петель. Минимально возможное число членов разложе-
ния G = S/GZ, где Gz—линейные графы, обозначим через D(G).
Оно называется размерностью G. Смысл этого названия связан
с теоремой 4, указывающей на возможность реализации G коор-
динатным отношением с ГЧ f на пространстве размерности D (G).
Утверждение 11. Для любого k существует граф G такой,
что D (G) > k.
Доказательство. Предположим противное. Число раз-
личных графов с N вершинами, представимых в виде f-суммы k
§5. СЛОЖНОСТЬ ДЕКОМПОЗИЦИЙ'
129
линейных, не превосходит 22 Число всех различных гра-
фов с N вершинами [без петель равно 2<ЛГ“’1)ДГ. Из сделанного
предположения следует, что при любом N
22*-(M)ft>2w-l,Jv. (51)
Заменим NI на большую величину УУУ Тогда в силу (51)
2i\NN)k = 22\Nk)N^(2N-1)N. (52)
Однако \vx$Nkl2N~l = 0 при любом k. Это значит, что (52), а сле-
/У->оо*
довательно (51), при достаточно больших N неверно. Полученное
противоречие доказывает утверждение.
Смысл последнего утверждения состоит в том, что нельзя
указать фиксированное число k, пусть даже очень большое, чтобы
произвольный граф имел размерность не более k. Однако это
число может быть ограничено для некоторых классов графов.
Положим
D(JV) = maxD(G), ' (53)
где максимум берется по всем графам без петель с N вершинами.
Приведенное доказательство теоремы 3 устанавливает, что D
^l+N(N —1)/2.
Обозначим минимальную размерность наретовской декомпози-
ции транзитивного графа G через DP(G); аналогично D{N) опре-
делим DP(N).
Утверждение 12. DP(G) не превосходит ширины k графа G.
Упражнение 27. Доказать, что DP(N)^.N.
Упражнение 28. Верно ли, что DP(G) равна ширине графа G?
Утверждение 13. Для любого k существует транзитивный
граф G такой, что Dp(G)>k.
Доказательство. Предположим противное. Если DP(G) ^.k,
то это значит, что G допускает ^паретовскую реализацию в Ek,
Рассмотрим граф G, содержащий" 2(k-f-1) вершин хг, ,xk+1,
Уъ • • - , У/i+i- Множество дуг G состоит из всех дуг вида (х{, у/},
где i Ф j. Транзитивность G очевидна.
Пусть Л' = <«1, ..., a‘k~>—точка, соответствующая вершине х,-
(i=l,£4-l); Bf=<b[, ..., b£>—точка, соответствующая вер-
шине у,- (j — l, &4-I). По построению G ясно, что
(s= 1, k\ i^j) (54)
и для любого р=1, k +1 найдется 1, ..., k} такое, что
If > <%. (55)
Положим ij = argminaf (s = 1, k). Ясно, что
р
(Э/) [у7 доминируется вершинами xZi, .... х£ ],
5 И. М Макаров и др.
130
ГЛ. 5. ДЕКОМПОЗИЦИЯ ФУНКЦИЙ ВЫБОРА
так как s < k +1. Но в силу (54) с учетом определения is имеем
(s = T7k-, i=l, £+1),
что противоречит (55). Утверждение доказано.
§ 6. Некоторые интерпретации декомпозиций и композиций
Любую декомпозицию можно интерпретировать как попытку
обосновать сделанный выбор в терминах некоторых аспектов или
критериев.
Теорема 4 позволяет обосновать выбор, сделанный по некото-
рому бинарному отношению, в терминах критериев, в качестве
которых можно интерпретировать оси Ет. Такие ситуации воз-
никают, например, при обработке результатов экспертной оценки,
когда на основании данных о попарном сравнении некоторых
проектов необходимо установить основные показатели и оценки
проектов по этим показателям.
Другой смысл имеет решение задачи композиции. При этом
по результатам решения более простых задач выбора ищется
решение исходной более сложной задачи. Теорема 1 показывает,
что всегда можно выделить отдельные „стороны, аспекты в описа-
нии объектов и установить взаимосвязь между ними так, чтобы
выбор описывался композицией нормальных функций, учитываю-
щих только выделенные аспекты. Такие ситуации могут возник-
нуть, например, при выборе проекта регионального развития.
Здесь обоснование проекта должно учитывать экономические,
социальные, демографические, экологические, энергетические и
другие аспекты проблемы, не сводящиеся непосредственно к ко-
личественным показателям.
Близкие соображения можно привести и для других видов
декомпозиций функций выбора. Заметим, что пересечения и объ-
единения функций выбора можно также интерпретировать как
результат коллективной деятельности нескольких ЛПР или экс-
пертов.
Литература. [2, 5, 9, 33, 70, 124].
ЧАСТЬ II
ПРОЦЕДУРЫ И АЛГОРИТМЫ
ПРИНЯТИЯ РЕШЕНИЙ
В части II рассмотрены конкретные реализации схемы при-
нятия решений, в соответствии с которой сначала подготавливают
варианты решений (формируют ИМА), а затем осуществляют выбор
наилучших решений. Информацию, необходимую для работы
алгоритмов формирования ИМА и выбора, получают экспертными
методами. Рассмотрены методы экспертного оценивания и дано
их унифицированное описание. Построены алгоритмы формирова-
ния конечных и бесконечных ИМА. Введены понятия простой,
частной и математической задач выбора. Приведен общий алго-
ритм решения задачи выбора, основанный на ее сведении к пере-
численным задачам с использованием методов декомпозиции функ-
ций выбора из части I. Рассмотрены модификации общего алго-
ритма для принципов оптимальности, заданных бинарным отно-
шением и функцией полезности.
В главе 1 рассмотрена задача экспертного оценивания, в главе
2—методы обработки экспертной информации, в главе 3—алго-
ритмы формирования ИМА, в главе 4—решение задачи выбора,
в главе 5—оценки мощности множества недоминируемых альтер-
натив, в главе 6—методы оптимизации функций полезности
и в главе 7—задачи выбора с заданным принципом оптималь-
ности.
Глава 1
ЭКСПЕРТНЫЕ ПРОЦЕДУРЫ ДЛЯ ПРИНЯТИЯ РЕШЕНИЙ
Как указывалось во введении, альтернативы, рассматриваемые
в процессе принятия решений, могут иметь вид элементов мно-
жества Q (целостное представление) или точек критериального
пространства, которое формально описывается Ет (критериаль-
ное представление). Кроме того, элементы й могут быть упоря-
дочены по некоторым аспектам, существенным для принятия
решений.
В практических задачах принятия решений альтернативы не
являются математическими объектами, а чаще представляют собой
конкретные физические системы (продукты, организационно-тех-
нические комплексы и т. д.). Поэтому получение описания аль-
тернатив в перечисленных формах требует разработки методов
5* И. М. Макаров и др.
132
ГЛ. 1. ЭКСПЕРТНЫЕ ПРОЦЕДУРЫ
решения следующих задач: построения множеств возможных и
допустимых альтернатив, формирования наборов аспектов, сущест-
венных для оценки альтернатив, критериального пространства,
упорядочения альтернатив по аспектам, получения оценок по
критериям или отображения Q в критериальное пространство.
Из дальнейшего изложения будет видно, что все они явля-
ются модификациями общей задачи .оценивания, суть которой
состоит в сопоставлении числа или нескольких чисел рассматри-
ваемой системе (объекту, альтернативе). Методы решения задач
оценивания основаны на использовании экспертных процедур.
В § 1 приведена постановка задачи оценивания; показано,
что ее можно представить как задачу принятия решения о наи-
более точной оценке. В § 2 рассмотрена общая схема экспертной
процедуры для решения задач оценивания. В § 3 рассмотрена
подготовка экспертизы. Вопросы обработки результатов экспер-
тизы выделены в отдельную главу 2.
§ 1. Задача оценивания
Смысл [задачиЦоцениванияJ состоит в сопоставлении рассмат-
риваемой системе (альтернативе, критерию) вектора из Ет. Рас-
смотрим некоторые примеры.
Пример 1. Пусть х g Q — альтернатива в задаче принятия
решений. Имеется т критериев. Требуется альтернативе xgQ
сопоставить вектор <h(x), ...»
Пример 2. Пусть ..., km — критерии, учитываемые при
выборе. При построении координатного отношения обобщенной
лексикографии их необходимо упорядочить по важности. В этом
случае системе S={k\, ..., km} сопоставляется упорядоченный
набор различных натуральных чисел от единицы до т\ и, ..., im,
где ik — номер fe-ro критерия при упорядочении по важности в
порядке убывания (иначе говоря, системе S сопоставляется пере-
становка ^./*1, ... , im^* € Ет) .
Пример 3. Пусть множество Q разбито на I подмножеств
Qi, .. •, Qb Для элемента х € Q необходимо указать, к какому
из подмножеств Qi (Z=l, I) он относится. В1 этом случае эле-
менту х сопоставляется одно из чисел 1, 2, ..., I в зависимости
от номера содержащего его подмножества.
Пример 4. Пусть х — отрезок, длину которого надо изме-'
рить. В этом случае отрезку сопоставляется действительное чис-
ло f(х) — его длина.
Назовем пространство Ет т-мерной шкалой (просто шкалой
при т~ 1), операцию сопоставления системе вектора — оценива-
нием, а нахождение указанного вектора —задачей оценивания.
Нетрудно заметить, что простейшей формой задачи оценива-
ния является обычная задача измерения (пример 4), гдет=1;
оценивание есть сравнение с эталоном, а решение задачи нахо-
S1. ЗАДАЧА ОЦЕНИВАНИЯ
133
дится подсчетом числа эталонных единиц в измеряемом объекте.
Более сложные формы оценивания, в которых, как правило, эталон
отсутствует кооперацию сопоставления системе вектора^ в явном
виде не удается указать, представлены в примере 2 (задача ран-
жирования) и в примере 3 (задача классификации).
Выделим следующие этапы решения задачи оценивания.
1. Определение множества допустимых оценок (МДО). На
оо
этом этапе определяется подмножество множества Е = U Ет,
в котором ищется оценка системы. Так, в примере 1—это Ет\
в примере 2—это подмножество Ет, состоящее из всех переста-
новок чисел 1,2, ..., /и; в примере 3—это подмножество {1, ...,/}
множества Е±, в примере 4—это множество всех положительных
чисел.
f'*: 2. Определение наиболее точной оценки. На этом этапе из
МДО выбирается та оценка, которая? наиболее точно выражает
свойства оцениваемой системы. Это позволяет представить задачу
оценивания в виде задачи принятия решений <Q, ОП>, в которой
Q есть МДО, а ОП—принцип оптимальности, выражающий пред-
ставление о наиболее точной оценке. Он задается функцией выбора
( а, если а£ X s Q,
Соп(Х)= I 0, если . (1)
. где а—оценка системы, которая является решением задачи <Q, ОП>.
Упражнение 1. К какому классу из описанных в § 1.2.4
принадлежит функция выбора (1)?
В соответствии с указанными этапами решение задачи оцени-
вания сводится к последовательному решению двух задач выбора:
<£, ОП!> и <й, ОП>, где ОП1—принцип оптимальности, задаю-
щий допустимость оценки; ОП—принцип оптимальности, задаю-
щий точность оценки из Q; решением 1-й задачи выбора является
Й = СОП (£); решением 2-й задачи выбора является искомая оценка
а = Соп (□).
Рис. 1.
Принципы оптимальности ОПХ и ОП (как и соответствующие
функции выбора С0П1 и Соп) зависят как от самой оцениваемой
системы, так и от оценивающего лица, роль которого аналогична
роли ЛПР в общей задаче принятия решений.
134
ГЛ. I. ЭКСПЕРТНЫЕ ПРОЦЕДУРЫ
Схема решения задачи оценивания представлена на рис. 1.
Видно, что она близка к рассмотренной во введении общей схеме
принятия решений, но несколько проще. В качестве здесь
выступает множество оценок Е — U Ет', вместо двух этапов по-
т= 1
строения ИМА—один этап построения МДО; решение задачи
выбора <Q, ОП> состоит из единственного элемента — результата
оценивания a==Con(Q).
§ 2. Общая схема экспертизы
Задачи оценивания, рассмотренные в § 1, возникают на раз-
личных этапах принятия решений. Они могут быть решены не-
посредственно ЛПР или с помощью консультантов (исследовате-
лей), когда оценивание сводится к измерению, к получению данных
из справочников и другим сравнительно простым операциям.
В общем случае из-за сложности оцениваемых систем и труд-
ности получения информации для решения задачи оценивания
привлекаются люди, обладающие специальными знаниями и опы-
том работы с данной (или близкой к ней) системой. Их называют
экспертами, а решение задачи оценивания — экспертизой.
В приведенной схеме решения задачи оценивания эксперты
участвуют в решении 2-й задачи выбора <Q, ОП>. Для построе-
ния Q необходимо иметь общее представление о свойствах системы,
которое не всегда есть у эксперта как специалиста в какой-либо
конкретной области. Поэтому эксперт решает не исходную задачу
выбора <й, ОП>, а, вообще говоря, отличную от нее задачу
выбора <£2Э, ОПЭ>, где £2Э—МДО для эксперта, ОПЭ —принцип
оптимальности эксперта, задающий точность его оценки, выби-
раемой из йэ. Например, в рассматриваемой далее задаче ран-
жирования системе из т объектов должна быть сопоставлена
перестановка чисел от единицы до т. При этом Q состоит из всех
возможных перестановок чисел. Однако, чтобы найти требуемую
перестановку, экспертам может быть предложено сделать попарное
сравнение всех объектов. При этом они решают задачу оцени-
вания с другим МДО йэ, состоящим только из перестановок двух
чисел. Результирующая перестановка определяется после обра-
ботки оценок экспертов. Вопросы, связанные с экспертизой, рас-
сматриваются и решаются исследователем (консультантом). Он
определяет Q, и все другие параметры схемы экспертизы, осу-
ществляет подбор экспертов, организует реализацию экспертизы.
Анализ существующих экспертиз показывает, что в процессе
их построения можно выделить следующую последовательность
действий:
1. Исследователь находит мнсжество допустимых сценск Q,
в котором содержится искомая оценка.
§2. ОБЩАЯ СХЕМА ЭКСПЕРТИЗЫ
135
2. Исследователь определяет множество допустимых оценок Й8,
из которого осуществляют выбор эксперты.
3. Каждый эксперт выбирает свою оценку (йэ) £йэ
(i=l,Af), т. е. решает задачу выбора наилучшей оценки из Й8.
При этом эксперты могут взаимодействовать между собой.
4. По заранее разработанному алгоритму (формуле) исследо-
ватель производит обработку полученной от экспертов информации
и находит результирующую оценку из й, являющуюся решением
исходной задачи оценивания.
5. Если полученное решение не устраивает исследователя, он
может предоставить экспертам дополнительную информацию, т. е.
организовать обратную связь, после чего они вновь решают соот-
ветствующие задачи выбора.
Рис. 2.
Выделенная последовательность действий представлена блок-
схемой экспертизы (рис. 2). Ее параметры: ,
й—исходное МДО;
Йэ—МДО для экспертов;
L—взаимодействие между экспертами;
Q—обратная связь;
<р—обработка (отображение й^ —>й).
Введем следующие понятия. Назовем схемой экспертизы пя-
терку параметров, представленных на блок-схеме. Под подготов-
кой экспертизы будем понимать предварительную разработку схемы
экспертизы и подбор экспертов, а под реализацией экспертизы —
получение от экспертов информации и ее обработку.
136
ГЛ. 1. ЭКСПЕРТНЫЕ ПРОЦЕДУРЫ
Рис. з.
Результат реализации экспертизы практически полностью опре-
деляется ее подготовкой, которая и будет рассмотрена далее.
Вопросы обработки "экспертных^оценок, в которых большое раз-
витие получили математические
методы, выделены в отдельную
главу 2.
Замечание. В ряде случа-
ев (например, при • многомерном
шкалировании, § 2.3) отображе-
ние <р представимо в виде
Ф = 9(1|?(С1, ..., CN)), (2)
где Ci—функция"выбора i-ro экс-
перта (i=],N)\ ф—композиция
функций выбора С{ и отображе-
ние q: йэ —► й. Это означает, что
сначала находится оценка экс-
пертов H3jQ3, а затем по ней на-
ходится результирующая оценка из й. Блок-схема обработки
для этого случая представлена на рис. 3.
Упражнение 2. Доказать, что при й = Йэ обработку всегда
можно представить в виде (2).
§ 3. Подготовка экспертизы
Подготовка экспертизы фактически состоит в конкретизации
выделенных параметров.
1. Множество допустимых оценок. МДО определяется решае-
мой задачей оценивания. Перечислим типы МДО и укажем опре-
деляющие их задачи'оценивания.
1) Й = {0, 1}. Соответствующая задача попарного (равнения
заключается в выявлении лучшего из двух имеющихся объектов
а и Ь. При этом
С(О)-( !' если “ лу,м ь- (3)
( 0 в противном случае.
2) й = {<1, 2, ..., и>,'<1, 3, ..., п, 2>, ..., <п, п—1, ..., 1 >},
т. е. состоит из множества перестановок длины п. Соответствую-
щая задача ранжирования заключается в упорядочении объектов,
образующих систему, по убыванию (возрастанию) значения неко-
торого признака. При этом’
С(й) = <гп i2, ..., « (4)
где ij—номер /-го объекта при указанном упорядочении.
3) й={1, ..., /}. Соответствующая задача классификации
заключается в отнесении заданного элемента x^S к одному из/
§3. ПОДГОТОВКА ЭКСПЕРТИЗЫ 137
подмножеств Slt .Sz. При этом
С (й) = 7 Лесли^х € £/• (5)
4) £1 = Ет. Соответствующая задача численной оценки заклю-
чается в сопоставлении системе ^одного или нескольких чисел.
При этом^
C(Q) = a9 если^оценкой системы является вектор а£Ет. (6)
Упражнение 3. Пусть задача состоит в том, что из пред-
ложенных нескольких вариантов ответа на вопрос нужно выбрать
один. К какой из перечисленных задач 1)—4) можно отнести эту
задачу?
2. Множество допустимых оценок для экспертов. Типы ьй9
для экспертов те же, что к типы й.
Для конкретизации йэ необходимо описать вид его представ-
ления эксперту, который зависит от формы опроса эксперта. Опрос
типа интервью предполагает беседу исследователя с экспертом,
в ходе которой исследователь ставит вопросы, в соответствии
с заранее разработанной программой, фактически определяющей йэ.
Большую роль в проведении интервью играет установление вза-
имопонимания ; между исследователем и > экспертом. К недо-
статкам такого метода опроса относятся сложность формализации
и высокие требования, предъявляемые к исследователю и эксперту.
Наиболее часто применяемой формой опроса экспертов является
анкетирование. Анкета—это* набор вопросов, на которые предла-
гается ответить'эксперту. Вопросы должны быть сформулированы
так, чтобы не допускать неоднозначного толкования. Сложные
вопросы разбиваются на более простые. Многочисленными экспе-
риментами установлено, что человек лучше отвечает на качест-
венные вопросы (лучше—хуже), чем на количественные. Поэтому
при составлении вопросов следует отдавать^предпочтение таким,
на которые^от эксперта требуется качественный ответ. Вопросы,
включаемые в анкеты, следует составлять по некоторой иерархи-
ческой схеме, т. е. сначала формулировать более общие вопросы,
а затем частные. Полезными для исследователя являются форма-
лизованные сведения о характере источников аргументации,
а также о степени влияния каждого' из источников на ответ
эксперта. Такие сведения предлагается получать путем заполне-
ния'’табл. 1. Вгкаждой строке эксперт должен указать соответ-
ствующую степень влияния (например, звездочкой).
Аналитическая форма опроса предполагает длительную само-
стоятельную работу эксперта, направленную на анализ характер-
ных свойств и тенденций исследуемой системы. Такую форму на-
зывают методом докладной записки. Эксперт в свободной форме
излагает свое мнение. Такая форма опроса является плохо фор-
мализуемой и трудоемкой для эксперта, но позволяет наиболее
точно выяснить его мнение. Форма докладной записки часто
138
ГЛ. 1. ЭКСПЕРТНЫЕ ПРОЦЕДУРЫ
применяется как первый этап более сложной экспертизы, позво-
ляющей уточнить направление исследований и содержание во-
просов, задаваемых на последующих этапах. Можно считать, что
08—множество всех возможных докладных записок по вопросам,
рассматриваемым в данной экспертизе.
Таблица 1
Источник аргументации Степень влияния источника
высокая средняя низкая
Проведенный теоретик, анализ *
Производственный опыт Обобщение отечественных работ Обобщение зарубежных работ * * *
Интуиция *
3. Взаимодействие экспертов. Выделяют три вида взаимодей-
ствия экспертов (параметра L):
1) эксперты могут свободно обмениваться информацией друг
с другом;
2) обмен информацией между экспертами регламентирован;
3) эксперты изолированы друг от друга.
В схеме типа круглого стола взаимодействие между экспер-
тами не регламентируется. Вся экспертная группа собирается для
определения общего мнения. Такая обстановка может способство-
вать созданию творческой атмосферы, так как эксперты будут
обогащаться идеями друг друга. С другой стороны, такой способ
имеет свои отрицательные стороны. Он предъявляет повышенные
требования к экспертам: умение высказывать мнение, не завися-
щее от мнения большинства; способность отказаться от своего
мнения, если оно окажется неверным.
Некоторая регламентация общения экспертов в схеме круглого
стола позволяет избежать указанных недостатков. Соответствую-
щая модификация называется методом мозговой атаки. Она со-
стоит в том, что в течение определенного промежутка времени
любое высказанное мнение не подлежит обсуждению и не может
быть отвергнуто. За это время каждый из экспертов успевает
хорошо обдумать высказанное другим мнение, и принятие или
отклонение этого мнения имеет в этом случае большую обосно-
ванность.
Когда эксперты изолированы, то каждый высказывает свое
мнение независимо от других (решает свою задачу выбора). При
этом используют статистические методы обработки экспертной
информации, поскольку оценки отдельных экспертов можно рас-
сматривать как независимые реализации случайной величины.
§3. ПОДГОТОВКА ЭКСПЕРТИЗЫ
139
4. Обратная связь в экспертизе. Идея обратной связи в экс-
пертизе заключается в следующем. Эксперты дают оценки, ко-
торые обрабатываются. После этого каждому из них предъявляют
результирующую оценку, вообще говоря, вместе с другой инфор-
мацией. На основании полученных данных эксперты уточняют
свои оценки, после чего процедура повторяется снова до тех пор,
пока не будет получена удовлетворяющая исследователя согласо-
ванность оценок.
К числу наиболее известных процедур с обратной связью
относится метод Дельфи. Экспертам предлагается ответить на
ряд вопросов и свои ответы аргументировать. Исследователь
изучает ответы экспертов и определяет их согласованность. Если
мнения экспертов недостаточно согласованы, то он сообщает
каждому из них дополнительные сведения о системе, а также
ответы на поставленные вопросы и аргументацию других членов
экспертной группы. С учетом вновь полученной информации
эксперты снова отвечают на поставленные вопросы.
Если рассматривать набор функций выбора экспертов как одну
функцию выбора, то процедуру метода Дельфи можно описать
динамической функцией выбора из § 1.2.6 (последующий выбор
зависит от результатов предыдущего). Применение метода Дельфи
для решения задачи численного оценивания будет рассмот-
ренно в § 2.1. Недостатками метода являются большие затраты
времени на проведение всех туров опроса и большая трудо-
емкость процедуры, связанная с пересмотром мнений экспертов.
5. Подбор экспертов. Первым шагом при подборе экспертов
является определение количественного состава экспертной группы.
Для каждой задачи этот вопрос решается, как правило, отдельно.
Число экспертов должно быть достаточно большим для того,
чтобы они в совокупности могли учесть существенные свойства
задачи и чтобы решение, найденное при их помощи, было доста-
точно точным. При слишком большом количестве экспертов их
мнения становятся несогласованными (за счет экспертов низкой
квалификации), возникают трудности в организации экспертизы.
С учетом этого целесообразно включить в группу от 10 до 20 че-
ловек. Возможны отклонения как в большую, так и в меньшую
стороны.
Когда численность экспертной группы определена, переходят
непосредственно к подбору экспертов. Для этого определяют
круг решаемых задач и составляют список лиц, компетентных
в рассматриваемой и близких областях. Для составления списка
экспертов можно предложить следующую итеративную процедуру.
Первоначально отобранным экспертам предоставляют список
вопросов, на которые в процессе проведения экспертизы должны
быть получены ответы, и просят рекомендовать специалистов,
способных дать заключение по представленным вопросам. Затем
список вопросов предоставляется каждому из названных специа-
140
ГЛ. 1. ЭКСПЕРТНЫЕ ПРОЦЕДУРЫ
листов, которые в свою очередь тоже называют людей, компе-
тентных в вопросах данного списка, и т. д. Этот процесс закан-
чивается, как только перестают называться новые специалисты.
Такая процедура позволяет составить достаточно полный список
компетентных лиц.
Помимо компетентности, хороший эксперт должен обладать
еще целым рядом качеств. Основными из них являются следую-
щие: креативность—способность решать задачи, метод решения
которых полностью или частично неизвестен; эвристичность —
способность выявлять неочевидные проблемы; интуиция—способ-
ность угадывать решение без его обоснования; предикатность —
способность предсказывать или предчувствовать будущее решение;
независимость—способность противостоять мнениям большинства;
всесторонность—способность видеть проблему с разных точек
зрения.
Требования, предъявляемые к экспертам, [зависят также от
метода организации экспертизы. Так, при работе эксперта в ко-
миссии, где эксперты вступают в непосредственный контакт друг
с другом, важное значение приобретают психологические факторы.
Часто специфические требования к эксперту непосредственно вы-
текают из формы организации и проведения экспертизы.
Для отбора экспертов из составленного списка, как правило,
используют тестирование. Пест состоит в следующем: эксперту
предлагают ответить в письменной форме на ряд вопросов, с тем
чтобы проверить его знания в области проводимой экспертизы и
выявить наличие качеств, перечисленных выше. В таких тестах
может применяться самооценка, т. е. эксперту предлагается оце-
нить свои знания (например, по пятибальной шкале) по каждому
вопросу теста. Для обработки и составления таких тестов прив-
лекают специалистов в области психологии.
При подборе экспертов следует учитывать заинтересованность
экспертов в том или ином результате^экспертизы. Наиболее бла-
гоприятным является тот 'случай, [когда эксперту безразличен
конечный 4 результат экспертизы. ЛЭто способствует его большей
объективности.
В ряде случаев ’при подборе экспертов используются некото-
рые численные оценки, характеризующие их качества. Такие
численные оценки носят статистический характер, и их примене-
ние возможно только тогда, когда эксперт достаточно часто
привлекался для решения задач экспертизы одного типа. Приме-
ром может служить определение экспертами качества продукции
в отделе технического контроля. Численные оценки могут быть
использованы для улучшения состава экспертной группы и повы-
шения достоверности результирующей оценки.
Остановимся Подробнее на определении весов экспертов az:
веса выражают их степень компетентности. Пусть одни и те же
эксперты многократно использовались для оценивания числовых
S I. СТАТИСТИЧЕСКИЕ МЕТОДЫ
141
величин. Относительная ошибка i-ro эксперта в /-й экспертизе
равна
8/у = | T^j Т ij\ fTfy,
где Тф,—фактическое значение; Т,,—оценка, данная i-м экспер-
том. Тогда
до / / */ \ . \ I / / I \
а/ = 2b \Д ) / \\ S 8 is J » (7)
где kt—количество оценок, которые дал /-й эксперт.
Упражнение 4*. Показать, что подбор экспертов можно
представить в виде задачи принятия решений.
Литература. [7, 15, 39, 43, 50, 77].
Глава 2
МЕТОДЫ ОБРАБОТКИ ЭКСПЕРТНОЙ ИНФОРМАЦИИ
В соответствии с общей схемой экспертизы, рассмотренной
в § 1.2, обработка оценок экспертов состоит в применении к ним
заданного отображения <р: (Q3)v-+Q. Смысл обработки заклю-
чается в нахождении результирующей оценки системы по оцен-
кам, даваемым экспертами.
В настоящей главе рассмотрены три основные группы методов
обработки: статистические методы (§ 1), алгебраические методы
(§ 2) и методы шкалирования (§ 3). Статистические методы осно-
ваны на предположении, что отклонение оценок экспертов от
истинных происходит в силу случайных причин; задача состоит
в том, чтобы восстановить это истинное значение с наименьшей
погрешностью. Суть алгебраических методов заключается в сле-
дующем: на множестве допустимых оценок задается расстояние
и результирующая оценка определяется как та оценка, сумма
расстояний от которой до оценок экспертов минимальна. Суть
методов шкалирования состоит в том, что по экспертной инфор-
мации о степени различия объектов устанавливается минимальный
или близкий к минимальному набор критериев и оценок объектов
по ним, обуславливающих указанные экспертами различия.
В главе рассмотрены наиболее распространенные методы обра-
ботки применительно к конкретным экспертизам.
§ 1. Статистические методы
Результаты оценок каждого из экспертов можно рассматривать
как реализации некоторой случайной величины, принимающей
значения из й8, и применять к ним методы математической ста-
тистики.
142
ГЛ. 2. МЕТОДЫ ОБРАБОТКИ ЭКСПЕРТНОЙ ИНФОРМАЦИИ
Статистические методы позволяют определить согласованность
мнений экспертов, значимость полученных оценок и т. д. Степень
согласованности указывает на качество результирующей оценки.
1. Численные оценки. Задача состоит в сопоставлении оце-
ниваемой системе одного числа. Для ее решения используется
экспертиза Э1:
L — эксперты изолированы;
Q—обратная связь отсутствует;
A N
..... xN) = 2 / У а,-. (1)
Результирующая оценка ищется по формуле средневзвешенного
значения, где az(i = l, N)—веса экспертов. При отсутствии ин-
формации о компетентности экспертов можно положить az = 1
(i = l, Степенью согласованности мнений экспертов в экспер-
тизе Э1 служит дисперсия о2:
N N
о2 = 2 (а—а.У <*i / 2 а/, (2)
i= 1 ' i = i
где а,-—оценка i-ro эксперта, а—результирующая оценка.
Приведем одну из модификаций экспертизы Э1, повышающую
(при некоторых предположениях) точность оценивания. Экспертиза
Э2 характеризуется параметрами
<р(х1, 4, xf, х22, xj,
й9 = £з,
VN VN VN\_
• ♦ • , Д'! , Л2 у Ag J ——
__ 'V Ч~ Х3,Уз
~~ i=l T1+Y2+V3
(3)
N
/ 2 az.
1 1
Остальные параметры те же, что и в экспертизе Э1. Степень
согласованности методу оценками определяется выражением
W A N N
О2 = 2 а< о? / 2 ai + 2 (а—а<)2«1 / 2 а,. (4)
1=1 ч=1 1=1 4=1
где а .—средняя оценка i-ro эксперта (i-e слагаемое в числителе
дроби (3)), or? = (a£—а{)2/?4; —степень неуверенности эксперта
своем ответе.
В,.экспертизе Э2 а[, а£, а» интерпретируются как оптимисти-
ческая, наиболее вероятная и пессимистическая оценки i-ro экс-
перта соответственно. Коэффициенты уц у2, уз, 74 определяются
эмпирически. По одной методике yi = l, у2=4, 73=1, 74=36, по
другой 71 = 3, 7» = 0, 78 = 2, у4 = 25 (по второй методике ух > ys,
$1. СТАТИСТИЧЕСКИЕ МЕТОДЫ
143
так как в ней считается, что человек склонен к занижению
оценки).
В экспертизах Э1 и Э2 можно определить статистическую
значимость полученных результатов. Задавшись вероятностью
ошибки Рош, укажем интервал, в который оцениваемая величина
попадает с вероятностью 1—Рош:
а—А a-f-A;
считается, что величина а распределена нормально с центром а
и дисперсией (2). Тогда A = Zcr|/Qv, где величина t имеет распре-
деление Стьюдента с N—1 степенью свободы. Ее определяют по
таблице, задавшись величиной Рош.
Г^р и м е р 1. Десять экспертов с одинаковыми весами а, = 1
(1 = 1, 10) оценивают величину Т. От них получены следующие
оценки:
Л = 33; Т2 = 35; Т8 = 32,2; 7\ = 34; Т6 = 38;
Т, = 34; 7\ = 37; Т8 = 40; Т9 = 36; Т10 = 35,5.
Значение Т, подсчитанное по формуле (1), в которую вместо х{
подставлены Tit будет равно 35,5. Дисперсия о2, рассчитанная
по (2), равна 4,9; 0 = 2,2136.
Задав вероятность ошибки Рош = 0,05, по таблицам распреде-
ления Стьюдента определим величину t: число степеней свободы
равно 9; 1 = 2,262. По формуле (5) А =1,583. Таким образом,
с вероятностью 0,95 оцениваемая величина Т находится в интер-
вале [33,917; 37,083].
Опишем применение метода Дельфи для численной оценки
в виде экспертизы ЭЗ:
Й = Л;
^a=|z €
S Z1 = 1.
1=1 ‘
zf>0
(5)
L—эксперты изолированы;
Q—экспертам предоставляется медиана q2 (7), диапазон кваш
тилей (8) и обоснования оценок, выходящих за этот диапазон.
Отображение <р зада-
ется следующим обра-
зом. Весь интервал до-
пустимых значений оце-
ниваемой величины раз-
бивается на k интерва-
лов tx, ..., tk\ эксперт
оценивает вероятность
попадания оцениваемой
величины в каждый из
Таблица 1
Эксперты Интервалы
tx t*
1 Р11 Р12 Plk
2 Р21 Р22 . . . P2k
N PNi PN2 • . . PNk
144 ГЛ. 2. МЕТОДЫ ОБРАБОТКИ ЭКСПЕРТНОЙ ИНФОРМАЦИИ
интервалов; по результатам их оценок составляется табл. 1,
где — оценка вероятности попадания оцениваемой величины
в /-й интервал, данная Z-м экспертом. На основе этой таблицы
определяется мнение экспертов о попадании оцениваемой| величи-
ны в каждый из интервалов tp
; * , _
2 Pij^i I 2 а,- O’ = 1 > k). (6)
J t=i
k
Упражнение Jl. Проверить, что 2^r==l'
/ = i i
Результирующей оценкой ф (Сх (Q3), ..., ‘ CAr(Q9)) является
медиана построенного распределения q2, определяемая|из условия
Р(Т <72)-0,5.
(7)
Помимо q2 вычисляется диапазон квантилей
= (8)
где Р (Т ^9з) = 0,75; Р(Т 0,25. Эмпирически установлено,
что процедуру можно прекращать, когда диапазон квантилей
уменьшился в 1,6 раза по сравнению с первоначальным.
2. Ранжирование. Строгое'ранжи рование. Задача со-
стоит в сопоставлении оцениваемой системе^одной перестановки.
Определим экспертизу Э4:
Q—множество всех перестановок;
Q9 = Q;
L—экспертизы изолированы;
Q—обратная связь отсутствует.
Отображение ф определяется следующим образом. Результаты
В i-й строке стоят места
(ранги), данные £-м экс-
пертом ранжируемым
объектам. В (N + 1 )-й
строке стоят суммы ран-
гов, полученных объек-
тами от экспертов. Все
п объектов упорядочи-
ваются в соответствии с
величиной rs, определя-
емой по формуле
rs = 2 rsi. (9)
/ = 1
опроса экспертов сводятся в табл. 2.
Таблица 2
Эксп ерты Объекты
1 2 п
1 Гц Г12 г 1п
2 Г21 Г 22 Г2П
N rNi . . . rNn
2 рангов Г1 г2 . . . гп
На первое место ставится объект, у которого rs минимально,
и т. Д. ‘
Степень согласованности мнений экспертов определяется при
помощи коэффициента конкордации W. Остановимся на этом под-
§1. СТАТИСТИЧЕСКИЕ МЕТОДЫ
14S
Y робнее. Рассмотрим два крайних^случая. Первый случай: ранжи-
ровки всех N экспертов совпадают. Каждый объект получил от
j всех экспертов одинаковый ранг, который для /-го объекта равен
u rjlN. Второй случай: полная несогласованность экспертов. Будем
' понимать под несогласованностью противоположность ранжировок^
даваемых экспертами. В силу (9) получаем
„ fn nN N / п \
'io>
( .. £ = 1 i = l/ = l i = = l JJ
i' Сумма рангов, даваемых каждым экспертом (т. е. выражение в скоб-
> ках в (10)), всегда равна п (« + 1)/2. Поэтому 2 rt — Nn (п-{- 1)/2.
, г = 1
; За средний ранг принимают величину
г{ ср = X С-М = N[(n 4-1)/2,
i -1
(11)
а за степень согласованности мнений—сумму квадратов отклоне-
ний rf от среднего значения rlcv.
Упражнение 2. При всех ли N и п существуют ранжи-
k ровки, у которых степень согласованности равна нулю?
Упражнение 3*. Доказать, что при четном W (n-|-1) ран-
,, жировки с нулевой согласованностью существуют, и указать регу-
лярный способ их построения.
I Коэффициентом конкордации W для случая строгого ранжи-
। рования, т. е. отсутствия равных рангов в ранжировке каждого
' эксперта, называется^ величина^
12 У, [г,—уЛ«(п+1)Г
(12)
где п — число объектов, N — число экспертов.^
Пример 2. Пусть проводится экспертиза по оценке техноло-
гического процесса выплавки стали в конверторе. Задан список из
шести признаков, влияющих на процесс. Десять экспертов ранжи-
ровали признаки по важности. Результаты их работы приведены
в табл. 3. Рассчитаем коэффициент конкордации. Суммы рангов
в соответствии с (9) равны: гг = 52, г2==46, г3 = 19, г4 = 28,
г5=17, гв = 48. Из (11) находим г{ ср = 35. Подставляя найденные
значения в (12), получим W — 0,690. '
Нестрогое ранжирование. Задача состоит в сопостав-
лении системе нестрогой ранжировки (вектора с определенными
свойствами). При этом некоторые объекты могут быть равноцен-
ными. Им приписываются равные ранги. Так, если два объекта
делят места 4—5, то каждый из них получает ранг 4,5.
146
ГЛ. 2. МЕТОДЫ ОБРАБОТКИ ЭКСПЕРТНОЙ ИНФОРМАЦИИ
Таблица 3
Номера экспертов
Признаки 1 2 3 4 5 6 7 8 9 10
Шум 6 1 6 6 6 6 4 5 6 6 52
Цвет футеровки 4 5 4 5 5 3 5 6 4 5 46
Цвет пламени 2 2 2 3 3 2 1 1 1 2 19
Цвет дыма 1 4 3 2 2 4 3 3 3 3 28
Качество дыма 3 3 1 1 1 1 2 2 2 1 17
Искры 5 6 5 4 4 5 6 4 5 4 48
У п"р а ж'н е н и’е 4. Описать множество Q для нестрогих ран-
жировок.
Экспертиза Э5 для нестрогого ранжирования отличается от
экспертизы Э4 только множеством Q.
Коэффициент конкордации для нестрогого ранжирования опре-
деляется формулой
12 Е [г<— 4jV(n+1)]2
W =-------J, (13)
N ki 7
»=i/=i
где k{—число групп равных рангов, введенных г-м экспертом; —
количество дробных рангов в /-й группе, введенной i-м экспертом.
Статистическую значимость ранжировки проверяют следующим
образом. Выбирают вероятность ошибки Рош. Предполагают, что
величина N (п— 1)F имеет х2-распределение с (n — 1) степенью
свободы. По Рош по специальным таблицам находят табличное
значение Wa. Если коэффициент W, полученный при реализации
экспертизы, больше или равен 1Га, то полученную ранжировку
считают статистически значимой.
Пример 3. Определим статистическую значимость ранжи-
ровки примера 2. Пусть требуется, чтобы вероятность ошибки,
т. е. вероятность того, что полученная ранжировка является слу-
чайной, Рош = 0,01. Вычислим величину N (п—1)IF = 10-5-0,69 =
= 34,5. Из таблиц распределения х4 для числа степеней свободы,
равного 5, находим x?,oi (5) = 15,086, что соответствует табличному
значению величины N (п—1)№о. Вычисленное значение, равное
34,5, больше^табличного. Следовательно, полученная ранжи ровка
статистически значима.
Выше подразумевалось, что эксперты имеют равную компе-
тентность. Однако, если компетентность экспертов различна и
§1. СТАТИСТИЧЕСКИЕ МЕТОДЫ
147
может быть оценена некоторым числом, то формулы (9) — (13)
нуждаются в уточнении.
Пусть компетентность j-го эксперта оценивается положительной
величиной а • (вес эксперта). Будете считать эти величины нормы-
/а X
рованными ( 2 = 1 ). Сумму рангов rt объектов будем рассчи-
\/ = 1 /
N
тывать по формуле rz = 2 rijar Коэффициент конкордации с уче-
/ = 1
том компетентности экспертов определяют той же формулой (13).
Проверку статистической значимости производят так же, как и
выше. Отметим, что проверяют статистическую значимость того,
что построенная групповая ^ранжировка отражает коллективное
мнение экспертов, т. е. проверяют значимость согласованности их
мнений.
Метод парных сравнений для нестрогого ран-
жирования. Экспериментально установлено, что большую труд-
ность для эксперта представляет построение ранжировки на основе
одновременного учета нескольких различных признаков, по кото-
рым оцениваются объекты. В этих случаях эксперты решают за-
дачи попарного сравнения (см. § 1.3).
Определим экспертизу Э6 для решения задачи нестрогого ран-
жирования:
Q—то же, что и в экспертизе Э5;
Яэ—множество всех матриц Л = (а(/), где __
«,/€{0, 1), а,7 + а71.= 1 (i=/=/), ап = 0 (/== 1, л); (14)
L—эксперты изолированы;
Q—обратная связь отсутствует.
Отображение <р определяется следующим образом. Вычисляют
и
матрицу A = (aqt)\= 2где^ Лу'= (а^)—оценка /-го эксперта.
/ = 1
п
Находят величины as= 2 ats (s=l> л)„ Объекты упорядочивают
i = 1
в соответствии с величинами as. Объект с минимальным as полу-
чает ранг 1 т. д.
В методе парных сравнений каждый из экспертов производит
Сп сравнений, т. е. сравнивает каждый.объект с каждым. Резуль-
тат сравнений /-го эксперта представляется матрицей размера
пхп, в которой а|*=1 тогда и только тогда, когда по мнению
/-го эксперта i-й объект предпочтительнее Л-го. Для любой пары
объектов <р, q> либо р предпочтительнее q, либо наоборот. Это
и выражено условиями (14); по определению.
Матрица AJ, представленная j-м экспертом (/ = 1, N), является
матрицей некоторого бинарного отношения, называемого отноше-
нием предпочтения э ксперта.
148
ГЛ. 2. МЕТОДЫ ОБРАБОТКИ ЭКСПЕРТНОЙ ИНФОРМАЦИИ
Упражнение 5. Доказать, что бинарное отношение, по-
строенное экспертом, является антирефлексивным, антисимметрич-
ным и, вообще говоря, не является ацикличным»
Сопоставим бинарному отношению граф. На рис. 1 приведен
пример графа отношения с матрицей
'0101 ( 1 '
0 0 1 0 0 0
л/ 10 0 1 11
Л 0 1 0 0 0 0’
110 10 1
,0 О 0 1 0 0у
Поскольку на отношение
то соответствующий граф
6, 2 на рис.
Говорят,
все 'объекты
наложено
не
может иметь
требование ацикличности,
циклы (например, 2, 3, 5,
1).
что предпочтение может быть выражено рангами, если
упорядочиваются так, что aik=l тогда и только
тогда, когда ранг i-ro объекта больше
ранга fe-ro.
Утверждение 1. Необходимым
и достаточным условием того, что
предпочтения выражаются рангами,
является ацикличность отношения пред-
почтения эксперта.
Доказательство. Необходи-
мость. Пусть предпочтения выражены
при помощи рангов. Покажем, что в этом
случае соответствующий граф не имеет циклов. Зададим на множестве
вершин графа функцию, поставив в соответствие каждой вершине
ранг представляемого этой вершиной объекта. В этом графе вер-
шины i и / соединим дугой тогда и только тогда, когда г (0 > г (/),
где г{1) к г(/) — ранги f-й и /-й вершин соответственно. Пусть
существует цикл с вершинами 1, 2; тогда по построению графа
г (1) < г (2) < ... < г(1), т.е. г (1) < г (1). Получили противоречие.
Достаточность. Пусть в графе отсутствуют циклы. Пока-
жем, что в этом случае предпочтения могут быть выражены при
помощи рангов. В графе без циклов существует хотя бы одна
вершина, в которую не входит ни одной дуги. Если такой вер-
шины нет, то, переходя по дугам от одной вершины к другой,
в силу конечности числа вершин графа получим цикл* Кроме
того, пос кол ьку^ дуги связывают любые две вершины, такая вер-
шина только одна. Поставим ей в соответствие ранг, равный 1,
и исключим ее из рассмотрения. Получим граф того же типа,
в котором число вершин на единицу меньше. В этом^графе про-
ведем аналогичные построения. В результате такой ^процедуры
предпочтения могут быть выражены при помощи рангов. Утверж-
дение доказано.
§2. АЛГЕБРАИЧЕСКИЙ МЕТОД .
149
Замечание. В рассматриваемом случае наличие циклов
эквивалентно наличию циклов длины 3 в силу свойств графа.
Упражнение 6. Доказать, что максимальное число цик-
лов длины 3 для четного п равно (га3 — 4п)/24; для нечетного —
(и8—п)/24.
КоэффициентомТсовместимости мнений эксперта называется
величина
I 1—24d/(/i3—л), если п нечетно,}
1 — 24d/(ns —4п), если п четно;
здесь d—число циклов длины 3. Величину v можно использовать
в качестве оценки компетентности эксперта] при экспертизах
типа Э6.
Ранговая корреляция. Укажем на один из способов
оценки связи между двумя различными ранжировками. Пусть
..., in>, </i, •••, /„>—две'нестрогие ранжировки. Положим
О-st
О, если is = it,
1, если is<Jt,
—1, если
аналогично определим величины bst для 2-й ранжировки. Коэф-
фициентом ранговой корреляции Кендалла называется величина
п п
X X astbst
S = 1 / = 1____
n(n —1)/2 •
(15)
Рассчитав коэффициент т, оценим значимость обнаруженной
связи между ранжировками. Для этого обозначим числитель (15)
через S. Если зафиксировать одну ранжировку (строгую) и рас-
сматривать все п\ остальных строгих ранжиророк, можно найти
частоту всех возможных значений S (и соответствующих т). При
и > 10 распределение S близко к нормальному со среднеквадра-
тичным отклонением <5^Уп(п—1)(2п + 5)/18. Прип^Ю рас-
пределение S можно найти в специальных таблицах.
В общем случае, если наблюдаемая величина S принимает
значение So такое, что случайное появление величины So или
большей маловероятно, то гипотеза о независимости ранжировок
отвергается. Если Pr{j S | > SJ < р0, то полученный коэффициент
т считается значимым. Величину р0 задают как уровень значи-
мости; сравнивают вычисленное значение S с табличным длиздан-
ного уровня значимости
§ 2. Алгебраический метод
" Как указывалось в начале главы, суть алгебраических методов
обработки экспертной информации состоит во введении некоторого
расстояния между оценками. Задача состоит в сопоставлении
150
ГЛ. 2. МЕТОДЫ ОБРАБОТКИ ЭКСПЕРТНОЙ ИНФОРМАЦИИ
системе нестрогой ранжировки. Для ее решения используется
экспертиза Э7:
Q—множество всех нестрогих ранжировок п объектов (вид й
будет указан ниже);
йэ = й;
L—эксперты изолированы;
Q—обратная связь отсутствует.
Отображение <р определяется следующим образом. Результи-
рующая оценка Ао находится из формулы
N
A0£Argmin У, d(A, А'),
Аеа i=i
где d—расстояние между ранжировками.
Дадим описание нестрогих ранжировок и определим расстояние
d между ними. Ранжировки (т. е. элементы й) будем задавать матри-
цами А = (а{у), в которых а(/- = 1 тогда и только тогда, когда
i-й объект предшествует /-му; если объекты i и j равноценны, то
а/7 = 0; кроме того, а/(- = 0 (1=1, п); а/у = 1 => aJ{ — — 1.
Упражнение 7*. Какие условия необходимо наложить на
элементы матрицы из 0, 1 и —1 для того, чтобы она задавала мат-
рицу некоторой ранжировки?
Будем говорить, что ранжировка С находится между ранжи-
ровками А и В, если а(/с,удля всех i, / = 1, п или
a{j Cq bij для всех i, / = 1, п.
Расстояние d между ранжировками вводится аксиоматически:
1) d(A, В)^0, причем d(A, В) = 0 тогда и только тогда,
когда А —В.
2) d(A, B) = d(B, А).
3) d(A, B) + d(B, C)~^d(A, С), причем равенство достигается
тогда и только тогда, когда В находится между А и С.
4) Расстояние d инвариантно относительно обозначений. Эта
аксиома означает, что при одинаковых перестановках объектов
внутри ранжировок А и В расстояние между новыми ранжиров-
ками А' и В' равно d(A, В).
5) Если две ранжировки отличаются друг от друга только н а
части объектов, то расстояние между ’исходными ранжировками
равно расстоянию между ранжировками только этих объектов.
6) Минимальное положительное расстояние между ранжиров-
ками равно единице.
Утверждение 2. Аксиомы 1)—6) однозначно определяют
расстояние d (А, В) при любой длине ранжировок п^2,а формула
d(A, В)=4 2 \аи-Ьи\ (16)
определяет единственное расстояние d, удовлетворяющее аксиомам
1)-6).
§2. АЛГЕБРАИЧЕСКИЙ МЕТОД
151
Упражнение 8**. Доказать утверждение 2.
Ранжировка Ло называется медианой Кемени —Снелла ранжи-
ровок А1, ..., AN. Наряду с медианой Кемени—Снелла в качестве
группового мнения используют ранжировку;
N
Д;'= Argmin 2 d*'t(A, А‘), J(17)
AeQ i=i
которая называется средним значением.5"*
Пример 4. Пусть три эксперта упорядочили три объекта и
полученные ранжировки имеют вид Л=<х, у, zy, В — <х, у, zy,
С = <у, х, zy. Выпишем соответствующие матрицы, обозначив их
теми же буквами, что и ранжировки:
/О 1 1\ / О — 1 1\
Л = В= 1 о 1), с= 1 о 1).
\ —1 —1 о/ \—1 —1 о/
Пользуясь выражением (16), вычислим расстояния; d(A, B) = Q,
так как а^^=Ьц (i, / = 1, 3), d(A, C)—d(B, С) = 2.
Если взять в качестве медианы ранжировку Л или В, то сумма
расстояний от нее до всех ранжировок равна 2. Если взять любую
другую ранжировку, то сумма расстояний от нее до всех осталь-
ных окажется больше. Например, для ранжировки D = <x, z, уу
матрица имеет вид
/ ° 1 1\
D=(—1 о -1 I,
\—1 1 о/
расстояния d(Л, D) = d(B, D) = 2, d(C, D) = 4. Сумма расстояний
от D до исходных ранжировок А, В, С равна 8.
Упражнение 9. Найти среднее значение по исходным дан-
ным примера 4.
Упражнение 10. Однозначно ли определяются медиана и
среднее значение?
Упражнение 11. Привести пример ранжировок, для кото-
рых медиана и среднее значение совпадают.
Упражнение 12. Найти медианы и средние значения^для
следующих ранжировок:
1) Л = <х, у, zy, B*=<z, х, уУ, С==<х, z, уУ\
2) А—<х, у, zy, В = (х, y\~zy, C — {y~\z, x>.
Здесь знак ~ означает эквивалентность объектов.
Упражнение 1S*. Какой будет медиана, если 51 эксперт
из 1С0 дают одинаковые ранжировки?
Упражнение 14**. Построить алгоритмы вычисления ме-
диан и средних значений.
52
ГЛ. 2. МЕТОДЫ ОБРАБОТКИ ЭКСПЕРТНОЙ ИНФОРМАЦИИ
§ 3. Методы шкалирования
Методы шкалирования в простейшем случае используются
в экспертизах следующего типа. Эксперты оценивают попарные
различия между объектами, указывая соответствующие числа.
Задача состоит в сопоставлении каждому объекту точки простран-
ства Ег, а всей системе, состоящей из п объектов, п точек в Ег
так, чтобы расстояния в Ег между точками были достаточно
близки к указанным экспертами числам. Таким образом, решением
задачи оценивания в этом случае является вектор длины nr. Для
его получения используется экспертиза Э8:
Q = £= и Ег\
Г = 1
Я8 = £С2;
L — произвольное;
Q—произвольное.
Отображение <р имеет вид£(1.2): <р = <?ф, где ф—произвольная
композиция функций выбора С,, ..., CN.
Дадим необходимые пояснения. В качестве множества допусти-
мых оценок Q взято Е = и Ег, поскольку во многих методах раз-
г — 1
мерность г заранее не указывается; Q3 = Ek, rpek = Cn, поскольку
эксперты задают матрицу попарных различий п объектов. Произ-
вольность некоторых параметров означает, что они не оказывают
влияния на отображение q\ Q3 —- Q. Различным типам отображе-
ния q соответствуют различные методы шкалирования. Поэтому,
далее, до метода одномерного шкалирования, который исполь-
зуется при отличной- от Э8 экспертизе, будут рассмотрены способы
задания q без указания остальных пара мет; св Э8. ,
Отображение q задается не формулами, а в виде алгоритмов,
сопоставляющих матрице различий D точку из Е. Во всех случаях
задача многомерного метрического шкалирования состоит в следую-
щем. Задана симметричная матрица различий D = (Dtj) между п
объектами Лх, . .., Ап. Нужно найти координаты точек^д/£Еп
сопоставленных объектам Л/ так, чтобы матрица Х — (х^) рас-
стояний между этими точками в Ег была возможно более близка
к исходной 'матрице различий D в смысле некоторого заранее
выбранного критерия. Если критерий обращается^ нуль, то гово-
рят, что задача имеет точное решение. >
1. Метод простой ординации. Пусть а1, ..., ап—точки в про-
странстве £и, соответствующие объектам Ль .Ап. Рассмотрим
способ их построения.
В качестве Лх и Л2 выберем объекты, расстояние Di} между
которыми tB исходной матрице D максимально. Сопоставим им
точки а1 и а2 по правилу д^==0, al = Djj, а} = а2=0 (1=2, п).
Полученные точки содержатся в подпространстве Еи образован-
ном первой осью Еп.
§3. МЕТОДЫ ШКАЛИРОВАНИЯ
153
Пусть Ег—r-мерное подпространство, образованное осями с но-
мерами 1......г, в котором уже найдены точки а1, а2, ..., ar+1,
являющиеся образами исходных объектов Лп Л2, Аг+1..
У этих точек в Еп все координаты, начиная с (г+1)-й, равны
нулю. Найдем проекции остальных точек аг+г, ..а„ъ Ег, исходя г
из заданных расстояний между объектами Л ,• и Л, (i, j = 1, n).
Зафиксируем k > г +1. Пусть проекция ак в Ег имеет координаты
ак, ..ак, пока неизвестные. Обозначим через hk расстояние
между ак и подпространством Ег. Тогда условие равенства рас-
стояния между точками а1 и ак и расстояния'^ между соответ-
ствующими объектами’имеет вид
D3jk=hk+ 2 (ai—aiY (1=1, f + l), -
i=t
отк уда
(aj-fl;)2 (/ = 1, г+1). (18)
i = i
Левая часть (18) не зависит от /. Приравнивая правые части (18)
при j и при /4-1, получим систему
Ofc- S (ai-aly— DU, J- S (а!+ч -tf)1 (/ = 177) (19)
i = 1 i - i
г уравнений относительно г неизвестных_‘гй1,"• ..., oj. Преобра-
зуя (19), получим систему
2а?|2Й!-»!+‘)]- 2 + ,‘~D‘t (/ = Т77)
/=1 1= '
(20)
г линейных уравнений [относительно г неизвестных а%, ..., ак.
Решив! ее” при & = г + 2, п,~ 'найдем проекцию точки ак в Ег
(fc = r + 2, п). С помощью (18) найдем ^"при k = r + 2, п и поло-
жим д*+1вЛй.
Выберем объект А, такой, что Лу= max hk. Сопоста-
А? = {г+2...................................п}
в им ему в пространстве Еп точку д/ = <а(, ..0 ... ,;0>,
где а{, ..., а1 г—решение системы (20). Перенумеруем объекты
Лг+2, ..., Ап так, чтобы выбранный объект имел номер г+ 2.
Таким образом, получим координаты точки ar+i и проекции точек
аг+3, ..., а” в пространство Ег+1.
Положим г = г + 1 и подсчитаем сумму
п г
Si= 2 2 04—<4)? (21)
i<! 6=1 V Г
I, / = 1
154
ГЛ. 2. МЕТОДЫ ОБРАБОТКИ ЭКСПЕРТНОЙ ИНФОРМАЦИИ
попарных расстояний между проекциями точек а1, ..., ап в Ег.
Введем критерий 1—Sx/S, где
S= S Dy. (22)
i<i
Если значение критерия меньше заранее заданной величины е, то
вычисление координат точек прекращают и образами объектов
А1, ..Ап считают проекции точек а1, ..., ап в Ег. В резуль-
тате построено отображение q: Q.
Упражнение 15. Доказать, что величина (21) всегда не
превосходит (22).
Упражнение 16*. При каком минимальном г можно гаран-
тировать равенство Sj и S в случае [Dy+D^k^Dik (i, /, k= 1, п)?
2. Метод троек. Положим
= (t, /, k=\7*). (23)
Утверждение 3. Величина Ь\к является произведением век-
торов из точки а‘ в а' и ак, где точки а1, ..., ап — образы
объектов Л1, ..., А".
Доказательство. Рассмотрим треугольник со сторонами
D,y, Dik и D/It (рис. 2). По теореме косинусов D]k = П2ц + D2ik —
— 2D,7Drt cos 0, откуда
DijDt, cos 0 = (Dj, + Dfk - D2k)/2, (24)
левая часть (24) представляет собой 'скалярное произведение,
а правая равна bjk- Утверждение доказано.
аз Таким образом, матрица B‘ = (b-k) является
«а матрицей попарных скалярных произведений
D-./ векторов, проведенных из точки а1 в точки
___________\ Упражнение 17. Какой размер имеет
a1_________ак матрица В'?
Ри‘с 2 Свойства матриц В' определяют существо-
вание точного решения задачи метрического
шкалирования и минимальную размерность пространства Ег, при
котором точное решение существует.
Теорема 1. 1. Если матрица В‘ (i£ {1, ..., п}) является
положительно полуопределенной*), то задача метрического шкали-
рования имеет точное решение.
2. Минимальная размерность r = minpz, где р,—ранг матри-
цы В1. ____
3. В качестве образов объектов As (s=l, n; s^=i) в про-
странстве Ег можно взять точки as = <.a{, ..., asr~> (s=l, п)
*) Матрица W называется положительно полуопределенной, если для всех
х выполняется (Wx, х)^0.
<3. МЕТОДЫ ШКАЛИРОВАНИЯ
155
такие, что
В‘ = Х-ХГ, X = (xpq), (25)
где xpq — apq (р=1, n; «7—1, г) и alt = 0 (/=1, г). (Знак Т
означает транспонирование.)
Часть 3 теоремы позволяет построить алгоритм, задающий
отображение q: —* Q.
3. Нелинейные методы. В рассмотренных методах отображе-
ния являются линейными. Однако для матриц D определенного
вида не удается построить линейное отображение q в простран-
ство достаточно малой размерности с сохранением требуемой точ-
ности. Поэтому используют нелинейные методы, основанные на
итеративных процедурах. Выбирают точки а1, ..., ап£Ег. На
каждой итерации смещают точки а1, ..., ап так, чтобы прибли-
зить матрицу расстояний между ними к исходной матрице раз-
личий D в смысле заданного критерия.
В частности, используют критерии вида
п
sp,q= 2 Dt^Dij-x^-,
h /=1
i < /
[ р, если хи < Dih
, $ — z J J
( q, если хи >DlJt
где p и q — произвольные действительные числа. Положим q =
=— р и обозначим Sp = SPi _р. При минимизации критерия
точность приближения элементов D(j матрицы D зависит от их
сравнительной величины: меньшие DtJ отображаются точнее. При
минимизации критерия точнее отображаются большие значения.
С учетом этого сначала используют критерий S^, а затем—кри-
терий Si.
4. Неметрическое многомерное шкалирование. Рассмотрим
матрицу различий D. Упорядочим по возрастанию п2 чисел,
являющихся элементами матрицы D, и обозначим полученный
порядок через г (Л). Отобразим объекты Л,- в пространство Ег и
упорядочим по возрастанию п2 чисел, являющихся элементами
матрицы расстояний между точками a1' (i— 1, ..., п); полученный
порядок обозначим через г (а).
Задача неметрического многомерного шкалирования состоит
в том, чтобы построить отображение q в пространство минималь-
ной размерности так, чтобы г(п) = г(Л). Для этого делают сле-
дующие операции:
1) Определяют ранжировку г (Л) и нормируют элементы матри-
цы D так, что минимальный равен нулю, а максимальный —
единице.
2) Помещают п точек в п вершин правильного (п — 1)-мерного
симплекса, центр которого находится в начале координат, а ребра
156
ГЛ. 2. МЕТОДЫ ОБРАБОТКИ ЭКСПЕРТНОЙ ИНФОРМАЦИИ
имеют длину 1. Координаты п точек а1, . ..,а" в [(п—1)-мерном
пространстве вычисляют по формулам
a^r = cos 1) л/п]/К n, [2^(i— 1) л/п]/]/п,
где 77=1, [(п —1)/2]. Щля^четного п проекция на (п—1)-ю\)сь
4-i =
3) Для построенных точек вычисляют ранжировку г (а) и срав-
нивают ее с г (Л). Если г(а) = г(Л), то вычисления прекращают.
В противном случае нормируют матрицу ^расстояний X между
точками a' (i=l, п) такаже, как матрицу D. Элементы пронор-
мированных матриц обозначают через bi} и xZ/- соответственно?
4) Находят новые [значения координат точек a1 (i = 1, п)’по
формулам
4=4.4-М (£ = 1. «—О,
где. Д4= S P’ti+Rti, Pfr =
/¥=1 *' Xij 1,1 11
₽[Д,—Д.о] (al—Jh . — ", -
= --—-.п.А ‘----,J DC9= Dij/n*, a = 0,2, 0 = 0,05.
5)^Полагают7а/ = (i = l, n), вычисляют ранжировку г (а) и
повторяют приведенные операции.
5. Одномерное шкалирование. Введем экспертизу Э9:
& = Еп\
Q3 — такое же, как в Э5;
L—эксперты изолированы;
Q—обратная связь отсутствует.
Отображение <р: —> Q будет описано ниже Л
Приведем операции, которые необходимо осуществить для по-
строения' <р. *!
| ' \
1) Вычисляют матрицу Р= A^N, где А1'—ранжировка, дан-
/=1
ная /-м экспертом. Элемент матрицы Р интерпретируют как
вероятность предпочтения i-ro объекта /-му.
2) Находят Zij по формуле л
V 1 - -
(26)
с использованием таблиц нормального распределения, исходя из
известных Связь между Zzy и pz/ показана на рис. 3, где
заштрихованная площадь под кривой равна pZy. Величина ZZy
измеряется в единицах стандартного отклонения.
'§3. МЕТОДЫ ШКАЛИРОВАНИЯ
157
3) Образуют [матрицу Z = (Zz,). Подсчитывают сумму оценок
Zi — S %.ц 11 среднее значение
/=1.
за искомую оценку объекта
Л,. (i = TT7i).
4) Определяют величины
Pi — G (Zi) по формуле (26),
которые нормируют по фор-
муле '
Р1 = Р,'1^Рр
1 i=i
Zi = Zi'n. Величину Z,- принимают
Эксперты i Параметры
S Я С р
1 3 2 1 4
2 1 2 3 4
3 3 1 2 4
4 1 2 3 4
5 3 1 2 4
6 3 1 2 4
7 3 2 4 1
8 3 4 1 2
9 2 4 1 3
10 2 ~ 1 3 4
Сумма рангов 24 20 22 34
Средний ранг 2,4 2,0 2,2 3,4
P*i называют показателями относительной важности' объектов.
5) Осуществляют проверку на непротиворечивость. Для этого
по формуле (26) находят == G (Z, —Zy) и вычисляют разности
Табл и а 4 между полученными значениями
Рц и исходными pij. Определяют
среднее отклонение
п
S |А,7|М(п-1);
«. /= 1
* < /
если оно мало, то это свидетель-
ствует о непротиворечивости по-
лученных экспертных ранжиро-
вок.
Пример 5 (использование Э9
для оценки относительной важности
параметров самолета). В качестве
экспертов приглашены 10 специ-
алистов. Рассматривались следую-
щие параметры: S—скорость поле-
та; R—радиус действия; С—бое-
вой потолок; Р—полезная на-
грузка. Экспертам было предложе-
но ранжировать названные пара-
метры в порядке их важности.
Результаты показаны в табл. 4. Эксперт 7 расположил пара-
метры по степени важности в порядке Р, R, S, С, а эксперт 2 —
в порядке S, R, С, Р.
Сформируем матрицу А размера 4x4, в которой указано число-
случаев, когда один параметр важнее другого (табл. 5). Разделив
элементы матрицы Л на 10, получим матрицу Р. С’ее элементами
осуществим все указанные выше операции. Матрица Z, величины
Z(- и оценки Zf приведены в табл. 6. Величины, необходимые для
158
Гл. 2. МЕТОДЫ ОБРАБОТКИ ЭКСПЕРТНОЙ ИНФОРМАЦИИ
Таблица 5
S R с Р
S 4 4 8
R 6 — 7 7
С 6 3 — 9
Р 2 3 1 —
расчета относительной важности пара-
метров, приведены в табл. 7.
Осуществим проверку на непроти-
воречивость. Необходимые данные соб-
раны в табл. 8. Среднее отклонение в
данном случае равно 0,45482//6 = 0,0758.
Наибольшее по абсолютной величине
расхождение между и pif равно
0,17094; это свидетельствует о непро-
тиворечивости ранжировок.
Таблица
Параметр i Параметр /
S R С Р zi zi
S R С Р 0 0.25334 0,25334 0,84161 -0,25334 0 -0,52441 -0,52441 -0,25334 0,52441 0 —1,28155 0,84161 0,52441 1,28155 0 0,33493 1,30216 1,01048 -2,64757 0,08373 0,35554 0,25262 —0,66189
Таблица 7
Параметр i zi />,- = G(Z.). Нормированная относительная важность P-
s 0,08373 0,53336 0,2647
R 0,32554 0,62761 0,3115
. С 0,25262 0,59972 0,2977
P —0,66189 0,25403 0,1261
Таблица 8
zi-zJ pif расчетное pij исходное Отклонение
Zx—Z2=0,08373 - 0,32554 = —0,24181 0,40447 0,400 - 0,0047
Z, — Z3 = 0,08373—0,25262 = —0,16889 0,43297 0,400 0,032295
Z, —Z4 = 0,08373 — (—0,6189) = 0,74562 0,77205 0,800 —0,02795
Z2—Z3 = 0,32554 — 0,25262 = 0,07292 0,52906 , 0,700 —0,17094
z3 — Z4 = 0,33554 - (-0,66189) = 0,98743 0,83828 0,700 0,13828
Z3—Z4 = 0,25262 - (—0,66189) = 0,91451 0,81977 0,900 —0,08023
Литература. [16, 39, 60, 61, 63, 64, 104, 109].
5 1. ОБЩАЯ ХАРАКТЕРИСТИКА АЛГОРИТМОВ
159
Г л а в а 3
ФОРМИРОВАНИЕ ИСХОДНОГО МНОЖЕСТВА
АЛЬТЕРНАТИВ
Воспользуемся методами решения задач оценивания для по-
строения алгоритмов формирования исходного множества альтер-
натив в задачах принятия решений. В § 1 дана общая характе-
ристика алгоритмов. В § 2 приведены алгоритмы формирования
конечных и бесконечных ИМА с разными способами порождения
альтернатив и проверки их допустимости.
§ 1. Общая характеристика алгоритмов
В соответствии со схемой, рассмотренной во введении, в зада-
чах принятия решений формируют исходное множество альтерна-
тив, а затем решают задачу выбора из ИМА. Алгоритмы форми-
рования ИМА составляют существенную часть алгоритмического
обеспечения задач принятия решений.
При отсутствии априорной информации о свойствах альтерна-
тив в качестве исходного используют универсальное множество
всех мыслимых альтернатив йу. Если решать задачу выбора при
таком ИМА, то она оказывается сложной и не всегда разреши-
мой. Чтобы избежать такой ситуации, используют свойства ре-
шаемой задачи и выделяют в йу некоторую область возможных
альтернатив йв. Можно считать, что йв = С0П1 (^у)> где С0П1 —
функция выбора, устанавливающая принадлежность альтернатив
к множеству возможных. Альтернативы, принадлежащие множе-
ству Qy\QB, никогда не могут быть решениями рассматриваемой
задачи. Наличие дополнительной информации о свойствах задачи
в виде технических, экономических и других ограничений позво-
ляет выделить из йв множество допустимых альтернатив й, кото-
рое примем за ИМА. Можно считать, что при этом решается
задача <йв, ОП2>, где ОП2—принцип оптимальности, выражаю-
щий условие допустимости альтернатив.
Таким образом, в общем случае процесс формирования ИМА
описывается схемой, включающей два этапа: порождения возмож-
ных альтернатив и проверки их на допустимость. В конкретных
алгоритмах этапы могут совмещаться. Это связано, в частности,
с тем, что порождение возможных альтернатив и проверка на
допустимость могут быть осуществлены с помощью одной и той
же процедуры экспертной классификации при разных параметрах
экспертизы.
Заметим, что алгоритмы формирования ИМА в конкретных
задачах принятия решений зависят от их специфики. В частно-
сти, альтернативы можно рассматривать как целостные объекты
(например, товары) или как объекты, наделенные структурой
160
ГЛ. 3. ФОРМИРОВАНИЕ ИМА
(например, план отрасли как совокупность планов~предприятий).
Способ рассмотрения альтернатив определяет схему^ экспертизы
для их порождения. В первом случае используют экспертов близ-
кой квалификации; во втором—требуются эксперты с разными
уровнями и областями знания.
В одних случаях получают сами альтернативы, в других —
•правила или модели их порождения. При этом модель используют
как генератор альтернатив.
При проверке допустимости альтернатив для конечных ИМА
проверяют каждую альтернативу, для бесконечных—устанавли-
вают границу допустимости для всею множества.
§ 2. Алгоритмы формирования ИМА
Для построения алгоритмов введем процедуру экспертного
перечисления в виде экспертизы ЭЮ.
Экспертиза ЭЮ:
Й = ^(Й);
йэ=О;
L—эксперты изолированы;
! Q—экспертам предоставляется множество Й и вероятности Р,
(формула (2)).
Отображение ф определяется следующим образом. Получить
от каждого из N экспертов множество Xz альтернатив, которые,
по его мнению, следует включить в й*. Построить множество
Й = и X,. (|Й1 = п).
i=i
Найти матрицу ^ = (/"//), *’=1, X; / = 1, и:
| 1, если /-я альтернатива принадлежит Xh
ГП~\ п (1)
I 0 в противном случае. ' '
Вычислить
/,/=2г?/Я (2)
1 = 1
(Величина Pj рассматривается как вероятность того, что /-я аль-
тернатива принадлежит множеству Q*.) Сформировать искомое
множество альтернатив Q*, включив в него альтернативы, для
которых Pj->P, где Р—заранее заданная величина, близкая
к единице.
Обратная связь в экспертизе ЭЮ организуется следующим
образом. Ответ каждого из экспертов рассматривается как ран-
§ 2. АЛГОРИТМЫ ФОРМИРОВАНИЯ ИМА
161
жировка множества Q; /-я альтернатива получает ранг г,7, вы-
числяемый по формуле (1). Подсчитывается коэффициент конкор-
дации IT полученных N ранжировок по формуле (2.13). Если W
меньше заранее заданного уровня то экспертам предостав-
ляются множество Q и вероятности Р; и проводится следующая
итерация экспертизы ЭЮ. В противном случае экспертиза закан-
чивается.
Алгоритм 1. Формирование конечного ИМА. Для порожде-
ния альтернатив и проверки их на допустимость используется
экспертиза ЭЮ.
Алгоритм реализуется следующей последовательностью шагов:
1. Выделить QB из Qv с использованием ЭЮ, в которой Q = QV,
Q‘ = QB.
2. Выделить й из QB с использованием экспертизы ЭЮ, в ко-
торой Q = QB, Q* = Q.
Алгоритм 2. Формирование ИМА с помощью модели.
Пусть непосредственное порождение £2В с помощью экспертизы
ЭЮ невозможно, но известен регулярный способ (модель) порож-
дения любой альтернативы из QB. Например, пусть заданы пра-
вила построения возможных расписаний авиарейсов; в то же время
число всех вариантов расписаний настолько велико, что их сов-
местный анализ эксперту провести не удается. Параметры модели
заранее не известны, но могут быть найдены экспертами.
Алгоритм 2 реализуется следующей последовательностью шагов:
1. С помощью экспертизы Э1 определить числовые параметры
модели.
2. Используя модель, найти множество йв возможных аль-
тернатив.
3. Найти множество Q с использованием экспертизы ЭЮ, в
которой Q = QB, Q* = Q.
4. Сравнить величину q — | Qj/|QB|, оценивающую качество ис-
пользованной модели, с заранее заданным числом р. Если р,
то алгоритм прекращает работу. В противном случае провести
корректировку модели и перейти к шагу 1.
Рассмотрим одну из модификаций общего алгоритма 2, извест-
ную под названием алгоритма, или метода морфологического
анализа.
Алгоритм 3. Морфологический анализ. Общая схема здесь
сохраняется той же, что и в алгоритме 2. Особенность состоит
в том, что фиксируется конкретная модель порождения альтер-
натив и используется другая процедура проверки допустимости.
Морфологический метод предполагает представление каждой аль-
тернативы в виде составных частей (компонент). Под компонен-
тами понимаются части, на которые условно разделена альтернатива.
Компонентами могут быть как некоторые измеряемые параметры,
так и отдельные структурные части альтернативы. Например,
6(0,5) И. М. Макаров и др.
162
ГЛ. 3. ФОРМИРОВАНИЕ ИМА
в задаче выбора комплекса технических средств для создания ав-
томатизированной системы управления альтернативу можно пред-
ставить с помощью следующих компонент: тип ЭВМ, число пери-
ферийных устройств, системное устройство ввода, системное уст-
ройство вывода, математическое обеспечение.
Обозначим множество возможных вариантов i-й компоненты
через Х{ = {хц, ..., xik.} (i®l, п). Тогда множество альтер-
натив QB представимо в виде QB = X1x ... хХп. Такое представ-
ление задает конкретную модель порождения возможных аль-
тернатив.
Для проверки допустимости используем экспертизу, в результате
которой выделим подмножество J — {/п ..., jj s {1, •.., п}, и
укажем множество V наборов вариантов компонент <x/idi, ..., х^у,
которые совместно недопустимы.
Алгоритм 3 реализуется следующей последовательностью шагов:
1. Найти множества Х{ возможных вариантов i-й компоненты
(i = l, п) с помощью п экспертиз 31(57" в которых Q — Qy/, Q* = X;-
(через Qyt. ^обозначено универсальное множество вариантов i-й
компоненты).
2. Сформировать множество] возможных альтернатив Пв=
=Х1Х...ХХ„.
3. Найти множество {/х, ..., /J, используя экспертизу ЭЮ,
В которой П = {1, . . ., п}, = .. ., /z}.
4. Найти множество V совместно недопустимых наборов вари-
антов компонент, используя экспертизу ЭЮ, в которой Й=Х71х ...
... X Xj^t И*=== V.
5. Построить функцию F(x), xgQB:
где xjidi, ..., х. di образуют i-й недопустимый набор, r = |V|,
( 1, если а = Ь,
v (0, если а^Ь.
6. Сформировать множество
Q = {x6Qb;F(x) = 0}.
Алгоритм 4. Формирование ИМА для иерархических струк-
тур. Пусть альтернативы разбиты на части, иерархически свя-
занные между собой. Например, допустимый план развития от-
расли основан на допустимых планах предприятий, а планы пред-
приятий—на планах цехов. Воспользуемся для формирования ИМА
§ 2. АЛГОРИТМЫ^ ФОРМИРОВАНИЯМ ИМА
163
иерархической экспертизой, которая представляет собой последо-
вательность экспертиз, где каждая экспертиза использует резуль-
таты предыдущих.
Рассмотрим два способа проведения иерархической экспертизы.
Первый заключается в проведении экспертизы снизу вверй. Сна-
чала проводят экспертизы на самом низком уровне иерархии.
Их результаты служат исходными данными для проведения экс-
пертиз на следующем уровне и т. д. Применительно к планированию
это означает, что сначала определяют допустимые планы цехов,
на их основе формируют допустимые планы предприятий и затем
планы развития отрасли.
Второй способ заключается в проведении экспертизы сверху
вниз. Здесь результаты экспертизы более высокого уровня слу-
жат ограничениями при определении допустимых альтернатив
более низкого уровня. Применительно к планированию сначала
определяют допустимые планы развития отрасли, затем допусти-
мые планы предприятий и допустимые планы цехов. Допустимыми
для предприятия будут только такие планы, которые обеспечи-
вают допустимость планов отрасли.
Воспользуемся первым способом проведения иерархической
экспертизы. Пусть .......—элементы нижнего уровня в ие-
рархической структуре альтернатив; элемент S* k-ro уровня свя-
зан с элементами S*/"1...(k — 1)-го уровня (6 = 2, d\ r =
Алгоритм 4 реализуется следующей последовательностью шагов:
1. Найти ИМА 2J, ..., 2Jt для элементов S}, ..., S},, поль-
зуясь в каждом случае алгоритмом 1.
2. Положить 2В (S’) = 2*i х ... X 2*i.
3. Найти множество 2i(SJ), используя экспертизу ЭЮ, в ко-
торой 2 = 2B(Si), 2* = 212(S12).
4. Повторить шаги 2 и 3 для всех элементов второго уровня.
5. Повторить шаги 2—4 при соответствующем изменении но-
меров уровней и элементов.
Упражнение 1. Построить алгоритм, соответствующий вто-
рому способу проведения иерархической экспертизы.
Алгоритм 5. Формирование бесконечного ИМА. Пусть аль-
тернативы являются точками из Ет. Тогда множества возможных
и допустимых альтернатив образуют некоторые области в Ет.
Формирование ИМА сводится к определению границ этих облас-
гей. Будем считать, что множество возможных альтернатив огра-
ничено, т. е. 2В = ХО, где Xe — {x£Em\ai ^.xt (i=l, т)} —
прямоугольный параллелепипед в Ет. Поэтому можно допустить,
что 2В известно и совпадает с Хо.
Идея алгоритма 5 состоит в аппроксимации множества 2 объе-
динением допустимых множеств в виде параллелепипедов. Экспер-
6*(0,5) И. М. Макаров и др.
164
ГЛ. 4. ЗАДАЧА ВЫБОРА
там предъявляют реализации х равномерно распределенной в QB
случайной величины. Они строят окрестность каждой реализации
в’виде параллелепипедов, состоящих из допустимых точек, если х
допустима, и из недопустимых точек в противном случае.
Алгоритм 5 реализуется следующей последовательностью шагов:
1. Определить минимальное значение aj и максимальное зна-
чение at оценок альтернатив по каждому из т критериев, исполь-
зуя экспертизу Э1 или Э2.
2. Положить Qq — Eq^=0.
3. Найти очередную реализацию х векторной случайной вели-
чины г], равномерно распределенной на QB = X0.
4. Если х содержится в Qq U Eq, то перейти к шагу 8, в про-
тивном случае—к шагу 5.
5. Рассмотреть пару {а, Ь}, где а означает, что альтернатива х
допустима, Ь—что х недопустима. Решить задачу ранжирования
пары {а, Ь} с использованием экспертизы Э4; точка х является
допустимой, если получена ранжировка <а, Ь>, и недопустимой,
если получена ранжировка <&, а>. Если х допустима, перейти
к шагу 6, в противном случае—к шагу 7.
6. Построить прямоугольный параллелепипед 6, состоящий из
допустимых точек, с использованием любой из экспертиз Э1—ЭЗ.
Положить Q(? = QqU6 и перейти к шагу 3.
7. Построить 6 аналогично шагу 6. Положить Eq = Eq\j8 и
перейти к шагу 3.
8. Положить 7V равным числу попаданий подряд точки х
в множество QqU-Eq (включая последнее попадание).
9. Определить вероятность
Рг= 1 —mes Qp/mes Хо—mes EQ/mes Хо *).
10. Найти величину N из соотношения Q = 1—е~йрг при за-
данной заранее доверительной вероятности Q.
1 Г. При N < N перейти к шагу 3, в противном случае поло-
жить Q равным Qq. Требуемая аппроксимация построена.
Литература. [38, 68, 78].
Глава 4
ЗАДАЧА ВЫБОРА
В главе рассмотрена общая задача выбора, которая является
частным случаем задачи принятия решений. В задаче выбора
исходное множество альтернатив известно. Решение^адачи выбора
получено путем ее сведения к частным и простым задачам с ис-
пользованием рассмотренных в главе 1.5 декомпозиций функции
♦) Через mes А здесь и далее обозначена мера множества А.
§ 1. МАТЕМАТИЧЕСКАЯ ЗАДАЧА ВЫБОРА
165
выбора. В § 1 сформулирована математическая задача выбора;
в § 2 приведен алгоритм 1 решения общей задачи выбора, в § 3
даны модификации алгоритма 1 для построения й^; в § 4 постав-
лена задача выделения й? в критериальном пространстве с ис-
пользованием функции полезности; соответствующие модификации
алгоритма 1 приведены в главе 6.
§ 1. Математическая задача выбора
Будем считать, что для любой функции выбора С известны
ее значения на некоторых подмножествах X £ 33* = 33 (й) и ее
принадлежность к некоторому множеству функций
Случай 33* = 0 и = соответствует отсутствию инфор-
мации о функции С; случай ®* = ®(й) соответствует полному
описанию функции С. Зададим описание функции С парой <<^*, 33*'>.
В отличие от общей задачи выбора, назовем математической
задачей выбора тройку <й, »<*, S*>, где й—множество альтер-
натив; С(Х) известны для всех
Решением задачи <й, 33*3 является множество Й* = С(Й).
Задача разрешима, если й* однозначно определяется по мно-
жеству аМ* и значениям С на всех X $ ^*. При й С S3* задача
разрешима и ее решением является значение С на й.
Введем на а/Я* отношение эквивалентности 7?! следующим об-
разом:
С R.C" & С (X) = С (X) для всех X € S3*.
Отношение эквивалентности Rx задает на <Л* разбиение ЗСй
каждый элемент разбиения состоит из всех эквивалентных по
отношению 7?! функций. Введем на <Ж* отношение эквивалент-
ности Т?2: С RtC” &С (Й) = С"(Й). Соответствующее разбиение
обозначим через 9?2.
Теорема 1. Математическая задача выбора <й, <М*,
разрешима тогда и только тогда, когда разбиение 3^х вложено
в разбиение
Доказательство. Вложенность разбиений означает, что
для любого элемента К разбиения 'К1 найдется элемент К раз-
биения 3^2 такой, что К '—К. По построению разбиений и
из К = К следует, что произвольное задание С на X € 33* одно-
значно определяет значение С на Й. Достаточность доказана.
Пусть произвольное задание С на всех Х^Й* однозначно
определяет значение С на Й. Это значит, что любой элемент К
разбиения 3^ содержится в некотором элементе К разбиения 3^2.
Теорема доказана.
Упражнение 1. Пусть задача <й, ©$*, ^*> разрешима,
Доказать, что задача <й, $?Г> разре-
шима.
6 И. М. Макаров и др.
166
ГЛ. 4. ЗАДАЧА ВЫБОРА
Приведем примеры математических задач выбора.
Пример 1. Пусть Ж*—множество всех нормальных функ-
ций выбора; 3S*—все двухэлементные и одноэлементные подмно-
жества Q. Задача <Q, с<*, ®*> разрешима; ее решением является
множество всех альтернатив, недоминируемых по отношению У?,
которое однозначно определяется по выбору из всех множеств,
принадлежащих S*.
Упражнение 2. Останется ли разрешимой задача из при-
мера 1, если из удалить одноэлементные множества?
Пример 2. Пусть Q^x^ х2, х3}; о//*—множество функций
выбора, являющихся объединением двух скалярных функций;
<53*—все двухэлементные подмножества Q.
Рассмотрим следующие четыре скалярные функции выбора:
О1 (Xj, х2) = х2,
С2 х2) = х1,
С3 (Xi, х2) = х2,
С4 (х^, х2) = х1,
С1 (Xj, х3) = Хз,
С?1 (хп х3) = х1,
С3 (Xi, х3) = х3,
С ^з) = ^1,
С1 (х2, Х3) — Х3,
б?2 (х2, х3) = х2,
С3(х2, х3) = х2;
^з) = Х3
(значения скалярных функций на остальных подмножествах оп-
ределяются однозначно). Легко видеть, что
C1(Q) = x3, C2(fi) = xl, C3(Q) = x2, 6?4(Q) = xx.
Положим C' = C1UC2, C" = C3UC4. Тогда
б> (Xi, Х2) == С (Xj, •^2)==={Xi,
(7 (Xi, х3) = б? (х1} х3) = (х1,
б? (х2, Х3) = С (Х2, Х3) = (Х2,
Поэтому С, С" попадают в один элемент К разбиения мно-
жества е^*. HoC'(Q)—(xn х3}, С"(П)={х1,х2}, т.е. С' (Q)#=C"(Q)
и, следовательно, К не содержится ни в одном элементе раз-
биения 3^2. Это значит, что не вложено в 3^2- В силу тео-
ремы 1 задача <Q, Ж*, 3}*> с указанными параметрами нераз-
решима.
Упражнение 3. Подсчитать числа элементов разбиений 3^
и Э?2 по данным примера 2.
§ 2. Алгоритм решения общей задачи выбора
Рассмотрим общую задачу выбора <Q, 0П>. Назовем задачу
<Q, 0П> простой, если ее решение Qon = б?оп (Q) может быть най-
дено непосредственно (например, указано ЛПР). Решение простых
задач не требует специальных алгоритмов.
Сведем задачу, не являющуюся простой, к математической
задаче выбора. Для этого нужно найти множество Ж*, содержа-
щее Соп (т. е. указать класс функций выбора, к которому при-
надлежит Соп), и найти ЗУ*—множество всех X^Q, для которых
задача <Х, 0П> с тем же принципом оптимальности является
§2. АЛГОРИТМ РЕШЕНИЯ ОБЩЕЙ ЗАДАЧИ ВЫБОРА 167
простой. Если полученная математическая задача оказалась раз-
решимой, то ее решение является решением исходной задачи
<Й, оп>.
Пусть соответствующая математическая задача неразрешима.
Введем понятие частной задачи выбора <Q, ОПг>, где ОП;—прин-
цип оптимальности при учете только i-ro аспекта, оказывающего
влияние на выбор из Q. Сформулируем частные задачи <Q, ОП,->
и укажем ф-композицию соответствующих функций С0Пд (i = l, п).
Решением исходной задачи <Q, ОП> является множество Qon=C (Q),
где С = С(С0П1, ..., Соп„; Ф). Проведенные построения соответст-
вуют выявлению основных аспектов, влияющих на выбор, и их
взаимосвязи.
Алгоритм 1. Решение общей задачи выбора.
1. Проверить, является ли задача <Q, ОП> простой. Если
задача простая, то алгоритм прекращает работу. В противном
случае перейти к шагу 2.
2. Сформулировать математическую задачу <Q, о<*, соот-
ветствующую исходной.
3. Проверить, является ли задача <Q, о<*, разрешимой.
Если задача разрешима, то алгоритм прекращает работу. В про-
тивном случае перейти к шагу 4.
4. Сформулировать частные задачи <Q, ОП;> (i=l, п).
5. Положить i = 0.
6. Положить i = i'4-l.
7. Проверить, является ли задача <Q, ОП,-> простой. Если
задача простая, то найти Й; = СОП. (й) и перейти к шагу 12, в
противном случае—к шагу 8.
8. Сформулировать математическую задачу выбора <Q,
соответствующую частной задаче <Q, ОП(>.
9. Проверить, является ли задача <Q, о<*, разрешимой.
Если задача разрешима, то найти й(-=С0Пд(Й) и перейти к шагу 12.
В противном случае перейти к шагу 10.
10. Найти и такие, что хотя бы одно-из
включений строгое.
11. Положить =<Л*1у — и перейти к шагу 9.
12. Сравнить i с п. Если i#»n, то перейти к шагу 6, в про-
тивном случае—к шагу 13.
13. Задать ф-композицию функций выбора СОП/ из частных
задач (i=l, п).
14. Найти йоп по формулам
Тп) = 1,
где
( 1, если х£йОп.,
( 0, если х^й0П/.
6* И. М. Макаров и др.
168 ГЛ. 4. ЗАДАЧА ВЫБОРА
Реализация шагов 1, 2, 4, 7, 8, 10, 13 может потребовать
участия ЛПР. На шаге 1 определяется решение исходной задачи
выбора из й, на шаге 7—решения частных задач. На шаге 2
получают информацию о принципе оптимальности ОП и о йно-
жествах, на которых задача выбора является простой; на шаге 8 —
соответствующую информацию о частных задачах. На шаге 10
уточняется информация о частных задачах. На шаге 4 опреде-
ляются основные аспекты, которые необходимо учитывать при
выборе; на шаге 13—их взаимосвязь и сравнительная важность.
Итак, при решении задачи выбора с помощью алгоритма 1
реализуется одна из трех возможностей:
исходная задача <Й, ОП> является простой;
математическая задача выбора <Й, еМ*, разрешима;
математическая задача выбора <й, <М*, 59*> неразрешима.
Такое построение алгоритма 1 позволяет использовать слож-
ные конструкции типа композиций частных функций выбора только
в случае необходимости. В остальных случаях достаточно ша-
гов 1—3.
Решение йоп, полученное на шаге 1, совпадает со значением
на й функции выбора С = С(С0П1, ..., С0Пп; Ф). Поэтому совпа-
дение найденного решения йоп с' Соп (й) обеспечивается построе-
нием соответствующей ф-декомпозиции функции выбора Соп с со-
ставляющими Con,.
Решение частной задачи <й, ОП,-> обеспечивается строгостью
одного из включений на шаге 10.
Любая функция выбора С допускает декомпозицию на нор-
мальные. Если функции С0П1, ..., Соп„ соответствуют нормальным
составляющим Соп, то математические задачи выбора <й, &Ю*, ^*>,
сформулированные на шаге 8, разрешимы и нет необходимости
находить <^1 и 38*.
Решение йоп может оказаться пустым. Это означает, что все
варианты, входящие в й, не устраивают ЛПР.
Общий алгоритм 1 может иметь много модификаций в зави-
симости от свойств решаемой задачи, которые отличаются шагами,
необходимыми для решения данной задачи, и способами реали-
зации отдельных шагов. Модификации для случая принципов
оптимальности, заданных бинарным отношением, приведены в §§3, 4
и в главе 6.
Операций шагов 2—4, 8—10, 13 реализуются при помощи
отдельных алгоритмов и процедур. В качестве примеров приведем
алгоритм решения математической задачи выбора (шаги 3 и 9)
и процедуру построения ф-композиции функций выбора Соп,. (шаг 13).
Пример процедуры, реализующей шаг 4, для случая, когда
аспекты сводятся к критериям, дан в § 4 (алгоритмы 8 и 9).
Алгоритм 2. Решение математической задачи выбора <й,
$}*'>. Алгоритм основан на теореме 1. Укажем его операции.
§2. АЛГОРИТМ РЕШЕНИЯ ОБЩЕЙ ЗАДАЧИ ВЫБОРА
16'9
1. Положить
^г = {С€^*| (VX£^*) [С(Х) = С(Х)]}.
2. Занумеровать все функции выбора, входящие в е<2:
G, .... С£.
3. Если  = 0, перейти к шагу 10. В противном случае
перейти к шагу 4.
4. Положить А = С1(Й).
5. Положить 1=1.
6. Положить i=7-f-1.
7. Если CZ(Q) = A, то перейти к шагу 8. В противном слу-
чае—к шагу 10.
8. Если i=#n, перейти к шагу 6. В противном случае —
к шагу 9.
9. Останов. Множество А является решением задачи <Q, &//*, S*>.
10. Останов. Задача <52, е^*, ^*> неразрешима.
Алгоритм 3. Процедура построения ^-композиции. Будем
искать ф в виде пороговой функции. Булева функция ..., Рг)
называется пороговой, если существуют числа alt ..., аг, назы-
ваемые весами, и число Т, называемое порогом, такие, что
£(&, •• №i>T.
1= 1
Пороговая функция обозн а чается через ga< т ф), где а = <ап ..., аг>.
Перечислим операции алгоритма.
1. Провести экспертизу Э9, в которой сравниваемыми объек-
тами являются аспекты; ее результатом являются числа alt ..., ап,
п
а^О, Sa( = l> задающие сравнительную важность аспектов.
1=1
2. Положить Т = 0, 1 = 0.
3. Положить i = i 4- 1.
4. Положить S, = 0.
5. Положить j = 0.
6. Положить j = j 4-1 •
7. Если X/CHoty, положить £, = £,•4-1.
8. Сравнить j с п. Если j^n, перейти к шагу 6, в против-
ном случае—к шагу 9. ,
9. Положить Si = Si/n.
10. Положить Т = Т4-S,-.
11. Сравнить i с N. Если i=£n, перейти к шагу 3, в гро-
g тивном случае—к шагу 12.
12. Положить T — T1N.
Построение пороговой 4УНКПИИ Для аспектов аналогично по-
строению линейной свертки в критериальном пространстве.
Теорема 1.5.1 о декомпозиции произвольных функций выбора
гарантируют возможность представления любой функции ф-ксм-
170
ГЛ. 4. ЗАДАЧА ВЫБОРА
позицией нормальных. Поэтому далее в этой главе рассмотрим I
реализацию шагов 3 и 9 алгоритма 1 в случае, когда множе- |
ство о/И* совпадает с множеством HP нормальных функций вы- i
бора. При этом решение задачи <й, HP, S*> совпадает с мно-
жеством й^ недоминируемых по бинарному отношению R элемен-
тов. Отношение У? однозначно определяется значениями CR на
всех двухэлементных подмножествах й, и задача построения й*
является математической задачей выбора.
§ 3. Алгоритмы построения Й^
Рассмотрим алгоритм построения й^ для произвольного би-
нарного отношения 7?.
Алгоритм 4. Построение й^.
1. Положить йя = 0.
2. Положить i = 0.
3. Положить i = i +1.
4. Положить / = 0. ' '
5. Положить / = / 4-1. '
6. Если XjRXi, перейти к шагу 7, в противном случае—к шагу 9. ।
7. Если j^N, перейти к шагу 5, в противном случае —
к шагу 8. |
8. Положить йл = йли{х(}.
9. Если перейти к шагу 3, в противном случае алго-
ритм прекращает работу.
Алгоритм 4 основан на переборе всех пар, образующих й2. 1
Можно избежать полного перебора, если наложить некоторые ।
требования на отношение <7?, й>. Напомним, что гомоморфиз- ;
мом <р отношения й^ в <Т?2, й2> называется такое отобра- (
жение ср: йх —► й2, при котором
x/?1t/^><p(x)T?2<p(t/). ;
Пусть существует гомоморфизм <р отношения </?, й> в отно- j
шение <>, Ег>, т. е. в линейный порядок на числовой прямой. \
Существование такого гомоморфизма для ацикличных отношений ।
устанавливается теоремой 1.1.2. !
Алгоритм 5. Выделение QR при заданном гомоморфизме <р
а линейный порядок. Идея алгоритма 5 состоит в том, что при
гомоморфизме отношения в линейный порядок недоминируемые ।
элементы переходят в максимальные. Приведем операции алго-
ритма. с
1. Положить й^=0, Х = й.
2. Найти шахф(х).
х
3. Положить й^ = Arg max <р (х), Z=0.
х ।
4. Положить X = X\(QR и Z). Если X =£ 0, перейти к шагу 5; 1
если Х = 0, перейти к шагу 8.
1
§3. АЛГОРИТМЫ ПОСТРОЕНИЯ а* 171
5. Найти Y = Argmax <р(х).
х _
6. НайтиУ^^бУКУхСаХХ)^]}.
7. Положить ^=0^11^1, Z = y\f\ и перейти к шагу 4.
8. Останов.
Замечание. Элементы, найденные на шаге 5, сравниваются
с ранее найденными недоминируемыми элементами из и не
сравниваются с остальными элементами.. Действительно, пусть
у£ Argmax <р(х). Тогда из xRy следует <р (х) > ср (у) и х(£Х. Но
тогда x£QR.
Упражнение 4. Доказать, что алгоритм 5 выделяет мно-
жество недоминируемых элементов.
Если отношение <7?, Й> транзитивно, то можно уменьшить
число необходимых сравнений.
Алгоритм 6. Выделение для транзитивного отношения R.
1. Положить й₽=0, X = Q.
2. Найти тах<р(х).
х
3. Положить QR=Argmax <p (х), Z — 0.
х
4. Положить X = Х\(ПЯ (J Z). Если X Ф 0, перейти к шагу 5;
если Х = 0, перейти к шагу 8.
5. Найти Y = Argmax <р(х).
х _
6. Найти У, = {y$Y I (Vx€ Ь2*)[*ЗД-
7. Положить Q* = Q«UTi, Z = Y\Y1 и перейти к шагу 4.
8. Останов.
Замечание. Алгоритм 6 отличается от алгоритма 5 только
шагом 6. Все элементы у, найденные на шаге 5, сравниваются
с элементами только из (в алгоритме 6) и со всеми просмот-
ренными ранее (в алгоритме 5). Это связано с тем, что элемент
может быть доминируем только элементами, не входящими в
если не требовать транзитивности R.
Упражнение 5. Доказать, что число попарных сравнений
в алгоритме 6 не больше, чем
|Q|.|Q«|-|Q^|.(|QR|-l)/2.
Пример 3. Пусть Q = ^xn х2, х8} и отношение R задается
графом, показанным на рис. 1. Гомоморфизм <р зададим формулой
[<р(х1) = 2, <р(х2)=1, <р(х8) = 0.
Применим для определения алгоритм 5. Получим
Q*={xJ, Z=0, Х = {х2, х8}, У = {х2}, Ух = 0,
Q* = {x,h Z = {x2}, Х = {х8}, У = {х3}, Уг = 0,
□«=1x4, Z = {x8}, Х = 0.
Таким образом,^Qff = {xj}.
172
ГЛ. 4. ЗАДАЧА ВЫБОРА
; Воспользуемся для определения алгоритмом 6. Получим
£2* = {*ib 2=0, Х = {х2, х3}, У = {х2}, Л = 0,
2 = {xJ, Х — {х3\, Y = {x3}, Ух = {х3},
Й^ = {хп х3}, 2 = 0, Х = 0.
Таким образом, получили й^ = {х1( x3}^fe{x1}, поэтому нельзя
пользоваться алгоритмом 6 для нетранзитивных отношений.
•----------------->. ... —>•
^7 ^3
Рис. 1.
В алгоритмы 5 и 6 входит функция ф, которая может быть
выбрана различными способами. Это влияет на число итераций
в алгоритмах 5 и 6, т. е. на число обращений к шагу 5. Чем
меньше | ф (й) |, тем меньше число итераций (при этом число
операций на шаге 6 возрастает).
Упражнение 6. Доказать, что существуют отношения
<7?, й>, для которых число сравнений (при любом гомоморфизме ф)
в алгоритме 5 не меньше, чем (|й| — 1)а/2.
Если множество альтернатив й расположено в пространстве Ет,
то наиболее удобным и простым является линейный гомоморфизм
Ф(х) = (Х, х). Существование линейного гомоморфизма отно-
шения </?, й> в линейный порядок эквивалентно отделимости R
на й. В силу теоремы 1.4.3 в случае конечного йс£я и аци-
кличного отделимого отношения можно сразу пользоваться алго-
ритмом 5 и алгоритмом б, если R транзитивно.
Для некоторых классов отношений вектор X, задающий ли-
нейный гомоморфизм, может быть найден следующим образом.
Утверждение 1. 1. Для отношения Парето
т
ф(х) =3 Мп
i= 1
где hi—люэые положительные числа.
2. Для отношения лексикографии
т
ф(х) = S Д'”"%,
i=l
где
Упражнение 7. Доказать утвер ждение 1.
Утверждение 2. 1. Пусть R— иерархическое отношение
Парето, 7?ч-»<7?1, ..., Rs>, К^='Х1, . . ., Xs>, X s Ekr и в каж-
§4. ЗАДАЧА ВЫБОРА В Ет
173
дом из Ек. задан линейный гомоморфизм <pf’: Х/—*Е1, где X*—
проекция X в Ек- Тогда линейный гомоморфизм <р: Х~—+Ех
задается формулой
ф(х) = 2фМ
1= 1
2. Пусть L—иерархическое отношение лексикографии. Тогда
линейный гомоморфизм ср: X—задается формулой
ф(х)=2 ^“'фДх,),
1
где
I Tn t <Р>' W)|
i, x>, x’ex J <pf (*!)-<₽/ (•*?) * 0}
Утверждение 2 позволяет строить гомоморфизм ф для иерархи-
ческого отношения Парето и/или лексикографии любого уровня,
если заданы соответствующие гомоморфизмы 1-го уровня, и ис-
пользовать алгоритмы 5 и 6.
Рассмотрим координатное отношение R на Ет. Алгоритм ре-
шения математической задачи выбора <Q, №т, 33*У проще, чем'
задачи <й, HP, 33*У, так как при <Ж* = °Х!т множество 33* со-
стоит не из всех двухэлементных подмножеств Q, а только из
некоторых подмножеств специального вида.
Алгоритм 7. Построение 33* для R(zfflm.
1. Занумеровать все вершины единичного куба Di;
х1 = <0, ..., 0>, х2 = <0, .... 1>, .... хд = <1, ..., 1>(L = 2“).
2. Положить
Х1 = {х\ х2}, .. .. Х£_1 = {х1, хЧ..Хм = {хд-1, хЧ (М = С1).
3. Положить 33* = {Xlt ХмЪЩх1}.
Замечание. 33* не зависит от множества мощность
S3* зависит только от размерности пространства.
Упражнение 8. Доказать разрешимость задачи т, й*>
при 33*, построенном алгоритмом 7.
§ 4. Задача выбора с функцией^полезности
На шаге 4 алгоритма 1 формулируют частные задачи <Q, ОП,>
выбора по аспектам; Известно, что аспекты могут сводиться
к критериям. Тогда каждая альтернатива x£Q описывается
точкой ф(х) = <фДх), ..., фт (х)> С Ет, гдесрДх)—оценка аль-
тернативы х по критерию т). Поэтому далее будем
считать, что Q s Ет и координатами точек из Q являются их
оценки по соответствующим критериям.
174
ГЛ. 4. ЗАДАЧА ВЫБОРА
Приведем алгоритм построения набора критериев, учитывае-
мых при выборе из й, и оценки альтернатив по ним.
Алгоритм 8. Порождение критериев.
1. Построить множество 9^ критериев с использованием экс-
пертизы ЭЮ, в которой Q = 9£y, й* = 3£1, где 9f у—универсальное
множество всех критериев.
2. Получить оценки всех альтернатив х£Й по всем критериям
k£3C1 с использованием любой из экспертиз Э1 —ЭЗ.
3. Определить ранжировки <i|, ..., t^>, ..., <#, ..., $>,
где d = 1| и ранжировка r* = <if, ..., определяется по-
рядком расположения альтернатив ..., xN, образующих й,
по критерию ks(s—l, d).
4. Найти коэффициент корреляции Кендалла t,7 между ран-
жировками г- и г' по формуле (2.15) для всех I, / = 1, d, i^j.
5. Положить 8=1.
6. Провести разбиение множества 9£i на группы критериев
по следующему правилу: критерии kt и kj отнести к одной группе
тогда и только тогда, когда т,7^1—8. Если такое разбиение
возможно, то перейти к шагу 8, в противном случае—к шагу 7.
7. Положить 8 = 8/2 и перейти к шагу 6.
8. Выбрать один (любой) критерий kp из каждой группы 9^f.
Замечание. Сходимость алгоритма следует из того, что
при 8 < 1 — шах т,7 требуемое разбиение существует: в каж-
<> / I ,ь ‘
дую группу надо включить критерии, ранжировки по которым
совпадают.
Приведем алгоритм построения набора критериев с использо-
ванием методов шкалирования.
Алгоритм 9. Порождение критериев и их интерпретация.
1. Построить матрицу различий между альтернативами из й
с использованием любой из экспертиз Э1—ЭЗ.
2. Отобразить с помощью метода простой ординации множе-
ство й в пространство Et.
3. Определить ранжировки г1, ..., г1 элементов множества й
по осям Ег.
4. Построить множество 9^1 критериев с использованием экс-
пертизы ЭЮ, в которой й = 9^у, й* = 9£1.л
5. Построить групповые ранжировки г' по каждому критерию
kt € 9^1 с использованием индивидуальных ранжировок и экспер-
тизы Э4.
6. Найти величины Гц—коэффициенты ранговой корреляции
Кендалла между’ранжировками г1 и p(i=l, /; / = 1, d), где
d=|3M.
7. Найти критерий kj. такой, что /,£ Argmax т,7. При этом
' /е{1..<0
Z-я ось пространства Et интерпретируется как критерий kj..
ГЛ. 5. ВЕРОЯТНОСТНЫЕ ХАРАКТЕРИСТИКИ МОЩНОСТИ 175
Пусть U — числовая функция с областью определения Е„.
Зададим на ££ отношение Rv:
xRvy&U(x)>U(y). (1)
Утверждение 3. Пусть QcE^. Тогда
йлу=Argmax U.
Q
Доказательство. Пусть х€йлу. Это значит, что для
всех yfz$i выполнено U (у) U (х), т. е. х£ Argmax U. Пусть
а
х С Argmax/7. Тогда для всех у£& выполнено U (у) U (х),
о_
т. е. yRx. Утверждение доказано.
Таким образом, для отношений R на Е^ специального вида
(1) задача построения йк сводится к задаче:
найти Argmax U. (2)
о
В отличие от задачи математического программирования,
в задаче (2) функция U в явном виде не задана. В силу утвер-
ждения 3 задача (2) является математической задачей выбора,
в которой состоит из некоторых двухэлементных подмно-
жеств Е^.
Функция U в задачах выбора называется функцией полезно-
сти. Алгоритмы и свойства решения задачи (2) при различных
предположениях о функции полезности U и множестве й рас-
смотрены в главе 6.
Литература. [22, 34, 38, 47, 68, 79, 85].
Глава 5
ВЕРОЯТНОСТНЫЕ ХАРАКТЕРИСТИКИ
МОЩНОСТИ МНОЖЕСТВА Q*
В ряде случаев элементы й являются случайными величинами,
принимающими значения из Ет. При этом мощность | й₽ | реше-
ния задачи выделения из й недоминируемых по отношению R
альтернатив можно оценить с помощью вероятностных характе-
ристик. В § 1 описана вероятностная модель, в рамках которой
оценивают | йл |, и даны способы вычисления функции распреде-
ления случайной величины |йл|. В § 2 приведены способы под-
счета среднего числа недоминируемых альтернатив. В § 3 рас-
смотрены вероятностные характеристики мощности множества
Парето.
176
ГЛ. 5. ВЕРОЯТНОСТНЫЕ ХАРАКТЕРИСТИКИ МОЩНОСТИ Q#
§ 1. Функция распределения числа
недоминируемых альтернатив
Пусть Q = {x‘, xN}cEa, где М —число элементов Q, и
7?—бинарное отношение на Ет. Мощность £2Л зависит от Q, N
и 7?.
Пример 1. На рис. 1 приведены шесть расположений мно-
жества Q из трех точек на плоскости. Если R—отношение Па-
рето, то | £2R | в случаях а) и б) равно 1, в случаях в)—д) равно 2
и в случае в) равно 3. Если /?—отношение лексикографии, то
• \2
•А1
•А2
‘А’
? а)
2
•А3
•Аг
•А1
е) 1
Рис. 1.
во всех случаях а)—е) | £2^1=1. При | £2 | = 2 | £2Л | не превосхо-
дит двух. ____
Упражнение 1. Доказать, что для любого k— 1, N можно
так расположить N точек в Д2, что число недоминируемых по
Парето будет равно k.
Упражнение 2. Доказать факт из упр. 1 для Ет (т > 2).
Упражнение 3. Доказать, что факт из упр. 1 верен для
транзитивного координатного отношения на Ет тогда и только
тогда, когда отлично от обобщенной лексикографии.
Упражнение 4*. Пусть координатное отношение R на Ет
таково, что для некоторого существуют наборы р1 и ра
такие, что
fz(P1) = f/(P1) = f/(P8) = 0, f/(P8)=l-
Доказать, что при этом можно расположить N точек в Ет таким
образом, что число недоминируемых по R элементов будет равно k,
где Л—любое число от 1 до У.
§1. ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ МОЩНОСТИ 177
Пусть т| = <г]1, т]т>—векторная случайная величина,
принимающая значения в Ет, с функцией распределения
F(tl, •••, Q = PrHlC|/i, Т12 < h, 1(1)
Будем рассматривать точки х1, ..xN из Q как реализации
случайной величины q с функцией распределения (1). Обозначим
через ф/Дх1, .... xN) число недоминируемых по отношению /?
альтернатив из Q. Величину <р^ можно считать числовой функ-
цией случайных величин т]1, ..., или числовой функцией
одной случайной величины v = <т|1, ..., . ,т|£> с функ-
цией распределения
G(t\, Рт, .... t%) = F(t{, ...,
(2)
Поэтому (р;?также является случайной величиной. Представление G
в виде (2) указывает на независимость различных реализаций
случайной величины т).
Функцией распределения числа недоминируемых альтернатив
называется функция распределения случайной величины
Ф/гСл1» •• •» при заданной функции распределения F случай-
ной величины т). Величина <р^ может принимать значения из
множества (0, 1, ...» N}. Вероятность того, что <p^ = fe, обозна-
чим через Рг{&, F, R, N, т}. Здесь т указывает на размерность
пространства.
Упражнение 5. Указать область значений ф^ для аци-
кличных отношений R.
Пример 2. Пусть альтернатива—одномерная случайная
величина т] с функцией распределения
F(/)
О, если /’<^0,
р, если 0 t < 1,
1, если t 1.
(3)
Рассмотрим в качестве R отношение Парето на Еи т. е. от-
ношение >. Положим N = 2. В соответствии с заданной функ-
цией распределения F (t) вида (3) г]—дискретная случайная ве-
личина, принимающая с вероятностью р значение 0 и с вероят-
ностью <? = (1—р) значение 1. Находим
, . ,, J 1, если хх=#х2,
фо(Хх, х2) = { ’ , .
’ I 2, если хх = х2.
Вычислим Pr{l,F, Р,2, 1) и Рг{2, F,P, 2, 1}=1— Pr {1, F, Р, 2,1}.
Реализации х1 и х2 случайной величины г| равны, если хх = х2=0
или х1 = х2 = 1. Отсюда
Рг{2, F, Р, 2, 1} = р2 + (1—р)2 = р2 + 1—2р+р2 =
= 1+2 (р2—р);
Рг{1, F, Р,-2, 1}= 1—[1 4-2(р2—р)] = 2(р—р2).
178 ГЛ. 5. ВЕРОЯТНОСТНЫЕ ХАРАКТЕРИСТИКИ МОЩНОСТИ
При изменении р в (3) величины Рг {I,/7, Р, 2, 1} и Рг {2, F, Р, 2, 1}
соответственно изменятся. Это показывает, что функция рас-
пределения значений <рЛ зависит от F (t)—распределения векто-
ра П-
Пусть гь ..., zd € Ет. Положим
d.
.... z&= иИ-(2/).» (4)
i=lj
Пусть известны г реализаций случайного вектора тр х1, ..., хг.
Определим условную вероятность того, что все следующие ре-
ализации хг+1, ..., xN будут доминироваться хотя бы одной из •
известных:
Q (х1, ..., х') = Рг (т)1........rf)
(i = r+l, N)lr^ = x1, i]2 = xa, ..., т)г = хг}. (5)
Поскольку реализации xr+1, ..., xN независимы, |то в силу (5)
Q[(x\ ..., xr) = [Pr{i}€ Д (х1....х'’)}]Л7-г. (6)
Найдем вероятность
L'(x\ ..., х') = Рг{т]€Л (х1....хг)}. (7)
Предположим, что функция распределения F (/1( ..., /т) аб-
солютно непрерывна, т. е. существует плотность вероятности
Р (it, • •» ^т)- Тогда вероятность попадания т] в область D<=Em
определяется формулой
/?(«!, ..., sjdsr.-.ds^ (8)
Из (5)—(8) получаем
По формуле полной вероятности
Pr{B} = $ J.. .JPr{B/x}dp(x)
Ет
находим Qr—безусловную вероятность того, что все реализации
с (г4-1)-й до N-й подчинены одной из г первых:
sm)ds1...dsm *~г х
X р(х}, .... хгт) р (х?...хгт)... p(xi, .... x^)dx}.. .dx„...
...dx[...dx^. (9)
§1. ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ МОЩНОСТИ 179
Вычислим вероятности Pk = Pr{k, F, R,N,m} для k—\,N.
Другие параметры фиксированы; Qt—вероятность того, что точки
х2, .. xN подчинены х1. В силу произвольности х1 вероятности
того, что все точки доминируются х2, х3 и т. д., также равны Qv
Поэтому
Р^СЩ.
Событие, заключающееся в том, что х8, .... xN доминируются
хотя бы одной из точек х1, х2, имеющее вероятность Q2, состоит
в объединении трех непересекающихся событий:
точки х2, Xs, ..., xN доминируются х1;
точки х1, х8, ..., xN доминируются х2;
точки х1 и х2—недоминируемые.
Вероятности первого и второго событий равны Qlt поэтому веро-
ятность третьего равна Q2—2Qn а искомая вероятность
/>2 = C^(Q2-2Q1).
Аналогично приходим к рекуррентной формуле
k-1
р __pk г\ __V4 р £...(& * 4~ 1)
— 4k #...(#
t. — ]
N-1
pN=l- £ Pi.
1 = 1
£=1, N — 1,
(10)
Таким образом, доказана
Теорема 1. Функция распределения числа недоминируемых
по транзитивному отношению R альтернатив определяется фор-
мулами (9), (10).
Упражнение 6. В каком месте доказательства теоремы 1
используется транзитивность R?
Упражнение 7**. Привести аналоги теоремы 1: а) для
ацикличных, б) для произвольных отношений R.
При определенных допущениях на отношение R и функцию
F (tlt вычисление вероятностей Pk (k=i, N) удается
упростить.
Будем считать, что R—координатное отношение и координаты
случайного вектора л = <Tli> • • • > г1га> — независимые одномерные
случайные величины с функциями распределения Fr (t), ..., Fm(t).
Это значит, что
P(ti, •••. = (И)
В этом случае обозначим Pk — Pr{k, F, R, N, т].
т т
Теорема 2. Пусть F, = ТТ f z и F2 = IJF2; функции F}, F}
____ 1=1 1 = 1
(1 = 1, т) непрерывны', R£9Cm. Тогда
Рг{&, Л, R, N, m} = Pr{k, F2,R, N, т} (k=l, N).
180 ГЛ. 5. ВЕРОЯТНОСТНЫЕ ХАРАКТЕРИСТИКИ МОЩНОСТИ
Доказательство. Пусть
X1 = <х}, • • •, *т>, • • • , XN = <Х?, ..., Х^>
—N реализаций случайной величины г| с функцией распределения
т
F = IJF1(/). Найдем т перестановок по N реализациям случай-
i-i
ной величины т] следующим образом. Расположим числа х^, х|, ...
..., Xs в порядке строгого возрастания;
х[‘<$<...< х‘*. (12)
Положим = ...» isN> (s = 1, т). Рассмотрим событие
В (ль ..., згга), состоящее в том, что N реализаций случайной ве-
личины т] задают по формуле (12) указанные перестановки. Найдем
Рг{В (ль ..., ля)} = ... ^dF...dF,
...» лт) ~
где Q(^j...лт)—часть пространства (Em)N, в которой
Xя* < хя* <... < Xя",
Хп1 < < <• Xя"
л2 Л2 Л2 ’
лт ТТт
т т т *
По условию теоремы и определению кратного интеграла
$ ... JdF...dF = n $ dFi...dFi,
«<"•...">»> ' —
где Q‘(л,)—часть пространства £$, в которой
хя1<... < Xя".
Здесь Е$—подпространство (Em)N, образованное i-ми осями каж-
дого из Ет; Е$ = UQ,(it/)Uo, где объединение идет по множе-
{Л}
ству (л) всех N\ перестановок, a S—множество точек из En,
у которых хотя бы две координаты совпадают. Из непрерывнос-
ти Ft непосредственно следует, что
JdF,....dFz = O.
s
(13).
Для любых двух перестановок л) и л?
• .$ (dF^= j (dF.)^v.
<?'(л)) <2г(л|)
§1. ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ МОЩНОСТИ 181
. Поэтому
2 $ $ (dFzyv= $ (dFz)"=l,
W Q'(nz) « Q‘(n.) jAft
откуда (dFz)w= l/AZ! и в силу (13)
<2'(nz)
> Рг{В(лх, .... nm)} = (l/W!)». (14)
। Пусть заданы перестановки лх, ..., лт и для N реализаций
f х1, ..., xN случайной величины г] выполнено событие В (лх, .... ли).
Поскольку по условию теоремы отношение R координатно, то
1 <рл (х1, ...,xN) принимает одно и то же значение для всех реа-
лизаций <х\ ..., xw> £ В (лх, ...,пт). Это значение зависит от
перестановок лх, ..., лт.
Вероятность Рг {k, F, R, N, т} равна сумме вероятностей всех
событий В (лп .... ли) таких, что <рл (х1, ..., xN) = k при <х\ ...
: хл'>^В(л1, ли). Вероятность каждого события
В(лп ...,лт) определяется равенством (14), а число L таких
’ наборов не зависит от F. Теорема доказана.
В силу теоремы 2 для вероятностей Pr{&, F, R,N,m} при
распределениях вида (И) и координатных отношениях можно
г пользоваться записью Рг{&, R,N,m}. Из доказательства теоре-
мы 2 следует, что эти вероятности зависят только от главного
члена ЛФО(/?). Поэтому можно использовать запись Рг {k, f, N, т},
где /(Pu ..pm)—главный член ЛФО(/?).
Вычислим интеграл (9) для отношения Парето и распределе-
! ния F вида (11). В силу теоремы 2 можно считать, что г|—слу-
чайный вектор, равномерно распределенный в единичном кубе,
т. е. p(slt . ..,sm)==l при 0s(гС 1 (i = l,/п). Тогда внутрен-
ний интеграл в (9) равен объему V (х1, ..., хг) части множества
А (хх, ..., хг), определенного формулой (4), содержащейся в еди-
‘ ничном кубе.
Для отношения Парето
* /?-(z) = (x€£„|x/<zz (i = 17m)}.
Объем V (х1, ..., хг) может быть найден по формуле
! V (х1, ..., хг) = 2 Х14-• -xsn—
S-I
г
— У min (xf, х{)min (х|, х0.. .min (xsm, х^)+ • • •
S, t=l
s 1
...+(—l)r-1min(x}, ..., x[)min(x|, ..., x0 ... min(x^, .. .,x^).
(15)
182 гл. 6. ВЕРОЯТНОСТНЫЕ ХАРАКТЕРИСТИКИ МОЩНОСТИ
Окончательно получим
Qr= $... $ (V (х\ .... x'^-'dx'.. .dxrm, (16)
0 0 0 0
где V(х1, ...,хг) определяется формулой (15).
Упражнение 8. Доказать формулу (15).
Упражнение 9. Привести аналог формул (15) и (16) для
произвольного транзитивного координатного отношения.
Утверждение 1. Пусть A(Pi, • •РСТ) = /2(Р^, • • •, Р’т)-
Тогда при всех k и N
Pr{k, ft, N, m} = Pr{k, f2, N, m}.
Упражнение 10. Доказать утверждение 1.
В некоторых случаях распределение числа недоминируемых
по координатному отношению альтернатив можно найти проще.
Утверждение 2. Для отношения из примера 1.4.5
РХ=(1-Л, NW-t + Pk, nPvn-\,
где
и Рп—вероятность того, что ровно v элементов из N будут
D^-оптимальны.
П р и мер 3. Пусть
f (Pi> Рз) = РзРг VPsPi • (17)
Найдем Рг{&, f, 3, 3} при £ = 0, 1, 2, 3. Вычисления будем про-
изводить по способу, изложенному при доказательстве теоремы 2.
Пользоваться формулами (15), (16) нельзя, так как отношение /?
с ГЧ, равным f, не является транзитивным.
Рассмотрим различные расположения точек х1, х2, х3 в Е3
Зададим их перестановками л1 = </}, il, и л2 = </2, i2, /*>, озна-
чающими, что по 1-й и 2-й осям выполнено х^1 < х*3 < х*3 и
•2 i2 i2
x2J <х/ <x23. Будем считать, что по 3-й оси х|< х3 < х3. По-
этому для каждого расположения укажем две перестановки по
2-й и 1-й осям и число недоминируемых точек. Результаты све-
дем в табл. 1. Здесь в каждой клетке слева указаны переста-
новки, а справа—число недоминируемых элементов по отноше-
нию Р с ГЧ f, задаваемым (17). Из табл. 1 находим
Р =-*2 = 1 р _16_± р _1_ р __1_
° 36 3’ 1 — 36— 9’ 2 — 36’ Гз —36’
Упражнение 11. При подсчете вероятностей Р( (i = Q,3>) в
примере 3 непосредственно по схеме доказательства теоремы 2
S 1. ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ МОЩНОСТИ О* 183
Таблица 1
123 123 123 123 123 123
1 0 1 0 0 0
123 132 213 231 322 321
132 132 132 132 132 132
2 1 1 0 1 0
123 132 213 231 312 321
213 213 513 213 . 213 213
1 0 1 0 0 0
123 132 213 231 312 321
231 231 231 231 231 231
2 1 2 1 1 1
123 132 213 231 312 312
312 322 312 312 312 312
2 1 1 0 1 0
123 132 213 231 312 312
321 321 321 321 321 321
3 2 2 1 2 1
123 132 213 231 312 321
необходимо было бы рассмотреть (ЛИ)га = 68 = 216 расположений
точек. Зафиксировав перестановку п3, удается в 3! раз умень-
шить число вычислений. Обосновать возможность фиксации л8.
Помимо функции распределения <рд представляет интерес сред-
нее число недоминируемых альтернатив, равное математическому
ожиданию <рд. Для его вычисления можно воспользоваться фор-
мулой
N
M(F, R,N,m)=%k-Pr{k,F, R,N,m}. (18)
k = 0
Однако в ряде случаев M(F, /?, N, tn) можно вычислить и не
зная функции распределения фд.
Утверждение 3. Пусть Р— вероятность того, что xN не-
доминируема реализациями х1, ...,xN~1 случайного вектора т).
Т огда
M(F, R, N,m) = P-N. (19)
Доказательство. Рассмотрим случайные величины
(1, если х' недоминируема, _____________
в,- = < . (i = 1, N).
(О, если х‘ доминируема
184 гл. 5. ВЕРОЯТНОСТНЫЕ ХАРАКТЕРИСТИКИ МОЩНОСТИ
Тогда
(W X W
=2jM(S/); (20)
i=l J i=l
здесь s, принимает значение 0 с вероятностью 1—Р и значение 1
с вероятностью Р. Поэтому
A4(s/) = 0-(l—Р) + 1Р = Р (i=TjV); (21)
равенство (19) следует из (20) и (21). Утверждение доказано.
В силу утверждения 3 нахождение М (F, R, N, т) сводится
к вычислению Р — вероятности того, что последняя реализация
недоминируема. Найдем вероятность Q=1—Р. Точка xN доми-
нируема тогда и только тогда, когда
xN^A(xY, ..., xJV"1).J
Поэтому условная вероятность того, что xN доминируема при
фиксированных х1, ...,хЛ/-1, равна
$ ... $ p(s1; ..., s^ds,.. .dsm,
A(x‘, xN~ !)
откуда
-S •••$••-Ш ••• ...,sm)ds1...dsm]>^
A(x«, ....
m m
...,xlm)...p(xr\ ...,x^)dx\...dx^-\ (22)
Таким образом, доказано
Утверждение 4. Среднее число недоминируемых по любому
бинарному отношению R альтернатив определяется формулой (19),
где P—\—Q, a Q определяется формулой (22).
Пример 4. Рассмотрим одномерную случайную величину г|
из примера 2. Найдем М (F, >, 2, 1). По формуле (18) получим
M(F, >, 2, l) = 2(p-p2) l+0 + 2(ps-p))-2 =
= 2р—2р2 + 24-4р2—4р = 2—2р + 2р« = 2(р2—р4-1).
Упражнение 12. Найти минимальное и максимальное зна-
чения среднего числа недоминируемых альтернатив при измене-
нии р от 0 до 1 в примере 2.
Упражнение 13*. Выполнить упр. 12 для любых F и лю-
бого координатного отношения R.
Упражнение 14. Изменится ли ответ в упр. 13, если R
ациклично?
Приведем другой способ подсчета М (F, R, N, т). Обозначим
через Р вероятность того, что х1 недоминируема реализациями
§2. СРЕДНЕЕ ЧИСЛО НЕДОМИНИРУЕМЫХ АЛЬТЕРНАТИВ
185
х2, ..xN. В силу независимости реализаций Р = Р. Зафиксируем
хх = х. Обозначим через вероятность того, что Z-я реализация
т] не доминирует х. В силу независимости реализаций Ux не зави-
сит от Z, поэтому LX = LX. Вероятность того, что х*-доминирует х,
обозначим через Dx. Положим Lx=l—Dx. Вероятность того, что
точка х останется недоминируемой при поступлении (N—1)-й
точки, равна
Вероятность Р определяется формулой
00 00
Р = $ ... $ ...,xlm)dx\...dxlm, (23)
— 00 — 00
где р—плотность распределения т|. Формула (23), как и (22),
справедлива для любых распределений т] и любых 7?. Заметим,
что
....., sjdsj.. .dsw. (24)
R + (x)
Величина M(Ft jR, N, m) находится по формуле (19).
§ 2. Среднее число недоминируемых альтернатив
tn
Будем считать, что 7? координатно, a F (7П ..., tm) =
£ = 1
Для обозначения среднего используем запись М (f, N, т), где
f—ГЧЛФО(7?).
1. Подсчет 7И (f, N, tri) для любых булевых функций •/. Как
и ранее, будем считать, что случайный вектор г) распределен
равномерно в единичном' кубе. Поэтому фурмулу (23) приведем
к виду
1 1
P = J...J(1— Vx)N~1dx, (25)
О о
где V х—объем пересечения области 7?+ (х) с единичным кубом.
Найдем Vx.
Напомним, что xRy <=> f (р) = 1, где
11, если Xj > у;,
(О, если х(-<«/,-.
Разложим f в СДНФ:
(26)
Для вектора 2 = <21, .... выполнено
<21, ..., 2„,>СР+(0)
186 ГЛ. 5. ВЕРОЯТНОСТНЫЕ ХАРАКТЕРИСТИКИ МОЩНОСТИ
тогда и только тогда, когда
sgn z = <sgn zlt sgn zm> = <al, ..., ol>
при некотором t £{1, ...,/}.
Введем функции от действительной переменной
( а. если о=1,
Ф°(а) = < , .
( 1—а, если о = 0,
и положим
Ф/ (ап ..., ат) = 2 П Ф°£ (а/). (27)
/=ii=i
Функция ф7 однозначно определяется по булевой функции f. Ив
построения фу следует, что
Ух = Фу(х). (28)
Теорема 3.
1 1
M(f, IV, m) = ivj... J [1 — Фу(Xx, ..., xj]"-1^.. .dxm. (29)
О о
Доказательство непосредственно следует из (28), (25) и (19).
В силу (27) функция Фу(хп ...,хт)—многочлен степени т,
поэтому 1—фу—тоже многочлен степени /п; подынтегральная
функция в (29) является многочленом, поэтому интеграл берется
в явном виде.
Пример 5. Найдем по формуле (29) М (f, 3, 3) для функ-
ции f из примера 3. Разложим f в СДНФ:
f (Р1» Рз) = Р3Р2Р1V Р3Р2Р1V Р3Р2Р1V Р3Р2Р1 •
Найдем фу по формуле (27):
фу= (1 — Х3) (1 — Х2) (1 — Xj)+(1 — Х3) (1 — Х2) Хх+х3 (1—х2) (1—хО+
4-х3х2 (1 — хг) = (1 — х3) (1 —х2) 4-х3 (1 —х2).
Отсюда
1 — фу = 1 — [(1 — х3) (1 —х2) + х3 (1 — xj] = х2 — х2х3 + х^,
(1 — фу)а = х|+х2х3+xfxl—2xfx3 + 2XjX2x3—2xtx2xt
Вычислим интеграл в (29), взяв его от каждого слагаемого:
1 _1_ । _L__L , _1_L —11
Утверждение 5. Пусть f(Р„ •.P„) = fi(Р?‘, ..Р’*).
Тогда М (fu N, т) = М (f, N, tri). _
Доказательство. При замене р,- на Р,- в фу член 1— х{
заменяется на х(. Но при замене переменной х,- на 1—х; интег-
1
рал ^XidXi не изменяется. Утверждение доказано.
О
§2. СРЕДНЕЕ ЧИСЛО НЕДОМИНИРУЕМЫХ АЛЬТЕРНАТИВ
187
2. Подсчет M(f, N, т) для классов булевых функций f.
Как следует из (27), число слагаемых в <jy может иметь поря-
док 2“, а число членов в подынтегральной функции может
иметь порядок 2mN. Для некоторых классов булевых функций
расчет М (j, N, т) можно упростить. Для этого сформулируем
несколько утверждений.
Утверждение 6. Пусть f (Рх, ..., Рга) = р(°'. Тогда M(f,
N, /и) = 1.
Доказательство. Предположим, что а, = 0. Тогда для
любых двух точек х\ х2£Ет функция [($(хг, х2)) равна 1, если
х) > х?. Пусть х1...xN—произвольные # реализаций вели-
чины я и
I = argmax xt.
i
Точка х1 является единственной недоминируемой точкой из
(х1, ..., xN}, поэтому <р/?(х1, ..., xN)=\ и среднее значение <рл
равно 1; в случае о,= 0 утверждение доказано. В случае az=l
положим / = argminxj и повторим предыдущие рассуждения.
i
У пражнен ие 15. Пусть f($lt ..., Рда) = ^(Р1, ..., Pz), т. е.
f не зависит от pz+1, ..., рт. Доказать, что для любого N
M(f, N, т) = М(ц>, N, I). (30)
Утверждение 7. Пусть 12, /, s {1, ..., т}, f($lt ..., 0OT)=
= A(P/.)V4(P/l), ЛП/а = 0. Тогда
M(f, N, т) = М(К, N, тг)М([2, N, m2)/N, (31)
где mr = |Л|. тг~ 141-
Доказательство. Пусть jx1, ..., xN—любые N точек и
f(P(x', х*)) = 0 (i=l, АГ-1). (32)
По условию утверждения это эквивалентно тому, что
4 (₽(*', ^)) = A(|3(x', х")) = 0 (1 = 1, JV-1). (33)
Из эквивалентности (32) и (33) событие
A = {xN недоминируема по отношению R с ГЧ f}
равно пересечению аналогичных событий С и В при f=4 и f = f2
соответственно. Из условия утверждения Л Г) /2 = 0 события В
и С независимы. Поэтому
Рг{4} = Рг{В}Рг{С}. (34)
Формула (31) следует из (19) и (34) с учетом (30).
Утверждение 8. Пусть ..., Pm)=₽zAfi (Pi,
P/+i, РД Тогда n
M(f, N, m) = 2 A4(fx, k, m—l)/k. (35)
k— 1
188 гл. 5. ВЕРОЯТНОСТНЫЕ ХАРАКТЕРИСТИКИ МОЩНОСТИ QR
Доказательство. Можно считать, что (=1 и что в лю-
бой последовательности реализаций х1, ..., xN первые коорди-
наты упорядочены в порядке убывания: xl > xf >... > х". Рас-
смотрим (т—1)-мерные векторы у' = <х'2, х^> (х/=<х{, у7>
(/ = 1, ЛО). Определим множества Тк (k=\, N), состоящие из
векторов у1, ..yN, по правилу
Т\=у1\
т = если А(р(«/Л yft)) = 0 (/=1, k — 1), —-
k Ufc-i в противном случае 1 ’ ’’
Докажем, что
Q-'? = {x/^Q|z//e7,v}) (36)
где Q = {x1, ..., xv}. Предположим противное: Xs£QR и ys^Ty.
Следовательно, по построению Тк получим ys^T3. Значит, су-
ществует t<s такое, что Д(Р(^, у'))=\, а так как х[>х1,
то по условию утверждения /(Р(х‘, х5))=1 и xs(£QR. Пусть
ysCTN, но XsСледовательно, для некоторого t < s
f(p(x‘, х0)=1.
Если t > s, то х{ < х|, Pj = 0 и, значит, / = Pi/i —0. Но
тогда по условию утверждения имеем
A (0(yf, ys)) = I (/<s),
т. е. по построению Тк получаем,• что ys(£Ts и, следовательно,
N. Формула (36) доказана.
Обозначим через множество недоминируемых точек из
у1, ..., ук по отношению с ГЧ Д. Введем случайную вели-
чину
( 1, если yk€.Th,
О, если ук$Тк. <37>
По построению Тк и формуле (37)
S ®т-1 = | Т'N | •
Л = 1
Поэтому
/ N \ N
м(|7\|)=м S 4-i = S м^)
\k=i j *=i
и в силу (36) получаем
M(f, N, tri)= S ^(8^). (38)
А=1
Определим случайные величины
fi* = J А если А(р(г/г, учУ) = О (1 = ТГк l=£v),
v I 0 в противном случае.
§2. СРЕДНЕЕ ЧИСЛО НЕДОМИНИРУЕМЫХ АЛЬТЕРНАТИВ
189
По определению 6*=1 тогда и только тогда, когда yv£Am-i-
Поскольку у1, ..., yN—реализации одной и той же случайной
величины т]* (,г) = <г11> ГГ> и т)*, ть независимы), то для всех
v k, ц k случайные величины 8% и одинаково распреде-
лены. Поэтому
М(6*) = М(6*).
(39)
k
Заметим, что = следовательно,
v= 1
/ k \ k
м(|ли|)=л1( 2б*)=2м(б*).
\v=l / V=1
Из (39) получаем при y = k:
k
2 М(8*) = 1г-М№,
V=1
откуда Л1(б0=М(|Л*_1|)/й. (40)
По построению следует, что — поэтому из (40) и определения Л^-х М(гкт_1) = М(К, k, (41)
Утверждение 8 следует из (41) и (38).
Приведем примеры, иллюстрирующие применение утвержде-
ний 5—8 для подсчета среднего числа недоминируемых альтер-
натив.
Пример 6. Рассмотрим отношение Парето; ГЧ ЛФО(Р)
т
имеет вид f(Pv ..., Р„)=А Р/ (см. пример 1.4.1). Изутвержде-
i=i
ния 8 следует
(т ' \ ( т—\
А ₽/, N, т )= У АП А ₽/» k, т— 1 ) k. (42)
i = l / k=l \i=l J'
В силу утверждения 6
Af(p, N, /п)=1. (43)
Для отношения Парето из (42) и (43) получаем рекуррентную
формулу
N
М(Р, N, М(Р, k, m—l)/k (44)
k=i
с начальным условием
М(Р, N, 1)=1.
(45)
190 ГЛ. 5. ВЕРОЯТНОСТНЫЕ ХАРАКТЕРИСТИКИ МОЩНОСТИ
Таблица 2
\ т N У. 1 2 3 4 5 6 7 8 9 10
1 1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00 .
2 1,00 1,50 1,75 1,87 1,94 1,97 1,98 1,99 2,00 2,00 ;
3 1,00 1,83 2,36 2,66 2,82 2,91 2,95 2,98 2,99 2,99
4 1,00 2,08 2,88 3,38 3,67 3,83 3,91 3,95 3,98 3,99
5 1,00 2,28 3,34 4,05 . 4,48 4,72 4,86 4,93 4,96 4,98 ;
6 1,00 2,45 3,74 4,67 5,25 5,60 5,79 5,89 5,94 5,97
7 1,00 2,59 4,12 5,26 6,01 6,46 6,71 6,85 6,92 ,6,96 !
8 1,00 2,71 4,45 5,82 6,74 7; 03 7,63 7,80 7,90 7,95
9 1,00 2,83 4,77 6,35 7,44 8,13 8,53 8,75 8,87 8,93 '
10 1,00 2,93 5,06 6,85 8,13 8,94 9,42 9,69 9,84 9,92 :
11 1,00 3,01 5,34 7,34 8,80 9,74 10,31 10,63 10,81 10,90 :
12 1,00 3,10 5,60 7,81 9,45 10,53 11,20 11,56 11,77 11,88 !
13 1,00 3,18 5,84 8,26 10,08 11,30 12,06 12,49 12,73 12,86 \
14 1,00 3,25 6,07 8,69 10,70 12,07 12,92 13,41 13,69 13,84
15 1,00 3,32 6,29 9,11 11,31 12,82 13,77 14,33 14,64 14,81
16 1,00 3,38 6,51 9,51 11,91 13,57 14,62 15,24 15,60 15,79
17 1,00 3,44 6,70 9,91 12,49 14,30 15,46 16,15 16,55 16,76
18 1,00 3,50 6,90 10,30 13,06 15,03 16,30 17,06 17,49 17,73
19 1,00 3,55 7,09 10,66 13,62 15,75 17,13 17,96 18,43 18,70
20 1,00 3,60 7,27 11,03 14,18 16,45 17,95 18,86 19,38 19,67
21 1,00 3,65 7,44 11,39 14,71 17,15 18,76 19,75 20,32 20,64
22 1,00 3,69 7,61 11,73 15,25 17,85 19,58 20,64 21,26 21,61
23 1,00 3,73 7,77 12,07 15,78 18,53 20,38 21,53 22,20 22,57
24 1,00 3,78 7,93 12,40 16,29 19,21 21,18 22,41 23,13 23,54
25 1,00 3,82 8,08 12,73 16,80 19,88 21,98 23,29 24,06 24,50
26 1,00 3,85 8,23 13,04 17,30 20,55 22,77 24,16 24,99 25,46
27 1,00 3,89 8,37 13,35 17,80 21,21 23,55 25,04 25,-92 26,42
28 1,00 3,93 8,51 13,65 18,29 21,86 24,33 25,91 26,65 27,38
29 1,00 3,96 8,65 13,95 18,77 22,51 25,11 26,77 27,41 28,34 '
30 1,00 3,99 8,79 14,25 19,24 23,15 25,88 27,63 27,77 29,29 ‘
31 1,00 4,03 8,92 14,53 19,71 23,65 28,49 29,61 28,17 30,25 ;
32 1,00 4,06 9,04 14,82 20,17 27,41 29,35 30,52 28,69 31,20 :
33 1,00 4,09 9,17 15,10 20,63 28,17 30,20 31,44 28,84 32,15
34 1,00 4,11 9,29 15,34 21,08 28,93 31,06 32,35 28,93 33,11
35 1,00 4,14 9,41 15,64 21,53 29,68 31,90 33,27 29,68 34,05
36 1,00 4,17 9,52 15,90 21,97 30,42 32,75 34,17 30,42 35,01
37 1,00 4,20 9,64 16,16 22,41 31,17 33,59 35,08 31,17 35,95 *
38 1,00 4,23 9,75 16,41 22,84 31,91 34,43 35,99 31,91 36,90 •
39 1,00 4,25 9,86 16,67 23,27 32,64 35,27 36,89 32,64 37,85 j
40 1,00 4,27 9,96 16,92 23,69 33,37 36,10 36,93 33,37 38,79
41 1,00 4,30 10,07 17,17 24,11 29,87 34,10 37,76 38,70 39,74
42 1,00 4,33 10,17 17,41 24,52 30,46 34,83 37,79 39,60 40,68 :
43 1,00 4,35 10,27 17,65 24,93 31,03 35.55 38,59 40,49 41,62 *
44 1,00 4,37 10,37 17,88 25,34 31,61 36,27 39,41 41,39 42,56 ;
45 1,00 4,39 10,47 18,12 25,74 32,18 36,98 40,24 42,28 43,50 :
46 1,00 4,41 10,57 18,35 26,14 32,75 37,70 41,06 43,17 44,44 >
47 1,00 4,44 10,65 18,57 26,54 33,32 38,40 41,87 44,07 45,38 ;
48 1,00 4,46 10,75 18,80 26,98 33,88 39,11 42,69 45,00 46,31
49 1,00 4,48 10,84 19,02 27,32 34,43 39,81 43,50 45,84 47,25 ;
50 1,00 4,50 10,93 19,24 27,70 35,00 40,51 44,30 46,73 48,18 ’
§2. СРЕДНЕЕ ЧИСЛО НЕДОМИНИРУЕМЫХ АЛЬТЕРНАТИВ
191
Из (44) и (45) получаем
N
М(Р, N, 2) = 2 Vk^lnN,
k=l
N N
M(P, N, 3)= S M(P, k, 2)/6 = S V(*0-
k=i k, i=i, i<k
(46)
Значения M(P, N, tn) при m=l, 10 и N=\, 50 приведены
в табл. 2.
Упражнение 16**. Доказать, что
lim М (Р, N, m)/ln”,_1 N —\/(т—1)!.
N -> со
Формула (46) показывает, что уже при т = 2 доля паретов-
ских элементов стремится к нулю, в то время как их число не-
ограниченно растет с ростом N. Для других отношений среднее
число недоминируемых альтернатив может быть ограниченным
при любой мощности Q.
Пример 7. Рассмотрим отношение V из примера 1.4.7.
Напомним, что при определении V задается семейство отноше-
ний Vk с ГЧ ЛФО (Vk), которые связаны рекуррентной формулой
fk (Рп • • •. Рл) = РД-1 (Ра-2 V Pft-8 V .... Pfc_4))
при начальных условиях
f1 (W = Pu f2 (Pi, P2)-PiP2, ,4~
HPi, p2, Рз)=PiP2p3, m, p2, Рз, р<)=р4рз <p2vPi). ( ’
Подсчитаем среднее число недоминируемых (7-оптимальных)
альтернатив. По формуле (35) получим
N
M(fk, N, ^) = zS^(pft_1(Pft_2VPft_8VfA-4), /, *-!)// =
= S ( 2 М (Pft-2 V Pft-3 V fk~\ S, k—2)!s\\l, (48)
Z=l\s = l /'
по формуле (31) —
M(Pft-2 VPft_3 S, k-2) =
= М($к_2, s, 1)M(P%_3, s, l)M(/ft~% s, A:—4)/s2; (49)
в силу утверждения 6
A4(Pfe-2, s, 1) = М(Р*_з, s, 1) = 1„ (50)
Подставляя (49) и (50) в (48), получим
N / I \
M(fk, N, k) = S 2 M{fk~\ s, A—4)/s3 ] I. (51)
z = l \s = l J1
192 ГЛ. 5. ВЕРОЯТНОСТНЫЕ ХАРАКТЕРИСТИКИ МОЩНОСТИ ЯЛ
В силу (47) и (46) получим
N 1
M(f\ N, 1)=1, M(f2, N, 2)=£~,
z=i
N 1 1
M(p, N, 3) = SLlT. (52)
l=1S=1
N 1 1
M(f*, N, 4) = ££-^.
1 = 1S=1
Рекуррентная формула (51) вместе с начальными условиями
(52) определяет M(fk, N, k) для всех k.
Упражнение 17. Доказать, что
lim M(f*, N, 4)=оо.
N -> со
Упражнение 18*. Доказать, что при всех N
M(f*, N, 4)<лЧпЛГ/6.
Утверждение 9. Для всех т>4
lim M(fm, N, т)—<х>.
N -> оо
Разобьем переменные на группы:
Pi, ..., р*,,
Р*,+it • • •, Р&8>
• • • » Р/д*
Введем отношение W, для которого ГЧ ЛФО(1Г) имеет вид
п=Фц_.+1 • • v
S=l, d; =
С помощью утверждений 5—8 можно найти М (f*, N, т), анало-
гично тому,"как это было сделано в примере 7 для отношения V.
Упражнение 19*. Пусть переменные разбиты на группы:
₽1. Ра; Рз, ₽«; Р5. ₽«;• •• Найти М (/„ N, т).
Упражнение 20*. Найти необходимые и достаточные усло-
вия на разбиение переменных на группы для того, чтобы М
N, т) было ограничено при всех N.
Булева функция называется симметричной, если
f(₽i, PJ = f(Pz,. PzJ
для любого набора <рп ..., ря> и любой перестановки <i1( ..., tm>.
Для любой симметричной функции существуют целые числа
klt kt, 0 < ki^.m, такие, что- f (Pi.pm) = 1
§2. СРЕДНЕЕ ЧИСЛО НЕДОМИНИРУЕМЫХ АЛЬТЕРНАТИВ
193
тогда и только тогда, когда число единиц среди значений пере-
менных равно одному из чисел klt ..kt. Соответствующая сим-
метричная функция обозначается через ...kt (0i...Pm).
Обозначим через Ак,г.к'1 множество всех наборов целых не-
отрицательных чисел <d°m, ..., таких, что
т ь ___
1) Sd^AZ-1; 2) dm'=0 (j=l, /). '
;=o
Для наборов из Ат должно выполняться только требование 1).
Для любого набора <d„, .... d„> положим
k
Dkm=^,dlm. (53)
1 = 0
У т в е р ж д|е н и е 10. Справедливо соотношение
N, m)~N V (54)
Aki..kl
т
где
р/ло dm}— 1 V 1?°/” cD"l~D'n~l с0"1 у
P(dm, ...» dm)--^ X
4_.
X[^4-(D^-D^_1)+ ... +(D^-D^)] !x
x[^-l-D«1-(D^-^_1)-... -(Z^-1-^)] ! X
XP(4-I, ...iCl) (55)
при
P(d°, AZ—1—d?) = l/AZ (0<d?<AZ — 1). (56)
Здесь Ca = Q, если b > a, и d! = 0, если d<0.
Доказательство. Обозначим через P (di....d|) вероят-
ность того, что имеется ровно d? точек, у которых первые t
координат не больше, чем у точки xN, ровно d} точек, у кото-
рых среди первых i координат одна больше, чем у точки AZ,
и т. д. ровно dj точек, у которых первые i координат больше,
чем у точки N. Положим i = m. Если d^*#=0 (s^p, •••» И)»
то точка xN доминируется одной из точек х1, ..., х-™-1. Поэтому
вероятность Р того, что xN недоминируема, равна сумме вероят-
ностей P(dm, dm) при условии d^ = 0 (s £ {1, ..., Z}), т. е.
при суммировании по Д**.’"’** формула (54) следует из (19).
Осталось найти вероятности P(d^, ..., d%). [Пусть имеется N
реализаций случайного вектора в пространстве £„,_!• Положим
Qm-i = {/||У} больше yN [ровно по i координатам} (i = 0, т—1).
Добавим к имеющимся векторам у! т-ю координату и получим
векторы х^ = <г/7, х/п>. Заметим, что любая перестановка номе-
194 ГЛ. 5. ВЕРОЯТНОСТНЫЕ ХАРАКТЕРИСТИКИ МОЩНОСТИ Я*?
ров 1, N, определяемая упорядочением х1, ..., х^’по по-
следней координате, равновероятна. Если /CQm-i и х^ > х^, то
так как xi больше xN по (t-f-l)-fi координате. Если
х‘т < хт, то / € О.т- Принадлежность j к одному из множеств Q‘m
определяет, находятся ли векторы х7 и хдгв данном отношении
ГЧ ЛФО которого—симметричная функция. Если j £Qm и I равно
одному из чисел /гг, ..., kt, то xJ'RxN\ в противном случае xJRxN.
Разобьем любое из множеств = {1, ..., N—1} на две
части: B^-i, состоящую из j£Qlm-i таких, что х^ < х%, и
состоящую из / С Qm-i таких, что х‘т > х" При этом получим
Q‘m = Вт-1ч Qm~ Cm-lU ..., Qm~
= ^m-iU Bm-i, Qm 1 = ^m-1 UQm==Qn-i- (67)
Положим
G-in-l ~ I Qm-1 |, = ^т-1== I ^m-1 |> ^m-i — I Cm-11 •
Вероятность того, что при разбиении Qfn_j получим \В^_1\ = Ь„-1,
\Clm_1\ = dfn-1—Ь1т_1, определяется формулой
О , „ , /т-1 \ / т-1 \
Л с те г.... с;:;< Е I (N-1 - £ 1. (58)
ат-1 ат-1 am-l\i=Q J \ £=0 /
С помощью (57) можно выразить Ъ1т_х через и df^.
bm-l = <im, = —d^—d^-i, •••
..^=1=4+ • • • +‘%-1-d°m-i- (59)
Подставляя (59) в (58) с учетом (53), получаем (55). Утвержде-
ние доказано.
Упражнение 21. Пусть f=PjP2 VPiPsVPaPs- Найти М (f, 3, 3)
по формулам (54)—(56).
Упражнение 21*. Доказать, что вычисление M(f, N, т)
для произвольной симметричной функции f требует порядка Nm
арифметических операций.
Обозначим через 33 класс булевых функций, который задается
следующим образом:
1. Р,-, 0, (s—любая симметричная функция).
2. A(P/,)Vfa(PZ1)€^, если’/1П/2 = 0, ft,
3. Р/ если %.
4. /(P?S ...» если f$!, ..., рг)е®.
Утверждения 5—8 и 10 позволяют находить M(f, N, т) для
всех функций
Выделим класс в который входят функции с числом
переменных не более т.
Упражнение 23**. Найти
Из условий транзитивности следует, что для любого транзи-
тивного координатного отношения R ГЧ ЛФО(/?) имеет вид
§3. ВЕРОЯТНОСТНЫЕ ХАРАКТЕРИСТИКИ МОЩНОСТИ 195
Л Поэтому среднее число недоминируемых по такому отно-
i е I
шению альтернатив совпадает со средним числом для отно-
шения Парето при zn = |/|.
§ 3. Вероятностные характеристики мощности
множества Парето
Пусть R—любое рациональное отношение. Тогда для любого
£2 s Ет множество £2* содержится в £2Р. Поэтому мощность мно-
жества Парето является оценкой сверху мощности £2* для любого
рационального R. Рассмотрим вероятностные характеристики
мощности множества Парето.
Утверждение 11. Справедлива формула
Pr{k, Р, N, 2} =
= 4-pr{£—Л 1, 2}+тРг^’ Р, АГ—1, 2} (60)
при начальных условиях
Рг{1, Р, N, 2}=l/N, Рг{£, Р, N, 2} = 0, если k>N. (61)
Формулы (60) и (61) позволяют легко найти распределение
числа паретовских элементов при /и = 2.
Приведем асимптотику М (F, Р, N, т), когда N —>оо, a F—
многомерное нормальное распределение. В случае нормального
распределения формула (24) запишется в виде
D _1Лг1/2.
* (2л)'"/2
GO 00
е~уТл. ly!^dy,
где Л—корреляционная матрица и знак Т означает транспони-
рование.
Утверждение 12. Для нормального распределения F с плот-
ностью
п = । Л ।_-__e~y*A~ty/2
M(F, Р, N, т)~ 2,”~" (In АГ)”-1 f n{(B*)-1e(<p)}(.J(<p)d<p, (62)
I Л I”17 J
11 Д(ф)
где матрица В приводит Л-1 к единичной-. В*Л~1В=Е', J(<р)г'“~1 —
\якобиан перехода к полярным координатам v = re(^ly ..., <pm-i).
vj = r; е—вектор, соответствующий точке на т-мерной единич-
ной сфере-, область £>(<р) находится из решения т тригономет-
рических неравенств с т—1 переменными-. (В*)-1е(<р) > 0. Вели-
чина M(F, Р, N, т) растет пропорционально (InAf)'"-1.
196 гл. 5. ВЕРОЯТНОСТНЫЕ ХАРАКТЕРИСТИКИ МОЩНОСТИ
Выражение (62) упрощается в случае трехмерного нормального
симметричного распределения с плотностью
р-у,А~1у/2 /1 Р Р\
dF(y) =----—------------dy, Л=(р 1 р I.
(2л)1/2 (1+2р)(1-р*) \р р 1/
При этом
M(F р N lnaJV J /Г^[(1-р)(1 +2р)_2p8J _|_
V ’ 21<1-р 1 1-гР
Н---;----1 arete-!---------1
- (1+2р)/1+р [ а Р •
(2р2-1)2р-(1-р)(1+2р)2 1-pl I
+ 1+p arctg V 1+p J /
Упражнение 24. Проверить, что при р = 0
M(F, Р, N, 3) ~1п2У/2.
Упражнение 25. Найти М (F, Р, N, 2) для двумерного
нормального распределения F.
Упражнение 26. Доказать, что для любых «/€[!, JV],
в > О и tn £ N найдется такая функция распределения F, что
\у—М (F, Р, N, т)|’<8.
Утверждение 13. При непрерывной функции распределения
вида (11) дисперсия D(P, N, т) числа паретовских элементов
выражается формулой
т- 1
У ск У _______________________________i—___________
_( у 1__________________Y+ у' 1,
Упражнение 27*. Доказать, что
D(P, N, 2)~lnAf,
D(P, N, 3)~ (y+?)ln2JV>
Dtp, n, 4)ULi+E(-UE-7-+-i-)in-«.
\z= 1 i = 2 4 1 j<i 1 /
Рассмотрим оценку сверху мощности множества Парето. В от-
личие от приводимых ранее оценок, она носит не вероятностный,
а детерминированный характер.
Пусть Й—m-мерная целочисленная решетка. Это значит, что
й состоит из всех точек х = <.х1г ..., хту с целочисленными коор-
§3. ВЕРОЯТНОСТНЫЕ ХАРАКТЕРИСТИКИ МОЩНОСТИ 197
динатами такими, что
(t^l, tri).
(63)
пользоваться обозначением
-2
2
\\\\\]
\\W\J
Двумерная 'решетка показана на рис. 2. Чтобы указать верхние
границы неравенств (63), будем
Й(пх, ..., пи). На рис. 2 показана
решетка й(5, 2).
Пусть X'^Q(nu ..., ram). Поло-
жим
V (щ, .... nm) = maxl Хр\.
Это значит, что V (nlt ..., пт)—
максимальная мощность множества
Парето по всем подмножествам X s
...........«J-
Рассматриваемая модель описывает многие ситуации, в кото-
рых число градаций по каждому критерию конечно, а объекты
могут оцениваться’произвольным набором оценок по каждому из
критериев.
Введем следующее обозначение:
1 2 3 4
Рис. 2.
О
L(0 = <[x€£m
т
2 Xj—t
/ = 1
Упражнение 28. Доказать, что множества Q(0), ...
(т \
2 п,), где Q (/) = L (/) Л й («1, •. •, пга), образуют разбиение
t = i J
й(пп .... пт).
Упражнение 29. Доказать, что все элементы из Q(t) не-
сравнимы между собой.
Из результата упр. 29 следует, что
V(nn .... n„)>max|Q(0|.
Заметим, что может быть несколько t, при которых Q (/) со-
держат наибольшее число элементов (см. рис. 2).
Число точек в Q(0 равно числу целочисленных решений
системы
2х, ==/, (t = 1, т). (64)
i=i
Утверждение 14. Число целочисленных решений системы (64)
равно коэффициенту при г* в разложении производящей функции
Fm(z, пи .... nm) = (z°+ ... +z^).. .(z°+ ... +zn“).
У тверждение 15.
t* = [y(«i + • • • +«»)]€ Argmax | Q (/)|.
198
ГЛ. 6. ФУНКЦИИ!ПОЛЕЗНОСТИ В ЗАДАЧАХ ВЫБОРА 3
У тверждение 16.
V(nlt ...,nJ = |Q(/*)|.
Упражнение 30 Л Доказать, что^
m ст
где qri определяются следующим образом.- Рассмотрим всевозмож-
ные наборы, содержащие г элементов из совокупности чисел
{пп ..., пт} для г = 0, т. Каждому фиксированному г поставим
в соответствие Сгт таких наборов, которые перенумерованы и
обозначены через Тг{, i=l, С^. Каждому набору \Trt "поставим
в соответствие число qrit равное сумме входящих в него чисел;
Полученная в утверждении 16 оценка зависит только от мно-
жества Q («j, ..., /гл), т. е. от числа градаций оценок по каж-
дому критерию.
Литература. [27, 29, 31, 54, 56, 111, 112, 113, 116, 122].«
Глава 6
ФУНКЦИИ ПОЛЕЗНОСТИ В ЗАДАЧАХ ВЫБОРА
В главе 4 рассмотрена математическая задача выбора <й, HP,
<®*>. Доказано, что решением этой задачи является множество
где 7?—бинарное отношение, задаваемое значениями функции
выбора С на множествах При отношение может
быть задано функцией полезности U’. xRyy U (х)> U (у). По-
строение сведено к решению задачи оптимизации
U(x) —<max. (1)
в
В настоящей главе приведены способы решения задачи (1).
В § 1 дано общее понятие функции полезности и приведены ее
основные свойства; в § 2 рассмотрены алгоритмы оптимизации
функции полезности; в § 3 исследовано влияние ИМА на реше-
ние задачи (1); в § 4 рассмотрено решение задачи оптимизации
при наличии помех.
§ 1. Общее понятие и свойства функции полезности
Понятие функции полезности возникло в теории потребитель-
ского спроса при сравнении различных наборов товаров. Значение
функции полезности на определенном наборе товаров выражает
ценность или полезность данного набора для потребителя. В за-
§ 1. СВОЙСТВА ФУНКЦИИ ПОЛЕЗНОСТИ
199
дачах выбора значение функции полезности выражает полезность
альтернатив.
Областью определения функции полезности U является Е^-
Областью значений—Е}. Если функция полезности известна, то
можно сравнить любые две альтернативы с помощью отношения Rv,
заданного формулой (4.1).
Упражнение 1. Какими свойствами из перечисленных в
§§ 1.1.4, 1.1.5 обладает отношение 7?у?
Будем считать, что все функции полезности обладают следую-
щими двумя свойствами, которые выделяют их из всех функций
на Е+:
а) Функции полезности монотонно возрастают по всем пере-
менным: для любых х=<хп .... хту, у—<уг, .... ут> £Е+,х=£у,
Х/>У} = U(x) > U(y).
Указанное свойство запишем в виде
хРу^и\х1>[и(у). (2)
б) Существуют две первые производные функции полезности U:
ыг = дЦ(х)/дхг, ____ ,3v
игх—дгиЦх}1дхТдх5 (r,s~\,m).
Гиперповерхность уровня функции U (хи ..., хт) определяется
как множество точек x = <xlt ..., хтУ^Е^, для которых U (х)=
= const. Гиперповерхности уровня функции полезности называ-
ются кривыми безразличия, а семейство всех кривых безразли-
чия—картой безразличия. Термин «кривая безразличия» связан
с тем, что полезность любых двух альтернатив х и у, лежащих
на одной такой кривой, одинакова: U (х) = U (у).
Введем на множестве 41 всех функций полезности отношение
R*; Uj^Uz, если существует возрастающая функция <р(-) такая,
что для всех х£Е£
<М*)~ф(СМ*))- (4)
Упраж'нение 2. Проверить, что отношение R* является
отношением эквивалентности.
Для отношения R* используем символ со.
Упражнение 3*. Доказать, что карты безразличия функ-
ций иг и t/2 совпадают тогда и только тогда, когда
Утверждение 1. Пусть U1tr>U2. Тогда для любого мно-
жества Q^E£.
Argmax = Argmax t/2.
□ о
Доказательство. Пусть x £ Argmax U2. Это значит, что
о
для всех у£ & выполнено U2 (x)ps U2 (у). В силу (4)
U1 (х) = д>({/2(х))>ф({/2(у)) = (/1 (у),
200
ГЛ. 6. ФУНКЦИИ ПОЛЕЗНОСТИ В ЗАДАЧАХ ВЫБОРА
т. е. U, (х)> Ui (у) и, следовательно, х£ Argmax U,. Этим дока-
Q
зано включение Argmax Ut £ Argmax Ut. Обратное включение
Q Q
доказывается аналогично.
Утверждение 1 означает, что решения задачи (1) для всех
функций из одного класса эквивалентности совпадают.
Утверждение 2. Пусть Тогда Rut = Rut-
Разные функции полезности могут порождать одно и то же
отношение которое, как следует из утверждения 4.3, одно-
значно определяет решение задачи (1). Поэтому далее будем ис-
пользовать только такие свойства U, которые являются общими
для всех функций, порождающих одно и то же отношение Rv.
Утверждение 3. Пусть Тогда
иУи\ = и}!и*.
Доказательство. По правилу дифференцирования слож-
ной функции „
И‘ = ^ = ^^ = ф'(^)^ = ф'([/а)«2.
С/А^» l/Aj»
Аналогично, п| = ф' (U2)и1, откуда
Ur фх (U2) Ur Ur
и$ ф* (U 2) uf uf
Утверждение доказано.
Величина ur(x)/us(x) называется предельной нормой замены
между r-м и s-м критериями в точке х^Е^. Предельная норма
замены между любыми двумя критериями в силу утверждения 3
является функцией на Е£, однозначно определяемой классом
эквивалентности [£/], содержащим U.
Упражнение 4. Доказать, что предельные нормы замены
положительны.
Пусть
Uj (хг)/и, (х2) < U/ (X^/Uj (х1)
для любых двух альтернатив х1 = <Xj, ..., х}, ..х], ..., х„> и
х2 = <xf, ... /х?, ..., х?, ..., х!> таких, что'
—"...IXIlgter -4
x}lx\> xj/x?.j
В этом случае говорят, что для функции полезности U выпол-
няется закон уменьшения предельных норм замены.
Положим Хм = {x^E^\U (х)М}. Говорят, что гиперповерх-
ности уровня выпуклы к началу координат, если множества Хм
выпуклы при всех М.
Упражнение 5*. Доказать, что из закона уменьшения
предельных норм замены следует выпуклость к началу коорди-
нат гиперповерхностей уровня.
S1. СВОЙСТВА ФУНКЦИИ ПОЛЕЗНОСТИ
201
Упражнение 6**. Следует ли закон уменьшения предель-
ных норм замены из выпуклости гиперповерхностей уровня к на-
чалу координат?
Общие свойства функции полезности одного класса определя-
ются их картами безразличия. Функцию полезности, для которой
гиперповерхности уровня выпуклы к
началу координат, назовем К-выпуклой.
Вид карты безразличия К-выпуклой
функции при т = 2 приведен на рис. 1.
Функцию полезности, для которой
все предельные нормы замены моно-
тонны по каждой переменной, назовем
К-гетеротонными. Знаки монотонности
могут зависеть как от номера пере-
менной /€{1, ..., т}, так и от точки
х=(хх, ..., хт>. Функцию полезности назовем К-линейной, если
ее гиперповерхности уровня представляют собой гиперплоскости.
Упражнение 7. Следует ли выпуклость функции U из ее
К-выпуклости?
Упражнение 8. Доказать, что К-линейная функция пред-
/ т \
ставима в виде t/=<p( 5 )» где<р(«)—возрастающая функция.
V=1 /
Приведем экономическую интерпретацию функций полез-
ности.
Пример 1. Сопоставим осям координат потребительские
товары. Точку х = <хп ...,хтУЕ^т рассмотрим как вариант
потребления, в котором х,-—
потребляемое количество i-ro
товара. Функция 1/(х) выра-
жает уровень удовлетворен-
ности потребителя вариан-
том х. Пусть р = <р±, ...
..., ря>—вектор цен на рас-
сматриваемые товары, а
средства на покупку товаров
равны М. Предполагают, что
потребитель расходует сред-
ства так, чтобы максимизи-
ровать свою функцию U (х)
на множестве всех вариан-
тов х, удовлетворяющих его
бюджетному ограничению
G={x£ Е„\(р,х)^М}, т. е. решает задачу U(х)—»-тах. На
О
рис. 2 изображены карта безразличия и три бюджетных огра-
ничения, задаваемые векторами цен и средствами. При векторе р1
и средствах М± потребитель выберет вариант А; при том же век-
7 И. М. Макаров и др.
202 ГЛ. 6. ФУНКЦИИ ПОЛЕЗНОСТИ В ЗАДАЧАХ ВЫБОРА
торе р1 и средствах Мг—вариант Б; при векторе р* и средст-
вах /Йя—вариант В.
Норма замены между r-м и s-м критериями равна числу еди-
ниц товара xs, потеря которых может быть компенсирована одной
единицей товара хг. Эта величина называется локальной ценой
r-го товара в единицах s-го товара. Приведем пример, иллюстри-
рующий понятие локальной цены.
Пример 2. В пункте, удаленном от населенных мест, встре-
чаются два туриста, у каждого из которых имеется определенный
продовольственный запас. Каждый из них хочет обменять часть
продуктов из своего запаса на продукты из запасов другого.
Пусть у первого туриста оказалось 2 пачки чая, 2 кг сахара
и 100 г хлеба. Второй турист согласен обменять 0,5 кг своего
хлеба на некоторое количество сахара. Если первый турист очень
голоден, то за 0,5 кг хлеба он
согласен отдать 0,5 кг сахара.
В этом случае локальная цена
хлеба в единицах сахара равна
единице. Если первый турист не
очень голоден, то за 0,5 кг хлеба
он согласен отдать 0,1 кг саха-
ра. В этом случае локальная
цена хлеба в единицах сахара
равна 1/5.
На рис. 3 точка х соответст-
вует набору <2 пачки чая, 2 кг
сахара, 0,1 кг хлеба>, точка
х1 — <2 пачки чая, 1,5 кг сахара,
0,6 кг хлеба>, точка хп—<2 пачки чая, 1,9 кг сахара, 0,6 кг
хлеба>. Функция полезности очень голодного туриста—U1, не
очень голодного туриста—Uli. Функции полезности U1 и Un—
разные, и поэтому локальные цены в точке х различаются.
При фиксированной функции полезности значение локальной
цены может зависеть от точки х, т. е. от наличия других това-
ров. Пусть U (х)—функция полезности туриста. Дополнительно
введем в продовольственный запас туриста сухари и рассмотрим
два набора: <2 кг сахара, 0,1 кг хлеба, 0,2 кг сухарей> и <2 кг
сахара, 0,1 кг хлеба, 2 кг сухарей>. При втором наборе локаль-
ная цена хлеба в единицах сахара меньше, чем при первом, за
счет значительно большего запаса сухарей.
В задачах выбора с использованием функции полезности счи- .
тают, что известна сравнительная полезность любых двух аль-
тернатив х, у, отличающихся не более чем по двум координатам.
Это значит, что известно, какое из трех соотношений
U(x)>U(y), U(x)<U(y), U(x) = U(y) (5)
выполнено для альтернатив х и у.
§2. АЛГОРИТМЫ ОПТИМИЗАЦИИ ФУНКЦИИ ПОЛЕЗНОСТИ
203
При таком предположении задача (1) является математической
задачей'выбора
<Й, $»> (6)
с параметрами
|Q|<oo,
где <₽у, й>—сужение [на Й бинарного отношения .53*—
множество, состоящее из всех двухэлементных подмножеств {х, у}
таких, что х отличается от у не более чем по двум координатам.
Соотношения (5) обеспечивают то, что задачи <Х, ОП> при X g 33*
являются простыми.
§ 2. Алгоритмы оптимизации функции полезности
Рассмотрим вспомогательную задачу компенсации. Пусть
выполняются предпосылки задачи (6) и даны альтернатива
х = <х1( ...,хт>, индексы /х, /2£{1, ...,«} й число Ах > 0.
Найдем с заданной точностью 8 число Д2 > 0 такое, что £/(х)=
= {7(х(А2)), где
хХА2) = <х1> ..., xj— An .... ха+А2,?*..., хи>.
Решение задачи компенсации обозначим через А2(х, jit /2, Ах).
Алгоритм 1. Решение задачи компенсации.
1. Положить A = AV
2. Положить А2 = А.
3. Если U (х) = U (х А2)), перейти к шагу 8; если U (х) >
>t/(x(A2))—к шагу 4; если U (х) < U (х (Д2))—к шагу 5.
4. Положить А2 = А24-Д и перейти к шагу 3.
5. Положить Д = А/2.
6. Если А < 8, то перейти к шагу 8, в противном случае —
к шагу 7.
7. Положить А2=А2—А и перейти к шагу 3.
8. Положить А2(х, /i, /2, Ax) = Aa.
Упражнение 9. Доказать сходимость алгоритма 1.
Воспользуемся алгоритмом 1 для решения задачи (6) при
Й = {х, у}, где х, у—произвольные альтернативы из Е^-
Алгоритм 2. Нахождение С(х, у).
1. Найти р—число координат, по которым х отличается от у.
2. Если р>2, перейти к шагу 3, в противном случае —
к шагу 10.
3. Если хРу, то перейти к шагу 8; если уРх—к шагу 9; в
остальных случаях перейти к шагу 4.
4. Найти /ь /2 такие, что хА>уА, хл<у/г.
5. Положить Ai=Xy,—уА.
6. Найти алгоритмом 1 Д2(х, Д, j2, Ax).
7* И. М. Макаров и др.
204 ГЛ, 6. ФУНКЦИИ ПОЛЕЗНОСТИ В ЗАДАЧАХ ВЫБОРА
7. Положить х=х(Аа) и перейти к шагу 1.
8. Положить С(х, у)~х и перейти к шагу 11.
9. Положить С(х, у)=у и перейти к шагу И.
10. Найти С(х, у) из условия (5).
11. Останов.
Решение на шагах 8 и 9 находится с использованием (2).
Решение на шаге 10 обеспечивается тем, что при х и у, отли-
чающихся не более чем по двум координатам, {х, у} £33*. Воз-
можность выполнения шага 4 обеспечивается тем, что при обра-
щении к нему точки х и у несравнимы по отношению Парето.
Алгоритм 2 основан на замене точки х точкой х(Аа), отли-
чающейся от у по меньшему, чем х, числу координат.
Алгоритм 3. Решение задачи (6).
1. Задать бинарное отношение Ru на й, воспользовавшись
для каждой пары <х, z/> £ Й2 алгоритмом 2.
2. Выделить множество й^</ недоминируемых по Ru альтер-
натив, воспользовавшись алгоритмом 4.6. (Алгоритм ’.6 можно
использовать в силу транзитивности Ry.}
Для реализации алгоритма 3 необходимо сравнить все (пары
из й2. Однако при наложении дополнительных требований на
функцию U (можно получить более эффективные градиентные
алгоритмы/^
^Обозначим градиент функции U веточке х^через V/.
- _/дЩх) дЦ(х)\ т
Направление вектора не изменяется, если все его |компо-
ненты разделить на одно и то же положительное число, например
на dUldxt. Имеем
V - Ух А дЩдх2 дЦ/дХпХ
Ух dUIdxi ~ У ’.. dU/dXi ’ ’ ‘ ‘ ’ dUldxJ ‘
Зафиксируем точку х = <хп ..., хт~> и положим
х = <Х], «••, хг А,, ..., Xj-^-Aj, ...,
Тогда
АУ = (x)«-^Ar + g%
откуда при ДУ = 0 получаем
ur/us « А,/Аг. (7)
Для построения вектора будем использовать приближенные
равенства (7).
Алгоритм 4. Определение вектора ^х.
1. Задать Аг и положить /1=1, Vi=l-
2. Положить i=l.
§ 2., АЛГОРИТМЫ ОПТИМИЗАЦИИ ФУНКЦИИ ПОЛЕЗНОСТИ
205
3. Положить i = i 4-1.
4. Положить /g=ai.
5. Найти алгоритмом 1 А3(х, /ь /2, Аг).
6. Положить V^ = A1/A2(x, /г, /2, Аг).
7. Если перейти к шагу 3. В противном случае алго-
ритм прекращает работу.
Алгоритм 4 является вспомогательным. Он используется в ка-
честве одного из'шагов в алгоритмах 5—8.
Утверждение 4. Пусть U-К-выпуклая функция, х1, х2 €
Utx^Utx1). Тогда
(Vx«, Х1)^^, х2).
Д о’к а|з а т е’л ь с’т’в о. Уравнение
|(Vx«, x) = (yxi, х1) (8)
является уравнением касательной гиперплоскости к гиперповерх-
ности уровня функции U (х), задающейся уравнением U (x) = U(x1).
Из условия /С-выпуклости U гиперплоскость (8) является опор-
ной к множеству Хм = (х С U (х)^М}, где Л4 = (/(х1). По
условию утверждения х3 С Хм, откуда в силу монотонности U
получаем требуемое неравенство. Утверждение доказано.
Упражнение 10. Пусть в условиях утверждения 4 U (х2) >
> U (х1). Доказать, что (?*«,. х1) < (?*>, х2).
Назовем функцию U строго К-выпуклой, если множества
ХД1 = {х £ £^|{/(х)^Л1} строго выпуклы при всех М. Строгая
выпуклость множества означает, что любая опорная гиперплос-
кость пересекается с ним только в одной точке.
Упражнение 11. Пусть в условиях утверждения 4 U строго
Х-выпукла. Доказать, что
(V*>, х1) < (Vx«, х2).
Утверждение 5. Пусть
(Vx«,x*) = max(vx., х). Тогда
х* £ Argmax U.
а
Доказательство.
Предположим противное. Тог-
да существует х £ £2 такое,
что U (х) > U (х*). Из резуль-
тата упр. И получаем
Рис. 4.
(Vx«,X‘)<(Vx‘,X),
что противоречит условию. Полученное противоречие доказывает
утверждение.
Геометрическая интерпретация утверждений 4 и 5 представ-
лена на рис. 4 (при т = 2), Все точки с большими значениями
функции полезности лежат на рис. 4 по одну сторону от каса-
тельной к линии уровня.
206 ГЛ. 6.ФУНКЦИИ ПОЛЕЗНОСТИ В ЗАДАЧАХ ВЫБОРА
Приведем алгоритм, позволяющий найти множество У, содер-
жащее решение задачи (6).
Алгоритм 5. Сужение ИМА.
1. Положить X = Q.
2. Занумеровать элементы X и обозначить через п мощ-
ность X.
3. Положить i=»0.
4. Положить i =
5. Построить вектор V*/ алгоритмом 4.
6. Положить Y = {х € X | (х, ух/) > (xl, V/)} U {xz}.
7. Сравнить Y и X. Если Y = X, перейти к шагу 9, в про-
тивном случае—к шагу 8.
8. Положить X = Y и перейти к шагу 2.
9. Сравнить i с п. Если i — n, перейти к шагу 10, в против-
ном случае—к шагу 4.
10. Останов. Решением является Y.
Упражнение 12. Доказать, что множество Y содержит
решение задачи (6).
Упражнение 13. Привести пример множества Q и функции
U, для которых множество Y, найденное в результате работы
алгоритма 5, совпадает с Q.
К* Алгоритм 5 позволяет при поиске решения задачи (6) заме-
нить ИМА на множество Y, т. е. уменьшает число альтернатив.
Для нахождения точного решения нужно воспользоваться алго-
ритмом 3 на множестве Y. При этом число попарных сравнений
соответственно уменьшается.
Приведем способ сужения ИМА, основанный на понятии ко-
нуса возможных направлений. Конусом Кд, натянутым на мно-
жество A s Ет, называется конус, являющийся пересечением
всех конусов, содержащих А. Если А={а1, ..., ак}, то
{к )
и конус К а замкнут.
Пусть {Vx}q — множество векторов V* во всех точках х£й.
Конусом возможных направлений назовем конус, натянутый на
множество {Vx}q. Этот конус обозначим через Kq. Приведем при-
меры различных конусов Ка-
Пример 3. На рис. 5, а, б, в изображены 'карты безразли-
чия для функций Ult Ut, U3 соответственно. Конус Ка «шире»
конуса Ка и расположен «выше» лУча хх = х8; конус Ка распо-
ложен «ниже» луча хх = х2; конус Ка состоит из единственного
вектора.
В случаях а) и в) второй критерий важнее, чем первый, так
как в любой точке множества Q за единицу приращения оценки
по второму критерию уменьшение оценки по первому критерию
§2. АЛГОРИТМЫ ОПТИМИЗАЦИИ ФУНКЦИИ ПОЛЕЗНОСТИ 207
превосходит единицу. В случае б), наоборот, 'первый [критерий
важнее второго. В случаях а), б) предельная норма замены пер-
вого критерия вторым зависит от точки; в случае в) она постоянна.
Упражнение 14. Доказать, что
Применим понятие конуса возможных направлений при реше-
нии задачи (6). Построим конус /С, двойственный к конусу Ка,
и рассмотрим отношение RK.
Рис. 5.
Утверждение#. Пусть U строго К-выпукла их* Argmax U.
Q
Тогда х*€йЧ
Доказательство. Предположим противное. Тогда для не-
которого х£Й получаем xRKx* или х—х*£К. По определению
двойственного конуса для всех V € Ко выполнено (х—х*, V) ^,0.
При V = VX получаем
l(V„ *)>(VX, х*). (9)
По условию U (х*) U (х). Поэтому в силу результата упражне-
ния 11 (Vx, х*) > (Vx, х). Полученное неравенство противоре-
чит (9). Утверждение доказано.
Упражнение 15*. Останется ли справедливым утвержде-
ние 6, если потребовать только /f-выпуклость функции 1Л
Упражнение 16*. Доказать, что [множество Qrk содер-
жится в множестве Y, построенном алгоритмом 5.
Алг о р[и т м 6. Построение
1. Найти алгоритмом 4 векторы Vx во всех точках х^Й.
2. Построить конус Дя.
3. Построить конус К, двойственный к конусу Да.
4. Найти алгоритмом 4.6 множество ЙЛ*.
- В силу утверждения 6 при строго Л-выпуклой функции полез-
ности множество й*к содержит решение задачи (6).
Нахождение Kq требует построения векторов во всех х £ й.
Пусть /CqsAj. Тогда Д=>Д[ и к». Поэтому решение
задачи (6) содержится в й *. На шагах 3 и 4 алгоритма 6 вместо
конуса Ка используем конус Д\, который строится следующим
208
ГЛ. 6. ФУНКЦИИ ПОЛЕЗНОСТИ В ЗАДАЧАХ ВЫБОРА
образом. Положим х/«тахх/, x/ = minx/. Обозначим через D&
Q О
множество 2т точек г из таких, чтсГ х{} (i = 1, т).
В каждой точке x^Dq построим алгоритмом 4 вектор Vx =
= <VJ, ..., ¥”>• Положим
at = max Vx, at = min'vj (i=>2, m)
и рассмотрим прямоугольный параллелепипед Пятв^£и:
пй = {^к1 = 1, aF”Oi<ai+j (i = 2Tm)}.
Обозначим через Кпа = К1 конус, натянутый на Па. На рис. 6
показан такой конус при т = 3.
Утверждение 7. ~
Тогда Ка^Кп .
Пусть U—К-гетеротонная функция.
Доказательство. Пусть х—произвольная точка Q. Из по-
строения множества Da следует, что любая точка также
принадлежит параллелепипеду с вершинами Da. Поэтому xz’^
построим VX==<1, V*.......V”>. При
движении х по любому отрезку, па-
раллельному одной из координатных
осей, V* по условию /<-гетеротонно-
сти изменяется монотонно. Выберем
направление движения так, чтобы
значение vj не убывало. Двигаясь
из х таким образом, всегда можно
прийти в одну из вершин X* С Da, от-
куда в силу определения величин afc
имеем
V^af. (10)
рис. 6. Аналогично доказывается, что
(П)
Поскольку неравенства (10) и (11) выполняются для любого i = 2, т,
то Vx^Hq. Следовательно, Ка^Кпа. Утверждение доказано.
В силу утверждения 7 для /С-гетеротонных функций полезности
Я к*
решение задачи (6) содержится в множестве Q \ где /Cx = 7<nQ.
Алгоритм 7. Построение KnQ.
1. Построить множество Da.
2. Найти алгоритмом 4 векторы Vx во всех точках x£Da.
3. Построить конус KnQ, натянутый на векторы vx, найден-
ные на шаге 2.
§3. ВЛИЯНИЕ ИМА НА ОПТИМИЗАЦИЮ
209
Построение конуса /Сх требует вычисления V* только в точках
из Dq. Мощность Dq не зависит от мощности £2 и определяется
размерностью пространства Ет.
Упражнение 17. Доказать, что Ка совпадает с конусом,
натянутым на множество {Vx | х €Dq}, если т = 2.
Пусть U—К-линейная функция. При этом конус возможных
направлений будет порождаться единственным вектором V, кото-
рый представляет собой нормаль к гиперплоскости уровня U. Все
гиперплоскости уровня параллельны. Задача (6) сводится к нахож-
дению Argmax (V, х).
Q
Утверждение 8. Пусть для функции U выполнен закон
уменьшения предельных норм замены и VX=V во всех точках
x^Dq. Тогда функция U является К-линейной.
Доказательство. Достаточно показать, что в любой точ-
ке £2 справедливо 7Ж=7. Рассмотрим a, b^Da, отличающиеся
только по i-й координате.
Пусть в а i-я координата меньше, чем в Ь. Из условия умень-
шения предельных норм замены следует, что во всех точках q
у ребра, соединяющего эти точки, Ve = V- Это верно, так как
для всех /#=i имеем йу/а,- > qjlqt >bjlbj. Тем самым утверждение
доказано для всех ребер, т. е. граней Г(1) параллелепипеда Па
размерности 1. Рассмотрим любую грань Г (2) размерности 2. Через
любую точку q этой грани проведем прямую I, [параллельную
одной из одномерных граней, ограничивающих Г (2). Как и выше,
можно показать, что в любой точке q отрезка прямой I, ограни-
ченного одномерными гранями, выполняется Аналогично
получим, что Ve = V для трехмерных и т. д., (т—1)-мерных гра-
ней и, наконец, для внутренних точек q параллелепипеда. Мно-
жество £2 по построению содержится в параллелепипеде Па. Утверж-
дение доказано. у
Алгоритм 8. Установление К-линейности функции полезности.
1. Построить по заданному £2 множество Dq.
2. Найти во всех точках x£Dq, воспользовавшись алго-
ритмом 4.
3. Сравнить между собой все полученные векторы. Их равен-
ство в силу утверждения 8 обеспечивает K-линейность функции
полезности U.
§ 3. Влияние ИМА на оптимизацию функции полезности
Пусть U (х)—функция [[полезности и существует ^£Ет такое,
что
Argmax U (х) = Argmax (%, х).
a q
В этом случае говорят, что задача (1) моделируется линейной зада-
чей. Возможность такого моделирования зависит от £2. Приведем
пример.
210
ГЛ. 6. ФУНКЦИИ ПОЛЕЗНОСТИ В ЗАДАЧАХ ВЫБОРА
Пример 4. Для множества Qic£2 (рис. 7, а) множество Qf
совпадает с частью границы множества Qi—ABCD. Все точки [Л, 5]
могут быть получены максимизацией функции (Хп х), точки [В, С] —
максимизацией функции (Х2, х) и точки [С, £>]—максимизацией
функции (Х3, х), и задача (1) на множестве Qi при любой функ-
ции полезности U моделируется линейной задачей.
Для множества Й2сД2 (рис. 7, б) множество Of совпадает
с* частью границы ABCDE. Точка С не может быть получена
максимизацией никакой функции вида (%, х), и задача (1) при
С Argmax U не может моделироваться линейной задачей.
Таким образом, возможность моделирования задачи (1) линей-
ной задачей определяется свойствами исходного множества альтер-
натив.
Обозначим через L(Q) выпуклую оболочку' множества Q, а \
через Q(Q)—множество L(Q)—Е^. Пусть |Q|<oo. S
Теорема 1. Пусть x*£Q(£2). Вектор Ь^Е^, Х=/=0, такой, |
что max (%, х) = (Х, х*), существует тогда и только тогда, когда I
.0(0) - i
x*$IntQ(Q). |
Доказательство. 1. Пусть a = <alt ..., amXи среди чисел ?
alt ..., ат есть числа с противоположными знаками. Тогда сущест- |
вует вектор х = <хп хда> такой, что’х,>0 (i = l,m) и ч
(а, х) = 0. Для любого е > 0 вектор х с указанными свойствами >
можно выбрать так, что | х | < 8. Обозначим через лъ ..., nr j
гиперплоскости, пересечение которых с Q (Q) образует границу Г ?
многогранника Q (Q)' (T = Q (Q)\Int Q (£2)). Положим Л/вл^ПГ .
0 = 177). ’ ___
Докажем, что для всех i = l, г вектор V, являющийся нор- }
малью *к гиперплоскости л,-, принадлежит Е%. Предположим про-
тивное. Пусть у^\гЛАь Тогда’существует точка у£А{ такая, j
что}’(/у—yj>^ (/= 1, т). Так KaK^^Q(Q), то по', построению f
у—Е^ Q'(Q).TaK как Р, где р = <рх, .... Ри> и Р/> 0 f
(/ = 1, т)/то у содержится в множестве "у—Е„ вместе с некото- а
§ 3. ВЛИЯНИЕ^ ИМА НА ОПТИМИЗАЦИЮ
211
рой окрестностью. Отсюда следует, что у € Int Q (й), что противо-
речит условию у$Т. Полученное]противоречие доказывает, что
уравнение любой гиперплоскости л,-, ограничивающей Q(Q), име-
ет вид
Xfx1+...-f-^xm=dC
где (s= 1, /и). В силу выпуклости ф(й) гиперплоскости л,
являются опорными к Q (й). Поэтому для любой точки х* Int Q (й)
в качестве требуемого вектора 1 можно взять нормаль к гипер-
плоскости л,- такой, что х*€Аг = л£ Л(?(й).
2. Пусть %€££, ^=#=0. Максимум линейной функции (Л, х)
на С(й) достигается, так как ее значение на Q(Q) не превосхо-
дит значения в точке у с координатами
у7^тахх,+1 (j = 1, tnj.
' Q
Максимум линейной функции не может достигаться во внутренней
точке многогранника, следовательно, Argmax (Л, х) f) Int Q (й) = 0.
<2(й)
Теорема доказана.
Из теоремы 1 при х* С Йр получим необходимые и достаточные
условия на точку х* для того, чтобы задача (1) с решением х*
моделировалась линейной задачей.
Сопоставим каждому элементу х* £ й₽ множество Лх. решений
следующей системы:
Мх?—xf)+ ~. . (х*т—х‘т) >Д, 1=1 ,"k, П2)
{х^х1, ..., х*} = Й₽, (/ = 1,/п). ' '
Множество Лх. является ’конусом.
Пример 5. Пусть множество ^«{х1, х2, Гх3, х4, x6}cz£^
имеет вид, изображенный на рис. 8.'Приведем способ]"построения
Рис. 8.
Axi (i=l,5). Для этого натянем на йр выпуклую оболочку, по-
строим в каждой’ вершине множество опорных гиперплоскостей
и параллельно* перенесем их в начало координат. Пример пока-
зывает, что конусы Ах для разных элементов разные: Axs = 0,
212
ГЛ. 6. ФУНКЦИИ ПОЛЕЗНОСТИ В ЗАДАЧАХ ВЫБОРА
так как ни одна функция (%, х) в соответствии с теоремой 1 не
достигает максимума в точке х2; Ал» порожден единственным век-
тором;. самым широким является конус Ах».
Упражнение 18. Доказать, что конусы, построенные спо-
собом, описанным в примере 5, задаются формулами (12).
Для сравнения конусов ограничим их сферой единичного ради-
уса с центром в начале координат. Часть единичной сферы, высе-
каемой конусом А*/, обозначим через Sh а через So—часть
сферы, высекаемую конусом Е^ (рис. 9). Размер конуса будем
характеризовать величиной mesSz, где mes Sf—мера S;. Для эле-
ментов х{ значения mesS,- могут меняться в пределах от О
до mesS0.
Утверждение 9. ¥ Пусть U—К-выпуклая функция и
Vx. £AX«. Тогда
х* С Argmax U (х).
Q
Доказательство. Из условия Т«»€АЛ, £и формул (12)
получаем, что для любого х'£йр выполняется
(V*., X*)>(Vx», х{),
откуда с учетом того, что XZ^'O (см. (12)), получаем
(Vx«, x*) = max(Vx„ х). (13)
о
Утверждение 9 следует из (13) и утверждения 5.
Пусть йр = {х*} состоит из единственного элемента х*.
При этом, какова бы ни была функция полезности, решение
задачи (6) всегда равно х*. Здесь конус Ах. совпадает с Д£.
Пусть й—любое множество из Ет-
Утверждение 10. Для любого К£Е^ найдется точка
х*£О.р такая, что (X, х*) = тах(Х, х).
о
Доказательство. Рассмотрим многогранник Q (й). Мак-
симум линейной функции с неотрицательными коэффициентами
достигается на одной из вершин Q (й), содержащихся в Йр. Утверж-
дение доказано.
Максимум линейной функции может достигаться только на тех
точках х* из йр, для которых Ах. =/= 0. Занумеруем такие точки:.
х1, х2, ..., xk. Для каждого Х£Д£ решением задачи максимиза-
ции функции (X, х) на множестве й является одна из точек
х1, ..., xft. Каждая из них максимизирует (X, х) при некотором
Х^Д^. Эти точки неравноценны: они различаются величиной
mes S{.
Пусть функция U (х) К-линейна, т. е. U (х) = ср((Х, х)), а век-
тор X б Дт неизвестен. Будем считать, что | X | = 1, т. е. X g So
(So—часть единичной сферы, высекаемая из нее положительным
ортантом Eii).
§4. ОПТИМИЗАЦИЯ ПРИ НАЛИЧИИ ПОМЕХ
213
Предположим, что вектор X—случайная величина, равномерно
распределенная b S0. Это значит, что вероятность попадания X
в любую область SsSe равна отношению mesS/mesS0. Если
X—случайный вектор, то точка х£.{х\ ..., хк}, максимизиру-
ющая линейную функцию (X, х), является случайной точкой.
Из утверждения 10 и формул (12) следует, что области Su ..., Sm
покрывают So. Точка х* максимизирует (X, х) только при Х£Ах..
Поскольку mesS(-—это площадь пересечения конуса А^ с единич-
ной сферой, то тем самым доказано
Утверждение 11. Вероятность Р{ того, что точка х1
принадлежит Argmaxi/, при сделанных допущениях определяется
о
формулой Рz=mesSz/mesS0.
Пусть х{—одна'из точек х1, ..., хк. Направление градиента
неизвестной функции полезности'!? может оказаться любым. Тогда
вектор v/| V | равномерно распределен в So и вероятность того,
что он попадет внутрь конуса Axi, равна mes S(/mes So. При попа-
дании yxi в функция U (х‘) максимальна (утверждение 9),
т. е. х‘ является решением задачи (1). Проведенные рассуждения
позволяют выбрать первую точку при нумерации множества Q
на шаге 2 алгоритма 5. Выбираем ту точку х1, для которой вели-
чина mesSz максимальна. Алгоритм построения точки х‘ приведен
ниже.
Упражнение 19. Дано множество йр = {х1, х2, х3, х4};
х1 = <1,5>, х2 = <3,4>, х3 = <4, 2>, х4 = <5, 1>. Найти вектор х* С
такой, что Рх. = max Р,.
<6{1.4}
Алгоритм 9. Максимизация mesSz.
1. Положить L равным пересечению й₽ с выпуклой^оболоч-
кой й; L — {a1, ..., as}.
2. Найти для каждой точки a1 £L конусы AflZ по формуле (12).
3. Найти площадь пересечения конуса Aai с единичной сферой.
4. Выбрать точку а1, для которой площадь пересечения мак-
симальна.
Упражнение 20**. Построить процедуру [для реализации
шага 3.
t§ 4. Оптимизация при наличии помех
В § 1 предполагалось, что известна сравнительная полезность
любых двух альтернатив х, у, отличающихся не более чем по
двум координатам. В основе предложенных в § 2 алгоритмов
решения задачи (1) оптимизации функции полезности лежит за-
дача компенсации. При ее решении (с помощью алгоритма 1)
сравнивают значения функции полезности в точках х и х(Д2).
Знак разности между U (х) и U (х (Д2)) известен в силу (5).
214 ГЛ. 6. ФУНКЦИИ ПОЛЕЗНОСТИ В ЗАДАЧАХ ВЫБОРА
!
В настоящем параграфе предполагается, что сравнений (5) мо-
гут быть осуществлены с ошибкой. Это означает, что известен
не знак разности U (х)—U (у), а знак выражения
U(x)-U(y) + n, (14)
где г]—случайная величина с нулевым математическим ожиданием.
Поэтому на шаге 3 алгоритма 1 в такой ситуации находят не
знак разности U (х)—£/(х(Д2)), а знак выражения U(x) —
— [/(х (Д2)) 4-я-
Рассмотрим решение задачи компенсации при этих условиях.
Задача компенсации, рассмотренная в [§ 2, состоит в решении
с заданной точностью 8 уравнения
<К(Д) = $, (15)
где?ф^(Д) = U (х (&.)), q = U(x), Д = Д2. При сделанных в § 1 до-
пущениях <р (Д) является монотонно возрастающей функцией от Д,
ф (0) < <7, lim ф(Д)><?. Поэтому уравнение (15) имеет единст-
Д-> оо
венный положительный корень. Этот корень Д2(х, /ь ja, Д2) и
находится в результате работы алгоритма 1.
В данном случае задача компенсации состоит в решении того
же самого уравнения (15), когда в любой точке Д известен только
знак выражения
<7—<Р(Д)-Н- (16)
Решение уравнения (15) при известном для любого Д знаке вы-
ражения q—ф(Д)4-1] можно найти с помощью стохастической
аппроксимации.
Дадим краткое описание этого метода применительно к реше-
нию (15). Корень Д* уравнения (15) можно найти с помощью
следующей рекуррентной формулы:
^l+1 = A, + rfsgn'(9—ф(Д/)+г]). (17)
Последовательность Д,, Д2, ... сходится по вероятности к корню Д*.
Это означает, что для всех 8 > О
lim Рг{| Д,—Д* I= 0. (18)
i -> оо
Для того £чтобы ^указанная сходимость имела место при любом
начальном Дп последовательность Гх, Г2, ... должна удовлетво-
рять условиям
5п<оо, 5Гу=оо. (19)
/=1 /=1
Например, условиям (19) удовлетворяет последовательность
Г7 = 1// 0«1, 2, ...)•
По формулам (17) можно найти приближенное решение задачи
компенсации, взяв в качестве начального значения Дх = 0. После
этого можно пользоваться любым алгоритмом из § 2.
§ 1. УПОРЯДОЧЕННЫЕ ПО ВАЖНОСТИ КРИТЕРИИ
215
Итак, если определение знака U (х)— U (у) делается с ошибкой,
то общая схема алгоритмов решения задачи оптимизации функции
полезности не изменяется. В такой ситуации вместо алгоритма 1
для решения задачи компенсации нужно использовать алгоритм
стохастической аппроксимации, задаваемый формулой (17). Это
может привести к меньшей точности решения и увеличению числа
вопросов к ЛПР по сравнению с рассмотренным ранее случаем
отсутствия помех.
Литература. [6, 10, 22, 49, 59, 60, 63, 73.J74, 87, 98, 120].
Глава 7
ЗАДАЧИ ВЫБОРА С ЗАДАННЫМ*ПРИНЦИП0М
ОПТИМАЛЬНОСТИ
На шаге 2 общего алгоритма 4.1 формулируется математиче-
ская задача выбора <Q, ЗИ*у. Если состоит из одного
элемента Соп, то функция Соп, выражающая принцип оптималь-
ности, полностью известна. Сама задача <Q, &^*, $•> в этом
случае эквивалентна общей задаче оптимизации <□, ОП>.
В задачах оптимизации практически используют функции
выбора из ограниченного набора. К их числу из ранее рассмо-
тренных следует отнести паретовскую, совокупно экстремальную,
турнирную, скалярную, а также нормальные функции выбора,
порожденные мажоритарным, лексикографическим и 'иерархиче-
скими отношениями.
В данной главе рассмотрены три задачи оптимизации. В § 1
принцип оптимальности выражается бинарным отношением спе-
циального вида, позволяющим учитывать сравнительную важность
критериев. В § 2 принцип оптимальности выражается функцией
выбора, определяемой близостью к идеальной точке; в’§ 3—функ-
цией выбора, определяемой максимальным числом неулучшаемых
оценок. Приведены определения перечисленных функций выбора,
указаны их свойства и алгоритмы решения соответствующих
задач оптимизации. Обоснованность того или иного принципа
оптимальности устанавливается с учетом условий, в которых
рассматривается конкретная задача оптимизации.
§ 1. Задачи с упорядоченными по важности критериями
Пусть 7 = {1, ..., т}—множество'номеров критериев. Для
любой пары (г, зададим два 'отношения на Ет—Sri и
Trt—формулами
xSrty& y=*xrt, (1)
xTrty&[y=!Xr*] и [x/>xt], (2)
216
ГЛ. 7. ЗАДАЧИ ОПТИМИЗАЦИИ
где через xrt обозначен вектор, полученный из х перестанбвкой
r-й и Z-й компонент: если х = <хх, хг, xit х^>, то
= ^Х19 • . •, X/,, . . ., Xrt • • •,
Упражнение 1. Доказать, что Srt является отношением
эквивалентности.
Упражнение 2. Пусть ..., zn~1Trizn. Чему равно п?
Упражнение 3. Доказать, что отношение Trt транзитивно.
Упражнение 4. Доказать, что Trt—отношение строгого
порядка.
Пусть задано множество Л s J8, т. е. задано некоторое мно-
жество пар (г, /). Определим отношение на £га:
xDj^y «Ф [существуют z°, z1, ..., z*+1, x = z°, zl+1 = y,
такие, что zlSr t zl+1 (i = 0, /) и (rh 1^^Лг (t = 0, /)].
Например, пусть Лх — {(1, 2), (2, 3), (3, 1)}. Тогда xD^y тогда
и только тогда, когда у отличается от х любой перестановкой
трех первых координат. В общем случае соотношение xD^y вы-
полняется тогда и только тогда, когда х отличается от у неко-
торой перестановкой координат, порожденной попарными пере-
становками (транспозициями) из заданного множества Лг.
Утверждение 1. Для любого Лг^1г отношение
является отношением эквивалентности.
Доказательство. Транзитивность следует из опре-
деления. Докажем его симметричность. Пусть xSrty. В силу (1)
это означает, что вектор у получен из х перестановкой r-й и
i-й координат. Но тогда х можно получить из у перестановкой
r-й и Лй координат, т. е. ySrix. Поэтому из
z^.t.z1, .... z‘Srz+ltx+1z‘+1, x = z°, zf+1=#,
следует, что zi+1Srz+lfz+1zf, •••, z^S^.z0, т.е. yD^x. Утвержде-
ние доказано.
Пусть теперь заданы два множества пар’Лх, J2, Лг П Л2=0.
Положим
Л == (Л}) л^,
= иТ,Л, (3)
где Р—отношение Парето на Ет.
Введем операцию транзитивного замыкания отношения. Тран-
зитивным замыканием отношения R (обозначается TC(R)) назы-
вается пересечение всех транзитивных отношений, включающих R
(т.е. пересечение всех транзитивных R' таких, что Д<Д').
Например, транзитивным замыканием отношения Д, граф которого
представлен на рис. 1, а, является отношение, граф которого
\ § 1. УПОРЯДОЧЕННЫЕ ПО ВАЖНОСТИ КРИТЕРИИ 217
\
представлен на рис. 1, б. Явный вид TC{(R) может быть найден
с помощью введенной в § 1.1.3 операции произведения отношений.
Утверждение 2. Для любого R
ТС(/?)=/?U/?2U ...иЯди ... (4)
Упражнение 5. Доказать утверждение 2.
Положим Pc4 = TC(Qe4), Тогда озна-
чает, что найдется цепочка z°, z1, ..., г1, zl+1, x = z°, zt+1 = y,
такая, что г1Н{г1+1 (i = 0, /) и ГЛ
Н^{Р, Srt, Trt((r, Д
Соотношение хРду означает, что / \ / \ Л,
в этой цепочке по крайней |мере у \ Хх-А
на одном месте не стоит отноше- _ |
ние Srt. \ \ /
По построению при а) б) \J
• При выпол- Рис. 1.
няется Pjt=R^-
Упражнение 6. Доказать, что для любых Лъ Лг^.1\
Л^Лг = 0, выполнено
,51
х£>Л/» гРЛУ^РЛУ- v
Упражнение 7. Какими свойствами из перечисленных
в § 1.1.4 обладает отношение (формула (3))?
Приведем примеры отношений R^ и Р^ н рассмотрим их
свойства в зависимости от множеств Лг и Л2.
Пример 1. Пусть т = 2, Л2 = {(1, 2)}, ^х = 0. При этих
исходных данных по построению R^ имеем
xR^y [существуют z°, z1, v’., zz+1, x = z°, zl+1 = y,
^такие, что zlPzi+1 или zzT,2z‘+1].
Отношения Srt отсутствуют, так как Лх=0. Покажем, что в
данном случае можно ограничиться цепочками длины не более
чем 2, т. е. любая цепочка может быть заменена цепочкой дли-
ны 1 или 2. Пусть z^u?2, z2Pzs, zsT12z4, z1 = <z{, z£>. Тогда
22 = <4, 21>> z|C2i, Zi — zf, zl = zf. Имеем z$<zt zj^zj,
t. e. z1/^4, и всю цепочку длины 3 заменили на z^Pz*—цепочку
длины 1. Два раза подряд в любой цепочке ТХ2 стоять не могут
(см. упр. 2). Два раза подряд стоящее Р заменяется на одно:
хРу, yPz^xPz.
Рассмотрим цепочку произвольной длины. Заменим фрагменты
вида zzTX2z/+1, zz+1Pzz+2, zz+2TX2zz+3 на z{Pzt+i и фрагменты
вида z'Pz,+I, zz+1Pzz+2 на zzPz/+a. Придем либо к цепочке дли-
ны 1, либо к цепочке длины 2, либо к цепочке zaPz\ z^^z9.
218
ГЛ. 7. ЗАДАЧИ ОПТИМИЗАЦИИ
z*Pz3. В ней zi<z®, zj<zj, zf = zl, z$=zj, z?<z?, $<z£.
Имеем z?<4, zf^z}, откуда zj^zj, z^sgCz?.
Рассмотрим следующие случаи. Пусть zj > z°. Положим
w = <z“, zj>. Тогда z°T12tt>, wPz8. Пусть zj^zj. Тогда из z°Pzx,
z1T12za получаем, что z°Pz3
и исходная цепочка эквива-
лентна z'Pz*, z3Pz3 или z3Pz3.
Таким образом, доказа-
но, что
xR^y &\хТ1ау\, или [хРу],
или [хТ1аг, гРу\,
или [хРг, гТ12у].
Рис. 2.
Отсюда получаем, что либо
Х1 У1, Ха > уа, либо Xi > ха,
Xi^xa, xa^yi. Итак,
ха> R'fcyi, &>>1*х>!/ь ха’»2].
или [Хх > ха, хх > уа, уа х,].
Верхнее и ’нижнее сечения отношения R^ в точке г показаны
на рис. 2. Здесь же показана отделяющая гиперплоскость (пря-
мая /).
У‘п р а ж н е н и е 8.^Доказать, что отношение R^ из примера 1
Х-отделимо при‘любых Х = <%|, Х2> таких, что ?v1>X3>0.
Смысл отношения R^ из. примера 1 состоит в следующем.
Пусть <хх, х2>—оценки школьника по двум предметам, из кото-
рых первый для него важнее второго. Тогда пара оценок <4, 3>,
с его точки зрения, лучше, чем пара <3, 4>, в силу большей
важности первого предмета (это выражается отношением Т1а.
<4, 3>7’i2<3, 4>). Пара <5, 3> лучше пары <4, 3> (это соответ-
ствует отношению Р: <5, 3>Р <4, 3>). Таким образом, пара <5, 3>
лучше пары <3, 4> по отношению R^, так как <5, 3>Р<4, 3>,
а <4, 3>Т12<3, 4>,
Приведем пример, показывающий, чти выбор по отношению Р^
уже, чем выбор по отношению Парето.
Пример 2. Пусть в Еа задано Q, состоящее из шести точек:
Xх = <5, 5, 4, 4>, х8 = <4, 4, 5, 4>, х8 = <5, 4, 5,'4>,
х* = <5, 4, 4, 5>, х? = <4, 4, 5, 5>, х* = <4, 3, 5, 5>.
Пусть£4х = {(ЦЗ)}, «4а = ((2, 4), (2, 3)}.^Найдем Q₽e^, не строя Р^
в явном видела 1 исключая точки, пользуясь только определе-
. р .
нием Р^. Легко видеть, что х8Рх’, х?Рх’, поэтому х2, х* £ Q л.
\ § 1. УПОРЯДОЧЕННЫЕ ПО ВАЖНОСТИ КРИТЕРИИ 219
Ясно также, что хгТих*, поэтому x4^QP^; [х^^х3, поэтому
х3 £ QP<^.
Остались две точки: х1 = <5, 5, 4, 4> и х? = <4, 4, 5, 5>.
Имеем <5, 5, 4, 4>Та4<5, 4, 4, 5>, <5, 4, 4, 5>S18<4, 4, 5, 5>,
откуда <5, 5, 4, 4> Р^<4, 4, 5, 5> и х5 Итак, Q состоит
из единственной точки х1; | | = 1. В то же время Qp={x*,
Xs, х4, х5}, т. е. |й₽|==4.
Рассмотрим случай, в котором отношение не ациклично.
Пример £3. ПустьЛ1 = 0, «4а = {(1, 2), (2, 3), (3, 1)},/п = 3.
Рассмотрим три точки: x*s=<4, 2, 2>, х2 = <2, 4, 2>, х3е=<2, 2, 4>.
Из формулы (2) получаем
х1Т1ах2, х2Т28х3, х3Т81х2.
Так^как (1, 2) С (2, 3)€«4а, (3, 1)С А» т0 по определению Рд
получаем, что х1Ре^х2, х2Р^х3, х’Р^х1.’ Получен [цикл. Итак,
в данном случае отношение Р^ не ациклично.^
Заметим, что отношение Р^ при- непустом всегдашне' ацик-
лично, поскольку D^x является симметричным и
xD^y, yD^x образуют цикл длины два.
При построении нормальных функций выбора требование
ацикличности порождающих их бинарных отношений является
существенным, так как при невыполнении свойства ациклично-
сти R выделяемое из ИМА множество й* может сказаться пу-
стым. Сформулируем условия, гарантирующие ацикличность Р^.
Пусть Лх, Л1[\Л2>=0. Определим на множестве
J = { 1, ..., ш} бинарные отношения Р1 = «41и Р2 = Л2. Положим
(6)
Из определения следует, что iW^j тогда и только тогда,
когда существует цепочка|(&0, kJ, (ku kJ, ..., (kt; k[+1), i = kt,
kl+1 = j, где (ks, ks+1) 6 Л2 U «4a (s —0, /), и [существует s£
€{0,1, ...,/} такое, что (ks, к3+1)£Л2.
Теорема 1. Отношение Рд ациклично тогда и только тогда,
когда отношение антирефлексивно.
Д о к[а з ательство. 1. Пусть Pfy не ациклично. [Поскольку" Р^
транзитивно, то это означает, что для некоторой точки х£Ет
выполнено хР^х. Учитывая определение Р^, получаем, что су-
ществует цепочка хгНгх3, хгН2х3, ... .х"//^1, где х2 = х и Ht £
€{Р, Trt, Srf} (/el, п). Заметим, что для всех i=l,n отноше-
ние Н, не равно Р, поскольку из x‘Pxi+l следует, что сумма
компонент х/+1 меньше суммы компонент х1, что противоречит
наличию цикла.
/
220 ГЛ. 7. ЗАДАЧИ ОПТИМИЗАЦИИ /
I
Рассмотрим исходный вектор х1 и проследим изменение места
его i-й компоненты при движении по элементам цепочки. Каждый
последующий вектор в цепочке в силу того, что H£{Trt, Srf},
получается из предыдущего перестановкой r-й и i-й компонент,
причем (г, Таким образом, i-я компонента может при
движении по цепочке:
а) оставаться на месте;
б) переходить на другие места и вернуться на i-e место;
в) попасть на i\-e место, I.
В последнем случае в силу того, что хР^х, выполняется равен-
ство xlt = x{, так как в исходном векторе ij-я компонента равна x/t,
в конечном равна и начальный^вектор совпадает с конечным.
Сама компонента с номером в исходном векторе переместится
на место i2, причем i2 Ф ilf так как ir-e место занято пришедшей
туда i-й компонентой. Аналогично, /2-я компонента переместится
на i3-e место и т. д. В силу конечности J = {1, ..., т} для не-
которого s получим, что 1в-я компонента переместится на i-e место.
В случае б) получим последовательность пар (i, jf), (Ju /2), ...
..., (Jft, i), где fa, .... jk—места, последовательно занимаемые i-й
компонентой при движении по цепочке. Для любого 1 = 0, k
пара (fa, fa+1) принадлежит Лл(]Лг (здесь /0 = /ft+1 = i).
Вернемся к случаю в). Аналогично случаю б) получим несколь-
ко последовательностей пар
(i, if), (Я, if),!•••> (/*,» О.
(h, if), (it, if).(ilt, if), (7)
Gs-i> if), (/i, if), • ••» (iks, 0»
Их объединение ’ приводит к замкнутой последовательности
V. А), •••. (is. 0-
Вернемся к исходной цепочке х1Н1хг, ..., хпН^с1. По опре-
делению Р^1 по крайней мере для одного ............п) выпол-
нено Ht = Trt. В исходном векторе х1 найдется компонента х].
такая, которая при движении по элементам цепочки перейдет
с r-го на i-e место. Рассмотрим полученную для нее замкнутую
последовательность пар (i*, /х), (fa, /2), ..., (г, t), ..., (jk, i*).
Поскольку (r, t) С Лг, то по определению W получим, что
i-^i*, т. е. Wл не антирефлексивно.^Тем самым доказано, что
из антирефлексивности Wл следует ацикличность Рл.
2. Если Wне антирефлексивно, то цикл в Е.. по отноше-
нию Рл легко строится непосредственно .по замкнутой цепочке .
(ii, if), (i3, if), , (ik, if), аналогично тому, как это было сде-
лано в пример'е 3. Теорема доказана.
Утверждение 3. При любых Лх и Л2 отношение Рл не-
строго ^-отделимо при Х = <1, ..., 1>.
§1. УПОРЯДОЧЕННЫЕ ПО ВАЖНОСТИ КРИТЕРИИ 221
Доказательство. Все’]циклы [по [отношению Рд лежат
т
в плоскости 2 xt = d, так [как сумма координат у всех точек
в цикле постоянна. У всех точек лучше данной сумма координат
не меньше, чем у нее, а у всех точек хуже данной (по отноше-
нию Р—не больше. Это^доказывает утверждение.^
Установим связь между ацикличностью и Х-отделимостьк/Р^г
Заметим, что пользоваться утверждениями из главы 1.3 нельзя,
поскольку отношения Р^ и не инвариантны относительно
переноса.
Упражнение 9. Доказать, что'|Р^ не инвариантно отно-
сительно переноса.
Пусть Л = (Ли Лг<=1\ Л1Г\Лг=0. Сопоставим
этим множествам систему линейных равенств и неравенств отно-
сительно положительных переменных X*, ..., Xm:
(8)
где Xf обозначает Xr = Xf при (г, И1 обозначает
Xr > Xf при (г, t) £ Л2, и]]в соотношении (8) участвуют все пары
(г, t) 6 Лх U Л*. Множество решений системы (8) обозначим через
Л^. Так как система (8)’ однородна, то является конусом.
Т е о р'е м а 2. Конус Л д является двойственным конусом от-
ношения Р^.
Доказательство. 1. Пусть хР^у. Это значит, что суще-
ствует последовательность z°, z1, ..., zl+1, x = z°, zl+l — y, такая,
что zQ7fz£+1 (i= 1 ,"7), где H, £{P, Srt, Пусть H{=P. Тогда
(X, z') > (X, zz'+1). Пусть ffi = Srt. Тогда
zls = z{s+1 (s=^j, r), zlt = z^+1, z' = zj+1
и "в силу системы ,(8)]]Xz = Xt, откуда XX,[!zz) = (X, г'+1).ППусть
Hi = Trt. Тогда
4 = zstl (S^=t, r), z‘>z‘t, zlr+1 = zit z{t+1 = z{r.
В^силу системы] (8) Xr>Xf. Учитывая это, имеем
(X, z')-(X, z^) = Xr(z'-zj)4-V(zj-z/) = (4-4^-zO>0,
т. e. (X, zl) > (X, zl+1). Итак, во всех случаях (X, z/+1),
откуда (X, х)>(Х, у). Строгое неравенство получаем в силу того’
что по крайней мере для одного i Hi=£Srt и, значит, (X, г1) >’
> (X, z'+1). Доказано, что любой вектор X из Л 'принадлежит
двойственному конусу отношения Р^.
2. Пусть Х^Л^. Если хотя бы одна (/-я) компонента у'X не-
положительна, то Х^7<р в силу того, что Р< Р^ (возьмем пару
222
НГЛ. 7. ЗАДАЧИ ОПТИМИЗАЦИИ
векторов х, у таких, что хРу, отличающихся только по /-й ком-
поненте, и получим, что (%, х) = (Х, у)). Пару х и у таких, что
xSrty и (X, х) < (X, у), легко найти, если Xr=/=Xf (взяв xr<_xt,
если X, >Xf, и хг>хъ если Xr<Xf). Наконец, в случае ХГ^Г. Xt
при (г, O f А имеем (Xr—Xf) (xr—xt) <0.
Таким образом, взяв произвольный вектор Х(£Л^, нашли
пару векторов' х^У таких, что хРду и (X, (X, у). Поэтому
X^K.R. Теорема доказана.
Пусть система (8) совместна. Тогда отношение Рд в 'силу
теоремы 2 Х-отделимо и, следовательно, ациклично. По теореме 1
это означает, что отношение Wна J антирёфлексивно. Наобо-
рот, пусть Wд не [антирефлексивно, [т. е. [существует цепочка
(G, У, («2, is), •••, (Ч« h) такая, что (if, i\+1)€AlM2 и по
крайней мере для одного s£{l, ..., q} выполнено (is, is+1)£d2
(iq+i — ii). Тогда соответствующая система (8) несовместна, т. е.
= 0. Тем самым доказано
У т в е р[ж д е’н[и е 4. Условия:
a) Pji ациклично,
б) W антирефлексивно,
в) 0»
г) Р^ Х-отделимо
эквивалентны.
Упражнение 10. Доказать, что отношение R^ нестрого
Х-отделимо при тех X, при которых Р^ Х-отделимо.
Установив свойства р^, рассмотрим решение соответствующей
задачи оптимизации <й, ОП>, где ОП выражается бинарным от-
ношением Р<£. Для работы с отношением Р^ необходимо сфор-
мировать множества и Л2, получив информацию о сравни-
тельной важности входящих в них пар критериев. Такую инфор-
мацию получают от ДПР, экспертов, а также в результате ана-
лиза исходной задачи выбора. Эта информация бывает двух типов:
а) сообщения о равноценности критериев: i-й критерий рав-
ноценен /-му;
б) сообщения о неравноценности критериев: i-й критерий
важнее /-го.
На основе этих сообщений формируют множества Л1г Л2 £ J2:
состоит из всех пар (i, /) номеров равноценных критериев,
Л2—из всех пар (i, /) номеров критериев таких, что i-й важнее./-го.
Затем по множествам и Л2 формулируют задачу оптимизации
<й, ОП>, в которой принцип оптимальности выражается бинарным
отношением Р^. Ее решением является множество недоминируе-
мых по отношению Р^ альтернативой^.
$ 1. УПОРЯДОЧЕННЫЕ ПО ВАЖНОСТИ КРИТЕРИИ 223 •
Ацикличность отношения Р^ 'рассматривают в качестве пока-
зателя непротиворечивости полученной информации Л. Теоремы 1
и 2 позволяют свести проверку непротиворечивости информации
к проверке антирефлексивности отношения на конечном мно-
жестве J и непосредственно по информации Л найти явный вид
линейного_гомоморфизма <р. отношения Q> в линейный по-
рядок поскольку” любой вектор задает ср формулой
<р(х) = (Х, х).-
Для того чтобы’^воспользоваться алгоритмом 4.6, необходимо
уметь сравнивать по отношению любые две альтернативы,
х, у € Е,п. Такую возможность дает
Утверждение 5. Любая цепочка z^HgZ1, zlHlzl+l, где
Hi^{P, Srt, Trt}, эквивалентна цепочке, в которой Н^Р при
1^1.
Доказательство. Рассмотрим фрагмент цепочки zlPzl+1,
zi+1Trtzl+a. Пусть zlr zlt. Так как z'+1 > zj+1 в силу (2) и гег+1
^г/, то вместе с неравенством zlr^Ztj получаем, что
4+а = Z*+1 < Zlr+1 < Zlr, Z/+2 = z'+l <Z* <z',
откуда z{Pzi+a. Пусть z£(> z^. Положим^"w = (ze)rt. При этом
wr = zl:^zt+1 = zf+2,[_a>t = z\ ~^z1^ = z‘+2 Г
откуда wPz^a и исходный фрагмент 'эквивалентен фрагменту .
z‘Trtw, wPzi+2.
Таким образом, либо Trt удаляется, либо меняется местами с Р.
Смена мест Р и Srt очевидна. Последовательное применение
указанных преобразований доказывает утверждение.
Таким образом, если хР^у, то либо хРу, либо найдется век-
тор z такой, 'что zPy и хРуг, причем вектор г получен из х \
некоторой перестановкой координат. Поэтому для проверки соот-
ношения хРуу достаточно найти все z, которые можно соединить
с х цепочкой вида
хН^г1, .... zlHtz,
где Trt} (i = Q, Г), а для каждого из полученных векто-
ров z проверить условие zPy,
Для нахождения всех указанных г можно сделать следующее.
Сопоставим каждой точке х”, полученной из х произвольной пере-
становкой компонент л, вершину графа G. Из каждой вершины,
сопоставленной некоторой точке w, проведем дуги во все вершины,
которые соответствуют точкам, полученным из точки w переста-
новкой r-й и Z-й компонент для всех (г, t) £ Ли и если wr > wt,
то для всех (г, f) С Лг. Множество точек z находится во взаимно
однозначном соответствии с множеством вершин, в которые ведут
пути из вершины, соответствующей начальной точке х. Таким
224
ГЛ. 7. ЗАДАЧИ ОПТИМИЗАЦИИ
образом, задача проверки соотношения хР^у сведена к известной
задаче нахождения множества вершин графа, достижимых из
данной.
Установление возможности сравнения любых двух точек х, у С
£Ет по отношению Рд и наличие указанного выше линейного
р .
гомоморфизма позволяют ’для нахождения й воспользоваться
алгоритмом 4.6.
В некоторых случаях проверку соотношения хР^у можно осу-
ществить более простым способом. Пусть информация о важности
критериев оказалась такова, что все критерии разбиты на п групп
следующим образом: внутри одной и той же группы любые два
критерия равноценны; любой критерий из группы с меньшим
номером важнее любого критерия из группы с большим номером.
Упражнение 11. Построить для этого случая отноше-
ние
Обозначим множество номеров критериев, составляющих /-ю
группу, через В1г указанную информацию о разбиении критериев
запишем в виде Si = <ВЬ ..., В„>, соответствующее отношение Р
обозначим через Р^, а Р^—через р^. Система (8) в этомслу-
чае принимает вид
I, i^Bp, р€{1,
при i£Bp, jZBq, p<q.
Введем необходимые обозначения. Пусть х, у^Ет. Положим
D(x, y) — <d1, ..., dkb,tyy>, d1>di>...>dk{Xtyi, где каждое из
чисел dj является компонентой х или у и для любой компоненты
х и у найдется равное ей dt. Пусть г С Ет, А, С Е%. Положим АЛ (z)=
= <A,J (z), ..., A.’’(z)>, где
1 ЦО противном случае.»
Обозначим через М(а) вектор-функцию, упорядочивающую ком-
поненты вектора а в порядке убывания. Например, М (<1, 5, 3» =
= <5, 3, 1>.
Теорема 3. Соотношение хР^у выполнено тогда и только
тогда, когда для Х^Е^, удовлетворяющего системе (9), выполнены
неравенства
(» = ~; <7 = 1, k(x, у)). (10)
Таким образом, для проверки соотношения хР^у нужно взять
любой вектор 7<£Е+, удовлетворяющий (9), и проверить для него
выполнение линейных неравенств (10).
Упражнение 12. Найти явный вид общего решения си-
стемы (9).
(9)
§2. МЕТОД ИДЕАЛЬНОЙ ТОЧКИ
225
§ 2. Метод идеальной точки
Пусть Q Определим функцию ^ыбора С/ на □ следую-
щим образом. Положим с; = тахх/ (i==l,'m). Таким образом,
Q
является максимально возможным значением по t-му критерию.
Точка xgQ такая, что х(-=а;-, является решением обычной одно-
критериальной задачи оптимизации. Предполагается, что Q—
замкнутое ограниченное множество в Ет, поэтому решения ука-
занных задач существуют.
Положим a = <.alt ..., am>. Точка а называется идеальной.
Смысл названия связан с тем, что такие точки оптимальны сразу
по всем критериям: получить большее значение ни по одному
критерию невозможно. Очевидно, что для всех х £ Q справедливо
аРх. (11)
Как правило, идеальная точка а не принадлежит Q.
Зададим для всех точек х£й функцию, являющуюся евкли-
довым расстоянием между точками х и а:
р(х,
(12)
' Введенные понятия позволяют задать функцию выбора’С/ фор-
мулой
C/(X)eArgminp^(x, а(Х)), ^(13)
х
где а(Х)—точка, идеальная для множества X.
Решение общей задачи оптимизации <Q, ОП>, в’которой]прин-
цип оптимальности выражается функцией выбора Соп = С/, 'сво-
дится к решению обычной однокритери-
альной задачи оптимизации
р(х, а) —>rnin. (14^
Q
Пример 4. Пусть
Й = {х*....х5}, х4 = <4, 0>,
х2 = <3, 1>, х3 = <2, 2>,
х4 = <1, 3>, х5 = <0, 4>.
Тогда идеальной точкой будет а(й) = <4, 4> и Cz(Q) = {x8}. Гео-
метрическая интерпретация данного примера показана на рис. 3.
Здесь_р(х\ й) = 4, р(х\ а) = )/Тб, р(х3, а) = 21^2, р(х*, а) —
= V10, р(х$, а) = 4. Окружность с центром в <4, 4> радиуса
226
ГЛ. 7»Г|ЗАДАЧИ ОПТИМИЗАЦИИ
2 |/2 проходит через точку <2, 2>, ближайшую к <4,[4>. Таким
образом, точка х3 * * * * = <2, 2> является решением задачи (14).
Утверждение 6. Пусть й выпукло. Тогда С/(&) состоит
из одной точки.
Доказательство. Пусть х1, xa€Cz(Q). Это значит, что
точки х1 и ха находятся на равном расстоянии от точки а. Про-
ведем двумерную плоскость через х1, _х2, а и обозначим через х3
середину отрезка с концами х1, ха. В прямоугольном треуголь-
нике хгх3а катет х3а меньше, чем гипотенуза хЧх. В силу выпук-.
В
Sl<.
Рис. 4.
^а(и)
лости й точка х3 принадлежит й. Так
как р(х3, а) < р(х1, а), то х^СДЙ).
Полученное противоречие доказывает ут-
верждение.
Для произвольных множеств С{ (й) мо-
жет состоять из нескольких точек. Уста-
новим, какими свойствами обладает функ-
ция выбора Cj. Приведем некоторые при-
меры.
Пример 5. Пусть [множества й и
й' = Е2 имеют вид, показанный на рис. 4
(здесь множество й—треугольник ДВО;
Й' — заштрихованная трапеция).
В рассматриваемом случае СДЙ) = Й' и (Cz (Й)ПЙ')Х С/(^)
(на рис. 4 СДО)™^1}, СДЙ') = {х8}). Таким образом, функция
Cj не обладает свойствами Н и О.
Упражнение 13. Доказать, что функция выбора Cz не обла-
дает свойством С.
О
Упражнение 14*. Установить, какими свойствами из рас-
смотренных в § 1.2.4 обладает и какими не обладает функция С,.
Функция выбора Cz обладает следующим свойством.
Теорема’ 1. Для любого Й^ДОТ имеет место включение
С, (й) е рр.
(15)
Доказательству. Пусть а—идеальная точка, х£СДЙ).
Предположим, что теорема неверна. Это значит, что для неко-
торой точки у$Д1 выполнено уРх. С учетом (11) имеем аРх,аРу
и уРх. Положим а—х — (а—у) + (у—х). В силу аРу и уРх все
компоненты векторов а—у и у—х неотрицательны. Поэтому
каждая компонента вектора а—х не меньше, чём соответствую-
щая компонента а—у, и найдется компонента, которая строго
больше. Следовательно, длина вектора а—х больше, чем длина
вектора а—у. Но это противоречит тому, чтох^СДЙ). Получен-
ное противоречие доказывает теорему.
Функции выбора С на Ет, для которых выполнено включе-
ние С < Ср, по аналогии с бинарными отношениями назовем ра-
циональными. Теорема 4 указывает, что рациональной является
и функция Cz.
§2. МЕТОД ИДЕАЛЬНОЙ ТОЧКИ
227
Пусть Тогда для любого i£{1, ...,т} выполнено
неравенство
x*i |<р(х*, а). (16)
Оно означает, что отклонение решения х* от максимально дости-
жимого уровня по каждому критерию, совпадающего с соответ-
ствующей координатой идеальной точки, не превосходит вели-
чины р(х*, а) расстояния от идеальной точки до х*.
Утверждение 7. Пусть Q—компактное множество в Ет.
Т огда Сt (Q) =0= 0.
Упражнение 15. Доказать утверждение 7.
При использовании функции выбора Сг в качестве единствен-
ного элемента множества е^* на шаге 2 алгоритма 4.1 соответст-
вующая математическая задача выбора является обычной одно-
критериальной задачей оптимизации. При ее формулировке и
решении не требуется получать дополнительную информацию, как
это делалось в предыдущем параграфе для отношения Р^. Идеаль-
ная точка строится непосредственно по ИМА.
Метод идеальной точки используют и при других функциях
расстояния. Пусть а, Ь£Ет. Положим
РЛ«, Ь) =
(17)
При s = 2 получаем обычное 'евклидово расстояние. При s^l
имеем
т
Pi (а. &)= —М-
При s=oo получим, равномерную метрику
' р.(а, &) = шах 1^—6, (18)
i
Используя метрики р^, определим семейство функций выбора С/.
Пример 6. Пусть Q совпадает с треугольником ОАВ, пока-
занным на рис. 4, |ОА| = |ОВ| = 1. Для любой точки х, лежа-
щей на отрезке [А, В], pt(x, a(Q))=l. Поэтому С} (Q) = [Л, В]
и утверждение 6 для функции С} не выполняется.
Пример 6 показывает, что метрика р^ влияет на свойства функ-
ции выбора С/. Здесь выбор метрики рх приводит к тому, что
множество С/ (Q) для выпуклого Q состоит из целого отрезка.
Упражнение 16. Какой вид имеет множество точек х на
плоскости, для которых рДх, 0) = 1?
Упражнение 17. Выполняется ли утверждение 6 для функ-
ций С"?
Упражнение 18. Доказать, что утверждение 6 выполнено
для С/ при всех s =/= 1, оо.
228
ГЛ. 7. ЗАДАЧИ ОПТИМИЗАЦИИ
^Утверждение 8. Пусть ~£1^Ет. Тогда для любого s£
€[1, оо) выполнено
Csi (Й)'= йр.
Доказательство. Утверждение 8 следует'из того, что
при аРЬ выполнено р5 (0, а) > рДО, Ь). В остальном доказатель-
ство совпадает с доказательством утверждения 6.
Пример 7. При s = oo и т = 2, как следует из формулы (18),
единичная сфера, т. е. множество точек, находящихся от начала
координат на расстоянии
единица, [имеет вид, [показанный на
Рис. 5<
Рис. 6.
рис. 5. Для 'точек а и b имеет место аРЬ, рм(0, а) = ра> (0, &),
т. е. условие, обеспечивающее верность утверждения 8, здесь не
выполнено. Множество точек, находящихся от заданной точки у
на фиксированном расстоянии I, совпадает с квадратом со сторо-
ной 21 и центром у.
Пусть Й имеет вид, показанный на рис. 6. Идеальной точкой
будет а = <2, 2>. Из рис. 6 и 5 видно, что для всех точек х£
€[Л, В] и [В, С] выполнено р(а, х)=1. Для всех остальных
точек г/С й выполнено р (a, z/) > 1. Поэтому С/Г(Й) = [Л, В]и[В,С].
Паретовскими в С"(Й) являются точки А и С. Таким образом,
функция выбора С“ даже не является рациональной, так как
С-ДЙ^ЙЛ
[i§ 3. Выбор с учетом числа доминирующих критериев
Пусть й = Ет. Рассмотрим х, у С й и определим число крите-
риев, по которым у имеет большие оценки, чем х. Можно найти у*,
для которого это число максимально, и задать числовую функ-
цию на й, которая принимает значения, соответствующие най-
денным максимальным числам. С помощью такой функции можно
построить функцию выбора С*, которая учитывает число домини-
рующих критериев. Пусть q(x, у)—число критериев, по которым
вариант у превосходит вариант х. Для X = й положим
Qx(x)=max^(x, у). (19)
У € X
§3. y4ETJ4HCJIA ДОМИНИРУЮЩИХ КРИТЕРИЕВ
229
Величина Qx(x) называется доминирующим показателем варианта
х при предъявлении X. Значением функции выбора СК(Х) является
подмножество всех вариантов х £ X с минимальным в X домини-
рующим показателем:
СК(Х) ш {х € XJ| (х) - min Qx (г)}. (20)
(«X
Величину Qq;= т!п’С^(х)^гназовем (доминирующим показателем
множества”®.
Пример 8. Пусть
£2 = {х\ х5}, хх = <1, 1, 5>, х2 = <3, 2, 4>,
х8 = <4, 3, 2>, х‘ = <7, 0, 1>, х5 = <2, 8, 0>.?
Подсчитаем Qq(x') (i=l, 5). Для этого сформируем матрицу А
размера 5x5 с элементами = х^):
/0 2 2 1 2\
/1 02 1 1\
А = 1 1 0 1 1 . (21>
\ 2 2 2] $ 1 I
\1 2 2 2 0/
В^'силу формул (21 )Jh' (19) имеем
Qp(x/) = 2 (/>3), Qq(x8)=1.W
Поэтому в силу (20) JCx(£2) = {x8}. В то же время С₽(£2) = £2;
Таким образом, выбор CK(Q) уже выбора по отношению Парето.
Пусть £2 с: Е3 и для всех х, у 6 И выполнено х{ Ф у( (i = 1, 3).
Это означает, что £28 = Е}, где J = {1, 2, 3}. Установим вид функ-
ции Ск(£1) в этом случае. Пусть х=<хр х2, x3>CC/r(Q). Рас-
смотрим три случая: Qa(x)=l, Qc(x) = 2, Qa(x) = 3.
В 1-м случае для любого у£&, у^х, имеем в силу (19)
<?(х, «/)=!. Но тогда для любого у=£х получим q(y, х) = 2,
откуда Qa(i/)>2 и, следовательно, С* (£2) состоит из единствен-
ного элемента х.
Во 2-м случае для любого х g £2 найдется у такой, что q (х, у)
2 и для всякого х € Ск(£2) и любого у q(x, у) = 2. Пусть х £ С₽(£2).
Тогда q(x, у)<3 для любого у. Если же х(£С₽(£2), то найдется
у£Ср(&) такой, что q(x, у)=3. Тем самым установлено, что
СЛГ(£2) = СЯ(£2).
В 3-м случае для любого х££2 найдется #££2 такой, что
q(x, у) = 3, т. е. х(£Ср(£2). Но условие Ср(£2) = 0 невозможно
(в силу ацикличности Р). Поэтому такой случай не может иметь
места.
Проведенными рассуждениями доказано
Утверждение 9. Для т—3 либо CK(Q) состоит из един-
ственного элемента, превосходящего все остальные хотя бы по двум
230
ГЛ. 7. ЗАДАЧИ_ОПТИМИЗАЦИИ
координатам, либо (при отсутствии такого элемента) Ск(Q) =
Упражнение 19**. При предположениях о распределении
элементов Q, которые сделаны в главе 5, найти среднюю мощность
Ж (/и = 3).
Упражнение 20. Доказать, что при т—2 имеет место
С*(Й) = ЙР.
Рассмотрим отношение В1 на Ет, которое задается формулой
х)>/. (22)
Утверждение 10. Пусть Qq = 1. Тогда Ск(Q)=QsZ+1.
Доказательство. Пусть x£Cx(Q). Этозначит, что для
всех у £ Q'
q (х, у) <Л, т. е. q (х, «/)</+!,,
откуда в силу (22) получаем, что
уВ^х. (23)
Это ^соотношение ^означает, что x£QsZ+I. Наоборот, пусть
Тогда’для всех у£& выполнено (23) или в силу (22) для
всех у С й справедливо q (х, у) I, откуда’^ (х)=max q (х, У)\^ I.
В силу’условия Qa—l получаем, что х£С*(Q). Утверждение
доказано
Упражнение 21. Проверить, что отношение В1 коорди-
натно при любых I.
Упражнение 22. Записать ГЧ ЛФО(В1).
Таким образом, при фиксированном значении доминирующего
показателя выбор CK(Q) совпадает с множеством недоминируемых
по некоторому координатному отношению элементов.
Докажем, .’что функция выбора Ск не является нормальной
при т > 2. Это означает, что найдется множество Q с Ет, на
котором функция Ск не может быть порождена никаким бинарным
отношением. Поэтому для доказательства достаточно построить
в явном виде такое множество Q. Это построение проведем при
т = 4 (аналогичная конструкция распространяется на произволь-
ное т > 4).
Пример 9. Пусть Х1 = {х1, х\ х3, х4}, где
х1.= <1; 2; 3; 4>, х2 = <10; 1; 2; 3>,
х3 = <9;. 10; 1,5; 2,5>, х4 = <8,5; 9,5; 10; 1,5>.
При этом ’Qx,(xz) = 3 (i = l, 4), поэтому
СК(Х1) = Х1.
Пусть у*}, где
i/i = x1 = <l; 2; 3; 4>, г/2 = <100; 100; 2,9; 3,9>.
§3. УЧЕТ ЧИСЛА ДОМИНИРУЮЩИХ КРИТЕРИЕВ
231
Имеем С*(Ха) = Ха. Таким образом,
С^(Х1)ПС^(Х,)«{<1; 2; 3; 4>}.
Положим X = X1(J Х2. ^Находим
Qx(x‘) = 3 (i=TT4), Q/.G/2) = 2
(так как q (у2, х1) = 2, q(y*, [х*) — д(уг, Jxs) = O, q(y2, х4)=1).
Поэтому
с*(Х)=Ш c^xj л c*(Xt) se сцх. и х2).
Следовательно, функция выбора Ск не удовлетворяет условию
С на множестве Й=Х1ДХ2 и в силу утверждения 1.2.13 не
является нормальной.
Упражнение 23*. Удовлетворяет ли функция Ск условиям
Н и О?
Упражнение 24. Доказать, что функция Ск не является
нормальной при /и = 3.
Функция выбора Ск «сужает» множество Парето йр.
Утверждение 11.
Доказательство. Отношение В1 рационально при любом
I £ {1, ..., tn}. Поэтому й^ sйр (/= 1, /и). Утверждение 11 сле-
дует из утверждения 10.
Важным свойством функции Ск является то, что выбор по
ней не зависит от элементов й, не входящих в множество Па-
рето. Таким образом, выбор СК(О) при разных йодинаков, если
множества Парето у них совпадают.
Утверждение 12. Ск(Q) = CK(Qp).
Доказательство. Пусть х£й₽. Если y$$ip, то найдется
z£Qp такой, что q (х, у)'^ q(х, г). Следовательно, Q«(х) = Qqp (х).
Если x$Qp, то Qo(x) = /n; если x^Q^, то Qa(x)<m. Поэтому
минимум в (20) можно брать только по множеству йр. Поскольку
Qo (х) = Qqp (х) (х £ Й₽), то утверждение 12 следует из формулы. (20).
Упражнение 25*. Пусть Сг—функция выбора, определяе-
мая идеальной точкой (см. § 2). Верно ли, что С7(й) s С*(Й)?
Верно ли это включение для множеств Й, у которых Qp содер-
жится в границе выпуклой оболочки й?
Задача оптимизации <Й, ОП>, где принцип оптимальности ОП
выражается функцией Ск, может быть решена при помощи сле-
дующего алгоритма, основанного на утверждении 12.
Алгоритм 1. Построение
1. Выделить из й множество йр, воспользовавшись алгорит-
мом 4.6 при ф(х)= 2 xi-
i = 1
2. Занумеровать элементы множества йр: х1, .... хг.
3. Положить Х — 0.
232
ГЛ. 7. ЗАДАЧИ ОПТИМИЗАЦИИ
4. Положить Q = m.
5. Положить i = 0.
6. Положить i = i -}- 1.
7. Сравнить i с г. Если i > г, перейти к 19, в противном
случае—к 8.
8. Положить Qi==Q.
9. Положить / = 0.
10. Положить j = j 4-1.
11. Найти число q координат, по которым xJ больше, чем х1.
12. Сравнить Q и q. Если </> Q, перейти к 6, в противном
случае—к 13.
13. Положить Qz = max(<7, Q;).
14. Сравнить / с г. Если j=£r, перейти к 10, в противном
случае—к 15.
15. Сравнить Qi и Q. Если Qf<Q, перейти к 16, в против-
ном случае—к 18.
16. Положить Q = QZ.
17. Положить Х = {х‘} и перейти к 6.
18. Положить Х — Х(){х1} и перейти к 6.
19. Положить CK(Q) — л.
Пусть Й = Ега. Занумеруем варианты из й: {х1, ..., xN] и
сопоставим множеству Q матрицу Aq размера NxN с элемен-
тами следующим образом:]
ац = Я{х{, х') (I, / = 1, N). (24)
Проиллюстрируем выбор [Ск на Q, используя матрицу Aq. Для
каждого i положим
a( = maxai7. (25)
/
Из формул (19), (20), (24) и (25) получаем, что
C/f(Q) = {x‘€Q| ArgminaJ. (26)
s
Таким образом, выбираются те строки матрицы Aq , максималь-
ные значения элементов которых минимальны.
Аналогичное правило выбора можно определить для произволь-
ных матриц, в том числе для матриц n-круговых турниров. Оста-
новимся начатом подробнее.
Пусть N игроков встречаются друг с другом в турнире «раз
и результатом каждой игры является победа или поражение.
Результаты всего турнира можно записать матрицей Т п-круго-
вого турнира размера NxN, в которой элемент равен числу
выигрышей /-го игрока у t-ro. В матрице Т для всех t
и /» *=#=/; по определению 1(1 = 0 (1=1, N).
Для определения победителей n-кругового турнира можно
использовать две функции выбора: Ст и Ск. Функция Ст, назы-
§ 3. УЧЕТ ЧИСЛА ДОМИНИРУЮЩИХ КРИТЕРИЕВ
233
ваемая турнирной п-круговой функцией выбора, задается формулой
СТ(Х)~{у£Х\МТАу)~гйпМтх(г)}, (27)
zeX
где
MTx(x)=%txz. (28)
zeX
При п=1 получаем в силу (27) и (28) турнирную функцию вы-
бора, рассмотренную ранее в примере 1.2.4.
С помощью формул (25) и (26), в которые вместо подстав-
лены tjj, определим на множестве й = {1, ...,N} функцию вы-
бора Ск. При этом функция Ст учитывает суммарное число
проигрышей игрока, а функция Ск—максимальное число про-
игрышей каждому игроку в отдельности и в определенном
смысле характеризует надежность данного игрока.
Произвольный n-круговой турнир называется критериальным,
если для некоторого его матрица T = Aq.
Упражнение 26*. Доказать, что n-круговой турнир яв-
ляется критериальным тогда и только тогда, когда для его мат-
рицы выполнены соотношения txz-[-tzy'^ txy.
Пусть Тх и Тг—матрицы n-круговых турниров одинакового
размера. Матрицы 7\ и Т2 называются эквивалентными в смысле
выбора, если для любого X s Q
сГ (X)=СГ (X), с* (X)=с? (X).
Утверждение 13. Матрицы Тг и T2 = p,T1-^-vE, где ц
и v — константы, Е—матрица, в которой еху=1 при х^у,
ехх = 0, эквивалентны в смысле выбора.
Упражнение 27. Доказать утверждение 13.
Теорема.5. Пусть 7\—матрица п-кругового турнира.
Тогда матрица Тг = Тх-\-гЕ является матрицей критериального
(п + 2г)-кругового турнира, если
_ Г^^-1)} ,]»+!
^ \_ 2 J 2 •
Итак, функция выбора Ск может быть использована в качестве
выражения принципа оптимальности при отсутствии информации
о сравнительной важности критериев. Она учитывает только
взаимные соотношения (типа больше—меньше) между оценками
альтернатив из Q и не учитывает абсолютные величины разно-
стей оценок по критериям.
Литература. [88, 89, 100].
8 И. М. Макаров и др.
ЧАСТЬ III
МНОГОКРИТЕРИАЛЬНЫЕ ЗАДАЧИ
ОПТИМАЛЬНОГО УПРАВЛЕНИЯ
В части III показана возможность совместного использования
аппарата теории выбора с классическим аппаратом оптимального
управления, математического программирования, дискретной
оптимизации, теории игр, марковских цепей. В задаче выбора
известно множество й, а принцип оптимальности в общем случае
неизвестен. В задаче оптимизации принцип оптимальности изве-
стен. Здесь рассмотрены задачи выбора и оптимизации, в которых
заданы множество 41, называемое множеством управлений, и
отображение ср: 41 —» Ет. Вектор ср (и) £ Ет интерпретируется как
доход от управления 41. Принцип оптимальности определен не на
исходном множестве 41, а на множестве доходов Ф = ср (ЭД) s Ет,
т. е. выбор управлений осуществляется не непосредственно, а на
основании доходов <р(ы), соответствующих управлениям и £41.
Задачи выбора, в которых строилось отображение й в Ет
или множество й предполагалось уже расположенным в Ет, рас-
сматривались в части II. Однако явный вид отображения ср не
был задан, а образ й в Ет находился экспертными процедурами.
Здесь же рассмотрены конкретные виды множеств 41 и отобра-
жений ср. Общая задача части III названа многокритериальной
задачей оптимального управления и состоит в следующем: найти
все или некоторые и* С 41 такие, что ср (и*) е Соп (Ф). Детализируя
принцип оптимальности ОП, вид множества 41 и отображение ср,
получаем конкретные виды задач. Основное внимание уделено
задачам, в которых принцип оптимальности выражается известным
бинарным отношением 7?. Кроме этого, рассмотрены задачи,
в которых принцип оптимальности выражается неизвестной зара-
нее функцией полезности, задачи со специальной структурой 41
и ср и игровые задачи.
Материал части III показывает, что совместное использование
аппарата теории выбора и классического аппарата позволяет
расширить известные постановки задач за счет использования
более общих принципов оптимальности. В главе 1 рассмотрены
общие свойства задач оптимального управления; 'в главе 2—
дискретные задачи; в главе 3—задача с непрерывным временем;
в главе 4—задачи, описываемые марковскими моделями. В главе 5
даны примеры прикладных многокритериальных задач оптималь-
ного управления.
§ 1. постановка задачи и ее свойства
235
Глава 1
ЗАДАЧА УПРАВЛЕНИЯ ПРИ МНОГИХ КРИТЕРИЯХ
В главе рассмотрена многокритериальная задача оптималь-
ного управления, представляемая тройкой <% <р, /?>, где 41—
множество управлений; <р—отображение ЭД в пространство дохо-
дов £m; R—бинарное отношение на Ет, по которому осущест-
вляется сравнение доходов. Исследованы вопросы существования
/^-оптимальных решений в зависимости от параметров задачи.
Показана возможность сведения многокритериальной задачи
к однокритериальной с использованием понятий отделимости и
1-отделимости. Приведен алгоритм решения для R = RV. Выделен
класс задач, в которых управление и£41 представимо в виде
набора частных управлений, а доход <р(ы) является их сепара-
бельной функцией.
В § 1 приведена постановка задачи и рассмотрены ее свойства;
в § 2 дан алгоритм решения задачи для R = R^, в § 3 выделен
класс динамических задач; в § 4 рассмотрена задача управления
при противодействии; в § 5—многокритериальная задача мате-
матического программирования.
§ 1. Постановка задачи и ее свойства]
Пусть 41—множество управлений для некоторого .объекта.
Управления и $ 41 могут иметь различную природу: стратегии
в игре, дуги в графе, непрерывные функции, правила остановки
и т. д. Природа и структура множества 41 для общей постановки
многокритериальной задачи оптимального управления несущест-
венны. Каждому управлению и £41 ставится в соответствие
m-мерный вектор дохода <р (u) С Ет. Вид <р (и) определяется свой-
ствами управляемого объекта. Будем интерпретировать Ет как
пространство доходов.
Вместо доходов можно рассматривать штрафы. В первом
случае оптимальные управления будут соответствовать мажоран-
там, во втором—минорантам; оба случая эквивалентны друг
другу в силу формулы (1.1.17')- Поэтому всюду в дальнейшем,
где не оговорено противное, будем рассматривать доходы.
Пусть на пространстве Ет задано бинарное отношение. Управ-
ление и* £41 является оптимальным, если при всех других
управлениях и £41 нельзя получить вектор доходов <р(м), более
предпочтительный по отношению R, чем <р(м*), т. е. <р(«) 7?<р(м*)
для всех и £41. Будем называть такие управления R-оптималь-
ными. Обозначим множество всех R-оптимальных управлений
через 6(41).
Многокритериальная задача оптимального управления состоит
в том, чтобы при заданных 41, <р и R выделить 6(41). Нетрудно
8* И. М. Макаров и др.
236
ГЛ. 1. ЗАДАЧА УПРАВЛЕНИЯ ПРИ МНОГИХ КРИТЕРИЯХ
видеть, что в приведенной формулировке рассматриваемая задача
является частным случаем задачи выбора, в которой альтерна-
тивами решений являются управления, а функция выбора задана
бинарным отношением 7?.
Если отображение ср сопоставляет каждому и £41 число
а отношение 7? является отношением «больше» на мно-
жестве действительных чисел, то получим классическую одно-
критериальную задачу оптимального управления. Как будет
видно далее, классические результаты используются для решения
рассматриваемой задачи.
Многокритериальная задача оптимального управления обычно
имеет множество решений. Решением 6 (ЭД, ср, R) задачи [опти-
мального управления <ЭД, ср, 7?> называется множество всех
7?-оптимальных управлений и*£ЭД; частным решением—любое
7?-оптимальное управление u*£4L.
Различные типы рассматриваемых далее задач будут отли-
чаться параметрами 41, <р, R.
Специфика конкретной задачи может привести к тому, что
оказывается необязательным выделение всего множества 6(41)'
достаточно бывает найти хотя бы один элемент и £6(41) или
часть 6(41), обладающую некоторыми дополнительными свойст-
вами.
Рассмотрим вопрос о существовании решения, т. е. вопрос
о непустоте множества 6 (41, ср, R). Приведем примеры, которые
показывают, что оно может быть пустым.
Пример 1. Пусть
ЭД = {и€Еа [«!>(), «2>0, 0 < Ui + Ujj < 1}, cp(u) = — и,
R—отношение Парето Р. При этом 6 (ЭД, <р, R)= 0, так как
единственная точка, которая доминирует все остальные—это
начало координат, а оно не принадлежит множеству ср (ЭД).
Пример 2. Пусть
ЭД = {а, Ь, с, d}, ср(а) = <0, 0, 0>, ср(Ь) = <—1, 1, 1>,
ср (с) = <0,2, —3>, ср (d) = <—1, 3, — 1 >,
R—мажоритарное отношение 7И3 (см. пример 1.4.5). При этом
6 (ЭД, ср, М3) = 0, так как ср (b) Rср (а), ср (с) Rq>(b), cp(d) 7?ср(с),
ср (a) Rср (d), т. е. точки ср (а),- ср (Ь), ср (с), y(d) образуют цикл.
Отсутствие решений в примерах 1 и 2 связано с различными
причинами: в примере 1—с незамкнутостью множества ср (ЭД),
в примере 2—с тем, что R не ациклично. Таким образом, как
и в однокритериальном случае, для существования решения
необходимо наложить некоторые требования на условия задачи.
Приведем требования общего характера, которые относятся к
любым задачам. Для некоторых задач они оказываются достаточ-
ными для существования решения.
51. ПОСТАНОВКА ЗАДАЧИ И ЕЕ СВОЙСТВА 237
При одном и том же множестве управлений ‘U и отображе-
нии <р на доходах ф(ы) могут задаваться разные бинарные
отношения" R.
Утверждение 1.
^<^=^0^, Ф,/?2) = 6(ЭД, Ф, RJ. (О
Следствие. Из существования решения задачи <ЭД, ф, R2>
следует существование решения задачи <flL, ф, Rx>.
Доказательство. Пусть и* £ 6 ((И, ф, R2). По определе-
нию ./^-оптимального решения для всех ивыполняется
Ф (и) /?2ф (и*). Из того, что Rx вложено в3#2, следует, что
R2 вложено в R^. Поэтому из ф (и) R2(p (и*) следует, что для всех
ы £ ЭД выполняется ф (м) Т^ф (и*), т. е. u^^Q^lL, ф, RJ. Это до-
казывает утверждение 1.
Хотя утверждение 1 помогает в некоторых случаях найти
частные решения задачи <ЭД, ф, /?>., оно не дает универсального
способа решения. Такой способ связан с введенными в главе 1.3
понятиями Х-отделимого и отделимого соотношений.
Утверждение 2. Пусть ф(ЭД)—замкнутое ограниченное
множество в Ёт', R—k-отделимое отношение. Тогда многокрите-
риальная задача оптимального управления <!U, ф, /?> имеет
решение.
Доказательство. Положим
Ф = Ф(ЭД). (2)
Из условия утверждения следует, что Argmax (а, ф) =/= 0. Пусть
ф
Ф* g Argmax (X, ф) и u* С ЭД таково, что ф(и*) = ф* (такое управ-
ф
ление и* существует в силу (2)). Докажем, что и*£б(ЭД, ф, R).
Предположим противное. Тогда для некоторой точки и £ R имеем
ф(м)7?ф (и*), откуда в силу Х-отделимости R и выбора и* выпол-
няется
(X, ф) = (Х, ф (u)) > (X, ф («*)) = (X, ф*). (3)
Полученное неравенство противоречит тому, что. ф* =
= Argmax (X, ф). Утверждение доказано, <
ф
Из утверждения 1 следует, что если задача <ЭД, ф, R> имеет
решение для Х-отделимого отношения R, то она имеет решение
и для любого отношения R', вложенного’в R. Для существова-
ния решения при замкнутом ограниченном Ф = ф (ЭД) достаточно
в силу утверждения 2 Х-отделимости R. Однако в доказательстве
утверждения 2 использовалась не компактность Ф, а лишь
непустота множества Argmax (X, ф).
ф
Пусть <ЭД, ф, R>—многокритериальная задача оптимального
управления, в которой ф: ЭД ->-Ет, и пусть ХС£т. Х-сверткой
238
ГЛ. 1. ЗАДАЧА УПРАВЛЕНИЯ ПРИ МНОГИХ КРИТЕРИЯХ
задачи <ЭД, ср, 7?> назовем однокритериальную задачу <41, g, >>,
где g = (X, ф) и указан конкретный вид отношения Л («больше»).
Переход к ^-сверткам представляет собой основной способ реше-
ния многокритериальных задач оптимального управления. Сфор-
мулируем соответствующие утверждения.
Утверждение 3. Пусть и*—любое решение задачи
<41, (X, ф), >>. Тогда и* £6(41, ф, /?) для любого ^-отделимого
отношения R.
Доказательство следует из того, что ф («*) £ Argmax (X, ф).
ф
Далее, оно в точности повторяет схему доказательства утверж-
дения 2.
Утверждение 3 позволяет находить частные решения задачи
<% ф, 7?>. Для того чтобы найти некоторое множество решений,
воспользуемся понятием двойственного конуса отношения* 7?.
Утверждение 4.
U 6 (Z, Ф), »s6(% ф, 7?). (4)
heKR
Упражнение 1. Доказать утверждение 4.
Утверждение 4 позволяет найти часть множества 6(41, ф, 7?).
Задача нахождения всего 6 (% ф, 7?) является сложной и часто
не сводится к однокритериальной. Однако здесь также существуют
условия на отношение R и множество Ф, позволяющие сформу-
лировать точные результаты.
Утверждение 5. Пусть К—конус, RK—отношение, по-
рожденное конусом К, RK^R и множество Ф = ф(^) (—К)-вы-
пукло. Тогда для любого u*$6(4L, ф, 7?) существует такое,
что и* ^6 (41, (X, ф), >) (X*—конус, двойственный к 7Q.
Доказательство утверждения непосредственно следует из ут-
верждений 1.3.8 и 1.
Следствие. Пусть Ф выпукло. Тогда для любого
и* £ 6(ЭД, ф, 7?) существует X £ X* такое, что и* £ Argmax(X, ф(^)).
В условиях утверждения 5 в силу утверждения 3 нахождение
6 (ЭД, ф, 7?) сводится к решению параметрической задачи: найти
Argmax (X, ф («)) при всех ZgTC, где X* — конус, двойственный
и
к конусу К, порождающему отношение RK, вложенное в R.
В общем случае невозможно ослабить требования на отноше-
ние R, отказавшись от Z-отделимости и заменив его значительно
более слабым свойством отделимости.
Утверждение 6. Пусть существует конечное множество
41*^41 такое, что для любого выполнено
41*0 6 (41, (Z, ф), >)у=0. Тогда для любого отделимого (неотри-
цательно отделимого) отношения R выполнено 41* П 6(41, ф, 7?)#=0.
Доказательство. Предположим противное. Это значит,
что для любого и* £41* существует и £41 такое, что ф(и) 7?ф(и*).
§2. АЛГОРИТМ ДЛЯ ФУНКЦИИ ПОЛЕЗНОСТИ
239
Рассмотрим множество ‘й, образованное ‘U* и управлениями и,
мажорирующими управления и* из 41*. По условию 41 конечно
(1*61 ^2В силу отделимости существует такое, что
для всех м1( и2^‘й
ф (г/t) /?<р (ы2) => (X, <р (mJ) > (X, ф (м2)). (5)
Рассмотрим Х-свертку задачи <% ф, 7?>. По условию сущест-
вует и* $ “U* s “W такое, что
(X, Ф), >).
Это значит, что для всех и С ‘й
(Х,ф(н*))>(Х,ф («')), _ (6)
что противоречит формуле (5) при ы2 = и*, и1 = и. Утверждение
доказано.
Пусть выполняются условия утверждений 5 и 6, т. е. для
некоторого конуса К. множество Ф (—Д')-выпукло и существует
конечное множество “U* управлений, оптимальных в любой
Х-свертке задачи при Х^/С*#
Через любую точку ф* С Ф^к проходит отделяющая гиперплос-
кость (X, ф) = (Х, ф*), где XgA* (утверждение 5). Однако все эти
точки можно получить, максимизируя на Ф конечное множество
функций (Хъ ф), ..., (Xd, ф). Тем самым доказано
Утверждение 7. Пусть Ф (—К)-выпукло и существует
конечное множество ‘U* управлений, оптимальных в любой ^-свертке
задачи <flL, ф, RKy при Х£/<*. Тогда множество совпадает
с частью поверхности выпуклого многогранника, каждая грань
которого соответствует одному управлению из 41*.
Итак, решение многокритериальной задачи оптимального
управления <СМ, ф, Ry для отделимых отношений R в определен-
ном смысле сводится к решению соответствующей однокритери-.
альной задачи. Это позволяет для отыскания частных (а иногда
и общих) решений задачи <% ф, Ry использовать хорошо разра-
ботанные в однокритериальном случае методы и алгоритмы.'
§ 2. Общий алгоритм решения для функции полезности
В предыдущем параграфе были сформулированы свойства
решения многокритериальной задачи оптимального управления
<ЭД, ф, Ry. Будем считать, что R = RV, где U—функция полез-
ности. Тогда оптимальными являются управления и*£еИ такие,
что
и* с Argmax U (ф («)). (7)
и
Задача вида (7) имеет существенную специфику, отличающую
ее от задач математического программирования и от задач, рас-
240 ГЛ. 1. ЗАДАЧА УПРАВЛЕНИЯ ПРИ МНОГИХ КРИТЕРИЯХ
смотренных в главе II.6. Здесь не предполагается, что ‘И^Е^
Это затрудняет применение обычных градиентных методов. Однако
при некоторых допущениях можно найти решение задачи (7).
Сформулируем необходимые допущения.
1. Множество Ф = <р(ЭД) (—Е^-выпукло. В таком случае
говорят также, что паретовская граница Ф₽ выпукла.
2. Функция полезности U (ф) вогнута на Ф, и ее градиент
на Ф имеет положительные компоненты.
3. В любой точке фСЕ^ известно направление градиента U.
4. При любых положительных А.х, . ..,Хт известно решение
однокритериальной задачи:
т
найти Argmax 2 Ч’Ф/(Ы)- (8)
«4 i = 1
5. Известна точка <р*, максимизирующая U (ф) на любом от-
резке [фп ф2] = Е„.
Решение задачи (7) можно получить, решив последователь-
ность задач типа (8) с линейной целевой функцией. Обоснованием
решения является метод условного градиента.
Приведем алгоритм, который при сделанных допущениях дает
решение задачи (7).
1. Выбрать произвольное управление и ^41.
2. Найти с помощью отображения ф вектор дохода ф! =
= у(и)£Ет.
3. Найти направление градиента ?Ф1 в точке <px.
4. Решить однокритериальную задачу (8) при %= ТФ1 и найти
соответствующее управление и*.
5. Положить ф2 = ф(^*).
6. Сравнить | фх — ф21 с заранее заданным 8. Если | фт—ф21< 8,
то алгоритм прекращает работу и решением задачи (7) является
управление и*. В противном случае перейти к шагу 7.
7. Найти ф* Argmax U (ф).
8. Положить Ф1== Ф* и перейти к шагу 3.
§ 3. Динамические многокритериальные задачи
Во многих случаях управление является конечным или
бесконечным набором u —<и0, и19 . ..> некоторых действий.
Например, и^41 представляет собой последовательность и —
= <Г4о, частных управлений, выбираемых в последова-
тельные моменты времени / = 0, 1, ... Тогда общую многокрите-
риальную задачу управления удается свести к последователь-
ности более простых задач, связанных с частными управлениями
«о, «п • • •
Наиболее важным является допущение о специальном виде
структуры доходов. Пусть доход представим в одной из следующих
трех форм:
§4. УПРАВЛЕНИЕ В УСЛОВИЯХ ПРОТИВОДЕЙСТВИЯ
241
. 1. В виде суммы конечного числа составляющих
Л- 1
Ф («) = 2 «/Фт («)> Ф/ («) = Фт («о. • • •. “/)• (9>
< = 0
2. В виде суммы бесконечного ряда
00
Ф(и) = 2 а»ф/(«)> Ф/(«) = (р'(и0, и,), (10)
1=0
где м = <«0, ... , и,-, .. .>, а{—заданные константы, обеспечиваю-
щие сходимость ряда в (10).
3. В виде определенного интеграла
г
<р(и)— J f (u(s))ds, (11)
о
где u = u(f) на отрезке [О, Т].
Существенно то, что во всех случаях доход ср (.'/.) является
суммой (интегралом) доходов, полученных от частных управле-
ний, а также что отношение R инвариантно относительно,
переноса. Будем называть динамическими многокритериальными,
задачами оптимального управления задачи, в которых
1) управление представимо в виде последовательности дей-
ствий;
2) доход аддитивен относительно частных управлений;
3) отношение инвариантно относительно переноса.
Поскольку динамическая задача является частным случаем
общей многокритериальной задачи оптимального управления, та
на нее переносятся все понятия и утверждения § 1, в частности
понятие 1-свертки задачи.
В главах 2—5 будут рассмотрены конкретные динамические
многокритериальные задачи оптимального управления. В каждом
случае сначала сформулирована задача в принятой для нее
терминологии, затем указаны множество управлений 41, отобра-
жение <р и бинарное отношение /?. После этого можно исполь-
зовать общие^утверждения настоящей главы.
§4 . ^Оптимальное управление в условиях противодействия
Рассмотрим задачу оптимального управления в условиях про-
тиводействия. Пусть 41 представимо в виде 41 = 41^... х41п и
имеется п элементов (игроков) Alt ..., Ап, каждый из которых
выбирает Доход элемента А{ задается функцией
Ф;(«1, ..., .....п„), т.е. зависит от управлений, выбранных
всеми элементами. Цель каждого элемента А{ состоит в макси-
мизации дохода ф(- (i=l,n).
Понятие оптимальности управления и£41 может быть задана
с помощью бинарного отношения /? на Еп следующим образом:
242
ГЛ. 1. ЗАДАЧА УПРАВЛЕНИЯ ПРИ МНОГИХ КРИТЕРИЯХ
и* /?-оптимально, если для всех u^'U
ф(и)7?ф(ц*), (12)
где ср(ы) = <ср1(и), <рп(и)>. В качестве 2? обычно рассматри-
вают отношения Парето и мажоритарное.
Задача поиска ^-оптимальных управлений совпадает с рас-
смотренной в § 1 многокритериальной задачей <fU, ср, /?>, где
... х Un, ср = <срп ..., ср„>, R—бинарное отношение
на Еп. Заметим, что при этом доходы ф, отдельных элементов —
скалярные функции. При переходе к векторным доходам (ф^СЕ^)
отношение R можно задать в Етп и задача остается прежней:
п
ф = <ф}, ф"*, ф1, ..., ф^>, R — бинарное от-
i=i
ношение на Етп. _____
Пусть ф(- (i=l, п)—скалярные функции. Зададим понятие
оптимальности управления с помощью принципа Нэша. Управ-
ление и* называется оптимальным по Нэшу, если
еArgmaxф,-^’, ..., и*_1г иь и*+1, .... и*) (i = T~n). (13)
Это означает, что каждому элементу в отдельности не следует
менять свое управление и‘, так как при неизменных управле-
ниях остальных элементов элемент Аг не может получить больше,
чем фДи*)—доход в точке и*, называемой точкой Нэша.
Заметим, что точка Нэша и* может не удовлетворять соотно-
шению (12) при R — P, т. е. при одновременном изменении
управлений все элементы могут увеличить свои доходы. В таких
случаях точка Нэша не является паретовской.
Упражнение 2*. Можно ли задать оптимальное по Нэшу
управление с помощью некоторого бинарного отношения R по
формуле (12)?
Запишем задачу оптимального по Нэшу управления в виде
<fU, ф, Н>, где йМ = 'И1х ... х^', Ф = <Ф1, .... ф„>, а Н указывает
на оптимальность по Нэшу. Частным решением задачи (U, ф, Н>
называется любое оптимальное по Нэшу управление и*^^,
а общим решением—множество всех частных решений. В отличие
от задачи оптимального управления из § 1, здесь принцип опти-
мальности управления не связан с максимизацией какой-либо
одной функции. ____
Пусть функции ф; (i=l,n) принимают значения из Ет, на
котором задано бинарное отношение R. Управление назо-
вем R-оптимальным по Нэшу, если для любого i£{l, ...,п} и
произвольного и;- g %-
ф/ (^1, . . ., UZ—i, , Wf+i, ...» Ил) (^1 > ‘ ' ч ^i+li ♦ • •» Hn).
(14)
§4. УПРАВЛЕНИЕ В УСЛОВИЯХ ПРОТИВОДЕЙСТВИЯ
243
При т=1 и отношении R на Еи являющемся отношением
«больше», приходим к приведенному выше понятию управления,
оптимального по Нэшу.
Задача оптимального управления в условиях противодействия
при векторных доходах состоит в нахождении всех или некото-
рых /^-оптимальных по Нэшу управлений. Используем для нее
запись <4М, ф, R, Н>. Понятия решения 6 (*?£, ф, R, Н), Х-свертки
задачи и другие переносятся на рассматриваемый случай из § 1.
Утверждение 8. Пусть и* R ^оптимально по Нэшу, Рг</?2.
Тогда и* Ц2-оптимально по Нэшу.
Доказательство. По условию /?2 >/?п откуда /?х>^2.
Следовательно, соотношение (14) выполняется для /?2. Утверж-
дение доказано.
Утверждение 9. Пусть R—^-отделимое отношение 'и
управление и* принадлежит 6 (41, (X, ср), Н). Тогда и* принадле-
жит 6(41, <р, 7?, Н).
Доказательство. Предположим противное. Тогда най-
дутся i' и Ир такие, что
Фг (Ui, ...,u’i.. и*п) /?ф,- (u*lt ..., u*t., ..., и’). (15)
По условию Х-отделимости R из (15) получаем, что
(X, Фр («?, .... и;.. и*)) > (X, фр (uj.u*t„ ..., и*)). (16)
Неравенство (16) противоречит условию и* £ 6 (% (X, ф), Н).
Утверждение доказано.
Утверждение 10.
U 6(41, (X, ф), Н)<=0(% ф, R, Н).
KeKR
Упражнение 3. Остается ли верным для задачи
<41, ф, R, Н> аналог утверждения 5?
Рассмотрим частный случай задачи <41, ф, R, Н> при « = 2
и ф2 = —фр
Утверждение 11. Пусть R—отношение, инвариантное
относительно переноса. Управление и* = <и}, ua> R-оптимально
по Нэшу тогда и только тогда, когда для всех их £ 4Lt
ф(их ,Ui)~R(p(Ui, «£) (17)
и для всех иг £ 41г
ф(пГ, «а) Я<р(«1, и3), (18)
где ф = фх = — ф2.
Доказательство. Формула (17) непосредственно следует
из определения /^-оптимальности по Нэшу. Из формулы (14)
получим, что для всех и2 £ 4la
— ф(и;, и2)^—ф(и;, и2). (19)
244
ГЛ. 1. ЗАДАЧА УПРАВЛЕНИЯ ПРИ МНОГИХ КРИТЕРИЯХ
В силу 'того, что R G Зт, R также принадлежит Зт.
Поэтому _из (19) имеем (<р (иЧ, и2*) — ср (и*, и2)) R0, откуда
«2) R<p(«i, ыз), что’ совпадает с (18). Тем самым доказана
эквивалентность (18) и (19). Утверждение 11 доказано.
Пусть /?х, ..., Rn—бинарные отношения на Ет, каждое из.
которых выражает предпочтения элементов Лп ...,Ап соответ
ственно. Положим R = </?х, ..., Rm> и введем следующее понятие'
Управление и* назовем совокупно оптимальным по Нэшу,
если для любого i С {1..п} и произвольного
(₽,-(«;, , и*) Ri<Pt (иЧ, ..., иЧ, ...,и*п). (20)
При Rj=R (i = \,ri) понятие совокупно оптимального управле-
ния перейдет в понятие R-оптимального управления.
Утверждение 12. Пусть R, — Неотделимое отношение,
фх=(Х;, <р() (i=l,n), = и управление и* принад-
лежит if, Н). Тогда и* принадлежит 6(41, <р, R, Н).
Упражнение 4. Доказать утверждение 12.
Рассмотрим теперь вопрос о существовании решений задачи
<elL, Ф, R,H>.
Утвержденае 13. Пусть выполнены следующие условия-.
1) s Er (1=1, п)—выпуклые компактные множества-,
2) при любых и{, ..., иЧ^, и"+1, .. .,и*п и любых Н£Ет
Argmax (X, ф,- (иЧ, ..., u*^, uh и*1+1, .... и*)) (i = 17п)
Ui
— выпуклое компактное множество-,
3) функции ф/ (и) (i = 1, п) непрерывны-,
4) R. (i=l, п)—Неотделимое отношение.
Тогда 6(41, Ф, R, Н)^=0.
Доказательство. В силу утверждения Г2 и условия
4) достаточно доказать существование решения задачи <% if, Н>,
где if=<ifx, ..., if„>, Ф, = (Х,-, фг). При условиях 1)—3), нало-
женных на параметры задачи <^IL, if, Н>, точка Нэша в задаче
КЭД, if, Н> существует*). Утверждение доказано.
§ 5. Многокритериальные задачи
математического программирования
Рассмотрим многокритериальную задачу оптимального управ-
ления <!U, ф, ОП>. Пусть 41— множество в пространстве Еп,
а ф,- (их, ..., ип)— непрерывные функции на Е„. Задачу <<!И, ф, ОП>
в этом случае назовем многокритериальной задачей математиче-
ского программирования. Это название связано с тем, что при
т= 1 и принципе оптимальности, выражаемом отношением > на
*) Это следует из теоремы 5.3 дополнения II в [86].
§ 5. МНОГОКРИТЕРИАЛЬНОЕ ПРОГРАММИРОВАНИЕ
245
Ei, задача <41, <р, ОП> становится известной задачей математи-
ческого’программирования. В общем случае при выпуклом 41 и
вогнутых <р(- имеем выпуклую задачу; при линейных срг- и 41,
заданном линейными неравенствами,— многокритериальную задачу
линейного программирования.
Рассмотрим подробнее многокритериальную задачу линейного
программирования. Пусть в пространстве Еп задана область 41,
представляющая собой множество решений системы линейных
неравенств
Bu^h, ((21)
где и — <их, ..., ип> £ Еп. Система, включающая в себя как нера-
венства, так и равенства, сводится к системе (21), включающей
только неравенства, с помощью замены равенства (&', «) = й,- на
два неравенства: (b‘, u)^hh (—b‘,
Отображение ср: 4L —+ Ет задано при помощи т линейных
функций ср(., определенных на Еп:
Ф/ («) = S Ф//«/» Ф («) = <Ф1 (м).Ф» («)>• (22)
/ = 1
Рассмотрим решения задачи <41, ср, ОП> при различных принци-
пах оптимальности.
1. Принцип оптимальности выражается функцией полезности
U, вообще говоря, неизвестной. В этом случае многокритериаль-
ная задача линейного программирования примет вид:
найти Argmax U (д>! (и), ..., <pm (w)) (23)
и
при 41, заданном системой (21). Эта задача является частным
случаем задачи (7), рассмотренной в § 2. Поэтому для нее можно
воспользоваться предложенным в § 2 алгоритмом, основанным
на последовательном решении задач (8). В рассматриваемом слу-
чае допущение 1 из § 2 всегда выполнено, поскольку множество
41, совпадающее с решением (21), выпукло, а Ф=±ц>(41) выпукло,
поскольку является образом выпуклого множества при линейном
отображении ср. Задача (8) при любом является однокри-
териальной задачей линейного программирования и может быть
решена стандартными способами, например симплекс-методом.
Итак, можно сказать, что линейность ограничений, задающих 41,
упрощает решение задачи (23) по сравнению с общим случаем,
рассмотренным в § 2.
2. Принцип оптимальности выражается известным бинарным
отношением R. В этом случае задача сводится к многокрите-
риальной задаче оптимального управления <41, <р, 7?>. Ее
Х-свертка принимает вид
т
У (и) -+ max
i = 1
246
ГЛ. 1. ЗАДАЧА УПРАВЛЕНИЯ ПРИ МНОГИХ КРИТЕРИЯХ
при условии Ви^/г, т. е. является7однокритериальной задачей
линейного программирования, решаемой стандартными методами.
В силу выпуклости ф (41) и утверждения 5 для любого отноше-
ния Л такого, что R^^R, нахождение 6(41, ф, R) сводится
к решению параметрической задачи линейного программирования:
найти Argmax (%, ф^(и))
при всех Х£/С*, где К*—конус, двойственный к конусу К. Эта
задача может быть решена стандартными методами; решением
может являться объединение всех граней многогранника 41, полу-
ченных при пересечении 41 с гиперплоскостями, задаваемыми
векторами X, содержащимися в К* (т. е. имеющими вид (X, u)=d,
где Х^К*).
3. Принцип оптимальности выражается функцией выбора CIt
определяемой близостью к идеальной точке. J3 этом случае при-
менение метода' идеальной точки состоит в следующем. Образуют
выражение
/?(«)= 2[ф?-ф>(«)]2,
• — 1
(24)
где ф£ = max ф,- (и), и’находят точку и £ 41, минимизирующую R (и).
Таким образом, решение многокритериальной задачи линейного
программирования в данном случае сводится к решению задачи
квадратичного программирования на многограннике 41. В ней
локальный минимум совпадает с глобальным, поэтому для ее
решения могут быть использованы численные методы, находящие
локальные экстремумы, в том числе и градиентные.
При использовании метрики рм и соответствующей функции
выбора С" решение сводится к минимизации функции
7 (u) = max 2 Ф<А—Ф?
(25)
« /=1
Точка, минимизирующая V (и), называется чебышевской точкой
для системы линейных уравнений
2 Ф//“/— Ф? = ° (i = 1, /«).
(26)
Пример 3. Пусть
Ф1 («)= —+ 2н2,
• , ф2(и) = 4ы1 + 3«2,
ф3 (m) = 2«x—5ы2.
Область 41 изменения переменных”задается неравенствами
—2«f—Зи2 + 18>0,
—2«!—ы2 4- 10> О,
ы1^0, «2^0.
§5. МНОГОКРИТЕРИАЛЬНОЕ ПРОГРАММИРОВАНИЕ
247
Применяя симплекс-метод, найдем, что линейная функция фх(ы)
достигает максимального значения ф?=12 в точке и1 = <0, 6>;
ф2 («>) = 18, ф8(и1) = —30. Линейная функция ф2(ы) максималь-
ного значения ф2 = 24 достигает в точке ы2 = <3, 4>; ф1(«2) =—1,
ф3(ы2) =—14. «Линейная функция ф3(м) максимального значения
Ф®=10 достигает в точке «3 = <5, 0>; ф1(«3) =—15, ф2(«3) = 20.
В соответствии с (24) составим функцию
Я («х, м2) = [12—(—3«х + 2м2)]2 + (24—(4«j + 3«2)]2 +
+ [10—(2ых—5м2)]2;
после преобразования имеем
R (иг, и 2) = 29«х + 38«|—8t/|U2 — 160ых— 92«2 + 820.
Минимальное значение данной функции достигается в точке
<«х, «2 > € “W с координатами
«х‘ = 1612/543 «2,97, м*2 = 827/543 « 1,52.
Упражнение 5. Как найти минимум квадратичной
функции?
В найденной точке «* = <ых, «2>, являющейся решением рас-
сматриваемой многокритериальной задачи линейного программи-
рования, фх =—5,87, ф2 =16,44, фз = —1,66. Для сравнения
вычислим значения в нескольких точках, соответствующих дру-
гим принципам оптимальности.
При максимизации суммы ф* = фх + ф2 + ф3 = Зых найдем
us = <5, 0>. ;Имеем ^i(us) = —15, ф2(ы5) = 20, ф3(ы4)=10. Точка
us совпадает с точкой и3, найденной при оптимизации только
3-й функции.
Вычислим чебышевскую точку для системы линейных урав-
нений
Ух («х, м2) =—Змх + 2«2—12 = 0,
V2(«x, ы2) = 4мх + 3«2—24 = 0,
У3(«х> «2) = 2ых—5«2—10 = 0
при В соответствии с (25) и (26) чебышевская точка опре-
деляется из условия минимума на 41 функции
V («1, «2) = max | Vt (ult и2) |.
i
Получаем точку ыс = <мх, ы2>:
«х = 82/54 « 1,52, «с2 = 518/378 « 1,37. .
В точке ис имеем
Фх(«<?) = —1,82, ф2 («с)= 10,19, ф3(ы<?) = —3,81.
Полученные результаты сведены в табл. 1. Приведенные в ней
данные позволяют провести сравнительный анализ разных реше-
248
ГЛ. 2. ДИСКРЕТНЫЕ МНОГОКРИТЕРИАЛЬНЫЕ ЗАДАЧИ
Таблица I
Условия задачи; линейные формы и ограничения Точка и - Условия поиска и Значе- ние Фх («) Значе- ние Фг (и) Значе- ние Фз («)
ф1 = —Зи± -р 2и% О о II II 'з* "а тах(—3«х4-2«г) 12 18 -30
ф2^= -р 3^2 фз = 2^1 5«2 СО 11 II «гЧ coei а а max (4«x-|-3u8) —1 24 —14
- ю о II II Мгч eow а а max(2«x—5«2) —15 20 10
——3^2 ”Ь 18 Ssj 0 —2^1—#2 “Ь10 0 II II О СЛ тахСфх+фа+ф,) -15 20 10
«1 0 #2 0 «1 = 1,52 «2=1,37 min V У(«)=тах|ф;—ф®| —1,82 10,19 —3,81
ь- сч сл «о сч II .11 *а *а min R (и) /?(«) = (фх-12)а+ + (Фа-24)2+ (ф3-10)а -5,87 16,44 —1,66
ний многокритериальной задачи линейного программирования и
выбрать среди них наилучшее.
Итак, решение многокритериальной задачи линейного про-
граммирования зависит от используемого принципа оптималь-
ности и может быть найдено на основе свойств соответствующих
функций выбора и однокритериальных задач математического
программирования.
Литература. [19, 46, 60, 86, 101, 120, 126].
Г л а в а 2
ДИСКРЕТНЫЕ МНОГОКРИТЕРИАЛЬНЫЕ ЗАДАЧИ
В главе рассмотрены многокритериальные задачи, в которых
управление представимо в виде набора частных управлений,
а доход от управления является суммой доходов от частных
управлений. Показано, что общие результаты § 1.1 позволяют
единообразно сводить многокритериальную задачу к однокрите-
риальной. В § 1 рассмотрена однокритериальная задача опта-
§1. ЗАДАЧА С ДИСКРЕТНЫМ ВРЕМЕНЕМ
249
мального управления с дискретным временем; [сформулирован
принцип Веллмана. В § 2 сформулирован многокритериальный
аналог принципа Веллмана. В § 3 рассмотрена задача независи-
мого выбора; в § 4—задача конструирования.
§ 1. Задача с дискретным временем
; Пусть xe, xlt ...,хп—состояния системы X такие, что
Хо~С, х1 = Т (х0), ..., хп = Т {xn—l). (1)
• Это значит, что на множестве состояний системы X действует
преобразование Т; в начальный момент t — О система находилась
в состоянии хо = х(О) = с, в момент t=l система находится
в состоянии ххвТ(х0) и т. д. Динамический процесс, описыва-
емый преобразованием (1), является неуправляемым. Для управ-
* ляемого процесса необходимо иметь возможность на каждом
шаге осуществлять не единственное преобразование Т (хк), а одно
, из множества преобразований {Т1(хк), ..., Тг(хк)}. Удобно счи-
тать, что конкретный вид преобразования определяется^ парамет-
1 ром ик, который на &-м шаге (в Л-й момент) может принимать
,J одно значение из множества значений Параметр ик будем
называть управлением, а ^—множеством допустимых управлений
( на k-м шаге. Для управляемого процесса последовательность (I)
будет иметь вид
\ хк+1 = Т(хк>ик), uk€Vk, k = 0, п — 1, „
i хо = х(О) = с. ' f
f Доход за один шаг зависит от состояния процесса в начале шага
! и примененного на этом шаге управления:
Qk — Q(xk> uk)> (3)
i За критерий качества управления будем принимать полный доход
за п шагов процесса:
/1—1
Q й^), (4)
k~0
। где и—последовательность управлений, & = <и0, .
Задача оптимального управления с дискретным временем для
• n-шагового процесса состоит в нахождении такой последователь-
ности управлений uQ, ulf ..un_lf при которой доход и)
будет максимальным. Управление u*=<j/q , , ..., назы-
вается Хц-оптимальным, если для любого другого управления
и^Щ
*^«(•^0, (*о, И*). (5)
250 ГЛ- 2- ДИСКРЕТНЫЕ МНОГОКРИТЕРИАЛЬНЫЕ ЗАДАЧИ |
1
Для нахождения оптимальных управлений воспользуемся •
принципом Веллмана. Суть этого принципа состоит в том, что,
каковы бы ни были начальное состояние х0 и начальное управ-
ление и0, последующее управление должно быть оптимальным 1
относительно состояния, являющегося результатом применения
начального управления.
Пусть = , Ui, ..., Un-!>—х0-оптимальное управление.
Тогда управление = , ..., по принципу Веллмана
^-оптимально (напомним, что Т (х0, и0) = х1).
Принцип Веллмана позволяет упростить нахождение опти-
мальных стратегий. Действительно, пусть |%. | = £z (<?Zz—множе-
ство управлений на i-м шаге). Тогда | |%| и поиск опта-
1-0
п—1 1
мальных стратегий полным перебором требует просмотра & = Ц kt
i = Q I
управлений. Воспользуемся принципом Веллмана. Пусть 1
У и •>У1—все состояния, из которых возможен переход за один
шаг в конечное состояние хп. Обозначим через и1, опти-
мальные управления, переводящие х0 за п—1 шаг в уи
соответственно, а через (х0, и1), ..., /„_! (х0, и1)—получаемые
при этом доходы. Тогда оптимальное управление, переводящее
начальное состояние х0 в конечное состояние [хп, имеет [вид
и* — <,иа, где ил находится из условия ” ь |
d €'Argmax [J„_i(x0, max Q (ys, «)], J(6)
se{i,.... 1}
в котором (s=l, I)—множество управлений, переводящих
ys в Un-i определяется из условия
Un-i € Argmax Q (if, и). (7)
«ti
Таким! образом, задача ^нахождения оптимальной стратегии 4
за п шагов сводится к I аналогичным (п—1)-шаговым задачам.
Число перебираемых вариантов управлений при этом уменьшается,
так как управление на последнем шаге выбирается в соответст-
вии с (7), а остальные управления из уже не рассматри-
ваются
§ 2. Многокритериальная задача^с дискретным временем
Рассмотрим обобщение задачи оптимального управления на
случай, когда качество управления определяется не скалярной,
а векторной целевой функцией Q; соответственно, векторным
является и полный доход J„(x0, и), вычисляемый по формуле (4).
Пусть R—бинарное отношение в /n-мерном пространстве доходов.
§ 2. МНОГОКРИТЕРИАЛЬНАЯ ЗАДАЧА
251
Управление «* = <м0‘, ..., «„_!> € называется (х0, R, ^-опти-
мальным, если для любого другого управления
(х0, и) RJп (хв, и*). (8)
Принцип Веллмана, сформулированный для многокритериаль-
ной задачи по аналогии с однокритериальной, требует, чтобы
последующее управление было (х1г 7?, п— 1)-оптимальным относи-
тельно состояния^ Xi,£ являющегося результатом применения
начального управления^. Однако для произвольных отношений
R это неверно.
Пример 5. Пусть ‘U, X, Т, Q, R заданы в следующем виде:
^ = {«1, ы2, м3, и4}, Х = {х0, х,, х2},
Т (Х3, W4) = Х4, Т (Xq, ^2)==Xj, ^з)==^2э Т ^4) == "^2»
Qo (^о> 1^, Qo(xo, 1^2)= ^1 > 0>,
Qita, ы3) = <0, 2>, Q1(x1, u4) = <2, 0>,
7? = {«3, 0>, <0, 3», «3, 0>, <2, 1»,
«3, 0>, <1, 2», «0, 2>, <2, 0»}.
Рассмотрим все управления, переводящие х0 в х2. Как следует
из задания Т, их всего четыре: (ut, и3), (ult и3), (и2, и3), (и2, и3).
Каждое из этих управлений по формуле (4) приводит к доходу
J„(x0, и): <0, 3>, <2, 1>, <1, 2>, <3, 0> соответственно. Доход <3,0>
при управлении (м2, jw4) мажорирует остальные доходы. В силу
задания R единственным (х0, R, 2)-оптимальным является управ-
ление (u2, и4). Однако управление и4 не является (х1( R, ^-опти-
мальным, поскольку Q(xn ы4) = <2, 0>, Q(x1( us) = <0, 2> и из
задания R имеем <0, 2> А* <2, 0>. Таким образом, в рассмотрен-
ной задаче со специально выбранным отношением R принцип
Веллмана не выполняется.
Принцип Веллмана* для задачи управления со многими кри-
териями формулируется в виде следующей теоремы.
Теорема 1. Пусть R—отношение, инвариантное относи-
тельно переноса, и и* — <и„, ..., u^_x>— (х0, R, пооптимальнее
управление. Тогда управление и* = <.и[, ..., u«-i> является
(Т (х0, и3), R, п—\)-оптимальным.
Доказательство. В силу (4)
п— 1 п—1
Jn (-^о, ^*) = 2 ^о)+ 2 Q ^k)=
л=о fe = i
= Q(x0, «;) + /„_!(Х1( u‘) = QXxo> «о)-Мп-1(т(Хо, «о), й*). (9)
Предположим, что управление «• = <«!, ..., w«-i> не является
(Т (х0, uj), R, п—1)-оптимальным. Это^ значит, что для некото-
рого управления й = <йп ...,
Jn-i (Т (х0, и*9), и) RJn_t (Т (х0, и*2), и*). (10)
252 ГЛ. 2. ДИСКРЕТНЫЕ МНОГОКРИТЕРИАЛЬНЫЕ ЗАДАЧИ
Положим
и== 1 Wi, • •«, * 00
Из (9)—(11) и инвариантности 7? относительно переноса получаем
J„(x0, u)7?J„(x0, и9),
что противоречит (х0, R, п)-оптимальности и*. Теорема доказана.
Схема использования принципа Веллмана для нахождения всех
(х0, R, п)-оптимальных управлений близка к схеме, рассмотрен-
ной в § 1: сначала ищутся все (х, /?, 1)-оптимальные управления
для всех х£Х, затем для каждого х£Х ищутся все (х, R, 2)-
оптимальные управления и т. д.
Если интерпретировать данную задачу в терминах общей по-
становки многокритериальной задачи оптимального управления,
то здесь в качестве 91 выступает множество всех наборов
<ы0, ult и^У, в качестве ср—отображение, сопоставляющее
каждому и £91 вектор доходов <p(u) = Jn(x0, и), вычисляемый
по (4); в качестве R—заданное бинарное отношение R, по кото-
рому сравниваются доходы J„(x0, и). Таким образом, рассматри-
ваемая задача является частным случаем общей задачи и на нее
переносятся все общие результаты и понятия из § 1.1.
Заметим, что понятий общей задачи недостаточно для полного
описания данной задачи. В частности, отображение ср, определяе-
мое (4), описывается с помощью дополнительных понятий: состоя-
ний X; преобразования состояний Г; дохода за один шаг Q;
начального состояния х0. С учетом сказанного общее описание
рассматриваемой задачи принимает вид
<91, X, Т, Q, х0, Ry.
Утверждение 1. К-сверткой задачи <91, X, Т, Q, х0, Ry
является однокритериальная задача <91, X, Т, Q, х0, >>, где
доход на k-м шаге
т
«й)= S «а)- (12)
Доказательство. Рассмотрим доход 7п(х0, и) в одно-
критериальной задаче, являющейся Х-сверткой исходной. В силу
определения k-свертки и формулы (4) имеем
и) = (л, Jд(х0, u))==^\, Qk(xk>
v k=0 /
п-1 п-1
== S (^, Qk(xkf Qk(xk> (13)
k= 0 = 0
что и доказывает утверждение.
Для поиска решений задачи <% X, Т, Q, х0, 7?> можно
воспользоваться утверждениями из § 1.1. В частности, из утвержде-
ния 1, конечности и утверждения 1.4 непосредственно следует
§ 3. ЗАДАЧА НЕЗАВИСИМОГО ВЫБОРА
253
Утверждение 2. 6(^1, X, Т, Q, х0, R) непусто для
любого отделимого отношения R.
'-^Упражнение 1. Доказать утверждение 2.
!?Для поиска частных решений можно воспользоваться утвержде-
ниями 1.3 и 1 и решать (применяя принцип Веллмана или дру-
гой метод) однокритериальную задачу, являющуюся Х-сверткой
исходной, как это сделано, например, в § 5.1.
§ 3. Задача независимого выбора
Пусть предъявляется последовательность множеств ..., й„,
каждое из которых содержится в Ет. Альтернативой является
последовательность <хх, ..., х"> g й = Qj х ... х й„; х1 С й,, i = 1, п.
Пусть R—бинарное отношение, заданное на Ет. Положим
ф(х) = 2 х‘£Ет для Всех х£й. (14)
i = i
Зададим бинарное отношение на Q по формуле
xRy&q>(x) Rq>(y), х, y^Q.
Задача состоит в том, чтобы найти Йй, т. е. недоминируемые
на й по отношению R последовательности <х*, ..., хп>. Будем
называть сформулированную задачу задачей независимого выбора,
так как альтернатива в задаче представляет собой последователь-
ность элементов, каждый из которых принадлежит одному мно-
жеству й0 а включение того или иного элемента в последова-
тельность не зависит от уже имеющихся в ней элементов. Задачи
такого типа возникают в различных прикладных областях, напри-
мер в оперативном планировании, в комплектации. Отметим, что
по схеме постановки их можно отнести к более широкому классу
задач, названных задачами конструирования, одна из которых
более подробно будет рассмотрена в § 4.
Установим соответствие между сформулированной задачей
и общей многокритериальной задачей оптимального управления.
Множеством управлений ‘IL здесь является множество й; частному
управлению соответствует точка из й(-. Последовательность
х = <хх, ..., х”> точек, выбранных из каждого й(., представляет
собой управление за п шагов. Отображение <р множества управ-
лений ‘IL в пространство доходов Ет определяется формулой (14).
Отношению R в общей задаче соответствует бинарное отношение,
заданное на пространстве доходов Ет.
Таким образом, задача независимого выбора представляет
собой ^частный случай общей многокритериальной задачи опти-
мального управления <flL, ср, Ry с определенными выше пара-
метрами. Для описания данной задачи достаточно использовать
запись <й, Ry. Параметр <р здесь исключен, поскольку он во всех
254
ГЛ. 2. ДИСКРЕТНЫЕ МНОГОКРИТЕРИАЛЬНЫЕ ЗАДАЧИ
задачах такого класса имеет один и тот же вид, определяемый
формулой (14). Далее в явном виде будут указываться только
те параметры, которые изменяются в задачах рассматриваемого
класса. Исключение какого-либо параметра означает, что он за-
дан в стандартном виде для любой задачи рассматриваемого класса.
Утверждение 3. к-сверткой задачи <й, R~> является одно-
п
критериальная задача <й, >>, где Й = ЦЦ и —образ Ц при
i= 1
линейном отображении g: Em—+Et, задаваемом формулой
т
g*(x) = (15)
/ = 1
Доказательство. По определению Х-свертки для любой
последовательности % g Q доход в однокритериальной задаче имеет
вид
т
{К <₽ (*))=.2 \ [ф (*)]/•! (16)
В силу (14)^и (15) из (16) получаем
т т п
(х, ф(х))= 2 х7 [<р (%)] .= 2 2*/=
/=1 /=1 i=l
ат л л
= 22 И= 2 х‘)= 2 г(х-). (17)
<=1 / = 1 М = 1 « = 1
Таким образом, доход (X, ф(х)) в Х-свертке исходной задачи
совпадает с доходом в однокритериальной задаче при указанном
в условии утверждения множестве Q. Утверждение доказано.
Заметим, что доказательства утверждений 1 и 2 аналогичны.
Это связано с линейностью структуры доходов относительно пред-
ставления общего управления и £ в виде набора частных управ-
лений « = <«!, ..., un>.
Рассмотрим однокритериальную задачу <Q, >>. Последова-
тельность точек <zn ..., z„> на прямой является ее решением
тогда и только тогда, когда zz—максимальное число в (i=17i).
Это позволяет найти все решения однокритериальной задачи.
УтвержДения 2, 1.2, 1.3 и 1.6 позволяют сформулировать
утверждение о решениях задачи <□, /?>.
Утверждение 4. 1. Если отношение R k-отделимо, то
любое решение k-свертки исходной задачи при любом к, содержа-
щемся в двойственном конусе RR отношения R, является реше-
нием исходной задачи.
2 в слУчае конечного множества Q для существования реше-
ния задачи <&» #> достаточно отделимости отношения R.
§4. ЗАДАЧА КОНСТРУИРОВАНИЯ
255
3. В случае выпуклого Q и отношения R такого, что R%^ R,
любое решение задачи <Q, /?> может быть получено как решение
^-свертки задачи <Q, Ry при некотором
Упражнение 2. Доказать утверждение 4.
Утверждение 4 позволяет в зависимости от свойств Q ги R
найти все или некоторые решения задачи <Q, Ry.
Приведем утверждения, позволяющие определять парето-опти-
мальные (недоминируемые по отношению Р) последовательности
<х\ ..и не являющиеся непосредственными следствиями
общих утверждений из § 1.1. Обозначим через конус норма-
лей ко всевозможным опорным гиперплоскостям к Qz, проходящим
через точку xz£Qz (см. формулу (II.6.12)).
Утверждение 5. Если Г) М#= 0, то последовательность
х = <^х1, ..., хпу парето-оптимальна.
Здесь никаких ограничений на множества Qz не накладывается.
Утверждение 6. Пусть Qz выпуклы. Последовательность
х = ..., хпу парето-оптимальна тогда и только тогда, когда
п
Л Л‘=/=0. (18)
1=1
Упражнение 3. Доказать утверждения 5 и 6. (При дока-
зательстве утверждения 6 воспользоваться частью 3 утвержде-
ния 4.)
Упражнение 4. Сформулировать и доказать аналоги утверж-
дений 5 и 6 для отношения /^.порожденного конусом К. (Рас-
смотреть пересечение конусов Л£ с конусом /С*.)
§ 4. Задача конструирования
В некоторых задачах исходное множество альтернатив задается
не в явном виде, а с помощью правила построения альтернатив
из других элементов. Именно такая ситуация была рассмотрена
в предыдущем параграфе. При этом альтернативами являлись -
последовательности
х = <х1, ..., хп>€й=ПО;
i — 1
одной и той же длины п. Если для некоторых пар (i, j) пере-
сечение непусто, то под альтернативой удобно понимать
множество Х = {х\ х*} элементов xl£Em, i=l, k, обладаю-
щее свойством ______________________
Хлй,¥=0, (i=177). (19)
Положим
k Л Л п
<р(Х)= S х1 Для всех X£Q(Q), Q= U Q,-; (20)
г=1 i=i
256
ГЛ. 2. ДИСКРЕТНЫЕ МНОГОКРИТЕРИАЛЬНЫЕ ЗАДАЧИ
Q(Q)—множество^всех подмножеств й, удовлетворяющих [усло-
вию (19).-Пусть на Ет задано бинарное отношение R. Определим
на Q (й) 'бинарное отношение R по” формуле
XRY X, Y$Q(Q). (21)
Задача конструирования состоит в том, чтобы выделить“из
множества Q (й) все недоминируемые по R элементы, которые
являются подмножествами й, удовлетворяющими (19). Название
задачи связано с ее интерпретациями. Можно считать, что все
элементы -множества й£ обладают некоторым i-м свойством. Эле-
мент, принадлежащий нескольким множествам, обладает всеми
свойствами элементов этих множеств. Множество X, удовлетво-
ряющееусловию (19), обладает всеми свойствами множеств
Й(. (i = TTn).
Таким образом, множество альтернатив интерпретируется как
множество некоторых систем с одним и тем же набором свойств.
Построение ^-оптимальных альтернатив можно рассматривать как
конструирование наилучших вариантов таких систем.
Установим соответствие между сформулированной задачей
и общей многокритериальной задачей оптимального управления.
Прежде чем определить множество управлений 41, введем следующее
понятие. Последовательности х = <хх, ..., х”>, у=<у1, .... г/">СЙ
п п
назовем эквивалентными, если Х = и (х'} равно Y — и {у'}. На-
1=1 1=1
пример, последовательности
х = <х1, х1, х3>, г/ = <хх, Xs, х3>
эквивалентны в указанном смысле, так как Х={хх, х3}, У={хх, х3},
т. е. Х = У.
Введение эквивалентных последовательностей задает на й отно-
шение эквивалентности. При этом множество й разбивается на
классы эквивалентности. Сопоставим множество классов эквива-
лентности множеству управлений 41. Заметим, что когда й£ не
пересекаются, каждый класс будет состоять ровно из одной последо-
вательности, как в § 3.
Отображение <р множества управлений 41 в пространство дохо-
дов Ет определяется формулой (20). Отношению R в общей задаче
соответствует бинарное отношение, заданное на пространстве дохо-
дов Ет.
Таким образом, рассматриваемая задача конструирования пред-
ставляет собой частный случай общей многокритериальной задачи
оптимального управления <4L, <p, Ry с определенными выше пара-
метрами 41, <р и R. Для ее описания, так же как в § 3, доста-
точно использовать запись <Й, Ry. На задачу конструирования
переносятся все результаты из § 3. Специфика задачи проявляется
§4. ЗАДАЧА КОНСТРУИРОВАНИЯ 257
в ее однокритериальном варианте. ^Однокритериальный вариант
задачи конструирования^имеет следующий вид.
Заданы числовые множества (т. е. = Elt i—\, ri).
Необходимо найти числовое множество X = Ег такое, что
X П Й/¥=0[£=1Гп), (22)
2 Х|—<-тах. (23)
х еХ
Легко видеть, что при непересекающихся Qz получаем одно-
критериальную задачу независимого выбора, которая, как ука-
зывалось в § 3, имеет простое решение. В рассматриваемом случае
ситуация ^значительно сложнее. Задача (22), (23) заведомо имеет
решение. Чтобы его найти, можно просмотреть все X, удовлетво-
ряющие (22), и выбрать среди них то, которое максимизирует
2 х, т. е. выполнить последовательность некоторых однородных
хех
~ п
•операций. Поскольку Q== U й(- конечно, такая процедура позво-
1 = 1
лит найти решение.
Существует достаточно много задач, в которых для получения
решения нужно выполнить конечное число «простых» операций.
Они отличаются друг от друга минимальным числом операций,
за которое находится решение. Это число естественно назвать
сложностью задачи *).
Пусть k—число переменных задачи, S (k)—ее сложность в ука-
занном смысле. Две задачи называются полиномиально связанными,
если существуют полиномы Рг (х) и Р2 (х) такие, что
saw^), х=$4(£),
x = S1(k)
при всех k = 1, ...
Задача называется NР-полной, если она полиномиально свя-
зана с задачей коммивояжера. Эта задача состоит в определении
кратчайшего циклического маршрута, проходящего через п горо-
дов при заданных расстояниях между ними.
Утверждение 7. Задача (22), (23) является N Р-полной.
П ~
Доказательство. Занумеруем все элементы Q= и Q,-:
L = 1
аи ..., aN. Каждое из множеств характеризуется булевым век-
тором Р' = <Pi, ..., Pw>, где р* = 1 О ак € Q,. Любое X s Q также
может быть описано булевым вектором Р£ = <Р?, , Р$>. Тогда
*) Строгие определения понятий, характеризующих сложность задачи,
можно найти в [8].
258
ГЛ. 3. НЕПРЕРЫВНАЯ МНОГОКРИТЕРИАЛЬНАЯ ЗАДАЧА
задача (22), (23) запишется в виде
N ~ ____
(i=l, п), (24)
/= 1
JV ~
5J —► шах, (25)
i = 1
где (24) эквивалентно (22). Задача (24), (25) о нахождении бу ле-
вого вектора является задачей целочисленного линейного про-
граммирования (ЦЛП). Значит, эквивалентная ей задача (22), (23)
является одной из задач ЦЛП.
Рассмотрим теперь частный случай задачи (22), (23). Пусть
все числа, входящие в каждое из множеств й(. (/=1, п), равны
единице; каждый элемент а С Q входит ровно в два множества из
семейства {йп ..., й„}, |й(| = 2 (i=l, п) и й(- =#П,- (i #= /). Рас-
смотрим граф G, вершинам которого сопоставлены множества
Qt, ..., Q„. Ребро (zh Zj) входит в граф G тогда и только тогда,
когда для некоторого выполняется а^й;пЙу. Таким обра-
зом,. множество ребер графа G находится во взаимно однозначном
соответствии с множеством й. Задача (22), (23) в рассматриваемом
частном случае является задачей, о минимальном вершинном по-
крытии графа G, т. е. о нахождении минимального (по количеству
элементов) множества ребер, инцидентных каждой вершине G.
Итак, доказано, что частным случаем задачи (22), (23) является
задача о минимальном вершинном покрытии графа.
Известно, что задача о минимальном вершинном покрытии
графа и задача ЦЛП являются АР-полными. Отсюда следует, что
и задача (22), (23) является jVP-полной. Утверждение доказано.
Результат этого утверждения означает, что задача (22), (23)
эквивалентна задаче полного перебора. Однако существует ряд
частных случаев задачи (22), (23), в которых точное решение
может быть найдено непереборно. Кроме того, известны алгоритмы,
которые позволяют существенно сократить перебор при решении
задачи конструирования в однокритериальном варианте. Они осно-
ваны на использовании необходимых, а также достаточных усло-
вий оптимальности решения.
Литература. [8, 60, 66].
v
Глава 3
МНОГОКРИТЕРИАЛЬНАЯ ЗАДАЧА
С НЕПРЕРЫВНЫМ ВРЕМЕНЕМ
В главе рассмотрена многокритериальная задача с непрерыв-
ным временем, в которой доход представим в интегральном виде
(1.11). Отображение <р: сИ—+Ет зависит от системы дифферен-
§ 1. ПРИНЦИП МАКСИМУМА
259
циальных уравнений, описывающих объект. Показана возможность
использования результатов из § 1.1, относящихся к сведению
задачи к однокритериальной. В § 1 приведены необходимые поня-
тия теории оптимального управления, в § 2 дана постановка
многокритериальной задачи, а в § 3 для нее приведены необходи-
мые условия оптимальности.
§ 1. Задача с одним критерием иТпринцип максимума
Рассмотрим стандартную модель системы автоматического управ-
ления:
•4(O = fi(Xi(z)> •••. xn(t), ur(t), ..., Mr(/), t),
= , xn(t), u^t), .... ur(t), t),
•••, xn(t), u^t), ..., ur(i), t),
или, в векторном виде,
= u(t), 0, (2)
где x(t) = <ixl(t), ..., х„(0>—вектор фазовых координат,
и(/) = <«1(/), ..., иг(/)>—вектор управлений.
Предположим, что функция /(-) — </i(-), ..., известна
и имеет такую гладкость, что все необходимые производные
существуют, а рассматриваемые уравнения имеют решения. Пусть
заданы начальные условия
х(0) = х° (3)
и отрезок [О, Т] изменения времени I. Обозначим через U мно-
жество возможных значений управления. Примем, что
и С Ul<=]Er. (4)
Будем считать, что управлением может быть любая кусочно-непре-
рывная вектор-функция и (/) на отрезке [О, Т] со значениями из U.
Зададим критерий качества управления в виде
т
<р(х, и) = Д (х, и, t)dt. (5)
о
Однокритериальной задачей оптимального управления называется
задача
т
ср (х, м)=^/0(х, и, t)dt —>-max, (6)
о
x = f(x, и, f), x(0) = x°, u£U,
при указанных выше предположениях.
260
ГЛ. 3. НЕПРЕРЫВНАЯ МНОГОКРИТЕРИАЛЬНАЯ ЗАДАЧА
Положим
t
Хо (t) = $ А (X (т), и (т), т) dx. (7)
о
Тогда, очевидно,
хо(О = /о(х(О, u(t), t) (8)
при начальном условии
х,(0) = 0. (9)
Добавйм уравнение (8) к системе (1), а начальное условие (9) —
к начальным условиям (3). Таким образом, получим’каноническую
форму задачи об оптимальном управлении:
х0(Т) —>тах, (10)—
x(t) — f (х, и, t), x(0) = x°, u£U,
где f = <fa, х = <х0, xlt ха>, х° = <0, х[, ...Л4>.
Наряду с этой задачей далее потребуется задача
\ п
X CjXi (Т) —> max, (11)
i=0
x=f(x, и, t), x(0) = x®, u$U.
Задача (И) эквивалентна (10) при с0=1, с; = 0 (i > 0).
Сформулируем для задачи (11) принцип максимума Понтря-
гина. Пусть u(t)—оптимальное управление и x(t)—соответству-
ющая ему траектория в задаче (11). Тогда существует вектор-
функция ф(t) = <ф0(0, •••, Ф„(0>> которая удовлетворяет системе
уравнений
4, (0 = ~ Z 4> (0 —(г = 0?п) (12)
i=o 1
и конечным условиям
%(Л = О (j = 6Tn), (13)
такая, что при почти всех t £[0, 7]
u(t) б Argmax Н (х(1), «> Ф(0> 0> (14)
и
где
Я(х, и, ф, /)= 5ф,Л-(х, и, f). (15)
1 = 0
Принцип максимума позволяет выделить управления, которые
могут оказаться оптимальными. Для этого надо выполнить сле-
дующее:
1) записать функцию Н (х, и, ф, f) в виде (15);
2) выразить из условия (14) управление и как функцию осталь-
ных переменных:
и = и(ху ф, /); (16^
§ 1. ПРИНЦИП МАКСИМУМА 261
3) сформировать систему
= — дН/дх{, = (i = 0Tn)> 07v
= дН/дф;, X{ (0) = x° (i = 0, n);
4) подставить в систему (17) управление (16) и найти все ее
решения <%(/), ф(/)>;
5) подставить найденные функции x(Z), ф(/) в (16) и полу-
чить управление u(t).
Принцип максимума дает необходимые условия оптимальности.
Его идея состоит в сведении задачи (11) к известной краевой
задаче (17).
Прежде чем перейти к многокритериальному случаю, сформу-
лируем результат, который понадобится в дальнейшем. Рассмотрим
систему дифференциальных уравнений с начальным условиями
x=g(x, и, /), х(0) = х°. (18}
Пусть и (0—произвольная кусочно-непрерывная функция, [задан-
ная на [0, Т], и (/) g U. Рассмотрим функцию
J vk, если t£(xk—&1к, Ч),
uk(t) = < ... .л.. . . U=l, а) (19)
(«(/), если /£(Tft—eZ*, тА) *"
(здесь N, lk, ek$Ef, vk^.U-, интервалы (хк — &1к, хк) не пере-
секаются). Разность 6м (Z) = ие (Z) — и (/) |называется игольчатой
вариацией.
Пусть x(t) и хе(/)—решения системы (18) при u(t) и ме(0
соответственно. Вектор
й(Т) = Нт Х^~ХЮ (20)
называется концевой вариацией.
Заметим, что при другой функции м8(/) (т. е. при других q,
тА, vk) получим другую концевую вариацию h(T). Обозначим
множество всех концевых вариаций, соответствующих всем функ-
циям ме(0 вида (19),- через {h(T)}. (Аналогично можно опреде-
лить {h (t)} при любом t £ [0, 71].) Заметим, что предел в (20)
существует, если g(x, и, t) удовлетворяет, предположениям о свой-
ствах /(•) в задаче (6).
Утверждение 1. Множество {h(T)} представляет собой
выпуклый конус.
Доказательство. Рассмотрим функцию m8(Z) специаль-
ного вида: q=l, xk = x, lk — l, vk = v. Основой для доказательства
является
Лемма. На отрезке [т, Т] вариация h(t) удовлетворяет
системе дифференциальных уравнений
п
= U(t), t)hj(t) (i = T77t) (21)
262
ГЛ. 3. НЕПРЕРЫВНАЯ МНОГОКРИТЕРИАЛЬНАЯ ЗАДАЧА
с начальными условиями
Щ?) =1 [g (* v, т)—g (х (т),^ (т), т)]. (22)
Пусть h^t)—решение системы (21), (22) при 1=1. Очевидно,
что
hl(t) = l-h1 (0 (23)
— решение той же системы при любом I. Для доказательства
утверждения рассмотрим следующий случай. Пусть tj < т2. Поло-
жим
и,, если
«8 (0 =) ,Л
(и(0, если
( и2, если
u*(Z)=< z.x
v' I и (0, если
/€(Т1—eZi, Ti),
8/j, Tj);
Z£(t2—sZ2, т2),
Z^(t2—eZ2, т2).
Пусть Zij(T), h2(T)—концевые вариации, соответствующие и\
и Докажем, что
МП = МП+МП. (24)
где h3(T)—концевая вариация, соответствующая w|(Z):
fug(i), если t (т1 + т2)/2,
(ы|(/), если t > (Tj + т2)/2.
(25)
Подставим в (19) вместо «(/) функцию Ug(Z) и вместо w8(Z) функ-
цию «!(/). Вариацию, определенную формулой (20), обозначим
через h(T). Очевидно, что
/1з(Т) = /г1(Т)+Й(Т). (26)
Докажем теперь, что h(T) = h2(T), откуда будет следовать (24).
В силу леммы на отрезке [т2, Т] функция h2(t) удовлетворяет
системе (21) с начальными условиями
lz[g(х(т:2), v2, т2)—g(x(r2), ы(т2), т2)],
а функция h(t) удовлетворяет на том же отрезке тому же урав-
нению с начальными условиями
limZ4[g(xJ(T2), v2, т2)—g(x|(t2), и (т2), т2)].
S-* О
Так как
»е (т2) = и (т2), Птх8(т2) = х(т2),
е-> О
то получаем, что начальные условия для h2(t) и h(t) совпадают,
поэтому совпадают и решения, и /i(T) = /z2(T). Утверждение дока-
зано.
Конус из утверждения 1 называют конусом концевых вариаций.
Упражнение 1. Показать, что для доказательства утверж-
дения 1 достаточно рассмотренного случая.
§2. МНОГОКРИТЕРИАЛЬНАЯ ЗАДАЧА И ЕЕ 1-СВЕРТКА
263
§ 2. Многокритериальная задача и ее Х-свертка
Рассмотрим систему
= и, t) (i = m+\, т + п), .
х,(0) = х? (i = m+l, /n-j-n).
Значения i = 1, т будут использованы далее для критериев.
Будем считать, что u(t)£U и выполняются другие предположе-
ния из § 1. Введем т критериев вида (5):
т
Ф/(х, «)=$ u(t\ t)dt (i=l, m). (28)
о
Будем считать, как и в общей постановке в главе 1, что на про-
странстве Ет задано бинарное отношение по которому сравни-
ваются различные управления. Определение оптимальности также
аналогично данному в § 1.1.
Установим соответствие между рассматриваемой и общей зада-
чами управления.
Управлениям и £41 общей задачи соответствуют все кусочно-
непрерывные вектор-функции, определенные на отрезке [О, Т] и
принимающие значения в заданной области U пространства Ег.
Отображение ср: 4L-+Em определяется формулой (28), которая
каждому управлению и £ 41 сопоставляет m-мерный вектор
<р(«) = <Ф1 (и), фт(и)>. Вектор x(t) однозначно определяется
по u(t) из (27). Следовательно, отображение ф в данном случае
зависит от функций Д-(-) в (27) и начальных условий х°.
Отношению R в общей задаче соответствует бинарное отноше-
ние, заданное на Ет.
С учетом сказанного задачи рассматриваемого типа будем запи-
сывать в виде <U9 f, х°, 7?>. Понятия оптимального управления,
решения и другие переносятся сюда из § 1.1 без изменений. Пре-
образуем критерии, как и в однокритериальном случае, введя
новые переменные
t
xi(t)=^^fi(x(x),u(x),x)dx,xi(G)^O (29)
о
Многокритериальная задача оптимального управления с непре-
рывным временем имеет следующий вид:
Г4 (/) С <3 (Л/, Л *°, R),
xi(t) = fi(x, и, t) (i=l,
%. (0) = х°- (i = m+ 1, m + n), (30)
x.(0)^0 (/=17^),
u(t)£U (ZG[O, T]),
где 6(t/, /, x°, 7?)—общее решение задачи.
264
ГЛ. 3. НЕПРЕРЫВНАЯ МНОГОКРИТЕРИАЛЬНАЯ ЗАДАЧА
Частным решением является любое управление u*t удовлетво-
ряющее (30). Для поиска решения задачи (30) воспользуемся
общим приемом из § 1.1—переходом'к Х-свертке задачи.
Утверждение 2. К-сверткой задачи (30) является однокри-
териальная задача
3 ^iXi (Т) — max,
i = 1
Xj = fi(x, и, t) (i=l,
(i=TT^), (31)
x,(0) = x? (i = m + l,
u(t)eU.
Заметим, что задача (31) эквивалентна задаче (11), в которой
Я° = <\0» •••» 0, Х%п+1, . .., Х%п+п>,
х=<х1, ..., хт+пУ, с = У-т, 0, ..., 0>.
Утверждение 2 непосредственно следует из определения
1-свертки и соотношений (И) и (30). Оно позволяет использовать
результаты из § 1.1 для поиска решений задачи (30). В частности,
из утверждения 1.3 следует, что любое решение задачи. (31) при
%-отделимом отношении R является ^-оптимальным.
Решения задачи (31) находятся с помощью принципа макси-
мума, который для задачи (31) принимает следующий вид.
Пусть <«(/), х(0>—оптимальное управление и соответству-
ющая ему траектория в задаче (31). Тогда существует вектор-функ-
ция ф(/) = <ф1 (/), ..., фт+л(0>, которая удовлетворяет системе
уравнений
ф,- (0=— х" Ф/ (о(i=Ь m+n) <32)
с конечными условиями
Ф/ (Т) = 1,- (t = 1, /л),_ (22)
ф,-(Т) — 0 (i = m-|-l, т + п),
такая, что при почти всех t £ [0, Т]
u\t) б Argmax H(x(t), и, ф(0> 0» (34)
где
Н(х, и, ф, 0= ^ifi(x, и, t). (35)
1 = 1
Схема использования принципа максимума для решения зада-
чи (31) не отличается от рассмотренной в § 1.
§ 3. НЕОБХОДИМЫЕ УСЛОВИЯ ОПТИМАЛЬНОСТИ
265
Множество
’ D=U{<x1(T), • • • > хт+п (?)>}
(36)
концов траекторий при всех допустимых управлениях и £41 назы-
вается множеством достижимости в задаче (31).
Упражнение 2. Доказать, что множество <р (41) в задаче (30)
является проекцией множества достижимости D е Ет+п в подпро-
странство Ет, образованное первыми т координатными осями.
Заметим, что множество D для задачи (31) не зависит от век-
тора А, поскольку определяется только последними четырьмя
соотношениями из (31). В качестве следствия упражнения 2 и
утверждения 1.5 получаем
Утверждение 3. Пусть множество достижимости D
выпукло и RK<ZR- Тогда для любого u*£6(U, f, х°, R) сущест-
вует А£/<* такой, что и* является оптимальным решением яа“
дачи (31) при А = Х.
§ 3. Необходимые условия оптимальности
Как было показано в § 2, утверждения из § 1.1 позволяют
находить частные решения задачи (30) для A-отделимых отноше-
ний R, а также общее решение 6 (U, f, х°, R) при Rk<R и неко-
торых предположениях относительно множества достижимости D.
Результаты, рассматриваемые в данном параграфе, не следуют из
результатов § 1.1.
Получим необходимые условия /^-оптимальности для задачи (30).
Пусть u*£6(U, f, х°, R) и R = RK, где К—конус. При всех
игольчатых вариациях вида (19) в силу утверждения 1 мно-
жество {h(T)} концевых вариаций представляет собой конус в про-
странстве Ет+п. Проекция этого конуса на Ет также является
конусом; обозначим его через L. Поскольку и* /^-оптимально,
то Lf]Int/<= 0. Поэтому существует А£/<* такой, что для
всех 21 СL,
(M*i)<0, (37)
(А, га)>0, ' (38)
откуда
f=l
ft;(T)Az^0 (А,- = 0 при i > т). (39)
i=i
Вернемся к задаче (31). Запишем для нее выражения типа (21),
(22) при этом же и* и соответствующем ему х*:
т + п
hJ (i = 1- « + t € [т, Т]), (40)
hi (т) = I [Л (х* (т), v, т)—Д- (х* (г), и* (т), т)]. (41)
9 И. М. Макаров и др.
266
ГЛ. 3. НЕПРЕРЫВНАЯ МНОГОКРИТЕРИАЛЬНАЯ ЗАДАЧА
Пусть ф = <фп фт+п>—любое решение (32), h = <h1, ...
•••> hm+n>—решение (40), (41). Найдем производную
т + п
37 (Ф> А)=(ф» М + (ф> й)= Ц (ф/Л/+ф/й/) =
/ = 1
т + п Г т+п т + п ~
-S -
/-1 L s= 1 J s= 1 _
т + п т + п т + п т + п
=-Е L*a£+£ 5>а^-о. (42>
/=1 5=1 J /=1 5=1 5
Выберем теперь конечные условия ф (Т) = <0, ..., 1, ..., 0>
i
и соответствующее решение (32) обозначим через ф^ = <ф;> ь ...
•••> Ф1, m+n>- В силу формулы (42) получим
(Ф'(т),
и в силу начального условия (41) имеем
л< (Т) =1 № (т). f (** (т)> v, т))—(ф'‘ (т), f (х* (т), и* (т), т))]. (43)
Напомним, что и* — /^-оптимальное решение задачи (30). Поло-
жим Z = 1 и подставим (43) в (39). При этом получим
2 [(Ф'(т). v, т))—(ф'(т), /(х*(т), «*(т), т))]А.( <0. (44)
1 = 1
Учитывая выражение (35), из (44) получим
2 [Я(х*(т), v, ф'’(т), т)—//(х* (т), и*(т), фг(т), т)]Х,,<0,
«=1 _______________________________________ (45)
\ = 0 при i — т + п.
Учитывая линейность (32) и (35) по ф, конечные условия (33)
т + п
и положив ф— S ^гФ'» из (45) имеем
1=1
Н (х* (т), v, ф, т)—Н(х* (т), и* (т), ф, т) 0.
В силу произвольности v U это значит, что
и* (г) Argmax Н (х* (т), и, ф (т), т) (46)
во всех точках непрерывности и* (t). Таким образом, взяв произ-
вольное /^^оптимальное решение и* задачи (30), доказали, что
для пары <«*, х*> существует решение ф системы (32) с конеч-
ными условиями (33), для которого выполнено (46), совпадающее
с (34). Тем самым доказана
§ 1. ОБЩИЕ ПОНЯТИЯ
267
Теорема 1. Пусть u*£0(U, f, х°, RK). Тогда существует
1g Д’* такой, что и* удовлетворяет необходимым условиям опти-
мальности в ^-свертке исходной задачи <JJ, f, х°, RK>.
В силу теоремы 1 решение многокритериальной задачи (30)
оптимального управления с непрерывным временем, в которой
отношение R порождено конусом К, сводится к однокритериаль-
ной параметрической задаче, в которой параметр X пробегает мно-
жество значений {lg/<*, |1|=1}.
В силу утверждения 1.1 аналогичные необходимые условия
справедливы для любого отношения R такого, что RK< R. В слу-
чае, когда задача (31) при любом 1g К* имеет единственное реше-
ние, каждое решение задачи (30) при RK<,R является решением
для 1-свертки исходной задачи при некотором 1g/С*.
Литература. [80, 91, 98].
Глава 4
МАРКОВСКИЕ МОДЕЛИ ПРИНЯТИЯ РЕШЕНИЙ
Одним из основных инструментов моделирования стохастичес-
ких систем являются марковские цепи. В главе поставлены и
исследованы многокритериальные задачи оптимального управле-
ния для систем, моделируемых марковскими цепями. В § 1 даны
необходимые понятия теории марковских цепей; в § 2 введено-
понятие управляемых марковских цепей с векторными доходами;
в § 3 рассмотрены свойства оптимальных управлений (стратегий);
в § 4—многокритериальное обобщение задачи об оптимальной
остановке. В § 5 поставлена задача двухуровневой оптимизации
марковских цепей с векторными доходами.
§, 1. Общие понятия
Пусть некоторая система (частица, объект) может находиться
в каждый момент времени / = 0, 1, ... в одном из состояний,
образующих конечное множество 3 = {1, ..., N}. Говорят, что
поведение системы описывается цепью Маркова (однородной) с
переходными вероятностями /?<7, если через единицу времени после
того, как система находилась в состоянии i g S, с вероятностью
Pij она оказывается в состоянии j g S независимо от того, когда
и каким путем она попала в состояние i. Если зависит от
момента времени t, в который осуществляется переход, то говорят
о неоднородной цепи Маркова. Матрицу Р — (р^) называют мат-
рицей переходов или переходных вероятностей.
Пример 1. Завод выпускает телевизоры определенного типа.
В зависимости от того, находит ли данный тип телевизора спрос
у населения, завод в конце каждого года может находиться в
одном из состояний: состояние 1—спрос есть, состояние 2—спроса
9* И. М. Макаров и др.
268
ГЛ. 4. МАРКОВСКИЕ МОДЕЛИ ПРИНЯТИЯ РЕШЕНИЙ
нет. Пусть вероятность сохранить состояние 1 в следующем году
с учетом возможного изменения спроса равна 4/5, а вероятность
изменить состояние 2 с учетом мероприятий по улучшению
выпускаемой модели равна 3/5. Тогда процесс производства на
данном заводе можно описать цепью Маркова с матрицей переходов
р _ /4/5 1/5\
<3/5 2/5/
Пример 2. Рассмотрим одномерное случайное блуждание час-
тицы на отрезке с поглощением на концах (рис. 1). Из состоя-
ний 1—4 частица с вероятностью 1/2 переходит в ближайшую
« j 4 J
Рис. 1.
слева или справа точку, а попав в'состояния 0 или 5, остается
там навсегда. В этом случае поведение частицы можно описать
цепью Маркова с матрицей переходов
( 1 0 0 0 0 0 \
1/2 0 1/2 О О ОД
О 1/2 0 1/2 0 01
0 0 1/2 0 1/2 0 •
0 0 0 1/2 0 1/2 /
0 0 0 0 0 1 /
В рассмотренных примерах поведение системы полностью-опре-
деляется матрицей переходных, вероятностей Р.
Усложним ситуацию, введя возможность управления цепью
Маркова.
Пример 3. Завод по изготовлению телевизоров, находясь в
состоянии 1, может увеличить спрос путем организации рекламы.
Это требует добавочных затрат и уменьшает доход. В состоянии
2 завод может увеличить вероятность перехода в состояние I
путем увеличения затратна исследования. Выделим две стратегии.
Первая состоит в отказе от затрат на рекламу и исследования,
а вторая—в согласии на них. Пусть матрицы переходных вероят-
ностей и матрицы доходов для данных стратегий имеют вид
, _ /0,5 0,5\ р /9 3\
1 — \0,4 0,6j ’ \3 — 1) '
/0,8 0,2\ „ /4 4\
2 \0,7 0,3/ ’ Л‘2— \1 —19/
В рассмотренной ситуации имеет место управляемая цепь Мар-
кова. Управление соответствует выбору стратегии.
Пусть каждому состоянию i£S = {l, ..., /V) соответствует ко-
нечное множество АД решений (или альтернатив), элементы которого
обозначим номерами 1, Пространством стратегий Л назы-
вается прямое произведение множеств решений /С = /<1х .. • xKn-
§ 1. ОБЩИЕ ПОНЯТИЯ
269
Пусть в i-м состоянии имеется не одно, a ki множеств пере-
ходных вероятностей {р1ц}, 1=1,1^. При | ! = 1 имеем рассмот-
ренную ранее ситуацию неуправляемой цепи Маркова.
Если система находится в состоянии i£S и принимается ре-
шение то
она получает доход г?;
ее состояние в следующий момент времени определяется вероят-
ностью где pf;—вероятность того, что система из состояния
i£S при выборе решения перейдет в состояние j£S.
Таким образом, смысл Л-го решения в f-м состоянии заклю-
чается в выборе одного набора переходных вероятностей из
/Q возможных. Предполагается, что доход ограничен при всех
i^S и Кроме того,
при I, jes,
/=1
Управляемой цепью Маркова называется конструкция, зада-
ваемая параметрами </С, Р, г>, где К—решения, Р—вероятности
переходов, г—доходы. Доход, полученный за несколько шагов,
является случайной величиной, зависящей от начального состоя-
ния и принимаемых в каждый момент времени решений.
Назовем решение, принимаемое в. конкретный момент, частным
управлением. Тогда управление есть последовательность решений
в моменты п= 1, 2, ... Качество управления можно оценить сред-
ним суммарным доходом (при конечном времени) или среднем дохо-
дом в единицу времени (при бесконечном времени).
Пусть
/ = <А, ..., £V>€K. (1)
Стратегией л называется последовательность решений
я = (Л» fa • • • > fn* • • •)>
где fn—вектор вида (1), i-я компонента которого, обозначаемая
через fn(i), является решением, принимаемым в состоянии i£S
в момент п. Другими словами, задание стратегии означает пол-
ное описание в каждый момент времени /=1, 2, ..., и, ...
конкретных решений, которые должны были бы приниматься в
i-м состоянии (i = l, N), если бы система находилась в нем в
рассматриваемый момент.
Стратегия (/, ..., f, ...) обозначается через f°° и назы-
вается стационарной. Стратегия л = (/ь /2, ...) называется мар-
ковской, если решение fn, принимаемое в каждом конкретном сос-
тоянии, не зависит от предшествующих состояний и принимавшихся
в них решений. В случае марковской стратегии решения fn могут
зависеть только от момента времени п.
Обозначим произвольную конечную часть стратегии через
Лл = (Л, fn)- Пусть зафиксированы произвольная стратегия
270
ГЛ. 4. МАРКОВСКИЕ МОДЕЛИ ПРИНЯТИЯ РЕШЕНИЙ
P = P(fn) =
я = (А, А, • • •, fw, • • •) и некоторый момент времени п. Если в этот
момент система находилась' в состоянии i £ S, то в следующий
(п + 1)-й момент времени она будет находиться в состоянии j£S
с вероятностью pkih где k=*fn(i). Тогда матрица переходных ве-
роятностей в момент п имеет вид
"11 • • • PtN \
Dfn (2) Dfn (2) \
Р21 • • * | (2)
л-?’/
Таким образом, при фиксированной стратегии л получаем цепь
Маркова с матрицами перехода Р (n) = Р (fn), п = 1, 2, ...
Упражнение 1. Доказать, что при стационарной стратегии
я определенная указанным образом марковская цепь является
однородной.
При фиксированной стратегии л = (/ъ /2, ...) вероятность пе-
рехода за п шагов из i-ro состояния (в первый момент) в /-е (в
момент n-Н) определяется матрицей
Рп(ял) = Р(Л)Р(/8).. .P(f„). (3)
Вычислим доход в момент п. Если при этом система нахо-
дится в /-м состоянии, то было принято решение fn(j) и на и-м
шаге получен доход Положим
^(/п) = <^(1). .... 4и(Л,)>. (4)
С учетом (4) получаем, что доход в момент п определяется век-
тором
Pn-A^r{fn), (5)
причем его i-я компонента соответствует f-му начальному состоя-
нию. Действительно, ья компонента вектора (5) равна
(6)
/ = I
где р/"”1’—вероятность попадания из i-ro состояния в j-e в мо-
мент п; г?п</)—соответствующий доход.
Тем самым установлено, что вектор иГ(л) суммарных средних
доходов, полученных до любого момента п включительно, для
любой стратегии n = ...) равен
П-1
«Г(л)= Р,-(л)г(Л+1), (7)
1 = 0
где Р0(л) —Е, а Е—единичная матрица. Действительно, доход в
§ 1. ОБЩИЕ понятия
271
момент и=1 равен г (/\) = Ег (/\). Положим
Г (л) = Пт inf "Г (л)/п. (8)
п -> 00
Заметим, что ЛГ (л) = ВГ (вл), где л = (/ъ ..., fn, ...), вл =
Стратегия л*, максимизирующая Г (л), т. е. удовлетворяющая
векторному покомпонентному неравенству
Г (л*) > Г (л) (9)
при всех л, называется оптимальной (для бесконечного времени).
Стратегия Лл* = (/^, /„), удовлетворяющая векторному нера-
венству
"Г (вл*) > "Г (Лл») (10)
при всех Лл = (/i, ...,/„), называется оптимальной (для времени п).
Пользуясь понятием отношения Парето, неравенства (9) и (10)
можно записать в виде
Г(л*)РГ(л), ВГ (вл*) РВГ (вл).
Заметим, что нижний предел в формуле (8) определяется по-
координатно. Время функционирования реальной системы не мо-
жет быть бесконечным, но может быть весьма большим. Поэтому
формула (8) выражает гарантированный результат: в какой бы
момент система ни остановилась, накопленный к этому моменту
средний доход в единицу времени будет не меньше, чем Г (л).
Пример 4. Пусть S = {1}, ./< = {1, 2}. При выборе решения
1 доход равен 1, при выборе решения 2—равен 0. Рассмотрим
следующую стратегию:
л —(1, 2, 1, 1, 1, 2...2, 1, ..., 1, 2, ..., 2, ...,.....).
"б ' *24 ' 12 0
Легко видеть, что у числовой последовательности •-= "Г (л)/п
(n = 1, 2, ...) множество предельных точек совпадает с отрезком
[0, 1], откуда
lim sup ВГ (л)/п = 1, lim inf ”Г (л)/п = 0,
Л->СЮ П->00
т. е. в рассматриваемом случае нельзя гарантировать доход больше
нуля.
Представляет интерес вопрос о существовании, свойствах и
способах нахождения оптимальных стратегий.
Утверждение 1. Для бесконечного времени существует опти-
мальная стационарная стратегия.
Утверждение 2. Для конечного времени существует оп-
тимальная марковская стратегия.
Таким образом, решение (при бесконечном времени) зависит
только от состояния, в котором находится система, и не зависит
ни от момента времени, ни от всей предыдущей траектории
ГЛ. 4. МАРКОВСКИЕ МОДЕЛИ ПРИНЯТИЯ РЕШЕНИЙ
272
(последовательности состояний и принятых решений). В случае ко-
нечного времени оптимальная стратегия является марковской, т. е.
может зависеть еще и от момента времени принятия решения.
Поясним вычисление среднего дохода Г (л) на примере.
Пример 5. Пусть имеется машина (станок), которая обслу-
живается периодически один раз в час. В каждый момент она
может находится в одном из двух состояний: рабочем (состояние 1)
и нерабочем (состояние 2). Если машина на некотором шаге про-
работала непрерывно 1 час, то доход равен 3 рублям. При этом
вероятность остаться на следующем шаге в состоянии 1 равна
0,7, а вероятность перейти в состояние 2 равна 0,3. Если машина
отказала на некотором шаге, то ее можно отремонтировать двумя
способами. Первый является ускоренным, требует затрат в 2 рубля
(доход равен —2) и обеспечивает переход в состояние 1 с вероят-
ностью 0,6. Второй, обычный способ требует затрат в 1 рубль и
обеспечивает переход в состояние 1 с вероятностью 0,4.
В рассматриваемом случае -1, |/<2| =2, т. е. /<! = {!},
Т'С2 = {1, 2}; остальные параметры таковы:
Рп = 0,7, р}2 = 0,3, /} = 3,
Ph = 0,6, ph = 0,4, r| = —2, (11)
Ph = 0,4, p22 = 0,6, r| = —1.
Положим f1 = < 1,1 >, f2 — < 1,2> и определим по формуле (2) Р (fx) и
«) ₽ <«=(":« м); <12)
по формуле (4) получим
г(Г) = <3, —2>, г(Г) = <3, -1>. (13)
Рассмотрим все четыре стратегии длины
%=(№)>
и определим по формулам (3) и (7) доход для каждой. из них.
Имеем
•Г(>Л1) = £г(/-) + Р(Л) r(f‘) =
2ГСлг) = Ег(Н + Р(/1)г(/г) =
= <3; -2> + (о’(б ол) (-= 2> + <1-8’ 1>4>=<4,8,— 0,6>,
2Г(2л3)=Ег(Н+Р(р)г(/1) =
= <3; J.’eXJH3-’ -1> + <1,5;0> = <4,5;-1>,
2Г (2Л4) = Ег (р) + Р(/2) г (Л) =
= <3; -Ч>+ (J) =<3; -1> + <1,8; 0,6> = <4,8; -0,4>.
§2. ЦЕПИ МАРКОВА С ВЕКТОРНЫМИ ДОХОДАМИ
273
Проведенные вычисления показывают, что на коне/шом времени
(до момента 2 включительно) оптимальной является стационарная
стратегия (f2, /2).
Принцип оптимальности Веллмана для управляемых цепей Мар-
кова имеет следующую формулировку. Пусть "л*==(Л, ..fn) —
оптимальная стратегия. Тогда стратегия «~1л* = (/2,
также является оптимальной. Получаем рекуррентное соотношение
N 1
л+1Г,- (л*) = гпах Г?+X Р?/"Г/Ю . (14)
и е Kj L i=i J
справедливое для всех i £ S и любого /ц>1, где
°Г((л*) = 0 (V/£S). (15)
Соотношения (14) и (15) позволяют находить оптимальную стратегию
(для конечного времени).
Упражнение2*.В цепи примера 3 доходы зависели не только
от i-ro состояния, в котором находится система, но и от /-го
состояния, в которое совершается переход, т. е. рассматривались,
не векторы /•/, а матрицы Rk= (rfy. Доказать, что задача нахож-
дения оптимальной стратегии в случае задания доходов матрицами
сводится к такой же задаче при задании доходов векторами.
У пражнениеЗ. Найти оптимальные стратегии управления це-
пями из примеров 3 и 5 при п = 3. (Воспользоваться^ формулами
(14), (15).)
§ 2. Управляемые цепи Маркова с векторными доходами
В ряде случаев доход (или штраф) системы при выборе решения
нельзя выразить одним числом. Примером могут служить ситуации,
возникающие при разрешении конфликтов в вычислительных сис-
темах, где важно не только общее время ожидания, но и времена
ожидания каждого ресурса в отдельности.
Итак, примем, что доходы г? являются не числами, а векторами:
d=<rHi), d(2), ..../•?(«)>• (16)
Зафиксируем q £ {1, ..., т} и рассмотрим управляемую марков-
скую цепь с множествами решений вероятностями переходов
рц и доходами г? = Г/(</). Для любой стратегии л = (/1, /2, ...)
можно определить вектор средних доходов за п шагов ЛГ« (л) и
вектор средних доходов за единицу времени Г® (л). Учитывая, что
лГ«(л) if Г? (л)—N-мерные векторы, i-я координата которых со-
ответствует доходу, полученному при i-м начальном состоянии,
имеем
ЛГ? (л) = <лП(л), ..., лГ^(л)>,
Г».(я) = <Г?(л), .... П(л)>, (17)
Г j (л) = li.n inf лГ?(п)/п.
274
ГЛ. 4. МАРКОВСКИЕ МОДЕЛИ ПРИНЯТИЯ РЕШЕНИЙ
Средним векторным доходом при начальном состоянии i и стратегии
л называется вектор
»Г'(л) = <»Г}(л), вГ?*(л)> (18)
(доход за п шагов), или вектор
Г'(л) = <Г£(л), .... 17(л)> (19)
(доход за бесконечное время), где ”1\в(л) и Г? (л) определяются
формулой (17).
Установим соответствие между рассматриваемой и общей зада-
чами управления отдельно для случая конечного и бесконечного
времени.
Случай А. Конечное время. Управлениям ЭД общей задачи в
данном случае соответствуют стратегии "л = (flt ..., f„), где
fiGK — KiX • • • хЛдг. При этом множество ЭД конечно, поскольку
конечны множества
Отображение <р: ЭД -+EmN определяется следующим образом: по
формулам (17) и (18) вычисляется m-мерный векторный доход
"Г1 (л), который образует первые т компонент вектора <р (и);
следующие т компонент (от (т + 1)-й до 2/п-й) вектора <р(и)
образуют т компонент вектора ”Г2 (л) и т. д., вплоть до вГл(л).
Отношению R соответствует бинарное отношение, задаваемое
на Emff формулой
xRy#(3ieS) [x'Ry1], (20)
где R—заранее заданное отношение на Ет,а a1...
..., ат1>—проекция вектора a£EmN на i-e подпространство Ет.
Чтобы указать параметры данного класса задач, будем писать
<К, Р, г, R, п>. Здесь К—пространство стратегий; Р—набор
переходных вероятностей; г—векторы доходов; R—бинарное от-
ношение на £т; п—время. Понятия оптимального управления, ре-
шения и другие переносятся в данный раздел из § 1.1.
Дадим эквивалентное определение оптимальности в терминах
отношения R. Стратегия л* называется ^-оптимальной, если для
любой другой стратегии л
вГ'(л) £вГ'(л*) (г = Т7"У). (21)
В дальнейшем будем пользоваться этим определением и обоз-
начать отношение R через R.
Утверждение 3. ^сверткой задачи (К, Р, г, R, п> является
однокритериальная задача <.К, Р, р, >, п>, где
rf-SdOA/ (i€S, (22)
/=1
Доказательство. В однокритериальной постановке доход
представляет собой вектор размерности N, каждая компонента
§2. ЦЕПИ МАРКОВА С ВЕКТОРНЫМИ ДОХОДАМИ
275
которого соответствует одному из N начальных состояний. Поэ-
тому свертка (X, <р) здесь понимается как вектор, i-я компонента
которого равна (X, <р7). Из формул (18), (17), (7) и (22) непосред-
ственно получаем
п-1 / т \
(X, ’Р(Л))=2Л(Л) 2 хЛ‘.(/)(/1+1) ,
i=0 \/=1 '
что доказывает утверждение.
Из утверждений 3, 2, 1.6 и конечности множества 41* мар-
ковских стратегий следует
Теорема 1. В любой задаче <.К, Р, г, R, п> с отделимым
отношением R существуют марковские R-оптимальные стратегии.
Способ поиска 7?-оптимальных стратегий л£б(К, Р, г, R, п)
для Х-отделимых отношений R основан на сведении исходной за-
дачи к однокритериальной и использовании имеющихся для нее
алгоритмов.
Случай Б. Бесконечное время. Управлениям и ^41 в данном
случае соответствуют стратегии n = (fu f2, ..., fn,...), где fj^K.
Множество 4L здесь бесконечно. Отображения <р: 41 -+EmN опре-
деляются, как в случае А. Чтобы указать параметры данного
класса задач, будем писать <К, Р, г, R>, где смысл параметров
тот же, что и ранее.
Главная особенность данной задачи состоит в том, что доход
в ней непредставим ни в одном из видов (1.9) — (1.11) (§ 1.3)
из-за нелинейности операции взятия нижнего предела. Поэтому
для нее не удается получить результат, аналогичный утвержде-
нию 3.
Основным фактором, позволяющим доказать существование ре-
шений у задачи <К, Р, г, R>, является
Утверждение 4. Для любой стратегии л, любого началь-
ного состояния i С S и любого вектора X £ £+
(X, Г'(л))<Г,.(л), (23)
где fz (п)—-средний доход за единицу времени для задачи <К, Р,
р, >>, в которой р определяется формулой (22).
Доказательство. Перепишем (8) с учетом (22):
Г (л) = lim inf nf (л)/п = lim inf ( 2 ХввГ« (л) ]ln —
\<7=1 /I
= lim inf 2 X, (ПГ« (л)/п)>
я->со <7=1
т т
> 2 X, lim inf ПГ? (л)/л = 2 \ Г"7 (л) • (24)
<7=1 п->а> <7=1
Неравенство в (24) справедливо в силу того, что Х^£^. Каждая
компонента векторного неравенства (24) записывается в виде (23).
Утверждение доказано.
276
ГЛ. 4. МАРКОВСКИЕ МОДЕЛИ ПРИНЯТИЯ РЕШЕНИЙ
Утверждение 5. Для любой стационарной стратегии л*
неравенство в (23) обращается в равенство.
Доказательство. В силу формулы (3) и определения стра-
тегии л имеем
(л‘) = Р (/)... Р(П=Р“ (fl. (25)
В силу (25) и (7) получаем
п-\ /п-\ \
"Г(л*) = X P'(fl/-(A=( S Р' НА, (26)
откуда в силу (8) и того, что для любой стохастической матрицы
существует
п- 1
lim 2 Р1 In,
п-+из i=0
получаем
Г (л*) = lim ПГ (л*)/п. (27)
п -> 00
Следовательно, нижний предел в (8) для стационарных стратегий
можно заменить на предел. В силу того, что
lim ax„ + pz/„ = alim xn4-piim^„,
n->ao n ->ao л->со
из (24) для стационарных л* получаем
Г,(л*) = (Х, Г'(л*)) (/=ГГдГ). (28)
Утверждение доказано.
Заметим теперь, что для рассматриваемой задачи <Х, Р, г, Ry
можно найти Х-свертку в виде
tn
(К Ф)= 2W (29)
17 = 1
Положим И*—множество всех стационарных стратегий.
Утверждение 6. Для любого выполнено
^‘ПбСМ, (X, <р), »#=0.
Доказательство. Предположим противное. Это значит,
что найдутся i £ S и нестационарная стратегия л, для которых
шах (А., Г‘(л*))<(А, Г'(л)). (30)
<11*
В силу утверждений 4 и 5 из (30) следует, что
max Г,- (л*) < Г,- (л), (31)
где й(л) —средний доход в однокритериальной задаче < /С, Р,
р,> > с функцией р вида (22). Последнее неравенство противоре-
чит утверждению 1. Утверждение доказано.
S2. ЦЕПИ МАРКОВА С ВЕКТОРНЫМИ ДОХОДАМИ 277
Из утверждений 6 и 1.6 следует
Теорема 2. В любой'задаче (К, Р, г, R> с неотрицательно
отделимым отношением R существуют стационарные R-опти-
мальные стратегии.
Способ поиска R-оптимальных стратегий п£б(К, Р, г, R),
как и в случае конечного времени, основан на сведении к одно-
критериальной задаче.
Условия на отношение R в формулировках теорем 1 и 2 га-
рантируют существование решения (и даже решения определенного
типа); отсутствие требований на R может привести к пустому
множеству 6 (К, Р, г, R).
Пример 6. Рассмотрим цепь Маркова из примера 4. Поло-
жим ^ = <1, 0>, г2 = <0, 1>. Пусть п—2. При стратегии
=(1, 1) получим 2Г(лх) = <2, 0>. При стратегиях л2 = (1, 2) и
л3 = (2, 1) имеем 2Г (л2) = *Г (л3) = <1, 1>; при стратегии л4=(2, 2)
имеем 2Г(л4) = <0, 2>. Пусть на £3 задано отношение R следую-
щего вида: xRy тогда и только тогда, когда хотя бы одна коор-
дината х больше, чем у у. Тогда можно записать
(2Г (л,)) R (2Г (л2)), (2Г (лх)) R (2Г (л,)),
(2Г (лх)) R (2Г (л4)), (2Г (л4)) R (2Г (лх)).«
Следовательно, оптимальных стратегий нет и множество 6 (Л, Р,
г, R, 2) пусто. .В примере 6 Q (R, Р, г, R, п) оказывается пус-
тым в силу неацикличности отношения R. Однако это может
произойти и при ацикличном отношении R.
Пример 7. Пусть отношение R в Ег задано следующим
образом: /? = {«2; 2>, <3; 3», «2,5; 2,5>, <2; 2»}. Рассмот-
рим задачу </(, Р, г, R, 2> со следующими параметрами: 5=
= {1,2}, Кх = {1}, /(, = {1,2}, ph = pls = l/2, рЪ = \, р?,=0,
Pai=O, p|i=l, г}=rl=< 1, 1>, г3 = <2, 2>. Занумеруем стратегии:
лх = (1, 1), л2 = (1, 2), л3 = (1, 2), л4 = (2, 2).
По формулам (7), (17), (18) получаем
2Г1(лх) = 2Г1(л3) = <2; 2>,
2Г1(л,)=8Г1(л4) = <2,5; 2,5>,i
2Г2(лх) = <2; 2>,
2Г2 (л,) = 2Г2 (л3) = 2Г2’(л4) = <3; 3>.
Пользуясь определением /^-оптимальной стратегии (R=R), за-
ключаем, что 6 (К, Р, r,'R, 2) — 0.
Упражнение 4. Построить пример, в котором 6 (К, Р, г, R)
не содержит стационарных стратегий для отделимого отношения
R. (Рассмотреть цепь из примера бив качестве R взять
отношение Парето на минимум: xRy^=>Xi^.yi (i=l, т) и
Х¥=у.)
278
ГЛ. 4. МАРКОВСКИЕ МОДЕЛИ ПРИНЯТИЯ РЕШЕНИЙ
§ 3. Оптимальные стратегии управления цепью Маркова
с векторными доходами
В настоящем параграфе приведены результаты, определяющие
существование и свойства решений задачи </С, Р, г, Ry при оп-
ределенных зависимостях между ее параметрами.
Утверждение 7. Пусть R—^.-отделимое отношение и
т
2 V* О') =1 О' = Cv; k е Ki). (32)
Тогда любая стратегия "л принадлежит 6 (К, Р, г, R, п) при
всех п и любая стратегия л принадлежит 6 (К, Р, г, R).
Доказательство. В однокритериальной задаче с дохо-
дами (22) оптимальна любая стратегия, так как р* = 1. Пусть
некоторая стратегия л* не принадлежит 6 (К, Р, г, R). Тогда
существуют стратегии л и i*£S, для которых выполнено (23) и
(А, Г'* (л)) > (А, Р*(л*)). (33)
Для любой стратегии л в однокритериальной задаче с дохо-
дами pi == 1 имеем
»Г(л)/п=1 (п = 1, 2, ...).
Поэтому lim inf "Г (л)/п = lim "Г (л)/п, откуда с учетом (24) по-
М СО П-*<Х>
лучаем
1=г(л)= £ауР(л), 1=г(л*)= 2Хг'(л»),
/=1 /=1
или
(%, Г'(л)) = (А, Г'(л*)) (i=TTN),
что противоречит (33). Доказательство утверждения для любого
п аналогично.
Пример 8. Пусть R—отношение Парето Р. Тогда для лю-
бого вектора А > 0 отношение Р является A-отделимым. Пусть
доходы г* не зависят от k и имеют вид rt = <0, ..., rz, ..., 0>.
Это значит, что с каждым состоянием связана своя компонента
векторного дохода. Размерность векторного дохода равна N —
числу состояний цепи. Очевидно, вектор А = <г-1.......г~^>
удовлетворяет (32). Следовательно, в силу утверждения 7 любая
стратегия является парето-оптимальной.
Рассмотрим выпуклую линейную комбинацию векторов г*
(t = 1, N-, k£.Ki). Полученный выпуклый многогранник обозначим
через А.
Утверждение 8. Пусть отношение R и многогранник А
таковы, что
§3. ОПТИМАЛЬНЫЕ СТРАТЕГИИ
279
а) для любых х‘ у£А выполняется txRty (£= 1, 2, ...);
б) для любой последовательности xlf гдех^А,
и любого у А
(lim inf хп) Ry. (34)
П CD
Тогда 1) любая стратегия л принадлежит 6 (К, Р, г, Р, п)',
2) любая стационарная стратегия л принадлежит 6 (К, Р, г, Р).
Доказательство. 1) Найдем каждое слагаемое в (7).
Зафиксируем l-ю координату у вектора d'==Р,-(л) г (fz+1); имеем
N
d^ — S (35)
h= 1
С учетом (18) получаем
N ____
di(j)= 2 (/) (/=l,m). (36)
ft=l
В силу (36) и того, что Р{—стохастическая [матрица, а много-
гранник А—выпуклый, имеем
<tf=<df(l), .... ^(т)>$А, (37)
п-1
«П(л)= 2 (38)
i=0J
Соотношение [(38) выполнено Гдля всех [стратегий л, откуда в
силу условия а) имеем л С 6 (/<, Р, г, Р,еп). Часть 1) утвержде-
ния доказана.
2) Пусть л—любая стратегия. В силу выпуклости А, формул
(37) и (38) получаем, что пГ1 (п)/п£А. Если л—стационарная
стратегия, то из формул (25) — (27) получаем, что
р (л) = lim “Г* (л)/п £ А |
Л-* <ю
Используя условие (34), получаем, что п£б(К, Р, г, Р). Часть
2) утверждения доказана.
Пусть многогранник А содержится в^гиперплоскости Л, за-
дающейся уравнением
и при этом X, > 0 (i=l, TV). Это значит, что для^ любого х£А
выполнено (39). Пусть отношение Р Х-отделимо, х, у^А. Тогда
т
очевидно, что ,SXz(xz—#/) = 0_и, следовательно, txPty (выпол-
нено условие а) утверждения 8). Более того, так как X,- > 0, то
280
ГЛ. 4. МАРКОВСКИЕ МОДЕЛИ ПРИНЯТИЯ РЕШЕНИЙ
для любой последовательности хп .х„, ...£Л
(X, lim inf хп) < d (40).
П -> 00
(выполнено условие б) утверждения 8).
Стационарную стратегию, R-оптимальную для любого конеч-
ного и для бесконечного времени, назовем R-канонической. Су-
ществование /^-канонических стратегий эквивалентно тому, что
( Г) 0(К, Р, г, R, и)') Лб(/<, Р, г, R)^0.
Утверждения 7 и 8 указывают на выполнение этого соотноше-
ния при определенных условиях на параметры задачи </С, Р, г, Ry.
Пусть цепь Маркова находится в некоторый момент в i-м
состоянии и принято решение k € К,-. Средний [доход в следую-
щий момент времени определяется формулой
N ____
^=1^/ N\ kSKft (41)
/=1
(рассматривается случай, когда доходы [зависят только от
состояния /). Обозначим через В,- многогранник, являющийся
выпуклой линейной комбинацией векторов D}, .... Dk{i.
Назовем цепь Р, гу бернуллиевской, если Bt = Bj = В для
всех i, j £ S. Это название связано с тем, что последовательность
испытаний Бернулли можно рассматривать как марковскую цепь,
в которой не зависит от i (вероятность наступления одного
из событий Alt Ad в каждом следующем опыте не зависит
от исхода предыдущих опытов).
Упражнение 5. Доказать, что цепь </С, Р, гУ бернулли-
евская, если — K (i, и ру не зависит от i.
Утверждение 9. Пусть СК, Р, гу—бернуллиевская цепь,
а вершина х£В и отношение R таковы, что
1) для всех i £S, t= 1, 2, ... и у £В
(ri + tyYRlrt + tx?, (42)
2) для любой последовательности xt, ..., хп, ... С В
(lim inf х„) Rx.
Тогда стационарная стратегия f™, определяемая по формуле
(i = TTN), (43)
является R-канонической.
Доказательство. Рассмотрим выражение (41). Ясно, что
при любой стратегии л средний доход за время п равен доходу
Г; в начальном состоянии плюс сумма векторов, каждый из ко-
§ 3. ОПТИМАЛЬНЫЕ СТРАТЕГИИ
281
торых лежит в одном из многогранников В(. По условию утвер-
ждения это значит, что при некотором уп£.В
"Г'(л) = г;4-(н—1) (44)
Для стратегии л*, определенной формулой (43), средний доход
за п шагов равен
’Т/(л*) = г/ + (п — 1)х. (45)
Из (42), (44) и (45) следует, что л* 6 6 (К, Р, г, R, п) для лю-
бого п. Из (44) следует, что для любой стратегии л
«Г' (л)/п = гj/ti + (п— 1) уп1п,
где уп£В. Поэтому
р (л) = Нт inf "Г (л)/п = Ит inf (г,/п-+-(п— 1) #„/«) = lim inf уп,
п оо . л -> со , п -► со
(46)
Г' (л*) = х. (47)
/?-оптимальность стратегии л* следует из (46), (47) и условия
2) утверждения. Таким образом, л* 6 6 (К, Р, г, R).
Пусть /?—Х-отделимое отношение и цепь <К, Р, г> бернул-
лиевская. Пусть argmax(X, у) — х. При Х>0 очевидно, что
в
вершина х и отношение R удовлетворяют условиям утверждения
9. Поэтому отыскание /^-канонических стратегий сводится к ре-
шению задачи линейного программирования с целевой функцией
(X, у) на многограннике В. Пусть Р— отношение Парето. Тогда
Р Х-отделимо при любом X > 0. Тем самым любая вершина х
многогранника В, на которой достигает максимума хотя бы одна
линейная функция с положительными коэффициентами, определяет
в соответствии с формулой (43) /^-каноническую стратегию.
Утверждения 7—9 в ряде случаев позволяют не только уста-
навливать существование /^-оптимальных стратегий, но и опре-
делять их свойства й способы нахождения.
Упражнение 6. Пусть /?—ацикличное координатное от-
ношение, <К, Р, г>—произвольная цепь. Доказать, что существует
/6(1, ..., т} такое, что любая стратегия, оптимальная в одно-
критериальной задаче с доходами р* = г* (/), будет /?-оптималь-
ной как для конечного, так и для бесконечного времени.
Упражнение?. Пусть /65 обладает следующими свойствами:
1) (Vi 6 5) £э&^бК; такие, что p^i = 1J;
2) (Vt‘65, ykeKt, V/=l, ..., Уу£А) _
[(r* + ty) R (г^+И)] :
3) для любой последовательности ylt у2, уп, ..., где
Уп&А (п=1, 2, ...), выполнено (lim inf у„) Rrfi.
282
ГЛ. 4. МАРКОВСКИЕ МОДЕЛИ ПРИНЯТИЯ РЕШЕНИЙ
Доказать, что стационарная стратегия где /(i) = ^, явля-
ется /^-канонической.
До сих пор шла речь о частных решениях задачи </С, Р, г, Ру
и их свойствах. Чтобы найти все множество решений 6 (К, Р, г, R),
введем необходимые понятия. Прежде всего расширим класс
используемых стратегий. Будем считать, что множеством реше-
ний в t-м состоянии является множество распределений на К;
т. е. множество наборов <рп ..., р^ > таких, что pz^0 (/=1, i),
ki
2 pi—1. При фиксированном распределении <рп ..., рк(> ре-
шение^ С К{ принимается с соответствующей вероятностью рг
(/=l,/ez). Для таких смешанных стратегий остаются в силе
утверждения 1 и 2 и теоремы 1 и 2.
В случае вырожденных распределений получим понятие
чистой стратегии, совпадающее с введенным в § 1. Ограничим-
ся рассмотрением случая бесконечного времени. При этом
Ф = £тЛг; Ф = ф(4/) представляет собой множество всех возмож-
ных векторных средних доходов за единицу времени; проекция
Ф на i-e подпространство Ет, образованное осями с номерами
от m(i —1)4-1 до mi, соответствует i-му начальному состоянию.
Учитывая, что Ф от R не зависит, будем писать Ф=Ф(/<, Р, г).
При этом R-оптимальным стратегиям соответствует множество ФЛ.
Пусть Г (nJ, Г (л2) £ —доходы, отвечающие двум страте-
гиям Л! и л2. Определим стратегию л3 = а1л14-а2л2 следующим
образом (а14-а2=1, aj^O, a2Z>0): будем пользоваться только
стратегией лх либо только стратегией л2. Выбор между страте-
гиями лх и л2 осуществим с вероятностями аг и а2. Очевидно,
что Г (л8) =а1Г (л!)4-а2Г (л2). Тем самым доказано
Утверждение 10. Множество Ф(/С, Р, г) выпукло.
Множество Фл {К, Р, г) может быть найдено с помощью
следующего утверждения.
Утверждение 11. Пусть L—конус такой, что L*^Em,
Rl<R. Множество Ф₽ (Д’, Р, г) совпадает с частью границы
выпуклого многогранника, каждая грань которого соответствует
одной чистой стационарной стратегии.
Утверждение 11 непосредственно следует из утверждений 10
и 1.7.
§ 4. Многокритериальная задача об оптимальной остановке
В ряде задач принятия решений нужно установить, окупает
ли прирост информации от новых данных плату за ее получе-
ние. Это характерно для задач теории статистических решений,
управления наблюдениями и экспериментами, остановки вычис-
лительного процесса и т. д.
§4. ЗАДАЧА ОБ ОПТИМАЛЬНОЙ ОСТАНОВКЕ
283
Пример 9. Осуществляются последовательные бросания
симметричной монеты; выпадение герба означает выигрыш одного
очка, выпадение решетки—проигрыш одного очка. Таким об-
разом, суммарный выигрыш за п шагов равен
п
В„= 2 X*,
Л=1
где Х.к— 4-1, если в результате fe-ro бросания выпал герб,
=—1 в противном случае. После каждого бросанияj мы
можем принять одно из двух решений: прекратить игру и соб-
рать накопившийся к данному моменту выигрыш или продолжить
игру и произвести по крайней мере еще одно бросание. Необ-
ходимо выйти из игры в такой момент, чтобы максимизировать
свой выигрыш.
Пример 9а. Та жа ситуация, что в примере 9, но имею-
щийся начальный кипитал ограничен и равен В. Однако, если
накопленный к моменту п выигрыш Вп становится равным —В,
то у игрока есть только одно решение: прекратить игру. Задача
по-прежнему состоит в том, чтобы найти оптимальный момент
выхода из игры, при котором выигрыш максимален.
Пример 10. Задача о стоянках. Пусть водителю авто-
мобиля известно, что на пути до места назначения имеется N
стоянок. Информации о том, какие стоянки свободны, у него
нет. Вероятность того, что стоянка свободна, равна р, а того,
что занята, равна 1—р. Поставив автомобиль на любую’стоянку,
оставшийся путь до места назначения водитель должен пройти
пешком. Примем соответствующее расстояние за штраф. Задача
состоит в том, чтобы поставить автомобиль, минимизировав
штраф.
Пример 11. Задача о наилучшем выборе. Пусть
в случайном порядке появляется п объектов. После ознакомле-
ния с очередным объектом его можно либо выбрать, либо от-
вергнуть; вернуться к ранее отвергнутому объекту нельзя.
Требуется выделить наилучший объект. (Эта задача называется
также задачей о выборе невесты.) Можно представить, что
объекты изображаются точками прямой; из двух объектов луч-
шим будет тот, которому соответствует точка, стоящая правее.
Так как появление объектов происходит в случайном порядке,
то с одинаковыми вероятностями точкой (первой встретив-
шейся) может оказаться любая из имеющихся точек. Порядок
появления точек определяет некоторую перестановку. Любая
из п\ перестановок точек, определяющих порядок появления,
может реализоваться с равной вероятностью. Перестановка ста-
новится известной по мере поступления точек: после появления
второй точки известно только относительное расположение at
и «2, после появления k-й—относительное расположение
284 ГЛ. 4. МАРКОВСКИЕ МОДЕЛИ ПРИНЯТИЯ РЕШЕНИЙ
аи а2, ак. Номер точек указывает на то, какой по порядку
она появилась. Задача состоит в том, чтобы распознать край-
нюю правую из всех «.точек в тот момент, когда она появляется.
Задачи рассмотренного типа могут быть решены с помощью
теории оптимальных правил остановки. Одним из основных ин-
струментов этой теории являются цепи Маркова. Построим цепи
Маркова и функции доходов для примеров 9—11.
В примере 9 выберем в качестве состояния системы общий
накопленный к данному моменту выигрыш. Иными словами,
S = {..., — AZ, — W +1, ..., О, 1, ..., АГ, ...}’—множество всех
целых чисел и
Г 1/2, / = i-f-l,
Pij=\ 1/2, j = (48)
I 0 для других /.
Доход F (;) в состоянии /£5 равен /, т.е. просто выигрышу в
данный момент.
В примере 9а марковская цепь и функция выигрыша опре-
деляются так же, как и в примере 9, однако в состояниях i,
где t —В, можно только выйти из игры. Таким образом,
здесь есть состояния с вынужденной остановкой. Множество
таких состояний обозначим через Ss.
В примере 10 в качестве состояний системы выберем пары
целых чисел (i, k), rpp i. пробегает значения —N, —Af-f-l, ...
...,0, 1, ...,a k принимает значения 0 и 1; i измеряет расстояние I
от данной стоянки до места назначения, a k отмечает, свободна
данная стоянка или нет. Переход из (t, k) в («4-1, 0) имеет
вероятность р, а в (i'4-l, 1)—вероятность 1—р. Этот пример от-
личается от предыдущих тем, что в нем есть состояния с вынуж-
денным продолжением, именно, все состояния вида (I, 1) (если
стоянка занята, то надо ехать дальше). Обозначим множество
таких состояний через Sc. Доход задается формулой
F (i, 0) = — I i |. (49)
В примере 11 положим S = {1, ..., п, «4-1}. Ясно, что вы-
бирать лучшую нужно среди тех точек ак, которые располагаются
правее всех предыдущих точек а1г ..., ak_t. Будем называть такие
точки максимальными. Максимальная точка остается таковой
до прихода следующей максимальной точки. В качестве состоя-
ния системы примем номер последней появившейся максимальной ।
точки. Выражение
pkl = k/(l(l-l)) (50)
задает вероятность того, что следующей максимальной точкой
будет az при условии, что предыдущей максимальной точкой
§ 4. ЗАДАЧА ОБ ОПТИМАЛЬНОЙ ОСТАНОВКЕ
285
была ak. По определению = если l^.k. Величина
п п п
1 — X = 11 Г77~Т)=1— k 11 (и“т)=|
/=*4-1 /=*4-1 к 7 /=*4-1 4 /
(51) .
представляет собой вероятность того, что после точки ак мак-
симальных точек больше не будет, т. е. точка ак является
искомой.
Введем в множество S фиктивное состояние «4-1, для которого
Pk, n+i = k/n (k = TTn). (52)
Состояние п + 1 является состоянием с вынужденной остановкой;
Pn+i, n+i=l- Вероятность того, что точка ак окажется макси-
мальной, определяется формулой (51). Возьмем в качестве зна-
чения функции дохода F (k) в состоянии k величину k/w,
F («-Не-
рассмотренные примеры приводят к следующему понятию.
Задачей об оптимальной остановке называется задача <Р, S, Sc,
Ss, i0, где P—матрица переходов цепи Маркова с множест-
вом состояний S; Sc и —произвольные непересекающиеся
подмножества S (Sc называют множеством состояний с вынуж-
денным продолжением, Ss—множеством состояний с вынужденной
остановкой)-, F—функция дохода, определенная на S; iQ—на-
чальное состояние.
Последовательность <i0, h, i„> называется останавлива-
ющей, если после наблюдения состояний i0, i\, ..., in принимается
решение остановиться в in.
Ясно, что in^Se; если in£Ss, то всякая последовательность,
оканчивающаяся в in, является останавливающей.
Правилом остановки называется любое конечное или беско- .
нечное множество L останавливающих последовательностей такое,
что
2Р(«0, in .... Q=l, (53)
где P(i0, - in) = Pl-„i, Pin-Mn-
Оптимальным правилом остановки^ называется правило LM,
для которого средний доход
X(b) = SP(io, ia)F(itt) (54).-
максимален. Величина maxM(L) называется ценой,
{М
Утверждение 12. Существует подмножество Т множест-
ва S такое, что оптимальное правило остановки состоит из тех
и только тех последовательностей, которые оканчиваются в Т.
Ясно, что Ss s Т, Sc £ S \ Т,
286
ГЛ. 4. МАРКОВСКИЕ МОДЕЛИ ПРИНЯТИЯ РЕШЕНИЙ
Из утверждения 12 следует, что оптимальное правило не
зависит от начального состояния. Однако цена от него зависит.
Обозначим через Н (I) цену, полученную при использовании
оптимального-правила при начальном состоянии i\ функция Н (i)
удовлетворяет уравнению
#(0=Ч
F(i), i£Ss,
^PuH(j), its,,
fes
max^F(i),
(55)
!• $ Sc u Sj.
Упражнение 8*. Пусть H(i)—решение уравнения (55) и
T = {i€S\Se|//(i)^Ft.(i)}. (56)
Доказать, что если Рг {попадания ’из i0 в Т}=1, то Т опреде-
ляет оптимальное правило остановки.
Уравнение (55) выражает принцип Веллмана в задаче об
оптимальной остановке. В некоторых случаях его решение можно
найти в явном виде.
Упражнение 9*. Всегда ли существует оптимальное пра-
вило остановки? Всегда ли оно существует в задачах, в которых
множество состояний S конечно?
Укажем на сходство и различие задач управления цепью
Маркова и оптимальной остановки. Пусть <К, Р, г>—управ-
ляемая цепь Маркова с множеством состояний S и j£S. Будем
рассматривать средние доходы за время до попадания из началь-
ного i-ro состояния в /-е и искать оптимальную стратегию л*,
которая определяется как стратегия, максимизирующая доход
Di (я). Такое понятие дохода’отличается от доходов в задачах,
рассмотренных в § 1. _____
Использование доходов £>/(л) позволяет свести задачу~Ъб
оптимальной остановке к одной из задач управления цепью
Маркова.|Для задачи <Р, S, Sc, S^, i0, F> определим цепь Мар-
кова. В качестве ее множества состояний возьмем S'Ux, где х—
фиктивное состояние, добавленное для учета факта остановки.
В каждом состоянии i С S множество решений К/ состоит из
двух элементов: при решении {1 осуществляется переход из i в
соответствии с цепью исходной задачи в одно из состояний j С S
и доход равен нулю; при решении 2 (остановка) происходит
переход в фиктивное состояние х с вероятностью 1 и доход
равен F(i). При попадании в х процесс останавливается.
Таким образом, определена управляемая цепь Маркова; стра-
тегия в такой цепи однозначно соответствует правилу остановки
для исходной задачи, причем оптимальная стратегия соответст-
вует оптимальному правилу остановки.
§5. ДВУХУРОВНЕВАЯ ОПТИМИЗАЦИЯ
287
Перейдем к многокритериальному варианту задачи об опти-
мальной остановке. При этом функция дохода F, заданная на S,
принимает значения из Ет, а не из Et (т. е. является вектор-
ной, а не числовой).
Правило остановки L* является /^-оптимальным, если для
всякого другого правила L
M(L)RM(L*). (57)
Запись векторной задачи принимает вид <Р, S, Sc, Ss, i0, F, Ry.
Утверждение 13. /.-сверткой задачи <Р, S, Sc, Ss, i0, F, Ry
является однокритериальная задача </’, S, Sc, Ss, i0, Fy, где
m
?<,1 = 2’-Л(0.
/= 1
Доказательство утверждения 13 аналогично доказательству
утверждения 3.
Упражнение 10*. Верно ли утверждение 12 для R-
оптимальных правил остановки при произвольном отношении R?
Теория для /^-оптимальных правил остановки практически
аналогична теории для /^-оптимальных стратегий. Например, для
них можно сформулировать утверждение, аналогичное теореме 2,
где вместо стационарных стратегий будут фигурировать правила
остановки, удовлетворяющие условию утверждения 12.
В силу указанного сведения задачи об оптимальной оста-
новке к задаче управления цепью Маркова связь многокрите-
риальной задачи об оптимальной остановке с общей многокрите-
риальной задачей оптимального управления очевидна.
§ 5. Двухуровневая оптимизация
управляемых цепей Маркова
Воспользуемся введенными в § 2 понятиями для выделения
задач двухуровневой оптимизации управляемых марковских про-
цессов принятия решений. Зафиксируем начальное состояние i0,
стратегию л и число шагов п. При этом оказывается возможным
лишь конечное число траекторий, т. е. последовательностей со-
стояний и решений вида
^1» ^1» • • •, ^п-1» ^п-1> ^пУ- (5®)
По сути дела каждая траектория есть реализация случайного
процесса, определяемого параметрами задачи. Вероятность реа-
лизации (58) равна
а получаемый на ней доход равен
r = r‘. + r‘«+...+rf»-.. (59)
Из конечности числа возможных траекторий следует конечность
числа возможных доходов г1, ..., гА. Вероятность получения
(61)
I
(62) -I
288 ГЛ. 5. ПРИКЛАДНЫЕ МНОГОКРИТЕРИАЛЬНЫЕ ЗАДАЧИ
дохода н (i = l, Л) обозначим через pt. Ясно, что средний доход
'Т‘" при начальном состоянии i0 равен
Л
^=^Р^. (60)
i= 1
Средние доходы "Г*’ исследовались в §§ 1—3.
В случаях одноразовых процессов, заканчивающихся после
фиксированного числа шагов, интерес представляют доходы на
отдельных траекториях и их вероятности. Положим D = {г1,..., гА).
Пусть на D задана функция выбора С. Для каждого вектора
r>$D возможно:
1) r^C(D); 2) r'$C(D).
Каждый доход г‘ может быть получен с определенной ве-
роятностью рг Занумеровав доходы, принадлежащие С (D),
индексами от 1 до g, получим, что вероятность реализации с
доходом из С(D) равна
g
Р(л)= У ps.
s — 1
Стратегию л* назовем слабо i-оптимальной, если
л* С Arg max Р (л),
п
Здесь П—множество всех чистых стратегий, i—начальное со-
стояние; рассмотрение чистых стратегий обеспечивает конечность
множества возможных доходов.
Для одноразового процесса задача состоит в том, чтобы найти
слабо оптимальную стратегию. В ней рассматриваются два уровня-
оптимизации: на первом выделяется С (D), а на втором находится
слабо оптимальная стратегия.
Заметим, что двухуровневый характер задачи сохраняется и
при переходе к ее однокритериальному варианту. Так, в задаче
о наилучшем выборе (пример 11) необходимо остановиться на
лучшем объекте с максимальной вероятностью.
Результаты, относящиеся к частным случаям задач двухуров-
невой оптимизации, приводятся в § 5.4.
Литература. [18, 51, 52, 71, 96].
Глава 5
ПРИКЛАДНЫЕ МНОГОКРИТЕРИАЛЬНЫЕ ЗАДАЧИ
ОПТИМАЛЬНОГО УПРАВЛЕНИЯ
В главе рассмотрены многокритериальные задачи, сводящиеся
к таким однокритериальным задачам, для которых найден конк-
ретный вид решения. В § 1 рассмотрена задача проектирования
§ 1. ПРОЕКТИРОВАНИЕ ПРОГРАММНОГО КОМПЛЕКСА
289
оптимального программного комплекса для вычислительных сис-
тем. В § 2 рассмотрена задача управления трехотраслевой эко-
номикой. В § 3 приведены результаты исследования задачи раз-
решения конфликтов в многопроцессорных вычислительных
системах. В § 4 рассмотрен класс задач об оптимальной оста-
новке на множестве частично упорядоченных объектов. В § 5
рассмотрена матричная игра с векторными доходами.
§ 1. Проектирование оптимального
программного комплекса
При проектировании программного комплекса необходимо
удовлетворить ряду противоречивых требований: увеличить точ-
ность определения выходных значений, уменьшить объем исполь-
зуемой оперативной памяти, занятой программами и данными,
уменьшить время выполнения программ, уменьшить загрузку
каналов между центральным процессором и внешними запоми-
нающими устройствами, сократить объем информации на внешних
запоминающих устройствах и т. д.
Пусть программный комплекс S должен реализовать множе-
ство операций 0 = 10^ ..., 0М}. Под операцией будем понимать,
например, решение систем дифференциальных уравнений данного
типа, печать результатов в заданном виде, вычисление интег-
рала, поиск информации по заданным признакам и т. д.
Каждая r-я операция 0Z£0 может быть реализована любой
программой из наперед заданного множества программ Uz=
= {ПП, ..., IT/,-.}, 1 = 1, М. Каждая из этих программ отличается
временем реализации, объемом требуемой памяти и/или другими
характеристиками. П рограммный комплекс S представляет собой
упорядоченный набор программ
л, = <111/,, ...,
где ГЦ—программа из множества IIZ, реализующая i-ю опера-
цию 0Z. (Заметим, что поскольку множества IIZ к Пу могут пересе-
каться, то на r-м к j-м местах в наборе может стоять одна
и та же программа.)
Под оптимальностью программного комплекса л, как и всюду
в части III, понимается недоминируемость его векторной оценки
по бинарному отношению R, выражающему принцип оптималь-
ности разработчика комплекса.
Будем считать, что разработчик учитывает критерии из мно-
жества 9C = {klf ..., km}, например время выполнения всех опе-
раций, общий объем занимаемой памяти, точность вычислений
и т. д. Поэтому оценка комплекса ср (л) — это вектор в Ет. Мно-
жеством управлений 4L, как и в §§ 2.3, 2.4, является множество
П = П1х ... хПм; отображение *11 Ет определяется прави-
290
ГЛ. 5. ПРИКЛАДНЫЕ МНОГОКРИТЕРИАЛЬНЫЕ ЗАДАЧИ
лом, по которому строится векторная оценка <р(л) комплекса л;
бинарное отношение 7?—это отношение, выражающее принцип
оптимальности разработчика. Таким образом, задача проектирова-
ния оптимального программного комплекса является многокрите-
риальной задачей оптимального управления <% <р, 7?> с указан-
ными параметрами. Специфика определяется отображением <р, т.е.
правилами построения векторной оценки программного комплекса.
Пример 1. Пусть П^Пц}, П2 = {П21} и Пп = П21 = П1,
т. е. две операции 61 и 62 реализуются одной и той же програм-
мой пх. При этом множество П = П1хП2 состоит из единственного
элемента л = <п1, п2>. Пусть разработчика интересует три крите-
рия: 1) общее время выполнения операций; 2) объем занимаемой
памяти; 3) точность вычислений. Ясно, что оценка всего комп-
лекса зависит от оценок входящих в него программ (в данном
случае от оценок программы пх).
Обозначим через х} и х2 время выполнения операций 6Х и 62
программой пх; через xf—объем памяти, занимаемой програм-
мой пх; через xf и xf —точность вычислений в операциях 6Х и 62.
Примем, что
Ф1 N = xl+xJ,
ф2 (л) = Х1,
Фз(я):==т1п(х|,
В данном случае время выполнения операций 6Х и 62 склады-
вается из времен выполнения каждой операции в отдельности,
память, занимаемая программой, не зависит от числа реализуемых
операций, а точность определяется по худшему случаю. Таким
образом, правила построения оценок по критериям могут разли-
чаться.
Будем рассматривать два основных типа критериев оценки
комплексов. Для комплекса л = <П1/1, ..., Пм/М> положим
= и ... U
Назовем критерий однократным, если оценка ср (л) комплекса л
по нему является суммой оценок по этому же критерию всех
программ из 5(л). В примере 1 однократным является критерий 2).
Пусть —оценка по некоторому критерию выполнения про-
граммой 1Ц. операции 6Z. Этот критерий назовем многократным,
если оценка <р(л) комплекса л = <ПНг. .Пм/7И> по нему является
значением числовой функции ..., а^). В примере 1 много-
кратными являются критерии 1) и 3).
Пример 2. Пусть
П1 = {П11, П12}, П2 = {П21, П22}, П3! = П21 = , П12 = и2, П22 = м3.
Программа реализует операции 6Х и 02; программа п2 —
только 61, программа п3—только 62.
$1. ПРОЕКТИРОВАНИЕ ПРОГРАММНОГО КОМПЛЕКСА
291
Рассмотрим два комплекса:
л1 = <«1. «2>, л2 = <п2, п3>.
Предположим, что объем, занимаемый каждой из программ, ра-
вен 1. Тогда
<р(лх)=1, <р(л2) = 2,
так как 5(ла) = {«!}, S(n2) = {n2, пя}.
Способ решения задачи проектирования комплекса состоит в
построении множества П* £ П такого, что
[ф (П)]* <= [ф (П»)]Я
В ряде случаев удается построить множество П*, мощность ко-
торого значительно меньше мощности множества П. Это облег-
чает решение задачи оптимального проектирования.
Упражнение 1. Пусть все критерии являются' однократ-
ными. Доказать, что в этом случае задача проектирования опти-
мального комплекса совпадает с задачей конструирования из
§ 2.4.
Упражнение 2. Пусть все критерии являются многократ-
ными, а все числовые функции в определении многократного
критерия являются суммами. Доказать, что в этом случае задача
проектирования оптимального комплекса совпадает с задачей не-
зависимого выбора из § 2.3.
Таким образом, в ряде случаев задача проектирования опти-
мального комплекса сводится к рассмотренным ранее в § 2.3 и
2.4 многокритериальным задачам оптимального управления. При
этом задача с многократными критериями является более простой,
так как задача независимого выбора проще задачи конструиро-
вания. _____
Упражнение 3. Пусть nznll7=0 (f, / = 1, М;
Доказать, что тогда понятия однократного и многократного кри-
териев совпадают.
Рассмотрим задачу с многократными критериями. Пусть
xjf. — оценка программы ГЦ., реализующей операцию 6Z, по s-му
критерию. Оценки набора л = <П1у1, ..., Пм/Л1> определяются
формулами
Фг(л) = ф,(х’д, ..., XSMIM) (s= 1, т).
Назовем задачу монотонной, если все функции ср5 являются
строго возрастающими по все?л переменным.
Упражнение 4. Является ли задача с непересекающи-
мися IIZ и с критериями из примера 1 монотонной?
Для монотонных задач имеет место
Утверждение 1. Пусть R — координатное отношение.
Тогда
[ф (П)Р S ф (П*) = [X (Пх)]«х ... X [X (ПМ)Г,
где X(IIZ)— множество оценок программ из П^.
292
ГЛ. 5. ПРИКЛАДНЫЕ МНОГОКРИТЕРИАЛЬНЫЕ ЗАДАЧИ
Доказательство. Предположим противное. Пусть
П = <ПV>> • • • > ПМ/Л>, ф € (НМ*
и при этом х (П171) (£ [X Это значит, что для некоторой
программы П*.-
Рассмотрим комплекс л* = <ПГ/,. •••> Пм/Л1>. отличающийся
от л только программой, стоящей на первом месте. Докажем,
что <р (л*) А?ф (л). Пусть <р = <ф!, ..., фт>—оценка комплекса л;
Ф* = <Ф1, Фт>—оценка комплекса л*. Зафиксируем
S^(l, ..., т}. В силу МОНОТОННОСТИ ф^
sgn (ф;—ф j=sgn (xs (п;Л)—<(П1Л)),
поэтому а(ф*—ф) == а (х (П?/() — х(П1Л)). В силу координатности R
X (Щ/ () Rx (П1Л) ф* Яф,
т. е. сделанное предположение неверно. Полученное противоречие
доказывает утверждение 1.
Упражнение 5. Останется ли в силе утверждение 1, если
не требовать: а) координатности R; б) строгой монотонности
функций ф4 (xf, ..., xsM)?
Упражнение 6. Пусть функции ф5 являются суммами
(s—1, т), Доказать, что утверждение 1 верно для любого
отношения R, инвариантного относительно переноса.
Смысл утверждения 1 состоит в том, что поиск недоминируе-
мой части на прямом произведении сводится к поиску недомини-
руемых частей на сомножителях.
Пример 3. В табл. 1 указаны номера программ и реали-
зуемых ими операций. Знак-(-означает, что программа реализует
Т аблица 1
№№ > операций Номера программ, реализующих данную операцию
«1 1 | «2 «3 «5 п9 «7 «8 | | «9 | «к» | I «ti i Л12 «13
1 2 3 4 + + + | + + + + + _L + +
операцию. Пусть при выборе комплекса учитывают три. крите-
рия: время выполнения всех операций; занимаемый объем опера-
тивной памяти; возможность промежуточного контроля вычисле-
ний. Оценки по этим критериям в условных единицах для каждой
из программ приведены в табл. 2. Исходные данные показывают,
что задача является монотонной.
§ 1. ПРОЕКТИРОВАНИЕ ПРОГРАММНОГО КОМПЛЕКСА 293
Пусть 7?—отношение Парето (на минимум по 1-му и 2-му
критериям). Из табл. 2 получим, что
[X (110]*={X(Пп)}, [X (П2)]*= {X (П23)},
[Х(П3)]« = {х(П31), х(П33), х(П34)}, [Х(П4)]* = (х(П42)}.
В силу утверждения 1 множество П», содержащее все оптималь-
ные комплексы, состоит из трех комплексов:
П* = <П11, П23, П31, П42>, П2 = <П11, П23, П33, П42>,
П3 = <П11, п23, п34, п42>.
Число всех возможных комплексов в данном примере равно
ЗхЗх4хЗ= 108.
'Х. х П \ xli „2 хи х3- хп
Пи 3 2 3
П12 3 3 3
Щз 5 6 1
Таблица 2
'Х. х II \ X2i X2. *21 у3
П21 2 2 6,
П22 6 7 4
П23 1 1 6
X П \ X3i Г 2 x3i х3. x3i
П31 6 1 5
Щг 6 2 2
П33 1 5 3
П34 1 5 4
\ X п xli v2 X4t v3 x4i
П41 4 1 1
П42 1 1 5
П43 4 4 3
Пример 3 показывает, что использование утверждения 1 поз-
' воляет существенно упростить задачу.
Рассмотрим задачу с однократными критериями.
Утверждение 2. Пусть
1) множество операций 6 = {6i, ..., 6 м} можно разбить на
два подмножества 6t и 6П такие, что = 0, если 6^6/,
€ &п',
2) отношение R инвариантно относительно переноса.
Тогда
[<Р (П)]* <= <р (П*) = [q> (П7)]*х [ф (П„)]*,
где П, и П7/—решения задач проектирования оптимального комп-
лекса, реализующего операции из 6f и 6П соответственно.
Доказательство. В силу условий утверждения для лю-
бого комплекса л имеем ф(л) = ф(л/) + ср(ля), где л7и яП—под-
комплексы комплекса, реализующие соответственно операции из
294
ГЛ. 5. ПРИКЛАДНЫЕ МНОГОКРИТЕРИАЛЬНЫЕ ЗАДАЧИ
6, и 6Ц. Очевидно, что, заменяя л, на доминирующий его под-
комплекс Л/, получим комплекс л* = <л/, л/7>, доминирующий
л = <л/, л„> (в силу аддитивности <р и инвариантности R отно-
сительно переноса). Это и доказывает утверждение 2.
Смысл утверждения 2 состоит в декомпозиции задачи по опе-
рациям.
Пример 4. Пусть множество операций 6Г задается табли-
цей 1, а 6ц—табл. 3; критерии те же, что и в примере 3.
Оценки по критериям даны в табл. 4.
Таблица 3
Ж операций Номера программ, реализующих данную операцию
«14 «15 1 ' «17 «1в «1» «20
5 6 + + + + + + + + +
\ х п 4» х2- Хо1 х3. ы
П51 3 4 3
П52 3 3 4
П53 3 2 3
П54 4 2 2
П55 4 4 3
Таблица 4
X6t X2- xei X3-
П«1 4 4 4
Пб2 2 3 3
Пб3 5 4 5
Пб4 4 4 6
Найдем Щ/ при R таком же, как в примере 3. Рассмотрим
табл. 4. Ясно, что программу и14 можно не включать в комп-
лекс, так как <3, 3, 4>Р<3, 4, 3>. То же относится к програм-
мам п17, п18, пи. Таким образом, получим табл. 5. Из нее
видно, что остается рассмотреть всего два подкомплекса: л)/=
=<п18, п15> и л?/ = <д1в, д20>. Выпишем их оценки
<р(л1//) = <6, 3, 8>, <р(л//) = <7, 6, 9>.
В силу утверждения 2 с учетом числа решений в примере 3
получим шесть возможных вариантов комплексов, так как П)
содержит три, а П}/—два подкомплекса. Общее число комплек-
сов в исходной задаче равно 3x3x4x3x5x4 = 2160.
Упражнение 7. Пояснить, почему в примере 4 можно
исключить из рассмотрения программы п17—п19, и сформулиро-
вать соответствующее общее правило исключения.
<S2. УПРАВЛЕНИЕ ТРЕХОТРАСЛЕВОЙ ЭКОНОМИКОЙ
295
Рассмотрим декомпозицию задачи по критериям. Назовем
задачу разложимой, если множество критериев можно разбить
на группы г, ..., такие, что отношение R является объеди-
нением отношений Rlt ..., Rr, каждое из которых зависит только
от критериев из сооответствующей группы.
Утверждение 3. В разложимой задаче
[<р (П)]« = [<р (П)]«> П • • • П [ф (П)]«с
Упражнение 8. Доказать утверждение 3.
Утверждение 3 позволяет в ряде случаев сводить общую
задачу к задачам с критериями одного типа. Если все критерии
из ЭТх многократны, из однократный R — RiU Re, то задача
сводится к решению двух задач—задачи независимого выбора
и задачи конструирования.
Упражнение 9*. Построить алгоритм решения задачи
выбора оптимального комплекса.
Упражнение 10. Привести пример, в котором ни один из
предложенных способов не приводит к сокращению перебора.
§ 2. Оптимальное управление трехотраслевой экономикой
Рассмотрим модель трехотраслевой экономики. Будем считать,
что первая отрасль производит средства производства, которые
могут расходоваться на развитие всех трех отраслей. Две другие
отрасли будем считать потребительскими. Обозначим через xt(t)
(/=1,3) мощность i-й отрасли в момент t. Развитие экономики
запишем следующим образом:
Xt = и(хх,
О)
296
ГЛ. 5. ПРИКЛАДНЫЕ МНОГОКРИТЕРИАЛЬНЫЕ ЗАДАЧИ
где uz(/) означает долю продукта xlt которая поступает на раз-
витие t-й отрасли в момент времени t. Введем ограничение
И14-а2 + и3=1, (i = l,2, 3), (2)
которое означает, что
ления
продукт используется целиком.
Будем считать, что начальные ус-
ловия имеют вид
хД0)=1, х2(0) = <(0) = 0. (3)
Это означает, что в первой отрасли
начальная мощность равна единице, а
во второй и третьей отраслях—нулю.
Используем в качестве критериев х2(0
и х3(/) в конечный момент времени
t = T. Положим Т = 2. Будем считать,
что задано отношение R = RKf которое
определяется некоторым конусом К в
£2. На рис. 1 показаны один из таких
возможных конусов /С, а также двой-
ственный конус К*.
Учитывая изложенное, запишем задачу оптимального управ-
x1 = u1xlf
Х2 ^2-^1»
' (1 * ’ Wj W 2) ^1»
ui + «2^1> «i>0, м2>0,
х1(0)=1, х2(0) = 0, х3(0) = 0,
<х8(2), х3(2)>£Фд.
(4)
Задача (4) является многокритериальной задачей оптимального
управления с непрерывным временем. В главе 3 было доказано,
что всякое 2?к-оптимальное управление в задаче (4) является
оптимальным в задаче
Xj = и^, Xi (0) = 1,
х2 = и2х1( х2(0) = 0,
х8 = (1— Ui-~. иг)хи х8(0) = 0, (5)
«2>0,
Х2х2 (2) 4-Х8х8 (2) —> шах,
которая представляет собой однокритериальную задачу оптималь-
ного управления. Решим задачу (5) при всех значениях пара-
метров Z.2 и Х3 таких, что Х24-^3=1 и Х = <Х2, A3>gK*, где
К—конус, порождающий отношение R.
§2. УПРАВЛЕНИЕ ТРЕХОТРАСЛЕВОЙ ЭКОНОМИКОЙ
297
Запишем для задачи (5) функцию Понтрягина Н (3.35), со-
пряженную систему (3.32) и конечные условия (3.33):
Н=Ф1ЫЛ 4- ф2«2Хх 4- ф3 (1 — «1—и2) Xi, (6)
— Фх = Фх«х4-фа«а4-фз(1 — «1—«а), * (7)
Фа = О, ф3 = 0,
Ф1(2) = 0, ф2(2) = А2, ф3(2) = Х3. (8)
Упражнение 11. Проверить, что функция Понтрягина,
сопряженная система и конечные условия в данном случае выра-
жаются формулами (6)—(8).
Из (7) и (8) получаем
Фа (О = ^-з, Фз(0=Лз* (9)
Поскольку > О И Xi (0) = 1, получим, что
М0>0, /€[0,2]. (10)
Управления и1г и2 находятся из условия максимума по U функ-
ции
4- 4- М1 — “1—“а) *1 • (11)
В силу (10) условие максимума (11) сводится к условию
(Ф1—^з)«14-(^а—М«а-*тах (12)
и
при ограничениях
«14-Ма^1, ы1^0, w2^0. (13)
Рассмотрим три случая: Х2>Х3, 12<Л3, Л2 = Х3.
1) Х2 > Х3. При этом управления выбираются следующим
образом:
J 1, фх>%2, _[ 0, Фх>%2,
U1~\ 0, фх < Х2; “a-l 1, фх<Л2.
Действительно, если фх^^2> то Фх—^з^^а—К и Фх—^з^
(фх—Mwx + (^a—А.3) а2; последнее неравенство следует из того,
что (фх—Х3) (1 — «х) (Х2—Х3) «2, 1 — «х «а • Аналогично, если
Фх < ^2, то фх Х3 Х2 Х3 И (Х2 Х3) (Х2 Х3)«24-(Ф1 %3) Wx>
которое следует из (%2—13)(1—«2)^(Фх—Мых» так как
1 — И2>Их.
Решим первое уравнение системы (7):
Фх = — Фх«х—Фа«а — Фз (1 — «х — «а) >
которое в силу (9) совпадает с
фх== Фх«х ^2W2 Xjj (1
Последний член равен нулю, так как либо «х = 1, либо иа = Г,
фх = —фх«х —^а«а» Фх(2) = 0.
10 И. М. /Макаров и др.
298
ГЛ. 5. ПРИКЛАДНЫЕ МНОГОКРИТЕРИАЛЬНЫЕ ЗАДАЧИ
Ясно, что %г > б, так как Х2 > Х3 и Х,-|-Х3=1. Поэтому
«1(2) = 0, М2)=1,
Ф1 =г /.^2 = /-3,
% (0----М+2Хг,
что выполняется при i|\ < Л2. При выполнено «1=1,
u2 = 0. Учитывая, что ф1(1) = Х2, получим
ф== — фх, ф1 = ?12е"‘+1,
ipi (1) = А.3, if j (0) = Х2е.
На рис. 2 изображен график функции [фх. Подставляя иг и и2
в систему (5), получим
Х1 = Х1, t £ [0, 1],
x1(/) = ef,
х1(/) = 0, t£(l, 2].
На рис. 3 показана функция хх(/). Для х2 имеем
х2 = 0, /£[0, 1],
х2 = е,. t €(1, 2];
х,(0эО, /6 [0,2].
X
На рис. 4 показана функция х2(/). Из предыдущих формул сле-
дует, что х2(2) = е, х3(2) = 0.
Заметим, что оптимальные управ-
ления и траектории не зависят от
значений параметров 12 и %3, а опре-
деляются неравенством Х2 > Х3.
2) Х3 > 12. В силу полной сим-
метрии задачи по 2-й и 3-й перемен-
ным получаем х2 (2) =0, х3(2) = е.
3) Х2 = Х3 = %. Максимизируемое вы-
ражение в (12) принимает вид^—%)wlr
§2. УПРАВЛЕНИЕ ТРЕХОТРАСЛЕВОЙ ЭКОНОМИКОЙ
299
откуда получаем
J 1, Ф1 X, ( 0, X;
И1—( 0, ы*в| любое «2С[0, 1], Ф1 < X.
Решаем систему (7) с учетом полученных и
ф = —%u2—Х(1 — «,) = — %, —М+2Х, t €(1, 2];
((), =—ф1=Хе",+1. [0, 1].
На рис. 5 показана функция Чч (0- На отрезке [1, 2] управле-
ние «2(0 произвольно. Зададим управление u2(f), показанное
на рис. 6. На рис. 7 и 8 показаны функции х8(01и]*»(0 ПРИ
этом управлении; xa(2)=xs(2) = e/2.
Упражнение 12. Получить формулы для ха(£) 'и x3f(t).
Итак, в случаях 1), 2) /^-оптимальные управления единст-
венны, а в 3) управление не единственно.
Рис. 7. Рис. 8.
Построим проекцию множества достижимости D для задачи (5)
на пространство критериев:
Ф = {«*!, ^Ш = х.(2), d2 = x8(2)j, (14)
где х2(/)> x3(t) являются решениями системы дифференциальных
уравнений
Xj = «Л, Xj (0) = 1,
х3 == w2Xi, х2 (0) == 0,
х8 = (1—«i—“а) *1, х8(0) = 0
3
10* И. М. Макаров и др.
300
ГЛ. 5. ПРИКЛАДНЫЕ МНОГОКРИТЕРИАЛЬНЫЕ ЗАДАЧИ
при всевозможных функциях их (/) и и2 (0 из множества кусочно-
непрерывных функций, удовлетворяющих ограничениям
М0 + М0<1» М0>0, и2(0>0
в каждый момент времени t.
Упражнение 13*. Доказать, что множество Ф имеет вид,
показанный на рис. 9.
Рассмотрим конус К (рис. 10), порождающий отношение RK.
Двойственный конус К* показан на рис. 11. Ясно, что конус К*
содержит только точки X такие, что Х2 > Х3/ В этом случае
имеется единственное R-оптимальное управление (рис. 12). Точка
<0, е> доминирует по отношению R все остальные точки_множе-
ства Ф.
Рассмотрим конус К. и двойственный конус К*, показанные
на рис. 13. Конус К* содержит точки, для которых может выпол-
няться любое из соотношений:
1) Х2 X3j 2) Х2 Х3; 3) Х2 = Х3.
Для такого конуса К проекция Ф множества достижимости D
состоит из недоминируемых по отношению Rk точек (рис. 14).
Таким образом, в зависимости от конуса К, задающего отно-
шение R, существует либо единственное оптимальное управление,
либо множество оптимальных управлений, приводящих к любой
точке из Ф.
§3. РАЗРЕШЕНИЕ КОНФЛИКТОВ В ВС
301
§ 3. Разрешение "конфликтов в многопроцессорных
вычислительных системах
При решении задач -на многопроцессорных вычислительных
системах несколько процессов могут одновременно потребовать
одного и того же ресурса (процессора, канала, таблицы), кото-
рый предоставляется только одному из них. Такая ситуация
называется конфликтом, а ресурс—неделимым.
Выделим основные типы неделимых ресурсов вычислительных
систем: информационные (^х), программные (512), аппаратные (5£3).
Примером ресурса типа является таблица распределения
памяти в операционной системе, таблица распределения внешних
устройств; примером ресурса Э12—нереентерабельные програм-
мы: симплекс-метод, вычисление логарифма; аппаратные типа
Si8—диск, магнитная [лента, канал ввода-вывода, устройство
печати.
Конфликты возникают многократйо. Внутри каждого процесса
можно выделить критические участки, где ему необходим неде-
лимый ресурс. В каждый момент времени не более чем один
процесс может использовать неделимый ресурс; при этом осталь-
ные процессы, претендующие на этот ресурс, временно блоки-
руются и должны ждать, пока он не освободится. Следовательно,
конфликты сопряжены с задержками процессов и снижают произ-
водительность системы.
Задача состоит в том, чтобы предоставлять неделимые ресурсы
процессам так, чтобы минимизировать потери из-за конфликтов.
Порядок предоставления неделимых ресурсов процессам назы-
вается стратегией S разрешения конфликтов.
В настоящем параграфе рассматривается многокритериальная
задача нахождения оптимальных стратегий.
Пусть i-й процесс (i = l, п) имеет /и 4-1 состояний А1} (/=0, tri)
(здесь j=l, т—номер неделимого ресурса). В отсутствие других
процессов поведение i-ro процесса (i = 1, п) описывается цепью
Маркова с вероятностями переходов (q—0, mr, i = 0, tri).
Состояние Л« не соответствует ни одному из критических участ-
ков i-ro процесса; состояние Л/ (j== 1, т) соответствует /-му
критическому участку. Множество процессов, находящихся в со-
стоянии, соответствующем критическому участку относительно
одного и того же неделимого ресурса, называется группой конф-
ликтующих процессов.
Пусть М;—множество состояний i-ro процесса. Состояние
всей совокупности процессов в любой момент времени представ-
ляет собой точку множества М = ... хМп. Рассмотрим под-
множество KjcM:
Ky = {s€Al|(3i^i') [st-A‘it «„-ЛЦ}, (15)
302
ГЛ. 5. ПРИКЛАДНЫЕ МНОГОКРИТЕРИАЛЬНЫЕ ЗАДАЧИ
где /€{1, т\. Подмножество Kj задает те состояния из М,
в которых по крайней мере два процесса претендуют на /-й
ресурс.
Введем величину
X(s’K/) = { о, s^Kj, (16)
и рассмотрим вектор
% = <%(s,K1)) .... X(s, Ки)>, (17)
определяющий штрафы в состоянии s£M за конфликты по каж-
дому из неделимых ресурсов. Штраф равен времени ожидания
каждого из ресурсов.
Зададим бинарное отношение 7? на множестве средних век-
торов штрафов за конфликты по каждому из ресурсов за время
функционирования системы (или векторов средних штрафов за
единицу времени, если время функционирования системы беско-
нечно). Задача разрешения конфликтов состоит в нахождении
2?-оптимальной стратегии.
Установим соответствие между рассматриваемой задачей и
зада чей z поиска 7?-оптимальных стратегий управления цепью
Маркова. Построим цепь Маркова. Примем М за множество со-
стояний цепи. Состояния s С М являются векторами: s=<s1,..., sm>,
где s(€{0, 1, ..., tn}—состояние i-ro процесса в данный момент
времени t; Sj(t) = j означает, что t-му процессу в момент t тре-
буется /-Й ресурс. Пусть n = 2, = j и s2 (/) = /. Тогда /-й
ресурс может быть предоставлен только одному из процессов.
Процессу, которому j-й ресурс в момент t не был предоставлен,
тот же ресурс требуется и в (/4-1)-й момент. Поэтому переход
из состояния <i, /> в состояние </', /">, где j'=£j, j" ф j, не-
возможен. Таким- образом, переходные вероятности зависят от
того, какому процессу предоставлен /-й ресурс. Если предоста-
вить ресурс 1-му процессу, то состояние <j, /> перейдет в со-
стояние </', j> с вероятностью р},, или в состояние </, /> с ве-
роятностью 1—Sp//' = P//- Если предоставить ресурс 2-му про-
i
цессу, то </, /> перейдет в </, j > с вероятностью рц,. Анало-
гично определяются переходные вероятности в общем случае п
процессов (п > 2).
В данном случае удобнее говорить о минимизации штрафов,
чем о максимизации доходов. Эквивалентность задач при этом
очевидна. Вектор штрафа не зависит от принятого решения,
а зависит только от состояния s: компоненты /и-мерного
вектора rs определяются по формуле (16). Задача^состоит в том,
чтобы найти 7?-оптимальную стратегию для такой цепи. Таким
образом, требуемое соответствие установлено. Это позволяет сво-
§ 3. РАЗРЕШЕНИЕ КОНФЛИКТОВ В ВС
303
дить исходную задачу к однокритериальной и использовать все
результаты главы 4 для задачи разрешения конфликтов.
Пример 5. Рассмотрим следующие неделимые ресурсы:
Pi—канал ввода-вывода;
р2—общая таблица;
р3—устройство печати.
Пусть ресурсы рг и р3 важнее, чем ресурс р2. Зададим кри-
терии ti, t2 и ts, оценки по которым являются средними време-
нами ожидания каждого ресурса. Зададим на множестве всех
возможных векторов времен ожидания 1 = <.'%л, %2, %3> иерархи-
ческое отношение?, определяемое графом на
рис. 15, учитывающее указанную неравноцен-
ность. Критерии и t3 важнее, чем t2, кри- t, f2
терии Zj и ts считаются равноценными. Логи- ./ *
ческая форма отношения Т (ЛФО (?)) имеет
вид \ /
/123 (Р1> 02> Рз)=Р1Рз, /12 (Р1> Рг) = Р1,
f is (Pi, Рз) = Р1Рз > /23 (Рг» Рз) = Рз, рис jg
Ш-)=Р/ (i=T73).
Мажорирующая последовательность <iCT> (Т), определяемая по
ЛФО(/?), имеет вид <ifr, ф, ф> = <1°, 2°, 3°>. Стратегия, мини-
мизирующая среднее время ожидания ресурса рп является
Т-оптимальной.
Упражнение 14. Доказать Т-оптимальность указанной
стратегии.
Стратегия, указанная в примере 5, не является единственной
Т-оптимальной. Учитывая, что критерии tt и ts равноценны,
можно установить, что Т-оптимальной будет стратегия, миними-
зирующая среднее время ожидания ресурса р3.
Пример 6. Рассмотрим частный случай задачи нахождения
оптимальной стратегии разрешения конфликтов. Пусть процессы
слабосвязаны. При этом
Ро/ = 8/ (i = 1, n; j=l, tn), pjk = Q /#=0, £=#0),
P// €(0,1) (i =T?n; / = f, m).
Утверждение 4. Пусть R—любое рациональное отноше-
ние. Существует 8 > 0 такое, что при любых е) <8 (i = Г, п;
j = 1, т) для конечного и для бесконечного времени:
а) R-оптимальная стратегия единственна-,
б) она задается следующим образом: ресурс предоставляется
процессу, имеющему меньшую вероятность рц остаться в состоя-
нии Af среди всех процессов данной группы.
Указанная стратегия является R-канонической.
Пример 7. Найдем количественную оценку выигрыша при
указанной в примере 6 /^-оптимальной стратегии. Рассмотрим
304
ГЛ. 5. ПРИКЛАДНЫЕ МНОГОКРИТЕРИАЛЬНЫЕ ЗАДАЧИ
Таблица 6
Начальное состояние Число шагов
5 10 20 j 1 25 i | 30
е|=0,035; в| = 0,04; 8^=0,035; 8^=0,25 -
00 0,04 0,193 0,662 0,929 1,207
0,043 0,229 0,871 1,256 1,663
01 0,134 0,327 0,783 1,043 1,315
0,150 0,404 1,041 1,414 1,809
11 2,832 3,559 4,226 4,507 4,788
3,405 4,736 • 5,911 6,334 6,743
12 0,038 0,247 0,897 1,239 1,574
0,040 0,290 1,188 1,693 2,197
22 3,119 4,170 5,215 6,610 5,974
3,750 5,657 7,660 8,338 8,933
е}=0,075; 82=0,1; б|=0,065; 82 = 0,06 5
00 0,170 0,700 2,060 2,781 3,514
0,183 0,832 2,675 3,690 4,730
01 0,296 0,820 2,115 2,819 3,540
0,329 0,994 2,753 3,737 4,754
11 2,888 3,823 5,140 5,815 6,516
3,444 4,982 . 6,959 7,902 8,877
12 0,085 0,524 1,881 2,624 3,375
0,090 0,612 2,424 3,467 4,535
22 -3,213 4,644 6,571 7,399 8,194
3,809 6,031 9,054 10,307 11,440
е} = 0,115; 82=0,160; 8^=0,095; 8®= 0,105
00 0,345 1,237 3,274 4,310 5,350
0,374 1,467 4,200 5,633 7,081
01 0,457 1,293 3,250 4,269 5,298
0,506 1,555 4,175 5,575 7,000
11 2,937 4,060 5,894 6,858 7,855
3,481 5,208 7,827 9,145 10,507
12 0,129 0,747 2,606 3,625 4,660
* 0,136 0,867 3,299 4,694 6,129
22 3,298 5,005 7,515 8,624 9,705
3,862 6,324 10,025 11,646 13,255
§4. ОПТИМАЛЬНЫЙ ПОСЛЕДОВАТЕЛЬНЫЙ ВЫБОР
305
Продолжение табл. 6
Начальное состояние Число шагов
5 10 1 20 | 25 | 30
е}=0,155 ; 4=0,220; 4=0,25; ф=0,145
00 0,535 1,713 4,214 5,457 6,698
0,582 2,027 5,357 7,061 8,771
01 0,608 1,702 4,129 5,357 6,589
0,673 2,035 5,256 6,929 8,617
11 2,984 4,263 6,473 7,634 8,828
3,517 5,404 8,493 10,065 11,683
12 0,168 0,927 3,141 4,349 5,576
0,178 1,070 4,929 5,559 7,137
22 3,373 5,284 8,184 9,488 10,760
3,911 6,554 10,720 12,586 14,372
однокритериальный вариант задачи со слабосвязанными процес-
сами. Сравним среднее число конфликтов при данной стратегии
со средним числом конфликтов при равновероятном выборе про-
цесса, которому предоставляется ресурс. Значения параметров:
пи2, ги = 2, р} = 0,9, />2 = 0,75, р, = 0,7, р| = 0,95;
при этом значения ^"меняются от 0,035 с шагом 0,04, значения
8g—от 0,04 с шагом 0,06, значения е%—от 0,035 с шагом 0,03 и
значения &1—от 0,025 с шагом 0,04.
В табл. 6 приведены результаты расчетов. Строка соответ-
ствует фиксированному начальному состоянию (запись 12 озна-
чает, что первый процесс находится в состоянии Л*, а второй —
в состоянии Л|; аналогичный смысл имеют обозначения 00, 01
и т. д.). Столбец соответствует времени функционирования си-
стемы Т (числу шагов); на пересечении строки и столбца запи-
сано в верхней части клетки среднее число конфликтов при
оптимальной стратегии, указанной в утверждении 4, а в ниж-
ней—при стратегии, предоставляющей ресурс равновероятно тому
или иному процессу. Табл. 6 разбита на части, каждая из кото-
рых соответствует фиксированным значениям ej (t, / = 1, 2).
Использование оптимальной стратегии уменьшает среднее число
конфликтов на 30—40%.
§ 4( Многокритериальная задача оптимального
последовательного выбора
Рассмотрим несколько ситуаций, в которых требуется осуще-
ствить выбор одного объекта из последовательно поступающих.
Геологическая партия заранее наметила для разведки шесть
мест, расположенных на определенном маршруте. Данные, харак-
306 .
ГЛ. 5. ПРИКЛАДНЫЕ МНОГОКРИТЕРИАЛЬНЫЕ ЗАДАЧИ
теризующие наличие полезных ископаемых и трудности разве-
дочного бурения, заранее не известны и могут, быть получены
только на месте. Разведочное бурение может быть произведено
только один раз. Как выбрать место для разведки в процессе
движения по маршруту?
У рыболовного корабля осталось девять дней до возвращения
на базу и только одна возможность провести улов (в один из
дней). Ценность рыбы и сложность ее добычи заранее не известны.
В какой из дней рыбакам забросить сеть? .
Пусть туристам необходимо выбрать место дневки во время
байдарочного похода. Заранее известно, что им встретятся пять
подходящих мест. Туристы плывут по течению и не могут вер-
нуться к пропущенному месту. При выборе места учитываются
два независимых критерия: качество пляжа (для отдыха) и нали-
чие дров (для приготовления пищи). Данные об оценках возмож-
ных мест дневок по этим критериям заранее не известны. Задача
туристов состоит в том, чтобы остановиться на отдых в таком
месте, которое не хуже любого из остальных четырех мест по
обоим критериям одновременно.
В рассмотренных и^других аналогичных ситуациях поступаю-
щие объекты характеризуются несколькими признаками; упорядо-
чение объектов по каждому признаку случайно, не зависит от
упорядочения по остальным признакам и заранее не известно.
Необходимо выбрать такой объект, который был бы в определен-
ном смысле оптимальным среди всех остальных.
Будем считать, что объекты являются точками из Ет. Опи-
шем конкретный механизм предъявления точек. Последовательно
предъявляется п точек из Ет'. А1, А2 и т. д.; при этом
Рг {А2 > Л}} = Рг {А1 > АЦ = ... = Pr|{А2т > Ak} = 1/2 (18)
и указанные события, относящиеся к разным координатам, неза-
висимы. При трех точках и двух осях общее число расположе-
ний точек в Е2, отличающихся порядком по осям, равно 31 31=36
и каждое из них имеет одну и ту же вероятность 1/36. Шесть
таких расположений были показаны на рис. II.5.1.
Заметим, что на рис. II.5.1 расположение по 1-й оси всегда
одно и то же: А} > AJ > А®, а по 2-й оси представлены все
3! = 6 возможных порядков. При т = 1 описанный механизм совпа-
дает с механизмом, рассмотренным в примере 4.11.
Задача состоит в том, чтобы выбрать с наибольшей вероят-
ностью одну из лучших в некотором смысле точек, используя
только данные о предъявленных точках. Как и в примере 4.11,
возвращение к отвергнутому варианту недопустимо.
Назовем многокритериальной задачей оптимального последова-
тельного выбора тройку <Q, С, п>, где
Q—механизм предъявления точек;
С—функция выбора, обладающая свойствами:
§4. ОПТИМАЛЬНЫЙ ПОСЛЕДОВАТЕЛЬНЫЙ ВЫБОР
307
а) если А = {А*, ..., А1}, В = {В1...В1},
sgn(4s'—4() = sgn(B|—B‘s) (i, j = l, /; s=l, m), (19)
то номера элементов 4Z, выбираемых из А, совпадают с номе-
рами элементов В1, выбираемых из В;
б) С наследственна;
п—заранее заданное число предъявляемых точек.
Точка 4‘ считается одной из лучших, если 4'С С (й). Счи-
таем, что Q совпадает с указанным выше механизмом.
Свойства функции выбора С позволяют по произвольной после-
довательности поступивших точек <4\ ..., Ak> однозначно опреде-
лить условную вероятность Рг(Л49 того, что 4* С С (41,...,4”)
при условии, что данная последовательность <4\ ..., 4*> уже
предъявлена, и безусловную вероятность Р2 (41, ..., Ак) предъяв-
ления данной последовательности. Под правилом выбора будем
понимать любое множество 2 последовательностей <4\ ..., 4*>»
s£{l, ..., п}, такое, что
У/Л(41, ..., 49=1, (20)
J5
а под оценкой правила 2—сумму
Р(^)в2Р2(41, ..., А^Р^А1, .... 49. (21)
JE
Точка 4-’ выбирается, как только последовательность
<41, ..., 45> принадлежит 2. Формула (21) задает безусловную
вероятность выбора некоторой точки 45СС(4*, ..., 4"). Опти-
мальным правилом 2* назовем такое, при котором Р (2) макси-
мальна. Решить многокритериальную задачу оптимального выбора
<Q, С, п>—это значит указать одно из оптимальных правил 2*.
Установим связь этой задачи с задачей двухуровневой опти-
мизации управляемых марковских цепей и приведем ее решения
в двух частных случаях. Построим цепь Маркова. Состоянием
цепи является любая последовательность точек вида <4Х, ..., 4*>
(£ = 1, га). Начальным состоянием является пустая последова-
тельность <0>. Добавим фиктивное состояние х, соответствую-
щее ситуации, в которой уже осуществлен выбор; х не является
последовательностью точек. В каждом состоянии i=/=x множе-
ство решений Д’,- состоит из двух элементов: Kf={l, 2}. Реше-
ние 1 означает, что осуществляются переходы с вероятностями,
определяемыми механизмом появления точек Q, т. е. из состоя-
ния <4\ ..., 4*> возможны только переходы в состояния вида
<4\ ..., 4s, 4J+1>, где 4i+1—вновь предъявляемая точка, с рав-
ными вероятностями. Доход г1 равен нулю. Решение 2 означает,
что происходит переход из состояния <4*, ..., 4S> в х с вероят-
ностью единица; доход при этом равен 4\ В состоянии х Кх—{ 1},
308
ГЛ. 5. ПРИКЛАДНЫЕ МНОГОКРИТЕРИАЛЬНЫЕ ЗАДАЧИ
доход равен 0, а переход возможен только в состояние х с вероят-
ностью 1.
Упражнение 15. Построить указанную марковскую цепь
и выписать ее матрицу переходов при п = 2 и п = 3.
Множество состояний построенной управляемой цепи—это
множество всех последовательностей вида <Л\ .... Л5> (s= 1, п),
к которому добавлено начальное состояние <0> и фиктивное
состояние х. Стратегия л однозначно определяет множество
состояний, в которых принимается решение 2, т. е. задает неко-
торое множество последовательностей. Задание любого множества
последовательностей типа <Лг.......Л8> (sС{1 > ..., «}) одно-
значно определяет некоторую стратегию, при которой решение 2
принимается на состояниях, соответствующих последовательностям
из этого множества.
Таким образом, между множеством всех стратегий для построен-
ной цепи и множеством всех правил выбора установлено взаимно
однозначное соответствие. При этом вероятность получения дохо-
да Ак в построенной цепи равна вероятности выбора точки Л*
в исходной задаче. Отсюда следует, что слабо оптимальная стра-
тегия для управляемой цепи Маркова определяет оптимальное
правило выбора для исходной задачи.
Решим задачу <Q, С, п> при паретовской и совокупно экстре-
мальной функциях выбора.. Различные расположения точек
Л1, ..., Л” в Ет можно описывать перестановками; г т-мерных
точек Л1, ..., Лг задают т перестановок символов 1, ..., г:
Л1в<4, *2, •••, #>> п2 — <»1> «1. •••. Ф, ...
.... = Z?........»«>,
каждая из которых определяется [проекцией точек Л1.....Аг
на соответствующую ось Ет.
С каждым расположением г точек <л[......лгту связаны две
вероятности:
F (лги ..., лгт\ k)—вероятность того, что при предъявлении
еще п—г точек Лг+1, ..., Л" выполняется Ак^С(А1, ..., Лп);
Н (л[, ..., л^)—вероятность того, что при дальнейшем предъяв-
лении точек лучшая точка окажется среди них при использова-
нии оптимального правила выбора.
1. Пусть С=СР—паретовская функция выбора. На рис. II.5.1
точка Л’СС^Л1, Ля,-Л8) только в случаях д) и е).
Рассмотрим одну ось. Точки Л1, ..., Аг определяют переста-
новку лг=<11, ..., iry. Пусть предъявлена еще одна точка Лг+1.
Тогда точки А1.....Ar, Ar+1 могут задать только одну из сле-
дующих перестановок:
< ii, .. •, ir, 1> =^z(0>
< ii, ..., ir, 2> =лг(2), (22)
< i'i, г-Ь1> = лг(г+1),
§4. ОПТИМАЛЬНЫЙ ПОСЛЕДОВАТЕЛЬНЫЙ ВЫБОР
309
где <ij,
i'r, k~> определяется так:
J is, если
is~ Vs + 1, если
is < k,
is>k-
(23)
Вероятность любого перехода из <i\, ..., ir> в одну из переста-
новок (22) равна 1/(г4-1).
Ясно, что
( 1, если Ак—паретовская точка,
Я(л", ..., л"; k) = { _ . (24)
* ( 0 в противном случае; '
Н(л1, ..., л£) = 0, (25)
поскольку г = п. Найдем Н(0), т. е. вероятность выбора паре-
товской точки. Это позволит найти оптимальное правило. Для цепи
Маркова, соответствующей данной задаче, уравнение Веллмана
(4.14) принимает вид
Я(л[, ..., л^) = тах|г(л[, ..., лгт-, г),
•£ Н(л[(4), .... ^0-77^} . (26)
1 < /1 //л<г + 1 (Т / J
где
F(n[, ..., Л^,; k)= Р •••, nrnGm)’^) (r-1-Пи •
(27)
Рекуррентные формулы (26), (27) вместе с начальными условиями
(24), (25) позволяют найти Н(0).
Упражнение 16*. Доказать, что оптимальное правило
находится при известной функции Н как множество последова-
тельностей, для которых H = F.
Приведем результаты расчетов Н и F по формулам (24)-'-(27)
при т = 2. Будем пользоваться моделью, показанной на рис. 16
для четырех точек Л1—А*; здесь л? = <3, 4,
2,1>, n‘ = <2, 3, 4,1>.
Пусть п = 5 и расположение предъяв-
ленных точек Л1, Л2 показано на рис. 17,
а. Вероятность F^A1, Л2; 2) того, что Л2
останется паретовской, равна 0,75; вероят-
ность Я (Л1, Л2) равна 0,69. Выбирается Л2,
так как Н < F. В расположении, показанном
на рис. 17,6, имеем ^(Л1, Л2; 2) = 0,54333
и Я (Л1, Л2) =0,745, т. е. Л2 не выбирает-
ся, так как Н >F. При расположении трех
точек, показанном на рис. 17, е, выбирает-
ся Л3, так как F = 0,78 > Я = О',6325, а при
казанном на рис. 17, г, Л3 не выбирается, так как F = 0,685
<#=0,7375.
Рис. 16.
расположении, по-
310 ГЛ. 5. ПРИКЛАДНЫЕ МНОГОКРИТЕРИАЛЬНЫЕ ЗАДАЧИ]
Обозначим вероятность оптимального выбора при п точках
и т критериях через И (п, т). В табл. 7 приведены значения
Н(п, т) при п^9 и /п=1, 2. Как видно из таблицы, геологи
могут найти одно из оптимальных мест с вероятностью 0,720;
рыбаки могут выбрать один из оптимальных дней с вероят-
ностью 0,726; туристы могут найти одно из оптимальных мест
дневки с вероятностью 0,730. Сами оптимальные правила не при-
Т аблица 7
п / / т 1 2 3 4 5 6 7 8 9
1 1 0,5 0,5 0,458 0,433 0,419 0,410 0,406 0,402
2 1 0,75 0,75 0,741 0,730 0,720 0,725 0,727 0,726
водятся в силу их громоздкости, так как число последовательно-
стей, содержащихся в J?*, при указанных параметрах велико.
Для Н(п, 1) имеет место
lim Я (га, 1) = <г». (28)
л->00
Для Н (п, т) верно
Утверждение 5. Для любого 8>0 существует т9 такое,
что для всех n = 1, 2, ... и т^та
Н (n, т) > 1—8.
Это означает, что, хотя при любом числе критериев отношение
числа паретовских точек к общему числу п всех точек стремится
к нулю с ростом п, вероятность выбора паретовской точки при
достаточно большом числе критериев и любом п может быть сде-
лана сколь угодно близкой к единице за счет использования
оптимальных правил выбора.
Упражнение 17*. Найти оптимальные правила выбора
и соответствующие вероятности Н при п = 2, т — 3 и и = 3,4,
т = 2.
§S. ИГРОВАЯ ЗАДАЧА С ВЕКТОРНЫМИ ДОХОДАМИ
311
2. Пусть С—совокупно экстремальная функция выбора.
Утверждение 6. При любом числе т критериев и числе п
точек существуют числа 1 . < sj п такие, что опти-
мальное правило задается следующим образом: если N-й предъяв-
ляется точка, которая лучше всех уже предъявленных по k кри-
териям, и N^Sk, то она выбирается. Числа s„, ..., s* нахо-
дятся^из условия максимума функции:
P(St....sm) =
т' ’fe-l"1 дг_1 . . \"^ IN И» С1
-ЕЛ £ П Hw-iy) Е
k = l N =S£ i~sk
где
ГП / m~i \
pk= П П
/=fc + l i=Sy \ i-q J
Л»=1.
Асимптотическое значение вероятности оптимального выбора при
росте п и т> \ равно
Н (т) = (\1т)Ч^-'\
Асимптотика чисел sj, задается формулой
lim -Ц-=1 — (1— Н(т)уй, i = l~in.
П -> 00
§ 5. Игровая задача с векторными доходами
Рассмотрим матричную игру. В ней участвуют два игрока
А и В. Игра задается матрицей Q размера пАхпв. Игрок А
выбирает строку матрицы Q, игрок В—столбец. Выигрыш игро-
ка А равен элементу матрицы Q на пересечении выбранных строки
и столбца. Проигрыш В равен выигрышу А. Строки матрицы Q
соответствуют чистым стратегиям игрока А, столбцы—чистым
стратегиям игрока В.
Если игрок А выбирает i-ю чистую стратегию с вероятностью xf
а игрок В—j-ю чистую стратегию с вероятностью yJt то гово-
рят, что игроки Л и В используют смешанные стратегии х=
=<хп .... хПд> и у=<уг....При этом средний выигрыш
пА пВл
игрокаЛ равен 2 где 4ij—элементы матрицы Q;
<%!, ..., хЛл>—смешанная стратегия игрока Л; <t/i, ..., Упв~> —
смешанная стратегия игрока В. Считают, что игрок Л стремится мак-
симизировать средний выигрыш, а игрок В—минимизировать его.
312
ГЛ. 5. ПРИКЛАДНЫЕ МНОГОКРИТЕРИАЛЬНЫЕ ЗАДАЧИ
Пусть игрок;/! выбрал, например, стратегию х. Тогда В избе-
рет такую стратегию у, которая делает выражение ХйШц
наименьшим. При этом стратегию у, минимизирующую 2 S
можно выбрать чистой. Действительно,
22w7z/e2^(2*zft/), *//>° (/=ъ «в). (29)
откуда следует, что левая часть (29) не может быть меньше,
чем наименьшая из сумм 2 xi4ij> которая соответствует /-й чистой
1
стратегии В. Итак, минимальный выигрыш игрока А при данной
стратегии х равен
Игрок А стремится максимизировать этот минимум. Поэтому он
будет выбирать свою стратегию х так, чтобы получить
= max min 2 4ijxi•
х I i
Величина называется максимином.
Упражнение^. Доказать, что чистый максимин, равный
max min q^, не больше, чем и,.
t I
Аналогичные рассуждения для игрока В показывают, что он
выбирает стратегию так, чтобы получить минимакс
u2=min тах^л^уу.
Утверждение 7 (теорема о минимаксе).
t»i = os. (31)
Пара стратегий х и у называется решением игры с матри-
цей Q, если
22^Л-У/=«1=»2;
величина v = vr = v.. называется значением или ценой игры.
Утверждение 8. Пара стратегий х', у* является реше-
нием тогда и только тогда, когда
22 ад%<22^«// для всех у, (32)
i i /
2 2 qtjXiy'i >22 qijXiy'i для всех х.
(33)
§5» ИГРОВАЯ ЗАДАЧА С ВЕКТОРНЫМИ ДОХОДАМИ
313
Доказательство. Из (32) и (33) имеем
max 2 2 qijXty'i = 22 ЯцхМ = min 2 2 ЧцХ'^. (34)
* i / i i у i i
При любых стратегиях х9 и у' имеют место неравенства
min max 22 <7/А^<тах22ад«//. (35)
У X i j х i j
max min 2 2 »in 2 2 ЧцХ'#,. (36)
[X l V. J j V i I
Левые части неравенств (35) и (36) равны в силу утверждения 7.
Поэтому они равны любой из сумм в (34). Это доказывает, что
пара х', у' является решением игры. Неравенства (32), (33) для
любого решения х', у' выполнены по определению решения.
Утверждение доказано.
Пусть Q1, ..., —квадратные матрицы размера пАхпв
с элементами q^, ..., q^. Положим qij — <q}j, .... <?“> (i = 1, пА,
i=l, п8). Определим матричную игру с векторными доходами.
По аналогии с однокритериальным случаем средний выигрыш
игрока А зададим формулой
2 2 ЯцХ{у/, (37)
i i
x = <Xj....хЯл>, У’^Уи •••> Упв}—смешанные стратегии игро-
ков А и В. Решением .матричной игры с векторными доходами
назовем пару х', у' такую, что
2 2 <hjX'iy'i Я 2 2 <Ц}х\У} Для всех у, (38)
22 4ijXiyiR'Si'^qijX'iy'i для всех х. (39)
При т=1 и отношении «больше» формулы (38), (39) перейдут
в (32), (33), т. е. получим понятие решения однокритериальной
матричной игры. Множество решений матричной игры с вектор-
ными доходами обозначим через 6(Q, Р), rAeQ = <Q\ ..., Qm>.
Задача нахождения 6(Q, Р) является задачей. поиска ^-опти-
мальных по Нэшу управлений.
Положим
пА пВ
Ф1 (х, у) = 2 2 ~x{yj qt/, ф, = — <рх.
В силу формул (38), (39), (1.16), (1.18) и утверждения 1.11
получаем, что 0(Q, /?) совпадает с <р, Р, Н) при указан-
ных значениях параметров задачи <^, <р, Р, Н>.
314 ГЛ. 5* ПРИКЛАДНЫЕ МНОГОКРИТЕРИАЛЬНЫЕ ЗАДАЧИ
В случае Х-отделимых отношений R поиск частных решений
в силу утверждения 1.9 можно свести’к решению однокритериаль-
ной игровой задачи. Такие задачи сводятся к задаче линейного
программирования.
ГГример 8. Пусть
( 1 3,\ Ц
4 ~ \—4 7/Й' ~йи\3 2J •
В матричной игре с матрицей оптимальной является чистая
стратегия (1, 1), в игре с матрицей Qs—чистая стратегия (2,2)
Рассмотрим игру <Q, R>, где Q = <Q‘, Q*>, т. е.
п /<1, 4> <3, 1>\
У = и^Тз> “7, 2>J •
Выражение (37) имеет вид
<9, 2>ху+<-4, -1>х + <-11, \уу, (40)
где %=%!, у=уг (х2 = 1 — xt, у2=1—У1)-
Для чистой стратегии (1, 1) х=1, у= 1 и’выражения^!.20)
о учетом (38) и (39) принимают вид
<—2, 3> Р2<—2у, Зу>,. <5х? х> Рх|<5, 1>;
для стратегии (2, 2) —
<0, 0> Р2<—Пу, у>, <—4х, —хН?! <0, 0>;
для стратегии (1, 2) —
<0, 0>Р2<—2у, Зу>, <—4х, — %>#!<—4, —1>;
для стратегии (2, 1)—
<—11, 1>R2<—Ну, у>, <5х, x>R1<0, 0>.
Положим /?!= Р2 = Р. Имеем
<—2, 3>Р<—2у, Зу>, <5х, х>Р<5, 1>,
<0, 0>Р5<—Ну, у>, <—4х, ”>Р<0, 0>,
<0, 0>Р<—Пу, у>, <5х, х>Р<0, 0>,
(—11, 1>Р<—Ну, У>, <5х, х>Р<0, 0>.
В силу (38) и (39) получаем, что стратегии (1,1) и (2,2) Р-опти-
мальны по Нэшу, стратегии (1,2) и (2,1)—нет.
Пусть R1=L<1( 2> (лексикография по 1-му критерию), R2 = L<2> 2>.
Тогда _
<—2, 3>Р2<—2у, Зуу, (5х, х>/?1<5, 1>,
<0, 0>Ra<—Ну, уу, <—4х, — х>Рх<0, 0>,
<0, 0>Р2<—2у, Зуу, <—4х, —x>Ri<—4, —1>,
<—11, 1>R2<—Пу, у>, <5х, х>Рх<0, 0>.
§5. ИГРОВАЯ ЗАДАЧА С ВЕКТОРНЫМИ ДОХОДАМИ;
315
Это значит, что единственной чистой совокупно оптимальной по
Нэшу стратегией является стратегия (2,2). При Ri = L<2, i>.
#2 = £<i, 2> имеем
<—2, 3>Ra<—2у, Зу>, <5х, х>^<5, 1>,
<0, 0>Ra<—11«/, у>, <—4х, —x>R1<0, 0>,
<0, 0>Ra<—2у, Зу>,
<5х, х> Rr <0, 0>,
т. е. единственной чистой совокупно оптимальной по’Нэшу стра-
тегией является (1,1).
Положим Rl = RUit Ra= Rut, где
^1(^1» 2г) = “ Z14* ^2(^1, 2а) =
где zx и z2—координаты доходов. Легко проверить, что совокупно
оптимальных по Нэшу чистых стратегий не существует.
Пример показывает, что обе седловые точки в матрицах
Q1 и Q2 определяют парето-оптимальные по Нэшу чистые страте-
гии. При различных отношениях у игроков совокупно оптималь-
ную по Нэшу чистую стратегию порождает не любая седловая
точка; совокупно оптимальные чистые стратегии могут отсутство-
вать при наличии седловых точек в матрицах Q1 и Q2.
Утверждение 9. Пусть Rj—^-отделимое отношение
(1 = 1,2). Тогда 0(Q, R)=£0.
Доказательство. Задача поиска 6 (Q, R) сводится к
задаче поиска совокупно оптимальных по Нэшу управлений в задаче
<<Й, Ф, R, Н> с параметрами
^1 = ; х
^2 = {i/
ЛА 1
S XZ=1, Х,>0
1= 1 J
пВ
/=1
"А пВ
Я>1(*, У) = X
i — 1 / = 1
ф2(*> 1/) = — Фх(*, У),
R = <Ri, Ra>.
Для ’ указанной задачи выполняются условия утверждения 1.13,
из которого следует существование решения в исходной игре. Ут-
верждение доказано.
Литература. [6, 11, 41, 45, 74, 113].
ЛИТЕРАТУРА
1. А г'а н бе г я н ГА. Г. Управление социалистическими предприятиями: воп
росы теории и практики.— М.: Экономика, 1979.
2. Айзерман М. А., Завалишин Н. В., Пятницкий Е. С. Глобаль-
ные функции множеств в теории выбора альтернатив. I.— Автоматика и
телемеханика, 1977, № 3, с. 111—125; II.— Автоматика и телемеханика,
1977, № 5, с. 103—113.
3. Айзерман М. А., Малишевский А. В. Некоторые аспекты общей
теории выбора лучших вариантов.—М.: Институт проблем управления,
4. Айзерман М. А., Малишевский А. В. Проблемы логического обосно-
вания в общей теории выбора.— М.: Институт проблем управления, 1980.
5. Алескеров Ф. Т., Завалишин Н. В., Литваков Б. М. О раз-
ложении функций выбора по системе более простых функций.—Автома-
тика и телемеханика, 1979, № 3, с. 107—117.
6. Аллен Р. Математическая экономика.— М.: ИЛ, 1968.
7. Архангельский Н. Е. и др. Экспертные оценки и методология их
применения. — М.: МЭСИ, 1974.
8. Ахо А., Хопкрофт Дж., Ульман Дж. Построение и анализ вычис-
лительных алгоритмов.— М.: Мир, 1979.
9. Бауман Е. В. Выбор на графе и в критериальном пространстве.—
Автоматика и телемеханика. 1977, № 5, с. 114—126.
10. Баумоль У. Экономическая ^теория и исследование операций.— М.:
Прогресс, 1965.
11. Березовский Б. А., Г^е'ни'нсон Б. А., Рубчинский А. А. За
дача об оптимальной остановке на частично упорядоченных объектах.-^
Автоматика и телемеханика, 1980, № 11, с. 69—75.
12. Бел ьский А. А. Теория графов и комбинаторика.—М.: МИИТ, 1979»
13. Бел ьс кий А. А., Липкина 3. С. Математическая логика и теория
графов.— М.: МИИТ, 1974. '
14. Б ер ж К- Теория графов и ее применения.— М.; ИЛ, 1962;
15. Б е ш е л е в С. Д.» Г у р в и ч Ф. Г. Экспертные оценки.— М.: Наука, 1973.
16. Б е ш е л е в С. Д., Г у р в и ч Ф. Г. Математико-статистические методы
экспертных оценок.— М.: Статистика, 1980.
17. Борисов В. И., Виноградская Т. М. Об одном алгоритме опре-
деления множества Парето.— В кн.: Материалы I Всесоюзной конферен-
ции по исследованию операций. Минск: Институт математики АН БССР,
1975, с. 264—269.
18. БрейманЛ. Задачи о правилах остановки.— В кн.: Прикладная комби-
наторная математика.— М.: Мир, 1968, с. 159—202.
19. Бурков В. Н. Основы математической теории активных систем.— М.:
Наука, 1977.
20. Вагнер Г. Основы исследования операций, т. 1—3. — М.: Мир, 1973.
21. В и л к а с Э. Й., М а й м и н а с Е. 3. Решения: теория, информация, моде-
лирование.— М.: Радио и связь, 1981.
22. Виноградская Т. М. Два алгоритма выбора многомерной альтерна-
тивы.— Автоматика и телемеханика, 1977, № 3, с. 90—95.
ЛИТЕРАТУРА
317
23. Виноградская Т. М. Иерархические отношения и алгоритм выде-
ления недоминируемых множеств.— ДАН СССР, 1979, 247, № 5,
с. 1073—1077.
24. Виноградская Т. М. Использование свойств частично упорядоченных
множеств в многокритериальных задачах принятия решений.— В кн.:
Проблемы принятия решений: Сб. трудов, вып. 5. М.: Институт проб-
лем управления, 1974, с. 56—60.
25. Виноградская Т. М. Принципы построения автоматизированной
системы «Выбор».— В кн.: Автоматизация проектирования, вып. 2. М.:
Статистика, 1979, с.176—184.
26. Виноградская Т. М. Согласованный выбор последовательности много-
мерных альтернатив в условиях неполной информации.— В кн.: УП Все-
союзное совещание по проблемам управления: Тезисы докладов, кн. 2.
Минск, 1977, с. 104—105.
27. Виноградская Т. М. Среднее значение числа неподчиненных р ешений
в многокритериальных задачах.— Известия АН СССР. Техническая кибер-
нетика, 1976, № 2, с. 36—38.
28. Виноградск ая Т. М. Тестовая процедура определения адекватной
модели выбора.— В кн.: Проблемы проектирования и применения диск-
ретных систем в управлении: Тезисы докладов. Минск, 1977, с. 220—221.
29. Виноградская Т. М., ГафтМ. Г. Точная верхняя оценка числа
неподчиненных решений в многокритериальных задачах.— Автоматика и
телемеханика, 1974, № 9, с. 111—118.
30. ВиноградскаяТ. М.,Генинсон Б. А. Многокритериальные модели
разрешения конфликтов в высокопроизводительных ВС.— В кн.: Высоко-
производительные вычислительные системы: Тезисы докладов, ч. 3.
Тбилиси, 1981, с 122—124.
31. Виноградская Т. М., Р у б ч и н с к и й А. А. Бинарные координат-
ные отношения в критериальном пространство. I.— Автоматика и телеме-
ханика, 1981, № 3, с. 95—<03; II.—Автоматика и телемеханика,
1981, № 4, с. 78—89.
32. Виноградская Т. М., РубчинскийА. А. Квазикоординатные от-
ношения в задаче выбора альтернатив.—Известия АН СССР. Техничес-
кая кибернетика, 1981, Ж 5, с. 22—29.
33. Виноградская Т. М., Рубчинский А. А. Логические формы би-
нарных отношений в критериальном пространстве.— ДАН СССР, 1980,
251, № 2, с. 300—304.
34. ВиноградскаяТ. М., Рубчинский А. А. Логические формы
функций выбора.— ДАН СССР, 1980, 254, № 6, с. 1362—1366.
35. Виноградская Т. М., Рубчинский А. А. Отделимые отношения
в задачах векторной оптимизации.— В кн.: Математические методы опти-
мизации и их применения в больших экономических и технических систе-
мах. М.:ЦЭМИ АН СССР, 1980, с. 74—77.
36. ВиноградскаяТ. М., Рубчинский А. А., Щербаков А. В."Ин-
терактивная процедура решения многокритериальной задачи оптимального
управления.— В кн.: I Всесоюзное совещание по статистическому и диск-
ретному анализу нечисловой информации, экспертным оценкам и дискрет-
ной оптимизации: Тезисы докладов. Алма-Ата, 1981, с. 310—311.
37. Вольский В. И. Выбор по Крамеру и его турнирное представление. —
В кн.: I Всесоюзное совещание по статистическому и дискретному ана-
лизу нечисловой информации, экспертным оценкам и дискретной оптими-
зации: Тезисы докладов. Алма-Ата, 1981, с. 312—313.
38. Вопросы анализа и процедуры принятия решений.—М.: Мир, 1976.
39. Вопросы кибернетики, вып. 58. Экспертные оценки.— М.: ВИНИТИ, 1979.
40. Гвишиани Д. М. Организация и управление.— М.: Наука, 1972.
41,ГенинсонБ. А., Рубчинский А. А. Оптимальное управление
слабосвязанными параллельными процессами в вычислительных системах.
— Автоматика и телемеханика, 1980, № 10, с. 180—187.
318
ЛИТЕРАТУРА
42. Глотов В. А., Павельев В. В. Экспертные методы определения ве-
совых коэффициентов.— Автоматика и телемеханика, 1976, № 12,
с. 95—107.
43. Глушков В. М. Введение в АСУ.—Киев: Техника, 1974.
44. Глушков В. М., Добров Г. М., Терещенко В. И. Беседы об
управлении.— М.: Наука, 1974.
45. Гнедин А. В. Многокритериальная задача об оптимальной остановке
процесса выбора.— Автоматика и телемеханика, 1981, № 7, с. 161—166.
46. Г у р и н Л. Г. О понятии точек равновесия и точек Парето в задачах
со случайными факторами.—ЖВА1 и МФ, 1981. № 6, с. 1411—1422.
47. Дертоузос М. Пороговая логика.— М.: Мир, 1967.
48. Джоффрион А., Дайер Д., Файнберг Б. Решение задач оптими-
зации при многих критериях на основе человеко-машинных .процедур.—
В кн.: Вопросы анализа и процедуры принятия решений. М.: Мир, 1976,
с. 126—145.
49. Добров Г. М., Ершов Ю. В., Левин Е. И., Смирнов Л. П.
Экспертные оценки в научно-техническом прогнозировании.— Киев: Нау-
кова думка, 1974.
50. Дубов Ю. А. Условия оптимальности в динамических многокритериаль-
ных задачах.— М.: ВНИИСИ, 1979.
51. Дынкин Е. Б., Юшкевич А. А. Теоремы и задачи о процессах Мар-
кова.— М.: Наука, 1967.
52. Дынкин Е. Б., Юшкевич А. А. Управляемые марковские процессы
и их приложения.— М.: Наука, 1975.
53. Ермаков С. Д. Метод Монте-Карло и смежные вопросы.—М.: Наука,
1975.
54. Емельянов С. В., На п пел ь ба ум Э. Л. Методы исследования слож-
ных систем/ Итоги науки и техники. Техническая кибернетика, т. 8.—[М.:
ВИНИТИ, 1977, с. 5 — 101.
55. Иванин В. М. Асимптотическая оценка математического ожидания числа
элементов множества Парето.— Кибернетика, 1975, № 1, с.’97—101.
56. Иванин В. М. Вычисление дисперсии числа элементов множества Парето
для выборки независимых векторов с независимыми компонентами.— В
кн.: Теория оптимальных решений. Киев: Институт кибернетики АН
УССР, 1976, с. 90—100.
57. Кал ужни н Л. А. Введение в общую алгебру.—М.: Наука, <1973.
58. К а р л и н С. Математические методы в теории игр, программировании ги
экономике.— М.: Мир, 1964.
59. Карманов В. Г. Математическое программирование.— М.: Наука, 1980.
60. К е м е н и Д., С н е л л Д. Кибернетическое моделирование.— М.:j Сов. ра-
дио, 1972.
61. Кендалл М. Ранговые корреляции.— М.: Статистика, 1975.
62. Кини Р. Л., Райфа X. Принятие решений при многих критериях: пред-
почтения и замещения.— М.: Радио и связь, 1981.
63. Китаев Н. Н. Групповые экспертные оценки/ Новое в жизни, науке,
технике. Математика, кибернетика, № 3.— М.: Знание, 1975.
64. Клигер С. А., Косолапов М. С., Толстова Ю. Н. Шкалирова-
ние при сборе и анализе социологической информации.— М.: Наука,
1978.
65. К о ж у х а р о в А. Н., Л а р и че в О. И. Многокритериальная задача о
назначениях.— Автоматика и телемеханика, 1977, № 7, с. 71—88.
66. К о р ш у н о в Ю. М. Математические основы кибернетики.— М.: Энергия,
1980.
67. Кукса А. И., Шор Н. 3. О методе оценки количества условно опти-
мальных траекторий дискретного сепарабельного динамического програм-
мирования.— Кибернетика, 1972, № 6, с. 37—44.
68. Ларичев О. И. Наука и искусство принятия решений.— М.: Наука, 1979.
69. Л а р и ч е в О. И. Человеко-машинные процедуры принятия решений (об-
зор).— Автоматика и телемеханика, 1971, № 12, с. 130—142.
ЛИТЕРАТУРА
319
70. Литваков Б. М. Минимальное представление совокупно-экстремального
выбора вариантов (функций Плотта).— Автоматика и телемеханика, 1981,
№ 1, с. 182—184.
71. Майн X., Осаки С. Марковские процессы принятия решений.—М.:
Наука, 1977.
72. Макаров И. М., Виноградская Т. М. Глобальная характеристика
структуры предпочтения в задачах выбора.— ДАН СССР, 1979, 245, № 2,
с. 312-315.
73. Макаров И. М., Виноградская Т. М. К теории многокритериаль-
ного выбора.—ДАН СССР, 1977, 232, № 1, с. 47—49.
74. Мак-Кинси Дж. Введение в теорию игр.— М.: Физматгиз, 1960.
75. Миллер Р. Теория переключательных схем.— М.: Наука, 1970.
76. Миркин Б. Г. Анализ качественных признаков.— М.: Статистика, 1976.
77, Миркин Б. Г. Проблема группового выбора.—М.: Наука, 1974.
78. Многокритериальные задачи принятия решений.—М.: Машиностроение,
1978.
79.. Моисеев Н. Н. Неформальные процедуры и автоматизация проектиро-
вания/ Новое в жизни, науке, технике. Математика, кибернетика, № 3.—
М.: Знание, 1979.
80. Моисеев Н. Н. Элементы теории оптимальных систем.— М,: Наука,
1975.
81, Моисеев Н. Н., Иванилов Ю,П., Столяров^ Е. М. Методы оп-
тимизации.—М.: Наука, 1978.
82. Мэдник С., Донован Дж. Операционные системы.— М.: Мир, 1978.
83. НайтенгейлМ. Е. Формальное определение ценности признаков.—
В кн.: Статистическое измерение качественных характеристик.— М.: Ста-
тистика, 1972, с. 155—166.
84. Нейман Дж., Моргенштерн О. Теория игр и экономическое по-
ведение.—М.: Наука, 1970.
85. Нормативные и дескриптивные модели принятия решений.— М.: Наука,
1981.
86. Опойцев В. И. Равновесие и устойчивость в моделях коллективного
поведения.— М.: Наука, 1977.
87. Оре О. Теория графов.— М.: Наука, 1980.
88, Подиновский В. В. Многокритериальные задачи^с упорядоченными
по важности однородными критериями.— Автоматика и телемеханика, 1976,
№ 11, с. 118—127.
89. Подиновский В. В. Коэффициенты важности критериев в задачах при-
нятия решений. Порядковые, или ординальные, коэффициенты важности.
— Автоматика и телемеханика, 1978, № 10, с. 130—141.
90. Подиновский В. В. Об относительной важности критериев в многокри-
териальных задачах принятия решений.— В кн.: Многокритериальные
задачи принятия решений. М.: Машиностроение, 1978, с. 48—82.
91а П о н т р я г и н Л. С., Б о л т я нск и й В. Г., Гамкрелидзё Р. В.,
Мищенко Е. Ф. Математическая теория оптимальных процессов.— М.:
Наука, 1976.
92. Поспелов Д. А. Логические методы анализа и синтеза схем.—М.:
Энергия, 1974.
93. Поспелов Г. С., Ириков В. А. Программно-целевое планирование
и управление.— М.: Сов. радио, 1976.
94. Райфа X. Анализ решений.— М.: Наука, 1977.
95. Раскин Л. Г’ Анализ сложных систем и элементы теории оптимального
управления.—М.: Сов. радио, 1976.
96. Роббинс Г., Сигмунд Д., Чао И. Теория оптимальных правил
остановки.— М.: Наука, 1977.
97. Роджерс К. Укладки и покрытия.— М.: Мир, 1968.
98. Ройтенберг Я- Н. Автоматическое управление.—М.: Наука, 1971.
99. Рубинштейн М. И. Разрешимость в комбинаторном программировании.
— М.: Институт проблем управления, 1980.
320
ЛИТЕРАТУРА
100. Салуквадзе М. Е. Методы векторной оптимизации.— Тбилиси: Мец-
ниереба, 1976.
101. Салуквадзе М. Е. О задаче линейного программирования с вектор-
ным критерием качества.— Автоматика и телемеханика, 1972, № 5, с. 99—
105.
102. Современное состояние теории исследования операций.—М.: Наука, 1979.
103. Соколов В. Б., Виноградская Т. М., Абрамов А. Л. Целе-
вые комплексные программы и иерархические отношения.—М.: Институт
проблем управления, 1980.
104. Статистические методы анализа экспертных оценок.—М.: Наука, 1977.
105. Статистическое измерение качественных характеристик.— М.: Статистика,
1972.
106. Субботин А. И., Ченцов А. Г. Оптимизация гарантии в задачах
управления.—М.: Наука, 1981.
107. Терехина А. Ю. Метрическое многомерное шкалирование.— М.: Инсти-
тут проблем управления, 1977.
108. Т е р е х и н а А. Ю. Неметрическое многомерное шкалирование.— М.:
Институт проблем управления, 1977.
109. Торгерсон У. С. Многомерное шкалирование. Теория и метод.— В кн.:
Статистическое измерение качественных характеристик. М.: Статистика,
1972, с. 95-118.
НО. Травкин С. И. Исследование одной модели многокритериального
выбора.— В кн.: Экспертные методы в системных исследованиях. М.:
ВНИИСИ, 1978, с. 46—54.
111. Травкин С. И. Этап выбора в экспертизе многомерных объектов.—
В кн.: Измерение и прогноз в культуре. М.: Научно-исслед. институт
культуры, 1978, с. 146—153.
112. Травкине. И. Распределение числа максимальных объектов в частично
упорядоченных системах сравнения.— В кн.: Вопросы кибернетики, вып 58.
Экспертные оценки. М.: ВИНИТИ, 1979, с. 109—117.
113. Трахтенгерц Э. А. Программное обеспечение автоматизированных
систем управления.—М.: Статистика, 1974.
114. Федоренко Н. П. Некоторые вопросы теории и практики планиро-
вания и управления.—М.: Наука, 1979.
115. Феллер В. Введение в теорию вероятностей и ее приложения, т. I.—
М.: Мир, 1964.
116. Фиш бе рн П. Теория полезности для принятия решений.— М.: Наука,
1978.
117. Фор Р., Кофм ан А., Дени-Па пен М. Современная математика.—
М.: Мир, 1966.
118. Цыпкин Я. 3. Адаптивные методы выбора решений в условиях неопре-
деленности.—Автоматика и телемеханика, 1976, № 4, с. 78—91.
119. Цыпкин Я. 3. Основы теории обучающихся систем.—М.: Наука, 1970.
120. Чар ин В. С. Линейные преобразования и выпуклые множества.—Киев:
Вища школа, 1978.
121. Ширяев А. Н. Вероятность.—М.: Наука, 1980.
122. Шо ломов Л. А. Логические методы в задачах согласованного выбора.—
М.: ВНИИСИ, 1978.
123. Шоломов Л. А. Основы теории дискретных^логических и вычислитель-
ных устройств.—М.: Наука, 1980.
124. Шоломов Л. А. Применение логических методов в задачах последова-
тельного выбора.— М.: ВНИИСИ, 1980.
125. Шрейдер Ю. А. Равенство, сходство, порядок.— М.: Наука, 1971.
126. Юдин Д. Б., Го ль штейн Е. Г. Линейное программирование.— М.:
Наука, 1969.
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Автомат 260
Алгоритм выделения для транзи-
тивного отношения Д 171
--------при заданном гомоморфизме
<р в линейный порядок 170
— максимизации mes Sz- 213
— морфологического анализа 161
—, общий для задачи управления с
функцией полезности 240
—- определения направления градиен-
та U (х) 204
-----с учетом числа доминирующих
критериев 231
-----функции полезности 203—209
— порождения (и интерпретации) кри-
териев 174]
- *па 208
-----й* 170
-----270
-----ф-композиции 169
— решения задачи компенсации 203
-----математической задачи выбора
168
-----общей задачи выбора 166
— сужения ИМА 206
— установления К-линейности функ-
ции полезности 209
— формирования бесконечного ИМА
163
-----ИМА для иерархических струк-
тур 162
-----ИМА с помощью модели 161
-----конечного ИМА 161
Альтернатива 10
— статус-кво 33
Аналитическая форма опроса 137
Анкета 137
Антицепь (максимальная) 128
Асимптотическое значение вероятнос-
ти оптимального выбора 311
Аспект 10
Бинарное отношение 14, 62
Блокировка 33
Бюджетное ограничение 201
Вариант 10
Вариация игольчатая 261
— концевая 261
Веса пороговой функции 169
Веса экспертов 140
Взаимодействие экспертов 138
Вложение отношений 19
Выбор из X 32
Выбор с учетом числа доминирующих
критериев 228—233
Гиперповерхность уровня 199
Главный член квази координатного от-
ношения 109
---ЛФО (ГЧ ЛФО) 80
Глубина функции выбора 127
Гомоморфизм отношений 24
Градиент функции полезности 204
Группа конфликтующих процессов 301
Декомпозиция общая ПО
— паретовская 129
— функций выбора 109
— частная ПО
Диагональ прямого произведения 108
Диапазон квантилей 144
Дизъюнктивная нормальная форма
(ДНФ) 115
Доминирующий показатель варианта
229
---множества 229
Дополнение отношения 20
— функции выбора 46
Евклидово расстояние 227
Единичная сфера 228
322
предметный указатель
Задание отношений графом 17
---матрицей 16
---сечениями 18
Задача выбора 10
---математическая 165
---независимого 253
---простая 166
---с заданным принципом оптималь-
ности 215—233
---с функцией полезности 173
---частная 167
— классификации 136
— коммивояжера 257
— компенсации 203
— конструирования 256
— многомерного метрического шкали-
рования 152
— о минимальном вершинном покры-
тии графа 258
— о наилучшем выборе (выборе не-
весты) 283
— оптимального управления в усло-
виях противодействия при векторных
доходах 243
--------однокритериальная 236, 259
— оптимизации общая 10
— о стоянках 283
— оценивания 132
— параметрическая 238
— попарного сравнения 136
— принятия решений 9
— проектирования монотонная 291
— WP-полная 257
Идеальная точка 225
Изоморфизм отношений 24
Исходное множество альтернатив
(ИМА) 11
Каноническая форма задачи об опти-
мальном управлении 260
Карта безразличия 199
Композиция 109
Конечный автомат, порожденный выбо-
ром 60
Конфликт 301
Консультант 11
Конус 64
— возможных направлений 206
— двойственный 67
— — отношения 67
— концевых вариаций 262
— , натянутый на множество 206
— острый 70
— телесный 64
Коэффициент конкордации 145
---для нестрогого ранжирования
146
— ранговой корреляции Кендалла 149
Коэффициент совместимости мнений
экспертов 149
Кривая безразличия 199
Критериальное пространство 10
Критерий 10
— доминирующий 228
— качества управления 259
— многократный 290
— однократный 290
Куб единичный 42
Лексикография обобщенная 97
Лемма Карлина 76
Линейный граф 121
Лицо, принимающее решение (ЛПР) 11
Логическая форма отношения (ЛФО) 80
----функции выбора (ЛФВ) 38
Мажоранта по отношению 30
Максимин 312
Максимум по отношению 30
Матрица переходов 267
— д-крутового турнира 232
Матричная игра 311
----с векторными доходами 313
Медиана Камени'— Снелла 151
— распределения 144
Метод алгебраический 149
— Дельфи 139
— докладной записки 137
— идеальной .точки 225—228
— мозговой атаки 138
— морфологического анализа 161
— нелинейный шкалирования 155
— парных сравнений 147
— простой ординации 152
— троек 154
— условного градиента 240
Метрика равномерная 227
Минимакс 312
Минимум по отношению 30
Миноранта по отношению 30
Многокритериальная задача дискрет-
ная 248
----линейного программирования 245
----математического программиро-
вания 244
----об оптимальной остановке 285—
287
---- оптимального управления 234
----------динамическая 241
----оптимального последовательно-
го выбора 306
---- прикладная 288
----с дискретным временем 250, 251
Множество альтернатив (универсаль-
ное) 11
— допустимых оценок (МДО) 133
-------для экспертов 137
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
323
Множество достижимости 265
— 'крайних элементов 99
— недоминируемых по R элементов 31
— Парето 65
— состояний с вынужденным продол-
жением 285
-----с вынужденной остановкой 285
— строго выпуклое 205
— Л-выпуклое 76
Модель Аумана 74
Неделимый ресурс 301
Норма замены (предельная) 200
НР-сложность 126
Область задания отношений 15
Обратная связь в экспертизе 139
Объединение отношений 20
— функций выбора 46
Опрос типа интервью 137
Оптимальное управление в условиях
противодействия 241
-----по Нэшу 242
-----совокупно по Нэшу 244
Оптимизация двухуровневая управля-
емых цепей Маркова 287
— при наличии помех 213
— функци! полезности 203—209
Ортант неотрицательный 67
Остов Т-дерева 124
Отделимость 68
Отказ от выбора 33
Отношение антидиагональное 19
— антирефлексивное 24
— антисимметричное 25
— асимметричное 25
— ацикличное 26
— бинарное 15
— ближайшее 86
----- сверху, снизу 87
— включения 29
— главное 89
— двойственное 22
— диагональное 19
— доминирования 29
— значимое 96
— иерархическое 101
-----лексикографии 102
-----Парето 102
—, инвариантное относительно пере-
носа 62
— квазикоординатное 104
— координатное 79
— лексикографии 66
— мажоритарное 83
— минимальное 36
— нестрогого порядка 28
— обратное 21
— отделимое 70
Отношение отделимое' на множестве
70
----- отрицательно транзитивное 26
— Парето 65
------на минимум 277
— подобное 96
— полное 18
— положительно отделимое 74
--------на множестве 74
-----Х-отделимое 74
—, порожденное конусом 65
— предпочтения эксперта 147
— пустое 18
— равенства 19
— рациональное 66
— рефлексивное 24
— сильно транзитивное 26
— симметричное 24
— строгого порядка 28
— транзитивное 25
— уномонотонное 96
— эквивалентности 28
— Х-отделимое 67
Оценивание 132
Оценка альтернативы по критерию
10
— комплекса 289
— правила выбора 307
— сверху мощности множества Парето
196
— численная 142
Пересечение отношений 20
— функций выбора 46
Подбор экспертов 139
Подготовка экспертизы 135
Показатели относительной важности
объектов 157
Полиномиально-связанные задачи 257
Порог 169
Порядок линейный 29
— нестрогий 28
— строгий 28
— частичный 29
Последовательность мажорирующая 99
— останавливающая 285
— Парето оптимальная 255
— эквивалентная 256
Правило выбора (опт?, льное) 307
— остановки 285
----- оптимальное 285
-----/?-оптимальное 287
— турнирио
Предпочтен
Принцип с на 250
-----в задаче об оптимальной останов-
ке 286
-----для многокритериальной задачи
251
324
[ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Принцип Веллмана для управляемых
цепей Маркова 273
— максимума для многокритериальной
задачи 264
---Понтрягина 260
— оптимальности 9
Программный комплекс 289
Проектирование оптимального прог-
раммного комплекса 289
Произведение отношений 22
— функций выбора 47
Пространство стратегий для управля-
емой цепи Маркова 268
Процедура экспертного перечисления
160
Разбиения вложенные 101
Разложение f в совершенную дизъюн-
ктивную нормальную форму (СДНФ)
87
Размерность графа 128
Ранговая корреляция 149
Ранжирование нестрогое 145
— строгое 144
Реализация паретовская 124
— экспертизы 135
Реализуемость отношения R координа-
тным отношением ПО
Решение задачи оптимального управле-
ния 236
----------с функцией полезности
239, 240
----------- частное, общее 236
---принятия решений 9
— игры 312
— матричной игры с векторными дохо-
дами 313
РЗ-сложность 126
Свертка линейная 75
Сечение верхнее 18
— нижнее 18
Сложность задачи 257
Совершенная дизъюнктивная нормаль-
ная форма 88
Состояние автомата 60
Способы задания отношений 15
Среднее значение ранжировки 151
— число недоминируемых альтерна-
тив 183
---элементов множества Парето 189
Средний векторный доход для цепи
Маркова 274
Стохастическая аппроксимация 214
Стратегия для управляемой цепи Мар-
кова 269
— марковская 269
— оптимальная для бесконечного вре-
мени 271
Стратегия оптимальная для конечного
времени 271
— разрешения конфликтов 301
— слабо /-оптимальная 288
— смешанная 282, 311
— стационарная 269
— чистая 282, 311
— /^-каноническая 280
Сужение отношения 24
Схема типа круглого стола 138
— экспертизы 135
Теорема о минимаксе 312
Точка максимальная 284
— Нэша 242
Транзитивное замыкание отношения
216
Транспозиция 216
Турнир д-круговой 232
----критериальный 233
Условие возможности и допустимости
альтернатив 11
— монотонности 49
— мультипликаторности 48
— наследования 48
— независимости от отвергнутых аль-
тернатив 48
— оптимальности (необходимое) для
многокритериальной задачи опти-
мального управления 267
— Плотта 48
— согласия 48
— сумматорности 48
Форма опроса эксперта 137
Формирование ИМА бесконечного 163
----для иерархических структур 162
---- конечного 161
----с помощью модели 161
Функция булева симметричная 192
— выбора 32
----антирефлексивная 54
---- ацикличная 54
----, ближайшая сверху (снизу) 44
----динамическая 60
---- запрета 113
----квазисумматорная 48
----конечно-нормальная 116
----мажоритарно-нормальная 115
----монотонная 50
----наследственная 50
----, независимая от отвергнутых
альтернатив 50
---- нормальная 34
----общая скалярная 57
---- паретовская 59
---- полная 54
----, порожденная отношением R 34
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
325
Функция выбора разрешения ИЗ
----- рациональная 226
-----рефлексивная 54
-----с запретом 59
----- скалярная 57
-----совокупно экстремальная 58
-----суммарно-нормальная 116
-----сумматор на я 50
-----транзитивная 54
-----турнирная п-круговая 233
-----, удовлетворяющая условию сог-
ласия 50
-----характристическая 58
— голосования (мажоритарная) 114
— переходов автомата 60
— полезности 198, 199
-----/(-выпуклая 201
-----/(-выпуклая строго 205
-----/(-гетеротонная 201
-----/(-линейная 201
— Понтрягина 297
— пороговая 169
— распределения числа недоминируе-
мых альтернатив 177
Цена игры 312
— локальная 202
Цепочка максимальная 44, 89
Цепь максимальная по отношению 31
— Маркова 267
-----бернуллиевская 280
----- неоднородная 267
Цепь Маркова однородная 267
----- управляемая 268, 269
-----с векторными доходами 273
Частное управление 269
Чебышевская точка 246
Ширина графа 128
Шкала т-мерная 132
Шкалирование многомерное метричес-
кое 152
— неметрическое многомерное 155
-----одномерное 156
Эквивалентность 28
Эксперт 11
F-сумма графов 109
— отношений 109
f-сумма графов 119
— отношений 119
— функций выбора 123
R-оптимальное управление 235
-----по Нэшу 242 *
/?-оптимальность 30
х0“Оптимальное управление 249
(х0, /?, п)-оптимальное управление 251
%-отделимость нестрогая 68
Х-свертка многокритериальной задачи
оптимального управления 237
ф-композиция 111
ОСНОВНЫЕ ОБОЗНАЧЕНИЯ
х£А — элемент х принадлежит множеству А
х(£а—элемент х не принадлежит множеству А
А^В—множество А включено в В
А$ЕВ—множество А не включено в В
{х£АЦ ^х)}—совокупность элементов х ^множества А, для которых выпол-
нено^ (*)
0—пустое множество 4
А [—число элементов конечного множества А
Л)—множество подмножеств А
mes Л—мерариножества Л
АхВ—декартово произведение множеств Л и В; М2 = ЛхЛ
Bi—числовая прямая (множество действительных чисел)
00
Ет—~/n-мерное действительное пространство; Е = (J Ег
Г= 1
1пЦЛ —внутренность^]
Л|;Ь В= {z | z — a i b, <2^Л| Ь^В}
L&A)—вЫпуклая оболочка множества|Л
N—множество^. туральных|чисел.
хт>—вектор из Ет
xRy—.^находится в отношении R с yj
т
(х, у) = х/у/—скалярное произведение векторов х и у (х, у£Ет)
<7?, В> —отношение R на множестве В (R^BxB)
~—эквивалентность
р(х9у)—евклидово расстояние между точками х и у (х, у£Ет)
А (/?)—матрица отношения R
Ф(Я)—граф^отношения R
R* (х)—верхнее сечение отношения R в точке х
Г-Тх) —нижнее сечение отношения R в точке х
R—дополнение к отношению R
Я1П#2 — пересечение ^отношений и R2
R R2—объединение отношений Rt и R2
jR-1—отношение, обратное к R
Rd—отношение, двойственное к R
R%—отношение, порожденное конусом К
ОСНОВНЫЕ ОБОЗНАЧЕНИЯ*
32Г
KR — двойственный конус отношения Р]
/(•—конус, двойственный к конусу К
К А—конус, натянутый на множество А
—множество мажорант на |Л по отношению R (множество недоминируе»
мых по R элементов из Л)
Л/?—множество максимумов на Л по отношению R
С (X)—выбор из X
CR—блокировка, порожденная R
C#—предпочтение, порожденное R
Argmaxg(x) = {x*gA|g(x*)==maxg(x)}, Arg min g (x) = {x*- £ A |g (x*) =-
А Ал
= ming(x)}’
A
{1, если 6|> 0,
0, если b—0,
—1,,если b < 0
A । V—знаки конъюнкции и дизъюнкции соответственно
р-мерный единичный куб
Рг{Л}—вероятность события Л
Рг{Л/В}—вероятность события Л при условии В
U (х)— функция полезности
Ru — отношение, порожденное функцией U (х)
h(Г)—концевая вариация
8u(t)—игольчатая вариация
(p/у)—матрица переходов цепи Маркова у
—стационарная стратегия для цепи Маркова
Я—функция Понтрягина
<0> — пустая последовательность
Е] = {<Х, уу с | xt * yt (I € /), Xi = У( (i £ I)}
Р —отношение Парето
L — отношение лексикографии
/И (т)) — среднее значение случайной величины г|
Игорь Михайлович Макаров,
Татьяна Мухаметовна Виноградская,
Александр Анатольевич Рубчинский,
Валерий Борисович Соколов
ТЕОРИЯ ВЫБОРА И ПРИНЯТИЯ РЕШЕНИЙ
Оформление художника Б. М. Рябышева
Редактор Е. Ю. Ходан
Техн/редактор Л. В. Лихачева
Корректоры Г, В. Подвольская, Е. В. Сидоркина
ИВ Xs 12077
Сдано в набор 16.04.82. Подписано к печати 18.11.82.
Т-20924. Формат 60Х90‘/1в. Бумага тип. Xs 2. Литературная
гарнитура. Высокая печать. Условн. печ. л. 20,5. Уч.-изд
л. 22,ОЬ Тираж 18 000 экз. Заказ Xs 462/515 Цена 1 руб.
Издательство «Наука»
Главная редакция физико-математической литературы
117071, Москва, В-71, Ленинский проспект, 15
Набрано в Ордена Октябрьской Революции
i и ордена Трудового Красного Знамени
Первой Образцовой типографии имени А. А. Жданова
Союзполиграфпрома при Государственном комитете ^СССР по
делам издательств, полиграфии и книжной торговли.
Москва, М-54, Валовая, 28.
Отпечатано в Подольском филиале ПО «Периодика»
Союзполиграфпрома при Государственном комитете* СССР
по делам издательств, полиграфии и книжной) торговли
г. Подольск, ул. Кирова, 25