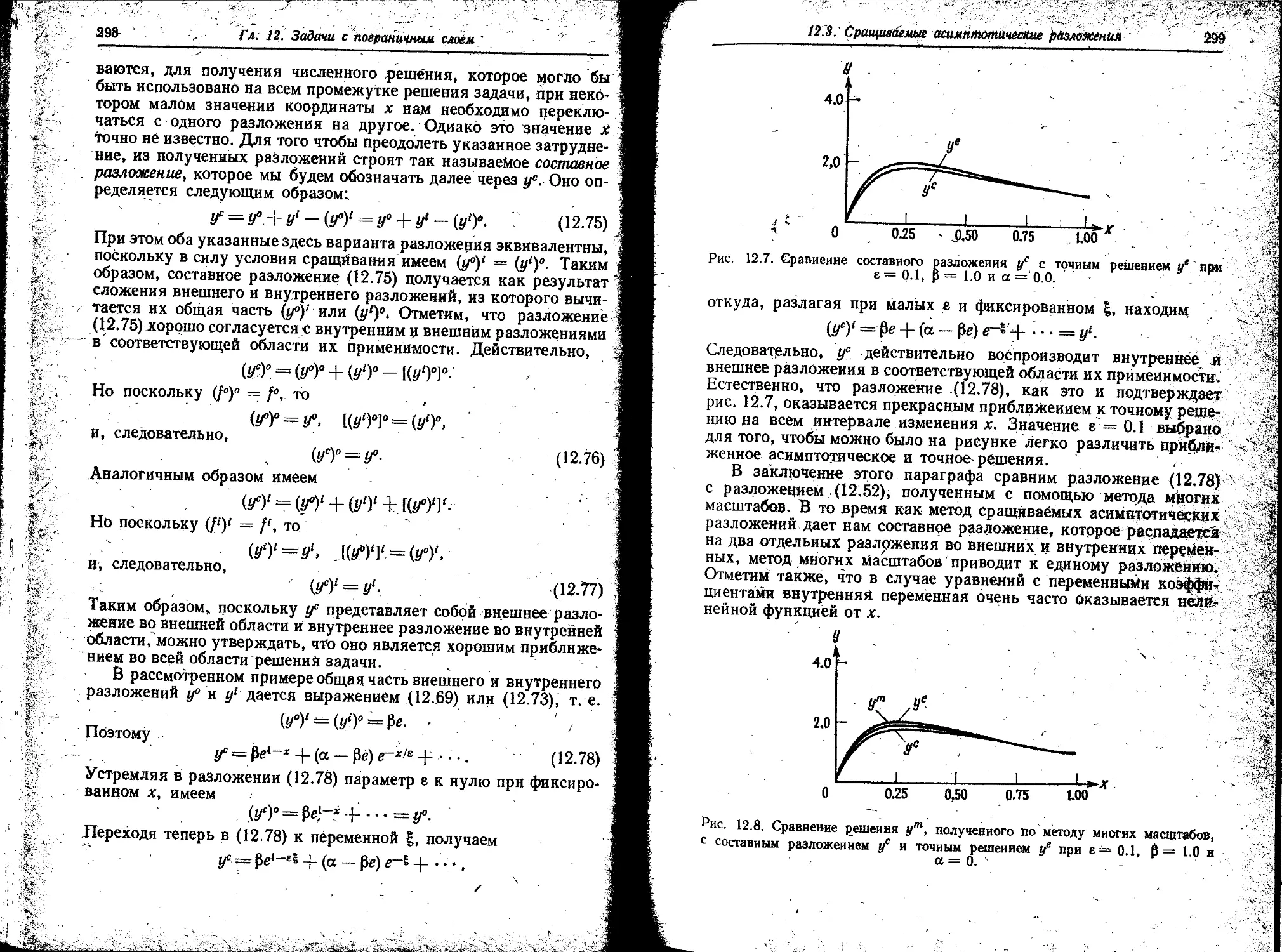
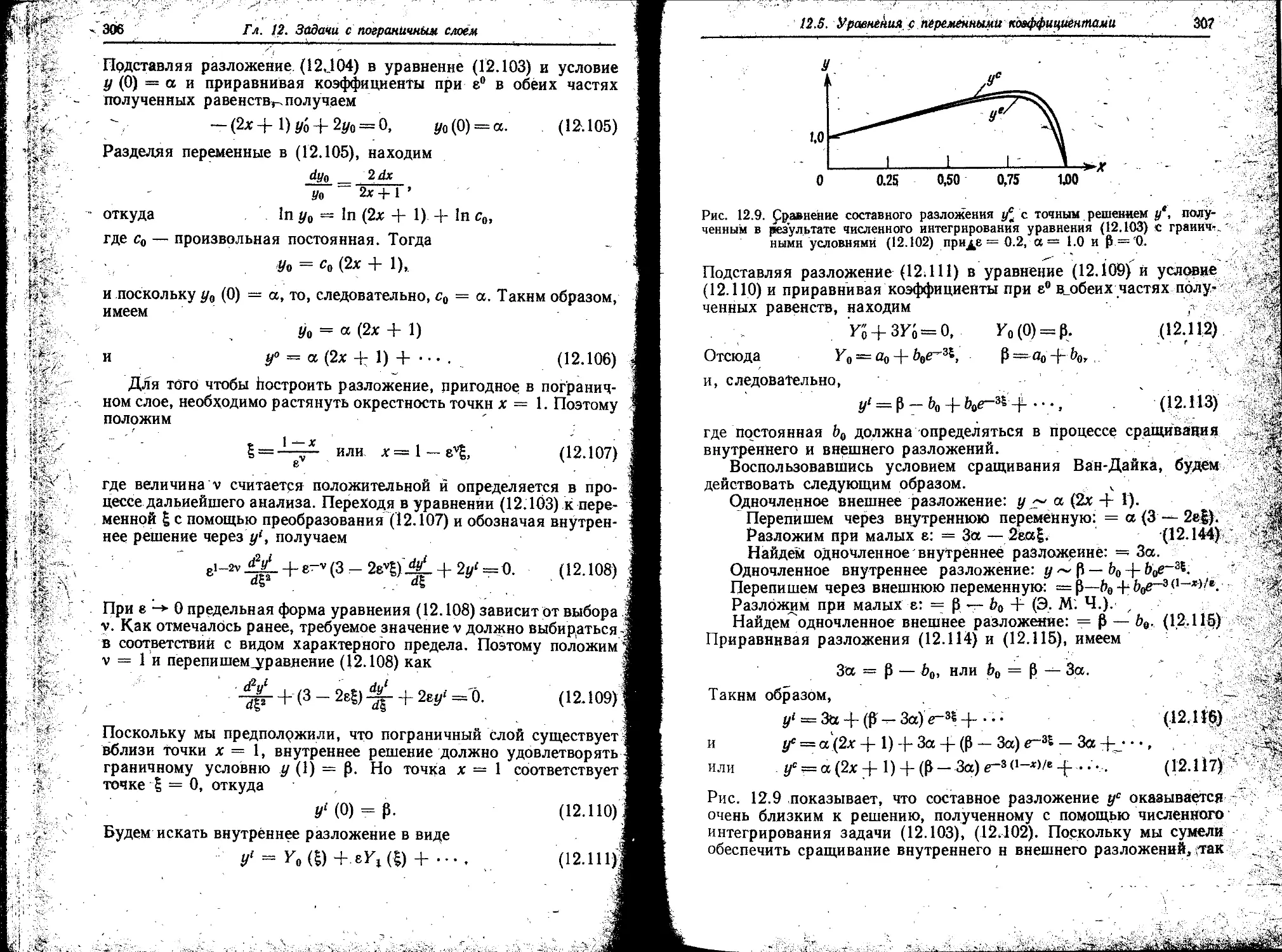
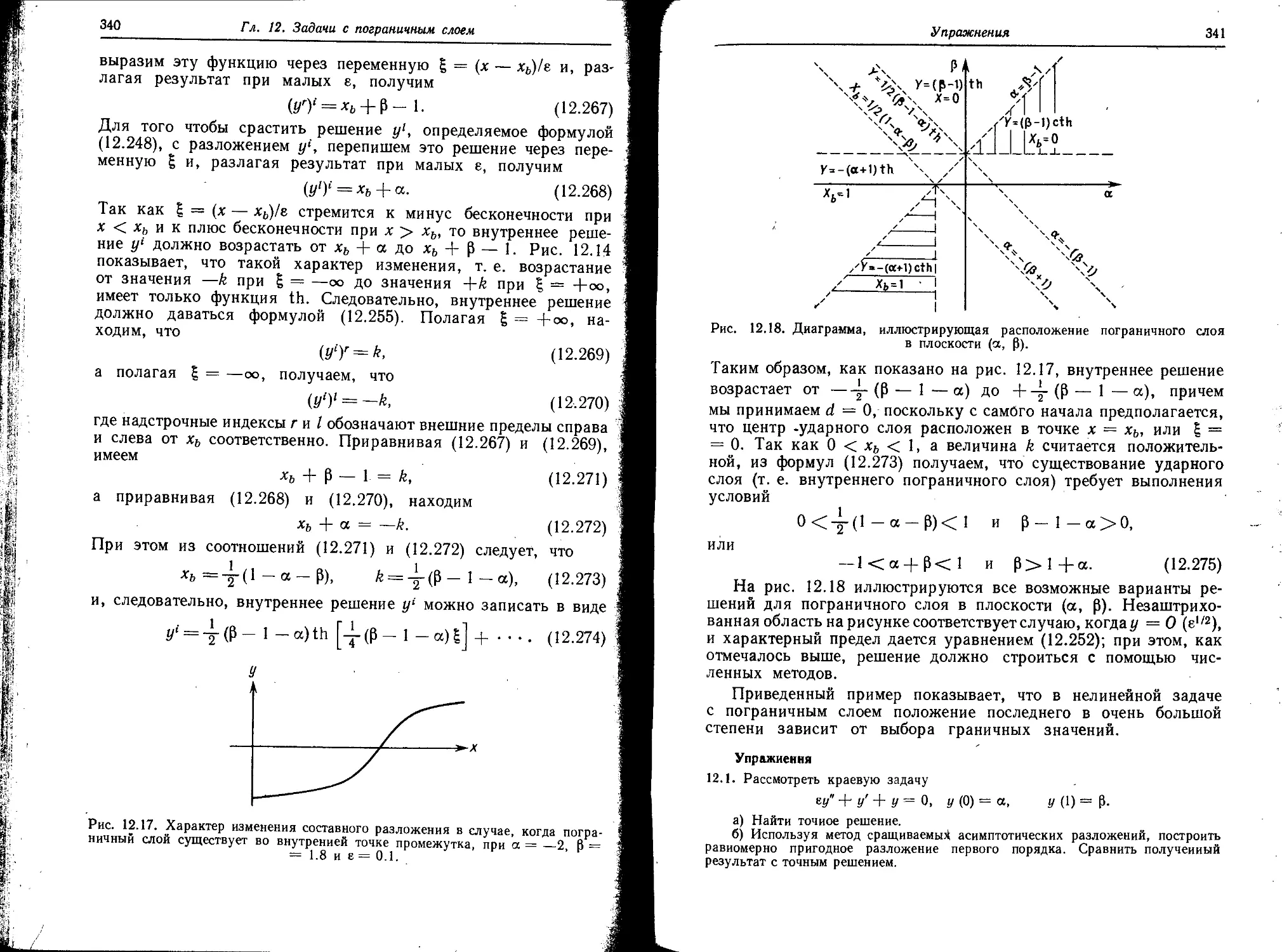
Введение в методы возмущений - Найфэ А., Зино И.Е., Тропп Э.А., Бранцев Р.Г.

Автор: Найфэ А. Зино И.Е. Тропп Э.А. Бранцев Р.Г.
Теги: дифференциальные, интегральные и другие функциональные уравнения конечные разности вариационное исчисление функциональный анализ математический анализ физика математическая физика переводная литература издательство мир введение в методы возмущений
Год: 1984
Похожие
Введение в методы возмущений
Хаос и интегрируемость в нелинейной динамике
Регулярная и стохастическая динамика
Интегрируемость и сингулярность
Текст
                    Introduction to
Perturbation Techniques
АЫ HASAN NAYFEH
University Distinguished Professor
Virginia Polytechnic Institute and State University
Blacksburg, Virginia
and
Yarmouk University, Irbid, Jordan
A WILEY INTERSCIENCE PUBLICATION
JOH N WILEY & SONS
New York Chichester Brisbane Toronto 1981
А. Найфэ
ВВЕДЕНИЕ В МЕТОДЫ
ВОЗМУЩЕНИЙ
Перевод с английского
И. Е. ЗИНО и Э. А. ТРОППА
под редакцией
Р. Г. БАРАНЦЕВА
МОСКВА «МИР» 1984
ББК 22.161.6
Н20
УДК 517.94
Найфэ А.
Н20 Введение в методы возмущений: Пер. с англ. — М.:
Мир, 1984, 535 с., ил.
Книга американского математика А. Найфэ, известного советскому чита-
телю по книге «Методы возмущений* (М.: Мир, 1976), представляет собой учебник
по асимптотическому анализу, в котором систематически излагаются современные
асимптотические методы решения дифференциальных уравнений и, в частности,
методы сингулярных возмущений, реализуемые в тех случаях, когда прямые
разложения по малому параметру не являютвя равномерно пригодными во всей
области решения задачи.
Для математиков-прикладников, инженеров, студентов и аспирантов тех-
нических специальностей, а также для всех лиц, приступающих к изучению асимп-
тотического анализа.
Н
1702070000—318
041(01)—84
38—84,
ч. 1
ББК 22.161.6
517.2
Редакция литературы по математическим наукам
1 0 В 1 8 7
5'“Ьиваиотека
5 Пермского
! универе.!:, 'г.
Copyright © 1981 by John Wiley & Sons, 1жс.
All Right Reserved. Authorized translation
from English language edition published by
John Wiley & Sons, Inc.
© Перевод на русский язык, «Мир», 1984
ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
Асимптотические методы, эффективность которых в самых
разных областях прикладной математики всеми признана, начи-
нают проникать в массовую учебную литературу. Предлагаемая
книга — один из первых учебников, предназначенных для студен-
тов и аспирантов не только университетов, но и технических вузов
разных профилей.
Суть асимптотических методов заключается в том, что при их
применении достигается синтез простоты и точности за счет лока-
лизации: в окрестности некоторого предельного состояния нахо-
дится упрощенное решение задачи, которое тем точнее, чем меньше
эта окрестность.
Аналитические методы обычно делятся на эвристические и точ-
ные. Совмещая в себе простоту эвристических представлений с точ-
ностью аналитических оценок, асимптотические методы не ограни-
чиваются ролью «золотой середины». В математике они занимают
особое место. Главное отличие от классической математики со-
стоит в том, что уровень точности конкурирует с размерами области
действия; в заданной области точность асимптотического разложе-
ния всегда ограничена. Такая плата за эффективность оказывается
вполне приемлемой не только на практике, но и в теории, если
этот «принцип неопределенности» допустить хотя бы в ту область
математики, которая занимается асимптотическими методами.
Жизненность и перспективность асимптотических методов под-
тверждается также тем фактом, что активное взаимодействие
численных методов с аналитическими происходит как раз через
асимптотику.
Учебник Али Хасана Найфэ появился на основе многолетнего
опыта преподавания и обладает рядом достоинств: простой уровень
изложения, богатый набор упражнений, сравнительный метод
демонстрации различных алгоритмов. Однако, естественно, автору
пришлось пойти и на некоторые жертвы. Так, в книге совсем не
обсуждается вопрос о строгой оценке остатков асимптотических
разложений. Но этот аспект не вполне освоен еще и в научной
литературе.
Проникновение асимптотических методов в массовую учебную
литературу — важный этап закономерного процесса освоения
этого самостоятельного раздела математической методологии.
6
Предисловие редактора перевода
Научная литература наполнилась книгами по асимптотике в тече-
ние двух-трех десятилетий. Если учесть, что темпы их освоения
в современном мире заметно возрастают, то можно ожидать, что
лет через десять асимптотические методы проникнут и в школьные
программы.
Библиография автора дополнена в основном книгами, издан-
ными на русском языке, тематическими сборниками и несколькими
статьями методологического характера. Замеченные опечатки
исправлены при переводе без специальных оговорок.
Предисловие, гл. 1—6, 12, 13 и приложения перевел И. Е. Зино,
гл. 7—11, 14, 15 — Э. А. Тропп.
Р. Г. Баранцев
ПРЕДИСЛОВИЕ
Многие задачи, с которыми сталкиваются сегодня физики,
инженеры и специалисты по прикладной математике, не поддаются
точному решению. Среди причин, затрудняющих точное решение,
можно указать, например, нелинейные уравнения движения, пере-
менные коэффициенты и нелинейные граничные условия на извест-
ных или неизвестных границах сложной формы. Для решения
подобных задач мы вынуждены пользоваться различного рода
приближениями, комбинируя аналитические и численные методы.
Среди аналитических методов весьма мощными являются методы
возмущений (асимптотических разложений) по большим или
малым значениям параметра или координаты. Настоящая книга
посвящена описанию этих методов.
Большинство используемых методов возмущений с учетом их
сходства и различия, а также преимуществ и ограничений было
систематически рассмотрено в моей предыдущей книге г. Хотя для
их,описания поначалу использовались примеры с простыми обык-
новенными уравнениями, допускавшими точное решение, и лишь
потом, по мере усложнения, исследовались уравнения в частных
производных, тем не менее изложение носило довольно сжатый
характер и было рассчитано в основном на специалистов. Цель
настоящей книги заключается в том, чтобы изложить этот материал
наиболее простым образом, что позволило бы освоить его хорошо
успевающим студентам и аспирантам самых различных научных и
технических специальностей. Основываясь на восьмилетием опыте
преподавания методов возмущений для аспирантов Политехниче-
«кого института и Университета штата Виргиния, я отобрал лишь
несколько определенных методов и существенно упростил их
описание. Кроме того, я попытался ответить здесь на вопросы,
которые чаще всего задавали мне мои слушатели. Все предлагае-
мые методы иллюстрируются с помощью простых примеров —
главным образом посредством алгебраических или обыкновенных
дифференциальных уравнений.
Материал, изложенный в гл. 3 и 15, а также в приложениях А
и В, в предыдущей нашей книге отсутствует. В гл. 3 рассматрива-
ются асимптотические разложения интегралов. Глава 15 посвя-
1 А. X. Найфэ. Методы возмущений. Пер. с англ. — М.: Мир, 1976.
8
П редис ловив
щена построению сопряженных линейных однородных уравнений
(алгебраических, дифференциальных — обыкновенных и в част-
ных производных, а также интегральных) и нахождению условий
разрешимости соответствующих неоднородных задач. В приложе-
нии А представлены некоторые тригонометрические тождества,
в приложении В описываются свойства обыкновенных линейных
дифференциальных уравнений, а также символический метод
решения однородных и неоднородных уравнений с постоянными
коэффициентами.
От читателя требуется лишь знакомство с основами анализа и
знание элементарных свойств обыкновенных дифференциальных
уравнений.
В каждой главе содержится большое число упражнений. За
дальнейшими задачами отсылаю читателя к моей предыдущей
книге, а также к монографии «Нелинейные колебания», написанной
мною совместно с Д. Му ком х. Ввиду учебного характера этой
книги в библиографию включен перечень лишь самых необходимых
работ, без каких бы то ни было ссылок на них в основном тексте.
Я глубоко благодарен К. Р. Асфару и Д. Т. Муку за чтение
всей рукописи, а также Л. Уотсону, М. Уильямсу, К. Пратеру,
С. А. Рагабу, И. Уикмену, А. Йену, Й. Лю, Г. Риду, Дж. Деде-
реру, Й. Ма и У. С. Сарику за чтение отдельных ее частей. Боль-
шинство рисунков были выполнены Т. X. Найфэ, К- Р. Асфаром,
И. Уикменом, Т. Дуньяком и Т. Макколи — всем им я хочу
выразить свою признательность. Наконец, мне хотелось бы
поблагодарить Патти Белчер, Джанет Брайант и Шарон Ларкине
за перепечатку рукописи.
Али Хасан Найфэ
Блэксберг, штат Виргиния.
Апрель 1980 г.
1	А. Н. Nayfeh, D. Т. Mook. Nonlinear Oscillations, — N. Y.: Wiley, 1979.
Глава 1
ВВЕДЕНИЕ
1.1.	Анализ размерностей
В большинстве задач гидромеханики, динамики твердого тела
и других разделов физики крайне редко оказывается возможным
получить точные решения — причиной этого служат обычно раз-
личного рода нелинейности, неоднородности или сложные гранич-
ные условия. Поэтому инженеры, физики и специалисты по при-
кладной математике вынуждены обращаться к приближенным
решениям, которые могут строиться либо численными методами,
либо аналитическими, либо путем комбинации численных и анали-
тических подходов. В этой книге мы будем рассматривать лишь
чисто аналитические процедуры, которые в сочетании с методами
численного анализа, например такими, как метод конечных разно-
стей или метод конечных элементов, позволяют создать весьма
мощный и гибкий аппарат решения современных физических
задач.
Ключом к решению той или иной задачи является, как известно,
построение ее математической модели. В процессе создания такой
модели мы стараемся принять во внимание одни особенности
задачи, полностью пренебрегаем другими и лишь в определенной
степени учитываем третьи. Для осуществления этих важных шагов
нам прежде всего нужно определить порядок величин различных
элементов системы (т. е. насколько они велики или малы), сравни-
вая их друг с другом и с заранее выбранными характерными
элементами. Этот процесс называется приведением переменных
к безразмерному виду. Прежде чем пытаться проделать какие-либо
аппроксимации, всегда нужно ввести безразмерные переменные.
Например, если некоторый элемент системы имеет длину один
сантиметр, является ли этот элемент большим или малым? Ответить
на такой вопрос можно лишь обратившись к исходной постановке
задачи. Ясно, что если мы, к примеру, исследуем движение спут-
ника на околоземной орбите, то один сантиметр будет пренебре-
жимо малым расстоянием. С другой стороны, если в какой-либо
предложенной.'-нам задаче нужно учитывать расстояния между
молекулами, то при этом один сантиметр оказывается уже гигант-
ской длиной. Точно так же масса в один грамм представляет собой
ничтожно малую величину по сравнению с массой спутника, но
в то же время оказывается невообразимо огромной по отношению
к массе электрона. Итак, представление уравнений в безразмерной
10
Гл. 1. Введение
форме выявляет наличие важных безразмерных параметров, кото-
рые определяют поведение исследуемой системы. Даже если мы не
собираемся обращаться к тем или иным аппроксимациям, тем не
менее, прежде чем приступить к анализу конкретной задачи или
к обработке экспериментальных данных, рекомендуется обяза-
тельно выполнить эту весьма существенную и важную операцию.
Разберем теперь насколько примеров, иллюстрирующих процесс
приведения к безразмерному виду различных физических задач.
Пример 1. Рассмотрим движение частицы массы т, закреплен-
ной на линейной пружине с коэффициентом жесткости k и испыты-
вающей сопротивление среды, коэффициент вязкости которой
равен (г (рис. 1.1). Используя второй закон Ньютона, имеем
/n-g- + p-^+b = °,	(1.1)
где и — смещение частицы и t — время. Предположим далее, что
частица начинает движение без начальной скорости из состояния
покоя, описываемого координатой w0; начальные условия при этом
запишутся как
«м=«0, 4rL=0-	(1-2)
Итак, в данном случае зависимой переменной является смещение и,
а независимой — время t. Их необходимо привести к безразмер-
ному виду, используя характерный размер и характерный масштаб
времени системы. Смещение и можно сделать безразмерным, при-
нимая в качестве характерной длины начальное смещение и0
в качестве же характерного масштаба времени выберем величину
обратную собственной частоте системы w0 = Уk/m. Таким обра-
зом, положив
w* = м/«о, t* = Ш<Т>
где звездочкой обозначены безразмерные величины, получим
du d (иои*\ dt*	du*
~dF ~ ~~dt* dT ~ “°"0 ~di*~ ’
1.1 Масса, связанная с пружиной и вязкостным демпферам.
Рис.
1.1. Анализ размерностей
11
при этом (1.1) представится в виде		
	2 d2u*	du*	* -ф рсо0м0	+ kuou = 0.	
Отсюда	d2u* ,	* du*	k . * n 	Г Ц ~77T- 		7-r U = 0, dt*	‘dt* 1 mtog	
или	d^ii*	du* 	i_ и* _2±_	,,* — о dt*‘ + ‘ dt* \ u —	(1-3)
где	LI* = —— . r	mco0	(1-4)
Начальные условия (1.2) в безразмерных переменных записы-
ваются как
«*(0) = 1- -gr(0) = 0.	(1.5)
Таким образом, решение данной задачи зависит от единственного
параметра р*, представляющего собой отношение силы сопротив-
ления к силе инерции, или возвращающей силе пружины. Если это
отношение мало, то при построении приближенного решения задачи
безразмерную величину р* можно рассматривать в качестве малого
параметра. В этом случае мы говорим о системе со слабым затуха-
нием. Следует отметить, что малость величины р вовсе не означает,
что данная система будет представлять собой систему с малым
затуханием; для этого необходимо, чтобы было мало р* = р/тсоо =
= р/j/ km.
Пример 2. Предположим теперь, что упругая сила пружины
описывается нелинейной функцией вида
fупр	ku -j- k2u ,	(1.6)
где k и k3 суть постоянные. Тогда (1.1) переходит в уравнение
*'d2u . du ,	, „	_
т ~di^ + ~di~ + ku +	= °'	О-7)
Используя те же самые безразмерные переменные, что и в преды-
дущем примере, получаем
2	d^u*	du*	♦ t_ 2 *8
тио^о ——г + P«owo + kuou +	= О,
dt* '	al
или
+ .4*	+ «* + ем*! = 0,	(1.8)
Г 1 ' dt* 1	‘	'•	>
где
11 e=2E <L9>
При этом начальные условия вновь преобразуются к виду (1.5).
Таким образом, данная задача будет зависеть уже от двух безраз-
12
Гл. 1. Введение
Рис. 1.2. Космический корабль в гравитационном поле двух фиксированных
масс.
мерных параметров ц* и е. Как и выше, р* представляет собой
отношение силы сопротивления к силе инерции, или линейной
возвращающей силе. Параметр же е представляет собой отношение
нелинейной и линейной составляющих упругой силы пружины.
В тех случаях, когда мы говорим о слабо нелинейной системе,
подразумевается, что величина k2u0lk мала. Вместе с тем даже при
малости постоянной k2 по сравнению с k нелинейность может ока-
заться весьма значительной, если и0 будет велико по сравнению
с отношением klk2. Таким образом, степень нелинейности системы
в целом характеризуется именно параметром е.
Пример 3. В качестве третьего примера рассмотрим задачу
о движении космического корабля с массой т в гравитационном
поле двух фиксированных притягивающих центров, массы которых
mi и т2 много больше массы т. В декартовой прямоугольной си-
стеме координат, показанной на рис. 1.2, уравнения движения
имеют вид
d2x __ rnrnfix	mmfi(x — I.)
(x2 + </2)3'2	[(x-l)2 + !/f2 ’
d2y __ __ mmfiy_____________mmfiy	. ...
(x2 + ^)3-'2	l(x-L)2 + </2]3/2 ’	1	’
где t — время, G — гравитационная постоянная и L — расстояние
между массами mj и т2.
В данном случае зависимыми переменными являются коорди-
наты х и у, а независимой переменной — время t. Ясно, что в ка-
честве характерной длины для этой задачи следует выбрать рас-
стояние L между притягивающими центрами. Выбор же характер-
ного масштаба времени далеко не так очевиден. Поскольку мы
предполагаем, что перемещения масс mi и т2 не зависят от харак-
тера движения космического корабля, то mj и т2 будут двигаться
по эллипсам вокруг общего центра масс. При этом период их
обращения будет равен
Т =	2л£3'2
Kg (m! +
1.1. Анализ размерностей
13
так что частота обращения оказывается равной
(оо = £~3;2 /0(т! + т2) •	(1.12)
Величину, обратную w0, мы и используем в качестве характерного
масштаба времени задачи. Далее, вводя безразмерные переменные
	X* =	X	У* =~r>	t* — <pot,	(1-13)
получаем					
dx 	 dt	d (x*L) dt*	dt* dt	r dx* — L(P0 d(i ,	d2x	. 2 d2x* dt2	L<a° dtS ’	
dy _ dt	d (y*L) dt*	dt* dt	_ i dy* — Z.tt)0	,	d2y _ i 2 d2y* dt2 ~L(i>0 dt*2 ’	
При этом (1.10) и (1.11) переписываются в виде
, 2 d2x* -___	mmfiLx*	mm2GL (х* — 1)
т “°	[L2 (х*2 + у*2)]3/2	I'.2 (X*— I)2 + £2|/*2]3/2 ’
I 2 d2y* ___________mmfiLy*	_______mmfiil.y*_______
т a°~dP [1.2 (х*2 + t/*2)]3/2 ~ [Z,2(x*— I)2 + L2y*‘]3‘2 ’
ИЛИ
d2x*	mfi	x*		mfi		(X*-1)		(1-14) (1.15)
dt*2 d2y*	mfi	(x*2 + y*‘ У*	!)3/2	mfi	[(X*-	- О2 + У* У*	2j3/2 ’	
dt*2 Использу	Ls<o‘q (x*! y* я (1.12), находим mfi	mx		!)3/2	L3W2 mfi	[(X*-	-1)2 + У* m2	2]3/2 •	
Поэтому,	L3o>2	4- m2 ’ если положить ma	~	~~			L3cog tnt	“ tnx	+ 1 — e,		(1.16)
	mi +	m2		mx 4- m	2			
и уравнения (1.14)—(1.15) принимают вид
d2x*	__	(1	— е)х*	е(х*—1)	И	I"7!
dt*’	~	(Х*2	+ </*Т2	[(х*-1)2+у*2]3/2	’
d2y*	= __ (1 — е) у*___________ еу*_______	.	. .
Щ*2	(х*’ + У*Т2 [(х* - I)8 + № ' U '
Таким образом, наша задача определяется только одним параме-
тром б, который обычно называют приведенной массой. Если тг
представляет собой массу Земли, а т2 — массу Луны, то
80	1
6 ~ .	1	~ 81
+ 80
14
Гл. 1. Введение
т. е. действительно является малой величиной. Она и может рас-
сматриваться в качестве параметра возмущения при построении
приближенного решения задачи о движении космического корабля
в гравитационном поле Земли и Луны.
Пример 4. В качестве следующего примера рассмотрим коле-
бания круглой пластины радиуса ах закрепленным краем, находя-
щейся под действием равномерно распределенной радиальной
нагрузки. Если обозначить через w поперечное смещение произ-
вольной точки пластины, то линейные колебания пластины будут
описываться уравнением
DV^-PV2^ + p-5L = 0>	(1.19)
где t — время, D — жесткость пластины, Р — равномерно распре-
деленная радиальная нагрузка и р — плотность материала пла-
стины на единицу площади. Граничные условия имеют вид
n dw п
w — 0, -ч— = 0	при	г~а,
J	л	(12°)
да<оо	при	г = 0.
В данном случае w представляет собой зависимую переменную,
a t и г — независимые переменные. Ясно также, что характерной
длиной для этой задачи является радиус пластины а; характер-
ный же масштаб времени Т мы определим ниже. Вводя безразмер-
ные переменные
	W* ~	W	*	г —, г* =		, t* = 4-
получаем		а ’	а	
	dw	д (aw*) dr*	dw*
	дг	~ dr* dr	dr*~ ’
dw "Эе"	д (aw*) ~ дб	= a	dw* dQ ’
dw	д (aw*)	dt*	a dw*
			
dt	dt*	dt	T dt*
Так как			
V2	_ di i 1	d	, 1
V —	dr* 1 г	dr	1 га d0a ’
то (1.19) дает			
р /	J__2_ ।	1	аа \2
аа \ дг*' ' г* dr* ' /•*’ d0a f W
Р ( d>	I д 1 а» \	.	pa
а \ дг*'	г* дг*	• г*г д№ )	'	Та	dt*'
или
(1.21)
1.1. Анализ размерностей
15
iepb мы можем выбрать Т из условия, чтобы коэффициент при
оказалея равным 1, т. е. полагая Т = а р/Р. В этом
гчае уравнение (1.21) приобретает вид
eV*V — V*V +	= 0,	(1.22)
D
е~ агР ’
(1.23)
ганичные условия (1.20) в безразмерных переменных переписы-
тся как
= 0 при г* == 1,
'	п	(1-24)
w* <Z оо при г* = 0.
^ак, наша задача вновь зависит от одного безразмерного пара-
Йгра в. При этом, если величина нагрузки Р велика по сравнению
В/а1, 8 оказывается малым и может рассматриваться в качестве
«раметра возмущения задачи.
* -Пример 5. В качестве последнего примера рассмотрим уста-
Йввшееся обтекание плоской пластины потоком несжимаемой
рДкости. Задача описывается уравнениями
du dv _______р
. дх ' ду
(1-25)
/ди . ди \ др .	/ dau dau \
Р +	дУ 11	+ ~dV* )	О’27)
Драничными условиями
f"	и = v = 0 при у = 0,	(1.28)
|	u-^Uoo, и—>-0 при х->- — оо,
и и v — составляющие вектора скорости вдоль осей х и у
ответственно, р — давление, р — плотность и р — коэффициент
Йкости жидкости.
| В данном случае зависимыми переменными являются величины
gsp и р, а независимыми переменными — координаты х к у. Для
№
f
^х,и
L
Рис. 1.3. Обтекание бесконечной пластины.
16
Гл. 1. Введение
того чтобы привести уравнения (1.25)—(1.27) к безразмерному
виду, выберем в качестве характерной длины L расстояние от
передней кромки пластины до некоторой заданной ее точки
(рис. 1.3), а в качестве характерного масштаба скорости — ско-
рость набегающего потока Uao. Вводя безразмерные переменные
по формулам
* “ 00		V	*	_ Р	* х	у* =	У
		и„ ’ р		Х — L		L ’
имеем						
ди	_ 5(^oo“	*) dx* _	иао ди*	дй 1	7я, ди*	
дх	дх*	dx "™	L дх* ’	ду ~	L ду* ’	
	дги	Уоо Л*	d2u 		д*и*		
	дх1	Lt дх*'	’ ду*	Lt м	9	
ди _	U <к> dv*	dv	иао dv*	d*v _	d*V*	
дх	L дх*	’ ду ~	L ду* ’	дх*	Li дх*'	9
d*v	d*v*	др	Ри1> др*	др	Ри1> др*	t
ду*	L* ду*'	’ дх	L дх* ’	ду	L ду*	। •
При этом из (1.25)—		(1.28) получаем				
		У» ди*	। U<x> dv*	= 0,		(1.29)
		L дх*	Г L ду*			
P^L * ди* L “* дх*	।	• оо 1 L	* ди* TV* —— == - ду*	Ри1, др* L дх*	। L*	/ д*и* . \ дх*'	д*и* \ ду*' / ’
						(1.30)
P^2J * dv* L и дх*	, Р^	.л dv*	P^L др*		/ д*у* . { - *1 1 \ дх*	d*v* \
	+ L	V ду* -	L ду*	1 L*		ду*' / ’
		и* = у*	= 0 при у	* = 0,		(1-31)
	U„u*-	v*	-> 0 при	х*->—	оо.	(1-32)
Соотношени	я (1.29)-	—(1.32) можно переписать в виде				
		ди* дх*	. dv* _ 1 ду*	= 0,			(1.33)
ди*			др* ।	1 /	’ д2и* .	д*и* \	(1-34)
дх*	1 V ду*		дх* 1	Re (	, дх*'	ду*' /’	
dv*	। * dv*		др* (	1 I	' d*v* ,	d*v* \	(1.35)
дх*	+ Р ду*		ду* 1	Re (	k дх*'	ду*' / ’	
	и* =	V* —	0 при	У*	==о,		(1.36)
	и*-> 1,	V* —>	0 при	X*		оо,		(1.37)
1.2. Разложения
17
где параметр
Re=-^i-	(1.38)
называется числом Рейнольдса.
Уравнения (1.33)—(1.35) с граничными условиями (1.36)—
(1.37) показывают, что наша задача зависит лишь от одного без-
 размерного параметра Re. В случае малой вязкости, т. е. когда р,
мало по сравнению,с произведением pUxL, параметр Re оказыва-
ется большим, и обратная ему величина может быть использована
-в качестве параметра возмущения при построении приближенного
^•решения данной задачи. Этот процесс приводит нас к широко
известным в механике жидкости уравнениям пограничного слоя.
Если же поток обтекает пластину с малой скоростью, т. е. в случае,
: когда pUoaL невелико по сравнению с р, параметр Re становится
малым и сам может служить в качестве параметра возмущения
•при построении приближенного решения. В этом случае мы
получаем так называемое течение Стокса—Озеена.
Г1.2. Разложения
При построении приближенных решений алгебраических, диф-
ференциальных и интегральных уравнений, а также при оценке
Различных интегралов нам приходится иметь дело с рядами по
степеням параметра или независимой переменной. Такие разложе-
1ия в степенные ряды строятся обычно либо с помощью формулы
мнома Ньютона, либо путем использования рядов Тейлора. О них
[ пойдет речь ниже.
Биномиальная формула
Простым перемножением находим
(а + b)2 = а2 + 2аЬ + Ь2,
(а + Ь)3 = а3 + За2Ь + ЗаЬ2 + Ь3,
(а + &)4 = ai + 4а3Ь + (за2Ь2 + 4аЬ3 + &4.
общением этого правила на случай произвольных целых п
ужит формула
4- Ь)п = ап-\- пап-'Ь + га(”71) ап~2Ь2 + «(«-!)(«-2) ап-з& + ... ,
4 1	О I
(1.39а)
Юторую можно переписать в виде
п
С +	(L396>
m=0
:и
п
(а + Ь)п = У,Сптап-т1Г, где С"=-Л7-^-?г. (1.39в)
1?
Гл. 1. Введение
Разложение (1.39а) справедливо для любых положительных или
отрицательных п, при условии если | Ыа\ < 1; в противном случае
ряд расходится, поскольку
Нш ____член _ ]jm	п (п— !)(»—2) ... (п—т-}-\)ап~тЬт
!)-й член ~ т^т! п(п~ 1)(п — 2) ... (п — т + 2) а”-т+,ь'п-1
— 11Ш '------—2— —------------.	(1.40)
т^оо «л	а	’
Так, например, мы имеем
5
(/1=0
= а5 + 5а4й + 1(W + 1(W + бай4 + й5,
6
(а _l b)6 = У .-.т.61—гт а6~'пЬт =
v 1 ’	т\ (6 — т)\
т~0
= а" + 6а8й + 15а4й2 + 2(W + 15а2й4 4- бай5 4- й\
(а + b)i/2 = ai/2 + ±а->/2Ь + 4 2 7	--/-а-^Ь2 +
+ Щ(Ч)..Н),зд,+._
□ I
= а‘/2 + -J- a~'!2b ~	а^/2Ь" -’
(а 4- b)-i = а-i—а-2й + (~4(-~'2)	+ (~^ (~Т	4  
= а'1 — а-2й + а-3й3 — а~4й3 4- • •  •
Отметим, что два первых разложения, соответствующие я = 5 и
п — 6, содержат конечное число членов. В последние два разложе-
ния, соответствующие п = -^-нп = —1, входит бесконечное число
членов; тем самым их справедливость имеет место лишь при
(й|<|а|.
Ряд Тейлора
Если функция f (х) бесконечно дифференцируема в точке
х х0, то ее можно разложить в ряд по степеням (х — хв)
f(x) = a0-|-a1(x-x0) + a2(x —х0)24-а,(х-х0)3-|---
= Lan(x-x0)",	(1.41)
1.2. Разложения
19
вде ап — постоянные, определяемые значениями функции f (к)
ре производных в точке х »= х9. Действительно, полагая в (1.41)
» = х0, находим, что а0 = f (х0). Дифференцируя разложение
И .41) по х, получаем
f Г (х) ~ аг + 2аа (х — х0) + За3 (х — х0)а +
Ц	+ 4at (х — х0)* + ...,	(1-42)
Вткуда, если положить х — х0, имеем at = f (х0). Далее, диффе-
ренцируя (1.42) по х, получаем
F f ,(•*) — 21 4" 3! о, (х — х0) 4~ 4 • 3 а4 (х — х0)4	• • • •	(1 -43)
ЯЭолагая х = х0, находим аа = f” (х0). Дифференцирование
Й1.43) по х дает
|	Г(х) = 31а3 + 4!а4(х-х0)+(1.44)
Откуда, полагая х — х0, имеем as =	f"' (х0). Неограниченно
Ййродолжая этот процесв, можно определить все остальные коэф-
фициенты
I	an=^-f^(x0),	(1.45)
|£де	и /<0) ~f(xo)- Таким образом, разложение (1.41)
ЯЙржно представить в виде ряда
I	1(х) = ^^^-(х-хоу,	(1.46)
п=0
рторый называется рядом Тейлора функции f (х) в окрестности
Очки х — х0.
* Так как t	(sin х) = cos х	и	(cos х) = Р ,	Sinx —X	31	+	5!	7! +	• — L	л»=о .	X*	.	X*	X»	V' 1	cosx=l	4!	6!+-'--2j г	Л—0 Аналогично, с помощью формулы 	4<e,)=e* Ьлучаем	x U + 2, + 3, + (=	= —sinx, 4.+1»  <l 47) .	(1.48) (2n)I	u t.Tr} (!«>
20
Гл. 1. Введение
а из соотношений
имеем
... I ч	Ха X3 X4 ,	\? (— 1)П+1ХП	/1 гслч
in(i 4-х)=х-——г+--- = 2j-—4—• о-50)
Вышеприведенные тейлоровские разложения мы будем часто
использовать в последующих главах.
1.3. Калибровочные функции
В этой книге мы будем заниматься исследованием пределов
различных функций, в частности предела функции f (е) при е,
стремящемся к нулю, что будем обозначать как е -* 0. Этот предел
может зависеть от того, стремится ли е к нулю справа (этот факт
мы будем записывать как е -► +0) или слева (такое стремление
обозначим как в -► —0). Например,
lime-1/® = 0, но lim е-1'8 = оо.
8->+0	е->~ 0
В дальнейшем мы будем предполагать, что все параметры выбира-
ются таким образом, что е 0. Если предел функции f (е) су-
ществует (т. е. у нее нет существенных особенностей при е = 0,
таких, как у функции sin е"1), то имеет место одна из трех возмож-
ностей
/(8)->0
Д8) + Л
оо
при 8->О, 0<|Л|<ОО.
(1.51)
Чаще всего такая классификация оказывается не слишком удоб-
ной, поскольку существует бесчисленное множество функций,
стремящихся к нулю при е -> 0. Так,
limsine = 0,	lim (1 — cose) = 0, lim (е — sine): О,
е-»-0	'	в->0	е-М)	/| сп)
lim [In (1 + е)]4 = 0, lim е-1/Е = 0.
8->0	8->0
Точно так же имеется бесконечно много функций, которые стре-
мятся к бесконечности при е -> 0, например
hm -с— ~ оо, lim-----------,-----------= оо,
е-М) sm е	е-о 1 __ ‘ еа — cos е
!	(1-53)
limе1/е = оо, lim in — = оо.
8->0	8->0	6
1.3. Калибровочные функции
21
Поэтому, для того чтобы уточнить вышеприведенную класси-
ацию, мы будем подразделять каждый из указанных классов
_кций в соответствии со скоростью, с которой они стремятся
улю или к бесконечности. Иначе говоря, мы будем сравнивать
рость соответствующего убывания или возрастания этих функ-
I со скоростью стремления к нулю или бесконечности некоторых
естных функций. Эти функции сравнения называются калибро-
чыми функциями. Простейшими и наиболее употребительными
них являются целые положительные степени параметра е
1, е, е2, е8, ...,
акже его обратные степени
е-1, е-2, е-8, е~4, ...;
I этом известно, что для малых е
1 > е > е? > е8 > е4 > ... и е-1 < е~2 < е~3 < е~4 < ... .
"Определим теперь скорость, с которой рассмотренные нами
|ее функции стремятся к нулю или бесконечности. Используя
Сюровское разложение (1.47), имеем
е3 . е5	е’
sine — е—ТГ+"51	7Г -
укдовательно, sin е —> 0 как е, поскольку
5’	,. sin е	1.	/ ,	е2	. е4	.
hm ___ = lim (1 - -5Г + -57- +
г	е->0	8	Е->0 \	3!	0 1
фее, с помощью (1.48) получаем
,	е2 е4 ,
1-СО§е=:-2Т--4Г+
— cos е —* О как е2, поскольку
lim.l-C0S8 1:_/1
е->0
[о так же
) следует
На
1
е
8’
— sin е —> О как
1
~ 2! '
4!
е8, поскольку из разложения
е3
е — sine = -х-г
□ I
F5
5Т

..	8— Sin 8	/ 1
S-7— =Й(-ЗГ-ТГ-Г-
югично, используя (1.50), получаем
(р2 сЗ
е —~ +
да [In (1 4- е) ]4 -> 0 как е4, поскольку
«-►0	8	8->0 \	О
22
Гл. 1. Введение
Для того чтобы определить скорость, с которой стремится
к нулю ехр (—1/е) при е -> О, попытаемся разложить эту функцию
в ряд Тейлора при малых е. Для этого нам необходимо знать ее
производные при е — 0. Но
=	(1.54а)
что при е = 0 приводит к неопределенности вида -у. Так как
е-1/е	х2
lim f (е) = lim —j— = lim x2e~x — lim —
e-»0	e->0	8	x->oo e
то, используя правило Лопиталя и дважды дифференцируя по х
числитель и знаменатель, имеем
lim f (е) = lim = 0,
е->0	х->оо е*
откуда
f (0) = 0.	(1.546)
Далее, дифференцируя по е соотношение (1.54а), находим
=	(1.55а)
откуда f" (0) = 0, поскольку, согласно правилу Лопиталя,
lim ( в-»0	' -V - -V) е’,/8 == Hm ** 2*3 = lim -Ц- = 0. < 84	в3 /	х— 0х	х^оо ех
Наконец, дифференцирование (1.55а) дает
Г(е)=(-^--?-+4)	<L56a>
откуда /" (0) = 0, так как
6	1 6 '		— Нт 6! - 0
			
е5		’	х->оо	е*	Х-ои е*
Продолжая этот процесс, получаем, что
(0) = 0	(1.57)
для веех п. При этом из (1.46) следует е~1/е =0+0+0+0+
+ .... что, конечно, неверно. Таким образом, функция ехр (—1/е)
не может быть представлена рядом по степеням е. Происходит это
потому, что при е -> 0 она стремится к нулю быстрее, чем любая
степень е. Действительно,
е 1/8	хп .. nl п
lim —— = hm — — hm —— = 0
«'-О	£	х-юо е х-оо е*
— этот результат легко получается с помощью последовательного
применения правила Лопиталя. Итак, одних лишь степенных
калибровочных функций нам оказывается недостаточно, и к ним
нужно добавить функцию ехр (—1/е).
1.3. Калибровочные функции
23
) Исследуем теперь, с какой скоростью стремятся к бесконеч-
рсти функции, представленные в соотношениях (1.53). Используя
1.47), получаем
£ 1  1
Sin 8	8s
	е~ 31
ткуда (sin е)-1 -> оо как е-1, поскольку
lim 1/sine — lim —®— = Hm —
в-*0 Vе	slne e->0 J.
1
е2
е
3!
1
е2
= 1.
3!
,алее из разложения (1.48) находим
1
<	1 я
1---g- 82 — COS 8
— е2 —
2 Е
1
е4 ев
4Т+ "бТ
|К что
lim
£ >0 I 1----е2 — cos е
= lim
е‘ е-*-0
как—е 4, поскольку
е4	__
е4 е*
“ТТ +"бГ н
= lim —
е->0 1
—4!
82
= — 4!.
lim
s->0
30 1
I Так как ехр (—1/е) стремится к нулю быстрее, чем любая
|ложительная степень е, то функция ехр (1/е) стремится к беско-
кности быстрее, чем любая обратная степень е; в самом деле,
^гласно правилу Лопиталя, имеем
е1/®	,.	е*	ех
—— = lim ——— hm —г= оо.
1/е" х -оо хп х-оо «!
|ким образом, мы должны пополнить совокупность калибровоч-
|х функций еще одной функцией, —ехр (1/е). Далее, функция
н1/е) при е -> 0 стремится к бесконечности медленнее, чем е-а,
I а — сколь угодно малое положительное число, так как
г	In (1/8)	1пХ ,.	1	1	1	„
lim —lim—— = hm----------—r = — lim-—= 0.
L »->0 e “ x-oo x“ X .oox a? 1 a x-»oo x“
едовательно, к набору калибровочных функций необходимо доба-
вь еще функцию 1п (1/е). Точно так же в этот набор нужно
яючить и функцию [1п (1/е) I-1, с тем чтобы иметь возможность
йсывать поведение функций, которые стремятся к нулю медлен-
p. чем любая степень е, в частности е“, где а — сколь угодно
йое положительное число.
[Итак, приведенные рассуждения показывают, что для получе-
и полного набора калибровочных функций кроме различных
24
Гл. 1. Введение
степеней е мы должны включать в него логарифмы, экспоненты; |
а также функции вида	I
//е, е-е'/е, Inln(-l), Inlnln(-l-),	(inит. д. I
1.4. Символы порядка	|
Вместо утверждения о том, что sin е стремится к нулю с той же |
скоростью, что и е, обычно говорят, что «sin е имеет порядок е I
при е -> 0», или «sin е есть «О большое» от е при е -> 0», и записы- I
вают это как
sin е = О (е) при е -> 0.
Вообще мы полагаем х)
f (е) = О [g (е) ] при е -> 0,	(1.58)
если существует такое число А, что
ПшЖ=д 0 < IАI < оо .	(1.59)
г-0 g (е)	11	\	/
Таким образом, при е -> 0
cos е — О (1), cos е — 1=0 (е2),
sh е = О (е), tg е = О (в),
cosec е = О (е-1), sec е = О (1),
Р3/2	j
ctg е = О (8-1),	-±_ = 0(81/2),	|
sh — = O(eI/s), sch — = О (е-1-'8).
В	в
Необходимо отметить, что введенное с помощью символа О мате-
матическое понятие порядка формально отличается от физического
понятия порядка величины, поскольку численное значение по-
стоянной А, т. е. выбранного коэффициента пропорциональности,
при этом совершенно не учитывается. Так, Ае = О (е), даже если А
равно ста тысячам. Вместе с тем всегда существует тайная надежда,
что эти две оценки в значительной степени связаны между собой. ?
Иными словами, обычно принимается, что соответствующие
коэффициенты пропорциональности порядка единицы и значение,
определяемое символом порядка, оказывается достаточно близким
к фактическому численному значению физической величины.
Ч В существующей литературе по асимптотическим методам символ О обычно ;
вводится несколько иначе. А именно, f (е) = О [g (е) ] при е—> 0, если |/ (е)|	
A |g (в) |, е^е0, А = const; при этом символ О фактически означает оценку
порядка сверху. Ограничиваясь, согласно (1.59), точной оценкой порядка, автор
отходит от традиционного определения и восстанавливает соответствие между j
звучанием и смыслом соотношения (1.58). Вопрос о новом символе для верх- 1
иих оценок у автора не возникает, поскольку такие оценки в книге ие исполь- I
зуются. — Прим. ред.	1
1.5. Асимптотические ряды.
25
о многих случаях имеющаяся у нас информация о заданной
:ции оказывается недостаточной для определения скорости,
орой эта функция стремится к пределу, однако с ее помощью
не можно установить, будет ли эта скорость больше или
ше скорости изменения соответствующей калибровочной
Кции. При этом мы используем символ порядка «о» (о малое),
оделяемый следующим образом:
(1.60)
f (е) = о [g (е) ] при е -> 0,
lim
8->-0
при
е -> 0
sine = о(1),
cos е = о(е-1),
e-i/e = o(e-10-8),
1П J- — 0(6-0.00001),
е2/® = о (ее*/е),
Ж = о.
g(e)
sin е = о(е1/2),
cos е = о(е~1/3),
е-ю‘»==0(е1/е),
1п 1п-~- — о fin
(1.61)
" Асимптотические ряды
'ассмотрим теперь вопрос
об оценке интеграла
и
/(«)==
(1.62)
о
.больших положительных со. Одним из способов построения
тствующей аппроксимации для функции f (со) является метод
1са, описываемый в § 3.3. Он заключается в разложении
!теля, стоящего в подынтегральном выражении при ехр (—х),
по степеням х и последующем почленном интегрировании
енного ряда. Действительно, используя биномиальную фор-
получаем ряд
____1	, х № х3	— V (—1)пхп
х 1 4- со-1*	со ‘ со2 со2 *	>
п=0
(1.63)
ай сходится при х < (о. Основная идея, лежащая в основе
i Лапласа, состоит в том, что при больших х ехр (—х) стре-
к нулю быстрее, чем растет к бесконечности любая степень х.
а следует, что величина нашего интеграла при больших о
!ляется в основном лишь поведением подынтегральной


Гл. 1. Введение
функции вблизи начала координат. Подставляя (1.63) в (1.62),
находим
О п=0	'1“0	О
Но повкольку для целых п
со
j хпе~х dx = n\,
о
то
(<«)
п=0
Применяя признак сходимости Даламбера, получаем
.. п-й член ..	(—1)п nl а>п-1	.. —п
lim ----гпг-----= 11П1 —г3 ---------------=? 11Ш —- = — оо,
п->«> («— 1)-й член п^х ш" (-1)"-' (п~ 1)1 П-.ОО 2®
и, следовательно, ряд (1.64) расходится для всех значений со.
Для того чтобы выяснить, можно ли все-таки каким-либо образом
использовать формулу (1.64) для вычисления / (со), вычислим
остаток, получающийся при усечении этого ряда на Д'-m члене.
Заметим при этом, что отрезок ряда
S(—l)4xn
<s>n
П=0
представляет собой геометрическую прогрессию с суммой
Отсюда следует, что
N	1
п=0
/	X \*+1	/	X \W+1	-
3 _ и ~ \	to )______k	to /	__	(—x)"+1
где KN — Q + x	i+JL	1 + ~ и" (to + x) ’
’’co	r®
или, окончательно,
®	= у (~l)nxn
® + x Zj w'1
>l=.O
(—x)"+1
<o" (® + x)
(1.65)
1.5. Асимптотические ряды
27
СО
Умножая (1.65) на ехр (—х) и интегрируя полученный ре-
гльтат от х ** 0 до х = оо, получаем
оо	W
(~1)п
<оп
f СО*
J со + X
о
остаток
чит
О
N
(—l)nnl
+ Rn (®),
(1.66)
Li ап
п=0
/ । Л+1
(1-67)
xN+ig-x
J W + x
0
аяется, очевидно, функцией со и N.
Теперь вместо того, чтобы применять признак Даламбера, мы
Кем заняться исследованием поведения RN (<о) при фиксирован-
но и N -► оо. При этом для сходимости ряда необходимо,
ы lim RN = 0. В нашем примере это не так: на самом деле
Af-»-oo
оо при N -> оо, так что ряд расходится для всех значений
I полном соответствии с результатом, полученным по признаку
мбера. Следовательно, для того чтобы можно было восполь-
?гься рядом (1.66), нужно зафиксировать число N и исследовать
5Цение RN (и) при фиксированном N. Для этого попытаемся
|ить величину RN (<о).
ак как со и х положительны, то
1	1
(й-рХ	X
АГ 1	w
=	о-1»)
о	о
ошибка,- обусловленная усечением исходного ряда на N-м
численно не превосходит первого отброшенного члена,
адно (N + 1)-го. Более того, при фиксированном N и со -► оо
RN -> 0. Поэтому хотя ряд (1.64) и расходится, но для
(рованного N первые N членов этого ряда могут представлять
(ию f (<о) с ошибкой, которая может быть сделана произвольно
! с помощью выбора достаточно большого значения а. Такой
взывается асимптотическим рядом типа Пуанкаре и обозна-
как ’
(—Ifni
(1.69)
28
Гл. 1. Введение
1.6. Асимптотические разложения
29
Рис. 1.4. Поведение членов расходящегося асимптотического ряда.
Вообще для заданного ряда (ап/ып), где ап не зависит от о,
п—О
мы говорим, что он является асимптотическим рядом, и пишем
оо
при со —оо	(1.70)
тогда и только тогда, когда ?
N
/((o)=S'5'+o(^r) при й)_*00-	(1,71)
п=0	'	7
При этом из (1.71) следует, что
f<“)=S-5-+5-+°(;H "р"
п=0	'	'
так что условие (1.71) можно переписать в виде
IN-1
f(®) = У ( 1 \при (0->оо.	(1.72)
(D	Ь \ и) /
п=0	" '
Необходимо отметить, что полезность асимптотических рядов
основана на том факте, что ошибка, совершаемая при усечении
ряда, по определению имеет порядок величины первого отброшен
кого члена и, следовательно, быстро стремится к нулю при <в -> оо
В приложениях обычно фиксируют достаточно большое значение о.
и пытаются минимизировать ошибку увеличением числа членов
ряда. Однако если ряд расходится, то в конце концов достигаете*
точка, за которой добавление новых членов лишь увеличивает
ошибку (рис. 1.4). Таким образом, для каждого заданного значе
ния о» существует оптимальное значение N, при котором ошибк;
будет наименьшей. На практике только в редких случаях вычис-
ляют более одного-двух членов разложения, и поэтому нет необхо-
димости заботиться о сходимости получающегося ряда. В тех же
случаях, когда требуется подсчитать достаточно много членов
ряда, их обычно получают посредством тех или иных алгебраиче-
ских операций, проводимых на ЭВМ. Затем ряд исследуется на
аналитичность, после чего он соответствующим образом преобра-
зуется с целью улучшения его свойств — например, с помощью
подстановок типа рациональных дробей, использования естествен-
ных координат или преобразования Эйлера. Вопросы преобразова-
ния расходящихся рядов в этой книге не рассматриваются, а чита-
телей, интересующихся этой проблемой, мы отсылаем к моногра-
фии Ван-Дайка (1975) и содержащейся в ней библиографии.
1.6.	Асимптотические разложения и последовательности
Как указывалось в § 1.3, существует множество функций, чье
поведение не может быть описано рядами по степеням малого
параметра. Более того, мы установили, что степени е следует
Дополнить другими калибровочными функциями — логарифмом,
экспонентой, логарифмом логарифма и т. д. Вместе с тем для
асимптотического представления заданной функции вовсе не
обязательно ограничиваться перечисленными функциями сравне-
ния. Вместо них можно воспользоваться произвольной последова-
тельностью функций общего вида б,( (е), удовлетворяющих усло-
вию
6„(e) = o[S„_1(e)] при е->0.	[(1.73)
Такая последовательность называется асимптотической последова-
тельностью. Примерами асимптотических последовательностей
являются
еп, еп/з> (|ne)“n, (sine)", (ctge)-".	(1-74)
В терминах асимптотических последовательностей мы можем опре-
СО
делить и асимптотические разложения. Так, сумму вида Tj апдп (е),
п=0
Где ап не зависит от в, a 6n (s) представляет собой асимптотическую
Последовательность, мы будем называть асимптотическим разложе-
нием функции f (е), если при е -> О
f(e)=Sa(e) + o(6«(8)),	(1.75)
п=0
Ли, что то же самое,
N-1
'	/(8)= Е «A(8) + 0(6jV(8)),	(1.76)
п=0
30
Гл. 1. Введение
записывая это соотношением
f (е) ~ £ ап8п(е) при е^О.	(1.77)
Очевидно, что асимптотический ряд есть частный случай асимпто-
тического разложения.
Отметим также, что асимптотическое представление заданной
функции / (е) не единственно. В самом деле, функция f (е) может
быть представлена бесконечным числом асимптотических разло-
жений, поскольку существует бесконечное число асимитотических
последовательностей, которые могут быть использованы для. такого
представления. Однако при задании последовательности функций
бп (е) асимптотическое представление функции f (е) с ее помощью
оказывается уже единственным. Действительно, положим
f (е) ~ а0«о (е) + alSl (е) + агд2 (е) + ....
Разделив (1.78) на i0 (е), имеем
И8) ,	1 д Me) ,
6e(e) а° + 01 60 (е) +
откуда, если устремить е к нулю,
поскольку lim [fin (е)/6в (е) ] — 0 для п 1. Перенося
е-»0
<Мо (е) в левую часть и деля полученное соотношение на
находим
f (в) — авбв (е)	„ ( _ ба (е)
----«ГФ------
е —> 0
откуда при
Продолжая

«1(8)
этот процесс, легко получить общую формулу
П-1
f (в) — a„6m (е)
в lim-----------------.
" ен-о	*»(•)
(1.78)
член
Si (е)-
(1.79)
1.7.	Сравнение сходящихся и асимптотических рядов
В гл. 13 мы получим два различных представления для функции
Бесселя нулевого порядка Jo (х), а именно
Л^)=1--5-+^ПГ--2Г^8Г+	(180)
1.8. Действия над асимптотическими разложениями
31
-^[wcos(x--J) + usin(x--J-)] при х->оо,
(1.81)
де
“W=1-4r^ + -S^+---«	(1-82)
J	о-83)
|д (1.80) сходится абсолютно и равномерно для всех значений
» время как ряды для и (х) и v (х), а следовательно, и правая
(1.81) расходятся для всех значений х. Однако при х -> оо
мые в и и v быстро убывают с ростом номера, так что пред-
:ние (1.81) действительно будет асимптотическим, поскольку
;а, совершаемая при обрывании рядов, имеет порядок пер-
>тброшенного члена.
я малых х первые несколько членов разложения (1.80)
вполне приемлемую точность. В самом деле, первые девять
i дают значение Jo (2) с точностью до 11 значащих цифр,
о по мере возрастания х число членов, необходимых для
чения той же точности, быстро растет. При х = 4 восемь
$ ряда дают точность до третьей значащей цифры, в то время
1кую точность обеспечивает уже первый член асимптотиче-
разложения (1.81). При дальнейшем росте х хорошую точ-
можно получать с гораздо меныцей затратой труда, именно
ьзуя расходящийся асимптотический ряд (1.81). Действи-
>, в случае очень больших х сходящийся ряд (1.80) оказы-
совершенно бесполезным с вычислительной точки зрения
ограниченности разрядной сетки современных ЭВМ. Таким
>м, любая попытка вычисления функции JQ (х) при больших
мощью ряда (1.80) потерпит неудачу, как только х окажется
е некоторого определенного значения; правда, это значение х
эгом определяется искусством программиста.
1ростейшие действия над асимптотическими разложениями
и построении приближенных решений алгебраических, диф-
циальных и интегральных уравнений, а также при оценке
>алов мы предполагаем, что асимптотические разложения
) подставлять в уравнения и выполнять над нйми простейшие
»ия, такие, как сложение, вычитание, умножение, возведение
ень, интегрирование и дифференцирование. Иногда примене-
екоторых из »тих операций оказывается необоснованным;
и случае они приводят к сингулярностям или неравномер-
м.
к
32
Гл. 1. Введение
Например, равенство
1/2
(1-84)
(1.85)
— ? Л L1 2 х ~	2	\ х /
=	•••) при
не обосновано при е/х — О (1), поскольку при этом второй, третий 1
и последующие члены разложения становятся сравнимыми по ।
порядку с первым его членом. Следовательно, ошибка, совершае-
мая в результате усечения ряда после N членов при х = О (е), уже i
не будет иметь порядок О т. е. не будет порйдка первого
отброшенного члена, и мы говорим о неравномерном разложении.
Аналогично, равенство
-—!— = 1 — ех -4- е2ха — е3ха 4-. •
1 + ех	1	1
не обосновано при ех = О (1), поскольку, по той же причине,
правая часть его будет неравномерна при больших х. Таким обра-
зом, необходимо всегда проверять, являются ли полученные разло-
жения равномерными или нет, — в этом, собственно говоря, и
заключается одна из главных целей методов возмущений.
Упражнения
1.1.	Найти первые три члена разложений следующих функций при малом е:
a)	f1 —4-“28 +-^'а4е2') ">
\ о	аЬЬ /
б)	cos К.1 — е/,
в)	У 1 —-1-е 4-2е2,	, .
г)	sin (1 4- е — е2).
1.2.	Разложить каждое из следующих выражений при малом е, сохранив
три члена:
а> ]Л —
б)	(1 + 8 COS/)-1,
в)	(1 + 80Ц 4- 82<02)-2,
г)	sin (s-f-e®xs 4-е2®^),
д)	sin 11 -—==),
1 + 2е — 82
е)	1п-з7т==йГ-
Упражнения
33
Ч	-	-
1.3.	Пусть р = |ч + еН1 + е% и Л =	[1 — /1 — Зц (1 — |*)J.
/ Разложить функцию Л при малом е, сохранив три члена.
1.4.	Определить порядок функций при малых е:
In (1+sine), In (2 +sine), e,n<1-e>.
1.5.	Определить порядок следующих выражений при в—> 0:
в (1 — е),	4л2в,
sech-1 е,	ete ®,
1000е.1/2, In (1 4- е),
1пС1 +2е) )
8(1—28) J’
1 — cos е	е3/2
1 + cos е ’	1 — cos е ’
In
,	14-2е
In —1---
е
1 —2е
e-chd/е), je'S'js?
о
1.8. Определить порядок следующих выражений при в—> 0:
6	1/* в	1	/	1 \
I + 5в), arcsin ——:,	1----в2 —cose, In ( sh—).
”	КТ+в’ sine ’	2	\ е /
1.7.	Определить порядок следующих функций при в—> 0:
, , , \	/ 1 \	е3/4	, Г, , , 1 + 2е 1
In(ctge), cth(—),	In 1 + ln—Г------ .
у & /	i — LUd &	L	о j
1.8.	Расположить следующие выражения в ряд по порядку убывания при
лх е:
в2,	в1''2,	1п(1пе-1),	1,	в1/2 In в-1, в In в-1,
е-1/®, In в-1,	в3/2, в, в2 In в-1.
1.9.	Расположить следующие выражения в ряд по порядку убывания при
ях в:
ехр (----J-'),	In ( —'j, в-1/100, ctg е, sh ( —.
1.10.	Расположить следующие выражения в ряд по порядку убывания
малых в:
ln(l + e), ctge, th(±),^
I	I 1 \ L I 1 \	, , / 1 \
Bine, ехр(-------Ь sh( —I, In 11 — 1.
\ В /	"~	\ В /	\ ® /
1.11.	Расположить следующие функции в порядке убывания при малых в:
е-1/®, 1п > Т~’ е1/,2>	'п (т-) ’
ТВ-. >• ТВ-.	ь(ь-г). '
gO.OOOl. g-0,0001( gO.OOOl jn 1 gl/B, 5-1/8.
2_Нвйфэ A. X.	10 6 < 1 8 7
SH5AHQ/TEKA~
/ Пермского
L университета
34
Гл. 1. Введение
1.12.	Расположить следующие функции в ряд по порядку убывания при
малых в:
в\ еЛ в»1, е^, 1,	в3/2,' в'3''2, ехр (-Ц, Inf—),
г \ е /	\ е /
ta[taG")l’ [,п(-г)Г’ e ta (4-)’ е/1п(-г)’ ех₽(—г)- е>
гДе v = 1О~100 и |1 = 10100.
। 1.13. Расположить следующие выражения в порядке убывания при малых е:
In(l-f-e), sech-1e, , C0Se , V"e(l—e),	e-^.U/e)
' 1 '	1'4-cose ’ r '	’
	1 +2e I
i ,	"	8	, ln(I+2e)1	e1/2
in 14~	. n “ , In I 1 z i"" n <" >	.
1 — 2e J	в (1 — 2e) J ’	1 — cose
1.14.	Какие из следующих разложений' по параметру не являются равно-
мерно пригодными для всех значений аргумента? Каковы области их неравно-
мерности?
а)	УТЦх, е) =-?-х3/24-е (-^-х372 4-К* —4-1п
0	\ 0	Z'
1	1 Ч-*?2
б)	ц(х, е) = е cos х 4- -g- еа у_ cos 2* +
. 3	2у*4-7?* + 2
16	(1 — 2?®) (1 — З?2)
Cos Зх 4- о (В*) ;
в)	о (k, в) = Vk? - 1 - -7==- + О (в®);
У й® — 1
г)	f (*> е) = 1 — ех 4-е®*® — е3*3 4~ О (е4);
д)	«</, е) = acos0 4- ва®^ t + -~cos 3 (1 4- -|-еа®) / 4-0 (е®)1
е)	u{t, ъ) = а<ж1 4- -е^~^-i-cos3< — 31 sto t4-0 (в®);
ж)	с (г, е) = I +	+ ° (е8):
3”(‘’1,“уйЙ7
cos xJK*(1— *) <1* 4-0(1) при Х~>оо;
о	J
и) f (х, е) = sinx 4- в cosx-i-e®sinx----в® cos х 4- О (в<),
Глава 2
АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ
5 этой главе мы займемся исследованием алгебраических
мнений, зависящих от малого параметра. Их приближенные
ения будут строиться в виде некоторых разложений, которые
Ом случае называются возмущениями по параметру. Сначала
«ерем этот метод для уравнений второго порядка, поскольку
них в целях сравнения можно легко воспользоваться точными
Вниями. Далее, в § 2.2 мы исследуем кубические уравнения,
£.3 — уравнения высших порядков и, наконец, в § 2.4 — неко-
Ье трансцендентные уравнения.
^Квадратные уравнения
Зачнём с анализа квадратных уравнений, и рассмотрим не-
1ько простых примеров, сравнивая полученные разложения
иными решениями.
«мер 1
эудем искать корни уравнения
|	х2 — (3 + 2е) х + 2 + е = 0	(2.1)
•малом е. В случае е = 0 имеем уравнение
I	х2 — Зх + 2 = (х — 2) (х — I) == 0	(2.2)
ариями х = I и х = 2. Уравнение (2.1) называется возмущен-
г уравнением,, а (2.2) — невозмущенным или вырожденным
шением. При малом, но конечном е естественно ожидать, что
1и уравнения (2.1) будут лишь немного отличаться от значений
2.
Первый шаг при нахождении приближенного решения заклю-
чи в выборе формы разложения. В нашем случае предположим,
искомые корни можно представить в виде
х = х0 + ехг + е2ха + ....	(2.3)
многоточие заменяет слагаемые со степенями е, для которых
Йатель степени п 2» 3. В большинстве приложений определяют
(ко один или два члена разложения, поскольку вычисление
Job высших порядков оказывается весьма громоздким; по
36
Гл. 2. Алгебраические уравнения
возможности подобные расчеты стараются проводить с помощью I
ЭВМ. Однако следует отметить, что во многих физических задачах, Ч
особенно нелинейных, нахождение членов высших порядков ока- 1
зывается достаточно сложной процедурой даже при использовании
ЭВМ. В этой книге мы будем ограничиваться рассмотрением лишь
нескольких первых членов соответствующих разложений. Обычно
первый член разложения хв называют членом нулевого порядка, '
второй, т. е. гхъ — членом первого порядка и т- д. Иными словами,
порядок соответствующего члена определяется видом функции
сравнения, а не его порядковым номером в асимптотическом
разложении.
Второй шаг заключается в подстановке выбранного разложения
(2.3) в исходное уравнение (2.1), что дает
(х0 + вхг 4* е2х2 4* ...)2 — (3 + 2е) (х0 4- 8Х2 4-
4* е2ха + ...) + 2 + в = 0.	(2.4)
Третий шаг представляет собой выполнение элементарных опе-
раций типа сложения, вычитания, умножения, возведения в сте-
пень и т. д. и, наконец, группировку коэффициентов при одинако-
вых'степенях в. Используя для разложения первого члена бино-
миальную формулу, получаем
(х0 + е*1 + 82Х2 -|--)2 = *0 + 2х0(8X1 4- 82Х2 + • • •) +
4- (еХ1 4- е2х2 4- .. .)2 = Хо 4- 28XqXi 4- 2в2ХоХ2 4~
4-е2х?4-2e3xix24-е4х24- =Xo4-2exoxI 4-е2 (2хьхг 4~ х?) 4*.. .4
(2.5)
здесь в соответствии с выбранной формой разложения (2.3) сохра-
нены лишь чле^ы порядка 82. ЕсЛи бы мы искали разложение
с точностью до членов порядка 8", где п 3, то в выражении (2.5)
следовало бы сохранить члены того же порядка. Выполнив умно-
жение во втором члене в (2.4), находим
(3 4- 2е) (х0 4- е'хд 4- е2х2 4* •••) = Зх0 4* Зехг 4- Зб2х2 4- 2ех0 4-
4* 2е2х! 4- 283х2 4-... = Зхо 4- е (3xj 4- 2х0) 4-
: 4- 82 (Зх2 4- 2хг) 4-....... .	. (2.6)
Здесь также в соответствии с выбранной формой исходного разло-
жения сохранены лишь члены порядка 82. Подставляя (2.5) и (2.6)
в (2.4), имеем
Xq 4“ 28XqXj 4- 8 (2XqX2 4- X?)—Зхо	8 (3Xj 4- 2xq)
— 82 (Зх2 4- 2xi) 4- 2 4- 8 4- • • • = о-
Собирая коэффициенты при одинаковых степенях 8, получаем
(хо — Зх0 4- 2) 4- 8 (2xqXi — 3xi — 2хо 4*1)4”
4-в2(2хоХ2 4-Х1 — Зх2 — 2xi)4* •••=0.	(2.7)
2.1. Квадратные уравнения	37
Четвертый шаг состоит в приравнивании нулю коэффициентов
ш последовательных степенях в. Для оправдания этого шага
’тремиме к нулю в выражении (2.7). В р^ул^-ате получим
равнение
I	*о — 3*о -(-2 = 0,	(2.8)
Г(2.7) примет вид
(2*0*1 — 3*1 — 2*о + 1) + в2 (2*0*2 4- *i — 3*2 — 2*i)	0.
разделив на в, приходим к равенству
f (2*o*i — 3*1 — 2*о 4- 1) + е (2*0*2 4- *? — 3*2 - 2*1) --=0,
I	(2-9)
Которое при в —> 0 дает
|	2*0*! — 3*1 — 2*в 4- 1 = 0.	(2 ДО)
|ри этом (2.9) переходит й равенство
?	8 (2*0*2 Д' *1 — 3*2 — 2*])	0,
Ьш после деления на'8
2*о*2 4-*i — 3*2 — 2*iО (8) = 0.	'	(2.11)
Г Устремив в (2.11) 8 к нулю, получаем
к	2*о*2 4~ *1 — 3*2 — 2*1 :- 0.	(2.12)
иметим. что соотношения (2.8), (2.10) и (2.12) можно получить
^посредственно из формулы (2.7), приравнивая нулю коэффи-
иенты при последовательных степенях 8.
I Пятый шаг состоит в последовательном решении упрощенных
равнений (2.8), (2.10) и (2.12). Уравнение (2.8) совпадает с вы-
ржденным уравнением (2.2), и, следовательно, его решениями
Ьдут
I	х° = 1,2‘
мая *0, из уравнения (2.10) мы можем найти хг. Отметим, что
|Д0) линейно относительно хх. Практически в большинстве задач
равнения каждого приближения также оказываются линейными,
и исключением, быть может, первого. В случае *0 = 1 уравнение
В. 10) дает
I	*i 4- 1 = 0, или *i = —1.
[на я *0 и *i, можно разрешить уравнение (2.12) относительно *2.
|ри *0 = 1,*1 = —1 из уравнения (2.12) получаем
|	4 *г — 3 = 0, или х2 = 3.
В случае х0 = 2 из (2.10) находим
|	*i — 3 = 0, или *! = 3,
[из (2.12)
Г;	• *а 4- 3 = 0, или *2 = —3.


38
Гл. 2. Алгебраические уравнения
Последний шаг заключается в подстановке полученных значе-
ний х0, Xi и х2 в исходное разложение (2.3). При х0 = 1, хг = —1
и х2 = 3 это разложение приобретает вид
х = 1 — е + Зе2 + ....	(2.13)
- а при х0 = 2, Xi — 3 и х2 = —3 разложение (2.3) можно пред-
ставить как
х = 2 + Зе — Зе2 + ...?	(2.14)
Формулы (2.13) и (2.14) дают иам приближенные выражения для
обоих корней уравнения (2.1). Для того чтобы выяснить, насколько
удачны эти приближения, сравним их с точным решением
х =-|-[3 + 2е Т У(3 4-2е)2 — 4(2 4~ е)]>
ИЛИ
х = -L [з + 2е =р У 1 + 8е + 4еа].
Используя биномиальную формулу, пблучаем
(2.15)
(1 4-8е + 4е2)>/2 = 1 4- Ц-(8е 4- 4е2) + V - <->- --7 (8е4-4е2)* + •
= 4 4-4е 4-2е2 —-j-(64е2-j--------)=1 4- 4е - бе2 + ...,
что при подстановке в (2.15) дает
х =
-j- (3 -}- 2е + 1 -J- 4е — 6s2 -}- • • •),
-^-(3 4-2е- 1 - 4е + 6е2-|-------)J

или
(2.16)
( 2 4-Зе-Зе2 4- ...
Х = ( 1 - е + Зе2 + ...
в полном согласии с (2.13) и (2.14)
Пример 2
В качестве второго примера исследуем уравнение, разложения
для корней которого могут включать в себя не только целые, но и
дробные степени параметра е. Так, рассмотрим уравнение
(х — 1) (х — т) — —ех.	(2.17)
При е = 0 оно сводится к уравнению
(х — 1) (х — т) — О,
имеющему корни х — 1 и х — т. Исходя из этого, будем искать
приближения для корней уравнения (2.17) в виде
х == х0 4- ехг 4- е2х2 4- ....
(2.18)
2.1. Квадратные уравнения	39
ь мы вновь ограничиваёмся членами порядка е2, и поэтому
ожение (2.18) будем называть разложением второго порядка,
гтавляя (2.18) в (2.17), получаем
(х0 — 1 4- ехг 4- е2х2 + ...) (х0 — т + ехг + е2х2 + ...) =
:	= —е (х0 4- exj + е2х2 + -..),
после перемножения дает
Со — 1) (хо — т) 4~ е(хп — 1) Xi 4-е (х0 — 1)х2 4^ е(*о — t)xi 4-
4- е Xi 4“ ® (*о — т) х2 4- ех0 4- £ xi 4“ "" * == 9"
гдиняя члены с одинаковыми степенями е, имеем
(х0 - 1) (х0 — т) 4- е [(2х0 — 1) х, 4- Хо] 4-
4~е [(2х0 — 1 — т)х2 4” -^1 4- Х11 4" ’   = 0.	(2-19)
и ранее в соответствии с выбранной формой разложения, мы
зияем лишь члены до порядка е2. Приравнивая нулю коэффи-
[ты при последовательных степенях е в соотношении (2.19),
гчаем
(х0 - 1) (х0 - т) - 0,	(2.20)
(2х0 — 1 — т) Xi 4- х0 = 0,	(2.21)
(2х0 — 1 — т) х2 4- Xi 4- Xi = 0,	(2.22)
позволяет последовательно найти значения х0, хх и х2.
Решение уравнения (2.20) дает
— Хо — 1 или х0 ~ т.
I х0 = 1 (2.21) переписывается в виде
(1 — т)х24“ 1 =0, или х2 = — -	.
[ее, из (2.22) находим
...	___ 1	।	1	т
(1—Т)Х2 (|_т)8Т|_г-	(1 — т)2 ’
или х2  -----(П=^Г-
им образом, один из корней можно представить разложением
(2-23)
По = т (2.21) переписывается в виде
(т — l)xi 4~т = 0, или Хд =	>
з соотношения (2.22) имеем
z х v _____ т	т2 ____ т
(т 1]х2—	1—т.	(1 —т)2 —	(1-т)4’
40	Гл. 2. Алгебраические уравнения
ИЛИ
_ т
Х«— (1— т)? •
Тем самым второй корень исходного уравнения дается разложе-
нием ,
Выражения (2.23) и (2.24) показывают, что при т -* 1 получен-
ные разложения перестают быть справедливыми (они оказываются
неравномерными), поскольку в этом случае «поправки» к решению
вырожденного уравнения будут стремиться к бесконечности.
Фактически же для того, чтобы построенные разложения дей-
ствительно оказались непригодными, т ие обязательно должно
строго равняться единице. Дело в том, что эти разложения нару-
шаются всякий раз, когда члены первого и последующих порядков
становятся сравнимыми по величине-с членом нулевого порядка,
так как в этом случае поправки к члену нулевого порядка будут
. уже не малыми, в противоположность предположению, лежащему
в основе описываемого метода. Чтобы определить порядок величин
г — 1, для которых разложения (2.23), (2.24) оказываются не-
пригодными (т. е. найти область их неравномерности), установим
условия, при которых последовательные члены разложения имеют
одинаковый порядок. Так, из формулы (2.23) Следует, что нулевой
и первый члены этого разложения оказываются одного и того же
порядка, когда
’ >j-~==O(l), или 1—т —0(e),
в то время как первый и второй члены будут иметь одинаковый
порядок, когда
Т^==0[“(Г=^р’]’ или 0-т)2^=0(е),
или же
1 — т = 0(в1''2).
Поскольку для малых ее'/2 больше, чем е, то областью неравномер-
ности будет наибольшая нз указанных двух областей, т. е. оиа
будет даваться соотношением 1—т = О (в1/2).
Как отмечалось в гл. 1, неравномерности в разложениях возни-
кают тогда, когда при построении этих разложений необоснованно
используется та или иная элементарная операция. Для того чтобы
выяснить, какая это операция, обратимся к точному решению.
С этой целью перепишем (2.17) в виде
х8 — х — тх + т + ех — О,
или	х8— (1 + Т — в) X + т = 0.
2.1. Квадратные уравнения
41
<орни этого уравнения даются формулой
X + т~ 8±/(l 4-Т — е)а — 4т],
1ЛИ
X = 4- [ 1 + т - 8 ± К(1 -т)а-28(1 + т) + 8а].	(2.25)
(алее, разложи^ (2.25) в случае малых 8 и сравним результат
(2.23) и (2.24). Используя биномиальную формулу, получаем
[(1 _ Т)2 _ 28 (1 + т) + В®]*'2 - (1 - Т) [ 1 - —((\"^Г--]1/2 =
=(1-т)[1-^<;±^^+
, (т)( г) (2е(1 + т)-е*]3 ,	}
2j |_ .
__/1_тчГ1	е0+т) ,	«3	1	4е«(1+т)* ,	1.
т'[	(1—т)» “г	2(1—т)»	8	(1— т)‘	*
(2-26)
$е вновь в соответствии с видом искомого разложения сохранены
Гишь члены порядка е®. Подставляя (2.26) в (2.25), с учетом
Юложительного знака перед радикалом для одного из корней
Получаем
t	.г — 1 Г1 I т	с I 1	e<1+T>	284 I____1
|	х~ 2 [1+Т	6+1	1-т	(1-т)а +	J’
1ЛИ
г	-=1—г^--(Т^-+---’'	(2-27)
| полном соответствии с (2.23). Подставляя (2.26) в (2.25), с учетом
Отрицательного знака перед радикалом для второго корня имеем
Г х=у[1+т-8-1+т+-гХ14--^—---------------J,
1ЛГ -
f	+Т^+1Т^)Г + ----	(“в)
I полном соответствии с (2.24).
? При выводе формул (2.27) и (2.28) из точного решения мы
Оыполиили возведение в степень в (2.26), а также сложение и вычи-
тание в (2.27) и (2.28). Сложение и вычитание являются обычно
ЙЭосиованными операциями, так что «подозрительной! представля-
йся операция возведения в степень. Действительно, при аппрокси-
42	Гл. 2. Алгебраические уравнения
мадии (1 — ы)1/2 разложением вида 1 — и 4-	1/2>~и* + ...
мы неявно предположили, что |и[ < 1. В нашем примере величина
мала по сравнению с единицей, только если f не слишком близко
к единице. В случае же т = 1 и обращается в бесконечность
независимо от того, насколько мало е, лишь бы оно было отличным
от нуля. Поэтому из (2.29) следует, что биномиальное разложение
Становится непригодным, когда и — О (1), или (1—т)2 = О (е),
или же 1 - т = О (е12).
Следовательно, для получения, равномерно пригодного разло-
жения в случае, Когда Г— т = О (е1^), нам необходимо видо-
изменить описанную выше методику с учетом этого обстоятельства.
Это можно осуществить, если ввести так называемый «параметр
расстройки», определяемый соотношением
1 -Т = е1/2Щ	(2.30)
где о не зависит от е. Подставляя (2.30) в (2.17), имеем
(*-1)(х-14-ei/2a)=,—(2,31.)
При е==0 уравнение (2.31) сводится к уравнению (х — I)2 == 0,
имеющему двукратной корень X 1. Этот факт, а также наличие
в уравнении (2.31) множителя е1/2 дают возможность предволо-
жить, что искомое разложение следует искать в виде
1-|_«i/2x14-ex24-....	(2.32)
Мы ограничимся вычислением лишь члена порядка е^2, поскольку
построение высших приближений представляется очевидным.
Подстановка первых двух членов разложения (2.32) в (2.31) дает
, . . (gi/2X1 _|_ ...) (eV2xx -f- е’Ат -|~  •.) — —е (1 + e1/2*i +•••)>
или	, . 
ехх 4- &тхх 4- е 4- '  • — О,
что приводит к уравнению
х?4* ОХ]}-1 ~ 0,
корни которого записываются как
,	Ха = (—ст ±f/ra3 — 4 ).
Таким образом, корни уравнения (2.17) в этом случае даются раз-
ложениями
х— 1 :—н-е1/2(а —	— 4 ) 4* * • • ,
______ (2.33)
х = 1  — — е1/2 (ст 4- iAj2 — 4 ) 4- • • • ,
равномерными при о = 0 или т = 1.
ИА-.!	-*.М' >' '1Л -и111" 1 1 L I'11 1
ДР-	. <	'	’ -у
д	 2.1. Квадратные уравнения 	\ 43	'
К Пример 3.	j
g" В-качестве третьего примера рассмотрим уравнение	 Jj
g	ех2 + х + 1 = 0,	(2.34)
ккотором малый параметр стоит множителем при наибольшей сте-
|ии х. Когда е -> О, уравнение (2.34) вырождается в уравнение
рвого порядка	\
Г	х + 1= 0,	(2.35) v,'Ь
Вйеющее только один корень. Таким образом, величина х претер-
Вйает разрыв при е = 0. Такую задачу принято называть задачей
ингулярнЫх возмушрний.	.	:
Ц Уравнение (2.35) дает возможность предположить, что один из
кр корней следует искать в виде разложения
Б	х = хб• + 8Xi 4- •  •.	(2.36)	*
КЛя упрощения вычислений мы ограничимся нахождением только
Шйенов первого порядка. Подставляя (2.36) в (2.34), имеем
I е (х0 4- 8Xt +• • )2 4- х0 4- 8X1 4---1-1=0,
Би
।	e(xo + 2eXoXi) 4~ Хо 4~ eXi 4~ 1 4~ ’ • — 0,	'
Би же ' .	'||
г	Хо 4~ 1 4~ е (xi + Хо) 4- • • • = о.
Приравнивая коэффициенты при одинаковых степенях е, получаем
вистему	J
I	(хо4-1 = О,	’
»	Xi 4- хо = 0,	-5
к» которой можно последовательно найти х0 и хх. В частности,
Ро — —1 и Xi — —Хо = —1, что дает для одного из корней	>
и	х = —1 — в 4----.	(2.37) Л
у Как и следовало ожидать, описанная выше методика позволяет
^айти только один корень уравнения (2.34). В целях разработки '
Модифицированной процедуры, позволяющей определить второй • 4
Корень этого уравнения, обратимся к его точному решению:
х = -^-(-1±<Г=Г4Г).	(2.38) Д
г	\
Используя биномиальную формулу, получаем
/1-4е =1-2е4-^г^-(—4е)24------------------ 1 — 2е—2е2 + ... .
(2.39)
Гл. 2. Алгебраические уравнения
L
Подставляя (2.39) в (2.38) с положительным знаком перед радика-
лом, имеем для одного из корней уравнения
х — —1 + 1—2в —2в»4-
1
2ё	-----1 — о -г- •••,	(2.40)
в полном соответствий с (2.37). Подставляя (2.39) в (2.38) с отрица1-
тельным знаком перед радикалом, для второго корня исходного
уравнения нахоДим
х==...^1г1±^+2е!, + --	£ + 1+е+... . (2.41)
Таким образом, оба корня описываются разложениями по
степеням е, но одно из них начинается с члена порядка е"1. Не
удивительно поэтому, что выбранная форма искомого разложения
не позволяет найти корень (2.41). Очевидно, что без знания особен-
ностей структуры второго корня оказывается невозможным опре-
делись его с помощью традиционной техники возмущений. Однако
в Общем случае, когда точное решение не известно, характер кор-
ней также заранее не известен и должен определяться в процессе
нахождения решения. Вместе с тем ясно, что при сохранении по-
рядка исходного уравнения второй корень становится неограни-
ченным при в -> 0, ^поэтому старший член.разложения следует
искать в виде
(2.42)

У
.	х-----7
р -	-
с положительным v, определяемым в процессе дальнейшего реше-
ния. Подставляя теперь (2.42) в (2.34), имеем
е1-2'#2 + е~vy 4-1-1--=0.	(2.43)
Далее, выделим в (2.43) члены, играющие определяющую роль.
ДлЯ восстановления структуры второго корня мы должны сохра-
нить первый член ef—2vy2; в противном случае мы будем вынуждены
сразу же остановиться. Так как v > 0, то второй член много
больше 1 и, следовательно, главная часть (2.43) будет
e»-2v^ + e-v^ = 0.	'	(2.44)
При этом степени е в обоих слагаемых соотношения (2.44) должны
быть одинаковы, т. е.
1 — 2v = —V, или v = 1,
для у, отличных от нуля. Затем из (2.44) получаем
у — 0 или у = —1.
/
Значение у — 0 соответствует первому корню (2.37), поскольку
в области О (е-1) он оказывается равным нулю; значение# = —1
соответствует второму корню исходного уравнения. Тем самым из
2.2. Кубические уравнения
45
 -.1
(2,45)
= 0,
и же
1
Я1
1
«
И
2х0
в
.42) следует, что первое приближение для второго корня можно
исать как
х = — ’ — + ... ,
е
. полном соответствии с (2.41). Для определения следующих
енов в разложении для второго корня попытаемся искать его
виде
~г~ + х0 4* •
с
одстановка (2.45) в (2.34) дает
е(---^-4-*о+ •••)2-4- + Л
—2х0 4" х0 4" 1 4" О (е) — 0.
тсюда х0 = 1, и разложение (2.45) приобретает вид .
x=-4- + i + ---,
полном соответствии с (2.41).
С другой стороны, как только величина v определена, можно
ассматривать (2.42) как преобразование переменной х к перемен-
ft у. Тогда, полагая в (2.34) х = у/е, получаем уравнение
/ + У + 8 = 0,	(2.46)
з которого могут быть найдены оба корня, поскольку параметр е
же не входит множителем в член высшего порядка.
2. Кубические уравнения
В этом параграфе мы также рассмотрим три примера. В первом
[римере корни уравнения представляются в виде ряда по целым
степеням малого параметра е, корни второго уравнения выража-
ется в виде ряда по дробным степеням е, а часть корней в третьем
римере включает в себя обратные степени параметра.
Пример 1
Рассмотрим уравнение
х® — (6 + е) № + (11 4- 2е) х — 6 + е2 = 0	(2.47)
попытаемся воспользоваться разложением по целым степеням е
х = ХО + 8Xi + ... .	(2.48)



	' .-\!Л- -у‘- ' 	: S. '•	'"'^- 4	. >	.' -.^~ -	- < ,	' 46	Гл. 2.Алге6раическиеуравнения
/ .'А	Подстановка (2.48) в (2,47) дает (х0 + ехх+--)3.—(6 + е)(х0 + ехх+-)2 +
	+ (И + 2е) (хр + ехх+ • • ) - 6 + е2 = 0, или
	Хр + 3expxi — (6 + е) (хр+2expxi) + ' _ ' -	+(11 4-2e)(XoH-8Xi)-6 4-e24	=0, или же Хо+ 3eXpXi — бхр — 12expXi — ех2 +
А	+ 11хр'+11ехх + 2ех0 - 6 + • • • =0.
	Группируя члены с одинаковыми степенями е, получаем х0 — 6xq 11х0 — 6 -|- 8 (3xoXi — 12xoXj -|-
 ft	+ 1 Ixi — хр + 2хр) + • • • — 0, где в соответствии с видом выбранного разложения сохранены лишь члены порядка е. Приравняв нулю коэффициенты при е° и в1» имеем	‘ Хо^6хо+11хо-6 = О,	(2.49)
Сч’"'*, Гм» . > ’ ^>ч *	•_	Зх^Х!-12хоХ1 +11Х!-Хо + 2х0 = О.	(2.50) Уравнение (2.49) можно представить в виде произведения (хв — 1) (х0 — 2) (х0 — 3) = 0, что дает
	Xq —1)	~Xq -+ 3.	□
	Из (2.50) следует, что	,	'
х'~	(Зхр — 12-tp + 11) Xi =з? Xp — 2х0> откуда xi=(4-2xp)/(3xi-12xo+ll).	-(2-51)
	При х0 = 1 из (2.51) получаем, что хх =	Таким образом,
»’ ' "s	оди+ из корней исходного уравнения дается разложением
	х-1	2 е+--.. При х0 = 2 нз (2.51) получаем, что хх = 0. Следовательно, разло- жение для второго корня можно записать как х = 2 + О-е + ... .
ч	При х0 — 3 из (2.51) получаем, что хх =	Исходя из этого, третий корень представляется в виде разложения х = 3	е + • • •.
2.2. Кубические уравнения	47
аким образом, в данном случае разложения для всех корней
>держат лишь целые степени е.
Пример 2
В качестве Второго примера исследуем уравнение
х® — (4 + е) х2 + (5 — 2е) х — 2 + е2 = 0.	(2.52)
,ак и в предыдущем случае, попытаемся воспользоваться разло-
жением вида
х = х0 + eXi 4* • • •.	(2.53)
[одстановка (2.53) в (2.52) дает
' (х0 + eXi + •••)8 — (4 + е) (х0 + еХ1+---)2 +
+ (5 - 2е) (х0 + exi + • • •) - 2 + е2 = 0
ли
$ — 4xq4- 5х0 — 2 е(ЗХ(£1,— 8xoXi — Хо 4- 5xi — 2х0) 4-=0.
приравнивая нулю коэффициенты при одинаковых степенях 8,
меем
Хо—4хо4-бхо — 2 = 0,	(2.54)
3x^xi — 8XoXi — Хо 4- 5x1 — 2х0 = 0.	(2.55)
Ля того чтобы решить уравнение (2.54), представим его левую
1сть в виде произведения
(х0 — I)2 (х0 — 2) = 0,
•куда получаем
х0 = -1,	х0 — 1, Хд = 2.
ля того чтобы иайти Xi из (2.55), перепишем это уравнение
виде
(Зхо — 8х0 4- 5) Xi = Хо 4- 2х0,
гкуда
<256>
ри х0 = 2 из (2.56) следует, что хх = 8. Таким образом, один из
>рней исходного уравнения может быть представлен как
х = 2 8е 4* • • •.	(2.57)
ри х0 = 1 из (2.56) получаем Xi — оо, что указывает на ошибоч-
сть выбранной формы разложения.
Для построения разложения, пригодного при х0 = 1, заменим
сложение (2.53) на следующее:
, х = 1 4-evXi 4~ е2^ 4~ • • • > v>0	(2.58)
48	Гл. 2. Алгебраические уравнения
и попытаемся найти значение v в ходе вычислений. Подставляя
(2.58) в (2.52), имеем
(1 + 8% 4- 82% + . • -)3 - (4 + е) (1 + 8% + 82% 4 . . .)2 4
4 (^ — 2е) (1 4 8vXj 4 e2vXg 4 * * *) ~=-2 4 * * * ==: О
или
1 4- Зе*Х1 3e2vX2 + 3g2v^2 _ 4 _ 8gvXi _ 8g2vX2 _ 4e2vx2 _ е __
- 28I+vXj 454 5evXi 4 5e2vx2 - 28 - 2eI+vX! - 2 4 • . • = 0,
.откуда
-x?e2v-3e4 ... =0.	(2.59)
Для того чтобы главные члены в (2.59) скомпенсировали друг
друга, 2v должно быть равно 1, или v — и, следовательно,
Xi = ±1^3 г. Тогда из (2.58) получаем, что второй и третий корни
исходного уравнения можно представить как
Х = 1 ± е1/2 /г i 4 ... .
Этот пример иллюстрирует трудности, возникающие в случае
неверного выбора вида исходного разложения. В то же время пра-
вильный выбор разложения позволяет сразу построить соответ-
ствующее решение. Отметим, что подобная ситуация оказывается
типичной для многих задач теории возмущений.
Пример 3
В качестве третьего примера рассмотрим уравнение
ех3 4 х 4 2 4 в == 0,	(2.60)
в котором малый параметр стоит множителем при наибольшей сте-
пени х. В случае е -» 0 уравнение (2.60) переходит в уравнение
х 4 2 — 0;
исходя из этого, положим, что один из корней (2.60) можно пред-
ставить в виде
х ~ хв 4 8хх 4 • • •.	(2.61)
Подстановка (2.61) в (2.60) дает
в (х0 4 ехх 4 • • •)’4 Jfo 4 8xt 4 • • • 4 2 4 е == 0
или
хо 42 4 е (*i 4 хо4 0 4 •• • — 0.
Приравнивая нулю коэффициенты при одинаковых степенях'8,
получаем
х0 4 2 = 0, X] 4 хо 41 ~ О»
2.3. Уравнения высших порядков
49
ркуда х0 = —2 и хх = 7. Таким образом, один из корней дается
азложением х — —2 + 7е + • • •. Прежде чем приступить к иа-
рждению остальных корней, отметим, что при е -> 0 они будут
Тремиться к бесконечности, поскольку е входит множителем
Кчлен наивысшего порядка. Поэтому при выборе разложений для
IX корней примем, что их главные члены имеют вид
х =	v>0.	(2.62)
вставляя (2.62) в уравнение (2.60), получаем
е1-зу^з_|_Е-^_|_2Н-------------------=0-	(2.63)
1я того чтобы определяющие члены в (2.63) скомпенсировали
уг друга, необходимо, чтобы
1 — 3v = —V или v = Ц- и у3 у = О,’
куда	у = 0, у = i, у = —i.
[учай у = 0 соответствует первому корню исходного уравнения
поэтому' здесь не рассматривается.
При построении уточненных приближений для второго и
етьего корней/ воспользуемся приведенной выше информацией
будем искать эти разложения в виде
х ~ "572 4- хо 4- • • • ,	(2.64)
е у = ±t. Подстановка (2.64) в (2.60) дает
е(~572	----) 4--Ь--------------}-24-е = 0
Iй
е~1/2(у34-у)4-3У%4-*в4-24-••• ==0- .
^иравнивая коэффициенты при одинаковых степенях е, имеем
У® + У = 0, Зу*х9 4- х9 4- 2 = 0.
t
тсюда, как и ранее, у = ±1 и
х9 = —2/(Зу2 4- 1) = 1.
аким образом, второй и третий корни уравнения (2.60) пред-
равляются разложениями
Л — ZE 1/2 I -г
С-
,3. Уравнения высших порядков
i В этом параграфе рассмотрим уравнения высших порядков,
делив особое внимание случаю, когда малый параметр стоит
Сожителем при наибольшей степени неизвестной. В частности,
сследуем уравнение
ex'1 = хт 4- am_iXm-1 4- ат-гХ"1-2 4-агх 4- а0)	(2.65)
50	Гл. 2. Алгебраические уравнения
где коэффициенты аа не зависят от е и х, п и т — целые числа и
ri > т. При е -> 0 уравнение (2.65) сводится к уравнению
хт± ат^хт~1 + ат_2хт~2 -|-------Н + а0 = 0,	(2.66)
имеющему корни аа, где 8=1, 2, ..., т. Для уточнения этих
корней положим
х = х0 + eXi 4- •••;	(2.67)
подставляя в (2.65), имеем
"8 (*0 4" 8X1 4* •  •)" — (х0 4* 8X1 + • • •/" + аот-1 (Хо 4” 8X1 4* • • -У1-1 4*
,	4- ^m-a (*0 4- 8X1 4- • • • У1-2 4- • • • 4- Я1 (х0 4- eXi 4- • • •) 4* ао
или
Xq1 4- ат^}Х^ 1 4~ От—2*0* 2 4~ • • • 4* “1*о 4~ °о 4~
4* 8 [тх0 4- (т — 1) am-t^o 2 4*
4- (т — 2) От—2^0 3 4- ' ' ' 4- а1 I X’l — 8Хо 4- О (в2) = 0.
Приравнивая коэффициенты при одийаковых степенях е, получаем
4 4- ат—4" 6lm—2^S -[-••• 4- Ц1Хо 4- CIq = 0,	(2.68)
[«4 4- (/и — 1) ат_14 4- (tn — 2) flm—г4 4~ * ’ * 4* ] xi — xb'*
(2.69)
Уравнение (2.68) совпадает с (2.66) и, следовательно, имеет те же
самые корни х0 = а„ где s = 1, 2, 3, ..., tn. Тогда из (2.69) сле-
дует, что
Х1 = №s [ffltts 4- (tn— l)flm_t<4 4- • • • 4-Д1]
Таким образом,
x = as 4- 8<zs [ma, 4- (tn — 1) am_i<xs 4~  •  4~ ®i 1 4~ ’ *  •
(2.70)
Следует отметить, что разложение (2.70) становится непригодным
всякий раз, когда член в квадратных скобках стремится к нулю.
Это соответствует случаю кратного корня уравнения (2.68).
При этом разложение должно включать в себя дробные степени е
и строится в соответствии с методикой, используемой в примере 2
предыдущего параграфа.
Прежде чем приступить к. определению оставшихся п — т кор-
ней, заметим, что они стремятся к бесконечности при е -> 0,
поскольку малый параметр е стоит множителем при наибольшей
степени неизвестной х. Поэтому разложения для них будем искать
в виде
х=-^-4-*о4- >	v>°-	(2-71)
2.4. Трансцендентные уравнении
51
Подставляя (2.71) в (2.65), имеем
е / у"	I	|______\	__ У"	 пиГ-'хд
1 gnv	'	g(zi—1) v	Т	I gnrv	Г g(m—1) v
L	4-	1 I —	2x0
g(m—1) v Г	g(m—2) V
[Выделяя главные члены, получаем
I	&(l-nv)yn — g—mvym
(2.72)
и, следовательно,
;	1 — nv = —mv, так что v —-----------,
Уп = ym.
1
(2.73)
(2-74)
|Для уравнения (2.74) нуль является корнем кратности т\ кроме
froro,
уп—т — ] — g2nir
[где r = 1, 2, ..., (n — tn). Отсюда
У = co, co2, • • •,	- ю — exp n — m ) ‘	(2.75)
[Корень у = 0 мы отбрасываем, так как он соответствует первым
Is корням.
[ Используя (2.73) и (2.74), перепишем. (2.72) в виде
пуп-'хуеУ = my”-1xoev am_ic/m-1ev + • • • .
Сравнение коэффициентов при ev в обеих частях этого равенства
дает
[	пуп-1х0 = тут-1х0-\-ап_1ут-1,
[откуда
;	х — —= —-g"*zi— = _gm=l_.	(2.76)
0 пуП-l _ myn-i пуП-М-т n — m	v ’
[Таким образом, оставшиеся п — т корней даются разложениями
I х = — 4-.	+ • • •,	г=1, 2,..., п — т, (2.77)
1где v и со определяются формулами (2.73) и (2.75).
12.4. Трансцендентные уравнения
I Рассмотрим теперь нули функции Бесселя Jo (х) при боль-
ыпих х, т. е. исследуем корни трансцендентного уравнения
I	Jo (х) = О
ири х -> оо. В гл. 13 будет построено разложение для Jo (х)
ртри х -> оо. Из формулы (13.141) следует, что
|к(*)~ [mcos(x - -£-) +vsin (х - -J-)] При Х-+СО,
I	(2.78)
52 .	Гл. 2. Алгебраические уравнения
где и и о в соответствии с (13.129) и (13.130) даются разложениями
1 ~	• * ’ »	(2-79)
(2-8°)
Полагая в (2.78) Jo (х) = 0, имеем
ИСОЗ^Х---= — О sin (х — -2-) •
или
ctg(v(2.81)
Из разложений (2.79) и (2.80), с использованием биномиальной
формулы, следует, что
_g-_ Л-1	75 । Wi ........? Г- • -Г1-
« “ \ 8х 1024ха	128х«	~
Г 1	75	,	\/.,__9__,	1 _ 33 ,
\.8х	Ю24х» “Г ’ * ’ 'Г 128х»~|	/ ~~ 8х 512ха	’
(2.82)
Подставляя (2.82) в (2.81), находим, что при больших значениях
аргумента нулй функций Jo (х) описываются уравнением
с‘8(л:-т)=-^-+т1Вп + --- •	(2.83)
Так как х велико, в первом приближении правой частью урав-
нения (2.83) можно пренебречь, что дает в рёзультате
/ ЧЕЙ ч
ctg^-^-O.
Откуда
х —y = (п + -|") я или; х. — (° + 4") п> (2-84)
где п — целое число, которое должно быть достаточно большим
для того, чтобы х было велико. Однако, как показано ниже, даже
при п — 0 мы имеем удивительно хороший результат.
Для уточнения полученных приближенных значений х поло-
жим теперь
х—= (п 4- 4") я или х= (п 4- -|“) я + 8 (2.85)
и, подставив в (2.83), получим
ctg [(« + -у)я + в] — 2л(4п + 3) + 86 +
’	+ [2л (4л -ь 3) -ь 86]а *	‘ 	(2.86)
2.4. Трансцендентные уравнения
53
использовавшись известными тригонометрическими формулами,
фепишем левую часть (2.86) как
Г/	т ctg (п +4"') «-ctg6 —1
“-«к=-*«в*-(в+тв1+-)-
)гда (2.86) приобретает вид
4 T 63 2л (4л 4-3) 4-86	[2л (4л 4- 3) 4- 86J3 + ’ ’ ' ’ (2-87)
>ичем это соотношение можно рассматривать как алгебраическое
>авнение относительно 6.
i Выберем в качестве малого параметра е = [2л (4га + 3) ]-1
перепишем (2.87) в циде
е I '1 в8  в	ЗЗв3 .
° -г з ° — 1 + 8еб (1 4-8еб)’ т- " *
1И
б-|__1-68 = е(1 — 8еб) — ЗЗе8-]--.
алее, воспользуемся следующим разложением для 6г
6 = e6i + ва62 + в868 + • • • •
одставляя (2.89) в (2.88), мы имеем
Вб1 + е262 + е363 + • ” + -4 ®38i = е - 8е3б! - ЗЗе3 Н-,
О
е сохранены лишь члены до порядка в8. Приравнивая коэффи-
[енты
(2.88)
(2.89)
куда
при одинаковых степенях е, получаем
= 6а==0 и 6з + 4-5? = -851 - 33,
_ о
68 = —41	Следовательно,
О
х = (п + л + е — 414-в8 + • ••»
1И

Х~ («+ 4)"+ 2л (4л 4-3)	6л»(4п+3)« +*••• (2>9°)
Сравнение приближенных значений нулей функции Бесселя
(х), подсчитанных по формуле (2.90), с точными значениями
едставлено в табл. 2.1. Соответствие оказывается весьма хо-
тим даже для первого корня, точное значение которого равно
40482 • • •, т. е. аргумент* при этом не очень велик. Приближен-
»е же значение при этом отличается от точного лишь в четвертой
54	Гл. 2. Алгебраические уравнения
Таблица 2.1
Сравнение приближенных и точных значений нулей функции Бесселя Je (*)
Порядковый
номер	1	2	3	4	S	6	7	-
нуля п
. Метод	2.40308 5.52004 8.65372 11.79153 14.93092 18.07106 21.21164
возмущений
Точное 2.40482 5.52008 8.65373 И Л9153 14.93092 18.07106 21.21164
значение	;		'
—— ............ - -
-..Л '.	.	\	.	_
значащей цифре, а относительная ошибка составляет примерно
0,07 %. По мере увеличения порядкового номера нуля п точность
увеличивается; для п — 4 значение, полученное по методу воз-
мущений, совпадает с точным табличным значением вплоть до
седьмой значащей цифры.
; Упражнения
. 2.1. Определить два члена разложения для каждого иорни следующих
уравнений при малых в:
а) х3 — (2 + в) х3 — (1 — е) х + 2 + Зе = 0,
б) х3 — (S-f'в) х — 2+в = 0, ;
в) х* + (3.— 2е) х3 + (3 + в) х + 1 — 2е = 0,
г) х* + (2 — Зе) х3 — (2 — е) х — 1 + 4е = 0,
. д) х4 * б) * + (4 — в) х3 4- (6 + 2е) х2 + (4 + е) х + 1 — в* = 0.	, .
2.2. Определить два члена разложения для каждого корня следующих
уравнений при малых е:
а)е (а3 + а3) + 4а2 — За — 1 = 0,
б) ей8 + и — 2=0,
в) ва3 + (а — 2)3 = 0,
г) ц3 — а — 2 + -i- в (а8 + 2а + 3) = 0,
А	' —	_
д)ва4 + а® — 2и2 — а + 2 = 0,
е) ей4 — а3 + За — 2 — 0,
ж) во4 — а2 + За — 2 = 0,
з) ва4 + а3 — За + 2 = 0,	;
и) 8а* — u3 + 2а — 1 — 0,
к) ei? + & — 2u + 1 = О,
л) в (а* +«*) — «*+ За — 2 = О,
м) в (а* + «* — 2а3) + 2а3 — За + 1 = О,
н) в (а4 + и4 — 2t?) — 4м2 + 4а — 1= 0,
о) в2ц® — еа4 — г? + 2а? + и — 2 = 0.
2.4. Трансцендентные уравнения
55
2.3. Найти двучленные разложения для решений следующих уравнений
и малых е:
.	8
a>s—3^
б) 1	®
^-=0,
Юз* .	’
____2!4=0.
3/s	5/s
2.4.	Найти двучленные разложения для корней следующих трансцендентных
авнений при больших значениях аргумента:
а) х tgx = 1,
б) х ctg х = 1.
2.5.	Дифференцируя (2.78) и используя (2.79) и (2.80), показать, что боль-
ie нули функции Jg (х) являются решениями уравнения
«(-т-)=-т+--
казать также, что
х^(п + 4-)"~ 2л(4Т+-1) + ••••
авнить полученный результат с точными табличными значениями для первых
ии нулей.
2.6.	Асимптотическое разложение функции Неймана нулевого порядка
:еет вид
оо.
»'«<«>- V"I»1 «
оказать, что нули Yo (х) даются формулой
Г= (л +-L) л + 2л(4^ + 1) + ••• •
авнить этот результат с точными табличными значениями для первых семи
лей.
2.7.	Используя асимптотическое разложение Yg (х) из предыдущего упраж-
няя, показать, что корни уравнения Yg (х) = 0 даются формулой
я--------3------ + ... .
2л(4« + 3)
>авнить этот результат с точными табличными значениями для первых семи
рней.
2.8.	Асимптотическое разложение функции Бесселя Jv(x) имеет вид
vn л \ 4va — 1 . I „ vn л \ ]
*~“2 —у	—-sm^x	2	4
при х -* оо.
а) Показать, что корни уравнения Jv (х) = 0 даются формулой
/ . 3 . v \	4v2 —1
х =
(*)
я — .	4- • • • .
2л (4л 4- 3 + 2v)
б) Показать, что корни уравнения (х) = 0 даются формулой
3 + 4v*
" 2л (4л + 1 + 2v) + ' ’ • •
X =
X
56
Гл. 2. Алгебраические уравнения
в)	Сравнить эти результаты с полученными в упр. 2.5 и в п. 2.4 при v .= 0.
г)	Сравнить эти результаты с точными табличными значенннмн для первых
семи корней при v = 1.
2.9.	Асимптотическое разложение функции Неймана Уv (ж) имеет вад
,, . ,	1/ 2 Г , / vn я \ . 4v*-l	/ уя л \ 1
r*(x)~ V ЯЖ [sto(* 2	4 ) + 8ж cos (*	§	”4~) J
при ж -» оо.
а)	Показать, что корни уравнения Уч (х) = 0 даются формулой
/ . 1 v \	4№— 1
х-(^п + —+ -г)л Щ4„ + 1+2у) +••••
Сравнить этот результат с результатом, полученным длн Ув (ж) в упр. 2.6.
б)	Показать, что корни уравнения У' (х) — 0 даются формулой
„	3 j. * \	'	3+4у»
\ + 4 + 2 )	2n(4n + 3 + 2v) +	‘
Сравнить этот результат с результатом, полученным дли У^х) в упр. 2.7.
в)	Сравнить эти результаты с точными табличными значениями для первых
семи корней при v = 1.
Глава 3
ИНТЕГРАЛЫ
Как известно, решения многих дифференциальных и разност-
ных уравнений не выражаются в элементарных функциях, но
Смогут быть представлены в виде определенных интегралов. Среди
^многочисленных методов, используемых для получения интеграль-
ных представлений решений дифференциальных уравнений, основ-
ное место занимают преобразования Лапласа и Фурье. Прежде
чем приступить к описанию приближённых методов оценки ин-
тегралов, покажем на примере, как можно получить в интеграль-
ной форме решение простого дифференциального уравнения,
другие примерьитого же рода приведены в § 13.5 и в упражне-
ниях 13.17 и 13.18.	>
 Будем искать общее решение следующего линейного дифферен-
циального уравнения первого порядка:
У' + У=±- .	(3-1)
Умножая обе части уравнения (3.1) на интегрирующий множитель
ехр (х), получаем соотношение
!	у’е* +	=	(3.2)
Которое может быть переписано как
:	'	1-^=4-	<з-з>
- >
Интегрируя уравнение (3.3), находим
7 е’
=	^4-с,	(3.4)
X,
Где т — переменная интегрирования, х0 — произвольно выбран-
ный нижний предел и с — произвольная постоянная. Подчиним
наше решение начальному условию у (1) = а. Это условие опреде-
58	Гл. 3. Интегралы
Подставляя выражение для с в (3.4), получаем
уех —	j-L-dr — ae-\-
x0	x0	1
Таким образом, имеем
у = ael~x + е~х J ~~ dr.	(3.5)
i
Данная глава посвящена методам приближенной оценки ин-
тегралов типа (3.5), являющихся решениями обыкновенных диф-
ференциальных уравнений и не выражающихся в элементарных
функциях.Мы рассмотрим такие методы, как разложение подынте-
гральной функции, интегрирование по частям,’’метод^Лапласа,
метод стационарной фазы и метод скорейшего спуска. Все эти
методы будут продемонстрированы на специальных примерах.
3.1. Разложение подынтегральной функции
В этом параграфе рассмотрим четыре примера.
Пример 1 _
Оценим величину интеграла
1
1 (е) — j sin ex2 dx	(3.6)
о
при малых e. Разложение подынтегральной функции в ряд Тей-
лора дает
мп^-= S (~'£-- 4-+w
П=1
(3.7)
Применяя к полученному ряду (3.7) признак Даламбера, имеем
Um у*. = нт (-1)n+1(e?)2,,;7-g~5L=
п-00 (л-О-й член п^х (2л — 1) I (—1)" (ах2)2'’-3
= I™ (2л-1) (2л- 2) = °'
Следовательно, ряд (3.7) сходится при любых значениях ех2.
Поскольку | х | < 1, а е мало, то остаточный член в формуле
. (3.7) есть величина порядка е7 для всех значений х из про-
3.1. Разложение подынтегральной функции
59
жутка интегрирования. Подставляя теперь ряд (3.7) в исход-
ш интеграл (3.6) и интегрируя почленно, получаем
n=I	О
S( —l)'l+1«2"-1	1	1 . ,	1 К , П/7Ч	/О 04
(2л — 1)1 (4n — 1) ~.3 6	42 6 + 1320 6 + ° (е )•	4 (3-8)
П=1
Пример 2
В качестве второго примера рассмотрим полный эллиптический
интеграл первого рода
/("l)— f J<1 _msinae	<3-9)
’ 0
[ри малых т.
Используя биномиальную формулу, можно записать
!	•.	( 4-)(-4)
(1 - msln>e)-'« = 1 +-l-mslnie + > -З— (-т>1п«е)Ч-
i + 3—123—LZ3——LL (_т sln2 0)4 + о (т5). (3.10)
Применение признака Даламбера дает
Л™ (п— 1)-й член “	-
_. (-I) (-4) (-1)  • • (-i— г>1	1=
; "’-(-|)(-1)(-4)...(-а4±)<”-->и-^ег ”
Г	11 ш 3) Sina0 ___	, 2 А
г	= lim —5—а ;	---= tn sin* и.
f 	п^оо 2(п-,1)
Гаким образом, ряд (3.10) сходится при всех значениях 0, для
которых т sin2 0 < 1. Поскольку Sin2 0 с 1, а параметр т
[самого начала предполагается малым, то остаточный член в фор-
муле (3.10) представляет собой величину порядка /и5 для любых
Значений 0.
60	— Гл. 3. Интегралы
-	Таблица3.1
Зависимость отношения Ijle от величины параметра т
т	0	0.2	0.4	0.5	0.6	0.7	0.8
- 1ане	1	1.0000	0.99917	0.99720	0.99216	0.98043	0.95382
Подставляя ряд (3.10) в формулу (3.9) и интегрируя почленно,
получаем '
Л/2	л/2	Л/2
\Jjjri) — j dO 4*4’m J sin2 0d0 +w2 j sln40d0 -|-
0	/2 O’	/2	°
+'-^-/n8 j sln’OdO+-g- j sin80dO + 0 (m5)- (3.11)
0	0	h
Воспользовавшись	формулой
:	л/2
.	j *1°"ед=	,	(3;i2)
можно	переписать	разложение	(3.9) в виде
ям=-т[1 +-rm +4-m'+im,+-rS<-"‘‘+o(m‘)].
(3.13)
В табл. 3.1 представлена зависимость от параметра т величины
отношения 1а11„ где 1а — приближенное значение - интеграла,
подсчитанное по формуле (3.13), а 1е — точное значение интеграла
I (/и), взятое из книги Абрамовица и Стигана (1979, с. 608). При
т -* 0 отношение IJIe стремится к единице. Так, при т < 0,5
относительная погрешность, возникающая при замене интеграла
, 1е приближенным выражением 1а, составляет менее 0,28 %;
при т = 0,7 эта ошибка не будет превышать 2 %. Таким образом,
разложение (3.13). является хорошим приближением к Ге; при
небольших значениях т.	\ '
Пример 3
В качестве третьего примера рассмотрим интеграл
Z (х) =	(3.14)
о
при малых х. Разложим экспоненту, входящую в по дынтеграль-
ное выражение, в ряд Тейлора
ОО .	-
S=1 - *+ 472 -4-/3 + -+ °(ЗЛ5>
П=0
3.1. Разложение подынтегральной функции	61
^Используя признак Даламбера, имеем
р lim —п'й ч;е; н = lim (-1)П<Пп(п~1)11 =lim^-=0 (3.16)
;для любых t. Следовательно, ряд (3.15) сходится при верх зна-
чениях t. Кроме того, если считать t малым, порядок ошибки в раз-
ложении (3.15) будет равномерным по t.
b Подставляя теперь ряд (3.15) в интеграл (3.14) и интегрируя
«почленно, получаем
л=0	0	жан п • (п + “Т*)
п=0 X * /
;	=4*1/4 __|_х5/4+_2_^/4 __^_х13/4 + О(Х17/4).	(3.17)
г Пример 4
5 В качестве последнего примера исследуем так называемый
Интеграл ошибок "
7(*) = ]е-1‘<Й	(3.18)
X	_
при малых х. Разлагая подынтегральную функцию в ряд Тейлора,
получаем ряд следующего вида:
е~“=Ё	<3-19’
л=0
который, как показано в предыдущем примере, сходится при лю-
бых значениях t. Заметим, однако, что функцию ехр (—/2) на
всей числовой оси нельзя представить с помощью конечного числа
членов ряда (3.19) (см. рис. 5.2). С другой стороны, разложение
(3.19) является асимптотическим при /-> 0, поскольку
w-i „„
=X +0	<3-20)
п=0
Поэтому интеграл (3.18) удобнее представить в следующей форме:
/(*)=. Je-t'dt-$e-fdi.	(3.21)
о	о
Для того чтобы вычислить первый из этих интегралов, заметим,
'что
Е '	/1== j)e-“,du= J e~v‘dv. ,	(3.22)
62
Гл. 3. Интегралы
Следовательно,
7? = Н е~и* duj J e~vt du = J J e~ du du. (3.23)
\0	/ \o Joo
Перейдем в последнем интеграле от декартовых координат и
й v к полярным г и 0. При этом элемент площади преобразуется
по формуле
ds = du dv = г dr dQ,	(3.24)
причем г будет меняться от нуля до бесконечности, а 0 — от
нуля до —. Таким образом, интеграл (3.23) преобразуется к виду
У? == J j re~r‘ dr dQ — I j dQ j I j re~r* dr j =
oo	\ о / 'o /
1	/	1 гЛ I00	1
.	)о=-Я>
откуда
Уп
~ ~~2~
(3.25)
о
Подставляя теперь ряд (3.19) во второе слагаемое в формуле (3.21),
интегрируя почленно и используя формулу (3.25), получаем
п=0
2(~l)nxlгn+, _ Уп~
n!(2n+ 1) ~	2
о
1
3	10 х8+ 42	(**)•
(3.26)
3.2. Интегрирование по частям
Проиллюстрируем данный подход также с помощью несколь-
ких примеров. При этом последний из них позволит выявить огра-
ничения метода интегрирования по частям и подведет нас к идее
метода Лапласа и метода стационарной фазы.
Пример 1
В качестве первого примера исследуем неполную гамма-
функцию, которая определяется интегралом вида
I(x) = \-^dt
X
при больших . значениях х.
(3.27)
1«,. Ч» I .И.»	--R,    ----------------—,	_ ‘'	-С" 4
3.2. Интегрирование no частям	63
| Метод интегрирования по частям основан, как известно, на
использовании тождества
I	d (uv) = и dv + v du,	(3.28}
^или	и dv = d (uv) — v du.	(3.29)
рели и и v являются функциями переменной t, то интегрирование
|обеих частей равенства (3.29) в пределах от до t2 дает
F	**	/* *•
|	j udv = uv — J vdu.	(3.30)
| Для того чтобы-иметь возможность воспользоваться формулой
1(3.30), нужно представить подынтегральное выражение в (3.27)
|в форме и dv, т. е. положив
I	- е~‘
|	—^~dt = udv.	(3.31)
ВОбычно разбиение на множители и и dv осуществляется таким
образом, чтобы выражение для dv можно было проинтегрировать.
ЕКроме того, и и dv следует выбирать так, чтобы последовательные
[члены разложения интеграла 7 (х), получающиеся при интегриро-
Йвании по частям, являлись бы величинами все более высокого
{порядка по малому параметру х-1. Для того чтобы проиллюстри-
ровать оба указанных требования, рассмотрим два варианта.
{Сначала положим
I	и = е-;,	(3.32)
[Тогда
I	du ——е~* dt,	v =----f-.	(3.33)
|Подстановка -выражений (3.32) и (3.33) в формулу (3.30) дает
К	'	ОО	ОО	,	00	,
r-r-fv*
!' * * х х
шли
J-L±dt = -^-J-^dt.	(3.34)
X	X
|Продолжая этот процесс, .положим
Б	ы = dv = -~.	(3.35)
Когда
к	du = —e-f dt, v = In t	(3.36)
К J ~.dt =	= Г + \e-t\ntdt. (3.37)
К	x	x	x X
64.	Гл. 3. Интегралы
. Поскольку в соответствии с правилом Лопиталя имеем
lime-* In t ~ lim = lim—~=0,
/•"►co}	/-*•«> С	/—>-ОО tv
то соотношение (3.37) принимает вид
J di ~ — е~х In х 4- j e-^ntdt.	(3.38)
X J	X
Подстановка этого соотношения в формулу (3.34) дает
7 е~* е~х	7	'
j —	— -|-e-*lnx - j e~‘In tdt. '	(3.39)
x	-	X
Отметим, что второе слагаемое в правой части (3.39) оказывается
существенно больше первого при х <х>. Таким образом, исполь-
зование выражений (3.32) и (3.35) не позволяет получить асимпто-
тическое разложение интеграла / (х) при л -* оо \
В качестве второго варианта выберем
u=-2-, dv — e^dt.	(3.40)
Тогда
'	du = — ^-dt,	v^—e-*.	'	(3.41)
Подстановка выражений (3.40) и (3.41) в формулу (3.30) дает
X	X	X	'
. или
\-^-dt = ^-2\-^-dt.	(3.42)
х	х
Продолжая, процесс интегрирования по частям, положим
dv — e^dt,	(3.43)
откуда
du = --^-dt, и —	(3.44)
Таким образом, имеем
X	X
1 Продолжая этот процесс интегрирования по частям, можно построить
(сходящееся) асимптотическое разложение интеграла / (х) 'при х->0. —Прим,
перев.
3.2. Интегрирование по частям
65
[ЛИ

(3.45)
(3.46)
одстановка соотношения (3.45) в формулу (3.42) дает
X -	X
| Продолжая'процесс интегрирования по частям и полагая на
каждом шаге dt = dv, находим
X
21 е
х»
31 е х 41 е~
х4	х?
!	+-bl>12i^ + (-l)"(„ + l)lj^2.d(.	(3.47)
I	'	X
^Поскольку при х < t < оо имеет место неравенство ("+2	хп+2,
1
______ 1
^”("2 "ч"’ ХП~^2
^Интегрируя полученное неравенство, имеем
е *
хп+2
? .	[	I [
J (п+2	дЛ+2 J
• * *
рГаким образом, формулу (3.47) можно представить в виде разло-
жения
N
СТ (—I)"-1 «1
J__
дЛ-Н -j- е "V ж#+2
которое по определению является асимптотическим. Отметим,
ито ряд (3.48) расходится-, поскольку
______________„	_____________== lim ——^-=г—ОО.
(m— 1)-й член_(—l)m~2(«—«-« х
Однако при фиксированном N остаточный член в разложении
|$.48) может быть сделан сколь угодно малым за счет выбора до-
статочно большого х.
Пример 2
В качестве второго примера рассмотрим интегра л вида
О
(3.48)
п=1
Ито ряд (3.48) расходится-,
^{га_hm
т-^со

(3.49)
3 Найфэ А. X.
66
Гл. 3. Интегралы
при больших положительных х. Как и в предыдущем примере,
разбиение на множители
и = е~*, dv = (х + tyi dt
не приводит к асимптотическому разложению при х -* оо.
Поэтому положим
и = (х + t)-1, dv = e-t dt,	(3.50)
откуда du = —(x + fy2 dt, v = —e~*.	(3.51)
Подстановка выражений (3.50) и (3.51) в формулу (3.30) дает
оо .	,	оо
Г р	p~~~t	1°° f р t
7 (х)= f x + t — ~ Т+Т о ~ I (X + di’
. '	0	.0
или
со
<3-52»
. - 0
Продолжая процесс интегрирования по частям, положим
и = (х + О'2. dv = е-1 dt, . '	(3.53)
откуда du — —2 (х + ty3dt, v = — еч.	(3.54)
Подставляя .выражения (3.53) и (3.54) в (3.30J, имеем
Г (х + О2 dt==~ (х + /)2 J - Г (х + о3 dt = I2' ~ 2 J (х И)3 dt'
О'	0	0	о
(3.55)
При этом" формула (3.52) принимает вид
со
'«=4-4-+2J	(’•“)
о
Повторяя процедуру интегрирования по частям п раз, мы при-
ходим к разложению
Пх}~ 1	1 д- 21 - 3! + • • ।
Нх)~ —	--р-Н Н------------—п--------+
-	+(-*)"»! J	(3-57)
Q (Х "Г О
Для оценки остаточного члена в (3.57) воспользуемся следующим
неравенством, справедливым при положительных х и t:
1 1
(х + 0”+1	х^-Ь*
1. m-й член
—1)-нчлен
Ц->-ао \	/
	3.2. Интегрирование no частям.	67	t
. . , < ~ ,
.Интегрируя это неравенство, получаем	_« I
I	J (X 4- on+1 dt <	dt =
ВТаким образом,
' 'W-S (~y7~1)l +o(-^r).
|?z	71=1 -	'	'
Ги, следовательно, разложение (3.57) является асимптотическим
I при х -* оо. Отметим, что ряд (3.58) расходится, поскольку
1в соответствии с признаком Даламбера
= Пщ (-О"1-1 (т-1)1 Xго-1 =
хт(~ 1)т-2(т- 2)!	J
rd^L^-oo.	V
_	Y
К"	7П-+СО
в Однако при фиксированном N остаточный член этого ряда может 'ч
 стать сколь угодно малым при достаточно большом х.	J.
к Пример 3	’
К В качестве третьего примера рассмотрим преобразование Лап- . л
 ласа от функции f (/), т. е. интеграл вида	-i
		оо	.
К.	7(х)= J e~xtf{t)dt.	(3.59) f
	0	'."S
К Построим асимптотическую оценку этого интеграла при больших
В положительных х в предположении, что функция f (0 является	?
 аналитической (т. е. на рассматриваемом интервале она обладает	f
№ производными любого порядка) и что исходный интеграл суще-
К ствует. Заметим, что интегралы типа (3.59) возникают при реше- ч
К нии дифференциальных уравнений с помощью преобразования
К - Лапласа.
I Положим	-!
I	и = f (/), dv = e~xt dt,	(3.60)
г так что	-
I	du~f{f)dt,	v =—~Y~'	(3.61)	|
I Если бы мы выбрали разбиение на множители вида и = ехр (—xt),	:
| dv = f (t) dt, то получили бы, что возникающее разложение не	]
г является асимптотическим при х -> оо. Подстановка выражений
I (3.60) и (3.61) в формулу (3.30) дает •	j
£	ОО	ОО	.	5
К	Г	Д—xt	|°° I Г	’"<
г	[ ^/(0^---^—/(о
Е'	*	1П'	*
I	0	- '	0-
! з*	,j
„:,Г
68	, Гл. 3. Интегралы
ИЛИ
Z(x) = -^1 + 2_J e-~xtf'(t)dt.	(3.62)
А>	Д, J	t	-
О
Продолжая процесс интегрирования по частям, положим в ин-
теграле в правой части (3.62)
u =	, dv — e~xt dt,	(3.63)
откуда
p—xi
du — f(t)dt,	(3.64)
Подставляя выражения (3.63) и (3.64) в формулу (3.30), а полу-
ченный результат в формулу (3.62), находим
1 w “ f W С + I
ИЛИ	'
со
/(х)==_Ш-4._т.+ _^.| e~xr(t)dt. (3.65)
о
Продолжая процесс интегрирования по частям, имеем
НН	^(°) । ПО)  ПО) . Г(0) 	. fw(V ,
' х № Т & “Г X* "Г." • ~Г ^.«+1 -г
оо
+	^n^(t}dt. (3.66)
х Q
Следовательно,
- N'	, ,
/W = S-V^ + o(7Sw) <367)
п=0	'	*
и разложение (3.67) является асимптотическим при х -*• оо. .
Пример 4
С помощью аналогичного процесса можно получить асимпто-
тическое разложение интеграла Фурье
7(а)= 1^f{t)dt	(3.68)
о
прн больших положительных а для случая, когда f (0 — беско-
нечно дифференцируемая функция от t. Интегралы такого типа
г возникают при решения дифференциальных уравнения с помощью
преобразования Фурье.
3.2. Интегрирование по частям
69
Пусть функция f (0 достаточно быстро стремится к нулю при
t -* оо, так что интеграл (3.68) существует 1 . Для того чтобы
проинтегрировать (3.68) по частям, положим
и — f (/), dv — eiatdt,	s (3.69)
откуда
/а/
du = f'(t)di, « = -V-	(3-70)
Подстановка выражений (3.69) и (3.70) в формулу (3.30) дает
j eiatf (0 dt = f (/) j” - 4- j e™f (0 di,
о	0 о
или
1 («)=- - 4- f eiatr &dt- <3-71>
-o



Продолжая процесс интегрирования по частям (а именно, инте-
грируя eiat и последовательно дифференцируя f (t)), как и в
предыдущем примере, получаем
	l о (_5—
(—ta)"+*__________\ aw+2
(3.72)
Разложение (3.72) является асимптотическим при a -* оо.
Пример 5
В качестве последнего примера рассмотрим обобщенный ин-
теграл Лапласа
6
I (х) = J е*л Wf (t) di, b> а,
a
(3.73)
при больших положительных х для случая, когда h (0 и f (t) —
дифференцируемые функции аргумента t. Для того чтобы проин-
тегрировать (3.73) по частям, необходимо представить подынте-
гральное выражение в виде udv. В данном случае мы не можем
положить
» = /(/), dv — exh <<> dt,	(3.74)
поскольку последнее выражение не интегрируется в общем виде
через известные функции. Чтобы получить интегрируемое выра-
жение, преобразуем формулы (3.74) следующим образом:
dv ^e^h' (t)dt.	(3,75)
л (0
1 При этом производные функции f (0 также должны затухать при I—> оо,
с тем чтобы существовали соответствующие интегралы, возникающие в резуль-
тате последовательного интегрирования по частям. — Прим, перев.
70
Гл. 3. Интегралы
При этом
du= [-///L ] и = ——— *	(3.76)
[ h (0 J	х
Подстановка выражений (3.75) и (3.76) в формулу (3.30) дает
ь	ь
f	<о f (/) dt = —<О/..(0 Г - -L f (О Г-Ш-1'd/,
J ' ’ xh (о |а X J L Л (О J
а	а
ИЛИ
1	xh' (b) xh' (a) X J e
a
(3.77)
Оценивая интегральный член в правой части соотношения (3.77),
находим, что
.. .	exh (b)	exh <a7 (a) w
v ’ xh (b)	xh (a) r
(3.78)
Формулы (3.77) и (3.78) получены в предположении, Что функции
f (f) и h (t) дифференцируемы и h'(t) =/= 0 на промежутке [а, &].
Если же какая-либо из точек этого промежутка оказывается для
функции h (t) стационарной (т. е.- в этой точке h' (t) == 0), то
интегрирование по частям становится незаконным и интеграл
в правой части (3.77) будет расходящимся. При h' (t) =/= 0 формула
(3.78) показывает, что основной вклад в величину интеграла
дают лишь ближайшие окрестности концевых точек промежутка
интегрирования. Более того, если h (a) #= h (b), то асимптотиче-
ское поведение нашего интеграла определяется окрестностью
только той концевой точки, в которой значение функции h (t)
больше. Это обстоятельство позволяет предположить, что основ-
ной вклад в асимптотическое разложение интеграла (3.73) дает
окрестность точки t = с £ (а, &], соответствующей наибольшему
значению h (t), независимо от того, является ли точка t = с
внутренней или граничной точкой промежутка интегрирования.
В этом, собственно, и заключается центральная идея метода
Лапласа. Если функция h (t) достигает наибольшего значения
в граничной точке, например при t — а, и если эта точка не яв-
ляется стационарной (т. е. h' (а) #= 0), то верхний предел в ин-
теграле (3.73) можно заменить на любую внутреннюю точку
t = с (при условии, что на отрезке [а, с! производная h' (t) не
обращается в нуль), проинтегрировать результат по частям и
получить требуемое асимптотическое представление интеграла
(3.73). Если же наибольшее значение h (t) достигается в стацио-
нарной точке, то метод интегрирования по частям становится
непригодным. В следующем параграфе рассмотрим построение
3.3. Метод Лапласа
71
асимптотических разложений интегралов типа (3.73) с помощью
метода Лапласа, причем ограничения, связанные с дифференци-
руемостью функции / (/) и отсутствием нулей у производной h' (t),
будут сняты.
3.3. Метод Лапласа
В этом параграфе мы рассмотрим интеграл общего вида
ь
Цх) —	(3.79)
а
в случае действительной функции h (i) и при больших положи-
тельных х, а также в предположении, что интеграл (3.79) суще-
ствует (т. е. имеет конечное значение). Как указывалось в предыду-
щем параграфе, основной вклад в асимптотическое представление
интегралов вида / (х) вносит ближайшая окрестность точки, в ко-
торой функция h (t) достигает своего наибольшего значения.
На этой идее Лапласа основан достаточно общий метод получения
асимптотических оценок интегралов типа (3.79). Ниже мы рас-
смотрим метод Лапласа на нескольких наиболее характерных
примерах.
Пример 1,
В качестве первого примера рассмотрим частный случай ин-
теграла (3.79), а именно интеграл
' ? е-**
TTi-dt.	(3.80)
о
Для того чтобы построить асимптотическое разложение I (х)
при х -> оо, разложим функцию (1 + t)1 в ряд по степеням t
и проинтегрируем полученное разложение почленно, заменив
верхний предел в (3.80) на оо. Возможность такой замены будет
обоснована ниже.
Из биномиальной формулы следует, что
(1	1 -/ + /2-*3Н-----= £ (—1)^"-	(3.81)
п=0
При этом, согласно признаку Даламбера, имеем
lim	(~17" i =lim =
п^> (Л —1)-й.член пч>оо (-I)*-1 t"-1 n-мх/
Следовательно, ряд (3.81) сходится только при |/| < 1, а значит,
подстановка ряда (3.81) и почленное интегрирование в пределах
от 0 до 10 являются незаконными, поскольку разложение (3.81)
\
72	Гл. 3. Интегралы
справедливо только при 111 < 1. Для того чтобы преодолеть ука- I
данное затруднение, разобьем промежуток интегрирования на I
два — [0, 61 и [6, 10], где 6 — некоторое малое положительное I
число. Таким образом, мы можем представить интеграл (3.80)	I
в виде	I
б	ю	I
(•	.—xt	(•	.—xt	I
/(^) = ]-ПП + J	(3-82) I
о	б	I
Покажем теперь, что второе слагаемое в правой части (3.82) I
экспоненциально мало при	х->оо. С этой целью заметим, что I
1 > (1 + О"1 при * > 0- Поэтому	1
ю	ю	•
(*	Р	p-—Xi Ю	о
J Т+7Л<]
б	о
При х -* оо ехр (—10х) стремится к нулю быстрее, чем любая
степень х-1. При конечном б и при х -> оо то же самое можно
утверждать и для слагаемого ехр (—бх). Следовательно, второй
интеграл в правой части (3.82) будет стремиться к нулю экспо-
ненциально, т. е. можно записать
б
Z(x) = J-р-р-Л+(Э. М. Ч.) при х-> оо, (3.83)
о
где сокращение (Э. М. Ч.) использовано для обозначения экспо-
ненциально малых членов. Таким образом, основной вклад в асимп-
тотическое разложение интеграла (3.80) действительно дает только
близкая окрестность точки t = 0.
Подставляя разложение (3.81) в формулу (3.83) и интегрируя
почленно, имеем
I(x)= fe~x4У (— 1)"/")<Й = У (— 1)" f tne~xtdt. (3.84) i
0	\л=0	/	п=0	0
Для оценки интеграла в правой части (3.84) введем замену пере-
менной т xt. При этом dt = dr/x и, следовательно,
б	бх
f lne~xt dt — —4т- [ i:ne~x dt.
-	/Ж J
о	о
(3.85)
3.3. Метод Лапласа
73
Последовательное интегрирование по частям в правой части соот-
ношения (3.85) дает
в	бх
j tne-xt di~ —ipp J Tne~xdT =
:	0	X 0
= ------^pp pt" + mt"-"1 + n (n — 1) t"-2 4- •" * + nty2 4*
4- nl т 4- e~'x >
. n!62	. n!6 . n! I
'~‘2xn~l xn + xn+' ]'
(3.86)
Поскольку, функция exp (—бх) при x -> оо стремится к нулю
быстрее, чем любая степень х'1, то член в правой части (3.86),
содержащий множитель ехр (—бх), будет экспоненциально ма-
лым. Поэтому
а	.
(tne~xt dt =	+(Э- М. Ч.),	(3.87)
J	Л '
0 '
причем этот результат не зависит от величины б, так как он
остается справедливым даже при б -* оо. Действительно,
(«-"<“=44-
о
Таким образом, приведенное рассуждение оправдывает описан-
ную выше процедуру вычисления асимптотики интеграла (3.80).
Подставляя разложение (3.87) в формулу (3.84), без учета
экспоненциально малых членов имеем
(3.88)
При этом, согласно признаку Даламбера, имеем
n-й член ,.	(—1)”п1х"	<•	— п 
(«—1)'й член x”+1 (—I)™-1 (« — 1) 1 ~ х
и, следовательно, ряд (3.88) расходится. Поэтому использование
знака равенства в формуле (3.88) является незаконным, и его
74
. Гл. 3. Интегралы
следует заменить на знак асимптотического соответствия. Окон-
чательно можно записать
оо
1(*) ~ 2	при х-> оо. (3.89)
п=0
Отметим также, что этот результат может быть получен и с по-
мощью метода интегрирования по частям.
Использованный выше прием — разбиение промежутка ин-
тегрирования и отбрасывание экспоненциально малых слагае-
мых — заимствован нами из доказательства так называемой леммы
Ватсона. С помощью этой леммы строятся асимптотические пред-
ставления интегралов вида
ь
I (х)= J f(t)e~*‘ dt, -	(3.90)
о
где функция f (t) непрерывна на промежутке [0, b ] и имеет асимп-
'тотическое разложение
Е amtm$rl при t-+0,	(3.91а)
ffl=l
причем показатель р считается положительным, что обеспечи-
вает сходимость интеграла (3.90). Кроме того, при й -> оо должно
иметь место неравенство
|/(/)|<КеЧ	(3.916)
где Киа — положительные постоянные. При указанных усло-
виях Лемма Ватсона утверждает, что полное асимптотическое раз-
ложение интеграла / (х) может быть получено с пОмОщью подста-
новки разложения (3.91а) в (3.90), дальнейшего почленного ин-
тегрирования и замены верхнего предела интегрирования на оо,
в результате чего получается формула
оо	оо •
I(x)~ S а™ J dt’
m=l 0
ИЛИ
/(х)~ Е а^Г (тр)/х^Р1 .	(3.92)
т=1
Пример 2
В предыдущем примере функция h (/) = —t (см. формулу
(3.79)) достигала своего наибольшего значения на нижнем пределе
1 Здесь Г (х) —• гамма-функция Эйлера, определение н свойства которой
указаны ниже на стр. 77. Полное же доказательство леммы Ватсона см., на-
пример, Ватсон Г. Н. Теория бесселевых функций. Ч. I—И. Пер. с англ.—
М.: Изд. иностр, лит., 1949. — Прим, перев.
3.3. Метод Лапласа
75
интегрирования. Поскольку в этом случае h' (0) = — 1, указан-
ная точка не являлась точкой относительного максимума. Поэтому
в качестве второго примера рассмотрим случай, когда наиболь-
шее значение h (/) и точка максимума совпадают, а именно иссле-
дуем интеграл
/(x)=f-fTr^,	(3.93)
о
у которого функция h (t) имеет относительный максимум в точке
t ~ 0. Как уже отмечалось в примере 5 предыдущего параграфа,
s метод интегрирования по частям в данном случае оказывается
- непригодным. При больших положительных х асимптотическое
: представление интеграла (3.93) определяется лишь вкладом от
' окрестности точки t = 0, в которой функция h (t) = —/2 дости-
гает своего наибольшего значения. Асимптотику интеграла I (х)
будем искать с помощью леммы Ватсона, т. е. подставляя степен-
ное разложение (3.81) функции (1 + 0-1 в интеграл (3.93) и ин-
тегрируя далее почленно в пределах от нуля до бесконечности.
В результате имеем
1(х)~ 2 (~tne~xt‘dt.	: (3.94)
п—О	0
ч /
Обозначая последовательные интегралы в формуле (3.94) через
In, т. е.
In = j tne-xit dt,	(3.95)
°
попытаемся вычислить эти интегралы при произвольных значе-
ниях п. Для случая п = 0 имеем
/0 = j e~xi*dt.	(3.96)
•о /	'
Полагая xt. = т и dt = dx/Ух, приведем интеграл (3.96) к виду
со
=	(3.97)
Г х о *
Интеграл в (3.97) мы вычисляли ранее (см. формулу (3.25)).
Таким образом, имеем
(3.98)
о
76	Гл. S. Интегралы
Дифференцируя обе находим	части соотношения (3.98) по переменной х,
	— f Ре~х** dt — ~ 0
откуда	00	ч ' Z2= f	(3.99) J	4*3  0
Далее, дифференцируя по х левую и правую части (3.99), в свою
очередь	находим — Г Per-*' dt — ~	,
X	
рткуда	Ц ~ j* Ре-*' dt ~	.	(3.100) о	x
Продолжая указанный процесс, можно получить выражение для
интеграла вида (3.95) при произвольном четном п. Итак,
=	(3.101)
Для того 'чтобы определить 1п при нечетном п, рассмотрим
прежде всего случай п = 1:
/1==j te~xttdt. '	(3.102)
о
Полагая xt* = т, имеем 2xtdt = dx и, следовательно,
'=44	=	(3.103)
о	о
Дифференцирование соотношения (3.103) по х дает
00
о
откуда
=	•	(3.104)
О
3.3. МетодУТапласа
77
алее, дифференцируя по х выражение для Ia, приходим к фор-
уле для.
/6 = J t*er*“dt = ±-.	(3AQS)
,	о
[родолжая указанный процесс, можно получить следующую
общую формулу для интегралов вида (3.95) с нечетными индек-
сами п:
1
(злоб)
^Окончательно с учетом формул (3.101) и (3.106) разложение
(3.94) переписывается в виде
;	-	оо
т=0	‘
1	V~5 . jdm , _n	1	. К л 1	।
2	) dxm	2х1/2 2х + 4хЗ/2	2х» +
т=0
+^-4-+--;- (зло7>
Гамма-функция
Интегралы вида (3.95) можно вычислить и другим способом,
выразив их через гамма-функцию Эйлера, определяемую при
положительных z соотношением
Г (z) =-j V'-'e-'1 dx.	(3.108)
о
С этой целью введем замену переменных
х = xt2, dx — 2xt dt. ''	(3.109)
Тогда интеграл (3.95) преобразуется к виду
1п == -l-x- ("+D/2 J	dx = -l-x-t'H-n/ar (^) • .
о
(ЗЛЮ)
Подстановка (3.110) в разложение (3.94) дает
п=0
78	Гл. 3. Интегралы
Покажем теперь, что разложения (3.111) и (3.107) совпадают.
Воспользуемся для этого следующим функциональным соотно-
шением для гамма-функции:
Г (z) = (z — 1) Г (z — 1)	13.112)
и докажем эту формулу для z > 1. Используя метод интегриро-
вания по частям, положим
и — тг-1, dv = е~х dx,
откуда
du = (г — 1) тг~2 dx, v = — е~х.
При этом из формулы (3.30) следует, что
Г (г) = —т2—1е~х |0	(г — 1) J х’~2е~х dx.	(3-113)
о
Интеграл в правой части при z > 1 существует и равен Г-(г — 1)
Тогда из формулы (3.113) сразу следует соотношение (3.112).
Отметим также, что рекуррентное соотношение (3.112) позволяет
найти Г (г) при z > 1, если Г (г) протабулирована на интервале
0 < z < 1. Например,
Г (5,3) = 4,ЗГ (4,3) = (4,3) (3,3) Г (3,3) ='(4,3) (3,3) (2,3) Г (2,3) =
= (4,3) (3,3) (2,3) (1,3) Г (.1,3) = (4,3) (3,3) (2,3) (1,3) (0,3) Г (0,3).
При натуральных г, а также при г, равных половине целого
положительного числа, интеграл, определяющий гамма-функ-
цию, может быть вычислен в явном виде. Так, в случае натураль-
ных z рекуррентная формула (3.112) дает
Г (z) =4z—1)Г(г—1) = (z—1) (z —2)Г(г —2) =
= (z — 1) (г — 2) (г — 3) ... 3-2-1 Г (1).	(3.114)
Полагая в формуле (3.108) z = 1, находим
T(l) = j е~х dx = -е-‘|"=1.	(3.115)
о
При этом из соотношения (3.114) следует, что
Г (г) = (г — 1)1,	(3.116)
где z — целое полбжительное число. Поэтому в случае п = 2т 4-
-j- 1, где т — произвольное натуральное число, имеем
Г (±±1) = Г ( 2m + -) = Г (m + 1) = т\.
1 Формулы (3.108) и (3.112) справедливы при всех г, за исключением
нуля и отрицательных целых чисел. См., например: Лебедев Н. Н. Специаль-
ные функции и их приложения. — М.—Л.: ГИФМЛ, 1963. — Прим, перев.
Г	3.3. Метод Лапласа	79
|------------------------------------------------- , ; ।
ЙГогда из формулы (3.110) получаем
/2m+i =4"m !y-(m+l) '	(3.117)	
•в полном соответствии с (3.106).	;;
В случае если г = т + -у-, где т — натуральное число,  “
из соотношения (3.112) следует, что	’
г(™ + 4) = (т-4)г4~4) = .
==(от-4)4-4)г(т~4)=;	'
= (т - 4) (т - 4) (т'~ 4) • • -4-4-4г (4) •
(3.118)
Полагая теперь в соотношении (3.108) z=-y, имеем	, ;
Г(4~) = J	(3.119)	\
0
С помощью подстановки т = у2 интеграл (3.119) можно привести ‘
к виду
г(4)==4 е~у2{&	'	(З.120)
о
Величина интеграла в (3.120), согласно формуле (3.25), равна ..
•/л/2, и, следовательно,	।
г(4-)=/л.	(3.121)	:
Таким образом, соотношение (3.118) принимает вид
г4+4) = 4~4) 4-4)(т-4)- • -4'4'4^’	|
(3.122)
где т — целое положительное число: Отсюда при п = 2т (т. —
целое) имеем
r(4L)=r(J4LL)=r('"+4-)=	?
-(-4)(—?)(—4)-44-1^.
(3.123)	,	:
- . ...
80	'	Гл. 3. Интегралы
Наконец, из формулы (3.110) следует, что
•	4-^л^[т+(1/2)]	<зл24>
в полном соответствии с (3.101).
Пример 3
В качестве третьего примера рассмотрим несколько более об-
щий, чем в предыдущем примере, интеграл, а именно
ь
/(x)=J	b>a,	(3.125)
а
где h' (<?) = 0, h" (а) < 0,	(3.126)
f (О ~ fo (t — а)х при t -► а	(3.127)
и /0 — некоторая постоянная. Условия (3.126) означают, что
функция h (0 имеет в точке t = а относительный максимум.
Мы предположим также, что этот максимум является наибольшим
значением h (t) (т. е. абсолютным максимумом) на промежутке
интегрирования (рис. 3.1). Для существования интеграла (3.125)
необходимо, чтобы показатель X был больше —1. Основной
вклад в асимптотическое представление / (х) дает только окрест-
ность точки t — а, в которой достигается наибольшее значение
h (0. Поэтому верхний предел интегрирования в (3.125) вполне
можно заменить/на а + б, где б — малое положительное число,
в результате ’jero получим
°+в
/(х)~ J f(t)exh ^dt.	(3.128)
Рнс. 3.1. Функция, имеющая относительный н абсолютный максимум в точке
3.3. Метод Лапласа	81	,'«>
j
Для того чтобы найти главный член разложения I (х), пред-	,! J
тавим функцию h (t) в окрестности точки t *= а ее рядом Тей-	‘ <
юра, положив -	И*]	, ' 	, '
или
h(t) = h(a) +-§y/i"(a)(/-a)2H----------------,	(3.129)-
поскольку h' (а) = 0. Подставляя теперь (3.127) и (3.129) в ин-	’
теграл (3.128), имеем
a-f-б
/ (х) ~ Де** (а) j (/-a)M1/2)^"W(/-°)s^.	(3.130)
а
Поскольку h" (а) < 0, верхний предел а 4- & можно заменить на
оо, что приведет к экспоненциально малой ошибке. Таким обра-
зом, перепишем (3.130) как
[ (^-а)хе0/2) **"(“) о-»)’d/.	(3.131)	,
а	-	'..	. 'Mr
Интеграл в правой части (3.131) можно-выразить через гамма-
функцию. С этой целью положим	1
	xh" (а) (/ — а)2 = т	(3.132)--
и получим-------------------------------------------------------’	;;
ОО
I^-'r\-^7a^YK+lV2foeXhW ( ^’^dx, (3.133)
a L	\~*'f J	v	. >
0	J
или, с учетом (3.108),
: ’ м ~ Т Г«г m при	г
(3.134) j
Отметим также, что для того, чтобы найти члены высшего по-
рядка в разложении I (х), необходимо сохранять члены более
высокого порядка и в разложениях функций / (/) и h (t).
Пример 4	?
В качестве четвертого примера рассмотрим интеграл вида	<
(3.125) в случае, когда функция h (t) имеет при t = а точку пере- -
гиба (рис. 3.2). При этом	'
:	' h' (а) = h" (а) = 0 и hm (а) < 0.	(3.135)
82
Гл. 3. Интегралы,
Рис. 3.2. Функция, имеющая точку перегиба и абсолютный максимум в точке
Л = а.
Как и в предыдущих случаях, основной вклад в асимптотическое
разложение нашего интеграла дает только окрестность 'Г'очки
t — а, поэтому верхний предел интегрирования можно заменить
на а + б, где б — малое положительное число.
Для того чтобы найти главный член асимптотического разло-
жения интеграла (3,128) при условиях (3.135), представим функ-
цию h (t) ее рядом Тейлора в окрестности точки t = а, положив
h (0 = h (а)+ h' (a) (t - а) + h" (a) (t - a? +
+ 4-Г(а)(/-а)з+...,
или
h(t) = h(a) + -±-hm(a)(t-а)3-|--.	(3.136)
Подставляя соотношения (3,127) и (3.136) в интеграл (3.128) и
заменяя а + б на оо, получаем
I (х) ~ faexh <а) J (/-а)ье(1/б)хЛ'Ча)('-я)3<й.	(3.137)
О
Интеграл в формуле (3.137) можно выразить через гамма-функцию.
С этой целью положим
- -i- xh’" (a) (t - а)’ = т.	(3.138)
Тогда
'	( х<к-2)/3е-*<1т, (3.139)
о
откуда, с учетом (3.108), следует, что
^Л(а)Г(-з-) при х->оо.
(3.140)
3.3. Метод Лапласа
83
Пример 5
Во всех предыдущих примерах наибольшее значение функции
h (/) достигается в граничных точках промежутка интегрирова-
ния. Теперь мы рассмотрим случай, когда h (t) достигает наиболь-
шего значения в некоторой внутренней точке (рис. 3.3). Итак,
рассмотрим интеграл вида
ь
I (x) = J	b>a,	(3.141)
а
при больших значениях х в случае выполнения условий
h' (с) = 0, h" (с) < 0, а < с < Ь,	(3.142)
f (t) ~ f0(t — СУ~ при t -*• с,	(3.143)
где X— целое число, большее —1, что гаранти]5ует сходимость
нашего интеграла. Для того чтобы найти асимптотическое пред-
ставление интеграла (3.141) при х -* оо, разложим функцию
,в ряд Тейлора, сохраняя в этом разложении первый член с нену-
левой производной:
/i(/) = /i(c) + 4r/i"(c)(/-c)2+ ....	(3.144)
Тогда имеем
С-1-6
I (х) ~ foexk j (t ~ c^e^^xh" dt, (3.145)
с— в
где S — некоторое Положительное число. Заменяя, как обычно,
.в интеграле (3.145) ё на оо, получаем
I (х) ~ [йех!г«) J (t -с)А.е(1/2)хЛ"(С)(/-С)’^.	(3.146)
Рис. 3.3. Функция, имеющая абсолютный максимум во внутренней точке про-
межутка.
84	Гл. 3. Интегралы
С помощью подстановки
— x/i" (с) (/— с)2 = та	(3.147)
асимптотическое представление (3.146) можно привести к виду
/(x)~f0 ГrA~L](X+1)/2^A (с) [ тхе—’’dr при х-> оо.
[_ЛП vvJ	J
—оо
-	(3.148)
В случае целых нечетных X интеграл в правой части. (3.148)
обращается в нуль, и поэтому необходимо искать следующий
член асимптотического разложения. Если же X — четное число, то
J тхе-т2 dx = 2 j Txe-1t‘cfr,	(3.149)
—со	О
откуда в результате подстановки т2 = 0 и с учетом формулы
(3.108) находим
j x^dx = j 0^-')/2е-е^0==Г	(3.150)
—co ***	0
Таким образом, окончательно имеем следующее выражение для
главного члена асимптотики I (х):
”Р“	.
(3.151)
Пример 6
Во всех предшествующих примерах функция f (t) в окрест-
ности точки t = с, т. е. в окрестности максимума h (t), имела
степенной характер:
f (0 ~fo	-1.	'	(3.152)
В качестве последнего примера рассмотрим случай, когда f (t)
при t -* с стремится к нулю быстрее, чем любая степень (t — с),
и, следовательно, не может быть представлена в виде (3.152).
Рассмотрим, например, интеграл вида
ь
z (X) = j е-1/(г-а)е-х (<-а)‘ dt, b> а, (3.153)
а
при больших положительных х. Поскольку функция f (t) —
= ехр [—(t — а)-1 ] стремится к нулю быстрее любой степени
(t — а), вклад в асимптотику от окрестности точки t =* а будет
экспоненциально малым. Поэтому непосредственное применение
3.3. Метод Лапласа	85
^алгоритма, используемого в лемме Ватсона, к интегралу (3.153)	Ч
|не позволяет получить требуемое асимптотическое разложение. _	$
I При нахождении главной части асимптотического представле-
Гния / (х) мы не можем отделить ехр [—(4 — a)rl ] от ехр [—х ft —	']
|— а)21. Напротив, нам следует объединить эти экспоненты и пере-	|
вписать (3.153) в виде		*
)	-	ь	-
Г	Цх) = JeH*. t)dt,	(3.154)
;Где	h (-Х, t) = — (t — а)-1 — х (t — а)2.	(3.155)'
[Стационарные точки функции h (х, t) находятся там, где обра-
щается в нуль производная
I	2*('-4	(3156)
(Решая уравнение (3.156), можно найти точку максимума h (х, t)
t = а + (2х)-’/3.	(3.157)
(Отметим, что в отличие от предыдущих случаев координата точки	' 1
(максимума в данном случае зависит от аргумента х. Таким об-
разом, для того чтобы найти асимптотическое разложение инте-	
ррала, мы должны прежде всего провести замену переменной ин-	[
Щгрирования с таким расчетом, чтобы координата точки макси-	*>
8мума (показателя) экспоненты не зависела от х. Полагая	>'
I	t~ а = x~i/3s,	(3.158)	 
перепишем интеграл (3.153) в виде	... j
I	,	(6-а) X1-'3 .	_	' Ч
I	=	|	е-х1/3 [s«+(i/s)j dS' (3.159)
!	. . \	°			' j'
t- Максимум функции h (s) = —(s2 + s-1), входящей в (3.159),	!
имеет место в точке s = 2'1/3. При условии что й-> 2-1/3, вклад =*
р асимптотику вносит именно окрестность этой точки. Следова-
тельно, нужно разложить функцию h (s) в ряд Тейлора в окрест-
ности точки s = 2-1/3. Сохраняя в разложении первый член с не-	7 j
рулевой производной, имеем	!
I	h (s) =-h (2->/3)	3 (s — 2-?/3)2 +h • • .	(3.160)
Иалее, полагая в (3.159)	t j
I	Зх1/3 (s — 2->/3)2 = т2	(3.161)

86
Гл. 3. Интегралы
и заменяя пределы интегрирования соответственно на +оо и
—оо, получаем
.-(3/2) (2x)V3	р°“
'W~ ГЗ-, J
—ОО
илй, с учетом формулы (3.125),
7(*)~ (4г)1/2е~(3/2)<2*)1/3-	(3-162)
3.4. Метод стационарной фазы
В этом параграфе мы исследуем обобщенный интеграл Фурье
I(a) = \f(t)elah<<) dt, b>a, '	(3.163)
а
в случае больших положительных а. При этом предполагается,
что f (t) и h (t) — вещественные функции и интеграл (3.163) су-
ществует. Подынтегральную функцию в (3.163) можно рассма-
тривать как некоторое комплексное выражение, представленное
в показательной форме, причем f (t) и ah (t) служат соответ-
ственно его модулем (амплитудой) и аргументом (фазой). Если
функции f (/) и h (t) непрерывно дифференцируемы, можно по-
пытаться применить метод интегрирования по частям, полагая
ц= ///]. , dv = eiah <*> h' (/) dt.
й (0	4 ’
При этом
du = Г1 dt, v = -4— eiah <<>.
L й (О J	»а
Интегрируя (3.163) по частям, находим
I — f $ etahm b ___1_ Г Г/ (0......1' gtafr «)
' iah'(t) [a la J [ h' (t) J	(3.164)
a	/
Интегральный член в правой части (3.164) мы можем оценить,
продолжив процесс интегрирования по частям. Окончательно
имеем следующее асимптотическое представление:
7(a)~ a[ h’(a)	h' (b)	] + Uka2/’ (-Э-165)
Как и в случае обобщенного интеграла Лапласа (пример 5
§ 3.2), метод интегрирования по частям становится непригодным,
если производная h' (t) обращается в нуль в какой-либо точке
промежутка [a, b 1. Если же /г' =/= О на промежутке [a, b 1, то,
согласно формуле (3.165), основной вклад в асимптотику'ин-
3.4, Метод стационарной фазы
87
U+7?)cos 50i
м
Рис. 3.4. Быстро колеблющаяся функция.
теграла / (а) вносят только окрестности концевых точек. При
этом быстрые колебания функции ехр Hah (t) ] уничтожают
вклад в интеграл от внутренних точек промежутка (рис. 3.4).
В данном случае в отличие от обобщенного интеграла Лапласа,
для которого асимптотика определялась только окрестностью
концевой точки с большим значением функции h (/), .обе гранич-
ные точки дают существенный вклад в асимптотику. Если же
h' (t) обращается в нуль на промежутке интегрирования (иначе
говоря, если фаза имеет стационарные точки), вклад в асимптоти-
ческое разложение вносят как окрестности концевых точек, так
и окрестности стационарных точек, причем вклад последних
значительнее. Этот факт хорошо иллюстрируется на рис. 3.5.
В точках, далеких от концевых и стационарных, положительные
и отрицательные полуволны взаимно погашаются. Кроме того,
из рис; 3.5 ясно, что взаимное погашение колебаний оказывается
меньшим в окрестности стационарной точки, чем в окрестностях
концевых точек. Поэтому главные члены асимптотического раз-
ложения интегралов Фурье должны определяться именно окрест-
ностями стационарных точек.
(1+7^)со550(2~2)г
Рис. 3:5. Функция со стационарной точкой.
wpw’"! '	—----- -
88	Гл. 3. Интегралы
При отсутствии стационарных точек хорошее приближение
для данного интеграла можно получить с помощью метода инте-
грирования по частям. При этом вклад концевых точек, как по-
казывает формула £3.165), представляет собой величину порядка
а-1. Для случая стационарных точек Стокс разработал так назы-
ваемый метод стационарной фазы, позволяющий учитывать вклад
стационарной точки t = с в асимптотику с помощью разложения
'' функций f (/) и h (t) по степеням1' (t с). К.ак показано далее,
. вклад окрестности стационарной точки в таком случае представ-
ляет собой величину порядка а-1/2, и, следовательно, именно
' стационарные точки определяют характер главного члена асимпто-
тического разложения интеграла 7(a). Ниже мы опишем метод
стационарной фазы в применении к четырем конкретным примерам.
Пример 1	\
Начнем со случая, когда у функции, h (t) существует един-
ственная стационарная точка (максимум или минимум), совпа-
дающая с левым концом промежутка интегрирования t — а.
Кроме того, принимается, что функция f (t) ограничена в точке
t — а, т. е. что |f (а) | < 4-оо. Как и при использовании метода
Лапласа, главный член разложения интеграла I (а) определяется
только вкладом окрестности точки а, и поэтому мы можем заме-
нить верхний предел интегрирования на a -F 6, где 6 — малое
положительное число. Таким образом, имеем
а-Н
I(a)~ \ f(t)elahW dt.	(3.166)
а
В первом приближении функцию f (t) можно заменить на f (а),
а функцию h (t) представить ее тейлоровским разложением вида
h(t) = h(a) + -^h"(a)(t — a)2H------------------
(поскольку h’ (а) — 0). При этом интеграл (3.166) можно пере-
писать как
a+в -
7(a)~f(a)eia/!<°) j № iah" <“> dt. (3.167)
а
Используя вновь допущение ‘о том, что наиболее существенный
вклад в асимптотику вносит ближайшая окрестность стационар-
ной точки, заменим верхний предел а + 6 на 4-оо. Полагая те-
перь t — а — z, перепишем формулу (3.167) в виде
7 (a) ~ f(a)eiah <°> j № iah" <°) 2‘ dz. (3.168)
3.4. Метод стационарной фазы
89
Рис. 3.6. Деформация~контура интегрирования.
(6) Л"(а) > О
| Для того чтобы вычислить интеграл в правой части (3.168),
^воспользуемся теоремой Коши, согласно которой, если функция
(Комплексного переменного F (z) имеет производную, непрерывную
(в некоторой области, ограниченной замкнутым контуром С,
;и на нем (т. е. F (г) является аналитической в указанной области),
(то
l	\F(z)dz = G.	(3.169)
*	' ’	с
(Основная идея вычисления интеграла 7(a) заключается в том,
(чтобы выбрать контур интегрирования С таким образом, чтобы
'исходный интеграл Фурье перешел в интеграл Лапласа, т. е.
в интеграл, главная часть подынтегрального выражения которого
^представляет собою экспоненту с вещественным показателем,
затухающую на бесконечности. В рассматриваемом случае имеем
	,	- F(z) = exp ^-|"ia/i" (a)z2^|,	(3.170)
так что производная F’ (z) существует при любых значениях г.
Следовательно, мы можем воспользоваться теоремой Коши в форме
(3.169). Для этого составим замкнутый контур С из отрезка‘дей-
ствительной оси х, отрезка прямой, выходящей из начала коорди-
нат под углом 45° к действительной оси, и дуги окружности до-
статочно большого радиуса 7? (рис. 3.6). Тогда
J F(z)dz-\- j F(z)dz-\- j F(z)dz=0.	(3.171)
-	Ci	cs	c.
На дуге C2
z = x + iy = R cos 0 + IR sin 0 = Rel&,
откуда	z2 = 2?2e21’0 = 7?2 cos 20 + i7?2 sin 20.
Следовательно, для того чтобы интеграл по дуге С2 стремился
• к нулю при R -> оо, мы должны выбрать аргумент 0 положитель-
90
Гл. 3. Интегралы
ным или отрицательным в зависимости от того, положительна
или отрицательна производная h" (а). Кроме того, для преобразо-
вания нашего интеграла в интеграл Лапласа угол между отрез-
ками С и С3 должен равняться + — или-------опять же в за-
висимости от знака h” (а). При h" (а) > 0 имеем (рис. 3.6, Ь)
о
Л/4
J F (z)dz — iR J g—0/2) ah" (a) R* sin 29+(1/2) (ah" (a) R« cos 29+(9^0
(3.172)
Тогда
Л/4
J F (г) dz < R j е-('/2) “h- w w sin 20 dQ =
. с,	о
R J e- (1/2) ah" (a) R« sin 29	_j_ R J '
0	s
(1/2) ah" (a) R« sin 29
de, (3.173)
где £ — малое положительное число. Поскольку h" (о) > 0,
а sin 20 > 0 при е < 0 < то подынтегральная функция при
R -* оо стремится к нулю равномерно относительно аргумента 0,
й, следовательно, второй интеграл в правой части (3.173) также
будет стремиться к нулю при R -* оо. Чтобы оценить интеграл
по промежутку [0, е], приближенно заменим sin 20 на 20, в ре-
зультате чего получим
е
е- (1/2) ah" (а) /?« sin 20
О
de ~ R J e~ah"(0) H’ede =
о
j е~ah" (a) R’e
= aRh" (a)
О при R -> oo.
Таким образом, при R -> оо весь интеграл по дуге С2 стремится
к нулю, и из соотношения (3.171) следует, что
J F (z)dz = — J F (z) dz при R->oo. (3.174)
с,	с,
На луче С2 z — хиг2=?, тогда как на луче С3 z = г ехр (йг/4)
и г2 = .га ехр (in/2) — ir9, где г — расстояние от начала коорди-
нат до текущей точки на луче С3. При этом подстановка выражения
(3.170) в равенство (3.174) дает
оо	О
j е( 1/2) (ah" (a) X‘ dx = е-1Л/4 j е- (1/2) ah" (a) дг =
О	ОО
оо
= ?л/4 j e~(imah" (a)rldr.	(3.175)
0

3.4. Метод стационарной фазы
91
Соотношение (3.175) показывает, что мы действительно преобразо-
вали интеграл Фурье в окрестности стационарной точки в инте-
. грал Лапласа путем поворота контура интегрирования на угол
ся/4 от действительной оси. Далее, используя подстановку
Г —
и учитывая формулу (3.25), преобразуем (3.175) к виду
ОО	оо
( *(|/2) iah"(a) хг^-~	f	- У™™	(3.176)
J	^ah’(a)J	/2аЛ"(а) v ’
Подставляя теперь выражение (3.176) в формулу (3.168), находим
'•	. . VHf (а\ eiah w+in^
[ (a ~	.	(3.177)
’	.	/2аЛ" (a)	'
= Как уже отмечалось выше, в данном случае вклад в асимптотику
’ от окрестности стационарной точки оказывается величиной по-
'рядка а-'/2, в то время как вклад от концевых точек представляет
собой величину порядка or1.
f В случае h" (а) < 0 контур интегрирования нужно повернуть
’ на угол —л/4, так чтобы
/	г = ге-‘пМ и
j Тогда представление (3.168) примет вид
г	/ (а) - f (а) eCah (а) - ‘я/4 f е((а} r' dr.
о
t-Интеграл в правой части (3.178) является интегралом
-поскольку h" (о) < 0. Используя подстановку
(3.178)
Лапласа,
;	-	у-----g-ссЛ (а) г=<т
и формулу (3.25), получаем вместо (3.178)
/	/л/ (a) eiah <“> -
1	!/(a)~—-	-------- при a->oo.
J	К-2аЛ”(а) Н
(3.179) .
' Отметим, что в общем случае поворот контура интегрирования
на угол 0 должен осуществляться таким образом, чтобы величина
pah" (a) г2 в интеграле (3.168) оказалась бы вещественной и от-
рицательной. Поскольку
z = rei6 и z2 = r2e2ie = г2 cos 20 -ф- ir2 sin 20,
гго указанное требование приводит к условию cos 20 = 0, или
fi — ;t л. При этом имеем za = ir2 sin 20 и
iah" (a) z2 = —ar2h" (a) sin 20.
92
Гл. 3. Интегралы
Таким образом, при h" (а) > 0 следует выбирать 0 = л/4, а при
. h" (а) < 0 необходимо полагать 0 = —л/4. Тогда в обоих случаях
интеграл в (3.168), т. е. интеграл по лучу Clt преобразуется в
интеграл типа Лапласа.
Пример 2
В качестве .второго примера рассмотрим случай, когда функция
h (t) имеет стационарную точку при t — с, где а < с < 6., Пред-
положим, что других стационарных точек у функции h (t) не
имеется; кроме того, будем считать, что функция f (t) ограничена
в точке с, т. е. |f (с) | < -f-оо. В соответствии с методом етацио-
, нарной фазы главный член асимптотического разложения инте-
грала (3.163) определяется характером изменения подынтеграль-
ной функции в окрестности стационарной точки t = с, что позво-
ляет записать
с+в
7(а)~ J f(/)^“MOrf/,	(3.180)
С—д
где 6—малое положительное число. Заменим функцию f (t)
ее значением в точке t ~ с, а функцию h (t) в окрестности этой
точки — ее рядом Тейлора, который Имеет вид
h(t) = h(c) + ±hH(c)(t-cY+'..,	(3.181)
поскольку h' (с) = 0. Подставляя разложение (3.181) в интеграл
(3.180), заменяя f (t) на f (с) и t — сна г, а также заменяя пределы
интегрирования на ±оо, получаем в итоге
ОО
/(^-/(с)/^^ J e(1/2)l“ft' (c)z!dz. (3.182)
—00
Для того чтобы вычислить интеграл в правой части (3.182)
в случае, если h" (с) > 0, повернем контур интегрирования на
угол л/4, так чтобы z = г ехр (in/4). В результате получим
00
—-оо
Вычисление этого интеграла с помощью подстановкиг
j/r-^-ah"(c)r = t
и использования формулы (3.25) приводит к следующему асимпто-
тическому представлению: .
.. .	/2л/ (й) eiah (с) +in/i	/о
------W73---------- прна-». (3.183)
3.4. Метод стационарной фазы
93
рочно так же, в случае если h" (с) < 0, мы поворачиваем контур
интегрирования на угол —л/4 и затем, используя подстановку
Г	----г = т,
получаем окончательно
t	j. ,	/2^ (с) eiah (с> -<я/4
г	/(a)~ —--------------- ПРИ а^°°'	(	}
Пример 3
, В качестве третьего примера рассмотрим случай,, когда h (t)
Имеет стационарную точку при t — а, причем
г	h' (a) = h" (а) = ... =	(a) = О,
po h(n) (a) #= 0. Разложим функцию h (t) в ряд Тейлора, который
р учетом равенства нулю первых п — 1 производных будет иметь
вид
,	h(t) = h(a) + ~hw(a)(t-a)n-[- ••• .	(3.185)
[одставляя разложение (3.185) в интеграл (3.163) и заменяя в нем
(/) на f (с), в первом приближении получаем
/ (a) ~ f (a) J еГаЛ(п) (а) (<“a)n/zh dt. (3.186)
j-	а
Полагая теперь t — а = г, перепишем представление (3.186)
й виде	оо
.	\ eiahWwznl"ldz.	(3.187)
о	I
Для того чтобы вычислить интеграл в правой части (3.187) в слу-
чае, если №> (а) > 0, повернем контур интегрирования на угол
п/2п. При этом имеем z — г ёхр (in/2n) и формула (3.187) преоб-
разуется к виду
I(a)^f(a)elah(a} + tnl2n\e-ah(n}(a}rn/nldr. (3.188)
'	о
Интеграл в правой части (3.1В8) выражается через гамма-функцию
<с помощью подстановки
Р	«А<"> (а) г" _
\	XT s-
При этом, учитывая формулу (3.108), находим
if «—a/И") (о) rn!n\ j ~ 1 Г л! 11/п
ц	-	«[ n) (а)
j s(l/n)-lg Sfa —
0
= Г я| 11/п Г \ /	(3.189)
[ ahw (а) ]	«

7(а)~[
94	Гл. 3. Интегралы
Таким образом, асимптотическое представление (3.188) можно
переписать как
I(а) ~ [—21—T/n Z (а) fel	(3.190)
v ' l«a( }(e) 1 п	~
В случае если /г<”> (а) < 0, контур интегрирования следует
повернуть на угол —-л/2п от действительной оси. Тогда, выражая
полученный в результате интеграл через гамма-функцию, имеем
,	П1, На)г(—
_____	\ п / giah(a) — 1Л/2п при ф —> оо,
— аЛ(п> (а) J	п
' ,	(3.191)
Из формул (3.190) и (3.191) следует, что главный член асимпто-
тики интеграла (3.163), определяемый вкладом окрестности ста-
ционарной точки, представляет собой величину порядка ст1''1,
где показатель п соответствует наименьшему порядку произ-
водной, не равной нулю в стационарной точке. Следовательно,
если функция h (t) обладает несколькими стационарными точками
на промежутке [a, b 1, то главный член асимптотического разло-
жения интеграла (3.163) определяется окрестностью стационар-
ной точки с наибольшим значением п. Если же наибольшему
значению п соответствует не одна, а несколько стационарных
точек, то главный член асимптотического разложения интеграла
(3.163) будет представлять собой сумму вкладов от всех этих
точек.
Пример 4
Во всех предыдущих примерах функция f (t) была ограничен-
ной в соответствующей стационарной точке. В данном примере
рассмотрим интеграл (3.163) при условии, что
f (0 ~ fo (t — а)к при t -> а,	(3.192)
где показатель К должен быть больше —1, для того чтобы инте-
грал (3.163) сходился. Относительно функции h (Т) используем
те же предположения, что и в предыдущем примере. Подставляя
выражения (3.185) и (3.192) в интеграл (3.163) и заменяя верхний
предел интегрирования на 4-е», получаем
\ (t~a)ke^	(3.193)
а
Для сходимости интеграла (3.193) на верхнем пределе потребуем
выполнения Неравенства А < п — 1. Полагая t — а — г, перепи-
шем представление (3.193) в виде
оо
/ (а) ~	j zKeiah<“> <а) z”/nt fa'	(3.194)
о
J
3.4. Метод стационарной фазы
95
Как и ранее, в случае если (а) > 0, преобразуем интеграл
(3.194) в интеграл Лапласа, повернув контур интегрирования
на угол п/2п от действительной оси так, чтобы z — г ехр (m/2n).
В результате имеем
/ (а) ~ f^iah Ю+( (*+]> J г\>-аА(',) (о) /-"/«i dr. (3.195)
о
Интеграл в правой части (3.195) можно представить через гамма-
функции с помощью подстановки
ай(п\а) гп _
—s-
Учитывая формулу (3.108), находим
п I
Г Г^ваЬ<.М (о) rn!n \ dr _1_ Г------f 5—1 4- (Х4~1)/пд—s ds =
J	п [ ай(п) (a) J J
= [—~—Г+')/П •->—я- >. (3.196)
L ай(л) (а) j	п '	7
Подстановка выражения (3.196) в (3.195) дает
I (а) ~ Г ——1U+1 ,/п	п—eiah (°) + ‘ (*+') п/2п	(3.197)
/	[ай<п) (а) J	п	v ’
при а~>оо.
В случае если (а) < 0, необходимо повернуть контур на
угол —л/2п. Выражая получающийся в результате интеграл
через Тамма-функцию, получаем окончательно
1(а)~ [----ГХ+‘>/п -°.....- - п ' e‘a!‘W - i (х+о я/2» (3.198)
ah' '(о)J	n	v ’
при a-> oo.
Отметим, что формулы (3.197) и (3.198) при X —0 переходят
в выражения (3.190) и (3.191). Еще одно замечание относится
к случаю, когда X + 1 > п. При этом, как видно из асимптотиче-
ских представлений (3.197) и (3.198), главный член асимптотиче-
ского разложения порождается не окрестностью стационарной
‘точки t — а, вклад от которой представляет собой величину по-
^грядка а-(х+0/«, а концевой точкой t = b, вклад от которой оказы-
вается величиной порядка а-1.
96	Гл. 3. Интегралы
3.5а Метод наискорейшего спуска 1 * *
До сих пор мы рассматривали только интегралы, у которых
показатель экспоненты в подынтегральной функции был либо
чисто вещественным (интегралы Лапласа), либо чисто мнимым
(интегралы Фурье). В этом параграфе исследуем случай ком-
плексных показателей экспоненты, т. е. обратимся к изучению
интегралов вида
/(а) =\ f (z) eWV dz,	(3.199)
с
где а — большое действительное положительное число, С — кон-
тур интегрирования в комплексной плоскости z, a f (г) н h (г) —
аналитические функции г, регулярные в некоторой области плос-
кости г, содержащей контур интегрирования. Как известно, функ-
ция h (г) называется аналитической в области D, если она опреде-
лена и Имеет производную в каждой точке этой-области. Функ-
ция /г (г), аналитическая в некоторой области D, за , исключе-
нием конечного числа точек, называется мероморфной в D. Эти
исключительные точки называются особенностями данной функ-
ции.
Функция h(z) комплексного переменного z = х + iy назы-
вается дифференцируемой в точке z0, если предел
lim	(3.200)
дг+о-	'
существует и не зависит от выбора Az. Этот предел называется
производной функции h (z) в точке z0 и обозначается как h' (z)
или dh (za)/dz. Подстановка zх + iy в выражение для h (z)
после отделения вещественной и мнимой частей дает
h (z) = h (х + iy) = <₽ (х, у) + гф (х, у).	(3.201)
Далее, подставляя выражение (3.201) в (3.200) и принимая Az
равным Ах, имеем	4
— (z ) = lim Ф(х° + Ах’ У») ~ Ф (х0’~У»)
д*-»о	Ах
4. i Нт +	Уо)~Ф(хо» Уо)
Дх->0	Ах
Таким образом,
> = > + '£ ”Р» г = г-	(3.202)
1 В новейшей литературе предпочитают иное название: метод перевала,
которое лучше отражает идею и суть метода. Прохождение седловой точки
в направлении .наискорейшего подъема и спуска — не обязательный, а лишь
удобный путь интегрирования в рамках этого метода. — Прим, ред.
3.5. Метод неострейшего спуска
97!
(алогично, выбирая Az — i &у, для выражения (3.200) находим
(ze) = lim ф(*°’ Уо + М-фС*»’ у») +
Ду->0
«Ау
, t- ijm Ф (XO, yt + Ay) — ф (x„, y0)
Ду-»0	ДУ	’
dh dil> . dip
— __3_ _ I —X. при 2 — 20.
dz dy dy r u
(3.203)
(3.207)
куда
ели функция h (z) дифференцируема, то величина производной
(z) не может зависеть от выбора Az, и поэтому выражения (3.202)
(3.203) должны быть равны друг другу. Таким образом, имеем
*	Й..	(3.204)
дх 1 dx dy ду	'	'
щеляя в равенстве (3.204) действительную и мнимую части, по-
даем так называемые уравнения Коши—Римана
'	(ЭМО.)
-§ = —S’-	(3.2056)
включение функции 'ф из системы уравнений (3.205) с помощью
фекрестного дифференцирования дает
^-4-^.==0.	(3.206)
dx2 1 ду2	'	'
«алогичным образом, исключая из системы (3.205) функцию ф,
шходим к уравнению
дх* "* ду* ~
Для того чтобы найти асимптотическое представление ин-
.грала / (а), воспользуемся свойством аналитичности подын-
тральной функции и, применяя теорему Коши в форме (3.169),
‘формируем контур С в новый контур С' с таким расчетом, чтобы
i С либо вещественная, либо мнимая части функции h (z) ока-
жись постоянными. Тем самым исходный интеграл преобразуется
1бо в интеграл Фурье, либо в интеграл Лапласа. Тогда асимпто-
та преобразованного интеграла может быть найдена с помощью
етода стационарной фазы или с помощью метода Лапласа. Во
Ногих случаях оказывается более предпочтительным трансфор-
ировать исходный интеграл в интеграл Лапласа (т. е. в интеграл,
у которого Im h = ф = const), поскольку полное асимптотиче-
ское представление интеграла Лапласа порождается лишь окрест-
ностью той точки иа контуре С, где функция ф = Re h (г) прини-
мает наибольшее значение. В то же время полное асимптотиче-
ское представление интеграла Фурье определяется, вообще го-
4 Найфэ А. X.

98
Гл. 3. Интегралы
воря, не только стационарными точками функции ф = Im h (z),
но и поведением подынтегральной функции в концевых/точках
промежутка интегрирования.
Отметим также, что линии постоянной£фазы ф = const яв-
ляются одновременно линиями наиболее быстрого изменения
(спуска или подъема) для функции <р. Чтобы показать это, восполь-
зуемся понятием градиента. Известно, что в плоском случае гра-
диент функции <р (х, у) представляет собой вектор с компонентами
£)•	(3-208)
а производная функции ф по направлению, задаваемому единич-
ным вектором й, определяется выражением
(3.209)
Таким образом, функция dyldn_достигает своего наибольшего зна-
чения в случае, когда п=Уф/|Уф|. При этом направление,
параллельное вектору Уф, будет направлением наибольшего
возрастания (подъема) функции ф, а противоположное направле-
ние, параллельное вектору —Уф,—направлением наибольшего
убывания ф, или направлением быстрейшего спуска. Кроме того,
из уравнений Коши—Римана (3,205) следует, что
z	уф.уф = 0,	(3.210)
т. е. что векторы Уф и Уф взаимно перпендикулярны, и, значит,
производная функции ф в направлении, определяемом вектором
будет равняться нулю. Таким образом, фунццияф оказывается
постоянной на линиях,, касательные к которым параллельны век-
тору Уф, откуда сразу следует, что линии постоянной фазы яв-
ляются бдновременио линиями наискорёйшего спуска (или подъ-
ема) для функции ф.
Отметим также, что функция ф (х, у) не может иметь в точках
регулярности h (z) ни максимума, ии минимума. Действительно,
Из уравнения (3.206) следует, что если, например,
^<0. то $>0.	(3-211)
и наоборот. Вместе с тем поверхность ф (х, у) может иметь точки,
в которых
- ' £• = £=<> <3-212)
однако они не являются точками экстремума функции ф. Такие
точки называются обычно седловыми точками (точками перевала).
Топография поверхности функции ф (х, у), имеющей седловую

3.5. Метод наискорейшего спуска
99
(3.213)
Сточку г0, изображена на рис. 3.7. Из уравнений Коши—Римана
н формул (3.212) следует также, что
йф _ дф _ п
дх
[Таким образом, седловая точка функции <р (х, у) является одно-
временно и седловой точкой функцииф (х, у), а значит, точкой, где
ft' (z) = 0. При этом, если z = z0 есть седловая точка и если '
[ft' (z0) = ft" (z0) = ... == ft<OT) (z0) = 0, но hSm+v (z0) ф 0, точку
-Zo называют седловой точкой порядка т + 1.
j l \ Через седловую точку z0 проходят две или более линий уровня
(т. е. кривых, вдоль которых функция <р сохраняет постоянное
значение), разделяющих окрестность седловой точки на отдельные
/ сектора. Кроме того, через седловую точку проходят две или более .
 линий постоянной фазы (т. е. кривых, вдоль которых функция ф
’ постоянна), являющихся линиями скорейшего спуска или подъема.
Хотя форма линий уровня и линий постоянной фазы, проходя-
« щих через седловую точку, если прослеживать их на всей ком-
плексной плоскости, может'быть достаточно сложной, однако
найти вид и расположение этих линий в окрестности седловой
[.Точки оказывается сравнительно нетрудно. Так, если седловая
точка имеет порядок /и, то в окрестности этой точки ряд Тейлора
[для функции ft (z) имеет вид
L Л<»> ЫIZ - г.?.

(3.214)
т; Рис. 3.7. Топография поверхности ф = Re Л(х) вблизи седловой
пичиой функции ft (г). Толстые сплошные кривые, выходящие
\ точки, обозначают срединные линии «хребтов» и «долин», пунктирные кривые —
' линии уровня ф = ф (*Ь. Уо) = const. Кривая АА' является линией иаискорей-
?	шего спуска.
точки для ти-
из седловой
4*
. Рве. 3.3. Топография поверхности <р = Re Л(г) вблизи седловой точки второго
порядка для случая X = 0. «Долины» на рис. заштрихованы, сплошные кривые
представляют собой линии уровня, кривые наискорейшего спуска обозначены
пунктиром, а стрелки на них указывают направление убывания функции <р.
Поэтому если положить
и z-z^re19,	(3.215)
то.	... < ,
J-* ,	-	Л(г)^.Л(^)4-КИввМ*+*’в)=ф-|-4ф,
или 	л
Ф ~ Фо 4~ Krm cos (% 4- т0), Ф == ф0 +	$1в (% + тФ> (3.216)
где <ра и фо представляют собой значения функций <р и ф в седло-
вой точке. Таким образом, линии уровня ф = <р0, проходящие
через седловую точку, приближенно описываются уравнением
cos (х 4- щ0) — 0, или х 4-4- 4“) л, (3.217)
где п = 1, 2, 3,	2т. Уравнение (3.217) дает нам 2т линий
•. уровня функций ф, задаваемых аргументами 0 —	4" 4") ” “
.	—1}!т. Эти линии делят окрестность точки z0 на т «холмов»
и т «ложбин». ’
'. - Точно так же из второго из уравнений (3.216) следует, что
линии постоянной фазы ф = ф0 приближенно задаются уравне-
--<•* кием	'	'
* .	' sin (х 4- от0) 0, или х 4- т& пл, (3.218)
где n = I, 2, 3, ..., 2т. Уравнение (3.218) описывает 2т кри-
. вых, т из которых являются линиями йаискорейшего спуска,
а другие т — линиями нанскорейшего подъема. _	.
В самом простом, случае, когда седловая точка имеет порядок,
равный ДЙум, существуют две линии наиекорейшего спуска и две
линии наискорейшего подъема (рис. 3.8). Кроме того, суще-
3.5. Метод наискорейшего спуска	101
Кствуют четыре линии уровня, разделяющие окрестность седло-	’I
	вой точки на два «долма» и две «ложбины». В случае седловой	1
	точки третьего порядка имеется, шесть линий уровня, разделяю-
В щих окрестность седловой точки на три «холма» и три «ложбины».
К Кроме того, через эти «ложбины» проходят трн линии наискорей- ’
К шего спуска, а через «холмы» — трн линии наискорейшего подъ- 4 |
К-ема (рнс. 3.9).	ГД
К Проведённый анализ показывает, что эффективным методом
i' построения асимптотических разложений для интегралов по кой- -
В турам, концевые Точки которых располагаются в двух различных 4
в «ложбинах», является метод наискорейшего спуска, развитый s
I Риманом н Дебаем. Идея этого метода заключается в деформации *
контура интегрирования С в некоторый новый контур С', удов-
| летворяющий следующим условиям:	.
г 1. Контур С'проходит через седловую точку (т. е. через нуль
Г функции h' (г)).
L 2. Мнимая часть ф функции h (г) на этом контуре должна быть
I постоянна.	'
I 3. Контур С' представляет собой кривую наискорейшего,
спуска.
I Если по условию задачи деформированный контур проходит
I более чем через одну седловую точку, то каждая из них может :
| дать свой вклад в асимптотику интеграла, причем основной вклад	- :
г вносится точкой, соответствующей наибольшему значению функ- J
F ции ф. Если же производная h’ (?) не обращается в нуль, то кон- . .
с тур интегрирования С выбирают таким образом, чтобы удовлет-
| Ворнть ^второму и третьему из перечисленных выше условий. ,	*
( Ниже метод наискорейшего спуска иллюстрируется тремя,
L типичными примерами.	-	 	*
Рнс. 3.9. Топография поверхности <р = Re й(г) вблизи седловой точки третьего
порядка дли случая % = 0. ^Долины» на рисунке заштрихованы, сплошные, кри-
вые представляют собой линии уровня, кривые наискорейшего спуска обозна-
чены пунктиром, а стрелки на них указывают направление возрастания функ-
ции <р.
102 ;	, Гл. 3. Интегралы
Пример 1
В качестве первого примера рассмотрим следующее интеграль-
ное представление функции Бесселя первого рода нулевого по-
рядка:
J0(a) = ~ J-p==-dz приа»1. (3.219)
Интегрирование по частям в этом случае не дает никаких ре-
зультатов, поскольку разбиение на множители
и — е‘аг,	dv = (.l-z?)-1/2dz
приводит к разложению, не имеющему асимптотического харак-
тера, а разбиение
M = (l-zT‘/2, dv = etnzdz
приводят к выражениям, содержащим особенности в точках
Z == Ч~ 1.
Для того чтобы найти приближенное "выражение для Уо (а)
при больших а с помощью метода наискорейшего спуска, дефор-
мируем Контур интегрирования в линию постоянной фазы. От-
метим, чтб h (z) = iz, так что фаза ф при z = 1 равна 1, а при
z = —1 она оказывается равной —1. Таким образом, контур
интегрирования ие удается деформировать непрерывным обра-
зом в единый контур, вдоль которого фаза ф оставалась бы по-
стоянной. Вместе с тем существует возможность деформировать
его в контур, изображенный на рис. 3.10 и состоящий из Трех
отрезков прямых: отрезка Сх, соединяющего точки —1 и —Г +
+ гК, отрезка С2, соединяющего точки —1 + iY и 1 + IY, и,
Рис. 3.10. Контур интегрирования для вычисления интеграла (3.219).
$.6. Метод наискорейшёго сЛуеКй
ИЗ
наконец, отрезка С3, соединяющего точки 1 + i Y и +1. Согласно
теореме Коши (3.169), имеем
4 1
f »iaz	г рмг
f Л...^ dz = Г dz. (3.220)
J V 1 _ z2 J 1< 1 — z2
C.+G+C,	-1 v
Строго говоря, контур следует деформировать так, как показано
на рис. 3.10 пунктирными линиями, с тем чтобы на него не по-
падали точки ветвления подынтегральной функции х = ±1.
Однако в пределе, при р'-> 0, интеграл по такому криволинейному
(т. е. с обходом углов) контуру стремится к интегралу по кон-
туру, состоящему из прямолинейных отрезков. Поэтому в даль-
нейшем мы можем не принимать во внимание наличие точек ветв-
ления на контуре интегрирования. При У<-> оо интеграл по участ-
ку Са стремится к нулю, поскольку в этом случае подынтеграль-
ная функция также стремится к нулю, причем равномерно отно-
сительно х = Re г. Следовательно,
—l+Zoo	г	1
J0(a) = — f	dz+ — I	(3.221)
0V ’ Л J Kl—г2 я J V\— Z2	v
— 1	1+foo
Используя подстановку z — —1 + iy в первом интеграле и
г — 1 + iy во втором, пёрепишем (3.221) в виде
я J У 2iy + у2 я J У—2iy 4- у2
ИЛИ
J0(a) = f у-^ (1-4- iy^2 e^dy-
v о
00
(3.222)
Интегралы в йравой части (3.222) представляют собой интегралы
Лапласа, и поэтому основной вклад в их асимптотику при a -► оо
вносит только точка у = 0. Таким образом, мы можем восполь-
зоваться леммой Ватсона, раскладывая предэкспоненциальные
множители, входящие в, состав подынтегральной функции, в ряд
при малых у и интегрируя полученный результат почленно.
При этом главный член асимптотического разложения Jo (a)
оказывается равным
»a+Zn/4	1а—1пЦ ?
•^°(a)---—J уг^е-чdy +	J y-‘/2e-“^dy.
'о	. о
\\'^Л'-	' /‘ -.	' -	'•	v" -•
tO4	Гл . 3. Интегралы
С помощью подстановки ay ~ t полученное выражение можно
привести к виду
СО
J0(a) ~^X-[e-‘“+‘^4 + e«6-i«/4] j	(3.223)
Окончательно, используя формулу (3.121) ^тождество
(е‘в + е"‘е) = 2 cos 0,
перепишем асимптотическое представление (3.223) в следующем
виде:
J0(a) ~ cos -----------j-11) при а->оо. (3.224)
Пример 2
В качестве второго примера рассмотрим интеграл Эйри •
* Ai (a) = j cos (-g- s3 + as) ds	(3.225)
о
В случаев » 1, Для того чтобы преобразовать (3.225) в интеграл,
имеющий форму (3.199), введем преобразование s — a1/2z. К ре-
зультате получим
,	? Ai(a) = -^-J cos [a3/2(4~ z34-z) J dz =*
о
1/2
. = ±_.j [gia3/2 (г3/з+г) + g-ia.3/2 (z3/3+z)j	=
0
00	00
=e««3/2dz +[ e-‘“3/2dz =
4л J	2л J
0 .	0
90	——90
= f gZa3/2P/3^)dz_^i [ ^/2(^/3+.)^
2л J	2л J
о.	о
.откуда
Ai (a) = Г eia3/2 (г3/з+г) dz.
' ХЛ J •
(3.226)
Интегрирование по частям дает тривиальный результат Ai (a) =
О’в-1 4- 0-a-’ + ..., поскольку, как будет показано ниже,
в асимптотическое разложение входит экспоненциальный мно-
житель, который стремится к нулю быстрее, чем любая сте-
пень а-1.
? Рис. 3.11. Кривые постоянной фазы (включая траектории нанскорейшего спуска),
< проходящие через седловые точки, для функции Эйри. Стрелки на рис. ука-
«	зывают направление, в котором функция Re ft(z) убывает.
Для того чтобы найти асимптотическое представление фунК-
? ции Ai (а), воспользуемся методом наискорейшего спуска. В дан-
; ном случае
(	h(г) = i (-j-z3 + г) и h' (z)—i(z2 4-1),
i так что седловые точки, т. е. нули производной h' (г), суть точки
i г = В этих точках
'г	h(±i) ~ ii 0 == ~F »
F и, следовательно, Imft(±i) =0. Полагая теперь в выражении
I для Л(г) z = х + iy, имеем
I /i(z)==f [4'(х+^)3+х+1^ ]=
J	<3-227)
Поскольку в седловых точках Im h ' = 0, то уравнение линий
i; наискорейшего спуска, проходящих через эти точки, получается
J из условия Im h = 0. В Соответствии с формулой (3.227) это
; уравнение имеет вид	;
I	jc(-Lx*-fA+l)==O.	(3.228)

V ’ • -V-^
106	Гл. 3. Интегралы
Уравнение (3.228) представляет собой кубическое уравнение,
определяющее три кривые иаискорейшего спуска: мнимую ось
х — 0 и две ветви гиперболы,
-^-х2-у2 + 1=0.	(3.229)
Эти линии изображены на рис. 3.11, причем стрелки на кривых
указывают направление, в котором убывает функция Re h (z).
Таким образом, для того чтобы применить метод наискорейшего
рпуска, деформируем исходный контур интегрирования в кон-
тур Съ который:
;	1) проходит через седловую точку z = i,
2) представляет собой кривую постоянной фазы,
3) является линией наискорейшего спуска из седловой точки.
Требуемая деформация вполне осуществима, поскольку в обла-
стях, расположенных между исходным и деформированным кон-
туром, подынтегральная функция затухает экспоненциально при
z—* оо. Поэтому мы можем заменить интеграл (3.226) на экви-
валентный ему интеграл
1/2
7	 А1(а)=4^-1е/“3/2(г3/з+г)с(2-	(3.230)
4	с,
На контуре Сх выполняется уравнение (3.229), и, значит, х2 —
3 (у2 — 1), так что соотношение (3.227) можно записать в виде
h(z) = y (2— -|-у2) при уг&1.	(3.231)
Кроме того, функция h (z) имеет максимум при г = I (т. е. при
у «=• 1). Следовательно, интеграл в формуле (3.230) представляет
собой обобщенный интеграл Лапласа, и его асимптотическое пред-
ставление может быть получено с помощью леммы Ватсона.
Для этого введем подстановку	Й
а3/% (z) = /аз/2 (= a»/2h щ _ т2 ----------1_ аз/2 _ т2 ^.232)
Тогда
za3'2(z2+ l)dz= — 2т dr,	(3.233)
и интеграл (3.230) принимает вид
.	(3 234)
Далее, нам нужно разложить функцию [z2 (т) + 1 ]-1 в ряд при
малых т, а для этого необходимо построить разложение по сте-
рецям т самой функции z (т). С этой целью разложим левую часть
3.S, Метод маискорейшего спуска	'	107
(3.232) в' ряд Тейлора по степеням (г — i), в результате чего
получим
(г_1)2__^_цг_ f-)3==a-j/2T2>	(3.235)	;
Решение этого уравнения при малых т имеет вид 1
z = i+ а-з/4+ •••.	(3.235а)
Таким образом,
(z2 + 1 )-1 = (2ia~3/4т)“' при т->0.	(3.236)
Подстановка выражения (3.236) в формулу (3.234) приводит к окон-
чательному асимптотическому представлению функции Ai (a):-. \
— (2/3) a3/2
A1 (a) ~ п₽и «- °0 • (3,237)
Нужно отметить, что строго следовать при интегрировании
вдоль всей линии йаискорейшего спуска оказывается не столь уж С
необходимым, поскольку асимптотическое разложение интегра-	J
лов типа (3.199) полностью определяется окрестностями точек,	”
где функция <р принимает наибольшее значение. Эти точки могут . 
быть как внутренними, так и концевыми точками отрезка инте-
грирования, причем если точка, в которой достигается макси-
мум ф, Является внутренней, то она необходимо будет и седло- -	'
вой. В данном примере для получения главного члена разложе-
ния оказывается вполне достаточным,строго следовать по кривой 1
наискорейшего спуска лишь на очень коротком ее участке*, про-
ходящем через седловую точку. Поскольку седловой точкой к
в нашем случае является точка z = i, то показатель экспоненты
в (3.230) можно приближенно представить как
 ia3/2 (-L z3 + г) = —Г а3/2 - «3/2 (г ~ О2 + * • • • (2.238)
При этом направление обхода контура интегрирования в точке
z — i должно выбираться с таким расчетом, чтобы величина	/
аз/2 (г — /)2 = т2 оказалась вещественной и положительной.	. \
Подставляя теперь (3.238) в интеграл (3.230) и заменяя в нем пре-
делы интегрирования соответственно на —оо и +<», вновь полу- х J
чаем для главного члена асимптотического разложения выра-
жение вида
е—(2/3)а3/2	“	<
Ai(«)~.....2^“ j e-^dx,
1 Разложение функции г (т) можно получить из уравнения (3.235) с по-
мощью метода-Неопределенных коэффициентов илн путем обращения степенных
рядов по формуле Бурмана—Лагранжа (см., например, Лаврентьев М. А.
и Шабат Б. В. Методы теории функций комплексного переменного. — М.: Наука,
1965). — Прим, перед.
♦
.- «ro^S^f
4 *> «.*%*« i,>«’5»	*	» f'	’	•» e	4	‘^'U t*	f
( '-^yi-.v'i' ‘/‘ .' 7-	".	, «
108	Гл, 3. Интегралы
или, с учетом формулы (3.25),
>	е— (2/3) а3/2
Ai(a)----2/£ai74 приа->оо.	(3.239)
Пример 3
В качестве последнего примера рассмотрим интеграл вида
I@)=J dz	(3.240)
о
при больших положительных а. Параметр 1 в данном случае
представляет собой комплексное число, не зависящее от а. Сед-
г"~ ловые точки задаются уравнением
' ’.	Л'(г) = -^-(ЗХг-г3)^0, или X-z2 = 0,
„ И, следовательно, они имеют координаты г ж ±^!/2. Если поло-
’ - •• Жить Й, *= о8 ехр (2iv), то координатами седловых точек будут
значения г = +оехр (iv). Поскольку вторая производная
(?) «= —6z в указанных точках отлична от нуля, то данные
. -седловые точки оказываются второго порядка.
Для того чтобы построить асимптотическое представление
интеграла (3.240), вновь воспользуемся свойством аналитич-
\ - ности подынтегральной функции и деформируем исхбдный Кон-
тур интегрирования в контур С, проходящий через начало коор-
{., динат и седловую точку г = о ехр (iv) и являющийся линией
Л наискорейшего спуска (рис. 3.12). Тогда интеграл (3.240) пере-
писывается в виде
'	/ (а) = j° е“ (3Xz~z,> dz = \^Wa-z>)dz.	(3.241)
- -	о	с
Как отмечалось выше, основной вклад в асимптотику инте-
Z трала I (а) вносит лишь небольшой отрезок С контура С, про-
; ходящий через седловую точку. Поэтому
7(a) — je“^2-z’>dz.	(3.242)
с
Поскольку точка г — о ехр (iv) является седловой, показатель
. экспоненты в интеграле (3.242) можно представить в виде' ряда
а (ЗХг-z8) = 2atfi^lv - 3aaeiv (г - ое'*)2 Ц-,	(3.243)
а направление С .выбрать таким образом, чтобы
3aaeiv (г — oe‘v)2 = т2,	(3.244)

О. Metnob наискорейшего спуска	id§
где т2 — вещественная и положительная величина. Таким обра-
' зом, контур интегрирования С будет задаваться параметрическим
j уравнением
«—(V/2
2_oe« = ±_t,	-	(3.245)
t Формула (3.245) показывает, что существуют два возможных
) направления интегрирования по контуру С, определяемые аргу-
ментами — v/2 и л — v/2. Для того чтобы выбрать здесь правиль-
/ ное направление, необходимо исследовать характер изменения
1 функций <р и ф на всей комплексной плоскости (рис. 3.12). Из
। рисунка ясно, что интегрирование следует проводить в направ-
я Ленин, определяемом аргументом —v/2. Таким образом, в фор-
муле (3.245) мы должны выбрать знак плюс, поскольку пред-
полагается, что х на контуре С изменяется от отрицательных
значений к положительным. При этом, согласно лемме Ватсона,
' в качестве пределов интегрирования можно выбрать соответ?-
1 ственно —оо и 4-оо. Подставляя теперь выражение (3.245) в ин-
г теграл (3.242), с учетом сделанных замечаний для главного члена
( асимптотики, исходного интеграла получаем выражение вида
i- iv 4- 2a<j3e3, v 1 (•
 г _-------------------------------------—- । е~т*^г,
V 3aa	J
f(a)
или ____________
I (а) ~ j/ехр [-------------Fiv + 2oKT?e3/v ] при а -> оо. (3.246)
Рис. 3.12. Деформированный контур интегрирования С для случая о = 1 и
v=22.5°.

у	. г- '	,	'	и
.«.Ш .	1.	1-	, 'ч *4.	‘	, I х_,,	^-^4^
/’4v'.;	:	" 4	^4. .	'-	.	,	- -	•'.
116	/л.З. Интегралы
Упражнения
3.1. Показать
что при е—> О
Г sine/ ,	1 . ,	1	.
_dZ_e__е. + _8б.
o
что при x—» O'
3.2. Показать,
x
-	f (-3/4e-id(^4xi/i_ 4 ж5/4 + '2
4	J	О	У
о
3-3. Показать, что при х->оо:
а)
-ж Г 1	11
е * Г —
L х
____	2!____3[
X» ’Г X®	X4
—i '-
' -Z—dt—-
tn J
п (п + 1) n (n + 1) (я + 2)
х2
х®
1 , 1-1 , (1-1)(1-2)
х Т- хъ т	“J5	1
3-4. Показать,, что при х—> оо
.	ОО
J dt ~ Л“х
X
3.5.	Показать, что при х—> оо
Г _й .. -	Г 1	1 .1-3	1-3-5 1
J е dt ~е	L 2х	22х® + 2®х®	2*х’ J '
X	1	,	•
3.6.	Рассмотреть полный' эллиптический интеграл второго рода
Я/2	'	-.
/ (m) = j Vl — msin20 d0.
о	'	'
Показать; что
, . ч 1 Г, 1	3	,	5	175	1
/(т) = -гя[1—4-т- — т2^ —т.__—
Сравнить полученный результат с результатами, приведенными в книге
Абрамовича и Стигаиа (1979).
3.7.	Показать, что при х —> со
Г cos/ Л /1,2!	4! \ .	/1	3! , 51 \
J —	— +T-^-)Slnx+(7-ir+-jr)cosx.
X
3.8.	Показать, что при х-* оо:
•	00
.	f COS / ..	1/х	.
a)	j ~yTdl ~ “j/T ^cos х~gsm х);
ОО	X
б)	[ --‘”2 dt ~ ' -J— (/ sin х g cos x).
J у t V x
Упражнения
,	1.	1-3-5 , 1-3-5-7-9 ,
- ~ 2х (2х)3 +	(2х)?	+ ’
1-3 , 1-3-5-7. ,
8	(2х)2 + (2х)4	+ '
3.9.	Показать, что при х —> оо:
. f cos (t — х) .	1	3!	5! .
a) j,- V._.
X
' J t	x x3 x3.
X	У
3.10.	Показать, что при х—>оо:
ОО
. Г	dt _	1
а' J	In / ~ xlnx ’
х
X	
, f dt ~ In X
' J t In In t In Inx
2
3.11.	Показать, что при x—> оо:
*> )"т^'~^-т^+тл
X
б)	j (?+i2)i/2 dt ~ a ?/2 + 4"x3/2;
0 \
x
• f dt x
J In t In X "
a
3.12.	Показать, что при х^->оо:
1
a)	j e~xt In (2 4-1) dt
о
1
6)	j e~xi In (1 4- t) dt ~
о
i
в)	j e~xi sin t dt-’
о
r)	[e-(x/0 + /4-x d/_ « .
112
Гл. 3. Интегралы
Я.
3.13.	Показать, что при (о—»со
f е J 1	1
j (О + х + Хр^О)	®	(03/2
3.14.	Показать, что при <о
оо:
а)
1
2<о ’
о
б)
In 2 .
2а> ’
да-
в)
Г- >•
< г)
*<
Й‘
о
j e-W(x«+2x) ln(1+x)dx~ _ll_;
б
7	(х«+2х)	Г —
J kjw " 2ш’
3.15. Показать, что при (о—>оо
’ *
j (х — а)ке~еЛ wdx----—
а
Где X > —1, b > а и h (х) > h (а).
3.18. Показать, что при ы—>оо:
[<вЛ' (a)Jx+‘
a) j е
1
e~~m In 2 .
2ю ’
б) J е ax*JI2\nxdx~S^.
1
3.17. Показать, что при <о-> оо
С е~шх‘ Г(“^)
а) I ‘"г:.;..;;;:.".'.л. dx-д—
J + X» 2®1/4
0
Г
б) I е-®* х5/2 In (1 + х) dx ~ -
о
3.18. Показать, что прн .ю—>оо:
a) j е-*х‘ In (2 + х2) dx
2<о9/4
—w
У я
2^'
Упражнения
11»
3.19. Показать, что при х—>оо:
J	2 Их
2
б) j е~х U + <‘/011П (1 + t) dt ~	е-2х ;
в) je х I* + In/ dt-----------------------------82х~ *
1
Г »-1,+|‘">1 д, г(т) .._ад
J Vi* — 1	2 К2х1/4
1,20. Показать, что при х—> оо:
3.21. Показать, что при а—> оо
\' а, (-«)=л j(4- ,> _«,) л ~	,i„ (4 «>«+4-«).
о
.22. Показать, что при а—> оо	.
’3.23. Показать, что при х—> оо
= vj C0S Sin 0) 40 ~ У "ST cos (* ~ “Г ") ‘
114	Гл. 3. Интегралы
3.24.	Показать, что при а->оо:
А	г (-i-') е‘я/6 ,п 2
- г) j ешг In (2 + /) dt ~ V ^)/з-.
А.. °
3.25.	Показать, что при х -» оо:
!'	Гт$^Г.л~/к Г*=
, «> »S”w—4J7= " - / S«'
<?:' . 1 4
•	Г '		..А
/ A) '/.W-±fZ—«—
3.2в. Показать, что при г -» оо
со
г (г) = J «’-’е-' dt~Y ^е~г'
о
3.27. Показать, что при х-> оо
— I
Упражнения
115
3.28.	Показать, что при <о—»оо
1
о
/Шш 'Т+-Г”
ш	ш
ОО
где V = — j е~‘ In t dt.
о
3.29.	Показать, что при а—»оо
/л fexp Г-------1- in 4- ае in/4
----------1-----8.........з-----------
J	“ 4
о
3.30.	Рассмотреть интегральное представление для полиномов Лежандра п-го
порядка
Рп (fi) — j ffi + /fi2 — 1 cos 0]" d6.
о
Показать, что
Рп (и) ~ при
3.31.	Рассмотреть функцию Эйри второго рода, определяемую интегралом
Bi (г) = V Г [в-Р/3+г/+ sin ("Г/3+г0]
о
а)	Используя метод Лапласа для оценки первого интеграла и метод
интегрирования по частям для второго, показать, что при г—> оо
J2/3) Z3/2
б)	Положить z — —а; далее, используя метод Лапласа для оценки первого
интеграла и метод стационарной фазы для второго, показать, что
в1Нг,~7^‘“‘(4-“м + т")-
* л" *> ,„'' ,ь'	"	"\ ' -Л	**>£’ 4
Глава 4
УРАВНЕНИЕ ДЮФФИНГА
Во многих случаях свободные колебания консервативных
систем с одной степенью свободы описываются уравнениями
Вида
-~£- + /(**) = 0, -	(4.1)
где f — некоторая нелинейная функция от х*; при этом член
-—^- определяет ускорение системы, а / (х*) — нелинейную
восстанавливающую силу. Пусть координата х* = xg определяет
положение равновесия системы; тогда ясно, что f (xg) = 0. Пред-
положим также, что функция f является аналитической’в точке
: х* = xg; тогда в окрестности этой точки ее можно разложить
в ряд Тейлора
/(х*)^^(х* -х0*)4-А2(х* - хо‘)2 4-А3(х‘ ^х0‘)3 4- . ., , (4.2)
,	1 W / .ч
kn ~
где
Таким образом, уравнение (4.1) можно представить в виде
'	-g. _|_ kl ix* д- xg) + k2 (X* - х0‘)2 + £ (х* - Хо*)3 + • • = 0. (4.3)
(И*
Уравнение (4.3) описывает Движение данной системы вблизи
, положения равновесия. Вводя для удобства преобразование
и* = х?xg, из (4.3) получаем
-^- + М* + ^в*2 + ^*3+--’=-0-	(4-4)
at*
, Большая часть этой главы посвящена исследованию специаль-
< ного вида уравнения (4.4), а именно уравнения
-g- + A1u* + A8M*8 = ft,	(4-5)
at*
где ki > 0, а k3 может быть как положительным, так и отрица-
тельным. Уравнение (4.5) называют обычно, уравнением Дюф-
финга. Как уже отмечалось в гл , 1,. прежде чем приступить к ре-
шению исходных уравйейий, следует принять за правило обя-
\	4.1. Прямое разло^ние	И?
|'зательно приводить их к безразмерному виду. С этой целью вы-
(берем некоторые характерные масштабы задачи —линейный U*
 и временной Т* — и положим
По правилу дифференцирования сложной функции имеем
d _ d _dt_	1 _d_	d2 _ I d3.	1
dt* dt dt*	T* dt ’	j/*2	j’*2 dt2 ’
при этом уравнение (4.5) преобразуется к виду
M + ^7’*2u + fesT*2f/*V=:0.	(4.6)
Выберем Т* таким образом, чтобы kxT*2 — 1, и положим е =	<
— k3T*2 U*2 = k3U*2lkr. Тогда (4.6) перепишется как	«
й + и + ей3 = 0.	(4.7)
Отметим, что параметр е представляет собой безразмерную вели- %
чину, которая характеризует степень нелинейности системы.
В качестве начальных условий примем, что
и(О) = хо, й(О) = хо.	(4.8)
Решение и нашей задачи является функцией независимой пере- , }
менной t и параметра е, что мы будем записывать как и = и (t; е),	\
отделяя параметр е от аргумента t точкой с запятой. В следую-
щем параграфе прямым разложением по параметру мы построим
приближенное решение задачи (4.7)—(4.8) при малых, но конец-
. ных е, однако это разложение не будет равномерно пригодным
для больших значений t. Далее, в § 4.2 мы получимточное решение
задачи, из которого будет видно, что частота системы <о является
функцией параметра е (т. е. степени нелинейности системы).
Это обстоятельство используется в § 4.3 для построения равно-
мерно'пригодного решения с помощью разложения функций и
и В'ряд по степеням параметра е — в этом состоит так назы-
ваемая Методика Линдштедта—Пуанкаре. В § 4.4 ряды для и
и сот подставляются непосредственно в прямое разложение реше-
ния, с дем чтобы сделать его равномерно пригодным — это так
называемый метод перенормировки. В § 4.5 мы описываем метод
многих масштабов, в §4.6 — метод вариации параметров (метод ?	-
специальных возмущений) и наконец в §4.7 — метод усредне- (
ниц.
4.L. .Прямое разложение
В случае е = 0 уравнение (4.7) сводится к уравнению
й + и = 0,	(4.9)
общее решение которого можцо записать в виде
«о = a0 cos (t + р0),	(4.10)
118	Гл. 4. Уравнение Дюффинга
где Оо, Ро — произвольные постоянные. При мрлом, но отличном
от нуля значении параметра е общее решение (4.7) уже нельзя
представить формулой (4.10), и к ней следует добавить некую
поправку. Будем искать эту поправку в виде ряда по степеням е,
т. е. положим
и (0 е) = и0 (0 4- еих (0 4- e2u2 (0 + e8us (0 + .... (4.11)
, Ограничим наше исследование нахождением лишь первого
поправочного члена ряда (4.11), т. е. будем искать приближенное
решение задачи в следующем виде:
и (0 е) == и0 (0 + еЫ1 (0 + О (в2).	(4.12)
При этом, поскольку мы сохраняем здесь лишь один поправоч-
ный член, будем называть разложение (4.12) разложением пер-
вого порядка.
Подставляя (4.12) в (4.7), имеем
Ко 4~	4“ О (в2) 4- «о 4- вК14- О (в2) 4~8 [и0 4~ suj 4“ 0 (е2)}3 = 0.
	> 	,	(4.13)
Используя биномиальную формулу для разложения последнего
члена, получаем
(«о 4- 8Wj 4“ О (в2)]3 = Ко 4~ Зко [eui 4* О (s2) J 4“ Зко [sui 4- О (в)) 4-
4-[еМ14-0(е2)13 = Ыо4-3еа?М14-0(82).
Далее, подставляя (4.14) в (4.13) и собирая члены с одинаковыми
сцепенями в, находим	>
• /	Ко 4- Ко 4- 8-(ki 4- «14- Ко) 4- О(е ) = 0.	(4.15)
Поскольку нас интересуют лишь члены порядка е, то в квадрат-
ных скобках в (4.13) необходимо учитывать лишь первое слагае-
, мое; это обстоятельство позволит нам существенно упростить
Дальнейшие выкладки. Полагая в (4-15) е “ 0, получаем
' ;	«о4~Ко = О-	(4.16)
При этом (4.15) принимает вид
e(ui4-ni4-Ko)4-0(e2) = 0-	(4.17)
Разделив иа е, имеем '
к\ 4-«! 4~ «0-4-О (s) — О’	(4.18)
’ откуда, полагая в (4.18) 8 = 0, находим
u14-ul4-^=0.	(4.19)
Сравнивая ($.16) и (4.19) с (4.15), можно заметить, чТо оба этих
соотношения легко получить, если просто приравнять нулю коэффи-
циенты при последовательных степенях е в выражении (4.15) —-

4.1. Прямое разложение
119
"i
{именно таким способом й находят уравнения для и0 и uv Заметим,
что уравнения (4.16) и (4.19) легко решаются последовательно. Дей-
ствительно, находя из (4.16) функцию и0, можно подставить ре-
зультат в уравнение (4.19) и затем найти функцию «х.
к Общее решение уравнения (4.16) можно представить в виде
и0 = а0 cos (t + Ро), _	(4.20)
{ где а0 и р0 — произвольные постоянные. Подставляя выражение
; для м0 в (4.19), получаем
Ui U\ = —а0 cos (t Po).	(4.21)
? Как известно, общее решение неоднородного уравнения (4.21)
складывается из общего решения соответствующего однородного
уравнения и некоторого частного решения (см. приложение Б).
{Для того чтобы найти это частное решение, разложим неоднород-
ность, в правой частщ_(4.21) в ряд Фурье, используя тригономе-
трическое тождество (формула (А. 18))
!	cos3 0 — cos 30 + Л-cos 0,
4	1 4'
{и перепишем (4.21) в виде
и\ Н- Й1 = —QqCos (/ -|- Ро) —га30cos (3/ -|- ЗРо).
Решение же соответствующего однородного уравнения
(представить как
|	«10дн = «1 cos (/ -)- РО,
:где ах и рх — также произвольные постоянные. В силу
{ности (4.22) частное решение этого неодцородного уравнения может
•быть представлено в виде суммы двух частных решений, соот-
ветствующих каждому из слагаемых неоднородности в правой
Участи (4.22). Таким образом, нам остается найти частные решения
’следующих двух уравнений:
(	г W1 -|- U\ —-------Oq cos (t -|- Ро),
{	Ui -|- ti\ =-OqCos (3/-|-ЗРо).	(4.25)
[астйым решением уравнения (4.24) является функция вида (фор-
улы (Б. 75) и (Б. 76))
“Части = — “Г а0* Sln (* + Ро)’
частным решением уравнения (4.25) — функция
улы (Б. 68) и (Б. 69))
“'части = 12 а° C0S
(4.22)
можно
(4.23)
лцней-
(4.24)
(4.&)
вида (фор-
(4.27)
..


й
¥<я

120	Гл. 4. Уравнение Дюффинга
Тогда, в силу принципа суперпозиции, для частного решения (4.22)
имеем
“’части -----1"Sln“Ь Ро) + "зЗ" cos (3Z + ЗРо) (4.28)
и, следовательно, его общее решение запишется как
щ = at cos (/• 4- 0,)	о*/ sin <Z +	+ i °» cos (3/ +	• (4-29)
Подставляя теперь выражения для u0 и их из (4.^0) й (4.29) соот-
> ветствейно в разложение (4.12), для общего решения уравне-
ния (4.7) получаем следующее -разложение первого порядка:
и Ц= а0cos(I + ро) 4- е jfl! cos (t 4- Pi) —§-c^t sin (/ 4 Po) 4
4-	$ cos (3/ + 3po)] 4- • • •,	(4.30)
где a0, аъ ро и px — некоторые произвольные постоянные. Таким
образом, начав с уравнения второго порядка, для которого ста-
вятся два начальных условия, мы в конце концов получили
четыре произвольные постоянные. Однако при этом оказывается,
что постоянные 4о> До До и рх связаны между собой и для их на-
хождения будет вполне достаточно двух начальных условий (4.8).
Действительно, подставляя разложение (4.30) в условия (4.8),
получаем
Хр = до cos р0 4* е (aiCosPi4--^-£4cos3Po)4- ••• > (4.31)
Xq~—др sin Ро — е	sltiPi 4—g- <*о 810 Ро 4" "gg" Op sin Зрр^ 4 • • • •
-	(4.32)
Перенося теперь в соотношениях (4.31) и (4.32) все. члены в одну
сторону и приравнивая нулю коэффициенты при, ’одинаковых
степенях е, или, что то же самое, непосредственно приравнивая
. коэффициенты при одинаковых степенях в, находим
при в0:
х0 — а0 cos рв,	(4.33)
х0 = —Оо sin р9;	(4.34)
при е1:	-
aiCosPi = —j4aoCOs3Pp,	(4.35)
4 sin Pi =---—a|sinPp-v 4-flpSin Зр0. (4.86)
Возводя (4.33) и (4.34) в квадрат и складывая, имеем
Тр -j- Хр == do cos2 Ро 4" Oq sin2 Ро — Op,
или
‘ '
4.7. Прямое разложение
121 '
и
(4.37)
вели-
(4.38)
(4.39)
. ao^C^ + xl)172.
Аналогичным образом из (4.33) и (4.34) можно найти
чину 0о
а	.	Хп	Хл
0О - - arcsin +	/2 - arccos + ^t/2 .
Далее, из 14.35)—(4.36) получаем
— -gg- fl® [cos2 30о 4* 9 (sin 30o 4- 4 sin 0O)2J / ,
. 3e®(4sin0O + sin 30n)	( a®cos30o\
0r = - arcsin-V 	i = arccos	0 j • (4.40)
Таким образом, вычислив постоянные «о и 0О по формулам (4.37)—
(4.38), постоянные аг и 01 можно найти по формулам (4.39)—(4.40)..
Возвращаясь вновь к разложению (4.30), заметим, что
a® cos (t 4- 0о) + ea! cos (t 4- 0i) =
= cos t cos 0o — a® sin t sin 0Q 4- cos t cos 0t—
—	вах sin t sin 0г = (a^ cos 0® 4- eaj cos 0X) cos t —
—	(<2o sin 0O 4- Ra1 sin 0i) sin t = a cos t cos 0
— a sin t sin 0 =a cos (t + 0),
a cos 0 — a® cos 0O 4~ eai cos 0i,
a sin 0 = Oo sin 0o + eai s*n 0i-
При этом из (4.42), (4.43) следует, что
fl® — а 4- О (в), 0о = 0 + О (в).
(4.41)
(4.42)
где
(4.43)

V4.!

ь’
3
(4.44)
Воспользовавшись соотношениями (4.41) и (4.44), перепишем (4.30)
в виде
и = a cos (/ + 0) 4-61-ffl + О (в)]31 sin {/ + 0 + О (в)] 4-


-4- [а 4- 0(e)]8 cos
откуда	.	-
и = acos«4- 0) 4- во3 £—slii(t 4- 0) + cos(3/ 4- 30)J 4- • • •.
(4.45)
Отметим, что это решение может быть получено непосредственно
из. уравнений (4.16) и (4.19) следующим образом. Выбирая реше-
ние (4.16) в виде	>
-	(4.46)
4
Uq = a cos (t + 0),


122	Гл. 4. Уравнение Дюффинга
перепишем уравнение (4.19) как
+ = — a8cos3(/ + ₽) =------|-a8cos(f+0) —
— -La8cos(3/ + 30).	(4.47)
Далее, при исследовании уравнения (4.47) ограничимся лишь
нахождением его частного решения, т. е. представим решение
этого уравнения в виде
«1 =а---Л sin (t + 0) + a3 cos (3/ + 30).	(4.48)
Подставив теперь выражения для и0 и из (4.46) и (4.48) в (4.12),
сразу получим разложение (4.45). Итак, при решении задач
подобного типа существуют две возможности. В одном случае при
- нахождении членов заданного порядка в них можно включать
соответствующее однородное решение, считая появляющиеся при
этом произвольные постоянные не зависящими от 8. При другом
подходе решения соответствующих однородных уравнений не
учитываются в членах всех порядков, за исключением первого,
но при этом произвольные постоянные считаются функциями от 8.
В этой книге мы будем пользоваться в основном вторым из опи-
санных здесь способов.
Возвращаясь вновь й разложению (4.45), находим, что в пер-
вом приближении искомое решение ^записывается как
- J	и = a cos (t -р- 0),
а первая поправка к этому решению есть
---------------1- a3&t sin (/ + 0) ч/за3 cos (3/ + 30).
Отметим, что поправочный член будет мал, как это н предпола-
гается . заранее, только тогда, когда произведение в/ мало по
сравнению с единицей. В случае если величина в/ имеет порядок
О (1), то член, относительно которого предполагается, что он
должен быть малой поправкой, оказывается того же порядка,
что и главный Член разложения. Если же е/ > О (1), то наша
«малая поправка» может оказаться даже больше главного член?
разложения. Поэтому прямое разложение (4.45) будет применимо
только для таких времён 7, при которых &t < О (1), т. е. для
t <О(е-1). Таким образом, можно утверждать, что подобные
разложения являются неравномерными по t, поскольку при боль-
* ших временах 7 их справедливость явно нарушается, и они ока-
зываются непригодными для использования — именно поэтому
мы будем называть такие разложения «медленными» разложениями.
Причина непригодности прямого разложения (4.45) заключается
в наличии члена t sin (t + 0), т. е. произведения алгебраической
4.2. Точное решение
123
V . ' "	i, -	г*”’	-‘-l?'.-.' чу,;
(линейной) и тригонометрической функций. В астрономической
литературе такие члены принято называть вековыми, или секу-
 лярными1), членами. Этим названием мы обязаны тому обстоя-
:тельству, что в астрономических приложениях величина в ока-
зывается обычно крайне малой, так что произведение st начинает
играть заметную роль в расчетах лишь по истечении очень ‘боль’-
г шого промежутка времени, например порядка столетия. Итак,.
: для того, чтобы данное разложение было равномерно пригодным .
= по t, в ием должны отсутствовать секулярные слагаемые. С тем,
чтобы выяснить, откуда же берутся такого рода члены, в следую-
[ щем параграфе мы построим и исследуем точное решение нашей
Ьзадачи, а в дальнейших параграфах опишем методы, позволяю-
; щие избежать появления секулярных членов и, следовательно,
1 дающие возможность получать равномерно пригодные разло-
жения.
г 4.2. Точное решение	.	1 ’ ? ’	(
’ Уравнение,,(.4.7) относится к классу' дифференциальных урав-
' иений '.второго порядка, -у которых отсутствует первая производ-
? ная. Такие уравнения легко могут быть проинтегрированы под-
£ стаиовкой 8) й = v, причем v рассматривается как новая неиз-
Е вестная функция аргумента и. Прн этом.-имеем
.._ . __ dv __ dv du dv
f,	.W ° dt du dt V du ’
i так что уравнение (4.7) приобретает вид
’ - °^ + ы + 8м3==0- •
(4.49)
(4,50)
Разделяя переменные, получаем
г	v dv = —(и + ем3) du, .	(4.51)
, что после интегрирования дает
-±-v2 = h -	+	— F(u),	(4.52)
где h — постоянная интегрирования. Так как v — й, то вели-
чина v2 оказывается пропорциональной кинетической энергии
.системы, а поскольку сумма и + su2 определяет собой восстанав-
ливающую силу, то выражение
F (и) = j (и + ей3) du = и2 + -$-еи*
г х) От французского- слова siScle—век, столетие.
8) Здесь более существенно то, что t входит в2(4.7) только через и. —
Прим. ред.
134	Гл. 4. Уравнение Дюффинга
оказывается пропорцциоальным потенциальной энергии, и, сле-
довательно, величина h будет определять собой полную энергию
нашей системы. При данном h. соотношение (4.52) представляет
собой некоторый интеграл исходного уравнения в плоскости uv,
называемой фазовой плоскостью. Этот интеграл можно исполь-
зовать для описания качественных характеристик движения
системы,
.’ Прежде чем приступить к построению на фазовой плоскости
отдельных интегральных кривых, проанализируем характер кри-
вей F (и), представленной на рис. 4.1. При в > О функция F (и)
имеет одну стационарную точку, а именно и — 0, которая соот-
ветствует минимуму функции F (и). С другой стороны, при 8 < О
у функции F (и) кроме и — 0 появляются стационарные точки
вида и ±Д|-1/2: первая из них- соответствует минимуму
F(u), в то время как две другие — Максимуму F (и). Три гори-
зонтальные линии, показанные на рис. 4.1, отвечают различным
значениям й. Из соотношения (4.52) также следует, что
v^±f2tf^F(u)}l/2.	... . (4.53)
Таким Образом, действительные значения о, а следовательно,
и реальные движения системы будут иметь место тогда и только
тогда, когда h F (и). Кроме того, эти движения будут-сим-
метричными относительно оси и. Наконец, поскольку й — v,
то при возрастании t Мы будем двигаться вдоль интегральной
кривой в отрицательном направлении, Т. е. обходя ее по часовой
стрелке.
В случае в > 0 реальные движения имеют место только при
й 2г й0 = 0. Если й = йр, то интегральная кривая вырождается
в точку, которая в этом случае называется центром,.. Если же
й > йр, то данная интегральная кривая будет представлять собой
замкнутую траекторию, соответствующую периодическому дви-
жгнйю системы. Таким образом, в указанной ситуации все воз-
можные движения Системы являются периодическими.
В случае е <0 реальные движения существуют при всех
значениях й. Из рис. 4.1, б видно, что при й = ho интегральная
кривая состоит из начала координат, т. е. центра, и Двух траек-
торий с ветвями, обращенными вправо и влево. Дри й — Jh ин-
тегральная кривая состоит из двух траекторий, проходящих
через точки а = |е|’/2, и = 0 и и — —]е|1/2, и = 0, которые
в этом случае называются седловыми точками (на рис. они обо-
значены буквой S) и соответствуют максимумам фУнкИии F (и).
При /этом сами траектории, проходящие через седловые точки,
обычно называют сепаратрисами. При й < й0 соответствующая
интегральная кривая состоит из двух отдельных траекторий,
обращенных ветвями влево и вправо. Наконец, при йо < й < hz
интегральная кривая состоит из трех отдельных траекторий —
замкнутой кривой, охватывающей начало крординат, н двух

.ветвей, открытых влево и вправо, т. е.^обращенных вершинами
к началу координат. Таким образом, периодические движения
Существуют только пр» h0 < Л < h2, а также при условии, что
Начальные данные ограничивают движение системы замкнутой
Ветвью соответствующей интегральной кривой.
У Обратимся теперь к интегрированию соотношения (4.52).
Используя начальные условия (4.8) и вспоминая, что- о — й,
{2в ,	Гл. 4. Уравнение Дюффинга ,
из (4.52) получаем
-^-Хо = ft — -у-*о +-^-е*о) »
откуда
ft — ~2~ i2o 4* ~2~ *о 4“ ~4~ ^0'	(4.54)
Поскольку v = й, то из (4.52) также следует, что
й = ± ^2Л — и2 — "5“eW*)12»	(4.55)
где знаки плюс и минус соответствуют движениям выше и ниже
оси и. После разделения переменных в (4.55) находим
' д°* Л' Л«’	14561
(2ft -ua —-^-eu4 j
причем интегрирование (4.56) дает
и •
Используем теперь полученное решение для исследования
периодических движений нашей системы. Из рис. 4.1 ясно, что
любая замкнутая траектория (соответствующая периодическому
движению системы) пересекает ось и в двух точках, координаты
которых обозначим через и = —х0 и и — х0 соответственно.
Подставляя значения и = ±х0 и и == Й ~ 0 в (4.54), получаем
Л =т	4~ *4“ ехо,
откуда
2ft—и2 —Ц-еи4 = х|Ч----8Хо—н?-------~еи4~
= (-«о - «2)(1 4- 4-	4- 4’ е“2) •	(*-58)
При этом (4.57) переписывается в виде,
и
Этот интеграл может быть приведен к стандартной эллиптической
форме с помощью подстановки
. < и = —хв cos 0.	' / (4.60)
ю < а ('4	"	
p 	'	i.,
4.2. Точное решение	127
Из (4.60) имеем du = х0 sin 9d9; кроме того, точки и = ±х0
соответствуют значениям 90	0, л. Таким образом, (4.59) можно
представить как
e
de
-K-g^C0S2e)
или
6
i f de
(4.61)
К1 — tn sin2 0 ’
где
(4.62)
m ?O+e*o)
Так как все замкнутые траектории симметричны относительно
осн и, то время, необходимое системе для ее перемещения из
’ точки и = —ха в точку и — +х0, составляет половину периода Т.
‘-Тогда из (4.61) следует, что "
‘ ‘	я
. ,	Т =	—
de
— m sin2 0
(4.63)
о
Поскольку величина интеграла в (4.63) одинакова как для про-
межутка f 0,nJ, так и для промежутка nJ, фор-
мулу (4.63) можно представить в виде
— m sin2 6
de
(4.64)
Интеграл в (4.64) называется полным эллиптическим интегралом
первого рода — значения его (как функции параметра т) -под-
робно протабулированы. Зависимость величины Т от пред-
ставлена в табл. 4.1. Из этой таблицы, так же как из формулы
* (4.64), видно, что период Т зависит от ел$ и, следовательно, яв-
ляется функцией нелинейности системы. Поскольку угловая
частота ® равна 2я/7’, то ясно, что она также будет зависеть от
степени нелинейности системы. Именно В этом кроется объясне-
ние того факта, почему Построенное нами прямое разложение
Доказывается несостоятельным — ведь в соответствии с видом
/разложения (4.45) угловая частота системы должна равняться
: единице независимо от характера ее нелинейности. Эго дает
возможность предположить, что всякое равномерно пригодное
/разложение должно учитывать зависимость угловой частоты от
--у- .	; ...- -7 
 128	Гл. 4. Уравнение Дюффинга
Таблица 4.1
Точные значения периода Т для периодических движений,
описываемых уравнением Дюффинга
т						
	0	0.02	0.04	0.06	0.08.	0.10
8Х$ Т	0 . 6.283	0.042 6.187	0.087 6.088	0.136 5.986	0.190 5.879	0.25 5.767
 •					Таблица 4.2	
Зависимость отношения Та/Т			от величины параметра ех^			
«4 т	0 .? 1000	. 0.042 1.0004	0.087 1.002	0.136 1.004	0.190 1.007	0.25 1.013
степени нелинеййости системы. Самым ранним, по времени под-
ходом, учитывающим это обстоятельство, явилась так назы-
ваемая методика Линдштедта-г-Пуанкарё, которая будет рас-
смотрена нами в следующем параграфе. Отметим также, что
- из формулы (4.62) при малом 8 следует малость величины т.
Тогда, разлагая в ряд подынтегральное выражение в (4.64) и
интегрируя почленно, имеем  . "	1
= ' ' ГI I
У1 4-еЛо |_
= 2я 0 — Tg- 8Хо 4- • •	1 Н—§- 8Хо 4“	,
откуда для двучленного приближения Та получаем
7\= 2л (1--|-его)-	(4.65)
А	’	A	v	< ,	5.	*	,
к	4.3. Методика Линдштедта—.Пуанкаре	129
К; 	/
в Таблица 4.2 показывает, что приближение Та оказывается весьма
I близким к точному значению Т: так, например, при ахо = 0,25
I ошибка составляет всего 1 ,3 %.
|> 4.3. Методика Линдштедта—Пуанкаре
I Как уже отмечалось в предыдущем параграфе, нарушение при-
I годности прямого разложения связано с тем, что с его помощью
| невозможно описать зависимость частоты системы от степени
| ее нелинейности. Таким образом, можно заранее утверждать, что
В любое разложение, не учитывающее эту зависимость, окажется
L несостоятельным. В настоящее время, однако, разработан целый
I ряд методов, позволяющих получать для подобного рода задач
[ равномерно пригодные разложения. Некоторые из этих методов
К мы обсудим в данной главе, начав прежде всего с рассмотрения
!i, методики Линдштедта—Пуанкаре.
L Для того чтобы выявить зависимость частоты от степени не-
I линейности системы, введем частоту <в непосредственно в диффе-
| ренциальное уравнение (4.7). С этой целью воспользуемся пре-
| образованием
I	т с= со/,	(4.66)
? где <в есть некоторая постоянная величина, определяемая только
| значениями параметра е. Тогда, переходя от аргумента i к новой
| независимой переменной т и используя правило дифференциро-
I вания сложной функции, получаем
I	d & 2
I	dt ~ dt dx , M dx ’ dt* ®	’
I в результате Чего уравнение (4.7) перепишется в виде
I	со2и" + и + ей3 = 0,	(4.67)
I где штрихи означают дифференцирование пц переменной т. Отме-
I тим, что фактическая частота системы со теперь явно входит в ис-
I ходное уравнение; правда, величины и и со остаются пока не
Г--определенными. Будем искать их в виде разложений по степе-
I иям в, т. е. положим	-
F	и = и0 (т) + &иг (т) + • • •,	(4.68)
со = 1+ £<ох + ... .	(4.69)
При этом первый член разложения для со представляет собой ча-
г стоту линейной системы, которая в нашем случае равна единице.
I Далее, исходя из требования, что разложение для функции и
| должно быть равномерным при всех т, в процессе вычислений
| можно определить все последующие поправки к частоте линейной
К системы.
I 5 Найфэ А. X.
. --------: _________________________________________ ,5.7..	................	, к-!
130	Гл. 4. Уравнение Дюффинга
.1  -  -  -. ' -    - - —	' - ......—.. . .	--- . .
Так, подстановка (4.68) и (4.69) в\ (4.67) дает
- (14-ЕСЙ14------)2 («о + еы'1 -}-) + u0-|-eui +
4" •_ • • е («о eui -|~ •••)== О,
откуда после выполнения всех необходимых действий имеем
Дд 4“ 2е<В1«о 4~	’ * 4~ 4~ eui 4~ * * * 4~ 8Но 4~ * * ’ —~ О,
или	"
Ц) 4- 4~ 8 (“1 4~ 4~ “о 4~ 2®|Uo) 4- • • • =. Q. (4.70)
Приравнивая нулю коэффициенты при е° и в1, получаем
“о 4- Но= 0,	(4.71)
- «1 4- Ui = — u3 — 2coiW0.	(4.72)
Общее решение уравнения (4.71) дается формулой
«о =• a cos (т 4- Р),	(4.73)
' где а и р—некоторые произвольные постоянные. При этом
уравнение (4.72) переписывается как
ui 4- “1 — — fl3 cos3 (т 4- Р) 4- 2(ot^cds (т 4" Р).
или
«1 4“ Ы1 — (2<dia - cos(t-4Р) — fl3 cos (Зт4-ЗР). (4.74)
Частное решение уравнения (4.74) (см. формулы (Б. 69) и (Б. 76))
можно представить в Виде
«1 = -5- ( 2<Bia-1- а3) т sin (т 4- Р) 4" -jg- flS cos (Зт 4- ЗР). (4:75)
Отметим, что данное частное решение для Hi содержит секуляр-
ный член, который делает разложение неравномерным. В то же
время, если исходить из требования равномерности искомого
' разложения для и, мы не должны допустить появления членов
подобного рода в соответствующих выражениях для ult иг, и3
и т. д. В противоположность методике построения прямого раз-
ложения (4.45), при которой эти члены не могли быть уничто-
жены (исключая случай а = 0, который приводил к тривиаль-
ному решению. и == 0), в данном случае мы можем подобрать
параметр «1 таким образом, чтобы исключить соответствующий
секулярный член. С этой целью положим коэффициент при нем
равным нулю, т. е. примем	-
2шга - ~^~а3 = 0;	(4.76)
ЦМ1! ijii m wjti i ainijniiyi i in i
4.3. Методика Линдштедта—Пуанкаре	131
при этом частное решение (4.75) приобретает вид
В	U1=-^a3cos(3T4-30).	(4.77)
Кк.
к. Если исключить тривиальный случай а = 0, то условие (4.76)
Е удовлетворяется при
I	®1=4а2-	(V8)
t Отметим также, что для получения условия (4.76), позволяю-
к.щего исключить секулярный член из выражения для ult нам
к вовсе нет необходимости строить в явном виде соответствующее
В частное решение, как это, например, делалось выше. Вместо этого
|. мы можем, исходя из вида неоднородности в правой части (4.74),
б которая собственно и определяет характер функции цх, просто
[ положить равным нулю коэффициент при cos.(t + Р), поскольку
I именно это слагаемое ответственно за появление секулярного
f члена в- «j.	~
I Подстановка (4.73) и (4.77) в (4.68) дает
Г	ы == a cos (т 4-Р) +-^-ea3cos(3r ЗР)-j-.	(4.79)
I Подставляя теперь значение (ох из (4.78) в разложение (4.69),
В имеем	•
I	4--1еа2+ ... .	(4.80)
[ Поскольку т = at, то разложение (4.79) можно переписать в виде
[	u==acos[(l 4--|-еа2)/4-Р] 4-
I	4-—ea’cos [3 (1 4--|-еаа)/ + Зр] 4-.... '	(4.81)
| Таким образом, разложение (4.81) будет равномерным разложе-
Вгнием первого порядка, поскольку секулярные члены в нем от-
g сутствуют, а поправка (т. е. член, пропорциональный е) оказы-
вается малой по сравнению с главным членом разложения.
I Сравним теперь период колебаний, получаемый с помощью
£ методики Линдштедта—Пуанкаре, с приближенным выраже-
| нием (4.65), полученным в предыдущем параграфе путем*разло-
I жения в ряд подынтегральной функции в точном решении задачи.
F Поскольку точка и = —х0 представляет собой пересечение замк-
| нутой траектории с осью х, то при и — —х0 имеем й = 0. Исполь-
| зуя эти соотношения в качестве начальных условий для раз-
I ложения (4.81), получаем
К	'	д , 1 ОД I	(4.82)
|	—x0 = acosP4-^2'£«8cos3P4-
I, 5*
I
'Я
.1
4
132	Гл. 4. Уравнение Дюффинга
откуда следует, что а2 = хо, поскольку 0 = 0 из условия й (0) =
== 0. При этом разложение (4.80) приобретает вид
< >	3	2 I
и — 1 4--g~ 8Xq 4“ ‘>	-
и поскольку Та — 2л/й, то, следовательно,
7в'=2л (1 +-|-ех02+ •••)"’ -2л (1 - -|"8Х02) + • • •, (4.83)
что оказывается в полном соответствии с формулой (4.65).
4.4. Метод перенормировки
-V	.	(
Вместо того чтобы вводить преобразование (4.66) в исходное
дифференциальное уравнение и строить новое разложение, как
это делалось в предыдущем параграфе (согласно методике Линд-
штедта—Пуанкаре), попытаемся теперь ввести это преобразование
непосредственно в прямое разложение (4.45). При этом из
(4.66) и (4.69) имеем
t ==(D-IT — (1 4*8®1 4* • • - )-1Т = Т(1 — efflj -|- • • .) = Т — 8<йхТ 4“ ‘ • • >
'	.(4.84)
так . что разложение (4.45) переписывается в виде
и — a cos (т 4- 0 — ехвхт +•••) +
4-	ва3 -g- (т — еа>хТ 4- • • •) + sin (т 4- 0 — ecojt 4-,,,) +
4-cos (Зт 4-30 — ЗешхТ 4-• ••)] 4“ • •' •	(4.85)
Разлагая косинусы и синусы в ряды Тейлора, получаем
cos (т 4- 0 — 8<BXT + • • •) =
= cos (т 4- 0) 4- вй)хТ sin (т 4* 0) + •  •,	(4.86а)
sin (т 4* 0 — ecoit 4- • • •) =
— sin (т 4- 0) 8йх^ cos (г 4* 0) + • • •,	(4.866)
cos (Зт 4* 30 — Звйх^ +  • •) =
— cos (Зт 4- 30) 4- ЗвйхТ sin (Зт 4- 30) 4- • • • •	(4.86в)
Используя эти разложения, можно представить (4.45) в виде
u = acos(T4-0)4-8 [(®ха —|-а8)т81п(т4-0) 4-
4--^-o8cos(3t4-30)] +	(4.87)
В противоположность методу построения прямого разложе-
ния, при котором не имелось возможности избавиться от секуляр-
4.5. Метод многих масштабов	133
(4.88)
г ного члена, если только не положить а = 0 (что соответствовало бы
Г тривиальному решению), мы ввели в разложение (4.87) новый
। параметр <bx, который можно выбрать та-ким образом, чтобы не
ь допустить появления секулярных членов. Так, полагая равным
|- нулю коэффициент при секулярном члене в (4.87), имеем
л.	з 3 п
Ь	(лга -—g- а3 ~ О
г	в результате чего (4.87) переходит в разложение	<:
I	и = a cos (т + 0) 4~ ей3 cos (Зт + 30) +	• • •.	(4.89)
К	Исключая из рассмотрения тривиальный случай а = 0,	мы	полу-	/
& ' чаем, что условие (4.88) удовлетворяется при <bx = -g- а2, в пол-
ном соответствии с значением (4.78), полученным по методу Линд-
Е штедта—Пуанкаре. Сравнивая разложения (4.89) и (4.79), легко - <
| видеть, что они тождественны, т. е. данный метод позволяет полу-
| чить то же самое разложение, что и методика Линдштедта—Пуан-
к каре. Описанный подход, при котором неравномерное прямое - s
I разложение (4.45) преобразуется в равномерное в результате
еС непосредственной подстановки в него преобразования (4.66)
Ь и (4.69), называют методом перенормировки.	'	|
К 4.5j Летод многих масштабов
|‘ Обратимся вновь к равномерному разложению (4.81), полу-
| ченному с помощью методики Линдштедта—Пуанкаре, и пере- S
| пишем-его в виде
I u = acos^ + 0 + -|-8ta2) +-^-ea3cos (3? + 30 + -g-eta2) + •••. -
I'	"	(4-90)
К Из разложения (4.90) видно, что мы не можем разделить функ-
циональную зависимость и от t и е, поскольку функция и затвисйт
в не только от этих аргументов в отдельности, но и от произве-
№ дения в/. Таким образом, вместо зависимости и = и (t; е) можно
писать и = и (t, st; е). Обращаясь теперь в’разложении (4.90) д
Р к членам более высокого порядка, легко видеть, что функция и
помимо прямой зависимости отТи е должна зависеть и от комбина-
вида st, s2t, s3t, .... Это означает, что можно записать
и (t; в) = й (/, st, s2t, s3t, ...; в),
и (f; е) = й (То, Тъ Та, Т3, ...; в),	(4.91) д
аргументы Тп определяются следующим образом:	'
Тв = t, 7\ = st, Tt = s*t, Т3 = s3t, ... .	(4.92)
а. дни
или
Б где
Ж;
134	Гл. 4. Уравнение Дюффинга
Отметим, что так как в является малым параметром, то ве-
личины Тп представляют собой разные временные масштабы
исходной задачи. Например, если в = 1/60, то изменения в мас-
штабе То могут быть охарактеризованы движением секундной
стрелки часов, изменения в масштабе 1\ определяются движением
их минутной стрелки, а изменения в масштабе Т2 связаны уже
с движением часовой стрелки. При этом, поскольку зависимость и
от t и в проявляется в различных масштабах времени, попытаемся
проследить за поведением функции и на разных временных шка-
лах.
Таким образом, вместо того, чтобы рассматривать и как функ-
цию аргумента t, мы будем определять ее как функцию пере-
менных То, Тъ Т2, ... С этой целью перейдем в исходном урав-
нении (4.7) от независимой переменной t к переменным То, Т1(
.... Используя правило дифференцирования сложной функции,
получаем
27=	+	+	’	(4-93)
d2 д2 . о д2 . , /о д2 ,	\ ,	,,
dt2 dT2Q +28ЗТвдТ1 +8 у дТадТ\ +	-.(4-94)
При этом уравнение (4.7) принимает вид
+ 2835^57 + * (2 «V +“ + “•+—= 0. (4.95)
Отметим, что в данном случае обыкновенное дифференциальное
уравнение (4.7) мы заменяем уравнением в частных производных
и тем самым, казалось бы, еще более усложняем задачу. Однако
практика использования данного метода показывает, что преиму-
щества подобного подхода оказываются гораздо более существен-
ными. При этом, как будет видно из последующих глав, данный
метод позволяет не только строить искомое равномерное разло-
жение, но и описывать разнообразные явления нелинейного ре-
зонанса, возникающие в исследуемой системе. 1
Будем искать приближенное решение уравнения (4.95) в виде
ы = Ц» (T’o, TltT 2, ...) + 8их (То, Ть Т2, ...) + • • •. (4.96)
Подстановка этого разложения в (4.95) дает
д2«0 , д2иг „	д»«0	.	.	। з ,	л /4
arf	28 дТо дТ1 + “° + е“1 + 8Ы0 Ч--- 0- (4-97)
J* tk1  ... 11114
 !
4.5.	Метод многих масштабов	13Й
Приравнивая нулю соответствующие коэффициенты при в0 и в1,
имеем ' .
^ + “•=0.	<498)
?г + “> = -2Ж^-“’'	<4">
S Общее решение уравнения (4.98) может быть представлено в виде
|	и0 ~а{Ти Тъ, ...)cos [То4- ₽.(?!, Т8, ...)!.	(4.100)
I Отметим, что в данном случае а и 0 оказываются не постоянными
F . величинами, а функциями медленных масштабов Тх, Т8,
поскольку ы0 представляет собой функцию То, Тъ 7\, ..., а ее
производные в (4.98) берутся по переменной То. На данной сту-
пени аппроксимации функциональная зависимость а и 0 от 7\, Тй,.'..
нам не известна н определяется на последующих этапах путем
исключения секулярных членов.
Подставляя теперь (4.100) в (4.99), получаем
+ ut = - 2 [а cos (То + 0)] - a3 cos3 (То + 0) =
;	=2^-sin(To + 0) + 2a^-cos(To + 0)-
Г	- -J- а3 cos (То + 0) - 4-а3 cos (ЗТ0 4- 30),
 или
. +2Дsln(T" + » + (2“Д--г°’)ав(7''>+Р>-
-4-a3cos(3To + 30).	(4.101)
Неоднородность в правой .части уравнения (4.101) служит источ-
ником секулярных членов для функции ut. В случае же равномер-
ного разложения подобного рода члены должны отсутствовать.
Этого можно добиться, приравняв нулю коэффициенты при
sin (То 4- 0) и cos (То 4- 0) в правой части (4.101), в результате
чего получаем
-^ = 0,	(4.102)
(4.103)
При этом частное решение уравнения (4.101) принимает вид
U1 = ^a3cos(3To4-30).	(4.Ю4)
136	Гл. 4. Уравнение Дюффинеа
Решение уравнения (4.102) есть функция а = а (Тъ, Т3, ...).
Тогда при а^О (4.103) можно переписать в виде уравнения
dTi ~ 8 и ’
решением которого будет функция
^=-§-а2Л + ₽о(Т8> Т5, ...).	(4.105)
Подставляя выражения для и0 и иг из (4.100) и (4.104) в разло-
жение (4.96), получаем
u = acos(T0 + ₽)+-^-ea3cos(3T0 + 3p)-f-... .	(4.106)
Подставляя теперь выражение для 0 из (4.105) в (4.106) и вспо-
, миная, что а — а (Т2, Т3, ...), находим
и = а(Т3, Т3, ...) cos [т0 + 4 Тз......) + Ро •••)] +
+ 4 ва3 (Т2, Ъ, ...) cos [ ЗТ0 + 4 Т’з. •  ) +
+ 3₽о(Т2, Т3, ...)] + ....	(4.107)
Если в разложении (4.107) ограничиться только выписанными
членами, то в рамках принятой точности функции а и 0О можно
считать постоянными. Действительно,
а(Т„ =	«Ч, ...) =
.	= а(0, 0, ...)	... =йр + О(в20,
	0о(Т2, Т3, ...)-0о(8% 82/, ...) =
= ₽0(0, 0, ...) + -^е«/₽о+ О(«80;
поэтому, заменяя а и 0О в (4.107) постоянными величинами а
и р0, мы имеем
и = d cos (То + 4	+ Ро") +
+ 4 ей3 cos (зТо + 4 Г1й2 + 3Р») + О (е2/),	(4.108)
|fc'	"	- Ь'
''	л
'	4.5. Метод многих масштабов	137
s или, после возвращения к исходной переменной t,
К'	'	4
I и = d cos (t + е/й2 -(- Ро) +
I	+	sda cos (3/ + е/d2 + Зр0) + О (ett), (4.109)
что полностью согласуется с разложением (4.90), полученным
Ь с помощью методики Линдштедта*—Пуанкаре или по методу пере-
Ц нормировки.
I Анализ формулы (4.109) показывает, что ошибка в ней будет
I иметь порядок О (1) и, следовательно, окажется порядка первого
I члена, если t = О (в-2). Таким образом, для значений t О (в-2)
I разложение (4.109) становится непригодным. Если же t = О (в-1),
| то ошибка будет иметь порядок в, т. е. окажется порядка второго
| члена разложения, и, следовательно, разложение, пригодное при
I t = О (в-1), должно включать в себя только первый член. Итак,
I для всех моментов времени вплоть до времен порядка г'1
|	u = dcos(t +Л-8/а2 + р0) +0(8).	-	(4.110)
t Это означает, что для того, чтобы построить равномерное разло-
К жение первого порядка, мы должны, не решая самого уравнения
к для «1, исключить из него члены, служащие источником секуляр-
| ных слагаемых, найдя тем самым только зависимость щ от Tj.
| Подобным же образом при построении равномерно пригодного
разложения первого порядка по методике Линдштедта—Пуанкаре
I или же с помощью метода перенормировки мы лишь исключали
I секулярные члены из уравнений для иг и тем самым определяли
I поправку Точно .так же при построении высших приближений
i мы полагаем
|	N—1
I-	Ur ЕЗД, Тъ ....Т^ + О^),	(4.111)
F	л=0
I т. е. если мы ищем разложение N-ro порядка, то должны учиты-
I вать масштабы Тв, Тъ .... TN, но не включать при этом в рас-
li. смотрение член порядка &N.
| В заключение этого параграфа обратимся к рассмотрению дру-
I гой формы решений для уравнений соответствующих приближе-
I ний, представив, в частности, решение уравнения (4.98) в комп-
| лексной форме. С этой целью воспользуемся .формулой (А.22)
р	- cos 0 = 4т(е‘в + е~,в)
Мша»	*


138	Гл. 4. Уравнение Пюффинга
и перепишем решение (4.ГО0) в виде
«о=4-а[е''<То+₽>+е“‘<Го+₽>] =4ае‘<л+₽) +4ае-,<7'”+₽,=
или
ий = Ае1Та\-Ае~11\	(4.112)
где А и А — комплексно-сопряженные величины и
A = ~aeip.	(4.113)
При этом в случае разложения первого порядка мы считаем А
функцией только переменной Тг.
~ Подставляя (4.112) в уравнение (4.99), имеем
^ + U1 = -2i^	+ 2t е~£Г" - (AeiT° + Ае~{Т^. (4.114)
дТо	1	1
Выполнив возведение в куб в последнем слагаемом правой части
уравнения (4.114) и собирая коэффициенты при соответствующих
экспонентах, получаем
SF + “* = - (2'^7 + ЗЛ’Л) е‘Г> + (2.	- З^Л)е-"- -
_ A3e3iT° - Л3е~3/7’°.	(4.115)
Ясно, что источником секулярных членов в частном решении
для служат именно слагаемые, пропорциональные ехр (t’T0)
и ехр (—iTo). Следовательно, для получения равномерно пригод-
ного разложения мы должны приравнять нулю каждый из коэф-
фициентов при этих экспонентах, т. е. положить
21-^- + ЗЛ2Л = 0,	(4.116)
011	1	4
21-^--ЗЛ2Л = 0.	(4.117)
Отметим еще раз, что для получения равномерно пригодного раз-
ложения первого порядка совершенно не обязательно решать
уравнение для и± — для этого вполне достаточно исключить из
уравнения (4.115) члены, порождающие в решении «х секулярные
слагаемые.
Сравнение (4.116) и (4.117) показывает, что эти уравнения,
поскольку они комплексно сопряжены между собой, не являются
независимыми. Следовательно, если удовлетворяется одно из
них, то другое будет выполняться автоматически. Для удобства
анализа уравнения (4.116) подставим в него величину Л из (4.113).
4.6. бариация произвольных постоянных
; При ЭТОМ получим
я(4-<-е'’ + т^“")+S-T -о,
или
1 * г»-а>е'’+тЛ'’=0. .
о! 1	оТ1 1 о
или
i<-<-+T«, = °-	(4.118)
Напомним теперь, что комплексное выражение равно нулю тогда
и только тогда, когда равны нулю его вещественная и мнимая
части. Поскольку а и 0 действительны, то, приравнивая нулю
вещественную и мнимую части равенства (4.118), имеем
 <4119)
а-~,--§-а3 = 0,	(4.120)
что полностью совпадает с соотношениями (4.102) и (4.103), полу-
ченными выше для случая, когда решение представлялось в дей-
ствительном виде. Сравнение вещественного и комплексного под-
ходов показывает, Что комплексное представление решений соот-
ветствующих уравнений оказывается более удобным. Именно
таким представлением мы будем часто пользоваться при даль-
нейшем изложений?
4.6. Вариация произвольных постоянных
В случае е = 0 решение уравнения (4.7) может быть представ-
лено в виде
?	и ~ a cos (t + 0),	(4.121)
; где а и 0 — некоторые произвольные постоянные. Кроме того,
\ из (4.121) следует, что
I	й = — a sin (t + 0). -	(4.122)
В случае 8	0 мы будем предполагать, что решение уравне-
Е ния (4.7) также описывается формулой (4.121), но при этом ве-
5 личины а и 0 являются функциями времени I. Иными словами,
мы рассматриваем формулу (4.121) как заданное преобразование
? переменной и (/) к переменным a (t) и 0 (/). Именно поэтому дан-
I ный подход обычно называют методом вариации произвольных
постоянных. Развивая эту идею, укажем, что в данном случае мы
имеем два уравнения, а именно уравнения (4;7) и (4.121) для трех
неизвестных функций и (/), a (t) и 0 (/), и, следовательно, можем
наложить на эти функции еще одно дополнительное условие
146	Гл. 4. Уравнение Йюффинёй
(т. е. ввести ^третье уравнение, их связывающее). Это, условие
может быть в достаточной степени произвольным, но обязательно
независимым от (4.7) и (4.121). Подобный произвол можно с успе-
хом использовать для получения простого и удобного преобра-
зования. С этой целью из всех возможных условий выберем ус-
ловие (4.122), предположив тем самым, что функции и и й имеют
тот же самый вид, что и для линейного случая. В результате мы
приходим к системе уравнений уже не второго, а первого порядка
относительно неизвестных функций a (i) и 0 (i).
Действительно, дифференцируя соотношение (4.121) по t
и учитывая, что а и 0 также являются функциями времени t,
имеем
" й = ~ a sin (/0)d cos (/+ 0) — а0 sin (<-}-0). (4.123)
Сравнивая (4.123) с (4.122), можно заметить, что
a cos (t -f- 0) — о0 sin (t 4- 0) = 0.	(4.124)
Дальнейшее дифференцирование (4.122) по t дает
й = — a cos (/4~ 0) — я sin (/4-0) — а0 cos (/4‘0)- (4.125)
Подставляя выражения для и и й из (4.121) ц ,(4.125)в уравне-
ние (4.7), находим
a sin (t 4- 0) 4- о0 cos (t 4“ ₽) = ®п8 cos3 (t 4- 0).	(4.126)
Соотношения (4.124) и (4.126) представляют собой систему
двух дифференциальных уравнений первого порядка относительно
й и 0. Эти уравнения можно еще более упростить, если умножить
первое из них на cos (t 4- 0), второе — на sin (t 4- 0) и резуль-
тат сложить; при этом, с учетам формулы (А.1), получаем
а. = еп3 sjn (t 4- 0) cos8 (t 4- 0).	(4.127)
Исключая теперь с помощью (4.127) величину а из уравнения
(4.124), находим
0 = ел2 cos4 (/ 4- 0),	(4.128)
если, конечно, а =/= 0. Таким образом, исходное дифференциаль-
ное уравнение второго порядка (4.7) относительно функции и (/)
мы заменили двумя уравнениями первого порядка (4.127) и (4.128)
относительно функций a (t) и 0 (/). Подчеркнем также, что при
выводе этих уравнений мы не пользовались никакими дополни-
тельными предположениями.
Из сравнения преобразованных уравнений (4.127) и (4.128)
с исходным уравнением (4.7) видно, что нелинейность преобра-
зованных уравнений оказывается более резко выраженной. При
этом, естественно, возникает вопрос, какова же ценность подоб-
ного преобразования. Ответ на этот вопрос зависит от величины
параметра е. Так, если е мало, то, как показано на рис. 4.2, глав-
ные части а и 0 меняются в зависимости от t медленнее, чем ис-
ходная функция «. Этот факт может быть с успехом использо-
4.7. Метод усреднения
141
Рис. 4.2. Зависимость величин а, 0 и и от времени t при а (0) = 1.5, 0 (0) =
= 0 и е = 0.05.
ван как при аналитическом решении, так и при численных рас-
четах. Аналитически он приводит к так называемому методу
усреднения, подробно описываемому в следующем параграфе;
при численном же анализе задачи исследование преобразованных
уравнений также оказывается более удобным, поскольку для их
решения можно выбрать существенно больший шаг интегриро-
вания. По этой причине астрономы используют метод вариации
произвольных постоянных для вывода уравнений, описывающих
параметры орбит небесных тел, после чего приступают к числен-
ному решению именно проварьированиых, а не исходных урав-
нений. При этом специалисты пр небесной механике называют
обычно подобный подход собственно «методом возмущений».
4.7. Метод усреднения
Воспользовавшись тригонометрическими тождествами
sin ф cos3 ф = ~ sin 2<р -j- -g- sin 4ф,
3	1	1
COS4 ф = -д- + -у COS 2ц> + -g- COS 4ф,
перепишем уравнения (4.127) и (4.128) в виде
а =-д-ео8 (2 sin 2ф-|- 81п4ф),	(4.129)
Р =еаг (34 cos 2ф	cos 4ф),	(4.130)
где положено ф = t + р. Так как —1 с sin пф < 1 и —1 <
с cos пф 1, то для любого ограниченного а получаем а —
— О (в) и р = О (е). Таким образом, при достаточно малом в
главные части аир оказываются медленно меняющимися функ-

US
Гл. 4. сравнение Дюффинга

циями времени (рис. 4.2). Это означает, что на интервале времени
длиной л они изменяются весьма незначительно и, следовательно,
в первом приближении на этом интервале их можно считать по-
стоянными.
Усредняя по интервалу [0, л] левые и правые части уравне-
ний (4.129) и (4.130), имеем
Л	л
-jj- j a dt = -^-e j а3 (2 sin2<p -J- sin4<p)d/, (4.131)
о	о
л	л
CQS 2<р cos 4<р) dt. (4.132)
,оо
Поскольку а и £ на интервале интегрирования [0, л] считаются
постоянными, то величины а, а и р в формулах (4.131) и (4.132)
можно вынести за знак интеграла, в результате чего получаем
Л
a	(2sin 2<р -J- sin4<p)cft,	(4.133)
о	)
Л -
Р =еа2 +-g^-ea2 J (4 cos 2<рcos 4<р)	(4.134)
°
Заменим теперь переменную интегрирования t на <р — t + Р;
тогда при условии постоянства Р на [0, л], dtp — dt и соотно-
шения (4.133) и (4.134) перепишутся в виде
а = -g^- еа3 j (2 sin 2<р + sin 4q>) dtp = .
. л+6.
= —g^~ ea3 ^cos 2q> -Ц- —cos 4<p) | = 0,	(4.135)’
Л+Р
’	3	1 f
P = -g- ea2 -g^- еа2 I (4 cos 2<p cos 4<p) dtp =
В
л-~3
=ea2ва2 2 sin 2<p.-j-sin 4<p )	= ea2. (4.136)
Описанная выше техника усреднения называется обычно мето-
дом Ван-дер-Поля или методом Крылова—Боголюбова.
Из соотношения (4.135) следует, что
а = а0 = const;	(4.137)
Упражнения	143
К далее, из (4.136) имеем
|	₽=4-ea»z+p<”	<4138)
 где ро — некоторая постоянная. Подставляя найденные значе-
I ния а и Р в (4.121), в первом приближении получаем
I	u = а0 cos 1 +еаоХ + Ро] г	(4.139)
| что полностью соответствует решениям, полученным по методике
i; Линдштедта—Пуанкаре, методу перенормировки и методу' мно-
Е:	гих масштабов.
I В заключение этого параграфа отметим, что соотношения (4.135)
В и (4.136) можно получить и без выполнения процедуры усредне-
I ния. В самом деле, правые части-уравнений (4.129) и (4.130)
I . представляют собой линейные комбинации быстро и медленно
I* меняющихся членов. При этом в первом приближении величина а
I в (4.129) определяется (равными нулю) медленно меняющимися
| членами в правой части этого равенства. Точно так же величина р
I в (4.130) в первом приближении определяется медленно меняю-
I щимися членами правой части, которые в свою очередь оказы-
I '	3 ,
I ваются равными еа.
| Упражнения
I 4.1. Используя метод перенормировки, преобразовать следующие разложения
| в равномерно пригодные:
I	а) и (t\ е) = a cos (о>0/ + 0) -j- e.a3t sin (о>в< + 6) + О (е2);
|	б) и (/; 8) = a cos (со0< - р 0) 4- е [ Л sin (со0£ -р 0) -р
| -Р (1 — а2) at cos (ci)of -р 0) ] -р О (в2).
г 4.2. Рассмотреть уравнение
|	й cooU = ей2и (8<^1).
I а) Построить двучленное прямое разложение решения и исследовать его
р равномерность.
К б) С помощью метода перенормировки сделать это разложение равномерно
| пригодным.
| в) Построить равномерно пригодное разложение первогоиторядка с помощью
I методики Линдштедта—Пуанкаре.
Is г) Используя метод многих масштабов, построить равномерно пригодное
| .разложение первого порядка:
t д) Используя метод усреднения, построить равномерно пригодное разло-
I жение первого порядка.
г 4.3. Рассмотреть уравнение	'
[	й + 4и + ви2й = 0.
| а) Построить двучленное прямое разложение решения и исследовать его
| равномерность.'
[ б) С помощью метода перенормировки сделать это разложение равномерна
I пригодным.

144	Гл.4. Уравнение Дюффинга
в)	Построить равномерно пригодное разложение первого порядка с по-
мощью методики Линдштедта—Пуанкаре.
г)	Используя метод многих масштабов, построить. равномерно пригодное
разложение первого порядка,
д)	Используя метод усреднения, построить равномерно пригодное разло-
жение первого порядка.
4.4.	Рассмотреть уравнение
а)	Построить двучленное прямое разложение решения н исследовать его
равномерность.
б)	С помощью метода перенормировки сделать это разложение равномерно
пригодным.
в)	Построить равномерно пригодное разложение первого порядка с по-
мощью методики Линдштедта—Пуанкаре.
г)	Используя метод многйх масштабов, построить равномерно пригодное
разложение первого порядка.
д)	ИспоЛьзуя метод усреднения, построить равномерно пригодное разло-
жение первого порядка.
4.5.	Рассмотреть уравнение
fi-|-(oow = ew5 (е<^1).
а) Построить двучленное прямое разложение и обсудить вопрос о его рав-
номерности.
• б) С помощью метода перенормировки сделать это разложение равномерно
пригодным.
в)	Построить равномерно пригодное разложение первого порядка с помощью
методики Линдштедта—Пуанкаре.
г)	Используя метод многих масштабов, построить равномерно пригодное
разложение первого порядка.
. д) Используя метод усреднения, построить равномерно пригодное разло-
жение первого порядка, используя метод усреднения.
4.6.	Движение математического маятника описывается уравнением
а
0 4- — sin 0 = 0.
а)	Разложить решение при малых 0, сохранив кубические члены. . 
б)	Построить равномерно пригодное разложение первого порядка при
малых, ио конечных 0.
4.7.	Рассмотреть уравнение
0 = Q2 sin 0cos0---f- sin 0.
К
а)	Разложить решение при малых 0, сохраини в разложении квадратичные
члены.
б)	Построить равномерно пригодное разложение первого порядка при ма-
лых, ио конечных 0.
4.8.	Движение точечной массы, перемещающейся по вращающейся параболе,
описывается уравнением
(1 + 4р2х2) х + Ах + 4р2х2х = 0,
где р н Л — некоторые константы. Построить равномерно пригодное разло-
жение первого порядка при малых, но конечных х,'
Упражнения
145<
4.9.	Рассмотреть уравнение
а)	Разложить решение при малых и, сохранив кубические члены.
б)	Построить равномерно пригодное разложение первого порядка при
малых, ио конечных и.
4.10.	Рассмотреть уравнение
(Р + г2 — 2г/ cos 0) 0 4- г/ sin 002 + gl sin 0=0,
где g, I н г — постоянные величины. Разложить при малых 0, сохранив ку-
бические' члены. Построить равномерно пригодное разложение первого порядка
при малых, но конечных 0.
4.11.	Рассмотреть уравнение
^/2+r202)0 + r2002 + gr0cos0 = O,
где г, lug — постоянные величины. Построить равномерно пригодное раз-
ложение первого порядка при малых, ио конечных 0.
4.12.	Рассмотреть уравнение	-
тх + kx (х2 + /2) ~1/2 рх2 + /2)1/2 —	/] = 0.
Построить равномерно пригодное разложение первого порядка при малых,
но конечных х.
4.13.	Разложить в ряд подынтегральное выражение в (4.64), сохраняя члены
порядка О (т2), н получить при этом разложение
Та ЛЦ. (1+ -lm+^-m2+... ).
]Л+ах2 \	, 4	64	'
Представить Та как функцию m в виде
та } = 2л 1 — 2m + -j-m +	+    )
и как функцию х0 в виде
Показать, что представляет собой более точное разложение, чем
сравнив их с протабулнрованным точным решением (4.64). Обратить внима-
ние, что можно получить нз с помощью преобразования Эйлера т =
2 (1 + ex2) ’
которое'часто расширяет область пригодности асимптотического
ряда.
Глава 5
(
ЛИНЕЙНЫЙ ОСЦИЛЛЯТОР С ЗАТУХАНИЕМ
В отличие от предыдущей главы, в которой рассматривались
консервативные системы, в этой главе мы рассмотрим системы
с затуханием. Для того чтобы свести к минимуму математические
выкладки, займемся исследованием простейшего уравнения для
системы с затуханием, а именно уравнения, описывающего сво-
бодные колебания частицы с массой т, связанной с жесткой опорой
посредством пружины с коэффициентом упругости k и успокои-
теля колебаний с коэффициентом затухания р (рис. 5.1). Урав-
нение, описывающее поведение такой системы, может быть за-
писано следующим образом:
OT.^4rfA^g._]_few* = 0.	(5.1)
При этом в случае отсутствия затухания угловая частота коле-
баний нашеюсистемы будет равна ®0 = у klm.
Как н ранее, введем безразмерные переменные
t = (()(/* и и = «7«о >
где Uo — некоторый характеристический масштаб длины, в ка-
честве которого можно выбрать, например, начальное смещение
частицы. Тогда уравнение (5.1) приобретает вид
й -|- 2е« -|- и ~ 0,	(5.2)
где параметр е — -i- р/у4km представляет собой меру отношения
демпфирующего усилия к упругой возвращающей силе пружины,
Ри?. 5.J. Масса, связанная с пружиной и демпфером,
5.1. Прямое разло№н.иё	14?
' а точки означают дифференцирование по времени. В данной главе
мы будем строить общее решение уравнения (5.2) при малых е.
Начнем, как и раньше, с построения прямого разложения,
после чего обсудим вопрос о его неравномерности. В § 5.2 для
выявления источника этой неравномерности мы исследуем точ-
ное решение нашей .задачи. Далее, в § 5.3 мы продемонстрируем,
что использование обычной методики Линдштедта—Пуанкаре
для описываемой системы приводит к тривиальному решению.
В § 5.4 покажем, как с помощью метода многих масштабов
г можно получить равномерно пригодное разложение решения.
 Наконец, в § 5.5 для построения равномерно пригодного первого
J приближения используем метод усреднения.
: 5.1. Прямое разложение
Будем искать разложение второго порядка в виде следующего
; ряда по степеням е:
;: • ,	« е) = w0 (0 + eWi (0 + е2«2 (/) + • • •.	(5.3)
' Подстановка (5.3) в уравнение (5.2) дает
«о + еЙ! + е.2й2-----р 2е (м0euj + е2й2-----) +
4" «о ez/j 4~ b2w2 4~   • — 0.
Группируя члены с одинаковыми степенями е, имеем
йо -|- и0 е (&i Ч- Ui -|- 2й0) 4" е2 (й2 4~ w2 + 2й1) 4- • • • = О,
откуда, приравнивая нулю коэффициенты при соответствующих
: степенях е, получаем уравнения
й# 4- и0 = 0,	(5<4)
,	й2 4~ == — 2uq.	(5.5)
й2 4- и2 = — 2iij',	ч (5.6)
~из которых последовательно могут быть найдены функции w0,
й «j.	’
Общее решение уравнения (5.4) может быть записано как
и0 = a cos \t 4- ₽), L	(5.7)
, где а и 0 — некоторые Постоянные. Тогда уравнение (5.5) пере-
писывается в виде
й2 + и-i — sin (1 + Р).	(5.8)
При этом, как отмечалось в §4.1, если для выполнения соответ-
ствующих начальных условий предположить, что а и р являются
i функциями от е, то нет необходимости искать решение соответ-
; ствующего (5.8) однородного уравнения. В связи с этим функцию их
; мы представим в виде только одного частного решения. Из фор-
14$	-	?л. 5. Линейный осциллятор с затухйниёМ
мул (Б.81) и (Б.82) приложения Б следует, что решение (5.8)
можно записать как
М1 = —at cos (t + Р).	(5.9)
Подстановка этого выражения для Uj в уравнение (5.6) дает
«2 + «2 = 2а cos (t + Р) — 2at sin (t + ₽).	(5.10)
Используя операторный метод, метод вариации произвольных
постоянных или метод неопределенных коэффициентов, 'можно
построить частное решение уравнения (5.10) следующего вида
(см. формулы (Б.69) и (Б.76) приложения Б):
а2 =a/2cos(f + Р) +-g-а/sin(f -f-0).	' (5.11)
Подставляя теперь полученные выражения для «0, и и2
из формул (5.7), (5.9) и (5.11) соответственно в уравнение (5.3),
находим
и = a cos (t 4- Р) sat cos (? + ₽) +
+ -i- e2a [i2 cos (t + p) +1 sin (t Р)Ц-.	(5.12)
Полученное прямое, или «медленное», разложение оказывается
непригодным при t О (е-1) из-за наличия в нем секулярных
членов. Отметим также, что по мере повышения порядка эти
секулярные члены становятся все более сложными. Так, в. первом
приближении секулярный член зависит от t линейно, тогда как
второе приближение содержит уже квадратичный секулярный
член. Выполнив разложение до п-го порядка, мы найдем, что
соответствующее n-е приближение будет содержать, секулярный
член, в который входит множитель tn. Перейдем теперь к иссле-
дованию точного решения и попытаемся выяснить причину появ-
ления подобных членов..
5.2. Точное решение '
х-Для того чтобы установить причину неравномерности полу-
ченного прямого разложения и разработать методы получения
равномерно пригодных разложений, обратимся к точному решению
уравнения (5.2). Поскольку это уравнение представляет собой
линейное дифференциальное уравнение с постоянными коэффи-
циентами, то оно допускает решения вида
и = с ехр (М),	(5.13)
где си X — некоторые, вообще говоря, комплексные постоянные.
Подстановка (5.13) в уравнение (5.2) дает
(%2 4- 2еХ + 1) с ехр (Xf) = 0,,
4
5.2. Точное решение
откуда, поскольку нас интересуют только нетривиальные решения,
X2 + 2еХ + 1 = 0,	(5.14)
или
1 = -- е±/^~Т.	(5.15)
Отметим, что в случае е < 1 формулу (5.15) удобно представить
в виде
—e±i^l—е2. t	(5.16)
Таким образом, общее решение уравнения (5.2) можёт быть за-
писано как
и = С! ехр [— et Ц- i1 — s2t] 4- qехр [— st — i^l — e2/J.(5.17)
Поскольку нас интересуют только действительные решения, по-
стоянная q должна быть комплексно-сопряженной с q. Для того
чтобы записать решение (5.17) через тригонометрические функции,
представим величины q и q в форме
q = -j- а ехр (ф), q = а ехр (— ф),
где а и Р — вещественные постоянные. Тогда решение (5.17) при-
обретает вид
и = ae~et cos (7/ 1 — ePt 4- р).	(5.18)
Для того чтобы выяснить причину неравномерности прямого
разложения, разложим выражение (5.18) при малых е, найдем
первые три члена этого разложения и сравним полученный ре-
зультат с прямым разложением (5.12), полученным непосредст-
венно из исходного дифференциального уравнения. G этой целью
разложим отдельно входящие в точное решение экспоненту и ко-
синус. Так, применяя формулу Тейлора, получаем
е-е<1 - е/4-е2/2 - eY= У-±-(-е/)п,(5.19)
£t •	О J	'* *
п=0
Прежде чем раскладывать в ряд тригонометрический косинус,
воспользуемся биномиальной формулой и представим входящий
в него корень в, виде
/1 - е2 = (1 — е2)1/2 = 1 —-е2 4~ 2~ 24——<?-
1_	— е® 4------- 1 - 4- е2 - 4- е4 4- • • • . (5.20)
	о 1	£•	о
ISO	Гл. 5. Линейный осциЛлЛ/Hofi t а&Шу)саНШМ
-- -	- 	_	--•		- - -- ---,	. - .	аи.
При этом
cos (ул 1 — е2/ 4~ Р) = cos р 4- ₽-yгЧ-е,Ч 4- ♦ J ==
== cos(/'4- Р) cos (4- &Ч 4- -g-e4t 4- • • • 'j 4-
4- sin (t 4- P) sin e2/ 4~ s4/ 4~ * ’ ’) ’
но поскольку
соз8=1-48»ч4г8‘+... = £<4§р	(5.21)
/1=0
и
^^. + ^+.,.-=£±^1, (5.22)
/1=1	-	Л
то, с точностью до членов порядка О (в4), имеем
cos (/1 — е2/ 4- Р) = cos (t 4- Р) [1 — ,4-(4-е2/4- * * * У ] +
+ sin(/4-P) [4-^ +4-^+ •••] + ••• =
= (1 - 4- 84/2) cos (t 4- Р) 4- (4- в2/ 4- 4" е4/)sln (/ + Р) Н-
и, следовательно,
cos (УГ^ТЧ 4- р) = cos (/ 4- Р) + 4" sln (Z + P) +
4-4" е4 [/sin (/4-Р) —/2 cos (/4-P)J 4- ••• .	(5.23)
Ддя того чтобы иметь возможность сравнивать с разложением
(5.12), нам нужно разложить выражение (5.18) с точностью до
членовхпорядка О (е3). Подставляя разложения (5.19) и (5.23)
для экспоненты и косинуса в формулу (5.18) и сохраняя в ней
члены до второго порядка включительно, находим
и=а(1 — 4-4®2^2 Ч-----)[cos(Z 4-P)4-4e2/sin(/4-P) Н--------] =
= a cos (t 4- P) — sat cos (/ 4~ P) +
4- 4-	[t*cos(/ 4- p) 4- / sin(/ 4- p)J 4- • • •	(5.24)
5.2. Точное решение
Г51
Рис. 5.2. Аппроксимация экспоненциальной функции с помощью конечного
числа членов ряда Тейлора.
в полном соответствии с разложением (5.12), полученным непо-
средственно из исходного дифференциального уравнения.
При построении прямого разложения нам пришлось раскла-
дывать экспоненту по формуле (5.19) и тригонометрический коси-
нус по формуле (5.23). Используя для ряда (5.19) признак Далам-
бера, имеем
п-й член
lim -г-—г.
n-*°D (п ~ !)-и член
lim
п-м» nA (— et)n 1,
— lim
П-*-оо
—nt
n
= 0.
Таким образом, ряд (5.19) сходится для всех значений et. Однако,
как показывает рис. 5.2, функция ехр (—е/) не может быть равно-
мерно аппроксимирована с помощью конечного числа членов ряда
при всех значениях е/. Следовательно, любая процедура разло-
жения, основанная на идее аппроксимации функции ехр (—et) ко-
нечным числом членов степенного ряда, заранее обречена иа не-
удачу при достаточно больших t.
В процессе разложения косинуса нам пришлось иметь дело
с тремя разложениями (5.20) — (5.22). Применяя признак Далам-
бера к ряду (5.20), имеем
n-й член
lim—;---гг-я--- =
(п — 0-й член
8«(2п— 1)	,
2» + 2 =е-
Следовательно, ряд сходится для всех е, удовлетворяющих усло-
jtyiK? еа <; 1. Это означает, что разложение (5.20) будет равномер-
152	Гл. 5. Линейный осциллятор с затуханием
но пригодным при достаточно малых е. Используя теперь признак
Даламбера для ряда (5.21), находим
Нт	в нт	= lim 2	= °-
п-оо(я—*)-и член п^м (2п) 1 (— I1 б2”-2 п^оо 2п^п
Таким образом, ряд (5.21) сходится при всех значениях 6. Однако
рьс. 5.3 показывает, что функцию cos 6 нельзя равномерно аппрок-
симировать конечным числом членов ряда (5.21) для любых зна-
чёний б. Аналогичным образом можно показать, что функцию
sin 6 также нельзя равномерно аппроксимировать конечной сум-
мой членов соответствующего ряда. Тем самым любое разложе-
ние, основанное на аппроксимации функций cos б и sin б конечным
отрезком степенного ряда, может оказаться непригодным при до-
статочно больших значениях б.
В заключение отметим, что несостоятельность прямого раз-
ложения при больших t обусловлена именно разложением функ-
ций ехр (—е/) и cos (j/ 1 — е*!--}- (i) в ряды по степеням параметра
е. При этом в соответствии с формой прямого разложения (5.23)
частота колебаний системы должна равняться единице незави-
симо от степени затухания. Фактически же наличие затухания
изменяет частоту от значения, равного 1, до значения у41 — 82.
Следовательно, любая процедура разложения, не учитывающая
зависимость частоты колебаний системы от величины параметра
в, окажется несостоятельной при больших значениях I. Перейдем
теперь к рассмотрению методики Линдштедта—Пуанкаре, кото-
рая, как мы покажем в следующем параграфе, может приводить
"К тривиальному решению.
Рис. 5.3. Аппроксимация косинуса с помощью конечного числа -членов ряда
Тейлора.
5.И. Методика Линдштедта—Пуанкаре	153
Е 5.3. Методика Линдштедта—Пуанкаре
 z Для учета того обстоятельства, что частота колебаний является
| функцией параметра е, введем новую переменную т = &t, в ре-
11 зультате чего уравнение (5.2) перейдет в уравнение
I	ю*и" + 2еии' 4- и = О,	(5.25)
| где штрихи означают дифференцирование по т. Далее, разложим
£ и и со в ряды по степеням е, т. е. примем, что
1	14 =- w0 (т) + 814х (т) + е2142 (т)4-,	(5.26)
t	io = 1 + еа»! + е2соа 4---.	(5.27)
к Заметим, что первый член в разложении (5.27) равен единице —
t он определяет собой частоту колебаний невозмущенной .системы,
или частоту свободных колебаний. Подстановка разложений (5.26)
I и (5.27) в уравнение (5.25) дает
;	(1 4- ecoi 4- е2<»2 4-—)2 (ио 4~ eui 4~ s2u2-}-) 4~
<	4- 2е (1 4- 8(0] 4- 8 0)2 4- • • • ) («О 4” 8W1 4- 82142 4* ’ ’ ’ ) 4“
4- «о 4-	4~е и2 4-    ~ 0.
/ Учитывая малость 8 и собирая члены с одинаковыми степенями е,
имеем
«0 4- uo 4- 8 [щ 4~ 44| 4- 2(й]44о 4“ 2Uq] 4"
4- е [^2 4- и% 4~ 2со2^о 4- ®i«о 4~ 2coiЩ 4~ 2coiUq 4~ 2ui ] 4~    ==,0-
Приравнивая теперь нулю коэффициенты при последовательных
степенях 8, можно получить следующие уравнения для определе-
[ ния функций «0, иг и иг:
I	и'о-\-и0 = 0,	'	(5.28)
I	«1 4г и1 = — 2и1«о — 244о»	(5.29)
|	^2 4~ ^2 =z — 2(iJ2U0 — ®1«0 — 2(0jU| — 2cO[44q — 2ui •	(5.30)
в Общее решение уравнения (5.28) может быть записано в виде
|	'	«о = a cos (т + 0),	(5.31)
I где а и 0 — некоторые постоянные. Тогда уравнение (5.29) при-
| нимает вид
|	ui 4~ wi = 2а®, cos (т 4- 0) 4- 2а sin (т 4~ 0)-	(5.32)
I Для того чтобы исключить секулярные члены из частного
решения для функции uit нам необходимо избавиться от правой
части уравнения (5.32). При произвольном т это условие может
быть выполнено, если потребовать, чтобы каждый из коэффициен-
-Л > >-^..А.----------Ж.	--- t	Г.»	-----... Г.	..
154
Гл. 5. Линейный осциллятор с затуханием
тов при sin (т + 0) и cos (т + 0) обращался в нуль независимо
друг от друга, т. е. чтобы
2аи! = 0 и а = 0.	(5.33)
При этом (5.32) принимает вид
ы; + и1 = 0.	(5.34)
Соотношения (5.33) нельзя удовлетворить одновременно, если
только а =/= 0. Если же а — 0, то, согласно формуле (5.31), и0 =
= 0, и тогда, если^не учитывать решение соответствующего одно-
родного уравнения, имеем их = 0. Далее, подставляя Up — их =
= 0 в уравнение (5.30), получаем для w2 уравнение вида
^ + «, = 0,	(5.35)
частным решением которого также является функция иа — 0.
Итак, мы в конце концов приходим к тривиальному решению.
Если бы мы воспользовались решением однородного уравне-
ния (5.34), то это решение можно было бы представить в виде
«!=(!! COS (т 4- Pi),	(5.36)
где tZj и рх — произвольные постоянные. При этом уравиеиие
(5.35) заменилось бы уравнением
,-j- и2 = 2о>1<21 cos (т + Pi) + 2tzi sin (т + РО, (5.37)
для которого условие отсутствия секулярных членов в свою оче-
редь привело бы к требованию ах = 0. Тем самым мы опять при-
шли бы к тривиальному решению.
Приведенное рассуждение показывает, что применение мето-
дики Линдштедта—Пуанкаре для нашей задачи в любом случае
дает только тривиальное решение. Аналогичным образом, лишь
тривиальное решение получается и при использовании метода
перенормировки. Причина того, почему с помощью этих методов
оказывается невозможным построить равномерно пригодное не-
тривиальное разложение решения, заключается в том, что в про-
цессе вычислений мы все время исходим из утверждения, что
равномерное решение должно иметь постоянную амплитуду, как
это следует, например, из формулы (5.31). Но поскольку из вида
точного решения (5.18) ясно, что амплитуда исходной задачи опи-
сывается выражением а ехр (—е£), то единственно возможным
равномерно пригодным решением с постоянной амплитудой
будет то, которое достигается по истечении произвольно большого
промежутка времени, т. е. при достижении стационарного со-
стояния. Таким образом, можно сделать вывод, что хотя методика
Линдштедта—Пуанкаре и метод перенормировки оказываются
достаточно эффективными при построении периодических решений,
они не позволяют описывать переходные характеристики систем
с затуханием.
5.3. Методика Линдштедта—Пуанкаре	155
| В данном, примере указанный недостаток методики Линд-
। штедта—Пуанкаре и метода перенормировки можно устранить,
| допустив, что величины соп могут быть комплексными. Для того
I чтобы проиллюстрировать эту идею, представим решение урав-
| нения (5.28) в комплексной форме
ue = Aetx + Ae~ix,	(5.38)
где А — некоторая комплексная постоянная. Тогда уравнение
| (5.29) примет вид
|	«1 + Ui = 2(<»1 — О Ае!х 4- (к. с.),	(5.39)
| где сокращение (к. с.) использовано для обозначения комплексно-
t сопряженного слагаемого. Исключая из (5.39) члены, которые
Г приводят к появлению секулярных слагаемых, мы приходим
I к выводу, что (Oj = i, причем уравнение (5.39) в этом случае сво-
I дится к уравнению (5.34), решением которого будет Uj = 0. Под-
I становка найденных значений w0, ut и u2 в уравнение (5.30) дает
I	+ «2 = (20)2 4- 1) Aeix + (к. с.).	(5.40)
| Условие отсутствия секулярных членов приводит к требованию
| со2 = — в результате чего мы вновь получаем м2 = 0. Таким
I образом,
|	? = (!)/= ie------^-824-'*')^	(5-41)
I	и ~ А ехр р 4-. ie--g-824-J 4" (к- с-) =
I	= А ехр (—8/) ехр р‘ 1-82) t j 4“ (к- с.j 4- • • • • (5.42)
| Полагая теперь А =-$- а ехр (ф), где а и £ — действительные
I числа, можно переписать разложение (5.42) в виде
I	M = «e-e'cos [(1 --^-82)/4-04---],	(5.43)
I что находится в полном соответствии с точным решением (5.18),
I в котором учитываются члены до второго порядка включительно-
[ Следует отметить, что успех применения описанной модифика-
 ции метода Линдштедта—Пуанкаре является чисто случайным.
 Фактически же подобная модифицированная методика, как по-
к казано в § 6.2, может приводить к совершенно ошибочным резуль-
V тэтам.

• f»	_ ,
156	Гл. 5. Линейный осциллятор с затуханием
5.4. Метод многих масштабов
Воспользовавшись разложением (5.20), перепишем (5.18)
в виде
и — cos (t Р------------^-82/-(5.44)
Отсюда ясно, что и (t; е) == и (t, st, 82/, е®/, ...), и поэтому для
решения данной задачи вполне может быть использован метод
многих масштабов. Для нахождения разложения второго порядка
нам необходимы только три масштаба То — t, Тх = е/ и Т2 e2t.
•Тогда, согласно правилу дифференцирования сложной функции,
производные по времени преобразуются в соответствии с форму-
лами (4.93) и (4.94). Однако в данном случае для упрощения формы
записи мы будем писать
4=D»+eZ)i+82D2+---’	<5-45а>
= (Do + eD, 4- s2D2 + • • • )2 =	+ 2eD(A +
-	+е2(2£><А-Н£)?)4-...,	(5.456)
где
=	(5-46)
При этом уравнение (5.2) принимает вид
[Z?o 4" 2e£*oZ>i -J- е2 (2DqDo 4- Df) -J- • • • J у
-	+ 2e(D0 +	+ e2D2 -}-••••)“+ u — 0-	(5-47)
Таким образом, исходная задача для обыкновенного дифферен-
циального уравнения (5.2) перешла в задачу для уравнения в част-
ных производных (5.47).
Будем искать решение уравнения (5.47) в виде ряда по степе-
ням е, т. е.
и = и0 (То, Tlt То) + еМ1 (То, Tlf То) + 88м2 (То. Тъ То)+ 
. (5.48)
Подставляя (5.48) в уравнение (5.47) и группируя члены с одина-
ковыми степенями 8, имеем
Т^о 4" tig -}- 8	-J- Uf 2DoDi«o 4~ 2Z)qUo] 4~
4- e2 [О&г 4- «2 4- 2D0D2U0 4“ rfuo 4- 2DgDtUt 4-
4-2D0Wi 4-2D,u0J 4-... == 0.	(5.49)
5.4, Метод многих масштабов	157
Приравнивая теперь коэффициенты при последовательных сте-
пенях е, получаем
D2u04-uo = O,	(5.50)
Dou( Uf = — 2Dg£)tuo ~ 2/)qUq,	(5.51)
Ж 4“ Wz — 2DoD2uo — HiUq — 2DqDiUi — 2D0ul — 2DiUq. (5.52)
Как указывалось в § 4.5, решение уравнения (5.50) удобнее
представить в комплексной форме
и0 = Д (Л, Тг) е‘г’ + Д(7\, Т2) е~‘Т°.	(5.53)
. Тогда уравнение (5.51) переписывается в виде
+ Щ = — 2i (DtА + Д) eiT° + (к. с.),	(5.54)
где комплексно-сопряженное слагаемое в данном случае будет
равно 21 (DrA + Д) ехр (—iT0).
Требование отсутствия секулярных членов в выражении для
Й! приводит к условию, чтобы каждый из коэффициентов при
ехр (iT0) и ехр (—iT0) независимо друг от друга равнялся нулю.
Обращение в нуль коэффициента при ехр (iT0) дает
DtA + А = 0.	(5.55)
Это же условие для коэффициента при ехр (—1Т0) приводит к со-
отношению, комплексно-сопряженному с (5.55), и, следовательно,
не. содержит никаких дополнительных ограничений, поскольку
если равенство (5.55) удовлетворяется, то комплексно-сопряжен-
ное с ним будет удовлетворяться автоматически. С учетом (5.-55)
уравнение (5.54) переписывается в виде
DqWi + wi = 0,	(5.56)
причем, согласно принятому нами ранее подходу, по которому
решения соответствующих однородных уравнений не принимаются
во внимание, за исключением уравнения для порядка е°, решение
(5.56) запишется как
Ы1 = 0.	(5.57)
Решение уравнения (5.55) имеет вид
А = В(Т2)е~т‘,	(5.58)
где постоянная интегрирования В (Т2) (поскольку в уравнение
(5.55) входит только производная по 7\) является функцией пере-
менной Т2. Она определяется из условия отсутствия членов, по-
рождающих секулярные слагаемые в задаче второго порядка, т. е.
в задаче для функции и2.
Подставляя выражения для и0 и uL в уравнение (5.52), полу-
чаем
Do«z + «г = — (2iD2A + О?А + 2О1Д) е‘т° + (к. с.). (5.59)
158	Гл. 5. Линейный осциллятор с затуханием
Условие отсутствия секулярных членов в выражении для «2 при-
водит к требованию обращения в нуль коэффициента при ехр (iT0),
т. е. к соотношению
2iZ)2X + Г>?Л 4-2£>1Л = 0.	(5.60)
Подстановка выражения для А из (5.58) в уравнение (5.60) дает
уравнение
2iD2Be~T1 - Ве~Т' = 0,
или
2iD2B — В = 0,	(5.61)
решением которого является функция
В = се'в12)1Тг ,	(5.62)
где с.— произвольная комплексная постоянная, поскольку В за-
висит только от переменной Т2.
Подставляя найденное выражение для В в формулу (5.58), на-
ходим
A=ce~Tl~W2}iT1,	(5.63)
так что (5.53) приобретает вид
_ „»-’>+< [Го—<1 /2) Г,] . - -Т,-ЦТ»-(1/2)Г,]
(40 Сс	“р" Се?	•
Представляя постоянную с в форме а ехр (i'P), перепишем
выражение-для и0 в виде
2	**	~< 2	*
(1/2)Т2+₽] _|_г-ЦТо-(1/2)Т2+₽]| =
= ae~Tlcos(T0-----g-Ta4-p),
или, после возвращения к исходной переменной t,
и0 — ае~г* cos	—g- ePt + р) •	(5.64)
Подставляя теперь соответствующие выражения для и0 и ut из
формул (5.64) и (5.57) в разложение (5.48), приходим окончательно
к разложению
и — ae~zt cos (t---- e?t -f- p) -|- 0 (e2),	(5.65)
которое уже является равномерным по t и полностью соответст-
вует разложению (5.44) с точностью до членов порядка е2. Таким
образом, в данном случае метод многих масштабов позволяет не
только построить полное описание переходного процесса, но и
найти приближенное выражение для частоты колебаний нашей
системы.
5.5. Метод усреднения
159
5.5.	Метод усреднения
В случае е = 0 решение уравнения (5.2) может быть записано
как
/	и —a cos (t + Р),	(5.66)
• где а и р—произвольные постоянные. При этом дифференци-
рование (5.66) по t дает
й = —a sin (t + р).	(5.67)
В случае е =/= 0 мы также будем считать, что решение исходной
задачи дается.выражением ,(5.66) с условием (5.67), но при этом
предполагается, что величины а и Р зависят от времени.
Поскольку а — a (t) и р = р (0, то дифференцирование (5.66)
I по t дает
w = й cos (t + Р) — а (1 + Р) sin (t + Р) —
•	— —a sin (i 4- Р) + a cos (t 4- Р) — ар sin (t + р). (5.68)
[ Сравнивая соотношения (5.67) и (5.68), можно сделать вывод, что
<	a cos (t + Р) — ар sin (t + Р) — 0.
' Дифференцирование (5.67) по t дает
<	й = —a sin (t + Р) — а (1 4- Р) cos (t + Р).
(5,69)
(5.70)
) Далее, подставляя (5.66), (5.67) и (5.70) в исходное уравнение (5.2),
। получаем
—a sin (i + Р) — a cos (i 4- Р) ~ ар cos (i 4- Р) —
— 2еа sin (£ + Р) + a cos (t + Р) — 0,
; или
a sin (t + Р) + ар cos (t 4- Р) = —2ъа sin (t 4- Р).	(5.71)
Умножая теперь равенства (5.69) и (5.71) соответственно на
cos (t + Р) и sin (t + Р), складывая полученные результаты и учи-
' тывая, что sin 2 0 4- cos2 0=1, находи^
f а — —2еа sin2 (t + р) == —еа 4- еа cos (2t + 2Р).
Подстановка (5.72) в соотношение (5.69) дает
>	—2еа sin2 (i 4- Р) cos (f + Р) — ар sin (t + Р) = 6.
«Если а ф 0, то из (5.73) следует, что
Р = —2е sin (i + р) cos (t + P) — —e sin (2i 4- 2p).
Как уже отмечалось в § 4.6, при решении уравнений (5.72) и
|(5.74) в случае малых е мы можем воспользоваться двумя различ-
ными подходами. С одной стороны, для построения первого при-
ближения можно усреднить правые и левые части уравнений (5.72)
(5.74) по промежутку [0, л ], а с другой — мы можем сохранить
pi этих уравнениях лишь медленно меняющиеся члены. Используя
(5.72)
(5.73)
(5-74)
Я
А
160	Гл. 5. Линейный осциллятор с затуханием
второй из этих подходов, в качестве первого приближения полу-
чаем
а = —еа,	(5.75)
0 = 0.	(5.76)
Решениями уравнений (5.75), (5.76) являются функции
л = и ₽ = 0о,	(5.77)
где а0 и 0О — произвольные постоянные. Тогда из (5.66) следует,
что
и ~ aop~et cos (t 4- 0О),	(5.78)
причем это выражение полностью соответствует (5.44) с точностью
до членов порядка е. Поэтому первое приближение метода усред-
нения хотя и позволяет определить переходные характеристики
нашей системы, но не дает возможности найти поправки к ее ча-
стоте, которые в данном случае имеют более высокий порядок,
чем первый. Следовательно, для нахождения этих поправок необ-
ходимо построить решения уравнений (5.72) и (5.74) с точностью
до членов более высокого порядка. Это можно осуществить, на-
пример, с помощью обобщенного метода усреднения (см. § 7.6).
Упражнения
5.1.	Рассмотреть уравнение
2epu -р и + ей3 = 0. (е < 1).
.Используя метод многих масштабов, и метод усреднения, построить равномерно
пригодное разложение первого порядка для функции и.
5.2.	'1>ассмотреть уравнение
й + ы^и ₽й3 = 0	.
Используя метод многих масштабов и метод усреднения, построить равномерно
пригодное разложение первого порядка для функции и.
5.3.	Рассмотреть следующее уравнение:.
й + wgu + 2btj«26 + ви3 = 0.
Показать, что в первом приближении
и = a cos (ti>oi + 0) + О (в),
и получить в$ц)тветствующие уравнения для нахождения а и 0 с помощью ме-
тода многих масштабов и метода усреднения.
5.4.	Используя метод многих масштабов и метод усреднения, построить равно-
мерно пригодное разложение первого порядка для общего решения уравнения
4 sin2
при малых, но конечных 0.
5.5.	Рассмотреть уравнение
й + <£и +Т^5 = 0.
Построить равномерно пригодное разложение первого порядка при малых р,
5.6. Используя метод многих масштабен н метод усреднения, построить равно-
мерно пригодное разложение первого порядка для уравнения
й + и4-ем8 = 0 (е<^1).
Глава 6
КОЛЕБАТЕЛЬНЫЕ СИСТЕМЫ С САМОВОЗБУЖДЕНИЕМ
В отличие от предыдущей главы, в которой рассматривались
системы с положительным затуханием, в этой главе мы займемся
исследованием систем, обладающих отрицательным затуханием.
А именно, мы рассмотрим системы с самовозбуждением, имеющие
одну степень свободы. Такие системы описываются уравнениями
типа
(6.1)
где р, — некоторый положительный параметр, а функция /* поло-
жительна при малых и*.
С целью упрощения математических выкладок будем рассма-
тривать уравнение следующего специального вида:
d2“* | L * fl 7 V 1
с положительным а. Это уравнение называется обычно уравне-
нием Рэлея. Как уже указывалось ранее, прежде чем приступить
к анализу уравнения (6.2), необходимо привести его к безразмер-
ному виду. С этой целью, выбрав в качестве исходных масштабов
задачи некоторое характерное смещение «о и собственную частоту
соответствующей линейной системы соо = 7/klm, введем следую-
щие безразмерные переменные:
и = и /«о и t = t* |/ klm-
Тогда уравнение (6.2) преобразуется к виду
(•' \
aun k 1
1-----й2I й,	(6.3)
где е = р/У"km. Выбирая величину ио таким образом, чтобы
auifk =-^~ т, можно записать уравнение (6.3) в стандартной
форме
й 4- м = е (й--(6-4)
Дифференцируя уравнение (6.4) по времени, имеем
и 4- й = е (й — й2й).	(6.5)
6 Найфэ А. X.
162	Гл. 6. Колебательные системы с самовозбуждением
Если положить й — v, то (6.5) можно представить в виде
v Ц- и — е (1 — о2) v.	(6.6)
Полученное уравнение обычно называется уравнением Ван-дер-
Поля.
В этой главе мы рассмотрим методы нахождения приближен-
ных решений уравнения (6.4), а следовательно, и уравнения (6.6)
при малых е. Начнем, как обычно, с построения прямого разло-
жения решения, после чего обсудим вопрос о его равномерности.
Далее мы покажем, что ни методика Линдштедта—Пуанкаре, ни
метод перенормировки не позволяют построить описание пере-
ходных режимов системы. В заключение покажем, что эти пере-
ходные режимы могут быть описаны с помощью метода многих
масштабов и метода усреднения.
6.1. Прямое разложение
Будем искать прямое разложение решения (6.4) в виде
и (/; е) = Uq (О Ц- e^i (О 4~ ' ’ ’ •	(6-7)
ограничиваясь членами первого порядка малости по е. Подста-
новка (6.7) в уравнение (6.4) дает
йо + ей1 4* ‘ ' 4~ ио 4" ewi 4~ '" • = е (йо 4" е«1 4~ • • •) —
---о- е (йо 4" ей1 4"  • ')3-	(6-8)
О
Используя биномиальную формулу для разложения кубического
члена в (6.8) и сохраняя члены порядка е, находим
йо 4~ ио 4*е (й1 Ц- wi) Н- • •  — е (йо —з~ йо) 4- • • • .	(6.9)
Приравнивание коэффициентов при одинаковых степенях е в обеих
частях (6.9) ведет к уравнениям
й0 4- «о — 0.	(6.10)
1	3
Й14-И1 — Йо----5-Йо,	(6.11)
О
которые могут быть решены последовательно относительно и0 и иг.
Общее решение уравнения (6.10) можно представить в виде
и0 — a cos (t 4- Р),	(6.12)
где а и Р — произвольные постоянные. Тогда (6.11) переходит
в уравнение
•• й14-И1 = — a sin (/ 4- Р) 4- 4” а3 sin3 “t" Р)-	(6-13)
6.1. Прямое разложение	163
к?Используя тригонометрическую формулу (А. 16)
Г	sin* 0 = -5- sln 0-j- sin 39,	i
| 44
I перепишем (6.13) как	i
I #i + “1 = (-5-~ 1) а sin (/4 0)—a® sin (3/4 30). (6.14)	
I Поскольку уравнение (6.14) линейно, то его частное решение мо-
I жет быть представлено как сумма двух частных решений следую-
| щих уравнений:
I	йР’4 Ы{1) = (4"а2-1)asin(^4 0)	(6.15)
| и	'
й!2) 4 «!2) — —-<V«3sin(3/4 30).	(6.16)	1
k.	1Z	<
t Частное решение первого из них (см. формулы (Б.81) и (Б.82) при- 1
ложения Б) есть	1
I «}ч)асТн = 4~(1 ~4a2)aZCOS(Z + P)’	(6Л7>	'
I частное решение второго (формулы (Б.68) и (Б.69)) —	j
|	<ас,н = -^- а» sin (3/4-30),	(6.18)	1
| откуда
j “1частн = части 4 ^1 части = ~2~ ^1	Clt COS (/ 4 0) 4
i	4-^-a3 Sin (3/ 4 30).	(6.19)
j Как уже указывалось в §4.1, в случае если а и 0 считаются
( функциями е, нам не нужно учитывать решение соответствующего i
I однородного уравнения, так что решение уравнения (6.14) будет
Si даваться именно формулой (6.19). Подставляя (6.12) и (6.19) в раз-
? ложение (6.7), получаем
) U = acos(/4P)+ 8 [4~(1-------------fl/COS(Z 4 ₽)+
S	4-^a*sin(3/4 30)] 4 ... .	(6.20)
Построенное таким образом прямое разложение неравномерно
при / О (в-1), поскольку при этом поправочный член из-за при-
сутствия в нем секулярного слагаемого оказывается по величине
[ порядка первого члена разложения или даже больше его. Эта
• неравномерность хорошо иллюстрируется иа рис. 6.1, где решение,
)	6*
164	Гл. 6. Колебательные системы с самовозбуждением
подсчитанное по формуле (6.20), сравнивается с решением, полу-
ченным с помощью численного интегрирования уравнения (6.4).
В начальные моменты времени прямое разложение решения и чис-
ленное решение близки между собой. Однако по мере возрастания
t аналитическое решение все более уходит от численного решения,
которое приближается к некоторому периодическому решению
с амплитудой, равной примерно 2 независимо от выбора началь-
ных условий. Это периодическое решение, к которому стремится
численное решение, называется предельным циклом. На рис. 6.2
показан типичный ход численных решений на фазовой плоскости
(плоскости uv, где v — й) для нескольких значений параметра е
и различных начальных условий. При этом, когда е мало, предель-
ный цикл имеет амплитуду, приблизительно равную 2, незави-
симо от выбора начальных условий.
Следует отметить, что секулярный член в (6.20) пропадает, если
(1-^а*)а = 0.	(6.21)
Если исключить тривиальный случай а = 0, то соотношение
(6.21) удовлетворяется при а — ±2. При положительных по опре-
делению амплитудах (а = 2) разложение (6.20) принимает вид
и = 2 cos (t + ₽) + 4"6 sin (3/ + 30) -|-.	(6.22)
1“
а
Рис. 6.1. Сравнение прямого разложения (а) с точным решением (б) при и (0) “
“ 0.5, й (0) «= 0 и в = 0.1.
6.2. Метод перенормировки
(6.23)
(6.24)
Рис. 6.2. Фазовые плоскости для уравнения Рэлея: а) в = 0.01; б) е= 0.1;
в) в= 1; г) е= 10.0.
Последняя формула представляет собой периодическое решение,
амплитуда которого, с точностью.до малых'первого порядка,
равна 2, т. е. дает нам предельный цикл.
6.2. Метод перенормировки
В этом параграфе для преобразования разложения (6.20) ис-
пользуем метод перенормировки. Так, полагая
т =	= (1 + e<Ox +• • •) t,

имеем
t в т (1 4- е<Ох . .)-1 = т — ecoft 4- • • • •
Подстановка (6.24) в разложение (6.20) дает
и — a cos (т 4- Р — вант 4- * • •) 4-
---а(т ~ е<й1т + •' •)cos (т + Р — e(°iT +•••) +
4-sin (Зт 4~ ЗР — 3e<0iT 4-•••)]+•'• •	(6.25)
166
Гл. 6. Колебательные системы с самовозбуждением
Используя разложения в ряды Тейлора вида (4.86), перепишем
(6.25) как
и — a cos (т 4* 0) + е (щп sin (т 4- 0) Ц-Ц- 1 ~4 а2^ ах cos (т4-0) +
+ ^aSsin(^T 4*	4* ’'(6.26)
Если coj принимает действительные значения, то условие отсут-
ствия секулярных членов в (6.26) приводит к соотношениям
= 0,	(6.27) .
(1 --^аг)а= 0.	(6.28)
Так как в случае нетривиального решения а =# 0, то из соотно-
шений (6.27) и (6.28) следует, что = 0 и а = 2. (Случай а —
— ;—2 может быть отброшен, если считать амплитуду положи-
тельной.) При этом из формулы (6.23) получаем, что т = t 4-
4- О (е8), и (6.26) переходит в разложение
и = 2 cos (t 4- 0) 4- -1- е sin (3/ 4- 30) 4-,	(6.29)
представляющее собой предельный цикл.
Возникает вопрос, нельзя ли нам все же построить равно-
мерно пригодное разложение, воспользовавшись введенным
в § 5.3 допущением о том, что соп могут принимать комплексные
значения. Для ответа на этот вопрос представим разложение
(6.26) в комплексной форме. G этой целью положим
cos0 = 4(е194-е-1'9) и Sin0 = -4(ef9-e-‘-9)
и перепишем разложение (6.26) в виде
и = 4 ае'(т+₽) 4- е |4 (1 — Т fl2) — Itoi] ахе'(х+₽) “
‘	aV*’(х+₽)) + (к-с-) 4- • • • • (б.зо)
Требование отсутствия секулярных членов в (6.30) дает
со1 = -41’(1 -"Га2)’	<6-31)
и, следовательно,
и = 4 ае1 (т+₽) 4- (к- е.) 4-•	(6.32)
При этом из (6.23) и (6.31) имеем
' x=t-4‘е(i -4а’)*+ •••»	(б-33)
6.3. Метод многих масштабов	167
В так что разложение (6.32) принимает вид
I «=уаехрр р --J-fl2)* + ₽4--------------]} + (к. с.) + • • • =
I =4аехР [“И1 ~~Та2) *] ехРI1’(* + ₽)] +(к- С)Н—•
|f Таким образом, окончательно получаем
I ы==аехр[4"е(1—г °2) d cos(^+₽)+• ••• (б-34)
г Из формулы (6.34) следует, что при t оо и оо, если |а| < 2,
г и и -> 0, если |а| > 2. Однако это неверно, поскольку из рис. 6.1
f и рис. 6.2 видно, что численные решения уравнения (6.4) стремятся
I к значению, приблизительно равному 2 независимо от начальных
I условий, а следовательно, и от величины а. Таким образом, пред-
f ложенный вариант методики Линдштедта—Пуанкаре и метода
| перенормировки, при котором допускаются комплексные значе-
| ния соп, может приводить к ошибочным результатам, как это и
I произошло в данном случае. В связи с этим следует избегать при-
I менения указанных методов для исследования решений, отличных
I от периодических.
I 6.3. Метод многих масштабов
| Для того чтобы построить равномерно пригодное разложение
[ первого порядка для решения уравнения (6.4) с помощью метода
i многих масштабов, введем масштабы То = t и 7\ — st. При этом
f производные по времени преобразуются следующим образом:
= Dq eDi 4* ‘— 2eDoDi -f- • • •,
| где Dn — д/дТп, а уравнение (6.4) примет вид
Г	D20u + 2rDqDiU + и = e. [Au —4- (ВД3] + • • • •	(6.35)
| Будем искать решение уравнения (6.35) в форме
|	u = Uo (Т’о»	+ еы1 (П, 1\) + • • • •	(6.36)
t Подставляя разложение (6.36) в (6.35) и приравнивая коэффи-
[ циенты при е° и е1 в левой и правой частях, получаем
|	£>o«o + «o = 0,	(6.37)
I	+ Ы1 — — 2Ро^1ыо + DqU0------— (ZJqHq)3. (6.38)
168	Гл. 6. Колебательные системы с самовозбуждением
Как и ранее, общее решение уравнения (6.37) запишем в комплекс-
ной форме	_
Ыо = Л(Т1)?г»4-Л(Т1)<Г/г’.	(6.39)
Тогда (6.38) приобретает вид
D{ux + «1 = — 2iA'eiT° Ц- 2iA'e~iT° + iAeiT° - iAe~iT° —
— -^-(iAe<r°- iAe~ir°)3,
'	о
или
Dfa =	(2A' - A + A2A) e‘r° + -j- iA3e3iT* + (к. c.). (6.40)
Требование отсутствия секулярных членов в решении для «1 при-
водит к соотношению
2А' -Д4-ЛМ = 0.	(6.41)
Как и ранее, представим А в форме
A = ±aeif>,	(6.42)
где а и р — действительные функции переменной 7\. При этом
решение (6.39) приобретает вид
№,=4-ж'|г'+в>+4-«-'<г-+”,
£	Л
или
u0 = acos(TQ + Р).	(6.43)
Подстановка (6.42) в условие (6.41) дает
ае^ + iap'?e - ~^aei& + -g- a3ei& = 0.
Опуская общий множитель ехр (t'P) и отделяя вещественную и
миимую части, получаем
а' = 4- а - 4- о3,	(6.44)
Р' = 0.	(6.45)
Решение (6.45) имеет вид
Р = Ро — const.	(6.46)
Уравнение же (6.44) представляет собой обыкновенное дифферен-
циальное уравнение с разделяющимися переменными, поэтому
(6’47>
-t	6.3. Метод многих масштабов	169
I   .Ill—», „.I III    I ~п	I I	II —। ни—	I IIIIII.I ~ Ulf
Разлагая правую часть (6.47) на простейшие дроби, находим
^ = ^ + ^7- 2$?.	(6.48)
Интегрирование (6.48) дает
7\ + с —2 Ina — In 12 — а | — 1п (2 + а),
или
Т14-с = 1п-гт-^-гг,
где с — произвольная постоянная. Отсюда
4 аа = еТ1+с = eei+c-	(6.49)
Решая уравнение (6.49) относительно а2, получаем
_ 4ехр (е< + С) _	4
“ — 1+ехр(е/+ с) 1 4-ехр (— st — с) '
Подставляя выражения (6.46) и (6.50) в решение (6.43) и полагая
То — t, находим
Wo— 2£ 1 —j—в 8 ] /2 cos (Z + ро) + • • •.	(6.51)
Наконец, подстановка (6.51) в (6.36) дает нам следующее разло-
жение первого порядка для общего решения уравнения (6.4):
и — 2 [1 4- ехр (— e,t — c)J-1/2 cos (^ + Ро) + • • • •	(6.52)
Используя начальные условия
и (0) = а0, й (0) = 0,	(6.53)
из разложения (6.52) находим
a0=2[l + e-cr1/2cosp0,	(6.54)
0 = —2[1 +е~с]~1/2 sinPo + O(e).	(6.55)
При этом из соотношения (6.55) имеем sin ро = О (е), или р0 =
= 0 + 0 (е), а из соотношения (6.54)
а2= 4 [1 +е-сГ*.
Выражая отсюда ехр (—с), находим
^=4- !•
“о
Таким образом, разложение (6.52) приобретает вид
cos t + • • •.
(6.56)
(6.57)
(6.58)
(6.59)
4- 1\е-8Т/2
.° )
Из формулы (6.58) следует, что при t -> оо
и -> 2 cos t + О (е)
u = 2 1 +
170
Гл. 6. Колебательные системы с самовозбуждением
Рис. 6.3. Сравнение приближенного (а) и точного (б) решений при и (0) =>= 0.5>
й (0) = 0 и е = 0.1.
независимо от значения а, если, конечно, а 0. Этот результат
вполне соответствует характеру численных решений, представлен-
ных на рис. 6.1 и рис. 6.3. Кроме того, из рис. 6.3 видно, что ре-
зультаты расчетов по формуле (6.58) оказываются в хорошем соот-
ветствии с численными решениями уравнения (6.4).
Вместе с тем из формулы (6.58) ясно, что решение и нельзя
представить в виде a cos (t + Р), где а — экспоненциальная функ-
ция времени. В то же время, согласно методике Линдштедта—
Пуанкаре и методу перенормировки, даже если предположить
со комплексным, амплитуда а обязательно будет представлять со-
бой экспоненциальную функцию. Это означает, что с помощью
указанных методов невозможно построить хорошее приближение
к решению исходной задачи. С другой стороны, метод многих
масштабов, который сводит исходную задачу для обыкновенного
дифференциального уравнения к системе уравнений в частных
производных, допускает достаточно широкий произвол при вы-
боре формы приближенного решения, что позволяет с помощью
этого метода получать весьма удачные аппроксимации.
6.4. Метод усреднения
Как указывалось в § 4.6 и 5.5, для того, чтобы применить метод
усреднения к уравнению (6.4), нам необходимо воспользоваться
идеей вариации произвольных постоянных и ввести преобразова-
ние
и (/; е) = а (/) cos [/ + ₽ (/) ],	(6.60)
й (t; е) = —а (/) sin [/ + р (/)].	(6.61)
6.4. Метод усреднения
171
Как и ранее, дифференцируя (6.60) по t, получаем
й = —a sin (t + Р) + a cos (t + Р) — ар sin (t + Р). (6.62)
При этом из соотношений (6.61) и (6.62) следует, что
a cos (/ + Р) — ар sin (t + Р) = 0.	(6.63)
Дифференцирование (6.61) по t дает
й = —a cos (t + Р) — a sin (t + Р) — ар cos (t + Р). (6.64)
Подставляя выражения (6.60), (6.61) и (6.64) в исходное уравне-
ние (6.4), находим
a sin (/ + ₽) + аР coS (^ + Р) = еа sin (^ + Р)-еа3 sin3 (t 4- Р).
(6.65)
Разрешая теперь (6.63) и (6.65) относительно аир, получаем сле-
дующие уравнейия в вариациях:
а = е |^asin(/ -|- Р)--|-a3 sin3 (^ + ₽)] sin(f + Р)>	(6.66)
ap = е р sin (t -|- Р)-a3 sin3 (t -f- Р) j cos (t -f- P).	(6.67)
Воспользовавшись известными тригонометрическими форму-
лами
sin2 0 = -к--s- cos 20,	sin4 0 = (cos 40 — 4 cos 20 4- 3),
2	2	o'
sin 0 cos 0 =	sin 20, sin3 0 cos 0 = -g- (2 sin 20 — sin 40),
перепишем уравнения (6.66) и (6.67) в виде
d=ea[i 0 _4a2) - Н1 -4fl2)cos(2'+2P>-
— a2 cos (4Z -|- 4Р),	(6.68).
р = е [-1- (1 - 4 fl2) sln (2/ + 2₽) + i a2 sln (4/ + 4₽)] ; (6>69>
кроме того, при выводе (6.69) используется предположение, что
a 0.
Как известно, в первом приближении мы сохраняем только
медленно меняющиеся члены, т. е. члены, не содержащие триго-
нометрических функций. Таким образом, в первом приближении
уравнения (6.68) и (6.69) заменяются усредненными уравнениями
а = га 1----------------------------а2) ,	(6.70)
Р = 0,	(6.71)
172	Гл. 6. Колебательные системы с самовозбуждением
Рис. 6.4. Сравнение решений проварьнрованных уравнений (6.68) и (6.69)
с решениями усредненного уравнения (6.70) при е = 0.3 в случае: а) а (0) =
= 0.5, ₽ (0) = 0; б) а (0) = 4.0, ₽ (0)	0.
которые полностью совпадают с уравнениями (6.44) и (6.45), полу-
ченными с помощью метода многих масштабов.
На рис. 6.4 приведено сравнение решений уравнений в вариа-
циях (6.68) и (6.69) с решениями усредненного уравнения (6.70)
при начальных условиях
а (0) = а0, ₽ (0) = 0.	(6.72)
Ясно, что решения усредненных уравнений представляют собой
средние значения решений уравнений в вариациях.
Упражнения
6.1.	Рассмотреть уравнение Ван-дер-Поля
й + и = е (1 — и2) й. ,
а) Построить двучленное прямое разложение и исследовать его неравно-
мерность.
б)	Преобразовать это разложение в равномерно пригодное, используя метод
перенормировки.
в)	Используя метод многих масштабов и метод усреднения, получить рав-
номерно пригодное разложение первого порядка.
г)	Сравнить результаты пп. б) и в) и указать ограничения метода пере-
нормировки.
Упражнения
173
6.2.	Используя метод многих масштабов и метод усреднения, построить рав-
номерно пригодное разложение первого порядка, описывающее переходный
режим для решения уравнения
й 4-	— е{й — й3 4- й2и] (е<^1).
6.3.	Рассмотреть уравнение
X 4- X 4- х — -±- (X — | X I) а (X — х0) = О,
где xtt — постоянная и 6 (х) — дельта-функция Дирака. Построить равномерно
пригодное разложение первого порядка при малых, но конечных х.
6.4.	Рассмотреть систему уравнений
й 4- <£»о« = 2е [(1 — о) й — vu],
v -4 v = и2.
Построить равномерно пригодные разложения первого порядка для и н v.
6.5.	Используя метод многих масштабов и метод усреднения, построить равно-
мерно пригодное разложение первого порядка для уравнения
й + и = е (1 — и4) й при е< 1.
6.6.	Используя метод многих масштабов и метод усреднения, построить равно-
мерно пригодное разложение первого порядка для уравнения
й + и — е (1 — и2) й + ей3 = 0. при е <g 1.
Глава 7
СИСТЕМЫ С КВАДРАТИЧНЫМИ И КУБИЧЕСКИМИ
НЕЛИНЕЙНОСТЯМИ
Рассмотрим свободные колебания частицы массы т, находя-
щейся под действием силы тяжести н связанной с пружиной, сила
упругости которой меняется по нелинейному закону (рнс. 7.1).
Уравнение движения такой системы имеет вид
Л2г*
rri~^ + f(x*'>==mS’	(7J)
аг*
где g — ускорение силы тяжести, a f (х*) — нелинейная возвра-
щающая сила пружины. Пусть f (х*) представляет собой полином
третьей степени от х* вида
f (х*) = V* + V*’.	(7.2)
где k- > 0. Подстановка (7.2) в уравнение (7.1) дает
т + k'x* +	= тВ-	(7-3)
аг*
Опуская в уравнении (7.3) член, описывающий ускорение
системы, можно найти координаты х’ ее положений равновесия
нз соотношения
+Ms ==t‘tlg.	(7.4:)
В этой главе мы будем исследовать малые колебания нашей си-
стемы около одного нз этих положений равновесия. С этой целью
положим в (7.3)
х‘ = х*(7.5)
в результате имеем
/п	5—h ki (xs	и ) -|- &з (xs u ) = mg.	(7.6)
at*
Возводя в куб и используя (7.4), перепишем уравнение (7.6) в виде
+	+ 3fe3*fW + 3Vs«’*+ М*’ = 0.	(7.7)
dt* v	1
Как и ранее, введем следующие безразмерные переменные:
U = u*/x*,	/ = (!)/*,
7.1. Прямое разложение
175
Рис. 7.1. Масса, связанная с нелинейной пружиной,
при наличии силы тяжести.
где а = V(fej -j- 3fe3x* )/m — собственная частота соответствую-
щей линейной задачи, предполагаемая вещественной. Тогда
уравнение (7.7) принимает вид
й + и + Зан2 + оси3 = 0,	(7.8)
где ос — йзХ*7/п(о2, причем мы будем считать, что а = 0(1).
В отлнчне от уравнения Дюффннга уравнение (7.8) содержит как
квадратичные, так н кубические члены. В дальнейшем вместо
(7.8) будем исследовать несколько более общее уравнение, а именно
й + и + сс2и* + ос3и3 = 0	(7.9)
с постоянными ос2 н ос3.
В следующем параграфе мы строим прямое разложение вто-
рого порядка для решения уравнения (7.9). В § 7.2 н 7.3 это раз-
ложение преобразуется в равномерно пригодное с помощью метода
перенормировки и методики Линдштедта—Пуанкаре. В § 7.4
равномерно пригодное разложение строится с помощью метода
многих масштабов. В § 7.5 мы покажем, что первое приближение,
полученное по методу усреднения, приводит к неполному реше-
нию. Поэтому в § 7.6 мы опишем обобщенный метод усреднения,
что позволит получить для решения уравнения (7.9) равномерно
пригодное разложение второго порядка. Наконец, в § 7.7 изложим
метод Крылова—Боголюбова—Митропольского.
7.1. Прямое разложение
Уравнение (7.9) не содержит явно малого параметра, поэтому,
для того чтобы получить прямое разложение решения в случае
малых, но конечных амплитуд, нам нужно ввести малый параметр
в исходное уравнение. С этой целью будем искать разложение
решения (7.9) в форме
и = euj (0 4- e2u2(0 + e3u3 (0 + • • •,	(7.10)
где е — малый безразмерный параметр, являющийся мерой ам-
плитуды колебаний. Мы используем этот параметр в качестве вспо-
176	Гл. 7. Системы с нелинейностями
могательного средства, с тем чтобы произвести «предварительный
учет» порядков величин, входящих в уравнение, а затем положим
его равным единице и будем считать малой амплитуду.
Подстановка (7.10) в уравнение (7.9) дает
£Ui —|- е2й2 4~ 83й3 —Н * * * ~t~ ewj e2u2 “J- 83u3 4~ * * *
• • • —<Z2 (eUj -|- 8U2 4“ 83U3 -f- • • • )2 OCg (eWj -f- 82W2 -|- 63W3 -|- • • • )3 = 0.
(7.И)
Возводя в соответствующую степень ряды, стоящие в скобках
в (7.11), и сохраняя члены до порядка О (б3) включительно, по-
лучаем
8 (й, +. Hi) 8 (йг —ы2 “Г*	1) +
6 (йз «з 4“ 2«2wiw2 4“	4~ • • • — 0.	(7.12)
Приравнивая нулю коэффициенты при соответствующих степенях
8, имеем набор уравнений
йг 4~ Ui = 0,	(7.13)
Й24-«2 = — «2м?,	(7.14)
йз4~ыз =— 2a2ulu2 — а5и?,	(7.15)
которые могут быть решены последовательно относительно неиз-
вестных ы1( и2 и и3.
Общее решение (7.13) представим в виде
иг — a cos (t + Р),	(7.16)
где аир — постоянные. При этом (7.14) принимает вид
й2 4- «2 = — а2°2 cos2 (t Ц- Р) =-«2а2-а2а2 cos (2/	2Р).
(7.17)
Как и ранее, мы не включаем в выражение для иг решение соот-
ветствующего однородного уравнения. Частное решение неодно-
родного уравнения (7.17) можно найти как сумму частных реше-
ний следующих уравнений:
uV)+^i)=-4"a2a2>	(7-18>
й^2> + 42) = - -L а2а2 cos (2t + 2р).	(7.19)
Г
Частным решением первого из них будет
4-<7-20>
7Л. Прямое разложение	177"
а частным решением второго (см. формулы (В.68) и (В.69)) —
ы2ч астн =	а2а2 cos(2/ 4- 20) •	(7.21)
Таким образом, имеем
W2 = Мгчастн 4" И2чаетн = — ~2~ Н--g“ а2^ COS (2Z -|“ 20).	(7.22)
Подстановка выражений (7.16) и (7.22) в уравнение (7.15) дает
й3 и3 = — 2ага cos (t Ц- 0) [---а2а2 + -у aaQ2 cos № + 20)]__
— o-3a3cos3(Z + 0),
или
#з + из — ("(Г а2-4~ аз) а cos (^ + Р) —
-(^аз+4-ai)a3c°s(^ + 30).	(7.23)
Поскольку уравнение (7.23) линейно, то
и3 = изчастн -|- ^зчастн,	(7.24)
где «зчастн и «зчастн — частные решения уравнений
й|1)+ыГ) = (4^-4аз)«3с°5(/ + 0),	(7.25)
«з ’ + ыз ’ — —	аз ”1—б” а2) а c^s + 30)'	(?-26)
При этом из формул (В.69) и (В.76) следует, что
«з'частн =	а2---§- а3) a3t Sin (t Ц- 0),	(7.27)
Изчастн —	аз -j—g- а2) a cos (3/ + 30).	(7.28)
Подставляя теперь решения (7.27) и (7.28) в (7.24), находим
ыз — ("jjr а^--------------g- аз) a3t sin (/ -|~ 0) +
Н—§~	аз “I—б" а2) а cos + ЗР)’
1
178	Гл. 7. Системы с нелинейностями
Наконец, подставляя (7.16), (7.22) и (7.29) в (7.10), получаем
следующее прямое разложение третьего порядка (с точностью до
членов порядка О (е3)):
и — ъа cos (t 4- 0) 4- -g- а282а2 [cos (2/ 4- 20) — 3J +
+ 83«3 [(-А-al - -1-аз) t sin(t 4- 0) +	(7.30)
+ “ аз 4~ “j-- Cos +130)] 4-  • • •
Заметим, что функциям зависит от 8 и а только через произве-
дение еа. Это дает возможность положить 8 = 1 и рассматривать
а в качестве параметра возмущения. Вместе с тем прямое разло-
жение (7.30) становится непригодным при t О (е-1а“1),. по-
скольку при этом второй поправочный член становится величиной
одного порядка с первым из-за наличия в нем секулярного слагае-
мого. Попытаемся теперь преобразовать разложение (7.30) в рав-
номерно пригодное, используя для этого метод перенормировки.
7.2. Метод перенормировки
Как указывалось в § 4.3 и 4.4, равномерно пригодное разло-
жение для решения уравнения (7.9) может быть построено либо
с помощью применения методики Линдштедта—Пуанкаре непо-
средственно к дифференциальному уравнению, либо путем ис-
пользования метода перенормировки для разложения (7.30).
И в том, и в другом случае мы вводим замену т = at, где со — «не-
линейная» частота в уравнении (7.9). Далее, мы раскладываем со
в ряд по степеням 8, причем первый член ряда оказывается часто-
той линейных колебаний (в нашем случае равной единице). Итак,
представим частоту со в виде разложения
(0 = 14- ecoi + е2(о2 + • • • •	(7-31)
Отметим, что в это разложение мы включили только члены вто-
рого порядка, поскольку секулярное слагаемое в (7.30) содержится
в члене третьего порядка. Далее, имеем
t== (1 4- 8(0! 4- 82(02 4- • • .)-! Т = [1 — (8i0i	82(02 -|-)4~
4-(8(0i 4-82(02 4- •••)2]Т.
Сохраняя члены порядка О (s2), получаем
t = т — 8(0iT 4- е2 ((о2 — (о2) т 4-  • • •	(7.32)
7.2. Метод перенормировки
179
{ Подстановка (7.32) в (7.30) дает
и — еа cos [т 4- Р — ecoiT Ц- е2 (со? — со2) т 4- • • • ] 4
4- -|-а282а2 {cos [2т 4- 2Р — 2ecoiT 4- 2е2(со2 — со2) т 4~ •  • ] — 3} 4
4- 83fl3 ^("ПГа2--|"аз) Iх ~ еС01Т + е2((02 — (Ог) Т 4- • • •] X (7.33)
X sin [т 4~ ₽ — е(0]Т 4- 82(й| - (02)т 4 • • • ] 4"
+ '8'(чТаз + T012) Х
X cos [Зт 4- Зр — Зе(01Т 4- Зе2 (со2 — со2) т 4* •' • 4* " ’ •
Исследуем теперь разложение (7.33) при малых е и фиксиро-
ванном т. Раскладывая тригонометрические функции в ряды Тей-
лора, находим
cos [т 4- Р — ecoiT 4- е2 (со2 — со2) т 4- • • • ] =
= cos (т 4- Р) + [ecoiT — е2 (со? — со2) т] sin (т 4- Р) —
—	[е<01Т — е2 (со? — со2) т 4- • • • ]2 cos (т 4- Р) =
= cos (т 4- Р) 4- ес°1г sin (т 4~ Р) — е2 f(со? — «2) т sin (т4₽)4 1
4 -i- ы2т2 cos (т 4- Р) 4- • • •,	(7.34)
cos [2т 4- 2р — 2e(0iT 4- 2е2 (со2 — со2) т 4* • • • ] =
= cos (2т 4- 2Р) 4- [2ecojT — 2е2 (<о2 — сог) т[ sin (2т 4- 2Р) 4 • • • =
= cos (2т 4- 2Р) 4- 2еы|Т sin (2т 4- 2Р) 4- • • ,	(7.35)
sin [т 4- Р — 6Ы1Т 4- е2 (со2 — со2) т 4- • • • ] — sin (т -|- Р) 4- • • •, (7.36)
cos [Зт 4- ЗР — 3s(0iT 4- Зе2 (со2 — со2) т 4- • • • J = cos (Зт 4- ЗР) 4~ •' •
(7.37)
Подставляя выражения (7.34)—(7.37) в (7.33) и сохраняя члены
до третьего порядка включительно, получаем
н — еа cos (т 4~ Р) 4-g2 ^ат sin (т 4- Р) 4*
4 4- а2°2 cos (2т 4- 2Р)---а2а2] +
4 е3 (—«2«т2 cos (т 4- Р) 4
180	Гл. 7. Системы с нелинейностями
+ [('Т2'а2--Газ) а3 ~ а(“1 — “2)] rsin(t + P) +
+ ссгинЛ sin (2т	20) -|-
+ -г(-Газ+4-а2)а3со5(3т+3Р)} + ••• •	(7-38)
Для того чтобы избавиться от секулярного члена порядка О (е2),
необходимо (в случае а =# 0) положить (Dj равным нулю. При этом
исчезают и все секулярные члены третьего порядка, кроме одного,
который пропадает при условии
-4-аз)а3 + а“2==0-	(7-39>
Отсюда
«)2 = — (-^ «2 - А аз) а2>	(7.40)
После уничтожения секулярных членов разложение (7.38) при-
нимает вид
и = еа cos (т 4- 0) e2a2tz2 [cos (2т 20) — 3J • • •, (7.41)
где
т^а/= [1 + (Ааз __5.а2)е2а2р^----------.	(7.42)
Отметим, что секулярный член порядка е3 в (7.38) исполь-
зуется для определения а2. Остальные члены порядка е3 ограни-
чены при т-> оо; они не включаются в (7.41), поскольку разло-
жение проводится до членов- второго порядка, так что ошибка
представляет собой величину О (е3) для всех t < О (е-1). Более
подробно этот вопрос обсуждался ранее в § 4.5.
Обращаясь вновь к разложению (7.30), отметим, что первый
секулярный член появляется лишь в членах порядка е3. Таким
образом, еще заранее мы могли бы заключить, что = 0, по-
скольку член eaj в разложении (7.31) порождает секулярные члены
второго, а не третьего порядка. Использование этого факта позво-
лило бы значительно сократить объем вычислений. Покажем те-
перь, что методика Линдштедта—Пуанкаре, требует проведения
еще меньшего объема вычислений, чем метод перенормировки.
7.3. Методика Линдштедта—Пуанкаре
Используя в уравнении (7.9) преобразование т = а/, получаем
<о2ы" + и + а2и2 + азы3 — 0.	(7-43)
7.3. Методика Линдштедта—Пуанкаре
181
це штрихами обозначено дифференцирование по т. Далее, рас-
ладываем (о и и в ряды по степеням е:
и =	(т) + еао2 (т) + е3ы3 (т) Н-,	(7.44)
ш = 1+ еа! + е2(о2 Н— • .	(7.45)
<ак указывалось в предыдущих главах, первый член разложения
ля со представляет собой частоту линейных колебаний, в нашем
лучае равную единице. Подставляя (7.44) и (7.45) в уравнение
г.43), имеем
(1 + 6(01 + 8 (02 + ‘	) (®«1 + 8 «2 + 8 U$ + • • * ) + 801 +
+ 6 «2 + 8 «3 + •  • “И а2 (е«1 + 8 «2 + 8 «3 + • • •) +
+ Og (eui + e2u2 + е3н3 + • • • )3 = 0.
Используя биномиальную формулу для разложения квадра-
тного и кубического членов и сохраняя члены до третьего по-
ядка включительно, находим
(1 + 2б<01 + е (01 + 2е (о2) (e«i + 8 о2 + е3о3) + e«i + е «2 + е «3 +
+ а2 (е «1 + 2е oi+) + a3e3«i + • • • = 0.
[еремножая выражения в скобках и приравнивая нулю коэффи-
иенты при последовательных степенях е, получаем
u"i +«i=0,	(7.46)
«2 + «2 = —2(0+1 — а2«ь	(7.47)
«3 + "з = —2(о 1«2 —	+ 2(о2) «1 — 2о^2«1«2 — сс3«|.	(7.48)
Общее решение уравнения (7.46) может быть представлено как
«! ±= a cos (т + Р),	(7.49)
je а и р — постоянные. Тогда (7.47) переписывается в виде
«2 + «2 = 2(0ia cos (т + 0) — а2а2 cos2 (т + Р),
ли
ы2 + ы2 = 2(oi« cos (т +Р)-ггагЯ2----cos (2т + ЗР).
(7.50)
(ля того чтобы в решении о2 отсутствовали секулярные слагае-
те, необходимо положить (ох = 0. При этом решение (7.50)
:троится аналогично тому, как это проводилось в § 7.1; оно имеет
1ИД
иг=-----^агр:2+-j-asa2cos(2T +20).	(7.51)
182
Гл. 7. Системы с нелинейностями
Подставляя решения (7.49) и (7.51) в уравнение (7.48) и учи-
тывая тот факт, что (Oj = 0, получаем
Нз —U3 = 2(02 cos (т —р) —
— 2а2а cos (т + Р) [-«2а2 + -±- а2а2 cos (2т 4- 2Р) j —
— Оза3со83(т + Р).	(7.52)
Используя теперь, как и в § 7.1, соответствующие тригономе-
трические тождества, перепишем (7.52) в виде
w3 + И3 = ^2(02Я--j- Озй3 4-COS (T 4- р) —
- (4- “з+4" аЭ cos (3т+зр)- <7-53)
При этом требование отсутствия секулярных членов приводит
к соотношению
2®2а----1- а3а3 +	«2«3 = О,
откуда
®2 = а3а2-------- ага2.	(7.54)
Отметим, что подстановка выражений (7.49) и (7.51) в (7.44) при-
водит к разложению (7.41), а подстановка (7.54) в (7.45) с учетом
преобразования т = cot и соотношения = 0 дает (7.42). Таким
образом, использование методики Линдштедта—Пуанкаре при-
водит к тому же самому разложению, что и методика перенорми-
ровки, но при заметно меньшем объеме вычислений.
7.4.	Метод многих масштабов
В этом параграфе мы построим равномерно пригодное разло-
жение третьего порядка с помощью метода многих масштабов,
используя для того три переменные: То = t, 7\ = &t и Т2 = е2/.
При этом для производных по времени получаем
~ = D0 + eZ)14-e2L>2 + ..-,	(7.55)
др — Do 4~ 2e.D0Di 4- e2 (D2 4- 2D0D2) 4~ • • •,	(7.56)
где Dn — д/дТп. С помощью (7.56) преобразуем уравнение (7.9)
к виду
Do^ 4~ 2eD0£>i« 4- е (OiW 4- 2DoD^) 4~ 4~ “2^ 4~ ®з“ 4~ ' ’' == 0.
(7.57)
IL	7.4. Метод многих масштабов	183
приближенное решение уравнения (7.57) будем искать в форме
в и = £и1 (То, 1\, Т2) + e2u2 (То, Tlt Т2) + e3u3 (То, 7\, Т2) +
|	+••••	(7.58)
Подставляя разложение (7.58) в (7.57) и приравнивая нулю коэф-
юициенты при последовательных степенях е, находим
Г	Dl^ + U] = 0,	(7.59)
е.	Z?o«2 “Ь ^2==: — 2D0Diu — a2«i,	(7.60)
D(,u3 4~ «3 = —.PiMi — 2DqD^i — 2DqDi42 — 2cc2f4ii42 — аз«3.(7.61)
I Решение уравнения (7.59) может быть представлено как
|	Ui = A(T1,T2)e^ + A(T1,T2)e-‘’"».	(7.62)
При этом (7.60) принимает вид
I	£>ou2 + «2 = ~2iDiAelT“ 4- 2iDlAe~iT° —
|	- a2 (A2e2iT° + 2AA + A2e-2‘r°).	(7.63)
Иля того чтобы избавиться от секулярных слагаемых в и2, поло-
вины
I'	DjA = 0, или А = А (Т2).	(7.64)
Ограничиваясь, как и в предыдущем параграфе, нахождением
вишь частного решения уравнения (7.63), можно получить его
I помощью принципа суперпозиции. В результате имеем
I u2=4- а2А2е2‘т« + 4- а2А2е-2/г» - 20,44.	(7.65)
r>	Ou
I Подстановка (7.62), (7.64) и (7.65) в уравнение (7.61) дает
| Z)2u3 + и3 = — 2iA'eiT° + 2iA'e~iT° - 2а2 (Ае‘г" + Ае~‘Г°) х
Lx (4- а2А2е2‘7’|> + 4-а2Л2е-2^«— 2а2АА) — а3 (Ае‘г° Ае_‘г»)3,
t	(7-66)
гае штрихом обозначается дифференцирование по переменной Т2.
При выводе (7.66) мы использовали уравнение (7.64), из которого
Еледует, что —D2u2 — 0. Воспользовавшись биномиальной
вормулой, перепишем уравнение (7.66) в виде
Ж + “з= [— 2iA' +-4-а22А2А-За3А2А] е1Т° -
L	-	“2 + *з) A3e3iTa + (к. с.).	(7.67)
При этом условие отсутствия секулярных членов приводит к соот-
ношению
[	— 2iA 4- (-4- «2 - За3) А2А = 0.	(7.68)
184
Гл. 7. Системы с нелинейностями
Представляя теперь комплексную амплитуду А в форме -
Д = _1-ае<₽,	(7.69)
где а и р — вещественные постоянные, приведем (7.68) к виду
—ia'e‘₽ ар'е,₽ ai----------|"аз)	= О,
или’	— *’«'+ «Р'+ (-jy-oa---д-аз)а3 = 0-	(7-70)
Отделяя вещественную и мнимую части в равенстве (7.70), имеем
а' = 0,	(7.71)
aP' = (Aa3-4-«22)fl3-	(7.72)
При этом из (7.71) следует, что а — а0 = const, а из (7.72) (при
а Ф 0), что
Р = (4- а3 - 4- а22) «а2Г2 + Ро,	(7.73)
где Ро — произвольная постоянная.
Подставляя (7.69) в формулы (7.62) и (7.65) и вспоминая, что
То = Л получаем
их — a cos (t + Р),	(7-74)
и2 =	a2a2 cos (2t + 2P)-- a2a2.	(7-75)
Разложение (7.58) в этом случае принимает вид
и = ea cos (/ + Р) + -§- e2a2a2 [cos (2/ 4* 2Р) — 3] + • • •. (7.76)
С помощью формулы (7.74) и с учетом того, что а = щ и Т2 =
— ePt, можно переписать (7.76) в виде
и — еао cos (mt ро) -Ь -g- [cos (2<о/ + ^Ро) — 3] + • • •,
(7.77)
где	® — 1 + ("в” аз —ПГ0^) е	(7.78)
что полностью согласуется с разложениями (7.41) и (7.42), полу-
ченными с помощью метода перенормировки и методики Линд-
штедта—Пуанкаре. Применим теперь к (7.9) первое приближение
метода усреднения.
7.5. Метод усреднения
185
7.5.	Метод усреднения
Как и ранее, для преобразования исходной функции и восполь-
зуемся методом вариации произвольных постоянных, положив
и = еа cos (t + Р),	(7.79)
й = —еа sin (t + Р),	(7.80)
где е — малый безразмерный параметр, являющийся мерой ам-
плитуды колебаний. При этом для нелинейной задачи величины
аир считаются переменными. Дифференцирование формулы
(7.79) по аргументу t дает
й == —еа sin (t -f Р) + ed cos (HP) — sap sin (/ + P). (7.81)
Сравнивая (7.80) и (7.81), заключаем, что
a cos (t + Р) — ap sin (t + P) = 0.	(7.82)
Аналогично, дифференцируя выражение (7.80) no t, имеем
й = —ea cos (t + P) — ed sin (t + P) — eaP cos (t + P). (7.83)
Подстановка (7.79) и (7.83) в исходное уравнение (7.9) дает
a sin (t + Р) + ap cos (t + P) = a2ea2 cos2 (^ + P) +
4- a3e2a3 cos3 (t 4- P)-	(7-84)
Разрешая уравнения (7.82) и (7.84) относительно аир, находим
а = a2ea2 sin (^ + Р) c°s2 (^ + Р) + a3e2a3 sin (t 4- Р) X
X cos3 (t + Р),	(7.85)
Р = а2еа cos3 (t + Р) + а3е2а2 cos4 (t + Р).	(7.86)
Кроме того, при выводе (7.86) предполагается, что а отлично от
нуля.
Поскольку а мало, то производные а и Р представляют собой
медленно меняющиеся функции t. При этом в качестве первого
приближения можно попытаться усреднить (7.85) и (7.86) по пере-
менной t. Преобразуя с этой целью уравнения (7.85) и (7.86) с по-
мощью известных тригонометрических формул, получаем
d =-i-a2ea2 [sin (/+ Р) + sin (3/+ ЗР)]+
4 -g- a3e2a3 [2 sin (2/ 4- 2P) + sin (4/ 4- 4p)],(7.87)
P = -L a3e« [3cos (/ + P) + cos (3t 4- 3p)] 4*
+ 4-a3e2a2[cos(4Z+ 4P) + 4cos(2/ + 2P)4-3]. (7.88)
186
Гл. 7. Системы с нелинейностями
Сохраняя в правых частях уравнений (7.87) и (7.88) только
медленно меняющиеся слагаемые, находим окончательно
а = 0,	(7.89)
Р=4-аз^2.	(7.90)
В то время как соотношения (7.89) и (7.71) полностью согласуются
между собой, уравнение (7.90) не совпадает с уравнением (7.72),
полученным с помощью метода многих масштабов, поскольку в нем
отсутствует член а2е2а2. Подробно прослеживая ход решения
в предыдущем параграфе, можно обнаружить, что этот член яв-
ляется результатом взаимодействия приближений первого и вто-
рого порядков, которое не принималось во внимание при выводе
(7.89) и (7.90). Чтобы учесть указанный эффект, нам нужно ввести
в рассмотрение высшие приближения для а и р в (7.87) и (7.88).
Это достигается с помощью обобщенного метода усреднения, опи-
сываемого ниже, или его варианта — метода Крылова—Бого-
любова—Митропольского, рассматриваемого в § 7.7.
7.6.	Обобщенный метод усреднения
Для того чтобы продемонстрировать применение этого метода,
введем новую переменную
Ф = t + р,	(7.91)
переписав соотношения (7.87) и (7.88) в виде
а — а2еа2 (sin <р + sin 3<р) -f- -g- а^а3 (2 sin 2<p + sin 4<p),
(7.92)
ф = 1 4~ -j-	(3 cos <p cos 3<p) + -g- (cos 4ф -f-
+ 4соз2ф + 3).	(7.93)
Приближенное решение (7.92) и (7.93) будем искать в следующей
форме:
а = а0 (0 4- еах	(а0,	ф0) 4- е2й2 (а0, ф0) 4--,	(7.94)
ф = Фо (0 4- ефх	(а0,	фо) 4- е2ф2 (а0, ;ф0) 4-,	(7.95)
d0 =	(а0)	4- еМ2 (а0) 4--.	(7.96)
Фо = 1 4~ еФх (й0) +	(а0) + • •  •	(7.97)
Функции ах, а2, ... и фх, ф2, ... представляют собой быстро ме-
няющиеся функции фо, в то время как а0 и, следовательно, Ап и
Фп — медленно меняющиеся функции I.
7.6. Обобщенный метод усреднения
187
; Используя правило дифференцирования сложной функции,
федставим первые производные выражений (7.94) и (7.95) в виде
		,	dat	.	даг	.	, „	да. .	,	,	да.	.	.
-	а	= а0 -4- е	д	а0 4-	е	д	ф0 -4- е2 -т-=- а0 4-	е2	. 2	(₽« 4-	• • •,
“ 1	daQ	° 1	дф0	т	да0 ° 1	ду	то '	’
?	(7.98)
| ^=^+e4!rd»+E-|r(p«+E2-IJ-do+e24lr(po + ----

:	(7.99)
Подставляя разложения (7.96) и (7.97) в (7.98) и (7.99) и сохраняя
мены вплоть до второго порядка, получаем
да,
да^
4~ Oj
(7.100)
*=1+' (ф- + »+е! (®>++Л. >+
(7.101)
Далее, необходимо подставить разложения (7.94) и (7.95) в (7.92)
I (7.93) и разложить правую часть при малых е, сохраняя члены
Ю второго порядка включительно. При этом для правой части
юотношения (7.92) имеем
еа2 (sin ф + sin Зф) =
= е (а,, + sa^2 [sin (<p0 + «Pi) + sin (3<p0 4- Зефх)] 4--
t=e (al 2ea0«i) [sin <p0 -f- e<Pi cos <po + sin 3<p0 -f- 3e<pi cos 3<p0] 4— • =
eoo (sin фо 4~ sin Зфо) 4~ 2e nto^i (sin фо 4~ sin Зфо) 4~
4- е2а$ф1 (cos фо + 3 cos Зф0) + • • • >	(7.102)
е2а3 (2 sin 2ф 4- sin 4ф) = e2flo (2sln 2фо + sin 4ф0) + • • •.
(7.ЮЗ)
для правой части (7.93) —
(3cos ф + cos Зф) = е (я0 4- еах) [3 cos (ф0 4- ефх) +
4- cos (Зф0 4- ЗеФ1) ] 4--------
= е (а0 4- 8Д1) [3 cos ф0 — Зефх х
X sin фо 4- cos Зф0 — Зефх sin Зф0 ] +
4- ••• =	(7.104)
= еа0 (3 cos ф0 4- cos Зф0) 4- еаах X
(3 cos фо 4- cos Зф0) — Зеааоф1 (sin ф0 4- sin Зф0) 4- • • •
188	Гл. 7. Системы с нелинейностями
И
e2a2(cos4<p + 4cos2<p 4-3) = е2До (cos 4<p0 + 4 cos 2<p0 + 3) + • • ••
(7.105)
Подставляя выражения (7.100)—(7.105) в (7.92) и (7.93) и прирав-
нивая нулю коэффициенты при одинаковых степенях е, находим
+	= -i-a2ao(slnTo + sin3<po), (7.106)
А +	+ А -Ц- + Ф1	<sln Фо + sin 3<р°) +
4—j-оДОоф! (cos фо -|- 3 cos Зфо) —g- &з#о (2 sin 2фо 4~ sln 4фо),
(7.107)
Фх -г = 4" а2«о (3 cos фо + cos Зф0),	(7.108)
Ф2 +	+ А + ф1 = 4- (3cos Фо +cos Зфо) -
— 4" “^оФ1 (sln Фо + sin Зфо) + 4" “зао (cos 4фо + 4 cos 2ф0 + З).
(7.109)
Для того чтобы выделить быстро и медленно меняющиеся члены
в формулах (7.106)—(7.109), используем метод разделения пере-
менных. При этом для медленно меняющихся членов в (7.106) и
(7.108) имеем
Л1-Ф1 = 0.	(7.110)
Аналогично, для быстро меняющихся членов получаем
= 4-«Л2 (sin фо + sin Зфо),	(7.1П)
= 4-^(3 cos Фо + cos Зф0).	(7.112)
Частные решения уравнений (7.111) и (7. М2) имеют вид
fli =----рОгОо (cos фо + 4" cos Зфо)	(7.113)
и	Ф1 = 4" а2ао (з sin фо + 4” sln 3 Фо) •	(7.И4)
К	7.6. Обобщенный метод усреднения	189	?
Г Подставляя теперь выражения (7.110), (7.113) и (7.114) в уравне-
| ния (7.107) и (7.109), находим
I А2 +	=-----g- (cos фо 4- -у cos Зфо) (sln фо + sin Зф0) 4~	;
I	+ «2ао (з sln Фо + -|" Sln Зфо) (sin фо + sin Зфо) 4*
[	+ аз^о (2 sin 2ф0 4~ 81п4ф0),	(7.115)
| ф2 4~	= —ПГ	(cos (f0 + 4"cos 3Ф°) (3 cos Ф° + cos Зф°) ~
[	----(З sln фо 4“sin Зфо) (sin фо 4* sin Зф0)4-
I	4--|-азао(со5 4фо4-4со5 2фо4-3).	(7.116)
I С помощью известных тригонометрических формул (см. прило-
! жение А) перепишем соотношения (7.115) и (7.116) в виде
I; Л2 + ^ = П^[(4а3~4"а2)81п2Фо +
|	+ (2а3 4-^-0^) sln фо 4“ “g-sln бфо] ,	(7.117)
|	(4”аз [у «2) ао4“ (4“аз------ПГ0^) аосоз2ф0 +
I 4“ (-§-а3 + 4“а2) a“COS4<;p0 4~cosбфо- (7.118)
i: Поскольку мы разыскиваем только разложение второго порядка,
нет необходимости решать уравнения (7.117) и (7.118) относительно
| аа и фг. Для этого требуется только выделить в (7.117) и (7.118)
[ медленно меняющиеся слагаемые и тем самым определить Аа и Фа,
f которые в этом случае имеют вид
|	Ла = 0,	(7.119)
Фа=(-|-аз-----[5"а2)ао*	(7.120)
Подстановка выражений (7.113) и (7.114) в (7.94) и (7.95) дает
а = Оо---|~а2еао (созфо 4““у cos ^Фо) 4“ • • •>	(7.121)
\	Ф = Фо 4~	(3 sin ф0 4-sin Зф0) 4--.	(7.122)
..—;.......-...' ...... '  ............ ' - .....................
190
Гл. 7. Системы с нелинейностями
Подставляя теперь выражения (7.110), (7.119) и (7.120) в (7.96)
и (7.97), получаем
d0 = 0,	(7.123)
Фо = 1 + (^---^Ч'	(7.124)
Решение (7.123) имеет вид а0 = const; при этом из уравнения
(7.124) следует
Фо = t + а3 -	а!) еЧ2/ + ₽0,	(7-125)
где р0 — постоянная интегрирования. Наконец, подстановка раз-
ложений (7.121) и (7.122) в (7.79) дает
и = е [а0--j- а2еяо (cos Фо + 4 cos ^о) + • • • ] X
X cos [ф0 + 4 (З sin фо 4“ 4 sln 3Фо) + •••]• (7-126)
Для того чтобы сравнить построенное решение с приближен-
ными решениями, полученными по методу многих масштабов и с
помощью методики Линдштедта—Пуанкаре, нужно разложить
cos [ф0 + О (е)] в (7.126) при малых 8 с точностью до членов по-
рядка 8, в результате чего получим
и = 8 [а0--a2ea2 (cos Фо + 4 cos ^Ч’о)] [cos Фо —
---^-aa8aosin ф0 (Зз1Пф0 -f- 481п3Фо)] + • • • =
= еа0 cos фо------агеЧ [cos2 фо + 4 coS (₽0 COS ^<₽0
4- 3 sin2 фо + 4 sin фо sin Зф01 4- •
О	J
= еа0 cos фо------а2в2ао [ 4 + 4 cos 2фо + 4 cos 2ф0 +
или
и = еа0 cos Фо 4“ 4 е2аоа2 (cos 2фо — 3) 4" " ' •	(7.127)
Разложение, даваемое формулами (7.125) и ’ (7.127), в точности
совпадает с разложениями (7.77) и (7.78), полученными по методу
многих масштабов. Оценка же объема вычислений, проделанных
здесь, и вычислений, проведенных в § 7.2 и 7.4, позволяет сде-
лать вывод, что метод перенормировки и метод многих масштабов
имеют в этом отношении преимущество перед обобщенным мето-
дом усреднения.
/ •
7.7. Метод Крылова—Боголюбова—Митропольского	191
[ 7.7. Метод Крылова—Боголюбова—Митропольского
| В этом параграфе мы опишем еще один вариант обобщенного
L метода усреднения, называемый обычно асимптотическим мето-
F дом Крылова—Боголюбова—Митропольского.
f Если пренебречь нелинейными членами, то решение уравнения
[ (7.9) можно записать в виде
'	и = еа cos (( 4- Р),	(7.128)
‘ где а и Р — некоторые постоянные, а е — малый безразмерный
параметр, определяющий амплитуду колебаний. При учете же
j нелинейных членов мы рассматриваем (7.128) лишь как первый
‘ член в приближенном решении (7.9), причем а и р считаются те-
• перь не постоянными, а медленно меняющимися функциями вре-
мени. Кроме того, введем так называемую быструю переменную
‘ Ф — t + р. В результате будем искать приближенное решение
; уравнения (7.9) в виде
и = га cos ф 4- е2и2 (а, ф) 4- е3ы3 (а, ф) 4- • • • •	(7.129)
Поскольку аир представляют собой медленно меняющиеся функ-
ции /, представим их рядами по степеням е с коэффициентами, за-
висящими от «медленной» переменной а. Таким образом, мы можем
записать
а — вЛ! (а) 4- е2Л2 (а) -,	(7.130)
	ф = 1 4. еФ± (а) 4- е2^ (а) --.	(7.131)
Иначе говоря, этот метод можно рассматривать как многомасштаб-
: ную процедуру с выбранными масштабами времени а и ф.
:	С помощью правила дифференцирования сложной функции
i выразим производные по i через новые независимые переменные
: а и ф:
:	+	(7.132)
at да а<р	'	'
d2 -2 & . .. д , о. . д2 , . д2 , .. д
— а2тт + а ~л—Ь2афд—д—ЬФтт + ф-з—• (7.133)
at* да2 1 да 1 да dtp 1 dtp2 1 dtp '	'
l При этом дифференцирование (7.130) по t дает
;	d = еЛ(а 4-еМга 4-• • • 	(7.134)
( где штрихами обозначено дифференцирование по а. Подставляя
[ теперь (7.130) в соотношение (7.134), имеем
• а = гА1 (еЛ1 4~е2Л2 4- • • •) 4'e2?Me^i +•••)+’••>
[ или
*	а = г2 Al А! + О (е3).	(7.135)
I Аналогично, дифференцирование (7.131) по t дает
1	ip = еФ[а 4- е2Ф2а 4~ • • •.	(7.136)
192
Гл. 7. Системы с нелинейностями
Подставляя (7.130) в (7.136), имеем
Ф = еФ1 (еЛ1 + е2Л2 + • • •) + е2Фг (еЛ1 + • • •) + • • •,
или
ф = ЕгЛ1Ф[ + О(е3).	(7.137)
Наконец, подставляя (7.130), (7.131), (7.135) и (7.137) в формулы
(7.132) и (7.133), находим
— (еЛх + еМ2 4~ • • •)	+ (1 + еФх + е2Ф2 + • • •)	-
= (еЛх + е2Лг + • • -)2-gr + (еМ,Л[ + • • -)-^ +
+ 2 (еЛх4- 82Л2 + ...) (1 + еФх + е2Ф2 + •  •) Д; +
+ (14- еФх + е2Ф2 + • • -)2~^- + е2Л1Ф1 + • • -)^">
откуда
-4г =	+ е (Лх + Фх + е2 ( Л2-j" 4- Ф2
dt dip 1	\ 1 да 1 dip / 1	\ 2 да 1	2 dip /
(7.138)
* +2г(ф1-Рт+41^ +
dt2 ду2 1	\ 1 д(р3 1	1 да ду 1
+«• [<®г+2®j -$-+2 <л+Л|ф>) А+
+л?+г+л,л;-ж-+л1®;+] + •••• (7лзэ)
в
При этом уравнение (7.9) принимает вид
4р" + 2е [ф1^±-+Лх^у + е2 [(Ф?+2Ф2)-|^- + 2(Л2 +
+ А‘ "У" + А,А‘ + Л1Ф‘ "v] + « + «г"2 +
+ а-у? 4--=0.	(7.140)
Подставляя разложение (7.129) в уравнение (7.140) и прирав-
нивая нулю коэффициенты при одинаковых степенях е, получаем
^22 + и, — 2Фха cos ф — 2ЛХ sin ф + а^а2 соз2ф = 0, (7.141)
1^-+“.+ 2®| -5^ + 2Л' 44 - W + 2®.)«os<P -
— 2 (Л2 + Л1ФХ) sin ф + Л1Л J cos ф — Л1Ф(а sin ф +
+ 202^0 008 ф + осза3 cos3 ф = 0. .	(7.142)
7.7. Метод Крылова—Боголюбова—Митропольского	193
Далее, с помощью тригонометрического тождества (А13) перепи-
шем (7.141) в виде
- 4- и2 = 2Фха cos <р + 2ЛХ sin ф-i- а2а2-а2а2 cos 2ф.
(7.143)
Для того чтобы исключить секулярные члены из решения и2, по-
требуем, чтобы
Фх = О и Лх = 0.	(7.144)
Тогда, как и ранее, решение (7.143) может быть представлено
в виде
и2 =---g- а^2 +	а2«2 cos 2ф.	(7.145)
Подстановка (7.144) и (7.145) в уравнение (7.142) дает
4-	и3 = 2Ф2а cos ф + 2Л2 sin ф — 2а2а cos ф х
X [----а2Д2 + -у а2а2 cos 2ф j — a^cos8 ф. (7.146)
С помощью соответствующих тригонометрических формул (см.
приложение А) перепишем теперь (7.146) в виде
-4^- + «з = (2Ф2---|-аза2 + a cos ф + 2А2 sin ф —
~ (4-a3 + 4"a2)fl3cos Зф‘ (7.147)
Условие отсутствия секулярных членов в решении и3 дает
Г	Л2 = 0,	Ф2=(4аз-4а^.	(7.148)
^Наконец, подстановка (7.144) и (7.148) в разложения (7.130) и
;(7.131) приводит к уравнениям
i	d = 0,	(7.149)
[	q>=l + (4a3-4a22)eV+...,	(7.150)
которые полностью совпадают с уравнениями (7.123) и (7.124),
 полученными с помощью обобщенного метода усреднения, а сле-
довательно, и с решением, построенным по методу многих мас-
; штабов.
7 Найфэ А. X.
194
Гл. 7. Системы с нелинейностями
Упражнения
7.1.	Рассмотреть уравнение
х — 2х — х? + х3 = 0.
Показать, что положения равновесия системы, описываемой^этим уравнением,
определяются координатами х= 0, —1, 2. Положить х = 2-р и и найти
уравнение для функции и. Затем построить равномерно пригодное разложение
второго порядка при малых, но конечных амплитудах с помощью:
а)	метода Линдштедта—Пуанкаре,
б)	метода многих масштабов,
в) обобщенного метода усреднения.
7.2.	Рассмотреть уравнение
й — и + и* — 0.
Показать, что точка и = 1 является положением равновесия системы. Построить
равномерно пригодное разложение второго порядка, описывающее малые коле-
бания около точки и — 1. Указание: положить и= 1 + х, получить уравне-
ние относительно х и затем использовать либо метод Линдштедта—Пуанкаре,
либо метод многих масштабов, либо обобщенный метод усреднения.
7.3.	Рассмотреть уравнение
й — и + ив = 0.
Показать, что точка « = 1 является положением равновесия данной системы.
Найти разложение второго порядка для малых, но конечных колебаний вблизи
точки и = 1.
7.4.	Рассмотреть уравнение
q
* + Х ~ 16(1 -х)	°’
Показать, что положения равновесия описываемой системы определяются ко-
ординатами х = 1/4 и х = 3/4. Изучить характер движения около этих поло-
жений равновесия. Построить разложения второго поряДка для решения
в окрестности устойчивого положения равновесия (т. е. соответствующего ко-
лебательным движениям).
7.6. Построить равномерно пригодное разложение второго порядка для урав-
нения
й + и + в2«3 +_вй2 =0 (в <§; 1).
7.6. Найти равномерно пригодное разложение второго порядка для уравнения
й -f- и + ей2- + ей? =0 (в < 1).
Глава 8
КОЛЕБАТЕЛЬНЫЕ СИСТЕМЫ СО СЛАБОЙ
НЕЛИНЕЙНОСТЬЮ ОБЩЕГО ВИДА
В этой главе мы рассмотрим системы с одной степенью сво-
боды, движущиеся под действием произвольных нелинейных сил.
Иначе говоря, будем исследовать уравнение
й + и = е/ (и, й),
(8-1)
где е — малый безразмерный параметр, точкой обозначено диффе-
ренцирование по безразмерному времени t и и — безразмерная
зависимая переменная. В этой главе, не ограничиваясь случаем,
когда f (и, й) является аналитической функцией своих аргумен-
тов, мы будем предполагать, что она представляет собой произ-
вольную кусочно-непрерывную функцию. При этом уравнения,
рассмотренные в четырех предшествующих главах, оказываются
частными случаями уравнения (8.1).
Как и ранее, начнем с построения прямого разложения пер-
вого порядка и обсудим вопрос о его неравномерности. В § 8.2
полученное прямое разложение преобразуется в равномерное
с помощью метода перенормировки. В § 8.3 и 8.4 мы используем
соответственно метод многих масштабов и метод усреднения.
Наконец, в § 8.5 полученные результаты распространяются на
случай неаналитических функций f, а также применяются для
описания некоторых систем, рассмотренных в предыдущих гла-
вах.
8.1. Прямое разложение
Как и в предыдущих главах, будем искать разложение первого
порядка в виде
и (t-, е) = и0 (0 -j- eux (О Ч-•	(8.2)
Подстановка (8.2) в уравнение (8.1) дает
[йо Ч- ®Й1 -)-••• Ч~ «о Ч- eUi Ч- • • • = е/ [Uo Ч~ е«1 + • • • > “о +
Ч~ 8iix -j- • • •] = ъ[(«о, й0) Ч~ • • • •	(8-3)
Приравнивая коэффициенты при е° и в1 в обеих частях соотноше-
ния (8.1), получаем
йо + «о = О,	(8.4)
Й1 Ч" «1--------f (и*)’ Йо).
(8-5)
7*
196
Гл. 8. Колебательные системы со слабой нелинейностью
Общее решение уравнения (8.4) можно записать в виде
и0 = a cos (t + Р),	(8.6)
где аи§ — произвольные постоянные. При этом уравнение (8.5)
принимает вид
+ «1 = f cos (t + P), —a sin (t + P) ].	(8.7)
Чтобы найти частное решение уравнения (8.7), правую часть этого
уравнения удобно представить в виде ряда Фурье. Заметим, что
правая часть (8.7) является периодической функцией с периодом
2л. Следовательно, ее ряд Фурье имеет вид
f [a cos (t Р), — asin(Z + P)J =
ОО	оо
= /о («) 4- Е fn (a) COS (nt + «Р) + Е gn (a)sln (nt ф- nP), (8-8)
n=l	n—l
где
2Л
/о (a) = J cos (₽’ ~a sin	(8.9)
о ,
2Л
f„(a) = —J f(acos<p, — a sin <p) cos шр dtp, (8.10)
о
2л
gn(d) = — J f(acos<p, — a sln <p) sin шр dtp. (8.11)
о
С помощью разложения (8.8) уравнение (8.7) можно переписать
как
«i4-«i = fo4- Е f„cos(nM-«P)+ Е gnsln(n/ + nP). (8.12)
П=1	П=1
Поскольку уравнение (8.12) линейно, мы можем использовать
принцип суперпозиции и найти частное решение в виде суммы
частных решений, соответствующих отдельным слагаемым в пра-
вой части. Из формул (Б.69), (Б.76), (Б.78) и (Б.82) (см. прило-
жение Б) следует, что частным решением уравнения (8.12) будет
“1 = /о +	sin (Z + ₽) “ 4“ & cos + 0) +
ОО
+ 2 cos (nt + rt₽) + sin (nt + «0)1 •	(8-13)
n—2
- 8.2. Метод перенормировки
197
Как и ранее, мы не включаем в лх общее решение однородного
уравнения. Подстановка выражений (8.6) и (8.13) в (8.2) дает
и = a cos (t + р) + е /0 + fit sin (/ + ₽)- -g” Sit cos (/ 4- p) 4-
CO
4- S Cos ^nt + + ёп sin ^nt
n^2
4- ••••
(8-14)
Отметим, что прямое разложение (8.14) становится непригодным
при t О (е-1) из-за наличия секулярных членов. Ниже мы пре-
образуем это прямое разложение в равномерное с помощью метода
перенормировки.
8.2. Метод перенормировки	>
Чтобы сделать разложение (8.14) равномерно пригодным, ис-
пользуем замену переменных
т = со/, <0 = 14- есох 4~ • • • .	(8.15)
Тогда
t = <о-1т = т (1 4- есох 4- • • )-1 = (1 — есох) т 4— • • (8.16)
Подстановка соотношения (8.16) в (8.14) дает
и = a cos (т 4~ Р — есохт 4~ • • •) 4~ е
/о 4- -у А (т - e®iT +.”•) X
X sln (т 4- Р — 8Q1T 4- • • •)-g- Si(т—есохт4-)cos (т-|-
со
4- р—есохт 4----) 4- уттр [fn cos (tn 4- zip - есох«т 4------) 4'
n=2
4-g„sln(ztr 4-«Р — ecoiZir-}-• • •)] 4* '• ••	(8-17)
Используя разложения
cos (zit + nfi — еа^пт 4- • • •) =
= cos (zit 4- zip) 4- ecojzrr sin (zit 4- zip) 4-,	(8.18^
sin (zit 4- «Р — ecOiZix 4-  • •) —
= sin (zit 4- ziP) — e(oxziT cos (zit 4- ziP) 4--.	(8.19^
198
Гл. 8. Колебательные системы со слабой нелинейностью
перепишем (8.17) в виде
и — a cos (т + Р) + е J/o -р 4* т sin (т -f- Р) —
ОО
— 4" C0S(T + 0) + 2 птр Ип cos («т + «Р) +
п^2
+ gn sin (пт + пР)]I 4- ....	(8.20)
Требование отсутствия вековых членов в (8.20) дает
®1Я + 4-А(«) = 0.	(8.21)
gi («) = 0.	(8.22)
Из уравнения (8.22) можно найти те значения амплитуды а, при
которых существуют периодические решения. При этом из соот-
ношений (8.15) и (8.21) следует, что указанные периодические ре-
шения имеют частоты
<0==1-i-A(fl)+ ••••	(8-23)
С помощью формул (8.10) и (8.11) переписываем соотношения
(8.22) и (8.23) для периодических решений в виде
2л
J f (a cos <р, — a sin ф) sin ф dq> = 0,	(8.24)
о
2Л
<о=1-----2Ha“J f(flCOS<P> ~a sin ф) cos ф </ф + • • •. (8.25)
о
В частности, для уравнения Дюффинга (4.7) f = —и8, и соот-
ношения (8.24) и (8.25) принимают вид
2Л
j a3 cos3 ф sin ф </ф = 0,	(8.26)
о
2Л
“=1 + '2Пг1 а8соз4ф^ф4---------= 1-р~ва2-|---------; (8.27)
о
при этом интегралы в (8.26) и (8.27) вычисляются по формулам
(А.31) и (А.37) приложения А. Отметим, что условие (8.26) вы-
полняется при произвольной амплитуде а. Что же касается соот-
ношения (8.2^), то оно полностью совпадает с (4.80).
8.3. Метод многих масштабов	199
В уравнении Рэлея (6.4) f = й---й3, и соотношения (8.24)
и (8.25) принимают вид
2л
J (—a sin <р + -g-a3sin3 <р) sin<р cZqp = О,
2л
и=1—2^7 J (~fl sin<P + sln3 ф) cos <pd<p 4- - • •.
о
Вычисляя интегралы с помощью формулы (А.32), имеем
— a+-J-a3 = O,	(8.28)
й=1+О(ё2),	(8.29)
что полностью совпадает с соответствующими выражениями (6.27)
и (6.28).
8.3.	Метод многих масштабов
Для построения равномерно пригодного разложения первого
порядка методом многих масштабов введем вместо переменной t
две новые переменные: То = t и 7\ — et. Тогда производные по
t примут вид
— Do 4* &Di 4* ’ ’ ’ >	"^2* ~ Do 4“ 2eDoDi 4~ • • ’ >
где£)п = д!дТп. Таким образом, уравнение (8.1) перейдет в урав-
нение вида
D& 4- 2eDoD[U 4- ... 4-и == Do и eDjU 4* • • • ] • (8.30)
Будем искать приближенное решение уравнения (8.30) в форме
и = и0 (То> Тi) 4~ euj (То, TJ 4~ • • • •	(8.31)
Подстановка разложения (8.31) в уравнение (8.30) дает
Dffto 4* ejDoMi 4- 2&D0D1U0 4~ • • • 4~ ио 4* eui 4~    =
= ef [ыо 4~ eui 4~ *  ’ > DqUq 4*	4~ &D0U14* • • • ]=
— vf (Но, D0Uq) 4- • • • •
Приравнивая коэффициенты при одинаковых степенях е в обеих
частях этого уравнения, получаем
£*и0 4-ы0 = 0,	(8.32)
jDoui 4- “i = — 2DqDiU0 4" f (мо> D^o)'	(8.33)
200 Гл. 8. Колебательные системы со слабой нелинейностью
Для того чтобы иметь возможность использовать ряды Фурье
(8.8), общее решение уравнения (8.32) удобно представить в дей-
ствительной форме
и0 = a cos (То + Р).	(8.34)
При этом
Douo = —a sin (То + Р),
Dfiouo = —a' sin (То + Р) — аР' cos (То + Р),
а уравнение (8.33) принимает вид
-|- и 1 = 2<z sin (То -|- Р) -j- 2ар cos (Т'о Н- Р) -|- f [a cos (Т о	Р),
-asin(7’0 + P)].	(8.35)
Используя представление функции f в виде ряда Фурье (8.8),
перепишем уравнение (8.35) следующим образом:
ul = 2а sin (Го + Р) 2ар cos (То	Р) ~Ь fo (а)
+ S tn (a) cos (пГ0 + пР) + S gn (a) sin (пТ0 + пР).
Я=1	Л=1
—	(8.36)
Для того чтобы в решении отсутствовали секулярные слагае-
мые, необходимо выполнение условий
2а' + gi (а) = 0,	(8.37)
2аР' 4- Л (а) = 0.	(8.38)
Подстановка выражений (8.10) и (8.11) в условия (8.37) и (8.38)
приводит к соотношениям
2Я
а' ------J /(acoscp, —a sin <р) sin ф dtp, (8.39)
о
2а
аР'=------2л~ J /(асовф, —a sin ф) cos ф с(ф. (8.40)
о
Подставляя теперь (8.34) в разложение (8.31) и полагая То — t,
находим, что в первом приближении решение ймеет вид
и = a cos (t + р) + • • •,	(8.41)
где аир даются формулами (8.39) и (8.40). В § 8.5 мы применим
полученное приближенное решение (8.41) к ряду частных слу-
чаев, а в следующем параграфе выведем формулы (8.39)—(8.41)
с помощью метода усреднения.
8.4. Метод усреднения
201
8.4.	Метод усреднения
Прежде всего в соответствии с идеей вариации произвольных
постоянных мы должны совершить переход от искомой функции и
к новым переменным — амплитуде а и фазе 0:
ы (0 = a (Ocos [/4-р (/)]	(8.42)
так, чтобы выполнялось равенство
й (0 = —a (t) sin [/ + 0 (/)],	(8.43)
т. е. чтобы и и й имели тот же вид, что и в невозмущенном слу-
? чае, когда е = 0. Дифференцируя формулу (8.42) по t, получаем
L	й = —a sin (t 4- 0) 4- a cos (t 4- 0) —
*	— <20 sin (t 4- 0).	(8.44)
• Из сравнения выражений (8.43) и (8.44) можно заключить, что
a cos (t 4- 0) — <20 sin (i 4- 0) = 0.	(8.45)
Дифференцируя еще раз по t соотношение (8.43), имеем
"	й = —a cos (t 4- 0) — й sin (t 4- 0) —
	— <20 cos (t 4- 0).	(8.46)
J Подстановка (8.42), (8.43) и (8.46) в уравнение (8.1) дает
f	a sin (t 4- 0) 4- <20 cos (t 4- 0) =
!	= —е/ [a cos (t 4- 0), —<2 sin (t 4- 0)1-	(8-47)
l Умножая соотношения (8.45) и (8.47) на cos (t 4- 0) и sin (t 4- 0)
’ соответственно и складывая полученные результаты, находим
г.	а = —е sin (t 4- 0) f I<2 cos (t 4- 0).
—<2 sin (/ 4- 0)].	(8.48
; Далее, подставляя (8.48) в соотношение (8.45) и разрешая его от-
носительно величины <20, приходим к уравнению
'	<20 = —е cos (t 4- 0) f la cos (t 4- 0),
—a sin (/4- 0)1.	(8.49)
Заменяя функцию f ее рядом Фурье (8.8), перепишем теперь
I уравнения (8.48) и (8.49) в виде
d = —е sin (/4-0) fo(a)4- S fn(a)cos(nZ4-n0)4-
L
4- S gB(<2)sin(«Z 4-П0) ,
n=l
<20 = — e cos (t + 0) fo(<2)4- S f„(<2)cos(^4-/i0)4-
n^=l
4- S gn (a) sin (nt 4- /20) •
'	ч=1	J
(8.50)
(8.51)
202 Гл. 8. Колебательные системы со слабой нелинейностью
Используя известные тригонометрические формулы, преобразуем
уравнения (8.50) и (8.51) к виду
4 — — ef0(a) sin (t + ₽) - -J-.е fn (а) {sin [(n 1) t (n + 1)0]—
n=l
—sin((n — 1)/ + (n — 1)Pl} j^(a){cos[(n- 1)/ +
+ (H-l)₽|-cos[(n+l)( + (n+1)₽]},	(8.52)
«0 = —e/0 (a) cos (t + 0) — e fn (a) {cos [(n + I) t + (n + 1) 0J+
/les 1
- +oos}(rt-l)/ + (n-1)01}--ЬеУ gn(a)|sln[(n+ l)/+
n=l
+ (n + 1)0] + Sin](n - 1) t + (n -1)0]}.	(8.53)
Как и в предыдущих случаях, в первом приближении мы сохра-
Л няем только медленней меняющиеся слагаемые в правых частях
(8.52) и (8.53). Эти слагаемые представляют собой члены, явно
\ не зависящие от t. Таким образом,
\	а~ — 4"egi(a).	(8.54)
a0=-l.ef1(a),	(8.55)
. t J -	-	• 	-
что полностью соответствует формулам (8.39) и (8.40), получен-
ным с помощью метода многих масштабов.
8.5. Приложения
В качестве первого приложения рассмотрим уравнение Дюф-
финга (4.7). В этом случае f——ua, и формулы (8.39) и (8 40)
принимают вид
2л
а' ~ ~^я~ J cosS ‘Р sin Ф = 0,	(8.56)
О	>
2л	*" «	.
a0'=J в® cos4 <р d<p =а8;	(8.57)
о
точно такой же результат был получен нами в гл. 4. Интегриро-
вание уравнений (8.56) и (8.57), как и других аналогичных соот-
6.5. Приложения	203
ношений, рассматриваемых в этом параграфе, осуществляется
с помощью соответствующих формул, представленных в § А.З
приложения А.
В качестве второго примера рассмотрим линейный осциллятор
с затуханием, описываемый уравнением (5.2). В этом случае
f = —2й, и формулы (8.39) и (8.40) принимают вид
2Я
а' =-----J 2а sin2 <p d<p = —а,	(8.58)
о	‘
2Л
а$' =-----J 2а sin ф cos ф dtp = 0,	(8.59)
о
что полностью согласуется с соответствующим приближением
первого порядка, полученным в гл. 5.
Рассмотрим теперь уравнение Рэлея (6.4). В этом случае
f = й----1-й8, и уравнения (8.39) н (8.40) принимают вид
О
2Л
а' —-----j аэЩф 4--д-а381п8ф) зШфЛр —-^-а—$-as,
о
(8;60)
2Л
=-----2я“ J (—а sin ф +-g-а8 sin8 ф) cos ф </ф = 0,
о
(8.61)
т. е. мы сразу приходим к результату, полученному в гл. 6.
В качестве четвертого приложения рассмотрим уравнение
(7.9). Это уравнение не содержит малого параметра явно. Вводя
его с помощью соотношения и = ev, получаем
v v 4- еа2р2 4- е2а3и3 — 0.	(8.62)
Таким образом, f = — а2и2, и система уравнений (8.39), (8.40)
приобретает вид
2л
а' = — [а2а2 cos2 ф sin ф t/ф = 0,	(8;63)
л£п J
0
2л
аР' = 	- J ago2 cos8 ф dtp = 0.	(8.64)
о
Аналогичный результат мы имели в гл. 7. Отметим, что влияние
нелинейности на амплитуду и фазу в данном случае сказывается
лишь во втором прнблнженнн.
204 Гл. 8. Колебательные системы со слабой нелинейностью
В следующих двух примерах обратимся к рассмотрению не-
аналитических функций f. В первом случае исследуем уравнение
й-\-и —— ей |й |.
(8.65)
При этом f — —й | й |, и система уравнений (8.39), (8.40) записы-
вается в форме
2Л
а'=-------j a2 sin2 ф | sin ф | с?ф,	(8.66)
о
2Л
ар'=------J а2 sin ф cos <р | sin ф| dq>. (8.67)
0 / '
Для того чтобы выполнить интегрирование в у8.66) и (8.67), за-
метим, что sin q> 0 при & < <р < л и sin <р < 0 при л < ф с
< 2л. Следовательно, в/первом промежутке | sin <р | — sin <р,
а во втором | sin sin <р. Поэтому промежуток интегриро-
вания в интегралах (8.66) и (8.67) мы разобьем на два, заменяя
| sin q> | соответственно на sin ф и —sin <р. Тогда уравнение (8.66)
перепишется в виде
Я	2 2Я
а' =------j sin3 ф с?ф + j sin3 ф dtp =
О	л
2 Я	2 2Я
=-----j (3 sin <р — sin 3<р) dtp + -gjj- J (3 sin <p — sin 3<p) dip =
о	л
= -&(3c°s<p-4-cos3<p) |o
^(ЗС08ф-4-С08 3ф)|2яЯ,
или
(8.68)
Аналогичным образом, уравнение (8.67) представим как
Л	2Л
ар' =-------J sin2 ф cos ф с?ф + j slns ф cos ф =
о	л
а2 • |л а2 . 3	|2Я
----д— sin3 ф +-д— 81П3ф
6л т |о 6л |л
или
ар' = 0.
(8.69)
f
8.5. Приложения
205
i Из уравнения (8.69) имеем р = р0, где р0 — произвольная по-
г стоянная. Уравнение (8.68) интегрируется с помощью разделе-
I ния переменных:
I	=	<8-7(»
| откуда	т+с“4-7'>-4'«<.	I8'7»
I где с — постоянная интегрирования. В случае если а (0) = а0,
I имеем с = —1/а0, и соотношение (8.71) принимает вид
t	11.4,
[	— == — Ч- а..,
к.	•	с Gq Зя
I откуда	а ~-----у----	'	(8.72)
|	1+-зГе/а»
I В заключение рассмотрим уравнение
|	= — eu|u|.	(8.73)
I В этом случае f = —и | и |, и уравнения (8.39) и (8.40) принимают
Г вид
|	2Л
I	а' = j a2 cos <р | cos <р | sin <р dtp,	(8.74)
f	°
|	ар' — j а2 cos2 <р | cos <р | d<p.	(8.75)
0
j Заметим, что cos <р 0 при —л < <р < -^-л и cos <р < 0
F	1	’ з
I при -g- л < <р < -у- л. Так как подынтегральные функции в
I (8.74) и (8.75) периодичны с периодом 2л, то значения интегра-
| лов не меняются при сдвиге промежутка интегрирования. Поэтому
В мы можем заменить промежуток интегрирования [0, 2л] на Про-
S'	г 1	3	1
К межуток------у л, — л I и разбить этот новый промежуток на два,
I заменяя | cos <р| в первом случае на cos <р, а во втором на —cos <р.
Г Таким образом, уравнение (8.74) можно переписать в виде
|	л/2	ЗЛ/2
I а’ = j cos2 <р sin <р сйр — j cos2 <р sin <р dtp =
Г	—Л/2	л/2
а2 Ч р/2 , а2 » ]Зл/2
-------C0S3 ф 4- -j— C0S3 Ф
6.Л т — л/2 6л I л/2
[ ИЛИ
а' = 0.
(8.76)
206 Гл. 8. Колебательные системы со слабой нелинейностью
Действуя аналогичным образом, уравнение (8.75) можно предста-
вить в виде
л/2	Зл/2
ар' = -^- j cos3<pd<p— j cos3<pd<p =
—л/2	л/2
Л/2	Зл/2
—j (3 cos <р + cos 3q>) dq— j (3cos<p-(-cos3<p)d<p=
—л/2	л/2
=-jc- ( 3sin <p + 4- sin 3qA I л/2--( 3 sin <p + sin 3<p) |3я'2,
olt \	О	/ I—Л/2	Oft \	т I 3	T ( |я/2
или	ар' =	а2.	(8.77)
Решением уравнения (8.76) будет a =p^ =const. При этом если
а0 =/= 0, то из уравнения (8.77) имеем /
л	/д,
Р —	аоТ 1 4~ Ро ,^ zta0 + Ро,	(8.78)
где р0 — произвольная постоянная. Тогда из формулы (8.41)
следует, что в первом приближении
и = Ооcos 1 Н—Зл"ей°) + Ро] Н- ‘ ‘ 	(8.79)
к
Приведенные примеры показывают, что метод многих масшта-
бов и метод усреднения могут эффективно использоваться для
построения равномерно пригодных разложений первого порядка
в случае слабо нелинейных колебательных систем.
Упражнения
8.1.	Построить равномерно пригодные разложения первого порядка для реше-
ний следующих уравнений:
а)	й + и + ей | и | = О,
б)	й + и + е (sin и + йщи) =0,
в)	й + и + е (sin й + щ й j й |) = О,
г)	й + и + е (2щй + щй | и |) = О,
д)	й + и -f- е (2^4 + sin и + p2ii | й |) = 0.
8.2.	Рассмотреть свободные колебания системы, описываемой уравнением
й + F (и) = 0,
Упражнения
207
где функция F (и) задана графически на рис. 8.1 для трех различных случаев
Показать, что в первом приближении
в)
„	,	/	2\1/2
=	^2-\)[arcsin
Глава 9
УРАВНЕНИЕ ДЮФФИНГА
СЛУЧАЙ ВЫНУЖДЕННЫХ КОЛЕБАНИЙ
В отличие от пяти предыдущих глав, где мы имели дело только
со свободными колебаниями, эту и последующую главы посвятим
анализу вынужденных колебаний. Для того чтобы сравнить ука-
занные два случая колебаний, обратимся к системе, которая уже
исследована в одной из предыдущих глав, а именно к системе,
описываемой уравнением Дюффинга (4.5), и попытаемся найти
реакцию такой системы на синусоидальное внешнее воздействие.
Иначе говоря, объектом нашего исследования будет уравнение
+ ktu* + £3ы*3 = F* cos	(9.1)
где F* и ®* — постоянные величины. Как и в гл. 4, введем без-
размерные переменные, используя для этого характерные мас-
штабы времени Т* и длины U*, т. е.
, t*	_ и*
‘ =? у*-» и 
Тогда уравнение (9.1) примет вид
+ kJ*2 и 4-	= F*T**- cos a>*T*t.	(9.2)
Выберем величину T* таким образом, чтобы выполнялось со-
отношение ktT*‘ = 1, или
у* = 1 ______ 1
VkT	®0 ’
где ®о —собственная частота соответствующей линейной задачи.
Далее, положим
,~*2,;*2 с F*T*2	W*
e = k3T*U*, F == utt  , (о = ю*Т* = —.
При этом уравнение (9.2) перепишется в виде
й + и + е.и3 = F cos.,®t	(9.3)
Отметим, что величина ® представляет собой отношение ча-
стоты внешнего воздействия к собственной частоте соответствую-
щей линейной системы. Ниже вместо уравнения (9.3) мы будем
рассматривать более общее уравнение
fi. + и + 2врй + eu3 = F cos ®/,	(9.4)
9.1. Прямое разложение	,209
где р, — некоторая положительная постоянная. При этом уравне-
ние (9.4) учитывает дополнительно затухание колебаний под дей-
ствием малой вязкости.
В данной главе будем искать приближенное решение уравне-
ния (9.4) с точностью до членов первого порядка малости по 8.
Прежде всего построим прямое разложение и, исследовав его,
найдем условия, при которых это разложение становится непри-
менимым. Эти условия определят нам так называемые резонанс-
ные значения частоты to. В § 9.2 и 9.3, используя соответственно
метод Многих масштабов и метод усреднения, построим разложе-
ния первого порядка для всех резонансных случаев с учетом сла-
бого вязкого затухания.
9.1.	Прямое разложение
Будем искать прямое разложение решения (9.4) в виде
и (t, е) = и0 (t) + еах (t) + • • • .	(9.5)
Подстановка разложения (9.5) в уравнение (9.4) дает
йо ейх 4” • • • а0 -j- 8UX 4~ • • • 2ер (й0 -j- 8ах -|-  • •) -J-
-|- е (и$ 8Uj * • • )3 = F cos со/,
или
Но Uq — F cos со/ -|- 8 (fij —j— U\ -j— 2рйо -|- Ug) * * * == 0* (9.6)
Приравнивая нулю коэффициенты при е° и е, имеем
й0 + «о = Р c°s со/,	(9.7)
й1+«1 = —2рй0 — «о-	(9.8)
Уравнение (9.7) представляет собой линейное неоднородное урав-
нение, так что его общее решение можно искать в виде суммы ре-
шения соответствующего однородного уравнения и некоторого
частного решения, определяемого видом правой части. Решение
соответствующего (9.7) однородного уравнения может быть за-
писано как
«о,одн = a cos (t + Р),	(9.9)
где аир — постоянные, а частное решение, согласно формуле
(Б.69) приложения Б, имеет вид
% =-1/(orcosm/.	(9.10)
Поэтому
и0 = a cos (/ + Р) + 2Л cos со/,	(9.П)
где	Л = -|-(1 -со2)-1 Л	(9.12)
210	Гл. 9. Уравнение Дюффинга. Вынужденные колебания
Подстановка (9.11) в уравнение (9.8) дает
iij И- Uj = 2р [tz sin (/ -j- p) -f-
+ 2Aco sin at ] — [a cos (t + P) +
+ 2Л cos to/]3 = 2pa sin (t + P) +
+ 4рЛсо sin at — a3 cos3(/ + P) —
— 6a2A cos2 (t + P) cos at. —
— 12aA2 cos (t + P) cos2 at — 8Л3 cos3 at. (9.13)
Далее, используя известные тригонометрические формулы (см.
приложение А), перепишем (9.13) в виде
дЗ
Si + «1 = 2pa sin (t Р) 4* 4pAto sin at-j- cos (3/ 4* ЗР) —
— a3 4- 6aA2^ cos (t 4- P) — 2Л3 cos 3 at — (6Л3 4- 3a2A) cos at —
- -|-a2Acos[(2 4-co)/4-2p] - cos [(2 - co)t 4-2p] -
— 3aA2 cos [(1 4- 2co) / 4- p] - 3aA2 cos [(1 - 2co) t 4- p], (9.14)
Как и ранее, решение однородного уравнения мы включаем только
в члены первого порядка. Поскольку уравнение (9.14) линейно,
его частное решение может быть представлено в виде суммы част-
ных решений, соответствующих отдельным слагаемым в правой
части. Из формул § Б.4 следует, что
— —pat cos (t 4- р) 4- - sin at 4~ -jgr a3 cos (3/ 4- 3p) —
— (-4- a3 4- 3aA2~) t sin (/ 4" P) ~ T"-^o»a cos ~
6Л2 + 3a2A . . 3a2A	,/O .	. , .	.
-----—cosco/4-2((i)2 + 4(0 + 3) cos [(2 4-to) / 4-2p] 4-
4-2 (W2 _ 4(o + 3) COS [(2 co) t 4- 2p] 4-	+	X
X cos [(1 4- 2co) t 4- Pl 4- 4(J^ cos Id - 2co) t 4- PJ. (9.15)
Подставляя выражения (9.11) и (9.15) в (9.5) н используя соотно-
шение (9.12), получаем
и = a cos (t 4- Р) 4~ 1 Ю2 cos at 4- 8^ —pa/ cos (/ 4~ P) 4~
4- (iT-SjrsinwZ + iaS cos(3z + 3P) ~
4~a [“a2 + p _ W2j2 ] slnG + P) ~
F3	„с, 4
4 (1 - и2)3 (1 — 9coa) cosoco?
9.2. Метод многий масштабов
211
2(1—ю*)* р~Г 2 (1 — W2)2 J C0S<B^ +
ОЛ2Г
+ 4 (1 - W2) (3 + 4ш + W2) C0S [(2 + ®) t + 20] +
4(1 —0)2) (3 —(0) (1 — ы) cos 1(2 — ®) + 2р1 +
“Ь 16(1— (1)2)2 (Ш2 w) C0S [(1 + 2®) t + р] 4-
+ W -OW-И) cos [(1 - 2(0) t + Pl} + • • • .	(9.16)
Заметим, Что наряду с секулярными членами разложение (9.16)
содержит дроби, знаменатели которых могут оказаться весьма
малыми. Такие члены разложения называют членами с малыми
знаменателями. Если условиться считать частоты колебаний
положительными, то малые знаменатели возникают в тех случаях,
когда и 1, и «=> 0, со 1/3 и со 3. Эти особые частоты назы-
ваются резонансными. Таким образом, прямое разложение ста-
новится непригодным по двум причинам: из-за наличия малых
знаменателей и в результате появления секулярных членов.
В случае когда со 1, малые знаменатели появляются уже
в главном члене разложения. Поэтому при со 1 говорят о пер-
вичном, нли главном, резонансе. При со 0, 1/3 или 3 малые зна-
менатели появляются начиная с членов первого порядка. Резо-
нансы, возникающие в этих случаях, называют вторичными.
Продолжая прямое разложение до членов более высоких по-
рядков, можно обнаружить и другие резонансы. Отметим, что
появление того или иного резонанса зависит от характера нели-
нейности системы. В общем случае резонансные частоты легко
определяются путем анализа прямого разложения, как это сде-
лано выше для уравнения Дюффинга.
В следующих двух параграфах, используя метод многих мас-
штабов н метод усреднения, построим равномерно пригодное раз-
ложение первого порядка для решения уравнения (9.4), не содер-
жащее секулярных членов нлн членов с малыми знаменателями.
9.2. Метод многих масштабов
Для того чтобы найти приближенное решение уравнения (9.4),
свободное от дефектов типа секулярных членов или малых знамена-
телей, необходимо различать случаи вторичных и первичных ре-
зонансов. Рассмотрим их в отдельности, обратившись поначалу
к исследованию вторичных резонансов.
9.2.1. ВТОРИЧНЫЕ РЕЗОНАНСЫ
В этом случае и отстоит достаточно далеко от 1, н малые дели-
тели появляются впервые в членах порядка 8. В дополнение
к быстрому времени То = t введем так называемое медленное
Гл. d. Уравнение Дюффинга. вынужденные колебаний.
..      *..."	...	........................ц ...г*”*
время Тг = е/. При этом производные по t преобразуются в выра-
жения вида
— Do Ц- e£>i + • • • ,
~	4~ 2e£>oDi 4- • • • ,
где Dn — д/дТп. Поскольку физическое время t входит в исходное
дифференциальное уравнение Явным образом, естественно воз-
никает вопрос, через какую переменную, То или Ть оно должно
быть выражено. Чтобы ответить на этот вопрос, попытаемся выяс-
нить, в каких случаях зависимость от времени t является быстрой
и в каких— медленной. В уравнении (9.4) такой проверке под-
лежит член cos at. Если частота ® достаточно далека от нуля,
cos at оказывается быстро меняющейся функцией, и мы пишем
cos at = cos аТ0,	(9-17)
представляя t через То. С другой стороны, если м «=> 0, функ-
ция cos at будет медленно меняющейся. В этом случае пишем
® — еа, где а = 0(1), чтобы выразить явно тот факт, что частота а
мала. Тогда имеем
।	<	cos at = cos aet = cos al\,	(9.18)
тем самым t представляется теперь через Тх. Таким образом, слу-
чай a 0 требует, по-видимому, специального рассмотрения.
Если значение <в оказывается достаточно далеким от нуля,
уравнение (9.4) можно преобразовать к виду
DqU + 2eDeDiU + 2epDoU + • • • + и 4- ем3 = F cos аТ0. (9.19)
Будем искать приближенное решение уравнения (9.19) в виде
-	«	«0 (Т9, 1\) + ей, (То, Л) + • • • .	(9.20)
Подставляя разложение (9.20) в (9.19) и приравнивая коэффи-
циенты при одинаковых степенях е, получаем
+ “о = Т cos ®Т0,	(9.21)
E%Ui -J- Wi = —DqDiUo — 2[iDoUq — u3-	(9.22)
Общее решение уравнения (9.21) может быть представлено
либо в действительной форме	$
и0 = а (Тх) cos [То 4- Р (Ti) 1 4- 2Л cos аТ0, (9.23)
либо в комплексной
«о = А (Т1)е{Т° 4- Ае‘“7'» 4- (й. с.),	(9.24)
где ' А — -^-ае^, Л = 2/т8)-	(9-25)
$.2. Метод многих масштабов	"213
При этом уравнение (9.22) принимает вид
Z&i -j-Uj=—2i (A -J- цА)#^’ -j-2i(Л 4_|*'<4)^ iT° —
— 2ip®Ae'MT» + 2ф®Ле~/м7’» — [Ле/Г» 4- Ле‘шТ° 4-
+ Ae~iT* + Ле-1'м7'»]3,
или
ti&x + ui = — [2i (A' + M) + 3 (AA + 2Л2) A] elT° -
— (2ip,® -J- 6ЛЛ 4" ЗА2) Aeiv>T‘i — A3^iT« — дэ^з/вт, _
— ЗЛ2А^ <2+®>г» — 34W	_ здд2е/ (i+2<o> r„ __
-ЗЛА2^<1-2»>г»4-(к. с.).	(9.26)
Как указано в предыдущем параграфе, частное решение уравне-
ния (9.26) содержит секулярные слагаемые и члены с малыми зна-
менателями при ®, близких к 3, 1/з и 0. Рассмотрим эти случаи
каждый в отдельности.
Случай ® *=« 3
Для того чтобы отразить близость безразмерной частоты ©
к 3, введем так называемый параметр расстройки ст = О (1),
определяемый соотношением
и = 3 4- ест.	(9.27)
Подстановка (9.27) в уравнение (9.26) дает
Dguj + Ы1 = - [2iA 4- 2щА 4- ЗЛ2Л 4- 6ЛА2] elT° - А3е31Т° -
— (2ф® 4* 6ЛЛ 4- ЗА2) Ae3irn+WeTt __ ДЗ^Т^З/аеГо —
— 3A2Ae5iT«+ioeT<>зл2Ае/7'"+/ае7'« — ЗЛА2е7*7'«+2‘ае7'» —
- ЗЛА2е-5‘г«-2гоеГ» 4-(к. с.).	(9.28)
Возникающие при этом в правой части уравнения (9.28) произве-
дения еТ0 следует выразить через медленную переменную Тх —
— гТ0. Поэтому уравнение (9.28) переписывается в виде
Dgut 4- ui = — [—2»Л 4- 2/р.Л 4- ЗЛ2! 4- 6ЛЛ21е/Го -
- [Л3 4- (2ip® 4- 6ЛЛ 4- 3A2)Ae/o7’-]e3ir» —А3езгог>е9'г» —
— 3A2AelaT<e5iT‘ — 3A2AeioT>eiT° — 3AA?e2taT*e!lT> —
— 3AA'2e^2:aT>e~5iTa 4- (к. с.).	(9.29)
Следует отметить, что введение параметра расстройки с по-
мощью соотношения (9.27) привело к преобразованию слагаемого
—ЗЛ2Л ехр Ii (® — 2) То),
214	Гл. 6. Уравнение Дюффинга. вынужденные колебания
которое определяло собой появление члена с малым знаменателем
в прямом разложении, к виду
—ЗЛ2Л ехр (ioTx) ехр (iT0),
которому соответствует секулярный член относительно перемен-
ной То. Подобный подход является общим для всех случаев, когда
возникают члены с малыми знаменателями: с помощью параметров
расстройки их преобразуют к виду, порождающему секулярные
члены.
Потребовав теперь, чтобы решение ut не содержало секуляр-
ных слагаемых, из уравнения (9.29) получаем
21А' + 21цА + ЗА2 А + 6ЛЛ2 + ЗЛ2Ле‘<^ = 0.	(9.30)
Заметим, что нет необходимости выписывать все члены в правой
части (9.28) и (9.29). Нужно учитывать лишь те слагаемые, кото-
рые порождают в разложении секулярные члены или члены с ма-
лыми знаменателями. Как и ранее, введем на этом этапе экспо-
ненциальное представление (9.25). В результате получим
ia'el& — сф'е‘Р 4~	+ -§-а3е‘₽ 4~ ЗаЛ2е/₽ 4"
4	4-(9.31)
Прежде чем отделить вещественную и мнимую части уравнения
(9.31), умножим его на ехр (—ip'), с тем чтобы избавиться от экс-
поненциальных множителей у величин а' и р'. Этот прием значи-
тельно упрощает результирующие уравнения. Действительно,
умножение (9.31) на ехр (—ip') дает
ia' — аР' + ЦШ + “§“ д3 + ЗаЛ2 a Ael (<’7'i-3P > = 0. (9.32)
В уравнении (9.32) только один член содержит экспоненциальный
множитель. Используя формулу Эйлера ехр (i0) = cos 0 +
4- i sin 0, переписываем (9.32) в виде
ia' — ар' 4- цш 4~ а3 4- ЗаЛ2 4-
4- а2Л [cos (а7\ — Зр) 4-i sin (<т7\ — Зр)] = 0,
или
i ^а' 4~	4~	& A sin (0Т1 — 30)] — ар' 4~
4- а3 4- ЗаЛ2 4- a2A cos (<тТх - Зр) = 0.	(9.33)
Поскольку комплексное выражение равно нулю тогда и только
тогда, когда равны нулю его вещественная и мнимая части, со-
9.2. Метод многих масштабов
215
отношение (9.33) эквивалентно системе двух	уравнений
а' = —ца-----а2Л sin (аТ^ — Зр),	(9.34)
ар' — ЗаЛ2 + cos — Зр).	(9.35)
Уравнения (9.34) и (9.35) являются искомыми уравнениями, опи-
сывающими модуляцию амплитуды и фазы того слагаемого в ре-
шении, которое определяет форму свободных колебаний.
Подставляя (9.23) в разложение (9.20) и вспоминая, что То = t,
получаем
и = a cos (t + Р) + 2Л cos to/ + О (е),	(9.36)
где а и р определяются уравнениями (9.34) и (9.35). Поскольку
медленное время Т\ входит явно в уравнения (9.34) и (9.35), эта
система называется неавтономной. Представляется удобным исклю-
чить явную зависимость от 7\, тем самым преобразовав уравне-
ния (9.34) и (9.35) в так называемую автономную систему. Этого
можно добиться, введя новую зависимую переменную у по формуле
у = <т7\ — Зр.	(9.37)
При этом
у'=о —Зр'.	(9.38)
Подстановка (9.37) в уравнение (9.34) дает
а' — —ра----1- а2Л sin у.	(9.39)
Подставляя теперь уравнение (9.35) в (9.38) и используя (9.37),
получаем
ау' = аа — 9аЛ2 — а3-----|-a2Acosy. (9.40)
Из формулы (9.37) также следует, что
Q 1 -г	1	1,1
р = _оТ1- —у = —ва/-—у.
Поэтому разложение (9.36) можно переписать в виде
и = a cos (t + -4- ео/-у4) + 2Л cos со/ + О (е),
что в свою очередь, с учетом соотношения (9.27), может быть
представлено как
и — acos ^-g-со/ — у) 4-2Лcosco/ + О(е).	(9.41)
Таким образом, в первом приближении решение и дается разложе-
нием (9.41), в котором величины а и у определяются из автоном-
ной системы уравнений (9.39), (9.40).
216
Гл. 9. Уравнение Дюффинга. Вынужденные колебания
Рис. 9.1. Зависимости величин а и у от времени t, полученные в результате
численного решения уравнений (9.39)—(9.40) при е=0.1, Л= 1^0.08,	=
= 0.1, а= 1.0, а (0) = 1.0 и у (0) = 1.0.
На рис. 9.1 представлены зависимости а и у от медленного вре-
мени Тг, полученные с помощью численного интегрирования си-
стемы (9.39), (9.40). На начальном участке кривые а и у имеют коле-
бательный характер, однако по мере возрастания они стре-
мятся к некоторым постоянным значениям. Эти постоянные зна-
чения обычно называют стационарными или установившимися.
При этом возможны два случая: установившееся значение ампли-
туды будет либо равно, либо не равно нулю. При ненулевой ам-
плитуде установившихся колебаний член, соответствующий сво-
бодным колебаниям, является периодическим с частотой, равной
в точности со/3, т. е. одной трети частоты внешнего воздействия.
О таком разонансе говорят как о субгармоническом резонансе
на частоте одна треть. В этом случае решение и, т. е. установив-
шаяся реакция колебательной системы на возмущение, оказы-
вается периодическим.
Для нахождения этой установившейся реакции нет необхо-
димости численно интегрировать систему (9.39), (9.40), описываю-
щую изменение а и у. Вместо этого используем тот факт, что ам-
плитуда и фаза в стационарном режиме постоянны, и, следова-
тельно, а' = 0 и у' = 0. В результате система (9.39), (9.40) при-
мет вид
9
—3[ia — -j- а2А sin у,
9	9		<9’42)
аа — 9аЛ2-----g- а? =	а2 Л. cos у.
Возводя каждое из уравнений (9.42) в квадрат и складывая полу-
ченные результаты, а также учитывая тождество
sin2 у + cos2 у = 1.
(9.43)
9.2. Метод многих масштабов
217
получаем
9ц2а2 + (а - 9Л2 - А а2)2 «2 = -|(Г	(9.44)
При этом из уравнения (9.44) следует, что а либо равно нулю,
либо удовлетворяет уравнению
9Н2 + (О - 9Л2 - А а2\2 = 81 Д2А2
Таким образом,
а4 - -у- (о - -Ц- Л2) а2 +	[9ц2 + (а - 9Л2)2[ = 0, (9.45)
и поскольку (9.45) представляет собой квадратное уравнение от-
носительно а2, его решения можно представить как
«2 = 4 (о -4-Л2) ±4 [(а - 4л2)2-9и2 - (о - 9A2)2f,
или
=4 (° - Д2) ± 4 [4-Д2 (2а - 4-Д2) - и2]1/2 • (9-46)
Соотношение (9.46) называют обычно амплитудно-частотной ха-
рактеристикой.
Из (9.46) следует, что для существования вещественных ре-
) шений подкоренное выражение и первое слагаемое в правой части
этого равенства должны быть положительными, т. е.
'Рис. 9.2. Области, где существуют субгармонические характеристики системы.
218	Гл. 9. Уравнение Дюффинга. Вынужденные колебания
Рис. 9.3. Субгармоническая характеристика для уравнения Дюффинга: ампли-
туда свободных колебаний в зависимости от: а) параметра расстройки, б) ампли-
туды возбуждения.
Таким образом, нетривиальные решения существуют только в том
случае, если выполняются неравенства
р \ и3 /	4р. р \ р2 /
Область, описываемая этими неравенствами, изображена на
рис. 9.2. На рис. 9.3а приведено несколько амплитудно-частот-
ных кривых, а на рис. 9.36 показана зависимость амплитуды а
от амплитуды возбуждения.
Заметим, что, хотя частота возбуждения втрое больше собст-
венной частоты системы, амплитуда отклика оказывается довольно
большой. Например, весьма сильные колебания отдельных частей
самолета могут возникать при работе его двигателя с угловой ча-
9.2. Метод многих масштабов
219
стотой, намного превосходящей их собственные частоты. Изве-
стен такой случай, когда вращение винтов самолета одной авиа-
компании послужило причиной возбуждения субгармонических
колебаний порядка Ц- в крыльях, которые в свою очередь инду-
цировали колебания руля поворота порядка -j-. При этом коле-
бания оказались настолько сильными, что самолет разрушился.
Случай <в -|-
Для того чтобы отразить близость со к введем параметр
расстройки о, определив его равенством
Зш = 1 + ео.	(9.47)
Как указывалось ранее, нет необходимости заменять величину со
на 1 + ео во всех членах уравнения (9.26). Замену следует про-
вести только в тех членах, в которых возникают малые знамена-
тели, т. е. в членах —Л8 ехр (±3zcoTo). С этой целью запишем
ЗсоТо = (1 + во) То = То + оеТ0 = То + оТх. (9.48)
Далее, преобразуем уравнение (9.26) к виду
+ ui = — [2г Л' + 2/рЛ + 6Л2Л 4- ЗЛ2Л] е1Т° -
—4-(к. с.) + (Н. С. Ч.),	(9 49)
где символом (Н. С. Ч;) обозначены невыписанные члены правой
части, которые не служат источником секулярных членов. Тре-
бование отсутствия секулярных членов в решении ых дает
2i (Л' + рЛ) + 6Л2Л 4- ЗЛ2Л 4- A3e‘w> = 0.	. (9.50)
Обратимся вновь к экспоненциальному представлению (9.25)
и перепишем условие (9.50) в виде
ia'e{^ — ор'е'Р 4" ip^^'P 4"	а3е‘& 4" ЗА2Ле'₽ 4- Л3е/аГ< = 0. (9.51)
Умножая (9.51) на ехр (—ip) с тем чтобы оставить лишь один член
с соответствующим экспоненциальным множителем, получаем
ia' — op' 4- f’pa + -|“а3 4" ЗЛ2а -|- Л3е' (’’’i-P) = О,
или
ia' — ар' 4- цш 4-	(z3 4- ЗЛ2а 4~
4- A3 cos (оТх - р) 4- «Л3 sin (оТх - р) = 0.	(9.52)
Отделяя вещественную и мнимую части, имеем
а' = —ца — Л8 sin (аТх — Р),	(9.53)
ар' = ЗЛ2а 4- -|-а3 4- A3 cos (оТх — р).	(9.54)
220
Гл. 9. Уравнение Дюффинга. Вынужденные колебания

Рис. 9.4. Зависимости величин а и v от Тъ нолученные с помощью числен-
ного решения уравнений (9.57)—(9.58) при е — 0.05, о = 0.1, А — 1.0, р= 0.1,
а (0) - 1.1 и у (0) = 2.5.
Как и в предыдущем случае, преобразуем систему уравнений
(9.53), (9.54) в автономную, вводя замену переменной
у = аТг — р.	(9.55)
Тогда
у' = а — р'.	(9.56)
Подстановка (9.55) в уравнение (9.53) дает
а' = —ра — Л3 sin у,	(9.57)
а подстановка (9.54) в (9.56) с использованием (9.55) приводит
к уравнению
ау' = аа — 3№а-----о3 — Л3 cos у.	(9.58)
Исключая величину р из (9.23) и (9.55), находим
и0 = a cos (То + oTj — у) + 2Л cos (оТ0,
или	и0 = a cos (t + sat — у) + 2Л cos at.	(9.59)
Наконец, подставляя (9.59) в разложение (9.20) и используя
(9.47), приходим к окончательному выражению:
и = a cos (3<в/ — у) + 2Л cos at + О (е).	(9.60)
Таким образом, в первом приближении решение и дается форму-
лой (9.60), в которой величины а и у определяются из системы
(9.57), (9.58).
На рис. 9.4 представлены кривые изменения амплитуды а
и фазы у в зависимости от медленного времени 7\, полученные
с помощью численного интегрирования системы (9.57), (9.58).
На начальном участке эти кривые имеют колебательный характер,
однако по мере увеличения 7\ амплитуда и фаза стремятся к по-
9.2. Метод многих масштабов
221
стоянным значениям. Как и в предыдущем случае, эти постоян-
ные значения называют стационарными или установившимися.
Из уравнения (9.60) следует, что установившийся отклик системы
на внешнее воздействие является периодическим. При этом для
определения установившегося отклика нам вновь не нужно чис-
ленно интегрировать систему (9.57), (9.58). Поскольку в установив-
шемся режиме а и у оказываются постоянными, то, полагая а’ = 0
и / = 0 в уравнениях (9.57), (9.58), получаем
—pa = A3siny,	(9.61)
са — ЗЛ2а —|-а3 — Л3 cos у.	(9.62)
Возводя в квадрат обе части уравнений (9.61) и (9.62), складывая
полученные результаты и используя (9.43), получаем следующее
кубическое уравнение относительно ст2:
ц2а2 + (ст - ЗА2 -	а2)2 а2 = Л6.	(9.63)
Это уравнение, как и (9.46), называется амплитудно-частотной
характеристикой. При известной амплитуде а фаза у может быть
найдена из любого из уравнений (9.61), (9.62). При постоянных
ст и у член, соответствующий свободным колебаниям, имеет ча-
стоту, равную 3to, т. е. утроенной частоте внешнего воздействия.
О таком резонансе говорят как о супергармонцческом резонансе
порядка три.
На рис. 9.5 приведена одна из характерных кривых реакции
системы, т. е. зависимости амплитуды а от амплитуды внешнего
воздействия. Отметим, что изгиб этой кривой обусловлен нелиней-
ностью возвращающейся силы, причем этот изгиб приводит к воз-
никновению так называемого срыва колебаний. Чтобы пояснить
сказанное, представим себе, что мы исследуем колебания системы
при фиксированной частоте (т. е. при постоянной ст) и медленно
Рис. 9.5. Скачок субгармонической характеристики для уравнения Дюф-
финга.
222	Гл. 9. Уравнение Дюффинга. Вынужденные колебания
меняющейся амплитуде возбуждения (т. е. F или Л). Если коле-
бания начинаются при малом значении Л, соответствующем точ-
ке А, а затем Л медленно увеличивается, то амплитуда а будет
медленно возрастать вплоть до точки В. При дальнейшем увели-
чении Л происходит скачок из точки В в точку С с соответствую-
щим возрастанием амплитуды а, после чего она начнет плавно убы-
вать с увеличением Л до точки Е. Дальнейшее увеличение Л
приводит к новому плавному нарастанию амплитуды. Если коле-
бания начинаются в точке Е и Л уменьшается, то амплитуда нач-
нет медленно возрастать, изображающая точка будет переме-
щаться через точку С и далее по верхней ветви вплоть до точки D.
При дальнейшем уменьшении Л происходит скачок из точки D
в точку А (резкое уменьшение а), после чего амплитуда вновь бу-
дет плавно уменьшаться с уменьшением Л. Заметим также, что
режим, соответствующий пунктирной линии BD, не может быть
реализован ни при увеличении, ни при уменьшении Л. Следова-
тельно, этот участок кривой соответствует неустойчивому режиму.
Случай о «=! О
В этом случае, как указывалось ранее, функцию cos at надо
выразить через переменную 7\ с помощью соотношения (9.18).
При этом уравнение (9.19) принимает вид
Do« + 2eDqDiu + 2ер£>ом + • • • + м + ем3 = F cos oTi. (9.64)
Подставляя разложение (9.20) в (9.64) и приравнивая коэффи-
циенты при одинаковых степенях е в обеих частях этого уравне-
ния, получаем
EfoUo 4- и0 = F cosaTi,	(9.65)
Domi4-ui = —2DoDiU0 — 2p.DoUo — «о-	(9.66)
Общее решение уравнения (9.65) может быть представлено
в виде	_
uQ = AeiT« 4- Ае~1Т° -(-FeosоТ^	(9.67)
Тогда уравнение (9.66) переписывается как
t DoUt + Mi = —2i (А' + рЛ) eiT° + 2i_(Л' + рЛ) е~‘т° -
— [Ае‘Г° -(- Ле-‘7’» + F cos oTj3,
или
£>g«i + «1 = — 2i (Л’ + рЛ) eiT° — A3e3iTa - 3A2AeiT° -
—3F2 cos2 uT1AeiT« — 3FA2 cos o7’1e2'7’» —
—3FAA cos oTx —^-F3 cos3 0^	(к. c.).	(9.68)
Исключая секулярные члены из решения ult имеем
2iА' + 2(цА 4- ЗЛ2Л + ЗЕ2Л cos2 оТ, = 0.	(9.69)
9.2. Метод многих масштабов	223
Представление А в форме (9.25) дает
— а$'е‘& Ц- щае‘& Ц- а?е‘& Ц- F2ae^ cos2 ст7\ = О,
или
ia' - а$' + ipa + -§- а3 4- А Р2а cos2 ст7\ = 0.	(9.70)
Отделяя в соотношении (9.70) вещественную и мнимую части, при-
ходим к системе
а' = ~ца,	(9.71)
«Р' =	а3 + Р2а cos2 ст7\.	(9.72)
При этом из уравнения (9.71) следует, что
а^аое-^,	(9.73)
где aQ— произвольная постоянная. Далее, из уравнения (9.72)
следует, что
о/ з 2 —2ц7\ |	3 г.2	2
Р = -g- Оо£ + -g-Р cos °Р 1 >
или
₽'=4 ^е~2^Т'+4- р2+4-F2 cos 2aTi ’	(9-74)
откуда после интегрирования получаем
₽=-щг а«^2цг*+4-р2т>+4?-sin 2аТ'+Ро» <9-75>
где р0 — произвольная постоянная. Подставляя (9.67) в разло-
жение (9.20) и используя показательное представление (9.25),
находим
и = a cos (То + Р) + FcosctT\ О (е).	(9.76)
Наконец, подставляя (9.75) в (9.76) и используя соотношения
То = t, 7\ = et и со = ест, перепишем (9.76) в виде
«=w-"cos [(1 +4ef’)f--Ar-*-!“' +
+ sl" 2m/+ ь] +f cos“(+ °(')-	(9-77)
Покажем теперь, что разложение (9.77) может быть получено
как частный случай общей зависимости при ®, отличных от 1.
Для этого заменим частоту со в последних членах правой части
уравнения (9.26) на величину ест, в результате чего получим
£^И1 + «1 = — [27 Л' + 21цА + ЗА2 А + 6Л2Л] eiT,‘ -
—ЗЛЛ2^7"» [е21Т^ + е~21Т^] + (к. с.) + (Н. С. Ч.).
г	(9.78)
224	Гл. 9. У равнение Дюффинга. Вынужденные колебания
Исключение секулярных членов из решения уравнения (9.78)
дает
21А' + 2фД + ЗА2 А + 6ЛМ + 6ДЛ2 cos 2ст7\ = 0. (9.79)
Поскольку и = ест, то из (9.25) следует, что Л « F/2. Тогда со-
отношение (9.79) принимает вид
2г Д' + 2грД + ЗА2 А + A FM (1 + cos 2ст7\) = 0,
или 2гА' + 2грД + ЗА2А + 3FM cos2 ст7\ = 0,	(9.80)
что полностью совпадает с условием (9.69).
9.2.2. первичный резонанс
В случае первичного резонанса и 1, и члены с малыми
знаменателями появляются непосредственно в слагаемых по-
рядка О (е°) прямого разложения (9.16). Следовательно, гг0 будет
резко возрастать при со -> 1. Однако при этом все большую роль
начинают играть нелинейное слагаемое в возвращающей силе и
член, описывающий затухание, что приводит к изменению поряд-
ков, приписываемых различным членам в уравнении (9.6). Более
того, «частное решение» и «решение однородного уравнения»
сливаются, так что их нельзя отличить друг от друга. В этой си-
туации для нас существуют две возможности. Первая из них со-
стоит в том, чтобы перенормировать нелинейный член и член, опи-
сывающий затухание, так, чтобы они имели порядок е° и тем са-
мым компенсировали эффект первичного резонанса на частоте воз-
буждения. Однако этот путь приводит к уравнению
uq -|- Uq 2цПогг0 -|- гг© — F cos соТ*о = 0,	(9.81)
совпадающему с исходным нелинейным уравнением. Вторая воз-
можность заключается в перенормировке внешнего воздействия,
с тем чтобы неоднородность появлялась в членах порядка е,
т. е. одновременно с нелинейностью и затуханием. Первый член
разложения оказывается при этом величиной порядка е и описы-
вается линейным уравнением. Именно такой подход, пригодный
для слабо нелинейный систем, применяется в этой книге. Чтобы
воспользоваться им в данном случае, положим F = е/ и перепи-
шем уравнение (9.4) в виде
й + и 4- 2ер,й + 8«® = е/ cos at.	(9.82)
При и, близких к 1, первые два члена прямого разложения
(9.16) имеют примерно одинаковую частоту, так что слагаемое
a cos (t 4- Р), описывающее свободные колебания, «сливается»
с реакцией на внешнюю силу F (1 — и2)-1 cos at. Этот факт оп-
равдывает перенормировку, проведенную в уравнении (9.82).
Для того чтобы получить приближенное решение уравнения
(9.82), введем переменные Тй = t и 7\ = е/ и представим cos со/
9.2. Метод многих масштабов	225
как cos аТ0. Тогда, как и в предыдущих случаях, уравнение (9.82)
примет вид
D20u 4" 2&DqDiU -|~ 2spZ?oU -|- и 4-'• • • 4" eu = е^cos coTg. (9.83)
Решение уравнения (9.83) будем искать в виде
« = и0'(Т0, Tj) 4- eczj (То, Тх) + • • • •	(9.84)
Подставляя разложение (9.84) в (9.83) и приравнивая коэффи-
циенты при одинаковых степенях е в обеих частях этого уравне-
ния, получаем
DqUq -f- uq — 0,	(9.85)
DqU\ -J- Щ == —2DqDiUq — 2y,DoiiQ — uq 4~ f cos coTg. (9.86)
Общее решение уравнения (9.85) можно представить как
и0 = Л(Тх)е^» Л(Т1)е-1'г».	(9.87)
При этом уравнение (9.86) переписывается в виде
Do«t 4- «1 = — 2i (Л' 4- рЛ) eiT° 4- 21 (Л' 4- р,Л) е-,‘г’ -
— (AeiT,> 4- Ле~‘г“)8
Или
Do«i 4- «1 = — (2М' 4- 2щА 4- ЗЛ2Л) /г° - ,Л3^Г° 4-
4- -i-+ (к. с.).	(9.88)
Поскольку мы рассматриваем случай со 1, то, введя параметр
расстройки по формуле
со = 1 4- ест,	(9.89)
. получим
аТ0 ==(14- ест) То = То 4- <теТ0 = То 4- аТх. (9.90)
^Подстановка (9.90) в уравнение (9.88) дает
Е?ощ 4- и, = — (21А 4- 2щА 4- ЗЛ2Л) eiT° - А3е3‘Г° +
;	4-	4- (к. с.).	(9.91)
Требование отсутствия секулярных членов в решении этого урав-
нения приводит к условию
21А' 4- 2щА 4- ЗЛ2Л - -1- fe‘°T‘ = 0.	(9.92)
Представляя Л в форме (9.25), переписываем соотношение
(9.92) в виде
iae1^ —- afi'e’fi 4-	4-~|~ a3eif> :—fe{aTl = 0,
8 Найфэ А. X.
226
Гл. 9. Уравнение Дюффинга. Вынужденные колебания
Рис. 9.6. Зависимости величин а н V от Tlt полученные в результате числен-
ного решения уравнений (9.98)—(9.99) при е = 0.5, а = 0.05, f = 0.5, и. = 0.1,
а (0) = 1.1 и у (0) = 0.5.
ИЛИ
ia' — а₽' + ща +	а3 —^-f cos(o7\ — 0) — if sin (ст7\ — 0).
(9.93)
Отделяя вещественную и мнимую части в соотношении . (9.93),
приходим к .системе уравнений
а' = — ра +-^-/sin(tf7\ — -0), •	(9.94)
а0' = -|-а8 - 4'^cos(ff7’1 “ 0)’	(9.95)
Как и раньше, преобразуем систему (9.94), (9.95) в автоном-
ную, вводя новую неизвестную
у = аТ1 — 0,	(9.96)
при ЭТОМ
у' = о — 0'.	(9.97)
Подстановка (9.96) в. (9.94) дает
а' = —pa + -i-fsiny. -	(9.98)
Подставляя выражение (9.95) в (9.97) и используя (9.96), полу-
чаем	-
ау'= аа—^-а3-^-/cosy.	-	(9.99)
Подстановка формы (9.25) в решение (9.87) приводит к выражению
«о = a cos (То + 0).
При этом из разложения (9.84) следует, что
и — a cos (То + 0) 4- О («X
Учитывая формулы (9.89), (9.96), а также равенства То — t и
Тг= е/, перепишем последнее разложение в виде
и = a cos (ш/ — у) + О (е).	(9.100)
На рис. 9.6 представлены зависимости амплитуды а и фазы у
от переменной 7\, полученные с помощью численного интегриро-
№£	' 9.2. Метод многих масштабов	227
.............. .............. .......,
Жвания системы уравнений (9.98) и (9 99). При этом поведение кри-
Квых а и у оказывается аналогичным их поведению в случае вто-
Кричных резонансов. При 7\ —оо а и у стремятся к предельным
К значениям, которые можно найти из решения системы уравнений
Е	pa = -^-/slny,	(9.101)
к	—ста + а3 = -g- f cos у.	ч (9.102)
Е Возводя соотношения (9.101) и (9.102) в квадрат и складывая по-
К. лученные результаты, приходим к кубическому уравнению от-
Е носительно величины а2 вида
I	. р2а2 + (ст-^-a2)2a2 = 4-^	(9. ЮЗ)
Е-Уравнение (9.103) определяет зависимость а от ст, обычно назы-
Е ваемую амплитудно-частотной характеристикой системы. Такое
Ц же название носит и кривая, изображающая эту зависимость.
Ц На рис. 9.7 представлена типичная амплитудно-частотная
Е характеристика. Резкое искривление этой характеристики при-
Е водит к явлению срыва. Поясним его, как и в предыдущем случае,
К- с помощью мысленного эксперимента, в котором амплитуда внеш-
R него воздействия поддерживается постоянной, а частота (и, сле-
Б доватедьно, ст) медленно изменяется, возрастая или убывая по
к сравнению с собственной частотой линейной системы. При этом
L в ходе эксперимента будем следить за амплитудой гармонического
Р отклика. Пусть начальная частота соответствует точке 1 на кри-
вой, изображенной на рис. 9.7. При уменьшении частоты ст умень-
Г шается; и амплитуда а медленно возрастает, ёледуя участку кри-
I вой 1—%—3. При дальнейшем уменьшении параметра расстройки
й- происходит скачок из точки 3 в точку 4, сопровождающийся уве-
£ личением амплитуды, после чего с дальнейшим ростом о ампли-
туда начинает медленно убывать. Если колебания начинаются
| в точке 5 и ст увеличивается, амплитуда а будет медленно возра-
|, стать, следуя участку кривой 5—4—6. При достижении точки 6
I происходит срыв — резкое уменьшение амплитуды до значения,
Рис. 9.7. Скачок в первичном резонансе для уравнения Дюффинга.
8*
228	Гл. 9. Уравнение Дюффинга. Вынужденные колебания
Рис. 9.8. Скачок в первичном резонансе для уравнения Дюффинга. ,
соответствующего точке 2, а затем медленное убывание амплитуды
с ростом частоты. Максимальная амплитуда, соответствующая
точке 5, достигается только при подходе к этой точке со стороны
низких частот. Участок амплитудно-частотной характеристики
между точками 3 и 6 соответствует неустойчивым движениям и,
следовательно, не может быть воспроизведен экспериментально.
Явление срыва может наблюдаться и в случае, когда колеба-
ния возбуждаются при фиксированной частоте внешнего воздей-
ствия со и медленно меняющейся амплитуде /. Предположим, что
колебания начинаются в точке 1 на кривой, изображенной на
рис. 9.8. При увеличении f амплитуда а будет медленно возрастать
вплоть до точки 3. При дальнейшем увеличении f происходит ска-
чок из точки 3 в точку 4, а затем увеличение' амплитуды а с ро-
стом /. При обратном ходе процесса изображающая точка следует
участку кривой 5—4—6, а в точке 6 происходит срыв в точку 2.
9«3« Метод усреднения
Применение к рассматриваемой задаче метода усреднения также
требует отдельного рассмотрения первичных и вторичных резо-
нансов. Мы начнем со второго случая.
9.3.1. ВТОРИЧНЫЕ РЕЗОНАНСЫ
Как известно, при использовании метода усреднения первый
шаг состоит в том, чтобы ввести вместо искомой функции и две
новые зависимые переменные — амплитуду и фазу свободных ко-
лебаний системы, а затем воспользоваться идеей вариации, по-
стоянных. Итак, при е = 0 общее решение уравнения (9.4) имеет
вид
и = a cos (t + Р) + 2A'.coSjdlf,	(9.104)
где аи^ — произвольные постоянные, а Л, определяется форму-
лой (9.12). Дифференцирование выражения (9.104) по t дает
й = -—a sin (t + Р) — 2Лсо sin toi. (9.105)
При е =/= 0 мы вновь представим решение в форме (9.104)
и подчиним 'его условию (9.105); но при этом будем считать а
9.3. Метод усреднения
229
и р функциями t. Дифференцирование выражения (9.104) по t
в этом случае дает	г
й — —а Sin (t + Р) + a cos (t + Р) —
— ар sin (/ 4- Р) — 2Лм sin at.	(9.106)
? Сравнивая формулы (9.105) и (9.106), находим
a cos (t + Р) — а$ sin (t + Р) = 0.	(9.107)
Далее, дифференцируя (9.105) по t, получаем
й = —a cos (t 4- Р) — a sin (/ + Р) ~ ар cos (t 4* Р) ~ 2Л®2 cos at.
(9.108)
Подставляя соотношения (9.104), (9.105) и (9.108) в (9.104), имеем
—a cos (/ 4- Р) — я sln (* 4~ Р) — яР cos (/ 4- Р) — 2Л®2 cos at —
— 2еца sin (t 4- Р)	4ецыЛ sin at 4- я cos (t 4- Р) +
J	4- 2Л cos at 4- e [я cos (t 4- P) 4" 2Л cos co/]3 — F cos at.
(9.109)
Поскольку, согласно формуле (9.12), 2Л = (1 — со3)-1/1', соотно-
шение (9.109) сводится к уравнению вида
:	a sin (t 4- Р) 4- яР cos (t 4- Р) = — 2ец [a sin (/4- Р) 4~
4-.2®Л sin ®/] 4- 8[я cos (t 4- Р) 4- 2Л cos®/]3.
(9.110)
Умножая (9.107) на cos (/ 4- Р), а (9.110) — на sin (t 4- Р) и скла-
дывая результаты, получаем
> d = —2ец sin (/ 4- Р) [я sin (/ 4* Р) + 2®Л sln ©/] 4-
4-8 sin (/4-Р) [a cos (/4-Р) 4-2Л cos ®/]3.	(9.111)
Подставляя (9.111) в уравнение (9.107) и разрешая его относи-
тельно ар, имеем
ар = —2ер, cos (t 4- Р) [я sin (/ 4~ Р) 4~ 2®Л sin ®/] 4~
4-	е cos (t 4- Р) [я cos (t 4- Р) 4- 2Л cos ®/]s.	(9.112)
Таким образом, задача свелась к решению системы уравнений
(9.111), (9.112) вместо уравнения (9.4).
Возводя в куб последние члены в уравнениях (9.111) и (9.112),
перепишем эту систему в виде
а — —2ер sln (/ 4- Р) la sin (/ 4- Р) + 2®Л sin ®/J + е sin (t 4- Р) X
X [a3 cos3 (/ 4- Р) + 6a2Acos2(/ 4" P)cos®/ 4- 12aA2cos (t 4- P) X
X cos2®/4-8A3cos3®/],	'	(9.113)
ap = — 2sp cos (/ 4- P) [a sin (/ 4- P) + 2®A sin ®/] 4-8 cos (/ 4- P) X
x [a3 cos3 (/ 4~ P) + 6a2A cos2 (/ 4* P)cos®/ 4- 12aA2cos(/ 4- P) X
X cos2®/ 4- 8A3cos3®/].	(9.114)
230 ' Гл. 9. Уравнение Дюффинга. Вынужденные колебания
Используя известные тригонометрические формулы (см. прило-
жение А), придадим системе (9.113),'(9.114) вид
а = е —ра + ра cos (2/ + 20) — 2сорЛ cos [(1 — со) / 4~ 0] 4~
+ 2сорЛ cos [(1 + со) t + 0] + (-1- а3 4- ЗаЛ2) sin (2/ 4- 20) 4-
+ о3 sin (4/ + 40) 4- (А а2Л + ЗА3) sin [(1 + со) / 4- 0] 4-
4. (-|_fl2A4-3A8)sin [(1 - со)/4-0] 4-
+ аЛ2 sin [(3 + со) Г-h 30] + a2 A sin [(3 - со) t + 30] +
4-4-aA2slnK2 + 2w)/ + 2₽J + -raAasin[(2-2co)/ + 20] +
+ A3sin[(l+3co)/ + 0] + A3sin[(l-3co)* + 0]},	(9.115)
a0 = e —pa sin (2/ 4~ 20) — 2copA sin [(co 4- 0^ + 0] —
— 2copA sin [(co — 1) / — 0] 4--|~aS 4“ ЗаЛ2 4-
+ (-j- a3 + ЗаЛ2) cos (2/ + 20) + -§- a3 cos (4/ + 40) 4-
+ (-J" °2 A 4~ ЗА3) cos [(l+®)/-]-0]4-
4-(Xa2A4-3A3)COS[(1-co)/4-0]4-
+ 4 a2Acos[(3 + co) t + 30] + 4«2Acos[(3- co)/ + 30] +
4- -y ate cos [(2 4- 2co) t + 20] 4-
4- 4" аД2 cos K2 — 2fi>) + 20I + ЗаЛ2 cos 2co/ 4-
4- A3cos [(1 4- 3co) t 4-0] 4- A’cos [(1 - 3co) t 4-0] J.
(9.116)
В первом приближении мы должны сохраййть в уравнениях
(9.115), (9.116) только медленно меняющиеся слагаемые. Члены
—ера и е	ЗаЛ2) не зависят от частоты со, во все же
остальные члены частота со входит явным Образом. Отметим, что
соответствующий член уравнения будет медленно меняющимся,
если коэффициент при t (т. е. частота) мал. Анализируя правые
$.3. Метод усреднения г	231
части уравнений (9.115), (9.116), приходим к выводу, что медленно
меняющиеся члены возникают при частоте со, близкой к значе-
ниям 0, 1, 3 и у. Случай со «=* Рследует^исключить [из рассмо-
трения, поскольку при этом малый знаменатель появляется уже
в главном приближении иа. Этот случай рассматривается в разд.
9.3.2. Остальные случаи последовательно рассмотрены ниже.
Случай со, отличной от 0, 3 и —
В этом случае медленно меняющимися оказываются только
члены, не зависящие от t. Поэтому из системы уравнений (9.115),
(9.116) следует, что
а = —ера,	(9.117)
а0 = ш3 ЗеаД2,	(9.118)
откуда
а —
Р == -	+ ЗеА2/ + ₽о,	(9.119)
1
где Оо и р0 — произвольные постоянные.
Случай со «« 3
В этом случае медленно меняющимися членами являются
sin 1(3 — со) / 4- Зр] в уравнении (9.115) и cos 1(3 — со) /Ч- Зр]
в (9.116). Следовательно,
а — —ера 4~е^2Л sin [(3 — со) / 4~ Зр],	(9.120)
ар = еа3 4- ЗеаД2 4- - еа2А cos [(3 - со)/ 4- ЗР)]. (9.121)
Система (9.120), (9.121) совпадает с системой (9.34), (9.35), полу-
ченной по методу многих масштабов, если учесть, что со — 3 = -
== ео.
Случай со -у
Здесь медленно меняющимися слагаемыми являются sin [(1 —
— Зсо) t 4- р] в уравнении (9.115) и cos [(1 —За») t 4- Pl в.урав-
нении (9.116). Следовательно,
а = —ера 4- еД3 sin {(1 —Зсо) t 4- pl,	(9.122)
ар = во3 4- ЗеаД2 4- еД3 cos [(1 - Зсо) t 4- fl. (9.123)
Система (9.122), (9.123) совпадает с системой уравнений (9.53)
и (9.54), полученной по методу многих масштабов, если учесть,
что Зсо — 1 = ест.
232	Гл. 9. Уравнение Дюффинга. Вынужденные колебания
Случай <в « О
В этом случае в уравнении (9.115) нет медленно меняющихся
членов, а уравнение (9.116) содержит медленно меняющееся сла-
гаемое cos2 <ot. Следовательно,
а ~ —еца,	(9.124)
ар = еа3 ЗеаЛ2 -J- ЗеаЛ2 cos 2со/,	(9.125)
что совпадает с системой (9.71), (9.72), полученной по методу мно-
гих масштабов, если учесть, что а = ео и Л « F/2.
9.3’2. ПЕРВИЧНЫЙ РЕЗОНАНС
При е = 0 общее решение уравнения (9.82) может быть запи-
сано в виде
. и = a cos (/ + р),	(9.126)
где а и р — произвольные постоянные. При этом
й — —a sin (t + р).	(9.127)
Если е =/= О* по-прежнему представляем решение в форме (9.126)
с наложенным на него условием (9.127), но при этом считаем,
; чТо аир зависят от времени. Дифференцирование выражения
(9.126) ио t дает
й — —a sin (t + Р) + a cos (/ + Р) — ap sin(f + р). (9.128)
Из сравнения формул (9.127Х и (9.128) следует, что
a cos (Г+ Р) — ap sin (t + р) = 0.	(9.129)
Дифференцирование (9.127) по t дает
й = —a cos (t + Р) — й sin (t + р) — ap cos (t + р). (9.130)
Подставляя выражения (9.126), (9.127) и (9.130) в уравнение
(9.82), получаем
й sin (t + р) -j- aP cos (t -|- p) = —2epa sin (/ + P)4-
Ц-ea3cos3(f-j-p) — efcos cof.	(9.131)
^Разрешая теперь (9.129) и (9.131) относительно а и ар, имеем
\	а = —2ера sin2 {t + Р) 4-
+ еа8 sin (t + Р) cos3 (t + р) — ef sin (/ .+ P) cos <ot, (9.132)
аРч== —2epa sin (t -f- p) cos (/ + P) +
+ ea3 cos4 (t + p) —- ef cos (t + p) cos (ot. (9.133)
Упражнения
233






(9.136)
(9.137)
Используя известные тригонометрические формулы (см. прило-
жение А), перепишем уравнения (9.132) и”(9.133) в виде
а = —ера Ц- ера cos (2/ -|- 20) -|- еа3 sin (2/	20) +
+еа3sin(4/40)-----------^-e/sin [(1 + со) t -|- 0] —
.	—-^-e/sin [(1 -a)t + 0],	, (9.134)
а0 = —ера sin (2t -f- 20) 4- еа3 + -g" cos (% + 20) +
+-g-ea3 cos (4/4-40)----^-e/cos [(1co) /₽1 —
- -i-e/cos[(l - co)/ + 0].	(9.135)
В первом приближении следует сохранить только медленно ме-
няющиеся слагаемые в правых частях уравнений (9.134), (9.135).
В случае первичного резонанса со 1, и медленно меняющимися
членами являются sin 1(1 — со) t + 0] в (9.134) и cos [(1 — со) t +
+ 0] в (9.135). Таким образом, приходим к системе
а =—е.ца-----i-e/sin [(1 — со)/0],
а0 = ~|-еа3 —e/cos [(1 — со) t -|- 0],
которая полностью совпадает с системой (9.94), (9.95), получен-
ной по методу многих масштабов, если учесть, что со — 1 = ео.
Упражнения
9.1.	Отклик системы с квадратичными нелинейностями на синусоидальное
возбуждение описывается уравнением
й + 0)§и = —2ерй + eau2 + К cos Qt.
а) Используя метод мйогих масштабов, показать, что
и0 = Де‘и“Го + AeiaT« + (к. с.),
£)3Uj + coJjUj — —2ia>0 (А' + рД) eib>°r° — 2ipAQezflr° —
'	_ a {д2е21а0т0 дг^сяго _|_ дд д2 2ДЛе‘ <а~<М т« _р
+ 2АЛе{<а+а1>) т’} + (к. с.).
' Чему равно Л?
• б) Для случая 2Q = а>0 + ео показать, что
2ia>o (Д' + рД) + aA2eiaT1 — 0.
Решить это уравнение относительно А и затем найти решение, соответствующее
- установившемуся режиму.
J / в) Для случая Я = 2а>0 + ео показать, что
t	геол (Д'+ рД) + аДЛе,оГ*.
234 - Гл. 9. Уравнение Дюффинга. Вынужденные колебания
Решить это уравнение относительно А. Указать условия, ирн которых ампли-
туда А будет неограниченной.
9.2.	Рассмотреть уравнение
й + о)3и = е (й----1- й3) + ей cos Sit.
Для случая □ '= <о0 + еа, используя метод многих масштабов н метод усред-
нения, показать, что
и = a cos (соо/ + Р),
где
Л = 4* 6 (1 — "J” ®^2) а + sin(ест/ ~ ₽).
а ей . ,
ap = 2^COS(eCT/~P)-
9.3.	Рассмотреть уравнение
й + <!>§« = е (й--------------i-
й3
+ К С05.Ш,
где Q не совпадает с частотами 3w0, соо/3 н 0. Используя метод Многих мас-
штабов и метод усреднения, показать, что
и = a cos (<М + Р) —	cos &t>
где	d =	----®§a2) а, (3 = °.
Определить величину т|.
9.4,	Рассмотреть уравнение
й + ®gu = е ^й-------i- й3^ + К cos Sit,
где $2 — ®о + еа. Используя метод многих масштабов и метод усреднения,
показать, что
и = a cos (<о0< + Р)-Q2~^r 608 >
- где	d = -i~e(fl------j-®oa2^ a + Tcos<ea^ — Р),
ap = еГ sin (ea< — p).
Определить величины i) н Г.
9.5. Рассмотреть уравнение
1
3

а +	= е { й
й3
где □ = 3<в0 + еа. Используя метод многих масштабов у.н метод усреднения,
Показать, что	. 1 *	1	.
IZ
и = a COS (G)ot + Р) —	------2 cos
м (Oq
где й = — е fi) — -j-®i)a2)fl+ 4_eo)°lcos(8<J< —3Р)>
ap = 4~ e«0£a2 sin(ea/ — зр).
|	-		' V. ч
ИГ-	УпраЛснениА	235 t
<!^—***—^*—****—«*—। «тши—Uli ——«I । ii и mu	—m»—*	«
F Определить величины т) и	;
Е 9.6. Рассмотреть уравнение
Е	й + и = —ей | й | + 2e£ cos □/,
К где □ = 1 + еа. Используя метод многих масштабов н метод усреднения, по-
£ казать, что
К'	и : a cos (t + Р) +...,
В	. 4еаа , , . , , о,
fcгде	а =----+ ek sin (eat — Р),
ft,	ар = —ek cos (eat — P).	;
£ 9.7. Рассмотреть уравнение	-
к:	й 4- и 4- 2еи2й 2ek cos Qt,
где □ = 1 4- ев. Используя метод многих масштабов и метод усреднения,
Е показать, что	i
и = a cos (tР),
£ где	й =----у- еа® + ek sln (eat — Р),
ар = — ek cos (eat — P).
? 9.8. Рассмотреть уравнение
J,	й 4-<i>§« + ей1 ==.2KcosQi.
t Показать, что резонансы первого порядка существуют при □ « 4<о0, 2©0, в>о/4,
, ®о/2, 2<оо/3 н Зш0/2. Используя метод многих масштабов и метод усреднения,
вывести уравнения, описывающие изменения амплитуды и фазы в каждом случае.

Глава 10
МНОГОЧАСТОТНОЕ ВОЗБУЖДЕНИЕ
В то время как в предыдущей главе мы имели дело с одноча-
стотным возбуждением, предметом исследования в данной главе
будет многочастотное возбуждение. Для того чтобы уменьшить
объем вычислений, будем рассматривать систему с квадратичной
нелинейностью, находящуюся под действием двухчастотного воз-
буждения. Итак, обратимся к уравнению
й + и + 2ерй+еи2 =? Ft cos со^ + F2 cos (®г/ + v), (10.1)
где v — постоянная фаза, a Fn и соп— некоторые постоянные.
Как и ранее, прежде всего построим прямое разложение и иссле-
дуем его равномерность, чтобы выявить малые знаменатели и,
следовательно, возможные резонансы. В § 10.2, с тем чтобы по-
строить равномерно пригодные разложения первого порядка для
некоторых из этих резонансов, мы используем метод многих мас-
штабов. В § 10.3 рассмотрим эти резонансы с помощью первого
приближения метода усреднения.
f	-  
10.1. Прямое разложение
Будем разыскивать (двучленное) разложение первого порядка
для решения и в виде ряда по степеням е	-
и (t, е) = и0 (/) + еих (/)+••• .	_ (10.2)
Подставляя (10.2) в уравнение (10.1), имеем
й0 + ей\ + • • • 4- и0 + £Uj + • • • + 2ер (й0 + • • • )+
+ е («о + • • )г = Fi cos ait + F2 cos (®а/ + v)>
йо -j- Uo ® («i 4“ wi 4“ 2p&o 4~ «о) 4~  *  —
= Fi cos + F2 cos(®2^ 4-Tvf-	(J0.3)
Приравнивая коэффициенты при последовательных степенях е
в обеих частях уравнения (10.3), получаем
«о 4~ «о = cos 4- F2 cos (®г/ 4- v),	(Ю.4)
й14-«1 = —2цйо — «о-	(10.5)
Ib.l. Прямое разложёниё	2з7
Общее решение уравнения (10.4) может быть получено так же,
как в § 9.1 или в приложении Б. Оно имеет вид
uQ = a cos (t + Р) + 2Ai cos + 2Л2 cos (©2/ + v), (10.6)
где а и Р — произвольные постоянные, а
- А(! _C02)-1Fn.
При этом уравнение (10.5) принимает вид
йг + ui — ta sin (^ + Р) + ZAjtOj sin ©^ + 2Л2©2Х
X sin (a>2t + v) ] — [a cos (t + P) + 2Aj cos ©^ +
+ 2Лг cos (®2Z + v)]2,
или	'	'
Hi + «i = 2р. [a sin (t 4- P)'+ 2Л1и1 sin ©4 + 2A2©2sln (ы2/ + v)] —
— a2 cos2 (/4-P) — 4Л] cos2 — 4A2 cos2 (<o2^ + v)—
— 4aAi cos (t + P) cos ©^ — 4aA2 cos \t 4~ P) cos (©2Z 4~ v) —
— 8AiA2cos ®iZ cos (ы2/ + v). (10.7)
Используя известные тригонометрические формулы, перепишем
уравнение (10.7) в виде
«1 + «1 — 2р [a sin (t + Р) 4~ 2Ai©! sin ф/ + 2Л2ы2 sin (©2/ + v)] —
- a2 + 2Л? + 2Л1) - a2 cos (2/+ 2Р)-
— 2Л2 cos 2©iZ — 2Л2 cos (2©2/ 4- 2v) —
— 2aAi cos [(1 + ©i) t + p] — 2aAj cos [(1 — ©iH + Pl +
4“ 2nA2 cos [(1 4- ©2)/ 4- p 4- v] -— 2&A2 x
X cos [(1 — ©2) t 4- p — v] — 4AjA2 cos [(©! 4- ©2)Z 4- v] —
— 4AjA2 cos l(®2 — ©i) t 4- *]•	(10.8)
Как указывалось ранее, решение однородного уравнения мы учи-
тываем только при построении решения и0. Частное решение урав-
нения (10.8) имеет вид (см. § Б.4)
«1 = [—P-at cos(t'4- Р) 4-	sinsin.(©2/ + v)] —
— ^~2~ a2 _h 2Л2 4~ 2A2^ 4—g- a cos (2t 4" 2p) —
~	cos 2®^ - i •cos <2®г/+2v) +
z + 2^-cosK1 +	' + N - 2^? cos[(1 -©j/ + PE4-
+^tUC0S[(1 4 <о2)/4 Р4 Ч -
2з8	Гл. 16. Многочастотное возбуждение
~2J^-COSKl-®2)^ + P + v]-.
- T-ffiw C0S [(й1 + ®а) * + v] -
,	~	cos^- eo^Z + v].	(10.9)
Подставляя (10.6) и (10.9) в уравнение (10.2) и используя опреде-
ление Лп, имеем
« = а cos (t -Ь Р) -Ь -д cos 4- cos (w2/ + v) +
4- e ра/ cos (/ + P) + sin '
-I- ^pfgtOg Sj_ /„ I I ___J_ a2____?!______
+ (1 — 0>i)2 sln	'	2	2(1 — O)2)2
—' 2 (1 — ©I)» + ~6" cos (2t + 2p) —
9 f	Fl- .
2(1 — a>|)2 (1 — 4o>|) C0S 2“1Г	2 (1 — <o2)2 (1 — 4<o|) X
X COS (2®2/ 4- 2v) 4- (1__Ю2)“2ш1+<в|) cos К1 + ®i) ^ + P1 —
~ '\1-^/(2^ -02) Cos [(1 - ®x} ' + ₽] +
+ -(T -o^^ + o)!) C0S К1 +	' 4- P + v] -
~ "(Г—m2)(Й2- о)2)	- O2)f 4-P - v) -
~ (1 - ®?) (1 - 4) [1 - (®1 + ®2)2] C0S K®1 + ®2) Z + ^ “
“ (1 - 04)-(l - ®2) Ц _ (ш1 _вг)2] COS [((02 - (A^t 4- vjj4- • • • •
(10.10)
Уравнение (10.10) показывает, что малые Знаменатели появляются
в тех случаях, когда «г 1, coj <=» 1/2, ©х 2, ®2	1, ш2
172, ш2 я» 2, ш2 4-«1« 1 и <о2 eij^ l. Поскольку при
®! <=» 1 и ®2 <=» 1 малые знаменатели возникают в первом члене
разложения, эти случаи называются первичными, или основ-
ными, резонансами. Все остальные резонансй называются вторич-
ными, поскольку соответствующие и малые знаменатели появ-
ляются в высших приближениях. Случаи 1/2 и (о2 е» 1/2
называются супергармоническими резонансами порядка 2, по-
скольку при этом в системе возбуждаются свободные колебания
с- частотой 1, равной приблизительно 2(0j или 2соа. Случаи 2
и ®2	2 называются субгармоническими резонансами порядка
f	10.2. Метод многих масштабов	239
1/2, так как при этом возбуждаются свободные колебания с ча-
стотой, примерно равной a>L/2 или ®2/2. Случай сог 4- <в3 <=« 1
называется комбинационным резонансом суммарного типа, а слу-
чай (о2 — oh — комбинационным резонансом разностного
типа. В следующем параграфе мы покажем, как метод многих
масштабов может использоваться для построения равномерно
пригодных разложений в случае вторичных резонансов. Что ка-
сается основных резонансов, толх исследование проводится так же,
как это описано в предыдущей главе.
10.2.	Метод многих масштабов
Если ограничиться членами первого порядка, то наряду с бы-
стрым временем То = t следует ввести медленное время 7\ = в/.
При этом -	, 	_	,
~dt~~ Do + eDt 4* • • • >
-^- = D?4-2eOoZ?i4----, '
где Dn = д!дТп. Тогда уравнение (10.1) примет вид
В^и 4- 2eDoDiU 4- • • • 4-и 4- 2ер (Dou 4- eDitT4- • • •) 4-ем2 —
= F1cosco1T04-/:'2Cos(®2To4-'v)-	(10.11)
Будем разыскивать приближенное решение уравнения (10.11)
в форме 1
; "Л!«- «о Ro. Л) Ч- еиЛТо, Л) + ••• •	(Ю-12)
Подставляя (10.12) в уравнение (10.11) и приравнивая коэффи-
циенты при одинаковых степенях е в обеих его частях, получаем
DoMo4r^ = ^iCos®iTo4-F2cos(®2'ro4-,v)> (10.13)
, Dlu^ ui — —2DqDiU — 2у.Д)Ио — «о-	(10; 14)
Общее решение (10.13) можно записать в следующей комплекс-
ной форме:	_
Мо = А (Л) eiT° 4- А (Л) е~‘т° 4-	4-
4-Л1^-№'г‘>4-Л2с'®’7’<’4-Л2е-,’ш’7’0,	(10.15)
гДе	&1= 2(1 —а>1) ’ Ла= 2(1 — ®|) '	(10.16)
При этом уравнение (Ю.,14) принимает вид
4-«, = —2i (А' 4- рА) ет° - 2фсоЛ1/“1Г° - 2ща2А2е!<ЛгТ° -
-A2e2iT°- A2te2(a'r° - A22e2ia’T° - АА - Л? - Л2Л2 - .
—2ДЛ^ <’+“*> г. _ 2ДЛ^ <’-“*> г» _ 2АА2е; 0+®.> т, _
—2ДА2с(1-ш») т» — 2А1А2е‘ («•+“»> т« ' —
(“«-“>> г» 4- (к. с.),	(10.17)
240	Гл. 10. Многочастошное возбуждение
Как и в предыдущем параграфе, частные .решения уравнения
(10.17) содержат секулярные члены и члены с малыми знаменате-
лями. Для того чтобы разложение было равномерным, эти плены
должны быть уничтожены с помощью подходящего выбора функ-
ции А. Тот или иной выбор А зависит от типа возникающего ре-
зонанса. Ниже мы рассмотрим два случая: а) Д- <о2 « 1
, б) ®2 - Й! « 1 И (О2	2.
10*2-1. СЛУЧАЙ <В1 +	® 1
В этом случае предполагаем, что	1, а все остальные
резонансы в членах первого порядка отсутствуют. Чтобы описать
близость суммы ©! Д- со2 к единице количественно, введем пара-
метр расстройки ст, определив его с помощью соотношения
®х Д- ®2 = 1 4- ест.	(10.18)
Единственными членами в уравнении (10.17), которые могут по-
рождать малые знаменатели, являются член —2AXA2 ехр [i (©х Д-
Д- ®г) То] и член, комплексно-сопряженный с ним. Используя
соотношение (10.18), перепишем этот член в виде
• —2A1Aaef	г» = —2AiAaef <1+е°) Т« = —2A1A2efr°+i<T7’>. .
При этом уравнение (10.17) примет вид
По»! Д- щ = —21 (Д' Д- Mhir“ - 2A1A2ejoT1eir’ Д- (к. с.) Д- (Н.С.Ч.),
(10.19)
где символ Н. С. Ч. обозначает члены, ие дающие вклада в секу-
лярные слагаемые. _ Требование отсутствия секулярных членов
~гВ решении уравнения (10.19) приводит к соотношению
2i (Д' Д- цД)Д- 2АхЛ2егаТ* = 0,
или	Д' Д-цД = iA1A24<j7'1 .	(10,20)
В данном случае уравнение (10.20) для комплексной ампли-
туды, поскольку оно является линейным неоднородным уравне-
нием первого порядкаг допускает точное решение; при этом пред-
ставлять А в показательной форме не требуется. Решение одно-
родного уравнения имеет вид
А = се~*т',		(10.21)
где с— комплексная постоянная. Так как правая часть уравне-
ния (10.20) содержит экспоненту, то соответствующее ей частное
решение можно искать в форме	- • ‘
A = beiaTt.	(10.22)
Подстановка (10.22) в уравнение (10.20) дает
ujbeiaT' Д- Д- iA1A2e‘a7’>,
ИЛИ	'	Mb + pb = iAjAj,
10.2. Метод многих масштабов
241
откуда
iAjAg
ц + ia
При этом общее решение уравнения (10.20) имеет вид
А = се~*Т> + elaTi.	(10.23)
Подставляя выражение для А в формулу (10.15), а затем подстав-
ляя полученный результат в разложение (10.12), получаем
и = [ce-wt 4- е£еа£] е£< +	4- Л2е,“«< 4- (к. с.) Ц- О (е).
(Ю-24)
Представим теперь постоянную с в показательной форме с =
= (1/2) а0 ехр (i’p0) и подставим выражения (10.16) для Лп в (10.24).
В результате имеем

„ _ «+8.> + 45; + а)(^;)(1^Ч) «+.«> <+» +
+ 2(1-<»В г“‘‘ + -(i/i-ioj) ‘‘ ‘“•'+v> + (к- с> + 0 <=)
(10.25)
Заметим, что 1 + ест = и1 4- <в2 (см. (10.18)) и
___L = 	_р— i aictg (а/ц)	"
р. + ta	-|- аг
Следовательно, мы можем переписать решение (10.25) в виде
и = а^е-^ cos (t 4- Во)---------—? 7==~ х
v 2(1— ©1)(1 — ®l)K|x2 + <*2
Т=Я" C0S“1Z+ .
х sin
+ T^Fc°sW+v)+0(e).	(10.26)
При t -> оо первый член в правой части (10.26) стремится к нулю,
и и стремится к следующему установившемуся решению:
и =  -------—т====г sln [koi 4- со2) t 4- v — arctg —1 4-
2(1 —®?)(1—®1)/н2 + ст2	L	и J
+ ilcos M д 1аЮ2 cos((W 4- v) + 0 (e).	(10.27)
10.2<2. СЛУЧАЙ ®, — J»! ~ 1 и w, «2
В этом случае предположим, что два резонанса существуют
одновременно, а именно и2 —	«=> Ги 2; другими словами,
имеем 2 и со2 3. Для того чтобы исследовать этот случай
более подробно, введем два параметра расстройки 04 и о2, опреде-
лив их соотношениями
Wj = 2 4- естр ®г = 3 4- естг. "	(10.28)
242	Гл, 10. .Многочастотное возбуждение
Подставляя (10.28) в уравнение (10.17), имеем
£>o«i + «1 = — 2i ,(Л' + р,Л) е‘Т° - 2А1Ле‘Гв+,'8аГ“ -
—2AiA2e; вг.+«го + (к. с.) 4- (Н. С. Ч),
или
ifoUt + Ut = —2i (Л' + рЛ) eiT° - 2AjAelaTlei't° -
—2А1АгеН<’г-<’1) пе;т»	(К,с.) + (Н. С. Ч).
(10.29)
Уничтожая секулярные члены, получаем
i (Л' + М) + А1Ле‘я-7'- + А1А2е1’ «*•-’*> = 0.	(10.30)
Уравнение (10.30) представляет собой неоднородное уравнение с
переменными коэффициентами. Прежде всего преобразуем его
в неоднородное уравнение с постоянными коэффициентами. Введя
с этой целью подстановку
Л = Ве^>,	(10.31)
где X — вещественное число, получим
i (В’ + &В + цВ) e‘KTi + АгВе1 «’-« г« + ЛгЛ2е; = 0,
или
i (В' + 1кВ + цВ) + AjBe‘ + А^е' П = о. (10.32)
Если выбрать 1 = <тг/2, то коэффициенты при В и В не будут за-
висеть от Т\, и тогда уравнение (10.32) примет вид
i (В' + мгВ + |лВ) + AjB + AjA^i (<ч-за./2) т, == 0. (10.33)
Ёместо того чтобы выражать В в показательной форме, как
в предыдущих случаях, представим В в виде
В == Вг 4-/В^4]	(10.34)
Возникаюпще при этом уравнения решаются легче, чем уравне-
ния относительно модуля и аргумента В. Подставляя (10.34)
в' уравнение (10.33) и используя (10.16), с тем чтобы предста-
вить в показательной форме, получаем
iBr — iB't — UiBr — -i- idjBi + ipB — pBt- -f-
AtBr — iAjBj 4- Г cos (oTj 4- v) 4- Л1 sin (oTt 4- v) = 0, (10.35)
где	° =	(Ю.36)
Отделение действительной и мнимой частей в (10.35) дает
в;4- ивг - (л, 4- -Lot) в- = -гsin(oTi 4- v),	(10.37)
в; 4- рв,- - (Al - -L о0 Вг = Г cos (о?! 4- V).	(10.38)
X .	± --‘1^	1
Метод многих масштабов	243
|г Поскольку (10.37) и (10.38) представляют собой систему ли-
. нейных неоднородных уравнений относительно ВТ и Bt, их общее
к. решение можно получить как сумму общего решения однородной
I системы и некоторого частного решения. Общее решение однород-
I ной системы можно получить, представив Вг и Вг в виде
|	Br = bre*\ Bi = bie^.	(10.39)
I Подставляя теперь (10.39) в’систему уравнений (10.37), (10.38)
К и приравнивая нулю ее правую часть, получаем
|	(v + H)br-(Ai + 4-ffOb‘ = 0’	(1°4°)
I	-(A1-4-a1)&r-h(T + »&i = 0.	(10.41)
I Таким образом, наша задача свелась к решению системы двух
I линейных однородных алгебраических уравнений. Поскольку нас
г интересуют нетривиальные решения для Ьг и bt, определитель
системы (10.40), (10.41)
j -	т + н —	+
|	т + и
I должен обращаться в нуль. При этом
[	(у+ Р)2-Л?+ 4*1 = °-	(Ю.42)
г Это условие можно было бы получить и путем исключения Ьг
L и bt из системы (10.40),<(10.41). Из уравнения (10.42) следует,
г что
I	? + и=±УA?--Lof.	(10.43)
I Следовательно, существуют два возможных значения у. Они даются
Г формулами	,
I 71 = -И—	—-А-ст? , у2 = - р + У А2 + 4 •	<10’44)
| Далее, из уравнения (10.40) получаем, что
|	bt = —l±J!^br.	(10.45)
I	Ai + ~2~ <Si
| Поэтому если
i	Br = b!^ +M*rS	(10.46)
I то из соотношения (10.45) имеем
I	~ Bi^=	b^ ------(Ю.47)
।	-	Ai + -g- ffi	Ai 4- -g- oi I
I где Ьг и b2 — произвольные постоянные.
244
Гл. !д. МногочасгЬотное возбуждение .
Частное решение системы (10.37), (10.38) можно построить
с помощью метода неопределенных коэффициентов. Поскольку
правые части системы содержат синусы и косинусы аргумента
оТ3 + v, а уравнения системы имеют постоянные коэффициенты,
будем искать ее частное решение в виде
Br = Cj_ cos (ог7\ + v)	+ сг sin (о?! + v),	(10.48)
Bt = с3 cos (oTj + v)	+ с4 sin (ffT/4 v).	(10.49)
Подставляя выражения (10.48),	(10.49) в уравнения	(10.37),
(10.38)	и	приравнивая коэффициенты при cos(a7'1	+ v) и
sin (oTj + v) в обеих частях этих уравнений, получаем
jui + стс2 — (лЛ + -g- щ) сз = °>	(10.50)
—CTCi +	pti - (л1 + -|-ст1)с’4 = — Г,	(10.51)
— (Ai-----g- (h) С! + цс3 4- ос4 = Г,	(10.52)
— (Лг-----g- oQ сг — ас3 4- |хс4 = 0.	(10.53)
Воспользовавшись правилом Крамера, найдем, что решение си-
стемы уравнений (10.50)—(10.53) имеет вид
(10.54)
0	-(Лх + 4-d)	0
-Г	0
,	Г	р,	о
0	" —о	~~ у
' (10.55)
сг	0	0
р,	—^A14--g_o1'j
0 ч	Г	чт	’
—	0	И
(10.56)
10.2. Метод мноАих масштабов
245
Г	(10.58)
I ч Складывая решения однородных уравнений (10.46), (10.47)
F с соответствующими частными решениями (10.48), (10.49), полу-
Р чаем следующее общее решение системы (10.37), (10.38):
j ’ Вг =	4- b2e^Ti 4-^1 cos (стТ1! 4- v) 4-c2sin(o7’i 4-v),	(10.59)
I Bl = 	4-...Va У....ЬгеъТ‘ 4-
|	Ai + -у <Ti	Ai + -y ai
I 4-c3cos(aTi4-v)4-c4sin(oTi4-v).	(10.60)
| Из соотношений (10.31) и (10.34) и того факта, что Л = ог/2,
I следует, что
|	А = (Вг + 1В1)е№‘°>Т>.	(10.61)
г Подставляя (10.61) в формулу (10.15), а затем подставляя получен-
[ ный результат в (10.12) и используя (10.16), имеем
j и = (Вг 4- iBi) е‘ 0 +. 0/2) еа,] t <вг - iBi) е~{ П + d /2>	4-
I	+	. cos <01/ 4-	cos 4- v) 4- О (e). .
| Так как Wj = 2 4- ест, то, следовательно,
I и — Вг [е^/г) «<»i< 4- е~ d/2)	4- iBt [е^/2)— е~ d/2) ‘“>4 4-
I + 1 ~ч>1 cos	cos + v) + 0 (е)>
I или и = 2Br cos -у он/ — 2Bj sin у (ог/ 4- i cos a>i/ 4*
I	4- cos (<o2/4-v)4- O(e).	(10.62)

Гл. it). Многочастотное возбуждение
, Подстановка (10.59) и (10.60) в (10.62) позволяет получить сле-
дующее выражение для первого приближения:
и — 2	4-	+ q cos (ест/ + v) 4- с2 sin (ест/ 4* V)1 COS у ®х/ —
' - 2
—— 51eeT’i< 4—У.2	— b^w,t 4- с3 cos (ест/ 4-v) +
Л14- у CTi ' Л14" у °!
4- с4 sin (ест/ 4- v)
,	1	. , Fi
siny®i/4--i-^
cos tOi/ 4-
+ i _2<й2 eos (^ + v) + 0 (e).	(10.63)
' Формула (10.63) показывает, что решение и становится не-
ограниченным по /, если вещественная часть ух или у2 положи-
тельна. При этом из соотношений (10.44) следует, что веществен-
ная часть у! всегда отрицательна, в то время как вещественная
часть у2 положительна при условии
А?>|о?'и |/л?-уст?-и>0,
или .	\ Л1>уст?4-р .
В этом случае пропорциональные cos (<ох//2) и sin (о)х//2) члены
в (10.62), которые описывают свободные колебания системы, бу-
дут стремиться к бесконечности при /-> оо. фактически же
решение и остается ограниченным, но член, описывающий свобод-
ные колебания, становится большим, и необходимо продолжить
разложение до членов Ьолее высокого порядка.
10.3. Метод усреднения
Как и ранее, применение этой Методики начинается с введе-
ния вместо искомой функции и двух новых зависимых перемен-
ных.—амплитуды а и фазы Р свободных колебаний и исйользо-
вания идеи вариации произвольных постоянных. С этой целью
заметим, что при е = 0 решение уравнения (10. Q имеет вид
ц a cos (/ 4- р) 4- - j1-!" cos а>1/ 4- t cos (<0i/ 4- v), (10.64)
где а и P — произвольные постоянные. -Тогда
. « = —а sin (/ 4- р) —	sin e>i/ - sin (с^/ 4- v). (10.65)
В случае е =# 0 вновь представим решение в форме (10.64), под-
чинив его условию (10.65), но при этрм будем считать амплитуду а
и фазу Р функциями времени /.
г,	'	. 10.3. Метод усреднения	~	247
| Дифференцирование (10.64) по t дает
ы = —a sin (£ ф р) ф drcos (/ф-Р) — ар sin (/ф-Р) —	'
~ \-&l sint°iZ ~ ~Уа2 sin (ю^ 4-v).	(10.66)
Сравнивая соотношения (10.65) и (10.66), заключаем, что
Г	a cos (t ф- р) — ар sin (t ф- 0) = 0.	(10.67)
Далее, дифференцируя (10.65) по t, находим	'
й = —acos(/ф-Р) ~ й sin(/ф р) — apcos(/ф р) — —	---
~ 1^2 cos --------- cos (со2/ ф- v).	(10.68)
Подставляя выражения (10.64), (10.65) и (10.68) в уравнение (10.1),
получаем	«.	. •
a sin (/ + Р) + ар cos (t ф- р) = в/,	(10.69)	1
где	ф
f = —2ц [asin(t фр) + -f^2-sinф /У* 2 sin(со2/ ф- v)] -ф
+ а2 cos2 (t ф р) 4- ц-^)г cos2 ф _^2)2 cos2 (со2/ ф- v) ф-	;j
+ cos U + P)cos + i-FL cos (t 4- p) cos (соф 4- -v) 4-	4
4- .....	cos (O^cos (c^t 4- v).	(10.70)
Разрешая уравнения (10.67) и (10.69) относительно ан ар, имеем
й = в/ sin (t 4- Р),	(10.71)	3
ар = ef cos(f 4-Р).	(10.72)	
Подставляя в систему (10.71), (10.72) соотношение (10.70) и ис-
пользуя известные тригонометрические формулы (приложениегА), ".
а == -ера 4- ера cos (2t ф- 2р) - yffig {cos [((ог -1)/-р] —
— cos[(ft)i4- 1)/4-РП ~ {cos^- \)t-рф-v] —
— cos{(«)24- l)/-bP4-v]| ф-еа2sin(^фр)ф-	'
+ -j" ва2 sin (3/ -ф Зр) -ф 2 (j _хш^2 ^sin (^ф-₽)ф-
ф-481п[(1-ф2(о1)/4-₽]+481пИ1-2“1)^ + Р1) +
+ 2 (1 — ш|)2 |sin “Ь 0) 4" "2" sin 1(1 + 2t0?) + Р + 2v) “Ь
i	S	.	-	-	-. ' .. .
248	Гл. 10. Многочастотное возбуждение
+ 4 sin [(1 - 2^)t + Р—2v] J 4- 27^2) {sin [(2 + (ог) t + 2p] +
+ sin [(2 - on) t + 2p]} +	{sin [(2 + o)2) / + 2p + v] +
+ sin [(2 -	+ 2P -v] | + 271-	X
X {sin [(1 4* ®i 4" ®a) 4" P 4- VJ 4" sin [(1 — (t>i — о)2) 14~ p — v] 4*
4-	sin [(1 4-®a — ®1)*4- P 4-V] 4- sin [(1 — 0)2 4- ©i) 14- P — v]{,
(10.73)
tz₽ = —ejw sin (2t 4- 2p) - jey^2 {sin [(<*>1 + 1) 14- p] 4-
,4- Sin [(О)г - 1) t-p] I - 4^- {Sin [(0)2 4- 1) t 4- P + V] 4-
4-sin [(o)2 — 1)^—p4-v}| + -|-a2cos(/4-p)4- -|-a2cos(3^4-3p)4-
+ 2 (1 — w'O2 (cos + P) + 4Г cos H1 Ч- 2°h) ^ + P1 +
4- 4 cos [(1 - 2oh) 14- p]| 4- 2 {cos $ + P) +
4- ~2 cos [(1 4“ 2о)г) 4- P 4- 2v] 4“ cos [(I — 2о)г) / 4~ P 4~ 2v]j 4"
+ (cos 4-4 cos K2 + “i)Z +
4- 4 cos [(2 - ®i) 14- 2p] j 4-	{cos fat 4- v) -p-
4- cos [(2 4- co2) 14- 2p 4- v] 4- cos [(2 — o)2) 14- 2p — v] j 4"
+ 2(1-ш|)д12—©I) {cos K1 + + ®«V 4- P 4- VJ 4-
4-cos[(l — о)г — o)a)/4-p — VJ 4-cos[(l 4-0)2 — ®1)/4-p4-v] 4-
4- COS [(1 ;— 0)2 4- (jOji) t 4” P — v]{.	(10.74)
Отметим, что в результате правые части уравнений (10.73)
и (10.74) оказались весьма громоздкими. Можно было бы значи-
тельно упростить их, если представить и и й в соотношениях
(10.64) и (10.65) не в действителвной, а в зКомплексной форме.
Для этого положим	• '
и = Ле‘74-Л1е‘’<в‘<4-Л2ег<в»<4-(к. с.),	(10.75)
й — iAeli 4-	i4h^l<s>,t 4* (к. с.).	(10.76)
Дифференцируя и по t с учетом того, что А = А (/), получаем
и == iAelt 4- АеИ 4*	4"	4* (к- М- (10.77)
1Ь.З. Метод усреднений.	249
I Сравнивая (10.76) и (10.77), заключаем, что
I -	Ае1/ + Ае~^ = 0.	'	(10.78)
| Дифференцирование соотношения (10.76) по t дает
I	и = — Л^ + 1‘Л^-®?Л1^“1<-о)1Л2е'“г< + (к. с.). (10.79)
I Подставляя теперь выражения (10.75), (10.76) и (10.79) в урав-
I нение (10.1) и используя (10.16), находим
I iAeH — iAe'" = — 2ie.fi [Ае“ + Ц-	—
I	- eAV1’'- еА^-' - еЛ^ги>1< - 2еЛА1е'(1+a>)f-
|	— 2еЛЛ2е‘(1+“2’' — еЛЛ — еЛ? — еА2А2—
I	— 2еЛЛгеН<в|-1) < _ 2вЛЛ^ (“vD < _
I	— 2еА1А^1	' — 2еЛгЛг^ ' + (к. с.).
|	.	(10.80)
| Из равенства (10.78) следует, что А ехр (—it) =—Л ехр (it).
Г Тогда из (10.80) имеем
L 1А = £—iep [Ае1/ +	co2A2ef“2/] —eAV17 —
[	- ±	± еЛ^2^' - еАА{е{ <“‘+1)' + еЛЛ^ (<в*+1>' - .
|	--4 е (АА + Л? + Л2Л2) - еАЛ^ (<в*'1)' - еЛЛ-/	!) * -
I	— eA1A2ef <“»+<B2) < — еЛгЛ^ <«>.-«>х) t -f. (к. с.)}«г".	(10.81)
г Наконец, представляя А в показательной форме и отделяя в соот-
I ношении (10.81) вещественную и мнимую части, приходим к сн-
I стеме (1Д73), (10;74).
I Перейдем теперь к рассмотрению случая Wj + <ог = 1 + ест,
I обсуждавшегося в п. 10.2.1, и случая юг = 2 + 80!, <о2 = 3 4-
I + 8<тг, обсуждавшегося в п. 10.2.2.
Г10.3.1. СЛУЧАЙ <», + <», и 1
| В первом приближении мы сохраним только медленно меняю-
| щиеся члены в правых частях уравнений (10.73), (10.74). В pe-
ls зультате имеем
I d = —ера +	sin [(1 - <ог - и,) / + 0 + v],	(10.82)
I	- 2 (1 - шВ (Г- < cos [(1 — — ша) / 4- р — V]. (10.83)
I Система уравнений (10.82), (10.83) эквивалентна уравнению (10.20),
| полученному с помощью метода многих масштабов. Отметим, что,
256	Гл. 10. Многочастотное возбуждение
в то время как уравнение (10.20) линейно, система (10.82), (10.83)
оказывается уже нелинейной. Именно по этой причине мы не пред-
ставляли амплитуду А в показательной форме, а решали урав-
нение (10.20) в комплексном виде.
Сохраняя в уравнении (10.81) лишь медленно меняющиеся
члены, находим
Д == —ерД + l'eAiA2ez	(10.84)
что полностью согласуется с уравнением (10.20).
10.3.2. случай — а,» г и в>, и2
Сохраняя в правых частях уравнений (10.73) и (10.74) мед-
ленно меняющиеся члены, получим уравнения
d — —в|и + ^(^4,.) Sln [(2 -	+ 2fj +
+ г(,'Х$^-й) sln[(l -<а, + и,)< + Р —v], (10.85)
cos К2 - “•) ‘ + ЭД +
+ 2(l"S(i-«,}) «>sl(l -«, +-Ji+ ?-?), (10.86)
которые эквивалентны уравнению (10.30), полученному с помо-
щью метода многих масштабов. Снова отметим, что уравнение
' в форме (10.30) представляется более удобным для решения, чем
система уравнений (10.85), (10.86).
I*» Если сохранить только медленно меняющиеся члены непо-
средственно в уравнении (10.81), то результат имеет вид
А — — ерД J- ieAAje1 <<в*'2> *	»еЛ1Л2е/ (“«-“i-i)	(10.87)
что полностью согласуется с (10.30). Вывод уравнений (10.84)
и (10.87) показывает, что комплексная форма записи решения
является более удобной по сравнению с действительной.
Упражнения
10.1.	Используя метод многих масштабов н метод усреднения, получить урав-
нения дли амплитуд и фаз первого приближения в случае системы, описывае-
мой уравнением	-
й +	'== ей2 + Ki cos fix/ + К2 cos Р2/, в 1,
при условии Qa ± Qj » <оо. Ограничиться случаем, когда значение частоты Рх
достаточно далеко от нуля.
10-2- Рассмотреть уравнение
й -р <oju -р ёи3 = Kt cos (Pj/ + 9х) -|- К2 cos (Р2/ + 02),
Упражнения
251
где <п0, Кп и 0П — постоянные. При условии что значения частот Qn доста-
точно далеки от о>0, с помощью метода многих масштабов показать, что
«о = А (Л) е£®»г» -|- 4x«iQ,r° + Лае*®’7» -(- (к. с.),
лп=4'к«(юо^й«)’1е<вл-
Далее показать, что
£^)и1 4-	= — [2г аэд4' 4- 3 (44 4- 24,4] 4- iA^A^) 4] eie>’T« —
- 3 (244 + 4,4, 4- 2Л2Л2) А^1^ - 3 (244+.24141 + 4242) X
X Л2егй,г° — Д3е3‘®»Г» — 43в3££г*Г» — 4^езгйгГ" —
— 342Лхе£ (2“°+Ql) Г» — 342Л2в£ <26)“+йг) Г" —
— 3424xe* (2“0_Ql) т” — 34242ег <2®»~Q4 Г» —	. . «
__(®о+2Й1) Т9__________ 34Л^в* (g>o+2Q2) т0_
— 3442ег (<й»"2й>) Г<> — 344^/ <“<>-2й4 т> _ '
— 644х42ег (®<>+й*+йг > Г" — 644хЛ2ег <®»-й1-в») Г« —
— 64Лх42е£ <“0-£21+£2г) т0 _ 6дЛ1д2е1' (а»+йх-йг) То __
— 3424гег (2Й*+йг> Г» — ЗА [Л/1 (2Й*-Й2> Г» —
— 34j4^; (й[+2йг) Г° — 3Aj4;e‘ (2Q,’Ql) Г’+ (к. с.).
а)	Показать, что при Р2> Р, резонансы возникают при условиях
as ЗОх или ЗЙ2, ©о as Р, или ’ Р2, со© Р2 -4- 2йх или 2Р, — Р2,
О	О
®0 2Й2 ± fij, ' ®о
б)	Показать, что резонансы разных типов существуют одновременно при
условиях
Йд Л? 9Q1	«3<ЙО,	Q2 a? Qj as	3®o,
О2	•	q" ЙО. О	Й2 & 5PX a	5. '' 3 “°’
Q2 zx?	7 T“0’	й2 a^	2 ® 3 “°
7 Q2 a? —r- Qi о	(a 7<Во,	p2«4q о	1 as 5®0.
в)	Для случая ш0 “ 2^1 + Й2 + ест показать, что
2iw04' + (344 + SAjAj + 64^) 4 + SA^^7"1 = 0.
г)	Для случая ЗЙх = ®о + sai и О, — Зш», + ео2 показать, что
2но04' + 3 (44 + 24,4, + 2А^ А + Л?е/о*Г* + 34s4Va,r* = 0.
д) Для случая ЗРх = <о<» + 80i и Р2 + Р, = 2<о0 + е<т2 показать, что
2<<о04' + 3 (44 + 24,4, + 24^) 4 + 4j/a*r* + 6441А2ега,Г1 = 0.
252	Гл. 10. Многочастотное возбуждение
е) Для случая 3St = о>0 4~ S04 и S2 ~	= 2а>0 + еСТ2 показать, что
2»<в0Д' + 3 (АА + гл^! + 2^^) А + Л3ега,г* + 6lA1A2ew,r* = 0.
ж) Для случая 3Sx = ш0 + ес^ и 2S2 —	= w0 + ест2 показать, что
21<о0л' + 3 (АА + 2A(At + 2Л2Л2) А + Л??а>г* + 3A^A/a’r* = 0.
з)	Для случая = 3tt>o + eoi и Q2 — 2Sx == <oo Ц- e<t2 показать, что
2i®0A' 4- 3 (АА + 2А1Л1 + гл^) А4- 3A2A1efai7’1 4- ЗА^е1°гТ' = 0.
и)	Для случая Sx = Зо>0 +’ еах и S2 — Pj — 2<в0 + ео2 показать, что
2Г<в0А' 4- 3 (АА 4- гд^ + 2Д2Л2) А 4- ЗА2Лхе£<,‘г* 4- бАЛхЛ/0*7* = 0.
10.3.	Рассмотреть уравнение из предыдущего упражнения. Пусть
и — A (t) е1(йо* 4- ЛхС‘й1/ 4-A2e/a»f 4- (к. с.),
—2<<о0а' = {3 (АА 4- 2AiXi 4- 2Д2Л2) А с^+.З (2АА+А1Х1+2Л2Х2) AieiQlt +
4- 3(2АА 4- 2A,A, 4- Л^) A^iQlt 4- A3e3‘““z 4- Afe3,01< 4-
• 4- л|е3;Й!< 4- ЗА?А^е1 (2Ио+й‘)' 4. ЗА2^1’ <2и»+а>)* 4.
4- 3A2Ajef (2®»’й,) < 4- ЗА2^1'	< 4- ЗАА3е1С20*.*®») < 4.
4	4- ЗАЛ^е1' (2йа+®0>* 4.'ЗАЛ2е* <“«-20>)* 4- ЗАХ$е{ (“»’2Й2)* 4-
4- 6AAxA2e‘ (в>+О»+®»> ‘ 4- бАЛ1А2е”‘ (й*+а«-®<>) <4.
4- 6АЛхЛ2е‘ (SVQt+®«) < 4.6AAxA2ez <ai-^+®o) t _|_
4- ЗЛ^Л2е/ (2a*+Й2>' 4- MfA^e' (2a*-a2>7 4.3A$pl (a*+2a»>1 4.
4- ЗЛхЛ^ f20*’0*»' 4- (к. c.)} e1^.
Усреднить последнее уравнение для случаев, указанных в предыдущем упраж-
нении.
10.4.	Используя метод многих масштабов и метод усреднения, построить рав-
номерно пригодные разложения первого порядка для системы уравнений
4" ®x^i	й2 4"	•— os2Wx
в случае малых, но конечных амплитуд, а также прн условии, что oig « 2<вх-
10.5. Используя метод многих масштабов и метод усреднения, построить урав-
нения для амплитуд и фаз системы уравнений
Йх 4-	=
“2 "Ь ®21,а = ®2U1U3>
Й3 4- ®з“з = а3«1«2 S 1-
в случае малых, ио конечных амплитуд, а также при условии, что а>з « о>х + <о2.
10.0. Используя метод многих масштабов и метод усреднения, построить рав-
номерно пригодные разложения первого порядка для системы уравнений
йх 4~	— ео*х^х^2 ~Н	1^х^’
и2 4- с)2и2 — 80*2^х 4- ®^2 cos Q2t
при условиях 1	•
а) <о2 « 2<Ох И Si я» о>х, б) со2 » 2ац и S2 « ац.
Глава 11
УРАВНЕНИЕ МАТЬЕ
В отличие от двух предыдущих глав, в которых внешнее воз-
действие входило в правые части исходных уравнений, в этой
главе мы рассмотрим возбуждение, описываемое переменными
коэффициентами уравнений. Такое возбуждение называется па-
раметрическим. Простейшим уравнением, описывающим пара-
метрическое возбуждение системы с одной степенью свободы,
является уравнение Матье
 + (б* + е* cos со*/*) и* = 0.	(11.1)
Как и ранее, введем безразмерные переменные, полагая
ц*	1
м	°
где Uq представляет собой некоторое характерное значение и.
При этом уравнение (11.1) можно записать в стандартной форме
й + (б2е cos 2/) ы = 0,	(11.2)
-	46*	4е* '
°	<о*2 ’	8	<0*2 
В следующем параграфе мы построим прямое разложение вто-
рого порядка при малых е и исследуем вопрос о его равномер-
ности. В § 11.2 мы изложим теорию Флоке, описывающую точные
' решения уравнения (11.2). В § 11.3 рассмотрим так называе-
(мый метод растянутых параметров, применяемый для построения
• приближенных периодических решений, а в § 11.4 построим при-
ближения к точным решениям. В § 11.5 и 11.6 мы покажем,
; как для получения равномерно пригодных разложений решений
уравнения (11.2) могут использоваться метод ^многих масштабов
и метод усреднения.
11.1. Прямое разложение
Будем искать прямое разложение решения уравнения (11.2)
> в виде следующего ряда по степеням е:
I	и (t\ е) = и0 (0 +	(f) + e2u2 (f) + ... .	(11.3)
254	Гл. 11. Уравнение Матье
Подставляя (11.3) в уравнение (11.2) и приравнивая нулю коэф-
фициенты при последовательных степенях е, имеем
й06и0 = 0,	(11.4)
«1 +	= —2«0 cos 2t,	(Н-5)
—	«2 + б«2 = —2мгСО5 2t.	(11.6)
Общее решение уравнения (11.4) можно представить как
и0 — a cos (<о/ + Р), 6 — со®,	(П-7)
где а и Р — произвольные постоянные. При этом уравнение
_ (11.5) принимает вид
йг 4~ (о®цг = —2а cos (®/ + Р) cos 21,
. или
+ (о2^ — —a cos [(со + 2) t 4- р ] — a cos ((со — 2) t 4- pi.
(П.8)
Как н ранее, исключая из рассмотрения решение соответствую-
щего однородного уравнения, запишем решение (11.8) в виде
“1------4(Т+ЪГ’ b 4(1-®)	’	1и'У'
При этом уравнение (11.6) принимает вид
«г +	совД® + 2) 14- Р) cos 2t -
— 271"^)-cos К® - 2)1 + й cos 2t,
или
fia 4- Ю2ц2 = - T(Tq7^- cos К® 4- 4) 14- pl - T(I^ -y x -,
x cos[(®-4)/ + P] [-—£-^-4- —-_]cos(w^4-P).	(11.10)
Опуская решение однородного уравнения, запишем решение (11.10)
в виде
а	।. tn । «cos ((© 4- 4) t + Р] ,
“2~	4©(1 — ©?)Лsm И + ₽) + 32(1 +<о)(24®) +
, acos [(« —4H4 0J Z1, 11Ч
+ ~32(Г-®Й2-®Г’- 1П Л11
Подставляя выражения (11.7), (И.9) и (11.11) в разложение
(11.3), получим	*	
. 1	( cos ((« 4 2) t 4 pp j cos ((® — 2) t 4 0] 1
и = a cos И 4- P) 4- Tffl (—+ — - !-© "-"j +
, 1	( 8fsin(®f4P) , cos [(M 4 4) / 4 0] ,
"* 32	|	®(1 —©4	। (1.4©) (2 4©)
i eos [(© 4) t 4 Pl) ,	/11 1 oi
+ {i-©)(2-®) J + • ’ • •	(H.^J
"	-<	if.2. Теория Флоке 	'25S
Полученное прямое разложение становится непригодным при
^больших значениях t из-за присутствия в разложении секуляр-
• ных членов. Кроме того, оно будет непригодным н при ® О,
1 и 2 из-за появления малых знаменателей. Если продолжить -
: разложение до членов высших порядков, то оказывается, что
j малые знаменатели возникают прн ® п, где п = 0, 1, 2, 3, ... .
Перейдем теперь к изложению теории Флоке, описывающей точ-
ные решения уравнения (11.2).
11.2. Теория Флоке
В этом параграфе мы изучим общие свойства решений урав-
нения (11.2), не решая уравнения в явном виде. Информация об
этих свойствах используется в последующих параграфах при
. построении соответствующих равномерных приближений.
Поскольку (11.2) представляет собой линейное однородное
уравнение второго порядка, оно обладает двумя линейно неза-
висимыми решениями иг (/) и и2 (/), удовлетворяющими началь-
ным условиям
«1(0)== 1,	«1 (0) = 0,	(11.13)
' и2 (0) = 0, йг (0) = 1,
так как определитель Вронского (см. § Б1) отличен от нуля. По-
кажем теперь, что если Ut (0 является решением уравнения
(11.2), то и иг (t 4=- л) также является решением. С этой целью
заменим независимую переменную t на z = t 4- л. Прн этом урав-
нение (11.2) примет вид
+ [б 4~ 2е cos (2г — 2л)] и = 0,
или	4-(б cos 2z) н = 0,	(11-14)
так как cos (2г!—2л) = cos 2z’ Но уравнение (11.14) совпадает
с уравнением (И-2), поэтому если функция (t) есть решение
(11.2), то функция (г) = иг (i 4- я) является решением урав-
нения (11-14) и, следовательно, и уравнения (11.2).
Из предшествующих рассуждений следует, что если ыг (0
н «а (0 — два решения уравнения (1L2), то и цг (t -F л) и w2 (t +
4- л) также представляют собой решения (11.2). Более того, если
функции иг (0 и н2 (0 линейно независимы, то их {t 4- л) должно
линейно зависеть от иг (0 и «2 (0, поскольку уравнение второго
порядка может иметь только два линейно независимых решения.
Следовательно, существуют две постоянные, ап н аи, не обра-
щающиеся в нуль одновременно, такие, что
«1 (t 4- л) = аииг (t) 4- Ни«2 (0-	(11.15)
256	Гл. 11. Уравнение Матье
Точно так же существуют две постоянные, по крайней мере одна
из которых не равна нулю, такие, что
«2 (t + л) = а2хих (t) + а22и2 (f),	(11.16)
поскольку ы2 (t + л) должно линейно зависеть от их (t) и u2(t).
Используя начальные условия (11.13), из соотношений (11.15)
И (11.16) находим, что
«Ц = «1 (л), «21 = «2 (л).	(11.17)
Дифференцирование (11.15) и (11.16) по t дает
Wi (t + л) = auWi (0 + ах2й2 (t),	(11.18)
й2 (t + л) =	(/) + а22й2 (/).
Подставляя условия (11.13) в (11.18), имеем
«12 = «1 (л), «22 = «2 (л).	(11.19)
Таким образом, если функции их (f) и и2 (/) известны, то коэф-
фициенты а1} в соотношениях (11.15), (11.16) определяются од-
нозначно по формулам (11.17) и (11.19).
Обращаясь вновь к соотношениям (11.15) и (11.16), запишем
их в матричной форме
u (t + л) = Ли (/),	(11.20)
„„„	.	«11	«12
где	А	=
L «21 «22
Далее, исследуем линейное преобразование вектора и (/) в век-
тор v (/), а/именно	положим
v(0=Pu(0,	(11.22)
где Р — постоянная невырожденная квадратная матрица 2-го
порядка. В скалярной записи соотношений (11.22) принимает вид
Н1 = Р11«1 + Р12«2, На = р21«1 + />22«2-	(11.23)
При этом из (11.22) следует, что
и (0 = P-^v (t),	(11.24)
где Р-1 — матрица, Ъбратная к Р, -т. е.
РР-1 = 7,	.	(11.25)
где 7 — единичная матрица
(П-21)
Подстановка (11.24) в формулу (11.20) дает
Р~гу(14- л) = ЛР~1у(/).	(11.26)
11.2. Теория Флоке
257
^Умножая соотношение (11.26) слева на матрицу Р н используя
ЙЧ1.25), получим
\	v (t + л) = PAP~lv (?),	(11.27)
'или
v (t + л) = Bv (/),	(11.28)
’где
"	В = РАР-1.	(11.29)
! Матрицы А и В называются обычно подобными, так как они об-
ладают одними и теми же собственными числами. Чтобы показать
это, заметим, что
[| В - X/1 = |РЛР-г - ХРР-11 = | Р (Л - V) Р-11 =
= |Р||Л-71Z11 J5"11 = | Л — XZ|,	(11.30)
поскольку | Р | | Р I"1 — 1.
Из курса линейной алгебры известно, что всякую невыро-
 жденную постоянную матрицу Р можно выбрать таким образом,
чтобы матрица В имела простейшую так называемую жорданову
каноническую форму. Эта форма определяется собственными чис-
лами и собственными векторами матрицы Л. Собственные числа
'матрицы Л (а следовательно, и матрицы В) находятся из урав-
нения
аи — аи	Q
#21	^22
. ИЛИ	(йц - ^) (^22	^12^21	0,
откуда
А,2	— (ап + а2г) А	+ аиа22 — а12а21	=	0.	(11.31)
Учитывая соотношения	(11.17)	и (11.19), а	также	тот факт,	что
вронскиан функций иг (/) и ы2 (t) равен 1, имеем
#11^22 - ^12^21 = «1 (Я) ^2 (Я)	" «2 (Я)	(Я)	1 •
При этом уравнение (11.31) принимает вид
V — 2аА + 1 = 0,	(11.32)
где
а = («и + М = 4"(я) + «2 (л)] •
Решения уравнения (11.32) даются выражением
А = а ± j/ а2 — 1 •	(11.33)
Если а +- ±1, формула (11.33) определяет два различных соб-
ственных числа ______________
Аг = a -j- / а2 — 1, А2 = а — / а2 — 1	(11.34)
и матрица В имеет диагональную форму
в = [ог Г •	(1L35)
9 Найфэ А. X.
258
Гл. 11. Уравнение Матье
ЕсЛи а =	= ±1, то формула (11.33) дает только одно собственное			
число, а	именно л, = а = ±1, и		матрица В имеет либо вид	
		' ±1	0 '	
	В =	0	±1 .	,	(11.36)
либо вид				
		' ±1	0 '	
	В =	1	±1 .	(11.37)
Если матрица В имеет форму (11.35) или (11.36), то соотно-
шение (11.28) можно переписать в следующей скалярной форме:
yi (< + л) =	(f), v2 (t + л) = X2v2 (i),	(11.38)
где = Х2 = ±1. если В имеет форму (11.36). Из соотношений
(11.38) следует, что
Vi (t + 2л) = Kiwi (t л) =	(i),
Vi (t + Зл) = XiUi (t 4- 2л) = kiVi (t),
Vi (t 4- 4л) — Mvi (t 4- 3л) = kjoj (/),
»1(/4-пл) = Х?»1(0,	(11.39)
где n — целое число. Аналогичным образом,
O2(f4-n^) = l?t»2(0.	(11.40)
Следовательно, при t —> оо имеем
Г о, |М<1,
1М|>1	(“-41)
и решение становится неограниченным по времени, если абсолют-
ная величина любого из собственных чисел больше единицы.
В случае когда = А,2 = 1, соотношение (11.38) показывает,
что решения vt периодичны с периодом л. Если же	=
= —1, то
иг (t 4- л) = — Vi (f),
vt (t 4- 2л) = —Vi (t 4- л) = Vi (t),	(11.42)
т. e. решения уг представляют собой периодические функции с пе-
риодом 2л. Таким образом, случаи = Z,2 = ±1 отделяют
устойчивые решения от неустойчивых. Эти значения X обычно
называют переходными значениями. т
Соотношения (11.38) можно использоватЬ'для того, чтобы за-
писать решения Vj{t) в так называемой нормальной форме, или
форме Флоке. Для этого умножим первое из равенств (11.38)
на ехр [—Vi (t 4- л) ], где показатель уг будет определен впо-
следствии, и получим
e-?i a+MV1 (t 4- л) — 'k1e~t'ne~f'ivi. (f).
(11.43)
11.2. Теория Флоке
259
роли положить Л,1 ехр (—урп) = 1, тогда ехр (Tior) = Aj и
Т1 = 4-1пА1.	(11.44)
В результате соотношение (11.43) принимает вид
e-v, </+л)У1 (/	= e-vi^^).	(11.45)
Следовательно, функция ехр (—YiO (/) является периодической
с периодом л, так что ее можно представить как
e~^vx (0 = Ф1 (0,	(11.46)
где Ф1 (t + л) = Ф1 (/). Таким образом, Vj (t) можно предста-
вить в нормальной форме
п1(/) = ^/ф1(/)>	(11.47)
где Yj = (1/л) In At — так называемый характеристический по-
казатель. Аналогичным образом можно представить в нормальной
форме и функцию v2 (I):
v2(0 = e^q>2(t),	(11.48)
где ф2 (t + л) = ф3 = (0 и у2 = (1/л) In А2.
Если матрица В имеет форму (11.37), соотношение (11.28)
переписывается в виде
иг (t + л) = Xvi (/), (11.49а) v2 (I 4- л) = Kv2 (t) + vx(t), (11.496)
где А = ±1. Используя рассуждения, аналогичные приведённым
выше, можно представить (t) в нормальной форме
Vi (О = е7<Ф1 (О,	150
Ф1 + л) = Ф1 (О и т = (1/л)1пХ.
При этом второе из соотношений (11.49) принимает вид
и2 (t + л) = м2 (t) +	(/).	(11.51)
Как и ранее, умножение равенства (11.51) на ехр [—у(£4-л)]
приводит к соотношению
е-ч (<+л)у2 (t + л) = Xe-v”e-v'u2 (t) +	(0>
которое может быть переписано в виде
e-v(/+n>v2(f _|_л) = е-тЧ)2(/) + у-ф1(0.	(11.51а)
В этом случае вид решения v2(t) отличен от (11.48) из-за присут-
ствия члена А-1ср1(/). Легко проверить, что вместо (11.48) нмеем-
= [фНО+^фНО]-	(11-52)
В случае |а| > 1 абсолютная величина одного нз собствен-
ных чисел А,,, будет больше единицы, в то время как абсолютная
величина другого собственного числа окажется меньше единицы,
9*
260
Гл. И. Уравнение Матье
Рис. 11.1. Неограниченные решения уравнения Матье.
поскольку XjA-2 = 1 в силу условия (11.32). Так как = (1/л) In Л,;
вещественная часть одного из показателей у, положительна,
а другого — отрицательна. Поэтому из соотношений (11.41)
или (11.47), (11.48) и (11.52) следует, что одно из решений неогра-
ниченно растет со временем, а другое остается ограниченным.
На рис. 11.1 показаны два возможных типа неограниченных
решений. Решение первого типа осциллирует с амплитудой,
экспоненциально растущей со временем, а решение второго типа
неосциллирующее, но также возрастает со временем экспонен-
циально.
В случае |а| < 1 собственные значения X/ представляют со-
бой сопряженные комплексные числа, модули которых равны еди-
нице, так что вещественные части характеристических показате-
лей уг оказываются равными нулю. Следовательно, нормальные
решения в этом случае будут ограничены. Эти ограниченные ре-
шения являются, вообще говоря, апериодическими, меняясь
' Рис. 11.2. Ограниченные решения уравнения Матье.
11.2. Теория Флоке
261
Рис. 11.3. Области устойчивости и неустойчивости (последние иа рис. заштри-
хованы) в плоскости параметров для уравнения Матье.
с двумя частотами — мнимой частью у и частотой возбуждения,
равной 2. В зависимости от отношения этих двух частот решение
может принимать разнообразные формы, кроме переходных пе-
риодических колебаний. Три возможных типа решения показаны
на рис. 11.2.
Переход от устойчивых движений к неустойчивым происходит
при | а | = 1, что соответствует кратным корням Aj = Х2 = 1
или Aj = А2 = —1. При этом Yi ==	= 0 или	= in.
Как указывалось выше, в первом случае существует нормальное
периодическое решение с периодом л, а во втором — нормальное
периодическое решение с периодом 2л. Эти свойства решений
уравнения Матье служат основой метода растянутых параметров,
применяемого для определения значений 6 и е, соответствующих
условию | оь | = 1 и, следовательно, переходу от устойчивости
к неустойчивости. Переходные кривые, разделяющие плоскость
8 — б на области устойчивости и неустойчивости, показаны на
рис. 11.3. Вдоль этих кривых по крайней мере одно из нормаль-
ных решений является периодическим с периодом л или 2л.
Характеристические показатели для уравнения (11.2) могут
быть получены с помощью численного расчета двух линейно неза-
висимых решений по начальным условиям (11.13) на отрезке,
равном периоду колебаний. Используя численные значения этих
решений и их первых производных при t = л, можно рассчитать
а = (1/2) 1«1/л) + «2 (л) ], затем по формулам (11.34) определить
и с их помощью вычислить Yi = (1/л) In А,г. Очевидно, что для
каждой пары значений б и е эту дорогостоящую процедуру, тре-
бующую значительных затрат машинного времени, необходимо
повторять. Для случая малых уг мы опишем в § 11.4 расчетную
262
Гл. 11. Уравнение Матье
схему, называемую методом Уиттекера, предназначенную для
приближенного определения характеристических показателей.
Проведенный анализ показывает, что применение метода рас-
тянутых параметров или метода Уиттекера требует информации
о качественном характере решения, а именно о нормальной форме
решения (форме Флоке). В § 11.5 и 11.6 будет показано, что
использование метода многих масштабов и метода усреднения по-
зволяет вполне обходиться без такой информации.
11.3.	Метод растянутых параметров
В § 11.1 мы выяснили, что прямое разложение становится
непригодным при 6^0, 1,4, ... . Это наводит на мысль, что
наряду с разложением по е решения и (t, е) следует разложить
в ряд по степеням е в окрестностях указанных значений и параметр
6. Итак, будем искать равномерно пригодное разложение вида
и (/, е) = и0 (0 + ецх (0 4- е2ы2 (0 + •   ,	(11.53)
6 = п2 + ебх + е262 + • • • ,	(11.54)
Определяя коэффициенты 6П из требования периодичности при-
ближенного решения. Получаемые в результате выражения для б,
как указывалось в предыдущем параграфе, будут определять
переходные кривые, отделяющие области устойчивости и неустой-
чивости решения.
Подстановка разложений (11.53) и (11.54) в уравнение (11.2)
дает
й0 + еих + е2ы2 4-  - • 4- (п2 4- ебх 4- е2б2 4-  • •) (ы0 +
- 4-	енх 4- е2ы2 4- • • •) 4- 2е cos 2t (и0 4- еых 4- е2ы2 4- • • •) = 0,
или
й0 4- п2и0 4- е (йх 4- «2«х 4- 6i«o + 2ы0 cos 20 4-
4-	е2 (й2 4- п2и2 4- бхых 4- б2ы0 4- 2ых cos 20 4- • • • = 0.
Приравнивая нулю коэффициенты при последовательных степе-
нях е, получаем
йо4-п2мо = О,	(11.55)
йх 4- «2«1	—6х«о — 2ы0 cos 2/,	(11.56)
й2 4- п2и2 = —6хих — 62ц0 — 2ux cos 2t.	(11.57)
Общее решение уравнения (11.55) можно ^представить в виде
и0 = a cos nt 4- b sin nt.	(11.58)
Из формулы (11.58) ясно, что функция и0 является периодической
с периодом л, если п четно, и с периодом 2л, если п нечетно.
Поэтому далее мы последовательно рассмотрим случаи ц =
11.3. Метод растянутых параметров
263
Случай п = О
В этом случае решение (11.58) сводится к и0 = а Тогда урав-
’ нение (11.56) принимает вид
й) = —— 2 acos 2t.	(11.59)
(Требование отсутствия в правой части (11.59) слагаемого, поро-
ждающего секулярный член в решении ut (т. е. подчинение их
; условию периодичности), приводит к условию
6Х = 0.	(11.60)
 В результате уравнение (11.59) сводится к виду
йх = —2а cos 2t.	(11.61)
Решение уравнения (11.61), не включающее в себя решение соот-
ветствующего однородного уравнения, имеет вид
ux = -^-acos2C	(11.62)
При этом уравнение (11.57) можно представить как
й2 = —62а — a cos2 2t
и с помощью известных тригонометрических формул преобразо-
вать его к виду
й2 = —62а—^-а—acos 41.	(11.63)
Для периодичности ы2 требуется выполнить условие
/	62а + а = 0,
откуда при а =# 0 (т. е. в случае нетривиального решения) имеем
б2=-4-	о1-64)
(Используя полученные результаты, находим решение во втором
приближении:
и = а + еа cos 2t -(-•••,	(11.65)
6 = —(1/2) е2 + • • • .	(11-66)
Таким образом, переходная кривая, отделяющая области устойчи-
вости и неустойчивости и выходящая из точки е = 0, 6 = 0, опи-
сывается уравнением (11.66). Соотношение (11.65) показывает,
что на этой кривой решение периодично с периодом л.
п Решение и$~ а не является общим решением, поскольку оно подчиняется
^условию ограниченности при I—> оо. — Прим, перев.
264
Гл. 11. Уравнение Матье
Случай п = 1
Подставляя (11.58) в уравнение (11.56) и полагая п. = 1,
получим уравнение
«1 + «1 = —6Х (a cos i + b sin t) — 2 (a cos t + b sin t) cos 2t,
которое с помощью простых тригонометрических формул преоб-
разуется к виду
«1 + «1 = —(1 + 6Х) a cos t — (6Х — 1) b sin t —
— a cos 3t — b sin 3t. (11.67)
Требование исключения слагаемых, порождающих секулярные
члены в ых, приводит к условиям
(6Х + 1) а = О,	(11.68)
(6Х —1)6 = 0,	(11.69)
в результате чего уравнение (11.67) принимает вид
йх + «1 = —a cos 3t — b sin 3t.	(11.70)
Условие (11.68) удовлетворяется при 6Х = —1 или при а = 0,
а условие (11.69) — при 6Х = 1 или 6 = 0. При этом в случае
6Х = —1 для выполнения соотношения (11.69) необходимо, чтобы
b равнялось нулю, а в случае 6Х = 1 для выполнения (11.68)
необходимо, чтобы а равнялось нулю. Таким образом, мы имеем
две возможности
6Х = —1,	6 = 0,	(11.71)
6i = l, а = 0.	(11.72)
Следовательно, решение уравнения (11.70), не содержащее ре-
шения соответствующего однородного уравнения, имеет вид
«i = -|-acos3/	(11.73)
или
«1 = Д-6 sin 3t.	(И-74)
Подстановка (11.71) и (11.73) в уравнение (11.57) дает
й2 -j- й2 = -|-acos3/ — 62acosZ—a cos 3t cos 2t,
или
й2 + и2 = — (б2 4- -i-) a cos t +-y acos3i—^-cos5i. (11.75)
Требование отсутствия слагаемого, которое приводит к появле-
нию секулярного члена в решении ы2, дает
68 =	(И-76)
11.3. Метод растянутых параметров	265
Таким образом, во втором приближении имеем
и — a cos t + -|-eacos 3t 4* • • •,	(11.77)
6=1 _e+±e2H---------.	(11.78)
Уравнение (11.78) описывает одну из ветвей переходной кривой,
выходящую из точки е = 0, 6 = 1, а соотношение (11.77) пока-
зывает, что на этой кривой решение является периодическим с пе-
риодом 2л.
Аналогичным образом, подстановка (11.72) и (11.74) в урав-
нение (11.57) дает
й2 + и2 —--g- b sin 3t — 62Ь sin t —j-b sin 3t cos 2t,
или
й2 + u2 = — ^62 4- -g-) b sin t —b sin 3t —b sin 5t. (11.79)
Требование отсутствия слагаемого в правой части (11.79), поро-
ждающего секулярный член в решении ы2, приводит к условию
62 = --g-	(Н.80)
Следовательно, во втором приближении имеем также
и = 5sin^ + -^-e&sin 3t -|- • • •,	(11.81)
6=1+е-±82 -Ь ....	(11.82)
Уравнение (11.82) описывает вторую ветвь переходной кривой,
выходящую из точки е = 0, 6 = 1, а соотношение (11.81) показы-
вает, что и на этой ветви решение имеет период 2л.
Случай п = 2
Подставляя (11.58) в уравнение (11.56) и полагая п = 2,
получаем
йх + 4ых = —6Х (a cos 2t + b sin 2t) —
— 2 (a cos 2t + b sin 2t) cos 2t,
или
йх 4- 4mx — —6X a cos 2t — д±Ь sin 2t —
— a — a cos 4/— b sin At.	(11.83)
Из условия уничтожения секулярного члена в ых следует, что
6Х = 0. При этом решение (11.83), не включающее в себя решение
соответствующего однородного уравнения, дается формулой
ых —---------------|-а +-jy cos4/4~-j7>-6sin 4/.	(11.84)
266
Гл. 11. Уравнение Матее
Тогда уравнение (11.57) с учетом (11.84) принимает вид
йа 4- 4ыа = — 6а (« cos 2t + b sin 2t) — 2 (—--a +~iy a cos 4t 4-
4- b sin 4^ cos 2t,
или
«а + 4«2 = —	—j7>-) a cos 2/ — (бг + -jy) & sin 2t 4- (H. С. 4).
(11.85)
Потребовав, как обычно, исключения секулярных членов из ма.
приходим к соотношениям
(бг-4-)а = 0,	^4-_^_)& = o. (11.86)
Таким образом, существуют два решения
ба = -^-> Ь=0	(11.87)
или
62 = — -{2, a = Q.	(11.88)
Итак, во втором приближении имеем
M=acos2Z—j-ea(l —|-cos 4/) 4- • • • ,	(11.89)
6 = 4 4- -^-е2 4-	(11.90)
или
и — 6 sin 2t 4~-]7>-efe sin it 4- • • •,	(11.91)
6 = 4---jye24---	(11-92)
Уравнения (11.90) и (11.92) описывают две ветви переходной кри-
вой, выходящие из точки е = 0, 6 = 4; при этом соотношения
(11.89) и (11.91) показывают, что на этих ветвях решение и пе-
риодично с периодом л.
11.4. Метод Уиттекера
В предыдущем параграфе мы установили, что метод растяну-
тых параметров позволяет найти переходные кривые и периоди-
ческие решения на этих кривых. Если же нас интересуют решения
в окрестности переходных кривых, необходимо воспользоваться
другим подходом. Для этого используем нормальную форму ре-
шения, или форму Флоке. Положим
и(0 = ^Ф(0,	(11.93)
11.4. Метод Уиттекера
267
где в соответствии с теорией Флоке <p (t + л) = <р (t). Но диффе-
ренцирование (11.93) по Z дает
й — е'^у	уе^ф,	(11.94)
и = е^ф	2уе^ф	у2е^ф.	(11.95)
Подставляя выражения (11.93) и (11.95) в уравнение (11.2), имеем

ф + 2уф + (6 + у2 + 2е cos 2t) <р = 0.	(11.96)
Таким образом, задача сводится к определению у и построению
периодических решений уравнения (11.96) при заданном 6. В ок-
рестности переходной кривой величина у мала, и поэтому будем
искать разложение в форме
ф (<ie) = Фо (0 + ефх (0 + е2фа (0 + • •  ,	(11.97)
6 = б0 + ебх + е2б2 + • • • ,	(11.98)
У = .®Ti- + е2?2 + • •  •	(11.99)
Для того чтобы дать лишь общее представление о методе Уитте-
кера, ограничимся нахождением членов порядка е. Подставляя
разложения (11.97)—(11.99) в уравнение (11.96), находим
Фо + еф1 + 2eyi (ф0 + еф2) + (бо + e6i + е2у2 + 2е cos 2t) X
X (фо Н~ 8ф1) + • • • — 0,
или
Фо + боФо + е (Ф1 + 6оФ1 + 2у1Фо +
+ 6хф0 + 2ф0 cos 21) + • • • =0.	(11.100)
Приравнивая нулю коэффициенты при е° и е в уравнении
(11.100), получаем
Фо+6оФо=О,	'	(11.101)
Ф1 + 60Ф1 = —2?1Фо — 6хФо — 2ф0 cos 2t.	(11.102)
Общее решение уравнения (11.101) можно представить как
Фо = а созд/б7t + b sin )/б71.	(11.103)
Поскольку, согласно теории Флоке, функция ф имеет период л,
то величина j/б0 будет равна п, где п — произвольное целое чи-
сло. При этом уравнение (11.102) примет вид
фх + п2фх = —2ух (—an sin ht + bn cos nt) —
— бх (a cos nt + b sin nf) — 2 (a cos nt + b sin nt) cos 2t. (11.104)
В случае n =# 1 источником секулярных членов в решении фх
оказываются первые два слагаемых правой части (11.104), про-
порциональные ух и 6Х; в случае п = 1 секулярный член поро-
268
Гл. 11. Уравнение Матье
ждается и последним слагаемым. Таким образом, уравнение
(11.104) можно переписать в виде
Ф1 + Ф1 = (2уха — &ib + b) sin t —
— (2yxfe + 6ха + a) cos t + (Н. С. Ч).	(11.105)
Уничтожая слагаемые, приводящие к появлению секулярных
членов в ф1, имеем
2V1a + (1 — 61) b = 0, (1 + 6Х) а + 2ТхЬ = 0. (11.106)
Условием существования нетривиального решения системы
(11.106) является обращение в нуль ее определителя, т. е.
4yi — (1 — 6?) = 0, или у1 = -^-(1 — 6?),
откуда
Ti = ±yfl-^	(11.107)
Из первого уравнения (11.106) с учетом формулы (11.107) следует,
что
Следовательно, в первом приближении получаем
и = zt j^cos t — g1 у/2 sin t J +
4- а2е* 0/2) е/ /i-6i j\Osi	у/2 sin^j 4- ... , (11.109)
где ах и а2 — произвольные постоянные, которые определяются
Из начальных условий задачи.
Соотношение (11.109) представляет собой первое приближение
к решению и на переходной кривой и в ее окрестности. При
этом характеристические показатели оказываются равными
±уб ]/1 — 6Х. Поэтому движение будет неограниченным при
6j < 1 и конечным при 6*	1. Значения 6Х = 1, или 6Х = ±1,
соответствуют переходу от устойчивого режима к неустойчивому.
Следовательно, переходные кривые, выходящие из точки е = 0,
6 = 1, описываются в первом приближении уравнениями
6 = 1 ± е 4- ... .	(11.110)
11.5. Метод многих масштабов	.,
Хотя метод Уиттекера и позволяет получить равномерную
аппроксимацию решения уравнения (11.2) на переходных кривых
и в их окрестностях, однако он пригоден только для линейных
задач, при решении которых можно обратиться к теории Флоке
с тем, чтобы с ее помощью заранее определить форму решения.
К нелинейным задачам теория Флоке неприменима, и априорная
11.5. Метод многих масштабов
269
информация о виде решения отсутствует, поэтому использовать
метод Уиттекера в таких задачах не представляется возможным.
Тем не менее существует эффективный метод приближенного ре-
шения и для нелинейных задач. Таким методом является метод
многих масштабов, не требующий к тому же задания какой бы
то ни было априорной информации о характере искомого решения.
Для того чтобы проиллюстрировать применение метода мно-
гих масштабов к уравнению (11.2), будем искать равномерно при-
годное разложение решения в виде
и (tye) =u(TQ, Ту, Т2, ..., Тп, е.) = и0 + елц + е2и2 +   • , (11.111)
где Тп = еМ. В этом параграфе мы получим только разложение
первого порядка, оставляя построение высших приближений чи-
тателю (см. упражнения в конце данной главы). Таким образом,
будем проводить вычисления с точностью до членов порядка е
и поэтому используем только два масштаба времени и соответ-
ственно две независимые переменные То и Ту. Подставляя раз-
ложение (11.111) в уравнение (11.2) с учетом формул (5.45) и (5.46),
получаем
(Do Н- 2eDoDi) (uq -j- eui) -|~ (6 -f" 2e cos 2To) (Но т e«i) • • • = 0,
(11.112)
где cos 2t представлен как функция быстрого времени. Приравни-
вая нулю коэффициенты при е° и е, имеем
О2н06н0 = 0,	(11.113)
Do«i.+ 6«1 = — 2DoD\u0 — 2ы0 cos2T0.	(11.114)
Общее решение уравнения (11.113) может быть представлено
в комплексной форме	_
н0 = A (TJ + А(Ту)е-^т»,	(11.115)
где	со = уг6 или со2 = 6.	(11.116)
При этом уравнение (11.114) принимает вид
П2оЫ1 + <Л1 = —2i(oA'e‘“r° + 2icoA	-
— (e2l7n е'2;г°) (Ае,шГ° -|- Ае~,<оГ°),
или
+ co2«i = — 2ia>A'е‘шТ° — ~Ael <2~ffl) 7'0 — Ae~‘(2+ffl) Ta + (к. c.).
(11.117)
Для нас интерес представляют два случая: 1 — со = О (1) и
1 — со = О (е).
Случай со, далеких от единицы
В этом случае условие уничтожения секулярных членов в ре-
шении иу сводится к уравнению А' — 0, откуда
А = Ао = const.	(11.118)
270	Гл. 11. Уравнение Матье
Следовательно, в первом приближении имеем
и = Лое‘иТ».
Если положить Ао = (1/2) Оо ехр (t0o), где а и 0 — вещественные
постоянные, то решение и примет вид
и = Оо cos (©/ + 0О),	(11.119)
из которого следует, что движение исходной системы является
ограниченным.
Случай © «=> 1	'
В этом случае введем параметр расстройки с помощью соот-
ношения
cd = 1 + есо±	(11.120)
и положим
(2 — ®) То =	= ©То — 2®!?!. (11.121)
Из вида правой части уравнения (11.117) следует, что секулярные
члены уничтожаются при условии
21©Л'+ Ле-21И‘Г> = 0.	(11.122)
Уравнение (11.122) можно решить, представляя комплексную
амплитуду Л либо в показательной, либо в алгебраической форме.
В первом случае имеем
Л = 4ае‘Э-	(11.123)
При этом уравнение (11.122) принимает вид
t© (а' + 1О0') е'Р + ае~‘ (Э+зиЛ) _ о>
или
I© (а' +ta0') + -g- а£-п — i© (o' + io0') +	a cos х —g- ia sin x = 0,
(11.124)
где	x = 20 + 2©1T1.	(11.125)
Отделяя в уравнении (11.124) вещественную и мнимую части,
имеем
©а' = -g- а sin х>	(11.126)
©00' = -g- a cos х• »	(11.127)
Исключение 0 из соотношений (11.125) и (11.127) дает
©ах' = 2©©хо + а cos X-	(11.128)
Из уравнений	(11.126) и (11.128)	в	случае а	#= 0	следует
, da ____ 1 sinX d%	1	d (cos %)
a	2 2<o<i>i f cos у =	2	2(0(0, 4- cos	x
11.5. Метод многих масштабов
271
Интегрируя это уравнение, получаем
а = с [2(0(0! + cosyj'1/2,	(11.129)
где с — произвольная постоянная. Уравнение (11.129) задает
связь между а и %• При этом, для того чтобы получить зависи-
мость а и, следовательно, % от времени 7\, нужно решить урав-
нение (11.126) или уравнение (11.128).
При изменении переменной % от —оо до 4-оо cos х меняется
от —1 до 1. Следовательно, выражение в скобках в (11.129)
будет обращаться в нуль, а амплитуда а — в бесконечность
(т. е. движение становится неограниченным) при условий 2(0(0х <
< 1 или 2(0(0! —1; в остальных случаях выражение в скобках
в нуль не обращается и амплитуда а остается ограниченной. Та-
ким образом, переход от устойчивого режима к неустойчивому
происходит при выполнении соотношений
2(0(01 = 1,	2(0(01 = —1.
При этом, поскольку (0^1, указанные условия дают (ох 1/2
или (ох —1/2. Следовательно, переходные кривые описываются
уравнениями
(о = 1 ± -у е + • • •.
Вспоминая, что 6 = со2, получаем для переходных кривых, вы-
ходящих из точки е = 0, 6 = 1, уравнения вида
6 = (1 ±у еН--------) ,
или	6 = 1 ± е + ... .	(11.130)
При втором способе решения прежде всего введем в уравнение
(11.122) преобразование
Л = Ве-«й1т1,	(11.131)
переводящее его в уравнение с постоянными коэффициентами
вида
2i(oB' + 2(О(охВ + В = 0.	(11.132)
Для решения уравнения (11.132) представим В в алгебраической
форме
B = BT + iBb	(11.133)
в результате чего получим
2ico (В; 4- IB-) 4- 2<o<oi (Br + iB() + ВГ- iB( = 0. (11.134)
Отделяя в (11.134) вещественную и мнимую части, находим
2(0# + (2®(0i — 1) Bt = 0,	(11.135)
2(0# — (2со(01 4~ 1) ВТ = 0.
272
Гл. 11. Уравнение Матье
——~;---------------------т
Уравнения системы (11.135) имеют достоянные коэффициенты,
поэтому решение этой системы можно искать в виде
Вг = ЬгеъТ', В^Ь^.	(11.136)
Подстановка (11.136) в (11.135) дает
2wy1b,. + (2(0(0! — 1) bt = О,
—(2(0(0t + 1) b,. + 2(оу1Ь; = 0.	(11.137)
Нетривиальное решение системы (11.137) существует при условии
обращения в нуль ее определителя:
4(о2у?-j-(4(O2(Oi — 1) = 0 или у2 =(о)”2 — 4(0?),
откуда
=	“4®i-	(11.138)
Поскольку (о«ь 1, соотношение (11.138) можно записать в виде
Vi ± 4 К1 ~ 4t°i-	(11.139)
При этом из (11.137) следует, что
Подставляя выражения для Л и В из формул (11.131) и
(11.133) в .решение (11.115) и далее — в разложение (11.111),
с учетом соотношения (11.120) имеем
и = (Вг 4- iBJe1'	+ (Вт - 1В()е-( <“г«-“хГ.)	=
= (Br + iB;) e{t 4- (Br - iB;) + ... =
= Br (е“ + e-lt) + iBi (elt - tr") =
= 2Brcost-2Bt sin t -]---.	(11.141)
Воспользовавшись теперь выражениями (11.136) и (11.140), пере-
пишем формулу (11.141) в виде
и = О1е- <>'2’ £/ [cos t - ( * r|~)1/2 sin +
+ а2е~ (*/2) е/ /1-4ш( [coSf ц_ J ~У 2 sin!j -j- • • • • (И.142)
Разложение (11.142) полностьюховпадает с разложением (11.109),
полученным по методу Уиттекера, если учесть, что 2(i)t = 6Г.
11.6. Метод усреднения
Для того чтобы применить к уравнению (11.2) метод усреднения,
прежде всего следует ввести вместо переменной и (О новые зави-
симые переменные*а (О и р (О, положив
и (0 = a{t) cos I®/ + ₽ (01,	(11.143)
11.6. Метод усреднения
273
где, как и ранее, 6 = со2. Дифференцирование (11.143) по t дает
,	й = —соа sin (at + Р) + a cos (at + ₽) —
— ар sin (at + P).	(11.144)
Как и ранее, подчиняя решение условию, что
й = —аа sin (at + Р),	(11.145)
получаем из (11.144)
а cos (at + Р)—аР sin (at + р) = 0.	(11.146)
Дифференцирование (11.145) по t дает
й = —а2а cos (at 4- Р) — cod sin (at + P) —
— coap cos (at + P).	(11.147)
Подставляя выражения (11.143) и (11.147) в уравнение (11.2),
имеем
—а2а cos (at + р) — cod sin (at + p) — coap cos (at + P) +
+ (6 + 2e cos 2t) a cos (at + p) = 0.
Упрощая последнее уравнение, с учетом равенства 6 = со2 полу-
чаем
cod sin (cot + Р) + coaP cos (cot + P) =
= 2ea cos 2t cos (cot + p).	(11.148)
Разрешая уравнения (11.146) и (11.148) относительно а и р,
находим
cod = 2ea cos 2t sin (cot + p) cos (cot + p),
coap = 2ea cos 2t cos2 (cot + P).	(11.149)
С помощью известных формул тригонометрии перепишем
(11.149) в виде
cod = -^-ea{sin[2(co+l)t + 2p]+ sin [2(со- 1) t -f-2p]},	(11.150)
coaP — ea |2cos2t -j-cos [2 (co 4- 1) t + 2p] 4- cos [2 (co — 1) t 4- 2P]}.
(11-151).
Приближенное решение имеет различный вид для со, близких
и далеких от единицы. В последнем случае все члены в правых
частях уравнений (11.150) будут быстро меняющимися, так что
в первом приближении имеем
а = 0, Р = 0,
что полностью согласуется с уравнением (11.118), полученным
по методу многих масштабов. При со 1 функция (со — 1) t + Р.
представляет собой медленно меняющуюся функцию t. При этом
274
Гл. 11. Уравнение Матье
из уравнений (11.150) и (11.151) следует, что в первом прибли-
жении
cod =еа sin [2 (со — 1)7 + 2р],
соа₽ =еа cos [2 (со - 1)/ + 2р],	(11.152)
что также согласуется с системой уравнений (11.125)—(11.127),
полученной по методу многих масштабов.
Упражнения
11.1.	Рассмотреть уравнение Матье
й 4* (6 + 2е cos 2t) и = 0.
Используя метод многих масштабов, построить равномерно пригодное разложе-
ние второго порядка при 6 « 0 н б « 4.
11.2.	Рассмотреть уравнение Матье
й + (6 + 2е cos 2Z) и = 0.
Используя метод Уиттекера, построить равномерно пригодное разложение вто-
рого порядка при 6 я 0 н 6 « 4.
11.3.	Рассмотреть уравнение
би _
U + 1 + е cos 2/
а)	Построить разложения второго порядка для уравнений переходных кри-
вых вблизи точек 6=0, 6=1нб=4.
б)	Используя метод Уиттекера, построить разложение второго порядка
для решения и в окрестности этих кривых.
11.4.	Рассмотреть уравнение
а)	Построить разложения второго порядка для уравнений первых трех
переходных кривых (т. е. прн 6=0, 1, 4).
б)	С помощью метода Уиттекера построить приближенное решение в окрест-
ности этих кривых.
11.5.	Рассмотреть уравнение
й + (6 + е cos3 1) и = 0.
Построить разложения второго порядка для первых трех переходных кривых
с помощью метода растянутых параметров н метода Уиттекера.
11.8.	Рассмотреть уравнение
й + ^6 4- е cos 2/-g- е2а sin 2t 4- -i- e2 cos 4/^ u = 0.
Найти два первых члена в уравнениях переходных кривых прн 6 « 1 н 6 я: 4.
11.7.	Рассмотреть уравнение
й +	(1 — в cos О"2 а~2 [2(1 — е cos t) (2 — еа2 cos t) 4- е2а2 sin2 /] и = 0.
Показать, что первые трн переходные кривые описываются уравнениями
а = 2±-4-е, а = 1 4- -^-е2.
Z	о
Упражнения
275
11.8.	Рассмотреть уравнение
й + (со2 + 2е cos 3/) и = 0, е <с 1.
а)	Используя метод вариации параметров, получить уравнения для ампли-
туды и фазы.
б)	Используя метод усреднения, получить уравнения, описывающие мед-
ленные изменения амплитуды и фазы. Рассмотреть все возможные случаи.
11.9. Используя метод многих масштабов и метод усреднения, получить урав-
нения первого приближения для амплитуд и фаз в случае системы, описы-
ваемой уравнением
й + <£>1и = ей2 cos Qt,
где Й существенно отлична от нуля и
а)	<оо далека от й и й/3,
б)	со,, « й,
в)	Зш0 « й.
11.10.	Рассмотреть уравнение
й 4- <ogu 4- 2eu3 cos 2/ = 0, е <с 1 
Используя метод многих масштабов и метод усреднения, получить уравнения,
описывающие в первом приближении амплитуду и фазу колебании данной си-
стемы прн следующих условиях:
а)	а>0 далека от 1 и 1/2,
б)	<о0 « 1.
в)	(Оо « 1/2 .
11.11.	Параметрическое возбуждение системы с двумя степенями свободы опи-
сывается системой уравнений
“1 +	+ е cos	= 0,
йц 4- (о^з + ® cos 4" /22^2) = 0-
Используя метод многих масштабов и метод усреднения, получить уравнения
для амплитуд и фаз колебаний прн условии й я: со2 =p Юр
Г лава'12
ЗАДАЧИ С ПОГРАНИЧНЫМ СЛОЕМ
В задачах, рассмотренных в гл. 4—11, влияние возмущений
было малым, однако они действовали в течение длительного вре-
мени. Поэтому соответствующие амплитуды и фазы оказывались
медленно меняющимися функциями времени и их можно было ис-
следовать путем введения медленных временных масштабов или
почти тождественных преобразований координат. В этой главе
мы будем рассматривать задачи с возмущениями, действующими
в очень узких областях, или зонах, в которых зависимые перемен-
ные испытывают достаточно резкие изменения. Ввиду наличия
малого параметра при старшей производной эти узкие зоны часто
оказываются лежащими вблизи границы области, в которой ре-
шается задача. Поэтому в задачах механики жидкостей и газов
такие зоны называют обычно пограничными слоями, в механике
твердого тела — областями краевого эффекта, в электрических
приложениях — поверхностными, или скин-слоям и. Во многих
физических задачах резкие изменения зависимых переменных
часто происходят внутри интересующих нас областей; в таких
случаях узкие зоны, где эти изменения имеют место, в механике
жидкостей и газов и в механике твердого тела называются обычйо
ударными слоями (скачками уплотнения), в квантовой механике —
точками перехода, в математике — стоксовыми линиями или
поверхностями. Указанные быстрые изменения мы не можем
исследовать с помощью обычных медленных масштабов; это при-
водит к необходимости вводить новые — быстрые, увеличенные
или растянутые — переменные.
Существует большое число методов исследования задач с по-
граничным слоем, как, например, метод сращиваемых асимптоти-
ческих разложений, метод составных разложений, метод многих
масштабов, метод ВК-Б и преобразование Лангера. Два послед-
них метода применяются только для линейных уравнений с боль-
шим параметром — мы обсудим их в гл. 14; В данной главе огра-
ничимся лишь анализом метода сращиваемых асимптотических
разложений, затем кратко рассмотрим метод составных разложе-
ний, и на одном примере исследуем возможности метода многих
масштабов.
Мы начнем с анализа простого примера, имеющего точное ре-
шение; это решение удобно использовать в дальнейшем для срав-
12.1. Простой пример
277
Енения и обоснования предлагаемых методов. Затем мы исследуем
^несколько линейных и нелинейных задач, у которых точные ре-
гшения отсутствуют.
Простой пример
|. Рассмотрим краевую задачу вида
|	е/ + (1 + е2)/ + (1 -е2)г/= 0,	.(12.1)
I	У (0) = а, У (1) = ₽,	(12.2)
!где е — малый безразмерный параметр, который мы считаем по-
1'Ложительным. При этом предполагается, что уравнение и гра-
кничные условия уже приведены к безразмерному виду.
I Для начала будем искать прямое разложение решения в форме
Г	у (х; е) = у0 (х) + еуг (х) Н---.	(12.3)
^Подстановка разложения (12.3) в уравнение (12.1) и граничные
Iусловия (12.2) дает
I е (Уо + £у"\ + •••) + ( 1 + е2) (уо + ег/1 + • • •) +
I	+(1 - е2) (z/o + ez/i Н-) = 0,
I	Уо (0) + еу! (0) + • • •	= а,
|	Уо (1) + &У1 (1) + • 	— Р-
['Приравнивая коэффициенты при одинаковых степенях е, имеем:
|для порядка е°:
В	Уо + уо = 0,	(12.4)
I	Уо (0) = а, у0 (1) = ₽;	(12.5)
|для порядка е1:
[	У1 + yi =~Уо,	(12.6)
I	У1(0) = 0, У1 (1) = 0.	(12.7)
[Общее решение уравнения (12.4) записывается в виде
Г	Уо = сое-х,	(12.8)
[где с0 — произвольная постоянная.
Г Отметим, что, согласно (12.5), на функцию у0 накладываются
[два граничных условия; в то же время общее решение (12.8)
[содержит лишь одну произвольную постоянную. Таким образом,
|мы оказываемся не в состоянии (кроме как по чистой случайности)
1-удовлетворить обоим граничным условиям. Например, восполь-
зовавшись условием у0 (0) = а, из формулы (12.8) имеем
I	а = с0, или у0 = ае~х.	(12.9)
278	Гл. 12. Задачи с пограничным слоем
Используя же граничное условие у0 (1) = 0, с помощью (12.8)
находим
р = сое~\ или с0 =	(12.10)
откуда	1/0 = ре1-*.	(12.11)
Сравнение выражений (12.9) и (12.10) показывает, что для того,
чтобы удовлетворить обоим граничным условиям, постоянная с0
должна принимать одновременно два различных значения, а именно
с0 = а и с0 — ре. Это конечно, невозможно, если исключить слу-
чайное совпадение, когда а = ре.
Сравнивая уравнение (12.4) с исходным уравнением (12.1),
можно заметить, что уравнение (12.1) является уравнением вто-
рого порядка, что позволяет использовать оба граничных усло-
вия, тогда как уравнение (12.4) оказывается уже уравнением
первого порядка — для него можно использовать лишь одно
граничное условие. Таким образом, мы не в состоянии удовлетво-
рить другому граничному условию и обязаны его опустить. Есте-
ственно, нельзя ожидать, что и результирующее разложение ока-
жется пригодным на том конце промежутка,) где опущено соот-
ветствующее граничное условие. При этом возникает вопрос,
какое же из заданных граничных условий должно быть отбро-
шено. Как будет видно из последующего изложения, на этот
вопрос можно ответить, привлекая как физические, так и матема-
тические соображения. Ниже мы покажем, что в случае, когда
коэффициент при у' в уравнении (12.1) положителен, следует
отбрасывать граничное условие на левом конце промежутка,
т. е. при х — 0.
Опуская граничное условие у (0) = а, получаем, что с0 = ре
и функция у0 дается выражением (12.11). Тогда (12.6) переходит
в уравнение
yi+yi = -№~x'	(12.12)
общее решение которого
Уг = сге~х — рхе1-*.	(12.13)
Поскольку уравнение (12.12) вновь оказывается уравнением пер-
вого порядка, решение z/x будет содержать только одну произ-
вольную постоянную, и мы опять не сможем удовлетворить обоим
граничным условиям (12.7). Таким образом, решение задачи
для уг не позволяет преодолеть указанную трудность. Точно так
же нет оснований ожидать каких-либо изменений и на после-
дующих стадиях итерационного процесса,' поскольку на каждом
шаге соответствующее дифференциальное уравнение будет оста-
ваться уравнением первого порядка. Таким образом, мы вновь
отбрасываем граничное условие при х = 0 и, используя гранич-
ное условие !/i(l) = 0, получаем из (12.13), что сх == ре. Окон-
чательно имеем
г/х = ре1-* — рхе1-* = Р (1 — х) е*~*.	(12.14)
12.1. Простой пример
279
Подставляя теперь выражения (12.11) и (12.14) в разложение
(12.3), находим
= J_ep(l-х)е>-*Н------------.	(12.15)
При этом в точке х = 0 имеем у = ре (1 + е), что, вообще го-
воря, отлично от значения а в первом из условий (12.2).
Для того чтобы выявить причину неравномерности получен-
ного разложения и способы ее устранения, обратимся к точному
решению нашей задачи.
Точное решение
Так как уравнение (12.1) представляет собой линейное диф-
ференциальное уравнение с постоянными коэффициентами, его
решение можно искать с помощью подстановки
У = esx,
которая приводит к характеристическому уравнению
или	es2 + (1 + е2) s + 1 — е2 = О,
(es + 1 — е) (s -f- 1 ф в) = О,
корни которого суть
si — — (1 + е) и s2 = — ——И 1 
Таким образом, общее решение (12.1) можно представить в виде
у — а-^ (|+8) х -j- а2е~ Ч х.	(12.16)
Подставляя решение (12.16) в граничные условия (1.2.2), имеем
а = п1-|-«2,	0 = п1е—(1+е) + «2б"[(|/е) “1],
откуда
_ р — ae-td 'e)- 1]	’ ае~ <*+е> — ₽
;	1<‘/е) — 1] ’	е-(1+е) _е-[(1/8)-1] •
^Следовательно, точное решение исходной задачи записывается как
i [р_0И!-[(1/е)-П]е-(1+е)х + (ае-(Ч-в) _р] е-Г(1/8)-1]х
V	е- (1+е) __е-[(1/е)-1]	•
Для того чтобы установить причину неравномерности прямого
^разложения вблизи начала координат, разложим точное решение
^12.17) в ряд для малых е. При этом обратим внимание на то
Обстоятельство, что при е -> 0 функция ехр (—1/е) будет меньше,
ряем любая положительная степень е. Поэтому мы можем перепи-
сать формулу (12.17) в виде
( г/ = ре<,+в)(1-лг) + [а_ре1+8]е-(лг/8) + лг+(э м. Ч.), (12.18)
Йде сокращение (Э. М. Ч.) используется для обозначения экспо-
[ненциально малых членов. При построении прямого разложения
и 12.15) предполагалось, что переменная х имеет некоторое фикси-
280
Гл. 12. Задачи с пограничным слоем
Рнс. 12.1. Сравнение внешнего разложения у0 с точным решением уе прн в =
= 0.01, ₽ = 1.0 и а = 0.0.
рованное значение, отличное от нуля, после чего разлагалось ре-
шение у при малых е. Если х фиксировано и положительно,
тогда функция ехр (—х/е) будет экспоненциально мала, и мы
можем переписать решение (12.18) в виде
г/ = ре(1+8)(1-^_]_(Э. М. Ч.).	(12.19)
Раскладывая выражение (12.19) при малых е, имеем
^_pei-Ares(i-Ar) (Э. м. Ч.) =
= ре'-ф+е(1 - х) + 4~е2(1-х)2-Н •• J ,
откуда	у — ре1-* + ер(1 — х) е1~х • • •	(12.20)
в полном соответствии с прямым разложением (12.15).
Как и в случае прямого разложения, формула (12.20) стано-
вится непригодной вблизи точки х — 0, поскольку при этом
у (0) = ре (1 + е), т. е., вообще говоря, отлично от значения а
в первом из граничных условий (12.2). Следовательно, в про-
цессе разложения решения (12.17) для случая малых е мы, по-
видимому, воспользовались одной или несколькими необоснован-
ными операциями, которые и послужили причиной возникновения
неравномерности полученного разложения? Для того чтобы про-
следить, какие это были операции, проанализируем более под-
робно процесс разложения в ряд точного решения. Прежде всего
мы предположили, что функция ехр (—1/е) экспоненциально
мала, и получили при этом выражение (12.18), которое остается
равномерным при х = 0, поскольку оно дает у (0) = а, т. е. удов-
летворяет первому из граничных условий (12.2). Далее, мы зафик-
сировали некоторое положительное значение х и, исходя из того,
что функция ехр (—х/е) экспоненциально мала, перешли к фор-
муле (12.19). Полагая в этом выражении х = 0, видим, что у (0) —
= р ехр (1 4- е), т. е. получаем значение, вообще говоря, отли-
чающееся от значения а из граничного условия (12.2). Таким об-
разом, именно этот шаг является причиной неравномерности
12.1. Простой пример
281
Рнс. 12.2. Влияние величины параметра е на толщину пограничного слоя
прн fj — 1.0 и а = 0.0.
-Нового разложения. Рассматривая указанный переход более
внимательно, можно заметить, что функция ехр (—х/е) будет
экспоненциально малой при е -> 0 только в том случае, когда зна-
чение х положительно и достаточно далеко от нуля. Поэтому не
; удивительно, что любое разложение, полученное на основе этого
допущения, становится непригодным, когда х «=* 0. Фактически
при х = 0 ехр (—х/е) = 1, что всегда будет много больше, чем
' любая степень еот, где т > 0. Если же х = е, то ехр (—х/е) = е-1,
т. е. эта функция оказывается величиной О (1) и уже никак не
экспоненциально малым членом.
Возникает вопрос, насколько применимо полученное прямое
разложение (12.15), если мы знаем, что оно непригодно вблизи
точки х = 0. Ответ на этот вопрос можно видеть из рис. 12.1,
на котором приведено сравнение решения у0, подсчитанного по
формуле (12.15), с точным решением уе (формула (12.17)) для слу-
чая е = 0,01. Нетрудно заметить, что при указанном малом е
^решение у0 хорошо согласуется с ys везде, за исключением малого
г участка вблизи точки х = 0, где уе быстро меняется, чтобы успеть
"удовлетворить граничному условию. Этот участок вблизи начала
/координат мы будем называть пограничным слоем. Рис. 12.2
: показывает, что по мере уменьшения величины е пограничный слой
/становится все более тонким; следовательно, решение у (х; е)
• непрерывно при е > 0, но претерпевает разрыв в точке е = 0,
(И мы не можем произвольно менять порядок предельных перехо-
/дов при х -+ 0 и е-> О: В самом деле, в соответствии с формулой
(12.17) имеем
lim у (х; е) = а,
х->0
откуда	lim lim у	(х;	е) = а.
<	е->0 лг->0
/С другой стороны, из решения (12.17) следует, что
/	lim у (х;	е) == ре1-*
г	е->0
282
Гл. 12. Задачи с пограничным Слоем
и, следовательно,
lim lim у (х; е) == $е.
Х~>0 Е->0
Таким образом,
lim lim у (х; е) у= lim lim у (х; е),
Е->0 *->0	Х->0 Е-^0
что и доказывает неравномерную сходимость прямого разложе-
ния у° к точному решению задачи у (х; е). Задачи такого рода
обычно называются задачами сингулярных возмущений. Анализ
точного решения (12.17) показывает, что функция у зависит от
х и е различными способами — в виде комбинаций (масштабов)
х/е, ех, а также прямо от х. При этом возникает вопрос, нельзя ли
построить равномерно пригодное разложение, используя в ка-
честве масштаба не переменную х, а некоторую функцию х и е.
Для того чтобы ответить на этот вопрос, исследуем теперь вли-
яние разных масштабов переменных на получающиеся в резуль-
тате разложения.
Влияние разных масштабов на разложение
Идея метода построения равномерно пригодных разложений
для задач сингулярных возмущений заключается в том, что мы
увеличиваем или растягиваем пограничный слой и исследуем
поведение решения в пограничном слое как функцию новой, рас-
тянутой переменной. Для облегчения этого исследования проана-
лизируем влияние смены масштаба непосредственно на результи-
рующем разложении (12.18).
Перейдем, например, от переменной х к растянутой (мелко-
масштабной) переменной g = х/е. Тогда выражение (12.18),
которое не содержит явно экспоненциально малых членов, пере-
пишется следующим образом:
у = 0еО+е) (i-e£) [а __ 0ei+E] + (Э. М. Ч.).
Раскладывая его при малых е и при фиксированном значении £,
получаем
1/ = 0е + (а- 0е)бК + е {0е(1 - В) + [— $е + (а - 0е)£] ₽-£} -.
(12.21)
Возвращаясь в разложении (12.21) вновь к переменной х, имеем
у — 0е(1 — х) + (а — 0е)(1 + х)е~х/& + efie [1 — е~х/е] +  • •. (12.22)
В начале координат у (0) = а, тогда как на правом конце про-
межутка у (1) = е$е. Поэтому разложение (12.22) оказывается
непригодным в окрестности точки х = 1, хотя оно, по-видимому,
остается в силе в начале координат. На рис. 12.3 показано, что
разложение (12.22) хорошо согласуется с точным решением лишь
в малой окрестности точки х = 0, но сильно отклоняется от него
вдали от этой точки.
Рис. 12.3. Сравнение так называемого внутреннего разложения (12.22), обо-
наченного на рис. через у1, с точным решением уе при е= 0.01, 0 = 1.0
и а = 0.
В качестве второго примера рассмотрим еще более мелкий мас-
1таб, а именно переменную £ = х/е2. Тогда разложение (12.18)
южно переписать в виде
у = ре(1+е) (1-е«С) + [а - е-вг+вч _|_ (Э. М Ц.),
ткуда при малых е и фиксированном £ получаем
у = а — е (а — $е) £ + • • ,	(12.23a)
ли	у = а---£-(« — ₽£)+••••	(12.236)
1 начале координат мы вновь имеем условие у (0) = а, в то время
ак на правом конце у (1) = а — (а — (Зе)/е, что отличается от
еличины 0 из условий (12.2). Таким образом, разложение (12.23)
называется"^ неприменимым вблизи точки х = 1. Фактически
:е оно будет пригодным только в очень малой окрестности
ачала координат (рис. 12.4).
:с. 12.4. Сравнение так называемого внутренне-внутреннего разложения (12.23),
означенного на рис. через у11, с точным решением уе при е= 0.01, 0 = 1.0
и а = 0.
284	Гл. 12. Задачи с пограничным слоем'
В качестве третьего примера исследуем случай умеренно рас-
тянутой координаты т) = х/е1/2. Для нее разложение (12.18)
переписывается в виде
У = 0е<1+е)(1-е1/2п) 4- [а — Ре’+Ч	+ (Э. М. Ч.),
откуда при малых е и фиксированном т] имеем
^==₽е(1+еН--------)(1-e’/2r]-|--l-eri2+ •••) =
= Ре[1— e’^ + eQ + ^-n2) Н---------],	(12.24а)
или	z/ = |tep— x + -^-x2-|-e-]---«J.	(12.246)
В начале координат у (0) = fie (1 + е) =И= а, а на правом конце
промежутка у (1) — fie (-5-+	¥= Р- Таким образом, разло-
жение (12.246) оказывается непригодным вблизи обоих концов/
Из рис. 12.5 видно, что это разложение хорошо согласуется е точ-
ным решением лишь на небольшом внутреннем интервале изме-
нения переменной х.
| Приведенное рассуждение показывает, что разложение функ-
ций, зависящей от некоторого аргумента и малого параметра, на-
пример функции у (х; е), очень сильно зависит от используемого ;
при этом*масштаба (т. е. от того,какой аргумент считается фикси- ;
рованным). В рассмотренном примере при фиксированном х 
мы получили разложение (12.20), пригодное везде, за исключе- i
нием малой окрестности начала координат. Зафиксировав пере- /
менную £ = х/е, мы получили разложение (12.22), справедливое
только в малой окрестности точки х — 0. Считая же фиксирован-
ной переменную С = х/еа, мы получили разложение (12.23), имею-
щее место в еще меньшей окрестности начала координат. Наконец,
фиксируя'переменную г)=х/е1/2, мы получили формулы (12.24), ко-
Рис. 12.5. Сравнение так называемого промежуточного разложения (12.24^
обозначенного на рнс. через 1/, с точным решением уе прн е== 0.01, Р=» 1.
и а — 0.
12.1. Простой пример	285
торые оказались непригодными вблизи обоих концов промежутка,
но хорошо описывали решение на малом внутреннем промежутке.
Таким образом, мы можем сделать вывод, что равномерно при-
годное разложение решения задачи сингулярных возмущений
нельзя получить, используя лишь один определенный масштаб
(т. е. определенную комбинацию х и е), как, например, х, х/е,
х/е3 или х/е1/2; тем самым подобные задачи оказываются идеаль-
ным объектом для применения метода многих масштабов. Однако
для нелинейных задач, и в особенности для тех, которые описы-
ваются не^ййейными уравнениями в частных производных, ис-
пользование метода многих масштабов в некоторых случаях’
может оказаться затруднительным, в связи с чем в таких задачах
довольно часто используется другой метод — метод сращиваемых
асимптотических разложений. Именно этот метод мы и будем рас-
сматривать в данной главе.
Основная идея, лежащая в основе метода сращиваемых асим-
птотических разложений, состоит в том, что приближенное ре-
шение данной задачи ищется не в виде единого разложения с за-
данным масштабом переменных, а в виде нескольких отдельных
разложений, в которых используются два или более различных
масштаба, пригодные лишь в части рассматриваемой области. Эти
масштабы выбираются таким образом, чтобы а) полный набор
разложений охватывал всю интересующую нас область и б) обла-
сти применимости соседних разложений перекрывались. При этом
ввиду условия б) нам необходимо срастить (т. е. согласовать
друг (с другом) соседние разложения и тем самым связать их ме-
жду собой. Рассмотрим процесс согласования или сращивания
решений в различных областях более подробно.
Сращивание
Для иллюстрации основной идеи сращивания попытаемся
в качестве примера срастить разложение (12.15), которое будет
пригодным везде, за исключением малой окрестности начала
координат, с разложением (12.21), которое применимо лишь вблизи
точки х — 0. При этом мы сумеем срастить их только в том слу-
чае, если эти два разложения имеют перекрывающиеся области
применимости. Разложение (12.15) было найдено путем разложе-
ния функции у (х; е) при фиксированном х, тогда как фррмула
(12.21) была получена в результате разложения функции у (х; е)
при фиксированном £ = х/е. В связи с этим возникает вопрос,
какое влияние на эти два разложения оказывает переход от од-
ного масштаба переменной к другому.
Прежде чем ответить на этот вопрос, обозначим разложение,
полученное при фиксированном х, надстрочным индексом «о»;
т. е. заменим в выражении (12.15) функцию у на у0. Разложение
же, полученное прн фиксированном значении f = х/е, будем
обозначать надстрочным индексом «», т. е. заменим в формуле

286	Гл. 12. Задами с пограничным слоем
(12.21) у на у‘. Далее, перейдем в разложении (12.15) от пере-
менной х к переменной в результате получим
iZo = pei-^ 4-ep(i _е|)е1-еЕ_]-.	(12.25)
Разлагая (12.25) для малых е и при фиксированном £, имеем
(^ = 0е + Ере(1-|)+...,	(12.26)
где верхний индекс «i» в разложении (12.26) использован для того,
чтобы показать, что функция у0 разлагается при фиксированном
значении £. Наконец, переходя в разложении (12.21) к перемен-
ной х и вспоминая, что следует заменить функцию у на у1, на-
ходим
у‘ = Ре(1 — х) + (а — £е)(1 +х) е~х/е-{-г$е [1 — е~х'е] + • • •. (12.27)
Разлагая (12.27) для малых е при фиксированном х, имеем
(у‘)° = &(1-х) + фе + .--,	(12.28)
где верхний индекс «о» в выражении (12.28) использован для того,
чтобы показать, что функция у1 разлагается при фиксированном
значении х. Заменяя теперь в (12.26) переменную t иа х/е, имеем
(£/“У = ₽е(1-х) + е₽е+....	(12.29)
Сравнение разложений (12.28) и (12.29) позволяет сделать вывод,
что
(^)о = (у°у.	(12.30а)
Другими словами,
внешнее разложение внутреннего разложения —
= внутреннему разложению внешнего разложения. (12.306)
Очевидно, что правило (12.30) применимо только в том случае,
когда два соседних разложения имеют перекрывающиеся области
применимости. Это правило называется обычно принципом сра-
щивания и служит для сшивания двух соседних разложений.
При этом объединение областей применимости разложений
(12.15) и (12.25) позволяет охватить всю интересующую нас
область, т. е. весь промежуток 10,1 ]. Следовательно, полученные
разложения можно использовать для представления решения у
на всем промежутке [0,1].
Выберем теперь в разложениях (12.15) и (12.23а) новые пере-
менные. Как и ранее, разложение, полученное при фиксирован-
ном х, будем обозначать верхним индексом «о». Кроме того, раз-
ложение, полученное при фиксированном £ = х/е8, будем обозна-
чать индексом «п». Такое разложение принято называть обычно
внутренне-внутренним разложением. Заменяя в разложении
(12.15) переменную х иа £, имеем	I
12;1. Прмпгрй пример
откуда, разлагая при малых е и фиксированном находим
(у°У‘ = ре Н- 8ре Н-.	(12.31)
Выражение (12.23а), которое после перехода к переменной х
принимает вид (12.236), в случае разложения для малых е и при
фиксированном х дает
(r)° = -(a-^)v + «+••••	(12.32)
Сравнение (12.31) и (12.32) показывает, что
Г'"	W¥=(^‘)°-	(12.33)
Таким образом, можно сделать вывод, что области применимости
разложений (12.15) и (12.23а) не перекрываются. Это и не удиви-
тельно, поскольку, как видно из рис. 12.4, разложение, (12.23)
будет справедливым в очень малой окрестности начала коорди-
нат — именно по этой причине мы и назвали его внутренне-
внутренним разложением. Отметим также, что существует бес-
конечное множество таких виутреиие-внутреииих разложений,
характеризуемых различными масштабами £ = х/еУ, где 1.
Итак, объединение областей применимости разложений (12.15)
и (12.23а) ие покрывает всю интересующую иас область, а именно
интервал 10,1 ].
В качестве третьего случая рассмотрим переход от одного
масштаба к другому в разложениях (12.15) и (12.24а). Будем обоз-
начать через у' разложение, полученное при фиксированном т] =
= х/е1/2; такое разложение мы будем называть промежуточным.
Переходя в разложении (12.15) от переменной х к переменной т],
имеем
У = Ре1-8’72” + ер (1 - е1/2т|)	_]-,	(12.34)
откуда, разлагая при малых е и фиксированном т], получаем
(у°У = ₽е — е1/2Рет)е ^Р« + -g-n2) Н-•	(12.35)
Замена т| иа х в формуле (12.24а) дает разложение (12.246), откуда,
разлагая при малых е и фиксированном х, находим
(/)° = ре(1-х + 4-х2)+ере+---.	(12.36)
Сравнивая разложения (12.35) и (12.36) и вспоминая, что г) =
= х/е|/2, можно видеть, что эти разложения совпадают, и, следо-
вательно, можно записать
(У°У = (/)’•	(12.37)
Таким образом, области применимости разложений (12.15) и
(12.24а) перекрываются, что позволяет путем взаимной замены
переменных получить из иих одинаковые разложения. В то же
время, хотя разложения (12.15) и (12.24а), как это видно из
288
Гл. 12. Задачи с пограничным слоем
рис. 12.5, имеют перекрывающиеся области пригодности, объеди- :
некие этих областей не позволяет покрыть целиком интересующий !
нас промежуток, поскольку ни одно из них не будет пригодным
в окрестности начала координат.	'
Приведенные рассуждения показывают, что соседние разло- 1
жения, полученные в результате использования разных масшта- ;
бов, не обязательно должны иметь перекрывающие друг друга j
области применимости. Более того, для двух соседних разложений 1
объединение их перекрывающихся областей применимости не 1
всегда будет охватывать всю интересующую нас область. Следо- 
вательно, целью метода сращиваемых асимптотических разложе- :
ний является получение таких разложений, которое покрывали
бы всю рассматриваемую область, причем таким образом, чтобы
соседние разложения имели перекрывающиеся области приме-
нимости. При этом соседние разложения сращиваются или сши- (
ваются с помощью принципа сращивания (12.30).	‘
В рассматриваемом случае следует воспользоваться разложе-
ниями (12.15) и (12.21), поскольку они охватывают всю интересу- 1
ющую нас область и одновременно обладают перекрывающими i
друг друга областями применимости. В то же время мы не можем 1
использовать разложения (12.15) и (12.23а) именно из-за того, что
их области применимости не перекрываются. Наконец, разложе-
ния (12.15) и (12.24а) нельзя использовать потому, что они не
перекрывают всю интересующую нас область. Следует отметить, (
что область применимости разложения (12.24а) перекрывается
с областью применимости разложения (12.21). Чтобы убедиться $
в этом, произведем в разложении (12.21) следующую замену I
переменных: ц = х/е1/2 = е1/2£. В результате имеем	,!
у1 == р<з (- (а — Ре) е^'г'е1-'2
4
ЁЪ2
е—п/е1/2
-ф е J fie 11
откуда при малых е и фиксированном т) находим
(у1)7 = Ре — Рее1/2ц -ф ере -ф- • • •.
Точно так же, заменяя в (12.24а) ц на g, имеем
у1 = ре [1 -еЬи(1 + 4^2)+ •••]’
откуда, разлагая при малых е и фиксированном £,
(12.38) |
получаем ;;
(12.39) j
Сравнивая формулы (12.38) и (12.39) и вспоминая, что ц = е'-Н, ф
можно сделать вывод, что эти разложения тождественны, и, j
следовательно,
(у1)' = (у'У-
(12.40)
jvieiuuu мписи.
Приведенные рассуждения показывают, что области применимости
разложений (12.15) и (12.21) перекрываются, а их объединение
покрывает весь интересующий нас промежуток. Разложение
(12.15) называется обычно внешним разложением и обозначается
через у°. Разложение (12.21) принято называть внутренним раз-
ложением и обозначать через у1. Переменная х при этом назы-
вается внешней переменной, а переменная £ = х/е — внутренней.
Отметим также, что область применимости разложения (12.24а)
перекрывает области применимости разложения (12.15), с одной
стороны, и разложения (12.21) — с другой. Поэтому разложение
(12.24а) обычно называется промежуточным разложением, а пе-
ременная т] = х/е1'2 — промежуточной переменной, поскольку
увеличение масштаба переменной, получаемое в результате вве-
дения переменной tj, лежит между х и х/е. Таким образом, лю-
бая переменная т] — х/еУ, где 0 < v < 1, оказывается промежу-
точной. Иногда вместо непосредственного сращивания сшивание
внешнего и внутреннего разложений производят путем пооче-
редного приравнивания их некоторому промежуточному разло-
жению. Мы продемонстрируем этот подход в § 12.3. В следующем
же параграфе будет показано, как для получения равномерно
пригодного разложения решения (12.1) можно использовать метод
многих масштабов.
12.2.	Метод многих масштабов
Как отмечалось в предыдущем параграфе, решение у (х; е)
зависит не только прямо от переменных хи е, но и от их комби-
наций вида х/е и ех. Это обстоятельство делает данную задачу
идеальным объектом для применения метода многих масштабов.
Поскольку область решения задачи конечна, величина ех оста-
ется малой, и, следовательно, в противоположность задачам для
бесконечных областей, рассматривавшимся в гл. 4—11, наличие
в нашей задаче секулярных членов вида ех, е2х2, е3х®, ... не бу-
дет служить причиной возникновения неравномерностей. Таким
образом, достаточно ввести лишь одну мелкомасштабную пере-
менную | = х/е, которая для данной задачи совпадает с обычной
внутренней переменной, и координату х0=х, которая в нашем
случае является внешней переменной. В этих координатах
П24П
dx е^Т дха ’ дхг е2 3g2 “г е д%дХ() г дхг ’
так что уравнение (12.1) принимает вид
~ S+2 яЙг- + е-й- + (1 +е2)( — # +	+(1 -е2)«/ = 0.
е 3g2 3g дх0 1 дх% 1 ' 1	' \ е 3g 1 дх0 / 1 v ’ а
(12.42)
Будем искать равномерно пригодное разложение первого
порядка в форме
У = Уо (I, х0) + ег/i (|, х0) + ... .	(12.43)
Ю Найфэ А. X.
290	 Гл. 12. Задачи с пограничным слоем
Как и в задачах о нелинейных колебаниях, для того чтобы опре-
делить произвольные функции, появляющиеся при решении
задачи для у0, нам необходимо исследовать член порядка е. Под-
ставляя разложение (12.43) в уравнение (12.42) и приравнивая
коэффициенты при одинаковых степенях е, имеем
> + > = 0,	(12-44)
+	~д^~ ~д^~Уа-	(12-45)
Общее решение уравнения (12.44) дается выражением
У о = А (х0) + В (х0) е-1,	(12.46)
где функции А и В на этом шаге аппроксимации остаются не-
определенными; их определяют на следующем этапе с помощью
соответствующих условий разрешимости. Подстановка получен-
ного выражения для г/0 в (12.45) дает
= 2В’е-1 — А' — В'е^ - А - Ве~1,
или ^.+'^_ = _(Л' + Л) + (В'-В)е-В.	(12.47)
Частное решение уравнения (12.47) имеет вид
у1ц = -(А'+А)1-(В'-В)&~Ъ,	(12.48)
так что при | оо величина е«/х оказывается много больше, чем
у0. Поэтому для получения равномерно пригодного разложения
коэффициенты при £ и при £ ехр (—£) в формуле (12.48) дол-
жны обращаться в нуль одновременно. Таким образом, имеем
А' + А = 0, В' — В = 0.	(12.49)
Решения уравнений (12.49) можно представить в виде
А — ае~х°, В = Ьех",
(12.50)
где а и b — произвольные постоянные. Тогда решение (12.46)
принимает вид
уй — ае~х<> 4- Ье~*+х«,
или, если перейти к исходной переменной,
уа~ае~х 4	+
Подстановка найденного выражения для уь в разложение (12.43)
дает
у = ае-хА-Ье-^х!^ + х Н----.	(12.51)
Удовлетворяя граничным условиям (12.2), имеем
a = a-\-b, р = ae~x + be~ U/e)-i-i _
12.3. Сращиваемые асимптотические разложения
291
Рис. 12.6. Сравнение решения (12.52), полученного с помощью метода многих
масштабов (и обозначенного на рис. через ут), с точным решением уе при в =
= 0.1, Р= 1.0 и а = 0.0.
Пренебрегая в этих соотношениях экспоненциально малым членом
ехр (—1/е) и разрешая их относительно а и Ь, получаем
а = Ре, b = а — Ре.
Таким образом, из разложения (12.51) находим, что в первом
приближении
у = ре1-* 4- (а — Ре) е-<*'е) + * -}-•••.	(12.52)
Рис. 12.6 показывает, что разложение (12.52) хорошо согласуется
с точным решением (12.17) во всех точках рассматриваемого про-
межутка. При этом значение параметра е мы выбрали равным 0,1,
для того чтобы иметь возможность различить на рисунке эти два
решения.
12.3.	Метод сращиваемых асимптотических разложений
Как отмечалось в § 12.1, главная идея, лежащая в основе ме-
тода сращиваемых асимптотических разложений, заключается
в представлении решения несколькими разложениями, каждое
из которых пригодно в некоторой части рассматриваемой области,
причем области применимости соседних разложений перекрыва-
ются, что позволяет провести их сращивание. В этом параграфе
мы проанализируем несколько примеров использования указанного
метода, начав с рассмотрения простой краевой задачи (12.1)—
(12.2).
При е —> 0 (12.1) вырождается в уравнение
у' + у = 0,
которое представляет собой уравнение первого порядка и, следова-
тельно, не позволяет удовлетворить обоим краевым условиям.
Поэтому одно из них должно быть опущено, и на соответствующем
конце промежутка должен появиться пограничный слой. В § 12.1
для того, чтобы показать, что пограничный слой возникает вблизи
10*
292
Гл. 12. Задачи с пограничным слоем
начала координат, мы воспользовались точным решением нашей
задачи. Конечно', на практике, когда мы пользуемся описываемой
методикой, точное решение задачи отсутствует; в противном случае
просто не было бы нужды прибегать к построению приближенного
решения. Таким образом, в данной задаче нам прежде всего необхо-
димо определить расположение пограничных слоев. Хотя во многих
случаях для этого можно воспользоваться различными физиче-
скими соображениями, в данной главе мы опишем, как можно
определить расположение пограничных слоев чисто аналитиче-
скими методами. Кроме того, в двух предыдущих параграфах мы
воспользовались структурой точного решения, для того чтобы
установить, что в качестве внутренней переменной следует выбрать
именно переменную | = х/е. В этом параграфе мы также попыта-
емся обосновать выбор именно этой внутренней переменной.
Чтобы определить местоположение пограничного слоя, предпо-
ложим, что он существует на одном, вполне определенном конце
промежутка, и построим соответствующие одночленные разложе-
ния. При этом если мы сумеем срастить соседние разложения, то
наше предположение будет правильным; в противном же случае
пограничный слой будет располагаться вблизи другого конца.
Предположим, например, что пограничный слой имеет место на
правом конце промежутка и, следовательно, условие у (1) = [3
должно быть опущено. Будем искать внешнее разложение в виде
у° (х; 8) = у0 (х) 4- ... .
Подстановка этого разложения в уравнение (12.1) и условие
у (0) = а дает
Уо + Уо ~ 0, у0 (0) = а.
Таким образом, имеем
Уо~ сое-'х и а = с0,
откуда	у0 == ае~х + • • •.	(12.53)
Для того чтобы проанализировать поведение решения в окрест-
ности выбранного пограничного слоя, нужно растянуть область
вблизи точки х = 1, т. е. растянуть малый участок 1 — х (х < 1)
вблизи конца х = 1. Поэтому выберем
1 =	(12.54)
где величина v должна быть больше нуля, для того чтобы £ оказа-
лось увеличивающим, или растягивающим, преобразованием.
Величина v, вообще говоря, заранее не известна и определяется из
последующих рассуждений. Отметим также, что, согласно опреде-
лению, координата £ является положительной,
12.3. Сращиваемые асимптотические разложения
293
и
Из соотношения (12.54) следует, что
х = 1 — evg
d = _d_dl_ l__d_
dx d% dx gv ’
d2 1 d2
dx2 e2v dg2 ’
Переходя в уравнении (12.1) к переменной 5, имеем
ei-2v __ e-v (1 + е2)	+ (1 _ е2) у _ °.	(!2.55)
При е -► 0 и фиксированном £ главными членами в (12.55) будут
е1-^^_Е-^ + у+...=0.	~	(12.56)
Предельная форма соотношения (12.56) при е -> 0 зависит от
величины V. При этом существуют три возможности: v > 1, v < 1
и v = 1.
В случае v > 1 соотношение (12.56) в пределе дает уравнение
dV =0
dg2
общим 'решением которого будет
г/‘' = а0 + М-	(12-57)
Поскольку предполагается, что пограничный слой существует при
х = 1, это решение должно удовлетворять условию у = р при
х = 1. Но точках = 1 соответствует точке £ =0, и, следовательно,
у[ = р при 5 = 0. Поэтому из решения (12.57) следует, что
р = Оо
у1 = р +	(12.58)
Для того чтобы срастить разложения (12.53) и (12.58), необходимо
построить пределы (у0)1 и (у1)0. Выражая (12.53) через перемен-
ную 5, получаем
и, значит,
y° = ae_|+eV5,
откуда, разлагая при малых е и фиксированном 5, находим
(у0)1 = ае-1.	(12.59)
Аналогичным образом, переходя в (12.58) к переменной х, получаем
^Р + -^\~—>
е
откуда, разлагая при малых е и фиксированном х, имеем
Р, если b0 — Q,
(у‘)°=\ Ml— х)	I. , г.
' '	_»д----L если Ьа ф 0.
v ,	-т-
(12.60)
294	Гл. 12. Задами с пограничныяслоем
Приравнивание в соответствен с принципом сращивания пределов
(12.59) и (12.60) приводит к соотношениям Ьо = 0 и осе-1 = 0,
что, вообще говоря, неверно. Таким образом, случай v > 1 исклю-
чается из нашего рассмотрения.
В случае v < 1 уравнение (12.56) в пределе дает
откуда
У1 = Оо-
Как и ранее, функция- у1 должна удовлетворять граничному
условию у (1) = 0, нли у1 — 0 при £ — 0. Поэтому а0 = 0 и
У' = 0.	(12.61)
Так как функция у1 постоянна, то
. -	(^)° = ₽-	(12.62)
Кроме того, как и в предыдущем 'случае, (у°)‘ = шт1. Поэтому
в соответствии с принципом сращивания имеем
(&°У = (1/‘)0,
откуда 0 — ае~\ что, вообще говоря, неверно. СлеДовательно,
случай v < 1 мы также должны исключить из рассмотрения.
: Наконец, в случае v = 1 предельной формой уравнения (12.56)
будет уравнение
общее решение которого записывается в виде
у1 =» о,, byfi.
Выполняя условие у1 ® 0 при & * 0, имеем
а0 + &о = Pi или Од ® 0 —1 Ьо.
Таким образом,
у‘ — 0 — Ьо + Ь6&
Для того чтобы выполнить процедуру сращивания, выразим у‘
через переменную х. В результате получим
У1 = 0 _ b0 4- Ьо ехр .
откуда, разлагая при малых е и фиксированном х, находим
0, если Ьо = О,
‘	({Н)°= .	/ 1 -х ч	.	(12.63)
о0ехр (—-—), если Ь0^=0.
При этом предельное соотношение (у°)‘ вновь дается выражением
(12.59). Далее, приравнивая в соответствии с принципом сращива-
ния выражения (12.59) и (12-63), получаем^ = Он, следовательно,
12.3. Сращиваемые асимптотические разложения	295
''	, 
Р = осе-1, что, вообще говоря, неверно. Тем самым мы должны
отбросить и этот последний случай. Отсюда следует, что пограйич-.-
нын слой вблизи конца х = 1 не существует.
Для того чтобы проверить, имеется лн пограничный слой вблизи
конца х = 0, введем преобразование растяжения ,	,
= или x = 8vE,	(12.64)
где величина v считается положительной. Тогда
_d__ d dg _ 1______________£_	. J_________^L
dx dg dx gv dg ’ dx* e2v dg2
и уравнение (12.1) принимает вид ~	’
e’-2v^. + e-v(1+e2)|l + (1_e2>// = 0.	'
Главной частью этого уравнения прн 8 -* О является уравнение
e,-2v^+e-V|r+^0- '	(12.65)
Как и ранее, здесь также существуют три возможности: v > 1, ,
V < 1 и V = 1.
В случае v > 1 предельная форма (12.65) при е, -*.0 приводит
к уравнению
-^г = 0,	 -- - (12.66а)
общее решение которого
^ДоШ
Поскольку предполагается, что пограничный слой существует
вблизи начала координат, это решение должно удовлетворять
граничному условию у (0) = а. Но, согласно (12.64), точка х = О
соответствует точке 1 = 0, н, следовательно, мЫ имеем у1 — а
при £ = 0. Тогда а = Оо и .
=	(12,668)
Ясно, что внешнее разложение должно оставаться справедли-
вым при х — 1, В связи с этим будем искать его в форме
у°(х; e) = yfl(x)+....
Подстановка этого разложения в уравнение (12.1) и условнее (1) =
= Р дает
Уо + Уо=0,	уо(1) = ₽.	'
Таким образом,
1/0 = 006-* и Со = Ре,	А
и	у° = Ре’-*-]--.	(12.67)"
296
Гл. 12. Задачи с пограничным слоем
Для того чтобы срастить, разложения (12.666) и (12.67), пере-
пишем первое из них через переменную х. В результате получим
ЬрХ
’ ev ’
фиксированном х, находим
если Ьо == О,
если />0 =$£ 0.
откуда; разлагая при малых е и
а,
(У1)° =
(12.68)

Далее, перепишем разложение (12.67) через переменную х, т. е.
“	Г-ре'-^+...,
откуда, разлагая при малых е и фиксированном 5, имеем
(у°У = ₽₽ + -...	(12.69)
Приравнивание в соответствии с принципом сращивания разложен
ний (12.68) и (12.69) дает Ьо = 0 и а = $е, что, вообще говоря,
наверно. Таким образом, случай у > 1 должен быть исключен из
рассмотрения.
В случае v<l предельная - форма уравнения (12.65) при
е -* 0 имеет вид
^- = 0,	(12.70а)
откуда	у1 ~ а0.
Используя условие у‘ — а при | = 0, получаем, что а0 — а, и,
следовательно,
( у1 = а.	(12.706)
Для того чтобы срастить разложения (12.67) и (12-706), заметим,
что (у0)1 и в этом случае дается выражением (12.69) и, кроме того/
МУ = а,	
поскольку у' есть постоянная величина. Как и ранее, использо-
вание принципа сращивания приводит к требованию а = ре, что,
вообще говоря, неверно. Следовательно, случай v < 1 также дол-
жен быть отброшен.	'
В случаеу = 1 предельной формой уравнения (12.65) при е -* 0
служит уравнение
(12.71)
общее решение которого имеет вид
у1 = а0 4- Ьае~Ъ.
Подстановка условия у1 = а при 5 = 0 дает
а0 + Ьо == а, или а0 = а — %
12.3. Сращиваемые асимптотические .разложения	297
и, следовательно,	.
yi = а _ b0 + b^e-i.	(12.72)
Для того чтобы срастить разложение (12.67) с (12.72), заметим, что
(у°У и в этом случае дается,той же самой формулой (12.69). Пере-
ходя в разложении (12.72) к переменной х, имеем
у1 = а — Ьо + Ьое~х!е,
откуда, разлагая при малых е и фиксированном х, находим
(у‘)° = а-Ьо.	(12.73)
Приравнивая теперь в соответствии с принципом сращивания
выражения (12.69) и (12.73), получаем
а — Ьо = ₽е, или Ьо = а — Ре.
Таким образом, в первом приближении имеем
у0 = ре1-* 4- • • •, у1 = ре -|- (ре — ре) е~х/й, + • • •. (12.74)
в полном соответствии с разложениями, полученными в § 12.1
с помощью преобразования точного решения.
Поскольку мы сумели добиться сращивания, наше предположе-
ние о местонахождении пограничного слоя оказывается правйль1-
ным. Кроме того, выбор в качестве внутренней переменной преоб-
разования £ = х/е позволяет построить внутреннее разложение,
перекрывающее соответствующее внешнее разложение, причем
именно случай v — 1 обеспечивает необходимое изменение мас-
штаба в пограничном слое. Отметим также, что лреобразодания
растяжения, соответствующие случаям v 1, приводят к требова-
нию а = ре, что, вообще говоря, является неверным. При этой
условия v < 1 и v > 1 остаются в значительной мере неопределен-
ными, поскольку каждое из них удовлетворяется бесконечный
набором значений v. С другой стороны, условие v = 1 оказывается
вполне конкретным; оно соответствует так называемому характер'
ному пределу задачи. При этом оказывается, что использование
характерного предела всегда дает нам надлежащее преобразование
координат. Кроме того, предельные формы (12.66а) й (12.70а)
исходного дифференциального уравнения при v S 1 представляют ?
собой частные случаи предельной формы (12.71) при v = 1. Таким
образом, мы будем, говорить об уравнении (12.71) как о наименее -
вырожденной форме предельного уравнения в пограничном слое.
Поэтому в последующих параграфах мы всегда будем определять
требуемые преобразования переменных путем выбора характерных
пределов.' .
Формулы (12.74) представляют собой два отдельных разложе-
ния, а именно разложение у° — пригодное везде, за исключением
малой окрестности порядка е вблизи точки х = 0, и разложе-
ние у( — пригодное только в малом промежутке порядка е вблизи
этой точки. Хотя области пригодности разложений у° и у‘ перекры-
398-	- Гл. 12. Задави- с пограничным слоем'	I
ваются, для получения численного решения, которое могло бы 1
быть использовано на всем промежутке решения задачи, при неко- I
тором малом значении координаты х нам необходимо переклю- '
чаться с одного разложения на другое. Одиако это значение £ ;
точно не известно. Для того чтобы преодолеть указанное затрудне- \
ние, из полученных разложений строят так называемое составное 1
разложение, которое мы будем обозначать далее через ус. Оно оп- ;
ределяется следующим образом:.
+ -({рУ^ + у* ~(у‘У.	(12.75) 
При этом оба указанные здесь варианта разложения эквивалентны, ,
поскольку в силу условия сращйвания имеем (у°)‘ — Таким j
образом, составное разложение (12.75) получается как результат 1
сложения внешнего и внутреннего разложений, из которого вычи- J
/ тается их общая часть (у0)' или (у‘}°. Отметим, что разложение-
(12.75) хорошо согласуется с внутренним и внешним разложениями '
в соответствующей области их применимости. Действительно, Д
(^)°-И0Ь('/‘')0-[(г/,')0]°.	/	;
Но поскольку (/°)° — р, то
0/°)°=^ Ют°=(^)°.
и, следовательно,
(*/с)° = Г	(12.76)
Аналогичным образом имеем
(^)г = (^)г + (^’У + КРУП-
НО поскольку (РУ = Р, то	- "
(уУ-у^ А№УУ=(у°У,
и, следовательно,
(У°У = у‘-	(12.77)
Таким образом, поскольку у представляет собой внешнее разло-
жение во внешней области и внутреннее разложение во внутренней
области, можно утверждать, чГо оно является хорошим приближе-
нием во всей области решения задачи. .
В рассмотренном примере общая часть внешнего и внутреннего
разложений у0 и у‘ дается выражением (12.69) илн (12.73), т. е.
„	(у°У = (Уе)° = ₽«• 	/
Поэтому	,
2	У = Ре1-* + (а - р€) е_*/е 4- • •.	(12.78)
Устремляя в разложении (12.78) параметр е к нулю прн фиксиро-
ванном х, имеем
. (^)° = №"*+••• = </°-
Переходя теперь в (12.78) к переменной £, получаем
у =	+ (а — 0е) е~* Ц- •.,
Рис. 12.7. Сравнение составного разложения ус с точным решением уе при
е = 0.1, р= 1.0 и а =0.0.	•
откуда, разлагая при малых е и фиксированном |, находим
(^У — & + (а — Ре) е~--------------------- у‘.
Следовательно, ус действительно воспроизводит внутреннее и
внешнее разложения в соответствующей области их применимости.
Естественно, что разложение (12.78), как это и подтверждает
рис. 12.7, оказывается прекрасным приближением к точному реше-
нию на всем интервале изменения х. Значение е == 0.1 выбрано
для того, чтобы можно было на рисунке легко различить прибли-
женное асимптотическое и точное-решения.	.
В заключение этого параграфа сравним разложение (12.78)
с разложением, (12.52), полученным с помощью метода многих
масштабов. В то время как метод сращиваемых асимптотических
разложений.дает нам составное разложение, которое распадается
на два отдельных разложения во внешних и внутренних перемен-
ных, метод многих Масштабов приводит к единому разложению.
Отметим также, что в случае уравнений с переменными коэффи-
циентами внутренняя переменная очень часто Оказывается нели-
Рис. 12.8. Сравнение решения ут, полученного по методу многих масштабов,
с составным разложением и точным решением р® при е=0.1, Р = 1.0 и
а = 0.
ЗЙ6	Гл. li. Задачи с мераиичным слоем
।
Устремляв е к нулю при фиксированном х, находим, что соотно-
шения (12.52) и (12.78) приводят к одному и тому же внешнему
разложению. Полагая теперь х — eg и устремляя е к нулю при
фиксированном g, получаем, что формулы (12.52) и (12.78) дают
одно и то же внутреннее разложение. Следовательно, разложения
(12.52) и (12.78) совпадают во внешней и внутренней областях.
Однако разложение (12.52) ввиду присутствия в нем дополнитель-
ного множителя ехр(х) лучше согласуется с точным решением при
больших значениях е (еда. рис. 12.8). Это, конечно, не означает, что
метод многих масштабов является более мощным по сравнению
с методом сращиваемых асимптотических разложений. Так,
например, использование метода многих масштабов для построе-
ния решений нелинейных дифференциальных уравнений, и осо-
бенно уравнений в частных производных типа уравнений Навье—
Стокса, представляет собой весьма сложную задачу.
12.4.	Высшие приближения
Как отмечалось выше, для того чтобы построить асимптотиче-
ское разложение более высокого порядка, описывающее решение
краевой задачи (12.1), (12.2), мы должны найти внешнее и вну-
треннее разложения, срастить их и, наконец, построить соответ-
ствующее составное разложение.
Внешнее разложение
Будем искать внешнее разложение в следующей форме:
У0 = Уо (*) + Ц/iАх) + ... •	(12.79)
При этом, поскольку мы предположили, что пограничный слой
существует вблизи начала координат, это разложение должно
удовлетворять граничному условию у (1) = р. Таким образом,
прдставляя разложение (12.79) в уравнение (12.1) и граничное
условие у (1) == § и приравнивая коэффициенты при одинаковых
степенях е, имеем
y'0^-y0 = Q, f/o(l) = P>	' (12.80)
. ’yi + yi = -yo, f/i(l) = 0.	(12.81)
Как и ранее, решение задачи для у0 можно “представить в виде
г/0 = ре1-*.
Тогда уравнение (12^81) переписывается как
y'i + yi = — Ре1-*.-
Общим решением этого уравнения является функция
У1 — cie~* — рхе1-*.
Но поскольку ух (1) = 0, то сг = Ре, и, следовательно,
г/° = Ре1-*-|-еР (1 -х)е'~х-\--.	(12.82)
i
12.4. Высшие: приближения .	•	* 301
Внутреннее разложение
Для того чтобы найти внутреннее разложение, прежде всего,
заменим в уравнении (12.1) независимую переменную х на перемен-
ную 5 = х/е. Тогда для внутреннего решения, которое будем
обозначать через у', получим уравнение
-^ + (l + e2)< + e(l-e2)V‘=0.	(12.83)
Посколькуt! согласно исходному предположению, пограничный
слой существует вблизи начала координат, внутреннее разложение
должно удовлетворять граничному условию у = а при х — 0.
Но координата х = 0 соответствует координате g = 0, поэтому
у* (0) = а.	(12.84)
Далее, будем искать внутреннее разложение в форме	z
У‘ = Уо(£) + гУ1 (5) +	(12.85)
Подставляя разложение (12.85) в уравнение (12.83) и граничное
условие (12.84)41 приравнивая коэффициенты при одинаковых сте-
пенях е, находим
FS + У^О, Го(О) = а,	(12.86)
УГ+И = -Г0,	У1(0) = 0.	(12.87)
Общее решение задачи для Уо имеет вид
У о = ао + Ь^.
Подстановка этого выражения в условие Уй (0) = а дает
а = а0 + Ьо, или а0 = а — Ьо,
откуда	Уо = а — Ьо + Ьое~Ь.	7
При этом уравнение (12.87) переходит в уравнение
Fi + ri = -(a-feo)-boe-4
общее решение которого записывается как :
У1 = й! +	— (а — bQ) I + Ь01е-^.
Подстановка в условие У-! (0) = 0 дает
01 4- 51 = 0, или «1	—bv
и, следовательно,
Л = _&1 + ь1е-1 - (а - Ьо) g + bege-&.
Таким образом, окончательно имеем
Ус = а — Ьо 4- btf-t -|- е [—bj 4- ^е-Ъ — (а — b0) g 4- 50£е~Ч 4-
(12.88)
где оставшиеся постоянные bQ и Ьг определяются из условия
сращивания.
302	Гл. 12. Задачи 6 пограничным слоем ’	'
Сращивание	\
Для того чтобы сшить внешнее и внутреннее разложения, вос-
пользуемся условием сращивания- (у°У =^= (у{)°. Поскольку оба
этих разложения содержат по два члена, нам нужно найти первые
два члена в каждом из разложений (у0)1 и (у1)0. Переходя в (12.82)
к переменной £ — х/е, имеем
у° = Ре1-е£ ер (1 — eg) + • • •,
откуда, разлагая при малых е и фиксированном %, находим
' (У°У = ре 4-ере (1 - |) + ••• .	(12.89)
Возвращаясь в разложении (12.88) к переменной х, имеем
yi = а — ьо 4- &ое-*/е +
+ e[-^i + ^-^y(a-fr0)^4-&0-^e--^] + ...,
откуда, разлагая при малых е и фиксированном х, находим
. 0/‘)° = a — — (а — &0) г — s&x + ... .	(12.90)
Наконец, приравнивая разложения (12.89) и (12.90) в силу прин-
ципа сращивания, получаем соотношение
Ре + Efte (1 — |) — a — b0 — (a — b0) x — Ebt,
которое с учетом того, что g = х/е, можно переписать в виде
Ре — Рех 4- Е$е — а. — Ьо — (а — Ь0) х — еЬ^ (12.91)
Приравниваний коэффициентов при одинаковых степенях в в ра-
венстве (12.91) приводит к условиям
Ре — Рех = а — Ьо — (а — Ьо) х, . (12.92)
ре = —Ьг.	(12.93)
“ Если пограничный слой существует там, где Мы и'предположили
заранее, и соответствующее растягивающее преобразование выб-
рано правильно, то полученные условия сращивания оказываются
непротиворечивыми, и из них .можно определить постоянные Ьо '
и Ьх. В самом деле, приравнивание коэффициентов при одинаковых,
степенях х в соотношении (12.92) дает	’	-	<
Ре = a — &о. Ре = a — &0,
откуда — a — ре. .Далее, из условия (12.93) следует, что = j
= —ре. Таким образом, разложение (12.88) приобретает вид
у1 = Ре 4- (а — ре) е~Ъ 4- е (Ре — рее~£ — peg 4~ (а — Ре) 4" • • • • 1
.	. .	(12.94)<
Как уже отмечалось в§ 12.1, сращивание можно производить,]
используя промежуточные разложения. Введем, например, про-1
межуточную переменную т] — х/е1/2, которая дает изменение?
42.4. Вжяиие приближения	303
масштаба, среднее между х и £=.х/е. Переходя от переменной
х к переменной tj, перепишем разложение (12.82) в виде
У» = ре1-в1/2я + е₽ (1 - е’^т]) ei-№i 4. ...;	(12.95а)
откуда, разлагая при малых 8 н фиксированном ц, имеем
(у0)1 = ₽е -	4. е₽е 4-1|------------.	(12.956)
Полагая теперь в разложении (12.88) £ = rj/e1''2, находим
yi^a-Jb^boe-^12 4-
4- е| — th 4- ^е-п/*1'2 — £-^*1 4. ^sl.e-n/e1/2J 4- ..., (12.96а)
откуда, разлагая при малых 8 и фиксированном’ tj, получаем
(у1)' = а - &0 - «J/2 (а - &0) т) - 8&J+ • • • •	(12.966)
Приравнивая разложения (12.956) и (12.966) в соответствии с прин-
ципом промежуточного сращивания, находим, что они согласуются
вплоть до порядка в1/2. Следовательно, на этом шаге аппроксима-
ции мы можем найти только постоянную Ь9. Для того чтобы сра-
стить разложения до О (е), необходимо продолжить внутреннее-
разложение до членов второгопорядка. С другой стороны, проме-
жуточное сращивание может проводиться путем вычитания разло-
жения (12.96а| из (12.95а), после чего следует устремить е к нулю
при фиксированном значении переменной tj. Этот процесс позво-
ляет определить обе постоянные Ьо и &х. Сопоставляя процесс'
промежуточного сращивания с прямым сращиванием, можно
сделать вывод, что промежуточное сращивание представляет собой
излишнее усложнение предлагаемого метода, и поэтому в дальней-
шем мы не будем им пользоваться.
Весьма удобный вариант прямого сращивания -представляет
собой так взываемый принцип сращивания Ван-Дайка: .	. .
m-членное внутреннее разложение
и-членного внешнего разложения равно
n-членному внешнему разложению
/я-членного внутреннего разложения, (12.97)
где тип — два произвольных целых числа, не обязательно рав-
ных друг другу. Чтобы определить m-членное внутреннее разло-
жение (я-членного внешнего разложения), перепишем первые п
членов внешнего разложения, выразив их через внутреннюю
переменную, и затем разложим их для малых е при фиксированном
значении внутренней переменной, учитывая в полученном разло-
жении лишь т членов. Аналогичным образом можно получить и
правую часть соотношения (12.97).	.	,
304	Гл. 12. Задали с пограничным слоем	- И
Для того чтобы продемонстрировать использование принципа
сращивания Ван-Дайка, применим его к сращиванию двучленного
внешнего разложения (12.82) с двучленным"внутренним разложе-
нием (12.88). При этом будем действовать следующим образом.
Двучленное внешнее разложение:	-j-еР(1—х)е1-*.
Перепишем через внутреннюю переменную: ="0е>-е5 4-
+ ер (1 - в?) б1-8®.
Разложим при малых в: = ре 1 — eg 4- -g-s2g2 -j- • •	-f- ;
+ epe(l - eg) (1-eg+•..).,
Найдем двучленное внутреннее разложение: = Ре 4- е£е (1 —g).
,	'	(12.98)
Двучленное внутреннее разложение: у ~ а — Ьо 4-	4-
4- е [— &1 4- ftje-5 — (а — &0) g 4- Ь01е~Ь].
Перепишем через внешнюю переменную: = а — Ьо 4-	4-
4-е [-&1 +	- (а-&0)+ ^е~^1.
L	©	с	J
Разложим при малых е: = а—Ьй—(а—Ь0)х—еЬ14-(Э. М. *1.).
Найдем двучленное внешнее разложение: =а — Ьо —
— (а — &0) х — s&i. (12.99)
/Приравняв теперь разложения (12.98) и (12.99) в соответствии
с условием сращивания (12.97) и выразив переменную, g через
переменную х, мы в точности получим соотношение (12.91). Следует
отметить, что существуют случаи, в которых принцип сращивания
Ван-Дайка может оказаться неприменимым. Тём нё менее он очень
удобен и потому широко применяется на практике.
В приведенном примере мы могли найти любое число членов
во внутреннем или внешнем разложениях, причем соответствующие
произвольные постоянные определялись в процессе сращивания.
Однако это оказывается возможным далеко не всегда. Например,
при построении асимптотики решения задачи обтекания тела про-
извольной формы потоком вязкой жидкости необходимо прежде
всего определить одночленное внешнее разложение, которое
используется для нахождения одночленного внутреннего разло-
жения; лишь затем переходят к нахождению второго члена внеш-
него разложения, который в свою очередь используют для нахож-
дения второго члена внутреннего разложения и т, д.
Составное разложение
После того как внешнее и внутреннее разложения найдены,
проведено их сращивание и тем самым определены все неизвестные
постоянные, можно построить составное разложение, которое будет
12.5. Уравнения с переменными, коэффициентами 	305
равномерно пригодным на всем промежутке решения -задачи.
С этой целью подставим выражения для у°, у1 и (y°)z из формул
(12.82), (12.94) и (12.89) соответственно в выражение (12.75) и
получим такое единое равномерно пригодное разложение:
ус = fie1-* -{- (а — Ре) е~$ -f- е [р (1 — х) е'~х — Ре1-» -|-
+ (а - ре)1е-5] + • • •.	(12.100)
12.5.	Уравнения с переменными коэффициентами
В этом параграфе мы воспользуемся методом сращиваемых
асимптотических разложений для построения асимптотического
решения первого порядка краевой задачи
«У* + Pi (х) у'+ Ро (х) у = 0,	(12.101)
у(0) = а, $r(l)W	(12.102)
в случае задания функций pt и р0 некоторого специального вида.
Эта задача исследуется также в гл. 14 с помощью метода ВКБ
и преобразования Лангера. Здесь мы рассмотрим два примера',
в которых функция рг (х)	0 на промежутке [0, 11, а также два
примера, в которых рх (х) обращается в нуль на этом промежутке.
Пример 1. Рассмотрим уравнение
.81/" - (2х + 1) у' + 2у = 0.	(12.103)
При 8 -* 0 это уравнение переходит в дифференциальное уравне-
ние первого порядка, и, следовательно, одно из граничных условий
(12.102) должно быть опущено. При'этом оказывается, что если
Pi (х) > 0 на промежутке [0, 1 ], то пограничный слой существует
на левом конце этого промежутка, а если pt (х) < 0 на [0,1 ], то
пограничный слой будет иметь место на правом конце. Таким обра-
зом, для рассматриваемого уравнения пограничный слой сущест-
вует в окрестности точки х = 1, и внешнее разложение должно
удовлетворять граничному условию у (0) = а. Во всяком случае,
наличие пограничного слоя на правом конце промежутка подтвер-
дится, если мы сумеем срастить полученные разложения, так
чтобы вся схема построения решения оказалась математически
непротиворечивой х).
Будем искать внешнее разложение в виде
У° = Уо (*) + e,yi (*) + •••.	(12.104)
х) В литературе по прикладному • асимптотическому анализу такие про- z
Цедуры, хотя и не имеющие строгого математического обоснорания, но обла-
дающие внутренней стройностью и логической завершенностью, .называют обычно
самосогласованными. — Прим, перев.
* '1*^	' 306	Гл. 12. Задачи с пограничным слоем
; -л;	Подставляя разложение. (12J04) в уравнение (12.103) и условие
-• <	У (0) = « и приравнивая коэффициенты при е° в обеих частях
7.,	- полученных равенств,-, получаем
:	-(2х+1)^+2у0 = О,	у0(О) = а.	(12.105)
Разделяя переменные в (12.105), находим
’ ts. ~	dy0 2 dx
; Ь	'	Уо “2х+1’
’Л- откуда	In у0 — In (2х 4- 1) 4- In с0,
4". где со — произвольная постоянная. Тогда
,	Уо = Со (2х 4- 1),
и поскольку у0 (0) = а, то, следовательно, с0 = а. Таким образом,
имеем
‘ ~	Уо = « (2х 4- 1)
'	и	у° = а (2х + 1) 4- ••• .	(12.106)
Для того чтобы Настроить разложение, пригодное в погранич-
п- ном слое, необходимо растянуть окрестность точки х = 1. Поэтому
4 > положим
!	£ = или. х=1-е^,	(12.107)
Л	6	'	- 
где величина v считается положительной и определяется в nPa-
's у цессе дальнейшего анализа. Переходя в уравнении (12.103) к пере-
менной с помощью преобразования (12.107) и обозначая внутрен-
j'4* нее решение через у1, получаем
\	8i-2v^-+-e-v(3_2evg^ + 2^=0.	(12.108)
•' X л	ds	.. ds
\ •’ "
<	" При в -► 0 предельная форма уравнения (12.108) зависит от выбора
4. У- Как отмечалбсь ранее, требуемое значение v должно выбираться-
к в соответствий с видом характерного предела. Поэтому положим
v = 1 и перепи тему равнение (12.108) как
! 5/ '		-^4-(3-28?)-^+ 28^ = 0.	(12.109)!
Поскольку мы предположили, что пограничный слой существует
вблизи Точки х = 1, внутреннее решение должно удовлетворять
граничному условию у (1) = 0. Но точка х = 1 соответствует
Л, точке £ = 0, откуда
. • ;	У1 (0) = 0-	(12.110)
;	Будем искать внутреннее разложение в виде
yl-Y0 (1)4- 8^ (;) + •••.	(12.111Й
12.5. Уравнения с переменными коэффициентами	30?
Рис. 12.9. ^равнение составного разложения у? с точным решением у*, полу-
ченным в результате численного интегрирования уравнения (12.103) с граиич-.
нымн условиями (12.102) при^е = 0.2, а = 1.0 и 0 = 0.
Подставляя разложение (12Л11) в уравнение (12.109) И условие
(12.110) и приравнивая коэффициенты при 8® в обеих частях полу-
ченных равенств, находим	,
Уо + ЗУ^ = 0, Уо(О) = 0.	(12.112)
Отсюда	Уо = Оо + &о^35>	₽—Oo-F&or.
и, следовательно,
У' = ₽-&о + *ое-3М---.	(12.113)
где постоянная Ьо должна определяться в процессе сращивания
внутреннего и внешнего разложений.
Воспользовавшись условием сращивания Ван-Дайка, будем
действовать следующим образом.	v
Одночленное внешнее разложение: у ~ « ( 2х 4 Г).
Перепишем через внутреннюю переменную: = а (3•— 2е£).
Разложим при малых в: = За — 2еа£.	(12.144) l
Найдем одночленное внутреннее разложение: = За.
Одночленное внутреннее разложение: у ~ 0 — b0 4- &ое~3£.
Перепишем через внешнюю переменную: =0—
Разложим при малых в: = 0—- Ьо 4 (Э. М. Ч.). z
Найдем одночленное внешнее разложение: =0 — Ьо. (12.115)
Приравнивая разложения (12.114) и (12.115), имеем	- 
За — 0 — Ьо, или Ьо = 0 — За.
образом,
у1 = За 4- (0 -= За) e~3%	• • •
ус = а (2х 1) 4- За -р (0 — За) е~3$ — За 4;
. а (2х + 1) + (0 - За) в-3 <•-*>/« 4- • • •,	(12.117)
12.9 показывает, что составное разложение ус оказывается
Таким
(.12.1 Гб)
и
или
Рис.
очень близким к решению, полученному с помощью численного
интегрирования задачи (12.103), (12Л02). Поскольку мы сумели
обеспечить сращивание внутреннего н внешнего разложений, /так
308	Гл. 12. Задачи с пограничным слоем
что вся процедура оказалась самосогласованной, следовательно, 1
наше предположений о существовании пограничного слоя на пра- |
вом конце промежутка является вполне оправданным.	1
Пример 2. В качестве второго примера рассмотрим уравне- |
ние (12.101), у которого функция рг (х) сохраняет знак на всем 1
промежутке [0, 1 ], но может быть как положительной, так и |
отрицательной.	1
Пусть теперь для определенности р! (х) > 0 на 10, 1 ]. В этом I
случае мы предполагаем, что пограничный слой существует на 1
левом конце промежутка, поскольку только такое предположение |
обеспечивает возможность сращивания соответствующих разложе- |
ний и получение математически непротиворечивых результатов. |
Тогда внешнее разложение должно удовлетворять граничному 1
условию у (1) = Р, а внутреннее — граничному условию у (0) = 1
'= а. Будем искать ^внешнее разложение в виде	1
/	У° = Уо(х) + г.у1(х) +	'	(12.118) |
Подставляя разложение (12.118) в уравнение (12.101) и условие |
у (1) = р и приравнивая коэффициенты при е° в обеих частях 1
полученных равенств, получаем	1
Р\Уо + роУо = 0,	у0(1) = р.	(12.119) j
Уравнение (12.119) представляет собой линейное дифференциаль- |
ное уравнение первого порядка, и, следовательно, его решение 1
может быть найдено	стандартными приемами.	Действительно, 1
разделяя переменные,	перепишем это уравнение в	виде	j
^ = —P2-dx,	1
Уо	Pi	I
откуда после интегрирования находим	1
1П Уо = ~	+ Со> 'I
или
Уо— Со £хр
Г Pi (т)
J Ро(т)
dx
При этом нижний предел интегрирования выбирается равным 1,
с тем чтобы Нам было удобнее удовлетворить граничному условию
на правом конце. Условие уй (1) — £ дает с0 = £, откуда
Уо = р ехр — Jy-dT
* Pl
и, окончательно,
= рехр
У° = рехр j-^-dx 4-----.
(12.120)
U.S. Уравнения с переменными коэффициентами	ЗОЛ
Для того чтобы найти внутреннее разложение, пригодное .
вблизи начала координат, введем преобразование растяжения
| = или x = sv£ (v>0).	(12.121)
Тогда уравнение (12.101) для внутреннего решения у1 перепишется
в виде
4	(^)	+ Ро М У{ = °-	(12-J22)
При 8 —* 0 р! (8v£) -► Pi (0) и р'о (8vg) -*.р0 (0), поскольку функ-
ция ро предполагается регулярной' в начале координат. Тогда
уравнение (12.122) переходит в уравнение
e’-2v-^- + e-vp1(O)-^-4-po(O)/4-"-=O, (12.123)
предельная форма которого при 8 -► 0 определяется величиной у.
Выбирая v = 1, что соответствует характерному пределу, находим^
что предельной формой (12.123) будет уравнение
- -^ + Р1Х0)-^- = 0,	(12.124)
общее решение которого записывается в виде
yi = ao^-boe-P‘ <«Н.	(12.125)
Из соотношения (12.121) следует, что координата х = 0 соответ-
ствует точке I — 0, и, следовательно, граничное условие у (0) » а.
переходит в условий у‘ (0) =* а. Тогда из формулы (12.125) полу-
чаем, что	‘
" а = а0 &0> илн а0 = а — Ьо,
и поэтому
yi^a-bo^bve-P^t.	(12.126)
Срастим теперь одночленное внешнее разложение (12.120) с одно-
членным внутренним разложением (12.126). При этом формально
будем действовать следующим образом.
Одночленное внешнее разложение: у ~ р ехр
J Pi
Перепишем через внутреннюю переменную: = Рехр
i^.dt
j pi
Разложим при малых в:
= Рехр j-g-dr Н------
1-0
310
Гл: 1$. Задачи с пограничным слоем
Найдем одночленное внутреннее разложение:
= £ехр f^dr. (12.127)
J pl
LO
Одночленное внутреннее разложение: у ~ а — Ьо &об~р‘(0>L
Перепишем через внешнюю переменную: == а—й0+ Ьое-р‘ <°>
Разложим при малых е: = a — b0 -j- (Э.М.Ч.).	}
Найдем одночленное внешнее разложение: — a —b0.	1
(12-128)
Отметим, что множитель^ ехр [—р1(0)х/е] при s-► О будет;
экспоненциально мал, поскольку р! (0) > 0. Если бы значение
р! (0) оказалось отрицательным, то член &0 ехр [— рг (0) х/в|
экспоненциально возрастал бы при е -> 0 и внутреннее разложений
невозможно было бы срастить с внешним. Именно поэтому отсут^
ствие экспоненциально растущих членов во внешнем и внутреннем!
разложениях является весьма существенным для успешного сра|
щивания. Итак, приведенные рассуждения показывают, что погра-j
ничный слой действительно'находится на правом конце промер
жутка.	' j
Приравнивая теперь разложения (12.127) и (12.128), имеем
а — Ь0=.Рехр [—Jr
J pl
Lo
Таким образом,
или b0 = a — 0 ехр (^- dr . I
J Pl	J
L0
^ = 0exp
f —dx + a —pexp f— dr
J Pl	Г Г }J>!
.(12.1
Ьо.
Наконец, складывая внешнее разложение (12.120) с внутреЙ
ним разложением (12.129) и вычитая из полученной суммы щ
общую часть (12.127), получаем следующее составное разложений
Lo
^ = ^exp J+ a—0exp j^-dx
6-74(0)5-1- ... . (12.131
L-X
i-о л	- q
Пример 3. В качестве третьего примера исследуем случаи
когда коэффициент рг (х) обращается в нуль в точке х = Q
А именно, рассмотрим уравнений	1
&у" + ху' — ху — 0	(12.131
с граничными условиями вида (12.102). Поскольку коэффициент
при у' положителен, мы предполагаем, что пограничный end
существует на левом конце' промежутка, даже если рг (х) =%
обращается на этом конце в нуль. В противном случае мы н
смогли бы срастить найденные разложения и полученные резулв
таты оказались бы математически несовместными.	3
12.5. Уравнения с переменными коэффициентами	311
Если искать внешнее разложение в виде
У0 (х) = у0(х) + ei/i (4 +	'
то из уравнения (12.131) можно получить следующее уравнение
для у0:
ху’ц — ху0 = О,
общее решение которого
Уо< =
Поскольку ^‘предположили, что пограничный слой располагается
вблизи начала координат, внешнее разложение должно удовлет-
ворять условию у (1) = р, или у° (I) = р. Таким образом, ймеем.
Уо (1) = Р И .	'
Р = Сдв, ИЛИ Сд ~ ре-1.
Тогда	,
у0 = Р^'1
и, окончательно,
уо = pe*-i + ... .	(12.132)
Для того чтобы исследовать пограничный слой вблизи начала
координат, введём растягивающее преобразование >
-5 = 4, или х =	(v>0),	(12,133).
в результате чего -уравнение (12.131) перепишется в виде"
£172v-^+^7ev^=°-	: (12-134>
При е -* О предельная форма уравнения (12.134) зависит от вели-
чины v. Как и ранее, ограничимся исследованием лишь характер-
ного предела, который в данном случае имеет вид
'	(12.135)
что соответствует значению v = Уравнение (12.135) представ-
ляет собой линейное-дифференциальное уравнение первого по-
-	,	du1
рядка относительно функция -^-, и, следовательно, его решение
может быть найдено стандартными приемами. Так, полагая
в (12.135)
v =	-
получаем уравнение
общее решение которого
v~age~^/2.
312
Гл. 12. Задачи с пограничным слоем
Поэтому
JeL — а„е-£!/2
. .	dl —а°е
откуда после интегрирования получаем	;
£
Ус = а0 J е-т’/2 dr + &0>	<
'° _ \
где нижний предел в интеграле выбран равным нулю, с тем чтобы;
нам было проще удовлетворить граничному условию на левом,
конце. Поскольку в соответствии с видом преобразования (12.133)J
точка х = 0 переходит в точку £ — 0, использование условия;
у (0) = а, или у1 (0) = а, дает а = Ьв* откуда
у* = Оо J е^х‘/2 dr 4- а,	(12.136)
о
где постоянная а0 должна определяться в процессе сращивания
внутреннего и внешнего разложений.
Для того чтобы срастить одночленное внешнее разложена
(12.132) с одночленным внутренним разложением (12.136), будеь
действовать следующим образом.
Одночленное внешнее разложение: у~0ех~|.
Перепишем через внутреннюю переменную: = 0е®1/2^ — 1.
Разложим при малых в: =06’’ (1 4-е1/2£4- • ••)•
Найдем одночленное внутреннее разложение: =0е~1.
(12.137
Одночленное внутреннее разложение: у а0 j e~x’/2dr + а.
о
Перепишем через внешнюю переменную:
. x/Sl/2
— а0 j е~х‘/2 dr +
о
ОО
Разложим при малых е: — а0 j е~х*12 dr 4- о. 4- •• •
о
Найдем одночленное внешнее разложение:	4-а>
.	(12.138:
где интеграл можно вычислить по формуле (3.25), полагая t =
= г т. е.
j е-х!/2 dr = /2 j е-‘г dt = J/ 2	•
о	о	г
12.5. Уравнения с переменными коэффициентами	313
Рис. 12.10. Сравнение составного разложения tf с точным решением уе, полу-
ченным в результате численного интегрирования уравнения (12.131) с гра-
ничными Условиями (12.102) при е— 0.2, а= 4.0 и ₽ = 1-0.
Далее,, приравнивая разложения (12.137) и (12.138), находим
а, или	(ре-1 - а).
Итак, внешнее и внутреннее разложения действительно допу-
скают сращивание, причем весь процесс решения оказывается
самосогласованным, оправдывая тем самым наше предположение
о том, что пограничный слой в данной задаче существует в окрест-
ности начала координат. Подставляя теперь найденное выражение
для Оо в (12.136), имеем
ц1 = а + фВг (₽е-> - а) j е~*Ч2 dr + • • •.	(12.139)
'п	о
Наконец, складывая введшее разложение (12.132) с внутренним
разложением (12.139) и вычитая их общую часть (12.137), находим
единое составное разложение, которое будет равномерно пригод-
ным да всем промежутке решения задачи. Оно имеет вид . -
1Л2"	г
, tf =	-|- а 4~ —?= (Р^-1 ~ а) J x>/2 dr — ре-1,
/	_	о .
или tf = ре*-1 - (ре-1 - а) (1 —	(е~^г/2 dt) ------. (12.140)
V /я,	/	,
Рис. 12.10 показывает, что составное разложение tf очень мало
отличается от точного решения уе даже при е = 0,2. В случае же
е = 0,1 разложение ус практически совпадает с точным решением.
Пример 4. В качестве последнего примера исследуем случай,
когда коэффициент р! (х) имеет простой нуль в некоторой внутрен-
ней точке промежутка [0, 1 ], что приводит к появлению так назы-,
III лиji; iujji 11Д111И ' ^ 111111	..1 ^wyj-
&c ' ..................... ’ 1	" v ' 1
• ’ ?	. ,314	Гл, 12. Задачи с пограничным слоем	1
•S'*, " '	. , ..................- . И.,..—W I' И'  1Ц1	! I»  I "' “IM     '.b.-lT-l _W Jl'll.l    Я
i.' ваемогр «внутреннего» пограничного слоя. Итак, рассмотрим]
> дифференциальное уравнение	.’	' 1
<	ер"+(х —(х —4-)«/ = ° - (12.141) j
’	. с граничными условиями (12.102). В данном случае функциям
,	1	1'1
Pi (х) = х--------------------g- меняет знак при переходе через точку -х = —, и |
; X' , потому наши рассуждения относительно расположения погранич- ]
V " ного слоя требуют более подробного рассмотрения. При этом ока-1
! . f_- зывается, что на обоих концах промежутка пограничный слой]
отсутствует, и вместо этого, как будет показано ниже, возникает!
i » пограничный слой в окрестности точки х = -L.	I
-Если искать внешнее разложение в виде	J
У"	у° = Уй (4+	(*) + • • •, - ,	~	|
( /	то из уравнения (12.141) получаем, что	|
Г*	(х 2~)	~ ~2~) У^~ 0*	i
X	Общим решением этого уравнения служит функция	3
Уо = ро^х< 	’
относительно которой естественно предположить, что она будет!
? пригодна всюду, за исключением'малой окрестности, примыкающей
• к точке х = -g-. В интервале х > -g- разложение у° должно!
удовлетворять граничному условию у0 (1) — р. Поэтому сое = р ц]
<’ ‘	^ = рех-1 + --->	(12.142W
где цндекс «п» . означает правую часть промёжутка. В интервале]
. х < -L- функция у° должна удовлетворять граничному условию!
Г	1
у0 (0) = а. Поэтому с0 — а и	1
=	_ (12.14з|
где индекс «л» указывает на левую половину промежутка. |
J , Исследуем теперь окрестность точки х = вводя следующее!
' преобразование растяжения:
1
х о	1
i=_—-—, илй x = -g- + e^ (v>0).
Уравнение-(12.141) при этом переписывается как
e'-2v-^- + ^_g^ = 0.
(12.144|
(12.145|
и ранее, выберем характерный предел в виде
+	=	(12.146)
значению v = -у. Общее решение уравнения
в виде (ср . с формулой (12.136))
£
. ^. = &04-a0 je-^dr,	(12.147)
..>	4л<;".7	;'да";   j,,J 7"
'12.5. Уравнения с переменными коэффициентами	315
При в -► О предельная форма уравнения (12.145) зависит от выбора
величины V. Как
что соответствует
(12.146) строится
* '
о
где нижний предел' в интеграле выбран равным нулю в соответ-
ствии с предположением о существовании пограничного слоя вбли-
зи точки х = Постоянные а0 и Ьо определяются в процессе
сращивания внутреннего и внешнего разложений.
Для того чтобы'срастить одночленное внешнее разложение
(12.142) с одночленным внутренним разложением (12.147), будем
действовать следующим образом.
Одночленное внешнее разложение: у ~ ре*-1.
Перепишем через внутреннюю переменную: = рее1/26_<1/2).
Разложим при малых в: = Ре_,/2(1-j-e,/2£4т ;•
Найдем одночленное внутреннее разложение: ^ре'1^2.
* (12.148)
Одночленное внутреннее разложение: р ~ J е~',/2Л.
Перепишем через внешнюю переменную:
= 6о+А) J e~t,/adr.
00
Разложим при малых в: = &04-Оо J е~т’/2^т + •••;
Найдем одночленное внешнее разложение: Ьо4~ . j
(12.149)
Приравнивая разложения (12.148) и (12.149), получаем соот-
ношение
fto-b-^l^pe-’/2,	(12.150)
1 Вычисление соответствующего интеграла, было проведено в предыдущем
примере.
316	Гл. 12. Задачи с пограничным слоем
связывающее постоянные а0 и Ьо. Чтобы найти второе соотношени
между этими постоянными, срастим внутреннее разложена
(12.147) с внешним разложением (12.143). Следуя обычной пре
цедуре асимптотического сращивания, находим
(у°пУ=^2
—оо	оо
и	(y‘)0==^o + ^0 f e~x,i2dr = b0 — nof e-^dx,
о	'	о
откуда	&o = а<>^П = ae^2.	(12.151
Решая уравнения (12.150) и (12.151) относительно а0 и &0, получае
а0 = -2=-(₽е-«/2_ае«/2),.	be^y&~l/2 + aeW),
и, следовательно,
1	1' F ’
у< ,= — (pe-V2 agi/2)	, (ре->/2 __ ае^2) | е-т’/2	_j_ ....
2	у 2л	о
(12.155
В данном случае мы не можем перейти к единому составном
разложению, которое оказалось бы равномерно пригодным н
всем промежутке решения задачи. Вместо этого образуем дв
составных разложения, одно из которых будет действовать н
промежутке £о, -у-}, а другое — иа промежутке £-|-, 1 j. С это
целью положим
Уа =“ Уа + 1? — МУ осе* + “j" (₽®~1/а 4- «е,/г) +
ч	Je-t2'2dT~a<1/2+ •••
А	0
ИЛИ -
/'	I \
Уа = ае* + (₽ё-1/а - ссе1/2) 4- + I dx + ’ ’' • <12-152
'	\ г 2л j	J
Аналогичным образом имеем
/	6	\_
£ = №~1 + (ае1/2 - ₽е-,/2 (4- -	( e~x,/‘ dx + • •.. (12.154
у Л у 2п J	J
Рис. 12.11 показывает, что разложение ус очень мало отличается о
точного решения уже при е = 0,1. -
12.6. Задачи с двумя пограничными слоями	317
Рис. 12.11. Сравнение составного разложения ус с точным решением у*, полу-
ченным в результате численного интегрирования уравнения (12-141) с гранич-
ными условиями (12.102) при е= 0.1, а— 1,0 и |5 — 1.0.	'	,
Отметим, что в данном примере коэффициент р£ (х) представляет
собой монотонно возрастающую функцию, и потому в задаче
имеется Только один внутренний пограничный слой. Если же
Pi (х)>будет монотонно убывающей функцией, структура решеййя
становится более сложной: кроме внутренней точки пограничные
слои»могут появиться и в граничных точках промежутка. Такого
рода задачи в последнее время привлекают все больший интерес'
исследователей.
12.6. Задачи с двумя пограничными сдоями	.	'
В предыдущих параграфах рассматривались задачи, имеющие
лишь одни пограничный слой. В этом параграфе исследуем задачу
с двумя пограничными слоями, а именно краевую задачу следую*
щего.вида:'	>
eyv_(i+x)s ^а.0,	(12.155)
у (0) - а, у' (0) - ₽, у (1) - у, у' (1) - 5. (12.156)
В данном случае порядок старшей производной на две единицы
превышает порядок производной во втором члене; это позволяет '
предположить, что в данной задаче имеются два пограничных
слоя по одному на каждом конце промежутка. Как обычно,
сделанное предположение будет подтверждено в дальнейшем
после проверки полученных результатов на самосогласованность.
Внешнее разложение
Будем искать двучленно^ внешнее разложение в виде
1Г = М«) + %И+'..,	(12.157)
Подставляя разложение (12.157) в уравнение (12.155) и приравни-
вая коэффициенты при одинаковых степенях е, получаем
-(i+«=i.	(12.158)
-(1 +х)2У; = 0,	’	{12.159)
318
Гл. 12. Задачи с пограничным слоем
Уравнение (12.158) можно переписать в виде
" — 1 . ’
Уо— (1+х)2 ’
откуда	yi — in (1 + х) + Аох 4- Во,	(12.16Q)
где Ае и Вй — произвольные постоянные. Общее решение уравне-
ния (12.159)	•	.
Л = Л^ + Л, .	.	(12.161)
где Ai и Bt — произвольные постоянные. Следовательно,
. у° = In (1 + х) + Аох + Во + е (А1Х + BJ + ........(12.162)
Отметим, что построенное внешнее разложение (12.162), вообще
' говоря, не удовлетворяет нн одному из граничных условий, По-
этому его необходимо срастить с двумя погранслойными (внутрен-
ними) разложениями, каждое из которых действует на своем койце
промежутка.		"
Внутреннее разложение вблизи точки х = 0 _
Для построения этого разложения, которое будем обозначать
через «Д.введем в уравнении (12.155) преобразование растяжения
= или. x = gV| (v>0),	(12.163)
переписав это уравнение в виде.	-	_
«-"О +	- Г.'
При в -> 0 характерный предел соответствует значению v =•» li
Поэтому у‘ должно удовлетворять предельному уравнений вида
-^-(l+2eg-he®^)-^-we> :	(12.164)
Будем искать двучленное внутреннее разложение в форме
. У1 - Го (£) + еУ1 (р.+ ....	(12.16^
Подставляя разложение (12.165)-в уравнение (12.164) и приравни-
вая коэффициенты при одинаковых степенях в, имеем
yiv-y;==0,	(12.166)
Иу-У1=МУо. '	(12.I6T
Разложение у1 должно удовлетворять также граничным усло-
виям к точке х — 0, которая соответствует значению § == 0.
Таким образом, условие у (0) — а переходит в условие
^(0)==а.	,	(12.168)
Кроме того, поскольку
< '	. dy dl 1 dy -	J
У dx di dx e	1
12.6. Задачи с, двумя пограничными £лМмр - .	319 -
граничное условие у' (0) = Д преобразуется в условие
^-(0) = е₽.	(12.169)
Подставляя разложение J( 12.165) в условия (12.168) и (12.169) и
приравнивая коэффициенты при одинаковых степенях е, находим
Уо(0) = а, Г6(0) == 0, ; . , .	(12.170) ...
Г1(б)=^о, Уг(О)==р;	(12.171)
Отметим, чт^ влияние величины Р сказывается только на членах
первого порядка, малости •— именно по этой причине мы ограни- z
чились построением двучленного разложения.
Общее решение уравнения (12.156) записывается в виде
Уа — °о +	4"	4* 4Л_
где постоянная <4 должна равняться нулю. В противном случае
функция Уо будет экспоненциально расти с увеличением что не
позволит срастить это решение с внешним разложением. Удовлет-
воряя граничным условиям (12.170), находим
' Це. + с0 == а, Ьа — с0 = 0. s ।
Таким образом, Ьв; = Со и ав ~ а — св, и, следовательно, .
Уо =а + ^'(е-В+ £-1).	.	(1^.172) ,
В данном случае удобнее проводить сращивание на этом шаге,
поскольку'постоянная Cq оказывается равной нулю.. Итак, для. -
того чтобы срастить одночленное внешнее разложение с одночлеш
ным внутренним разложением, положим в (12.97) т п 5= 1 .
и будем действовать следующим образом-. / -
Одночленное внешнее ^разложение: у ~ In (1 4--0 +	+ йф-
Перепишем через внутреннюю переменную:
'Г;	=1п(1+4)4-еА£+Дь\>
Разложим при малых ef = е£ 4-	4- Ва 4- - •«.
Найдем одночленное внутреннее разложение: = Во. (12.173)
Одночленное внутреннее разложение:. у ~ а 4- с0 (еЧ 4- £ — 1).
Перепишем через внешнюю переменную:	‘;
= а 4-со (е-х/е 4- -j- — 1).
Разложим при малых в: == а — с0 4- -fr ~Н (Э. М. Ч.).
Найдем одночленное внешнее разложение:
• \	х \ -
(12.174)
а при св —и,
при .с0¥=0-
320
Г л. 12. Задачи с пограничным РЛоем
Условие равенства (12.173) и (12.174) дает
с0 = О, Во = а
(12.175)
и	Уо = а.	(12.176)
Подставляя найденное выражение для Уо в (12.167), получаем
уравнение	....
y’v_y;=o,
общее решение которого записывается в виде
У1 = ai 4- &15 4- Ci«-E 4- 4А
Как и ранее, постоянная должна7 равняться нулю, поскольку
в противном случае. функция будет экспоненциально расти
с увеличением В, что не позволит срастить это решение с внешним
разложением. Выполняя граничные условия (12.171), .имеем
Oi 4- Ci — 0,	&1 — ci = Э.'
Поэтому аг = —q и Ьг =	4- Р, и, следовательно,
—	>! = Р5 4- q (е~* 4- I - 1).
Окончательно находим
' ^=а4-е [₽5 4-с1(е-5 + ^-1)14-.-
(12,177
(12.178
Срастим теперь двучленное внешнее разложение (12.162) с двучлен
ным внутренним разложением (12.178), действуя следующим обра
зом:	-
Двучленное внешнее разложение:
у In (1 4- х) 4- AqX -f- Bq 4- ® (^ix Bj_t
Перепишем через внутреннюю переменную:
.	== In (1 -f- е£) еДоВ 4- & 4~ е 4~
Разложим при малых е:
= 4т еД05 4~а 4- e2^i£ 4- ,®^i 4- * * ,
Найдем Двучленное внутреннее разложение:
•	„	+	+	+	(12.17$
- Двучленное внутреннее разложение:	' • f J
> У ~ а 4-в [₽S 4-/1 (в~6 4-5-1)|
Перепишем через внешнюю переменную:	7

=«+<^+^(«-"•+4—i)]j
Разложим при малых s:
= a 4- Рх 4~ Cix — e^i 4~ (Э. М; Ч.)
Найдем двучленное внешнее разложение:
= а 4- рх + CjX — ecj
r	(12.18g
12.6. Задачи с двумя пограничными слоями
321
Далее, переписывая разложение (12.179) через переменную х и
приравнивая его (12.180), имеем
а + х + Аох + sBx — а + fix + схх — есх,
откуда 1 + Ло = Р + Cj и = —с,.	(12.181)
Внутреннее разложение вблизи точки х — 1
Для построения этого разложения, которое мы будем обозна-
чать через у1, введем в уравнении (12.155) следующее преобразова-
ние растяжения:
£ = 1=^-, или	(v>0).	(12.182)
Тогда уравнение (12.155) перепишется в виде
e2-4v	~ £“"2v (2 - £V?)2^- = I-
При е-> 0 характерный предел соответствует значению v = Е
Поэтому функция у1 должна удовлетворять предельному уравне-
нию вида
_ (4 - 4^ +	=	(12-183>
Будем искать двучленное разложение у1 в виде
/ = У0(О + гУ1(£)+ ••••	(12.184)
Подставляя разложение (12.184) в уравнение (12.183) и приравни-
вая коэффициенты при одинаковых степенях 8, находим
F’v-4F; = 0,	(12.185)
Hv-4F;=-4^.	(12.186)
Внутреннее разложение у1 должно удовлетворять также гранич-
ным условиям в точке х = 1, которая в данном случае соответ-
ствует точке £ = 0. При этом условие у (1) = у дает
У’ (0) =	(12.187)
а поскольку
» _ dy _ dy <%' _	1 dy
y dx di dx ~	e di ’
то второе граничное условие у1 (1) = б переходит в условие
^-(0) = -вб.	(12.188)
Подставляя разложение (12.184) в условия (12.187) и (12.188)
и приравнивая коэффициенты при одинаковых степенях е, полу-
чаем
Уо(О)-у,	Fj(O) = O,	(12.189)
7,(0) = 0,	Й(0) = -б.	(12.190)
1 1 Найфэ А. X.
322	Гл. 12. Задачи с пограничным слоем	з
Общее решение уравнения (12.185)	?
Yo —	4*	-|_ dfjg2^,	j
где постоянная 3q должна равняться нулю. В противном случае
функция Ya будет экспоненциально расти с увеличением £, что не
позволит срастить это решение с внешним разложением. Далее,
используя граничные условия (12.189), находим, что
Йо Со = у, — 2с0 = 0.
Поэтому 50 = 2с0 и й0 = у — с0, и, следовательно,
?о = т + со(е-2£ + 2С-1).	(12.191)
Как и ранее, срастим одночленное внешнее разложение с одно-
членным внутренним разложением, действуя по следующей схеме.
Одночленное внешнее разложение: у ~ In (1 + *) + Аох + а-
Перепишем через внутреннюю переменную:
= ln(l — 2б£) + Ло(1 — 8?;) + а, 
Разложим при малых б:
— In 2---б£ -|- Ао — бЛ0£ к ®	' •
Найдем одночленное внутреннее разложение:
= Л0 + а + 1п2. (12.192)
Одночленное внутреннее разложение:
у^у-\-с0(е~^ + 2^- 1).
Перепишем через внешнюю переменную:
= У + Со (с~2 <'-*>/* + 2(1е~х) ~ 1).
Разложим при малых б:
^у+ .2м..^1_ёв + (э. М. Ч.). j
Найдем одночленное внешнее разложение:	J
у при со = О,	j
2М1-Ч	(12.193)3
—-------,присо=#О.	|
Условие равенства разложений (12.192) и (12.193) дает с0 = 0 и1
Ло + а + In 2 = у, или Ло = у — а — In 2, (12.194Ц
и, следовательно,	1
Уо = У- _	(12.195)|
Подставляя найденное выражение для Yo в (12.186), получаема
уравнение	i
р;у-4У\=0,	j
12.6. Задачи с двумя пограничными слоями	323
общее решение которого записывается в виде
Л = «i+ к +^е-2^ + Э^.
Как и ранее, для того чтобы можно было срастить разложение у'
с внешним разложением, постоянная З.г должна равняться нулю.
Далее, используя граничные условия (12.190), находим, что
arHi = 0,	—2ёх =—6.
Поэтому йх = —ёх и йх — 2ёх — 6, и, следовательно,
Кх = -6С + Ме-2г + 2С-1).	(12.196)
Срастим теперь двучленное внешнее разложение с двучленным
внутренним разложением yJ, действуя следующим образом.
Двучленное внешнее разложение:
У ~ In (1 4 х) AqX 4 а 4- е (Ахх 4 BJ.
Перепишем через внутреннюю переменную:
= In (2 — е£) 4 Ао (1 — еС) 4 а 4 е (А — еАхС 4 Bi)-
Разложим при малых е:
= 1п 2 —g- е£ 4 Ао — еА0^ 4 а 4 вАх — е2АхС 4	4    •
Найдем двучленное внутреннее разложение:
= А04а41п2-|-б ^Ах 4 Bi-------j- С — Ао0 •
(12.197)
Двучленное внутреннее разложение:
У ~ У 4 е (-6С 4 ёх (с-2? + 2С - 1)))
Перепишем через внешнюю переменную:
= т + е	6,(1 - х) + сг [е-2 <»-*>/* + -L4-*.). — 1 ] }.
Разложим при малых е:
= у — 6(1 — х) 4 2ёх(1 — х) — вех 4 (Э. М. Ч.).
Найдем двучленное внешнее разложение:
= У 4 (2ёх - 6) (1 - х) — есх.
(12.198)
Переписывая разложение (12.197) через переменную х и приравни-
вая его разложению (12.198), имеем
Ао 4 а 4 1п 2 — ^-g- 4	(1 — *) 4 6 (^i 4 Вг) —
= у 4 (2сх — 6) (1 — х) — есх,
11*
324
Гл. 12. Задачи с пограничным слоем
Рис. 12.12. Сравнение составного разложения ус с точным решением уе, полу-
ченным с помощью численного интегрирования уравнения (12.155) с гранич-
ными условиями (12.156) при е = 0.2, а = 0 = 1.0 и у — 6 =—1.0.
откуда следует соотношение (12.194), а также соотношения
— 2_ _ л0 = 2Ci - 6,	+ Ср (12.199)
Подставляя теперь значение Ло из (12.194) в (12.181), находим
Bi = —ci = —У + а + Р — 1 + In 2,	(12.200)
а подставляя значения Ло и Вг из (12.194) и (12.200) в соотношения
(12.199), окончательно имеем
^ = 4-(a + 6-Y-4 + ln2),	(12.201)
Л! = —4-(За + 2р-Зу + 6--|- + 31п2). (12.202)
Таким образом, все произвольные постоянные во внешнем и вну-
тренних разложениях оказались выраженными через граничные
значения.
Соответствующее составное разложение может быть построено
следующим образом:
Ус = Уа + У1 + У1 - (</')’ - (/)’.
где (у*)’ и (у7)’даются формулами (12.180) и (12.198). В результате
имеем
У°= In (1 -f- х) -|- АдХ -|- а 8 (Лхх -|- Bi) -f- а -|-
+ е[Р$-В1(<?-Е + 5- 1)] + е [—6СН- гх(е-2С4_ 2g — 1)] —
— а — p.r BiX — eBi — у — (2Ci — 6) (1 — х) eci.
12.7. Случай нескольких зон
325
ИЛИ
jic = a + ln(14-x)4-(v — a — ln2)x4-
+ е[-4-(3а + 2Р-3? + б--г + 31п2)х-
— (у - a — р + 1 — In 2) (1 - е-*/£) +
+	+ 6 - у - А-_|_ In 2) в-2 <»-*>/е] -|-. (12.203)
Рис. 12.12 показывает, что составное разложение if хорошо соот-
ветствует точному решению задачи.
12.7.	Случай нескольких зон
Во всех рассмотренных ранее примерах в области пограничного
слоя существовал только один характерный предел. В этом пара-
графе обсудим случай, когда в данном пограничном слое имеется
несколько характерных пределов. При этом, если в задаче сущест-
вуют, например, два характерных предела, результирующее
разложение, кроме внешнего, будет включать в себя два внутрен-
них разложения. Области пригодности каждого из этих разложе-
ний обычно называют зонами г), а сама задача именуется в этом
случае трехзонной задачей. Таким образом, если в данном погра-
ничном слое существует не один, а несколько характерных пре-
делов, то говорят соответственно о многозонной задаче. Ниже мы
исследуем случай двух характерных пределов в пограничном слое,
т. е. трехзонную задачу.
Итак, рассмотрим краевую задачу
е3у" + х3//' + (х3 — е) у = 0,	(12.204)
у (0) = а, у (1) = р.	(12.205)
Поскольку коэффициент при у' положителен, пограничный слой
должен существовать вблизи начала координат. Поэтому внешнее
разложение должно удовлетворять граничному условию у (1) = Р,
однако, вообще говоря, не предполагается, чтобы оно удовлетво-
ряло условию на левом конце у (0) = а.
Будем искать внешнее разложение в виде
У0 = Уо (х) + e*/i (х) + ••••
Подставляя разложение у0 в уравнение (12.204) и граничное
условие у (1) = р и приравнивая коэффициенты при е° в обеих
частях полученных равенств, получаем
х3у' + хяу0 = 0,	г/0(1) = р.	(12.206)
Общее решение уравнения (12.206)
Уо = сае~х.
!) У автора используется слово deck (палуба). — Прим. ред.
326
Гл. 12. Задачи с пограничным слоем
При этом из условия у0 (1) = р следует, что с0 = ре. Поэтому!
Уо = Ре1-'	1
и	у° = ре1-* + ....	(12.207)|
Ясно, что полученное разложение не удовлетворяет граничному |
условию при х = 0.	j
Как и ранее, для того чтобы исследовать окрестность точки!
х = 0, введем преобразование растяжения	3
5 = -^-, ИЛИ x = evg (v>0).	(12-208)1
В результате уравнение (12.204) перепишется в виде	1
e3"2v‘0' + 62^3< + (e3^3“e^==0-	(12-209) ]
При е'-> 0 член О (e3v) оказывается малым по сравнению с e2v, |
поскольку v > 0. Поэтому главной частью уравнения (12.209) 1
будет	|
e3'2v-^- + e2vg3-|--8z/+...=0.	(12.210)1
Соответствующие характерные пределы получаются в результате 1
«уравновешивания» (компенсации) двух любых членов в (12.210). 1
Так, чтобы скомпенсировать первый и второй члены этого разло- я
3	1
жения, следует положить 3 — 2v = 2v, или v = При этом |
(12.209) переходит	в уравнение ,	1
63/2	+ е3/^3~< + (е9/4?3 “ е) У = °’	I
главная часть которого соответствует тривиальному решению 4
у = 0. Поэтому данный случай должен быть исключен из нашего |
рассмотрения. Если теперь скомпенсировать в (12.210) первый и 1
третий члены, мы должны выбрать 3 — 2v = 1, или v = 1. Тогда I
уравнение (12.209) переходит в уравнение	1
+	+	'	(12.211а) I
с нетривиальной главной частью, и поэтому данный случай необхо- |
димо учесть при дальнейшем рассмотрении. Если же, наконец, |
скомпенсировать в разложении (12.210) второй и третий члены, то |
необходимо положить 2v = 1, или v = -±-. В отличие от предыду- |
щего случая, где преобразование пограничного слоя имело вид .1
£=х/е, здесь мы используем новую мелкомасштабную переменную j
С, так что С = х/е1/2. При этом уравнение (12.209) переходит I
в уравнение	1
8з^. + 8?з^. + (83/2^_8)^ = о	(12.2116) |
12.7. Случай нескольких эон
327
с нетривиальной главной частью, и, следовательно, этот случай
также следует учитывать при анализе. Изменение масштаба £ =
= х/е, соответствующее v = 1, описывает некоторую область
(подслой) вблизи начала координат, которую будем называть
левой зоной. Изменение масштаба £ = х/е1/2, соответствующее
v = -i-, определяет другую область, лежащую между левой зоной
и областью внешнего разложения (правой зоной). Поэтому будем
называть ее средней зоной. Отметим, что в задачах вязко-невязких
взаимодействий эти зоны обычно называются нижним, средним и
верхним подслоем соответственно.
Из формулы (12.211а) следует, что главный член Yo разложения
левой зоны у1 удовлетворяет уравнению
_ у — О
Общее решение этого уравнения можно записать в виде
Ya = aoe~t + Ьйе\
где постоянная b0 должна равняться нулю, так как в противном
случае функция Yo будет с увеличением £ экспоненциально расти,
что не позволит срастить ее с разложениями средней или правой
зоны. Поскольку разложение левой зоны пригодно в окрестности
начала координат, оно должно удовлетворять граничному условию
у (0) = а. Но точка х = 0 соответствует точке 5 = 0, и, следова-
тельно, у1 (0) = а. Тогда из этого условия имеем а0 = а и
откуда	у1 = ае~%	.	(12.212)
Точно так же из формулы (12.2116) следует, что главный член
Yo разложения средней зоны ут удовлетворяет уравнению
£3?о —Ро=О.
Разделяя переменные, имеем	,
dY0 _ 4
Го ? ’
Интегрирование этого соотношения дает
In Гц = — -2£j- + In do,
откуда	У0 = Ч0е~Г2^
и	ут = doe-'/^1 Ч--.	(12.213)
Так как начало координат соответствует точке £ = 0, то из разло-
жения (12.213) следует, что ут —» 0 при £ ->• 0, и поэтому данное
Разложение не может удовлетворить граничному условию у (0) =
= а. Таким образом, постоянную d0 следует определять из условия
сращивания ут либо с разложением у1, либо с разложением у0.
328
Гл. 12. Задачи с пограничным слоем
Рис. 12.13. Сравнение составного разложения ус с точным решением уе, полу*
чеииым с помощью численного интегрирования уравнения (12.204) с граничными
условиями (12.205) при е = 0.05, а= 2.0 и 0= 1.0.
Отметим, что разложение у1 нельзя срастить прямо с разложе-
нием у0, поскольку
(У1)0 = 0 и (у"У =
Поэтому для ликвидации разрыва между у1 и у0 нужно воспользо*.
ваться разложением ут. Для того чтобы срастить разложения ут
и у0, заметим, что
(Г)о = 4> и \у°Г = $е.
Отсюда d0 = ре, и, следовательно,	;
^ = Ре>-1/2£!^----.	.	(12.214)
Аналогично, для того чтобы срастить разложения ут и у1, заметим,^
что
(Г)' = 0 и (t/z)m = 0,	'
и, следовательно, их сращивание вполне возможно.
Наконец, образуем составное разложение по следующей схеме:;
Vе = У0 + Ут + У1 - (Г)т - (У1)т-
Таким образом,
= ре1-*Ре1 ~(1/2^>-|-oce-s — Ре-]-------------------.	(12.215
При этом из разложения (12.215) имеем
Ш = ре1-* = у0,
(tf)m = Pe*-(W> = ут,
(у0)1 - ае~Ъ = у1,
и, следовательно, мы можем утверждать, что разложение ус буде:
равномерно пригодным на всем промежутке [0, 1]. Рис. 12.15
показывает, что разложение ус действительно оказывается доста
Точно близким к точному решению.
12.8. Нелинейные задачи
329
12.8.	Нелинейные задачи
В заключение этой главы рассмотрим две нелинейные задачи.
Задача 1. Прежде всего исследуем случай, когда в процессе
построения асимптотического решения приходится вводить не
растягивающее, а сжимающее преобразование масштаба. Рас-
смотрим следующую краевую задачу:
У" + ^ГУ' + ^' = °>	е«1,	(12.216)
У (1) = 0, у(оо) = 1.	(12.217)
Здесь разложение нулевого порядка оказывается равномерным,
а неравномерность будет проявляться только в членах первого
порядка. Отметим также, что в данном случае малый параметр
стоит не при старшей производной, и, следовательно, причиной
неравномерности, как и в задачах о нелинейных колебаниях, явля-
ется неограниченность области изменения аргумента х.
Будем искать двучленное прямое разложение в виде
У = Уо (*) + et/i (х) + ....	(12.218)
Подставляя разложение (12.218) в уравнение (12.216) и граничные
условия (12.217) и приравнивая коэффициенты при одинаковых
степенях е, имеем
для порядка е°:
*/S + 4^ = °-	(12.219)
. ’ f/o(l) = O, t/0(oo)=l;	(12.220)
для порядка е1:
У\ + 4 У1 = —УоУо,	(12.221)
^(1) = 0, Jh(oo) = 0.	(12.222)
Умножая уравнение (12.219) на х2, перепишем его в виде
^;+2эд=4(12^-)=о,
откуда, после интегрирования, находим
Уо = —^ + Ьо.	(12.223)
Используя граничные условия (12.220), получаем
—а0 + Ьо = 0 и b0 = 1.
Отсюда а0 = Ьо = 1, и, следовательно,
//о=1-4-	(12.224)
330
Гл. 12. Задачи с пограничным слоем
Таким образом, первый член разложения (12,218) оказывается
равномерным по х, поскольку он удовлетворяет вырожденному
уравнению (12.219) и исходным граничным условиям.
Подставляя найденное выражение для у0 в (12.221), получаем
уравнение
У\ +4^ = -(! -т)
которое после умножения на х2
x2y"i + 2ху\ — — 1 + , или
Интегрируя его, имеем
хъ—т^- =—*4-lnx + ai> или -
dx	1
Повторное интегрирование дает
, In х
У1 = ~ 1ПХ----—-
._L = _J_+JL
X2	«2 Х3 >
приобретает вид
dx \ dx /	1 х
dyt __	1	In x
dx	x	x2	x2 "
3-4А.	'	(12.225)
Используя граничное условие f/i (1) = 0, получаем, что Ьг =
=	+ 1, откуда
У1 = _1пх__!Е£+Ь1^ _±у	(12.226)
При х->оо функция уг является неограниченной, и поэтому мы
не можем удовлетворить второе из граничных условий (12.222),
а именно условие уг (оо) = 0. Таким образом, прямое разложение,
которое будем называть внешним и обозначать через у0, т. е.
у>=\ -± + е[-(1 +±)1пх4-Ц1-±)] + ••• (12.227)
оказывается непригодным при больших х.
Для того чтобы исследовать поведение решения в случае боль-
ших х, введем следующее преобразование сжатия:
£ = xev (v > 0).	(12.228)
При этом
_±_& ,v
dx ~ dl dx d% ’ dx* ь d£* ’
и уравнение (12.216) переписывается в виде
2v £yL ।	l gi+vy,- _ о
e d^ + g + e y dg ~u-
Характерным пределом для него является уравнение
-^-+т4+!''#=<)’	<,2-229>
соответствующее значению v = 1. Получающееся в результате
разложение будем называть внутренним и обозначать через у1.
12.8. Нелинейные задачи
331
Далее, вместо того чтобы задавать вид разложения у1, после-
довательно находить и решать уравнения для членов различного
порядка и, наконец, сращивать у‘ с внешним разложением, мы
поступим иначе, а именно: используем внешнее разложение в
качестве критерия для определения формы внутреннего разло-
жения у{. Такой подход оказывается очень удобным в случае
уравнений в частных производных и интегродифференциальных
уравнений, особенно нелинейных. Кроме того, в этом случае
первый член разложения, даваемый формулой (12.224), оказы-
вается пригодным на всем промежутке решения задачи и, следо-
вательно, его можно использовать и во внутренней области.
Тогда, переписывая этот член через внутреннюю переменную,
имеем
!/о=1--|-.	(12.230)
Устремляя теперь е к нулю при фиксированном	получаем
у0 = 1; эта функция и будет первым членом внутреннего разло-
жения. Кроме того, вид функции у0, даваемой формулой (12.230),
позволяет предположить, что у1 разлагается в ряд по целым по-
ложительным степеням е. Таким образом, мы будем искать внут-
реннее разложение в форме
f/'=l+ey1(g)+... .	(12.231)
Подставляя разложение (12.231) в уравнение (12.229) и прирав-
нивая нулю коэффициент при е1, получаем
П + (у+1)И = 0.	(12.232)
С помощью интегрирующего множителя
ехр [J l)d|] =exp(21ng + g) = ^
перепишем уравнение (12.232) в виде
Интегрируя, имеем
или
dYt __	_е^_
d£ ~C1 52 >
откуда после повторного интегрирования находим
6 -т
y1 = z?1J _S-dr +d1;	(12.233)
00
332
Гл. 12. Задачи с пограничным слоем
где q и di — произвольные постоянные. В связи с тем что внут-
реннее разложение должно удовлетворять граничному условию
на бесконечности, нижний предел интегрирования в этой формуле
мы положили равным бесконечности (поскольку точка х = оо
соответствует точке | — оо). При этом из (12.217) и (12.231)
следует, что (оо) = 0, и, значит, постоянная dx в формуле (12.233)
должна равняться нулю. Таким образом, формулу (12.233) можно
переписать как
S _т
Yi = Ь j -^5- dx,
СО
а разложение (12.231) принимает вид
СО
yi=\-ec1\-^-dx+---,	(12.234)
где мы поменяли пределы интегрирования, с тем чтобы значение
интеграла оставалось положительным. Постоянная же q опреде-
ляется в процессе сращивания внутреннего и внешнего разло-
жений.
Срастим теперь двучленное внешнее разложение (12.227)
с двучленным внутренним разложением (12.234), действуя сле-
дующим образом.
Двучленное внешнее разложение: у~1 — уе —(1 + у)х
X In X Н- ( 1 -4)j •
Перепишем через внутреннюю переменную: = 1 — -|- 4-
+ е[-(1 +у)1п	-т)]*
Разложим при малых е: =1-----------4- е In е — е In g -j-
+ + ''' •,
Найдем двучленное внутреннее разложение: = 1 — е (-|- +
+ lng- Ine-ftj) * .	(12.235)
ао	J
Г	?
Двучленное внутреннее разложение: у ~ 1 — ecj J dx. j
оо
Перепишем через внешнюю переменную: = 1 — J drj
1 Обратим внимание читателя на наличие в разложении (12.235) логарифм
мического члена.	1
12.8. Нелинейные задачи
333
Разложим при малых е: =1— еСхГ-—— + In exl + • ’ ••
I	J
Найдем двучленное внешнее разложение: =1 —j—
— ecx(—1	In х + In e). (12.236)
При вычислении интеграла мы воспользовались интегрированием
по частям:
— I 1п те‘т dx — —-[- e~zx In ex + О (e In e).
ex
Переписывая разложение (12.235) через внешнюю переменную
х и приравнивая его разложению (12.236), получаем
1 —j— elnx Ц- ebj = 1 —j— ecj (—1-[- Inx + In e). (12.237)
Таким образом, = 1 и bL = 1 — Ine, и, следовательно,
y«=l - ± + e[-(l +±)lnx + (l-lne)(l -±)]+ ...
(12.238)
и	yt=\ — e	---.	(12.239)
'	I
Наконец, складывая внешнее разложение (12.238) с внутрен-
ним разложением (12.239) и вычитая их общую часть (12.236)
при cr = 1, находим искомое составное разложение
~т + е[‘“(1 +v)lnz + (1 “1пе)(1 ~т)] +
+ 1 - е	1 +^- + е (~1 +lnz+ 1пе)Н---,
или ^=l-eJ^LctT-er41+-1~xln8 ]+•••• (12.240)
J I	L Л	" J
Задача 2. В качестве второго примера, следуя Коулу (1968),
рассмотрим следующую задачу:
ер" + уу' — у = 0, _ 0 с х с 1,	(12.241)
У(0) = а, р(1) = ₽,	(12.242)
где 0 < е « 1 и а и р не зависят от е. В этом случае малый па-
раметр стоит множителем при старшей производной, в результате
334	Гл. 12. Задачи с пограничным слоем
чего в задаче возникает пограничный слой, причем разложение
этого пограничного слоя зависит от знака коэффициента при у'.
В то же время поскольку функция у определяется значениями а
и 0 на границе области, то в конечном счете местоположение по-
граничного слоя также оказывается зависящим от граничных
значений а и 0.
Будем искать внешнее разложение в виде
= Уо (х) + су,, (х) + ....
Подставляя это разложение в уравнение (12.241) и условия (12.242)
и приравнивая коэффициенты при е°, получаем
УоУо — Уо = 0,	(12.243)
Уо (0) = а, Уо (1) = 0-	(12.244)
Решение уравнения (12.243) состоит из двух ветвей, а именно:
у0 = 0	(12.245)
и	у о — х + с0.	(12.246)
Первую ветвь следует отбросить, потому что с ее помощью мы
не можем удовлетворить произвольным граничным условиям.
Вторая ветвь дает два специальных внешних решения
= х + 0 — 1,	(12.247)
у1 = х + а, 1	(12.248)
где уг удовлетворяет граничному условию на правом конце, а
у1 — условию на левом конце. При этом из (12.247) и (12.248)
следует, что
£/ЧО) = 0-1 И (1) = а + 1.
Таким образом, если а у= 0 — 1, то функция уг оказывается
непригодной вблизи точки х = 0, а функция у1 — вблизи точки
х = 1, и, следовательно, возникает необходимость ввести погра-
ничный слой. Если пограничный слой существует на левом конце
промежутка, то решение у1 следует исключить из рассмотрения;
если пограничный слой имеет место на правом конце, то из рас-
смотрения исключается решение уГ. Если же пограничный слой
располагается в некоторой внутренней окрестности данного про-
межутка (ударный слой), то нам необходимо учитывать оба этих
решения. Если теперь а = 0 — 1, то функция уг = у1 = х + ;
+ 0 — 1 будет удовлетворять дифференциальному уравнению
(12.243) и граничным условиям и, следовательно, она является
точным решением задачи.
Как отмечено выше, в случае а =/= 0 — 1 пограничный слой
располагается в некоторой внутренней точке промежутка [0,1].
12.8. Нелинейные задачи
335
Для того чтобы исследовать поведение функции у в этом погранич-
ном слое, введем преобразование растяжения
£ =	ИЛИ x = *b + evl (v>0),	(12.249)
где координата хь задает положение пограничного слоя и заранее
не известна. При этом для линейных задач нет необходимости
изменять масштаб зависимой переменной, поскольку он не ока-
зывает влияния на решение задачи. Однако в случае нелинейной
задачи может возникнуть необходимость изменить масштаб и у
зависимой переменной. Поэтому положим
у1 = Y (|; е) 4--= у(х^ е) ,	(12.250)
где величина X подлежит определению из дальнейшего анализа.
Подставляя (12.249) и (12.250) в уравнение (12.241), имеем
e!-2vn + ^-»у.	_ eKyi = 0,
или
+ e>.+v-lyi dj- _ е2У-1 yi = 0.
ag2 1	& dt.	?
Если X = 0, характерным пределом будет уравнение
+ У1 = 0,	(12.251)
соответствующее значению v = 1. Если же % =/= 0,.то характерный
предел будет иметь вид
^ + у^-у‘ = °>	(12.252)
что соответствует случаю
X Ц-v — 1=0 и 2v—1=0, или v = 4' и =
При этом из разложения (12.250) следует, что в первом случае
(т. е. при X = 0) у = О (1), тогда как во втором случае (т. е.
при % = функция у = О (е1/2). Во втором случае характер-
ный предел совпадает с исходным дифференциальным уравнением.
Таким образом, уравнение для характерного предела приходится
интегрировать численно, и, следовательно, обращаясь к методу
асимптотических разложений, мы практически не получаем ни-
какого упрощения исходной задачи. Однако Коул (1968) показал,
что данные граничные условия являются каноническими, и поэ-
тому численное интегрирование может быть проведено сразу
для всех задач. Здесь мы ограничимся исследованием только пер-
вого случая, когда у = О (1) и v = 1, а характерный внутренний
336
Гл. 12. Задачи с пограничным слоем
предел (12.251) оказывается более простым, чем исходное диффе-
ренциальное уравнение.
В первом приближении можно заменить у‘ на V в уравнении
(12.251), откуда после интегрирования находим
Y' = или у'=	р),	(12.253) \
где b — произвольная постоянная. Эта постоянная b должна
быть положительной, поскольку в противном случае при £ -* ±оо 1
функция Y будет стремиться к +оо, и, следовательно, мы не/
сумеем срастить разложение у1 с соответствующим внешним раз-
ложением.
Разделяя переменные в (12.253), имеем
=	(12.254)
где постоянную b мы заменили на положительную величину k2.
При интегрировании уравнения (12.254) будем рассматривать два
случая: Y2 < k2 и Y2 k2. В первом случае положим
Y = k th е
и, учитывая, что dY = &sch20d0, из уравнения (12.254) получим .
2k sch2 0 dQ _	2
ft2 - ft2 th2 0 “ ~ ~ T
Таким образом, имеем
0 = ife(l + d)
и
y‘ = Y-]----= Hh	H----,	(12.255)
где d — постоянная интегрирования. Во втором случае положим
Y = k cth 0
и, учитывая, что dY = —&csch20d0, из уравнения (12.254) по-
лучим
2k csch2 0 d& _	__ 2
~ k* - A2 cth2 0 ~a*~~k aV-
Следовательно,
0=-^(В + Ф	;
и	yl = Y -f- • • • = &cth (B + d)] + • • • •	(12.256)
Отметим, что величину k также можно считать положительной,
поскольку функции th и cth нечетные. Постоянные интегрирова-
ния k и d в обеих формах внутреннего разложения определяются
в процессе сращивания внутреннего и внешнего разложений.
12.8. Нелинейные задачи
337
Исследуем теперь три возможных случая расположения погра-
ничного слоя: на левом конце промежутка, на правом его конце
и в некоторой внутренней точке.
Если пограничный слой существует на левом конце проме-
жутка, т. е. координата хь = 0, то внешнее решение (12.248)
следует отбросить и надлежащим внешним решением будет
(12.247). Затем это внешнее решение сращивается с одной из форм
внутреннего разложения, в результате чего получаются условия
для пограничного слоя на левом конце. Выражая уг через пе-
ременную В и разлагая найденное выражение при малых е,
имеем
ОЛ)‘ = Р- 1.
(12.257)
Далее, выражая у1 из разложений (12.255) или (12.256) через
внешнюю переменную х, раскладывая при малых е и замечая,
что х > 0, получаем
(^ = £>0.
Следовательно, k = Р — 1 и
(Р-l)th [-!(₽-l)(l + d)] при У<р-1,
(₽- l)cth	l)(l + d)] при Е^Р-1.
(12.258)
(12.259)
Поскольку предполагается, что пограничный слой сущест-
вует в точке х = 0, которая соответствует точке | = 0, он должен
удовлетворять условию у (0) = а, или Y (0) = а. Тогда из
(12.259) следует, что
а = (р- l)th !)d]	(12.260)
или
а = (р-l)cth [^-(р -l)d].	(12.261)
Учитывая поведение функций th и cth (рис. 12.14), из соот-
ношения (12.258) можно сделать вывод, что величина р должна
быть больше единицы, так что внутреннее решение либо убывает,
либо возрастает до значения Р — 1 > 0. Кроме того, если а >
> Р—1, внутреннее решение выражается через cth, который
убывает от значения а до значения р — 1. Если же а < р — 1,
то должно быть также а > —(Р — 1), так что внутреннее реше-
ние будет выражаться через th, который возрастает от значения
а до значения р — 1. Оба этих решения приведены на рис. 12.15.
Перейдем теперь к анализу случая, когда пограничный слой
существует на правом конце. При этом имеем = 1, и, следо-
вательно, решение (12.247) должно быть отброшено, а надлежа-
щее внешнее решение будет даваться формулой (12.248). Для того
чтобы срастить это внешнее решение с одной из форм внутреннего
338
Гл. 12. Задачи с пограничным слоем
Рис. 12.14, Поведение функций th £ и cth
разложения, выразим у1 через переменную £ = (х — 1)/е и раз-
ложим полученное выражение при малых е. В результате получив
(у°У = а + 1.	(12.262);
Кроме того, выражая у‘ в (12,255) и (12,256) через внешнюю пе-;
ременную х, имеем
+ d)].
Рис. 12.15 Характер изменения составного решения в случае, когда погранич-
ный слой существует в окрестности точки х = 0, при 8=01, Р = 3 и a) a=»i
= —0.5; б) a= 4.
12.8. Нелинейные задачи
339
Рис 12.16. Характер изменения составного решения в случае, когда погранич-
ный слой существует в окрестности точки х= 1, при е = 0.1, а= —3 и
а) Р = 1; б) Р = —4.
Устремляя е к нулю и замечая, что х < 1, находим, что аргумент
в этих выражениях стремится к —оо, и, следовательно,
(y*)° = -k.	(12.263) ,
Приравнивая в соответствии с принципом сращивания выражения
(12.262) и (12.263), получаем, что k = — (а + 1). Таким образом,
— (а+ l)th Г— 4“(а+ 1)(£ + d)] ПРИ ^>а+1>
У=	Г 1	1
— (a-(-l)cthl—j"(a -|- 1) (| -j-d) J при Y < а 4-1,
(12.264)
причем функция Y должна удовлетворять граничному условию
у (1) = р, или Y (0) = р, поскольку точка х = 1 соответствует
точке | = 0. Наконец, находим
р = — (а 4- l)th [—4~(а+ l)d] (12.265)
или	р = — (а 4- l)cth [— 4~(а+ l)d] •	(12.266)
Поскольку предполагается, что k > 0, величина a 4- 1 должна
быть отрицательной. Если р < a + 1 <0, внутреннее решение
выражается через cth, причем оно будет возрастать от значения
Р до значения - a 4- 1. Если же |Р|<|«+1| и a 4- 1 .<
< 0, то внутреннее решение будет выражаться через th, который
убывает от значения р до значения a 4- 1. Оба этих решения пред-
ставлены на рис. 12.16.
Наконец, исследуем случай, когда пограничный слой существует
в некоторой внутренней точке промежутка.. При этом с внутрен-
ним разложением необходимо сращивать уже оба внешних ре-
шения. Для того чтобы срастить уг из (12.247) с разложением у1,
340	Гл. 12. Задачи с пограничным слоем
выразим эту функцию через переменную £ = (х — хь)/е и, раз-
лагая результат при малых 8, получим
(f/7-^ + р- 1.	(12.267)
Для того чтобы срастить решение у1, определяемое формулой
(12.248), с разложением у1, перепишем это решение через пере-
менную В и, разлагая результат при малых 8, получим
(у1У = хь±а.	(12.268)
Так как | — (х — хь)/е стремится к минус бесконечности при
х < хь и к плюс бесконечности при х > хь, то внутреннее реше-
ние у‘ должно возрастать от хь + а до хь + р — 1. Рис. 12.14
показывает, что такой характер изменения, т. е. возрастание
от значения —k при | = —оо до значения -\-k при 5 = +°о,
имеет только функция th. Следовательно, внутреннее решение
должно даваться формулой (12.255). Полагая В = +оо, на-
ходим, что
(yl)r = k,	(12.269)
а полагая | = —оо, получаем, что
(у1У = — k,	(12.270)
где надстрочные индексы г и I обозначают внешние пределы справа
и слева от хъ соответственно. Приравнивая (12.267) и (12.269),
имеем
хь + р — 1. = k,	(12.271)
а приравнивая (12.268) и (12.270), находим
хь + а = — k.	(12.272)
При этом из соотношений (12.271) и (12.272) следует, что
-а“Р)>	=	1 -“)> (12.273)
и, следовательно, внутреннее решение у‘ можно записать в виде
у‘ = 4(Р~ 1 -a)th	1	+ • • •• (12-274>
Рис. 12.17. Характер изменения составного разложения в случае, когда погра-
ничный слой существует во внутренней точке промежутка, при а = —2, Р =
Упражнения
341
Рис. 12.18. Диаграмма, иллюстрирующая расположение пограничного слоя
в плоскости (а, Р).
Таким образом, как показано на рис. 12.17, внутреннее решение
возрастает от i- (Р — 1 — а) до + Ц- (Р — 1 — а), причем
мы принимаем d = 0, поскольку с самбго начала предполагается,
что центр -ударного слоя расположен в точке х = хь, или | =
= 0. Так как 0 < хь < 1, а величина k считается положитель-
ной, из формул (12.273) получаем, что существование ударного
слоя (т. е. внутреннего пограничного слоя) требует выполнения
условий
0<4(1-СС-РХ1 и Р- 1-а>0,
или
— 1<а + р<1 и р>1+а.	(12.275)
На рис. 12.18 иллюстрируются все возможные варианты ре-
шений для пограничного слоя в плоскости (а, Р). Незаштрихо-
ванная область на рисунке соответствует случаю, когда у — О (е1/2),
и характерный предел дается уравнением (12.252); при этом, как
отмечалось выше, решение должно строиться с помощью чис-
ленных методов.
Приведенный пример показывает, что в нелинейной задаче
с пограничным слоем положение последнего в очень большой
степени зависит от выбора граничных значений.
Упражнения
12.1.	Рассмотреть краевую задачу
еу" + у' + у = 0, у (0) = а, у (1) = р.
а)	Найти точное решение.
б)	Используя метод сращиваемый асимптотических разложений, построить
равномерно пригодное разложение первого порядка. Сравнить полученный
результат с точным решением.
342
Гл. 12. Задачи с пограничным слоем
в)	Используя метод многих масштабов, построить равномерно пригодное
разложение первого порядка. Сравнить полученный результат с результатами
пунктов а) и б).
12.2.	Рассмотреть краевую задачу
еу" — У’ + У = 0, у (0) = а, у (1) = 0.
а)	Найти точное решение.
б)	Используя метод сращиваемых асимптотических разложений, построить
равномерно пригодное разложение первого порядка. Сравнить полученный
результат с точным решением.
в)	Используя метод многих масштабов, построить равномерно пригодное
разложение первого порядка. Сравнить полученный результат с результатами
пунктов а) и б).
12.3.	Рассмотреть краевую задачу
е/ —/=1, z/(0)=a, у (1)•= 0.
а)	Найти точное решение.
б)	Используя метод сращиваемых асимптотических разложений, построить
равномерно пригодное разложение первого порядка. Сравнить полученный
результат с точным решением.
в)	Используя метод многих масштабов, построить равномерно пригодное
разложение первого порядка. Сравнить полученный результат с результатами
в пунктах а) и б).
12.4.	Рассмотреть краевую задачу
е/ + У’ = 1, У (0) = а, у (1) = 0.	!
а)	Найти точное решение.	'!
б)	Используя метод сращиваемых асимптотических разложений, построить
равномерно пригодное разложение первого порядка. Сравнить полученный ре- ;
зультат с точным решением.	
в)	Используя метод многих масштабов, построить равномерно пригодное
разложение первого порядка. Сравнить результат с результатами, полученными
в пунктах а) и б).
12.5.	Построить равномерно пригодные разложения первого порядка для ре- j
шенин краевых задач
еу" ± (Зх + 1) у' = 1, у (0) = а, у (1) = 0.
12.6.	Построить равномерно пригодные разложения первого порядка для ре-
шений краевых задач
ъу" ±у' = 2х, у (0) = а, у (1) = 0.	i
В обоих случаях сравнить полученный результат с точным решением.
12.7.	Построить равномерно пригодные разложения первого порядка для ре-
шений краевых задач
еу" ± (2х2+ х+ 1) у' = 4х+ 1, у (0) = а, у (1) = 0.
12.8.	Построить равномерно пригодные разложения первого порядка для ре-
шений следующих краевых задач:
а)	еу" + ху' — ху = 0,
У (0) = а, У (П = 0.
б)	еу” + (1 — х) у' — (1 — х) у = 0,
у (0) = а, у (1) = 0.
12.9.	Построить равномерно пригодное разложение первого порядка для ре-
шения краевой задачи
ez/’ + х2у' — х?у =0, у (0) = а, у (1) = 0.
Упражнения
343
12.10.	Рассмотреть задачу
еу +	— хту = 0, у(0)=а, у (!) = £.
При каких условиях существует пограничный слой вблизи начала координат?
Построить для этого случая равномерно пригодное разложение первого порядка.
12.11.	Построить равномерно пригодное разложение первого порядка для ре-
шения краевой задачи
в/ + ху' — ху= 0, у (— 1) = а, у (1) = р.
12.12.	Рассмотреть задачу
еу” — у'=1,
у (0) = а, у' (0) = Р, у (1) = у.
а)	Найти точное решение и с его помощью показать, что в общем случае
пограничный слой существует иа обоих концах промежутка.
б)	Построить равномерно пригодное двучленное разложение и сравнить
полученный результат с точным решением.
12.13.	Рассмотреть задачу
еу* — у' + у=0, у (0) = а, у' (0) = Р, у (1) = у.
а)	Найти точное решение и с его помощью показать, что в общем случае
пограничный слой существует иа обоих концах промежутка.
б)	Построить равномерно пригодное двучленное разложение и сравнить
полученный результат с точным решением.
12.14.	Рассмотреть задачу
еу” — (2х + 1) у' = 1,
у (0) = а, у' (0) = Р, у (1) = у.
Построить равномерно пригодное двучленное разложение первого порядка.
12.15. Рассмотреть задачу
IV "	(
е/ — У = 1,
У (0) = а, у' (0) = Р, у (1) = у, у' (1) = б.
а)	Найти точное решение и с его помощью показать, что в общем случае
пограничный слой существует на обоих концах промежутка.
б)	Построить равномерно пригодное разложение первого порядка и сравнить
полученный результат с точным решением.
12.Г	О. Рассмотреть задачу
eylv - (2х + 1)/= 1,
у (0) = а, у' (0) = Р, у (1) = у, у' (1) = б.
Построить равномерно пригодное разложение первого порядка.
12.17.	Рассмотреть задачу
е2/ + хру — (х2 + е1/2) у = 0,
у (0) = а, у (1) = р.
Показать, что для иее существуют два характерных предела. Далее построить
равномерно пригодное трехзоииое решение первого порядка.
12.18.	Рассмотреть задачу
о
и” -J- — и' + еии' = 0, и (1) = 0, и (оо) — 1.
Построить равномерно пригодное двучленное разложение.
12.19.	Рассмотреть задачу
и" и' + еии' = 0,	и(1) = 0, и(оо) = 1.
344
Гл. 12. Задачи с пограничным слоем
Построить равномерно пригодное одночленное разложение. Обратить внимание
на то, что неравномерность проявляется уже в первом члене разложения.
Ответ: и0 = [1п(1/е)]~1 1п /+...,
и‘ = 1 + Qn j dx + • • •, ис = и1.
er
12.20.	Рассмотреть задачу
Показать, что
tc =	Х3/2 + 8	— 1П 2 4- 1П 8 +
+ 4*3/2 + 1п 0 + xV2) + & - /И1+ 1) + Arsh КГ1 + • ••
О	J
где
I = (1 — х)/е.
12.21.	Рассмотреть задачу
в/ — УУ' — У = 0, у (0) = а, у (1) = р.
Построить равномерно пригодное разложение первого порядка для случая
У = О (1).
12.22.	Рассмотреть задачу
еу" + уу' — ху= 0, у (0) = а, у (1) = р.
Построить равномерно пригодное разложение первого порядка для случая у =
12.23.	Рассмотреть задачу
еу" —у2=0, у (0) = а, У(1)=Р-
Построить равномерно пригодное разложение первого порядка.
12.24. Рассмотреть задачу
еу" ± (2х + 1) у'+ у2 = 0, у (0) == а, у (1) = р.
Построить равномерно пригодное разложение первого порядка.
Глава 13
ЛИНЕЙНЫЕ УРАВНЕНИЯ
С ПЕРЕМЕННЫМИ КОЭФФИЦИЕНТАМИ
В этой главе мы займемся исследованием линейных дифферен-
циальных уравнений с переменными коэффициентами следую-
щего вида:
y'(x) = F(x)y(x)4-h(x),	(13.1)
где у и h — вектор-столбцы с п компонентами, a F (х) — квадрат-
ная матрица n-го порядка, составленная из переменных коэф-
фициентов. При этом нас будут интересовать лишь решения од-
нородной задачи
y'(x) = F(x)y(x),	(13.2)
поскольку, если они известны, для нахождения частного решения,
а затем и общего решения исходной неоднородной задачи всегда
можно воспользоваться методом вариации произвольных поста-,
янных. Действительно, пусть уг (х), у2 (х),..., уп (х) — п линейно
независимых векторных решений уравнения (13.2); тогда решение
неоднородной задачи (13.1) можно представить в виде
У (х) = с, (х) у! (х) 4- с2 (х) у2 (х) -|-)- сп (х) у„ (х),	(13.3)
где сп (х) — некоторые скалярные функции от х, подлежащие
определению в дальнейшем. Дифференцируя выражение (13.3)
по х, имеем
У (х) = с[у 1 4~ сгУг + • • • 4" спУп 4“ С1У1 4~ с2Уг 4- • • • + спУп- (13.4)
Подстановка (13.4) в уравнение (13.1) дает
С1У1 4~ сгУг 4- • • • 4- спУп 4“ С1У1 4" сгУг 4~ ’ ’' 4” спУп —
= CiFyi 4- c2Fy2 Н----4 cnFyn 4- h. (13.5)
Поскольку у'п = Fyn, соотношение (13.5) можно упростить:
<4yi С2У2 4~    4“ спУп — ь,	(13.6)
что дает нам систему из п линейных уравнений относительно п
скалярных функций с'т. Обозначив составляющие вектора ут
через у , равенство (13.6) можнс^ переписать в виде
Ус' = Ь,	(13.7)
346
Гл. 13. Уравнения с переменными коэффициентами
где
	Уи	У12	 У1П	С1		
	У-и	Уж	• Угп	И	с =	С2
	_Ул1	Упг 	Упп _			_ Сп
Поскольку уп у2, .... уп линейно независимы, матрица Y оказы-
вается невырожденной и будет иметь обратную матрицу, которую
обозначим как У-1. Умножая уравнение (13.7) слева на К"1,
получаем соотношение
с' = У-Ч1,	(13.8)
определяющее собой систему п независимых уравнений относи-
тельно неизвестных ст. Поскольку у и h — известные функции,
решение (13.8) может быть представлено в квадратурах
с = J У-i (х) h (х) dx. '	(13.9)
Таким образом, если решения соответствующего (13.1) одно-
родного уравнения известны, то частное решение уравнения (13.1)
может быть найдено по формуле (13.9). Именно поэтому будем
рассматривать только однородные уравнения вида (13.2). При
этом сначала рассмотрим скалярные уравнения первого порядка,
а затем перейдем к исследованию уравнений второго порядка.
13.1.	Скалярные уравнения первого порядка
Начнем со случая, когда у (х) и F (х) представляют собой ска-
лярные функции, поскольку тогда точное решение уравнения
(13.2) можно записать в виде
у = ce F dx,	(13.10)
где с — постоянная интегрирования, определяемая из начального
условия.
D*? Если функция F (х) представима в виде ряда Тейлора, сходя-
щегося при | х — х01 < /?, то говорят, что х0 есть обыкновенная
точка данного дифференциального уравнения; в противном случае
точка х0 называется особой. Кроме того, если считать переменную
х комплексной, тогда F (х) будет аналитической функцией, ре- \
гулярной в некоторой окрестности | х — х01 < R точки х0.
Если точка х0 конечна, ее всегда можно перевести в начало
координат, положив
В = х-х0.	(13.11)
Тогда уравнение (13.2) переписывается в виде
^- = F(g + x0)f/,	(13.12)
13.1. Скалярные уравнения 1-го порядка
347
причем функция F (£ + х0) разлагается в ряд Тейлора, сходя-
щийся для всех | £| < R. Таким образом, не уменьшая общности,
можем считать, что интересующая нас точка является началом
координат.
В случае если ряд
F(x)=SF„xn,	(13.13)
л=0
где Fn — некоторые постоянные коэффициенты, сходится при
|х| < R, решение (13.10) можно записать как
или
z/ = t?exp
— с ехр
оо
S Fn J Хп dx
п=0
у — сехр
V FnXn+'
Li n + i
L л=о
(13.14)
Заметим, что ряд под знаком экспоненты сходится, так как
lim
/г->оо
я-й член
(п— 1)-й член
Рпхп^п
(» + ^Fn-i>?
(13.15)
а ряд (13.13) по условию представляет собой сходящийся ряд с
радиусом сходимости R. Поскольку функцию ехр (z) всегда
можно представить в виде ряда Тейлора, сходящегося при любых
значениях z, правая часть (13.14) также оказывается разложимой
в ряд Тейлора, который будет сходиться при | х| < R.
Если точка х = 0 представляет собой изолированную особую
точку функции F (х), например полюс порядка N, то F(x) можно
разложить в ряд Лорана вида
rt—0
(13.16)
где Fn — некоторые постоянные и Fo 0. Подстановка ряда
(13.16) в формулу (13.10) дает
у -= с ехр
(оо	\
2 Fnxn~N dx
л=0	/
00
= с ехр У, Fn j xn'N dx ,
L«=0
ИЛИ
У = с ехр Г---------° N , —-------F1 N о— • • • —+
L	(2V—I)**’1	(N~2)xn-2	х
4“ Fн-i In x -f~ Fnx	FN+^x2 -|- -у FN+ix2	(13.17)
348	Гл. 13. Уравнения с переменными коэффициентами
В случае N = 1 разложение (13.17) принимает вид
у = сехр	+	-J-^-FaX2 4- -j-F3r*-|- •••] ,
или
z/ = cxF” ехр ^Frx +-|-Faxa+-^F3x3 + • • • J.	(13.18)
Если представить экспоненциальный член в виде ряда по степе-
ням х, то формулу (13.18) можно записать как
у = cxF* ^.апхп,	(13.19)
п=0
где ап — постоянные, не зависящие от х. В случае. N = 2 разло- ;
жение (13.17) принимает вид
z/ = cexp [—+	+	+-^-Fsx2 + yF4r‘+ •••],
или
у — cxFi ехр ( —ехр [Fax + ± F^2 + ± F4x* + • • • ] • (13.20)
Член ехр (— F0/x) нельзя представить в виде ряда по степеням х ,
или аг1, поскольку при х -> 0 эта функция стремится к нулю j
быстрее, чем любая степень х, если Fo > 0, или к бесконечности 
быстрее, чем любая степень х-1, если Fo < 0. В то же время вторую 
экспоненту в (13.20) можно представить в виде ряда по степеням
х, так что разложение (13.20) переписывается как
у = cxF*e~F°x~l J] апхп,	(13.21)
п=о
где постоянные коэффициенты ап не зависят от х. Аналогичным
образом можно переписать разложение (13.17) в случае /V^2:
у = cxFn~* ехр [-------— „-г-------ы 1
у	Ч (N — I)?'1 (N — 2) х*’2
ОО
(13.22)
где ап — постоянные коэффициенты, ие зависящие от х.
Сравнение формул (13.19), (13.21) и (13.22) показывает, что
полюс первого порядка всегда можно отличить от полюсов бо-
лее высокого порядка. Действительно, в случае простого полюса
решение (13.19) отличается от решения в обыкновенной точке
множителем xF°. Если же полюс имеет более высокий порядок,
чем первый, то соответствующая форма решения будет отличаться
от представления решения в обыкновенной точке на экспоненци-
альный множитель, который нельзя разложить в ряд по степеням
х, и, кроме того, на множитель х°, где а — некоторая постоянная.
13.2. Уравнения 2-го порядка
349
Отметим, что в случае N = 1 рассматриваемая точка, т. е. на-
чало координат, называется регулярной особой точкой, а в случае
/V =2 2 —иррегулярной особой точкой.
Отметим также, что полученные выше представления решений
не меняют своего вида и в случае, когда у есть вектор-столбец,
a F — квадратная матрица n-го порядка.
13.2.	Уравнения второго порядка
Рассмотрим теперь решения уравнения
у" + р (х) у' + q (х) у = 0	(13.23)
вблизи начала координат. Если р (х) и q (х) являются аналити-
ческими функциями, регулярными в окрестности х = 0, то точка
х=0 называется обыкновенной точкой данного дифференциального
уравнения. В этом случае функции р (х) и q (х) разлагаются в
сходящиеся степенные ряды с ненулевым радиусом сходимости,
причем решение у 'также можно представить в виде сходящегося
степенного ряда по степеням переменной х. В случае если одна
из функций р (х) и q (х) или обе они одновременно оказываются
нерегулярными в начале координат, тогда точка х = 0 называ-
ется особой точкой исходного дифференциального уравнения. Если
р (х) имеет в этой точке полюс максимум первого порядка, а
q (х) — полюс второго порядка, тогда точка х — 0 называется
регулярной особой точкой. При этом по крайней мере одно из
решений уравнения (13.23) имеет вид (13.19). Если р (х) имеет
в точке х = 0 полюс порядка выше, чем первого, или q (х) имеет
в этой точке полюс выше второго порядка, или это имеет место
одновременно, тогда'угочка х = 0 называется иррегулярной осо-
бой точкой, и по крайней мере одно из решений уравнения (13.23)
имеет вид (13.22). Покажем теперь, как строятся решения уравне-
ния (13.23). Для уменьшения объема вычислений рассмотрим лишь
несколько частных случаев, иллюстрирующих характерные свой-
ства получаемых решений. В этом параграфе исследуем случай,
когда начало координат представляет собой обыкновенную точку
дифференциального уравнения.
Обратимся, например, к уравнению
у" + ху' + 2у = 0.	(13.24)
Здесь р (х) = х и q (х) = 2, так что точка х = 0 является обыкно-
венной точкой уравнения (13.24), и, значит, функцию у можно
разложить в ряд Тейлора вида
У(х)=^апхп.	(13.25)
350
Гл. 13. Уравнения с переменными коэффициентами
Дифференцируя (13.25) по х, имеем
у' (х)~ папхпЛ.	(13.26
п=0
Дальнейшее дифференцирование (13.26) по х дает
у" (х) = £ п (п — 1) апхп~2,	(13.27
п=2
поскольку члены, пропорциональные а0 и аг, пропадают. Под-
ставляя разложения (13.25)—(13.27) в исходное уравнение (13.24),
имеем
(13.28

S п(п — 2)апхп~2 4- S папхп~' 4- 2 £
п=2	л=0	л=0
Следующий шаг заключается в том, чтобы приравнять коэффици
енты при одинаковых степенях х. Для этого сделаем замену
индекса суммирования п таким образом, чтобы степени х под
знаком каждой суммы оказались одинаковыми, а именно положи»
п == т 4- 2 в первой сумме и п — т во второй и третьей суммах
В результате находим



S (т 4- 2) (т 4- 1) ат+2хт 4- £ mc^x”1 4- 2 £	= 0,
т=0	т=0	т=0
или
S [(/«+ 1)И4-2)0^24- (m4-2)aj хт = 0.
т—0
Далее, приравняв нулю коэффициенты при х”, получим
рентное соотношение вида
«т+2 = -^Т. /п = 0, 1, 2...........
При этом из (13.30) следует, что
___________	__ аг
ilg — aOf	—	2 9
(13.29
рекур*
(13.30


а3 а1
аъ =--Г = ТТ- а« = ~
а*~	3	3 ’
Др
5
з-5 ’ • '
Таким образом, коэффициенты ап с четными и нечетными
сами оказываются не связанными друг с другом: все четные ко-
эффициенты выражаются через а0, а все нечетные — через ах
В результате мы имеем два линейно независимых решения, в одно
из которых входит множителем коэффициент а0, а в другое —
коэффициент flx. Следовательно,
индек-

У (х) =	(х) 4-	(х),
13.3. Регулярная особая точка
351
где
, \	1	а,**	*'	1	*®	।	Х'' (—2)тт\х2т
— 1 х + 3	3 5 4- 3 5 7 + • • • — 2j (2/п)1
т=0
(13.32)
и
оо т
, \	„ X3 . Xs х? .	VM—l)*2zn	N/9^2
^(х) = х-_д^--—- + ... =	-0/2)*,
т—0
(13.33)
Ясно, что ряд в формуле (13.33) сходится, поскольку мы смогли
записать его сумму в замкнутой форме. Применяя теперь признак
Даламбера к ряду (13.32), имеем
lim --”г-й 7Н - » Пт (-2)™/ni^ (2m-2)1
«->» (« - 1)-й член	(2/п) 1 (-2)'”-1 (т - 1)! х2т"2
..	—2тх2	„ ..	1
= hm \ ,6-------тт- = —х2 lim -s---г
т.оо (2/п) (2т-1)	2т-1
О,
и, следовательно, ряд (13.32) также сходится для всех значений
х. Таким образом, общее решение уравнения (13.24) при любых
значениях х дается формулой (13.31).
13.3.	Решение в окрестности регулярной особой точки
В этом случае каждая из функций р (х) и q (х) или обе одно-
временно имеют особенности в точке х = 0, но в то же время
функции хр (х) и x2q (х) могут быть разложены в ряды Тейлора
по степеням х. Простейшее уравнение такого 'типа имеет место
в том случае, когда
р (х) = рох~1 и q (х) = 70х'2,
где р0 и q0 — постоянные величины. При этом уравнение (13.23)
записывается как
У" +-^-у' + -^y = Q-	(13.34)
Это уравнение называется уравнением Эйлера', как показано ниже,
можно легко построить его точное решение.
Уравнение Эйлера
Перепишем уравнение (13.34) в виде
хгу" + Роху' + qoy = 0.	(13.35)
Ясно, что данное уравнение принадлежит к классу так называе-
мых однородных уравнений, каждый член которых содержит
352
Гл. 13. Уравнения с переменными коэффициентами
из самой
или
(13.
уравнением
1/2
(13.38;

х в той же степени, что и соответствующий порядок производной
от у. Такие уравнения имеют решения вида
z/ = x®,	(13.36)
где а — некоторая постоянная, которая называется обычно
характеристическим, показателем и определяется
уравнения. Подстановка (13.36) в (13.35) дает
а (а — 1) х° 4~ роах® + УоХ° = 0,
о2 + (Ро — 1) о + q0 = 0.
Это уравнение принято называть определяющим
корнями его будут
05,2 = 4"(! ~Ро)± [-у(1 - Ро)2 -
Если корни Oj и а2 различны, то функции х®1 и х®* представляю!
собой два линейно независимых решения исходного уравнения,
Тогда общее решение уравнения (13.35) можно записать Kai
у (х) = CjX®> с2х®* ,	(13.39
где и с2 — произвольные постоянные. В случае если о2 = а2 =s
=	(1 — ро), т. е. при (1 — р0)2 = 4<7о, описанный способ дае!
нам только одно из двух возможных линейно независимых ре
шений, а именно
У1 (х) = х®«.
Второе линейно независимое решение можно получить с помощи
преобразования
где функция и (х)
новка выражения
z/a (х) = и (х)у! (х),
подлежит определению в дальнейшем. Подста
для р2 в (13.35) приводит к уравнению
x2yiu -J- 2х ущ 4~ х?ущ pQxu у 1 4~ рохиу{ 4* Убчу\ — О,
которое после упрощения принимает вид
х*ухи (Ъ?у\ + рохух) и = 0,	(13.40
поскольку у± является решением исходного уравнения (13.35)
Соотношение (13.40) представляет собой уравнение первого па
рядка относительно функции и'. Таким образом, указанный под
ход является общим; он всегда позволяет найти еще одно линейц
независимое решение произвольного уравнения второго порядка
Подстановка выражения для в уравнение (13.40) дает
х®*+2м' + (2<h + Ро) х^+хи — 0,
хи" + и1 = 0.
или
13.3. Регулярная особая точка
353
Таким образом,
и" 1
~ + ~7 —О, или 1пи' + 1пх = О,
и, следовательно , и' = -i-, или и = 1пх.
Окончательно имеем
уг (х) = ха‘ 1п х.	(13.41)
Решение (13.41) можно получить и другим способом. Так,
полагая в уравнении (13.35) у = ха, имеем при ох = о2
+ Роху' + ЯоУ = (о2 + (р0 - 1) а + ft] х° = (а- oj2 х°. (13.42)
Дифференцирование (13.42) по о дает
х^ (#) + ^4 (-Й-) +	= 2(О-О1)х° + (o-o^x’lnx.
(13.43)
Полагая теперь а = ©j в (13.42) и (13.43), мы видим, что функции
у и ду/да должны удовлетворять исходному дифференциальному
уравнению при о = Следовательно, одним из решений ис-
ходного уравнения будет функция ух = х°«, а вторым — функция
= -й- Ц =	l’=°*=x<5i 1п х
в полном соответствии с формулой (13.41).
Приведенный пример показывает, что случай одинаковых
показателей требует специального рассмотрения. Как показано
ниже, такое рассмотрение может потребоваться даже тогда, когда
Oi и о2 различны, но их разность равна некоторому целому числу.
Перейдем теперь к рассмотрению уравнений более общих,
чем, уравнение Эйлера, причем мы начнем со случая неравных
показателей, разность между которыми не есть целое число.
Случай, когда о2 — ©i =+ целому числу
Рассмотрим уравнение
4х/ + 2у' + 0 = 0.	(13.44)
Здесь р (х) —	х"1 и q (х) = ~ х-1, и, следовательно, х = 0
есть регулярная особая точка этого уравнения. Поэтому уравнение
(13.44) обладает решениями в так называемой форме Фробениуса
у = ха^апхп=^апхР+п.	(13.45)
п=0	п=0
Подстановка (13.45) в уравнение (13.44) дает
4 S (о + п) (о + п — 1) a/>xa+ft'1 + 2 S (о + п.) апха+п~1 +
л=0	л=0
+ алх®+л = 0.	(13.46)
п=0	।
12 Найфэ А. X.
354
Гл. 13. Уравнения с переменными коэффициентами
Главные члены первых двух сумм в (13.46) пропорциональи
х°~', тогда как главный член в последней сумме оказывается пр
порциональным х°. Поэтому основное соотношение, определяют
вид характеристических показателей, можно получить, полож1
коэффициент при х”^1 равным нулю, т. е.
4а (а — 1) й0 + 2ад0 = 0-	(13.4
Тогда соотношение (13.46) принимает вид
У 2 (а + п) (2а + 2п — l)Ja„x<5+n-1 + £ апха+п = 0.
л=1	п=0
Показатели степени х в каждой сумме можно сделать одинаковым:
полагая п — т + 1 в первой сумме и п = т — во второй,
результате имеем уравнение
00
S [2(а4-/п+ 1)(2а + 2/п+ 1) ат+1 + ат] х°+т = О,
/71=0
из которого, последовательно приравнивая нулю коэффициент
при хГ+т, можно получить рекуррентное соотношение
«т+1 = — 2(а + т+ 1)^20 +2т + 1)’	(134i
При этом из формулы (13.47) следует, что либо а0 = О (что с<
ответствует тривиальному решению), либо
4а2 — 4а + 2а = О,
откуда	а1 = 0 и а2 = -|-.
В данном случае показатели а2 и а2 не равны друг другу, а и
разность равна Ц-, т. е. отлична от целого числа. Поэтому можг
построить два линейно независимых решения, соответствуют^
разным значениям а.
Так, полагая в формуле (13.48) а = 0, находим
“m+i—	2 (тп + 1) (2т + 1) ’
откуда
п __ __ °о „ ____	°1	_ во п ______ а2	__ во
1	2	,	«2 —	2 2	3 — 41	,	«3—	2 3 -5	~	6!	’ ‘	‘
Следовательно, выбирая а0 — 1, имеем
оз*
т=0
Этот ряд сходится при всех х, поскольку
lim __от2й.член = ит bl)CT<(,2/n-2)l =Q
(m - 1)-й член	(2/П)! (-1)'”-1 Хт'1
13.3. Регулярная особая точка
355
Полагая теперь в формуле (13.48) а = получаем
am+i = — 2(/n + l)m(2/n + 3) ’
откуда
______Q0__________________	fll _ а0	_______а2	а0
2-3 ’	2-2-5 — 5! ’	3"“	2-3-7 ~_71 ' ' " '
Следовательно, выбирая а0 = 1, имеем
УЛх>~х (J 31' 5!	71'91'	/	Д)(2/п+1)!
т=0
(13.50)
Легко показать, что построенный ряд сходится при любых зна-
чениях х. Таким образом, в данном случае как и для уравнения
Эйлера, мы получим два линейно независимых частных решения,
соответствующие разным корням характеристического уравнения.
Случай, когда а2—о1 равно целому числу
Рассмотрим здесь два уравнения: решение одного из них мы
получим, используя описанный выше способ, решения же второго
получаются в результате некоторого видоизменения указанной
процедуры. Начнем с уравнения
(1 — х2) у" + 2ху' + у = 0.	(13.51)
Действуя как и ранее, будем искать решение у (х) в форме (13.45)
Подставляя (13.45) в уравнение (13.51), имеем
(1 — х2) £ (а 4-п)(а 4-п— 1)<^х0+п-2 4-
+ 2 2 (а + п) апха+п 4- 2 апх°+п » 0,
П«0	Па>0
ИЛИ
S (о п) (а + п — 1) а„х°'+п’2 4-
п=0
4- Zj [1 4"3(а4~п) — (а4~я)2]«„x<5+n = 0- (13.52)
п=0
Главными членами в разложении (13.52) являются члены с х°~2 и
Xе7'1; они соответствуют значениям индекса п = 0 и п = 1 в
первой сумме. Приравнивая нулю коэффициенты при указанных
степенях х, находим
а (а — 1) а0 = 0,	(13.53)
(а 4- 1) <зах = 0.	(13.54)
12*
356
Гл. 13. Уравнения с переменными коэффициентами
Тогда (13.52) переписывается в виде
2 (о + п) (а 4- п — 1) апк°+п-2 4-
п=2
оо |
+ S 11 + 3 (а + п) — (а п)2] апха+п = 0.
п=0
Как и ранее, приведем показатели степени при х в обеих суммах
к одинаковому виду; с этой целью положим п — т 4- 2 в первой :
сумме и п = т во второй сумме. В результате получим
ОО 1
{(о 4~т 4- 2) (° 4*т 4- 0 йт+2 4-
т—0
4- [ 1 + 3 (а 4- т)—(а 4- т)21 ат} ха+т — 0.
Далее, приравнивая нулю коэффициенты при последовательных
степенях х, находим
п _ _ 1 + з (ст + т) — (ст + /п)2
"1+2 (g + т + 2) (g + т + 1) т‘
(13.55)
Из соотношения (13 53) следует, что при а0 =4= 0 а = 0 или
а = 1. В случае когда а = О, уравнение (13.54) удовлетворя-
ется автоматически, а значение может быть выбрано произ-
вольно. Если же а = 1, то из соотношения (13.54) следует, что
а± = 0.
При а = 0 формула (13.55) принимает вид
п —	1 + 3m — та
От+2--------(т+ 1)(т + 2) а”'
откуда
п ___ ао __________ аа _ °о _ __________	____до
Оа —	2	>	«4 —	4 — 8	> ав —	10 — 80	> • • • »
п _ _ «1	„ _ «э _ «1	„ _ За5 _ Зв!
 3	2 ’	6	20	40 ’	14 — 560 ........
Следовательно, получаем решение
Pi х® . х4 .	.	1 .
у(х) — Пор — т+т + -§0-+ ••'] +
। Г. х8 , х6 , Зх7 . "I
[Х 2 + 40 + 560	' ’] ’	(13.56)
которое содержит две произвольные постоянные и которое поэ-
тому должно быть общим решением исходного уравнения. При
этом суммы в квадратных скобках представляют собой два ли-
нейно независимых частных решения уравнения (13.51). Исполь-
зуя признак Даламбера, легко, показать, что оба ряда в решении
(13.56) сходятся при любых значениях X.
13.3. Регулярная особая точка
357
При а = 1 из соотношения (13.54) следует, что аг — 0, а
формула (13.55) принимает вид
п —	1+3(т+1)-(т +Л)а „
(/n + 2)(m + 3) ат‘
Тогда
аз ~ аъ= ai ~	~ tyn+i = • • • = О,
_____ а0	__ а2 _____ а0 п 	 3^4 	 ЗОд
«2 —	2 ’	~	20 — 40 ’_14_560 ’ ’ ’ ' ‘
В результате имеем разложение
, Г, х2 *, х4 , '3х« ,	1	ло
у~OqX И 2 + 40 + 560 + •••]>	(13.57)
лишь постоянным множителем отличающееся от второго част-
ного решения в разложении (13.56), которое, как уже упоминалось
выше, дает общее решение уравнения (13.51).
Перейдем теперь к исследованию случая, в котором требуется
несколько видоизменить описанную выше процедуру, а именно
рассмотрим уравнение Бесселя первого порядка
х*у" + ху' + (х2 - 1) у = 0.	(13.58)
Как и ранее, подстановка разложения (13.45) в уравнение (13.58)
приводит к соотношению
У (о + п) (ст + п — 1) a,1xo+n 4-2 (ст + п) апха+п 4-
п~0	п=Л
4-(х2-1) 2 а„х°+п« 0,
п*0
которое можно переписать в виде
2 [(ст 4- п)8 — 1 ] апх0+п + £ ОяХ’*"*8 — 0,
ИЛИ
(ст2 — 1) айх° 4- ст (ст + 2) СхХ®*1 + 2 1(я 4~ л)2 — 1] апх’+п +
п=2
+ 2й^+п+2 = 0' (13.59)
п=0
Полагая коэффициенты при главных членах разложения, т. е.
членах с хР и x?+l в (13.59), равными нулю, имеем
(ст2 — 1) а0 = (ст — 1) (ст + 1) а0 — 0,	(13.60а)
[(ст + I)2 — 11 ах = ст (ст 4- 2) ах = 0.	(13.606)
При этом соотношение (13.59) принимает вид
2 [(о 4- п)2 ~~ 1] апх°+п -р 2 апха+п+2 == 0.	(13.61)
п=?	n—Q	’
358
Гл. 13. Уравнения с переменными коэффициентами
Для того чтобы привести показатели степени х в каждой сумме Я
к одинаковому виду, положим п = т + 2 в первой сумме и п = Я
— т — во второй. В результате получим	|
S U(O + т + 2)2 —l]am+2 + ат\ ха+т+2 = q	j
т=0	Я
Приравнивание коэффициентов при последовательных степенях 1
х приводит к рекуррентному соотношению	И
ат+2 = (а + т + 2)2— 1 = ~(а + /п+ 1)(о + /п + 3) * (13’62) 1
Из формулы (13.60а) следует, что при а0 =^= 1 показатель 1
о равен ± 1- Тогда из (13.606) находим, что аг = 0 и, следо- я
вательно, а3 = аь = а7 = ... —а2п+1 = ... =0. Полагая в (13.62) |
о —1, имеем	,1
(13-63)|
Если положить теперь в формуле (13.63) т = 0, то коэффи- я
циент а2 оказывается равным бесконечности. Таким образом, |
описанная выше метвдика не позволяет получить решение при |
а = —1.	'Я
В случае когда а = 1, из рекуррентной формулы (13.62) |
следует, что	|
а —___________“т_______	’ I
т+2 (м + 2) (т + 4) •	I
Поэтому	I
_______go п ________ а»________Др
2~	ТТ’	4~	4.6 “* 2-4»-6 ’	|
п    а*   До	|
6-8 ~	2-4» 62-8..................... 1
и, следовательно,	1
У1 (х) — Л(х) = аоХ [ 1	+ 2.42.6	2-42-62'8
(13.64)
Построенный ряд представляет собой одно из решений урав- |
нения (13.58); при а0 = ~ он обычно называется функцией )
Бесселя 1-го рода первого порядка и обозначается через /j (х). s
Для того чтобы найти второе линейно независимое решение j
уравнения (13.58), можно воспользоваться одним из приемов, -
применявшихся для построения второго решения уравнения Эй-
лера в случае равных показателей, т. е. равных корней определяю-
щего уравнении, Здесь мц используем второй из описанных там '
13.3. Регулярная особая точка.
355
способов, а именно выразим коэффициенты ат через а0, не подстав-
ляя соответствующее значение о. Тогда из формулы (13.62) имеем
д ____________а»
2~ (О +1)(а + 3)’
д ___ а%'	_ а0
(а + 3)(а + 5) (а + ]) (а + з?(о + 5) ’
=__________«л _______________________«о____________
(а + 5) (а + 7) (а + 1) (а + 3)* (а + 5)2 (or + 7) ’
и, следовательно,
z \ _ л Г	аох2 ।	ао*4
У ~ Г°	(а + I) (а + 3) + (а + 1) (а + З)2 (а + 5)
(а+1)(а + ЗНа + 5р(а + 7р ]’
Как и ранее, если положить в разложении (13.65) о = —1, то
соответствующие коэффициенты обратятся в бесконечность ввиду
наличия в их знаменателях множителя (а + 1). Для того чтобы
обойти это затруднение, выберем а0 равным b (о + 1). При этом
из разложения (13.65) имеем
у = Ьха [(о -j- 1) — а + 3 + (Ст + 3)2 (а + 5) “
(а + З)2 (а + 5)2 (а + 7) + '']’	(13.66)
откуда после подстановки в дифференциальное уравнение (13.58)
находим
х2у" + ху' + (х2 — 1) у = b (о + I)2 (а — 1) х°. (13.67)
С другой стороны, уравнение (13.67) можно получить прямо из
формулы (13.59), полагая в ней а0 = Ь (о + 1),	= 0 и учитывая
соотношение (13.61). Как и для уравнения Эйлера в случае рав-
ных корней определяющего уравнения, наличие квадратичного
множителя (а + I)2 в правой части (13.67) приводит к тому, что
функции у и ду/да должны удовлетворять исходному дифферен-
циальному уравнению при о = —1. Полагая теперь в (13.66)
а = —1 и принимая b — 1, приходим к разложению
^1(х)-х-1[-4+•••]’ <13-68а)
которое лишь постоянным множителем отличается от (13.64).
Далее, дифференцируя (13.66) по о и полагая 5=1, имеем
^2 = ~да ~ У1° х + х° Р + (or + З)2
Г 2 г 1	1 л [	1
L (or + З)2 (<т + 5) + (сг +З)2 (СТЧ-J ' J’
360	Гл. 13. Уравнения с переменными коэффициентами
откуда, полагая о = —1, находим
^(х) = ^(х)1пх + ^[1	. • .] .	(13.686)
Таким образом, разложения (13.64) и (13.686) представляют co6oij
два линейно независимых решения уравнения (13.58). Используя
признак Даламбера, можно легко показать, что построенные для
Hi и Уг ряды сходятся при любых значениях х.
Случай о2 = 0!
В качестве следующего примера рассмотрим уравнение Бес-
селя нулевого порядка
ху" + у' + ху = 0.	(13.69)
Как и ранее, подставляя разложение (13.45) в уравнение (13.69),
имеем
S (о + п) (о + п - 1) апх<’+«-1 + £ (о + п) апха+п~1 +
п=о	п==о
+ Ё anx°+n+l = 0,
л=0
ИЛИ
S (а + п}2апхП+п~х 4- S а„ха+'1+1 = 0,
п=о	п=0
ИЛИ
о2670х°-1 + (о + I)2 а1*°+ S (а + пУ апха*п~' + У, anxa+n+l = 0. (13.70)
п=2	п=о
Приравнивая нулю коэффициенты при первых двух степенях х,
т. е. при х”-1 и ха, находим
аЧ = 0,	(13.71а)
(о + I)2 ах = 0.	(13.716)
Соотношение (13.70) в этом случае переписывается в виде
S (а 4- п)2 а^0^-1 + £ anx°+n+l = 0,	(13.72)
л=2	zi=0
откуда, полагая п = т + 2 в первой сумме и п — т — во второй,
получаем
£ l(a + tn + 2)2 ат^ + ат] ха+т+1 = 0.
ГП=О
Приравнивание коэффициентов при последовательных степенях
х приводит к рекуррентной формуле
ат+а = ~ (а + mm+2)* ’	(13’73)
13.4. Бесконечно удаленная точка
361
Из соотношения (13.71а) следует, что при а0 0 оба характе-
ристических показателя равны нулю; при этом из (13.716) получаем,
что аг = 0. Следовательно, используя прямую методику Фро-
бениуса, можно построить только одно решение уравнения (13.69).
Поэтому прежде всего попытаемся найти зависимость решения
у от величины о. Из формулы (13.73) имеем
аЯ — аЬ — а1 —    = аЯп+1 = • • • — 0
И
_____ а0	_ ________а2____________а0______
2~ (ст 4-2)2 ’	4 (ст 4-4)2	(<т 4-2)2 (ст 4-4)* ’ ' ' ' ’
Таким образом, получаем
у =	[ 1 — ((Т + 2)2 + (ст + 2)2 (ст + 4)2 —
X®	"1
~ (ст + 2)2 (а + 4)2 (а + 6)2 + ' J'	(13.74)
Подстановка разложения (13.74) в уравнение (13.69) дает
ху" + у' 4- ху = atfjx0-1.	(13.75)
С другой стороны, уравнение (13.75) можно получить из (13.70),
полагая = 0 и используя соотношение (13.72). Как и ранее,
наличие квадратичного множителя о2 в правой части (13.75)
приводит к тому, что функции у и ду/да должны удовлетворять
исходному дифференциальному уравнению при а = 0.
Полагая теперь в (13.74) а = 0 и выбирая а0 = 1, приходим
к решению следующего вида:
г/1(х) = Л(х)^1--^+ 2^2- - 22.12.62 + ••••	(13.76)
Далее, дифференцируя (13.74) по а и принимая а0 = 1, получаем
du t _ (	24
^=//lnx + x-’(-FW--
__ Г______2________I______2______1 4 I ... 1
L (ст + 2)а (ст 4-4)2 (а + 2)2 (а + 4)3 J Л “
откуда при 0 = 0 находим второе решение исходного уравнения
^(х) = й(х)1пх + 4--^§-+ ••••	(13-77)
Воспользовавшись признаком Даламбера, можно легко показать,
что ряды для z/i и сходятся при всех значениях х.
13.4.	Сингулярность в бесконечно удаленной точке
В § 13.2 и 13.3 мы строили решения дифференциальных урав-
нений в виде рядов в окрестности некоторой конечной точки.
В этом параграфе мы рассмотрим решения в окрестности беско-
362
Гл. 13. Уравнения с переменными коэффициентами
нечно удаленной точки. Для того чтобы выяснить, является ли!
бесконечность обыкновенной или особой точкой данного урав-|
нения, а также выяснить характер ее особенности, бесконечно!
удаленную точку обычно переводят в начало координат с помощью]
подстановки z = х~г. При этом	1
d d dz 1 d <, d	|
dx dz dx x2 dz	dz ’	|
d2 =_2_	_O,3_£. i JL	1
dx2 x2 dz “г x^ dz2 dz ' dz2 '	1
Тогда уравнение (13.23) переписывается в виде	1
+ 2‘	(4) 4+ч (4) у=».
ИЛИ	.1
4-+[4-4'’(4)]4+4?(4)('=0- <13-78)|
Таким образом, х = оо будет обыкновенной точкой уравнения 1
(13.23), если точка г = 0 будет обыкновенной точкой для уравне-1
ния (13.78). Следовательно, бесконечно удаленная точка будет ]
обыкновенной точкой для уравнения (13.23), если функции 1
и ТГ'Цт)	1
представляют собой аналитические функции, регулярные в ок- ]
рестности точки г = 0; в противном случае бесконечно удаленная I
точка будет особой точкой исходного уравнения. Указанные yc-J
ловия равносильны требованию, чтобы функции	1
2х — х2р (х) и xiq (х)	i
разлагались в сходящиеся ряды Тейлора по обратным сте- j
пеням х.	1
В качестве	примера рассмотрим	уравнение	|
у' + (4 + 4-) у' +(4- + т-)у = °-	(13 79)1
Подстановка	z	= х-1 переводит его	в уравнение	1
-й--з4+(2г+1)^=°-	(13-8°)1
Поскольку точка г = 0 является обыкновенной точкой для урав- -з
нения (13.80), то бесконечно удаленная точка также будет обы- |
кновенной точкой для уравнения (13.79). Следовательно, решения I
уравнения	(13.79)	могут	быть	представлены	в	виде сходящегося |
ряда	I
(13-81)|
п=Э	ч
где ап — некоторые	постоянные	коэффициенты.	1
1$.S. Иррегулярная особая точка	563
В качестве второго примера рассмотрим уравнение
*'+G-+4>' + (t + i-)» = 0-	(13.82)
После преобразования z = х"1 оно принимает вид
S- + (t-3)->+(t+I2)«=°-	<13-83’
Поскольку z = О есть регулярная особая точка уравнения (13.83),
то бесконечность будет регулярной особой точкой для уравнения
(13.82). Следовательно, по крайней мере одно из решений урав-
нения (13.82) можно представить в виде сходящегося ряда
Го©
<13М)
с постоянными коэффициентами ап. Второе частное решение этого
уравнения строится с помощью формулы (13.84), как это делалось,,
например, в предыдущем параграфе.
В качестве последнего примера исследуем уравнение Бесселя
нулевого порядка
ху" + у' + ху = 0.	(13.85)
После подстановки z — х-1 оно приобретает вид
Й + —#+-rZ/ = °-	(13.86)
dz2 ' г dz ' z4	v ’
Поскольку г — 0 есть иррегулярная особая точка уравнения
(13.86), то бесконечность также будет иррегулярной особой точ-
кой уравнения (13.85). Приближенные представления решений
дифференциальных уравнений второго порядка вблизи иррегу-
лярной особой точки рассмотрим в следующем параграфе.
13.5.	Решение в окрестности иррегулярной
особой точки
Как указывалось в § 13.1, если начало координат есть ирре-
гулярная особая точка уравнения (13.23), то решения этого урав-
нения имеют вид
- у (х) = еЛ (*)хаи (х),	(13.87)
где функция и (х) может быть представлена в виде ряда (не обя-
зательно сходящегося) по степеням xm/n, Л (х) — некоторый
полином от x~m/n, а т и п —простые числа. В случае п = 1 та-
кое решение называется нормальным, если же п 1, то оно на-
зывается субнормальным решением. В этом параграфе мы рас-
смотрим три примера — уравнение, для которого существует
нормальное решение, уравнение, для которого имеется субнор-
мальное решение, и уравнение с иррегулярной особой точкой на
бесконечности.
364
Гл. 13. Уравнения с переменными коэффициентами
Пример 1. В качестве первого примера рассмотрим уравнение
х2/ — (1 — Зх) у' 4- у = 0,	. (13.88)
которое, как мы покажем ниже, обладает нормальным решением
вблизи начала координат, являющегося в этом случае иррегу-
лярной особой точкой. Для того чтобы определить вид много-
члена Л (х), прежде всего найдем его главный член. Принимая,
что главный член в Л (х) имеем форму Xx-V, положим
	у-	еКх v.	(13.89)
Тогда			
и' ~ — Zv Р/х^ У	xv+i е »	У” ~	Г X2v2 , [^v+2	h	eKx'V' (13-9°)
Подставив выражения для у, у' и у" в уравнение (13.88) и раз-
делив на х2, получим
x2v+2 1	Ху (v + В , xV+2	।	Ху xv+3	— —J- J_ _L . . . = 0 xV+2 1 x2 ’	(13.91)
Поскольку сохраняя в	при x-> 0 (13.91) лишь	X'2v~2 X» x-v-2 и x-v-3	x- основные члены, находим		v-2, jo,
	Л2 ,	Xv		(13.92)
	x2v+2 ।	xv+3 1		
Далее нужно приравнять соответствующие показатели степени
у переменной х. Поскольку эти показатели степени зависят от
величины v, то здесь возможны три варианта:
2v + 2 = v + 3, 2v 4-2 = 2 и v + 3 = 2;
соответственно получаем три значения v: v = 1, v = 0 и v=—1.
Однако из этих значений нужно выбрать лишь самое большее,
поскольку в противном случае мы не сумеем скомпенсировать
главный член в (13.92). Например, если выбрать значение v = О,
то первый член этого разложения будет иметь порядок х"2, вто-
рой член — порядок х~3 и третий — порядок х-2. 'Следовательно,
мы не сможем подобрать величину X таким образов, чтобы исклю-
чить главный член, которым в этом случае окажется второе сла-
гаемое в разложении (13.92). В случае же v = —1 многочлен
Л (х) -> 0 при х 0, и поэтому функция ехр [Л (х)] будет
представима рядом по степеням х, что позволит объединить ее
с функцией и (х).
В то же время в случае v = 1 главными членами разложения
(13.92) окажутся первые два слагаемых. Их можно скомпенсиро-
вать, положив
Vv2 + Xv = О, или X2 + % = О,
откуда X = О или —1.
1$.5. Иррегулярная особая точка
365
В случае X = 0, подставляя ряд
У(х)=Ъап^ ,	(13.93)
ftssO
в уравнение (13.88), получаем
S (ст + п) (ст + п — 1) апха+п — (1 — Зх) £ (ст + п) а,.ха+п-1 +
+ S а/+»=0,
л=р
или
S (ст + п+ I)2 апха+п - S (стЧ-п)а„х<г+"'! = 0.	(13.94)
п=0	п=0
При этом главный член в (13.94) оказывается пропорциональным
ха-1, что соответствует слагаемому с индексом п = 0 во второй
сумме. Если положить коэффициент при ха-1 равным нулю, то
имеем
ста0 = 0,	(13.95)
и разложение (13.94) приобретает вид
2 (о + п + I)2 апх°+п — £ (ст 4- и) anxa+rt*1 = 0.
п=0	л=1
Отсюда, полагая п = т в первой сумме и п = т 4* 1 — во вто-
рой сумме, находим
S [(ст + т + I)2 ат — (ст 4- т + l)am+i] xa+m = 0.
m«=0
Приравнивая нулю коэффициенты при последовательных степе-
нях х, получаем
«m+i = (ст 4- т 4- 1) ат.	(13.96)
Из формулы (13.95) следует, что при а0 =/= 0 ст = 0. Тогда из (13.96)
получаем
«m+i = (т 4- 1) ат,
и, следовательно,
== Uqi @2 —	— 2£Zq, tZg — 3tZg 31
a4 == 4a3 = 41 a0,	a6 = 5a4 = 5!«0, . .
или
i/1(x) = a0[l 4-x4-2!x24-3lx34-4lx*4-5lx54------].
Таким образом, имеем
уг(х) ~ а0 £ ш\хт.	(13.97)
т=0
366	Гл. 13. Уравнений. с Переменными коэффициентами	|
Используя признак Даламбера, легко показать, что ряд (13.971
расходится для всех значений х; именно поэтому мы воспользо!
вались вместо знака равенства знаком асимптотического соот*
ветствия. То, что построенный ряд оказался расходящимся^
не должно являться для нас неожиданным — ведь начало коор-;
динат представляет собой иррегулярную особую точку рассмат-?
риваемого уравнения.
В случае X = —1 положим
у’(х) = v (х)+хр (—	,	(13.98>
откуда
У = (У'+-^)ехр(~4-)-	I
•Подставляя выражения для у, у' и у" в уравнение (13.88), имеем!
xV + 2у' — ~ v + v — v' — ^-и + Зхи' + v + v = О, I
или	j
xV'+(l +3x)v' + (l +-L)v = 0.	(13.99)]
Поскольку экспоненциальный множитель ехр [А (х)] уже вклю-
чен нами в выражение (13.98) для у (х), будем искать решение
v (х) в форме Фробениуса
v (*) — S	(13.100)
п=о	•
Подстановка ряда (13.100) в уравнение (13.99) дает	;
S (ст + п.) (ст + п - 1) апх°+п + £ (ст + п) апха+п-1 +	;
п=0	п=0
+ 3 2 (ст + h) апх°+п + 2 апха+п~1 + 2 о„ха+п = 0,
п=0	п=0	п=0
ИЛИ
£ (ст + п+ Оа^-Ч- 2 (ст + « + рг^х^^О. (13.101)-
п=0	п=0
Полагая главный член в (13.101) равным нулю, находим
(0+1)00 = 0.	(13.102)
При этом (13.101) принимает вид	:
£ (ст + п + 1) апха+п-' +2 (ст + п + I)2апха+п = 0,	.!
П=0	•;
13.5. Иррегулярная особая точка
367
откуда, полагая п = т + 1 в первой сумме и п = т — во вто-
рой сумме, имеем
S [(ст +/и + 2)tzm+1 + (ст + m + \yam]x^m^Q.
т=0
Наконец, приравнивая нулю коэффициенты при последователь-
ных степенях х, получаем
W = -	(13.103)
Из соотношения (13.102) следует, что в случае а0 0 ст —
= —1; тогда из формулы (13.103) находим
__ т2
— — m + ]
откуда (Zj = а2 — as = ... = ат = 0 для т =/= 0, и, следовательно,
ряд (13.100) обрывается на первом члене. Таким образом, если
принять а0 = 1, имеем окончательно
f/2(*) = 4-!exP	(13.104)
При этом, поскольку экспонента в формуле (13.104) включает
в себя обратные степени х, функция у2 (х)’есть нормальноё ре-
шение исходного уравнения.
Пример 2. В качестве следующего примера рассмотрим урав-
нение, обладающее субнормальными решениями вблизи начала
координат, а именно уравнение
х3/ — х2у’ — у = 0.	(13.105)
Поскольку точка х = 0 является иррегулярной особой точкой,
то решения уравнения (13.105) будут иметь вид (13.87). Для того
чтобы определить явным образом функцию А (х), предположим,
что главный член решения имеет форму (13.89). Подстановка
выражений (13.89) и (13.90) в уравнение (13.105) приводит к
соотношению
^+24Н-1+-£г~1+---=0' (13-106)
основными членами которого являются первое слагаемое и,
возможно, последнее. Чтобы скомпенсировать эти члены, потребуем
выполнения условий v = и XV = 1. Тем самым X = ±2,
и, принимая в (13.106) v = мы лишь подтверждаем предпо-
ложение о том, что основными членами в этом соотношении яв-
ляются первый и последний.
Итак, в данном случае решение у имеет вид
y = e±2x-i/2y^	(13.107)
368
Гл. 13. Уравнения с переменными коэффициентами
Поскольку экспонента в формуле (13.107) включает в себя дроб- i
ные обратные степени х, такое решение называется субнормальным
решением. При этом из '(13.107) следует, Что
у' = (v' =Р %-3/2и) ехр (±2х-1/2),
у" = (у" Т 2х“3/2и' 4- x~3v ±	ехр (±2х~’/2).
Подставляя выражения для у, у', у" в уравнение (13.105), получаем
x3v" =F 2х3/2п' D ± -g- xx/2v — x2v' ± xx/2v — v= 0,
или	x3v" — (x2 ± 2X3/2) a' ±-|-Xi/20 —q.	(13.108)
Далее, будем искать решение уравнения (13.108) в виде ряда по
степеням х1/2, т. е.
v ~ £ anx(<J+n)/2.	(13.109).
п=0
Подстановка этого разложения в (13.108) дает
ОО	оо
24"(° +	+ п — 2)anx^+nW2 —	-^-(о 4- n)anx(<I+n+2)/2T ’
п=0	п=0
ИЛИ
^2 у (о + л) апх<0+'г+1>/2 ± -|- anx<cr+rt+1 = 0,
п=0	п=0
2 -4 (° + П) (° + П — 4) dnx(a+n+2)/2 4-
п=0
2 (±-ГТОТП)а'‘Х(О+П+1)/2:=0-	(13.110);
п=о	;
Главный член в разложении (13.110) представляет собой слагае-
мое, пропорциональное х(0+1^2, что соответствует члену с ин-
дексом п = 0 во второй сумме. Приравнивая этот член нулю,
находим
(±4-Тст)0о = 0-	(13.111)
Далее, полагая п — т в первой сумме и п = т + 1 — во второй
сумме, перепишем разложение (13.110) в виде
ОО
X {"Г (° + т^а + т ~ ^ йт +
т—0
4- (±4" + ° т + 0Qm+1} x(o+m+2)/2 = 0,
13.5. Иррегулярная особая точка
369
Приравнивание нулю коэффициентов при последовательных сте-
пенях х дает рекуррентную формулу
«г,1 + 1 =
(<т + т) (<т + « — 4)
/5	X и,п'
4 ( ± -у 4= а Т т Т 1 )
(13.112)
Из соотношения (13.111) следует, что при а0 #= 0 o = -g-.
Тогда формула (13.112) принимает вид
^т+1 — i "	[ + ю| сл 'Т ьэ| СО	ат,	(13.113)
	4(m + 1)	
3-5	7-1	3.5-7
откуда аг = =Р	а0,	а2 И" ' 16.2 а1~	162-2
«з = ±
9.1 „	, 3-5-7.9
16-3 а2 — ± 163.3! а°’
, 1L3 „	32-5.7.9.1!
16-4 С^~	164-41
и, следовательно,
У1 (х) ~ ^-1/2х5/< [1 -	+
3.5-7-Эх3/2	32.5-7-9.llx2	1	.
+	16»-3!	+	16*-4J	+ j
у2 (х) ~	[1 +	+	- •
3.5-7-9Х3''2 , 32.5-7-9.11x2	1
------16М!~ +--------16М!— + •••]•	(13Л15)
Используя признак Даламбера для ряда (13.109), в соответствии
с рекуррентным соотношением (13.113) получаем
lim
m-*oo
(т + 1)-й член ______
/n-й член
lim
m-*oo
am+^+m+l>'2
атЛ
^xVMim
Щ-юо аТП
±00.
Таким образом, ряды (13.114) и (13.115) являются асимптоти-
ческими, в связи с чем мы воспользовались в них не знаком
равенства, а знаком асимптотического соответствия.
Пример 3. В качестве последнего примера рассмотрим построе-
ние приближенного решения для уравнения Бесселя нулевого
порядка
(13.116)
ху" + у' + ^ = 0
370	Гл. 13. Уравнения с переменными коэффициентами
при больших х. Как было показано в § 13.4, точка х = оо явля-
ется для этого уравнения иррегулярной особой точкой. Поэтому
решение уравнения (13.116) при больших х имеет вид
у(х)~еМх)хаи(х),	(13.117)
где Л (х) — полином от хт/п (т, п — простые числа), а функция
и (х) может быть представлена рядом по обратным степеням хт/'г.
Для того чтобы определить вид функции Л (х), предположим,
что главный член (13.117) можно представить в форме
(13.118)
Тогда
у' ~ A/vxv~'eXxV, у" ~ [X2v2x2v~2 + Xv (v — 1) xv~2] eKxV,
и подстановка выражений для у, у' и у" в уравнение (13.116) дает
X,2V2X2V-I Xv (v - 1) xv~1 + Xvxv-1 + х J--= 0. (13.119)
При x-> оо основными членами в (13.119) будут первое и послед-
нее слагаемое, причем для того, чтобы они скомпенсировали друг
друга, необходимо выбрать
v=l и X = ±i.	(13.120)
В случае X = i положим
у — eix v (х)
и, подставив в уравнение (13.116), получим
х (и" + 2iv' — v) + v' + iv + xv — 0,
или	xv" + (2ix + 1) v' + iv = 0.	(13.121)
Будем теперь искать решение уравнения (13.121) в форме
v ~ £ апх~а~п,	(13.122)
п=0
что при подстановке в это уравнение дает
2 (о + п) (о + п + 1) апх~а-п^’ — 21 У (о + ti) апх~а~п —
я==0	л=0
— S (° + «) апх-°-п-1 + i S апх~а~п 0,
п=0	п=0
или
S (о -ф- п)2 апх~а~п-' + i 2 (1 — 2о — 2п) апх~а~п = 0. (13.123)
п=0	п—й
Главный член в этом разложении пропорционален х~а; он соответ-
ствует индексу п = 0 во второй сумме. Приравнивая этот член
нулю, получаем
(1 — 2о) а0 = 0.	(13.124)
13.5. Иррегулярная особая гйочкй
371
Далее, полагая п = т в первой сумме и п = tn + 1 — во второй
сумме, перепишем разложение (13.123) в виде
S [(ст + т)2 ат — t (2ст + 2/и + 1) а„+1] х~а-т~1 = 0.
т=0
Положив коэффициент при соответствующей степени х равным
нулю, находим
«т+1 = — 2а + 2m + 1 йт'	(13.125)
Из соотношения (13.124) следует, что при а0 0 ст = в ре-
зультате рекуррентная формула (13.125) приведется к виду
 _	'НУ
«т+1—	2(т+1)	°"’
откуда
_ iao п _	_	1-32а0
“1	4.2 ’	°2	' 4-22	42-23 ’
52»а2 _ 1-32-52<а0	„	72ш3 _ 1-32-52-72а0
йз—'	4-3! ~ 43-23-3! ’	4-2-4 ~ 44-24-4! ........
Таким образом,
, ч _|/9 Г, 1	•	1-32	,	1-32-52	. ,
У(х) — е *	[1	4-2х 1	42-22-2!х2 "I 43-23-31лг3 1 +
. 1-32-52-72 .	]	1<мп
+ 44.24.4 |Х4 + • • • J прих+оо. (13.126)
Поскольку отношение двух последовательных членов этого раз-
ложения
i(2m+l)2
— —гтг—*- —100	при т оо,
8 (т + 1) х	к
то ряд в (13.126) расходится при любых значениях х. Однако
при больших х он все же представляет собой асимптотическое
разложение решения, поскольку его старшие члены с ростом т
убывают очень быстро.
Отделяя в (13.126) вещественную и мнимую части, получаем
следующие два линейно независимых решения уравнения (13.116):
ух ~ x-1''2(«cosx + vsinx)	(13.127)
и	Уг ~x~!/2(usinx — vcosx),	(13.128)
где
, ч	1	12-32	, 12-32-52-72 .	,,о 10Q,
и (х)	1	42-22-2!х2 + 4*-24-4!х4 + ’’’’	(13.129)
, ,	1	12-32-52	.	/JQ	1ОЛ\
и (.х) = Т-5---лч о-г-'о , . 4- • • • •	(13.130)
\ /	4-2х	48-23-3!х3	1	4
372
Гл. 13. Уравнения с переменными коэффициентами
Таким образом, имеем
J0(x) ~ Аух + В уч при х^-оо, (13.131) ।
где А и В — постоянные, определяемые из обычных начальных 1
условий типа Jo (0) = 1 и J'o (0) = 0. Вместе с тем формула (13.131)
теряет силу при малых х, поскольку при х-> 0 правая ее часть!
становится неограниченной. Следовательно, мы не можем прямо 1
воспользоваться полученным асимптотическим разложением, чтобы |
удовлетворить заданным начальным условиям. Для того чтобы 1
преодолеть это затруднение, обычно пытаются построить интег-1
ральное представление рассматриваемой функции, которое удов- I
летворяло бы исходным начальным условиям. Тогда, определив !
главный член в асимптотическом разложении полученного ин-1
теграла, можно связать постоянные в асимптотическом представ- 1
лении типа (13.131) с соответствующими начальными условиями. I
Интегральное представление функции Ja (х) можно найти I
следующим образом. Разложим функцию ехр (ixsinO) в ряд по I
возрастающим степеням х, т. е.	I
p»*sin6_ 1 । «sinO । («х sin б)* (ix sin б)3	I
e ~ 1 + —П	'----2!----'----3!----H------ I
SQ'xsin 6)”
n!
n=0
(13.132)
Поскольку
lim _ч„лен .. = lim (tx sin 6)” (n — 1)! =	j
«^=0 (n - 1)-и Член	n!(ix sin O)”-1	|
то ряд (13.132) сходится для всех значений х. Интегрируя обе|
части разложения (13.132) по 0 в пределах от нуля до 2л, имеем!
2л	оо	2Л	1
” 1 Г -	J
--2H-J sin"0d0. (13.133)!
о	1

^sin9^
о
п=0
Из формулы (А.38) приложения
следует,
что
2л
-J— [ sin” 0 dO =
/Л J
О
О,
если
п нечетное,
(n-l)(n-3)...3.1
n(n — 2)...4-2	’ если
п четное.
А
Тогда с учетом этой формулы из (13.133) находим
2Л
A_J	+	.... (13.I34)
О
£
13.5. Иррегулярная особая точка
373
Так как, согласно формуле (13.76), ряд в правой части (13.134)
представляет собой функцию Jo (х), то тем самым получаем иско-
мое интегральное представление для Ja (х)
2Л
/о(лг) = -2^ / <?'*sin0d0,	(13.135)
о
удовлетворяющее начальным условиям Jo (0) = 1 и J'o (0) = 0.
Найдем' теперь главный член асимптотического разложения
интеграла (13.135) для больших х. С этой целью воспользуемся
методом стационарной фазы, заметив, что соответствующие ста-
ционарные точки даются соотношением cosO = 0, или 0 = ±л/2.
Поскольку в окрестности точек 0 = ±л/2
sin0=±[l -4-(0 + 4-л)2+ •••]’	(13.136)
то главный член в асимптотическом разложении нашего интег-
рала в соответствии с рекомендациями § 3.4 будет даваться вы-
ражением
j9(x)^-^-eix ] e-{l/2)ixt,dt + -^r^ix J eWVixttdt, (13.137)
—оо	—оо
где /=0±-^- л. Интегралы в формуле (13.137) можно преобра-
зовать в обычные интегралы Лапласа путем поворота из контуров
интегрирования на углы------^-ли 4~—л соответственно. В ре-
зультате получим
j0(x)~_Leix J e~txt*^dt + 4~e~ix f etxt*/2 dt.
-~(e-fn/4)	-~(е«Л/4)
(13.138)
Далее, положив t — ^2 rx-1/2exp ------in) в первом интеграле
и t = -^2 тх~1/2ехр^-^- in) во втором интеграле, перепишем (13.138^
в виде
ОО
J0(x)-----’	Ге-г^г-Ь
яу2х	J
—«о
।---1g-,- (х-л/4) С g-^dr,
л/2х	J
—об
3?4	Гл, 1S. Уравнения с ЦерёменнЫми коэффициентами
или с учетом формулы (3.25)
Jo (х) ~ [el	+ е- ‘ (*—«/<>],
у 2лх
откуда	___
Jo(х) ~ jZcos(х---------Гп) ПРИ х->0°- (13.139|
Из формул (13.127)—(13.130) при х-> оо следует, что
ух ~ x~1/2cosx и у2 ~ x~I/2sin х.
Поэтому из (13.131) получаем
Jo(x) ~ х~,''2(А cosx-f- В sinx).	(13.140’
Сравнивая выражения (13.139) и (13.140), находим
j/ (cos xcos-^- + sin х sin= A cosx Ц- В sinx,
откуда Л = ]/4"Cos-T’ " в = У 4"sln"Г’
Подставляя найденные значения Л и В в (13.131) и использу
(13.127) и (13.128), получаем окончательно
Jo (*) ~ 1/ ——	( cos х cos -£- + sin х sin-^-) -f-
г ЛХ ц \	4	* /
+ v (sin x cos-j— cos x sin	j ,
или
J0(x)~]Z[ucos(x + usin (x --£-)] (13.141
при X -+ сю.
Формулы (13.76) и (13.141) описывают два различных пред
ставления одной и той же функции Jo (х). Первая из них дае'
ряд, сходящийся при всех значениях х, тогда как ряды в формул
(13.141) расходятся при любых х. Как уже отмечалось в гл. 1
хотя сходящийся ряд (13.76) прекрасно описывает функцию Jo (х
при малых х, при больших значениях аргумента он оказываете!
бесполезным с вычислительной точки зрения вследствие огранй
ченности разрядной сетки современных ЭВМ. На практике лю
бая попытка вычисления на ЭВМ функции Jo (х) при больших j
с помощью сходящегося ряда (13.76) будет терпеть неудачу
как только х превысит некоторое заданное значение, которое
правда, в значительной степени определяется мастерством пре
граммиста. В то же время, хотя расходящийся ряд (13.141) окг
зывается совершенно непригодным при малых значениях х, о
Упражнения
375
будет давать очень хорошее приближение к Jo (х) при больших х,
причем точность этого приближения с ростом х будет увеличи-
ваться.
Упражнения
13.1.	Найти два линейно независимых решения для каждого из следующих
уравнений:
а)	ху" + у' — О,
б)	О,
в)	х2/ + ху' - у = О,
г)	х2у" + 2ху' — 4у = О,
д)	х2у" — ху' + у = 0.
13.2.	Найти три линейно независимых решения для каждого из следующих
уравнений:
а)	х2у" -f- 2х(/” — 2у' = 0,
б)	х?уя — Зху’ + Зу = 0,
в)	х3/ + 2х2/ — Зху' + Зу = 0,
г)	х?у" — 6x4/* 4“ 7ху' — 7у = 0.
13.3.	Для каждого из следующих уравнений построить два линейно независи-
мых решения в окрестности точки х = 0 и найти радиус сходимости получен-
ных рядов:
а)	у" — ху= 0,
б)	у" + ху’ -2у=0,
в)	у’ + У' — %ху = 0,
г)	у" — ху' — у = 0.
13.4.	Рассмотреть уравнение Эрмита
у" — 2ху'+ уу = 0.
Найтн два линейно независимых частных решения этого уравнения, представляя
их в виде степенных рядов в окрестности точки х = 0, н показать, что один
из них вырождается в конечную сумму в случае, если у = 2п, где п — 0,
I, 2..
13.5.	Рассмотреть уравнение Лежандра
(1 — х2) у’ — 2ху' + уу = 0.
Построить два линейно независимых решения этого уравнения, представляя
их в виде степенных рядов в окрестности точки х = 0, и показать, что один из
них^ вырождается в конечную сумму в случае, если у = п (п 4- 1), где п = 0,
13.6. Построить два линейно независимых решения уравнения Чебышева
(1 — х2) у’ — ху' 4- уу = 0,
представляя нх в виде степенных рядов в окрестности точки х = 0, и показать,
что один из ннх вырождается в конечную сумму в случае, если у = п2, где п =
376	Гл. 13. Уравнения с переменными коэффициентами
13.7.	Для каждого из следующих уравнений построить два линейно незави-
симых решения, представляя их в виде соответствующих степенных рядов
в окрестности точки х — 0:
а)	4х/ + 2у" — у = 0,
б)	(2х + х2) у’ + у' — 6х{/ = 0,
в)	9х (1 — х) у’ — 121/' + 4у = 0,
г)	2х (1 — х) у’ + (1—х) у' + Зу = 0.
13.8.	Для каждого из следующих уравнений построить два линейно независи-
мых решения, представляя их в окрестности точки х = 0 в виде степенных рядов:
a)	xV + х (х — 1) у' — ху — 0,
б)	х2/ + ху' + (х2 - 4) у = 0,
в)	(1 - х2) у’ - 2ху' + 2у = 0,
г)	х (1 — х) у’ — Зху' — у = 0,
д)	у" + х2у = 0,
е)	(2 + х2) у" + ху' + (1 + х) у = 0.
13.9.	Для каждого из следующих уравнений построить два линейно независи-
, мых решения, представляя их в окрестности точки х = 0 в виде степенных
рядов:
а)	ху" 4- (1 + х) у' + 2у = 0,
б)	(х — х2) у" + (1 — х) у' — у = 0,
в)	(х — х2) у" + (1 — 5х) у' — 4г/ = 0,
г)	4 (х4 — х2) у" + 8xV — у = 0.
13.10.	Для каждого из следующих уравнений построить два линейно неза'
виснмых решения, представляя их в окрестности точки х = 0 в виде степенны)
рядов:
а)	х2/ 4- х2{/' — 2у = 0,
б)	х/— (1 4-х) / 4-2 (1 — х){/= 0.	;
13.11.	Показать, что точка х = 0 является устранимой особой точкой для урав
нения	а
х2у" — (4х 4- >ч*2) У' 4- (4 — Х2х) у = 0,	J
если: а) Х2 = — X,; б) Х2= —2>.г; в) = —ЗХГ (Указаний: Показать, что. вв
построенные решения регулярны при х = 0.)	3
13.12.	Показать, что функции	я
У1=х’,/3[1+^х+^+4т~х3+---]’	- I
№==тг + тгх+тгх2 + жх8 + --'’	|
№ = х'/3 [2т+тгх+угх2+-т-х3+---]	j
являются линейно независимыми решениями уравнения	Я
Му1" + 27ху” + Ъу' — у == 0.	Я
Упражнения
377
13.13.	Показать, что функции
х®
Ух I 4“ * 4 22" "1 22-32 4* ” * *
у2 = уг In х + 2 [-х- ± (1 + _!_) х*_	+ Л. + -1) Xs + ... ] ,
Уз = 2у2 In х — Уг (In х)2 + ^6х +	)х2 Н----]
представляют собой три линейно независимых решения уравнения
х2< + Зху" + (1 - х) у’ - у = 0.
13.14.	Показать, что выражение
У = ciexp (х-Ь-L) 4-с2ехр х —-L
представляет собой общее решение уравнения
X4 (1 — X2) у" + 2xV — (1 — X2)3 у = 0.
Показать, что точки х — 0 и х = оо являются иррегулярными особыми точками
этого уравнения.
13.15.	Для каждого из следующих уравнений построить два линейно незави-
симых решения, пригодных в окрестности точки х = 0:
а)	^у" + х (1 — 2х) у' — 2у = 0,
б)	х*у" + 2х3у' — у = 0,
в)	х2у" + 2 (1 — х) у' — у = 0.
13.16.	Для каждого нз следующих уравнений построить два линейно незави-
симых решения, пригодных при больших х:
а)	16х2/ + 32xi/' — (4х + 5) у = 0,
б)	ху" + 2 (1 - х) у' - у = 0,
в)	4х2у" + Зху' — (4х2 + 3) у = 0.
13.17.	Рассмотреть модифицированное уравнение Бесселя нулевого порядка
ху" + у' — ху = 0.
а)	Показать, что в окрестности точки х = 0 оно имеет следующее ограни-
ченное решение:
X2 X4	Xе
(х)	1 + 22 "Ь 22.42	22-42.62 Ч- • • • ’
Найти второе линейно независимое решение этого уравнения.
б)	Построить асимптотическое решение для больших х, включающее в себя
произвольную постоянную.
в)	Показать, что
/о(х)=-^Г J e*sin0d0.
о
г)	Построить асимптотическое разложение интеграла, полученного в п. «в»,
при больших х и с его помощью определить произвольную постоянную, вве-
денную в п.«б».
13.18.	Рассмотреть уравнение Бесселя первого порядка
х2/ + ху’ + (х2 — 1) у = 0.
378
Гл. 13. Уравнения с переменными коэффициентами
а)	Показать, что одно из решений этого уравнения можно представит
в виде ряда
. . . X Г X2	X4	1
2 ['	2-4 + 2-42-6 +”]’
сходящегося при любых значениях х. Найти второе линейно независимо
решение этого уравнения.
б)	Разложить функцию sin 0 ехр (<х sin 0) в ряд по~степеням х, проинте
грировать полученный результат по 0 в пределах от нуля до 2л и получить фор
мулу
2Л
(х) = 2п J s'n Sln 6
О
в)	Построить асимптотическое разложение решения этого уравнения npi
больших х, включающее в себя две произвольные постоянные.
г)	Найти главный член асимптотического разложения полученного в п. б
интеграла при х—> оо и с его помощью найти значения постоянных из в).
13.19. Для каждого из следующих уравнений построить асимптотические раз
ложения трех линейно независимых решений при больших х:
а)	хву" + 6х&у" — у = О,
б)	ху" - (2х +!)/_(! + х) у' + (2х + 3) у = 0.
13.20. Рассмотреть уравнение Бесселя порядка v
х*у" + ху’ + (х2 — V2) у = 0.
а)	Показать, что одно из решений этого уравнения есть
J = V (-l)n(^/2)2,,+v
v 2jnir(v + n+ !)•
n=0
Показать, что в случае, когда v отлично от целого числа, решением этого ypaj|
нения служит также функция
J fx\ = V (~l>n(x/2)2n-v
"v()	п|Г(—v+«+ 1) •
n=0
б)	Показать, что при больших х
у ~ Ауг + Ву2,
где
Ух ~ -±=- eix Г1 +	+ • • • 1 и
ух L хх j
в)	Воспользовавшись интегральным представлением
1
Jv (х) = —_	———- Г (1 — /2)v~i/2 cos v >----------
Клг(ну) J
показать, что
~ J^-^~cos (х — 4" W~ Т П) при х">00-
г)	Используя результат в), найти постоянные А и В из б).
Глава 14
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
С БОЛЬШИМ ПАРАМЕТРОМ
В этой главе мы будем строить приближенные решения одно-
родных дифференциальных уравнений второго порядка, содер-
жащих большой параметр. Такие уравнения имеют вид
у" + р(х, K)y' + q(x, К)у = О,	(14.1)
где X — безразмерный параметр, причем А 1. Уравнение (14.1)
можно преобразовать к так называемому нормальному виду,
т. е. к виду, не содержащему первой производной, если восполь-
зоваться подстановкой
У (%) И и W-
При этом
у’ = Р'и + Ри’, у" = Р"и + 2Р'и’ + Ри".
Подставляя выражения для у, у' и у” в уравнение (14.1), при-
ведем его к виду
Р"и + 2Р'и' + Ри" + рР'и + рРи' + qPu = 0. (14.2)
Полагая коэффициент при и' равным нулю, находим
2Р' + рР - 0.	(14.3)
Тогда уравнение (14.2) переписывается как
и" + [-£-4- ^-+ф»0.	(14.4)
Интегрирование (14.3) дает
In Р = —j- J pdx,
или
Р = ехр^—(14.5)
Дифференцируя выражение (14.5), имеем
Р' = — -уР ехР [— Т f Р ’
Р" = (“ ~ТР' + ехр [— -J- J Р ^] •
При этом уравнение (14.4) принимает вид
и'' + [<7-уР2-Т^]и = 0’	(14.6)
ЗЙО
Гл. 14. Уравнения с большим параметром
Таким образом, мы можем ограничиться исследованием урав-
нения
у" + Q (х, X) у = 0,	(14.7)
поскольку исходное уравнение (14.1) всегда может быть преобра-
зовано к виду (14.7). В качестве примера рассмотрим уравнение
Бесселя нулевого порядка
ху" + у' + ху = 0.	(14.8)
В данном случае р = х-1, q = 1, так что преобразованное урав-
нение (14.6) имеет вид
“" + 0 +1^)ы==0-	(14-9>
Заметим, что нормальная форма (14.7) оказывается удобной
для построения асимптотического решения дифференциального
уравнения при больших значениях аргумента х.
В этой главе будем исследовать специальный класс уравнений
(14.7), а именно уравнения
у" + Wqi(x) + q2(x)]y = 0.	(14.10)
Уравнения вида (14.10) называют обычно уравнениями Лиу-
вилля. Прежде всего мы рассмотрим ВКБ-приближение, затем
преобразование Лиувилля—Грина и, наконец, преобразование
Лангрена для случая уравнений с точками поворота.
14.1.	ВКБ-приближение
Предположим, что в интервале, на котором разыскивается
решение уравнения (14.10), функция qt (х) дифференцируема,
а функция (х) непрерывна. Разделив обе части уравнения (14.10)
на X*, имеем
-fir у" + qiy-jr qty — °-	(14. п)
Если формально устремить X в уравнении (14.11) к бесконечности,
то (14.11) перейдет в уравнение вида
<Ы/ = 0,	(14.12)'
которое имеет только тривиальное решение у = 0. Следовательно,
мы не сможем построить приближенное решение уравнения (14.10),
если станем искать его в форме
У (х) = у0 (х) + уг (х) Н-,	(14.13)
как это делалось в предыдущих главах.
Поясним идею используемого ниже метода на простом примере
уравнений, в котором коэффициент равен постоянной, а коэф-'
14.1. ВКБ-приближение
381
фициент g2 равен нулю. В этом случае решение уравнения (14.10)
имеет вид
f/ = ftexp (й-j/ft х) + с2ехр (—a/ftx),	(14.14)
где сг и с.2 — произвольные постоянные. Если коэффициент qr
отрицателен, общее решение уравнения (14.10) можно записать
в виде
t/ = c1exp(2.y<^91x) + с2ехр(—X,-/—ftx).	(14.15)
В том и в другом случае оба линейно независимых решения можно
выразить через показательные функции, причем параметр X
будет входить в показатель соответствующей экспоненты. Рас-
смотренный пример наводит на мысль вместо прямого разложе-
ния по обратным степеням А, искать приближенное решение урав-
нения (14.10) в виде
у = ехр [A.G (х, X)],	(14.16)
а для функции G строить прямое разложение по обратным степе-
ням %. Вычисляя первую и вторую производные выражения (14.16),
имеем
у' = НЗ'е^, у" = (Х2ОЛ + A.G") е™.
Подставляя выражения для у, у’ а у" в линейное уравнение
(14.10), преобразуем его в следующее нелинейное уравнение:
X,2G'* + XG" + Vft + ft = 0,
или
G', + ft + xG' + 4-^ = 0-	(14.17)
Как указывалось выше, прямое разложение для функции G
мы будем искать в форме
G(x, X) = G0(x)+4-giW+-’--	(14-18)
Подставляя разложение (14.18) в уравнение (14.17), имеем
(Go “Ь ‘ ‘ + ft -by (б®
или	Go GqGi -|- ft -|—Go + . • • = 0.	(14.19)
Приравнивая нулю коэффициенты при %® и X-1, получаем
G’o 4~ ft = 0,
GS + 2GiGi' = 0.
Из уравнения (14,20) следует, что
_	±»/ft, если ft > 0,
Go = Л-------
, ±У~ft, если ft<0.
(14.20)
(14.21)
(14.22)
382
Гл. 14. Уравнения с большим параметром
При этом
±i J /qtdx,
± J —<7i dx,
если
если
<7i>°-
<71 <0.
(14.23)
Для того чтобы решить уравнение (14.21), разделим обе его части
на 2Gq. В результате получим
1 Go'
2 Go
+- GJ = 0,
что после интегрирования дает
Gi In Go — 0.
Из дальнейшего будет ясно, что постоянную интегрирования в по-]
следнем соотношении можно опустить. Переписывая это соот-|
ношение в виде	1
Gi—~ ln/GT	(14.241
и подставляя (14.23) и (14.24) в разложение (14.18), имеем |
G = ±i j y/"qldx — -i-[In/'±7'4* In --------- при <?i>0 |
(14.2M
или	1
G==± J[in/±1 -j-lny^—7i] H----------------------- при <7i<i
(14.21
Подстановка выражения (14.25) в формулу (14.16) дает
У = ехр{±й J y^qidx - [In/±7 + In. •},
что с учетом соотношения ехр (—In z) » z-1 может быть nepeni
сано в виде
ехр /X j dx
Формула (14.27) доставляет нам приближенные выражения Д5
двух линейно независимых решений уравнения (14.10). Выраж|
экспоненты через тригонометрические функции, общее решен|
уравнения (14.10) можно приближенно записать в форме j
<?i cos X K<7i dx + <?2 sin X dxl
у -----------LJ----------------------1_Д----------1,	(14,:
у 41
где <?i и с2 — произвольные постоянные.
В случае < 0 подстановка выражения (14.26) в форму.
(14.16) и использование основного логарифмического тождест
14.2. Преобразование Лиувилля—Грина	383
позволяет приближенно записать общее решение уравнения (14.10)
в виде
ехр X —gi dx + с2 ехр —%	dx
-------L_^. L-----j-------1. (14.29)
Соотношения (14.28) и (14.29) называются обычно ВКБ-прибли-
жениями в честь Вентцеля, Крамерса и Бриллюэна.
Отметим, что соотношения (14.28) и (14.29) становятся непри-
годными в окрестностях нулей функции qx (х) (и в самих этих
точках). Эти нули называются обычно точками поворота или
точками перехода. Задачи для уравнений с точками поворота
рассматриваются в § 14.5 и 14.6.
Рассмотрим в качестве примера уравнение
' у" + V(1 + х)*у = 0.	(14.30)
В этом уравнении <71 = (1 + х)2 > 0, так что соотношение (14.28)
дает
Щ cos Г % ( х 4- -Ь- хг\ 1 + sin Г% ( х + 4- х2%) 1
—L-s—-	- - - •
В качестве второго примера рассмотрим уравнение
у" — V(1 +x)2z/ = 0.	(14.32)
При этом <7Х = —(1 + х)2 < 0, и приближенное решение, согла-
сно формуле (14.28), имеет вид
cxexp Гх(х 4--Lx2\1 4-с2ехр Г — A. f х 4--i-х2\ 1
------------2_22_1—V—(14.зз)
14.2. Преобразование Лиувилля—Грииа
В этом параграфе мы рассмотрим другой способ построения
приближенного решения уравнений с большим параметром. Этот
способ включает в себя использование так называемого преобра-
зования Лиувилля—Грина. При этом производится замена как
зависимых, так и независимых переменных по формулам
z = <р (х), v (г) = ф (х) у (х),	(14.34)
где функции <р (х) и ф (х) выбираются таким образом, чтобы урав-
нение (14.10) перешло в новое уравнение, в котором наиболее су-
щественные при А -> оо члены имели постоянные коэффициенты.
Из формул (14.34) следует, что
<14-35>
+	=	+	(14-36)
384
Гл. 14. Уравнения с большим параметром
d2y	d / $' \ri	хр'	dv	dz	,	d / <f>' \ dv	,	<р'	d2v dz	_
dx2	dx \ф2 /	ф2	dz	dx	'	dx \ ф ) dz	'	ф	dz2 dx
_ <p'2	d2v	,	/	tp"	2<р'ф'	\	dv	/ ф"	2ф'2	\	...	n.
,ф	dz2	'	\	ф	ф2	/	dz	\ ф2	ф3	/	'
Подставляя выражения для у и у" в уравнение (14.10), получае]
<р'2	d.2v	.	/	ф" _ 2ф'ф'	\	dv _ / ф" __ 2ф'*	\	।
ф	dz2	'	\	ф	ф2	/	dz	\ ф2	ф3	/
+ (А2<71 + <7г)	= 0>
или	<
d2v л_ 1 (xh" 2<Р'Ч>' \ dv _1_ V<?1 -4- 92	। 2Ф'? „ С
dz2 + ф'2 V	Ф / dz +	ф,. "г ф,2 фф,2 ।
(14.31
Как указывалось выше, выбор функций <р и ф обусловлю
требованием, чтобы главная часть преобразованного уравнещ
(14.38) имела постоянные коэффициенты. С этой целью преж,
всего обратим в нуль коэффициент при первой производной dvld
полагая
<р" —	= 0.	(14.3
Уравнение (14.39) можно решить с помощью разделения пер
менных. В результате получим
-у In <р = 1п ф,	.1
или	ф = 1/ ф'-	(14-^
При этом уравнение (14.38) принимает вид
-5-+(^?-+«)»=»•	(и-1
w	+-£?-•	(|4-|
ф ФФ Ф2Ф	i
Уравнение (14.41) имеет два переменных коэффициента,Ц
именно ft/g/2 и 6. Поскольку на функции <р и ф наложено толя
одно условие, у нас есть возможность связать их еще одним с<Я
ношением. Мы используем это второе условие, чтобы сделя
постоянным коэффициент А,2<7х/ср'! при главном члене в уравне»
(14.41). Не теряя общности, постоянную в соотношении АЛ/хф.'Я
= const можно выбрать равной 1 при qx > 0 или равной Я
при <7Х < 0. Таким образом,	Я
( ^2<7i>	если qr > 0,	-Я
I —А,2^!, если <71 < 0.	Я
14.3. Задачи на собственные значения
385
При этом
iXj/^dx, если «/j > О,
2 = Ф =	____
+Х J у —</! dx, если < О,
а из уравнения (14.40) следует, что
ЛА/2у qt, если qt > О,
Х1'2^—qt, если ^СО.
(14.43)
(14.44)
После сделанного выбора функции <р уравнение (14.41) прини-
мает вид
1	-5-±v = —Sv,	(14.45)
где знаки «плюс» и «минус» относятся соответственно к случаям
положительной или отрицательной функции qx.
В первом приближении можно пренебречь малым членом
—би в правой части уравнения (14.45). В результате имеем урав-
нение вида
общее решение которого можно представить как
v = сг cos z + с2 sin z при	qx > 0,	(14.46)
v = сг ехр z + с2 ехр (—г) при qt < 0.	(14.47)
Подставляя теперь выражения для г, ф и v в формулу (14.35),
получаем в первом приближении соотношение (14.28) в случае,
когда <71 > 0, и соотношение (14.29) при qt < 0.
14.3. Задачи на собственные значения
В этом параграфе мы используем ВКБ-приближение, чтобы
найти собственные числа и собственные функции некоторых
краевых задач для дифференциальных уравнений второго по-
рядка с переменными коэффициентами. В качестве первого при-
мера рассмотрим задачу на собственные значения для уравнения
у" + W У = 0	(14.48)
с краевыми условиями
у (0) = 0, у (1) = 0	(14.49)
при больших значениях параметра X. Предполагается также, что
Функция <71 положительна на отрезке [0, 1 ]. Поскольку qr > 0,
общее решение уравнения (14.48) в первом приближении может
быть представлено формулой (14.28). Кроме того, мы должны удов-
летворить граничным условиям (14.49). Для упрощения вычис-
13 Найфэ А. X.
386
Гл. 14. Уравнения с большим параметром
Г. *
лений выберем нижние пределы интегрирования в формуле (14.2
равными нулю. Тогда формула (14.28) перепишется в виде
X
я J 1^91 (г) dr +
. о
ci cos
с2 sin
j К<71 (т) dr
.0 .
(14.5
V 91 W
где г — переменная интегрирования. Подставляя выражени
(14.50) в граничное условие
0	—-С1 
4/9i(0) ’
у (0) = 0, имеем
или Ci = 0,
откуда
У 1/4 Sin
Подстановка этого выражения
дает
X
h f /<7i (т) dr .
L о
в граничное условие у (1) =
У


0 = 6’2[<7i(l)]')/4sin
j /<71(т)с/т .
Lo
Для существования нетривиального решения задачи необходим,
чтобы постоянная с2 была отлична от нуля. Поэтому
sin А ] 4<?i (т) dr
. о
= 0,
или
J 4/<7i (т) dr = пл,	п = 1, 2, 3, ...
о
Отметим, что случай п — 0 приводит к тривиальному решени!
задачи (14.48), (14.49); по этой причине значение п — 0 не вклк
чено в формулу (14.51)*. Таким образом, в первом приближена
собственные числа определяются формулой
(14.51






= пл
J / <7i (т) dr
о
(14.51
а соответствующие им собственные функции— формулой
-1.4
Уп == <71
sin J । <71 (т) dr .
о
(14.55
1 В формулу (14.51) не включены также и отрицательные значения п : п
= —1, —2, —3, ... . Случай отрицательных п легко сводится к описываемо.
случаю ввиду нечетности функции sin х. — Прим, перев.
14.3. Заадачи на собственные значения
387
Таблица 14.1
Сравнение приближенных значений собственных чисел,
подсчитанных по методу возмущений, с точными численными
значениями
Порядковый номер соб- ственного числа	1	2		3	4	5	6	7
Метод	* 2.0944	4.1888	6.2832	8.3776	10.4720	12.5664	14.6608
возмущений Точное	2.0604	4.1686	6.2691	8.3668	10.4632	12.5590	14.6545
значение Ошибка (%)	1.65 ‘	0.49	0.23	0.13	0.08	0.06	0.04
Рассмотрим численный пример. Пусть qt (х) = (1 + х)г, тогда
формула (14.51а) примет вид
А.Д — пл
(1 Ц- т) dx
-1
2
= у лп.
В табл. 14.1 приведены для сравнения собственные числа, подсчи-
танные по предыдущей приближенной формуле, и собственные
числа, полученные с помощью численного интегрирования урав-
нения (14.48) и применения итерационного метода Ньютона—
Рафсона *. Совпадение оказывается очень хорошим даже в самом
неблагоприятном случае, т. е. для наименьшего собственного
числа Xi 2,0604. Как и следует ожидать, точность решения,
полученного методом возмущений, увеличивается с ростом номера
собственных чисел.
В качестве второго примера рассмотрим задачу на собственные
значения для уравнения (14.48) при краевых условиях
у' (0) - 0, у (1) = 0.	(14.53)
Для того чтобы иметь возможность подставить приближенное
решение в первое из условий (14.53), продифференцируем выраже-
ние (14.50) по х. В результате получим
У'
—X у q1 Ci sin
 X
J /91 (т) dx
. о
— с2 cos
 х
f / 9i (т) dx
.о
+ 0(1).
(14.54)
Отметим, что слагаемые, появляющиеся при дифференцировании
множителя +'/4, суть величины О (1) при Л оо. Они малы
1 Итерационный метод Ньютона—Рафсона используется при этом для
решения трансцендентного уравнения, получающегося в результате выполне-
ния исходных граничных условий. — Прим, перев.
13*
388
Гл. 14. Уравнение с большим параметром
Таблица 14
Сравнение приближенных значений собственных чисел,
подсчитанных по методу возмущений, с точными численными
значениями
Порядковый номер соб- ственного числа	1	2	3	4	Б	6	7
Метод	1.0472	3.1416	5.2360	7.3304	9.4248	11.5192	13.6131
возмущений Точное	1.1879	3.2089	5.2793	7.3621	9.4497	11.5397	13.63 к
значение Ошибка (%)	11.84	2.10	0.82	0.43	0.26	0.18	0.13
по сравнению со слагаемыми, которые возникают при диффере!
цировании тригонометрических функций. Последние растут пр<
порционально X при X-> оо. Воспользовавшись теперь условие
у' (0) = 0, имеем с2 = 0, так что выражение (14.50) принимае
вид	'

cos X j (т) dx .
. о
Подставляя последнее выражение в граничное условие у (1) = (
приходим к уравнению
Г 1
cos	(т) dx
= 0,
. о
решения которого имеют вид
л,
п = 0, 1,2,...
рг 0
Таким образом, в первом приближении собственные числа задач
(14.48), (14.53) определяются формулой
(14.5;
Lo	J
а соответствующие им собственные функции — формулой
X
Уп = ?Г1/4 COS X„ j /<7! (т) dx .
о
(14.51
Если при ЭТОМ ВНОВЬ ПОЛОЖИТЬ <71 = (1 + *)а, то
К = (п + Т-) л
- 1 -1
j (1 4-T)dr
14.5. Уравнения с точкой поворота
389
В табл. 14.2 приведены для сравнения приближенные значения
собственных чисел, подсчитанные по методу возмущений, и зна-
чения тех же собственных чисел, найденные с помощью численных
методов. Как и следует ожидать, точность приближенного решения
быстро возрастает с ростом номера собственных чисел. При этом
уже для третьего собственного числа относительная погрешность
не превышает одного процента.
14.4.	Уравнения с медленно меняющимися коэффициентами
В этом параграфе рассмотрим уравнения вида
“77г + <71 СО = °>	(14.57)
где т = е/ и е — малый безразмерный параметр. Таким образом,
т представляет собой по отношению к t «медленную» переменную.
Переходя от t к т, имеем
du dy dr du	d2u „ d2u
~dF ~ ~dr ~dT ~ & ~dT ’	-dif-b-dT-2’
в результате чего уравнение (14.57) принимает вид
е25 + ^(т^ = 0-	(14.58)
Полагая е = V1, перепишем уравнение (14.58) в виде
-§- + ^(^ = 0.	(14.59)
Уравнение (14.59) совпадает с уравнением (14.10), поэтому к нему
применимо ВКБ-приближение, рассматривавшееся в § 14.1. Сле-
довательно, учитывая соотношение , h МУ
X j dt = еХ j d/ = j d/,
можно записать выражения, аналогичные (14.28) и (14.29), через
исходную переменную t:
<7r1/4{cicos[j/'<7id^] с2 sin [ j-/<71 d/]}, <?i>0,	(14.60)
^c2e-^'dt], <71 <0.	(14.61)
14.5.	Уравнения с точкой поворота
Как указывалось в § 14.1, ВКБ-приближеиия (14.28) и (14.29)
становятся непригодными в окрестностях нулей функции qr (х).
Эти точки называются точками поворота, или перехода. Пусть,
393
Гл. 14. Уравнения с большим параметром
например, qx = 1 —х3. В этом случае формулы (14.28) и (14.2!
можно представить в виде
ci cos
1
A j /1 — dr
X
+ с2 sin
+ а2 ехр
1
% j К1 — т3 dx
х
И
У
а± ехр
% j /т3 — 1 dr
1
4/х3 — 1
-% j /т3 - 1 dT
1
если х < 1
(14.62;
если х > 1
(14.63’
где а2, q и с2 — произвольные постоянные, а верхний и ниж-
ний пределы интегрирования в первой и второй формулах соот-
ветственно выбраны равными 1, с тем чтобы входящие в них инте-
гралы оказались положительными. Отметим, что при рассмо*
трении уравнений с точками
рования в формулах
ВКБ
поворота один из пределов интегри?!
приближения
удобнее всего
принимать
равным координате точки поворота. Можно считать, что формул!*:
(14.62) и (14.63) дают два различных представления одной и той же!
функции у (х), причем одно из этих представлений пригодно при!
х < 1, а другое при х > 1. При этом ясно, что постоянные ап.
и сп должны быть линейно связаны между собой, поскольку наше
дифференциальное уравнение имеет второй порядок и его решение^
определяются лишь двумя произвольными постоянными. Один;
из рассматриваемых ниже методов нахождения связи между;
этими постоянными предусматривает построение разложения,;
пригодного в окрестности точки х = 1 (или так называемого вну-;
треннего разложения), и сращивание этого разложения соответ-?
ственно с разложениями (14.62) и (14.63). В следующем пара<
графе обсуждается также другой метод, позволяющий связать^
константы в (14.62) и (14.63); он основан на использовании пре-
образования Лангера.
Для того чтобы построить разложение, пригодное в окрестно-;
сти точки х = 1, введем «растягивающее» преобразование неза-:
висимой переменной х, с тем чтобы координаты точек, близких
к х = 1, оказались величинами О (1) при А, -> оо. С этой целью;
положим
£ = (х — 1) V, так что х = 1 + A,-Vg, (14.64)’
причем показатель v, точное значение которого будет определено;
ниже, считается положительным, чтобы преобразование (14.64)(
действительно было растягивающим. Производные по исходной
переменной х преобразуются следующим образом:
dy _ dy dg _ , v dy	&У _ is* а2У
dx dl dx dl’	dx2 ~л dg2 •
14.5, Уравнения с точкой поворота	391
При этом уравнение (14.10) в случае qr — 1 — х3 и </2 = 0 прини-
мает вид
Vv^ + Z2[l-(l+V^)3]^ = 0,
или
_ 32?-3vg (1 +	+ V2vg2) у = о. (14.65)
Если X -> оо, то второе и третье слагаемые в скобках в уравнении
(14.65), поскольку v > 0, будут стремиться к нулю, и уравнение
(14.65) примет вид
_g__3V-3^ = o.	(14.66)
Уравнение (14.66) имеет различную предельную форму при
А, —> оо в зависимости от величины показателя v. В случае v > 2/3
коэффициент Х2-3^ стремится к нулю, и уравнение (14.66) пере-
ходит в уравнение вида
-^ = 0.	(14.67)
В случае v < 2/3 коэффициент A,2-3v стремится к бесконечности,
и уравнение (14.66) имеет предельную форму
1у = 0.	(14.68)
Наконец, при v = 2/3 коэффициент A,2-3v равен единице, и урав-
нение (14.66) принимает вид
-^--3^=0.	(14.69)
Предельная форма (14.69) является «наименее вырожденной»
из трех; она включает в себя уравнения (14.67) и (14.68) в каче-
стве частных случаев. Кроме того, первые два случая соответствуют
бесконечным наборам значений v, в то время как третий случай
определяется вполне определенным значением показателя v.
Следовательно, наиболее подходящей предельной формой является
уравнение (14.69), соответствующее значению v = 2/3.
С точностью до коэффициента 3 уравнение (14.69) представляет
собой так называемое уравнение Эйри, решения которого хорошо
известны. Для того чтобы использовать эти решения, представля-
ется удобным видоизменить преобразование (14.64), с тем чтобы
результирующее уравнение не содержало множителя 3. Таким
образом, вместо замены переменных (14.64) используем преобра-
зование
z = 31/3(х — 1)АА'3 или х = 1 + З-'/ЗА,-2^,	(14.70)
в результате чего вместо уравнения (14.69) придем к уравнению
Эйри в стандартной форме:
=	(14.71)
392
Гл. 14. Уравнения с большим параметром
Общее решение уравнения (14.71) обычно выражают в виде
у(3) =	(z) + b2Bi (z),	(14.7:
где bi и b2 — произвольные постоянные, a Ai (z) и Bi (z) пре;
ставляют собой функции Эйри первого и второго рода соотве1
ственно.
Теперь необходимо провести сращивание решения (14.71
с ВКБ-решениями (14.62) и (14.63). Для этого потребуются аси«
птотические разложения функций Ai (z) и Bi (z) при больши
положительных z (т. е. при х > 1), чтобы срастить (14.72) с р<
шением (14.63), и при больших по абсолютной величине отриц;
тельных z (т. е. при х < 1), чтобы срастить (14.72) с решение
(14.62).
Если мы будем искать указанные асимптотические разложени!
исходя из дифференциального уравнения (14.71), то обнаружив
что первые члены этих разложений экспоненциально растут и.
затухают в случае положительных z и совершают синусоидальш
колебания в случае отрицательных г. Более точно, использ'
ВКБ-приближение (14.28) и (14.29) при = —г, имеем
и
у ~ Z“1/4 JXcos Z3'2) + ^2 Sin Z3/2)J
при z->
оо
у ~ г-'/< [а^3')г3/2 + а2е- <2/3> *3/2]
при z->oo.
Однако при этом нам по-прежнему не известны соотношения м(
жду постоянными ап, сп и ап, сп, с одной стороны,, и ап, t
и Ьп — с другой. Для того чтобы обойти это затруднение, обычй
представляют решения уравнения (14.71) в интегральной форм
и затем определяют главные члены асимптотических разложенй
полученных интегралов, подобно тому как мы делали это в при
мере 3 § 13.5.
Интегральные представления построенных выше двух линейн
независимых решений уравнения Эйри можно получить с помощь]
модифицированного преобразования Лапласа. Функции Эйр;
первого и второго рода обычно определяют. как
ОО	.
Ai (z) = J cos t3 4- zi^ dt,	'	(14.72
о
ОО
Bi (z) = -^- j j^exp (-L/3_|_z0-|- sin 4-z/)j dt. (14.74
°	i
Главный член асимптотического разложения функции Ai (i
при z -> сю найден в § 3.5 с помощью метода перевала. Таи
из формулы (3.239) следует, что
.... ехр [(—2/3) 23/2]
Al (г) ~ о м ПРИ	(14.75
2 -у л z
14.5. Уравнения с точкой поворота
393
Используя метод стационарной фазы, можно получить главный
член асимптотики Ai (z) при z —оо. Из упражнения 3.21
следует, что
At~ sin Г4(~г)3/2 + ~т] при (14-76)
Главные члены асимптотических разложений интегралов в (14.74)
при г оо можно найти с помощью метода Лапласа и интегриро-
вания по частям.'ТакимЪбразом, мьГимеем (см. упражнение 3.31)
Bt (г)--—-j—— при z-> оо. (14.77)
При больших по абсолютной величине отрицательных значениях г
асимптотика интегралов, входящих в (14.74), определяется с по-
мощью метода Лапласа и метода стационарной фазы. В этом слу-
чае имеемл'(см. упражнение’3.31)
cos [4(~г)3/2+~т] при (14-78)
Асимптотические представления (14.75)—(14.78) дают нам иско-
мые соотношения между сп, ап и Ьп. Устремляя теперь в решении
(14.72) z к бесконечности и используя представления (14.75)
и (14.77), находим
ехр [— (2/3) г372]	62 ехр [(2/3) z3/2]	/14 7СП
у TyvT73 +	(	}
Точно так же, устремляя в (14.72) z к —оо и используя пред-
ставления (14.76) и (14.78), получаем
+	+ т] •	(|О0>
Для того чтобы найти соотношения между постоянными ап и сп
в ВКБ-приближениях (14.62) и (14.63), необходимо срастить эти
разложения с решением (14.72), справедливым в окрестности
точки поворота. Чтобы срастить разложения (14.62) и (14.72),
выразим в интегралах, входящих в (14.62), переменную х через z
и устремим X к бесконечности при фиксированном z. Таким об-
разом, имеем 	О ,
1 1
k j уД — т3 dx = X j	У1 — х3 dx,
394
Гл. 14. Уравнения с большим параметром
откуда, полагая т = 1 + 3-1/3V2/31, находим
1	о
X | 1/ 1 — Т3 dX = X J [-3-W-2/3/ - 3>/ЗХ-4/3/2 -----------J1/2 з-1/зх-2/з dt
х	г
О
~ J (—/)1/2^ = _2_ (—г)з/2.
Z
Тогда
<1 cos Г 2 (-г)3/2] + с2 sin	(— Z)3/21	'
lim У<1) =----------—------ГтНпй-------ГлА~~--------“• (14.811
x-^co a	3/6Х“/6 (~z)1/4	v 7
афикс.
Для того чтобы использовать условие сращивания, необходим!
выразить решение г/<3) через х при х < 1 и совершить предельны!
переход Z. ->оо при фиксированном х. Эта процедура эквивалента?
вычислению асимптотики при z -> —оо; в результате имеев!
представление (14.80). Приравнивая разложения (14.80) и (14.81)
в соответствии с принципом сращивания, получаем
„1/2X1/63-1/6 Lcos	(_z)3/2j + С2 sin [4(-
= bl sin [4- (-2)3/2 + 2L] + bi COS [4 (-2)3/2 +	.
Далее, используя тригонометрические формулы для синуса и ко-
синуса суммы двух аргументов и приравнивая коэффициенты при
[2	1 г 2	1
(—г)2/3j и sin -у (—г)2/3 в обеих частях полученногс
равенства, находим
c1 = 31/6n,-1/2V1/6 ^iSiny- +^2cos-p]>
сг = 31/6л~1/2%-1/б [\cos у---------^sin~4] •
Перейдем теперь к сращиванию асимптотических представле-
ний (14.63) и (14.72). Выразим переменную х в формуле (14.63)
через z и совершим предельный переход % оо при фиксирован-
ном положительном г, что соответствует х > 1. С этой целые
запишем
14.5. Уравнения с точкой поворота	395
и, полагая т = 1 4- 3~1/3Х~2/3/, преобразуем этот интеграл к виду
X j	dT = X j [32/ЗХ-2/3/	3V3X-4/3/2 ----] 1/2 3-1/3X-2/3 dt
1	. о
j /‘/2л = -|-z3^2.
°
Тогда из формулы (14.63) следует, что
lim i/(2> = 3-W/62-i/4[aiexp [(2/3)г3Д’+а2ехр[(—2/3)z3/2]. (14.83)
Х->оо
z фикс.
Далее, необходимо выразить в решении (14.72) переменную г
через х и совершить предельный переход Л -> оо при фиксирован-
ном х, большем 1. Это эквивалентно нахождению асимптотики
функции у<3> при z —> оо; результат дается формулой (14.79).
Приравнивая выражения (14.79) и (14.83) в соответствии с прин-
ципом сращивания, получаем соотношение вида
3-1/бХ1,ел1/2 ^aiexp	гз/г^ а^ехр -------L гз/2^ _
= ехр ( —	z3/2) + b2 ехр (-|- z3''2) ,
из которого после приравнивания коэффициентов при каждой
из экспонент в левой и правой частях находим искомые связи ме-
жду постоянными ап и Ьп:
а2 = -уЗ1/6^1^-!/2^.	(14.84)
Итак, решение нашей задачи дается тремя отдельными разло-
жениями: разложением (14.62), пригодным при х < 1, разложе-
нием (14.63), пригодным при х > 1, и разложением (14.72), спра-
ведливым в окрестности точки х = 1. При этом мы срастили по-
лученные разложения с помощью координатной асимптотики для
интегральных представлений функций Эйри. Результатом сращи-
вания явились соотношения (14.82) и (14.84), которые связали
коэффициенты ап, Ьп и сп всех трех разложений. Подобно тому
как это было проделано в гл. 12, можно получить и составное
равномерно пригодное разложение. Однако используемая при
этом процедура оказывается сравнительно громоздкой. Другой
метод получения разложения, пригодного всюду, включая окрест-
ность точки поворота, заключается в применении преобразования
Лангера и приводит к единому представлению решения во всей
области через функции Эйри. Этот метод рассматривается в сле-
дующем параграфе.
396	Гл. 14. Уравнения с большим параметром
14.6.	Преобразование Лангера
Суть преобразования Лангера состоит в том, чтобы заменить^
зависимые и независимые переменные по формулам (14.34) и по-’
добрать функции (риф таким образом, чтобы преобразованное’
уравнение, будучи возможно более простым по форме, в то же
время имело решения, поведение которых совпадало бы в основных?
чертах с поведением решений исходного уравнения. Например,?
если во всех точках интересующего нас интервала коэффициент
<7i > 0. то решения исходного уравнения (14.10) имеют колеба-'
тельный характер, и поэтому функции (риф следует выбрать
так, чтобы главная часть преобразованного уравнения совпадала,
с уравнением
-§- + у = 0,	(14.85а)'
которое представляет собой простейшее уравнение, обладающее-
осциллирующими решениями. Если же во всех точках рассматри-
ваемого промежутка для уравнения (14.10)	< 0, то с ростом х
одно из решений этого уравнения будет экспоненциально расти,
а другое — экспоненциально убывать. Поэтому функции (риф
в этом случае следует выбрать так, чтобы преобразованное урав-
нение с точностью до малых слагаемых совпадало с уравнением
= 0,	(14.856)
которое является наиболее простым уравнением, обладающим
экспоненциально растущим и экспоненциально затухающим ре-
шениями. Наконец, если функция qt в интересующем нас интер-
вале один раз меняет знак, как, например, функция = 1 —х3
в рассмотренном нами в предыдущем параграфе случае, то реше-
ния исходного уравнения (14.10) будут иметь колебательный'
характер при х < 1 и экспоненциально расти или затухать при
х> 1. Поэтому функции (риф следует выбрать таким образом,
чтобы преобразованное уравнение оказалось близким к такому -
уравнению, решения которого в заданной точке меряют свое по-
ведение, переходя от осцилляций к экспоненциальному росту или
затуханию . Простейшим уравнением с такими свойствами яв-
ляется уравнение Эйри
d%v
^-zv = 0,	(14.86);
рассматривавшееся нами в предыдущем параграфе. При г> 0 ;
одно из решений уравнения (14.86) растет, другое убывает, s
в то время как при z < 0 оба решения имеют колебательный
характер.
1 При этом существенно, чтобы сохранялся порядок поведения коэффи-
циента в точке перехода. В целом этот метод называют методом эталонных ,
уравнений. — Прим. ред.	;
14.6. Преобразование Лангера
397
Приведенные рассуждения объясняют, почему ВКБ-прибли-
жение или преобразование Лиувилля—Грина становятся непри-
годными в окрестности точки поворота. В § 14.1 и 14.2 мы стре-
мились представить решения уравнения (14.10) через элементар-
ные функции — тригонометрические или показательную. По-
скольку ни одна из указанных элементарных функций не может
описать поведение решений уравнений с точкой поворота, справед-
ливость ВКБ-приближений в окрестности этой точки должна на-
рушаться. Таким образом, разложение, равномерно пригодное
для любых значений аргумента х, должно выражаться через не-
элементарные функции, поведение которых качественно совпадает
с поведением решений исходного уравнения.
С другой стороны, нарушение пригодности ВКБ-приближения
в окрестности точки поворота можно объяснить тем, что преоб-
разование (14.34) имеет особенность в этой точке. Согласно фор-
мулам преобразования Лиувилля—Грина, ф ~ yz<7i. Поскольку
функция обращается в нуль в точке поворота, то и функция ф
в этой точке также должна обращаться в нуль. Поэтому пред-
ставление (14.35) становится непригодным в окрестности точки
поворота, так как оно содержит деление на нуль. Следовательно,
для того чтобы получить равномерно пригодное разложение,
мы должны найти преобразование, регулярное всюду в интересу-
ющем нас интервале. В частности, функция ф в этом интервале дол-
жна быть регулярной и не иметь нулей. Кроме того, из формулы
(14.40) следует, что аналогичными свойствами должна обладать
и функция <р' (г). Исходя из этого, положим
= <Р'Ч (г),	(14.87)
так что (14.41) принимает вид
-^ + £(2)а = -6и,	(14.88)
и постараемся подобрать по возможности наиболее простую по
форме функцию £ (г), которая вместе с тем привела бы к преобра-
зованию, не содержащему особенностей. Для того чтобы функция <р'
была регулярной и не имела нулей в рассматриваемом интервале,
функция £ (г) должна иметь особенности и нули того же порядка,
что и функция <?!•	\
Пусть, в частности, функция (х) регулярна и имеет един-
ственный нуль первого порядка (простая точка поворота), как,
например, функция 1 —х3. Тогда функцию £ (г) надо тоже вы-
брать так, чтобы она была регулярна и имела один простой нуль.
Простейшей функцией, удовлетворяющей этим требованиям, яв-
ляется. функция £ (г) = г. Если qt (х) регулярна и имеет един-
ственный двойной нуль в интересующем нас интервале (т. е. в этом
интервале существует точка поворота второго порядка), то и
функция £ (г) должна быть регулярной и иметь один двойной
398
Гл. 14. Уравнения с большим параметром
нуль. Простейшей функцией этого типа является функция £ (г) =1
= z2. В случае точки поворота n-го порядка, когда функция qx (хн
регулярна и имеет единственный нуль порядка п, в качестве]
функции £ (z) следует выбрать функцию zn. Если, наконец, qx (хи
имеет два нуля в точках х = аих = £(£>а) порядка т и /ы
соответственно, то полагают £ (z) = zm (1 — z)n.	J
Существует еще одна причина, по которой происходит наруше?!
ние точности ВКБ-приближения и преобразования Лиувилля—4
Грина. Слагаемое в уравнении (14.45) мало по сравнению с Дру-У
гими членами уравнения только вдали от точки поворота. В самой
же этой точке функция 6 (?) имеет особенность и, следовательно!
± v = 0	1


в противоречии с нашим исходным предположением не являете^
уже главной частью преобразованного уравнения. Так, в примере!
рассмотренном в предыдущем параграфе, <7i = 1 — xa, и в соо/
ветствии с (14.43) и (14.44),	|
ф — О [Х1/2(х — 1)1/4], ф'2 = О(Х2(х — 1)) при х-+1 и Х->оо;
При этом из формулы (14.42) следует, что
1
Х-> оо.
при
б-%2(х_ 1)3/2
Следовательно, коэффициент 6 будет мал по сравнению с единицей
при X-* оо только при х, далеких от 1, т. е. вдали от точки
поворота. Таким образом, чтобы убедиться в равномерности полу|
чающегося в результате разложения, необходимо проверить!
всегда ли отброшенные члены преобразованного уравнения буду®
малы по сравнению с оставшимися.	I
Остановимся подробнее на случае простой точки поворота]
когда функция в рассматриваемом интервале имеет единствен!
ный простой нуль, а функция £ (z) должна быть регулярной в этом
интервале и иметь в соответствующей точке единственный проа
стой нуль. Простейшими функциями этого типа являются функций
£ = ±z. Ниже мы используем функцию £ = —г, для того чтобы
.преобразованное уравнение имело форму стандартного уравнения
Эйри (14.86). Иначе говоря, запишем соотношение (14.87) в виде
фф'2 = —Х2^,	(14.89|
поскольку, согласно первой из формул (14.34), z = ф. Извлекая
квадратный корень из обеих частей (14.89), получаем уравнение
Ф1/2Ф' = ±Х /—<71 (х) ,	1
которое после разделения переменных приводится к виду I
ф‘/2 rfq — -j-X у —qv (Х) dx
14.6. Преобразование Лангера
399
Интегрируя это уравнение, имеем
_|_ срЗ/2 = j /—<?! (т) dx,
где буквой т обозначена переменная интегрирования. В качестве
нижнего предела интегрирования удобно выбрать координату
точки поворота. Пусть это будет, например, точка х = р. Тогда
можно записать окончательно
' „ „ х
А гз/г = А Ф3/2 = ±М -91 W	(14.90)
О	О	J
Из уравнения (14.89) следует, что
ф'2 = —Л2ф-191
и, следовательно, в соответствии с уравнением (14.10)
ф = V'V'/i (-(14.91)
Как уже отмечалось выше, общее решение уравнения (14,86)
выражается через функции Эйри в виде
и (г) = ctAi (z) + c2Bi (z).	(14.92)
Подстановка выражений (14.91) и (14.92) в формулу (14.35) дает
у ~	(_f?1)-i/4 [C1Ai (г) + C2Bi (?)],	(14.93)
при этом множитель V'2 включается в постоянные Ci и с2.
Проверим теперь регулярность преобразования (14.34) и по-
рядок величины слагаемого 6, отброшенного в преобразованном
уравнении (14.41). Поскольку предполагается, что р— простая
точка поворота, то — О (х — р) при х —> р. При этом из соот-
ношения (14.90) вытекает, что
ф3/2 ±Х j (fl) (т - р) + • • • ]V2 dx ъ
И_______. ___________________________ \
А, /—q{ (р) j (т — р)1/2 dx = ± A A y~q{ (р) (х — \i)3/2.
и	\
Следовательно,	\
Ф = О [Х2/з(х — р) ]	\
и <р' = О (А,2/3) при х-» р, Х-» сю.
Наконец,
ф =: уЛф = О (А1'3) при х-> р, ОО,
что и доказывает регулярность преобразования всюду, включая
точку поворота. Подставляя полученные выше оценки в соот-
ношение (14.42), находим, что 8 = 0 (А-4/3) равномерно относи-
тельно х. Это означает, что слагаемое 8v будет мало по сравнению
400
Г л. 14. Уравнения с большим параметром
с членами, оставленными в уравнении (14.86), при всех значея
ниях х. Таким образом, единое асимптотическое представления
(14.93), в котором z дается соотношением (14.90), оказываете»
справедливым всюду, включая точку поворота.	Я
14.7.	Задачи на собственные значения для уравнений	а
с точкой поворота	Я
В этом параграфе мы применим полученные выше результатЫи
к двум задачам на собственные значения. Сначала мы рассмотри
рим задачу	Я
у" + V (1 - х3) у = 0,	(14.94»
у (0) = 0, у 0 при хоо, (14.95»
которая является прототипом задач, встречающихся в квантовой!
механике. Здесь q± = 1 — х3, так что соотношение (14.90) приниЯ
мает вид	
-j-z3/2 =-|-ф3/2 = X j у т3 — 1 dx.	(14.Эби
1	я
В формуле (14.96) выбран положительный знак перед квадратны»
корнем, с тем чтобы z было положительно при х > 1. Поэтом»
при х-» оо, z. —> оо, и решение (14.93) в соответствии с асимптоЯ
тическими представлениями (14.75) и (14.77) будет вести себя как!
у ~ — —И------сге~ г3/2 с2е(2/3) г3/2j при х оо. I
г 2	1	а
Поскольку ехр -g-z3/2J стремится к бесконечности намного!
быстрее, чем стремится к нулю множитель (х3 — 1)-1/4 при х—► оо,|
то из условия ограниченности решения (т. е. второго из условий!
(14.95)) следует, что с2 = 0- Таким образом, соотношение (14.93)1
принимает вид	|
oyd^x3 — I)-1/4 Al(z). -	(14.97)1
Подчиняя решение граничному условию у (0) = 0, имеем |
су [z (О)]1/4 Al [z (0)1 = 0,	1
откуда с учетом требования нетривиальности решения находим!
Al [z (0)1=0.	(14.98)1
Поскольку z является функцией X, корни уравнения (14.98) дают!
нам искомые собственные значения. Из соотношения (14.96)1
следует, что	'	1
о	।	(
[z(0)]3/2 f /т3 - 1 dx = ~ik J/l - - т3 dx, j
1	о	1
14.7. Задачи для. уравнений с точкой поворота
401
Таблица 14.3
Сравнение приближенных значении собственных чисел,
подсчитанных по методу возмущении, с точными численными
значениями
Порядковый номер собственного числа	1	2	3	4
Метод возмущений	2.892	6.535	10.27	14.00
Численное значение	2.807	6.540	10.27	14.00
1	“12/3
|J//l-T3dT
о
откуда
z (0) = —Х2/з
(14.99)
Следовательно, z (0) -> —оо при Х-» +оо ив соответствии с асим-
птотическим представлением (14.76) мы получаем оценку
м I2(°)1 ~	sl" (-г I-2(°)'” + т)• (14 10°)
Подставляя (14.99) и (14.100) в уравнение (14.98), имеем
sin
X J /1 - т3 dx 4-
о
Решения этого уравнения имеют вид
(14.101)
Таким образом, собственные функции даются формулой (14.97),
где z определяется соотношением (14.96), а собственные числа А,п —
формулой (14.101).
В табл. 14.3 приведены для сравнения собственные числа, под-
считанные по приближенной формуле (14.101), и собственные
числа, полученные с помощью численного интегрирования урав-
нения (14.94) и использования итерационного метода Ньютона—
Рафсона. Совпадение оказывается очень хорошим, даже в самом
неблагоприятном случае, т. е. для наименьшего собственного
числа 2,807. При этом относительная погрешность опреде-
ления первого собственного числа составляет 3 %, второго —
0,08 %. Третье же собственное значение вычисляется по асимпто-
тической формуле (14.101) с четырьмя вернымй знаками.
402
Гл. 14. Уравнения с большим параметром
В качестве второго примера рассмотрим задачу
у" + V (1 — х2) у = 0,	(14.102)
у (0) = 0, у (1) = 0,	(14.103)
возникающую при расчете теплообмена в плоском канале в слу-
чае полностью развитого ламинарного течения. При этом qr =
= 1 — х2, так что уравнение (14.102) имеет две точки поворота:
одну при х = 1, а другую при х = —1. Однако в промежутке
интегрирования находится только одна точка поворота, а именно
х — 1. Поскольку задача решается на конечном промежутке,
удобнее выразить решение уравнения Эйри не через функции
Эйри, а через функции Бесселя.
Выбирая функцию £ (г) равной г, полагаем
А,2 (1 — х2) = ф''ф,	(14.104)
так что преобразованное уравнение с отброшенными малыми сла-
гаемыми принимает вид
^ + zv^0.	(14.105)
Решение уравнения (14.104) запишем как
2_гз/2 =2_фз/2 = _х j/1 -x2dx = XH. (14.106)
1
В формуле (14.106) выбран знак минус перед квадратным корнем
с тем, чтобы г было положительно при х £ [0, 1 ]. Общее решение
уравнения (14.105) можно представить через функции Бесселя
порядка 1/3 (см. упражнение 14.3). В результате имеем
v = Yz [ctJ_1/3 (-|г3/2) +W(423/2)] • (14.107)
Из уравнения (14.104) следует, что
ф' = Хф~1/2 •[/1 — х2,
и поэтому в соответствии с (14.40)
г|р = ХЬ2г-1/4(1 _ x2)i/4.	'	(14.108)
Подставляя теперь выражения (14.107) и (14.108) в формулу (14.35)
и используя соотношение (14.106), получаем окончательно
^^//1/2(1 _а.2)-1/4[С17_1/з(Х//) + с271/з(Х//)].	(14.109)
Для того чтобы подчинить решение граничному условию у (1) =
= 0, необходимо вычислить предел выражения (14.109) при х->1.
С этой целью заметим, что при х —» 1
1	I
Н— Jy1 — т2 dx->y 2 J (1 — г)’/2dx =	2(1 — х)3/2.
X	X
14.7. Задачи для уравнений с точкой поворота
403
Кроме того, из упражнения 13.20 следует, что
J_I/3=O(//-1/3),	J13 = O(//>/3) при /7 —> 0,
и, следовательно,
J_1Z3 = O(1 -x)-V2,	J1/3 = O(1 -X)1/2 прих—>1.
Таким образом,
у = О\(\ -х)3/4(1 -x)-V4 [С1(1 _х)-1/24-с2(1 -х)1''2]},
ИЛИ у = Cj О (1) + с2О (1 — х) при х-> 1.
Это означает, что мы можем удовлетворить граничному условию
у (1) = 0 только при сг = 0, так что соотношение (14.109) прини-
мает вид
-x2)-'/*Jl/3(Mi).	(14.110)
Удовлетворяя второму граничному условию у (0) = 0, получаем,
что собственные значения А,л должны быть корнями уравнения
или
J1/3
1
Л. j У1 — т2 dx
(14.111)
Поскольку X велико, можно воспользоваться асимптотическим
представлением функций Бесселя при больших значениях ар-
гумента
<Л/з(г)~ ]/^-cos	при z->oo
(см. упражнение 13.20). При этом вместо уравнения (14.111) имеем
/ лл 5л \ Л	лл 5л /	.	1 X
СОЦ~4-----12/= °’ или ~1----------1Г=(П+—)я-
n = 0, 1, 2..
Таким образом, собственные функции даются формулой (14.110),
а собственные числа определяются соотношением
Xn = 4(n+4-).	(14.112)
В табл. 14.4 приведены для сравнения собственные числа, подсчи-
танные по приближенной формуле (14.112), и собственные чибла,
полученные с помощью численного интегрирования исходного
уравнения и использования итерационного метода Ньютона—
Рафсона. Совпадение результатов оказывается очень хорошим,
даже для наименьшего собственного числа, приближенно равного
3.6723. Как и следует ожидать, точность приближенной формулы
быстро растет с увеличением номера собственных чисел. Так,
уже пятое приближенное собственное значение имеет пять вер-
ных значащих цифр.
404
Гл. 14. Уравнения с большим параметром
Таблица 14.
Сравнение приближенных значений собственных чисел,
подсчитанных	по методу возмущении, с точными численными значениями
Порядковый номер собственного числа	1	2	3	4	5	6
Метод возмущений Численное значение Ошибка (%)	3.6667	7.6667	11.6667	15.6667	19.6667	23.6667 3.6723	7.6688	11.6679	15.6675	19.6673	23.6672 0.152	0.027	0.010	0.005	0.003	0.002
Упражнения
14.1.	Рассмотреть уравнение Бесселя порядка 1/2
+ ху' + (х2 — Ц-) у = 0.
Ввести преобразование, исключающее первую производную, и получить ура]
ненне
и" + и = 0.
Показать также, что
Л/2 (х) = х-"1/2 (С] sin х + с2 cosх)-
14.2.	Рассмотреть общее дифференциальное уравнение Бесселя
х2Г + xt,' + (х2 - v2) £ = О
для цилиндрических функций t,v (х). Положив х = уг$ и	и (г), ил
и = г₽''-^(тг₽),
далее показать, что функция и удовлетворяет дифференциальному уравнени
г2 + (2а — 20v +	+ [02у2г2₽ + а (а — 2v₽)]u = 0.
14.3.	Рассмотреть уравнение Эйри
(Ри
-^-+2« = 0.
Используя результаты предыдущего упражнения, выразить общее решен!
этого уравнения через функции Бесселя дробного индекса	/
“ = Кг ^е/-1/з	г3'2) + е2Л-/з *3'2)] •
Указание: Представить уравнение в виде
, d2u , „
г + г “ = °-
аг‘
Сравнить это уравнение с уравнением из упражнения 14.2, положив
2а — 2v0 = 1,	02?2 = 1,
20 = 3, а (а — 2v0) = 0.
Упражнения
405
14.4. Используя результаты упражнения 14.2, показать, что общее решение
уравнения
^+Л-«
может быть представлено в виде
“ -	G4vw,,!) + ‘V- (т|тг'"+ад)] •
где v = (п + 2)*1.
14.5. Рассмотреть задачу на собственные значения
е2у" + (х2 + 2х + 2) у = О, 8 < 1,
Показать, что
У (0) = О,
У (1) = 0.
= +2х + 2 dx-
о
14.6. Показать, что большие по номеру собственные числа
и" + X2/ (х) и = О,
и (0) = О,
даются приближенной формулой
/ (х)> О,
« (1) = О
j W (х) dx
_о
14.7. Показать, что большие по номеру собственные числа
и" + X2/ (х) и = 0,	/ (х) > 0,
и (0) = 0,
даются приближенной формулой
Кп = пп
и' (1)= О
LO	J
14.8. Рассмотреть задачу о собственных значениях вида
у" + Wy = О,
у (1) = 0, у (2) = 0.
Показать, что
.	2
---— лл.
14.9. Показать, что большие по номеру собственные числа
и" + X2/ (х) и = О,
и' (а) = 0, и (Ь) = 0,
даются приближенной формулой
f (х)> о,
5> а
краевой
краевой
краевой
задачи
задачи
задачи
ь
Un
14.10. Рассмотреть задачу
у" +	(1 - х2) у = 0,
у' (0) = 0, у (1) = 0.
406
Гл. 14. уравнения с большим параметром
Показать, что собственные числа с большим номером описываются приближен
ным соотношением
X„ = 4(«+
14.11. Применить метод ВКБ непосредственно к уравнению
ху" + у' + Х2х (1 — х2) у = 0, X > 1.
Указать область применимости полученного приближения.
14.12. Рассмотреть краевую задачу, описывающую теплообмен в плоском ка
нале при полностью развитом турбулентном течении,
у" + к2 (1 - х2) f (х) у = 0,
у (0) = 0, у (1) = 0,
где f (х) = f (—х) > 0 при х [0, 1 ]. Показать, что
14.13.
К(1 — "г2) f (х) dx
Рассмотреть задачу из
предыдущего упражнения при краевых условия^
Показать, что
</(0)=0, у (1) = 0.
Хп=(”+Лт)л J К(1-x*)f(x)dx
Lo
14.14.	Рассмотреть уравнение
у” + X2 (1 — х2)2 = 0.
Показать, что при X—> хи х> —1 имеет место асимптотическое представлени
У — Н (1 •’-2) 1,2	+ с2^—1/4 (^0] ,
где -
X	'
Н = j (1 — т2) di = х — 1------(х— I)3.
1
14.15.	Рассмотреть уравнение
у" +	(х) У = о,
где q (р) = q’ (р) = 0 н q" (р) =/= 0. Показать, что при X—> оо имеет место аснмг
тотнческое представление
у~^ '29-1/4 PjJj/4 (ХЯ) + c2J_1/4 (ХЯ)],
где
х
И = [ К7 dx.
н
14.16.	Рассмотреть уравнение
е/ + (2х + 1) у' + 2у = 0,	0 < е « 1.
Провести преобразование, исключающее средний член уравнения, а затем прн
менять к полученному уравнению метод ВКБ.
14.17.	Рассмотреть уравнение
е/ + (2х + 1) у' + 2у = 0,	0 < е < 1.
Представить решение в форме у = ехр [e-1G (х, е)] и найти два члена разлс
жения функции G.
Г
Глава 15
УСЛОВИЯ РАЗРЕШИМОСТИ
В процессе использования методов возмущений, и в частности
метода многих масштабов, нередко возникают совокупности за-
дач, которые должны решаться последовательно, одна за другой.
При этом задача первого порядка обычно оказывается однород-
ной, в то время как задачи высших порядков будут неоднород-
ными, но линейными. Для того чтобы получить зависимость ре-
шения от медленных переменных, нам необходимо исследовать
задачи высших приближений, после чего функции медленных
переменных подчиняются условиям, позволяющим преобразовать
асимптотическое разложение в равномерно пригодное. В простых
задачах о нелинейных колебаниях указанный процесс приводит
к исключению секулярных членов и членов с малыми знаменате-
лями. В задачах с одной степенью свободы такая операция вы-
полняется легко. Все, что мы должны при этом сделать, — это
положить равными нулю коэффициенты при тех слагаемых, ко-
торые порождают соответствующие секулярные члены. Однако
для динамических систем со многими степенями свободы, которые
описываются несколькими связанными между собой дифферен-
циальными уравнениями, уничтожение секулярных членов пред-
ставляет собой несколько более сложную задачу. Эта задача и ее
приложения к динамическим системам с двумя степенями свободы
составляют содержание первой части настоящей главы.
В других задачах неравномерность получаемых разложений
проявляется в том, что мы не можем удовлетворить всем гранич-
ным условиям. Такую несогласованность удается устранить только
наложением некоторых условий, называемых условиями раз-
решимости (иначе условиями согласования, интегрируемости
или совместности). Ниже эти условия выведены для случая
неоднородного дифференциального уравнения второго порядка
при различных краевых условиях. Полученные результаты ис-
пользуются затем при решении двух простых задач на собствен-
ные значения, задачи о волнах в канале с волнистыми стенками и
задачи о колебаниях мембраны, близкойГ по форме к кругу.
В § 15.10 и 15.11 выведены условия разрешимости для случая
неоднородного уравнения четвертого порядка при различных
краевых условиях. Эти результаты применяются затем еще к двум
задачам, одна из которых возникает в теории устойчивости по-

408
Гл. 15. Условия разрешимости
граничного слоя, а другая — при рассмотрении колебаний пла- 1
стин, близких по форме к круговому кольцу. Далее, в § 15.12 1
с помощью развитой теории решается вырожденная задача на ]
собственные значения. В § 15.13 рассматривается система диф- 1
ференциальных уравнений специального вида. Краевые задачи 1
для систем дифференциальных уравнений первого порядка об- |
щего вида изучаются в § 15.14. § 15.15 посвящен рассмотрению 1
краевых задач для дифференциальных уравнений с внутренними |
граничными условиями. В § 15.16 рассматриваются интегральные |
уравнения, а в § 15.17 — краевые задачи для дифференциальных |
уравнений с частными производными.	|
15.1. Алгебраические уравнения	1
Рассмотрим прежде всего систему двух алгебраических урав- |
нений:	Я
%! — х2 = Ьъ	(15.1) j
2xj — 2х2 = Ь2.	(15.2) I
Очевидно, что эта система не имеет решения, если только не 1
выполнено условие b2 = 2ftx. В самом деле, умножив первое урав-я
нение на 2, получим	и
2xi — 2х2 — 2Ьг.	(15.3) 1
Сравнивая уравнения (15.2) и (15.3), мы приходим к выводу, что.1
для совместности уравнений (15.1) и (15.2) необходимо, чтобыЯ
b2 — 2bv Если Ь2 2Ь1У то уравнения (15.1) и (15.2) оказыва-Я
ются противоречивыми, и, следовательно, у системы (15.1), (15.2)Я
решений нет. Если же Ь2 ~ 2Ь1У то уравнения (15.1) и (15.2)Я
будут линейно зависимы, и фактически имеем лишь одно исходноея
уравнение. Например, можно решить любое из уравнений (15.1),Я
(15.2) относительно х2, записав	Я
х2 = *i —
В этом случае значение хг остается произвольным, и, следова-Я
тельно, имеем бесчисленное множество решений исходной системы Я
Если положить в уравнениях (15.1), (15.2) Ьп = 0 и рассмо®
треть возникающую при этом однородную систему уравнений»
Xi — х2 = 0,	Я
2хг — 2х2 = 0,	Я
то нетрудно видеть, что эта система имеет нетривиальное решениш
х2 = хх.	Я
Видоизменим систему уравнений (15.1), (15.2) так, чтобыЯ
однородная система не имела нетривиальных решений. Рассмотрим®
например,	систему	,®
Xi — х2	= blt	(15.5®
2xj + 2х2	= b2.	(15.6®
15.1. Алгебраические уравнения	409
Умножение уравнения (15.5) на 2 дает
2%! — 2х2 = 2ЬГ.	(15.7)
Складывая уравнения-(15.6) и (15.7), получаем
4%! = Ь2 + 2ЬЪ
а вычитая' (15.7) из (15.6), получаем '
4х2 = Ь2 — 2ЬХ.
Следовательно, система уравнений (15.5), (15.6) имеет решение
xi = ~ (^2 4 2fti), х2 = —£ (Ь2 — 2^),
существующее при любых значениях Ьг и Ь2. В этом случае од-
нородная система, соответствующая (15.5), (15.6), а именно система
— х2 = 0,
2хг + 2х2 = 0
обладает лишь тривиальным решением. В случае системы (15.1),
-(15.2) для существования решения требуется подчинить посто-
янные Ьг и Ь2 условиям разрешимости, а соответствующая од-
нородная система может иметь нетривиальное решение. В случае
системы (15..5), (15.6), напротив, неоднородная система не требует
наложения никаких условий на Ьг и Ь2 для своей разрешимости,
а соответствующая однородная система должна иметь только три-
виальное решение.
Далее, рассмотрим систему третьего порядка
х2 + 2х2 — Зх3 = blt	(15.8)
2х± 4" х2 4" х3 — Ь2,	(15.9)
3xj + х2 — 4х3 = Ь3.	(15.10)
Сложение уравнений (15.9) и (15.10) дает
хг + 2х2 — Зх3 = Ь2 4- Ь3.	(15.11)
Сравнивая уравнения (15.8) и (15.11), замечаем, что они совме-
стны только при условии
bi + b3 = Ьъ
которое и представляет собой требуемое условие разрешимости.
При этом уравнения системы (15.8)—(15.10) оказываются ли-
нейно зависимыми, и для нахождения решения достаточно ис-
пользовать любые два из них.	(
Например, из уравнений (15.8) и (15.9) можно выразить хг и х2
через х3. В результате имеем
*i — *з Ч—д- (^i — 2й2),	х2 = х3 -j—g-(2&i + &а), (15.12)
410
Гл. 15. Условия разрешимости
причем значение х3 остается произвольным; следовательно, си-;
стема (15.8)—(15.10) при выполнении условия разрешимости
имеет бесчисленное множество решений. К условию разреши-:
мости Ьх — Ь2 = Ь3 можно прийти иначе, подставив решение (15.12)^
в уравнение (15.10). Однородная система, соответствующая (15.8)—
(15.10), имеет нетривиальное решение хг = х2 = х3.
Приведенные рассуждения показывают, что в случае, если;
однородная система имеет нетривиальное решение, неоднородная?
система имеет решение тогда и только тогда, когда правая часть
удовлетворяет условию разрешимости. Покажем это теперь для*
системы линейных алгебраических уравнений общего вида •
Лх = Ь,	(15.13)
где А представляет собой квадратную матрицу порядка N, а X
и b — вектор-столбцы с N компонентами. Эта система имеет;
единственное решение при произвольных правых частях b тогда
и только тогда, когда однородная система
/1х —0	(15.14)
обладает только тривиальным решением. Если у однородной си-?
стемы существует нетривиальное решение, то неоднородная си-j
стема не имеет решений, если только компоненты вектора b не|
удовлетворяют специальным условиям разрешимости. В принципе^
эти условия разрешимости можно получить с помощью процесса:
исключения неизвестных. Другой способ получения условий раз-^
решимости состоит в использовании так называемой расширен-^
ной матрицы В. Матрица В представляет собой N X (N + l)j
матрицу, получающуюся добавлением столбца Ьъ Ь2, ..., b^i
к так называемой матрице коэффициентов А. Таким образом,;
если матрица коэффициентов имеет вид
А =
ап a12
a2i a22
alN
(15.15);
aN1 aN2

то расширенная матрица
имеет
вид
ап
а21
а12
а22
bi
alN
a2N b2
(15.16) •

__aNi aN2
aNN bN _
При этом условие разрешимости можно сформулировать следу-.
ющим образом: система линейных алгебраических уравнений имеет,
решение тогда и только тогда, когда ранг расширенной матрицы В
совпадает с рангом матрицы коэффициентов А.
15.1. Алгебраические уравнения
411
Отметим, что однородная система имеет нетривиальное ре-
шение тогда и только тогда, когда определитель матрицы коэф-
фициентов обращается в нуль, т. е.
И 1 = 0.
При этом ранг матрицы А меньше N, и поэтому ранг матрицы В
тоже меньше N. Следовательно, определитель любой квадратной
матрицы N-vo порядка, образованной из матрицы В вычеркиванием
одного из столбцов, должен равняться нулю. Любое такое условие,
например,
Q12	а1з	a1N	bl	
°22	а23	a2N	b2	= 0	(15.17)
aNz aN3    (Inn
дает некоторое условие разрешимости. Это условие разрешимости
можно интерпретировать еще и по-другому. Если | А |	0, то
для нахождения решения хъ х2, ..., xN можно использовать
правило Крамера. Например,
frl	“12	“13		• •	alN
^2	“22	“23	‘	‘ ‘	“гУ
fry	“у2	O-N3		• 	aNN
(15.18)
Если | А | = 0, то, как видно из формулы (15.18), хг обращается
в бесконечность. Следовательно, система уравнений (15.13) не-
разрешима, если только одновременно не обращается в нуль и
определитель в числителе дроби (15.18). При этом мы имеем не-
определенность вида 0/0.
Условие разрешимости системы (15.13) в случае, когда соответ-
ствующая однородная система обладает нетривиальным реше-
нием, можно выразить еще и следующим образом. Рассмотрим век-
торное уравнение, транспонированное по отношению к уравне-
нию (15.13), и умножим его справа на вектор-столбец и, где черта
сверху означает комплексное сопряжение, а так называемый
сопряженный вектор-столбец и определяется ниже. В результат^
имеем
(4x)Tu = bTu,	(15.19)
412	Гл. 15. Условия разрешимости
где верхний индекс Т означает операцию транспонирования, т. е. 1
Оц	012	• • •	alN Т
а21	а22	• • •	a2W
ап	а21		 	аН1
а12	а22	•	 •	°W2
alN	a2N		 	aNN
_ aNl aN2  • • aNN
- ьх у
— [Й1 &2 ... bN].	|
_ &N _	j
Поскольку (Лх)т = хтЛт, соотношение (15.19) можно переписать !
в виде	_	_	I
хтЛти = Ьти.	|
Следовательно,	  |
хтЛти —bTu,	|
или	хтЛ*и = bTu,	. (15.20)|
где матрица Л* = Лт представляет собой матрицу, сопряженнук/Я
к матрице Л. Матрица Л называется самосопряженной, если!
Л* = Л, т. е. такая матрица будет либо эрмитовой, либо сим-1
метричной, в зависимости от того, является ли она комплексной!
или вещественной. Если однородная система (15.13) имеет нетритЗ
виальное решение х, то |Л| — |Л*| = 0. Последнее равенстве®
означает, что однородная система	я
Л*и = 0	(15.21И
имеет нетривиальное	решение.	|
Определив вектор	и как решение однородной системы (15.21)!
обратимся вновь к неоднородной системе (15.13), т. е. к случаи!
b #= 0. Подставляя соотношение (15.21) в (15.20), получаем елея
дующую форму условий разрешимости:	'	а
bTu = 0,	<15-22|
где и — любое решение сопряженной системы. Иначе говоря!
условие разрешимости требует, чтобы правая часть систем™
(15.13) была ортогональна к любому решению однородной соя
пряженной системы.	Я
Если определить	внутреннее	произведение вектор-столбцов и
и	v как	I
(u, v)=uTv,	(15.231
то соотношения (15.19) и (15.20) можно переписать в виде Я
(Лх,	и) = (х,	Л*и) = (Ь,	и),	(15.24ая
15:1. Алгебраические уравнения
413
а соотношение (15.22) — в виде
(b, и) = 0.
(15.246)
Хотя мы показали только необходимость условия (15.246),
на самом деле оно является и достаточным условием разрешимости
системы (15.13).
Рассмотрим в качестве примера систему (15.8)—(15.10). В этом
случае
(15.25)
и А* = Ат, поскольку матрица А
ряженная система имеет вид
вещественная. Далее, соп-
1	—2	3'			
2	1	1	4^2	= 0,	(15.27)
—3	1	—4.	_и3_		
или
Uj — 2па + Зп3 — 0,
2«! + и2 Н- ыз “ 0»
—3«! + и2 — 4и3 = 0.
(15.28а)
(15.286)
(15.28b)
Система уравнений (15.28) имеет нетривиальное решение,
поскольку таким свойством обладает система (15.8)—(15.10).
Умножая уравнение (15.286) на 2 и складывая с (15.28а), имеем
5иг + 5п3 = 0.
В то же время вычитая из уравнения (15.286) уравнение (15.28в),
имеем снова
5их + 5п3 = 0.
Следовательно, и3 — —иг. При этом из уравнения (15.286) вы-
текает, что иа ~ —«1- Таким образом, сопряженная задача имеет
решение вида
Г 11
U — с
Подчиняя теперь вектор b условию ортогональности к решению
однородной сопряженной системы, находим, что условие разре-
шимости имеет вид
К — — Ь3 — 0,
414	Гл. 15. Условия разрешимости
что полностью согласуется с условием, полученным выше с по--'
мощью исключения неизвестных. Заметим, что условие разре-i
шимости в форме (15.17) удобно для применения, и поэтому мы-
будем часто использовать его в дальнейшем.	<
Применим теперь полученные выше результаты к двум зада-
чам о колебаниях гироскопических систем с двумя степенями
свободы.
15.2.	Нелинейные колебания гироскопических систем
с двумя степенями свободы
Рассмотрим свободные колебания гироскопической системы
с двумя степенями свободы с учетом квадратично нелинейных;
возвращающих сил. Такая задача сводится к исследованию^
системы уравнений
«1 + «2 +	= 2U!U2,
Й2 — й1 + 2«2 — Ul
при малых, но конечных амплитудах.
Будем искать равномерное разложение с помощью метод;
многих масштабов в виде
«1 = виц (То, Л) + е2«12 (То, Л) + • •  , J.
X
«2 = ен21 (То, 7\) + е2и22 (7о, 7\) + • •  ,	1
где То = t, 7\ = e.t и & — малый безразмерный параметр, харай
теризующий амплитуду колебаний. Подставляя разложения
(15.30) в уравнения (15.29) и используя соотношение (5.45), пс|
лучаем	_	я
(Do 4' 2eDqD\) (eun 4~ е Ui2) 4“ (Do 4~ ®Di) (eu2i 4* е ^22) 4~	1
4“ 2 (еиц 4- е2и12) 1- • • • = 2 (еиц 4~ е2м1г) (ем21 4* 82«2г) 4"	' а
(Do 4- 2eD0Di) (eu2i 4“ е н2г) — (Do 4“ e^i) (e“n 4“	12) 4*	..я
-|- 2 (еи21 4~ е2и22) -{-••• = (еНц 4“ е2и1г)2 4" ''" Ц
Приравнивая коэффициенты	при одинаковых степенях е в обеиЯ
частях этих уравнений,	имеем	1
для порядка е:	Ц
Down 4“ D0U21 4“ 2нц = 0,	(15.31м
DoH2i •— D0«n 4- 2u2i = 0;	(15.31м
для порядка е2:	м
D0U12 4“ Df)ll22 4“ 2ui2 = —2DoDj«u —Di«21 4“2Uji«21,	Я
DqU22 — D0U12 4- 2ll22 — —2D0D1U21 4“ D]U11 4- Иц.	05.3Я
15.2. Гироскопические системы с 2 степенями свободы
415
Уравнения (15.31) образуют систему двух дифференциаль-
ных уравнений с постоянными коэффициентами. Следовательно,
их решения можно получить, полагая
«и = <4 ехр (ссоТ0), и2 = с2 ехр (ico То). (15.33)
Подстановка (15.33) в уравнение (15.31) дает
(2 — co2) Cj + icoc2 = О,
—tcocj + (2 — со2) с2 = 0.	(15.34)
Для того чтобы существовало нетривиальное решение системы
(15.34), определитель матрицы ее коэффициентов должен обра-
щаться в нуль, т. е.
2 — со2 ico
—ico 2 — со2 0-
Следовательно,
(2 — со2)2 — со2 = 0,
или	со4 — 5со2 + 4 = (со2 — 4) (со2 — 1) = 0,
откуда со = 1 и со = 2, если рассматривать только положитель-
ные частоты. При со~= 1 из первого из уравнений (15.34) следует,
что
Ci + ic2 = 0, или с2 = ici.
При со = 2 из того же уравнения имеем
—2сг + 2ic2 = 0,' или с2 = —ic1.
Следовательно, общее решение системы (15.31) можно записать
в виде
«н = Ai (Л) е‘т<> + Аг (7\) e~iT° Д А2(7\) е2‘т° + Д2 (7\) е~2‘т°,
«21 = iAr (7\)	- iAr (7\) е~‘г° - iA2(T\)e2iT° + iA2 (Л) е~2‘'г°.
(15.35)
Как и в случае колебательной системы с одной степенью свободы,
амплитуды А± и А2 нельзя определить на этом этапе итерацион-
ного процесса. Они будут определены на следующем этапе из
условий разрешимости неоднородной задачи.
Подставляя решения (15.35) в систему уравнений (15.32),
имеем
DqU\2 4” Оо«22 + 2uI2 = —2iAieiT° — 4iA2e2‘ ° — iA\e‘^’>
+МЙ2'7'” + (К. с.) 4- 2 (Ле'7"” 4- Aie“''r° 4-
4-A2e2iT’> 4- A2e~2ir«) (iA\eiT<> —
—iA1e~‘7'» — iA2e2lTa 4- iA2e~2iT,>),
DqU22 — DqUi2 4" 2u22 = 2A1£?77"“ — 4A2£?2< ° 4- AtC?17"0 4"
+A2e2/7'“ + (к. c.) 4- (AxetTa + А^1Т° 4-
+А2е2(Г« 4- A2e~2‘r«)2.
416
Гл. 15. Условия разрешимости
После некоторых преобразований и упрощений последняя
система примет вид
^о^12 4~ D0U22 -j- 2ui2 = —i (ЗЛ, -j- 4ЛгЛ1) е‘ ° -\-
4"» (—ЗЛ2 -j- 2Л1) е ‘ ° 4~ (к. с.) 4~ (Н. С. Ч.),
(15.31
D0U22 — D0U12 4* 2u22 = (ЗЛ ।	2ЛгЛ,) е ’4~
+ (-ЗЛ2 + Л,) e2iT° 4- (к. с.) + (Н. С. Ч).
(15.3:
Поскольку однородная система, соответствующая (15.36), (15.37
имеет решения, пропорциональные ехр (±1Т0) и ехр (±2iTa
слагаемые в правых частях, пропорциональные этим экспонента»
порождают в решении ы12, и22 секулярные члены. Заметим, чт
правая часть каждого из уравнений (15.36) и (15.37) содержг
слагаемые, пропорциональные ехр (±гТ0) и ехр (±2гТ0), и по;,
тому нет необходимости полагать коэффициент при каждой и
этих экспонент в обоих уравнениях равным нулю. Более того, есл
бы мы поставили такое условие, то получили бы четыре несовмес
ных комплексных уравнения относительно Аг и Л2. Поэтому для т<
го чтобы уничтожить секулярные члены (т. е. чтобы найти соотве'
ствующие условия разрешимости), будем искать частное решен»
не содержащее резонансных слагаемых, соответствующих ехр (iT
и ехр (2iT0), в виде
«12 = Л(Л)^» + Л(Л)^Ч
U22 = Q1(7’1)^7’4-Q2(7’1)^T».	(
Подставляя решения (15.38) в уравнения (15.36), (15.3'
имеем
(Pi 4- tQi) eiTo + (-2Рг + 2iQ2) e2iT° = -i (ЗЛi + 4A2Ar) x
X eir<>+i (^3A2A-2A^)e2i
(~tPt 4- Qi) elT° 4- (-2^2 - 2Q2) e2iT° = (3л; 4- 2Л2Л,) x
x 4- (—ЗА'2 + А2) e2i‘
Приравнивая коэффициенты при каждой из экспонент в обе
частях полученных уравнений, находим
Р 4~ iQi — —i (ЗЛ 1 4- 4Л2Л,),	(15.31
—/Р14-е1 = ЗЛ14-2Л2Л1,	(15.31
~2Р2 4- 21Q2 = i (~ЗА2 + 2Л?),
,	<>	(15.*1
—2.1Р2 — 2Q2 = —ЗЛг 4" Л1 •
15.3. Параметрическое возбуждение
417
Уравнения (15.39) образуют неоднородную систему двух линей-
ных алгебраических уравнений относительно Рг и Соответ-
ствующая однородная система имеет нетривиальное решение,
так как определитель матрицы ее коэффициентов равен нулю:
При этом условие разрешимости системы (15.39) может быть за-
писано в одной из двук форм:
1	—i (ЗЛI 4- 4Л2Ло
—i ЗА[ 4- 2A2Ai
= 0, или
—i (ЗД1 4* 4ЛгЛ1) i
3A't 4- 2Л2Л1	1
= 0.
В двумерном случае оба этих условия приводят к одному и тому же
результату, но в случае систем более высокой размерности это,
вообще говоря, не так. В настоящем случае оба равенства экви-
валентны условию вида
А\ = —А2А\.
(15.41)
Аналогичным образом, определитель системы (15.40) равен нулю,
и эта система имеет решение тогда и только тогда, когда выпол-
няется следующее условие разрешимости:
—2 i (-ЗА2 + 2Л?)
—2i
—ЗА2 4" Aj
= 0,
равносильное уравнению
A2 = -^-Ai.
(15.42)
Уравнения (15.41) и (15.42) описывают модуляцию амплитуд Аг
и А2, т. е. их изменение с медленным временем 7\. Как и в случае
динамических систем с одной степенью свободы, амплитуды А±
и А2 обычно представляют в показательной форме и в уравнениях
(15.41) и (15.42) отделяют вещественные и мнимые части. Решением
этих уравнений завершается построение разложения первого
порядка. Мы не будем здесь входить в детали этого решения,
а отошлем заинтересованного читателя к книге Найфэ и Мука.
15.3.	Гироскопические системы с параметрическим
возбуждением
Рассмотрим параметрически возбуждаемую линейную систему
с двумя степенями свободы. Иначе говоря, будем исследовать
решения системы уравнений вида
йх 4- «2 + 2«i 4- 2е cos Qt (fnUi 4- /12«2) =0,	^543^
й2 —• «1 + 2«2 + 2е cos Qt (f2i«i + f22«2) = 0
14 Найфэ A. X.
418
Гл. 15. Условия разрешимости
при малых е. Предположим для определенности, что частота £
положительна. Используя метод многих масштабов, будем ис
кать решение в виде
«1 = «ю (То, Тх) 4- е«и (То, Л) 4- •   ,
«2 ~ «го (П, ^1) “Ь e«2i (Т’о» ^1) 4~ •   •	(15.44
Подставляя разложения (15.44) в систему (15.43), учитывая соот
ношение (5.43) и выражая cos Qt в виде cos ЙТ0, получаем
(£)2 4~ 2eZ?oZ)i) (що f е«п) 4" (^о Т eDj) (и2о 4“ e«2i) 4~
+ 2 («ю 4~ е«и) 4~ 2е cos ПТ'о (Л1«ю + /12«го) + • • • — 0.
(Do -k 2eDoOi) («го 4~ е«21) — (По 4“ еП1) («ю 4~ е«п) 4*	•;
4-	2 («го 4~ e«2i) 4~ 2a cos НТо (/21«ю 4“ /г2«го) 4~  ’  ~ О
Приравнивая коэффициенты при одинаковых степенях е, имее^
для порядка е°:	J
DqUio Z)q«20 “Ь 2«10 = О,
D0II20 — DqUiq 4~ 2«20 — О;
(15.45
для порядка е1:
По«11 + D0U21 ф- 2«11 = —2DqD\U\q — D\U2Q — 2 COS QT^/nHlO 4“/12«2э}
(15.41'
D0U21 — DqU\i + 2«2i — —2D0DlU20 4- Пщю — 2 cos Q7o(/2i«io + /22^20
(15.4'
Как и в предыдущем параграфе, общее решение системы ди(
ференциальных уравнений (15.45) можно представить как
«ю = Аг (Л)	+ Аг (Тг) е~‘г° + Л2 (7\) e2ir° + Л (Л)
и2№ = 1А1е‘г° — г» —	7’® 4~ M2e~2‘7'»,	(15.4
где Аг и Л2 подлежат определению из условий разрешимости i
следующем этапе итерационного процесса. Подстановка выр;
жений (15.48) в уравнения (15.46) и (15.47) дает
П?«н 4" DqU2i 4- 2«ц = —ЗЛ16 0 — 3iA2e ° 4~ (к- с-) — (е ° 4~
4- е-еаг<>) (fuA1e‘r« 4- /11Л2е2‘г» 4- i'A2/l1e,T» — 1/12А2е2!7'° 4- (к. с.)
По«21 — О0«п 4- 2«2i 4~ ЗЛ|6 0 — ЗЛ2<? °	(к. с.) — (е ° I--
4- е-/й7'«) (/21Лхе‘т° 4- /aiAe2'7" 4- «Лг^^1'7'0 — if22A2e2tT« 4- (к. с.)
или
D^Ujj 4" D(/i2i 4~ 2нц = —3Aie‘ ° — ЗА2е ° —
-(/11 + »712)Л1[е'<1+а)г»4-^<1-й>Ч-	:
- (Ах - 1/12) Ао [е‘ <2+й> + е‘ <2-й) ч + (к. с.), (15.41
15.3. Параметрическое возбуждение	4J9
D(,u.2i 7-<E^ouii 4~ 2u2I — ЗА[в ° — ЗЛ2е ° —
-	(/2i + */22) Аг [е‘ <>+«)	+ е1 Ч _
-	(/21 ~ »/22) Л2 [е‘ <2+«) Т° + е‘ <2-®) Ч + (к. с.). (15.50)
Когда амплитуды Аг и Л2 постоянны, как в случае прямого
разложения, правые части уравнений (15.49) и (15.50) содержат
слагаемые, которые могут порождать в решении секулярные члены
при определенных значениях й. Так, резонансные члены поя-
вятся в,«ц и и21, если любой из показателей экспонент в (15.49)
и (15.50) будет равен ±1 или ±2, поскольку функции
ехр (±iT0) и ехр (±2tT0) являются решениями соответствующей
однородной системы. Итак, условия появления секулярных
членов суть следующие:
1 + Q = ±2, 1— Q = _|-2, 1 + й = ±1, 1— й = ±1,
2 + й = ±2, 2 — й — +2, 2 + й = ч-1. 2 •—- й = ч- 1.
т. е. параметрический резонанс наступает при й = 0, 1, 2, 3, 4.
Если заменить точное равенство на приближенное, то вместо се-
кулярных членов появятся члены с малыми знаменателями. Рас-
смотрим случай й 3.
Для того чтобы уничтожить члены с малыми знаменателями,
мы прежде всего преобразуем их в секулярные члены, вводя
параметр расстройки по формуле
7 у	й = 3 + ест	(15.51)
и соответственно записывая
ЙТ0 = ЗТ0 + 8стТ0 = ЗТ0 + аТг. (15.52)
Подставляя соотношение (15.52) в уравнения (15.49) и (15.50),
имеем
DqUh + Oo«2i + 2«ц = — [З1Л1 Ц- (/п Ц- i/i2) Азе1аГ1] e‘Tl> —
-	[3i%4-(/n — i/i2) Де'011] е2,Г° 4-(к. с.) 4-(Н. С. Ч.), (15.53)
й^«21 — DoU\\ 4" 2«2i — [ЗЛ1 — (/2i 4- i/22) Л2е1<,Г1] etT" —
-	[ЗЛ; 4- (/21 - i/22) AieiaT'] e2iT“ 4- (к. с.) 4- (Н. С. Ч). (15.54)
Для того чтобы вывести соответствующие условия разреши-
мости, будем искать частное решение системы (15.53), (15.54),
не содержащее секулярных членов, в виде
«и = Pi (Л) ехр (гТ0) + Р2 (Л) ехр (2iT0),	(15.55)
«21 = Qi (7\) ехр (iT0) + Q2 (Ti) ехр (2iT0).
Как и в предыдущем параграфе, подставляя решения (15.55) в
уравнения (15.53) и (15.54) и приравнивая коэффициенты при
14*
420	Гл. 15. Условия разрешимости	я
ехр (iT0) и ехр (2iT0) в обеих частях каждого из уравнений, пой
лучаем	j
Pi + iQ\ = — 3<А{ — (/и + if\2) Д2ехр (ioTi),	j
—iPi Ч- Qi — ЗЛ{ — (/21 4- I/22) A2 exp (icsT 1), (15.56)?
—2P2 + 2iQ2 = —ЗМ2 — (/11 — if 12) At exp (iaTi),	1
— 2iP2 — 2Q2— —ЗД.2 — (f2i — if22)Аехр(ю7\). (15.57|
Поскольку однородная система (15.56) обладает нетривиальным^
решением, неоднородная система разрешима тогда и только тогда!
когда выполняется следующее условие:	,	?
1	— 3iA; — (fn -j- if\2) Д2ехр (ioTi)
—i	ЗЛ{ — (/21 + I/22) Aexp(ioTi)	I
Это условие можно переписать в виде	|
А{ = Ц- [f2t — f\2 + i(fu +fi2)l ^2exp(ioTi). (15.5^
Условие разрешимости системы (15.57) имеет вид
—2	—ЗМг — (/п — i/12) A exp(ioTi)	4
—2i —ЗА — (/21 — i/22) Ai ехр (ioTi) ’	4
или Л2 =-----------[/21 —/12 —^(/11-4-/22)] Aexp(ioTi). (15.59|
Уравнения (15.58) и (15.59) описывают модуляцию амплитуд!
Аг и А2. За деталями анализа этих уравнений мы вновь отсы-)
лаем читателя к книге Найфэ и Мука.	j
15.4.	Краевые задачи для дифференциальных уравнений |
второго порядка	|
В этом параграфе будут выведены условия разрешимости
краевых задач для линейных неоднородных дифференциальны!
уравнений второго порядка с неоднородными граничными услоЗ
виями общего вида. Итак, рассмотрим задачу	|
Р2 (х) у" + рх (х) у' + р0 (х) у =	1
= / (х), а < х < Ь,	(15.601
«и//' (а) + «21^ (а) + а1Йу' (Ь) + а14р (b) = 0Х,	|
<х21У' (а) + «221/ (а) + «2з//' (b) + a2iy (b) = 02,	(15.61|
где граничные операторы линейно независимы, т. е. матрица
«11 «12 «13 «14
СС22 «23 «24 J	Л
15.4. Краевые задачи для уравнений 2-го порядка
421
имеет ранг 2, и, следовательно, существует по крайней мере одна
невырожденная субматрица размером 2x2. Иначе говоря, по
крайней мере один из определителей
Л12			а11 а12 0^21 ^22	>	Л13 				СО	со i-Ч а	8 W	Я а	а		—		а а W а а	1
Дгз —		Я	Я to	М Ю	tO Я	я с5	со		, Д21 —		а12 ос14 0^22 ^24		>	^34 —		«13 а14 «23 «24	
отличен от нуля.
Граничные условия (15.61) называют смешанными или нераз-
деленными, поскольку они содержат значения искомой функции
и ее производной на обоих концах промежутка.
В этом параграфе рассмотрим случай, когда определитель
Д13 =0= 0. Разрешая уравнения (15.61) относительно у' (а) и у' (&),
имеем
У' («) = УпУ (а) + у1гу (Ь) + бх,	(15.62)
У' (Ь) = у21у (а) + у22у (Ь) + б2,
где
.. __	Л23	.. ___ Д34	,,	Д12	..	_	^14
711 ------д-->	712 --"д-->	721 ------д >	722 - д >
“13	Л13	Л13	“13
g* : ' Р1«23 — Р2«13	g  Р2«ц — Pl«21	(15 63)
Предпошлем подробному выводу условий разрешимости пояс-
няющий дальнейшее простой пример. Рассмотрим задачу вида
у" + л2у = л sin лх,	(15.64)
У (0) = ₽1, у (I) = ₽2.
В данном случае граничные условия разделены, а соответствую-
щая однородная задача
У* + я*у «0, у (0) = у (1) = 0	(15.65)
имеет нетривиальное решение у = sin лх. Поэтому неоднородная
задача не будет иметь решения, если только не окажется удовлет-
воренным соответствующее условие разрешимости. Для того
чтобы получить указанное условие, будем искать решение задачи
(15.64) в предположении, что оно существует. Общее решение
уравнения (15.64) представляет собой суперпозицию общего
решения однородного уравнения и некоторого частного решения
(см. приложение Б). В результате имеем
у — q sin лх + с2 cos лх — 0,5®cos лх, (15.66)
гдесх и с2 — произвольные постоянные. Подчиняя решение (15.66)
граничным условиям (15.64), получаем
С2 — Р1> . ---С2 Н- ~2~ ~ Ра’
422	Гл. 15. Условия разрешимости
Эти уравнения несовместны, и, следовательно, исходная задач!
(15.64) не имеет решения, если только не выполнено соотношение
Pi + 02 = 4’	(15’67>
которое и представляет собой искомое условие 'разрешимости^
При этом решение задачи (15.64) имеет вид
у = сх sin лх + Pj cos лх-^-xcosjix. (15.68|
Для того чтобы найти условия разрешимости в общем случае^
нет необходимости проводить указанную выше процедуру, в осо|
бенности если не представляет интерес явный вид решения, как^
например, в задачах теории возмущений. Вместо этого восполь^
зуемся идеей обращения к сопряженной задаче. Умножим урав^
нение (15.60) на функцию нх (х), которую будем называть сопря-t
женным решением, подлежащим определению в дальнейшем!
В результате получим	5
р2иу" + р^иу' + р<>иу = fu.	(15.69)5
Почленное интегрирование соотношения (15.69) от а до b (т. е|
по интересующему нас промежутку, на котором решается крае!
вая задача) дает	|
ь	ь	ь	ь
J р2иу"dx j pyiy' dx + j рйиу dx = j fu dx. (15.70|
a	a	a	a
Далее, проинтегрируем по частям первые два слагаемы^
в (15.70), чтобы перейти отдифференцирования функции у к диф|
ференцированию	функции	и.	Таким	образом,	имеем	«
ь	ь	ь	I
J	р^иу" dx = Р2,иу' |	—	j (р2п)' у' dx	I
а	а	а
b	ЪЬ	I
И	J (р2«)' у' dx — (p2u)' у | — j (р2н)" у dx,
а	а а
откуда	';
b	ь	1
J руну" dx - = [руну' — (p2u)' у]а + J (р2и)" у dx. (15.711
а	а	1
Кроме того,	I
Ь	b ь	1
j рулу' dx — ррлу | — j (pyi)' ydx.	(15.72|
15.4. Краевые задачи для уравнений 2-го порядка
423
Подставляя соотношения (15.71) и (15.72) в (15.70), имеем
ь
[р2иу — (р2и)' у + Piuy\a + j (Р2«)” ydx —
а
b	b	ь
 — J (ptu)’ ydx-f- J роиу dx= j fu dx,
a	a	a
ИЛИ
b
J [p2U + (2/?2 - Pl) w + (p2 — pi + Po) u]ydx -I-
a
b
+ {p2uy + I(pi — p2) и — p2u] y]a = J fu dx. (15.73)
a
Приравнивая нулю подынтегральное выражение в левой части
соотношения (15.73), получим уравнение относительно функции и:
р2и + (2рг — Pi) W + (р2 — р[ + ро) и = 0,	(15.74)
которое обычно называют сопряженным по отношению к одно-
родному уравнению (15.60). Для того чтобы найти вид граничных
условий, необходимых для замыкания сопряженной задачи,
рассмотрим, однородную задачу, соответствующую (15.60), (15.62),
т. е. положим f = 0 и бх = 62 = 0. Тогда соотношение (15.73)
и условие (.15.62) примут вид
/ \P2uy’ + [(pi - р2) и - р2и'] у\х=ь -
—	+ 1(Р1 — Pi) и — р2и]у\х=а=0,	(15.75)
У' (а) = упу (а) + у12у (Ь), у' (Ь) = у21у(а) + у22у(Ь). (15.76)
Подставляя выражения для у' (а) и у' (Ь) в соотношение (15.75)
и собирая члены, содержащие у (а) и у (b), получим
[Y21P2U	— (V11P2 + pl — р2) Ux=a + р2и' |ж=0] у (а) —
— [Y12P2U |x=a — (Y22P2 + Pl — Р2) U [x=b + p2U |X=ZJ у (Ь) = 0. (15.77)
Выберем граничные условия сопряженной задачи так, чтобы ко-
эффициенты при у (а) и у (Ь) обращались в нуль каждый в отдель-
ности, т. е.
Y21P2U |х=* — (Y11P2 + Pi — рг) и |х=0 + р2и' |х=0 = 0,
Y12P2U |х=а — (Y22P2 + Р1 — р2) И ь=& + Р2«' |х=б = о.	(15.78)
Таким образом, функция и представляет решение краевой за-
дачи для уравнения (15.74) с граничными условиями (15.78).
Однородное дифференциальное уравнение, соответствующее
(15.60), называется самосопряженным, если оно совпадает с сопря-
женным ему уравнением (15.74). Эти уравнения совпадают в слу-
чае, если
2рг —Р1=Р1, Рг —pi = 0,	(15.79)
424
Гл. 15. Условия разрешимости
или pi = р2. При этом однородное уравнение, соответствующее
(15.60), имеет вид
Р2У" + р2у' + РоУ = 0,
или
(РгУУ + РоУ = 0-	(15.80;
Сопряженное уравнение (15.74) можно тогда записать как
(р2м')' + Ро« = 0.	(15.81
а граничные условия (15.78) примут вид
и (а) = уп« (а) - у21р2 (Ь) р2' (а) и (Ь),
и (Ь) = — у)2р2 (а) р21 (Ь) и (а) -|- у22м (Ь).
Отметим, что граничные условия (15.82), вообще говоря, отлича
ются от граничных условий (15.76), если только не выполнена
равенство
—Т21Р2 (Ь) = —?12р2 (а).	(15.83
Если же соотношения (15.79) и (15.83) выполнены, то сопряженно
дифференциальное уравнение (15.81) и граничные условия дл)
него (15.82) совпадают с исходным однородным дифференциальньй
уравнением (15.80) и граничными условиями (15.76). В этом сл$
чае самосопряженной называют краевую задачу в целом. j
Если однородное дифференциальное уравнение второго порядй
не является самосопряженным (т. е. pt р2), его всегда можи
преобразовать в самосопряженное, умножив на подходящую
функцию v. Для того чтобы найти функцию v, умножим одна
родное уравнение, соответствующее (15.60), на v. В результат)
получим	j
Ptvy" + ptvy' + povy = 0.	(15-И
Условие самосопряженности уравнения (15.84) имеет вид ‘
Piv = (p2v)' = p2v’ + p2v,	1
откуда	'	|
o' = Pl____P2	I
° Po	P* ’	J
ИЛИ
In v = I — dx — In p2.	1
j	Pi	3
Таким образом,	"i
v — рУ	exp j -y- dx.	(15.8|
Следует отметить, что дифференциальное уравнение	порядка выф
второго преобразовать в самосопряженное не всегда возможет
Определив сопряженную	краевую задачу	(15.74),	(15.78
вернемся к неоднородной задаче (15.60), (15.62), с тем чтобы найя
вид соответствующего условия разрешимости. С учетом того, ч|
15.4. Краевые задачи для уравнений 2-го порядка
425
функция и удовлетворяет уравнению (15.74), соотношение (15.73)
принимает вид
1рч.чу' + (pi — Рг) чу — Рч.ч’у\х^ь —
ь
— [ptuy + (pi — pfiuy — P2U'y]x=a = j fudx. (15.86)
a
Подставляя выражения для у' (а) и у' (Ь) из условий (15.62)
в соотношение (15.86), имеем
62P2W |х=й — 61P2W |х=а + [?21 Р2Ч |х=6 — (Y11Р2 +
+ Pl — Р2) и |х—a -J- Р2Ч |х=а] у (я) —
b
— (У12 Р2Ч |х=0 — (Т22Р2 + Pl — р'2) U |X=ZJ y(b)=^ fu dx. (15.87)
а
Поскольку члены в квадратных скобках в соответствии с усло-
виями (15.78) обращаются в нуль, соотношение (15.87) сводится
к искомому условию разрешимости:
^р2 (Ь) и (Ь) -ф 6tp2 (а) и (а) — j / (х) и (х) dx, (15.88)
а
где и представляет собой решение сопряженной краевой задачи
(15.74), (15.78).
В качестве частного случая рассмотрим неоднородную задачу
Ш турма—Лиувилля
1р (х) у'] + q (х) у — кг (х) у = f (х),	(15.89а)
У' (а) = уиу (а) + у12 у (Ь),	(15.896)
У' GO = Y21 у (а) + у22у (Ь).	(15.89в)
При формулировке задачи (15.89) предполагается, что выполнено
соотношение (15.83) и, кроме того, что г (х) >0 при х £ [а, Ь].
Если значение параметра X не совпадает ни с одним из собствен-
ных чисел однородной задачи (т. е. однородная задача имеет только
тривиальное решение), то неоднородная задача имеет единствен-
ное решение при любой непрерывной функции f (х). С другой сто-
роны, если параметр X равен какому-либо собственному числу од-
нородной задачи (т. е. однородная задача имеет нетривиальное
решение), йеоднородная задача разрешима лишь при условии
ь
j/(х) u(x)dx = 0,	(15.90)
а
т. е. при условии ортогональности функции / (х) собственной функ-
ции, отвечающей собственному значению X. Этот результат состав-
ляет содержание теоремы, обычно называемой альтернативой
Фредгольма:
426
Гл. 15. Условия разрешимости
При заданном значении X либо неоднородная задача
имеет единственное решение при любой непрерывной i
функции f, либо однородная задача имеет
нетривиальное решение.
В следующем параграфемы рассмотрим краевую задачу с гра-
ничными условиями общего вида (15.61). В § 15.6 и 15.7 применим
развитую теорию к двум задачам о собственных значениях,’
а в § 15.8 — к задаче о звуковых волнах в канале с волнистыми^
стенками. В § 15.9 мы видоизменим полученные выше резуль-j
тэты, с тем чтобы применить их к задаче для дифференциального^
уравнения с регулярной особой точкой, и используем модифици-i
рованную теорию в задаче о колебаниях мембраны, близкой по;
форме к кругу.
15.5. Граничные условия общего вида
Сопряженный оператор
Обозначим через L дифференциальный оператор второго по-
рядка, определяемый дифференциальным выражением (15.60),’
т. е.
Ь(«/) = [рЛх)^ +Pi(x)~-£- +Ро(х)]у, (15.91>
где р2, Pi и р0 представляют собой непрерывные функции в промер
жутке 1а, Ь]. Если у (х) и и (х) — дважды непрерывно дифферент]
цируемые на 1а, Ь] функции, то имеем
X	X
J и Цу) dx = J [(р2«) у" + (Plu) у' + (р0«) у] dx, а « х < Ь. (15.92)
а	а
Как и в предыдущем параграфе, интегрирование соотношений
(15.92) по частям дает	\
X	I
j uL (у) dx = fp2uy' — (p2u)' у + PlUyYa +	1
a
x	!
+ J KP2«)" — (Piu)' + Poll] ydx.	(15.93)
a
Обозначим дифференциальный оператор, входящий в подынтег-i
ральное выражение в правой части (15.93), через L*, т. е. !
L’(ц) = (рги)"— (рщУ-j-р0« =	(
== [/’2-|^- + (2P2-pi)-^- + Po + P2-p;j и. (15.94Х
При этом соотношение (15.93) перепишется как
х	'
J [uL {у) - yL* (u)J dx = ]р2 {иу - у'и) + (pi - р2) иу]*. (15.95^
15.5. Граничные условия общего вида
427
Оператор L* называется сопряженным по отношению к опера-
тору L. Умножая соотношение (15.94) на у и интегрируя полу-
ченный результат по частям, легко показать, что L является со-
пряженным оператором по отношению к оператору L*. Таким
образом, операторы L и L* взаимно сопряжены.
Как и в предыдущем параграфе, дифференциальное уравнение
L* (ц) = 0	(15.96)
будем называть сопряженным дифференциальному уравнению
L (у) = 0.	(15.97)
Если же L = L*, то оператор L и дифференциальное уравне-
ние L (у) = 0 будем называть самосопряженными. Сравнивая
выражения (15.91) и (15.94), приходим к выводу, что L = L*
тогда и только тогда, когда
2р2-Р1 = Рь
Таким образом, оператор L будет самосопряженным тогда и
только тогда, когда pt = р2. При этом
L — L _р2—+ р2—4- р0.
Как указывалось в § 15.4, любое дифференциальное уравнение
вида (15.97) можно преобразовать в самосопряженную форму,
умножив на функцию v, определяемую равенством (15.85).
Дифференцируя соотношение (15.95) по х, получаем так на-
зываемую формулу Лагранжа
иЦу)~ уL* ф) = ^~[р2(иу' - и у) + (/?! -р'2)иу]. (15.98)
Выражение в квадратных скобках называется билинейной диффе-
ренциальной формой от и и у, поскольку при заданном у это выра-
жение линейно по и, в то время как при заданном и оно линейно
по переменной у. Полагая в соотношении (15.95) х = Ь, получаем
формулу Грина
ь
j luL (р) - yL* (и)] dx = [p2 (uy — uy) + (pi - p2) uy]ba. (15.99)
a
Правая часть этой формулы может быть записана как
Р = [Р2 фу' - и'у) + (р, - р2) иу]ь = р2 ф) и ф) у' ф) -
—р2 ф) и ф) у ф) + [р, Ф) - Р2 (&)] и Ф) у (а) - р2 (а) и (а) у' (а) +
+р2(а)и (а)у\а) - [р, (а) - р2 (а)] и (а) у (а) = ulPyb, (15.100)
428
Гл. 15. Условия разрешимости
где
«' («) "
и -
и’(Ь) ’
_u(fe)
О	р2(а)
р_ ~Р2(а) p2(a) — pi(a)
О	О
О	о
~	у' («) "
Уь	У'(Ь)	’
!/(^)
о	о
о	о
OJ — Р2 (Ь)
Р2 (b) Pl (Ь) - Р2 (Ь)
(15.101)
Отметим, что
IР | =1Р2 (а) р2 (6)]2,
и, следовательно, матрица Р — невырожденная. Подстановка
выражения (15.100) в соотношение (15.99) дает
ь
J[mL(z/) — yL* (u)]dx = ut>Pyb.	(15.102)
Сопряженная однородная задача
Поскольку граничные условия общего вида (15.61) включают
в себя линейные комбинации компонент у' (а), у (а), у' (Ь) и у (Ь)
вектора уь, введем следующее невырожденное линейное преобразо-
вание уь в вектор Y:
Y = Ay6,	(15.103)
где
			«11	«12	«13	«14	
Y =	г2 Уз	А = 9	«21 «31	«22 «32	“23 «33	«24 «34	. (15.104)
	Ул		«41	«42	«43	«44 _	
Заметим, что указанное преобразование может быть выполнено
бесчисленным множеством способов в зависимости от выбора мат-
рицы А. Правда, мы уже наложили некоторые ограничения на А,
потребовав, чтобы первые две строки этой матрицы совпадали
с коэффициентами a;J- в граничных условиях (15.61). Однако две
нижние строки матрицы А остаются при этом произвольными, за "
исключением того, что они должны быть линейно независимы друг ;:
от друга и от двух верхних строк с тем, чтобы определитель | А |(
не обращался в нуль. При заданном ненулевом векторе уь две :
последние строки матрицы А можно выбрать так, чтобы придать^
любые требуемые значения компонентам Y3 и Yt. Это замечание-
используется в дальнейшем при нахождении вида сопряженных
граничных условий.
15.5. Граничные условия общего вида
429
Поскольку | А | #= 0, мы можем обратить преобразование
(14.103) и получить
уь = Л-1У.
При этом формулу (15.102) можно переписать как
ь
j [uL (у) — yL* (и)] dx = и\РА~х\,
а
ИЛИ
b
J [uL (у) - yL*(u)]dx = UTY =	+ U2Y2 + U3Y3 + UtYt, (15.105)
а
где
UT=u£PA_!, и=(Д“')тРЧ.	(15.106)
Билинейная форма UTY в соотношении (15.105) называется
каноническим представлением билинейной формы в правой части
тождества (15.102). /
Для того чтобы найти граничные условия сопряженной задачи,
положим в соотношении (15.105) L (у) = 0 и L* (и) = 0 и полу-
чим
t/iKi + U2Y2 + U3Y3 + UtYt = 0.	(15.107)
Из формулы (15.103) и граничных условий (15.61) следует, что
однородные граничные условия, соответствующие (15.61), экви-
валентны равенствам
Vi = ацу' (а) + а12у (а) + а13у' (Ь) + аиу (Ь) = 0, (15.108а)
Yi = <х21у' (а) + а22у (а) + а2зу' (b) + a2iy (b) = 0. (15.1086)
С учетом равенств (15.108) соотношение (15.107) принимает вид
U3Y3 + t/4K4 = 0.	(15.109)
Как указывалось выше, при ненулевом векторе уь последние две
строки матрицы А могут быть выбраны так, чтобы компоненты Y3
и Yi принимали любые требуемые значения, лишь бы Y3 и У4
не обращались в нуль одновременно. В частности, нижние строки
матрицы А можно выбрать из условия Y3 = 1, У4 = 0. При этом
из соотношения (15.103) следует, что U3 = 0. Аналогичным об-
разом, нижние строки матрицы А можно выбрать так, чтобы
выполнялись равенства Y3 = 0 и У4 = 1. Тогда из соотношения
(15.103) вытекает, что t/4 = 0. Таким образом, задача, сопряжен-
ная задаче
L (у) = 0,	= Y2 = 0,	(15.110)
имеет вид
L* (и) = 0, U3 = Ui = 0,	(15.111)
где U3 и Ut связаны с компонентами и' (а), и (а), и' (Ь) и и (Ь)
вектора соотношением (15.106). Краевая задача (15.110) на-

430
Гл. 15. Условия разрешимости
зывается самосопряженной тогда и только тогда, когда L — L
и каждая из двух компонент U3 и [/4 является линейной комбин
цией Y\ (иь) и К2 (uft), т. е. и (х) пропорциональна у (х).
Поскольку граничные условия (15.61) линейно независим]
по крайней мере один из определителей
А;У —	«1>«2г> I /
матриц-блоков
Г «п av ’
. «г; a-z;.
должен быть отличным от нуля. Чтобы иметь возможность сра
нить эти результаты с теми, которые были получены в предыдуцц
параграфе, предположим, что А13	0. Далее, выберем такие 1
и Y4, чтобы строки матрицы А были линейно независимы. Н
пример, положим Y3 = у (а) и Yi = —у (Ь). При этом матрица
примет вид
«11	«12	«13	«14
д _ «21	«22	«23	«24
0	10 о
10	0—1
Из формулы (15.112) следует, что		Ml	—	^13	^0.	Тогда
	«23	0	«21	0 "	
/Д —IV —	«13	0		«11	0	(15.11
V1 '	Л а13	А 23	—	-А13	А12	0	
	^34	0		А14	Ай _	
Подставляя матрицы (15.101) и (15.113) в соотношение (15.1
имеем
	U = —	--Л— X А13
0	а2зР2 (°)	0	а21Р2 (^)
0	И13Р2 (а)	0	—«11Р2 (А)
х — Д13Р-2 (о)	^2зРг° —Д13 [р-2 (а) — Pl (а)]	0	А12Р2 (^)
0	—Л34Р2 (а)	~А1з₽2 (^)	А1*Рг(Ч + А13 1Р1 (Ь) — р'2 (*)]
(15.lt
Следовательно, граничные условия сопряженной задачи имеют в|
С'з = р2 (а) и' (а) + ^2 (а) — Pi (а) +	?2 (а)] и (а) -
_^_p2(fe)w(fc) = 0, (15.11
15.5. Граничные условия общего вида
431
С4 = р2 (Ь) и (Ь) + р2 (а) и (а) -
- [Pi(b)~ p2(b) --|1*-р2(&)] и(Ь) = О, (15.1156)
что полностью совпадает с граничными условиями (15.78), если
учесть соотношения (15.63).
Для того чтобы краевая задача (15.60), (15.61) была самосопря-
женной, необходимо, чтобы L = L* и чтобы каждая из компо-
нент U3 и являлась линейной комбинацией Кх (иь) и К2 (ufc).
Как указывалось выше, L = L* тогда и только тогда, когда рх =
= р2. При этом условия (15.115) принимают вид
и’ (a) ф- ф2- и (а) —д12^2- и (Ь) = 0,
A	А	(15.116)
Разрешая равенства (15.61) относительно у (а) и у' (Ь) при рх =
= р2 = 0 и заменяя у на и, получаем
и' («)=- Ф-«(«)+-4м*и
Л13	t13	(15.117)
Сравнивая граничные условия (15.116) и (15.117), заключаем, что
они совпадают тогда и только тогда, когда
р2 (а) Лги = Рз (5) ЛХ2.	(15.118)
Соотношение (15.118) представляет собой равенство (15.83), по-
лученное в предыдущем параграфе. Следовательно, краевая за-
дача (15.60), (15.61) при ДХз 0 самосопряжена тогда и только
тогда, когда выполнены соотношение (15.118) и равенство рх =
= Pi-
Условие разрешимости
Определив сопряженную краевую задачу, вернемся к решению
неоднородной задачи (15.60), (15.61). Используя определение
(15.111), перепишем формулу Грина (5.105) в виде
ь
^uL^dx^YiUi-^Y^.	(15.119)
а
В силу уравнения (15.60) и граничных условий (15.61) L (у) =
= / (х), Y1 = рх и Уг = р2; тогда из соотношения (15.119) выте-
кает, что условие разрешимости имеет вид
' ь.
Р/Л + p2f/2 = J / (х) и (х) dx.	(15.120)
а
432
Гл. 15. Условия разрешимости
Для того чтобы сравнить условие (15.120) с условием разреши-^
мости (15.88), полученным в предыдущем параграфе, используей
связь Ui и Uг с вектором иь, описываемую формулой (15.114),’
т. е.	1
и __ а23Р2 (й) и	(Ь)	,ь.	;
А1з v А1з v '
{/а =	(g) ц (а) + W ц (у).	(15.121)
^13	^13
При этом соотношение (15.120) принимает вид
^ЧТз0121-1	« («) № -
ь
= j f (х) u (х) dx,
а
что полностью совпадает с условием (15.88), если учесть соотно-
шения (15.63).
Сравнивая вывод условия разрешимости в настоящем и преды-
дущем параграфах, можно заметить, что процедура, использован-
ная в § 15.4, требует меньшего объема вычислений. Поэтому, если
приходится иметь дело с граничными условиями общего вида, по-
добными (15.61), можно порекомендовать выразить какие-либс
два из граничных значений (функции или производной) через два
других, аналогично тому как это проделано в (15.62), и затем
действовать, как в предыдущем параграфе.
15.6. Простая задача на собственные значения
Рассмотрим задачу на собственные значения
у" + [X + e.g (х)1 у = 0, е « 1,
у (0) = 0, у (л) = 0,	'
где X — собственные числа. Поскольку значения X-зависят от ма-
лого параметра е, будем искать равномерное разложение первогс
порядка с помощью метода растянутых параметров, раскладывав
в ряды по степени е не только решение у, но и собственные числа X
У = Уо (х) + ez/i (х) + • •,	(15.123
л = Л(( 4-
Подставляя разложения (15.123) в уравнение и граничные услови!
(15.122), имеем
Уо + e.yi + ft-o + (Уо + »У1) 4---------=0,
Уо (0) + eyi (0) 4- • • • = 0, у0 (л) 4- еу! (л) 4-=0.
15.6. Простая задача
433
Приравнивание коэффициентов при одинаковых степенях е дает
для порядка e°:	Уо	1-оУо — 0, /п/	7 \ л	(15.124) Уо (0) = уо (л) = 0;
для порядка e:	у"\ + M/i = — gyo — Мо,	(15.125) У1 (0) - уг (л) = 0.	(15.126)
Общее решение дифференциального уравнения в (15.124) можно
записать как
Ро = Ci cos ул0 х -j- с2 sin •/Хо х.
Воспользовавшись краевым условием у0 (0) = 0, находим = 0.
При этом второе граничное условие приводит к уравнению
c2Sinj/ А«о л == 0.
Для того чтобы существовало нетривиальное решение (т. е. при
с2 =/= 0), Ло должно удовлетворять уравнению
sinт/А0п = 0, или | Л0 л = пл, п = I, 2,.. . .
Таким образом, с точностью до членов первого порядка малости
собственные функции имеют вид
Ро = sin пх,	(15.127)
а собственные числа равны
= п\	(15.128)
Подставляя выражения (15.127) и (15.128) в уравнение (15.125),
получаем
у\ -f-n2pi = —g(x)sinnx — XjSinnx.	(15.129)
Поскольку однородная задача, соответствующая (15.129), (15.126),
имеет нетривиальное решение, неоднородная задача обладает ре-
шением, только если выполнено некоторое условие разрешимости.
Вместо того чтобы применять общие результаты предыдущего
параграфа, на наш взгляд, будет более поучительным вновь
вывести это условие для рассматриваемого частного случая.
В уравнении (15.129) р2 = 1 и = 0, так что р'2 = рх, т. е. ус-
ловие (15.118) выполнено, и задача является самосопряженной.
Следовательно, в качестве решения сопряженной задачи можно
взять функцию и = Уо sin пх. Умножая уравнение (15.129) на и
и интегрируя полученный результат от х = 0 до х = л, после
некоторых преобразований получим
Л	л
j yi (tT n2u) dx [у\и\ — y\ti \ = — j [g (x) + Xi] и sin x dx.
о	0
(15.130)
434
Гл. 15. Условия разрешимости
Поскольку и = sin пх и уг (0) — 0, уг (л) = 0, левая часть соот--
ношения (15.130) обращается в нуль, и условие разрешимости
принимает вид
Л	л
j g (х) sin2 пх dx Xi J sin2nxdx = 0.
о	о
С учетом того, что второй интеграл равен л/2, последнее соотно
шение переписывается как
Л
Хх =------g (х) sin2 пх dx.	(15.131
о
Подставляя выражения (15.127), (15.128) и (15.131) в разложена
(15.123), находим, что в первом приближении
у = sin пх + О (е),
2е г"	(151323
X = п2----— J g (х) sin2 пх dx 4-0 (е2).
о	4
15.7. Вырожденная задача на собственные значения
Рассмотрим следующую задачу на собственные значения: 5
у" + [X + е/ (х)) у = 0, е < 1,	(15 133
У (0) = У (1), У' (0) = у’ (1).	’ '
Как и в предыдущем параграфе, будем искать равномерное раз
ложение первого порядка, раскладывая у и X в ряды по степеням
у (х, в) = у0 (х) + &У1 (х) + ,  	,15 12
X = Хо + еХ2
Подставляя разложение (15.134) в уравнение и граничные услов
(15.133) и приравнивая коэффициенты при одинаковых степени?
в обеих частях этих соотношений, получаем
для порядка е°:
Уо + ^оУо = 0,	Н51'
г/о(О) = z/0(l), Уо(О)= i/o(l);
для порядка е:
z/i + Xoz/i = (Xi + /) уо,
y,(0) = ^(i),	y;(0) = yi(i).	( • г
Общее решение уравнения в (15.135) можно записать как
у0 — аг cos -j/ Хо х 4~ п2 sin у'Хо х.
15.7. Вырожденная задача
435
Удовлетворяя граничным условиям (15.135), имеем
— ai cos у' Ао 4' ch. sin )/Х0,
а2 = — ar sin р/.о 4- а2 cos ^0>
или	(cos yzA.o - - 1) а, 4- sin УXoa„ — 0,
—	.	.	(15.137)
—sin У	+ (cos ]/ /.(, — l)n2 = 0.
Для того чтобы существовало нетривиальное решение системы
уравнений (15.137), ее определитель должен равняться нулю, т. е.
(cosy A0— 1)24-sin2y Ао = 0,	(15.138а)
что при действительных дает 1
sin у Ао = 0 или cos у Хо = 1,
откуда Хо = 4пала, /у== 0, 1, 2,...,	(15.1386)
причем из системы уравнений (Т5~. 137) вытекает, что а± и а2 мо-
гут быть произвольными числами.
Тогда
у0 = aL cos 2плх + а2 sin 2плх	(15.139)
при произвольных а± и а2.
Таким образом, при любом Хо = 4п2л2, где n 1, существуют
две линейно независимые собственные функции, а именно cos 2лпх
и sin 2лпх. Задачи на собственные значения с двумя или более
собственными функциями, отвечающими одному и тому же соб-
ственному числу, называются вырожденными. Вырождение яв-
ляется результатом симметрии и может быть снято, если эта сим-
метрия будет нарушена. Покажем, что в данном примере асим-
метрию, устраняющую вырождение исходной задачи, может
вносить член f (х) у (х).
Подставляя решение (15.139) в уравнение (15.136) и учитывая,
что = 4пазха, имеем
у'{ 4- 4п2лД/1 — — (Xi + /) (ai cos 2лпх 4- «2 sin 2л пх). (15.140)
Поскольку задача для однородного уравнения, соответствующего
(15.140), совпадает с задачей (15.135) и поэтому имеет нетривиаль-
ное решение, неоднородная задача относительно уг имеет реше-
ние, только если выполнены условия разрешимости. Для нахож-
дения этих условий умножим уравнение (15.140) на и (х) и проин-
тегрируем полученный результат от х = 0 до,х = 1. В результате
некоторых преобразований получим
1
[у\и — ytu Jo 4- j У\ (и 4~ 4/z2n2«) dx =
о
1
= — | и (7И 4- f) (Qi cos 2лпх а2 sin 2л/гх) dx.	(15.141)
___________ о
1 Комплексных решений уравнение (15.138а) не имеет. — Прим, перев.
436
Гл. 15. Условия разрешимости
Для того чтобы найти вид уравнения и граничных условий cd
пряженной задачи, рассмотрим прежде всего задачу для однород
ного уравнения, соответствующего (15.140), т. е. положим в фор
муле (15.141)	= 0 и f = 0. Сопряженное уравнение получаем
как обычно, обращая в нуль коэффициент при у в интегрально!
члене в соотношении (15.141), т. е.
и" + 4палац = 0.	(15.14!
При этом соотношение (15.141) принимает вид
У\ (1) и (1) - У1 (1) и (1) - у\(0) и (0) + yt (0) и' (0) = 0. (15.14£
Но в силу граничных условий (15.136) У1 (0) = У1 (1) и у[ (0) =
= у[ (1), и, следовательно, соотношение (15.143) можно переп:
сать как
[«(1) _ „(0)] (1) — [«'(1)-«'(0)]^(1) = 0.	(15.14-
Выбирая сопряженные граничные условия так, чтобы коэфф]
циенты при У1 (1) и у[ (1) обращались в нуль одновременно, имее
и (1) = и (0), и' (1) = и (0).	(15.14
Таким образом, однородная краевая задача, соответствующа
(15.136), является самосопряженной, и поэтому
и = sin 2лпх или cos 2лпх.	(15.14’
Определив сопряженную задачу, вернемся к неоднородной кра
(вой задаче. Используя уравнение (15.142) и граничные условг
(15.145), приведем формулу Грина (15.141) к виду
1
j и (х)	-j- f (•*)] («i cos 2тх + а2 sin 2лпх) dx= 0, (15.14j
о	1
откуда и получаются искомые условия разрешимости. Отмети!
что соотношение (15.147) должно выполняться для всех допуст
мых функций и (х), удовлетворяющих условиям сопряженн
задачи. В данном случае, если 1, и (х) = sin 2лпх и<
cos 2лпх. Следовательно, неоднородная задача (15.140) разр
шима относительно у1г только если условие (15.147) выполняет
при и (х) = sin 2лпх и и (х) = cos 2лпх.
Полагая в соотношении (15.147) функцию и (х) равн
sin 2лпх и cos 2лпх соответственно, получаем
/12 а1 + (^1 + /11) «2 = 0	(15.1
и	(А.! + /22) Qi + /12 0.2 — 0,	(15.1
15.7. Вырожденная задача
437
где
fu = 2 J f (х) sin2 2тх dx,
oj
i
/12 = 2 j f (x) sin 4лях dx,
о
i
/22 = 2 J f (x) cos2 2anxdx.
°
Требование существования нетривиального решения системы урав-
нений (15.148), (15.149) приводит к условию обращения в нуль
определителя этой системы, т. е.
4~ (/11 4" /22) ^1 -f- /11/22 — /12 = О,
откуда
х|’’2) =-----(fn + /22) Т 4 [(/>1 - /22)2 4- 4/122]'/2. (15.150)
Тогда из уравнения (15.149) следует, что
а2 = ~
>Г> + /22
/12
(15.151)
Таким образом, в первом приближении имеем либо
i/(1) = cos2лих —^L_+_/22_ sin 2лпх	О (е),
А,(1) — 4п2л2---g-e {/и 4- /22 4~ [(/п — /гг)2 4" 4/?2]1/2} 4~ О (е2),
(15.152)
либо
z/(2) — cos 2лях —-уЛ ^22 sin 2ллх 4- О (е),
Х<2) = 4и2л2----е {/и -f- /22 — [(/и — /22)2 4- 4/i2],/2j О (е2).
(15.153)
Следовательно, при условии, что ХР отличается от к[2) (т. е.
/п =/= и =^= 0), вырождение снимается, поскольку каждому
из собственных чисел Х(т) соответствует только одна собственная
функция y(m). Если М0 = ^[2), то вырождение может быть снято
в высших приближениях теории возмущений.
438
Гл. 15. Условия разрешимости
15.8. Звуковые волны в канале с волнистыми стенками
Рассмотрим задачу о распространении линейных гармонически:
звуковых волн в плоском канале (волноводе), ширина которого ме
няется по синусоидальному закону. Математически задача ста
вится так:
Фхх + фто + <оаф = 0,	(15.154
<ру — 0 при у = 0,	(15.15?
= е^и,фх cos kwx при у = 1 4~ е sin kwx, (15.15?
где со и kw — постоянные величины и е — малый безразмерны;
параметр. За исключением формы граничных условий, данна
задача является прототипом задач о распространении по волне
водам электромагнитных и упругих волн.
В качестве первого шага для получения равномерно пригоД;
ного разложения первого порядка построим прямое разложение
вида
ф = Фо (х, у) + еф! (х, у) + • • • .	(15.15'
Отметим, что граничное условие (15.156) поставлено при у =
= 1 +esin&u,x. Поэтому при подстановке разложения (15.15'
в граничное условие малый параметр е будет входить не толы
в коэффициенты при последовательных членах разложения, й
и в аргумент функции ф. Поскольку обычная процедура мето,!
возмущений состоит в приравнивании коэффициентов при один!
ковых степенях е, мы не сможем провести ее до тех пор, пока 1
исключим параметр е из аргумента ф. Чтобы добиться этого, пр
ведем так называемый перенос граничных условий. В данном сл'
чае мы перенесем граничные условия с поверхности у == 1 -
+ е sin kwx на плоскость у = 1 с помощью тейлоровского степе;
ного разложения. Запишем при у = 1 + е sin kwx в условг
(15.156) как
сру (х, 1 + е sin kwx).
Раскладывая эту функцию в ряд Тейлора в окрестности у = !
имеем
qy(x, 1 + 6 sin kwx) — q>y (х, 1) 4~Ф</у(х, 1) е sin kwx -f-
+ ПГГ (х’ 1 )е2 sin2 kwX +
+ Чуууу 1) е3 sin3 -j .
Аналогичным образом раскладываем в ряд Тейлора произвр
ную фж:
фж(х, 1 4- е sin kwx) = <рх(х, 1)4-фхг/(х, l)esin£u>x +
21 tyxyy (Х> 1) В3 Sin3 kwX 4“
4 зу фхг/jij, (х, 1) е sin3 kwX 4- • • • .

15.8. Звуковые волны в канале
439
Подставляя полученные тейлоровские разложения в граничные
условия (15.156), находим
фг/(х, 1) + &4>уу (х, l)sin£wx = e,kwq>x (х, l)coskwx -f- • • • . (15.158)
Тем самым мы совершили перенос граничных условий с поверх-
ности у = 1 + е sin kwx на плоскость у = 1 и исключили е из
аргументов функций <рж и фу. Теперь можно продолжить процесс
построения прямого ^разложения.
Подставляя разложение ,'(15.157) [в уравнение (15.154) и гра-
ничные условия ;(15.155) и'(15.158)4имеем.
фохх + 8<Р1 XX + Фои, +	“Чо 4- е(°гф1 4 • • • = о,
ф0|/ (х, 0) + 8<р1г/ (х, 0) Н-- 0,
<Роу(х, 1)4-еф1г,(х, 1)4-еф0^(х, l)sinfewx = e^„,cfOx(x, l)cos^xH-.
Приравнивание коэффициентов при одинаковых степенях е
в обеих частях каждого из написанных выше соотношений приво-
дит к последовательности задач следующего вида:
для порядка е°:
фохх + фода 4* ®2ф0 = 0,	(15.159)
ф0!/ (х, 0) = 0,	(15.160)
ф04, (х, 1) = 0;	(15.161)
для порядка е:	
Ф1хх 4 Ф1да 4 ®афх = 0,	(15.162)
Фху (х, 0) = 0,	(15.163)
Ф1У (х, 1) = —фОда(х, 1)81пЛшх4-Лш(г0ж(х;	l)cos^u>x. (15.164)
Поскольку уравнение (15.159) имеет постоянные коэффициенты,	
соответствующая задача может быть решена	с помощью метода
разделения переменных. С этой целью положим	
Фо = X (х) Y (у).	(15.165)
В результате имеем	
X"Y + XY" + (о2ХУ = 0,	(15.166)
X (х) Y' (0) = 0,	(15.167)
X (х) Y' (1) = 0.	(15.168)
Разделив (15.166) на произведение XY \	и перегруппировав
члены уравнения, получим	•
X"	У" .	
у = — 4	(15.169)
440
Гл. 15. Условия разрешимости
Поскольку левая часть (15.169) зависит только от х, а правая
часть только от у, обе части этого уравнения должны равняться
одной и той же постоянной, т. е.
-2£- = Ь,	(15.170)
=	(15.171)
Уравнение (15.170) можно записать как
X" + ЬХ = 0.
В случае распространяющихся волн функция X должна ме-
няться по синусоидальному закону, поэтому b должно быть поло-
жительным.
Обычно полагают b — k2, так что
X = ехр (± ikx),	(15.17!
где k — так называемое волновое число. Полагая b = k\ перепи-
шем уравнение (15.171) в виде
Y" + (о>2 — k2) Y = 0.	'
Общее решение этого уравнения имеет вид	’
Y = схsin)/со2 — k2у -j- c2cos)/со2 — k2у. (15.173»)
Поскольку X (х) не обращается в нуль тождественно, из соотнес
шений (15.167) и (15.168) следует, что
Y' (0) = Y' (1) = 0.	(15.174)
Подчиняя этим условиям решение (15.173), находим, что сх = (
и )/ (О2 — k2 = лп, или
^ = (02_ nV, n = 0, 1, 2,.. . .-	(15.175)
Т гда
Y = costing.	(15.176’
Подставляя выражения (15.172) и (15.176) в формулу (15.165),
имеем
<р0 = elknX cos лпу или e~th'nX cos tiny, (15.177
где одно из решений соответствует волне, распространяющейся
в прямом направлении, а другое решение — волне, распростри^
няющейся в обратном направлении. Решение, соответствующе
заданному номеру п, называется п-и модой.
15.8. Звуковые волны в канале
441
fk,.X
Возьмем решение со знаком плюс в показателе экспоненты.
Подставляя его в граничное условие (15.164), имеем
ФьДх, 1) — (—1)пп2л2е‘кпХ sin kwx ф- i (—\)п knkwelknX cos k^x —
= (-irnW?»* ±^L(e‘^x - e~ika>x) +
+ i(~ 1)" knk^{knx.-L(e'
=	(**+*»)x 4- ^e‘ (**-*»)x,	(15.178)
где £i=-|-(—\)ni(knkw~ n2n2), ^ = -L(_l)',t(Mw + «M-
(15.179)
Чтобы найти решение задачи (15.162), (15.163), (15.178) отно-
сительно <р!, заметим, что граничное условие (15.178) неоднородно
и его форма позволяет воспользоваться разделением переменных
в следующем виде:
<Р1=Ф1(г/)^^+^х+ Фг(у)е{(кп-^)^.	(15.180)
Подставляя выражение (15.180) в уравнение (15.162) и граничные
условия (15.163) и (15.178), имеем
[Ф1 + а2Ф1] е {kn+kw} х + [Ф; + а|ф21 е ^~k^ x = о,
4- Ф2 (0) el (kn~kw)х = о,
=	(4п+М х 4- l2el (kn~kw)х,
(15.181)
в обеих
ф; (0) el (i'i+k4>)х
ф[ (1) е{ (*«+*“’)х -f- Ф2 (1) е1 (кп-~кш)х
где	а? = со2 — (kn + kw)2, а% = ы — (kn — kw)2 •
Приравнивая коэффициенты при каждой из экспонент
частях этих соотношений, получаем
Ф, + а2Ф1 = 0,
ф; (О)=о, Ф1(1) = £ь
Ф2 + «2 = 0,	1
(15.182)
(15.183)
Общее решение уравнения (15.182) записывается как
Ф1 = сг cos 4- с2 sin Л1У-
С учетом граничных условий (15.182) находим, что
с2 = 0, ci = —^af1 sin-1 ai
и, следовательно,
ф _ _ £icos а1У
1	ах sin ах
442
Гл. 15. Условия разрешимости
Аналогичным образом, решение задачи (15.183) можно представ
вить в виде	I
Ф _ _ & cos «2у .	J
2	а2 sin а2 '	j
Таким образом, имеем
_	gi COS «1У i (bn+kw) х
’Р* aisina!
Подставляя теперь решения (15.177) и (15.184) в разложений
(15.157), получаем	;
Ф = cos nnyeik»x - в [&V (*п+М *	J
т	v	L “1 sln al	i
g2cosa2y ci (kn-kt
a2sina2
(15.18$
Анализ разложения (15.185) показывает, что оно становится
непригодным при sin = О (в) или sin а2 = О (е). Если sin d
или sin а2 обращается в нуль, второй член разложения (15.18Г
оказывается неограниченным. При sin = О (е) появляют^
члены с малыми знаменателями, и разложение становится неравн
мерным.
Поскольку равенство sin at = 0 означает, что at = л
т = 0, 1, ..., пригодность прямого разложения нарушается п
условиях
со2 — (kn + kw)2 л2т2 или со2 — (kn — kw)2 л2т2 (15.18
в соответствии с равенствами (15.181). Учитывая дисперсионно
соотношение (15.175), формулам (15.186) можно
(kn + kw)2 k2m ИЛИ (kn — kw)2 k2m,
kw^ ±kn± km.
говоря, прямое разложение перестает быть
когда волновое число, характеризующее
волновода, равно сумме или разности волновых чисел t
Ё
придать в
(15.18i
(15.18
справедлив
«волнистое
или
Иначе
тогда,
стенки
и kn двух распространяющихся мод, т. е. при наличии комбий
ционного резонанса.
Для того чтобы найти разложение, пригодное при k,
«=< kn — km, введем параметр расстройки о по формуле
kw = kn — km + во.	(15.18
Кроме того, будем использовать метод многих масштабов и й|
кать решение в виде
Ф (х, у, е) = ф (х0, хх, у, в) = ф0 (х0, хь у) +
+ 8фх (х0, хп у) +  • ,
15.8. Звуковые волны в канале
443
где х0 = х и хх = ех. При этом
д _____________ д । д д _______________	д2
дх дх0 ' 6 дхг ’ дх2 дх$ ' 6 дхв дхг
(15.190)
Подставляя разложения (15.189) и (15.190) в уравнения (15.154)
и граничные условия (15.155) и (15.158) и приравнивая коэффи-
циенты при одинаковых степенях е, получаем
для порядка е°:
д2Фо , д2Фо । f _ о
дх2 + ду2 + w Фо — 0,
(15.191)
-^2- = 0 при у = 0, -^- = 0 при у = 1;
для порядка е:
-?V- + -?v- + (o2<Pi:=-2a?T->	(15.192)
dxg 1 ду* 1	дх0 дхг	4	'
-^- = 0 при у = 0,	(15.193)
= ~ ~ly^~ sin kwX° + kw cos kwX° ПРИ У=1>
(15.194)
где sin kwx и cos kwx выражены через переменную х0 в предполо-
жении, что величина kw достаточно далека от нуля.
Решение (15.191) можно получить с помощью метода разде-
ления переменных, как это сделано выше. Однако теперь вместо
решения (15.177), содержащего одну моду, выберем <р0 в виде,
содержащем две взаимодействующие моды, т. е. запишем решение
в виде
Фо = Ап (xt) cos туе‘&пХ° -ф- Ат (х^ cos я,туе1кт\ (15.195)
где krtl и kn определены соотношением (15.175), а функции Ат
и Ап подлежат определению в дальнейшем из условия разреши-
мости задачи второго приближения. Подставляя выражение
(15.195) в уравнение (15.192) и граничное условие (15.194), имеем
+ “2ф1 ~ 2^«Л« cos nnyeiknX° - '
(15.196)
— 2ikmA’m cos ятуе‘ктК°,
(kn+Aw) x° + ЬгЛ/	x° +
+ £lmAme‘ xo + ^тАте‘	При у = 1, (15.197)
где £1л, £2л и £1,„, ?2,л определены соотношениями (15.179) при
значениях индекса, равных соответственно п и т.
444
Гл. 15. Условия разрешимости
Для того чтобы найти вид условий разрешимости для задгй
второго приближения, "йодставим прежде всего соотношей
(15.188) в граничное условие (15.197), с тем чтобы преобразов^
члены с малыми знаменателями в секулярные члены. В резул
тате получим
= £1пАпе<	хо + Го2яД„/ +	J
+ Ате‘ (ftn+E°)+ £2тАте‘ PW*-) \ уЛ
или
= ЪпАпе^е1	х° + t2nAue-iox^xo +
+ tlmAmeiaX1e‘knX° + ^тАте~‘ах^ (2кт~кп) *0> у = 1. (15.1|
Заметим, что только члены, пропорциональные ехр (ikmx0)
ехр (ifenx0) в правых частях (15.196) и (15.198), могут привес
к несовместности, поэтому условия разрешимости должны 6yi
наложены лишь на эти слагаемые. Эти условия разрешимо^
можно получить, если искать частное решение, соответствую!^
указанным членам, в виде	|
Ф1 = Фп (Х1, У) е1к*х° + Фтг(хь у) е‘ктхо. (15.1|
Подставляя выражение (15.199) в уравнение (15.196) и граничй
условия (15.193) и (15.198) и приравнивая коэффициенты п|
ехр (iknx0) и ехр (ikmx0) в обеих частях этих соотношений, с у|
том формулы (15.175) получаем	|
д^2п + я2л2Фп = — 2iknA'n cos лпу,	J
(1И
тН »-»	»=1; j
+ я2л2Фт = —2ikmA'm cos лту,	J
(15.2^
^- = 0, у = 0, ^ = ^пАпе~^, у=\.	|
Таким образом, нахождение условий разрешимости для <рх d
дится к определению условий разрешимости для функций |
и Фт.	I
Уравнение задачи (15.200) самосопряженное благодаря той
что в этом уравнении р2 = 1 и = 0. Поэтому решение сопряги
ной задачи можно выбрать в виде и (у) = cos лпу. Умножая у|
15.8. Звуковые волны в канале	445
занное уравнение на и (у) и интегрируя полученный результат
по частям от у = 0 до у = 1, получаем
1 1
[ (и + л2п2и) Фпс1у + Г-^2- и — Фпи'1' — 2iknAn [ и cos лпу dy.
J	L &У	J О	J '
о	о
(15.202)
Поскольку и = cos лпу, соотношение (15.202) переходит в равен-
ство
ЭФП	I1 'At, Л'
-Q - cos лпу I = — toknAn,
где 6 = 1 при л :js 1 и 6 = 2 при п — 0. Используя граничные
условия задачи (15.200), имеем
(-1)”	= ~i6knA'n,
или	A'n — (~i)n %imk~l8~lAmeioXi .	(15.203)
Аналогичным образом, при т #= 0 можно найти условие разреши-
мости задачи (15.201)
Ат - (-1)т i^mAne~£ax‘.	(15.204)
Если положить
А„ = ап ехр (iyiXi),	Ат = а,п ехр (iy2Xi),	(15.205)
где ап, ат, ylt у2 — постоянные величины, то из уравнений
(15.204), (15.205) следует, что
iV1an = (-1)"	(15.206)
t?2am = it2nk~'an,	(15.207)
7г = 7i — a-	(15.208)
Исключение и am из системы уравнений (15.206)—(15.208)
дает	\
7i (71 - а) = (-1 )п+т (Мтб)’1 J
или	7? - о?1 - (—l)n+m (knkm^yx
Следовательно,
71 = 2. а Т [4-Of2 + (~1)n+m(Mm6)-4im^]1/2. (15.209)
Подстановка этих выражений в (15.205) позволяет определить
зависимость амплитуд двух взаимодействующих мод от медленной
переменной хР
446
Гл. 15. Условия разреиш/юсти
15.9. Колебания мембраны, близкой по форме к кругу
Рассмотрим малые колебания мембраны, форма которой
к кругу. В безразмерном виде математическая постановка
сводится к следующему:
Э2ш	।__1	dw	___1_ d2w	q2w ___
dr2	'г	dr	' г2 Э62	dt2	’
< оо При Г =0,
w = 0 при г = 1 -Hf (0),
причем средний радиус мембраны равен 1, так что
2л
j f(0)d0 = O.
о
Рассматривая гармонические по времени колебания,
ш (г, 0, 0 = ф (г, 9 )cos (и/ 4- т),
где со — безразмерная частота. Подставляя выражение (15.2:
в условия задачи (15.210)—(15.212), для амплитуды колебав
(15.2
(15.2;
(15.2'
(15.2
полож
(15.2
получаем
д2ф 1 Эф 1 Э2ф
dr2 + г dr + г2 Э62 Тмф —°>	(,5 2
I ф| < ОО при г =0,	(15 2
Ф = 0 при г = 1 + if (0).	(15.2
Как и в предыдущем параграфе, необходимо перенести гран
ные условия с линии г = 1 + е/ (0) на окружность г — 1 с
мощью разложения в ряд Тейлора. Таким образом, уело
(15.217) перепишем в виде
ф(1-0)4-8-^ (1, О)/(0)+ ... = 0	(15.3
Для того чтобы построить равномерно пригодное разлож»
первого порядка для функции ф, используем метод растяи^
параметров, раскладывая ф и со в ряды следующим образ
ф = Фо (г, 0) + еф! (г, 9) + . ..,	5
СО = (О0 + 8(01 + • •• .
Подставляя разложение (15.219) в уравнение (15.215) и- услй
(15.216) и (15.218) и приравнивая коэффициенты при одинакей
степенях в, получаем	?
15.9. Колебания мембраны
447
для порядка е°:
i 1	д<Уо >	1	д2ф0	2 _п	99П,
дг2	'г	дг '	г2	Э92	г (0чФо — v,	(1D.ZZU)
| ф0 (0,	0) |	< оо,	(15.221)
Фо(1, 0) = 0;	(15.222)
для порядка е1:
+ + = <15-223)
| Ф1 (0, 0) I < ОО	(15.224)
Ф1(Ь 0) = -^-(1, 0)/(0).	(15.225)
Решение задачи нулевого порядка можно получить с помощью
метода разделения переменных. Так, полагая в уравнении (15.220)
Фо = R (г) 0 (0),	(15.226)
имеем
R"0 + 4- R'0 + 4- ^0" +	= °>
или	^R + rR' + r2“o7?) + "F = °'
Следовательно,.
0" = — 00, r2R 4. rR' + <&2R = 0/?.
I Решение уравнения для функции 0 можно представить как
0 = Cr cos уЛ0й0 + с2 sin /0 0.
Для однозначности 0, а значит, и ф0 следует положить j/0 — п,
где п — некоторое целое число.
Тогда	\
>	0 = c1cosn0-j-c2sinn0,	(15.227)
| и уравнение для функции R принимает вид
|	i^R Ц- rR + (g)2/2 - /г2) R = 0.
> Это уравнение представляет собой уравнение Бесселя порядка л;
I его общее решение записывается в виде
I	R = caJn (юог) +	(gv)-	(15.228)
I Подставляя выражение (15.226) в условия (15.221) и (15.222),
I получаем граничные условия для функции R : | R (0) | < оо
I и R (1) = 0. Поскольку при г0 Y,. оо (см. § 13.3), условие
448
Гл. 15. Условия разрешимости
.—.---------------------------------------------------------
| R (0) | < оо требует, чтобы с4 = 0. При этом граничное услов]
R (1) = 0 приводит к характеристическому уравнению
J„(«o) = 0.	(15.22!
Таким образом, имеем
®0 = Огт>	(15.23'
где Qnm — корни уравнения Jn (Q) = 0.- Следовательно,
ф0 = Jn $lnmr) let cos «0 + с2 sin л0 ],
или	<р0 = Jn (Пп„/)(Лпте,,г0 + Апте-‘'пв), (15.23
Где Апт — комплексные постоянные. Решение вида (15.231) nj
заданных п и т называется л/п-й модой; полное же решение в
дачи содержит сумму вкладов всех мод. Исследуем теперь влц
ние отклонения формы мембраны от круга на частоту Qn:n пт
моды.
Заметим, что при заданной частоте £1пт существуют две кол
бательные моды, а именно
Jn cos пВ и Jn (£lnmr) sin пВ.
Следовательно, о круглой мембране можно говорить как о выро
денной системе, поскольку одному собственному значению (
стоте) соответствуют две линейно независимые собственные фу]
ции (моды). Вырождение является результатом высокой сим
трии системы и, как показано ниже, м&жетбыть снято при нару!
нии симметрии.
Подставляя выражение (15.231) в уравнение (15.223) и гран
ное условие (15.225) и полагая ®0 = Qmn, имеем
д2Ф1 . 1 дф1 I 1 d2<Pi Q2 __
dr2 + г дг + дб2 + ^т<Р1 —
= —Jn (йптг) (Апте -|- Апте е)>	(15.2
ф1 (1, 9) = -—QnmJ п (йщ) f (9) [Апт6 ~f~ Апте I- (15.2
Далее, разлфкщм функцию f (9) в ряд Фурье:
оо	2л
/(0)=	=	(15.2
g=—оо	О
где /о = 0 в соответствии с условием (15.213). Следуя мет
разделения переменных, представим в виде ряда Фурье и иско»
функцию фх:
оо
ф.= 2 Фл(г)^0.	(15.5
k——оо
15.9. Колебания мембраны
449
Подставляя ряд (15.235) в уравнение (15.232), имеем
[ф; + -L-ФА +	Ф*]	=
к
= —2Qnm<»1/n (Qnmr) [Anmein* -j- ~Anme~inQ]t
что после умножения на ехр (—ts0) и интегрирования от 0 = О
до 0 = 2л дает
ф; +	+ (рпт - ф„ = ~2Qnm^AnmJn (Qnmr),
(15.236)
Ф'з + 4^ + (й^--Л-)ф5 = 0’ s*«-	(15.237)
Аналогичным образом, подставляя ряды (15.234) и (15.235) в гра-
ничное условие (15.233), имеем
Е Фк(1) е1М = -QnmJ'n (Qnm) 2 [Anmf,.e‘ (<+”> » +
A	q
+ ~Апт^^в],
что после умножения на ехр (—is0) и интегрирования от 0 = О
до 0 = 2л дает
Ф«[(1) ~ QnmJп [Anmfs-n -|- Anmfs^.n]. [(15.238)
Наконец, подставляя ряд (15.235) в условие (15.224) приходим
к выводу, что функции Ф8 (г) должны удовлетворять условию ог-
раниченности:
|Ф8(0)|<со.	(15.239)
В случае если s п, задача (15.237)—(15.239) для функции Ф8
имеет единственное решение, потому что соответствующая одно-
родная задача имеет только тривиальное решение. Поскольку мы
не собираемся продолжать разложение до членов более высоких
пбрядков по е, нет необходимости находить функции Ф8. При
s = п однородная задача, соответствующая (15.236), (15.238),
(15.239), имеет нетривиальное решение.йпоэтому неоднородная
задача имеет решение только при выполнении некоторого условия
разрешимости. Для нахождения упомянутого условия умножим
уравнение (15.236) на г, с тем чтобы это уравнение можно было
переписать в самосопряженной форме
(гФп)	Ф„ = —2^inm^lAnmrJn
(15.240)
15 Найфэ А. X.
‘J'1 ------------"l;... -...’lr:	—
I-.-  -	'	 '•'	•
j 450 .	Гл. 15. Условия разрешимости
Кроме того, полагая в граничном условии (15.238) s — п, имеет
Фл(1) = QnmfznJ п (S2nm^4nm)>	(15.24Й
поскольку f0 — 0 в соответствии с (15.213).	|
Заметим, что уравнение (15.240) имеет регулярную особу!
точку в начале координат, и поэтому вместо условия типа (15.(м!
в роли граничного условия в этой точке выступает условие он
раниченности (15.239). В связи с этим придется рассмотреть п<я
строение сопряженной задачи и вывод условия разрешимости ба
лее подробно.	Я
Умножая уравнение (15.240) на и (г) и интегрируя получея
ный результат по частям в пределах от г = 0 до г — 1, находи!
1 1
j Ф„ [(гм')' + (о?птг-mJ dr + [гмф; — гм'Ф„]£ =	j
° 1
1 1
= — 2Qnm©1z4nm J ruJп (Qnmr) dr. (15.24Я
0	Я
Для того чтобы определить вид уравнения н граничных услови|
сопряженной задачи, прежде всего используем формулу (15.24а
для случая однородного уравнения, соответствующего (15.24(1
(т. е. положим правую часть (15.242) равной нулю). Как и ране®
полагая равным нулю коэффициент при Фл в подынтегральна
выражении в левой части (15.242), получаем следующее сопряжеж
ное уравнение:	j
(гм')' + (Q^mr - и = 0.	(15.24Й
у
Учитывая, кроме того, граничные условия однородной задачу
Фл (1) = 0 и |Ф„ (0) | < оо, приведём соотношение (15.242) к вид!
и (1) ф; (1) — Jim [гцф; — гм'Ф„] = 0.	(15.24 J
Выберем сопряженные граничные условия так, чтобы оба член!
в соотношении (15.244) обращались в нуль независимо, т.
и (1) = 0, lim [гиФ„ — ги’Ф„] = 0.	|
r-*0	J
Второе условие удовлетворяется, если функция м ограничен^
при г -> 0. Таким образом, сопряженные граничные условия, ко*
торым подчинена функция м, имеют вид	g
м(1) = 0, |м(0)|<оо.	(15.24б|
Следовательно, рассматриваемая однородная задача являете^
самосопряженной, и в качестве решения сопряженной задач®
можно взять функцию и = Jn (£inmr).	3
J5.9 Колебания мембраны . 	.	451
Возвращаясь к неоднородной задаче, и'з соотношения (15.249)
получаем искомое условие разрешимости
(Q„m) f2nAnm = — 2Qnmwj Апт J 'rJ2n (Qnmr) dr. (15.246)
о
Для вычисления интеграла в левой части (15.246) применим фор-
мулу
jrfy(ar)dr = -Lr2J'n‘(ar) + ~^~r2 (1 — Л-} J*n(ar).
о
(15.247)	
Полагая в (15.247) а = Qnm и используя тот факт, что Jn (Qnm) =
= 0, находим
\rJ2n(Qnmr)dr = -^-J'n (Qnm).	(15.248)
Подстановка соотношения (15.248) в условие (15.246) дает
&nmNnAnm~ (‘ilAnm-	(15.249)
'	-	• J
Для того чтобы исследовать соотношение (15.249), представим
коэффициенты Апт и f2n в Тюказательной форме, а именно
Апт = ±апте1^, hn~F2ne1^ '	(15.250)	'
В результате получим	“
=	(15.251)
Поскольку поправка toi к частоте является вещественной величи-
ной, то из отношения (15.251) следует, что
vtn — 20rtm = 0 или я.
Следовательно,
₽пт = -^- или"^(у2п-я),	(15.252)
и соотношение (15.251) может принять одну из двух форм
СО1 = — QnmF2n ИЛИ - (Oi^QnmFzn- (15.253)
Подставляя выражения (15.250), (15.252) и (15.253) в формулу
(15.231), полученный результат — в разложение (15.219) и, на-
15*
452	Гл. 15. Условия разрешимости
конец, разложение (15.219) — в формулу (15.214), получаем в пер-
вом приближении
®(|) =anm4(&nm'')cos(rt9 + -|-van) cos(to6)/ + т)Ч-,
(15.254)
^(2) = anmJn $lnmr) sin (n9 + 4" v2n) cos	+ т) H-, (15.255)
где
®(') = Q„m(l-eF2„)+...,	(15.256)
W(2) = Qnm(l+eF,J+-.-.
Заметим, что в случае круглой мембраны одному собственному
числу Q„m соответствуют две линейно независимые собственные
функции. Однако в случае почти круглой мембраны различные
собственные функции отвечают различным собственным числам wW
и со»2), если Fin =# 0. Если же F2n = 0, то для того, чтобы снять*
вырождение, нам необходимо продолжить разложение до членов
более высокого порядка.
15.10.	Краевая задача для дифференциального уравнения 1
четвертого порядка	|
В этом параграфе рассмотрим вопрос о построении сопряжен^
ной задачи и найдем условия разрешимости краевых задач для
линейных неоднородных уравнений четвертого порядка при не!
однородных граничных условиях. Точнее говоря, мы будем ис|
следовать задачу	/2
Pi (х) ф1у + Ра (х) ф'" + Ра (х) ф* +	I
+ Р1 (х) ф' + рв (х) ф = f (х),	.	(15.25тЦ
ф (0) = Pi, ф' (0) = Pi, ф (1) - р„ ф' (1) = р4. (15.251
Краевую задачу для уравнения четвертого порядка при смешан!
ных граничных условиях общего вида обсудим в следующем па|
раграфе, а в § 15.12 изучим задачу о собственных значениях для
уравнения четвертого порядка.	я
Для того чтобы найти условия разрешимости задачи (15.257я
(15.258), умножим уравнение (15.257) на функцию и (х), которая
является решением сопряженной задачи и подлежит определении
р дальнейшем, и проинтегрируем полученный результат почлепЙЯ
i5,10. Краевая задача для уравнения 4-го порядка	453
в пределах от х = 0 до х = 1 (т. е. по всему промежутку, опреде-
ляемому граничными условиями). В результате получ,им
i	til
j PiUty™ dx 4- J РзНф” dx Ц- j ргиу dx'-\- J pi«<p' dx 4-
o	о	о	о
i	i
4- j p^uydx = [ ufdx.	, (15.259)
0	0
Далее, проинтегрируем члены, содержащие производные функ-
ции <р, по частям, чтобы «перебросить» дифференцирование на
функцию и. Выпишем результаты интегрирования по частям для
каждого члена в левой части (15.259) в отдельности:
1 1
J р4«Ф1У dx = р4«ф” IJ - J (р4и)' <ря dx —
о	о
1
= [р4«ф” - (РМ ф"Н + J (Piu)" q"dx ==
1
= [р4«ф'" - (piU)' ф' 4- (р4и)" ф'и - j (р4и)" ф' dx =*
' о
 1
«= [Р4“Ф* - (р4«)' ф’ 4- (р4«Г ф' “ (р4цГ ф]£ 4- J (р4и)1У ф dx,
о
t	1
( pgUtp1* dx . [р,иф' - (paUY ф' 4- (Рз«)’ ф]J - J (Рз“Г ф d*.
1 1
J раиф' dx = [раиф' - (раи)' ф]} 4- J (раи)" ф dx,
1 1
j РхНф' dx « рхиф |J р j (P1U)' ф dx.
С помощью найденных выражений перепишем соотношение
(15.259) как
1
j ф l(p4«)IV 4- (Рз«)” 4- (Р»иГ - (Pi«)' 4- Po«J dx 4-
0
4- {р4иф” - [(р4н)' - р3и] ф" 4- [(р4и)' - (р3н)' 4- р2и] ф' -
1
Цр4и)" - (Рз«)’ 4- (Р2«)'	Р1«] ф)о = jfudx. (15.260)
J* ,	-	' . ' ' '-
;>	454 ч ,	Гл. 15. Условия разрешимости
Как и ранее, сопряженное уравнение получим, приравняв нулюИ
коэффициент при ф в подынтегральной функции в левой частиД
(15.260). В результате имеем	Д
(p4n)IV — (рз«Г + (ргм)" — (Piu)'+ рои = 0. (15.261)Я
Для того чтобы однородное уравнение, соответствующееД
(15.257), было самосопряженным, оно должно совпадать с уравне-Я
нием (15.261). Раскрывая производные и перегруппировывая члены®
в (15.261), приведем это уравнение к виду -	Д
p4MIV + (Apt — р3) и" + (6/?4 — Зр3 -f- р2) и +	Д
-4-(4р4—Зрз-|-2д2 — Pi)u + (p4V — Рз + Рг— Pi + Ро)и = 0•	.JU
(15.262)1]
Условие совпадения уравнений (15.257) и (15.262) дает S
4^~Рз = Рз, 4р4 — Зрз+2рг-Р1=Р1,	Д
6р4 — Зрз 4~ Рг = Р2> p\v — рз + р2 — Pl Ро — Ро, Д
ИЛИ р3 = 2р^р'з = 2р\, Р1 = 2р’ - Рз + Рг = — р” + Рг- . J
При этом уравнение (15.257) принимает вид	 Д
Аф + 2р4ф Аф {Рг — Pt) ф + Роф = 0>	Д
или (a -g-) + 4- [(А - я) -g-] + РоФ » 0. (15.263)1
Таким образом, произвольное самосопряженное дифференциальное Я
уравнение четвертого порядка без правой части может быть за- Я
писано в виде	Д
(15.264)]
Заметим, что в то время, как любое дифференциальное уравнение Д
второго порядка может быть приведено к самосопряженному виду и
путем умножения на специально подобранную функцию, произволь- Я
ное дифференциальное уравнение порядка выше второго, вообще Д
говоря, не может быть преобразовано в самосопряженное. Я
Для того чтобы найти сопряженные граничные условия, рас-Ц
смбтрим соотношение (15.260) для однородной задачи (т. е. при f — ’1
= 0, рл = 0):	I
{р4мфж — [(р^и)' — р3и] ф" + [(р4м); - (Рз«)' + р2и] ф' —	I
- [(р4и)7 - (рзП)" + (р2и)1 - Рги] фЕ = о.	j
Учитывая уравнение (15.261) и однородные граничные условия J
ф (0).= ф' (0) = ф (1) = ф' (1) = 0, получаем	|
Piu |i ф'" (1) - [(Р4и)' ~ Рз«11 ф" (1) - РзР |о ф'" (0) +	1
+ [(М'-М1»Ф’(°М (15.265) |
15.10. Краевая задача для уравнения 4-го порядка	455
Выберем сопряженные граничные условия так, чтобы соотноше-
ние (15.265) выполнялось при произвольных значениях ф" (0),
ф" (1), ф" (0) и ф'" (1). Для этого необходимо положить равным
нулю коэффициент при каждой из указанных величин. В резуль-
тате имеем
и (0) = 0, и (1) = 0, и' (0) = 0, и' (1) = 0.	(15.266)
Таким образом, сопряженная задача включает в себя уравнения
(15.261) ng краевые условия (15.266).
Для того чтобы найти условие разрешимости неоднородной
задачи, вернемся к соотношению (15.260). Используя уравнение
и граничные условия, которым подчинена функция и, находим
1
[р4« ф' — (р4н” -|- Spiii — р5и ) ф]о = J ufdx.. (15.267)
Подставляя в соотношение (15.267) граничные условия (15.258),
перепишем (15.267) как
(р4и р4 — р^и рз — Зр4и Рз Рзы Рз) |i —
1
— (Р4« Рг — Pi — Зр4« Pi -f- p'J4 Pi) |о = j fu dx. (15.268)
0
Выбирая в качестве функции и любое нетривиальное решение од-
нородной сопряженной задачи, из соотношения (15.268) можно
получить условие разрешимости задачи (15.257), (15.258). Ясно,
что в случае, когда сопряженная однородная задача имеет лишь
тривиальное решение, условие (15.268) удовлетворяется при лю-
бых значениях рл и при произвольной функций f (х).
Применим теперь полученные результаты к двум модельным
задачам.
Пример 1	/
При исследовании вопросов устойчивости пространственных
течений вблизи плоских поверхностей, если сформулировать со-
ответствующую гидродинамическую задачу с помощью функции ,,
тока и пользоваться методом многих масштабов-, возникает так
называемая неоднородная задача Орра—Зоммерфельда следую-
щего вида:
~ *2)2<р ~iR(Vk - ~ + ikR(15-269) '
<p(0) = 0, ^(O)=o,
ф| ^0,	^0,	(15.270)
1	dy	v
456
Гл. 15. Условия разрешимости
где величины /?, k и со не зависят от у, a U и f являются заданными
функциями у. При этом соответствующая однородная задача пред
ставляет собой задачу на собственные значения, у которой су
ществует нетривиальное решение, только если выполнено опре
деленное условие разрешимости.
Раскрывая производные в (15.269), перепишем это уравнен»
как
ф1У _ (2^ + ikRU — i<pR) q>" + (k* +
+ ik3RU — iwk2R + ikRU") =	(15.271
Здесь
Pt = 1, p3 = 0, p2 = — (2k2 + ikRU — i&R),
Pi = 0, p0 = k* + ik3RU — ia&R 4- ikRU".
При этом сопряженное уравнение (15.261) переписывается в ви,
' «iv _ [(2^ + ikRU — iu>R) и]" +
+ (fe4 +.ik3RU — iiok2R + ikRU") и = О,
или
uIV — (2& + ikRU — i^R) и" — 2ikRU'u' +
+ (^ + ik3RU — i^k2R) и = 0.
После некоторых преобразований последнее уравнение мож!
представить как
(~ - k*Yu - iR(kU - <о)	~ 2ikR- =
\dy2 /	'	' \ dy2 1	dy dy >,
(15.2'
(15.27
Граничные условия для функции и имеют вид
и (0) = 0, и' (0) = 0,
и, и' -> 0 при
Определив таким образом сопряженную задачу,
соотношением (15.268), заменяя в нем верхний предел, равный
на оо. Тогда условие разрешимости сводится ,к соотношенц
воспользуем)
j fudy~ 0.
о
(15.271
Пример 2	.3
Исследование колебаний пластины, имеющей форму, близку
к круговому кольцу, в случае жестко закрепленной кромки, eci
пользоваться при этом методом растянутых параметров, привод,
к следующей неоднородной задаче: .
[G&+ -7-3F-	О5'27
Ф (а) =	<р' (а) = 02, ф (Ь) = 0з, ф' (Ь) = В4, (15.27
. •> '-улу- уу.-у-уу-. уу'-у --..t . JUJ u_ '- U !
' -  . . ;•!«
15.10. Краевая задача для уравнения 4-го порядка	457
где п, pft (k — 1, 2, 3, 4) и <дпт — постоянные величины и b > а.
Соответствующая (15.276), (15.275) однородная задача имеет не-
тривиальное решение, поэтому-для разрешимости неоднородной
задачи требуется выполнить специальное' условие.
Вместо того чтобы раскрывать дифференциальный оператор
в круглых скобках в (15.275), группировать члены с производными
одного порядка и применять затем условие разрешимости, выве-
денное в предыдущем параграфе, покажем, что удобнее иметь дело '
непосредственно с уравнением (15.275), которое можно преобразо-
вать в самосопряженное, умножая его на функцию v (г) = г.
При этом для вывода условия разрешимости уравнение (15.275) /
следует умножить на ги (г), где и (г) — решение сопряженной од-
нородной задачи, которое подлежит определению в дальнейшем.
Производя указанное умножение и интегрируя полученный ре-
зультат от f = а до г = 5, получаем
ь	-	ь
f ги [(-$ + 7Т - -у-)2 - “>-] <Рdr = I ruf dr- (15-277)
а	а
Если положить
<Р<р , 1 dtp	пг
dr« г dr	f2	(15.278)
то первое слагаемое в левой части (15.277) можно преобразовать
следующим образом:
ь	ь
а	а
Ъ
- =['“£-	+Н4 ('£) -
7
Подставляя выражение (15.278) в (15.279) н вновь/Интегрируя по
частям, имеем
ь
% Г 1 d / du X п*и 1, Г Г d / dtp X п2 1	,
х |ттЫ~“ J*=Jr*v-aF)-—=
а
- Ъ
= ['ТТ х - Ч	[4 (г $) - V*]dr’ <15-280)
а
1
X —
где
d / du X
~dr\r~dr)
=	(15.281)
г2 , \аг2 1 г dr г* )	'	7
458
Гл. 15. Условия разрешимости
Подставляя выражение (15.281) в (15.280), имеем
ь
г , Г d / du \ п2и 1 , г dtp / d2u . I du n2u\
M^v*)—rj*=[r^(₽ + — T~—) ~
a
d fd2u .	1 du
ST
b
+ Jr<^+44:-4),“^(15’28
a
Наконец, подставляя (15.282) в (15.279), а полученный результат -
в соотношение (15.277), получаем
ь
г Г / d2 . 1 d п2 \2 г! , । '
J Г(( [\-37-2+—-37~-7г) ~^nm\udr +
а
г	а ! d2<p 1	dtp	п2ф \ du [d2tp	f__1	dtp	n2tp \
' [rU	dr \ dr2	' r	dr	r2 )	Г dr \ dr2	'	r	dr	r2 /
। dtp j d2u 1 du n2u\
' Г dr \ dr2 r dr r2 )
b
d / d2u ,	1 du n2u \ 1 b f ,	,. - o.
)].=)* <15'2'
a
Как обычно, приравнивая нулю коэффициент при <р в подынт
ральной функции в левой части (15.283), получаем сопряжет
уравнение
Г / d2 1 d п2 \2	2 1 л	/1 г
|д’272’ + "7''57~75’) —tonsil— 0,	(15.
которое полностью совпадает с однородным уравнением, соотв
ствующим (15.275). Следовательно, это уравнение ^является саз
сопряженным. Далее, полагая в граничных условиях (15.2
— 0, (k = 1, 2, 3, 4) и подставляя полученный результат в
отношение (15.283), а также полагая в нем / = 0, имеем
\rutp'" Ц- «ф* — ru'^ja — 0,
или
Ьи (Ь) ф" (b) + [и (b) - bu' (b)]-tp” (b) —
— аи (a) tp'" (а) — (и (а) — аи' (а)] <р" (а) = 0. (15.2
Сопряженные граничные условия, как и ранее, найдем из 
условия,- чтобы левая часть (15.285) обращалась в нуль при i
Извольных значениях (а), <р" (6), q>'" (а) и tp" (Ь). Для э'
15.11. Сравнение 4-го порядка с граничными условиями общего вида 459
следует приравнять нулю коэффициенты при каждой из указан-
ных производных, т. е.
и (а) = и (Ь) = 0, и' (а) и' (Ь).— О? (15.286)
Сравнивая’, наконец, уравнение (15.284) с уравнением (15.275),
а граничные условия (15.286) с условиями (15.276), замечаем, что
однородная краевая задача, соответствующая (15.275), (15.276),
является самосопряженной.
Опре^блйв сопряженную однородную задачу, вернемся к не-
однородной задаче (15.275), (15.276), с тем чтобы найти недостаю-
щее условие разрешимости. Используя уравнение (15.284) и гра-
ничные условия (15.286) для функции и и подставляя граничные
условия (15.276) в соотношение (15.283), получаем искомое ус-
ловие разрешимости в виде
(6) — &рзи'" (6) — рзц" (Ь) — ар2и" (о) 4-
ь
+ ар1и'я(а)4-р1и"(а) = j rufdr.	(15.287)
а
15.11.	Краевая задача для уравнения четвертого порядка'
с граничными условиями общего вида
В этом параграфе мы выведем условие разрешимости для крае-
вой задачи вида
Pi (х) ф1 v + ря (х) ф” 4- р2 (х) ф" 4- /?! (х) ф’ 4- ро (-0 <р = f (х),	. . .
сКх<Ь,	(15.288) -
£аоф, = 0о i=l, 2,3, 4, \	(15.289)
где ф; представляют собой соответствующие компоненты ф” (а),
ф" (а), ф' (а), ф (а), ф”' (5), ф"(Ь), ф' (Ь), ф (Ь) вектор-столбца ф»..
Предполагается, что граничные условия (15.289) линейно неза-’
висимы, т. е. существует по крайней мере одна невырожденная
квадратная субматрица 4-го порядка матрицы (а,/!.
Для того чтобы определить вид сопряженной задачи, обозна-
чим дифференциальный оператор в левой части уравнения (15.280)
через L, т. е.
ь (ф) = р4ф1У 4- w’ + р2ф” 4- Р1Ч> + РоФ. а < х < b, (15.290)
JV ftr ff г	'
где р4 , рз, р2, pi и ро предполагаются непрерывными на проме-
жутке 1а, Ь]. Пусть ф (х) и и (х) — две произвольные функции,,
непрерывные на 1а, Ь] вместе со своими производными до четвёр-
того порядка включительно. Тогда имеем
ь	ь
J uL (ф)dx	1р4«ф1у 4- Рзиу" 4- Р2«ф” +'PiU<p 4- Ро«ф] dx-
(15.291.)
4бд
Гл. 15. Условия разрешимости
Интегрируя соотношение (15.291) по частям, с тем чтобы «пере
бросить» дифференцирование с функции ф на функцию и, полу
чаем
ь	ь
J uL (<р) dx = j <р {(p4u)IV - (рзы)” + (р2и) - (р&У -ррои] dx +
а	а
+ \р^т - ((р4и)' - (РзИ)] ф" + [(Р^У - (р3и)' + р2и] ф' —
— Кр^У" — (Рз«)" + (Рг«)' — P1U] ф|а- (15.292
Далее, обозначим дифференциальный оператор в подынтегрально!
выражении в левой части (15.292) через L*, т. е.
L“ (и) = (р4и)” - (р3и)" + (рЛи)” - (Р1и)' + рои. (15.293
При этом соотношение (15.292) может быть переписано в виде еле
дующей формулы Грина:
6
j [uL (ф) — ф£* (u)l dx = {р4шр" — [р4и	(р4 — р3) и] ф’ + ;
а
+ lP4U “F (2р4 — Рз) U 4“ (Р4 — Рз ф- Рг) и] ф — [р4и '
+ (зр;-р3)и+(зр4-2р;+р2)«+	;
+ (Р4—Рз -ф- Рг — Р1)и1ф}а*	(15.291
Оператор L* называют сопряженным по отношению к оператору !
Нетрудно проверить, что оператор L сопряжен оператору L?
так что L и L* взаимно сопряжены друг с другом. Как и в пред!
дущем параграфе, дифференциальное уравнение
L* (и) = 0	(15.29!
будем	называть	сопряженным дифференциальному	уравнени
L (ф) = 0,	(15.29
и наоборот.	Если	же L —	L*, то будем	говорить,	Что оператор
и дифференциальное уравнение L (ф) = 0 являк^гся самосопр
женными. Сравнивая уравнения (15.290) и (15.293), заключав
как и в предшествующем параграфе, что оператор L будет сам
сопряженным тогда и только тогда, когда
рз — 2р4, Р\—Рз — р4 •
При этом уравнение (15.290) можно переписать как
=	+	ЪРоФ. (15.29'
Правая часть тождества (15.294) называется билинейной ди(
ференциальной формой относительно ф и и, поскольку при з;
данной функции ф она линейна по и, а при заданной и — линей!
15.11. Уравнение 4-го порядка с граничными условиями общего вида 461
по ф. Используя векторно-матричную форму записи, перепишем
формулу (15.294) в виде
v	ь
j [и£(ф) — ф£* (и)]<1х: = иГРфг>,	(15.298)
а	1
где вектор ф6 определен ранее, и6 представляет собой вектор-
столбец с компонентами и'" (а), и" (а), и'(а), и (а), ит (Ь), и" (Ь),
и' (Ь), «(£>), а матрица Р определяется соотношением				(15.299)
	р =	Лв о - . 0 Ль.		
причем матрицы-блоки / 0	0 0	0	\а,ь имеют вид 0 ~ Р<		Рл Зр'л - рз	-
Ла>6 =	0	р4	Рз	— 2/74	3/?4 — 2/?3 + р2	•
 Р4 Рз	Рз-	Pi — Р2	Рл — Рз Р2 — Р\	х=а, b (15.300)
Заметим, что |Р|	[р4	(а) Рл	(b) J4 и, следовательно, матрица Р		
невырожденная.
Для того чтобы найти сопряженные граничные условия,
преобразуем правую часть формулы Грина (15.298) в каноническую
билинейную форму. С этой целью введем невырожденное линейное
преобразование вектора фЬ в вектор Ф согласно формуле
Ф = ЛфЬ1	--- (15.301)
где А — квадратная матрица 8-го порядка с постоянными эле-
ментами а;,. Матричные элементы аг/, входящие в первые четыре
строки матрицы, совпадают с коэффициентами в граничных ус-
ловиях (15.289). Нижние четыре строки остаются при этом совер-
шенно произвольными, за исключением того, что оци должны быть
линейно независимыми между собой и с четырьмя верхними стро-
ками. Следовательно, при заданном ненулевом векторе фь произ-
волом в выборе нижних четырех строк матрицы А можно восполь-
зоваться, чтобы получить любые наперед заданные значения ком-
понентФ8, Ф6, Ф7 и Ф8. Ниже мы используем этот факт при нахожде-
нии граничных условий сопряженной задачи.
Преобразование (15.301) можно обратить, что-дает
Фь = Л-1Ф.
Тогда имеем
ь
J [м£ (ф) - ф£* (м)] dx = итьРА~'ф = игФ, (15.302)
а
где
иг = и?РЛ-1, или U = (Л-1 )тРтиь. (15.303)
462
Гл. 15. Условия разрешимости
Из соотношения <15.301) и граничных условий (15.289) следуе
что
8
Ф|=2ам<р/ = ₽г,	»=1, 2,3, 4.	(15.30
/=1
Чтобы завершить построение сопряженной задачи, рассмотри:
однородный случай (т. е. = 0) и положим левую часть соотш
шения (15.302) равной нулю. В результате имеем
8
£Цфг = 0, Ф; = 0, i=l, 2, 3, 4.
4=1
Следовательно,
и6Ф6 + ивФв + и7Ф? + и*Ф8==0.	(15.301
Как указывалось выше, при заданном ненулевом в кторе <j
последние строки матрицы А можно выбрать так, чтобы придат
любые требуемые значения компонентам Ф6, Фе, Ф7 иФ8 в соотщ
шении (15.301). Выберем эти четыре строки, например, такиг
образом, чтобы выполнялись равенства Ф6 = ,1, Ф6 = Ф7 = Ф8
"= 0. Тогда из (15.305) следует, что U6 = 0. Точно так же мож
выбрать последние четыре строки матрицы А из условия Фв =
Ф6 — Ф7 = Ф8 = 0, откуда следует, что Ue = 0. Кроме то:
с помощью аналогичных рассуждений нетрудно показать, i
U, = V, = 0.
Таким образом, задача, сопряженная задаче
L (<р) = 0, Ф, = Ф2 = Ф3 = Ф4 = 0,	(15.31
имеет вид
L* (и) = 0, lh= U, = U7 = U8 = 0.	(15.31
Определив сопряженную краевую задачу, вернемся к не^д]
родной задаче, чтобы найти условие ее разрешимости. С учет
(15.307) формула Грина (15.302) принимает вид
ь	4 
J ыТ(ф)б1х = £ЦФг.	(15.31
a	/=1
Наконец, из соотношений (15.288) и (15.304) следует, что L (ф)
= f (х) и Ф; = при i = 1, 2, 3, 4. С учетом этих равенств со<
ношение (15.308) переходит в искомое условие разрешимое'
Ь	4
\u(x)f(x)dx =	(15.31
а	4=1
15.12.	Задача на собственные значения для дифференциально
уравнения четвертого порядка
Применим развитую в двух предыдущих параграфах теорг
к следующей задаче на собственные значения:
Ф1У + 10ф" + [X + е/ (х)]ф = 0, е « 1,	(15.31
Ф (0) = ф" (0) = ф (л) = ф" (л) = 0.
15.12. Задача на собственные значения
463
Будем искать равномерно пригодное разложение первого по-
рядка для решения задачи (15.310) с помощью метода растянутых
параметров, т. е. полагая	.	'	'
Ф (х, е) = ф0 (х) + ефх (х) + ...,	(15.311)
х = %о ®х^ ....
Подставляя разложения (15.311) в уравнение и граничные условия
(15.310) и приравнивая коэффициенты при одинаковых степе-
нях е, получаем
для порядка е°:	й
фГ	1 Офо -J- Хофо = 0,		‘ .
фо(О) = Фо(О}= фо (л) = фо (л) = 0;	(15.312)	;
для порядка в:	'	'
ф1V —|- 1 Оф] —Л,оф1 = — (Х1+/)фо?	(15.313)
ф! (0) = ф! (0) = ф! (л) = фЦл) == 0.	(15.314)	. J
Нетрудно проверить, что решением задачи (15.312) является -
функция	' *>
Фо = sin пх при %о = па (10 — п2).	(15.315)
Заметим, что, согласно приведенной формуле, собственные Числа
при п = 1 и п = 3 совпадают, т. е. Хо О) — К (3) = 9. Следова-
тельно, собственные функции sin х и sin Зх отвечают одному и
тому же собственному числу Хо = 9, а при п = 1 и п — 3 задача
на собственные значения (15.312) оказывается^ вырожденной. 5:
При всех остальных значениях п каждому собственному числу со-
ответствует только одна линейно независимая функция, и, зна-
чит, вырождение отсутствует. Оба эти случая, вырожденный и не- < -У
вырожденный, рассмотрим ниже.
Неоднородная задача имеет решение, только если выполнены .
условия разрешимости. Для нахождения этих условий прежде
всего сформулируем соответствующую сопряженную задачу.
С этой целью умножим уравнение (15.313) на функцию и (х), про-
интегрируем это произведение от х = 0 до х = л, а затем преобра-
зуем полученный результат с помощью интегрирования,по ча-
стям, «перебрасывая» дифференцирование с функции фх на функ-
цию и. В результате получим
j ф! (miv.+ 10и” 4- XG«) dx + [фГы — фХ + фХ — Ф1«”]о +
о
Л
+ 10[фщ ~ фХ]о = — j (Х+ЛфоИ^х- (15.316)
о
Следовательно, сопряженное уравнение имеет вид
Mlv+ 10м"+Х9м= 0,	(15,317)
464
Гл. 15. Условия разрешимости
что полностькГсовпадает с однородным уравнением, соответствую-
щим (15.313). Этот факт не является неожиданным, поскольку
однородное уравнение, соответствующее (15.313), имеет форму
(15.263). Для того чтобы найти сопряженные граничные условия,
положим в соотношении (15.316)	= 0 и f = 0, так-что (15.316)
примет вид
„ [ф1 и — ф1« 4” Ф1 О* “И 10и) — ф1 (и Юи )]о — 0.
Учитывая в соотношении (15.318) граничные условия
имеем
Ф1(л)ы(л)4-фЦл)[и’(л)-|-10и(л)) —
— фГ(0)«(0)-ф1 (0)[«’(0) + 10tz(0)J = 0.
(15.318;
(15.314),,

получим
(15.319'
Как и ранее, выберем сопряженные граничные условия, требуя
чтобы выражение (15.319) обращалось в нуль при произвольны!
значениях фГ (л), ф! (л), <р” (0) и""ф1 (0), т. е.
и (0) = и" (0) = и (л) = и" (л) = 0.	(15.320
Таким образом, однородная краевая задача, соответствующе!
(15.313), (15.314), является самосопряженной.
5 Вернемся теперь к неоднородной задаче и, используя уравне
ния и граничные условия сопряженной задачи,
(15.316) искомое условие разрешимости:
f (^i + f) Фо« dx = 0.
о
Рассмотрим теперь в отдельности вырожденный
денный случаи, начиная со случая простого (т. е.
собственного значения.
Невырожденный случай
В этом случае параметр п отличен от 1 и 3, и решение зада1
нулевого порядка дается формулой (15.315). При этом решен:
сопряженной задачи можно взять в виде и = sin пх, что пос.
подстановки в условие (15.321) дает
j [^i + f (*)] sin2 пх dx = 0,-
о
Такум образом,
(15.321
и невыро?
некратноп
Л
=-------j f (х) sin2 пх dx,
о
15.12. Задача на собственные значения	. 465
и из разложения (15.311) следует, что в первом приближении
,	<р = sin пх + О (в),	(15.322а)
. ^ = n2(10-n2)-^- jf(x)sln2nxdx + O(82). (15.3226)
п о
Вырожденный случай
В этом, случае параметр п равен 1 или 3, и решение задачи
нулевого порядка имеет вид
фо ~ ai sin х + а3 sin Зх, — 9,	(15.323)
где постоянные at и а3 на данном этапе итерационного процесса,
считаются независимыми, что в данном случае и служит проявле-
нием вырождения задачи. При Хо = 9 решениями сопряженной
задачи будут функций и = sin х и и — sin Зх. Подставляя реше-
ние (15.323) в условие разрешимости (15.321), имеем
j [%i + f (x)J (fli sln х Ц- а3 sin Зх) и (х) dx = 0.	[(15.324)
о
Соотношение (15.324) должно выполняться для любого решения
сопряженной задачи. Полагая в соотношении (15.324) и = sin х
и ы = sin Зх, получаем соответственно
fUi + /(x)](aiSin х + а3 sin Зх) sin х^х = 0,
о
I л
J [Ь1+ /(*)] (01 Sin х + а3 sin Зх) sin 3xdx = 0,
о
или	+ fu) at + f13a3 = 0,	(15.325)
fi3ai + (^i + /зз) й,з = о,
где	f f sin2 х dx,	[ f sln2 3x dx,
Л J	- JI J
о	0
л
2 f
/i3 = — J f sin x sin 3x dx.
о
Для того чтобы существовало нетривиальное решение системы
уравнений (15.325), необходимо и достаточно, чтобы определи-
тель этой системы обращался в нуль, т. е.
^>1 + /11	/13	__ _
/гз ^ + /зз
466
Гл. 15. Условия разрешимости
Раскрывая этот определитель, получаем квадратное уравнение
вида
11	(/11 —Ь /зз) 11 + /11/зЗ — /13 = О
с корнями
l('i2) =----2~(/и /зз) ± [(/п ~ /зз)2 + 4/1з]'2 • (15.326)
Если lj совпадает с одним из корней (15.326), то из системы
(15.325) находим
Окончательно, подставляя найденные выражения в разложение
(15.311), получаем, что в первом приближении
х (1) _1_ f
Ф = sin х--------j-----sm Зх 4- • • •,
/13
1(1> = 9 -	(/„ + /33) +	[(/и - /33)2 + 4/?3]1/2 4- • • • (15.327)
Ф(2) = sin х----1—_tAl_ Sin Зх 4- • • •,
/13
И
1(2) = 9 -	(/н 4- /зз) -	[(/п - /зз)2 4; 4/1з]"2 + •  • • (15.328)
Таким образом, если lj(l) =f= Х*2) (т. е. /п =4= /33 или /13	0), то
в первом приближении вырождение задачи снимается.
15.13.	Система дифференциальных уравнений первого порядка
В этом параграфе выведем условия разрешимости краевой
задачи для одной системы дифференциальных уравнений первого
порядка. В следующем параграфе рассмотрим систему уравнений
первого порядка общего вида, а в § 15.15 — краевую задачу для
дифференциального уравнения второго порядка с внутренними
граничными условиями на поверхностях раздела.
При изучении распространения затухающих звуковых волн
в сжимаемой Жидкости, движущейся по каналу кольцевого се-
чения, возникает следующая неоднородная задача:
—»(ю - Ли0) Ф4 + ^роФ1 -Ь -у^-фз 4--у- 7г(гРо<₽2) = Л, (15.329)
— ip0 (<о — ku0) <Pj 4- рс«оф2 + 1^ф5 = /г, (15.330)
— ipo(«— &«о)ф2 + ф5 = /з> (15.331)
— i р0 (<о — kue) <р3 + -у- <р5 = /4, (15.332)
15.13. Система уравнений 1-го порядка '	46?
— 1р0(® — ^и0)<Рб+ РоТ’офгЧ* i (? — 1)(® - йм0)ф5 = /5, (15.333)
_£l=Tj. + 1!L	(15.334)
Фа (^?1) Р1фб (^?i) = aii фз (Rz) Рзфб (Rz) ~ a2i (15.335)
где и0, ро, р0, То и fn (г) представляют собой известные функции
переменной г, а параметры ®, т, k, ап, f}rt и у не зависят от г.
Отметим, что четыре приведенных уравнения из шести являются
алгебраическими, следовательно, система дифференциальных
уравнений имеет второй порядок. Предполагается, что соответ-
ствующая однородная задача имеет нетривиальное решение,
поэтому для разрешимости неоднородной задачи требуется вы-
полнить специальное условие.
Для того чтобы получить требуемое условие разрешимости,
умножим каждое из уравнений (15.329)—(15.334) соответственно
на фх, ф2, фз, 4’4, фз и ф6. Далее, сложим полученные произведения
и проинтегрируем результат по г в пределах от Rt до R2. Затем
преобразуем полученное соотношение с помощью интегрирования
по частям, перенося дифференцирование с функций <рп на функ-
ции ф„. В результате получим
Яг	Да
J фоф! [— ®ф2 4- £ф1] dr + J p0q>2 [— !®фз + «оф2 — Г (-7-) +
Я.	Я.
4- Т0ф6^ dr 4- j фофз ®ф4 4- -у-ф1 ] dr 4- J q>4 [— *®ф1 —
«I	Я1
«2
— RоРоФб] dr 4~ | ф5 ^1^4'2 — фз 4- —р~ ф4 4~ * (? — 1) ®ф’5 4-
я,
«2
4- РоТ’оФб] dr 4- j рофб [— гюфб — Рофб] dr 4-
«1
5
4- [Р0Ф2Ф1 4- Фбфз]^ = J фл/л dr,
nS К,
(15.336)
где (о = а) — ku0. Отметим, что члены в левой части соотношения
(15.336) сгруппированы так, что в подынтегральное выражение
в каждом интеграле входит только одна из функций <р„. Прирав-
468	Гл. 15. Условия разрешимости
нивая нулю коэффициенты при каждой из функций фя, получаем
сопряженную систему уравнений вида
—	—0> (15.337)
— 1<вфз Н- иофз — г -jp (“У") Т’офб — 0> (15.338)
—	+-у-Фх = 0> (15.339)
— 1шф1 + То/’офв = О, (15.340)
1Ъ|-2 — фз + -у^ф4+ »(у— 1)юф5+ роГофб = О, (15.341)
1<Ьф5 + /?офв = 0. (15.342) .
Система уравнений (15.337)—(15.342) сопряжена системе уравне-;
ний (15.329)—(15.334). Для того чтобы получить граничные уело-'
вия, которым подчинены функции фя, положим в соотношении -
(15.336) /я = 0 и воспользуемся уравнениями (15.337)—(15.342).'
В результате получим
[рофгфг + ФбФз]₽, — 0-	(15.343);
Полагая в граничных условиях (15.335) а„ = 0, а затем выражая;
граничные значения ф2 через граничные значения ф6, перепишем;
(15.343) в виде
(Р0Р2Ф1 Фз)г=«2Фб (^г) — (роР1фх ~Ь Фз)г=₽1Фб (^?1) = 0. (15.344),
Сопряженные граничные условия выбираем, как и ранее, из!
условия обращения левой части (15.334) в нуль при произвольных?
значениях ф6 (Ri) и ф6 (Т?2). В результате получаем	•
Фз (Rz) Р0Р2Ф1 (Rz) = о,	?
(15.345)’
Фз (Ri) + poM'i (Я1) = 0.	•
Таким образом, сопряженная краевая задача определяется Си-;
стемой уравнений (15.337)—(15.342) и граничными условиями;
(15.345).	•
Возвращаясь к неоднородной задаче, прежде всего упростим!
соотношение (15.336) с помощью уравнений (15.337)—(15.342)1
и условий (15.345).	В	результате	получим	|
5 R,	•’
[Р0Ф2Ф1 + ФбФз]₽; = S j Фп/п dr.	(15.346);
Л=1 я,	-4
Выражая	граничные	значения	ф3	через	граничные значения ф!
с помощью соотношений (15.345), а граничные значения ф2 череж
15.14. Общая краевая задача	469
граничные значения <р6 и постоянные 04 и а2, перепишем (15.346)
как
5 R,	..	.
«аРо(/^2)(^2) — «1Р0 (Я1)Ф1(#1)= S j fn^ndr, (15.347)
Л=1 «1
что и служит искомым условием разрешимости. ’	• <
15.14. «Общая краевая задача для системы обыкновенных
дифференциальных уравнений
Рассмотрим вывод - условий разрешимости для задачи вида '
^-4(x)<p = f(x),	(15.348)
Фг (0) = ₽i> / — 1. 2, . . ., т, . х
(15.349)	;
фг (1) = рг, I = т 4- 1, т 4- 2, . п,
где ф и f — вектор-столбцы с п компонентами, А — квадратная
матрица n-го порядка, а рг — известные постоянные величины.
Отметим., что граничные условия краевой задачи для системы
уравнений первого порядка не всегда могут быть разделены,
как в соотношениях (15.349). Нетрудно, однако, развить теорию
и для граничных условий, содержащих п линейно независимых
комбинаций ф; (0) и фг (1). Более общие, чей (15.349), случаи <*
рассматриваются в конце настоящего параграфа.	-J"-"
Предположим, что однородная задача, соответствующая
(15.348)—(15.349), обладает нетривиальным решением, так что , .
неоднородная задача имеет решение, только если удовлетворено., ...4‘
некоторое условие разрешимости. Для того чтобы вывести уело- :'4-.
вие разрешимости задачи (15.348), (15.349), умножим /-е уравне- < ф
ние (15.348) (/=1,2, . . ., га) на ф, и сложим полученные резуль-- /• 4.
тэты. Эта операция эквивалентна умножению векторного урав* 4*".
нения (15.348) слева на фг, гдеф7 представляет собой транспони- Тч
рованный сопряженный вектор-столбец ф с п компонентами.
Таким образом, имеем	>
^--М’г^ф=фЧ
что после интегрирования по переменной х в пределах от 0 до t
дает	1	- дн|
1 1 1
j фг dx — j фтЛф dx = j фт1<£г.	(15.350)
ооо
470
Гл. 15. Условия разрешимости
Интегрируя по частям в первом интеграле в левой части (15.350)
находим
1 1 Т 1 1
фгф| — j	— |фтЛ<р<£г = j ij)Tf dx,
оо	о	о
(15.351;
или
Я’т<р | — J (^- + Я’Т^)«Р^= J фт1 dx-.
0	0	о
_	_		Б
Приравнивая нулю коэффициент при <р в подынтегральном
выражении в левой части (15.351), получаем сопряженное век*
торное уравнение	Д
-^.|фгЛ = 0.	1
dx 1 т
Выполняя транспонирование, имеем
или
-^+Лгф= 0.	(15.352)
ИЛИ
(15.353);
• Сравнивая уравнения (15.348) и (15.352), приходим к выводу,
что уравнения окажутся сопряженными, если А = —Лт. Для-з
того чтобы вывести граничные условия для вектора ф, рассмотрим >
однородную задачу. Полагая в соотношении (15.351) f = 0, j
получим
фт<р|о = О,
1Ф1ф1.+ Ф2Ф2• • • Д'Флфп]о = 0.	(15.354);
Полагая в граничных условиях (15.349) |)( = 0и подставляя ;
граничные значения функций <р(- в (15..354), находим
Д1(1)ф1(1) + Д2(1)ф2(1) Н------1~ Дт(1)фт(1) -	j
Фт+1 (0) фт+1 (0)	Фт+2 (0) фт+2 (0) — • • • — фп (0) <рп'(0) = 0.
(15-355);
Как и ранее, сопряженные граничные условия определяем из 
требования, чтобы левая часть соотношения (15.352) обращалась
в нуль при произвольных значениях <pz (1), i = 1, 2, . . ., т и >
фг (0), i = т + 1, т + 2, . . ., п. В результате имеем	;
фг (0) = 0,	i = т + 1, т + 2, . . ., п, (15.356) *
фг (1) = 0,	i = l,2,.. ., т.
15.14. Общая краевая задача	471
Возвращаясь к неоднородной задаче, подставим выражения
(15.349), (15.356) в формулу (15.351). Это дает соотношение
Рт+1Фт+1 “1“ Рт+гФт+2 Н- ’ ‘ ' “1“ РпФп 0)	,
- Ml (0) ~ М2 (0) - ... - Мт (0) = J ФТ f dx, (15.357)
о
которое и служит искомым условием разрешимости.
Рассмотрим теперь более общий случай граничных условий,
чем (15^349), а именно	'
<р(0) = ^<р(1) + р,	(15.358)
где — квадратная матрица n-го порядка с постоянными эле-
ментами, р — вектор-столбец с п компонентами. В этом случае
соотношения (15.350)—(15.354), выведенные выше, сохраняют
силу, причем изменяется лишь последний этап вывода сопряжён-
ных граничных условий. Так, полагая f = 0 и р = 0,.из соотно-
шений (15.353) и (15.358) находим, что
фт (1)<р(1)- фт (0)<р(0) = фт (1)<р(1)-фТ (0)Л<р (1) = 0,
или
[фт (1)-фГ(0)Л]<р(1)= 0.	(15.359)
Как и раньше, сопряженные граничные условия определяем
с учетом требования, чтобы левая часть соотношения (15.359)
обращалась в нуль при произвольных значениях компонент век-
тора фг (1). В результате получим
фт (1) — фг (0) si- — 0,
откуда после транспонирования находим
ф(1) = ^тф(0).	(15.360)
Обращаясь вновь к неоднородной задаче и используя урав-
нение (15.352), приведем соотношение (15.351) к виду
1
фг (1)<р(1) — фг (0)<р(0)=	(15.361)
о
Подставляя выражение (15.358) в формулу (15.361)f имеем
1
фг(1) <р(1)-фг(0)^<р(1)~фг(0)р = fdr. (15.362)
о
Принимая во внимание условие (15.360), убеждаемся, что первые
два члена в левой части (15.362) взаимно уничтожаются, так что
это соотношение сводится к равенству
1
< — фг(О)р= /фг fdx,	(15.363)
Q
472
Гл. 115. Условия разрешимости
которое и является искомым условием разрешимости. Таким же^
образом можно рассмотреть и другие задачи с аналогичными 1
краевыми условиями.	?
Наконец, обратимся к случаю граничных условий самого об? 1
щего вида
2n	j
Saf/pj=*₽h i— 1, 2, ...,п,	(15.364)1
/=1	а
где <р; представляют собой компоненты граничного вектор-столбца ,
<рь, причем первые п компонент вектора <рь совпадают с составля- з
ющйми вектора <р (1), а последние п компонент — с составляю- ‘
щими вектора <р (0). Соотношения (15.350)—(15.354) остаются ';
в Силе и в этом случае. Следующий шаг состоит в том, что мы •]
вводим невырожденное линейное преобразование вектора <рь по
формуле, аналогичной (15.103) и (15.301)
Ф = ^<рь,	(15.365) ?
где st- — квадратная матрица 2п-го порядка с постоянными эле- '
ментами. Элементы первых ее п строк совпадают с коэффициентами '
в граничных условиях (15.364), поэтому
2п
Фг = S =	*=1, 2,-.., п. (15.366)
/=1
Как и в других подобных случаях, последние п строк матрицы
остаются произвольными, за исключением того, что они должны ;
быть линейно независимы одна от другой и от первых п строк. ,
При ненулевом векторе <рь последние п строк матрицы А можно <
выбрать так, чтобы компоненты Фг, i п + 1, принимали любые .’
наперед заданные значения.	J
Перепишем соотношения (15.353) в виде
фгф I * = фг (1) /<р (I) _ фг (0) Iff (0) = о,	i
или
г г v т 1R Гф 0) 1	'	"
[<<!)<(<»40 ,][; ;О)']=о.-	;
или, наконец,
=	0,	(15.367),
где / — единичная матрица порядка п, а через Р обозначена
матрица вида
Г/ 0]
Р~ [0
Разрешая уравнения (15.365) относительно <рь, имеем
<р6 = ^-1Ф.
15.15. Внутренние граничные условия	473
Подстановка этого выражения в (15.367) дает
г<р ft = ф^РА-1 ф — о,
или	Vr<p ft = YT Ф = 0,	(15.368)
где
, ЧгТ='фь^-1> откуда W = (^~1)TPT^b.	(15.369)
Учитывая однородные граничные условия, соответствующие
(15.366) (при 0(- = 0), приведем соотношения (15.368) к виду
2п
S ^Фг = 0.	(15.370)
*=л4-1
Левая часть (15.370) представляет собой линейную форму от
компонент Yj, i = п + 1, п + 2, .... 2га. Поскольку эта форма
должна обращаться в нуль при произвольных ненулевых значе-
ниях коэффициентов Фг, то все компоненты также должны
обращаться в нуль
V; = 0, i = п. + 1, п + 2, . . ., 2п.	(15.371)
Определив вид сопряженных уравнений (15.352) и граничных
условий (15.371), вернемся к неоднородной задаче. С помощью
уравнения (15.352) и соотношения фт<р ft = ЧГФ придадим фор-
муле (15.351) следующий вид
1
= JtTfdr.	(15.372)
о
Используя теперь граничные условия (15.366) и (15.371), получим,
искомое условие разрешимости z
л	1
= J/fdr,
/=1	о
которое должно выполняться для произвольного вектора ф,
являющегося решением сопряженной задачи.
15.15.	Краевые задачи с внутренними граничными условиями
При исследовании распространения волн в составных телах
часто приходится сталкиваться с краевыми задачами для неодно-
родных дифференциальных уравнений с неоднородными гранич-
ными условиями на поверхностях раздела. В этом параграфе
мы рассмотрим в качестве примера задачу о крутильных колеба-
ниях стержня, покрытого оболочкой из другого материала при
474
Гл. 15. Условия разрешимости
синусоидальном возмущении поверхности раздела «ядро—обо-;
лочка». Эта задача формулируется следующим образом:	j
5^7^ + (“" ~ ?г) = Л (И. О < г < а, (15.373)'
+	а < г < 5, (15.374)'
|ф1(0)|<оо, ф2 (6) — бфг (&) = 0,	(15.375)“,
Ф1(а) — Фг («) = ₽!, Фг(а) —Н1Ф1’(«) —Н2ф1(б) = ₽2,
где а„, yh, l^n, Рп, а и b — заданные постоянные.	j
Как указывалось в § 15.9, однородные уравнения, соответ-J
ствующие (15.373) и (15.374), можно привести к самосопряжен^
ному виду, умножив каждое из них на независимую перемен-^
ную г. Таким образом, для того чтобы вывести условие разреши-’;
мости задачи (15.373)—(15.375), следует умножить уравнение^
(15.373) на гиг (г), а уравнение (15.374) — на гщ (г). Интегрируя?
результат первого умножения по переменной г от 0 до а, получим?
а	а
j [“1 (гф1Т + (а2пг---фА \dr = j ruifidr, (15.376).
о	J о	s
что после интегрирования по частям дает
' а
[гЦ1ф1 - ru’itpi Jo + J Ф1 [('“О + (“«Г —
о
а
0
(15.377)
Аналогичным образом, интегрируя результат умножения (15.374)"
на ги2 (г) по промежутку [а, 5], получим	*
ь		ь	I

а	а
бткуда после интегрирования по частям имеем
Ь	, ъ

7
(15.378)j
, находим
а
Складывая теперь соотношения (15.377) и (15.378)
[ ГИгфг — ^2ф21а -f- [ ГИ1ф1 — ГЫ1ф1]о -|~
а

4
а2пг —
О
ь
а
а	b
-J-) U^dr = J ruifidr + J ruj2dr. (15.379):
0	a	• 4
15.15. Внутренние граничные условия	475
Далее, приравнивая нулю коэффициенты при <рх и <р2 в подын-
тегральных выражениях в левой части соотношения (15.379),
получим сопряженные уравнения
W' + (anr--4-)“i = °>	(15.380)
(г«2)'-(т»г+-4-)“2 = °-	(15.381)
При этом соотношение (15.379) примет вид
&«2 (Ь) фг (Ь) — Ьи2 (Ь) фг (6) — lim [rui— ru^] +
'-•о
+ aui (a) (pj (а) — аи\ (а) ф, (а) — аи2 (а) ф2 (а) -j- аи2 (а) ф2 (а) = 0
(15.382)
Уравнение (15.380) имеет регулярную особую точку г — 0, так
что одним из граничных условий для него служит условие | ф! (0) |<;
<оо. Как показано в § 15.9, сопряженным этому условию яв-
ляется условие ограниченности решения
[|М0)|<оо.	-	(15.383)
Если условие (15.383) выполнено, то должно обращаться в нуль
слагаемое в левой части (15.382), содержащее предельный пере-
ход г -> 0.
Из однородных граничных условий, соответствующих (15.375),
следует, что
фг (Ь) =; bq>2 (&),
Фг (а) = Ф1 (а),
фг (а) = Ц1Ф1 (а) + Ц2Ф1 (а).
Подставляя эти выражения в соотношение (15.382), приводим
его к виду
b [«2 (&) — Ьи2 (&)] ф^ (Ь) 4- a [ui (а) — ptiU2 (а)] Ф^ (а) +
+ а [и2{а) — и\ (а) — ц2а2 (а)] ф1 (а) = 0 (15.384)
Как обычно, выбираем сопряженные граничные условия из тре-
бования, чтобы левая часть соотношения (15.384) обращалась
в нуль при произвольных значениях ф£ (6), ф{ (а) и ф1 (а), т. е.
«2 (b) = bu2 (b), Ui (а) = ^«2 (а),
и2 (а) — til (а) — Цги2 (а) = 0.	(15.385)
Таким образом, сопряженная краевая задача состоит в решении
уравнений (15.380) и (15.381) с граничными условиями (15.383) и
(15.385). Сравнивая сопряженную задачу с исходной однородной
задачей, замечаем, что несмотря на то, что дифференциальные
476
Гл. 15. Условия разрешимости
уравнения этих задач Самосопряжены, краевые задачи не яв-J
ляются самосопряженными, за исключением случая fXj = 1. j
Определив теперь сопряженную задачу, вернемся к неодно--.
родной краевой задаче, чтобы завершить вывод условия разре-j;
шимости. Соотношение (15.379) с учетом сопряженных уравне-.;
ний (15.380), (15.381) и условия ограниченности (15.383) преобра-J
зуем к виду
bu2 (t) фг (6) — bu'z (6) ф2 (5) +	(а) Ф1 (а) — (fl) Ф1 (а) —
в	а	|
—	аи2 (а) фг (а) + аи2 (а) <р2 (а) = J ^i/i dr Ц- J ru2f2 dr. (15.386)
о	о	i
Выражая <р2 (Ь), <р2 (а) и фг (д) с помощью граничных условий’.
(15.375) и подставляя результат в (15.386), имеем	'
Ь [и2 (Ь) — bll2 (fc)] ф2 (&) + Я [Ы1 (й) — Р1Ы2 (а)] Ф1 (fl) +
+ а [и2 (а) — u'i (а) — ц2м2 (а)] Ф1 (а) — (фА (а) — а₽1«2 (а) =
а	Ь
= J rujfidr -J- J ru2f2dr
0	а	Ц
Упрощая последнее соотношение с помощью условий (15.385),
приводим его к виду
а	b
—	аРг^г (д) — дР]П2 (а) = J ruji dr	J ги^2 dr.	(15.387)
0	а
Соотношение (15.387) и служит искомым условием разрешимости.
15.16.	Интегральные уравнения
В этом
трального
параграфе выведем условие разрешимости для инте*.
уравнения Фредгольма второго рода
Ф (s) = f (s) + X J К (s, /) Ф (0 dt _	(15.388)’
когда соответствующее однородное уравнение (т. е.
в случае, j ..
при f = 0) имеет нетривиальное решение. Для'этого умножи»
уравнение (15.388) на функцию ф (s) и проинтегрируем получен'
ный результат по промежутку 1а, Ь]. В результате получим
b	ь	ь ь
J Ф (s) ф (s) ds = j f (s) ф (s) ds + X j J К (s, t) qp (t) dt ф (s) ds,
a	a	a
ИЛИ
b	b	b b
J ф (s) ф (s) ds = J f (s) ф (s) ds + X j j к (s, t) ф (/) Ф (s) ds,
9	9	9 9

а
15.16. Интегральные уравнения	477
—...... .  -
что после смены порядка интегрирования в двойном интеграле
дает
b	. b b	ь
j Ф (s) ф (s) ds — X j j К (s, t) ф (s) <p (0 dsdt = - j f (s) ф (s) ds. (15.389)
a	' a a	a
He меняя значения двойного интеграла в левой части (15.389),
поменяем местами обозначения переменных интегрирования s и t.
Тогда соотношение (15.389) перепишется как
*	ь ъ	ь
J ф (s) ф (s) ds — X J J /С (/, s) ф (0 <р (s) dt ds = j f (s) ф (s) ds,
a	a a	a
ИЛИ
6	b	~	b
J 4>(s) — 1J К (t, s) ty(t)dt qp (s) ds = j f (s) ф (s) ds. (15.390)
fl	а	ч J	fl
Для того чтобы определить вид сопряженного интегрального
уравнения, рассмотрим соответствующее однородное уравнение
(т. е. положим в (15.390) / = 0). При этом соотношение (15.390)
примет вид
ь г	ь
j ф (s) — X J K{t, s) ^{t)dt
a L	c
Ф (s) ds = 0.
(15.391)
По аналогии с уже рассмотренными случаями выберем сопряжен-
ное уравнение так, чтобы обратился в нуль, коэффициент при
<р (s) в подынтегральном выражении в (15.381):
ь
ф ($) = X J к (/, s) ф (0 dt.	(15.392)
Сравнивая уравнение (15.392), с однородным интегральным урав-
нением, соответствующим (15.388), замечаем, что они отличаются
друг от друга лишь порядком аргументов ядра Д’(s, 0. Следо-
вательно, однородное интегральное уравнение Фредгольма вто-
рого рода будет самосопряженным тогда и только тогда, когда
его ядро К. (s. 0 симметрично, т. е. К (s, 0 = К (t, s).
Возвращаясь к тождеству (15.390) и предполагая, чтовходя-
щая в него функция ф является решением сопряженного уравне-
ния (15.392), получаем искомое условие разрешимости
ь
J f (s) Ф (s) ds —
а
(15.393)
которое можно сформулировать следующим образом: неоднород-
ное интегральное уравнение Фредгольма второго рода разрешимо
при условии, что его правая часть ортогональна любому нетри-
виальному решению сопряженного интегрального уравнения,
478	Гл. 15. Условия разрешимости
Мы доказали необходимость этого условия, но на самом дел$
оно является и достаточным. Если однородное уравнение имеет'
только тривиальное решение, то условие (15.393) удовлетворяется;
автоматически, поскольку в этом случае ф (s) — 0.
Эти предложения составляют содержание так называемой;
альтернативы Фредгольма: либо интегральное уравнение (15.388^
разрешимо при произвольном неоднородном члене f (s) и соответ^’
ствующее однородное уравнение имеет только тривиальное ре»,
шение, либо однородное уравнение имеет нетривиальные решения*;
и неоднородное уравнение разрешимо тогда и только тогда!
когда его правая часть ортогональна всякому решению сопряжен^
ного однородного уравнения.	|
В качестве приложения развитой выше теории рассмотри}^
случай интегрального уравнения с вырожденным ядром. Ядр^
К (s, t) называют вырожденным, если оно может быть представ^
лено конечной суммой слагаемых, каждое из которых являете^
произведением функции переменной s на функцию переменной
т. е.	' 	’’i
N	-	3
K(s,t)= S a, (s) p;(0.	[(15.394
i=i	*4
В случае вырожденного ядра уравнение (15.388) можно запи-я
сать в виде
n	ь	1
<р (s) = f (s) +	X S a( (s) j	рг (t) <p (t) dt.	(15.3951
i=i	°	1
Для того чтобы решить	уравнение	(15.395),	положим	,|
6	i
j Pi (0 Ф(/) dt = xh i~l, 2......У. (15.396®
a	Ji
Тогда уравнение (15.395) примет вид	|
*	J
ф(«) = /(з)Ч-Х 2 Xtat(s).	'	(15.39Я
f=l	••
Умножив уравнение (15.397) на pj (s) и проинтегрировав получем
ный результат по промежутку [а, 6), получим	3
b	b	N b
- J₽;(s)<P («)<& = JP/(s)/(«)<* + Jcc4(s)pj(s)ds. (15.39^
a	a	а
Интеграл в левой части уравнения (15.398) равен х} (см. 15.396Щ
поэтому данное уравнение можно	переписать как	.1
N	1
Х1 = !1А-^^ацХь	(15-39$
15.17. Уравнения с частными производными	 479
где	°	‘
fj= J P7(s)/(s)ds,	/
а
b
ап = I ₽/ (s) “i (s)	(15.400)
а
Отметим, что решение интегрального уравнения (15.388)
свелось к .решению системы линейных алгебраических уравне-
ний (15.380). Эту систему уравнений можно записать в векторной
форме как
[/-M]x = f,	'	(15.401)
где / — единичная матрица порядка N, А — квадратная ма-
трица порядка N, элементами которой являются коэффициенты
ахи! — вектор-столбцы с компонентами и ft.
Как указывалось в § 15.1, если однородное векторное уравне-
ние, соответствующее (15.401), имеет только тривиальное реше-
ние, неоднородное уравнение имеет единственное решение при
произвольном f. С другой стороны, если однородное уравнение
имеет нетривиальное решение (т. е. 11 — кА | — 0), то уравне-
ние (15.401) имеет решение тогда и только тогда, когда
(u, f) = 0,	(45.402)
где вектор и представляет собой любое решение сопряженного
уравнения
{/- М]*и = 0.	(15.403)
Поскольку матрица А вещественна, уравнение (15.403) можно
переписать как
[/ —kAT]u = 0,
или, в тензорных обозначениях,
N
tij — к S aijui = 0.	(15.404)
«=«. . .
Таким образом, исходное интегральное уравнение является само-
сопряженным тогда и только тогДа, когда матрица А симметрична,
т. е. atj = ал, что имеет место, например, при условии
a-t (s) =	,(s).
15.17. Дифференциальные уравнения с частными производными
В предыдущих параграфах данной главы мы изучали различ-
ные краевые задачи для обыкновенных дифференциальных урав-
нений. В этом параграфе мы рассмотрим вывод условий разре-
шимости краевых задач для уравнений в частных производных.
Алгоритм, с помощью которого выводятся условия разрешимо-
сти в этом случае, аналогичен алгоритму, который мы приме-
480
Гл. 15. Условия разрешимости
няли в задачах для обыкновенных уравнений, за исключением i
того, что интегрирование производится не по отрезку числовой !
оси, а по многомерной области. Продемонстрируем процедуру 
вывода условий разрешимости на двух примерах.
Пример 1
При исследовании распространения "звуковых волн по аку-
стическому волноводу с переменным по длине прямоугольным
сечением возникает следующая неоднородная задача:
^+-g + ^ = /(//, z), 0<у<а, 0<z<6, (15.405) .
ф (0, z) = 0, ф (у, 0) = 0,
-а1ф = ₽1(г) при у~а,
-g -а2ф = ра(у) при z = 6.
(15.406)
(15.407)
Для того чтобы найти условие разрешимости задачи (15.405)—
(15.407), умножим уравнение (15.405) на функцию и (у, z) и про-
интегрируем полученный результат по интересующей нас обла-
сти, т. е. по прямоугольнику 0 < у < а, 0 < z < b. В резуль-.
тате получим
b а	b а
J J [u^ + u^- + Xu(p]dydz==i iufdydz- <15-41
ч	0 0.	00
Преобразуем теперь соотношение (15.408) с помощью интегрир
вания по частям, чтобы «перебросить» дифференцирование с фун
ции ф на функцию и:
Ь а
b
а
0 о
0 Lo
Ь г
iUl&-dy dz~
a
ди	\ |° . f
dy |o J
о
dy dz, (15.41
0
а
Ь а
b
Jp-g-dz/dz-J ju-^-dz dy =
0 Lo
о L
О а
ди \ р
дг *Р/ |о
b
+ jcp-^-dz dy. (15.41-
о
15.17. Уравнения с частными производными
481
Подставляя (15.409) и (15.410) в соотношение (15.408), имеем
Ь а	;
I Ии ['В’+-S-+М -ф [$+$+4}dydz=
0 0	-
Ь	а	Ь
=j (“ % - т I." *+1 (” < ’) к-(is41»
о	о	о
Соотношение (15.411) можно получить и другим способом, непо-
средственно используя формулу Грина для произвольной обла-
сти
jj(«VV--TVWS=	(15.412)
s	г	'
где Г представляет собой границу области S.
Сопряженное уравнение определим, как и ранее, из условия
равенства нулю коэффициента при ср в подынтегральном выраже-
нии в левой части соотношения (15.411), т. е.
д2и 32« , . п	_	.
др2 + дг2 “Ь 0’	(15,413)
Для того чтобы найти вид сопряженных граничных условий,
обратимся к однородной задаче (т. е. положим f = 0,	— 0).
В случае,если f — 0, соотношение (15.411) принимает вид
ft	а
(>5;414>
о	о
Перепишем теперь однородные граничные условия, соответству-
ющие (15.407), разрешая их относительно производных
L = “1Ф \у~а,	|#=6 = сад, |г=*.	(15.415)
Подставляя в формулу (15.414) вместо левых частей граничных
условий (15.406) и (15.415) соответствующие правые части, имеем
J [(а1“-|04_ы1НоРг +
о
а
о
Поскольку соотношение (15.416) должно выполняться для любой
функции ф (у, г), удовлетворяющей однородному уравнению,
соответствующему (15.405), и однородным граничным условиям,
соответствующим (15..406) и (15.407), то коэффициенты при'каж-
дом из следующих членов:
<P(a,z), -^-(0,2), <р(у, Ь), -^(£,0)
х/а 16 Найф9 А. X.
482
Гл. 15. Условия раврешимости
должны обращаться в нуль, т. е.
ы (0, г) = О, и (у, 0) = О,	(15.417)
(а, г) - а^а, г) = О, (у, Ь) - с^и (у, &) = 0. (15.418)
Определив таким образом сопряженную задачу, обратимся
вновь к исходной неоднородной задаче. Учитывая (15.405) и
(15.413), вместо соотношения (15.411) имеем
b а	Ь	а
ООО	о	-
что с помощью граничных условий (15.406), (15.407), (15.417) и
(15.418) легко приводится к виду
j J ufdydz = j p1(z)u(a, z)dz-]- J 02 (y)u(y, b)dy. (15.419)
0 0	0	0
Таким образом, неоднородная задача (15.405)—(15.407) имеет
решение лишь при условии, что соотношение (15.419) удовлет-
воряется для любого решения и (у, г) сопряженной задачи, вклю-
чающей уравнение (15.413) и граничные условия (15.417) и
(15.418). Сравнивая сопряженную задачу с исходной однородной
задачей, замечаем, что они полностью совпадают друг с другом,
и, следовательно, эти задачи являются самосопряженными.
Пример 2
В качестве второго примера рассмотрим задачу, состоящую
в решении уравнения (15.223) с граничными условиями (15.224) и
(15.225). В § 15.9 мы раскладывали функции <р± и / в ряды Фурье
и сводили задачу к решению обыкновенного дифференциального
уравнения. Вместо этого в данном параграфе будем оперировать
непосредственно с исходным уравнением в частных производных.
Для этого запишем уравнение (15.223) как
V2<pj +	= — 2(о0(О!ф0.	.	(15.420)
В качестве следующего шага можно либо умножить уравнение
(15.420) на решение сопряженной задачи и (г, 0), проинтегриро-
вать полученный результат по интересующей нас области и пре-
образовать его с помощью интегрирования по частям, либо при-
менить непосредственно формулу Грина (15.412). Первым спо-
собом мы только что воспользовались при рассмотрении преды-
дущего примера, поэтому здесь пойдем по второму пути. Чтобы
избежать' трудностей, связанных с наличием у уравнения (15.420)
решений, неограниченных, в начале координат, в качестве обла-
сти интегрирования в формуле Грина возьмем кольцо r0 < г < 1,
где г0 — малая величина. Перепишем формулу (15.412) в поляр-.
15.17. Уравнения с частными производными
483
ных координатах, учитывая, что dS = rdrdG и ds = rdf). Произ-
водные по нормали, входящие в левую часть (15.412), выразятся
как д<р/дп — ду/дг при г = 1 и dyldn = —dqldr при г = г0,
так как предполагается, что нормаль п внешняя. При этом фор-
мула Грина (15.412) принимает вид
2л 1	2л
f J («V2<P1 - <P1V2«) г dr de = J - <P1 |r=i —
0 0	0
2Л
-1 (|5“2')
0
Подставляя в (15.421) вместо лапласиана V2<P! его явное выраже-
ние из формулы (15.420), имеем
2л 1	2л' 1
— j j 2соо®/фо« dr de — j j ф] [V2« -|- (Оо«] r dr de =
0 0	0 r0
2л	2л -	!
о	0
По виду соотношения (15.422) определяем, что сопряженное урав-
нение совпадает с однородным уравнением, соответствующим
(15.420), т..е.
V2« + <oo« = 0.	(15.423)
Следовательно, оба эти уравнения являются самосопряженными.
Обращаясь к однородной задаче (т. е. полагая в (15.422)
©j = 0 и f = 0) и используя (15.423), из соотношения (15.422)
получаем, что
2л	2л ,	'
J и- J (-&-*-3f)U/.<«»-<>- <1М24>
Граничным условием, сопряженным условию в начале координат,
т. е. | ф! (0, 0)| < оо, является условие ограниченности решения
сопряженной задачи |« (0, 0)|-< оо. При этом второй член в ле-
вой части соотношения (15.424) обращается в нуль. Далее обычное
рассуждение приводит к требованию обращения в нуль коэффи-
циента при д^/дг в подынтегральном выражении в первом
члене левой части (15.424). Таким образом, сопряженные гранич-
ные условия имеют вид
|ы(0, 0)|<оо,	ы(1, 0)=О.	(15.425)
Сравнивая краевую задачу (15.423), (15.425) с однородной крае-
вой задачей, соответствующей (15.223)—(15.225), убеждаемся
в том, что обе эти задачи являются самосопряженными.
484	Гл. 15. Условия разрешимости
Для того чтобы вывести соответствующее условие разреши-
мости, вернемся к исходной неоднородной задаче. Используя 1
уравнение (15.423) и граничные условия (15.425) и переходя к Прет |
делу при го^О, из соотношения (15.422) получаем	|
2л 1	2л
2®0®1 j j ф0«г dr dQ = j <Pi IT L dQ'	1
00 ° '
откуда с учетом граничных условий (15.225) находим	<
2л 1	2л	;
2(00(0! f (Tourdrd0 = - [ -4^-g-l f(0)d0. . (15.426) X
J J	J \JT (Jl
оо	о	5
Соотношение (15.426) является искомым условием разрешимости '
задачи (15.223)—(15.225).	’j
Подставляя теперь в (15.426) выражение (15.231) для функ- '
ции ф0 и вспоминая, что ю0 = имеем
2л 1
2®! j ^rJn(pnTnr)(Anmeine + Annie~ine)udrdd =
0 0	"
2 л
= - Jn (Q„m) J (Л„те‘«е + Апте-^) -gIf (0) dQ. (15.427)
о
Поскольку рассматриваемая задача является самосопряжен-
ной, в качестве функции и можно взять решение соответствующей
однородной задачи
u = Jn (Qnmr) е1п® или Jn (Qnmr) е~‘пв,
причем соотношение (15.427) должно удовлетворяться для лю-
бого из этих решений.
Используя второе решение, из (15.427) получим	!
2л 1
2®1 J j гJ* (Qnmr) (Апт + Апте~21пв) dr dQ =
0 0
2л
= -VnmJn (Qnm) J [Лш^(0) + Л„те~2'"7(0)]-(/0. (15.428)
о
Вычисляя интеграл ОТ функции rJn (&птг) с помощью формулы
(15.427) и вспоминая, что
2л
J eimedd = o,
о
если т — произвольное целое число, из (15.428) получаем соот-
ношение	_
®1Лпт~ ^nmfinAnm,
которое полностью совпадает с (15.249), выведенным другим спо-
собом.
Упражнения '	485
Упражнения
15.1.	Найти условия разрешимости системы уравнений
4
Й1 + “г + 2«i = У Рпем,
n=i
4
— ^14" 2и^=	»
n=l
где Рп и Qn — заданные постоянные величины.
15.2.	Найти условия разрешимости системы уравиений
j х + У + х = Pi ехр (2«7) + Р2 ехр («7//2 ),
| у — 1,5* + 2у = Qi ехр (2i7) + Q2 ехр («7/1^Ю>
где Рп и Qn—заданные постоянные величины.
15.3.	Найти условия разрешимости следующих краевых задач:
а)	и" + 0,25u = f (х), и’ (0) = а, и (я) = Ь;
б)	u" + х-1и' + k2u = f (х), и (а) = с1; и (Ь) = с2.
В задаче б) предполагается, что 6> а> 0 и, кроме того, что соответствующая
однородная задача имеет нетривиальное решение.
15.4.	Найти условие разрешимости краевой задачи
и” + х-1и' + (X2 — л2х~2) и= f (х),
| «(0) | < оо, и’ (а) = g,
где а и g — заданные постоянные величины, а X — корень уравнения 7' (Ха) =
= 0.
15.5.	Найти условия разрешимости следующих задач:
а)	ф" + п2л2 d~2<p = f (х),
. ф'(0)=0, <р'(7)=Р;
б)	ф" + Уп Ф = f (х)>
ф' (0) = О, ф' (1) — а ф (1) = Р,
где уп tg уп = —а.
15.6.	Найти условие разрешимости краевой задачи
<?2Ф , <?2Ф , / л2я2	т2л2	X ,
+ SF + (— + —	)<р = f {у’ г}'
фу (0, Z) = 0,	фг (у,	0) = 0,
фи (d, г) = Рп	фг (у,	Ь) = Р2.
15.7.	Найти условие разрешимости краевой задачи
dr2 + г dr г Vn/n г2 ) У ‘ {
- |ф(0)|<оо,	ф'(1) —Рф(1) = а,
где У пт — корень уравнения yj'n (у) — PJ п (у) = 0.
15.8.	Найти условие разрешимости краевой задачи
дг2 + г дг + г2 дв2 +	' О ’
| Ф (0, 0) | < оо, фг (1, 0) = а ехр (1П0),
где упт — корень . уравнения J'n (у) = 0.
16 Найфэ А. X.
486
Гл. 15. Условия раврбшимосМи
15.9.	Найти условие разрешимости краевой задачи
d2u 2 du .
-d^ + —-dr + lU = F(r)’
и (а) = иа, и (Ь) — иъ
при условии, что параметр X равен одному из собственных значений соответству
ющей однородной задачи.
15.10.	Найти условие разрешимости краевой задачи
4-	Хш = F (г),
| w (0) | < оог w (1) = Pi,
I (1) I = Рг. .
где X — одно из собственных чисел соответствующей однородной задачи
» Э® , 1	d
dr2 г	dr '
15.11.	Найти условие разрешимости краевой задачи
Ф?+ г~‘ф!+ («« — r~2)tfl=fl(r),
Фг + *Фг ~ (?л + г~2) Фг = h (f)>
ф'1 (1) = Н1Ф1 (0 + РгФг (О’ Фг (0 = ИзФ1 (0 + И 1Фг (0>
| Ф1 (°) | < 00 > афг (а) — ф2 (а) = О,
при условии, что соответствующая однородная задача
решение.
15.12.	Найти условие разрешимости краевой задачи
Э2Ф , Г J_ ,	,	2^о ~1 Эф Г (и — ku0)2 _
dr2 + L г То + со — kUo J dr + L
имеет нетривиальное
к2 - ~-г\ Ф = f
Та
|ф(0)|<оо, Ф' (1) - РФ (1) = а,
где Та. «о и f — известные функции переменной г; и, k, р и а — заданные
постоянные величины и m — целое число. Предполагается, что соответствующая^
однородная задача имеет нетривиальное- решение.
15.13. При исследовании распространения волн в плоском канале возникает
задача	. .
+ 5^2ф = f (у) sin 2лх,
ил '•'У
=0,
ду |у=о
Эф I
ду [
= a sin 2лх.
|</=1
Показать, что условие разрешимости данной задачи имеет вид
j cos пу f (y')dy = —a.
о
15.14.	Найти условие разрешимости краевой задачи
д Г . Эф 1 Э Г , - - .
-5“ Р (X, У) -т*- + -ч— У (X, У)
дх [ v - дх J ду L ' '
фх (0, у) = О,
Фх (а> У) — «1 (У) Ф (а. У) = Pi (У).
+ Хг(х, у) ф = /(х, у),
Фу (х, 0) = О,
Фу (х, Ь) — а2 (х) ф (х, Ь) = Р2 (х).
Упражнения
48?
15.15.	Рассмотреть систему уравнений
( х — У + 2х + Зех2 + 2В1/2 =0,
1 у + i + 2бу + 4еху = 0,
где б = 1 + ео, е<1. С помощью метода многих масштабов' показать, что
х = Лг (TJ ехр (1Т0) + Л2 (TJ ехр (2iT0) + (к. с. ) + • • •,
причем функции (TJ и Л2 (TJ удовлетворяют системе уравнений
Л2 = -д-юЛ2----2~ iAj,
1 _
Ai — —/оЛ2 *— i Л2Л2 •
15.16.	Нелинейные колебания динамической системы с двумя степенями свободы
описываются системой уравнений
( Hi + 0,5й2 + 6и2 — BUxUj,
]. й2 — 0,5«i + 0,5^2 = euf,
где е<1, d= 0,5+80. Показать, что система уравнений относительно ком-
плексных амплитуд имеет вид
ЗЛ2 = «оЛ2 + 2Л^,
ЗЛ2 — «oAj *— 4Л^Л2.
15.17.	С помощью метода многих масштабов получить уравнения, описывающие
изменения амплитуд и фаз колебаний следующей системы:
Hi 4-
й2 + ®2^2 —
«з + ®з“з = «з“1“2
при условии, ЧТО <В8 « <£>i + <02.
15.18.	Рассмотреть параметрически возбуждаемую колебательную систему из
§ 15.3. Получить уравнения относительно комплексных амплитуд в случае, если
а) Л « 1, б) й « 2 и в) й « 4.
15.19.	Определить разложение первого порядка для собственных чисел задачи
и" + Хи = е/ (х) и,
и (0) = 0, и (1) = О
при условии, ЧТО 8« 1.
15.20.	Рассмотреть задачу о собствейных значениях
и’ + [X + ef (х)] и = О,
и (0) = 0, и' (1) = 0.
Показать, что
' 1
Х=(п + -£-^ я2 — 2е j f (х) sin2 + ~у-^ nxdx + • • •.
О
15.21.	Рассмотреть краевую задачу
uIV + 5«” + [X + 8/ (х)] и = 0, е<с 1,
и (0) = и" (0) = и (я) = и" (я) = 0.
Показать, что при X « 4
к. — 4 4-
16»
488
Гл. 15. Условия разрешимости
где ki — один из корней уравнения
^1 + (/11 + /22) ^1 + f Ilf 22 — /12 — О,
л	л
Zu = J / (х) sin* х dx, /*2 = "JT f / (х) sinS 2х dx’
о	о
л
flt = JL j f (х) sin х sin 2х dx.
о
15.22.	Найти условие разрешимости для уравнения
Рз (*) У" + Pi (*) У' + Ро(х) У = f (*)
при краевых условиях
а)	У (0) = Pi, У (1) = Р2;
б)	у' (0) = а^у (0) + Pi, у'(0 = «21/(0+ Рз!
с) У (0) = «п»' (0) + a12y' (1), у (1) = a»»' (0) + а22»' (1).
15.23.	Найти условия, при которых уравнение
РзУт + Р2У” + Р1У' + РвУ = 0
является самосопряженным. Ответ: р2 = 1,5р3, р0 — 0,5 (р3 — Рг + Pi)-
15.24.	Найти условия разрешимости для уравнения
Рз (х) у” + pt (х) у" + Pi (х) у’ + р0(х)у = f (х)
при краевых условиях
а)	У (0) = Pi, у' (0) = р2, у (1) = Р3;
б)	у" (0) = Оцу (0) + а2у' (0) + а13» (1) + аиу' (1),
у" (1) = «21» (0) + «22»' (0) + «28» (1) + «24»' 0)>
О = «31» (0) + «32»' (0) + «33» (0 + «34»' (О-
15.25.	Доказать, что произвольное однородное самосопряженное уравнен»
шестого порядка можно представить в виде
++(*£)+^=«-
15.26.	Доказать, что произвольное однородное самосопряженное уравнен»
порядка 2т можно представить в виде
dm /„ dmy\ , dm~l /„	dm-ly\ ,
dx”1 \ т dxm j+ dxm~i m-1 dxm-1 J +
"• + i(Ai ^) + Aoy^°-
15.27.	Найти условия разрешимости краевой задачи
Рз (х) yv + Pi (х) ylv + рз (х) у" + рг (х) у + Р1 (х) у + д, (х) у = f (х),
У (0) = Pi, »' (0) = Рз, »" (0) = Рз, » (1) = Р4, »' (1) = Рз-
15.28.	Рассмотреть задачу о собственных значениях
л
<р (s) = X j [cos (s + t) + еД’х (s, /)] <p (0 dt, e < 1.
0
Упражнения
489
Показать, что
<р<1> = cos s + • • •, <р(2)..= sin s + • • •,
' %<i> = 2л'1 + eXj Н--, Х<2> = —2л-1 + бХ2 + • • •.
Найти коэффициенты Хп.
15.29.	Найти равномерно пригодное разложение первого порядка для решения
интегрального уравнения
1
<р (s) = X J [si + s2/2 + eKi (siOl <р(0 dt, 1.
—1
15.39.	Найти равномерно пригодное разложение первого порядка для решения
интегрального уравнения
<р (s) = X j [s — t + еД’! (s, OJ <P (0 dt, e«l.
о
15.31.	Показать, что дифференциальный оператор
oi dx vs dx Vi
будет самосопряженным тогда и только тогда, когда о8 = ±0£.
15.32.	Показать, что дифференциальный оператор
, , .	1 d 1 d	1 d у
L (У) = — -j------j--------т ~
vt dx v3 dx vs dx Oj
является самосопряженным тогда и только тогда,.когда
vt = ±vlt v3 = ±vt.
15.33.	Показать, что дифференциальный оператор
L .	1	J_____£ J____d_j£_
vn+i dx vn dx ‘ ‘ ' v8 dx os dx Oj
является самосопряженным тогда и только тогда, когда
П»+1 = ± П1> Пл = ± v3, fn_i — ± Og, • • • •
Рассмотреть задачу иа собственные значения
д®ф 1 дф , 1 д2ф , п
/ дф
^1	=о-
dr |r=ft+eg.(0)
разложения первого порядка для собственного числа <в.
Течение несжимаемой жидкости вблизи волнистой стенки описывается
краевой задачей вида
\7*Ф = 0,
(	+ в sin kx\ I =0,
\ ду дх / |^=е cos kx
ФЪ-ОО
15.34.
'	=0,
|гя=а4"в1 (0)
Найти
15.35.
Показать, что
<р = U (х + в sin kxe~ky + 0,5e2fc sin 2fca—2*1' + • • • )•
Обсудить вопрос о равномерности этого разложения.
490	Гл. 15. Условия раврешимости
_____------------------—.--------------------:--------------------------43
15.36.	Обтекание тела, близкого по форме к телу вращения, несжимаемым не-'
вязким потоком жидкости описывается следующей краевой задачей:
д2ф , 1 дф , 1 д2ф п	;
дг2 + г дг + г2 ~ '
tlr-»»-: Ur sin0- 11г=а (1-e sin* 6) = °-
Показать, что
ф = {/£г- -у-)	^y-sinO— -^-sin30) 4--------.
Рассмотреть вопрос о равномерности этого разложения.
15.37.	Найти условия разрешимости краевой задачи
У*Ф — ХФ = f (г> °)-
Ф (а, 0) = 0, Ф(Ь, 0) = 0,
-^-(а, О)=Н0)- ^-(b, 0)=g(0)-
.fe
15.38.	При исследовании устойчивости двумерного течения несжимаемой жидко-'
оти вблизи волнистой стенки возникает краевая задача
iau + v' = fi (у),
—i (<о — aUj и + U'v + iap---— (и’ — a2u) = f2 (y),
A
—i (w — aU) v + p' — -i- (v" — a2v) = h (y),
К
и (0) = ct, V (0) = c2,
“I^OO- 0.	^Uoo-*0-
где U и fn— известные функции переменной у, со, a, R, k и сп — некоторые
постоянные величины, а штрихом обозначается производная по у. Показать,;
что условие разрешимости данной задачи имеет вид
3 оо
J Ф,Л dy == 4" С1Ч>2 (0) + 4" с2*Рз (°)>
п^1 О
где фп удовлетворяет уравнению и граничным условиям соответствующей со-
пряженной задачи
»аф2 — фз = О,
1’осф! — i (® — аЦ) ф2 — R*1 (ф2 — а2ф2) = О,
• — ф[ + и'Чг — i (® — at/) Фз — R"1 (Фз — “2Фз) = О,
Фз (0) = фз (0) — О,
фп-* 0, у-> оо.
Указание: Умножить исходные уравнения на ф„ ф2 и ф8 соответственно. Далее,
проинтегрировать полученный результат от у — 0 до у = оо, преобразовать
полученные соотношения с помощью интегрирования по частям, с тем чтобы
«перенести* дифференцирование с функций и, v и р на функции фп. Затем
сложить полученные уравнения и собрать коэффициенты при и, v и р, после
чего провести остальные этапы вывода, следуя § 15.13.
Упражнения
491
15.39.	Прн исследовании устойчивости трехмерного пограничного слоя, сущест-
вующего прн течении несжимаемой жидкости вблизи плоской поверхности,'
возникает следующая задача:
iau + фю + v' =	(у),
—i&u + U’v + iap — У?-1 («" — k2u) — f2 (у),
—&v + p' — R~l (v" — k2vj = f3 (y),
—i&w + фр + Wv — R'1 (w" — k^w) = ft (y),
и = v — w = 0, у — 0,
и, v, w—> 0	у—> оо,
где й> = со — aU — PW' н k2 = а3 + р2. Здесь U, W и fn — известные функции
переменной у, а а, Р, R и со — заданные постоянные величины. При условии что
однородная задача имеет нетривиальное решение, показать, что условие раз-
решимости имеет вид
4 оо
V [ /пфп dy — 0,
П=1 6
где функции фп (п — 1, 2, 3, 4) удовлетворяют системе уравнений
1СХф2 + фф4 — ф' = 6,
|«Ф1 - Iшф2 — R-1 (М — £2ф2) = О,
— ф[ + У/'ф2 — 1шф3 — У?-1 (Фз — й2ф3) + ®"ф4 = О,
«РФ! — <6<₽4 — R'1 (ф4 — ^4) = О,
<Ра (0) = Фз (0) = ф4 (0) * О,
|	~* О’
15.40.	Рассмотреть задачу о собственных значениях
ф.тх + Ф^у + Хф = е№ф,
ф (х, 0) = ф (х, я) = ф (0, у) = Ф (я, у) = 0.
Найти разложения первого порядка для случая, когда значение параметра X
близко к значениям 2 н 5.
15.41.	Рассмотреть краевую задачу для уравнения
у2Ф + Хф = ef (х, у, х) ф
с условиями обращения функции ф в нуль на поверхности куба с ребром, рав-
ным Л. Найти разложения первого порядка при X « 3 и X « 6, если a) f = х2
н б) f = х2у.

Приложение А
ТРИГОНОМЕТРИ ЧЕСКИЕ ФОРМУЛЫ
А.1. Основные формулы	1
sin2 а + cos2 а = 1,	(А.1)
, sin а , cos а .	1	, к П\ 3
tga==------, ctga = —:-----, tga = —г-----,	(А.2)1
° cos а 5 sin а ° ctg а ' .jt
sin (а + Р) = sin a cos р ± cos a sin р, (А.З)Ц
cos (a ± P) = cos a cos p T sin a sin p.	(A.4)j
1
Складывая формулы (А.З), имеем	1
sinacosp =-g-[sin (a-|-Р) + sin (a — Р)];	(A.5)*j
вычитая формулы (А.З), получаем	J
cos a sin p = [sin (a 4- P) — sin (a — P)).	(А.6Ш
Аналогичным образом, складывая и вычитая формулы (А. 4)4
находим	1
cos a cos р == -4- [cos (a + Р) + cos (a — P)],	I
*	(A.Ti
sina sin P =-g-[cos(a — P) — cos (a + P)].	Л
Из соотношений (A.2)—(A.4) следует, что
t /„ .	= sin («± P) _ sin a cos P± cos a sin P »	.
( ± Pi cos(a±P)	cos a cos P 4= sin a sin [J ‘
Разделив числитель и знаменатель на cos a cos p, получим ,<j
Аналогично	“ у
ctg(a±P)=	M
Положим теперь	. |
a + p = x и a — p = y,	J
тогда	a = 4j-(x-±- у) и ^ = -L(x — у).	|
Тригонометрические формулы	493
При этом равенства (А.5)—(А.7) переписываются в виде
sin х	sin у = 2 sin х + у cos * ~,
sin х — sin у = 2 cos * у sin * у ,	(А. 10)
I	г> X + у X— у
cos х cos у = 2 cos —cos —~,
cosy — cosx = 2sin sin x 2(A H)
Подстановка в формулу (A.5) p = а дает
sin 2a = 2 sin a cos a,	(A. 12)
подстановка p = a в формулы (A.7) приводит к соотношениям
cos 2a = 2 cos2 a — 1,
cos 2a = 1^ 2 sin2 a,	'	(A. 13)
складывая которые, получаем
cos 2a = cos2 a — sin2 a.	(A. 14)
Для того чтобы выразить sin За через sin a, положим в (А.З)
Р = 2a:
sin 3a = sin a cos 2a + cos a sin 2a.
Используя формулы (A. 12) и (A.13), имеем
sin 3a = sin a (1 — 2 sin2 a) + 2 cos a sin a cos a.
Поскольку cos2 a = 1 — sin2 a, to
sin 3a = sin a — 2 sin8 a + 2 sin a (1 — sin2 a),
или	sin 3a = 3 sin a — 4 sin8 a.	(A.15)
Выражая отсюда sin8 a, приходим к часто используемой формуле
sin8a= ~ (3cosa — sin 3a).	(A.16)
Аналогичным образом, можно выразить cos За через cos а.
Действительно, полагая в (А.4) р = 2a, имеем
cos За = cos a cos 2а — sin a sin 2а,
откуда, используя (А. 12) и (А. 13), получаем
cos За = cos а (2 cos2 а — 1) — 2 sin a sin a cos а =
= 2 cos8 а — cos а — 2 sin2 a cos а =
= 2 cos8 а — cos а — 2 (1 — cos2 a) cos а.
Таким образом,
cos За = 4 cos8 а — 3 cos а,	(А. 17)
или	cos8 а =	(3 cos а cos За).	(А. 18)
494
Приложение А
А.2. Комплексные величины
Полагая в (1.49) х = t‘0, где i = У —1 > находим
1 , ‘0	, G+2 , GQ)3	, (*>)4 ,	R5 ,	(»е)6	,
е ~	' 11	21 + 3!	41	'	5!	'	61
Поскольку i2 = —1, имеем разложение
eze = ir2L_JL_10!. + ±_4--^_-^+ ...
-г и 21	31 ' 41 I 51	6! '
которое можно переписать в виде
“М1-£+£-£+--)+'(9-£+£+"')-
(А. 19)
Сравнивая ряды в круглых скобках с разложениями (1.47) и
(1.48), заключаем, что
е‘е = cos 0 + i sin 0.	(А.20)
Переходя в (А.20) к комплексно сопряженным величинам, полу-,
чаем
е~1в = cos 0 — i sin 0.	.	(А.21)
Сложение формул (А.20) и (А.21) дает
cos 0 = -i- (е‘е + е~‘е).	(А. 22)
Вычитая (А.21) из (А.20), находим
sin 0 = ^г(е‘е —£>-“>).	(А.23)
Покажем теперь, как с помощью формул (А.20)—(А.23) можно
представить cos" 0 и sin" 0 в виде рядов Фурье. Из (А.22) в соот-
ветствии с биномиальной формулой следует, что
cos3 о=[ -|- (е'е+е-1в)]3=4 (е'е+e-i6)3 = 
=_L(e3ie + Зе1в + Зе~"> + e~3ie).
Перегруппировывая соответствующие члены и учитывая (А.22)»
имеем
cos3 о=4 +е-зге) + 4	=
= 4 • 2 cos 30 + 4 • 2 coS 6.
О	о
Таким образом,
cos3 0 = 4 (Cos 30 + 3 cos 0),
Тригонометрические формулы
495
что полностью совпадает с (А. 18). Аналогичным образом, из
(А.22) с помощью формулы (А. 16) получаем, что
sin3 0 = [-1- (е'0 — е~‘в) ] = -gL (е.е _ е-<е)з =
= — А. (^9 — Зе‘е + Зе-‘е - е-3/е) =
3 e^_e-ie 1 e3ie_e-3ie 3	i 
= —-----Я--------—-------2Г— = — sm 0 - — sin 30
в полном соответствии с формулой (А.16).
Для того чтобы разложить cos" 0 при произвольном нату-
ральном п, заметим, что
cos" 0 = [-у- (е‘е + е~1в) j П — (е‘е + е~£в)п-
Полагая теперь в формуле (1.396) а = ехр (i0) и b = ехр (—70),
находим
(е/е _|_	— V  п 1—— е‘ £п-т> ее-1те _
v 1	'	ml (л — т) I
т=0
п
= V--------—-----el («-2m) 6 — е<«0 4- пе‘ <«-2) 9 4-
т I (л — т) I	1	1
т=о
+ " ("2~ ei (л-4) е _|_ ... "(".zzlle-i (л-4) е + „g-z (л-2) е +
g—inS — eiiO g—Гл0 _|_ п [gZ (л—2) е g— i (п—2) 0|
+ " (п~ Ц [е( (л-4) е _|_ е-i (л-4) 0] +
[ П (п~!)	2) [е( (л-6) 0 _]_ е-1 (л-6) 0] _|_ . . . .
3!
Поэтому для нечетных п
cos" 0 = —Li • £cos nS + n cos (n — 2) 0 + " ^n~ cos (n — 4) 0 -|-
+ »(»-П(»-2) cog (n _ 6) 0	... ] , (Д.24)
а для четных п
cos" 0 =
1
2л-1
cosn0 + n cos (и — 2) 0 + "(”2[ cos(n — 4)0 + • • •
_____л!_____
2(т”)'(т")'
(A.25)
••• +
496
Приложение А
Аналогичным образом, для того чтобы разложить в ряд sin" 0,
заметим, что
sin" 0 = [-i- (е‘в — е_/е)У = -^г(е‘в — е-‘в)п.
Полагая в формуле (1.396) а = ехр (i0) и b = —ехр (—i0),
имеем
п
(gi0___ g-t’0)n — Ур 1~~ 1) gi (п-т) Og-imQ —
m=0
= У	ei (п-2т) 0
т! (л — т)!
т=0
Тогда в случае четных п
(g(0___e~ie)n — ein®__nel <-n~2>6 [ n el (n~4)6 -j-
, "("—I)
g-i (n-4) 0_	(rt"2) G I g-in& — gin® I g-inQ_
— n [e‘ (-n~2'i 6 + e-‘ 0J + ” __________________________________- [el ("-4>0 + e~‘ (n-4>e] + • • •.
Следовательно, для четных n
2 Г
sin" 0 = cos n0 — n cos (n — 2)0 +
" <"2[ -- cos (n — 4) 0 —
_ UlfL.2) cos (n. - 6) 0 + ••• + (- 1)"/2 -	.~ .
2 (ЖЖ
(A.26)
В случае нечетных п имеем
(gi0 e_<6)n -—	__fie{ (n-2) 0 । n	("~4>0 
 n(n~l) c-i (n-4) 0 ne-i (n-2) 0 _ e-in6 _ einO _ g-ine _
21
__n [gi (n-2) 0 _ g-l (n-2) 0] n (n^~ *) [gi (n-4) 0 _ g-i (n-4) 0]	.
Поэтому для нечетных n
sin"0 = —: Fsinn0 — nsin(n — 2)0 + " %7~-- sin (n — 4)0 —
(2i) L
n(n 0(n 2) sin (n_6)QH----j. (A27)
Полагая в (A.25) n = 4, имеем
cos4 0 = -§- (cos 40 + 4 cos 20 + 3).
Тригонометрические формулы
497
Полагая в (А.24) п = 5, находим
cos50 = (cos 50 + 5 cos 30 -|- 10 cos 0).
Полагая в (A.26) n = 4, имеем
sin4 0 = (cos 40 — 4 cos 20 + 3).
Полагая в (A.27) n = 5, находим
sin5 0 = (sin 50 — 5 sin 30 -j- 10 sin 0).
Для того чтобы разложить в ряд Фурье произведение cos" 0 X
X sinm 0, мы можем либо непосредственно использовать формулы
(А.22) и (А.23), либо предварительно разложить каждый из со-
множителей по степеням cos 0 и sin 0 и затем воспользоваться
формулами (А.22) и (А.23).
А.З. Интегралы
j cos ах cos dx = -у J cos (a 0) x dx у J cos (a — p) x dx —
sin (a + fl) x . sin (a — fl) x
2 (a + fl) ' + 2 (a — fl)
sin 2ax , 1
-4^-Ь — X’
(A.28)
p = a;
j sinax sin flx dx = J cos (a — fl) x dx-у j cos (a -|- fl) x dx =
sin (a — fl) x _sin (a + fl) x
2 (a—fl) 2 (a + fl)
1 sin 2ax
~cTX------л---->
2	4a	’
P#=a,
(A.29)
P = a;
j sin ax cos px dx =	j sin (a P) x dx -y j sin (a — P) x dx =
	cos (a + fl) x	cos (a - fl) x 2 (a —fl) ’	
~ 	2 (a + fl) cos 2ax		(A.30)
	4a ’	P = a;	
j	cos” 0 sin 0 d0 =	cos”+1 6 n + 1 ’	(A.31)
	j sin" 0 cos 0 d0 =	_ sin”+1 0 n 1	(A.32)
Интегрируя левые	и правые части	формул (A.24)—(A.27),	полу-
чаем
498
Приложение А
для. нечетных n
J cos"0d0 =	[-jj- sinn0 4- sin (n - 2)0 +
+	sln <» - 4>6 + "W-V*510 <“ - 6>0 + • • • ] 
(A.33)
для четных n
f cos" 0d0 = —~
3	2n~‘
— sin Л0 -|----
n	1 n — 2
sin (л — 2) 0 —
5i%-=T)Sin(«-4)6+--
nl 0
(A.34)
2
для четных n
[ sin"0J0 = -£-
J	2"i".
' 1 , n n
— SianQ-~2
sin (n- 2)6-1-
+ ?j'J-_4j Sin (л —4)0-j H-
(- l)"/2nl 0
(A. 35)
для нечетных n
f sin"0d0 =——r Г
J	(2<)"-‘ L
--J- cos n0 -I—cos (n — 2) 0 —
n	1 n — 2	*	'
(A.36)
Окончательно из
-5iTr=%cos(rt-4)0+'”]
соотношений (A.33)—(A.36) находим
2л j cos" 0 dB ~  0	°’ nl n	если , если	п п	‘нечетное, четное; -
				
2л	0,	если	п	нечетное,
f sin" 0 dB = 	(— l)n/2nl Л	—. если	п	четное.
(A.37)
(A.38)
Приложение Б
ЛИНЕЙНЫЕ ОБЫКНОВЕННЫЕ
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Дифференциальным уравнением называется уравнение, ко-
торое связывает неизвестную функцию (называемую часто зави-
симой переменной), производные этой функции, а также неко-
торые известные величины. Если зависимая переменная пред-
ставляет собой функцию одной переменной (называемой обычно
независимой переменной или аргументом), то такое уравнение
называется обыкновенным дифференциальным уравнением. Если
же зависимая переменная является функцией двух или более
независимых переменных, тогда данное дифференциальное урав-
нение называется уравнением в частных производных. Итак,
обыкновенное дифференциальное уравнение общего вида записы-
вается в форме
Л dn~‘u
dxn’ dxn-x’
d2u
dx2’
du
u, x
dx ’ ’
(Б.1)
где порядок старшей производной называется порядком диффе-
ренциального уравнения. Например, уравнение (Б.1) представ-
ляет собой дифференциальное уравнение порядка п.
Обыкновенное дифференциальное уравнение n-го порядка
называется линейным, если оно линейно относительно функции и
и ее производных и', и"....Таким образом, самое
общее линейное дифференциальное уравнение п-го порядка имеет
вид
рп 7? + Р*-1 (х)	----+ Р1 (*) + Ро (х) и =	(Б,2)
. ЛХ	ЛХ
где рт (т = 0, 1, 2, . . ., п) и f — известные функции от х.
Если f (х) = 0, то уравнение (Б.2) называется однородным;
в противном случае оно будет неоднородным.
Положим, что функции рт(х) (/и = 0, 1, 2......п) непре-
рывны на промежутке I = (х £ [а, &]}, включающем в себя
некоторую точку х0, причем рп (х) не обращаются в нуль ни
в одной точке этого промежутка. Тогда для любых вещественных
чисел а0, аг, . . ., ап_г существует единственное решение и (х),
удовлетворяющее уравнению (Б.2) на всем промежутке I, а также
начальным условиям
u(x0) = a0,	и'(х0) = а1, ....	(х0) = ап_г
500
Приложение Б
Приведенное утверждение представляет собой основную теорему
существования для обыкновенных линейных дифференциальных п
уравнений.	’
Часто бывает удобным выразить уравнение (Б.2) в оператор- ;
ной форме. С этой целью обозначим через D дифференциальный";
оператор d/dx. Тогда
du ,
' Du = ~т- = и ,
dx	
D2u == D (Du) = D (u')~ u",
(Б.з):
Dnu = D(Dn~lu) = D = uw
Кроме того, будем считать, что D°u = и. При этом уравнение.
(Б.2) можно переписать как
Рп&и + Pn_iDn-'u 4------f- PyDyU + p0D°u = f (х),
или, в более удобной, сокращенной форме
L (и) = f (х),
где оператор L определяется с помощью соотношения
L = pnDn 4- pn-iDn-1 -I-------------4- pyD 4- p0D°.
Оператор L называется линейным, оператором и обладает
ющими свойствами. Так, если с — постоянная и и (х) — произволь- ,,
ная функция, имеющая по крайней мере п производных, то ’
L (си) = cL (и),	(Б.6) j
(Б 4) ;
(Б.5)
следу-
поскольку
L (си) = рп (си)<п> 47 рп_1 (си)<"-» - г • • • 4- Pi (си)' 4- Ро (си) =
= рпси^ 4- Pn-yCU^-V 4- • • • 4- P1CU' 4- Роси =
= с[рпи(п) 4-рп_1Ц(п-1) 4---4- P1U' 4- PoU] = cL (и).
Если Uj и Uj — две произвольные п раз дифференцируемые функ-
ции, то
(Б.7)...-
&
я
L (uy 4~ Uz) — L (uy) 4- L (u2),
поскольку
L (ui ~ Pn (ui	4" Pn-i (ui 4- и2)<-п~С) 4~ • • •
• • • 4- Pi (wi “Г ua) 4- Po (ui 4- ыг) — Рп 1и1П> “г u2 Ч 4~
4-	Pn-i lui l> 4~ u2 4~    4- Pi (“i 4- “2) 4" Po(ui ~r ua)=
=	(Pnui 4- Pn-iui ) 4~    4~ Piut 4“' PomJ 4-	'j
4-	1Рпи2П) 4- Рп-1и2П 11 4~ • • • 4~ Plu2 4- Pou21 = L (Uy) 4- L (u2)-1
Из соотношений (Б.6) и (Б.7) следует, что
T (cyUy 4- с2и2) = CyL (uy) 4- c2L (u2),
(Б.8)
Линейные дифференциальные уравнения	501
или, в более общем случае,
£ (CiUj 4- c2u2 -р' • • + стит) = CjL (ui) 4~ c2L (us) -р- • • • 4- cmL (um),
(Б.9)
где ci — некоторые произвольные постоянные.
Б.1. Однородные уравнения
Полагая в уравнении (Б.4) /(х).= 0, получаем однородное
дифференциальное уравнение n-го порядка вида
L (и) = 0.	(Б. 10)
Если функция есть решение уравнения (Б.10) и с — произ-
вольная постоянная, то произведение сих также является реше-
нием уравнения (Б.10), поскольку
L (сиг) = cL («i) = 0.
Принцип, суперпозиции
Если функции иг и и2 являются решениями уравнения (Б. 10),
a Ci и с2 — две произвольные постоянные, тогда выражение с^ +
+ с2и2 также будет решением уравнения (Б. 10), поскольку
L (ср!! 4- с2и2) = сгЬ (uj) 4- c2L (u2) = сг0 4- с20 = 0.
В более общем случае, если функции их, и2, . . ., ит являются
решениями уравнения (Б.10), a clt с2,   , ст — произвольные
постоянные, то сумма
CjU.! + с2и2 4- • • • 4- стит
также будет решением этого уравнения, поскольку
£ (CiUi 4- с2и2 4- ... 4- стит) = c-iL (ых) 4- c2L (ы2) 4--(- cmL (и,„) =
= сх0 4- с20 4- • • • 4- ст0 = 0.
Данное свойство называется обычно принципом суперпозиции,
а выражение с1и1 4- с2и2 4- • • • 4- стит линейной комбинацией
функций иъ и2, . . ит.
Линейная независимость
Пусть функции (х), и2 (х), . . ., ит (х) представляют собой
множество функций, определенных на промежутке I = [а, Ь].
Говорят, что функции и1г и2, . . ., ит линейно зависимы между
собой, если найдутся такие постоянные clf с2, . . ., ст, не равные
нулю одновременно, что условие
CiUj. (х) 4- с2и2 (х) 4--к стит (х) = 0	(Б. 11)
выполняется для всех х из промежутка la, Ы; в противном случае
данные функции называются линейно независимыми. Ограниче-
ние, что не все сг должны равняться нулю одновременно, яв-
502
Приложение Б
ляется существенным, поскольку соотношение (Б. 11) в случае,
если все с, равны нулю, выполняется для любых функций ит (х).
Например, функции 2х — 1 и 6х — 3 будут линейно зависимыми,
потому что —З'(2х — 1) + 1 -(6х — 3) = 0.
В то же время функции 2х — 1 и 5х — 3 являются линейно не-
зависимыми, поскольку невозможно подобрать такие постоянные сх
и с2, не равные нулю одновременно, чтобы
су (2х — 1) + с2 (5х — 3) = 0.
Другим важным методом проверки функций th (х), и2 (х), . . .,
ит (х) на линейную независимость служит исследование их опре-
делителя Вронского, т. е. определителя вида
		Ui	
W = W(ult и2, .	 > ^т) —	U\	U2	11т
		.,(т-1)	(т-1) IZj	и<>	и(т~!) • •
(Б. 12)
Так, если функции иЛ (х), и2 (х), . . ., ит (х) —линейно зави-
симы на промежутке /, тогда существуют постоянные съ с2, . . .,
ст, не равные нулю одновременно, такие, что
Ci«i + с2и2 + • • • + стит = 0.	(Б. 13)
Дифференцируя соотношение (Б. 13) (т — 1) раз, имеем
С1Щ -|- с2и2 -]-••• -|- cmtim = 0,	(Б. 14)
C]Ui с2и2 • И- cmtim = 0,	(Б. 15)
С1Н(-0 +	+ • • • + сти£-1) = о. (Б. 16)
При произвольном фиксированном х из промежутка I соотноше-
ния (Б. 13)—(Б. 16) образуют неоднородную систему линейных
алгебраических уравнений относительно постоянных сь с2, . •
ст. Так как постоянные сг одновременно не равны нулю, опре-
делитель матрицы коэффициентов этой системы должен равняться
нулю. Но поскольку указанный определитель является опре-
делителем Вронского для функций «х, и2, . . ., ит, то, следо-
вательно, W (х) = 0 в каждой точке промежутка I. Если же
определитель Вронского не равен нулю во всех точках х £ /,
тогда система (Б. 13)—(Б. 16) имеет только тривиальное решение
= с2 = • • •= ст = 0, так что функции иг (х), и2 (х), . . .,
ит (х) оказываются линейно независимыми. Таким образом,
функции ип (х) (и = 1, 2, . . ., т) являются линейно зависимыми
на промежутке I тогда и только тогда, когда их определитель
Вронского равен нулю во всех точках промежутка I. Например,
Линейные дифференциальные уравнения
503
определитель Вронского для функций 2х — 1 и 6х — 3 имеет вид
W =
2х - 1
2
6х- 3
и, следовательно, эти
для функций 2х — 1
нулю, поскольку
W
функции линейно зависимы. В то же время
и 5х — 3 определитель Вронского не равен
2х - 1 5х — 3
2	5
Таким образом, указанные функции являются линейно незави-
симыми .
Общее решение
Уравнение (Б. 10) имеет не более чем п линейно независимых
решений. В самом деле, допустим, что функции щ (х), м2 (х), . . .,
uN (х), где N > п, являются решениями, уравнения (Б. 10). Тогда
определитель
U1	и2	• • •	UN
я		•	
Ml	и2	. Un	. .	u'n
и\п)	и{2п) .		„(п)  UN
u[N-"	U2		• UN
(Б-17)
117 (щ, м2, •  •, Up/') —
равен нулю, поскольку с помощью уравнения (Б. 10) мы всегда
можем представить (п + 1)-ю строку в виде линейной комбина-
ции первых п строк. Следовательно, решения щ (х), м2 (х), . . .,
uN (х) при N > п оказываются линейно зависимыми.
Покажем теперь, что уравнение (Б. 10) на промежутке / имеет
ровно п линейно независимых решений. С этой целью заметим,
что согласно основной теореме существования уравнение (Б. 10)
имеет п единственно возможных решений ил (х), м2 (х), . . .,
ип (х), удовлетворяющих начальным условиям
Ы1(х0) = 1, и[ (х„) = щ (х0) = • • • = u(in~" (х0) = 0;
«2 (*о) = 0, и2 (х0) = 1, «2 (*о) = • • • = м?'1’ (х0) = 0;
м3 (х0) = «з (*о) = 0, из (х0) = 1, Из' (х0) = • • • = и(3п~‘ * (х0) = 0;
ит (*о) — ’ ‘	’ (^о) — 0, Um ’ (Xg) — 1,
ит ' (Хо) — • • • = Um *' (Х0) - - 0;
ип (ХО) = и’п (х0) = ... — и(пп~2> (Х0) = 0, (Хо) = 1.
504
Приложение Б
‘ Легко показать, что определитель Вронского для этих п реше-:
ний в точке х0 равен единице. Следовательно, этот определитель
не равен нулю в каждой точке промежутка У1’, и потому функции;
Ы1 (х), ы2 (х), • • •,	(х) линейно независимы.
Произвольная совокупность п линейно независимых решений)
уравнения (Б. 10) называется фундаментальной системой, причем;
произвольная линейная комбинация этих решений также будете
решением уравнения (Б. 10). Таким образом, если функции иг (х),
и2 (х), . . ., ип (х) представляют собой фундаментальную си-)
стему решений уравнения (Б.10), то комбинация
и (х) =	(х) + с2и2 (х) + • • • 4- спип (х)	. (Б. 18)
при любых значениях постоянных си сг, . . ., сп в соответствии
с принципом суперпозиции будет решением уравнения (Б. 10).
При этом, поскольку любое решение уравнения (Б. 10) может
быть получено из выражения (Б. 18) путем надлежащего выбора
постоянных ст, выражение (Б. 18) называется общим решением
уравнения (Б. 10).	v
В заключение этого параграфа выведем соотношение, связы-
вающее значение определителя Вронского для фундаментальной
системы решений в произвольной точке промежутка / с его зна-
чением в некоторой заданной точке х0. С этой целью запишем
определитель Вронского в виде
Ui	Ug	• • •	цп
Uf	«2	‘ *	U'n
up-1’	... up’”
(Б. 19)
Дифференцируя выражение (Б. 19)
свойства определителей, имеем
по х и используя известные
U1	^2	•	 •	Цп
Щ	U2	•	 •	Un
up’”	up’1’	up-1’
Wi U2 * * * Un
। ' U\	* * • un
Up-’’ up-1’ ... Up-’’
«1
Ui
u2	... un
«2	•• •	Un
tfUi)
U[ 1*2	• • • Un
(Б.20)
См. также формулу (Б.24). — Прим, перев.
Линейные дифференциальные уравнения
&05
Все определители в (Б.20), за исключением последнего, равны
нулю вследствие наличия в каждом из них одинаковых сурок.
Поэтому
«1	«2	... ип
flZ' = Ul	U2	...	Un	(Б.21)
и[п}	... и(пп)
Воспользовавшись уравнением (Б. 10) для того, чтобы выразить
член и(п} через ит, ит, . . Um~l\ и используя известные свой-
ства определителей, перепишем определитель (Б.21) в виде
		W' = —	Рп-1 Рп	“1 «1 и/"'1	Н2 «2 ’ «Г” .	aS • S R Д а ' 3	— 
рП-2	U1	«2 «2			__ _ р»	Щ	«2	. . • , «л	
Рп	и[п'2)	u^-2) .	.. и	(п-2) п	Рп	„(п-2)	i-2)	tJ(n-2) * « • ип
	и(Г2)	«Г2’.	.. и	(п-2) п		иг и	2	••'
(Б.22)
Все определители в соотношении (Б.22), за исключением пер-
вого, также равны нулю ввиду наличия в каждом из них одина-
ковых строк. Кроме того, легко видеть, что первый из определи-
телей в (Б.22) есть определитель Вронского (Б. 19). Таким обра-
зом, мы получаем дифференциальное уравнение
W = - W,
Рп
(Б.23)
решение которого можно представить в виде
Г(х) = Г(хи)ехр
Рп-1 (Т)
Рп (Т)
dx
Найденная формула позволяет выразить значения
W (х0).
(Б.24)
W (х) через
Б.2. Неоднородные уравнения
Уравнение (Б. 10) называется однородным по отношению
к уравнению (Б.4). При этом оказывается, что мы можем решить
неоднородное уравнение (Б.4), если нам известны общее решение
соответствующего однородного уравнения и какое-либо частное
решение уравнения (Б.4). Так, если, функции ur (х), и2 (х), . . .,
17 Найфэ А. X".
506
Приложение Б
ип (х) представляют собой п линейно независимых решений '
однородного уравнения (Б. 10), а функция ир (х) есть некоторое ‘
частное решение уравнения (Б.4), то общее решение уравнения
(Б.4) будет иметь вид
и =	+ с2и2 + • • • + спип + ир,	(Б.25) <
где сп — произвольные постоянные. При этом комбинация 4
ис = Ci«i + с2и2 + • • • + спип	(Б.26) 5
часто называется дополнительной функцией. Таким образом, "
общее решение неоднородного уравнения (Б.4) есть сумма не-
которого частного решения и дополнительной функции. Пока-
жем прежде всего, что всякое решение вида (Б.25) является ре- Л
шением уравнения (Б.4). Поскольку L (ит) =0 при т — 1,
2, . . ., п и L (ир) = f, то -
Б G’lWl 4“ ^2Ы2 4"  • • 4- CnUn -|- Up) = CyL (Uj) -\-c2L (u^) -]--•• -j-
+ cnL (un) 4- L (up) = f.
Тем самым мы получаем, что выражение (Б.25) является реше-
нием уравнения (Б.4). Покажем далее, что всякое решение урав-
нения (Б.4) имеет вид (Б.25). Пусть функция и (х) является ре-
шением уравнения (Б.4). Тогда
L (и) =f,
и поскольку
L (ир) = f,
то
L (и — ир) = L (и) — L (ир) = f — f = 0.
Таким образом, разность и — ир является решением соответ-
ствующего однородного уравнения L (v) =0. Следовательно,.
V — U — Up = CrUr + C2U2 + • • • + cn^n>	?
откуда мы сразу получаем формулу (Б.25).
Кроме того, если
T(H) = /(0(x)+/<2)(x)+.-. + /W(x)	(Б.2 7)
И	j
Z,	(х),	(Б.28) '
то	•	-
«p==w‘I>+«(2>+...+«(«	(Б.29)
поскольку
^(ыр) ~ L Lupl) + ир2) + • • • 4~ upk)] = L [ыр1’] 4~ [wp2) 1 + •  •
• • • + L [«<*> ] = /(1) (х) + /(2) (х) + • • • +	(X).
Линейные дифференциальные уравнения	507
Б.З. Однородные уравнения с постоянными коэффициентами
В этом параграфе мы рассмотрим построение общих решений
однородных уравнений с постоянными коэффициентами, т. е.
уравнений вида
L (и) .= 0,	(Б.ЗО)
где L = Dn + Pn-iD*-1 + Pn^D"'2 + • " + Ро®'1 + Pi® + Po, (Б.31)
а коэффициенты рн являются постоянными величинами. Каждому
оператору L поставим в соответствие некоторый многочлен вида
Р (s) = sn + /2n_iSn-! 4- pn_2s"-2 н-h p2s2 4-	+ Po, (Б.32)
так что P (D) = Dn 4-	4- pn_2D”-2 4--4-p2O2 + PiD 4~ Po-
/	'	(Б.ЗЗ)
Назовем P (D) операторным многочленом и перепишем уравне-
ние (Б.ЗО) как
Р (D) и = 0.	(Б.34)
Поскольку
Desx = sesx, D*esx ~ s2esx, Dme5X = smesx,
то	P (D)es* = P (s) esx.	(Б.35)
При этом P (s) обычно называется характеристическим много-
членом, соответствующим операторному многочлену Р (D). Из
соотношения (Б.35) следует, что если sm является корнем много-
члена Р (s), то функция ехр (smx) будет решением уравнения
(Б.34). Поэтому если многочлен Р ($) имеет п различных дей-
ствительных корней sn s2, .... sn, то каждая из функций
'	eS1X, ё^, eSnX
является решением уравнения (Б.34). Поскольку эти функции
линейно независимы, общее решение уравнения (Б.34) будет
записываться в виде
и = С1е*4- с^*х 4- ... 4- спе>пХ,	(Б.36)
где с„ — произвольные постоянные.
Обратимся, например, к уравнению
и" — Зи' 4- 2и = 0,	(Б.37)
которое можно переписать как
(D2 — 3D 4- 2) и = 0.	(Б.38)
Соответствующий характеристический многочлен имеет вид
s2 — 3s 4- 2 = (s — 2) (s — 1);
корнями его будут значения $1 = 1 и $2 = 2. Поэтому каждая
из функций ехр (х) и ехр (2х) является решением уравнения
. 17*
508	Приложение Б
(Б.37)-. Поскольку эти функции линейно независимы, общее
решение уравнения (Б.37) можно представить как	'Ц^В
и = c^x.
В качестве второго примера рассмотрим уравнение	J^B
и'" + 2и" — и' — 2 = 0,	(Б.38)
для которого соответствующий характеристический многочлен |^В
имеет вид
s3 + 2 s2 — s — 2 = (s — I) (s + 1) (s-+ 2);
Корнями его будут значения Sj = 1, s2 = — 1 и ss = —2. Поэтому я^Е
каждая из функций	ШВ
е* е~х е2х	'“ЕВ
является решением уравнения (Б.38). Так как эти функции ли- JBB
н§йнр независимы между собой, общее решение (Б.38) можно IBE,
записать в виде	/
и = с1ехС2е-ХСзе-2х.	>JBB
Следует отметить, что в общем случае корни характеристике- >|йВ
ского многочлена могут оказаться равными друг другу или ком-. ЯЕ
плексными. Рассмотрим эти возможности более подробно, начав
со случая комплексных корней,
,  Случай комплексных корней	jjaB
- /Рассмотрим уравнение второго порядка, у которого, соответ- f
ствующий характеристический многочлен имеет два комплексно :**аВ-
сопряженных корня р + ico и р — iсо, где р и со — вещественные	'Зш
величины.: Отметим также, что если один из корней характери-
стического многочлена оказывается комплексным, то второй
корень обязательно должен быть комплексно сопряженным > -^В
с первым, поскольку сам этот многочлен (т, е. его коэффициенты.—
Прим,. перед.) является вещественным. Таким образом, каждая *aB*
из функций	. т	'лОЗВ
g(n+i<>>)x и	'	«В
будет' решением исходного уравнения. Поскольку эти -решения ^ЦВ
линейно независимы между собой, общее решение этого ура вне- ''ЯИ'
ния дается формулой
,7 (j	и =	4-с2е<^-га)х.	(Б.39)	яВ
Используя равенства
eia>x — cos едя { sin щх,
e-ia>x _ cos _ j Sjn /х-	ЯК
перепишем выражение (Б.39) в следующей вещественной форме:	JB
и = ъе^ (cos сох 4- i sin сох) 4- (cos сох — i sin сох) =	.^В
/• а= е^ [(Сх + с2) cos сох 4- i (ci — с2) sin tex], .
или	и — е^х (A cos сох 4- В sin сох),	(Б.40)
Линейные дифференциальные уравнения	509
где А = ct + с2 и В = i (сх — с2) — произвольные постоянные,
которые можно считать вещественными. Формула (Б.40) показы-
вает, что каждая из вещественных и мнимых частей обеих функ-
ций ехр [(р + io) х] и ехр 1(р — tco) х] является решением
исходного уравнения.
Отметим также, что решение (Б.40) можно переписать в сле-
дующей более удобной для использования форме:
и = ae^cos (сох— р),	(Б.41)
или	и = ae^sin (сох + 0),	\	(Б.42)
где а = (Л2 +В2)'/2, P = arctg4> 0 =
Рассмотрим, например, уравнение
и -|- <»о« = 0,	(Б.43)
соответствующий характеристический многочлен для которого
записывается в виде
s2 + (Оо-
Он имеет корни s1>2 = ±tco0. Поэтому каждая из функций
ехр (ico0x) и ^ХР (—*®ох) является решением уравнения (Б.43);
точно так же решениями уравнения (Б.43) являются функции
cos со0х й sin со0х, т. е. вещественная и мнимая части ехр (ссо0х).
Таким образом, общее решение уравнения. (Б.43) можно пред-
ставить в Одной из следующих форм:
и = A cos со0х + В sin со0х,
или	и = a cos (соох — Р),
или, наконец, и = a sin (<о0х + 0).
В качестве второго примера исследуем уравнение
и" 4- 2и' + 5и = 0.	(Б.44)
Соответствующий характеристический многочлен имеет вид '
s2 + 2s + 5 = (s + Г+ 2t) (s + 1 — 2i).
Корнями его будут значения Sj = — 1 —2i ns2 = —1 + 2i, так
что каждая из функций ехр (—х — 2ix) и ехр (—х 4- 2ix) Яв-
ляется решением уравнения (Б.44). Аналогичным образом можно
утверждать, что функции ехр (—х) cos 2х и —ехр (—х) sin 2х,
т; е. вещественная и мнимая части ехр (—х — 2ix), также
являются решениями уравнения (Б.44). Следовательно, общее
решецие уравнения (Б.44) может быть представлено в виде
и — е~х (Л cos 2х + В sin 2х).
В качестве третьего примера рассмотрим уравнение
uIV — coou — 0,	(Б.45)
510
Приложение Б
соответствующий характеристический многочлен для которого
есть	' .	
4	2
s — (О0-	__ _______________
Корнями этого многочлена будут s1>2 = ±	<о0 и s3,4 — ±t у/(о0.
Это означает, что каждая из функций
gVa>ox g-jAo^x gf/<oox
ИЛИ	eVre><)Xi e-lfe>ox) Cos^—x> Sln/^x,
является решением уравнения (Б.45). ТакикГ образом, общее
решение уравнения (Б.45) записывается в виде
и — A cos (о0х + В sin у4©ох 4-	£)е~
В качестве последнего примера исследуем уравнение
uIV + 2u"' + 6w" + 2w' + 5u = 0.	(Б.46)
Характеристический многочлен для него имеет вид
s4 + 2s3 + 6s2 + 2s + 5 - (s2 + 1) (s2 + 2s 4- 5);
корнями его будут s112 = ±t, s3 = —1 — 2i, s4 = — 1 + 2i.
Поэтому каждая из функций
eix, eix e~x~2fx e'x+2ix,
или	cos x, sin x, e~x cos 2x, e~* sin 2x,
будет являться решением уравнения (Б.46). Следовательно, об-
щее решение уравнения (Б.46) может быть записано в виде
и = A cos х + В sin х + ё~х (С 90s 2х + D sin 2х).
Случай равных корней
Рассмотрим уравнение
и" — 2а.и' + а2« = 0,	(Б .47)
или	(7)2 — 2aD + а2) и — (D — а)2 и =‘0.	(Б.48)
Соответствующий характеристический многочлен
(s — а)2
имеет двукратный корень s = а. Следовательно, мы имеем только
одно решение экспоненциального вида, а именно функцию ехр (ах).
Так как уравнение (Б.47) представляет собой уравнение вто-
рого порядка, нам необходимо построить второе решение, кото-
рое было бы линейно независимым с функцией ехр (ах). С этой
целью положим
и = е“*и(х).	(Б.49)
Поскольку
D (е“*и) = vDeax 4- e?xDv = аг>е“* 4- e?xDv ==
— (^х (Dv 4- ао) — 6°“ (D 4* а) v
Линейные дифференциальные уравнения	511
и	D2 (e“*v) = D [D (е“*и)] = D [е“* (D + a) и] = е®* (D 4- a)2 v,
то	P (D) (caxv) = eaxP (D + a) v.	(Б.50)
При этом подстановка выражения (Б.49) в (Б.48) приводит к
уравнению
e^xD2v — 0, или D2v = 0,
решением которого является функция v = сг + с2х. Таким обра-
зом, общее решение уравнения (Б.47) есть
и — (<?! + с2х) еах.	(Б.51)
Другими словами, функции ехр (ах) и х ехр (ах) представляют
собой два линейно независимых решения уравнения (Б.47).
. В качестве второго примера рассмотрим уравнение
(D — а)8и = 0,	(Б.52)
у которого соответствующий характеристический многочлен
(s — а)3
имеет корень s = а третьей кратности. Это означает, что существует
лишь одно линейно независимое решение уравнения (Б.52),
которое можно представить в виде экспоненты, а именно функция
ехр (а^). Для того чтобы найти два других линейно независимых
решения, подставим выражение (Б.49) в уравнение (Б.52), откуда,
воспользовавшись формулой (Б.50), получим
(D — а)3 и — (D — а)3 еах v (х) = e^D^v == 0.
Таким образом, мы приходим к уравнению
D3v = 0,
общее решение которого имеет вид
V = сг + с2х + Г3Х2.
Следовательно, общее решение уравнения (Б.52) можно записать
как
и = (<\ + с2х + г3х2)	(Б.53)
При этом из формулы (Б.53) следует, что функции
gax х2ё3,х
являются линейно независимыми решениями уравнения (Б.52).
В качестве третьего примера исследуем уравнение
(D—a)mu = 0.	(Б.54)
Как и ранее, используя формулы (Б.49) и (Б.50), для функции
получаем уравнение
Dmv = 0,
решение которого есть
V = Ci + CtX + С3Х2 4- • . • 4-стхт-'..
512	Приложение Б
----------------------------------------------г
Окончательно имеем
и = еах (сх + с2х + с3х2 + • • • + стхп-1).
В качестве четвертого примера рассмотрим следующее урав-
нение общего вида, характеристический многочлен которого
имеет два кратных корня:
(D - (D - а2)« v = 0.	(Б.55)
Уравнение (Б.55) можно переписать как
(D-ax)'n[(D-a2)n4=0.
Отсюда следует, что ему удовлетворяет любое решение более
простой задачи •
•_(D-a2)«u = 0.	(Б.56)j
Поскольку операторы (D — a.j)m и (D — а2)п обладают свой- ).
етвом коммутативности, уравнение (Б.55) можно переписать в »
виде	\
(D — а2)п [(£) — ах)”1 и] = 0.
Таким образом, уравнение (Б.55) удовлетворяется также с по-
мощью любого решения более простого уравнения вида
(D — а^и = 0.	(Б.57)
Общее решение уравнения (Б.55) представляет собой сумму
общих решений (Б.56) й (Б.57), содержащих (т + п) произволь-
ных постоянных, т. е.
и = еа'х (<?х -j- с2х-+ • • • + стхт-1) -J- (Ьх + Ь2х + • • • 4- Ьп*"'')-
(Б.58)
В качестве примера использования формулы (Б.58) рассмо;
трим уравнение
(D* — 8D2 + 16) и = 0, или (D2 — 4)2 и = 0. (Б.59)
Соответствующий характеристический многочлен г($2 — ’4)2 имеет
корни
зх = 2 (двукратный корень) и з2 = —2 (двукратный корень).
Тогда в соответствии с формулой (Б.48) общее решение уравне-
ния (Б.59) можно представить в виде
и = (сх + с2х) е2х + (&х + Ь2х) ег2х.
В качестве второго приложения формулы (Б.58) рассмотрим'
следующее уравнение с комплексными корнями:
(О2 + а2)2 (£>2 + а^)3 « = °-	(Б.60)
Соответствующий характеристический многочлен	;
(з2 + a?)2 (s2 + «22)3
имеет корни
X
Линейные дифференциальные уравнения
513
Si = iax (двукратный корень), s2 = —iax (двукратный корень);
«з = ta2 (трехкратный корень) и s4 = —ia.2 (трехкратный корень).
Поэтому общее решение уравнения (Б.60) записывается как
и ~ (ai + а2х) 4- (&1 + &2х) e~ia‘x 4-
+ (^i + с2х + CjX2) eia*x + (dx + d2x 4- d3x2) e-la*x,
или, в действительной форме,
и — (Лх 4- Л2х) cos ахх 4- (Вх 4- В2х) sin ахх 4- (Сх + С2х 4-
4- С3х2) coS а2х 4- (£>х 4- D2x 4- D3x*) sin а2х.
Б.4. Частные решения неоднородных уравнений с постоянными
коэффициентами
Перейдем теперь к построению частных решений для уравне-
ний вида
Р (О) и = f (х),	,	(Б.61)
где правая часть f (х) может включать в себя экспоненты, триго-
нометрические функции, положительные степени х и их произ-
ведения. Частные решения такого уравнения, соответствующие
функциям f (х) общего вида, могут быть найдены другими мето-
дами, отличными от используемого здесь символического метода,
например, с помощью метода вариации произвольных постоян-
ных, широко применявшегося в гл. 4—11. Ниже для обозначе-
ния частного решения уравнения (Б.61) мы будем пользоваться
следующей символикой:
“ = Р (£>) ?
Случай f (х) = ехр (ах)
Поскольку - Р (D) еах = еахР (а),
то при условии, что Р (а) =# 0, частное решение (Б.62) может
быть записано в виде
1	еах
и = P(D)	Р (а) •	(Б.63)
Легко видеть, что выражение (Б.63) является частным решением
уравнения (Б.61), поскольку
₽(D)U = P(D)[^-] = ^>.= e~.
В случае если Р (а) = 0, в выражение для Р (D) должен
входить множитель (D — а). Мы предположим, что а есть корень
кратности т для многочлена Р (а); следовательно, в Р (D) будет
входить множитель (D — а)т. Поэтому Р (D) = (D — a)mQ (D),
где Q (а) у= 0. Тогда, используя формуду (Б.62), частное решение
уравнения (Б.61) можно записать в виде
ц —______?_____gax___	1 Г 1 g<Xx 1
(D — а)т Q (D) (D — а)п LQ (Р) J ‘
(Б.62)
514
Приложение Б
Поскольку Q (а) у= О, то
1	еах
____ мх — ___
Q(D)^ ~ Q (а) •
(Б.64)
Таким образом,
1 еах 1 1
ц —__________________________—	* мх
(D — а)т Q (а)	Q(a) (D — a)m
Воспользовавшись формулой (Б.50) для случая v — 1, из (Б.64)
имеем .
(Б.65)
е“х 1
U~ Q (а) ‘ТЙ" ’О)’
где выражение 1/D обозначает величину, обратную D, т. е. опе-
ратор однократного интегрирования по переменной х, тогда
как выражение l/Dm представляет собой оператор /п-кратного
интегрирования по х. Таким образом,
1 ...  1	, .  хР
Dm и —	'\Х> —	>
и, следовательно, частное решение уравнения (Б.61) в случае
когда Р (D) = (D — a)mQ (D), где Q (а) у= 0, будет иметь вид
е<хх хт
U Q (а) ‘ ~тГ *
поскольку	'
(D - a)- Q (D) и = (D — а)" Q (D)	=
{Г tfxx т Т)	( Лх _ г
(D-aH-L^ =Q(D)*	=
'	LQ (a) mlJJ	x’ [Q (a)	[ ml JJ
f >>ax 1
Случай f (x) = cos ax
Поскольку
D2 (cos ax) = —a2cos ax и D* (cos ax) = (—a2)2 cos ax,
то	Q (D2) cos ax = Q (—a2) cos ax.
Это дает возможность предположить, что мы можем найти нуж-
ное нам частное решение, заменив во всех случаях, где это необ-
ходимо, величину D2 на величину —а2. Таким образом, частное
решение уравнения
Q (D2) и = cos ax	(Б.66)
дается выражением
1	cos.ax
U ~ Q (D2) C0S аХ ~ Q (—аэ)	(Б. 67)
Линейные дифференциальные уравнения
515
(Б.68)
(Б.70)
решение
(Б.71)
при условии, что Q (—а2) =И= 0. Действительно,
Q (D2) и = Q (D*)	Q (D*) {cos ах} =
О (— аа) cos ах
= л ,	>;--= cos ах.
Q (— а2)
Важным частным случаем уравнения (Б.66) и решения (Б.67)
является уравнение
й -|- tt>ou = cos (at,
решёние которого имеет вид
cos (at	r-rw
U= (Б-69)
В случае если Q (—а2) = 0, описанную процедуру надлежит
несколько видоизменить. С этой целью заметим, что
cos ах — Re (е‘ах),
так что уравнение (Б.66) может быть переписано в виде
Q (D2) (Re и) = Re (eiax).
Поэтому частное решение уравнения (Б.66) можно будет построить,
если мы сумеем найти частное решение уравнения
Q (Ое) и = е‘ах
и затем отделить его действительную часть. Частное
уравнения (Б.70) можно представить как
Q (Da) е ‘
Поскольку теперь Q (—а2) = 0, то
Q (D) = (D + ia)m (D — ia)mF (О2),
где F (—а2) у= 0. Таким образом, решение (Б.71) переписывается
в виде
и — ------------:------------giax _-----}--- f------!-------
(D + ia)m (D — ia)m F (D2)	(D — ia)m ((D + ia)m F (Da)	J
(Б.72)
если выделить часть оператора, для которой знаменатель обра-
щается в нуль. Выполняя в формуле (Б.72) действия в фигурных
скобках, имеем
1	( е‘ах 1	1	1
и —------:--1--------------I = ------:-----------:___/е‘ах}
(D — ia)m[(2ia)mF(—a2)j	(2ia)mF(—a2) (D~ia)mV ”
откуда, используя формулу (Б.50) для случая v = 1, находим
.	t (ах— —- тя)
i	е‘ах 1	... хте v 2	’
и =----------------(О =--------------------
(2:.а)т F (— а2) Dm v (2а)т F (— а2) т\
(Б.73)
516
Приложение Б
Отделяя в выражении (Б.73) действительную часть, получаем
следующее частное решение уравнения (Б.66):
/	1	\
и —----------------cos (ах--/пл).	(Б.74)
(2а)"1 F (— а2) т\ \	2	)	v
Важным частным случаем формул (Б.66) и (Б.74) является урав-
нение
и (oqU = (О -j- coo) u = cos (Од/,	(Б.75)
частное решение которого имеет вид
u=icos(^—rn) = i^sln(0o/-	(Б-76)
Случай f (х) = sin ах исследуется аналогичным образом. Так,
частное решение уравнения
Q (О2) и = sin ах.	(Б.77)
дается формулой
Q(-a2)#=0.	(Б.78)
Если теперь Q (—а2) = 0, мы можем искать частное решение
таким же способом, как и в случае f (х) = cos ах, за исключе-
нием того, что теперь мы будем выделять не действительную,
а мнимую часть решения (Б.73). Так, например, частное решение
уравнения
(О2 + а2)"1/7 (О2) и = sin ах	(Б.79)
имеет вид
и  --------—-------sin fax —~ тп) .	(Б.80)
(2а) F (- а2) т\ \	2	/	\	/
Важным частным случаем формул (Б.79) и (Б.80} является урав-
нение
U (OqU = (Z) (Оо) и = sin (OgZ,	(Б.81)
частное решение которого записывается как
u = isin((0o/-4-n)==-2i-0ZcoS(0oZ-	(Б-82>
Если полином Р (D) явно зависит от D и О2, описанную про-
цедуру также необходимо видоизменить. При этом вместо иссле-
дования общего случая рассмотрим конкретное уравнение
(О2 + 2D + 3) и = cos ax,	(Б.83)
частное решение которого может быть записано как
’U = D4^D + 3C0SaX-	<Б'84)
Линейные дифференциальные уравнения	-517
Заменяя в (Б.84) величину D2 на —а2, находим
« = 2D + 3+—2C0SCTX'	<Б'85>
Преобразуем, теперь правую часть формулы (Б.85) таким обра-
зом, чтобы получить в знаменателе разность квадратов двух
величин, одна из которых оказалась при этом равной D2. Для
этого умножим числитель и знаменатель в (Б.85) на оператор
2D — (3 —п а2), в результате чего получим
2D — (3 — а2)	2D — 3 + а2 ~
“ ~ (2D + 3 — а2) (2D — 3 + а2) C0S аХ~ 4D2 — (3 — а2)2 C0S ~
= (2D — 3 -j- а2) 4д2 _ (з _ сс2)2 cos ах~
-(2^-3+a2),_4CT2cis^T =
2а sin ах—(3 — а2) cos ах
~	а4 — 2«2 4- 9	'
Случай f (х) = х™, где т — положительное число
Рассмотрим уравнение
Р (D) и = хт,	(Б.86)
частное решение которого может быть записано в виде.
и^~Р7р)хт-	(Б-87)
Разлагая функцию 1/Р (D) в ряд Лорана по степеням D, находим
u = -pXD)xm = ^(a0+a1D + a^+ ... +flft+mD^+...)X'” =
___________________________,
(tn + k) (т + k — l)...(/n + 1) '
а1хт+к~х
+ (m + fe—l)(m + fe —2).;.(m +.1) + * ’ ‘ Qm+h-
В качестве примера рассмотрим уравнение
D (D2 + 3D + 2) и = х2.
Тогда
и = D(D> + 3D + 2) 'х* = 2D^ + ^D + ^ х2 =
=4г [М4 D+т0’) +	+-W-
-(4D+4D°)‘ +
518
Приложение Б
"-2!o(1-4D+tD!-
= (_J____*L I _7_ р _ 15 рг . \ х2 —
\ 2D 4 ' 8 ^16 17 '	/
= ±xs_J_x2 . _LX_J£
6	4^4	8’
Отметим, что все члены ряда порядка выше чем D2 дают нам
нули, поскольку они воздействуют на функцию х2. Кроме того,
15
постоянный член —g- в этом выражении может быть опущен,
поскольку его можно включить в решение однородного уравне-
ния.
Общий случай
Рассмотрим, наконец, уравнение
(D2 + 4а2) и — х2 cos 2ах.
Поскольку Р (—а2) = 0, то мы можем найти его частное решение
как действительную часть частного решения уравнения
- {D2 + 4а2) u = x2e2iajc.
Таким образом, имеем
и — I vlpliax — _________1________ уЧрНах —
Da + 4aa r (D — 21а) (D + 21а) с ~
1	2 ^iaX I 1	1 D > Di ,
D (D + 41a)	41a \ D 4ia 16a2 ' 64ias '
\	JJlOCX  / 1	y2	y2	J \
_L . . Л r2 = Z-_( — X3 * — —__— 4- —— \
' j	41a \ 3 4ia 8a2 32ias ) ’
и, следовательно,
“ = 1^-Re p'“ (-4+ 4 + ₽ - 3^)] =
=(^ ~ 4)cos 2a*+4 - 4)sin 2a*-
ЛИТЕРАТУРА
(Абрамович М., Стиган И). Справочник по специальным функциям с фор-
мулами, графиками и математическими таблицами. Под ред. М. Абрамо-
вича, И. Стиган. Пер. с англ.—М.: Наука, 1979.
Айне Э. Л. Обыкновенные дифференциальные уравнения. Пер. с англ. —
Харьков: Гос. иаучно-технич. изд-во Украины, 1939.
Алфорс (Ahlfors L. V.). Complex Analysis. — New York: McGraw-Hill; 1953.
Андронов А, А., Витт А. А., Хайкин С. Э. Теория колебаний. — M.: Наука,
1981.
Арскотт (Arscott F.). Periodic Differential Equations. — New York: Pergamon,
1964.
(Бабич В. M.). Математические вопросы теории дифракции и распрост-
ранения волн. Под ред. В. М. Бабича. Записки научных семинаров
ЛОМИ им. В. А. Стеклова. Вып. 1—12. — Л.: Наука, 1968—1981.
Баумеи (Bowman F.). Introduction to Bessel Functions. — New York: Dover,
1958.
Бейер (Beyep R. T.). Nonlinear Acoustics. — Washington-, D. C.: Naval Ship Sy-
stems Command, 1974.
Бейтмен (Bateman H.). Partial Differential Equations of Mathematical Physics. —
Cambridge: Cambridge University Press, 1959.
Веллман (Bellman R.). Perturbation Techniques in Mathematics, Physics and
Engineering. — New York: Holt, 1964.
Беллмаи P. Теория устойчивости решений дифференциальных уравнений, Пер.
с англ. — М.: Изд. иностр, лит., 1954.
Бендер, Opcar (Bender С. М., Orszag S. A,). Advanced Mathematical Methods
for Scientists and Engineers. — New York: McGraw-Hill, 1978.
Биркгоф, Рота (Birkhoff G., Rota G. C.). Ordinary Differential Equations. —
Boston: Ginn and Company, 1962.
Блакьер О. Анализ нелинейных систем. Пер. с англ. —М.: Мир, 1969.
Блейстейн, Ханделсмаи (Bleistein N., Handelsman R. A.). Asymptotic Expan-
sions of Integrals. — New York: Holt, Rinehart and Winston, 1975.
Блум, Казаринов (Bloom С. O., Kazarinoff N. D.). Short Wave Radiation Prob-
lems in Inhomogeneous Media: Asymptotic Solutions. — New York: Sprin-
ger-Verlag, 1976.
Боголюбов H. H., Митропольский Ю. А. Асимптотические методы в теории
нелинейных колебаний. — М.: Наука, 1974.
Бойс, Ди Прима (Воусе W. Е., Di Prima R. С.). Elementary Differential Equa-
tions and Boundary Value Problems.— New York: Wiley, 1977.
Болотин В. В. Неконсервативные задачи теории упругой устойчивости. — М.:
Физматгиз, 1961.
Ьрауер, Ногел (Brauer F.,Nohel J. A.). The Qualitative Theory of Ordinary Dif-
ferential Equations. — New York: Benjamin, 1969.
Бриллюэн Л., Пароди M. Распространение волн в периодических структурах.
Пер. с англ. — М.: Изд. иностр, лит., 1959.
Брокетт (Brockett R. W.). Finite Dimensional Linear Systems. — New York:
Wiley, 1970.
520
Литература
Бутеннн Н. В. и др. Введение в теорию нелинейных колебаний. — М.: Наука,
1976.
Бхаттачария Р. Н., Ранга Рао Р. Аппроксимация нормальным распределением
н асимптотические разложения. Пер. с англ. — М.: Наука, 1982.
Бюргерс (Burgers Т. М.). The Nonlinear Diffusion Equation: Asymptotic Solu-
tions and Statistical Problems.—Amsterdam: North-Dordrecht—Holland,
1974.
Вазов В. Асимптотические разложения решений обыкновенных дифференциаль-
ных уравнений. Пер. с англ.—М.: Мир, 1968.
Ван-Дайк М. Методы возмущений в механике жидкости. Пер. с англ. —М.:
Мир, 1967.
Ватсон Г. Н. Теория бесселевых функций. Ч. I—II. Пер. с англ. — М.: Изд.
иностр, лнт., 1949.
Ган (Hahn W). Stability^ Motion. — New York: Springer-Verlag, 1967.
Гарабедян (Garabedian P.R.). Partial Differential Equations. — New York: Wi-
ley, 1964.
Грабмюллер (Grabmflller H.). Singular Perturbation Techniques Applied to
Integro-Differential Equations. — San Francisco: Pitman, 1978.
Градштейн И. С., Рыжик И. М. Таблицы интегралов, сумм, рядов и произве-
дений.— М.: Наука, 1971.
Гринберг (Greenberg М. D.). Foundations of Applied Mathematics. — Eng-
lewqod Cliffs: Prentice-Hall, 1978.
Де Брейн H. Г. Асимптотические методы в анализе. Пер. с англ. — М.: Изд,
иностр, лит., 1961.
Дейвис (Davis Н.) Introduction to Nonlinear Differential and Integral Equations.—
New York: Dover, 1962.
Деи Хартог (Den Hartog J. P.). Mechanical Vibrations. — New York: McGraw-
Hill, 1947.
Деттман (Dettman J. W.). Introduction to Linear Algebra and Differential Equa-
tions. — New York: McGraw-Hill, 1974.
Джакалья Г. Методы теории возмущений для нелинейных систем. Пер. с англ.—
М.: Наука, 1979.	'
Джеффрис (Jeffreys Н.). Asymptotic Approximations. — Oxford: Oxford Uni-
versity Press, 1962.
Джеффрис.Г., Свирлс Б. Методы математической физнкн. Вып. 1—3. Пер.
с англ. — М.: Мир, 1969—1970.	z
Диментберг Ф. М. Изгибные колебания вращающихся валов. — М.: Изд.
АН СССР, 1959.
Дингл (Dingle R. В.). Asymptotic Expansions: Their Derivation and Interpre-
tation.— New York: Academic, 1973?
Дьюар M. Дж. С., Догерти P. Теория возмущений молекулярных орбиталей
в органической химии. Пер. с англ. — М.: Мир, 1977.
Еругин Н. П. Линейные системы обыкновенных дифференциальных уравнений
с периодическими и квазиперноднческими коэффициентами. — Минск:
Изд-во АН БССР, 1963.
Ивен-Ивановскнй (Evan-Iwanowski R. М.). Oscillations in Mechanical Systems.—
New York:. Elsevier, 1969.
Кдмке Э. Справочник по обыкновенным дифференциальным уравнениям. Пер.
с нем. — М.: Наука, 1971.
Каннингэм (Cunningham W. J.). Introduction to Nonlinear Analysis. — New
York: McGraw-Hill, 1958.
Каплун.(Кар1ип S.). Fluid Mechanics and Singular Perturbations. Lagerstrom P. A.,
Howard L. N., Liu C. S., Eds. — New York: Academic, 1967.
Карпман В. И. Нелинейные волны в диспергирующих средах. — М.: Наука,
1973.
Карриер, Крук, Пирсон (Carrier G. F., Krook М., Pearson С. Е.). Functions,
of a Complex Variable. — New York: McGraw-Hill, 1966.
Литература
521
Карриер, Пирсон (Carrier G. F., Pearson С. Е.). Ordinary Differential Equa-
tions.— Waltham, Mass.: Blaisdell, 1968.
Като T. Теория возмущений линейных операторов. Пер. с японск. — М.:
Мир, 1972.
Каудерер Г. Нелинейная механика. Пер. с ием. — М.: Изд. иностр, лит.,
1961.
Коддингтон Э. А., Левинсон Н. Теория обыкновенных дифференциальных
уравнений. Пер. с аигл. — М.: Изд. иностр, лит., 1958.
Кононенко В. О. Колебательные системы с ограниченным возбуждением. — 
М.: Наука, 1964.
Копсон Э. Т. Асимптотические разложения. Пер. с англ. — М.: Мнр, 1966.
Копсон (Copson Е. Т.). An Introduction to the Theory of Functions of a Complex
Variable. — Oxford: Oxford University Press, 1935.
Коул Дж. Методы возмущений в прикладной математике. Пер. с англ. —М.:
Мир, 1972.
Коул Р. Г. (Cole R. Н.). Theory of Ordinary Differential Equations. — New
York: Appleton-Century-Crofts, 1968.
Крылов H. M., Боголюбов H. H. Введение в нелинейную механику. — Киев:
Изд-во АН УССР, 1937.
Кумар К- Теория возмущений и проблема многих тел для атомного ядра. Пер.
с англ. — М.: Мир, 1964.
Кураит Р. н Гильберт Д. Методы математической физики. Пер. с нем. —
Т. 1—2. — М,—Л.: ГИТТЛ, 1951.
Лйитхнлл (Lighthill М. J). Introduction to Fourier Analysis and Generalized
Functions. — Cambridge: Cambridge University Press, 1960.
Ландау Л. Д., Лифшнц E. M. Теоретическая физика. T. 3. Квантовая ме-
. хаинка. Нерелятивнстская теория. — М.: Наука, 1974.
(Лейбович, Сибасе). Нелинейные волны. Под ред. С. Лейбовича н А. Сибасса.
Пер. с англ. — М.: Мир, 1977.
Лейпхольц (Leipholz Н. Е.). Stability Theory. — New York: Academic, 1970.
Лефшец С. Геометрическая теория дифференциальных уравнений. Пер. с аигл.—
М.: Изд. иностр, лит., 1961.
Лю (Lu Y. -С.). Singularity Theory and an Introduction to Catastrophe Theory.—
New York: Springer-Verlag, 1976.
Ляпунов A. M. Общая задача об устойчивости движения. — М.—Л.: Гостех-
нздат, 1950.
Магнус, Оберхеттнигер (Magnus W. and Oberhettinger F.). Formulas and
Theorems for the Functions of Mathematical Physics. — New York: Chel-
sea, 19475
Магнус, Уинклер (Magnus W. and Winkler S.). Hill’s Equation. — New York:
Wiley, 1966.
Мак-Лахлан H. В. Теория н приложения функций Матье. Пер. с англ.—
М.: Изд. иностр, лнт., 1953.
Мак-Лахлан (McLachlan N. W.). Ordinary Nonlinear Differential Equations
in Engineering and Physical Sciences. — Oxford: Clarendon Preess, 1950.
Малкин И. Г. Некоторые задачи теории нелинейных колебаний.—М.: Гос- ,
техиздат, 1956.
Мейровнч (Meirovitch L.). Methods of Analytical Dynamics. — New York:
McGraw-Hill, 1970.
Мерцбахер (Merzbacher E.). Quantum Mechanics. — New York: Wiley, 1970.
Миллер (Miller K. S.). Linear Differential Equations in the Real Domain. — New
York: W. W. Morton, 1963.
Минорскнй (Minorsky N.). Non-Linear Mechanics. — Ann Arbor, MI: J. W. Ed-
wards, 1947.
Мннорскнй (Minorsky N.). Nonlinear Oscillations. — Princeton: Van Nostrand,
1962. .
Митропольский Ю. А. Проблемы асимптотической -теории нестационарных
колебаний. —'М.: Наука, 1964.
522
Литература
Мбрс Ф. М. и Фешбах Г. Методы теоретической физики. Т. 1—2. Пер. с нем.—
М.: Изд. иностр, лнт:, 1958—1960.
Мэтьюз Дж., Уокер Р. Математические методы физики. Пер. с англ.—М.:
Атомиздат, 1972.
Мюррей (Murrey J. D.). Asymptotic Analysis. — Oxford: Clarendon, 1974.
Найфэ А. Методы возмущений. Пер. с англ. — М.: Мир, 1976.
Найфэ, Мук (Nayfeh A. and Mook D. Т.). Nonlinear Oscillations. — New York:
Wiley, 1979.
Олвер Ф. Введение в асимптотические методы и специальные функции. — Пер.
с англ. — М.: Наука, 1978.
О’Малли (O'Malley R. Е.). Introduction to Singular Perturbations. — New York:
Academic, 1974.
Пиаджио (Piaggio H. T. H.). An Elementary Treatise on Differential Equations
and their Applications. — London: G. Bell and Sons, 1954.
Пуанкаре А. Избранные труды. В 3-х т. Т. I. Новые методы небесной меха-
ники. Пер. с франц. — М.: Наука, 1971.
Рабенстейн (Rabenstein A. L.). Introduction to Ordinary Differential Equations. —
New York: Academic, 1972.
Реллих (Rellich F.). Perturbation Theory of Eigenvalue Problems. — New York:
Gordon and Breach, 1969.
Рид M., Саймон Б. Методы современной математической физики. Т. 1—4. Пер.
с англ. — М.: Мир, 1977—1982.
Рокленд (Rockland С.). Hypoellipticity and Eigenvalue Asymptotics. — New
York: Springer-Verlag, 1975.
Poco (Roseau M). Asymptotic Wave Theory. — Amsterdam: North-Holland, 1976.
Сагдеев, Галеев (Sagdeev R. Z. and Galeev A. A.). Nonlinear Plasma Theory. —
New York: Benjamin, 1969.
Сибуя (Sibuya Y.). Global Theory of a Second Order .Linear Ordinary Differen-
tial Equation. — Amsterdam: North-Holland, 1975.
Силяк (Siljak D. D.). Nonlinear Systems. — New York: Wiley, 1969.
Сирович (Sirovich L.). Techniques of Asymptotic Analysis. — New York: Sprin-
ger-Verlag, 1971.
Скотт (Scott E. J). Transform Calculus. — New York: Harper and Brothers, 1955.
Смирнов В. И. Курс высшей математики. Т.1—5.—М.: Наука, 1957—1959.
Стейнманн (Steinmann О.). Perturbation Expansions in Axiomatic Field Theory.—
New York: Springer-Verlag, 1971.
Страбл (Struble R. A.). Nonlinear Differential Equations. — New York: McGraw-
Hill, 1962.
Татарский В. И. Распространение волн в турбулентной атмосфере. — М.: Наука,
1967.
Тондл А. Динамика роторов турбоагрегатов. Пер. с анл. — Л.: Энергия, 1971.
Уизем Дж. Линейные и нелинейные волны. Пер. с англ. — М.: Мир, 1977.
Уили (Wylie С. R.). Advanced Engineering Mathematics. — New York; McGraw-
Hill, 1965.
Уилкокс (Wilcox С. H.). Asymptotic Solutions of Differential Equations and
their Applications. — New York: Wiley, 1964.
Уилкокс (Wilcox С. H.). Perturbation Theory and its Applications in Quantum
Mechanics. — New York: Wiley, 1966.
Уиттекер (Whittaker E. T.). Analytical Dynamics of Particles and Rigid Bodies.
4th ed. — Cambridge: Cambridge University Press, 1937.
Уиттекер (Whittaker E. T.). A Treatise on the Analytical Dynamics of Partic-
les and Rigid Bodies. —Cambridge: Cambridge University Press, 1961.
Уиттекер Э. T., Ватсон Г. H. Курс современного анализа. Ч. I—II. Пер.
с аигл.— М.: Наука, 1963.
Фене (Fans W. G.). Self-Adjoint Operators. — New York: Springer-Verlag, 1975.
Фещеико С. Ф., Шкиль H. И., Николенко Л. Д. Асимптотические методы в тео-
рии линейных дифференциальных уравнений. — Киев: Наукова
думка, 1966.
Литература
523
Фреман Н., Фреман П. У. ВКБ-приближение. Пер. с англ. — М.: Мир, 1967.
Фридрихе (Friedrichs К. О.). Advanced Ordinary Differential Equations. — New
York: Gordon and Breach, 1965.
Хагедорн (Hagedorn P.). Nichtlineare Schwingungen. — Wiesbaden: Akademische
Verlagsgesellschaft, 1978.
Хаяси T. Вынужденные колебания в нелинейных системах. Пер. с англ. — М.:
Изд. иностр, лит., 1957.
Хаяси Т. Нелинейные колебания в физических системах. Пер. с англ. — М.:
Мир, 1968.
Хедииг Дж. Введение в метод фазовых интегралов. (Метод ВКБ.) Пер. с аигл. —
М.: Мир, 1965.
Хейл Дж. К. Колебания в нелинейных системах. Пер. с англ. — М.: Мир, 1966.
Хейл (Hale J. К.). Ordinary Differential Equations. — New York: Wilgy, 1969.
Хилдебранд (Hildebrand F. B.). Methods of Applied Mathematics. — New York:
Prentice-Hall, 1952.
Хоффман (Hoffman K.). Linear Algebra. — Englewood Cliffs: Prentice-Hall, 1961.
Хохштадт (Hochstadt H.). Differential Equations. — New York: Holt, Rinehart
and Winston, 1964.
Чезари Л. Асимптотическое поведение и устойчивость решений обыкновенных
дифференциальных уравнений- Пер. с англ. — М.: Мир, 1964.
Чернов Л. А. Распростраиеиие волн в среде со случайными неоднородностями. —
М.: Изд-во АН СССР, .1958.
Шмидт Г. Параметрические колебания. Пер. с нем. — М.: Мир, 1978.
Штокало И. 3. Линейные дифференциальные уравнения с переменными коэф-
фициентами. (Асимптотические методы и критерии устойчивости и неу-
стойчивости решений.) — Киев: Изд-во АН УССР, 1960.
кхаус (Eckhaus W.). Matched Asymptotic Expansions and Singular Perturba-
tions. — Amsterdam: North-Holland, 1973.
Экхаус (Eckhaus W.). Studies in Nonlinear Stability Theory. — New York: Sprin-
ger-Verlag, 1965.
Эрдейи А. Асимптотические разложения. Пер. с англ. — М.: Физматгиз, 1962.
Эрдейи, Магнус, Оберхеттингер, Трикоми (Erdelyi ~А., Magnus W., Oberhettin-
ger F. and Tricomi F. G.). Higher Transcendental Functions. 3 Vols. — New
York: McGraw-Hill, 1953.
Якубович В. А., Старжинский В. M. Линейные дифференциальные уравнения
с периодическими коэффициентами и их приложения. — М.: Наука, 1972.
Литература, добавленная редактором перевода
1.	Арнольд В. И., Варченко А. Н., Гусейн-Заде С. М. Особенности диффе-
ренцируемых отображений. — М.: Наука, 1982.
2.	Асимптотика решений дифференциальных уравнений: Материалы к семи-
нару «Дифференциальные уравнения и их применение». — Вильнюс: Инет,
математики и кибернетики АН СССР, 1981.
3.	Асимптотические и качественные методы в теории нелинейных колебаний.—
Киев: Иист. Мат. АН УССР; 1971.
4.	Асимптотические методы в динамике систем. — Новосибирск: Наука, 1980.
5.	Асимптотические методы в механике. — Иркутск: СЭИ СО АН СССР, 1979,
1981.
6.	Асимптотические методы в механике жидкости и газа. — Иркутск: ИГУ, 1979.
7.	Асимптотические методы в нелинейной механике. — Киев: Инет. Мат.
АН УССР, 1974.
8.	Асимптотические методы в теории нелинейных колебаний. — Киев: Наукова
думка, 1979.
9.	Асимптотические методы в теории нестационарных процессов. — М.: Наука,
10.	Асимптотические методы в теории систем. — Иркутск: ИГУ и СЭИ СО
АН СССР; в. 1, 1970; в. 2, 1972; В. 3,	4, 5, 1973; в. 6, 7, 1974; в. 8,
1975; в. 9, 1976; в. 10. 1977; в. 11. 1978; в. 12, 1980; в. 13. 1982.
524
Литература
11.	Асимптотические методы нелинейной механики. — Киев: Инет. Матеи,•’«BL
АН УССР, 1979.	•' -Ж
12.	Асимптотические методы решения дифференциальных уравнений: Мате-
риалы к семинару «Дифференциальные уравнения и их применение». — Виль-, .egr
нюс: Инет. Матем. и киберн. АН Лит. ССР, 1980.
13.	Асимптотические методы теории дифференциальных и интегро-дифферен-
циальных уравнений и их приложение. — Фрунзе: Кирг. Гос. ун-т, 1981.
14.	Асимптотическое поведение решений дифференциально-функциональных
уравнений. — Киев: Инет. Матем. АН УССР, 1978.
15.	Бабич В. М., Булдырев В. С. Асимптотические методы в задачах дифрак-
ции коротких волн.—М.: Наука, 1972.	’’
16.	Бабич В. М., Булдырев В. С. Искусство асимптотики. Вести. Ленингр.
ун-та, № 13, 1973.
17.	Бабич В. М., Кирпичникова Н. Я- Метод пограничного слоя в задачах
дифракции.—Л.: Изд-во ЛГУ, 1974.	А.
18.	Баранцев Р. Г. Об асимптотологии. Вести. Ленингр. ун-та, № 1, 1976.
19.	Баранцев Р. Г. Дефиниция асимптотики и системные триады. В кн.: Асимп-
готические методы в теории систем. — Иркутск: СЭИ420 АН СССР, 1980.
20.	Баренблат Г. И. Подобие, автомодельность, промежуточная асимптотика.—
Л.: Гидрометеоиздат, 1978.	ж
21.	Бартман А. Б., Перельман Т. Л. Новый асимптотический метод в анали-
тической теории переноса. — Минск: Наука и Техника, 1975.
22.	Боголюбов Н. Н., Митропольский Ю. А. Асимптотические методы в теории '
нелинейных колебаний. — М.: Наука, 1974.
23.	Брекер Т., Ландер Л. Дифференцируемые ростки и катастрофы. . Пер. .
с англ. — М.: Мир, 1977.
24.	Бутузов В. Ф., Васильева А. Б., Федорюк М. В. Асимптотические методы
в теории обыкновенных дифференциальных уравнений. В кн.: Итоги науки.
Математический анализ. — М.: ВИНИТИ, 1969.	. 2
25.	Вайнберг Б. Р. Асимптотические методы в уравнениях математической фи- .
зики.—М.: Изд-во МГУ, 1982.
26.	Васильева А. Б., Бутузов В. Ф. Асимптотические разложения решений
сингулярно возмущенных уравнений. — М.: Наука; 1973.
27.	Васильева А. Б., Бутузов В. Ф. Сингулярно возмущенные уравнения в. крц-/ .
тических случаях. — М.: Изд-во МГУ, 1978.
28.	Волосов В. М., Моргунов Б. И. Метод осреднения в теории нелинейных-,
колебательных систем. — М.: Изд-во МГУ, 1971.	-А
29.	Всесоюзная конференция по асимптотическим методам в теории сингулярно- '4/,
возмущенных дифференциальных и интегро-дифференциальных уравнений
и их приложениям. Тезисы докладов. — Фрунзе: Илим, 1975.	1
30.	Всесоюзная конференция по асимптотическим методам в теории сингулярно-
возмущенных уравнений. Тезисы докладов. — Алма-Ата: Наука, . 1979. А'
31.	Гийемин В., Стернберг С. Геометрические асимптотики. Пер. с англ. — М.: JS
Мир, 1981.
32.	Голубицкий М., Гийемин В. Устойчивые отображения и их особенности.
Пер. с англ. —М.: Мир, 1977.	к-
33.	Гольденвейзер А. Л., Лидский В. Б., Товстик П. Е. Свободные колебания -If
тонких упругих оболочек.—М.: Наука, 1979.
34.	Гребенников Е. А., Рябов Ю. А. Резонансы и малые знаменатели в небес- А
.ной механике.—М.: Наука, 1978.	жС
35.	Гребенников Е. А., Рябов Ю. А. Конструктивные методы анализа нели- Д
нейных систем. — М.: Наука, 1979.	ж
36.	Дифференциальные уравнения с малым параметром. Свердловск: УНЦ
АН СССР, 1980.	.t-
7.	Зино И. Е., Тропп Э. А. Асимптотические методы в задачах теории тепло-
проводности и термоупругости. — Л.: Изд-во ЛГУ, 1978.
38.	Ибрагимов И. А., Хасьминский Р. 3. Асимптотическая теория оценива-
ния. — М.: Наука, 1979.
Литература
525
39.	Ломов С. А. Введение в общую теорию сингулярных возмущений. — М.:
Наука, 1981.
40.	Мазья В. Г., Назаров С. А., Пламеневский Б. А. Асимптотика решений
эллиптических краевых задач при сингулярных возмущениях области. —
Тбилиси: ИПМ ТГУ, 1981.
41.	Маслов В. П. Теория возмущений и асимптотические методы. — М.: Изд-во
МГУ, 1965.
42.	Маслов В. П. Комплексный метод ВКБ в нелинейных уравнениях.—М.:
Наука, 1977.
43.	Маслов В. П., Федорюк М. В. Квазнклассическое приближение для урав-
нений квантовой механики.—М.: Наука, 1976.
44.	Методы возмущений в механике. — Новосибирск: Наука, 1982.
45.	Методы малого параметра и их применение. — Минск: ИПМ АН СССР, 1982.
46.	Митропольский Ю. А. Метод усреднения в нелинейной механике. — Киев-'
Наукова думка, 1971.
47.	Митропольский Ю. А., Мосеенков Б. И. Асимптотические решения урав-
нений в частных производных. — Киев: Высшая школа, 1976.
48.	Мищенко Е. Ф., Розов Ц. X. Дифференциальные уравнения с малым па-
раметром и релаксационные колебания. — М.: Наука, 1975.
49.	Моисеев Н. Н. Асимптотические методы нелинейной механики. — М.: Наука,
1981.
50.	Панасюк А. И., Панасюк В. И. Асимптотическая оптимизация нелиней-
ных систем управления. — Минск: Изд-во БГУ, 1977.
51.	'Панченков А. Н. Основы теории предельной корректности. — М.: Наука,
52.	Панченков А. Н. Асимптотические методы в экстремальных задачах меха-
ники. — Новосибирск: Наука, 1982.
53.	Постон Т., Стюарт И. Теория катастроф и ее приложения. Пер. с англ. —
М.: Мир, 1980.
54.	Применение метода согласования асимптотических разложений к краевым за-
дачам для дифференциальных уравнений.—Свердловск: УНЦАНСССР, 1979.
55.	Проблемы асимптотической теории нелинейных колебаний. — Киев: Наукова
думка, 1977.
56.	Проскуряков А. П. Метод Пуанкаре в теории нелинейных колебаний. —
М.: Наука, 1977.
57.	Риекотыньш Э. Я- Асимптотические разложения интегралов. — Рига: Зи-
натне, Т. 1, 1974; Т. 2, 1977; Т. 3, 1981.
58.	Рождественский К- В. Метод сращиваемых асимптотических разложений
в гидродинамике крыла. — Л.: Судостроение, 1979.
59.	Смирнов Б. М. Асимптотические методы в теории.атомных столкновений. —
' М-: Атомиздат, 1973.
60.	Федорюк М. В. Метод перевала. — М.: Наука, 1977.
61.	Федорюк М. В. Асимптотические методы для линейных дифференциальных
уравнений. — М.: Наука, 1983.
62.	Фещенко С. Ф., Шкиль Н. И., Николенко Л. Д. Асимптотические методы
в теории линейных дифференциальных уравнений.— Киев: Наукова думка,
1966.
63.	Фещенко С. Ф., Шкиль Н. И., Пидченко Ю. П., Сотничеико Н. А. Асимп-
тотические методы в теории линейных дифференциальных уравнений с от-
клоняющимся аргументом. — Киев: Наукова думка, 1981.
64.	Филатов А. Н. Методы усреднения в дифференциальных' н интегродифферен-
циальных уравнениях. — Ташкент: Фан, 1971.
65.	Фридрихе К- Возмущение спектра операторов в гильбертовом пространстве.
Пер. с англ. — М.: Мир, 1969.
66.	Цирулис Т. Т. Метод градиентных линий для асимптотического представле-
ния контурных интегралов. — Рига: Зинатне, 1973.
67.	Eckhaus W. Asymptotic analysis of singular perturbations. — Amsterdam:
North-Holland Publ. Co, 1979.
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Автономная система 215, 220, 226
Акустические волны
в каналах, заполненных сжимаемой
жидкостью 466
в каналах с переменным поперечным се-
чением 480—482
в каналах с синусоидальными стенками
438-445
Алгебраические уравнения 35—56
высших порядков 49—51
квадратичные 35—45
кубические 45—49
условия разрешимости 408—414
Альтернатива Фредгольма,
для задачи Штурма—Л иувилля 426
для интегрального уравнения 477
Амплитудно-частотная характеристика 217
в случае первичного резонанса 227—228
в случае субгармонического резонанса
216—218
в случае супергармоннческого резонанса
221—222
Анализ размерностей 9—17
для линейного осциллятора 146
для осциллятора с самовозбуждением 161
* для системы с квадратичными нелиней-
ностями 174—175
для уравнения Дюффинга 116—117
для уравнения Матье 253
Аналитическая функция 67, 89, 97. 108,
116, 346, 349, 362
определение 96
Апериодические решения 260
Асимметрия 435, 448.
Асимптотическая последовательность 29
логарифмические члены 29
по дробным степеням параметра 38—42,
48—49, 50
по обратным степеням параметра 44, 45
Асимптотический ряд 25—29
его точность 30—31
определение 27—28
погрешность 28
сравнение со сходящимся рядом 30—31,
374.
См. также Асимптотическое разложение
Асимптотического соответствия знак 28,
74, 366, 369
Асимптотическое разложение 29—30
для уравнений с большим параметром 380
единственность 30
интегралов 57—115
определение 29
по параметру 35
равномерное 32
расходящееся 27, 31
функций Бесселя 31, 102—104, 114,
369—374, 378
функций Эйрн 104—108
элементарные операции над ними 31, 41.
См. также Асимптотический ряд
Биномиальная формула 17—18, 25, 36,
38, 41, 52, 59, 71, 1 18, 149, 162, 181,
183, 494
Быстрые колебания 87
Вариация произвольных постоянных 148,
345—346, 513
в случае многочастотного возбуждения
246 — 249
в случае слабой нелинейности общего
вида 201 — 202
для линейного осциллятора 159—160
для линейных неоднородных дифферен-
циальных уравнений 345—346
для систем с квадратичными нелинейно-
стями 185—186
для уравнения Дюффинга 139—141
для уравнения Дюффингав случае вы-
нужденных колебаний 228—233
для уравнения Матье 272—274
для уравнения Рэлея 170—1/2
Векторное решение 345
Ветвь внешнего разложения 334
Взаимодействие,
вязко-невязкое 327
приближений 186
Взаимодействующие моды 443, 445
ВКВ-прнблнженне 380—383, 389
несостоятельность 397—398
применение к решению задачи иа соб-
ственные значения 385—389
Внешнее разложение 285—286, 289, 298
для задачи с двумя пограничными слоями
317—318
для нелинейной задачи 329—330, 334
для простой краевой задачи 300
для трехэонной задачи 325—326
для уравнений с переменными коэффи-
циентами 305—306, 308v‘ 311, 314
Внешняя переменная 289
как критерий прн выборе внутреннего
разложения 331
Внутренне-внутреннее разложение 283,
286, 287 ’
Внутреннее произведение 412
Внутреннее разложение 285—286 , 289,297—
299
для задачи с двумя пограничными слоями
318—323
для задачи с точкой поворота 390—391
для нелинейной задачи 331—333, 335—
338
для простой краевой аадачн 282—283.
301
для уравнения с переменными коэф*
фнцнентами 306—307, 311 — 313, 31®
Внутренняя переменная 289
выбор 292—298, 306, 309, 311
Возбуждение,
внешнее 208, .209, 216. 221
параметрическое 253
Предметный указатель
527
порядок 224.
См. также Многочастотное возбуждение
Возмущение,
по параметру 11, 12,' 13, 15, 17, 34
сингулярное 43
Возмущенное уравнение 34
Волновод 438
Волновое число 440, 442
Восстанавливающая (возвращающая) сила
11, 116, 123,	146, 174
Вронскиан 255, 257, 502—505
Вторичный резонанс 211—224, 228—232
определение 211.
См. также Комбинационный резонанс,
Субгармонический резонанс, Супер-
гармоннческнй резонанс
Вынужденные колебания,
многочастотные 236—252
с одной частотой 208—235
Вырождение 435, 448, 465
в задаче о колебаниях мембраны, близ-
кой по форме к кругу 448—452,
482-484
снятие 437, 452, 466
Вырожденная задача на собственные зна-
чения,
для уравнения второго порядка 434 — 437
для уравнения четвертого порядка 408,
463, 465—466
Вырожденное уравнение 35, 37, 40, 117,'
291
Вырожденное ядро 478
Гамма-функция 81, 82, 93, 95
асимптотическое представление 114
неполная 62
определение 77—80
Геометрическая прогрессия 26
Гипербола 106
Гироскопические системы 414 — 420
нелинейные 414—417
с параметрическим возбуждением 417 —
420
Главный резонанс,
См. Первичный резонанс
Градиент 98
Граничные условия,
на поверхности раздела 408, 473 — 476
общие 420, 426 — 432. 472 — 473
перенос 439, 446
потеря 278, 292
смешанные (неразделенные) 421
сопряженные 429—430
Дельта-функция Дирака 173
Демпфирование 146—209
отрицательное 161
Деформация контура интегрирования 89,
101, 102, 106, 109
Дифференцируемая функция комплексного
переменного 96
Дифференциальное уравнение,
общее решение в линейном случае 503
определение 499
Дробные степени параметра 38
Естественные координаты 29
Жорданова каноническая форма 257
Задача иа собственные значения,
вырожденная, для уравнения второго
порядка 434—437
для уравнения четвертого порядка 462—
466
решение с помощью метода ВКБ 385—389
с регулярной особой точкой 446 — 452
с точкой поворота 400—406
Задача Орра—Зоммерфельда 455
Задача с двумя точками поворота 402—404
Задача сингулярных возмущений 43, 282
Задача с точкой поворота 380
на собственные значения 404—406
n-го порядка 398
определение 383, 389
решение методом сращиваемых асимпто-
тических разложений 310—317, 389—
395
Задача Штурма—Лнувнлля 425
Замкнутая траектория 124—127
Затухание 466
Изменение масштаба зависимой перемен-
ной 335
Интеграл,
асимптотическое разложение 57—115,
373, 378
движения 124
Интеграл Лапласа 89, 91, 95, 96, 97, 103,
373
обобщенный 69, 86, 106
интегрирование, по частям 67—68
Интеграл ошибок 61
Интеграл Фурье 96, 97
главный член 86—87, 88
обобщенный 86
преобразование в интеграл Лапласа 89,
91
Интегральное представление,
решений дифференциальных уравнений
57-58,- 373, 377, 378
функций Эйри 392—393
Интегральное уравнение Фредгольма 476—
479
Интегрирование по частям 62—71
в приложении к функции Эйрн 115, 393
несостоятельность 69, 71, 75, 86, 102, 104
Интегрирующий множитель 57, 331
Исключение первой производной 379—380
Калибровочные функции 20—24, 36
Каноническое представление 429, 461
Колебания пластины 14, 15, 456—459
Комбйнационный резонанс 251, 252
для акустических волн в каналах 442
для гироскопических систем с парамет-
рическим возбуждением 419
при многочастотном возбуждении 239
расчет методом многих маештабЬв 239—
246
расчет методом усреднения “246—250
Консервативные системы 116, 146
Корин характеристического уравнения,
комплексно сопряженные 510
кратные 510—513
Коррекция частоты 129, 215, 220, 226
Краевая задача,
нелинейная 329—341
решение с помощью метода ВКБ 406
с двумя пограничными слоями 317—325
см. также Задача на собственный зна-
чения, Условия разрешимости
Кривая,
интегральная 124—125
наискорейшего спуска 100, 101
см. также Линия нанскорейшего спуска
Лемма Ватсона 74—75, 85, 103, 106, 109
формулировка 74
Линейная комбинация 501 •
Линейная независимость 501— 503 _
Линейные дифференциальные уравнения
499—518
с большим параметром 379—406
с переменными коэффициентами 345—
378
528
Предметный указатель
Линейный оператор 500
Линейный осциллятор с затуханием 146—
160, 203
использование метода многих масшта-
бов 156—158
использование метода усреднения 159—
160
использование методики Линдштедта —
Пуанкаре 153—155
прямое разложение 4 47—148
точное решение 148—152
Линия ианскорейшего спуска 99—101, 108
Линия * постоянной фазы 102, 106
Линия уровня 99
Малые знаменатели 211, 407
в задаче для гироскопических систем
с параметрическим возбуждением 419
в задаче об акустических волнах 442
в задаче о вынужденных колебаниях
для уравнения Дюффинга 211
в задаче о миогочастотном возбуждении
236, 238
для уравнения Матье 255
преобразование к секулярным членам
213 — 214, 444
приводящие к комбинационному резо-
нансу 238, 239, 419, 442
приводящие к первичному резонансу
224, 230 — 231
приводящие к субгармоническому резо-
нансу 213
приводящие к супергармоническому ре-
. зонансу 219
Масштабы 134, 135, 191
влияние на вид разложения 282—285
их комбинация 282, 289
Матрица, невырожденная 428, 461
Матрица-блок, 430 .
Мембрана 407, 426, 482
колебания 446—452
Мероморфная функция 96
Метод ван-дер-Поля 142
Метод ВКБ 277, 305, 406
Метод Лапласа 25, 71 — 86
в приложении к функциям Эйри 115, 393
сравнение с методом стационарной фазы
97
Метод многих масштабов 117, 144, 147,
160, 162, 172—173, 175, 186, 190,
191, 193, 194, 202, 209, 231, 232,
233 — 235, 407, 455
для задачи об акустических волнах
442 — 445
для задачи о линейном осцилляторе
156—158
для краевых задач 276, 289—291
для нахождения вторичных резонан-
сов 21 1 — 224
для нахождения первичных резонан-
сов 224 — 228
для нелинейной гироскопической си-
стемы 414—417
для нелинейных уравнений в частных
производных 300
для систем с квадратичными нелинейно-
стями 182—184
для систем с нелинейностями общего
вида 199— 200
для систем с параметрическим возбуж-
дением 417—420
для уравнения Дюффинга 133—139
для уравнения Матье 268—272
для уравнения Рэлея 167—170
сравнение с методом сращиваемых асимп-
тотических разложений 299—300
упражнения 274 — 275
Метод ианскорейшего спуска (метод пере-
вала) 96—109, 392	.
Метод неопределенных коэффициентов 148.
244
Метод перенормировки 117, 133, 137, 143,
144, 162, 172, 175, 182, 184, 190 ,
для произвольных нелинейных систем
197—199
для системы с квадратичными нелиией^
костями 178—180
для уравнения Дюффинга 132^-133
для уравнения Рэлея 165—167
недостатки 155, 167, 170
Метод растянутых параметров 253, 261,
456
в вырожденной задаче на собственные
значения 434—437 .
в задаче на собственные значения для
уравнения четвертого порядка 462 —
466
в задаче о колебаниях мембраны 446 —
452
в простой задаче на собственные значе-
ния для уравнения второго порядка
432—434
для уравнения Матье 262—266
Метод сращиваемых асимптотических раз-
ложений 276, 299, 300
для простой краевой задачи 291—300
для уравнений с переменными коэф г
фициеитами 305—317
основная идея 285, 291
сравнение с методом многих масшта-
бов 299, 300
Метод стационарной фазы 86—95.
в приложении к функциям Бесселя 373
для интеграла Эйри 115, 393
сравнение с методом Лапласа 97
Метод Уиттекера 262, 266—268, 272
ограничения 268—269
упражнения 274
Метод усреднения 117, 143, 144, 147, 162,
170—173, 175, 209, 228—235
для линейного осциллятора 159—160-
для общего нелинейного уравнения
201—202, 206
для систем с квадратичными нелинейно-
стями 185—186
для случая многочастотного возбужде-
ния 246—250
для уравнения Дюффинга 141 —143,
228—233
для уравнения &1атье 272—274
для уравнения Рэлея 170—172
методика Крылова— Боголюбова— Мит-
ропольского 191 —193 и
недостатки 185—186
обобщенный 160, 186—190, 193, 194
сравнение с методом растянутых пара-
метров 262
упражнения 274—275
Методика Крылова— Боголюбова—Мит-
ропольского 175, 186, 191 —193
Методика Линдштедта—Паункаре 117,
133? 137, 143, 144, 147, 162, 175, 178,
184, 190, 194
в задаче о линейном осцилляторе 153—>
155
для системы с квадратичными нелиней-
ностями 180—182
для уравнения Дюффинга 129—132 ,
недостатки 154, 167, 170
Методика Ньютона—Рафсона^387, 401, 403
Многочастотное возбуждение 236-^252
использование метода многих масшта-
бов 239—246
использование метода усреднения 246—
250
прямое разложение 236—239
Предметный указатель
529
Мода,
акустическая 440, 442
прн колебаниях мембраны 448.
Модуляция амплитуды н фазы 215, 417, 420
Наименее вырожденная форма 279, 391
Неавтономная система 215
Неаналнтнческне функции 195, 204—207
Невырожденное преобразование 428
Нелинейные колебания 290
Неограниченные решения 246, ^268, 271
для уравнения Матье 258, 260
Неоднородные уравнения 407—491
определение 499.
с постоянными коэффициентами, их ре-
шения 513—518.
свойства 505—506
связь с соответствующим однородным
уравнением 505, 506
Неравномерная сходимость прямого, раз-
ложения 282
Неравномерное разложение 40, 117, 122
Неравномерность 40, 130, 147
в разложении 32
для линейного осциллятора 147—152
для простой краевой задачи 278—282
для уравнения ' .Дюффинга 122,	129
для уравнения Рэлея 163
область 34, 40
Несовместные уравнения 416
Неустойчивые движения 222, 228, 258, 261
Неэлемеитарные функции 397
Нормальная форма Флоке 258, 262, 266
Нормальное решение 363, 367
Область,
бесконечная 329
внешняя 297—300
внутренняя 297—390
конечная 289
применимости 285, 288, 298.
См. также Перекрывающиеся области
Обтекание бесконечной пластины 15—17
Обыкновенная точка дифференциального
уравнения 346, 348, 349
решения вблизи нее 349—351
Ограниченные решения уравнения Матье
260
Однородное дифференциальное уравнение,
определение 499
с постоянными коэффициентами, реше-
ния 507—513
свойства 501 — 505
Оператор 500
коммутативный 512
сопряженный 460
четвертого порядка 459
Операторный метод 148
Операция,, не обоснованная 41, 280
Определяющее уравнение 352
Особая точка,
изолированная 347
иррегулярная 349
решения вблизи нее 363—375
классификация 348—349
на бесконечности 361 — 363
регулярная 349, 426, 450
решения вблизи нее 351—363
устранимая
Осциллятор с самовозбуждением 161 — 173
использование метода многих масшта-
бов 167 — 170
использование метода перенормировки
165—167
использование метода усреднения 170—
172
прямое разложение 162—165
Парабола 144
Параметр 20,
безразмерный 11, 12, 13—14, 15, 17
в уравнении Дюффинга 117
малый, при старшей производной 276—
344
Параметр расстройки 42, 213, 219, 225,
240, 241, 270, 4-19, 442
в случае первичного резонанса 225
в случае субгармонического резонанса
213
в случае супергармоинческого резо-
нанса 219
для акустических воли в канале 442
для гироскопических систем с пара-
метрическим возбуждением 419
для уравнения Матье 270
прн комбинационном резонансе 240, 241
Параметрическое возбуждение 253
гироскопической системы 417—420
системы с двумя степенями свободы 275.
См. также Уравнение Матье
Первичный резонанс 238
исследование методом многих масшта-
бов 224 — 228
Исследование методом усреднения 232—
233
определение 211
Переключение с одного разложения на дру-
- гое 298
Перекрывающиеся области 285—289, 297,
298
Перенос граничных условий 438—439, 446
Переходная характеристика 154, 158, 160,
162, 173
Переходные кривые 262—274
периодические 261, 262
Периодическое решение 124—126, 154* 164
в случае первичного резонанса 227
в случае субгармонического резонанса
216
в случае супергармоинческого резонанса
221
произвольной нелинейной системы 198
уравнения Дюффинга 127—129, 131, 132
уравнения Матье 258—259
см. также Предельный цикл
Пограничный слой 281
внутренний 313—317,	334, 339—341
высшне приближения 300—305 .
определяющие уравнения 17
Подобные матрицы 257
Подынтегральное выражение, 128
разложение в ряд 58—62
Полиномы Лежандра 115
Полная энергия 123—124
Положение равновесия 116, 174, 1.94
Порядок,
величины 9
дифференциального уравнения 499
члена 3$, 224
Правило Крамера 24.4, 411
Правило Лопиталя 22—23, 64
Преобразование,
интегрального уравнения к системе ал-
гебраических уравнений 478—479
невырожденное 397, 428, 461, 472
обратное 429
регулярность 399
Преобразование Лангера 276, 380, 390,
396—400
Преобразование Лапласа 57, 67
модифицированное 392
Преобразование Лиувилля—Грина 380»
383 — 385, 397, 398
Преобразование растяжения 276, 282,
292, 295, 311, 314, 318, 321, 326,
335, 390
См. также Внутренняя переменная
530
Предметный указатель
Преобразование сжатия 329, 330
Преобразование Фурье 57, 68
Преобразование Эйлера 29, 145
Приведенная масса 13
. Признак Даламбера 18; 26, 27, 59, 61, 65,
67, 71. 73, 151, 152, 347, 351. 354,
360, 369, 372
Принцип асимптотического сращивания,
См. Сращивание
Принцип сращивания Ван-Дайка 303—304
Принцип суперпознцнн 119, 120, 183,
196, 421, 501. 504
Производная по направлению 98
Промежуточная переменная 289
Промежуточное разложение 284, 287, 289
для простой краевой задачи 302 — 303
Пружина 10, 11, 146, 174, 175
Прямое разложение 117, Г47, 162, 175,/
195, 209, 236, 253, 277	'
в задаче для уравнения Дюффинга в слу-
чае вынужденных колебаний 209—211
в задаче об акустических волнах в ка-
нале 438—442
в задаче о Многочастотном-возбуждении
236—239
для линейного осциллятора 147—148
для произвольных нелинейных систем
195-197
для простой краевой задачи 277
для систем с квадратичными нелинейно-
стями 175—178
для тригонометрической функции 149—
150
для уравнения Дюффинга 117—123
для уравнения Матье 253—255, 262
для уравнения Рэлея 162—165
для экспоненты 149
причины несостоятельности 127, 151,
152, 163—164
Радиальная нагрузка 14, 15
Разделение переменных 123, 126, 168,
188, 205, 306, 308, 327, 336, 379,
384, 398
в задаче о колебаниях мембраны 447
в задаче об акустических волнах в ка-
нале 439—441, 443
Разложение 17—20
неравномерное 32, 122
перекрывающееся 285
подынтегральных функций 58—62.
См. также Асимптотическое разложе-
ние, Внутреннее разложение, Внеш-*
нее разложение
Растянутая переменная 276, 282, 292
См. также Внутренняя переменная
Расширенная матрица 410
Резонанс 134, 235
одновременный 241, 251, 252
см. также Комбинационный резонанс,
^.-Первичный резонанс, Субгармоннчес-
. кий резонанс, Супергармоннческий ре-
зонанс
Резонансные частоты 209, 211
Рекуррентные соотношения 350, 354, 360,
365, 367,. 369, 371
Решение в форме фробеннуса 353—355(
361, 366
Ряд,
См. Асимптотический ряд. Геометриче-
ская прогрессия. Ряд Тейлора
Ряд Лорана 347, 517
Ряд Тейлора 18—19, 58, 60, 61, 81, 82,
83, 85, 88, 92, 93, 107, 116, 132,
166, 179, 346 — 347, 349, 351
для косинуса 149—152
. для экспоненты 149, 150
разложение с целью переноса гранич-
ных условий 438—439, 446
Ряд Фурье 119, 198, 200, 201, ,448, 482
для трнгонометрнческнх функций 494 —
Самосопряженный 433, 435 444, 484
алгебраическая система 479
дифференциальное уравнение четвер-
того порядка 454—455. 464
задача для уравнения в частных произ-
водных 482, 483
задача с внутренними граничными усло-
виями 475—476
интегральное уравнение 477
матрица 412 ’
оператор 427, 460
система дифференциальных уравнений
второго порядка 424, 430
система уравнений первого порядка -470
уравнение с регулярной особой точкой
449—450
Седловая точка 98—101, 105—107, 108, 124
Секулярные члены 123
более сложный вид при увеличении по-
рядка 148
их исключение 130, 138, 153, 155, 157,
158, 180—182, 193, 200, 407
в решении для произвольной нелиней-
ной системы 198
в решении для систем с квадратичными
нелинейностями 180, 181, 183
в решении уравнения Дюффинга 123,
130-133, -135
в решении уравнения Матье 263—266
в решении уравнения Рэлея 164,
166, 168
в случае вынужденных колебаний
Для уравнения Дюффинга 211
не приводящие к неравномерности 289
Сепаратрисы 124
Сила инерции 11
Символический метод 513—518
Символы порядка 24—25
Симметричная матрица 412, 479
Симметричное ядро 477
Симметрия 435, 448
Системы с квадратичными нелинейностями
174-194, 236, 250
прямое разложение 175—178
решение методом многих масштабов 182—
184
решение методом перенормировки 178—
180
решение методом усреднения 185—186
решение обобщенным методом усредне-
ния 186—190
решение с помощью методики Крылова —
Боголюбова — Митропольского 191 —
193 .
решение с помощью методики Линдш-
тедта—П уанкаре 180—182
случай ' ненулевого внешнего воздей-
ствия 233—235
См. также Многочастотное возбуждение
Системы со слабой нелинейностью общего
вида 195—207
прямое разложение 195—197
решение методом многих масштабов
199—200
решение методом перенормировки 197—
199
решение методом усреднения 201—202
Скачок характеристики 221, 222, 227, 228
Собственное значение матрицы 257, 258
Собственный вектор матрицы 257
Составное разложение 298—300
Предметный указатель
531
I
для задачи с двумя пограничными слоями
324—325
для задачи с точкой поворота 313, 316,
317
Для многовонной задачи 328
для нелинейной задачи 333
для уравнения с переменными коэффи-
циентами 307, 310
для уравнения с постоянными коэффи-
циентами 304—305
Составное тело 473
Сращивание
в многозонной задаче 327—328
основная идея 285—289
принцип 286
промежуточное 289, 302—303
сравнение промежуточного и прямого
303
См. также Принцип сращивания Ван-
Дайка
Сращивание внешнего и внутреннего раз-
ложений
в задача» с точиамн поворота 392—395
в многозонной задаче 327—328
в простой краевой задаче 302—304
для задачи с двумя пограничными слоями
319—324
для нелинейной задачи 332—333, 337—
340
для уравнений с переменными коэффи-
циентами 307, 309—310, 312—313,
315—316
Стационарная точка 70, 85, 87, 88, 91, 92,
93, 94, 98, 124, 373
вклад в главный член' 94
Стационарное решение 154, 216, 221, 241
Стержень, покрытый оболочкой 473
Стоксовы линии н поверхности 276
Субгармонический резонанс 213—219, 238,
определение 216
Субнормальное решение 363, 367—369
Супергармоннческнй резонанс 219—222,
231-232, 238
определение 216
Существенно особая точка 20, 349
на бесконечности 363, 364, 370
решения вблизи нее 363—375
Сходимость 27
асимптотического ряда 31
Неравномерная 282
радиус 347,, 349
см. также Признак Даламбера
Тензорная запись 479
Теорема Коши 89, 97, ЮЗ
Теорема существования 500, 503
Теория Флоке 253, 25S—262. 267
Теплообмен в канале 402, 406
Течение
вблизи волнистой стенки 489
ламинарное 402
сжимаемой жидкости 466
турбулентное 406
ем. также Акустнчесине волны
Течение Стокса—Озеена 17
Точка ветвления 103
Точки перегиба 81
Точки перехода 27S, 383, 38 9
Точное решение
алгебраических уравнений 38, 41
в случае линейного осциллятора 148—152
для простой задачи на собственные зна-
чения 279
уравнения Дюффинга 123—129
Точность асимптотического ряда 28—29
Точность решения, построенного по методу
возмущений 387, 388, 401, 403
Траектории 124—126
Транспонирование 411, 468, 471
Трансцендентные уравнения 51 — 54
Тригонометрические формулы 492—498
Ударный слой 276, 334, 341
Упругие волны 438
Уравнение Бесселя
в нормальной форме 380
модифицированное 377
n-го порядка 378, 447
нулевого порядка 360
Уравнение Ван-дер-Поля 162, 172
см. также Осциллятор с самовозбужде-
нием
Уравнение Дюффинга 116—143, 175, 198,
202
вариация произвольных постоянных
139-141
прямое разложение 117—123
решение методом многих масштабов
133-139
решение методом перенормировки ЮЗ-
ЮЗ
решение методом усреднения 141 — 143
решение с помощью методики Линдш-
тедта— Пуанкаре 129—132
случай вынужденных колебаний 208—235
точное решение 123—129
фазовая плоскость 124—125
явление скачка 221 — 222, 227—228
Уравнение Лиувилля 380
Уравнение Матье 253—275
прямое разложение 253—255
решение методом многих масштабов
268—272
решение методом растянутых парамет-
ров 262—266
решение методом Уиттекера 266—268
решение методом усреднения 272—274
Уравнение Рэлея 161, 165, 199, 203
случай вынужденных колебаний 234
см. также Осциллятор с самовозбужде-
нием
Уравнение Эйлера 351—353, 355, 358, 359
Уравнение Эйри 391, 396, 399, 404
Уравнения Коши—Римана 97—99
Уравнения Навье—Стокса 15, 16, 300
Уравнения с большим параметром 379—406
ВКБ-прнблнженне 380—383
задачи на собственные значения 385—389
задачи на собственные значения с точ-
ками поворота 400—404
преобразование Лангера 396—400
' преобразование Лиуеилля—Грина 383—
385
случай медленно меняющихся коэффи-
циентов 389
Уравнения с медленно меняющимися ко-
эффициентами 389
Уравнении с постоянными коэффициентами
неоднородные 513—518
однородные 507—513
Уравнения, совместные 408, 409
Условия разрешимости 290, 407—491
в случае общей краевой задачи для си-
стемы дифференциальных уравнений
первого порядка 469—473
для алгебраических уравнений 408—414
для граничных условий общего вида
426—432
для дифференциального уравнения чет-
вертого порядка с граничными усло-
виями общего вида 459—462
для интегральных уравнений 476—479
для системы дифференциальных уравне-
ний с внутренними граничными усло-
виями J473—476
532
Предметный указатель
для системы обыкновенных дифферен-
циальных уравнений 466—469
для системы обыкновенных дифферен-
циальных уравнений второго порядка
420 — 432
для системы уравнений четвертого по-
рядка 452 — 459 -
для уравнений в частных прфнзводных
479 — 484
достаточность 478
простой модельный пример 421—422
Успокоитель колебаний 146
Устойчивость
пограничного слоя '407—408, 490, 491
пространственного течения 455
См. также Переходные кривые
Устранимая особая точка 376
фазовая плоскость
для уравнения Дюффинга 124—126
для уравнения Рэлея 164, 165
Формула Грина 427, 431, 436, 460, 462,
481, 483
Формула Лагранжа 427
Фундаментальная система решений 504
Функции Бесселя
асимптотические разложения 113—114,
374, 378, 403
интегральное представление 102, 373,
377, 378
модифицированные 377
n-го порядка 448
нулевого порядка 30, 102—104, 360 —
361, 369-374
нули 51 — 56, 448
первого порядка 357—'360, 378
порядка 1/2 404
порядка 1/3 402, 404
Функция, дополнительная 506
Функция тока 455
Функции Эйри 391, 395, 402
второго рода 115
интегральное представление 104, 392
первого рода 104—108, 113
связь с функциями Бесселя 402, 404
Характеристический показатель 259, 261,
262, 268
Характеристический полином 507—513
Характерный предел 297, 306, 309, 311,
315, 318, 321, 330, 335, 341, 343, 393
случай нескольких характерных пре-
делов 325—328
Целые степени параметра 38
Центр, притягивающий 12
Частота
иелииейиой системы 178, 198
собственная 10, 175
Численное интегрирование 335, 387, 401,
403
Число Рейнольдса 17
Экспоненциальная форма разложения 381
Электромагнитные волны 438
Электрон 9
Элементарная функция 397
Эллиптический интеграл
второго рода НО
первого рода 59, 127
Эрмитова матрица 412
Ядро, 'Вырожденное 478
ОГЛАВЛЕНИЕ
Предисловие редактора перевода................................... 5
Предисловие.....................................................  8
Глава 1. Введение.............................................    9
1.1.	Анализ размерностей.....................................  9
1.2.	Разложения.............................................. 17
1.3.	Калибровочные функции................................... 20
1.4.	Символы порядка ........................................ 24
1.5.	Асимптотические ряды...................................  25
1.6.	Асимптотические разложения и последовательности......... 29
1.7.	Сравнение сходящихся и асимптотических рядов............ 30
1.8.	Простейшие действия над асимптотическими разложениями 31
Упражнения................................................... 32
Глава 2. Алгебраические уравнения. .	  35
2.1.	Квадратные уравнения..................................... 35
2.2.	Кубические уравнения.....................................  45
2.3.	Уравнения высших порядков . ............................. 49
2.4.	Трансцендентные уравнения ............................... 51
Упражнения....................................................  54
Глава 3. Интегралы............................................... 57
3.1.	Разложение подынтегральной функции...................... 58
3.2.	Интегрирование по частям................................ 62
3.3.	Метод Лапласа .......................................... 71
3.4.	Метод стационарной фазы ................................ 86
3.5.	Метод наискорейшего спуска.............................. 96
Упражнения.................................................. ПО
Глава 4. Уравнение Дюффинга................................... 116
4.1.	Прямое разложение .................................... 117
4.2.	Точное решение ....................................... 123
4.3.	Методика Линштедта—Пуанкаре........................... 129
4.4.	Метод перенормировки.................................. 132
4.5.	Метод многих масштабов................................ 133
4.6. Вариация произвольных постоянных........................ 139
4.7. Метод усреднения ....................................... 141
Упражнения................................................... 143
Глава б. Линейный осциллятор с затуханием..................... 146
5.1.	Прямое разложение ........................‘........... 147
5.2.	Точное решение..........'............................. 148
5.3.	Методика Линштедта—Пуанкаре .......................... 153
5.4.	Метод многих масштабов................................ 156
5.5.	Метод усреднения ..................................... 159
Упражнения................................................. 160
Оглавление
534
Глава 6, Колебательные системы с самовозбуждением ...
6.1.	Прямое разложение ..................................
6.2.	Метод перенормировки...........,....................
6.3.	Метод многих масштабов.......	.............
6.4.	Метод усреднения ...................................
Упражнения........... ...................................
Глава 7. Системы с квадратичными и кубическими нелинейностями
7.1.	Прямое разложение ...................................
7.2.	Метод перенормировки...........................
7.3.	Методика Линштедта—Пуанкаре ........................
7.4.	Метод многих масштабов..............................
- 7.5. Метод усреднения ....................................
7.6. Обобщенный метод усреднения..........................
7.7. Метод Крылова—Боголюбова—Митропольского.............
Упражнения..........................'.......... .........
Глава 8. Колебательные системы со слабой нелинейностью
общего вида..........................................
8.1.	Прямое разложение ...................................
8.2.	Метод перенормировки ................................
8.3.	Метод многих масштабов...............................
8.4.	Метод усреднения ....................................
8.5.	Приложения...........................................
Упражнения...............................................
Глава 9. Уравнение Дюффинга. Случай вынужденных колебаний
9.1.	Прямое разложение ..................................
9.2.	Метод многих масштабов..............................
9.3.	Метод усреднения ...................................
Упражнения...............................................
Глава 10. Многочастотное возбуждение.........................
10.1.	Прямое разложение...................................
10.2.	Метод многих масштабов .............................
10.3.	Метод усреднения . ,'...............................
Упражнения ...............................................
Глава 11, Уравнение Матье....................................
11.1.	Прямое разложение..........:...........'............
11.2.	Теория Флоке .............................
11.3.	Метод растянутых параметров.....................- . .
11.4.	Метод Уиттекера ....................................
11.5.	Метод многих масштабов . . .-.......................
11.6.	Метод усреднения............'.......................
Упражнения................................................
Глава 12, Задачи с пограничным слоем.........................
12.1.	Простой пример ................................
12.2.	Метод многих масштабов..............................
12.3.	Метод сращиваемых асимптотических разложений ......
12.4.	Высшие приближения..................................
12.5.	Уражнения с переменными коэффициентами..............
12.6.	Задачи с двумя пограничными слоями . ...............
12.7.	Многозонная задача..................................
12.8.	Нелинейные задачи...................................
Упражнения.....................................L..........
161
162.
165
167
170
172
174
175
178
180
182
185
186
191
194
195
195 .
197
199
2Э1
202
206
208
209
211
223
233
236
236
239
246
250
253
253
255
262
266 ’
268
272
274
276
277
289
291
300
305
317
325
329
341


я
Li
Оглавление	j--	535
Глава 13. Линейные уравнения с переменными коэффициентами 345
13.1.	Скалярные уравнения первого порядка........................ 346
13.2.	Уравнения второго порядка.................................. 349
13.3.	Решение в окрестности регулярной особой точки.............. 351
13.4.	Сингулярность в бесконечно удаленной точке . .............. 361
13.5.	Решение в окрестности иррегулярной особой точки ...	363
Упражнения.....................................................   375
Глава 14, Дифференциальные уравнения с большим параметром 379
14.1.	ВКБ-приближение ................................  .	380
14.2.	Преобразование Лиувилля—Грина .............................383
14.3.	Задачи на собственные значения............................ 385
14.4.	Уравнения с медленно меняющимися-коэффициентами ....	389 ’
14.5.	Уравнения с точкой поворота............................... 389
14.6.	Преобразование Лангера.................................... 396
14.7.	Задачи на собственные значения для уравнений с точкой по-
~ _ ворота....................................................... 400
Упражнения.....................................................   404
Глава "16. Условия разрешимости ..................................... 407
15.1.	Алгебраические уравнения.................................. j4O8
15.2.	Нелинейные колебания гироскопических систем с двумя сте-
пенями свободы ............................................ 414
15.3.	Гироскопические системы с параметрическим возбуждением . .	417
15.4.	Краевые задачи для дифференциальных уравнений второго
порядка...................................................  420
15.5.	Граничные условия общего вида. ...........................  426
15.6.	Простая задача на собственные значения..................... 432
15.7.	Вырожденная задача на собственные значения ......	434
15.8.	Звуковые волны в канале с волнистыми стенками.............. 438
15.9.	Колебания мембраны, близкой по форме к кругу............... 446
15.10.	Краевая задача для дифференциального уравнения четвертого
порядка..................................................   452
15.11.	Краевая задача для уравнения четвертого порядка с гранич-
ными условиям? общего вида ...............................  459
15.12.	Задача на собственные значения для дифференциального урав-
нения четвертого порядка . ...............................  462
15.13.	Система дифференциальных уравнений первого порядка. . .	466
15.14.	Общая краевая задача..для системы обыкновенных дифферен-
циальных уравнений......................................... 469
15.15.	Краевые задачи с внутренними граничными условиями . . . .	473
15.16.	Интегральные уравнения ................................... 476
15.17.	Дифференциальные уравнения с частными производными . . .	479
Упражнения......................................................  485
Приложение А. Тригонометрические формулы . .......................... 492
Приложение Б. Линейные обыкновенные дифференциальные
уравнения....................................................... 499
Литература........................................................... 519
Литература, добавленная редактором перевода.......................... 523
Предметный указатель................................................  526
53
Г/
:	'	УВАЖАЕМЫЙ ЧИТАТЕЛЬ!
Ваши замечания о содержании книги, ее оформ-
'	лении, качестве перевода и другие просим присылать
по адресу: 129820, Москва, И-110, ГСП, 1-й Рижский
пер., 2, издательство-«Мир».
Г
Али Найфэ
ВВЕДЕНИЕ В МЕТОДЫ ВОЗМУЩЕНИЙ
Старший научный редактор А. А. Бряндннская
Художник А. Я. Мусин
Художественный редактор В. И. Шаповалов '
Технический редактор В., П. Сизова	.
Корректор Т. П. Пашковская
ИБ № 3611	1
Сдано в набор 12.01.84. Подписано к печати 29.06.84.	j
Формат бОХЭО'/ц. Бумага типографская № 2.	я
Гарнитура литературная. Печать высокая. Объем бум. л. 16,75	|
Усл. печ. л. 33,50. Усл. кр-отт. 33,59. Уч.-изд. л. 27,92. Изд. № 1/2701. Я
Тираж 1С500 экз. Зак. № 35. Цена 2 р. 30 к.	1
ИЗДАТЕЛЬСТВО «МИР»	j
129820, Москва, И-110, ГСП, 1-й Рижский пер., 2.
Ленинградская типография № 6 ордена Трудового Красного
Знамени Ленинградского объединения «Техническая книга»
нм. Евгении Соколовой Союзполнграфпрома прн Государственном
комитете СССР по делам издательств, полиграфии и книжной
торговли.
193144, г. Ленинград, ул. Моисеенко, 10.