Курс дифференциального и интегрального исчислении. Том 2

Автор: Фихтенгольц Г.М.
Теги: математика
Похожие
Курс дифференциального и интегрального исчисления. Том 2.
Курс дифференциального и интегрального исчисления. Том 2
Курс дифференциального и интегрального исчисления. Том 3.
Курс дифференциального и интегрального исчисления. Том 3
Текст
                    Г.М. Фихтенгольц
КУРС ДИФФЕРЕНЦИАЛЬНОГО И ИНТЕГРАЛЬНОГО ИСЧИСЛЕНИЯ
ТОМ 2
Содержание
ГЛАВА ВОСЬМАЯ. ПЕРВООБРАЗНАЯ ФУНКЦИЯ
(НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ)
§ 1. Неопределенный интеграл и простейшие приемы его вычисления	11
263.	Понятие первообразной функции (и неопределенного интеграла) 11
264.	Интеграл и задача об определении площади	14
265.	Таблица основных интегралов	17
266.	Простейшие правила интегрирования	18
267.	Примеры	19
268.	Интегрирование путем замены переменной	23
269.	Примеры	27
270.	Интегрирование по частям	31
271.	Примеры	32
§ 2. Интегрирование рациональных выражений	36
272.	Постановка задачи интегрирования в конечном виде	36
273.	Простые дроби и их интегрирование	37
274.	Разложение правильных дробей на простые	38
275.	Определение коэффициентов. Интегрирование правильных дробей 42
276.	Выделение рациональной части интеграла	43
277.	Примеры	47
§ 3. Интегрирование некоторых выражений, содержащих радикалы	50
278.	Интегрирование выражений вида Щ х,т\	 . Примеры	50
^ \ ух + 8 J
279.	Интегрирование биномиальных дифференциалов. Примеры	51
280.	Формулы приведения	54
281.	Интегрирование выражений вида Я\х,л1ах2 + Ьх + с). Подстановки -^
Эйлера
282.	Геометрическая трактовка эйлеровых подстановок	59
283.	Примеры	60
284.	Другие приемы вычисления	66
285.	Примеры	72
§ 4. Интегрирование выражений, содержащих тригонометрические и	74

показательную функции
286.	Интегрирование дифференциалов i?(sin x, cos x) dx	74
287.	Интегрирование выражений sinv xcosKx	76
288.	Примеры	78
289.	Обзор других случаев	83
§ 5. Эллиптические интегралы	84
290.	Общие замечания и определения	84
291.	Вспомогательные преобразования	86
292.	Приведение к канонической форме	88
293.	Эллиптические интегралы 1-го, 2-го и 3-го рода	90
ГЛАВА ДЕВЯТАЯ. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
§ 1. Определение и условия существования определенного интеграла	94
294.	Другой подход к задаче о площади	94
295.	Определение	96
296.	Суммы Дарбу	97
297.	Условие существования интеграла	100
298.	Классы интегрируемых функций	101
299.	Свойства интегрируемых функций	103
300.	Примеры и дополнения	105
301.	Нижний и верхний интегралы как пределы	106
§ 2. Свойства определенных интегралов	108
302.	Интеграл по ориентированному промежутку	108
303.	Свойства, выражаемые равенствами	109
304.	Свойства, выражаемые неравенствами	110
305.	Определенный интеграл как функция верхнего предела	115
306.	Вторая теорема о среднем значении	117
§ 3. Вычисление и преобразование определенных интегралов	120
307.	Вычисление с помощью интегральных сумм	120
308.	Основная формула интегрального исчисления	123
309.	Примеры	125
310.	Другой вывод основной формулы	128
311.	Формулы приведения	130
312.	Примеры	131
313.	Формула замены переменной в определенном интеграле	134

314.	Примеры	135
315.	Формула Гаусса. Преобразование Ландена	141
316.	Другой вывод формулы замены переменной	143
§ 4. Некоторые приложения определенных интегралов	145
317.	Формула Валлиса	145
318.	Формула Тейлора с дополнительным членом	146
319.	Трансцендентность числа е	146
320.	Многочлены Лежандра	148
321.	Интегральные неравенства	151
§ 5. Приближенное вычисление интегралов	153
322.	Постановка задачи. Формулы прямоугольников и трапеций	153
323.	Параболическое интерполирование	156
324.	Дробление промежутка интегрирования	158
325.	Дополнительный член формулы прямоугольников	159
326.	Дополнительный член формулы трапеций	161
327.	Дополнительный член формулы Симпсона	162
328.	Примеры	164
ГЛАВА ДЕСЯТАЯ. ПРИЛОЖЕНИЯ ИНТЕГРАЛЬНОГО
ИСЧИСЛЕНИЯ К ГЕОМЕТРИИ, МЕХАНИКЕ И ФИЗИКЕ
§ 1. Длина кривой	169
329.	Вычисление длины кривой	169
330.	Другой подход к определению понятия длины кривой и ее	171
вычислению
331.	Примеры	174
332.	Натуральное уравнение плоской кривой	180
333.	Примеры	183
334.	Длина дуги пространственной кривой	185
§ 2. Площади и объемы	186
335.	Определение понятия площади. Свойство аддитивности	186
336.	Площадь как предел	188
337.	Классы квадрируемых областей	190
338.	Выражение площади интегралом	192
339.	Примеры	195
340.	Определение понятия объема. Его свойства	202
341.	Классы тел, имеющих объемы	204

342.	Выражение объема интегралом	205
343.	Примеры	208
344.	Площадь поверхности вращения	214
345.	Примеры	217
346.	Площадь цилиндрической поверхности	220
347.	Примеры	222
§ 3. Вычисление механических и физических величин	225
348.	Схема применения определенного интеграла	225
349.	Нахождение статических моментов и центра тяжести кривой	228
350.	Примеры	229
351.	Нахождение статических моментов и центра тяжести плоской
фигуры
352.	Примеры	232
353.	Механическая работа	233
354.	Примеры	235
355.	Работа силы трения в плоской пяте	237
356.	Задачи на суммирование бесконечно малых элементов	239
§ 4. Простейшие дифференциальные уравнения	244
357.	Основные понятия. Уравнения первого порядка	244
358.	Уравнения первой степени относительно производной. Отделение _.,
переменных
359.	Задачи	247
360.	Замечания о составлении дифференциальных уравнений	253
361.	Задачи	254
ГЛАВА ОДИННАДЦАТАЯ. БЕСКОНЕЧНЫЕ РЯДЫ С
ПОСТОЯННЫМИ ЧЛЕНАМИ
§ 1. Введение	257
362.	Основные понятия	257
363.	Примеры	258
364.	Основные теоремы	260
§ 2. Сходимость положительных рядов	262
365.	Условие сходимости положительного ряда	262
366.	Теоремы сравнения рядов	264
367.	Примеры	266
368.	Признаки Коши и Даламбера	270

369.	Признак Раабе	272
370.	Примеры	274
371.	Признак Куммера	277
372.	Признак Гаусса	279
373.	Интегральный признак Маклорена—Коши	281
374.	Признак Ермакова	285
375.	Дополнения	287
§ 3. Сходимость произвольных рядов	293
376.	Общее условие сходимости ряда	293
377.	Абсолютная сходимость	294
378.	Примеры	296
379.	Степенной ряд, его промежуток сходимости	298
380.	Выражение радиуса сходимости через коэффициенты	300
381.	Знакопеременные ряды	3 02
382.	Примеры	303
383.	Преобразование Абеля	305
384.	Признаки Абеля и Дирихле	307
385.	Примеры	308
§ 4. Свойства сходящихся рядов	313
386.	Сочетательное свойство	313
387.	Переместительное свойство абсолютно сходящихся рядов	315
388.	Случай неабсолютно сходящихся рядов	316
389.	Умножение рядов	320
390.	Примеры	323
391.	Общая теорема из теории пределов	325
392.	Дальнейшие теоремы об умножении рядов	327
§ 5. Повторные и двойные ряды	329
393.	Повторные ряды	329
394.	Двойные ряды	333
395.	Примеры	338
396.	Степенной ряд с двумя переменными; область сходимости	346
397.	Примеры	348
398.	Кратные ряды	350
§ 6. Бесконечные произведения	350
399.	Основные понятия	350

400.	Примеры	351
401.	Основные теоремы. Связь с рядами	353
402.	Примеры	356
§ 7. Разложения элементарных функций	364
403.	Разложение функции в степенной ряд; ряд Тейлора	364
404.	Разложение в ряд показательной, основных тригонометрических
функций и др.
405.	Логарифмический ряд	368
406.	Формула Стерлинга	369
407.	Биномиальный ряд	371
408.	Разложение синуса и косинуса в бесконечные произведения	374
§ 8. Приближенные вычисления с помощью рядов. Преобразование рядов 378
409.	Общие замечания	378
410.	Вычисление числа п	379
411.	Вычисление логарифмов	381
412.	Вычисление корней	383
413.	Преобразование рядов по Эйлеру	3 84
414.	Примеры	386
415.	Преобразование Куммера	388
416.	Преобразование Маркова	392
§ 9. Суммирование расходящихся рядов	394
417.	Введение	394
418.	Метод степенных рядов	396
419.	Теорема Таубера	398
420.	Метод средних арифметических	401
421.	Взаимоотношение между методами Пуассона—Абеля и Чезаро	403
422.	Теорема Харди—Ландау	405
423.	Применение обобщенного суммирования к умножению рядов	407
424.	Другие методы обобщенного суммирования рядов	408
425.	Примеры	413
426.	Общий класс линейных регулярных методов суммирования	416
ГЛАВА ДВЕНАДЦАТАЯ. ФУНКЦИОНАЛЬНЫЕ
ПОСЛЕДОВАТЕЛЬНОСТИ И РЯДЫ
§ 1. Равномерная сходимость	419
427.	Вводные замечания	419

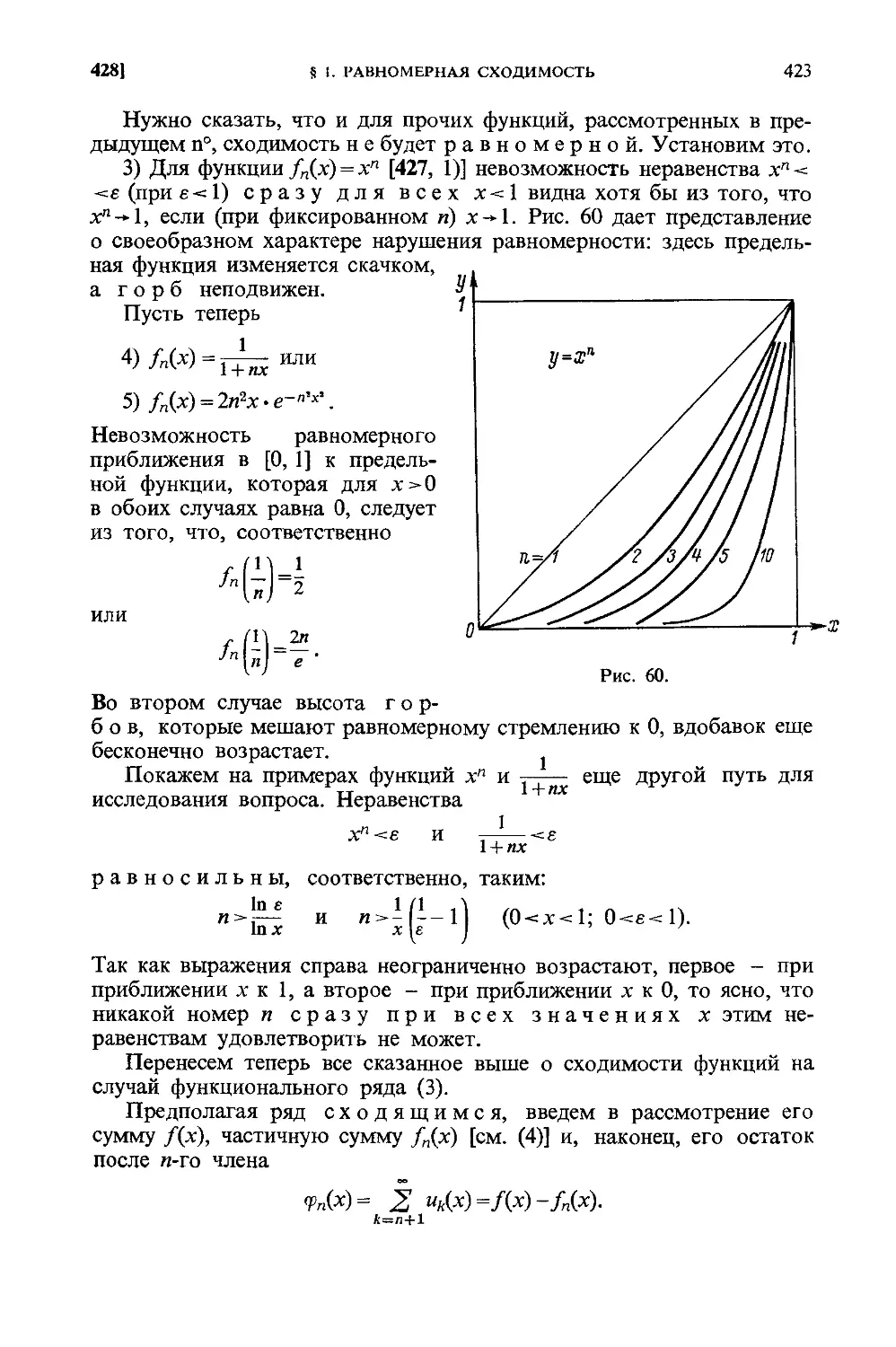
428.	Равномерная и неравномерная сходимости	421
429.	Условие равномерной сходимости	425
430.	Признаки равномерной сходимости рядов	427
§ 2. Функциональные свойства суммы ряда	430
431.	Непрерывность суммы ряда	430
432.	Замечание о квази-равномерной сходимости	432
433.	Почленный переход к пределу	434
434.	Почленное интегрирование рядов	436
435.	Почленное дифференцирование рядов	438
436.	Точка зрения последовательности	441
437.	Непрерывность суммы степенного ряда	444
438.	Интегрирование и дифференцирование степенных рядов	447
§ 3. Приложения	450
439.	Примеры на непрерывность суммы ряда и на почленный переход к
пределу
440.	Примеры на почленное интегрирование рядов	457
441.	Примеры на почленное дифференцирование рядов	468
442.	Метод последовательных приближений в теории неявных функций 474
443.	Аналитическое определение тригонометрических функций	477
444.	Пример непрерывной функции без производной	479
§ 4. Дополнительные сведения о степенных рядах	481
445.	Действия над степенными рядами	481
446.	Подстановка ряда в ряд	485
447.	Примеры	487
448.	Деление степенных рядов	492
449.	Числа Бернулли и разложения, в которых они встречаются	494
450.	Решение уравнений рядами	498
451.	Обращение степенного ряда	502
452.	Ряд Лагранжа	505
§ 5. Элементарные функции комплексной переменной	508
453.	Комплексные числа	508
454.	Комплексная варианта и ее предел	511
455.	Функции комплексной переменной	513
456.	Степенные ряды	515
457.	Показательная функция	518

458.	Логарифмическая функция	520
459.	Тригонометрические функции и им обратные	522
460.	Степенная функция	526
461.	Примеры	527
§ 6. Обвертывающие и асимптотические ряды. Формула Эйлера—Маклорена 531
462.	Примеры	531
463.	Определения	533
464.	Основные свойства асимптотических разложений	536
465.	Вывод формулы Эйлера—Маклорена	540
466.	Исследование дополнительного члена	542
467.	Примеры вычислений с помощью формулы Эйлера—Маклорена 544
468.	Другой вид формулы Эйлера—Маклорена	547
469.	Формула и ряд Стерлинга	550
ГЛАВА ТРИНАДЦАТАЯ. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
§ 1. Несобственные интегралы с бесконечными пределами	552
470.	Определение интегралов с бесконечными пределами	552
471.	Применение основной формулы интегрального исчисления	554
472.	Примеры	555
473.	Аналогия с рядами. Простейшие теоремы	558
474.	Сходимость интеграла в случае положительной функции	559
475.	Сходимость интеграла в общем случае	561
476.	Признаки Абеля и Дирихле	563
477.	Приведение несобственного интеграла к бесконечному ряду	566
478.	Примеры	569
§ 2. Несобственные интегралы от неограниченных функций	577
479.	Определение интегралов от неограниченных функций	577
480.	Замечание относительно особых точек	581
481.	Применение основной формулы интегрального исчисления.	,оп
Примеры
482.	Условия и признаки существования интеграла	584
483.	Примеры	587
484.	Главные значения несобственных интегралов	590
485.	Замечание об обобщенных значениях расходящихся интегралов 595
§ 3. Свойства и преобразование несобственных интегралов	597
486.	Простейшие свойства	597

487.	Теоремы о среднем значении	600
488.	Интегрирование по частям в случае несобственных интегралов	602
489.	Примеры	602
490.	Замена переменных в несобственных интегралах	604
491.	Примеры	605
§ 4. Особые приемы вычисления несобственных интегралов	611
492.	Некоторые замечательные интегралы	611
493.	Вычисление несобственных интегралов с помощью интегральных ,.. ,
сумм. Случай интегралов с конечными пределами
494.	Случай интегралов с бесконечным пределом	617
495.	Интегралы Фруллани	621
496.	Интегралы от рациональных функций между бесконечными
пределами
497.	Смешанные примеры и упражнения	629
§ 5. Приближенное вычисление несобственных интегралов	641
498.	Интегралы с конечными пределами; выделение особенностей	641
499.	Примеры	642
500.	Замечание по поводу приближенного вычисления собственных
интегралов
501.	Приближенное вычисление несобственных интегралов с	,.„
бесконечным пределом
502.	Использование асимптотических разложений	650
ГЛАВА ЧЕТЫРНАДЦАТАЯ. ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ
ПАРАМЕТРА
§ 1. Элементарная теория	654
503.	Постановка задачи	654
504.	Равномерное стремление к предельной функции	654
505.	Перестановка двух предельных переходов	657
506.	Предельный переход под знаком интеграла	659
507.	Дифференцирование под знаком интеграла	661
508.	Интегрирование под знаком интеграла	663
509.	Случай, когда и пределы интеграла зависят от параметра	665
510.	Введение множителя, зависящего лишь от х	668
511.	Примеры	669
512.	Гауссово доказательство основной теоремы алгебры	680
§ 2. Равномерная сходимость интегралов	682

513.	Определение равномерной сходимости интегралов	682
514.	Условие равномерной сходимости. Связь с рядами	684
515.	Достаточные признаки равномерной сходимости	684
516.	Другой случай равномерной сходимости	687
517.	Примеры	689
§ 3. Использование равномерной сходимости интегралов	694
518.	Предельный переход под знаком интеграла	694
519.	Примеры	697
520.	Непрерывность и дифференцируемость интеграла по параметру 710
521.	Интегрирование интеграла по параметру	714
522.	Применение к вычислению некоторых интегралов	717
523.	Примеры на дифференцирование под знаком интеграла	723
524.	Примеры на интегрирование под знаком интеграла	733
§ 4. Дополнения	743
525.	Лемма Арцела	743
526.	Предельный переход под знаком интеграла	745
527.	Дифференцирование под знаком интеграла	748
528.	Интегрирование под знаком интеграла	749
§ 5. Эйлеровы интегралы	750
529.	Эйлеров интеграл первого рода	750
530.	Эйлеров интеграл второго рода	753
531.	Простейшие свойства функции Г	754
532.	Однозначное определение функции Г ее свойствами	760
533.	Другая функциональная характеристика функции Г	762
534.	Примеры	764
535.	Логарифмическая производная функции Г	770
536.	Теорема умножения для функции Г	772
537.	Некоторые разложения в ряды и произведения	774
538.	Примеры и дополнения	775
539.	Вычисление некоторых определенных интегралов	782
540.	Формула Стерлинга	789
541.	Вычисление эйлеровой постоянной	792
542.	Составление таблицы десятичных логарифмов функции Г	793
Алфавитный указатель	795
Алфавитный указатель

Абелевы интегралы 84
Абель 290, 292, 527
Абеля лемма 306
-	подстановка 69, 608
-	преобразование 305, 312, 403
-	признак равномерной сходимости
ряда 429
-	- сходимости интеграла 564
-	- - ряда 307
-теорема328, 397, 516
Абеля—Пуассона метод
обобщенного суммирования
рядов 401, 409
Абсолютно интегрируемая функция
563, 586
-	сходящееся произведение 356
-	сходящийся несобственный
интеграл 563, 586
--ряд 296, 356, 513
	переместительное свойство 315,
332, 356, 513
	умножение 321, 513
Адамар 300
Аддитивная функция промежутка
225
Аддитивность объема 203
-	площади 188
Алгебраическая часть интеграла,
выделение 68
Амплитуда 252
Аналитическая функция 449, 450,
491,499,502
Аргумент комплексного числа 510
Арксинус, главное значение 525
-	степенной ряд 458, 467, 503, 526
Арктангенс, главное значение 524
-	степенной ряд 368, 457, 524
Архимедова спираль 175, 199
Арцела433,438,743,745
Асимптотический ряд 534, 650, 793
-	- действия 536
-	- дифференцирование 540, 793
-	- единственность 534
-	- интегрирование 538
-	- потенцирование 538
Астроида 175, 184, 185, 202, 210, 218
Барроу 15
Бернулли Иоганн 95
Бернуллиевы числа 494, 541, 703, 704
Бертрана признак 279
Бесконечно малых элементов
суммирование 221, 228
Бесселевы функции 345, 464, 468,
709, 734
Бесселя дифференциальное
уравнение 468, 675
Бета-функция 750
-	- рекуррентная формула 751
-	- связь с гамма-функцией 755
-	- симметричность 751
Биномиальный дифференциал,
интегрирование 51
-	ряд 372, 452, 468, 487, 526
Био и Савара закон 242, 557
Бонне формула 119
Бореля метод обобщенного
суммирования рядов 411
Буняковского неравенство 153, 590
Валлиса формула 145, 352, 371, 377,
613, 704
Ван-дер-Варден 479
Варианта комплексная 511
-	- предел 511
Вейерштрасс 424, 479, 488
Вейерштрасса формула 362, 473, 775,
778
Вивиани кривая 186, 223
Виета 352
Винтовая линия 186
Вороного методы обобщенного
суммирования рядов 408
Выделение алгебраической части
интеграла 68
-	рациональной части интеграла 44
Вычисление интегралов:

n
- j\n(\-2rcosx+ r2)dx 122, 140,464,
673
n
-	JlnsinjB&611, 616, 726, 785
о
00
-	je'^dx 612, 704, 719, 757
cosbxdx 701, 726
614,621,718,742
706, 721, 729, 740, 741
dx 721, 729, 740
699, 717
ou
0
00
a +x
a +x
—	jsmx2dx,jcosx2dx 721,729
о	о
Вычисление определенных
интегралов,
дифференцирование по
параметру 673, 674, 717, 721,
723, 782
—	интегральные суммы 120, 615,
617
—	интегрирование по параметру
679, 718, 721, 722, 732, 756, 786
—	интегрирование по частям 131,
603, 632, 634, 636
—	искусственные приемы 611, 621,
623
—	основная формула интегрального
исчисления 124, 554, 582
—	подстановка 134, 143, 605, 611,
630,631,764
	предельный переход по
параметру 704, 717, 719, 722,
735,788
	разложение в ряд 457—467, 614,
632, 670, 671, 672, 697, 710
Гамма-функция 361, 753
-	Вейерштрасса формула 362, 775
-	Гаусса формула 772
-	график 755
-	дополнения формула 377, 757
-	Коши формула 771
-	Лежандра формула 760, 774
-	логарифмическая производная 473,
770, 774
-	максимумы и минимумы 755, 780
-	определение ее свойствами 760, 762
-	Раабе интеграл 759
-	распространение 780
-	рекуррентная формула 361, 754
-	Стерлинга формула и ряд 792, 793
-	таблицы логарифмов 793
-	Эйлера произведение 758
-	Эйлера—Гаусса формула 361, 754,
769, 775, 780
Гармонический ряд 263, 267, 270, 289
Гаусс 281, 680, 769
Гаусса признак 280
-	формулы 142, 772
Гаусса—Эйлера формула 361, 754,
769, 775, 780
Гельдера методы обобщенного
суммирования рядов 411
Гипербола 177, 195
Гиперболические подстановки 29
-	функции, сопоставление с
тригонометрическими 196, 523
Гипергеометрический ряд 280, 297,
359, 470, 769
Гипергеометрическое
дифференциальное уравнение
470
Гипоциклоида 185
Главное значение аргумента
комплексного числа 510

-	- арксинуса 525
-	- арктангенса 524
-	- логарифма 525
-	- несобственного интеграла 591, 594
-	- степени 526
Гладкая кривая 192
-	поверхность 204
Гольдбах 338
Гульдина теоремы 229, 232
Даламбера признак 271, 278, 296, 513
Дарбу 97
-	интегралы, верхний и нижний 100
-	- как пределы 106
-	суммы, верхняя и нижняя 97
-	теорема 106
Двойной ряд 333, 452
Декартов лист 200
Дзета-функция 264, 287, 362, 469,
769, 777
Дини290,291,292
-	теорема 431
-	- обобщение 657, 695, 711
Дирихле 290, 754, 769
-	признак сходимости интеграла 564
	равномерной ряда 429
	ряда 307
-	разрывный множитель 633, 640, 741
-ряды 309, 451, 469
-	функция 105, 106, 587
Дифференциальное уравнение 244
-	- Бесселя 469, 675
-	- Гипергеометрическое 470
-	- составление 253
Дифференцирование интеграла по
верхнему (нижнему) пределу
116,600
-	- по параметру (дифференцирование
под знаков интеграла) 661, 666,
669, 710, 749
-	ряда, почленное 447, 517
Длина кривой 169, 171
-	- выражение интегралом 169
	производная 169
-	- пространственной кривой 185
е (число), трансцендентность 146
Ермакова признак 285
Живой силы закон 235
Зайдель 424
Знакопеременный ряд 302
-	- оценка остатка 303
Инерции момент плоской фигуры
241
-	- тела 241
Интегральная сумма 97
-	- верхняя, нижняя 97
Интегральный косинус 83, 566, 639,
652
-	логарифм 83, 593, 650
-	признак Маклорена—Коши 282
-	синус 83, 566, 639, 652, 709
Интегралы, не выражающиеся в
конечном виде 36, 52, 83, 86, 92,
459
Интегрирование биномиальных
дифференциалов 51
-	в конечном виде 36
-	интеграл по параметру
(интегрирование под знаком
интеграла) 663, 669, 714, 749
-	по частям 31, 130, 602
-	подстановкой (путем замены
переменнойJ3,135, 143, 602
-	правила 18
-	простых дробей 37
-	радикальных выражений 50, 51, 56,
66, 529
-	рациональных выражений 43
-	ряда почленное 447, 668, 697, 710
-	тригонометрических и
показательных выражений 74,
83, 529
Интегрируемая функция 97
-	- классы 101
-	- свойства 103
-	- с квадратом 590
Интегрируемость предельной
функции 437, 659

Интерполирование параболическое
156
Канторович 642
Кардиоида 178, 185, 200, 218
Каталана постоянная 168, 460, 734
Квадратура 16
Квадрируемая фигура 187
Квадрируемости условие 187, 189,
191
Квази-равномерная сходимость 433
Кеплера уравнение 509
Кнопп 311
Комплексная варианта 511
-	переменная, функция от нее 513,
519, 520, 522, 526
-	плоскость 509
Комплексное число 508
-	- аргумент 510
-	- вещественная часть 508
-	- действия 508
-	- мнимая часть 508
-	- модуль 508
-	- тригонометрическая форма 510
Конус круговой 208, 239, 240, 241
Корень из комплексного числа 511
Корни из вещественных чисел,
вычисление 383
Косинус, аналитическое определение
477
-	бесконечное произведение 377
-	в комплексной области 523
-	гиперболический, бесконечное
произведение 378
-	- степенной ряд 367
-	степенной ряд 367, 523
-	для логарифма 497
Котангенс, Адамара теорема 300
-	гиперболический, разложение на
простые дроби 473
-	разложение на простые дроби 472
-	степенной ряд 484, 496, 524
Коши 290, 502, 591
-	Гёльдера неравенство для
интегралов 151
	рядов 293
-	Маклорена признак 282
-	признаки 270, 290, 561, 584
-теорема321, 326
-	формула 321
Кратный ряд 350
Кубируемое тело 202
Куммера преобразование рядов 388
-	признак 277
Лагерра (Чебышева) многочлены 604
Лагранжа ряд 504
Ламберта ряд 311, 341
Ландау 310
Ландена преобразование 143
Лаплас 508, 701, 721, 729
Лежандр 92, 677, 703, 750, 753, 794
Лежандра многочлены 138, 148, 491,
508, 530, 671
-	формула 760, 774
-	функции К (к), Е (к) 142, 166, 177,
214, 224, 252, 352, 465, 675, 734,
768
--К(к,<р),Е(к,<р)93, 116, 177
Лейбниц 15, 95, 395
Лейбница и Ньютона теорема 15
-	правило 661
-	теорема 302, 308
Лемниската 178, 200, 219
Лиувилль 92
Лобачевский 614
Лобачевского формулы 634, 672
Логарифм комплексного числа 520
Логарифмическая спираль 176, 184,
185
-	функция в комплексной области 520
-	- степенной ряд 368, 453, 457, 484,
503, 522
Логарифмы, вычисление 381
Мажорантный интеграл 685
-	ряд 427
Мажорантных рядов метод 502
Маклорена—Коши признак 281
Маркова преобразование рядов 392
Маятник математический 250

Мертенса теорема 328
Механическая работа 233
Минковского неравенств 293, 590
Многозначные функции комплексной
переменной 513, 521, 524, 525,
526
Множитель сходимости 718, 722
Моавра формула 374
Модуль комплексного числа 509
-	перехода от натуральных
логарифмов к десятичным 382
-	эллиптического интеграла 93
Момент инерции плоской фигуры,
тела 241
Мэшина формула 380
Направление в промежутке 108
Натуральное уравнение кривой 180
-	- эволюты 185
Натуральный логарифм
комплексного числа 520
Начальное значение величины 14
Начальные условия 14, 244
Неабсолютно сходящееся
произведение 356
-	сходящийся интеграл 563, 565, 569,
586
--ряд 296, 304, 336, 516
Неопределенный интеграл 11
-	- геометрическое истолкование 14
-	- свойства 13
-	- существование 116
-	- таблица 17
Неопределенных коэффициентов
метод 42, 45, 67, 91, 470, 488,
492
Непрерывная функция без
производной 479
Непрерывность интеграла по
параметру 660, 675, 678, 710
-	предельной функции 420, 657
-	суммы ряд 430
-	- степенного ряда 444, 446
-	функции комплексной переменной
513
Неравенства для интегралов 151
-	для рядов 293
Неравномерная сходимость
интеграла 683, 689
-	- последовательности, ряда 429, 446
Неравномерности точки 425, 444
Несобственный интеграл от
неограниченной функции 577,
578
-	- с бесконечным пределом 552, 580
-	- сходящийся, расходящийся 552,
578
	аналогия и связь с рядами 558,
586,713
	признаки сходимости 561, 564,
584
	свойства 597
	условия существования 562, 585
Нечетная функция, интеграл по
симметричному промежутку
138
Неявные функции 474, 498
Ньютон 15, 248, 372
Ньютона—Лейбница теорема 15
-	- формула 124
Обвертывающий ряд 534, 544, 550,
651, 792
Обратные тригонометрические
функции
-	Арксинус и Арктангенс
Обращение степенного ряда 502, 506
Объем тела 202
-	- аддитивность 203
-	- внутренний, внешний 202
-	- вращения 207
-	- выражение интегралом 205
-	- как предел 203
-	- по поперечным сечениям 206, 207
-	- условие существования 203, 204
Определенный интеграл в
собственном смысле 96
-	- вычисление с помощью
интегральных сумм 120
	первообразной 124

-	- свойства 108
-	- схема применения 225
-	- условия существования 100, 105,
107
Ориентированный промежуток 108,
598
Основная последовательность
разбиений промежутка 96
-	теорема алгебры 680
-	формула интегрального исчисления
123, 127, 128, 554, 582
Особая точка функции 577, 580, 581
Особенности выделения при
вычислении интегралов 642,
646
Остаток ряда 260
Остаточное произведение 353
Остроградского метод выделения
рациональной части интеграла
43
-	формула 45
Ось вещественная 509
-	мнимая 509
Оценка остатка ряда 283, 303, 378
Парабола 16, 174, 197, 232, 233
Параметр 654
Первообразная функция 11
-	- восстановление с помощью
определенного интеграла 129,
583
Переместительное свойство
абсолютно сходящегося
произведения 356
	ряда 315, 332, 513
Перестановка двух предельных
переходов 442, 443, 658
Периодическая функция, интеграл по
периоду 138
тт(число), приближенное вычисление
379
Площадь криволинейной трапеции
192
-	как первообразная 16
	предел суммы 94
-	плоской фигуры 187
	аддитивность 188
	внутренняя, внешняя 187
	выражение интегралом 192
-	как предел 188
	условия существования 187, 189,
191
-	поверхности вращения 214
-	цилиндрической поверхности 220
Повторный ряд 330
Подынтегральная функция 12
Подынтегральное выражение 12
Подстановка (замена переменной) 23,
134, 143, 604
-	Абеля 69
-	гиперболическая 29
-	дробно-линейная 70, 87
-	ряда в ряд 485
-	тригонометрическая 29
-	Эйлера 57, 59
Показательная функция в
комплексной области 517
-	- связь с тригонометрическими
функциями 519, 523
-	- степенной ряд 367, 452, 454, 468,
518
Последовательных приближений
метод 474
Почленное дифференцирование ряда
438,517
-	интегрирование ряда 436, 669, 697,
710
-	умножение рядов 321, 328, 333, 407,
456, 513
Почленный переход к пределу 434,
515
Правильная дробь, разложение на
простые 21, 39
Предел интеграла по параметру
(предельный переход под
знаком интеграла) 442, 659, 668,
694, 696, 745, 748
-	функции комплексной переменной
514

Пределы интеграла нижний и
верхний 97
Предельная функция,
дифференцируемость 443
-	- интегрируемость 443, 657
-	- непрерывность 657
Предельный переход в ряде
почленный 434, 515
-	- под знаком интеграла 443, 659,
668, 694, 696, 745, 748
Преобразование рядов по Куммеру
388
-	Маркову 392
-	- - Эйлеру 384
Приближенное вычисление
интегралов несобственных 641,
647, 650
-	собственных 153, 646
Приближенные вычисления с
помощью рядов 378, 388, 390,
459, 460, 466, 650
Приведения формулы для
биномиальных дифференциалов
54
-	интегралов от sinA\nux cosA\mu x
78
-	определенных интегралов 130
Произведение бесконечное 351
-	- абсолютно сходящееся 356
-	- признаки сходимости и
расходимости 354
-	- расходящееся 351
-	-сходящееся 351
-	остаточное 353
-	частичное 351
Производная функции комплексной
переменной 515
Производящая функция для
бесселевых функций 345
	многочленов Лежандра 492, 508
Простые дроби 37
-	- интегрирование 37
-	- разложение правильной дроби 21,
39,42
-	- разложение функций ctg x, cth x, tg
х, х, х, х, l/sinA2, 1/sh, 1/sin, 472,
473
Прямоугольников формула 154
-	- дополнительный член 159
Псевдоэллиптнческие интегралы 86
Пуассон 122, 140, 612
Пуассона—Абеля метод
обобщенного суммирования
рядов 396
Пуассона формула 256
Раабе интеграл 759
-	признак 273, 278
Равномерная сходимость интеграла
682, 687, 688
	признаки 684, 688
	связь с рядами 684, 688
	условие 684, 687
-	- ряда, последовательности 419, 422,
424, 515
	признаки Абеля 429
	Вейерштрасса 427
	Дирихле 429
	условие 425
-	- степенного ряда 444, 446
Равномерное стремление к
предельной функции 654
Разрывный множитель Дирихле 633,
640, 736, 741
Расходящиеся бесконечные
произведения 351
Расходящийся интеграл 552, 578
-	- обобщенное значение 595
-	ряд 258, 333
Расходящихся рядов суммирование,
см. Суммирование рядов
обобщенное
Рационализация подынтегрального
выражения 50, 51, 57, 74, 85
Рациональная функция, интеграл
между бесконечными
пределами 623
-	часть интеграла, выделение 44
Регулярный метод суммирования 395

Решение уравнений рядами 498
Риман 97, 264
Римана теорема 317
Риманова (интегральная) сумма 97
Ряд (бесконечный) 257, 512
-	гармонический 263, 267, 270, 289
-	гипергеометрический 280, 297, 359,
470, 769
-двойной 333, 513
-	знакопеременный 302
-	кратный 350
-	лейбницевского типа 303
-	повторный 330
-	расходящийся 258, 292, 333
-	сходящийся 258, 292, 333, 512
-	- абсолютно 296, 336, 513
-	- неабсолютно 296, 317, 336, 516
-	остаток 260
-сумма258, 333, 512
-	условие сходимости 294
-	частичная сумма степенной, ряд,
также, см, 257, 333, 512
Сапогова признак 291
Симпсона формула 159
-	- дополнительный член 162
Синус, аналитическое определение
477
-	бесконечное произведение 376
-	в комплексной области 523
-	гиперболический, бесконечное
произведение 378
-	- разложение обратной величины на
простые дроби 473
-	- степенной ряд 367
-	разложение обратной величины на
простые дроби 472
-	степенной ряд 367, 454, 522
	для log sin x/x 497
Сочетательное свойство ряда 313,
332
Спрямляемая кривая 169
Сравнения теоремы для
несобственных интегралов 560
-	рядов 264
Среднее значение, теорема 113
	вторая 117,600
	обобщенная 114, 600
	связь с формулой Лагранжа 124
Статический момент кривой 228
-	- плоской фигуры 231
-	- поверхности вращения 240
-	- тела 239
-	- цилиндрической поверхности 240
Степенная функция, главное
значение 526
Степенной ряд 298, 364, 515
--действия 481, 485, 518
--деление 492, 518
-	- дифференцирование 447, 449
-	- единственность 445
-	- интегрирование 447
-	- круг сходимости 515
-	- непрерывность 444, 446
-	- обращение 502, 506, 518
-	- промежуток сходимости 299, 516
-	- радиус сходимости 300, 515
-	- с двумя переменными 346
-	- с несколькими переменными 350
Стильтьес 651
Стерлинг 360
Стерлинга ряд 550, 792
-	формулы 369, 550, 793
Стоке 424
Сумма ряда 257, 333, 512
Суммирование рядов обобщенное
395
	метод Бореля 411
	Вороного 408
	Гельдера411
	Пуассона—Абеля 396
	Чезаро401,409
	Эйлера 416
Сфера (полусфера) 241
Сходимости пограничная абсцисса
309
-	принцип 308, 512
Сходимость бесконечного
произведения, признаки 354

-	- ряда, признаки: Абеля 307,
Бертрана 279, Гаусса 279,
Даламбера 271, 288, 296, 513,
Дирихле 307, Ермакова 285,
Коши 270, Коши—Маклорена
282, Куммера 277, Лейбница
302, 308, Раабе 273, 278,
Сапогова291
	условие 293
-	несобственного интеграла,
признаки 561, 563, 584
	условие 560, 584
Сходящееся бесконечное
произведение 351
Сходящийся бесконечный ряд 258,
292
-	несобственный интеграл 552, 578
Тангенс в комплексной области 523
-	разложение на простые дроби 472
-	степенной ряд 493, 497, 524
Таубера теорема 398,405
Тейлора ряд 364, 449, 450
-	формула 364
-	- дополнительный член 146, 366
Теплица теорема 325
Тождество степенных рядов 445
Тор 230, 233
Торичелли 242
Трактриса 179, 248
Трапеций формула 155
-	- дополнительный член 161
Тригонометрическая форма
комплексного числа 510
Тригонометрические подстановки 29
-	функции, аналитическое
определение 477
-	- в комплексной области 522, см.,
также, Синус, и, т.д.
-	- связь с гиперболическими
функциями 1966, 523
	показательной функцией 519,
523
Улитка 177, 199
Умножение рядов 321, 328, 333, 407,
456, 513
Уникурсальная кривая 85
Френель 721, 729
Фробениус 401
-	теорема 403
Фруллани интегралы 621, 635, 636,
638, 639
Харди 576, 740
Харди—Ландау теорема 403
Центр тяжести кривой 229
-	- плоской фигуры 232
-	- поверхности вращения 240
-	- тела 239
-	- цилиндрической поверхности 240
Цепная линия 174, 184, 195, 209, 217
Циклоида 175, 184, 185, 199, 209, 218,
230, 233
Цилиндрический отрезок 210, 222,
240
Частичная сумма 257, 333, 512
Чебышев 52
Чебышёва—Лагерра многочлены 604
Четная функция, интеграл по
симметричному промежутку
138
Шаровой пояс 217
Шлёмильх 373
Штейнер 339
Штольца теорема 326
Эвольвента круга 175, 183, 185
-	цепной линии 189
Эволюта, натуральное уравнение 185
Эйлер 57, 255, 263, 358, 361, 362, 363,
376, 377, 395, 611, 699, 717, 756,
758, 764, 778
Эйлера метод обобщенного
суммирования рядов 412
-	преобразование рядов 384
-ряд 462, 490, 496, 671
-формулы 519, 527
Эйлера—Гаусса формула 361, 754,
775

Эйлера—Маклорена формула 540,
547
—	дополнительный член 540, 548
Эйлера—Маклорена ряд 543, 549
—	приближенные вычисления 546
Эйлерова постоянная 270, 285, 319,
353, 772, 775, 776, 782, 793
Эйлеровы интегралы первого и
второго рода 750, 753
—	подстановки 57, 59
Эллипс 176, 195, 198, 199, 201, 202,
229, 233
Эллипсоид 209, 211, 212, 219
Эллиптические интегралы 86
-	- в форме Лежзндра 93, 111
-	- 1-го—3-го рода 90
-	- полные 143, 166, 177, 179, 214,
224, 252, 352, 465, 675, 734, 768
Эллиптический синус 252
Эпициклоида 185
Эрмит 146

ГЛАВА ВОСЬМАЯ
ПЕРВООБРАЗНАЯ ФУНКЦИЯ
(НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ)
§ 1. Неопределенный интеграл и простейшие
приемы его вычисления
263. Понятие первообразной функции (и неопределенного интеграла).
Во многих вопросах науки и техники приходится не по заданной функ-
функции искать ее производную, а наоборот - восстанавливать функцию
по известной ее производной. В 91, предполагая известным уравнение
движения s = s(t), т. е. закон изменения пути с течением времени, мы
ds
путем дифференцирования нашли сначала скорость v = -j-, а затем
и ускорение я=-зг • На деле, однако, часто приходится решать обрат-
обратную задачу: ускорение а задано в функции от вре-
времени t: a = a(t), требуется определить скорость си
пройденный путь s в зависимости от/. Таким обра-
образом, здесь оказывается нужным по функции a=a(t) восстановить ту
функцию v = v(t), для которой а является производной, а затем, зная
функцию v, найти ту функцию s = s(t), для которой производной бу-
будет V.
Дадим следующее определение:
Функция F(x) в данном промежутке называется первообраз-
первообразной функцией для функции f(x) или интегралом от f(x), если
во всем этом промежутке f(x) является производной для функции
F(x) или, что то же, f(x)dx служит для F(x) дифференциалом
F'(x)=f{x) или dF{x) = f(x)dx*.
Разыскание для функции всех ее первообразных, называемое ин-
интегрированием ее, и составляет одну из задач интегрального исчисле-
исчисления; как видим, эта задача является обратной основной задаче диф-
дифференциального исчисления.
* В этом случае говорят также, что функция F(x) является первообразной
(или интегралом) для дифференциального выражения fix) dx.

12	ГЛ. VIII. ПЕРВООБРАЗНАЯ ФУНКЦИЯ	[263
Теорема. Если в некотором {конечном или бесконечном, замкну-
замкнутом или нет) промежутке X функция F{x) есть первообразная для
функции /(*), то и функция F(x) + С, где С - любая постоянная, так-
также будет первообразной. Обратно, каждая функция, первообраз-
первообразная для/(х) в промежутке X, может быть представлена в этой форме.
Доказательство. То обстоятельство, что, наряду с F(x),
и F(x) + C является первообразной для /(х), вполне очевидно, ибо
№	F()
) ]()
Пусть теперь Ф(х) будет любая первообразная для f(x), функ-
функция, так что в промежутке X
Ф'(*) = /(*)•
Так как функции F(x) и Ф(х) в рассматриваемом промежутке имеют
одну и ту же производную, то они разнятся на постоянную [131, след-
следствие]:
Ф
что и требовалось доказать.
Из теоремы следует, что достаточно найти для данной функции
f(x) только одну первообразную функцию F(x), чтобы знать все
первообразные, так как они отличаются друг от друга постоянными
слагаемыми.
В силу этого выражение F(x) + С, где С — произвольная постоян-
постоянная, представляет собой общий вид функции, которая имеет
производную f(x) или дифференциал f(x)dx. Это выражение называется
неопределенным интегралом f(x) и обозначается сим-
символом
\f(x)dx,
в котором неявным образом уже заключена произвольная постоянная.
Произведение f(x)dx называется подинтегральным выра-
выражением, а функция f(x) - подинтегральной функ-
функцией.
Пример. Пусть f(x) - х2; тогда, как нетрудно видеть, неопре-
неопределенный интеграл этой функции будет
х3
C
Это легко проверить обратным действием - дифференцированием.
Обращаем внимание читателя на то, что под знаком «интеграла»
J пишут дифференциал искомой первообразной функции, а не
производную (в нашем примере: х2dx, а не- х2). Такой способ
записи, как будет выяснено ниже [294], создался исторически; к тому
же он предоставляет ряд преимуществ, и его сохранение вполне це-
целесообразно.

263]	§ 1. ПРОСТЕЙШИЕ ПРИЕМЫ ВЫЧИСЛЕНИЯ	13
Из определения неопределенного интеграла непосредственно вы-
вытекают следующие свойства:
1.	d\f(x)dx-^f(x)dx,
т. е. знаки d и\, когда первый помещен перед вторым, взаимно сокра-
сокращаются.
2.	Так как F(x) есть первообразная функция для F'(x), то имеем
ffiA -i С*
что может быть переписано так:
J
Отсюда видим, что знаки d и\, стоящие перед F(x), сокращаются
и тогда, когда d стоит после , но только к F(x) нужно прибавить
произвольную постоянную.
Возвращаясь к той механической задаче, которую мы поставили
вначале, мы можем теперь написать, что
v=
s=\v(t)dt.
Предположим для определенности, что мы имеем дело с равноуско-
равноускоренным движением, например под действием силы тяжести; тогда
a-g (если направление по вертикали вниз считать положительным)
и - как нетрудно сообразить -
Мы получили выражение для скорости о, в которое, кроме вре-
времени t, входит еще и произвольная постоянная С. При различных
значениях С мы будем получать и различные значения для скорости
в один и тот же момент времени; следовательно, имеющихся у нас
данных недостаточно для полного решения задачи. Чтобы получить
вполне определенное решение задачи, достаточно знать величину
скорости в один какой-нибудь момент времени. Например, пусть нам
известно, что в момент t = t0 скорость v=v0; подставим эти значения
в полученное выражение для скорости
v0=gt0 + C,
откуда
C=vo~gto,

14	ГЛ. VIII. ПЕРВООБРАЗНАЯ ФУНКЦИЯ	[264
и теперь наше решение принимает уже вполне определенный вид
Найдем, далее, выражение для пути s. Имеем
s = J [g(t -' о) + oj dt = \ g(t - tof + vo(t -t0) н С
(дифференцированием легко проверить, что первообразная функция
может быть взята в такой форме). Неизвестную нам новую постоян-
постоянную С" можно определить, если, например, дано, что путь s = s0 в мо-
момент t = t0; найдя, что C' = s0, перепишем решение в окончательном
виде
s = 2Sif-Q2-^ vo(t-to)-i V
Значения t0, s0, v0 условно называются начальными значе-
значениями величин t, s и v.
Мы знаем, что производная функции y = F(x) дает угловой коэф-
коэффициент касательной к соответствующему графику. Поэтому задачу
разыскания первообразной
F(x) для заданной функции
f{x) можно истолковать так:
требуется найти кривую у =
— Fix), для которой имел
бы место заданный закон
изменения углового коэффи-
коэффициента касательной:
tg a =/(*).
Рис.1.	Если y = Fix) есть одна
из таких кривых, то все ос-
остальные могут быть получены из нее простым сдвигом (на произволь-
произвольный отрезок С) параллельно оси у (рис. 1). Для того, чтобы индиви-
индивидуализировать кривую в этом множестве кривых, достаточно, напри-
например, задать точку (х0, j0), через которую кривая должна пройти; н а-
чальное условие yQ = F(x0) + C даст C=yo-F(x0).
264. Интеграл и задача об определении площади. Гораздо важнее
истолкование первообразной функции как площади криволинейной
фигуры. Так как исторически понятие первообразной функции было
теснейшим образом связано с задачей об определении площади, то
мы остановимся на этой задаче уже здесь (пользуясь интуитивным
представлением о площади плоской фигуры и откладывая точную
постановку этого вопроса до главы X).
Пусть дана в промежутке [а, Ь] непрерывная функция y=fix), при-
принимающая лишь положительные (неотрицательные) значения. Рас-

264)
1. ПРОСТЕЙШИЕ ПРИЕМЫ ВЫЧИСЛЕНИЯ
15
я
смотрим фигуру ABCD (рис. 2), ограниченную кривой у = fix), двумя
ординатами х = а и х = Ь и отрезком оси х\ подобную фигуру будем
называть криволинейной трапецией. Желая определить
величину площади Р этой фигуры, мы изучим поведение площади
переменной фигуры AMND, заключенной между начальной ор-
ординатой х = а и ординатой, отвечающей произвольно выбранному
в промежутке [а, Ь] значению х.
При изменении х эта последняя
площадь будет соответственно из-
изменяться, причем каждому х от-
отвечает вполне определенное ее
значение, так что площадь криво-
криволинейной трапеций AMND явля-
является некоторой функцией от х;
обозначим ее через Р(х).
Поставим себе сначала зада-
задачей найти производную
этой функции. С этой целью
придадим х некоторое (скажем, положительное) приращение Ах; тогда
площадь Р(х) получит приращение АР.
Обозначим через т и М, соответственно, наименьшее и наиболь-
наибольшее значения функции f(x) в промежутке [х, х + Ах] [85] и сравним
площадь АР с площадями прямоугольников, построенных на осно-
основании Ах и имеющих высоты т и М. Очевидно,
Рис. 2.
откуда
m Ax<AP<M Ax,
AP
^ Ax "^
Если Ах—О, то, вследствие непрерывности, т и М будут стремиться
к f(x), а тогда и
Таким образом, мы приходим к замечательной теореме (обычно
называемой теоремой Ньютона и Лейбниц а):* производная
от переменной площади Р(х) по конечной абсциссе х равна конечной
ординате у = f(x).
Иными словами, переменная площадь Р(х) представляет собой
первообразную функцию для данной функции у = f(x). В ряду
других первообразных эта первообразная выделяется по тому при-
признаку, что она обращается в 0 при х = а. Поэтому, если известна
* В действительности это предложение - хотя и в другой форме - опублико-
опубликовал еще Барроу (Is. Barrow), учитель Ньютона.

16
ГЛ. VIII. ПЕРВООБРАЗНАЯ ФУНКЦИЯ
B64
какая-либо первообразная F(x) для функции f(x), и по теореме
предыдущего п°
то постоянную С легко определить, положив здесь х = д
О - F(d) I С, так что С= - F(a).
Окончательно
В частности, для получения площади Р всей криволинейной тра-
трапеции ABCD нужно взять х = Ь:
P = F(b)-F(a).
В виде примера, найдем площадь Р{х) фигуры, ограниченной п а-
раболой у = ах2, ординатой, отвечающей данной абсциссе х, и от-
отрезком оси х (рис. 3); так как парабола пересекает ось х в начале коор-
координат, то начальное значение х здесь 0. Для функции /(х) = ах2 легко
найти первообразную: F{x) = ^- . Эта
функция как раз и обращается в 0 при
#=ахг/ x = 0, так что
"	[ср. 32, 4)].
Ввиду той связи, которая существует
между вычислением интегралов и нахож-
'	дением площадей плоских фигур, т. е.
квадратурой их, стало обычным и самое
-*~х вычисление интегралов называть квад-
квадратурой.
Для распространения всего сказанного
выше на случай функции, принимающей
и отрицательные значения, достаточно условиться считать отрица-
отрицательными площади частей фигуры, расположенных под осью х.
Таким образом, какова бы ни была непрерывная в промежутке
[а, Ь] функция f(x), читатель всегда может представить себе перво-
первообразную для нее функцию в виде переменной площади фигуры,
ограниченной графиком данной функции. Однако считать эту геоме-
геометрическую иллюстрацию доказательством существования пер-
первообразной, разумеется, нельзя, поскольку самое понятие площади
еще не обосновано.
В следующей главе [305] мы сможем дать строгое и притом чисто
аналитическое доказательство того важного факта, что каждая не-
0\ х
Рис. 3.

265)	§ 1. ПРОСТЕЙШИЕ ПРИЕМЫ ВЫЧИСЛЕНИЯ	17
прерывная в данном промежутке функция f(x) имеет в нем первооб-
первообразную. Это утверждение мы принимаем уже сейчас.
В настоящей главе мы будем говорить о первообразных лишь для
непрерывных функций. Если функция задана конкретно и имеет точки
разрыва, то рассматривать ее будем лишь в промежутках ее непре-
непрерывности. Поэтому, допустив сформулированное выше утверждение,
мы освобождаемся от необходимости всякий раз оговаривать суще-
существование интегралов: рассматриваемые нами инте-
интегралы все существуют.
265. Таблица основных интегралов. Каждая формула дифферен-
дифференциального исчисления, устанавливающая, что для некоторой функ-
функции F(x) производной будет /(*), непосредственно приводит к соот-
соответствующей формуле интегрального исчисления
Перебрав формулы п° 95, по которым вычислялись производные эле-
элементарных функций, а также некоторые формулы, выведенные даль-
дальше (для гиперболических функций), мы можем теперь составить сле-
следующую таблицу интегралов:
1.	Jo.tfx=C.
2.	Jbtfx=Jtfx=x+C.
4. Jirfx=jf = ln|x|
5-
6 f—L=tfx= f-J^
j l/i-x* J yi-ж2
7.	Ja*tfa- = j2l + C IV <& = «*+С
8.	fsinxrfx= -cosx + G
9.	fcosxrfx = sinx f C.
2 Г. М. Фихтенгольц, т. II

18	ГЛ. VIII. ПЕРВООБРАЗНАЯ ФУНКЦИЯ	[266
12.	Jshxtfx = chx i С.
13.	Jchxtfx = shxH С.
14.
По поводу формулы 4 сделаем пояснение. Она приложима в любом
промежутке, не содержащем нуля. Действительно, если этот проме-
промежуток лежит вправо от нуля, так что я:>0, то из известной формулы
дифференцирования [1пя:]' = - непосредственно следует
jf=lnx + C.
Если же промежуток лежит влево от нуля и х < 0, то дифференциро-
дифференцированием легко убедиться в том, что [In ( — х)]' = - , откуда
Обе эти формулы и объединены в формуле 4.
Рамки приведенной выше таблицы интегралов раздвигаются при
помощи правил интегрирования.
266. Простейшие правила интегрирования. I. Если а — постоянная
(я^О), то
ja-f(x)dx = a- \f(x)dx.
Действительно, дифференцируя выражение справа, мы получим [105,1]
d[a • J/(x) dx] = a-d[ J f(x
так что это выражение является первообразной для дифференциала
a-f{x) dx, ч. и тр. д. Итак, постоянный множитель можно выносить
из-под знака интеграла.
И. J[Дх)±*С*I dx= J/(x)dx± Jg(x)dx.
Дифференцируем выражение справа [105, II]:
d[ I fix) dx± \g{x) dx] = d\fix) dx+d\gix) dx = [fix)±g(x)] dx;

267]	S 1- ПРОСТЕЙШИЕ ПРИЕМЫ ВЫЧИСЛЕНИЯ	19
таким образом, это выражение является первообразной функцией для
последнего дифференциала, ч. и тр. д. Неопределенный интеграл от
суммы {разности) дифференциалов равен сумме {разности) интегра-
интегралов от каждого дифференциала в отдельности.
Замечание. По поводу этих двух формул заметим следующее.
В них входят неопределенные интегралы, содержащие каждый произ-
произвольное постоянное слагаемое. Равенства подобного типа понима-
понимаются в том смысле, что разность между правой и левой частями его
есть постоянная. Можно понимать эти равенства и буквально, но то-
тогда один из фигурирующих в них интегралов перестает быть про-
произвольной первообразной: постоянная в нем устанавливается
после выбора постоянных в других интегралах. Это важное замеча-
замечание следует иметь в виду и впредь.
III. Если
то
[ f{ax + b)dx = -- F(ax + b) + C.
Действительно, данное соотношение равносильно следующему:
-~ F[f) = F{t) =/@-
Но тогда
-у- F(ax+b) = F'(ax + b)-a = a -/(ax + b),
так что
— Г
т. е. - F(ax + b) действительно оказывается первообразной для функ-
функции f(ax + b).
Особенно часто встречаются случаи, когда а = 1 или Ъ = 0:
\ f(x
[На деле правило III есть весьма частный случай правила замены
переменной в неопределенном интеграле, о чем будет речь ниже, 268.]
267. Примеры. Г Fxs - Ъх+5) dx.
Пользуясь правилами II и I (и формулами 3, 2), имеем
fFx2-3;c+5)rf;c= Гбх2<*с- $3xdx+ [sdx =
-6 Гл:2^д:-3 fxd.v + 5 рх=2*з	*2 I 5x + C.

20	ГЛ. VIII. ПЕРВООБРАЗНАЯ ФУНКЦИЯ	[267
2) Легко проинтегрировать многочлен и в общем виде
Г (а^л + а1хп-1 + ...+an_1x+an)dx =
= Оо \хп dx + at xn~1dx+ ...+an-i \xdx+an \ dx =
"" хп+1+хп++а±х* + ах+С (II, I; 3, 2)
и + 1
3) fBx2 + l)»dx = f(8x6+12x4+&e!+•
8 12
= — хЧ—xs+2x3+x+C.	(пример 2)
4) f(l+yjcLdr=
|
8 —	R — 1
—x*+3x2+—x2H—д:3 + С. (II, I; 3, 2)
r(*+l)(x*-3)	гх'+д;г-3д:-3
5)	dx= 	dx-
J Зл2	J	3*2
з 3 x xaj	3J	3J	J л:
(-11	1
- A:-2dx=-x2+-x-lnx+-+C. (II, I; 3, 2, 4)
J	6 3	x
6-6-
e«
f- ci 6-6-
= \x*dx- x»dx = — xe	x«+C. (II; 3)
Дадим ряд примеров на применение правила III:
7) (а) Г~^~ = 1п |х-в|+С.	(III; 4)
J х-а
(б) Гт-^т-.- f(jc-e)-ft Л =
J (x-a)" J
=-	+С. (III; 3)
(/c-lXx-a)*-1
Г	1
8) (a) sinwxdA:-	cosmx+C,	(HI; 8)
J	/и
(m^O)
f	1
(б)	cos тих dx = — sin ж + С,	(III; 9)
J m
(в)	I e-i>*rfx-=	e-зх ( c.	(IIT; 7)
J	3

2671	§ 1- ПРОСТЕЙШИЕ ПРИЕМЫ ВЫЧИСЛЕНИЯ	21
9) (а)	| г^== = - I _ ,	= arcsin -+С.	(III; 6)
r dx 1 I ax i	x
™!*4*~* ~^aarCtg«+C-	(Ш;5)
J1+U
Примеры на все правила:
10) f-	l—^—dx= ("(
J	ex	J
„,}
_е2х_ех+А. + е-х+с. (II, III; 7, 2)
ах -1-6
cx+d
dx.
Разделив числитель на знаменатель, представим подинтегралыгое выражение
в виде
a be-ad I
с с cx+d
Отсюда искомый интеграл равен
с2
\n \cx + d\+C.	(II, I, Ш; 2, 4)
г2х"-Зх+1 г( 6 \
12)	dx= 2х-5Ч	?
Интегрирование дроби со сложным знаменателем часто облегчается разложе-
разложением ее на сумму дробей с более простыми знаменателями. Например,
1	1
.=if_L__L).
хг-аг (x-a)(x+a) 2a\x-a x + al'
поэтому [см. пример 7) (a)]
1 x-a
13)
f
-Ф 2a[J x-a J x+a\ 2а
Для дроби более общего вида
x+a
1
+ С
(х+а)(х+Ь)
можно указать, например, такой прием. Очевидно, (x+a)-(x+b) = a-b. Тогда
имеем тождественно
1	1 {х+а)-{х+Ь) 1/1	1
{x+a){x+b) a-b {x+a)(x+b) a-b \x+b x+a
Таким образом,
dx	I
,„. Г dx	I x+b
И) т—	rln	+С.
+а)(.х+Ь) а-Ь
x+b
х+а

22
ГЛ. VIII. ПЕРВООБРАЗНАЯ ФУНКЦИЯ
1267
В частности,
15) (
Знаменатель следующим образом разлагается на вещественные множители:
A(x-<x)(x-(i), где
-В+ fB*-AC	-В- УЖ^АС
А тогда, согласно примеру 14), полагая в нем а- -@,Ь= -а, получим
dx	1
J:
¦In
+ С.
Некоторые тригонометрические выражения, после тех или иных элементар-
элементарных преобразований, интегрируются также при помощи простейших приемов.
Очевидно, например,
1 + cos 2тх 1 - cos 2mx
cos2 mx =	, sin2 mx =	,
откуда
Г	1	1
17) (a) cos2 mx dx = — x -i	sin 2mx + C,
J	2 Am
F) {sin2mxdx = — x	sin2mx+C.
J	2 Am
Аналогичным образом, имеем
sin mx cos nx = — [sin (in + n) x+sin (m - n) x],
cos mx cos nx=— [cos (m+ri) x + cos (m - n) x],
sin mx sin nx = — [cos (m - n) x -
Считая m±n*Q, получим следующие интегралы:
1
18) (a) Jsi:
F) J
sin mx cos nx dx = - ¦
cosroc cos ил: Ac =
2{m+n)
1
1
-sin
2{m-ri)
1
cos (т-и)д:+С,
-sin(ra- ri)x+C,
2(m+ri)	2{m-ri)
(в) sin mx sin nx dx =	sin (m -n)x	sin (m + и) •*+C.
J	2(m-n)	2(m+n)

268]	§ 1. ПРОСТЕЙШИЕ ПРИЕМЫ ВЫЧИСЛЕНИЯ	23
В заключение рассмотрим немного более сложный пример.
(•sin 2nx
19) (а) —	dx (й-1, 2, 3,...).
J smx
р sin 2nx
(а)/
Так как
л	л
sin 2их = 2 ts'n 2&x - sin Bk - 2) х] = 2 sin x 2 cos B/c - 1) х,
/с=1	4=1
л
то подинтегральное выражение приводится к 2 2 cos B? - 1)х, и искомый
интеграл будет равен
2 2	1-С.
Аналогично
fsinBn + l)A:
sin л:
fsinBn+l);<:	"sin2ytx
(б) 	.	dx=x + 2 2 ., +С.
J sin л:	a-=i 2A:
268. Интегрирование путем замены переменной. Изложим один из
сильнейших приемов для интегрирования функций — метод замены
переменной или подстановки. В основе его лежит сле-
следующее простое замечание:
если известно, что
/ио тогда
а>{х))са'(х) dx = G(co(x)) + С.
[Все фигурирующие здесь функции g(t), oipc), m\x) предполагаются
непрерывными.]
Это прямо вытекает из правила дифференцирования сложной функ-
функции [98]
если учесть, что G'(t)=g(t). Xo же можно выразить и иначе, сказав,
что соотношение
dG(t)=g(t)dt
сохраняет силу и при замене независимой переменной t на функцию
(о(х) [106].
Пусть требуется вычислить интеграл
\f(x)dx.

24	ГЛ. VIII. ПЕРВООБРАЗНАЯ ФУНКЦИЯ	[268
Во многих случаях удается в качестве новой переменной выбрать
такую функцию от х: t = co(x), чтобы подинтегральное выражение
представилось в виде
(	A)
где g(t) - более удобная для интегрирования функция, чем f(x).
Тогда, по сказанному выше, достаточно найти интеграл
чтобы из него подстановкой t = co(x) получить искомый интеграл.
Обыкновенно пишут просто
B)
подразумевая уже, что в функции от t, которая представлена инте-
интегралом справа, произведена указанная замена.
Найдем, например, интеграл
J sin3 л- cos х dx.
Так как dsinx = cosxdx, то, полагая t = siax, преобразуем подинте-
подинтегральное выражение к виду
sin3 х cos x dx = sin3 x d sin x= t3 dt.
Интеграл от последнего выражения вычисляется легко:
Остается лишь вернуться к переменной х, подставляя sin x вместо V.
Г • 1	j sin4* „
I sur a* cos x ax = —j—h С.
Обращаем внимание читателя на то, что при выборе подстановки
t=co(x), упрощающей подинтегральное выражение, нужно помнить,
что в его составе должен найтись множитель а>'(х) dx, дающий диф-
дифференциал новой переменной, dt [см. A)]. В предыдущем примере
удача подстановки t = sin x обусловливалась наличием множителя
cos xdx = dt.
В этой связи поучителен пример
J sin3 x dx;
здесь подстановка t=sinx была бы непригодна именно ввиду отсут-
отсутствия упомянутого множителя. Если попробовать выделить из под-
интегрального выражения, в качестве дифференциала новой перемен-
переменной, множитель sinxdx иди лучше -sinxdx, то это приведет к под-

268]
§ 1. ПРОСТЕЙШИЕ ПРИЕМЫ ВЫЧИСЛЕНИЯ
25
становке t = cos x; так как остающееся выражение
-sin2 х=cos2 x- 1
этой подстановкой упрощается, то подстановка оправдана. Имеем
jsm3xdx^j(t2-l)dt = ~-t + C=^^-cosx + C.
При некотором навыке в производстве подстановки можно самой
переменной t и не писать. Например, в интеграле
sin3 х cos x dx=\ sin3 xdsin x
мысленно рассматривают sin x как новую переменную и сразу
переходят к результату. Аналогично
dx
dx
Подстановка t = - здесь подразумевается.
Читатель видит теперь, что правило III, 266, по существу, сво-
сводится к линейной подстановке t = ax-\b:
Иной раз подстановка применяется в форме, отличной от указан-
указанной. Именно, в подинтегральное выражение f(x) dx непосредственно
подставляют, вместо х, функцию x=(p(t) от новой переменной t и по-
получают в результате выражение
f(<p(t))cpV)dt=g(t)dt.
Очевидно, если в этом выражении произвести подстановку t = co(x),
где (о{х) - функция, обратная для cp(t), то вернемся к исходному под-
интегральному выражению f(x)dx. Поэтому, как и прежде, имеет
место равенство B), где справа, после вычисления интеграла, следует
положить t = co(x).
Для примера найдем интеграл
dx
fx(l+fx)

26	ГЛ. VIII. ПЕРВООБРАЗНАЯ ФУНКЦИЯ	[268
Если положить x = te (чтобы все корни «извлеклись»), то получим
3
6
Теперь остается перейти к переменной х по формуле t = ylc, и
окончательно
ее
J
Более интересен пример
Разность квадратов под корнем (из которых первый постоянен) под-
подсказывает нам тригонометрическую подстановку x = asmt*. Имеем
У а2-.*2 = a cos t, dx = a cos t dt
и
J fdT^1 dx = a2 J cos2 f fifr.
Но мы уже знаем интеграл
a2 fcos2 t dt = a2 Г^ r+^ sin 2*1 + C
[267, A7) (а)]. Для перехода к л: подставляем t = arc sin -; преобра-
преобразование второго слагаемого облегчается тем, что
я3	1	1 /
-^sm2t=-=asm t-acos г^л'Уа2-*2.
Окончательно
I Yd2 - х2 dx = = xYa2 -x2 + y arcsin - + С.
Уменье разыскивать выгодные подстановки создается упражне-
упражнением. Хотя общих указаний по этому поводу дать нельзя, но отдель-
отдельные частные замечания, облегчающие это разыскивание, читатель
найдет в следующем п°. В канонических случаях подстановки будут
просто указаны в курсе.
* Уместно указать, что х мы считаем изменяющимся между - а и a, a t между
71 Л	X
	и — . Поэтому t = arc sin — .
2 2	а

26J>]	§ t. ПРОСТЕЙШИЕ ПРИЕМЫ ВЫЧИСЛЕНИЯ	27
/*	{* X (Ix	С X^
269. Примеры. 1) (a) \exxdx, 6) 	, в) 	dx.
J	J i+Xl	J COS2 X3
(а) Решение. Полагая t = x\ имеем dt--=lx dx, так что
d	t Cx*C
J
ex'x dx = -L dt e + C
2 J	2	2
(б) Указание. Та же подстановка. Ответ: — arctgx2+С. В обоих случаях
интегралы имели вид
где g - удобная для интегрирования функция; для таких интегралов естественна
подстановка t=xs. Аналогично интегралы вида
берутся подстановкой t - х3 и т. д. Под последний тип подходит третий интеграл,
(в) Ответ: —tgx3+C.
2)
Решение. Можно положить здесь / = х2; но проще сразу взять и = ссхг+/?,
ибо множитель xdx лишь числовым коэффициентом отличается от du-2ovcdx.
Имеем, таким образом,
3) (а)
Указ
и берутся ]
РУх dx =
fln*
J дг
а н и е. Все
подстановкой
1 Г
2J
(б)
эти
1
2аСв+1)
Г dX (в)
J х\пх
J
интегралы имеют
jgQnx)— = Jg
[ t = In X.
(In
дг1п2х
вид
x)rfln
1
2<x(fi+l)
X
Ответ: (а) — In2 х+С; (б) In In x+С; (в)	h С.
2	\ах
4) Интегралы вида
dx
g(sva x) cos x dx,	g(cos x) sin x dx,	g(tg x) ¦
J	J	J	(
cos2 x
берутся, соответственно, подстановками
t=smx, u = cosx, v^tgx.

28
ГЛ. VIII. ПЕРВООБРАЗНАЯ ФУНКЦИЯ
[269
Например,
г cosxdx с dt
(а) 	:	= г— = arctg/+C = arctgsinx+C;
J l+sm2* J 1 + r8
г	(¦ sin jc	г du
(б)	tgx dx = 	dx= - —= -In Ы+С= -In IcosA-l+C;
J	J cos л:	J и	i i >
du
—
и
' dx
00 J
dx
COS2 X
-J;
dv
A2 sin2 лг-1-.В2 cos2 x J Л2 tg2 *+.B2 J ^2«2+Ба
1	Л»	1
ctg	hC= —
e2x
5) (a) j'^, F) fctgxdr, (в) \-^-dx, (r) f ,
1 e2=c+l	J sin л: cos л:
Решение, (а) Если положить / = л:2+1, то числитель 2х dx дает в точности
dt; интеграл сведется к
Заметим, что всегда, когда предложенный интеграл имеет вид
¦/'(*) rdf(x)
так что в подинтегральном выражении числитель представляет со-
собой дифференциал знаменателя, подстановка t=f(x) сразу при-
приводит к цели
\f(x)\+C.
По этому образцу имеем
г	г dsin х
(б) ctgx dx=	= ln |sin л:| +C [cp. 4) F)];
J	J sin л:
r e2x	1 j-c
J e2x+i X~~2J '
i- dx
(r)
J sin л со
dx
I COS2 X
= ln |tgjc| +C.
: COS x J tg л:
6) Из последнего интеграла легко получаются два полезных интеграла:
Г*	г*
(а)
(б)
dx
dx
COS*
X	X
sin—cos—
2 2
-И)
sin \x+
- = ln
= ln

§ 1. ПРОСТЕЙШИЕ ПРИЕМЫ ВЫЧИСЛЕНИЯ	29
с	Г ,		2	-?
-dx= \ Varctg л; rf arctg д: = — (arctg х)*+С;
г 1 ах г 1 I	1
(в) tg	= - tg-rf — = ln cos	hC
J x .r2 J x x	x
[см. 4) F)].
Дадим теперь несколько примеров интегрирования выражений, содержащих
двучлены вида аг-х2, х'+а* и х*-а2. В этих случаях обычно бывает выгодно
заменить х тригонометрической или гиперболической функ-
функцией от новой переменной t, используя соотношения
1
sinsf+cossr=l, 1-t-tg2 ? = sec2?"
cos21
ch3f-sh2?-l, 1 - th2 / =
ch2/
8) Г dx
adt	a"
Подстановка: x-atgt*, dx =	, х2 + я2=- , так что
cos21	cos2 /
г it If	1
	= — cos2 tdt= — (f+sin rcos/)+C [см. 267, 17) (a)].
x
Перейдем теперь к переменной х, полагая t = arc tg — и выражая sm / и cos t
х	а
через tg t = —. Окончательно
а
С dx	1x1	х
J (л:2+а2J 1ФхгЛ-аг 2а3	а
С dx
9) -=¦
J Y
Здесь удобнее применить гиперболическую подстановку. Останавливаясь для
примера, на нижнем знаке, положим: х = a ch t (при х и / =- 0), dx = a sh t dt, Ух2 - а2 =
= ash/. Интеграл приведется просто к I Л=/+С. Для перехода к х вспомним
выражение обратной для гиперболического косинуса функции [49, 3)]
Г dx	(х ] Г(х Y
= 1п -+ / - -
J }<х*-а* \а У \а)
причем в постоянную С мы включаем и слагаемое - in a.
10) (а) Г dX , (б) f dX , Г- dX .
J (x*+a*)'U	J(x2-a2)V.	J (a2-x2)'h
л л
Причем достаточно предположить / изменяющимся между	и — .

30
ГЛ. VIII. ПЕРВООБРАЗНАЯ ФУНКЦИЯ
[269
В данном случае одинаково просто приводят к цели и тригонометрическая
и гиперболическая подстановки. Для примера, во втором интеграле возьмем
a sin / dt atgtdt
х = asset, dx =	=	, тогда x2 - a2 = a3 tg21 и
cos21 cos t
dx 1 rcostdt 1 1
(x--a~)"' aK) sin2/ e2 sin f	а2 т/ЗГГ
г dx 1 r cos
J (х*~~а~У>' a2.) sin
ID
Подстановка: x = a sin t, dx = a cos / dt приводит этот интеграл к такому [см.
6) (а)]:
Но
так что окончательно
1 г dt 1
a J sin t a
In
+ C.
? 1-cos/ a- l'c2-.\-2
		„ '
2 sin t	x
J;
+ C.
В заключение рассмотрим еще два примера интегрирования путем замены
переменной, где подстановка не столь естественна, как в предыдущих случаях,
но зато быстро ведет к цели.
dx
Положим Yx*+a=t-x и примем t за новую переменную. При возведении
в квадрат, х2 в обеих частях можно опустить, и в результате
так что
Окончательно
¦ =	 ,
It It
(тw,
=	dt.
2t2
Jdx rdt	,	, ,	,
	;= — = ln t\+C = la \х+]Гх2+а\+С.
1/V2 4-W J t
[Cp. 9)]
dx
Положим, д-^acos2
0<:у< —I где <р - новая переменная; тогда
Таким образом,
ал: = 2(jS - a) sin y cos у rfip.
f dr	Г
= 2 d<p =
J Yix-аЮ-х) J

270]	§ 1. ПРОСТЕЙШИЕ ПРИЕМЫ ВЫЧИСЛЕНИЯ	31
270. Интегрирование по частям. Пусть м=/(х) и v=g{x) будут две
функции от х, имеющие непрерывные производные u' = f'(x) и»' =
=g'(x)- Тогда, по правилу дифференцирования произведения, d{uv) =
= udv + v du или и dv = d(uv) - v du. Для выражения d(uv) первообраз-
первообразной, очевидно, будет uv; поэтому имеет место формула
\udv = uv- \vdu.	C)
Эта формула выражает правило интегрирования по
частям. Оно приводит интегрирование выражения и dv = uv' dx к
интегрированию выражения v du = vu' dx.	,
Пусть, например, требуется найти интеграл! xcos x dx. Положим,
и = х, dv = cosxdx, так что du-dx, w = sinx*,
и, по формуле C),
xcosxJx = J х Jsinx = xsin x- sinx dx = xsin x + cosx + C. D)
Таким образом, интегрирование по частям позволило заменить
сложную подинтегральную функцию х cos x на простую sin x. По-
Попутно для получения v пришлось проинтегрировать выражение cos x dx
- отсюда и название: интегрирование по частям.
Применяя формулу C) к вычислению предложенного интеграла,
приходится разбивать подинтегральное выражение на два множителя:
и и dv =»' dx, из которых первый дифференцируется, а второй инте-
интегрируется при переходе к интегралу в правой части. Нужно стараться,
чтобы интегрирование дифференциала dv не представляло трудностей
и чтобы замена и на. du. я dv яа. v ъ совокупности влекла за со-
собой упрощение подинтегрального выражения. Так, в разобранном
примере было бы явно невыгодно взять, скажем, х dx за dv, a cos x
за и.
При некотором навыке нет надобности вводить обозначения и,
v, и можно сразу применять формулу [ср. D)].
Правило интегрирования по частям имеет более ограниченную
область применения, чем замена переменной. Но есть целые классы
интегралов, например,
хк lnm х dx, x4 sin bx dx, xk cos bx dx, xk e°x dx и др.,
* Так как для наших целей достаточно представить cos x dx хоть одним спо-
способом в виде dv, то нет надобности писать наиболее общее выражение для », содер-
содержащее произвольную постоянную. Это замечание следует иметь в виду и впредь.

32	ГЛ. VIII. ПЕРВООБРАЗНАЯ ФУНКЦИЯ	[271
которые вычисляются именно с помощью интегрирования по
частям.
Повторное применение правила интегрирования по частям при-
приводит к так называемой обобщенной формуле интегри-
интегрирования по частям.
Предположим, что функции и и v имеют в рассматриваемом про-
промежутке непрерывные производные всех порядков, до (и f 1)-го вклю-
включительно: и', г/, и", v", ..., z/n\ i?n\ t/n+1>, г^п+3>.
Заменяя в формуле C) v на »<">, будем иметь
J hd("+1) dx = J и ddn) = ш/п> - J ю<") du = мгХ"> - J и' »<"> dx.
Аналогично
J t/n^' <& = t/n'w - J ц("+Щ dx.
Умножая эти равенства поочередно на +1 или на -1 и склады-
складывая их почленно, по уничтожении одинаковых интегралов в правой
и левой частях придем к упомянутой формуле:
E)
Особенно выгодно пользоваться этой формулой, когда одним из
множителей подинтегральной функции служит целый многочлен. Если
и представляет собой многочлен л-й степени, то ы<п+1> тождественно
равно нулю, и для интеграла в левой части получается окончательное
выражение.
Перейдем к примерам.
271. Примеры. 1) I x8 In x dx.
Дифференцирование In x приводит к упрощению, поэтому полагаем
dx	1
и = In х, dv = x3 dx, так что du = — , v = — xl
x	4
du =
1
	X1.
4
dx
x '
Чп x
V
1

16
f xs\r\xdx = -x4nx	| x3
J	4	4J
2) (a) lnxdx, F) \arctgxdx, (в) arcsinxcfc,

' 271]	§ 1- ПРОСТЕЙШИЕ ПРИЕМЫ ВЫЧИСЛЕНИЯ	33
Принимая во всех случаях dx-dv, получим
(а)	Inхdx = xIn x- I xd\TLX = x\TLX- dx = x(lnx-\) + C;
(б)	arctgxdx = x arctgx- \xdarctgx =
r x 1
=г* arctg х- - — dx = xarctgx	In(x2+1)+C [см. 269, 5) (a)];
J X -j- 1	^
в) j arcsin x dx = х arcsin л: - J xrf arcsin x =
г xrfr
=.v arcsin x - -	= x arcsin x+}ll-x2 + С [см. 269,2)].
J /b^
3)	Г x2 sin ж dr.
Имеем
xsrf(-cosx)= -л:2 cos л:- (-cosx) «bca= -x2cosa- + 2 x cos л; dr.
Таким образом, мы привели искомый интеграл к уже известному [270 D)]; подстав-
подставляя его значение, получим
x2smxdx= -x2cosx+2(xsinx+cosx) + C.
В общей сложности здесь правило интегрирования по частям пришлось при-
применить двукратно.
Так же, повторным применением этого правила, вычисляются интегралы
Г Р(х)е°* dx, Г Р(х) sin Ьх dx, Г Р(х) cos bx dx,
где Р(х) — целый относительно х многочлен.
4)	Если воспользоваться обобщенной формулой интегрирования по частям,
то можно получить сразу общие выражения для интегралов этого вида.
Полагая v(n+v>=eaxt будем иметь
(ОХ	еах	еах
гХ")= —, f)(n-l)=— е(л-2)=— и т. д.
а	аъ	аа
Поэтому, считая Р(х) многочленом и-й степени, по формуле E) получим
Г	ГР Р' Р"	1
P(x)e<>xdx = eax	+	... +С.
J	La а2 я3	J
Аналогично, если взять t<n+i) = sin bx, то
cos bx	sin bx	cos bx
я(п)=	_	?Xn-l)=	г<"-2)=	 и т. д.
Ь	Ъ*	Ь3
Отсюда формула
г \Р' Р'" Л [Р Р"	1
P(x)smbx dx = sinbx- —	 + ... \-cosbx •	i"+••• +С-
3 Г. М. Фихтенгольц, т. II

34	ГЛ. VIII. ПЕРВООБРАЗНАЯ ФУНКЦИЯ	[271
Подобным же образом устанавливается и формула
[Р Р" I	\Р' Р'"
ь+cos Ъх
г	[Р Р" I	\Р' Р'"	л
Р[х) cos bxdx = %mbx • -	ь... +cos Ъх •	1	+С.
J	lb Ь3 1	Ш б4	J
х3 In2 х dx. Имеем
с	х* 1	1 г	1	1 г
\n*xd — = -x* In2*-- x4rfln2x = -x4ln2 х-- x3lnxdx,
J	44	4J	4	2 J
и мы свели дело к интегралу 1). Окончательно
-хЧп*х	(-х* In х	x4j+C = -x4(ln2x	in*+
Так, последовательно, вычисляется интеграл
[xk\nmxdx,
где к — любое вещественное число (к* -1), а т-1, 2, 3, ... Если применить к
этому интегралу формулу интегрирования по частям, положив и=Ытх, то получим
рекуррентную формулу
г	1	tn с
хк\пт х dx=	хк+Чптх	хкlnm-iхdx,
J	k+\	k+li
по которой вычисление рассматриваемого интеграла сводится к вычислению
интеграла такого же типа, но с меньшим на единицу показателем при In x.
Впрочем, подстановка f = lnx приводит рассматриваемый интеграл к виду
tmeQi+\)t d(t уже изученному в 3) и 4).
6) Любопытный пример представляют интегралы
еах cos bx dx,	eax sin bx dx.
J	J
Если к ним применить интегрирование по частям (в обоих случаях взяв, скажем,
dv = eaxdx, v = — eaX), то получим
а
С	1	b С
еах cos bxdx= — eax cos bx ч— е0* sin bx dx,
J	a	a J
e^sinbx dx= — eax sin bx	е0* cos bx dx.
j	a	a j
Таким образом, каждый из этих интегралов оказался выражением через другой *.
* Если под интегралами разуметь определенные первообразные [ср.
замечание в 266], то, желая во второй формуле иметь те же функции, что и в первой,
мы, строго говоря, должны были справа присоединить еще некоторую постоян-
постоянную. Конечно, она была бы поглощена постоянными С и С в окончательных
выражениях.

271]	§ 1. ПРОСТЕЙШИЕ ПРИЕМЫ ВЫЧИСЛЕНИЯ	35
Однако если в первую формулу подставить выражение второго интеграла
из второй формулы, то придем к уравнению относительно первого интеграла,
из которого он и определится:
,~ b sin bx+a cos bx
eax cos bx dx =	—	eax+C.
Аналогично находим и второй интеграл
г
J
asmbx-b cos bx
еах sin bx dx ¦¦	eax f C".
? b*
7) В качестве последнего примера применения метода интегрирования по
частям выведем рекуррентную формулу для вычисления интеграла
С dx
Jn=	„_ (и=1, 2, 3, ...)•
Применим к нему формулу C), полагая
1	2пх ¦ dx
, dv = dx, так что du= --
Мы получим
X	С	X*
Jn =	Ь 2п 	dx.
(ха+аг)" J (д:2+й2)"+1
Последний интеграл можно преобразовать следующим образом:
г х2	г(х2 + а-)-а2	г dx	r dx
J	J	J
г(х2 + а-)-а2	г dx	r
*~ J (xi+d')n+1~ X ~ J (x* + a*)n °J
""
Подставляя это выражение в предыдущее равенство, придем к соотношению
откуда
1	х	2л-1 1
Полученная формула сводит вычисление интеграла Jn+i к вычислению интег-
интеграла Jn с меньшим на единицу значком. Зная интеграл
1	х
/, = —arctg—
а а
[267, 9) (б); мы берем одно из его значений], по этой формуле, при и = 1 найдем
1x1	х
J, =	1	arctg — ,
' 2a2x2 + a2 2а3	а
3*

36	ГЛ. VIII. ПЕРВООБРАЗНАЯ ФУНКЦИЯ	[272
[что мы выше получили другим путем, см. 269, 8)]. Полагая в формуле F) п = 2,
мы получим далее
\ х	3	1 х	3 х 3	х
3~4^B2J+4 2" 4^
а2J + 8а* х2 + а2 + 8
и т. д. Таким образом можно вычислить интеграл Jn для любого натурального
показателя и.
§ 2. Интегрирование рациональных выражений
272. Постановка задачи интегрирования в конечном виде. Мы по-
познакомились с элементарными приемами вычисления неопределен-
неопределенных интегралов. Эти приемы не предопределяют точно пути, по ко-
которому надлежит идти, чтобы вычислить данный интеграл, предо-
предоставляя многое искусству вычислителя. В этом и следующих пара-
параграфах мы остановимся подробнее на некоторых важных классах
функций и по отношению к их интегралам установим вполне опре-
определенный порядок вычислений.
Теперь выясним, что именно нас будет интересовать при инте-
интегрировании функций упомянутых классов и по какому принципу будет
произведено самое их выделение.
В 51 было охарактеризовано то многообразие функций, к кото-
которым в первую очередь применяется анализ; это - так называемые
элементарные функции и функции, которые выражаются через эле-
элементарные с помощью конечного числа арифметических дей-
действий и суперпозиций (без предельного перехода).
В главе III мы видели, что все такие функции дифференцируемы
и их производные принадлежат к тому же многообразию. Иначе об-
обстоит дело с их интегралами: очень часто оказывается, что интеграл
от функции, принадлежащей упомянутому классу, сам этому классу
не принадлежит, т. е. не выражается через элементарные функции с
помощью конечного числа названных выше операций. К
числу таких заведомо невыражающихся в конечном
виде интегралов относятся, например,
I е~х' dx, J sin х2 dx, J cos x2 dx,
psinx ,	fcos;t ,	r dx
j — ax, j — dx, j ^;
другие примеры подобного рода будут приведены ниже [280, 289.
290 и ел.].
Важно подчеркнуть, что все эти интегралы реально суще-
существуют *, но они лишь представляют собой совершенно н о-
* См. сказанное по этому поводу в 264. Мы вернемся к этому ниже, в 305.

273J	§ 2. ИНТЕГРИРОВАНИЕ РАЦИОНАЛЬНЫХ ВЫРАЖЕНИЙ	37
вые функции и не приводятся к тем функциям, которые мы назвали
элементарными *.
Известны сравнительно немногие общие классы функций, для ко-
которых интегрирование может быть выполнено в конечном виде; этими
классами мы ближайшим образом и займемся. На первом месте среди
них надлежит поставить важный класс рациональных функ-
функций.
273. Простые дроби и их интегрирование. Так как из неправильной
рациональной дроби можно исключить целую часть, интегрирование
которой не представляет трудностей, то достаточно заняться интегри-
интегрированием правильных дробей (у которых степень числителя
ниже степени знаменателя).
Из них мы остановимся здесь на так называемых простых
дробях; это будут дроби следующих четырех типов:
т А	тт А	ттт Mx+N	TV Mx+N
х-а'	{x-d)k'	x*+px + q' Y- (x*+px+q)™ '
(k=2,3,...)	(m=2, 3,...)
где A, M, N, a, p, q - вещественные числа; кроме того, по отношению
к дробям вида III и IV предполагается, что трехчлен x2+px + q не
имеет вещественных корней, так что
^--<7<0 или #-^г=~0.
Дроби вида I и II мы уже умеем интегрировать [267, 7)]
dx
	±__
-а)Ь к-\ (х-а)к-1
Что же касается дробей вида III и IV, то их интегрирование об-
облегчается следующей подстановкой. Выделим из выражения x2+px + q
полный квадрат двучлена
* Для того чтобы помочь читателю освоиться с этим фактом, напомним ему,
что интегралы
dx	r dx
J 1+Х2
от рациональных функций сами уже не являются рациональными функ-
функциями. Таким образом, если бы для нас «элементарными» были лишь рацио-
рациональные функции, то уже названные интегралы от «элементарных» функций не
выражались бы через «элементарные» функции, представляя собой «неэлементар-
«неэлементарные» функции новой природы: In л: и arctgx!

38	ГЛ. VIII. ПЕРВООБРАЗНАЯ ФУНКЦИЯ	[274
Последнее выражение в скобках, по предположению, есть число поло-
положительное, его можно положить равным а2, если взять
Теперь прибегнем к подстановке
x+^ = t, dx = dt,
Mx+N=Mt+iN~-~A.
В случае III будем иметь
Mx+N j.. |	i 2 j ^ Mr 2tdt . („_Mp\ r dt
2
или, возвращаясь к х и подставляя вместо с его значение:
dx = ^r ln(^2 + p^ + fir) + —	-arctg-
J
Для случая IV та же подстановка даст
Mx+N
Мр\ Г
2 J J
Первый из интегралов справа легко вычисляется подстановкой
um m-lu"*	^)
Второй же из интегралов справа, при любом т, может быть вычис-
вычислен по рекуррентной формуле F) п° 271. Затем останется лишь по-
2х+р	_
ложить в результате t = —-=—, чтобы вернуться к переменной х.
Этим исчерпывается вопрос об интегрировании простых дробей.
274. Разложение правильных дробей на простые. Остановимся теперь
на одной теореме из области алгебры, которая, однако, имеет фун-

274]	§ 2. ИНТЕГРИРОВАНИЕ РАЦИОНАЛЬНЫХ ВЫРАЖЕНИЙ	39
даментальное значение в теории интегрирования рациональных дро-
дробей: каждая правильная дробь
Q(x)
может быть представлена в виде суммы конечного числа простых
дробей.
Это разложение правильной дроби на простые дроби теснейшим
образом связано с разложением ее знаменателя Q(x) на простые мно-
множители. Как известно, каждый целый многочлен с вещественными
коэффициентами разлагается (и притом единственным образом) на
вещественные же множители типа х — а и x2+px + q; при этом квад-
квадратичные множители предполагаются не имеющими вещественных
корней и, следовательно, неразложимыми на вещественные линейные
множители. Объединяя одинаковые множители (если таковые име-
имеются) и полагая, для простоты, старший коэффициент многочлена
Q(x) равным единице, можно записать разложение этого многочлена
схематически в виде
О(х) = (х-аУ ...W+px+qT ...,	О)
где к, ..., т, ... суть натуральные. числа.
Заметим, что если степень многочлена Q есть п, то, очевидно,
сумма всех показателей к, сложенная с удвоенной суммой всех
показателей т, в точности даст л:
Zk + 2Zm = n.	D)
Для доказательства теоремы установим предварительно следую-
следующие два вспомогательных предложения:
1°. Рассмотрим какой-нибудь линейный множитель х-а, входя-
входящий в разложение знаменателя с показателем &з*1, так что
G(*)=(*-«)*&(*),
где многочлен Qx уже на х-а не делится. Тогда данная правильная
дробь
Р(х) ___ Р(х)
Q{x) {х-а)Шх)
может быть представлена в виде суммы правильных дробей*
A	Pt(x)
из которых первая является простой, а знаменатель второй со-
содержит множитель х-а в более низкой степени, чем раньше.
* Буквы Р, Q (с различными указателями) обозначают здесь целые многочлены,
а буквы А, М, N — постоянные числа.

40	ГЛ. VIII. ПЕРВООБРАЗНАЯ ФУНКЦИЯ	[274
Для доказательства достаточно подобрать число А и многочлен
Рх(х) так, чтобы выполнялось тождество
Определим сначала А так, чтобы левая часть делилась на х-а,
для чего достаточно (по известной теореме Б е з у), чтобы ее зна-
значение при х = а было нулем; это приводит к следующему выражению
для А:
Л
Оно имеет смысл именно потому, что (также по теореме Б е з у)
Qx(a) т* 0. При указанном выборе А многочлен Р1 определится просто
как частное.
2°. Пусть теперь x2+px + q будет какой-нибудь из квадратичных
множителей, входящий в разложение знаменателя с показателем т.» 1,
так что на этот раз можно положить
где многочлен Qx на трехчлен x2+px + q не делится. Тогда данная
правильная дробь
Р(х)	Р(х)
может быть представлена в виде суммы правильных дробей
Mx+N	Pt(x)
из которых первая уже будет простой, а вторая содержит в зна-
знаменателе упомянутый трехчлен снова - в низшей степени.
Для доказательства достаточно подобрать' числа М, N и много-
многочлен Рх(х) так, чтобы имело место тождество
Определим М и N так, чтобы на этот раз левая часть делилась
на квадратный трехчлен x2+px + q. Пусть остатками от деления Р
и Qx на этот трехчлен будут, соответственно, хх+(} и ух+д. Тогда
вопрос сведется к тому, чтобы на x^+px + q делилось выражение
olx+/3 - (Мх + N)(yx + д) = - уМх2 + (а - дМ - yN)x + (/3 - dN).
Выполнив здесь деление, на самом деле, в остатке будем иметь
[(ру - S)M-yN+x]x+ [qyM-
Мы должны приравнять нулю оба эти коэффициента и, таким обра-
образом, для определения М и 2V получим систему из двух линейных

274]	§ 2. ИНТЕГРИРОВАНИЕ РАЦИОНАЛЬНЫХ ВЫРАЖЕНИЙ	41
уравнений; ее определитель
ру-ь -у =b^PYb+qf
ЧУ -<5
отличен от нуля. Действительно, при у ^ О его можно написать в виде
но выражение в квадратных скобках есть значение нашего трехчлена
x2+px + q в точке х= — и, следовательно, не может быть нулем,
ибо трехчлен этот не имеет вещественных корней. При у = 0 опре-
определитель сведется к <52, а в этом случае д заведомо не нуль, поскольку
многочлен 2i на x2+px+q не делится.
Установив указанным путем значения М i&N, многочлен Рг и здесь
также определим без труда как частное.
Обратимся теперь к доказательству высказанной вначале теоремы.
Оно сведется к повторному применению предложений 1° и 2°, кото-
которые обеспечивают возможность последовательного выделения про-
простых дробей из данной правильной дроби, вплоть до ее исчер-
исчерпания.
Если множитель х-а входит в Q лишь в первой степени, то, в силу
1° (при к = 1), мы поставим ему в соответствие единственную про-
простую дробь вида
А
х-а
В случае же, если показатель степени х — а есть к>\, то, выделив,
на основании 1°, простую дробь
Ак
(х-а)*'
мы к оставшейся дроби снова применим 1°, выделим простую
дробь
(х-я)*-1'
и т. д., пока множитель х — а вовсе не исчезнет из разложения знаме-
знаменателя. Таким образом, в рассматриваемом случае множителю
(х-а)к (к> 1) будет отвечать группа нз к простых дробей
Такое же рассуждение мы поочередно применим и к каждому из
оставшихся еще линейных множителей, пока знаменатель не исчер-
исчерпается или в его разложении не останутся одни лишь квадратичные
множители.

42	ГЛ. VIII. ПЕРВООБРАЗНАЯ ФУНКЦИЯ	[275
Аналогично этому, пользуясь 2°, квадратичному множителю
х2 +рх + q мы поставим в соответствие одну лишь простую дробь
вида
Mx+N
x*+px+q '
если он входит в первой степени, и группу из т простых дро-
дробей
M2x+N2	Mmx+Nm	. „
x*+px+q + (x*+px+qY+ '	(x*+px+q)™ '	W
если этот множитель входит с показателем т>1.
То же можно сделать и с прочими квадратичными множителями,
если они еще имеются; этим и завершается доказательство теоремы.
275. Определение коэффициентов. Интегрирование правильных дро-
дробей. Таким образом, зная разложение C), мы тем самым знаем зна-
знаменатели тех простых дробей, на которые разлагается данная
дробь гг. Остановимся на вопросе об определении числителей,
т. е. коэффициентов А, М, N. Так как числители группы дробей E)
содержат к коэффициентов, а числители группы дробей F) 2т коэф-
коэффициентов, то ввиду D) всего их будет я.
Для определения упомянутых коэффициентов обычно прибегают
к методу неопределенных коэффициентов, который
Р
состоит в следующем. Зная форму разложения дроби ^, пишут
его с буквенными коэффициентами в числителях справа.
Общим знаменателем всех простых дробей, очевидно, будет Q; скла-
складывая их, получим правильную дробь *. Если отбросить теперь слева
и справа знаменатель Q, то придем к равенству двух многочленов
(л - 1)-й степени, тождественному относительно х. Коэффициентами
при различных степенях многочлена справа будут линейные одно-
однородные многочлены относительно л коэффициентов, обозначенных
буквами; приравнивая их соответствующим численным коэффициен-
коэффициентам многочлена Р, получим, наконец, систему п линейных уравнений,
из которых буквенные коэффициенты и определятся. Ввиду того, что
возможность разложения на простые дроби наперед установлена,
упомянутая система никогда не может оказаться противоре-
противоречивой.
Больше того, так как упомянутая система уравнений имеет реше-
решение, каков бы ни был набор свободных членов (коэффициентов много-
многочлена Р), то ее определитель необходимо будет отличен от нуля.
Иными словами, система всегда оказывается определенной.
Это простое замечание попутно доказывает и единственность
* Сумма правильных рациональных дробей всегда представляет собой пра-
правильную же дробь.

276]	§ 2. ИНТЕГРИРОВАНИЕ РАЦИОНАЛЬНЫХ ВЫРАЖЕНИЙ	43
разложения правильной дроби на простые дроби. Поясним сказанное
примером.
2х+2дг+13
Пусть дана дробь 	¦—	. Согласно общей теореме, для нее имеется
(х-2)(д:2 + 1J
разложение
2хЧ-2х+13 А Вх+С Dx+E
Коэффициенты А, В, С, D, Е определим, исходя из тождества
2х2 + 2х +13 = А(х* +IJ + {Вх+О(дг2 + 1)(* - 2) + фх + Е)(х - 2).
Приравнивая коэффициенты при одинаковых степенях х слева и справа, придем
к системе из пяти уравнений
откуда
А = \,
Окончательно
X"
X3
X3
X1
х°
В=-
2х* + Ъ
-2В+С = 0,
2A+B-2C+D = 2,
-2B+C-2D+E=2,
А-2С-2Е=13,
-1, С=-2, Z)=-3,
-+13 1 х + 2 Зх+4
Е= -4.
(х-2)(х2 + 1J х-2
Алгебраический факт, который мы только что установили, имеет
непосредственное применение к интегрированию рацио-
рациона льных дробей. Как мы видели в 273, простые дроби инте-
интегрируются в конечном виде. Теперь мы то же можем сказать о любой
рациональной дроби. Если всмотреться в те функции, через которые
выражаются интегралы от целого многочлена и от правильных дро-
дробей, то можно сформулировать более точный результат:
Интеграл от любой рациональной функции выражается в конечном
виде - с помощью рациональной же функции, логарифма и арктан-
арктангенса.
Например, возвращаясь к только что рассмотренному примеру и вспоминая
формулы п° 273, имеем
г 2х2+2х+13 ,
\(х-:	dx=
,- dx rx + 2	г Зх + 4	1 3-4* 1 (х-2J
=	ах- 	dx=	1—In—	4arctgx+C.
J x-2 J *2+l J (*2 + lJ 2jc2 + 1 2 x2 + l
276. Выделение рациональной части интеграла. Существует прием,
принадлежащий М. В. Остроградскому, с помощью кото-
которого нахождение интеграла от правильной рациональной дроби зна-
значительно упрощается. Этот прием позволяет чисто алгебраиче-
алгебраическим путем выделить рациональную часть интеграла.

44	ГЛ. VIII. ПЕРВООБРАЗНАЯ ФУНКЦИЯ	1276
Мы видели [273], что рациональные члены в составе интеграла
получаются при интегрировании простых дробей вида II и IV. В пер-
первом случае интеграл сразу можно написать
Установим теперь, какой вид имеет рациональная часть интеграла
Прибегнув к знакомой уже нам подстановке x+^ = t, используем
равенства A), B) и формулу приведения F) п° 271 при п = т- 1. Если
вернуться к переменной х, то получим
г Mx+N ,	M'x+N'	г	dx
где М', N' и a означают некоторые постоянные коэффициенты. По
этой же формуле, заменяя т на т — 1, для последнего интеграла най-
найдем (если т=-2)
С	a dx	M"x+N" о с	dx
и т. д., пока не сведем показатель трехчлена x2+px + q в интеграле
справа к единице. Все последовательно выделяемые рациональные
члены суть правильные дроби. Объединяя их вместе, получим резуль-
результат вида
г Mx+N ,	R(x)	. г dx
J (рс*+рх+ЯУ""л (x*+px+q)m-^ J x*+px+q '	W
где R{x) — целый многочлен, степени низшей, чем знаменатель *, а
А - постоянная.
Р
Пусть имеем правильную дробь ^, которую будем предполагать
несократимой, и пусть знаменатель ее Q разложен на простые мно-
множители [см. C)]. Тогда интеграл от этой дроби представится в виде
суммы интегралов от дробей вида E) или F). Если к (или т) больше
единицы, то интегралы всех дробей группы E) [или F)], кроме пер-
первой, преобразуются по формуле G) [или (8)]. Объединяя все эти ре-
результаты, окончательно придем к формуле вида
M	(9)
* См. сноску на стр. 42.

276]	§ 2. ИНТЕГРИРОВАНИЕ РАЦИОНАЛЬНЫХ ВЫРАЖЕНИЙ	45
Р,
Рациональная часть интеграла ^ получена от сложения выделенных
выше рациональных частей; следовательно, прежде всего она является
правильной дробью, а ее знаменатель Qx имеет разложе-
разложение
Qx{x) ^{x-af-1... (х2 +рх + q)'1...
Что же касается дроби -^ , оставшейся под знаком интеграла, то она
получилась от сложения дробей видаI и III, так что она также пра-
правильная и
Q2(x) = (x-a).. \x2+px+q)...
Очевидно [см. C)], 6 = 6162-
Формула (9) и называется формулой Остроградского.
Дифференцируя, можно представить ее в равносильной форме
Р tP л> Р
Ий +й •	A0)
Мы видели, что многочлены Qx и Q2 легко находятся, если из-
известно разложение C) многочлена Q. Но они могут быть определены
и без этого разложения. Действительно, так как производная Q' со-
содержит все простые множители, на которые разлагается Q, именно
с показателями на единицу меньшими, то Qx является наибольшим
общим делителем Q и Q', так что может быть определено по этим
многочленам, например, по способу последовательного деления. Если
6i известно, то 6г определится простым делением Q на Qx.
Обратимся к определению числителей Рх и Р2 в формуле A0). Для
этого также пользуемся методом неопределенных коэф-
коэффициентов.
Обозначим через п, пх, и2, соответственно, степени многочленов Q,
6i> 62» так что Л1 + Иг = и; тогда степени многочленов Р, Рх, Рг будут
не выше и -1, пх-\, щ-Х. Подставим в качестве Рх и Рг многочлены
степеней ^-Ih^-Ic буквенными коэффициентами;
всего этих коэффициентов будет пх + щ, то есть п. Выполним в A0)
дифференцирование
Q\	йг Q '
Покажем теперь, что первую дробь всегда можно привести
к знаменателю Q, сохраняя целым числитель. Именно
р'о r Q'lQ*
Q\	"	Q1Q2	Q

46	ГЛ. VIII. ПЕРВООБРАЗНАЯ ФУНКЦИЯ	[276
если Н означает частное Ц^. Но это частное можно представить
в виде целого многочлена. Действительно, если (х — а)к, при кз*1,
входит в состав Qx, то {х-а)к~х войдет в Qi,a. х-аъ состав Q2; такое
же заключение можно сделать и о множителе вида (х2 +рх + q)m при
/яэ»1. Следовательно, числитель Н нацело делится на знамена-
знаменатель, и впредь под Н можно разуметь целый многочлен (степени
«2-1).
Освобождаясь от общего знаменателя Q, придем к тождеству двух
многочленов (степени п - 1)
Отсюда, как и выше, для определения п введенных буквенных ко-
коэффициентов получим систему из п линейных уравнений.
Так как возможность разложения A0) установлена, каково бы ни
было Р, то упомянутая система должна быть совместной при
любых свободных членах. Отсюда само собой вытекает, что опре-
определитель ее отличен от нуля, а значит - система необходимо ока-
оказывается определенной, и разложение A0) - при указанных
знаменателях Q1 a Q2 - возможно лишь единственным обра-
образом*.
Пример. Пусть требуется выделить рациональную часть интеграла
С 4xi+4х3 + 16лг2 + 12х+8
	dx.
J (х+1J(л:2+1J
Имеем
4д:Н4л3+16д:2+12х:+8 f ах^+Ьх+с Т*
х3+хг+х+\
откуда
= Bах+Ь)(х3+х*+х+1) - (ах*+Ьх+с)Cх"+2х+1)+(dx2+ex+f)(x* 4-ха+х +1).
Приравнивая коэффициенты при одинаковых степенях х в обеих частях,
получим систему уравнений, из которых и определятся неизвестные а, Ь, ...,/:
d=0 (в последующем уже d в расчет не берем),
х*
-2b+e+f=4,
a-b-3c+e+f=16, e=-l, b=l, с=-4,
2а-2с+е+/=12, </=0, е = 3, /=3,
х°
* Ср. аналогичное замечание по поводу разложения правильной дроби на
простые дроби, стр. 42.

277J	§ 2. ИНТЕГРИРОВАНИЕ РАЦИОНАЛЬНЫХ ВЫРАЖЕНИИ	47
Итак, искомый интеграл
dx-
x*-x+4	r dx	x2-x+4
г+3 \;тт= --.—;	—+3arctgx+C.
В этом примере вычисление последнего интеграла легко было произвести сразу.
В других случаях приходится снова разлагать на простые дроби. Можно, впрочем,
и этот процесс объединить с предыдущим.
277. Примеры. Приведем дальнейшие примеры на интегрирование рациональ-
рациональных функций.
Разложение на простые дроби здесь достигается путем незамысловатых пре-
преобразований:
1	(\+х*)-х°-	1	1
A+х2J
-x2 1	1 1
1 1 х 3
Ответ:	¦	arc tg x + С.
х 2 1+х* 2
г 4* + 4х11
2) 	dx.
J B*-l)B*+3)Bx-5)
Имеем
1 И
Bx-l)B«+3)Bx-5)
откуда следует тождество
ABC
	- +	; ,
f l)( 3W 5\	1	3	5
\х	л:Н—\\х	х	х-\— х
{ 2){ 2){ 2)	2	2	2
Вместо того чтобы приравнивать коэффициенты при одинаковых степенях
х слева и справа, можно поступить иначе. Положим в этом тождестве последо-
13 5 113
вательно х = — , - — , —; сразу получим А= — , Б=	, С= — (ибовсякий раз
2 2 2	4	8	8
справа останется лишь одно слагаемое).

48
ГЛ. VIII. ПЕРВООБРАЗНАЯ ФУНКЦИЯ
[277
1
Ответ: —In
4
1
1
	In
8
3
X+12
3
5
X~2
+ C
iln
3)
dx
+С *.
Так как
то разложение ищем в виде
1
Ах + Б
Cx+D
Из тождества
1 =(Ax+B) {x*-xf2+\) + {Cx + D) I
получаем систему уравнений
x3
откуда
Таким образом,
Г dx
А= -С=
1 Г X+V2	1 Г х
2^2 J x*+xfi+\	2]/'2 J x*-
-V2
arctg
_ arctg
4f2 x2-xy2+l 2]/2	' ' 2]/2
Использовав формулу сложения для арктангенсов [50], можно этот результат
представить и в такой форме:
1 , х'+х ]/2+1 1 х]/2
—г In	Ц;	1	 arctg—'	\-С .
Нужно заметить, однако, что это выражение годится лишь отдельно для
промежутков (-~, -1), (-1, 1), A, +«•), ибо в точках х= ±1 оно теряет смысл.
Постоянная С для этих промежутков, соответственно, равна
С—
С, С+-
2]/2	2]/2
Скачкообразное изменение постоянной компенсирует разрывы самой функции
при х= ± 1.
4)
'2л*-4х3+24х2-40д:+20
¦dx.
1
* Очевидно, постоянная С разнится от постоянной С на	In 2.

277]	§ 2. ИНТЕГРИРОВАНИЕ РАЦИОНАЛЬНЫХ ВЫРАЖЕНИЙ
Прибегнем к выделению рациональной части интеграла. Имеем
49
Таким образом,
2x4-4x3+24x2-40x+20 r
I
fx+g
J + х^Т + x2
причем мы заодно уже разлагаем на простые дроби то выражение, которое еще
подлежит интегрированию (после выделения рациональной части интеграла).
Тождество
(х -1) -
2 - 40х+20 = (
-(ax*+bx*+cx+d)- 2Bдг-2) (*-
приводит к системе уравнений:
откуда
Xе
X3
JC°
6,
«+/=0,
-a-6e-5f+g = 0,
-a-2b+lSe+12f-5g=2,
8a+2b-3c-32e-16f+12g= -A,
-	6a+4b + 5c-4d+36e+12/-16?= 24,
-	46 + Sd- 24e -4f+12g= - 40,
-	2c-4rf+8e-4^ = 20,
Ответ:
5)
О2-2л:+2J
1" In ¦
-1J
3, е = 2, /=-2,
+ 2arctg(x-l) + C.
dx.
Выделим рациональную часть интеграла. Имеем
Разложение ищем в виде
Г
fx2+gx+h
Из системы уравнений:
Xs
Xs
х1
X3
X1
х°
/=0,
a-2b+3g+h~-l,
5a-b-3c+5g+ih=l,
2c-d-1e+g + 3h
t Г. М. Фихтенгольц, т. II

50	ГЛ. VIII. ПЕРВООБРАЗНАЯ ФУНКЦИЯ	[278
находим
e=-l, b = 0, c=-2, d=0, e=-l, f=g = h = O.
Таким образом, здесь интеграл весь сводится к рациональной функции
2l
+
§ 3. Интегрирование некоторых выражений,
содержащих радикалы
278. Интегрирование выражений вида R \х, У ах+г\ . Примеры.
Вьппе мы научились интегрировать в конечном виде рациональные
дифференциалы. В дальнейшем основным приемом интегрирования
тех или других классов дифференциальных выражений будет разыс-
разыскивание таких подстановок t = оз(х), которые привели бы подинтеграль-
ное выражение к рациональному виду и дали бы возможность пред-
представить интеграл в конечном виде в функции от t. Если при этом
сама функция со{х), которую надлежит подставить вместо t, выра-
выражается через элементарные функции, то интеграл представится в ко-
конечном виде и в функции от х.
Назовем этот прием методом рационализации под-
интегрального выражения.
В качестве первого примера его применения рассмотрим интеграл
вида	т
J V г ух+д)	v '
где R означает рациональную функцию от двух аргументов,
т - натуральное число, а а, /3, у, д - постоянные.
Положим
t = i
ух+д'	ух+д'	YVJ *-yt"i •
Интеграл перейдет в
JR(<p(t), t)<p'(t)dt;
здесь дифференциал имеет уже рациональный вид, так как R, q>, <p' -
рациональные функции. Вычислив этот интеграл по правилам преды-
предыдущего параграфа, к старой переменной вернемся, подставив t =
К интегралу вида A) сводятся и более общие интегралы
rR(xD?±PYf f^V,...
J	\ух + д) ' \ух+д)
\ \ i	\ '
* Условимся раз навсегда буквой R обозначать рациональную функцию
от своих аргументов.

279]
§ 3. ИНТЕГРИРОВАНИЕ РАДИКАЛЬНЫХ ВЫРАЖЕНИЙ
51
где все показатели г, s, ... рациональны; стоит лишь привести эти
показатели к общему знаменателю т, чтобы под знаком интеграла
т
получить рациональную функцию от х и от радикала
1^+1+2
ах+р
Примеры
¦ « к
-dx.
Здесь дробно-линейная функция
ух + д
к линейной функции. Полагаем t = Ух+1, dx = 2tdt; тогда
Г yI+T+2	ЛГ'+2^ ГГ 2 2t+2 \
	'	dx = 2	dt=	dt =
J (x+iy-VxTl	J'3-l Jl'-l f2 + /+lj
, в частности, свелась просто
= ln-
2	2t + \
arctg	hC,
]/3	у
где остается лишь подставить t =
з
2)
/x+l.
dx
x-\x+l
Полагаем t =
x+l
x~^l
C-Г
6t*dt
dx = - ——— ; тогда
x+l dx
t + 2
l
= — In
2
2/-1
arctg -^ +C,
уз
где /=
дс-1
279. Интегрирование биномиальных дифференциалов. Примеры. Би-
Биномиальными называются дифференциалы вида
хт(а + Ьх"У dx,
где а, Ъ - любые постоянные, а показатели т, n, p - рациональные
числа. Выясним случаи, когда эти выражения интегрируются в ко-
конечном виде.
Один такой случай ясен непосредственно: если/) - число
целое (положительное, нуль или отрицательное), то рассматривае-
рассматриваемое выражение относится к типу, изученному в предыдущем п°. Имен-
Именно, если через X обозначить наименьшее общее кратное знаменателей
и
дробей т и п, то мы имеем здесь выражение вида R (fx) dx, так что
я
для рационализации его достаточна подстановка t = Yx.

52	ГЛ. VIII. ПЕРВООБРАЗНАЯ ФУНКЦИЯ	[279
Преобразуем теперь данное выражение подстановкой z = xn.
Тогда
1	2±1-1
xm(a + bxnydx=-(a + bz)Pz " dz
и, положив для краткости
будем иметь
f хт{а + Ъхп)р dx=X-Ua + bz)Pz4 dz.	B)
Если q — число целое, то мы снова приходим к выраже-
выражению изученного типа. Действительно, если обозначить через v зна-
»»
менатель дроби/), то преобразованное выражение имеет вид R(z, ^a + bz).
Рационализации подинтегрального выражения можно достигнуть и
сразу - подстановкой
Наконец, перепишем второй из интегралов B) так:
z )
Легко усмотреть, что при p + q целом мы также имеем изучен-
9
ный случай: преобразованное выражение имеет вид R\z, У-—-I .
Подинтегральное выражение в данном интеграле рационализируется
и сразу подстановкой
Таким образом, оба интеграла B) выражаются в конечном виде,
если оказывается целым одно из чисел
р, q, p + q
или (что то же) одно из чисел
7Я+1	7Я+1
Р>—> —+Р-
Эти случаи интегрируемости, по существу, известны
были еще Ньютону. Однако лишь в середине прошлого столетия
П. Л. Чебышев установил замечательный факт, что других слу-
случаев интегрируемости в конечном виде для биномиальных дифферен-
дифференциалов нет.

279J
§ 3. ИНТЕГРИРОВАНИЕ РАДИКАЛЬНЫХ ВЫРАЖЕНИЙ
53
Рассмотрим примеры,
з
1)
-dx-
1	1
Здесь т=	, n = —,
dx.
P = — ', так как
= 2,
то имеем второй случай интегрируемости. Заметив, что v = 3, положим (по общему
правилу)
тогда
fe
2)
dx
Ух
с	з
06-*3)Л = -
J	I
и т. д.
На этот раз т = 0, п = 4, р=	; третий случай интегрируемости, так как - +р =
1 1	4	п
=	= 0. Здесь v = 4; положим
4 4
*-04-1) " ,
л:
_5^
dx
и т. д.
3)
dx
-= j
г t*dt 1 г( 1 1 ) I г dt 1
.=	=_	\dt	-—In
J г4-1 4J U+l г-l j 2J /=+1 4
f+1
--arctg/+C
Здесь m= -1, и*5,
1	/Я+1
=	; второй случай:	= 0; v = 3. Положим
3	и
dt;

54	ГЛ. VIII. ПЕРВООБРАЗНАЯ ФУНКЦИЯ	[280
dx 3 с tdt 1 (( 1	(-1 ] 1 (t-\y Уз	2/+1
1	¦'	1^1-	+J_ arctg	+с
3 f /Л 1 с 1
= —	= -
5 J /3— 1 5JU-1
; ю t*+t+i 5
280. Формулы приведения. Так как интеграл от биномиального
дифференциала всегда может быть [см. B)] преобразован к виду
C)
то в дальнейшем ограничимся рассмотрением именно этих интегра-
интегралов.
Установим ряд формул приведения, с помощью которых
интеграл C) может быть, вообще говоря, выражен через подобный
же интеграл Jp\q', где р' и q' разнятся от р и q на произвольные це-
целые числа.
Интегрируя тождества
{а + bz)P+1zi = а(а + bz)Pzi + Ъ(а + bz)Pzi+1,
d
-г- [{а + bz)P+1zc'+1] = (р + l)b(a + bz)pzQ+1 + (а +1)(
найдем
•'p+l, Я~ ® Р* Q^ p, Q+1*
(а + bz)P+lz4^ = (р + l)bJPi q+l + (q + l)/p+1>,.
Отсюда получаются первые две формулы
JP- 9=	^ГГП +И(р~+Т) JP+1- 1'
(a+bz)P+1z4+1 up+q+2
которые позволяют увеличить показатель р или # на единицу
(если только он отличен от -1).
Разрешая эти равенства относительно Jpn q, /рд+1 и заменяя/) и q
соответственно на р - 1 и q - 1, придем к формулам
ГТТП	. _(a + bz)Pz<l+1 ар .
JP1
которые позволяют уменьшать показатель р или q на единицу
(если только сумма p + q отлична от -1).

280]	§ 3. ИНТЕГРИРОВАНИЕ РАДИКАЛЬНЫХ ВЫРАЖЕНИЙ	55
Если ни р, ни q, ни р + q не будут целым числом (так что инте-
интеграл Jp q не вьфажается в конечном виде через элементарные функции),
то формулы приведения могут последовательно прилагаться без вся-
всякого ограничения. С их помощью параметры/) п q могут быть
сделаны, например, правильными дробями.
Остановимся на более интересном для нас случае, когда интеграл
берется в конечном виде. При этом можно предположить, что целым
оказывается показатель р или q, так как случай целого р + q подста-
1
новкой z=- приводит к случаю целого q.
Тогда последовательное применение выведенных формул позво-
позволяет свести этот целый показатель, р или q, к 0 (если он был поло-
положительным) или к — 1 (если он был отрицательным). Этим обычно
либо заканчивается интегрирование, либо - во всяком случае - зна-
значительно упрощается.
Примеры. 1) Рассмотрим интеграл *
хт
(/я - целое).
1	ти+1
Здесь п = 2, р =	; поэтому при т нечетном оказывается целым числом 	=
2	п
т+\ тя + 1 тя+1 1 т
=	, а при m четном - число	\-р =	= —. так что во всех
2	и	2 2 2
случаях интеграл в конечном виде берется. Подстановкой г=хг сведем его к ин-
интегралу
Если, считая т>\, применить к этому последнему интегралу формулу (IV),
то получим
1 /П — 1
V-z)*z~T~ m-\
или, возвращаясь к данному интегралу,
1		т-1
ш	/я
Эта формула, уменьшая значение т на 2, последовательно сводит вычисление
Ят либо к
* Аналогично можно исследовать и интегралы

56	ГЛ. VIII. ПЕРВООБРАЗНАЯ ФУНКЦИЯ
при т нечетном, либо же к
[281
Г dx
На = —==== = arcsin x-\-С
при т четном.
Пусть теперь т -= -1, так что т = -fi,(i>l. Применим на этот раз формулу (II)
1 Я1+1
\Ч^~
i.ffl
откуда
С помощью этой формулы мы имеем возможность уменьшать значение ^ на
2 и, последовательно, свести вычисление H_li либо к
+ С
при [I нечетном, либо же к
г etc угг
я_2= 	--I
J х2УТ^Г2 *
+с
при ,if четном.
2) Если к интегралу *
jn =
с dx	\ с
J(x2+a2)n+1 2J
(п=1,2,3 ...)
применить формулу (I):
(n+
2и-1 1
2л а2 -п,-J-'
то, возвращаясь к /п» получим уже известную нам [271, F)] формулу приведения
1	х 2и-1 1
281. Интегрирование выражений вида R(x, Уал^ + Ьж + с). Подста-
Подстановки Эйлера. Переходим к рассмотрению очень важного класса ин-
интегралов
|	D)
, Уах2 + Ъх + с) dx.
* Аналогично можно исследовать и интеграл
dx
г
J (ха-

28Ц	§ 3. ИНТЕГРИРОВАНИЕ РАДИКАЛЬНЫХ ВЫРАЖЕНИЙ	57
Предполагаем, конечно, что квадратный трехчлен не имеет равных
корней, так что корень из него не может быть заменен рациональ-
рациональным выражением. Мы изучим три подстановки, называемые под-
подстановками Эйлера (L. Euler), с помощью которых всегда
можно достигнуть здесь рационализации подинтегрального выраже-
выражения.
I подстановка приложима в случае, если а>0. Тогда пола-
полагают
f	= t - Yax *.
Возводя это равенство в квадрат, найдем (по уничтожении членов ах2
в обеих частях) bx + c = t2-2fatx, так что
=±	L
ijat+b
Все остроумие эйлеровой подстановки именно в том, что для опре-
определения х получается уравнение первой степени, так что х, а одно-
одновременно с ним также и радикал УахР + Ьх + с выражаются рацио-
рационально через t.
Если полученные вьфажения подставить в D), то вопрос сведется
к интегрированию рациональной функции от t. В результате, воз-
возвращаясь к х, нужно будет положить t = У ах2 + bx + c + Yax.
II подстановка приложима, если с >0. В этом случае можно
положить
Если возвести в квадрат, уничтожить с в обеих частях и сократить
на х, то получим ax + b = xt2 + 2Yct - снова уравнение первой степени
относительно х. Отсюда
Подставив это в D), очевидно, осуществим рационализацию подин-
подинтегрального выражения. Проинтегрировав, в результате положим
* Можно было бы положить и
** Или Yax*+bx+c=xt-Yc.

58	ГЛ. VIII. ПЕРВООБРАЗНАЯ ФУНКЦИЯ	[281
Замечание I. Случаи, рассмотренные выше (а > 0 и с > 0), при-
приводятся один к другому подстановкой х = -. Поэтому всегда можно
избежать пользования второй подстановкой.
Наконец, III подстановка пригодна в том случае, если квад-
квадратный трехчлен ах2 + Ьх + с имеет (различные) вещественные корни
А и /л. Тогда этот трехчлен, как известно, разлагается на линейные
множители
ах2 + Ьх + с = а{х - Х)(х - [i).
Положим
Возводя в квадрат и сокращая на х — А, получим и здесь уравнение
первой степени а(х - /л) = t2(x - А), так что
*-
,.-а
и т. д.
Замечание II. При сделанных предположениях радикал
-Х)(х-[г) (считая для определенности, скажем, х>А) можно пре-
преобразовать к виду
так что в рассматриваемом случае
R{x, Ya
и мы, в сущности, имеем дело с дифференциалом изученного в п° 278
типа. III подстановка Эйлера, которую можно записать, в форме
тождественна с подстановкой, уже указанной в 278.
Покажем теперь, что I и III подстановок Эйлера одних доста-
достаточно для того, чтобы осуществить рационализацию подинтеграль-
ного выражения в D) во всех возможных случаях. Дей-
Действительно, если трехчлен ах2 + Ьх + с имеет вещественные корни, то,
как мы видели, приложима III подстановка. Если же вещественных
корней нет, т. е. й2-4ас<0, то трехчлен
ах2 + Ьх + с=^ [Bах + ЬJ + (Аас - Ь2)]
при всех значениях переменной х имеет знак а. Случай а<0 нас не
интересует, ибо тогда радикал вовсе не имел бы вещественных зна-
значений. В случае же а>0 применима I подстановка.

82]	§ 3. ИНТЕГРИРОВАНИЕ РАДИКАЛЬНЫХ ВЫРАЖЕНИЙ	59
Эти соображения приводят вместе с тем к общему утверждению:
ттегралы типа D) всегда берутся в конечном виде, причем для пред-
представления их, кроме функций, через которые выражаются интегралы
>т рациональных дифференциалов, нужны еще лишь квадратные корни.
282. Геометрическая трактовка эйлеровых подстановок. Эйлеровы
юдстановки, кажущиеся столь искусственными, могут быть все по-
1учены из наглядных геометрических соображений.
Рассмотрим кривую второго порядка
у = ± У ах2 + Ьх + с или у1 = ах2 + Ьх+с.
Если взять на этой кривой произвольную точку (х0, j0), так что
yl = ax% + bxo + c,	E)
го проходящая через нее секущая y-yQ = t(x-x0) пересечет кривую
:ще только в одной точке (х, у). Координаты последней найдутся
грюстым вычислением. Исключая у из уравнений кривой и секущей,
толучим
[у0 + t{x - xo)f = ax2 + bx + с,
эткуда, с учетом E),
2yot(x - xQ) + t2(x- х0J = а(х2 - х§) + Ь(х - х0)
1ли - по сокращении на х-х0 -
2y0t +t\x- х0) = а(х + х0) 4 Ъ.
Гаким образом, абсцисса х, ас нею и ордината у второй точки пере-
пересечения выражаются рациональными функциями от пере-
переменного углового коэффициента t. При этом очевидно, что, надле-
каще изменяя t, можно заставить точку (х, у) описать всю кривую.
Теперь ясно, что зависимость
У ах2 + bx + c-yo = t(x- x0)
i определит ту подстановку, которая заведомо рационализирует под-
подынтегральное выражение в случае D).
Пусть трехчлен ах2 + Ьх + с имеет вещественные корни Я и /л; это
шачит, что наша кривая пересекает ось х в точках (Я, 0) и (jj,, 0); взяв,
например, первую из них за точку (х0, у0), придем к III подстановке
Эйлера
fax2 + bx + с = t(x - X).
Если с >0, то кривая пересекает ось у в точках @, ± /с); взяв одну
аз них за точку (xo,jo), получим II подстановку Эйлера
Уах2 + bx + с ± У~с = tx.

60	ГЛ. VIII. ПЕРВООБРАЗНАЯ ФУНКЦИЯ	[283
Наконец, в сущности, в том же порядке идей получается и I под-
подстановка Эйлера, лишь за точку (х0,у0) мы принимаем беско-
бесконечно удаленную точку кривой. Именно, предполагая а>0
(в этом случае кривая будет гиперболой), рассмотрим асимптоту
кривой у- ±У~ах и станем пересекать кривую прямыми у = t + У~ах,
параллельными асимптоте (они будут проходить через упомянутую
бесконечно удаленную точку). Каждая такая прямая пере-
пересекает кривую во второй точке (х, у), координаты которой будут ра-
рациональными функциями от t. Отсюда подстановка
У ах2 + bx + c = t + Уах.
283. Примеры. Нам уже известны два основных интеграла [269, 9)
и 12); 268]:
dx	, ,	,
= ln \х+ух2±а*\+С,
Ji
dx	x
• = arcsin—\-С,
а
относящихся к рассматриваемому типу. Отправляясь от них, можно вычислить
и другие интегралы.
С dx
1) ——==. При вычислении этого интеграла будем различать два случая:
<х=»0 и
Если ос» 0, то интеграл легко преобразуется к первому из основных
(при —= +аА
- +С.
Можно еще умножить аргумент логарифма на а, что введет дополнительное сла-
слагаемое — In а и, следовательно, отразится лишь на С. Окончательно получим
Г
J
^	1\УфЧ^)\+С.	F)
<a=-0)
Если же а-=0, так что <х= - |а|, радикал перепишем в виде Ур- \л\х2. Для
того чтобы радикал вообще мог иметь вещественные значения, необходимо пред-
предположить здесь /? =¦ 0. Интеграл преобразуется ко второму из основных интегралов
при-—- = i
> и
dx	1
и
.		 „ 		О)
УИ

283]
§ 3. ИНТЕГРИРОВАНИЕ РАДИКАЛЬНЫХ ВЫРАЖЕНИЙ
61
К интегралам F) и G) с помощью элементарных приемов приводятся многие
другие. Например,
2) I У<хх%+@ dx берется интегрированием по частям
[
-J'
-Jl
_p
H/?)-/?
r 	 r
- l/axz+fidx+P
dx
Справа у нас снова получился искомый интеграл; перенося его налево и разде-
разделив все равенство на 2, найдем
= —х
dx
(8)
Для получения окончательного результата остается лишь вместо последнего
интеграла подставить его выражение F) или G), смотря по тому, будет ли <х^0
или <х-=0.
3) (а)
L-
dx
(б)
J;
dx
(в)
;¦
dx
(ax*+pyl,
сводятся к уже известным интегралам простой подстановкой х = — , dx=	dt.
Имеем (для определенности, пусть д:и(>0):
(а) Г dx	Г
J xVxxz+в J VS
- дальнейшее вычисление производится по формуле F) или G), смотря по знаку /?.
Далее,
(б)
Г ^__ f_if_
/?*
9
+ C
и аналогично
(в) Г dx - Г Ы< ! J
4) Тождественные преобразования подинтегрального выражения приводят к
уже вычисленным следующие, например, интегралы:
(а)
;;
х* dx
(б)
dx.

62
ГЛ. VIII. ПЕРВООБРАЗНАЯ ФУНКЦИЯ
[283
Имеем
(а)
Г x2dx 1 Г(а*2+/3)-/3 1 Г 	 В Г
Р Г dx
или, воспользовавшись формулой (8),
jfldx 1
Г
J
2а
2а J
dx
ад;2+/д
и т. д. [см. 1)].
Затем
(б)
ГУо^Т^	Г од;2+^	Г xdx	Г
	 </х= —==== Ас = а	+/3
J •<	J x Vax*+e	J V<xx2+B J
х Уод:2+/3
первый из интегралов берется сразу, второй вычислен в 3). Наконец,
(в)
Г х*	\_ Г dx р Г
J (ах*+0)Ч. a J у^Тй « J
dx
(«•+/»)•/.
[см. 1) и 3)].
5) Если под радикалом стоит полный квадратный трехчлен ах*+Ьх+с,
часто выгодно линейной подстановкой свести его к двучлену. Выделяя пол-
полный квадрат
1
ах2 + Ьх+с = — [Bах+ЬJ+Аас - №],
4а
полагают t = 2ax+b. Таким путем, например, из формул F) и G) получается
при «=>0
Jl
dx
.JLta
Va(ax*+bx+c)\+C=
]Га
-In
ахЛ	h
+ C,
а при а«=0
h
dx
1	2ax+b
	arcsin	+C.
F*)
G*)
6) Обратимся теперь к эйлеровым подстановкам. В 269, 12)
мы фактически применили I подстановку к вычислению интеграла
dx
Хотя второй основной интеграл
dx

283]
§ 3. ИНТЕГРИРОВАНИЕ РАДИКАЛЬНЫХ ВЫРАЖЕНИЙ
63
нам известен из элементарных соображений, но - для упражнения - мы все же
к нему применим эйлеровы подстановки.
(а) Если воспользоваться сначала III подстановкой У а2 - х2 = t(a - х), то
х = а	,
t*+l'
dx =
4at dt
lat
Г dx Г dt ЛГа+х
————=2 	= 2arctgf+C=2arctg /	\-C.
J Уа2-х2 J ?2 + !	Г a~x
Так как имеет место тождество
2arctg
. х л
arcsin—|—
а-х	а 2
то этот результат лишь формой разнится от уже известного нам.
Читателю и впредь следует считаться с возможностью для интеграла полу-
получаться в разных формах, в зависимости от примененного для его вычисления
метода.
(б) Если к тому же интегралу применить II подстановку ]/а2 - х2 = xt-a,
то аналогично получим
dx Г dt
	 _ 2 1	= _
a x	j
2arctgf+C= -2arctg
+ С.
Здесь мы сталкиваемся с другим любопытным обстоятельством *, этот результат
годится отдельно для промежутка ( - а, 0) и для промежутка @, а), ибо в точке
х = 0 выражение
- 2 arctg -
лишено смысла. Пределы этого выражения при х*-0и при х-*+0 различны:
они равны, соответственно, я и -я; выбирая для упомянутых промежутков раз-
различные же значения постоянной С так, чтобы второе из них было на In больше
первого, можно составить функцию, непрерывную во всем промежутке (-а, а),
если принять за ее значение при х=0 общий предел слева и справа.
И на этот раз мы получили прежний результат лишь в другой форме, ибо
имеют место тождества
- 2 arctg ¦
G)
dx
x+][x2-x+l
arcsin	л для
arcsin —1-я для
a
- a -= x ¦= 0.
: Ср. пример 3) n° 277.

64
ГЛ. VIII. ПЕРВООБРАЗНАЯ ФУНКЦИЯ
[283
(а) Сначала применим I подстановку: \х*-x+l = t-x,
f2-!
f
J x
2t-\
2t*-2t+2
t
dx = 2
Bt-\)>
dt,
Ч\т-
3 , 3
2/-1 Bf-l)
Если подставить сюда 1 = х+ух2-х+1, то окончательно получим
dx	3	1
J
-|m
l-l|+2In
(б) Применим теперь II подстановку: Ух3-х+1 = tx— 1,
2/-1	t2-t+l		 ;2_/_i_1
x =	, dx=-2	dt, yx2-x+l=-
х+ух*-х+1 =	,
t-\
Гг2 113 1
2 '~ J L7"/^T"hT
_
Остается подставить сюда t-
получим	x
; после очевидных упрощений
I
dx
+ 21п
1
	In Vx*-x+l-x+l
2
--In \TJxz-x+l+x+l +C.
Это выражение хотя и разнится от ранее полученного по ф о р м е, но при С =
= С+— отождествляется с ним.
8)
Г	dx
J (xz + a*)^^

283)	§ 3. ИНТЕГРИРОВАНИЕ РАДИКАЛЬНЫХ ВЫРАЖЕНИЙ	65
(а) Так как корни подкоренного выражения вещественны, то можно применить
III подстановку fa?-x2 = t(a-x); здесь -а-=х<а и t>0. Имеем
/2-1	4а/ dt	„	 2а?	2а2(/4+1)
/2+1'	(?2+1J'	/2+1'	(г2+1J
и
Г «far I f2<2+2 Iff 1 1 1
		=— _	 л = —-	1	Л =
= -— tarctg (/ у2+1) + arctg (/ fi -1)] + С,
куда еще нужно подставить для получения окончательного результата
Воспользовавшись формулой для суммы арктангенсов, а также очевидным
соотношением
1	л
arctg—= - arctg <х ± — (при ое S 0),
а	2
можно придать результату более простую форму
1	xfl	{
- —arctg	+C, где Сг
2a2 fl.
(б) Если к тому же интегралу применить II подстановку f^ ~ л'2 = tx-a,
то получим, что
и
dx 1 г	,,,- N	, ,- N .
	—— =	[arctg (У2+1>+ arctg (У2-1)/] +С
а+Уал;
при ? =	. Этот результат годится в отдельности для про-
х
межутка (-в, 0) и для промежутка @, а); легко сообразить, что изменяя зна-
значение постоянной С" при переходе х через 0, можно сделать его пригодным во всем
промежутке (-а, а). Наконец, если преобразовать его по формуле для суммы
арктангенсов, то он отождествится с предыдущим результатом.
•J
dx
I подстановка: yx"+fi = t-x. Имеем
С dx	г	ltdt	с	du
г	it at	r
J/4+2BA-«)f*+Ju«-2.
5 Г. М. Фихтенгольц, т, П

66	ГЛ. VIII. ПЕРВООБРАЗНАЯ ФУНКЦИЯ	1284
Таким образом, вопрос сводится к вычислению элементарного интеграла; в резуль-
результате надлежит подставить
284. Другие приемы вычисления. Хотя подстановки Эйлера прин-
принципиально во всех случаях решают вопрос о вычислении интеграла
типа D) в конечном виде, но иной раз - при их применении - даже
простые дифференциалы приводят к сложным выкладкам. Ввиду важ-
важности интегралов рассматриваемого типа мы укажем и другие приемы
для их вычисления.
Для краткости положим
Рациональная функция R(x, у) может быть представлена в виде част-
частного двух целых многочленов относительно х и у. Заменяя у2 всюду
на У, мы приведем R(x, у) к виду
где Р,(х) - целые многочлены. Умножая числитель и знаменатель
этой дроби на выражение Р3(х) - Pt(x)y (и снова заменяя у2 на У),
придем к новой форме для R
Интеграл от первого слагаемого справа мы уже умеем выражать
в конечном виде: следовательно, нам надлежит заняться лишь вторым
слагаемым. Умножая и деля его на у, окончательно получим такое
выражение
интегрированием которого мы и займемся.
Прежде всего выделим из рациональной функции R*(x) целую
часть Р(х), а правильно-дробную часть представим себе разложенной
на простые дроби [274]. В таком случае интегрирование полученного
выражения сведется к вычислению интегралов следующих трех типов;
I. -=== dx,
J Уахг+Ьх+с
Adx
где все коэффициенты вещественны, а корни трехчлена x2+px + q
мнимые. Остановимся на каждом из них в отдельности.

284)	8 3. ИНТЕГРИРОВАНИЕ РАДИКАЛЬНЫХ ВЫРАЖЕНИЙ	67
I. Положим (для т = 0, 1, 2, ...),
Легко установить рекуррентную формулу для этих интегралов. С этой
целью, считая т е=-1, возьмем производную
(х-' /Г)' = (т -	^f
2(т-
хт [ \
=r + (ml)c?=
и проинтегрируем полученное тождество
X»-lYY=maVn + [т -i) bVm-i 4 (m - l)cFm_2.
Беря здесь т-l, найдем
1 а ' 2а °'
полагая затем т — 2 (и используя выражение для Уг), получим
У1 =
Поступая так дальше, придем к общей формуле
где рт-\(х) есть многочлен (/я-1)-й степени, aAm = const. Таким обра-
образом, все интегралы Ут приводятся к Уо.
Если в интеграле I многочлен Р(х) будет и-й степени, то этот ин-
интеграл представит собой линейную комбинацию интегралов Уо, Vlt ...
..., Vn, а значит, по предыдущей формуле, напишется в виде
ЩЩ,	(9)
где Q(x) - некоторый многочлен (и - 1)-й степени, а Я = const.
Самое определение многочлена Q(x) и постоянной А обычно про-
производится по методу неопределенных коэффициен-
коэффициентов. Дифференцируя (9) и умножая полученное равенство на /У,
получим
с) + \ Q(x)Bax + Ь) + А.

68	ГЛ. VIII. ПЕРВООБРАЗНАЯ ФУНКЦИЯ	[284
Если вместо Q(x) подставить сюда многочлен (и - 1)-й степени с бук-
буквенными коэффициентами, то в обеих частях мы будем иметь много-
многочлены и-й степени. Приравнивая их коэффициенты, придем к системе
и + 1 линейных уравнений, из которых и определяется п коэффициен-
коэффициентов многочлена Q(x) и постоянная Я *.
Замечание. Формула (9) осуществляет выделение алге-
алгебраической части из интеграла
Подобное же выделение могло бы быть произведено и по отноше-
отношению к интегралу общего вида
г Щ
J у? '
где R — знак произвольной рациональной функции. На этом мы не
останавливаемся.
II. Интеграл
р dx
1
приводится подстановкой х - а=- к только что рассмотренному типу.
Действительно, имеем
,	dt	„ ,	(ax*+ba.+c)t'+Ba<x+b)t+a
ах=	ax2 + bx + c=^
так что (считая для определенности х>а и t>0
/ft-» dt
f	*	=-f
y(aaa+6a+c)fa+B«x+&)f+a '
Если ас/.2 + bx + с = 0, т. е. а оказывается корнем трехчлена Y, то дело
еще упрощается: мы получаем интеграл типа, рассмотренного в 278.
III. (а) Обращаясь к последнему интегралу, рассмотрим особо слу-
случай, когда трехчлен ах^ + Ьх + с лишь множителем а отличается от
трехчлена x2+px + q. Тогда искомый интеграл имеет вид
I
Mx+N	,
ах.
2m+l
* Из доказанного явствует, что эта система будет совместной при любых
значениях свободных членов, а в таком случае ее определитель необходимо отли-
отличен от 0, и система оказывается всегда определенной. Этим попутно устанавли-
устанавливается и единственность представления (9). (Ср. стр. 42 и 46).

284]	§ 3. ИНТЕГРИРОВАНИЕ РАДИКАЛЬНЫХ ВЫРАЖЕНИЙ	69
Его легко представить как сумму двух интегралов:
М Г 2ах+Ь	, , /лг МЬ\ Г	dx
г 2ах+Ь	, („ МЬ\ Г
2a	2/n+i --«•'" 2a] \	2m+i
из которых первый сразу берется подстановкой t = ax + bx \ с.
Для вычисления интеграла
dx	r dx
/•	ах	р
2m+T=
J (ny2j-hr4-r\ 2 J
2m+T= 2m+l
всего удобнее так называемая подстановка Абеля (N.-H. Abel)
Ь
ах+-
2
Возводя в квадрат и умножая на 4Y, получим равенство
4/2У = (УJ = 4а2х2 + Aabx + Ь\
которое вычтем из умноженного на Аа равенства
В результате получится
откуда
4 J (a-t*r
Дифференцируя теперь равенство
ПО)
tfY=axv\,
найдем
так что
Из A1) и
и, наконец,
(Ю)
f:
dx
2m + l
у 2
Vdt + t2dx = adx,
dx dt
YY a-t1 '
A1)

70	ГЛ. VIII. ПЕРВООБРАЗНАЯ ФУНКЦИЯ	1284
Таким образом, весь вопрос сводится к вычислению интеграла от
многочлена.
В частности, например, при т = 1 имеем
г dx	_ 2	2ax+b
J (ax2+bx+с)'Т.~ Аас- ba f^+fx+c '
(б) В общем случае для большей симметрии обозначений положим
ах2 + Ьх + с = а(х2 +р'х + q'),
причем теперь мы можем предположить, что трехчлен в скобках не
тождествен с трехчленом x2+px + q. Поставим себе задачей пре-
преобразовать переменную х так, чтобы в обоих трехчленах
одновременно исчезли члены первой степени.
Пусть сначала р^р'. Тогда нашей цели можно достигнуть с по-
помощью дробно-линейной подстановки
A3)
надлежаще подобрав коэффициенты \х и v. Имеем
х
и аналогично - для второго трехчлена. Искомые коэффициенты опре-
определяются из условий
2\iv л р(ц + v) + 2q = 0, 2 ixv +
или
„=-2
^
Р-Р r P-P
Таким образом, ц и v суть корни квадратного уравнения
О» ~P'V + 2(<7 - q')z + (p'q -pq') = 0.
Для того чтобы эти корни были вещественны и различны * (необхо-
(необходимо и), достаточно условие
pq')^0;	A4)
удостоверимся в его выполнении.
Перепишем условие в равносильной форме
[2{д + q') -pp'f > (Ад -p2)Dq' -p'%	A4*)
Дано, что 4q-p2>0 (ибо трехчлен x2+px + q имеет мнимые корни),
поэтому неравенство A4*) заведомо выполняется, если одновременно
* При ц~ v подстановка теряет смысл, ибо сводится к

284]	§ 3. ИНТЕГРИРОВАНИЕ РАДИКАЛЬНЫХ ВЫРАЖЕНИЙ	71
4q'-p'2<0. Остается исследовать случай, когда и 4q' -р'2>0. Тогда
<7>0, q'>0 и 4 Уда'>рр', и мы имеем последовательно*
-р'2) + 4(^' - //^(^ -p2)Dq' -/,'*).
Здесь дважды знак неравенства соединяется со знаком равенства, но
равенство не может иметь место в обоих случаях одновременно: если
q^q', то равенства, наверное, нет в первом случае, а при q=q', на-
наверное, нет во втором. Таким образом, неравенство A4*), а с ним
и (,14), доказано.
Выполнив подстановку, мы преобразуем искомый интеграл к виду
J(f8+Aynya74-/S
где P(t) есть многочлен степени 2т-I (и Я >0). Снова прибегнув (при
т>1) к разложению правильной дроби
Р@
на простые, мы придем к сумме интегралов вида
Г At+* ,Л (*-l,2,...,ni).
J (<2+A)*yafs+/?
В исключенном случае, когда /?=/>', уничтожение членов первой
р
степени достигается еще проще - подстановкой x = t—^, и мы не-
непосредственно приходим к интегралу только что указанного
вида.
Полученный интеграл, естественно, разлагается на два:
Первый из них легко берется подстановкой и = Vaf2+j3. Ко второму
же приложима уже знакомая нам подстановка Абеля
_ at
ы —
Именно, в силу A1), имеем
dt du
(/<«*+/? а-'
a -j- a'
* Поскольку

72	ГЛ. VIII. ПЕРВООБРАЗНАЯ ФУНКЦИЯ	[285
кроме того, как легко вычислить,
«(ос-и")
Поэтому
Г	*	(
J (/«
и искомый интеграл привелся к интегралу от рациональной функции.
Замечание. Помимо того что мы в настоящем п° указали ряд
новых приемов для вычисления интегралов типа D), совокупность
приведенных соображений дает независимое от прежнего доказатель-
доказательство утверждения, сформулированного в конце п° 281.
J уз?
Г x'-x + l	a	v-	 Г
J Уха+2х+2	J
285. Примеры. 1) | __	dx.
Полагаем
{2ах+Ь)(х*+2х+2)+(ах*+Ьх+с)(.х+1) + д.
Система уравнений
3a=l, 5a+2b = 0, 4а+ЗЬ+с=-1,
15	15
приводит к значениям а = —, Ь=	, с = —, д = — . Таким образом, если учесть
3	6	6	2
стример 5) пс 283, окончательно получим
>-х+\ . 1
"б
2)
ь
Подстановка jc—1=— (если, скажем, х^1 и /=-0) приводит интеграл к виду
У1 - 2/а
Этот интеграл легко берется элементарными средствами [см. 283, 4)].
Ответ: — t У1-2*2	arcsin / У2"+ С=
4	4У2	'
1 	 1	уг
= —	--У^-2х-1	-arcsin -~-+C.
4(х-1J'	4У2	*-1
J

285]	§ 3. ИНТЕГРИРОВАНИЕ РАДИКАЛЬНЫХ ВЫРАЖЕНИЙ	73
Подстановка Абеля
4х-1
t=—_—__
преобразует интеграл следующим образом:
64 (¦
3375 J ~ ''
при этом можно либо повторить для частного случая общие выкладки п° 284,
III (а), либо воспользоваться готовой формулой A2).
64
Ответ:
3375
)^тй
4х-1	1 Dх-1K 1 Dх1)
Bx2-x+2)Vt 6 Bx2-x+2)'/i 160 Bxa-x+2)V.
4)
Ух"+х+1
Дробно-линейная подстановка
И-1
дает
Требования
2fj.v±(fi+v)+2 = 0
O, (tv=- -1 удовлетворяются, например, при fi = 1, i> = - 1. Имеем
f-1	2Л
М-1
если - для определенности - считать t+1 =»0 (т. е. ж< 1). Таким образом,
Г (x+3)dx	Г (8t+4)dt
J (ха-х+1)Ух2+х+1 J Ц*+У)УЪ?Ч
(ха-х+1)Ух2+х+1
Полученный интеграл разбивается на два:
dt
С tdt	С
J ——^=+4j -
8
Первый легко вычисляется подстановкой и = УзТм-Т и оказьшается равным
yiarctg / —	ьС. Ко второму применим подстановку Абеля
у	О
3/
и=	-.
У7
з7»+Т

74	ГЛ. VIII. ПЕРВООБРАЗНАЯ ФУНКЦИЯ
которая приведет его к виду
'и 1 31/5+2У2ы
:	— +С".
Остается лишь вернуться к переменной х.
5) I " ' """ '		dx.
[286
С du	1
12	= —In
J 27-8«2 ye
Указание. Представить подынтегральную функцию в виде
к третьему слагаемому применить метод п° 284, I, а к последнему - подстановку
§ 4. Интегрирование выражений, содержащих
тригонометрические и показательную функции
286. Интегрирование дифференциалов i?(sin x, cos x) dx. Дифферен-
Дифференциалы этого вида всегда могут быть рационализированы подстанов-
подстановкой t = tg^ (-л<х<я). Действительно,
It
япдс-
2tg-
2
1-tg2
1+tg2—
1+tg2
так что
Д(яп x, cos x) Л = R | IT?i , ш-2
2Л
Таким образом, интегралы типа
A)
всегда берутся в конечном виде; для их выражения, кроме функций,
встречающихся при интегрировании рациональных дифференциалов,
нужны лишь еще тригонометрические функции.
Упомянутая подстановка, являющаяся универсальной для
интеграла типа A), приводит иной раз к сложным выкладкам. Ниже
указаны случаи, когда цель может быть достигнута с помощью более

286]	§ 4. ИНТЕГРИРОВАНИЕ ТРИГОНОМЕТРИЧЕСКИХ ВЫРАЖЕНИЙ	75
простых подстановок. Предварительно сделаем следующие элементар-
элементарные замечания из области алгебры.
Если целая или дробная рациональная функция Щи, v) не меняет
своего значения при изменении знака одного из аргументов, например,
и, т. е. если
то она может быть приведена к виду
содержащему лишь четные степени и.
Если же, наоборот, при изменении знака и функция R(u, v) также
меняет знак, т. е. если
R(~u,v)=-R(u,v),
то она приводится к виду
это сразу вытекает из предыдущего замечания, если его применить
к функции —	 .
I.	Пусть теперь R(u, v) меняет знак при изменении знака и; тогда
R(sin х, cos х) dx = ^(sin2 x, cos x) sin x dx = - R0(l - cos2 x, cos x) d cos x,
и рационализация достигается подстановкой t = cos x.
II.	Аналогично, если R(u, v) меняет знак при изменении знака v, то
R(sin х, cosx)dx=R$(smx, cos2 x) cos x dx = i?$(sin x, 1 -sin2 x)dsin x,
так что здесь целесообразна подстановка t = sin x.
III.	Предположим, наконец, что функция R(u, v) не меняет своего
значения при одновременном изменении знаков и и v
R(-u, -v) = R(u,v).
В этом случае, заменяя и на - v, будем иметь
По свойству функции R, если изменить знаки и и v (отношение - при
этом не изменится),
а тогда, как мы знаем,

76	ГЛ. VIII. ПЕРВООБРАЗНАЯ ФУНКЦИЯ	[287
Поэтому
R(sin х, cos х) = Rf(tg x, cos2 x) = Rf | tg х, y^j- 1,
т. е. попросту
/?(sinx, cos x) = R(tg x).
Здесь достигает цели подстановка t = tgx I ~f <Л:<5 >
i?(sinx, cos x) dx = R(t) j-— и т. д.
Замечание. Нужно сказать, что каково бы ни было рацио-
рациональное выражение R{u, v), его всегда можно представить в виде суммы
трех выражений рассмотренных выше частных типов. Например, мо-
можно положить
. . _й(н, v)-R(-u, v) R(-u, v)-R(-u, -о) , JR( —i/, -v)+R(u, v)
Щи, V)	2	'	2	2	'
Первое из этих выражений меняет знак при изменении знака и, вто-
второе меняет знак при изменении знака v, а третье сохраняет значение
при одновременном изменении знака и и v. Разбив выражение i?(sin x,
cosx) на соответствующие слагаемые, можно к первому из них при-
применить подстановку t=cosx, ко второму - подстановку ?=sinx, и,
наконец, к третьему - подстановку t = tgx. Таким образом, для вы-
вычисления интегралов типа A) достаточно этих трех подстановок.
287. Интегрирование выражений sin" x • cos" x. Будем считать v и
/и, рациональными числами, а переменную х - изменяющейся в про-
промежутке 10, ~\ . Тогда подстановка z=sin2x, dz = 2 sin x cos x dx дает
1	—
sirT л: cos^ x dx = -z sin" x(l - sin2 x) 2 2 sin x cos xdx =
так что дело сводится к интегрированию биномиального диф-
дифференциала [279]
sin-хcos" x dx = ~ A -z) 2
B)
Вспоминая случаи интегрируемости биномиальных дифференциалов,
мы видим теперь, что интересующий нас интеграл берется в конеч-

287]	§ 4. ИНТЕГРИРОВАНИЕ ТРИГОНОМЕТРИЧЕСКИХ ВЫРАЖЕНИЙ	77
ном виде, 1) если ^--—(и™ ~~т~) есть Челое число> т е- если /"
11-A-V
(или v) есть нечетное целое число, либо же 2) если Чу~ есть
целое число, т. е. если /i+v есть четное целое число.
Сюда же, в частности, относится случай, когда оба показателя
ц и v - целые; впрочем, тогда выражение sin" х cos" х рационально
относительно sin x и cos x, т. е. принадлежит классу выражений, уже
рассмотренному в предыдущем п°.
В этом случае, если показатель v (или /i) будет нечетным, то
рационализация сразу достигается подстановкой t=cos х (или t=sin x).
Если же оба показателя vh/j четные (а также если они оба н е-
четные), то можно для той же цели применить подстановку t=tg x
или t=ctgx.
Заметим, что если показатели v и ц оба суть положительные
четные числа, то предпочтительнее другой прием, основанный на
применении формул
sin2x . , 1-cos 2л: „ l+cos2,r
Sin X COS X = —j—, Sin2X =	^	> COS'!X =	_-	.
Именно, если v = 2n, /л = 2т, то при vs^/л пишут
-cos 2x1"-
. ,, тЛ /sin 2^2™/
sin2<n-m>x= —2"-
а при v<fi
• on ,„ ,. v> w „, /¦sin2x"\2nM+COs2x1l'"-n
sm2nxcos2mx=-(sinxcosxJncos2<m-")x= —y— 	2
В развернутом виде получится сумма членов вида
С sin"'2:* cos"'2.x,
где v'+n'*sin + m=v-Y^. "^е члень1' У которых хоть один из показа-
показателей v', /л' есть нечетное число, легко интегрируются по указан-
указанному выше способу. Остальные члены подвергаем подобному же раз-
разложению, переходя к sin 4x и cos 4x, и т. д. Так как при каждом раз-
разложении сумма показателей уменьшается, по крайней мере, вдвое, то
процесс быстро завершается.
Вернемся к установленной выше зависимости B). Мы можем теперь
воспользоваться формулами приведения биномиальных интегралов
[280], чтобы, полагая там а = \, 6= -1, •Р=/-2—> 9 = -~> установить
формулы приведения для интегралов рассматриваемого типа.

78	ГЛ. VIII. ПЕРВООЬРАЗНАЯ ФУНКЦИЯ	B88
Таким путем получатся следующие формулы (которые, конечно,
могут быть выведены и самостоятельно):
(I) J sin" х cos'1 x dx =
=	-:	+ —^-j— sin1" x cos''+2 x dx (a * - 1).
(II) j sin" x cos'1 x dx =
sin^1 ж cos/<+1 л v+u + 2 Г.-.,	j	,	,ч
=	—-j	+ —~— J sin"+2 x cos" x dx (v * - 1),
(III) ("sin" x cos^ x dx =
=	;	+-— J sin" x cos''-2 x dx (y f /г ^ 0),
(IV) (sin1' x cos'' x dx =
=	¦	-+	sin" x cos'1 x dx (v + и т± 0).
Эти формулы вообще позволяют увеличить или уменьшить показа-
показатель v или [I на 2 (за указанными исключениями). Если оба показа-
показателя v и /^ - целые числа, то последовательным применением формул
приведения можно свести дело к одному из девяти элементарных
интегралов (отвечающих различным комбинациям из значений v и /<,
равных -1,0 или 1)
* = *,	6) Jg?<fc=-
2) JcosxJx=sinx,	7)
o\ (COS* , .
8) Jito-.^^1
4)	I sin x dx - - cos x,	9)
5)	J sinxcosxrfx = -
sin2x
288. Примеры. 1) I sina x cos8 x dx. Подынтегральное выражение меняет знак от
замены cos х на - cos x. Подстановка /=sin x:
г г t3 tb
sin2xcos3xdx = \t2O-t") dt =	\-C
J	J	J	J
t3 tb _ sin3* sin5*

288J	§ 4. ИНТЕГРИРОВАНИЕ ТРИГОНОМЕТРИЧЕСКИХ ВЫРАЖЕНИЙ	79
ч psin5x
2) 	dx. Подинтегральное выражение меняет знак от замены sin х
J cos4 х
- sin х. Подстановка t = cos x:
(¦sin5*	f/4-2/2 + l	2 1	2	1
rfx-	Л= -t	f — + C= -cosx-	4	+ C.
J cos4*	J г4	/ 3r3	,cosx 3cos3x
С	</x
3)	I	. Подинтегральное выражение не изменяет своего значения
J sin4 x cos2 x
при замене sin х на - sin х и cos х на — cos л. Подстановка t = tg л:
Г </х	f(l+<2J	2 1	1
	= 	-A-f	+ C=tgx-2ctgx--ctg3x4C.
J sin4 л: coss л: J /4	* 3f3	3
4)	sin2 x cos4 x dx. Здесь пригодна та же подстановка, но проще пользоваться
формулами удвоения угла
sin2 х cos4 х = — sin2 2x(cos 2.v-h 1) = — sin2 2x cos 2x4— A - cos Ax)
8	8	16
и
Г	111
sin2*cos4* dx = — sin3 2x-\—x	sin4x:+C.
J	48	16 64
Jdx 1 г dx
	= — 	. Пригодна подстановка / = sin x, но проще
sin x sin 2x 2 J sin2 x cos x
прибегнуть к II формуле приведения:
1	г dx	1 1 г dx	1 1	(х л]\
— 	=	4— 	=	Ь—In tg - + - +С.
2	Jsin8*cosx 2sinx 2 J cos* 2sin* 2	^2 4 /1
г dx
6) 	. Пригодна подстановка t = sin x, но проще дважды прибегнуть
J cos5 *
к I формуле приведения:
dx sin* 3 r dx
г dx sin * i r
J cos5 x 4cos4* 4 J
' cos5 x 4cos4* 4 J cos3 x '
в свою очередь,
с dx sin х 1 г dx sin x 1	(x n \ I
=	+— 	= —	4—In tg —4— 4C,
J cos3x 2cos2x 2 J cosx 2cos2x 2	\2 4j\
так что
dx sin x 3 sin x 3
cos5 x 4cos4x 8cos2x 8
x n
+ 4

80
ГЛ. VIII. ПЕРВООБРАЗНАЯ ФУНКЦИЯ
|288
7) Г4
J si;
COS4 л:
dx. Пригодна подстановка / = cos x, но проще воспользоваться
sin3 л:
II и III формулами приведения:
гcos4;
J sin3 x
lx
I sin3 x
cos5 x 3
2 sin2 x
3 rcos4x
—г ——dx<
2 J sin *
Г cos4* 1	pcos2x 1
	 dx=— cosax+ 	dx- — cos3 л+cos л:+In
J sin x	3	J sin x 3
+ C,
так что (после упрощающих преобразований)
*cos4x	cosx	3
(•cos'x	cosx	5
	dx= -—	cos x--ln
J sm3 x	2 sin2 x	2
+C.
8)
dx
с J si
dx
J sin л: cos 2x J sin дгB cos8 x -1)
. Подстановка / =
«fcc
- ])
¦!*=
dt
- = — In
1 + /У2
1-/У2
1 , 1-/
+2пы7-
= — In
n
1 + Y2COSX
+C.
f SI
9) -
J si;
sin4 x cos x
dx. Так как при изменении знаков у sin x и cos x подин-
sin Х+ COS X
тегральное выражение не терпит изменения, то пригодна подстановка t = tgx:
sin2 x cos x
sinx+cosx
dx =
-J
t-\ 1 /-1
4 r2
2 (f
¦+C =
1-Й 1
УП72 4
= —In |sinx+cosx|	cosx(sinx+cosx)+C.
4	4
10) f
J
dx
-при.
ж	ж
О. Предполагая	¦<х«= —,
с помощью подстановки t = tg x приведем интеграл к виду
Ответ:
arctg

288]	§ 4. ИНТЕГРИРОВАНИЕ ТРИГОНОМЕТРИЧЕСКИХ ВЫРАЖЕНИЙ	81
С dx с dt
11) 	=
Ja+btgx J (a+bt)(l+t2)
(я	л\
	-=x<— .
Разлагая на простые дроби
1	A Bt+C
(a+bt)(l + t*) a+bt
для определения коэффициентов А, В, С получим уравнения
0, аВ+ЬС=0,
b* b a
откуда А =	, В=	, С=
a	b a+bt
Ответ: 	arc tg H	In ———— + С ¦-
а*+Ьг	a*+b* тАГТг
[ах+Ып \acosx+b sinx\]+C.
аг + Ь
12) К этому же интегралу приводятся следующие два:
r sinxdx	г cosxdx
*р __ I 		гр 	 1
J acosx+usinx'	2 J acosx+bsinx '
Впрочем, проще вычислить их, исходя из связывающих их соотношений
ЬТх+аТ2= dx = x+Clt
r -asinx+bcosx
-аТу+ЬТг= 	dx =
J dcosx+osmx
f d(a cos x+bsinx)
= 	:	= ln lacosx+ftsmxl +C2,
J acosx+6sinx
откуда и получаем
• [bx -a In
T2=	[ax+bln \acosx+bsmx\]+C.
a*+ba
1-r2
¦—	dx @<r-=l, -я<х-=я). Применим здесь универ-
l-2rcosx+ra
сальную подстановку t = tg — . Имеем
1 f 1~г* j /•, Л<"	dt
2rcosx+r2
6 Г. М. Фихтенгольц, т. II
^ /j+c=arctg j^tg|

82	ГЛ. VIII. ПЕРВООБРАЗНАЯ ФУНКЦИЯ
К этому интегралу приводится и такой:
\-r cos х
l-2rcos;t+
ffl 1	1-r2 л 1	(l + r x]
— dx= —I	dx-=— x+arctg	tg—
r*	J 12 2 l^rcosx + rO	2	[l-r 2)
[288
+ C.
r dx
14) I	, в предположении, что lei Э 161 (-л«=л:-=я).
J a+ocosx
Пусть сперва | а | > 161 и (что не умаляет общности) а =- 0. Подстановка / - tg —,
как и в только что рассмотренном частном случае, дает
dx	2	ПГа^Ъ х
arctg
e+ftC0SJC y
Можно преобразовать это выражение к виду
1
acosx+b
arcsm	1 С,
+6
причем верхний знак берется, если 0=ех-=я, а нижний - если - я-= je«sO, и значение
постоянной С возрастает на
при проходе х через 0.
Пусть теперь \а\ «= \Ь\ и b =-0. Та же подстановка:
2*	1
J (
-In
-In
Это выражение легко преобразуется к виду
-In
6+a cos л+ Уба - a2 sin л
а+6 cos л
Интеграл I
+ С-
+С.
я
приводится к предыдущему подстановкой x = — ±t.
2
г
15) Наконец, к интегралу 14) приводится и интеграл
J
ввести угол а под условием, что
dx
. Если
cos a = -
sm a =
W+c*

2891	§ 4. ИНТЕГРИРОВАНИЕ ТРИГОНОМЕТРИЧЕСКИХ ВЫРАЖЕНИЙ	83
то интеграл перепишется в виде
dx
a+ftf+c* cos {х -а)
подстановка t = x-a.. И здесь, конечно, интересен случай |а| ^ уЬ2+сг.
289. Обзор других случаев. В 271, 4) мы уже видели, как интегри-
интегрируются выражения вида
Р{х)е?х dx, P(x)sin bx dx, P(x) cos bx dx,
где Р{х) - целый многочлен. Любопытно отметить, что дробные
выражения
ех , sin х , cos* , / 1 л т \
— dx, -^~dx, -^rdx (и = 1, 2, 3, ...)
уже не интегрируются в конечном виде.
С помощью интегрирования по частям легко установить для ин-
интегралов от этих выражений рекуррентные формулы и свести их,
соответственно, к трем основным:
I. Г — dx = f-^- = h\y* («интегральный логарифм»);
тт fsinx , . ,	„	>
II. 	ах=six («интегральный синус»);
III. f—^-dx = c\x («интегральный косинус»)**.
Мы знаем уже [271, 6)] интегралы
j>sin bx dx =
je-cos bx <fa =
Отправляясь от них, можно в конечном виде найти интегралы
Г хперх sin bx dx, Г хпе^ cos bx dx,
где л = 1,2,3, ... Именно, интегрируя по частям, получим
г . „ • , , „ a sin bx - b cos bx
xneF- sin bx dx = xn	т—т-.	e°x -
J	a*+b3
^j"-1^ sin bxdx-\ ^—Jx^^^cos bx dx,
J x^x cos bx dx = x- *-sin bxJ
n~1^sinbxdx~^TF*ixn~]eax cos bx
* Подстановка x = hiy.
** Впрочем, во всех трех случаях надлежит еще фиксировать произвольную
постоянную; это будет сделано впоследствии.

84	ГЛ. VIII. ПЕРВООБРАЗНАЯ ФУНКЦИЯ	[290
Эти рекуррентные формулы позволяют свести интересую-
интересующие нас интегралы к случаю и = 0.
Если под Р{...) по-прежнему разуметь целый многочлен, то, как
окончательный результат, можно утверждать, что в конечном виде
берутся интегралы
|>(,v, еа'х, е°"х, ..., sin b'x, sin Ь"х, ..., cos b'x, cos b"x, ...) dx,
где a', a", b', b", ... - постоянные.
Дело сводится, очевидно, к интегрированию выражения
хпе°х sin'1'b'x sin*" b"x ... cos™' b'x ...
Если использовать элементарные тригонометрические формулы
. „ , l-cos2ta
sin2 bx =	1	,
sin b'x sin b"x = \ [cos (b' - b") x - cos (b' + b") x]
и им подобные, то легко разбить рассматриваемое выражение на сла-
слагаемые типа Axnef*x sin bx и Ъхпё1Х cos bx, с которыми мы уже умеем
справляться.
§ 5. Эллиптические интегралы
290. Общие замечания и определения. Рассмотрим интеграл вида
JR(x,y)dx,	A)
где у есть алгебраическая функция от х, т. е. [205] удо-
удовлетворяет алгебраическому уравнению
Р(х,у) = 0	B)
(здесь Р - целый относительно х и у многочлен). Подобного рода
интегралы получили название абелевых интегралов. К их числу от-
относятся интегралы, изученные в § 3,
dx, JR(x, Уах* + Ьх + с) dx.
Действительно, функции
удовлетворяют, соответственно, алгебраическим уравнениям
{ух + $)ут - (ах +/S) = 0, f- {ax2 + bx + c) = 0.

290]	§ 5. ЭЛЛИПТИЧЕСКИЕ ИНТЕГРАЛЫ	85
Становясь на геометрическую точку зрения, абелев интеграл A)
считают связанным с той алгебраической кривой, которая
определяется уравнением B). Например, интеграл
\r{
dx	C)
связан с кривой второго порядка у2 = ах2 + Ьх-\с.
Если кривая B) может быть представлена параметрически
так, что функции r^t) и r2(t) оказываются рациональными (в
этом случае кривая называется у н и к у р с а л ь н о й *), то в инте-
интеграле A) становится возможной рационализация подинтегрального вы-
выражения: подстановкой x = r1(t) оно приводится к виду
К этому классу и относятся оба упомянутые выше случая. В част-
частности, возможность рационализации подинтегрального выражения в
интеграле типа C) связана именно с тем фактом, что кривая вто-
второго порядка уникурсальна [281, 282].
Очевидно, что переменные х и t связаны алгебраическим уравне-
уравнением, так что / является алгебраической функцией отх
Если расширить класс элементарных функций, включив в него и все
алгебраические функции, то можно сказать, что в случае уникурсаль-
ности кривой B), интеграл A) всегда выражается через элемен-
элементарные функции в конечном виде.
Однако подобное обстоятельство является в некотором смысле
исключением. В общем случае кривая B) не уникурсальна, а тогда,
как можно доказать, интеграл A) заведомо не всегда, т. е. не
при всякой функции R, может быть выражен в конечном виде (хотя
не исключена возможность этого при отдельных конкретных К).
С этим мы сталкиваемся уже при рассмотрении важного класса
интегралов
JR{x, Yax* + bx2 + cx + d)dx,
r		D)
J R (x, fax* + bx3 + ex2 + dx + e) dx,
содержащих квадратный корень из многочленов 3-й или 4-й степени
и естественно примыкающих к интегралам C). Интегралы вида D) -
как правило — уже не выражаются в конечном виде через элемен-
элементарные функции даже при расширенном понимании этого термина.
Поэтому знакомство с ними мы отнесли к заключительному пара-
параграфу, чтобы не прерывать основной линии изложения настоящей
* Можно дать и чисто геометрическую характеристику уыикурсальной кривой,
но мы на этом останавливаться не будем.

86	ГЛ. VIII. ПЕРВООБРАЗНАЯ ФУНКЦИЯ	[291
главы, посвященной, главным образом, изучению классов интегралов,
берущихся в конечном виде.
Многочлены под корнем в D) предполагаются имеющими веще-
вещественные коэффициенты. Кроме того, мы всегда будем считать, что
у них нет кратных корней, ибо иначе можно было бы вынести ли-
линейный множитель из-под знака корня; вопрос свелся бы к интегри-
интегрированию выражений уже ранее изученных типов, и интеграл выра-
выразился бы в конечном виде. Последнее обстоятельство может иметь
место иной раз и при отсутствии кратных корней; например, легко
проверить, что
rl+xl dx	х
Jl
Интегралы от выражений типа D) вообще называют эллиптиче-
эллиптическими [в связи с тем обстоятельством, что впервые с ними столк-
столкнулись при решении задачи о спрямлении эллипса, 331, 8)]. Впрочем
это название, в точном смысле, относят обычно лишь к тем из них,
которые не берутся в конечном виде; другие же, вроде
только что приведенных, называют псевдоэллиптическими.
Изучение и табулирование (т. е. составление таблиц значений)
интегралов от выражений D) при произвольных коэффициентах я,
Ь, с, ..., разумеется, затруднительно. Поэтому естественно желание
свести все эти интегралы к немногим таким, в состав которых
входило бы по возможности меньше произвольных коэффициен-
коэффициентов (параметров).
Это достигается с помощью элементарньк преобразований, кото-
которые мы рассмотрим в последующих пп°.
291. Вспомогательные преобразования. 1°. Заметим, прежде всего,
что достаточно ограничиться случаем многочлена 4-й степени под
корнем, ибо к нему легко приводится и случай, когда под корнем
многочлен 3-й степени. Действительно, многочлен 3-й степени ах> +
+ Ьх2 + сх + д с вещественными коэффициентами необходимо
имеет вещественный корень [81], скажем, Я - и, следовательно, до-
допускает вещественное разложение
ах3 + Ьх2 + сх + д = а{х - Х)(х2 +рх + q).
Подстановка х - Я = t2 (или х - Я = -12) и осуществляет требуемое при-
приведение
.77Jtdt.
Впредь мы станем рассматривать лишь дифференциалы, содержащие
корень из многочлена 4-й степени.

291]	§ 5. ЭЛЛИПТИЧЕСКИЕ ИНТЕГРАЛЫ	87
2°. По известной теореме алгебры, многочлен четвертой степени
с вещественными коэффициентами может быть представлен в виде
произведения двух квадратных трехчленов с вещественными же коэф-
коэффициентами:
ах* + Ъу? + Ъхг +дх + е = а(х2+рх + q)(x2 +p'x + q').	E)
Постараемся теперь надлежащей подстановкой уничтожить в обоих
трехчленах сразу члены первой степени. Мы имели уже дело с по-
подобной же задачей в 284, III (б).
Если р =р', то наша цель достигается, как указывалось, простой
подстановкой x-t~^. Пусть теперь р^р'; в этом случае мы вос-
воспользуемся, как и выше, дробно-линейной подстановкой
flt+V
t+l
Возможность установить вещественные и притом различные значения
для коэффициентов /х и v, как мы видели, обусловлена неравенством
{q-q'f-ip-pXp'q-pq'^O.	F)
Мы уже доказали это неравенство в предположении, что один из
рассматриваемых трехчленов имеет мнимые корни, и это играло
существенную роль в наших рассуждениях. Пусть же теперь трех-
трехчлены E) оба имеют вещественные корни, скажем, первый - корни
а и /3, а второй — корни у и д. Подставляя
р=-{*+Р), q = *p, p'=-(y + 8), q'=yb,
можно переписать F) в виде
(«-У)(«-Л)(|3-У)(/3-«)*О,	F')
а для осуществления этого неравенства достаточно лишь позабо-
позаботиться, чтобы корни трехчленов не перемежались (например, чтобы
было а>/3>у>5), что в нашей власти*.
Таким образом, надлежаще выбрав /х и v, с помощью указанной
подстановки мы получим
* Заметим попутно, что представление неравенства F) в форме F') может
быть использовано для доказательства его и в тех случаях, когда корни а, /3,
невещественны. Если лишь первый трехчлен имеет невещественные, т. е. комплекс-
комплексные сопряженные корни а и /S, а числа у и 6 вещественны, то множители
а-у и ji-y будут сопряженными, так что их произведение будет, как
известно, положительным вещественным числом; то же относится и к множителям
а -/? и /3- 6. Если же как корни а, (I, так и корни у, 6 суть попарно сопря-
сопряженные комплексные числа, то сопряженными же будут множители
а - у и /3 - й, а также а-йи(?-'/, и их произведения снова дадут положительные
вещественные числа.

88	ГЛ. VIII. ПЕРВООБРАЗНАЯ ФУНКЦИЯ	[292
что можно также (если исключить случаи вырождения, когда какой-
либо из коэффициентов М, N, M', N' оказывается нулем) переписать
в виде
при А, т и т' отличных от нуля.
3°. С помощью соображений, совершенно аналогичных тем, кото-
которые были применены в начале п° 284, можно свести этот интеграл,
с точностью до интеграла от рациональной функции, к такому:
J
*'"»
л.
Разложим теперь рациональную функцию R*(t) на два слагаемых
д,^ Д*@+Д*(-0 | R40-R4-0
Первое не меняет своего значения при замене t на —t, следовательно
сводится к рациональной функции от t2: R^t2); второе же при указан
ной замене меняет знак, а потому имеет вид R^t2)t *. Рассматриваемый
интеграл представится в форме суммы интегралов
J \A(l + mt*)Q+m't') J
Но второй из них подстановкой u = t2 сразу приводится к элементар-
элементарному интегралу
R2(u)du
и берется в конечном виде. Таким образом, дальнейшему исследова-
исследованию подлежит лишь интеграл
Г , VV"' 	.	G)
292. Приведение к канонической форме. Покажем, наконец, что
каждый интеграл типа G) может быть представлен в форме
J]
где к есть некоторая положительная правильная дробь: 0</:<1. На-
Назовем эту форму канонической.
Положим для краткости
* Ср. замечания по аналогичному поводу в 286,

292]	§ 5. ЭЛЛИПТИЧЕСКИЕ ИНТЕГРАЛЫ	89
Не умаляя общности, дозволительно считать здесь А= ±1; кроме
того, для определенности ограничимся положительными значениями
t. Рассмотрим теперь различные возможные комбинации знаков А,
т, т' и укажем для каждого случая подстановку, непосредственно
приводящую интеграл G) к канонической форме.
1) А- + 1, т= -h2, т'= -Л'2 (Л>й'>0). Для того чтобы радикал
имел вещественные значения, нужно, чтобы было ?<т или t^-r, ¦
Полагаем
ht = z, где 0 •< z «= 1 или z =» -г, .
Тогда
dt _	dz
У
„|/(l-^l-_.
так что за к здесь следует принять -г .
2) A=+l, m=-h2, m' = h'2 (h, й'>0). Для того чтобы радикал
имел вещественные значения, ограничимся значениями /<т . Пола-
Полагаем
ht=Yl-z2, где С
Тогда
dt_	1_	dz
У ~ УАЧ1/
и можно взять к =.,,
3) ^4 = + 1, m = Л2, т' = Л'2 (Л > К > 0). Изменение ? ничем не стеснено.
Полагаем
ht = , , где
yi-z2
В этом случае
А_	dz
у~
4) J= -I, m= -h2, m' = h'2 (h, А'>0). Изменение < ограничено не-
неравенством *=-т. Берем
1
ht = ~	, где 0«=z«=l,
Vl^z2

90	гл. via. первообразная функция	[293
так что
dt	dz
У	"I/	/A2
2+А'а
и к =
5) А—-\, т= -А2, т'= -Л'2 (Л>Л'>-0). Переменная f может из-
1 1
АИА^
меняться лишь между т и Т7. Полагаем
Имеем
dt _ _	dz
у
я к = -—т— • Этим исчерпываются все возможные случаи, ибо
в случае, когда А= — 1 и оба числа т, т' >0, радикал вообще не мог
бы иметь вещественных значений. О множителе R^t2) мы не гово-
говорили ничего, ибо во всех случаях он, очевидно, преобразовывался в
рациональную функцию от z2.
Отметим еще, что, рассматривая интеграл (8), мы можем огра-
ничиться значениями z<l; случаи z>t приводится к этому подста-
1
новкой fcz = ~, где С<1-
293. Эллиптические интегралы 1-го, 2-го и 3-го рода. Теперь остается
изучить простейшие из интегралов вида (8), к которым могли
бы быть сведены все интегралы этого вида, а следовательно, в ко-
конечном счете, и все вообще эллиптические интегралы.
Выделим из рациональной функции R(x), фигурирующей в под-
интегральном выражении (8), целую часть Р(х), а правильно-дробную
ее часть разложим на простые дроби. Если не объединять сопряжен-
сопряженные комплексные корни знаменателя (как мы это делали в 274), а рас-
рассматривать их порознь, подобно вещественным корням, то R(x) пред-
представится в виде суммы степеней *п (и = 0, 1, 2, ...) и дробей вида
, _ .т (т = 1, 2, 3, ...), где а может быть и мнимым числом, умно-
умноженных на числовые коэффициенты. Отсюда ясно, что интеграл (8),
в общем случае, является линейным агрегатом следующих интег-
интегралов:
т _ Г	2Ш dz	гт _ Гfb
" J VCb^Xfr:^ И	m ~ J (r2_e)
(л=0,1,2, ...)	(

293]	§ 5. ЭЛЛИПТИЧЕСКИЕ ИНТЕГРАЛЫ	91
Остановимся на интегралах /„. Если проинтегрировать (легко про-
проверяемое) тождество
' = Bи-3Ja"-4Vr(l-z2)(l-A:2z2)
+
2n_3
то получится рекуррентное соотношение
Bл - 1)/с2/„ - Bл - 2)(&2 + 1)/л_, + Bи - 3)/п_2 =
= z2n-3f(T^2Xl~"/c2^), (9)
связывающее три последовательных интеграла /. Полагая здесь п = 2,
выразим /2 через /0 и 1г; если взять и = 3 и вместо /2 подставить его
выражение через /0 и /х, то и /3 выразится через эти интегралы. Про-
Продолжая так дальше, легко убедиться, что каждый из интегралов /„(яэ= 2)
выражается через /0 и /1( и даже, учитывая (9), можно установить и
вид связывающей их формулы
где <хп и /3„ - постоянные, а #2n-3(z) есть нечетный многочлен
степени 2и - 3. Отсюда ясно, что если Рп(х) есть многочлен и-й сте-
степени от х, то
(Ш)
где а и /3 - постоянные, а Sn-2(^) есть некоторый многочлен (и-2)-й
степени от х. Определение этих постоянных и коэффициентов много-
многочлена Q может быть произведено (если многочлен Р конкретно за-
задан по методу неопределенных коэффициентов
[ср. 284, Ц).
Заметим, что из (9) можно было бы выразить через /0 и /j инте-
интегралы /„ и при отрицательных значениях (и = - 1, - 2, ...).
так что в интегралах Нт достаточно ограничиться случаем а 5*0.
Переходя к интегралам Нт (скажем, при вещественных а), подоб-
подобным же образом установим для них рекуррентное соотношение
Bт - 2) [ - а + (к2 + 1)а2 - к2ср] Нт -
- B/и - 3)[1 - 2а(к2 + 1) + 3/t2a2] Ят_х +
+ B/и - 4)[(&2 + 1) - 3&2a] Ят_2 - Bт - 5)А:2Ят_3 =

92	ГЛ. VIII. ПЕРВООБРАЗНАЯ ФУНКЦИЯ	1293
справедливое и при отрицательных и нулевом значениях т. Отсюда
все Нт выразятся через три из них:
dz
tfo=J__|__=/o5
(z*-a)dz
т. е. окончательно через /0, /г и Д^.
Подчеркнем, что все это сохраняет силу и при мнимых значе-
значениях параметра а; однако мы не станем входить здесь в разъяснения
по этому поводу, отсылая читателя к § 5 главы XII.
Итак, в результате всех наших рассуждений мы приходим к такому
общему заключению: все эллиптические интегралы с помощью эле-
элементарных подстановок — и с точностью до слагаемых, выражаю-
выражающихся в конечном виде, - приводятся * к следующим трем стандарт-
стандартным интегралам:
h
dz	г г2 dz
y(l-z2)(l-/c2z2)
f
dz
J A + hz") УA-г2)A-?2г2)
(последний получается из Н1 введением, взамен а 5*0, нового пара-
параметра h= --). Эти интегралы, как показал Лиувилль (J. Liou-
ville), в конечном виде уже не берутся. Их Лежандр назвал элли-
эллиптическими интегралами, соответственно, 1-го, 2-го и 3-го рода. Пер-
Первые два содержат лишь один параметр к, а последний, кроме него,
еще (комплексный) параметр h.
Лежандр внес в эти интегралы еще дальнейшие упрощения,
выполнив в них подстановку z=sin ср ш изменяется от 0 до ^1 . При
этом первый из них непосредственно переходит в интеграл
• Хотя выше даны достаточные указания для того, чтобы вопрос о приведении
произвольного эллиптического интеграла к упомянутым трем мог считаться
принцигиально решенным, но на практике на этом пути могут
встретиться трудности. В специальных монографиях, посвященных эллиптическим
интегралам и смежным вопросам, можно найти другие практически удобные
приемы для этой цели.

293J	§ 5. ЭЛЛИПТИЧЕСКИЕ ИНТЕГРАЛЫ	93
Второй преобразуется так:
г sm2<pdm 1 г dip	1 с-,п	, 9 • о— _»
г ~—— г;		т-у У1 —A;2 Sin2 (p п(р,
т. е. приводится к предыдущему интегралу и к новому интегралу
4k?siaFq> dtp.	A2)
Наконец, третий интеграл при указанной подстановке переходит в
f	dip
A+Asin2,p)yi-A:2sin2?> '
A3)
Интегралы A1), A2) и A3) также называются эллиптическими инте-
интегралами 1-го, 2-го и 3-го рода - в форме Лежандра,
Из них особую важность и частое применение имеют первые два.
Если считать, что эти интегралы при <р = 0 обращаются в нуль, и тем
фиксировать содержащиеся в них произвольные постоянные, то по-
получатся две вполне определенные функции от гр, которые Л е ж а н д р
обозначил соответственно через Р(к,<р) и E(k,q>). Здесь, кроме неза-
независимой переменной у, указан также параметр к, называемый мо-
модулем, который входит в выражения этих функций.
Лежандром были составлены обширные таблицы значений
этих функций при различных у и различных к. В них не только аргу-
аргумент ср, трактуемый как угол, выражается в градусах, но и модуль
к (правильная дробь!) рассматривается как синус некоторого угла в,
который и указывается в таблице вместо модуля, и притом также
в градусах.
Кроме того, как Лежандром, так и другими учеными были
изучены глубочайшие свойства этих функций, установлен ряд отно-
относящихся к ним формул и т. д. Благодаря этому функции F и Е Ле-
Лежандра вошли в семью функций, встречающихся в анализе и его
приложениях, на равных правах с элементарными функциями.
Низшая часть интегрального исчисления, которой в основном мы
вынуждены пока ограничиться, занимается «интегрированием в ко-
конечном виде». Однако было бы ошибочно думать, что этим ограни-
ограничиваются задачи интегрального исчисления вообще: эллиптические
интегралы F м Е являются примерами таких функций, которые пло-
плодотворно изучаются по их интегральным выражениям и с успехом
применяются, хотя и не могут быть представлены через элементар-
элементарные функции в конечном виде.
Мы еще вернемся к интегралам F и Е в следующей главе и во-
вообще не раз будем с ними встречаться в дальнейших частях курса.

ГЛАВА ДЕВЯТАЯ
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
§ 1. Определение и условия существования
определенного интеграла
294. Другой подход к задаче о площади. Вернемся к задаче об опре-
определении площади Р криволинейной трапеции ABCD (рис. 4), которой
мы уже занимались в 264. Мы изложим сейчас другой подход
к решению этой задачи *.
Разделим основание АВ нашей
фигуры произвольным образом на
части и проведем ординаты, со-
соответствующие точкам деления;
тогда криволинейная трапеция
разобьется на ряд полосок (см.
рисунок).
Заменим теперь приближенно
каждую полоску некоторым пря-
прямоугольником, основание кото-
которого то же, что и у полоски, а
высота совпадает с одной из ординат полоски, скажем с крайней
слева. Таким образом, криволинейная фигура заменится некото-
некоторой ступенчатой фигурой, составленной из отдельных прямоуголь-
прямоугольников.
Обозначим абсциссы точек деления через
Рис. 4.
i = a<Xi-=:
A)
Основание /-го прямоугольника (г = 0, 1, 2, ..., п- 1), очевидно, равно
разности xl+1-xh которую мы будем обозначать через Axt. Что же
касается высоты, то, по сказанному, она равна .у, = /(*,). Поэтому
площадь z-го прямоугольника будет у(Ах1	А
* Обобщая при этом идею, уже однажды примененную в частном примере
[32, 4].

294]	§ 1. ОПРЕДЕЛЕНИЕ И УСЛОВИЯ СУЩЕСТВОВАНИЯ	95
Просуммировав площади всех прямоугольников, получим при-
приближенное значение площади Р криволинейной трапеции
^1 или P^2
1=0
Погрешность этого равенства при безграничном убывании всех zlx,
стремится к нулю. Точное значение площади Р получится как пре-
предел:
P=1ua2ytAx, = ]im2f(xd Axn	B)
в предположении, что все длины Axt одновременно стремятся к 0.
Тот же прием применим и к вычислению площади Р(х) фигуры
AMND (рис. 2), лишь дробить на части пришлось бы отрезок AM.
Заметим еще, что случай, когда у = f(x), принимает и отрицательные
значения, исчерпывается заключенным в 264 условием считать пло-
площади частей фигуры под осью х отрицательными.
Для обозначения суммы вида %УАх (вернее сказать - пре-
предельного значения этой суммы) Лейбниц и ввел символ
у dx, где у dx напоминает типичное слагаемое суммы, а I есть сти-
стилизованная буква S - начальная буква латинского слова «Summa» *.
Так как площадь, представляющая это предельное значение, в то же
время является первообразной для функции у, то тот же символ со-
сохранился и для обозначения первообразной функции. Впоследствии,
с введением функционального обозначения, стали писать
\f(x)dx,
если речь идет о переменной площади, и
ь
i dx
/л*).
- в случае площади фиксированной фигуры ABCD, отвечающей из-
изменению х от а до Ъ.
Мы воспользовались интуитивным представлением о площади,
чтобы естественно подойти к рассмотрению пределов своеобразных
сумм вида B) (которые исторически и были введены в связи с за-
задачей о вычислении площади). Однако самое понятие площади ну-
нуждается в обосновании, и - если речь идет о криволинейной трапе-
трапеции - оно достигается именно с помощью упомянутых пределов.
Разумеется, этому должно быть предпослано изучение пределов B)
• Термин «интеграл» (от латинского integer - целый) был предложен учеником
и сподвижником Лейб ница Иоганном Бернулли (Ioh. Bernoulli); Лейб-
Лейбниц первоначально и говорил «сумма».

96	ГЛ. IX. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ	[295
самих по себе, отвлекаясь от геометрических соображений, чему и
посвящена настоящая глава.
Пределы вида B) играют исключительно важную роль в матема-
математическом анализе и в разнообразных его приложениях. К тому же
в различных видоизменениях развиваемые здесь идеи будут неодно-
неоднократно повторяться на всем протяжении курса.
295. Определение. Пусть функция f(pc) задана в некотором про-
промежутке [а, Ь]. Разобьем этот промежуток произвольным образом
на части, вставив между а и Ъ точки деления A). Наибольшую
из разностей Ах{, = xi+1 - xt (i=0, 1,2, ..., п- 1) будем впредь обозна-
обозначать через А.
Возьмем в каждом из частичных промежутков [xj, xi+1] по про-
произволу точку х =?,•*
Xi'sii'sxt^ (/=0, 1, ..., п - 1)
и составим сумму
о= ЛЬ) Да.
Говорят, что сумма а при А-<-0 имеет (конечный) предел I, если для
каждого числа е >¦ 0 найдется такое число й =» 0, что, лишь только
А<<5 (т. е. основной промежуток разбит на части, с длинами /Ьс,<й),
неравенство
\\
выполняется при любом выборе чисел ?,-.
Записывают это так:
/=1Ш1G.	C)
Этому определению «на языке г-й», как обычно, противопоста-
противопоставляется определение «на языке последовательностей». Представим
себе, что промежуток [а, Ь] последовательно разбивается на части,
сначала одним способом, затем - вторым, третьим и т. д. Такую по-
последовательность разбиений промежутка на части мы будем называть
основной, если соответствующая последовательность значений
Я = ЯХ, Д2, Х3, ... сходится к нулю.
Равенство C) можно понимать теперь и в том смысле, что по-
последовательность значений суммы а, отвечающая любой основной
последовательности^ разбиений промежутка, всегда стремится к пре-
пределу I, как бы ни выбирать при этом !,-.
Доказательство равносильности обоих определений может быть
проведено в том же порядке идей, что и в 53. Второе определение
• Выше мы в качестве!,- брали во всех случаях наименьшее значение

296|	§ 1. ОПРЕДЕЛЕНИЕ И УСЛОВИЯ СУЩЕСТВОВАНИЯ	97
позволяет перенести основные понятия и предложения теории преде-
пределов и на этот новый вид предела.
Конечный предел 1 суммы о при Д-»0 называется определен-
определенным интегралом функции f(x) в промежутке от а до Ь и
обозначается символом	0
в случае существования такого предела функция f(x) называется и н-
тегрируемой в промежутке [а, Ь].
Числа аяЬ носят название, соответственно, нижнего и верх-
верхнего пределов интеграла. При постоянных пределах опреде-
определенный интеграл представляет собой постоянное число.
Приведенное определение принадлежит Риману (В. Riemann),
который впервые высказал его в общей форме и исследовал область
его применения. И самую сумму а иногда называют римановой
суммой*; мы же будем предпочтительно называть ее интеграль-
интегральной суммой, чтобы подчеркнуть ее связь с интегралом.
Поставим теперь себе задачей — выяснить условия, при которых
интегральная сумма а имеет конечный предел, т. е. существует опре-
определенный интеграл D).
Прежде всего заметим, что высказанное определение в действи-
действительности может быть приложено лишь к ограниченной функ-
функции. В самом деле, если бы функция f(x) была в промежутке [а, Ь]
неограничена, то - при любом разбиении промежутка на части - она
сохранила бы подобное свойство хоть в одной из частей. Тогда за
счет выбора в этой части точки ? можно было бы сделать /(?), а с ней
и сумму а, - сколь угодно большой; при этих условиях конечного
предела для а, очевидно, существовать не могло бы. Итак, интегри-
интегрируемая функция необходимо ограничена.
Поэтому в дальнейшем исследовании мы будем наперед предпо-
предполагать рассматриваемую функцию f(x) ограниченной
x)*zM (если
296. Суммы Дарбу. В качестве вспомогательного средства иссле-
исследования, наряду с интегральными суммами, введем в рассмотрение,
по примеру Дарбу, еще другие, сходные с ними, но более простые
суммы.
Обозначим через /и,- и М,, соответственно, точные нижнюю и верх-
верхнюю границы функции f(x) в /-м промежутке [х,-, х, , J и составим
суммы
;=о	,=о
* На деле еще К о ш и отчетливо пользовался пределами подобных сумм,
но лишь для случая непрерывной функции.
Г. М. Фихтенгольц, т. II

98	ГЛ. IX. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ	[296
Эти суммы и носят название, соответственно, нижней и верх-
верхней интегральных сумм, или сумм Дарбу.
В частном случае, когда f(x) непрерывна, они являются
просто наименьшей и наибольшей из интегральных сумм, отвечаю-
отвечающих взятому разбиению, так как в этом случае функция Дх) в каждом
промежутке достигает своих точных границ, и точки ^ можно
выбрать так, чтобы - по желанию - было
|и, или
Переходя к общему случаю, из самого определения нижней и верх-
верхней границ имеем
Умножив члены обоих этих неравенств на Axt {Axt положительно)
и просуммировав по /, получим
При фиксированном разбиении суммы s я S будут постоянными
числами, в то время как сумма а еще остается переменной ввиду
произвольности чисел !,-. Но легко видеть, что за счет выбора ?/ мо-
можно значения /(!/) сделать сколь угодно близкими как к mh так и к
М-,, а значит — сумму а сделать сколь угодно близкой к s или к S.
А тогда предыдущие неравенства приводят к следующему уже об-
общему замечанию: при данном разбиении промежутка суммы
Дарбу s и S служат точными, соответственно, нижней и
верхней границами для интегральных сумм.
Суммы Дарбу обладают следующими простыми свойствами:
1-е свойство. Если к имеющимся точкам деления добавить
новые точки, то нижняя сумма Дарбу может от этого разве
лишь возрасти, а верхняя сумма - разве лишь уменьшиться.
Доказательство. Для доказательства этого свойства до-
достаточно ограничиться присоединением к уже имеющимся точкам де-
деления еще одной точки деления х'.
Пусть эта точка попадет между точками хк и хк+1, так что
Если через 5" обозначить новую верхнюю сумму, то от прежней
S она будет отличаться только тем, что в сумме S промежутку [хк, хк+1]
отвечало слагаемое
а в новой сумме S" этому промежутку отвечает сумма двух слагае-
слагаемых
Мк(х' - хк) + Мк(хк+1 - х'),

2961	§ 1. ОПРЕДЕЛЕНИЕ И УСЛОВИЯ СУЩЕСТВОВАНИЯ	99
где Мк и Мк суть точные верхние границы функции f(x) в проме-
промежутках [хк, х'] и [л"', Xfc+J- Так как эти промежутки являются частями
промежутка [xk,xk+i], то
так что
Мк(х' - xk)*sMk(x' - хк),
Mk(xk+1-x')*zMk(xk+1~x').
Складывая эти неравенства почленно, получим
Мк(х' - хк) + Мк(хк+1 - x')*sMk(xk+1 - хк).
Отсюда и следует, что 5" «s S. Для нижней суммы доказательство ана-
аналогично этому.			__
Замечание. Так как разности Мк-Мк и Мк-Мк, очевидно,
не превосходят колебания Q функции f(x) во всем промежутке [а, Ь],
то разность S— S' не может превзойти произведения QAxk. Это оста-
остается справедливым и в том случае, если в к-оы промежутке взято
несколько новых точек деления.
2-е свойство. Каждая нижняя сумма Дарбу не превос-
превосходит каждой верхней суммы, хотя бы отвечающей и другому раз-
разбиению промежутка.
Доказательство. Разобьем промежуток [а, Ь] произволь-
произвольным образом на части и составим для этого разбиения суммы Дарбу
«1 и -S,.	A)
Рассмотрим теперь некоторое другое, никак не связанное с пер-
первым, разбиение промежутка [а, Ь]. Ему также будут отвечать его суммы
Дарбу
s2 и S2.	(И)
Требуется доказать, что .у^.^. С этой целью объединим те и дру-
другие точки деления; тогда получим некоторое третье, вспомогательное,
разбиение, которому будут отвечать суммы
s3 и S3.	(Ill)
Третье разбиение мы получили из первого добавлением новых то-
точек деления; поэтому, на основании доказанного 1-го свойства сумм
Дарбу, имеем
Сопоставив теперь второе и третье разбиения, точно гак же за-
заключаем, что

100	ГЛ. IX. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ	B97
Но s~*sS3, так что из только что полученных неравенств выте-
вытекает
что и требовалось доказать.
Из доказанного следует, что все множество {s} нижних сумм огра-
ограничено сверху, например, любой верхней суммой S. В таком случае
[11] это множество имеет конечную точную верхнюю границу
и, кроме того,
какова бы ни была верхняя сумма S. Так как множество {S} верхних
сумм, таким образом, оказывается ограниченным снизу числом /*,
то оно имеет конечную точную нижнюю границу
причем, очевидно,
Сопоставляя все сказанное, имеем
s*sI^I**sS	E)
для любых нижней и верхней сумм Дарбу.
Числа /.,. и /* называют, соответственно, нижним и верхним ин-
интегралами Дарбу [ср. ниже 301].
297. Условие существования интеграла. С помощью сумм Дарбу
теперь легко сформулировать это условие.
Теорема. Для существования определенного интеграла необходимо
и достаточно, чтобы было
lim(S-j) = 0.	F)
л-»о
Сказанное в 295 достаточно для уяснения смысла этого предела.
Например, «на языке е-д», условие F) означает, что для любого г=-0
найдется такое д>0, что лишь только А<<5 (т. е. промежуток разбит
на части с длинами Axt ¦= 8), тотчас выполняется неравенство
Доказательство. Необходимость. Предположим,
что существует интеграл D). Тогда но любому заданному е > 0 най-
найдется такое й~-0, что лишь только все Zbc,<#, тотчас
а -7|<е или /-е-=(Т-</+г,
как бы мы ни выбирали |,- в пределах соответствующих промежут-
промежутков. Но суммы s и S, при заданном разбиении промежутка, являются,

298]	§ 1. ОПРЕДЕЛЕНИЕ И УСЛОВИЯ СУЩЕСТВОВАНИЯ	101
как мы установили, для интегральных сумм, соответственно, т о ч-
н ы м и нижней и верхней границами; поэтому для них будем иметь
так что
lims=/, \im S=I,	G)
Д-»0	А-»0
откуда и следует F).
Достаточность. Предположим, что условие F) выполнено;
тогда из E) сразу ясно, что /*=/* и, если обозначить их общее зна-
значение через /,
s^kS.	E*)
Если под о разуметь одно из значений интегральной суммы, отве-
отвечающей тому же разбиению промежутка, что и суммы s, S, то, как
мы знаем,
Согласно условию F), если предположить все Axt достаточно малыми,
суммы s я S разнятся меньше, чем на произвольно взятое е>0. Но
в таком случае это справедливо и относительно заключенных между
ними чисел о и /:
\в -/|<е,
так что / является пределом для а, т. е. определенным интегралом.
Если обозначить колебание М,- - mt функции в г-ом частичном про-
промежутке через со,-, то будем иметь
S-s=Z (М,- - т,) Axi=5 <°М >
1=0	/=0
и условие существования определенного интеграла может быть пере-
переписано так:
lim 24^ = 0.	(8)
А-»0 (=0
В этой форме оно обычно и применяется.
298. Классы интегрируемых функций. Применим найденный нами
признак к установлению некоторых классов интегрируемых
функций.
I. Если функция f{x) непрерывна в промежутке [а, Ь], то она ин-
интегрируема.
Доказательство. Раз функция f(x) непрерывна, то на осно-
основании следствия из теоремы Кантора [87] по заданному е>0
всегда найдется такое <5=-0, что лишь только промежуток [а,Ь] раз-
разбит на части с длинами Ах^д, то все со;<г. Отсюда
л-1	п-1
xj =e(b - а).

102	ГЛ. IX. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ	[298
Так как Ь-а есть постоянное число, а е произвольно мало, то
условие (8) выполняется, а из него и вытекает существование инте-
интеграла. Можно несколько обобщить доказанное утверждение.
И. Если ограниченная функция f{x) в [а, Ь] имеет лишь конечное
число точек разрыва, то она интегрируема.
Доказательство. Пусть точки разрыва будут х', х", ..., х^кК
Возьмем произвольное е>0. Окружим точки разрыва окрестностями
(х'-е\ х'+е'), (х"-е", х"+е"), ...,(*<*>-е<к>, *<« + е<*>)
таким образом, чтобы длина каждой была меньше е. В оставшихся
(замкнутых) промежутках функция f{x) будет непрерывной, и мы
можем применить к каждому из них в отдельности следствие из
теоремы Кантора. Из полученных по е чисел д выберем наимень-
наименьшее (его мы также будем обозначать буквой 8). Тогда оно будет
годиться для каждого из указанных выше промежутков. Ничто нам
не мешает взять при этом <5<е. Разобьем теперь наш промежуток
[а, Ь] на части так, чтобы их длины Axt все были меньше д. Полу-
Полученные частичные промежутки будут двух родов:
1)	Промежутки, лежащие целиком вне выделенных окрестностей
около точек разрыва. В них колебание функции ш,-<е.
2)	Промежутки, либо заключенные целиком внутри выделенных
окрестностей, либо частью на эти окрестности налегающие.
Так как функция fix) предположена ограниченной, то колебание
ее Q во всем промежутке [а, Ь] будет конечно; колебание же в любом
частичном промежутке не превосходит Q.
Сумму
разобьем на две:
распространенные, соответственно, на промежутки первого и второго
рода.
Для первой суммы, как и в предыдущей теореме, будем иметь
^(Oi'Axf-^e^Axi'^si}} - a).
Что касается второй суммы, то заметим, что длины промежутков
второго рода, целиком попавших внутрь выделенных окрестностей,
в сумме <fce; промежутков же, лишь частично налегающих на них,
может быть не больше 2к, и сумма их длин <2кд, а значит и подавно
<2&е. Следовательно,
=Q - Ъке.

299J	§ 1. ОПРЕДЕЛЕНИЕ И УСЛОВИЯ СУЩЕСТВОВАНИЯ	103
Таким образом, окончательно, при Axt-<5 имеем
«[(* - а) + Зкп].
Это и доказывает наше утверждение, так как в квадратных скоб-
скобках содержится постоянное число, а е произвольно мало.
Наконец, укажем еще один простой класс интегрируемых функций,
не покрывающийся предыдущим.
III. Монотонная ограниченная функция Дх) всегда интегрируема.
Доказательство. Пусть f(x) - монотонно возрастаю-
возрастающая функция. Тогда ее колебание в промежутке [xh xi+1] будет
Зададимся любым е>0 и положим
t	e
ЯЬ)-/(а) •
Как только /Ьс,<й, тотчас будем иметь
2щЛх^Ь Z[f(xi+1)-/(*,)] = д\ДЬ)-Да)] =е,
откуда и следует интегрируемость функции.
299. Свойства интегрируемых функций. Из признака п° 297 можно
вывести и ряд общих свойств интегрируемых функций.
I. Если функция f(x) интегрируема в промежутке [а, Ь], то и функ-
функции \f(x)\ и kf(x) (где k = const) интегрируемы в этом промежутке.
Доказательство проведем для функции |/(х)|. Так как
для любых двух точек х', х" промежутка [xh xi+1] имеем [17]
то и колебание tof функции \f(x)\ в этом промежутке не превосходит
«о,- [85]. Отсюда
так как последняя сумма стремится к нулю (при А-»0), то первая и
подавно, что влечет интегрируемость функции |Дх)|.
II. Если две функции f(x) и g(x) интегрируемы в промежутке [а, Ь],
то их сумма, разность и произведение также интегрируемы.
Доказательство ограничим случаем произведения f(x)g(x).
Пусть \f(x)\=*sK, \g(x)\*sL. Взяв в промежутке [Xj, x,+1] любые
две точки х', х", рассмотрим разность
f(x")g{x") -f(x')g(x') = [/(*") - Д

104	ГЛ. IX. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ	[299
Очевидно,
|/(*'W) -Я*'Ж*')| ^ьщ+кщ,
если через coh щ обозначить, соответственно, колебания функций f(x),
g(x) в промежутке [xt, x,+1]. Но тогда [85] и для колебания Qt функ-
функции f(x)g(x) в этом промежутке будем иметь
откуда
Так как две последние суммы стремятся к нулю (при Я->О), то пер-
первая и подавно, что и доказывает интегрируемость функции f(x)g{x).
III.	Если функция f(x) интегрируема в промежутке [а, Ъ], то она
интегрируема и в любой части [а, /3] этого промежутка. Наоборот,
если промежуток [а, Ь] разложен на части, и в каждой части в от-
отдельности функция f(x) интегрируема, то она интегрируема и во всем
промежутке [а, Ь].
Доказательство. Предположим, что функция f{x) интегри-
интегрируема в промежутке [а, Ь], и построим для этого промежутка сумму
2}(QjAxt (считая, что а и /? входят в состав точек деления). Аналогич-
Аналогичная сумма для промежутка [а, /?] получится отсюда, если опустить
ряд (положительных) слагаемых; она наверно стремится к нулю, если
стремится к нулю первая сумма.
Пусть теперь промежуток [а, Ь] разложен, скажем, на две части
[а, с] и [с, Ь] (где а<с<?), и в каждой из них функция f(x) интегри-
интегрируема. Возьмем снова сумму ^со^х,- для промежутка [а, Ь]; если
точка с оказалась в числе точек деления, то названная сумма соста-
составится из двух подобных же сумм для промежутков [а, с] и [с, Ь] и вме-
вместе с ними стремится к нулю. Заключение это остается в силе и для
случая, когда с не является точкой деления: присоединив эту точку,
мы изменим лишь один член суммы, который сам, очевидно, стре-
стремится к нулю.
IV.	Если изменить значения интегрируемой функции в конечном
числе ( = &) точек, то интегрируемость ее не нарушится.
Доказательство очевидно, ибо упомянутые изменения кос-
коснутся не более чем к членов суммы ^со,/1л:,-.
Легко понять, что и значение самого интеграла при этом не по-
потерпит изменения. Это вытекает из того, что для обеих функций -
исходной и измененной - точки |,- в интегральной сумме всегда мо-
можно выбирать так, чтобы они не совпадали с теми точками, для ко-
которых значения их разнятся.
Замечание. Благодаря этому свойству мы получаем возмож-
ь
ность говорить об интеграле f(x)dx даже тогда, когда функция f(x)

300]	§ 1. ОПРЕДЕЛЕНИЕ И УСЛОВИЯ СУЩЕСТВОВАНИЯ	105
не определена в конечном числе точек промежутка [а, Ь]. При этом
можно приписать в этих точках нашей функции совершенно произ-
произвольные значения и рассматривать интеграл от функции, определен-
определенной таким образом во всем промежутке. Как мы видели, ни суще-
существование этого интеграла, ни величина его не зависят от значений,
приписанных функции в точках, где она не была определена.
300. Примеры и дополнения. В качестве упражнения приведем еще примеры
применения признака п° 297 к конкретным функциям.
1) Вернемся к функции, рассмотренной в 70, 8): /(*) = —, если х есть несокра-
р	Я
тимая правильная дробь —, и равно 0 в прочих точках промежутка [0, 1].
а
Пусть промежуток [0, 1] разбит на части с длинами zbc,=sA. Возьмем произ-
произвольное натуральное число N. Все частичные промежутки распределим на два
класса:
р
(а)	К первому отнесем промежутки, содержащие числа — со знаменателями
q
q=sN; так как таких чисел существует лишь конечное число к = к^, то и промежут-
промежутков первого рода будет не больше 2к, а сумма их длин не превзойдет 2кк.
(б)	Ко второму отнесем промежутки, не содержащие указанных чисел; для
них колебание о>,-, очевидно, меньше —.
N
Если соответственно этому разложить сумму JZcoiAxj на две и оценить каждую
порознь, то получим в результате
Взяв сначала N-—, а затем А-=	= <5, будем иметь ?ацАх(~=?, что доказывает
г	4км
интегрируемость функции.
Пример этот интересен тем, что функция здесь имеет бесчисленное
множество точек разрыва и все же интегрируема. [Впрочем, примеры такого рода
можно построить и на основе теоремы III.]
2)	Теперь рассмотрим вновь функцию Дирихле [46; 70, 7)] %(х)=1, если
х — рациональное число, и 0, если х иррационально. Так как в любой части про-
промежутка [0, 1] колебание этой функции а>=1, то и ]?щАх1=\, так что функция
заведомо не интегрируема.
3)	Критерий существования определенного интеграла, выведенный в 297,
может быть представлен в следующей форме:
Для существования определенного интеграла необходимо и достаточно, чтобы
по заданным числам е=»0 и сг=-0 можно было найти такое д>0, что, лишь только
все Ax;~zd, сумма
длин тех промежутков, которым отвечают колебания
сама

106	ГЛ. IX. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ	[301
Необходимость ясна из неравенства
4Jj
С
если, за счет выбора <5, сделать первую сумму меньшей чем га.
Достаточность же вытекает из оценок:
2j	^j	]%	Qa +e(b - a).
i	i'	I"	i'	I"
(Здесь Q, как всегда, означает колебание функции во всем рассматриваемом про-
промежутке; значком i" отмечены частичные промежутки, в которых колебания
ео/"-=е.)
4)	Применим критерий в этой новой форме к доказательству следующего
предложения:
Если функция fix) интегрируема в промежутке [а, Ь], причем значения
ее не выходят за пределы промежутка [с, d], в котором непрерывна функция
<р(у), то сложная функция <p(f(x)) также интегрируема в [а, Ь].
Возьмем по произволу числа г>0 и <г>0. По числу е, в силу непрерывности
функции (р(у), найдется такое jj»O, что в любом промежутке значений у с длиной
-=?7 колебание функции <р будет <=е.
Ввиду интегрируемости функции / по числам г/ и а теперь найдется такое 5,
что лишь только промежуток разбит на части с длинами Ах(<д, сумма 2jAxi'
i'
длин тех из них, для которых колебания функции /: a>j'[/]B= т/, сама меньше а [см.
3)]. Для прочих промежутков имеем a>rlf]^v> a следовательно, по самому выбору
числа rj, ш;"[<р(/)] < е. Таким образом, для сложной функции qj(f(x)) колебания
могут оказаться э=е лишь в некоторых из промежутков первой группы, сумма длин
которых заведомо -=<г. Применяя к сложной функции критерий 3), убеждаемся
в ее интегрируемости.
5)	Если и относительно функции <р предположить лишь интегрируемость,
то сложная функция может оказаться и неинтегрируемой. Вот пример:
В качестве функции fix) возьмем ту, которая была уже изучена выше в 1);
она интегрируема в промежутке [0, 1], причем значения ее также не выходят за
пределы этого промежутка. Далее, пусть
для 0
Функция <р0') также интегрируема в [0, 1].
Сложная же функция q>(f(x)), как легко видеть, совпадает с функцией Дирих-
л е [см. 2)]: она не интегрируема в [0, 1].
301. Нижний и верхний интегралы как пределы. В заключение мы вернемся к ниж-
нижнему и верхнему интегралам, которые в п° 296 были определены как точные
границы сумм Дарбу s и S. Мы покажем теперь, что вместе с тем они
являются и пределами названных сумм.
Теорема Дарбу. Какова бы ни была ограниченная функция f(x), для нее
всегда
Доказательство проведем, например, для верхних сумм.
Прежде всего, по наперед заданному е>0, возьмем такое разбиение проме-
промежутка [а, Ь], что для отвечающей ему верхней суммы 5" будет
5'-=/*+!;	(9)

301)	§ 1. ОПРЕДЕЛЕНИЕ И УСЛОВИЯ СУЩЕСТВОВАНИЯ	107
но возможно, так как /* служит точной нижней границей для множества
верхних сумм. Пусть это разбиение содержит т' (внутренних) точек деления.
Положим теперь
~ Zm'D'
rjafiji означает колебание функции f(x) во всем промежутке [а, Ь], и рассмотрим
произвольное разбиение промежутка, для которого все /Ьс,--= 6; пусть ему
отвечает сумма S.
Для того чтобы оценить разность между S и /*, введем еще третье разбиение
нашего промежутка, объединив точки деления первых двух разбиений. Если соот-
соответствующая ему верхняя сумма есть S", то, по 1-му свойству сумм Дарбу
[296], S"=sS\ так что и подавно [см. (9)]
S"^I*+t-.	(Ю)
С другой же стороны, по замечанию п° 296 разность S-S" не превосходит произ-
произведения Q на сумму длин Ах( тех промежутков второго разбиения, внутрь которых
попали точки деления первого разбиения. Но число таких промежутков не больше
т', а длина каждого из них меньше 8, так что
-,
откуда, в связи с A0),
S^l*+e.
Так как, с другой стороны, S&/*, то, лишь только /U,-= 8,
так что, действительно, S-I*.
Из доказанной теоремы непосредственно следует, что всегда
Это соотношение позволяет высказать критерий существования интеграла в сле-
следующей форме [ср. 297]:
Для существования определенного интеграла необходимо и достаточно, чтобы
пилений и верхний интегралы Дарбу были между собой равны
При выполнении его, очевидно, их общее значение и дает величину определенного
интеграла.
Новая форма условия имеет некоторое преимущество перед прежней. Для
того чтобы убедиться в равенстве интегралов Дарбу, достаточно установить,
что неравенству
при произвольном е удовлетворяет хоть одна пара сумм s и 5. Действительно,
в силу E), тогда будет также
0/=S*-/,-=?,
откуда, ввиду произвольности е, и вытекает требуемое равенство.
Легко сообразить, как в соответствии с этим может быть облегчено и условие
интегрируемости, высказанное в предыдущем п° [см. 3I.

108	ГЛ. IX. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ	[302
§ 2. Свойства определенных интегралов
302. Интеграл по ориентированному промежутку. До сих пор, говоря
об «определенном интеграле в промежутке от а до Ь», мы всегда под-
подразумевали, что а-<Ь. Устраним теперь это стеснительное ограни-
ограничение.
С этой целью мы, прежде всего, устраним понятие направ-
направленного или ориентированного промежутка. Под ори-
ориентированным промежутком [а,Ь] (где может быть и а<Ъ и
а>Ь) мы будем разуметь множество значений х, удовлетворяющих
неравенствам, соответственно,
a=sx*sb или
и расположенных или упорядоченных от а к Ь, т. е.
в порядке возрастания, если а-<Ь, или убывания, если а>Ь. Таким
образом, мы различаем промежутки [а, Ь] и [Ь, а]: совпадая по своему
составу (как числовые множества), они разнятся по направле-
направлению.
То определение интеграла, которое было дано в 295, относится
к ориентированному промежутку [а, Ь], но лишь для случая,
когда а^Ъ.
Обратимся к определению интеграла в ориентированном проме-
промежутке [а, Ь], в предположении, что а>Ь. Можно повторить для этого
случая обычный процесс дробления промежутка путем вставления
точек деления, идущих в направлении от а к i:
Выбрав в каждом частичном промежутке [х,-, х,+1] по точке ?,-, так
что л:,-э=?г-з= xi+1, составим интегральную сумму
i=o
где - на этот раз - все Axt = xi+1 - xt < 0. Наконец, предел этой суммы
при Д = тах |^х;| ->0 и прртведет нас к понятию интеграла
| f(x)dx = lim a.
Если для промежутков [а, Ь] и [Ь, а] (где а^Ь) взять те же точки
деления и те же точки |, то отвечающие им интегральные суммы будут
разниться лишь знаками. Отсюда, переходя к пределам, полу-
получаем такое предложение:

303)	§ 2. СВОЙСТВА ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ	109
1°. Если f(pc) интегрируема в промежутке [Ь, а], то она интегри-
интегрируема и в промежутке [а, Ь], причем
Впрочем, можно было бы именно это равенство принять за опре-
ь
деление интеграла при я=-й в предположении, что интеграл
а	и
существует.
ь
Заметим еще, что по определению же полагают
303. Свойства, выражаемые равенствами. Перечислим дальнейшие
свойства определенных интегралов, выражаемые равенствами*.
2°. Пусть f(x) интегрируема в наибольшем из промежутков [а, Ь],
[а, с] и [с, Ь]**. Тогда она интегрируема в двух других, и имеет место
равенство
) dx = \f{x) dx + \f(x) dx,
каково бы ни было взаимное расположение точек а, Ъ и с.
Доказательство. Положим сначала, что а^с-^b и функ-
функция интегрируема в промежутке [а, Ь].
То, что функция интегрируема в промежутках [а, с] и [с, Ь], сле-
следует из 299, III.
Рассмотрим разбиение промежутка [а, Ь] на части, причем точку
с будем считать одной из точек деления. Составив интегральную сум-
сумму, будем иметь (смысл обозначений ясен)
* Здесь и впредь, если речь идет об интеграле , мы считаем возможным
и
(при отсутствии специальной оговорки) оба случая: а-= b и а =-Ь.
** Вместо этого можно было бы предположить, чгго функция f(x) интегрируема
is каждом из двух меньших промежутков: тогда она была бы интегрируема и в
большем.

110	ГЛ. IX. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ	[304
Переходя к пределу при А-*0, мы и получим требуемое равенство.
Другие случаи расположения точек а, Ъ, с приводятся к этому.
Пусть, например, Ъ-^скс и функция f(x) интегрируема в проме-
промежутке [с, Ь], или - что то же ввиду 1° - в промежутке [Ь, с]. В этом
случае, по доказанному, будем иметь
откуда, перенося первый и второй интегралы из одной части равен-
равенства в другую и переставив пределы (на основании свойства 1°), при-
придем опять к прежнему соотношению.
3°. Если f(x) интегрируема в промежутке [а, Ь], то и kf(x) (где
к = const) также интегрируема в этом промежутке, причем
4°. Если f(x) и g(x) - обе интегрируемы в промежутке [а, Ь], то
и f(x)±g(x) также интегрируема в этом промежутке, причем
ь	ь	ь
J [/(*) ±g(x)] dx = J/(x) dx ± fax) dx.
В обоих случаях доказательство строится аналогично, исходя из
интегральных сумм и переходя к пределу. Проведем его, например,
для последнего утверждения.
Разобьем промежуток [а, Ь] произвольно на части и составим ин-
интегральные суммы для всех трех интегралов. При этом точки |,- в
каждом частичном промежутке выбираем произвольно, но для всех
сумм одни и те же; тогда будем иметь
Пусть теперь А-0; так как для обеих сумм справа пределы суще-
существуют, то существует предел и для суммы слева, чем устанавливается
интегрируемость функции f{x)+g(x). Переходя в предыдущем равен-
равенстве к пределам, приходим к требуемому соотношению.
Замечание. Обращаем внимание на то, что при доказатель-
доказательстве двух последних утверждений не было надобности опираться на
предложения 299, I и II: интегрируемость функций kf(x) и f(x)±g(x)
устанавливается непосредственно переходом к пределу.
304. Свойства, выражаемые неравенствами. До сих пор мы рас-
рассматривали свойства интегралов, выражаемые равенствами; перейдем
теперь к таким, которые выражаются неравенствами.

304]	§ 2. СВОЙСТВА ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ	111
5°. Если функция f(x), интегрируемая в промежутке [а, Ь], н е-
отрицательна и а<Ь, то
Доказательство очевидно.
Труднее доказать более точный результат:
Если функция /(.*), интегрируемая в промежутке [а, Ь], положи-
положительна и а^Ь, то
ь
>0.
Доказательство проведем от противного. Допустим, что
ъ
Тогда при Я—0 и верхняя сумма Дарбу ? также стремится к нулю
[297 G)]. Взяв произвольное %>(), можем сделать эту сумму мень-
меньшей чеме^б - а). При этом хотя бы одна из верхних границ Мг- окажется
меньшей е1, иными словами, найдется в [а, Ь] такая часть [ах, Ьг], в
пределах которой все значения f(x) <ег.
Так как и
то, аналогично, из [flx,^] выделится часть [а2,Ь^\, в пределах кото-
которой Дх)<?2, где е2 - любое положительное число <ех, и т. д.
Взяв последовательность положительных чисел ек-~0, можно опре-
определить такую последовательность вложенных один в другой (и - если
угодно - убывающих по длине до 0) промежутков [ак, Ьк], что
0</W-=eA, если ак^х^Ък (к= 1, 2, 3, ...).
* Действительно, по 2°:
6 ах 6j b
1 = 1 + 1 + 1 и, так как Г з=0, Г =»0,
а а аг Ьх
ТО
ь, ь

112	ГЛ. JX. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ	[304
Тогда по лемме п° 38 существует точка с, общая всем этим про-
промежуткам; для нее должно быть
0</(c)<efc при *= 1,2,3, ....
что невозможно, ибо ек-*0. Теорема доказана.
Простым следствием отсюда (и из 4°) является
6°. Если две функции Дх) и g(x) интегрируемы в промежутке [а, Ь]
и всегда /(x)=s^(.x) [или f(x)-<g{x)\ то и
b	b	b	!>
f(x) dx*s \g(x) dx [или J7(x) dx < \g{x) dx\
a	a	a	a
в предположении, что а<Ь.
Нужно лишь применить предыдущее свойство к разности g(x) -f(x).
Так же легко получается:
7°. Пусть функция f(x) интегрируема в npoAi ¦т,с\тке [а, Ь] и а<Ъ,
тогда имеем неравенство
Ь	b
Существование последнего интеграла следует из 299, I. Свойство
6° применяем затем к функциям
-1 Л*) |*Я*)*|/(*)!•
Впрочем неравенство легко получить и непосредственно, исходя
из интегральных сумм*
и переходя к пределам.
8°. Если f(x) интегрируема в [а, Ь], где а-<Ь, и если во всем этом
промежутке имеет место неравенство
то
ь
m{b — a)=s f(x) dx =s M(b — a).
Можно применить свойство 6° к функциям т, f(x) и М, но проще
непосредственно воспользоваться очевидными неравенствами
и перейти к пределу.
* Так как я«=Л, то вес

304)
§ 2. СВОЙСТВА ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
ИЗ
Доказанным соотношениям можно придать более удобную форму
равенства, освобождаясь в то же время от ограничения а-<Ь.
9°. Теорема о среднем значении. Пусть f(x) интегрируема
в [°> b] (a'S-b) и пусть во всем этом промежутке т?г==/(х)==М; тогда
где
Доказательство. Если а <Ь, то по свойству 8° будем иметь
откуда
Положив
т(Ь - a) =s J/(x) dx *s Мф - a),
a
b
mss±- J/(;
получаем требуемое равенство.
a
Для случая, когда а > Ъ, проводим эж ох рассуждение для J , а
б
затем, переставив пределы, приходим к прежней формуле.
Только что доказанное равенство принимает особенно простой
вид, когда функция Дх) непрерывна. Действительно, если
считать, что т и М суть наибольшее и наименьшее значения функции,
существующие по теореме В е й-
е р ш т р а с с а, 85, то и проме-
промежуточное значение /*, по теореме
Больцано-Коши, 82, дол-
должно приниматься функцией Дх)
в некоторой точке с промежутка
[а, Ь]. Таким образом,
ь
0	Рис. 5.
где с содержится в [а, Ь].
Геометрический смысл последней формулы ясен. Пусть
Рассмотрим криволинейную фигуру ABCD (рис. 5) под кривой y=f(x).
Тогда площадь криволинейной фигуры (выражаемая определенным
Г. М. Фихтенгольц, т. П

114	ГЛ. IX. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ	[304
интегралом) равна площади прямоугольника с тем же основанием
и с некоторой средней ординатой LM в качестве высоты.
10°. Обобщенная теорема о среднем значении. Пусть 1) f(x)
и g{x) интегрируемы в промежутке [а, Ь]; 2) m*sf(x)=*sM; 3) g(x) во
всем промежутке не меняет знака: g(x)s*0 [g(.x)*s&]. Тогда*
где
До казательство. Пусть сначала g(x)s»0 и а<Ь\ тогда имеем
mg{x) *zf(x)g(x) *sMg(x).
Из этого неравенства, на основании свойств 6° и 3°, получаем
ь	ь	ь
т J g(x) dx *s J/(x)g(x) dx =s M J g(x) dx.
a	a	a
Ввиду предположения о функции g{x), no 5°, имеем
ь
Если этот интеграл равен нулю, то из предыдущих неравенств ясно,
что одновременно также
и утверждение теоремы становится очевидным. Если же интеграл
больше нуля, то, разделив на него все части полученного выше двой-
двойного неравенства, положим
а
и придем к требуемому результату.
* Самое существование интеграла от произведения f(x)g(x) следует из 299,
II. Впрочем, можно было бы вместо интегрируемости функции f(x) непосредствен-
непосредственно предположить интегрируемость самого произведения f{x)-g(x).

30S|	§ 2. СВОЙСТВА ОПРЬДЫЮШЫХ иНТЫРАЛОВ	J15
От случая a-<b легко перейти к случаю а>Ь, равно как от пред-
предположения g(x)=2=0 — к предположению g(x)s=0: перестановка преде-
пределов или изменение знака g(x) не нарушат равенства.
Если f(x) непрерывна, то эта формула может быть записана
следующим образом:
jf(x)g(x)dx=f(c)jg{x)dx.
где с содержится в [а, Ь].
305. Определенный интеграл как функция верхнего предела. Если
функция/(х) интегрируема в промежутке [a, b] (a^b), то [299, III]
она интегрируема и в промежутке [а, х], где х есть любое значение
из [а, Ь]. Заменив предел Ъ определенного интеграла переменной х,
получим выражение *
X
Л
0)
которое, очевидно, является функцией от х. Эта функция обладает
следующими свойствами:
11°. Если функция f(x) интегрируема в [а, Ь], то Ф(х) будет не-
непрерывной функцией от х в том оке промежутке.
Доказательство. Придав х произвольное приращение Ах = h
(с тем лишь, чтобы x + h не выходило за пределы рассматриваемого
промежутка), получим новое значение функции A)
х+Л	х x+h
[см. 2°], так что
Х+Л
Применим к этому интегралу теорему о среднем значении 9°
Ф(х + А)-Ф(х)= fj.fi;	B)
здесь {г содержится между точными границами т' и М' функции f{x)
в промежутке [х, х 4- А], а следовательно, и подавно между (посто-
(постоянными) границами ее т и М в основном промежутке [а, Ь]**.
* Переменную интегрирования мы обозначили здесь через t, чтобы не сме-
смешивать ее с верхним пределом х; разумеется, изменение обозначения пере-
переменной интегрирования не отражается на величине интеграла.
** Напомним, что интегрируемая функция ограничена [295].

116	ГЛ. IX. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ	|305
Если устремить теперь h к нулю, то, очевидно,
Ф(х)-0 или Ф(х-ьп)-*Ф(х),
что и доказьшает непрерывность функции Ф(х).
12°. Если функцию f(t) предположить непрерывной в точке
t = х, то в этой точке функция Ф(х) имеет производную, равную f(x)
Ф'(х) =/(*).
Доказ ателье гво. Действительно, из B) имеем
А)-Ф(*)
h
где
Но, ввиду непрерывности функции f(t) при t = x, по любому е>0 най-
найдется такое <5>0, что при |/г|<5
f(x)-s^f(t)^f(x) + e
для всех значений t в промежутке [х, х + п]. В таком случае имеют
место и неравенства
f[x) -e^.m'=sy=sM'=sf(x) +e,
так что
|/i-/(*)|*e.
Теперь ясно, что
Ф\х) = lim -^	1	— = hm у. = f{x),
/l-O	"	Л-0
что и требовалось доказать.
Мы пришли к заключению, имеющему огромное принципиальное
и прикладное значение. Если предположить функцию f(x) непре-
непрерывной во всем промежутке [а, Ь], то она интегрируема [298, I],
и предыдущее утверждение оказывается приложимым к любой
точке х этого промежутка: производная от интеграла A) по пере-
переменному верхнему пределу х везде равна значению f(x) подынтеграль-
подынтегральной функции на этом пределе.
Иными словами, для непрерывной в промежутке [а, Ь] функ-
функции f(x) всегда существует первообразная; примером ее является опре-
определенный интеграл A) с переменным верхним пределом.
Таким образом, мы, наконец, установили то предложение, о ко-
котором упоминали еще в 264.
В частности, мы теперь можем записать функции F и Е Лежандра [293]
в виде определенных интегралов
<р	<р
F(k, <р)= !	, E(k, <f)~
J yi-/t2si

306]	§ 2. СВОЙСТВА ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ	117
По доказанному только что, это будут первообразные функции, соответственно,
для функций
}f ki
и притом обращающиеся в 0 при <р = 0.
Замечание. Утверждения, доказанные в настоящем п°, легко
распространяются на случай интеграла с переменным нижним пре-
пределом, так как A°)
Ь	х
\f(t)dt=-\f(t)dt.
Производная от этого интеграла по х, очевидно, равна — f(x)
(если х есть точка непрерывности).
306. Вторая теорема о среднем значении. В заключение установим
еще одну теорему, относящуюся к интегралу от произведения двух
функций
ь
I=\f(x)g{x)dx.
а
Ее представляют в разных формах. Начнем с доказательства сле-
следующего предложения:
13°. Если в промежутке [а, Ь] (a-=Z>) f(x) монотонно убывает (хотя
бы в широком смысле) и неотрицательна, a g(x) интегрируема, то
ь	{
jf(x)g(x)dx=№Jg(x)dx,	C)
а	а
где I есть некоторое значение из названного промежутка.
Разбив промежуток [а, Ъ] произвольным образом на части с по-
помощью точек деления лг, (i = 0, 1, ..., и), представим интеграл / в виде
Л —1 f*
Ы2 J
,=0 J
¦>J
Л—1 г
1=0 J
Если через L обозначить верхнюю границу для функции \g(x)\, a
через (Of (как обычно) колебание функции f{x) в г-ом промежутке

118	ГЛ. IX. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ	[306
[xit xi+1] длины Axh то, очевидно,
< + 1
J
I еI *Д J |/(*) -ЛхдЫх)I
Отсюда ввиду интегрируемости функции /(х) [298, 111] ясно, что
2-0 при 1 = таахАхг~ О, так что
/=lim a.
Введем теперь функцию
и с ее помощью перепишем сумму а так:
+1)
1=0
или, наконец, раскрывая скобки и иначе группируя слагаемые,
5
1=1
Непрерьшная функция G(x) [305, 11°], при изменении х в проме-
промежутке [а, Ь], имеет как наименьшее значение т, так и наибольшее зна-
значение М [85]. Так как все множители
/(*,_i)-/(*,) (при i= 1, 2, ..., п - 1) и f(xn-x),
в силу сделанных относительно функции f(x) предположений, неот-
неотрицательны, то, заменяя значения G соответственно через т и М, мы
получим два числа:
mf(a) и Mf{a),
между которыми содержится сумма в. Между теми же числами, оче-
очевидно, содержится и интеграл / как предел этой суммы, или иначе
где /WsSjUasM. Но, по непрерывности функции G(x), в промежутке
[a, b] найдется такое значение I, что /х = С7(|) [82]. Тогда
что равносильно формуле C).

306]	§ 2. СВОЙСТВА ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ	119
Аналогично, если функция f(x), оставаясь неотрицательной, моно-
монотонно возрастает, то имеет место формула
где a*s?*sb. Эти формулы обычно называют формулами Бонне
(О. Bonnet). Наконец,
14°. Если сохранить только предположение о монотонности функ-
ции f(x), не требуя ее неотрицательности, то молено утверждать:
ь	s	ь
\f{x)g{x) dx =f(a)\g{x) dx +f(b)jg(x) dx	D)
Действительно, пусть, например, функция f(x) монотонно убывает;
тогда, очевидно, разность f(x)—f(b)^0, и стоит только к этой функ-
функции применить формулу C), чтобы после легких преобразований по-
получить D).
Доказанная теорема и носит название второй теоремы о среднем
значении [ср. 304, 10°].
Следующее простое замечание позволяет придать ей несколько
более общую форму. Если изменить значения функции f{x) в точках
а и Ь, взяв вместо них любые числа А я В под условием лишь
As*f(a + 0) и B*ef(b-0) (если / убывает),
+ G) и Bs*f(b-0) (если / возрастает),
то не только значение интеграла / не изменится, но и сохранится
монотонность функции f(x), так что по образцу D) можно утвер-
утверждать
ь	f	ь
g(x) dx=A jg(x) dx + BJg(x) dx.	E)
В частности,
b
\f{x)g{x) dx = f{a+0)\g{x) dx + f(b - 0)\g(x) dx.	E*)
Здесь, как и выше, I означает некоторое число из промежутка
[а, Ь], но оно, вообще говоря, зависит от выбора чисел
А и В.

120	ГЛ. IX. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ	[307
§ 3. Вычисление и преобразование определенных
интегралов
307. Вычисление с помощью интегральных сумм. Приведем ряд
примеров вычисления определенного интеграла, непосредственно как
предела интегральных сумм - в согласии с его определением. Зная
наперед, что интеграл для непрерывной функции существует, для в ы-
числения его мы можем выбирать разбиение промежутка и точки
I, руководствуясь исключительно соображениями удобства.
ь
1) хк dx {a, b - произвольные вещественные числа, а к - натуральное
а
ЧИСЛО).	а
Сначала вычислим интеграл I xk dx (a*0). Промежуток [0, а] разобьем на
о
п равных частей, а в каждом частичном промежутке функцию хк вычислим
для его правого конца, если а=-0, и для левого - при я-=0. Тогда интегральная
сумма
' а , . 1к+2к+...+пк
и, если учесть пример 14) п° 33,
а
ak+i
хк dx = lim an =	.
л~~ к + 1
о
Отсюда уже нетрудно получить и общую формулу
Ь	Ь а
к+1
а	0 0
ь
2) I xi1 dx (Ь^а^О, (I - произвольное вещественное число).
в
На этот раз мы разобьем промежуток [а, Ь] на неравные части, а именно
между а и Ъ вставим л-1 средних геометрических. Иными словами, положив
л
а
г
рассмотрим ряд чисел
а, ад, ..., aql,
Заметим, что при л-=° отношение <? = <?п-*1, разности же aql+1-aql все меньше
величины b(q -1) — 0.
Вычисляя функцию для левых концов, имеем
л-1
2
(=0

307]	§ 3. ВЫЧИСЛЕНИЕ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ	121
Предположим теперь р* -1; тогда
F"+' - Р+1)
и, используя уже известный предел [пример 5), (в), 77], получим
h
j x>1 dx = lim on ™ FU+1 - af+*) lim
q-\
a
В случае же /i = -1 будет
11/ a I»
и на основании другого известного результата [там же, (б)]
— = lim ап = lim л I I /	1 I = In b - In a,
J х п~оо п-*~ \\ а )
г	Ь-а
3) I sin х dx. Разделив промежуток [а, Ь] на п равных частей, положим h =	;
J	п
а
функцию sinx вычислим для правых концов, если а^Ь, и для левых при
а^Ь. Тогда
л
on = h^j sin (a + ih).
(=.1
Найдем сжатое выражение для суммы справа. Умножив и разделив ее на
2 sin —, а затем представляя все слагаемые в виде разности косинусов, легко
получим
л	1 "	h
2 sin (a+ih)	2! 2 sin (a+ih) sin - =
f~i	. . A /-1	2
2sm —
 tcos
2sin-' L v	> v	1X	2sin-
2	2	A)
Таким образом,
h
"n
sin —

122	ГЛ. IX. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ	[307
Так как /; »0 при л-»<*>, то
h
^
&\nxdx = lim	 cos \a + — h -cos \ЬЛ—h\ = cos a -cos b.
J	h~o hi { 2 )	\ 2I
sin
sin —
Аналогично, исходя из элементарной формулы *
'	1
In	SU1
2 cos (a+ili) = —	—	"-L ,	B)
'=1	2 sin —
2
легко установить, что
Ь
cos x dx=sin b - sin a.
a
4) Чтобы дать менее тривиальный пример, рассмотрим интеграл
я
In A - 2r cosx+r2) dx,
о
обычно связываемый с именем Пуассона (S.-D. Poisson). Так как
то, предполагая \г\ * 1, видим, что подинтегральная функция непрерывна, и ин-
интеграл существует.
Разделив промежуток [0, л] на п равных частей, имеем
"""вы I rC°S I+rj=^L +Г Д1
где П есть знак произведения. С другой стороны, из алгебры известно
z2"-l=(za-l) TT l-2zcos —+
л
* Которая получается из A) заменой а на аЛ—.
** Учитывая значения корней степени 2и из единицы, имеем такое разложение
zm - 1 на линейные множители:
Пп~г ( кл	кл)
Iz-cos	ism— ,
A—«I	"	">
где / есть мнимая единица. Если выделить множителиz= ± 1 (отвечающие к- -п

308]	§ 3. ВЫЧИСЛЕНИЕ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ	123
Используя это тождество при z=r, представим ап в виде
n
Пусть теперь | г \ ¦<¦ 1, тогда г-п - О и
л
j In A - 2r cos х + г2) Л = lim an = 0.
о
Если же \г\ =-1, то, переписав t/n так:
Г2П_ ¦
найдем
л
I* In A - 2r cos х + г2) Л = 2л In | г |.
о
Читатель видит, что прямой способ вычисления определенного
интеграла, как предела сумм, требует даже в простых случаях зна-
значительных усилий; им пользуются редко. Наиболее практичным яв-
является прием, излагаемый в следующем п°.
308. Основная формула интегрального исчисления. Мы видели в 305,
что для непрерывной в промежутке [а, Ь] функции f(x) интеграл
оказывается первообразной функцией. Если F(x) есть любая
первообразная для f(x) функция (например, найденная методами
§§1-4 предыдущей главы), то [263]
Постоянную С легко определить, положив здесь х = а, ибо Ф(а) = 0;
будем иметь
0 = ф(а) = Л(а) + С, откуда C= -F{a).
Окончательно
и к = 0) и собрать вместе сопряженные множители, то мы и получим, что z2" - 1
равно
^ I	кп	кп\ I	кп	кп\
(г2- 1) II г-cos	i sin — z-cos —yi sin— =
ДД I	n	n)\	n	nj
Л—1 /	,	,
= (z2"l)TT 1 -2zcos—+z4.
til I	« /

124	ГЛ. IX. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ	[308
В частности, при х = Ъ получим
ь
W dx = F(b) - F(a).	(A)
Это - основная формула интегрального исчисления *.
Итак, значение определенного интеграла выражается раз-
разностью двух значений, при х = Ъ и при х = а, любой первообраз-
первообразной функции.
Если применить к интегралу теорему о среднем [304, 9°] и вспом-
вспомнить, что f(x) = F'(x), то получим
читатель узнает в этом формулу Лагранжа [112] для функции
F{x). Таким образом, с помощью основной формулы (А) устанавли-
устанавливается связь между теоремами о среднем в дифференциальном и ин-
интегральном исчислении.
Формула (А) дает эффективное и простое средство для вычисле-
вычисления определенного интеграла от непрерывной функции f(x). Ведь для
ряда простых классов таких функций мы умеем выражать первооб-
первообразную в конечном виде через элементарные функции. В этих случаях
определенный интеграл вычисляется непосредственно по основной
формуле. Заметим лишь, что разность справа обычно изображают
символом F{x) |? («двойная подстановка от а до Ь») и формулу пишут
в виде
ь
\f(x)dx~F{x)\l	(A*)
а
Так, например, сразу находим:
a
b
2) Г*-
J х
\пх
-\nb-\na (а=-0,
* Эту формулу называют также формулой Ньютон а-Лейбниц а.
Читатель видит, что рассуждения здесь вполне аналогичны тем, которыми
мы пользовались в 264 при вычислении функции Р(х) и площади Р. Сама
формула (А) легко могла бы быть получена сопоставлением результатов
пп° 264 и 294.

309J	§ 3. ВЫЧИСЛЕНИЕ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ	125
3) sin* dx = -cos x ba= cos a -cos b,
ь
b .
cos л dx = sm x „= sin b -sin a
- результаты, не без труда полученные нами в предыдущем п° [ср. примеры 1,)
2), 3)] *.
309. Примеры. Приведем дальнейшие примеры использования формулы (А):
п
Г sin (m - ri)x sin (m + и) xl
r	Irs
4) (a) I sin mx sin nxdx = —\-
-| =0
m-л	m + n J _я
F)
—я
Аналогично
г	1 Г sui2t?m:i |+л
sm2mjc*te = — Ь:	=я [см. 267, 17), 18)].
J	2 l 2т ] 1-я
(в) sin 777Л cos ты: rfx = 0,
(г) I cos mx cos nx dx = 0 или л, смотря по тому будет ли лит или л = и?.
— я
5) Найти значения интегралов (т, п - натуральные числа):
С sin Bm-l).v
(a) J 	:	dx,
sin л
о
Лет nxY
-.	 dx.
sin х J
о
Указание, (а) Из формулы B), полагая в ней а = 0, h = 2х и и = т - 1, можно
вывести, что
1	"U1 sinBm-l)jc
—+ 2/ cos 2(>=	.
2	j=i	2sinA:
* Пример 4) предыдущего п° уже не может быть исчерпан так просто, ибо
соответствующий неопределенный интеграл в конечном виде не выражается.

126
ГЛ. IX. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
1309
Отсюда, так как отдельные слагаемые легко интегрируются по формуле (А),
сразу получается
psin Bи
J sin
rsin Bm- l)x л
- dx = — .
sin*	2
(б) Из формулы A), полагая а = - x, A = Ix, найдем
1 - cos 2nx sin2 nx
sin Bm -
m=l	2 sin л: sin л
Отсюда, если использовать предыдущий результат,
if
sinn*"»2	я
	 dx = n — .
sin x I	2
6) Вычислить интеграл
dx
где 0-=a, /?-= 1.
Если в формуле [283 F*)]
dx
I
¦ = — In
^ + bx+c
ах-\—
отождествить
= (l -lax + a2
+ С
то, дифференцируя, найдем
b
ах + -= -<хA-2
Отсюда легко вывести, что при х = 1 выражение, стоящее под знаком логарифма,
получит значение
а при д: = - 1 значение
Таким образом, окончательно для искомого интеграла получается простое выра-
выражение
зависящее только от произведения а/?*.
* Наши вьжладки безупречны лишь при а^Д, но легко видеть, что результат
верен и при а = /?.

3091
§ 3. ВЫЧИСЛЕНИЕ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
127
Заметим, что при выводе основной формулы нам на деле не было надобности
требовать, чтобы функция F(x) была для /(*•) первообразной в замкнутом
промежутке [а, Ь]. Опираясь на следствие п° 131, достаточно было бы предположить
это для открытого промежутка (а, Ь), лишь бы только и на кот/ах его функция
F(x) сохраняла непрерывность.
Поэтому, например, мы имеем право писать [268]
яа2
XI а я»2
— =—,
а] -а 2
хотя при х= ±а вопрос о производной найденной первообразной еще требовал
бы исследования.
Некоторое затруднение мы встречаем при вычислении интеграла
dx
так как найденная в 288, 13) первообразная
1 + г х)
^-— tg-j
не имеет смысла при х= ±ж. Однако существуют, очевидно, пределы
lim F(x)= -л, lim F(x)=n,
х-^я+0	х->-я-0
и если, как обычно, положить F(-ra) и F(n) равными именно этим пределам, то
функция F(x) будет не только определена, но и непрерывна на концах промежутка.
Поэтому все же имеем
Jit
1-г2
- 2r cos
— я
9) Аналогично вычисляется и интеграл
п
%
j
A cos2 х+2В cos x sin x+С sin2 x
Мы уже имели [288, 10)] выражение первообразной
1
arctg
Ctgx+B
л	п
пригодное для	¦=*-=—. Отсюда
2	2
J
dx
A cos2 x + 2В cos x sin x + С sin2 x
¦F(x)
Vac-в*

128
ГЛ. IX. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
[310
п п
причем значки	ьО,	0 символизируют необходимость брать соответствую-
соответствующие предельные значения функции F(x).
10) Если при вычислении интеграла
dx
исходить из формально вычисленной первообразной
	 arctg
и подставить сюда л = 0 и х=1, то для интеграла получится парадоксальное зна-
значение 0 (интеграл от положительной функции не может иметь нулевое
значение!).
Ошибка в том, что это выражение испытывает скачок при х = у 2 - /3 = х0.
Если порознь вычислять интегралы от 0 до х0 и от х0 до 1, то получится правиль-
правильный результат
о
х„-0
о
х«+0 3
11) Легко вычислить, с помощью первообразных, интегралы
2
dx
- = ln х
= 1п2,
• dx
1+х'
= arctg x
Если вспомнить о стремлении к ним соответственных интегральных сумм, то
можно получить, например, такие предельные соотношения:
1
/
lim
п-оДл+1
lim
1	1 \
	+...+-— =ln 2,
л + 2	2л!
+...Ч
2л1
—
4
310. Другой вывод основной формулы. Установим теперь основную
формулу (А) при более общих предположениях. Пусть функция /(х)
интегрируема в промежутке [а, Ь], а непрерывная в [а, Ь]
функция F(x) имеет f(x) своей производной
*"(*)=/(*)
C)
повсюду в (а, Ь) или даже лишь повсюду, исключая конечное
число точек.

310]	§ 3. ВЫЧИСЛЕНИЕ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ	129
Разобьем промежуток [а, Ь] произвольным образом на части точ-
точками
[позаботившись лишь о том, чтобы в их числе были все те
точки, где не имеет места соотношение C), если
такие точки есть]. Очевидно, будем иметь
- F(a) =
2
(=0
Применим к каждой из разностей, стоящих под знаком суммы,
формулу конечных приращений, - условия для ее применения все
выполнены. Тогда получим
F{b) - F{a) = 2F'(SMxt+1 - х,),
1=0
где I,- есть некоторое определенное (хотя нам не известное) значение
х между xt и х1+1. Так как для этого значения ^"(?/)=/(?/)> то мы
можем написать
2
Справа получилась интегральная сумма а для функции f[x). Мы
предположили, что для суммы а при Я-<-0 существует определенный
предел, не зависящий от выбора чисел !,-. Следовательно, в частно-
частности, наша сумма, сохраняющая (при указанном выборе этих чисел)
постоянное значение, также стремится к интегралу, откуда и вытекает,
что
F(b)-F{a)=lf{x)dx.
В предыдущем п° мы с помощью основной формулы вычисляли
определенный интеграл. Но она может быть использована и в дру-
другом направлении. Заменив в основной формуле Ъ на х, a f(x) на F'{x),
можно написать ее в виде
Таким образом, с помощью предельного процесса (ибо определен-
определенный интеграл есть предел), по заданной производной F\х) «вос-
«восстанавливается» первообразная функция F(x).
Впрочем, это предполагает, что производная не только ограни-
ограничена, но и интегрируема в согласии с римановым определением, что
осуществляется не всегда.
9 Г. М. Фихтенгольц, т. И

130	ГЛ. IX. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ	[311
311. Формулы приведения. Мы видели, что основная формула при
благоприятных условиях сразу дает значение определенного интеграла.
С другой стороны, с ее помощью различные формулы приве-
приведения в теории неопределенных интегралов преобразуются в ана-
аналогичные формулы уже в определенных интегралах, сводящие вы-
вычисление одного определенного интеграла к вычислению другого (во-
(вообще более простого).
Мы имеем в виду прежде всего формулу интегрирования по частям
\и do = uv — \vdu
и ее обобщение [270 C) и E)], а также другие формулы приведения
[271 F); 280; 287], частично на ней же основанные. Общая форма их
такова:
\f(x)dx=<p(x)-\g(x)dx.	D)
Если областью применения подобной формулы является промежу-
промежуток [а, Ь], то ей в определенных интегралах отвечает формула
*	ь
\f(x)dx=<p{x)l-\g{x)dx.	E)
а	а
При этом функции /, g будем считать непрерывными.
Для доказательства обозначим последний интеграл в формуле D)
через Ф(х). Тогда
J/(*) dx = [ф) - Ф(х)] Ц=ф) I - Ф{х) \Ь
а
Так как, в то же время,
то мы и приходим к доказываемой формуле.
В частности, формула интегрирования по частям примет теперь вид
ь	ь
)udv = uv\ba- \vdu,	F)
а	а
а обобщенная формула перейдет в такую:
ь	ь
h(-l)n+1J dn+v>vdx; G)
а

3121	§ 3. ВЫЧИСЛЕНИЕ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ	131
при этом по-прежнему функции и, v и все встречающиеся их произ-
производные предполагаются непрерывными.
Формула E), устанавливающая соотношение между числами,
принципиально проще формулы D), в которой участвуют функции;
она особенно выгодна, если двойная подстановка равна нулю.
312. Примеры. 1) Вычислить интегралы
Jm = sinm х dx, j'm -= cosm x dx
(при натуральном т).
Интегрируя по частям, найдем
./,„ = I sinm~1 xd( - cos v) - — sinm ~> x cos x
2 4 (m - 1) sinm'2 x cos2 x dx.
Двойная подстановка обращается в нуль. Заменяя cos-.v через 1 -sin2.v, получим
Jm = О' - 1)Л?1-» ~ ('» ~ Шш.
откуда рекуррентная формула:
т-\
Зт~	~ Jт — 2>
т
по которой интеграл Jm последовательно приводится к /0 или Jx. Именно, при
т~2п имеем
.	Bii-l)Bi!-3)...3.1 л
J*n = sm2" x dx =
\п = Sin2" л ил	,
.1	2д.Bи-2)...4-2 2
о
если же т = 2п +1, то
п
2п-Bп-2)...4-2
С
1= sin
о
Такие же точно результаты получаются и для Jm.
9*

132
ГЛ. IX. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
[312
Для более короткой записи найденных выражений воспользуемся символом
от!! *. Тогда можно будет написать
sinm х dx = cosm x dx =
о	о
2) Доказать формулы
от-1)!! я
	•— при т четном.
/я!! 2
(от-1)!!
те!!
при т нечетном.
(а)	cosm х cos (от + 2)х dx - О,
о
л
2
(б)	cosm х sin (от+2)х dx = 	,
J	от+1
о
2	sin -
(в)	sinm х cos (m+ 2)x dx
m+\
(8)
Г
(r) sinm л sin (m+2)x dx -=
J
ot4 1
(где т - любое положительное число).
Рассмотрим интеграл
cosm+2 x cos
x
о
и дважды произведем в нем интегрирование по частям:
л
2
cosm+2 х cos (m +¦ 2)х <йс =
О
от + 2
[cosm+2 х sin (от +2)х - со8т+г х sin x cos (от+2)х]
1 г
[-
-?2J
l)cos
2)x dx.
* Напомним, что «!! означает произведение натуральных чисел, не превосходя-
превосходящих от и одной с ним четности.

312]	§ 3. ВЫЧИСЛЕНИЕ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ	133
Двойная подстановка обращается в 0. Заменяя под знаком интеграла sin2 x через
1 - cos3 х, придем к равенству
я/2
cosm *¦2 х cos (m + 2)х dx =
О	л/2	л/2
т +1 г	С
=	 cosm xcos(ot + 2);c<&+ cosm+2 xcos(m + 2)xdx,
m + 2 J	J
о	о
откуда и следует (а).
Аналогично устанавливаются остальные равенства.
3) Вычислить (при натуральном и) интегралы
я	л
2	2
Кп = cos" х sin nx dx, Ln = cos" x cos nx dx.
о	о
Интегрируя по частям, будем иметь
л/2
1 г
Кп-	I cos" х sin x cos nx dx.
n J
0
Если к обеим частям прибавить по Кп> то преобразуя выражение под знаком
интеграла справа, легко получить
1	1 (I
2Кп = —\-Кп_1 или Кп = —\—Ь
п	2\п
По этой рекуррентной формуле легко уже найти
1 B 2- 2з	2"
Аналогично
л
4) Найти интеграл
1
Hk,m= [xk\r\mxdx,
о
где i>0, a m - натуральное число.
Интегрирование по частям [ср. 271, 5)]
С
xk\amxdx =
1
1	|1 т
к+1\т\
х\
| + о Аг+1.
о	о
приводит к рекуррентной формуле
т
Нк,т= ~Т~~7 Hk,m-i>
K-j-1
откуда и получается
хк In x dx

134	ГЛ. IX. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ	[313
Особенность этого примера в том, что в точке х = 0 значения как подинтеграль-
ных функций, так и функций под знаком подстановки определяются как предель-
предельные при х- +0.
5) По формуле (III) п" 280 имеем (считая р и q натуральными числами)
г	A~х)РхЯ+1 р г
A - х)РхЧ dx =	h —	 A -x)P"lx4 dx,
J	p+q + 1 p + q + U
что при переходе к определенным интегралам в промежутке от 0 до 1 дает
1	1
f A - х)РхЯ dx =	-	f A - x)P-lx4 dx.
J	p+q+\J
о	0
Последовательно применяя эту формулу, получим
1
I {\-x)Pxidx =
xQdx
о	о
и окончательно
p\q\
(l-x)Px4dx =
6) Если в формулах (IV) п° 287 при натуральных fi и v перейти к определенным
интегралам, то, используя результат примера 1), можно получить более общую
формулу
-1)!! л
— (при четных /< и i>),
(у+,«)!! 2
sinv х cos''
(во всех прочих случаях).
313. Формула замены переменной в определенном интеграле. Та же
основная формула (А) позволит нам установить правило замены пере-
переменной под знаком определенного интеграла.
ь
Пусть требуется вычислить интеграл I fix) dx, где f{x) - непре-
а
рывная в промежутке [а,Ь] функция. Положим х=q>(t), подчинив функ-
цяю q)(t) условиям:
1) (pit) определена и непрерывна в некотором промежутке [ос,/5]
и не выходит за пределы промежутка [а, Ь] *, когда t изменяется
в [о,Д;
* Может случиться, что функция fix) определена и непрерывна в более широ-
широком, чем [а, Ь], промежутке [А, В], тогда достаточно потребовать, чтобы значения
(p(t) не выходили за пределы промежутка [А, В].

314]	§ 3. ВЫЧИСЛЕНИЕ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ	135
2)	ф) =
3)	существует в [а, /5] непрерывная производная
Тогда имеет место формула
jf(x)dx=$f{v(t))v'(t)dt.	(9)
а	а
Ввиду предположенной непрерывности подынтегральных функций
существуют не только эти определенные интегралы, но и соответ-
соответствующие им неопределенные, и в обоих случаях можно воспользо-
воспользоваться основной формулой. Но если F(x) будет одной из первооб-
первообразных для первого дифференциала f(x)dx, то функция 0(t) = F(q>(t)),
как мы знаем, будет первообразной для второго дифференциала
f{f{t))q>'(t)dt [ср. 268]. Поэтому имеем одновременно
- Ф(а) = F(qW) - F(rfx)) = F(b) - F(a),
откуда и вытекает доказываемое равенство.
Замечание. Отметим одну важную особенность формулы (9).
В то время как при вычислении неопределенного интеграла с по-
помощью замены переменной, получив искомую функцию выраженной
через переменную t, мы должны были возвращаться к старой пере-
переменной х, здесь в этом нет надобности. Если вычислен
второй из определенных интегралов (9), который представляет собой
число, то тем самым вычислен и первый.
314. Примеры. 1) Найдем интеграл Ya2-x* dx с помощью подстановки
J
о
л
= asin/; рель аир здесь играют значения 0 и —. Имеем
а	я/2
г	a2 j sin 2Л
с = а2 \ cos2 tdt = — \t+ -
J	2{ 2 J о
о	о
[cp. 268].
2) Вообще при и натуральном с помощью той же подстановки получим
2)n& = a2"+1 f
я/2
2и!!
Bл+ 1)!!

1 36	ГЛ. IX. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ	1314
[см. (8)], и аналогично
2~-~-i-	Bл-1)!! л
.*) • ^2"
3)	J ^ dx.
a
Подстановка x = a sec /; пределам а и 2а переменной х отвечают пределы О
и я/3 переменной /. Находим
71/3	_
1 sin3/
sin2 / cos tdt = —
1 г .
- Si:
a2 J
о
4) Рассмотрим интеграл
л
J
a2 3
о
л; sin x
dx.
l+cos2x
о
Подстановка х^л-t (где / изменяется от л до 0) приводит к равенству
я	п
г xsinx г(л-t) sin t
	—• dx= 	 dt
J 1+COS2 /	J 1+COS2/
dx = n I	—dt- Г	dt.
J 1+cos2/ J 1+cos2/
г xsinx	г sin/	(¦ /sin/
о	о
Перенеся последний интеграл (в котором вместо / снова можно написать х) на-
налево, получаем
С х sin х	л с sin /	л	"л"
	dx = — 	dt=	arctg (cos /) =¦ — .
J 1+cos2 x 2 J 1+cos2/	2	jo 4
о	о
Ср. ниже И), где этот пример будет обобщен.
1
rln(l+x)
5) Вычислить интеграл J= 	dx.
J l+x2
о
l	л\
Подстановка x = tg<p где <р изменяется от 0 до — переводит его в
я/4
ln(l+tgy>)rfy. Но
cosy

3141	§ 3. ВЫЧИСЛЕНИЕ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ	137
так что
л/4	л/4
Л
•J — '
71	Г	i71 \	Г
= — In 2 = In sin —\-<p\d<p- In cos cp d(p.
8	J	\4 }	J
Так как оба интеграла равны (например, второй приводится к первому подстанов-
п	л	\
кой <р =—v'> причем у> изменяется от — до 0 , то окончательно
4	4	j
л
/=-1п2.
8
г arctg х
Заметим, что то же значение имеет и интеграл I 	— dx, в чем легко
J 1+х
убедиться интегрированием по частям.	°
6) Установить, что
1	л/2
,<¦ arctg х	1
С arctg д:	If',
	dx = — 	dt.
J x	2 J sin t
о	о
t
Указание. Подстановка х = tg — .
7) Преобразовать один в другой интегралы
Л	7Х
)nd<p= Г
о v '
считая х =-1 и п - натуральным.
Это достигается путем преобразования переменной по формуле
(х + fx--i cos ip) (х - fx^l cos В) = 1.
Отсюда
- Ух2 -1 + х cos б
х - ух2-1 cos б
причем выражение справа по абсолютной величине не превосходит единицы,
и каждому 0 в промежутке [0, я] однозначно отвечает некоторое <р в том же проме-
промежутке. При 0 = 0 или л также иу = 0 или л. Имеем
sin 0 d9
sin <p dq> = ——
и так как
sin0	de
sin <p =	—===	, то dtp =	===	,
x - Уха-1 cos 0	x - Ух2 - 1 cos 0
так что окончательно
откуда и следует требуемое равенство.

138	ГЛ. IX. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ	[314
[Заметим, что оба интеграла (с точностью до множителя л;) выражают п-й
многочлен Лежандра Рп(х), 118, 6).]
8) Какова бы ни была непрерывная в промежутке [0, а] (<з»0) функция f(x),
всегда
о	о
(л Л
(подстановка x = a-t, aa=/=»0). В частности, так как cosх = sin	х , то при
любой непрерывной функции F(u) будет
я/2	я/2
F(sin x)dx= F(cos х) dx.
о	о
9) Пусть f(x) непрерывна в симметричном промежутке [ - а, а] (а >• 0). Тогда
в случае четной функции [99, 25)]
jf(x)dx=-2Jf(x)dx,
-а	О
а в случае нечетной
а	0 я
В обоих случаях интеграл представляется в виде суммы интегралов +
— а	—а О
и к первому из них применяется подстановка х= -t.
10)	Пусть имеем непрерывную периодическую функцию f(x) с перио-
периодом ш, так что при любом х: f{x+ai)=f(x). Тогда в любых промежутках с дли-
длиной го, равной периоду, интеграл от этой функции имеет одно и то же значение
a-\-ta	о)
f = J/(X) dx.
а	0
a-i-ot 0 а> а+(о
Для доказательства разлагаем: = М- I + и, применяя к третьему
а	а 0	<о
интегралу справа подстановку x = t+w, убеждаемся, что он лишь знаком разнится
от первого.
11)	Доказать, что
xf(sin x)dx = — /(sin x) dx,
о	о
где /(и) - любая непрерывная в промежутке [0, 1] функция.

314]	§ 3. ВЫЧИСЛЕНИЕ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ	139
Указание. Воспользоваться подстановкой х = л -1.
12) Доказать, что
I rp(a cos 9 4 Ь sin в) db =-- 2 I g?(Уаг+б'2cos Я) rfA,
о
где (р(и) - любая функция, непрерывная для \u\=sYa° + b'-.
Определяя угол а соотношениями
a	b
cos a = ———— ,	sin a = ——-
a cos 0 f 6 sin в -- У^ + й2 cos @ - а).
В силу A0) можно написать
2 л	сс+я
|?>(acos0 + />sin в) с1в= Г <p(Y& +b*cos (в-aj) d6
О	а—я
или, если положить 0 - а = / и использовать 9),
л	л
L( Уоч!^ cos Я) <tt = 2 Гу( УоЧ^ cos Я) dl.
-л	О
13) Доказать, что
л/2	л/2
g- (sin 2м) cos udu= g (cos- и) cos г> «/г>,
о	о
где g(z) - любая непрерывная функция от z в промежутке [0, 1].
/	/	/
Представив первый интеграл в виде суммы интегралов = + ,
л/2 л/1 л/2
= +
0	0	л/1
подстановкой и =	и приводим и второй из них тоже к промежутку [0, гт/4]
и получаем
л/4
g (sin 2h)(cos м+sin и) du.
Здесь мы делаем замену переменной, исходя из соотношения sin 2м = cos2 v;
возрастанию и от 0 до л;/4, очевидно, отвечает убывание v от я/2 до 0. Дифферен-
Дифференцируем cos 2« du = - sin v cos v dv; учитывая, что
cos2m= У1 -sin2 2m= yi-
и
1 + cos2 «=1+2 sin
находим окончательно
(sin и + cos и) du = - cos v dv.
Теперь уже нетрудно получить требуемый результат.

140	ГЛ. IX. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ	[314
14) В заключение вернемся к интегралу Пуассона
l(r) = j In (I - 2r cos x + r2) dx
[ср. 307, 4)]. Мы уже знаем, что при \г\ т* 1 подинтегральная функция непрерывна
и интеграл существует. Мы наново вычислим его с помощью некоторого искус-
искусственного приема, в котором замена переменной будет играть существенную
роль.
Заметим предварительно, что из очевидных неравенств
A - |г|J==1 -2r cosx + r2=s;(l + |г|J,
логарифмируя и затем интегрируя от 0 до ж, получаем (при |г|-=:1)
Отсюда ясно, что при г-0 и /(г)-О.
Рассмотрим теперь интеграл
л
7(-r)= fln(l+2rcosx+r2)<&.
о
Если в этом интеграле положить х = л~(, причем t изменяется от л до 0, то ока-
окажется, что
0	л
Ц-г)= {in (l+2r cos (n-t) +r*) d(n-t) = fln(l-2rcos( + r2) dt = I(r).
л	0
В таком случае
л
2/(г) = /(/¦)+Д - г) = I In [A - 2r cos x+ ra)(l + 2r cos x-\- r2)] dx
2/(r)= i"ln(l-2
о
Полагая х = t/2 (где t меняется от 0 до 2ж), получим
2я	л	1л
2/(»0 = - fln(l-2r2cosr + r4)A = - Г+- Г .
2 J	2 J 2 J
0	(I	я
Последний из полученных интегралов подстановкой / = 2тс - и (где и меняется
от л до 0) приводится к первому, так что у нас получается
2/(г)=/(г2), откуда 7(г) = _/(г2).
Заменяя здесь г на г2 и т. д., легко получить общую формулу
/(/-) = 1/(г2") (и=1, 2, 3, ...).

315]	§ 3. ВЫЧИСЛЕНИЕ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ	141
Пусть теперь | г | -= 1, так что f2" - 0 при и — ~; так как при этом (согласно заме-
замечанию вначале) 1{г2")-0, то должны иметь тождественно
/(#•) = О при |г|-=1.
Легко теперь вычислить этот интеграл и при \г\ =-1. В самом деле
1 -2rcosx4 ;-2=г2 1 -2	cosx + —
I	г	г2
и
( I	11
In(l-2ccosx+r2)-21n If I +ln 1 -2. — cosx + — ,
I	r	r-)
гак что, интегрируя от 0 до л, будем иметь
Но, по предыдущему, Л — = 0; следовательно, при | г \ =-1 имеем
Дг) = 2-1п \г\.
Те же результаты мы получили и в 307.
315. Формула Гаусса. Преобразование Ландена. В качестве еще одного примера
на замену переменной рассмотрим замечательную формулу, установленную
Гауссом (С. F. Gauss) для преобразования интеграла
G-
Положим здесь
л/2
I	9
I
•' ]fa2 cos2 q> + й2 sin2 <p
2a sin 0
sina>=
	;
(a+ b)+(a -b) sin2 9
легко видеть, что при изменении 0 от 0 до л/2 и <р растет в тех же пределах. Диф-
Дифференцируем
cosq>d<p = la——rr—r—„,„„.,, cos в de.
Ho
так что
f(a+6)(<36)sin0
cosro =	cos 6,
(a+6) +(a-6) sin2 6
(a + 6) + (a - 6) sin2 0 y(a + 6J _ (e _ ^J sin2 в
С другой стороны,
(а+6)-(а-6)sin2 0

|/а2 cos2 да+б2 sin2 <р = а
и окончательно
	cos2 0 I- ab sin2 б

142	ГЛ. IX. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ	[315
а + b	„—
Если положить ах=	, Ъх= yab, то
л/2	п/2
in2 m J
sin2 0
и
Это и есть формула Гаусса.
Применяя это преобразование повторно, получим, что
Г	dw
С-	(и=1, 2, 3, ...),
J У я2 cos2 оз 4 ft2 sin2 о?
где варианты й;1 , bn определяются рекуррентными соотношениями
ап =	, Ьп = Уап^Фп-i ¦
Мы уже знаем [35, 4], что эти варианты стремятся к некоторому общему пределу
fi=/i(a, b), который мы назвали «средним арифметико-геометрическим» чисел а и Ъ.
Из легко получаемых неравенств
л	л
x1-1	2Ьп
переходя к пределу, находим теперь, что
G = x/2/i(a, b), откуда ц{а, Ь) = тг/2С.
Таким образом, каждое из чисел G и fi просто выражается одно через другое.
Пусть, например, требуется вычислить интеграл
я/2	л/2
С	dB	r	de
G= ^^--^-^
J fl+cos20 J
Здесь а = /2 и Ъ = 1; варианты ап и Ъп, определенные выше, стремятся к^быстро:
уже at и bt оба приближенно равны 1,198140, и можно ;i положить равным этому
числу. Тогда получаем приближенно
G = — =1,3110288.
Обратно, интеграл G приводится к полному* эллиптическому интегралу
первого рода
о
и легко может быть вычислен по таблицам; а уже отсюда получается /;.
* Полными называют интегралы F(k, (p) и Е{к, <р) Лежандра [293,
305] при <р = тт/2: в этом случае в их обозначении обычно опускают второй аргумент
и пишут К(к), Щк). Для полных интегралов существуют особые таблицы.

316]	§ J. ВЫЧИСЛЕНИЕ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ	143
Рассмотрим теперь полный эллиптический интеграл первого рода
п/2
dcp
= J
при любом значении модуля А он получается из G при
а=\ и b=yi-k2 = k'.
Желая применить к нему формулу Гаусса, вычисляем прежде всего
l + yi^fc2 \+к'	-
bl/k'
a
я/2	я/2
Г	dm	г
Эта формула, равносильная формуле Гаусса, на деле была получена до
Гаусса и представляет частный случай так называемого преобразования Ландена
(Landen). Последовательно применяя ее, получим
где вариант кп определяется индуктивно
так что 0-=&„<1 и кп^кп—к чем обеспечивается быстрое стремление кп к О
при п-~. В то же время
я/2	я/2'
~ VI К-п Sill Ф	Л 1 V I Кп
Уg	2 J yi-/t*sin2y	2 y
о	о
л
откуда K(fcn) - — при п -~ <= и, наконец,
K(fc) = - lim (l+fc1)(l+A2)...(l+A:n).	A0)
2 п—«•
На этом основывается метод приближенного вычисления интеграла К(к), который
- при достаточно большом и - попросту полагают равным
316. Другой вывод формулы замены переменной. Мы дадим теперь
другой вывод формулы (9) при измененных предположениях.
Прежде всего (и это - самое важное) мы не станем предполагать
функцию f(x) непрерывной, а только лишь интегрируемой.

144	ГЛ. IX.-ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ	1316
Зато от функции q>(t) мы дополнительно потребуем, чтобы при изме-
изменении t от а до /S она переходила от значения а=<р(ос) к значению Ъ =
=(рф), монотонно изменяясь.
Для определенности допустим, что а<Ь и я</3, так что функция
монотонно возрастает.
Разобьем промежуток [ос, $] произвольно на части с помощью точек
если положить Х(=срA,) (г = 0, 1, 2, ..., п), то одновременно будем
иметь
а = х0 -< хх ¦= х2 < ... < X; -= Xj+i -=...< л:„ = 6.
Если наибольшая из длин dti = ti+1-tj (обозначим ее через А) стре-
стремится к нулю, то ввиду (равномерной) непрерывности функции х-
=f(t) то же будет справедливо относительно наибольшей из длин
Axi = xi+1-xi=(p(ti+1)-(p(ti) [см. 87].
Возьмем теперь по произволу число т,- в каждом промежутке
[ti> tj+1] и составим интегральную сумму для второго из интег-
интегралов (9)
Положим |,-=qp(T,-), так что x,-=s=f,=s=xi+1. Если к функции <p(t) в про-
промежутке {/,, tj+i] применить формулу конечных приращений, то по-
получим
Axt = xi+1 - xt=cp(ti+1) -cp(t,) =q>'(rd Ath
где также /,- -= т,- -= ?,-+1, но т,- (нам не известное) вообще отлично от
наудачу взятого значения xt. Вместе с тем интегральной сумме для
первого из интегралов (9)
теперь можно придать вид
I
Эта сумма при А-*0, очевидно, имеет своим пределом интеграл
ь
J f(x) dx. Для того чтобы показать, что к тому же пределу стремится
а
и сумма а, достаточно установить, что разность а -а стремится к
нулю.
Задавшись произвольным числом е>0, ввиду (равномерной) не-
непрерывности функции <p\t), можно найти такое 8 =-0, чтобы при Д<6
выполнялись неравенства

317]	§ 4. ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ	145
[см. 87, следствие]. Тогда
если через L обозначить верхнюю границу для \f(x) | и сумму
заменить через /?-а.
ь
Теперь ясно, что при А-«-О сумма а стремится к пределу \j\x)dx,
/3	а
а это значит, что существует интеграл I f(f{t))f'(t) dt и имеет место
а
формула (9). Доказательство завершено.
Замечание. Подчеркнем особо, что на основании доказанного
простые и часто полезные формулы, установленные в упражнениях
8), 9), 10) п° 314, распространяются теперь на случай любой инте-
интегрируемой функции f(x).
§ 4. Некоторые приложения определенных интегралов
317. Формула Валлиса. Из формулы (8) п° 312 легко вывести знаменитую фор-
формулу В а л л и с a (J. Wallis).
Предполагая 0<л:-=я/2, имеем неравенства
sin2"+1 x-=sinan x-^sin2"-1 х.
Проинтегрируем эти неравенства в промежутке от 0 до л/2:
я/2	я/2	я/2
lsmm+1xdx~= Г sin2nxdx-= \sin2n-1xdx.
о	оо
Отсюда, в силу (8), находим
2га!! Bп-1)!! л Bга-2)!!
Bга+ 1)!!* 2га!! 2""Bл-1)!!
или
г 2л!! 1» 1 яг 2га!! I2 1
Ц2я-1)!П 2га + 1 *Т 4Bra-l)!!j 2и"
Так как разность между двумя крайними выражениями
1 Г 2га!! 1* 1 ж
2nBra+l)LBra-l)!!J 2га 2
очевидно, стремится к 0 при и - <», то тг/2 является их общим пределом. Итак,
1
л	г 2я!! I*
— = lim
2 п~ДBга-1)!П :
2я+1
или
ж	2.2-4.4 ...2и-2л
— = hm
2 л^-ЬЗ-3.5 ...Bл-1
Это и есть формула Валлиса. Она имеет исторический интерес, как первое
представление числа л в виде предела легко вычисляемой рациональной варианты.
В теоретических исследованиях ею пользуются и сейчас [см., например, 406].
10 Г. М. Фихтенгольц, т. II

146	ГЛ. IX. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ	[318
Для приближенного вычисления числа л теперь существуют методы, гораздо более
быстро ведущие к цели [410].
318. Формула Тейлора с дополнительным членом. Положим в обобщенной
формуле интегрирования по частям G) [311] v = F - х)п. Тогда
и'=-лF-*)"-', v" = n(nT\){b-x)n-\ ...,
при х = 6 все функции и, г/, ..., гХ") обращаются в нуль. Пользуясь для и, м',
«", ... функциональным обозначением f(x), f'(x), f"(x), ..., перепишем G) в виде
0 = ( -1)" [n\f(.b)-nlf(a)-n\fXa)(b - а) - ^/"(а)F - fl)! - • • • -/С>(а)F-а
Отсюда получается формула Тейлора с дополнительным членом в виде
определенного интеграла
ь
f'(a)	f"(a)	f("Xa)	1 г
/(ft) = /(я) + ~- № " а) + --- Ф - аУ + ... + —-^ F - в)"+- /<« +D(X)F - х)" Л.
1!	2!	и!	«!J
0:
Переходя к обозначениям пп° 124 -126, заменим здесь b через х, а через х(
/у •, л- ч ^'W / ч /"(*о), ч	/(п)(*о) , .„
/(х) =/(*„) + - - - (х-хо)+-——(х-хо?+...+	— (х-хо)п +
V.	2!	п\
X
+ -[f(n+i)(t)(x-t)ndt.
х«
Новое выражение для дополнительного члена, в отличие от изученных в 124
и 126, не содержит никаких неизвестных чисел.
Если угодно, из этого выражения можно было бы вывести и уже знакомые
нам формы дополнительного члена. Например, воспользовавшись тем, что мно-
множитель (x-t)n подинтегральной функции не меняет знака, можно применить к по-
последнему интегралу обобщенную теорему о среднем [304, 10°]
\ с	1	г	/¦("+')(?)
- /("+1)(О(х-ОпЛ =—/("+1)(с) (х-О" *=	 (х
n\J	n\	J	(я+1)!
где с содержится в промежутке [х0, х]. Таким образом, мы вновь получили лагран-
жеву форму дополнительного члена.
319. Трансцендентность числа е. Та же формула G) п° 311 может послужить
отправным пунктом для доказательства одной замечательной теоремы Э р м и т а ,
относящейся к числу е.
Все вещественные (а также и вообще комплексные) числа распределяются на
два класса - алгебраические и трансцендентные. Число назы-
называется алгебраическим, если оно является корнем алгебраического уравне-
уравнения с рациональными коэффициентами (очевидно, не умаляя общности, эти

319J	§ 4. ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ	147
коэффициенты можно считать целыми); в противном случае число называют
трансцендентным.
Примером алгебраического числа может служить любое рациональное число
или иррациональное число, выражающееся через рациональные в радикалах:
11	1/
число	служит корнем уравнения 17лч-11=0, а число |/ 1 + ]/2 - корнем
уравнения х6 - Зх4+Ъхг - 3 = 0 и т. д.
Э р м и т установил, что е является трансцендентным числом*.
Мы приведем доказательство этой теоремы.
Допустим, что е служит корнем уравнения
c0 + c,e + c2e2+...+cmem = 0,	A)
где все коэффициенты со> ci> - • •> ст ~ целые числа.
Пусть в формуле G) п° 311 u=f(x) будет произвольный многочлен
п-й степени, а « = (- 1)"+'е~х; тогда, если взять а = 0, эта формула примет вид
\f(.x)e-xdx=-e-x[J
о
так как f^+^Xx) = 0. Полагая для краткости
Лх)+Г(х)+ ... +/(")(*) = Пх),
имеем отсюда
е »ДО) = F(b) + е » Г f(x)e ~* dr.
Возьмем здесь последовательно 6 = 0, 1, 2, ..., т; умножая получаемые равен-
равенства соответственно на с0, с1; с2, ..., ст и складывая, в силу A), придем к оконча-
окончательному равенству
т	/•
0 = c0F@) + c,F(l)+ .. . + cmF(m) + 2^Cie' f(x)e~xidx,	B)
о
которое, напомним это, должно иметь место для любого многочлена f(x).
Теперь мы покажем, что этот многочлен можно выбрать так, чтобы равенство
B) стало невозможным; этим теорема и будет доказана.
Положим, с этой целью,
1
/Ос) =	хР~\х- \)Р{х-2)Р...(х-т)Р,
где р - простое число, большее та \со\. Производные этого многочлена порядка
р и выше имеют целые коэффициенты и притом делящиеся на р; это вытекает
непосредственно из того, что произведение р последовательных натуральных чисел
делится на р\. Поэтому при любом целом значении х все эти производные имеют
целые значения, кратные р. Так как при х = 1, 2, ..., т многочлен f(x) и его первые
* Вслед за этим Л и н д е м а н (F. Lindemann) доказал трансцендентность,
числа я, чем впервые установил неразрешимость исстари знаменитой задачи о
квадратуре круга.

148	ГЛ. IX. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ	[320
р— 1 производных обращаются в 0, то F(l), FB)	F(m) будут целыми числами,
кратными р.
Иначе обстоит дело с F@). При х = 0 многочлен f(x) обращается в 0 лишь
с р - 2 своими производными, так что
Все слагаемые, начиная со второго, как мы видели, суть целые числа, кратные р;
но /Ср~1Ч0) = (-1)Р(/п!)Р, ас ним и ДО), на р не делится. Так как при сделанных
относительно р предположениях и с0 не делится на р, то приходим к заключению,
что первая сумма, стоящая в равенстве B) справа, есть целое число, не делящееся
на р и, следовательно, заведомо не равное нулю.
Обратимся ко второй сумме в B). В промежутке [0, т], очевидно,
1
11 0D!
Поэтому
mmp+p-i
(x)e~x dx
P+P-i (•
	 e~xdx-
—	1)! J
о	о
и, если сумму | с01 + | сг \ + .. ¦ + \ ст \ обозначить через С,
m
mmp+p-i
Сеттт
Но мы знаем [35, 1)], что последний множитель при р — со стремится к 0, так что
вторая сумма в B), при достаточно большом р, будет по абсолютной величине
меньше первой. В таком случае их сумма не может равняться 0, и мы пришли
к противоречию.
320. Многочлены Лежандра. Поставим себе задачу — найти такой многочлен
и-й степени Хп(х), чтобы для любого многочлена Q(x) степени ниже и выполня-
выполнялось равенство
ь
{dx = 0,	C)
где а и b — произвольные, но фиксированные числа.
Каждый многочлен n-й степени Хп(х) можно рассматривать как n-ю произ-
производную от некоторого многочлена R(x) степени 2и, который из Хп(х) получается
и-кратным последовательным интегрированием. Если при каждом интегрирова-
интегрировании произвольную постоянную выбирать так, чтобы при х-а интеграл обращался
в 0, то для многочлена R(x) окажутся выполненными еще условия
R(a) = 0, Л'(в) = 0	Жл-ОСя) = 0.	D)
Итак, задача наша сводится к нахождению такого многочлена R(x) степени
In, чтобы было
ь
jC)(xJW«fcc = 0	E)

320]	§ 4. ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ	149
для любого многочлена Q{x) степени ниже п и, кроме того, выполнялись равенства
D). Но по формуле G) п° 311, если заменить в ней п на п - 1,
a
Если принять во внимание D), а также то, что &пХх) = О, то условие E) приведется
к виду
Ввиду полной произвольности многочлена (и-1)-й степени Q{x) значения
Q(b), Q'(b), ..., Q("-1X6) этого многочлена и его последовательных производных
при х = Ь можно рассматривать как произвольные числа, а тогда условие
F) равносильно следующим:
R{b) = 0, R'{b) = 0, .... В/^-Ъф) = 0.	G)
Из D) и G) видим, что многочлен R(x) должен иметь числа а и b корнями и-й
кратности и, следовательно, лишь постоянным множителем может отличаться
от произведения (х—а/Чх—ЬУ1. Таким образом, окончательно
Хп(х) = сп~^ [Се - аГ(х - Ы).
Если, в частности, взять <з=-1и6=+1, то придем к уже знакомым нам много-
многочленам Лежандра
Хп(х) сп.
dxn
Мы условились в 118, 6) обозначать многочлены Лежандра через Рп(х),
если постоянные сп выбраны так:
1 1
для этих многочленов имеем РпA) = 1, Рп(-1) = (-1)п. Обыкновенно полагают
еще Р0(х) = 1. Все члены многочлена Рп имеют показатели одинаковой с п четности.
Старший коэффициент, очевидно, будет
2ЙМ	и! '
По самому определению многочленов Лежандра имеем всегда
1
(8)
каков бы ни был многочлен Q(x) степени ниже и. В частности, если пит- два
неравных неотрицательных числа, то
1
lPn(x)Pm(x)dx=Q,	(9)
	1

150	ГЛ. IX. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ	1320
1
Найдем значение интеграла РЩх) dx; он лишь множителем с* =	 отлича-
J	Bw!!J
ется от интеграла
J
-dx.
dxn	dxn
	1
Если применить к последнему снова формулу G) п° 311, заменив п на п -1 и по-
положив
dn(x2 - 1)"
dxn
то он сведется к интегралу
1	1
(-1)" 	\ п <х*-irdx = 2.2nl <X-
J dxm	J
-1	о
(все внеинтегральные члены исчезают, потому что функция v и ее производные
до (и-1)-й включительно при х±1 обращаются в 0). Полагая здесь x = siat [ср.
314, 2)], получим
2л!!	2
2-2и!	=	Bи!!J,
B+1)!! 2 + 1
так что окончательно
1
[pttddx^-^-^.	A0)
В заключение, используя свойства многочлена Лежандра, выведем
рекуррентное соотношение, связывающее три последовательных таких много-
многочлена.
Заметим предварительно, что степень хп может быть представлена в виде
линейной однородной функции от Ро, PL	Рп с постоянными коэффициентами;
тогда то же справедливо и для любого многочлена степени п. Поэтому
где Ц), а1( аг, а3, ¦¦¦ - постоянные коэффициенты. Легко установить, что <з3 = а4 =
= ... = 0. Например, чтобы определить а3, умножим обе части этого равенства
на ХП-2 и проинтегрируем от - 1 до +1
ill
ГРп-хРп-г dx = a0 tPn+iPn-t dx+ax [pnPn-idx+
-l
-l	-l
Ввиду (8) и (9) все интегралы, кроме одного, будут нулями, и мы получим
1
«3
-1
\Р„ _ 2 dx - 0, откуда а3 = 0.

321]	§ 4. ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ	151
Коэффициент аг также равен 0, ибо левая часть равенства не содержит вовсе члена
с хп. Для определения а0 приравняем коэффициенты при хп+1 в обеих частях равен-
равенства
Bя-1)!! Bл+1)!!	п+\
)_	_
\ а° ~г , 141 > откуда а0 = - ——
п\	(/г+1)!	2/г+1
Наконец, чтобы найти о2, приравняем обе части равенства при х—1:
1
так что
" 2и+1
Подставляя найденные значения коэффициентов, окончательно получаем
Это и есть искомое рекуррентное соотношение, которое позволяет находить много-
многочлены Лежандра последовательно, отправляясь от Ро = 1 и PL = x:
Зх2-1	5л:3-Зх
321. Интегральные неравенства. В п° 133 и 144 был выведен ряд неравенств
для сумм, покажем теперь, как подобные же неравенства могут быть установ-
установлены для интегралов. Все рассматриваемые здесь функции р(х), <р(х), v'W будем
считать интегрируемыми*.
1) В п" 133 мы имели неравенство D), которое можно переписать так:
е ^y.	A2)
2Pi
Рассмотрим в промежутке [а, Ь] положительные функции р(х) и <р{х). Разделив
промежуток точками
а = хо-=х1-= ...-=х,«=.х,+1< ...~=хп = Ь
на части, с длинами Axj-xj+1 — xj, положим теперь в написанном неравенстве
Pi=p(xj)-Axi, ai=<p(xj); мы получим
Все суммы здесь имеют вид интегральных сумм и при Axj -* 0 стремятся
к соответствующим интегралам. Таким образом, в пределе получим «интеграль-
«интегральный аналог» неравенства A2):
ь
j P(x)<p(x) dx
ь
р(х) dx
а
* Из этого предположения вытекает уже интегрируемость и других встре-
встречающихся ниже функций: для обоснования этого достаточно сослаться на п° 299,
II и п° 300, 4).

152
ГЛ. IX. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
[321
В частности, при р(х) = 1, будем иметь:
~ \ф) dx.
i-a J
Выражение справа называется «средним арифметическим» значений функции (р{х)
в промежутке [а, Ь], а выражение слева - их «средним геометрическим».
2) Вьгаедем теперь интегральные аналоги неравенств Коши - Гельдера
и Минковского [133, E) и G)]:
atfAIM'?
A3)
A4)
Пусть в промежутке [а, Ь] даны положительные функции <р(х) и у(х); разложив,
как и выше, этот промежуток точками х,-, положим в A3):
а в A4):
Будем иметь:
Переходя к пределу, при Axj—О, получаем окончательно
Ь	6	16	1
k.[ U^'dxY'
i ь	16
Uq>+y]kdx\ =s| Гр"л|* + ! | у'*ЛГ.
а	а	а
Отметим частные случаи этих неравенств при к = к' = 2;
I 9
$
A3*)
A4*)
A3')

322]
§ 5. ПРИБЛИЖЕННОЕ ВЫЧИСЛЕНИЕ ИНТЕГРАЛОВ
153
I <p2 dx +
A4')
Первое из них принадлежит В. Я. Буняковскому. Второе легко приводится
к первому возведением в квадрат.
3) Перейдем, наконец, к неравенству И е н с е н а [144 A2*)]:
A5)
здесь функция f(x) предполагается выпуклой в некотором промежутке X,
которому принадлежат точки л:,-; pi - положительные числа. Пусть в некотором
промежутке [а, Ь] задана функция<р(х), значения которой содержатся в^,и по-
положительная функция р(х). Теперь Xj будут означать точки деления про-
промежутка [а, Ь]; прежние х,- в A5) заменим науСх,-), ар,-положим равными p(xi)-Axj.
Переходя, как и выше, от интегральных сумм к интегралам, получим интегральное
неравенство Ие нее на:
р(х)<р(х) dx
p(x)-f(<p(x))dx
x) dx
§ 5. Приближенное вычисление интегралов
322. Постановка задачи. Формулы прямоугольников и трапеций. Пусть требуется
ь
вычислить определенный интеграл /(*) dx, где f(x) есть некоторая заданная
а
в промежутке [а, Ь] непрерывная функция. В § 3 мы имели много примеров вычисле-
вычисления подобных интегралов, либо с помощью первообразной, если она выражается
в конечном виде, либо же — минуя первообразную - с помощью различных
приемов, большей частью искусственных. Нужно отметить, однако, что всем
этим исчерпывается лишь довольно узкий класс интегралов; за его пределами
обычно прибегают к различным методам приближенного вычисления.
В настоящем параграфе мы познакомимся с простейшими из этих методов,
в которых приближенные формулы для интегралов составляются по некоторому
числу значений подинтегральной функции, вычисленных для ряда (обычно равно-
равноотстоящих) значений независимой переменной.
Первые относящиеся сюда формулы проще всего получаются из геометри-
ь
ческих соображений. Истолковывая определенный интеграл f(x) dx как площадь
а
некоторой фигуры, ограниченной кривой y = f(x) [204], мы и ставим перед собой
задачу об определении этой площади.

154
ГЛ. IX. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
C22
Прежде всего, вторично используя ту мысль, которая привела к самому поня-
понятию об определенном интеграле, можно разбить всю фигуру (рис. 6) на полоски,
Ь-а
скажем, одной и той же ширины* Ах,=	, а затем каждую полоску прибли-
п
женно заменить прямоугольником, за высоту которого принята какая-либо из ее
ординат. Это приводит нас к формуле
ь
f(x) ifei
где je,-=ss?I-asx,-+1 О'=0, 1, ..., п- 1). Здесь искомая площадь криволинейной фигуры
заменяется площадью некоторой состоящей из прямоугольников ступен-
ступенчатой фигуры (или - если угодно - определенный интеграл заменяется
интегральной суммой). Эта приближенная формула и называется формулой
прямоугольников.
Л
/7т " а х,
На практике обычно берут ?,- = —	'— = л:,-ц_7,; если соответствующую сред-
среднюю ординату f($i)=f(xj^4t) обозначить через yi+1/,, то формула перепишется
в виде
1>
Ь-а
A)
Впредь, говоря о формуле прямоугольников, мы будем иметь в виду
именно эту формулу.
Геометрические соображения естественно приводят и к другой, часто при-
применяемой, приближенной формуле. Заменим данную кривую вписанной в нее
ломаной, с вершинами в точках (л:,-, yi), где у,-=f(xj) (j=0, 1, ..., и- 1). Тогда наша
криволинейная фигура заменится другой, состоящей из ряда трапеций (рис. 7).
Если по-прежнему считать, что промежуток [а, Ь] разбит на равные части, то пло-
площади этих трапеций будут
Ь-а
Ь-а
п 2	и 2	и
Складывая, придем к новой приближенной формуле
B)
* Мы сохраняем обозначения п° 294.

3221
5. ПРИБЛИЖЕННОЕ ВЫЧИСЛЕНИЕ ИНТЕГРАЛОВ
155
Это так называемая формула трапеций.
Можно показать, что при возрастании п до бесконечности погрешности фор-
формулы прямоугольников и формулы трапеций безгранично убывают. Таким обра-
образом, при достаточно большом п обе эти формулы воспроизводят искомое значение
интеграла с произвольной степенью точности.
Для примера возьмем известный нам интеграл
dx тт
— = - = 0,785398...
2 4
и применим к нему обе приближенные формулы, беря н = 10 и вычисляя на четыре
знака.
По формуле прямоугольников имеем
x1/2 =0,05
x*h =0'15
х1ы =0,25
*7/2 =0,35
Xtji =0,45
xn/2 = 0,55
x13/2 = 0,65
Xl5/2 = 0,75
x^j i = 0,85
x19/2 = 0,95
уЩ
Ущ
Ущ
Уу,
Ущ
Уп/г
Уп,2
у»/,
Уи,г
сумма
= 0,9975
= 0,9780
= 0,9412
= 0,8909
= 0,8316 7>8562
= 0,7678 10
= 0,7030
= 0,6400
= 0,5806
= 0,5256
7,8562
По формуле же трапеций
хо =
х«,=
0,0
1,0
7о=1,0000 *1 =
yw = 0,5000 х2 =
сумма 1,5000
1 /1,5000	
Го(-2- + 7'°"Г
= 0,78498
t = 0,9901
2	= 0,9615
3	= 0,9174
, = 0,8621
5 = 0,8000
0,7 у7 = 0,6711
0,8 у8 = 0,6098
0,9 у9 = 0,5525
сумма 7,0998
Оба полученных приближенных результата обладают примерно одинаковой
степенью точности - они разнятся от истинного значения (в ту и в другую сторону)
меньше чем на 0,0005.
Читатель, конечно, дает себе отчет в том, что погрешность мы смогли оценить
здесь лишь потому, что наперед знали точное значение интеграла. Для того чтобы
наши формулы были действительно пригодны для приближенных вычислений,

156	ГЛ. IX. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ	[323
нужно иметь удобное выражение для погрешности, которое позволяло бы не
только оценивать погрешность при данном п, но и выбирать п, обеспечивающее
требуемую степень точности. К этому вопросу мы вернемся в п° 325.
323. Параболическое интерполирование. Для приближенного вычисления интег-
ь
рала I f{x) dx можно попытаться заменить функцию f(x) «близким» к ней много-
а
членом
у = Рк(х) = аох'< + а1хк-1+ ... +ak_lx+ak	C)
и положить
Иначе можно сказать, что здесь - при вычислении площади - данная «кривая»
у=/(*) заменяется «параболой Ахго порядка» C), в связи с чем этот процесс получил
название параболического интерполирования.
Самый выбор интерполяционного многочлена Ри(х) чаще всего производят
следующим образом. В промежутке [а, Ь] берут к+1 значений независимой пере-
переменной ?0, ?г, ..., i^ и подбирают многочлен P^ix) так, чтобы при взятых значениях
х его значения совпадали со значениями функции fix). Этим условием, как мы
знаем [128], многочлен Pkix) определяется однозначно, и его выражение дается
интерполяционной формулой Лагранжа:
(*&(*&• • -(xh)
(f. -1№ о ~?2) • • • «о -^)	«1 -loXli -«• • • (f i ~
При интегрировании получается линейное относительно значений /(?0),...
• ¦ •, /(?ft) выражение, коэффициенты которого от этих значений уже не зависят.
Вычислив коэффициенты раз навсегда, можно ими пользоваться для любой функ-
функции fix) в данном промежутке [а, Ь].
В простейшем случае при к = 0, функция fix) попросту заменяется п о с т о я н-
а + Ь
ной /(?д), где f0 - любая точка в промежутке [а, Ь], скажем, средняя: ?0 =	.
Тогда приближенно
ь
/Д—) .	D)
Геометрически - площадь криволинейной фигуры заменяется здесь площадью
прямоугольника с высотой, равной средней ее ординате.
При к = 1 функция fix) заменяется линейной функцией Pjix), которая имеет
одинаковые с ней значения при х=!„ и х=|х. Если взять |0 = а, ?, = Ь, то
~ fid) + *^ /F)	E)
а-Ь	Ь-а

323]
§ 5. ПРИБЛИЖЕННОЕ ВЫЧИСЛЕНИЕ ИНТЕГРАЛОВ
157
и, как легко вычислить,
Таким образом, здесь мы приближенно полагаем
x)Jx-(b a)m+m
F)
На этот раз площадь криволинейной фигуры заменяется площадью трапеции:
вместо кривой берется хорда, соединяющая ее концы.
Менее тривиальный результат получим, взяв к = 2. Если положить ?0 = а0,
а+Ь
?j =	,?2 = b, то интерполяционный многочлен Pz(x) будет иметь вид
а + Ь
J а+ь\
Ь-Ъ-Ь)	ia+b) 	I 2 ,
(а+Ь \(а+Ь ,\{ 2 } {ь_а)[ь_а+П
"{ 2 )
С помощью легкого вычисления установим
6
и аналогично
2 \(х-ЬK Ь-а (х-ЬУ
G)
Ь-а
Ь-а
(х-
( а+Ь\
ф-а)\Ь-—-.
2 ) Ь-а
ах =	.
6
Таким образом, приходим к приближенной формуле
6
(8)

158	ГЛ. IX. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ	C24
Здесь площадь фигуры под данной кривой заменяется площадью фигуры,
ограниченной обыкновенной параболой (с вертикальной осью), проходящей через
крайние и среднюю точки кривой.
Увеличивая степень к интерполяционного многочлена, т. е. проводя параболу
C) через все большее число точек данной кривой, можно рассчитывать добиться
большей точности. Но более практичным оказывается другой путь, основанный
на сочетании идеи параболического интерполирования с идеей дробле-
дробления промежутка.
ь
324. Дробление промежутка интегрирования. При вычислении интеграла fix) dx
а
можно поступить так. Разобьем сначала промежуток [а, Ь] на некоторое число, п,
равных промежутков
[х0, х,], [*!, х2]	[*n-i. хп] ixo = a, хп = Ь),
в связи с чем искомый интеграл представится в виде суммы
Xj	X,	Хя
j f{x) dx + |/(дг) dx-\ ... + J Дх) dx.	(9)
X,	X,	ЬН-1
Теперь же к каждому из этих промежутков применим параболическое интерполи-
интерполирование, т. е. станем вычислять интегралы (9) по одной из приближенных формул
D), F), (8), ...
Легко сообразить, что, исходя из формул D) или F), мы таким путем вновь
получим уже известные нам формулы прямоугольников и тра-
трапеций, A) и B).
Применим теперь к интегралам (9) формулу (8); при этом, для краткости,
положим, как и выше,
2
Мы получим
b-a
г	Ь-(
fix) dx~ -
J	6n
I
b-a
J f{x) dx~ -~ iyn
Наконец, складывая почленно эти равенства, придем к формуле
6
--—
O/7
6
{fix) dx'--
J

325]	§ 5. ПРИБЛИЖЕННОЕ ВЫЧИСЛЕНИЕ ИНТЕГРАЛОВ	159
Она носит название формулы Симпсона (Th. Simpson); этой формулой пользуются
для приближенного вычисления интегралов чаще, чем формулами прямоуголь-
прямоугольников и трапеций, ибо она - при той же затрате труда - дает обычно более точный
результат.
1
г dx
Для сравнения вычислим снова интеграл I - - [см. 322] по формуле
J \+х%
о
Симпсона. Мы возьмем п = 2, так что число использованных ординат на этот
раз будет даже меньшим, чем раньше. Имеем (вычисляя на пять знаков)
_1	1	3
Л-1; 4Л/,= 3,76471; 2л-1,б; 4Л/1 = 2,5б; л = 0,5.
— A + 3,76471+ 1,6 + 2,56 + 0,5) = 0,78539...
- все пять знаков верны!
Конечно, по отношению к формуле A0) могут быть повторены замечания,
сделанные в конце п° 322. К оценке погрешности приближенных формул мы сейчас
и переходим.
325. Дополнительный член формулы прямоугольников. Начнем с формулы D).
Предположим, что в промежутке [а, Ь] функция f(x) имеет непрерывные произ-
производные первых двух порядков. Тогда, разлагая fix) [по формуле Тейлора,
а+Ь
126 A3)] по степеням двучлена х	вплоть до квадрата его, будем иметь
для всех значений х в [а, Ь]
Ч
O (а
a + b
где f содержится между х и	и зависит от х.
Если проинтегрировать это равенство в промежутке от а до Ъ, то второй член
справа исчезнет, ибо
ь
К-
)±с = 0.	(П)
Таким образом, получаем
ъ
так что дополнительный член формулы D), восстанавливающий ее
точность, имеет вид
Обозначив через т и М, соответственно, наименьшее и наибольшее значения
непрерывной функции f"(x) в промежутке [а, Ь] [85] и пользуясь тем, что

160	ГЛ. IX. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ	[325
второй множитель подынтегрального выражения не меняет знака, по
обобщенной теореме о среднем [304, 10°] можем написать
ь
1 с( a+by {Ь-аУ
J
где ц содержится между т и М. По известному свойству непрерывной функции
[82], найдется в [а, Ь] такая точка f*, что [i=f "(?*), и окончательно
(Ь -аK
9-—~ /"(**).	A2)
Замечание. Естественно было бы, разлагая функцию /(*) по степеням
а+Ь
х	, оборвать разложение уже на первой степени этого двучлена, т. е. восполь-
воспользоваться формулой
Это привело бы нас, при интегрировании, к равенству
b	Ь
а	а
так что дополнительный член выразился бы интегралом
ь
содержащим лишь первую производную fix). Но здесь второй множитель
подинтегралъного выражения меняет знак в промежутке [а, Ь], и применение
обобщенной теоремы о среднем - в целях упрощения выражения для р - оказы-
оказывается невозможным. Продвижение в тейлоровом разложении еще на один член,
в связи с равенством A1), обеспечило нам успех.
Если теперь разделить промежуток [а, Ь] на и равных частей, то для каждого
частичного промежутка [л:,-, х/+{[ будем иметь точную формулу
f /(*) dx = — /(*,+•/,) + %^ /"(?*) (*,*1*=е х,+J.
J	n	TAtP
Сложив эти равенства (при i = 0, 1, ..., и- 1) почленно, получим при обычных
сокращенных обозначениях
ь
/(x) dx= —- (У
а
где выражение
Jb-аУ /"(

326]	§ 5. ПРИБЛИЖЕННОЕ ВЫЧИСЛЕНИЕ ИНТЕГРАЛОВ	161
и есть дополнительный член формулы прямоугольников A). Так как выражение
/"(?*)+• ••+/"(?*-!)
п
также содержится между т и М, то и оно представляет одно из значений функ-
функции /"(*).
Поэтому окончательно имеем
1
При возрастании п этот дополнительный член убывает примерно как —*.
1	л2
г dx
Вернемся для примера к вычислению интеграла 	, произведенному
1 о Зх2-1
в 322. Для подинтегральной функции f{x) =	имеем / (х) = 2 -	— ; эта
1 ~т~ X	\* ~т~ X )
производная в промежутке [0, 1] меняет знак, но по абсолютной величине остается
меньшей 2. Отсюда, по формуле A3) | Rlo | -= 0,85 • 10"~3. Мы вычисляли ординаты
на четыре знака с точностью до 0,00005; нетрудно видеть, что погрешность от
округления ординат может быть включена в приведенную выше оценку. Истинная
погрешность, действительно, меньше этой границы.
326. Дополнительный член формулы трапеций. Займемся теперь формулой F)
при прежних предположениях относительно функции f(x). Воспользовавшись
интерполяционной формулой Лагранжа с дополнительным членом [129 G)],
можем написать [см. E)]
Интегрируя эту формулу от а до Ь, найдем
*	ь
ГШх-aXx-b) dx,
так что дополнительный член формулы F) будет
ь
Рассуждая, как выше, и пользуясь тем, что второй множитель подинтеграль-
подинтегральной функции и здесь не меняет знака, найдем
ь
1	г	(Ь- аK
? = у /"(г/*) | (* - а)(х -b)dx=- —^— f"(r,*
* Мы говорим: примерно, ибо и I может изменяться с изменением п.
Это следует помнить и впредь.
11 Г. М. Фихтенгольц, т. 11

162	ГЛ. ГХ. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ	[327
Наконец, для случая деления промежутка на п равных частей
(Ь - аK
Rn=- -—r f"(ri) (a^srj^b).	A4)
Таков дополнительный член формулы трапеций B). При возрастании п он
также убывает примерно как -. Мы видим, что применение формулы трапеций
л2
приводит к погрешности того же порядка, что и для формулы прямоугольников.
327. Дополнительный член формулы Снмпсона. Обратимся, наконец, к формуле
(8). Можно было бы, аналогично тому, как это было сделано только что, снова
воспользоваться интерполяционной формулой Лагранжа с дополнительным
членом [129 G)] и положить [см. G)]
/(*) = Р2(х) +f~- (* -а)(х- п ~) {х -Ь) («< С - Ь).	A5)
Но мы сталкиваемся здесь снова с таким положением вещей, какое имели в п°
325 (см. замечание). Именно, проинтегрировав равенство A5), мы не могли бы
упростить интегральное выражение для дополнительного члена с помощью тео-
( а+ь\
ремы о среднем, так как выражение {х-а) \х	¦ (х-Ь) в подынтегральной
функции уже меняет знак в промежутке [а, Ь]. Поэтому мы поступим иначе.
Выражение
( а+Ь\
RJ,z) + K{z-a) z—— I (z-i),
а+ b
каково бы ни было число К, в точках z = а, 	, b принимает те же
значения, что и функция /(г). Легко подобрать теперь число К так, чтобы и п р о-
а+b (а+Ь\
изводная этого выражения при z=	 совпадала с производной /' 	 .
Таким образом, при этом значении К, мы имеем в лице написанного выражения
не что иное, как интерполяционный многочлен Э р м и т а [130], отвечающий
а+Ь
простым узлам a, b и двукратному узлу	. Воспользовавшись формулой Э р-
мита с дополнительным членом [130 A1)] - в предположении существования
для функции fix) производных до четвертого порядка включительно - получим:
K(x_a-)(x_ajb)( _ил /(<)(б _ )(x_a + bY( _b)	^?^Ь)
"Х	Г 2 ) Х	4! Х ° Г 2 j
Теперь проинтегрируем это равенство от а до Ь; мы найдем, что
ь
b-af
=	f(a)+4/1 — I +f{b) I + — I /0)@(x - a) I x - ~—- \(x-b) dx,
6 L	12/	J 24J	12
'-tJ*-1

327]	§ 5. ПРИБЛИЖЕННОЕ ВЫЧИСЛЕНИЕ ИНТЕГРАЛОВ	163
так как
ь
?, J a + b\, tw C( a + b\\(
]
Если предположить производную /D)(л:) непрерывной, то, как и в предыдущих
случаях, дополнительный член формулы (8)
ь
1
р =
о
1 г	/ а + Ь\-
— \/ЩО(х-а)\х- ~—\(x~b)dx,
24 J	{ 2 )
пользуясь тем, что второй множитель в подинтегральном выражении не меняет
знака, можно представить в такой форме*:
ь
г	( a+bV
J (x-e)lx-—J
1	г	( a+bV
—У<4>(С*) J (x-e)lx-—J (x-b)dx =
b
а-[Ь\- (Ь-а)°
)
Если промежуток [а, Ь] разделен на п равных частей, то - для формулы С и м-
пеона A0) - получим дополнительный член в виде
При возрастании п это выражение убывает примерно как —; таким
п*
образом, формула Симпсона действительно выгоднее двух предшествующих
формул.
1
с dx
Обратимся снова к примеру интеграла 	. Для того чтобы избежать
J 1+ха
о
вычисления четвертой производной, фигурирующей в формуле A6), мы заметим,
что функция f{x)=	сама является производной от y=arctgx, так что мы
можем воспользоваться готовой формулой из 116, 8). В согласии с ней
/¦D)(х) *- j'E) = 24 cos5 у sin 5 ly + -1 = 24 cos5 у cos 5y;
* Если f(x) есть многочлен степени не выше третьей, то, очевидно, ? обра-
обращается в 0. Значит, для такого многочлена формула (8) будет точной (в чем
легко убедиться И непосредственно).

164	ГЛ. IX. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ	[328
это выражение, по абсолютной величине, не превосходит 24, так что по формуле
1
A6) |Л2Н	=0,0006. Истинная погрешность, как мы видели, значительно
меньше этой границы.
Замечание. На этом примере бросается в глаза, что граница погрешности,
найденная по нашей формуле, оказывается довольно грубой. К сожалению - и в
этом практический недостаток выведенных формул, - подобное обстоятельство
встречается нередко.
Тем не менее именно с помощью этих формул, позволяющих все же оценивать
погрешность наперед, можно осуществлять приближенное вычисление определен-
определенных интегралов. Обратимся к примерам.
2
rdx
328. Примеры. 1) Вычислим интеграл — = 1п2 с точностью до 0,001, во-
J х
1
спользовавшись формулой прямоугольников.
1	2
Так как для f{x) = — имеем 0</"(x) = —=s2 (если 1 asx=s2), то по формуле A3)
х	х2
0 «=*„-=-!;.
12л2
Если взять п= 10, то дополнительный член нашей формулы будет Л10-=	-=
\2\J\j
-= 0,84 • 10~3. Нам придется внести еще погрешность, округляя значения функции;
постараемся, чтобы границы этой новой погрешности разнились меньше чем на
0,16 • 10~3. С этой целью достаточно вычислять значения функции — с четырьмя
х
знаками, с точностью до 0,00005. Имеем:
*1/а = 1,05 ущ = 0,9524
х,/2=1,35 Л/| = 0,7407
л-9/2=1,45 Л/г = 0,6897
*ii/,= 1.55	*!,, = 0,6452 _^ = о,69284
*13,2=1>65	л,/,-0,6061 10
*U/l=l,75	y»,r 0,5714
«it/,-1,85	yB,t- 0,5405
л1в/г = 1,95	л»/г = 0,5128
сумма 6,9284
Учитывая, что поправка к каждой ординате (а следовательно, и к их среднему
арифметическому) содержится между ±0,00005, а также принимая во внимание
оценку дополнительного члена Rla, найдем, что In 2 содержится между границами
0,69279 = 0,69284-0,00005 и 0,69373 = 0,69284+0,00005 + 0,00084, а следовательно,
и подавно между 0,692 и 0,694. Таким образом, In 2 = 0,693 ±0,001.

328|	§ 5. ПРИБЛИЖЕННОЕ ВЫЧИСЛЕНИЕ ИНТЕГРАЛОВ	165
2)	Провести то же вычисление по формуле трапеций.
В этом случае по формуле A4)
I
г! 6л2'
Попробуем и здесь взять и= 10, хотя тогда гарантировать можно лишь что | Rl0 \ --
-=	= 1,7-10—3. Ординаты (вычисленные с той же точностью, что и выше)
600
будут
л-^1,1 ух = 0,9091
.т., = 1,2 у2 = 0,8333
*¦"!* Л"Ж *-!-° >-1'0000
х. = 1,4	у* = 0,7143 v — 9 О i> — П WVl
2:1.6	^S су^а-15000^
л, = 1,7	у, = 0,5882
л:8=1,8	у8= 0,5556	i /1,5000 \
л-9=1,9	у9 = 0,5263	-|——+6,1877j= 0,69377
сумма 6,1877
Учитывая все поправки, найдем, что In 2 содержится между границами 0,69202 =
= 0,69377-0,00005-0,00170 и 0,69382 = 0,69377+0,00005, т. е. снова между 0,692
и 0,694, и т. д.
3)	С помощью формулы Симпсона, при том же числе ординат,
можно получить более точный результат. Так как четвертая производная под-
24
интегральной функции есть —, то по формуле A6)
.г5
24
180- BнL 15 -BпУ
При и = 5 (тогда число ординат будет то же, что и в предыдущем случае) имеем
s| -=1,4-10—в. Вычисление поведем на пять знаков, с точностью до 0,000005:
*i/2 = l,l	Л/ =0,90909
л. = 1,4 у2 = 0,71429 *s/2=1>3	,v8/22 = 0,76923
*з=1,6 Уз = °.625О0 x&lit=\,5	ybji = 0,66667
хЛ=1,8 ^4 = 0,55556 х?^=1,7	у, / =0,58824
сумма 2,72818-2	*9/?.= J'9 y*h° °'52632
5,45636	сумма 3,45955-4
13,83820
*о=1,О уо= 1,00000
х5 = 2,0 уъ = 0,50000
сумма 1,50000
— A,50000+5,45636+13,83820) = 0.693152.

166	ГЛ. IX. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ	[328
Отсюда In 2 содержится между границами
0,693133 = 0,693152-0,000005-0,000014
0,693157 = 0,693152 + 0,000005,
так что, например, можно положить In 2 = 0,69315±0|OO002.
В действительности In 2 = 0,69314718..., и истинная погрешность оказывается
меньшей чем 0,000005 [ср. замечание в конце предыдущего п°].
4) Поставим себе задачей вычислить полный эллиптический ин-
интеграл 2-го рода*
п
2
1
1 - — sin2 х dx
г
о
с точностью до 0,001 по формуле Симпсона.
Л[ I	л
Для функции f{x) = I / 1	sin2 х, при изменении л- от 0 до — , имеем
I/WH12**, поэтому [см. A6)]
2 1
• 2-=—	, так как I —
1 180-BиL 3 BлL
Возьмем и = 3, так что | Rs | -= 0,00052. Тогда
*о = О @°)	л =
л-1; =— A5°) 4уц ,-/l2 +/12 = 3,9324
'¦'¦ 12	/2
хх^ C0°)	2Л=/14/2= 1,8708
с3 =- D5е) 4у31 =/12 = 3,4641
л 15,4771
л	_	= 1,35063...
я-2 = - F0°)	2^2=/10/2=1,5811	2 18
=/12-/12 = 2,9216
л
xs^- (90°)	v3=/2/2 = 0,7071
сумма 15,4771
* См. сноску на стр. 142.
** Очевидно, y=f(x)s*—; дифференцируя тождество уг=\ — sin2я:, легке
/2	2
последовательно получить оценки (сверху) абсолютных величин производныз
у', у", у'", №¦

328J
5. ПРИБЛИЖЕННОЕ ВЫЧИСЛЕНИЕ ИНТЕГРАЛОВ
167
К полученному результату, кроме поправки 2?3, следует добавить еще (неотрица-
0,0003. п
тельную) поправку на округление, которая не превссходит 	-=0,00003.
36
Таким образом,
и можно утверждать, что Е
36
1,35011-= e|— U 1,35118,
1,351+0 0
У
(На деле в полученном результате все знаки верны.)
5) Вычислить интеграл
1
о
с точностью до 0,0001 по формуле Симпсона.
Непосредственно вычислив четвертую производную от подинтегральной
функции, убеждаемся, что по абсолютной величине она не превосходит 12; поэтому
180-BпL
Достаточно взять и=5, ибо |.R5|-=0,7-10-5. Имеем
*о = О,О у„ = 1,00000	Xl/ =0,1
ДС.-1.0 у5 = 0,36788	-*8/22 = 0,3
=0,99005
]-0,91393
x,-0,2	у, =0,96079
л:, = 0,4	y» = 0,85214
^3 = 0,6	уд = 0,69768
^4 = 0,8	y4 = 0,52729
сумма 3,03790-2
Jf9/, = 0,9 y9/o = 0,44486
сумма 3,74027-4
14,96108
1,36788 + 6,07580+14,96108
30
= 0,746825
6,07580
0,746813-= W^ 0,746837
^=0,7468+0>00005.
(И здесь в полученном результате верны все шесть знаков!)
6) Найдем интеграл
1
-
J
arctgx
dx

168
ГЛ. IX. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
[32
[ср. 314, 6)] по формуле С и м п с о н а, при п = 5, вычисляя на пять знаков
Уо-1
75=0,78540
сумма 1,78540
Л = 0,98698
У2 = 0,95127
уа = 0,90070
у^ 0,84343
Л/2 = 0,99668
у8/22 = 0,97152
Л/2 = 0,92730
Л/2 = 0,87246
уа,г 0,81424
сумма 4,58220 • 4
18,32880
1,78540 + 7,36476 +18,32880
__	,
= 0,915965.
сумма 3,68238-2
7,36476
В полученном результате все знаки верны. Предоставляем читателю оценить
погрешность по формуле A6).
Значение G иногда называют постоянной Ката л ана (Е. Catalan) [см.
также 440, 6) (а)].
Замечание. Последние три примера интересны в том отношении, что
соответствующие первообразные функции в конечном виде не выражаются, так
что ими воспользоваться для вычисления определенных интегралов было бы не-
невозможно.
Наоборот, если эти первообразные представить в виде определенных инте-
интегралов с переменным верхним пределом, то можно было бы вычислить значения
этих интегралов, отвечающих ряду значений верхнего предела. Этим, с принци-
принципиальной стороны, выясняется возможность составления для функций, заданных
лишь их интегральными выражениями, таких же таблиц, какие известны читателю
для элементарных функций.
На этом пути можно также получить для упомянутых функций и приближен-
приближенные выражения.

ГЛАВА ДЕСЯТАЯ
ПРИЛОЖЕНИЯ ИНТЕГРАЛЬНОГО ИСЧИСЛЕНИЯ
К ГЕОМЕТРИИ, МЕХАНИКЕ И ФИЗИКЕ
§ 1. Длина кривой
329. Вычисление длины кривой. Пусть на плоскости параметриче-
параметрическими уравнениями
задана непрерывная простая кривая АВ. В первом томе [247] было
установлено понятие длины кривой как точной верхней гра-
границы S периметров, вписанных в кривую ломаных
S = sup{^}.	B)
В предположении, что функции A) имеют непрерывные производные,
было доказано [248], что кривая спрямляема, т. е. длина дуги
конечна. Больше того, если рарсмотреть переменную дугу AM,
где М - любая точка кривой, отвечающая значению t параметра, то
было установлено, что длина
есть дифференцируемая функция от t, производная которой выра-
выражается так:
или - короче -
YW^	C)
[248 A0)] и, очевидно, тоже непрерывна.
Владея понятием интеграла, мы можем теперь перейти и к вы-
вычислению длины s кривой АВ. По основной формуле интеграль-
интегрального исчисления, сразу получим

170	ГЛ. X. ПРИЛОЖЕНИЯ ИНТЕГРАЛЬНОГО ИСЧИСЛЕНИЯ	[329
или
AB=S= \ixf+y? dt = jfW(t)Y+ WU)f dt.	D)
Длина переменной дуги AM, о которой выше шла речь, как легко
понять, выразится формулой
xJVy} dt.	E)
Может случиться, что за начальную точку отсчета дуг берется какая-
либо внутренняя точка Мо. Если t0 по-прежнему определяет
именно эту точку (в этом случае t0 уже не будет концом проме-
промежутка, где изменяется t), то формула E) дает, очевидно, величину
дуги AM со знаком, именно, со знаком плюс, если t > t0 и точка
М лежит с положительной стороны от начала отсчета дуг Мо, и со
знаком минус, если t-^t0 и точка М лежит с отрицательной стороны
от Мо.
Если кривая задана явным уравнением в прямоугольных коор-
координатах
y=f(x) (xo*sx*sX),
то, принимая х за параметр, из формулы D), как ее частный случай,
получим
х	х
S = J /ТТ^ dx = J /TTL/W dx.	Da)
Наконец, случай полярного задания кривой
как известно, также приводится к параметрическому с помощью обыч-
обычных формул перехода
х = г cos в = gF) cos в, y = r sin в = gF) sin в;
роль параметра здесь играет в. Для этого случая
в	в
s= \Y7^T^d6=|/Ш?7Ш?^ •	Dб)
Легко для этих двух частных случаев задания кривой написать
и выражения для величины переменной дуги AM, если М отвечает
абсциссе х или полярному углу в:
х
\	Ea)

330)	S i. длина кривой	171
или, соответственно,
AM = .9 = s(d) = J fr*+~rf dd.	E6)
e.
330. Другой подход к определению понятия длины кривой и ее вы-
вычислению. При определении самого понятия длины непрерывной про-
простой кривой A) мы исходили из равенства B). Докажем теперь, что
-	в случае незамкнутой кривой — ее длина S является не
только точной верхней границей для множества длин
{/>}, вписанных в кривую ломаных, но и попросту пределом для р
-	при условии, что стремятся к 0 длины всех сторон ломаной (р)
(или, точнее, длина Я* наибольшей из этих сторон):
S = \irap.	F)
л*-о
Впрочем, удобнее исходить из значений параметра t:
/0-=*i-= .. .<?,<?,+1-= ... **„=Г,	G)
определяющих положение на кривой вершин ломаной (р), и предпо-
предположить, что стремятся к нулю все приращения Atj = ti+1-t( (или,
точнее, наибольшее из них Х = max At,). Две леммы п° 245 обеспечи-
обеспечивают равносильность обеих характеристик предельного процесса. Итак,
подлежит доказательству предельное соотношение
S = \imp.	F*)
Сначала отметим следующее важное свойство периметра р. Если
он отвечает некоторому способу G) разложения промежутка [tQ, T],
и затем мы вставим еще одну точку деления t:
то периметр р разве лишь увеличится, причем увеличение его не прев-
превзойдет удвоенной суммы колебаний функций y(t) и tp(t) в промежутке
[tk, tk+1]. Действительно, добавление новой точки t заменяет в сумме
р одно слагаемое (длину стороны):
-V(tk)f	(8)
суммой двух слагаемых (суммой длин двух сторон)
^Ш (9)
которая во всяком случае не меньше, чем слагаемое (8).

172	I Л. X. ПРИЛОЖЕНИЯ ИНТЕГРАЛЬНОГО ИСЧИСЛЕНИЯ	[330
С другой стороны, вся сумма (9) не превосходит суммы
I «КО - 9(h) I + I f@ -V(h) I
и, следовательно, увеличение периметра/7 и подавно не превос-
превосходит этого числа, которое, очевидно, меньше упомянутой удвоенной
суммы колебаний.
В дальнейших рассуждениях ограничимся случаем конечного S.
Для произвольно малого числа е >0, по определению точной верх-
верхней границы, найдется такой способ разбиения промежутка [t0, T] на
части точками
tf = to^t?^t$^...t* = T,	A0)
что для соответствующего периметра р* будет выполняться неравен-
неравенство
Ввиду равномерной непрерывности функций <р@ и tp(t) существует
столь малое число й>0, что
лишь только \t"-t'\<d. Разобьем же промежуток [t0, T] на части
точками G) под единственным условием, что А«=# (т. е. что все Zl?,<<5),
и составим соответствующую сумму р.
Рассмотрим третий способ дробления промежутка [t0, T] на части,
при котором точками деления служат как все точки t, способа G),
так и все точки t* способа A0); пусть ему отвечает периметр р0. Так
как этот способ получен из A0) путем добавления новых точек, то
в силу сказанного вначале
Р0**Р*-	A2)
С другой стороны, тот же способ получен и из G) добавлением
точек t%. Добавление каждой точки t * увеличивает р не более, чем
на удвоенную сумму соответствующих колебаний функций cp(t) и ip(t),
т. е. меньше, чем на ^— . Так как этот процесс повторяется меньше,
чем m раз, то р0 превзойдет р меньше чем на -^:
ро^р + ~.	A3)
Из неравенств A3), A2), A1) следует, что

330]	§ 1. длина кривой	173
так что 0<S—p<e, откуда вытекает доказываемое утверждение F*),
а значит и F).
Так как из F) обратно вытекает B), то равенство F) можно рас-
рассматривать как новое определение длины кривой, равносильное преж-
прежнему.
Замечание. Однако, как нетрудно видеть, в случае замкну-
замкнутой кривой такое определение не может быть применено безогово-
безоговорочно: ведь даже при соблюдении
указанного условия ничто не ме-
мешало бы ломаной стягиваться в
точку, а ее периметру стремиться
к 0 (рис. 8). Суть дела в том,
что при незамкнутой кри-
кривой одно убывание всех звеньев
ломаной (р) до нуля уже обеспе-	">ис"
чивает все более тесное примы-
примыкание их к соответствующим частичным дугам; поэтому-то и естест-
естественно предел ее периметра р принять за длину всей дуги. В случае
же замкнутой кривой дело обстоит уже не так.
[Отметим, что если вместо стремления к 0 длин всех сторон
ломаной, потребовать того же относительно диаметров соответствую-
соответствующих дуг, то новое определение было бы в равной мере приложимо
как к незамкнутым, так и к замкнутым кривым.]
Покажем теперь, как из определения F) или — что то же - F*)
непосредственно вывести выражение D) для длины S кривой. Будем
исходить из готового выражения для периметра р ломаной [см. 248
G)]:
2
1=0
где т,, т, - некоторые значения t из промежутка [?,, ti+1].
Если заменить во втором слагаемом под знаком корня везде т,
на t,, то преобразованное выражение
л-1
/=0
очевидно, представит собой интегральную сумму как раз
для интеграла D). При стремлении Я к нулю, эта сумма и будет иметь
своим пределом упомянутый интеграл*. Для того чтобы показать,
что к тому же пределу стремится и периметр р ломаной, достаточно
обнаружить, что разность р - а стремится к нулю.
* Существование его не вызывает сомнений, ибо подинтегральная функция
непрерывна [298, I].

174	ГЛ. X. ПРИЛОЖЕНИЯ ИНТЕГРАЛЬНОГО ИСЧИСЛЕНИЯ
С этой целью произведем оценку этой разности
[331
'ет - У W(*S?
Элементарное неравенство
если применить его к каждому слагаемому написанной выше суммы
в отдельности, даст нам
/> - ff Н2>'(*<)-У (*/) И,-•
Ввиду непрерьшности функции y>'(t), по любому заданному е>0
найдется такое й>0, что \ip'(t)-y>'(t)\<e, лишь только \t-t\<b. Если
взять А«=<5 (т. е. все At^b), то и |г,~т(|<й, так что |f'(T/)~?'(^)He и
Это доказывает формулу D).
331. Примеры. 1) Цепная линия: >^och- (рис. 9). Мы имели уже в
а
252, 1):
у
х
а
Тогда по формуле Eа), если за начало от-
отсчета дуг принять вершину А кривой
s----AM =
г х	х
= \ch-dx = ash-.
J а	а
Рис. 9.
способ графического спрямления цепной линии.
хг
2) Парабола: у= — .
2
Вспоминая, что tg а = у'х - sh —, имеем
а
также s = a tg а. Таким образом, в д МР5
(рис. 9) катет MS=a tga в точности равен
(по длине) дуге s. Мы получили простой
* Неравенство это очевидно при а = 0; если же а#0, то оно непосредственно
вытекает из тождества
= F-*>i),
так как множитель при разности в скобках по абсолютной величине меньше
единицы.

331]	§ 1. ДЛИНА КРИВОЙ	175
Приняв за начало отсчета дуг вершину О (х = 0), для произвольной точки М
с абсциссой х имеем
If	1 Г 1		 р2		. 1
=- ]/л?Тр2Лс = - 1-х Vx2 +р2+- \п(х+]/х*+р*)\
pJ	p L2	2	J
р
— In
2
3) Астроида: x = acos31, y = asin31.
Пользуясь уже вычисленными [224, 4)] значениями х\ и у\, имеем
У*/2 +y'f = За sin * cos г (если 0=s?=e- .
Длина четверти астроиды между точками А(а, 0) и В@, а), по формуле D), равна
2
За
За
АВ = За sin / cos t dt = — sin21
J	2
о
так что длина всей кривой будет 6а.
4) Циклоида: x = a(t-sin t), y = a(l -cost).
Здесь (при 0=в?«г2л)
ТхР+УР = аУA-со8 02+81П^7= 2а sin —;
2
длина одной ветви циклоиды, по формуле D), будет
2я
Г t	t
2а sin — dt = - 4а cos —
J 2	2
5) Эвольвента круга: *=a(/sin ?+cos/), y = a(sin /-
Имеем (при /=-0)
Yxf+y'f = a]f{t cos ty+{t%\atj2 = at,
так что переменная дуга AM от точки A (t = 0) до любой точки М (t =- 0) выразится
так:
-w о*2
ЛЛ/=1 = —.
2
При /<:0 в предшествующей формуле справа нужно лишь поставить знак
минус.
6) Архимедова спираль: /- = ав.
По формуле E6), отсчитывая дугу от полюса О до любой точки М (отвечаю-
(отвечающей углу 8), получаем
о
ом=а( yiТе* de = a- [в
J	2
О

176
ГЛ. X. ПРИЛОЖЕНИЯ ИНТЕГРАЛЬНОГО ИСЧИСЛЕНИЯ
[331
Любопытно, что подставив здесь в = —, мы придем к выражению, формально
а
сходному с выражением для длины дуги параболы [см. 2)].
7) Логарифмическая спираль: /- = аетв (рис. 10).
1	-w
Так как г'о = тг, то г = — г«, и для дуги М0М между двумя точками с координа-
т
тами (/-„, 0О) и (/% 0) будем иметь по той же формуле E6)
-J,
- I r'udB-
1 +-(г-го).
Если вспомнить, что для логарифмической спирали tg со = —, то полученный
т
результат можно написать так:
J
COS ft)
Приближая точку Мо к полюсу О,
т. е. устремляя /-„ к нулю и прини-
принимая получаемый при этом
предел длины дуги М0М з а
длину дуги ОМ, мы придем к еще
более простому результату
COS О)
С помощью этой формулы из
А МОТ (см. рисунок) уже легко усмо-
усмотреть, что дуга s равна полярному
отрезку касательной tp:
ОМ=ТМ*.
Мы получили весьма простой способ
графического спрямления нашей кривой.
Рис. 10.	хг yi
8) Эллипс: — + — =1.
аг Ьг
Удобнее, впрочем, взять уравнения эллипса в параметрической форме х=a sin t,
6 cos/. Очевидно,
1г+У12=Уа* cos2 r + 62sin2 /= ]/(Г2 - (а2 - б2) sin2 f = efl -?2sin2/,
fa2 - Ь*
где f	 есть численный эксцентриситет эллипса.
а
* Это свойство логарифмической спирали позволяет легко установить такое
предложение: когда эта кривая катится без скольжения по прямой МТ,
то полюс О (если считать его неизменно связанным с кривой) описывает некото-
некоторую прямую. Предоставляем читателю доказательство.

331]	§ 1. длина кривой	177
Вычисляя длину дуги эллипса от верхнего конца малой оси до любой его точки
в первом квадранте, получим
= a{ /I -e2sin2 f Л = пЕ(е, t).
Таким образом, длина дуги эллипса выражается эллиптическим инте-
интегралом 2-го рода [293, см. также 305]; как указывалось, этот факт послужил
поводом для самого названия «эллиптический».
В частности, длина четверти обвода эллипса выражается через полный
эллиптический интеграл*
a I ]/l
о
]?2sin2f<# =
о
Длина же всего обвода будет
х
Интересно отметить, что для длины одной волны синусоиды у - с sin — , где
		Ь
с = /а2 - № получается в точности такой же результат. Геометрически это совпаде-
совпадение объяснить легко. Вообразим прямой круговой цилиндр; в пересечении его
поверхности с плоскостью, наклонной к образующим, получится эллипс. Если
разрезать поверхность цилиндра по образующей, проходящей через вершину
малой оси, и развернуть, то обвод эллипса перейдет в синусоиду.
Аналогично к эллиптическим интегралам (обоих родов) при-
приводится и вычисление дуги гиперболы.
9) Улитка: r=acos0+6.
Здесь г[) = - a sin в и
[Aab	в 1
1	sin2 — .
(а+ЬУ 2J
Поэтому (при b * а) для длины дуги от точки, для которой в = 0, до точки с любым
в-= л получим выражение в виде эллиптического интеграла B-го
рода)
Л/ Aab	в
/ 1	sin2 —
' {+ЬУ 2
о
_е
2
(а+ЬУ	[
\а+Ь 2
о
Длина всей кривой выразится полным эллиптическим интегралом:
* См. сноску на стр. 142.
12 Г. М. Фихтенгольц, т. II

178
ГЛ. X. ПРИЛОЖЕНИЯ ИНТЕГРАЛЬНОГО ИСЧИСЛЕНИЯ
[331
Однако для частного случая - кардиоиды (Ь = а) дело значительно
упрощается. В этом случае
0
г2 +/"а2 = 4а2 cos2 —,
так что (О<0=вл)
о
в
СО	V
s = 2а \ cos — d6 = 4а sin - .
J 2	2
Если (рис. 11) из полюса О радиусом 2а описать дугу AL до пересечения с продолжен-
продолженным радиусом-вектором ОМ, то хорда AL, очевидно, будет равна дуге s=AM.
Длина всей кардиоиды будет 8а.
10) Лемниската:
г2 = 2а2 cos 20.
Вычислим длину дуги лемнискаты от вершины, отвечающей 9 = 0, до любой
л
точки с полярным углом 8-= — .
4
Имеем
гг'0= -2л2 sin 20,
2а2 sin 20
откуда гв =	.
В таком случае
и по формуле E6)
0
Рис. 11.
мы снова приходим к эллиптичес-
эллиптическому интегралу A-го рода). Так
как таблицы вычислены для интегралов, в которых множитель кг при sin2 8 меньше
единицы, то прибегаем к замене переменной. Положим 2 sin2 8= sin2 у (так как
л
9-=-, то 2sin29<l, и угол д> отсюда определить действительно можно); тогда
4
cos 9 d6 = — cos q> d(p,
n
У1-2 sin2 q> = cos <f
и окончательно

331]	§ 1. ДЛИНА КРИВОЙ	179
л	л
Полагая в предельном случае* 0 = -, а д> = -, для длины четверти лемнискаты
получим выражение через полный эллиптический интеграл
'(#
длина всей лемнискаты будет 5=4аК
У
Замечательно, что задача спрямления дуги кривой столь часто приводит именно
к эллиптическим интегралам.
11) В заключение приведем пример использования формулы для длины дуги
при построении эвольвенты кривой [256].
Рассмотрим цепную линию. Если текущие координаты ее точки обо-
обозначить через ?, ?7 (применительно к обозначениям п° 256), а дугу ее, отсчитываемую
от вершины, - через а, то уравнение кривой напишется в виде
а
а дуга представится формулой [см. 1)]
а = a sh — .
а
Отсюда можно выразить ( и t] непосредственно в функции от а:
? = e[ln (о + Уаг + а2) - In в], т}=Уа'+а*.
Теперь по формулам A7) п° 256, учитывая, что здесь [см. A8)]
а	а
cos В = ————— , sin В =
можно написать параметрические уравнения произвольной эвольвенты
а
Остановимся на той из эвольвент, которая отвечает с = 0; она исходит из вер-
вершины цепной линии и имеет в ней точку возврата (рис. 12). Исключая а, эту кривую
(называемую трактрисой) можно выразить и явным уравнением
х= ±
* Мы вынуждены рассматривать этот случай именно как предельный, пере-
п	п
ходя в полученном выражении для s к пределу при в—— или ф-+-, так как при
л	4	2
в = - производная г» = » и формула E6) непосредственно неприложима.
4
12*

180	I Л. X. ПРИЛОЖЕНИЯ ИНТЕГРАЛЬНОГО ИСЧИСЛЕНИЯ
Если вспомнить выражение «отрезка касательной» [230 D)]
[332
i - —
Ух
то отсюда легко получить, что t = a. Этим выражено замечательное свойство
трактрисы: отрезок касательной для нее имеет постоянную величину*.
Этот результат легко получается и непосредственно из свойств цепной линии
[см. в 1) ее спрямление, рис. 9].
О	Т
Рис. 12.
332. Натуральное уравнение плоской кривой. Представление кривой
с помощью уравнения между координатами ее точек (по отношению
к какой-либо системе координат), несмотря на всю полезность та-
такого представления, часто носит искусственный характер, поскольку
координаты не являются существенными геометрическими элементами
кривой. Такими существенными элементами, наоборот, являются д у-
г а кривой s, отсчитываемая в определенном направлении от некото-
некоторой начальной точки, и радиус кривизны R (или сама кри-
кривизна Jk = i] [см. 250, 251].
Для каждой кривой между этими элементами можно установить
зависимость вида
которая и называется натуральным уравнением кривой*
* С этим связано и самое название трактриса (происходящее от латин-
латинского глагола trahere - влечь, тащить): если движущаяся по горизонтали
точка Т при помощи нити ТМ тащит за собой точку М, то последняя будет
описывать как раз трактрису.
** Перевод немецкого термина: natiirliche Gleichung; не менее выразителен
и французский термин: equation intrinseque (т. е. «внутреннее уравнение»!.

332]	§ I. длина кривой	181
Докажем, что кривые, имеющие одно и то же натуральное урав-
уравнение, могут отличаться только своим положением на плоскости,
так что форму кривой натуральное уравнение определяет вполне
однозначно.
Пусть же две кривые (I) и (II) имеют одно и то же натуральное
уравнение, которое мы возьмем в виде
j-g(s).	A4)
Для того чтобы доказать их конгруентность, сначала перенесем одну
из кривых так, чтобы совпали точки, от которых на обеих кривых
отсчитываются дуги, а затем повернем эту кривую так, чтобы сов-
совпали положительные направления касательных в этих точках.
Отметим указателями A и 2) соответствующие одному и тому же
значению s элементы обеих кривых:
координаты переменной точки: (х1г jx) и (х2. >>2);
угол касательной с осью х: х1 и а2;
радиус кривизны: Rt и R^.
В силу A4) будем иметь при всех s: ^-=^-, т. е. [250, B)]
 Л2
J
ds ds
Кроме того, как предположено, при s =0
¦*i = *8. уг=у2	A6)
и
Из A5), по следствию п° 131 вытекает, что ху и а2 могут разниться
лишь на постоянную; но, как мы видели, при s = 0 эти величины сов-
совпадают, следовательно равенство A7) имеет место всегда. В таком
случае для всех значений s будет [249, A5)]
dx,	dx,
~ = cos x, = cos a, = — ,
ds	*	^ ds '
dy, ¦	¦	dy°
откуда аналогичным образом заключаем, что и равенства A6) имеют
место всегда, т. е. кривые совпадают.
Покажем теперь, как по натуральному уравнению A4) кривой
восстановить координатное представление ее. Прежде всего из A4)
da . ч
имеем -r=g\s), так что
S
*0,	A8)

182	ГЛ. X. ПРИЛОЖЕНИЯ ИНТЕГРАЛЬНОГО ИСЧИСЛЕНИЯ	C32
где а0 - постоянная. Затем, исходя из равенств
dx — coscr.ds, dy = sina.ds,	A9)
интегрируя, находим
о
y= sma.ds + y0,	B0)
где х0 и у0 - новые постоянные.
Нетрудно понять, что вращение кривой влечет за собой измене-
изменение постоянной а0, а параллельное перенесение ее связано с измене-
изменением постоянных х0, у0*. Равенство этих постоянных нулю означает,
очевидно, что кривая расположена так, что начальная точка для от-
отсчета дуг совмещена с началом координат, а положительное направ-
направление касательной в ней совпадает с положительным направлением
оси х.
Пусть теперь уравнение A4) взято произвольно [лишь функцию g(s)
мы будем предполагать непрерывной]. Тогда, определив сначала
а формулой A8), а затем х и у - уравнениями B0), получим пара-
параметрическое представление некоторой кривой. Дифференцируя B0),
вернемся к A9), откуда прежде всего усматриваем, что
так что ds, действительно, является дифференциалом дуги этой кри-
кривой, a. s - дугой (если надлежаще выбрать начальную точку отсчета).
Затем те же равенства A9) приводят к заключению, что а служит
углом касательной к той же кривой с осью х. Наконец, дифферен-
дифференцируя A8), найдем, что кривизна будет равна
и, таким образом, уравнение A4) действительно оказывается нату-
натуральным уравнением для нашей кривой. Итак, каждое урав-
уравнение вида A4), где функция g(s) непрерывна, может быть рассматри-
рассматриваемо как натуральное уравнение некоторой кривой.
Обращаем внимание читателей на то, что за счет выбора началь-
начальной точки и направления отсчета дуг на кривой в ее натуральное урав-
уравнение можно вносить (впрочем несущественные) изменения.
* Обращая эти утверждения, легко получить новое доказательство того предло-
предложения, которое было высказано выше.

333]
§ I. ДЛИНА КРИВОЙ
183
В заключение заметим еще, что две симметрично располо-
расположенные кривые* (рис. 13) имеют натуральные уравнения вида A4),
разнящиеся лишь знаком правой части
1
и j=-
B1)
Действительно, при согласном выборе начальных точек и направления
для отсчета дуг на обеих кривых, радиусы кривизны их будут иметь
противоположные знаки. Обратно, две кривые, имеющие, соответ-
соответственно, уравнения B1), передви-
передвижением по плоскости могут быть
приведены в симметричное поло-
положение. Можно не считать и такие
две кривые существенно разнящи-
разнящимися по форме.
333. Примеры. 1) Найти кривую, отве-
отвечающую натуральному уравнению R" = las.
Имеем
doc 1
ds
-w-
Рис. 13.
так что ds=aoc da.. Выбирая а в качестве параметра, получим затем
<?e = cosa ds = ах cos ос drt, dy = sm a ds = az sin ос doc,
откуда
jc=-a(cosa+asina), у - a(sin a - a cos a).
Кривая оказалась эвольвентой круга [225, 8)].
2) То же для натурального уравнения Rl+st = l6at. Здесь
da
ds у 16a»-.Я
a=»arcsin —, s-4asina,
4a
ds-= 4a cos ос doc.
Тогда
dx = cosa ds-4a cos2 a aa,
и отсюда, интегрируя,
dy = sin a ds = 4a sin a cos a doc
x = 2a\oc-{—sin2al=aBa+sin2a),
y= -
= a-a(l+cos2a).
* Совместить их перемещением по плоскости нельзя; для этого по-
понадобилось бы вращение в пространстве.
** Так как нам нужно восстановить хоть одну кривую, то выбирать постоян-
постоянные интегрирования мы будем лишь по соображениям удобства. Это замечание
следует иметь в виду и впредь.

184	ГЛ. X. ПРИЛОЖЕНИЯ ИНТЕГРАЛЬНОГО ИСЧИСЛЕНИЯ	[333
Если перейти к параметру / = 2а-я, то уравнения полученной кривой примут вид
x=na+a(t -sin t), ya-a(\-cost),
и мы узнаем циклоиду [225, б)], лишь сдвинутую и перевернутую по сравне-
сравнению с обычным ее расположением.
3) То же для натурального уравнения R^ms.
Очевидно,
da. I	In j
— = —, а =	, s = em, ds*=menmda,
ds ms	m
dx = cos a- memt* da, dy = sin a • mem da
и, наконец,
m	m
(m cos a +sm a)emct, у =	(m sin a - cos a)em".
l+2
x	(m cos a +sm a)e, у
1+m2	l+/n
Перейдем к полярным координатам. Прежде всего
„	т
г=
Затем, вводя постоянный угол со под условием tg со = —, будем иметь
т
1
tg a
у т sin a - cos a	m
- =	=	= tg (a - со),
л: mcosa+sina	1
И—tga
т
так что полярный угол в можно принять равным а-со, откуда а = со+0. Оконча-
Окончательно полярное уравнение найденной кривой будет таково:
это - логарифмическая спираль [226, 3)]. Величина коэффициента
при етв роли не играет, его можно свести к 1 поворотом полярной оси.
4) Займемся теперь задачей другого рода: станем по заданной кривой уста-
устанавливать ее натуральное уравнение.
(а)	Для цепной линии > = ach— имели [331, 1); 252, 1)]
а
х		у*
s*	a	a
отсюда R = a\— .
а
(б)	Для астроиды х = а cos31, у = a sin31, если за начало для отсчета дуг
выбрать середину ее ветви в первом квадранте, будет [ср. 331, 3)]
За	За
s = — sm21	, R = За sin t cos t.
2	4
Поэтому
За	За
R* = 4—sin2/-—
2	2
и окончательно натуральное уравнение астроиды может быть написано в виде
9а2
(За Л(Ъа Л 9а2
= 4 — + s\\	s \=
14 Д4 J 4

334]	§ 1. длина кривой	185
(в)	В случае кардиоиды /- = e(l + cos 0) у нас было [331, 9); 252, 6)]
9	4	9
j=4asin —, R = — a cos— ;
2	3	2
очевидно, 9R2 + s2 = 16a2.
(г)	Последние два результата содержатся как частные случаи в следующем.
Для эпи- и гипоциклоиды [225, 7)] натуральное уравнение будет A +
+ 2тJ R* + л3 = 16/я2A + т*)а\
(д)	Нетрудно вновь получить натуральные уравнения эвольвенты кру-
круга, циклоиды и логарифмической спирали, известные нам
из 1)-3).
5) По натуральному уравнению кривой можно установить натуральное уравне-
уравнение ее эволюты. Мы имели соотношение [255, 15)]
dR
Р = Д-т-.	B2)
ds
Если начало для отсчета дуг на эволюте выбрать так, чтобы было R = a [см.
255, 2°], то, исключая R и s из этих двух соотношений и натурального уравнения
данной кривой, придем к зависимости между рист, т. е. к натуральному
уравнению эволюты.
(а)	Для логарифмической спирали R = ms; тогда р = mR = та.
С точностью до обозначений мы вернулись к прежнему уравнению, отсюда заклю-
заключаем, что эволютой будет такая же логарифмическая спираль, которая от исходной
может отличаться лишь положением [ср. 254, 5)].
(б)	Для эвольвенты круга
dRlfa 1 a
ds [/2 Vs a>
4 = — ,
1л
a
a
(результат, который следовало предвидеть).
(в) Если натуральное уравнение кривой имеет вид R2+?2.s2 = c2, то ее эволюта
будет такой же кривой, но в к раз увеличенной по линейным размерам.
Действительно, имеем
и, наконец,
Отсюда и вытекает сделанное утверждение.
Полученный результат применим к циклоиде [ср. 254, 4)], к э п и -
и гипоциклоиде, в частности, к кардиоиде и к астроиде
[ср. 254, 3)].
Замечание. Указанный метод во всех случаях позволяет судить лишь
о форме эволюты, оставляя открытым вопрос об ее положении.
334. Длина дуги пространственной кривой. По отношению к простой
пространственнойкривой

186	ГЛ. X. ПРИЛОЖЕНИЯ ИНТЕГРАЛЬНОГО ИСЧИСЛЕНИЯ	[335
определение длины дуги может быть дано в таком же виде, как и
для плоской кривой [249, замечание]. Здесь также для длины дуги
получается формула, аналогичная D),
и т. д. На этот случай, почти без изменений, переносится все сказан-
сказанное относительно случая плоской кривой. Не задерживаясь на этом,
приведем примеры.
1) Винтовая линия: x = acos/, y=asin t, z=ct.
Так как здесь
то длина дуги кривой от точки А (/ = 0) до точки М (t — любое) будет
- результат очевидный, если вспомнить, что при разворачивании цилиндрической
поверхности винтовая линия на ней превратится в наклонную прямую.
2) Кривая Вивиани: x = R sin21, y=Rsint cos t, z = R cos /.
Имеем
В таком случае длина всей кривой выразится полным эллиптическим
интегралом 2-го рода
S=4R У1+8Ш»/Л = 4Д yi+cos«/<U = 4y2fl I \f I—sin1 / dt = 4У2ЛЕ1 —
0	0
§ 2. Площади и объемы
335. Определение понятия площади. Свойство аддитивности. Мно-
Многоугольной областью, или - короче — многоуголь-
многоугольником, мы будем называть произвольную конечную (возможно, и
несвязную) плоскую фигуру, ограниченную одной или несколькими
замкнутыми ломаными. Для такой фигуры понятие площади было
достаточно изучено в школьном курсе геометрии, его мы положим
в основу.

335]	S 2. ПЛОЩАДИ И ОБЪЕМЫ	187
Возьмем теперь произвольную фигуру (Р) на плоскости, пред-
представляющую собой ограниченную и замкнутую область.
Ее границу или контур (К) мы всегда будем себе представлять
в виде замкнутой кривой (или нескольких таких кривых)*.
Станем рассматривать всевозможные многоугольники (Л), цели-
целиком содержащиеся в (Р), и много-
многоугольники (В), целиком в себе со-
содержащие (Р) (рис. 14). Если А и
В означают, соответственно, их пло-
площади, то всегда А^В. Множество
чисел {Л}, ограниченное сверху лю-
любым В, имеет точную верхнюю
границу Р* [11], причем P*=*sB.
Точно так же множество чисел {В},
ограниченное снизу числом Р*, имеет	Рис- 14-
точную нижнюю границу Р*»
2&Р*. Эти границы можно было бы назвать первую - внутрен-
внутренней, а вторую - внешней площадью фигуры (Р).
Если обе границы
совпадают, то общее их значение Р называется площадью фи-
фигуры (Р). В этом случае фигуру (Р) называют квадрируемой.
Как легко видеть, для существования площади необходимо и до-
достаточно, чтобы для любого е=-0 нашлись такие два многоугольника
(А) и (В), что В-А^е.
Действительно, необходимость этого условия вытекает из основ-
основных свойств точных границ [11]: если площадь Р существует, то най-
найдется А>Р-~ и В<Р + ~. Достаточность сразу же следует из нера-
неравенств
Пусть теперь фигура (Р) разложена на две фигуры (Pt) и (Р2)**;
можно себе представить, например, что это осуществлено с помощью
кривой, соединяющей две точки ее контура, или целиком лежащей
внутри (Р) (рис. 15, а и б). Докажем, что
* В этом параграфе, говоря о кривой, мы всегда будем иметь в виду не-
непрерывную простую кривую, допускающую параметрическое представление.
Как доказал Ж о р д а н (С. Jordan), замкнутая кривая этого типа всегда раз-
разбивает плоскость на две области, внутреннюю и внешнюю, для которых и служит
общей границей.
** Они могут иметь частично общую границу, но не налегают одна
на другую, т. е. не имеют общих внутренних точек.

188
ГЛ. X. ПРИЛОЖЕНИЯ ИНТЕГРАЛЬНОГО ИСЧИСЛЕНИЯ
1336
квадрируемость двух из этих трех фигур (Р), (i\), (Р2) влечет за
собой квадрируемость третьей, причем всегда
Р = Р^Р2,	A)
т. е. площадь обладает свойством аддитивности.
Предположим для определенности, что имеют площади фигуры
(Pj) и (Р2). Рассмотрим соответствующие им входящие и выходящие
многоугольники {Аг), (В-^ и (А2), (В^). Из взаимно неналегающих
многоугольников (Aj), (A2) составится многоугольная область (А)
с площадью А=А1+А2, целиком содержащаяся в области (Р). Из
Рис. 15.
многоугольников же EХ) и (В2), возможно и взаимно налегающих,
составится область (В) с площадью В^Вх + Вг, содержащая в себе
область (Р). Очевидно,
так как при этом Вг от Ах и В2 от А2 могут отличаться произвольно
мало, то это же справедливо относительно В и А, откуда и вытекает
квадрируемость области (Р).
С другой стороны, имеем одновременно
Л, + А2=
В2
В2,
так что числа Р я Рх + Р2 содержатся между одними и теми же и при-
притом произвольно близкими границами А1+А2к В1+В2, следовательно,
эти числа равны, ч. и тр. д.
Отметим, в частности, что отсюда Р^Р, так что часть фигуры
имеет площадь, меньшую чем вся фигура.
336. Площадь как предел. Условие квадрируемости, сформулиро-
сформулированное в предыдущем п°, может быть перефразировано так:
1) Для того чтобы фигура (Р) была квадрируема, необходимо и
достаточно, чтобы существовали такие две последовательности много-

§ 2. ПЛОЩАДИ И ОБЪЕМЫ
189
угольников {(A-ri)} и {{Вп)} и соответственно, содержащихся в (Р) и со-
содержащих (Р), площади которых имели бы общий предел
lim Ап = Иш В„ = Р.
B)
Этот предел, очевидно, и будет площадью фигуры (Р).
Иногда вместо многоугольников выгоднее использовать другие
фигуры, квадрируемость которых уже установлена:
2)	Если для фигуры (Р) можно построить такие две последова-
последовательности квадрируемых фигур {(Qn)} и {(Rn)}, соответственно,
содержащихся в (Р) и содержащих (Р), площади которых имеют об-
общий предел
]\mQn = Mm.Rn = P,	C)
то фигура (Р) также к в а д р и р у е м а, причем упомянутый пре-
предел и будет ее площадью.
Это сразу вытекает из предыдущего утверждения, если заменить
каждую фигуру (?>„) содержащимся в ней многоугольником (Ап), а
фигуру (Rn) - содержащим ее
многоугольником (Вп), настолько
близкими к ним по площади,
чтобы одновременно выполнялось
и B).
Хотя на практике выбор фи-
фигур (Ап), (Вп), (Qn), (Rn), упоми-
упоминавшихся в двух сформулиро-
сформулированных выше признаках, и не
создает затруднений, но все же
представляет принципиальный ин-
интерес устранение связанной с этим
выбором неопределенности. С этой целью можно поступить,
например, так:
Заключив рассматриваемую фигуру (Р) внутрь некоторого прямо-
прямоугольника (R) со сторонами, параллельными координатным осям,
разобьем его на части с помощью ряда параллелей его сторонам.
Из прямоугольников, целиком содержащихся в области (Р), составим
фигуру (А) (на рис. 16 она заштрихована), а из прямоугольников,
имеющих с (Р) общие внутренние точки, но могущих частично и вы-
выходить из этой области, составим фигуру E). Эти фигуры представ-
представляют, очевидно, частный случай тех многоугольников (А) и (В), о ко-
которых была речь в определении понятия площади; их площади А я В
зависят от способа разложения на части прямоугольника {К). Будем
через d обозначать длину наибольшей из диагоналей частичных прямо-
прямоугольников.
3)	Если при d-~ 0 обе площади А и В стремятся к общему пределу
Л и только в этом случае, область (Р) будет квадрируема;
Рис. 16.

190	ГЛ. X. ПРИЛОЖЕНИЯ ИНТЕГРАЛЬНОГО ИСЧИСЛЕНИЯ	1337
при выполнении этого условия упомянутый предел и будет площа-
площадью фигуры (Р).
Читатель легко сам выразит понятие предела, которое здесь фи-
фигурирует, как «на языке е-д», так и «на языке последовательностей».
В доказательстве нуждается только необходимость ука-
указанного условия. Допустим же, что площадь Р существует, и устано-
установим, что тогда
limi=limi? = .P.	D)
По заданному е=-0 найдутся [335] такие многоугольники А а В,
что В-А^е; при этом можно предположить, что их контуры
не имеют общих точек с контуром {К) фигуры (Р). Обо-
Обозначим через д наименьшее из расстояний между точками кон-
контуров обоих многоугольников, с одной стороны, и точками кривой (К)
- с другой*. Если взять теперь d<d, то каждый частичный прямо-
прямоугольник, хотя бы в одной точке задевающий кривую {К), заведомо
лежит вне многоугольника (Л) и внутри многоугольника (В). Отсюда
следует, что
так что Р-А^е и В-Р<е, что и приводит к D).
Ясно, что на равенстве D) можно было бы построить и самое
определение понятия площади, очевидно, равносильное прежнему.
Такое определение представляется весьма простым и естественным;
недостатком, однако, является его (конечно, кажущаяся) зависимость
от ориентации координатных осей.
337. Классы квадрируемых областей. Кривая (К) — контур области
(Р) - играет существенную роль в вопросе о квадрируемости
этой области.
Если квадрируемость налицо, то, как мы видели в 335, по задан-
заданному е=-0 кривая (К) может быть заключена в некоторую много-
многоугольную область (В-А), содержащуюся между контурами обоих
многоугольников (А) и (В) (см. рис. 14) и имеющую площадь В-А^е.
* Пусть имеем две конечные непрерывные кривые на плоскости; пред-
предположим, например, что они заданы параметрически
(I) х=9>0), У=Ч>(.О; (II) х =?>*(«), y=V*(u),
где q>, v, 9*, у>* - непрерывные функции, каждая от своего аргумента. Тогда рас-
расстояние между двумя произвольными точками этих кривых
будет непрерывной функцией от (/, и) в замкнутой области [/„, Т;и0, U] и, следова-
следовательно, достигает там своего наименьшего значения [173]. Если кривые не пере-
пересекаются, то это наименьшее расстояние будет отлично от нуля.

337]
6 1. ПЛОЩАДИ И ОЁЪЁМЫ
191
Допустим теперь, обратно, что контур (К) может быть заключен
в многоугольную область (С) с площадью С<е, где е - любое на-
наперед заданное положительное число. При этом, без умаления общ-
общности, можно предположить, что (С) не покрывает всей фигуры (Р).
Тогда из точек области (Р), не попадающих внутрь (С), составится
многоугольная область (А), содержащаяся в (Р); если же к (А) при-
присоединить (С), то получится многоугольная область (В), уже содер-
содержащая в себе (Р). Так как разность В-А = С^е, то - по критерию
п° 335 - отсюда следует квадрируемость области (Р).
Для облегчения речи условимся говорить, что (замкнутая или не-
незамкнутая) кривая {R) имеет площадь 0, если ее можно
покрыть многоугольной областью с произвольно малой площадью.
Тогда приведенное выше рассуж-
рассуждение позволяет сформулировать
следующее условие квад-
квадрируемости:
для того чтобы фигура (Р)
была квадрируема, необходимо и
достаточно, чтобы ее контур
(К) имел площадь 0.
В связи с этим приобретает
важность выделение широких
классов кривых с площадью 0.
Прежде всего легко показать, что этим свойством обладает лю-
любая непрерывная кривая, выражаемая явным уравнением вида
F
*~х
Рис. 17.
или x=g(y)
E)
(/ и g - непрерывные функции).
Пусть, например, мы имеем дело с первым из этих уравнений.
По заданному е>0 можно промежуток [а, Ь] разложить на части
[Xj, х,+1] (/=0, 1, ..., л-1) так, чтобы в каждой из них колебание
со,- функции / было ^tzt 187]. Если обозначить, как обычно, через
/и,- и Mt наименьшее и наибольшее значения функции / в i-ом про-
промежутке, то вся наша кривая покроется фигурой, составленной из
прямоугольников
[Xi, xi+1; mh M,] (/=0, 1, ..., п-1)
(см. рис. 17) с общей площадью
2 (Mi - тд(х1+1 - х,) = 2 "И*, *iTi2 Axi =е>
что и требовалось доказать. Значит, кривая E) имеет площадь 0.
Отсюда следует:

192	ГЛ. X. ПРИЛОЖЕНИЙ ИНТЕГРАЛЬНОГО ИСЧИСЛЕНИЯ	C38
Если фигура (Р) ограничена несколькими непрерывными кривыми,
каждая из которых порознь выражается явным уравнением E) (того
или другого типа), то эта фигура квадрируема.
Действительно, поскольку каждая из упомянутых кривых имеет
площадь 0, то и весь контур, очевидно, также будет иметь площадь 0.
Из этого критерия можно получить другой, более частный, кри-
критерий, который на практике, однако, оказывается более удобным.
Назовем кривую, заданную параметрическими уравнениями
*=9>@, y=W),	F)
гладкой, если 1) функции уи^ имеют непрерывные производные
во всем промежутке [t0, Т] изменения параметра, и 2) на кривой нет
ни кратных, ни вообще особых точек. В случае замкнутой кри-
кривой, потребуем еще равенства
4>'(to)=<p\T), y'(to)=V'(T).
Установим теперь, что гладкая кривая имеет площадь 0.
Возьмем на кривой любую точку М, определяемую значением t
параметра. Так как эта точка - не особая, то, как мы видели [223],
существует такой промежуток:
ff = (F-5", 7+8),
что соответствующий участок кривой может быть выражен и явным
уравнением.
Применим теперь лемму Боре ля [88] к промежутку [t0, T] и
к покрывающей его системе 2!= W окрестностей; весь промежуток
перекроется конечным числом таких окрестностей, так что кривая
распадается на конечное число частей, каждая из которых выражается
явным уравнением E) (того или другого типа). Остается лишь со-
сослаться на доказанное выше. Итак,
если фигура (Р) ограничена одной или несколькими гладкими
кривыми, то она заведомо квадрируема.
Заключение это сохраняет силу даже в том случае, когда кривая
имеет конечное число особых точек: выделив эти точки с по-
помощью окрестностей произвольно малой площади, мы будем иметь
дело уже с гладкими кривыми.
338. Выражение площади интегралом. Обратимся теперь к вычи-
вычислению площадей плоских фигур при помощи интегралов.
На первом месте рассмотрим, впервые - в строгом изложении,
уже встречавшуюся нам задачу об определении площади криво-
криволинейной трапеции ABCD (рис. 18). Эта фигура ограничена
сверху кривой DC, имеющей уравнение
У=Дх),

3381
§ 2. ПЛОЩАДИ И ОБЪЁМЫ
193
где Дх) есть положительная и непрерывная в промежутке [а, Ь] функ-
функция: снизу она ограничена отрезком АВ оси х, а с боков — двумя
ординатами AD и ВС (каждая из которых может свестись к точке).
Собственно, существование площади Р рассматриваемой фи-
фигуры ABCD следует из доказанного в предыдущем п°, и речь идет
лишь об ее вычислении.
С этой целью разобьем промежуток [а, Ь], как обычно, на части,
вставив между а и b ряд точек
Обозначив через w,- и А/,-, соответственно, наименьшее и наибольшее
значения функции f(x) в г-ом промежутке [xh xi+1] (/=0, 1,..., и-1),
составим суммы (Дарбу)
Они, очевидно, представляют со-
собой площади ступенчатых фигур,
составленных, соответственно, из
входящих и выходящих прямо-
прямоугольников (см. рисунок). По-
Поэтому
Рис. 18.
Но при стремлении к нулю наибольшей из разностей Axt обе суммы
имеют своим пределом интеграл I f(x) dx*, следовательно, ему и равна
искомая площадь	°
G)
Если криволинейная трапеция CDFE ограничена и
снизу и сверху кривыми (рис. 19), уравнения которых
•то, рассматривая ее как разность двух фигур ABFE и ABDC, получим
площадь названной трапеции в виде
6	Ь
-Уд dx = J Шх) - Мх)} dx.
(8)
* В силу 336, 1) это само по себе доказывает квадрируемость криволинейной
трапеции ABCD; чтобы получить упоминавшиеся там последовательно-
последовательности фигур, можно было бы, например, делить промежуток на равные части.
13 Г. М. Фихтенгольц, т. II

194
ГЛ. X. ПРИЛОЖЕНИЯ ИНТЕГРАЛЬНОГО ИСЧИСЛЕНИЯ
[338
Пусть теперь дан сектор АО В (рис. 20), ограниченный кри-
кривой АВ и двумя радиусами-векторами ОА и ОВ (каждый из которых
может свестись и к точке). При этом кривая АВ задается полярным
уравнением r=gF), где gF) - положительная непрерывная в про-
промежутке [а, /3] функция. И здесь вопрос стоит лишь о вычисле-
вычислении площади Р сектора, так как существование площади
обусловлено свойствами контура фигуры.
Вставив между а и /3 (см. рисунок) значения
проведем соответствующие этим углам радиусы-векторы. Если ввести
и здесь наименьщее и наибольшее из значений функции gF) в [6t, б,+1]:
Ж~А
Рис. 19.
Рис. 20.
,и, и М,-, то круговые секторы, описанные этими радиусами, будут,
соответственно, входящими и выходящими для фигуры АО В. Со-
Составим отдельно из входящих секторов и из выходящих секторов две
фигуры, площади которых будут
и, очевидно, <7<P~=Z-
В этих суммах а и 2! легко узнать суммы Дарбу для инте-
/з
грала ^ I [gF)]2 ^0; ПРИ стремлении к нулю наибольшей из разностей
а
Ад, обе они имеют пределом этот интеграл*, так что и
(9)
* Здесь можно было бы сделать замечание, аналогичное замечанию на стр.
193, но со ссылкой на 336, 2).

339)
§ 2. ПЛОЩАДИ И ОБЪЕМЫ
195
339. Примеры. 1) Определить площадь Р фигуры, ограниченной цепной
х
линией у = а сп —, осью х и двумя ординатами, отвечающими абсциссам
а
О и х (рис. 9).
Имеем
»= ach-,
J a
о
x
— = as,
a
где 5 - длина дуги AM цепной линии
[331, 1)]. Таким образом, искомая
площадь АОРМ оказалась равной пло-
площади прямоугольника, построенного
на отрезках PS и SM (ибо SM=AM).
2) Даны эллипс — + — = 1 и
точка М(х, у) на нем (рис. 21). Определить площадь криволинейной трапеции
ВОКМ и сектора ОМВ.
Из уравнения эллипса имеем у = — У а- - х-, так что по формуле G)
а
X
г b ,r	 ab х Ъ ,		ab x ху
Р, - пл. ВОКМ - — ]'а2 - х2 dx - — arcsin —\— х }'аг - .г2	= — arcsin —Ь — .
1 J а ' 2 а 2а '	2 а 2
О
Так как последнее слагаемое представляет площадь д ОКМ, то, отнимая ее,
для площади сектора получим выражение
ab	х
Р„ = пл. ОМВ -- — arcsin — .
2	а
Ttab
При л: = а для площади четверти эллипса найдем значение — , так что площадь
4
всего эллипса P=nab. Для круга a = b = r и получается известная формула Р=лг/-2.
Xs у2
3) Пусть даны гипербола	=1 ина ней точка М(х, у) (рис. 22).
аг Ьг
Определить площадь криволинейных фигур АКМ, О AM и OAML.
b
Из уравнения гиперболы имеем у - — Ух'2 - а2, и - по формуле G) -
а
Рг = ши АКМ =
a J
b rl
TIT
	аг .
*-a*-- In (x
2
	л h
J „
1	ab x -t l^x2 - fl-
-Л'	In

196
ГЛ. X. ПРИЛОЖЕНИЯ ИНТЕГРАЛЬНОГО ИСЧИСЛЕНИЯ
[339
Так как
форме
a у
	= —, то это выражение можно представить в более симметричной
a b
х у
- +
а Ь
Отсюда уже легко получить
ab (х
—\\
2
а Ъ)
1	1	(х у\
= — xy + -ab\n \ — + — \.
2	2	\а Ь)
Замечание. Полученный результат позволит нам несколько углубить
аналогию между тригонометрическими (круговыми) и гиперболическими
Рис. 22.
функциями. Сопоставим круг радиуса 1: х2+>'2=1 и ра внобочную гипер-
гиперболу: л-3-у2=1 (рис. 23, а и б). Эти кривые параметрически могут быть пред-
представлены так:
для круга:	OP = x = cos t, PM = у = sin t,
для гиперболы: OP = x = cht, PM=y = sht.
Но в то время как в случае круга ясна геометрическая роль t - это <$АОМ, для
гиперболы так истолковать числовой параметр / невозможно. Можно, однако,
для круга дать и другое истолкование параметра t, именно: t есть удвоен-
удвоенная площадь сектора АОМ (или площадь сектора М'ОМ). Оказывается,
что это истолкование переносится и на случай гиперболы.
В самом деле, если координаты точки М суть
у = sh t = -
то х+у = е* и t = \n(x+y). Если вспомнить найденную выше для Р2 формулу и
положить в ней а = b = 1, то получим, что t равно удвоенной площади
сектора А ОМ (как и для круга).
Итак, в круге отрезки РМ и ОР представляют круговые синус и ко-
косинус от удвоенной площади кругового сектора АОМ, а для гипер-
гиперболы аналогичные отрезки выражают гиперболические синус и коси-
косинус от удвоенной площади гиперболического сектора АОМ. Роль

339]
§ 2. ПЛОЩАДИ И ОБЪЕМЫ
197
гиперболических функций по отношению к гиперболе вполне аналогична роли
круговых (тригонометрических) функций по отношению к кругу.
Ш)
Рис. 23.
С указанным истолкованием аргумента гиперболических функций, как некоей
площади, связаны и обозначения обратных им функций [см. 49, 3) и 4)],
Arsh х, Arch х и т. п.
Буквы Аг являются начальными от латинского слова Area, означающего «площадь».
4)	Найти площадь Р фигуры, ограни-
ограниченной осями координат и параболой
Vx + уу — уа (п > 0).
а
Ответ: Р= у dx = — а2. (Читателю
J	6
о
самому предоставляется сделать чертеж.)
5)	Определить площадь фигуры, за-
заключенной между двумя конгруентными
параболами уг = 2рх и хг-2ру (рис. 24).
Очевидно, нужно воспользоваться фор-
формулой (8), полагая там
У1="Тр' У^2рХ-	Рис.24.
Для установления промежутка интегрирования решим совместно данные
уравнения и найдем абсциссу точки М пересечения обеих парабол, отличной от
начала: она равна 2р. Имеем
2р
У2^-1Ц- 1 }г2рх*--\ =-/*
2р) {3	вр) |о 3

198
ГЛ. X. ПРИЛОЖЕНИЯ ИНТЕГРАЛЬНОГО ИСЧИСЛЕНИЯ
|339
6) Найти площадь Р эллипса, заданного уравнением
АхЧ2Вху-\ Су°-=1 (АС-Вг>0, С=-0).
Решение. Из этого уравнения
-Bx-
-Вх +
У&х2-
с
УВ*х2-
С(Ах2~
С(Ах2-
1)
1)
причем j>1( y\ получают вещественные значения лишь для х, удовлетворяющих
неравенству
т. е. содержащихся в промежутке [-а, а], где а =
Тогда искомая площадь будет
АС-В2
^ j УС-
-dx =
2 ,	f ,	2 ,	1	5
= - УАС-В* У<х.2-х*<1х+ - УаС-В*—ло.-= -—
7) Пусть, наконец, эллипс задан общим уравнением
ах2 + 2Ьху + су2 + 2дх+2еу-\ -/= 0:
требуется найти его площадь Р.
Задача эта может быть сведена к предыдущей.
Если перенести начало в центр (?, rj) эллипса, определяемый, как
из уравнений
то уравнение примет вид
ах2 + 2Ьху + су2 +/' = 0,
где
известно,
(И)
A2)
Исключая f, rj из равенств A1) и A2), найдем
I a b д
\Ь
,) е f-f
=0,
откуда
Г' —
Л
ас-Ь2'
где
а Ь д
bee
д е f
* Очевидно, /' и А отрицательны (иначе уравнение не выражало
ственной кривой).
бы веще-

веще339]	§ 2. ПЛОЩАДИ И ОБЪЕМЫ	199
Полученное уравнение легко приводится к виду, рассмотренному в 6), если
положить
a	b	с
А	В	С
Значит, площадь эллипса будет
/'|	пЛ
p*
8)	Формула G) может быть использована и в том случае, если кривая, ограни-
ограничивающая криволинейную трапецию, задана параметрически или уравнениями
вида F). Произведя замену переменной в интеграле G), получим (в предположе-
предположении, что х = а при t = t0 и x = b или t=T):
т	т
y>(t)<pXt)dt.	A3)
'.	t.
Если, например, при вычислении площади эллипса исходить из его пара-
параметрического представления
х = a cos /, y^bsmt
и учесть, что х возрастает от - а до а, когда t убывает от п до 0, то найдем
О	я
Р = 2 6 sin t-{-a sin t)dt = 2ab sin21 dt = nab.
n	0
Мы вычислили здесь площадь верхней половины эллипса и удвоили ее.
9)	Аналогично вычисляется площадь фигуры, ограниченной циклоидой
x = a(f-sinO, у = а{\ -йоъ t). Имеем по формуле A3)
2л
2л
Г	/	1
д2A - cos О2 dt = а1 — t-2smt+ — sin
J	V.2	4
Зла2.
о
Таким образом, искомая площадь оказалась равна утроенной площади обра
зующего круга.
10) Найти площадь одного витка архимедовой спирали г=ав
(рис. 25).
Имеем по формуле (9)
2л
2л 4
о = З"
в то время как площадь круга радиуса 2ла будет Ал3аг. Площадь витка спирали
равна трети площади круга (этот результат был известен еще Архимеду).
Предоставляем читателю показать, что площади фигур, заключенных между
последовательными витками, составляют арифметическую прогрессию с раз-
разностью 8л3а2.
Ш Найти площадь улитки
при

200	гл. х. приложения интегрального исчисления
Имеем по формуле (9)
_ 1
~~2
0 + —a2sin20 + 2a6sin
4
В частности, площадь кардиоиды F = а) равна-™2.
12) Найти площадь лемнискаты г- = 2а2 cos 28.
Рис. 25.
Достаточно удвоить площадь правого овала, которому отвечает
1339
П	71
угла 0 от	до — :
4 4
изменение
i	4
' = 2.-2as j cos29a?0 = 4e2 fcos20dO = 2а2.
13) Найти площадь декартова листа д:+^3-3олг^ = 0.
Перейдем к полярным координатам. Полагая в уравнении кривой
x=rcos6, y
до сокращении на г2 придем к такому полярному уравнению;
За sin б cos 0
sin8 e+cos3 9 '

339]	S 2. ПЛОЩАДИ И ОБЪЕМЫ	201
Так как самый виток кривой отвечает изменишю угла в от 0 до —, то по формуле (9)
я
2
9а2 г sin2 в cos3 в
Р	de
Р	de.
2 J (sin3 0+cos3 0J
о
Заменяя sin в через tg 6 cos 8, приведем подинтегральное выражение к виду
tg2 9d tg 0
(l+tg30J '
откуда сразу находится первообразная функция
1 1	1 cos30
Таким
образом,
3
Р-
l + tg3(
За2
2 si
) 3
COS30
sin3 0+cos3 б
>S30
1 За2
о 2 '
14) Решить задачу 6) наново, воспользовавшись полярными координатами.
Решение. Вводя полярные координаты, представим уравнение A0) эллипса
в виде
1
2
Г	.
A cos2 в + 2В cos 0 sin 0 + Csin20
Тогда по формуле (9) сразу получаем [309, 9)]
Р=9._
J /4cos20 + 2Bcos0sin 0 + Csin2 0
Площадь всего эллипса мы здесь приравняли удвоенной площади той его
части, которая лежит в I и IV координатных углах. Какие затруднения встретились
бы при использовании результата 10) 288 для вычисления непосредственно всей
площади эллипса?
15) Формулу (9) можно приспособить к случаю, когда кривая задана своими
параметрическими уравнениями вида F). Так как
V	.ХУ/ — XtV
r* = x*+y\ 0 = arctg- и В\=—	-,
х	х*+у2
ТО
1	1
-r*dO=-(x/t-xiy)dt.

202	ГЛ X. ПРИЛОЖЕНИЯ ИНТЕГРАЛЬНОГО ИСЧИСЛЕНИЯ	[340
Если изменению угла в от а до [> отвечает изменение параметра t от /0 до Т, то
г	г
'.	t.
Ввиду большей симметричности эта формула зачастую приводит к более простым
выкладкам. Например, если по ней вычислить плошадь эллипса, исходя из
его параметрических уравнений х = a cos t, y = b sin t, то получим
In	2я
1 Г	If
Р = — \{aco&t-bcost >r asm t-bunt) dt = — ab \dt = nab.
о	о
16) Вычислим еще по формуле A4) плошадь астроиды х = а cos3 t, y = asina t.
Имеем
2я
1 г
Р = — [a cos3 «• За sin2 /cos/ + 3acos2 «sin t-asin3t]dt =
о
3 ( sin 40
sin21 cos2 / dt = — а2 Г-
16 I 4 J
о
340. Определение понятия объема. Его свойства. Наподобие того,
как в 335, исходя из понятия площади многоугольника, было уста-
установлено понятие площади для произвольной плоской фигуры, мы
сейчас дадим определение объема тела, опираясь на объем много-
многогранника.
Итак, пусть дано произвольной формы тело (К), т. е. ограничен-
ограниченная замкнутая область в трехмерном пространстве. Границей E) тела
пусть служит замкнутая поверхность* (или несколько таких поверх-
поверхностей).
Мы будем рассматривать многогранники (X) объема X, целиком
содержащиеся в нашем теле, и многогранники (У) объема Y, содер-
содержащие в себе это тело. Существует всегда точная верхняя граница У%
для X и точная нижняя граница V* для Y, причем V* =s V*; их можно
было бы назвать, соответственно, внутренним и внешним
объемами тела.
Если обе границы
совпадают, то их общее значение V называется объемом тела
(У).
В этом случае тело (V) иногда называют кубируемым.
* Мы имеем в виду непрерывную поверхность, допускающую параметрическое
представление.

3401	^ 2. ПЛОЩАДИ И ОБЪЕМЫ	203
И здесь легко видеть, что для существования объема необходимо
и достаточно, чтобы для любого е=»0 нашлись такие два многогран-
многогранника (X) и (У), для которых Y -Х-^е.
Далее:
Если тело (V) разложено на два тела (Fj) и (К2), то из существо-
существования объема для двух из этих трех тел вытекает существование
объема для третьего. При этом
т. е. и объем обладает свойством аддитивности.
Легко перефразировать для объемов и те предложения 1), 2), 3),
которые в 336 были доказаны для площадей.
1) Для того чтобы тело (V) имело объем, необходимо и доста-
достаточно, чтобы существовали такие две последовательности, соответ-
соответственно, входящих и выходящих многогранников {(Хп)} и {(Yn)}, объемы
которых имели бы общий предел
Этот предел и будет объемом тела (F).
Полезно отметить и такое предложение, где вместо многогран-
многогранников фигурируют произвольные тела, заведомо имеющие объемы.
2) Если для тела (V) можно построить такие две последователь-
последовательности, соответственно, входящих и выходящих тел {(Тп)} и {(?/„)},
которые имеют объемы, причем эти объемы стремятся к общему
пределу
то и тело (К) имеет объем, равный упомянутому пределу.
В заключение упомянем о возможности выбирать многогранники,
приближающиеся к рассматриваемому телу, «стандартным» образом.
Заключив тело внутрь некоторого прямоугольного параллелепипеда
(W) с гранями, параллельными координатным плоскостям, разобьем
его на части с помощью ряда плоскостей, параллельных его граням.
Из частичных параллелепипедов, входящих в (V), составим тело (X),
а присоединив к ним и частично выходящие из (F) параллелепипеды,
получим тело Y. Эти тела представляют частные случаи тех много-
многогранников (X) и (У), о которых была речь выше. Будем обозначать
через d наибольшую из диагоналей тех прямоугольных параллеле-
параллелепипедов, на которые был разложен параллелепипед (W).
3) Если при d^-О оба объема X и Y стремятся к общему пределу
V и только в этом случае тело (V) будет иметь объем;
при выполнении этого условия упомянутый предел и выразит объем
тела (V).
Доказательство всех этих утверждений мы предоставляем чита-
читателю; их легко скопировать с рассуждений п° 336-

342]
2. ПЛОЩАДИ И ОБЪЕМЫ
205
окружить точку (и, v) на плоскости uv такой окрестностью
а = (и - д, и + д; v-8, v + S),
чтобы соответствующий участок поверхности выражался явным урав-
уравнением. Остается лишь применить к замкнутой области (Q) и к по-
покрывающей ее системе окрестностей J? = М лемму Б о р е л я [175],
чтобы установить возможность разложения рассматриваемой глад-
гладкой поверхности на конечное число частей, каждая из которых выра-
выражается явным уравнением одного из трех типов. Отсюда - по преды-
предыдущему - следует, что гладкая поверхность имеет
объем 0.
Теперь ясно, что
тело, ограниченное одной или несколькими гладкими поверхностями,
заведомо имеет объем.
Допустимо, впрочем, и наличие на ограничивающей тело поверх-
поверхности конечного числа особых точек, которые могут быть выде-
выделены окрестностями с произвольно малым объемом.
342. Выражение объема интегралом. Начнем с почти очевидного
замечания: прямой цилиндр высоты Н, основанием которого служит
квадрируемая плоская фигура (Р), имеет объем, равный произ-
произведению площади основания на высоту: V=PH.
Рис. 26.
Возьмем [336, 1)] многоугольники (Ап) и (ДО, соответственно со-
содержащиеся в (Р) и содержащие в себе (Р), так, чтобы их площади
Ап и Вп стремились к Р. Если на этих многоугольниках построить
прямые призмы (Хп) и (Yn) высоты Н, то их объемы
Хп=АпН и Yn=BnH
будут стремиться к общему пределу V=PH, который в силу 1) п° 340
и будет объемом нашего цилиндра.
Рассмотрим теперь (рис. 26) некоторое тело (F), содержащееся
между плоскостями х = а и х = Ь, и станем рассекать его плоскостями,

342]
2. ПЛОЩАДИ И ОБЪЕМЫ
205
окружить точку (и, v) на плоскости uv такой окрестностью
а = (и - д, и + д; v-8, v + S),
чтобы соответствующий участок поверхности выражался явным урав-
уравнением. Остается лишь применить к замкнутой области (Q) и к по-
покрывающей ее системе окрестностей ]? = {а} лемму Б о р е л я [175],
чтобы установить возможность разложения рассматриваемой глад-
гладкой поверхности на конечное число частей, каждая из которых выра-
выражается явным уравнением одного из трех типов. Отсюда - по преды-
предыдущему - следует, что гладкая поверхность имеет
объем 0.
Теперь ясно, что
тело, ограниченное одной или несколькими гладкими поверхностями,
заведомо имеет объем.
Допустимо, впрочем, и наличие на ограничивающей тело поверх-
поверхности конечного числа особых точек, которые могут быть выде-
выделены окрестностями с произвольно малым объемом.
342. Выражение объема интегралом. Начнем с почти очевидного
замечания: прямой цилиндр высоты Н, основанием которого служит
квадрируемая плоская фигура (Р), имеет объем, равный произ-
произведению площади основания на высоту: V=PH.
Рис. 26.
Возьмем [336, 1)] многоугольники (Ап) и (!?„), соответственно со-
содержащиеся в (Р) и содержащие в себе (Р), так, чтобы их площади
Ап и Вп стремились к Р. Если на этих многоугольниках построить
прямые призмы (Хп) и (Yn) высоты Н, то их объемы
будут стремиться к общему пределу V=PH, который в силу 1) п° 340
и будет объемом нашего цилиндра.
Рассмотрим теперь (рис. 26) некоторое тело (F), содержащееся
между плоскостями х = а и х = Ь, и станем рассекать его плоскостями,

206
ГЛ. X. ПРИЛОЖЕНИЯ ИНТЕГРАЛЬНОГО ИСЧИСЛЕНИЯ
1342
перпендикулярными к оси х. Допустим, что все эти сечения к в а д-
р и р у е м ы, и пусть площадь сечения, отвечающего абсциссе х,
- обозначим ее через Р(х) - будет непрерывной функцией от х (для
)
Если спроектировать (без искажения) два подобных сечения на
какую-либо плоскость, перпендикулярную к оси х, то они могут либо
содержаться одно в другом (как на рис. 27, а), либо частично одно
на другое налегать или лежать одно вне другого (см. рис. 27, б, в).
Рис. 27.
Мы остановимся сначала на том случае, когда два различных се-
сечения, будучи спроектированы на плоскость, перпендикулярную к оси
х, оказываются всегда содержащимися одно в
другом.
В этом предположении можно утверждать, что тело (V) имеет
объем, который выражается формулой
V=
A5)
Для доказательства разобьем отрезок [а, Ь] на оси х точками
на части и разложим плоскостями х ¦-*,-, проведенными через точки
деления, все тело на слои. Рассмотрим /-й слой, содержащийся между
плоскостями
х = Х(Пх = х!+1 (i = 0, 1, ..., п~ 1).
В промежутке [xt, xi+1] функция Р(х) имеет наибольшее значение Mt
и наименьшее значение от,; если сечения, отвечающие различным зна-
значениям х в этом промежутке, поместить на одну плоскость, скажем,
x = xt, то все они (при сделанном предположении) будут содержаться
в наибольшем, имеющем площадь Л/,-, и содержать в себе наимень-
наименьшее, с площадью w,-. Если на этих, наибольшем и наименьшем, се-
сечениях построить прямые цилиндры высоты Axj--=xi+1-xh то боль-
больший из них будет содержать в себе рассматриваемый слой нашего
тела, а меньший сам будет содержаться в этом слое. На основании

342J
§ 2. ПЛОЩАДИ И ОБЪЕМЫ
207
сделанного вначале замечания объемы этих цилиндров будут, соот-
соответственно, MtAxt и nijAxj.
Из входящих цилиндров составится тело (Г), а из выходящих -
тело (?/); их объемы равны,
соответственно,
и, когда стремится к нулю
А = max Ax[, имеют общий пре-
предел A5). В силу 340, 2) таков
же будет и объем тела (К)*.
Важный частный случай,
когда заведомо выполняется
указанное выше предположе-
предположение о взаимном расположении
сечений, представляют тела
вращения. Вообразим на
плоскости ху кривую, задан-
заданную уравнением j = /(x) (a=s
=е;с=ег6), где f(x) непрерывна и
неотрицательна; станем вра-
вращать ограниченную ею криво-
криволинейную трапецию вокруг оси
х (рис. 28, а и б). Полученное
тело (F), очевидно, подходит под рассматриваемый случай, ибо сече-
сечения его проектируются на перпендикулярную к оси х плоскость в виде
концентрических кругов. Здесь
Рис. 28.
так что
V=n\fdx=n\[f(x)]2dx.
A6)
Если криволинейная трапеция ограничена и снизу и сверху кри-
кривыми y1 = fi(.x) и у2 = /2{х), то, очевидно,
ь	ь
?} dx,
A7)
хотя предположение о сечениях здесь может и не выполняться. Во-
Вообще доказанный результат легко распространяется на все такие тела,
* Деля, например, промежуток на равные части, легко выделить те после-
последовательности входящих и выходящих тел, о которых говорится в цитиро-
цитированном предложении.

208
ГЛ. X. ПРИЛОЖЕНИЯ ИНТЕГРАЛЬНОГО ИСЧИСЛЕНИЯ
[343
которые получаются путем сложения или вычитания из тел, удовлет-
удовлетворяющих упомянутому предположению.
В общем случае можно утверждать лишь следующее: если тело
(V) имеет объем*, то он выражается формулой A5).
В самом деле, задавшись произвольным е>0, мы можем между
плоскостями х — а и х = Ъ построить такие два тела, [X) и (У), с о-
ставленные из параллелепипедов, чтобы первое со-
содержалось в (F), а второе содержало в себе (К), и притом бьшо Y-X^e.
Так как к этим телам формула наша, очевидно, приложима, то, обо-
обозначив через А{х) и В(х) площади их поперечных сечений, будем иметь
X =
ь	ь
JA(x) dx, Y= JB(x) dx.
С другой стороны, так как A(x)=sP(x)=sB(x), то и
P(x
B(x) dx = Y,
так что объем V и интеграл j P(x) dx оба содержатся между одними
и теми же границами X и Y,
разнящимися меньше, чем на е.
Отсюда и вытекает требуемое за-
заключение.
О
343. Примеры. 1) Вычислить объем
V кругового конуса с радиу-
радиусом основания г и высотой h.
Проведем через ось конуса секу-
секущую плоскость и выберем эту ось за
ось х, считая начальной точкой вер-
вершину конуса; ось у проведем перпендикулярно к оси конуса (рис. 29). Уравнение
образующей конуса будет
г
Рис,
и - по формуле A6) - получим
\\—х\ dx =
J \h j	IP 3
Результат этот известен читателю из школьного курса.
* Так будет, например, если тело ограничено одной или несколькими глад-
гладкими поверхностями [341].

343]	§ 2. ПЛОЩАДИ И ОБЪЕМЫ	209
х^ v^
2) Пусть эллипс —I—=1 вращается вокруг оси х. Так как
а2 Ь%
б2
;у2 = --(а2-л:2),
а2
то для объема эллипсоида вращения найдем
г Ь2	б2 г	ь% (
Jfl!	а2 J	вЧ
х3\ Iя 4
3 j о 3
Аналогично для объема тела, полученного от вращения вокруг оси у, найдем
4
выражение — жагЬ. Предполагая же в этих формулах а = 6 = г, мы получим для
4
объема шара радиуса г известное значение ~пг3.
3)	Определить объем тела, полученного от вращения цепной линии
х
у = a ch — вокруг оси х, между сечениями, соответствующими точкам 0 и х.
а
Имеем
с х 1 г( 2х\
У=ла*\ ch*-dx = -na4 1 + ch— <fe =
J a 2 J \	a J
о	о
1	/ a 2x) 1 I	x	x\
= —яа2 |л: + — sh — \= — ла ал: fa ch — -a sh — .
2	{ 2 a) 2 {	a	a)
X
Вспоминая [331, 1)], что ash— есть длина дуги s нашей кривой, окончательно
a
получим
V = — ла(ах+sy).
4)	То же - для ветви циклоиды
* = a(f-sin/), j> = a(l-cosO @=в?ае2я).
Параметрические уравнения кривой облегчают выполнение подстановки
* = a(f-sinO> dx = a(l - cos t)dt в формуле
2ла
y*dx.
о
Именно:
2л
У=ла3 I (I -cosГ)аdt=ntP I — f-4sinH—sin lt + — sin3
J	\2	4	3
И Г. М. Фихтенголъц, т. II

210	ГЛ. X. ПРИЛОЖЕНИЯ ИНТЕГРАЛЬНОГО ИСЧИСЛЕНИЯ	{343
L L L
5) То же для астроиды х3 +у* = а3.
Имеем
г/
J
-\3 32
In	1 |Z	т>	lid	Oil	1
y=\a3 -Xя/ , V=n \cr -Xs/ dx =	na3.
\	I	\\	7	Ю5
Предлагается повторить вычисления, исходя из параметрических уравнений
астроиды и прибегнув к замене переменной (как в предыдущей задаче).
6) Найти объем общей части параболоида 2аг=хг+у* и сферы
y
Решение. Вместе с обоими этими телами и общая часть их будет телом
вращения вокруг оси z. Пересечение указанных поверхностей происходит
по плоскости z = a.
Плоскости, перпендикулярные к оси z, пересекают рассматриваемое тело по
кругам; квадраты радиусов этих кругов равны 2az, пока z=sa, и 3a2-z2, лишь
только z становится >а. Пользуясь формулой, аналогичной A6), будем иметь
а	а Уз"
К=2ла [zdz+n j Ca2-z2)<fe = —(бУЗ-5).
О	а
7) Найти объем общей части сферы x2+y2+z2 = R2 и конуса xz = y*+z2
(xs*0).
R
Указание. Пересечение поверхностей происходит по плоскости х = —^.
У2
Имеем
R
Уг"	r
=л x*dx+n \(R--x2) dx =	B- ]/2).
О	_R_
yf
До сих пор мы рассматривали примеры применения частной формулы A6).
Перейдем теперь к общей формуле A5). Так как самое существование
объема во всех случаях легко может быть обосновано, например, исходя из со-
соображений п° 341, то мы на этом останавливаться не будем и займемся лишь
вычислением объема.
8) Определить объем цилиндрического отрезка. Так называют
геометрическое тело, отсекаемое от прямого кругового цилиндра плоскостью,
проходящей через диаметр основания (рис. 30).
Положим, что основание цилиндра есть круг радиуса а:
и что секущая плоскость проходит через диаметр А А' и составляет угол а с пло-
плоскостью основания. Определим площадь сечения, перпендикулярного к оси х
и пересекающего ее в точке М(х). Это сечение будет прямоугольным тре-
треугольником; очевидно,
Р(х) = пл. MNP = — у- tg а = — (аг - х") tg а,

343)
§ 2. ПЛОЩАДИ И ОБЪЕМЫ
211
так что по формуле A5)
If
К= —tga Uai-
2	2
= — a3tga = — a2h,
где h = KL есть высота цилиндрического отрезка.
Интересно отметить, что тот же объем можно было бы получить, заставив
ось у играть ту роль, какую до сих пор играла ось х, т. е. рассекая тело плоскостя-
плоскостями, перпендикулярными оси у (рис. 31). Такая плоскость, проведенная через точку
Рис. 30.
Рис. 31.
М с ординатой у, пересечет наше тело по прямоугольнику SQ, площадь
которого будет
Р(у) = 2ху tg a = 2 tg a-yftf-y2.
Поэтому, аналогично A5),
= 2 tg а Ufa2 - уг dy = — tg a(a2 -
2
= — a3 tga.
о 3
9) Найти объем трехосного эллипсоида, заданного каноническим урав-
уравнением
а2 Ъг с2
(рис. 32).
Плоскость, перпендикулярная к оси х и проходящая через точку М(х) на этой
оси, пересечет эллипсоид по эллипсу; уравнение проекции его (без искажения)
на плоскость yz будет таково:
-(¦-ЗЧ-г)
= const).
Отсюда ясно, что полуоси его будут, соответственно,
И*

212	ГЛ. X. ПРИЛОЖЕНИЯ ИНТЕГРАЛЬНОГО ИСЧИСЛЕНИЯ
а площадь [см. 339, 2), 8), 15)] выразится так:
/ х2\ nbc
Р(х) = лЬс 1 - - =	(а2-*2).
V аг) а2
Таким образом, по формуле A5) искомый объем
а
жЬс с	. 4
C43
жос (¦	4
I' =	 (а2 - л-2) а"* = — Tiabc.
аг J	3
10) Найти объем эллипсоида, отнесенного к центру,
А х2 + 2Вху + Сгг + 2Fyz+IGzx+2Hxy = 1.
Z1
Рис. 32.
Решение. Если фиксировать z, то уравнение соответствующего сечения
(или - вернее - его проекции на плоскость ху) будет
ахг + 2Ьху+ су* + 2dx+2ey+f= О,
где положено
По 339, 7), площадь этого сечения равна
пА*
(АВ-Ю)'г
если через /1* обозначить определитель
^ Я й
Н В Fz =Az*-(AB-H2),
Gz Fz Сгг-\
A H G
H В F
где
Подставляя, получим
G F С
(АВ-Н"K'°-

343]
§ 2. ПЛОЩАДИ И ОБЪЕМЫ
213
Очевидно, г может изменяться лишь в пределах
от -
ГАВ-Н*
	д0
Л
АВ-Н-
	;
А
интегрируя в этих пределах, найдем окончательно
4 1
3 1/^|
11) Рассмотрим два круговых цилиндра радиуса г, оси которых пересекаются
под прямым углом, и определим объем тела, ограниченного ими.
Тело OABCD, изображенное на рисунке 33, составляет восьмую часть интере-
интересующего нас тела. Ось х проведем через точку О пересечения осей цилиндров
перпендикулярно к обеим осям. Тогда в
сечении тела OABCD плоскостью, проведен-
проведенной на расстоянии х от О, перпендикулярно
к оси х, получится квадрат KLMN, сто-
сторона которого MN= 1/г2-х2, так что Р(х) =
= гг-хг. Тогда по формуле A5)
J
16
12) Решим, в заключение, ту же задачу,
но в предположении, что цилиндры имеют
различные радиусы: г и R =- г.
Разница, по сравнению с прежним, будет
лишь в том, что, вместо квадрата, в сечении
рассматриваемого тела плоскостью на рас-
стоянии х от О получится прямоуголь-
прямоугольник со сторонами Уг% - ха и
б	б
Рис. 33.
У	У2 - хг. Таким
образом, в этом случае объем V выразится уже эллиптическим инте-
интегралом
V= 8
*-*") dx
или, если сделать подстановку jc=/-sirup и положить к = —,
R
К= 8Rra f cos2у ¦ уГ-~к*Щп*<р d<f = 8Яг2 • /.
О
Займемся сведением интеграла / к полным эллиптическим интегралам обоих
видов. Прежде всего
q> cos2 a
С cos3 rp	Г sin2 q> cos
/=	— dp - k*	y
J yi-k2sin'p	Jy\-k2sm

214	ГЛ. X. ПРИЛОЖЕНИЯ ИНТЕГРАЛЬНОГО ИСЧИСЛЕНИЯ	[344
Но
л	л
2	2
j= —	- d<p= -¦ - -
J Vl-k*sm*(p	k2 J 1
d(p
0
С другой стороны, интегрируя по частям, имеем
1 |>	I 1 ~1	1
— У\ - k*sm*<p d<p= I - — К (к) + — Е(Л).
Л2 J	\ A:2 J	А:2
24Jsir
1
= — sin у |/l-A:2sm2<p
2-
- cos 2<p ¦ Vl - к2 sin2® dip = I (
J	'	r r J
О	о
Отсюда
Таким образом, окончательно
к- !^ Ki+*») е да - A - *•) к да].
344. Площадь поверхности вращения. Пусть имеем на плоскости
ху (именно, в верхней полуплоскости) некоторую кривую АВ (рис. 34),
заданную уравнениями вида F), где у, у - непрерывные функции с
непрерывными же производными <р', \р'. Предполагая отсутствие осо-
особых и кратных точек на кривой, мы можем ввести в качестве пара-
параметра дугу s, отсчитываемую от точки A(t^), и перейти к представ-
представлению
х = Ф(я), y = W(s).	A8)
Параметр s изменяется здесь от 0 до S, если через S обозначить длину
всей кривой АВ.
Если вращать кривую вокруг оси х, то она опишет некоторую
поверхность вращения. Поставим своей задачей - вычи-
вычислить площадь этой поверхности.
Мы лишены возможности установить здесь в общем виде понятие
площади «кривой» (т. е. н е п л о с к о й) поверхности; это будет еде-

344]
§ 2. ПЛОЩАДИ И ОБЪЕМЫ
215
лано в третьем томе. Сейчас же мы определим это понятие специ-
специально для поверхности вращения и научимся вычислять ее площадь,
причем будем исходить из данных еще в школьном курсе правил вы-
вычисления боковых поверхностей цилиндра, конуса и усеченного ко-
конуса. Впоследствии мы убедимся, что полученная нами формула вхо-
входит как частный случай в общую формулу для площади кривой поверх-
поверхности.
Возьмем на кривой АВ в направлении от А к В ряд точек (см.
рис. 34)
и рассмотрим ломаную ААХ.. .Ап^В, вписанную в кривую. Станем
вместе с кривой вращать вокруг оси х эту ломаную; она опишет
некоторую поверхность, площадь которой мы умеем определять по
правилам элементарной геоме-
геометрии. Условимся под пло-
площадью поверхности, опи-
описанной кривой, разуметь
предел Р площади Q по-
поверхности, описанной
ломаною, при стремлении к
нулю наибольшей из частичных
дуг. Это определение площади
поверхности вращения дает нам
ключ к ее вычислению.
Мы уже знаем, что ряд то-
точек A9) может быть получен, ис-
исходя из ряда возрастающих значений s, вставленных между 0 и S:
0 = 5'0< JX<J2< . . . <.У,<.У,+1< . . . ^Sn-1<Sn = S.
Каждое звено ломаной при вращении вокруг оси х будет описывать
поверхность усеченного конуса*. Если обозначить ординаты точек
Aj и Ai+1 соответственно через yt и j,+1, а длину звена AtAi+1 через
/,, то площадь поверхности, описываемой i-u звеном, будет
х
Рис. 34.
Площадь же поверхности, описываемой всей ломаной линией, будет
л-1
(=0
i + УНг
* В частности, эта поверхность может выродиться в поверхность конуса или
цилиндра; площадь ее, однако, и в этом случае можно вычислить по общей формуле
для поверхности усеченного конуса.

216
ГЛ. X. ПРИЛОЖЕНИЯ ИНТЕГРАЛЬНОГО ИСЧИСЛЕНИЯ
[344
Полученную сумму можно разбить на две суммы следующим образом:
Q = Ъг  yih +п (J«+i-ydh¦
( = 0	1=0
Так как функция y = W(s) непрерывна, то (по свойству равномер-
равномерной непрерывности) можно предположить нашу кривую разложен-
разложенной на столь мелкие части, что все разности yt+1-yi по абсолютной
величине не превзойдут произвольно малого положительного числа е.
Тогда
л-1
( = 0
л-1
2
i=0
отсюда следует, что эта сумма стремится к нулю при max As(-*O.
Что касается суммы:
л— 1
2ж 2 yih,
о
то ее можно разложить на две суммы:
Ъг
2
= 0
yL Ast - In 5 y,{ds, - /,).
Так как функция W(s) непрерывна, то она ограничена, так что все
|j,|=sM, где М - некоторое постоянное число. Обозначая послед-
последнюю сумму через т, имеем
¦¦2л
л-1
-.2nM\S-2h\-
2
При дроблении кривой на все более и более мелкие части раз-
разность
л-1
s- 2 it,
1=0
по определению длины дуги, как предела периметра вписанной ло-
ломаной*, должна стремиться к нулю. Но тогда и т-»0.
Оставшаяся сумма
л-1
а = 2я 2 У1 Asi
1 = 0
* Это непосредственно следует из определения лишь для простой незам-
незамкнутой кривой, но затем легко получается и для простой замкнутой кри-
кривой, путем разложения на две незамкнутые кривые.

345]	§ 2. ПЛОЩАДИ И ОБЪЕМЫ	217
является интегральной суммой для интеграла
s
2я J у ds,
о
который вследствие непрерывности функции у = W(s) существует, так
что при maxz1s,—0 сумма а стремится к этому интегралу.
Мы получаем окончательно, что - при сделанных предположе-
предположениях - площадь поверхности вращения существует и выражается фор-
формулой
S	S
j	^(s)ds.	B0)
Если вернуться к общему параметрическому заданию F) нашей
кривой, то, произведя в предшествующем интеграле замену пере-
переменной [см. 313, (9)], преобразуем его к виду
т	т
Р = 27i$yfx't*+y't2 dt = 2л jf(t)Y\^pr(iW^W(tW dt.	B1)
'•	и
В частности, если кривая задана явным уравнением у = f(x) (a*&x*sb),
так что в роли параметра оказывается х, будем иметь
(x)Yl + [f'(x)fdx.	B2)
345. Примеры. 1) Определить площадь поверхности шарового пояса.
Пусть полукруг, описанный около начала радиусом г, вращается вокруг оси х.
Из уравнения круга имеем у = \г*-хг; далее,
Ух
В таком случае площадь поверхности пояса, описанного дугой, концы которой
имеют абсциссы xt и дг2=»л-1( по формуле B2) будет
г\
2пг{х„ - хх) =
где А есть высота пояса. Таким образом, площадь поверхности шарового пояса
равна произведению окружности большого круга на высоту пояса.
В частности, при хг = - г, х2 = г, т. е. при h = 2r, получаем площадь всей шаровой
поверхности Р=Апгг.
2) Найти площадь поверхности, образованной вращением дуги цепной
линии y = ach —, концы которой имеют абсциссы 0 и х.
а

218	ГЛ. X. ПРИЛОЖЕНИЯ ИНТЕГРАЛЬНОГО ИСЧИСЛЕНИЯ	[345
Так как \ \+у'х =сЬ. —, то по формуле B2)
я Ich2- dx = -V,
j a	a
где V - объем соответствующего тела вращения [см. 343, 3)].
3) То же для астроиды х = а cos3 /, у = a sin31.
Достаточно удвоить площадь поверхности, описанной дугой астроиды, лежа-
(	л\
щей в 1 квадранте lO^s/^— I . Мы имели уже
Уx^+y't* = ~iasm f cos t;
в таком случае по формуле B1)
sin5/
л 12
г a sin3 /¦ За sin /cos /Л = 12яа2 sin4 /cos tdt=12nefi
J	J	5 о 5
4) To же для циклоиды x = a(z-sin /), y = a(l-cos/)-
/	/
Так как у = 2а sin2 —, ds = la sin — dt, то
2л
" 64
С / г /"cos3 и	\
Р=2л 4a2sin3 —Л=16яа2 sin8 и du = 1 бяа2	cos и
= — яа*.
О 3
5) Найти площадь поверхности, образованной вращением кардиоиды
a(l+cos0) вокруг полярной оси.
Следует в основной формуле B1) перейти к полярным координатам:
S	/3
yds = 2n{rsmey7*Tifd6-	B3)
О	a
В нашем случае <х = 0, /? = л, и
во	о
y=rsind = аA +cos б) sin в = 4a cos3 — sin — , rfs = 2а cos — rfO,
поэтому
Г 0 0	32
= 2л ¦ 8а2 cos4 —	sin — dO^ — na*.
J 2 3	5
о

345]	§ 2. ПЛОЩАДИ И ОБЪЕМЫ	219
6) То же для лемнискаты r2 = 2Ф cos 26.
ау2
Здесь у = а ]/2 ]/cos 26 sin 0, ds = - ¦ dd, так что по формуле B3)
Vcos29
4
Г
\2\
— L=7,361e2.
о
Наконец,
7) определим поверхность эллипсоида вращения как вытянутого,
так и сжатого (сфероида).
х2 у*
Если эллипс —I— = 1 вращается вокруг оси х, и а>Ь, то имеем последо-
а2 Ьг
вательно
Ъ2	Ь2
у> = Ь>— х\ у/= — х,
а2	а2
+ (у/У = I/ Ь*-- х2 + -х2 = - ]Га* -
I/	2 4
a2
Но а" - bz = с2, где с - расстояние фокуса от центра и — равно эксцентриситету
а
к эллипса. Таким образом,
	 Ь
а
П ,,	 а2	гл;
— д: Va8-e2x2H—arcsin —
V2	2e	a
= 2я — (а Уаг-г2л2+а2 arc sin e);
но в2 - f 2в2 = в2 - с2 = б2, так что окончательно имеем
/¦ а	^
Р = 2пЬ\ЬЛ—arc sine .
Если эллипс вращается вокруг малой оси, то для того, чтобы удобнее было
воспользоваться уже произведенными выкладками, мы будем считать, что ось
х и служит малой осью. Тогда в полученном для у у\ +у'% выражении нужно лишь
обменять а и Ъ местами, так что теперь
а "I/ а2-Ьг а
Ь /	Ь2	Ь

220	ГЛ. X. ПРИЛОЖЕНИЯ ИНТЕГРАЛЬНОГО ИСЧИСЛЕНИЯ
в таком случае
[346
с=?а, так что окончательное выражение для Р будет такое
( Ь* , а+с\ „ /" б2 1 И-еЛ
Р=2па \а+— In	=2м о+	In	 .
V 2с а-с)	[ 2а е 1-е)
346. Площадь цилиндрической поверхности. Рассмотрим еще один
частный тип кривой поверхности, для которой мы также здесь
определим понятие площади {предвосхищая то общее определе-
определение, которое будет дано лишь впоследствии). Мы имеем в виду ци-
цилиндрическую поверхность.
Вернемся к кривой АВ на плоскости ху, о которой была речь в 344.
Приняв ее за направляющую, представим себе цилиндрическую по-
поверхность с образующими, параллельными оси z (рис. 35). По этой
поверхности проведем кривую CD, которая с каждой образующей
пересекается в одной точке; эта кривая определится, если к уравне-
уравнениям F) присоединить еще третье
(Х-0).	B4)

346)	§ 1. ПЛОЩАДИ И ОБЪЕМЬ!	221
Речь идет о вычислении площади Р части цилиндрической поверх-
поверхности «под этой кривой».
Как и в п° 344, введем дугу s в качестве параметра; тогда не только
уравнения F) кривой АВ заменятся уравнениями A8), но и уравнение
B4) перейдет в
z = X(s).
Вписав в кривую АВ ломаную ААХ ... Ап_гВ и, в соответствии с этим,
в кривую CD - ломаную CQ ... Сп-хТ> (см. рисунок), из трапеций
AjAi+1Ci+1Ci составим призматическую поверхность, вписанную в рас-
рассматриваемую цилиндрическую поверхность. Под площадью
этой последней будем понимать здесь предел Р
площади Q упомянутой призматической поверх-
поверхности при стремлении к нулю наибольшей из частичных дуг.
Полагая z,=y4,Q, имеем (сохраняя в остальном прежние обозна-
обозначения)
С помощью таких же соображений, что и в 344 (провести их пол-
полностью читатель сможет сам), вопрос приводится к вычислению пре-
предела суммы
л-1
в которой легко узнать интегральную сумму. Окончательно*
s	s
Возвращаясь к произвольному параметру /, легко получить и об-
общую формулу
Р = jzYtfTy? A = J Х@ YWWWUW*.	B5)
Наконец, для случая явного задания кривой А В: j=/(x)
эта формула перепишется так:
B6)
* Этот результат становится совершенно наглядным, если представить себе
цилиндрическую поверхность развернутой по плоскости, так что рассматриваемая
фигура превратится в «криволинейную трапецию».

212
ГЛ. X. ПРИЛОЖЕНИЯ ИНТЕГРАЛЬНОГО ИСЧИСЛЕНИЯ
[347
347. Примеры. 1) Пусть на рис. 36 кривая АВ представляет собой параболу
с вершиной в точке В. Ее уравнение (при обозначениях рисунка)
Ьх*
у = Ь	-.
а2
Построенная на ней цилиндрическая поверхность пересечена плоскостью ОВС
с уравнением
с
z= -х.
а
Найти площадь Р части ABC цилиндрической поверхности.
Решение. По формуле B6)
= {zfiW2dx = -a [хуа
2) Если кривая АВ будет четвертью окружности у = ]/а2 - х2 @=s x =s. а), то восполь-
воспользоваться формулой B6) - безоговорочно - нельзя, ибо при х^а производная
Рис. 36.
ух обращается в °°. Прибегнув к параметрическому представлению
x = acost, y
мы по общей формуле B5) будем иметь
2 Ж = ас icostdt^ac.
Если вернуться к цилиндрическому отрезку, о котором была
речь в 343, 8), то боковая поверхность его, как следует из полученного только
что результата, окажется равной 2оЛ (с = А).
3) Наконец, решим ту же задачу в предположении, что кривой АВ будет чет-
четверть эллипса
х = a cos Л y = bsint 0=s/=s — .

347|	§ 1 ПЛОЩАДИ И ОБЪЕМЫ	223
[Явным уравнением здесь не следует пользоваться по той же причине, что
и выше].
(а) Пусть сначала а =- Ь. Вводя эксцентриситет в =	эллипса по формуле
а
B5), получим
л
2	а
Р=с Г cos t fa2 sin21 + b2 cos2 / dt = — j Yb2+e2u2~du
о	о
(подстановка « = asinO. и окончательно
1-Е2 1+61
2 I 2e
}
(б) В случае e-=Z>, эксцентриситет е = -
In	\.
1-е/
P = 6c Г yi-?2sinz/ cosr & = — jyi-еЧ— arcsinej.
о
4) Рассмотрим часть цилиндрической поверхности хг+у2 = Ях, ограниченной
сферой хг+у2+z2 = Л2; кривая, получающаяся в пересечении [кривая В и в и а н и ,
229, 1)], как мы знаем, может быть представлена параметрически так:
х = R sin2 /, у = R sin t cos t, z = R cos /.
Если ограничиться первым октантом, то / здесь надлежит изменять от 0 до —.
Очевидно, первые два уравнения играют роль уравнений (б), а последнее - уравне-
уравнения B4).
Площадь упомянутой поверхности по формуле B5) будет
5) Определить площадь поверхности тела, общего двум цилиндрам радиуса г,
оси которых пересекаются под прямым углом [ср. 343,11)]. Введем систему коорди-
координат, как на рис. 33.
Ограничиваясь одной из цилиндрических поверхностей, для первого октанта
имеем
х = г cos ?, у - г sin /
и, наконец,
По формуле B5) половина искомой площади равна
—) .
sin

114	ГЛ. X. ПРИЛОЖЕНИЯ ИНТЕГРАЛЬНОГО ИСЧИСЛЕНИЯ	|347
6) Та же задача - но для случая, когда цилиндры имеют различные радиусы
/• и R^r [ср. 343, 12)].
Вычислим сначала площадь части цилиндрической поверхности радиуса г.
Имеем
x-rsmt, у = г cost
z = YR*^x* = yR*-r2sirtl = R ]Al - Jt2 sin2 /
По формуле B5)
(	п\
j к = -) .
i = 8Rr f fl - к" ske~t dt = 8ЯгЕ (к).
о
Обращаясь теперь к цилиндрической поверхности радиуса R, обменяем ролями
ось z и ось у. На этот раз
x = Rsint, z^Rcosr,
причем / может изменяться (если, как всегда, ограничиться первым октантом)
лишь от 0 до arcsin к. Тогда, по формуле, аналогичной B5), получим
arcsin A-	arcsin к
"к*'
О
Подстановка
к cosy d<p
yYx',2 + z?dt = 8Rr
sin f = k sin <p,
71
где у изменяется от 0 до —, дает
arcsin к
J
о	о
С последним интегралом мы уже встречались в 343, 12); он равен
(l-i
Таким образом,
рг-.
Окончательно
- A - к)Щк)}.
Этим исчерпываются простейшие геометрические приложения опре-
определенного интеграла. С вычислением геометрических протяжений в бо-
более сложных и более общих случаях мы встретимся в третьем томе.

348J
§ 3. ВЫЧИСЛЕНИЕ МЕХАНИЧЕСКИХ ВЕЛИЧИН
225
§ 3. Вычисление механических и физических величин
348. Схема применения определенного интеграла. Прежде чем перейти
к применениям определенного интеграла в области механики, физики
и техники, полезно наперед уяснить себе тот путь, по которому в
прикладных вопросах обычно приходят к определенному интегралу.
С этой целью мы набросаем об-
общую схему применения интеграла,
иллюстрируя ее примерами уже из-
изученных геометрических задач.
Вообразим, что требуется опре-
определить некоторую постоянную ве-
величину Q (геометрическую или иную)
связанную спромежутком
[а, Ь]. При этом пусть каждому час-
частичному промежутку [а, /?], содержа-
содержащемуся в [а, Ь], отвечает некоторая
часть величины Q так, что разло-
разложение промежутка [а, Ь] на частич-
частичные промежутки влечет за собой
разложение на соответствующие ча-
части и величины Q.
Точнее говоря, речь идет о не-
некоторой «функции от промежутка»
?№> Д]), обладающей «свойством
аддитивности»; это значит, что, если промежуток [а, /3] состоит из
частичных промежутков [ос, у] и [у, /5], то тогда и
Задача же состоит в вычислении ее значения, отвечающего всему про-
промежутку [а, Ь].
Для примера возьмем на плоскости кривую y=f(x) (a=sx=«6) (рис. 37)*. Тогда
1) длина S кривой АВ, 2) площадь Р ограниченной ею криволинейной
трапеции АА'В'В иЗ) объем V тела, полученного от вращения этой трапеции
вокруг оси х, - все три являются величинами указанного типа. Нетрудно дать
себе отчет в том, какие «функции от промежутка» ими порождаются.
Рассмотрим «элемент» AQ величины Q, отвечающий «элементар-
«элементарному промежутку» [х, х + Ах]. Исходя из условий вопроса, стараются
найти для AQ приближенное выражение вида q{x) Ax, линейное от-
относительно Ах, так чтобы оно разнилось от AQ разве лишь на бес-
* Функция f(x) предполагается непрерывной и имеющей непрерывную произ-
производную. Для определенности мы допустим, что кривая все время идет вверх
и выпукла вниз.
15 Г. М. Фихтенгольп. т. II

226	ГЛ. X. ПРИЛОЖЕНИЯ ИНТЕГРАЛЬНОГО ИСЧИСЛЕНИЯ	[348
конечно малую порядка высшего, чем Ах. Иными словами, из бес-
бесконечно малого {при zlx-*0) «элемента» AQ выделяют его главную
часть. Ясно, что тогда относительная погрешность приближенного
равенства
AQ~q(x)Ax	A)
будет стремиться к нулю вместе с Ах.
Так, в примере 1) элемент дуги MMt можно заменить отрезком касательной
МК, так что из AS выделяется линейная часть
'х2 Ах = ]/1 + [/Хх)]2 Лх.
В примере 2) естественно заменить элементарную полоску АР входящим прямо-
прямоугольником с площадью
у Ах = fix) Ах.
Наконец, в примере 3) из элементарного слоя AV выделяется его главная часть
в виде входящего кругового цилиндра, с объемом
яу* Ax=>n[f(x)\* Ах.
Во всех трех случаях нетрудно показать, что погрешность от такой замены
будет бесконечно малой высшего порядка, чем Лх. Именно*, в случае 1) она будет
меньше КМЛ = Ау - dy, в случае 2) - меньше Лх Лу, а в случае 3) - меньше
лBу + Ау) Ах Лу.
Лишь только это сделано, можно уже утверждать, что искомая
величина Q точно выражается интегралом
ъ
B)
а
Для пояснения этого разложим промежуток [а, Ь] точками хг,х2, ...
..., х„_1 на элементарные промежутки
[a, xj, [*!, х2], ..., [xh хш], ..., [хп_:, Ъ].
Так как каждому промежутку [xt, xi+1] или [xhXj +Ax,] отвечает
элементарная часть нашей величины, приближенно равная q(x^Axt,
то вся искомая величина Q приближенно выразится суммой
Степень точности полученного значения будет тем выше, чем мельче
частичные промежутки, так что Q, очевидно, будет пределом упомя-
упомянутой суммы, т. е. действительно выразится определенным интегралом
\q(x)dx.
* При предположениях, сделанных в сноске на предыдущей странице.

348]	§ 3. ВЫЧИСЛЕНИЕ МЕХАНИЧЕСКИХ ВЕЛИЧИИ	227
Это в полной мере относится ко всем трем рассмотренным примерам. Если
выше мы получили формулы для величин S, Р, V несколько иначе, то это потому,
что задача наша состояла не только в вычислении их, но и в доказатель-
доказательстве их существования - в согласии с ранее данными определениями.
Таким образом, все дело сводится к установлению приближен-
приближенного равенства A), из которого непосредственно получается оконча-
окончательный результат B).
Обыкновенно, впрочем, вместо Ах и AQ пишут dx и dQ, а равен-
равенство A) для «элемента» dQ величины Q записывают в форме
dQ = q(x)dx.	C)
Затем «суммируют» эти «элементы» (на самом деле беря интеграл!),
что и приводит к формуле B) для всей величины Q.
Мы подчеркиваем, что пользование здесь интегралом, вместо
обыкновенной суммы, весьма существенно. Сумма давала бы лишь
приближенное выражение для Q, ибо на ней отразились бы погреш-
погрешности отдельных равенств типа C); предельный же переход, с по-
помощью которого из суммы получается интеграл, уничтожает погреш-
погрешность и приводит к совершенно точному результату. Итак, сначала
в интересах простоты, в выражении элемента dQ отбрасываются бес-
бесконечно малые высших порядков и выделяется главная часть, а за-
затем, в интересах точности, суммирование заменяется интегрирова-
интегрированием, и просто получаемый результат оказывается точным.
Впрочем можно было бы подойти к вопросу и с иной точки зре-
зрения. Обозначим через Q{x) переменную часть величины Q, отвечаю-
отвечающую промежутку [а, х], причем Q(a), естественно, полагаем равным 0.
Ясно, каким образом рассмотренная выше «функция промежутка»
6(К РЪ выражается через эту «функцию точки» Q{x)
В наших примерах функциями точки являются: 1) переменная дуга AM,
2) площадь переменной трапеции АА'М'М и, наконец, 3) объем тела, полученного
от вращения именно этой трапеции.
Величина AQ есть попросту приращение функции Q(x), а произ-
произведение q(x) Ax, представляющее собой его главную часть, есть
не что иное, как дифференциал этой функции [103, 104]. Таким обра-
образом, равенство C), написанное в дифференциальных обозначениях,
на деле является не приближенным, а точным, если только под
dQ разуметь именно dQ(x). Отсюда также сразу получается требуемый
результат:
ь
('q(x) dx =Q(b) -б(в) = Q([a, b])^Q.

228
I Л. X. ПРИЛОЖЕНИЯ ИНТЕГРАЛЬНОГО ИСЧИСЛЕНИЯ
!349
Отметим все же, что в приложениях более удобной и плодотвор-
плодотворной является идея суммирования бесконечно малых
элементов.
349. Нахождение статических моментов и центра тяжести кривой. Как известно,
статический момент М материальной точки массы т относительно некоторой
оси равен произведению массы т на расстояние d точки от оси. В случае с и с т е -
м ы п материальных точек с массами т1, т2,
d d
тп, лежащих в одной плоскости
Рис. 38.
1 2
с осью, соответственно, на расстояниях dlt d2, ¦ ¦ ¦, dn от оси, статический момент
выразится суммой
При этом расстояния точек, ле-
лежащих по одну сторону от оси, бе-
берутся со знаком плюс, а расстояния
точек по другую сторону - со знаком
минус.
Если же массы не сосредоточены
в отдельных точках, но расположены
сплошным образом, заполняя линию
или плоскую фигуру, то тогда для вы-
выражения статического момента вместо
суммы потребуется интеграл.
Остановимся на определении ста-
статического момента М относительно
оси х масс, расположенных вдоль некоторой плоской кривой АВ (рис. 38). При
этом мы предположим кривую однородной, так что ее линейная плот-
плотность р (т. е. масса, приходящаяся на единицу длины) будет постоянной; для
простоты допустим даже, что р = 1 (в противном случае придется полученный
результат лишь умножить на р). При этих предположениях масса любой дуги
нашей кривой измеряется просто ее длиной, и понятие статического момента
приобретает чисто геометрический характер. Заметим вообще, что когда говорят
о статическом моменте (или центре тяжести) кривой - без упоминания о распре-
распределении вдоль по ней масс, - то всегда имеют в виду статический момент (центр
тяжести), определенный именно при указанных предположениях.
Выделим теперь какой-нибудь элемент ds кривой (масса которого также
выражается числом ds). Приняв этот элемент приближенно за материальную
точку, лежащую на расстоянии у от оси, для его статического момента получим
выражение
dMx = у ds.
Суммируя эти элементарные статические моменты, причем за независимую пере-
переменную возьмем дугу s, отсчитываемую от точки А, мы получим
М,
-J
у ds.
D)
Аналогично выражается и момент относительно оси у
S
Mv~ \xds.
E)

350)	§ 3. ВЫЧИСЛЕНИЕ МЕХАНИЧЕСКИХ ВЕЛИЧИН	22*
Конечно, здесь предполагается, что у (или х) выражено через s. Практически в этих
формулах * выражают через ту переменную (t, х или в), которая играет роль не-
независимой в аналитическом представлении кривой.
Статические моменты Мх и Му кривой позволяют легко установить положение
ее центра тяжести C(f, if). Точка С обладает тем свойством, что если в ней сосре-
сосредоточить всю «массу» S кривой (выражаемую тем же числом, что и длина), то
момент этой массы относительно любой оси совпадает с моментом кривой
относительно этой оси; в частности, если рассмотреть моменты кривой относи-
относительно осей координат, то найдем
S	S
S? = My= [xds, Stj = Mx = [yds,
0	О
откуда
« = —— = — \ х ds, ri =	= — \ у ds.	F)
s si	' s sJ
Из формулы для ординаты rj центра тяжести мы получаем замечательное
геометрическое следствие. В самом деле, имеем
• I у ds, откуда 2nr)s = 2n\ у ds;
J	J
но правая часть этого равенства есть площадь Р поверхности, полученной от вра-
вращения кривой АВ [см. 344, 20)], в левой же части равенства 2лг] обозначает длину
окружности, описанной центром тяжести кривой при вращении ее около оси х,
a S есть длина нашей кривой. Таким образом, приходим к следующей теореме
Г у льдина (P. Guldin):
Величина поверхности, полученной от вращения кривой около некоторой не
пересекающей ее оси, равна длине дуги этой кривой, умноженной на длину окружно-
окружности, описанной центром тяжести С кривой (рис. 38)
Эта теорема позволяет установить координату г/ центра тяжести кривой, если
известны ее длина S и плошадь Р описанной ею поверхности вращения.
х2 уг
350. Примеры. 1) Найти статический момент обвода эллипса —у — = I
относительно оси х (предполагая а ¦>¦ Ь).	°2 ^2
Для верхнего (или нижнего) полуэллипса этот момент только отсутствием
множителя 271 отличается от величины соответствующей поверхности вращения.
Поэтому [см. 345, 7)]
(а
Мх = 26\ЬН— arcsine
{
1
2) Если рассматриваемая дуга симметрична относительно некоторой
прямой, то центр тяжести дуги необходимо лежит на этой прямой.
Для доказательства примем ось симметрии за ось у, а точку ее пересечения
с кривой - за начальную точку для отсчета дуг. Тогда функция х = 0(s) окажется
нечетной функцией от j и, если на этот раз длину всей кривой обозначить
через 25, будем иметь [см. 314, 9)]
s
-5
откуда и f = 0.

230
ГЛ. X. ПРИЛОЖЕНИЯ ИНТЕГРАЛЬНОГО ИСЧИСЛЕНИЯ
|351
3) Пользуясь теоремой Гульдина, определить положение центра тяжести
дуги АВ (рис. 39) круга радиуса г.
Так как эта дуга симметрична относительно радиуса ОМ, проходящего через
ее середину М, то ее центр тяжести С лежит на этом радиусе, и для полного опре-
определения положения центра тяжести необходимо лишь найти его расстояние ?;
от центра О. Выбираем оси, как указано на рисунке, и обозначим длину дуги АВ
через s, а ее хорды АВ (=А'В') - через d. От вращения рассматриваемой дуги
вокруг оси х получается шаровой пояс, площадь поверхности Р которого, как мы
знаем [345, 1)], равна Irtrd. По теореме Гульдина та же поверхность равна
Inrjs, так что
st] = rd
rd
и v = —
В частности,
окружности d
для
2r, s =
полу-
r и
2
7 = -г= 0,637г.
л
4)
ветви
Определить центр тяжести
циклоиды
= a{t-smt), y = a(l-cosO
Если принять в расчет симметрию, то сразу ясно, что ?=.та. Учитывая же
4
результаты примера 4) п° 345, легко получить затем rj = — a.
5) В тех случаях, когда наперед ясно положение центра тяжести, теоремой
Гульдина можно воспользоваться для определения площади поверхности
Рис. 40.
вращения. Пусть, например, требуется определить величину поверхности кольца
(тор а), т. е. тела, образованного вращением круга около оси, не пересекающей
его (рис. 40). Так как очевидно, что центр тяжести окружности совпадает с ее цен-
центром, то (при обозначениях рисунка) имеем
351. Нахождение статических моментов и центра тяжести плоской фигуры.
Рассмотрим плоскую фигуру АА'В'В (рис. 41), ограниченную сверху кривой АВ,
которая задана явным уравнением y=f(x). Предположим, что вдоль по этой
фигуре равномерно распределены массы, так что поверхностная плот-
плотность их р (т. е. масса, приходящаяся на единицу площади) постоянна. Без
существенного умаления общности можно тогда принять, что р = 1, т. е., что масса

351]
§ 3. ВЫЧИСЛЕНИЕ МЕХАНИЧЕСКИХ ВЕЛИЧИН
231
любой части нашей фигуры измеряется ее площадью. Это всегда и под-
подразумевается, если говорят просто о статических моментах (или о центре тяжести)
плоской фигуры.
Желая определить статические моменты Мх, My этой фигуры относительно
осей координат, мы выделим, как обычно, какой-нибудь элемент нашей фигуры
в виде бесконечно узкой вертикальной полоски (см. рисунок). Приняв эту полоску
приближенно за прямоугольник, мы видим, что масса ее (выражаемая тем же
числом, что и площадь) будет у dx. Для определения соответствующих элементар-
элементарных моментов dMx, dMy предположим всю массу полоски сосредоточенной в ее
Рис. 41.
центре тяжести (т. е. в центре прямоугольника), что, как известно, не изменяет
величины статических моментов. Полученная материальная точка отстоит от оси
1	I 1 J Л
х на расстоянии — у, от оси у - на расстоянии лН—dx\ ; последнее выражение
можно заменить просто через х, ибо отброшенная величина —dx, умноженная
на массу у dx, дала бы бесконечно малую высшего порядка. Итак, имеем
dMx = — y- dx, dMy = xy dx.
Просуммировав эти элементарные моменты, придем к результатам
ь	ь
Мх =
= — \у2 dx, My = xy dx,
G)
причем под у разумеется, конечно, функция f{x), фигурирующая в уравнении
кривой АВ.
Как в случае кривой, по этим статическим моментам рассматриваемой фигуры
относительно осей координат легко определить теперь и координаты |, t] центра
тяжести фигуры. Если через Р обозначить площадь (а следовательно, и массу)
фигуры, то по основному свойству центра тяжести

232	ГЛ. X. ПРИЛОЖЕНИЯ ИНТЕГРАЛЬНОГО ИСЧИСЛЕНИЯ	[352
откуда
ь
¦ If	Mx 1 f
- = — xy dx, n =	= — у2 dx.
Pi	' P 2PJ
ь
(8)
И в данном случае мы получаем важное геометрическое следствие из формулы
для ординаты т] центра тяжести. В самом деле, из этой формулы имеем
2лг)Р = п \y*dx.
Правая часть этого равенства выражает объем V тела, полученного от враще-
вращения плоской фигуры АА'В'В около оси х [342 A6)], левая же часть выражает произ-
произведение площади этой фигуры Р на 2иг\ - длину окружности, описанной центром
тяжести фигуры. Отсюда вторая теорема Г у льдина:
Объем тела вращения плоской фигуры около не пересекающей ее оси равен произ-
произведению площади этой фигуры на длину окружности, описанной центром тяжести
фигуры:
V=P-birj.
Заметим, что формулы G), (8) распространяются на случай фигуры, ограни-
ограниченной кривыми и снизу и сверху (рис. 19). Например, для этого случая
Ga)
отсюда ясно уже, как преобразуются формулы (8). Если вспомнить формулу (8)
п° 338, то легко усмотреть, что теорема Гульдина справедлива также и для
этого случая.
352. Примеры. 1) Найти статические моменты Мх, Му и координаты центра
тяжести фигуры, ограниченной параболой уг = 2рх, осью х и ординатой,
соответствующей абсциссе х.
Так как у= ^2рх, то по формулам G)
X
J-pxK
о
С другой стороны, площадь [338, G)]
о
В таком случае по формулам (8)
t_3	_3
~1Х' V~~8

353]	§ 3. ВЫЧИСЛЕНИЕ МЕХАНИЧЕСКИХ ВЕЛИЧИН	233
Пользуясь значениями ? и т], легко найти - по теореме Гульдина -
объем тела вращения рассматриваемой фигуры вокруг осей координат или вокруг
конечной ординаты. Например, если остановиться на последнем случае, так как
2
расстояние центра тяжести от оси вращения есть — х, то искомый объем будет
8
К= — лх2у.
15
2)	Найти центр тяжести первого квадранта эллипса —I— = 1, восполь-
воспользовавшись результатами 339, 2) и 343, 2).	°2 &
Аа ЛЬ
По теореме Гульдина | = — , г)=> — .
Ъп Ъл
3)	Если фигура имеет ось симметрии, то центр тяжести фигуры необходимо
лежит на этой оси.
Докажем это для случая фигуры, ограниченной снизу и сверху кривыми ух =/i(x)
и j'2=/2W. Если взять ось симметрии за ось у, то обе функции ух и уг окажутся
четными; промежуток же изменения х в этом случае будет иметь вид [-а, а].
Тогда, по второй из формул Gа) [см. 314, 9)]
а
вместе с чем и ? = 0.
4)	Найти центр тяжести фигуры, ограниченной ветвью циклоиды х =
= a(t - sin t), у = аA - cos t) и осью х.
Воспользовавшись 339, 9) и 343, 4), по теореме Гульдина легко устано-
установить: г] = —а. По симметрии | = яа.
6
5)	То же для фигуры, ограниченной двумя параболами уг = 2рх и х' = 2ру
(см. рис. 24).
Вспоминая пример 5), 339, по формуле Gа) находим
2р	_рЗ
,7=1 = 1 fjc(y^--]d*=--- =-p.
Pi У	2р)	4 10
о	-р2
6)	Подобно первой теореме Гульдина [ср. 350, 5)] и вторая теорема также
может быть использована в том случае, когда положение центра тяжести ясно,
для определения объема соответствующего тела вращения. Например, для тора
(рис. 40) получается объем V= 2n2r2d.
353. Механическая работа. Из элементарной механики читателю известно,
что если сила, приложенная к двужущейся точке М, сохраняет постоянную вели-
величину F и постоянный угол с направлением перемещения точки, то работа А этой
силы на перемещении s точки выразится произведением Fcos(F, s)-s, где (F, s)
обозначает угол между направлениями силы и перемещения точки. Произведение
Fs = Fcos(F, s), очевидно, представляет собой проекцию силы F на перемещение
s; вводя эту проекцию, можно выражение для работы представить в виде А = Fss.
Если направление силы совпадает с направлением перемещения точки, то 4= Fs;
в случае же, когда оба направления прямо противоположны, А= - Fs.
Вообще говоря, однако, и величина силы F и угол (F, s) ее с направлением
перемещения могут не оставаться постоянными. При непрерывном изменении
хоть одной из этих величин для выражения величины работы приходится прибег-
прибегнуть снова к определенному интегралу.

234
ГЛ. X. ПРИЛОЖЕНИЯ ИНТЕГРАЛЬНОГО ИСЧИСЛЕНИЯ
1353
Пусть путь s, проходимый точкой, будет независимой переменной: при этом
предположим, что начальному положению А нашей точки М соответствует зна-
значение s = s0, а конечному В - значение s= S (рис. 42). Каждому значению s в про-
промежутке (s0, S) отвечает определенное положение движущейся точки, а также
определенные значения величин F и cos (F, s), которые, таким образом, можно
рассматривать как функции от .$. Взяв точку М в каком-нибудь ее положении,
определяемом значением s пути, найдем теперь приближенное выражение для
элемента работы, соответствующего приращению ds пути, от * до s+ds, при
котором точка М перейдет в близкое положение М' (см. рисунок). В положении
М иа точку действует определенная сила F
под определенным углом (F, s); так как
изменение этих величин при переходе точки
из М в М' - при малом ds - также мало,
пренебрежем этим изменением и, считая
величину силы F и угол (F, s) приближенно
постоянными, найдем для элемента работы
на перемещении ds выражение
dA = F cos (Fty-ds,
так что вся работа А представится инте-
интегралом
S
Л= I F cos (F,s)-ds.
(9)
Из этого общего выражения для работы
силы F ясно, что при (F, s) = — работа об-
Рис. 42.	2
ращается в нуль; действительно, при этом
cos (F, s) = 0, так что подинтегральная функ-
функция оказывается нулем. Таким образом, сила, перпендикулярная к направлению
перемещения, механической работы не производит.
Если действующую на точку силу F разложить (по правилу параллелограмма)
на две составляющие - по касательной к пути, т. е. по направлению перемещения,
и по нормали к нему, то, согласно сказанному, работу будет производить лишь
касательная составляющая Fs = Fcos(F, s):
= \Fsds.
(9а)
Положим теперь, что F есть равнодействующая всех приложенных к точке
сил; тогда, по закону движения Ньютона, касательная составляющая Fs
равна произведению массы т точки на ее ускорение а, и выражение для работы
А можно написать в виде
Вспомним теперь, что
dv
а = — и
dt
А = I та ds.
So
ds	dv ds dv
¦¦ — , так что а = —¦ — = — v;
dt	ds dt ds

354)	§ з. ВЫЧИСЛЕНИЕ МЕХАНИЧЕСКИХ ВЕЛИЧИН	235
в таком случае
S	S
г du	г (X \ 1 s 1	1
А = mv — ds- I и — me» = — mv- = — от И	/m;*,
J ds J {2 ) 2 s, 2	2 °
где через v0 и К обозначены величины скорости, соответственно, в конечной и на-
начальной точках пути.
1
Как известно, — тог есть живая сила или кинетическая энергия
2
точки; таким образом, мы пришли к важному предложению: механическая работа
А, произведенная силой, под действием которой происходило движение точки, равна
приращению кинетической энергии точки. (Разумеется, работа А и приращение
кинетической энергии могут одновременно
оказаться и отрицательными). Этот прин-
принцип, который можно распространить и
на системы материальных точек, и на	Щ
сплошные тела, играет в механике и физике	Щ_
очень важную роль. Его называют «за-
коном живой силы».
354. Примеры. 1) Применим в ви-	Р с 43
де примера формулу (9) к вычислению
работы растяжения (или сжатия) пру-
пружины с укрепленным одним концом (рис. 43); с этим приходится иметь дело, на-
например, при расчете буферов у железнодорожных вагонов.
Известно, что растяжение s пружины (если только пружина не перегружена)
создает натяжение р, по величине пропорциональное растяжению, так что p = cs,
где с - некоторая постоянная, зависящая от упругих свойств пружины («жест-
(«жесткость» пружины). Сила, растягивающая пружину, должна преодолевать это натя-
натяжение. Если учитывать только ту часть действующей силы,
которая на это затрачивается, то ее работа при возрастании растя-
растяжения от 0 до S выразится так:
I = \ р ds = (
s = c I sds = c —
о	о
Обозначив через Р наибольшую величину натяжения (или преодолевающей
ее силы), соответствующую растяжению S пружины (и равную cS), мы можем
представить выражение для работы в виде
A = -PS.
Если бы к свободному концу пружины сразу была приложена сила Р (на-
(например, подвешен груз), то на перемещении S ею была бы произведена вдвое
большая работа PS. Как видим, лишь половина ее затрачивается на растяжение
пружины; другая половина пойдет на сообщение пружине с грузом кинетической
энергии.
2) Пусть некоторое количество газа (пара) содержится в цилиндре (рис. 44)
по одну сторону поршня, и предположим, что газ этот расширился и передвинул
поршень направо. Поставим себе задачей определить работу, произведенную
при этом газом. Если начальное и конечное расстояния поршня от левого дна
цилиндра обозначить через Sj и s2, давление (на единицу площади поршня) -

236
ГЛ. X. ПРИЛОЖЕНИЯ ИНТЕГРАЛЬНОГО ИСЧИСЛЕНИЯ
[354
через р, а площадь поршня - через Q, то вся сила, действующая на поршень, будет
pQ, и работа, как мы знаем, выразится интегралом
,l = QJpds.
Обозначая через V объем рассматриваемой массы газа, очевидно, будем иметь
V=Qs. Нетрудно теперь перейти от переменной s к новой переменной V; мы
получим
V,
A0)
v,
Рис. 44.
где У1 и V.z означают начальное и
конечное значения объема V.
Если бы нам известно было
давление р как функция от объема
V, то этим определилась бы работа
А. Предположим сначала, что при расширении газа температура его остается
постоянной, так что необходимая для его расширения энергия в виде тепла при-
притекает извне; в этом случае процесс называют изотермическим. Считая
газ «идеальным», по закону Бойля - Мариотта будем иметь: pV= с = const,
так что р = — , и для работы получаем значение
V,
-J-
= с In — .
Если обозначить через рг и рг давления в начале и в конце процесса, то рг Уг = р„ V.,
V, />i
и —- = — . Поэтому работу расширения, связанного с переходом от давления р,
Vi Рг
к давлениюp.^Pi, можно представить в виде
. , Pi
А = с In — .
Pi
Наконец, вместо с в эти формулы можно подставить произведение р^Ух-
Часто бывает, однако, естественнее предположить, что во время расширения
не происходит теплового обмена между газом и окружающей средой, и на произ-
производство работы затрачивается энергия самого газа, температура которого при
этом понижается; такой процесс называется адиабатическим. В этом
случае зависимость между давлением р и объемом V рассматриваемой массы
газа имеет вид
pVk-c = const
[эта зависимость будет выведена ниже, 361, 3)], где к есть характерная для каждого
газа (пара) постоянная, всегда большая единицы. Отсюда p = cV~k и
V,
Л=
= °— Vl~k
\-k
, с
=	(VI'
v, \-k 2
yk-i

355)	§ 3. ВЫЧИСЛЕНИЕ МЕХАНИЧЕСКИХ ВЕЛИЧИН	237
Этот результат можно представить в более удобной форме, если вспомнить,
что с Кг* =Pi,c V^~k = р2; подставляя, придем к следующему выражению для работы:
fc-1
Мы лишь для простоты рассуждения и наглядности предположили расширяю-
расширяющийся газ заключенным в цилиндр. Основная формула A0), равно как и получен-
полученные из нее частные формулы, сохраняют силу независимо от формы, которую
имеет в каждый данный момент рассматриваемая масса газа. Разумеется, те же
формулы выражают и работу сжатия газа от объема К2 до объема Vx -= Vz
(сопровождаемого повышением давления от р2 до р1^-р2), т. е. работу внешней
силы, заставляющей газ сжиматься; работа самого газа в этом случае отрица-
отрицательна!
355. Работа силы трения в плоской пяте. Пятой вообще называют опорную
часть вертикального вращающегося вала; неподвижная опора, в которой вращает-
вращается пята, называется подпятником. В настоящем п° мы рассмотрим вопрос
о мощности, затрачиваемой на преодоление трения в пятах, ограничиваясь простей-
простейшим случаем - плоской пяты.
Плоская пята представляет собой цилиндрическое тело, которое на подпятник
опирается своим плоским основанием (рис. 45). Это основание имеет, вообще,
форму кругового кольца, с внешним радиусом R и внутренним радиусом г0; в част-
частном случае, при го = О, мы получаем сплошное круговое основание.
Обозначим через Р полное давление, передаваемое пятой, через ы A/сек.) -
угловую скорость вращения вала, через ft — коэффициент трения, наконец, через
р - давление на единицу площади пяты в рассматриваемой ее точке. Не касаясь
пока вопроса о распределении давления, отметим лишь одно очевидное
обстоятельство: точки пяты, равноудаленные от ее центра О, находятся в одина-
одинаковых условиях, и в них давление должно быть одинаково. Таким образом, р во-
вообще можно считать функцией от радиуса-вектора г. Ниже будут указаны допуще-
допущения, которые обычно делаются относительно этой функции: по одному условию
она должна удовлетворять во всяком случае, именно полное давление на пяту
должно уравновешиваться давлением Р со стороны вала.
Для того чтобы вычислить это полное давление, прибегнем снова к методу
суммирования бесконечно малых элементов по схеме п° 348, причем за независи-
независимую переменную примем радиус г, изменяющийся от га до R. Разбивая этот про-
промежуток на части, мы в то же время можем разложить все кольцо на элементарные
концентрические кольца, так что все давление Р сложится из элементарных давле-
давлений, соответствующих отдельным кольцам. Рассмотрим теперь кольцо, ограни-
ограниченное окружностями радиусов гиг+dr (на рис. 45, б оно заштриховано). Площадь
этого кольца есть я(г+«?#¦)*-яг2 = 2яг dr+n(drJ; отбрасывая бесконечно малую
второго порядка n(drJ, можно принять эту площадь приближенно равной 2лг dr.
Если р есть давление (на единицу площади) в точке, отстоящей от центра на рас-
расстояние г, то рассматриваемому кольцу отвечает элементарное давление
так что, суммируя, получаем равенство
[	A1)
Оно, повторяем, и выражает тот факт, что суммарное давление, распределенное
по пяте, равно давлению со стороны вала.

238
ГЛ. X. ПРИЛОЖЕНИЯ ИНТЕГРАЛЬНОГО ИСЧИСЛЕНИЯ
[355
Определим теперь момент М силы трения во вращающейся пяте относительно
оси вращения. Рассмотрим снова элементарное кольцо, о котором шла речь выше;
развивающаяся в нем сила трения, противодействующая вращению, будет
fidP=2n/iprdr,
так что соответствующий ей элементарный момент dM выразится произведением
из этой силы на плечо г (общее для
всех точек кольца)
Ш)
dM=2nfipr"dr.
Отсюда полный момент трения будет
я
M=2n/i\pr*dr.	A2)
Как известно из механики, рабо-
работа А, производимая таким постоян-
постоянным вращательным моментом М в
одну секунду, получается умножением
момента М на угловую скорость cj
A/сек.) вращения
Для того чтобы довести до конца
вычисление работы А, теперь нужно
сделать те или иные допущения от-
относительно закона распределения р на
поверхности пяты.
Самым простым является предпо-
предположение, что давление распределяется
равномерно, т. е. что р = с = const.
Величина этой постоянной определя-
определяется из условия A1). Впрочем, в этом
случае непосредственно ясно, что если
давление Р равномерно распределяет-
распределяется по площади кольца .т(Л2 - г%), то на единицу площади придется давление р =
Р
Рис. 45.
Подставляя это значение вместо р в A2), найдем далее
я
М = 2л [I -
2
dr = -fiP
3^
К--г0
В частности, для сплошной пяты будем иметь: М =—fiPR.
Однако эти результаты прилагают лишь к новым, не обтершимся еще пятам.
Дело в том, что при вращении вала точки пяты, дальше отстоящие от центра О,
движутся с большей скоростью, в них работа трения больше и, соответственно,
больше и изнашивание как пяты, так и подпятника; благодаря этому часть давления
перелагается на более близкие к центру части пяты. Для старых приработавшихся
пят обычно допускается, что давление на них распределяется так, что работа
трения (на единицу площади), а с нею и изнашивание, всюду сохраняют постоян-

356]	§ 3. ВЫЧИСЛЕНИЕ МЕХАНИЧЕСКИХ ВЕЛИЧИН	239
ную величину. Разделив элементарную работу dA = w dM на площадь 2лг dr эле-
элементарного кольца, запишем наше допущение в виде
cufipr- const, откуда и />/-=e = const;
итак, мы предполагаем, что р изменяется обратно пропорционально расстоянию
г от центра. Подставляя с вместорг в условие A1), найдем величину этой постоянной
Р = 2пс dr = 2nc(R - г0), откуда с =
Наконец, заменив и в A2) рг полученным выражением, придем к такому результату:
1
-ro)J	2
1
Для сплошной же пяты М = — цРЯ.
Легко видеть, что потеря мощности на трение в случае приработавшихся
пят меньше, чем в случае новых пят.
356. Задачи на суммирование бесконечно малых элементов. Приведем еще ряд
задач, решаемых методом суммирования бесконечно малых элементов.
1) Найти формулу для выражения статического момента М тела (V) относи-
относительно данной плоскости, если известны площади поперечных сечений тела парал-
параллельно этой плоскости (в функции расстояния х от нее). Плотность предполагается
равной единице.
При обозначениях п° 342, масса (объем) элементарного слоя тела на расстоя-
расстоянии х от плоскости есть Р(х) dx, его статический момент dM= xP(x) dx, так что,
суммируя, получим
ь
М= [xP(x)dx.
Расстояние ? центра тяжести тела от данной плоскости выразится так:
б
I xP(x) dx
, м i
V ь
jp(x)dx
а
В частности, для тела вращения
ь
ху2 dx
ь
y2dx

240	ГЛ. X. ПРИЛОЖЕНИЯ ИНТЕГРАЛЬНОГО ИСЧИСЛЕНИЯ	[356
Если применить этот результат (а) к круговому конусу и (б) к полусфере, то
найдем, что расстояние центра тяжести от основания составит (а) — высоты,
3	4
(б) — радиуса.
о
2) Найти формулу для выражения статического момента М поверх-
поверхности вращения относительно плоскости, перпендикулярной к оси враще-
вращения. «Поверхностная плотность» предполагается равной единице.
Примем ось вращения за ось х, а за начало координат возьмем точку пересе-
пересечения ее с упомянутой плоскостью. При обозначениях п° 344 масса (площадь)
элементарного кольцевого слоя на расстоянии s от начала дуги есть 2лу ds, его
статический момент dM=2nxy ds и, окончательно,
S	S
С	Г
М=2л \ xyds = 2л 0(s)lF(s)ds.
J	J
о	о
В частности, если вращающаяся кривая задана явным уравнением y=f(x)
Расстояние f центра тяжести поверхности от данной плоскости будет
S	Ь
\ ху ds xy^l +y'^ dx
.. М {	а
\yds Jj
о
Применить последнюю формулу к поверхности (а) кругового конуса, (б) полу-
полусферы.
Ответ. Расстояние центра тяжести от основания равно (а) — высоты, (б)
1	3
— радиуса.
3) Определить статические моменты Myz , Мгх, Мху относительно координатных
плоскостей для цилиндрической поверхности [346, рис. 35] и поло-
положение ее центра тяжести. Применить полученные формулы к боковой поверхности
цилиндрического отрезка [343, 8)].
Ответ. Общие формулы
S	S	S
Муг = xz ds, Мгх = I yz ds, Mxy = — I z2 ds,
oo	о
,. Myz	Mzx	Mxy
л	л
где Р - площадь поверхности. В предложенном примере: ? = 0,т] = —а, ? = — А.
4) Моментом инерции (или квадратичным моментом) мате-
материальной точки массы m относительно некоторой оси (или плоскости) называется
произведение массы я? на квадрат расстояния d от точки до оси (до плоскости).

356]
§ 3. ВЫЧИСЛЕНИЕ МЕХАНИЧЕСКИХ ВЕЛИЧИН
241
Исходя из этого, предполагается найти выражение для момента инерции 1У относи-
относительно оси у плоской фигуры А1В1В2А2 (рис. 46), в предположении, что «поверх-
«поверхностная плотность» распределения масс есть единица.
Имеем
ь
dly = х2О2 - Л) dx, Iy= \ х2(у2 - Уг) dx.
Например, для случаев, изображенных на рис. 47, получим:
(а)
1У=Ъ
12'
bh*
в частности, при е = О будет /у= — ;
(Ь)
с+г
Iy=2
яг4
в частности, при с = 0 будет /у = —.
5) Определить момент инерции тела (V), рассмотренного в задаче 1), отно-
относительно упомянутой там плоскости. Применить полученную формулу
к вычислению момента инерции (а) кру- п
гового конуса, (б) полусферы - относи- "
тельно плоскости основания.
Ответ. /= х2Р(х) dx;
в частности,
(a) /=^-
-
15
а:
х
6) Давление жидкости на какую-ни-
какую-нибудь площадку, расположенную на глу-
глубине Ым) под ее поверхностью, равно весу
цилиндрического столба жидкости высоты
А, имеющего эту площадку своим осно-
основанием. Таким образом, давление (в кГ/мг)
на глубине h (м), приходящееся на единицу
площади, равно hy, если у означает удель-
удельный вес жидкости (кГ/м3).
Предположим, что в жидкость вертикально погружена плоская фигура А^
(рис. 46)*.
Найти полное гидростатическое давление W на эту фигуру и его момент М
(относительно свободной поверхности жидкости).
Рис. 46.
* Мы берем ось у лежащей на свободной поверхности жидкости.
16 Г. М. Фихтенгольц, т. II

242	ГЛ. X. ПРИЛОЖЕНИЯ ИНТЕГРАЛЬНОГО ИСЧИСЛЕНИЯ
Элементарная площадка dP=(y%-y^)dx испытывает давление
[356
момент которого относительно оси у равен
dM = y**(yt-yJ dx.
Отсюда
Первый интеграл, очевидно, представляет собой статический момент
My фигуры относительно оси у; второй же дает момент инерции 1у фигуры
относительно той же оси.
0°
lOj
h
с
1
h
—у
Рис. 47.
Если | есть расстояние центра тяжести С фигуры от свободной поверхности,
а Р - ее площадь, то можно написать, что W = yP?. Центр давления, т. е.
точка приложения равнодействующей всего давления, от свободной поверхности
отстоит на расстоянии
~W~ly~'
Приложим эти формулы к случаям, изображенным на рис. 47.
В случае a): f = с, P=bh и W = ybhc. Далее, так как в 4) мы уже вычислили 1у-
bh3	№
= ЪсгИл	, то можем сразу написать I* = сн	. В частности, если c = h/2 (т. е.
12	12с	1
верхняя сторона прямоугольника лежит на уровне жидкости), имеем W = — yb№,
7	'	2
ш
В случае б): ? = е, Р = лг% и W = успгг. Здесь 1у-ттг2с2^	[см. 4)]. Поэтому
гг	4
|* = с+—.
Ас
7) Если в стенке резервуара, наполненного водой, на глубине h (м) под поверх-
поверхностью воды имеется горизонтальная щель, то через нее вода будет вытекать
со скоростью
	U=V2iA*.
сек)
* Эта формула, доказываемая в гидродинамике, известна под названием
формулы Торич елли. Отметим, что она имеет такой же вид, как и фор-
формула для скорости, приобретаемой тяжелой материальной точкой при падении
с высоты И.

356)
§ 3. ВЫЧИСЛЕНИЕ МЕХАНИЧЕСКИХ ВЕЛИЧИН
243
Предположим теперь, что в стенке резервуара имеется прямоугольное от-
отверстие (рис. 48). Требуется определить расход воды, т. е. объем воды Q(m3), вы-
вытекающий в 1 сек.
Рис. 48.
Рис. 49.
Элементарной полоске ширины dx на глубине х отвечает скорость v - ^2gx;
так как ее площадь есть b dx, то расход воды через эту полоску выразится так:
dQ= l[2gx-bdx. Суммируя, найдем
-4)
К
Фактический расход несколько менее вычисленного, ввиду наличия трения
в жидкости и сжатия струи. Влияние этих факторов обыкновенно учитывают
с помощью некоторого эмпири-	п\
ческого коэффициента ,а-=1 и т
пишут формулу в виде
2 	 / I 1\
= -fipgb\h*-hl).
При ha = 0 отсюда получается фор-
формула для расхода воды через
прямоугольный водослив
л
2 _ -
][2bh\
\ л,
L-—m)
8) Изучая магнитное поле t
тока, Био и Савар пришли
к заключению, что сила, с кото-
которой ток действует на «магнитный	Рис. 50.
заряд», может быть рассматри-
рассматриваема как равнодействующая сил, как бы исходящих от отдельных бесконечно
малых «элементов тока». По установленному ими закону, элемент тока ds
(рис. 49) действует на магнитный заряд т, помещенный в точке О, с силой*
lm sin cp ds
где / - сила тока, г - расстояние ОМ, а <р - угол (ds, r).
* Формула имеет место в таком виде лишь при надлежащем выборе единиц
(например, если силу выражать в динах, расстояние - в см, магнитный заряд
и силу тока - в электромагнитных единицах).

244	ГЛ. X. ПРИЛОЖЕНИЯ ИНТЕГРАЛЬНОГО ИСЧИСЛЕНИЯ	[357
Сила эта направлена по перпендикуляру к плоскости, проходящей через О
и ds, и притом - в случае, изображенном на рисунке, - в сторону от читателя.
При желании установить действие конечного отрезка тока на магнитный
полюс, приходится суммировать эти элементарные силы.
Для примера определим силу, с которой действует на единицу «магнитного
заряда» прямолинейный отрезок тока ВС (рис. 50), при указанных на рисунке обо-
обозначениях.
а
Так как sin <р = sin < ОМА = — , то dF можно представить в виде
aids aids
dF=
Элементарные силы здесь можно непосредственно складывать, ибо они все имеют
одно и то же направление. Поэтому
§ 4. Простейшие дифференциальные уравнения
357. Основные понятия. Уравнения первого порядка. В главе VIII мы рассматри-
рассматривали задачу об определении функции у=у(х) по заданной ее производной
/=/(*)	A)
[или - что то же - по ее дифференциалу dy=f(x)dx] и учились производить
операцию интегрирования или квадратуру, с помощью которой
она решается,
>•= jf(x)dx+C*.
B)
В этом общем решении фигурирует постоянная С. Как мы видели
на примерах [263, 264], если даны начальные условия
у=у0 при х = х0,	C)
то этим определяется конкретное значение постоянной С=С0. Подставив его
в B), мы придем к частному решению нашей задачи, т. е. к конкретной
функции у = у{х), которая не только имеет наперед заданную производную, но
и удовлетворяет начальным условиям C).
Часто, однако, приходится определять функцию у = у{х) из более сложных
соотношений вида
Fix, у, у', у", ...) = 0,
связывающих значения независимой переменной х со значениями как самой искомой
функции у, так и ее производных у', у", ... Такого рода соотношения вообще
называются дифференциальными уравнениями.
Остановимся на уравнении первого порядка, содержащем лишь
первую производную у',
Fix, у, /)-0.	D)
Решением его является любая функция y=yix), которая удовлетворяет ему
тождественно относительно х. Как можно показать (при известных предполо-
* В этом параграфе под символом f(x) dx мы будем разуметь хотя и произ-
произвольную, но определенную первообразную функцию, так что постоянную
интегрирования мы в этот символ не включаем и будем писать ее отдельно.

358|	§ 4. ПРОСТЕЙШИЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ	245
жениях относительно функции F), общее решение его, подобно упомяну-
упомянутому вначале простейшему случаю [см. B)], и здесь также содержит произвольную
постоянную С, т. е. имеет вид
v=<p(x, С).	E)
Иногда, впрочем, это решение получается в неявной форме
Ф(х, у,С) = 0 или ц)(х,у) = С.	F)
Разыскание общего решения дифференциального уравнения, в той или иной
форме называется интегрированием уравнения.
Для примера рассмотрим такую задачу: найти кривые, для кото-
которых поднормаль постоянна. Если представить себе такую кривую
выраженной явным уравнением у = у{х), то вопрос сведется к разысканию таких
функций, которые удовлетворяют условию уу' =р, где р = const [230 C)]. Перепишем
его в виде (у2)' = 2р; теперь ясно, что общим решением его будет
у* = 2рх + С или у** ±]/2рх+С.	G)
Таким образом, поставленному требованию удовлетворяет целое семейство пара-
парабол, получающихся одна из другой смещением параллельно оси х.
Здесь ответ на задачу дает именно общее решение, поскольку требовалось
разыскать все кривые, обладающие упомянутым свойством. Если бы в задаче
было дополнительно указано, что кривая должна проходить через заданную точку
(*о> Уо>' то> подставив эти значения х и у в полученное уравнение G), мы сможем
определить значение С:
Полагая в G) С =С0, мы придем к частному решению уг = 2рх+С0, выра-
выражающему уже конкретную кривую.
Нужно сказать, что чаще всего бывает именно так, что задача, приведшая
к дифференциальному уравнению, требует конкретного частного решения.
Обычно последнее определяется начальными условиями типа C),
выдвигаемыми самой задачей. По этим условиям, как и только что, прежде всего
может быть установлено конкретное значение С=С0; оно определится из уравне-
уравнения, которое получится, если в общем решении E) [или F)] положить х = х0, у = уа.
Если теперь в это общее решение подставить найденное решение С„ вместо С,
то и придем к тому частному решению, которое удовлетворяет задаче.
358. Уравнения первой степени относительно производной. Отделение переменных.
Предположим теперь, что в уравнение D) производная у' входит в первой
степени, т. е., что уравнение имеет вид
Р(х, y)+Q(x, y)y' = 0,
dy
где Р, Q суть функции от х и у. Полагая здесь у' = — , можно представить уравне-
ах
ние в форме
Р(х, у) dx + Q(x, у) rfy = 0,	(8)
которая часто более удобна.
Мы остановимся здесь подробнее лишь иа тех простейших частных случаях
уравнения (8), когда интегрирование его непосредственно сводится к
квадратурам; рассмотрение этих случаев, таким образом, служит естественным
дополнением главы VIII,

246	ГЛ. X. ПРИЛОЖЕНИЯ ИНТЕГРАЛЬНОГО ИСЧИСЛЕНИЯ	[358
Если в уравнении (8) коэффициент Р на деле зависит только от дг, а коэффи-
коэффициент Q - только от v, т. е. если уравнение имеет вид
Р(х) dx+Q(y) dy = 0,	(9)
то говорят, что переменные отделены. В этом случае интегрирование
производится очень просто.
Пусть функции Р(х) и Q(y) непрерывны (в соответствующих промежутках).
Тогда Р(х) dx будет дифференциалом функции Р(х) = Р(х) dx, a Q(y) dy - диффе-
дифференциалом функции Q(y) = Q(y) dy, даже если под у разуметь функцию у(х), удовлет-
удовлетворяющую уравнению (9)*. В таком случае левая часть уравнения (9) представит
собой дифференциал от суммы P(x) + Q(y). Так как этот дифференциал, в силу
уравнения (9), равен 0, то сама функция сводится к постоянной
P(x) + Q(y) = C.	A0)
Легко видеть, что и обратно, если функция у = у(х) удовлетворяет (при любом х)
этому уравнению, то удовлетворяется и уравнение (9). Равенство A0) дает общее
решение уравнения (9).
При решении уравнения (9) иногда предпочитают члены с dx и dy помещать
в разных частях уравнения
Q(y)dy=-P(x)dx.	A1)
Интегрируя каждую часть порознь и не забывая о произвольной постоянной,
которую достаточно присоединить к одному из интегралов, придем к результату
=- jp(x)dx+C,
тождественному с полученным выше.
Предположим, что требуется удовлетворить начальным условиям
C). Вместо того чтобы сначала находить общее решение, а затем подбирать по-
постоянную С, исходя их этих условий, можно поступить проще: «просуммировать»
элементарные величины A1), справа между х„ и х, а слева - между соответствую-
соответствующими им значениями уа и у. Мы получим равенство
JQ(y)dy=-jp(x)dx,
которое и дает требуемое частное решение; самый вид его подчеркивает, что оно
заведомо выполняется при х=х„ и у=у0. Читатель легко уяснит себе, что этот
прием лишь формой отличается от прежнего.
Пример 1): Пусть дано уравнение
dy
sa\xdx-\	= 0.
Интегрируем
с	г dy
I sin x dx+ — = С или -cosx +2Уу= С,
J	J уу"
откуда
(cos*+CJ
У
* Ввиду инвариантности формы дифференциала [106].

359]	§ 4. ПРОСТЕЙШИЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ	247
Таково общее решение предложенного уравнения. Если даны началь-
начальные условия, например у = 1 при х = 0, то, подставляя эти значения, сразу
находим С= 1, что приводит к частному решению
A+COSJtJ
у = __________
Как упоминалось, можно в этом случае избежать необходимости предвари-
предварительно составлять общее решение, написав сразу
г dy г	_ .
—— = - sinxrfx, т.е. 2( уу-l) = cosх-1,
1 *'	О
откуда
,- l + cosx
2 ' - { 2 J
Часто случается, что хотя уравнение (8) и не имеет вида (9), но может быть
преобразовано к этому виду, после чего интегрируется, как указано выше. Такое
преобразование и носит название отделения переменных. Переменные
легко отделяются в том случае, когда коэффициенты Р и Q представляют собой
произведения множителей, зависящих каждый только от одной переменной, т. е.
когда
Р(х, у) = Pi{x)Pz(y) и Q(x, у) = Q\{x)Q«(y).
Действительно, достаточно разделить обе части уравнения
0	A2)
на P2(y)Qi(x), чтобы этим уже отделить переменные:
. Q4y) , .
dx-\	dy = 0.
P&)
X	X'
Пример 2): у sin — dx - cos — dy = 0.
Уравнение имеет вид A2); отделяем переменные
х
sin —
dy г
— -•	dx
и интегрируем
¦У х
cos—
2
- 2 In cos— + с.
Потенцируя, определяем отсюда у
ес	2ес
X 1+COSX*
COS2 —
2
Полагая еще С- 2ес, приведем общее решение к виду
С
1 + COSX
359. Задачи. Рассмотрим ряд задач из различных областей знаний, ИёпОсред-
ственно приводящих к дифференциальным уравнениям с отделяющимися1 йбре-
менными.

248
ГЛ. X. ПРИЛОЖЕНИЯ ИНТЕГРАЛЬНОГО ИСЧИСЛЕНИЯ
[359
1) Найти кривые, у которых отрезок п нормали (до пересечения с осью х) со-
сохраняет постоянную величину г.
Воспоминая выражение для и [230, D)], записываем условие, которому должна
удовлетворять искомая функция у от х, в виде дифференциального уравнения
Отсюда
или
ydy
= ±dx.
У	~][г<>-у*
Интегрируем:
- ]/гг-уг = + (х+С) или (х+О2+у2=г2.
Как и следовало ожидать, мы получили семейство окружностей радиуса г с
центром на оси х.
2) Найтн кривые, у которых отрезок / касательной до пересечения с осью х со-
сохраняет постоянную величину а.
В силу 230 D), дифференциальное уравнение задачи имеет вид
dy
Полагая у' = — , его легко преобразовать так:
dx
Интегрируем:
мы получили семейство трактрис [ср. 331, 11)].
3) Закон охлаждения. Пусть охлаждающееся тело температуры 6° С
окружено средой с температурой 0° С. Ньютон установил закон, по которому
скорость охлаждения пропорциональна самой температуре 8, т. е.
dt
где к - положительная постоянная. Определить закон, по которому убывает тем-
температура тела, начиная с момента / = 0.
Имеем
откуда, интегрируя, найдем In в= -kt+lnC*. Очевидно, в = Се~ш. Полагая здесь
t = 0, видим, что С есть не что иное, как начальная температура 0О.
Подставляя, придем к окончательной формуле
которая определяет температуру Тела в любой момент, если только она была
известна в начальный момент (80).
In С.
* Предвидя потенцирование, мы сразу оерем постоянную для удобства в виде

359]	§ 4. ПРОСТЕЙШИЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ	249
Коэффициент к зависит от свойств тела и среды; он определяется опытным
путем.
4) Экстратоки размыкания и замыкания. Если в электри-
электрической цепи действует постоянное напряжение V, то, обозначая через R сопротив-
сопротивление цепи и через / - силу тока, по закону Ома будем иметь V- RI. Когда же
напряжение К меняется (а также в момент размыкания или замыкания тока постоян-
постоянного напряжения), во многих случаях имеет место явление самоиндукции, которое
состоит в появлении дополнительной электродвижущей силы, пропорциональной
dl
скорости изменения силы тока — ,но имеющей обратный знак.
dt
Таким образом, величину этой электродвижущей силы самоиндукции можно
dl
представить так: - L— , где L - «коэффициент самоиндукции» (JL =- 0).
dt
Если налицо самоиндукция, то при размыкании тока его сила не сразу падает
до нуля, а при замыкании - не сразу достигает своей нормальной величины. Иссле-
Исследуем эти явления аналитически.
Закон Ома теперь принимает следующую форму:
dl	dl R V
V-L — = RI или	h—/= —.	A3)
dt	dt L L
(а)	Пусть постоянный ток силы 10 в момент t = 0 размыкается. Так как тогда
V=0, то имеем
dl R	dl R
—I—/=0 или —=	dt
dt L	I L
и (аналогично З))
--(
/=v L ¦
Этот ток, проходящий в цепи под действием одной лишь электродвижущей
силы самоиндукции, называется экстратоком размыкания. С возра-
возрастанием / его сила быстро стремится к 0, и через короткое время он становится
неощутимым.
(б)	Если цепь в момент ? = 0 замыкается, в ней начинает действовать
постоянное напряжение V, то из уравнения A3), снова отделяя переменные, получим
-Rdl R	R	-т>
	=	dt, ln(V-Rl) =	t+lnC, V-RI=Ce L .
V-RI L	L
Постоянную С определим из начальных условий 1=0 при t = 0; оче-
очевидно, С= V, так что окончательно
v( -?/]
/=— 1-е L .
R {	'
V
Мы видим, что наряду с током —, отвечающим закону Ома, одновре-
R
у _«,
менно протекает в обратном направлении ток — е . Это и есть экстра-
R
ток замыкания; его сила также быстро убывает с возрастанием t.

250	ГЛ. X. ПРИЛОЖЕНИЯ ИНТЕГРАЛЬНОГО ИСЧИСЛЕНИЯ	C59
5) Уравнение химической реакции. Рассмотрим химический
процесс, состоящий в превращении взаимодействующих веществ А, В, ... в ве-
вещества М, N, ... Для оценки количества вещества, участвующего в реакции, его
выражают в грамм-молекулах или молях. Молем какого-нибудь вещества
называется такое его весовое количество, которое выражается в граммах числом,
равным его молекулярному весу. В моле любого вещества всегда содержится одно
и то же количество молекул, независимо от вещества.
Если предположить, что во взаимодействие вступают на каждую молекулу
одного вещества по одной молекуле другого, то на каждый моль одного придется
один моль другого. По истечении времени t от начала реакции, от каждого из
взаимодействующих веществ вступит в реакцию одно и то же количество х молей.
dx
Скорость возрастания х относительно времени, т. е. производная —,
at
называется скоростью химической реакции.
Пусть в процессе участвуют два вещества А и В, первоначальные количества
которых (в молях) обозначим через а и Ь (при этом пусть, скажем, b^-d). Через
промежуток времени t будем иметь количество а-х вещества А и количество
Ь-х вещества В. Естественно допустить, что скорость химической реакции в момент
t пропорциональна произведению реагирующих масс, т. е. произведению
количеств реагентов, не подвергшихся еще превращению. Это приводит к такому
дифференциальному уравнению
dx	dx
— = k{a-x){b-x) или	——- = kdt.
dt	(a~x)(b-x)
Интегрируя, получим
1 а-х
In	= -kt+C.
b-a b-x
1 a
Так как при t = 0 мы должны иметь и х = 0, то С =	In — . Подставляя это зна-
значение С: Ъ-а b
(а-х)Ь	i-e-Kb-ayt
In	=-k(b-a)t, легко находим затем x-ab	——т.-
ф-х)а	b-ae-Kb-a)t
При возрастании / показательное выражение стремится к 0; через конечный
промежуток времени оно становится настолько малым, что х практически уже не
отличить от а, и реакция заканчивается.
6) Математический маятник. Пусть материальная точка массы
т подвешена на нерастяжимой нити или стержне длины / (весом которых пренебре-
пренебрегаем) так, что может двигаться по дуге окружности (рис. 51). Эта система называется
математическим маятником. Выведя маятник из положения равновесия ОА
в положение О В (а -= я/2), предоставим маятник самому себе, не сообщая ему началь-
начальной скорости.
Маятник перейдет в симметричное положение ОВ\ потом вернется в положе-
положение ОВ и т. д. Задача состоит в установлении характера колебаний маятника, т. е.
в выяснении зависимости между углом 6 = <$АОМ и временем /. Для определен-
определенности рассмотрим движение точки М по дуге АВ, отсчитывая пройденный путь
s=AM = IB от точки А, а время t - от момента прохождения маятника через поло-
положение равновесия.
Разлагая силу тяжести F= mg, действующую на точку М, как указано на ри-
рисунке, видим, что ее касательная составляющая Fs= - mg sin 6*,

3591
4. ПРОСТЕЙШИЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
251
в то время как нормальная составляющая уничтожается сопротивлением нити
или стержня. Если через v обозначить скорость точки М, то ее кинетическая энергия
в рассматриваемом положении будет — mv* и сведется к 0 при переходе М в В.
С другой стороны, работа А, произведенная силой Fs на пути MB выразится так
[352 (9а)]:
Л = ¦- mg sin 6 ds
(здесь S=AB) или, если перейти к
переменной 6,
Л= -mgl | sin
0
= - mgl(cos в - cos а).
Тогда, по закону живой силы [352],
имеем:
— mv2 = mgl (cos 0 - cos a),
Рис. 51.
v= y^/]/2(cos0-cosa).
ds d6
Так как v = — = / — , то для определения зависимости между 6 и t получаем
dt dt
дифференциальное уравнение
de ~\[g~ ,		~\fl	de
— = / — V2(cos0-cosa) или dt=\
dt \ I '	У g
где переменные уже отделены.
Интегрируя слева от 0 до /, а справа от 0 до в, приходим к искомой зависи-
зависимости:
]/2(cos0-cosa)
-V?/
]/2(cos 0 - cos a)
A4)
Однако, квадратура на этот раз в конечном виде не берется: как сейчас увидим,
интеграл справа непосредственно приводится к эллиптическому интегралу 1-го
рода.
Переписав A4) в виде
и положив sin— = k @-=?«=!), введем новую переменную интегрирования <р по
* Сила направлена против движения!

252	ГЛ. X. ПРИЛОЖЕНИЯ ИНТЕГРАЛЬНОГО ИСЧИСЛЕНИЯ	[359
формулам
9	1 в
sin — = fc-smp, — cos— de = k-cosq>'dq>;	A5)
при этом изменению 6 от 0 до а отвечает изменение у от 0 до я/2. Тогда
\ 8 J yl-ka'Sin2ip
8
Так как по первой из формул A5) легко выразить <р через 6, то зависимость / от 6
можно считать установленной.
Желая выразить, наоборот, 8 через /, мы нуждаемся в обращении эллипти-
эллиптического интеграла
<р
С
J yi-
dv
Это равенство определяет и как монотонно возрастающую непре-
непрерывную (и даже дифференцируемую) функцию отр в промежутке (-<», +«¦), кото-
которая и сама при этом изменяется от —<*> до +•=. В таком случае [83] переменная
<р оказывается однозначной функцией от и в промежутке (—~, +~); ее Я к об и
обозначил через am и*. Из A6) теперь ясно, что
1/7
i/—
. в . а . 1/7
и, значит, sin— = sin — -sin am I/ — /.
Функцию sin am и («синус амплитуды» или «эллиптический синус») обычно обозна-
обозначают просто через sn и**. Итак, окончательно, зависимость 6 от / выражается ра-
равенством
.8 .a ][g
sm —= sm—sn I/ —/.
2 2 |/ /
Определим, в заключение, продолжительность Т одного размаха маятника
из положения ОБ' в положение ОБ; она вдвое больше промежутка времени,
нужного для перехода из ОАь ОБ. Полагаяв A4) 0=осиливA5)?>=я:/2***, получим
(после удвоения) выражение для Т через полный эллиптический интеграл
1-го рода:
л/2
Отметим, что период колебания Т на деле зависит от угла а, на который
маятник первоначально был отклонен, ибо к зависит от а. Заменяя - при малых
* am — начальные буквы от слова amplitude (амплитуда).
** Функция sn и, рассматриваемая как функция комплексного аргумента,
является одной из простейших (введенных Абелем и Якоб и), так назы-
называемых, эллиптических функций.
*** Если верхний предел интеграла A4) взять равным а, то интеграл станет
«несобственным» [см. ниже 479], ибо на этом пределе подинтегральная функция
обращается в «°. Это затруднение исчезает при пользовании интегралом A6).

360j	S 4. ПРОСТЕЙШИЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ	253
углах а - модуль к нулем, получим простую приближенную формулу
которая обычно и приводится в элементарных курсах физики.
360. Замечания о составлении дифференциальных уравнений. Ограничиваясь
уравнением первого порядка вида (8), мы остановимся на вопросе о составлении
подобного уравнения. Наши замечания по этому поводу читатель сопоставит со
сказанным в 348 относительно простейшего уравнения dQ = q(x) dx.
Как правило, при составлении уравнений приходится рассматривать беско-
бесконечно малые элементы входящих в рассмотрение тел и бесконечно малые прира-
приращения тех величин, о которых идет речь. Правда, в задачах предыдущего п° нам,
как будто, удалось избежать этого, но лишь ценой использования уже гото-
готового выражения для углового коэффициента касательной, готового выра-
выражения для скорости изменения той или иной величины, коюрые сами поя-
появились из рассмотрения бесконечно малых элементов.
При установлении зависимости между бесконечно малыми элементами сле-
следует пользоваться всеми возможными упрощающими допущениями
и приближенными заменами, сводящимися в сущности к отбрасы-
отбрасыванию бесконечно малых высших порядков. В частности, все бесконечно малые
приращения рассматриваемых величин рекомендуется
заменить их дифференциалами; как читатель знает, это также
сводится к отбрасыванию бесконечно малых высших порядков. Истинный смысл
всех этих указаний лучше всего выяснится на примерах (см. следующий п°).
Здесь же мы хотим остановиться еще на разъяснении того важного обстоя-
обстоятельства, что получающееся в результате всех этих упрощений и отбрасываний
дифференциальное уравнение вида (8)
Р(х, у) dx+Q(x, y)dy = 0
оказывается отнюдь не приближенным, а вполне точным*.
Итак, предположим, что заменяя приращения Ах и Лу дифференциалами dx
ndyn отбрасывая - в случае надобности - бесконечно малые слагаемые в ы с ш е -
г о, чем Ах, порядка, мы пришли к уравнению (8). Если бы мы не делали этой
замены, то вместо dx и dy имели бы Лх и Лу. Восстановим, сверх того, все отброшен-
отброшенные бесконечно малые высших порядков и, перенеся в правую часть, обозначим
их сумму через а; очевидно, а также будет бесконечно малой высшего порядка.
Таким образом, рассуждая строго, мы пришли бы не к равенству (8), а к такому:
Р(х, y)Ax + Q(x, у)Лу = а,
которое вполне точно. Разделим теперь обе части его на Лх
Лу а
Р(х, y)+Q(x, У) — - —
Лх Лх
а
и перейдем к пределу при zbc-O. Так как при этом	'О, то в пределе получим
равенство	^х
dy
Р(х, y) + Q(x, у)у'= 0 или Р(х, y) + Q(x, у) — = 0,
dx
которое тождественно с (8). Поэтому и уравнение (8) оказывается точным.
Хотя при обычном методе составления уравнения мы явным образом не при-
прибегаем к предельному переходу, но фактически мы его именно и выполняем, когда
* Это аналогично сказанному в конце 348 о равенстве dQ = q(x) dx.

254
ГЛ. X. ПРИЛОЖЕНИЯ ИНТЕГРАЛЬНОГО ИСЧИСЛЕНИЯ
C61
отбрасываем бесконечно малые высших порядков и заменяем приращения диффе-
дифференциалами.
Обращаем внимание читателя на то, что мы вовсе не утверждаем, что всякое
отбрасывание бесконечно малых высшего порядка приводит к точному ре-
результату. Лишь в том случае, если это отбрасывание доведено «до конца», и в ре-
результате получилось уравнение вида (8), линейное и однородное отно-
относительно дифференциалов, можно уже ручаться за его точность. [Опять аналогия
с п° 348!]
361. Задачи. 1) Барометрическая формула. Поставим своей
задачей установить зависимость между высотой И(м) места над уровнем моря
и давлением воздуха р (кг/м2).
Вообразим над уровнем моря площадку в 1 мг и рассмотрим призматический
столб воздуха, опирающихся на эту площадку. Давление воздуха р в сечении этого
столба на высоте h обусловлено весом той части столба, которая опирается на
упомянутое сечение. Увеличение высоты h на бесконечно малую величину
dh влечет за собой убыль давления - dp, которая измеряется весом слоя воздуха
между площадками {К) и (Ji+dh) (рис. 52)
-dp= s dh,
где 5 есть вес (в кг) 1 м3 воздуха под давлением р. Мы пренебрегаем здесь тем,
что на деле s меняется при переходе от нижней площадки рассматриваемого
слоя к верхней.
Как легко вывести из закона Бойля -Мариотта, величина 5 сама
пропорциональна давлению р: s = kp, так что окон-
окончательно
dp
dp= -kp dh или — = -?k dh
- уравнение уже знакомо
3) и 4) (а)].
Отсюда
нам типа [ср. 359, задачи
Если решить это уравнение относительно //,
то получим формулу
, 1 . Ро
h = — In —,
k p
Уровень моря
Рис. 52.
позволяющую судить о высоте h подъема над уровнем
моря по давлению р воздуха.
Постоянная \jk, как устанавливается в физике, равна (с округлением) 8000
A + 0,004г), где t — средняя температура воздуха. Если перейти к десятичным
логарифмам (умножив и разделив на модуль М=0,43) и заменить отношение
давлений pjp отношением барометрических отсчетов bjb, то получим окончатель-
окончательную формулу h = 18 400A +0,0040 log bjb.
Эта формула годится и для определения разности высот h любых двух точек,
в которых показания барометра соответственно равны Ьо и Ь.
2) Трение канатов и ремней. Представим себе, что через непо-
неподвижно укрепленный цилиндрический барабан перекинут канат (ремень и т. п.),
который прилегает к цилиндру по некоторой дуге АВ (рис. 53а), соответствующей
центральному углу со («угол обхвата»). Пусть к концу А каната приложена сила
So, а к концу В - сила 5:.
Если между канатом и барабаном существует трение, то сила So может уравно-
уравновесить даже ббльшую ее силу, приложенную на другом конце. Какова же та наи-
наибольшая сила S,, которая при наличии трения может быть уравновешена дан-
данной силой Sn ?

36Ц
§ 4. ПРОСТЕЙШИЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
255
Для решения этого вопроса рассмотрим сначала, как распределится натя-
натяжение ? вдоль части АВ каната в тот момент, когда лишь начинается сколь-
скольжение. Что это натяжение не будет постоянным, явствует уже из того, что в точках
А а В оно, соответственно, равно So и Sx.
Возьмем на дуге АВ какую-нибудь точку М, положение которой определяется
углом 6 = <$АОМ, и установим, какие силы действуют на элемент ММ' каната,
отвечающий центральному углу dd. Прежде всего в точке Мдействует натяжение
S=S{Q), а в точке М' - натяжение S+dS (рис. 536). Обе эти силы направлены
М-	М'
ib^L
по касательным к окружности барабана. Для того чтобы определить силу трения
на рассматриваемом элементе, нужно вычислить нормальную силу dN, прижи-
прижимающую этот элемент к поверхности барабана. Она слагается из радиальных
составляющих обоих натяжений, так что
d6	de
dN= Ssin	h(S+dS) sin — .
d6
Здесь можно отбросить произведение dS sin — как бесконечно малое высшего
d6	de
порядка и заменить sin — эквивалентной ему бесконечно малой — (что снова
2	2
равносильно отбрасыванию бесконечно малой высшего порядка). Окончательно
dN=Sd6. Так как сила трения пропорциональна этой нормальной силе, то, обо-
обозначая множитель пропорциональности (коэффициент трения) через ц, получим
dR=fidN=fiSde. Трение противодействует начинающемуся движению, так что
сила dR вместе с натяжением S в точке М должны уравновешивать натяжение
S+dS в точке М', откуда dS=/iSd6. Мы снова получили дифференциальное урав-
уравнение знакомого типа. Можно сразу написать его решение (с учетом начального
условия S= So при в = 0): S-Soe№. Наконец, полагая здесь 0 = а>, найдем St = Suei"».
Эта важная формула принадлежит Эйлеру.
3) Формула Пуассона (S. D. Poisson). Предложим себе установить
зависимость между объемом V и давлением р одного моля идеального газа при

256	ГЛ. X. ПРИЛОЖЕНИЯ ИНТЕГРАЛЬНОГО ИСЧИСЛЕНИЯ	[361
адиаб атическом процессе (т. е. в случае полного отсутствия теплового
обмена между газом и окружающей средой).
Состояние газа, кроме величин V и р, характеризуется еще его (абсолютной)
температурой Т. Впрочем эти величины не независимы; они связаны известной
формулой Клапейрона
pV=RT (R - газовая постоянная).	A7)
Установим, какое количество энергии dU, в единицах тепла, нужно затратить,
чтобы перевести газ из состояния (р, V, Т) в бесконечно близкое состояние (p+dp,
V+dV, T+dT).
Процесс перехода можно представить себе состоящим из двух стадий. Во-
первых, объем V газа увеличивается на dV и, во-вторых, температура Т газа -
при постоянном объеме — изменяется на dT.
Чтобы вычислить элементарную работу расширения газа, предположим
для простоты, что рассматриваемая масса газа находится в цилиндре по одну
сторону поршня [ср. 354, 2)]. Сила, действующая со стороны газа на поршень,
будет pQ, где Q - площадь поршня. Если при расширении газа поршень сдви-
сдвинулся на расстояние ds, то работа, произведенная газом, будет равна pQ ds или
р dV (так как Qds = dV). Так выражается работа - в обычных единицах работы,
например, в кем (если р дано в кг/м2, V - в ма). Желая установить потраченное
на эту работу тепло, нужно полученное выражение умножить на так называемый
«термический эквивалент работы» А =	 кал/кгм, что даст Ар dV.
Изменение температуры на dT потребует cv dT кал, где с„ есть теплоемкость
газа при постоянном объеме. Складывая, получим
dU=cvdT+ApdV.	A8)
Исключить отсюда dT легко. Если продифференцировать формулу A7)
pdV+Vdp = RdT	A9)
и определить dT
dT = —(pdV+Vdp),
К
то остается лишь подставить это выражение в A8)
с„	Cv+AR
dU=— Vdp+-	pdV.
R	R
Можно показать, что cv+AR есть как раз теплоемкость ср газа при постоян-
постоянном давлении*, так что окончательно
cv	Cn
du = — Vdp+ —
Вернемся теперь к сделанному вначале предположению, что процесс протекает
адиабатически; тогда dU-О. Таким образом, мы приходим к дифферен-
дифференциальному уравнению, связывающему р и V,
dp dV	(	с„ \
cvVdp+cppdV=O или	Ь&	= 0 где ? = — =• 1 .
d V	\	cv J
Интегрируя, найдем \np+kbi V=0 или pVk = C.
Это и есть формула Пуассона.
* Если из A9) определить pdV=RdT- V dp и подставить в A8), то получим
dU=(cv+AR) dT-AVdp. Полагая здесь р = const, т. е. dp = O, придем к равенству
dU'= (с„+AR) dT, которое и показывает, что cv+AR есть ср.

ГЛАВА ОДИННАДЦАТАЯ
БЕСКОНЕЧНЫЕ РЯДЫ С ПОСТОЯННЫМИ ЧЛЕНАМИ
§ 1. Введение
362. Основные понятия. Пусть задана некоторая бесконечная по-
последовательность чисел
«1, а%, a.j, ..., ап, ...	A)
Составленный из этих чисел символ
а1+а, + а3+ ... +ап+ ...	B)
называется бесконечным рядом, а сами числа A) - ч л е-
н а м и ряда. Вместо B), пользуясь знаком суммы, часто пишут так:
2ап;	Bа)
л=1
указатель п пробегает здесь все значения от 1 до ~*.
Станем последовательно складывать члены ряда, составляя (в бес-
бесконечном количестве) суммы;
= ах + а2 + а3, |
их называют частными суммами (или отрезками) ряда.
Эту последовательность частичных сумм {Ап} мы всегда будем сопо-
сопоставлять с рядом B): роль этого символа и заключается в порождении
упомянутой последовательности.
Конечный или бесконечный предел А частичной суммы Ап ряда B)
при и-»~:
А = lim An
называют суммой ряда и пишут
А = ах+а2+ ...+ап+ ... = 2 ап,
п=1
* Впрочем, нумерацию членов ряда иногда бывает удобнее начинать не с
единицы, а с нуля или же с какого-либо натурального числа, большего единицы.
17 Г. М. Фихтснгольп, т. II

258	ГЛ. XI. БЕСКОНЕЧНЫЕ РЯДЫ С ПОСТОЯННЫМИ ЧЛЕНАМИ	1363
придавая тем самым символу B) или Bа) числовой смысл. Если ряд
имеет конечную сумму, его называют сходящимся, в про-
противном же случае (т. е. если сумма равна + <», либо же суммы вовсе
нет) — р а с х о д ящим с я*.
Таким образом, вопрос о сходимости ряда B), по определе-
н и ю, равносилен вопросу о существовании конечного предела для
последовательности C). Обратно, какую бы варианту х = хп {п = 1,2,
3, ...) наперед ни взять, вопрос о наличии для нее конечного предела
может быть сведен к вопросу о сходимости ряда
х1 + (х2-х1) + (х3-х2) + ... +(х„-*„_!)+...,	D)
для которого частичными суммами как раз и будут последовательные
значения варианты:
Х[, Х2, Xj, . . ., Хп, . . .
При этом сумма ряда совпадает с пределом варианты.
Иными словами, рассмотрение бесконечного ряда и его суммы
есть просто новая форма изучения варианты (или последова-
последовательности) и ее предела. Но эта форма, как читатель увидит из даль-
дальнейшего изложения, представляет неоценимые преимущества как при
установлении самого существования предела, так и при его вычис-
вычислении. Это обстоятельство делает бесконечные ряды важнейшим ору-
орудием исследования в математическом анализе и его приложениях.
363. Примеры. 1) Простейшим примером бесконечного ряда является уже
знакомая читателю геометрическая прогрессия:
a+aq+aq2+ .
Ее частичная сумма будет (если q и 1)
a-aqn
Если знаменатель прогрессии, q, по абсолютной величине меньше единицы, то
[как мы уже знаем, 25, 7)] sn имеет конечный предел
т. е. наш ряд сходится, и s будет его суммой.
При |«[з&1 та же прогрессия дает пример расходящегося ряда. Если
то его суммой будет бесконечность (определенного знака), в прочих случаях суммы
вовсе нет. Отметим, в частности, любопытный ряд, который получается при а = 1
* Об этом уже была речь в первом томе [25, 9)].

363]	§ 1. ВВЕДЕНИЕ	259
и q= - 1:
1-1 + 1-1 ! ... = 1 + (-1)+1+(-1)+...*.
Его частичные суммы попеременно равны то 1, то 0.
2)	Вещественное число а, разложенное в бесконечную десятичную дробь
С„, сгс2с3 ... сп ...
[9], очевидно, представляет собой сумму ряда:
0+io'io*+i03 "•• ' ю" "¦•
3)	По образцу D) построен ряд
2 In (l + -)=2 [1п(и+1)-1пи],
n=i V л / п=г
явно расходящийся, ибо In (и+1) —+•=.
4) На той же идее построены следующие ряды (где а обозначает произвольное
число, отличное от - 1, -2, -3, ...):
А	" ' ' '
2
_ у1 Г	i
и, вообще, при любом целом
2
5) Аналогично трактуется ряд
где х есть любое фиксированное число, отличное от ±1. Так как «-я частичная
сумма равна
1	1
1-Х 1-.Y2»'
X	1
то при I х I -= 1 ряд сходится к сумме — , а при I х I =-1 — к сумме
1-х	1-.
* Если какой-либо член а ряда оказывается отрицательным числом:
а- -Ь (где 6 =»0), то вместо того, чтобы писать:
• • • +{-Ь) + • •., пишут: . ..-6+...
Подчеркнем, что членом ряда здесь будет все же - Ь, а не Л.
17*

260	ГЛ. XI. БЕСКОНЕЧНЫЕ РЯДЫ С ПОСТОЯННЫМИ ЧЛЕНАМИ	[364
6)	Легко установить расходимость ряда
- 1	11	1
?ifi У2 /3 }fJt
В самом деле, так как члены его убывают, то его и-я частичная сумма
1	11
1 +	h ¦¦¦-)—-=~и	=уп
fi yn fn
и растет до бесконечности вместе с п.
7)	Наконец, менее тривиальный пример нам доставит уже известное [37] раз-
разложение числа е:
11	1	- 1
112
Вспоминая приближенное вычисление числа е в 37, читатель на этом примере
сможет оценить выгоду последовательного введения все менее и менее значитель-
значительных поправок, постепенно улучшающих получаемые в лице частичных сумм при-
приближенные значения е.
364. Основные теоремы. Если в ряде B) отбросить первые т чле-
членов, то получится ряд:
«т + 1 + Ят + 2+ ¦ • • +ат + к+ ¦ ¦ ¦ = 2 ап,	E)
называемый остатком ряда B) после т-т о члена.
1°. Если сходится ряд B), то сходится и любой из его остатков
E); обратно, из сходимости остатка E) вытекает сходимость ис-
исходного ряда B).
Фиксируем т и обозначим k-ю частичную сумму ряда E) че-
через А'к:
А'к = ат+1 + ат+2+ ¦ ¦ ¦ +am+i,.
Тогда, очевидно,
A\l'=Amjrii — Am,	(р)
Если ряд B) сходится, так что Ап-+А, то - при безграничном возра-
возрастании к - существует конечный предел
А' = А-Ат	G)
и для суммы А'к, что и означает сходимость ряда E).
Обратно, если дано, что сходится ряд E), так что А'к-*А', то пере-
перепишем равенство F), полагая в нем к — п-т (при а^-т), так:

3641	S i введение:	261
отсюда можно усмотреть, что - при безграничном возрастании п -
частичная сумма Ап имеет предел
А=А,п-гА',	(8)
т. е. сходится ряд B).
Иными словами, отбрасывание конечного числа начальных членов
ряда или присоединение в начале его нескольких новых членов не от-
отражается на поведении ряда (в смысле его сходимости или
расходимости).
Сумму ряда E), если он сходится, обозначим вместо А' символом
ат, указывая значком, после какого члена берется остаток. Тогда
формулы (8) и G) перепишутся следующим образом:
А=Ат-\-хт, хт=А-Ат.	(9)
Если увеличивать т до бесконечности, то Ат^А, а ат—0. Итак:
2°. Если ряд B) сходится, то сумма <хт его остатка после т-го
члена с возрастанием т стремится к нулю.
Упомянем следующие простые свойства сходящихся рядов:
3°. Если члены сходящегося ряда B) умножить на один и тот же
множитель с, то его сходимость не нарушится (а сумма лишь умно-
умножится на с).
В самом деле, частичная сумма Ап ряда
очевидно, равна
Ап = саг - са2 - - ... •+- сап = с(а^ - а2 - ... + ап) = сАп
и имеет пределом сА.
4°. Два сходящихся ряда
А = ах -г а2 f ... + ап -г ...
и
B = b1 + b2 i- ... +bn+ ...
можно почленно складывать {или вычитать), так что ряд
также сходится, и его сумма равна, соответственно, А + В.
Если Ап, Вп и Сп означают частичные суммы упомянутых рядов,
то, очевидно,
Сп = (а, ± 6,) 4 (а2 ± Ь2) + ... + (в„ + Ьп) =
b?+ ... -'-bn)=An + Bn.

262	ГЛ. ХГ. БЕСКОНЕЧНЫЕ РЯДЫ С ПОСТОЯННЫМИ ЧЛЕНАМИ	[365
Переходя к пределу, найдем, что lim C,,^lim An + lim Bn, что и дока-
доказывает наше утверждение.
В заключение сделаем еще одно замечание.
5°. Общий член ап сходящегося ряда стремится к нулю.
Это может быть доказано совершенно элементарно: раз Ап (а с
ним и Ап-2) имеет конечный предел А, то
В предыдущем утверждении содержится необходимое усло-
условие для сходимости ряда, которым мы будем часто пользоваться. При
нарушении его ряд заведомо расходится. Однако
важно подчеркнуть, что это условие не является само по себе доста-
достаточным для сходимости ряда. Иными словами, даже при вы-
выполнении его ряд может расходиться. Примерами
этого служат ряды
'1+3 и k-fn
рассмотренные выше [363, 3) и 6)]; многочисленные другие примеры
этого же рода читатель найдет в последующем.
§ 2. Сходимость положительных рядов
365. Условие сходимости положительного ряда. Займемся теперь
вопросом об установлении сходимости или расходимости ряда. Этот
вопрос всего проще решается для рядов, члены которых неотрица-
неотрицательны; для краткости такие ряды мы будем называть просто поло-
положительными.
Пусть ряд
2 ап =
2,
1
ап = ах f а2 + ... -;- ап f ...	(А)
будет положительным, т. е. апг=0 (п= 1, 2, 3, ...). Тогда, очевидно,
т. е. варианта Ап оказывается возрастающей. Вспоминая тео-
теорему о пределе монотонной варианты [34], мы непосредственно при-
приходим к следующему основному в теории положительных рядов пред-
предложению:
Положительный ряд (А) всегда имеет сумму; эта сумма будет
конечной (и, следовательно, ряд - сходящимся), если частичные суммы
ряда ограничены сверху, и бесконечной (а ряд - расходящимся) в про-
противном случае.
Все признаки сходимости (и расходимости) положительных рядов
в конечном счете, основаны на этой простой теореме, Но н е п о-

365)	§ 2. СХОДИМОСТЬ ПОЛОЖИТЕЛЬНЫХ РЯДОВ	263
средственное ее применение лишь в редких случаях позволяет
судить о характере ряда. Приведем примеры этого рода.
1) Рассмотрим ряд
у 1	11	1
п=1«	2 3	п
известный под именем гармонического ряда*.
Имеем очевидное неравенство:
11	111
Если, отбросив первые два члена, остальные члены гармонического ряда после-
последовательно разбить на группы, по 2, 4, 8, ¦ •., 2'?~1, . •. членов в каждой
1 1 !
Т^4~'
2
то каждая из этих сумм в отдельности будет больше —; в этом легко убедиться,
полагая в A) поочередно п= 2, 4, 8, ..., 2к~1, ... Обозначим и-ю частичную сумму
гармонического ряда через Нп; тогда, очевидно,
Мы видим, что частичные суммы не могут быть ограничены сверху: ряд имеет
бесконечную сумму.
Упомянем уже здесь, что Нп с возрастанием п возрастает очень медленно.
Эйлер, например, вычислил, что
#юоо = 7,48 ..., #! 00оо00 = 14,39 ..., и т. д.
Впоследствии мы будем иметь случай точнее охарактеризовать возрастание сумм
Нп [367, 10)].
2) Рассмотрим теперь более общий ряд:
^,1	11	1
2, — = 1+—Ь—!-...+ — +•••,
Zi\ ns	2s 3«	ns
где 5 - любое вещественное число; он содержит в себе, как частный случай (при
s= 1), предыдущий ряд. По сходству с рядом 1), и этот ряд тоже называют гар-
гармоническим.
Так как при 5 «= 1 члены рассматриваемого ряда больше соответствующих
членов ряда 1), то, в этом предположении, частичные суммы и подавно не огра-
ограничены сверху, так что ряд расходится.
* Каждый член его, начиная со второго, представляет собой среднее гар-
гармоническое двух соседних членов. [Число с называется средним гар-
1 ! I Ml
адоническим чисел а и Ь, если — = — —|— .
с 2 U Ь] \

264	ГЛ. XI. БЕСКОНЕЧНЫЕ РЯДЫ С ПОСТОЯННЫМИ ЧЛЕНАМИ	[366
Займемся случаем, когда s>l; положим для удобства s= I +a, где сг^О.
Аналогично A), имеем на этот раз:
1	1	1	11
"' (iny""' ns п<>'
Выделяя, как и выше, последовательные группы членов:
с помощью B) легко показать, что эти суммы соответственно меньше членов
прогрессии
11111	1	1
2"' 4" B")»' 8я B<>K ' ¦"' B''-1)" B")*-1'
В таком случае ясно, что какую бы частичную сумму рассматриваемого ряда
ни взять, она будет меньше постоянного числа
следовательно, ряд сходится.
[Его сумма, зависящая от s, представляет знаменитую функцию C(s) P и м а н а,
играющую важную роль в теории чисел.]
366. Теоремы сравнения рядов. Сходимость или расходимость по-
положительного ряда часто устанавливают путем сравнения его с дру-
другим рядом, заведомо сходящимся или расходящимся. В основе такого
сравнения лежит следующая простая теорема.
Теорема 1. Пусть даны два положительных ряда
2ап = а1 + а2+ ... +ап+ ...	(А)
Л = 1
и
Z ьп=ъ±+ь2 + ... + ъп + ...	(в)
л=1
Если, хотя бы начиная с некоторого места (скажем, для п >iV), вы-
выполняется неравенство: ап=^Ьп, то из сходимости ряда (В) вытекает
сходимость ряда (А) или - что то же - из расходимости ряда (А)
следует расходимость ряда (В).
Доказательство. На основании того, что отбрасывание ко-
конечного числа начальных членов ряда не отражается на его поведе-
поведении [364, 1°], мы можем считать, не нарушая общности, что ал*&Ьп

366]	§ 2. СХОДИМОСТЬ ПОЛОЖИТЕЛЬНЫХ РЯДОВ	265
при всех значениях и= 1,2,3, ... Обозначив частные суммы рядов
(А) и (В), соответственно, через Ап и Вп, будем иметь:
Ап-*Вп.
Пусть ряд (В) сходится; тогда, по основной теореме [365], суммы
Вп ограничены:
Bn=sL (L = const; n= 1, 2, 3, ...).
В силу предыдущего неравенства, и подавно
а это, по той же теореме, влечет за собой сходимость ряда (А).
Иногда на практике более удобна следующая теорема, вытекаю-
вытекающая из первой:
Теорема 2, Если существует предел*
On
то из сходимости ряда (В), при К-< + ~, вытекает сходимость ряда
(А), а из расходимости первого ряда, при К>-0, вытекает расходимость
второго. [Таким образом, при 0 < К< + ~ оба ряда сходятся или оба
расходятся одновременно.]
Доказательство. Пусть ряд (В) сходится и К< + ~. Взяв
произвольное число е>0, по самому определению предела, для до-
достаточно больших п будем иметь
~^К+е, откуда ап^(К+е)Ьп.
On
В силу 364, 3°, одновременно с рядом (В) будет сходиться и ряд
2^{К+е)Ь„, полученный умножением его членов на постоянное число
К+е. Отсюда, по предыдущей теореме, вытекает сходимость ря-
ряда (А).
Если же ряд (В) расходится и К>0, то в этом случае обратное
отношение — имеет конечный предел; ряд (А) должен быть расходя-
Оп
щимся, ибо если бы он сходился, то, по доказанному, сходился бы
и ряд (В).
Наконец, приведем еще одну теорему сравнения, также представ-
представляющую собой следствие первой.
Теорема 3. Если, хотя бы начиная с некоторого места (скажем,
для п >-N), выполняется неравенство**
* Мы предполагаем при этом, что Ьп^0-
** При этом ап и Ьп, конечно, предполагаются отличными от нуля.

266	ГЛ. XI. БЕСКОНЕЧНЫЕ РЯДЫ С ПОСТОЯННЫМИ ЧЛЕНАМИ	[367
то из сходимости ряда (В) вытекает сходимость ряда (А) или -
что то же — из расходимости ряда (А) вытекает расходимость
ряда (В).
Доказательство. Как и выше, при доказательстве теоремы
1, не умаляя общности, можно считать, что неравенство C) справед-
справедливо для всех значений п= 1, 2, 3, ... В таком случае будем иметь:
«1 ^i ' а, ^Ьг' " ' ' ' ап_г ^bn-i '
Перемножив почленно эти неравенства, получим:
afjf или пп^.Ъп (п = 1,2,3,...).
Пусть ряд (В) сходится; вместе с ним сходится ряд J>' — -Ьп, полу-
ченный умножением его членов на постоянный множитель -^ . А то-
гда, по теореме 1, сходится и ряд (А), ч. и тр. д.
Перейдем теперь к примерам установления сходимости или рас-
расходимости рядов непосредственным применением теорем срав-
сравнен и я.
Х7 1
367. Примеры. 1) Л 	 (а=>0).
п=1 1+ап
Если ва=1, то нарушается необходимое условие сходимости, 364, 5°
и ряд расходится. При а=-1 члены ряда оказываются меньшими членов сходя-
сходящегося ряда У — Г: ряд сходится (теорема 1).
2) ^ — сходится, так как
л=1 Bи)!
(и!J	и!	1
Bга)! ~ 2".Bя-1)!!"" 2"
(теорема 1).
3) 2 2" • sir> — (° -= х -= Зя).
п=!	3"
Так как
2" • sin —• -= л ,
3" [З
— I сходится, то это же справедливо и для данного ряда (теорема 1).

367)	§ 2. СХОДИМОСТЬ ПОЛОЖИТЕЛЬНЫХ РЯДОВ	267
4) Рассмотрим вновь гармонический ряд 2 — и сопоставим его,
л=1 И
по теореме 2, с заведомо расходящимся рядом
2 [1п(я+1)-1пи]= 2'mfl+-) [363, 3)].
1	V П)
V. П
Так как [77, 5) (а)]
lim—	-1,
n
то отсюда уже вытекает расходимость гармонического ряда.
Или иначе: применяя к функции In x в промежутке [я, п+\} формулу конеч-
конечных приращений, найдем, что
1
1п(и+1)-1пя-	 @*0*1).
п + 0
В таком случае гармонический ряд, члены которого соответственно больше, и по-
подавно расходится (теорема 1).
5) Аналогично можно установить вновь сходимость ряда 2	(ПРИ ° ^ 0),
сопоставляя его с заведомо сходящимся рядом
1 Ч
-1Г пЛ'
Применяя к функции — в промежутке [и — 1, и] формулу конечных приращений,
ха
найдем:
1	1	а
001
Таким образом, при и*2
откуда, по теореме 1, и вытекает сходимость испытуемого ряда.
6) Чтобы подобным же приемом получить новый результат, рассмотрим
ряд У	(члены которого еще меньше, чем соответствующие члены гармони-
-ей1пй
ческого ряда).
Сопоставим его с заведомо расходящимся рядом
In In (и г 1)-In In и].

268	ГЛ. М. БЕСКОНЕЧНЫЕ РЯДЫ С ПОСТОЯННЫМИ ЧЛЕНАМИ	|367
Применяя формулу конечных приращений к функции In In x в промежутке [я,
я+l], получим:
I
In In (;г+1)-1п 1пя =	@-= 0-= 1),
(и + 0Iп(и+0)
откуда, по теореме 1, заключаем, что данный ряд, члены которого соответственно
больше, и подавно расходится.
7) Сравнение с гармоническими рядами 4) и 5) позволяет установить поведение
многих рядов. По теореме 1:
I 11
(а) у — ¦¦¦¦ расходится: —=—— -	;
(в) V	— (р=»0) расходится: Aпи)Р<и (для достаточно больших и);
еAп)р
- л! и! 2
(г) У —	сходится:	=— (для и=-3);
~	1	111
| Г1 |	"\* . , .,. .	*-*v/Л ТТfXTf*О •		 —- 	 ~~-
^2(\ппУпп	AпиIп" И1п1пд „1
(для достаточно больших и);
~1	111
(е)	V	 сходится: 	=	; — (то же);
^з С" 1п "Iл "	Aп1пяIпп и'"!11'1 л2
I	1111
(ж)	У	расходится:	=	=> — - —
^ On «)ln 1п"	Aпл)|п1пп eOnin.i? einn „
(то же).
8) По теореме 2:
(а) У	F =- 0) сходится при s =- i, расходится при i=s 1:
1	1 1
™ 1	11
(б)	V —	расходится: 	:—-*1;
1 п	п П
п \jn	п |/я
°°	X	X I
(в)	^ sin—	@-=х-=я) расходится; sin — :—-i; аналогично,
расходятся и ряды У In И— (х>0) и

367J	§ 2. СХОДИМОСТЬ ПОЛОЖИТЕЛЬНЫХ РЯДОВ	269
(г) 2 1-cos — сходится: 1-cos — :•—>—.
n=i V	nj	n n" 2
9) Вот более сложные примеры этого же типа:
Обозначим через хп отношение общего члена этого ряда к — :
и
In хп = In п+п In 11
I n
Пользуясь разложением In A + х), о котором была речь в 125, 5), можно написать:
( 1пл*| In л 1 /In л^2	(\пп\-
I п )	п г\п )	\ п )
где <хп~0 при л-~. Поэтому
1	In2 л	In2 л
2	и	п
следовательно, хп -* 1, и предложенный ряд расходится.
Пользуясь и здесь упомянутым разложением log A+х), будем иметь:
2л+1 ( 2 \ 2 \ ( 2 \* \ ( 2 \*	( 2
1	1A	() 1) ^(
где /?„ -~ 0 при и - «=, так что
2л+1	2и + 3 ( 1 V	8л [ 1\!
и In	1 =	 +вп ¦	 .
2и-1	3Bл-1) l.2«-lj	2л-1 12л- lj
1
Таким образом, отношение общего члена испытуемого ряда к	имеет
1	Bл -1J
пределом —: наш ряд сходится.
10) Наконец, рассмотрим ряд
^ С1 "+1\
2	In	¦
п = 1 \п	п )
Мы знаем [133, 4)], что
0, -1-= х-
Пользуясь им, можем написать:
>Н 1 I 1 \ 1
In 	= ln 1+-U-,
я	\ л / л

270	ГЛ. ХГ. БЕСКОНЕЧНЫЕ РЯДЫ С ПОСТОЯННЫМИ ЧЛЕНАМИ	[368
я в то же время
. й+1 , п	( 1 \ 1
In — • = - In	= — In 1 —	=>	.
п	и+1	I. л+lj и+1
Поэтому
1 и+1 11	11
0<_-1п	-=	=	«-¦ — .
п	п и и + 1 и(и + 1) п"
Таким образом, члены данного ряда положительны и меньше соответственных
членов сходящегося ряда у — [365, 2)]; следовательно, и данный ряд сходится.
-° и2
Если обозначить его сумму через С, то частичная сумма
" !\ к+\\
2 г-In—- =Я„-1п(«+1ЬС
(Нп обозначает, как всегда, частичную сумму гармонического ряда). Можно за-
/ ! 1
менить здесь In (и+1) на In и, так как их разность, равная In 11H— , стремится
I п)
к нулю. Окончательно: обозначая через уп некоторую бесконечно малую, имеем
для Нп замечательную формулу
Нп = Ып + С + уп.	D)
Она показывает, что при бесконечном возрастании п частичная сумма Нп гармо-
гармонического ряда растет, как In п.
Фигурирующая в формуле D) постоянная С называется эйлеровой по-
постоянной. Ее численное значение (которое удается вычислить из других
соображений) таково:
С = 0,577 215 664 90...	E)
368. Признаки Коши и Даламбера. Сравнение данного ряда
2 а,г--а| + ао+ ... +а„+ ...	(А)
п=1
с различными стандартными рядами, заведомо сходящимися
или расходящимися, может быть проведено и в другой, так сказать,
более организованной форме.
Возьмем для сравнения, в качестве ряда (В), с одной стороны,
сходящуюся геометрическую прогрессию
4 + <72+ • • • +Чп+ ¦ ¦ ¦ @-=#-=1),
а с другой стороны - расходящуюся прогрессию
21 = 1 + 1+•¦.+!+...
Сравнивая испытуемый ряд (А) с этими рядами по схеме теоремы 1,
придем к следующему признаку:
Признак Коши. Составим для ряда (А) варианту

368]	§ 2. СХОДИМОСТЬ ПОЛОЖИТЕЛЬНЫХ РЯДОВ	271
Если, при достаточно больших п, выполняется неравенство
где q — постоянное число, меньшее единицы, то ряд сходится;
если же, начиная с некоторого места,
то ряд расходится.
п	п
Действительно, неравенства /а„«=дили Ya~n»l равносильны, соот-
соответственно, таким: an=sqn или ап»1; остается применить теорему 1*.
Чаще, однако, этот признак применяют в другой, предельной,
форме:
Допустим, что варианта Qn имеет предел (конечный или нет):
Тогда при B-=1 ряд сходится, а при B=~1 ряд расходится.
Если g< 1, то возьмем положительное число е, меньшее чем 1 - (?,
так что и B + е<1. По определению предела, для n>N будет:
Число (?+? играет роль числа q в предыдущей формулировке: ряд
сходится.
Если же б=-1 (и конечно), то, взяв е = (?-1, так что B-е=1, для
достаточно больших значений п на этот раз будем иметь (?п>\: ряд
расходится. Аналогичный результат и при Q= +~.
В случае, когда B=1, этот признак не дает воз-
возможности судить о поведении ряда.
Варианту Qn будем называть вариантой Коши.
Если сравнение ряда (А) с указанными стандартными рядами про-
производить по теореме 3, то придем к такому признаку:
Признак Далалгбера (J. d'Alembert). Рассмотрим для ряда (А) ва-
варианту
Если, при достаточно больших п, выполняется неравенство
* Расходимость ряда, конечно, может быть установлена и простой
ссылкой на нарушение необходимого условия сходимости - 364, 5°.

272	ГЛ. XI. БЕСКОНЕЧНЫЕ РЯДЫ С ПОСТОЯННЫМИ ЧЛЕНАМИ	[369
где q — постоянное число, меньшее единицы, то ряд сходится;
если же, начиная с некоторого места,
то ряд расходится*.
И в этом случае удобнее пользоваться предельной формой
признака:
Допустим, что варианта <5j)n имеет предел {конечный или нет):
Тогда при @<1 ряд сходится, а при ®>1 ряд расходится.
Доказательство — такое же, как и в случае признака К о ш и.
И этот признак ничего не дает, если оказыва-
оказывается, что <5?) = 1.
Варианту ®„ назовем вариантой Даламбера.
В примере 77, 4) мы видели, что из существования предела для
варианты ®„ вытекает уже существование предела и для варианты
Bл» причем оба предела равны. Таким образом, во всех случаях, когда
признак Даламбера дает ответ на вопрос о поведении ряда,
ответ может быть получен и с помощью признака К о ш и. На при-
примерах мы увидим ниже, что обратное утверждение неверно, и при-
признак К о ш и сильнее признака Даламбера. Однако на практике
пользование признаком Даламбера обыкновенно проще.
369. Признак Раабе. В тех случаях, когда указанные простые при-
признаки не дают ответа, приходится прибегать к более сложным при-
признакам, основанным на сравнении испытуемого ряда уже с другими
стандартными рядами, так сказать, «медленнее» сходящимися
или «медленнее» расходящимися, чем прогрессия**.
Мы рассмотрим здесь еще признак Раабе (J. L. Raabe); он
осуществляет сравнение данного ряда (А) с гармоническими рядами
- сходящимися:
и расходящимися:
i
* И здесь расходимость прямо вытекает из нарушения необходимого
ап+1 Л
условия сходимости: ведь если	=в1 или Оп+^ап, то ап не может стре-
стремя
мяться к 0.
** Ср. 375, 7).

369]	§ 2. СХОДИМОСТЬ ПОЛОЖИТЕЛЬНЫХ РЯДОВ	273
- именно с помощью теоремы 3. При этом приходится рассматри-
рассматривать варианту Раабе:
Признак Раабе. Если, при достаточно больших п, выполняется не-
неравенство
где г - постоянное число, большее единицы, то ряд сходится;
если же, начиная с некоторого места,
то ряд расходится.
Итак, пусть, при достаточно больших п, имеем:
'П+1
или
Возьмем теперь любое число s между 1 и г: r>s>\. Так как по из-
известному предельному соотношению [77, 5)]:
.. КГ-
lim	:	s>
n
то для достаточно больших п будет
1 'и
1+- -1
я)	Л Ц» , . г
г или 14-1
+»)
<: Г ИЛИ I1	1 +
1	' nJln { п)	п
п
а следовательно, и
Это неравенство можно переписать следующим образом:
1
Справа мы имеем отношение двух последовательных членов ряда
применив теорему 3, убеждаемся в сходимости ряда (А).
Если же, начиная с некоторого места,
18 Г. М. Фихтенгольц, т. 11

274	ГЛ. XI. БЕСКОНЕЧНЫЕ РЯДЫ С ПОСТОЯННЫМИ ЧЛЕНАМИ	f37O
то отсюда сразу находим, что
п
и+1
ап и+1 1 '
п
применив к рядам (А) и (Н) теорему 3, заключаем о расходимости
ряда (А).
Признак Р а а б е тоже применяется преимущественно в пре-
предельной форме:
Допустим, что варианта §1п имеет предел {конечный или нет):
lim $,„ = $.
Тогда при §{,> 1 ряд сходится, а при §{,<\ ряд расходится.
Сравнивая признаки Даламбера и Ра а бе, видим, что по-
последний значительно сильнее первого. Если предел @ = lim <g)n суще-
существует и отличен от единицы, то для <$,„ = п —— 1 существует пре-
дел Ц, равный + ~ при <5j) -< 1 и - ~ при <5j) > 1. Таким образом, если
признак Даламбера дает ответ на вопрос о поведении данного
ряда, то признак Р а а б е и подавно его дает: больше того, все такие
случаи охватываются всего двумя из возможных значений <$,,
именно ±~. Все остальные значения Л, (исключая $1=1), также даю-
дающие ответ на вопрос о сходимости, соответствуют, таким образом,
случаям, когда признак Даламбера заведомо ответа не дает,
потому что @ = 1.
Но все же и здесь при §{=\ мы не имеем ответа на
вопрос о поведении ряда; в подобных случаях (которые
очень редки) приходится прибегать к еще более тонким и сложным
признакам [см., например, ниже п° 371].
Обратимся к примерам.
370. Примеры. 1) Применим признак К о ш и к следующим рядам:
~ 1	_ 1
(<i) 2, -.—пг. tn=,—-» <S^0: Ряд сходится;
п = 2 (In n)"	111 И
(б)	2 {-} (*»0), &,= -, B = 0: ряд сходится;
(в)	2 I — I (х^О; ап - положительная варианта, имеющая предел а):
л=г \ап)
X
t/; = —. Если а = 0, то B=+~, и ряд расходится, еслиа=+~, то B = 0, и ряд
°п	а
сходится; наконец, при 0-=а«=+™ будет (i! = — и поведение ряда зависит от х:
х

370]	§ 2. СХОДИМОСТЬ ПОЛОЖИТЕЛЬНЫХ РЯДОВ	275
при х-=а ряд сходится, при х>а - расходится. При х = а в общем случае и пове-
поведении ряда ничего сказать нельзя, оно зависит уже от характера приближения
ап к а.
2) Применим признак Даламбера к следующим рядам:
"° Х^	X
(а)	1+2 — (х^-0), )„=	, '3) = 0: ряд сходится;
п=1 и!	й+1
(б)	2j пхп~Цх^0), ~irn = x	. '3) = х: ряд сходится при л¦< 1
п = ]	И
и расходится при хз=1 (при л = 1 в этом убеждаемся непосредственно).
Z, хп	_ / и И
(в)	Л — (л: =- 0, 5 =- 0), >2)„ = х	, *2Р = л" ряд сходится
п=ш5	\п+1)
при л-= 1 и расходится при х=-1; при л = 1 получается гармонический ряд, пове-
поведение которого, как мы уже знаем, зависит от s.
(г)	2 «'• I — I "(* =- °) ®" = 7	Пп' ® = ~": при ¦* * е ряд сходится> °РИ
. W	A)
х>-е расходится; при х = е признак Даламбера в предельной форме ничего
{ 1V
не дает, но так как варианта 11 +— I приближается ке возрастая, так что
I )
©n^l, то первоначальная форма признака позволяет все же заключить о рас-
расходимости ряда.
(д) 2	(х»0), ^п=х- 1ч— , б$) = х-е: при х-=— ряд сходится, а
л=1 n!	I n)	e
1	1
при х =— расходится; при х = — на этот раз при помощи признака Д а л а м -
е	е
б е р а ничего установить нельзя, так как б$п приближается к ® = 1 снизу. Мы вер-
вернемся к этому случаю ниже, в 5) (г).
3) Возьмем ряд
где а и b - два различных положительных числа. Здесь ®2n-i = a> ©2п = 6> и при-
признак Даламбера (в первоначальной форме) позволяет сделать заключение
о сходимости или расходимости ряда, лишь если оба числа a, b меньше единицы
или оба - больше.
В то же время
2л-1	2л
так что i? = Yab; по признаку К о ш и , при ab -= 1 ряд сходится, а при аб =-1
(очевидно, и при ab = 1) - расходится.
4) Рассмотрим ряд ^т(п)х", где х=-0 и т(и) означает число делителей
натурального числа п. Ввиду прихотливого хода изменения функции т(я) не пред-

276	ГЛ. XI. БЕСКОНЕЧНЫЕ РЯДЫ С ПОСТОЯННЫМИ ЧЛЕНАМИ	[370
ставляется возможным применить здесь признак Даламбера. Между тем
признак К о ш и вполне приложим:
п	п
x^Qn= V?(ri)-x=*sYn-x, так что & = х,
и при л-= 1 ряд сходится, а при *=-1 (очевидно, и при х= 1) - расходится.
5) Приведем примеры применения признака Р а а б е .
(а) 1+2
п=1 \?пу.\ 2л + 1
Признак Даламбера к этому ряду неприложим, ибо
(и притом ®„ ¦= 1). Составим варианту Р а а б е :
^	3
Так как Si = lim аЯп = — =-1. то ряд сходится.
2
,,. -^	и!	. ..
Так как ®п =	, @ = 1, то здесь признак Даламбера неприло-
х+п+1
жим. Имеем, далее, Sin	х> так что	$1 = х. Таким образом, при x-=l ряд
п+\
расходится, а при х =-1 сходится; при л: = 1	получается расходящийся гармониче-
гармонический ряд (без первого члена).
¦?,	и!х"
(в) 2-
n=i (х+а^ (Ьс+а^	(пх+ап)
где х >• 0, и яп - положительная варианта, имеющая конечный предел о.
Имеем: ©„ = —		, @ = 1. Далее, Лп= Ш"+1 , Ц = -. Итак, при
(+l)+a	(п+\)х	х
+i	)
х<а ряд сходится, при х>а он расходится. При х = а в общем случае ничего
сказать нельзя: поведение ряда тогда зависит от характера приближения ап к а.
(г) Наконец, рассмотрим ряд
Для него
р
-1
(¦4)"
чтобы вычислить предел этой варианты, заменим ее более общим выражением:
1
Л ¦-
1A+*)*

371)	§ 2. СХОДИМОСТЬ ПОЛОЖИТЕЛЬНЫХ РЯДОВ	277
к которому уже можно применить методы дифференциального исчисления. По
правилу Лопиталя, переходим к отношению производных:
,	.	In A+*)--•*-
У	1 „ 1-4	е	1 + х
1 I	[ х2) х	\	!	Y2
[A+*)*]=	A+*>v
Полагая
1	х
In A + .г) = х	х- + о(лг2), 	= х - х- + о{х-),
2	1+х
1
сразу получаем, что искомый предел равен — . Ряд расходится.
371. Признак Куммера. Теперь мы выведем один весьма общий признак, при-
принадлежащий Куммеру (Е. Е. Кшшпег); его скорее можно рассматривать как
общую схему для получения конкретных признаков.
Признак Куммера. Пусть
Clt С2, •-., Сп, •¦•
будет произвольная последовательность положительных чисел, такая, что ряд
°° 1
2-
1 Сп
расходится*. Составим для испытуемого ряда (А) варианту
Если (для n>N) выполняется неравенство
где б - постоянное положительное число, то ряд сходится. Если же (для
то ряд расходится.
Доказательство. Пусть
Жп = СП'-—-
(неравенство это, очевидно, можно считать выполненным при всех и).
Умножив обе части этого неравенства на ап+1, получим:
CnOn-Cn+iOn+i^^'in+i,	F)
значит,
* Обращаем внимание читателя на то, что последним предположением мы
будем пользоваться только при выводе признака расходимости: признак
сходимости в нем не нуждается,

278	ГЛ. XI. БЕСКОНЕЧНЫЕ РЯДЫ С ПОСТОЯННЫМИ ЧЛЕНАМИ	[371
Отсюда следует, что переменная спап монотонно убывает и, следовательно,
стремится к конечному пределу (так как она ограничена снизу нулем).
Итак, ряд
2
сходится, ибо сумма его п первых членов:
c1a1-cn + lan+i
имеет конечный предел. Но тогда из неравенства F), по теореме I, следует, что
сходится ряд 2 <5вп+1> а с ним и данный ряд (А).
п = 1
Если же, для n>N,
Жп = Сп	 сп+i=e0,
Яп + 1
то имеем:
]
аП+1 СП+1
Так как ряд у — предположен расходящимся, то, по теореме 3, расходится и
Сп
испытуемый ряд (А), ч. и тр. д.
В предельной форме признак К у м м е р а выглядит так:
Допустим, что варианта Жп имеет предел (конечный или нет):
Тогда при Ж^Оряд сходится, а при ЗС-=О - расходится.
Покажем теперь, как при помощи признака К у м м е р а можно получить
некоторые важные признаки сходимости как частные случаи его.
а)	Положим, например, сп=1; условие, чтобы ряд Jj?— расходился, соблю-
соблюдено. Имеем:	сп
3Cn__5L..-l-J_-1.
ап+1	6J)n
Если варианта @„ стремится к пределу ®, то Жп стремится к пределу Ж =	1
(е){=+°°, если ® = 0, Ж= — 1, если ©= + ~). При @>-1, очевидно, Ж^О, и по
признаку Кум мер а ряд расходится; если же @-=1, то Ж>0, и ряд сходится.
Таким образом, мы пришли вновь к признаку Даламбера.
б)	Положим, далее, сп = п и отметим, что ряд V — расходится. Выражение
Жп получит вид:	"
сг	ап
Если варианта §1п стремится к пределу §1, то Жп стремится к пределу Ж = Л -1
(ЭС=±~, если Ji=±~). При Л>1 имеем Ж^О, и по признаку Куммера
ряд сходится; если же Л, •< 1, то Ж^О, так что ряд расходится. Мы вновь получили
признак Р а а б е .

372]	§ 2. СХОДИМОСТЬ ПОЛОЖИТЕЛЬНЫХ РЯДОВ	279
1
в) Наконец, возьмем сп = п In n (лз=2), такой выбор допустим, ибо ряд V
-" п In п
расходится [367, 6)]. Имеем в этом случае
Ж \пп
что можно также представить в виде:
nl~n--l j-lj-ln 1+-
если обозначить через §hn новую варианту:
Отсюда получается уже новый
Признак Бертрана (J. Bertrand). Допустим, что варианта §hn имеет
предел (конечный или нет):
ей = lim Sbn.
Тогда при 3d =¦ 1 ряд сходится, а при об *= 1 — расходится.
{ 11n+1
Действительно, так как lim In 1ч— =log e=l, то варианта Кум-
I п)
мера §in стремится к пределу |С= §}>- 1 (Ж= ± °°? если ^= ± ~). Остается со-
сослаться на признак Куммера.
Сопоставляя признаки Раабе и Бертрана, можно было бы повторить
те же замечания, которые мы выше сделали по поводу признаков Даламбера
и Р а б б е [369]. Эта цепь все более и более чувствительных (но и более сложных!)
признаков может быть неограниченно продолжена.
372. Признак Гаусса. Из признаков Даламбера, Раабе и Бер-
Бертрана легко может быть получен следующий признак Гаусса (С. F. Gauss).
Признак Гаусса. Допустим, что для данного ряда (А) отношение
может быть представлено в виде:	ап+\
l1,
«n+i	» n8
где А и fi - постоянные, а вп есть ограниченная величина: | вп \ *г?; тогда
ряд сходится, если А=-1 или если А=1, /и=-1, и расходится - если Я-=1 или Х=\,
Случаи X^ 1 приводятся к признаку Даламбера, ибо lim — + = —.
Пусть теперь Я = 1; тогда	ап *•
31п = «\—-—1 =<" + — . 3l=ft,
\an+i I	n
и случаи /I% 1 исчерпываются признаком Раабе. Наконец, если (i-l, то имеем:
<$л = 1пи(Ил-1) = —<0Л.
п
In и
Так как —, как известно, стремится к нулю при и - °°, а бп ограничена, то ой =*
п
= limс^„ = 0, и по признаку Бертрана ряд расходится.

280	ГЛ. XI. БЕСКОНЕЧНЫЕ РЯДЫ С ПОСТОЯННЫМИ ЧЛЕНАМИ	1372
Примеры. 1) Рассмотрим так называемый гипергеометрический ряд
(Гаусс):
F(u, ft у, х)=1+2
л=1
11д; |д;
Ьу	Ь2.у.(у+1)
предполагая пока а, /?, у, х =- 0. Здесь
-V — X,
так что по признаку Даламбера сразу устанавливается сходимость при
х-= 1 и расходимость при х> 1. Если же л: = 1, то возьмем отношение
и, пользуясь разложениями:
1	a a2 I
	_j	|	 .. ._
a	«	2>
a	« a я2>	jff	n /ff я2'
i+_ i+_	i+L г+L
n n	n n
представим его в виде:
ап	y-a-/?+l вп
ап+1	л	и2'
где @п ограничена. Применяя признак Гаусса, видим, что ряд F(a, /?, у, 1)
сходится при у-а-{1^0 и расходится при y-a-$=sO. Ниже мы вернемся к ги-
гипергеометрическому ряду при более общих предположениях относительно а, ^,
у и *.
2) Другим примером на применение признака Гаусса может служить ряд
1 +
ге'-+Ш+-
который сходится прир>2и расходится прир=&2. Здесь - по формуле Тейлора
2я Ь2 Bи)«
откуда
an , 2 fln
	= 1Н	1— (вл ограничена),
вп+i и я3
и т. д.

373|	§ 2. СХОДИМОСТЬ ПОЛОЖИТЕЛЬНЫХ РЯДОВ	281
373. Интегральный признак Маклорена—Коши. Этот признак по
форме отличается от всех предыдущих. Он построен на идее сопо-
сопоставления ряда с интегралом и представляет собой обобщение того
приема, которым мы уже пользовались для выяснения сходимости
или расходимости ряда в примерах 4), 5), 6) п° 367.
Пусть предложенный ряд имеет форму
%ап= %№,	G)
где /(я) есть значение при х = п некоторой функции f(x), определен-
определенной для хэ=1*; функцию эту предположим непрерывной, положитель-
положительной и монотонно убывающей.
Рассмотрим какую-либо первообразную функцию F(x) для
f(x); так как ее производная F'(x) = f(x)>0, то F(x) возрастает вместе
с х и, при х — + ~, наверное, имеет предел, конечный или нет. В пер-
первом случае ряд
2[F{n+\)-F{ri)}	(8)
сходится, а во втором - расходится. С этим рядом мы и сравним
испытуемый ряд.
По формуле конечных приращений, общий член ряда (8) пред-
представится в виде:
так что вследствие монотонности функции f(x)
ап+1 = /(и +1) - F{n +1) - F(n) < fin) = ап .	(9)
В случае сходимости ряда (8), по теореме 1, сходится ряд
— 2 f(n + 0) члены которого меньше соответственных членов ряда
п=1
(8); значит, сходится и данный ряд G). В случае расходимости ряда
(8), расходится и данный ряд G), ибо члены его больше соответствен-
соответственных членов ряда (8).
Таким образом, мы приходим к следующему интересному при-
признаку (впервые найденному в геометрической форме М а к л о р е-
н о м, но позабытому и лишь впоследствии вновь открытому Коши):
* Начальным значением номера и, вместо 1, может быть и любое другое
натуральное число пв; тогда и функцию /(х) надлежит рассматривать при

282	ГЛ. XI. БЕСКОНЕЧНЫЕ РЯДЫ С ПОСТОЯННЫМИ ЧЛЕНАМИ	[373
Интегральный признак. При сделанных предположениях ряд
G) сходится или расходится в зависимости от того, имеет ли
функция
при х — + «¦ конечный предел или нет.
Приведем примеры применения этого признака (помимо рассмо-
рассмотренных в 367).
Здесь f(x) =—, ., ; F(x) =	г	'0 при jc — +°=>: ряд схо-
дится.
v
2)
л=з n-ln и-ln In n
Имеем f(x) - х1пхЛа1пх ', F(x) = In In In д:- + °°: ряд расходится.
3) 2 ~.	,} , ,гг- (cr>0).
' л=зй-1п«-Aп1пйI+я v '
В этом случае
' ^ = ~а.Aп1пл-)сг~" *
ряд сходится, и т. д.
Первообразную функцию F(x) можно взять и в форме определен-
определенного интеграла
Предел его при х — + <*> называют «интегралом от 1 до + ~»* и обо-
обозначают так:
Итак, предложенный ряд G) сходится или расходится, смотря по
тому, имеет ли этот интеграл конечное значение или нет**.
* Это так называемый несобственный интеграл; подобными инте-
интегралами мы будем заниматься в главе XIII.
** При такой формулировке признака доказательство легко провести без
предположения о непрерывности функции fix) и используя только опре-
определенный интеграл (который для монотонной функции существует, 298, III).

373|
§ 2. СХОДИМОСТЬ ПОЛОЖИТЕЛЬНЫХ РЯДОВ
283
В такой форме интегральный признак допускает простое геоме-
геометрическое истолкование, близкое к идее Маклорена. Если изоб-
изобразить функцию f(x) кривой (рис. 54), то интеграл F(x) будет вы-
выражать площадь фигуры, ограниченной этой кривой, осью х и двумя
ординатами; интеграл же F( + ¦»), в некотором смысле, можно рас-
рассматривать как выражение для площади всей бесконечно прости-
простирающейся направо фигуры под кривой. С другой же стороны, члены
X
¦Пх)
Ш&Шк
я i
Z 3	л
Рис. 54.
ах,аг, ..., ап ... ряда G) выражают величины ординат в точках х =
= 1, 2, ..., п, ... или, что то же, площади прямоугольников с осно-
основаниями 1 и с высотами, равными упомянутым ординатам.
Таким образом, сумма ряда G) есть не что иное, как сумма пло-
площадей выходящих прямоугольников, и лишь первым чле-
членом отличается от суммы площадей входящих прямоугольни-
прямоугольников. Это делает совершенно наглядным установленный выше резуль-
результат: если площадь криволинейной фигуры конечна, то и подавно
конечна площадь заключенной в ней ступенчатой фигуры, и предло-
предложенный ряд сходится; если же площадь криволинейной фигуры
бесконечна, то бесконечна и площадь содержащей ее ступенчатой
фигуры, так что в этом случае ряд расходится.
Сделаем теперь некоторые замечания относительно дальнейшего
использования неравенств (9).
а) В случае существования конечного предела
lim
можно указать удобную оценку остатка предложенного ряда.
Именно, просуммировав неравенства
при к-n + l, ...,п + т, получим
2 ak^F(n +
п+т—1
2
2
«*¦

284	ГЛ. XI. БЕСКОНЕЧНЫЕ РЯДЫ С ПОСТОЯННЫМИ ЧЛЕНАМИ	|373
Перейдем к пределу, увеличивая здесь т до бесконечности:
ИЛИ
^+-)-Дв+1)* 2 а*-в/;( + -)-Ди);	(Ю)
это и дает искомую оценку как сверху, так и снизу*.
Например, для ряда _/, 	(ст>0) будет
п=1И1+о
11 ~ 1 11
—-—	=e 2i	^	•	O1)
a («+1)<* i, = n+lk1+a о na
б) Если же F{x) возрастает до бесконечности вместе с х, то эта
функция позволяет судить о быстроте роста частичной суммы
предложенного ряда. Рассмотрим неравенства
О < /(к) - [F{k + 1) - F(k)] <= f(k) -f(k+l)
и, просуммировав их от к = 1 до к = п, получим возрастающую,
но ограниченную варианту
2 № - \F[n+1) - ад < /A) - /(«+о - /A),
* Так как
п+т
F{n+m)-F(n)~ J fit)Л,
л
то, переходя к пределу при лг- =°, получаем несобственный интеграл
+•>
F(+~)-F(ii)= J ДОЛ-
п
Поэтому неравенства A0) могут быть переписаны так:
Г/(О<Й=е 2 акт 2 f(k)*&\
ЛОЛ.	A0а)
я

374]	§ 2. сходимость положительных рядов	285
которая стремится к конечному пределу. То же справедливо и отно-
относительно варианты
2
*=1
Если через С обозначить ее предел, а через <хп - бесконечно малую,
которой она разнится от своего предела, то придем к формуле:
1
Например, при fix) = —, Fix) = In x, отсюда вновь получается формула D) п° 367.
374. Признак Ермакова. Примерно ту же область применения, что и интеграль-
интегральный признак, имеет и своеобразный признак, предложенный В. П. Ермако-
Ермаковым. Формулировка его не содержит понятий интегрального исчисления.
Признак Ермакова. Предположим по-прежнему функцию fix) непрерыв-
непрерывной*, положительной и монотонно убывающей для х=»1**. Тогда, если для
достаточно больших х Скажем, для *э*л:0) выполняется неравенство
f(e*)-e*
-———-=s<7«=l,
fix)
то ряд G) сходится, если же (для xs*x0)
f(ex)-e*
fix)
то ряд G) расходится.
Доказательство. Пусть выполняется первое неравенство. При любом
будем иметь (подстановка / = еи)
fit)dt= j fie")-e" du^qJ fit) dt.
отсюда
e	x	e	e.	e	e
-4) J /(/) *•?<?[ J ДО *- J Д0л]=е?[|/(ОА~ J/@*]=e<7 J
так как
ex>x,	A2)
* На деле требование непрерывности может быть опущено. См. сноску **
на стр. 282.
** См. сноску на стр. 281.

286	ГЛ. XI. БЕСКОНЕЧНЫЕ РЯДЫ С ПОСТОЯННЫМИ ЧЛЕНАМИ	|3?4
в вычитаемое в последних скобках положительно. В таком случае
J /(/) dt,
rx.	xt
прибавляя к обеим частям интеграл /(?) dt, получим
,х
1
ех.
1
1-
и тем более - учитывая A2) -
Так как с возрастанием х и интеграл возрастает, то для него существует конеч-
конечный предел х — ":
и - по интегральному признаку - ряд G) сходится.
Пусть теперь имеет место второе неравенство. Тогда
и - если к обеим частям прибавить интеграл f{t)dt
I
X	Хо
(так как, ввиду A2), лго<е**). Определим теперь последовательность
полагая хп = ехп-г; по доказанному
хп
м
у Г
1 = 1 J

S 2. СХОДИМОСТЬ ПОЛОЖИТЕЛЬНЫХ РЯДОВ	287
Отсюда ясно, что
Г= lim
Г
J
и - по интегральному признаку - ряд G) расходится.
Примеры предыдущего п° легко исчерпываются и с помощью доказанного
признака:
1) 2 -Аг— (*=-<»¦
п=2 И'1П1+О П
1
В этом случае fix) =	, и выражение
х-\п1+а х
/(<•*)•<•* 1п1+".«
	=	— 0 при .V —~,
fix)	х"
так что при достаточно больших х оно становится меньшим любой правильной
дроби q: ряд сходится.
1
2) 2
п=зй-1п и-In In п
1
Здесь fix) =	, а выражение
х • In х • In In х
= 1п1пд:-*оо при х-*<*>,
fix)
и при достаточно больших х превзойдет единицу: ряд расходится.
л=зя-1пя-Aп1пиI+а
Имеем на этот раз
f{x) =
хЛп л:-Aп In xI+a
-0 при х-~: ряд сходится.
fix)	1п° х
Заметим в заключение, что функция ех, фигурирующая в признаке Ерма-
Ермакова, может быть заменена любой другой функцией (fix), монотонно возра-
возрастающей, положительной, имеющей непрерывную производную и удовлетворяю-
удовлетворяющей неравенству
Ф>х,	A2*)
которое заменяет A2). Доказательство может быть скопировано с приведенного
выше. Таким образом, в общей форме признак Ермакова является источни-
источником для получения ряда конкретных признаков, отвечающих различному выбору
функции (fix).
375. Дополнения. 1) Мы воспользуемся оценками A1), чтобы охарактеризовать
поведение функции Р и м а н а [365, 2)]
(которая определена лишь для п => 0) при приближении а к 0.

288	ГЛ. XI. БЕСКОНЕЧНЫЕ РЯДЫ С ПОСТОЯННЫМИ ЧЛЕНАМИ	[375
Прежде всего, полагая и=0 в первом из неравенств A1) и п= 1 во втором из
них, легко получить
1
откуда
lim а - СA + ст) = 1.
а-0
Можно прийти к более точному результату, если, исходя из очевидного ра-
равенства
применить неравенства A1) при произвольном и:
п1+" О ЦЛ+1)
1	1 1 /1 A
+^+"-+тг+-—] ¦
z	и о \n j
Переходя здесь к пределу при ст->0, мы получим
Г	1 1
k(l+a)--Us
L	О \
И	1- ...Л	1п(и+1)=е lim
2	и	—„
lim f(l + cr)	UslH	1-...+	In и*.
<r»oL	cr J	2	и
Наконец, ввиду произвольности и, устремим здесь п к бесконечности. Так как
первое и последнее выражения, в силу D) п° 367, при этом стремятся к эйлеровой
постоянной С, то наибольший и наименьший пределы совпадают, так что суще-
существует обычный предел и равен
limfcd + ff)	] = С.
о—о L	о!
[Эти результаты принадлежат Дирихле.]
2) Пусть члены ряда (А) монотонно убывают; тогда ряд (А) сходится
или расходится одновременно с рядом 2 2л-а2* (К о ш и).
* = 0
Действительно, с одной стороны,
d2k^a1 + (a2 + aj+ ... +(а2к+ .. ¦ +o2t+1~i)<a1 + 2a2+ ... +2ка2к,
а с другой -
— al + a2 + 2al+ ... +2к~1а2к = — (al + 2a2 + 4ai+ ... +2ка2к)-
* Мы пока не знаем, существует ли предел выражения СA+<?)	при а-*О,
а
и потому пользуемся наибольшим и наименьшим пределами [42]. Пределы
1 Г 1 I 1 Г 1	1
жений —	1 и —	1 находим по формуле 77, 5), (б).
а \п" \ сг |(л-И)о I

375] § 2. СХОДИМОСТЬ ПОЛОЖИТЕЛЬНЫХ РЯДОВ	289
Отсюда и следует требуемое заключение.
Например, поведение ряда,2"— совпадает с поведением	ряда_2" 2Л-—=
1 и	о 2"
=^1, явно расходящегося. Ряд ^	(р^О) сходится вместе с рядом 2 ^¦!с'~п—<П=
о i л1+	о 2"A+ I
• Ряд ^—	 расходится, ибо расходится ряд
о 2fco	2 я In /г	i 2*ln2" i Ып2
и т. д.
В этой теореме ряд сравнения _2'2*а2* может быть заменен и более общим
рядом J^m*»aa*, где т - любое натуральное число.
к = 0
3) Пусть (А) будет произвольный сходящийся ряд. Какие заключения
1
можно сделать о порядке малости общего члена ап по сравнению с — ?
п
Прежде всего, очевидно, что если эти бесконечно малые вообще сравнимы
между собой [60], т. е. если существует предел
hm ¦— =
то необходимо с = 0, так что
(-).	A3)
п )
Действительно, иначе - ввиду расходимости гармонического ряда 2	и Дан"
1 п
ный ряд был бы расходящимся [366, теорема 2].
Однако существование такого предела, вообще говоря, не обязательно, как
видно на примере ряда
111111111
]
1
Сходимость этого ряда ясна из сопоставления с рядом У! — ; в то же время, если
1 и2
п не есть полный квадрат, то для него пап = —, в противном же случае: пап=1.
п
Впрочем, если члены ряда монотонно убывают, то для сходи-
сходимости его условие A3) все же необходимо. Действительно, при любых
т и п>т:
¦+an~=<*-m,
ат - остаток ряда. Отсюда
п
— -ат.
пт
11) Г. М. Фихтенгольц, т. II

290	ГЛ. XI. БЕСКОНЕЧНЫЕ РЯДЫ С ПОСТОЯННЫМИ ЧЛЕНАМИ	1375
Пусть сначала т взято так, чтобы ат бьшо меньше произвольно заданного числа
?>0; если предположить теперь я настолько большим, что
то одновременно пап^е, ч. и тр. д.
Заметим в заключение, что даже для рядов с монотонно убывающими членами
условие A3) отнюдь не является достаточным для сходимости. Это видно
на примере ряда
2 иши
4) Если ряд 21 dn расходится, и Dn означает его п-ю частичную сумму, то
1
ряд ^—¦ также расходится, в то время как ряд 2 " у+~в {а =- 0) сходится. [Абель
(N. H. Abel) и Дин и (U. Dini).]
Имеем:
dn+i	dn+m dn+1+ •.. +dn+m	Dn
1.
Dn+m	Dn+m
Сколь большими ни взять п, всегда можно выбрать такое т, чтобы было
Dn I	dn+1	dn+m 1
	=—и, следовательно, —-—[-¦••+	-
		n+1	Dn+m 2
Для ряда 2 —— нарушено основное условие сходимости [364, 5°] - ряд рас-
1 Dn
ходится.
- dn
Для доказательства сходимости ряда 2i —1+о~ м*1 прибегнем к приему,
сходному с примененным К о ш и [373].
р dx 11
К функции I	=	•— в промежутке от x = Dn_1 до x = Dn применим
J х1+а а ха
формулу конечных приращений:
1 ( 1
где
Таким образом, члены рассматриваемого ряда соответственно меньше членов
сходящегося ряда 2j — I	1» что и доказывает высказанное утверж-
утверждение. ^ "-1 п'

375]	§ 2. СХОДИМОСТЬ ПОЛОЖИТЕЛЬНЫХ РЯДОВ	291
5)	Если ряд 2 cn сходится и уп означает его остаток после п-го члена, то ряд
1
°° с
2	 расходится, в то время как ряд
1 Уп-1
2^ »-=-!)
сходится (Дини).
Доказательство аналогично предыдущему.
6)	Следующий признак сходимости недавно был указан Н. А. Сапого-
вы м:
Если ип — положительная монотонно возрастающая варианта, то ряд
V (л "п \\	V (Un+1 Л\
^1	равно как и ? I	- II
л=1 V ип+1) [	л=1 V ип )\
сходится при условии ограниченности этой варианты и расходится - в противном
случае.
Положим (при л= 1, 2, 3, ...)
тогда предложенный ряд перепишется так:
и его поведение совпадает с поведением ряда
n=\Dn'
DO
а значит - и с поведением ряда 2 dn (в случае расходимости его можно со-
сослаться на результат Абеля - Дин и, 4)). Последний же ряд сходится или
расходится в зависимости от того, будет ли варианта ип ограниченной или нет.
7) Пусть даны два сходящихся ряда:
2
л=1
1

292	ГЛ. XI. БЕСКОНЕЧНЫЕ РЯДЫ С ПОСТОЯННЫМИ ЧЛЕНАМИ	[375
Второй называется медленнее сходящимся, чем первый, если
остаток у'п второго ряда есть бесконечно малая низшего порядка чем
остаток уп первого:
lim — = 0.
Уп
Для каждого сходящегося ряда 2 сп можно построить ряд, медленнее
сходящийся. Достаточно рассмотреть, например, ряд
2 с'п^ 2
п=1	п=1
так как в этом случае уп /
Рассмотрим теперь два расходящихся ряда:
2 dn и 2 d'n ¦
n=L	л=1
Про второй говорят, что он расходится медленнее, чем первый, если
его частичная сумма Dn является бесконечно большой низшего порядка,
чем частичная сумма Dn первого:
D'n
lim — = 0 .
Для каждого расходящегося ряда 2 dn молено построить ряд, медленнее
1
расходящийся. С этой целью можно, например, взять ряд
2 d'n = Wi+ 2
n = l	n=2
здесь D'n = YDn.
Аналогичные заключения можно получить и с помощью рядов Абеля
и Д и н и , рассмотренных в 4) и 5).
Построенные примеры приводят к такому принципиально важному утвержде-
утверждению: никакой сходящийся (расходящийся) ряд не может служить универсаль-
универсальным средством для установления путем сравнения с ним** сходимости (расходи-
(расходимости) других рядов.
Это ясно из того, что
Уп-х-Уп
dn
d'n
* За у0 принимаем всю сумму 2 сп ¦
1
** С помощью любой из теорем п° 366.

376J	§ 3. СХОДИМОСТЬ ПРОИЗВОЛЬНЫХ РЯДОВ	293
8) Пусть даны две последовательности положительных чисел
Oi, а2, ..., ап, ... и Ь1г bo, ..., Ьп, ...
Каково бы ни было и, для первых п чисел этих последовательностей имеет место
неравенство Коти - Гельдера:
,-=1 \=1
и неравенство Минковского:
[133 E) и G)]. Здесь к - произвольное число =-1, а к' другое число тоже =-1, кото-
которое связано с к соотношением
1 1
h
Переходя в этих неравенствах к пределу при и->~, получим подобные же не-
неравенства для бесконечных рядов:
причем из сходимости рядов в правых частях вытекает сходимость рядов в левых.
§ 3. Сходимость произвольных рядов
376. Общее условие сходимости ряда. Обратимся к вопросу о схо-
сходимости рядов, члены которых могут иметь произвольные знаки. Так
как, по определению, сходимость ряда
Z ctn^^ + a^ ... +с„+...	(А)
л = 1
приводится к сходимости последовательности
составленной из частичных сумм ряда, то естественно при-
применить к этой последовательности принцип сходимости [39J. Из двух

294	ГЛ. XI. БЕСКОНЕЧНЫЕ РЯДЫ С ПОСТОЯННЫМИ ЧЛЕНАМИ	C77
номеров п и п', которые в нем упоминаются, можно, не умаляя общ-
общности, считать л'>яи положить п' = п + т, где т - любое натураль-
натуральное число. Если вспомнить, что
¦ ¦ ¦ + ал+т,
то принцип сходимости применительно к ряду можно перефразировать
так:
Для того чтобы ряд (А) сходился, необходимо и достаточно, что-
чтобы каждому числу ?>0 отвечал такой номер N, что при n>N нера-
неравенство
|яп+1 + яп+2+ • • • +ап+т\ <е	B)
выполняется, каково бы ни было т = \,2,Ъ, .. .*
Иными словами: сумма любого числа членов ряда, следующих
за достаточно далеким, должна быть произвольно
мала.
Если, предполагая ряд сходящимся, в неравенстве B) взять, в
частности, т = 1, то получим:
[а„+1|-се (при n=-N),
так что an+i^-0 или (что то же) ап-*0, и мы вновь приходим к извест-
известному необходимому условию сходимости ряда [364, 5°]. Оно
требует гораздо меньшего, чем принцип сходимости: необходимо,
чтобы не только далекие члены, в отдельности взятые,
были малы, но и сумма далеких членов, взятых в любом
количестве, должна быть мала! В этом смысле поучительно вер-
вернуться к гармоническому ряду [365, 1)] и к неравенству A), установ-
установленному для его членов. Хотя общий член здесь и стремится к 0, но
неравенство B) (настоящего п°) при е = = и т-п не выполняется ни
при одном п, и гармонический ряд расходится!
Нужно сказать, однако, что проверка выполнения приведенного
общего условия сходимости ряда в конкретных случаях обычно бы-
бывает затруднительна. Поэтому представляет интерес изучение класса
случаев, когда вопрос решается с помощью более простых средств.
377. Абсолютная сходимость. Мы видели в предыдущем параграфе,
что в отношении положительных рядов сходимость, по большей ча-
части, устанавливается легко, благодаря наличию ряда удобных при-
признаков. Поэтому естественно начать с тех случаев, когда вопрос о
сходимости данного ряда приводится к вопросу о сходимости поло-
положительного ряда.
Если члены ряда не все положительны, но начиная с некоторого
места становятся положительными, то отбросив достаточное количе-
* Оба автора принципа сходимости - Больцано и Коши сформу-
сформулировали его именно как условие сходимости бесконечного ряда.

377]	§ 3. СХОДИМОСТЬ ПРОИЗВОЛЬНЫХ РЯДОВ	295
ство начальных членов ряда [364, 1°], сведем дело к исследованию
положительного ряда. Если члены ряда отрицательны или, по край-
крайней мере, с некоторого места становятся отрицательными, то мы вер-
вернемся к уже рассмотренным случаям путем изменения знаков всех
членов [364, 3°]. Таким образом, существенно новым случаем будет
тот, когда среди членов ряда есть бесконечное ко-
количество как положительных, так и отрицатель-
отрицательных членов. Здесь часто бывает полезна следующая общая
Теорема. Пусть дан ряд (А) с членами произвольных знаков. Если
сходится ряд
2 К| = К| + |flss|.+ ... + \ап\ + ...,	(А*)
k=l
составленный из абсолютных величин его членов, то и дан-
данный ряд также сходится.
Доказательство сразу получается из принципа сходимо-
сходимости: неравенство
|#n + l + #n+2+ • • • ~^~ап+т\ == |#n+l| + |fln+2| + . . . + |йл+т|
показывает, что если условие сходимости выполняется для ряда (А*),
то оно тем более выполняется для ряда (А).
Можно рассуждать и иначе. Из положительных членов
ряда (А), перенумеровав их по порядку, составим ряд
2 Pk=Pi+p2+---+Pk+---;	(P)
/с=1
так же поступим с отрицательными членами и составим ряд
из их абсолютных величин
со
^-i Чт
т=1
Сколько бы членов того или другого ряда ни взять, все они содер-
содержатся среди членов сходящегося ряда (А*), и для всех частичных
сумм Рк и Qm выполняются неравенства
так что оба ряда (Р) и (Q) сходятся [365]; обозначим их суммы соот-
соответственно, через Р и Q.
Если взять п членов ряда (А), то в их составе окажется к поло-
положительных и т отрицательных, так что
Здесь номера к и т зависят от п. Если в ряде (А) как положительных,
так и отрицательных членов бесчисленное множество, то при ?z-"¦<*>
одновременно к-+°° и т—<*>.

296	ГЛ. XI. БЕСКОНЕЧНЫЕ РЯДЫ С ПОСТОЯННЫМИ ЧЛЕНАМИ	[378
Переходя в этом равенстве к пределу, приходим снова к заклю-
заключению о сходимости ряда (А), причем его сумма оказывается
равной
A=P-Q.	C)
Можно сказать, что при сделанных предположениях сумма дан-
данного ряда равна разности между суммой ряда, составленного из одних
положительных его членов, и суммой ряда, составленного из абсолют-
абсолютных величин отрицательных членов. Этим мы в последующем будем
пользоваться.
Если ряд (А) сходится вместе с рядом (А*), составленным из аб-
абсолютных величин его членов, то про ряд (А) говорят, что он аб-
абсолютно сходится. По доказанной теореме, одной сходимо-
сходимости ряда (А*) уже достаточно для абсолютной сходимости
ряда (А).
Как увидим ниже, возможны случаи, когда ряд (А) сходится, а
ряд (А*) - нет. Тогда ряд (А) называют неабсолютно схо-
сходящимся.
Для установления абсолютной сходимости ряда (А) - к по-
положительному ряду (А*) могут быть применены все признаки схо-
сходимости, изученные в предыдущем параграфе. Но нужно быть
осторожным с признаками расходимости: если даже ряд (А*)
окажется расходящимся, то ряд (А) может все же сходиться (н е а б-
с о л ю т н о). Исключение представляют только признаки К о ш и
и Даламбера, и именно потому, что когда они констатируют
расходимость ряда (А*), то это значит, что общий член \ап\ ряда (А*)
не стремится к нулю, а тогда ио„к нулю не стремится, так что и ряд
(А) также расходится. Поэтому упомянутые признаки могут быть пере-
перефразированы применительно к произвольному ряду. Сделаем это,
например, для признака Даламбера (который преимущественно
и применяется на практике):
Признак Даламбера. Пусть для варианты @* = 1^2±ii сущест-
\ап\
вует определенный предел:
<g)*=lim<g)*,
тогда при <Ц)*-с 1 данный ряд (А) абсолютно сходится, а при
@* > 1 он расходится.
378. Примеры. 1) Применить признак Даламбера ко всем рядам (а)—(д),
о которых была речь в 2) п° 370, но отбросив требование х=-0. Мы получим,что:
(а)	ряд абсолютно сходится для всех значений х;
(б)	ряд абсолютно сходится при -1-=л:«=1 и расходится при дэ=1 или
x=s -1 (при х = ± 1 нарушается необходимое условие сходимости);
(в)	ряд абсолютно сходится при -1-=л-=1 и расходится при х=~1 или х-= -1,
если б>1, то при х= ±1 ряд также абсолютно сходится, если же0-=,$==1,

378]	§ з. сходимость произвольных рядов	297
то при х — 1 ряд заведомо расходится, а при х= -1 вопрос пока остается
открытым;
(г)	ряд абсолютно сходится при -е^х^е и расходится при хз=е или
x=s - е (при х - + е нарушается необходимое условие сходимости);
1	1	1
(д)	ряд абсолютно сходится при	-х^— и расходится при хз=—
1/1	ее
или х~=—• при х= - — вопрос пока остается открытым)
е \	е
HJX1 ,
^ia+x)(.i+x*)-...-(i+x")
Имеем
| х |, если - 1 -=;
1*1
\\+хп\
О, если л:-= -1 или
итак, ряд абсолютно сходится для всех значений х^ - 1.
хп
3)
Л = 1 1-Х"
Здесь
н1;,1
лс|, если -l<x-=l,
если д: =-1 или л; -= - 1.
При | х | «= 1 ряд абсолютно сходится; при | х | =-1 признак Даламбера
ничего не дает, но все же можно заключить о расходимости ряда, ввиду нарушения
необходимого условия сходимости.
4) Вернемся к гипергеометрическому ряду [372]
, „	ч , ^т а.(а-1-1)	(а+и-1
F(a, ft у, x)=\+Z
n\y-{y+i)- ¦ ¦ --{у+п- 1)
- при любых а, /?, у, х (параметры а, /?, у предполагаются лишь отличными от
нуля и от целых отрицательных чисел).
Применяя признак Даламбера в новой форме, убеждаемся, что при [ х \ -= 1
этот ряд абсолютно сходится, а при |*|^1 расходится.
Пусть теперь х=\; так как отношение
ап+1	п	и3	" ~~
для достаточно больших п будет положительно, то члены ряда, начиная с неко-
некоторого места, будут иметь один и тот же знак, а тогда к ним (или к их абсолют-
абсолютным величинам) приложим по-прежнему признак Гаусса, который показывает,
что ряд сходится (конечно, абсолютно) при у-а-/?=-0 и расходится при
y/
Пусть, наконец, х= -1. Из только что сказанного ясно, что при у-а-/?=»0
будет сходиться ряд, составленный из абсолютных величин членов данного ряда

298	ГЛ. XI. БЕСКОНЕЧНЫЕ РЯДЫ С ПОСТОЯННЫМИ ЧЛЕНАМИ	[379
F(a, /?, у, -1), так что данный ряд в этом случае сходится абсолютно. При
у—а-/?-= -1 будем иметь, начиная с некоторого места,
ап
¦Л, т. е. \ап\-= \ап+1\,
ап не стремится к 0, ряд расходится.
В случае х=-\ и -1я?у-а-/?==0 вопрос о сходимости ряда
F(.a, Р,У> -1) остается пока открытым.
379. Степенной ряд, его промежуток сходимости. Рассмотрим сте-
степенной ряд вида
2 опхп = ао + ахх + а^х2 + ... + апхп + ...,	D)
л=0
представляющий собой как бы «бесконечный многочлен», расположен-
расположенный по возрастающим степеням переменной х(а0, а1,а2,... здесь обо-
обозначают постоянные коэффициенты). Выше мы не раз имели дело с
такими степенными рядами [см., например, в предыдущем п° 1)
(а)- (Д)].
Предложим теперь себе выяснить, какой вид имеет «область
сходимости» степенного ряда, т. е. множество % = {х} тех значений
переменной, для которых ряд D) сходится. Это послужит снова важ-
важным примером применения изложенного выше.
Лемма. Если ряд D) сходится для значения х = х, отличного от
О, то он абсолютно сходится для любого значения х, удовле-
удовлетворяющего неравенству: |х|<|3с|.
Из сходимости ряда:
2 я„хп = ао=а^с + оус2 + ... +апхп+ ...
п=0
вытекает, что его общий член стремится к 0 [364, 5°], а следователь-
следовательно, - ограничен [26, 4°]:
\апхп\^М (и = 0, 1,2,3, ...).	E)
Возьмем теперь любое х, для которого |х|-=|3с|, и составим
ряд
2 \апхп\ = |ао| + {а^х] + IflgX2! + ... + \апхп\ + ...	F)
п->0
Так как [см. E)]:
X
X

379]	§ 3. СХОДИМОСТЬ ПРОИЗВОЛЬНЫХ РЯДОВ	299
и члены ряда F) оказываются меньшими соответствующих членов
сходящейся геометрической прогрессии со знаменателем
м+м-\=\+м
xl*	,, \x
_ + ... +M-\ =
X>	X
то, по теореме 1 п° 366, ряд F) сходится. В таком случае, как мы
знаем, ряд D) сходится абсолютно, ч. и тр. д.
При х=0 сходится, очевидно, всякий ряд D). Но есть степенные
ряды, которые - помимо этого - не сходятся ни при одном значе-
значении х. Примером такого «всюду расходящегося» ряда может служить
ряд ^ п- х"> как в этом легко убедиться с помощью признака Д а-
1
л а м б е р а. Подобные ряды для нас не представляют интереса.
Предположим же, что для ряда D) вообще существуют та-
такие отличные от 0 значения х=х, при которых он сходится, и рас-
рассмотрим множество {\х\}. Это множество может оказаться либо
ограниченным сверху, либо нет.
В последнем случае, какое бы значение х ни взять, необходимо
найдется такое х, что |х| -= |3ё|, а тогда, по лемме, при взятом зна-
значении х ряд D) абсолютно сходится. Ряд оказывается «всюду
сходящимся».
Пусть теперь множество {|3с|} сверху ограничено, и R будет его
точная верхняя граница. Если- |х| >jR, to сразу ясно, что при
этом значении х ряд D) расходится. Возьмем теперь любое х, для
которого \х\ <Л. По определению точной границы, необходимо най-
найдется такое ~х, что \х\ < |3c[==jR; а это, по лемме, снова влечет за
собой абсолютную сходимость ряда D).
Итак, в открытом промежутке (-R, R) ряд D) абсолютно
сходится; для x>R и х< -R ряд заведомо расходится,
и лишь о концах промежутка х = ± R общего утверждения сделать
нельзя - там, смотря по случаю, может иметь место и сходимость,
и расходимость.
Поставленная нами задача решена.
Для каждого степенного ряда вида D), если только он не является
всюду расходящимся, «область сходимости» % представляет собой
сплошной промежуток от -R до R, со включением концов или нет;
промежуток этот может быть и бесконечным. Внутри промежутка,
к тому оке, ряд сходится абсолютно.
Упомянутый промежуток называют промежутком сходи-
сходимости, а число R @< jR«s + ¦») - радиусом сходимости ряда.
Если вернуться к примерам 1) (а) - (д) предыдущего п°, то, как легко
видеть, в случае
(a) R= + -; (б), (в) Д = 1; (г) R = e; (д) R = \ .

300	ГЛ. XI. БЕСКОНЕЧНЫЕ РЯДЫ С ПОСТОЯННЫМИ ЧЛЕНАМИ	[380
Для всюду расходящегося ряда принимают R = 0: его «область
сходимости» сводится к одной точке х = 0.
380. Выражение радиуса сходимости через коэффициенты. Теперь мы докажем
более точную теорему, в которой не только вновь устанавливается существование
радиуса сходимости, но и определяется его величина в зависимости от коэффи-
коэффициентов самого ряда D).
Рассмотрим последовательность:
п
Pi=KI, Ра = V"I«2J	 ?п=Т\<*п\, ¦¦¦
Обозначим наибольший предел этой последовательности [который
всегда существует, 42], через р, так что
л
р = Tim рп = lim У | о.ч | ¦
П -* «	Л -* =»
Теорема Коши — Адамара. Радиус сходимости ряда {А) есть величина,
п
обратная наибольшему пределу р варианты рп = У\ап\:
1
R = —
9
(при этом, если р = 0, то R = + ~, еслир ~ + ~, то R = 0).
Теорема эта, открытая Коши, была забыта; А д а м а р (J. Hadamard)
вновь нашел ее и указал важные приложения.
Доказательство. I случай: р = 0. Докажем, что в этом случае i?=+==,
т. е. что при любом х ряд D) абсолютно сходится.
("	)
Так как последовательность []/|ап\ | состоит из положительных элементов,
то из того, что р = 0, следует, что она имеет определенный предел:
п
lim У\ап\ =0;
отсюда варианта Коши
л	л
&.= У\ап\-\х\п= \х\ -ГЫ -0
при и-оо, каково бы ни было х. Следовательно, по признаку Коши [368], ряд,
составленный из абсолютных величин членов ряда A), сходится, а значит сам
ряд A) сходится абсолютно.
// случай: р = + •=. Докажем, что в этом случае R = 0, т. е. при всяком х * 0 ряд
A) расходится.
Так как
п
р= Пт УТо^Т= +~»
то, очевидно, можно найти такую частичную последовательность {и,}, чтобы
щ
lim У\ащ\ ~ •!-<».

380]	§ з. сходимость произвольных рядов	301
Следовательно, при каждом х^О найдется такой номер г0, что для всех js-i0 будет
выполняться неравенство:
	 1
/|ол4|=-	 или \a4-x"i\ =-l.
Видим, что в этом случае не выполняется необходимое условие сходимости
ряда (общий член ряда не стремится к нулю). Следовательно, ряд D) расходится.
Ill случай: р - конечное положительное число: 0 <= р «= + <*=. Докажем, что в этом
1	1	1
случае R = — , т. е. что при | х \ ~? — ряд абсолютно сходится, а при | х | =
Р	Р	Р
1
ряд расходится. Возьмем любое х, для которого |х| -=—-. Выбереме=-0 настолько
Р
малым, чтобы выполнялось неравенство
I г I
р+е
По этому г, очевидно, всегда можно найти такое число Nf, чтобы для всех n-~Nt
было:
на основании 1-го свойства наибольшего предела последовательности 42].
Отсюда следует, что варианта К о ш и
еп = У\^х"\ = \х\ ¦ УКИ \х\ .(Р+е)* 1
при всех n>-Ns. По признаку К о ш и , ряд, составленный из абсолютных величин
членов ряда D), сходится, а значит сам ряд D) сходится абсолютно.
Возьмем теперь любое х, для которого | jc | =— . Выберем е настолько малым,
Р
чтобы было
По 2-му свойству наибольшего предела [42], для сколь угодно больших
п будет выполняться неравенство:
У|в„|>р-е,
так что
Следовательно, для сколь угодно больших п общий член ряда
и ряд D) расходится.

302	ГЛ. XI. БЕСКОНЕЧНЫЕ РЯДЫ С ПОСТОЯННЫМИ ЧЛЕНАМИ	[381
381. Знакопеременные ряды. Знакопеременными назы-
называются ряды, члены которых поочередно имеют то положительный,
то отрицательный знаки. Знакопеременный ряд удобнее записывать
так, чтобы знаки членов были выявлены, например
сх-с2 ic3-c4i ...+( -1)"-]сп1 ...(с„=-0).	G)
По отношению к знакопеременным рядам имеет место следующая
простая теорема.
Теорема Лейбница. Если члены знакопеременного ряда G) моно-
монотонно убывают по абсолютной величине:
сл+х^сп (л = 1,2, 3, ...)	(8)
и стремятся к нулю:
lim cn = 0,
то ряд сходится.
Доказательство. Частичную сумму четного порядка
dm можно написать в виде:
Qm = (Ci ~ Cj) + (С3 - С4) + . . . + (C2m_i - С ).
Так как каждая скобка, ввиду (8), есть положительное число, то от-
отсюда ясно, что с возрастанием т сумма С2т также возрастает. С дру-
другой стороны, если переписать Сгт так:
Сът = С1 - (С2 - С3) - . . . - (c2m-2 - C2m-l) ~ С2т ,
то легко усмотреть, что Сгт остается сверху ограниченной:
В таком случае, по теореме о монотонной варианте [34], при без-
безграничном возрастании т частичная сумма Сгт имеет конечный
предел
limC2m = C.
Переходя к частичной сумме нечетного порядка C2m+i, имеем,
очевидно, C2m+i = C2m+C2m. Так как общий член стремится к нулю,
то и
lim Czm+i = С.
Отсюда следует, что С и будет суммой данного ряда.

382]	§ 3. СХОДИМОСТЬ ПРОИЗВОЛЬНЫХ РЯДОВ	303
Замечание. Мы видели, что частичные суммы четного по-
порядка Сгт приближаются к сумме С ряда возрастая. Написав
Сът-i в виде
-l = С1 ~ (С2 ~ Сз) ~ • ¦ • ~ (c2m-2 - C2m-l),
легко установить, что суммы нечетного порядка стремятся к С убы-
убывая. Таким образом, всегда
В частности, можно утверждать, что
Это позволяет дать весьма простую и удобную оценку для остат-
остатка рассматриваемого ряда (который и сам представляет собою та-
такой же знакопеременный ряд). Именно, для
очевидно, имеем:
наоборот, для
У%т-\= -
будет:
Таким образом, во всех случаях остаток ряда лейбницев-
ск о г о типа* имеет знак своего первого члена и меньше его по
абсолютной величине.
Это замечание часто используется при приближенных вычислениях
с помощью рядов [см. 409].
382. Примеры. 1) Простейшими примерами рядов л е й б н и ц е в с к о г о
типа служат ряды
(a)
2	1+
л=1 и	2 3
п=1 2л-1	3 5	2и-1
Сходимость обоих вытекает из доказанной теоремы.
В то же время ряды, составленные из абсолютных величин их членов, расходят-
расходятся: для ряда (а) это будет гармонический ряд, для ряда же (б) получится ряд
1 1	1
1
* Так мы называем знакопеременный ряд, удовлетворяющий условиям теоремы
Лейбница.

304	ГЛ. XI. БЕСКОНЕЧНЫЕ РЯДЫ С ПОСТОЯННЫМИ ЧЛЕНАМИ	[382
расходимость которого ясна из того, что его частичная сумма
Таким образом, в лице рядов (а) и (б) мы имеем первые примеры н е а б с о-
лготно сходящихся рядов. [Ниже мы увидим, что сумма первого из них
п
есть In 2, а сумма второго равна — ; 388, 2); 405, 404].
4
2) По теореме Лейбница сходятся ряды
3
\	,	E0).
л = 1 /2s ' n=2n-\nsn' л=3 nln И-Aп In ri)s
Если заменить все члены их абсолютными величинами, то, как мы знаем,
при 5>1 получатся сходящиеся ряды, а при ,y=s=l расходящиеся. Таким образом
исходные ряды при s =-1 оказываются абсолютно сходящимися, а при .?=sl -
неабсолютно сходящимися.
00 хп
В частности, про степенной ряд У! —, который мы рассматривали в 370
п=1Иа
и 378, теперь можно сказать, что на конце х- -1 своего промежутка сходимости,
при s=sl он все еще сходится, но неабсолютно.
^	х
3)	Рассмотрим ряд л (-l)nsin —, при любых лг^О. Теорема Лейб-
Лейбла	п
н и ц а применима, если не к этому ряду, то к его достаточно далекому (по но-
х
меру) остатку. Действительно, при достаточно большом п, sin — приобретает
п
знак л: и по абсолютной величине убывает с возрастанием п. Итак, ряд сходится
[очевидно, неабсолютно, см. 367, 8) (в)].
4)	Для того чтобы выяснить, что требование монотонного убывания чисел сп
в теореме Лейбница отнюдь на является лишним, рассмотрим знакопере-
знакопеременный ряд
-+-
fi-\ p+\ уз-i уз+i ya-i уп+i
общий член которого стремится к нулю. Сумма 2п его членов равна
2
у*+Г
и бесконечно возрастает вместе с п: ряд расходится! Нетрудно проверить, что
монотонность убывания нарушается всякий раз при переходе от члена
1 1
	— к члену ——==	.
Уи+1	уй+1-i

383]	§ з. сходимость произвольных рядов	305
Для той же цели может служить и расходящийся ряд
в чем убедиться предоставляем читателю.
5)	Последний ряд дает повод к такому замечанию. Если его сопоставить со
сходящимся рядом 2j	—" > т0 оказывается, что отношение их общих
ч=1 Уп
членов стремится к 1. Таким образом, теорема 2 п° 366 не имеет аналога в теории
рядов с членами произвольных знаков.
6)	Использование в выкладках расходящихся рядов и действий над
их бесконечными суммами может привести к парадоксам. Вот, например,
один из них:
111	/11	^ A 1
1- + г + ?+.	2
Если то же преобразование применить к сходящемуся ряду
Р=1	1	h--. 0s=-0),
2» 3» 4s
то получим, что
где
1 1 1
9=И	1	1	h...
2s 3s 4s
При s -= 1 (в этом случае последний ряд расходится!) снова приходим к пара-
парадоксу: р-=0 [ср. 381, замечание]. При i=-l мы имеем дело с сходящимися рядами,
и получается правильный результат.
383. Преобразование Абеля. Часто приходится иметь дело с сум-
суммами парных произведений вида
S = 2 ««А = «I/3! + «2& + • • • + «mjSm •	(9)
Во многих случаях при этом оказывается полезным следующее эле-
элементарное преобразование, указанное Абелем (N. H. Abel).
Введем в рассмотрение суммы
Вг = /31, В2=/?1+/52, Вз=/51+& + /5з, ...,
20 Г. М. Фихтенгольц, т. II

306	ГЛ. XI. БЕСКОНЕЧНЫЕ РЯДЫ С ПОСТОЯННЫМИ ЧЛЕНАМИ
Тогда, выражая множители /5,- через эти суммы,
[383
сумму S можно написать в виде
S = а1Вх + ъ(В2 - Вх) + а3(В3 - В,) + ... + ocm(Bm - В,^).
Если раскрыть скобки и иначе сгруппировать члены, то и получим
окончательную формулу*
(=1
(«2 -
• • • +(<Zm-l—«т)Вш-
[Если переписать ее в виде
m-1
/- am)B/+ amBm •
m-l
то станет ясно, что эта формула для конечных сумм является ана-
аналогом формулы интегрирования по частям для интегралов: диффе-
дифференциал здесь заменен разностью, а интеграл - суммой.]
Основываясь на формуле A0), выведем теперь следующую оценку
для сумм указанного вида:
Лемма. Если множители щ не возрастают (или не убывают), а
суммы Bt все ограничены по абсолютной величине числом L:
(/-1,2,..., m),
то
\S\ =
Действительно, так как все разности в A0) одного знака, то
+ 2|ат|).
т-1
¦-2
Нетрудно видеть, что если множители а,- не возрастают и поло-
положительны, то оценку можно упростить:
\S\ =
(И)
Этими оценками мы будем ниже не раз пользоваться по разным
поводам. Сейчас мы их применим к выводу критериев сходимости,
более общих, чем установленный выше критерий Лейбница.
* По сути дела, мы уже пользовались подобным преобразованием при дока-
доказательстве второй теоремы о среднем значении [306].

384]	§ 3. СХОДИМОСТЬ ПРОИЗВОЛЬНЫХ РЯДОВ	307
384. Признаки Абеля и Дирихле. Рассмотрим ряд:
2 anbn = a1b1 + a2b2 + ... +anbn+ ...,	(W)
л=1
где {ап} и {Ьп} - две последовательности вещественных чисел.
Следующие предположения относительно каждой из них в отдель-
отдельности обеспечивают сходимость этого ряда.
Признак Абеля. Если ряд
2 bn = b1 + b2+ ...+bn+...	(В)
л = 1
сходится, а числа ап образуют монотонную и ограниченную последо-
последовательность
\an\*sK (и = 1,2, 3, ...),
то ряд (W) сходится.
Признак Дирихле. Если частичные суммы ряда {В) в совокупности
ограничены *:
\Вп\^М (и= 1,2,3,...),
а числа ап образуют монотонную последовательность, стремящуюся
к нулю:
lim ап=0,
то ряд (W) сходится.
В обоих случаях для установления сходимости ряда (W) мы при-
прибегнем к принципу сходимости [376]. Рассмотрим поэтому сумму
п + т	т
2 аФк = 2 an + ibn+i',
к=п + 1	( = 1
она имеет вид (9), если положить щ = ап+ь J3i=bn+i. Попытаемся оце-
оценить эту сумму с помощью леммы.
При предположениях Абеля, по заданному е>0 найдется такой
номер N, что при п >-N неравенство
будет выполняться, каково бы ни было р (принцип сходимо-
с т и). Следовательно, за число L, упоминавшееся в лемме, можно
принять е. Имеем тогда при n>N и т-1, 2, 3, ...:
п+т
2 аФ>к
что и доказывает сходимость ряда (W).
* Это требование шире предположения о сходимости ряда (В).
20*

308	ГЛ. XI. БЕСКОНЕЧНЫЕ РЯДЫ С ПОСТОЯННЫМИ ЧЛЕНАМИ	[385
При предположении Дирихле, по заданному е>0 найдется
такой номер N, что при п >N будет
\ап
Кроме того, очевидно,
и можно в лемме положить L-2M. Тогда, при n>N и т— 1, 2, 3, ...,
=s2M-f|an+i| +
и сходимость ряда (W) доказана.
Замечание. Признак Абеля вытекает из признака Д и-
р и х л е. Ведь из предложений Абеля следует, что ап имеет ко-
конечный предел а. Если переписать ряд (W) в виде суммы рядов
2 {an-a)hn\-a 2 Ьп,
то второй из них сходится по предположению, а к первому применим
уже признак Дирихле.
385. Примеры. 1) Если ап, монотонно убывая, стремится к нулю, а Ьп — (—1)п~',
то условия теоремы Дирихле, очевидно, выполнены. Следовательно, ряд
2 (- \)п'1ап = а1- а, + а3- ... +(- 1)"-»й„+ . -.
п = 1
сходится. Таким образом, теорема Лейбница получается, как частное след-
следствие теоремы Дирихле.
2) При тех же предположениях относительно ап, рассмотрим ряды (х - любое):
2 ctn-sinnx, 2an'cosnx.
n=i	л=а
Полагая а = 0ий = л;в тождествах A) и B) п° 307, которые там были установ-
установлены по другому поводу, мы найдем
п	cos—л--cos
2 sin ix =
1	( 1)
— х-cos «+— ¦
2 sin — x
sin n-\—
1
sin I n-\—I x-sin— x
v .	\ 2)	2
2j COS IX	,
*~	2 sin — x

385]	§ 3. СХОДИМОСТЬ ПРОИЗВОЛЬНЫХ РЯДОВ	309
в предположении лишь, что х не имеет вида 2кп (к = 0, +1, ±2, .. .)• Таким обра-
образом, если только х ^ 2кж, обе суммы при любом п по абсолютной величине ограни-
1
чены числом
х
sin —
2
По признаку Дирихле, оба ряда сходятся при любом значении х, отлич-
отличном от 7кп, впрочем, первый ряд сходится и при х = 2кл, ибо все члены его обра-
обращаются в 0.
В частности, например, сходятся ряды
^, sin пх	?-, ( 1	1 1 sin пх
2 	. 2 i+;r+--^— 	и т- п-
л=1 п	п=1 I 2	п) п
3) Большой интерес представляют ряды вида
2 -х ,	A2)
где {ап} - произвольная последовательность вещественных чисел; они носят
название рядов Дирихле.
Для них может быть доказана лемма, имеющая сходство с леммой п° 379,
относящейся к степенным рядам:
Если ряд A2) сходится при некотором значении х = х,то он сходится при всяком
Это сразу следует из теоремы Абеля, так как при х => х ряд A2) получается
из сходящегося ряда
умножением его членов на монотонно убывающие положительные множители
-Л;	A1=1,2,3,...).
пх-х
^ 1 1
Существуют ряды A2) «всюду сходящиеся», вроде 2	> и «всюду
1 2" пх
расходящиеся», вроде 21 — • Если исключить эти случаи, то с помощью при-
1 пх
веденной леммы легко установить существование пограничной абсцис-
абсциссы сходимости А, такой, что ряд A2) сходится при х =-Я и расходится при
х^к. Например, для ряда 21 — > очевидно, Я = 1, а для ряда 21
1 пх	1 пх
имеем /1 = 0. Если угодно, для «всюду сходящегося» ряда можно считать Я= -¦*>,
а для «всюду расходящегося» положить Я= +<*>.
Читатель легко усмотрит сходство со степенными рядами: в обоих случаях
«область сходимости» представляет собой сплошной промежуток. Но есть
и существенное отличие: область абсолютной сходимости здесь может не
°° (—I)"
совпадать с областью сходимости вообще. Так, указанный только что ряд 21
1 пх
сходится для х>0, а абсолютно сходится лишь для л' =-1.

310	ГЛ. XI. БЕСКОНЕЧНЫЕ РЯДЫ С ПОСТОЯННЫМИ ЧЛЕНАМИ	[385
4) Сопоставим с рядом Дирихле A2) ряд
^т	п\ап
n=ix{x+ !)•... -(х+п)'
A3)
при тех же значениях коэффициентов а„. При этом, естественно, будем считать
х отличным от 0, -1, - 2, ... и т. д.
С этим ограничением имеет место такое предложение, принадлежащее Лан-
Ландау (Е. Landau): ряды A2) и A3) сходятся при одних и тех оке значениях х.
Ряд A3) получается из ряда Дирихле A2) путем умножения его членов,
соответственно, на множители:
(и= 1,2,3,...).	A4)
При достаточно больших значениях и эти множители приобретают определен-
определенный знак. Кроме того, начиная с некоторого места, они изменяются уже моно-
монотонно.
Действительно, отношение (н+1)-го множителя к n-му будет таково:
\ п
КГ
Но [125, 4)]
( 1
v+n+1	х+1
1 +
п
\\ +1 х+1 (х+\)х I
1 +1+о\
и	2н2	[п2
и, аналогично,
1	х+1 (х + \У
= 1	+—— + о\-\,
x+i	п	и2
1 + —
п
откуда
6с+1)а- М-
= 1 + ——-—\-o\-\.
Из последней формулы явствует, что при {х+\)х>-0 упомянутое отношение
в конце концов становится бблыпим единицы, а при (x+l)x«=0 — меньшим еди-
единицы.
Для того чтобы установить ограниченность множителей A4), мы сошлемся
на то, что [как это будет доказано ниже, в п° 402, 10)] для выражения A4) при
п-~ существует конечный предел. Таким образом, по признаку Абеля,
сходимость ряда A2) влечет за собой сходимость ряда A3).

385J	§ 3. СХОДИМОСТЬ ПРОИЗВОЛЬНЫХ РЯДОВ	311
Так как названный предел (как мы увидим) всегда отличен от 0, то подобные
заключения применимы к множителям, обратным по отношению к A4). В таком
случае, по той же теореме, и сходимость ряда A3) влечет за собой сходимость
ряда A2). Этим доказано все.
5) Подобного же рода взаимность может быть установлена между поведе-
поведением так называемого ряда Ламберта (J. H. Lambert):
х
2ап-^—п	A5)
л=1 1-х"
и степенного ряда [379]
2 апхп,	A6)
л=1
с теми же коэффициентами ап (значения х = ±1, конечно, исключаются). Точнее
говоря:
Если ряд
2 ап	(А)
л=1
сходится, то ряд Ламберта A5) сходится при всех значениях х; в противном
же случае он сходится как раз для тех значений х, для которых сходится степен-
степенной ряд A6). [К н о п (К. Кпорр).]
(а) Пусть сначала ряд (А) расходится, так что радиус сходимости ряда
(А) будет R=ml. Покажем, что для \х\ ¦< 1 поведение рядов A5) и A6) одинаково.
Если сходится ряд A5), то сходится и ряд, полученный умножением его членов
на хп*, а следовательно, и ряд A6), который является разностью обоих рядов
[364, 4°]:
хп=2 \ап~.	Z-an-j—^
л=1 L 1-х" \-хп
2 апх2 \ап.Zanj^
n=i	л=1 L 1-х" \-хп
Пусть теперь сходится ряд A6); тогда, по признаку Абеля сходится
ряд, полученный умножением его членов на монотонно убывающие мно-
1
жители	:
1-х2"
2 йпхп	, равно как и 2
* Если какой-либо ряд, скажем, 2 Ьп сходится, то это значит, что степенной
1
Ряд 2 ЬпХп сходится при л: = 1, а тогда, по лемме п° 379, этот ряд заведомо сходится
при любом х, для которого |х|-=1. Этим замечанием мы еще дважды будем
пользоваться в рассуждении, проводимом в тексте.

312
ГЛ. XI. БЕСКОНЕЧНЫЕ РЯДЫ С ПОСТОЯННЫМИ ЧЛЕНАМИ
[385
Следовательно, сходится и ряд A5), который представляет сумму этих рядов
[364, 4°]:
v x" v
Для |х|=-1 ряд A6) заведомо расходится; мы утверждаем, что при этом
значении л: расходится и ряд A5). Действительно, в противном случае, из сходи-
сходимости ряда
У *"	у	1
вытекала бы сходимость рядов [364, 4°]:
у
c-r
2'*«=
л=1
«л-
fir
1 Ui
вопреки предположению.
F) Если ряд (А) сходится (так что if s=l), то для |л:|*=1 ряд A6) сходится,
и сходимость ряда A5) устанавливается как и выше. Остается показать, что ряд
A5) сходится и при |л:| »1.
=1 и ряд
Действительно, тогда
у
1L
как упомянуто, сходится, следовательно, сходится и ряд [364, 4°]:
n=l
_=_ У л	J	у
я,1 + а„
6) В заключение, в качестве примера непосредственного применения преобра-
преобразования Абеля A0), приведем тождество
2
л=1
= (!-*) 2 А„х",
1
2
л=1
где
(п-0, 1, 2, ..

386]	§ 4. СВОЙСТВА СХОДЯЩИХСЯ РЯДОВ	313
При этом |л:| предполагается не только меньше радиуса сходимости Я первого
ряда, но и меньше 1.
В самом деле, имеем:
л	л—1
2 «/*'= 2 Al(x'-xi + l)+Anxn.
i = 0	1 = 0
Отсюда при и-»»» и получается требуемое равенство, если только установить
еще, что Апхп - 0. С этой целью возьмем число г под условиями
\x\-=r-=R, rf-1.
Тогда |о,| r'=sL (для / = 0, 1, 2, ...) и
11	П	L (\х\\п Lr
+-+-+¦••+-= 1*1"=;— — — I
ГГ2	,."/	1Г\Г/1
Последнее же выражение при сделанных предположениях, очевидь стремится к 0.
§ 4. Свойства сходящихся рядов
386. Сочетательное свойство. Понятие суммы бесконечного ряда
существенно отличается от понятия суммы конечного числа слагаемых
(рассматриваемого в арифметике и алгебре) тем, что включает в себя
предельный переход. Хотя некоторые свойства обычных
сумм переносятся и на суммы бесконечных рядов, но чаще всего лишь
при выполнении определенных условий, которые и подлежат изуче-
изучению. В иных же случаях привычные нам свойства сумм разительным
образом нарушаются, так что, вообще, в этом вопросе надлежит
соблюдать осторожность.
Рассмотрим сходящийся ряд
2 ап = а1 -I а2 -\- ... -I ап + ...	(А)
и станем объединять его члены произвольным образом в группы, не
меняя при этом их расположения:
йх + ... + а„г, ащ f.i-\- ... + аПг, •..,
Ял*_,+1+ ... +ап/с, .. ¦
Здесь {пк} есть некоторая, извлеченная из натурального ряда, ча-
частичная возрастающая последовательность номеров.
Теорема. Ряд, составленный из этих сумм:
... (А)
всегда сходится и имеет ту же сумму, что и исходный ряд. Иными
словами: сходящийся ряд обладает сочетательным свой-
свойством.

314	ГЛ. XI. БЕСКОНЕЧНЫЕ РЯДЫ С ПОСТОЯННЫМИ ЧЛЕНАМИ	[386
Действительно, последовательность частичных сумм нового ряда
А л	А
1' Л2> • • • у ЛА» • • •
есть не что иное, как частичная последовательность
А А	А
сумм исходного ряда. Этим [40] и доказывается наше утверждение.
Мы видим - пока - полную аналогию с обычными суммами; но
эта аналогия нарушается, если мы попытаемся применять сочетатель-
сочетательное свойство, так сказать, в обратном порядке. Если дан сходя-
сходящийся ряд (А), члены которого каждый в отдельности представ-
представляют собой сумму конечного числа слагаемых, то, опустив скобки,
мы получим новый ряд (А), который может оказаться и расходя-
расходящимся.
Вот простые тому примеры: ряды
A-1) + A-1) + A-1)+... =0 + 0 + 0+... =0
и
1-A -1) - A-1)-... = 1-0-0-...=1,
очевидно, сходятся, между тем как полученный из них опусканием
скобок ряд
1-1 + 1-1 + 1-1 + ...
будет расходящимся.
Конечно, если — опустив скобки — мы получим сходящийся
ряд (А), то его сумма будет та оке, что и у ряда (А). Это вытекает
из данного выше.
При некоторых условиях можно наперед гарантировать, что ряд
(А) будет сходиться. Простейшим случаем этого рода является тот,
когда все слагаемые в (А) внутри одних и тех же
скобок будут одного знака*.
Действительно, тогда при изменении п от пн-i до пк частичная
сумма Ап будет изменяться монотонно, следовательно, будет содер-
содержаться между A^i_1=Aic-1 и Ащ=Ак. При достаточно большом/:
эти последние суммы произвольно мало разнятся от суммы А ряда
(А), следовательно, то же справедливо и относительно суммы Ап при
достаточно большом и, так что Ап->-А.
Этим замечанием мы не раз будем пользоваться в последующем.
* Этот знак от одних скобок к другим может меняться.

387]	§ 4. СВОЙСТВА СХОДЯЩИХСЯ РЯДОВ	315
Рассмотрим и сейчас такой
" (-1)Ё(Ул)
Пример. Установить сходимость ряда 2i 	•
n=i n
Здесь сначала идут 3 отрицательных члена, за ними 5 положительных и т. д.
Если объединить каждую такую группу членов одного знака в один член, то полу-
получится знакопеременный ряд
Легко установить неравенство
к	к + 1
2 1 1
например, так как сумма первых к слагаемых меньше, чем к— = —, а сумма
кг к
последних (к+1) слагаемых меньше, чем (к + 1)	= —, то вся сумма, действи-
2	№+к к
тельно, будет меньше, чем —. Отсюда заключаем, что члены ряда A) будут стре-
к
миться к нулю, монотонно убывая по абсолютной величине. Тогда, по теореме
Лейбница, ряд A) сходится, следовательно, в силу сделанного выше заме-
замечания, сходится и предложенный ряд.
387. Переместительное свойство абсолютно сходящихся рядов. Пусть
дан сходящийся ряд (А), имеющий сумму А. Переставив в нем члены
произвольным образом, мы получим новый ряд:
2а'к = а1 + а'2+...+а'к+...	(А')
Каждый член а'к этого ряда отождествляется с определенным членом
пщ. исходного ряда*.
Возникает вопрос, сходится ли ряд (А') и - в случае сходимости -
будет ли его сумма равна сумме А исходного ряда. При рассмотрении
этого вопроса нам придется провести резкое различие между абсо-
абсолютно и неабсолютно сходящимися рядами.
Теорема. Если ряд (А) абсолютно сходится, то ряд (А'), полу-
полученный из него перестановкой членов, также сходится и имеет ту
же сумму А, что и исходный ряд. Иными словами: абсолютно
сходящийся ряд обладает переместительным свойством.
Доказательство, (а) Проведем доказательство в два при-
приема. Предположим сначала, что ряд (А) - положительный.
* Причем последовательность номеров {щ} без пропусков и повторений вос-
воспроизводит - с точностью до порядка - натуральный ряд.

316	ГЛ. XI. БЕСКОНЕЧНЫЕ РЯДЫ С ПОСТОЯННЫМИ ЧЛЕНАМИ	[388
Рассмотрим произвольную частичную сумму А'к ряда (А'). Так
как
то, взяв п' большим всех номеров щ, и2, ..., пк, очевидно, будем иметь
A'k=sAn,, а следовательно, и подавно
В таком случае (А') будет сходящимся [365] и его сумма А' не пре-
превзойдет А:
А'^А.
Но и ряд (А) из (А') получается перестановкой членов, поэтому
аналогично:
A<sA'.
Сопоставляя полученные соотношения, придем к требуемому равен-
равенству: А'=А.
(б) Пусть теперь (А) будет произвольный абсолютно сходящийся
ряд.
Так как сходящийся положительный ряд:
2 |а„| = |о,| + |о2| + ••¦ + Ы + ••¦,	(А*)
п = 1
по доказанному, при любой перестановке членов останется сходя-
сходящимся, то по теореме п° 377 сохранит при этом свою (абсолютную)
сходимость и ряд (А).
Далее, мы видели в 377, что, в случае абсолютной сходи-
сходимости ряда (А), его сумма выражается так:
A=P-Q,
где Р и Q суть суммы положительных рядов
2
/.=1
2 Чт,	(Q)
т = 1
составленных, соответственно, из положительных и абсолютных ве-
величин отрицательных членов ряда (А).
Перестановка членов в ряде (А) вызовет перестановку членов и
в этих рядах, но не отразится (по доказанному) на их суммах Р и Q.
Следовательно, и сумма ряда (А) останется прежней, ч. и тр. д.
388. Случай неабсолютно сходящихся рядов. Обратимся теперь к
рассмотрению неабсолютно сходящихся рядов и установим,

388]	§ 4. СВОЙСТВА СХОДЯЩИХСЯ РЯДОВ	317
что они переместительным свойством не обладают: в каждом таком
ряде надлежащей перестановкой членов можно изменить его сумму
или даже вовсе нарушить сходимость.
Предположим, что ряд (А) сходится, но неабсолютно. Из
сходимости следует, что limon = 0 [364, 5°]. Что же касается рядов
(Р) и (Q), о которых мы упоминали в предыдущем п°, то, хотя, оче-
очевидно,
lim/>ft-0 и lim<7m=0,	B)
к-*~ °°	тп-*- °°
но в данном случае они оба расходятся.
Действительно, имеют место равенства
An = Pk-Qm, A*=Pk + Qm,	C)
если кат означают число положительных и отрицательных членов
в составе первых и членов ряда (А). Подчеркнем, что из трех номе-
номеров п, к, т один может быть взят произвольно, а другие два по нему
подбираются. Из сходимости одного из рядов (Р) или (Q), ввиду пер-
первого из равенств C), вытекла бы с необходимостью и сходимость
другого, а сходимость обоих, ввиду второго из этих равенств, имела
бы следствием сходимость ряда (А*) - вопреки предположению!
Докажем теперь следующую замечательную теорему, принадле-
принадлежащую Р и м а н у:
Теорема Римана. Если ряд (А) неабсолютно сходится, то
какое бы ни взять наперед число В (конечное или равное ± ~), можно
так переставить члены в этом ряде, чтобы преобразованный ряд имел
своей суммой именно В.
Доказательство. Остановимся на случае конечного В. За-
Заметим, прежде всего, что из расходимости рядов (Р) и (Q), в силу
364, 1°, вытекает, что и все их остатки также будут расходя-
расходящимися, так что в каждом из этих рядов, начиная с любого
места, можно набрать столько членов, чтобы сумма превзо-
превзошла любое число.
Пользуясь этим замечанием, мы следующим образом произведем
перестановку членов ряда (А).
Сначала возьмем столько положительных членов нашего
ряда (в том порядке, в каком они в нем расположены), чтобы их сумма
превзошла число В:
PiJrp2+ ..	B
Вслед за ними выпишем отрицательные члены (в том по-
порядке, в каком они расположены в данном ряде), взяв их столько,
чтобы общая сумма стала меньше В:
Px+Pi-v ... +Pk~ 11-42- ¦¦¦ -Чт^В.

318	ГЛ. XI. БЕСКОНЕЧНЫЕ РЯДЫ С ПОСТОЯННЫМИ ЧЛЕНАМИ	C88
После этого снова поместим положительные члены (из числа
оставшихся) так, чтобы было
• + PK — <7l — ¦ ¦ ¦ — qml +Pki+1 + ¦ ¦ ¦ +Pk, ="-O.
Затем наберем столько отрицательных членов (из числа остав-
оставшихся), чтобы было
РХЛ- . . . + Ркх - #i - • • • - <7т, +Ркх + \ + ¦ ¦ ¦ +Рк, — Чтх+Х - ... - #т, ¦= В
и т. д. Процесс этот мы мыслим продолженным до бесконечности;
очевидно, каждый член ряда (А), и притом со своим знаком, встре-
встретится на определенном месте.
Если всякий раз, выписывая члены р или q, набирать их не больше,
чем необходимо для осуществления требуемого неравенства, то укло-
уклонение от числа В в ту или другую сторону не превзойдет по абсо-
абсолютной величине последнего написанного члена. Тогда из B) ясно,
что ряд
(рх+ ... +Pkl)-(q1 +¦¦¦ +qmd +•¦•
¦ ¦ ¦ +(Pk(.1+i+ ¦ ¦ ¦ +Pk()-(qmt-r+i+ ¦ ¦ ¦ -<7m<)+ • • •
имеет своей суммой В. В силу замечания п° 386, это останется вер-
верным и после раскрытия скобок.
Если В = + °°, то, взяв последовательность возрастающих до бес-
бесконечности чисел Вь можно было бы набор положительных чисел
подчинить требованию, чтобы суммы последовательно становились
больше Вх, В2, Bs и т.д., а из отрицательных членов помещать лишь
по одному после каждой группы положительных. Таким путем, оче-
очевидно, составился бы ряд, имеющий сумму + <=. Аналогично можно
получить и ряд с суммой - ~*.
Установленный результат подчеркивает тот факт, что н е а б с о-
л ю т н а я сходимость осуществляется лишь благодаря взаимно-
взаимному погашению положительных и отрицательных
членов, и потому существенно зависит от порядка, в котором они
следуют один за другим, между тем, как абсолютная сходи-
сходимость основана на быстроте убывания этих членов — и от порядка
их не зависит.
Примеры. 1) Рассмотрим заведомо неабсолютно сходящийся ряд:
* Читатель легко сообразит, как разместить члены данного ряда, чтобы частич-
частичная сумма преобразованного ряда имела в качестве наименьшего и наи-
наибольшего пределов два наперед заданных числа В и С>С.

388]	§ 4. СВОЙСТВА СХОДЯЩИХСЯ РЯДОВ	319
сумма которого, как легко показать [см. 2)], есть In 2. Переместим его члены так,
чтобы после одного положительного следовали два отрицательных:
11111	1	11
1	E)
мы утверждаем, что сумма ряда от такого перемещения умень-
уменьшит с я вдвое.
В самом деле, если обозначить частичные суммы этих двух рядов, соответ-
соответственно, через Ап и Ап, то
л' -$( 1 - J -1]- У( Х _ М 1 У( 1 -1}-1 j
зт ё\2к-\ 4fc-2 4к}~кй[4к-2 4к} = 2,й{2к-1 2к)~2 2т>
, 1
так что Azm -— In 2. Так как
1	1
'	А
4/и	4/и - 2
стремится к тому же пределу — In 2, то ряд E) сходится и имеет суммой именно
это число.
2) Более общий результат можно получить, если исходить из формулы для
частичной суммы Нп гармонического ряда [367 D)]
#л = И—+...Н— = In n+C+yn,
2	п
где С есть эйлерова постоянная, а. уп - бесконечно малая. Отсюда,
прежде всего, имеем
Расположим теперь члены ряда D) в таком порядке: сначала поместим р поло-
положительных и q отрицательных, потом снова р положительных и q отрицательных
и т. д. Для того чтобы определить сумму ряда
1	11	11	11
+ з"+'"+27м 2~---~2	F>
нам удобнее объединить последовательные группы из р или q членов. Частичная
сумма Ат полученного таким путем ряда равна
т = \п\2 |/-

320	ГЛ. XI. БЕСКОНЕЧНЫЕ РЯДЫ С ПОСТОЯННЫМИ ЧЛЕНАМИ	[389
( \П\
и стремится к пределу In 2 / — ; к тому же пределу стремится и сумма Avl_x.
\ 1 1)
Наконец, в силу замечания п° 386, и ряд F) будет иметь суммой это же число
1
В частности, для ряда D) получается In 2 (р = <? = 1), для ряда E), как и в 1),
1
— In 2 0>=1, Ч~2). Аналогично:
11111
(р=2, q=l)
11111 1 1 1 11
1	f.	+	...=0
2 4 6 8 3 10 12 14 16 5
(р=1, q=4)
и т. п.
Заметим, что если численность последовательных групп положительных и
отрицательных членов еще изменять от группы к группе, то легко закон этого
изменения подобрать так, чтобы для преобразованного ряда действительно полу-
получить любую наперед заданную сумму. Предоставляем читателю убедиться
в этом.
389. Умножение рядов. О почленном сложении (или вычитании) двух
сходящихся рядов, равно как о почленном умножении сходящегося
ряда на постоянный множитель - уже была речь в 364, 3° и 4°. Те-
Теперь мы займемся вопросом об умножении рядов.
Пусть даны два сходящихся ряда:
..+ап+...	(А)
В = Zbm = bl + b2+...+bm+...	(В)
т = \
Подражая правилу умножения конечных сумм, рассмотрим и здесь
всевозможные парные произведения членов этих рядов: af)k\ из них
составится бесконечная прямоугольная матрица:
аф1 ajZ»! a3bl ... афх .. ¦
аф„ аф* аф2 ... аф2 ¦ ¦ ¦
аф3 аф3 аф3 ... аф3 ...	G)
афк ... афк

389]
§ 4. СВОЙСТВА СХОДЯЩИХСЯ РЯДОВ
321
Эти произведения можно многими способами располагать в виде
простой последовательности. Например, можно выпи-
выписывать произведения по диагоналям или по квадратам:
a A
я А
a A
a2b2
a2b3
aA
(кЬг
a3b3
. . .
. . .
. . .
что, соответственно, приводит к последовательностям:
или
«А; ДА>
«A» #2^2' °2^
(8)
(9)
Составленный из подобной последовательности ряд называется
произведением рядов (А) и (В).
Теорема Кохии. Если оба ряда (А) и (В) сходятся абсолютно,
то их произведение, составленное из произведений G), взятых в л ю-
б о м порядке, также сходится и имеет своей суммой произведение
сумм АВ.
Доказательство. По предположению, ряды
... +\an\+ ...
(А*)
(В*)
сходятся, т. е. имеют конечные суммы, скажем, А* и В*.
Расположив произведения G) произвольным образом в виде по-
последовательности, составим из них ряд:
2 аФк. = афЬх + aubk, + ...
(Ю)
Чтобы доказать сходимость соответствующего ряда из абсолютных
величин:
2 I афк. | = | в/А, | + | я/А. I + • • • +1 аФь.\ +¦¦¦>
s=l
(И)
21 Г. М. Фихтешольц, т. II

322	ГЛ. XI. БЕСКОНЕЧНЫЕ РЯДЫ С ПОСТОЯННЫМИ ЧЛЕНАМИ	[389
рассмотрим его s-ю частичную сумму; если через v обозначить наи-
наибольший из значков il5 къ i2, к2, ..., /s. ks> т°, очевидно,
Отсюда [365] вытекает сходимость ряда A1), следовательно, и абсо-
абсолютная сходимость ряда A0).
Остается определить его сумму. Мы вправе придать членам ряда
A0) более удобное для этого расположение, ибо ряд этот, как абсо-
абсолютно сходящийся, обладает переместительным свойством [387].
Разместив эти члены по квадратам, как в (9), мы объединим
последовательные группы, которые отличают один квадрат от другого
афх + (афг + аф2 + афг) + {аф% + аф3 + аф3 + аф2 + аф^ + ... A2)
Если через Ап и Вт, как обычно, обозначить частичные суммы рядов
(А) и (В), то для ряда A2) частичные суммы будут
они стремятся к произведению АВ, которое, таким образом, является
не только суммой ряда A3), но и ряда A0).
При фактическом умножении рядов чаще всего представляется
удобным размещать произведения G) по диагоналям, как в
(8); обычно члены, лежащие на одной диагонали, при этом объеди-
объединяются:
АВ - афх + (афг + афу) + (аф3 + афг + аф^) + ...	A3)
В этом именно виде К о ш и впервые и представил произведение
двух рядов. Так, написанный ряд мы впредь будем называть произ-
произведением рядов (А) и (В) в форме Коши.
Пусть, например, перемножаются два степенных ряда
2^	0 1 2 ... +апхп+ ...,
л=0
... +bmxm+ ...
[причем л: взято внутри соответствующих промежутков схо-
сходимости, 379]. Тогда, как нетрудно сообразить, указанный прием
отвечает приведению подобных членов в произведении:
2 апхп • 2 Ьтхт = аф0 + (афг + афо)х + (аф2 + аф1
Л = 0	Л! = 0
Таким образом, произведение двух степенных рядов в форме К о-
ш и непосредственно представляется в виде степенного же ряда.

§ 4. СВОЙСТВА СХОДЯЩИХСЯ РЯДОВ	323
390. Примеры. Во всех примерах, кроме последнего, произведения рядов бе-
берутся в форме К о ш и.
1)	Помножив ряд
1 ^
— = Z хп~1+х + хг+...+хп+... (|х|-=1)
1 - х о
на самого себя, таким путем получим:
1	°°
	= У. их"-1 = 1 + 2x4- Зх2 + ... + пхп~г + ...
A - хУ 1
2)	Умножение рядов:
1 °°
	= 2(
1-f-JC 0
^	Хт	X2 X3	Хт
2 (- ])"•-! —^х- +--...+(- iyn-i—+...	A4)
1	m	2 3	/и
(где | л: | -= 1) даст такой результат:
Ниже мы увидим [405], что сумма ряда A4) есть ln(l+x), так что последнее
,	In A4-х)
разложение представляет функцию 	.
1+х
3) Произвести возведение в квадрат:
(z - любое).
Указание. Воспользоваться элементарно доказываемой формулой:
„ 2v\
4) Тождество [см. 385, 6)]
2,Апхп = -	2<
п-0	1—Хп=0
21*

324	ГЛ. XI. БЕСКОНЕЧНЫЕ РЯДЫ С ПОСТОЯННЫМИ ЧЛЕНАМИ	1390
2апхп = A-х) 21 Апхп
л=0 п-й
(где Ап^па+а^Л-	Ьял)
легко доказывается путем почленного умножения.
При этом, если в промежутке (-7?, 7?) @-=/{=sl) сходится один из двух рядов,
отсюда уже следует сходимость в том же промежутке и другого ряда.
5) Доказать тождество (я=»0):
/1 1 х ЬЗ х2	W 1 ЬЗ
l	I	t
6) Как мы знаем уже [378,1) (а)], ряд
^,а" л: .v2 Xs
?1
абсолютно сходится при всех значениях х, обозначим его сумму через Е(х).
Заменив здесь л: на у, получим аналогичный ряд с суммой Е(у). Произведение
обоих рядов в форме К о ш и имеет общий член:
уп х уП-1 Х2 уп-г	хк уп-к	хп
' л!" + 7Г (п- 1)!+2Т'(и-2)! +'"+к\' (п-к)\+ "'+ri'
2 L
ЩУ	и! ¦
Таким образом, для неизвестной нам пока функции Е(х) получается соотно-
соотношение
— при любых вещественных хм у. Впоследствии это даст нам возможность уста-
установить, что Е(х) есть показательная функция [439, 3); ср. 75, Г].
7) С помощью признака Даламбера легко показать, что ряды
•?,	Хт	X2 X*	Хт
(-1)"
1+ ...+A)
Bл)!	2! 4!	2п!
™-1	х3 хъ
(l)mi
S(xJ (l)x+...+(l)+..
i	Bm-l)!	3! 5!	Bm-l)!
абсолютно сходятся при всех значениях х. Путем умножения рядов можно
доказать соотношения
С(х+у) = С(х)-Оу) - S(x).S(y),

391]	§ 4. СВОЙСТВА СХОДЯЩИХСЯ РЯДОВ	325
Так как на деле S(x) и С(х) есть не что иное, как sin x и cos х [404], то мы узнаем
здесь известные теоремы сложения для этих функций.
8) Рассмотрим, наконец, положительный ряд
который сходится для х=-1 [365, 2)] и представляет функцию С Р и м а н а. Вы-
Вычислим, с помощью умножения рядов, ее квадрат.
Всевозможные произведения
111
пх тх (п-т)х
на этот раз мы разместим так, чтобы члены с одним и тем же числом к=п ¦ т
в знаменателе стояли рядом, а затем - объединим их. Каждому к будет отвечать
столько (равных между собой) членов, сколько делителей п имеет число к, т. е.
т{к). Итак, окончательно,
391. Общая теорема из теории пределов. Для упрощения изложения в ближай-
ближайшем п° и в последующем мы установим здесь одну теорему из теории пределов,
дающую широкое обобщение известных теорем Коши и Штольца [33].
Эта теорема принадлежит Теплицу (О. Toplitz). Мы докажем ее в два приема.
I. Предположим, что коэффициенты tnm {l=sm=sn) бесконечной ^треугольной»
матрицы
hi
hi hz
hi Ы t33
		A5)
hii tnz 'лз • • • 'л/1
удовлетворяют двум условиям:
(а)	Элементы, стоящие в любом столбце, стремятся к нулю:
tnm — Q nPu я-*°° (т фиксировано).
(б)	Суммы абсолютных величин элементов, стоящих в любой строке,
ограничены все одной постоянной:
I ttn I + \tnz 1+ • • ¦ +1 Inn \*sK (К = const).
Тогда, если варианта хп — 0, то это псе справедливо и относительно варианты
составленной из значений исходной варианты с помощью коэффициентов мат-
матрицы A5).

326	ГЛ. XI. БЕСКОНЕЧНЫЕ РЯДЫ С ПОСТОЯННЫМИ ЧЛЕНАМИ	C91
Доказательство. По е=-0 найдется такое т, что при п=-/и будет:
е
| Хп | -= — ; для этих п имеем, используя (б):
2л
Так как т здесь уже постоянно, то - ввиду (а) — существует такое Ns&m, что
Е
при n^N ж первое слагаемое справа будет <—, следовательно, \х'п\^е, что
и тр. д.
II. Пусть коэффициенты tnm, кроме условий (а) и (б), удовлетворяют еще условию:
(в)	2Wni + fnj+...+fmi-l прип-~*.
Тогда, если варианта хп-*а (а — конечно), то также и
Хп = tniXi + /Л2*2 + • • • + tnn*n - О.
Доказательство. Выражение для х'п, очевидно, можно переписать
так:
х'п = tni(xi- a)+tn«(x,_- a)+ ¦ ..+tnn(.Xn-a)+Tn-a.
Применяя теорему I к варианте хп-а^0 и опираясь на (в), непосредственно при-
приходим к требуемому заключению.
1°. Теорема К о ш и [33] отсюда получается, если положить
1
'щ = 'П2 = • • • = tnn — •
П
Выполнение условий (а), (б), (в) очевидно.
2°. Обратимся к теореме Штольца [33], сохраняя прежние обозначения.
Итак, пусть имеем две варианты хп и уп, из которых вторая стремится монотонно
к +оо. Предположим, что варианта
-а,
Уп-Уп-i
(я= 1,2,3,...; хо=Л=О):
и применим к ней теорему II, полагая tnm =	. Выполнение условий
Уп
(а), (б), (в) легко проверяется. Тогда получим, что варианта
хп irt Хт — Хт—г
— = ^i tnm	' а>
Уп ш=1 Ут~Ут—1
ч. и тр. д.
Приведем ряд других полезных следствий теоремы Теплица.
3°. Пусть даны две варианты хп -* 0 и уп - 0, причем вторая из них удовлетворяет
условию:
(л=1, 2, 3, ...; АГ= const).
Тогда и варианта
yn -1 + • • • + ХпУ1 "* 0.
В применениях обычно Тп = 1.

392]	§ 4. СВОЙСТВА СХОДЯЩИХСЯ РЯДОВ	327
Простое применение теоремы I при tnm = yn—m+i-
4°. Если варианта хп-а, а варианта уп-Ь, то варианта
2П =	-аЬ.
п
Пусть сначала я-0 и требуется доказать, что zn—0. Это просто вытекает из
следствия 3°, если заменить в нем уп на — . Условие, наложенное там на уп, легко
п
проверяется с учетом того, что здесь уп ограничено: \yn\*sK.
Обращаясь к общему случаю, перепишем гп в виде
¦+уп
Первое слагаемое справа стремится к 0, по только что доказанному. Второе же
слагаемое стремится к ab, ибо множитель при а имеет пределом Ъ по теореме
Коши A°).
5°. Если хп-*а, то и*
2"
Применяем теорему II, полагая
Так как С™ «= л771 и	-0 [32, 9)], то условие (а) выполнено. Выполнение условий
(б) и (в) вытекает непосредственно из того, что
2
т = 0
6°. Если хп-*а и z = const (z»0), то и
хп
Это - простое обобщение предыдущего утверждения, и доказывается оно анало-
аналогично. Можно коэффициенты расположить и в обратном порядке, так что и
'¦•Х2+...+1-Хп
*'———1г^	*
392. Дальнейшие теоремы об умножении рядов. Как указал М е р т е н с
(F. Mertens), результат Коши может быть распространен на более общий случай.
* Конечно, несущественным является то, что нумерацию значений варианты
мы начинаем с 0 вместо 1.

328	ГЛ. XI. БЕСКОНЕЧНЫЕ РЯДЫ С ПОСТОЯННЫМИ ЧЛЕНАМИ	[392
Теорема Жертенса. Если ряды (А) и (В) сходятся, причем хоть
один из них сходится абсолютно, то разложение A3) имеет место.
Доказательство. Пусть, скажем, ряд (А) сходится абсолютно, т. е.
сходится ряд (А*).
Объединяя члены на л-й диагонали, положим
сп = a1bn+a2bn-i+ ¦ ¦ ¦ +an-l
так что нужно доказать, что Сп-~АВ.
Прежде всего, нетрудно видеть, что
Сп = ахВп + агВг _!+ ... +an-1Bi+anBl.	A6)
Если положить Вт = В - /?т (гле остаток /?т -* О при т - °°), то сумма Сп пере-
перепишется так:
Сп = АпВ-уп, где уп=*афп+афп-\Л- ¦ ¦¦+an-iP2+anpi;
так как Ап -~А, то весь вопрос сводится к доказательству соотношения: lim yn = 0.
А это утверждение сразу следует из 3°, 391 (при хя=/?п и уп = ап), если учесть,
что
где А* - сумма сходящегося, по предположению, ряда (А*).
В виде примера применения теоремы, вернемся к задаче 4) п° 390. Упомянутое
там равенство, как мы видим теперь, имеет место и на конце х = ± R промежутка
сходимости ряда ^ апхп, если Я<1 и ряд на этом конце вообще сходится (хотя
о
бы и н е а б с о л ю т н о).
Заметим, что если бы оба ряда (А) и (В) сходились лишь
неабсолютно, то уже нельзя было бы ручаться за сходи-
сходимость ряда A3). Для примера попробуем умножить ряд
~ (-1)"	1 1	1
2 —-— = i—+—..^(-ly-1—+...
»-1 Тп	V* УЗ	fn
[как мы знаем, 382, 2] сходящийся неабсолютно] на самого себя. В этом
случае
(XI	1	X \
так как каждое слагаемое в скобках больше — , то | сп\ =» 1 (при п> 1) и ряд _2" сп
п	1
расходится [364, 5°].
Однако если аналогично поступить с также неабсолютно сходящимся
[382, 1)] рядом
44
2 3

393]	§ 5. ПОВТОРНЫЕ И ДВОЙНЫЕ РЯДЫ	329
то окажется, что
Здесь, при возрастании п, \сп\ стремится к 0, монотонно убывая, так что [по тео-
теореме Лейбница, 381] ряд 2сп все же будет сходящимся. Какова же
1
его сумма, будет ли она равна (In 2)a ? На этот вопрос отвечает
Теорема Абеля. Лишь только для двух сходящихся рядов (А) и (В) и их
произведение, взятое в форме Кош и, оказывается сходящимся, то его
сумма С необходимо равна А • В.
Доказательство. Сохраняя прежние обозначения, из A4) легко полу-
получаем:
d + C.,+ ... + Сп = А1Вп+А2Вп_1 + ... +АпВ1.
Разделим это равенство почленно на п и перейдем к пределу при п-°°. Так как
Сп~С, то по теореме Коши [33; см. также 391, Г] и среднее арифметическое
Q+C.+•••+<:„
л
С другой стороны, в силу 391, 4° (если положить там хп = Ап, уп = Вп),
AlBn+AiBn_l+ ... +
¦~АВ.
Отсюда С=А-В, ч. и тр. д.
§ 5. Повторные и двойные ряды
393. Повторные ряды. Пусть задано бесконечное множество чисел
ej» (/=1,2,3, ...;*= 1,2,3, ...),
зависящих от двух натуральных значков. Представим себе их рас-
расположенными в виде бесконечной прямоугольной матрицы:
4 4	/
42> 42) • • • af
43) 43) ••• 43
Такого рода матрица носит название бесконечной прямоугольной
матрицы с двумя входами.

330	ГЛ. XI. БЕСКОНЕЧНЫЕ РЯДЫ С ПОСТОЯННЫМИ ЧЛЕНАМИ	[393
Теперь остановимся на одном понятии, связанном с рассмотрением
матриц вида A) - понятии повторного ряда.
Если в бесконечной прямоугольной матрице просуммировать каж-
каждую строку отдельно, то мы получим бесконечную последователь-
последовательность рядов вида
%а?\	B)
Просуммировав теперь эту последовательность вторично, будем
иметь
2 2 <№¦	C)
Полученный символ и носит название повторного ряда. Если
заменить строки столбцами, т. е. если суммировать члены нашей бес-
бесконечной матрицы по столбцам, то мы получим второй повторный
ряд
2 2 "Г-	D)
Повторный ряд C) называется сходящимся, если, во-пер-
во-первых, сходятся все ряды по строкам B) (их суммы, соответственно,
обозначим через А(®) и, во-вторых, сходится ряд
его сумма и будет суммой повторного ряда C). Легко перефразиро-
перефразировать все это и для ряда D).
Элементы матрицы A) можно многими способами представить
в виде обыкновенной последовательности
иг,щ, ...,щ, ...	E)
и по ней составить простой ряд
2 щ	F)
[Об этом мы уже говорили в связи с частного типа матрицей G)
п° 389]. Обратно, если имеем обыкновенную последовательность E),
то разбив все ее члены (не считаясь с их расположением) на беско-
бесконечное множество бесконечных групп, можно ее представить мно-
многими способами в виде матрицы с двумя входами A), и по этой ма-
матрице составить повторный ряд C). Естественно встает вопрос о связи
между рядами F) и C), состоящими из одних и тех же членов.

393]
§ 5. ПОВТОРНЫЕ И ДВОЙНЫЕ РЯДЫ
331
Теорема 1. Если ряд F) сходится абсолютно к сумме U, то,
как бы его члены ни расположить в виде матрицы A), сходится и по-
повторный ряд C), причем имеет ту же сумму.
Доказательство. Ряд
2Ы
1
F*)
по предположению, сходится; обозначим его сумму через U*.
Тогда, прежде всего, при любых пак,
(=1
откуда следует сходимость ряда 2 I Я/А)! [365], а значит и сходимость
ряда 2 а\к) [377] (при любом к).
Далее, для любого числа е>0 найдется такое г0, что
2 I
следовательно, и подавно
2 щ
и-2 «г
г=\
G)
(8)
Члены Их, «2, ..., иг ряда F) содержатся в первых п строках и пер-
первых т столбцах матрицы A), если пят достаточно велики, скажем,
при п>п0 и т>т0. Тогда для указанных пит выражение
2 2
к=\ (=1
представляет сумму группы членов щ с номерами, большими г0, и
ввиду G) по абсолютной величине <е. Переходя к пределу при ш-<-~,
получим (для и>и0)
так что - в связи с (8) -
откуда следует сходимость повторного ряда C), и именно к сумме U.

332	ГЛ. XI. БЕСКОНЕЧНЫЕ РЯДЫ С ПОСТОЯННЫМИ ЧЛЕНАМИ	[393
Замечание. Некоторые строки матрицы A) могут состоять
и из конечного числа членов; легко распространить результат и на
этот случай.
Если вспомнить, что в 386 мы разбивали члены простого ряда
лишь на конечные группы, не нарушая при этом их
расположения, то станет ясно, что теорема 1 формулирует да-
далеко идущее распространение (совместно) сочетательного и переме-
стительного свойства абсолютно сходящегося ряда.
Обратная теорема имеет место лишь при усилении предположений
о повторном ряде.
Теорема 2. Пусть дан повторный ряд C). Если по замене его чле-
членов их абсолютными величинами получается сходящийся ряд, то схо-
сходится не только ряд C), но и простой ряд F), состоящий из тех же
членов, что и ряд C), расположенных в любом порядке, и притом -
к той же сумме.
Доказательство. По предположению ряд
2 2ИАI
сходится; пусть А* - его сумма. При любых пат, имеем
1 ii
/с=1 (=1
Возьмем теперь произвольную частичную сумму ряда F*):
При достаточно больших п и т, члены щ,щ, ...,иг будут содер-
содержаться в первых п строках и первых т столбцах матрицы A). Тогда
из (9) следует, что
U*^A*
и ряд F*) сходится, т. е. ряд F) сходится абсолютно.
Остается применить теорему 1.
Так как, очевидно, все сказанное о повторном ряде C) справед-
справедливо и для повторного ряда D), то как следствие из доказанных тео-
теорем получается следующее важное предложение, которое часто бы-
бывает полезно*.
Теорема 3. Пусть дана матрица A). Если по замене членов ряда
C) их абсолютными величинами получается сходящийся ряд, то схо-
сходятся оба повторных ряда C), D) и имеют ту же сумму:
2 24»= 2 2<Ф-
к-\ /=1	(=1 к=\
* В немецкой литературе это предложение носит название «grosser Umord-
nungssatz».

394]	§ 5. ПОВТОРНЫЕ И ДВОЙНЫЕ РЯДЫ	333
394. Двойные ряды. С бесконечной прямоугольной матрицей A)
связано и понятие двойного ряда. Так называется символ
-t ¦<#> I 4*° i 4k) f ¦ • • t af i ...
+	= 2 «$*>•	(io)
Ограничившись первыми т столбцами и первыми п строками, рас-
рассмотрим конечную сумму
1=т, Л = п
l,k=l
называемую частичной суммой данного двойного ряда. Ста-
Станем увеличивать числа тип одновременно, но независимо друг от
друга, устремляя их к бесконечности. Предел {конечный или бесконеч-
бесконечный)
называют суммой двойного ряда, и пишут
Z 4
l,k=\
Если ряд A0) имеет конечную сумму, его называют схо-
сходящимся, в противном же случае — расходящимся.
Вернемся для примера к матрице G) предыдущего параграфа, с
общим членом
В этом случае частичная сумма, очевидно, равна (если сохранить
прежние обозначения)
С (л) _ Л R
так что двойной ряд, соответствующий упомянутой матрице, всегда
С=ПтАтВп=АВ.
сходится и имеет сумму*
* Таким образом, если произведение двух сходящихся простых рядов пред-
представить в виде двойного ряда, то суммой последнего всегда будет произ-
произведение АВ; трудность была в доказательстве того же по отношению к произ-
произведению рядов, представленному простым рядом.

334	ГЛ. XI. БЕСКОНЕЧНЫЕ РЯДЫ С ПОСТОЯННЫМИ ЧЛЕНАМИ	[394
На двойные ряды легко перенести теоремы [364, 3° и 4°] об умно-
умножении членов сходящегося ряда на постоянное число и о почленном
сложении или вычитании двух сходящихся рядов; предоставляем сде-
сделать это читателю.
Точно так же для сходимости двойного ряда необходимо
стремление к 0 общего члена:
lima}*) = 0
[ср. 364, 5°]. Это сразу видно из формулы
а?>=Af> -А& - /*{*"« + А<??\
Естественно сопоставить двойной ряд A0) с повторными
рядами C) и D), рассмотренными выше. Так как
то, переходя здесь при фиксированном п к пределу при т -*¦ ~ (в пред-
предположении, что ряды по строкам сходятся), получим
Теперь ясно, что сумма повторного ряда C) есть не что иное, как
повторный предел
lim
л-™
Вопрос же о равенстве сумм двух повторных рядов C) и D) является
частным случаем вопроса о равенстве двух повторных пределов.
Применяя к рассматриваемому случаю общую теорему п° 168 о
двойном и повторном пределах*, придем к результату:
Теорема 4. Если 1) сходится двойной ряд A0) и 2) сходятся все
ряды по строкам, то сходится повторный ряд C) и имеет ту оке
сумму, что и двойной ряд
2 #
i,k=\
Аналогичная теорема имеет место и для второго повторного
ряда D).
* Здесь т и п играют роль независимых переменньк, а частичная сумма Am ~
роль функции от них.

394]	§ 5. ПОВТОРНЫЕ И ДВОЙНЫЕ РЯДЫ	335
Вопрос о сходимости двойного ряда A0) просто решается для
случая положительного ряда, т. е. ряда с неотрицательными
членами: а^з»0.
Теорема 5. Для сходимости ряда A0), если в^г^О, необходимо
и достаточно, чтобы его частичные суммы были ограничены.
Доказательство. Необходимость этого утверждения ясна.
Докажем достаточность. Пусть Affi*sL. Возьмем точную верхнюю
границу множества сумм А$:
А=тр{А%>}
и покажем, что она и будет являться суммой нашего ряда.
Зададим любое е=-0. По определению точной верхней гра-
границы, можно найти такую частичную сумму А^«\ что
Если взять т>т0, п > п0, то и подавно
А^^А -б
так как А$ с возрастанием обоих значков п и т, очевидно, воз-
возрастает.
Так как всякая частичная сумма не превосходит А, то можно на-
написать, что
\А^-А\^е (при/и=»/и0, и>и0),
а это и означает, что
т. е. ряд A0) сходится.
На основе этой теоремы можно установить теорему о сравнении
положительных двойных рядов, аналогичную теореме 1 п° 366; пре-
предоставляем это читателю.
Рассмотрим теперь двойной ряд, составленный из матрицы, в ко-
которой не все элементы положительны. Очевидно, что, как для про-
простых рядов, мы можем исключить из рассмотрения те случаи, когда
все элементы матрицы отрицательны или когда есть только конеч-
конечное число положительных или отрицательных элементов, так как все
эти случаи непосредственно приводятся к только что рассмотрен-
рассмотренному. Поэтому мы предположим, что в рассматриваемой матрице
A), а значит и в ряде A0), есть бесконечное множество как положи-
положительных, так и отрицательных элементов.

336
ГЛ. XI. БЕСКОНЕЧНЫЕ РЯДЫ С ПОСТОЯННЫМИ ЧЛЕНАМИ
[394
Кроме матрицы A), составим еще матрицу из абсолютных вели-
величин элементов.
i
42>
<#>| ... \аР\ ...
42)| ••• !я;2)! ...
4*>! ... №\ ...
и по этой матрице составим двойной ряд
A0*)
Подобно теореме п° 377 о простых рядах, и здесь имеет место
Теорема 6. Если сходится ряд A0*), составленный из абсолютных
величин членов данного ряда A0), то и данный ряд сходится.
Доказательство. Представим а\к^ в виде:
где
> =pf
Л*)
Ф
.(*) = J
Так как ^^la^l, gp:)=s|ap:)|, то из сходимости двойного ряда
A0*) вытекает сходимость двойных рядов
Но тогда сходится и ряд
2
1,к=1
а именно имеет сумму
2{
1,к=\
= P-Q.
Если одновременно с рядом A0) сходится и ряд A0*), то ряд A0)
называется абсолютно сходящимся. Если же ряд A0) сходится,
а ряд A0*) расходится, то ряд A0) называется неабсолютно
сходящимся.
Докажем теперь теорему о связи между двойным рядом A0) и
простым рядом F), состоящим из тех же членов. Она аналогична
теоремам 1 и 2.
Теорема 7. Пусть даны двойной ряд A0) и простой ряд F), состоя-
состоящие из одних и тех же членов. Тогда абсолютная сходимость

394J	§ 5. ПОВТОРНЫЕ И ДЙОЙНЫЕ РЯДЫ	337
одного из них влечет за собой абсолютную же сходимость дру-
другого и равенство их сумм.
Доказательство. Предположим сначала, что сходится аб-
абсолютно двойной ряд A0), т. е. сходится ряд A0*); сумму последнего
обозначим через А*. Взяв любое натуральное число г, составим ча-
частичную сумму ряда F*):
Как и при доказательстве теоремы 2, легко устанавливается неравен-
неравенство U*<A*, а с ним и абсолютная сходимость ряда F).
Пусть теперь дано, что сходится абсолютно простой ряд F), т. е.
сходится ряд F*); его сумму обозначим через U*. Какую бы частич-
частичную сумму
А=1 1 = 1
ряда A0*) ни взять, найдется столь большое г, что все слагаемые
этой суммы будут содержаться среди первых г членов ряда F*), так
что
В таком случае, по теореме 5, двойной ряд A0*) сходится, а значит
ряд A0) сходится абсолютно.
Наконец, для вычисления суммы U ряда F) - ввиду его абсо-
абсолютной сходимости — можно члены его расположить в любом удоб-
удобном для этой цели порядке [387]. Мы расположим их по квад-
квадратам схемы A); тогда, если еще объединить члены, отличающие
один квадрат от следующего за ним, получится:
что и завершает доказательство.
Сопоставляя теоремы 1, 2 и 7, сформулируем, в заключение,
такое
Следствие. Пусть матрица A) и последовательность E) состоят
из одних и тех же членов. Тогда двойной ряд A0), повторные ряды
C), D) и, наконец, простой ряд F) - если хоть один из них
оказывается сходящимся по замене его членов
их абсолютными величинами - все четыре сходятся и
имеют одну и ту же сумму.
В случае положительных рядов (т. е. при а^»0), очевидно, до-
достаточно сходимости одного из указанных рядов, чтобы сходились
все четыре и притом к одной и той же сумме.
22 Г. М. Фихтенгольц, т. II

338
ГЛ. XI. БЕСКОНЕЧНЫЕ РЯДЫ С ПОСТОЯННЫМИ ЧЛЕНАМИ
[395
395. Примеры.
1) Интересный пример дает матрица @«=х< 1):
X
x(l-x)
X\\ — X)"
-x2
-X2(l
-X2(l
-x2)
-x2J
X2
x2(l-x2)
^2A _ _j-2J
-x»
-X3(l
-X8(l
-Xs)
-X8J
хз
X8(l
xKl
-**) ..
-х*У ..
Здесь ряды по строкам абсолютно сходятся и имеют, соответственно,
суммы х, хA-х), хA-х)8, ... Ряд, составленный из этих сумм, также абсо-
абсолютно сходится; его сумма равна 1. Между тем другой повторный ряд не схо-
сходится, так как ряды по столбцам имеют суммы, попеременно равные +1 или - 1.
Этот факт нисколько не противоречит теореме 2, ибо для матрицы из аб-
абсолютных величин ни один повторный ряд не сходится. Мы видим лишь,
что предположение об абсолютной сходимости рядов по строкам (по
столбцам) и об абсолютной же сходимости ряда, составленного из их
сумм, не может заменить требования, чтобы сходился повторный ряд для матрицы
абсолютных величин.
2) Приведем знаменитый «парадокс Йог. Бернулли». Рассмотрим поло-
положительную матрицу (недостающие члены можно заменить нулями):
1
Ь2
1
1
гТз
1
1
1
	>¦
1
1
1
1
и приравняем сумму двух соответствующих ей повторных рядов. Если сначала
суммировать по строкам, то получим суммы [ср. 25, 9)]: 1, —, —, —, ..., из кото-
2 3 4
рых составится гармонический ряд; его сумму обозначим через s. Суммируя же
по столбцам (все они содержат по конечному числу членов!), придем к результатам
1111
—,—,—,—, ...; из них составится гармонический ряд без первого члена, что
2 3 4 5
в сумме даст s-1. Итак, ,$=,$-1!
На деле, конечно, этот «парадокс» является лишь доказательством от против-
противного того факта, что сумма s не может быть конечной, т. е. что
гармонический ряд расходится.
3) Пусть q пробегает всевозможные степени с натуральными основаниями
и показателями (бблыпими единицы), и притом - каждую однажды.
Доказать, что
j
[X. Гольдбах (Ch. Goldbach)].

395]	§ 5. ПОВТОРНЫЕ И ДВОЙНЫЕ РЯДЫ	339
Если т принимает всевозможные натуральные значения (^1), не являю-
являющиеся степенями, то
= Z{ — + — +... I- — Н—+... + — + —+... +...
_ у f 1
Отсюда
где и пробегает на этот раз уже все натуральные значения, начиная с 2, так что,
действительно, G = l [25, 9].
[Обоснование, со ссылкой на доказанные теоремы, предоставляем читателю].
Любопытно сопоставить этот результат с результатом Штейн ера
(J. Steiner):
~ °° 1 ~ 1
2 Z -— = 2 ——— =i-
т=2 к=2 тк т=2т(т-\)
Здесь степени могут появляться и не однажды!)
4) Рассмотрим матрицу с общим членом
<*) =	(к-1)	(/-1I
' (
Воспользовавшись установленным в 4), 363 соотношением
i	l	..	l	- (,,)
л=1 (а+и)(а + " + 1)	(ct + n+p) />(<*+!)•.. .'(а+р)
(при а = 0, р~к), легко просуммировать члены А>ой строки:
~да (k-Vfi j_.
отсюда сумма повторного ряда
Ввиду симметрии выражения л/ относительно i и А:, второй повторной ряд
тождествен с первым, и приравнивание их сумм ничего нового не даст.
22»

340
ГЛ. XI. БЕСКОНЕЧНЫЕ РЯДЫ С ПОСТОЯННЫМИ ЧЛЕНАМИ
[-195
Видоизменим теперь матрицу так: сохранив в ти-ой строке первые т - 1 членов
прежними, вместо т-то члена подставим сумму rm всех членов тя-й строки, начиная
с m-го, а остальные члены отбросим. Для новой матрицы
4m)
Ят—1 fjn
„(т + 1) „(т + 1)
Суммы рядов по строкам, а с ними и сумма первого повторного ряда останутся
прежними [см. A2)]. Для суммирования рядов по столбцам вычислим сначала
rm = 2j 77Г
(т-1)!
(/п-1)!
n=i (m-l+n)-...-Bm-l+n) mKm+X)-.. .-{2т- 1)'
здесь мы снова воспользовались соотношением A1), при а = тя-1, р = т. Сумма
же остальных членов тя-го столбца равна
(m-l)!
(т-\)\
... 'Bт+л)
)-. ¦. -2т
[в A1) мы положили а=р = т]. Окончательно же, сумма членов /л-го столбца
хжазывается равной
m{in+\)- ...•
- = 3-
К/и-1)!]2
2т!
Приравнивая, по теореме 3, суммы обоих повторных рядов, мы приходим к инте-
интересному соотношению:
Ъп\
A3)
Так как ряд справа сходится очень быстро, то он облегчает приближенное
вычисление суммы важного ряда, стоящего слева. Больше того, ниже [440, 7]
мы увидим, что выведенное соотношение позволяет выразить сумму первого
л2
ряда «в конечном виде»: она равна — (этот результат принадлежит Эйлеру).

395]	§ 5. ПОВТОРНЫЕ И ДВОЙНЫЕ РЯДЫ
5) Остановимся на ряде Ламберта:
341
<р(х)=
л=1 1-хк
ограничиваясь предположением, что |х|^1. Мы видели [385, 5)], что при этом
предположении ряд Ламберта сходится при тех же значениях х, что и сте-
степенной ряд
Z
k=\
Допустим же, что радиус сходимости R этого ряда ^0 [379], и будем считать
Очевидно:
Составим теперь матрицу из этих членов, умноженных еще на a/f, помещая оди-
одинаковые степени х в один столбец (пустые места можно заполнить нулями):
а2х2
а2хе
а7х'
Повторный ряд по строкам как раз и имеет сумму <р(х). Так как сте-
степенной ряд, а с ним и ряд Ламберта, сходится при замене х на | х \ и а^ на
Iafi|, то можно применить теорему 3 и просуммировать по столбцам. Мы
получим разложение ср(х) в степенной ряд
{х) = 2 "-пх", причем лп = 2 ак>
п=1	(г/л
значок к/n условно означает, что сумма распространяется лишь иа делители А;
числа п.

342	ГЛ. XI. БЕСКОНЕЧНЫЕ РЯДЫ С ПОСТОЯННЫМИ ЧЛЕНАМИ
Например, полагая я/( - 1 или а^ - к*, будем иметь соответственно
STI X*	sr,	sr, КХК	sr,
2 ~.	г=2 Ф)-х", 2 :	т. = 2 a{ri)xn,
где т(н) означает число, a o(ti) - сумму делителей п.
6) Расположив те же члены иначе, без пропусков:
[395
а,*1-
мы сохраним те же суммы по строкам, по столбцам же получим, по порядку:
fix), Дх2), f(x3), f(x*), ... Таким образом, мы приходим к тождеству, связываю-
связывающему функции (р и /:
те
Ф) = Z fix").
Например, взяв а^ = ак, где |a[ssl, будем иметь
ах
/(*) =
1-ах'
так что
7) Полученный результат можно обобщить. Пусть даны два степенных ряда
и
2
п=1
Ограничимся значениями х, для которых |x|-= 1, и оба ряда абсолютно сходятся.
Составим матрицу из элементов anbmxmn. Так как (для т=»1 и л>1)
шз=и+л, то
[ =s | апхп | • | omxm |.
Отсюда легко заключить, что двойной ряд, соответствующий взятой матрице,
абсолютно сходится. Приравнивая, на основании следствия, суммы повторных
рядов, найдем тождество:
2
т=1
2
п=1
* В обоих случаях, как легко проверить, R=l, так что достаточно
сто |лг|<1.
считать
просто |

395]	§ 5. ПОВТОРНЫЕ И ДВОЙНЫЕ РЯДЫ	343
Отсюда тождество предыдущего упражнения получается при Ьт = 1 [так что
1-х
8) Ряд
2 *<
к 0
получается умножением рядов 2 х' и 2 Ук> которые (абсолютно) сходятся при
i = 0	/с=0
[х\^1 и |>|-=1; для этих значений (абсолютно) сходится и двойной ряд.
Если 1*1^1 или |>|^1, то нарушается необходимое условие сходимости:
общий член не стремится к 0, ряд расходится. Легко проверить непосредственно,
что расходимость налицо и в случае, если | х | = 1 или | у | - 1.
9)	Рассмотрим ряд
¦^ 1
2, 	 (а^О, |б=>0).
i,k=l i'kP
Он также получается умножением рядов 2 ~г и 2 ~s • которые сходятся при
а =-1 и /? =-1, так что и двойной ряд при этих предположениях сходится.
Наоборот, если a=sl (или |6=sl), то двойной ряд наверное расходится, ибо
тогда расходятся все ряды по строкам (по столбцам) (ср. следствие предыду-
предыдущего п°).
10)	Исследуем сходимость ряда
i т.'
Для этого представим его в виде простого ряда, расположив члены его по
диагоналям. Так как члены, лежащие на одной диагонали, равны, то, объеди-
объединив их для удобства подсчета, получим ряд
2 <«-»-.
Ввиду очевидных неравенств
— и=еи - 1 -= п,
деля на па, будем иметь
1	1 ^	1^1
2	па~1	па па~1
Отсюда ясно, что полученный нами простой ряд сходится при а >¦ 2 и расходится
при стяз2. По теореме 7, то же справедливо и для двойного ряда.
11) Рассмотрим теперь более сложный ряд

344
ГЛ. XI. БЕСКОНЕЧНЫЕ РЯДЫ С ПОСТОЯННЫМИ ЧЛЕНАМИ
[395
где форма Ахг+2Вху+СУ предполагается определенной положи-
положительной, так что А = АС-В*>-0, а также А и С^О.
Если через L обозначить наибольшее из чисел \А\, \В\, \С\, то, очевидно,
AP+2Bik+Ck>*sL(i+k)\
В таком случае из 10) ясно, что при g=sl наш ряд расходится.
С другой стороны, имеем
так что
a l	ш а? 1
s—•— и, аналогично, a) J^—•—.
A? j2P	A? kt9
Отсюда легко получить, что
Сопоставляя это с 9), видим, что при р =-1 рассматриваемый ряд сходится.
12) В теореме 4, вместе с предположением о сходимости двойного ряда, делает-
делается особо предположение о сходимости всех рядов по строкам. Следующий простой
пример показывает, что без второго предположения обойтись нельзя - оно не
вытекает из первого. Двойной ряд по схеме
1
— 1
1
2
1
~2
1
3
1
~3
-1
1
1
~2
1
2
1
3
1
3
1
— 1
1
2
1
~2
1
3
1
з
	,—r-
-1
1
1
~2
1
2
1
3
1
3
сходится, его сумма равна 0. Между тем все ряды по строкам расходятся.
13) Установить суммы следующих двойных рядов:
(в) 2
1
m,T=lDn-lJ'"+i 8 2
(д) i
1	з
= 1п2;
= -ln2;

395]	§ 5. ПОВТОРНЫЕ И ДВОЙНЫЕ РЯДЫ	345
Указание. Перейти к повторному ряду, начав с суммирования по т.
Использовать разложения
1	+	f ...-In 2
2 3 4
111	л
1
как известные.
14) Рассмотрим функцию двух переменных
фс,г) = е
Перемножая абсолютно сходящиеся ряды
.Kif-V--. х
получим для этой функции (также абсолютно сходящийся) двойной ряд
™ ( х У"^ ( — 1)^
Ч\л, Z) - ^_i — I —— i.
lt A — U V. *- /	i.п..
Собирая (следствие) члены с одинаковыми степенями z, можно преобразовать
его в повторный ряд
где для лз=О
а для я-=0
xYk+n
Впрочем, легко видеть, что
Функция Уп(х) (и = 0,1,2, ...) называется функцией Бесселя со значком
н; эти функции играют важную роль в математической физике, небесной механике
и т. д. Функция <р(х, г), из разложения которой они получаются, носит название
«производящей функции» для бесселевых функций.
* Сумма 2 ат по определению, есть сумма двух рядов
2ап+2а-п-
л=0 п=1

346	ГЛ. XI. БЕСКОНЕЧНЫЕ РЯДЫ С ПОСТОЯННЫМИ ЧЛЕНАМИ	[396
396. Степенной ряд с двумя переменными; область сходимости.
Степенным рядом с двумя переменными х, у на-
называется двойной ряд вида
2 «/,/с*'/,	A4.
(,/с=0
расположенный по целым положительным степеням переменных х и у
Как мы сделали это в 379 по отношению к простым степенные
рядам, мы и здесь поставим себе задачей выяснить вид «области схо
димости» ряда A4), т. е. множества в^={М(х, у)} тех точек плоско
сти, для которых ряд сходится.
Лемма. Если ряд A4) сходится в некоторой точке М(х, у), коор
динаты которой обе отличны от О, то он абсолютно схо
дится во всех точках М(х,у), удовлетворяющих неравенствам: | х | -
-=1*1> IjM^IjM (т- е- во всем открытом прямоугольнике с центров
в начале координат и с вершиной в точке М).
Доказательство вполне аналогично доказательству леммы п° 37
Из ограниченности членов ряда A4) при х = х, у=у
гД = О, 1,2, ...)
получается
так что - если только |х|<|х|, |j|<|j>| - справа мы имеем о(
щий член сходящегося ряда [395, 8)]; отсюда и следует абсолютна
сходимость ряда A6).
Мы станем изучать лишь такие ряды, для которых подобные точк
М существуют - другие ряды для нас не представляют интерес
Самый характер леммы позволяет нам ограничиться рассмотрение
лишь первого координатного угла; полученные результаты - г
симметрии - легко можно будет распространить и на остальнь
углы.
Возьмем же в первом угле луч OL, исходящий из начала, п<
углом в к оси х (рис. 55). Как и в 379, пользуясь леммой, можно п
казать, что найдется такое положительное число Щв) (которое м
жет оказаться и бесконечным), что во всех точках М на этом лу*
для которых
ряд A4) сходится абсолютно, в то время как при условии
он расходится.

396]
§ 5. ПОВТОРНЫЕ И ДВОЙНЫЕ РЯДЫ
347
Если хоть для одного луча Л(в) = + °°, то, в силу леммы, ряд ока-
оказывается сходящимся (и притом — абсолютно) на всей плоскости,
которая и играет роль «области сходимости» вЖ.
Исключим теперь этот случай всюду сходящегося ряда.
Тогда RF) будет конечной функцией от в, и на каждом луче OL най
дется пограничная точка Мо, для которой
Она отделяет точки М луча, в которых ряд (абсолютно) сходится,
от точек, где он расходится; в самой точке Мв, смотря по случаю-
может иметь место и сходимость, и расходимость.
L'
Если провести через Мв вертикаль РР' и горизонталь QQ' (см.
рисунок), то внутри прямоугольника OPMeQ ряд заведомо схо-
сходится, а внутри угла Q'M0P' - заведомо расходится (по лемме!).
Поэтому на новом луче OL', отвечающем какому-нибудь другому
углу в', вдоль OR будет сходимость, а вдоль SL' - расходимость.
Следовательно, пограничная точка Мь, на этом луче должна лежать
между R и S. Отсюда легко усмотреть, что, при изменении в от О
до j, Я@) изменяется непрерывным образом, так что точка Мо
описывает в первом координатном угде непрерывную погранич-
пограничную кривую.
Так как при уменьшении в абсцисса х0 точки Мв не убывает, а ор-
ордината ее у0 не возрастает, то обе имеют предельные значения при
0-0. Тогда, очевидно, имеет предельное значение и RF). Если этот
предел

348
ГЛ. XI. БЕСКОНЕЧНЫЕ РЯДЫ С ПОСТОЯННЫМИ ЧЛЕНАМИ
[397
конечен, то, точка Мо стремится к некоторой предельной точке Мо(Яо, 0)
на оси х, в противном же случае пограничная кривая имеет асимптоту,
параллельную оси х (которая может совпадать и с самой осью х).
Легко перефразировать все сказанное и для случая, когда 0 -*"=, меняя
ролями оси х и у.
Замечание. Не следует, однако, думать, что предельная точ-
точка Мо, о которой только что шла речь, необходимо совпадает с п о-
граничной точкой Мо на самой оси х. Точка Мо может ока-
оказаться и правее М§ (и даже лежать в бесконечности). Возможность
эта не должна удивлять читателя, ибо лемма и построение на ней
рассуждения относятся лишь к точкам вне координатных осей.
Дополним теперь построенную в первом координатном угле кри-
кривую симметричными ей (относительно обеих осей и начала координат)
кривыми в остальных углах. Таким путем мы получим полную п о-
граничную кривую, которая в существенном и определит ин-
интересующую нас «область сходимости» ©#: в той части плоскости,
которая извне ограничена этой кривой, ряд A4) сходится {и притом
абсолютно), во внешней части плоскости ряд расходится*, в точках
оке самой пограничной кривой может иметь место как сходимость,
так и расходимость.
Рассмотрим примеры.
397. Примеры. 1) Для ряда
У i k
+ 1
как мы видели в 395, 8), «область сходимости» &% сводится к открытому пря-
прямоугольнику (-1, 1; -1, 1) (рис. 56), в пре-
1 1
делах которого суммой его будет — • -
1-х 1-у
2) Для аналогично ряда
Z
Рис. 56.
(где указатели г, к изменяются, начи-
начиная от 1) «область сходимости» будет
состоять из этого же прямоугольника, н о
с присоединением обеих коор-
координатных осей. В этом случае, хотя
пограничная точка Мо, о которой речь шла
выше, и стремится при G ^ 0 к предельной
точке М* A, 0) на оси х, но сходимость имеет место на всей этой оси (см. за-
замечание).
* Если не считать координатных осей, вдоль которых в иных случаях, как
указывалось, ряд может сходиться и за пределами этой кривой.

397]
§ 5. ПОВТОРНЫЕ И ДВОЙНЫЕ РЯДЫ
349
3) Ряд
очевидно, абсолютно сходится на всей плоскости.
4) Для того чтобы сходился абсолютно ряд
i
т. е. сходился ряд
2 Цр
необходимо и достаточно, чтобы сходился ряд
1
который получается из предыдущего сум-
суммированием по диагоналям. Это при-
водит нас к условию |х| + |^|<1. Следо-
Следовательно, здесь «область сходимости» пред-
представляет собой косо поставленный квад-
квадрат с вершинами в точках (± 1, 0), @, +1)
(рис. 57).
ху=1
Рис. 58.
5) Рассмотрим, в заключение, следующий двойной ряд:
...+хт-\
...+хту+
.+хту2+	\-xmy"i+.
Если, предположив его абсолютную сходимость, просуммировать его по
строкам, то получим:
¦ ¦ ¦)И+ху+(хуУ-+ .. .]
1-х 1-ху'

350	ГЛ. XI. БЕСКОНЕЧНЫЕ РЯДЫ С ПОСТОЯННЫМИ ЧЛЕНАМИ	[398
Отсюда ясно, что для абсолютной сходимости необходимо: | х | ¦= 1 | ду | -= 1;
вместе с тем, эти неравенства и достаточны. «Область сходимости» изобра-
изображена на рис. 58; кривые на ней - равнобочные гиперболы.
398. Кратные ряды. Дальнейшее расширение понятия бесконечного
ряда происходит совершенно естественным образом. Пусть задана
бесконечная система чисел
занумерованных s(s»2) значками i,k, ..., 1, каждый из которых - не-
независимо от других - принимает всевозможные натуральные значе-
значения. Тогда символ
2 ui,k,...,i
i, It,... ,(=1
носит название кратного (точнее: s-к ратного) ряда.
Предел частичной суммы ряда
n m	p
Un,m	p= 2 2 ¦ • ¦ 2 ui,k,...,l
(=1 t=
при и-»~, m -> ~, ...,/>-* ~ (конечный или бесконечный) есть сумма
ряда. Ряд назьгеают сходящимся, если он имеет конечную
сумму.
Важнейшим классом кратных рядов являются степенные
ряды с несколькими переменными:
2 °i,k	,xy...z'.
На кратные ряды также распространяются основные понятия и
предложения изложенной выше теории.
§ 6. Бесконечные произведения
399. Основные понятия. Если
P\-.Pi,Pzi ---уРп, ¦¦¦	A)
есть некоторая заданная последовательность чисел, то составленный
из них символ*
Pi-Рг'Рз' ¦¦••Рп--- = ПРп	B)
л=1
назьгеают бесконечным произведением.
* У нас уже встречалось такое обозначение для произведения, но лишь конеч-
конечного числа сомножителей.

400]	§ б. БЕСКОНЕЧНЫЕ ПРОИЗВЕДЕНИЯ	351
Станем последовательно перемножать числа A), составляя ч а-
стичные произведения
Р\ =Pl> Р2 =Л 'Pz> PS =Р\ -Р-2 -Рз> • • • >
Рп=РГР2----'Рп, ¦¦¦	C)
Эту последовательность частичных произведений {Рп} мы всегда будем
сопоставлять символу B).
Предел Р частичного произведения Рп при п -*• ~ {конечный или бес-
бесконечный)
называют значением произведения B) и пишут:
Р=рх-р2-...-рп- ... = Прп.
п = 1
Если бесконечное произведение имеет конечное значение Р и при-
притом отличное от 0, то само произведение называют сходя-
сходящимся, в противном же случае — расходящимся*.
Достаточно одному из сомножителей произведения быть нулем,
чтобы и значение всего произведения также было равно нулю. В даль-
дальнейших рассмотрениях мы этот случай будем исключать, так что для
нас всегда рпт^0.
Читатель легко установит аналогию с бесконечными рядами [362]
и уяснит себе, что - подобно рядам - и рассмотрение бесконечного
произведения также есть лишь своеобразная форма изучения варианты
(или последовательности) и ее предела. С этой формой полезно по-
познакомиться, так как в иных случаях она представляется более удоб-
удобной, чем другие.
400. Примеры. 1)
Так как частичное произведение
я И).
то бесконечное произведение сходится, и его значением будет —.
2) Формула В а л л и с а [317]
п .	2-2.4-4-...2л.2л
* Таким образом (подчеркнем это), если Р=0, то произведение для нас будет
расходящимся. Хотя эта терминология идет в разрез с терминологией,
принятой для бесконечных рядов, но она общепринята, ибо облегчает формули-
формулировку многих теорем.

352	ГЛ. XI. БЕСКОНЕЧНЫЕ РЯДЫ С ПОСТОЯННЫМИ ЧЛЕНАМИ	[400
я
очевидно, равносильна разложению числа — в бесконечное произведение
я 2 2 4 4	2п 2п
2 13 3 5	2и-1 2и + 1
Она же приводит к формулам
П Fi—L—1-" ua«/7 (i__
mill Bm+lJJ 4' mill 4mV я
3) Докажем, что (при |х|-=1)
1-х
Действительно, как легко убедиться последовательным умножением,
_l-x"'
"~ 1-х '
Отсюда в пределе и получается требуемое равенство.
4) Мы имели в п° 54, 7а) предел:
Ф ф	ф sin ф
limcos— -cos—•... -cos — =
n~» 2 22	2" ф
Теперь мы можем записать это так:
В частности, при ф = — , придем к разложению:
2	я я	я
— = cos—-cos—•... -cos —— •
я	4 8	2"+!
Если вспомнить, что
то разложение это можно переписать в виде
я ПМ	а ]/ 1 1
s-=^- и cos-=^-+-
2 1/ lAl
К
Т \[
[В и е т a (F. V i e t а)]. Эта формула вместе с формулой В а л л и с а представ-
представляет первые примеры бесконечных произведений в истории анализа.
5) В 315 A0) для полного эллиптического интеграла 1-го
рода мы установили-формулу
К(к) - -- lim A + *,)(! + к2) ¦... • A + кп\

401J	§ 6. БЕСКОНЕЧНЫЕ ПРОИЗВЕДЕНИЯ	353
где варианта кп определяется рекуррентным соотношением:
Эта формула дает разложение К(к) в бесконеченое произведение
6) Рассмотрим еще такое бесконечное произведение:
и
В данном случае частичное произведение имеет вид
, 1 1
Л+1	Л+1	й+1
где С - эйлерова постоянная, а уп бесконечно малая [367 D)]. Таким
образом, произведение сходится, и его значение
401. Основные теоремы. Связь с рядами. Отбросив в бесконечном
произведении B) первые т членов, получим остаточное произ-
произведение
пт =Рт+1 -Рт+2 * • • • 'Рт+1:' • • • = П Рп>	D)
которое вполне аналогично остатку бесконечного ряда.
1°. Если сходится произведение B), то сходится, при любом т,
и произведение D); обратно, из сходимости произведения D) вытекает
сходимость исходного произведения B)*.
Доказательство предоставляем читателю [ср. 364, 1°].
Таким образом, и в случае бесконечного произведения отбрасы-
отбрасывание конечного числа начальных множителей или присоединение вна-
вначале нескольких новых множителей на его поведении не отражается.
2°. Если бесконечное произведение B) сходится, то
lim nm = 1
[см. D)].
* Напомним, что мы раз навсегда предположили рп ^ 0.
23 Г. М. Фихтенгольп, т. II

354	ГЛ. XI. БЕСКОНЕЧНЫЕ РЯДЫ С ПОСТОЯННЫМИ ЧЛЕНАМИ	[401
Это следует из равенства
и из того, что Рт стремится к
3°. Если бесконечное произведение B) сходится, то
\impn=l.
Действительно, вместе с Рп, и Pn_i стремится к Р,
limPn P ,
"	1
п
[Ср. 364, 5°.]
Не перечисляя других свойств бесконечных произведений, анало-
аналогичных свойствам бесконечных рядов, мы обратимся к установлению
связи между сходимостью бесконечных произведений и рядов, что
позволит нам непосредственно использовать для произведений под-
подробно развитую для рядов теорию.
В случае сходящегося произведения, множители рп, начиная с не-
некоторого места, будут положительны C°). Впрочем, ввиду 1°, мы не
нарушим общности, если будем впредь предполагать
все рп>0.
4°. Для того чтобы бесконечное произведение B) сходилось, необ-
необходимо и достаточно, чтобы сходился ряд
2
п=1
При выполнении этого условия, если L есть сумма ряда, имеем
P = eL.
Обозначив через Ln частичную сумму ряда E), будем иметь:
Из непрерывности логарифмической и показательной функций теперь
следует, что если Рп стремится к конечному положительному пре-
пределу Р, то Ln стремится к In P, и обратно - если Ln имеет конечный
предел L, то для Рп пределом будет eL.
При исследовании сходимости бесконечного произведения B) часто
представляется удобным, полагая
записывать его в виде
л),	B*)
л=1

401]	§ 6. БЕСКОНЕЧНЫЕ ПРОИЗВЕДЕНИЯ	355
а ряд E) - в виде
aJ.	E*)
п=1
В этих обозначениях имеем простую теорему:
5°. Если, по крайней мере для< достаточно больших п, будет
а„=>0 (или а„<0),
то для сходимости произведения B*) необходима и достаточна схо-
сходимость ряда
2ап.	F)
п = 1
Так как для сходимости как произведения B) так и ряда F) во
всяком случае необходимо, чтобы было
Итал = 0	G)
[см. 3°], то предположим это условие выполненным. Тогда имеет
место соотношение
[77, 5) (а)]. В таком случае, ввиду того, что члены обоих рядов E*)
и F), начиная с некоторого места, сохраняют определен-
определенный знак, по теореме 2 п° 366 эти ряды сходятся или расходятся
одновременно. Отсюда, в связи с 4°, и следует наше утверждение.
Возвращаясь к общему случаю ап<0, докажем еще такое предло-
предложение:
6°. Если, вместе с рядом F), сходится и ряд
2а2п,	(8)
л=1
то бесконечное произведение B*) сходится.
В самом деле, из (8) прежде всего следует G). Вспоминая разло-
разложение функции 1пA+х) по формуле Тейлора [125, 5)], имеем:
In A + ап) = ап-^а2п
так что
По теореме 2 п° 366 сходимость ряда (8) влечет за собой сходимость
ряда
1 [в„ - In A+«„)].	A0)
1
23*

356	ГЛ. XI. БЕСКОНЕЧНЫЕ РЯДЫ С ПОСТОЯННЫМИ ЧЛЕНАМИ	[402
Так как ряд F) предположен сходящимся, то отсюда следует сходи-
сходимость и ряда E*), как разности двух сходящихся рядов. Остается при-
применить предложение 4°.
Остановимся бегло на случае, когда бесконечное произведение
«расходится» к 0.
7°. Для того чтобы бесконечное произведение [B) или B*)] имело
нулевое значение, необходимо и достаточно, чтобы ряд E) или
[E*)] имел суммой — °°.
В частности, это будет так, если а„<0 и ряд F) расходится, или
если ряд F) сходится, но расходится ряд (8).
Предоставляем доказательство читателю. Лишь по поводу послед-
последнего предположения заметим, что из расходимости ряда (8), в силу
(9), вытекает расходимость ряда A0), который будет иметь суммой
+ ~. А тогда, ввиду сходимости ряда F), ясно, что суммой ряда E*)
будет ¦- ~.
В заключение используем связь между произведением B) [или B*)]
и рядом E) [или E*)] для установления понятия абсолютной
сходимости бесконечного произведения. Произведение называют а б-
с о л ю т н о сходящимся именно в том случае, когда абсолютно
сходится соответствующий ряд из логарифмов его множителей.
Исследования пп° 387 и 388 сразу же позволяют заключить, что
абсолютно сходящиеся произведения обладают переместитель-
ным свойством, в то время как неабсолютно сходящиеся за-
заведомо им не обладают.
Легко доказать по образцу 5°, что
8°. Для абсолютной сходимости произведения B*) необхо-
необходима и достаточна абсолютная же сходимость ряда F).
402. Примеры. 1) Применим доказанные теоремы к бесконечным произведе-
произведениям:
(а)	77 H— (*=-0) сходится при *>1и расходится при л;«=1, в согласии с
таким же поведением ряда 2 — E°); аналогично, 77 И	пРи х =-1 сходится
/1=1 Пх	л=2 V Пх)
E°), а при 0-=a-=s1 расходится к нулю G°).
°° г (_ 1)« — Л	1
(б)	77 1 Ч	|при х-— сходится: именно, при х>\ произведение аб-
л=1 L	nx J	1
" 1	1
солютно сходится, поскольку сходится ряд У, — (8°), а при —-=x=el про-
n=i пх	2
изведение неабсолютно сходится, так как сходятся ряды 2
°° 1	1
и ^ — F°); наконец, при 0<х==— значение произведения есть 0, ибо первый
n=i и2*	2
из этих рядов сходится, а второй уже нет G°).

402J	§ 6. БЕСКОНЕЧНЫЕ ПРОИЗВЕДЕНИЯ	357
( л\
2) Пусть хп - произвольная варианта, содержащаяся в промежутке 0, — I.
Тогда произведения
Ятт si
cosxn и .//
л = 1	п = 1 Хп
сходятся или нет, смотря по тому, сходится ли ряд 2 хп или нет.
п=1
Предположим сначала, что варианта хп-+0; тогда эти заключения вытекают
из-5° и 7°, если воспользоваться разложениями [125, 2) и 3)]
Если же хп к 0 не стремится, то одновременно и ряд расходится, и оба произ-
произведения имеют нулевые значения*.
3)	Из теории бесконечных произведений легко получить теорему Абеля:
если ^ ап - данный положительный ряд, и Ап означает его частичную сумму, то
л=1
ряд ^ — сходится или расходится одновременно с данным [ср. 375, 4)]. В дока-
л=1 Ап
зательстве нуждается лишь случай расходимости. Если Ап — °°, то бесконечное
Я™ (л °п\ тт Ап-\	/	„	-V пп
1	= // -- расходится к 0, а тогда (в силу 5 ) ряд 2i —
п=2\, Ап) л=2 Ап	п-ЧЛп
расходится.
4)	Рассмотрим важное произведение
П 1 -
П = 1 I	П*Л-
[ниже, в п° 408, мы увидим, что оно представляет функцию sin x]. Пусть х^кл,
где /с = 0, ±1, ±2, ...
Его сходимость (конечно - абсолютная) сразу вытекает из сходи-
¦^г X2	I
мости ряда Л 	. Если каждый множитель разложить на два и написать
1 и2л2
произведение в виде:
X
то - так как 1	> 1 - сходимость при указанном расположе-
пл
нии множите л е й сохранится, сохранится и значение произведения. Но
* Что произведения имеют определенные конечные значения, явствует из
того, что все множители их - правильные дроби; однако значения их не могут
быть отличны от 0, так как нарушено необходимое для этого условие C°).

358	ГЛ. XI. БЕСКОНЕЧНЫЕ РЯДЫ С ПОСТОЯННЫМИ ЧЛЕНАМИ	1402
на этот раз сходимость станет неабсолютной, ввиду неабсолютной сходи-
сходимости ряда
х л х х	хх
л х 2л. 2л	пл. пл.
так что множители эти произвольно перемещать нельзя.
*	( х\ ± —
Заменим теперь каждый множитель 1 :р— множителем II т—\е пл; легко
пл	{ пл)
видеть, что это не отразится ни на сходимости, ни на значении бесконечного
произведения. В то же время новое произведение будет уже абсолютно сходя-
сходящимся, ибо [125, 1)]
±~г	х х* A\	( х\ ±~	х2 П
е п"=1± —+ -- +о - ,	1+— \е пл=\	+о -
пл 2и2л2 \пг)	{ пл)	2п2л2 [п*
и множители, начиная с некоторого места, становятся положительными правиль-
правильными дробями.
5) Доказать тождество (при 0-=#~= 1)
1
(Э й л е р).
Указание. Сходимость обоих произведений устанавливается с помощью
5°. Представить первое из них в виде
6) Доказать, что (при а=-/?
lim 	= 0.
A)A)
Для этого достаточно установить расходимость бесконечного произведения
или [см. 7°] расходимость ряда
А это легко вытекает из сравнения написанного ряда с гармоническим.
Замечание. Этот пример, равно как и следующие, получительны в том
отношении, что показывают, как иной раз действительно выгодно сводить разыска-
разыскание предела варианты (или последовательности) к исследованию бесконечного
произведения, с использованием развитой для бесконечных произведений теории.

402]	§ 6. БЕСКОНЕЧНЫЕ ПРОИЗВЕДЕНИЯ	359
7) Вернемся к ряду 2j	> который мы уже рассматривали в 370, 2) (д)
л=1 и!
и 378. 1) (д). Мы оставили открытым вопрос о поведении его на конце х= — его
е
промежутка сходимости.
В этом случае получается знакопеременный ряд
члены которого по абсолютной величине монотонно убывают. Вспоминая теорему
Лейбница [381], видим, что заключение о сходимости ряда зависит от наличия
равенства
и" 1
lim	= 0,
„-™ и! е"
Так как отношение (и+ 1)-го значения этой варианты к n-му есть
\\п
КГ
то задачу можно представить в равносильной форме - разыскания значения
бесконечного произведения
е n=l e
Логарифмируя, получим [125, 5)]
так что ряд логарифмов типа E) расходится и имеет суммой -°°. В таком случае
G°) значение бесконечного произведения (а с ним - и искомый предел), действи-
действительно, есть 0. Ряд сходится.
8) Исчерпаем вопрос о поведении гипергеометрического ряда
F(*,p, у, х)=1+2
n=i
[см. 372 и 378, 4)] при х= -1, в предположении, что -l=ey-a-/J=sO (именно
этот случай остался без рассмотрения).
Отношение (и+ 1)-го коэффициента к n-му здесь равно:
п%

360
ГЛ. XI. БЕСКОНЕЧНЫЕ РЯДЫ С ПОСТОЯННЫМИ ЧЛЕНАМИ
1402
Для достаточно больших значений и это отношение положительно; пусть у—а.—
-/8=- — 1, тогда оно окончательно становится меньшим единицы. Таким образом,
ряд
1+^(M)	A2)
если отвлечься от некоторого числа его начальных членов, оказывается знако-
знакопеременным, с монотонно убывающими по абсолютной величине членами. И здесь
нахождение предела (абсолютной величины) общего члена удобнее свести к опре-
определению значения бесконечного произведения:
п
Если у-а-/3=--1 (как мы предположили), то из A1), в силу 7°, следует, что это
произведение имеет значение 0: ряд сходится.
В случае же, когда у-а-/3 = -1, формула A1) получит вид
(а-щХ/Н-и)
Я,
A+пХу + и) и2
по теореме 5°, значение бесконечного произведения отлично от 0, для ряда A2)
нарушается необходимое условие сходимости, ряд расходится.
Мы, наконец, завершили исследование поведения гипергеометри-
гипергеометрического ряда. Результаты могут быть сведены в таблицу
1*Н1
1*1*1
х=1
х= -1
у-а-Р>0
y-x-P&sO
y-a-/S*0
0s*y-a.-P> -1
y-a —/3=s- 1
абс. сходится
расходится
абс. сходится
расходится
абс. сходится
неабс. сходится
расходится
9) Доказать, что ряд
2 агХ
п=1
2 - 2-)... (х- - п*
сходится для всех значений х, если сходится хоть для одного нецелого
значения х = х0 [С т и р л и н г (Т. Stirling)].
Члены этого ряда отличаются от членов сходящегося ряда
л=1
* Начальное значение л = и0 предполагается настолько большим, чтобы все
множители были положительны.

402]	§ 6. БЕСКОНЕЧНЫЕ ПРОИЗВЕДЕНИЯ	361
множителями
(х2-1)(л:2-23)...(л;2-и2)
которые при достаточно больших и изменяются монотонно.
Остается еще установить их ограниченность (ибо тогда можно будет
применить признак Абеля), а для этой цели проще всего убедиться в сходи-
сходимости бесконечного произведения
00 v2 — «2
тт*	"_.
л = 1 X2,-/!2
мы предоставляем это читателю.
10) Рассмотрим (вместе с Эйлером) бесконечное произведение
аз)
считая х огличным от нуля и от всех целых отрицательных чисел.
Легко представить его общий множитель так:
X	ZW"
и
отсюда, в силу 8°, вытекает, что наше произведение (абсолютно) сходится. Опре-
Определяемая им функция Г(х) является (после элементарных) одной из важнейших
рассматриваемых в анализе функций. Ниже [глава XIV, § 5] мы дадим другое
определение этой функции и глубже изучим ее свойства.
Так как и-е частичное произведение имеет вид
п\пх
п ) х(.х+1)(х+2)	(х + п)
то можно положить и
п\пх
Г(х)= lim 	.	A4)
х(х+1)(х + 2){х+п)
Написав аналогичную формулу для Г(х+1), легко видеть, что
пх
= lim	= х,
+1+
li
Г(х) п
и мы приходим к простому и важному соотношению:
Г(х+1) = х-Г(х).	A5)
Если положить х равным натуральному числу т, то получим рекур-
рекуррентную формулу

362	ГЛ. XI. БЕСКОНЕЧНЫЕ РЯДЫ С ПОСТОЯННЫМИ ЧЛЕНАМИ	D02
Так как РA) = 1 (что легко проверить), то отсюда
Еще одну важную формулу для функции Г мы получим, если перемножим
почленно равенства
Г
КГ
-
/7
IVе
11 +
л
"КГ
из которых первое следует из A3) и A5), а второе легко выводится из 400, 6). Мы
найдем:
X
еО.Г(х+1)= П --
л
или
1	°° ( х\ --
	= еСх /7 11 ч— 1-е " .	A6)
Г(х+1) П=Ц nj
Это - формула Вейерштрасса.
11) Приведем замечательный пример преобразования бесконечного произ-
произведения в ряд, также принадлежащий Эйлеру. Если перенумеровать про-
простые числа, в порядке возрастания:
Л = 2, р» = Ъ, р3 = 5, ¦•¦, Рк
то при л:=-1 имеет место тождество
1	1111
	=1 + — Н	Ь — + ...+¦—+•••
2х 3х 4х	пх
~ 1	°° 1
Л = 1	1 п=1 Пх
так что это произведение представляет функцию ?(х) Р и м а н а [365, 2)].
Имеем, по формуле для суммы геометрической прогрессии:
111	1
Если перемножить конечное число таких рядов, отвечающих всем простым
числам, не превосходящим натурального числа N, то частичное произведение
окажется равным
—^— = 2' — = 2 — + 2' —
i_i п=1"х п=1йХ '
*2

402]	§ 6. БЕСКОНЕЧНЫЕ ПРОИЗВЕДЕНИЯ	363
где штрих означает, что суммирование распространяется не на все натуральные
числа, а лишь (не считая единицы) на те из них, которые в своем разложении на
простые множители содержат только уже введенные простые числа (первые N
натуральных чисел этим свойством, конечно, обладают). Отсюда и подавно
IV ,	- 1
2-< 2 iz-
п=1 Пх л=Л>+1 И*
Ввиду сходимости ряда ? — , выражение справа, представляющее его
п-1 Iх
остаток после N-то члена, стремится к 0 при iV- °=; переходя к пределу, и полу-
получим требуемый результат.
12) При л:=1 соотношение A7) еще сохраняет силу, отсюда
р*=гЛГ 1 п=1 и
Рк
так что при N— ~ на этот раз Рх' - + °°, т. е. произведение
1	°° 1
1	п
ИНН)	ю-.".-
1
Рк
расходится и имеет значение + ~.
В этом состоит данное Эйлером новое доказательство того, что мно-
множество простых чисел бесконечно (чем, по существу, в проведенном рассуждении
мы не пользовались); ведь при конечности этого множества и произведение имело
бы конечное значение. Если полученный результат переписать так:
\ 2){ зД 5)	{ Рк)	ИЛ Рк)
то, в связи с 5°, можно заключить о расходимости ряда
111	1	^,1
	h	Ь	h ...+ — +••• = 2j —¦
2 3 5	рк	к=1Рк
Это важное предложение дает, сверх того, еще некоторую характеристику роста
простых чисел. [Подчеркнем, что оно гораздо сильнее утверждения о расходи-
расходимости гармонического ряда 2 — > иб° здесь речь идет лишь о части его
п=1 и
членов],

364	ГЛ. XI. БЕСКОНЕЧНЫЕ РЯДЫ С ПОСТОЯННЫМИ ЧЛЕНАМИ	[403
13) Аналогично может быть установлено (при х>1) тождество:
1	1111
	 ._- 1	I	I
Зх 5х 7х 9х '"'
где знак плюс или минус в знаменателе левой части берется в зависимости от
того, будет ли (нечетное) простое число вида 4и-1 или 4н+1.
§ 7. Разложения элементарных функций
403. Разложение функции в степенной ряд; ряд Тейлора. Мы уже
рассматривали в 379 степенные ряды вида:
2 апхп = а0 + ахх+ а^ + ... + апхп + ...,	A)
о
расположенные по степеням х. Если исключить «всюду расходящиеся»
ряды, то для каждого такого ряда существует промежуток схо-
сходимости с центром в точке х = 0, от - R до R, где радиус
сходимости R >0, но может быть и бесконечным. Концы этого
промежутка включаются или нет, смотря по случаю.
Рассматривают и степенные ряды более общего вида:
2ап(х-х0)п = а0 + а1(х-х0)+ ... + ап(х - хо)п + ...,	B)
о
расположенные по степеням двучлена х-х0 (вместо х). Такой ряд
не разнится существенно от ряда вида A), ибо приводится к нему
простой заменой переменной: х-хо=у (с точностью до обозна-
обозначения переменной). Для ряда B) - если он не будет «всюду расхо-
расходящимся» - также существует промежуток сходимости,
но на этот раз с центром в точке х0, от xo-R до xo + R. Концы его,
как и в случае ряда A), могут принадлежать, но могут и не принад-
принадлежать промежутку.
В последующих параграфах мы детально изучим свойства степен-
степенных рядов, которые во многом уподобляются многочленам. Отрез-
Отрезками степенного ряда являются многочлены, что делает степенные
ряды удобным средством для приближенных вычислений. В связи со
всем этим приобретает большую важность вопрос о возможности на-
наперед заданную функцию разложить по степеням х — х0 (в частности,
по степеням х), т. е. представить ее в виде суммы ряда типа B) или A).
Мы займемся здесь подобным разложением по отношению к эле-
элементарным функциям, причем путь к решению поставленного вопроса
нам открывает формула Тейлора, подробно изученная в 124 -126.
В самом деле, предположим, что рассматриваемая функция f(x) в

403)	§ 7. РАЗЛОЖЕНИЯ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ	365
промежутке [хо,хо + Н] или [хо-Н,хо] (Н>0) имеет производные
всех порядков (тем самым — непрерывные). Тогда, как мы видели
в 126, для всех значений х в этом промежутке имеет место формула
/(х) + Н[Г (х-х)+^(х-хJ+ +
где дополнительный член гп{х) может быть представлен
в одной из указанных в п° 126 форм. При этом я мы можем
брать сколь угодно большим, т. е. доводить это разло-
разложение до сколь угодно высоких степеней х-х0.
Это естественно приводит к мысли о бесконечном разложении:
J \л) ~J \ЛО'
¦ ¦ • +~1й (х-хо)п + ¦¦¦ D)
Такой ряд - независимо от того, сходится ли он и имеет ли, на самом
деле, своей суммой f(x), — называется рядом Тейлора для функ-
функции f(x). Он имеет вид B), причем коэффициенты его:
ао=/(Л'о)> ai = ~TT ' а = —?*-,..., ап = —^
носят название коэффициентов Тейлора.
Так как разность между /(х) и суммой п +1 членов ряда Тей-
Тейлора, ввиду C), есть как раз гп(х), то, очевидно: для того чтобы
при некотором значении х действительно имело место разложение D),
необходимо и достаточно, чтобы дополнительный член гп(х) формулы
Тейлора - при этом значении х — стремился к 0 с возраста-
возрастанием п:
lim г„(х) = 0.	E)
При исследовании вопроса, имеет ли место это равенство и при
каких именно значениях х, нам и будут полезны различные формы
дополнительного члена гп{х), выявляющие его зависи-
зависимость от и.
Чаще всего приходится иметь дело со случаем, когда хо = 0 и
функция /(х) разлагается в ряд непосредственно по степеням х:
• • "I ~\ х" + ... ;	(о)
* Этот ряд обыкновенно называют рядом Маклорена; см. сноски на
). 247 и 251 первого тома.

366	ГЛ. XI. БЕСКОНЕЧНЫЕ РЯДЫ С ПОСТОЯННЫМИ ЧЛЕНАМИ	[404
этот ряд имеет вид A), с коэффициентами:
«„=/@), a,J-f, 0,-q»,. ..,«„=«,...	G)
Выпишем теперь подробнее дополнительный член гп(х) примени-
применительно именно к этому частному предположению: хо = 0 [126]
в форме Лагранжа: гп(х) = (и+1м х"+\	(8)
в форме К о ш и: rn(x) =/(n+^Sx> (i _ 0yixn+\	(9)
При этом о множителе б известно только то, что он содержится между
0 и 1, но он может меняться при изменении х или п (и даже - при
переходе от одной формы к другой).
Перейдем к конкретным разложениям.
404. Разложение в ряд показательной, основных тригонометрических
функций и др. Докажем сначала следующее простое предложение,
которым сразу будет охвачен ряд важных случаев:
Если функция f(x) в промежутке [0, Н] или [-Н, 0] (Я>0) имеет
производные всех порядков, и все эти производные при изменении
х в указанном промежутке оказываются по абсолютной величине огра-
ограниченными одним и тем же числом:
\f(n\x)\^L	A0)
{где L не зависит от я), то вр всем промежутке имеет место
разложение F).
В самом деле, взяв дополнительный член гп(х) в форме Лаг-
Лагранжа [см. (8)], имеем, в силу A0):
При безграничном возрастании и выражение , ., стремится к 0,
как мы видели в 35, 1); впрочем, это же [в силу 364, 5°] следует и из
сходимости ряда
1 + у нп+х
[370, 2) (а)]. Но в таком случае и гп(х) имеет пределом 0, что и до-
доказывает наше утверждение.
(а) Это предложение приложимо к функциям
f(x) = ех, sin х, cos x

404]	§ 7. РАЗЛОЖЕНИЯ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ	367
в любом промежутке [ - Н, Н], ибо производные их, соответ-
соответственно, равные
будут в нем по абсолютной величине ограничены числом е" - для
функции ё*, и единицей - для sin х и cos х.
Так как коэффициенты Тейлора мы уже вычисляли для этих
функций в 125, 1)-3), то можем сразу написать разложения:
sinx = x-f + J- ... +(- i)*-i J^ + ...,	A2)
f J^...	A3)
Все они имеют место при любом значении х.
(б) Нетрудно подобным же образом получить разложения и для
основных гиперболических функций, но проще, вспомнив их
определение:
, ех-е~х	, ех+е~х
SD X	т ,	СП X= ^j ,
вывести эти разложения путем почленного вычитания или сложения
ряда (И) и следующего ряда, который из него получается заменой
х на -х:
р-*=\— — 4-— — +(-Un — 4-
1! 2! ¦ ¦ ¦ +\ L) и!
Таким путем мы находим:
X3 Xs	Х2к~х
+ +	+
3! '5! ' ¦¦" B/fc-l)!
х2 х*	xlk
(в) К функции у = arctg x доказанное вначале предложение уже
не приложимо. Действительно, общее выражение для ее и-й произ-
производной, найденное в 116, 8):
(U	A4)
не гарантирует существования общей границы для всех j(n).
Так как соответствующий ряд Тейлора [см. 125, 6)]:

368	ГЛ. XI. БЕСКОНЕЧНЫЕ РЯДЫ С ПОСТОЯННЫМИ ЧЛЕНАМИ	[405
сходится лишь в промежутке [-1, 1]*, то вне этого промежутка не
приходится уже говорить о выражении функции arctg х этим рядом.
Наоборот, для |x|=el имеем по формуле Лагранжа (8) [с уче-
учетом A4)]:
n+l.
где уе = arctg дх. Отсюда ясно, что rn(x)->-0, так что для всех значе-
значений х в промежутке [-1, 1] имеет место разложение
arctgx=x--j + -7-—... +(—I)'''1 , _ + ...	A5)
Мы еще раз подчеркиваем, что хотя arctg x и вне этого проме-
промежутка имеет определенный смысл, но разложение A5) там уже не
действительно, поскольку ряд не имеет суммы.
Из ряда A5) при х=1, в частности, получается знаменитый ряд
Лейбница
^i_i.+i-...+(-i)^^LI+...	Aб)
- первый ряд, дающий разложение числа я.
405. Логарифмический ряд. Если в качестве функции /(х) взять
1пA + х) (х > - 1), то соответствующий ряд Тейлора будет таков
[125, 5)]:
Он сходится лишь для значений х в промежутке ( —1, 1]**; значит,
только для этих значений и имеет смысл исследовать поведение до-
дополнительного члена гп{х).
Возьмем его сначала в форме Лагранжа (8). Так как
J	W-K L) (l+xyn+i
[116, 2)] то
Если 0«x=sl, то последний множитель не превосходит единицы, и
отсюда
так что r"W "*° ^ПРИ п "* ")•
* По признаку Даламбера [377] легко убедиться, что ряд (абсолютно) схо-
сходится, если |лг|<1, и расходится при |х|^1. Сходимость (неабсолютная) при
х = ± 1 вытекает из теоремы Лейбница [381].
** Ср. предыдущую сноску; при х= -1 получается (с точностью до знака)
расходящийся гармонический ряд.

406]	§ 7. РАЗЛОЖЕНИЯ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ	369
Но при х<0 поведение этого множителя становится неясным, и
приходится прибегнуть к форме К о ш и дополнительного члена
[см. (9)].
Имеем
так что
\х "+1
Так как при х > — 1 будет 1 + вх =-1 — в, то последний множитель
меньше единицы; следовательно, лишь только |*|<1, заведомо
г„(*Ь0.
Любопытно, что хотя форма К о ш и вполне исчерпывает вопрос
для всех значений х между -1 и 1, она ничего не дает при х=\; в
этом случае мы получаем
КО) Н A-0)",
но ввиду возможности для в меняться вместе с п, нельзя заключить
о том, что A-0)п-О.
Итак, по совокупности для всех значений х в промежутке (-1, 1]
действительно будет
f y^	A7)
В частности, при х = 1 получаем уже знакомый нам ряд
1п2=1-1 + {-...+(-1)"-1^+...	A8)
Из ряда A7) можно вьюеети и другие полезные разложения. Напри-
Например, заменяя в нем х на -х и вычитая полученный ряд почленно из
ряда A7) (при этом мы считаем |х| < 1), придем к следующему ряду:
A9)
406. Формула Стирлинга. В качестве приложения покажем, как с его помощью
может быть выведена одна важная формула анализа, носящая имя Стирлинга
(J. Stirling).
Возьмем в A9) х=	, где и - произвольное натуральное число. Так как
2и+1
тогда
1 +
\+х 2и + 1 и+1
Т^х	Т~~~п~'
2и+1
24 Г. М. Фнхтенгольц, т. II

370	ГЛ. XI. БЕСКОНЕЧНЫЕ РЯДЫ С ПОСТОЯННЫМИ ЧЛЕНАМИ	[406
то мы получим разложение
которое можно переписать в виде:
11 11
l
Это выражение, очевидно, больше единицы, но меньше, чем
1 г 1	1
Итак, имеем:
1* \п + - In 1+- Ul +
{ 2) { п)
откуда, потенцируя, найдем
'(•4)
е<|]+-| -=е I2n(n+i)_
п\е"
Введем теперь варианту ап=	. Тогда
и из предыдущих неравенств следует, что
1
J	 „12/1
ап
O/J+1
так что, с одной стороны, ап >O/i+i, с другой же,
	i_		i_
ап-е 12п	'"'"'
Таким образом с возрастанием и варианта ап убывает (оставаясь ограниченной
снизу, например, нулем) и стремится к конечному пределу а, варианта же ап-е Пп
возрастает, стремясь, очевидно, к тому же пределу а \ибо е 12"- 1/. Так как при
любом и вьшолняются неравенства
	1^_
ап-е w^a-zan,
то найдется такое число в, заключенное между нулем и единицей, что
	в_	j_
а=ап-е 12п или я„ = а-е12л.

407]	§ 7. РАЗЛОЖЕНИЯ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ	371
(Заметим, что число в, вообще говоря, зависит от и). Вспоминая определение пере-
переменной ап, находим:
(П\п Л-
n\ = afn- - -е12" @«=й<1).	B1)
Остается теперь определить величину постоянной а. С этой целью вспомним
формулу В а л л и с а [317], которую можно записать в виде:
1 Г 2и!! I2
+Т 1Bи-l)!lj "
л
-= lim
2 „-„, 2и +
Выражение в скобках преобразуем следующим образом:
2и!! Bи!!J 22П-(и!J
Bп-\)\\~~2п\	2и! '
подставив сюда вместо и! его выражение по формуле B1), а вместо 2и! аналогичное
выражение
Bп\гп
Bп\
—
после элементарных упрощений получим
2и!! 1 / п
Bи-1)М С 2
так что
= а\ —е
24л
л	1	и Ц^- а-
li	п12П
lim	ае
2 п-»~2и+1 2	4
Отсюда:
а- = 1л и а = У2л.
Подставляя это значение а в формулу B1), мы и придем к формуле Стир-
линга
которая позволяет легко оценивать величину факториала и! при больших зна-
значениях и.
Для упражнения предлагаем читателю фактически найти сумму ряда
vF . 2/1+1 ,1
n=i L 2и-1 J
сходимость которого была доказана в п° 367, 9) (б).
Указание. Вычислить и-ю частичную сумму и, преобразовав ее с по-
помощью формулы Стирлинга, перейти к пределу. Отв. — A - In 2).
407. Биномиальный ряд. Возьмем, наконец, f(x) = (l+x)m, где т
- любое вещественное число, отличное от 0 и от всех натуральных
чисел (при натуральном т получается известное конечное разложение

372	ГЛ. XI. БЕСКОНЕЧНЫЕ РЯДЫ С ПОСТОЯННЫМИ ЧЛЕНАМИ	D07
по формуле Ньютона). В этом случае ряд Тейлора имеет
вид [125, 4)]:
I-тх
т(т-1) „	т(т- 1)... .-(т-п Ь1) „
- \2 х2 + ...+ ¦-	/^ттт!1^	"х л ¦¦¦>
его называют биномиальным рядом, а коэффициенты его
- биномиальными коэффициентами. При сделанных
относительно т предположениях ни один из этих коэффициентов не
будет нулем (наоборот, если бы т было натуральным числом, то ко-
коэффициент при xm+1 и все следующие обратились бы в нуль). С по-
помощью признака Даламбера [377] легко установить, что при
|х|<1 биномиальный ряд (абсолютно) сходится, а при |х| =-1 рас-
расходится. Исследование дополнительного члена гп{х) мы будем произ-
производить в предположении, что |х|<1, причем сразу возьмем его в
форме К о ш и (9) (форма Лагранжа и здесь дает ответ не при
всех значениях х).
Так как
f.«+i\x) = m(m- 1).. .{т-п\ \)(т-п){\ +х)т-п~\
то будем иметь:
гп(х) =	?
Представим его, перегруппировав множители, в виде:
ГпУХ)~	. 1-2....-и	xmxv + ox) [1 + exJ ¦
Первое из этих трех выражений представляет собой обидай член
биномиального же ряда, но отвечающего показателю т-\; так как
при |дг| < 1 биномиальный ряд сходится, каков бы ни был показатель,
то это выражение при а — оо стремится к нулю. Что же касается двух
других выражений, то второе по абсолютной величине содержится
между границами
\тх\ -A - I*!)-1 и |mjc| »A+ Ix])™-1,
не зависящими от п, а третье, как и в 405, меньше единицы. Таким
образом, гп(х)-0, т. е. для |х|<1 имеет место разложение
A+*)" =
•••+	1.2-...-и
которое также связано с именем Ньютона.

407|
§ 7. РАЗЛОЖЕНИЯ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ
373
Мы не рассматривали вопроса о применимости его при значениях х = +1.
Легко сообразить, что биномиальный ряд есть частный случай гипергеометри-
гипергеометрического ряда и получается из последнего при а= -т, E = у и замене х на -х.
Вследствие этого, по таблице в 402, 8), легко составить такую таблицу, характе-
характеризующую поведение биномиального ряда на концах х = ± 1 его промежутка
сходимости:
х=\
х=-1
7П=>0
0>т=- -1
m=s-l
т=-0
абс. сходится
неабс. сходится
расходится
абс. сходится
расходится
Можно показать, что всякий раз, когда биномиальный ряд сходится, его
суммой будет A+л)т. Здесь мы на этом не останавливаемся, желая избежать
кропотливого исследования дополнительного члена, так как этот результат просто
вытекает из одной общей теоремы, которая будет доказана ниже [см. 437, 6°].
Отметим некоторые частные случаи биномиального ряда, отвечающие, на-
. 1 1
пример, т= -1, — ,	:
1
(обыкновенная геометрическая прогрессия), затем,
B3)
1
2
3
- ]
8
¦хг-
5
— Л? +
16
35
128
B4)
Важно подчеркнуть, что в случае рационального т сумма биномиального
ряда дает всегда арифметическое значение радикала.
Замечания. I. На этом построено, например, следующее любопытное
разложение, принадлежащее Шлёмильху (О. Schlomilch). Прежде всего, полагая
в B3) х= -у\ где -1 «=>¦«= 1, получим, что
1-]/1-.у2 у Bи-3)!!
~у	n=i 2л!! У"П К
А затем, вместо у подставим сюда выражение
-~ и +оо. Окажется, что
Bи-3)!!
2
2п\\
2z
l+z2j
, где z изменяется уже между

374	ГЛ. XI. БЕСКОНЕЧНЫЕ РЯДЫ С ПОСТОЯННЫМИ ЧЛЕНАМИ	[408
Этот пример интересен тем, что для функции, определяемой в разных проме-
1
жутках различными аналитическими выражениями z и —, дается в то же
Z
время и единое аналитическое выражение - в виде суммы ряда [ср. 46; 363, 5)].
II. Во всех рассмотренных выше примерах разложения функций в ряд Тей-
Тейлора выходило так, что для всех значений х, при которых ряд сходился, его
сумма равнялась той функции, для которой ряд был построен. Поэтому у чита-
читателя могло возникнуть подозрение, что вообще достаточно установить сходимость
ряда, даже не проверяя соотношения E), чтобы было обеспечено разложение
D) или F).
На деле, однако, это не так. Если, например, вернуться к функции, рассмотрен-
рассмотренной в замечании п° 138:
1
f(x) = e *' (при х*0), /@) = 0,
то для нее, как мы видели, существуют даже при х = 0 производные всех порядков,
но все в этой точке обращаются в нуль. Ряд Тейлора вида F) со сплошь нуле-
нулевыми коэффициентами, конечно, сходится везде, но ни при одном значении х
(кроме х = 0) не воспроизводит значения исходной функции.
408. Разложение синуса и косинуса в бесконечные произведения. Мы познако-
познакомились выше с разложениями важнейших элементарных функций в бесконечные
ряды, расположенные по степеням х, т. е. с представлением этих функций в виде
«бесконечных многочленов». В заключение этого параграфа мы представим функ-
функции sin х и cos х в виде бесконечных произведений, которые как бы осуществляют
разложение на множители соответствующих «бесконечных многочленов».
Начнем с вывода одной вспомогательной формулы. Известна из алгебры
формула М о а в р а *:
(cos z+ i sin z)m = cos mz+ г-sin mz,
где т будем считать натуральным числом. Раскрыв слева скобки - по обычному
правилу - и приравняв слева и справа коэффициенты при «мнимой единице»
i = У -1, получим
т{т-\)(т-2)
sin mz=m cosm~1z-sinz	cosm 3z-sm3 z+ ...
1.2-3
Если /п = 2и+1 нечетно, то, заменяя четные степени косинуса по формуле
cos2fc z = A - sin2 z)k, мы представим результат в виде:
sin B7i+l)z = sin z-i>(sin2 z),	B5)
где Р(и) есть целый многочлен и-й степени.
Этот многочлен, если через %, и2, ..., ип обозначить его корни, можно следую-
следующим образом разложить на множители
Корни щ, и2, ..., ип легко определить из B5), заметив, что если z обращает в нуль
sin Bи+l)z, но оставляет sin z отличным от нуля, то sin2 z необходимо будет корнем
п	п	п
многочлена Р(и). Очевидно, значениям z =	, 2		и	, содержа-
содержать 2и+1 2и+1 2и+1
щимся между 0 и — и идущим в порядке возрастания, отвечают возрастающие
: См., например, ниже, 453.

408]
§ 7. РАЗЛОЖЕНИЯ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ
375
же (следовательно, различные) корни:
! = sin2
2и + 1 '
и, = sin2 2 -
2и+1
i sin2 n = ¦
2n + l
Наконец, коэффициент Л = Р@) определяется, как предел отношения sin Bи + l)z/sin z
при г^О; отсюда Л = 2л+1.
Таким образом, приходим к формуле
sin Bи + l)z=Bn+l)sinz| 1-
ina z \
sm:
1 —
sin2 z
sin2
2я+1/
2и+1
Полагая z = -
2и + 1
, перепишем ее так:
sin x =
2n+l
sin2
2и+1
sma
2и+1
sin2
sin2 и
X
2и + 1
B6)
Будем считать х отличным от 0, ±л, ±2л, ..., так что sin х^О. Возьмем нату-
натуральное число к под условием: (&+1)я:=- \х\, и пусть и будет =»&. Представим
теперь sin x в виде произведения:
smx=U(kn)-vin),	B7)
где
х \
sin2		I sin2
2n+l
2и+1
1
1
2и+1
sin2 А:
2и + 1
содержит лишь к множителей в скобках, а
\
sin2-
2и+1
sin2(A;+l)
2и+1
sin2 и
2и+1
охватывает все остальные.
Пусть к пока фиксировано; легко найти предел с4"' при и-~, поскольку это
выражение состоит из определенного конечного числа сомножителей. Так как
limBn+l)sin
2и+1
¦ х,
lim
п—=
2и+1
sin2 A
(А-1,2, ..., А),
2и + 1
то
х- Л
	.
A:2W

376	ГЛ. XI. БЕСКОНЕЧНЫЕ РЯДЫ С ПОСТОЯННЫМИ ЧЛЕНАМИ	[408
Ввиду B7), существует и предел
Vk = lim Vk , причем sinx= U^- V^.
Займемся оценкой предела Vk.
л
Известно, что для 0«p-z— имеют место неравенства
[54, (9); 133, 1)]. Поэтому
2
—
71
2и + 1 Bи+1J
л 4 №л2
sin2 /г	=-	(h = kr\, ¦-., п),
2и + 1 л2 Bи + 1J
так что
Бесконечное произведение
f
?).....U-J?-).	B8)
II fl
~ x°
(где h0 выбрано так, чтобы было 4Aq=-x2) сходится, ибо сходится ряд ^ ттг
л=л, чп
[теорема 5°, 401]. Поэтому остаточное произведение
Л=Л + 1
при fc~~ должно стремиться к 1 [401, 2°]. Очевидно, мы лишь усилим второе из
неравенств B8), если напишем
переходя (при фиксированном к) к пределу при п — °°, получим
Отсюда следует, что
lim Vk = 1, так что lim Uk = sin x,
и мы приходим, окончательно, к замечательному разложению:
впервые установленному Эйлером.

408]	§ 7 РАЗЛОЖЕНИЯ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ	377
Оно имеет место, разумеется, и для исключенных ранее значений х = 0, ±л,
+ 2л, ..., ибо тогда обе части этого равенства суть нули. Легко видеть, что от-
отдельные множители как раз и отвечают различным корням sin x*.
л
Если в полученном разложении положить х = —, то найдем:
откуда снова вытекает формула В а л л и с а [317; ср. 400. 2)].
Укажем еще одно интересное применение этого разложения, которое, заменяя
х на пх, можно представить в виде:
= лх U 11	.
л=11 и2/
Вспомним определение функции Г{х) [402, A3)]:
х л=1	х
п
и соотношение Г(х+1) = х-Г(х) [там же, A5)]. Тогда
1\~х
-К
ГA-х)--х.Г{-х)-П
и
Умножая, сразу приходим к так называемой формуле дополнения
sin лх
также найденной Эйлером; она имеет место при любых нецелых зна-
значениях л:**.
Аналогично разложению sin x выводится разложение
n=i( Bn-l)W) „^i
i i —
2
2и-1
выявляющее корни cos x: ±	л. Впрочем, оно может быть получено и из
разложения sin x, по формуле
sin 2x
cosx=sin | — -х] или cos* = —	.
2 sinx
* Относительно возможности переставлять сомножители - см. 402, 4).
** Положив здесь х = —, в частности, найдем, что \Г I - = л; так как при х =- 0
и Г(х)=-0, тоГ - =Уя.

378	ГЛ. XI. БЕСКОНЕЧНЫЕ РЯДЫ С ПОСТОЯННЫМИ ЧЛЕНАМИ	[409
Наконец, упомянем о разложениях
n(l +\,
n=i\ /2я-1 J» '
CD
которые также могут быть установлены с помощью сходных соображений.
§ 8. Приближенные вычисления с помощью рядов.
Преобразование рядов
409. Общие замечания. На примере полученных нами конкретных разложений
мы разъясним, как бесконечные ряды могут быть использованы для целей при-
приближенных вычислений. Предпошлем ряд общих замечаний.
Если неизвестное нам число А разложено в ряд:
А = а1+а2+а3+ ¦ ..+ап+ ...,
где аи а2, а3, ¦ ¦ ¦ - легко вычисляемые (обыкновенно рациональные) числа, и мы
положим приближенно:
то поправка на отбрасывание всех остальных членов выразится остатком
При достаточно большом и эта погрешность станет сколь угодно малой, так
что Ап воспроизведет А с любой наперед заданной точностью.
Мы заинтересованы в возможности просто производить оценку остатка
ап; это позволило бы нам и вовремя остановиться при вычислении последователь-
последовательных частичных сумм, когда уже будет получено приближение требуемой точности.
Если рассматриваемый ряд оказывается знакопеременным и притом с моно-
монотонно убывающими по абсолютной величине членами («лейбницевского типа»),
то, как мы видели [381, замечание], остаток имеет знак своего первого члена и по
абсолютной величине меньше его. Эта оценка в смысле простоты не оставляет
желать лучшего.
Несколько сложнее обстоит дело в случае положительного ряда.
Тогда обыкновенно стараются найти легко суммируемый положи-
положительный же ряд, члены которого были бы больше членов интересующего
нас остатка, и оценивают остаток суммой этого ряда.
°° 1
Например, для ряда 2 — можно получить:
1 тг
2 !«= 2 * 2 LL-IUI
m=n+i тг т--п+1 т(т-1) m=n+i\tn-l т) п

410]	§ 8. ВЫЧИСЛЕНИЯ С ПОМОЩЬЮ РЯДОВ	379
[эта оценка совпадает с оценкой сверху, полученной в 373 A1) с помощью интегри-
интегрирования], а для ряда 1+2 —
\
У
m^n+im\ 'и! т=п+1 (и+1)-	т и! m=u+i (и+1)т-« п\п
[этой оценкой мы фактически и пользовались при вычислении числа е в 37].
Обыкновенно ищется десятичное приближение числа А, в то время
как члены ряда могут и не быть выражены десятичными дробями. При обращении
их в десятичную дробь, округление их служит источником новой погрешности,
которую также следует учесть.
Наконец, отметим, что далеко не всякий ряд, имеющий суммой интересующее
нас число А, пригоден для фактического вычисления этого числа (даже
если его члены просты, и оценка остатка производится легко). Вопрос - в быстроте
сходимости, т. е. в быстроте приближения частичной суммы к числу А.
Возьмем для примера ряды [см. 404 A6) и 405 A8)]:
111	1111
1	\~	(-... и 1	1	1	...,
3 5 7	2 3 4 5
л
дающие соответственно разложение чисел — и In 2. Для того чтобы с их помощью
4
вычислить эти числа, скажем, с точностью до 1/105, нужно было бы сложить пять-
пятьдесят тысяч членов в первом случае и сто тысяч - во втором; это,
конечно, осуществимо лишь с помощью быстродействующих вычислительных
машин.
Ниже мы без особого труда вычислим упомянутые числа даже с большей
точностью, но использовав более подходящие ряды.
410. Вычисление числа п. Воспользуемся известным рядом для арктангенса
[404 A5)]:
X3 ХЪ X1
arctgx = ;t	1	1-... (
1	л
Если взять х = — , то arctg х = —, и мы получим ряд
УЗ	6
я 1 / 111111	\
'6~Ш~~3+~5'*~ТУ+"Г
уже пригодный для вычисления.
Вспоминая формулу сложения для арктангенса*
х+у
arctg x+arctg у = arctg -
1—ху
и выбирая в качестве х и у какие-нибудь две правильные дроби, удовлетворяющие
соотношению
х+у
1-ху
= 1 или (х+1H>+1) = 2,
* Которая в этом виде верна лишь в предположении, что сумма углов по абсо-
я
лютной величине -= — [50].

380	ГЛ. XI. БЕСКОНЕЧНЫЕ РЯДЫ С ПОСТОЯННЫМИ ЧЛЕНАМИ	[410
п ( х3 \ ( у3	\
будем иметь — = arctg х+arctg у = \х	f ... + \у	ь .... Например,
4	\ г ] \ г )
поло-
жив дг = —, у- — , получим
Существуют, однако, ряды, еще более удобные для вычисления числа л. Поло-
1
жим ос = arc tg —, тогда
5	2	10
1	Т 5	Б 120
а	*4
25	144
Ввиду близости этого числа к 1, ясно, что угол 4а близок к —; положив /S = 4а	,
будем иметь:	4	4
120
119~ 1	1
t8^125239'
Отсюда
^ 15 3 53 5 55 7
1 1 _ 1 1	1 ( 1
9"Ja~ П*5" + "' } 4 1239
Это - формула Машина (J. Machin).
Вычислим по ней число л с 7-ю знаками после запятой. Для этого достаточно
тех членов формулы, которые фактически выписаны, Так как оба ряда - типа
Лейбница, то поправки в уменьшаемом и вычитаемом на отбрасывание
невыписанных членов, соответственно, будут:
16 J	.41
0А0А
И
0<А-=:	=		И	0<=А"=—	¦«=	.
13-513 108	5-2395 108
Сохраненные члены обратим в десятичные дроби, округляя их (по правилу допол-
дополнения) на 8-м знаке. Вычисления сведены в таблицу (± в скобках указывает знак
поправки):	j,	j,
	3,20000000	—- = 0,04266667 ( - )
16 16
+	_ = 0,00102400	+	 = 0,00002926 ( - )
— = 0,00000091 (+) -^-^- = 0,00000003 (-)
3,20102491	0,04269596
^1 = 0,01673640 (+)
_ 3,20102491	_1_ = 0,00000010 ( - )
0,04269596	3-239'
3,15832895	0,01673630

411]
§ 8. ВЫЧИСЛЕНИЯ С ПОМОЩЬЮ РЯДОВ
381
Учитывая все поправки, имеем:
3,15832895* 16а* 3,15832898
-0,01673632* -4/S* -0,01673630,
так что
3,14159263*л*3,14159268.
Итак, окончательно, я =^3,1415926..., причем все выписанные знаки верны.
411. Вычисление логарифмов. В основе вычислений лежит ряд
In-—1
и
fl++
2и+1 L 3 B/1+1)' 5 Bи+1L
О)
которым мы уже пользовались в п° 406 [см. B0)] при выводе формулы С т и р -
л и н г а . При и = 1, получим разложение для In 2:
2/ 11 111111 11 11 11 11
In 2 = — 1-1	1	1	1	1	1	1	1	t- .
3 \ 3 9 5 92 7 9** 9 94 11 9^ 13 9** 15 9' 17 9**
Этот ряд вполне пригоден для вычислений. Покажем, например, что, ограничи-
ограничиваясь лишь выписанными членами, можно найти In 2 с 9-ю правильными десятич-
десятичными знаками.
В самом деле, если отбросить члены этого ряда, начиная с десятого, то со-
соответствующая поправка будет:
11	Л	1	2
+ 9" + 9~2+ "'' I ~12-19-98*1о™
Вычисления, на 10 знаков, сведены в таблицу:
3
3
3
з.
з.
з.
3-3
2
•5-
2
-7-
2
•9-
2
11
2
13
2
¦15
2
i-9
92
93
94
¦ 95
•9«
•9'
3-17-98
— = 0,66666 66667
= 0,02469 13580 (+)
= 0,00164 60905 (+)
= 0,00013 06421 (+)
= 0,00001 12901 (-)
= 0,0000010264 (-)
= 0,00000 00965 (-)
= 0,0000000093 (-)
= 0,00000 00009 (+)
Учитывая все поправки, имеем:
0,69314 71802* In 2* 0,69314 71809,
так что
In 2 = 0,69314 7180...,
и все написанные 9 знаков верны.
0,69314 71805

382	ГЛ. XI. БЕСКОНЕЧНЫЕ РЯДЫ С ПОСТОЯННЫМИ ЧЛЕНАМИ	[411
Полагая теперь в A) п = 4, найдем:
Пользуясь уже вычисленным значением In 2, по этой формуле легко вычислить
In 5, а затем и In 10=ln2+ln5. После этого, с произвольной степенью точности,
может быть вычислен модуль
М=
In 10
для перехода от натуральных логарифмов к десятичным; он равен М=
=0,434294481... Умножив на модуль, найдем десятичные логарифмы: log 2 и log 5.
Перейдем к десятичным логарифмам и в основной формуле A):
2М г 1 1 1 1	-,
]0gG1+l)-log71=	 1+	+	+... .	B)
2и+1 I 3 Bи + 1J 5 Bи+1L	J
Полагая здесь и = 80 = 2М0 и принимая во внимание, что и+1 = 81 = 34,
найдем
4 log 3-3 log 2-1=	[l +	+	+•••],
161 L 3 25921 5 25921»	J
откуда легко найти log 3. Полагая, далее, в формуле B) и = 2400 = 3-2М02, будем
иметь
так что найдем и логарифм log 7. Подбирая подобные числовые комбинации,
можно с произвольной степенью точности найти логарифмы простых чисел, а по
ним путем умножения на натуральные множители и сложения найдутся логарифмы
составных чисел.
Можно было бы поступить и иначе, непосредственно вычисляя логарифмы
последовательных натуральных чисел и переходя от log и к log (и+1) при помощи
формулы B). Так, для вычисления логарифмов чисел от 1000 до 10 000 возьмем
в формуле B) только один член, т. е. приближенно положим
гм
log (и+1)-log n=
2и + 1
Поправка при этом будет
. 2М rl 1 1 1
2и+1
гм г 1	1	1	гм	гм
3Bи+1)з L Bи+1)! Bи + 1L	J 3Bи + 1)-2и-Bи+2) 24»3
Так как у нас игЛО3, а 2А/-= 1, то
24-10" 2-1010

412J	§ 8. ВЫЧИСЛЕНИЯ С ПОМОЩЬЮ РЯДОВ	383
Если бы даже все ошибки суммировались, то в общем все же погрешность
101 1
была бы меньше, чем 	=	. Но легко избегнуть такого накопления
погрешностей, вычислив целый ряд контрольных логарифмов по первому
методу. Таким путем можно достигнуть гораздо большей точности, сохранив
в то же время присущий второму методу автоматизм вычислений (который
очень ценен, особенно при составлении обширных таблиц).
412. Вычисление корней. Проще всего корни вычисляются с помощью таблицы
логарифмов. Однако если отдельные корни нужны с большой точностью, то целе-
целесообразно прибегнуть к биномиальному ряду [407 B2)]:
пАт -1) т(т - 1)(/и - 2)
JC2 +Х»+
Предположим, что нужно вычислить fA, причем уже известно приближенное
значение а этого корня (по недостатку или по избытку), но требуется его улучшить.
Если, скажем,	,
где \х\ есть небольшая правильная дробь, то можно преобразовать корень сле-
следующим образом:
к лГа
а
— = а-(\+х)к
и использовать биномиальный ряд при т = — . Иногда выгоднее исходить из ра-
равенства	^
если \х'\ снова - небольшая правильная дробь, и прибегнуть к другому пре-
преобразованию:	/{	j
после чего применить биномиальный ряд, взяв т - - — .
к
Для примера, вычислим с большой точностью У2, исходя из его приближен-
приближенного значения 1,4. С этой целью преобразуем корень по одному из указанных двух
образцов:
1
,4.A-1Г*
2 К	2
Для облегчения вычислении естественно предпочесть второй путь. Итак, имеем:

384	ГЛ. XI. БЕСКОНЕЧНЫЕ РЯДЫ С ПОСТОЯННЫМИ ЧЛЕНАМИ	[413
Ограничимся написанными членами; все они представляются конечными
десятичными дробями:
-	— = 0,00000004375
128 504
63 1
	= 0,0000000007875
256 505
1,0101525445375 x 1,4 = 1,41421356235250.
Так как коэффициенты при степенях — убывают, то поправка может быть
оценена, как обычно:
... 231 Л 1 1	^ 1,4-231 2,1
1024-506 i 50 502 ] 1024-505-49 10»
Поэтому
1,414213562352<: ]^2«= 1,414213562373,
]/2 = 1,4142135623...;
все десять знаков после запятой верны.
Использовав преобразование
легко получить значительно большее количество знаков. Приведем еще несколько
примеров подобных преобразований (предоставляя вычисления с помощью бино-
биномиального ряда читателю):
]
v з I. iooJ
125.
413. Преобразование рядов по Эйлеру. При использовании ряда для прибли-
приближенных вычислений иной раз оказывается выгодным предварительно подвергнуть
его преобразованию. Так называется замена данного сходящегося ряда - по тому
или иному правилу - другим рядом с той же суммой. Конечно, применять такое
преобразование целесообразно лишь в том случае, если новый ряд быстрее сходится
и удобнее для вычислений.
Выведем формулу для классического преобразования, носящего имя Эйлера.
Пусть дан сходящийся ряд
S(x)= 2i (~ 1У1якхк = ао-а1х+а2хг- ¦ ¦. +(- 1У'акхк+ ...,	C)
где х=-0. Мы лишь для удобства представляем А>ый коэффициент его под видом
(- 1)лйй, вовсе не предполагая все а&=-0. Для варианты а^к=0,1, 2, ...) мы введем
в рассмотрение последовательные разности (наподобие того, как сделали
это в 122 по отношению к функции fix) от непрерывно меняющегося аргумента х):

413]	§ 8. ВЫЧИСЛЕНИЯ С ПОМОЩЬЮ РЯДОВ	385
и, вообще,
D)
Перепишем данный ряд так:
°° ai*~°o* в2*2-в1*2 агХ3-а2х3 {
1 + х 1+х 1+х	1+х
Это дозволительно, так как к-я частичная сумма нового ряда разнится от анало-
аналогичной суммы ряда C) лишь слагаемым 	(- 1)к+*ак+гхк+\ стремящимся к О
1 + х
при fc — <*> ввиду сходимости исходного ряда [364, 5°]. Введем теперь разности для
упрощения записи:
1
5(х) = —— {ao~Aao-x+Aal-x2-Aa.,'X3+...}.
1+х
«о
Сохраняя первый член 	, остающийся ряд
1+х
X
~1+1с
перепишем, как и 5(х), в форме
х 1
-{Аа0-
1 + д: 1+х
так что, если снова выделить первый член, имеем:
а, Аа
Продолжая поступать так и дальше, после р шагов получим:
а0 Аа0	А2а0	АР~1ай
5(х) = —	^-л:+	°—.х*- ...+(-DP-1	-xP-i + RJx); E)
1+х A + хJ A+х)»	A+х)Р	р
где
Обратимся к доказательству того, что Rp(x) при р — <*> стремится к 0.
Заменив р-ую разность АРак ее разложением D) и переставив суммирования,
получим
25 Г. М. Фяхтенгольц, т. II

386	ГЛ. XI. БЕСКОНЕЧНЫЕ РЯДЫ С ПОСТОЯННЫМИ ЧЛЕНАМИ	[414
Если ввести обозначение для остатка исходного ряда C), положив
ею
гп(х)= 2(-1)к+пак+пХк+" (и = 0, 1, 2, ...),
то выражение для Rp(x) окончательно может быть написано в виде
Z
1- грлЛх) Z С'рх"'1 ¦ г,<х)
и так как /•„(*) ¦» 0, то в силу 391, 6°, и Rp(x)~O.
Переходя в E) к пределу при р - ~, найдем, что
If х I х Y I х \Р )
S(x) =	\аа-Ла0	+/Ра0-	 • • • +{-1)РАРаЛ	 +... .
Подставляя вместо S(x) его выражение C), мы и придем к преобразованию Э и л ера:
27 (- l)kai(Xk =	 2 (~ 1)р^ра0-|	 .	F)
к=0	1+Хр=0	ll+*7
Чаще всего его применяют при дг=1; тогда оно преобразует числовой ряд
в числовой же:
2 (-1L = 2, -р..— •	G)
А = 0	р=0 2Р+1
1
414. Примеры. 1) Положим а^	, где z - любое постоянное число, от-
z+k
личное от 0, -1, - 2, - 3, ... Ряд
а=0 z+к
если отбросить в нем достаточное число первых членов, окажется рядом «лейбни-
цевского типа» и, следовательно, сходится.
Легко вычисляются последовательные разности Ла/,, Лга^, ..., и с помощью
математической индукции находим:
).. .(z+k+p) '
в частности,
/1Ро A)Р
Таким образом, по формуле G)
у
(-Р* у J
у
?a z+k p-fo 2P+iz(z+1)	(z+p) '

414J	§ 8. ВЫЧИСЛЕНИЯ С ПОМОЩЬЮ РЯДОВ	387
Если положить здесь z=l, то получится преобразование известного ряда для
In 2:,
In2= У (-1)-1 — = У	.
пТ±1	т п=1И-2"
Читателю ясно, что вторым рядом для приближенного вычисления In 2 поль-
пользоваться гораздо выгоднее; чтобы получить точность в 0,01 в первом ряде потре-
потребовалось бы 99 членов, в то время как во втором достаточно было бы взять 5
членов!
1
2) Пусть аь = — (z отлично от 0, —2-, - 4, .. .)• Представив аи в виде:
1 1	z+2k
а^ = —•	, для выражения ЛРаа мы можем воспользоваться прежней формулой:
2Р+1-р1
2 z(z+2)-....(z+2p)
В этом случае преобразование Эйлера имеет вид:
2ptoz(*+2).....(z+2/>)
В частности, при z = 1 отсюда получается преобразование ряда Лейбница,
я
выражающего —:
4
-г "	1 1 ~	п!
4 а^о	2к+1 2 ^о
3) Для 0«sxa=l мы имели в 404 (в) разложение
arc tg x = 2 ( -
/,=о
Желая применить к этому общему ряду преобразование Эйлера, положим
в F) а/; =	; тогда для ЛРа0 можно использовать формулу предыдущего при-
примера (при z=\):
2р\\
(-ПР	.
Bр+Щ
Кроме того, заменим в F) д: на х"- и обе части равенства еще умножим на х. В ре-
результате получим:
(8)

388	ГЛ. XI. БЕСКОНЕЧНЫЕ РЯДЫ С ПОСТОЯННЫМИ ЧЛЕНАМИ	[415
4) Не следует думать, что эйлерово преобразование сходящегося ряда всегда
приводит к улучшению сходимости. [При этом, сравнивая качество сходимости
двух рядов _2" ск и ^ c'k с членами любых знаков, мы, как и в 375, 7), исходим
*=° "=°	.	Уп .
из поведения отношения их соответственных остатков уп и уп: если — ¦» 0, то
Уп
первый ряд сходится быстрее, а второй - медленнее.]
Вот примеры:
~	1	^,11
2i (-l)ft-r переходит в быстрее сходящийся ряд 2i	>
к=о	2"	р=о2 4Р
Xj ¦— переходит в медленнее сходящийся ряд X
А-о2х	р=о
5) При использовании преобразования ряда для вычислений часто бывает
выгодно первые несколько членов ряда вычислить непосредственно
и преобразованию подвергнуть лишь остаток ряда. Проиллюстрируем это
на примере вычисления числа п с помощью ряда, выведенного в 2):
I 1 1-2 1-2.3	\-2-...-р	)
Р 1
Так как отношение последующего члена к предыдущему	-= —, то отбрасы-
2/>+1 2
ваемый остаток ряда всегда будет меньше последнего вычисленного члена.
Например, мы получим шесть верных цифр числа л после запятой, вычислив 21
член написанного ряда, ибо 21-й член
1-2-3-...- =0000000 37...*0,0000005.
1.3-5-...-41
Если же, скажем, первые семь членов исходного ряда вычислить непосредствен-
непосредственно, и лишь остаток после 7-го члена преобразовать, мы получим
{ 1 1 1 1 1 \\
1-—+	+	+— -
{ 3 5 7 9 11 13J
1	1	1-2-
15-17 15-17-19	15-17-....A5 + 2/))
Здесь уже восьмой член ряда в скобках меньше требуемой границы:
1-2-3-4.5.6-7
15-17-...-29
= 0,000000 2...
и для достижения той же точности достаточно, кроме 7 сохраненных членов, вы-
вычислить еще 8 членов, т. е. всего 15, против прежних 21!
415. Преобразование Куммера. Мы видели, что преобразование Эйлера,
основывающееся на точно сформулированном правиле, приводит к однозначному
результату, правда не всегда выгодному [414, 4)]. Метод же преобразования рядов,
предложенный Куммером, допускает большой произвол, многое предо-
предоставляя искусству вычислителя, но зато является более целеустремленным,
в смысле облегчения приближенного вычисления. Мы ограничимся изложением

415]	§ 8. ВЫЧИСЛЕНИЯ С ПОМОЩЬЮ РЯДОВ	389
идеи, положенной в основу названного метода, и осветим его немногими при-
примерами.
Пусть дан сходящийся ряд
AW+AW+...+AW+...	(9)
и требуется вычислить его сумму с заданным приближением. Очевидно, ЛСО-0
при к-*<». Выберем другую бесконечно малую ai , эквивалентную AW [62], так,
чтобы ряд
не только сходился к конечной сумме А1, но и чтобы эта сумма легко вычислялась.
Если положить
и вычисление суммы исходного ряда приводится к вычислению суммы пре-
преобразованного ряда, члены которого заведомо быстрее стремятся к нулю.
°° 1
Например, желая вычислить сумму ряда 2j 7~ > мы вспоминаем про ряд
1 Л
Л	с суммой 1 [25, 9)] и отмечаем, что (при к — <*>)
1 к(к+\)
1	1
Так как разность
то
и преобразованный ряд оказывается более выгодным для вычисления.
Указанный процесс можно повторить и, взяв новую бесконечно малую аг ,
эквивалентную <^*^, так чтобы ряд
сходился к конечной и легко вычисляемой сумме Аг, мы сведем вычисление суммы
исходного ряда, по формуле

390	ГЛ. XI. БЕСКОНЕЧНЫЕ РЯДЫ С ПОСТОЯННЫМИ ЧЛЕНАМИ	[415
к вычислению суммы последнего ряда, члены которого
стремятся к нулю быстрее, чем oq '.
Повторив процесс р раз, придем к формуле
2 AW = A1+A,+ ... +АР+ 2
А=1	к=0
где
суть известные суммы последовательно выделяемых рядов, и сведем дело к вы-
вычислению суммы ряда 2 a/j •
1
v J
Так, в приведенном выше примере вычисления суммы ряда Л — можно
h=ik2
пойти дальше:
= ii k(k+W+2)+ 'k
так что
1	1 (
= 1+ ^+2! i
i^i к* = 1+ 2^+2! ,r=Ti кЧк+Щ+2) '
затем,
2
1	11
^_l — = 1 + —-I—•-
и т. д. После р шагов получим
2— = Н	Н	I	Vp\ 2	•	(Юа)
/ГГ1/с2	2* > 1,1^ + 1)	{к+р)
При этом мы все время пользуемся уже известной нам формулой
f	J	=J_
ift-Lk{k+\)-...-{k+p-l){k+P) p.pl
[получающейся из выведенного в 363, 4) соотношения при а = 0].
Таким образом, вычисление суммы медленно сходящегося ряда 2 —
к=\№
приводится к вычислению суммы р его членов и суммы быстро сходя-
сходящегося - уже при умеренных значениях р - преобразованного ряда,
Приведем еще один более сложный пример.

415]	§ 8. ВЫЧИСЛЕНИЯ С ПОМОЩЬЮ РЯДОВ	391
Обозначим через Sp (p - натуральное) сумму ряда
°°	1
iTi/c2(/c+D2- • • --{к+р- IJ"
При неопределенном пока з> имеем
к+у	к+1+у	, Bр-1)к*
к°(к+1J- ¦ ¦ -{к+р- IJ (/c + lJ0fc + 2J-... .(к+ру кКк+1У- ¦ ¦ ¦ -(к+р- Шк+р)
Отсюда видно, что (при к - =*>)
1 Г	к+у	к+1+у	1
2^1 [кКк+1J- ¦ ¦ • -{к+р- \у~'(к+тк+2У-... -{к+р)Ч
Если заменить члены ряда Sp этими эквивалентными им разностями, то
получится ряд с легко вычисляемой суммой
1	1+у
2р~1 (l-2-З-...-рУ
Дополнительный (шреобразованный») ряд будет иметь общий член
Вот теперь мы воспользуемся произвольностью у и выберем его так, чтобы в
числителе здесь исчез член, содержащий к:
у---\.
Учитывая все сказанное, получаем для ряда Sp такую формулу преобразо-
преобразования
Отсюда, подставляя вместо р последовательно значения 1,2, ..., р, имеем
-?, 1	3 1
1	3 1 B!)s
S	+	S
3 (р-1)\ t (р\У
\ р 2Р'B1уУ 2РBр1)\\' р+и
2Р-\2р-Ъ)\\ р р-2Р'Bр-1уУ 2Р-Bр-1)\\

392	ГЛ. XI. БЕСКОНЕЧНЫЕ РЯДЫ С ПОСТОЯННЫМИ ЧЛЕНАМИ	[416
Наконец, складывая почленно все эти равенства, придем к результату
+
1
№ \2 2-22 3 3-235!!. "" p-2P
+ -
>-!)!!*?
A06)
Взяв, например, р= 5 и сохранив в преобразованном ряде тоже 5 членов, можно
1
вычислить сумму исходного ряда с точностью до —-.
416. Преобразование Маркова. Прием для преобразования данного сходя-
сходящегося ряда (9)
указанный А. А. Марковым, также оставляет много произвола вычисли-
вычислителю. Разлагая каждый член AW каким-либо образом в сходящийся же
ряд:
2
1=1
Из членов всех этих рядов составляется бесконечная прямоугольная матрица с
двумя входами [ср. 393 A)]
4° 4°
42)	42) 42) ••• 42) •••
43)	43) 43) ••• 43) •¦•
A2)
так что искомое число А оказывается попросту суммой повторного ряда
л- 2 2#\
А=1 (=1
соответствующего этой матрице. Предполагая, далее, еще сходимость всех рядов
по столбцам:
А=1
Марков устанавливает условие, необходимое и достаточное для того, чтобы
ряд 2 At сходился к той же сумме А. Преобразование Маркова и состоит
i=i
в замене одного повторного ряда другим
а- 2лт- 2а,,

416]	§ 8. ВЫЧИСЛЕНИЯ С ПОМОЩЬЮ РЯДОВ	393
Достаточные условия для применимости преобразования Маркова
даются, например, в теореме 3 п° 393. [Сама теорема Маркова, впрочем,
значительно шире, ибо не предполагает даже упоминающиеся в ней ряды а б-
с о л ю т н о сходящимися.]
Примером применения преобразования Маркова может служить соот-
соотношение A3) п° 395. Речь идет о ряде ^ — , и его &-ый член представляется в виде
суммы, на этот раз, конечного числа членов
1	1
2.3	(Л+2)
(к-1)к-...-Bк-
Затем производится суммирование по столбцам, которое и приводит к упомяну-
упомянутому соотношению [см. 395, 4)].
Любопытно отметить, что, если воспользоваться разложением
1 vj« ^ (fr-D'-i
то преобразование Маркова, как уже подчеркивалось в 395, 4), ничего нового
не даст, ибо просто вернет нас к исходному ряду.
Можно построение матрицы A2) связать с повторным применением преобра-
преобразования К у м м е р а. Об этом уже была речь в предыдущем п° [см. A0)], но там
процесс К у м м е р а повторялся лишь конечное число раз, а здесь мы мыслим
это повторение продолженным до бесконечности. При этом всякий раз надлежит
лишь проверять стремление к нулю, при р - =, «дополнительного члена» фор-
формулы A0):
lim
Для того, чтобы убедиться в этом, например, по отношению к A06), отметим,
что фигурирующая в дополнительном члене сумма не превосходит выражения
у±
)<4=ifc*'
так что весь доцолнительный член не превосходит величины

394	ГЛ. XI. БЕСКОНЕЧНЫЕ РЯДЫ С ПОСТОЯННЫМИ ЧЛЕНАМИ	[417
и, очевидно, стремится к нулю при р-~. Переходя к пределу в A06), придем к ра-
равенству
+4 +
2-22 3 3-23 5!! "" p-2PQ.p~\)\\
+... =
которое, как нетрудно видеть, тождественно с равенством A3) п° 395.
Однако подобный предельный переход вовсе не всегда приводит к полезному
результату: если, например, осуществить его в равенстве A0а), то получим просто
тождество
Таким образом, прием, предложенный Марковым, дает очень общую схему,
предоставляя вычислителю широкие возможности, но многого требуя от его
искусства.
§ 9. Суммирование расходящихся рядов
417. Введение. До сих пор на всем протяжении настоящей главы
заданному числовому ряду
со
2 ап = а0 + ах + а2+ ... +ап+...	(А)
в качестве его суммы мы приписывали предел ее частичной суммы
А = lim An
в предположении, что этот предел существует и конечен (или же ра-
равен бесконечности определенного знака). «Колеблющийся» расходя-
расходящийся ряд для нас всегда оказывался лишенным суммы, и подобные
ряды мы систематически из рассмотрения исключали.
Различные факты из области математического анализа, как, напри-
например, расходимость произведения двух сходящихся рядов [392], естест-
естественно выдвинули во второй половине прошлого века вопрос о воз-
возможности суммирования расходящихся рядов в некоем новом смы-
смысле, конечно, отличном от обычного. Некоторые методы такого «сум-
«суммирования» оказались особенно плодотворными; ими мы займемся
подробнее.
Нужно сказать, что до создания К о ш и строгой теории пределов
(и связанной с нею теории рядов) расходящиеся ряды нередко встре-
встречались в математической практике. Хотя применение их при доказа-
доказательствах и оспаривалось, тем не менее иной раз делались попытки
придавать им даже числовой смысл. Так, колеблющемуся ряду

417]	§ 9. СУММИРОВАНИЕ РАСХОДЯЩИХСЯ РЯДОВ	395
еще со времен Лейбница в качестве «суммы» приписывалось чи-
число -_-. Эйлер, например, мотивировал это тем, что из разложения
т—— = 1 - х + х2 - х3 + xi - х5 + ...
1+х
(которое в действительности имеет место лишь для | х | < 1) при под-
подстановке вместо х единицы как раз и получается
В этом уже содержалось зерно истины, но постановке вопроса не
хватало четкости; самый произвол в выборе разложения оставлял от-
открытой возможность, скажем, из другого разложения (где п и т -
любые, но т^п)
i rm~i I — y^i
• ¦ 'tJ	i x _ i _ xm i xn _ xn+m _j_ д-2п _
l+x+ ...+xn~1 1-х"
получить одновременно
Современный анализ ставит вопрос по-другому. В основу кла-
кладется то или иное точно сформулированное определение «обобщен-
«обобщенной суммы» ряда, не придуманное только для конкретно интересую-
интересующего нас числового ряда, но приложимое к целому классу таких
рядов. Законность этого не может вызвать сомнения: читатель дол-
должен помнить, что даже обычное понятие «суммы ряда», сколь про-
простым и естественным оно ни кажется, тоже было введено на основе
условно принятого определения, оправдываемого лишь целесообраз-
целесообразностью! Определение «обобщенной суммы» обычно подчиняется двум
требованиям.
Во-первых, если ряду ^ ап приписывается «обобщенная сумма» А,
а ряду ^Ьп - «обобщенная сумма» В, то ряд ]?pan + qbn, где р, q -
две произвольные постоянные, должен иметь в качестве «обобщенной
суммы» число рА + qB. Метод суммирования, удовлетворяющий этому
требованию, называется линейным.
Во-вторых, новое определение должно содержать обычное опреде-
определение как частный случай. Точнее говоря, ряд, сходящийся в обычном
смысле к сумме А, должен иметь «обобщенную сумму», и притом
также равную А. Метод суммирования, обладающий этим свойством,
называют регулярным. Разумеется, интерес представляют лишь такие
регулярные методы, которые позволяют устанавливать «сумму» в бо-
более широком классе случаев, нежели обычный метод суммирования:
лишь тогда с полным правом можно говорить об «обобщенном сум-
суммировании».

396	ГЛ. XI. БЕСКОНЕЧНЫЕ РЯДЫ С ПОСТОЯННЫМИ ЧЛЕНАМИ	[418
Мы переходим теперь непосредственно к рассмотрению двух особо
важных с точки зрения приложений методов «обобщенного суммиро-
суммирования».
418. Метод степенных рядов. Это метод, в существенном, принад-
принадлежит Пуассону (S.-D. Poisson), который сделал первую попытку
применить его к тригонометрическим рядам. Он состоит в следую-
следующем.
По данному числовому ряду (А) строится степенной ряд
21 апхп = а0 + ахх + й2х2 + ...+ апхп + ...;	A)
если этот ряд для 0<д:-=1 сходится и его сумма f{x) при л-»-1-0
имеет предел А:
lim f(x)=A,
то число А и называют «обобщенной (в смысле Пуассона) суммой»
данного ряда.
Примеры. 1) Ряд, рассмотренный Эйлером:
1-1 + 1-1 + 1-1+...,
здесь уже в силу самого определения приводит к степенному ряду,
1	1	1
сумма которого	при х -1 - 0 стремится к пределу —. Значит, число — , дей-
ствительно, является «обобщенной суммой» указанного ряда в точно установлен-
установленном здесь смысле.
2) Возьмем более общий пример: тригонометрический ряд
^-+2'cosne	B)
2 n=i
является расходящимся при всех значениях в, -я
Действительно, если в и
значений п, кратных q, будет
р
Действительно, если в имеет вид — л, где р и q - натуральные числа, то для
1
cos/i9= +1,
так что нарушено необходимое условие сходимости ряда. Если же отношение
в
— иррационально, то, разлагая его в бесконечную непрерывную дробь
, т
и составляя подходящие дроби — , будем иметь, как известно,
л
в т 1
п п пг'
откуда
71
п

418]	§ 9. СУММИРОВАНИЕ РАСХОДЯЩИХСЯ РЯДОВ	397
Таким образом, для бесконечного множества значений п
п
так что
|cosn0| =»1	.
п
Это также свидетельствует о нарушении необходимого условия сходимости.
Если образовать степенной ряд
1	°°
—+ 2 гпсо&пв (()-=/•< 1)
2	л=1
(здесь буква г заменяет прежнюю букву х), то его сумма при значении в, отличном
от 0, будет
1	I-/-2
2"l-2/-cose + r2
[см. 440 E)] и при г -1 - 0 стремится к 0. Таким образом, для 0^0 «обобщенной
суммой» ряда будет 0. Если 6 = 0, то ряд B), очевидно, имеет сумму, равную + ~;
1 1 + г
впрочем, и выражение C), которое в этом случае сводится к	, также
имеет пределом +~.
3) Аналогично ряд
2 sin нб (-jr=s=9=syr),
л=1
который сходится лишь при 6 = 0 или ±ж, приводит к степенному ряду
г sin 9
2! rn sin пв = -
1 1
[461, 6) (а)], так что «обощенная сумма» на этот раз оказывается равной — ctg — 0
при в * 0 и равной нулю при 9 = 0.
Непосредственно ясно, что рассматриваемый метод «обобщенного
суммирования» является линейным. Что же касается регуляр-
регулярности этого метода, то она устанавливается следующей теоремой,
принадлежащей Абелю:
Если ряд (А) сходится и имеет сумму А (в обычном смысле), то
для 0<л-=1 сходится степенной ряд A), и сумма его стремится к
пределу А, когда д:-*1-0*.
* Эта теорема была доказана Абелем в его исследованиях по теории би-
биномиального ряда [мы к ней вернемся в п° 437, 6°]. Нельзя сомневаться, что именно
она привела к общей формулировке метода «обобщенного суммирования», который
Пуассоном был применен лишь в частном случае. В связи с этим и самый
метод часто называют методом Абеля, хотя самому Абелю идея
«суммирования» расходящихся рядов была в высшей степени чужда. Мы будем
в дальнейшем говорить об этом методе, как о методе Пуассона - Абеля.

398
ГЛ. XI. БЕСКОНЕЧНЫЕ РЯДЫ С ПОСТОЯННЫМИ ЧЛЕНАМИ
[419
Прежде всего, ясно [379], что радиус сходимости ряда A) не меньше
1, так что для 0-=x-=l ряд A), действительно, сходится. Мы имели
уже тождество
71=0
(где Ап = а0 + ах + ... + ап) [см. 385, 6) или 390, 4)]; вычтем его почленно
из очевидного тождества
A=(\-x)ZAxn.
п=0
Полагая А-Ап = а.п, придем к тождеству
A- Zanxn = (l~
Z
п=0
Z
л=0
D)
Так как <х„->-0, то по произвольно заданному е>0 найдется такой
номер N, что |а„| <-у е, лишь только n>N.
Разобьем сумму ряда в правой части D) на две суммы
Z
n=0
A-х) 2 *п*п-
n=N+l
Вторая оценивается сразу и независимо от х:
) Z *nXn
n=N+l
2
- _ A _ \Л V v" «- _
z	n=JV+l	z
Что же касается первой, то она стремится к 0 при х — 1 и при доста-
достаточной близости х к 1 будет
A-х) V
так что окончательно
Z
п = 0
2
л=1
что и доказывает утверждение.
419. Теорема Таубера. Если ряд (А) суммируем по Пуассону — Абелю
к сумме А, то в обычном смысле, как мы видели, он может и не иметь суммы.
Иными словами, из существования предела
lim Z апхп~А,
10 0
E)

419]
§ 9. СУММИРОВАНИЕ РАСХОДЯЩИХСЯ РЯДОВ
399
вообще говоря, не вытекает сходимость ряда (А). Естественно возникает вопрос,
какие дополнительные условия надлежит наложить на поведение членов этого
ряда, чтобы из E) можно было заключить о сходимости ряда (А), т. е. о существо-
существовании для него суммы А в обычном смысле.
Первая теорема в этом направлении была доказана Таубером (A. Tauber);
она гласит:
Пусть ряд A) сходится при 0-=л:-= 1, и имеет место предельное равенство E).
Если члены ряда (А) таковы, что
а1
hm
= 0
F)
2 ап = А.
п = 0
Доказательство разобьем на две части. Сначала предположим, что
lim пап = 0 или в„ = 0 — .
Если положить
dn = max\kak\,
то при п - <*> величина дп, монотонно убывая, стремится к нулю.
Имеем при любом натуральном N
N	N	Г ~
2<*п-А = 2ап(.1-хп)- 2 апХп+\2
О	О	N+1	[О
так что **
N
О
N+1
(ЛН-1)A-*Г
2 апхп-А
Взяв произвольно малое число е>0, положим
(l-jcJV=e или х=\~-^,
* Отсюда, по известной теореме К о ш и [33, 13)], уже следует выполнение
условия F), но не обратно, так что мы исходим теперь из более частного
предположения, нежели F).
** Мы пользуемся очевидными при 0<л:"=1 неравенствами:
)-=йA -х)
у ,
JV + 1
1-Х 1-Х

400
ГЛ. XI. БЕСКОНЕЧНЫЕ РЯДЫ (^ПОСТОЯННЫМИ ЧЛЕНАМИ
[419
так что х~1 при i\T*~. Пусть теперь N выбрано достаточно большим, чтобы 1)
выполнялось неравенство 6^+1-=ег и 2) соответствующее х было настолько близко
к 1, что
2 апхп-А
Тогда
2 ап-А
= B+<5„)- s,
что и доказывает утверждение теоремы.
К рассмотренному частному случаю теоремы приводится и общий случай.
Положим
так что
и затем
г п
(н+1)
G)
Но из предположения теоремы, т. е. из того, что — -О при п-~, легко полу-
чить, что
lim (l-xJ — хп = 0.
х-1-0	1 п
Для доказательства этого достаточно разбить здесь сумму на две:
(8)
N
2
N+1
и выбрать N таким, чтобы во второй сумме все множители — были по абсолютной
п
величине меньшими наперед заданного числа е =» 0, тогда и вторая сумма по аб-
абсолютной величине будет меньше в, каково бы ни было х; относительно первой
суммы, состоящей из определенного конечного числа слагаемых, того же можно
достигнуть за счет приближения л: к 1.
Таким образом, ввиду G), E) и (8) имеем
lim 2 ¦
¦хп+1=А-а„.
Но здесь уже можно применить доказанный частный случай теоремы, так что и
V Vtl	A
lAa

420]	§ 9. СУММИРОВАНИЕ РАСХОДЯЩИХСЯ РЯДОВ	401
С другой стороны,
•у vm	yVm _ -у Ут _ уЧп _"у vm-_i _ _ Vn S,
i m(/n+l) l m i m + l i m i m	и + l i"
Отсюда, так как первое слагаемое справа стремится к нулю
п
lim _^ ctm~А — й0,
что и завершает доказательство теоремы.
Впоследствии различными авторами бьш установлен целый ряд тонких теорем
подобного типа (их принято называть «тауберовскимн» теоремами), видоизменяю-
видоизменяющих и расширяющих условия Таубера. На них мы не будем останавливаться.
420. Метод средних арифметических. Идея метода в простейшем
его осуществлении принадлежит Фробениусу (G. Frobenius), но
связывают его обычно с именем Ч е з а р о (Е. Cesaro), который дал
методу дальнейшее развитие. Вот в чем самый метод состоит:
По частичным суммам Ап данного числового ряда (А) строятся
их последовательные средние арифметические
	, „ _Aa+Aj	_A0+Al+...+An
а0~л0> а1~ 2 ' "¦' "	и+1	' "¦"'
если варианта хп при п - °° имеет предел А, то это число и называют
«обобщенной (в смысле Чезаро) суммой» данного ряда.
Примеры. 1) Возвращаясь к ряду
1-1 + 1-1 + 1-1+...,
имеем здесь
k+1	1
1
так что а.п-—. Мы пришли к той же сумме, что и по методу Пуассона
Абеля [418, 1)].
2) Для ряда
— + 2 cosnfl (-jr=s9asjr)
2 n=l
частичные суммы будут (если только б # 0)
sin |n+ij в
26 Г. М. Фихтенгольц, т. II
1
2 sin —9

402	ГЛ. XI. БЕСКОНЕЧНЫЕ РЯДЫ С ПОСТОЯННЫМИ ЧЛЕНАМИ	[420
Теперь нетрудно подсчитать средние арифметические:
1	" / 1 "\
(и+1К =	г- 2 sin \т+-\в
. 1 „m=o I 2)
2sin-e
Итак, окончательно
1	"
,	 2 [cosmfl -cos(m+lH] =
1 ш=0	.
4sinIS	/sin (« +1)-I
^	l-cos(n+l)e 1	2 '
1	~2	f
4 sin2 — б	I sin —
sin («+!) — ]
.
Vsin —
2
Очевидно, ап-*0: для значений 0^0 «обобщенной суммой» и здесь служит 0 [ср.
418, 2)].
3) Наконец, пусть снова предложен ряд
2 sin пв
Имеем при
1	( 1\
s-0-cos \п+- \в
1
2sin-0
(n+l)ar!=^r^ctg — 0	2 [sin(m+l)e-sin/ne] =
2	2	1 m — l
4 sin2 - 0
й+1 1 sin (и+2H-sine
= — ctg-0	j	.
4 sin2 - 0
Отсюда ясно, что ап -— ctg — 0.
Во всех случаях по методу Ч е з а р о получилась та же «обобщенная сумма»,
что и выше, по методу Пуассона - Абеля. Ниже [421] будет выяснено,
что это - не случайность.
И здесь также непосредственно ясна линейность метода.
Известная же теорема К о ш и [33, 13)] в случае существования пре-
предела
lim An=A

421]
§ 9. СУММИРОВАНИЕ РАСХОДЯЩИХСЯ РЯДОВ
403
удостоверяет наличие того же предела и для средних арифметиче-
арифметических хп. Таким образом, метод Ч е з а р о является регулярным.
421. Взаимоотношение между методами Пуассона—Абеля и Чезаро.
Начнем с простого замечания: если ряд (А) суммируем по методу
средних арифметических к конечной «сумме» Л, то необходимо
ап ---= о{п).
Действительно, из ап-х-~А и 	<*„-»-Л следует, что
а тогда и
п~~ п п и-1 '
что и требовалось доказать.
Поставленный в заголовке вопрос исчерпывается следующей тео-
теоремой, принадлежащей Фробениусу:
Если ряд (А) суммируем по методу средних арифметических к ко-
конечной «суммеъ А, то одновременно он суммируем также по методу
Пуассона - Абеля и притом к той же сумме.
Итак, пусть ап—Л. Ввиду сделанного вначале замечания очевидна
сходимость степенного ряда
2
для 0 < х < 1. Выполнив дважды преобразование Абеля [см.
383 и особенно 385, 6)], последовательно получим*
= A - х)]?Апх« = A - xfZin +
n=0	n=0
¦ В справедливости этого тождества легко убедиться и непосредственно, от-
отправляясь от заведомо сходящегося, ввиду ограниченности ос„, ряда справа:
n - 2яа„ _х + (л - 1)ап_2]хп =
- па„_х] - [nan_! - (и - 1)ссп_
[При этом мы полагаем а._1-а_
здесь получается сама собой.
2апх".
о
Сходимость последнего ряда
26*

404	ГЛ. XI. БЕСКОНЕЧНЫЕ РЯДЫ С ПОСТОЯННЫМИ ЧЛЕНАМИ	[421
[при этом следует помнить, что А0+Ах+ ... +Ап=(п+ 1)а„]. Известно,
что (для 0-=*<l)(l-x)-2 = j?(n + l)*" или
Умножим обе части этого тождества на А и вычтем из него почленна
предыдущее тождество:
А -/(*) = A - х?2 (и + \){А - ап)х".
л=0
Сумму справа разобьем на две:
?2
0	N
причем число N выберем так, чтобы при n>N было
где е - произвольное наперед заданное положительное число. Тогда
вторая сумма по абсолютной величине и сама будет меньше в (не-
(независимо от *!), а для первой суммы того же можно добиться за счет
приближения х к 1. Этим и завершается доказательство [ср. с доказа-
доказательством теоремы Абеля в 418].
Итак, мы установили, что во всех случаях, где приложим метод
Ч е з а р о, приложим и метод Пуассона-Абеля с тем же ре-
результатом. Обратное же неверно: существуют ряды, суммируемые
методом Пуассона-Абеля, но не имеющие «обобщенной сум-
суммы» в смысле Ч е з а р о. Рассмотрим, например, ряд
1-2 + 3-4+...
Так как здесь явно не соблюдено необходимое условие сумми-
суммируемости по методу средних арифметических, указанное вначале, то
этот метод не приложим. В то же время ряд
¦имеет (при 0<х-=1) сумму . ,а, которая при х-*1-0 стремится
к пределу j. Это и есть «обобщенная сумма» нашего ряда по П у а с-
сону-Абе л ю.
Таким образом, метод Пуассона-Абеля является более
мощным, т. е. приложим в более широком классе случаев, чем ме-
метод Ч е з а р о, но не противоречит ему в тех случаях, когда они
оказываются приложимыми оба.

422J	§ 9. СУММИРОВАНИЕ РАСХОДЯЩИХСЯ РЯДОВ	405
422. Теорема Харди— Ландау. Как и в случае метода Пуассона —
Абеля, для метода Ч е з а р о также могут быть доказаны теоремы «тауберов-
ского» типа, устанавливающие те дополнительные условия относительно членов
ряда, при наличии которых из суммируемости ряда по методу средних арифмети-
арифметических вытекает его сходимость в обычном смысле слова.
Ввиду теоремы Фробениуса ясно, что каждая тауберовская теорема
для метода Пуассона - Абеля приводит, в частности, к такой же теореме
для метода Ч е з а р о. Например, сама теорема Т а у б е р а перефразируется
теперь так: если а.п^А и выполняется условие
^+^2+ ...+пап
ton	=	= 0,	(9)
л--	П
то одновременно и Ап-*А. Впрочем, здесь она непосредственно вытекает из легко
проверяемого тождества
.. .+пап*
которое для данного случая указывает даже на необходимость усло-
условия (9).
Харди (G. H. Hardy) установил, что заключение от а,г —А к Ап -*А можно
сделать не только, если ап = о — (это содержится в предыдущем!), но и при более
широком предположении, что
\тат\^С (C=const; т=\, 2, 3, ...).
Ландау (Е. Landau) показал, что можно удовольствоваться даже «односторон-
«односторонним»- выполнением этого соотношения:
Если ряд (А) суммируется к %суммеч А по методу средних арифметических
и при этом выполняется условие
тат>-С (C=const; т-\, 2, 3, ...),
то одновременно и
[Изменяя знаки всех членов ряда, видим, что достаточно также предположить
неравенство другого смысла:
В частности, теорема, очевидно, приложима к рядам с членами постоянного
знака.]
Для доказательства рассмотрим сначала сумму
п + к
1
* Имеем
(» + \)Ап-(п-f- 1)а,, = (n + i)An-(A0+A1+ ... +Ап) =
= (Ап-А0)+(Ап-А1)+ ...+(Ап-Ап_1) =
(	)(	• +вч)+ • • • +а„ =

406	ГЛ. XI. БЕСКОНЕЧНЫЕ РЯДЫ С ПОСТОЯННЫМИ ЧЛЕНАМИ	[422
где пик- произвольные натуральные числа; путем тождественного преобразо-
преобразования она легко приводится к виду
п + к	л
S= 2Am- 2Лт = (п+к+1)<хгцк-(.п+1)*п^koLn+h + (n + l)(txn+k-an). A0)
т=0	т=0
Если взять любое Ат (при н«= т=^п+к), то, используя предположенное неравенство
С
ат=-	, можно получить такую оценку снизу:
т
к
Am=An+(an+i+ ¦ ¦ ¦ +ат)>Ап--С,
откуда, суммируя по т, найдем
к2
п
Отсюда, сопоставляя с A0), приходим к такому неравенству:
Ап<*п+к+—,— (<*п+к-Ъп)-\—С.	A1)
к	п
Станем теперь произвольно увеличивать п до бесконечности, а изменение к
к
подчиним требованию, чтобы отношение — стремилось к наперед заданному
п
числу е>0. Тогда правая часть неравенства A1) будет стремиться к пределу А+еС,
так что для достаточно больших значений п будет
A2)
Совершенно аналогично, рассматривая сумму
п
S'= 2 Am^ku.n-.h + (.n+1)(<*n-<x-n-k)
m = n-/.f 1
и проведя для Ат (при п-к^т^п) оценку сверху:
к
Am=An-(am + i+ • ¦ ¦+ап)<Ап-\	 С,
придем к неравенству
к*
п-к
Отсюда
п+1	к
An =~<*п-к + —,— (а« " a»-ft) - '	, С-
к	п-к
с	к	I	М
Ьсли и-~ и одновременно — -е, как и прежде но на этот раз пусть (¦'-=—, то
п	{	2]
правая часть этого неравенства стремится к пределу А	С--А- ЪС. Следо-
1-е
вательно, для достаточно больших п окажется
Ап^А-2еС.	A3)
Сопоставляя A2) и A3), видим, что, действительно,
Теорема доказана.

423]	§ 9. СУММИРОВАНИЕ РАСХОДЯЩИХСЯ РЯДОВ	407
Замегим, что подобная же «тауберовская» теорема была установлена затем
и для суммирования по Пуассону-Абелю - для нее только что дока-
доказанная теорема является частным следствием. Но ввиду сложности доказательства
мы его не приводим.
423. Применение обобщенного суммирования к умножению рядов. Остановимся
на применении обобщенных методов суммирования в вопросе об умноже-
умножении рядов по правилу К о ш и [389]. Пусть, кроме ряда (А), дан еще ряд
2X = 60+*>i+ ••¦+Ьп+---;	(В)
тогда ряд
2сп = 2(aobn +aibn-i+ ¦ ¦ • +an-1b1+anb0)	(С)
п—0 п—0
и называется произведением рядов (А) и (В) в форме К о ш и. Если
данные ряды сходятся и имеют обыкновенные суммы А и В, то ряд (С) все же
может оказаться расходящимся [пример этого мы имели в 392].
Однако во всех случаях ряд (С) суммируем по методу Пуассона - Абеля
и именно к сумме АВ.
Действительно, для 0*х«= 1 ряд A) равно как ряд
2ьпхп = Ь0+Ь1х+Ь,х"+ ... +Ьпхп+ ...
п=0
оба абсолютно сходятся [379]; обозначим их суммы, соответственно, через
f(x) и g(x). Произведение этих рядов, т. е. ряд
^ф афп -1 + • • • + ап - А+anb0) хп,
гс=0	п=0
по классической теореме К о ш и [389] также сходится и имеет суммой произ-
произведение f(x)-g(x). Эта сумма при л:-1-0 стремится к АВ, ибо, как мы видели,
по отдельности
lim f(x) = A, lim g(x) = B.
X-.1-0	x-1-0
Итак, «обобщенной (в смысле Пуассона - Абеля) суммой» ряда (С) дей-
действительно будет АВ, что и требовалось доказать.
Отсюда как следствие получается теорема Абеля об умножении рядов
[392]. Равным образом из самого доказательства ясно, что то же заключение
остается в силе, если ряды (А) и (В) - вместо того, чтобы сходиться в собствен-
собственном смысле - лишь суммируемы по методу Пуассона- Абеля к суммам
А и В.
В таком случае, учитывая теорему Фробениуса [421], можно сделать
и следующее утверждение: если ряды (А), (В) и (С) суммируемы в смысле Чезар о
и имеют, соответственно, ^обобщенные суммы* А, В и С, то необходимо
С = АВ.
В качестве примера рассмотрим возведение в квадрат ряда
1	1ЬЗ	Bт-1)!!
— = 1	f	... + (- l)m	—+ • •.,
fl 2 2-4	Bm)!!

408	ГЛ. XI. БЕСКОНЕЧНЫЕ РЯДЫ С ПОСТОЯННЫМИ ЧЛЕНАМИ	[424
который получается из биномиального разложения
1	11-3	Bш-1)!!
-f\+x	2 2-4	B/л)!!
при х=1. Умножая указанный числовой ряд на самого себя, придем к хорошо
знакомому нам ряду
1-1 + 1-1 + 1-1 + ...*,
«обобщенная сумма» которого, как по методу Пуассона - Абеля, гак
1 ( 1
и по методу Ч е з а р о, есть — = I
2
Далее, «возведем в квадрат» и этот расходящийся ряд. Мы получим ряд
1-2+3-4+...,
1 A\*
«обобщенная сумма» которого в смысле Пуассона - Абеля есть — = I — I
4 1.2;
(в смысле Ч е з а р о он не суммируем!).
424. Другие методы обобщенного суммирования рядов. 1) Методы Г. Ф. Воро-
Вороного. Пусть имеем положительную числовую последовательность {рп} и
Ро=Ро, Pn=P0+Pi+---+Pn (н=~0).
Из частичных сумм Ап ряда (А) составим выражения
PnA0+Pn-iAi+ ¦ ¦ ¦ +РоАп
Если wn ^A при п - ~, то А называется «обобщенной суммой» ряда (А) в смысле
Вороного - при заданном выборе последовательности {рп}.
Линейность метода как в этом случае, так и в следующих - очевидна,
и мы на ней не будем останавливаться.
Для регулярности метода Вороного необходимо и достаточно
условие
lim— = 0.
Необходимость. Допустим сначала регулярность рассматриваемого
метода: пусть из Ап--А всегда следует и wn-*A. Если, в частности, взять ряд
1-1+0+0+0+...,
для которого Ао - 1, а прочие Ап = 0 (так что и А - 0), то необходимо
Рп
* Мы пользуемся здесь числовым тождеством
ДBт-1)Н Bn-2m-l)ll
о B/я)!! Bи-2т)!!
где (- 1)!! и 0!! означают условно единицу.

424]	§ 9. СУММИРОВАНИЕ РАСХОДЯЩИХСЯ РЯДОВ	409
Достаточность. Предположим теперь условие теоремы выполненным
и докажем, что из Ап —А вытекает и гоп -~А.
Обратимся к теореме Теплица [391] и заменим там хп на Ап и tnm на ——— .
Рп
Условие (а) этой теоремы удовлетворено, ибо
Рп—т Рп—т «
t	°
*п Гп—т
Выполнение условий (б) и (в) очевидно, так как
л	п
2j I tnm I = 2j tnm = !•
ra=0	m=0
Следовательно, как и требовалось доказать, wn—A.
2) Обобщенные методы Че з ар о. Мы уже знакомы [420] с методом средних
арифметических; он является простейшим из бесконечной последовательности
методов суммирования, предложенных Чезаро. Фиксируя натуральное число
к, Чезаро вводит варианту
*
7
скп+к
и ее предел при и — ~ рассматривает как «обобщенную сумму» (А>го порядка) ряда
(А). При к= 1 мы возвращаемся к методу средних арифметических.
В дальнейшем нам не раз понадобится следующее соотношение между коэффи-
коэффициентами С:
CkkZ\+ct1+Ckk+l+ .. - +Ck+U--Ck+k ;	A4)
оно легко доказывается по методу математической индукции относительно и,
если исходить из известного соотношения
Сп+к = С(л-1Я-* + Cn-K/t-i) •
Прежде всего, покажем, что методы Чезаро всех порядков являются
частными случаями регулярных методов Вороного. Для этого достаточно
положить рп = Сп+?-1, ибо из A4) тогда следует, что Рл = ?¦*+*, и к тому же, оче-
очевидно,
Рп 1
— =	>О при и~"».
Рп п+к
С помощью того же равенства A4), пользуясь самим определением величин
?>п , устанавливается, что
$-1)+&-1)+ ... I #~х>- .#> *.	A5)
Это дает возможность выяснить взаимоотношение между суммированием по
Чезаро fc-го и (к — 1)-го порядка. Пусть ряд (А) допускает суммирование (к - 1)-го
Под Srf* разумеется Ап,

410	ГЛ. XI. БЕСКОНЕЧНЫЕ РЯДЫ С ПОСТОЯННЫМИ ЧЛЕНАМИ	[424
порядка, так что >'п*~1)^Л. В силу A4) и A5) имеем
c\ft) Лк—l) i e\k—i}, , rik—l)
(А) л &o "r^l т • ¦ ¦ t On ^
У n - k	7.
Cn+k
п+
Применяя сюда теорему Теплица [391], причем полагаем
. = 0,1,..., и),
придем к заключению, что и yh -~А. Таким образом, если ряд (А) допускает сум-
суммирование по методу Че з ар о какого-нибудь порядка, то он допускает и сумми-
суммирование любого высшего порядка, и притом к той оке сумме.
Приведем теперь обобщение уже известной нам теоремы Фробениуса
[421]: если ряд (А) суммируем по какому-либо из методов Чезаро (скажем
k-xo порядка), то он суммируем к той же сумме и по методу Пуассона —
Абеля.
Пусть дано, что
М)
^lim-— =A.	A6)
Легко заключить отсюда, что ряд
2^	A7)
2
п=0
для — 1 -=jc-= 1 сходится. Действительно, так как Сп+*~— , то из A6) имеем:
Если A*Q, то
так что, по теореме Коши - Адамара, радиус сходимости ряда A7) равен 1.
Он во всяком случае не меньше 1, если /1 = 0.
Рассмотрим теперь ряд тождеств
2п ( 2
п — 0	п=0
i
л=0
n=0
* Здесь и дальше учитываются соотношения тина A5).

424]	§ У. СУММИРОВАНИЕ РАСХОДЯЩИХСЯ РЯДОВ	411
Выше мы установили сходимость последнего ряда в промежутке (-1, 1); от-
отсюда вытекает [см. 390, 4)] сходимость и всех предшествующих рядов. Кроме
того,
2	2+	A8)
п = 0	л=0	л=0
Сопоставим с этим тождеством другое:
1 = A-х)"+^2Сп+кхп,	A9)
л = 0
которое имеет место в том же промежутке (-1, 1); оно получается /с-кратным
дифференцированием прогрессии
Умножив обе части тождества A9) на А вычитая из него почленно равенство A8),
получим, наконец,
А - 2V" - A - х)*+> j? [A - j^lcJt**"-
л=0	л=0
Дальнейшие рассуждения [с учетом A6)!] вполне аналогичны тем, с помощью
которых была доказана теорема Абеля в 418 и теорема Фробениуса
в 421; они могут быть представлены читателю. В результате мы и получим:
lim 2j апхп = А,
1-1-0 п=0
ч. и тр. д.
Отметим, что существуют расходящиеся ряды, суммируемые по методу
Пуассона-Абеля, но не суммируемые ни одним из обобщенных методов
Ч е з а р о. Таким образом, первый из названных методов оказывается сильнее
всех последних даже вместе взятых!
3)	Методы Гельдера. Эти методы состоят просто в повторном приме-
применении метода средних арифметических. Все вопросы, относящиеся к их регуляр-
регулярности и взаимоотношению, исчерпываются ссылкой на теорему К о ш и .
Можно доказать, что к-кратное применение метода средних арифметических
совершенно равносильно применению метода Чезаро k-го порядка, т. е. сумми-
суммирует тот же класс рядов и притом к тем же суммам.
4)	Метод Б о р е ля. Он состоит в следующем: по ряду (А) и его частичным
суммам Ап строится выражение
У А ХП
о п\

412	ГЛ. XI. БЕСКОНЕЧНЫЕ РЯДЫ С ПОСТОЯННЫМИ ЧЛЕНАМИ	{424
Если последний ряд сходится, хотя бы для достаточно больших значений х, и его
сумма при х— +<*> имеет предел А, то это число и является чобобщенной суммойь
в смысле Бор е л я для данного ряда (А).
Докажем регулярность метода Б о р е л я. Допустим сходимость ряда (А)
и обозначим его сумму через/1, а остатки А - Ап — через ап. Имеем (для достаточно
больших х)
хп	°° хп	°° хп	°° хп
и!	о л!	о л!	о л!
Зададимся произвольно малым числом г^О; найдется такой номер N, что для
е
n^N будет |<хп| -=—. Представим последнее выражение в виде суммы,
О П1	N + 1 Л!
E
Второе слагаемое по абсолютной величине -= —, каково бы ни было х, а первое,
представляющее собой произведение е~х на многочлен, целый относительно х,
е
становится абсолютно ^— при достаточно больших х. Этим все доказано*.
5) Метод Эйлера. Для ряда
Z(-04
мы имели в 413 [см. G)] формулу
B0)
выражающую «преобразование Эйлера». При этом, как было доказано, из
сходимости ряда в левой части уже вытекает сходимость ряда в правой части
и равенство между их суммами.
Однако и при расходимости первого ряда второй ряд может оказаться
сходящимся; в подобном случае его сумму Эйлер приписывал в качестве «об-
«обобщенной суммы» первому ряду. В этом собственно и состоит метод Эйлера
суммирования рядов; сделанное только что замечание гарантирует регулярность
метода.
Если писать рассматриваемый ряд в обычном виде (А), не выделяя знаков ±,
и вспомнить выражение D) п° 413 для^-й разности, то можно сказать, что по методу
суммирования Эйлера в качестве «обобщсшгой суммы» ряда (А) берется обыч-
обычная сумма ряда
у
р=о	2Р+1
(в предположении, что последний сходится).
* Читатель отметит сходство этого доказательства с доказательством теоремы
Абеля [418] и других.

425]	§ 9. СУММИРОВАНИЕ РАСХОДЯЩИХСЯ РЯДОВ	413
На этом мы закончим обзор различных методов суммирования расходящихся
рядов, так как и приведенных уже достаточно, чтобы создать у читателя впечатле-
впечатление о многообразии подходов к этому вопросу. Регулярность метода, как необ-
необходимую его особенность, мы устанавливали во всех случаях. К сожалению лишь,
мы не всегда имели возмояшость достаточно углубиться в вопрос о взаимоотно-
взаимоотношении различных методов. А между тем может случиться, что два метода имеют
пересекающиеся (но не покрывающие одна другую) области приложи-
приложимости; может оказаться и что два метода приписывают одному и тому же расходя-
расходящемуся ряду различные «обобщенные суммы».
425. Примеры. 1) Пусть {ап} положительная монотонно убывающая последо-
последовательность, сходящаяся к 0. Положим
А1) = а0, Ап-«„•!-«!-I- ...-I ап 0?=-0).
Доказать, что знакопеременный ряд
AB-Al+As-A3+...
суммируем по методу Чезаро A-го порядка), и его ^обобщенная сумма» равна
половине суммы сходящегося ряда лейбницевского типа
[X а р д и (G. H. Hardy)].
Указание. Подсчитать среднее арифметическое первых 2т частичных
сумм данного ряда; оно представится в виде
A (ao~ai) + (ao"gi + a2~g3)+ • • ¦ +(Др- ai+ ¦ • •+«2m-2-agm-i)
2	т
и, по теореме К о ш и [33, 13)], стремится к — а. Затем легко уже показать, что
к тому же пределу стремится и среднее первых 2т+ 1 частичных сумм.
1	и + 2
2) Взяв ап =	 или а„ = 1п	(п-0, 1, 2, ...), установить на основании
л+ J	п+\
теорехмы 1), что расходящиеся ряды
In 2- In 3 + In 4- In 5+...
оба суммируемы по методу Чезаро, и их «обобщенные суммы» соответственно
1	1 ж
равны — In 2 и — In — .
2	2 2
Указание. Во втором случае используется формула В а л л и с а [317].
3) С помощью той же теоремы доказать, что при -1-=х<0 расходящийся
ряд Дирихле
2	jh) (f , г)
/1 = 1 И*	п = 1
суммируется по методу Чезаро.
* Нп (как обычно) обозначает n-ю частичную сумму гармонического ряда.

414	ГЛ. XI. БЕСКОНЕЧНЫЕ РЯДЫ С ПОСТОЯННЫМИ ЧЛЕНАМИ	[425
Указание. Представить п$ в виде суммы
и методами дифференциального исчисления доказать, что с возрастанием п варианта
в?-л- 1* убывает (при этом, ввиду 32, 5), она стремится к О!).
4) Если «разбавить» члены сходящегося ряда нулями, то это никак не отразится
ни на сходимости ряда, ни на его сумме. Как видно из следующих примеров,
с обобщенным суммированием расходящегося ряда дело может обстоять иначе.
Рассмотрим ряды
(а)	1-1 + 1-1 + 1-1+...
0 12 3 4 5
(б)	1-1+0 + 1-1+0 + 1-1+0...
0 12345678
(в)	0+1-1+0+1+0+0 + 0-1+...*
012345678
Про первый ряд мы уже знаем, что его «обобщенная сумма» по Ч е з а р о
равна 1/2. Показать, что ряд (б) имеет уже другую сумму, именно 1/3, а ряд (в)
вовсе не суммируем по Ч е з а р о.
Указание. В случае ряда (в), при изменении п от 22т~х до 22т - 1, среднее
арифметическое первых и+1 членов колеблется
1 22т-1 2	1 22т- 1 1
3"*2am-i+i "* з Д° У"~2«т~"*7'
5) Считая к любым натуральным числом, рассмотрим ряд
и докажем, что ^и не суммируется методом Чезаро к-го порядка, но сумми-
суммируется (к асумме» 1/2к+1) методом Чезаро (к+1)-го порядка.
Используя равенство A8) и - дважды - равенство A9) (в первый раз заменяя
х на - х, а второй раз х на х2), последовательно получим:
Приравнивая коэффициенты при одинаковых степенях х в первом и в последнем
из этих рядов [мы пользуемся здесь «теоремой о тождестве степенных рядов»,
которая будет доказана лишь ниже, в 437, 3°], приходим к заключению, что
•SiS = cHi+k, S&Vi = 0 (m = 0, 1, 2, 3, ...)	B1)
* Член ± 1, стоявший в (а) на /и-ом месте (где /я = 0, 1, 2, 3, ...), в (в) пере-
перемещен на 2т-е место; остальные места заполнены нулями.
** Сходимость последнего ряда в промежутке (-1, 1) легко устанавливается
с помощью теоремы Коши-Адамара, а отсюда уже вытекает и сходи-
сходимость первого ряда.

4251	§ 9. СУММИРОВАНИЕ РАСХОДЯЩИХСЯ РЯДОВ	415
Таким образом,
'	1	к
2к
и предложенный ряд не имеет ^обобщенной суммы Чезаро А-го порядка.
С другой стороны, ввиду B1), A5) и A4) как для п = 2т, так и для и-2м + 1
будет &+1> = Скк + с!?+к+... I C^+t-C*V*+i. Отсюда
гк+1
7 2m —
юдливо и для Угт+и что и }
6) Ряд
то же справедливо и для у\т+1> что и доказывает наше утверждение.
2
п=0
- любое натуральное число, также суммируем по методу Чезаро (& + 1)-го
порядка. Это можно установить, опираясь на предыдущий результат. Действи-
Действительно, разложим Сп+k п0 степеням и+1:
здесь <х/*^ - постоянные коэффициенты, причем oq*^ = I/A;! ^ 0. Написав еще ряд
таких равенств, заменяя ?на&-1,&-2	1, легко затем, наоборот, представить
* в виде суммы
с постоянными коэффициентами ^. Но тогда
Так как все ряды ^i («=I, 2, ..., fc) суммируемы по методу Чезаро
порядка (мы учитываем здесь свойства методов Чезаро последова-
последовательных порядков!), то ввиду линейности названного метода это справед-
справедливо и для предложенного ряда.
Самое вычисление «обобщенной суммы» мы в состоянии будем осуществить
лишь впоследствии [449].
Приведем еще несколько простых примеров на непосредственное применение
методов Гельдера, Бореля и Эйлера.
7)	Просуммировать по методу Гельдера ряды
(а)	1-2+3-4+...
и
(б)	1-3 + 6-10+...
Ответ, (а) Двукратное усреднение дает 1/4.
(б) Трехкратное усреднение дает 1/8.
8)	Просуммировать ряд 1-1 + 1-1 + 1-1+... по методу Бореля.
ех+е-х 1
Ответ, lim е~х •	= — .
х—	2	2

416	ГЛ. XI. БЕСКОНЕЧНЫЕ РЯДЫ С ПОСТОЯННЫМИ ЧЛЕНАМИ	[426
9) Просуммировать по методу Эйлера ряды
(а)	1-1 + 1-1 + ...
(б)	1-2+3-4+...
(в)	1-2 + 22-24+...
(г)	1=>-
Указание. Во всех случаях удобно воспользоваться преобразованием
Эйлера в форме B0).
Ответ, (а) А -~\ (б) А°а„- \, JIa0=l, ЛРао = О для р>\,
111	111	1
'244	0>. 248	3
6, Ма^-О для р>Ъ
1	7 12 б 1
А-=	-j	= --.
2	4 8 16 8
426. Общий класс линейных регулярных методов суммирования. Приведем
в заключение некоторую весьма общую схему для построения класса линейных
регулярных методов суммирования, содержащего в частности все методы, упоми-
упоминавшиеся выше.
Пусть в некоторой области % изменения параметра х задана последователь-
последовательность функций
Vo(x), <Pi(x), (р2(х)	<рп(х), ...	(Ф)
Допустим, что область ЗС имеет точкой сгущения число со, конечное или нет. По
данному числовому ряду (А) строится ряд, состоящий из функций:
) + ... +Ап<рп(х) +... = 2АпЧ>п(.х)	B2)
л=0
(где Ап - а0 Ь at + ... + ап~). Если этот ряд, по крайней мере для х, достаточно близких
к а), сходится и его сумма при х-*си стремится к пределу А, то это число и прини-
принимается за «обобщенную сумму» данного ряда.
Мы получаем, таким образом, некий метод суммирования рядов, связанный
с выбором последовательности (Ф) и предельной точки а>. По самому построению
метода ясна его линейность. Предположим теперь, что функции (рп(х) удов-
удовлетворяют следующим трем требованиям:
(а) при любом постоянном п
(б)	при значениях х, достаточно близких к о,*
2\<Pn(x)\*sK №= const);
л=0
(в)	наконец,
lim
Тогда метод суммирования оказывается регулярным.
* Т. е. для | х - <п | "- 6', если о> конечно, или для л- =- /У, если со = + ~.

426]	§ 9. СУММИРОВАНИЕ РАСХОДЯЩИХСЯ РЯДОВ
Доказательство. Итак, пусть
lim An = A.
417
Тогда по произвольно заданному е=-0 найдется такой номер »', что для и=-и'
будет
\Ап-А\
ЪК
B3)
Ввиду ограниче1шости Ап и абсолютной сходимости ряда 2ч>п(х), по крайней
л = 0
мере для |л:-со| -= й' (х>А') будет сходиться также и ряд 2 Апфп(.х)- При этом,
л=0
очевидно,
„'	«,	Г ~	I
А\<рп(х)+ 2 lAn-A]<pn(x)+A\2<Pn(.x)-l\,
л=л'+1	[yj=O	J
2
п=0
так что, переходя к абсолютным величинам,
п=0
Anq>n(x)-A
2[Ап-А]<рп{х)
- 2 \An-A\\<pn(x)\
л=л'+1
л=0
Второе слагаемое справа < —, в силу B3) и условия (б). Что касается первого
и третьего слагаемого, то каждое из них можно сделать -=—, приблизив доста-
достаточно х к со, в силу условия (а) и условия (в). Следовательно,
lira
т. е. «обобщенная сумма» оказывается существующей и равна обычной сумме.
Если х есть натуральный параметр т (так что си = + ~0, то последовательность
функций (Ф) заменяется бесконечной прямоугольной матрицей:
ho hi '12
*20 21 '22
(Т)
'по 'щ ^nг
27 Г. М. Фихтенгольц, т. II

418	ГЛ. XI. БЕСКОНЕЧНЫЕ РЯДЫ С ПОСТОЯННЫМИ ЧЛЕНАМИ	[426
За «обобщенную сумму) ряда (А) принимается предел при т-~ю варианты
Г' 	At Д- Л t Л- Д- Л t _l
в предположении, что этот ряд сходится, по крайней мере для достаточно больших
значений т.
Условия регулярности преобразуются для этого случая следующим
образом:
(а)	при любом постоянном п
lim tnm - 0,
(б)	при достаточно больших т
2\1пт\^=К (АГ= const),
л=о
(в)	наконец,
lim ^ fnm= !•
т~-л=0
По существу все эти идеи принадлежат Теплицу [ср. 391], у которого
лишь, как читатель помнит, матрица предполагалась треугольной. Этого част-
частного случая нам по большей части и было достаточно.
Упомянем еще, что под упомянутую выше схему непосредственно подходит как
суммирование по Пуассону - Абелю, так и суммирование по Б о р е л ю .
В первом случае имеем
2	2п,
л=0	л=0
так что роль <рп(х) в области ЗС = @, 1) (со = 1) играет множитель A - х)хп. Во втором
же случае <рп(х) = е~х-— в ^ = @, +¦») (со =+¦»). Соблюдение условий (а), (б),
п\
(в) легко проверяется, и тем - на основании доказанной выше общей теоремы -
снова устанавливается регулярность этих методов.
Общее определение метода суммирования, данное выше, и теорему об его
регулярности легко перефразировать так, чтобы в них участвовали не частичные
суммы Ап, а непосредственно члены ап суммируемого ряда (А). Останавливаться
на этом не будем.

ГЛАВА ДВЕНАДЦАТАЯ
ФУНКЦИОНАЛЬНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И РЯДЫ
§ 1. Равномерная сходимость
427. Вводные замечания. Мы изучали выше бесконечные последо-
последовательности и их пределы, бесконечные ряды и их суммы; элемен-
элементами этих последовательностей или членами рядов были постоянные
числа. Правда, иной раз в их состав и входили, в роли параметров,
те или иные переменные величины, но во время исследования им не-
неизменно приписывались определенные постоянные значения. Так, на-
например, когда мы устанавливали, что последовательность
1 -г у ,
имеет пределом ех или что ряд
х2 х3	, .,„_, хп
имеет суммой 1пA + х), для нас х было числом постоянным. Функ-
Функциональная природа элементов последовательности и ее
предела или членов ряда и его суммы - нами вовсе не учитывалась;
сейчас же именно к этому моменту будет привлечено наше внимание.
Предположим, что дана последовательность, элементами
которой являются функции
fix) fix)	fix)	(П
от одной и той же переменной х, определенные в некоторой области
ее изменения Х = {х}*. Пусть для каждого х из X эта последователь-
последовательность имеет конечный предел; так как он вполне определяется зна-
значением х, то также представляет собой функцию от х (в X):
B)
которую мы будем называть предельной функцией для по-
последовательности A) [или для функции fn(x)].
* Чаще всего это будет промежуток; но мы сохраняем пока наибольшую общ-
общность, разумея пол х любое бесконечное числовое множество.
27»

420	I л. XII. ФУНКЦИОНАЛЬНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И РЯДЫ	[427
Теперь мы будем интересоваться не одним лишь существованием
предела при каждом отдельном значении х, но функциональ-
функциональными свойствами предельной функции. Чтобы читатель уяс-
уяснил себе наперед, какого характера новые задачи при этом возникают,
упомянем для примера об одной из них.
Допустим, что элементы последовательности A) все суть непре-
непрерывные функции от х в некотором промежутке % = [а, Ь\, гарантирует
ли это непрерывность предельной функции ? Как видно из следующих
примеров, свойство непрерывности иногда переносится и на предель-
предельную функцию, иногда же нет.
Примеры. Во всех случаях %— [0, 1].
1)	/п(х)-хп, Дх) = 0 при х<1 и Д1) = 1 (разрыв при х=1);
2)	fnix) = y^, > /(*) = 0 при л--0 и Д0) = 1 (разрыв при х = 0);
3)	fnix) =} "^, Дх) = 0 при всех х (везде непрерывна);
4)	fn(x) = 2n2x-e-n'x\ Дх) = 0 при всех х (то же).
Естественно возникает задача - установить условия, при которых
предельная функция сохраняет непрерывность; этим мы займемся в
431 (и 432).
Мы уже видели [362], что рассмотрение числового ряда и его
суммы есть лишь другая форма исследования последовательности
чисел и ее предела. Рассмотрим теперь ряд, членами которого явля-
являются функции от одной и той же переменной х в некоторой обла-
области X:
2ип(х) = щ(х) + 1ф) + ...+ ип(х) + ...	C)
Пусть этот ряд сходится при каждом значении хъ%; тогда его сумма
также представит собой некоторую функцию от х: f(x). Эта сумма
определится предельным равенством вида B), если под fn(x) раз-
разуметь частичную сумму
Ш = 1фс) + гфс) + ... + «„(*).	D)
Обратно, вопрос о предельной функции для произвольно заданной
последовательности A) можно рассматривать под видом суммирова-
суммирования ряда C), если положить
Щ(х) =Л(х), щ{х) =/2(х)-fiix), ...,
Нам чаще придется иметь дело именно с функциональными рядами,
так как эта форма исследования предельной функции на практике
обычно удобнее.

428)	§ i. равномерная сходимость	421
И здесь также следует подчеркнуть, что предметом наших бли-
ближайших исследований будут не одни лишь вопросы сходимости ряда
C), но функциональные свойства его суммы. В виде примера можно
назвать вопрос о непрерывности суммы ряда, в предположении не-
непрерывности всех его членов; это - та же задача, которая уже упо-
упоминалась выше.
Как оказывается, функциональные свойства предельной функции
(или - что то же — суммы ряда) f(x) существенно зависят от самого
характера приближения fn(x) к Дх) при различных значениях х.
Изучением типических возможностей, которые здесь представляются,
мы займемся в следующем п°.
428. Равномерная и неравномерная сходимости. Допустим, что для
всех х из X имеет место равенство B). По самому определению пре-
предела это значит следующее: лишь только фиксировано
значение х т % (для того чтобы иметь дело с определенной
числовой последовательностью), по любому заданному е>0 найдется
такой номер N, что для всех n>N выполняется неравенство
\Ш-Лх)\^е,	E)
где под х разумеется именно то значение, кото-
которое было заранее фиксировано.
Если взять другое значение х, то получится другая число-
числовая последовательность, и - при том же е - найденный номер N
может оказаться уже непригодным; тогда его пришлось бы заменить
большим. Но х принимает бесконечное множество зна-
значений, так что пред нами бесконечное же множество раз-
различных числовых последовательностей, сходящихся к пределу. Для
каждой из них в отдельности найдется свое N; возникает вопрос: су-
существует ли такой номер N, который (при заданном е) способен был
бы обслужить сразу все эти последовательности?
Покажем на примерах, что в одних случаях такой номер N суще-
существует, а в других - его нет.
1) Пусть сначала-
Так как здесь
то сразу ясно, что для осуществления неравенства /Цх)~=е доста-
достаточно, каково бы ни было х, взять «>s~- Таким образом, например,
число N=еB~ в этом случае годится одновременно для
всех х.

422
ГЛ. XII. ФУНКЦИОНАЛЬНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И РЯДЫ
[428
2) Положим теперь [427, 3)]:
Для любого фиксированного х >0 достаточно взять п =» ЕI— ,
чтобы было: fn(x)< — <e. Но, с другой стороны, сколь боль-
большим ни взять и, для функции fn{x) в промежутке [0, 1] всегда
1	~	1
найдется точка, именно точка х = -, в которой ее значение равно ^:
"
Таким образом, за счет увеличения и сделать
для всех значений х от 0 до 1 зараз - никак нельзя. Иными
1
словами, уже для е = = не существует
9
-1
О L
-1
~—^о
*-х
п = Ч0
Ш
Рис. 59.
номера N, которое годилось бы для
всех х одновременно.
На рис. 59 изображены графики
этих функций, отвечающие и = 4 и
п = 40: характерен горб высоты
-z, передвигающийся с возрастанием
п справа налево. Хотя по каждой
вертикали, в отдельности взятой,
точки последовательных кривых с
возрастанием п бесконечно прибли-
приближаются к оси х, но ни одна кривая
в целом не примыкает к этой
оси на всем протяжении
от х = 0 до х = 1.
Иначе обстоит дело с функциями, рассмотренными на первом
месте; мы не приводим их графиков, ибо они, например при и = 4 или
я = 40, получаются из графиков, изображенных на рис. 59, путем умень-
уменьшения всех ординат, соответственно, в 4 или в 40 раз. В этом случае
кривые сразу на всем своем протяжении примыкают к оси х.
Дадим теперь основное определение:
Если 1) последовательность A) имеет в X предельную функцию
fix) и 2) для каждого числа е>0 существует такой не завися-
зависящий отх номер N, что при n>N неравенство E) выполняется сразу
для всех х из X, то говорят, что последовательность A) сходится
[или - функция fn{x) стремится] к функции f(x) равномерно
относительно х в области %'.
Таким образом, в первом из приведенных примеров функция fn(x)
стремится к нулю равномерно относительно х в промежутке
[0, 1], а во втором - нет.

428]
§ 1. РАВНОМЕРНАЯ СХОДИМОСТЬ
423
Нужно сказать, что и для прочих функций, рассмотренных в пре-
предыдущем п°, сходимость н е будет равномерной. Установим это.
3) Для функции fn(x) = хп [427, 1)] невозможность неравенства хп<
<е (при е< 1) сразу для всех х<1 видна хотя бы из того, что
х"-*1, если (при фиксированном п) х-+1. Рис. 60 дает представление
о своеобразном характере нарушения равномерности: здесь предель-
предельная функция изменяется скачком,
а горб неподвижен.
Пусть теперь
4)/„(*) =
5) /п(х) =
1
1 + пх
или
Невозможность равномерного
приближения в [0, 1] к предель-
предельной функции, которая для х>0
в обоих случаях равна 0, следует
из того, что, соответственно
или
2л
е
Рис. 60.
Во втором случае высота гор-
горбов, которые мешают равномерному стремлению к 0, вдобавок еще
бесконечно возрастает.
Покажем на примерах функций хп и
исследования вопроса. Неравенства
1

еще другой путь для
хп-
и
равносильны,
lne
и>.—
In л:
\ + пх "
соответственно, таким:
и
п
¦мн
0<е<1).
Так как выражения справа неограниченно возрастают, первое - при
приближении л- к 1, а второе - при приближении х к 0, то ясно, что
никакой номер п сразу при всех значениях х этим не-
неравенствам удовлетворить не может.
Перенесем теперь все сказанное выше о сходимости функций на
случай функционального ряда C).
Предполагая ряд сходящимся, введем в рассмотрение его
сумму f(x), частичную сумму /„(*) [см. D)] и, наконец, его остаток
после и-го члена
*+1

424	гл. xii. функциональные последовательности и ряды	1428
При любом фиксированном х
lim/n(x) = f(x) и lim rpn(x) = 0.
Если частичная сумма fn(x) стремится к сумме ряда f(x) равно-
равномерно относительно х в области X [или, что то же, остаток ряда
<рп(х) равномерно стремится к 0], то говорят, что ряд C) рав-
равномерно сходится в этой области.
Это определение, очевидно, равносильно следующему:
Ряд C), сходящийся для всех х из области X, называется равно-
равномерно сходящимся в этой области, если для каждого числа е =- 0
существует такой независящий от х номер N, что при n>N
неравенство
\fn(x)-fn{x)\^e или \срп(х)\-<е	F)
выполняется одновременно для всех х из %*.
Примеры равномерно и неравномерно сходящихся рядов, конечно,
можно составить, преобразовав приведенные выше примеры после-
последовательностей. Мы присоединим к ним еще несколько новых при-
примеров.
6)	Рассмотрим прогрессию 2 хп~1; она сходится в открытом промежутке
п = 1
ЗС = (- 1,1). Для любого хизл остаток после и-ro члена имеет вид:
хп
4>п<-х) = -	.
1-х
Если п произвольно фиксировать, то очевидно:
lim \<pn{x)\= —, Hm <pn(x)=">°.
х——1+о	2 х-1-о
И то, и другое доказывает, что осуществить для всех х одновременно
неравенство
1?>л(*)|-=е (если е< —I
при одном и том же номере и невозможно. Сходимость прогрессии в промежутке
(-1, 1) неравномерна; это же относится к промежуткам (-1, 0] и [0, 1)
по отдельности.
7)	Ряд У!	 при любом значении х из и/ = (- ~, + =о) сходится, ибо
1 хг+п
он удовлетворяет условиям теоремы Лейбница [381]. По замечанию, сде-
* Понятие равномерной сходимости ряда было введено в науку одно-
одновременно (в 1848 г.) Зайделем (Ph. L. v. Seidel) и Стоксом (G. С. Stokes),
но еще до них применялось Вейерштрассом на его лекциях.

429]	§ 1. равномерная сходимость	425
данному после доказательства теоремы, остаток ряда оценивается, по абсолют-
абсолютной величине, своим первым членом:
\фп{х) I -
Отсюда ясно, что во всем бесконечном промежутке ряд сходится равномерно.
8) Аналогично, и ряд ]?——-^- сходится равномерно ъХ = {— «., + <*,),
ибо при х * О
\<Рн(х) I ¦
X
Любопытно отметить, что ряд, составленный из абсолютных величин ^	,-
1 V^ ~т~ X )
хотя и сходится, но неравномерно. Действительно, его остаток, при х * О,
таков:
<Рп(х)=
1 + д:2
при любом фиксированном п он стремится к 1, когда х-0.
Замечание. Если в примере 2), вместо промежутка [0, 1], рассмотреть
любой промежуток [а, 1], где 0< а-= 1, то в нем сходимость уже будет равно-
равномерной. Действительно, для всех
В любом же промежутке [0, а] сходимость, очевидно, неравномерна. Таким
образом, вокруг точки х = 0 как бы «сгущается» свойство неравномерности; назовем
ее точкой неравномерности. То же относится и к примерам 4), 5)
и 8). Аналогичную роль в примере 3) играет точка х = 1, а в примере 6) - обе точки
х= -1 и х= 1.
В более сложных случаях точки неравномерности могут встречаться в беско-
бесконечном количестве.
429. Условие равномерной сходимости. Теорема Больцано-
К о ш и [39], устанавливающая условие существования конечного пре-
предела для заданной числовой последовательности («принцип сходимо-
сходимости»), естественно приводит к следующему условию равномерной
сходимости для заданной в области % последовательности функций A):
Для того чтобы последовательность A) 1) имела предельную функ-
функцию и 2) сходилась к этой функции равномерно относительно
х в области %, необходимо и достаточно, чтобы для каждого числа
?>0 существовал такой не зависящий от х номер N, чтобы

426	ГЛ. XII. ФУНКЦИОНАЛЬНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И РЯДЫ	[429
при п >N и любом т= 1, 2, 3, ... неравенство
|/л+т(*)-/„(*) |-е	G)
имело место для всех х из X одновременно.
[Требование это можно кратко сформулировать так: принцип схо-
сходимости для последовательности A) должен осуществляться равно-
равномерно для всех х из X.]
Доказательство. Необходимость. Если последова-
последовательность A) имеет предельную функцию f(x) и сходится к ней рав-
равномерно в X, то по заданному е>0найдется не зависящий
от х номер N, такой, что при n>N будет
для всех х. Аналогично и
\fn+m(x)-f(x)\^^e (m = 1,2,3, ...),
а из этих обоих неравенств вытекает G).
Достаточность. Пусть условие, указанное в теореме, выпол-
выполнено. Тогда, какое бы значение х из Xни фиксировать, в лице
последовательности A) мы будем иметь числовую последова-
последовательность, для которой выполняется условие Больцано-Коши.
Следовательно, для этой последовательности существует конечный
предел, чем доказано существование для последовательности A) пре-
предельной функции f(x).
Теперь, взяв по произволу n>N и х из X, станем в неравенстве
G) безгранично увеличивать т (при постоянных п и х). Переходя к
пределу, получим:
\f(x)-fn(x)\^e.
Этим устанавливается равномерное стремление fn(x) к f(x).
Нетрудно перефразировать доказанное условие для случая функ-
функционального ряда:
Для того чтобы ряд C) сходился равномерно в области X,
необходимо и достаточно, чтобы для каждого числа е>0 существовал
такой не зависящий от х номер N, что при п>N и любом т =
= 1, 2, 3, ... неравенство
n+m
2
+ ...+ иП+т(х) | < е	(8)
имеет место для всех х из X одновременно.
Отсюда, в частности, вытекает полезное следствие:

430]	!) 1. РАВНОМЕРНАЯ СХОДИМОСТЬ	427
Если все члены ряда C), равномерно сходящегося в области
%, умножить на одну и ту же функцию v(x), ограничен-
ограниченную в %:
то равномерная сходимость сохранится.
Для установления на практике равномерной сходимости конкрет-
конкретных последовательностей или рядов выведенные условия мало при-
пригодны. С этой целью пользуются — на них же основанными, но более
удобными в применении - достаточными признаками, которые фор-
формулируются обычно применительно к рядам.
430. Признаки равномерной сходимости рядов. Вот простейший и
чаще всего применяемый признак:
Признак Вейерштрасса. Если члены функционального ряда C)
удовлетворяют в области X неравенствам
к(*)|"*еп (и= 1,2,3,...),	(9)
где с„ суть члены некоторого сходящегося числового ряда
2^ = ^ + ^+ ... +сп+ ...,	(С)
л = 1
то ряд C) сходится в % равномерно.
При наличии неравенства (9) говорят, что ряд C) мажориру-
мажорируется рядом (С), или что (С) служит мажорантным рядом
для C).
Действительно, из (9) получаем неравенство
un+i(x) + ип+2(х) 1-... гип+т(х)\ =scn+i + сл+2-т ... -г сп+т,
справедливое одновременно для всех х из области X. Согласно прин-
принципу сходимости, который мы применяем к числовому ряду (С), для
любого е>0 найдется такое N, что при n>N правая часть предыду-
предыдущего неравенства будет уже меньше е, а с нею - и левая, притом
для всех х одновременно. Этим, по условию п° 429, наше утвержде-
утверждение доказано.
Таким образом, например, в любом промежутке равномерно
сходятся ряды
2}ап sin nx, 2!an cos nx,
/1 = 1	Л = 1
если только ряд 2 ап сходится абсолютно. Ведь
л = 1
ап sin nx
ап cos nx =s= \an
так что роль мажорантного здесь играет ряд 2!Iап

428	ГЛ. XII. ФУНКЦИОНАЛЬНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И РЯДЫ	D30
Замечание. Каждый равномерно сходящийся в ЭС ряд 2ип(х)
п = 1
путем расстановки скобок может быть преобразован в ряд, к кото-
которому уже применим признак Вейерштрасса.
Действительно, возьмем какой-нибудь положительный сходящийся
ряд 2ick- По числу сх [429] найдется такой номер тх, что \ит +i(x) +
+ ... +ип(х)\ <сх в X для п^-т1. Затем, по числу с2 найдется такой
номер т2>тг, что \итг+х(х)+ ... +ип(х)\ <с2 в X для и=-т2, и т- Д-
Тогда, группируя члены данного ряда следующим образом:
[щ(х) + ...+ umi(x)] + [umi+1(x)+ ...+ ит,{х)\ + [иП1г+1(х)+ ...+ ип1,(х)] + ...
получим ряд, члены которого - начиная со второго - по абсолют-
абсолютной величине не превосходят в X последовательных членов взятого
числового ряда.
Если к данному ряду C) признак Вейерштрасса оказался
применим, то ряд C) необходимо абсолютно сходящийся. Боль-
Больше того, одновременно с рядом C) будет равномерно сходиться
и ряд, составленный из абсолютных величин его членов:
Между тем возможны случаи, когда ряд C) сходится равно-
равномерно, будучи неабсолютно сходящимся. Примером этого
служит ряд 7) п° 428 (что ряд этот не сходится абсолютно, следует
из сравнения с гармоническим рядом). Возможно даже такое поло-
положение вещей, когда ряд C) сходится абсолютно и равномерно, но ряд
A0) все же сходится неравномерно [см. ряд 8) в 428]. Подобные слу-
случаи заведомо не охватываются признаком Вейерштрасса; для
их исследования нужны более тонкие признаки.
Сейчас мы установим два признака, относящихся к функциональ-
функциональным рядам вида:
2а„(х) • bn(x) = а,{х) • Ь&) + <фс) ¦ Ь2{х) +...+ ап{х) • bn(x) * ..., (W)
1
где an(x), bn(x) (п = 1, 2, 3, ...) суть функции от х в X. Мы скопируем
эти признаки с признаков Абеля и Дирихле [384] из теории
числовых рядов; условно будем называть и их по именам этих
ученых.

430]	§ i. равномерная сходимость	429
Признак Абеля. Пусть ряд
х) = Ь,(х) + Ъ2(х) +...+ Ъп(х) +...	(В)
сходится равномерно в области X, а функции ап(х) (при каждом х)
образуют монотонную последовательность и а совокупности - при
любых х и п - ограничены:
\ап(х)\*&К.
Тогда ряд (W) сходится равномерно в области %.
Доказательство аналогично прежнему. Ввиду равномерной
сходимости ряда (В) номер N находится независимо от х, с ссылкой
на условие п° 429 (вместо принципа сходимости), а затем с помощью
леммы Абеля [383] получаем, как и выше (считая n>N):
2
ak(x)-bk(x)
2\an+m(x)\)*s3Ke,
сразу для всех х ш %. Этим наше утверждение доказано.
Признак Дирихле. Пусть частичные суммы Вп(х) ряда (В) в сово-
совокупности - при любых х и п — ограничены:
а функции ап(х) (при каждом х) образуют монотонную последователь-
последовательность, которая сходится к 0 равномерно в области %. Тогда
и ряд (W) сходится равномерно в этой области.
И здесь доказательство проводится так же, как и в 384. Отметим
лишь, что номер N можно выбрать независимо от х именно ввиду
равномерного стремления ап(х) к 0.
На практике часто на месте функциональной последова-
последовательности {ап(х)} оказывается обыкновенная числовая последо-
последовательность {ап} или на месте функционального ряда
1
- обыкновенный числовой ряд ~2Jbn. Нужно заметить, что этот
1
случай, конечно, входит как частный в рассмотренный выше; ведь
сходящуюся последовательность {ап} и сходящийся ряд
}п можно рассматривать как равномерно сходящиеся
1
(зависимости от х нет).
Например, если {ап} есть последовательность положительных чисел,
монотонно стремящихся к 0, то оба ряда
2^ап sin nx, 2jan cos их
л=1	п=1

430	гл. хп. функциональные последовательности и ряды	1431
- по признаку Дирихле - равномерно сходятся в любом зам-
замкнутом промежутке, не содержащем точек вида 2кж (где А; = 0, ±1,
±2, ...). Это следует из того, что, например [см. 385, 2)],
1	IV
cos—х-cos | п+—\ х ,
2
гх
1
2 sin — х
sm —х
и в названном промежутке sin - х не обращается в 0, так что для суммы
можно установить границу, не зависящую и от х.
Дальнейшие примеры применения признаков равномерной сходи-
сходимости читатель найдет в п° 439 и следующих.
§ 2. Функциональные свойства суммы ряда
431. Непрерывность суммы ряда. Мы переходим теперь к изучению
функциональных свойств суммы ряда, составленного из функций, в
связи со свойствами этих последних. Выше уже указывалось на экви-
эквивалентность точки зрения последовательностей и точки
зрения бесконечных рядов. В изложении мы отдаем пред-
предпочтение последней точке зрения, потому что в приложениях встре-
встречаются почти исключительно именно бесконечные ряды. Перенесению
сказанного о функциональных рядах на случай последовательностей
функций будет посвящен особый п° [436].
Введенное выше понятие равномерной сходимости во всем
дальнейшем будет играть решающую роль, так что важность его вы-
выявится с полной силой.
Начнем с вопроса о непрерывности суммы ряда, которого мы уже
касались в 427.
Теорема 1. Пусть функции ип(х) (и = 1, 2, 3, ...) определены в про-
промежутке X = [а, Ь] и все непрерывны в некоторой точке х = х0 этого
промежутка. Если ряд C) в промежутке X сходится равномерно,
то и сумма ряда f{x) в точке х = х0 также будет непрерывна.
[Подобное утверждение впервые было сформулировано К о ш и;
но знаменитый автор придал ему слишком общую форму, не выдви-
выдвинув требования равномерности, без которого оно перестает быть вер-
верным.]
Доказательство. Сохраняя прежние обозначения, имеем при
любом и = 1, 2, 3, ... и любом х из Ж:
/(*)=/„(*)+?>„(*)	(И)
и, в частности,
откуда
\/(х) -Л*„)| * \Ш ~fn(x0)\ + Ы*)| + Ы*о)|.	A2)

4311	§ 1. ФУНКЦИОНАЛЬНЫЕ СВОЙСТВА СУММЫ РЯДА	431
Зададимся теперь произвольным е>0. Ввиду равномерной схо-
сходимости ряда можно фиксировать номер п так, чтобы нера-
неравенство
\*е	A3)
выполнялось для всех значений х в промежутке X (в том числе
и для x = Xq). Отметим, что при фиксированном и функция fn(x) есть
сумма определенного конечного числа функций ик(х), непрерывных
в точке х = х0. Поэтому она также непрерывна в этой точке, и по за-
заданному е>-0 найдется такое <3>0, что при х-х0 -=<3 будет
A4)
Тогда, ввиду A2), A3) и A4), неравенство
бой
влечет за со-
что и доказывает теорему.
Естественно, если функции ип(х) непрерывны во всем промежутке
X = [а, Ь], то при наличии равномерной сходимости и сумма
ряда C), f(x), будет непрерывна во всем промежутке.
Что требование равномерной сходимости в тексте теоремы не может
быть опущено, показывает, например, ряд
[см. 428, 8)], сумма которого равна 1 при х * О и равна 0 при х = 0. Однако равно-
равномерная сходимость фигурирует в теореме лишь как достаточное условие,
и не следует думать, что это условие необходимо для непрерывности суммы
ряда*: например, ряды
2 2x[n2e-"'*1-(B-l)i!e-(n-i)'x'], 2 \——		-1	A5)
п=1	?iU + n*x" l+(n-lJ*2J
[ср. 428, 5) и 2)] в промежутке [0, 1] имеют непрерывную сумму 0, хотя оба в нем
сходятся неравномерно.
Впрочем, есть классы случаев, когда равномерная сходимость все
же оказывается необходимой. В этом направлении мы докажем сле-
следующую теорему, принадлежающую Д и н и (U. Dini).
Теорема 2. Пусть члены ряда C) непрерывны во всем промежутке
Х=[а,Ь] и положительны. Если ряд имеет сумму f(x), так-
также непрерывную во всем промежутке, то он сходится в этом про-
промежутке равномерно.
См. следующий п°

432	ГЛ. XII. ФУНКЦИОНАЛЬНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И РЯДЫ	D32
Доказательство. Рассмотрим остатки ряда C):
?>„(*)= 2 uk(x)=f(x)-fn(x).
Функция уп{х) от х, как разность двух непрерывных функций, также
непрерывна. Ввиду положительности членов ряда, последовательность
{(рп(х)}, при постоянном х, является убывающей (невозрастающей):
Наконец, поскольку ряд C) сходится в промежутке X, при любом по-
постоянном х
lim ц>п(х) = 0.
Для того чтобы установить равномерную сходимость ряда, доста-
достаточно доказать, что для каждого числа е>0 существует хоть одно
значение и, при котором срп(х)-<е одновременно для всех х (ибо тогда
для больших значений и это неравенство выполнялось бы и подавно).
Доказательство этого будем вести от противного. Предположим,
что для некоторого е >0 такого номера и не существует. Тогда
при любом и = 1,2, 3, ... в промежутке^ найдется такое значение
х = хп, что срп(хп)з*е. К последовательности {хп}, все элементы которой
содержатся в конечном промежутке X, применим лемму Больцано
-Вейерштрасса [41] и выделим из нее частичную последова-
последовательность {xnt}, сходящуюся к пределу х0.
Ввиду непрерывности <рт(х), имеем:
lim<pm(xnt)=<pm(x0),
каково бы ни было т. С другой стороны, при любом т, для доста-
достаточно больших к:
так что <рт{хп^»(рПк(хп^е.
Переходя здесь к пределу при &->¦¦», найдем, что
Ит<рт(хПк)=<рт(х0)»е.
А это неравенство, имеющее место при любом т, противоречит тому,
что
limcpm(x0) = 0.
Теорема доказана.
432. Замечание о квази-равномерной сходимости. Итак, если функциональный
ряд C) состоит из непрерывных в промежутке X - [а, Ь] функций и сходится в этом
промежутке к сумме fix), то для непрерывности этой последней достаточна

432|	§ 2. ФУНКЦИОНАЛЬНЫЕ СВОЙСТВА СУММЫ РЯДА	433
равномерная сходимость ряда, но - в общем случае - вовсе не необходима.
Было замечено еще Д и н и и другими, что достаточным условием является
некая «ослабленная» равномерность сходимости: она состоит в том, что для каж-
каждого числа е>• О и каждого номера N' существует хоть один не зависящий
от х номер п >N', такой, что неравенство F) выполняется одновременно для всех х
из X. Действительно, при доказательстве теоремы 1 мы и использовали лишь
один номер п, при котором неравенство A3) выполняется для всех х из X.
Однако даже эта «ослабленная» равномерность все же не является необхо-
необходимой для непрерывности суммы fix) ряда C). Она не имеет места, например,
для рядов {15), сходящихся к непрерывной сумме fix) = 0.
Арцела (С. Arzela) ввел в рассмотрение в 1883 г. особый тип сходимости
(впоследствии получивший название квази-равномерной сходимости),
который решает вопрос о точной характеристике сходимости ряда, обеспечи-
обеспечивающей непрерывность его суммы.
Про ряд C), сходящийся в промежутке X = [а, Ь], говорят, что он сходится
квази-равномерно в % к сумме f(x), если для каждого числа ?>0а каждого
номера N' промежуток X может быть покрыт к о не чны м числом открытых
промежутков
(alf ад, (в., *,),..., (в,-, ьд,..., (ак, ад,
и им в соответствие могут быть поставлены к номеров
пх, п2, ..., щ, ..., пк (*¦№)
так, что для всех значений х (из X), содержащихся в (о,-, Ь[) (/=1, 2, ..., А), не-
неравенство
|/(*)-/n,(x)| = |?4toH«
выполняется одновременно.
Т1ри упомянутой выше «ослабленной» равномерной сходимости всем значе-
значениям х из X ставился в соответствие один и тот же номер п, а здесь все х
разбиваются на группы, которым в соответствие ставятся разные значения п, но
всякий раз - в конечном числе.
Пользуясь этим понятием, Арцела установил следующее предложение:
Теорема 3. Пусть функции ип{х) определены и непрерывны в промежутке
X = [а, Ь], и ряд C) сходится в этом промежутке. Для того чтобы сумма ряда f(x)
также была непрерывна в X, необходимо и достаточно, чтобы ряд
сходился в X к f(x) квази-равномерно.
Необходимость. Предположим сначала непрерывность функции fix),
а значит и всех остатков <рп(х). Возьмем в X любую точку х'. По заданным
числам в и N для нее найдется такой номер л' >N, что
По непрерывности функции <рП'(х) подобное же неравенство
будет выполняться и в некоторой окрестности а'=(х'-д', х'+8') точки х'. Из всех
этих открытых промежутков а', построенных для всевозможных х' из X, соста-
составится некая бесконечная система 2> покрывающая промежуток X. Тогда,
по лемме Б о р е л я [88], из нее выделяется и конечная подсистема про-
промежутков
2* = {(г1, ст2, ..., ак),
28 Г. М. Фихтснгпльц, т. II

434	ГЛ. XII. ФУНКЦИОНАЛЬНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И РЯДЫ	[433
также покрывающая X. Эти промежутки и будут теми, о которых идет речь в
определении квази-равномерной сходимости.
Достаточность. Допустим теперь, что ряд C) сходится к своей сумме
/(*) квази-равномерно. Задавшись числами е и N', построим промежутки (а,-, 6,)
и выберем номера щ (i=l, 2, ..., к) с указанными в определении свойствами.
Возьмем по произволу в Сточку хп; пусть она содержится в промежутке (а,„, />/„).
Как и при доказательстве теоремы 1 [431 A2)], можем написать
-/(хо)\^\/„,(х)-Мх0)\ + \<рП((х)\ + \<рщ(хо)\.	A2а)
При этом, очевидно,
если х тоже принадлежит этому промежутку (я,„, 6,„), то и
\<Рт(х) | -= е.
Можно найти такое число <5 ^ О, что, при | х - х0 \ «= S, не только х содержится
в указанном промежутке, но и первое слагаемое в A2а) справа будет <=f, а значит
и непрерывность f(x) в точке х0 доказана *.
Из этой теоремы с легкостью выводится теорема Д и н и предыдущего п°.
Действительно, если ряд C) состоит из положительных непрерывных функций
и сходится к непрерывной же сумме, то, как мы видели, сходимость необходимо
будет квази-равномерной.
Пользуясь тем, что в данном случае остатки <рп(х) с возрастанием п убывают,
достаточно взять номер N бблыпим всех и, (/= 1, 2	к), чтобы для n>N не-
неравенство F) выполнялось одновременно для всех х из ЗС: сходимость оказывается
равномерной.
433. Почленный переход к пределу. Приведем еще одну теорему,
которая является обобщением теоремы 1. В ней X = {х} есть про-
произвольное бесконечное множество, имеющее точку сгущения а
(конечную или нет) [52]; эта точка сама может и не принадлежать
множеству.
Теорема 4. Пусть каждая из функций ип{х) (и= 1, 2, 3, ...) опре-
определена в области X и имеет, при стремлении х к а, конечный предел:
\\тип{х) = сп.	A6)
Если ряд C) в области X сходится равномерно, то 1) сходится
ряд, составленный из этих пределов:
2сп = С,	(С)
* Как читатель заметил, предположение, что все номера л,- могут быть выбраны
сколь угодно большими, на деле нигде не используется.

433]	§ 2. ФУНКЦИОНАЛЬНЫЕ СВОЙСТВА СУММЫ РЯДА	435
и 2) сумма ряда C), f(x), также имеет при х — а предел, именно:
C.	A7)
Доказательство. Согласно условию равномерной сходимо-
сходимости п° 429, для произвольно взятого е>0 существует такой номер N,
что при n>N и т — \, 2, 3, ... неравенство (8) выполняется для всех
х из X. Переходя здесь к пределу при х-»а с учетом A6), найдем,
что
так что для ряда (С) выполняется условие сходимости [376].
Если С, Сп и уп означают, как обычно, его сумму, частичную сумму
и остаток, то
С—С -4-v
v^ — к^п -г уп.
Вычитая это равенство почленно из A1), легко получить:
\Лх)-С\*\Мх)-Сп + \<рп(х)\ + |у„|.	A8)
Ввиду равномерной сходимости ряда C) и сходимости
ряда (С), по любому е>0 можно фиксировать и столь боль-
большим, чтобы для всех х из X было:
•	\yn{x)\<-z, а также |ул| <е.	A9)
Так как, очевидно,
limfn(x) = lim 2Чх)•= ДсЛ = Сп,
то - если ограничиться случаем конечного а - найдется такое <5=-0,
что при |х-а|<й будет:
:Р.	B0)
Тогда, при указанных значениях х, в силу A8), A9) и B0), будет
выполняться неравенство
|Д*)-С|*3е,
что и приводит к A7) *.
Равенство A7) можно написать в форме [см. A6)]:
lim 2"n(x)= 2"{lim
* Читатель узнает в этом рассуждении то, которое уже было применено для
доказательства теоремы 1.
28»

436	I Л. XII. ФУНКЦИОНАЛЬНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И РЯДЫ	[434
таким образом, при наличии равномерной сходимости, предел суммы
ряда равен сумме ряда, составленного из пределов его членов, или,
иными словами, в ряде допустим предельный переход почленно.
434. Почленное интегрирование рядов. Перейдем теперь к рассмо-
рассмотрению вопроса об интегрировании суммы сходящегося функциональ-
функционального ряда.
Теорема 5. Если функции ип(х) (и = 1, 2, 3, ...) непрерывны в про-
промежутке X = [а, Ь], и составленный из них ряд C) сходится в этом
промежутке равномерно, то интеграл от суммы f(x) ряда C)
представляется следующим образом:
\Лх)<1х= 2j«n(x)dx =
и	а
1>	Ь	Ь
= щ(х) dx+ \ м2(х) dx-r . . . т \ ип(х) (fci ...	B1)
а	а	а
Доказательство. Ввиду непрерывности функций ип(х) и /(х)
[431, теорема 1], существование всех этих интегралов очевидно. Про-
Проинтегрировав тождество
Дх) = и^х) + гфе) + .. . + ип(х) +<рп(х)
в промежутке [а, Ь], получим:
ll	Ь	b	Ь	Ь
J /(х) dx = J щ(х) dx + J щ{х) dx+ ... f J ип(х) dx + J <pn(x) dx.
a	a	a	a	<i
Таким образом, сумма п членов ряда B1) разнится от интеграла
f{x) dx дополнительным членом ) <рп(х) dx. Для доказательства раз-
а	а
ложения B1) нужно лишь установить, что
lim {<pn(x)dx = 0.	B2)
В силу равномерной сходимости ряда C), для любого е>0 най-
найдется номер N такой, что при п >N

434]	§ 2. ФУНКЦИОНАЛЬНЫЕ СВОЙСТВА СУММЫ РЯДА	437
сразу для всех х в рассматриваемом промежутке. Тогда для тех же
значений и будет:
J<Pn(x)dx =sJ \q>n(x)\dxt(b-a)-e,
что и доказывает предельное соотношение B2).
Равенство B1) может быть написано в виде
J ^ 2ип(хЦ dx = Д | J un(x) dxj,
так что в случае равномерно сходящегося ряда интеграл от суммы
ряда равен сумме ряда, составленного из интегралов его членов, или,
иными словами, допустимо почленное интегрирование ряда.
Как ц в случае теоремы 1, требование равномерной сходимости суще-
существенно для верности разложения B1), т. е. не может быть просто опущено,
но все же не является необходимым. Ряды A5), рассмотренные в 431,
как раз и иллюстрируют это обстоятельство. Оба они в промежутке [0, 1] сходятся
к функции fix) = О неравномерно. Но, интегрируя первый почленно, мы
в качестве суммы ряда интегралов получим
lim 2«s
lim 2«sx-e-n!-\J<fc = lim(l-e-4')=l, хотя
для второго же ряда аналогично найдем
1	1
г их In A + л2)	г
lim 	dx = lim 	= 0= \ f(x) dx.
n-~.J \+П2Х2	п-- In	J
о	n
Любопытен пример ряда
1
Здесь
так что ряд можно интегррпзовать почленно, хотя при х = 1 он и вовсе рас-
расходится.
Укажем теперь обобщение теоремы 5, связанное с отказом от
требования непрерывности рассматриваемых функций.
Теорема 6. Если функции ип(х) (и= 1, 2, 3, ...) интегрируемы * в
промежутке X — [а, Ь], и составленный из них ряд C) сходится равно-
* В смысле п° 295.

438	I Л. XII. ФУНКЦИОНАЛЬНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И РЯДЫ	[435
мерно, то сумма f{x) ряда также будет интегрируема, и имеет
место разложение B1).
Доказательство. Остановимся на интегрируемости функ-
функции f(x).
Ввиду равномерной сходимости ряда, по заданному наперед е, мы
можем фиксировать п столь большим, чтобы во всех точках
промежутка [а, Ь] было:
\f(x)-fn(x)\ <| или /„(*)-|</(х) </„(*)+|.	B3)
Возьмем какую-нибудь часть [a, fl промежутка [а, Ь], и пусть т, М
будут точные границы функции fn{x) в [a, /S], a ю = М-т - ее коле-
колебание; соответствующее колебание функции /(х) обозначим через Q.
Ввиду B3), в пределах промежутка [к, /5]:
т — ~<j{x)-^М — х, так что iJ=so> +е.
Разобьем теперь промежуток [а, Ь] обычным образом на частич-
частичные промежутки [xj, xi+i] и станем значком i отмечать колебания, от-
относящиеся к /-му промежутку. Тогда ??,=sa>, + ?, и
]?Q[ • Ах^^са! • Axj + e(b - а).
i	i
Так как второе слагаемое справа произвольно мало, а первое стре-
стремится к нулю вместе с ?. = max Axt, то это же справедливо и относи-
относительно выражения слева, откуда и следует интегрируемость функции
/00 [297 (8)].
Что же касается равенства B1), то оно доказывается буквально
так же, как и выше.
Покажем на примере, что при нарушении равномерности ряд, состоящий
из интегрируемых функций, может иметь неинтегрируемую сумму. Положим ип(х)
(для я=1, 2, 3, ...) равным 1, если х выражается несократимой дробью
т
—, и равным 0 - в прочих точках промежутка [0, 1]. Эти функции, имеющие
п
лишь конечное число разрывов, интегрируемы в [0, 1], а суммой ряда будет ча-
ведомо неинтегрируемая функция Дирихле [300, B)].
Вместе с тем, разумеется (мы это видели на примерах), равномерная сходи-
сходимость не является необходимым условием для интегрируемости суммы
ряда, составленного из интегрируемых функций. И для этого случая А р ц е л а
указал условие, одновременно необходимое и достаточное («квази-
(«квазиравномерная сходимость вообще»), ср. п° 432.
435. Почленное дифференцирование рядов. С помощью теоремы 5
предыдущего п° легко доказывается следующая
Теорема 7. Пусть функции ип(х) (и = 1, 2, 3, ...) определены в про-
промежутке % = [а, Ь] и имеют в нем непрерывные производные и'п(х).

4351	§ 2. ФУНКЦИОНАЛЬНЫЕ СВОЙСТВА СУММЫ РЯДА	439
Если в этом промежутке не только сходится ряд C), но и р а в но-
номе р н о сходится ряд, составленный из производных:
2!u'n(x) = ui(x) + U2(x) + • ¦ • + u'n{x) + ...,	B4)
л=1
то и сумма f(x) ряда (З) имеет в X производную, причем
2и'п(х).	B5)
Доказательство. Обозначим через f*(x) сумму ряда B4);
ввиду теоремы 1, это будет непрерывная функция от х. Воспользо-
Воспользовавшись теперь теоремой 5, проинтегрируем ряд B4) почленно в про-
промежутке от а до произвольного значения х из X; мы получим
\f*(t)dt=z\u'n(t)dt.
J	n=lJ
а	а
х
Но, очевидно, I u'n{t) dt = ип(х) - ип(а), так что
= 2К(х) - ип(а)} = JX(x) - JX(a)
л=1	л=1	п=1
а
[Это преобразование оправдано наперед известной сходимо-
сходимостью рядов 2ип(х) и 2un(fl)> CM- 364, 4°.] Так как интеграл слева,
ввиду непрерывности подинтегральной функции, имеет производную,
равную f*(x) [305, 12°], то ту же производную имеет и функция f{x),
которая от интеграла отличается лишь на постоянную.
Равенство B5) можно переписать (если воспользоваться, следуя
К о ш и, обозначением D для производной) в виде
Таким образом, при указанных условиях, производная от суммы ряда
оказывается равна сумме ряда, составленного из производных его
членов, или, иными словами, допустимо почленное дифференци-
дифференцирование ряда,

440	ГЛ. XII. ФУНКЦИОНАЛЬНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И РЯДЫ	[435
Рассмотрим ряды
ln(l+;^2[;rln(l + «*)in
2	2	2A)
Первый из них сводится к 0 при х = 0 и к 1 в остальных точках, а сумма второго
везде равна 0. Если продифференцировать их почленно, то получатся уже знако-
знакомые нам ряды A5) [431], сходящиеся во всем промежутке [0, 1] к 0, но оба н е-
равномерно. В первом случае ряд из производных сходится и при х = 0,
где сумма первоначального ряда производной иметь не может, ибо разрывна
в этой точке. Во втором случае, наоборот, почленное дифференцирование повсюду
приводит к верному результату. Этими примерами иллюстрируется роль требо-
требования, чтобы ряд производных сходился равномерно: оно существенно,
но не необходимо.
Теорема 7 может быть освобождена от некоторых лишних пред-
предположений ценою небольшого усложнения доказательства.
Теорема 8. Пусть функции ип(х) (и= 1, 2, 3, ...) определены в про-
промежутке X = [а, Ь] и имеют в нем конечные производные и'п(х). Если
ряд C) сходится хоть в одной точке, например при х = а, а ряд B4),
составленный из производных, равномерно сходится во всем
промежутке ЭС, то тогда 1) ряд C) сходится равномерно во
всем промежутке и 2) его сумма f(x) имеет в X производную, вы-
выражаемую равенством B5).
Доказательство. Возьмем в промежутке [а, Ь] две различ-
различные точки х0 и х и составим ряд
Д —о •	B6)
Мы докажем, что при любом фиксированном х0 этот ряд сходится
для всех х9^х0 и притом равномерно относительно х.
С этой целью, задавшись произвольным числом е>0, ввиду рав-
равномерной сходимости ряда B4), найдем такой номер N, что при
я >N и т = 1, 2, 3, ... неравенство
п+т
> и I
JLa n\
B7)
выполняется для всех значений х одновременно. Фиксируя на момент
пят, рассмотрим функцию
п+т
[/(х)= 2 "*(*);
*=л+1
ее производная
k=n+l

436J	§ 2. ФУНКЦИОНАЛЬНЫЕ СВОЙСТВА СУММЫ РЯДА	441
в силу B7), по абсолютной величине всегда <е. Но, очевидно,
п+т ип(х) - «„(*„) _ Ц(х) - Щх0)
у- у	v-y
X Хо	X Хо
где с содержится между х0 и х [по теореме Лагранжа, 112]. По-
Поэтому, окончательно, для всех
n+m un{x)-un(xa)
ПГ+i x~xo
I
так как это неравенство имеет место, лишь только n>N, каково бы
ни было т = 1, 2, 3, ..., то равномерная сходимость ряда B6)
этим доказана. Отсюда уже вытекают все нужные нам заключения.
Прежде всего, взяв хо = а, из равномерной сходимости ряда
^, ип(х) - ип(а)	^,г , N , Ч1
2 '	' а с ним и 2Шх) - ип{а)]
[см. следствие п° 429], и из сходимости ряда 2ип(а) заключаем о
равномерной же сходимости ряда 2ип(х)-
Если через f(x) обозначить его сумму, то суммой ряда B6), где
х0 есть снова любое значение х в промежутке [а, Ь], - очевидно, бу-
дет j	. Так как в равномерно сходящемся ряде можно пере-
переходить к пределу почленно (по теореме 4), то, устремляя х к х0,
получим:
/'(*„)= lim ^-^= 2 I lim и^р^-\ = i -и^0), ч. и тр. д.
Замечание. Все эти теоремы о почленном предельном пере-
переходе, почленном интегрировании и дифференцировании устанавливают
аналогию между функциональными рядами и суммами конечного
числа функций. Аналогия эта, однако, ограничена известными усло-
условиями, в характеристике которых равномерная сходимость
занимает исключительное место.
436. Точка зрения последовательности. Представляет интерес пере-
перефразировать полученные результаты с точки зрения последователь-
последовательности функций. Это позволит отчетливо поставить в связь рассматри-
рассматриваемые вопросы с общим вопросом о перестановке двух
предельных процессов, который играет столь важную роль

442	ГЛ. XII. ФУНКЦИОНАЛЬНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И РЯДЫ	[436
во всем анализе. С другой стороны, наметится и путь к обобщению
этих результатов.
Итак, мы снова сопоставляем последовательность функций A) и
функциональный ряд C), считая, что они связаны соотношениями:
/„(*)=!«*(*) («=1,2,3,...)
или равносильными им:
щ{х) = Л(х), ип(х) = /„(*) - Гп-г{х) (п = 2, 3, ...).
Предельная функция для последовательности есть то же, что и сумма
соответствующего ряда. Равномерная сходимость может иметь место
лишь одновременно и для последовательности, и для ряда.
I. Рассмотрим сначала вопрос о пределе упомянутой предель-
предельной функции. Пусть множество ЗС = {х}, в котором определены все
рассматриваемые функции, имеет точкой сгущения а. Тогда теорема
4 п° 433 перефразируется так:
Теорема 4*. Если функции fn(x) имеют пределы
lim/„(*) = /(*) (х из X)	B8)
lim/„(*) = С„ (« = 1,2,3,...),	B9)
x-~a
причем в первом случае стремление к пределу происходит равно-
равномерно относительно х {в %), то существуют оба конечных пре-
предела
НтДх) и limCn,
х—а	л-» —
которые равны между собой.
Равенство
lim/(x)= lim С„,
х-*а	л —о»
если принять во внимание B8) и B9), может быть переписано так:
lim lim/„(*)= lim lim/„(a-).
x-~an-*°°	n-~°°x-*a
Таким образом, рассматриваемая теорема устанавливает для функ-
функции fn(x) от двух переменных, х и и, условия существования и
равенства двух повторных пределов и непосредственно примыкает
к исследованиям п° 168.
Предоставляем читателю перефразировать для последовательно-
последовательностей и две теоремы п° 431.

436]	§ 2. ФУНКЦИОНАЛЬНЫЕ СВОЙСТВА СУММЫ РЯДА	443
П. Теперь пусть область % представляет собой промежуток \а,Ъ\
и рассмотрим вопрос об интеграле предельной функции. Вот
аналог теоремы 6 [434]:
Теорема 6*. Если последовательность {fn(x)} состоит из функций,
интегрируемых в промежутке [а, Ь], и сходится к своей предельной
функции f(x) равномерно относительно х в [а, Ь], то функция
f(x) будет интегрируема в [а, Ь], причем
а	о
Последнее равенство перепишем в виде:
ь	ь
lim Г/„(х) dx = Г flim /„(*)} dx,	C0)
так что предел, относящийся к интегралу, оказывается возможным
отнести непосредственно к подинтегральной функции. В этом случае
говорят, что допустим предельный переход под знаком инте-
интеграла.
В равенстве C0) переставляются знаки предела и интег-
интеграла. Так как определенный интеграл также получается в резуль-
результате некоего предельного процесса, то рассматриваемый здесь во-
вопрос оказывается родственным тому, который изучался в 168.
III. Наконец, перейдем к вопросу о производной предель-
предельной функции. Перефразируем теорему 8 [435]:
Теорема 8*. Пусть все функции fn{x) дифференцируемы в проме-
промежутке [а, Ь], и последовательность производных {/„'(*)} сходится во
всем промежутке, равномерно относительно х. Если известно,
что последовательность функций {/„(*)} сходится хоть в одной точке
промежутка [а, Ь], то можно утверждать, что 1) эта последова-
последовательность сходится во всем промежутке, и даже равномерно,
2) предельная функция f(x) дифференцируема, причем
Если переписать это равенство более выразительно:
то сразу станет ясно, что речь идет о перестановке знаков предела
и производной. Так как производная также есть предел, то
и этот вопрос связан с перестановкой двух предельных переходов.
В заключение заметим следующее. Если стоять на точке зрения
бесконечного ряда, то натуральный параметр п, естественно, не мо-

444	ГЛ. XII. ФУНКЦИОНАЛЬНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И РЯДЫ	|437
жет быть заменен более общим. Иначе обстоит дело, если речь идет
о последовательности функций. Здесь функция fn{x) может быть за-
заменена функцией f(x, у) от двух переменных, где у изменяется в про-
произвольной области °Ц = {.)>}, имеющей точкой сгущения число у0 (ко-
(конечное или нет). Предельный переход при л->-~ заменяется предель-
предельным переходом при у—у0. Формулировка и доказательство теорем,
относящихся к этому общему случаю, не представляют трудности.
К некоторым из этих обобщений мы вернемся ниже, в главе XIV.
437. Непрерывность суммы степенного ряда. Важнейшим примером
применения всей изложенной теории является изучение свойств сте-
степенных рядов. Мы ограничимся степенными рядами вида
2,апхп = а0 + агх + агх2 + ... + апхп t . ..,	C1)
ибо, как мы видели в 403, ряды более общего вида
Zan(x - хоу = а0 + а?х - х0) + <фс - xof + ... + ап{х - х0)" +... C1 *)
л=0
непосредственно приводятся к виду C1) простой заменой переменной.
Пусть ряд C1) имеет радиус сходимости /?>0 [379].
Прежде всего, можно утверждать:
1°. Какое бы положительное число r<R ни взять, ряд C1) будет
сходиться равномерно относительно х в замкнутом промежутке
Действительно, так как r<R, то при х = г ряд C1) сходится аб-
абсолютно, т. е. сходится положительный ряд:
2\ап\ • гп=\а0\ + \ах\ • г + \аг\ • г2 + ... + \ап\ -гп+ ... C2)
л=0
При [х]==г члены ряда C1) по абсолютной величине не превосходят
соответствующих членов этого ряда, который, таким образом, играет
роль мажорантного ряда, и по признаку Вейерштрасса
ряд C1) для указанных значений х сходится равномерно.
Хотя число г и может быть взято сколь угодно близким к R, но
из доказанного все же н е вытекает равномерная сходимость в про-
промежутке [-R, R]. На примере прогрессии [428, б)] читатель видит,
что как раз концы промежутка сходимости могут оказаться т о ч-
ками неравномерности.
Теперь, как следствие теоремы 1, получаем:
2°. Сумма f(x) степенного ряда C1) для всех значений х между
- R и R представляет собой непрерывную функцию от х.

437]	§ 2. ФУНКЦИОНАЛЬНЫЕ СВОЙСТВА СУММЫ РЯДА	445
Какое бы значение х = х0 внутри промежутка сходимости ни взять,
можно выбрать число г-^R так, чтобы было |дго| -=г. Применив тео-
теорему 1 в промежутке [ - г, г], ввиду 1°, установим непрерывность функ-
функции fix) в этом промежутке, следовательно, в частности, и при
X — Хо.
[Обращаем внимание читателя на то, что мы избежали примене-
применения теоремы 1 в промежутке ( — R, R), где равномерная сходимость
не может быть гарантирована.]
Непрерывность суммы степенного ряда может быть использована
для доказательства теоремы о тождестве степенных
рядов (напоминающей подобную же теорему для многочленов):
3°. Если два степенных ряда
2,
п = 0
1 = a0 + axx + a<pc2 4- ... 4- anxn + ...
1 = Ь0 + Ь±Х 4- Ь2Х2 4- ... + ЬпХп 4- ...
в окрестности точки х = О* имеют одну и ту же сумму, то эти ряды
т о ж д с с т в е и н ы, т. е. соответственные коэффициенты их по-
попарно равны:
Полагая х = 0 в тождестве
а0 4- ахх 4-... = Ьо 4- Ьхх + ...,
сразу убеждаемся в равенстве ао — Ьо. Отбрасывая эти члены в обеих
частях написанного тождества и деля их на х (в этом случае
мы вынуждены считать х^О), получим новое тождество
аг + а^х 4-... = bx -t- b2x + ... ,
которое также имеет место в окрестности точки х = 0, но исклю-
исключая саму эту точку. Не имея права положить здесь х = 0, мы,
однако, можем устремить х к 0; в пределе, пользуясь непрерывно-
непрерывностью, мы все же получим, что % = &!¦ Отбрасывая эти члены и снова
деля на х^О, при х-*0 найдем, что a<l = b2, и т. д.
Эта простая теорема, устанавливающая единственность
разложения функции в степенной ряд, имеет частые применения. С ее
помощью, например, сразу устанавливается, что разложение четной
(нечетной) функции в степенной ряд вида C1) может содержать лишь
четные же (нечетные) степени х.
* Здесь имеется в виду не только двусторонняя окрестность (- 6,
точки д- = 0, но и односторонняя окрестность вида [0, <5) или (- '5, 0].

446	ГЛ. XII. ФУНКЦИОНАЛЬНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И РЯДЫ	[437
Рассмотрим теперь более тонкий вопрос о поведении ряда вблизи
одного из концов x=±R его промежутка сходимости (считая
впредь этот промежуток конечным). Мы можем ограничиться пра-
правым концом x = R; все сказанное о нем, с помощью простой замены
х на -х, переносится и на случай левого конца х= -R.
Прежде всего ясно, что
4°. Если степенной ряд C1) на конце x = R его промежутка сходи-
сходимости расходится, то сходимость ряда в промежутке [О, R)
не может быть равномерной.
Действительно, при наличии равномерной сходимости, можно было
бы, по теореме 3, перейти в нашем ряде к пределу при x—R-0 по-
почленно, и тем установить сходимость ряда из пределов:
2,anRn = a0 + a1R + a2R?+ ... +anRn+ ...,
л=0
вопреки предположению.
Имеет место и следующая, в некоем смысле — обратная теорема:
5°. Если степенной ряд C1) сходится и при x = R {хотя бы и не-
неабсолютно), то сходимость ряда будет необходимо равномерной
во всем промежутке [О, R].
Действительно, если представить ряд C1) в виде
л=0	\
то требуемое заключение непосредственно вытекает из признака
™	(х\п
Абеля, так как ряд ]?anRn сходится, а множители -= образуют
л=0	\К)
монотонную и равномерно ограниченную последовательность
Доказанное предложение позволяет применить теорему 1 ко всему
промежутку [О, R]. Таким образом, в виде дополнения к теореме 2°
о непрерывности суммы степенного ряда в открытом промежутке
(-R, R), мы получаем такую теорему (принадлежащую Абелю)*:
6°. Теорема Абеля. Если степенной ряд C1) сходится при x = R,
то его сумма сохраняет непрерывность и при этом значении х (разу-
(разумеется слева), т. е.
lim 2<*пХп = 2апКп-
X— R-0 0	О
* Другое доказательство этой теоремы (в предположении #=- 1) мы дали и
п° 418 - в связи с вопросом о регулярности метода Пуассона- Абеля
суммирования расходящихся рядов.

438]	S 2. ФУНКЦИОНАЛЬНЫЕ СВОЙСТВА СУММЫ РЯДА	447
Теорема Абеля имеет важные приложения.
Если для функции f{x) получено разложение в степенной ряд лишь
в открытом промежутке (— R, R):
но функция сохраняет непрерывность, а ряд продолжает сходиться, -
и на каком-либо из концов этого промежутка, например, при x = R,
то разложение остается верным и для этого кон-
конца. В этом легко убедиться, переходя в написанном равенстве к пре-
пределу при x—R-0.
Таким образом, например, получив разложение
*-?-+^--...+(-iy-1 — +...
2 3	п
лишь для - 1 -= а- -= 1, но, зная, что ряд
1 1	1
i(iy.+
сходится, заключаем, что сумма его есть In 2. Точно так же оправдывается и утвер-
утверждение п° 407 о том, что биномиальный ряд
т(т-\)	m(m - 1)(т - 2) • ...•
1 + П7Х+2++
Ь2	Ь2-3	п
и при х= + 1 имеет своей суммой A +л;)т,если только ряд оказывается сходящимся.
р ^
438. Интегрирование н дифференцирование степенных рядов. При-
Применим теперь к степенным рядам теоремы пп° 434 и 435.
Сопоставляя доказанные уже свойства 1° и 5° с теоремой 5 п° 434,
получим:
7°. Степенной ряд C1) в промежутке [0,х], где \x\<R, всегда
можно интегрировать почленно, так что
.. +^х»+ ...	C3)
Значение х здесь может совпадать и с одним из концов промежутка
сходимости, если на этом конце ряд C1) сходится.
Переходим к вопросу о дифференцировании степенного ряда.
8°. Степенной ряд C1) внутри его промежутка сходимости можно
дифференцировать почленно, так что
ео
"~1 - ...	C4)

448
ГЛ. XII. ФУНКЦИОНАЛЬНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И РЯДЫ
[438
Утверждение сохраняет силу и для конца промежутка сходимо-
сходимости, если только написанный ряд на этом конце сходится.
Возьмем любое х внутри промежутка сходимости исходного
\\	\\	\\
ряда, так что \х\ <R, и вставим число г' между \х
Ввиду сходимости ряда
и R: \x\
...+anr'n
его общий член ограничен:
= const; и = 1, 2, 3, ...).
Тогда для абсолютной величины и-го члена ряда C4) получается
оценка
аг,
х]"-1 = н|ап| • r'n•
л-1
У^У
и-1
Ряд
... + п
л-1
сходится; в этом легко убедиться с помощью признака Д а л а м-
б е р а [368], если учесть, что |—j -= 1. В таком случае абсолютно схо-
i r
дится ряд C4). Отсюда ясно, что радиус сходимости R' этого ряда
не меньше R.
Если теперь взять любое r<R, то одновременно и г<R'; в
силу Г ряд C4) равномерно сходится в промежутке [ - г, г],
так что - по теореме 7 п° 435 - в этом промежутке допустимо по-
почленное дифференцирование ряда C1). Так как r<R произвольно, то
основное утверждение теоремы доказано.
В случае сходимости ряда C4), скажем, при x = R, эта сходимость
равномерна [5°] в промежутке [О, R], и теорема 7 приложима
ко всему этому промежутку - почленное дифференцирование оказы-
оказывается допустимым и при x = R.
Замечание. Мы убедились в том, что R's*R. С другой сто-
стороны, члены исходного ряда C1) не превосходят по абсолютной ве-
величине соответственных членов ряда
2}
п=1
= агх +
... + папхп + ...,
имеющего тот же радиус сходимости R', что и ряд C4). Следова-
Следовательно, Rs^R'. Таким образом, окончательно, R' = R: радиусы схо-
сходимости степенного ряда C1) и ряда C4), полученного из него почлен-
почленным дифференцированием, совпадают. Это, впрочем, легко устанавли-

438J	§ 2. ФУНКЦИОНАЛЬНЫЕ СВОЙСТВА СУММЫ РЯДА	449
вается и с помощью теоремы Коши-Адамара [380], если вспом-
п
нить, что Ул"-»1 при и-*-°° [32, 10)].
Так как ряд C1) получается почленным дифференцированием из
ряда C3), то и эти ряды имеют один и тот же радиус сходимости.
Последняя теорема 8° открывает возможность последовательно
многократного дифференцирования степенного ряда. Таким
образом, по-прежнему обозначая Через f(x) функцию, представляемую
степенным рядом C1) в его промежутке сходимости, будем иметь
повсюду внутри этого промежутка:
... + anxn + ...
f'(x) = 1 • ax + 2 • а%х + 3 • a3x2 + ... + и • «„x" + ...
f"(x) = l-2'O2 + 2-3'a.ix+ ... +{n-\)-n-anxn-2+ ...
/"'(*) = 1-2-3-a3+ ... +(n-2)(n-l)n-anx"-3+ ...
fw(x)=l -2-3 •... -(л-1). пап+ ...
Если положить во всех этих равенствах х = 0, то придем к хорошо
нам знакомым выражениям коэффициентов степенного ряда:
a2=q, *=q, .... an=, ...
[ср. 403 G)]. Если бы речь шла о ряде общего вида C1*), то лишь
пришлось бы здесь вместо значения х = 0 подставить х = х0. Итак:
9°. Функция, представляемая степенным рядом в его промежутке
сходимости, имеет внутри этого промежутка производные всех по-
порядков. Самый ряд, по отношению к этой функции, является не чем
иным, как ее рядом Тейлора.
Это замечательное предложение проливает свет на вопросы раз-
разложения функций в степенные ряды, которыми мы занимались в пре-
предыдущей главе. Мы видим, что если функция вообще разлагается
в степенной ряд, то необходимо - в ряд Тейлора; поэтому-то мы
и ограничивались исследованием возможности для функции быть
представленной именно своим рядом Тейлора. Заметим, что функ-
функция, которая разлагается в ряд Тейлора по степеням х-х0, на-
называется аналитической в точке х0.
29 Г. М. Фихтенгольц, т. II

450	ГЛ. XII. ФУНКЦИОНАЛЬНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И РЯДЫ	[439
Изложенная теория распространяется и на кратные степенные
ряды. Остановимся для определенности на ряде с двумя переменными:
2 ik
t,k=O
Внутри области сходимости [396] такой ряд также можно почленно
дифференцировать по любой из переменных и любое число раз. От-
Отсюда, как и только что, легко получаются выражения для коэффици-
коэффициентов
a -f(x уЛ а -Жхо'У^ а _
aw>-J\xo> Уо)> "м-: ^ » 1
„ _1 дУ(х0, у0)
^°~2! дх* ' "•
и, вообще,
1
'* ИМ
, у„)
ИМ дх'ду" '
Таким образом, разложение функции f(x, у) (если только оно воз-
возможно) необходимо имеет вид
их v\- У l di+kf(-x»> yJ(x vVCv vV
J(x, у)- ?ом dxidyk (x-xj (y-y0) .
И этот ряд называется рядом Тейлора; он естественно примы-
примыкает к формуле Тейлора, о которой была речь в 195. При на-
наличии такого разложения функция f(x,у) называется анали-
аналитической в точке (х0, у0).
§ 3. Приложения
439. Примеры на непрерывность суммы ряда и на почленный переход к пределу.
1) Исследовать на непрерывность суммы ряда
/с*)- 2
в предположении, что^-^э=0 и один из этих показателей »1 (чем обеспечивается
сходимость ряда для всех значений х). Очевидно, достаточно ограничиться неотри-
неотрицательными х.
Если р>\, то для x*sxa (xo>Q - любое число) ряд мажорируется сходя-
сходящимся рядом
ХC ?j I »
п=1ПР
следовательно, по признаку Вейерштрасса сходится равномерно, и его
сумма в промежутке [0, д;0] непрерывна. Ввиду произвольности х0 это относится
ко всему промежутку [0, +~)-

439)	§ 3- приложения	451
Если же p«sl, но д =-1, то, переписав ряд, для х =-0, в виде
1
2
л=1
заключаем, по предыдущему, о непрерывности его суммы для всех х=-0. Таким
образом, нужно лишь решить вопрос о точке х = 0.
Методами дифференциального исчисления можно установить, что л-й член
ряда достигает своего наибольшего значения при х = п 2 и это значение равно
1 1
п 2
Если p+q>2, то наш ряд мажорируется сходящимся рядом
2 n=i т.
п 2
чем обеспечивается непрерывное ь функции fix) для всех х, включая точку
Остается открытым вопрос о непрерывности f(x) при х = 0 в случае, если
р«= 1, G=-1, но p + qss.2. Мы увидим ниже [491, 13)], что при этих условиях функция
fix) в точке х = 0 имеет разрыв.
2) Рассмотрим ряд Дирихле [385, 3)]
2 —
где {ап} — некоторая последовательность вещественных чисел. Предположим,
что он не будет «всюду расходящимся», так что для него существует пограничная
абсцисса сходимости А-= +~. Какое бы число хо>А ни взять, ряд
¦у оп
л~1^
сходится. Отсюда можно заключить, что рассматриваемый ряд сходится равно-
равномерно для всех xs^xa [аналог теоремы 1°, 437]. Это утверждение следует из
признака Абеля, если переписать наш ряд в виде
У пп . *
и заметить, что множители 	убывают с возрастанием п, будучи все вместе
ограничены единицей. А тогда, по теореме 1, сумма ряда будет непрерывна для
х^х0, а следовательно (ввиду произвольности х0), - для всех х=>А [аналог тео-
теоремы 2°].
29*

452	ГЛ. XII. ФУНКЦИОНАЛЬНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И РЯДЫ	[439
Если X конечно, и ряд
у о-п
сходится, то таким же образом убеждаемся в равномерной сходимости рассматри-
рассматриваемого ряда для х=&/1 [ср. 5°] и в непрерывности его суммы при х=1 справа
[ср. 6°].
3) В п° 390, 6), определив функцию Е(х) равенством
л=1 и!
мы убедились в том, что она удовлетворяет такому соотношению:
Е(х+у) = Е(х)-Е(у).	A)
Теперь, согласно теореме 2°, 437, функция Е{х) оказывается непрерывной
во всем промежутке от - ~ до + <=. В силу же доказанного в 75, Г, непрерывное
решение уравнения A) необходимо имеет вид: Е(х) = ах. Наконец, основание а,
очевидно, определится равенством
у 1
л=1 и!
Итак, окончательно, Е(х) = ех [ср. 404 A1)].
4) Дадим новую трактовку биномиального ряда [407 B2)]
1 + тяН	хг-\	х*+ ... Н	хп+ ...,
Ь2	Ь2-3	1-2.....И
который абсолютно сходится при любом т, если | х \ ¦<¦ 1. Поставим задачей опре-
определить его сумму. Обозначим эту сумму как функцию от т (при фиксированном х,
\х\ -= 1) через <р(т).
Из элементов алгебры известно, что при любом натуральном т (ряд
тогда обрывается на (т+1)-м члене) <р(т) = A + х)т; покажем же, что это верно
для всех т.
Взяв любое к, рассмотрим подобный же ряд
Kk-i) ' Цк-Ш-2)	к(к-1)-...-(к-п+1)
х2-\	х3+...Н	хп+ ...
х+х+...+
L2	1-2-3	1.2
с суммой (р(к) и перемножим оба ряда по правилу К о ш и. Нетрудно написать
несколько первых членов этого произведения:
rm(m-l)	/t(/t-l)
1 +(т+к)х+
хп
Коэффициентом при — будет, очевидно, некий целый многочлен и-й степени
л!
относительно т и к. Каков вид его? Если т и к - любые натуральные

439]	§ з. приложения	453
числа, большие я, то из элементарных соображений явствует, что названный коэф-
коэффициент будет
(т+к){т+к-\).. .(т+к-
Следовательно (как это вытекает из алгебраической теоремы о тождестве целых
многочленов с двумя переменными), этот же вид он будет иметь при любых
тик. Итак, искомая функция <р(гп) удовлетворяет функциональному соотно-
соотношению
<р(т)-<р(к)=<р(т+к).
Установим теперь непрерывность функции<р(т). Это следует из равно-
равномерной сходимости биномиального ряда для всех значений т, не превосходящих
по абсолютной величине произвольно взятого числа /яо=»О: для этих значений
он мажорируется сходящимся рядом
m0(m0+l)(ra0+2)
с|* +|дс|3+
+	|дс| +1 2
В таком случае, как мы знаем [75, 1°], необходимо
<р(т) = ат.
Так как а=<рA)= 1+х, то окончательно
5) Известный уже читателю логарифмический ряд [405 A7)] можно получить
из биномиального ряда [407 B2)], с помощью соотношения [77, 5 (б)]
к _
lne=lim*(ye-l) (*=1, 2, 3, ...)
Положим а=1 + х (где |х|«=1) и подставим вместо A+дс)* его разложение
Тогда In A+х) представится как предел при &-«= выражения
Члены этого ряда (при постоянном х) содержат, в качестве переменной,
натуральный параметр к. Во всей области его изменения ряд B) сходится равно-
равномерно относительно к; это (по признаку Вейерштрасса) следует из
того, что он мажорируется рядом
|х|2 \х\3	\х\п
\x\ + -^-+1^-+...+—L-+... (x=const, |jc|<1),
2 3	п

454	ГЛ. XII. ФУНКЦИОНАЛЬНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И РЯДЫ	[439
уже не содержащим к. В таком случае, по теореме 4*, в ряде B) можно перейти
к пределу при А-»~ почленно, что и приводит к логарифмическому ряду.
6) Интересный пример того же рода дает вывод показательного ряда [404 A1)]
из соотношения
(х\к
1+- (*=1, 2, 3, ...)
к
Имеем, разлагая степень бинома по формуле Ньютона,
к
ы -
х\п
На деле здесь, при каждом к, членов всего лишь конечное число (
но мы можем считать, что пред нами «бесконечный ряд», если остальные члены
положить равными 0. Этот «ряд» сходится равномерно для всех к, ибо,
очевидно, сходящийся ряд
служит для него мажорантным. В таком случае по теореме 4 в «ряде» C) можно
перейти к пределу при &-~ почленно. Так как (и+1)-й член этого ряда,
равный 0, покуда к^п, при всех ks&n имеет уже вид
1
к
хп
то его предел при к - «> есть — . Таким путем мы приходим вновь к разложению
л!
показательной функции ех.
7) Исходя из формулы М о а в р а, мы уже вывели в 408 формулу
m(m-l)(m-2)
sin mz = mcosm~1 z-sin z	cosm~3z-sin3z+ ...
Покажем, как отсюда может быть получено разложение функции sin x в степенной
ряд.
х	х
Положим z-— и вынесем cosm— за скобки; наша формула перепишется
т	т
в виде:
х\ х ( 1Л( 2
-W	1	1
т [ т \ т)\ т
+ ...
Считая х неизменным, перейдем в ней справа к пределу при /«-<*>.
* Напомним, что область изменения % переменной х, о которой шла речь
в теореме 4, могла быть какой угодно; в частности, она могла свестись и к нату-
натуральному ряду (с тем, что а = + ~).

439]	§ з. приложения	455
X	X
Так как cosm — -1 [например, см. 79, 4) при А = 0], а т tg—-~х, то в пределе,
т	т
действительно, получается требуемое разложение [404 A2)]
Xs
smx = x	1-...
Остается обосновать почленный предельный переход в скобках, где число членов
при каждом т конечно, но неограниченно возрастает вместе с т [ср. 6)].
1	1
Пусть взятое х содержится между	тал и Ч—тал; будем считать т^-гщ.
X
Легко показать, что тогда выражение т tg — по абсолютной величине убывает
т
с возрастанием т и, следовательно, ограничено:
X
/«tg —
m
\x\
:=motg	 (m>m0).
Щ
В таком случае разложение в скобках мажорируется сходящимся рядом
U
L + -+...
Рассуждение завершается как и в предыдущем примере.
Аналогично может быть получено и разложение cos x в степенной ряд.
Замечание. Примеры 5), 6) и 7) воспроизводят в уточненном изложении
вывод разложений элементарных функций, данный Эйлером в его «Введении
в анализ бесконечно малых» A748).
8) Доказать, что
°° С — \\п—1 -гП 1
(a) lim 2—	— = -1п2,
х»1-0п=1 п 1 + хп 2
™ (-l)n-l	Хп
(а) Пусть 0<х-=1; так как ряд 2j ¦	¦— сходится, а множители
T n	1 + x"
ограниченные сверху единицей, монотонно убывают с возрастанием и, то при-
приложим признак Абеля, так что ряд сходится равномерно для всех х
в @, 1). Переходя в нем к пределу при х ^ 1 - О почленно (теорема 4), получим
требуемый результат.
(б) Пусть и здесь 0-=л:-= 1; имеем:
У п-г	х"
л=1
На этот раз ряд ^(-l)" не сходится, но его частичные суммы ограничены.
1
хп
Зато множители 	 не только монотонно убывают с возрастанием
l+x++х2"-1

456	ГЛ. XII. ФУНКЦИОНАЛЬНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И РЯДЫ	[439
и, но и равномерно для х в @,1) стремятся к 0, ибо
хп	хп	хп 1
~1 пхп п
В таком случае приложим признак Дирихле, ряд сходится равно-
равномерно, допустим почленный предельный переход при х- 1 -0, и т. д.
9) Говоря о степенном ряде, мы всегда подразумевали, что члены его располо-
расположены в порядке возрастания показателей. Если внутри промежутка сходимости
это не имеет значения, поскольку ряд сходится абсолютно, то, например, теорема
Абеля становится неверной без этой оговорки.
Проверить это на ряде
Xs X* X3 X6 Xs
полученном перестановкой членов из логарифмического ряда [ср. 388, пример 1)]
10) Применим теорему Абеля [6°] к доказательству его же теоремы об
умножении рядов [392]. Рассмотрим два сходящихся ряда
А = 2ап	(А)
В-2Ьп	(В)
л = 1
и предположим, что их произведение (К о ш и)
с=2сп,	(С)
п = 1
где cn = a1bn+a2bn_l+ .. .+апЬх также сходится. Нужно доказать, что тогда
А-В=С.
Из сходимости ряда (А) прежде всего заключаем, по лемме п° 379, что ряд
A(X) = Zanx"	(A*)
л = 1
абсолютно сходится для | х \ •< 1, так что радиус сходимости R этого ряда
наверное з»1. Таким образом, во всяком случае имеет место соотношение
lim А(х) = А = 2ап.
х-*1-0	л = 1
именно, при R = 1 - по теореме 6° А б е л я, а при R >• 1 - по теореме 2° [437]
Если рассмотреть, аналогично, ряды (при |х| -= 1):
2Х	(В*)
(С*)
л = 1
то для них будет справедливо все сказанное о ряде (А*)

4401	§ з. приложения	457
Применяя теперь к абсолютно сходящимся рядам (А*) и (В*) теорему
К о ш и [389], будем иметь
А(х)-В(х)
Остается лишь перейти к пределу здесь при х ¦* 1 - 0, чтобы получить требуемый
результат:
А-В=С.
440. Примеры на почленное интегрирование рядов. 1) Суммирование ряда
-^ (-1)"
> 	 можно осуществить так:
п=о Зл+1
X
°° ( — IV	°° (— IV	г "
2 -——= lim 2-—-х™+1 = lim 2 (-1)"*3" dx=
л=0 Зи+1 х^1-0л=0 3/1+1	I-.1-0 J п=С
о
= lim f
dx A (x+1J 1	2x-l » ] 1	л
—-= lim -In-	—+—arctg——-+—- =-ln2+-
уз б]/з» 3 зуз
Мы использовали сначала теорему Абеля, а затем - почленное интегри-
интегрирование степенного ряда [437, 6°; 438, 7°].
2) Почленным интегрированием рядов
= 1-Х+Х-- ...+(- 1У>-1хп~1+ ...,
1+x
1
1+x2
в промежутке [0, x] (где | x | -= 1) сразу получаются разложения
x
г
J
dx	х- Xs	хп
I A )	A)">
1+х	2 3	п
о
/^--н**-*-у+т—¦+(-iyii'
2й-1
о
которые в 405 [см. A7)] и 404 [см. A5)] были получены более сложным путем.
Справедливость первого разложения при х = 1 и второго при х = ± 1 устанавли-
устанавливается дополнительно с помощью теоремы Абеля [437, 6°].
3) Если вспомнить, что производная функция arcsin х, равная —rr^rr. разла-
разлагается в ряд следующим образом [407 B4)]:
.	1 + /. —' л 71 X	\ 1'<Хчс:1),

458	ГЛ. XII. ФУНКЦИОНАЛЬНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И РЯДЫ	[440
то почленным интегрированием этого ряда легко получить (новое для нас) разло-
разложение самого арксинуса:
dx	- Bл-1)!! хт+г
arsin x+ уAх1)
г dx
2!! 2л+1
Так как этот ряд сходится и при х = ± 1 [370, 5) (а)]*, то, по теореме Абеля,
разложение действительно и при этих значениях. В частности, при х = 1 будем
иметь такой ряд для числа л:
п	™Bи-1)!! 1
тт -1 + Z
2 n=i 2л!! 2и+1
Аналогично, разложив производную
[1(уг7)]'
в ряд и почленно проинтегрировав его, найдем разложение
Bл-1)!! х'-п+1
In (х+ УГ+х5) = х+
2л!! 2и+1
Функция эта есть не что иное, как Arsh x, т. е. функция, обратная sh x [49, 4); 339,
замечание].
4) С помощью почленного интегрирования рядов получаются разложения
в бесконечные степенные ряды для некоторых ннтегралов, не выражающих-
выражающихся в конечном виде через элементарные функции [см. 272]. Эти разложения
могут быть использованы для приближенных вычислений.
Так, исходя из известного разложения
* Впрочем, сходимость ряда 1 + У!	теперь может быть дока-
„=1 2л!! 2й + 1
зана проще. Имеем - при любом т —
¦йBи-1)!! хт+1	ж
х+ 2j	•	' arcsinx-=— .
n=i 2и!! 2n+l	2
Переходя здесь к пределу при х-*1, получим
1,-1I! 1 ^
t=i 2и!! 2й+1 2'
откуда [365] и следует требуемое.

440]	§ з. приложения	459
[ср. 404 A1)], найдем
х3 1 х5	1 х2"+х
И
2! 5	п\ Ъг+1
о
Поставим себе задачу: вычислить с точностью до 0,0001 интеграл
1
W= f e-*s dx.
о
Взяв верхний предел интеграла равным 1, получим для W знакопеременный чи-
числовой ряд с убывающими по абсолютной величине членами:
11111 1	1
Т 10 42 + 216 1320 9360 75600
Так как восьмой член уже значительно ниже заданной границы, то мы сохра-
сохраним лишь первые семь членов. Соответствующая (отрицательная) поправка А
легко оценивается
1 1,5
Ы|-=	-=—.
' 75600 105
Вычисляя оставленные члены с пятью знаками после запятой, найдем:
1 + —= 1,10000	- = 0,33333 (+)
	= 0,00463 (-) — = 0,02381 (-)
11	1 10474
	= 0,00011 (-) 	= 0,00076 (-) - '
9360	1320	0,35790 .
1,10474	0,35790	0,74684
Если учесть все поправки, то окажется, что
0,74681 <= W^ 0,74685, W= 0,7468...
и все четыре знака верны. [Ср. 328, 5).]
5) Аналогично, так как [ср. 404 A2)]
sin х х2 х4	х2Л~2
	= 1	+	. ..+(-1)"-!	+...,
х	3! 5!	Bй-1)!
то
X
/•sinx	х3 х5	хт~1
	dx=x	+	... + (-1)"-»	+...
J х	3!3 5! 5	Bи-1)!Bи-1)
о
Предложим себе вычислить, с помощью этого разложения, интеграл
л
rsin х
ps
J
dx,
X
о
с точностью до 0,001.

460	ГЛ. XII. ФУНКЦИОНАЛЬНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И РЯДЫ	[440
Имеем, полагая х=л,
111	1	1
I =в	я3Н	лъ	-яЧ	я9	ли+ ¦¦¦,
18 600 35 280 3 265 920 439 084 800
т. е. снова знакопеременный ряд с убывающими по абсолютной величине членами.
Так как шестой член меньше, чем 0,0007, то мы ограничимся пятью членами.
Вычисляем на четыре знака:
1
600
1
3 265 920
я= 3,1416
я5 = 0,5100
л9 -0,0091
(-)
(+)
(+)
— л3
18
1
35 280
'= 1,7226
'-0,0856
(-)
(+)
3,6607
1,8082
3,6607	1,8082	1,8525
Учитывая поправки, приходим к заключению:
1,8517-=/*^ 1,8527, ц= 1,852 ±0,001.
6) Поставим себе задачей представить в виде рядов интегралы
1	1
arctg х
г arctg х	г
(a) J —~- dx,	(б) J
о	о
(а) Вспоминая разложение арктангенса, имеем:
1	г
(• arctg х	г! 1 2 1 4 1
J х *~ J 1 ~1Х2 + 1Х ~~7Х +'"
arctg х г / 1 1 1 "l 111
& 1 *+*х6+ db= I	+
32 52 72
Так как ряд, стоящий под знаком интеграла, сходится при дс=1, то почленное
интегрирование допустимо [438, 7°].
Мы уже упоминали [328, 6)], что значение этого интеграла
G = 0,915965...
известно как «постоянная К а т а л а н а». Теперь мы видим, что
б) Переписав подинтегральное выражение в виде e~xinx, разлагаем его в по-
показательный ряд
хп In" х *
n=i
* При х = 0 члены ряда, начиная с и=1, заменяем предельными значениями,
т. е. нулями.

440J	§ 3. ПРИЛОЖЕНИЯ	461
который сходится равномерно для 0-=x=sl, ибо максимум функции |xlnx|
(как легко установить методами дифференциального исчисления) есть —, так что
е
написанный ряд мажорируется рядом
IV
л^о и!
Итак, допустимо почленное интегрирование. Так как [312, 4)]
1
г	и!
xnlnnxdx=(-l)n	,
J	(л+1)«+1
то окончательно
m = 1 т"
Г
J
о
7) Мы имели [414 (8K разложение
х ^i 2р\\ I хг \Р
arctg х = - Zi —-— 	 @=sx=? 1).
У	У
Полагая здесь х - -^^г= и учитывая, что arctg —=== = arcsin у [50] найдем:
arcsin у
Проинтегрируем это равенство от 0 до у, причем справа выполним интегрирование
почленно:
1	.	2р!! ^р+2
— (arcsm уJ = у.	= у.
2	?оBр+Щ2р+2
2	?ZoBp+l)l\2p+2 m=i Bm-1)!! 2т
Этот результат можно переписать так:
2 (arcsin уУ = У.—	— BvJm.
т=\ 2га!
При у = — получим отсюда
у [(га-1)!]2_тг2
?\ 2та! II"
Но мы видели уже [395 A3); см. также 416], что
™ 1	Z. ГГт-ПП*
у. — = 3
=1 2га!

462	ГЛ. XII. ФУНКЦИОНАЛЬНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И РЯДЫ	[440
так что, окончательно,
°° 1	7Г2
п=1й2 6
К этому интересному результату Эйлера мы будем возвращаться еще
не раз.
8) Вычислить интеграл
1
о
1
pln(l + x)
	dx.
J х
Если воспользоваться логарифмическим рядом [405 A7)], то для подинтеграль-
ной функции получим разложение
1- — Х+-Х1- ... + (-l)"-1-x"-1+ ...,
2 3	п
которое действительно во всем промежутке [0, 1]. Интегрируя почленно, найдем
Мы только что установили равенство D); из него следует:
1
2
и2	п=!й2 п=гBл)г 12'
Таким образом, мы приходим к «конечному» выражению для искомого интеграла
i-Z.
12
9) Пусть требуется найти интеграл (|а| -= 1)
л
с In A + a- cos x)
	Же.
J	COSX
о
/	л
При д: = — приписываем подинтегральному выражению предельное при
л
х — — значение а.
Пользуясь разложением логарифма, имеем:
In(l+jcosx)
COSX
причем ряд сходится равномерно в промежутке [0, л]. Заметив, что [312 (8)]
я
я	я	2
cos2 х dx = 0, fcos2mx</x = 2 f cos2 x dx = —^—— n,

440]	§ з. приложения	463
произведем почленное интегрирование:
fln(H-ecosx)	( у Bти-1)!! а2т+1 \
J cos л:	1 m = i 2»?!! 2ти+1 J '
о
В полученном ряде мы узнаем разложение функции арксинус [см. 3)]. Таким обра-
образом, окончательно находим (в конечном виде!)
п
fin A+acosx)
	dx=n-arcsin a.
J cos л:
о
10) Рассмотрим разложение (при \r\ -= 1):
1-r2
= 1+2 2rn-cosnx.	E)
I	- 2r cos x+ r2	n=i
Доказать его легко, умножив правую часть на знаменатель 1 - 2r cos x+ гг;
мы получим:
оо	ею
+ 2^rn cosnx-2]>l
II	1
Если заменить 2 cos их• cos я: через cos(;j+l)x+cos(n- l)x и соответственно
разбить вторую сумму на две, то после сокращений останется лишь 1 - г2, что
и завершает доказательство.
Ввиду сходимости ряда J? \ г \п (при | г | -= 1), ряд в E) справа сходится равно-
1
мерно относительно х в промежутке [-л, л]. Возьмем теперь интегралы от
-л до я и слева и справа, причем ряд можно интегрировать почленно (теоре-
п
ма 5). Так как cos nxdx=Q, то мы получим:
J 1 -
1-г2
2r cos х + г2
— л
[ср. 309, 8)].
Аналогично, умножив обе части тождества E) на cos тих (#я=1, 2, 3, ...) и
интегрируя почленно, легко получить
я
С
J l
cos mx	гт
d 2
dx 2n.
l-2rcosx+r2	1-r2
— л
При этом используется известный результат [309, 4) (г)]
л
г	| 0 при т^п,
cos mx cos пх dx = \
J	I л при т-п.

464	ГЛ. XII. ФУНКЦИОНАЛЬНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И РЯДЫ	[440
11) Если в тождестве E) перенести единицу налево и разделить обе части на 2г,
то получим:
cos х - г	Z,
> f" COS ИХ.
На этот раз фиксируем по произволу х и станем рассматривать г, как перемен-
переменную с областью изменения (-1, 1). Проинтегрируем обе части равенства по г
от 0 до любого г в этом промежутке, причем степенной ряд справа будем интегри-
интегрировать почленно; так как слева числитель (с точностью до числового множи-
множителя) есть производная знаменателя по г, то в результате получим:
In(l-2rcosx+r2) = -2,2/ —cosnx (|r|<l).
n=l n
Теперь снова фиксируем г, а х будем изменять от 0 до л. Легко видеть, что
ряд справа сходится равномерно относительно х в этом промежутке, так что
допустимо почленное интегрирование (теорема 5). Выполнив его придем
к интегралу:
л
In(l-2rcosx+r2)rfxr = 0 (|г|«1)
[ср. 307, 4); 314, 14)]. Отсюда, как мы уже видели, легко получить значение инте-
интеграла и при \г\ =-1.
12) Следующие интегралы, зависящие от х:
л
2
2
= - I* cos {x sin 0)d0,
л J
2
2х"
2х" г
	 cos (xsin 0) cos2" 0 dO (n= 1, 2, 3, ...),
-1)!!jzJ
представляют так называемые бесселевы функции [ср. 395, 14)]. Разла-
Разлагая подинтегральные выражения по степеням х sin в и интегрируя почленно, легко
получить уже знакомые нам разложения этих функций в ряды по степеням х.
Например, интегрируя ряд
-
cos (xsin 0)= 1 + Z (- 1)" zr,
и вспоминая формулу [312 (8)]
F)

4401	§ з. приложения	465
найдем для бесселевой функции с нулевым значком
^	. х*
13) Нам уже встречались так называемые полные эллиптические
интегралы 1-го и 2-го рода [315 и др.]:
2	2
Г dm	Г ,
К(*)=	Е(*)= ]/\-к* sin* (p dip.
J yi-Ar2sin2y>	J
о	о
Поставим себе задачей - разложить их по степеням модуля к @ «= к -= 1).
Полагая в формуле B4) п° 407 х = - кг sin q>, получим:
Этот ряд сходится равномерно относительно <р, ибо мажорируется при
всех значениях w сходящимся рядом
~B«-Ш
+ п-^1 2й!! * '
следовательно, по теореме 5, здесь допустимо почленное интегрирование,
которое мы и выполним. Используя снова формулу F), таким путем получим:
2
С dm	л [ ~ ГBл-1)!!~|2 1
J yi^FiuT^ 2 [ „f i [ 2я!! | J
о
Аналогично, исходя из формулы B3) п° 407, найдем
Этими рядами также можно воспользоваться для приближенных вычислений.
Для примера рассмотрим ряд
- , - I 1 3 5 175	441
2\ 8 256 2048 262144 2 097152
Если сохранить здесь только написанные члены, то соответствующая поправка
будет отрицательна и оценивается следующим образом:
U2!!
30 Г. М. Фихтенгольц, т. II

466
ГЛ. XII. ФУНКЦИОНАЛЬНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И РЯДЫ
[440
можно ждать трех верных знаков после запятой. Действительно, вычисляя с пятью
знаками, имеем:
^-=1,57080 (-)
2
_ 1,57080
0,21997
1,35083
1,35057 <=Е
1,35085,
ж 5
n 175
2 262 144
п 441
2~'2О97 152
= 0,00105 (-)
0,00033 (+)
0,21997
El —1=1,350... [ср. 328, 4)].
Нужно сказать, что лишь при малых значениях к указанные выше ряды для
полных эллиптических интегралов К(к) и Е(&) на самом деле выгодны для вы-
вычислений. Но существуют преобразования, позволяющие сводить вычисление
названных интегралов к случаю сколь угодно малого к [ср. 315].
14) Можно использовать полученное разложение функции Е(&) для вычисления
следующего интеграла:
Е(й sin в)
sin в dO
Прежде всего, легко проверить, что имеет место разложение
например, умножая правую часть равенства на 1 - к2.
Подставляя & = A.sin0 и умножая еще на sin б, мы можем интегрировать
почленно по в от 0 до —, поскольку полученный ряд сходится в этих пределах
равномерно (он, например, мажорируется предыдущим рядом при к = А).
Так как [312 (8)]
Г •
2п\\

440]	§ з. приложения	467
то находим:
с E(Asir>8)	nil 1-3 1-3-5	) л< ^,Bи-1)!!	]
—	—-sine</e = - 1+-A2 +	A4+	A6+... =-U + 2i	A	,-
J l-A2-sin2e	21 2 2-4 2-4-6	1 2 1 n=i 2и!!	]
о
Сопоставив выражение в скобках с формулой B4) п° 407, получаем значение
искомого интеграла даже в конечном виде:
ism в) . „ ,„ я 1
С К(Л sm В)
J l-A2-sin2(
2 1/1-й*
15) Наконец, рассмотрим вопрос о разложении по степеням х (но н е целым!)
функции у - arcsin A - х) при хз=0 *.
Имеем (используя биномиальный ряд):
1	1	1
У = --=г
УЙ1 4 32	I уг	4f2 32|2
причем, если опустить первый член, который при х=0 обрашается в ~, сходи-
сходимость ряда будет равномерной в любом промежутке [0, х], где 0-=х<2.
Первообразная функция для первого члена есть - ]/2х2; для остального ряда
первообразную получаем почленным интегрированием. Так как при х = 0 должно
быть у = —, то окончательно находим такое разложение по дробным сте-
степеням х (действительно для 0asx<2):
?	У2хА;Х	х
2	61/2 80 У 2
Аналогично получается и разложение
I §L 1 5- 1 —
222
1+х*
для 0^х-= 1.
* О разложении обычного типа по целым положительным степеням х здесь
не может быть речи, ибо иначе, по теореме 9°, 438, наша функция имела бы конеч-
конечную производную и при х = 0, чего на деле нет.
зо«

468	ГЛ. XII. ФУНКЦИОНАЛЬНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И РЯДЫ	1441
441. Примеры на почленное дифференцирование рядов.
1)	Вернувшись снова к функции [ср. 390, 6); 439, 3)]:
^ хп
l+Z -г.
п—1 П\
мы можем теперь легко установить ее производную; для этого достаточно [438,
8°] почленно продифференцировать этот ряд. Мы получим, что Е'{х) = Е(х), так что
рассматриваемая функция удовлетворяет дифференциальному уравнению: у'=у.
Отсюда у=Сех; так как при х = 0, очевидно, у=\, то окончательно находим, что
Е(х) = е*.
2)	Аналогичный прием применим к определению суммы биномиального ряда
т(т-1)	т(т-\)	(яг-и+1)
У= /(*)= 1 + J7W + —	 Х2+ . . . +—	 Хп+ . . .
1-2	1«2-.. .-и
[на этот раз т фиксировано, а х изменяется в промежутке (-1, 1); ср. 439, 4)].
Дифференцируя его почленно, получим:
1.2-...-и
Теперь нетрудно убедиться в том, что*
A+х)./'(*) =/я-Дх).
Таким образом наша функция удовлетворяет дифференциальному уравнению
Отсюда
Так как при х = 0, очевидно, у=\, то постоянная С= 1 и, окончательно,
3) Мы знаем уже, что сумма ряда Дирихле [385, 3)]
<Р(х)= 2 —
* При умножении f'(x) на 1+дс надлежит воспользоваться свойством бино-
биномиальных коэффициентов:
(т-1)(т-2)-...-(т-п) (/я-1)(/я-2)-	(т-й+1) т(т-\)	.(от-и+1)
+
1.2-....И	+	1-2-.. ..(и-1)	1.2-...-и
частным случаем которого является известное соотношение
r" j-r"~1 -г"

441)	§ з. приложения	469
для х=-Я (где Я - пограничная абсцисса сходимости, Л-= +~) есть непрерывная
функция [439, 2)].
Почленным дифференцированием можно найти производную этой функции:
Л = 1П*
Пока мы получили этот результат лишь формально. Для того чтобы оправдать
его, достаточно удостовериться в том, что последний ряд сходится равно-
равномерно относительно х для всех xs&x0, где х0 - любое (но фиксированное)
число, ббльшее А. Это устанавливается, как и в 439,2), с помощью признака Абеля,
Inn
опираясь на то, что множители	, начиная с п = 2, убывают с возраста-
возрастанием л, будучи все вместе ограничены числом In 2. Какое бы значение х =- А ни
взять, его можно заключить между границами х' =- А и х" >¦ х'\ к промежутку [х', х"\
применима теорема 7 [435].
Таким же путем можно убедиться в существовании для функции <р(х) произ-
производных всех порядков и получить их выражение в виде рядов.
Все сказанное, в частности, приложимо к функции
1
Р и м а н а при х»0.
4) Мы уже встречались с разложением бесселевой функции с нуле-
нулевым значком J0(x) в степенной ряд
7fv1=1_i ~У ( —\\к
[395, 14); 440, 12)].
Покажем теперь, что эта функция удовлетворяет дифференциальному уравнению
Бес селя:
хи"+и'+хи = 0.
Имеем, полагая u = J0(x),
а затем, дважды почленно дифференцируя разложение и,
н'= У Г-IV* ——-—— -хЖ-1
Если сложить эти равенства, то коэффициент при х2* окажется равным
что и доказывает требуемое утверждение.

470	ГЛ. XII. ФУНКЦИОНАЛЬНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И РЯДЫ	D41
Аналогично можно убедиться в том, что бесселева функция с произ-
произвольным натуральным значком Jn(x), о которой также была речь выше, удовлет-
удовлетворяет общему уравнению Бе с с е ля:
х*и" + хи' + (х2 - л2)и = 0.
5) Поучительнее другая постановка задачи: пусть требуется найти функ-
функцию, разлагающуюся в ряд для всех х и удовлетворяющую уравнению Бес-
Бесселя.
Выполним это, например, для простейшего случая п = 0. Напишем разложение
искомой функции в виде ряда с неопределенными коэффициен-
коэффициентами:
ш=0
и, считая его всюду сходящимся, дважды продифференцируем почленно. Подстав-
Подставляя все эти разложения в уравнение, получим:
«1+ 2 (/И2ат + вт-2)*т~1 = 0.
т=2
По теореме 3° [437]:
aL = 0, т2ат + ат^., = 0 (т = 2, 3, ...).
Отсюда, прежде всего, коэффициенты с нечетными индексами а2/{_1 = 0 (fc=l, 2,
3, ...), что же касается коэффициентов с четными индексами о2/(> то по рекуррент-
рекуррентной формуле все они выразятся через а„:
Итак, с точностью до произвольного множителя а0 мы возвращаемся к функции
Ux).
Что полученный ряд, действительно, всюду сходится, проверяется непосред-
непосредственно. А из самого способа его получения явствует, что представляемая им
функция удовлетворяет уравнению.
[Обращаем внимание читателя на своеобразное использование метода не-
неопределенных коэффициентов; здесь у нас оказалось уже бесконечное множество
этих коэффициентов и пришлось прибегнуть к теореме о тождестве степенных
рядов, взамен обычно применяемой теоремы о тождестве многочленов].
6) Гауссом была введена функция
а(а + 1)...(а + и1) fl/J+1). ..(/Мл1)
u=F(a, р,у, х) = 1+2 	—,	г;	;	^	х
!(+1)(+1)
[гипергеометрический ряд (см. 372, 378, 4)]. Дважды дифференцируя этот ряд по-
почленно (считая |х|<1), можно установить, что эта функция удовлетворяет так
называемому гипергеометрическому дифференциальному уравнению
Предоставляем несколько громоздкие, но нетрудные выкладки читателю.
И здесь можно изменить постановку задачи, как это сделано в упражнении 5.

441]	§ 3. ПРИЛОЖЕНИЯ	471
7)	Определим для 0=s:x=sl функцию fix) равенством
/(*)= 2 -г •
Покажем, что для 0-=л-«=1 эта функция удовлетворяет интересному функциональ-
функциональному уравнению:
fix) +/A - х)+In x ¦ In A - х) = С = const.
Для этого достаточно доказать, что производная по х от выражения слева
тождественно обращается в нуль:
/'(*)-/'Ц-*)+-In A-*)	— 1пх = 0.
X	1-Х
Дифференцируя почленно ряд, определяющий функцию fix), найдем:
°° л:" 1
/'(*)- 2	—In A-х);
71 = 1 П	X
заменяя х на 1-х, получим, что
/'A-*)=--,-—In*.
1-х
Этим и завершается доказательство.
Самую величину постоянной легко определить, устремляя в доказанном со-
соотношении х к 1. По теореме Абеля левая часть его будет иметь пределом
lim /(x)-/(l)-2-.-7
Х~1-0	71=1 Л2 6
Я»
[440 4)]; значит, С=— .
6
8)	В 400, 4) рассматривалось бесконечное произведение
Предполагая 0-=р-=—, сначала прологарифмируем это равенство [401, 4°]:
2j In cos — =lnsiny-lna>,
n=x	2n
а затем продифференцируем полученный ряд почленно:
Так как ряд из производных мажорируется сходящейся геометрической про-
прогрессией, то почленное дифференцирование оправдано.

472	ГЛ. XII. ФУНКЦИОНАЛЬНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И РЯДЫ
9) В 408 мы вывели разложение sin x в бесконечное произведение
sin х = х [j
Вводя абсолютные величины, получим отсюда:
[441
1-
\«пх\-\х\П
Если х отлично от чисел вида кп (к = 0, ±1, ±2, ...), то, логарифмируя, придем
к бесконечному ряду:
In |sinx| =ln
2:
л=1
1-
X2
Почленное дифференцирование дает нам такое разложение:
cosx	1 ^ 2х
-— = ctgx— +2г ———,.
sin х	х п=1хг-пЬ1г
Для оправдания его достаточно убедиться в том, что полученный ряд сходится
равномерно в любом замкнутом конечном промежутке, не содержащем точек
вида кп. Действительно, при изменении х в этом промежутке его абсолютная
М
величина остается ограниченной: |х|-=М, так что, по крайней мере для л=-—,
2х
2\х\
гм
гм
Так как ряд
сходится, то требуемый результат получается с помощью признака Вейер-
ш т р а с с а.
Разложению ctg x можно придать форму:
cosx	1 ^, [ 1	1 1
8ШХ	X п=1 \Х-ПП Х + ПЯ)
в этом виде оно является как бы разложением ctg x на простые д р о-
б и, отвечающие отдельным корням 0 и ± ял знаменателя sin x.
По формуле tgx= -ctgI*-—I, отсюда можно получить разложение
tgx на простые дроби:
2и-1	2и-1
[х	—л дм—-—я|
V
1

441]
§ з. приложения
473
Точно так же. если воспользоваться формулой:
1 1 ( х х\
".— = тг ctg-+tg- ,
sm х 2 I 2 2/
1
можно получить разложение и для —
11^,	( 1	1 ^i 1 ™	2х
Sin X X л=1	\Х-П71 Х + Пп) X п = 1	Х2-Пг712
Продифференцировав почленно разложение для ctg x (предоставляем читателю
убедиться в дозволительное™ этого), получим еще одно полезное разложение:
1 1
sin2 х х2
к\*к
10) Если исходить из представления shx бесконечным произведением [408],
то аналогично можно прийти к разложениям
shx x n=i
ит.п.
11) Для функций Т(х) мы вывели в п° 402 формулу Вейерштрасса
[см. A6)]:
=есх;7.
Учитывая, что Г(х+1) = Х'Г(х), и переходя к логарифмам, отсюда легко полу
тать (при х, отличном от 0 и от целых отрицательных чисел)
lnir(x)|«-ln|x|-Cx+J? | —— In
Дифференцируя ряд почленно, формально отсюда получим
Г(х)
п-ця х+п)
Покажем теперь, что ряд справа сходится равномерно в любом конеч-
конечном промежутке (не содержащем целых отрицательных чисел). Действительно,
так как при этом \х\ остается ограниченной: |х| -=М, то по крайней мере для
п>М, имеем:
1 1
« х+п
1*1 м
=	-KZ
п(п+х) п(п~М)

474	ГЛ. XII. ФУНКЦИОНАЛЬНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И РЯДЫ	1442
Так как ряд _/, 	 сходится, то, по признаку Вейерштрасса,
мп{пМ)
{
равномерная сходимость обеспечена. Мы получаем возможность сослаться на
теорему 7 п° 435 и тем докажем и самое существование производной от In | Г(л:) |,
а следовательно, и от Г(л;) и т. д.
Прибавляя к правой части полученной формулы ряд
1 + ^
n = l V«+l
можно привести ее к виду:
„А	С+
Легко убедиться в существовании для функции Т(х) производных всех порядков.
442. Метод последовательных приближений в теории неявных функций. Для
того чтобы показать в действии теорию функциональных рядов (или последова-
последовательностей), рассмотрим вновь вопрос о существовании «неявных» функций [206
и след.]. Ограничимся для простоты случаем одного уравнения:
F(x, у) = 0,	G)
из которого у подлежит определению, как однозначная функция от х. На этот
раз мы прибегнем к методу последовательных приближений, который позволит
нам не только установить существование этой функции, но и дать указания отно-
относительно ее фактического вычисления.
Пусть функция F(x, у) непрерывна, вместе со своей производной Fy(x, у) в неко-
некотором квадрате
с центром в точке (х0, у0), причем
(8)
Тогда уравнение G) в окрестности точки (хо,уо) определяет у как однозначную
и непрерывную функцию от х, которая при х = ха обращается в уа.
Нам удобнее рассмотреть сначала частный случай, когда уравнение
G) имеет форму
У = Уо+<р(х, у),	G*)
где функции у вместе с <р'у удовлетворяет тем же условиям непрерывности, что и F,
но с заменой условий (8) следующими:
9><Л>. Уо) = 0, | <р'у(х0, у0) | -= 1.	(8*)
Ввиду непрерывности производной мы можем с самого начала считать область
<2Й настолько малой, чтобы в ее пределах вообще было
у)\^К	(9)
где X есть некоторая постоянная, меньшая единицы. Затем, сохраняя
промежуток изменения переменной у, нам придется еще сжать промежуток изме-
изменения переменной х, заменив его столь малым промежутком [хо-д, хо+д], чтобы

442]	§ з. приложения	475
в его пределах непрерывная функция от х: <р(х, у0), которая обращается в 0 при
х = х0, удовлетворяла неравенству
Таким образом мы подготовили область
®*= [хо-д, хо + д; уо-А, уо+А],	A0)
к которой и будут относиться наши дальнейшие рассуждения.
Подставив в правую часть уравнения G*) вместо у постоянную у0, мы
получим некоторую функцию от х:
х, у0).
Аналогично, полагаем последовательно
*, y2),
и вообще
оФ Уп-i)-	A1)
Эти функции
ЛОО. Уг(х), •••» Уп(х), ...
и осуществляют последовательные приближения к искомой функции у(х).
Правда, остается еще проверить, что все они не выходят за пределы проме-
промежутка [уа-Д, Уо+Л\ ибо, если бы какая-нибудь из них вышла из этого промежутка,
то ее уже нельзя было бы подставлять вместо у в правую часть уравнения G*).
Установим это индуктивно. Пусть, скажем,
а
Из A1):
Уп~Уо=<Р(х, yn-i).
Но
| <р(х, Уп-i) | =s | q>(x, у„_х) -q>(x, у0) | + | q>(x, у0) |.
Первое слагаемое справа преобразуется по теореме о среднем значении, и, на
основании (9),
\<р(х, yn-i)-<P(x, yo)\ = \q>y(x, п)-(Уп-1-Уо>\^^'А
а второе меньше A - Х)А, в силу A0), так что по совокупности
что и доказывает наше утверждение.
В то же время индуктивно устанавливается, что все построенные указанным
путем функции будут непрерывны.
Обратимся теперь к вопросу о пределе для последовательности функций
{уп}. Удобнее, однако, рассмотреть ряд
Уо+ 2(Уп-Уп-1>-	A2)
л=1
Из самого определения нашей последовательности ясно, что
Уп-Уп-1*=<р(.х, yn-i)-<p(x, Уп-i)-
Воспользовавшись снова теоремой о среднем и неравенством (9), найдем

476	ГЛ. XII. ФУНКЦИОНАЛЬНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И РЯДЫ	|442
Отсюда, заменяя и на п- 1, на п- 2 и т. д., окончательно получим
ввиду A0). Таким образом, ряд A2) мажорируется геометрической прогрессией
A-Х)А-2Хп-\	A3)
1
а следовательно, сходится и притом равномерно для всех значений х
в промежутке [ха-д, хо + д]. А тогда, по теореме 1 п° 431, и предельная функция
у = у(х) = lim yn(x)
будет в указанном промежутке непрерывна.
В том, что эта функт1чя удовлетворяет исходному уравнению, легко убедиться
переходя к пределу при и— °° в равенстве A1). Остается еще доказать, что не су-
существует других значений у, кроме доставляемых ею, которые удовлетворили
бы уравнению G*). В самом деле, если бы, при некотором х, наряду с G*) имели
У = хо+(р(х, у),
то, вычитая и оценивая разность значений <р, как обычно, получили бы
\У-У\ - \<р(х,у)-<р{х, у)\*=Х-\у-у\,
что невозможно, если
Отсюда уже вытекает, что
это, впрочем, непосредственно ясно и из того, что все уп(х0) = у0.
Теорема - в рассматриваемом частном случае - доказана. Общий случай
легко приводится к частному; именно, уравнение G) можно переписать в виде
F(х, у)
У
	J.
0, yB)\
который отождествляется с G*), если положить
Fix, у)
<Р(х,у)-У-у0
, yB)
Эта функция удовлетворяет требованиям (8*), в частности второму из них, потому
что <ру(х„, у0) оказывается равной 0.
Как уже упоминалось, изложенный процесс облегчает и фактическое вычисле-
вычисление искомой функции у(х) по приближению. Погрешность от замены X*) на уп(х)
легко оценивается, так как остаток ряда A2) после и-го члена мажорируется соот-
соответствующим остатком геометрической прогрессии A3). Отсюда и получается:
\у(х)-уп(х)\^А.к" (и=1, 2, 3, ...)•
Весьма поучительно сопоставление доказательства теоремы о неявной функ-
функции в 206 и только что проведенного. Там мы имели дело с чистым «доказатель-
«доказательством существования», здесь же - с построением искомого объекта.

443)	§ з. приложения	477
Подобным же образом могут быть эффективно доказаны и общие
теоремы п° 208. Мы ограничились простейшим случаем, чтобы лучше выявить
идею метода.
443. Аналитическое определение тригонометрических функций. Читатель видел,
какую важную роль в анализе играют тригонометрические функции. Между тем
вводятся они на основе чисто геометрических соображений, анализу совершенно
чуждых. Поэтому приобретает принципиальную важность вопрос о возможности
определения тригонометрических функций и изучения их основных свойств -
средствами самого анализа. Бесконечные ряды как раз и есть то орудие, с помощью
которого все это может быть осуществлено, и мы посвятим этот п° изучению
тригонометрических функций по их аналитическому определению, в качестве
нового примера приложения изложенной выше теории.
Итак, рассмотрим две функции С(х) и Six), формально определяемые для
всех вещественных значений х всюду сходящимися рядами:
см-1+ 2 (-О" *-"-, ад= 2 (-D"-1 т^г.,
л=1	Bл)!	л=1	Bи-1)!
ни в какой мере не отождествляя их покуда с ранее известными нам функциями
cos х и sin х. Мы уже имели однажды дело с так определенными функциями [390,
7)]; с помощью умножения рядов, как там указывалось, для них можно установить
две основные формулы:
С{х+у) = С(х) ¦ С(у) - Six) • Siy),	A4)
S{x+у) = ад • СО)+С(х) • S(y),	A5)
справедливые при всех значениях х и у.
Продолжим исследование свойств функций С(х) и Six). Заменяя х на - х,
сразу усматриваем, что С(х) есть функция четная, a S{x) - нечетная,
С(-*) = С(х), Si-x)=-S(x).
Полагая же х = 0, найдем, что
С@)=1, 5@) = 0.
Если теперь, сохраняя х произвольным, положить в A4) у= -х, то - с учетом
только что установленных равенств - получим соотношение, алгебраически
связывающее обе функции
ОМ+ЭД=1.	A6)
Легко получить и формулы удвоения или деления пополам аргумента.
Из теоремы 2°, 437 и 9°, 438 заключаем, что обе функции с{х) и SO*) не только
непрерывны, но и имеют производные всех порядков. В частности, применив
к рядам, определяющим наши функции, почленное дифференцирование 8°, 438
легко убедимся в том, что
С'С*)=-ад, У(х) = С(х).	A7)
Все эти свойства, как видим, устанавливаются легко. Несколько бблыпих
усилий требует доказательство периодичности рассматриваемых функций,
к чему мы теперь обратимся.
Установим сначала, что в промежутке @, 2) существует, и притом единственный,
корень функции С(х). В самом деле, мы знаем, что С@) = 1. Значение же СB) можно

478	ГЛ. XII. ФУНКЦИОНАЛЬНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И РЯДЫ	D43
написать в следующем виде (отделив первые три члена соответствующего ряда,
а остальные члены объединив попарно):
2»
Так как все скобки положительны:
2т I	2-2 "\
2\[ ~B + 1)B + 2» '
2л! Bл+2)Г2п\[
а сумма первых трех членов дает	, то СB)«=	, т. е. СB) заведомо отрица-
отрицательно. Ввиду непрерывности функции С(х), отсюда следует, что в промежутке
(О, 2) действительно лежит корень этой функции.
С другой стороны, в том же промежутке функция
очевидно, сохраняет положительный знак, а производная С'(х) = - S(x) - отрица-
отрицательный, следовательно, функция С(х) убывает, когда х растет от 0 до 2, и обра-
обращается в 0 лишь однажды.	п
Обозначим теперь упомянутый корень функции С(х) через —, причем п, таким
образом, вводится здесь совершенно формально, и отождествлять его с отно-
отношением окружности к диаметру пока нельзя.
Итак, имеем:
последнее равенство следует из A6), с	учетом положительности функции S(x)
при 0-=x=s2.	л
Полагая в формулах A4) и A5) сначала х = у=— , а затем х = у=п, последова-
последовательно, найдем:	2
С(я)=-1, 5(л) = 0;	СBя)=1, SBn) = 0.
Если в тех же формулах, сохраняя	х произвольным, взять у = л или
у = 2л, то получим:
С(х+я)= -С(х),	?(а-+л) =-?(*) A8)
и, наконец,
С(х+2л) = С(х),
Последние соотношения устанавливают, что функции С(х) и S(x) имеют п е-
риод 2л.
Нетрудно было бы вывести и другие «формулы приведения»; мы предоставляем
это читателю.
Теперь попытаемся доказать совпадение рассмотренньк функций С(х) и S(x)
с тригонометрическими функциями cos x и sin x, а также отождествить формально
введенное нами число л с тем числом л, которое играет столь важную роль в гео-
геометрии.
С этой целью рассмотрим кривую, заданную параметрически уравне-
уравнениями:
х-ао, у=*),
где параметр t изменяется от 0 до 2я. Ввиду A6), все точки ее удовлетворяют урав-

444]
§ 3. ПРИЛОЖЕНИЯ
479
нению: x2+y2= 1, т. е. лежат на окружности, описанной вокруг начала радиусом 1
(рис. 61). Покажем, что при этом получится каждая точка ее и лишь по разу;
исключение представит, естественно, начальная точка А, отвечающая значениям
? = 0 и t = 2n.	п
Мы видели, что 5@ =- 0, пока 0 -= /==2, а следовательно, и подавно при 0 -= t=s— .
Заменяя во второй из формул A8) л: на -/, получим	2
5{я-0=5@;
отсюда можно усмотреть, что 5@ =¦ 0 и при —
=<-< л. В таком случае, функция
С@> производная которой равна - S(t), монотонно убывает при изменении г от О
до л, проходя по разу через каждое значение от 1 до -1. Отсюда ясно, что про-
промежутку [0, л] изменения параметра взаимно однозначно отвечает верхняя часть
нашей окружности. Аналогичное утверждение можно сделать относительно про-
промежутка [л, 2л] значений параметра и
нижней части окружности, ввиду того,
что [см. A8)]
C(t +7i) = - C(t), S(t + л) = - S(t).
Теперь вычислим, по формуле D)
п° 329, длину дуги AM, считая, что точка
М отвечает значению t параметра. При-
Принимая во внимание A7) и A6), мы полу-
получим
t
о
Это показывает, что t совпадает с углом
0= -йАОМ, выраженным в радианах, а
тогда:
С@) = х = cos 0, 5@) = у = sin в.
М
Рис. 61.
В то же время, длина всей окружности по нашей формуле оказывается равной
2л; следовательно, введенное нами число тождественно с тем, которое рассматри-
рассматривается в геометрии.
444. Пример непрерывной функции без производной. Первый пример такого
рода был построен Вейерштрассом; его функция определяется рядом:
/00
2
л=0
' где 0
мажорируется сходящейся прогрессией
(	3
1, a b есть нечетное натуральное число причем ab =¦ 1Н—-я
Этот ряд
а"> следовательно [430, 431, теорема 1],
__
сходится равномерно, и его сумма является всюду непрерывной
функцией от х. Кропотливым исследованием Вейерштрассу удалось по-
показать, что тем не менее ни в одной точке для нее не существует конечной произ-
производной.
Мы приведем более простой пример ван-дер-Вардена (В. L. van
der Waerden), построенный по существу на той же идее, лишь колеблющиеся
кривые у = cos их заменены колеблющимися ломаными.

480
ГЛ. XII. ФУНКЦИОНАЛЬНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И РЯДЫ	1444
Итак, обозначим через щ(х) абсолютную величину разности между числом х
и ближайшим к нему целым числом. Эта функция будет линейной в каждом
+11
[S
_
у
S 5+11
_ 	 ,
б
где s - целое; она непрерывна и имеет период 1.
[
Ее график представляет собой ломаную, он изображен на рис. 62, а; отдельные
звенья ломаной имеют угловой коэффициент ± 1.
Положим, затем, для fc=l, 2, 3, ...:
"к(.х)--
4*
Г S	5+11
Эта функция будет линейной в промежутках вида ——-, —~Л > она также
непрерывна и имеет период — . Ее график также ломаная, но с более мелкими
4"
зубчиками; на рис. 62, б, например, изображен график функции иг(х). Во всех слу-
случаях угловые коэффициенты отдельньк звеньев ломаной и здесь равны ± 1.
Определим теперь, для всех вещественных значений х, функцию f(x) равен-
равенством
/(*)= 2 «/((*)•
А=0
Так как, очевидно, 0=sHftW=s—-^ (fc = 0, 1, 2, ...), так что ряд мажорируется
сходящейся прогрессией 2	г • то (как и в слУчае Функции Вейерштрасса)
О 2-4"
ряд сходится равномерно, и функция fix) всюду непрерывна.
Остановимся на любом значении х = х0. Вычисляя его с точностью до ^-^
(где и = 0, 1, 2, ...), по недостатку и по избытку, мы заключим его между числами
вида:

445]	§ 4. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ О СТЕПЕННЫХ РЯДАХ	481
где sn - целое. Очевидно, что замкнутые промежутки
Лп = \-—, i^t.| (л = 0, 1, 2, ...),
L2-4" 2-4" J
оказываются вложенными один в другой. В каждом из них найдется такая точка
хп, что расстояние ее от точки х0 равно половине длины промежутка;
ясно, что с возрастанием п варианта хп^х0.
Составим теперь отношение приращений
у
/i=0
Но, при к>п, число —— есть целое кратное периода — функции ик(х), так что
Art 4" 1	ЛК
Ukixn)= Ик(х0), соответствующие члены ряда обращаются в 0 и могут быть опущены.
Если же ?=зл, то функция щ(х), линейная в промежутке Л^, будет линейной и в со-
держащиемся в нем промежутке Лп, причем
ик(хп)-ик(х0)
	=±1 (fc = 0, 1, ..., л).
Таким образом, имеем окончательно
Хп-Х0	А=0
иными словами, это отношение равно четному целому числу при нечетном п и
нечетному целому числу при четном п. Отсюда ясно, что при я^<» отношение
приращений ни к какому конечному пределу стремиться не может, так что наша
функция при х = х0 конечной производной не имеет.
§ 4. Дополнительные сведения о степенных рядах
445. Действия над степенными рядами. Этот п° мы посвятим обзо-
обзору - в основном уже известных - действий над степенными рядами,
что послужит отправной точкой для дальнейшего продвижения.
Рассмотрим два ряда:
2апхп = а0 + ахх + а2х2+ ... +апхп+ ...,	A)
л=0
?Ьпхп = Ь0 + Ь1х + Ь2х2+ ... +bnxn+ ...	B)
л = 0
Предполагая радиусы сходимости обоих рядов отличными от 0,
обозначим через г наименьший из них. Тогда для | х \ < г, как мы
31 Г. М. Фихтенгольц, т. II

482	ГЛ. XII. ФУНКЦИОНАЛЬНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И РЯДЫ	[445
знаем [364, 4°; 389], эти ряды можно почленно складывать, вы-
вычитать и перемножать, причем результаты вновь распола-
располагаются по степеням х:
Zanx«± Zbnx«= 2(ап±Ъп)хп,
л=0	л=0	л=0
2 апхп • 2 ьпхп = 2 № + афп_х + афп-2 + • • • + апЬ0)хп. C)
л=0	л=0	п=0
Допустим, что ряд B) тождествен с A); тогда получится, что
внутри промежутка сходимости степенной ряд можно следующим об-
образом возводить в квадрат:
«1	\2 ~
2 апхп = 2 (аоап + а&п-х + • • • + апа0)хп.
п=0	} п=0
Если последний ряд, по указанному выше правилу, снова помножить
на ряд A) и повторить это неопределенное число раз, то придем к
заключению, что степенной ряд, внутри промежутка сходимости,
можно вообще возводить в степень с любым нату-
натуральным показателем т, причем результат представляется
также в виде степенного ряда:
2 ап*п = 2 а^х" (т = 1, 2, 3, ...).	D)
0	)	0
Коэффициент dfi^ зависит от коэффициентов а0, ах, а2, ..., ап ис-
исходного ряда и - как это следует изC) - получается из них
лишь с помощью сложений и умножений. Это за-
замечание нам ниже понадобится.
Теперь особо остановимся на сложении бесконечного
множества степенных рядов, с чем нам часто придется
иметь дело ниже. Итак, пусть дана бесконечная последовательность
степенных рядов
2аптхп (т = 0, 1,2, ...);
л=0
из них составим повторный ряд
m=0ln=O
Если при выбранном значении х сходится ряд, полученный отсюда
заменой всех членов их абсолютными величинами, то сходится и ряд

445J	§ 4. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ О СТЕПЕННЫХ РЯДАХ	483
E), причем сумма его А(х) может быть разложена в степенной ряд
просто путем объединения подобных членов:
А(х)= %Апхп, где Ап= %апт (и = 0, 1, 2, .. .)•
п=0	m=0
Доказательство исчерпывается ссылкой на теорему 3 п° 393.
Применение этой важной теоремы осветим примерами.
Примеры.
1) Разложить функции
а)
Л
(считая jjc| -= 1 и 0-=а-=1) в ряды по степеням х.
(а) Имеем
ат	у	f
l + aimx* п=о
и, подставляя и изменяя порядок суммирования,
~ аBл + 1)т
Х)= Z — 2 (-1)"аBл + 1>пд:2л= 2* (-
Так как повторный ряд
Z, — Z оBл+1)'"х2л= ^
о'я!О
1-агтх2 \-
сходится, то перестановка суммирований оправдана,
(б) Аналогично
Z
п=0
2) Исходя из разложения функции *ctg;*; на простые дроби [441, 9)], пред-
представим ее теперь степенным рядом. Для упрощения заменим лишь х на пх, так что
^ 1-2 7.
1Ш2
Если |дг| -= 1, то для любого т= 1, 2, 3, ...
хг
от2 - д:2	х2
-if-l"
31*

484	ГЛ. XII. ФУНКЦИОНАЛЬНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И РЯДЫ	[445
Ввиду положительности всех членов, по теореме сразу получаем:
'хП> гпе sin~ ? ~ ("=1, 2, 3, ...).
т=\ТПг-Хг л = 1
Таким образом, при | х | -= 1 имеем:
-тх-ctgлх = 1 - 2 2 smxm.
п=1
3) Совершенно аналогично, исходя из разложения функции x-cth x на простые
дроби [431, 10], получим разложение в степенной ряд
Впоследствии 449 мы дадим и другое выражение для коэффициентов разложений
в 1) и 2).
4) Теорема сохраняет свое значение и в том случае, когда складываемые в
бесконечном количестве ряды вырождаются в обыкновенные конечные много-
многочлены. Для примера выведем логарифмический ряд, исходя из биномиального
и показательного путем следующего рассуждения.
При | х | «= 1 и произвольном а имеем [407 B2)]:
а(а-1)(а-2)
3+
х +*+...
Фиксируя х, станем рассматривать члены этого ряда как целые многочлены отно-
относительно а. Так как ряд
сходится, как легко убедиться с помощью признака Даламбера, то в пред-
предшествующем ряде, согласно теореме, можно объединить подобные члены:
I хг х3	I
A+х)«=1+а \х-— + — -...+...
С другой стороны, очевидно,
Так как оба разложения должны быть тождественны, то, приравнивая коэффи-
коэффициенты при а, получим:
х2 х3
A)
Заметим, что доказанная теорема непосредственно распростра-
распространяется и на кратные ряды, например на ряд
2 \ 2 апк
Действительно, стоит лишь заменить двойной ряд простым, чтобы
свести дело к уже рассмотренному случаю.

446]
§ 4. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ О СТЕПЕННЫХ РЯДАХ
485
446. Подстановка ряда в ряд. Рассмотрим функцию у =f(x), которая
в промежутке (-R, К) разлагается в степенной ряд A). Пусть, кроме
того, дана функция q>(y), также разлагающаяся в степенной ряд
т=0
... \-hmym+ ...
F)
для значений у в промежутке (- р, р).
Если \ао\ = |/@) | <р, то и при достаточно малом х будет |/(х)| <р,
так что имеет смысл сложная функция <p(f(x)).
При единственном условии: |ао|<р, эту функцию q>(f(x)) в окрест-
окрестности точки х = 0 можно разложить в ряд по степеням х, если под-
подставить в F) вместо у ряд A) и, произведя все возведения в степень
согласно D), объединить затем подобные члены.
Доказательство. Считая х I < R, рассмотрим ряд
2
п=0
а,Х
= \ап
\О2\'\Х
по непрерывности суммы его [437, 2°], ввиду \ао\
малых х выполнится неравенство
для достаточно
2\
п=0
так что ряд
2 Ы
л=0
будет сходящимся.
Полагая, аналогично D),
2
л=0
*л
предыдущий ряд можно переписать в виде
1*0
2\К
711 = 1
•(Я").
л=0
G)
Так как <4т) получается из \ао\, fa], ..., \ап\ с помощью сло-
сложений и умножений [445] совершенно так же, как о*,т) из
аа, alt .. .,ап, то очевидно: |a?m)| =sa(,m\ Поэтому для упомянутых зна-
значений х сходится, и ряд
,(ш)| . iv In

486	ГЛ. XII. ФУНКЦИОНАЛЬНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И РЯДЫ	[446
а тогда к ряду
применимо последнее утверждение предыдущего п°, что и доказывает
теорему.
Область изменения х, для которой наше рассуждение обеспечи-
обеспечивает возможность разложения функции <р(/(х)) в ряд по степеням х,
характеризуется, таким образом, кроме само собою разумеющегося
неравенства |х|<Л, еще неравенством G). При Я=+~ нет надоб-
надобности вводить первое ограничение, при р = + ~ отпадает второе.
В большинстве приложений теоремы достаточно знать, что раз-
разложение имеет место для малых значений \х\. Если представляет
интерес вся область применимости полученного ряда, то этот вопрос
требует отдельного исследования.
Для примера проведем его в простом случае. Рассмотрим функцию
сю
т = 0
в промежутке (-1, 1) [р = 1] и, вместо у, подставим функцию /(х) = 2х-х'г [R =
= +«•]. Сложная функция
имеет смысл, лишь если
-1-=2х-х2«=1, т. е. 1 — УТ^х-^ 1 + У2, но
Ее разложение по степеням х нам известно*
1
A-*)»
этот ряд сходится для -1-=х<1. По совокупности, равенство
2 Bх - х*)™ = 1 + 2х+Ъх* + • • •
т=0
имеет место при условии, что
1-У2-=х-=1.
Интересно сопоставить это с тем, что дает наше рассуждение. В согласии с ним
надлежало бы потребовать, чтобы было [см. G)]
1 или 1-Y2^x^f2.-1.
Как мы видели, полученное равенство на деле применимо в более широкой области.
* См. 390, 1). Можно получить это и почленным дифференцированием [438,
8°] прогрессии
	= 1 -ГХ+Х2 + Х3+ ..,
1-х

447]	§ 4. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ О СТЕПЕННЫХ РЯДАХ	487
И здесь надлежит отметить возможность дальнейших обобщений
теоремы. Пусть, например, дан двойной ряд
?<y,z)= 2 hmykzm,
к,т = 0
сходящийся при | j'l <е и lzl ^б» и даа Ряда
у=/(*) = 2 ап*п, *=«(*) = 2 ьпхп,
л=0	п=0
сходящиеся при |х| <R; тогда, при условии: \ао\<р и |60|<р, слож-
сложную функцию <p{f{x), g(xj) в окрестности х = 0 можно разложить в ряд
по степеням х, если подставить вместо у и z соответствующие ряды
и, выполнив возведения в степень и умножения, сделать приведение
подобных членов.
ЛАП. Примеры. 1) Найти несколько первых членов разложения функции
L
по степеням х.
е
Имеем для | х \ -= 1
- 1
)x =-
е
2 х3 х* \* 1 / х хг х3
х хг
1	11 7 2447 959
= 1	х-\—хг	х3 н	х4	гЧ...
2	24 16 5760 2304
[Подобного типа задачи близки к тем, которые рассматривались уже в 125.]
2) Поставим себе задачей получить биномиальный ряд, исходя из логарифми-
логарифмического и показательного рядов.
При \х\ ¦< 1 и любом а, очевидно, будет:
¦к-
х*	\ а?[ х- х3	у	а(а-1)
+	...+... 1 + ex+
Вид нескольких первых коэффициентов устанавливается сразу. Коэффициент
же общего члена, содержащего хп, можно получить из таких соображений. Не-
Непосредственно ясно, что он представляет собой целый многочлен относительно а,
степени и: gn(a). Так как при «(=0,1,2,..., л-1в разложении чдеца с хп нет, то

488	ГЛ. XII. ФУНКЦИОНАЛЬНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И РЯДЫ	[447
этот многочлен в названных точках обращается в 0, а следовательно, имеет вид:
При а = и коэффициент при хп есть 1, Qn(n)=l; отсюда с = —, и окончательно:
п\
3) Пусть/(х) будет некоторая функция, разлагающаяся в ряд по степеням х,
без свободного члена:
тогда, по общей теореме, для тех же значений х разлагается в ряд и функция g(x) =
= еД*), причем свободный член, очевидно, равен 1. Требуется найти это разло-
разложение.
Покажем, как для этого может быть использован метод неопределенных коэф-
коэффициентов. Пусть
... +Ьпхп+ ...
Продифференцировав это равенство, найдем:
ef(x)-fXx) = bl + 2bzx + 3bsx2+ ... +nbnxn+ ...,
или, подставляя вместо множителей левой части их разложения,
Это условие приводит к такой системе уравнений:
2 + albn-i = nbn	, (8)
из которой неизвестные коэффициенты b последовательно и определятся.
Для примера приложим указанный прием к решению следующей задачи (В е й-
е р ш т р а с с).
Доказать, что разложение функции
X X*	Х'п~ *
+ + +
хт
начинается членами 1	1-..., и что все его коэффициенты по абсолютной
т
величине меньше единицы.
Напишем g(x) в виде
l
g(x) = e
12	m-l =
тогда первая часть утверждения становится очевидной. Вторая же часть докажется
индуктивно. Допустим, что все коэффициенты bk со значком, меньшим п,
по абсолютной величине меньше единицы. Так как в данном случае
аь = 0 при k^m и аи=	(faty=-l) при
к
то л-е из равенств (8) обнаружит, что и | bn \ ¦< 1.

447]	§ 4. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ О СТЕПЕННЫХ РЯДАХ	489
[Предлагается применить указанный здесь метод к примерам 1) и 2).]
4) Те же уравнения (8) могут пригодиться и в другом вопросе. Пусть дано
разложение функции
+ ... +bnxn+...,
а ищется разложение функции
f(x) = In g(x) = alx+aix2 + asx3+ ... +anxn + ...
Легко понять, что коэффициенты а и b связаны теми же соотношениями (8), но на
этот раз подлежат определению коэффициенты а.
5) Показать, что бесконечное произведение
, F(x)= na+qmx) = (l+qx)(l+q"x){l + q3x)... (k|-=l),
,71 = 1
при достаточно малых х разлагается по степеням х, определить коэффициенты
этого разложения.
При | х | -= 1 произведение сходится и имеет положительное значение; логариф-
логарифмируя, получим
m=l	m=l
В частности, этот ряд сходится при замене всех членов в скобках их абсолютными
величинами. Отсюда [445] следует, что In F(x) в окрестности нуля разлагается
в ряд по степеням х, а с ним [уже по теореме п° 446] разлагается и выражение
Итак, для достаточно малых х, имеем:
F(x)= I +blX+b2x*+ ... +bnxn+ ¦ ¦.,
где коэффициенты bu Ьг, ..., bn, ¦¦¦ еще подлежат определению. Проще всего
это выполнить, если исходить из очевидного равенства:
которое, воспользовавшись разложением, можно переписать в виде:
1 + 61*+62X2+ ... +Ьпхп+ .. .=(l+qx)(\ + blqx+btq2x2+ .. . +bnqnxn+ ¦
По теореме о тождестве степенных рядов, i сюда
. q . bii2 , bn-iqn
Ь-t = 	 , Уо= 	 , . ... Оп = —	 , ...
\-q	I-?2	\-qn
и, окончательно,
n(n-l)
b =_?_ b q3	q 2
1 iq' 2 A<?)A?2)' ¦"' n~(iq)uq2)

490	ГЛ. XII. ФУНКЦИОНАЛЬНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И РЯДЫ	[447
sin х
6) Возьмем разложения функции 	 в бесконечное произведение [408] и в
х
бесконечный ряд [404] A2)] и приравняем их логарифмы [401, 4°]:
sin х ~
или
х2 1 х1	1 (х* xi	\ 1 (х* xi
JlJl
Разложив левую и правую части по степеням х [445, 446] и отождествив коэффи-
коэффициенты, придем к равенствам
1 " 1 _Ь	1	у 1_ I
5 1 л"г?' 2л1 1 п4~Ш> "¦'
откуда
Впрочем, ниже [449] мы найдем эти формулы из других соображений.
7) Если функция f(x) в промежутке (-R, К) разлагается в степенной ряд A)
их- произвольная точка этого промежутка, то в ее окрестности функция раз-
разлагается в ряд по степеням х-х.
Действительно, положим в A) х = х+у; по общей теореме (меняя лишь роли
х и у), покуда \х\ + \у\ ~^R или \у\ -<R— \x\, можно перейти к разложению по
степеням у, т. е. по степеням х-х:
Вьшолнив в ряде 2 ап(х+у)п все возведения в степень и собрав подобные
л = 1
члены, легко определить и коэффициенты этого разложения:
п=0
и, вообще,
" п{п-\)...(п-к+\) _
А" = ?к	b2^Jfc	ппХП =
Результат этот, ввиду 438, 9°, не является неожиданным.
* Этот результат нам уже известен [см. 440 D)|.

447]	§ 4. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ О СТЕПЕННЫХ РЯДАХ	491
Мы лишь для простоты взяли исходный ряд расположенным по степеням
х - дело не изменилось бы, если бы функция f(x) была дана разложенной по
степеням разности х-х0.
Напомним, что функция f(x), которая в окрестности точки х = х0 разлагается
в ряд по степеням х-xj, называется аналитической в этой точке. Мы
доказали, таким образом, что функция, аналитическая в какой-либо точке, будет
аналитической и во всех точках некоторой ее окрестности.
Это утверждение распространяется и на случай функции от нескольких пере-
переменных.
8) В качестве последнего примера рассмотрим разложение функции
1	_!
[1 (*2)] 2
по степеням а, при произвольно фиксированном х. Возможность такого разло-
разложения гарантируется нашей теоремой, если только |а|2+2|х|-|а|-=1. Легко
усмотреть, что коэффициентом при а" (ив»1) будет некий многочлен Рп = Рп{х)
степени и, так что
1
1 Р Р	¦ +Р„ап+ ¦ ¦ ¦	(9)
Для определения этих коэффициентов, продифференцируем равенство (9)
по а:
• ¦ ¦ + пРп<хп
Сопоставляя этот результат с (9), легко получить:
Приравниваем теперь коэффициенты при одинаковых степенях а в обеих частях.
Мы найдем, прежде всего,
Зх*-1
Pj = x и 2P2-2xPi= -1+хР1у откуда Р2 = —-—.
Затем, вообще,
n+i - Bя+ 1)хРп +яР«-1 = 0.
Зная первые два многочлена, по этой рекуррентной формуле последовательно
можно вычислить остальные.
Бросается в глаза, что многочлены Рх и Рг совпадают с первыми двумя много-
многочленами Лежандра, а упомянутая только что формула тождественна с анало-
аналогичной формулой A1) п° 320, по которой вычисляются многочлены Лежандра.
Отсюда заключаем, что коэффициентами разложения (9) являются именно много-
многочлены Лежандра.
В связи с этим функцию от двух переменных аил:
1
* Этот ряд, необходимо, будет ее рядом Тейлора [438, 9].

492	ГЛ. XII. ФУНКЦИОНАЛЬНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И РЯДЫ	[448
называют «производящей функцией» для многочленов Лежандра. Разло-
Разложение (9) с успехом может быть использовано для изучения свойств этих много-
многочленов.
448. Деление степенных рядов. Важным примером применения тео-
теоремы о подстановке ряда в ряд является вопрос о делении сте-
степенных рядов.
Пусть свободный член а0 ряда A) отличен от 0; представим этот
ряд в виде
полагая
«о «о	а0
— х + — x2i + — хп+ ...
Тогда
а0	s
Последний ряд играет роль ряда F), причем д здесь есть 1. Согласно
общей теореме, это выражение может быть разложено по степеням х:
	;	;	тг,	 =Са + СлХ+ . . . + СпХп + . . .,
по крайней мере, для достаточно малых значений х, например для
тех, которые удовлетворяют неравенству
XJ2+...+
Рассмотрим второй степенной ряд
Ьо + Ьхх + Ь2х2 + ... + bnxn + ...
с отличным от 0 радиусом сходимости. Тогда частное
для достаточно малых х может быть заменено произведением
(Ь0±Ь1х+ ... -bnxn+ .. .)(со + с1х+ .. .+cnxn+ ...)
и, следовательно, снова представимо в виде некоторого степенного ряда
d0 + dYx + d2x2 + ... + dnxn + ...
Коэффициенты этого ряда проще всего определятся по методу не-
неопределенных коэффициентов, исходя из соотношения
+ ... +dnxn+ .. .) =
= Ь0 + Ьхх+ ... +bnxn+ ...,

448]	§ 4. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ О СТЕПЕННЫХ РЯДАХ	493
в которых коэффициенты а и Ь предполагаются известными. Пере-
Перемножив ряды слева по общему правилу [445], мы затем приравняем
коэффициенты при одинаковых степенях х слева и справа. Таким
путем получится бесчисленное множество уравнений:
..., aodn + a^-i + • ¦ • + ап-Л + and0 = Ъп. A0)
Так как коэффициент а0 предположен отличным от 0, то из пер-
первого уравнения сразу получим: d0 = —, затем второе даст нам: dt =
=———= ° * 1 " и т. д. В общем случае, если п коэффициентов
dQ,dx, ..., dn_± уже найдены, то (п+ 1)-е уравнение, содержащее един-
единственную неизвестную dn, позволит установить ее значение. Так, п о-
следовательно, уравнениями A0) определяются все коэффи-
коэффициенты частного и притом вполне однозначно.
Примеры. 1) Найти несколько первых членов частного
хх	1
In
Уравнения A0)
1
здесь
do =
X2 X3
принимают
1
1 2 '
1
X4
вид:
1
X
1
1
X2 Xs
1
1	1	1
и т. д.; отсюда rfo=l, dt= - —, rf2= -—, d3= -— , ••• Итак,
r	111
-=1--д;-— Л-2-— X3-...
1	2 12 24
In
1-х
2) Найти разложение tg x в окрестности нуля, рассматривая tg д: как частное
sinx и cosx, разложения которых известны [404, A2) и A3)].
Существование такого разложения наперед известно - по общей теореме.
Так как tgx есть функция нечетная, то это разложение содержит только
нечетные степени х. Коэффициент при хгп~г в искомом разложении удобно
Т
взять в форме 	. Итак, имеем
B1)!
X
п=1 "Bи-1)!л=о^ ' 2и! п=

494	ГЛ. XII. ФУНКЦИОНАЛЬНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И РЯДЫ	D49
Очевидно, 7\ = 1. Для определения остальных чисел Тп, приравнивая коэффициенты
при хгп~1 слева и справа, получим последовательность уравнений вида:
Bя-1)! Bя-3)! 2! Bл -5)! 4!	Bл-1)!
(п=2,3,„.)
или, по умножении на Bл-1)!,
Так как все числа C2n-i суть целые, то последовательно убеждаемся, что и коэффи-
коэффициенты Тп все целые. Вот значения нескольких первых из них:
Г, = 1, Г2 = 2, Г3=16, Г, = 272, Г6 = 7936, ...
Таким образом,
1 2 17	62
..*	,
В следующем п° будет указан другой способ вычисления коэффициентов этого
разложения и точно установлена область его применимости.
449. Числа Бервулли и разложения, в которых они встречаются. Рассмотрим
еще один пример деления, который будет иметь важные приложения:
хх	1
ех-1 хг	х"
Согласно общему утверждению п° 448, это частное, по крайней мере для доста-
достаточно малых значений х, представляется в виде степенного ряда
f.ir
ех-\	л=1л!
Коэффициенты его мы взяли в форме: /?„/л!, что (как увидим) сделает более удоб-
удобным их последовательное определение.
Исходя из соотношения:
приравняем нулю коэффициенты при различных степенях хп (и= 1, 2, 3, ...) слева.
Мы получим уравнения вида
или - по умножении на (л+1)! -

449)	§ 4. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ О СТЕПЕННЫХ РЯДАХ	495
Использовав сходство с биномом Ньютона, можно эти уравнения сим-
символически записать так:
(fi+l)n+1-fin+1 = 0 (я = 1, 2, 3, ...);
после возвышения двучлена в степень по обычному правилу и сокращения старшего
члена, степени /3* должны быть заменены здесь коэффициентами /% Итак, для
определения чисел рп (и= 1.2, 3, ...) будем иметь бесконечную систему уравнений:
из которых последовательно находим:
Pi~~k' Рг~т /Зз=0' /?
А-~. А-о. А.4- At
3617	43867	174611
Так как числа /3 определяются из линейных уравнений с целыми коэффициен-
коэффициентами, то все они являются рациональными. Легко установить, в общем
виде, что числа /3 с нечетными значками (кроме первого) - нули. Действи-
х
тельно, перенося в равенстве A2) член	налево, будем иметь в левой части
равенства, очевидно, четную функцию
х хх ех+1 х е2+е г х х
	Ь^=-	=	= — cth -.
ех-\ 2 2 е*-1 2 >L _=? 2 2
ег-е 2
В таком случае ее разложение
не может содержать нечетных степеней х, ч. и тр. д.
Для чисел р с четными значками введем более привычное обозначение, полагая*
An-C-i)"-1^,
так что
1111
1 б ' 30 3	42	30
5	691	7
5s=66' 5б = 2У30'	5' = "б"' •¦•
3617 43867	174611
Эти именно числа Вп и называют числами Берну л ли, по имени Якова
Бернулли, который впервые пришел к ним при изучении сумм степеней
* Мы скоро убедимся, что все Вп положительны.

496	ГЛ. XII. ФУНКЦИОНАЛЬНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И РЯДЫ	[449
последовательных натуральных чисел с натуральными же показателями. Числа
Бернулли играют важную роль во многих вопросах анализа.
Итак, заменяя для удобства х на 2х, окончательно имеем разложение
1гВх
jc-cth *=1 + —-х2
2!
2!	4!	2л!
Y/.nn-i2'"
п=1	2й!
действительное для достаточно малых значений х.
В 445, 3) мы уже имели разложение
л=1
где через s.2n была обозначена сумма ряда _2 	• Заменив и в равенстве A3) х на
лх, перепишем его так:
у	п_1BлУпВп
п=1	2и!
Оба разложения, разумеется, должны быть тождественны; отсюда
Вп =	s,n,
BлJ"
так что все числа Вп оказываются положительными. Так как при л -•¦ °°,
очевидно, ssn-»l, то из полученной формулы явствует, что числа Бернулли
бесконечно возрастают* при возрастании их номера.
Отметим попутно полезные выражения, получающиеся для сумм s2n:
g — ^^ 	 = 	, . D .
в частности [ср. 447, 6)]
m=i т2 6 '	m=i mi 90
Вспомним теперь, что и для ^x-ctgrrx мы имели [445], 2)] разложение, коэффи-
коэффициенты которого также зависели от сумм s2n'
nx-ctgnx=l-2 2 s2nx2n.	A4)
Заменяя здесь лх на х и подставляя вместо s2n найденные их выражения через
бернуллиевы числа, получим:
x-ctgx=l- ^	^л:2".	A5)
п=1 2и!
* Хотя, как мы видели, не монотонно, а по весьма прихотливому закону.

449)	§ 4. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ О СТЕПЕННЫХ РЯДАХ	497
Так как про разложение A4) мы знаем, что оно имеет место при \х\ -= 1, то разло-
разложение A5) действительно при |х|«=я. Но при х^+л левая часть равенства A5)
бесконечно возрастает, следовательно, ряд справа не может сходиться ни при
х= ±л, ни тем более при |л:| =-да его радиус сходимости в точности равен я; *.
Отсюда, между прочим, ясно, что таков же будет радиус сходимости ряда
A3), между тем как исходный ряд A2) имеет радиус сходимости 2тг.
Пользуясь тождеством
tg х = ctg x - 2 ctg 2x,
из A5) легко наново получить разложение для tg x:
- 2*"B2" -1)
tg*- 2 \, вп.#п-\	Об)
Оно тождественно с полученным раньше [см. A1)], но его предпочитают писать
именно в этой форме потому, что числа Бернулли хорошо изучены, и для
них имеются обширные таблицы. Радиус сходимости ряда, представляющего
л
tg х, есть —; это видно теперь из самого способа его получения.
I С числами Бернулли связаны и многие другие полезные разложения.
Например, так как
, sinxV cos л: 1 1	^ 2тВп
In	 = — -_ = _(*.ctgx-l)=- 2, 	 xsn~\
x ) sin x x x	n=i 2n\
то, интегрируя почленно, находим (для \х\ «я)
sin х	^ 2тВп х-п
In	= - 2j	•
х	„=i 2л! In
(	л\
Аналогично, из разложения A6) почленным интегрированием получаем для | х | -= -1
- 22"B2"l)S *n
=- 2
i
2	.
n=i 2л!	2л
tgx
Из этих разложений легко получить разложение для In	. Ряды эти полезны
х
при составлении логарифмо-тригонометрических таблиц.
* Впрочем все вопросы, связанные с определением радиуса сходимости сте-
степенного ряда, легко решаются с помощью теоремы Коши - Адамара [380].
Например, для ряда A5) имеем
2л	2л
Л[2Вп \[2 2-2п\
Р«-х-О, Р2„= \1 —= |/ -_.
lim рл
m-fo
1
71
l
R~ — ~7l.
P
32 Г. М. Фяхтенгольц, т. II

498	ГЛ. XII. ФУНКЦИОНАЛЬНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И РЯДЫ	[450
Вернемся, в заключение к расходящемуся ряду
который мы рассматривали в задаче 6) n° 42S. Там была установлена суммируе-
суммируемость этого ряда по методу Ч е з а р о к-ro порядка, но самой «обобщенной сум-
суммы» (обозначим ее через А(кУ) мы не нашли; выполним это сейчас. Впрочем, мы
просуммируем ряд по методу Пуассона - Абеля, что - как мы знаем
[424, 2)] - должно привести к тому же результату.
При /=»0 будет 0<е"~'«=1 и, суммируя прогрессию, получим
е(-1 e*'-l t e'-l t e2t-\
Используя разложение A2), для достаточно малых / будем иметь
2 (- iye-
о
2
2 ( iyec = - 2 -—— i-
л=о	л=1 я!
Продифференцируем оба ряда п_ ленно к раз; для степенного ряда справа мы
опираемся на теорему 8° п° 438, она1 же служит основанием и для дифференциро-
дифференцирования ряда слева, который тоже оказывается степенным, если ввести переменную
х = е~1. В результате найдем
2 B""~~1)/?"(и-1)(я-2)-¦¦¦•(«--*:)'"-*-'•
л=А + 1	и!
Устремим теперь t к 0, а следовательно, л: к 1. Слева в пределе получится именно
искомое AW, а справа — свободный член
Вспоминая, что числа /? с нечетными знaчкa^ш, ббльшими единицы, все нули,
а с четными - приводятся к числам Б е р н у л л и, окончательно приходим
к формулам:
450. Решение уравнений рядами. Мы еще раз вернемся к вопросу
об определении переменной у, как функции от х, из неразрешенного
уравнения:
F(x,y) = 0	A7)
[ср. 206 и 442!], но в иной постановке:
Предположим, что функция F(x,y) в окрестности точки (хо,уо)
разлагается в ряд по степеням х — х0 и у—у0, причем постоянный член

4S0J	§ 4. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ О СТЕПЕННЫХ РЯДАХ	499
в нем равен О, а коэффициент при у -у0 отличен от О *. Тогда и функ-
функция у = у(х), определяемая уравнением A7) в окрестности указанной
точки, также разлагается в ряд по степеням х-х0 вблизи х - х0.
Иными словами, если функция F, фигурирующая в левой части
уравнения A7), будет аналитической в точке (хо,уо), то и
функция у=у(х), определяемая уравнением, оказывается аналити-
аналитической в точке х0. Таким образом, здесь речь идет уже не только
о существовании или вычислении значений искомой функции, но и об
ее аналитическом представлении.
Доказательство. Без умаления общности можно принять
хо=уо = О; это, по существу, сводится к тому, что в качестве новых
переменных мы выбираем разности х-х0 и у-у0, но сохраняем ста-
старые' обозначения. Если выделить член с первой степенью у, то, пере-
перенося его в другую часть и деля на коэффициент при нем, можно будет
переписать данное уравнение так:
у = с1Ох + с20х2 + спху + с^У2 + СзоА-3 + с21х2у + с12ху2 + сюу* +... A8)
Ряд для функции у от х будем искать в виде:
а3х3+...	A9)
Прежде всего, если подобное разложение в окрест-
окрестности нуля имеет место, то коэффициенты его
вполне однозначно определяются самим соотно-
соотношением A8).
Действительно, заменяя в нем у (при указанном предположе-
предположении) разложением A9), получим:
ахх +
=с1Ох + cwx2 + Cuxfax + Оа*2 +...) + с02 • {агх + а^х2 + ... J +
+ с21х2 • (агх +...) + с12х • (а^ + .. .J +
...K+... A8а)
По теореме п° 446, для достаточно малых х, справа здесь можно вы-
выполнить все возведения в степень и сделать приведение подобных
членов. Если после этого воспользоваться теоремой о тождестве сте-
степенных рядов и приравнять коэффициенты при одинаковых степенях
х слева и справа, то мы придем к (бесконечной!) системе уравнений:
ах = с10, Яг = с20 + спаг
аг = спа2 + Ic^fljf^ + с30 + с21ах + с12а\ + сйга\, ...	B0)
* Это в точности соответствует обычным требованиям
32*

500	ГЛ. XII. ФУНКЦИОНАЛЬНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И РЯДЫ	[450
относительно искомых коэффициентов а1Уа2,а3, ..., ап, ... Так как
в A8) справа все члены, содержащие у, не ниже второго измерения
(т. е. содержат либо высшую степень самого у, либо у в первой сте-
степени, но умноженное на какую-либо степень х), то в и-м уравнении
системы B0) коэффициент ап оказывается выраженным через коэффи-
коэффициенты а1г а^, ..., а„_! с меньшими номерами (и известные коэффи-
коэффициенты с). Этим и обеспечивается возможность
определять коэффициенты ап последовательно
один за другим:
а1 ~ С10 > а2 ~ С20 + С11С10 + С02С10 >
аг = (си + 2с02с10)(с20 + спс10 + c02cf0) + с30 + с21с10 + с12с\0 + созс|о, ... B1)
Попутно сделаем такое, важное для дальнейшего, замечание. Так
как при раскрытии скобок в A8а) над буквами а и с не приходится
производить иных действий, кроме сложения и умножения, то в пра-
правых частях уравнений B0) мы будем иметь целые многочлены относи-
относительно этих букв, с заведомо положительными (даже - на-
натуральными) коэффициентами. А тогда и в формулах B1) справа
также будут целые многочлены с положительными же коэф-
коэффициентами относительно букв с.
Составим теперь ряд A9) с коэффициентами а, вычисленными
именно по этим формулам. Про него можно сказать, что он «фор-
«формально» удовлетворяет соотношению A8а). Если бы была удосто-
удостоверена сходимость этого ряда для достаточно малых х, то уже не
было бы надобности доказывать, что для представляемой им функции
условие A8) выполнено, ибо в этом случае равенства B0), которым
коэффициенты ряда удовлетворяют, вполне равносильны A8а). Итак,
весь вопрос теперь сводится к доказательству
того лишь, что ряд A9), коэффициенты которого
определяются формулами B1), сходится в неко-
некоторой окрестности нуля.
Рассмотрим, одновременно с A8), аналогичное соотношение
У=ушх + у2ах2 + упху+уюу2 + узох3 + у21х2у + упху2 + уюу3+ ..., A8*)
где все коэффициенты yik положительны и, кроме того, удо-
удовлетворяют неравенствам
M=sy(ft.	B2)
Построим для него - пока формально - ряд, аналогичный A9):
... +хпхп+ ...,	A9*)

450]	§ 4. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ О СТЕПЕННЫХ РЯДАХ	501
причем коэффициенты его, наподобие B1), определим формулами:
«з=(Ун + 2уо2Ую)(У2о + УпУю + У02У10) +
+ У30 + У21У10 + У12У10 + У03У10, •¦• B1*)
Самый состав этих формул, ввиду отмеченного выше, обеспечивает
положительность чисел а„. Кроме того, сопоставляя с B1) и
учитывая B2), видим, что и (при всех п)
\ап\ >*«.„.	B3)
Если бы удалось выбрать положительные коэффициенты yik так, чтобы
не только выполнялись условия B2), но и чтобы соответственно по-
построенный ряд A9*) имел отличный от нуля радиус сходимости, то,
ввиду B3), это же было бы справедливо и для ряда A9) - и теорема
была бы доказана. Займемся же выбором чисел yik.
Существуют такие положительные числа г и д, что двойной ряд
cu\
\cO2\q2
будет сходящимся, так что его общий член \clk\ r'Qk стремится к 0
и, следовательно, ограничен:
! cik | • rlqk^M, откуда | cik \ =s-^-.
Положим yik = -Yk и> в согласии со сказанным, рассмотрим соотно-
соотношение:
м м 9 м м „	м	,, м
или, наконец,
2	Ы~	iviQ2	X	л
у ~~о+мул"о+м'Т^х =
Здесь оказывается возможным фактически найти функцию
у=у(х), удовлетворяющую уравнению - именно ту ее ветвь, кото-
которая обращается в 0 при х = 0. Решая квадратное уравнение, мы по-
получим (считая Ы<г):
х ]*
* Знак минус перед корнем взят как раз для того, чтобы при л: = 0 иметь и
у=0.

502	ГЛ. XII. ФУНКЦИОНАЛЬНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И РЯДЫ	1451
Если, для упрощения записи, ввести обозначение
B4)
то выражение для у можно написать в виде:
[-НГИ
откуда уже ясно, если воспользоваться биномиальным рядом, что
оно для |х| -=>!-=:/• разлагается по степеням х. Так как упомянутое
разложение должно быть тождественно с A9*), то этим и завершается
доказательство сходимости ряда A9*), а значит, и ряда A9), по край-
крайней мере для \х\ -<г1.
Отметим, что теорема устанавливает лишь возможность разло-
разложения у по степеням х (или, в общем случае, по степеням х - х0) вбли-
вблизи х = 0 (х = х0). Определение точного промежутка сходимости этого
разложения требует особого исследования.
Подобным же образом можно трактовать и общий случай, когда
система функций определяется из системы уравнений.
Замечательный метод рассуждения, примененный выше, принад-
принадлежит К о ш и. Сущность его заключается в замене данных степен-
степенных рядов, с одной или несколькими переменными, - более удоб-
удобными для исследования «мажорантными» рядами, все коэффициенты
которых положительны и, соответственно, превосходят абсолютные
величины коэффициентов данных рядов. В связи с этим и сам метод
получил название метода мажорантных рядов. Им часто пользуются
в теории дифференциальных уравнений.
451. Обращение степенного ряда. Как частный случай решенной
задачи, рассмотрим теперь вопрос об обращении степенного
ряда. Пусть функция у =f(x) в некоторой окрестности точки х = х0
представляется рядом, расположенным по степеням х - х0. Обозначая
свободный член (выражающий значение у при х = х0) через у0, напишем
это разложение в виде
У-Уо = а1(х-хо) + сфс-хоУ+ ... +ап(х-х0)п+ ...
При ао^О, в окрестности у=у0, х определяется отсюда как функ-
функция от у, разлагающаяся, в свою очередь, е ряд по степеням у-у0.
Таким образом, если у является аналитической функцией от
х в точке х0, то в соответствующей точке у0 (при указанном усло-
условии) и обратная функция будет аналитической.
Все это непосредственно вытекает из доказанной теоремы. Поло-
Положив для простоты хо=уо = 0, напишем соотношение, связывающее

451]	§ 4. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ О СТЕПЕННЫХ РЯДАХ	503
у с х, по примеру A8), в виде
X = Ьу + С2Х2 + CjX3 + С4Х4 + . . . *
Тогда коэффициенты искомого разложения
х = Ьху + Ь2у2 + Ь3у3 + ...
последовательно определятся из уравнений:
ЬХ = Ъ, Ьг = сф\, Ь3 = 2сфф2 + сф\,
Ъ, = с2BЬф3 + Ъ\) + Ъсф\Ъ2 + сф\,
Ъь = 2с2(&А + Ьф3) + Зс3A%Ьг + Ьф%) + Асф\Ъ2 + сф\.
Например, зная разложение синуса
1	1 ,
у = sin х = х - — х3 I	х° - ...,
6 120
можно найти разложение
х = arcsinу = у + b3y3 fЬъуь + ...
(мы выписываем лишь нечетные степени у, ибо, ввиду нечетности функции у = sin x
наперед ясно, что и обратная функция будет нечетной). Уравнения, определяющие
коэффициенты Ъ, в этом случае имеют вид:
Другой пример: пусть
хч. хз
, = **_!-*+_ + _+...;
отсюда
дс = 1п {l+y) = bly+b2y2+b3y3+ ¦ ¦ ¦
Коэффициенты Ъ определяются последовательно:
fti-1. ъг--х-ъ\--х~, ь3=-ьфг-1-ь\=^,
h = - ФА+bzb3) - j ф\ь3+bjb\) - j ь\ь2 - ^ ь\ - i
- _^+у>-3—-у'+--уь-...
Область изменения у, в которой гарантируются существование обратной
функции и действительность полученного для нее разложения, может быть уста-
установлена из соображений n° 4S0, но оказывается обычно очень заниженной. Если,
* Нужно помнить, что здесь - по сравнению с предыдущим п° - х и у обменя-
обменялись ролями,

504	ГЛ. XII. ФУНКЦИОНАЛЬНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И РЯДЫ	[451
скажем, в первом из приведенных примеров переписать уравнение, связывающее
х и у в форме A8):
X3 Xs
х=у-{	—+ ...
6 120
л
и ограничиться х и у, удовлетворяющими неравенствам |x|=s—, |j;]=sl, т. е.
взять q = — , г = 1, то получим М= 1 и - по формуле B4) -
л у
-=0,2,
в то время как истинная область применимости полученного результата есть
промежуток [-1, 1]!
Замечание. Полезно дать себе отчет в значении условия ах * 0,
при котором только и справедливо сформулированное выше утвер-
утверждение. Пусть 0^ = 0, но а2^0, скажем, с^^О; итак, вблизи х = 0 (для
простоты мы полагаем хо=уо=О) имеем
у =
1
так что j=-0. Обозначая через у2 арифметическое значение корня,
видим, что
причем поставленный двойной знак совпадает со знаком х. В силу
теоремы п° 50, последний радикал вблизи х = 0 сам представляется
степенным рядом с свободным членом 1. Таким образом, оконча-
окончательно (если двойной знак перенести налево):
где уже ai = /a^>0. Используя теорему настоящего п° (роль у играет
величина ± Yyl), мы получим два различных разложения для х, в
зависимости от выбранного знака:
-0 (ft*
Обращаем внимание читателя как на двузначность обрат-
обратной функции, так и на то, что каждая из ее ветвей разлагается уже не
по целым, а по дробным степеням переменной у.

452]	§ 4. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ О СТЕПЕННЫХ РЯДАХ	505
452. Ряд Лаграюка. Применим теорему п° 450 к частному уравнению вида
у = а+х<р(у),	B5)
где функция <р(у) предполагается аналитической в точке у = а. Тогда, как мы знаем,
для достаточно малых значений х, отсюда у определяется, как функция от х, анали-
аналитическая в точке х - 0 и обращающаяся в этой точке в а.
Пусть, далее, и=/(у) будет какая-либо функция от у, аналитическая при у=а.
Если вместо у подставить сюда упомянутую функцию от х, то и окажется функцией
от х, которая также является аналитической при х=0. Поставим себе задачей
найти разложение и по степеням х, точнее - найти удобные выражения для коэф-
коэффициентов этого разложения.
Заметим предварительно, что - при переменном а - из уравнения B5), у
определяется как функция двух переменных хна, аналитическая в точке @, а)*.
Тогда и переменная и будет функцией от тех же двух переменных.
Дифференцируя B5) по д; и по а, получим:
да
откуда, очевидно,
а также и вообще,
[1-
при
х-
и
ду
<р'(у)] {¦
дх
-/(у),
=<р(у),
ду
ди
Tx=4t
[1-
ду
ди
V)Ta
B6а)
С другой стороны, какова бы ни была функция F(y), для которой существует
производная по у, имеем:
д Г ди] д
ди] д
да! да
dxl да! да
В этом легко убедиться непосредственно дифференцированием, с ссылкой на
тождества B6) и B6а).
Всеми этими замечаниями мы воспользуемся для доказательства важной
в дальнейшем формулы:
дпи д"'1 Г	ди] **
дхп дап 11	да!
При п= 1 она приводится к B6а). Допустим теперь, что она верна для некоторого
значения йэ=1, и установим справедливость ее для производной (/?+1)-го порядка.
Дифференцируя B8) по х и пользуясь правом переставлять дифференцирования
[190], получаем
дп+1и дп'1 д Г	ди]
	=	— \фп(у)— .
дхп+1 да"-1 дх I	да!
Но, в силу B7) и B6а) имеем последовательно
дх L	да! да L	дх! да [	да!'
* Это утверждение предполагает, что теорема п° 450 распространена на слу-
случай, когда в уравнении фигурируют три переменные, и одна из них определяется
как функция от остальных двух.
** Здесь <рп(у) означает степень: [<р(у)]п.

506	ГЛ. XII. ФУНКЦИОНАЛЬНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И РЯДЫ	[452
Подставляя это в предыдущее равенство, получим:
дх"+1 дап1	да
Таким образом, формула B8) индуктивно оправдана.
Обратимся, наконец, к интересующему нас разложению функции и по степеням
х. При постоянном а оно необходимо имеет вид разложения Тейлора [438, 9°].
ди
где указатель 0 означает, что функция и ее производные взяты при х = 0. Но тогда
у обращается в а, так что ио=/(а), и затем, по формуле B8),
дпи\ d"'1
дхп!о da"-1
Подставляя эти значения коэффициентов, мы приходим к разложению:
/(у)-Яа) + х-ф)/\а) + ^-у №(а)./'(«)]+ • • • +^ ^- 1<Рп(а)•/'(«)]+ • • -, B9)
2! da	n\ dan~1
которое и называется рядом Л а г р анж а. Оно замечательно тем, что ко-
коэффициенты его представлены в виде явных функций от а.
Если /0>)=/, то, в частности, получаем
у = а+х-<р{а)+Х--—{<р\а)\+...+ — --	 [?>"(«)]+•••	B9а)
2! da	и! dan~l
Существует тесная связь между задачей, рассматриваемой в настоящем п°,
и задачей обращения степенного ряда. Если (в предположении, что у(а)^0) пере-
переписать уравнение B5) в виде
х = ^ Ь0+Ь1(у
то задача Лагранжа окажется равносильна обращению этого ряда, располо-
расположенного по степеням у - а. Наоборот, если поставлена задача обращения степен-
степенного ряда
v = alx+azx1+a3x3+... (о^О),
то, переписав это соотношение так:
обозначим сумму ряда в скобках через у(х). Тогда приходим к уравнению типа B5)
1
здесь а = 0, <р{х) =	, и кроме того, х и у обменялись ролями. Последнее заме-
V(*)
чание важно потому еще, что позволяет сразу дать общее выражепие для результата

452]	§ 4. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ О СТЕПЕННЫХ РЯДАХ	507
обращения по формуле B9а):
1 у* Г d I I	yn\ dn~* 1
@) 2! L&2(
1 у Г d I I	y\ d	1 1
V>@) 2! L<&v>2(*)J*=o "я! Lrfx"-1v'IwJx=o
Приведем примеры.
1) Начнем именно с использования формулы C0). Пусть дано уравнение
у = х(а+х)
Гак как
то приходим
dx>
к такому
1 (-
-х)"
разложению:
а а3
О"
-1)
1
а+х
~hi-(n+l)-.
(а+хуп-
B.п — 2)!
(л-1)!л!
..-Bи-2)
1
уП
а2П-1 ' ' ' '
То же разложение получается, если решить квадратное уравнение относительно х,
выбрав то из его значений, которое обращается в 0 вместе с у.
2) Будем исходить из уравнения типа B5)
х
у=ал— ,
У
так что здесь <р(у) = — . Полагая f(y)-y~k, по формуле Лагранжа B9) найдем
У
11	к х* к(к+3) х3 к(к+4)(к+5) х* k{k+S){k + 6){k+l)
ук ак дА+2 2! ak+i 3!	ак+е	4!	ak+s
Так как данное уравнение приводится к квадратному:
у2 - ау - х = 0,
то, очевидно,*
Например, если а = 2, то получается (по умножении на 2к) такое разложение:
2 \к
'4
4 2!
* Знак плюс перед корнем взят в связи с тем, что при х = 0 должно быть у = а.

508	ГЛ. XII. ФУНКЦИОНАЛЬНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И РЯДЫ	D53
3) В теоретической астрономии важную роль играет уравнение Кеплера:
где Е есть эксцентрическая аномалия планеты, М - ее средняя аномалия, а е -
эксцентриситет планетной орбиты. Воспользовавшись рядом Лагранжа
B9а), можно найти разложение Е по степеням эксцентриситета, с коэффициентами,
зависящими от М:
е2 d	en dn~x
?= М4е• sin Мн	sin2M+ ...Л	sin" M+ ...
2! dM	n\ dM"-i
Здесь представляет важность знать точные размеры промежутка сходимости:
Лаплас [P. S. Laplace] первый установил, что сходимость имеет место для
е-= 0,6627...
4) Наконец, рассмотрим уравнение
Его решение, обращающееся в х при а = 0, будет
2х - а
а	1 + У1
Разложение этой функции по степеням а имеет вид:
f
«fa"
Продифференцируем обе части этого равенства по х (причем из аналитического
характера у как функции от двух переменных а и х, можно заключить, что
для ряда допустимо почленное дифференцирование). Мы получим разложение
: dx	2!22 etc2	и!2" dxn
Его коэффициентами, как мы в этом случае непосредственно усматриваем
[ср. 447, 8)], являются многочлены Лежандра:
n"
iiJ2" dx"
§ 5. Элементарные функции комплексной переменной
453. Комплексные числа. Хотя наш курс целиком посвящен веществен-
вещественным переменным и вещественным же функциям от них, настоящий
параграф - отступая от этой основной линии - мы посвятим элементарным
функциям комплексной переменной. Изложение этого вопроса
примыкает к теории степенных рядов и, в свою очередь, проливает свет на некото-
некоторые принципиальные моменты этой теории. Кроме того, знакомство с функциями
Здесь х играет роль а, а a - роль х.

453]
§ 5. ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ
509
комплексной переменной оказывается полезным для вещественного анализа и
в вычислительном отношении [ср. примеры в 461, а также главу XIX, посвященную
рядам Фурье, в третьем томе курса].
Мы предполагаем, что читатель уже знает комплексные числа из алгебры.
Поэтому мы ограничимся здесь лишь кратким обзором основных свойств этих
чисел.
Комплексное число z имеет вид: z=x+yi, где i есть мнимая единица,
i = У— 1, а. х я у - вещественные числа. Из них х называется вещественной,
а. у — мнимой составляющей или частью числа г, и обозначаются так:
x = R(z), у = I(z).
Два комплексных числа x+yi и x'+y'i равны тогда (и только тогда), когда
порознь х = х' и у = у'.* Сложение и умножение комплексных чисел производятся
по формулам:
(x+yi)(x'+y'i) = (xx' - yy') + (xy'+x'y)i;
легко проверить существование разности и частного, выражаемых так:
x+yi хх'+уу' х'у-х/
-Л	:	:.-«
x'+y'i х'2+у'* х'2+у'-
(последнее - в предположении, что х'+y'i^O, т. е. что х'2+у^0). При этом
для комплексных чисел соблюдаются все обычные свойства действий, не свя-
связанные с понятиями больше и меньше (эти понятия для комплексных чисел
не устанавливаются). Точнее говоря, имеют
место свойства II 1°-4° п° 3 и III 1°-5°
п° 4.
Возьмем на плоскости прямоугольную
систему координатных осей хОу (рис. 63).
Тогда каждое комплексное число z=x+yi
может быть изображено на этой плоскости
точкой М(х, у), координатами которой яв-
являются вещественная и мнимая составляю-
составляющие этого числа. Очевидно, и обратно -
каждой точке М плоскости отвечает вполне
определенное комплексное число. В связи
с этим рассматриваемую плоскость назы-
называют плоскостью комплексной
переменной z или просто комплекс-
комплексной плоскостью.
Вещественные числа x = x+0-i изобра-
изображаются точками на оси х (ибо для них
j> = 0), а чисто мнимые числа yi-0+yi (х=0) - точками на оси у. Эти оси
и называют первую - вещественной осью, а вторую - мнимой.
Важную роль играют также полярные координаты г, в точки, служащей
изображением числа z=x+yi (см. чертеж). Неотрицательное число г называется
модулем или абсолютной величиной комплексного числа z и
Рис. 63.
* Иными словами, и здесь для нас равенство сводится к простому тождеству
[ср. п° 2].

510	ГЛ. XII. ФУНКЦИОНАЛЬНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И РЯДЫ	D53
обозначается так: r= \z\. Модуль однозначно определяется комплексным числом z:
и обращается в нуль в том и только в том случае, когда 2 = 0. Угол 0 называется
аргументом комплексного числа z, 0 = Argz. При z*0, он определяется из
равенств
х	у
cos0=—, sin0 = —,
г	г
но лишь с точностью до слагаемого вида 2кл (к - целое). Для г=0 аргумент
остается вовсе не определенным. За исключением этого случая для каждого числа
z существует один и только один аргумент в, удовлетворяющий неравенствам
его называют главным значением аргумента и обозначают через argz.
Если б-=тг, то
0 sin б	г sin в	у
+2 — = ^————— = —————— = ___^__^^__^^_
2 l + cosfl r+rcosO х+ух2+уг'
и угол arg z можно определить равенством
V
argz=2arctg-
оно годится для всех комплексных чисел, кроме вещественных отрицательных
(и нуля).
Отметим, что для модулей комплексных чисел z=x+yi и z' = x'+y'i также
выполняется неравенство:
столь привычное для абсолютных величин вещественных чисел. Действительно,
в настоящем случае оно приводится к известному неравенству:
которое представляет частный случай неравенства Минковского [133 G)];
см. также сноску на стр. 346 1-го тома.
Справедливы и вытекающие из него следствия [см. 17].
Если в обозначении комплексного числа z=x+yi положить x=r-cos &,
у= r-sin &, то получим так называемую тригонометрическую форму
комплексного числа:
z = r(cos в + i sin ©).
Возьмем второе комплексное число z' также в тригонометрической форме:
z'= f'(cos @'+/sin ©')•
Тогда произведение zz'b тригонометрической форме напишется так:
zz'=rr'[cos @+0O+»sin @+001;
это непосредственно следует из теорем сложения для косинуса и синуса. Отсюда
|zz'| = |z|-|z'|, Arg zz' = Arg z+Arg z'.

454]	§ 5. ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ	511
Аналогично, для частного чисел z и z' (z' ^ 0) находим:
Z
Arg — = Arg z - Arg z'.
z
Из формулы произведения получается формула для степени с натуральным
показателем п:
zn =
в частности, при г- 1, приходим к формуле М о а в р a (A. de Moivre):
(cos в + i sin в)п = cos пв+i sin пв.
Наконец, для корня и-й степени из z имеем
"_ "_/ 0	0"|
Уг=\г cos—I-/sin — ,
I п	п)
л
где УТ есть арифметический корень из г. Полагая здесь поочередно,
например,
0 = 0, 0 + 2л, 0 + 4л, ..., в+2(п-1)тт,
п
мы получим п различных значении корня Уг (конечно, считая z*0); при
других значениях 0 будут уже лишь повторяться эти же значения корня.
454. Комплексная варианта и ее предел. Рассмотрим последовательность {zn},
состоящую из комплексных чисел zn = хп+yni {п- 1,2, 3, ...), и переменную
z, принимающую эти значения в порядке возрастания номеров.
Предел такой комплексной варианты определяется в тех же терминах,
что и в случае вещественной варианты [23]:
Постоянное число с=а+Ы называется пределом варианты z = zn, если
сколь мало бы ни было число е^О, для него существует такой номер N, что все
значения zn с номерами n^N удовлетворяют неравенству
|г„-с|<е.
При этом пишут
lim zn = c или zn — с.
Точно так же переносятся на рассматриваемый случай определения беско-
бесконечно малой и бесконечно большой величин.
Отметим, что теперь не может быть речи о стремлении варианты к бесконеч-
бесконечности определенного знака, поскольку комплексным числам знак
вообще не приписывается. Если zn есть бесконечно большая, т. е. \zn\ — +~, то
говорят, что zn-«> (без знака!).
Рассмотрим, например, варианту zn = z", где z есть комплексное число. Если
при этом \z\ ¦< 1, то zn—0, если же \z\ =-1, то zn - «>; легко видеть, что при \z\ - 1
(но z^ 1) для варианты zn предела вовсе нет.
Для комплексной варианты легко непосредственно передоказать основные
утверждения теории пределов, почти дословно повторяя прежние рассуждения.
С другой стороны, все эти утверждения автоматически переносятся на случай
комплексной варианты на основании следующей простой теоремы:
Комплексная варианта zn = xn+yni стремится к пределу с = а+Ы тогда и только
тогда, когда вещественные варианты хп и уп стремятся соответственно к пределам
а и Ь.
Ее доказательство сразу следует из неравенств:
\Уп-Ь\ I

512	ГЛ. XII. ФУНКЦИОНАЛЬНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И РЯДЫ	[454
Таким образом исследование комплексной варианты может быть заменено
исследованием двух вещественных вариант. В частности, этим путем можно до-
доказать для комплексной варианты и принцип сходимости [39].
Рассмотрим теперь бесконечный ряд
2 Сп = С1 + С2+...+Сп+...
л=1
с комплексными членами cn = an+bni. Суммой ряда и здесь называется предел
частичной суммы
сп= 24-
А = 1
Так, например, для геометрической прогрессии
(где z - комплексное число, отличное от 1), частичная сумма равна
отсюда ясно, что при \z\ -= 1 ряд имеет сумму
1
1-z'
а при |z|s»l у него (конечной) суммы нет.
Все основные понятия и теоремы пп° 362, 364 (с их доказательствами) сохра-
сохраняются.
Исследование комплексного ряда может быть сведено к исследованию двух
вещественных рядов, на основании теоремы:
Сходимость комплексного ряда
Zcn^Z(an+bni)	(С)
л = 1	л=1
к сумме С-A + Bi равносильна сходимости двух вещественных рядов
2 an (А) и УЪП (В),
л=1	п=1
соответственно, к суммам А ж В.
Это утверждение, очевидно, есть лишь перефразировка теоремы, доказанной
выше в терминах варианты.
Теперь докажем теорему, аналогичную теореме п° 377.
Если сходится положительный ряд
2\сп\,	(с*)
л=1
составленный из модулей членов ряда (С), то и этот последний ряд также
сходится.

4551	§ 5. функции комплексной переменной	513
Действительно, ввиду очевидных неравенств
сходимость ряда (С*) влечет за собой сходимость обоих рядов
2 1«л1 и 2 \Ьп\-
Отсюда [377] следует, что сходятся ряды (А) и (В), а тогда - по предыдущей тео-
теореме - сходится и ряд (С).
В случае сходимости ряда (С*) ряд (С) называется абсолютно сходя-
сходящимся, отметим, что при этом, как мы видели, и ряды (А), (В) также сходятся
абсолютно.
Благодаря этой теореме, для комплексных рядов сохраняет свою силу, на-
например, признак Даламбера [377].
На абсолютно сходящиеся комплексные ряды переносятся теорема п° 387
о перемещении членов ряда и правило п° 389 о почленном умножении рядов. В пер-
первом случае доказательство осуществляется сведением к вещественным рядам,
а во втором - в принципе может быть сохранено прежнее доказательство.
Наконец, аналогичным образом можно на комплексный случай перенести
основные понятия и теоремы из теории двойных рядов.
455. Функции комплексной переменной. Пусть комплексная переменная z =
= x+yi принимает всевозможные значения из некоторого множества % = {z),
которое геометрически интерпретируется, как область (открытая или нет) в ком-
комплексной плоскости. Если с каждым значением z из области % сопоставляется
одно или несколько значений другой комплексной переменной w = u+vi,
то последнюю называют (соответственно, однозначной или многознач-
многозначной) функцией от z в области %> и пишут:
iv = /(z) или w=g(z), и т. п.
Примерами однозначных функций (и притом - во всей комплексной пло-
плоскости) могут служить: \z\,zn или вообще - целая рациональная функ-
функция, т. е. целый многочлен
с произвольными комплексными коэффициентами с0, clt ...,cn. Дробная
рациональная функция, т. е. несократимое частное двух многочленов,
также однозначно определена во всей плоскости, но в точках, отвечающих корням
знаменателя, она обращается в бесконечность. В качестве примеров неоднознач-
п
ных функций назовем Argz, ]Az. Ниже, в 457-460 мы изучим другие важные
функции комплексной переменной.
В последующем, если не оговорено противное, мы будем рассматривать
однозначные функции.
Если w=u+vi есть функции от z=x+yi в области %> = {z} = {x+yi}, то ее
составляющие и, v, очевидно, также будут функциями от z или - что то же -
от х, у в соответствующей области %* = {(х, у)} (которая геометрически изобра-
изображается той же фигурой, что и %>):
и = и(х, у), v = v(x, у).
33 Г. М. Фихтенгольп, т. II

514	ГЛ. XII. ФУНКЦИОНАЛЬНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И РЯДЫ	[455
Например, для вещественных функций w= |г| или w=arg z имеем, соответственно:
V
или и = 2 arctg -
для функции iv = zn = (x+,y0n, очевидно,
п(п-\)
и = хп	хп~*у*+ ...,
и(и-1)(и-2)
в-ихл-1?	-хп~3у3+ ...
1-2-3
Пусть с будет точкой сгущения области %. Говорят, что функция w=/(z)
при стремлении z к с имеет предел С *, если для каждого числа е >• О найдется такое
число д^О, что |/(z)-C| -=е, лишь только \z-c\ -=й (аг^с).
Записьшают этот факт, как обычно:
lim»c=lim/(z) = C.
Легко перефразировать это определение для случая, когда с (или С) есть ~; можно
выразить его «на языке последовательностей».
Если с-а+Ы, C=A+Bi, то [как нетрудно вывести из п° 454] предыдущее
соотношение равносильно таким двум:
\imu(x, y)=A, Шпг>(х, у) = В.
у—Ь	у-*Ь
Непрерывность функции/(z) в какой-либо точке z0 = xo+yoi области %
определяется равенством:
ton/(z)=/(z0).
Она, очевидно, равносильна непрерывности обеих составляющих и(х, у), v(x, у)
в точке (х0, у0).
Таким образом, вспоминая только что приведенные выражения для |г| и со-
составляющих г", видим, что эти функции непрерьшны для всей плоскости комплекс-
комплексной переменной. Аналогично, argz оказывается непрерывным повсюду, исклю-
исключая отрицательную часть вещественной оси.
Конечно, непрерывность может быть устанавливаема и непосредственно из
комплексных соображений. Например, для функции |z| она сразу следует из
неравенства
||Г|
Для функции гп имеем:
При достаточной близости г к z0 значения г будут ограничены некоторой постоян-
постоянной: |z|«eM, так что
^^- |г-го|,
откуда и следует требуемое заключение.
* Здесь с и С - комплексные числа.

456]	§ 5. ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ	515
Легко теперь доказать непрерьшность целой и дробной рациональной функции
(в последнем случае - исключая корни знаменателя).
Определение производной для функции w=f(z) в точке z=z0 имеет
тот же вид, как в обычном дифференциальном исчислении:
,	/(zo+zlz)-/(zo)	/(z)-/(z0)
w —j (zo)= lim 	= lim 	.
Jz-o	Az	z-~2, z-zQ
Например, для функции w=z" имеем
г*-г*
O
так что, переходя к пределу при z~z0, получаем снова знакомую формулу:
Формула п° 94 для производной обратной функции и все правила дифферен-
дифференцирования пп° 97, 98 переносятся без изменений. Аналогично устанавливается
и понятие производных высших порядков.
Упомянем еще о рядах:
членами которых являются функции от комплексной переменной z в одной и той
же области %.
Здесь, прежде всего, может быть установлено понятие равномерной
сходимости в тех же терминах, что и в 428. В случае комплексных функцио-
функциональных рядов убеждаться в равномерной сходимости также можно по наличию
положительного мажорантного ряда, так как признак Вейерштрасса со-
сохраняет силу и здесь. Из теорем о функциональных рядах нам понадобится в даль-
дальнейшем теорема о почленном предельном переходе в равно-
равномерно сходящемся ряде 433, теорема 4; доказывается она так же, как и выше.
Теперь мы обращаемся к рассмотрению, в частности, степенных рядов,
которые в теории функций комплексной переменной играют исключительно важ-
важную роль. Им мы посвятим особый п°.
456. Степенные ряды. Пусть имеем ряд
2 cnzn = c0 + c1z+c2z2+ .. . + cnzn+ ¦ ¦.,	A)
где с0, с1г с2, • • ¦ - постоянные комплексные коэффициенты, a z - переменная,
изменяющаяся во всей комплексной плоскости. Совершенно так же, как это было
сделано в 379 [или 380], для него может быть установлено существование такого
неотрицательного числа R, что для \z\ -= R (если R ^0) ряд A) абсолютно сходится,
а для \z\ >R (если й< +«.) ряд расходится. Таким образом, если отбросить случай
i? = 0, мы имеем при R— +~ ряд, сходящийся на всей комплексной плоскости,
а при конечном R - ряд, сходящийся внутри круга, описанного около начала
радиусом R, и расходящийся вне этого круга. Вместо промежутка схо-
сходимости здесь появляется круг сходимости, и термин «радиус»
впервые оказывается оправданным.
33*

516	ГЛ. XII. ФУНКЦИОНАЛЬНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И РЯДЫ	[456
Например, как легко убедиться с помощью признака Даламбера, ряд
1+ Z "Г
п=1 и!
абсолютно сходится при любом комплексном значении z, в то время как ряды
имеют радиусы сходимости R = 1.
На границе круга сходимости поведение степенного ряда может быть различ-
различным. Например, из только что приведенных трех рядов - первый расходит-
расходится во всех точках окружности \z\ =1, ибо нарушено основное условие сходимости
- общий член не стремится к нулю; второй ряд во всех точках этой окружности
°° 1
абсолютно сходится, так как сходится ряд У. —; наконец, третий ряд,
1 И2
если положить в нем z = cosO+/sin6, принимает вид
_ -^,sm nO
2
и (исключая случай в = 0, т. е. z= 1) сходится [385, 2)], но неабсолютно.
Замечание. Если коэффициенты степенного ряда - вещественные числа
(как в приведенных примерах), то ясно, что радиус R «круга сходимости» на ком-
комплексной плоскости совпадает с прежним радиусом «промежутка сходимости»
на вещественной оси.
Перечислим теперь дальнейшие теоремы о степенных рядах, которые пере-
переносятся на комплексные степенные ряды.
Теоремы 1° и 2° п° 437 сохраняются полностью, так что внутри круга сходи-
сходимости сумма степенного ряда A) является непрерывной функцией от г.
Что же касается теоремы Абеля [437, 6°], то теперь изложим ее в такой
форме:
Если ряд A) сходится в некоторой точке z0 окружности \z\ =й, то при при-
приближении точки z к точке z0 изнутри вдоль по рад и у с у имеем
lim 2 <=nzn = 2 сп4 *¦
г-2, п=0	л=0
В частном случае, когда za-R, можно считать, что z=r есть вещественная
положительная переменная, и доказываемое равенство представится в виде
lim 2 спГп = 2 cnRn.
r-~R—O л=0	п = 0
* Можно доказать это равенство и при более общем законе приближения
z к z,,, на чем мы, однако, не будем здесь останавливаться.

456]	§ 5. ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ	517
Если положить cn = an+bni, то оно распадается на такие два равенства:
lim 2 апг" = 2 anRn, lim 2 bnrn = 2 bnRn.
r-R-0 n=0	n=0	r—R-0 n=0	л=0
Так как ряды в правых частях сходятся, ввиду предположенной сходимости ряда
2cnR"= 2(.an+bni)-Rn,
то для доказательства этих равенств остается лишь сослаться на обычную теорему
Абеля.
Переходя к общему случаю, обозначим через в0 аргумент числа z0. Тогда
можно положить:
z0 = i?(cos в0+i sin в0), z - r(cos 0a+i sin в0),
и подлежащее доказательству равенство напишется так:
lim 2 cn(cosne0+i-smne0)rn= 2 cn(cos пво+isin пво)Яп.
r-R-0 n=0	n=0
Если множители в скобках отнести к коэффициентам, то вопрос, очевидно, све-
сведется к уже рассмотренному случаю.
Теперь (не ссылаясь на общую теорему о дифференцировании рядов) непо-
непосредственно докажем, что внутри круга сходимости степенной ряд молено диффе-
дифференцировать почленно, т. е. если для | z \ -= R положить
№=Zcnz", то /'(z)= 2 ncnzn-K
Прежде всего, отметим, что и радиус сходимости последнего ряда также
есть R, в чем легко убедиться, например, с помощью теоремы Коши-Ада-
мар а.
Остановимся на определенной точке z0, |zo| -=i?. Имеем:
/(z)-/(Zo)= i cn !!ll« 2 €№-*+*?-*+ ¦ ¦ ¦ +*;-). ™
Z-Zo	n = l	Z-Zo n=l	°
Если взять q между |zo| ий,то можно считать и |z| -=g; тогда
Ряд 2n\cn\qn^1 сходится, ибо q меньше R, который (как мы указали) служит
1	»
радиусом сходимости и для ряда 2 ncnzn~1. В таком случае, применяя признак
1
Вейерштрасса, заключаем о равномерной сходимости ряда B); в нем
при z — z0 можно перейти к пределу почленно, что и приведет к требуемому
результату.
Отсюда уже вытекает, что предложения 8 и 9 п° 438 также переносятся на
комплексный случай без изменений.
Таким образом, внутри круга сходимости сумма степенного ряда
непрерывна вместе со всеми производными. Иными словами, если мы разлагаем

518	ГЛ. XII. ФУНКЦИОНАЛЬНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И РЯДЫ	D57
функцию в ряд по степеням z, то расстояние от начала до ближайшей к нему точки
разрыва функции (или какой-либо ее производной) является естественной гра-
границей для радиуса сходимости этого разложения.
В случае прогрессии
1
1+Z
такой точкой будет z=-l; она лежит на вещественной оси, поэтому и
раньше было ясно, что радиус сходимости разложения функции	 не может
1+Z
быть больше единицы. Иначе обстоит дело с прогрессией
1+Z2
Ее сумма терпит разрыв в точках г == ±i мнимой оси, на расстоянии единицы
1
от начала; оставаясь на вещественной оси, вдоль которой функция	непрерывна
1+х2
вместе со всеми производными, нельзя было уяснить себе, почему радиус сходи-
сходимости ее разложения равен единице.
Подобного рода примеры, когда переход в комплексную область помогает
выяснить истинные причины тех или иных особенностей разложения вещественной
функции от вещественной переменной, мы встретим и ниже.
В заключение упомянем, что все правила действий над степенными рядами
[445], теорема о подстановке ряда в ряд [446], о делении рядов [448] и, наконец,
об обращении степенного ряда [451] сохраняют свою силу и здесь; доказательства,
носящие формальный характер, в полной мере годятся и для комплексных степен-
степенных рядов.
457. Показательная функция. Мы видели в 404 A1), что при произвольном
вещественном х имеет место разложение
х х3	хп
Если заменить в этом ряде вещественную переменную х комплексной пере-
~ 2п
менной z = x+yi, то получится ряд 1+2 — . пр° который мы уже знаем [456],
1 и!
что он сходится, т. е. имеет определенную конечную сумму во всей плоскости
комплексной переменной. Его сумму и принимают, по определению, за зна-
значение показательной функции ег при любом комплексном z, т. е. полагают
z z2	zn
...1+_ + . + ... + _+...	C)
Это определение, как мы видели, не противоречит обычному определению для
случая вещественного показателя и является естественным его обобщением.
Если воспользоваться правилом умножения степенных рядов, то, как и в 390,
6), легко убедиться, что при любых комплексных значениях гиг' будет
ez.ez' = ez+z't	D)
так что это характерное свойство показательной функции
оказывается соблюденным и в комплексной области.

457J	§ 5. ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ	519
Функция ег непрерывна во всей плоскости, больше того - она имеет произ-
производные всех порядков; почленно дифференцируя определяющий ее ряд, получим
как и раньше.
Пусть z = x+yi, где х и у - вещественные числа; заменяя в D) z на х, а г' на>>/,
будем иметь
Займемся теперь особо степенью еУ1 с чисто мнимым показателем. Если в основ-
основном определении C) подставить yi вместо z, то получим
или, отделяя вещественную часть от мнимой,
(у2 V4	у2П
1-_+--...+(-1)"-+.
В этих рядах мы узнаем разложения cos у и sin у [404, A2) и A3)] и, таким образом,
приходим к замечательной формуле
еУ1 = cos у+i sin j,	E)
которую впервые установил Эйлер; отсюда, например,
-/	— j
ег =if e"i=-\, е* =-/, е«"'=1.
Итак, если z = x+yi, то
ег_ ex(cos д,^.,• sjn у) *j	F)
мы видим, что
ех = ei?(z) = | ez 15 j, =/(z) = Arg ez.
Так как ех> 0 при любом вещественном х, то ег отлично от нуля при любом
комплексном z.
Заменяя в E) у на -j, путем сложения и вычитания обеих формул, получим
соотношения
G)
выражающие тригонометрические функции от вещественного аргумента
через показательные функции от чисто мнимых аргументов. Мы еще
вернемся к этому замечательному факту ниже.
Если в равенстве F) заменить у на у+2п, то значение правой (а значит, и левой)
части равенства не изменится; иными словами,
* Можно было бы положить и это равенство в основу определения показатель-
показательной функции от комплексного аргумента; тогда D) вытекало бы из теорем сложения
для косинуса и синуса.

520	ГЛ. XII. ФУНКЦИОНАЛЬНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И РЯДЫ	[458
и показательная функция оказывается периодической, с чисто мнимым
периодом 2я|.
Легко показать, что, кроме периодов вида Tkni (к - целое), других периодов
функция ег иметь не может. В самом деле, если ег+т = ег, то (полагая z-0) em~l.
Пусть, скажем, со = a+/S/, так что [см. F)] e«(cos/9+/sin/S) = l; отсюда е«=1 иа=0,
а затем: cos /9=1, sin^ff=0, следовательно, @ = 2кл, ч. и тр. д.
Теперь лишь, когда мы знаем, что e±*"' = l, становится понятным, почему
разложение функции	 в степенной ряд [449 A2)] имеет радиус сходимости
«х-1	х
2я; хотя на вещественной оси у функции 	 нет особенностей, кото-
ех- 1
рые могли бы это мотивировать, но на мнимой оси есть точки, где функция обра-
обращается в бесконечность, и ближайшими из них к началу как раз и будут точки
2= ±2л/, лежащие от него на расстоянии 2л.
В связи с обобщением показательной функции на случай любого комплексного
показателя, вспомним об одной интересной функции, которую мы рассматривали
в 138, 407:
	_
) = в *'
Д0) = 0.
Невозможность разложить ее по степеням х в какой бы то ни было окрестности
нуля, несмотря на непрерывность самой функции со всеми производными вдоль
вещественной оси, включая точку х = 0, становится непосредственно очевидной
при переходе к комплексной переменной z = x+yi. Действительно, функция
_ j_
е 2' (zaO) при z-*0 не имеет даже предела, ибо, например, при приближении z
к нулю вдоль мнимой оси, когда z=yi и у-*0, будет:
458. Логарифмическая функция. Возьмем любое комплексное число w, отличное
от 0, и поставим себе задачей найти число z, удовлетворяющее уравнению:
(при w = 0 это уравнение, как мы знаем, не имеет решений). Такое число г назы-
называется {натуральным) логарифмом w и обозначается символом
z = Lnw.	(8)
Если w= r(cos в + isin в) и положить z=x+yi, то, ввиду F), уравнение (8) распа-
распадается на такие:
ex = r, cos>> = cos0, sin .у=sin 0,
откуда
х = \пг*, у = в+2кл (к - целое).
Мы приходим к заключению, что логарифм w (при w^Q) всегда существует; он
равен
Ln w = ln |и>| +/-Arg w = in \w\ +i-a.igw+2kni	(9)
* Здесь имеется в виду о б ы ч н ы й натуральный логарифм положительного
числа г.

458]	§ 5. ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ	521
и, таким образом, оказывается многозначным. Впрочем, это легко было
предвидеть, исходя из периодичности показательной функции. Взяв /с = 0, получим
так называемое главное значение логарифма:
In w = ln |>e|+/>argw,	A0)
которое характеризуется тем, что его мнимая составляющая содержится в про-
промежутке (-я, л]:
Например, имеем
lnl = 0, Lnl = 2faii; 1п(-1) = яг, 1л(-1) = BА:+1)я/,
я .	4к+1 .
In i = — г, Ln i =	т и т. д.
2	2
При переменном w формула A0) выражает главную ветвь много-
многозначной логарифмической функции Lnie. Другие ветви получаются
при различных целых значениях к по формуле
Ln w = ln w+2kni.
Легко видеть, что функция A0) непрерывна на всей плоскости комплексной
переменной w, за исключением начальной точки и отрицательной части веще-
вещественной оси. Разрыв при w = 0 неустраним, ибо при w-О, очевидно, lnw — °°.
Иначе обстоит дело с отрицательными вещественными значениями wo = uo^O.
Разрыв здесь создается, в некотором смысле, искусственно из-за нашего условия
брать argw в промежутке (-я, я].Когда w = u+vi-~w0 при v>0, то argw-*Ji = argn'o,
если же при этом г>-=0, то arg w- -п. Если бы от главной ветви: In w во
второй четверти мы перешли к другой ветви: 1п>е+2ш - в третьей, то
непрерывность была бы восстановлена. Таким образом, желая избегнуть много-
многозначности и расчленяя многозначную функцию на однозначные ветви, мы тем
самым для каждой отдельной ветви создаем разрывы. Наоборот, одна ветвь
в другую переходит непрерывным образом. В этой связности различных ветвей
многозначной функции и заключается замечательная особенность комплексной
плоскости, не имеющая аналога в многозначных вещественных функциях, опреде-
определенных на вещественной оси.
По общей теореме о производной обратной функции, имеем (исключая точки
разрыва)
QnwY--^-----.	(П)
(е*) ег w
Заменив w на 1+и>, рассмотрим функцию z = ln(l+>e) (w^-1). Тогда
z
"
—, так что w= 2 — ¦
и!	n=l П\
Отсюда следует, что для достаточно малых (по абсолютной величине) значений
w функция z=ln A+иО разлагается в ряд по степеням w:
Z=W-{ CtW* + C3W*+ ¦• .+CnWn+. ..
Производная от этой функции по w представится рядом:
[In A +>?)]'= 1 + 2c2w+3c3w2+ ... +ncnwn-~1+ ...;
в то же время, ввиду A1), она выразится и так:
1
[In

522	ГЛ. XII. ФУНКЦИОНАЛЬНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И РЯДЫ	D59
Сравнивая эти два разложения, видим, что
2с2=-1, 3cs=l, .... йсп = (-1)"->, ....
откуда
11	1
с% — Z" > ^з~*Г"» ¦•¦> Сп=()	» •••
2	3	л
Итак, окончательно, в окрестности нуля имеем разложение:
ln(l + w) = >v	+	...+(-1)""—+...	A2)
2 3	n
Легко проверить, что полученный ряд имеет радиус сходимости R=\. Мы
видели, что при достаточно малых г, его сумма будет главное значение
логарифма: In A + w)\ будет ли это так и во всем круге | w | «= 1 ?
Так как ряд A2) формально удовлетворяет равенству
то он и фактически ему удовлетворяет, покуда сходится. Таким образом,
во всем круге |>v| -=1 сумма ряда A2), наверное, представляет собой одно из
значений Ln (I + w); весь вопрос теперь в том, всегда ли это будет именно
главное значение.
Если |»е|-=1, так что точка, изображающая число 1 + w, лежит внутри
л л
круга радиуса 1, с центром в точке w=l, то arg(l + ie) лежит между	-и—,
другие значения Arg(l+w) лежат в промежутках	2 2
5л ЗтЛ ( 9я 7л\
"У
Зя 5я^ Пп Чп\
Т ~г}' Кг' TJ- ¦-
Мнимая составляющая суммы ряда A2) и есть Arg (I + w) [см. (9)]. Для доста-
достаточно малых w = u+vi она дает главное значение arg (I + w), т. е. содержится
я п
между	и —; в то же время, как непрерывная функция от и и в, она не может
перескочить в другие указанные промежутки, следовательно, при всех |и>|-=1
равна именно главному значению arg A+w). Этим доказано, что равенство A2)
имеет место во всем круге \w\ -= 1.
Заменяя в A2) w на -wm вычитая полученный ряд из ряда A2), получим полез-
полезное разложение *:
1 1+w w3	н*™-1
1+	<»>
которое годится для | w | ¦< 1.
459. Тригонометрические функции и им обратные. Мы знаем [404 A2) и A3)],
что при вещественном х функции cosx и sin x представляются следую-
следующими рядами:
_~	хт	-	хгп-\
l 2(l)	iZ (ir1
, sinxZ
2и!	п=Х
* Так как мнимая составляющая разности In A + w)- ln A - w) лежит между
1+w
-л и л, то эта разность дает именно главное значение ш	.
\-w

459]	§ 5. ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ	523
Естественно функции cos z и sin z для любого комплексного z определить
с помощью аналогичных рядов:
cosz-l+^C-l)" —, sinz=Z (-I)»-*-	—,	A4)
n=x	2n!	„=i	Bn-l)!
сходящихся на всей плоскости переменной z.
Этот способ введения тригонометрических функций для нас уже не нов: в 443
мы воспользовались им даже в вещественной области (для того, чтобы обосно-
обосновать эти важные для анализа функции без обращения к геометрии). Подражая
проведенным там рассуждениям, можно было бы и здесь установить для косинуса
и синуса теоремы сложения, формулы приведения, свойство периодичности, а
также правила дифференцирования их — но уже для комплексных значений не-
независимой переменной.
Впрочем те же результаты можно получить и другим путем, установив связь
тригонометрических функций с показательной. Именно, при любом комплексном
z, обобщая сделанное в 457 для z=yi, можно вывести, что [ср. E)]
n z,
а отсюда [ср. G)]
gzi + g-zi ezi-e—zl
cosz=	, sinz=——	.	A5)
Эти формулы целиком сводят изучение тригонометрических функций к изучению
показательной функции. [Их можно было бы положить в основу определения
тригонометрических функций вместо A4).] Предлагаем читателю, исходя из формул
A5), наново доказать упоминавшиеся выше свойства косинуса и синуса, а также
установить, что 1) cos z и sin z не имеют других периодов, кроме 2кл (Jc - целое),
и 2) что все корни этих функций вещественны.
Если в A5) взят z=yi (у - вещественное), то найдем
еУ + еУ еУеУ
cosyi=	= chy, sinyi=	i=i-shy.	A6)
Таким образом устанавливается непосредственная связь между гипер-
гиперболическими функциями от вещественного аргумента и тригонометрическими -
от чисто мнимого. Любопытно отметить, что cos .у/ есть вещественное число,
всегда большее единицы.
Теперь, воспользовавшись теоремами сложения, можно написать, что
cos (x+yi) = cos x • cos yi - sin x -sin yi,
sin (x+yi) = sin x • cos yi+cos x • sin yi
или [во внимание к A6)]
cos (x+yi) = cos л>сп у - j-sin x-sh y,
sin (x+yi)=sin x-chy+i-cosx-shy,
и тем разложить косинус и синус на их составляющие.
Функции tg z и ctg z определяются формулами
sinz I ezi-e~zi
cosz / ezi+e~zi
cosz ezi+e~zi
CtK Z =	= /
sinz ezl-e~zt
причем оказываются имеющими период п.
¦НИ-

524	ГЛ. XII. ФУНКЦИОНАЛЬНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И РЯДЫ	[459
Разложения, полученные в 449 для tg х и х • ctg х, сохраняют свою силу и после
подстановки комплексной переменной z на место вещественной х. Сходство раз-
разложений для х ¦ ctg х и х • cth х становится совершенно понятным, если учесть
получающиеся из A6) соотношения
tgyi=i-thy, ctg yi= -j-cthy.
Из функций, обратных тригонометрическим, мы остановимся на арктангенсе
и на арксинусе.
Ввиду того, что тригонометрические функции приводятся к показательной,
естественно ждать, что обратные им окажутся связанными с логарифмом.
Начнем с указания, что w = tg z не принимает значения ± i (в этом легко убе-
убедиться, рассуждая от противного). Пусть w a ±i; тогда уравнение
1 ezi-e~zi 1 е2г'-1
может быть решено относительно z:
. 1+wi	I 1+wi
1 - wi	2/ 1 - wi
Таково выражение для обратной функции Arctgw, очевидно, бесконечно
многозначной вместе с Ln.
Если для логарифма взять его главное значение, то получим главное
значение арктангенса:
1 1 + wi
arctg w = — ln	 (w * ± 0,
2/ 1 - wi
которое характеризуется тем, что его вещественная часть содержится в проме-
71 лЛ
п	п
---=i?(arctgw)-=-.
Остальные значения получаются по формуле
Arctg w = arctg w+кп {к - целое).
Заменив в ряде A3) w на wi, придем к разложению для главной ветви
арктангенса
И
arctg w = w	+...+(-
3
+...+( l)
3	In -1
которое действительно для \w\ «= 1*.
Обратимся, наконец, к решению уравнения
sin z ¦=
w
2;
относительно z:
e2iz_2wi-eiz-1 = 0, eiz = wi± ^l-w\
откуда
z = Arcsin w = — Ln (wi± yi-w2);
i
и здесь получаем бесконечно многозначную функцию.
* При w = ± i функция arctg w обращается в ~.

459]	§ 5. ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ	525
Ограничимся для логарифма его главным значением:
л
При w = +1 или - 1 радикал обращается в 0, и мы получим, соответственно, z = —
л	2
или —, что и примем за главное значение арксинуса. Пусть
теперь w * ± 1, и нам предстоит выбор из двух значений г. Очевидно,
— In (wi+ УГ^) -I - In {wi- УГ^) = ±л,
следовательно, и
R |- In (wi+УТИ?)} + R {- In (wi- УТ^ЙГ2)) = ±ж,
\i	I \i	1
в то время как мнимые части разнятся лишь знаками. Так как каждая из веще-
вещественных частей не выходит за пределы промежутка (-я, я] ,то лишь одна из них
Л 71
будет содержаться между	и —; соответствующее значение арксинуса при-
принимаем за главное. Исключение представится лишь в случае, когда обе
л п
вещественные части равны — или	; тогда за главное принимается то значение,
которому отвечает положительная мнимая часть*. С этой оговоркой можно ска-
сказать, что главное значение арксинуса определяется условием
я	л
	=s/J (arcsin tv)=s—.
Легко проверить, что остальные значения выразятся формулами:
Arcsin w = arcsin w + 2kn,
Arcsin w = Bk+1) л -arcsin w (к - целое).
В заключение, упомянем о разложении arcsin w по степеням w. В области ве-
вещественных переменных мы уже видели, что для ряда
х3	х2п~х
[выражающего sin x], обращением будет ряд
1 у3 1-3 у5	Bл- 1)!! у*п+1
[выражающий arcsin у; см. 440, 3)]. Так как и в случае комплексных переменных
коэффициенты определяются совершенно одинаковым образом, то ясно, что
в результате обращения ряда
z3 z5	z2n—1
W = z	1	...+(-I)"	h ••¦
3! 51	Bn-l)!
* Например, arcsin 2 = —h i In B+ УЗ).

526	ГЛ. XII. ФУНКЦИОНАЛЬНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И РЯДЫ	[460
должен получиться ряд
1	w3 1-3 и>5	Bп-1)
2	3 2-4 5	2и!! 2и + 1
Его радиус сходимости R=l*; при |w|«=l он дает одно из значений Arcsin>e.
Покажем, что это будет именно главное значение arcsin w. Действительно
\R(z)\ не превосходит
11 1-3 1	Bи-1)!! 1	л
|| 1+++ +	+
откуда и вытекает требуемое заключение.
460. Степенная функция. Пусть а и Ъ будут два комплексных числа, из которых
а^О. Тогда общее определение степени cfi будет такое
(fi = ebhna = eb(}na+2k7ii) (fc - целое),
так что степень оказывается вообще многозначной. При к = 0 получается
так называемое главное значение степени
Для отличия общее выражение степени, следуя К о ш и , иногда обозначают
так: ((а))&. Таким образом
{(ft))b = d>-e^"bi (к - целое).
Если Ъ равно целому числу, то второй множитель обращается в единицу:
в этом случае степень будет иметь лишь одно значение. Когда b есть несократимая
р
рациональная дробь — (д >¦ 1), то степень будет иметь ровно q различных значений.
Я
Наконец, при всяком другом значении b степень будет иметь бесконечное
множество значений.
Например,
2' = enn2 = Cos(ln2)+i-sin(ln2), (B))' = 2'-е-2/от {к - целое),
Ц~е1\щ=е~* , (@)' = е DА+1J (А; _ целое).
Если т есть любое постоянное комплексное число, то степенная
функция ((z))m вообще многозначна. Ее главная ветвь есть (z * 0) **
2т = emAn z.
Из соотношения
(l+z)m = em.ln(l + z)
совершенно так же, как в п° 447, 2), можно получить биномиальный ряд
m{m-V)	m(m-Y).. .(/п-и
z2+...+	-4—^
1-2	1-2-...-и
* При w = ± 1 нарушается непрерывность производной арксинуса:
1
** Иногда при z = 0 полагают zm = 0, если R(m) >¦ 0.

461]	§ 5. ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ	527
Этот ряд сходится при любом комплексном т, если [z| -= 1*, и воспроизводит,
как видно из самого способа его получения, именно главное значение степени
бинома. Исследованием его занимался Абель.
461. Примеры. В этом п° на нескольких примерах мы покажем, какие услуги
оказьшает вещественному анализу комплексная переменная и элементарные функ-
функции от нее.
1) Последовательные производные функции у--	легко вычисляются,
Х2+1
если представить ее в виде:
2i'vx-i x+i
Именно,
2i
i X '
[x + i]
-1У
24- ^
,r-(*-»r
n(n-
1
l)(n-2)
•2-3
Например,
Одновременно, очевидно, получаются и последовательные производные функ-
функции arctg х [ср. 116, 8) и 118, 4)].
2) Формулы Эйлера, выражающие косинус и синус через показатель-
показательную функцию, могут быть многообразно использованы. Например, желая найти
сжатое выражение для суммы
п
s= 2 cosfcc,
1
можно свести дело просто к суммированию геометрической про-
прогрессии:
— \ У ekxl+ У е~кх1\= — \
2 If	Г	) 2{ 1-е*
-\xi -{п+\)Х,\
2 - е v 2/ |
* При z= — 1, если не сама степень (l+z)m, то достаточно далекие ее произ-
производные терпят разрыв; исключение представляет лишь случай, когда т равно
О или натуральному числу.

528	ГЛ. ХП. ФУНКЦИОНАЛЬНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И РЯДЫ	D61
3) Целые положительные степени sin x и cos x, а также произведения таких
степеней можно представить линейными комбинациями синусов и косинусов
кратных дуг. Выполнить это легко с помощью тех же формул Эйлера, раз-
развернув выражения
jexl-e-xi\n
sin" x =
по биному Ньютона. Например,
sin5 x- — (esxi- 5e3xi I- 10exl'- 10e~xi + 5e-*xl-e 5X<) =
32/
gixl — g — SXi	gXi —g — X	1
-5	:	HO	:	 = — (sin 5x-5sin3x+]Osinx);
16 V 2/	2/	2/ j 16
cos4 л: sin3 x —
e-xf-vs
=	_
128/
=
128/
	(e7
128/
=	(sin 7x+sin 5x— 3 sin Злг- 3 sin лг).
64
Можно установить и общие формулы:
(-1)" f
(a) sin2" х = -j—[ cos 2vx ~ 2v cos Bv""
2vBv-l)
-rr- cos Bv-4),-...
+ ———s\nBv-y)x+...+(-\)>	—	sin x ,
(в) cos" лг=-^^ |cosnAt+ncos(«-2)xH	cos(n-4)x+ •• •
причем в формуле (в) последний член имеет вид
1 2vBv- 1) •.. (v+l)	Bv + lJv ... (v+2)
.ИЛИ
2	1-2...V	1-2... v
COS*,
смотря по тому, будет ли и=2v или 2v +1.
Подобные преобразования выгодны при интегрировании [ср. 287].
4) На комплексные функции от вещественной или комплексной переменной
распространяются простейшие формулы интегрального исчисления (относящиеся
к разысканию первообразных).

461]	§ 5. ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ	529
Пусть требуется найти интегралы:
Г	Г
еах cos bx dx,	eax sin bx dx.
J	J
Эта задача равносильна нахождению интеграла:
Г
= Г e{fl+Ы)х
который - по элементарной формуле - равен
1 . ... costa+isinix acosbx+bsmbx	asmbx-bcosbx
е(а+Ы)х —	еах —	еах _j- /.
аЛ-Ы	а+Ы	a2+b2
Приравнивая порознь вещественные и мнимые, получим искомые интегралы
[ср. 271, 6)].
Формулу для вычисления интеграла типа
J
где Р(х) - целый многочлен [271, 4)], можно распространить и на случай комплекс-
комплексного а. Тогда к ней приведутся не только интегралы
Г Р(х) cos bx dx, Г Р(х) sin bx dx,
f P(x)eax cos bx dx, j* P(x)eax sin bx dx
но и интегралы
[271, 4); 289].
5) Связь между логарифмической и обратными тригонометрическими функ-
функциями объединяет многие формулы интегрального исчисления, казавшиеся со-
совершенно различными, и позволяет устанавливать новые формулы. Например,
интегралы
dx 1	х
	= —arctg—
х2+а2 а а
или
г dx	, ,.	.	г dx	х
= lnU+]/a'2+x2) и	^arcsin —
г dx 1 х-а	с
	= — In	 и
J хг-Ф 2а х+а	J
приводятся один к другому заменой х на xi.
6) Отделяя вещественную и мнимую части в известных комплексных разложе-
разложениях, можно иной раз просто получить интересные разложения в вещественной
области.
(а) Возьмем, при |г|-=1, прогрессию
и положим z = r(cosE+j'sin б). Справа получим ряд
2 r"(cos пв + i sin пв),
л=1
34 Г. М. Фнхтенгольц, т. П

530	ГЛ. Xtt. ФУНКЦИОНАЛЬНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И РЯДЫ	[461
а слева - выражение
r(cose+ism6)	r cos в-г2	г sin 0
-Н	i.
(l-rcos0)-/rsinO l-2rcos0+r2 l-2rcosO+r2
Приравнивая вещественные и мнимые составляющие в обеих частях равенства
(и сокращая на г), придем к разложениям:
cos 0 - г	^,
= 2j г" cos пО,
l-2rcos0 + r2 nZ
sin в . ^,
l-2rcos0 + r2 n=l
[cp. 440, 11)].
б) Аналогично поступив с логарифмическим рядом:
2	|И
п=1 И
получим для г-= 1 [ср. 440, 11)]:
1	г, cos пв
— In(l-2rcos0+r2)= - ^ г"	,
2	n=l к
г sin E ¦?, sin пв
arctg-	-= Z '¦"	•
1-rcosO n=i л
Пусть О-=0^я; так как при г=\ ряды справа продолжают сходиться [385,
2)], то можно, воспользовавшись теоремой Абеля [437, 6°], перейти здесь к
1	. О
пределу при г -* 1 - 0. Слева получим в первом случае: — In B - 2 cos в) = In 2 sin —,
I в\ I л-в) п-в гт
втором: arctg ctg — = arctg tg	1 =	. Итак,
в .г, cos пв л-в ^т sin пв
In 2 sin —=-Z 	. 	=2
2	i n	2	i
Z	.	2(О
2 n=i n	2 n=i л
[В третьем томе курса мы встретимся со многими замечательными тригоно-
тригонометрическими разложениями.]
7) В п° 447, 8) мы имели разложение
l 2>()"
где Рп(х) - многочлены Лежандра. Изменяя х между -1 и +1, положим
здесь x = cos0:
_L	°°
(l-2acose+a») ! =1+ 2 рп (cosб)-а".
п=1

462]	§ б. ОБВЕРТЫВАЮЩИЕ И АСИМПТОТИЧЕСКИЕ РЯДЫ	531
Заменим теперь 2 cos 0 на eoi+e~oi; мы получим
_i_	_t_	_i_	1
l-2acos6+a2) 2 = [1 -a(e<"' + e-eO + a2] 2=A-ае'9) 2-A-ае-'в) *" =
( 1	1-3	У 1	ЬЗ	"\
¦= Ц—ае'0-|	а2е2'° + ... 1 + —ае-'»Ч	а%-2'в + ....
Перемножив эти два ряда по обычному правилу и приравняв коэффициенты при
а" в обоих разложениях, мы придем к выражению для Рп (cos 0):
P,;(cos0)= "~ ("'в + -"'») +
2лП	Bл-2)!! 2
+ —	_._l_(
Bи-4)П 2-4
Скобки теперь можно заменить последовательно на 2 cos пО, 2 cos (и-1N,
2 cos (и - 2N и т. д. Так как все коэффициенты здесь положительны, то совершенно
очевидно, что наибольшего значения это выражение достигнет при 6 = 0, т. е. при
х = cos 0=1. Таким образом, воспользовавшись соображениями из области функций
комплексной переменной, мы нашли интересный результат, всецело относящий-
относящийся к вещественной области: при изменении х в промежутке [— 1, +1] все многочлены
Лежандра своего наибольшего значения достигают на конце х-\.
§ 6. Обвертывающие и асимптотические ряды.
Формула Эйлера—Маклорена
462. Примеры. В § 9 предыдущей главы мы познакомили читателя с некото-
некоторыми важнейшими определениями «обобщенной суммы» для расходящихся рядов,
причем сами частичные суммы ряда всего менее были пригодны для
приближенного вычисления такой «суммы». Сейчас мы вновь займемся расходя-
расходящимися рядами, но совсем в другом плане: мы покажем, что при наличии
определенных условий и в известных границах именно
частичные суммы расходящегося ряда могут служить превосходными
приближениями для числа, в том или ином смысле «породившего» этот ряд. Для
того чтобы читатель ощутил наперед практическую важность применения расходя-
расходящихся рядов в приближенных вычислениях, достаточно упомянуть о том, что этим
методом привычно пользуются астрономы для предвычисления положения небес-
небесных тел, причем точность получаемых результатов оказывается вполне удовлетво-
удовлетворительной.
Мы постараемся сначала выяснить нужные нам идеи на двух простых при-
примерах.
1") Рассмотрим логарифмический ряд
JC2 JC3	Хп
*-- + --...+(-1Уг-1- + (-1)" — 7+-"	W
2 3	п	п+1
Хорошо известно [405], что этот ряд сходится и представляет функцию 1пA+л:)
лишь для -1<л:«=1. Вне этого промежутка (например, для х=»1) ряд будет рас-
расходящимся и лишен суммы. Однако и для значений х=-1 функция In A+х) про-
продолжает быть связанной с отрезками этого расходящегося ряда, ибо, по формуле
Те й л ор а,
34*

532	ГЛ. XII. ФУНКЦИОНАЛЬНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И РЯДЫ	[462
где «дополнительный член» гп(х) может быть взят, скажем, в форме Лагранжа
[126]
°^1) „тг ^ ^»-
Оказывается, что дополнительный член абсолютно меньше первого отбрасываемого
члена ряда и имеет одинаковый с ним знак (как и в случае сходящегося ряда лейб-
ницевского типа!). Итак, если заменить значение 1пA+х), при х=-1, отрезком
расходящегося ряда A), то мы имеем удобную оценку погрешности (и даже знаем
ее знак). Этого достаточно для того, чтобы можно было воспользоваться упомя-
упомянутым отрезком для приближенного вычисления числа \п(\+х)\
Конечно, при 0<;c=sl, с возрастанием п до бесконечности погрешность стре-
стремится к 0, а при заданном и, но х~0, будем иметь даже
^-О, т.е.
т. е. погрешность будет, по сравнению с х, бесконечно малой тем более высокого
порядка, чем больше п. При любом фиксированном х>1 оценочный член
сам растет до бесконечности с возрастанием п, и не может быть речи о том, чтобы —
для данного х - за счет и сделать погрешность произвольно малой. Однако,
как показывает сама оценка
хп+1
кМ1
л + 1
при х, достаточно близком к 1, все же можно сделать погрешность произ-
произвольно малой\ Если л: фиксировано, но близко к 1, то члены ряда A), даже при
л=-1, будут сначала убьгеать по абсолютной величине, именно, покуда отношение
хп+1 хп п	1
1 или
и+1 п п+1	х-1
а затем лишь начнут возрастать. Выгоднее всего оборвать ряд на члене с номером
п = Е \	1 : так - при данном х - получается наилучшее приближение для числа
\1)
В изложенном примере рассматриваемый ряд A) все же для -l-sxssl был
сходящимся. Второй пример поучительнее в том отношении, что здесь рассматри-
рассматривается постоянно расходящийся ряд.
2) Положим теперь (для х>0)
где 0-=с-=1 (ряд сходится!).
При к-<х имеем
1 \ к кг к3
х+к х х2 х3 xi '"'
если же кз^х, то этот ряд расходится. Тем не менее, формально подставив
это разложение в ряд, определяющий функцию F(x), объединим подобные члены
и получим таким путем ряд
4 + 4+...+^+....	B)
2	п

463]
где
6. ОБВЕРТЫВАЮЩИЕ И АСИМПТОТИЧЕСКИЕ РЯДЫ
533
Легко убедиться, что ряды, определяющие коэффициенты Ап, все сходятся.
Но предшествующий ряд явно расходится, ибо
Ап
а последнее выражение при и-*~ стремится к °=.
Для написанного расходящегося ряда B) и-й отрезок будег:
х'Чх+к
так что «дополнительный член»
И здесь имеем
2
1
Снова налицо привычная особенность ряда лейбницевского типа, хотя рассматри-
рассматриваемый ряд и расходится. Конечно, приближенно приравнивая F(x) частич-
частичной сумме Sn(x) этого расходящегося ряда, при фиксированном х, заведомо
нельзя получить произвольную точность, но можно добиться любой
точности при достаточно большом х. Для рассматриваемого случая со-
сохраняет силу замечание о том, что наращивание числа сохраняемых членов выгодно
(в смысле увеличения точности) лишь до тех пор, пока члены по абсолютной
величине убывают, т. е. —1
Очевидно, при фиксированном и, дополнительный член гп(х) стремится к 0,
если х ->• ~. Более того, так как при этом
хпг„(х) =
0,
C)
так что гп(х) оказывается бесконечно малой выше и-го поряд-
к а. Чем больше членов расходящегося ряда B) мы удерживаем для приближен-
приближенного представления функции F(x), тем более высокого порядка малости при х-*~
можно ждать от погрешности этого приближения!
463. Определения. Перейдем теперь к общим формулировкам и определениям.
Пусть дан числовой ряд
2 вл =
в
D)

534	ГЛ. XII. ФУНКЦИОНАЛЬНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И РЯДЫ	[463
(а) Если его частичные суммы поочередно то меньше, то больше некоторого
числа А, т. е. если дополнительный член, определяемый формулой
А = аа+а1 + ...+ап+гп,	E)
оказывается знак опере м е пны м, то говорят, что ряд D) обвертывает
число А.
Простое равенство
делает очевидным, что это определение равносильно такому:
(б)	Ряд D) называется обвертывающим число А, если, во-первых, этот
ряд — знакопеременный и, во-вторых, дополнительный член гп формулы
E) меньше числа Оп+i по абсолютной величине и имеет одинаковый с ним знак*.
В предыдущем п° мы уже имели дело с такими рядами: ряд A) явно был об-
обвертывающим для ln(l+x) (при любом х>0), а ряд B) - обвертывающим для
функции F(x), определенной в 2) (тоже при х=-0).
Заметим, что в случае расходимости ряда D) он может одновременно обверты-
обвертывать и бесконечное множество чисел А. Например, ряд
1-2 + 2-2 + 2-...
с частичными суммами 1, -1, 1, -1, 1, ..., очевидно, обвертывает каждое из
чисел промежутка (-1, 1).
Свойство обвертывающего ряда, сформулированное в определении (б), часто
делает его ценным средством для приближенного вычисления числа А, но само
собою ясно, что далеко не всякий ряд, обвертывающий число А, может служить
для этой цели.
Пусть, вместо ряда D) с постоянными членами и числа А, имеем функциональ-
функциональный ряд
2ап{х) = а0(х) + а1(х)+ ... + ап(х) + ап+1(х) + ...	F)
о
и некую функцию А(х), причем все функции ап(х) и А(х) заданы в одной и той же
области %. Только что приведенные определения числового ряда, обвертываю-
обвертывающего данное число, естественно распространяются и на случай функционального
ряда, обвертывающего данную функцию. Не останавливаясь на этом, мы дадим
новое определение, относящееся специально к случаю, когда члены ряда, подобно
F), содержат еще параметр х, область изменения которого ЗС имеет в качестве
точки сгущения конечное или бесконечное число со. Как всегда, дополнительный
член гп(х) определим равенством
А{х) = ао(х)+ах(х)Л-... +ап{х) + гп{х).
(в)	Ряд F) называется асимптотическим разложением вблизи
х = со функции А{х), если при любом фиксированном п
limr"W=0**.	G)
()
* Мы сохраним термин «обвертывающий» и в том случае, если предполо-
предположенное в определении выполняется лишь для достаточно больших п (скажем,
для из=по=-1).
** При этом, естественно, предполагается, что ап(х) отличны от 0 (по крайней
мере, для х, достаточно близких к си).

463J
§ 6. ОБВЕРТЫВАЮЩИЕ И АСИМПТОТИЧЕСКИЕ РЯДЫ
535
Этот факт записывается так:
А{х) со ао(х
гп{х) = ап
Ввиду
ап(х) +...
an(.x) an{x)
как следствие из G), получается, что
lim
an+i(x) г гп+1(х)!
\
г гп
[ ап
+1(х)\
lim	^
(8)
Легко доказывается такое утверждение:
Если ряд F) обвертывает функцию А(х), причем выполняется (8), то названный
ряд служит и асимптотическим разлозкением функции А(х) вблизи x = w.
Действительно, имеем
так что
гп(х)
Тогда из предположения (8) непосредственно вытекает G).
Оба ряда A) и B), приведенные выше в виде примеров, служат асимптоти-
асимптотическими разложениями соответствующих функций, первый - вблизи х = 0, а вто-
второй - вблизи х = °°.
В последующем изложении нам, как правило, предстоит иметь дело
с асимптотическими разложениями вида
«*'4Л^ЪЪ* ¦¦¦+->¦¦¦	<»>
вблизи х=~. Напомним, что смысл написанного соотношения состоит лишь
в том, что, как бы ни было фиксировано и, всегда
или - подробнее
гп{х) = о —
\хп
lim
хх2	хп
Таким образом, для «больших» х имеет место приближенная формула
A0)
хп
«качество» которой характеризуется равенством A0).
Если переписать это равенство так:
A0*)
то станет ясна единственность асимптотического разложения, вида (9),
функции А{х), - конечно, в предположении, что она вообще допускает такое

536	ГЛ. XII. ФУНКЦИОНАЛЬНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И РЯДЫ	[464
разложение. По формуле A0*) все коэффициенты ап последовательно
определяются вполне однозначно!
Обратное утверждение, однако, неверно: различные функции могут
иметь одно и то же асимптотическое разложение. Например, известно, что
е~х-хп-~0 при х-*~; поэтому, очевидно, все функции вида А(х)-\ С-е~х будут
иметь то же асимптотическое разложение, что и функция А(х).
Замечание. Иногда для удобства мы будем писать
где В(х), (р(х) и у(х) - функции, определенные в ЗС> разумея под этим, что
) .?, ап
да 2, — •
п=о хп
464. Основные свойства асимптотических разложений. Говоря об «асимптоти-
«асимптотических разложениях», мы здесь и впредь разумеем разложения вида (9)*. Все рас-
рассматриваемые функции предполагаются определенными в области ЗС с точкой
сгущения +~.
1°. Если
А(х)а>2 ~„, В(х)а>2 -п,	(Щ
п=0Хп	п=0Хп
то, очевидно, и
л=0 X"
т. е. асимптотические разложения мозкно складывать и вычитать почленно.
2". Покажем теперь, что асимптотическое разложение произведения А(х)-В(х)
может быть получено путем формального умножения — по «правилу К о ш и» —
разложений A1).
Имеем, при любом п,
а^ a<i	an
А(х) = a$-i	1—- +•••"!	Ь
х х2	хп
хх2	хп [хп
Перемножая, получим:
ci
х л-3
где
т
Сщ= 2 Oibm-i-
1 = 0
¦ Теория таких разложений была развита Пуанкаре (Henri Poincare),
который дал важные приложения их как в теории дифференциальных уравнений,
так и в небесной механике.

464]	§ 6. ОБВЕРТЫВАЮЩИЕ И АСИМПТОТИЧЕСКИЕ РЯДЫ	537
Это и равносильно утверждению
которое подлежало доказательству.
Если отождествить В{х) с А(х), то получим асимптотическое разложение для
квадрата: [Л(х)]г. Так же может быть получено асимптотическое разложение для
функции [Л(х)]т, где т - любое натуральное число.
3°. Далее, пусть дана некоторая функция F(y), аналитическая в точке у = 0,
т. е. разлагающаяся в окрестности этой точки в степенной ряд:
F(y) = 2 $тУт = А> +РлУ+РгУ~ + • • • +РтУт +¦•¦
0
Кроме нее рассмотрим функцию А{х), допускающую асимптотическое разложение
без свободного члена:
а* а<>	an
A(x)w —+— + ...+— + ...,	A2)
3	п
так что А(х) -*0 при х -»=». В таком случае, по крайней мере для достаточно больших
х, сложная функция
F(A(x))= ZPmlAW"
т = 0
имеет смысл.
Функция F(A{x)) тоже допускает асимптотическое разложение, которое
может быть получено из предыдущего разложения, если вместо каждой степени
[А(х)]т подставить ее асимптотическое разложение и формально выполнить при-
приведение подобных членов [ср. 446!].
Заметим, прежде всего, что в окрестности точки у = 0 функция F(y) имеет не-
непрерывную (а следовательно - ограниченную) производную, и для любых двух
точек этой окрестности у и у будет вьшолняться неравенство
\F(y)-F(y)\*sL-\y-y\ (? = const).
Обозначим и-й отрезок ряда A2) через Ап(х):
Ап(х)~—+ — +...+—.
X Хг	Хп
При фиксированном п, для достаточно больших х, обе функции А{х) и Ап(х) попадут
в упомянутую только что окрестность, так что
\xn[F{A(x))~F{An(x))]\^L-x"\A{x-)-An(x)\ = ?.х"|/¦„(*)| -0
При Л-^оо, И

538	ГЛ. XII. ФУНКЦИОНАЛЬНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И РЯДЫ	D64
С другой стороны, на основании известной нам теоремы п° 446, для достаточно
больших х:
хп
'-o\ — \;
ввиду предыдущего соотношения такое же равенство может быть написано
для F(A(x)), что и доказывает справедливость асимптотического разло-
разложения
F(A(x)) »/?„ +	f	;	Н	+ ... +	+ ...,
X	X1	X3	Хп
о котором была речь.
Например, если взять
то окажется, что
а, Га., а\ 1 1 уая 2аха«
— уГП
m=i т\
¦А(х) оо1Ч—-+ -^Ч	- I	1-1 —
С
Интересным приложением этой теоремы о подстановке ряда в ряд является
[как и в случае сходящихся степенных рядов, 448] деление асимптотических разло-
разложений функций В(х) и А{х), в предположении, что свободный член а0 второго из
них отличен от нуля. Так как, по сравнению с п° 448, здесь не приходится привле-
привлекать никаких новых идей, мы не будем на этом останавливаться.
4°. Обратимся к интегрированию асимптотического разложения.
Пусть функция А(х) непрерывна в промезкутке % = [а, +~) и допускает асим-
асимптотическое разложение
А{х)со-+—+... + _+...,	A3)
начинающееся членом, содержащим — . Тогда для этой функции
х2
существует конечный интеграл от любого xs=a до +«>*, и этот интеграл (как
* Напомним [см. стр. 282], что интегралом функции f(x) от о до + ~ называется
предел
\f(x)dx= lim \f{x)dx.

464]	§ 6. ОБВЕРТЫВАЮЩИЕ И АСИМПТОТИЧЕСКИЕ РЯДЫ	539
функция от х) в свою очередь имеет асимптотическое разложение
со
Г	а2 л, 1	ап 1
А(х) dxx -i+ 3. + ... +._L	+ ...,	(И)
J	х 2 х2	п-\ х"~1
которое из A3) формально получается почленным интегрированием.
Действительно, полагая
Ап(х) = 2 1- > гпМ = А{х)-Ап{х),
при произвольно взятом е - 0 и любом фиксированном и, для достаточно больших
х будем иметь
хп- 1г„(УI «=<¦¦	A5)
Если Х>х, то
х	х	х	х
rn{x)dx- У ',—:
X	XX	X
При Х^ж, получим
t" а% 1 а% 1 ап 1
j	\ х 2х2	п	] г"—^
X"
где
X
lim rn(x)dx= rn(x) dx.
Так как, в силу A5), для достаточно больших х
X
dx
то, переходя к пределу при Х-~°=, будем иметь (для указанных х)
так что
а это, вместе с равенством A6), и доказывает справедливость асимптотического
разложения A4),

540
ГЛ. XII. ФУНКЦИОНАЛЬНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И РЯДЫ
[465
Можно показать, что наличие в асимптотическом разложении функции А(х)
члена — (при ау ф 0) сделало бы невозможным существование конечного интеграла
х
для этой функции от х до +~. [См. ниже 474.]
Замечание. Любопытно отметить, что формальное почленное дифферен-
дифференцирование асимптотического разложения, вообще говоря, недопустимо.
Для примера рассмотрим функцию F(x) = e-Xsinex. Так как, при любом п,
lim F(x)'Xn=0,
х-*-<*>
то F{x)aiQ, т. е. асимптотическое разложение функции F(x) состоит из нулей.
Между тем для производной F'(x) = e-Xsm ex + cosex такое разложение вообще
невозможно, ибо не существует даже предела lim F'(x).
х-*°°
465. Вывод формулы Эйлера—Маклорена. Эта формула играет важную роль
в анализе; в частности, ею нередко пользуются для получения конкретных обвер-
обвертывающих и асимптотических разложений. Мы дадим ее вывод и укажем при-
приложения.
Будем исходить из формулы Тейлора с дополнительным членом в форме
определенного интеграла [318]:*
где дополнительный член
6 m\ J
г
= /
J
x,	0
Возьмем здесь, вместо /, поочередно функции
m!
z
-Я	dz.
!
), hf\x), АУ"Сх),
одновременно заменяя т соответственно на
т, т-1, т-2, т-3,
Мы получим систему т равенств:
hA}\X,)=
Am-i
* Мы здесь и впредь, не оговаривая этого специально, всегда предполагаем
существование и непрерывность всех упоминаемых производных.

465]
§ 6. ОБВЕРТЫВАЮЩИЕ И АСИМПТОТИЧЕСКИЕ РЯДЫ
541
Исключим из этой системы все производные в правых частях; для этого сложим
почленно первое равенство со всеми остальными, умноженными соответственно
на числа А1г А2, ..., Лт_1; которые мы выберем так, чтобы было
1
m\ (w-1)!
В результате найдем:
Оя-2)!
A7)
Д-ГоЬт
A8)
где .
г- -
--iP
-z). —-
hzm~1 h2zm~2
	тгЛЛ,-	-
(пг-1I (m-2)!
1
dz,
или - короче -
- z)<pm(z) dz,
A8*)
где положено
hzm~1 A2zm~2
-	-+A2-	—
(w-1)! (m-2)!
A9)
Очевидно, из системы линейных уравнений A7) коэффициенты А1г Аг, ...
..., Ат—х однозначно определяются один за другим, и притом независимо
от выбора функции/и чисел х0 и h. Впрочем, эти коэффициенты нам уже известны —
это коэффициенты — разложения	 по степеням х [449 A2)]. Действительно,
к\	ех-1
если вспомнить символические уравнения:
которым удовлетворяют числа /9, то легко убедиться в том, что именно числа
— и будут решениями уравнений A7). Из сказанного о числах Д в п° 449 явствует,
к\
что
-^1--1 A -
1 1! 2' ^""
для
5D
B0)
где Вр есть р-е число Б е р н у л л и.

542	ГЛ. XII. ФУНКЦИОНАЛЬНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И РЯДЫ	[466
Пусть функция f{x) рассматривается в конечном промежутке {а, Ь\\ положим
Ъ-а
h =	, где п - натуральное число, и, взяв за х0 поочередно числа
п
a, a + h, a\-2h,..., a + (n-1)h- b~h,
для каждого промежутка [a-\-(i-\)h, a+ih] (/=1, 2, ..., л) в отдельности напишем
равенство типа A8), с дополнительным членом A8*), и все эти равенства почленно
сложим. Мы получим:
2f(a+J^\h)^ 2fW=T (V(*> dx + AJfib)-/(e)] +
1 = 1	a	nJ
+ A,h[f'(b)-f'(a)}+ ¦ ¦ ¦ +Am-1hm-4f("''2Xb)-f<-'n'2Xa)] + R, B1)
где дополнительный член
Л
2 (V(m)( ih~)() d^2 \f{m)( h^() d B1')
Эта формула и есть формула Эйлера - Маклорена, и притом с до-
дополнительным членом (которого авторы ее, разумеется, не писали). Числу т
можно давать различные значения, начиная с 2.
466. Исследование дополнительного члена. Сначала сделаем некоторые замечания
относительно функций <pm{z).
Прежде всего, дифференцируя A9), получаем:
_ium-1.	B2)
Далее, каково бы ни было /я==2, имеем
<рт@) = 0, ?>,„№> = 0.	B3)
Первое ясно по самому виду многочлена tpm{z) [см. A9)], а второе следует из по-
последнего равенства системы A7).
Докажем теперь такое утверждение: функция (p2ic(z) {четного порядка)
не может принимать в промежутке [0, h) какое-либо значение больше двух раз.
Допустим противное; тогда ее производная [см. B3)] cp'2k{z)=<p2/t-i(z) (ведь^12^_1 = 0!),
кроме концов промежутка [0, К), обращалась бы внутри промежутка в 0 - по
теореме Рол ля - не менее двух раз. В таком случае производная 9?2fc-i(z)-
=<?2k-2(z)+A2i<_1h!!k~~2 - по той же теореме - должна была бы обращаться в 0
внутри промежутка [0, h] не менее трех раз, т. е. функция <р2/г_2(.г) принимала бы
внутри этого промежутка одно и то же значение: - Аги.-^"г не менее трех раз.
Так, постепенно понижая порядок функции (р2к на две единицы, мы пришли бы
к заключению, что функция cp2(z) = — z2	(квадратичный двучлен) при-
принимает некоторое значение не менее трех раз, что невозможно! Этим наше утвер-
утверждение доказано.
Из него вытекает такое важное следствие: функция (p2ii(z) сохраняет знак
в промежутке @, К), ибо, обращаясь в 0 на концах промежутка [B3)], она внутри

466]	§ 6. ОБВЕРТЫВАЮЩИЕ И АСИМПТОТИЧЕСКИЕ РЯДЫ	543
промежутка больше уже в 0 обратиться не может. Легко установить, какой именно
знак сохраняет функция q>2k(z): для малых значений г (а, значит, и повсюду между
О и А) этот многочлен имеет знак младшего члена А2к-Л-к~7г- (А2к_1 = 0), т. е. -
так как А2к^2-{- 1)*~2	 ~ знак (~1)к-
Таким образом, две последовательные функции четного порядка, <p,k(z) и y2k+»(z),
сохраняют — каждая — определенный знак в (О, И), но знаки их противопо-
противоположны^. Это замечание нам сейчас понадобится.
Возвращаясь к дополнительному члену R, будем считать теперь т четным
числом, т = 2к, и предположим на этот раз, что производные /Bft)(z) и f(ik+2\z)
в промежутке [а, Ь] о бе положительны или обе отрицательны.
Из выражения для R, дважды интегрируя по частям, с учетом B2) и B3) по-
последовательно получаем:
h
\ Ь г.
R-	2 4>2k(z)fBl<Xx + h-z)dz =
h п J
ft
1 »
a
0
= Т2 Г
n a J
2
ft
It a
ft
1 b r
-- У <p->k+*(z)f{2k+iXx+h-z) dz
h a J
0
Так как подчеркнутые суммы интегралов в силу сделанных предположений имеют
противоположные знаки, то первая из них имеет тот же знак, что и
выражение
и меньше его по абсолютной величине. Таким образом, окончательно
R - R«k= O.A2kh*i<-4f№-i)(b) -/С*"-1)(а)] =
0A)'{~1Л2'с

544	ГЛ. XII. ФУНКЦИОНАЛЬНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ Й РЯДЫ	D6*7
Если предположить теперь, что все производные f(ik\z) четного порядка
сохраняют в промежутке {а, Ь] один и тот же знак, и написать вместо конечной
формулы B1) бесконечный ряд, учитывая вдобавок значения B0) коэффициентов
А т, то получится бесконечный ряд Эйлера - Маклорена:
ь
= у Г
h J
-\Уф)-Да)] + §
2	Z!
_!_(_ \)k-i —*__ ^2fc-i[/Bfc-i)(^,)_yBfc-i)(a)]_j_.., B4)
Bk))
Этот ряд, вообще говоря, расходится (так что знак=поставлен здесь услов-
условно!). В силу сделанных предположений, он - по крайней мере, начиная с третьего
члена - оказывается знакопеременным. Учитывая еще B1*), можно сказать,
ь
что написанный ряд обвертывает сумму ^f(x), стоящую слева. Если
а
ь
переставить эту сумму и интеграл — I f(x) dx, изменив при этом знаки всех
л J
а
прочих членов на обратные, то получится ряд, обвертывающий назван-
названный интеграл.
Частичные суммы этих рядов позволяют иной раз с большой точностью
ь
вычислять сумму ~У , зная интеграл, или интеграл — I , зная сумму. Конечно,
a	h j
а
во всем этом основную роль играет тот факт, что нам наперед известна оценка
дополнительного члена!.
467. Примеры вычислений с помощью формулы Эйлера—Маклореиа. 1) Найти
приближенное значение суммы 900 (!) слагаемых
1 = 999 л 1000 1
1=100 I 100, X
положив /(z) = 1/z, a= 100, b= 1000, A= 1. Так как
/'(z)=-i /"(z) = -. /'"&=--., /IV() ^ fto
ZZ	-3	z*
и, вообще,
то условия на счет производных четного порядка соблюдены.
Мы продолжим разложение до члена, содержащего /'", так что в дополни-
дополнительный член выйдет уже/v. В этом случае формула Эйлера -Маклорена

467]	§ 6. ОБВЕРТЫВАЮЩИЕ И АСИМПТОТИЧЕСКИЕ РЯДЫ	545
дает:
dx 1 С 1	11
	I 	, —	I -
x 2 \.1OO 1000 j
100
1/1	1 Л 6/1	1 ^	12/1	1 \
	I	 +0.	I		@-= б < 1)
12 {1002 10002J 720 (, 100* 1000V 3024 V 100е 10006J
Так как
юоо
Г — = In 10 = 2,302 585 092 994 045 ....
J x
100
fU,0045
2 (.100 1000]
1	1
12/1	1 )
3024 \ 100е 1000е)
2,307 093 342 910 720
= 0,000 000 000000 004,
1	1000 1
то с точностью до —- можно положить	^7 — = 2,307 093 342 910 72.
10"	100 л:
1
г dx 1
2) Вычислим теперь 	= 1п2. Здесь /(z) =	, а = 0, 6
J1+X	1+2
Л =1/10 (и = 10). Имеем
возьмем
l+X	- ' ' 1+2
0
A+2)"' у w A+z)
^ и, вообще, /WB) = -
так что наши условия снова выполнены. Воспользуемся видоизмененной фор-
формулой Эйлера- Маклорена, оборвав ее и на этот раз на члене, содер-
содержащем /'":
1
rcfel 1 1 1 1 1 1 1 1 1
/ П 1 / 11	6 / П	12	/ П
~2"]~Г20о[ "J+7 200 000 I ~ lij ~ 'з024 000 000 1 64J
W. П 1 (. П 6 Г.П . 12 (. П
20 I,
(О-=0-=1).
35 Г. М. Фихтенгольи, т. II

546	ГЛ. XII. ФУНКЦИОНАЛЬНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И РЯДЫ	[467
Находим, далее,
Й+П+Й+-+БГ °'718771403
	(l	1= -0,000 625
1200 i 4)
1	=+0,000 000 781
72000001.
3 024 000 000 V 164
1
Поэтому с точностью до	получаем:
0,693 147 184
(\——U 0,000 000 004.
2-108
1
12 = 0,693 14718.
J 1 + x
0
3) Покажем, наконец, как с помощью формулы Эйлера - Маклорена
может быть приближенно вычислена сумма бесконечного ряда, сходящегося,
но медленно. В виде примера остановимся на ряде:
Положим в общей формуле B1) [и B1*)]
№=- A-1, b
х*
где аи п - пока любые натуральные числа. Интеграл и производные вычисляются
легко; подставляя вместо Ат их выражения, получим:
п-1 1	Г 1	11 1 Г 1	11
М (а+02 = ~ lo+n "^J ~ 2 Ш + пУ ~ а*\~Bl
При фиксированных а и к перейдем здесь к пределу, устремив п к +¦». Легко
убедиться, что множитель вп тоже стремится при этом к некоторому пределу 0,
0== 0=^1, и в результате:
-1111	1	1	1
Д	ВвВ
-•^г.-^-"' '%*+.¦

468]	§ 6. ОБВЕРТЫВАЮЩИЕ И АСИМПТОТИЧЕСКИЕ РЯДЫ	547
Возьмем теперь конкретно а = 10 и к = 10; воспользовавшись известными значе-
значениями чисел Бернулли [449], окончательно найдем:
9 16 3	1	1	1	1
2 6^	+
5-1(Р + 7-10' 5-109 +
5	691	7 3617 43867 174611
_|	[	|	О
1Ы011 455-1013 1015 85-Ю17 133-Ю19 55-Ю21
Вьиисления проведем с 19 знаками после запятой:
э 1
6У7= 9,238 606 386 999 244 142 1
> У-
6 3 1
io+Too+Tooo~ >631
= -0,000 002
5-Ю5
1
7.10'
1
-109
5
= 0,000 000 014 285 714 285 7
= -0,000 000 000 2
= 0,000 000 000 004 545 454 5
691
= -0,000 000 000 000 151868 1
455-1013
—-= 0,000 000 000 000 007
3617
85-10"
43867
133-1019
= -0,000 000 000 000 000 425 5
= 0,000 000 000 000 000033 0
9,869 604 401 089 358 621 7
Если учесть поправки на округление и дополнительный член, то окажется, что
я2 = 9,869 604 401 089 358 62
с точностью до 1/2-10—17.
Этот пример очень поучителен: сумму л2 сходящегося ряда мы вычис-
вычислили с очень большой точностью по формуле Эйлера- Маклорена,
по сути дела прибегнув к частичной сумме расходящегося ряда, обверты-
обвертывающего число л2. Если бы мы захотели достигнуть того же, пользуясь самим
сходящимся рядом, то пришлось бы взять больше миллиарда его членов!
468. Другой вид формулы Эйлера—Маклорена. Вернемся к формуле B1) и
BГ), но предположим, что производные функции fix) всех порядков существуют
в бесконечном промежутке [а, +°°) и удовлетворяют условиям:
(а) производные f^'tk\z) четного порядка все имеют в этом промежутке один
и тот же определенный знак,
35*

548	ГЛ. XII. ФУНКЦИОНАЛЬНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И РЯДЫ	[468
(б) производные /Bfc—1)(z) нечетного порядка при z» + °° все стремятся
к нулю.
Пусть число т четное: т = 2к. Числа а и А мы фиксируем, a b = a+nh (вместе
с я) будем считать переменным. Дополнительный член R [см. BГ)] представим
теперь в следующем виде:
A	h
h	Л
Л
s-72 {<
а
Л
* ь о
Объединив первую из этих сумм со всеми членами формулы B1), содержащими
а, в одну постоянную:
h
Ск= -AJ(.a)-A2hf'(.a)- ... -^2Л_гА^-з/BЛ-з)(а)_ 1 jr f y
явно не зависящую от Ь, перепишем формулу B1) так:
ь
7- f/W dx+A1№+Aihf(b)+ ... +Alk-.!h*k-*f№-*Xb)+S', B5)
h J
где
"~^х о
1
*"UJ'
"
Для обоснования проведенного преобразования нужно лишь еще убедиться
1 оо
в сходимости использованных бесконечных рядов; начнем с ряда — У" •
"а
Из B4) следует
л
1 л-1
" ' ¦ 	 -ih-z)dz
1 л-1 (¦

468]	§ 6. ОБВЕРТЫВАЮЩИЕ И АСИМПТОТИЧЕСКИЕ РЯДЫ	549
По свойству функции?>2/((z) [466] и в силу предположения (а), все слагаемые
в числителе имеют один и тот же знак, совпадающий со знаком
знаменателя. Отсюда, переходя к пределу при п ¦» ~ и учитывая предположение
(б), заключаем о сходимости ряда
h	h
1 ~ г	1 ~
причем его сумма имеет тот же знак, что и выражение A2kh2k~1-fBk~1)(a), и по
абсолютной величине не превосходит его. Заменяя в проведенном рассуждении
числа а на Ь, убедимся в сходимости ряда
~2 \<p2kW<2kKx+h-z)dz=T У \<P«.hW<?4b+ih-z)dz,
h„ J	hJ
а также в том, что его сумма имеет тот же знак, что и выражение ^A2
а по абсолютной величине не превосходит его.
Итак, мы не только убедились в сходимости примененных бесконечных рядов,
но попутно установили, что дополнительный член R' формулы B5) можно написать
в виде:
Ви
R' = e-A2kh2k-1-fBk-1Xb) = e-(-l)k-i—h2k-
7к\
B5*)
Весьма любопытно, что постоянная Ск в формуле B5), для которой - по са-
самому способу ее составления - не исключена была возможность зависеть от
указателя к, на деле от к не зависит! Для того чтобы в этом удостовериться, доста-
достаточно сопоставить формулы B5) и B5*) с такими же формулами, написанными
для к= 1:
6
= Ci + - I f(x)dx+AJ(b) + R',
п •>
где
R'=B-AJi-f'{b) @-=<Г-=1).
Имеем
Если перейти здесь к пределу при Ь - °°, то - с учетом предположения (б) - полу-
получим: Cic = С2 = С. Постоянная С, которую естественно было бы назвать постоянной
Эйлера - М а к лор е на для функции f(x), кроме этой функции зависит еще
от выбора а и h.
Замечание. Переходя в неравенствах к пределу, нам следовало бы к
знакам неравенства присоединить знаки равенства и для множителя 0 в B5*) писать
0=s9=sl. Что равенство нулю исключается, это сразу ясно - сумма бесконечного
ряда с членами одного знака не может быть нулем. Если же предположить 0 = 1,
то - при увеличении в формуле B5) номера к на единицу - имели бы R'=0,
что (как мы только что разъяснили) невозможно. Итак, на деле: О-=0<1, как мы
и писали.

550	ГЛ. XII. ФУНКЦИОНАЛЬНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И РЯДЫ	[469
Напишем вместо конечной суммы B5) бесконечный ряд. Мы получим ряд
Эйлера-Маклорена в следующем виде:
6
J = C+i jf(pc)dx~f(b) + ^ hf\b)~ ?f'"(Jb)+ ¦..
-1)»-» ^ АЛ-
2!
Bк — 2)!
[Знак = и здесь также имеет лишь условный смысл!] В силу предположения (а),
все производные /B'с~1)F) с возрастанием Ъ изменяются в одном направлении;
а так как, по предположению (б), при Ъ — °° они стремятся к нулю, то все они имеют
один и тот же знак. Отсюда [и из B5*)] заключаем, что и в новой форме ряд Э й-
6
лера- Маклорена обвертывает сумму ^f(x), стоящую справа.
а
Замечание. Сделаем, в заключение, пояснение относительно возмож-
возможности определить саму постоянную С, фигурирующую в написанном выше разло-
разложении. Выбрав некое Ь*-а, для которого и сумма и интеграл вычисляются без
труда, можно дл? числа С получить о вертывающий его ряд:
ь
х)--г \f{x)dx+l-
" J	2
2	2!	4!
a
который во многих случаях и позволяет найти приближенное значение С.
469. Формула и ряд Стирлинга. В качестве примера использования полученных
в предыдущем п° разложений применим их к вычислению
л-1
In (л!) = In л + 2 In i.
Взяв а -1, h = 1 и (заменив л на л -1) b = л, мы положим
/(г) = In г, так что /<m)(z) = ( - l)m~
zm
и условия (а) и (б) выполнены. Мы приходим, таким образом, к асимптотическому
разложению для 1п(я!) *:
1\	Bi I В2 I	2?fc	1
I	I Jfl ft — 72 _j	.	.	L ( — JVC — 1 	 .	Ь • • •
2)	1-2 n 3-4 и3	Qk-\Jk nik~x
B6)
Это - так называемый ря<) Стирлинга; он явно расходится, ибо абсолютная
s2k Bk-2)\
величина его общего члена [449], равная 	•	— , стремится к ~.
* К сумме логарифмов прибавляется отдельно написанный In п. Число 1, полу-
получающееся в виде слагаемого при интегрировании, включено в С.

469]	§ 6. ОБВЕРТЫВАЮЩИЕ И АСИМПТОТИЧЕСКИЕ РЯДЫ	551
Из асимптотического разложения 1п(я!), как указывалось в 464, 3°, можно
получить разложение и для самого факториала. Именно, подставляя вместо ко-
коэффициентов В/с их численные значения, получим:
(п\п( 1 1	139	571
y {1+
Если оборвать ряд B6), удовольствовавшись выписанными членами, но при-
прибавив дополнительный член, то получим формулу Стирлинга:
Bk
+(i)	.+e(i
'"+К ' B*:-1J* и*"»
которая, как увидим, уже вполне пригодна для приближенных вычислений.
Положив к=1, получим простой и важный частный случай формулы Стир-
Стирлинга:
( 11	в
In (я!) = С+ \п-\— In л-лн	;
I 2)	12л
потенцируя, ее обычно пишут в виде:
Эта формула в п° 406 уже была выведена другим путем; там же мы нашли, что
еС = а- ]/2я( так что нешвестная нам до сих пор постоянная С оказывается равной
-In 2л.
2
Вычислим для примера In A00!) с десятью знаками после запятой - по формуле
B7), взяв к = 2. Сложив всего пять чисел
-1п2я= 0,91893 85332 04
(« + -] In n = 100,5 In 100= 462,81960 36918 03
-и=-100=-100
— =	= 0,00083 33333 33
2и 1200
	-=	=- 0,00000 00027 77,
12и<> 36-10'
получим для In A00!) значение 363,73937 55556, точное до 	 (с учетом до-
дополнительного члена и поправок на округление). Точность приближения можно
еще весьма значительно увеличить, взяв больше членов и выписав в каждом
из них больше верных знаков. Эта точность будет возрастать - для данного
случая - примерно, до 300-го члена (покуда члены по абсолютной величине про-
продолжают убывать).
Замечание. Читатель на ряде примеров видел, что отрезки заведомо
расходящихся рядов иной раз позволяют находить значения нужных величин
и даже с большой точностью. Подобные ряды и в старину, и в наше время неко-
некоторые авторы называли «полусходящимися». Мы, однако, предпочли отказаться
от применения этого термина, поскольку затрудняемся дать ему достаточно общее
и в то же время точное определение.

ГЛАВА ТРИНАДЦАТАЯ
НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
§ 1. Несобственные интегралы с бесконечными
пределами
470. Определение интегралов с бесконечными пределами. В главе IX
было изучено понятие определенного интеграла I fix) dx для случая
а
конечного промежутка [а, Ь]я ограниченной функции /(х).
Настоящая глава посвящена обобщению этого понятия в различных
направлениях. Начнем с рассмотрения интеграла, распространенного
на бесконечный промежуток.
Пусть функция f{x) определена в промежутке [а, + °°), т. е. для
а, и интегрируема в любой конечной его части [а, А], так что ин-
А
теграл I f{x) dx имеет смысл при любом А > а.
а
Предел этого интеграла {конечный или бесконечный) при А -+ + °°
называют интегралом функции f(x) от а до + ~ и обо-
обозначают символом
А
\f(x)dx=\im \f(x)dx.	A)
J	A-- J
В случае, если этот предел конечен, говорят, что интеграл A) схо-
сходится, а функцию fix) называют интегрируемой в беско-
бесконечном промежутке [а, + ¦»]. Если же предел A) бесконечен или вовсе
не существует, то про интеграл говорят, что он расходится. В
отличие от изученного ранее интеграла в собственном смысле или
собственного интеграла, только что определенный интеграл A)
называется несобственным*.
* Мы уже сталкивались с понятием несобственного интеграла в п° 373.

470J	§ 1. ИНТЕГРАЛЫ С БЕСКОНЕЧНЫМИ ПРЕДЕЛАМИ	553
1
Рассмотрим примеры. 1) Функция	 интегрируема в любом конеч-
конечном промежутке [О, А] 04=-0), причем имеем
А
г ах
J iTjc2 =
А
= arctg A.
о
л
Так как для этого интеграла при А •» + ~ существует конечный предел —, то ин-
интеграл от 0 до + <*> сходится и имеет значение
+ ~	А
dx
С dx	r я
	= hm = — .
J 1+Х* А- + - J 2
о
2) Изучим вопрос, при каких значениях показателя А => 0 существует несобствен-
несобственный интеграл
\% <^	&
а
Пусть А^ 1, тогда
А
cdx 1
а 1-Я
Это выражение при А -<¦ °= имеет пределом <*> или конечное число ;	а1-;' в зависи-
/ — 1
мости от того, будет ли А -= 1 или А =-1. Если 1 = 1, имеем
А
dx	a
— = In х = In A - In a
X	а
а
и при А -+ со в пределе получается ~.
Таким образом, интеграл B) при А=-1 сходится и имеет значение -—ах~л ,
1	А— 1 /
а при А^1 расходится.
Аналогично A), определяется и интеграл функции f(x) от -
<3<з а:
[Лх)йс= lim Г/(х)Л (Л'<а),	C)
J	A'--~ J
-~	А'
равно как и интеграл функции f{x) от - ~ до + ~:
+ ~	А
Г/(х)^х= lim [f{x)dx.
А'

554	ГЛ. ХШ. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ	[471
При этом сохраняется и терминология, введенная по поводу инте-
интеграла A).
В последнем случае, взяв любое а, можно положить
А	а	А
\f(x) dx = J/(x) dx + \f(x) dx,
A'	A'	a
и существование предела при А'->¦ — °°, А— + ~ для интеграла слева,
очевидно, равносильно существованию порознь пределов A) и C)
для интегралов справа *. Таким образом, интеграл от - ~ до + °°
можно определить и равенством
+-	а	+-
<\f{x)dx= jf(x)dx-r \f(x)dx
в предположении существования порознь интегралов справа. Опреде-
Определение это не зависит на деле от выбора точки а.
Примеры:
о	о
г dx	f dx	я
3) 	 = lim ¦— = lim (-arctg^') = -;
J 1+X2 A'--~ J 1+X2 A'—oo	2
-=	A'
dx
471. Применение основной формулы интегрального исчисления. В
приведенных выше примерах интеграл по конечному промежутку вы-
вычислялся с помощью первообразной функции, а затем осуществлялся
переход к пределу. Можно объединить оба момента в одной фор-
формуле.
Пусть, например, функция Дх) определена в промежутке [а, + °°)
и интегрируема в каждой конечной его части [а, А]. Если для Дх)
при этом существует первообразная функция F(x) во всем проме-
промежутке [а, + ~), то по основной формуле интегрального исчисления
[308]
Отсюда ясно, что несобственный интеграл A) существует в том и
только в том случае, если существует конечный предел
* Исключается лишь случай, когда оба этих интеграла равны бесконечности,
но разных знаков.

472]	§ 1. ИНТЕГРАЛЫ С БЕСКОНЕЧНЫМИ ПРЕДЕЛАМИ
и тогда
555
Аналогично
\f(x)dx=F(x)
если под F{ - ~) разуметь предел lim F{A'). Самая возможность вы-
числения двойной подстановки, связанная с существованием и ко-
конечностью фигурирующего в ней предела, свидетельствует уже о схо-
сходимости интеграла.
Обратимся к дальнейшим примерам.
472. Примеры. 1) е~ахsin bxdx (a>0).
Так как первообразная функция
F(x)=-
asinbx+bcosbx
так что ДО) =	и F(~) = 0, то
а2 + 62
fe-°*si
sin bx
Аналогично
e-axcos
b sin bx-a cos bx
e-ax
2) \*-
Jl+де*
х*-хУ2+1
+ —= arctg (x V2+1)+	arctg {x f2- 1) 1
2f2	2У2	J
2У2
о 2У2
3) — sin — dx = cos —
x 2

556	ГЛ. XIII. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ	[472
4) sin х dx. Первообразной функцией здесь будет - cos x, но двойная под-
о
становка -cos x |" не имеет смысла, так как cos л: при х-»~ не стремится ни
к какому пределу: интеграл не существует.
л: In х
¦dx.
о
С помощью интегрирования по частям и разложения на простые дроби нахо-
находим первообразную функцию
J
xlnx	I In* 1	1	11
	dx=	1—In x	1пA+х2)ч	.
A+x2K	4 A+x2J 4	8	8 1+x2
При х -» 0 имеем lim Fix) = —, этот предел и принимаем за значение функции при
8
х = 0. С другой стороны, F(+=o)=0. Таким образом, значение интеграла есть
1
6) Для тела, полученного вращением гиперболы ху = 1 вокруг оси х, вычислить
объем и боковую поверхность части, определяемой неравенством хв=1.
Конечная часть тела, отвечающая изменению х от 1 до А (А =-1), имеет объем
и боковую поверхность
А	А
1
X'	J X
1	1
Естественно за объем V и боковую поверхность S всего (простирающегося в беско-
бесконечность) тела принять пределы этих величин, т. е. положить
rdx	г 1 1/ 1
J хг	J х 1 x
dx.
Однако, в то время, как первый интеграл сходится [470, 2)], и для объема полу-
получается конечное значение я, второй интеграл расходится, что указывает на беско-
бесконечное значение боковой поверхности.
Для того чтобы убедиться в последнем, достаточно заметить, что
А
-dx
cdx
—
J х
X
1
н Sa стремится к ~ при А-~<™.
7) Пусть в начале координат О находится масса т, которая притягивает ма-
материальную точку М массы 1, находящуюся на оси х на расстоянии х от О, с силой
(по закону Ньютона). Какую работу А произведет сила F при перемещении
точки М вдоль оси х из положения, отвечающего х= г, в бесконечность?

472]	§ 1. ИНТЕГРАЛЫ С БЕСКОНЕЧНЫМИ ПРЕДЕЛАМИ	557
Работа, очевидно, будет отрицательной, так как сила направлена
против движения. Распространяя на этот случай формулу (9) п° 353, найдем:
ею
С т т - т
А =	dx = — =—.
J X2	X г	Г
г
При обратном перемещении точки М из бесконечности до расстояния х = г
т
сила ньютоновского притяжения произведет положительную работу — .
г
Эта величина называется потенциалом рассматриваемой силы на точку М и служит
мерой, накопленной в точке потенциальной энергии.
8) Для работы, производимой газом при расширении его от объема Vx до
объема V2 (У^^У^, мы имели формулу [354 A0)]:
jpdV.
Пусть дана некоторая масса идеального газа, занимающая объем V^ при
давлении рх. Предположим, что газ расширяется до бесконечности и
притом адиабатически, т. е. без теплообмена с окружающей средой. В этих условиях,
как известно [361, 3)], имеет место формула Пуассона
Тогда работа, которая могла бы быть выполнена газом при таком расширении,
будет
1— к Vk~J
к-\
Принимая во внимание, что c=plVk, и подставляя это в полученную формулу,
окончательно .найдем
A -PlVl
9) В задаче 8) п° 356 мы установили силу F, с которой на единицу «магнитного
заряда» действует конечный прямолинейный отрезок тока:
f
J
ds.
h
Рассмотрим теперь случай бесконечного (в обе стороны) проводника,
т. е. положим st= -<», s2= +~. Тогда
С al
- 21
а
Разумеется, бесконечный проводник - это фикция; тем не менее полу-
полученный результат может оказаться полезным: в случае очень длинного проводника
его выгодно приближенно рассматривать как бесконечный, ибо этим дости-
достигается значительное упрощение формулы!
10) Если в электрической цепи с самоиндукцией в момент времени f = 0 ток
силы /0 разомкнуть, то в ней возникает экстраток размыкания, под-
подчиняющийся закону:	_

558
ГЛ. XIII. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
[473
[см. 359, 4) (а); мы сохраняем здесь прежние обозначения]. Предложим себе вы-
вычислить полное количество джоулева тепла Q, выделяемое этим током.
Элементарное количество тепла за промежуток времени [t, t+dt], очевидно,
будет
dQ = PR-dt.
Суммируя за весь бесконечный промежуток, получим:
L
о	о
Отметим, что хотя практически ток через конечный промежуток времени
становится неощутимым, все же для определения полного количества энергии
тока, переходящей в тепло, приходится интегрировать по бесконечному
промежутку.
473. Аналогия с рядами. Простейшие теоремы. В последующем мы
ограничимся интегралами вида A): все сказанное о них легко пере-
переносится на случаи B) и C). При этом мы всегда будем предполагать,
что функция f{x) интегрируема в собственном смысле ме-
между любыми пределами а и А > а, так что вопрос относится только
к несобственному интегралу от а до ~.
Между несобственными интегралами ]f(x)dx и числовыми ря-
—	а
дами 2 ап существует глубокая аналогия, которую полезно под-
1
черкнуть.
Если процесс суммирования по л заменить процессом ин-
тегрирования по х, то аналогами будут
общий член ряда
частичная сумма ряда
N
сумма ряда
как предел частичной суммы
при JV-»- —
остаток ряда
JV + 1
подынтегральная функция
Ах)
собственный интеграл
А
jf(x)dx
а
несобственный интеграл
как предел предыдущего
интеграла при А-+°=
интеграл
\f{x)dx

474]	§ 1. ИНТЕГРАЛЫ С БЕСКОНЕЧНЫМИ ПРЕДЕЛАМИ	559
Мы перечислим простейшие теоремы о несобственных инте-
интегралах, сходные с теоремами п° 364 о рядах. Доказательство их -
с использованием указанной аналогии — предоставляем читателю.
1°. Если сходится интеграл I f(x) dx, то сходится также инте-
оо	а
грал \f(x)dx (A^a), и наоборот. При этом
А
J/(x) dx = J/(x) dx + If(x) dx.
a	a	A
2°. В случае сходимости интеграла \f(x)dx имеем
о
оо
lira \f(x)dx = O.
3°. Из сходимости интеграла \f(x)dx вытекает и сходимость
•о	а
интеграла \c-f(x)dx (с = const), причем
а
\c.f(x)dx~c.\f{x)dx.
а	а
Наконец:
4°. Если сходятся оба интеграла \f{x)dx и \ g{x)dx, то сходится
о*	а	а
интеграл I [f(x)±g(x)]dx, и
а
оо	оо	оо
J [/(*) ± *(*)] dx = J/(x) dx±\ g(x) dx.
474. Сходимость интеграла в случае положительной функции. Если
функция Дх) положительна (неотрицательна), то интеграл
А
<?>(A)=\f(x)dx	D)

560	ГЛ. XIII. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ	[474
представляет собой монотонно возрастающую функцию от
переменной А. Вопрос о существовании для нее конечного предела при
А-*°° решается очень просто — на основании теоремы о пределе мо-
монотонной функции [п° 57]:
Для сходимости несобственного интеграла A) - в случае поло-
положительной функции f(x) - необходимо и достаточно, чтобы
интеграл D) при возрастании А оставался ограниченным сверху:
(JL = const).
Если же это условие не выполнено, то интеграл A) имеет значе-
значение ~ [ср. п° 365].
На этом основана следующая «теорема сравнения» для интегралов
от положительных функций:
Теорема 1. Если хотя бы при хг^-А (А»а) имеет место неравен-
неравенство f(x)*eg(x), то из сходимости интеграла g(x) dx следует схо-
сходимость интеграла J f(x) dx или, что то оке, из расходимости J f(x) dx
а	а
следует расходимость J g(x) dx.
а
Доказательство можно скопировать с доказательства теоремы 1
п° 366.
Часто полезна следующая теорема, являющаяся следствием первой:
Теорема 2. Если существует предел
fix)
lira -т-г= К
g(x)
то из сходимости интеграла I g(x) dx, при К< + °°, вытекает схо-
димость интеграла \f(x)dx, а из расходимости первого интеграла,
а
при К>-0, вытекает расходимость второго. [Таким образом, при
О-г^Г< + °° оба интеграла сходятся или оба расходятся одновремен-
одновременно.]
Доказательство такое же, как и для аналогичной теоремы
2 п° 366 [см. 473, 3°].
Выбирая конкретную функцию для сравнения, можно отсюда по-
получить частные признаки сходимости или расходимости интеграла

475]	§ 1. ИНТЕГРАЛЫ С БЕСКОНЕЧНЫМИ ПРЕДЕЛАМИ	561
f(x) dx. Практическое значение имеет сравнение с функцией ~х >
а
которая интегрируема от а>0 до ~ при А>1 и не интегрируема при
А=?=1 [ц° 470, 2)]. На этом построены следующие признаки Коши:
Пусть для достаточно больших х функция f(x) имеет вид
Тогда: 1) если А=-1 и q>(x)*sc-< + ~, то интеграл I f(x) dx сходится,
а
2) если оке A=sl к <р(х)э=>с=-О, то этот интеграл расходится.
Для доказательства надо воспользоваться теоремой 1; функцией
сравнения является —х [п° 473, 3°].
Если при х-* ~ функция /(х) является бесконечно малой порядка
со
А=>0 по сравнению с-, то интеграл \f(x)dx сходится или рас-
ш
ходится в зависимости от того, будет ли А=-1 или A==sl.
Здесь следует сослаться на теорему 2; роль функции g(x) играет —х.
Примеры:
Подинтегральные выражения при х-*~ представляют собою бесконечно
малые, соответственно, порядка V2 и 2. Следовательно, первый интеграл расходится,
а второй - сходится.
2) I	dx, где Р(х) есть целый многочлен степени т, a Q(x) - целый много-
J Q(x)
а
член степени п =- ш, не имеющий корней в промежутке [а, ~).
Для достаточно больших х подинтегральное выражение сохраняет определен-
определенный знак. Поэтому (изменяя в случае надобности знак) можно применить изло-
изложенные выше признаки. Подинтегральная функция является (при х - ~) бесконечно
малой порядка п-т. Поэтому при п = т+1 интеграл расходится, а при лэ»тя+2
сходится. (При л=?=л! он, очевидно, расходится.)
475. Сходимость интеграла в общем случае. Вопрос о существова-
нии несобственного интеграла f(x) dx, согласно определению A),
а
36 Г. М. Фихтенгольц, т. II

562
ГЛ. ХШ. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
[475
приводится к вопросу о существовании конечного предела при А ¦
для функции от А:
А
D)
Применяя к этой функции признак Больцано-Коши [58],
можно условие существования несобственного интеграла представить
в следующей форме:
Для сходимости несобственного интеграла I J\x) dx* необходимо
а
и достаточно, чтобы каждому числу е^О отвечало такое число Ло>
>а, чтобы при А>А0 и А' >Л0 выполнялось неравенство
А'	А	А'
|Ф(А') - Ф{А) | = | J/(x) dx - If{x) dx\ = \ \f{x) d
= ?.
Этот критерий позволяет с легкостью установить такое предло-
предложение:
Если сходится интеграл I \f{x)\dx, то* и подавно сходится
—	ш
jf(x)dx.
а
В самом деле, применяя изложенный критерий к интегралу
I \f{x)\dx, который предполагаем сходящимся, видим, что для лю-
а
бого ?>0 найдется такое А0>а, что
А'
А'
лишь только А'>А=-А0. Но, очевидно,
\f{x)dx
и,
следовательно, для тех же А, А' тем более выполняется неравенство
А'
\f{x)dx
-е,
* В предположении, что в каждом промежутке [а, А], А>а, функция /О) интегри-
интегрируема (в собственном смысле).

476]	§ 1. ИНТЕГРАЛЫ С БЕСКОНЕЧНЫМИ ПРЕДЕЛАМИ	563
откуда, в силу нашего критерия, вытекает сходимость интеграла
со
\f{x)dx.
а
Отметим, что из сходимости последнего интеграла, вообще го-
говоря, не следует сходимость интеграла J \f(x)\dx. Это обстоятель-
а
ство дает основание особо отличать следующий случай. Если наряду
со	со
с интегралом J f{x)dx сходится и интеграл I |/(х)| dx, то интеграл
<=	а	а
I f(x) dx называют абсолютно сходящимся, а функцию f(x) - аб-
а
солютно интегрируемой в промежутке [а, + ~]. Пример интеграла,
сходящегося неабсолютно, будет дан в следующем п°.
По отношению к знакопеременной функции /(х) признаки
п° 474 непосредственно неприложимы. Но можно попытаться с их
помощью установить сходимость интеграла от положитель-
положительной функции |/(х)|: если эта функция оказывается интегрируемой,
то функция /(х) также будет интегрируема и притом абсолютно.
Отсюда вытекает и следующее предложение, которое часто бывает
полезно:
Если функция f(x) абсолютно интегрируема в промежутке
[а, + «•], а функция g(x) ограничена, то и произведение их /(х) • g(x)
будет функцией, абсолютно интегрируемой в промежутке
[а, + -].
Для доказательства достаточно сослаться на неравенство
|/(x)-g(x)|^L.|/(x)|.
г cos ax
Пусть, например, дан интеграл ——- dx. Здесь функция f(x) =
о
оказывается (абсолютно) интегрируемой, в то время как g(x) = cosax, очевидно,
ограничена. Отсюда - абсолютная сходимость предложенного интеграла.
Как видно, для знакопеременной функции изложенные
здесь соображения - в благоприятном случае - могут установить
лишь абсолютную сходимость. Если же интеграл от данной
функции расходится или сходится, но не абсолютно, то различить эти
случаи с помощью установленных здесь признаков нельзя.
476. Признаки Абеля и Дирихле. Мы дадим сейчас признаки дру-
другого типа, основанные на применении второй теоремы о среднем
значении [306]. Они аналогичны признакам Абеля и Дирихле
36*

564
ГЛ. XIII. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
[476
сходимости бесконечных рядов [384], ввиду чего удобно и их связать
с теми же именами. Эти признаки позволяют устанавливать сходи-
сходимость несобственных интегралов в ряде случаев, когда абсолютная
сходимость отсутствует.
Признак Абеля. Пусть функции f(x) и g(x) определены в про-
промежутке [а, •»), причем
1)	функция f(x) интегрируема в этом промежутке, так что ин-
интеграл A) сходится (хотя бы и неабсолютно),
2)	функция g(x) монотонна и ограничена:
\g(x)\*sL (L = const,
Тогда интеграл
\fix)g(x)dx
E)
сходится.
Доказательство. По второй теореме о среднем значении,
при любых А'^-А^а, будем иметь
A'	S	А'
\f(x)g(x)dx^g(A) \f(x)dx + g(A') \f(x)dx,	F)
A	A	I
где A*s!;=sA'. Ввиду предположения A), для произвольно заданного
е>0 найдется такое А0>а, что при А>А0 будет
Z	А'
В связи с 2), это дает нам, при А'=~А>-А0,
А'	С	А'
\
| J f(x)g(x)
A
| g(A') | • | J
х) dx
что и влечет за собой [475] сходимость интеграла E).
Можно и в случае интегралов дать другую комбинацию условий,
налагаемых на функции f(x) и g(x), при которых сходится интеграл
от их произведения:
Признак Дирихле. Пусть
1) функция f(x) интегрируема в любом конечном промежутке
[а, А] (А>а), и интеграл D) оказывается ограниченным:
А
I Г
\f(x)dx
(K= const,

476]	§ 1. ИНТЕГРАЛЫ С БЕСКОНЕЧНЫМИ ПРЕДЕЛАМИ	565
2) функция g{x) монотонно стремится к 0 при х — °°:
lim
Тогда интеграл E) сходится.
[Как читатель видит, прежнее условие A) несколько ослаблено,
ибо мы здесь не требуем сходимости интеграла A); зато условие B)
заменено более сильным!]
Доказательство проводится как и выше, исходя из равен-
равенства F), но в этом случае первые множители g(A) и g(A') могут быть
сделаны сколь угодно малыми, если взять А и А' достаточно боль-
большими, а вторые множители ограничены числом 2К.
Замечание. И здесь признак Абеля вытекает из признака
Дирихле. Действительно, для ограниченной монотонной функции
g(x) необходимо существует конечный предел
g(-) = lim g(x).
Представив f(x)-g(x) в форме
/(*) • *(*) = /(*) • g (~) + /(*) • Ш - «<-)],
видим, что для второго произведения уже выполняются условия
Дирихле [см. 473, 3° и 4°].
Легко видеть, например, что при X => 0 сходятся интегралы
а	а
Пользуясь признаком Дирихле, мы полагаем f(x)=sin x или cos x, a g(x) = —.
Xх
Условия 1) и 2) выполнены, так как
А	А
sinxdx
= |cosa-cos^4|=s2 и, аналогично,
I cos х dx
и функция— , монотонно убывая, стремится к 0 при х-»~.
хх
В частности, отсюда при X = 1 вытекает сходимость интеграла
rsin х
dx
J х
о
(мы могли взять здесь а-0, потому что подинтегральная функция при л:-0 имеет
конечный предел). Можно показать, что этот интеграл сходится неабсолют-
но, т. е. что интеграл
J-
X
о
dx

566	ГЛ. XIII. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ	[477
расходится. В самом деле, если бы этот интеграл сходился, то по теореме 1 п°
474 сходился бы и интеграл
г sin2 х
	dx (a=~0),
J х
а
ибо sin2 x=s | sin x |. Иными словами, сходился бы интеграл
1 р 1 - cos 2x
прибавив к нему заведомо сходящийся интеграл
cos 2x
dx,
х
а
мы пришли бы к заключению, что сходится интеграл
а
чего на деле нет [470, 2)].
Замечание. Теперь, когда мы установили сходимость интегралов
¦sin х
(¦sin x	ccosx
	dx и 	dx,
J x	J x
мы можем, наконец, уточнить определение иеэлементарных функций six
(«интегральный синус») и ci;t («интегральный косинус»), о которых мы упоминали
в п° 289. Именно, полагают
С sin t	r cos /
si x = - 	dt, ci x = - 	dt.
J t	J t
(xs=0)	(x-^0)
Если, например, вторую из этих формул написать в виде:
х	«>
f cos / сcos t
cix= -	dt-	dt,
J t	J t
l	l
то - по известному свойству определенного интеграла [n° 305, 12°] - ясно, что
cos л:
производная от а х действительно равна 	.
х
477. Приведение несобственного интеграла к бесконечному ряду. Мы
знаем, что понятие предела функции может быть выражено двояко -
«на языке е-д» и «на языке последовательностей» [52, 53]. Если к
функции Ф(А) [см. D)] применить второе определение предела, то

477]	§ 1. ИНТЕГРАЛЫ С БЕСКОНЕЧНЫМИ ПРЕДЕЛАМИ	567
определение A) несобственного интеграла может быть истолковано
так: какую бы ни взять последовательность возрастающих до бес-
А„
конечности чисел {Ап} (Ап > а), последовательность интегралов 11 f(x) dxf
а
должна стремиться к одному и тому же конечному пределу *, который
и дает значение несобственного интеграла \f(x)dx.
а	Ап
С другой стороны, вопрос о пределе последовательности {J/(*)<
а
тождествен вопросу о сумме ряда [362]:
Ах А, Ах	Ая А4	Ах Аг А|
а	а а	а а	а А, А,
Таким образом, можно утверждать: для существования несобст-
несобственного интеграла f(x) dx необходимо и достаточно, чтобы - какова
а
бы ни была варианта Ап-~°° (Ап>а) - ряд
2 \ f{x)dx
п=1 .->
А„_,
сходился к одной и той же сумме, которая и дает значение несобст-
несобственного интеграла.
Отметим, что в случае положительной (неотрицательной)
функции f(x) - для существования интеграла достаточно сходимости
указанного ряда при одном частном выборе варианты
Ап-+°°. Действительно, тогда возрастающая функция D) от А будет
ограничена суммой этого ряда и, следовательно, имеет конечный пре-
предел при у4-*~ [474].
Сведение вопроса о сходимости интеграла к вопросу о сходимости
ряда представляется часто очень выгодным, так как дает возможность
использовать многочисленные признаки сходимости или расходимости
рядов.
я»
* Достаточно предположить, что все последовательности -I I f(x) dx\
а
сходятся, чтобы отсюда уже можно было заключить, что предел у них будет один
и тот же [53].

568	ГЛ. XIII. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ	[477
г sin x
Для примера рассмотрим снова интеграл I	dx, о котором уже была
J х
речь в предыдущем n°.	°
Так как sinx при возрастании х принимает попеременно то положительные,
то отрицательные значения, меняя знак в точках ля (л = 1, 2, 3, ...), то естественно
именно эти числа взять в качестве Ап и рассмотреть ряд
°° г sin х
2 J —dx.	G)
л=0 J	X
пп
г sin х
Произведя в общем члене vn= I	dx подстановку х = пл+1, получим
J	X
X
лл
J
sin/
dt.
пл+t
о
Отсюда видно, что члены ряда имеют чередующиеся знаки и по абсолютной вели-
величине монотонно убывают. Далее, при л>0,
71	71
с sin t	r 1 1
К = \—Л^ —dt = -
J пя+t J пп п
о	о
и, следовательно, абсолютная величина членов ряда стремится к нулю с увели-
увеличением их номера. Ряд G) будет типа Лейбница и, по известной теореме
[381], сходится. Обозначим его сумму через /. Таким образом, для любого е=-0
найдется такое N, что при ns^N имеет место неравенство
psin х
J х
-dx-1
X
о
(8)
Теперь уже завершить доказательство существования интеграла проще «на
языке е.-6». Пусть A >Nn; тогда существует такое натуральное число щ, что «„я=^Л -=
-= (и„+ 1)тг, причем, очевидно, no&=iV. Так как в промежутке от щл до (ло+ 1)л функ-
А
ция sin х сохраняет знак, то интеграл будет содержаться между интегралами
О
и I , каждый из которых лежит, в силу (8), между 1-е и 1+е. Следовательно,
0	0	А
то же можно утверждать и об интеграле I . Итак, окончательно, для A >Nti имеем
о
А
sinx
	dx-I
-х
Q

478]	§ 1. ИНТЕГРАЛЫ С БЕСКОНЕЧНЫМИ ПРЕДЕЛАМИ	569
так что существует
А
rsinx rsinx
	dx = hm 	dx=I*.
J X	A-*+«. J X
о	о
Мы уже знаем [476], что этот интеграл сходятся неабсолютно, т. е.
г I sin jc I
что интеграл 	dx расходится. Этот факт также легко установить, обра-
о
щаясь к представлению интеграла в виде ряда. Действительно, если бы интеграл
сходился, то имели бы, как и только что,
со	(п+1)я	Я
f ^U=i f
J x ?oi
л0	?o
О	лл	О
Но яя+/ге(л+1)я, так что
л	п
sin t	1 с	2
Лd
f sin t	1 с	2
J tm+t (п+1)л J	(л+1)я
о	о
2 1
между тем как ряд — 2И	расходится! [365, 1)].
я л+1
478. Примеры. 1) Исследовать сходимость интегралов:
dz
FO)
(a)
о
г arctg х	с
	— dx, (б)
J *	JVz(z-
Решение, (а) Подинтегральная функция при дс ->+<»» является бесконечно
малой первого порядка; интеграл расходится.
(б)	Бесконечно малая порядка 3/2: интеграл сходится.
(в)	При х-*0 подинтегральная функция стремится к 0. Разлагая в ряд, видим,
что выражение
"*	*' J.2 г
-j, --, б2-а*
е -е =	Ь- ¦•
х*
при х — + «> является бесконечно малой 2-го порядка: интеграл сходится.
(г)	Разлагая е±х в ряд, легко получить
<-e~x 2 12
* Здесь (как и в предыдущем п°) нас интересует лишь вопрос о сходимости
Этого интеграла. Ниже мы увидим, что его значение /= —.

570	ГЛ. XIII. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ	[478
1
так что при х — 0 подинтегральное выражение стремится к	. При х-*°° оно
будет бесконечно малой 2-го порядка. Интеграл сходится.
2) То же для интегралов:
г г xdx (¦ In л:
(a) \xfe-axdx (ft a=-0), (б)	. (в)	dx.
а	0	1
Решение, (а) Взяв любое А =-1, имеем:
х»е~ах
-0;
интеграл сходится.
(б) Заметим сначала, что при х^О подинтегральная функция стремится к 0.
Взяв теперь снова любое А =-1, получим:
х	1	1
*0 при л- + ~;
интеграл сходится.
(в) При х^\ подинтегральная функция имеет пределом 0. Пусть
1
тогда отношение этой функции к — можно написать в виде:
Xх
Xя- In х Ых 1
	>0 при л:— со;
интеграл сходится.
3) То же для интегралов:
(a) -S'n "Х (о=-0), (б) \ xiJe-"xcosxdx (/*, а=-0).
Указание. В обоих случаях имеем произведение ограниченной функции
на (абсолютно) интегрируемую.
4) Исследовать сходимость интеграла (<х>0)
а	а
[dx fsin(/32jc3)cfJS= I" { [sin
10
Постараемся оценить порядок убывания при *-•» «внутреннего» интеграла.
Полагая в нем /З2*3 = z, имеем:
[sin
1 г sin z
	dz.
* Примем здесь без доказательства, что «внутренний» интеграл представляет
непрерывную функцию от х.

478]	§ 1. ИНТЕГРАЛЫ С БЕСКОНЕЧНЫМИ ПРЕДЕЛАМИ	571
г sin г
Ввиду сходимости интеграла 	fife [476], найдется постоянная L такая, что
о V*
при всех Л=-0
А
• sin г
— fife
о
а
Следовательно, интеграл sin (fSV) df! по абсолютной величине не превосходит
1	о
выражения —— . Отсюда вытекает абсолютная сходимость предложенного ин-
х'2
теграла.
5) Установить сходимость интегралов {а, к, А=»0)
г л;- sin ах	г . sin 2x
(а) —	-dx,	(б) \e™x——dx,
J к2+х2	J	хх
о
(В) 11ПАГ|
J
sin х	г sin (х+х2)
Лd	(г)	Цi
О
Решение. Во всех случаях пользуемся признаком Дирихле.
х
(a) g{x) =	 для достаточно больших х монотонно убывает и при х ¦* ¦
к2 + х2	а
стремится к нулю; интеграл sin ax dx, очевидно, ограничен.
1	о
(б) g(x) = — , монотонно убывая, стремится к нулю при х -» ~ f(x) = esin x-sin 2x,
хх
так что (если положить sin x = t)
A	sin A
fix) dx
tel dt
О	О
--2е.
(в) g(x)= ] In л: ]д —, для достаточно больших значений х
X
так что g(x) убывает, очевидно, стремясь к нулю, и т. д.
(г) g(x) = — ;f(x) = sin(x+x2), так что (полагая z = х+х2)
хх
А + А'
sin 2
f	f sin 2
\ьш(х+хг) dx=	dz.
a	a+a'

572
ГЛ. XIII. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
[478
Это выражение по абсолютной величине остается ограниченным, ввиду того,
Г sinz
- dz сходится (в чем можно удостовериться с помощью
что интеграл
a+a'
того же признака Дирихле).
6) Доказать следующее утверждение:
Пусть функция f(x) определена в промежутке [а, + °°) и имеет период а>>0,
а функция g(x) монотонна в том же промежутке и стремится к 0 при х-* +¦».
Если интеграл (собственный)
то интеграл (несобственный)
сходится. Если же, наоборот,
jf(x)g(x)dx
(9)
E)
{f(x)dx = K*0,
(9*)
то интеграл E) сходится или расходится в зависимости от того, сходится или
расходится интеграл
c) dx.
A0)
(а) Предположим сначала выполнение условия (9) и покажем, что интеграл
А
J/W dx
в этом случае остается ограниченным при всех А =- а.
Ввиду 314, 10) и замечания в 316, очевидно, и
а+Ы
= 0 (* = 1, 2, 3, ...),
и тогда, каково бы ни было А =~а, если взять к = Е\	 , будем иметь
\ ш )
А	А	А—ки> a+to
\fix)dx = J -
а	а+кю	а	а
требуемое заключение следует непосредственно из признака Дирихле.

478]	§ 1. ИНТЕГРАЛЫ С БЕСКОНЕЧНЫМИ ПРЕДЕЛАМИ	573
(б) В предположении (9*), заменим f(x) на f(x)	. Так как эта функция
(О
удовлетворяет условию типа (9), то интеграл
J [/(*)--*
E*)
по доказанному сходится. Отсюда уже ясно, что интегралы E) и A0) сходятся
(или расходятся) одновременно.
7) Если, например, положить /(х) = sin2 х в промежутке [0, +~) и ш=л, то
видим, что интеграл
г	п
sin2 х dx = — * 0;
о
следовательно, интеграл
sin2 x-g(x)dx
{при прежних предположениях относительно g) сходится или расходится одно-
одновременно с интегралом A0).
Напротив, интеграл
Г| — -sin2 x\g(x) dx = — \cos2x-g(x)dx
сходится во всяком случае, независимо от поведения интеграла A0)!
8) Исследовать сходимость интегралов
г	их	г	dx
(a) ecos x-sin (sin x) — , (б) esin *.sin (sin x) — .
J	x	J	x
о	о
(а)	Имеем
2л	л 2л
jV°sx.sin (sin x) fife = f + [=0,
О	О л
ибо второй из двух последних интегралов разнится от первого из них лишь знаком
(подстановка z=2rc-x). В силу 6), интеграл (а) сходится.
(б)	На этот раз
2л
esln х.8щ (sjn
о
так что [см. 6)] - ввиду расходимости интеграла
г dx
- (а=-0)
J х
а
- интеграл (б) расходится.

574	ГЛ. XIII. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ	[478
9) Исследовать интеграл
г sin л:
	dx
J xf+sinx
о
на сходимость, в зависимости от значений параметра ц =» 0.
Имеем тождество
sin х sin x	sin2 x
XIх+sin x xf x" (xv + sin x)
Интеграл от первого члена справа
J .да
как мы знаем [476], всегда сходится. Обратимся к интегралу от второго члена
справа
г sin2 х
	dx.	A1)
J xf (xf+sinx)
о
Так как
sin2 x	sin2 x	1
xf(xf+l) xi<(xf+sinx) xf(xf~l)'
1
то при ft,-—интеграл от выражения справа, а с ним и интеграл A1) сходится;
при /t=e— рассмотрим выражение слева: интеграл от него, в силу 7), ведет себя
так же, как и интеграл
с dx
т. е. расходится, а с ним расходится и интеграл A1).
1
Окончательно, предложенный интеграл сходится при /г-— и расходится
1
при ,a=s—.
1
Пример этот, в случае ,и=д—, поучительно сопоставить с признаком сходи-
сходимости Дирихле. Интеграл от первого множителя, sin x, ограничен, в то время
как второй множитель
1
xf+sinx
стремится к 0 при х-»<*>. Нарушено лишь требование монотонности этого
множителя, и предложенный интеграл оказывается расходящимся!

478]	§ 1. ИНТЕГРАЛЫ С БЕСКОНЕЧНЫМИ ПРЕДЕЛАМИ	575
10) Исследовать интеграл
г x*dx
J 1+xi3-sin2*
о
на сходимость, в зависимости от значений параметров а, /?=»0.
Обозначив подинтегральную функцию через fix), будем иметь при изменении
х между ял и (л+1)л:
l+|(«+l)rc|/»sin2x	1 + (ил)/? sin2 х
Интегрируя эти неравенства, учтем, что
dx	c dx	л
A2)
мы получим
т
Теперь суммируем по л от 0 до ~:
с	ах	г ах	л
j I+A sin2 x	J 1+А sin2 x ~\[~\+A
nn	0	'
;	J fix)dx
Так как оба крайних ряда сходятся или расходятся одновременно с рядом
i»-1'.
о
то это же справедливо и для интеграла.
Итак, предположенный интеграл сходится при /?=-2(а+1) и расходится при
/S=s2(a+1).
11) То же - для интеграла
Г ха dx
(a, /5-0).
Метод рассуждения тот же, что и в предыдущем примере. Вместо интеграла
A2) здесь придется рассматривать интеграл [см. 288, 14)]:
dx
Это легко вывести из 288, 10) или 309, 9).

576	ГЛ. XIII. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ	[478
Так как при А - <»
Ы(А+УА*-1) ЫА
У^гЗТ " А
то сравнивать предложенный интеграл достаточно с рядами
In гФ
т. е., в конечном счете, с рядом:
¦у
Ответ. При ^=-а+1 интеграл сходится, а при |8«га+1 расходится.
Примеры 6), 7), 9), 10), 11) принадлежат X а р д и (G. H. Hardy).
12) Произвести полное исследование случаев сходимости и расходимости
интеграла:
dx
J ! + *«• 1st
в зависимости от значений параметров а и f) (а, /? =- 0).
(а) Пусть a=sl. Так как
1	1
l] 1+х*'
то в этом случае интеграл расходится [474].
(б) Пусть aag/?. Переходя к ряду [477], имеем в этом предположении:
(л+1)л	п	(л+1)я
у [	dX	у Г	dz	у Г
=о J l+x4sinx|0 n-f0 J l+^+z^sin^z"^ J
ля	О	0
Но для 0-=z
=1,
так что члены последнего ряда оказываются бблыпими соответствующих членов
расходящегося ряда
Итак, интеграл снова расходится.
(в) Пусть а.?-р>\. Представим / в виде суммы Jt+Jz, где
= у f
1 AJ
fife	. Z. Сdz
п—О х T\"'L-t-z>~ :>u"' z	п—1 •* * "г V'-'f ~z)a SinP Z
о

479]	§ 2. ИНТЕГРАЛЫ ОТ НЕОГРАНИЧЕННЫХ ФУНКЦИЙ	577
п
Затем, для 0«=z-= — и лз=1,
B Y	}~г
\л )
откуда
2
8 я
» -С-2
г dz 1 г dt с* 1 г dt
——	 =	 	=s— , где с* = — I	.
Таким образом,
Аналогично и /2^™. Так что интеграл сходится.
(г) К случаю а=-|8=»1 приводится и общий случай, когда одновременно а=»1
и а;»/?. Действительно, в этом случае легко найти такое ^'ssft чтобы было а >|8' =-1.
Так как при уменьшении § сходимость лишь усиливается, то и в упомянутом
общем случае налицо сходимость.
Резюмируя все исследование, видим, что интеграл / сходится при одновре-
одновременном выполнении условий i>1 и а>[) и расходится во всех прочих случаях.
Можно сказать и короче: если а=>тах A, /?), интеграл сходится, а при a=smax
A, Р) — расходится.
§ 2. Несобственные интегралы от неограниченных
функций
479. Определение интегралов от неограниченных функций. Рассмо-
Рассмотрим теперь функцию f(x), заданную в конечном промежутке [а, Ь],
но неограниченную в этом промежутке. Предположим более
определенно, что в любом промежутке [a, b-rj\ @<rj<Z?-a) функция
ограничена и интегрируема, но оказывается неограниченной в каж-
каждом промежутке [b-rj, b] слева от точки Ь. Точка Ъ носит в этом слу-
случае название особой точки.
Ь-п
Предел интеграла \f(x)dx при Г]-*0 (конечный или бесконечный)
а
называется (несобственным) интегралом функции f(x) от а до Ъ и
обозначается как обычно:
Ь	b—q
а	' а
= \im\f(x)dx.	A)
37 Г. М. Фихтенгольц, т. II

578	ГЛ. XIII. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ	[479
В случае, если этот предел конечен, говорят, что интеграл A) схо-
сходится, а функцию f{x) называют интегрируемой в про-
промежутке [а, Ь]. Если же предел A) бесконечен или вовсе не существует,
то про интеграл говорят, что он расходится.
1
Пример. 1) Функция -—== ограничена и интегрируема в любом промежутке
[0, l-rj\ (O-=r;-=l), и
"" dx
r ax
J Vf31
- = arcsin x
= arcsin A-т;).
В точке х-\ функция обращается в бесконечность. Напомним, что под этим
1
разумеется лишь то, что при х — 1 функция ——=^; стремится к бесконечности.
У
Очевидно, в любом промежутке A-г/, 1) функция неограничена, т. е. точка х=\
является особой. На практике обыкновенно приходится иметь дело именно с такого
рода особыми точками.
л
Так как вычисленный интеграл при т)-0 стремится к пределу arcsin 1=— ,
то существует несобственный интеграл
1	1-7)
dx
г dx	г п
Пусть теперь функция f(x) ограничена и интегрируема в любом
промежутке [a+rj',b] @< ?]'<&-а), но оказывается неограниченной
в каждом промежутке [а, а + щ'] справа от точки а (особая точка).
Тогда {несобственный) интеграл функции fix) от а до b определяется
равенством
ь	ь
f/l(jc)«&=lim \ f(x)dx.	B)
а	' a+rf
В общем случае, в промежутке [а, Ь] может быть конечное число
особых точек с0, q, ..., cm_1( cm, вблизи которых функция f(x)
неограничена, между тем как в каждой части этого промежутка, не
содержащей особых точек, функция ограничена и интегрируема.
Пусть (для простоты письма) таких точек три, причем две из
них совпадают с концами а, Ь промежутка, а третья, с, лежит между
ними. Тогда определение интеграла от а до Ъ дается равенством
6-7I
C)
J}-

479]	§ 2. ИНТЕГРАЛЫ ОТ НЕОГРАНИЧЕННЫХ ФУНКЦИЙ	579
Взяв внутри каждого из промежутков [а, с], [с, Ь] соответственно
по точке d, e, будем иметь
с—rl3	d c—rl3
I = J + J-
Легко видеть, что существование предела C) равносильно существо-
существованию порознь пределов для всех четырех этих интегралов, так что
определение C) можно заменить таким:
b	d	с	е	Ь
\f{x) dx = \f{x) dx + J/(x) dx + J/(x) dx + J f(x) dx,
a	a	it	с	е
в предположении, что все несобственные интегралы справа сущест-
существуют *. Это определение не зависит от выбора точек d и е.
По отношению к несобственным интегралам B) и C) сохраняется
та же терминология, что и выше.
Примеры.
о
Г dx
2) 	, особая точка - 1,
J Vl-л:2
— 1
о	о
г dx	г dx	n
= lim	= lim [-arcsin (-1+т)')] = — >
— 1	—1 + т/
+1
г dx
3)	, две особые точки -1 и 1,
1	0 1
Г dx	Г Г 71 71
	 — I Г	I	I	—ту
J 1/ГЗ^ J J ~2 + 2
-1 '	-10
4)	Исследуем, при каких значениях показателя .Я=»0 сходится несобственный
интеграл
ь
1(^я «•->•	«>
а
При А ^ 1 интеграл
а+т;
* За исключением случая, когда два из этих интегралов равны бесконечности
разных знаков.
37*

580	ГЛ. XIII. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ	[479
при т;-0 имеет пределом °° или конечное число	-(Ь-аУ~х в зависимости
1 — К
от того, будет ли А =-1 или Х< 1. Если А = 1, то
ь
dx
a+rq
с dx
	= In {Ь - а) - In г] - ~ (при 1] - 0).
J х-а
Итак, интеграл D) при А-=1 сходится и имеет значение 	F-аI—я, а при
1 — Я
расходится [ср. 470, 2)].
6) Аналогичный результат может быть установлен относительно интеграла
который несущественно разнится от предыдущего.
Замечание. Полезно заметить следующее: если функция f(x)
в промежутке [а, Ь] интегрируема в собственном смысле (так что
ь
интеграл \f{x)dx уже определен), то предельное равенство A) [B)
а
или C)] для нее все же имеет место. Оно непосредственно вытекает
из непрерывности интеграла по переменному верхнему (ниж-
(нижнему) пределу [305, 11°]. Таким образом, для несобственного интеграла
мы приняли за определение то равенство, которое для соб-
собственного выполняется само собою.
Наконец, рассмотрим функцию fix), заданную в бесконечном про-
промежутке, например в [а, + ~), и имеющую в нем конечное число
особых точек*, вблизи которых она перестает быть ограниченной.
Предположим, что в каждом конечном промежутке [а, А] интеграл
А
\f[x)dx существует, как собственный или как несобственный, со-
а
гласно данному выше определению. Тогда, переходя еще раз к пре-
пределу при А-~~>, можно равенством A) [470] определить несобствен-
несобственный интеграл в промежутке [а, + ~].
В случае бесконечного промежутка точка ± ~ играет ту же роль,
что и особые точки, требуя подобно им дополнительного предель-
предельного перехода. На этом основании и точку ± ~ также называют осо-
особой, независимо от того, будет ли функция f(x) при безграничном
возрастании х оставаться ограниченной или нет.
* Особых точек может быть и бесконечное множество, лишь бы в каждом
конечном промежутке [а, А] (А^а) их было лишь конечное число (кото-
(которое может расти до бесконечности вместе с А).

480J	§ 2. ИНТЕГРАЛЫ ОТ НЕОГРАНИЧЕННЫХ ФУНКЦИЙ	581
480. Замечание относительно особых точек. Рассмотрим функцию f(x), опреде-
определенную в конечном промежутке [а, Ь], и предположим, что она в этом промежутке
в собственном смысле не интегрируема. Тогда в промежутке [а, Ь] необходимо
найдется такая точка с, в каждой окрестности которой функция оказывается
не интегрируемой (в собственном смысле).
Действительно, если бы подобных точек не было вовсе, то каждую точку х
промежутка [а, Ь] можно было бы окружить такой окрестностью а, чтобы в ее
пределах функция была интегрируема. Применив к системе 2 = М> покрываю-
покрывающей промежуток [а, Ь], лемму Б о р е л я [88], легко в таком случае разложить
промежуток [а, Ь] на конечное число частей, в которых порознь функция интегри-
интегрируема. Но отсюда вытекала бы ее интегрируемость во всем промежутке [а, Ь],
вопреки предположению.
Упомянутую точку с и естественно назвать особой: в ней как бы «сгущается»
свойство функции не быть интегрируемой. Особых точек может быть несколько,
даже - бесконечное множество; в случае функции Дирихле [300, 2)], например,
особые точки заполняют сплошь весь промежуток [0, 1].
Ограничимся случаем конечного числа особых точек с0, ct, с2, ¦¦•, ст.
В этом случае природа «особенности», осуществляющейся в названных точках, легко
вскрывается: в окрестности каждой из них функция попросту неограничена
(так что именно неограниченность и является причиной неинтегри-
неинтегрируемости в собственном смысле). Чтобы убедиться в этом, достаточно рас-
рассмотреть случай, когда единственной особой точкой будет Ь.
Итак, пусть при любом r/^0 (rj^b-d) функция f{x) интегрируема (следова-
(следовательно, необходимо - и ограничена) в промежутке [a, b-rj\, но не интегрируема
в промежутке [Ь - т), Ь]. Нужно доказать, что при этих условиях вблизи точки b функ-
функция не может оставаться ограниченной. Допустим противное: пусть для всех х
в [в, Ь] имеем:
\f(x)\=sL (? = const).
е
Задавшись произвольным числом е > 0, возьмем ?; -= — . Для промежутка
6L
Е
[a, b-TJ], в котором функция f(x) интегрируема, по числу — можно найти такое
<5=-0, чтобы при разделении этого промежутка на части с длинами 4х/'-=<5 было
Z^'Ax,^,
где cot' означают, как всегда, соответствующие колебания функции [297]. Можно
предположить сверх того, что <5«=т;. Разобьем теперь весь промежуток [а, Ь]
на части с длинами Axj^6, и пусть Ах? будут отвечать тем частям, которые не
выходят за пределы [a, b-rj\, a Axr - остальным частям; из них только одна
может выходить за пределы [a, b-rj\ - если точка b-r/ сама не входит в состав
точек деления. Тогда по-прежнему
Z,<m xc=-,
с другой же стороны:
2

582	ГЛ. XIII. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ	[481
и окончательно
А этим обусловливается [297] интегрируемость функции f(x) во всем промежутке
[а, Ь], и точка Ь оказывается не особой, вопреки предположенному о ней. Этим
и завершается доказательство.
Таким образом, в случае конечного числа особых точек, их можно характери-
характеризовать именно тем, что вблизи них функция перестает быть ограниченной; это
мы и возвели в определение особых точек в предыдущем п°.
481. Применение основной формулы интегрального исчисления. При-
Примеры. Пусть функция /(jc) определена в промежутке [а, Ь] и интегри-
интегрируема (в собственном смысле) в каждом промежутке [a, b-rj\, в то
время как Ъ служит для нее особой точкой. Если для f(x) в проме-
промежутке [а, Ь), т. е. для а^х^Ь существует первообразная функция F(x),
то
6—г?
J f{x) dx = F(b -г])- F(a) = F(x)
b—7j
i
a
и существование несобственного интеграла A) равносильно суще-
существованию конечного предела lim F{b - rj). Если последний существует,
1}--0
то его естественно принять за значение F\b) первообразной функции
при х = Ь, достигнув этим непрерывности F(x) во всем промежутке
[а, Ь]. Для вычисления интеграла A) мы имеем тогда формулу обыч-
обычного вида:
E)
Та же формула имеет место и в том случае, если особая точка
лежит внутри промежутка или при наличии нескольких особых точек,
но (это нужно твердо помнить) при непременном условии, чтобы пер-
первообразная функция F(x), имеющая f(x) своей производной всюду,
исключая особые точки, была непрерывна и в этих последних. Суще-
Существование такой первообразной обеспечивает существование несоб-
несобственного интеграла.
Замечание. Говоря о «первообразной» функции F(x), мы могли
бы понимать ее в еще несколько более широком смысле: F(x) должна
иметь своей производной f(x) повсюду, исключая не только особые
точки, но и, быть может, еще некоторые точки в конечном числе,
лишь бы и в них не нарушалась непрерывность функции F(x)
[ср. 310].

4811	§ 2. ИНТЕГРАЛЫ ОТ НЕОГРАНИЧЕННЫХ ФУНКЦИЙ	583
Заменив в основной формуле E) Ъ на х, a f{x) на F'(x), мы, как
и в 310, можем написать ее в виде
X
Таким образом, по заданной производной F'(x) восстанавли-
восстанавливается первообразная функция F(x), если только производная ин-
интегрируема, хотя бы в несобственном смысле.
Обратимся к примерам.
8
1) —-, особая точка х = 0; так как первообразная функция— x'U непрерывна
-ф	2
и в этой точке, то интеграл существует:
9
-1 ~г
-1 Ух
2
~2х dx
J ',- 2
2) 	 не существует, так как первообразная In | хг -11 обращается
J хг~\
-2
в с» в особых точках х= +1.
1
3)	—	rfx, особая точка х=1; здесь первообразная — (arcsin л;J не-
J yi-^2	2
0	( я*\
прерывна при х = 1; следовательно, интеграл существует = — I.
18/
1
4) In х dx, особая точка л: = 0; здесь первообразная xlnx-x при х^О имеет
о
пределом 0. Приписывая ей при х = 0 именно это значение, будем иметь
1
Г
lnxdx = x\nx-x
= -1.
о
2
г	dx
5) —	— , особая точка дс=1; имеем:
J vlAv2_?v_1
J;
- = - arcsin
хУ$х2х1	2х
2 я	3
= — arcsin —.
1 2	4
2
f fifcc
6) —j	, особая точка х= 1; интеграл не существует, так как первообраз-
J х in х
1
ная In In х обращается в °° при х = 1.

584	ГЛ. XIII. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ	[482
482. Условия и признаки существования интеграла. Мы остановимся
лишь на случае, связанном с определением A), так как перефрази-
перефразировка для других случаев не представляет трудностей. Ввиду полной
аналогии с несобственным интегралом, распространенным на бес-
бесконечный промежуток [а, ¦*>], мы ограничимся формулировкой неко-
некоторых основных предложений. Доказательства аналогичны приведен-
приведенным выше.
Для сходимости несобственного интеграла A) - в случае поло-
положительной функции fix) — необходимо и достаточно, чтобы
при всех г}=-0 выполнялось неравенство
Ь-т,
x)dx=siL {L = const).
Теоремы сравнения п° 474 формулируются и доказываются и в
рассматриваемом случае почти в тех же выражениях. Приведем без
доказательства вытекающие отсюда признаки К о ш и.
Пусть для достаточно близких к Ъ значений х функция f(x) имеет
вид:
Тогда, 1) если А<1 и g(x)=sc< + <», то интеграл \f(x)dx сходится,
а
2) если же А=з=1 и g(x)s*c>0, то этот интеграл расходится.
Более частная форма, удобная на практике:
Если при х^-b функция f(x) является бесконечно большой порядка
ь
%>0 \по сравнению с -— I, то интеграл f(x)dx сходится илирас-
а
ходится в зависимости от того, будет ли Л<1 или Аг»1.
1
dx
r dx
Примеры. 1)	. Подинтегральная функция при х-1 предста-
yi4
y
вляет бесконечно большую порядка V4:
11	11
	:	=	>— при х-
Следовательно, интеграл сходится.
1
dx
7rrz^=^z: (л2<1). Бесконечно большая порядка 1/г, интеграл
сходится.

482]	§ 2. ИНТЕГРАЛЫ ОТ НЕОГРАНИЧЕННЫХ ФУНКЦИЙ	585
3) xflnxdx. Если /i^O, /(х) = х/*\пх-~0 при х-*0, интеграл существует
о
как собственный. При ju==O подинтегральная функция обращается в бесконечность
при х = 0.
Если /х=— 1, то взяв А под условием 1 =- А> |,«| = -ц,, будем иметь
хР In х
	= x>.+ii In х » 0 (при х - 0);
1/дся
1
г Ас
так как интеграл — сходится, то и предложенный интеграл сходится [по теореме,
о
аналогичной теореме 2 п° 474] *.
1
Наконец, если ,u=s-l, то интеграл xi' dx расходится, тем более расходится
предложенный интеграл, ибо	°
хр \мх
	= 1пх^~ (при дс — 0)
[по той же теореме].
Дальнейшие примеры читатель найдет в следующем п°.
Далее, применяя признак Больцано-Коши, имеем такое
общее условие сходимости:
ь
Для сходимости несобственного интеграла J f(x) dx (где Ъ - осо-
а
бая точка) необходимо и достаточно, чтобы каждому числу е>0
отвечало такое число <5>0, чтобы при 0<??<<$к0<?/<<5 выполнялось
неравенство
6-7,'
J Ax)dx
)-7J
Отсюда, как и выше, вытекает:
б
Если сходится интеграл I \f{x)\dx, то** и подавно сходится ин-
ь
теграл f(x) dx.
* Мы применяем к функции х^ In х признаки, предназначенные для положи-
положительных функций, ибо она приводится к положительной простым изменением
знака.
** В предположении, что в каждом промежутке [a, b-rj\ (т/^0), функция f(x)
интегрируема (в собственном смысле).

586	ГЛ. XIII. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ	1482
Обратное, вообще говоря, неверно. Поэтому и здесь особо отли-
ь	ь
чают случай, когда наряду с интегралом f(x) dx сходится и I \f(x) \ dx;
а	а
тогда первый интеграл называют абсолютно сходящимся, а функ-
функцию f(x) — абсолютно интегрируемой в промежутке [а, Ь].
Подобно последнему утверждению п° 476 легко доказать и здесь:
Если функция f(x) абсолютно интегрируема в промежутке
[а, Ь], а функция g(x) интегрируема в [а, Ь] в собственном смысле, то
и функция f(x)• g(x) будет абсолютно интегрируема в указан-
указанном промежутке.
Связь с бесконечными рядами дается теоремой:
б
Для сходимости несобственного интеграла f(x) dx (где Ъ — осо-
а
бая точка) необходимо и достаточно, чтобы - какова бы ни была
варианта ап^-Ъ - ряд
2
л=0
A ]f(x)dx (ao = a,
a»
сходился к одной и той оке сумме; последняя и дает значение несоб-
несобственного интеграла.
Дадим пример интеграла, сходящегося, но не абсолютно. Положим для
л Ъг п
л:-sin ^ ^ 'COSX2 '
она непрерывна при л:=-0, и единственной особой точкой для нее в промежутке
[О, 2] будет 0. С другой стороны, первообразной для fix), как нетрудно проверить,
является функция
п
хг '
которая имеет при х-»0 пределом F(+0) = 0. Таким образом, интеграл
2
[
сходится.
Для того чтобы обнаружить, что интеграл \f{x)\dx расходится, прибегнем
о
к представлению этого интеграла в виде ряда. Возьмем варианту ап-*-0, положив
Z7—г> a2fc = — №=1,2,3,...)-

483]	§ 2. ИНТЕГРАЛЫ ОТ НЕОГРАНИЧЕННЫХ ФУНКЦИЙ	587
Тогда
/, II/ уХ) | дл:э= > I I / №) их.
л=1 J	А = 1 J
art
Л	ЯЛ	Я
В промежутке [а2^, a2ft-il> т' е- Для &лэ=—э=?я	, sin — и cos — имеют противо-
х2	2 х2	х2
положные знаки, так что f(x) сохраняет определенный знак, и поэтому
J/W
dx
1
2k-l к
- 1
Ввиду расходимости гармонического ряда У1 — расходится и рассматриваемый
1 *
ряд, а с ним и предложенный интеграл.
483. Примеры. Исследовать на сходимость интегралы
в	11
ycosp-совв
я/а	я/*
г с /"cos fl - sin
(г) (tg x)P dx,	(дМ 	~
я/2	я/4
соя fl —sin в\1
de.
О	-я/4 '
Решение, (а) Особая точка ср - в. Ввиду существования производной
cos q> - cos в
lim 	= - sin в
q,-~s ?>-e
подинтегральное выражение будет (при <р — 6) бесконечно большой порядка г/2
Iотносительно 	1. Сходимость.
(б)	Особая точка х = 0. Так как
ех-е~х
lim	=2,
х-^о х
то порядок подинтегрального выражения относительно — I будет 2/з- Схо-
I	х)
ди мост ь.
(в)	И здесь
lnx
	--1 при х-*\,
х-1
порядок относительно	равен 1. Расходимость.
I	1-х)
(г)	Если р =»0, то особой точкой является л/2, при р^О особая точка 0. В обоих
случаях подинтегральное выражение является бесконечно большой порядка \р\.
Итак - сходимость при |р|^1 и расходимость при

588	ГЛ. XIII. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ	[483
П	Л
(д) При р=»0 особой точкой будет	, а при р«=0 особая точка —. Ответ
тот же, что и в примере (г).	4	4
1	1
2) (a) \-^=dx, (б) Г ' X" l dx,
0	0 (a, 6*0)
(в) flnsinxufe, (r) fln|sin
Решение, (а) При х -1 подинтегральная функция стремится к 0. Особая
точка х = 0. Пусть 0-=А«=1, тогда
In х 1 хх In х
:-r= , ~0 при х-0;
сходимость.
(б)	При х — 1, раскрыв неопределенность, найдем, что подинтегральная функ-
функция имеет конечный предел ( = 6-а). Особая точка х=0 (если хоть одно из чисел
а, Ь меньше 1, что мы и предположим). Отношение подинтегральной функции
1
1	р
к числителю равно	0 (при х -0). Ввиду сходимости интеграла (xt>~1 -ха~1) dx
lnx	J
сходится и предложенный интеграл.	°
(в)	Особая точка х = 0. Пусть 0-=А-=1, имеем:
In sin х ( х \х
———=	 -sin-1 л:-In sin л:-0 при (дг-О);
\/х'- vsin x)
сходимость.
I	л\
(г)	Положим к = sin со p-=co=s—-I, особая точка б = со. Пусть снова 0-=/-=1,
тогда
In [sin2 6-sin2со|
fl-ш
sin в - sin со
стремится к нулю при в¦*со; интеграл сходится.
1	1
3) (а)
Hl-*)»-1***, (б) Г х<»-1A - дс)Ь-1 In jc dtc.
о	о
Решение, (а) При а-= 1 особая точка 0, при 6-^1 особая точка 1. Разложим
1
1 2 1
предложенный интеграл на два, например, так: = + I . Так как подинте-
о о i_
2
тральная функция при х—0 является бесконечно большой (если а-=1) порядка
1 - а, то первый интеграл сходится лишь при условии 1-а«=1, т. е. а=-0.

483]	§ 2. ИНТЕГРАЛЫ ОТ НЕОГРАНИЧЕННЫХ ФУНКЦИЙ	589
Аналогично, второй сходится при Ь=~0. Итак, предложенный интеграл сходится
в том и только в том случае, если одновременно а=»0 и 6=»0.
(б) По отношению к точке х = 0 положение осталось прежним. Достаточно
1
2
рассмотреть интеграл и притом в предположении a=sl (при а=-1 интеграл
о
существует, как собственный). Рассуждения те же, что и в примере 3) п° 482. Ин-
Интеграл сходится при а=-0, как в случае (а).
Что касается точки х = 1, то здесь положение изменилось, так как Inx при
1
х-1 является бесконечно малой 1-го порядка. Интеграл существует
1
При Ь> — 1.	2
Окончательно, условия сходимости предложенного интеграла: а =- О, Ь =- - 1.
я
г $\a.n~1<pd<p
Решение. Так как случай к-^0 приводится к случаю &=-0 подстановкой
<р=п-<р1, то можно ограничиться предположением: кз*0. Кроме того, для сходи-
сходимости интеграла во всяком случае необходимо: л^О - иначе при <р-0 (или <р-я)
подинтегральная функция становится бесконечно большой порядка &1.
Если &«=1, то этого условия и достаточно. При к = \ интеграл сходиться не
может, ибо при g?-n имеем бесконечно большую порядка 1.
Пусть, наконец, к>\. Тогда налицо еще одна особая точка. a = arccos I	,
V к)
при q>-~ а подинтегральное выражение обращается в бесконечность порядка л,
значит для сходимости интеграла нужно еще потребовать: л< 1.
Итак, интеграл сходится, если 1) 0=^к^1 и л=»0 или 2) к>1 и 0<и^1;
в прочих же случаях - расходится.
rxa~1	f In х	г
5) (а) I	dx, (б) I	dx, (в) \ xP~le~* dx.
J 1 + х	J 1+х2	J
0	0	0
Решение, (а) Особые точки: <*> и (при а-= 1) также 0. Если разбить интеграл:
| = | + |, то первый сходится при а=»0 (бесконечно большая порядка 1-а-=1
0 0 1	Г
относительно х), а второй - при а<\ (бесконечно малая порядка 2—а>1 относи-
1} „	I n
тельно — I. Итак, интеграл сходится при 0^о-=1.
(б) Особые точки ~ и 0, = + . Взяв 0-=Л-= 1, имеем
0 0 1
In х 1 Xх In д-
	г:-г = -|	г~0 при х-0,
1+Х2 Xх 1+Х3

590	ГЛ. XIII. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ	[484
сходится. Пусть теперь !<,«-= 2, тогда
In х 1 хг In х
• —— -0 при х-°°,
значит, и I сходится. Отсюда следует сходимость
1	о
1
(в) Особые точки ~ и О (при р -= 1). I существует лишь прир =- 0 бесконечно малая
о
1\ г
порядка 1 —р по отношению к — I. существует, каково бы ни было р, так как,
х) J
1
взяв А=-1, имеем
1 При ЛГ-оо.
J
Vxx	ех
существует при р^О.
В следующих двух упражнениях рассматриваемые в конечном (или бесконеч-
бесконечном) промежутке [а, Ь] функции предполагаются имеющими в нем (или в каждой
его конечной части - если промежуток бесконечен) разве лишь конечное число
особых точек.
6) Доказать, что
(а)	если интегрируема функция /2, то и сама функция / необходимо будет
абсолютно интегрируема (про такую функцию говорят, что она «интегрируема
с квадратом»);
(б)	если обе функции /и g интегрируемы с квадратом, то и сумма nxf+g также
интегрируема с квадратом;
(в)	при тех же предположениях и произведение fg будет (абсолютно) интегри-
интегрируемой функцией.
По теореме сравнения все это просто вытекает из неравенств
7) Для функций указанного класса могут быть установлены те же интеграль-
интегральные неравенства, какие были выведены в п° 321 в предположении интегрируемости
рассматриваемых функций в собственном смысле. Например, если единственной
особой точкой во всех случаях является Ь (которое может быть и °=), то стоит
лишь написать то или иное интегральное неравенство для промежутка [а, х0],
где a-=xo~=6, а затем перейти к пределу при ха~Ь, чтобы установить справедли-
справедливость неравенства и для несобственных интегралов. При этом из сходимости
интегралов в правой части неравенства вытекает сходимость интегралов в левой
части, сходно с тем, что мы имели в 375, 8) по отношению к бесконечным рядам.
484. Главные значения несобственных интегралов. Допустим, что в промежутке
[а, Ь] задана функция f(x), которая имеет одну лишь особую точку с внутри

484J	§ 2. ИНТЕГРАЛЫ ОТ НЕОГРАНИЧЕННЫХ ФУНКЦИЙ	591
промежутка и интегрируема (в собственном смысле) в каждой части его, не со-
содержащей с. Несобственный интеграл от а до Ь определяется равенством
c—rj b
+
т/-*0 a
I Г
c= htn|
причем предел должен существовать при независимом предельном
переходе по г\ и по rf. В некоторых случаях, когда этот предел не существует,
оказывается полезным рассмотреть предел того же выражения, если ijhi)' стремятся
к нулю, оставаясь равными: r/'-rj-O. Если этот предел существует,
его называют (по примеру К о ш и) главным значением несобственного интеграла
ь
I f(x) dx и обозначают символом
а
b	с—т]Ь
V.p.J/W*-Jm{J+ J}.
a	a c+7j
[V. p. — начальные буквы от слов «Valeur principale», означающих по-французски
ь
«главное значение»]. В этом случае говорят, что интеграл f{x)dx существует в
ь	•>
Г	"
смысле главного значения. Если интеграл f(x) dx существует как несобственный,
а
то он, очевидно, существует и в смысле главного значения; обратное же, вообще
говоря, неверно. Рассмотрим примеры.
ь
с dx
1) Интеграл 	(а-=с-=Ь) как несобственный не существует, ибо выражение
J х-с
а
С — 7J	Ь
dx с dx b-c
г dx г dx b-c ri
	+ 	= ln	+ ln-
J x-c J x-c c-a rf
не имеет определенного предела, если г\ и rf стремятся кО независимо друг
° т друга. В то же время, если связать г) и rf требованием rf = г), то получим
выражение
с— т]	Ь
С г Ь-с
+ =1п	,
J	J	c-a
a	c+tj
на деле не зависящее от г\, так что главное значение интеграла существует.
dx .b-c
r ax ь-с
/. р. 	= 1п	.
J x-c с-а

592	ГЛ. XIII. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ	[484
ь
г dx
2) Интеграл I	(а^с^Ь, п»2) при и четном имеет бесконечное значение,
J {х-с)п
а при п нечетном вовсе не существует, как несобственный.
Рассмотрим выражение
V dx с dx	1 с 1	1	1	1 1
)(х-с)п ) (х-с)п n-llfa-c)»-1 F-c)"-1 J?"-1	гр-Ч'
a	c+tj
При п нечетном оно сводится к постоянному числу; таково же будет в этом случае
и главное значение:
f dx	! Г 1	1 ] г	ч
V. р. 	=	(и - нечетное).
J {х-с)п и-1 LCa-c)"-1 ф-с)п-Ч
а
3) Рассмотрим, далее, расходящийся интеграл
2
-sin 8
J k-sin
о
Особой точкой будет a = arcsin к, и при 8-а подинтегральная функция обраща-
обращается в бесконечность 1-го порядка. Имеем:
f dB	1
	, = _____ jn
J fc-sin 8 l/i _i-2
1 -ksin 8-Vl -к2cos
sin a-sin 9
l-cos(a-8)
Поэтому
a—7]	z
Г Г	If sin a - sin (a - rj) l-cosai
+	-Пп	+ln	}.
J	J Vi _?2 I sin (a.+rj)-sin a	sin a J
0	«+7J	'
При ?;—0 выражение под знаком логарифма в первом слагаемом стремится к 1
(в чем нетрудно убедиться, раскрывая неопределенность по правилу Лопиталя).
Окончательно,
f rffl	1	1 - У1 - A:2
V.p. 		In	 (O-=/fc-=l).
JAr-sinfl Т/Г7Г2	A:

484]	§ 2. ИНТЕГРАЛЫ ОТ НЕОГРАНИЧЕННЫХ ФУНКЦИЙ	593
В некоторых случаях можно наперед установить существование главного
значения интеграла. Остановимся на одном таком случае. Пусть дан интеграл
ь
г dx
J /Ос) '
а
где функция f(x) непрерывна в промежутке [а, Ь] и обращается в 0 в одной лишь
точке с внутри промежутка. Предположим, что в окрестности точки с существует
первая производная /'(*)> не обращающаяся в 0 при х = с, а в этой точке суще-
существует и вторая производная /"(с).
Так как 	 при х-с является бесконечно большой 1-го порядка, и притом
/(*)
меняя знак при прохождении х через с, то предложенный интеграл не существует.
Покажем, что он существует в смысле главного значения.
Положим
/(х) f'(c)(x-c)
эта функция для х ^ с непрерывна. Вблизи х = с имеем, по формуле Тейлора
с дополнительным членом в форме П е а н о [124]:
где а0с)-0 при х^с. Тогда, очевидно,
i [/"(с)+«(*)]
так что <р(х) вблизи х = с остается ограниченной и, следовательно, интегрируема
1
даже в собственном смысле. Так как для функции	 интеграл существует
f'(c)(x-c)
в смысле главного значения [см. 1)], то это справедливо и относительно предло-
предложенного интеграла.
С помощью этого признака, например, легко установить существование глав-
главного значения в примере 3). Другим примером может служить определение одной
важной неэлементарной функции, так называемого «интегрального логарифма»:
а
dx
г Г ах
Ьа=	.
J 1пх
о
Этот интеграл сходится лишь при 0 -= а -= 1; при а >¦ 1 его понимают именно в смысле
главного значения.
Нетрудно распространить понятие главного значения и на случай любого
конечного числа особых точек внутри рассматриваемого промежутка.
До сих пор мы исключали возможность особенностей на концах проме-
промежутка; можно этого не делать, если только при построении главных значений
этих именно особенностей в расчет не принимать.
4) Пусть, например, предложен заведомо расходящийся интеграл (а^О)
2
dx.
J 1-х
о
38 Г. М. Фихтенголыд, т. II

594	ГЛ. XIII. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ	[484
Особыми здесь будут точка х=1 и (если а<1) конец промежутка х = 0. Легко
показать, что в этом случае
2	1-») 2
О	О 1 + т)
приводится просто к интегралу
1
¦dt
Л
(при а< 1 - несобственному).
В заключение рассмотрим еще одну разновидность «главного значения», кото-
которою нередко приходится пользоваться. Именно, остановимся на интеграле, рас-
распространенном на бесконечный в обе стороны промежуток (-°°, + °°),
причем внутри промежутка мы не предполагаем наличия особых точек. Как из-
известно, такой интеграл может быть определен предельным равенством
+-	А
f(x) dx= lim /(*) dx,
J	a~+°- J
—	A'--" A'
где предельный переход по А а по А' предполагается не-
независимым один от другого. Может оказаться, однако, что в этом
смысле предела нет, но существует предел, отвечающий частному предположению
А' = -А. Его также называют главным значением интеграла f(x)dx и обозна-
чают символом
V.p. \f(x)dx= lim \ f(x)dx.
J	A-*+oe J
—	-A
Например, если функция f(x) нечетная, то ее интеграл в симметричном
относительно 0 промежутке {-А, А) будет равен 0, так что и
V.p. J f(x)dx = 0,
хотя несобственного интеграла f(x)dx может и вовсе не существовать (как,
скажем, для функции sin x).
Если функция /Ос) четная, то
-А

485J	§ 2. ИНТЕГРАЛЫ ОТ НЕОГРАНИЧЕННЫХ ФУНКЦИЙ	595
предел для этого интеграла существует в том и только в том случае, когда суще-
А
ствует предел для интеграла f(x) dx, т. е. существует несобственный интеграл
о
fix) dx, а с ним и интеграл f(x) dx. Таким образом, для четной функции
о
главное значение интеграла существует лишь одновременно с несобственным
интегралом (и, естественно, равно ему).
Любую функцию fix) (интегрируемую в каждом конечном промежутке) можно
представить в виде суммы двух функции, четной и нечетной
, , /(*)+/(-*) , . /(*)-/(-*)
<р(х) =	 и у>(х) =
(сохраняющих то же свойство интегрируемости).
Из сказанного выше теперь ясно, что
V. p. J Д*) dx= J ф) dx,
если последний несобственный интеграл существует. Например, замечая, что
1+х 1 х
функция —- состоит из четной части — и нечетной части 	, сразу
J. "т* Х^	I. ~j~ X	X т X
можно написать
1+х . с dx
1+>
Г1+х j Г
.р. 	dx= —-п.
J 1+х' J " -
485. Замечание об обобщениях значениях расходящихся интегралов. В § 9 главы
XI мы занимались суммированием расходящихся рядов, приписывая
такому ряду - по тому или иному правилу - «обобщенную сумму». Подобно
этому, существуют методы, позволяющие в иных случаях и расходящимся
интегралам приписывать «обобщенные значения». Собственно говоря, мы
делали это и в предыдущем п° именно тем, что вносили некоторые упрощающие
частные ограничения в предельные процессы, которые приводят к обычным не-
несобственным интегралам. Здесь же мы имеем в виду уже существенно иные про-
процессы, сходные с теми, какими мы пользовались по отношению к расходящимся
рядам. Мы ограничимся двумя примерами таких процессов, которые служат
аналогами метода Ч е з а р о и метода Пуассона - Абеля для рядов.
1. Пусть функция fix) определена для дгэ=О и интегрируема в. собственном
смысле в каждом конечном промежутке [0, х], но не интегрируема в промежутке
[О, ~]. Определим функцию
о
и составим среднее ее значение
X
- [ Fiu) du.
х J
38'

596	ГЛ. XIII. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
Если для него существует конечный предел
[485
litn — F(u)du = I,
х-.,» x J
о
то это число и рассматривают как «обобщенное значение» интеграла.
Применим этот процесс, для примера, к известному нам расходящемуся
интегралу
sin х dx
о
[472, 4)]. Здесь f(x) = sin x, F(x) = 1 - cos x, и
F)
1 с
lira — I F(u)du = li
х-»= х J	х-
.--sinx
hm	= 1.
В качестве «обобщенного значения» расходящегося интеграла F) получилось,
таким образом, число 1.
Естественно, и здесь возникает вопрос о регулярности изложенного
метода: приписывает ли этот метод сходящемуся интегралу
J/(*)&,
G)
имеющему по определению п° 470 конечное значение Див качестве «обобщенного
значения» - то же число /. Покажем, что это именно так.
По произвольному числу е =- 0, ввиду сходимости интеграла G), найдется такое
хо>0, что для х»х0 будет
где
Предполагая х>х0, имеем
X	X	Хо
- [F(u)du-I=- [ [F(u)-I]dv=- [ l
X J	X J	X J
X
-—)—— [
X j X-XaJ
/]du,
так что
i-I
= -| | [F(u)-I]du
(u)-I\du.

486]	§ 3. ПРЕОБРАЗОВАНИЕ НЕСОБСТВЕННЫХ ИНТЕГРАЛОВ	597
Второе слагаемое справа -=— (по самому выбору числа х0); первое же тоже станет
-=—, при достаточно большом х, и одновременно:
1 р
- F(u)du-
х j
о
Таким образом, действительно
lim - [ F(u) du = I,
х»~ х J
о
ч. и тр. д.
II. На этот раз по заданной функции fix), для которой интеграл G) не суще-
существует, введем в рассмотрение другой интеграл
о
Если последний интеграл при к => 0 сходится и существует конечный предел
im [e-^
—О J
lim
A-
0
то этот предел и принимается за «обобщенное значение» расходящегося инте-
интеграла G).
Чтобы дать пример, рассмотрим вновь интеграл F). Так как
e-kxs'mx dx=
о
[472, 1)] стремится к 1 при &—+0, то и здесь в качестве «обобщенного значения»
интеграла F) получается 1.
К вопросу о регулярности второго метода мы вернемся ниже [520].
§ 3. Свойства и преобразование несобственных интегралов
486. Простейшие свойства. Мы будем рассматривать функции, ин-
интегрируемые (в собственном или несобственном смысле) в конечном
или бесконечном промежутке [а, Ь]. Таким образом, а и Ъ могут озна-
означать не только конечные числа, но также и ± ¦». Простейшие свой-
свойства несобственных интегралов, которые мы лишь перечислим, вполне
аналогичны свойствам собственных интегралов [302-306] и полу-
получаются из них единообразным приемом. Так как несобственные ин-
интегралы суть пределы собственных, то обычно достаточно написать
для этих последних равенство или неравенство, выражающее требуе-
требуемое свойство, и перейти к пределам.

598	ГЛ. ХШ. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ	I486
Здесь, прежде всего, также можно ввести понятие об интеграле
по ориентированному промежутку и установить:
1°. Если fix) интегрируема в промежутке [Ь, а], то она интегри-
интегрируема в промежутке [а, Ь], причем
a	b
[Можно принять это просто за определение интеграла
для случая, когда а>Ь \.
а
Далее:
2°. Пусть fix) интегрируема в наибольшем * из промежутков [а, Ь],
[а, с] и [с, Ь]. Тогда она интегрируема в двух других, и имеет место
равенство
\f{x)dx=\f{x)dx+\f{x)dx.
3°. Если f{x) интегрируема в [а, Ь] и с = const, то и с •/(*) также
интегрируема, и
ь	ь
4°. Пусть функции f(x) и g(x) — обе интегрируемы в промежутке
[а, Ь]; тогда интегрируема и функция fix) ± g(x), и
ь	ь	ь
J [f(x) ± g(x)] dx = \f(x) dx±\ g(x) dx.
a	a	a
При доказательстве** этого (и следующего) свойства следует
иметь в виду замечание п° 479. Пусть, скажем, Ъ будет единственной
особой точкой для той или другой из функций f{x), gix). Тогда, на-
написав равенство
J [fix) ± gix)] dx = jfix) dx ± I gix) dx (a -= x0 < b),
* Точнее: в том из промежутков, который содержит в себе оба других.
** По отношению к интегралам с бесконечным пределом свойства 3° и 4°
уже упоминались в п° 473 и даже использовались 8 доследующих п°. Здесь они
приводятся в более общей формулировке.

4861	§ 3. ПРЕОБРАЗОВАНИЕ НЕСОБСТВЕННЫХ ИНТЕГРАЛОВ	599
можно из него получить предшествующую формулу, переходя к пре-
пределам при хо-&, как в том случае, когда все интегралы от а до & не-
несобственные, так и в том, когда один из них собственный.
5°. Если для двух интегрируемых в [а, Ь] функций f{x) и g{x) вы-
выполняется неравенство f{x)^gipc), то при а<Ъ
§f(x)dxsjg(x)dx.
6°. Если функция f(x) в промежутке [а,Ь] абсолютно инте-
интегрируема, то (при а^Ь)
о
\1
Ах) dx
¦ \\f(x)\dx.
1°. Если функция f(x) интегрируема в [а, Ь], то при любом х из
этого промежутка существует интеграл
0)
и представляет собой непрерывную функцию от х.
Пусть a^xo*sb; докажем, например, непрерывность функции Ф(х)
при х - х0 слева. Взяв с между а и х0 так, чтобы в промежутке [с, х0]
не было особых точек, исключая разве лишь х0> имеем для c
llt	B)
а	с
и достаточно установить, что
X	X,
lim \f(t)dt= \f(t)dt.
ЗС—Xo-OJ	J
с	с
А это равенство имеет место [см. замечание п° 479] как в случае, когда
интеграл справа — собственный, так и в случае, когда он несобствен-
несобственный.
Если хо = Ь= + ~, то непрерывность функции Ф(х) при х= + «¦ по-
понимается в том смысле, что
lim Ф(х) = Ф( + -) = Г ДОЛ.

600	ГЛ. XIII. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ	[487
8°. При тех оке предположениях, если в точке х = х0 функция f(x)
непрерывна, существует производная для функции Ф(х) [см. A)] в этой
точке, и
Ф'(*о) =/(*<>)•
Для доказательства используется разложение B), с ссылкой на
аналогичное свойство собственного интеграла.
Легко перефразировать свойства 7° и 8° для случая, когда пере-
переменным является нижний предел интеграла.
487. Теоремы о среднем значении. Первая теорема о среднем зна-
значении в первоначальной форме [304, 9°] существенно предполагает
функцию f(x) ограниченной, а промежуток конечным, и потому не
может быть перенесена на случай несобственного интеграла. В обоб-
обобщенной же форме [304, 10°] ее перенести можно:
Первая теорема о среднем значении. Пусть функции fix) и
g{x) обе интегрируемы в промежутке [а, Ь], причем f{x) ограничена:
a g(x) не меняет знака; тогда и функция f{x)-g(x) интегрируема и
&	ь
где m=sfi=sM.
Существование интеграла вытекает из заключительной теоремы
п° 475 и аналогичной ей теоремы п° 482. Само же равенство дока-
доказывается формально так же, как и для собственных интегралов.
Если функция fix) непрерывна в замкнутом промежутке
[а, Ь], то за т, М можно взять наименьшее и наибольшее значение
fix) в [а, Ъ], и множитель \i оказывается равным одному из значений
функции f(x):
ь	ь
\fix).g(x)dx=f(c).\gix)dx,
где с содержится в [а, Ь]. Это верно и в том случае, если промежу-
промежуток [а, Ь] бесконечен, ибо теоремы Вейерштрасса и Б о л ь-
цано-Коши [85, 82] для этого случая также справедливы, в чем
предлагаем читателю убедиться самому.
Имеет место также [ср. 306, 14°]:
Вторая теорема о среднем значении. Пусть функция f(x)
монотонна и ограничена в промежутке [а, Ь], а функция g(x) интегри-
интегрируема в этом промежутке. Тогда и функция fix)'gix) также

487J	§ 3. ПРЕОБРАЗОВАНИЕ НЕСОБСТВЕННЫХ ИНТЕГРАЛОВ	601
интегрируема, и
Ь	4	6
Остановимся для определенности на случае, когда а конечно,
Ъ = + - и других особых точек для g(x) нет. Существование интеграла
вытекает из признака Абеля.
Без умаления общности можно считать функцию f(x) убываю-
убывающей. Ввиду ограниченности ее, существует конечный предел
/(+-)= lim/(x).
х—+°°
Тогда f*(x)=f(x)-f(+°°)s>0. Для конечного промежутка [а, А]
имеем [306, 13°]:
А	П
//*(*)«(*) dx =f*(a) \g(x) dx {a^r)^A).	C)
a	a
A
Непрерывная в промежутке [a, + ~] функция I g(x) dx от А имеет
a
конечные границы т, М, так что [см. C)]
A
m
и, в пределе при А-
m
Отсюда
/(*)«(*) dx =ii •/•(«) {m*p*M).	D)
Но непрерывная функция g(x) dx достигает своих границ т, М и
а
принимает любое содержащееся между ними значение, т. е.
()d где a=s!«s + ~.
Полагая в D) f*{x) =f(x) -/(+ ~) и подставляя только что най»
денное выражение для ft, и придем к доказываемой формуле.

602	ГЛ. ХШ. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ	D89
488. Интегрирование по частям в случае несобственных интегралов.
Пусть функции и = и(х) и v = v(x) определены и непрерывны вместе
со своими первыми производными во всех точках промежутка [а, Ь],
исключая точку Ъ (которая может быть равна и + ~). Тогда имеет
место равенство
\udv = uv - I v du,
если под двойной подстановкой понимать разность
lim u(x)v{x) - u{d)v(a).
При этом предполагается, что из трех входящих в равенство выра-
выражений (два интеграла и двойная подстановка) имеют смысл два:
существование третьего отсюда уже вытекает.
В самом деле, взяв а^хо<Ь, напишем обычную формулу инте-
интегрирования по частям для промежутка [а, х0], где все интегралы -
собственные:
= [u(xo)v(xQ) - n(d)v(a)] - J v du.
Пусть теперь в этом равенстве х0 стремится к Ъ. По условию, два из
входящих в него выражений имеют конечные пределы при х-*х0*.
Следовательно, имеет конечный предел также третье выражение, и
доказываемое равенство оправдывается с помощью предельного пере-
перехода.
489. Примеры.
2	Ш 2"	2
\d
1) In sin х dx = х In sin x - \x	dx=- 	dx
J	о J sin x	J tg x
\
о J sin x	J tg x
0	0	0
— интегрированием по частям здесь удалось свести несобственный интеграл
к собственному и тем доказать существование несобственного интеграла
[ср. 483, 2) (в)]. Ту же особенность имеют и следующие примеры:
2)
11	11
J- Inx г ! гarctgx гarctgx
	dx= In xd arctg x = m x-arctg x — 	dx= - I
1+x* J о J x J x
oo q о
dx.
* См. замечание n° 477,

1	1
In л: .	farcsinx
489]	§ 3. ПРЕОБРАЗОВАНИЕ НЕСОБСТВЕННЫХ ИНТЕГРАЛОВ	603
(б) Аналогично
J
о '"	о
rsinx	rdcosx cos* - /-cosx
3) 	<fe= - 	=	 	dx (a=-0).
J X	J X	X a J X1
a	a	a
Так как и двойная подстановка и интеграл справа имеют смысл, то этим снова
доказано существование интеграла слева [ср. 476, 477].
Совершенно аналогично можно установить существование интеграла —— dx
а
х
(а, Л=»0), если функция fix) непрерывна и интеграл от нее F(x)= fix) dx ограни-
а
чен для всех х =- а. [Это вытекает и из признака Дирихле.]
Путем интегрирования по частям иной раз получаются рекуррентные формулы,
с помощью которых затем уже легко осуществляется вычисление предложенных
интегралов. Проиллюстрируем это на следующих примерах (л и к - натураль-
натуральные числа):
4)	In" JV
о
Имеем:
In=-e-f-tn +n\
о J
о
откуда 1п = л!
Уничтожение двойной подстановки здесь (и в дальнейших примерах) создает
преимущество для применения формулы интегрирования по частям именно к опре-
определенным интегралам (а не к неопределенным).
5) Еп= {е-™ sin" х dx (a=-0).
о
Прежде всего, интегрируя по частям, найдем:
1
Еп=	e""axsiri
а
Н— е~ах sin" 1 х cos x dx.
о a J
Так как двойная подстановка равна нулю, то, снова прибегая к интегрированию
по частям, получим далее:
л
Еп = - — е~ах sin"-1 х cos x
а%
' и(л -1) г	п г
Н	е~ах sin" х cos2 x dx	е-™ sin" x dx,
i в2 J	a* J
о	о

604	ГЛ. XIII. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ	[490
Если заменить здесь cos2 х на 1 - sin2 x, то легко прийти к рекуррентной фор-
формуле:
Е П{П~Х) е
1	1
Так как Ео = — и J5i= 	, то окончательно для случаев нечетного и четного
а	1 + а2
п найдем соответственно:
2k-V.
(l+a2)C2 + a2)...Bfc-
2k\
aB2 + a2)D2 + a2)... (U2 + a8)
6) Легко распространяется на случай несобственных интегралов и обоб-
обобщенная формула интегрирования по частям [311 G)].
Пусть, например, предложен интеграл
= f
где р>0 и Ln(x) означает так называемый н-й многочлен Чебышева - Ла-
Лаге р р а (Е. Laguerre)
^yp (я-0, 1,2,...).
Пользуясь упомянутой формулой, будем иметь
К= \e~Px	йх= \е~Рх	• • •+(-1)п~1
J	dxn	{	dxn	dxn 1
о
+ (-1)" xne-*	dx = pn ;
J	dxn	J
о	о
и, окончательно [(см. 4)]:
Pn
K=	4—-и!
+
о
Аналогично устанавливаются результаты:
О, если
!J если к = п.
490. Замена неременных в несобственных интегралах. Пусть функция
f(x) определена и непрерывна в конечном или бесконечном проме-
промежутке [а, Ь) и, следовательно, интегрируема в собственном смысле
в каждой его части, не содержащей точки Ь, которая может быть и
4 -; эта точка, по предположению, является единственной особой
точкой для функции fix).

491]	§ 3. ПРЕОБРАЗОВАНИЕ НЕСОБСТВЕННЫХ ИНТЕГРАЛОВ	605
Рассмотрим теперь монотонно возрастающую функ-
функцию x=q>(t), непрерывную вместе со своей производной cp'(t) в про-
промежутке [ос, /?), где /? может быть и + ~, и допустим, что <р(а) = а и
<p(fi) = b. Последнее равенство надлежит понимать в том смысле, что
lim (p{t) = b.
При этих условиях имеет место равенство
ь	а
E)
в предположении, что существует один из этих интегралов (суще-
(существование другого отсюда уже вытекает). Второй интеграл будет либо
собственным, либо несобственным - с единственной особой точкой /?.
По теореме об обратной функции [83] ясно, что и t можно рас-
рассматривать как монотонно возрастающую и непрерывную функцию
от х в [a, b): t = 6(x), причем Итв(х)=р.
Пусть теперь х0 и t0 будут произвольные, но соответствующие
одно другому значения х и t и из промежутков (а, Ъ) и (а, /?). Тогда
с помощью замены переменной в собственном интеграле будем иметь
х.	4,
\f{x)dx=\f{cp{t)).9'{t)dt.
а	а
Если существует, скажем, второй из интегралов E), то станем при-
приближать произвольным образом хок Ь; при этом t0 = в(х0)
устремится к ]3, и мы установим формулу E), одновременно с дока-
доказательством существования интеграла слева.
Наше рассуждение одинаково применимо в случае монотонно
убывающей функции y(t), когда а>/?. Так же исчерпываются и
другие возможные случаи распределения особых точек. При расста-
расстановке пределов в преобразованном интеграле всегда следует помнить,
что нижний предел а должен соответствовать нижнему пределу а,
а верхний предел ]3 - верхнему пределу Ь, независимо от того, будет
ли а< или >/3.
г	dx	1
491. Примеры. 1) Интеграл I-—======= {к2 -= 1-=х0) подстановкой х = —,
Ух(.х-1)(х-к")
0
2
dx =	dt приводится к интегралу
t3
*	2 f	*
_2 J _=_^__=2 J

606	ГЛ. XIII. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ	D*>1
Здесь а = х0, & = «>, а =	, /3 = 0. Несобственный интеграл преобразуется в
собственный.
2) Вычислить интеграл
ь
dx
подстановкой
х = a cos2 <p+b sin2 <р.
я:
Указание. Здесь а = 0, /3 = —, и искомый интеграл приводится к собствен-
собственному интегралу
71
2
2
о
2 d(p = n.
о
3) Для установления сходимости интеграла sin хг dx выполним в нем замену
о
переменной: x=V7, dx=	а = а = 0, 6 = /3=~. Мы получим заведомо сходя-
1 f sin /
щийся [476 или 489, 3)] интеграл — 	dt, следовательно, сходится и предло-
2J ут
женный интеграл. Интересно отметить, что подинтегральная функция в нем при
х - ~ не стремится ни к какому пределу, колеблясь между — 1 и +1.
Аналогично исчерпывается вопрос о сходимости интеграла cos х'2 dx. В сле-
о
дующем примере устанавливается более общий результат.
4) Доказать, что интегралы
Jsin (/(*)) dx, J cos (/(*))<&
а	а
сходятся, если fix) монотонно возрастает и стремится к ~ при х-~.
Прежде всего, fix) =-0 для достаточно больших х и fix) монотонно возрастает;
будем считать, что это имеет место уже начиная с х = а. С помощью формулы
конечных приращений получаем
/<*+1) = /(*)+/'(*+ 0>/(а)+/'(*),
следовательно, сама функция f(x) - =• при х — =». Введем новую переменную t=fix),
так что
x = giO, dx = g'(t)dt [a=/(а), /3 = ~]>
1
если через g обозначить функцию, обратную / Но производная g'it)-——-

491]	§ 3. ПРЕОБРАЗОВАНИЕ НЕСОБСТВЕННЫХ ИНТЕГРАЛОВ	66?
монотонно убывает и стремится к 0 при t-*<*>. Поэтому преобразованные ин-
интегралы
| &mt-g'(t)dt, \ cos t-g'(t)dt
по признаку Дирихле сходятся, а с ними сходятся и предложенные интегралы.
г 1пх
5) Для вычисления интеграла 	dx [его сходимость мы уже установили
J 1+х2
1+х2
о
1
в 483, 5) (б)] разобьем его на два: = + . Во втором из них сделаем под-
0 0 1
становку х = — (а= 1, Ь = ~, а= 1, /3 = 0) и придем к результату
о	1
р In x	pint	г Ых
	dx=	dt= - 	dx,
J 1+** J 1+/2	J 1+x*
0
откуда следует, что предложенный интеграл равен 0.
6) Пусть дан несобственный интеграл
интегралу
подстановкой x = sin/ \а = 0, 6=1, а = 0, /3 = — он приводится к собственному
2"
| e
/- Г dx
7) Вычисление интеграла
о
[ср. 472, 2)] может быть очень упрощено применением целесообразных подста-
подстановок.
Прежде всего, к нему приводится интеграл
rx2dx
J lTx4

608
ГЛ. XIII. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
[491
подстановкой х=— (а = 0, 6 = °°, а =<*=,/? = 0), так что можно написать
— \dx
2 1 + х1 2
I
Если теперь прибегнуть к подстановке х	= z (a = 0, 6= +«, а= — ~, /? = + °°),
то сразу получим	х
1 г dz 1	z
/=— I -—-=—— arctg —
2У2	У2
'4 b
r dd	,.
8) Для вычисления интеграла —	естественно положить f=ytg0, т. е.
о
в = arctg /21 а = 0, 6 = —, а = 0, /3 = ~; мы придем к только что вычисленному
г dt я
интегралу: 2 	= —.
J 1 + г4 у?
о	'
9) Установить формулы:
1
dx	л
(a) f
J Ггу2 _
С	dx	arcsin a
(б) 		=——zr
1
1
г	dx	n
(в) 	___ =
_J (х2+а2)У1-л:2 аУ1 + а
@-=а-=1);
(а=-0);
p	<&	1п(а
(г) 	?= =
J (х2+а2)Ул:2-1 а
1п(а+У1+а2)
(ц)
1п(а+У52"Л)
(а=-1),
= 1 (в-1),
arccos а
Указание. Во всех случаях воспользоваться подстановкой Абеля
[284].

491|	§ 3. ПРЕОБРАЗОВАНИЕ НЕСОБСТВЕННЫХ ИНТЕГРАЛОВ	609
10) Вопрос о сходимости интегралов
Jx\nxx J л>1пл>1пАAпдг)
сразу решается, если подстановкой
/=1пдг, и=1пAпдг)
привести их к интегралам
г dt	r du
J 7*' J И*
In a	ln(lnA)
- оба сходятся при А=-1 и расходятся при Assl.
В следующих упражнениях под /(и) разумеется произвольная непрерывная
для иг=0 функция.
11) Доказать, что
Jlx a\ dx	с (х a\dx
/-+- lnx — lne /-+- - (e»0),
если только интегралы сходятся.
Указание. Прибегнуть к подстановке х = аеи (а= -°=, /3 = + <*>).
12) Доказать, что (при ^=-0)
Г	dx
(а) ДхР+х- Р) In д: — = 0,
J	х
(б) Г ЯхР+х-Р) In х—-= 0,
J	1 + х2
о
если только интегралы сходятся.
1	оо	1
Например, для (а) имеем: = I + , но = - I , как в этом легко убе-
0 0 1	1	О
1
диться подстановкой х = —, и т. д.
13) В предположении, что сходится интеграл справа, доказать формулу
о
39 Г. М. Фихтенгольц, т. II

610	ГЛ. XIII. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ	[491
в
Подстановка у = Ах	(а = - ~, 6 =+<*=, а = 0, /? = + ~) дает
х
о
в
Но последний интеграл подстановкой х =	(я=0, 6= +<*=, а= -~, /5=0) при-
водится к
так что
J f(y*)dy = A J
Отсюда (ввиду четности подинтегральной функции) и вытекает требуемая фор-
формула.
13) В заключение, владея заменой переменной в несобственных интегралах,
вернемся к одному незавершенному выше вопросу. В п° 439, 1) мы исследовали
на непрерывность функцию
но не установили ее поведения в точке х = 0 в том случае, когда 0=sp-= 1, <?=-1 и
q
Воспользовавшись формулой A0а) в сноске стр. 286, можно оценить сумму
ряда снизу с помощью интеграла:
f
J
xdt
	2_
Полагая здесь t = x q-p-v, заменим это неравенство таким:
Р+1-2 г dv
X q-p -
J n
При х¦* + 0 интеграл стремится к конечному положительному пределу
dv
vP+v4
о

492]	§ 4. ОСОБЫЕ ПРИЕМЫ ВЫЧИСЛЕНИЯ	611
а множитель при нем либо равен 1 (если p+q = 2), либо даже стремится к °° при
х- +0 (если p + q-^2). Так как /@) = 0, то справа в точке х = 0 во всяком случае
налицо разрыв; то же - и слева.
Замечание. Интеграл с бесконечным пределом I f{x) dx всегда
а
может быть надлежащей подстановкой приведен к интегралу с конечными преде-
пределами (собственному или нет). Например, если а =-0, можно положить х=— :
а	О
6
Наоборот, несобственный интеграл f{x) dx с единственной особой точкой b
а
всегда может быть приведен к интегралу с бесконечным пределом (без других
особых точек). Например, полагая х = b	, получим:
§ 4. Особые приемы вычисления несобственных
интегралов
492. Некоторые замечательные интегралы. Начнем с вычисления
некоторых важных интегралов с помощью искусственных приемов.
1°. Интеграл Эйлера (L. Euler):
J= In sin x dx.
В его существовании мы уже убедились. Вычисление интеграла Э й-
л е р а основано на использовании замены переменной. Имеем, по-
полагая л: = 2?:
J=2 j In sin 2t dt=| In 2 + 2 J In sin t dt + 2 J In cos t dt.
39»

612	ГЛ. XIII. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ	D92
Подставляя в последнем интеграле t = = -u, приведем его к виду
2 I In sin и du, так что, окончательно, для определения J получаем
4
уравнение
=^-In 2 + 2/, откуда /=~1п2.
К этому же интегралу, с точностью до знака, приводятся н соб-
собственные интегралы [ср. 489, 1) и 2) (б)]:
Г х ,	Г arcsin x ,
-— ах, 	ах.
J tgx ' J х
tgx
2°. Обратимся к вычислению интеграла Эйлера-Пуассона:
K= J е~* dx,
о
встречающегося в теории вероятностей. С этой целью предварительно
установим некоторые неравенства.
Обычными в дифференциальном исчислении методами нетрудно
установить, что функция A + t)e~* достигает своего наибольшего зна-
значения 1 при / = 0. Следовательно, для t^O будет
A+-*>?-'< 1.
Полагая здесь t = ± х2, мы получим
откуда
Ограничив в первом из этих неравенств изменение х промежутком
(О, 1) (так что 1 -д:2=-0), а во втором считая х любым, возвысим все
эти выражения в степень с любым натуральным показателем п; это
дает нам *
И — х2)п<е~пх' и с~пх'
* Для неравенств с положительными членами допустимо возвышение
в натуральную степень почленно.

492]	§ 4. ОСОБЫЕ ПРИЕМЫ ВЫЧИСЛЕНИЯ	613
Интегрируя первое неравенство в промежутке от 0 до 1, а второе
- от 0 до + ~, получим
1	1	+~	+~
— x2Ydx- -"~* * Г _~л j.. Г dx
о	о
Но
(e~nx'dx = —--K (подстановка и = ~fnx),
}	уп
J (l-x2)"dx= J sin2n+11 dt = Bn+' (подстановка x=cos t),
о	о
и, наконец,
= S-2)!! '\ (подстановка x = ctg/).
Мы воспользовались здесь известными выражениями для sinm x dx,
о
312 (8) . Таким образом, неизвестное нам значение К может быть
заключено между следующими двумя выражениями:
так что, возводя в квадрат и преобразуя, получим
пBи!1)»	„2 п
2л+1 Bл-1!!JBл+1)	2л-1 Bи-2!!J \2) "
Из формулы В а л л и с а [317]:
л _..	[Bи)!!]2
2 ~п™ [Bл- 1)!!]2Bл +1)
легко усмотреть теперь, что оба крайних выражения при и -*• ~ стре-
стремятся к одному и тому же пределу j, следовательно,
К2=% я К=±?- (так как А>0).

614	ГЛ. XIII. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ	[492
3°. Рассмотрим, наконец, интеграл
т С sin х ,
1= 	dx.
J X
о
Мы знаем уже, что он сходится [476; 477; 489, 3)]. Представим инте-
интеграл в виде суммы ряда
i=2 \ .
v—0 J
Положив v = 2fi или 2/J, - 1 и прибегнув, соответственно, к подстановке
x=fin + t или x=\m-t, будем иметь:
!	2
Г =(_iy\lELdt
J	V ' J [171+1
[171+1
0
f =(_i),-
J	v '
Отсюда
fin-t
0	0
/= f!Ei^+ у fc-iv [—^— + —^-1 sin / dt.
Так как ряд
в промежутке0=s?=s| сходится равномерно, ибо мажорируется
сходящимся рядом - 2!	г' то его можно интегрировать п о-
" ' "
ч л енн о.
Это дает нам право написать выражение для / в виде:

493]	§ 4. ОСОБЫЕ ПРИЕМЫ ВЫЧИСЛЕНИЯ	615
Но выражение в квадратных скобках есть разложение на простые
дроби функции -.— [441, 9)]. Таким образом, окончательно,
i-\*-\.
Приведенный изящный вывод принадлежит Лобачевскому,
который первым обратил внимание на нестрогость тех приемов, с
помощью которых этот важный интеграл вычислялся раньше.
493. Вычисление несобственных интегралов с помощью интегральных
сумм. Случай интегралов с конечными пределами. Если функция f(x)
в промежутке [а, Ь] неограничена, то произвольными инте-
интегральными (римановыми) суммами пользоваться для вычисления ее
интегралов в этом промежутке, разумеется, нельзя. Однако всегда
можно так выбирать эти суммы, чтобы они — при дроблении
промежутка - стремились к значению несобственного интеграла.
Мы установим это для простейшего случая монотонной функции.
Итак, пусть функция/(х) в промежутке [0, а] (а>0) положительна,
монотонно убывает и при х^-0 стремится к + °°; в то же время, пусть
для нее существует несобственный интеграл от 0 до а. Разделив про-
промежуток [0, а] на п равных частей, будем иметь
л
л—1 f	п	л —1
J Дх) dx < \f(x) dx + 2 /f Й • a~,
и тем более
'-V
— a
о	о
В то же время, очевидно,
О
так что, по совокупности,

616	ГЛ. Х1Н. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ	[493
Так как последний интеграл при и-*~ стремится к нулю*, то окон-
окончательно
а
В случае положительной возрастающей функции /(*), стремящейся
к + ~ при х-* а, получается аналогично
Наконец, изменяя знак/, легко получить такие же формулы и для
монотонной отрицательной функции.
Рассмотрим примеры. 1) Для вычисления интеграла I Inд:dx (с особой
точкой 0) имеем:	°
1	"
I In xdx=Yim— J? In—=lim In ¦— .
0
Л
Ш 1
Так как [77, 4)] lim-—= —, то предыдущий предел равен - 1; таково, в действи-
п-~ =о п е
тельности, и есть значение предложенного интеграла.
я
~2
2) В качестве второго примера возьмем более сложный интеграл: In sin x dx.
о
В этом случае
ГС
г	ж "zi	vn	п "jr?- vn
In sin x dx= Km — У In sin — = lim — In // sin — .
J	п-™2л,^1	2л п-*-2и »=i 2л
о
Желая получить простое выражение для последнего произведения, рас-
рассмотрим целый многочлен, получающийся от деления z2"-l на z2-l, и раз-
разложим его на линейные множители, собирая вместе множители, отвечающие
* Он представляет собой разность между несобственным интегралом и
а	0
стремящимся к нему собственным интегралом .

494]	§ 4. ОСОБЫЕ ПРИЕМЫ ВЫЧИСЛЕНИЯ	617
сопряженным корням. Мы получим (при любом вещественном г, отличном от ± 1):
-cos — +sin2 — .
л )	л J
z2-l /_'i
При z^l отсюда найдем:
Л— 1 г/	VTt]1	V7l~\	n — 1	V7l
"= /7 1-cos— +sin2 — U4"-1 JJ sin2— ,
»=i LI	n)	n\	,,=i 2л
так что, наконец,
][
sin — = -'— .
2n 2"-i
Поэтому искомый интеграл оказывается равным:
"	-1пи-(л-1Iп2
Jir 2 я
In sin x dx^lim-	=	In 2
„™ 2 л 2
о
[ср. 492, П.
494. Случай интегралов с бесконечным пределом. Пусть функция
определена и интегрируема в промежутке от 0 до + ~. Разлагая этот
промежуток на бесконечное множество равных промежутков длины
h ¦>¦ 0, составим сумму ^f(vh) • h, напоминающую по своему стро-
»=о
ению риманову сумму. Сходится ли этот ряд, будет ли его сумма
при h ->0 стремиться к несобственному интегралу I f(x) dx - вот
о
вопросы, которыми мы займемся при некоторых частных предполо-
предположениях относительно f(x).
Предположим сначала, что /(х) положительна и, монотонно убы-
убывая, стремится к 0 при х-* + ~. Тогда
0	vh
=2 \
v-0 J
vh
а с другой стороны, очевидно,
Г Я*) dx>h • l/(vA) = A 2f(vh) - h -ДО),
¦ См. сцрску на стр. 122.

618	ГЛ. XIII. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ	[494
так что
Прим
2) Зная
?=о
0
еры. 1) Положим /(ж)
0
значение интеграла
j
0
Л-»0
¦.!«-
Тогда
hi- h
л-»о1-е~л
A)
го других соображений, мы все же можем применить выведенную формулу и
получим, таким образом, что
2
л^о v=o	2
Если положить е-л' = г, то А= / In —со yi-г при /-1. Отсюда - интересное
предельное соотношение:
)
/-1-0	2
Может случиться, что требование монотонного убывания функ-
функции f(x) выполняется лишь для xs*A>0. Это обстоятельство не ме-
мешает применению указанного для монотонных функций приема; нужно
лишь озаботиться тем, чтобы отношение -=- было целым. Тогда
п
„=А_1	А
lim 2 Л"й)-А= [f(x)dx	B)
о
по самому определению собственного интеграла, а
во
lim Z f(.vh)-h= \f(x)dx
- по доказанному выше,

494]	§ 4. ОСОБЫЕ ПРИЕМЫ ВЫЧИСЛЕНИЯ	619
Пример. 3) Пусть f(x) = xe~x; эта функция монотонно убывает, начиная
с х= 1. Тем не менее
л-о \eh-\
что легко проверить интегрированием по частям.
Перейдем к более общему случаю, не требуя от f(x) пока ничего,
кроме интегрируемости. Имеем
\f(x) dx = J/(x) dx + I fix) dx.
При достаточно большом А последний интеграл по абсолютной вели-
величине будет произвольно мал *. Каково бы ни было А, станем и здесь
h брать таким, чтобы A jh бьш целым. Тогда, при А = const, как и только
что, будет выполняться B).
Теперь ясно, что для справедливости равенства A) достаточно,
чтобы еще выполнялось условие:
lira a2'/(vA)-A = 0.	C)
А-+~ _А_
Действительно, тогда все слагаемые правой части равенства
при достаточно большом А и достаточно малом h будут произвольно
малы.
Условие C) автоматически выполняется при ранее сделанных от-
относительно f(x) предположениях, ибо
А
\f(x)dx.
* Он представляет собой разность между несобственным интегралом и стрел
A	Q
мящимся к нему при 4 - ~ собственным интегралом .

620	ГЛ. XIII. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ	[494
Оно также выполняется, если f(x)=<p(x)>y>(x), где <р(х) (хотя бы для
хз*х0 >0) удовлетворяет тем условиям, которые выше были наложены
на f(x), а у(х) ограничена: | гр(х) \ =ssL. В этом случае
2" <p(vh) • y>(vh)
A
v=—
Л
•2
A
\cp(x)dx,
и т. д.
4) В качестве примера рассмотрим интеграл 	dx; здесь <р(х) = — ,
J х2	х2
о
гр(х) = sin2 х. Имеем
r sin2 х ^, sin2 j>A I -v s'n2 "^
I	dx=lim А- Л	= Iim — ^	.
J x2 л-о „=i OA)a wb=i v2
о
Для вычисления последней суммы сообразим сначала, что
f^rsin2»*!' ^,sin2vA я-2А тс
U = l >-2 /Л „=1 V	2	2
[461, 6) (б)]. Почленное дифференцирование для А^О допустимо по теореме 7 п°
435, ввиду равномерной сходимости ряда, составленного из производных [по
признаку Дирихле, 430]. Интегрируя, найдем выражение для интересующей
n-h ,
нас суммы: 	-Л. Отсюда наконец,
- sin2 х	л- h я
rf li
0
В других случаях выполнение условия C) приходится проверять непосред-
непосредственно.
с sin х
5) Пусть, например, предложен интеграл 	dx. Ограничимся (на что
J х
о
мы, очевидно, имеем право) значениями А = — и А => тп, где к, т - натуральные
к
числа.
Представим интересующую нас сумму в виде:
»- 2 + z +¦¦¦
n=km ?lft	n=hm n = A(m
Нетрудно убедиться в том, что слагаемые в пределах каждой конечной суммы
справа будут одного знака, который меняется при переходе к следующей сумме.

495]
§ 4. ОСОБЫЕ ПРИЕМЫ ВЫЧИСЛЕНИЯ
621
В общем, ряд справа будет типа Лейбница. Поэтому его сумма по абсолют-
абсолютной величине будет меньше абсолютной же величины первого слагаемого. С другой
стороны, так как kmh = mn = A,
2
n—km
7
Ш1
1	i
-A-= — 2j Isin nh\ -A = — ? s'n 'A-A.
А п = кт	A /=0
Последняя же сумма, как интегральная сумма для интеграла sinxdx=2, при
о
достаточно малом А будет меньше любого числа С =-2, а тогда
Zj 	r~
n=km nil
откуда и вытекает выполнение условия C).
Самое же вычисление предложенного интеграла, оправданное изложенными
соображениями, проводится весьма просто [см. 461, б) (б)]:
г sin х	.?, sin nh
	rfx = lim 2i 	= lim
J x	h-On=i n h—o
л- h я
	= —,
2 2
что выше [492, 3°] мы получили иным путем.
495. Интегралы Фруллани. Рассмотрим вопрос о существовании
и вычислении одного частного вида несобственных интегралов, обычно
называемых интегралами Фруллани (G. Froullani):
I. Относительно функции fix) сделаем следующие предположения:
1°/(д:) определена и непрерывна для хйи 2° существует конечный
предел
/(+-)= lim/(x).
Из 1° ясно, что существует (при 0<<5<Zl< +«>) интеграл
tKax)-f{bx)dx= («л. ГЛадл =
J	X	J X	J X
аЛ
ЪЛ
Ьв
ЬА
ад
Ь6
ад
J z

622	ГЛ. ХШ. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ	[495
Предложенный же интеграл определяется равенством
И	ЬА
гл«о
J
Применяя к последним двум интегралам порознь обобщенную тео-
теорему о среднем значении, получим
Ьд	Ь6
j j-~ dz =/(?) j у =/(!) • In - (где
ад	ад
и, аналогично,
с f(z)	ь
-^ dz =/(«) • In - (где аЛ *s у
J z	a
аЛ
Так как, очевидно, ?-*0 (при 5—0), а г?— + ~ (при ZI— + ~), то отсюда
)]-lni	D)
о
Примеры. 1)В случае интеграла
ге~ах — е~ь*
	dx
J х
о
имеем:
/(х) = е-*, Д0)=1,
Ь
так что значение интеграла будет In — .
а
2) Пусть предложен интеграл
p+qe~ax dx
г p+qe~ax dx
In l	— (A 9-0).
о
Заменяя логарифмы частного разностью логарифмов, можно положить здесь
f() \(), так что f(O) = ln(p + q) и	)
I q\ Ъ
Ответ. In 1 Л— -In — .
I PJ а
3) Вычислить интеграл
г arctg ах - arctg Ъх
	dx.
J	х
о

496]	§ 4. ОСОБЫЕ ПРИЕМЫ ВЫЧИСЛЕНИЯ	623
В этом случае
f(x) = arctg x, ДО) = 0, /(+¦») = |.
я а
Ответ. — In —.
II. Иной раз функция f(x) не имеет конечного предела при х-* + <*>,
но зато существует интеграл
z
А
Заменяя в приведенном рассуждении Л сразу на + °°, придем, вза-
взамен D), к результату
n^	Da)
о
Пример 4):
г
J
cos ax - cos 6x
х
о
( *	pcosz	"\
ибо интеграл I	dz, как мы знаем, существует .
{	J z	)
III. Аналогично, если нарушена непрерывность функции f(x) при
= 0, но существует интеграл
то
№)_z/(to)^=/( + oo).ln«	Dб)
J	X	О
о
Впрочем, этот случай приводится к предыдущему подстановкой
_1_
496. Интегралы от рациональных функций между бесконечными пре-
пределами. В заключение рассмотрим еще один частный тип интеграла
с бесконечными пределами:
J Q(x) йХ>

624
ГЛ. ХШ. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
[496
где Р(х) и Q(x) — целые многочлены. Предположим, что многочлен
Q(x) вещественных корней не имеет и что степень Р(х), по
крайней мере, на две единицы ниже степени Q(x). При этих условиях
интеграл существует [474, 2)]; вопрос лишь в его вычислении.
Если хх = <хх + ф1 ((Зя$0; А = 1, 2, ...) суть различные корни много-
многочлена Q(x), то дробь P(x)lQ(x) следующим образом разлагается на
простые дроби
Q(x) i
причем число дробей в каждой скобке равно показателю кратности
соответствующего корня *.
Распространяя на случай комплексной функции от веще-
вещественной переменной элементарные способы вычисления интегра-
интегралов, видим сразу, что, при /и=-0,
J&T
dx
1
=о,
следовательно,
С другой стороны,
1	1
х~хх
:+ I-
-л
.Г
L
При й — + ~ первое слагаемое в последнем выражении стремится к О,
а второе к +да или -т в зависимости от того, будет ли /?д>0 или
* В главе VIII [274] мы имели подобное же разложение, но там мы старались
избежать мнимости и, в случае мнимых корней, рассматривали дроби, знамена-
знаменателями которых служили степени квадратного трехчлена уже с вещественными
коэффициентами. Здесь же мы мнимые корни трактуем так же, как там вещест-
вещественные.

496]	§ 4. ОСОБЫЕ ПРИЕМЫ ВЫЧИСЛЕНИЯ	625
Таким образом, приходим к результату:
где при Ах стоит знак плюс, если соответствующее /?я > 0, и знак ми-
минус в противном случае. Эту формулу можно несколько видоизме-
видоизменить на основании следующих соображений. Умножим обе части
тождества E) на х. При х-*~ левая часть будет стремиться к 0, так
как степень х • Р(х) все же ниже степени Q{x). В правой части в пре-
пределе уничтожатся все члены с нелинейными знаменателями, так что
и предел суммы остальных членов также 0. Отсюда 2 Ах = 0, так
а
что ^(+^д= -2^~^а.> если знаком ( + ) и (-) обозначить суммы
тех Ах, которые отвечают /?л>0 и /?я<0. Теперь полученную формулу
можно написать в виде
F)
Что касается вычисления коэффициентов Ах, то мы ограничимся
указанием, относящимся к случаю простого корня хх, для кото-
которого Q{xx) = 0, но б'С^д) ^ 0; ему отвечает в разложении E) один
Ах
только член	¦. Если обе части равенства E) умножить на х — хх,
х — хх
то оно представится в виде
Q(.x)-Q(xx) ^ ¦ ч" "» "*¦"'>
х-хх
где R(x) означает группу членов, остающихся конечными при при-
приближении х к хх. Переходя к пределу при х—хх, получим
Обратимся теперь к примерам применения формул F) и G).
1) На первом месте рассмотрим интеграл
dx,
где тип- натуральные числа, причем /и<л. Все условия для при-
применения установленной формулы здесь соблюдены.
*0 Г. М. Фихтенгольц, т. II

626	ГЛ. XIII. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ	1496
Корнями знаменателя являются числа
А ~	2и	2я
(А = 0, 1,2, ...,и-1;и, ...,2и-1),
но лишь первые и из них имеют положительные мнимые части. Оче-
Очевидно, хх = х%х+1, где
"	Я . . Я
Xn = COS х- + I Sin тг~ .
и	2л	2л
По формуле G), при А = 0, 1, ..., п- 1,
¦*	А	_ _ J_ V2m+1 _ _ _L
2п
(
°
(с учетом того, что xf'= -1). Суммируя прогрессию, получаем:
, П-1	1 г2Ш + 1_ v-Bm+l)
	L У у Bт+1) BД+1)= __L._»9
Я" 2«Я0	2
L У у (
2«Я=0
или, так как х\п= -1,
Подставляя
Х	1
	= -
Bm + 1) It
о
2m+l , . . 2т+\
= cos __!^ я± J • Sin -^—
окончательно представим нужную нам сумму в виде
1 1
2ni 2т +1
sin	я
2п
Отсюда же, по формуле F),
, л	1
Г х*
sta
2л
2) Несколько более общий пример:
где т,т'п - натуральные числа и т, т'-*п.
Условия выполнены, за исключением того, что знаменатель имеет веществен-
вещественные корни ±1. Это обстоятельство здесь не существенно, ибо эти корни имеет
и числитель, так что дробь могла бы быть сокращена на х2-1. Впредь эти корни
не будем принимать во внимание.

496]	§ 4. ОСОБЫЕ ПРИЕМЫ ВЫЧИСЛЕНИЯ	627
Остальные корни знаменателя суть
1л	In
хх = cos —hi- sin — = х*-
п	п 1
(yUl, 2, ..., л-1; л+1, ..., 2и-1)
Из них положительные мнимые части имеют первые и - 1. По формуле G)
х\т> - х]т 1
так что
\ ] 1
_	 =	(хгт'+1- v!m + i\
1 л-1	1 л-1
2" А=1	2и Л=1
Полученное выражение последовательно преобразуется так *:
1
-1	l J
2m + l	2m+l	2m'+l
2л I 2m + l	2m + l	1m' +1	2m'+l
v 2	v	2	v 2	v
2ni
Окончательно,
1 Г 2m + l	2m'+l 1
— ctg—	я-ctg—	я .
.nil In	In J
rx*m-x2m' л Г 2m + l	2m'+1 1
	dx = —I ctg	я - ctg	л
J 1-х2"	и L 2л	2и J
(m, m'^ri).
Заметим, что из этой формулы легко можно было бы получить и предыдущий
результат, если заменить л на 2л и положить tri = тл-п (при т-= л).
3) Наконец, рассмотрим интеграл
J—	^	Л,
где т-=л и -я-=9-=я.
* Учитывая, что х"= -1.
40*

628	ГЛ. XIII. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
Вводя угол 0'=л-0, О-=0'-=2я, перепишем интеграл так:
[496
Г__^__
dx.
Для вычисления корней знаменателя положим х2п = z, тогда z определится из уравне-
уравнений z2-2z-cos в' + 1 = 0, именно, z = cos 6'±i-sin 6'. Для л: получаются две серии
значений
0'
где
и x,, = .vo-e1', где
л
e = cos—\-i
л
0'
0 2л
л
? = COS •
Л
л
• sin —
п
в'
l'SlTl2n
л
/sin— .
л
0, 1, ..., и-1;
и, .... 2и-1)
При этом положительную мнимую часть будут иметь первые л из первой
серии и последние л ю второй.
Соответствующие корням xv (i>= 0, 1, ..., л-1) коэффициенты Av вычисляются
по формуле G):
XVT
1
4л'
1
Bп - Cos 0) 4л (cos в' + i sin 0') • i sin в'
Суммируя эти коэффициенты и умножая на 2я/, получим*
Bт+1 \	Bт+1 Л
cos—	1 e'+j.sin	10'
л { 2л /	У 2п j l-(e"
2л
sin0'
cos 1	¦
л \ 2п
0' - i- sin 1 -
2л j
2m + l 1 2m+l
- cos	л I — /• sin	л
sin0'
Для второй группы корней jc, (v = n, и+1, •••, 2и-1) аналогично получится
выражение, сопряженное с этим; их сумма даст удвоенную вещественную часть.
После элементарных преобразований эта сумма сведется к
г/ 2т+П 2т+1 1
sin 1	— 0'+——л
я I	2л I	2л J
2m+l
sin 0'-sin	л
2л
* е"= -1.

497]	§ 4. ОСОБЫЕ ПРИЕМЫ ВЫЧИСЛЕНИЯ	629
Возвращаясь к углу В-л—В', окончательно получим
( 2т+\\
+ -	sin 1	О
хгт	я { 2п )
I
n	2т+\
sin 6-sin	я
2л
497. Смешанные примеры и упражнения. 1) Доказать существование интеграла
dx
J X2-(S1B
Особых точек бесконечное множество: х = пя (п = 1, 2, .. .)• В любом конечном
промежутке их конечное число, и интеграл сходится. Вопрос лишь о сходимости
интеграла в бесконечном промежутке.
Имеем:
(п + 1)я	п	п
dx	с dx	1
—у J ^Ti J (x+nJtJ-(sinxJ/3 J (sin хJ/з ^ п2л
пл	О	О
2)	Если в сходящемся [478, 5) (в)] интеграле
o%t\^~~dt (Я=-0)
о
сделать подстановку t = ex, x=\n t, придем к интегралу
\х\х-&ш ех dx;
последний, таким образом, сходится, несмотря на то, что подинтегральная функ-
функция при безграничном возрастании \х\ колеблется между - ~ и +~.
3)	Мы видели только что, что для сходимости интеграла
J/W dx	(8)
вовсе не необходимо даже, чтобы было
/(.*) = оA) (прих-~).	(9)
Доказать, что, однако,
(а)	если существует предел
lim f(x),
то - в случае сходимости интеграла (8) - этот предел необходимо равен 0; больше
того,
(б)	если существует предел
lim х •

630	ГЛ. XIII. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ	[497
то и этот предел необходимо равен 0, т. е.
A0)
(в) если интегрируемая в промежутке [а, ~] функция монотонно убывает, то
это условие A0) необходимо выполняется.
Доказательство [для (б) и (в)] сходно с доказательством аналогичных предло-
предложений для положительных рядов [375, 3)].
Отметим еще (тоже по аналогии с рядами), что даже для монотонно убываю-
убывающей функции fix) вьшолнение условия A0) не гарантирует сходимости интеграла
(8): примером может служить расходящийся интеграл
Г dx
(«
J хЛпх
a
4) Распространить утверждение, доказанное в 6), 478, на случай, когда функция
fix) в промежутке [а, а+ш] интегрируема в несобственном смысле (при
сохранении прочих условий). С помощью этого установить, что - в предполо-
предположении, что gix) монотонно стремится к 0 при х -» °=, — интеграл
I In [ sin д: | •gix)dx
о
сходится или расходится одновременно с интегралом
в то время как интеграл
сходится во всяком случае.
5) Вычислить интегралы
f In 21 sin
l
In x	r x dx
С	r In x	r xdx
(a) \x-\nunxdx,	F) 	dx,	(в)
J	J V\-Xz	J ye2x_i
о	'	о '
ние, а) Подста
я/2
к In sin x dx = 2 In sin t dt.
о	о '
Указание, а) Подстановкой x=n — t убеждаемся, что интеграл приводится
я/2
я/2
(б), (в) Интегралы приводятся к I In sin t dt подстановками x = sin t, In — .
J	sint

497]	§ 4. ОСОБЫЕ ПРИЕМЫ ВЫЧИСЛЕНИЯ
6) Вычислить интеграл
1
J= [УГ^Чп 1-4 dx.
631
Имеем (полагая х = sin 0)
J=2 I cos20-lnctg 0</0« f cos20-ln ctg6d6.
о	о
Интегрируя по частям, затем получим:
/=-sin29-lnctg0
2+-[si
о 2J
sin 20
1 1
ctg 0 sin2 в '
г л
\ав=2-
7) Найти интеграл
= f
Положив a = sin a> и использовав тождество
sin2 в - sin2 со = sin (в - со) sin @ + «>)>
получим, что
К= Г ln|sin0|rfe= flnsin0</0= -я1п2.
8) Вычислить интеграл
-ax'-~-.
2
dx (a,
Решение. Воспользовавпшсь формулой [491, 13)], имеем
2 i a
[Cm. 492, 2°].
9) Вычислить интегралы
2 г
71 J
COS— Ф
2
9	COS — Q)
2 г	2

l/2(cos?)-cose)
2 г
= -
n J
7=
l/2(cos?)-cos0)

632	ГЛ. XIII. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ	[497
Решение. Обозначим cos б через х и сделаем подстановку z=cosq>; тогда
5I _1/I±* cos- ^TT?
2 i 2	2
cos-
1
1 г	dz	If Bz-l)dz
51J У(г-х)A-г) ' ' ^J f(z-x)(l-z)'
ременную / no i
/o~ J/ч-Г1'
Вводя еще раз новую переменную / по формуле У(г-х) (I -z) = /(l -z),
получим:
2 р/2+2д:-1 2
/,=_ 	<# = —
о
2A)
0	0	0
Итак, /0=1 и /! = cos0. Ниже [511, 3)] мы установим более общий результат.
10) Интегрированием по частям установить следующие результаты:
cos ax- cosbx n
хг	2	'
(б)Г
о
(в) J'—	'х2	- <Ь-ф-b).
о
11) Легко видеть, что [492, 3°, 494, 5)]
ж
— при а =- 0,
- sin ах I
-dx=< 0 при а = 0,
х	\
о	я
I	при а-=0.
Отсюда, так как
sin ох а _, 1 i rsin(a+/S)x т fsin(a-/S)
0	0	0
то, очевидно (если считать для простоты а и /S > 0),
(
|- при
г sin осх	I
	cos (Ix dx = \n
J x	j — при /S = a,
о	|4
|
\0
при

497]
§ 4. ОСОБЫЕ ПРИЕМЫ ВЫЧИСЛЕНИЯ
633
Этот интеграл многократно применялся Дирихле и известен под назва-
названием разрывного множителя Дирихле.
К нему приводятся многие другие интегралы. Например (если а,Ду>Ои« -
наибольшее из них):
" sin ах ¦ sm px • sin ух
dx-
— при а =
8
О при а^
(замена произведения двух синусов разностью косинусов) или (снова считая а,
/S-0):
— при а^в+у,
4
J
sin ax sm px
-dx=\
при /?=sa,
— а при p=»a
(интегрирование по частям).
Последний результат может быть обобщен следующим образом.
Если a, alt а2, ..., an=>0 и a^^a,-, то
/=
г sin ax sinatjc sinanx
= -at a2... an.
2
Доказательство проводится по методу математической индукции (интегрирование
по частям!).
12) Вычислить интеграл
г	dx
(sin ax - sin Ьх)г — .
J	хг
Указание, Проинтегрировать по частям; использовать разрывной мно-
п
житель Дирихле. Ответ: —\а-Ъ\.
13) Вычислить
СZx-sin ax
.р. —	—dx (a, r>0).
J x2 - г2
Решение. Особая точка х = г. Пользуясь тождеством
2х 1 1
x2-r2 x+r x-r
сразу выделяем сходящийся интеграл
Г sin ax
г sin ax	г sin ay	rcosa^
	dx = cosar- 	 dy-sin ar- 	dy.
J x+r	J у	J У
о

634	ГЛ. XIII. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ	[497
Затем, с помощью легких преобразований, находим
Г—В	оо	оо	оо	г
а г *\ sin ах р sin ay . р cos ау р sin ay
+ 	dx = cosar- 	dy+smar-	dy+2cosar- 	dy,
J J x-r J у J у J у
0 r+e
так что
г sin ax
V. p. 	dx
J x- r
получается, если в последнем интеграле положить просто е = 0.
Окончательно,
p 2*sina*	psinay
о	о
14) Пусть функция f(x) @«=л:< ~) удовлетворяет условиям
/Ос+я)=/(х) и /(я -х)=Дх).
В предположении, что существует интеграл слева, доказать формулу
[Она принадлежит Лобачевскому и доказывается с помощью разло-
разложения функции 	 на простые дроби так же, как и в частном случае f{x)=\;
sin x
см. 492, 3°.]
Применить эту формулу к вычислению интегралов:
sin2" л:	г	sin*
р sin" х	г	sin л:
(а) 	dx= sin2" л:	dx (v=l, 2, ...);
J х	J	x
x	J	x
о	о
_ г	dx ra.rctg(a-sinx) sin x
F) arctg(a-sinx)— = 	—	dx (a=~0).
J	x J sin*	x
о	о
Интеграл (а) приводится к уже известному [312 (8)] интегралу
p., J n Bv-l)!!
sin2l>xdx =
J	2 2v!!

497]	§ 4. ОСОБЫЕ ПРИЕМЫ ВЫЧИСЛЕНИЯ	635
а интеграл (б) - к интегралу
1
г arctg at
—	at
J /yi_fS
о '
(подстановка: t = sin *), значение которого
-inCa+yr+o2)
будет установлено ниже [511, 9)].
15) Налагая те же условия на функцию /(*), доказать формулу (снова - в
предположении существования интеграла слева):
л
2
sin2*
Указание. И здесь применим метод Лобачевского, лишь с ссыл-
ссылкой на разложение функции 	на простые дроби [441, 9)].
sin2*
При /(*) = 1 отсюда снова получается известный нам интеграл
г si
J
sin2* n
2
о
[см. 494, 4)].
16) Вычислить интегралы (а, 6=-0)
ео	во	1
г smaxsinbx с 1-cosa* гха~1~хь ~1
(а)	dx, (б) 	cos bx dx, в) 	dx.
J	X	J	X	J	In *
о	о
Указание. Все приводятся к интегралам Фруллани; первые два
интеграла при а=Ь расходятся.
a
\-Ь\	b	Ь
17) Вычислить интегралы (а, 6=-0)
r b-
(a)
J
0
b-smax-a-sinbx
rb In A +ax)-a In A+bx)
r
(б)	.1	?
о
(в)	("(e-ax_e-63cJ_f .
J	X2

636	ГЛ. XIII. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ	[497
Указание. Все три приводятся к интегралам Фруллани интегриро-
интегрированием по частям.
18) Найти интеграл (а=»0)
о
Решение. Имеем тождество
|1	(х**)
Ях \\dx
ex-e~x~l.)~x*
1A 1 1 Л 1/1	1 1 _ \
-х 2) 2х
Интегралы от второго и от третьего выражений взаимно уничтожаются (в чем
легко убедиться заменой переменной), и все сводится к интегралу Фру ллани.
1
Ответ.	In 2.
2
19) Найти интеграл (а, 6>0)
г е~ах - е-Ьх+х(а- Ь)е-Ьх
	dx.
J	X*
О
Решение. Имеем (для г\ =- 0)
g—bx
П V	1
Первый из интегралов справа преобразуем интегрированием по частям.
dx=
{¦be-bx-ae-ax
+ 	dx,
v ¦>
X
V	1
так что, окончательно
ге~ах~е~Ьх+х(а-Ь)е-Ьх е~а'1-е~ь1 г е~Ьх-е~ах
	dx =	ha 	dx.
J	Хг	7]	J	X
n	n
При 77—0 первое выражение справа стремится к b - а, а второе к интегралу Ф р у л-
л а ни:
«I
х
о
Эти интегралы не сходятся при г) = 0.

497]	§ 4. ОСОБЫЕ ПРИЕМЫ ВЫЧИСЛЕНИЯ	637
20)	Установить формулу
г A cosax+Bcosbx+ .. .+Kcoskx	,
	dx = -{A \na+B\nb+ ...+K\nk)
о
в предположении, что а, Ь, ..., к>0иА+В+...+К=0 (последнее условие, оче-
очевидно, необходимо для существования интеграла).
Указание. Полагая К = -А-В- ..., воспользоваться формулами
г A cosax-A coskx
	ах= -А Ыа+А In k и т. п.
J	х
Легко обобщить предложенную формулу на случай любой функции fix),
удовлетворяющей условиям п° 495, II.
21)	Найти выражение для интеграла
(•sin11*
(•sin11*
	dx,
J хт
о
где пит- натуральные числа и
Решение. Распространяя на случай бесконечного промежутка обоб-
обобщенную формулу интегрирования по частям [311], сразу получим (так как
двойная подстановка здесь исчезает):
f sin" x	1 г d'1	dx
dx =	 	sin" х-—.	A1)
(m-DUdx"»-!	x
J xm
0
Для вычисления последнего интеграла удобно воспользоваться известными
нам разложениями sin" x по синусам или косинусам кратных дуг [461, 3), (а) и (б)].
Рассмотрим различные могущие представиться здесь случаи,
(а) и = 2к+1, m = 2[i+\. Тогда
sin2- + 1 х=	 Bj> +1J" sin B»+ l)x-
B^+1J,		1
и, по формуле A1),
о
(б) n = 2v, m = 2fi+l. В этом случае:
J2fl	(-1>+СГ
	sin2' х =	 Bv)V cos 2v x - 2v ¦ Bi> - 2Jл cos Bv - 2)x+
dx^	22*-1 L
1
v-4)V cos Bv-4)x- ....

638	ГЛ. ХШ. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ	[497
Легко видеть, что левая часть (так как i>=-|«) при jc = O обращается в 0, так что
сумма коэффициентов при косинусах равна 0, и мы можем использовать преды-
предыдущее упражнение 20). Отсюда
rsin2'* (- l)"+f+1 г
	dx =	 Bvyf In 2v - Ivilv - 2L In Bv - 2) +
J Л+i	22--42u!) L
,	N—r ._, 	v—	.J ...
Аналогично устанавливаются формулы для случаев: (в) n=2v+l, m = 2fi и (г)
n-2v, m = 2(i. Отметим, что, в частности, для любого лэ=2
о
22) С помощью того же разложения 461, 3) (б) легко получить, что (при р > 0)
О,+ 1J,_	_
1-2
Впрочем, с помощью элементарных соображений, это выражение приводится
к более простому:
я B).-1)!!
 2г>!! '
г sin2» />jc
Интеграл 	dx расходится. Интеграл Фруллани
J х
¦ sin2l>/«-sin2''<7*
	—dx (p.q^O)
не удовлетворяет условиям п° 495, но с помощью разложения 461, 3) (а) легко
установить, что он приводится к случаю II интеграла Фруллани, если sin211 x
заменить на
sin*
2"	1-2...V
Окончательно, по формуле 4а):
с sin2' рх - sin2" qx	Bi> - 1)!! q
	dx= ——— In - .
J	x
2v\\	p

497]
§ 4. ОСОБЫЕ ПРИЕМЫ ВЫЧИСЛЕНИЯ
639
г cos"х
Интеграл 	dx ни при каком натуральном п не сходится. Но при
J х
о
n = 2v+l сходится I и, по формуле Фруллани 4а), сразу имеем
J-
1 qx	q
p'
0
При n=2v, используя разложение в 461, 3) (в), как и выше в случае синусов,
получим
cos^px-cos2" qx ( Bj>-1)!!\ q
dx = 11	In —.
2И!
J
о
23) Установить следующие формулы *:
с г cos /
(a) cos ух dx 	dt=
Ту ПРИ
г г sin t
(б) sin ух dx 	dt =
—	при |у|=1,
4
О при |у|-=1.
—	при |у|=-1,
2
— при |у|=1,
г	г sin t I
(в) cos ух dx 	dt = — In
J	J /	2y
О при
1+y
при y^O, ± 1,
1-y
при у = 0**.
С	p cos t 1
(r) sinyjctfcc 	dt = — In[ 1 — y21 при y^O, ±1,
J	J f	у
С	pe~' 1
(д) e~^d!x: 	Л = —1п
J	J /	у
0 при у = 0**.
при у=-0,
* Интегралы
CD	OO
г sin t	с cos /
-J— * И -J— *
X	X
и представляют собой функции si x и ci x («интегральный синус» и «интегральный
косинус»), о которых упоминалось в п° 289.
** При у = ± 1 интеграл расходится.

640	ГЛ. XIII. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ	[497
Доказательство, (а) Предполагая у <0, интегрируем по частям:
г г cos t 1 г cos / - 1 р sin yx
cos yx dx 	dt = — sin yx • 	dt -\— 	cos x dx.
J	J t	у	J )	О У J X
Так как
г cos t	I г cos/
	dt =s
J /	| J /
+
j
J
X
dx
X
то двойная подстановка обращается в 0, и интеграл приводится к разрывному
множителю Дирихле [A1)].
Особо рассмотрим случай у = 0. При любом А>0, повторно интегрируя по
частям, получим:
Г	CCOSt	CCOSt \А г
Л 	Л = л 	dt + \
С cos t
cos x dx=A I	Л+sin A --
0	A
= А-
sin/
~ с sm t	г sin /
+А 	tft+sin A =A	dt.
4 J /3	J t2
По второй теореме о среднем значении [487], последнее выражение приводится
А
р sin / _
к виду: 	dt (А >А), а этот интеграл стремится к 0 при А - ~, в силу условия
А
г sin /
Больцано - Коши [475], примененного к сходящемуся интегралу 	dt.
Итак,
dt = 0.
0	х
Доказательства в прочих случаях аналогичны.
24) Доказать следующие формулы (а, /9=-0):
, ч f , f f COS f	f COS / 1
О	ах
/3x
sin
—
0	ax
71
2a'
n
20'
n
Ъх'
n
w
если a>/3,
если a=s/S.
если a>/3.
если a«s/?.

498]
§ 5. ПРИБЛИЖЕННОЕ ВЫЧИСЛЕНИЕ
641
, ч г , f г cos f , p sin f | 1 ,
(в) Jafc J—-A.J—*} = —In
fix
2a
=--ln2
a
1 1
(a
0	ax
fix
a*
1 , k2-
-\—In
20
при
при
Доказательство, (а) Интегрированием по частям предложенный ин-
интеграл приводится к интегралам типа, рассмотренного в 23) (а):
( г cost г cost ) г cost г cost х=°°
	dt- 	dt\=x- 	dt.	dt +
Г I Г COS Г	Гcos « I	С COSt	r COS
dx\ 	dt- 	dt\=x- 	dt- —
J U t ]t\ j t J t
0	ax	fix	ax	fix
x=0
Г	Гcos 1	С	Г COS t
+ cosotxdx 	dt+ cospxdx 	dt =
fix
1 f a	rcos' 1 /¦ j3 г cos t ж
= — cos— xdx	dt-\— cos — xdx 	dt= —
8J в it	aJa J t	2o
— или —,
2a	2/8
смотря по тому, будет ли as»/3 или a^/S.
Сделаем еще пояснение относительно обращения в 0 двойной подстановки.
Из уже знакомой нам оценки
Г cos г
\'Tdt
\\пх\
явствует, что выражение под знаком подстановки стремится к 0 вместе с х. С другой
стороны,
r cost
sin t
t
psinf	I reost
+	dt,		dt
¦it*	|J <2
2
: j
x
откуда следует, что упомянутое выражение стремится к 0 и при х^°*.
Доказательство остальных формул проводится аналогично, со ссылками
на формулы, установленные в 23) (б), (в) и (г), (д).
§ 5. Приближенное вычисление несобственных интегралов
498. Интегралы с конечными пределами; выделение особенностей. Выше, в
322-328, нами изучены были различные приемы для приближенного вычисления
определенных интегралов в собственном смысле. К несобственным интегралам
эти приемы и указанные для них оценки погрешностей непосредственно непри-
неприменимы. Иногда удается, путем замены переменной или интегрирования по частям,
41 Г. М- Фихтешольц, т. II

642	ГЛ. XIII. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ	[499
свести несобственный интеграл к собственному. Тогда и приближенное вычисле-
вычисление несобственного интеграла приводится к уже знакомой задаче.
Во многих случаях приближенное вычисление несобственного интеграла
ь
f(x) dx (с конечными пределами) облегчается путем выделения особенностей *.
а
Последний прием состоит в подыскании функции g(x) простого вида, которая
как бы впитывает в себя все особенности функции fix), так что разность (р(х) =
=f(x)-g(x) оказывается уже лишенной особенностей, т. е. интегрируемой в соб-
собственном смысле. При этом выбором функции g(x) стараются распорядиться
так, чтобы интеграл от g(x) выражался в конечном виде, а функция q>(x) имела
нужное число производных, чтобы при приближенном вычислении интеграла от
нее можно было использовать существующие формулы для погрешности.
Подбор функции g(x) производится различным образом, смотря по случаю.
В виде примера мы укажем общее правило построения этой функции для одного
часто встречающегося класса интегралов.
Пусть подинтегральная функция имеет вид:
где h(x) для a'S.X'Sib разлагается в степенной ряд
h(x) = со + с1(х-хо) + с.г(х-хоУ+ ¦ ¦ ¦ +сп(х~х0)"+..
Тогда полагаем
g(x) = {х - х0)- «• [с0 + сх(х -хо)+...+сп(х-х0У]
Интеграл от g(x) берется легко; с другой стороны, f(x), очевидно, имеет в [а, Ь],
включая в точку х0, п непрерывных производных.
499. Примеры. 1) Пусть требуется вычислить интеграл
1	V»
с _i	_i.	r _i_	_i_
\х Hl-x) a<& = 2 х "A-х) * dx;
о	о
в последнем интеграле единственной особой точкой является 0.
Разлагая A-х) 2 по степеням х, остановимся на члене, содержащем х*, и
положим
63 '
«*•* Т-* Л-[1+-+ШХ')]-*
Тогда
2"	2"
¦ Этот прием был предложен Л. В. Канторовичем.

499]	§ 5. ПРИБЛИЖЕННОЕ ВЫЧИСЛЕНИЕ	643
Значение Д легко вычисляется:
715801 1Г-
Что же касается /2, то его найдем по формуле Симпсона, деля промежуток
[0, — I на 2я= 10 частей и ведя вычисление на 6 знаков:
2J
/ -0
2
2y, =0,000018
4y8/2 = 0,000225
2y\ = 0,000431
4ув/2 = 0,002496
2^3 = 0,003017
4ylj2 = 0,012901
2^ = 0,012632
4ув/2 = 0,046350
75 = 0,020239
0,098309!
/^1,5691585
/2 = 0,0016385
/=1,5707970
60
0,0016385
Истинное же значение / равно [как это вытекает из теории функции «Бета» 529
Eа)],
^= 1,5707963...
Произведем оценку погрешности (не пользуясь, разумеется, тем, что мы - из
других соображений - можем здесь получить точное значение интеграла). Имеем:
хК...0,
256 2 2 2 2
и 9?IV возрастает вместе с х, так что наибольшего значения достигает при х = — .
Отсюда легко получить, что max?)iv(^) = 288.	2
Погрешность формулы Симпсона выражается по известной формуле
[327]:
'IV
R
lO4 180
Таким образом,
288 5
1 104 180 10е
С другой стороны, погрешность полученного для 12 значения, проистекающая
5-Ю-6
из округлений, абсолютно меньше 	<10~'. Такова же абсолютная по-
5,2 0,2
грешность значения /,. Общая погрешность лежит между	и —, так что
10е 10е
1,5707918^/^1,5707972 или 1,570791-=/-= 1,570798.
41»

644	ГЛ. XIII. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ	[499
Окончательно,
/= 1,57О79+о,оооо1 .
1
2) Для интеграла /= \х а A - х) 4 dx обе точки 0 и 1 являются особыми; со-
о
ответственно этому разбиваем его на два:
1
1 2 1
/= I = I + =/t+/2. Полагаем для вычисления Д
3 31 . 77 . 1155
2048
так что
1	1
2	2~
h=\g(x)dx +
0	О
Сразу получаем
576293 „
Интеграл /12 вычисляем по формуле С и м п с о н а, 2л = 10, на шесть знаков:
/12 = О,0О3813. Отсюда /,==1,661938. Оценивая погрешность, как и только что,
найдем:
/t = 1,66193+о,оооо1.
Аналогично,
1
1	2
с -1. -*-
2= х SU-*) * ^=
1	0
2
]
2
1	35
2
+ J*"*[(! -*)"«-(!+. •
Найдем, что
/21 = 3,580291, /22 = 0,002033, /2 = 3,582324.

499]	§ 5. ПРИБЛИЖЕННОЕ ВЫЧИСЛЕНИЕ	645
Если оценить погрешность, как выше, то получим
/2= 3,58232+о,ооооо5.
Таким образом,
/=5,24425+о,оооо15 или /=5,24426±o,ooooi.
1
гЫх
3) Пусть предложен интеграл /= 	dx; особенность при х = 0.
J 1-х
о
Для выделения ее прибегнем к приему, сходному с примененным выше.
Положим:
1	1
х^ In х
Ь11
г	г х^ In
1= \(l+x+x2+x3+xa)lnxdx +
J	J 1-
Легко найти (с помощью интегрирования по частям): Д= -1,46361... Интеграл
же /2 вычисляем по формуле Симпсона Bи= 10, на пять знаков); мы получим:
/2=0,18135. Таким образом, 1= —1,64496. Истинное значение искомого интеграла
[519, 1) (б)] есть - — = -1,644934...
6
При оценке погрешности производная д>М(х) вычисляется по формуле Лейб-
Лейбница [117]. При этом удобно воспользоваться легко доказываемой формулой:
(где с лежит между а и х), взяв f(x) = Ых, а=1. Грубая оценка дает \q>iv(x)| -= 200,
отсюда
|Д|<	=0,00011.
' ' 104 180
Общая погрешность ±0,00013. Окончательно,
|/| =1,645±о,ооо2.
4) Рассмотрим, наконец, пример другого типа
Г= log sin x dx,
о
с особой точкой 0.
Естественно сопоставить подиитегральную функцию с функцией g(x) = \ogx,
для которой интеграл вычисляется легко *:
/,= \loexdx = M. \]nxdx = MxQnx-l) T = -•(log--м) = -0,374123.
J	J	0 2^2;
* Буквой М ниже обозначен модуль перехода от натуральных логарифмов
к десятичным.

646	ГЛ. XIII. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ	[500
sin х
Интеграл же /„ от функции fix) = log	вычисляем по формуле Симпсона,
х
при 2л = 18, на шесть знаков. Имеем:
h = - f Bog x ~ log sin x] dx = - 0,098733.
о
Поэтому
I=I1+I2~ -0,472856.
На деле интеграл / лишь множителем М отличается от известного уже нам
[492, 1°] интеграла:
lnsinxdx=	1п2
и, следовательно,
/= --.log 2= -0,4728568...;
мы видим, что в полученном выше значении все шесть знаков верны.
Не зная истинного значения, мы вынуждены были бы пользоваться оценкой
погрешности формулы Симпсона. Здесь
6(х* - sin4 х) - Ах* sin8 x
= М-	.
х4 sin4 х
Можно показать, что 0<ipiV(x)«— М-=3,6, откуда Ji<0 и |Л| *0,000002. Учиты-
Учитывая и погрешность от округлений, мы могли бы лишь установить, что
|/|=0,47285+0,00001.
500. Замечание по поводу приближенного вычисления собственных интегралов.
Метод выделения особенностей может оказаться полезным и при вычислении
собственных интегралов, если подинтегральная функция, даже будучи
непрерывной, не имеет нужного числа непрерывных производных (что затрудняет
оценку погрешности). Поясним это на примере.
Рассмотрим интеграл
1
h
Легко видеть, что при х —0 подинтегральная функция стремится к 0, так что эту
функцию можно считать непрерывной во всем промежутке интегрирования. Но
уже первая производная подинтегральной функции обращается при х = 0 в беско-
бесконечность. Воспользовавшись разложением логарифма, представим нашу функцшо
в виде суммы двух функций
(Y-2 v-3 v«
Л- Л Л
*~-Г + ^	7
2 3 4

501]	§ 5. ПРИБЛИЖЕННОЕ ВЫЧИСЛЕНИЕ	647
Интеграл от первой функции берется легко: его значение есть - 0,20528...
Интеграл же от второй функции (имеющей уже четыре непрерывных производных!)
вычислим по формуле С и м п с о н а, 2и = 10, на пять знаков. Мы получим
-0,00348, так что общий результат будет -0,20876.
Так как |?>IVW| -=36, то \R\ -=0,00002. Окончательно,
|/| =0,20876±о,ооооз = 0,2087+0,0001.
(На деле же в полученном приближенном значении все знаки будут верны, так как
истинное значение / будет -0,2087618...)
Любопытно отметить, что если формулу Симпсона (при том же 2л = 10
и по-прежнему вычисляя на пять знаков) применить к подинтегральной функции
без предварительного выделения особенности, то получим /= - 0,2080, т. е. всего
три верных знака.
Таким образом, если не прибегнуть к выделению особенности, то мы не только
испытаем затруднение в оценке погрешности, но можем столкнуться и с факти-
фактическим понижением точности результата^.
501. Приближенное вычисленне несобственных интегралов с бесконечным пределом.
Редко удается вычислять интеграл fix) dx, на основе его определения, как
а
А
предела собственного интеграла fix) dx, приближенно полагая (при достаточно
а
+~ А
большом А) = I причем последний интеграл вычисляется уже изученными
а а
приемами. Это может оказаться полезным разве лишь при очень быстром убывании
подинтегральной функции с возрастанием х, так что - даже при небольшом А —
написанное выше приближенное равенство имеет уже достаточную точность.
1) Так, например, будет обстоять дело в случае интеграла /= е-** dx.
Из неравенства x2s=2Ax-A2 следует, что	°
и
А	А
При А = 3:
[e-*dx^ 0,00002.
з
3
Что же касается интеграла е-*'dx, то его вычислим по формуле Симп-
о
с о н а, при л = 30, на пять знаков; это дает нам 0,88621. Нетрудно получить оценку:
|(e-x=)iv|^i2, |Д|-=2.10-5. Общая погрешность содержится между -0,00004
и 0,00006. Таким образом,
0,88617 -= /^ 0,88627, /= 0,8862±o,oooi.

648	ГЛ. XIII. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ	[501
Точное значение /, как мы знаем [492, 2°], есть —=0,886226...
Чаще бывает выгодно либо преобразовать интеграл к конечным пределам,
А "	а
либо разбить его на два: I + I , и второй преобразовать к конечным пределам.
а А
2) Возьмем снова тот же интеграл /= е-*2 dx и представим его в виде суммы:
о
0 0 1
/, вычислим по формуле Симпсона, 2л = 10, на пять знаков, |i?| «=0,00001;
/t = 0,74683 ±0,00002. /2 подстановкой х = — преобразуем к виду:
1
1 --
/„= —е р dt.
о
Обычным путем получим /2=0,13945, так что /=0,88628.
Оценкой погрешности заниматься не будем.
Если интеграл с бесконечным пределом имеет особую точку и на конечном
расстоянии, то надлежит разбить интеграл на два, содержащих каждый лишь одну
особенность.
3) Рассмотрим (при 0«=а-= 1) интеграл
Г — dx= f — dx+ f —<
J1+x J1+x Jl+x
0	0	1
Интеграл /, находится путем выделения особенности:
1	1
Г	12	ГЛЯ+4
J i ""~ I t и^^ """" и^^ 'j" Ик^ "^ Ик^	I ,л^ / (Лл ~~ I ¦ ^ ~"" иЛ У i i *** if 94
J	J l + x
0	0
11111
/,,=	1	1	, a /,» вычисляется по формуле Симпсона.
a e+1 a+2 e+3 e+4
У2
Пусть, например, а = — = 0,7071068...; тогда /n = 1,14052... Для /12 Bn = 10,
на пять знаков) получаем значение 0,09518. Итак, /,==1,04534.
Интеграл /2 подстановкой х = — приводим к виду
г

501]	§ 5. ПРИБЛИЖЕННОЕ ВЫЧИСЛЕНИЕ	649
где Ь- 1-а = 0,2928931... Аналогично прежнему получим: /2 = 2,90289. Оконча-
Окончательно, /= 3,94823. Впоследствии [522, 1°] мы узнаем, что истинное значение / есть
—^— = 3,948246...
i
Иногда в случае «медленно сходящегося интеграла» f(x) dx все же удается
а
выделить из него (например, путем повторного интегрирования по частям) легко
вычисляемые члены с тем, чтобы остающийся интеграл был уже мал.
4) Пусть предложен интеграл
«о
г sin л:
= 	dx.
J х
I
о
Представим его в виде суммы интегралов: + , не стремясь, однако, к тому,
0 А
чтобы второй из них был мал. Интегрируя затем по частям, будем иметь:
(¦sinx I cosx sin x cosx smi
	dx=\	-+2	+ 6——-
J X	(XX*	X3	X1
A
+ 720
A
\~^rdx-
A
Взяв, например, A = 2л, получим:
rsiax 1 2 24	rsinx
	dx =	+	+720 	dx.
J x	Ьг Bл)з BлM	J x>
+
Bл)з BлM
in	2л
Сумма проинтегрированных членов равна 0,15354.. • Далее
°° dx 120
rsinx	rdx 120
0^720 	dx -=720 — =	=0,002.
J x->	J x> (bif
BяN
2л
Вычисляя интеграл по формуле Симпсона Bи = 40 на четыре знака),
о
найдем: 1,4182.
Оценка погрешности:
„1-1Г-Ч-	.?, (-1)тХгт
о Bm+l)! '	о 2m!Bra+5)'
\/Щх) | -= - ch 2п-- 54, | R| * 0,0012.

650	ГЛ. ХШ. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ	[502
Отсюда, учитывая общую погрешность,
1,5702-=/-= 1,5752, /=1,57+о,01.
п
Как мы знаем, 492, 3°, на деле /= — = 1,5707...
502. Использование асимптотических разложений. При приближенном вычисле-
вычислении интегралов вида
\fit)dt
часто оказывается выгодным использовать их асимптотические разложения.
Поясним это на примерах.
Iе. Интегральный логарифм. Если 0<а-=1, интегральный логарифм На опре-
определяется так:
а
-;	02)
в случае же а>1 этот интеграл расходится, и его понимают в смысле главного
значения:
lH-p
+ \
О	0 1 + е
[см. 484].
Пусть сначала а<1. Положим а = е~х прих^О и сделаем в интеграле A2)
подстановку и = е~1:
li(e-^)-- j — Л.	A3)
X
Полагая t^x+v, мы придем к интегралу
с e~v civ
li(e-x)=_e-x 	.	A4)
J x+v
H-V.p. f?- lim ([+[)?¦	A2*)
J 1ПН е— +0 \ J J ) Ши
0
Так как
1 1 v v1	о"-1	«л
	|	 _i_f_1Vl—I	Lf_iyi
x + v x x*+x* '"+( ' x« +( l) x"(x+v)'
то отсюда [489, 4)]
li(e-*)- -е-х\---Л---Л ¦¦¦+(-1)"-'^+^)) ,	A5)
U X2 X3 Xi	Xn	J
где дополнительный член выражается интегралом
с Vй <e~v dv
(-l)" -—	-.	A5а)
J xn(x+v)
xn(x+v)
о

529]	§ 5. ЭЙЛЕРОВЫ ИНТЕГРАЛЫ	751
Рассматриваемый интеграл, как мы знаем [483, 3) (а)], для поло-
положительных значений а и Ъ (хотя бы и меньших единицы) сходится *
и, следовательно, действительно может быть положен в основу опре-
определения функции В. Установим некоторые ее свойства.
1°. Прежде всего, почти непосредственно (подстановкой х = 1 -1)
получаем:
так что функция В является симметричной относительно а и Ъ.
2°. С помощью интегрирования по частям из формулы A), при
Ь>\, находим **
В(а, Ъ)= f A -
a	a
i
.-(I — \[ Л	-v-\b — 1 elv
Л	II Л, l	Нл —
о	о
=^iB(a, b-\)-b^ B(a, b),
откуда
b-\).	B)
Эту формулу можно применять с целью уменьшения Ъ, пока Ъ остается
больше 1; таким образом всегда можно достигнуть того, чтобы второй
аргумент стал =sl.
Впрочем, того же можно добиться и в отношении первого аргу-
аргумента, так как - ввиду симметричности В - имеет место и другая
формула приведения (а > 1)
B(a,b) = ^YB(.a-l,b).	B')
Если Ъ равно натуральному числу п, то, последовательно применяя
формулу B), найдем:
п-\ и-2
* Наоборот, если значение хоть одного из параметров a, b будет ==0, то
интеграл расходится.
** Мы используем ниже тождество

652	ГЛ. XIII. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ	[502
Сумма первых двух интегралов есть не зависящая от х постоянная С *. Остается
лишь последний интеграл разложить по степеням х, чтобы получить требуемый
результат:
X2 X3 X1	Хп
li(e-*) = C+ln \x\-x	...-¦	...	A7)
2! 2 3!3 4! 4	п\п
Однако этим разложением невыгодно пользоваться при больших значениях
\х\, и расходящееся разложение A6) имеет перед ним в указанном случае суще-
существенное преимущество. Так, Стилтьес, взяв 23 члена ряда A6), нашел
И 10'° = 455055614,586;
в ряде же A7) понадобилось бы больше 1010 членов, чтобы осуществить ту же
точность!
2°. Интегральный косинус и синус:
г cos t	r sin /
P=cix=- 	dt, <2=six=- 	dt.
j t	j t
X	X
Для упрощения выкладок введем в рассмотрение интеграл от комплексной
функции по вещественной переменной:
Последовательным интегрированием по частям получается формула
gtx elx	gix	gix	eix
P+Qi =	1	h2!	h3!	h ¦. .+(n-l)!	h rn(x),
ix (ixJ (ixK («L	(ix)n
где
re"
dt.
Если выведенную формулу разделить почленно на -eix и отдельно прирав-
приравнять вещественные и мнимые члены в обеих частях равенства, то получим более
удобные для вычислений формулы:
(¦cos(Z-x)
	dt= -P cos x - Q sin x =
A8)
* Как увидим ниже, она на деле тождественна с эйлеровой постоянной [538, 3)].

502]	§ 5. ПРИБЛИЖЕННОЕ ВЫЧИСЛЕНИЕ	653
sin (t-x)
dt Р si x Q cos x
г sin (t-x)
	dt = Р sin x - Q
1 I 2!	Bm-2)! \
- - {l --+... +(- т-г -^-p-j + rlm_,C*)*, A9)
где, соответственно,
sin (t-x)
Bm+1)! J^+t Л
Легко установить [например, с помощью формулы Бонне, 306, C)], что
х
sin (/ — j

tn
dt
2
V1'
Переходя к пределу при А"-»», получим, что дополнительные члены в формулах
A8) и A9) по абсолютной величине не превосходят каждый удвоенного
члена (соответствующего разложения), следующего за выписанными членами.
Отсюда явствует, что, продолжив разложения A8) и A9) до бесконечности, мы
придем к асимптотическим представлениям интегралов в левых частях.
В частности, например, из A9), полагая там х-кп (&=1, 2, 3, ...), найдем
!™sin t	, ( 1 2! 4! 6!
ok = si(k7i)= - 	Aco(-i)ft+i J	)-	+ .
Wt	' it ~	\kn (кпУ (Ы)* (кяу
Ал
При к =-2 отсюда легко найти приближенные значения д^:
0з = 0,1040, &= -0,0786, е5 = 0,0631, е„= -0,0528, ...
Например, для вычисления gl достаточно трех членов в скобках:
0,07958 - 0,00101 +0,00008 = 0,07865;
так как погрешность абсолютно меньше 2-0,000015 = 0,00003, то |g4| содержится
между 0,07862 и 0,07868, и окончательно
&= -0,0786...
* Любопытно отметить, что члены в {...} оказываются как раз обрат-
обратными величинами по отношению к членам известных степенных рядов
для синуса и косинуса [404, A2) и A3)].

ГЛАВА ЧЕТЫРНАДЦАТАЯ
ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА
§ 1. Элементарная теория
503. Постановка задачи. Рассмотрим функцию f(x,y) двух пере-
переменных, определенную для всех значений х в некотором промежутке
[а, Ь] и всех значений у в множестве <у = {у}. Пусть, при каждом по-
постоянном значении у из ^, f(x, у) будет интегрируема в промежутке
[а, Ь], в собственном или в несобственном смысле. Тогда интеграл
A)
будет, очевидно, функцией от вспомогательной переменной
или параметра у.
Говоря в 436 о последовательности функций {/„(*)}, мы рассма-
рассматривали интегралы
которые представляют собой частный случай интегралов A): в роли
параметра здесь фигурирует натуральный указатель п.
По отношению к функции 1(у) естественно возникает ряд вопро-
вопросов - о существовании и выражении ее предела при определенном
предельном переходе, в частности, об ее непрерывности по у, об ее
дифференцируемости и выражении для ее производной, наконец, об
ее интеграле. Всем этим вопросам и посвящена настоящая глава.
Изучение свойств функции, выраженной интегралом A), завися-
зависящим от параметра, может представить самостоятельный интерес (в
этом отношении см., например, § 5). Но, помимо того, эти свой-
свойства, как читатель увидит, имеют и многообразные применения, в
особенности, к вопросу о вычислении несобственных интегралов.
504. Равномерное стремление к предельной функции. Решающую
роль в предстоящих исследованиях будет играть указанное в заго-
заголовке понятие. Пусть функция f(x, у) определена, в общем случае,

504]	§ 1. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ	655
в двумерном множестве еЛ?=%хв$, где ^ и<| означают множества
значений, принимаемых порознь переменными х и у, причем ^ имеет
своей точкой сгущения, скажем, конечное число у0.
Если 1) для функции f(x, у) при у -+у0 существует конечная пре-
предельная функция
lim f{x, у) =ф) (х из I),	B)
У-~Уо
и 2) для любого числа е>0 найдется такое не зависящее от х
число <5>0, что
при \у-уо\^д будет \f(x,y)-cp(x)\ ^e	C)
сразу для всех х из X, то говорят, что функция fix, у) стре-
стремится к предельной функции <p(x) равномерно относительно х
в области X.
Нетрудно перефразировать это определение и на тот случай, когда
у0 есть несобственное число, например, + ~: при этом лишь нера-
неравенство вида |j-Jo| ^ заменяется неравенством вида у>А. В главе
XII [428] мы имели уже дело с частным случаем такого равномер-
равномерного приближения к предельной функции; там речь шла о функции
fnix), содержащей в качестве параметра натуральный значок п.
В 429, имея дело с последовательностью функций, мы установили,
что для равномерной сходимости необходимо и достаточно, так ска-
сказать, равномерное выполнение принципа сходимости. То же можно
сделать и в общем случае. Именно (если ограничиться предположе-
предположением, что у0 конечно):
1°. Для того чтобы функция fix, у) при у-*у0 имела предельную
функцию и стремилась к ней равномерно относительно х в об-
области %, необходимо и достаточно, чтобы для каждого числа е=-0
существовало такое не зависящее от х число Ь =-0, что не-
неравенство
\Лх,У)-Лх,у)\^е	D)
выполняется для всех х из % сразу, лишь только
\у-Уь\*Ъ> Ь'-ЛМ iy,y'm%.	E)
[В случае у0 = + °° взамен последних неравенств появляются не-
неравенства у>А, у'^А.]
Необходимость. Пусть имеет место равномерная сходи-
сходимость. Заменив в определении е на я и соответственно выбрав 6,

656	ГЛ. XIV. ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА	[504
возьмем теперь два значения у и у' из °JI, так чтобы выполнялись
условия E). Тогда будем иметь, каково бы ни было х,
\f(x, у') -9(х)\ <| и \ф) -f(x, у)| <|.
откуда и следует D).
Достаточность. Если упомянутое условие выполнено, то
прежде всего ясно существование предельной функции B). Переходя
затем к пределу в неравенстве D) при у' -*у0 (причем у фиксировано
так, что ly-yol^S), получим:
\<p(x)-f(x,y)\*se.
Этим и установлено равномерное стремление функции f(x,у)
к предельной функции (р(х).
Установим теперь возможность сведения рассматриваемого вопро-
вопроса к равномерной сходимости последовательностей функ-
функций:
2°. Для того чтобы функция f{x, у) при у-*у0 стремилась к функ-
функции <р(х) равномерно (относительно х в областиX), необходимо
и достаточно, чтобы к <р(х) равномерно сходилась каждая последо-
последовательность {/(х, уп)}, по какому бы закону варианта уп (со значениями
из '-у) ни стремилась к у0.
Доказательство ограничим случаем конечного у0.
Необходимость. Предполагая равномерное стремление
f(x, у) к <р(х), по произвольно взятому е >0 найдем соответствующее,
в согласии с определением, число <5>0 [см. C)]. Какова бы ни была
варианта уп-»у0, для нее существует такой номер N, что |^п—>-0| -= 5
лишь только п >iV. Но тогда, при тех же значениях «, в силу C), вы-
выполняется неравенство
\Лх,уп)-(р(х)\^е
и притом сразу для всех х. Таким образом, доказана равномер-
равномерная сходимость последовательности {f(x, Уп)}.
Достаточность. Пусть теперь дано, что каждая такая по-
последовательность сходится к q>(x) равномерно.
Для того чтобы доказать равномерное стремление функции f(x, у)
к <р(х), предположим противное. Тогда для некоторого е>0,
какое бы ни взять <5 = с>'>0, найдется такое значение у—у' из ^), что
хотя |/-уо| <(^ все же по крайней мере для одного значения х=х'
из ЗС будет выполняться неравенство: \f(x',y')-<p(x')\s*e.
Возьмем теперь последовательность положительных чисел {дп},
сходящуюся к нулю. Каждому дп, по сказанному, можно сопоставить
два значения уп и хп такие, что
\Уп-Уо\<дп, но \f(xn,yn)-(p(xn)\z*e.	F)
Ясно, что уп-+у0 (ибо <5п->-0), но последовательность {f(x, yn)} равно-
равномерно сходиться к у(х) не может, ввиду F). Мы пришли к противо-
противоречию с тем, что дано.

505J	§ 1. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ	657
Пусть теперь множество X представляет собою конечный
промежуток [а,Ь]. Мы знаем [436], что если последователь-
последовательность {fn(x)} функций, непрерывных (или интегрируемых в соб-
собственном смысле), равномерно сходится к предельной функции,
то и последняя необходимо будет непрерывной (интегрируемой).
Ввиду 2° непосредственно ясно, что все это переносится и на общий
случай:
3°. Если функция f(x, у) при любом у из ^ непрерывна (интегри-
(интегрируема) по х в промежутке Х = [а,Ь] и при у-*у0, равномерно
стремится к предельной функции <р(х), то и эта функция также будет
непрерывна (интегрируема).
В интересах дальнейшего изложения мы установим еще следую-
следующее предложение, обобщающее теорему Д и н и п° 431. При этом
мы будем считать, что все у<у0.
4°. Пусть функция f(x, у) при любом у из ^ будет непрерывна по
х в промежутке X = [а, Ь] и при возрастании у, монотонно воз-
возрастая, стремится к непрерывной же предельной функции
q>(x). Тогда стремление это необходимо будет равномерным от-
относительно х в промежутке X.
Выделим из <*у монотонно возрастающую последовательность {уп}
значений у, сходящуюся к у0, и рассмотрим соответствующую по-
последовательность функций (f(x, >'„)}, очевидно, также монотонно воз-
возрастающую вместе с п. Так как ряд
/(*, Уд + 2\Лх> Уп) -/(*, Уп-д] =<К*)
2
состоит из положительных членов (возможно, за исключением
первого члена), то теорема Д и н и позволяет утверждать, что этот
ряд сходится равномерно относительно х в промежутке X. Сле-
Следовательно, по заданному е>0 найдется такой номер я0, что нера-
неравенство
окажется выполненным сразу для всех х из X. Ввиду монотонного
возрастания функции / вместе с у, тогда подавно выполняется и не-
неравенство
\cp(x)-f(x,y)\^e,
лишь только у^Уп,', этим доказывается наше утверждение.
Хотя установленный частный признак равномерного приближения
и кажется очень узким, но он нередко бывает полезен, избавляя от
необходимости иным путем убеждаться в наличии равномерного при-
приближения.
505. Перестановка двух предельных переходов. В настоящей главе
через все изложение красной нитью проходит вопрос о переста-
перестановке двух предельных процессов того или иного
42 Г. М. Фихгенгольи. т. II

658	ГЛ. XIV. ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА	[505
типа. В простейшей форме этот вопрос впервые встретился нам в 168,
когда речь шла о существовании и равенстве повторных пределов:
lim lim fix, у) = lim lim f{x, у)	G)
x-x, у-~Уе	y~y, x-x0
в предположении, что существует двойной предел:
lim fix, у).
х-х.
Затем в 436 мы видели, что теорема о почленном переходе к пределу
в равномерно сходящемся функциональном ряде также может быть
выражена в подобной форме:
lim lim fn(x) = lim lim fn(x)
x-*a n-*-°°	л-*-1» x-*-a
на этот раз - в предположении равномерной сходимости при
п -> о= функции fn(x) к своей предельной функции.
Пользуясь введенным в предыдущем п° понятием, мы сформули-
сформулируем сейчас общую теорему того же типа. Мы будем предполагать,
что функция fix, у) определена в двумерном множестве ©#=^X^J,
причем множества Х-{х} и ^ = {j} имеют порознь точки сгущения
х0 и у0 (конечные или нет).
Пусть при каждом х из X существует простой предел
lira fix, у)=ф),
У-У'
а при каждом у из <%) - простой предел
Пт/(х,у)=ц>(у).
х~х.
Если при у-*у0 функция f{x, у) стремится к предельной функции
(р(х) равномерно относительно х в области X, то существуют
и равны оба повторных предела G).
Легко было бы свести эту теорему к упомянутому выше частному
случаю ее, но - для большей отчетливости - мы предпочитаем дать
здесь независимое доказательство (предполагая — для определенно-
определенности - оба числа х0 и у0 конечными).
Задавшись произвольным числом е>0, в силу теоремы 1° 504,
найдем соответствующее ему число 6>0 такое, что неравенства E)
влекут за собою D), каково бы ни было х из X. Фиксируем значения
у и у', удовлетворяющие условиям E), а х предположим стремящимся
к х0; переходя в D) к пределу, получим:
"-	(8)
Таким образом, для функции ц>(у), при предельном переходе у-*уп>
выполняется классическое условие Больцано — Коши [58],

506]	§ 1. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ	659
откуда и следует существование конечного предела
lim гр(у)=А.
У~У«
Теперь ясно, что, лишь только {у-у^^Ь, будет (при любом х
из X)
\<р(х)-fix, y)\*se, а также \ip(y)-A\*se;
в этом легко убедиться, переходя к пределу в неравенствах D) и (8)
при у' —у0 и фиксированных х и у. Сохраняя выбранное значение у,
найдем такое 5'>0, что
при \х-хо\<д'. Тогда из всех этих неравенств следует, что при тех
же значениях х выполняется и неравенство
так что и
lim q>(x)=A.
Теорема доказана.
Замечание. Можно показать, что число А, о котором только
что шла речь, в то же время будет и двойным пределом
функции f(x, у) при совместном предельном переходе х-+х0,
у-*у0. Это обстоятельство сближает доказанную теорему с теоре-
теоремой п° 168.
506. Предельный переход под знаком интеграла. Обращаемся теперь
к рассмотрению интеграла A), зависящего от параметра у, ограни-
ограничиваясь вначале случаем конечного промежутка [а,Ъ\ и функ-
функции, интегрируемой в собственном смысле.
Предполагая, что область ^ изменения параметра имеет точку
сгущения уй, поставим вопрос о пределе функции A) при у-*у0.
Теорема 1. Если функция f(x, у) при постоянном у интегрируема
по х в [а, Ь) и при у-*у0 стремится к предельной функции B) равно-
равномерно относительно х, то имеет место равенство
ь	ь
lim 1{у) = lim \f{x, у) dx = |>(;c) dx.	(9)
Доказательство*. Интегрируемость предельной функции
<р(х) уже известна [504, 3°]. Задавшись произвольным числом е>0,
* Для определенности мы предполагаем, что уа конечно.
42*

660	ГЛ. XIV. ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА	[506
найдем такое число д >0, чтобы имело место C). Тогда при \у-уо\ <д
будем иметь
ь	ь	ь
\f{x, у) dx - \фс) dx = | J [f(x, у) -ф)] dx ^
а	о	а
Ь
« J \Лх, У) - <р(х) | dx <e(Z> - а),
а
что и доказывает формулу (9).
Формула (9) может быть переписана в виде:
ь	ь
lim [f(x, y)dx= flim/(x, y)dx.
y~y« J	J y-y,
a	a
При наличии ее говорят, что предельный переход по параметру до-
допустим под знаком интеграла.
Предполагая, что все у-^уй, имеем:
Следствие. Если функция f(x, у) при постоянном у непрерывна
по х в [а,Ь] и при возрастании у стремится к непрерывной же
предельной функции, монотонно возрастая, то справед-
справедлива формула (9).
Ссылка на обобщенную теорему Д и н и [504, 4°].
В предположении, что область ^ сама представляет собой конеч-
конечный промежуток [с, д], рассмотрим в заключение вопрос о непре-
непрерывности функции A).
Теорема 2. Если функция f(x, у) определена и непрерывна, как функ-
функция от двух переменных, в прямоугольнике [а, Ь; с, д], то интеграл
A) будет непрерывной функцией от параметра у в промежутке [с, д].
Доказательство. Ввиду равномерной непрерывности функ-
функции f(x,y) [174], по произвольному е=-0 найдется такое <5>0, что из
неравенств
следует неравенство
Положим, в частности, х' =х" = х, у' ~у0, у"=У, тогда при |j-J0|
каково бы ни было х, будем иметь
Таким образом, функция f(x, у), при стремлении у к любому
частному значению у0, стремится к f(x, y^) равномерно

507|	§ 1. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ	661
относительно х. В таком случае, по теореме 1,
ь	ь
lim \f(x,y)dx = \f(x,yo)dx
У"*Уо ^	^
а	а
ИЛИ
lim
что и доказывает наше утверждение.
Так, например, не вычисляя интегралов
]	1
| arctg — dx, \ In (хг+у2) dx,
сразу видим, что они представляют собой непрерывные функции от параметра у
для любых положительных его значений.
507. Дифференцирование под знаком интеграла. При изучении свойств
функции A), которая задана интегралом, содержащим параметр у,
важное значение имеет вопрос о производной этой функ-
функции по параметру.
В предположении существования частной производной /у'(х, у)
Лейбниц дал для вычисления производной Г(у) правило, которое
в обозначениях Лагранжа записывается так:
y)dx,	cm)
или - если воспользоваться более выразительными обозначениями
К о ши -
»	*
Dy \f(x, y)dx=\ Dyf(x, у) dx.
Если такая перестановка знаков производной (по у) и интеграла
(по х) допустима, то говорят, что функцию A) можно дифференци-
дифференцировать по параметру под знаком интеграла.
Самое вьиисление производной по указанной формуле и получило
название «правила Лейбница».
Следующая теорема устанавливает простые достаточные условия
для применимости этого правила.
Теорема 3. Пусть функция f(x, у), определенная в прямоуголь-
прямоугольнике [а, Ь; с, д], будет непрерывна по х в [а, Ь] при любом постоянном
у в [с, д]. Предположим, далее, что во всей области существует

662	ГЛ. XIV. ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА	[507
частная производная fy(x, у), непрерывная как функция двух переменных *.
Тогда при любом у из [с, д] имеет место формула A0).
Непрерывность функции f(x, у) по х обеспечивает существование
интеграла A).
Фиксируя любое значение у=у0 придадим ему приращение Лу = к.
Тогда
ь	ь
1(Уо) = J/(*> Уо) dx, I(y0 + k)= \f{x, j0 + A;) dx,
а	а
так что
ь
1(У<,+к)-1(у0) [f(x,yo+k)-f(x, у0)^	,|n
	к	= J	к	dX-	(U)
a
Интеграл справа зависит от параметра к. Нам предстоит дока-
доказать, что при А:-*0 здесь допустим предельный переход под знаком
интеграла. Этим будет установлено и существование производной
/(-О
и наличие требуемого равенства
Г{Уо) = H
/с—О J
Ц
= cf;(
С этой целью, сначала по формуле Лагранжа напишем
/С*. У»+к)-Ях, у0) „^ + щ @<:е<1)	A2)
Пользуясь же равномерной непрерывностью функции fy\x,у),
по произвольному е>0 найдем такое 6>0, что при
\х"-х'\<д и l/'-y'l^b
будет вьшолняться неравенство
\f'y(x",y")-f'y(x',/)\^e.
Полагая здесь х' = х"=х, у'=у0, у"=уо+вк и считая |A;j -= й, полу-
получим, с учетом A2), что сразу для всех х будет
-г.
* Из этих условий, собственно, уже вытекает и непрерьшность функции f(x, у)
по обоим аргументам, но мы ею пользоваться не будем.

508]	§ 1. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ	663
Отсюда ясно, что подинтегральная функция A2) при к~+0 равномерно
(относительно х) стремится к предельной функции f'y{x, yQ). Этим, по
теореме 1, и оправдывается предельный переход под знаком инте-
интеграла A1).
В виде примеров снова рассмотрим интегралы, о которых была речь
в предыдущем п°. Очевидно, для у=»0
f	X	Г	X	С
Dy] и*,-*- J Dym-d*- - J
1
x ax
0	0	0
11	1
d 2 tg
= f Dy\a(x2+y*)dx = [—— dx = 2 arctg
J	J x2+y2
хг+уг
0	0	0
Легко проверить полученные результаты, непосредственно вычислив эти инте-
интегралы в конечном виде:
1
г х	1 1	у2
= arctg — dx = arctg —h — у In	,
J	У	у 2 \+y2
о
1
Г
hb>)= ln
J
и затем продифференцировав по у.
При у = 0 условия теоремы 3 нарушены; посмотрим, как обстоит дело
с производными функций Ii(y) и 12{у) при у=0. Если в первом интеграле подин-
тегральному выражению при у = 0 и x=-0, чтобы сохранить его непрерывность,
л	л
приписать значение —, то получим /,@) = —, так что функция ДОО будет непрерывна
по у и при у = 0. Но
h(y)-Ii(P) 1 , Уг arctg у
У	2 1+у* у
при у-*0, так что конечной производной при у=0 не существует. Для функции
же 12(у) имеем:
,,т , /iGO-Ш 1пA+у)	1
/2@) = - 2, 	=	Н2 arctg —
>'	У	У
при у —0. Здесь /2@)=гг, между тем как производная по у от подинтегральной
функции при у = 0 равна нулю, так что и интеграл от нее тоже нуль: правило
Лейбница не приложимо.
508. Интегрирование под знаком интеграла. Поставим, наконец,
вопрос об интеграле по у от функции A), скажем, в
промежутке [с, д].

664	ГЛ. XIV. ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА	1508
Нас особо будет интересовать случай, когда этот интеграл выра-
выразится формулой:
д	а ь	ь а
J 1{у) dy=\[\f{x, y)dx)dy=\{If{x,у)dy) dx,
с	с a	a c
которую - без скобок - пишут обычно так:
а ь	ь а
J dy \f(x, y)dx=\ dx \f{x, y)dy.	A3)
с a	a с
При наличии ее говорят, что функцию A) можно интегрировать по
параметру у под знаком интеграла (взятого по перемен-
переменной х).
Простейшие условия, достаточные для равенства двух повторных
интегралов A3), дает
Теорема 4. Если функция f(x, у) непрерывна (по обеим перемен-
переменным) в прямоугольнике [а, Ъ; с, д], то имеет место формула A3).
Докажем более общее равенство
v ь	ь ч
\dy //(*, у) dx= \dx\f{x,y)dy,	A3*)
с а	ас
ГДе C°?Z7]=sid.
В левой и в правой его частях мы имеем две функции от пара-
параметра % вычислим их производные по г\.
Внешний интеграл в левой части имеет подинтегральную функ-
функцию A), непрерывную по у в силу теоремы 2. Поэтому его произ-
производная по переменному верхнему пределу будет равна подинтеграль-
ной функции, вычисленной при у=% т. е. интегралу
В правой части A3*) стоит интеграл
Ь	I)
\ср(х, rj) dx, где ф, rj) = J/(x, у) dy.
Функция q>(x, rj) удовлетворяет условиям теоремы 3. Действительно,
<р{х, г]) непрерывна по х *, в силу теоремы 2, Затем производная
f'rix, rj) =/(x, rj)
Который играет здесь роль параметра.

509]	§ 1. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ	665
непрерывна как функция двух переменных. Поэтому к упомянутому
интегралу применимо правило Лейбница:
ь	ь	ь
Dr,]<p{x, rj) dx = )<р'г,{х, rj) dx = J f(x, rj) dx=I(rj).
a	a	a
Таким образом, левая и правая части равенства A3*), как функ-
функции от щ, имеют равные производные, следовательно, могут разниться
разве лишь на постоянную. Но при rj = с оба упомянутых выражения
обращаются, очевидно, в нуль; следовательно, они тождественны при
всех значениях rj, и равенство A3*) доказано.
При г) = д из него, в частности, и получается равенство A3).
Рассмотрим примеры. 1) Пусть f(x, у) = хУ в прямоугольнике [0, 1; а, Ь],
где 0«=а-=6. Условия теоремы соблюдены. Имеем
6 1	16
[dy [хУс1х= [
a 0	0 a
Слева легко получается окончательный результат
ь
г dy	l + b
	= ln	,
J1+y 1+a
и
1
справа же мы приходим к интегралу I	dx. Таким образом, благодаря
J \пх
о
перестановке интегрирований, мы находим его значение [ср. 497, 16) (в)].
2) В случае функции fix, у)=	; в прямоугольнике [0, 1; 0, 1] условия
теоремы не выполнены: налицо разрыв в точке @, 0). Имеем:
1
х
х=0
e=arctgy
о 4
о о
в то время как
1 1
509. Случай, когда и пределы интеграла зависят от параметра. Об-
Обратимся к рассмотрению более сложного случая, когда не только под-
интегральное выражение содержит параметр, но и самые пределы ин*
теграла здвисят от него.

666	ГЛ. XIV. ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА	[509
В этом случае интеграл имеет вид
«у)
КУ)= ]Ax,y)dx.	A4)
«у)
Ограничимся исследованием вопроса о непрерывности и дифферен-
цируемости по параметру подобного интеграла.
Теорема 5. Пусть функция f[x, у) определена и непрерывна в прямо-
прямоугольнике [а, Ъ; с, д], а кривые
х=х(у), х=Р(у) [c*sy*sd]
непрерывны и не выходят за его пределы. Тогда интеграл A4) пред-
представляет собой непрерывную функцию от у в [с, д].
Если у0 есть любое частное значение у, то интеграл A4) можно
написать в виде
ЭЫ	«у)	Чу)
/00= J /(*, y)dx+ \ f{x, y)dx- J f(x, у) dx.	A5)
Чу.)	«у.)	«(у*)
Первый интеграл, в котором пределы уже постоянны, при у -»у0 стре-
стремится к
«У.)
A>*o)= \ f(x,yo)dx,
по теореме 2. Остальные же два интеграла допускают оценку
«У.)
где M=max \f(x, y)\, и в силу непрерывности функций х(у), j3(j) -
при у-*у0 стремятся к нулю.
Таким образом, окончательно
У-Уо
что и доказывает теорему.
Теорема 6. Если, сверх сказанного, функция f(x,y) допускает в
прямоугольнике [а, Ъ; с, д] непрерывную производную f'y(x, у), а также
существуют и производные <х.'(у), fi\y), то интеграл A4) имеет

509]	§ 1. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ	667
производную по параметру, которая выражается формулой
«у)
г(у) = J /X*, y)dx + ПУ) -ЛКу), у) - Лу) -№у)> у)- 06)
Чу)
И здесь мы будем исходить из равенства A5). Первый интеграл
при j=yQ имеет производную, представляемую интегралом от произ-
производной
«У.)
J f'y(x,yo)dx
<у„)
- по теореме 3. Для второго интеграла (значение которого при у=у0
есть нуль) имеем, по теореме о среднем:
«у)
«у.)
где Зс содержится между j3(j0) и /?(>>). Отсюда производная второго
интеграла при у=у0, которая совпадает с пределом предшествую-
предшествующего выражения при у~*у0, будет
Р'(Уо)-АКУо)>Уо)-
Аналогично, для производной третьего интеграла при у=у0 получим
-<*-'(Уо)-/«Уо),Уо)-
Объединяя все эти результаты, убедимся в том, что производная
Г(Уо) существует и дается указанной формулой.
Замечание. Заключения обеих теорем сохраняют свою силу
и в предположении, что функция f(x, у) задана (и обладает указан-
указанными свойствами) лишь в области, содержащейся между кривыми
х=л(у) и x=jS(>>).
Возможность рассматривать функцию и вне этой области использо-
использована была для упрощения рассуждений.
Поучительно взглянуть на установленные результаты и с такой
точки зрения. Интеграл 1(у) получается из интеграла
и, v)= ]f(x,y)dx,
зависящего от трех параметров у, и, v, подстановкой и=х(у), v =
=/?(>>). Вопрос исчерпывается применением общих теорем о непре-
непрерывности и о дифференцировании сложной функции. В частности,

668	ГЛ. XIV. ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА	1510
формула A6) написана по классической схеме:
dl dl dl ,, ч Ы
510. Введение множителя, зависящего лишь от х. Легко получить
некоторое обобщение установленных выше результатов, и притом -
без привлечения новых идей. Именно, можно вместо A) рассмотреть
интеграл
ь
\x,y)-g{x)dx,	A*)
где g(x) является функцией от х, которая абсолютно интегри-
интегрируема в промежутке [а, Ь] (возможно, и в несобственном
смысле). Таким путем удается частично распространить изложенную
элементарную теорию и на несобственные интегралы.
Сформулируем предложения, аналогичные теоремам 1, 2, 3 и 4:
Теорема 1*. При предположениях теоремы 1 имеет место фор-
формула
ь	ь
lim \f{x,y)-g{x)dx = \<p{x)-g(x) dx.
a	a
Прежде всего заметим, что все интегралы, фигурирующие в этих
формулах, существуют. Интегрируемость предельной функции у(х)
была уже доказана. Существование же интегралов от /• g и q> • g (во-
(вообще говоря, несобственных) следует из п° 482.
Теперь, задавшись числом е >0, найдем, ввиду равномерного стрем-
стремления f(x, у) к (р(х), такое число 5=-0, что имеет место C)*. Тогда при
|j->>0|<<5 справедлива будет такая оценка:
*	*
\lf(x,y)-g(x)dx- [cp(x)-g(x)dx =s
a	a
Ь	b
* J |Л*. У) -Ф)I • ШI dx-= e • J \g(x)| dx,
a	a
что и доказьгоает нашу формулу, ибо справа произвольно малое число
ь
умножается на постоянное конечное число
\\g{x)\dx.
В частности, подобная теорема имеет место и для последо-
последовательности функций {fn(x)} с « в роли параметра. Мы
* Мы и здесь, как всегда, для примера рассматриваем случай конечного
распространение на случай у$= +*¦ не представляет трудности.

511]	§ 1. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ	669
сформулируем этот результат «на языке бесконечных рядов», так как
в таком виде он чаще применяется.
Следствие. Если 1) члены ряда
л=1
— интегрируемые в [а, Ь] (в собственном смысле) функции, и ряд схо-
сходится равномерно, 2) g(x) - абсолютно интегрируемая в [а, Ь]
функция (хотя бы и в несобственном смысле), то ряд
Zun{x)-g(x)
л=1
можно интегрировать почленно.
Далее, совершенно так же, как и теоремы 2 и 3 (но лишь со ссыл-
ссылкой на теорему 1* вместо 1), доказывается:
Теорема 2*. При предположениях теоремы 2 интеграл A*) будет
непрерывной функцией от у в промежутке [с, д].
Теорема 3*. При предположениях теоремы 3 функция A*) будет
дифференцируема по параметру, и имеет место формула:
Наконец:
Теорема 4*. При предположениях теоремы 4 справедливо равенство
повторных интегралов
\l(y)dy=\dy If(x, y) .g{x) dx= jg(x) dx\f{x, y)dy.
Доказательство буквально воспроизводит доказательство теоремы
4 (лишь со ссылкой на теоремы 2* и 3* вместо теорем 2 и 3).
Многочисленные примеры применения этих (равно как и пред-
предшествующих) теорем читатель найдет в следующем п°.
511. Примеры. Используя разложение в ряд функции ех, представить в виде
суммы ряда интеграл
1	г
(a) [e'lnxdx, (б) [e—^—dx.
о

670	ГЛ. XIV. ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА	[511
По
(а)
(б)
следствшо из теоремы
/-
0
1
i 1
1
:ln xdx= In х- jl
0
l
0
1
0
1* имеем:
¦у X"\
+ 2 —7 \dx
1
dx+ У1 —— [
0
m— — -^
m =
2) Разложением в ряд вычислить интеграл
1
hnx-ln
о
По теореме п° 437, 5°, ряд
хп
равномерно сходится в промежутке [0, 1]. Так как Inx абсолютно интегри-
интегрируема в этом промежутке, то, по тому же следствшо из теоремы 1*,
1	П	J	I H(H+1J
0
Ввиду тождества
111	1
л(и+1J п л+1 (л+1J'
учитывая притом известные разложения
*
Z
1п2,
v	,>=i J>2	12
вьфажение для / можно представить в виде:
и+1 (n+l)
Здесь для 7 получилось значение «в конечном виде». Разумеется, это удается
не всегда.
* 405 A8); 440, 8).

511]	§ 1. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ	671
3) Обозначая через Рп{х) n-ый многочлен Лежандра, доказать, что
« ( М j
¦ cos п+— \<ра<р
71 J
Pn(COS0) =
0
Если вспомнить происхождение многочленов Лежандра Рп(х), как ко-
коэффициентов разложения по степеням а выражения	—— [447, 8)], то доста-
достаточно, рассмотрев ряд yi-2oor+a2
п COS | П + — |
-1Н-^=^=,	A7)
л „=о J ]/2(cosip-cos0)
установить, что сумма его равна указанному выражению при х = cos 0.
Так как [ср. 461, 2)], при |а| -= 1,
1
cos — q>
и ряд сходится равномерно относительно <р (ибо мажорируется геометри-
ческой прогрессией 2^lal" > то РЯД A7) - снова потому же следствию - можно
о 1
преобразовать так:
в	1
cos — q>
2---	2	¦"¦
Л J
~\/2(.cos<p-cosO)
Прибегая к тем же подстановкам, что и в задаче 9) 497 (где, собственно, был
установлен частный результат, для л = 0 и 1), последовательно получим:
1
1 - а г	1	dz
I - a (•	1	dz	2	(•
		= -(l-a) —
я J Y(z-x)(l-z) l-2az+a2 л	J A —
что и завершает доказательство.
4) Воспроизведем один из приемов, с помощью которых Эйлер получил
свой результат:
1 я2
Вычислим интеграл
1
2 — = — •
n=in2 6
г	ах г	л2
Е= arcsin х • ^^^= = arcsin x d arcsin x = —
J	yi_^ J	8
о

672	ГЛ. XIV. ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА	[511
еще иначе, воспользовавшись известным разложением арксинуса
^, Bл-1)!!
которое в промежутке [0, 1] сходится равномерно. Будем иметь
Я ^т 1 dx r xdx ^r Bи-1)!! г хт+х
х-\- У >	= 1	\- / 	 I 	dx
n=i"Jyfr^2 J уГ^Зс5- n=i2n!!Brt+l)J УПГ^г
о ' о ' о '
Так как
то получается, что
1
1-
0
Е
Х2П+
п^
Я2
8
1
— dx =
= 1 +
л
2
= fsin2'1+
0
^i Bл+1
2п!!
Bл+1)!!
V 1
)» п^1Bл-1J
откуда уже легко прийти к упомянутой вначале формуле.
5) Показать, что прием Лобачевского, с помощью которого в 14)
и 15) п° 497 были выведены формулы
г sin х	г	г sin^ х	г
J № —- - dx = J f(x) dx, J f{x) --r <fe = J
[4]
применим и в том случае, когда функция fix) в промежутке 0, — I интегрируема
в несобственном смысле (при сохранении прочих условий).
С помощью этих формул получаются, например, следующие интегралы:
(a) I In | sin jc |	dx= In sin x dx = - — In 2;
•'	x	j	z.
f In I cos x I p In I cos x I sin2 x f In cos x n
F) 	dx =	dx = 	ал: =
J x2	J sin2* x2	J sin2*	2
oo	о
(интегрирование по частям);
rln2|cosx|	fln2cosx
(в) 	<fe= 	«be =-я In 2 (тоже).
J x2	J sin2*
о	о

511]
§ 1. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ
673
6)	Установить непосредственно, что для интегралов (где у>0)
1	1	f
(а)	— dx, (б) \ — е у dx
J (*2+>>2J	J у*
о	о
предельный переход при у-0 не может быть произведен под знаком интеграла.
Удостовериться в нарушении условий теоремы 2.
7)	Применить правило Лейбница к вычислению производной по пара-
параметру от интеграла
Легко проверить, что условия теоремы 3 здесь соблюдены. Имеем
г lade	я
Ja2-sin20 УсП
о	'
Отсюда, интегрируя по а, восстанавливаем значение Да):
Для того чтобы определить постоянную С, представим интеграл Да) в виде
п
~2
Г ( 1	"\
7(в)=л1па+ In I	sin2 б ей,
О
так что, если использовать и найденное для Да) выражение,
п
~2
С= In 1-— sin2e\de-nln-—'	 .
J { a2 J	a
о
Перейдем здесь к пределу при е- +°°; так как
то интеграл стремится к нулю, и находим: С= -лIn 2. Окончательно, для я
[ср. 497, 7)]:
Весьма замечательно, что дифференцирование по правилу Лейбница
позволило найти конечное выражение предложенного интеграла. Этот метод
нередко приводит к цели.
8) Еще проще вычисляется уже известный нам [307, 4); 314, 14); 440, 11)] ин-
интеграл
f
ln(l-2rcosx+r2)<?c

674	ГЛ. XIV. ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА	[511
По правилу Лейбница
/'(,)= J-
-2cosx+2r
J
о
X
2rcosx+r2
о
dx,
С помощью подстановки r-tg— легко установить, что полученный интеграл
равен 0; в таком случае
/(r) = C = const.
Но /@) = 0, значит, С = 0. Итак, при | г\ * 1 интеграл /(г) = 0.
г arctg х
9) Вычислить интеграл /= 	==== dx.
Вводя параметр, рассмотрим более общий интеграл
1
arctg xy
г arctg
/00 = —
oJ л: У1-
<&
из которого предложенный интеграл получается при у=\. Условия теоремы 3*,
если положить
arctg xy	1
f(x, у) =	 и g(x)
вьшолнены. Дифференцируя по у (под знаком интеграла), найдем
1
dx
г
J
о
этот интеграл легко вычисляется, например, с помощью подстановки x=cos6:
2
dd	1	tg в
л	F ~ ' *"	Г ~ ' • 0
* л 1
Отсюда, интегрируя, находим
Так как /@) = 0, то С = 0; при у = 1 получаем, наконец, искомый интеграл
10) Доказать, что выражения
я	я
(а) и = хп- Г cos (д: cos б) sin2" 6^0 и (б) и= Г cos(n6-x-sin 6) с/9

511]	§ 1. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ	675
(при целом rts»0) удовлетворяют так называемому дифференциальному уравнению
Б е с с е л я:
х V+хи' + (х2 - и2)м = 0.
Здесь роль параметра играет х. Дифференцируя под знаком интеграла дважды
(теорема 3), найдем, что сумма в левой части уравнения (при подстановке вместо
и указанных выражений) будет равна:
л
(a) xn+l I [x.cos(xcos0)sin2"+20-Bn+l)sin(xcos0)-cos0-sin2" 0]d0 =
= -sin2n+1 0-sin (х cos в)
= 0,
(б) - ("[(я2 sin2 0 + Ф - х2) cos (пв - х sin в) -х sin 0 -sin (пв-х sin в)] dO =
= - (п+х cos в)- sin (пв - хsin в)
= 0.
11) Доказать, что уравнению
d2u I du
(при целом и) удовлетворяет функция Aux+Bi^ {А, В - произвольные постоян-
постоянные), где
«!= fenrcose d6,
о
„2= fgnrcose in (r sin2 б) dO.
Очевидно, достаточно проверить, что уравнению удовлетворяют функции
«1, и2 порознь. Это выполняется, как и выше, с помощью дифференцирования
под знаком интеграла, причем к функции иг применяется теорема 3, а к функции
п
«2 = Ьг- enrcose dB + 2 gn/-cos
ose in sin 6 с/б
о	о
еще и теорема 3*.
12) Найти производные от полных эллиптических интегралов
Е(к)= У1 — A:2 sin2 q> dq>,
о
л
кда-Г' d<p
J
по модулю A: @-= A:-= 1).
У1 - A:2 sin2
0 '

676	ГЛ. XIV. ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА	[511
Имеем
л
— =- \к sin2 <р-(\-кг sin2 <p) 2 d<p =
dk J
о
л	л
2"	Т
1 ( Г	-	Г	-i-
= -] A-A:2sin»2 «fy- A-A;2sin29)) 2
E-K
Аналогично
л
~	Т
1 I г	-I
= _J In-t2s,-n2m1 2/Jm-
dk
Но
2	?
— I A - Л2 sin2 93) 2 d<p - A - A:2 sin2 m) 2 c/95! .
A: U	J	J
= 	 Г A-
1 К J
*« sin» pM"
так что
с/К Е	К
«ft Щ-к2) к
Полученные формулы имеют интересные применения. Например, если ввести
сопряженный модуль k' = Yl-k* и функции
и К'(А:)
d
то легко получить — (ЕК'+Е'К-КК') = 0, откуда следует, что ЕК'+Е'К-КК' =
dk
= с = const.
Для определения величины этой постоянной с установим предел левой
части при к — 0 (к' -1): этот предел, очевидно, и будет с. Прежде всего, легко полу-
получить, что
Г	с/т	г	я
limK = lim	—= с/ю = -;
/,-0 J /I _ ?2 sjn2 д, J	2
/,-0 J /I _ ?2 sjn2 д,
0 '	^
limE' = lim У1 — A:'2 sin2 ip «f^ = \cosq>dqi =
4—0 k'—lJ	J
k
0
* Это вытекает из легко проверяемого тождества:
A - к* sin2 q>f* = —- A - к* sin2 уJ - -^- — Lsin <p cos уA - к2 sin2
1 - кг	\-№ а<р

511]	§ 1. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ	677
[теорема 2, 506]. Затем имеем:
п
~2
f	d&	71	1	Ж
K' =
J Vl - J-'2 sin
2 sin2 p
2 fl^T* 2k'
2
так что
f к2 sin2 <р	л:
S-K|=K-E= 	— <fy«= — А;2,
J У1 - A:2 sin2 <р 2
|К'(Е-К)|<= — к и ШпК'(Е-К) = 0.
4	А—О
л
Искомый предел оказывается равным —, и мы приходим окончательно к извест-
известному соотношению Лежандра:
ЕК'+Е'К-КК' = -.
13) Доказать тождество
где /(О есть произвольная функция, непрерывная в промежутке [а, Ь] и a*ex=sb.
Решение. Прибегнем к методу математической индукции. При и = 1 тожде-
тождество очевидно. Допустим теперь, что оно справедливо при каком-нибудь лэ=1
и докажем его справедливость и при замене п на п+1.
Для краткости положим
=7n~hy. J(
~t)n'
Продифференцируем по х выражение
X
1
с применением теоремы 6. Так как нижний предел здесь постоянен, а на верхнем
пределе, т. е. при t = x, подинтегральная функция обращается в нуль, то внеин-
тегральные члены формулы A6) исчезают, и мы получим
Ввиду того, что /п(а) = 0, отсюда
X
In+i(x)= \In(tn)dtn.

678
ГЛ. XIV. ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА
[511
Подставляя вместо 1п его выражение в виде повторного интеграла, придем
к такому же выражению и для /„+,.
Совершенно так же доказывается и более общий результат:
V('n-i) dtn-x J v'ifn-i) Лп-2 ¦ • • j7@ dt = J—^
где /и <р - непрерывные функции в промежутке [а, Ь], причем д> имеет и непрерыв-
непрерывную производную.
14) Найти производную по параметру а интеграла
где <р(х) непрерывна вместе со своей производной <р'(х) в промежутке [0, а] и
Применить формулу A6) непосредственно мы не можем, ибо подинтеграль-
ное выражение при * = <х, вообще говоря, обращается в бесконечность. Мы при-
прибегнем к обходному пути, именно, подстановкой x = a.t преобразуем интеграл
к виду:
1
здесь применима уже теорема 3*. Найдем, дифференцируя интеграл по правилу
Лейбница:
1 о
или, если вернуться к прежней переменной,
а
1 С Ф) _,_. . 1 f хд>'{х)
о
,„. If Ф) , 1 Г хд>'
/'(а)=	dx+-
2aJ Vo^lx	aJ Vk
dx.
Преобразовав первый из этих интегралов путем интегрирования по частям,
можно придать формуле более простой вид:
15) Пусть
fix, ^) =
/@, y) =
при

511]	§ 1. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ	679
1
Установить непосредственно, что к интегралу fix, у) dx правило Лейбница
о
при у = 0 неприложимо.
То же для функции
X'
f(x,y) = x-e у при 0==*=й1, 0<,у=е1,
fix, 0) = О
16) Представим вычисление интеграла
7- \^^L-dx,
J.yi-,2
который мы нашли в 9) дифференцированием по параметру, в другом виде.
arctg х
Заменяя в подинтегральном выражении 	— равным ему интегралом
х
1
arctg х г dy
о
перепишем / в форме повторного интеграла
г	1
/= i - . ^
Г dx r dy
J 1/1 _ V-2J 1+Х2у"
о '	о
Применяя теорему 4*, переставим интегрирования:
11	1
/= I ^.. .	dX	71 { dy	Л
С , С "х	я г
\dy\	= -r
J Jo (l+x2y2)Yl-x2 2J
o (l+xy)Ylx
17) Вычислить путем интегрирования под знаком интеграла интеграл
2
a+bsinx dx
r a+bsmx dx
К= In	(я=>6=»0).
J a - b sin x sin x
о
Представим подинтегральную функцию в виде интеграла
1 a+bsmx _ , с dy
- ln-
sin л: а - b sin х	J а2- Ьгуг sin2 x'
о
так что
K=2ab
2 1
dy
a2 - b2y2 sin2 x
о о

680	ГЛ. XIV. ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА	E12
Переставляя интегрирования (по теореме 4), получим:
1 ~2
о о
Так как
п
dx
J a*-l
- b2y2 sin2 x 2e]/a2-6V'
и
то, окончательно
l
гг и f dy	¦ b
K=nb 	 =n.arcsin—.
18) Приведем еще примеры случаев, когда перестановка двух интегрирований
оказывается недопустимой:
11	11
(а) J ^ J (*+,K 2 ' J * J tc+ ^ ^ 2 '
0 0	0 0
(; J*J 17 l^i	«' J"¦ j ь* у3)' "' «¦ 2
oo	oo
Само собою разумеется, что в этих случаях условия соответствующей теоремы
нарушаются: подинтегральная функция терпит разрыв в точке @, 0) *.
512. Гауссово доказательство основной теоремы алгебры. Опираясь на теорему 4,
Гаусс дал весьма своеобразное доказательство основной теоремы алгебры.
Эта теорема гласит, что всякая целая функция
(с вещественными или комплексными коэффициентами) имеет вещественный или
комплексный корень.
Положим х = r(cos в + / sin в); тогда
xk = rk (cos kO + /-sin кв),
так что
/M-P+QI,
где
P=r"cosnO+...,
* В случае (б), при ^ = 0, но х&О, подинтегральную функцию можно считать
непрерывной, если положить ее здесь равной нулю.

512]	§ 1. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ	681
причем ненаписанные члены содержат лишь низшие степени г, а члены, свободные
от г, сводятся просто к постоянным.
Теорема, очевидно, будет доказана, если будет установлено, что выражение
Рг+0,2 обращается в нуль для некоторой системы значений г и 0.
Введем в рассмотрение функцию
Р
tf-aictg-.
Тогда
BU дг'	Ifr dU По	'~дТ
~дг	P2 + Q2 ' дО
так что
д2 U Н(г, 0)
здесь Н(г, 0) есть непрерывная функция г и 0, точное выражение которой для нас
не представляет интереса.
Составим, наконец, повторные интегралы
2.1
"—_ dO
'•-И
оо	о и
где R есть положительная постоянная, значение которой мы установим ниже.
Если бы функция P2+Q2 никогда не равнялась нулю, то подинтегральная
функция была бы непрерывна, и, по теореме 4, необходимо было бы: 1Х=12- Мы
покажем, однако, что при достаточно большом R подобное равенство
заведомо не выполняется; это будет свидетельствовать о том, что в круге радиуса
R вокруг начала функция P2+Q2 должна принимать и нулевое значение, и теорема
будет доказана.
Вычисляя внутренний интеграл для /х, получаем:
дги ja ди
г д*и
УдгдО
= 0,
в=о
о
ди
так как из самого выражения для	 видно, что это и есть функция от в с периодом
дг
2л. Отсюда следует, что /х = 0.
Обращаясь к интегралу /2, имеем
с d2U dU
Здгдв дв
/•=0
0
Для дальнейшего важно теперь рассмотреть старшие относительно г члены числи-
теля и знаменателя дроби — .
ВО
Так как
дР	BQ
—•= -пгп&тпв+ ..., — = n
то

682	ГЛ. XIV. ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА	[513
С другой стороны,
P-+Q2=r2n+...,
так что, окончательно, имеем:
dU -пгт+...
~дв =
Так как ненаписанные члены содержат низшие степени г, коэффициентами
которых служат ограниченные функции от в, то не только
v dU
но самое стремление к пределу - п происходит равномерно относительно в.
t)JJ(	йР ЯО Л
Поскольку при г = 0 и — = О I ибо в этом случае — = — = 0 , внутренний
dU
интеграл для 12 сводится к значению 	 при r = R. Когда Л~~, это значение
дв
стремится к -л равномерно относительно в. А тогда, по теореме 1,
lim /2 = - Ъгп.
Таким образом, для достаточно больших R интеграл /2 будет отрицательным,
и равенство Iy = L станет невозможным.
§ 2. Равномерная сходимость интегралов
513. Определение равномерной сходимости интегралов. При рас-
распространении изложенной теории интегралов, зависящих от пара-
параметра, на случай несобственных интегралов особую роль иг-
играет понятие равномерной сходимости интегралов, кото-
которое мы предварительно и выясним.
Предположим, что функция fix, у) задана для всех значений х^а
и всех значений у в некоторой области ^Ц. Пусть, далее, при каждом
у в этой области существует интеграл
I{y)=\f{x,y)dx.	A)
а
По самому определению несобственного интеграла с бесконечным
пределом [470]:
[f(x, у) dx = lim f/(x, у) dx.
а	а
Таким образом, интеграл
А
F(A,y)=\f{x,y)dx,	B)

513J	§ 2. РАВНОМЕРНАЯ СХОДИМОСТЬ ИНТЕГРАЛОВ	683
представляющий собой функцию от А и у, при у = const и А - •» имеет
пределом /(.у). Если стремление этого интеграла к 1(у) происходит
равномерно относительно у в области °У, то интеграл 1(у) на-
называют равномерно сходящимся относительно у для указан-
указанных значений параметра.
Это значит, что для любого е =-0 найдется такое не зависящее
от у число Aos*a, что, лишь только А>А0, неравенство
->	А	-.
\f(x, у) dx - \f{x, у) dx | = | \f(x, у) dx
будет выполняться одновременно для всех значений
У в %
Для примера рассмотрим интеграл
I уе-хУ dx,
который сходится при каждом фиксированном значении
Вычислим непосредственно интеграл
е-ху dx.
При у = 0 он равен 0, каково бы ни было А; если же у *¦ 0, то с помощью подстановки
ху = t легко находим
[уе~*У dx= [
A	Ay
Когда у фиксировано, это выражение при А-*•*•, очевидно, стремится к 0, и,
каково бы ни было е =»0, неравенство
е-^У-ге	C)
1п-
е
будет выполняться для всех А >А0(у), где Аа(у)	зависит от у.
У
Если изменение у ограничено промежутком [с, В], где с =- 0, то найдется и н е
зависящее от у число Аь, такое, что при А>*А0 неравенство C) будет вы-
выполняться сразу для всех у: достаточно за Ао принять А0(с), ибо при А>А„
будет тогда
Иными словами, наш интеграл сходится равномерно относительно у
в промежутке [с, 9].
Иначе обстоит дело, если параметр у изменяется в промежутке [0, 3] (#=-0).
На этот раз такого Ао уже не существует (по крайней мере, если е-= 1). Это видно
хотя бы из того, что, сколь большим ни взять А, выражение е~АУ стремится к 1
при у ¦* 0, так что для достаточно малых значений у оно будет больше любого

684	ГЛ. XIV. ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА	[515
числа е-=1. Сходимость интеграла при изменении у в промежутке [0, д] уже не
будет равномерной относительно у.
514. Условие равномерной сходимости. Связь с рядами. Пользуясь
общим критерием равномерного стремления функции к пределу [504,
1°], можно применительно к рассматриваемому случаю сформулиро-
сформулировать его так:
Для того чтобы интеграл A) сходился равномерно относительно
у в области ^j, необходимо и достаточно, чтобы при любом задан-
заданном е>0 нашлось такое число Ао, не зависящее от у, чтобы
неравенство
А'	А	А'
\f{x, у) dx - \f{x, у) dx = jf(x, у) dx
выполнялось одновременно для всех у в °Ц, лишь только
А'>А>А0.
И здесь, как обычно, дело сводится к тому, чтобы для всех рас-
рассматриваемых значений у равномерно выполнялся принцип
сходимости [ср. 475].
Несобственный интеграл с бесконечным пределом мы в 475 уже
сопоставляли с бесконечным рядом. Связь с бесконечными ряда-
рядами существует и в вопросе о равномерной сходимости инте-
интеграла A).
Как мы знаем из 504, 2°, для равномерного (относительно у) при-
приближения функции F(A, у) [см. B)] при А •* °° к интегралу A) необ-
необходимо и достаточно, чтобы к этому интегралу равномерно сходи-
сходилась каждая последовательность функций {F(An,у)}, какова
бы ни была варианта Ап, стремящаяся к +<*¦.
Если, наконец, от «языка последовательностей» перейти к «языку
бесконечных рядов», то придем к окончательному заключению, что
равномерная (относительно у) сходимость интеграла A) совершенно
равносильна равномерной же сходимости всех рядов вида
2 \ /(•*> У) dx Ц0 = а, Апз* а),
л=0 J
Ап
где Ап есть любая варианта, стремящаяся к + ~.
515. Достаточные признаки равномерной сходимости. Установим
теперь некоторые признаки, по которым обыкновенно на практике
судят о равномерной сходимости интегралов.
Они построены по образцу признаков Вейерштрасса, Абеля
и Дирихле равномерной сходимости функциональных рядов [430],
а также близки к признакам сходимости несобственных интегралов

515]	§ 2. РАВНОМЕРНАЯ СХОДИМОСТЬ ИНТЕГРАЛОВ	685
[476], которые мы также связывали с именами Абеля и Ди-
Дирихле.
1°. Мы будем предполагать, что функция f(x, у) интегрируема
по х в каждом конечном промежутке [a, A] (As*a). Если существует
такая, зависящая лишь от х, функция <р(х), интегрируемая в бес-
бесконечном промежутке [а, + ¦»], что при всех значениях у в °J)
I fix, у) | =s (р(х) (для х э= а),
то интеграл A) сходится равномерно относительно у {в ука-
указанной области его значений).
Это непосредственно вытекает из неравенства
А'	А'
)f{x,y)dx =s j(p(x)dx,
если воспользоваться критерием предыдущего п°.
При указанных условиях иногда говорят, что функция f(x, у) имеет
интегрируемую мажоранту ср(х), или что интеграл A) мажо-
мажорируется сходящимся интегралом
j dx,
не содержащим параметра.
2°. Более тонкие признаки, как и в 476, доставляет нам примене-
применение второй теоремы о среднем.
Рассмотрим интеграл от произведения двух функций:
D)
предполагая функцию f(x, у) интегрируемой по х в любом проме-
промежутке [а, А], а функцию g(x, у) монотонной по*.
Если интеграл
\f{x,y)dx
сходится равномерно относительно у в области <^, а функция
g(x,у) равномерно ограничена:
\g(x,y)\^L (L = const, xs*a, у из <*J),
то интеграл D) сходится равномерно относительно у в обла-
области ^).

686	ГЛ. XIV. ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА	|515
Вместо F) п° 476, имеем на этот раз:
А'	?	А'
J/(*, y)gix, у) dx = g(A, у) j/(x, >•) dx + g(A', y) \f(x, у) dx.
Л	Л	?
Если на основании 514 взять Ао настолько большим, чтобы при
А' >А >А0 было
А'
$f(x,y)dx <~
А
одновременно для всех у, то (как и в 476) нетрудно получить оценку
А'
Г
)f(x,y)g(x,y)dx <e,
i
что [514] и доказывает наше утверждение.
3°. Аналогично п° 476, можно указать и другую комбинацию усло-
условий, налагаемых на функции fug.
Если интеграл
А
jf(x,y)dx
а
будет равномерно ограничен, как функция от А и у:
\f(x,y)dx
(K= const, As*a, у из
a g(x,jO-0 при х-~ равномерно относительно у (в области
^)), то интеграл D) сходится равномерно относительно у в об-
области *у.
Доказательство предоставляем читателю.
4°. В заключение заметим, что на практике чаще встречается слу-
случай, когда из двух множителей / и g на деле лишь один содержит
параметр у. Таким образом, каждый из критериев 2°, 3° дает два
частных признака (в зависимости от того, какой из этих множи-
множителей содержит у).
Сформулируем один из признаков, вытекающих из 2°, который
наиболее часто применяется на практике:
Если интеграл

516]	§ 2. РАВНОМЕРНАЯ СХОДИМОСТЬ ИНТЕГРАЛОВ	687
сходится, а функция g(x, у), монотонная по х, равномерно ограничена,
то интеграл
\f(.x)g{x,y)
dx
сходится равномерно относительно у.
В качестве примера, отсюда следует равномерная относительно у, для уз^О,
сходимость интеграла типа
[e-xy-f(?c)dx, [e-*y.f(x)dx (аэ=0)
в предположении, что интеграл f(x) dx сходится. Действительно, обе функции:
а
е-ху, е-х'у, монотонно убывающие по х, ограничены единицей.
Это замечание не раз будет нам полезно в дальнейшем.
516. Другой случай равномерной сходимости. Рассмотрим теперь
функцию f(x,у), определенную для значений х в конечном про-
промежутке [а, Ь] и значений у в некоторой области <^j; пусть при у = const
она интегрируема по х (в собственном смысле или нет) от а до Ъ.
Тогда интеграл
ь
Ky)=\f(x,y)dx,	E)
а
будь он собственный или нет, является пределом при
tj-О интеграла
Ь-7,
cp{%y)=\f(x,y)dx.	F)
а
Если стремление этого интеграла при ^-*0 к пределу 1{у) проис-
происходит равномерно относительно у для значений у в области
% то говорят, что интеграл E) сходится равномерно отно-
относительно у в указанной области.
Это значит, что для любого е>0 найдется такое не завися-
зависящее от у число д > 0, что, лишь только г] < д, неравенство
О	О —7J	О
\f(x, y)dx- J Дх, у) dx\ = | J f{x, у) dx
будет выполняться одновременно для всех значений
У в %

688	ГЛ. XIV. ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА	[516
Нетрудно сформулировать для этого случая условие, необходимое
и достаточное для равномерной сходимости. И здесь оно сводится
к равномерному выполнению принципа сходимости: по числу
е>0 должно найтись такое не зависящее от у число б=-0, что при
О < т{ -= г\ -= б выполняется неравенство
Ь-г,'
\)f{x,y)dx
b
каково бы ни было у в области ^.
Точно так же здесь можно свести вопрос о равномерной сходи-
сходимости интеграла E) к вопросу о равномерной сходимости бесконеч-
бесконечного ряда:
\
J
2
л=о
какова бы ни была варианта ап-*Ь [ср. 514].
Наконец, переносятся на рассматриваемый случай и достаточные
признаки п° 515. Предоставляем это читателю.
Мы рассматривали интеграл E) от а до b как предел интеграла
F) от а до Ъ- щ, и нас интересовал характер приближения послед-
последнего интеграла к своему пределу. Таким образом, особую роль
здесь играет точка х = Ъ (как в 513 — точка х = °°). Может понадо-
понадобиться (в зависимости от обстоятельств, которые выяснятся дальше)
отвести подобную же роль и другой точке промежутка. Например,
тот же интеграл E) можно рассматривать как предел при г]-0 ин-
интеграла
\f(x,y)dx.
Если последний при г]-0 приближается к своему пределу равно-
равномерно относительно у, то также говорят о равномерной
сходимости интеграла E). Все сказанное выше переносится и на
этот случай.
Если может возникнуть сомнение относительно того, о каком виде
равномерной сходимости идет речь, говорят, что интеграл сходится
равномерно (относительно у в определенной области), соответственно,
при х- + °°, при х = Ь, при х = а и т. п.
Отметим, что, как правило, равномерная сходимость интеграла
E), скажем, при х=Ь, нас будет интересовать в тех случаях, когда
именно точка х = Ъ оказывается особой для интеграла E) [в смысле
п° 479] - при тех или иных значениях у.
Но определение не только формально сохраняет силу и тогда,
когда интеграл E) при всех значениях у оказывается

517]	§ 1. РАВНОМЕРНАЯ СХОДИМОСТЬ ИНТЕГРАЛОВ	689
собственным, но, как увидим, может оказаться реально полезным также
и в этом случае.
Например, интеграл	i
Г V
dx
для каждого значения у в промежутке [0, д], где д=-0, будет существовать как
собственный. Однако для указанного промежутка изменения у его сходимость
не будет равномерной при х = 0. Действительно, неравенству
J х*+у*
О
п
если только е-= —, нельзя удовлетворить одновременно для всех значений у>0:
2	я
сколь малым ни взять г), его левая часть при у -» 0 стремится к — и для достаточно
малых значений у будет, наверное, больше, чем е.
517. Примеры. 1) Доказать непосредственно равномерную относительно у
сходимость интеграла
¦dx
(для всех значений у).
Имеем:
dx
1
А2+у* А
откуда и вытекает требуемый результат.
2) Установить с помощью мажоранты, что интегралы
(а) Г е ~ ix! dx, (б) ie-txx0 cos x dx (as= 0)
сходятся равномерно относительно t для o
Указание. Мажорантой будет (а) е—'«**, (б)
3) Доказать непосредственно, что интеграл
для значений п= 1, 2, 3, ... не сходится равномерно относительно п.
Это следует из того, что, каково бы ни было А = const,
П
f-
А
-1-е ZA -1 при
А

690	ГЛ. XIV. ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА	[517
г sin ад:
4) Доказать непосредствено, что интеграл I	dx сходится равномерно
J х
о
относительно а в области азка0 =¦ 0, и неравномерно - в области
Если Ао настолько велико, что при А>А0
-dz
Z
А
-=?,
где е=-0 - произвольное наперед заданное число, то
р sin а.х г sin z
	dx- 	dz	G)
J X	J Z
Ao
по абсолютной величине будет меньше е для всех аг&Оо^О, лишь только А>-—.
«о
Этим доказывается первая часть утверждения.
Вторая же часть следует из того, что выражение G) при любом А = const стре-
стремится к пределу
г sinz п
	йг=—
J z	2
2 '
о
когда а-0.
5) Доказать равномерную относительно а сходимость интеграла
г sin ax
	cos х dx
J х
о
в любом замкнутом промежутке, не содержащем ± 1.
Указание. Преобразовать интеграл к виду
1 г sin (a+ l)x+sin (a - \)х
г)	—	dx-
6) Исследовать вопрос о равномерной (относительно /) сходимости интеграла
х sin х3 sin tx dx.
о

517]	§ 2. РАВНОМЕРНАЯ СХОДИМОСТЬ ИНТЕГРАЛОВ	691
Указ г. ни е. С помощью двукратного интегрирования по частям интеграл
!¦
приводится к виду:
А
cos х3 • sin tx t sin x3 ¦ cos tx
3.x	3	3x3
1 с cos x3-sin tx t r sin a:3-cos tx
°° 1 г cos A:d-sm tx t p
_ _ 	.	dx + —
A 3J	Л	3J
t2 fsin^-sini
отсюда ясна равномерная сходимость относительно / в любом конечном
промежутке.
7)	Установить, что интегралы
1	1
(а) Г хР'1 dx, (б) xP~l lnm х dx
о	о
(т - натуральное число) сходятся равномерно относительно р (при х = 0) в области
рэ=/?0>0 и неравномерно - в области р^О.
Мажоранта: (а) хР°~1, (б) хР'~1\^пх\т (для области рз*ра =-0). С другой сто-
стороны, какое бы ни взять ??= const,
\xP~1dx =	-~, когда р^О.
J	p
о
8)	Аналогично устанавливается равномерная сходимость интеграла
1
относительно р для/>»=ро=-0 (при д: = 0) и относительно q для q»qa>0 (при л= I).
9) Доказать, что сходимость интеграла
1
rsin*
	dx
J хУ
о
(при х = 0) будет равномерной относительно >> для у*?-.уа<2ине будет равномер-
равномерной для у <=2.
Мажоранта	для случ&я у =s,y0^2. Далее фиксируем rj>0 произвольно,
хУ"	sinx 1
но настолько малым, чтобы при x*&v было	э=—; тогда
х 2
V	V
г sin х 1 г dx	1
	dx =- —	=	эт2"У -* ~ при у - 2.
J ^	2J хУ-1 2B-у)

692	ГЛ. XIV. ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА	[517
10) Доказать равномерную относительно п (и=1, 2, 3, ...) сходимость ин-
интеграла
Ul+x+x2+ .. .+xn~1)\l \n- dx
о
(как при х = 0, так и при х •= 1).
Так как 1+д:-\-х2 + . ¦. +Д:"*:	 , то мажорантой служит функция
l—, которая в промежутке [0, 1] интегрируема.
11) Непосредственно установить, что сходимость интеграла
¦dx
1
Г У
не будет равномерной (при л: = 0) относительно у в промежутке [0, 1] изменения у.
Имеем, при произвольном т; = const,
V
г у*-х2	х \x=v t] 1
	dx =	 =	-—, если y~0.
J (x2+y2J	x2jry |x=o rf+y* tj
о
12) To же для интеграла
l
г 8х?у - %ху*
	dx.
J (х2+у2J
о
Здесь интеграл
v
Г
(.V+У2J
о
при у — rj обращается в	.
V
13) Доказать, что интеграл
С
\
J
cos х
е~ху
Xй
сходится равномерно относительно у для у»0 (как при л: = 0, так и при л; = =°).
По отношению к х = 0 это ясно из наличия мажоранты —, а для х=~ это
Xй
следует из сходимости интеграла
CCOSX
dx
CCOSX
J
J
о
[476] в связи с заключительным замечанием п° 515.

517J	§ 2. РАВНОМЕРНАЯ СХОДИМОСТЬ ИНТЕГРАЛОВ	693
14) Пусть функция ДО непрерывна для t^O. Если интеграл
сходится при /1 = <х и А=/5 (<х</3), то он сходится - и притом равномерно относи-
относительно А (при ? = 0 и при / = ¦»)- для всех значений /I между а и /5.
1
Доказательство. Интеграл I t*f(t)dt сходится, а *д~а для значений
о
Ав=а является монотонной функцией от I и ограничена единицей. Отсюда ин-
интеграл
1	1
Г f */(<)#= [t*-*'
для указанных значений А сходится равномерно (при t = 0). Аналогично убеждаемся
в том, что интеграл
t= it'-P-tPftt) dt
i	i
сходится равномерно относительно А для А«=/3 (при t= ~).
15) Установить равномерную относительно у сходимость (при х = ~) интеграла
rcosxy
J__rfx @<e*l)
о
для узву0 =- 0, и нарушение равномерности в случае, если изменение у ограничено
лишь неравенством >>=-0.
В отношении первой части утверждения можно было бы воспользоваться
признаком 515, 3° (ср. 4°), так как при любых у4э=0 и уз^у0
А
sin Ay
sin Ay I
cos xy dx
У Уа
о
а функция —, монотонно убывая, стремится к нулю при х ¦* °°.
Xй
То же замечание можно сделать, непосредственно рассматривая выражение
(•cosxv	rcosz
	dx^y0'1	dz.
) x?	) z
A	Ay
1
Вторая часть утверждения вытекает из того, что это же выражение при А- —
У
и у-*0 бесконечно возрастает.
(Легко видеть, что при х=0 интеграл сходится равномерно относительно
у - в любой области изменения у.)

694	ГЛ. XIV. ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА	[518
16) Доказать, что интеграл
равномерно сходится относительно /?, для /?э=/?0=»0.
Это следует из 515, 3°. Действительно, для /?в=/?0
sin fix dx
1-cosAfJ 2
о
С другой стороны, выражение
не содержащее /3, убывает с возрастанием х (по крайней мере для д:э=а) и стремится
к 0 при х-+~.
§ 3. Использование равномерной сходимости интегралов
518. Предельный переход под знаком интеграла. Мы займемся сей-
сейчас, главным образом, вопросом о предельном переходе под знаком
интеграла, распространенного на бесконечный промежуток. Теорема
1 п° 506 на этот случай не распространяется: если даже во всем бес-
бесконечном промежутке функция f(x,у) при у-+у0 равномерно
стремится к предельной функции у{х\ предельный переход под зна-
знаком интеграла может оказаться недопустимым.
Рассмотрим, в виде примера, функцию (и = 1, 2, 3, ...)
Обычными методами дифференциального исчисления легко устано-
установить, что наибольшего значения эта функция достигает при х = [/ \
з	' J
ЗУз ~2
и равно оно —~е . Так как при и-"-<*> это значение стремится к
нулю, то отсюда ясно, что функция fn(x) при h — ~ во всем проме-
промежутке [0, + ~) равномерно стремится к qo(x) = 0. Тем не менее
интеграл
о
при «->•« вовсе не стремится к нулю.

518]	§ 3. ИСПОЛЬЗОВАНИЕ РАВНОМЕРНОЙ СХОДИМОСТИ	695
Условия, достаточные для допустимости предельного перехода,
даются следующей теоремой:
Теорема 1. Пусть функция f(x, у) при у из «у интегрируема {в соб-
собственном смысле) по х в промежутке [а, А] при любом А>а, и в каж-
каждом таком промежутке при у-*у0 равномерно относительно
х стремится к предельной функции ср{х). Если, сверх того, интеграл
I{y)=\Ax,y)dx	A)
а
сходится равномерно относительно у (в <^)), то имеет место
формула
оо	оо
Mm \f(x,y)dx=\<p{x)dx.	B)
У~*Уо
а	а
Положим, как и выше,
А
F(A,y)=\f{x,y)dx.	C)
а
Для этого интеграла выполнены условия теоремы 1 п° 506, поэтому
А
MmF{A,y)= \<p(x)dx.	D)
У~*Уо
а
С другой стороны, очевидно,
lim F{A,y) = \f(x,y)dx,	E)
а
причем дано, что здесь стремление функции F{A, у) к своему пределу
происходит равномерно относительно у. В таком случае мы
имеем право сослаться на общую теорему п° 505 о перестановке пре-
предельных переходов и утверждать существование и равенство повтор-
повторных пределов, что непосредственно и приводит к B).
Отсюда, применяя обобщенную теорему Д и н и [504, 4°], можно
получить такое
Следствие*. Пусть неотрицательная функция f{x,y) непре-
непрерывна по х в промежутке [а, + ~) и стремится, возрастая
с возрастанием у, к предельной функции <р(х), также непре-
непрерывной в указанном промежутке. Тогда из существования инте-
интеграла
" x)dx	F)
* Мы считаем, что здесь все

696	ГЛ. XIV. ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА	[518
уже вытекает как существование интеграла A) (при всех у из 40,
так и наличие формулы B).
По упомянутой теореме при указанных условиях стремление функ-
функции f(x,у) к <р(х) будет равномерным относительно х в любом
конечном промежутке. Далее, в силу теоремы 1 п° 474, существует
интеграл A), так как
f(x,y)*scp(x).
Функция (р(х) играет одновременно и роль мажоранты [515], обеспе-
обеспечивающей равномерную (относительно у) сходимость интеграла
A). Таким образом, соблюдены все условия для применения преды-
предыдущей теоремы.
Читатель легко докажет, что предположение о существовании ин-
интеграла F) от предельной функции может быть заменено здесь пред-
предположением о существовании конечного предела
lim \f(x,y)dx
- отсюда уже будет вытекать и существование интеграла F), и на-
наличие формулы B).
В том же порядке идей можно получить и некоторое обобщение
теоремы 1 п° 510, относящейся к конечному промежутку.
Теорема Г. Пусть функция f(x, у) (для у из ^)) интегрируема (в
собственном смысле) в промежутке [a, b-rj], при любом rj>0 (но
<Ь-а), и в каждом таком промежутке при у-*у0 равномерно
относительно х стремится к предельной функции у(х). Если, сверх
того, интеграл
ь
\f(x,y)dx
сходится (при х = Ь) равномерно относительно у в ^, то имеет
место формула
ь	ь
lim J/(x, у) dx= )cp(x)dx.
Доказательство ничем не отличается от только что проведенного.
Легко распространяется на этот случай и следствие.
Конечно, роль точки Ъ может играть и любая другая точка про-
промежутка. Кроме того, подобных точек в промежутке может быть и
несколько.
Как и выше, с предельным переходом под знаком интеграла чаще
всего приходится иметь дело применительно к последова-
последовательности функций [fn(x)}. Переходя от последовательностей

519]	§ 3. ИСПОЛЬЗОВАНИЕ РАВНОМЕРНОЙ СХОДИМОСТИ	697
к бесконечным рядам, можно получить, таким образом, новые
теоремы о почленном интегрировании функциональных рядов.
Вот, например, какую форму получает следствие:
Пусть ряд
2 ип(х),
состоящий из положительных непрерывных для х»а
(или для a=sx-^b) функций, имеет для этих значений х непрерыв-
непрерывную же сумму (р(х). Если последняя в промежутке [а, + ~] (или [а, Ь])
интегрируема, то в этом промежутке ряд можно интегрировать
почленно. Здесь так же, как и выше, вместо интегрируемости
суммы ряда, можно было бы предположить сходимость ряда инте-
интегралов:
2 \ип(х) dx [или 2 f "п(*) dx \.
л=1 J	l	n=l J	J
Утверждение, очевидно, остается в силе и в том случае, когда все
члены ряда отрицательны: он приводится к предыдущему простым
изменением знака.
519. Примеры. 1) С помощью разложения в ряд вычислить интегралы:
1	1
f In A - л:) f In x
(a) 	dx, F)	dx.
J	X	J1-Х
о	о
Решение, (а) Разлагаем подинтегральную функцию в ряд
In A-х)	х хг х3
х	~ ~2"~Т~~'"''
все члены которого имеют отрицательный знак. Нарушается равномерность
сходимости вблизи х=\. Эта точка и является для суммы ряда особой; тем не
менее, в промежутке [0, 1] сумма интегрируема. Применяя последнее предложение
предыдущего п°, интегрируем почленно
х	„fi	A
[440 D)].
(б) Второй интеграл подстановкой x=\—z приводится к первому. Тем не менее,
1
для упражнения, вычислим его заново, разлагая в ряд	:
1-х
\пх
1-х л=о
все члены здесь тоже отрицательны. Равномерность сходимости на этот раз нару-
нарушается вблизи двух точек; # = Ои;с=1, так что упомянутое предложение

698	ГЛ. XIV. ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА	[519
п п
применить порознь, например к промежуткам I О,
тельно,
следует применить порознь, например к промежуткам 0, — и I — , II. Оконча-
о
2) (а) Вычислить сумму ряда
о * "=°о	"~"
11111
G = И	1	1	...,
3 5 7 9 11
исходя из того, что
1
йгт/*"* с-0'1.2'-)-
о
Решение. Имеем:
11	1
а= У(~1)п Uxln+xln+2) dx= f dx^ (- l)nxin • A + х2)= f-
1+JC*	Ttfl
0	J	J 0
oo
Хотя особенностей сумма ряда не имеет, но равномерная сходимость нару-
нарушается вблизи х=1. Так как для частичной суммы ряда имеем:
"—1	1±х*п	1+х2
то в роли мажоранты оказывается просто постоянная и интеграл от этой
суммы сходится (при х=1) равномерно относительно п. Этим оправдывается
почленное интегрирование (теорема 1').
(б) Аналогично:
1111	п 1 + V2
1- —+	+	••• =	— .
7 9 15 17	4 2
3) Исходя из формулы
1	1 г
—	- = - \(\-xy*xP
...(р+п) и! J
вычислить сумму ряда:
I	I	I
4567 78910
J-2-3-4 4-5-6-7 7-8-9-10

519]	§ 3. ИСПОЛЬЗОВАНИЕ РАВНОМЕРНОЙ СХОДИМОСТИ	699
Ответ.
о
1 r(l-xJx 3
(б)- 	dx = --\n2,
2j 1-х2	4
о
1 r(l-xK	1 1
(в)-	-dx =	1пЗ +
6J 1- °	' '
х3	6 4	2 VI 6
о	'
4) Вычислить интегралы Эйлера:
оо	mm
(а) 7=	dx, (б) JiT= —	dx.
J1+х	J 1-х
о	о
Решение, (а) Разбив интеграл на два интеграла:
1	оо
О 1
вычислим их порознь.
Для 0<;с< 1 имеем разложение в ряд
х0 ^
который сходится равномерно, лишь если О-=г==л;«=1-г'<: 1. Но частичная сумма
имеет интегрируемую в [0, 1] мажоранту
следовательно, интеграл от нее сходится равномерно (как при х = 0, так и при
х = 1). Интегрируя почленно, по теореме 1 получим:
1
/i=l Г(-о-*¦+'-***= 1^.
,'=о J	>.=о а + г>
0
Интеграл /2 подстановкой х=— приводим к виду
Z
2 J1+х Х J 1+х
о	о
Применяя уже полученное выше разложение, найдем:
h= 2-—-
r=i a-v

700	ГЛ. XIV. ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА	[519
Таким образом,
1 ¦?,	11 1
a v=i	\a-{-v a — v
Мы узнаем в этом выражении [см. 441, 9] разложение на простые дроби функции
п
—	. Окончательно,
	dx = -r
J 1+х smj
(б) Разбивая интеграл на два, как и выше, и делая во втором ту же подстановку,
получим
1	1
С х°~1 - х~а	г -х6 -х~ь
К^ —	dx- —	dx^Kt-Kf.
J 1-х	J 1-х
о	о
Очевидно, достаточно найти Кг. Прибегая к разложению подинтегральной
функции в ряд, как и только что, найдем:
1 Ъ( 1 М
х = -+2\	+	 .
a r=i\a + v a-vj
но [441, 9)] здесь мы узнаем разложение на простые дроби функции я-ctg па.
Итак,
	dx=n{z\%na- ctgnb).
J 1-х
о
5) Найти значения интегралов (| г\ -= 1)
1- г cos fix
г	1- г cos fix
1 ~ J (l + x2)(l-2rcos/SA:+r2)
FO2=J
ln(l+2/-cos/SA:+r2)
о
1+х-
причем в обоих случаях интеграл
С cos kx n
dx,
J 1+х2	2
о
считать известным [см. 522, 4°, а также 523, 9)].
* В обоих интегралах при х = 1 особенности не будет, особая точка х = 0; ин-
интегралы сходятся.

519]	§ 3. ИСПОЛЬЗОВАНИЕ РАВНОМЕРНОЙ СХОДИМОСТИ	701
Решение, (а) Исходим из разложения
1 - г cos fix
l-2rcos/?A:+r2 r=o
= 2 r" cos vflx *;
1
умножая на	, интегрируем почленно
1 + х-
,,=0 J
cosvfix
. , dx.
1+X2
0
1
Так как исходный ряд - по умножении на дробь 	 - сходится равномерно
1+х2
относительно х даже во всем бесконечном промежутке, а частичные суммы его
с
имеют мажоранту вида	, то почленное интегрирование оправдано (теорема 1).
1+х2
Если использовать теперь значение указанного интеграла, то окончательно
получим
2о	2 1-re P 2 еР-г
(б) Указание. Исходить из разложения [461, 6) (б)]
In (I - 2r cos fix + r-) = - 2 2 — cos i>|0x.
r = l V
Ответ. /2=я1пA- ге~Р).
6) Разложить интегралы (Лаплас)
(а) Г е - *! cos 2bx dx, (б) Г е - х2 ch 2bxdx,
о	о
(в) Г е-х! cos2bxdx
о
в ряды по степеням 6 F=-0), причем во всех случаях считать известным интеграл
2
о
[492, 2°].
(а) Решение. Пользуясь известным разложением косинуса и интегрируя
почленно, получаем
f.-*co,2fa*- [,-^1 (-1)VB^ rf,- j (-1)Ч2*J' Г.-
J	J >.=o	2i>!	t.=o 2i'! J
: Оно легко получается из разложений в 10) и 11) п° 440.

702	ГЛ. XIV. ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА	E19
Равномерная сходимость нашего ряда в любом конечном промежутке [О, А]
очевидна; частичные суммы его имеют мажоранту:
¦?, BЬхУ
интегрируемую от 0 до ». Этим установлена законность почленного интегри-
интегрирования.
со
Остается определить интеграл I e-^-x2* dx = Ir. Интегрируя по частям, легко
о
придем к рекуррентной формуле:
2j>-1	Bг>-1)!' г-
h = —j-h-i, откуда 7„=__-уя.
Подставляя это в полученное разложение, найдем окончательно:
Ответ: —е~'г.
(б) Аналогично получается разложение:
но на этот раз к «конечной» формуле оно не приводит. Впоследствии, другим путем,
мы выясним характер новой (уже неэлементарной) функции, которая нужна
была бы для выражения нашего интеграла [523, 5) (б)].
7) Найти значение интеграла
k-i
- dx
1, 2, 3, ...).
Решение. Разложив
в прогрессию, получим положительный ряд
* Мы воспользовались очевидньпл преобразованием:

519]	§ 3. ИСПОЛЬЗОВАНИЕ РАВНОМЕРНОЙ СХОДИМОСТИ	703
который сходится равномерно в любом промежутке [??, А] @<т;-=у4-=+~]. Так
как сумма ряда интегрируема в промежутке [0, + ¦»), то почленное интегрирование
Л JхЬ
о
Вспоминая, что &-е_число Бернулли В^ имеет выражение
2-B*I ^J_
[449], окончательно получим
4А:
8) Найти выражение для интегралов (Л е ж а н д р):
sin тес	с sin mx
d (б)
С sin тес с sin mx
(а) 	dx, (б) 	«& (т=-0).
о
Решение, (а) Разложение
sin mx
тоже сходится равномерно в любом промежутке [q, А], его частичные суммы
|sinmx|
мажорируются функцией 	. Поэтому допустимо почленное интегриро-
2лХ 1
вание:
р sin mx	^т г
¦——-dx= X e~2r"x sin mxdx =
J еых-\ v=iJ
у т 4 1	I+iLi
;я2+4г>2л2 2 ^ef"-l пг 2j 4em-l 2m
(б) Аналогично получаем (пользуясь той же мажорантой):
т	1 1	1
=1	т2 + 4р2жг 2т 2
Замечание. Естественно было бы также искать значения предложенных
интегралов путем разложения sin mx в ряд. В случае (а), например, мы пришли
* Мы пользуемся здесь (и в следующей задаче) сразу и теоремой 1 и теоре-
теоремой Г предыдущего п°, примененными, скажем, к промежуткам [1, +~] и [0, 1]
порознь.
** Эти результаты получаются из разложений на простые дроби функций
cth* и	 [441, 10)].
sh х

704	ГЛ. XIV. ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА	[519
бы к интегралам, рассмотренным в 7), а для получения результата в конечном
виде могли бы использовать известное разложение
+ jj(Dm
ет-\ т 2 *=1	2к\
[449] и т. д. Но этот метод имеет принципиальный недостаток - он требует пред-
предположения т^2п, в то время как результат верен для любого т.
9) Если в элементарной формуле [ср. 492, 2°]
p dx Bи-3)!!я
J A+х2)п ~Bп-2)\\~2
z
положить х = —, то получим:
Уп
I
dx Bн-3)!' я
Функция 	, монотонно убывая с возрастанием п, стремится к пределу
е~г\ Опираясь на следствие п° 518 (которое сохраняет силу и для монотонно убы-
убывающей функции), можно здесь перейти к пределу при л —<» под знаком инте-
интеграла. Если для определения предела правой части воспользоваться формулой
В а л л и с а 317, то окончательно получим результат
dz
С	г dz	|/я
J «---& = lim |__—= _.
о	о 1+-
[Ср. 492, 2°.]
10) Известный интеграл Ф е й е р а [309, 5) (б)]
1 г /sin nz\2 л
п J \ sin z j 2 '
о
х
если положить здесь z = —, может быть переписан в виде
п
Переход к пределу при л—><*> здесь затруднен тем обстоятельством, что от
параметра л зависит не только подинтегральная функция, но и верхний предел
интеграла.

519J	§ 3. ИСПОЛЬЗОВАНИЕ РАВНОМЕРНОЙ СХОДИМОСТИ
Полагая, однако,
705
(sin лЛ* п
{ X ) . X
Ism —
п
для
fn(x) = 0 для прочих значений х,
можно написать и так:
Очевидно, каково бы ни было лг>0,
lim fn(x) =
. (sin x\z
I х )
G)
причем приближение функции fn(x) к своему пределу в любом конечном проме-
промежутке [0, А] будет равномерным. С другой стороны, известно, что для 0-=z==—
2
sinz 2
поэтому для 0-=л:=ёя-
/sin х'\2 л2
\ х I 4
это неравенство тем более выполняется при х>п-~ , ибо тогда fn(x) = 0.
Применяя теорему 1, п° 518, можем в равенстве G) перейти к пределу при
л-*°° под знаком интеграла, что приводит нас к результату
[Ср. 494, 4); 497, 15).]
11) Другой пример того же рода. Известно [см. 440, 10)],
что
cos тес
- dx = n
-2rcosx+r2
о
где т - натуральное число и | г \ ¦= 1. Положим здесь х = — и г=\	(где h =» 0);
считая m^h, получим:	т	т
cos z dz
z\( h
1-cos- 1--
m)\ m
cos z dz
f ¦
sm
т
z
2т j
1 --
к
т

706	ГЛ. XIV. ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА	[519
Переходя здесь к пределу при т ¦» <» «под знаком интеграла», не стесняясь тем,
что и верхний предел здесь растет вместе с т (его мы заменим на °=), получим:
с cosz л
	dz = —e~h.
J	2A
Но верно ли это? Постараемся обосновать выполненный предельный переход.
Введем и здесь функцию
cosz
/m(z) =	;	—	 при 0«sz=snnr,
I sin—\
г \ т)
2т j
/m(z) = O при г>пи,
так что левая часть интересующего нас равенства перепишется так:
|'/тИ dz.
О
Очевидно,
lim /т(г) = -
причем в конечном промежутке стремление происходит равномерно. Наконец,
мажорантой может служить функция
1
4 f /г V
если nto^ha рассматривать только значения те=т0. Остается сослаться на теорему
1 п° 518.
12) Необходимость обоснования предельного перехода в примерах 10) и 11)
подчеркивается следующим сходным с ними примером, где, однако, такого
обоснования дать нельзя; результат же не подкрепленного обоснованием
предельного перехода оказывается неверным.
Рассмотрим интеграл
Г п
7'1=	ldx>
если с ним поступить, устремляя п к ~, как в предыдущих примерах, то полу-
получится, что
На деле же (как легко убедиться с помощью замены переменной) интеграл /„ со-
п
храняет постоянное значение —!
4

519]	§ 3. ИСПОЛЬЗОВАНИЕ РАВНОМЕРНОЙ СХОДИМОСТИ	707
Приведем еще два нешаблонных примера, интересных, как увидим, в другом
отношении.
13) Вычислить интеграл (где а - любое число)
/= feo(:0SXsin(asm.x:) —
J	х
о
[ср. 478, 8)(а)], считая известным интеграл
р sin t n
—л=-
J t	2
[см. 492, 3°; 494, 5).
Удобно ввести комплексную переменную
z = a (cos x+i sin x);
тогда [457, F)]
ez-eacosx [cos (a s;n x) _|_ ,¦ sjn (a s;n xy)
разлагается в ряд
-у an(cos nx+i sin nx)
n=i	«!
Приравнивая мнимые части, мы и получим разложение того выражения, кото-
которое стоит первым множителем под знаком интеграла:
gacosx sjn (a s;n x)= 2j — sin nx,
л=1 П\
отсюда
Ъ ап sin /tx
= 1 я! л;
о
Если бы можно было здесь произвести интегрирование почленно, то сразу
получили бы:
ап г sin nx л %, ап л
1=2-
п=\ п\ J
х	2п=1и! 2Ч '
о
Но обосновывать право на это в данном случае приходится своеобразно.
Так как ряд, стоящий под знаком интеграла, мажорируется постоянным
рядом
V-0 VI
то в конечном промежутке [О, А] интегрирование можно произвести почленно:
А
г ^, ап sinnx	^a" psin nx	^ an r sin t
\2—.	dx=Z—\	dx=2—\	dt.	(8)

708	ГЛ. XIV. ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА	[519
Остается перейти к пределу при А-"". Но, как нетрудно видеть, ввиду самого
rsint rsiat
существования интеграла 	at, интеграл	dx при всех значениях
J t	J t
о	о
tf^O будет равномерно ограничен:
'.
pin/
	dx
J t
о
Тогда ряд (8), члены которого зависят от переменного А, мажорируется постоян-
постоянным рядом
и, следовательно, сходится равномерно относительно А. В таком случае,
по известной теореме [433], в нем можно перейти почленно к пределу при А-+°°,
чем и завершается доказательство.
14) Другой пример того же рода. Пусть ряд
2
п = 0
СХОДИТСЯ, И ПОЛОЖИМ ДЛЯ ЛГЭ=О
¦Гт хп
Z ап-—;
п=0	П\
этот ряд также сходится, и притом - в любом конечном промежутке [0, А] -
равномерно относительно х [по признакам Абеля - Дирихле, см. 430],
так как множитель хп/п\, по крайней мере для л >А, убывает с возрастанием п.
Доказать, что тогда
e-xg(x)dx=s.	(9)
о
Результат получается сразу, если проинтегрировать почленно
СО	СО
Г -v хп	^, ап с	¦?!
е~х Zj аП'—dx= 2i — \е~х-хп dx= 2j an = s,
J л=о и! л=о я! J	n=o
о	о
ибо е~х-хп dx = n\ [489, 4)]. Обратимся теперь к обоснованию права на это.
6
Как и только что, в конечном промежутке почленное интегрирование до-
допустимо:
А	А
С	°°	Хп	™	I С
е~х 2 ап— dx= 2 ап— е~х-хп dx.
(Ю)

519]	§ 3. ИСПОЛЬЗОВАНИЕ РАВНОМЕРНОЙ СХОДИМОСТИ	709
Интегрируя по частям, легко показать, что
Л	А
1 г	1 (¦
- \e-*-x*dx^-	— <
n\ з	(и - 1)! J
0
так что множители
А
- [e~x-xndx,
о
зависящие от А и л, монотонно убывают с возрастанием п (при А = const), оста-
оставаясь равномерно ограниченными. В таком случае (по только что указанному
признаку) ряд в A0) справа сходится равномерно относительно А, а значит, в нем
можно перейти к пределу при А-*" почленно, и т. д.
Приведем два примера применения полученной изящной формулы (9).
(а) Рассмотрим так называемый интегральный синус
х3 х5
rsin/ п	х3 х*
-six= 	dt =	хЛ	Ь...
J t	2	3! 3 5! 5
х
Этот ряд составляется по типу g(x), исходя из ряда
л	11
___ + +_+ ---+...
По формуле (9) тогда
11	\ п п п
~3~+5"~ "¦]4~4'
(б) Другая интересная функция - функция Бесселя с нулевым
значком /0(д:) имеет разложение [441, 4), 5):
которое составляется по типу g(x), если положить
2v\\
* Это разложение легко вывести, если написать:
х
rsin/ psm/
d
rsin/ psm
-six= 	dt-
dt
t
о
и во втором интеграле заменить синус его разложением в ряд, а затем проинтегри-
проинтегрировать прчленнр.

710	ГЛ. XIV. ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА	[520
Тогда, в силу (9),
Bл-1)!! 1
.г,
2 (-
2v!!
окончательный результат получается здесь, если вспомнить разложение функции
в биномиальный ряд [407 B4)] и положить в нем х = 1.
Замечание. Поучительно разобраться, в чем состоит особенность при-
примененного в двух последних примерах метода рассуждения - по сравнению с
прочими примерами на почленное интегрирование рядов в бесконечном проме-
промежутке.
Если вернуться к общему вопросу о предельном переходе под знаком интеграла
с бесконечным пределом [518], то он оказывается равносильным вопросу о су-
существовании и равенстве обоих повторных пределов для некоторой функции
F(A, у) двух аргументов [см. C)]. Согласно общей теореме п° 505 достаточным
условием в этом случае является - при наличии обоих простых пределов -
равномерное стремление функции к одному из них, D) или E), и притом все равно
к какому. Обычно мы предполагали такую равномерность в отношении предела
E), что и отвечало «равномерной сходимости интеграла» с бесконечным пределом.
Но заключение оставалось бы в полной силе, если бы вместо этого равномерным
было приблшнсение функции F к пределу D)!
В случае ряда 2 ип(х) с частичными суммами fn(x) можно, таким образом,
1
либо устанавливать равномерное (относительно и) приближение функции
А
Fn(.A)=jfn(x)dx
а
при А - ~ к пределу fn(x) dx, т. е. «равномерную сходимость» этих интегралов,
а
что мы обычно и делали, либо же убеждаться в равномерном (относительно
А
А) приближении названной функции при п - ~ к пределу ср(х) dx, т. е. в равно-
а
мерной (относительно А) сходимости ряда
2 un(x)dx= \<p(x)dx,
что оказалось более удобным для нас в примерах 13) и 14)!
520. Непрерывность и дифферевцируемость интеграла по параметру.
Займемся и здесь сначала переносом теорем 2 и 3 пп° 506 и 507 на
случай бесконечного промежутка.
Теорема 2. Пусть функция f(x,y) определена и непрерывна
(как функция двух переменных) для значений хз*а и значений у в

520]	§ 3. ИСПОЛЬЗОВАНИЕ РАВНОМЕРНОЙ СХОДИМОСТИ	711
промежутке [с, д]. Если интеграл
I(y)=\f(x,y)dx	A)
а
сходится равномерно относительно у в промежутке [с, д], то он пред-
представляет собою непрерывную функцию от параметра у в этом про-
промежутке.
Это следствие из теоремы 1. Действительно, как мы видели в 506,
при изменении л; в любом конечном промежутке [а, А], функция f(x, у)
при у-*у0 (где у0 - любое частное значение у) равномерно
относительно л; стремится к предельной функции f(x, _y0). А тогда,
по теореме 1, в интеграле A) можно перейти к пределу под знаком
интеграла:
lim /О) = lim f(x, у) dx = f(x, у0) dx=I(y0),
У~У>	У~Уо а	а
что и доказывает наше утверждение.
В п° 485, описывая методы, с помощью которых расходящимся интегралам
приписываются «обобщенные значения», мы оставили открытым вопрос о регуляр-
регулярности второго из этих методов. С помощью только что доказанной теоремы
мы в состоянии теперь восполнить этот пробел. Если интеграл /(х) dx сходится,
г	°
то интеграл е~ kxf{x) dx равномерно сходится относительно параметра к,
о
для ?э=0 (см. замечание в конце п° 515) и, следовательно - по крайней мере, в
случае непрерывности f(x) - представляет непрерывную функцию от параметра к,
для ks*Q. В частности, имеем:
im \e~kxf(x)dx= f /(x) dx.
*+об'	oJ
lim
Таким образом, величина сходящегося интеграла совпадает с его «обобщенным
значением»; в этом и состоит упомянутая регулярность.
Замечание. В случае, если функция f(x,y) неотрица-
неотрицательна: f(x,y)s»0, имеет место в некотором смысле обратная
теорема: из непрерывности интеграла A), как функции от параметра,
вытекает равномерная его сходимость.
В этом случае непрерывная функция от у
А
F(A,y)=jf(x,y)dx	C)
а
при возрастании А возрастает и, следовательно (по обобщенной тео-
теореме Д и и и, 504,4°), стремится к своему пределу A) равномерно
относительно у, ч. и тр. д.

712
ГЛ. XIV. ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА
[520
Теорема 3. Пусть функция f(x, у) определена и непрерывна по х
для xs*a и у в [с, д] и, сверх того, имеет для указанных значений не-
непрерывную по обеим переменным производную /у{х, у). Предположим,
далее, что интеграл A) сходится для всех у в [с, д], а интеграл
сходится равномерно относительно у в том оке промежутке.
Тогда при любом у из [с, д] имеет место формула *
Взяв частное значение y—yQ, рассмотрим отношение
»+*)-/(л)
'dx
A2)
и докажем, что здесь допустим предельный переход по параметру
к-+0 под знаком интеграла.
Мы уже видели в 507, что если х изменяется в любом конечном
промежутке [а, А], подинтегральная функция ——— Л*, w CTpe.
мится при к->-0 к предельной функции fy(x,y0) равномерно от-
относительно х Для того чтобы иметь право применить теорему 1, нам
следовало бы еще убедиться в равномерной сходимости инте-
интеграла A2) относительно к.
Ввиду предположенной равномерной сходимости интеграла A1),
по любому ?>0 найдется такое Aos*a, что, лишь только А'>А>Ай,
будет
л.
A3)
для всех у зараз [514]. Покажем, что одновременно будет и
Г/(х,
J
,
A4)
для всех возможных значений к.
* Вычисление производной по этой формуле и здесь называют правилом
Де йбиица.

520]	§ 3. ИСПОЛЬЗОВАНИЕ РАВНОМЕРНОЙ СХОДИМОСТИ	713
Для этой цели (фиксируя А и А') рассмотрим функцию
А'
По теореме 3 п° 507 ее производная вычисляется по правилу Лейб-
Лейбница:
А'
и, ввиду A3), по абсолютной величине всегда <е. Но тогда и отно-
отношение
А'
которое по формуле Лагранжа равно Ф'(Уо + вк), тоже по абсо-
абсолютной величине будет -=г, т. е. выполняется A4). Отсюда, по при-
признаку п° 514, следует равномерная сходимость интеграла A2), чем и
завершается доказательство.
Легко получить и обобщение теорем 2* и 3* п° 510, относящихся
к конечному промежутку fa, b]: стоит лишь, ничего не меняя по су-
существу в приведенных здесь формулировках и рассуждениях, заме-
заменить точку х = ~ точкой х = Ъ (как это сделано, например, при пере-
переходе от теоремы 1 к теореме Г).
Замечание. В излагаемой здесь теории мы не пользуемся
связью интегралов с рядами, предпочитая выдвигать повсюду ту
идею, которая в действительности является основой всех умозаклю-
умозаключений, - идею равномерного стремления к предельной функции. Од-
Однако в иных случаях ссылка на уже развитую теорию рядов могла
бы создать формальное упрощение в рассуждениях. Разъясним это,
дав новое доказательство теоремы 3 (где упомянутое упрощение бо-
более значительно).
Заменим интеграл 1{у) радом [477]
'00 = 2 ] fix, у) dx {An - °°),
Члены этого ряда
«пО0= f(x,y)dx,
А я.,

714	ГЛ. XIV. ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА	[521
в силу теорем 2 и 3 пп° 506 и 507 непрерывны и имеют непрерывные же произ-
производные
А„
"п(у)= J fy(x,y)dx.
К тому же ряд, составленный из этих производных, сходится равномерно относи-
относительно у в промежутке [с, s], как это следует из равномерной сходимости инте-
интеграла A1) [514]. Тогда, по теореме о почленном дифференцировании ряда [435],
существует производная
А„
во	со	л	Л
Г (у) = 2 »'пЬ>) = 2 fi(x,y)dx=\fy(x,y)dx,
1	1 J	J
что и доказывает требуемое.
Тот же прием можно применить и к доказательству теорем 1 и 2 п° 518 и 520
(а также теоремы 4 из следующего п°), со ссылкой на соответствующие теоремы
из теории функциональных рядов. Осуществление этого предоставляем читателю.
521. Интегрирование интеграла по параметру. Сначала докажем сле-
следующую теорему:
Теорема 4. При предположениях теоремы 2 имеет место фор-
формула:
д	д	-
\l(y) dy=\dy If{x, у) dx = \dx\j\x, у) dy.	A5)
с	со	ас
Действительно, по теореме 4 п° 508 для любого конечного А»а
справедливо равенство
д А	Ад
\dy \f{x, у) dx= \dx\j\x, у) dy.
с а	ас
Но, по предположению, функция C), непрерывная по у, при Л->-~
стремится к своему пределу A) равномерно относительно у.
Следовательно, по теореме 1 п° 506, в интеграле слева можно перейти
к пределу по А -* ~ под знаком интеграла, т. е.
д А	д
Jim J dy J/(x, y)dx=\ dy \f(x, y) dx.
°° с а	с а
В таком случае существует и предел при А -* ~ интеграла справа, т. е.
интеграл
д
\dx\f{x,y)dy,
а с
и имеет то же значение, ч. и тр. д.

521]	§ 3. ИСПОЛЬЗОВАНИЕ РАВНОМЕРНОЙ СХОДИМОСТИ	715
Если воспользоваться замечанием к теореме 2 [520], то легко
вывести отсюда такое
Следствие. В случае неотрицательной функции f(x, у)
одна непрерывность интеграла A) по у влечет за собой формулу A5).
Таким образом, мы - при известных условиях — установили право
переставлять два интеграла, из которых лишь один распростра-
распространен на бесконечный промежуток, а другой - на конечный.
Между тем во многих случаях как раз приходится переставлять
интегралы, взятые оба в бесконечных промежутках, по формуле
A6)
Оправдать такую перестановку часто представляется делом сложным
и кропотливым, чему читатель ниже найдет много примеров.
Лишь для узкого класса случаев удается обосновать формулу A6)
общими соображениями:
Теорема 5. Пусть f(x, у) определена и непрерывна для х»а и у»с.
Предположим, далее, что оба интеграла
\f(x,y)dx и \f(x,y)dy	A7)
сходятся равномерно: первый - относительно у, а второй - отно-
относительно х, в любом конечном промежутке. Тогда, если хоть один из
двух повторных интегралов
\dy\\f{x, у)| dx, jdx J\f(x, y)\dy	A8)
с а	а с
существует, то существуют и равны повторные интегралы A6).
Допустим, что существует второй из интегралов A8). Ввиду
равномерной сходимости интеграла \fdx, по предыдущей теореме,
а
для любого конечного С>с будем иметь
J dyjf{x, у) dx =jdx \f{x, у) dy.

7 16	ГЛ. XIV. ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА	[521
Остается доказать, что в интеграле справа при С-*°° допустим
предельный переход под знаком интеграла, ибо
тогда будет существовать
»	с	с
jdyjf(x,y)dx = lim jdyjf(x,y)dx = lim jdx^f(x,y)dy =
ас
С
• lim J/(x, j) ф = Jrfx J/(X; y) dy.
Оправдать упомянутый предельный переход можно, опираясь на
теорему 1 [518]. Функция от х и С
с
\f{x,y)dy,
непрерывная по х [теорема 2, 506], при С ¦* <*> стремится к предельной
функции
равномерно относительно я: в любом конечном промежутке. Интеграл
же
с
\dx\f(x,y)dy
сходится равномерно относительно С, потому что мажорируется вто-
вторым из интегралов A8), поскольку
\f{x,y)dy
Таким образом, все условия теоремы 1 здесь выполнены, и наше утвер-
утверждение оправдано.
Несколько проще обстоит дело в случае функции, не меняющей
знака. Например, для неотрицательной функции (этим случаем до-
достаточно ограничиться) имеет место
Следствие. Пусть для неотрицательной непрерывной
функции f(x, у) оба интеграла A7) также представляют собой н е-
прерывные функции, первый — от у, а второй — от х. Тогда,
если существует один из повторных интегралов A6), то существует и
другой и притом - равный первому.

522]	§ 3. ИСПОЛЬЗОВАНИЕ РАВНОМЕРНОЙ СХОДИМОСТИ	717
По теореме 2 и замечанию к ней явствует, что предположение о
непрерывности интегралов A7) равносильно требованию их равно-
равномерной сходимости. Остается применить предыдущую теорему, от-
отметив, что в данном случае \f(x, у) \ =f(x, у).
Предложения настоящего п° также могут быть перефразированы
на случай конечных промежутков; при этом особая точка х = ~ лишь
заменяется конечной особой точкой х = Ъ, а также (если нужно) точка
у = «• точкой у— д.
522. Применение к вычислению некоторых интегралов. Применим
вышеизложенную теорию к вычислению некоторых важных интегралов.
1°. Интегралы Эйлера:
h
3fl-xdx
о
@«=а, 6
Из результатов п° 496, 1) сразу получается:
Положив здесь z = xn, найдем первый из эйлеровых интегралов:
!'¦
2л
2m+l
при частном значении а = —— .
Для того чтобы отсюда получить значение искомого интеграла
при любом а, удовлетворяющем неравенствам 0<д-=1, убедимся в
гом, что этот интеграл представляет собой непрерывную функцию
>т а для указанных значений параметра.
При 0-=х-= +~ и 0<д<1 подинтегральная функция сохраняет не-
непрерывность по обеим переменным. Далее, рассматриваемый инте-
рал сходится равномерно относительно а: при х = 0 для az=ao>0, a
[ри л: = ~ для a^ayzl. Действительно, разбивая интеграл на два:
¦ с
+ J , легко видеть, что последние мажорируются, соответственно,
1
[нтегралами:
"~'dx.

718	ГЛ. XIV. ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА	[522
Прилагая к интегралу J теорему 2, а к интегралу ) - аналогич-
1	О
ную ей теорему для конечного промежутка, убеждаемся в непрерыв-
непрерывности обоих интегралов как функций от параметра.
К любому значению а, 0 < а < 1 можно произвольно приблизиться
2т+\ ,	ч _
с помощью значении вида —— (т и п - натуральные, т -= и). Пере-
Переходя в формуле A9) к пределу при —	>-а и используя доказанную
непрерывность интеграла, найдем окончательно:
[f^dx^-Л- [ср. 519, 4)].
о
Совершенно аналогично, из 496, 2) и 3) получим:
г ха~1 —
J
2°. Интеграл
г ха~ — х°~
	dx = л (ctg arc - ctg bri)
J 1 -x
0
xa~1 dx	sin(l-aH
+ 2x-cos0+l
о
J
x
[cp. 492, 3°].
Рассмотрим интеграл
dx
W
sm ax
0
Вычислим его с помощью дифференцирования по параметру а. Од-
Однако непосредственное применение правила Лейбница приводит
здесь к расходящемуся интегралу
со
Г cos ax dx.
о
Поэтому мы введем «множитель сходимости» е~кх (&>0) и станем
искать значение интеграла
/= {e-kxS-^-^dx (сс==О).
о

522]	§ 3. ИСПОЛЬЗОВАНИЕ РАВНОМЕРНОЙ СХОДИМОСТИ	719
Для него дифференцирование по а под знаком интеграла уже до-
дозволительно, ибо соблюдены условия теоремы 3: подинтегральная
функция и ее частная производная по а непрерывны по л: и а для
и аз»0, а интеграл, получаемый в результате дифференцирования:
J
е-** cos хх dx =
b
сходится равномерно относительно ос, так как мажорируется интегра-
интегралом е~кх dx, не содержащим а.
о
Итак, для а> О
dl к
rfa ofi+k3 '
Интегрируя по а, найдем
7= arctg |
(постоянного слагаемого здесь вводить не приходится, так как оба
эти выражения при <х = 0 обращаются в нуль).
Эта формула выведена в предположении, что А;>0. Но, при а =
= const, интеграл / оказывается функцией от к, непрерывной
и при к = 0; это следует по теореме 2 из равномерной сходимости
интеграла / относительно к при kz*Q [см. 515, 4°]. Иными словами,
Если а>0, то
/0= lim
к0
/0= lim arctg- = arctg (+~) = -.
В частности (при а = 1) и
о
3°. Интеграл Эйлера-Пуассона
/=
[ср. 492, 2°].
Положив здесь х = Ш, где и — любое положительное число, полу-
получим

720	ГЛ. XIV. ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА	[522
Умножим теперь обе части этого равенства на е~и' и проинтегрируем
по к от 0 до ~:
Г e-u= rfw = /2 = f е""' и di J е-"'1'
Нетрудно видеть, что перестановка интегралов ведет здесь весьма
быстро к результату. В самом деле, после перестановки получим
откуда
(так как,
J-j*j,
0 0
очевидно,
''" и с
0)
/ 1 Г *
0
я
4
Для оправдания произведенной перестановки интегралов попро-
попробуем прибегнуть к следствию из теоремы 5 п° 521. Но в то время как
интеграл
есть непрерывная функция от t для всех /=в0, интеграл
непрерывен лишь для и>0, а при м = 0 обращается в 0, терпя в этой
точке разрыв. Поэтому применить следствие непосредственно к
прямоугольнику [0, ~; 0, ~] нельзя! Мы его применим к прямоуголь-
прямоугольнику [и0, ~; 0, ~], где wo=~O, пользуясь тем, что интеграл
то
С	•	11
J е"Aт'" "'и du=2'T+T*'e~<1+rya'
является непрерывной функцией от t для всех ts*0. Этим оправды-
оправдывается равенство
j du j e~A+B>u*w dt=- \dt j e-(}+A)"' u du.
"o 0	0 u0

522J	§ 3. ИСПОЛЬЗОВАНИЕ РАВНОМЕРНОЙ СХОДИМОСТИ	721
Остается лишь, уменьшая и0, перейти здесь к пределу при мо-*О, что
в правой части можно вьшолнить под знаком интеграла — на осно-
основании следствия п° 518.
4°. Интегралы Лапласа (P. S. Laplace):
у = \-~-.dx, z= —=—~dx (a,
J J X2 + X2	J Ofi + X2	\ >
Полагая в первом из них
1
-/(аЧх«)
получим
у= \cosPx
о	о
Переставим здесь, по теореме 5, интегрирования по я: и по t
у=\ e~*'t dt \ e~tx' cos fix dx.
о	о
Но внутренний интеграл нам известен [519, 6) (а)]
так что
-а<2!-
?-,
Вспоминая 497, 8), окончательно находим
Второй интеграл Лапласа получается из первого дифференци-
дифференцированием по параметру /J:
Z_ _ *	 р—Хр
ар 2
Применение правила Лейбница оправдывается тем, что интеграл
сходится равномерно относительно р1 для /}в=/}0=-0 [517, 16)].
5°. Интегралы Френеля (A. J. Fresnel):
J sin x2 dx, cos x2 dx.
о	о

722	ГЛ. XIV. ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА	[522
Полагая x2 = t, получим:
J si
СО	со
lfsin/,. с	„. 1с cos t
¦? j j=-dt j cos x*dx = ^-~-
sin **<& = ¦? j j=-dt, j cos	^
о	о	о	о
станем искать первый из этих интегралов в преобразованной форме.
Заменяя (под знаком интеграла) выражение l//7 равным ему ин-
интегралом
приведем искомый интеграл к виду:
J V7 VSJ
Перестановка интегралов здесь сразу привела бы к окончательному
результату:
rsin/ , 2 с , г /и" • ^ j 2 г du 2 я ТАл *
) Vt	VSJ J	y^J l + «4 1^ 2f2 Г 2
Так как непосредственное обоснование такой перестановки требует
кропотливых преобразований и оценок, мы предпочтем и здесь (ср. 2°)
прибегнуть к «множителю сходимости» е~ы (fc>0).
Имеем
Г !iL? e-kt rft = f e-w sin f ^ f e-;u! ^M =
j yi	yaj	j
о	о	о
\2 *
На этот раз возможность перестановки интегралов устанавливается
с помощью теоремы 5. Остается, наконец, перейти к пределу при к-*0,
что - как легко проверить - может быть проведено под знаком ин-
интеграла.
* См. 472, 2) или 491, 7).

523)	§ 3. ИСПОЛЬЗОВАНИЕ РАВНОМЕРНОЙ СХОДИМОСТИ	723
Итак, окончательно
с cos t
То же значение получается и для интеграла -— dt. Отсюда
о
sin л:2 dx = cos х2 dx-^У^ .
523. Примеры на дифференцирование под знаком интеграла. 1) Исходя из из-
известных интегралов (при а =¦ 0)
(a) (V«! </*=-]/-,
J	2 i a
о
г dx 1 л
(б) 	; =	,
v ' a + xz о i/
О	'
1
(в)
о
путем последовательного дифференцирования их по параметру вывести новые
интегралы.
(а) Решение. По правилу Лейбница, после и-кратного дифферен-
дифференцирования, найдем:
{е-ах'хт
Так как получающиеся при этом интегралы все равномерно сходятся отно-
относительно а, для аз=ао=-О (например, написанный интеграл мажорируется интегра-
интегралом е-"«*2л:2Г! dx I, то применение правила Лейбница оправдано,
о	/
f dx	1 Bи-1)П 1 л
(б) Ответ. —	v '
•J (йЧ
2 2п\\ ап
1
(в) Ответ. [х?-1 log" xdx = {- 1)" —
J	an+
ап+1
о

724	ГЛ. XIV. ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА	[523
2) Дифференцированием по параметру вычислить интегралы (a, (i, к >¦ 0):
¦ 1 - cos оис
о
[• sin ocx sin /fa:
г 1 - cos хх
(а)	J= \	e~kxdx,
J x
о
С
(б)	Я=
J
x x
о
(a) Решение. Производная / по а выражается интегралом (сходящимся
равномерно относительно а)
dJ ( ,	а
— = \ е~кх sin оис dx =
da J
о
отсюда
1
/1п
Так как при а = 0 интеграл / обращается в 0, то С- — In &2 и окончательно
(б) Дифференцируя Н по а под знаком интеграла, получим:
-= е~КХ	dx.
dH r _^sin/?x-cosa;t
о
Применение правила Лейбница законно, ибо условия теоремы 3 соблюдены,
как в этом легко убедиться.
Преобразуя произведение синуса на косинус в разность двух синусов, сведем
полученный интеграл к интегралам знакомого нам вида [522, 2°]:
dH 1 г г , sin(a+/5)x г , sin(a-/?)x т 11 a+fi	a-p]
— = - \e-kx— H'dx- \e-b*—-—— dx =- arctg—--arctg—" .
da. 21J	x	J	*:	J2V	к	к j
о	о
Интегрируем по а:
а+в	а + в a-/5	a-S k A:2 + (a-/SJ
Я= — arctg -li-	 arctg —"+- In	——+ C.
2	Л 2	A 4 A2 + (a+/SJ
Постоянная C= 0 (ибо Я= 0 при a = 0).
3) Вычислить интеграл
Г 1-е-'

J t
cos t dt.

523J	§ 3. ИСПОЛЬЗОВАНИЕ РАВНОМЕРНОЙ СХОДИМОСТИ	725
Указание. Рассмотреть более общий интеграл, введя параметр:

J t
cos t at,
вычислить его с помощью дифференцирования, а затем положить а = 1.
Ответ. In Jl.
4) Вычислить интегралы:
F) 4-Г^А fr>0),
J A+2)
(в) Л= f^08^'8 Xdx (.a,b>0).
J	хг
о
(а) Указание. Jt непрерывен по а для яэ»0; мажоранта
для 0=sn=se,. Производная для о=-0
dJi Г
~da~ J(
dx = -
мажоранта ^j^^ Для
я
Ответ. 7, = — In (ab+1).
6
(б) Указание. Производная при гз=0:
dx	л 1
fli= Г
rfr J
2 1 + r'
о
1	п
мажоранта 	. Ответ. Л = — In A + г).
1 + х1	2
(в) Указание. Производная по а приводится к интегралу типа />:
Г	? Ь
I	I arctg — /
dJ3 I 1 arctg bx	I	a n a+b
da I l + o2x2 x	I r(l + B) 2 я
о	о
л (а+ЬУ+ь

726	ГЛ. XIV. ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА	[523
Замечание. Из Jlt при r—i, подстановкой х = tg t получается интеграл
Г t	л
J tg t 2
о
а отсюда интегрированием по частям находим вновь [ср. 492, 1°]:
f	-я
Insin/*=	In 2.
J	2
о
DO
5) (а) Вычислить интеграл J= I e~x' cos 2bx dx.
6
Решение. Имеем
dJ с
— = - e-**-2x-sm2bxdx.
db J
о
Интегрируя по частям, получим затем:
dJ	7
— = -2b e-x-CO52bxdx= -2bJ.
db	J
о
Таким образом, для определения J получилось простое дифференциаль-
дифференциальное уравнение с отделяющимися переменными [358]. Интегрируя, на-
находим
J=Ce~»\
Так как при Ь = 0 должно быть /= —, то именно этому и равно С. Оконча-
Окончательно,
[ср. 519, 6) (а)].
(б) Если тот же прием применить к вычислению интеграла Н= е-*1 sin 2bxdx,
то придем к дифференциальному уравнению
db
Умножив обе его части на е*\ слева получим, очевидно, производную от произ-
произведения еь'-Н по Ь; интегрируя от 0 до Ь, найдем

523]	§ 3. ИСПОЛЬЗОВАНИЕ РАВНОМЕРНОЙ СХОДИМОСТИ	727
(так как Н=0 при Ь = 0). Таким образом,
Н=е-Ь'. [et'dt.
Здесь для выражения интеграла пришлось ввести новую, «неэлементарную»
функцию
х
[ср. 519, 6) (в)].
6) Вычислить интеграл (я,
I e	dx.
о
Решение. Искомый интеграл лишь множителем 1/Уа отличается от
интеграла
где сг = аЬ (подстановка у=Уах).
Имеем:
dc
о
(	«I
подстановка у = — I . Отсюда
Ответ. -V-e~''m. [Ср. 497, 8)].
21 и
7) Вычислить интеграл
- e~at cos bt - e~ail cos byt
re~al cos bt-e~a*' cos b,t
T= —	 dt (a, ay > 0).
7=
о
Решение. Дифференцируя по а и по Ъ порознь, получим:
— = - I e~at cos btdt =
da
о
dJ
— = - e-atsmbtdt=	.
db J	а*+Ьг
о

728	ГЛ. XIV. ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА	E23
Нетрудно по этим частным производным восстановить самую функцию *
J= --1п(а*+Ь2) + С,
где С не зависит ни от а, ни от Ь. Так как при а = «! и b = bt будет 7=0, то
так что
j1
2
8) Вычислить интегралы (я=-0, 6э=0):
и =. е~ах* cos bx2 dx, v = e-axZ sin 6x2 rfx.
о	о
Решение. Найдем производные этих интегралов по параметру Ь, поль-
пользуясь правилом Лейбница:
du г	dv с
— = - х2-е~ах2 sin bx2 dx,	— = x2-e~axl cos bx2 dx.
db J	db J
о	о
Интегрированием по частям отсюда легко получить
</u 1 b dv dv 1 b du
— =	v	•—, — = — и4—• —
db 2a a db db 2a a db
или - решая эти уравнения относительно производных -
du bu+av	dv au-bv
db~(a2+b*)' db{a2+b2)'
B0)
Таким образом, для определения неизвестных функций и, v от b мы получили
систему дифференциальных уравнений.
Вводя комплексную функцию и> = и+го от вещественной переменной 6, легко
свести дело к одному уравнению (с отделяющимися переменными). Именно,
если второе из уравнений B0) умножить на i и почленно сложить с первым, то
придем к уравнению
dw -b+ai i w
db 2(as+62) "'" l'a-Ы'
Его можно интегрировать обычным путем, отделяя переменные. Чтобы из-
избежать пользования логарифмами комплексных чисел, можно и непосредственно
убедиться, что
d
db
в силу дифференциального уравнения, откуда
w • Уа-Ы= с - const.
* Впоследствии мы займемся этим вопросом сиетематически, здесь же «перво-
«первообразная функция» устанавливается на глаз.

523]	§ 3. ИСПОЛЬЗОВАНИЕ РАВНОМЕРНОЙ СХОДИМОСТИ	729
Полагая 6 = 0, легко найти с = — , так что
_ft 1 _1[л fa+bi
Под символом Уа±Ы мы разумеем те ветви корней, которые при 6 = 0 обращаются
в арифметический корень + У а.
Известно, что
таким образом,
Приравнивая отдельно вещественные и мнимые части, получим, наконец:
„= I e-ax2cosbx2dx = — U -
1 \ я / -й+У^+62
Эти формулы выведены нами при существенном предположении, что а>0.
1о так как оба интеграла, как легко убедиться с помощью теоремы 2 [см. и 515,
°], являются непрерывными функциями от а и при а = 0, то, переходя в полученных
авенствах к пределу при а-*0, найдем (если 6=»0):
7	Г	1 ][~я
cos Ъх% dx = sin bx2 dx = — / — ,
J	J	2 Г 26
о	о
e. интегралы Френеля [ср. 522, 5°].
9) Покажем, как с помощью дифференциального уравнения могут быть просто
лчислены интегралы Лапласа [ср. 522, 4°]:
г cos их	гх sin вх
y-\-T-.dx и z- [—-?-. dx («,/?=><>).
J a2+x2	J as + x2
* Полагая Ya+bi=x+yi, будем иметь: а=хг-у\ b = 2xy. Отсюда и полу-
ются:
^.Г . ~~	~..Г-а+ Vo2+62
х= ±
)ичем оба корня здесь берутся с плюсрм, вр внимание к заключенному только
о условию и к тому, что ху~ — 6=-0,

730	ГЛ. XIV. ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА	[523
Мы уже видели, что
dy=_
dp Z-
Дальнейшее дифференцирование по Р производить под знаком интеграла невоз-
невозможно, ибо в результате такого дифференцирования получился 'бы уже расходя-
расходящийся интеграл.
Однако если к написанному равенству почленно прибавить равенство
п f sin/?.*
— = 	dx
2 J x
о
[522, 2°] *, то получим:
dy п а р sin/Sx
- dx.
ay n с
	I— = а2
dp 2 J
x(az+x2)
о
Здесь дифференцировать под знаком интеграла снова можно и таким путем мы
найдем
d2y 2 г cos /?x
dPz J a2 + x2
о
т. е.
Для этого простого дифференциального уравнения второго порядка с постоян-
постоянными коэффициентами, по корням ± а «характеристического уравнения», легко со-
составить общее решение
где QhC. - постоянные. Но при всех значениях /3 величина у ограничена:
dx л
2а'
о
значит Су необходимо равно 0 (ибо иначе, при р —+<*>, и величина у безгранично
возрастала бы).
Для определения же постоянной С2 положим р - 0; очевидно:
Окончательно,
«-?•
у = —
2а
Отсюда дифференцированием получается и z.
* Впрочем, для дальнейшего нам вовсе не нужно значение этого интеграла;
достаточно лишь знать, что при всех р^О он сохраняет постоянное значение,
а в этом легко убедиться простой подстановкой t=px.

523]	§ 3. ИСПОЛЬЗОВАНИЕ РАВНОМЕРНОЙ СХОДИМОСТИ	731
10) Вычислить интегралы
С	а2	га2
и= е~*2 cos—dx,	v= I e~*!sin— dx.
J x2	J	x2
о	о
Существование и непрерывность интегралов при всех значениях а обеспечи-
обеспечивается наличием мажоранты: е-*2. По правилу Лейбница:
du r	а2 2а	г -—¦
— = - е-*2sin	dx= -2\ е у' йпу- dy.
da 1	х2 хг	J
'И)
Второй интеграл сходится равномерно - как при у=0, так и при _у = ~ - для
зсех значений а, значит, первый сходится равномерно - как при х=~, так и при
с = 0 - для значений а, удовлетворяющих неравенствам 0-= ao=*sa.*sA -= +~. Таким
эбразом, для а »0 применение правила Лейбница оправдано.
Дальнейшее дифференцирование по а (которое оправдывается аналогично)
iacT нам:
— = — 2 I е у' sin у2-	dy = 4\ e-*!sin — dx = 4v.
da?	J	у2	J	x2
о	о
Точно так же
—;=-4и.
Полагая w-u+iv, имеем для определения w дифференциальное уравнение
—— = - 4/w.
da2
доставим «характеристическое» уравнение: As+4i=0 и по корням его А= ± У2т /2'
гапишем общее решение дифференциального уравнения.
'ак как функция w при всех а ограничена, то необходимо: В- 0; но при a = 0 должно
ыть iv = —, так что А = — . Окончательно,
11) Доказать тождество
Р

732	ГЛ. xrv. ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА	[523
Обозначим первый интеграл через и, а второй - через v. Полагая в и: хг + а2 = у1,
преобразуем его к виду:
и = е«!- е-У' dy.
а
Введем новую переменную ив», полагая x = az; получим
Продифференцировав v по а (по правилу Лейбница), представим производ-
dv
ную — в виде:
da
dv la
dv 2a I r	re-aV I
— =	f e-o'z'dz- 	dz\,
da lC|J	Jz' + l I
L
|o	о
откуда для определения v получается линейное дифференциальное уравнение
	2я-«)= -1.
da
Умножив обе части его на («интегрирующий») множитель е~а', придем к равенству
d
— [v-e-a*]= -e-fl";
da
если проинтегрировать его по а от 0 до а, то получим:
а
V.e-a' = Vo- e-t'dt,
о
о
где под «о разумеется предельное значение
1 F dz ys
»0= lim« = —	= —.
e-o y^Jz«+l 2
о
Так как это же число есть значение интеграла I е-''dt, то для v окончательно
°
v = e<-'-1 e-''dt,
получается
т. е. то же выражение, что и для и.
12) Доказать тождество (при к>0)
Се кх	rsm(x-k)
	dx= 	dx,
J l + л:8 J x
g—kx
l + x*
О	к

524J	§ 3. ИСПОЛЬЗОВАНИЕ РАВНОМЕРНОЙ СХОДИМОСТИ	733
Оба интеграла, как функции от к, удовлетворяют дифференциальному уравне-
уравнению
По отношению к первому в этом убеждаемся, дважды дифференцируя его по пра-
правилу Лейбница. По отношению ко второму проще исходить из его пред-
представления в виде:
rsmt . f cos г
cos A:- 	dt-smk- 	dt.
it	it
Так как разность обоих предложенных интегралов z = z(k) удовлетворяет
однородному уравнению: z"+z-Q, то она имеет форму
где сх и с2 - постоянные. Но оба интеграла, а с ними и их разность z, стремятся
s 0 при ?-~. Отсюда ^ = 0, z(k) = 0 и требуемое тождество доказано.
524. Примеры на интегрирование под знаком интеграла. 1) Найти значения
интегралов
r-e-ax-g-bx г cos ax-cosbx
(a) J	dx, (б) J-	—	dx (e,A>0)
о	о
гутем интегрирования под знаком интеграла.
Решение, (а) Интеграл
— Cf=-O)
j	у
о
годится равномерно относительно у для уз*уо>О. Интегрируя это равенство
ю у от а до Ь, причем слева интегрирование можно произвести под знаком ин-
еграла, получим
ь	ь
(* г	г g—ax — g—bx	Г dy Ь
dx e~y%dy= 	dx= — = ln—.
J J	J	x	J v a
О а	о	а
Cp. 495, 1).]
б) Аналогично, исходя из интеграла
(•sin j
J x
ух л
о
оторый также сходится равномерно относительно у для yz^yo>O, найдем:
с»	ft
dx с	г cos ах - cos bx л
\id	d (b)
С dx с	г
— \sinyxdy=
i x i	.1
\sinyxdy	dx
x i	.1	хг	2
On	0
-p. 497, 10) (a).]

?34	ГЛ. XIV. ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ Of ПАРАМЕТРА	E24
2) Рассмотрим полный эллиптический интеграл 1-го рода
ко*)-
J
о
f * _.
J У1 — A;2 sin2 (р
как функцию от модуля к, и. найдем интеграл от этой функции в промежутке
[О, 1].
Имеем
л	л	я
J	J J yi-^sin2^ J
L==
fl-^sin2^
0	0	0
что подстановкой x-tg — приводит к удвоенному интегралу
&_c_	5 _
J х
о
[G - «постоянная К а т а л а н а», см. 328, 6) и 440, 6а)].
Перестановка интегралов производится на основании (модифицированного)
следствия из теоремы 5. Подинтегральная функция повсюду в прямоуголь-
\ л	Л	(л \
нике 0,—; 0, 1 положительна и непрерывна, за исключением точки —, II, где
она обращается в «. Интеграл
Л
2
dcp
J
У1 - к2 sin2 (p
о
есть непрерывная функция от к для значений к ¦<¦ 1, а интеграл
1
elk
-A:2 sin2?;
о
л
- непрерывная функция от <р для значений <р-= —. Наконец, второй из повторных
интегралов, очевидно, существует. Таким образом, все условия названного след-
следствия выполнены.
В ближайших нескольких примерах будем вновь иметь дело с уже знакомой
нам функцией Бесселя с нулевым значком [440, 12); 441, 4)]
2 г
= - cos (x sin в) dO,

524]	§ 3. ИСПОЛЬЗОВАНИЕ РАВНОМЕРНОЙ СХОДИМОСТИ	735
но в основу наших умозаключений положим «асимптотическую» формулу для
J0(x), которую примем без доказательства. Вот эта формула:
%^,	B1)
4; х3 '2
где <pu(*) при безграничном возрастании х остается ограниченной:
3) Вычислить интеграл
Имеем
n
о
с cos (л: sin в) dO =
2	°°	2
2 г Г	2 ,-
=-[de f
ni a2+sin20
о
Перестановка интегралов дозволительна ввиду равномерной (относительно О
сходимости интеграла
fe-ax cos (x sin 0)dx
(мажоранта: е~ах).
Так как из B1) явствует, что интеграл
J0(.x) dx
сходится *, то интеграл А будет непрерывной функцией от а и при а = 0 [теор. 2;
515, 4°]. Поэтому значение этого интеграла может быть получено из выражения
для А предельным переходом при а -» 0. Таким образом,
]и
* Это сразу станет ясным, если первое слагаемое в B1) справа написать в
виде:
ГУ (	я	я) 1 /cos х sin x
-cos—Hin x-sin— =—	H
)	{
(
— cos лг-cos—Hin x-sin
\	4	4

736	ГЛ. XrV. ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА	[524
4) Вычислить интеграл
(¦sin ax
=	Ja{x)dx (a=-0).
J х
Имеем
2	2
2 rsmax .г . . „ „ 2
2 r sin ах г 2 г г sin ax
Я=_ ——dx cos (л: sin Q)dQ = -\ dO 	cos (x sin 0) dx.
TlJ X	J	7lJ J X
0	0	0 0
Но внутренний интеграл есть «разрывный множитель» Дирихле [497, 11)]
°°	/71
J1 sin ах	I—, если sin9-=a,
	cos(xsinO)ax=J 2
х
о { 0, если sin в =- а.
Поэтому
rsin (
В= )~~х~
а* ,, s , 1т ПРИ a3sl>
о	I arcsin а при в-=1.
Установим дозволительность перестановки интегралов. Имеем
п	п
А	?	~2 А
2 rsin ах г	lc rsin ax
— 	dx cos (x sin 0)dO = —\de\ —— cos (x sin 0) ax.
nj x J	7iJ J x
oo	oo
Но можно написать внутренний интеграл в виде:
A	I A	A	\
г sin ax	I I r sin (a+sin 0)x	с sin (a - sin 0) x I
	cos (x sin 0) dx = — <	dx+ I 	axf =
J x	2 IJ	x	J	x
о	lo	о	'
A(a-sinO)	\
sinz	r sinz I
	dz+		dz). B2)
z	J г
о	о	'
Если a=-l, так что a-sin 0=»a-1 =-0, то это выражение при А-~~ стремится к
своему пределу равномерно относительно 0, иными словами, интеграл
sin ax
	cos (x sin б) dO сходится равномерно, и перестановка интегралов оправ-
х
о
дана. При a=sl равномерность нарушается вблизи 0 - arcsin а. Но так как выражение
B2) остается равномерно ограниченным при всех А и б (мажорируется постоян-
постоянной!), то наружный интеграл при б = arcsin а сходится равномерно относи-
относительно А, так что предельный переход при А — ~ под знаком интеграла все же
допустим, чем снова оправдана перестановка интегралов.
J

524]
§ 3. ИСПОЛЬЗОВАНИЕ РАВНОМЕРНОЙ СХОДИМОСТИ
737
5) Из интеграла В, дифференцированием по параметру а, получаем другой
интересный интеграл:
0 при а=-1,
cos ax dx-
1
/1-я2
при а-=1.
Для обоснования права на дифференцирование под знаком интеграла заметим,
что интеграл С сходится равномерно относительно а в любом замкнутом проме-
промежутке значений а, не содержащем единицы. Это следует из асимпто-
асимптотической формулы B1). Переписав ее в виде *
1	Фо(.х)
Jo(x) =	 (cos л: 4 sin х) H	,
]/^х	хУ'
умножим обе части на cos ал::
J0(x) cos ax =
1 cos(l+a)x + cos (I -a)x + sin (l+a)x+sin A -a)x <pu(x)-cosax
L
Второе слагаемое мажорируется функцией — . Что же касается интеграла от
x'h
первого слагаемого, то при 11 - а \ =?6^0 и он сходится равномерно.
Та же формула показывает, что при а = 1 интеграл С расходится.
6) Вычислить интеграл
г
1
x (a=-0).
Имеем
2 г 1 - cos ax г
?> = - 	dx cos(xsmO)dO =
Л J	X	J
о
л
2 р fl
1 - cos ах
cos (x sin 0) ах
о о
п
2
=— Г [in У | а2 - sin2 01 - In smO)
[см. 497,16) (б)]. Таким образом [497, 7) и 511, 7)]:
о
* См. сноску на стр. 735.
47 Г. М. Фихтенгольц, т. II
dO
при
при

738	ГЛ. XIV. ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА	[524
Для обоснования перестановки интегралов напишем сначала для конечного А:
л	л
А	2~	2 А
2 г 1 — cos ах с	2 ее 1 - cos ax
— 	dx cos (x sin в) dO =— \ d6 \	cos {x sin 0) dx.
TtJ	X	J	71J	J	X
О	О	0 0
Весь вопрос теперь в том, можно ли справа здесь перейти к делу при А -<• «¦ под
знаком интеграла.
Чтобы исследовать характер стремления внутреннего интеграла к своему
пределу, рассмотрим интеграл
А'
г 1-cosах	. т ,
	cos (x sin 0) dx =
J х
А
А'
1 cdx
=— — [2 cos (х sin 0) - cos (а 4 sin в)х - cos I a - sin 01x1 =
21 x	¦
A
A'sinO A'@ + sin 6)	А'[а- sin f}|
-I[2 f - f	-	j"	l^A-
21 J	J	J	1 z
A sin [J A(a-t-sin(<)	A|a—sin9|
A(a + sin 0) A'(a + sin 6) A |a —sin f. | А'|я—sin 0 |
1Г Г	Г	Г	Г 1cos z ,;
A sin 0	A' sin 0	A sin 0	A' sin I)
Г COST
Ввиду существования интеграла I	dz (z0 =- 0) ясно, что, взяв А я А' достаточно
г,
большими, можно сделать эту сумму сколь угодно малой сразу для всех значений 0
в любом замкнутом промежутке, не содержащем ни 0, ни arcsin a (если a«sl).
Таким образом, равномерность стремления внутреннего интеграла к
своему пределу при А ¦* ~ нарушается лишь вблизи одного или двух указанных
значений 0.
Но, с другой стороны, этот внутренний интеграл мажорируется функцией
[In /[a2-sin2 01 -In sin б], которая интегрируема в промежутке [0, л/2]; значит,
наружный интеграл равномерно сходится как при 0 = 0, так и при 0 = arcsin a
(если a=sl). Тогда, по теореме Г п° 518, упомянутый выше предельный переход
допустим.
7) Отсюда дифференцированием по параметру найдется интеграл:
1
при а =
Е= I Jo(x) sin ax dx = ¦
о
0	при а <= 1.
Обоснование проводится сходно с 5), опираясь на формулу B1). При а = 1
интеграл расходится.
8) (а) Проверить непосредственно допустимость перестановки интеграла
в случае

524]
3. ИСПОЛЬЗОВАНИЕ РАВНОМЕРНОЙ СХОДИМОСТИ
739
Имеем:
J (хЧу")
dx
так что
J=
С dy
= - ——- = - arctg у
\+у-
е=1	1+У2
™	Л Л	.7
i = ~ 2"+4~ ~4
В то же время для другого повторного интеграла
V2 - х2
г с V2
\<1х\ —
1 1
7Г
7Г
аналогично получается значение ./=-—: перестановка недопустима.
4
Любопытно отметить, что [как мы убедились в 517, 1)] интеграл
• yz-x*
Ра-
Расходится равномерно относительно у для всех ys^l: аналогично устанавливается
и равномерная относительно х (для xss\) сходимость интеграла
	'¦	dy.
J 0е2+.у2J
Теорема 5 здесь неприменима потому, что (как легко проверить непосред-
непосредственно) интегралы
Г , Г \У2~хг\ .	Г , С \У2-Х*\
dx 	dy,	dy 	dx
J J {хг+у*У	J J (.x*+y*y
11	11
расходятся!
(б) Легко установить недопустимость перестановки интегрирований и в сле-
следующем случае:
у-х	1
(х+уу х" ~Т
10
Здесь интеграл
(х+уУ

740	ГЛ. XIV. ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА	[524
- как это ясно уже из теоремы 4 - не может быть равномерно сходящимся
относительно у в промежутке [0, 1] (в чем легко убедиться и непосредственно),
(в) Еще изящный пример того же типа (X а р д и) *:
j dx I (pe-Pxy-qe-Яху) dy- I dy j (pe'Pxy-qe'W) d
0	1	1 (I
= Г
„
-
p
что не равно нулю, если взять р> О, q> О,
9) Приведем два новых приема для вычисления интеграла Лапласа:
r-cos
JiT
7= j _' dx
о
[ср. 522, 4°].
Так как
— = I e^ysin y dv
2 J
\+x-
0
то, подставляя, представим J в виде
J= cos fix dx е~хУ sin v dy.
Переставляя интегрирования, получим
С с г у sin у с х sin fix
/= sin^ fljy e~x-v cos fix dx- I —;	ov=	dx.
0	0	0	0
dJ
Но последний интеграл, с точностью до знака, представляет собой —, так что
dp
J удовлетворяет простому дифференциальному уравнению
dJ
— =-./, откуда J=Ce~P.
dp
71	,	Л
Так как J-C=— при /5 = 0, то, окончательно, J=—e~P.
* Интеграл Ф р у л л а н и [495, 1)].

524)	§ 3. ИСПОЛЬЗОВАНИЕ РАВНОМЕРНОЙ СХОДИМОСТИ	741
Остается еще обосновать перестановку интегралов. Если 0<а-=Л<+~, то
легко убедиться в справедливости равенств:
А	А	А
pcos/Jx	г	г	[•	г
	 dx = cos Px dx е~хУ sin у dy = sin у dy е~хУ cos px dx =--
а	о	О	О	о
С	гй sin A4 - у cos /?Л	р sin Pa ~ у cos pa	I
= sinvf/v	е~АУ	е~°У =
J	L у2+р2	у*+р*	1
sin v	С v sin у
-^rf+ p
С v sin у
pa- 	е~аУ dy.
J y2+p2
Равномерная сходимость всех интегралов, соответственно, относительно а
и А позволяет перейти под знаком интеграла к пределу при а-0 и при /4-»~. От-
Отсюда ясно, что рассматриваемое выражение при указанном двойном предельном
С у sin у
переходе действительно стремится к пределу 	dy.
J у*+р2
10) Используя другое тождество
	= I е~У sin xy dy,
1 + х2 J
о
можно написать:
- cos Р
г cos px (•
J= 	dx е~У sin xy dy.
о
Переставляя здесь интегралы
с г sin ху
J= е~У dy 	cos/fo dx,
мы в качестве внутреннего интеграла получаем «разрывный множитель» Дирих-
Дирихле [497, 11I
О при
Г sin xy
	cos Px dx =
x	— при

742	гл. xiv. интегралы, зависящий от параметра	|524
Таким образом,
Р
Для обоснования перестановки интегралов заметим, что интеграл
sin ху
е"У-	cospxdy
х
сходится равномерно относительно х (мажоранта уе~~У). Поэтому
А	А	А	~А
С cos fix	(• cos fix г	C	г sin лгу
—— dx= 	— dx е-У&ш xydy= е~У dy 	cosfixdx.
J i+x2	J x J	J	J x
0	0	0	0	0
Можно ли в последнем интеграле (по у) перейти к пределу при А — ~ под знаком
интеграла? Подинтегральное выражение есть произведение е~У на
А	А
I rsm(y+0)x+sm(y-fi)x
(sinxy I rsm(y+0)x+sm(y-fi)x
	cos вх dx =—	dx =
J X	l)	X
(У+«А	(У
sin z	r sin z
— *+ J -T~
о
sin z
P	0
и стремится при А~°° к своему пределу равномерно относительно у, исключая
окрестность точки y = fi. Так как второй множитель равномерно ограничен при всех
А и у, то подинтегральное выражение имеет мажоранту вида Се~Уу так что при
у = @ и _у=оо (наружный) интеграл сходится равномерно относительно А. Этим
оправдывается предельный переход под знаком интеграла, а с ним и перестановка
интегралов.
11) В заключение укажем еще один изящный вывод значения интеграла
1 sin x
	dx.
X
0
Так как
-= \e~xydy,
х J
х
о
dy n
oo	oo	о
г	r	С С	Г
/= sin л: ал: е~хУ dy= dy е~хУ smxdx= -
J	J	J J	J \ + v2 2

525]	§ 4. дополнения	743
Займемся вопросом о законности перестановки интегралов. Взяв О^а^А^
-= + ~, легко оправдать равенства
А '	А	-	А
J"sinx	г	г	ГС
	dx= sin x dx e-xy dy= \dy\ е~хУ sin x dx =
a	a	О	О я
= [• fysing+cosg	ysin^ + cos^ J
J I 1+J-»	l+J'2	j
0
Jy г 1
	-e-oyrfv+cos a- 	e~aydy-
1+y* J l+y2
erfv+cos a
1+y*	J l+y2
о	о
-sin/)- f
е~АУ dy-cosA I
Так как последние два интеграла сходятся равномерно относительно А (для
I), то, переходя к пределу при А — °° под знаком интеграла, видим, что оба
они стремятся к 0. Второй интеграл, равномерно сходящийся относительно а
п
(для оз»0), очевидно, стремится к — при а-0. Остается убедиться в том, что
первый интеграл, умноженный на sin а, при этом предельном переходе стремится
к 0. Имеем:
оо	оо	1	во
J J
о
l l
г с tdt 1	с с dt
-= 	=-ln(l+a2)-lna, -= —- = С.
J .1 а2 + г2 2	J J te'
о о
Отсюда и вытекает требуемое заключение.
§ 4. Дополнения
525. Лемма Ариела. Хотя для вычислительных целей чаще всего достаточно
того материала, который изложен в первых трех параграфах, но в теоретических
построениях иной раз бывают нужны некоторые более тонкие теоремы, дающие,
кстати сказать, более простые условия применимости рассмотренных процессов.
Начнем с доказательства одного вспомогательного утверждения, относя-
относящегося к системам промежутков; оно принадлежит А р ц е л а (С. Arzela).
Лемма. Пусть в конечном промезкутке [а, Ь] содерзкатся системы Di,D2,
..., Dit, ... промезкутков, казкдая из которых состоит из конечного числа не
налегающих друг на друга замкнутых промезкутков. Если сумма длин промезкут-
промезкутков каждой системы D^ (k= I, 2, 3, ...) больше некоторого постоянного положи-
положительного числа д, то найдется, по крайней мере, одна точка х = с, принадлежащая
бесконечному множеству систем Die.
Доказательство. Если промежуток какой-нибудь системы Dk (fc=»l)
налегает на промежутки предшествующих систем Dx, ¦¦¦> A<-i и их

744	ГЛ. XIV. ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА	[525
концами делится на части, то эти части мы впредь будем рассматривать как от-
отдельные промежутки системы Dk- Таким образом, если id' есть промежуток системы
Dk1, a d" - промежуток системы Dk", и к' ¦< к", то либо d' и d" не налегают друг
на друга, либо же d" содержится в d'.
Однако целиком система А<+1 может в предшествующей системе ?>/< и не со-
содержаться. Так как это обстоятельство неудобно, то мы заменим системы Dk
другими системами промежутков Ак, по следующему правилу. Для получения
Ак мы кладем в основу Dk, присоединяем к ней не содержащиеся в Dk промежутки
системы Dk+1, затем не содержащиеся в Dk и в Dk+i промежутки системы Dk+г,
и т. д. до бесконечности.
Построенная таким образом система Лк может состоять уже из бесконечного
множества промежутков. Но зато 1) каждый из промежутков системы dk+i ча-
верно содержится в одном из промежутков системы Ак ¦ К тому же 2) сумма длин
(или точнее - сумма ряда длин) промежутков, составляющих Ак, и подавно
больше <5, как это имело место для Dk.
Следующий шаг будет состоять в том, что мы и эти системы Ак заменим их
конечными частями AW, сохраняя, однако, при этом первое из только что
указанных свойств систем Ак. Сделаем мы это так.
Если число промежутков системы А1 конечно, то просто положим А'-А^.
В противном случае мы из Ах выделим конечную систему А' промежутков
di, d2, • •., dr так, чтобы сумма длин остальных промежутков dr+i, dr+z,... системы
Ах была меньше <5*. Некоторые из промежутков системы Аг содержатся в проме-
промежутках А', ибо, если бы все они содержались в промежутках ar+i, dr±2, ..., то
сумма их длин была бы меньше <5, вопреки второму свойству систем Ак. Если
промежутков системы А2, содержащихся в А', конечное число, то из них и составим
систему А". В противном случае мы выделим из них конечную систему А"
так, чтобы сумма длин всех прочих промежутков 4 (вместе с теми из них,
которые не содержатся в А') была меньше Ь *. Продолжаем этот процесс до беско-
бесконечности, последовательно выделяя из zK конечную систему А'", ..., из Ajc —
конечную систему AW, ... При этом каждый из промежутков системы
/Цк-t-i) содержится в одном из промежутков системы А(к). (Второе свойство си-
системы Ак, вообще говоря, утеряно, но ценой этого мы восстановили конеч-
конечность систем, наподобие Dk.)
Наконец, последний этап заключается в выделении из систем AW по о д-
н о м у промежутку dW так, чтобы каждый из них содержался в предыдущем.
Именно среди промежутков системы А' найдется хоть один (обозначим его
через d'), в котором содержатся промежутки бесконечного множества
последующих систем. Действительно, пусть это не так, ив каждом промежутке
А' содержатся промежутки лишь конечного числа последующих систем; тогда
это же было бы справедливо и относительно всей системы А' в целом (именно
потому, что она состоит из конечного числа промежутков). Иными словами,
можно было бы найти столь большой номер ко, чтобы ни один из промежутков
системы А(к«) не содержался в А', а это противоречило бы свойству 1) систем AW.
В d' содержатся некоторые промежутки системы А" (ибо, в противном случае,
в нем вовсе не было бы промежутков А'" и т. д.). Больше того, хоть один из
содержащихся в d' промежутков системы А" (обозначим его через d') должен
обладать подчеркнутым выше свойством промежутка d', т. е. содержать проме-
промежутки бесконечного множества последующих систем, ибо иначе этим
свойством не мог бы обладать и а" (здесь снова играет роль конечность
системы А"). Продолжая этот процесс до бесконечности, мы последовательно
из каждой системы AW выделим промежуток dW, содержащийся в ранее выделен-
выделенном промежутке d^k~1\
Получив последовательность вложенных один в другой промежутков dW =
= l"k, bk] (k=l, 2, 3, ...), мы - как и при доказательстве известной элементар-
* Это можно сделать цр свойству остатка сходящегося ряда.

526]	§ 4. дополнения	745
ной леммы [38] - установим, что для монотонных переменных ак и b/t существуют
пределы
lim ak = a=s/9 = lim bu.
Так как о длинах промежутков «/(*) мы ничего не знаем, то равенства пределов
мы здесь утверждать не можем. Но любая точка с, взятая под условием asscss/3,
принадлежит, очевидно, всем промежуткам dW (при к = 1, 2, 3, .. .)• Вместе с тем
точка с принадлежит каждой системе А^ (при к= 1, 2, 3, ...); значит, каково бы ни
было к, точка с необходимо принадлежит (если учесть правило построения А/;)
и некоторой системе ZV, где k's*k. Отсюда уже ясно, что точка с принадлежит
бесконечному множеству систем D^, ч. и тр. д.
526. Предельный переход под знаком интеграла. Теперь вместо теоремы 6 *
п° 436 мы установим следующую теорему, где требование равномерного
стремления функции fn(x) к своему пределу заменено более общим условием
ограниченности ее:
Теорема 1 (Арцела). Пусть дана последовательность функций
fn(x) («=1,2,3,...),
интегрируемых (в собственном смысле) в промежутке [а, Ь] и ограниченных в их
совокупности:
(? = const; a^x^b; и = 1, 2, 3, ...).
Если для всех х в [а, Ь] существует предел
lim/„(*),
и функция <р(х) также интегрируема, то
ь
lim fn(x) dx = <р(х) dx.
Доказательство. Ограничимся вначале частным предположением,
что функции fn(x) неотрицательны:
и имеют пределом нуль:
) = 0.	A)
В этом предположении нам нужно будет доказать, что
*
lim [/„(*) <2г = 0.	B)

746	ГЛ. XIV. ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА	[526
Взяв последовательность положительных чисел г/п — 0, мы для каждого п можем
разложить промежуток [а, Ь] на части щ"' (/=1,2, ..., й„) так, чтобы соответствую-
соответствующая нижняя сумма Дарбу*:
№)
удовлетворяла неравенству
ь
0=s fn(x) dx-sn^r)n.
а
Тогда, очевидно,
ь
ton [|/„(х)&-*„]-<>,
а
и для доказательства B) нам достаточно установить, что
lim sn = 0.	C)
С этой целью, взяв произвольно малые числа г=-0 и д^О, установим, что
найдется такой номер N, что при ns»JV сумма длин тех из промежутков d\n^ и-го
подразделения, которым отвечают нижние границы т/'з^е, будет =ss<5.
Действительно, допустим, что это не так. Тогда для бесконечного множества
значений п:
сумма длин тех промежутков d^"h\ для которых mff'^s^e, была бы =- 6. К системам
В/;, составленным из этих промежутков, применима лемма предыдущего п°. В со-
согласии с ней нашлась бы в [а, Ь] такая точка с, которая принадлежала бы беско-
бесконечному множеству систем Z)^. Таким образом, для бесконечного
множества значений и выполнялось бы неравенство
а это противоречит предположению A), которое должно выполняться и при
х = с.
Итак, упомянутый номер N существует; пусть же ns^N. Обозначим через г"
и i" номера тех промежутков и-ro подразделения, для которых, соответственно,
будет
ту ^е или myls^s.
Сообразно с этим разобьем и сумму:
•Sh= Z mi d) '= Z Щ' <Ч> +Z т\,Щ,1.
* Мы обозначаем через dj" и самый частичный промежуток, и длину его; щ'
есть inf f{x) в промежутке d\n'.

526)	§ 4. ДОПОЛНЕНИЯ
Теперь легко видеть, что
747
ибо, конечно, mj'ssL (по условию теоремы). Отсюда
что - ввиду произвольности чисел г и 6 - и доказывает утверждение C).
Общий случай легко приводится к исчерпанному только что частному случаю.
В самом деле, ввиду неравенства
ь ь
rn4x)dx-
0
J |/„(х)- rf(x) I dx,
достаточно применить доказанное к неотрицательной функции \fn(x)-(p(x)\,
стремящейся к нулю.
Следствие, При выполнении всех условий теоремы, кроме предположения
об интегрируемости предельной функции, во всяком случае можно утверждать
существование конечного предела
ь
lim fn{x) dx.
Для доказательства достаточно [39] установить, что для любого е>0 найдется
такой номер, N, что при ri'^n'^-N будет
ь ь
fn"(x)dx- [fn'{x)dx
JI/л-
Допустим противное. Тогда существует такое число fo>On такие две после-
последовательности неограниченно возрастающих чисел п'т и пт (т= 1, 2, 3, ...; пт>пт),
что всегда выполняется соотношение
D)
С другой стороны,
Если к функции
и lim
применить предыдущую теорему, то получим:
I)	Ь
lim
lim \f*{x)dx= lim \[fn'
что противоречит соотношению D). Это противоречие и доказывает наше утвер-
утверждение.

748	ГЛ. XIV. ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА	E27
От параметра п, принимающего лишь натуральные значения, легко перейти
и к произвольному параметру у [ср. теорему 1 п° 506]:
Теорема 2. Пусть функция fix, у) определена для значений х в промежут-
промежутке [а, Ь] и значений у в области СУ, интегрируема по х в [а, Ь] {при постоянном
у) и равномерно ограничена
\f{x, y)\*sL (L = const)
для всех упомянутых значений хи у. Если для всех х существует предельная функция
<р(х)= lim f(x, у)*,
у-л
также интегрируемая в [а, Ь], то
ь	ь
lim \f(x,y)dx= [<p{x)dx.	E)
у-у. •>	¦>
а	а
Достаточно применить теорему 1 к функции fn(x) =f(x, yn), где {уп} есть произ-
произвольная последовательность значений у из ^), стремящаяся к у0. Получаемое
таким путем соотношение
ь	ь
lim \f(x,yn)dx= \y(x)dx
a	a
равносильно E).
527. Дифференцирование под знаком интеграла. На основе теоремы Арцела
легко получается и следующий результат, как аналог и обобщение теоремы 3 п° 507.
Теорема 3. Пусть функция fix, у), определенная в прямоугольнике [а, Ь; с, д]>
будет интегрируема по х в [а, Ь] при любом постоянном у в [с, Э]. Предположим,
далее, что во всей области существует частная производная fy{x, у), также ин-
интегрируемая по х. Если эта производная, как функция двух переменных, ограни-
ограничена:
\fy(x, Jf)|=s? (L = const; assx=ssb;
то при любом у из [с, д] для функции
ь
/О)= \f(x,y)dx
а
имеет место формула
I'iy)-
fy{x, у) dx.
Доказательство. Взяв любое значение у = у0> как и при доказательстве
в п° 507 [см. 1A1)], будем иметь
	— I
ь
, yo+k)- f{x, y0)
* При этом, конечно, предполагается, что область ^у допускает предельный
переход при у~уй.

528]	§ 4. дополнения	749
Гак как, по теореме Лагранжа,
Ях,уо+к)-/(х,у0)
	т	=fy(x, уа+Ок),
го подинтегральная функция, зависящая от х и к, будет при всех значениях этих
юременных ограничена (по абсолютной величине) постоянной L. Применяя к
пому случаю теорему 2, мы можем перейти к пределу при к~0 под знаком ин-
интеграла, что и даст нам требуемый результат.
528. Интегрирование под знаком интеграла. В этом направлении имеет место
гредложение, значительно обобщающее теорему 4 п° 508.
Теорема 4. Пусть функция f(x, у), определенная в прямоугольнике [а, Ь\ с, д],
ттегрируема по х в {а, Ь] (при постоянном у) и по у в [с, д] (при постоянном х). Если,
верх того, функция f(x, у) ограничена
\f(x,y)\*sL (L = const)
Us всех упомянутых значений х и у, то существуют оба повторных интеграла
1 равны между собой.
Доказательство. Положим
»> д
\dx\f(x,y)dy
1(У) = | fix, у) dx, K(x) = j f(x, у) dy.
Рассмотрим произвольную последовательность разбиений промежутка [с, д]
а части с длинами
#°, Ь\п\..., й?> (я =1,2,3,...),
одчиненных лишь тому условию, что max \<3/ } с возрастанием и стремится к 0.
S каждой 1-й части (/=1,2, ..., hn) п-то разбиения по произволу возьмем значение
¦=У1 и составим интегральную сумму для функции 1(у);
Если положить
о ап перепишется в виде:
2 Ах, y<in)Ln)-fn(x\

750	ГЛ. XIV. ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА	[529
Так как, очевидно, существует предел
а
lim /*(*) = Г fix, у) dy = K(x)	F)
л—~	J
с
и к тому же для всех значений х и и
то, по следствию п° 526 заключаем о существовании предела
lim 6п.
Итак, предел этот существует., как бы ни делить промежуток на части (лишь
бы наибольшая из длин их стремилась к нулю) и как бы ни выбирать в них значе-
значения у\"\ Отсюда ясно, что предел этот должен быть одним и тем же во всех слу-
случаях, т. е. что существует интеграл
д	ь
j I(y) dy = lim an = lim [ /*(*) dx.
с	и
b
Но подобным же образом можно доказать и существование интеграла К(х) dx,
a
т. е. интегрируемость предельной для /*(*) функции [см. (С)]. Тогда, применив
к f*(x) теорему 1, окончательно получаем
в	ь	ь
т. е.
\l(y)dy= lim \f*(x)dx= \K(x)dx,
С	II	U
д I)	b д
(* dy J fix, y) dx = j dx j f{x, y) dy,
ч. и тр. д.
Мы ограничились здесь случаем собственных интегралов. Если положить
в основу доказанные для них теоремы, то можно было бы соответственно обоб-
обобщить и результаты, относящиеся к несобственным интегралам; этим, однако,
мы заниматься не будем.
§ 5. Эйлеровы интегралы
529. Эйлеров интеграл первого рода. Так называется (по предложе-
предложению Лежандра) интеграл вида
1
B(a,b)= \xa-\\-x)b-1dx,	A)
ii
где a,b>0. Он представляет функцию от двух переменных пара-
параметров а и Ь: функцию В («Бета»).

529]	§ 5. ЭЙЛЕРОВЫ ИНТЕГРАЛЫ	751
Рассматриваемый интеграл, как мы знаем [483, 3) (а)], для поло-
положительных значений а и Ъ (хотя бы и меньших единицы) сходится *
и, следовательно, действительно может быть положен в основу опре-
определения функции В. Установим некоторые ее свойства.
1°. Прежде всего, почти непосредственно (подстановкой х = 1 -1)
получаем:
B(a,b) = B(b,a),
так что функция В является симметричной относительно an b.
2°. С помощью интегрирования по частям из формулы A), при
Ь>\, находим **
1	1
В{а, Ь)=
о
1
о
Л-±Ща,Ъ-\)-Ь-± Ща, Ъ),
откуда
и~ЛтВ(а, Ь-\).	B)
Эту формулу можно применять с целью уменьшения Ь, пока Ъ остается
больше 1; таким образом всегда можно достигнуть того, чтобы второй
аргумент стал =sl.
Впрочем, того же можно добиться и в отношении первого аргу-
аргумента, так как - ввиду симметричности В — имеет место и другая
формула приведения (я>1)
^\,Ь).	B')
Если Ъ равно натуральному числу п, то, последовательно применяя
формулу B), найдем:
п ~ 2.
* Наоборот, если значение хоть одного из параметров а, Ь будет ==0, то
интеграл расходится.
** Мы используем ниже тождество

752	ГЛ. XIV. ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА	[529
Но
1
г	1
ТО(п \\= уО— 1 Лу = _
о
Поэтому для В(а, и) и - одновременно — для В(п, а) получается
окончательное выражение
Если и а равно натуральному числу пг, то
^ ' ' (m+n-1)! '
Эту формулу можно применять и при т = 1 или п = 1, если под сим-
символом 0! разуметь 1.
3°. Дадим для функции В другое аналитическое представление,
которое часто бывает полезно. Именно, если в интеграле A) произ-
V
вести подстановку х = y—i, где у - новая переменная, изменяющаяся
от 0 до оо, то и получим
4°. Положим в формуле D) Ъ — 1 - а, считая, что 0 -= а < 1; мы най-
найдем
Читатель узнает уже вычисленный выше интеграл, также связываемый
с именем Эйлера [см. 519, 4) (а) или 522, 1°]. Подставляя его зна-
значение, приходим к формуле
@-=в-=1).	E)
Если, в частности, взять а=1-а = ^, то получим:
В ± i =я.	Eа)
Мы ограничимся этими немногими свойствами функции «Бета»
потому, что - как увидим сейчас - она очень просто выражается
через другую функцию — «Гамма», которая и будет главным пред-
предметом нашего изучения в настоящем параграфе.

530]	§ 5. ЭЙЛЕРОВЫ ИНТЕГРАЛЫ	753
530. Эйлеров интеграл второго рода. Это название было присвоено
Лежандром замечательному интегралу:
I\a)=\ji°-1er*dx,	F)
о
который сходится при любом а>0 [483, 5 (в)]* и определяет функ-
функцию Г («Гамма»). Функция Г, после элементарных, является одной из
важнейших функций для анализа и его приложений. Обстоятельное
изучение свойств функции Г, исходя из ее интегрального определения
F), послужит одновременно и прекрасным примером применения из-
изложенной выше теории интегралов, зависящих от параметра.
В главах XI и XII 402, 10); 408; 441, 11) мы встречали уже функцию
Г, но определяли ее иначе; покажем же, прежде всего, тождество обоих
определений (конечно, для а>0).
Полагая в F) х = 1п —, найдем:
(
о
Как известно [77, 5) (б)];
1
In — = lim
п \\ - zn),
причем выражение п\\ - zn) при возрастании п стремится к своему
пределу возрастая**. В таком случае, на основании 518, оправ-
оправдано равенство
1
r(a)=\imna-4{l-z») dz
или - если прибегнуть к подстановке z=yn -
1
Г(а) = lim па Г>'"-1A - y)a~l dy.
о
Но, согласно C),
* При a=sO интеграл расходится.
** В этом можно убедиться методами дифференциального исчисления, рас-
l-z«
сматривал выражение 	как функцию от а.
а
48 Г. М. Фихтенгольц, т. II

754	ГЛ. XIV. ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА	[531
Таким образом, окончательно, приходим к знаменитой формуле
Эйлера-Гаусса:
Да) = lim п° • , Л'2/3";^"	jt ,	G)
в-(в+1).(в + 2)..(в + и-1)	w
которая выше послужила нам отправной точкой [402 A4)]. В даль-
дальнейшем свойства функции Г, как указывалось, мы будем извлекать
из ее интегрального представления F).
531. Простейшие свойства функции Г. 1°. Функция Г(а) при всех
значениях а>0 непрерывна и имеет непрерывные же производные всех
порядков. Достаточно доказать лишь существование производных.
Дифференцируя интеграл F) под знаком интеграла, получим
r\a)=\xa-x-\nx-e-xdx.	(8)
о
Применение правила Лейбница оправдано тем, что оба интеграла
1
J	J
о	1
сходятся равномерно относительно а: первый при х = 0 для
а=&ао>0 (мажоранта х^~х jIn x\), а второй при х = ~ для а==Л<°°
(мажоранта хАе~х) *).
Таким же путем можно убедиться и в существовании второй про-
производной
Г"(а)= Jjc0-1- (In xfe-'dx	(8*)
о
и всех дальнейших.
2°. Из F), интегрированием по частям, сразу получаем:
г	°° г
и I л с ил л с	-г I л с ил,
J	о J
о	о
т. е. [ср. 402 A5)]
Да+1) = а.Да).	(9)
Эта формула, повторно примененная, дает
A0)
Таким путем вычисление Г для сколь угодно большого значения
аргумента может быть приведено к вычислению Г для аргумента < 1.
Для х>0, очевидно, In x

531]	§ 5. ЭЙЛЕРОВЫ ИНТЕГРАЛЫ
Если в A0) взять A=1 и принять во внимание, что
= (e'xdx=\,
и
Ди+1) = я!
то окажется, что
755
(И)
A2)
Функция Г является естественным распространением - на область
любых положительных значений аргумента - факториала п\, опре-
определенного лишь для натуральных значений п.
3°. Ход изменения функции Г. Теперь мы можем со-
составить себе общее представление о поведении функции Г(а) при воз-
возрастании а от 0 до ».
Из A1) и A2) имеем: ГA)=ГB) = 1, так что, по теореме Р о л ля,
между 1 и 2 должен лежать корень а0 производной Г'(а). Эта произ-
производная постоянно возрастает, ибо вторая производная Г"(а), как видно
—
If
J
-3
1
-2
\
1
/
/
f
1
3
2
1
-0
\
1
1
I
\
\
I
-3
1
-.5
\
	^
г
~7
1
/
1
3
</= Г(х)
j
\
1
-
Рис. 64.
из ее выражения (8*), всегда положительна. Следовательно, при 0<
<а<а0 производная Г'(а)<0, и функция Да) убывает, а при ао<а-<°°
будет Г {а) >0, так что Да) возрастает; при а = а0 налицо минимум.
Вычисление, которого мы не приводим, дает
ао = 1,4616 ..., rain Да) =Дао) = 0,8856 ...
48*

756	ГЛ. XIV. ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА	[531
Интересно установить еще предел для Да) при приближении а к
О или к ~. Из A1) [и из Г] ясно, что
при а - + 0. С другой стороны, ввиду A2)
Да)>я!, лишь только а>п+\,
т. е. Да) — + ~ и при а — + ~>.
График функции Да) представлен на рис. 64. (Сейчас нам инте-
интересна его часть, лежащая в первом координатном углу.)
4°. Связь между функциями В я Г. Для того чтобы
установить эту связь, мы подстановкой x = ty (?>0) преобразуем F)
к виду:
A3)
о
Заменяя здесь а на а + b и одновременно t на 1 +1, получим:
Умножим теперь обе части этот равенства на Р*-1 и проинтегри-
проинтегрируем по t от 0 до ~:
В интеграле слева мы узнаем функцию Б(а, Ь) [см. D)]; справа же
переставим интегралы. В результате получим [с учетом A3) и F)]:
b)-B(a,b) = (ya+b^1e-ydyha-1<
у = Г(а)[у*-1е-У dy = I\a).I\b),
откуда, наконец,
В^Ь^ Па+Ь) ¦
Приведенный изящный вывод этого соотношения Эйлера при-
принадлежит Дирихле. Впрочем, для обоснования его надлежит еще
оправдать перестановку интегралов.
Мы сделаем это, ограничиваясь поначалу предположением, что
а > 1, Ъ > 1. Тогда для функции
(d-lya+b-l e-(l+t)y

5311	§ 5. ЭЙЛЕРОВЫ ИНТЕГРАЛЫ	757
оказываются выполненными все условия следствия п° 521: эта функ-
функция непрерывна (и притом положительна) для у»0 и ts^O, a
интегралы
o-ie-y
в свою очередь представляет собою непрерывные функции:
первый — от t для ts&O, второй — от у для js=0. Ссылка на упомя-
упомянутое следствие оправдывает перестановку интегралов, а с нею и фор-
формулу A4) - для случая а>\, Ь>1.
Если же известно лишь, что а > 0 и Ъ > 0, то - по доказанному -
имеем
Г(а+\)Г(Ь+\)
В(а+\,Ь+\) = -
Г(а+Ь+2)
А отсюда, используя формулы приведения B), B') для функции В и
(9) для функции Г, легко вновь получить формулу A4) уже без не-
ненужных ограничений.
5°. Формула дополнения. Если в формуле A4) положить b = 1 - а
(считая 0<а<1), то, ввиду E) и A1), получим соотношение [ср. 408
C0)]
которое и называется формулой дополнения.
При а=-у отсюда находим (так как Дд)>0):
Если в интеграле
сделать подстановку z = xL, то вновь получим значение интеграла
Эйлера-Пуассона:

758	ГЛ. XIV. ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА	[531
6°. В качестве применения формулы дополнения определим (вместе
с Эйлером) величину произведения (где п — любое натуральное
число)
Переписав это произведение в обратном порядке:
перемножим оба выражения:
и к каждой паре множителей Г1-/4-—-I применим формулу до-
дополнения. Мы получим
я"
я	я	я
sin — sin 2—... sin (и-1)—
ии	и
Теперь для вычисления произведения синусов (ср. стр. 621), рас-
рассмотрим тождество
z" -1 "^} I	2vn . . 2vri
—=- I \z-cos	1sin —
z-\ *_5i ^	и	и
и устремим в нем г к 1. В пределе:
"fr1 I.	2vn , . 2vn\
И=ЯA-со8 — -ism—j
или, приравнивая модули,
v=\
,	2»я . . 2vn
1 - cos	j sin —
n	n
v=l
так что
""! . г>я И
Подставляя это в выражение для Е2, окончательно получаем:
п-1

531)	§ 5. ЭЙЛЕРОВЫ ИНТЕГРАЛЫ	759
7°. Интеграл Раабе. С формулой дополнения связано и вычис-
вычисление важного интеграла:
1
До =J In Да) йа,
о
очевидно, существующего, так как [см. (9)]
In Да) = In Да+ 1)-In а.
Заменяя а на 1 - а, можно написать
Ro = [1пД1-а)оа
и, складывая:
1
2R0 = Jin Да)Д1 -а)оа =
я	2
1 г	2 г
= 1пя-- In sin x dx = In я - - lnsinxax
о	о
Подставляя сюда значение уже известного нам [492, 1°] интеграла,
найдем:
1
Ro = Г In Да) </а = In /2л.	A8)
о
Р а а б е рассмотрел интеграл (при а >0)
о+1	a+1 a
Д(а)= |1пДа)аа= Г -Г.
а	0 0
Так как, очевидно,
Ща) = In Да + 1) - In Да) = In a
[см. (9)], то интегрируя, находим для а>0
Л(а) = аAпа-1) + С.
Но R(a) сохраняет непрерывность и при а = 0; переходя здесь к пре-
пределу при а-0, убеждаемся, что C=R0. Подставляя значение A8), при-
приходим к формуле Раабе:
а+1
Ща) = Jin Да) da = a(ln а - 1) + Ь /2т?,	A9)

760	ГЛ. XIV. ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА	[532
8°. Формула Лежандра, Если в интеграле
сделать подстановку ^-х = ^У1> то получим
Заменим в обоих случаях функцию В ее выражением A4) через Г:
Г Bа)
- ,к) ¦
Сокращая на Г (а) и подставляя вместо fU его значение ]/я [см. A6)]
придем к формуле Лежандра:
^.	B0)
532. Однозначное определение функции Г ее свойствами. Мы знаем, что функция
Г(а) непрерывна вместе со своей производной для положительных значений аргу-
аргумента. Кроме того [см. (9), B0) и A5)], она удовлетворяет функциональным уравне-
уравнениям:
(I)
(II) Ф(а)ф\ а +- = -~t ФBа),
V	/
(III) Ф(а)ФA - а) = —
sin ая
Мы покажем, что эти свойства в совокупности вполне характеризуют функцию
Г (так что каждая функция, обладающая этими свойствами, тождественна с Г).
Одних свойств (I) и (II) для этого недостаточно, так как, наряду с Г, ими обла-
обладает и функция
Ф(а) = Г(а) • [4 sin2 an]f (при fi>0).
Точно так же недостаточно и свойств (И) и (III), ибо они принадлежат и функции
<*>(«) = Да)-г г (при г»0).

532J	§ 5. ЭЙЛЕРОВЫ ИНТЕГРАЛЫ	761
Наконец, свойства (I) и (III) явно оставляют произвольными значения функции
Ф(а) для 0«=а«= —. Иначе обстоит дело, если налицо все три свойства. Впрочем,
свойство (III) может быть заменено более слабым требованием, чтобы функция
Ф(а) при а>0 не обращалась в 0, что как раз и вытекает из (III) *.
Итак, пусть функция Ф(а) для а=»0 непрерывна вместе со своей производной,
отлична от 0 и удовлетворяет соотношениям (I) и (II). Докажем, что тогда
Ф(а)=Г(а).
Положим Ф(а) = М(а)-Г(а); очевидно, функция М(а) также непрерывна вместе
со своей производной и отлична от 0. Кроме того, так как Ф(а) и Г(а) обе удовлет-
удовлетворяют условиям (I) и (II), то М(а) удовлетворяет соотношениям
(Г) М(а+1) = М(а) и (И') М(а)М\а+- =МBа).
Из (Г) явствует, что при а^ +0 для М(а) существует конечный предел. Если
принять его за значение Af(O), то М(а) окажется непрерывной вместе со своей
производной вплоть до а = 0.
1	/It
Заметим, что из AГ) при в= — следует, что iW 1—1 = 1; значит, М(а)=~0 для
всех as=0. Это дает нам право рассматривать функцию
Да) = In M(a),
которая также непрерывна вместе со своей производной для ав=0, но удовлетворяет
условиям:
(I") Ца+1) = Ца) и (И") L(a) + L fe + ij =Д2в).
Наконец, введем еще непрерывную функцию
она выполняет соотношения:
(Г") А(а+1) = А(а) и (И'") А(а) + А\а + ^\=2АBа).
а
Из (И'"), заменяя а на —, получим
а а + 1
Если здесь снова заменить а сначала на —, а затем на 	и сложить полученные
равенства, то найдем, что
Методом математической индукции легко установить обшее соотношение
* Для 0«=а<1; соблюдение этого требования для прочих значений а следует
уже из (I).

762	ГЛ. XIV. ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА	[533
Но, каково бы ни было а, сумму слева можно рассматривать как интеграль-
интегральную сумму для интеграла
1
Г Л(х) dx *.
о
Поэтому
1
1 z"-1 (a+v\ r
Л(а)= lim - 2 лКтг =
[ввиду (I")]. В таком случае Да) = const, значит и М(а) = const. Но мы видели, что
М - = 1, так что М(а) = 1 и Ф{а) = Г{а), ч. и тр. д.
В заключение отметим еще, что требование дифференцируемости играет
при этом существенную роль и не может быть отброшено. Если, например, по-
положить
то в лице L(a) будем иметь непрерывную функцию, удовлетворяющую условиям
(I") и (II")- Вместе с тем ?@) = 0 и L I—I = —, так что ?(а) не сводится к постоянной!
W 2
533. Другая функциональная характеристика функции Г. В предыдущем п° была
дана характеристика функции Г(а), как единственной непрерывной вместе со своей
производной функции, удовлетворяющей функциональным уравнениям (I) и (II)
и не обращающейся в 0 (для а =- 0). Здесь же мы дадим более простую характеристику
функции Г(а), используя лишь одно функциональное уравнение (I), но налагая
на функцию еще требование «логарифмической вьшуклости», смысл которого мы
сейчас выясним.
В п° 141 было дано определение выпуклой функции f(x). Положительная
функция f(x), заданная в промежутке ЗС, называется логарифмически
выпуклой в этом промежутке, если ее логарифм In f(x) оказывается выпуклой
функцией. Так как
то в силу 142, 3°из логарифмической выпуклости функции f(x) вытекает
ее выпуклость; обратное заключение, вообще, неверно. Таким образом, лога-
логарифмически выпуклые функции составляют лишь часть всего класса выпуклых
функций.
Пользуясь теоремой 2 п° 143, можно установить условие логарифмической
выпуклости: пусть положительная функция fix) непрерывна вместе со своей произ-
производной fix) в промежутке % и имеет внутри промежутка конечную вторую
производную f'(x); тогда для логарифмической выпуклости функции f(x) в % необ-
необходимо и достаточно, чтобы внутри % было
Доказательство состоит в применении упомянутой теоремы к функции 1пДх).
* Учитывая при этом периодичность функции Л(а), в силу (I'").

533]	§ 5. ЭЙЛЕРОВЫ ИНТЕГРАЛЫ	763
Вернемся теперь к функции Г(х). Ее первая и вторая производные выражают-
выражаются формулами (8) и (8*). По неравенству Буняковского [321, A3'); 483, 7)]:
J [<p(xW dx- J W*)]2 dx-
если положить здесь
a = 0, b = ~; <p(x) = У*"-^-*, уW = Ух"*"*-In x,
получим:
Отсюда, по только что приведенному условию, функция Г"(а) в промежутке @, °°)
оказывается логарифмически выпуклой. Вот этим-то свойством, совместно с урав-
уравнением A), функция Г и определяется с точностью до постоянного
множителя. Иными словами:
Если 1) в промежутке (О, ~) Ф{а) удовлетворяет уравнению (I)
2)	Ф(а) логарифмически выпукла и
3)	ФA) = 1, то Ф(а) = Г(а).
Допустим, что для Ф(а) выполнены все эти три условия.
Повторно применяя уравнение (I), придем к общему равенству
{а+п-\){а+п-2)-	(а+1)-а-Ф(а),	B1)
где и - любое натуральное число; отсюда, полагая а = 1 [см. 3)] и заменяя и на
и- 1, найдем:
Ф(и) = (и-1)!	B2)
Отметим, что достаточно доказать совпадение Ф(а) с Г(а) в промежутке @, 1],
ибо, вследствие (I), эти функции будут совпадать и повсюду. Пусть же 0
Вспомним неравенство F) п° 143
имеющее место для выпуклой функции f(x) при единственном условии: Х\ •< хг *.
Применив дважды это неравенство к выпуклой, ввиду 2), функции In Ф(а) при
любом ns=2, получим
1пФ(-1 + и)-1пФ(и) 1пФ(а + и)-1пФ(и) 1пФA+и)-1пФ(и)
(-1 + и)-и	(а + п)-п	A + и)-и
или - с учетом B2) -
Ф(в+иIп(и1)!
In (и- l)=eln	=sln п.
а
Отсюда следует
In (п - 1)" • (л - 1)!=е1п Ф(а+/i)=sln ifi ¦ (и -1)!,
а значит:
(п- 1)а-(п- 1)!*еФ(в+и)*Ела.(н- 1)!
* Правда, в указанном месте было предположено, что xt < jc -= дг2, но нетрудно
убедиться, что написанное неравенство справедливо при любом положении точки х,
лишь бы она не совпадала с х% и *8,

764	ГЛ XIV. ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА	[534
Переходя теперь, с помощью формулы B1), к самому значению Ф(а), придем
к неравенствам
Наконец, заменяя в первом из них и на и+1, представим полученные неравенства
в виде:
1.2-3.....(и-1) л,
Отсюда уже ясно, что
Ф(а) = Km rfi —~^~-' V". " <ч - Па)
- в силу формулы G) Эйлера-Гаусса.
534. Примеры. 1) Найти интеграл
1
ГхР-\\-х™)?-1 dx (p, q,m>0).
о
Указание. Полагая хт=у, сводим его к эйлерову интегралу первого
рода.
Ответ.
т (р
Предлагается с помощью этого результата доказать, например, что при любом
натуральном и
1	1
С dx г хп dx n
__._—- = _ (Эйлер).
J V\ _ хт J у i _ xin 2n
2) Вычислить интеграл
1
г xP'^l-xy^1
	dx
J [алг+/?A -х)+у]Р+1
о
С помощью подстановки
= . ——, х~гг- - ' [ах+рA_х)+у]г=
предложенный интеграл приводится к виду
1
1	Г.	,. 	 ,. B(p,q)
(<*+у)Р(Р+у)Я

534)	§ 5. ЭЙЛЕРОВЫ ИНТЕГРАЛЫ	765
3) Найти интегралы
1	+i
	dx, (б) 	7~т+п	^*"
О	-1
(a, 6, p^O)	(m, n=»0)
Указания, (а) Подстановка у = A +/>)	. (б) Подстановка и =
1+х2 '
Ответ, (а) 	В(а, 6); (б) 2"> + п-2Д(|я, „)
A +)V
( p)V
Отсюда, в свою очередь, может быть получен ряд любопытных интегралов.
Например, если в последнем взять и=1-т, положить 2т-1 = cos 2a и сделать
подстановку x = tg<p, то найдем:
4
г |'cos<p+sin<p'\c0s2';'
	:—
J vcosffi-sina»/
2 sin (л cos2 a)
4) Найти интегралы
л
2
(а)	\sina~1 <p cosb~l<pd<p (a, 6=-O);
о
л	л
2	г
(б)	\sina~1(pd<p= \ cos"-1 <pd<p (a=-O);
о	о
л
(В) jt&ipdq,	(|C|-1).
О
Решение, (а) Полагая х = sin <p, приведем предложенный интеграл к ин-
интегралу
о
так что, используя задачу 1), будем иметь
-	1а\ (Ь
2	г -\Г -
f • а_1 „_, _! /а 6)_ J W U
.'	2 1.2' 2J 2

Гл. XIV. ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ Of ПАРАМЕТРА	[534
(б) В частности, при Ь=\, получим отсюда
С помощью формулы Лежандра этот результат может быть переписан
в виде:
Г (а
\г\-
L U
(в) Наконец, полагая в (а) а=1 + с и 6=1-с, где |с|-=1, найдем (используя
формулу дополнения)
л
8
2/1,2/	ел
о	2 cos —
5) Определить площадь Р фигуры, ограниченной кривою
г1 = sin3 0 cos9.
Решение. Кривая имеет две петли - в одну и в три четверти; достаточно
удвоить площадь одной из них. По формуле для площади в полярных координатах
[338 (9)] имеем:
2J	2ГB)	8 [4) {4! 3
о
[см. зад. 4) (а) и соотношения (9), A2), A5)].
6) Определить (а) площадь Р фигуры, ограниченной одним витком кривой
(пг - натуральное число)
,-m = am cos mQt
и (б) длину S этого витка.
л	л
2т	2
2	, Л 2
о» Г 2-	«2 Г
Решение, (а.) Р=2— I cosm mO dO = —
cos"
6
а2 Ул \т 2) лсР \т
~т~2 Т\
Г -+1
\т
[см. зад. 4) (б) и соотношения (9), B0)].
* Легко проверить, что в этой формуле как частные случаи содержатся обе
формулы (8) п° 312.

534)	§ 5. эйлеровы интегралы	161
(б) По формуле для длины дуги в полярных координатах [329 D6)]
2m	2
r i-i	la г -1--!
cos тв dd = — cos
J	m J
[см. зад. 4) F)].
7) Вычислить интералы
(a)
о
(а) Указание. Подстановка: cos 6 = 1-2 Ух.
1
Ответ.
4 y^L Uj
в 1 [T^k <f
(б) Указание. Подстановка: tg—= / 	tg—.
2. у I ~f~ /С 2.
0
Ответ.
- №
8) Доказать, что
1
ГA-jc3)~i"rfjc= ]/3 | (лгЗ-1) 2 dx.
Решение. Положим
1
,-,, j
о
J (l-x3)"^» U
-=o	0
Подлежит доказательству равенство
L	_I
Применяя к этим интегралам подстановки (соответственно) x = tz, x=t 3,
x = (t~1 — lK, приведем их к эйлеровым интегралам первого рода. Затем придется
лишь несколько раз использовать формулу дополнения.
* 9) Доказать формулу (принадлежащую Дирихле)

768	ГЛ. XIV. ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА	[534
Указание. Подставить
J4±_= [e-(g+x)yyr-idy _^Xf)_= \e-(f+y)xxs-idx
(g+xY J	y *' {f+yf J
о	о
и использовать перестановку интегралов по х и по у (случай положительной
функции).
10) В задаче 12) п° 511 мы доказали тождество
ЕК'+Е'К - КК' = с = const
(относительно обозначений см. в указанном месте). Затем, с помощью некоего
я
предельного перехода было установлено, что с =—. Этот же результат можно
было бы получить, вычислив величину левой части при каком-нибудь частном
значении к.
Пусть k = l/Y2; тогда к' = к, Е' = Е и К' = К, и тождество принимает вид
2ЕК-К2 = BЕ-К)-К = с.
Интегралы
о |/l--sin2<p	о
последовательными подстановками cos <p = t, tf = x приводятся к эйлеровым ин-
интегралам первого рода:
1
1 Г -- --
К =	 л: 4A-х) 2 dx,
ifi)
о
iff-- -- С -- -- 1
	< х 4 A - х) 2 Л+ л: 4 A -х) 2 dx\ ,
4
v о	о
так, что
1
1 г _i _!
-К=-^ х 4A-х) 2Л.
2V2J
2Е
21/1
о
Отсюда искомая постоянная
11) Разложить в ряды интегралы:
г xs~1	г Xs
fa) —-dx,	(б) -—Л.
J ex-l	J ex+l
о	о
(s=»l)	(s=-0)

534)	§ 5. ЭЙЛЕРОВЫ ИНТЕГРАЛЫ	769
Решение.
(a) f^—rf.x= [Xs-lZe-nxdx = 2 f xs-»e-"* <**=/»• j? — =Г(*)-С(Д
J ех - 1 J	I	I J	i /Is
оо	о
если через C(s) [функция «дзета» Р и м а н а], как обычно, обозначить сумму по-
последнего ряда. Мы воспользовались здесь теоремой об интегрировании положи-
положительного ряда [518] и формулой A3).
г xs~'	°° (—1)"~'	2х3~г
(б) 	— dx = r(s)y,	. Мажоранта: 	.
J ех+1	1 и»	ех+1
о
Если j=-1, то этот результат можно представить в виде
ибо
12) Некоторое обобщение предыдущей задачи представляют разложения:
- 1
	 dx= Г(*). 2^	 (**1, в»0)
l-e~x	n=o(a + n)s
о
[11) (а) отсюда получается при а= 1];
(а)
J l-e~x
(б) —
J ex-
~l dx	-у z" (-l=sz«=l ks>0,
Z	n = l«S	ИЛИ Z=l И S^l)
0
[11) (а) отсюда получается при z = 1, a 11) F) - при z= - 1].
13) Обозначая сумму гипергеометрического ряда [см. 441, 6)]
через F(a, /S, у, х), доказать соотношение:
(Гауе с).
Считая а=-0 и у-а=-0, рассмотрим интеграл
) = J z«-41 -
о
49 Г- М. Фихтенгольи, т. II

770	гл. xiv. интегралы, Зависящие от Параметра	153$
при 0<х~=1. Так как ряд
п=о	Ь2...и
сходится (при фиксированном х) равномерно относительно z в проме-
промежутке [0, 1], то - умножая на интегрируемую в этом промежутке функцию zc(~1(l -
-z)y~"~1 - полученный ряд можем интегрировать почленно. Мы придем к раз-
разложению
/м=2"/„•*",
о
где
-(/3+"~1) Г(х+п)-Г(у-в.у
Г{а)Г(у-а) а(
[см. A0)].
Таким образом,
Г(а)Г(уа)
/(*) = '.	--F(<x, /?, у, х).
Для получения формулы Гаусса остается лишь перейти здесь к пределу при
х-\ (считая у-а-/?»О). В ряде этот переход можно выполнить почленно -
по теореме Абеля [437, 6°]. В интеграле же можно перейти к пределу под знаком
интеграла - ввиду наличия мажоранты:
2»-1A-гM'-«-1 (при /3«=0) или z*- \\-г)у-я-!>-1 (при ?=-0).
В результате [см. A4)]
Г(у-Р)	Г(у)
откуда и следует доказываемое соотношение.
Из него, в частности, при у=\, /3= -а получается [с учетом A1), (9), A5)],
любопытное разложение @-=а-= 1).
«пая а2 а2(а2-1) а2(а2-1)(а2-4)
ая ~Т+ A-2J	(Ь2-3J +'"'
535. Логарифмическая производная функции Г. Продолжая изучение
свойств функции Г, обратимся к рассмотрению ее логарифми-
логарифмической производной, т. е. выражения
d In Г(а) Г'{а)
1а = Г{а) '
9°. Различные представления этого выражения в виде интегралов
можно получить и из формулы (8). Но проще исходить из следующих
* Оно, впрочем, может быть выведено и преобразованием известного бесконеч-
бесконечного произведения, выражающего синус [408].

S3S]	§ 5. ЭЙЛЕРОВЫ ИНТЕГРАЛЫ	771
соображений. Имеем:
Г{а)Г(Ь) _ Г(Ь)-Ь Г(а+Ь)-Г(а) _
' Г(а+Ь) ~ Г(а+Ь) '	~Ъ	"
Г(а+Ь)-Г(а)
так что, если перейти здесь к пределу при Ь-*0,
Возьмем сначала [см. F) и D)]:
1*-* dx, B(a, Ъ)=
о	о
Тогда
и, вьшолняя предельный переход под знаком интеграла, получим фор-
формулу Кош и:
Да) J
в-*
Да) J Г A+хГ\ х ¦
о
Для оправдания предельного перехода заметим, что вблизи х = 0,
= 0 выражение
1 \с-г	1
х[	A + х)а+
будет непрерьшной функцией от х и Ъ, а л* < 1. Для достаточно боль-
больших х и Z>=sfe0 имеется мажоранта:
i	е-х]
+х)"	J-
1A +х)"
Если же в выражении A) для 5 сначала сделать подстановку х =
В(а, Ъ) =
о
то можно написать
-е-^)*-1] dx.
49 .

772	ГЛ. XIV. ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА	[536
Переходя здесь к пределу под знаком интеграла (что оправдывается
аналогично), придем к другой формуле:
Наоборот, можно вовсе устранить показательные выражения из
подинтегральной функции. С этой целью положим в B3) а = 1:
Г'О) r,,iv
где С есть так называемая эйлерова постоянная *. Вычитая почленно
это равенство из B3), получим
Ш . с= ff_i
Г(а)	J Yl+х
о
Наконец, подстановка / = г— приведет нас к формуле Гаусса:
штС=|~А	B5)
536. Теорема умножения для функции Г. 10°. Опираясь на пред-
представление B5) для логарифмической производной, установим теперь
следующую замечательную формулу, также принадлежащую Гауссу:
П—1
/ (а) Г [а + -)•¦¦ Г [а + -^-J = • ' Г (па)	B6)
п 8
(п - любое натуральное число). Она выражает теорему умно-
умножения для функции Г.
Полагая в B5) t = un, получим:
Ла)"
С=П) Х-Ф d«>
* Мы имели в главе XI [367, 10)] другое определение этой постоянной. Ниже
мы убедимся в тождестве обоих определений.

536]	8 5. ЭЙЛЕРОВЫ ИНТЕГРАЛЫ	773
откуда, заменяя а на а + - (v = 0, 1, ..., и- 1),
-К)
= n\	-.—	du
J	1-й"
и, суммируя по v от 0 до и-1,
Сопоставим это равенство со следующим:
1
"(.па) r_ f 1-ц™-'
\па)+^~ J 1-й
ГО
о
Умножив последнее равенство на и и вычитая из предыдущего, най-
найдем:
I v
v
= - п In л,
о
что можно написать в виде:
Отсюда, интегрируя, получим
in
или
Для определения постоянной С положим здесь а=-. Очевидно,
С=пЕ, где ?есть то произведение Эйлера, которое мы вычис-
* Предвидя потенцирование, мы заранее берем произвольную постоянную
под видом In С.

774	ГЛ. XIV. ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА	[53П
ляли в 531, 6°. Подставляя его значение из A7), придем к формуле
B6).
Частным случаем формулы Гаусса является ранее выведенная
независимо формула Лежандра B0). Действительно, если в B6)
взять и = 2, то получим формулу
которая равносильна B0).
537. Некоторые разложения в ряды и произведения. 11°. Источни-
Источником их является та же формула B5). Разложим подинтегральное вы-
выражение в ряд:
* ~~_[	(\ 	fa—1\ 'V fv	 "V ( *v ta + v—14
1 _ t — V	^ ^J — -^—i ^	*>
1 l	v=0	i>=0
все члены которого имеют один и тот же знак. Почленное интегри-
интегрирование дает:
B7)
Ряд этот сходится равномерно для 0-=я=еао, ибо мажорируется рядом
Если его почленно продифференцировать по а, то получим заме-
замечательное по простоте разложение
^	B8)
Так как и этот ряд сходится равномерно для а>0 (мажорируется
рядом 2 ~? > т0 почленное дифференцирование оправдано.
»=i v )
12°. Проинтегрировав почленно ряд B7) по а от 1 до а>0 (что
законно, ввиду равномерной сходимости ряда), получим
B9)
Заменяя здесь а на а +1 (при а => -1), перепишем разложение в виде

538]	§ 5. эйлеровы интегралы	775
или
Отсюда, потенцируя, приходим к уже известной нам формуле
Вейерштрасса [ср. 402 A6)], дающей разложение yq—^- в бес-
бесконечное произведение:
U?~n {a^l)- C0)
13°. Возвращаясь к B9), положим здесь а = 2. Так как In Г B) =
= In 1 = 0, то получим:
1(^^)	О.)
Заметим попутно, что отсюда
и мы приходим к уже знакомому нам определению эйлеровой по-
постоянной [367, 10)]. Наконец, умножая C1) на а-\ и вычитая по-
почленно из B9), мы исключим С:
или, что то же,
Отсюда, потенцируя, мы вновь находим формулу G) Эйлера
Гаусса, выше установленную другим путем.
538. Примеры и дополнения. 1) Пользуясь тем, что
-'-Km I— ,
п~~\ п)
е
доказать, что (при а>0)
Т(а)= f/a-'e-'^lim f t0'1 \ 1 --) dt,
J	л—.J	V П]
0	0
и вывести отсюда формулу G).

776	ГЛ. XIV. ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА	[538
Указание. Предельное равенство устанавливается так же, как это было
сделано в задачах 10) и 11) п° 519. Подстановкой т = г/и преобразуем интеграл
1
fa-^fl--) dt = na Г
и используем формулу C).
2) Из формулы B3)
Да) J
о
непосредственно вывести формулу B4)
и r~r~7i~Adu-
J L и	1 — 0 MJ
Г'(а)
Л«) =
о
Заметим, что трудность здесь в том, что нельзя интеграл B4) рассматривать
как разность двух интегралов (иначе вопрос был бы исчерпан преобразованием
второго подстановкой х = е"-1). Поэтому, обходя ее, напишем:
Ли) f'-foiJ
в-xdx г dx )
Ли) f'-foiJ х
t
-lim[ [в-^.~ [ -L-!L«
»-oU и	J 1-е-»
t-o J L и l-e~HJ J I u 1-е"
>	о
так как
С e-au
lim I 	du = 0.
e^o J 1-е-"
[Это видно из того, что интеграл оценивается выражением
е-ln A+е)	е
-1 2A+е)а-
3) Исходя из определения эйлеровой постоянной равенством
("I	^
?	In и I,
v=l V	)

538]	§ 5. ЭЙЛЕРОВЫ ИНТЕГРАЛЫ	777
установить интегральные формулы
1	«,	«,
(a) C= f(l-e-*)-- IV*-, (б) С= f(— -e-A'-
J	X J	X	J \\+U	j
0	1	0
к
1	1	1
X7	 1 X7 tV — 1 fit — I 	 /УI — I	Ле
ds
l
TO
1
s	J s
0	l
л
| г Г ( х\т] dx rdx)
= lira 1-1—	_
Предельный переход во втором интеграле проводится, как и в 1). Относительно
преобразования (а) в (б) см. 2).
4) Полагая (при в>0 и s>l)
Us, a)= 2! ;	гг. доказать, что lim \Z(s, a)- —-U -
Г'{а)
Па)'
Мы имели [534, 12) (а)]
1 rxs-ie-ax
C(s a) =	dx
Hs)} l-e~x
о
Поэтому
1 1 I rxs-4-ax	, ) 1 r r e-flx <?-*!
5-1 ГE) U 1-е-*	j r(s) J ll-e-x x J
о	о
Предельный переход при 5-1 можно произвести под знаком интеграла, так
как подинтегральное выражение, в промежутках [0,1] и [1, +~] порознь, стремится
к своему пределу монотонно 518. Затем использовать формулу B4). При а=1
в частности, получается
> 1+0
[Ср. 375, 1)].
lim Г«*)--Л-1-С.
е-»1+01	5- 1J

778	ГЛ. XIV. ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА	[538
5) Вычислить величину бесконечного произведения
где
{n+ai)(fl+a^...(,. , _„,
и„ =	 (a/, bi^—1).
(n+b1)(n+b2)...(n+bk)
[Э й л е р].
[Так как
-ИЬНКГ-ИГ-
(в!+ .¦¦+ак) -№!+...+ ад j4n
и	и2
то сходящимся бесконечное произведение будет лишь при условии
в этом предположении и предлагается вычислить Р].
Указание. Представив ип в виде
ип--
1 + — в " ... 1ч—-\ е л
использовать формулу Вейерштрасса C0).
Ответ. Р = -
6) Предполагая 0 •= | а,-1, 16,-1 -<1, вывести из 5) другой результат Эйлера:
""ri" sin i^-sin 62л-... -sin Ь^л
11 un «	:
11 n	::
л--- sin д^т-sin Oj-t. ...-sm о;,д
Указание. Воспользоваться формулой
которая вытекает из (9) и A5).
7) Вернемся к формуле Гаусса:
которая в 534, 13) была установлена в предположении, что
а=»0, у-а>0 и у-а-/9=-0.
Сейчас предлагается доказать ее другим путем, предполагая лишь положительными
аргументы функции Г в правой части формулы и опустив ненужное
условие »>0.

538]	§ 5. ЭЙЛЕРОВЫ ИНТЕГРАЛЫ	779
Укажем план доказательства. Обозначим, соответственно, через ап, Ьп, сп
общие члены гипергеометрических рядов
А = F(oc, В, у, 1), В= F(oc, - 1, В, у, 1), С= F(a, /9, у+1, 1).
Непосредственно проверяются соотношения
и доказывается, что иа„ -* 0. Складывая эти соотношения при изменении указателя
от 1 до и и переходя к пределу, получим:
уВ = (у-В)С, (у-а)(А-В) = ВА,
откуда
С.
Рассмотрим теперь выражение
F(a, В, у, 1).-	' г -¦;	C2)
предыдущее соотношение [в связи с (9)] показывает, что значение этого выражения
не изменится при замене у на у +1. Таким образом,
F(a, В, у, 1)	= №, А у + т, 1)
Перейдем здесь справа к пределу при т-~ <*>. Из равномерной, относительно /я,
сходимости ряда F(a, В, у+т, 1) следует [433], что его сумма стремится к 1. Таков
же будет предел и множителя
Г(у+т-а)-Г(у + т-В)
Г{у + т)-Г(у+т-*-В)'
так как он представляет собой остаточное произведение для сходящегося
[в силу 5)] произведения
/7
/
n=i(y+n)(y-a-B+n)'
В таком случае выражение C2) оказывается равным 1, а это равносильно
формуле Гаусса.
Из этой формулы теперь можно, при у = 1, а = В= -1j2, получить разложение
1+UJ Цгц} +{^
-1-3.5^	1
можно доказать и более общий результат, что сумма биномиальных коэф-
коэффициентов, отвечающих показателю т бинома, при т> -1/г, равна
Л1+21И)
( 1 S)
Раньше мы это сделать не могли из-за ограничения а=»0.

780	ГЛ. XIV. ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА	E38
8) Распространение Г(а) на случай отрицательных а. По формуле (9),
так что значение Г (а) определяется через значение Г(а+1). Если -1<а<0, то
а+1=-0, и Г(а+1) имеет смысл. Определим Г(а) по предыдущей формуле;
таким образом, определение функции Г(а) распространено и на случай -1^а«=0.
Вообще, если -п^а^ -(и-1), то, распространяя на этот случай формулу A0),
определим Г(а) равенством
Если для большей отчетливости положить здесь а= -и + а, где 0-=а-=1, то
определение это перепишется так:
Г(<х)
r(a-«) = (-l)"	———	.	C4)
(l-«X2-«)...&i-«)
Отсюда сразу видно, что знак Г(а) для -и-=а-=-(н-1) дается множителем
(-1)". При приближении я к -и или -(и-1) (т. е. при приближении а к 0 или
к 1) Г{а) обращается в ~ (первого порядка!).
9)	Предлагается, основываясь на 8), обобщить на случай любых веществен-
вещественных значений аргументов формулы G), (9), A5), B0), B6), C0) (избегая лишь целых
отрицательных и нулевого значений аргументов).
Указание. При распространении формулы [30] учесть равенство C3).
Если воспользоваться распространением Г(а) на случай отрицательных а,
то и формула Гаусса, о которой речь была в 7), окажется верной при един*
ственном предположении: у-а-/3=-0, которое необходимо для сходимости самого
ряда F(oc, /?, у, 1) [378, 4].
10)	Основываясь на формуле C4), доказать, что, при изменении а от 0 до 1,
Г'(а-п) однажды (скажем, при а = ос„) проходит через 0, меняя знак (-1)"+' на
(-1)". При соответствующем значении а=а„- п функция Г(а) имеет, таким обра-
образом, положительный минимум (при п четном) либо отрицательный максимум
(при п нечетном). См. график функции Г на черт. 64.
Предлагается доказать также, что (при возрастании п) как ип, так и
Гп — \Г(а.п-п)\, монотонно убывая, стремятся к 0.
Указание. Основанием для этих заключений служат равенства @<а¦< 1):
Я+1-« ' l*v»4'l „+]_a ^(„+1_aJ
11) Доказать, что при -и-=а<= -(и-1) функция Г(а) выражается интегралом
Указание. Применить интегрирование по частям; см. 8).
12) В главе XI [402, 10)], исходя из определения функции Г(а) формулой Э й-
лера - Гаусса G), - и притом сразу для любых вещественных значений

538]	§ 5. эйлеровы интегралы	78i
аргумента (исключая нуль и целые отрицательные числа) - мы установили не-
некоторые простейшие свойства этой функции [см. также 408]. То же можно сделать
и по отношению к другим изученным свойствам.
Точно так же отправной точкой для изучения функции Г(а) при любых веще-
вещественных а (за теми же исключениями) может служить ряд
Z
при дополнительных условиях 7X1) = -ГB)=1.
13) Наконец, отметим, что функция Г(а) может быть определена, как однознач-
однозначная аналитическая функция, во всей плоскости комплексной переменной
а *. Это может быть сделано, исходя из самого интегрального определения F),
если разбить
о»	1	оо
f на два Г + Г = P(a)+Q(a).
о	о 1
Тогда функция
'-/¦
и! J	о и! а + п
естественно распространяется на всю плоскость комплексной переменной как
мероморфная функция, с простыми полюсами в точках 0, - 1, -2, ..., -и, • •.,
которым отвечают вычеты 1,-1, — ,...,(-1)"— , ... Функция же
2!	и!
QW-J:
имеет смысл и при комплексных значениях а и представляется целой функцией.
Свойства функции Г(а), доказанные для положительных вещественных значений
аргумента, автоматически распространяются на всю плоскость, по известной
теореме об аналитических функциях (мы имеем в виду свойства, выражаемые
равенствами между аналитическими функциями). В частности, из формулы допол-
дополнения A5), которую можно написать так:
1	1	1
	= — sin ал- Г{а) = — sin ал[Р(а) + Q(a)\ **,
77A — а) л	л
явствует, что 1/Г(а) голоморфна во всей плоскости. Таким образом, Г(а) не имеет
корней.
В заключение упомянем, что как формула Эйлера - Гаусса G), так
и формула Вейерштрасса C0) с успехом могут быть положены в основу
определения функций Г(а) сразу во всей плоскости.
* Это последнее замечание о распространении функции Г может быть понято
лишь теми, кто знаком с основными понятиями и терминами теории функций
комплексной переменной.
** В тех точках, где Р(а) имеет полюс, sin an обращается в нуль.

¦?82	ГЛ. XiV. ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА	[539
539. Вычисление некоторых определенных интегралов. Обратимся к рассмотре-
рассмотрению некоторых интегралов, при вычислении которых используется функция Г{а)
и ее свойства.
1) Дифференцируя по а формулу
Г(а)= [
о
мы получили в 531, 1° формулу (8):
о
Полагая здесь в= 1, так как Г'A)= -С, получим:
е~х In xdx= -С.
о
Подстановка х = - In и приведет к любопытному интегралу
Г1п(-1пи)<Л/= -С.
о
Если взять a=lj2 и положить х = t2, то найдем:
(V'4n / Л =-^ Г'(^) = - ^j (C+2 In 2),
J	4 \2)	4
О
как это легко получается из разложения B7) - с учетом логарифмического
ряда.
Повторяя дифференцирование по а, мы пришли к равенству (8'):
Г"(а)= [ хР-Ч-х In2 х dx.
о
При а = 1 оно дает нам:
г	яг
е-х1п2хЛ = Г"A)=С2 + — .
J	6
о
Последний результат получается из B8), если при этом воспользоваться известным
°° 1 л2
рядом У. — = — . Наконец, полагая и здесь а = */г. с помощью подстановки х = /2
1 и2 6
получим еще такой интеграл:
во
Г	Ул Г	я21
е-'1п«/А=- (С+21п2)г+—
.'	о I	2 J
и т. д.

530j	| 5. ЭЙЛЕРОВЫ ИНТЕГРАЛЫ	?83
2) Вычислить интеграл
rsinP x
J= 	dx,
J x
0
где p есть рациональная дробь с нечетными числителем и знаменателем.
Указание. Воспользоваться формулой Лобачевского [497, 14)];
в согласии с ней
См. 532, 4) (б) Ответ. J-
у,
' 2
3) Вычислить интегралы
Имеем [см. A3)]:
1
0
1 1 с si _at
0
Переставив интегрирования,
л- 1
Г-
2
1 2 J
F=»0):
cos 6л:
:1)
, так что А =
получим
s-i Лт Го-гхгг.<! А
Л.
.['
т
Ар)
со
1
0
1
sin ft
jcos-
0
1
ОС
bxdxj
0
С zs«fe
г
zs~4~zx dz.
J
о	о
или, полагая Ьг( = гг,
«. s—i
— А =	В.
о	sin	я 27 (.s)-cos —
[см. D), E)]. Аналогично
ir{s) sin —
Обоснование перестановки интегралов проводится так же, как и при вычисле-
вычислении интеграла 	dx в 524, 11).
J х
х
о

784	гл. xiv. интегралы, зависящие от г1а{>амет1>а
4) Вычислить интегралы
fsin х	rsinx
I	In x ax,	I	In2 x ax.
J x	J x
о	n
Согласно З), интеграл @«:s-=2)
г sin x л
J= 	dx =	.
J Xs	S7l
о	2r(s) sin —
Дифференцируя его по параметру s (пользуясь правилом Лейбница),
найдем:
sin х л If
	lnxcfe =	/"
с sin
J x
sn л	sn
r()
/(.s)sin jr(j)cos
2 Г	зял*{	2 2	2
r(*).sin —I
Применение правила Лейбница оправдывается равномерной сходимостью
полученного интеграла относительно i как при х = ~ (для ss=so^O, см. 515, 4°),
так и при х = 0 (для J=ssi, мажоранта | In лг| ixSi-1)- Продифференцировав полу-
полученное равенство еще раз (что обосновывается аналогично), найдем:
Г Sin X	Л	I	S7l Tt	S7l\ 2
	ln*xdx =	 r'(s)sin— + -rO)cos—
J Xs	Г , ч . *л1» I	2 2	2 J
о	(i)-Sm~2
	I F"(s) sin	hлГ"($) cos	— P(s) sin —J-.
2 Г„, . . «П* I	2	2 4	2 I
r(s)sinyj
Полагая в обоих равенствах s= 1, найдем значения искомых интегралов
г sin х

о
Учитывая, что [ср. 1)] Г'A)= -С, /"'A)=С2Н— , окончательно будем иметь:
6
со	оо
• sin х _ . я	г sin х. . я	л3
2"С +24'
J' sin х я с sin л:
	\nxdx=	С, 	\r&xdx =
х 2 J х
о
формулу
г	Ул Г(а)
I Sin20"!!)!/!!)»	•	 (<3 =*()).
J	2 Г П
о	о
5) Мы имели уже [см. 534, 4 (б)] формулу
я/2

539J	§ 5. ЭЙЛЕРОВЫ ИНТЕГРАЛЫ	785
Дифференцируя по а [с применением правила Лейбница, 520], получим
"Я	Г	dlnr[a+-\
1 У^ Г(а) \dlnr(a)_	{ 2)
"l'~2 1 Г\ Та	da
J	V
¦И)
Если воспользоваться формулой Гаусса B5), то выражение в скобках пере-
перепишется в виде
1 о_1
rt 2-/0-1
	dt.
J \-t
Положим теперь 2а - 1 = 2л, где и - любое натуральное число или нуль, и сделаем
подстановку t = и2. Тогда получим
Л	,	|
"	Г\пЛ
г	~\[л \ 2) г ит
sin2" <p In sin <p dq> =	•	 I 	<Л/,
J	^ 2 Г(и+1) J 1 + и
о	о
При и = 0 эта формула дает уже известный результат:
г	л
h\sm(pdq>- — In 2.
о
При «s= 1 мы приходим к новому интегралу
л Bи-1)!! С 1 1
о
6) Вычислить интегралы (а =- 0, р =- 0)
оо	во
к= \ е~аххР~1 cosbxdx, ю= I «~exxP-1sin bxdx.
о	о
Решение проводится аналогично 8) п° 523. Для функции w = u+vi от Ь, как
и там, получается дифференциальное уравнение
dw	p
— =	(b-ai)w,
db
которое можно переписать в виде:
dw
db	а- Ы
Легко проверить, что - в силу этого уравнения -
w • (а - Ы)Р = с = const *.
* Под (а ± Ы)Р здесь и ниже мы разумеем ту ветвь степенной функции, которая
при 6 = 0 обращается в положительное вещественное число аР.
50 Г. М. Фихтеагольп, т. II

786	ГЛ. XIV. ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА	[539
Полагая здесь 6 = 0, находим, что c = F(d). Таким образом,
Г(р)	Г(Р) (	Ь .	Ь\
	(а+60р =	{cosparctg—i-ismp arctg—}
\	а	\
w	(а+60	{cosparctgiismp arctg
{а-Ы)Р (я2 + 62)Р	(а2 + 62)Р/2\	а	а
Приравнивая порознь вещественные и мнимые части, получим, наконец;
Г(р) .
cos об, v =	sinpO,
(а2+62)Р/2
(Й2+62)Р/2
b
где для краткости положено: в = arctg —.
а
.		Ь	а
Заменяя Ца2+Ь2 через 	 или через 	, можно переписать результат
sin 0	cos О
в виде
Г(р)	Г(р)
и =	sinP Ocos рв =	cosP в cos рв,
ЬР	аР
Г(р)	Г(р)
«=—- -sinP0sinp(?=	cosP0sinpO.
ЬР	аР
Предлагается получить отсюда интегралы А я В задачи 3), полагая p=l — s и
устремляя а к О I при 6>0 угол в = arctg — будет тогда стремиться к — .
I	a	2)
Дифференцируя по р интегралы и, v, можно получить ряд новых интегралов;
предоставляем это читателю.
7) Найденные для интегралов и, v значения позволят нам вычислить другие
интересные интегралы. Умножим обе части равенства
- — cosP6-cospO= \ е~аххР~1 cosbxdx
аР	J
о
на
cos2i9
71
(считая O^q^p ив<1)и проинтегрируем слева по б от 0 до —, а справапоботО
до ¦» *. В результате получим
я/2	-	«. '
г	аР~1 г	г
Л= cosP~4~^0¦sinQ~1 0-cosрв d9 =	 Ьч~х db e~axxPcosbxdx.
J	Г(р) J	J
о	oo
Если переставить справа интегралы, то это сразу приведет к вычислению
* Связь между переменными b и 0 дается формулой Ь = аЛ%в (а = const).

539]	8 5. ЭЙЛЕРОВЫ ИНТЕГРАЛЫ	787
интеграла J^.
Из 3) легко установить, что значение внутреннего интеграла будет Г(д) cos — х~ч,
так что
и, окончательно,
я/2
qn
) COS — ~
Г0>)	J
J, = Г cosP-9->.sin9-' O-cospB
J
-cos-
Г0>)	2
о
Аналогично можно вывести:
я/2
• «-in ¦	Г(д)Г(р-д) .
2= Г
Лр)	2
о
Покажем теперь, как обосновать перестановку интегралов, без чего, разумеется,
результат не может считаться установленным. Так как интеграл
хР~1е~ахЬЧ~1 cos bx dx
о
сходится равномерно для 0-=60=^6=sJ5«= +~, то
в	«в
b4~1db xP~xe~ax cos bxdx= e"axxP~ldx W cos bxdb =
Bx
Г - - - Г -
= J e axxP	x J иЯ
b,x
Ввиду существования интеграла и? cos и du, внутренний интеграл при
о
и J5—+~ стремится к нему, оставаясь ограниченным:
II
Bx
?-1 -cos и du
50*

788	ГЛ. XIV. ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА	1539
так что все подинтегральное выражение мажорируется функцией
и предельный переход при йо»0иВ-+=» допустим под знаком интеграла и т. д.
8) Положим
1
y(t) = D\nr(t)= 	dx-C
J 1-х
о
[см. B5)]. Тогда
i
схР-хЯ
	dx=y(q+l)-ip(p+\)
J 1-х
(при p+1*0, q+1^0).
Заметив это, рассмотрим интеграл
гAх)Aх/) .
/= 	dx
J (l-x)lnx
о
Его производная по а.
doT ~ } 1-;
о
Поэтому
Так как /=0 при а = 0, то необходимо C=ln /'(/S+l), следовательно,
Аналогично находятся интегралы
f^(l-^(l-^)^	{	(
J (l-x)lnx	Г(а+1)А<х+^+У+1)' -+r—-i.-+/»+r>-¦)
(l-x)lnx
о
f(l-x«)(l
J	(\-
x)\nx

540]	> 5. ЭЙЛЕРОВЫ ИНТЕГРАЛЫ	789
1 а	Ь~а
Если в интеграле К взять у = —, <х =	1, р=~ — и сделать подстановку
л: = t2, то придем к интегралу
¦@ — 1— F — 1
о
При 6 = 1 - а отсюда получается любопытный интеграл
1
Приведенных примеров достаточно, чтобы показать, насколько расширяются
наши возможности представления интегралов конечной формулой благодаря
введению функции Г. Даже в тех случаях, когда конечная формула не содержит
иных функций, кроме элементарных, получение ее все же часто облегчается исполь-
использованием функции Г, хотя бы в промежуточных выкладках.
540. Формула Стврлинга. Обратимся теперь к выводу удобных приближенных
формул для In Г(а) и к вопросу о вычислении значений этого логарифма (и самой
функции Г).
Отправной точкой нам будет служить формула B4) для логарифмической
производной Г:
Яе е
	dx.
х 1-е-*)
о
Так как подинтегральное выражение представляет собой непрерывную функ-
функцию от обоих аргументов х я а при хэ=0 ив>0 (при * = О в этом можно убедиться
разложением в ряд), а при х = °° интеграл сходится равномерно относительно а
для assao^O - мажоранта
е~х е-а^с
то можно проинтегрировать по а, от 1 до а, под знаком интеграла:
Яе~х-е~ах\е1х
(e-l)e-*	 — (в^О).
1-е~х J х
о
Изменяя знак переменной интегрирования, перейдем к промежутку [-<», 0]:
о
, [еах-ех	Idx
In/'(«)- —-—— (е-IV* -.	C5)
р геах-ех	Лйх
J I. ex-\	J х
И этот интеграл сходится равномерно при х- -~ для O-=ao=«a=s/4-= +~; проин-
проинтегрируем снова по а, от а до а 4-1, под знаком интеграла
a+l
R(a)= In r(a)da=	\a	e< - .
J	J I x ex -1 { 2) 1 x

790	ГЛ. XIV. ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА	[540
Мы используем полученный интеграл, равно как и элементарный интеграл Ф р у л-
л а н и [495]:
о
1	re-x_e-ax dx re^-e* dx
_tae.J_	-.j — .-.	C7)
о	--
для упрощения выражения C5). Именно, вычитая из него C6) и прибавляя C7),
получим:
о
Полагая, для удобства,
Я1 1 \
о
1 1 \-\e°xdx
и подставляя вместо R(a) известное уже нам выражение A9) интеграла Р а а б е,
получим
	1 1па-а+си(а).	C9)
В главе XII [441, 10] мы имели разложение на простые дроби гиперболического
котангенса:
2х
действительное для всех значений х^О. Заменяя здесь х на х/2, можно преобра-
преобразовать его к виду [ср. 449]:
хх	ъ 1хг
12^
e*-l 2
или, наконец,
"'	х- 2,
В лице f{x) мы узнаем функцию, входящую в подинтегральное выражение C8).
Фиксируем любое неотрицательное целое число т и заменим каждый член
ряда тождественной ему суммой
11 v2 v-4	-у-2ГП — 2
	_	I	_|_ t	 1 ЛТП —1 ,.,	|
1 +
Суммируем отдельно слагаемые вида

540]	fe 5. ЭЙЛЕРОВЫ ИНТЕГРАЛЫ	791
при к= 1, 2, 3, ... Полагая, как обычно,
2 TTn = s-m, получим результат (-1)" —-—-¦ s,n-x2n~2;
если ввести n-е число Бернулли [449];
2-Bи)!
то этот результат перепишется так:
AI12П2
A)Х_
2-Bи)!
( х 1
Что же касается последних слагаемых, снабженных множителями 11+	 ,
V 4&22/
представляющими положительные правильные дроби, то, суммируя их, придем
к члену
(pm.0.	.Хтг
2Bт + 2)!
где 0 также есть положительная правильная дробь.
Окончательно получим такое выражение для f{x):
Вл В*	Въ	Вт
»-«x2+ixi---+(-1)m~1M.x2m~*+
A)т0^
Bm + 2)!
Подставив это в C6), проинтегрируем почленно. Так как
О	о.
2и!
Г eaxxindx= Г е-аххт dx._
о
о
C 1т\
еах.(,.хгт^х = 0. e°xx2m dx = 0	(О-=0-=1)*.
то находим, что
1-2 а 3-4 а3 5-6 a5	B/w-lJm а2
1
Bт+Щ2т + 2) as
* Обращаем внимание читателя на то, что в зависит от х, а 0 - нет.

792	ГЛ. XIV. ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА	[541
Наконец, если в C9), вместо си(а), подставить полученное выражение, то мы
придем к формуле:
л+\а -j па в + ь2'в
В2 1	В„	1
П	1
(O*0-=l), D1)
носящей имя Стирлинга (J. Stirling).
В простейшем случае при т = 0 формула принимает вид
D \	Л
а	1па-а+— @*0-= 1).
2)	12а
Если, отбросив дополнительный член (содержащий множителем в),
продолжить ряд членов в формуле до бесконечности, то получится так назы-
называемый ряд Стирлинга:
а	\\па-а+—	—
2) 1-2 а 3-4 а3
Bт-1)-2т а
Этот ряд будет расходящимся. Действительно, ввиду D0), абсо-
абсолютная величина общего члена ряда Стирлинга при п - ~
Вп	1 1 Bи-2)!
Bя- lJwew-1 я
Тем не менее этот ряд очень полезен для приближенного вычисления функции
In Г(а), являясь ее асимптотическим представлением и в то же
время обвертывая ее. Мы уже сталкивались как с формулой, так и с рядом
Стирлинга для In (n!) [см. 469, B6) и B7)]. Только что полученные разложения
имеют более общий характер. Если пожелать вывести из них прежние результаты,
то следует положить а = п и, кроме того, прибавить еще In п, таж как Г(п) = п - 1!
а не л! И в рассматриваемом общем случае также, потенцируя [464, 3°], можно
получить асимптотическое разложение для самой функции Г(а) [см. 469].
541. Вычисление эйлеровой постоянной. Вернемся к формуле C9), которую
продифференцируем по а:
о
1	С
D In Г(а) = In а	+ш'{а), где ш\а) = xeaxf(x) dx.
2а	J
Повторяя прежние выкладки, получим
А 1 Bj 1	Вт 1
о,'(а)= —- — +—	...-(-iyn—	+
2 а2 4 а1	К	2т aim
^±I@-в'*1). D2)
2m+2

542]	§ 5. ЭЙЛЕРОВЫ ИНТЕГРАЛЫ	793
Отсюда и приходим к асимптотическому разложению
1 Вг 1 В2 1	Вп 1
----- + ----...+(-1)'г^—-+...
2а 2 а2 4 а4	2и а2'1
Формально оно может быть получено почленным дифференцированием
ряда Стирлинга*.
Из выведенной формулы D2) можно извлечь удобный прием для вычисления
эйлеровой постоянной С.
Полагая в формуле Гаусса B5) а равным натуральному числу к, найдем
Но
с
1
1
1
0
1-t
	 t
1-
- =
tit
-t
1+/+.
-IV
Z>ln
ДА:).
1
"Ч-i
о
Используя формулу D2) при а = к, окончательно получим
1	1	1111
С~1 + 2"+'"" +А^Т~ П +гА: + 12А:2~~Т20А7 +
In к™
По этой формуле, взяв А: =10 и вычисляя члены вплоть до содержащего к12,
Эйлер нашел значение С с 15-ю знаками:
С = 0,577 215 664 901 532...
542. Составлепие таблицы десятичных логарифмов функции Г. Укажем вкратце
путь для составления упомянутой таблицы.
Вернемся к формуле B7), которую, заменяя а на 1 +а, напишем в виде
	=	е 4- / I	-
da	k=i\k
Последовательным дифференцированием придем к формуле для и-й производной
dan	- " - "-^ia+kT
(равномерная сходимость получаемых рядов оправдывает почленное дифферен-
дифференцирование).
* Таким образом, в данном случае оказалось допустимым почленное
дифференцирование асимптотического разложения [ср. замечание в п° 464).

794	ГЛ. XIV. ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА	E42
Таким образом, находим коэффициенты ряда Тейлора:
~Т 	Т~п	 =(-!)" — , где sn=Zrn-
nil dan Ja=o	n	k=\kn
Тогда для | a | -= 1 будем иметь:
In ГA + a) = -Ca-\— s.za2 — s3a3н— J4e4- ...
Так как числа s/,- (особенно для больших А:) близки к 1, то выгодно прибавить
почленно разложение (также справедливое для | а | -= 1)
что дает нам
1пГA
Умножив на
li
+в)=-1
модуль
1A+
In(l-)
Ми
а)-а--а>
полагая
1
1а+—¦ (j
1
~~4
получим
1пГA+а)= - In (I + a)+ CIa + C2a2-Qai' + c4a*- ...	D3)
Заменяя в на -а, вычтем получаемое разложение
In ГA -a)= -In (I -a)-Cla+C1a*+C3a3+Cia4+ .
из предыдущего. Так как, по формуле дополнения,
ал
=	 и 1пГA-а)=-1пГA+а)+1п
sin a	sin
sin an
то найдем:
1	ал 1 1 + а
1пГA+а) = -1п —	In	+Сха-С^-Сьаъ- ...	D4)
2	sin ал 2 1 - а
Л ежа ндр дал значения коэффициентов Сп (для n=sl5) и их логарифмы
и вычислил с помощью формул D3) и D4) десятичные логарифмы Г{а) для а от 1
до 2 через 0,001, сначала с 7, а затем и с 12 десятичными знаками.
Заканчивая этим изучение функции «Гамма», мы видим, что, ис-
исходя из ее представления с помощью интеграла, содержащего пара-
параметр а, мы не только ознакомились с глубокими ее свойствами, но
и научились вычислять ее. Новая функция эта является в такой же
мере освоенной нами, как и элементарные функции.

АЛФАВИТНЫЙ УКАЗАТЕЛЬ
Абелевы интегралы 84
Абель 290, 292, 527
Абеля лемма 306
—	подстановка 69, 608
—	преобразование 305, 312, 403
—	признак равномерной сходимости ряда 429
	сходимости интеграла 564
	ряда 307
—	теорема 328, 397, 516
Абеля — Пуассона метод обобщенного сум-
суммирования рядов 401, 409
Абсолютно интегрнруемая функция 563, 586
—	сходящееся произведение 356
—	сходящийся несобственный интеграл 563,
586
	ряд 296, 356, 513
	—, переместительное свойство 315, 332,
356, 513
	 —, умножение 321, 513
Адамар 300
Аддитивная функция промежутка 225
Аддитивность объема 203
—	площади 188
Алгебраическая часть интеграла, выделение 68
Амплитуда 252
Аналитическая функция 449, 450, 491, 499, 502
Аргумент комплексного числа 510
Арксинус, главное значение 525
—, степенной ряд 458, 467, 503, 526
Арктангенс, главное значение 524
—, степенной ряд 368, 457, 524
Архимедова спираль 175, 199
Арцела 433. 438, 743, 745
Асимптотический ряд 534, 650, 793
	, действия 536
	, дифференцирование 540, 793
	, единственность 534
	, интегрирование 538
	, потенцирование 538
Астроида 175, 184, 185, 202, 210, 218
Бонне формула 119
Бореля метод обобщенного суммирования рядов
411
Буняковского неравенство 153, 590
Валлиса формула 145, 352, 371, 377, 613, 704
Ван-дер-Варден 479
Варианта комплексная 511
¦	, предел 511
Вейерштрасс 424, 479, 488
Вейерштрасса формула 362, 473, 775, 778
Вивиани кривая 186, 223
Виета 352
Винтовая линия 186
Вороного методы обобщенного суммирования
рядов 408
Выделение алгебраической части интеграла 68
— рациональной части интеграла 44
Вычисление интегралов:
ln(l
122, 140, 464, 673
\lnsiaxdx 611, 616, 726, 785
о
612, 704, 719, 757
J г-*1 cos 2bx dx 701, 726
0
со
^l^dx 614, 621, 718, 742
Ъарроу 15
Бернулли Иоганн 95
Бернуллиевы числа 494, 541, 703, 704
Бертрана признак 279
Бесконечно малых элементов суммирование 221,
228
Бесселевы функции 345, 464, 468, 709, 734
Бесселя дифференциальное уравнение 468, 675
Бета-функция 750
	, рекуррентная формула 751
	, связь с гамма-функцией 755
	, симметричность 751
Биномиальный дифференциал, интегрирование
— ряд 372, 452, 468, 487, 526
Био и Савара закон 242, 557
706, 721, 729, 740, 741
- dx 721, 729, 740
1+х
dx 699, 717
f sin x' dx, { cos x1 dx 721, 729
о	и

796
АЛФАВИТНЫЙ УКАЗАТЕЛЬ
Вычисление определенных интегралов, диффе-
дифференцирование по параметру 673, 674, 717,
721, 723, 782
	, интегральные суммы 120, 615, 617
	, интегрирование по параметру 679, 718,
721, 722, 732, 756, 786
—	, интегрирование по частям 131, 603,
632, 634, 636
	, искусственные приемы 611, 621, 623
	, основная формула интегрального ис-
исчисления 124, 554, 582
	, подстановка 134,143, 605, 611, 630, 631,
764
	, предельный переход по параметру 704,
717, 719, 722, 735, 788
— ¦	, разложение в ряд 457—467, 614, 632,
670, 671, 672, 697—710
Л. амма-функция 361, 753
—, Вейерштрасса формула 362, 775
—, Гаусса формула 772
—, график 755
—, дополнения формула 377, 757
—, Коши формула 771
—, Лежандра формула 760, 774
—, логарифмическая производная 473, 770, 774
—, максимумы и минимумы 755, 780
—, определение ее свойствами 760, 762
—, Раабе интеграл 759
—, распространение 780
—, рекуррентная формула 361, 754
—, Стерлинга формула и ряд 792, 793
—, таблицы логарифмов 793
—, Эйлера произведение 758
—, Эйлера—Гаусса формула 361, 754, 769, 775,
780
Гармонический ряд 263, 267, 270, 289
Гаусс 281, 680, 769
Гаусса признак 280
—	формулы 142, 772
Гаусса—Эйлера формула 361, 754, 769, 775, 780
Гёльдера методы обобщенного суммирования
рядов 411
Гипербола 177, 195
Гиперболические подстановки 29
—	функции, сопоставление с тригонометриче-
тригонометрическими 196, 523
Гипергеометрический ряд 280, 297, 359, 470, 769
Гипергеометрическое дифференциальное урав-
уравнение 470
Гипоциклоида 185
Главное значение аргумента комплексного числа
510
	арксинуса 525
	арктангенса 524
	логарифма 525
	несобственного интеграла 591, 594
	степени 526
Гладкая кривая 192
—	поверхность 204
Гольдбах 338
Гульдина теоремы 229, 232
признак 271, 278, 296, 513
Дарбу 97'
—	интегралы, верхний и нижний 100
	как пределы 106
—	суммы, верхняя и нижняя 97
—	теорема 106
Двойной ряд 333, 452
Декартов лист 200
Дзета-функция 264, 287, 362, 469, 769, 777
Дини 290, 291, 292
—	теорема 431
	, обобщение 657, 695, 711
Дирихле 290, 754, 769
—	признак сходимости интеграла 564
—	— — равномерной ряда 429
	ряда 307
—	разрывный множитель 633, 640, 741
—	ряды 309, 451, 469
—	функция 105, 106, 587
Дифференциальное уравнение 244
	Бесселя 469, 675
	гипергеометрическое 470
	, составление 253
Дифференцирование интеграла по верхнему
(нижнему) пределу 116, 600
го параметру (дифференцирование под
:ом ингеграла) 661, 666, 669, 710, 749
	по.
знаке-- 	 .	 _, ,
—	ряда, почленное 447, 517
Длина кривой 169, 171
—	—, выражение интегралом 169
•	>-, производная 169
—	—, пространственной кривой 185
С (число), трансцендентность 146
Ермакова признак 285
#1\.ивой силы закон 235
.Эайдель 424
Знакопеременный ряд 302
¦	, оценка остатка 303
.кЪнерции момент плоской фигуры 241
	тела 241
Интегральная сумма 97
	, верхняя, нижняя 97
Интегральный косинус 83, 566, 639, 652
—	логарифм 83, 593, 650
¦— признак Маклореиа—Коши 282
—	синус 83, 566, 639, 652, 709
Интегралы, не выражающиеся в конечном виде
36, 52, 83, 86, 92, 459
Интегрирование биномиальных дифференциа-
дифференциалов 51
—	в конечном виде 36
—	интеграл по параметру (интегрирование под
знаком интеграла) 663, 669, 714, 749
—	по частям 31, 130, 602
—	подстановкой (путем замены переменной) 23,
135, 143, 602
—, правила 18
—	простых дробей 37
—	радикальных выражений 50, 51, 56, 66, 529
—	рациональных выражений 43
—	ряда почленное 447, 668, 697, 710
—	тригонометрических и показательных вы-
выражений 74, 83, 529
Интегрируемая функция 97
	, классы 101
	, свойства 103
—	— с квадратом 590
Интегрируемость предельной функции 437, 659
Интерполирование параболическое 156
Канторович 642
Кардиоида 178, 185, 200, 218
Каталана постоянная 168, 460, 734
Квадратура 16
Квадрируемая фигура 187
Квадрируемости условие 187, 189, 191
Квази-равномерная сходимость 433
Кеплера уравнение 509
Кнопл 311

АЛФАВИТНЫЙ УКАЗАТЕЛЬ
797
Комплексная варианта 511
—	переменная, функция от нее 513, 519, 520,
522, 526
—	плоскость 509
Комплексное число 508
	, аргумент 510
	, вещественная часть 508
—; ¦—¦, действия 508
	, мнимая часть 508
	, модуль 508
	, тригонометрическая форма 510
Конус круговой 208, 239, 240, 241
Корень из комплексного числа 511
Корни из вещественных чисел, вычисление 383
Косинус, аналитическое определение 477
—, бесконечное произведение 377
—	в комплексной области 523
—	гиперболический, бесконечное произведение
378
—	—, степенной ряд 367
—, степенной ряд 367, 523
—,	для логарифма 497
Котангенс, Адамара теорема 300
—	гиперболический, разложение на простые
дроби 473
—, разложение на простые дроби 472
—, степенной ряд 484, 496, 524
Коши 290, 502, 591
—	Гёльдера неравенство для интегралов 151
—	рядов 293
—, Маклорена признак 282
—, признаки 270, 290, 561, 584
—, теорема 321, 326
—, формула 321
Кратный ряд 350
Кубнруемое тело 202
Куммера преобразование рядов 388
—	признак 277
Лагерра (Чебышева) многочлены 604
Лагранжа ряд 504
Ламберта ряд 311, 341
Ландау 310
Ландена преобразование 143
Лаплас 508, 701, 721, 729
Лежандр 92, 677, 703, 750, 753, 794
Лежандра многочлены 138, 148, 491, 508, 530, 671
—	формула 760, 774
—	функции К (к), Е №) 142, 166, 177, 214, 224,
252, 352, 465, 675, 734, 768
	К (к, ч>), Е (к, <р) 93, 116, 177
Лейбниц 15, 95, 395
Лейбница и Ньютона теорема 15
-— правило 661
—	теорема 302, 308
Лемниската 178, 200, 219
Лиувнлль 92
Лобачевский 614
Лобачевского формулы 634, 672
Логарифм комплексного числа 520
Логарифмическая спираль 176, 184, 185
—	функция в комплексной области 520
	, степенной ряд 368, 453, 457, 484, 503, 522
Логарифмы, вычисление 381
Ма
Мажорантный интеграл 685
— ряд 427
Мажорантных рядов метод 502
Маклорена—Коши признак 281
Маркова преобразование рядов 392
Маятник математический 250
Мертенса теорема 328
Механическая работа 233
Микковского неравенств 293, 590
Многозначные функции комплексной перемен-
переменной 513, 521, 524, 525, 526
Множитель сходимости 718, 722
Моавра формула 374
Модуль комплексного числа 509
—	перехода от натуральных логарифмов к де-
десятичным 382
—	эллиптического интеграла 93
Момент инерции плоской фигуры, тела 241
Мэшина формула 380
Нап
аправление в промежутке 108
Натуральное уравнение кривой 180
	эволюты 185
Натуральный логарифм комплексного числа 520
Начальное значение величины 14
Начальные условия 14, 244
Неабсолютно сходящееся произведение 356
—	сходящийся интеграл 563, 565, 569, 586
	ряд 296, 304, 336, 516
Неопределенный интеграл 11
	, геометрическое истолкование 14
—: —, свойства 13
—	—, существование 116
—	•—, таблица 17
Неопределенных коэффициентов метод 42, 45,
67, 91, 470, 488, 492
Непрерывная функция без производной 479
Непрерывность интеграла по параметру 660, 675,
678, 710
—	предельной функции 420, 657
—	суммы ряд 430
	степенного ряда 444, 446
—	функции комплексной переменной 513
Неравенства для интегралов 151
—	для рядов 293
Неравномерная сходимость интеграла 683, 689
	последовательности, ряда 429, 446
Неравномерности точки 425, 444
Несобственный интеграл от неограниченной
функции 577, 578
	с бесконечным пределом 552, 580
	сходящийся, расходящийся 552, 578
	, аналогия и связь с рядами 558, 586, 713
	—, признаки сходимости 561, 564, 584
	, свойства 597
	, условия существования 562, 585
Нечетная функция, интеграл по симметричному
промежутку 138
Неявные функции 474, 498
Ньютон 15, 248, 372
Ньютона—Лейбница теорема 15
	формула 124
Обвертывающий ряд 534, 544, 550, 651, 792
Обратные тригонометрические функции — см.
Арксинус и Арктангенс
Обращение степенного ряда 502, 506
Объем тела 202
	, аддитивность 203
	, внутренний, внешний 202
	вращения 207
	, выражение интегралом 205
	 как предел 203
	по поперечным сечениям 206, 207
	, условие существования 203, 204
Определенный интеграл в собственном смысле
96
	, вычисление с помощью интегральных
сумм 120
	,	первообразной 124
	, свойства 108
	, схема применения 225
— —. условия существования 100, 105, 107

798
АЛФАВИТНЫЙ УКАЗАТЕЛЬ
Ориентированный промежуток 108, 598
Основная последовательность разбиений про-
промежутка 96
—	теорема алгебры 680
—	формула интегрального исчисления 123, 127,
128, 554, 582
Особая точка функции 577, 580, 581
Особенности выделения при вычислении интег-
интегралов 642, 646
Остаток ряда 260
Остаточное произведение 353
Остроградского метод выделения рациональной
части интеграла 43	-
—	формула 45
Ось вещественная 509
—	мнимая 509
Оценка остатка ряда 283, 303, 378
Парабола 16, 174, 197, 232, 233
Параметр 654
Первообразная функция 11
	, восставновление с помощью определен-
определенного интеграла 129, 583
Переместнтельное свойство абсолютно сходя-
сходящегося произведения 356
	ряда 315, 332, 513
Перестановка двух предельных переходов 442,
443, 658
Периодическая функция, интеграл по периоду
138
п (число), приближенное вычисление 379
Площадь криволинейной трапеции 192
	как первообразная 16
•—¦	предел суммы 94
—	плоской фигуры 187
	, аддитивность 188
	, внутренняя, внешняя 187
	— —, выражение интегралом 192
	как предел 188
	, условия существования 187, 189,
191
—	поверхности вращения 214
—	цилиндрической поверхности 220
Повторный ряд 330
Подинтегральная функция 12
Подинтегральное выражение 12
Подстановка (замена переменной) 23, 134, 143,
604
—	Абеля 69
—	гиперболическая 29
—	дробио-линейная 70, 87
—	ряда в ряд 485
—	тригонометрическая 29
—	Эйлера 57, 59
Показательная функция в комплексной области
517
	, связь с тригонометрическими функциями
519, 523
	, степенной ряд 367, 452, 454, 468, 518
Последовательных приближений метод 474
Почленное дифференцирование ряда 438, 517
—	интегрирование ряда 436, 669, 697, 710
—	умножение рядов 321, 328, 333, 407, 456,
513
Почленный переход к пределу 434, 515
Правильная дробь, разложение на простые 21,
39
Предел интеграла по параметру (предельный
переход под знаком интеграла) 442, 659, 668,
694, 696, 745, 748
—	функции комплексной переменной 514
Пределы интеграла нижний н верхний 97
Предельная функция, дифференцируемость 443
	, интегрируемость 443, 657
—	—, непрерывность 657
Предельный переход в ряде почленный 434,
515
	под знаком интеграла 443, 659, 668, 694,
696, 745, 748
Преобразование рядов по Куммеру 388
—	Маркову 392
	Эйлеру 384
Приближенное вычисление интегралов несоб-
несобственных 641, 647, 650
	собственных 153, 646
Приближенные вычисления с помощью рядов
378, 388, 390, 459, 460, 466, 650
Приведения формулы для биномиальных диф-
дифференциалов 54
	интегралов от sin" x cos*1 х 78
—	определенных интегралов 130
Произведение бесконечное 351
	, абсолютно сходящееся 356
	, признаки сходимости и расходимости 354
	, расходящееся 351
	, сходящееся 351
—	остаточное 353
—	частичное 351
Производная функции комплексной переменной
515
Производящая функция для бесселевых функций
345
	многочленов Лежандра 492, 508
Простые дроби 37
•	, интегрирование 37
	, разложение правильной дроби 21, 39, 42
—	¦—, разложение функций ctg x, cth я, tg xt
-r^—, -Jr- , 4— 472, 473
sin x sm! x sh x
Прямоугольников формула 154
¦	, дополнительный член 159
Псевдоэллиптические интегралы 86
Пуассон 122, 140, 612
Пуассона—Абеля метод обобщенного сумми-
суммирования рядов 396
Пуассона формула 256
Я?аабе интеграл 759
—	признак 273, 278
Равномерная сходимость интеграла 682, 687,
688
	, признаки 684, 688
	, связь с рядами 684, 688
	, условие 684, 687
	ряда, последовательности 419, 422, 424,
515
	, признаки: Абеля 429, Вейерштрасса
427, Дирихле 429
	, условие 425
—	-— степенного ряда 444, 446
Равномерное стремление к предельной функции
654
Разрывный множитель Дирихле 633, 640, 736,
741
Расходящиеся бесконечные произведения 351
Расходящийся интеграл 552, 578
	, обобщенное значение 595
—	ряд 258, 333
Расходящихся рядов суммирование, см. Сум-
Суммирование рядов обобщенное
Рационализация подинтегрального выражения
50, 51, 57, 74, 85
Рациональная функция, интеграл между беско-
бесконечными пределами 623
—	часть интеграла, выделение 44
Регулярный метод суммирования 395
Решение уравнений рядами 498
Риман 97, 264
Римана теорема 317
Риманова (интегральная) сумма 97

АЛФАВИТНЫЙ УКАЗАТЕЛЬ
799
Ряд (бесконечный) 257, 512
—	гармонический 263, 267, 270, 289
—	гипергеометрвческий 280, 297, 359, 470, 769
—	двойной 333, 513
—	знакопеременный 302
—	кратный 350
—	лейбницевского типа 303
—	повторный 330
—	расходящийся 258, 292, 333
—	сходящийся 258, 292, 333, 512
—	— абсолютно 296, 336, 513
—	— неабсолютно 296, 317, 336, 516
—, остаток 260
—, сумма 258, 333, 512
—, условие сходимости 294
—, частичная сумма 257, 333, 512 см. также
Степенной ряд
Сфера (полусфера) 241
Сходимости пограничная абсцисса 309
—	принцип 308, 512
Сходимость бесконечного произведения, при-
признаки 354
	ряда, признаки: Абеля 307, Бертрана 279,
Гаусса 279, Даламбера 271, 288, 296, 513,
Дирихле 307, Ермакова 285, Коши 270,
Коши—Маклорена 282, Куммера 277, Лейб-
Лейбница 302, 308, Раабе 273, 278, Сапогова 291
—	¦	, условие 293
—	несобственного интеграла, признаки 561, 563.
584
	•—, условие 560, 584
Сходящееся бесконечное произведение 351
Сходящийся бесконечный ряд 258, 292
—	несобственный интеграл 552, 578
i-^апогова признак 291
Симпсона формула 159
—	—, дополнительный член 162
Синус, аналитическое определение 477
—, бесконечное произведение 376
—	в комплексной области 523
—	гиперболический, бесконечное произведение
378
—	—, разложение обратной величины на про-
простые дроби 473
—	—, степенной ряд 367
—, разложение обратной величины на простые
дроби 472
—, степенной ряд 367, 454, 522
_, __ да log s-
497
Сочетательное свойство ряда 313, 332
Спрямляемая кривая 169
Сравнения теоремы для несобственных интегра-
интегралов 560
¦—	рядов 264
Среднее значение, теорема 113
—	—, — вторая 117, 600
	, — обобщенная 114, 600
¦	, —, связь с формулой Лагранжа 124
Статический момент кривой 228
—	— плоской фигуры 231
	поверхности вращения 240
	 тела 239
	цилиндрической поверхности 240
Степенная функция, главное значение 526
Степенной ряд 298, 364, 515
	, действия 481, 485, 518
—	—, деление 492, 518
	, дифференцирование 447, 449
	, единственность 445
	, интегрирование 447
	, круг сходимости 515
	, непрерывность 444, 446
	, обращение 502, 506, 518
	, промежуток сходимости 299, 516
	, радиус сходимости 300, 515
.	с двумя переменными 346
	с несколькими переменными 350
Стильтьес 651
Стерлинг 360
Стерлинга ряд 550, 792
—	формулы-369, 550,'793
Стоке 424
Суммц ряда 257, 333, 512
Суммирование рядов' обобщенное 395
	, метод Бореля 411
	, — Вороного 408
	, — Гёльдера 411
	. — Пуассона—Абеля 396
	—, — Чезаро 401, 409
	, — Эйлера 416
Аангенс в комплексной области 523
—, разложение на простые дроби 472
—, степенной ряд 493, 497, 524
Таубера теорема 398, 405
Тейлора ряд 364, 449, 450
—	формула 364
	, дополнительный член 146, 366
Теплица теорема 325
Тождество степенных рядов 445
Тор 230, 233
Торичелли 242
Трактриса 179, 248
Трапеций формула 155
	, дополнительный член 161
Тригонометрическая форма комплексного числа
510
Тригонометрические подстановки 29
—	функции, аналитическое определение 477
	в комплексной области 522 см. также
Синус и т. д.
	, связь с гиперболическими функциями 196,
	, — — показательной функцией 519, 523
Улитка 177, 199
Умножение рядов 321, 328, 333, 407, 456, 513
Уникурсальная кривая 85
Ф
'ренель 721, 729
Фробениус 401
—, теорема 403
Фруллани интегралы 621, 635, 636, 638, 639
Аарди 576, 740
Харди—Ландау теорема 403
Центр тяжести кривой 229
	плоской фигуры 232
	поверхности вращения 240
	тела 239
	цилиндрической поверхности 240
Цепная линия 174, 184, 195, 209, 217
Циклоида 175, 184, 185, 199, 209, 218, 230, 233
Цилиндрический отрезок 210, 222, 240
ТЖастичная сумма 257, 333, 512
Чебышёв 52
Чебышёва—Лагерра многочлены 604
Четная функция, интеграл по симметричному
промежутку 138

800
АЛФАВИТНЫЙ УКАЗАТЕЛЬ
Шаровой пояс 217
Шлёмильх 373
Штейнер 339
Штольца теорема 326
-Эвольвента круга 175, 183, 185
—	пепной линии 189
Эволюта, натуральное уравнение 185
Эйлер 57, 255, 263, 358, 361, 362, 363, 376, 377,
395, 611, 699, 717, 756, 758, 764, 778
Эйлера метод обобщенного суммирования рядов
412
—	преобразование рядов 384
—	ряд 462, 490, 496, 671
—	формулы 519, 527
Эйлера—Гаусса формула 361, 754, 775
Эйлера—Маклорена формула 540, 547
	"чпопнительный член 540, 548
Эйлера—Маклорена ряд 543, 549
—	— —, приближенные вычисления
546
Эйлерова постоянная 270, 285, 319, 353, 772, 775,
776, 782, 793
Эйлеровы интегралы первого и второго рода
750, 753
—	подстановки 57, 59
Эллипс 176, 195, 198, 199, 201, 202, 229,
233
Эллипсоид 209, 211, 212, 219
Эллиптические интегралы 86
	в форме Лежандра 93, 111
	1-го—3-го рода 90
	полные 143, 166, 177, 179, 214, 224, 252,
352, 465, 675, 734, 768
Эллиптический синус 252
Эпициклоида 185
Эрмит 146