ГМ. Фихтенгольц
КУРС ДИФФЕРЕНЦИАЛЬНОГО И ИНТЕГРАЛЬНОГО ИСЧИСЛЕНИЯ
ТОМЗ
Содержание
ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ.
ИНТЕГРАЛ СТИЛТЬЕСА
§ 1. Криволинейные интегралы первого типа	11
543.	Определение криволинейного интеграла первого типа	11
544.	Сведение к обыкновенному определенному интегралу	13
545.	Примеры	15
§ 2.	Криволинейные интегралы второго типа	20
546.	Определение криволинейных интегралов второго типа	20
547.	Существование и вычисление криволинейного интеграла второго __
типа
548.	Случай замкнутого контура. Ориентация плоскости	25
549.	Примеры	27
550.	Приближение с помощью интеграла, взятого по ломаной	30
551.	Вычисление площадей с помощью криволинейных интегралов	32
552.	Примеры	35
553.	Связь между криволинейными интегралами обоих типов	38
554.	Физические задачи	40
§ 3.	Условия независимости криволинейного интеграла от пути	45
555.	Постановка задачи, связь с вопросом о точном дифференциале 45
556. Дифференцирование интеграла, не зависящего от пути	46
557.	Вычисление криволинейного интеграла через первообразную 49
558. Признак точного дифференциала и нахождение первообразной в
случае прямоугольной области
559.	Обобщение на случай произвольной области	52
560.	Окончательные результаты	55
561.	Интегралы по замкнутому контуру	56
562.	Случай неодносвязной области или наличия особых точек	57
563.	Интеграл Гаусса	62
564.	Трехмерный случай	64
565.	Примеры	67
566.	Приложение к физическим задачам	71
§ 4.	Функции с ограниченным изменением	74
567.	Определение функции с ограниченным изменением	74
568.	Классы функций с ограниченным изменением	76
569.	Свойства функций с ограниченным изменением	79
570.	Критерии для функций с ограниченным изменением	82
571.	Непрерывные функции с ограниченным изменением	84
572.	Спрямляемые кривые	87
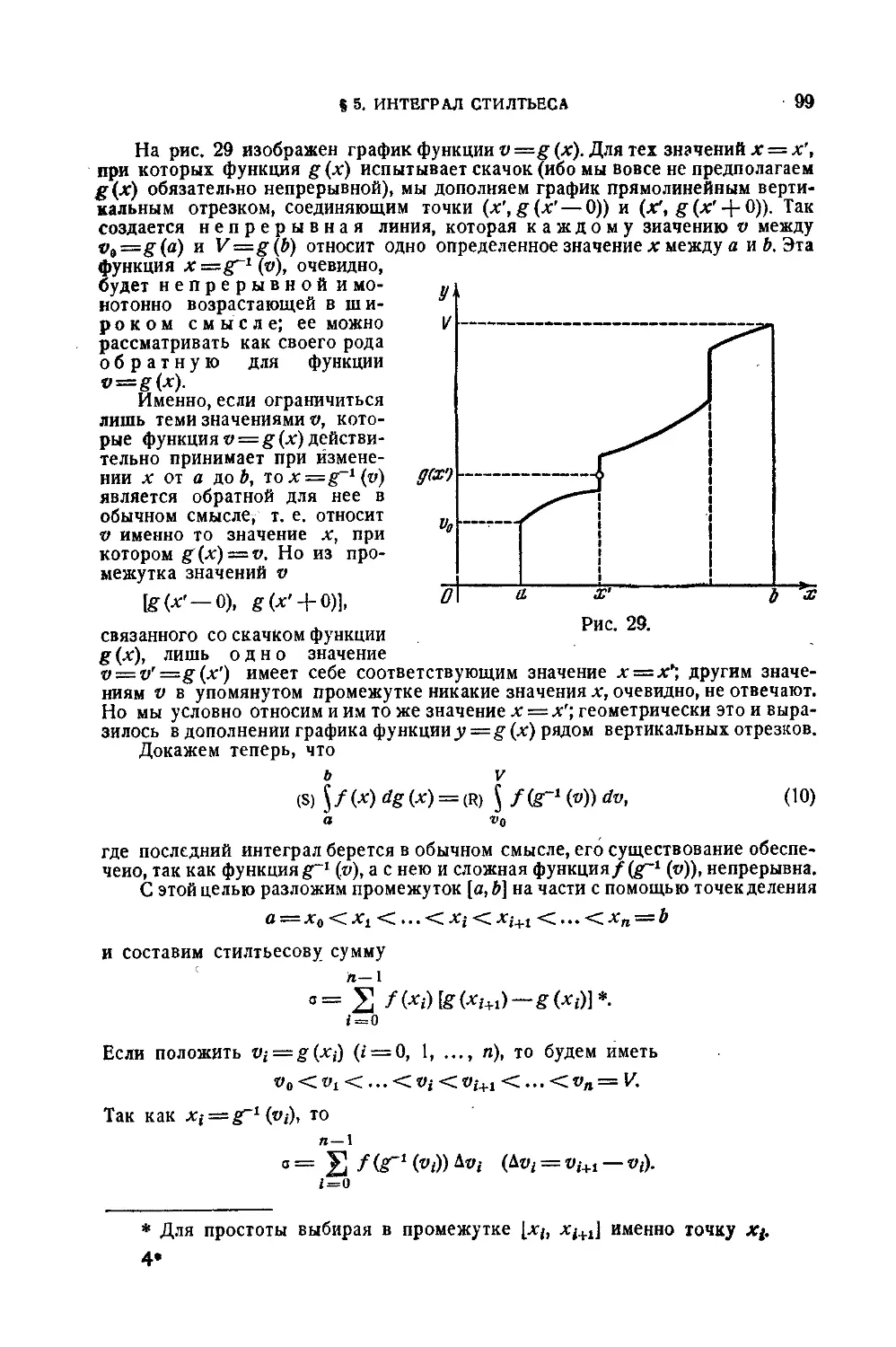
§ 5. Интеграл Стилтьеса	89
573.	Определение интеграла Стилтьеса	89
574.	Общие условия существования интеграла Стилтьеса	91
575.	Классы случаев существования интеграла Стилтьеса	92
576.	Свойства интеграла Стилтьеса	95
577.	Интегрирование по частям	97
578.	Приведение инйгоааа Стилтьеса к интегралу Римана	98
579.	Вычисление интегралов Стилтьеса	100
580.	Примеры	104
5	81. Геометрическая иллюстрация интеграла Стилтьеса	111
582.	Теорема о среднем, оценки	112
583.	Предельный переход под знаком интеграла Стилтьеса	114
584.	Примеры и дополнения	115
585.	Сведение криволинейного интеграла второго типа к интегралу
Стилтьеса
ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
§ 1. Определение и простейшие свойства двойного интеграла	122
586.	Задача об объеме цилиндрического бруса	122
587.	Сведение двойного интеграла к повторному	123
588.	Определение двойного интеграла	125
589.	Условия существования двойного интеграла	127
590.	Классы интегрируемых функций	128
591.	Нижний и верхний интегралы как пределы	130
592.	Свойства интегрируемых функций и двойных интегралов	131
593.	Интеграл, как аддитивная функция области; дифференцирование по ^4
области
§ 2. Вычисление двойного интеграла
594.	Приведение двойного интеграла к повторному в случае
137
137
прямоугольной области
595.	Примеры	141
596.	Приведение двойного интеграла к повторному в случае
криволинейной области
597.	Примеры	152
598.	Механические приложения	165
599.	Примеры	167
§ 3. Формула Грина	174
600.	Вывод формулы Грина	174
601.	Приложение формулы Грина к исследованию криволинейных
интегралов
602.	Примеры и дополнения	179
§ 4. Замена переменных в двойном интеграле	182
603.	Преобразование плоских областей	182
604.	Примеры	184
605.	Выражение площади в криволинейных координатах	189
606.	Дополнительные замечания	192
607.	Геометрический вывод	194
608.	Примеры	196
609.	Замена переменных в двойных интегралах	204
610.	Аналогия с простым интегралом. Интеграл по ориентированной	-
области
611.	Примеры	207
§ 5. Несобственные двойные интегралы	214
612.	Интегралы, распространенные на неограниченную область	214
613.	Теорема об абсолютной сходимости несобственного двойного 2р
интеграла
614.	Приведение двойного интеграла к повторному	219
615.	Интегралы от неограниченных функций	221
616.	Замена переменных в несобственных интегралах	223
617.	Примеры	225
ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ.
ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
§ 1. Двусторонние поверхности	241
618.	Сторона поверхности	241
617. Примеры	243
620.	Ориентация поверхностей и пространства	244
621.	Выбор знака в формулах для направляющих косинусов нормали 246
622.	Случай кусочно-гладкой поверхности	247
§ 2.	Площадь кривой поверхности	248
623.	Пример Шварца	248
624.	Определение площади кривой поверхности	251
625.	Замечание	252
626.	Существование площади поверхности и ее вычисление	253
627.	Подход через вписанные многогранные поверхности	258
628.	Особые случаи определения площади	259
629.	Примеры	260
§ 3.	Поверхностные интегралы первого типа	274
630.	Определение поверхностного интеграла первого типа	274
631.	Сведение к обыкновенному двойному интегралу	275
632.	Механические приложения поверхностных интегралов первого типа 277
633.	Примеры	279
§ 4.	Поверхностные интегралы второго типа	285
634.	Определение поверхностного интеграла второго типа	285
635.	Простейшие частные случаи	287
636.	Общий случай	290
637.	Деталь доказательства	292
638.	Выражение объема тела поверхностным интегралом	293
639.	Формула Стокса	297
640.	Примеры	299
641.	Приложение формулы Стокса к исследованию криволинейных
интегралов в пространстве
ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ
ИНТЕГРАЛЫ
§ 1.	Тройной интеграл и его вычисление	308
642.	Задача о вычислении массы тела	308
643.	Тройной интеграл и условия его существования	309
644.	Свойства интегрируемых функций и тройных интегралов	310
645.	Вычисление тройного интеграла, распространенного на
параллелепипед
646.	Вычисление тройного интеграла по любой области	314
647.	Несобственные тройные интегралы	315
648.	Примеры	316
649.	Механические приложения	323
650.	Примеры	325
§ 2.	Формула Гаусса—Остроградского	333
651.	Формула Остроградского	333
652.	Приложение формулы Остроградского к исследованию
поверхностных интегралов
653.	Интеграл Гаусса	336
654.	Примеры	338
§ 3.	Замена переменных в тройных интегралах	342
655.	Преобразование пространств и криволинейные координаты	342
656.	Примеры	343
657.	Выражение объема в криволинейных координатах	345
658.	Дополнительные замечания	348
659.	Геометрический вывод	349
660.	Примеры	350
661.	Замена переменных в тройных интегралах	358
662.	Примеры	359
663.	Притяжение со стороны тела и потенциал на внутреннюю точку	364
§ 4.	Элементы векторного анализа	366
664.	Скаляры и векторы	366
665.	Скалярное и векторное поля	367
666.	Градиент	368
667.	Поток вектора через поверхность	370
668.	Формула Остроградского. Дивергенция	371
669.	Циркуляция вектора. Формула Стокса. Вихрь	372
670.	Специальные поля	374
671.	Обратная задача векторного анализа	378
672.	Приложения	378
§ 5.	Многократные интегралы	384
673.	Задача о притяжении и потенциале двух тел	384
674.	Объем n-мерного тела, n-кратный интеграл	386
675.	Замена переменных в n-кратном интеграле	388
676.	Примеры	391
ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
§ 1.Введ	ение	414
677.	Периодические величины и гармонический анализ	414
678.	Определение коэффициентов по методу Эйлера—Фурье	417
679.	Ортогональные системы функций	419
680.	Тригонометрическое интерполирование	424
§ 2.	Разложение функций в ряд Фурье	427
681.	Постановка вопроса. Интеграл Дирихле	427
682.	Первая основная лемма	429
683.	Принцип локализации	432
684.	Признаки Дини и Липшица сходимости рядов Фурье	433
685.	Вторая основная лемма	436
686.	Признак Дирихле—Жордана	438
687.	Случай непериодической функции	440
688.	Случай произвольного промежутка	441
689.	Разложения только по косинусам или только по синусам	442
690.	Примеры	446
691.	Разложение In Г(х)	461
§ 3.	Дополнения	463
692.	Ряды с убывающими коэффициентами	463
693.	Суммирование тригонометрических рядов с помощью
аналитических функций комплексной переменной
694.	Примеры	472
695.	Комплексная форма рядов Фурье	477
696.	Сопряженный ряд	480
697.	Кратные ряды Фурье	483
§ 4.	Характер сходимости рядов Фурье	484
698.	Некоторые дополнения к основным леммам	484
699.	Признаки равномерной сходимости рядов Фурье	487
700.	Поведение ряда Фурье вблизи точки разрыва; частный случай	490
701.	Случай произвольной функции	495
702.	Особенности рядов Фурье; предварительные замечания	497
703.	Построение особенностей	500
§ 5.	Оценка остатка в зависимости от дифференциальных свойств функции 502
704.	Связь между коэффициентами Фурье функции и ее производных 502
705.	Оценка частичной суммы в случае ограниченной функции	503
706.	Оценка остатка в случае функции с ограниченной k-й производной 505
707.	Случай функции, имеющей k-ю производную с ограниченным
изменением
708.	Влияние разрывов функции и ее производных на порядок малости
коэффициентов Фурье
709.	Случай функции, заданной в промежутке [0, л]	514
710.	Метод выделения	особенностей	516
§ 6.	Интеграл Фурье	524
711.	Интеграл Фурье как предельный случай ряда Фурье	524
712.	Предварительные замечания	526
713.	Достаточные признаки	527
714.	Видоизменение основного предположения	529
715.	Различные виды формулы Фурье	532
716.	Преобразование Фурье	534
717.	Некоторые свойства преобразований Фурье	537
718.	Примеры и дополнения	538
719.	Случай функции двух переменных	545
§ 7.	Приложения	547
720.	Выражение эксцентрической аномалии планеты через ее среднюю
аномалию
721.	Задача о колебании струны	549
722.	Задача о распространении тепла в конечном стержне	553
723.	Случай бесконечного стержня	557
724.	Видоизменение предельных условий	559
725.	Распространение тепла в круглой пластине	561
726.	Практический гармонический анализ. Схема для двенадцати
ординат
727.	Примеры	565
728.	Схема для двадцати четырех ординат	569
729.	Примеры	570
730.	Сопоставление приближенных и точных значений коэффициентов
Фурье
ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
§ 1.	Операции над рядами Фурье. Полнота и замкнутость	574
731.	Почленное интегрирование ряда Фурье	574
732.	Почленное дифференцирование ряда Фурье	577
733.	Полнота тригонометрической системы	578
734.	Равномерная аппроксимация функций. Теоремы Вейерштрасса 580
735.	Аппроксимация функций в среднем. Экстремальные свойства
отрезков ряда Фурье
736.	Замкнутость тригонометрической системы. Теорема Ляпунова	586
737.	Обобщенное уравнение замкнутости	589
738.	Умножение рядов Фурье	592
739.	Некоторые приложения уравнения замкнутости	593
§ 2.	Применение методов обобщенного суммирования к рядам Фурье	599
740.	Основная лемма	599
741.	Суммирование рядов Фурье по методу Пуассона—Абеля	601
742.	Решение задачи Дирихле для круга	605
743.	Суммирование рядов Фурье по методу Чезаро—Фейера	607
744.	Некоторые приложения обобщенного суммирования рядов Фурье 609
745.	Почленное дифференцирование рядов Фурье	611
§ 3.	Единственность тригонометрического разложения функции	613
746.	Вспомогательные предложения об обобщенных производных	613
747.	Риманов метод суммирования тригонометрических рядов	616
748.	Лемма о коэффициентах сходящегося ряда	620
749.	Единственность тригонометрического разложения	621
750.	Заключительные теоремы о рядах Фурье	623
751.	Обобщение	626
ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
752.	Различные виды пределов, встречающиеся в анализе	631
753.	Упорядоченные множества (в собственном смысле)	632
754.	Упорядоченные множества (в обобщенном смысле)	633
755.	Упорядоченная переменная и ее предел	636
756.	Примеры	637
757.	Замечание о пределе функции	639
758.	Распространение теории пределов	640
759.	Одинаково упорядоченные переменные	643
760.	Упорядочение с помощью числового параметра	644
761.	Сведение к варианте	645
762.	Наибольший и наименьший пределы упорядоченной переменной 647
Алфавитный указатель
650
Абель 237
Абсолютная сходимость рядов Фурье
593
Аддитивная функция от области
плоской 134, 165
-	— пространственной 311
-	— определение ее по производной
136,312
—	промежутка 119, 137
Аппроксимация функции в среднем
583
-	- равномерная 579
Архимеда закон 340
Арцела119, 591,626, 627
Астроида 35
Бернштейн 505, 593
Бесселевы функции 144, 235, 401,
411,422, 478, 541,548, 561
Бессель 584, 585, 586
Био и Савара закон 44
Бу ваковского неравенство 146, 169
Бэта-функция 213, 230
Валле-Пуссен 626
Вейерштрасс 580, 610
Вектор 366
-	потока тепла 370
Векторная линия, поверхность 367,
368
-	трубка 368, 376
Векторное поле 367
-	произведение 45, 367
Вивиани тело 163, 208, 210, 261, 263,
265
Винтовая поверхность 265
Виртингер 596
Вихревая линия 383, 384
-	поверхность 383
-	трубка 383, 384
Вихрь 373
Вихря поток 373
Вольтерра 158
Алфавитный указатель
Вращение плоской фигуры 170
Вращение тела 331, 332
Вращения поверхность 264, 266
- тело 170, 355
Гамильтон 369
Гамма-функция 159, 161, 230, 392,
394—, 403, 407, 411, 461, 541
Гармоники 492
Гармоническая функция в круге 605
---области плоской 180
-	— пространственной 339, 381
Гармонические колебания 492
Гармонический анализ 492
-	- практический, схема на ординат,
12, 563
---схема на ординаты, 24, 568
Гаусс 62, 336, 412
Гаусса—Остроградского формула
333
Гауссовы коэффициенты
поверхности 256
Гейне—Кантора теорема 621
Гельмгольц 383
Гиббс 495, 497
Главное значение несобственного
интеграла 240, 533
Градиент 368
Грам 413
Грина формула 174
Гульдина теорема 171, 355
Гурвиц 596
Дарбу верхние и нижние интегралы
128
-----как пределы 130, 649
-	- Стилтьеса суммы 91
-	суммы для интеграла двойного 127
-	— тройного 310
Двойной интеграл 123, 126
-	- выражение через первообразную
147
-	- как аддитивная функция области
135
-	- классы интегрируемых функций
128
-	- несобственный 214, 221
Двойной интеграл, приведение к
повторному 123, 137, 149
-	- свойства 131
-	- условия существования 128, 131
-	ряд, сопоставление с двойным
интегралом 240
-	- Фурье 483
Двусторонняя поверхность 242, 248
Декартов лист 36
Диаметр точечного множества 126
Дивергенция 371
Дини признаки 434, 487, 528, 531
Дирихле—Жордана признаки 438,
489, 529, 531,609
-	задача для круга 605
-	интеграл 423
-	лемма 436, 486
-	разрывный множитель 536
-	условие 439
-	формулы 158, 231, 237, 394, 407
Дифференциал точный,
интегрирование 50, 52, 65, 68
- - признаки 50, 65, 178
- - связь с криволинейным
интегралом 46, 65, 66, 306
Дифференциальное уравнение
гидродинамики 379, 382
-	- колебания струны 550
-	- теплопроводности 380, 554, 561
Дифференцирование по области 135,
312
-	ряда Фурье, почленное 577, 611
Длина дуги 14, 358, 643
Дю Буа-Реймонд 497, 625, 626
Жидкий контур 381, 383
Жордан 74, 87, 88
Жордана—Дирихле признаки 438,
489, 529, 531,609
Замена переменных в интегралах
двойных 204
-	— несобственных 223
-	— тройных 358
-	— и-кратных 388
Замкнутая ортогональная система
функций 585
Замкнутости уравнение 585, 586, 589,
590
Замкнутость тригонометрической
системы 586
Изгибающий момент 108
Изопериметрическая задача 596
Инверсия 186, 344
Инерции главные оси 169, 170, 332
-	момент плоской фигуры 166
Инерции момент полярный 168
-	- поверхности 277
-	- прямолинейного отрезка 106
-	- тела 324
-	- цилиндрического бруса 167
Интегральная сумма 12, 20, 90, 126,
274, 286, 308
Интегральное уравнение 158, 237,
534, 535, 539
Интегральный косинус 540
-	логарифм 542
-	синус 541
Интегрирование по частям для
интегралов Стилтьеса 97
-	— обыкновенных интегралов ПО
-	рядов Фурье, почленное 574, 590,
591
-	точных дифференциалов 51, 52, 65,
68
Интегрируемая функция 90, 127, 310
Интегрируемости условие (для
дифференциальных выражений)
46, 50
Источники 372
-	плотность 372
-	производительность 372
Кантор 620
Кантора—Гейнс теорема 621
Каталан 405
Каталана формула 160, 232, 270, 407,
409
Квадрируемая поверхность 251
Квази-стационарный процесс 43
Кеплера уравнение 547
Кинетическая энергия вращающегося
тела 331
Колмогоров 502
Конфинальная
подпоследовательность 646
Координатные линии 184
-	поверхности 343
Косинус-преобразование Фурье 535,
545
Косинус-преобразование Фурье для
функции двух переменных 547
Котангенс, разложение на простые
дроби 452
Коши 524, 533, 535
Кратные интегралы 126, 309, 386
-	- Фурье 545
-	ряды Фурье 483
Кривизна поверхности, гауссова 272
Криволинейные координаты в
пространстве 343
-	- на плоскости 184
-	- элемент объема 348
-	- элемент площади 192, 257
Криволинейный интеграл второго
типа 20, 21
-	— вычисление через
первообразную 49, 65
-	— дифферренцирование 46
-	— независимость от пути 29, 46,
55, 65, 121, 178, 306
-	— наведение в случае
неодносвязной области 57, 70
-	— по замкнутому контуру 25, 56,
67, 178, 305
-	— приближение интегралом по
ломаной 30
-	— сведение к интегралу Стилтьеса
120
-	— сведение к обыкновенному
интегралу 22
-	— связь с криволинейным
интегралом первого типа 38
-	- первого тина 11
-	— сведение к обыкновенному
интегралу 13
Крылов 516, 578
Куммер 461
Кусков 355
Лагранж 383, 470
Лаплас 381, 536, 605
Лебег 98, 497, 502, 624
Левая координатная система 26, 246
Левая ориентация плоскости 26
-	- пространства 245
Лежандр 230, 271
Лежандра многочлены 233, 422
Лейбниц 234, 278, 376, 410, 448
Лемниската 196
Линейный интеграл 372
Липшиц 77, 93, 435, 489, 593
Липшица признаки 435, 489
Лиувилль 234, 405, 412
Лиувилля формулы 161, 213, 214,
231,396, 403,407
Ляпунов 586
Малиев 515
Масса кривой 11, 17
-	- поверхности 277, 281
-	плоской фигуры 137, 165
-	тела 308, 323
Мёбиус 242, 248
Многократные интегралы 387
-	- замена переменных 388
-	- сведение к повторному 387
Монотонная переменная,
возрастающая и убывающая 641
Мур 632
Набла 369
Направление на замкнутом контуре
26
Напряжение поля 40
Начальные условия 550, 555, 556,
557, 560, 561
Неравномерная сходимость рядов
Фурье 495, 497
Неразрывности уравнение 379
Несобственный двойной интеграл
215, 222, 240
— абсолютная сходимость 217, 222
— замена переменных 223
— приведение к повторному 219
—	признаки сходимости 226
-	тройной интеграл 315
Нечетная функция 442, 533, 535, 546
Нормальная ортогональная система
функций 420
Ньютона закон притяжения 18, 72,
277, 324, 364, 371, 384
Объем в криволинейных координатах
345, 349
-	выражение поверхностным
интегралом 298, 333
-	различные формулы 301
-	тела по поперечным сечениям 323
-	формула Кускова 355
-	цилиндрического бруса 122, 323
-	«-мерного параллелепипеда 386
-	- симплекса 391
-	- тела 386
-	«-мерной сферы 392
Ограниченного изменения функции
74
—	классы 76
—	критерии 82
—	непрерывные 84
—	ограниченность частичных сумм
ряда Фурье 611
—	порядок коэффициентов Фурье
508
—	свойства 79
Односвязность плоской области 53,
178
-	пространственной области 305, 336
Односторонняя поверхность 242
Ориентация плоскости 26
-	поверхности 244, 245
-	- связь со стороной поверхности 245
-	пространства 245
Ориентированная область, интеграл
по ней 207, 359
Ортогональная система функций 420,
583
Ортогональные функции 420
-	- с весом 423, 562
Особенностей выделение как метод
улучшения сходимости 516, 578
Особенности рядов Фурье 497
Остаток ряда Фурье, оценка 505, 508
Остроградский 333, 335, 371, 379, 388
Остроградского—Гаусса формула
333
Парсеваль 585, 589
Первообразная функция 46, 60, 65,
136, 147
Перерезывающее усилие 108
Периодическая функция 414
-	- интеграл по периоду 427
Плотность линейная 11
-	объемная 308, 324
-	поверхностная 135, 277
Площадь винтовой поверхности 265
- кривой поверхности 248, 251, 356
---особые случаи 259
— параметрическое задание 252,
273
---явное задание 257, 273
-	плоской фигуры в криволинейных
координатах 189, 194
---выражение криволинейным
интегралом 32, 121, 176
-	поверхности вращения 264, 266
-	- «-мерной сферы 393
-	цилиндрической поверхности 266
Поверхностные интегралы второго
типа 285, 287
-	— независимость от формы
поверхности 336
---по замкнутой поверхности 335
---сведение к двойному 288, 291
-	— связь с поверхностными
интегралами первого типа 289,
291
-	- в «-мерном пространстве 388, 405
-	- первого типа 274
-	— сведение к двойному 275
Поверхность вращения 264, 266
-	уровня 367
Поле векторное 367
-	магнитное 44
-	ньютоновского притяжения 72, 369,
371
-	силовое 40, 71, 372
-	скалярное 367
Поле скорости 42, 370, 374
-	температуры 369
Полное изменение функции 74, 82, 86
Полнота тригонометрической
системы 578, 610
Положительное ядро 600, 603, 608,
610,612,619
Полярное уравнение поверхности 266
Полярные координаты в
пространстве 344
-	- в «-мерном пространстве 401
-	- на плоскости 184
-	- обобщенные 198
-	- элемент площади 192, 195
Потенциал векторный 375
- ньютоновский, созданный
материальной точкой 72
---поверхностью 278
---сферическим слоем 285
---сферой 329
---телом 325, 364
---эллипсоидом 363
-	- тела на само себя 385
-	— другое тело 385
Потенциальная функция 71, 374
Потенциальное попе 71, 374
Поток вектора через поверхность 370
-	тепла 370
-	- вектор 371
Правая координатная система 26, 246
-	ориентация плоскости 26
-	- пространства 245
Предел упорядоченной переменной
636
---наибольший, наименьший 648
---условие существования 642, 648
Предельные условия 550, 555, 556,
557, 559, 561
Преобразование плоских областей
182
---сохраняющее площадь 203
-	пространственных областей 342
Приложения к механике и физике:
интеграла двойного 137, 165,
173, 208
-	криволинейного второго типа 41,
43, 44, 72, 73, 382
-	- первого типа 11, 17, 42
-	многократного 384
-	поверхностного 277, 281, 370, 379,
380
-	Стилтьеса 106, 108
-	- интеграла тройного 308, 324—332,
340, 362, 364, 379, 380
-	Фурье 558
-	- рядов Фурье 551, 555, 557, 560,
565, 570
Притяжение материальной точки
кривой 19
---поверхностью 277
---сферическим слоем 284
---сферой 328
---телом 325, 364
-	тела телом 385
Произведение инерции 169, 331
Производная обобщенная, первая и
вторая 613, 614
-	по направлению 368
-	- области 135,312
Простой слой 277
Пуассон 228, 280, 407, 603, 606
Пучности 553
Работа силового поля 40, 71, 372
Равномерная сходимость рядов
Фурье 419, 487
Расходимость 371
Расходящихся рядов суммирование,
см. Суммирование рядов
обобщенное
Регулярная точка 434
Риман 429, 432,619, 631
Римана метод суммирования 616, 618
Ротор 373, 374
Рунге 564, 569
Силовая функция 71
Силовое поле 40, 71, 372
Синус-преобразование Фурье 535,
545
—	для функции двух переменных
547
Синус, разложение обратной
величины на простые дроби 452
Скаляр 366
Скалярное поле 367
-	произведение 367
Смит 632
Соленоидальное поле 375
Сонин 400, 407, 409
Сопряженные функции первого и
второго рода 536
Сопряженный тригонометрический
ряд 480
Спрямляемая кривая 11, 88, 89
Среднее значение, теорема 112,116,
134,311
Среднее квадратичное отклонение
583
Статические моменты кривой 18
—	поверхности 281
-	- плоской фигуры 166
-	- прямолинейного отрезка 106
-	- тела 324
-	- цилиндрического бруса 166
Стеклов 585, 595
Стилтьеса—Дарбу суммы 91
-	интеграл 90
-	- вычисление 100
-	- геометрическая иллюстрация 111
-	- интегрирование по частям 97
- - классы случаев существования 92,
98
-	- непрерывность по верхнему
пределу 118
-	- оценка 112
-	- предельный переход 114, 119
-	- приведение к обыкновенному 98
-	- свойства 95
-	- теорема о среднем 112,116
-	- условие существования 96
Стилтьеса сумма 90
Стокса формула 297, 373
Сторона поверхности 241, 242, 248
Стоячих волн метод, см. Фурье метод
Струны колебание 549
Суммирование рядов обобщенное,
метод Римана 619
-	тригонометрических рядов в
конечном виде 469
---обобщенное, метод Пуассона—
Абеля 601
-----Римана 616
-----Чезаро—Фейера 607
Сфера, притяжение и потенциал 328,
329
Сферические координаты 266
-	- обобщенные 360
-	- элемент площади кривой и
поверхности 267
Сферический слой, притяжение и
потенциал 284, 285
Сходимость интеграла Фурье,
признак Дини 528, 531
-	— Дирихле—Жордана 529, 531
-	рядов Фурье абсолютная 593
	неравномерная 495, 497
	признак Дини 434
Сходимость рядов Фурье, признак
Дирихле 438
-	— Дирихле—Жордана 438
-	— Липшица 435
---равномерная 419
-	— признак Дини 487
----Дирихле—Жордана 489
----Липшица 489
Телесный угол 272, 337
Тепла распространение в круглой
пластине 561
---стержне бесконечном 557
----конечном 553, 559
-	— полубесконечном 559
—	теле 370
Тепло, поглощенное газом 43, 73
Теплопроводности уравнение 380,
554, 561
Томсон 383
Тригонометрическая система
функций, замкнутость 586
---полнота 578, 610
Тригонометрический многочлен 424,
580, 585
-	ряд 416
-	- лемма о коэффициентах 620
-	- не являющийся рядом Фурье 624
-	- сопряженный 480
Тригонометрическое
интерполирование 424
Тройной интеграл 309
-	- как аддитивная функция области
311
-	- классы интегрируемых функций
310
-	- несобственный 315
-	- приведение к повторному 312, 314
-	- свойства 310
-	- условие существования 310
Угол видимости кривой 63
-	- поверхности 338, 371
Узлы 553
Улучшение сходимости рядов Фурье
516
Умножение рядов Фурье 592
Упорядоченная переменная 636
-	- предел 636
-	- сведение к варианте 645
Упорядоченное множество 632, 633
Фату теорема 611
Фейер 497, 607
Фурье 417
-	интеграл 524
-	коэффициенты 419, 432, 586
-	- обобщенные 424, 560, 562
-	- порядок малости 509
-	- экстремальное свойство 584, 586
-	метод 550, 553, 555, 560, 561, 606
-	преобразование 534, 537
-	- для функции двух переменных 547
-	ряд 419, 427
-	- двойной 483
-	- комплексная форма 477
-	- обобщенный 424
-	формула, различные виды 525, 532
-	- для функции двух переменных 545
Центр тяжести кривой 18
-	- поверхности 277
-	- плоской фигуры 166
-	- тела 324
-	- цилиндрического бруса 167
Центробежная сила 332
Центробежный момент 169, 331
Циклическая постоянная 59, 70
Цилиндрические координаты 343,
354
Цилиндрический отрезок 172
Циркуляция вектора 372
Частичная сумма ряда Фурье,
ограниченность 610
-	— оценка 503
-	- сопряженного ряда, оценка 504
Чебышев 146
Четная функция 443, 534, 535, 546
Шатуновский 632
Шварц 248, 603, 614, 616, 629
Эйлер 417
Эйлера метод суммирования 470
-	- Фурье формулы 419
Эйлерова постоянная 463
Эквивалентная нулю функция 579
Экстремальное свойство отрезков
ряда Фурье 584, 586
Элемент площади в криволинейных
координатах 192, 195, 257
---полярных координатах 192, 195
---сферических координатах 267
- объема в криволинейных
координатах 348, 350
---сферических координатах 350
---цилиндрических координатах 350
Эллипс 35
-	инерции 169
Эллипсоид 172, 173, 268, 269, 363,
396
Эллипсоид инерции 332
Эллиптические интегралы 270, 363
-	координаты 189, 228, 229, 345, 355
Энтропия 74
Юнг 463, 590
Ядро положительное 600, 612, 619
-	Дирихле 610
-	Пуассона 603
-	Фейера 608
Якоби 230, 394, 403
Якобиан как коэффициент
растяжения 193, 349
ГЛАВА ПЯТНАДЦАТАЯ
КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
§ 1. Криволинейные интегралы первого типа
543. Определение криволинейного интеграла первого типа.
Для того чтобы естественным путем прийти к этому новому понятию,
рассмотрим одну механическую задачу, которай к нему приводит.
Пусть на плоскости дана непрерывная простая * спрямляемая кри-
вая (К) (рис. 1), вдоль которой расположены массы, причем из-
вестна их линейная плотность р (Л1) во всех точках М кривой. Тре-
буется определить массу т всей
кривой (Д').
С этой целью между концами
А и В кривой вставим произвольно
ряд точек Аь А2, ... , АлЛ (А#
и А„ для симметрии обозначений
отождествляются с А и В). Мы
считаем, что точки эти перенумеро-
ваны в направлении от А к В
[см. 246], хотя ничто не мешало бы
нам нумеровать их и в обратном
направлении.
Взяв какую-нибудь точку Mt на дуге А,- А;+1 кривой, вычислим
плотность р(2И;) в этой точке. Приближённо считая, что
такова же плотность во всех точках этого участка,
и обозначая длину дуги A,-Af+i через аг, для массы mi этой дуги
будем иметь приближенное выражение
отг = р(Ж,) аг,
а для всей искомой массы — выражение
п— 1
2 р(М,-)аг.
1 = 0
Ограничимся для определенности случаем незамкнутой кривой.
12 ГЛ. XV. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА |543
Погрешность этого последнего, связанная с сделанным выше
приближенным допущением, будет стремиться к нулю, если длины
аг всех участков стремятся к нулю. Таким образом, обозначая через
X наибольшую из длин аг, для получения точной формулы остается
лишь перейти к пределу:
п— 1
т = lim У р (Л1,-) а,.
Станем же изучать вообще пределы этого рода и, отвлекаясь от
рассмотренной задачи, возьмем произвольную «функцию точки»
f(M)—f(x,y), заданную вдоль непрерывной простой спрямляемой
кривой (К)*, и повторим указанный процесс: разбив кривую (А7) на
элементарные дуги At A(+i и выбрав на них произвольно по точке
7j(-), вычислим значения f (Mt) =f ($f, т]г) в них и составим
сумму
п—1	л—1
I=0	i=0
она представляет собой также своего рода «интегральную сумму».
Аналогичный процесс может быть применен и в случае замкну-
той кривой, если за точку Ао (А„) выбрать любую ее точку, а
остальные точки А{ расположить в соответствии с тем или другим
направлением на кривой [246].
Если при стремлении X = max а к нулю интегральная сумма
имеет определенный конечный предел I, не зависящий ни от спо-
соба дробления кривой (К)> ни от выбора точек на участках
A;Ai+1, то он называется криволинейным интегралом
(первого типа**) от функции f(M)=f(x,y), взятым по
кривой или по пу ти (К), и обозначается символом
/=S f(M)ds = 5 f(x,y)ds	(1)
(Ю	(К)
(где s есть длина дуги кривой и ds напоминает об элементарных
длинах о;). Точную характеристику предельного процесса можно пре-
доставить читателю.
Таким образом, полученное выше выражение для массы матери-
альной кривой может быть переписано так: •
щ = 5 ?(M)ds.	(2)
W
* При этом предполагается, что в основу положена некоторая прямоуголь-
ная система координат.
** В отличие от криволинейных интегралов второго типа, рассматри-
ваемых ниже [546].
644]	§ I. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ ПЕРВОГО ТИПА	13
Отметим особо, что в приведенном определении не играет
никакой роли направ ле ние, которое может быть придано
пути {К}- Если, например, эта кривая не замкнута и под (АВ) и
(ВА) разуметь разно направленные кривые, то
S f(M)ds = f(M)ds.
(АВ)	(BA)
Аналогично рассмотренному, мы могли бы ввести понятие интег-
рала, распространенного на пространственную кривую (/С):
] f(M)ds=\ f(x,y,z)ds*.
U0	(К)
Ввиду отсутствия новых принципиальных моментов нет надоб-
ности вдаваться здесь в подробности.
544. Сведение к обыкновенному определённому интегралу.
Предположим, что на кривой (К) произвольно установлено направ-
ление (одно из двух возможных), так что положение точки М на
кривой может быть определено длиной дуги $ = AM, отсчитываемой
от начальной точки А. Тогда кривая (К) параметрически выразится
уравнениями вида:
х = х (з), у =у (s) (0 sg s S),
а функция f(x, у), заданная в точках кривой, сведется к сложной
функции f(x(s), y(s)) от переменной з.
Если через з, (I = 0,1, ... , п) обозначить значения дуги, отвечаю-
щие выбранным на кривой точкам деления At, то, очевидно,
a; = sz+i — з; = Дзг. Обозначив через зг значения з, определяющие
точки М; (причем, очевидно, зг «С зг з;+1), видим, что интегральная
сумма для криволинейного интеграла
п-1	п-1	_	_
2 /(М,.) аг = £ 7(х (зг), У (з;))
1 = 0	1 = 0
является в то же время интегральной суммой для обыкновенного
определенного интеграла, так что сразу имеем:
з
f (Al) ds = (R) $ f (x (s), у (з)) ds **,	(3)
(К)	о
причем существование одного из интегралов влечет за собой суще-
ствование другого.
* В основу кладется некоторая прямоугольная система координат. Функ-
ция f определена лишь в точках кривой (X).
** Значок (R) указывает, что интеграл понимается здесь в согласии с обык-
новенным, римановым определением.
14 ГЛ. XV. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА [544
Эта непосредственность сведёния криволинейного интег-
рала первого типа к обыкновенному интегралу, разумеется, понижает
его теоретическое значение, но методическое значение он все же
сохраняет.
Интеграл, очевидно, существует, например, в случае непрерыв-
ности функции f (М) *, что мы будем впредь предполагать.
Пусть теперь простая кривая (/С) задана произвольными парамет-
рическими уравнениями
х = ?(0> р = ф(О	Т),
где функции ср и ф непрерывны со своими производными ср' и ф'.
Тогда кривая заведомо спрямляема, и если возрастание дуги
s = AM = s(ty отвечает возрастанию параметра t, то
[248 (10)]. Заменяя переменную в интеграле (3) справа, сразу по-
лучим:
т
\f{M)ds = \ /(ср (0, ф (0) V l?W + bpW dt.	(4)
ОТ	<0
Таким образом, для вычисления криволинейного интеграла перво-
го типа надлежит заменить в подингцегральной функции пере-
менные х и у выражениями координат через параметр, а мно-
житель ds — дифференциалом дуги, как функции параметра.
Подчеркнем, что нижний предел определенного интег-
рала (4) должен быть меньше верхнего.
В случае кривой, заданной явным уравнением
у=у(х) (а^х^Ь),
формула (4) принимает вид:
ь
5 f(M)ds = \f(x, _у(х))/1 + 1У(х)]а dx.	(5)
(А)	а
Этому соотношению можио придать и другую форму. В предположении
непрерывности функции у (х) вместе с ее производной у' (х), кривая (/<) в
каждой точке будет иметь определенную касательную, не параллельную оси у.
Обозначив через а угол касательной с осью х, получим;
* Мы имеем в виду непрерывность в точках кривой (/<) вдоль нее.
На языке <s-8> это означает, что по е > 0 найдется такое 8 > 0, что
|/(М’)—/(М)|<г при ММ' < 8 (М и М'— точки кривой). При этом пред-
положении и сложная функция f(x (з), у (s)), поскольку х(з) и у (з) непре-
рывны, есть также непрерывная функция от з.
545J	5 1. КРИВОЛИНЕЙНЫЙ ИНТЕГРАЛЫ ПЕРВОГО ТИПА	15
Поэтому
ъ
£ f(M) ds=[	dx.
J	J | COS a |
(К)	a
В частности, так как, очевидно,
$ ds = S,
(А)
где через S обозначена длина всей кривой (АВ), то
ь
s _ С dx
J | COS а | ’
a
(6)
Замечание. Формула (7) получена нами в результате формальных пре-
образований. Если бы мы определили длину дуги кривой, как предел периметра
описанной (а не вписанной) ломаной, то это определение — в случае
явного задания кривой — непосредственно привело бы к формуле (7). Пред-
лагаем читателю самому убедиться в этом.
545. Примеры. 1) Вычислить интеграл I=^xy ds, если (Л) есть чет-
. <*)
х3 у8 .
верть эллипса	лежащая в первом квадранте.
Решение, (а) Имеем
У = ~Уа3 — х3 , у'
Ьх
а У а3 — № *
так что по формуле (5)
/ =
а
1 Га*— (a3 — b3)x3
а V	а3 — х3
dx —
О
У а* — (а3 — Ь'2) x3-xdx.
Выполняя интегрирование, найдем:
2а‘(а3 — Ь2.
3
2 . .	.	... . -о I а ab а3 + aft + ft3
3 (a ~<a ~ b ) X 3 I о = 3 -~Ta + b ’
Следует заметить, что проведенная выкладка на деле требует еще неко-
торых оговорок, поскольку при х = а угловой коэффициент касательной обра-
щается в бесконечность. От этого недостатка свободно следующее
решение.
(б) Если перейти к параметрическому представлению эллипса: х = a cos t,
у — б sin t, так что
x‘t = — a sin	j^ = ftcos7, У x'f -\-у'3 = У a3sin31 -|- ft3 cos%
16
ГЛ. XV. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА [545
то вычисление можно произвести по формуле (4):
Я
*2
I — a cos t • b sin t • У a2 sin21 -J- b2 cos3^ dt =
о
Я
T	_______________'________,
ab C .	i Г „	1—cos2i	, 14-cos2Z	..
= 2- \ sin It •	у a2--g---b b	* —----- dt'
о
Положим здесь cos It = z, тогда sin It dt = — i- dz и
, аЬ C i/'«3 + *2 , *s-aa .
/==4)кУ -^-4—Zd2 =
_~ab 2	2 Га3 + &г —a2 __ ab a2 + ab + b2
“4 b2 — a23[	2	+	2 Z\ |_i“*3 a+b '
2)	Вычислить интеграл Z=( yds, где (Доесть участок параболы у2 = 2рх
(Ю
от начала координат до то^ки (х0, у/).
Решение. Из уравнения кривой имеем уу' = р, так что
 у ds =у У1 +У2 dx = Уу2 -/у2у'2 dX = Ур2 Ipx dx
и
х0	2
/= УУ + 2р^ах=1[(р2+у2У-р2].
о-5	Зр
3)	Вычислить интеграл L = (х2 +з+ <Zs, где (А) есть прямолинейный
(X)
отрезок, соединяющий точки (а, а) и (Ь, Ь) (Ь > а).
2 1^2”
Указание. У равнение прямой: у — х. Ответ; —— (Ь2 — а2).
О
4)	Вычислить интеграл ЛГ= ( уе~х ds, где (С) есть участок кривой
(С)
х = In (1 4-12), у = 2 arctg t — 14- 3
между точками Z = 0 и < = 1.
Указание: Ух/ 4"У? = Ь
С 2arctgZ-Z4-3 к2 1 Зя
\-----Г+72------Л-Тб~2 1П 2 + Т-
5) Для большинства постоянно встречающихся кривых (эллипс, гипербола,
синусоида, лемниската и пр.) длина дуги не может быть выражена в элемен-
тарных функциях, так как ds не интегрируется в конечном виде. Тем не ме-
545]	$ 1. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ ПЕРВОГО ТИПА	17
нее, интеграл j f(x,y)ds и для таких кривых часто может быть вычислен
(Ю
в элементарных функциях [см., например, упр. 1)], так как присоединение мно-
жителя f (х, у) меняет всю структуру подинтегрального дифференциала. Пред-
лагаем читателю построить примеры интегралов f f(x,y) ds, распространенных
(Ю
на синусоиду у = sin х или гиперболу ху — 1 и выражающихся через элемен-
тарные функции.
6)	Вычислить интеграл /=Д xyz ds, где (С) есть дуга кривой
(С)
х = t, у = /8Z3 г = Ь t2 между точками t — 0 и t = 1,
О	£,
Решение: ds = V x't2 y't2 z't2 dt = (1 +1) dt,
-19	_
T К2 С Л/1 , л л 16/2
0
7)	Дать формулу для вычисления интеграла I=\f(x, у) ds в случае,
(Л
когда кривая (К) задана уравнением г = г(0) (0^0 <А) в полярных коор-
динатах.
е»	_____
Ответ. 1= ( f (г cos 0, г sin 0) У г2 г'2 «70.
ех
f ds
8)	Вычислить интеграл Н = I	з , если (К) есть отрезок гипер-
J (х’+УР
(К)	_
болической спирали г0 — 1 от 0 = /3 до 0 = 2/2.
/о 19
Ответ.
О
9)	Найти массу участка кривой у = 1п х между точками с абсциссами х,
и х2, если (линейная) плотность кривой в каждой точке равна квадрату абс-
циссы точки.
Решение. По формуле (2), так как в нашем случае р = х2, имеем:
т = \ х" ds. Но ds = K-Lzt/L dX,
J	x
Xi
так что
x%	3	3
и= yr+^.xrfx = g-[(l+xD2-(l+x!p].
Xl
10)	Найти массу участка цепной линии у = a ch — между точками
х = 0 и х = а, если плотность кривой в каждой ее точке обратно пропорцио-
нальна ординате танк*
18
ГЛ. XV. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА [545
k	XV
Указание, р = —, rfs = ch — dx= — dx, m = k.
г у ’	a a
И другие вопросы, связанные с массами, непрерывно распределенными
вдоль материальной кривой, естественным образом приводят к криволинейным
интегралам рассмотренного типа.
11)	Мы уже имели дело в главе X [349] с вычислением статических момен-
тов плоской кривой относительно осей координат, а также координат ее центра
тяжести, в предположении, что «линейная плотность» р=1. Читатель легко
распространит полученные там формулы на общий случай непрерывного рас-
пределения масс. Если использовать введенное понятие криволинейного интег-
рала, то результаты напишутся в следующем виде:
Му fX ds,
Мх = J РУ ds,
(К)
т f р ds
(X)
5 РУ 8
v _____________
Ус~ т - f pds
(К)
12)	Укажем еще одно применение криволинейного интеграла первого
типа — к вопросу о притяжении материальной точки материальною же
кривою.
Как известно, по закону Ньютона, материальная точка М массы т
притягивает материальную точку Ма массы т0 с силой, направленной от Мо
,,	« тто
к М и численно равной k •	, где
г — расстояние М0М, a k — коэффи-
циент, зависящий от выбора основных
единиц измерения; впрочем, для про-
стоты мы будем обычно считать его
равным единице.
Если точка Мо притягивается си-
стемой точек Mlt М2, ... , Мп, с мас-
сами т„ т2, ... , тп, то результирую-
щая сила, или равнодействующая, по-
лучается геометрическим сло-
жением сил притяжения отдельными
точками. В то же время проекции ре-
зультирующей силы на координат-
ные оси равны алгебраическим
суммам проекций отдельных сил.
Если обозначить проекцииравнодействующей на оси через X и Y, а угол,
составленный вектором rt = MaMi с осью х, через 0, (рис, 2), то, очевидно,
п	п
1	*	1
(где Г{, как обычно, означает длину вектора г,).
Пусть теперь притягивающая масса распределена непрерывным образом
по кривой (К). Для нахождения притяжения разобьем кривую на участки и,
сосредоточив массу каждого участка в произвольно выбранной на нем
545]	$ 1. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ ПЕРВОГО ТИПА
19
точке Л4(-, найдем приближенные значения проекций равнодействующей иа оси:
X=2	cos 0it Г =	«п Ч
i 1	i 1
ибо в этом случае масса отдельного участка приближенно равна р(Л1,-)аг.
Если устремить все а,- к нулю, то в пределе получатся точные равенства,
г = „. С	(8)
W
причем суммы заменятся интегралами:
„ Ср (М) cos 0 .
X = т0 I r v -----ds,
(Ю
здесь г означает длину вектора ~г = Л40Л(,
13) Найти притяжение, оказываемое
р — 1) на единицу массы, помещен-
ную в центре.
Решение. Поместим начало
координат в центр полуокружности и
ось абсцисс проведем через ее концы
(рис. 3).
По соображениям симметрии
Х = 0, так что дело приводится к на-
хождению лишь проекции У. По фор-
а 0 — уГол, составленный им с осью х.
однородной полуокружностью (при
Но в нашем случае г = R (радиус полуокружности) и ds = /? dd. Поэтому
1 С	2
лУ1пИ9=л
14) Найти притяжение, оказываемое бесконечной однородной прямой (р= 1)
на точку единичной массы (т0=1), лежащую на расстоянии Л от прямой.
Решение. Рассмотрим искомое притяжение, как предел притяжения,
оказываемого конечным отрезком названной прямой при условии, что концы
удаляются в разные стороны до бесконечности. Если саму прямую принять
за ось х, а ось у провести через заданную точку, то получим (учитывая, что
в данном случае ds = dx)
Аналогично, X = 0 (что; впрочем, ясно из соображений симметрии).
15) Найти притяжение, оказываемое дугой астроиды х = a cos31, у=а sin31,
лежащей в первом- квадранте, на единицу массы, помещенную в начале коор-
динат, если плотность кривой в каждой ее точке равна кубу расстояния этой
точки от начала координат.
„	За8
Ответ. Х = У=-^-.
о
20 гл. XV. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА (546
§ 2. Криволинейные интегралы второго типа
546. Определение криволинейных интегралов второго типа.
Переходя к практически более важному понятию криволинейного ин-
теграла второго типа, мы здесь начнем прямо с его определения,
отложив приложения этого понятия до дальнейших номеров [см., на-
пример, п° 554]. Пусть дана непрерывная кривая (АВ) (которую мы
для простоты предположим незамкнутой) и пусть вдоль нее снова
задана некоторая функция f(x, у)*. Разложив кривую точками
Л,- (х{, у{) на части, выберем на отрезке кривой А[А1+1. по произволу
точку М;(^1, т],) и вычислим в ней, как и раньше, значение функции
f(Mi) =f' (5/( т]/). Но это значение мы умножим на этот раз не на
длину дуги AiAi+l, а на величину проекции этой дуги, скажем,
на ось х, т. е. на х1+1 — хг = Дх,-; затем составим сумму
г=о	;=о
Если при стремлении fi = max AtAi+l к нулю эта сумма имеет
конечный предел I, не зависящий ни от способа дробления кривой,
ни от выбора точек Mir то этот предел называется кри в о ли-
нейным интегралом (второго типа) от f(M)dx, взя-
тым по кривой или по пути (АВ), и обозначается символом
1= f(M)dx — f(x,y)dx.	л)
(ЛВ)	(ЛВ)
Аналогично, умножая значение f(Mt) не на Дхг, а на Ду;, т. е.
на проекцию дуги Л;Л,-+1 на ось у, и составляя сумму
п—1	п—1
С* = 2 f(Mi) tyi = £	71,.) йУ1
i=0	i=0
как предел ее получим криволинейный интеграл (второго
типа) от f (Af)dy
1*= f(M)dy= f(x,y)dy.	(2)
(ЛВ)	(ЛВ)
Если вдоль кривой (АВ) определены две функции Р(М) = Р(х,у),
Q(M) = Q(x, у) и существуют интегралы
$ Р (Af) dx = § Р (х, _у) dx, Q (AT) dy — Q (х, у) dy,
[АВ)	{АВ)	{АВ)	{АВ)
* См. примечание на стр. 12.
546]	§ 2. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ ВТОРОГО ТИПА	21
то и их сумму называют криволинейным интегралом («общего вида»)
и полагают
Р(х, y)dxA-Q(x,y)dy= Р(х,у) dxA- J Q(x,y)dy.
(AB)	(AB)	(AB)
Сопоставим теперь определение криволинейного интеграла вто-
рого типа (1) [или (2)] с определением криволинейного интеграла
первого типа [см. 543 (1)]. При очевидном сходстве оба опре-
деления имеют существенное различие: в случае интеграла первого
типа при составлении интегральной суммы значение функции /(Л1г)
умножается на длину ai = ^st участка АгА;+1 кривой, а в слу-
чае интеграла второго типа это значение /(2Й,-) умножается на
проекцию bxi (или &у.) упомянутого участка на ось х (или на
ось у).
Мы видели, что направление пути (АВ), вдоль которого произво-
дится интегрирование, не играет роли в случае интеграла первого
типа, ибо длина <зг дуги Л;А,+1 от этого направления не зависит.
Иначе обстоит |дело с интегралом второго типа: проекция упомя-
нутой дуги на ту или другую из осей существенно зависит от на-
правления дуги и меняет знак с изменением этого направления
на обратное. Таким образом, для интегралов второго типа
будет
5 f-(x> y)dx = —	f(x> J) dx
(BA)	(AB)
и, аналогично,
J f(x, y)dy = — f(x> J) dy,
(BA)	(AB)
причем из существования интегралов справа уже вытекает существо-
вание интегралов слева, и обратно.
Подобным же образом можно ввести понятие криволинейного
интеграла второго типа, распространенного на пространствен-
ную кривую (АВ). Именно, если функция f(M)=f(x,y,z) задана
в точках этой кривой, то, как и выше, строим сумму
п— 1
>=0
и рассматриваем ее предел при условии стремления к нулю р.=
= тахАгЛг+1. Этот предел называется криволинейным ин-
тегралом (второго типа) от f (М) dx и обозначается сим-
волом
f(M) dx —	(х, у, z) dx.
(АВ)	(АВ)
22
ГЛ. XV. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА [547
Аналогично определяются интегралы вида
5 /(М) dy =	/(х, у, z) dy
(АВ)	(АВ)
И
f(M) dz= f(x, у, z)dz.
(АВ)	(АВ)
Наконец, рассматривается и интеграл («общего вида»)
Р dx + Q dy 4~ R dz — Р dx-\- Qdy -j- § Р dz.
(АВ)	(АВ)	(АВ)	(АВ)
Здесь также изменение направления интегрирования меняет знак
интеграла.
Заметим в заключение, что простейшие свойства обыкновенного
определенного интеграла [302, 303] легко переносятся на рассматри-
ваемый криволинейный интеграл; останавливаться на этом не будем.
547. Существование и вычисление криволинейного интеграла
второго типа. Пусть кривая (ЛГ) = (АЯ) задана параметрическими
уравнениями
x=.<?(f), y = ty(t),	(3)
причем функции ® и ф непрерывны, и при изменении параметра t от
а до р кривая описывается именно в направлении от А к В. Функ-
цию f(x,y) вдоль кривой (АВ) также будем предполагать непре-
рывной.
Если речь идет об интеграле (1), то дополнительно обусловим
еще существование и непрерывность производной </(£).
При этих предположениях криволинейный интеграл (1) суще-
ствует, и имеет место равенство
₽
5 f (х, у) dx = (^)\f(^(t), ^(t))^'(t)dt.	(4)
(АВ)	«
Таким образом, для вычисления криволинейного интеграла (1) над-
лежит заменить в подинтегральной функции переменные х и у
их выражениями (3) через параметр, а множитель dx — диффе-
ренциалом переменной х, как функции от параметра. Поря-
док расстановки пределов в последнем интеграле
отвечает на этот раз выбранному на кривой на-
правлению.
Переходим к д о к а зате л ь ств у. Пусть точки A,(Z = O, 1, 2,...
,.. , п), взятые на кривой, определяются значениями tt параметра, а
547]	§ 2. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ ВТОРОГО ТИПА	23
выбранная на дуге Л;А/+1 точка Л4г — значением (очевидно, лежа-
щим между tt и /,+1). Тогда интегральная сумма
в==
i=0
если учесть, что
Zi+1
Дх,= <р(^+1) —?(Q= 5
‘i
может быть переписана в виде
n-l	‘i+l
*= £/(?«), фсч» $ ?(о^.
i = 0	tt
/
С другой стороны, и интеграл в (4) справа * можно представить
в виде суммы:
0	п-1 z» + i
/=$/(?	ф (0) ?' (0 dt = £ 5 /(т (/), Ф (0) т' (0 dt.
a	i = 0 tt
Отсюда
п-1 Zi + 1
S	ф(^))-/(?(0, ФСОИтЧО^.
« = 0 t.
t
Задавшись произвольным е^>0, предположим теперь все на-
столько малыми, чтобы в промежутках 7(+1] колебания непре-
рывной функции /(ср (t), ф (7)) были е. Так как непрерывная
функция <р' (7) ограничена | ср' (t) | L, то будем иметь
| а — 7| <е£ | р — а|.
Таким образом, при стремлении к 0 величины К = max | Д7£ | **,
lima=7,
чем одновременно доказано как существование криволинейного интег-
рала, так и требуемое равенство.
* Самое существование интеграла очевидно ввиду непрерывности подин-
тегральной функции.
** А это (в случае незамкнутой кривой) равносильно стремлению к 0 наи-
большей из хорд [245].
24 ГЛ. XV. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА (547
Переходя к интегралу (2), подобным же образом можно устано-
вить его существование и доказать формулу
₽
$ f(x, у) dy = (R) ^/(? (0> Ф (0) Ф' (0 dt	(5)
(АВ)	а
при условии существования непрерывной производной ф'(t).
Наконец, если речь идет об интеграле общего вида
Р (х, y)dx-]- Q (х, у) dy,
(АВ)
где Р и Q суть непрерывные функции, то на кривую (АВ) наложим
требование, чтобы обе функций (3) имели непрерывные произ-
водные. В этом предположении будет справедлива формула
§ Р dx -|- Q dy —
(АВ)
-₽
= Ф (0) ?' (0 + Q (<р (0. ф (0) У (01 dt. (6)
а
Определение криволинейного интеграла и указанный здесь способ
сведения его к обыкновенному определенному интегралу непосред-
ственно распространяются и на случай кривой (3), которая сама
себя пересекает, если только направление на ней по-прежнему
определяется монотонным изменением параметра t от а до р.
В заключение укажем некоторые случаи, когда вычисление криво-
линейного интеграла представляется особенно простым. Пусть интег-
рал (1) берется по кривой, заданной явным уравнением:
у=у(х),
причем перемещение точки из А и В происходит при изменении х
от а до Ь. Тогда без каких-либо предположений о кривой, кроме ее
непрерывности, имеем
ь
f(x,y)dx — (^.)\f(x,y(x))dx.	. (7)
(АВ)	а
Аналогично, если интеграл (2) распространяется на непрерывную кри-
вую, заданную явным же уравнением, но другого типа:
х = х(у)
(где у изменяется от с до d), то
а
$ f(x> y)dy — (R) f(x(y),y)dy.	(8)
(AB)	c
548]	§ 2. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ ВТОРОГО ТИПА	25
Наконец, если интеграл (1) распространяется на прямолиней-
ный отрезок {АВ), параллельный оси у, то он равен О
(ибо в этом случае равны 0 все Дх;, а с ними и все суммы а). Ана-
логично равен 0 и интеграл (2), взятый по прямолинейному
отрезку, параллельному оси х.
Если путь интегрирования (А) распадается на конечное число
примыкающих одна к другой кривых и вдоль каждой из них в от-
дельности криволинейный интеграл
существует и вычисляется по одной
из указанных формул, то, как легко ( С ------------------аХ
показать, существует интеграл вдоль	___у
всей кривой (К) и равен сумме ин-	х
тегралов по ее частям.	----'	'
548. Случай замкнутого кон- .	.s'
тура. Ориентация плоскости. Об-	__________—'п
ратимся к рассмотрению замкнутого
контура (А), т. е. к случаю, когда	-РйС. %.
начало А и конец В пути интегри-
рования совпадают. Взяв на кривой отличную от А точку С, пола-
гают по определению, с учетом выбранного на кривой направления
(на рис. 4 оно указано стрелкой):
Ь $ + S
(Д) (АМС) (САГА)
в предположении, что интегралы справа существуют.
Легко показать, что существование и величина интеграла не зави-
сят от выбора точек ‘А и С. Кроме того, и для замкнутого кон-
тура (А) оказываются применимыми формулы (4), (5) и (6), выведен-
ные в предыдущем номере.
Замечание. Впрочем, можно и здесь криволинейный интеграл полу-
чить в результате предельного перехода (как и в случае незамкнутой
кривой), но ограничив предельный переход, например, требованием,
чтобы две наперед фиксированные точки'А, А' неизменно входили в со-
став точек деления. Ничем не ограниченный предельный переход при
max МгА;+1 — 0 здесь к цели не привел бы [ср. 330].
Особенность рассматриваемого случая заключается в том, что ука-
зание начальной и (совпадающей с ней) конечной точки на этот раз
не определяет направления, в котором описывается кривая (К).
Можно было бы в каждом случае указывать особо, какое именно на-
правление имеется в виду. Так и приходится делать, если речь идет
о пространственной кривой. В случае же плоского замкнутого кон-
тура (Ю обыкновенно поступают иначе.
Из двух возможных для данной плоскости направлений вра-
щения — «против часовой стрелки» и «по часовой стрелке» — одно вы-
бирается за положительное: этим создается определенная ориентация
26
ГЛ. XV. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА (548
плоскости. Если положительным считается вращение против часо-
вой стрелки, то ориентация плоскости называется правой, в дру-
гом же случае — левой.
В случае правой ориентации плоскости мы именно вращение про-
тив часовой стрелки положим в основу определения п о л о-
жительного направления на простом замкнутом контуре
а)	б)
Рис. 5.
(рис. 5, а). Правда, это определение имеет достаточно ясный харак-
тер лишь для контуров, близких к окружности. Поэтому мы усло-
вимся более точно так:
положительным направлением
обхода (простого) замкнутого контура на-
зывается то, при котором ближайшая к
наблюдателю часть области, ограниченной
контуром, оказывается лежащей слева от
наблюдателя (рис. 5, а). В случае левой
ориентации плоскости положитель-
ным будет обход контура по часовой
стрелке, так что область остается
справа от наблюдателя (рис. 5, б).
Заметим, что самое расположение ко-
ординатных осей на плоскости всегда ста-
вится в связь с ее ориентацией: ось у по-
лучается из оси х поворотом ее на 90° про-
тив часовой стрелки при правой
ориентации плоскости и по часовой стрелке — при левой
(см. рис. 6, а, б). В первом случае сама координатная система назы-
вается правой, а во втором — левой.
После этих пояснений заключим раз навсегда такое соглашение:'
если путь интегрирования {К) есть простая замкнутая кривая,
то под символом
Pdx4- Qdy
(Ю
при отсутствии указаний на направление обхода контура разумеется
интеграл, взятый в положительном направлении. Конечно,
549]	s 2. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ ВТОРОГО ТИПА
27
это соглашение не мешает нам рассматривать в случае надобности
и интеграл, взятый в отрицательном направлении, но обозначать его
мы будем через
— Р dx + Q dy.
(К)
549. Примеры. 1) Найти интеграл /= (ха—у2) dx, если (К) есть от-
резок параболы у = х2 от точки с абсциссой х = 0 до точки с абсциссой х = 2.
Решение. Так как кривая интегрирования задана явным уравнением, то
применим формулу (7); мы получим
2
/ = (х2 — x*)dx = —
V
о
2) Найти интеграл J—	(х2—y*)dy, где (К) означает ту же кривую,
(Д)
что и выше.
Решение. Здесь следует воспользоваться формулой (8). Заметив, что
из уравнения кривой х2—у и что пределы
изменения у суть 0 и 4, будем иметь
4
. С .	.. .	40
/=\ (У— y^dy= — —.
3) Вычислить значение криволинейного ин-
теграла
77 = § 2ху dx -|- x*dy,
взятого по пути (Z.),
(О, 0) и А (1, 1), если
у = х, (б) парабола
бола у = х3 (рис. 7).
соединяющему точки О
путь (Z.)
V — V2
есть: (а) прямая
(в) парабола х = у2, (г) кубическая пара-
Решение, (а) Так как
dy э= dx, то j 2ху dx 4- x2dy= § 3xsdx = 1;
(i)	0
1
(6) dy = 2xdx,' /7 = ?4x3dx=l;
о
1
(в) dx = 2y dy, . H — {5yidy—\;
(r)
dy — 3x2 dx,
5x’ dx — 1.
28 ГЛ. XV. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА [549
4) Вычислить криволинейный интеграл
0= § ху dx + (У — x)dy
при тех же путях интегрирования.
Ответ, (а) 1, (6)1, (в) g, (г)-1
5) Найти криволинейный интеграл
7 = ( (х—у2) dx + 2 ху dy,
(ОА)
если в качестве пути интегрирования берется одна из следующих линий, со-
единяющих точки 0(0, 0) и А(1, 1) (см. рис. 7): (а) прямолинейный отрезок
ОА(у — х); (б) ломаная ОРА, состоящая йз отрезка ОР оси х(у = 0) и
отрезка РА прямой х =1; (в) ломаная OQA, состоящая из отрезка OQ оси
у(х = 0) и отрезка QA прямой у.= 1.
Решение, (а) Так как у = х и dy = dx, то
1
(•	ч
7= \ (х4-х2) rfx= у.
(б) В этом случае естественно разбить путь интегрирования на два
отрезка:
7 = ( = =Л + Л>
(ОРА) (ОР) (РА)
Вдоль ОР имеем: _у = 0 и dy = 0, так что
1
7 С Л 1
\ xdx=
Вдоль РА будет: х=1 и dx = 0, поэтому
1
Is = \ 2у dy = l.
Таким образом, окончательно 1 = -^-.
(в) Аналогично предыдущему найдем (так как интеграл вдоль отрезка OQ
равен нулю):
7 =	(х—l)rfx=—1.
(QA) О
6)	То же для интеграла
J = ( Су2 + 2ху) dx 4- (2ху 4- ха) dy.
(ОА)
Ответ. Во всех случаях J — 2.
549]
§ 2. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ ВТОРОГО ТИПА
29
Замечание. Читатель, вероятно, уже обратил внимание на различие
между результатами упражнений 3)и6), с одной стороны, и 4) и 5) — с другой.
Величины интегралов, рассмотренных в 3) и 6), оказались не зависящими от
л и н и и, соединяющей начальную и конечную точки. Напротив, в примерах 4),
5) мы столкнулись с интегралами, значения которых зависят от того, какой
линией соединены начальная и конечная точки. Ниже [§ 3] мы займемся
этим вопросом специально и выясним его важность.
7)	Вычислить интеграл
/ = ? (х2 + 2ху) dy,
(С)
д*2 v2
где (С) означает верхнюю половину эллипса	1, пробегаемую
против часовой стрелки.
Решение. Воспользуемся параметрическим представлением эллипса:
x = acosT, y = b sin Z; t изменяется здесь от 0 до л,- Подставляя вместо х и
у их выражения через t и заменяя dy через bcostdt, получим [по фор-
муле (5)]
те
I =	(a3 cos31 -|- 2ab cos t sin t} b cos t dt ==
’ о
те	те
(•	С	4
= a?b \ 60s31 dt + 2aZ>2 \ cos2 t sin t dt == -у ай9.
У	Л	о
8)	Вычислить интеграл
К— у2 dx — х2 dy,
(I)
где (£) есть окружность раДиуса 1 с центром (а) в начале координат или (б)
в точке (1, 1).
Решение, (а) Исходя из параметрических уравнений x = cosf, _y==sinT,
где t меняется от 0 до 2л, по формуле (5) будем иметь
2те
К= — (sin31 + cos31) dt — 0.
Аналогично с помощью параметрического представления
х — 1 = cos t, у — 1 — sin t
*
получим
2те
К=—	(2 + sin t + cos t + sin31 -f- cos3 f) dt=—4л.
9) Найти значение’интеграла
J= Ах2 + 2Вху + Су2 (-А’ с п АС — В2 > 0),
W
где (/<) есть окружность х2 у2 — г2.
Указание. Ср. 339, 14). Ответ. —===.
у АС —В2
30
ГЛ. XV. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА (550
10) Вычислить интеграл
.___ С х dx , dy
~ д У + У~“ '
(Л)
если (Д) есть отрезок циклоиды
x — a(t — sin/), _y = e(l—cos/)
от точки t = ~ до точки / = -^-.
О	3
Решение.
те
"3
L= $ [a (/-sin/)-^p = e(^ + ^^)-|ln3.
те
Т
11) Вычислить интеграл
.__ С ха dy — у3 dx
'	5 Ъ- >
' & х*+у3
если (Уф есть часть астроиды
х = a cos3 /, у = a sin’ /
от точки А (а, 0) до точки В (0, а).
Решение.
те
_41~	J
/=3а 3 \ sin* £ cos* t dl= па3 .
J 16
550. Приближение с помощью интеграла, взятого по лома-
ной. Во многих случаях, имея дело с криволинейным интегралом,
представляется удобным приблизиться к нему с помощью интеграла,
взятого по ломаной. Такое приближение основывается на следующем
предложении, которое нам не раз будет полезно.
Кривая (£), которая в нем упоминается, предполагается простой
и незамкнутой. Она задается уравнениями вида (3), где функции
и ф непрерывны вместе со своими производными; этим обеспечи-
вается существование криволинейного интеграла в написанном ниже
равенстве [547], а также спрямляемость самой кривой (£) [248].
Лемма. Пусть функции Р(х,у) и Q(x,y) непрерывны в открытой
области (Е), а (£) — содержащаяся в ней кривая указанного класса.
Если вписать в (£) ломаную (Л), то при стремлении к нулю
наибольшей из ее сторон будем иметь
lim Pdx-\-Qdy = Р dx -|- Q dy.
(л)	(1)
55OJ	$ 2. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ ВТОРОГО ТИПА	ЗГ
Достаточно остановиться на интегралах ? Pdx и \ Pdx\ для
(А)	(I)
интегралов Qdy и \ Qdy рассуждения вполне аналогичны. Пусть
(А)	(1)
вписанная в (Z.) ломаная (А) имеет вершины в точках
А = Aq, Aj, ..., A;, Aj+j,..Ал = Д,
обозначим через xt, Pj значения х, Р в точке А,-. Задавшись произ-
вольным числом е^>0, можно звенья АгА1+1 представить себе на-
столько малыми, чтобы 1) колебание непрерывной функции Р вдоль
звена А;А;+1 было <^е и 2) интегральная сумма У] РгДх^ отличалась
i
от своего предела Pdx тоже меньше, чем на е.
(X)
Имеем, очевидно,
Pdx=^i Pdx
• W	i (Ai'Ai+l>
и, с другой стороны,
$ Pidx>
i	1 (AiAi+l>
так что
Pdx = 2р^+2 $ [Р — PiJdx.
(A)	i	i (А .А -+1)
Но первое слагаемое справа разнится от интеграла Pdx меньше,
(М
чем на е [см. 2)], а второе по абсолютной величине не превосходит
е S А,-А;+1 [см. 1)], т. е. и подавно L • е, где L — длина
кривой (L).
Итак, окончательно,
| Pdx— § Pdx|<e(l+L),
(А)	(I)
что и доказывает наше утверждение.
Замечание. 'Доказанное утверждение в некотором смысле
может быть распространено и на случай замкнутой простой
кривой (А), если разложить ее на две незамкнутые кривые и к
каждой из последних в отдельности применить лемму. Предельный
переход здесь ограничен требованием, чтобы в числе точек деления
были две наперед фиксированные точки [ср. замечание в п° 548].
32 гл. XV. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА (551
551. Вычисление площадей с помощью криволинейных инте-
гралов. Покажем теперь,\ как с помощью криволинейных интегралов
(второго типа) можно вычислять площади плоских фигур.
Рассмотрим сначала (рис. 8) фигуру (D) = PQRS, ограниченную
отрезками PS и QR прямых, параллельных оси у (они в частных
случаях могут стягиваться и в точ-
ку), и двумя кривыми PQ и SR,
которые любой параллелью.к оси_у
пересекаются каждая только в од-
ной точке. Пусть явные уравнения
кривых (PQ) и (SR) будут
(PQ): у=у0(х),
(SR): у = Y (х),
причем х изменяется в проме-
жутке [а, Ь\. •
Рассматривая площадь D «кри-
волинейной трапеции» PQRS как
разность площадей двух «криволинейных трапеций» abRS и abQP,
можем написать
»	ь
D — Y(x)dx— y0(x)dx.
а	а
С другой стороны, по формуле (7)
ъ	ь
у dx— уй (х) dx, у dx —	Y(х) dx.
(.PQ)	a	(SJ?)	а
Поэтому
D= у dx_у dx;
(SP) (QP)
мы изменили знак перед вторым интегралом, но зато изменили и
направление интегрирования. Если прибавить к правой части равенства
интегралы
\ у dx и \ у dx,
(PS)	(Я<?)
равные нулю (так как они взяты по отрезкам, параллельным оси _у),
то равенство не нарушится. В результате получим
D = \ у dx,
(PSKQP)
причем контур пробегается в порядке букв, указанных под символом
интеграла.
551]
$ 2. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ ВТОРОГО ТИПА
33
Если обозначить контур области (D) через (L), то символ у dx
(Р
по заключенному в п° 548 условию будет означать интеграл, взятый
в положительном направлении. При
осей, которая принята на рис. 8, это будет
оставляющее область слева, в то время как
оставляет эту область справа. Поэтому
f ydx ——
(PSPQP)	(L)
и, следовательно,
правой ориентации
направление обхода,
направление PSRQP
D =
(А)
Предположим теперь, что хотя фигура (О) ограничена контуром
более сложного вида (который может даже состоять из нескольких
отдельных кривых), но эту фи-
гуру прямыми, параллельными У
оси у, можно разложить на ко-
нечное число частей рассмот-
ренного типа (рис. 9). Каждая из
этих частей будет иметь пло-
щадь, выражающуюся по фор-
муле (9). Сложив все эти ра-
венства, мы получим слева пло-
щадь всей фигуры (О),.а справа _
сумму интегралов, распростра-
(9)
ненных на все частичные кон-	Рис. 9.
туры. Эти интегралы, однако,
приводятся к одному, взятому по общему контуру (Z.), ибо интегралы
по каждому из вспомогательных отрезков равны нулю. Таким образом,
и в этом случае площадь D выражается по формуле (9).
Для фигуры PQRS (рис. 10), ограниченной прямолинейными
отрезками PQ и 5R, параллельными оси х, и двумя кривыми
(PS):	х=ха(у)
(QR):	х = Х(у)
(с У d),
с помощью сходных рассуждений получается формула
D= \ xdy.	(10)
(Z) '
Впрочем, она может быть выведена и непосредственно из формулы (9),
если обменять ролями оси х и у. Знак при этом придется изменить
именно потому, что, несмотря на изменение ролей координатных осей,
положительное направление обхода все же осталось прежним.
34 гл. XV. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА [551
Легко понять, что формула (10) будет справедлива и для более
сложной фигуры, которая прямыми, параллельными оси х, разлагается
на конечное число «криволинейных трапеций» второго типа.
Полученный результат на деле имеет уже вполне достаточную
общность. Однако проверка в конкретных случаях возможности раз-
ложить предложенную фигуру на части упомянутых специальных типов
представляется обременительной. Поэтому мы укажем и другое —
тоже весьма общее, но легко проверяемое условие, при котором ока-
Рис. 10.
зываются приложимыми одновре-
менно обе формулы (9) и (10).
Именно, предположим, что об-
ласть (D) ограничена произволь-
ной кусочно-гладкой кривой
(£) *. Так как эта область квад-
рируема [337], то можно по-
строить входящую и выходящую
многоугольные области (Л) и (В)
так, чтобы было
A<jD<5; В — 4<е,
где е — наперед заданное положительное число [335]. При этом
можно предположить также, что контуры всех этих областей попарно
не имеют общих точек. Обозначим через 3 наименьшее расстояние
между точками различных контуров [см. 336, сноска]. Если вписать в (L)
ломаную (Л) так, чтобы ее звенья все были <^8, то эта ломаная
уже не может иметь общих точек с контурами многоугольников
(А) и (В), так что ограниченный ею многоугольник (Д) содержит в себе
(Л) и сам содержится внутри (В). Отсюда
]Д — D|<e,
так что Д—>jD при стремлении к нулю наибольшего из звеньев впи-
санной ломаной.
Теперь нетрудно убедиться, что к вычислению площади Д много-
угольника приложимы как формула (9), так и формула (10), т. е.
Д = — у dx = х dy
(Л)	(А)
(ибо прямыми, параллельными оси у или оси х, легко разложить
этот многоугольник на трапеции того или другого типа). Если, опи-
раясь на лемму предыдущего п° (см. замечания), перейти здесь к
пределу, то и получим окончательно: площадь фигуры (D), ограни-,
ченной кусочно-гладкой кривой, выражается любой из названных
формул.
* Напомним, что кусочно-гладкой называется кривая, состоящая из
нескольких гладких дуг [см. 337; ср. 261].
552]
§ 2. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ ВТОРОГО ТИПА
35
Чаще всего, впрочем, для вычисления площади применяется Дру-
гая, более симметричная, формула:
£)=-g- xdy—ydx,	(11)
(О
которая легко получается из формул (9) и (10) [ср. 339 (16)].
Замечание. Легко убедиться, что и наличие на кривой конеч-
ного числа особых точек не мешает на деле справедливости выве-
денных формул. Если выделить эти точки с помощью их окрест-
ностей, то к остающейся части фигуры формулы приложимы. Затем
нужно лишь перейти к пределу, предполагая диаметры упомянутых
окрестностей стремящимися к нулю.
552. Примеры..!) Найти площадь эллипса с полуосями а и Ь.
Решение. Воспользуемся параметрическими уравнениями эллипса:
x = acost, у = ft sin/ (0 t sg 2тс). По формуле (11)
2-я	2-я
1 С	аЬ С
D = — \ a cost- bcost dt — bsmt •(— a sint) dt ==	\dt — nab.
0	о
Для вычисления криволинейного интеграла мы применили формулу (6); при
расстановке пределов интегрирования было принято во внимание, что положи-
тельный обход контура отвечает возрастанию
параметра.
2) Найти площадь астроиды
х = a cos’ t, у = a sin81
(0«£/«£2л).
Ответ.
2-я
D = sin2/cos2/= —рД .
z J	о
0
3) Найти площадь фигуры, ограниченной од-
ной аркай! эпициклоиды
х = а [(1 + т) cos mt — т cos (1 т) /],
y==a[(l-|-m) sinm/— т sin(l -]-m)/]
и соответствующей дугой круга (рис. 11).
Решение. Интеграл (11) нужно взять сначала по кривой (АВС), а затем
по кривой (CDA). В -первом случае мы можем воспользоваться написанными
выше уравнениями, изменяя t от 0 до 2тс. Тогда
х dy—у dx = a3 * sm (1 + т) (1 -|- 2m) (1 — cos t) dt,
так что
i \ — ла2т (1m) (1-|-2m).
(ABC)
2*
36 гл. XV. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА (552
Что же касается дуги круга (CDA), то, сохраняя тот же параметр, ее можно
выразить уравнениями
х = a cos mt,
у = a sin mt,
изменяя t на этот раз от 2я до 0. Соответствующий интеграл будет
о
у ? =^a?m^dt = —па-т.
(CDA)	2п
Итак, искомая площадь равна
D = nasm2 (2т + 3).
4)	Найти площадь петли декартова листа (рис. 12)
х3 + у3 — Заху.
Решение. Для получения параметрических уравнений контура положим
y = tx*. Тогда [ср. 224, 5)]
3at	3ats
1 +*3 ’ у~ 1 +*3 ’
ясно, что петля описывается при измене-
нии параметра t от 0 до со ^ибо t — —^ =
= tg 0, где fl изменяется от 0 до
Имеем
1 —2Z3
dx = За	dt,
2t—t3
и
с»
9as г t* dt _ 3
2 3(1+t3)3 ~ 2
Отметим, что здесь мы использовали
несобственный интеграл с бесконечным
пределом, в то время как при выводе формулы (6) мы считали, что промежуток
изменения параметра конечен. Оправдать сделанное легко, если предвари-
тельно ввести другой параметр с конечным промежутком изменения (например,
у
угол fl), а затем уже перейти к параметру
5)	То же для кривой:
(а) (х-\-у)3 — ах2у, (б) (х + y)2n+I = ахпуп (п — натуральное).
Указание. Ввести t = меняя t от 0 до оо. В случае (б)
х dy—y dx =	”^+2dt-
* Такая подстановка оказывается удобной, как правило, в тех случаях,
когда в уравнении алгебраической кривой имеются две однородные группы
членов, причем степени этих групп различаются на единицу.
552]	§ 2. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ ВТОРОГО ТИПА
37
При интегрировании разложение на простые дроби можно получить, исходя
из тождества
2п
tin = [(1 +0 _ 1]!Я = 2 С*п (- 1)* (1 + i)ft.
й=0
2/1	С6
Оте.. (.)!>=£;	'
ft = 0
6)	Найти площадь фигуры, ограниченной осями координат и кривой
х34-У = х24-у2.
Ответ. D = 4- + 4=
3	9/3 •
7) В качестве примера применения общей формулы (10) для вычисления
площадей плоских фигур любой формы * остановимся в заключение на такой
задаче.-
Пусть основанием некото-
рого тела служат две произволь-
ного вида фигуры, лежащие в
двух параллельных плоскостях,
а боковая поверхность его яв-
ляется линейчатой и образована
прямыми, соединяющими по
произвольному закону точки
контуров упомянутых фигур
(рис. 13). Доказать, что объем
V тела выражается формулой
V=± (Qe + ^ + Qi), (12)
где h означает высоту тела,, а
Q(l, Qi и Qs суть площади его
оснований и среднего сечения.
Мы знаем, что объем V по
площади Q = Q (х) поперечных
сечений выражается формулой
ь
V= j Q (х) dx
а
[см. 342]<С другой стороны,
формула Симпсона:
ь
^Q(x)dx=^ (Qo+^ + Qs),
а
если Q (х) есть многочлен степени не выше третьей, является точной [см.
327, сноска]. На деле, как мы увидим, Q (х) представляет собой многочлен
второй степени.
Пусть
у = ах + ₽,	2 = 7x4-8	(13)
* С соблюдением, конечно, высказанных условий, о которых для простоты
мы здесь уже не будем упоминать.
88
ГЛ. XV. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА (553
будут уравнения образующей той линейчатой поверхности, которая ограничи-
вает наше тело. При этом можно предположить, что коэффициенты а, р, 7,8 яв-
ляются функциями от некоторого параметра t, при изменении которого (скажем,
от до Г) образующая и описывает поверхность. Если теперь пересечь по-
верхность плоскостью, параллельной плоскости yz, на расстоянии х от нее, то
в сечении получится кривая, проекция которой (без искажения!) на плоскость
yz как раз и будет иметь уравнения (13) своими параметрическими уравне-
ниями. Предположим, что при изменении t от до Т контуры всех сечений
описываются ('соответствующими точками образующей) в положительном на-
правлении. Тогда площадь сечения, например, по формуле, аналогичной (10),
выразится так:
т
Q (х) = у dz = (ах ₽) d (fx + 8) =
/о
т	т	т
= х2 • adf -f- х Л (a d8 р d'() -f- J ₽ rf8,
4	»о	'о
т. е. действительно представится квадратным трехчленом от х.
Легко показать, что формула, аналогичная формуле (12), применима и к вы-
числению статического момента нашего тела относительно плоскости yz. Этот
момент выражается интегралом
ь
Муг = xQ (х) dx
а
[356, 1)[, и здесь подинтегральная функция будет полиномом третьей
степени.
553. Связь между криволинейными интегралами обоих типов.
Рассмотрим гладкую кривую (К)=(АВ) и, выбрав в качестве
параметра дугу $ = д./и, представим ее уравнениями
х — х ($), У—У ($),	(0 s S).
Функции x(s), y(s) будут иметь непрерывные производные- x'(s),
у'(з). Если через а обозначить угол, составленный с осью х каса-
тельной, направленной в сторону возрастания дуг, то,
как известно [249 (15)],
cos a = V (s),	sin a =y'(s).
Если вдоль кривой (К) задана непрерывная функция /(2И) =
=/(.£, у), то последовательно имеем
$
f(M)dx = ^f(x (s), у (s)) х’ (s) ds —
(К)	о
S
= f (х (s), у ($)) cos a ds = f (Л1) cos a ds,
0	(X)
и криволинейный интеграл второго типа оказался сведенным к
криволинейному интегралу первого типа.
553]
§ 2. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ ВТОРОГО ТИПА
39
Аналогично получается
J f(M)dy = /(Af) sin ads.
m	(Ю
Если же заданы две непрерывные вдоль кривой (К) функции
Р (М) = Р (х, у) и Q (Af) = Q (х, у), то
§ Р dx + Q dy = $ (Р cos a -j- Q sin a) ds.
(Ю	w
(14)
Подчеркнем, что во всех этих формулах угол а связан с тем
направлением касательной, которое отвечает направлению самой кри-
вой (К). Если изменить направление кривой, то не только интеграл
слева изменит знак: ввиду изменения направления касательной угол а
изменится на ±к, в связи с чем изменит знак и интеграл справа.
Очевидно, выведенные формулы остаются справедливыми и для
кусочно-гладкой кривой без кратных и особых точек; в этом
легко убедиться, если написать их для каждого из гладких кусков
кривой и почленно сложить.
В виде упражнения предложим себе преобразовать формулу (11) для пло-
щади к криволинейному интегралу первого типа:
1 С	1 С
D = -^ 1 X dy—ydx—-^ \ (xsina — ycosafds.
W	(к)
Если перейти к полярным координатам г, 6, то получим, далее,
D = -^- ? г (sin a cos 0 —cos а sin 0) rfs=-^- г sin (а — 0) ds.
(К)	w
Заметив, что а — 0 есть угол (г, f) между радиусом-вектором точки и касатель-
ной в ней, можно придать формуле такой окончательный вид:
Р==-^- 1 г sin (г, t)ds.
ОТ
Аналогичные соображения можно развить и для криволинейных
интегралов по пространственной кривой. В результате полу-
чится формула
Р dx 4~ Q dy 4~ R dz = § (Р cos а Q cos р -|- R cos у) ds,
ОТ	ОТ
где cos а, cos р, cos у-суть направляющие косинусы касательной, в
предположении, что ее направление отвечает направлению пути ин-
тегрирования.
Для случая плоской кривой иногда удобна формула, связываю-
щая криволинейные интегралы обоих типов и содержащая угол между
40
ГЛ. XV. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА [554
осью х и нормалью к кривой, на которую распространены инте-
гралы. Если приписать нормали такое направление, чтобы угол
<£(t, л) между касательной и нормалью был равен-}--у*, так что
ЗС(х, п) = ^(х, + л) = а-}-£,
то
cos а = sin (х, п),
sin а = — cos (х, л).
Тогда, например, формула (14) может быть написана в виде
Pdx-]- Qdy = [Р sin (х, л) — Q cos (х, л)] ds. (15)
(Ю	(Ю
554. Физические задачи. Остановимся в заключение на нескольких
физических задачах, в которых криволинейные интегралы находят себе
применение.
1) Работа силового поля. Пусть в каждой точке М плоскости ху (или
определенной части плоскости) на помещенную в нее единицу массы действует
определенная сила F, величина и направление которой зависят только от
положения точки М; если масса т помещенной в точке М материальной точки
отлична от единицы, то действующая на
„I	нее сила будет равна mF. При этих усло-
" '	виях плоскость (или рассматриваемая ее
часть) называется (плоским) силовым
___________________полем, а сила F, действующая на единицу
-___________________массы, — напряжением поля. Задание
Г	С—	]	силы F по величине и направлению рав-
!___ носильно заданию ее проекций X, Y на
МI	।	*" оси, очевидно, являющихся функциями от
1	•	координат х, у точки М:
-----------!---------!----	Х=Х(х,у), Y=Y(x,y).
Если обозначить через <р угол, составлен-
Рис. 14.	ный вектором F с осью х, то (рис. 14)
X=Fcos<?, Y=Fsin<?. (16)
Предположим теперь, что материальная точка М с единичной массой, на-
ходящаяся в поле, движется и описывает некоторую непрерывную кривую (X)
в определенном направлении. Задача состоит в вычислении работы А, кото-
рую при этом движении совершают силы поля.
Если бы действующая на точку сила сохраняла постоянную величину F и
постоянное направление, а само перемещение точки происходило прямоли-
нейно, то, как известно, работа А выразилась бы произведением перемеще-
ния I на проекцию силы на направление перемещения:
A=Fl cos 0,
где 0—угол между силой F и направлением перемещения.
* Направление отсчета углов должно быть согласовано с ориентацией
плоскости!
554]
§ 2. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ ВТОРОГО ТИПА
41
В случае непрямолинейного движения и непостоянной силы работа опре-
деляется с помощью некоторого предельного процесса. Можно, впрочем, при-
бегнуть для краткости к привычному в приложениях «методу суммирования
бесконечно малых» [ср. 348]. Станем определять положение точки М на кривой
(К) (рис. 15) длиной s дуги AM. Рассмотрим бесконечно малый элемент
MV= ds кривой и будем приближенно считать, что сила F и угол 9 на пере-
мещении ds сохраняют свою вели-
чину. Тогда соответствующий эле-
мент работы будет
dA — Feos 0 ds.
Теперь остается лишь «просумми-
ровать» эти элементы вдоль всей
кривой (АГ), в результате чего ра-
бота А выразится криволиней-
ным интегралом первого
типа:
А = J F cos0 ds.	(17)
W
Введем угол а между напра-
влением элемента ds (т..е.направле-
нием касательной к кривой в точке М) и осью х. Очевидно, 6 = <р — а, так что
cos 0 = cos <р cos а + sin с sin а,
и элемент интеграла пишется так: (Fcos<p • cosa /-"sintp • sina) ds или, ввиду (16):
(X cos a -f- У sin a) ds.
Само выражение (17) для работы примет вид:
А = ( (X cos a + Y sin a) ds.
W
Если теперь учесть ф&рмулу (14), устанавливающую связь между криволиней-
ными интегралами обоих типов, то, окончательно, работа силового поля выра-
зится к рьи волинейным интегралом второго типа:
А = ? Xdx+Ydy.	(18)
(К)
Это и есть наиболее употребительное выражение для работы, удобное для
исследования ряда важных, связанных с нею вопросов: зависит ли произведен-
ная работа от формы траектории, соединяющей данные две точки; будет ли
работа по замкнутой траектории всегда равна нулю (об этом см. ниже
п°п° 555—562).
2) Плоское установившееся течение несжимаемой жидкости. Такое
движение характеризуется тем, что, во-первых, все частицы, лежащие
на одной вертикали к некоторой плоскости, имеют одну
и ту же скорость, параллельную этой плоскости, так что для характе-
ристики всего движения достаточно изучить движение в одной лишь пло-
скости *, и, во-вторых, с к о р о с т ь с частицы жидкости зависит
только от положения частицы, но не от времени. Таким об-
разом, с каждой геометрической точкой рассматриваемой плоскости (или ее
* Которую мы и выберем за плоскость ху.
42
ГЛ. XV. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА 1554
части) связана определенная по величине и направлению скорость; иными
словами, задано некоторое «поле скорости».
Если обозначить угол, составленный вектором с с осью х, через <j>, а про-
екции этого вектора на координатные оси (слагающие скорости по осям) через
и и v, то (рис. 16, а)
и — Сх = С COS ср, V = Су = С sin ср.
Возьмем теперь в плоскости ху какую-нибудь кривую (К) и постараемся
определить количество Q жидкости, протекающей через нее в определен-
ную от нее сторону в единицу времени. Предполагая жидкость несжи-
маемой, можно количество жидкости измерять площадью закрытой ею фигуры.
Рис. 16.
Если фактически жидкость течет в сторону, противоположную выбранной, то
количество протекающей жидкости будем считать отрицательным.
Рассмотрим элемент ds = AB кривой (АГ). За время dt через этот элемент
протечет количество жидкости, равное
сп ds dt,	(19)
где сп есть проекция скорости с на нормаль п к,элементу ds, направлен-
ную в выбранную сторону от кривой. Действительно, это коли-
чество равно площади параллелограмма со сторонами ds и с  dt, высотой кото-
рого как раз и является произведение cndt (рис. 16, б). Для подсчета коли-
чества жидкости, протекающей через элемент ds в единицу времени, суммируем
выражения (19) по элементам dt, что дает cnds. Суммируя же найденные вы-
ражения по всем элементам кривой (АГ), мы представим искомое количество Q
жидкости в виде криволинейного интеграла первого типа
Q= j cnds.	(20)
т
Если угол между осью х и нормалью к кривой есть (х, п), то угол между
нормалью и скоростью с будет
(и, с) = (х, с) — (х, п) = ф — (х, п);
поэтому
с„ = с cos (п, с) = с [cos <j> cos (х, п) 4- sin <р sin (х, п)[ — и cos (х, п) v sin (х, п),
и выражение (20) принимает вид
Q = [и cos (х, п) 4- v sin (х, n)J ds.	(21)
554]
§ 2. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ ВТОРОГО ТИПА
43
Теперь, согласно формуле (15) п* 553, этот интеграл можно представить
и в форме криволинейного интеграла второго типа:
Q = vdx— udy,	(22)
(К)
причем важно подчеркнуть, что направление на этой кривой должно быть
взято так, чтобы угол между соответствующим направлением касательной и
выбранным заранее направлением нормали был равен [ибо именно в
этом предположении и выведена была формула (15)].
Если (АГ) есть замкнутый контур и интеграл (22) считать взятым
(как обычно, 548) в положительном направлении, то нормаль в формуле (22)
должна была бы быть направлена внутрь области; ограниченной конту-
ром (К) (чтобы было соблюдено упомянутое только что условие). Следова-
тельно, в этом случае формула (22) дает количество жидкости, протекающей
через контур (А) в единицу времени внутрь области. Если желаем полу-
чить количество жидкости, вытекающей наружу из области, ограниченной
контуром (А), то следует лишь в формуле (22) изменить знак.
Далее, если поле.не имеет ни «источников», ни «стоков» жидкости, то
в любой ограниченной области количество жидкости остается постоянным.
Поэтому, какую бы замкнутую кривую ни взять, интеграл (22), взятый по ней,
должен быть равен нулю.
Итак, если ина суть слагающие скорости в плоском установив-
шемся течении несжимаемой жидкости, то при отсутствии
источников и стоков
v dx — udy —О,
(К)
каков бы ни был замкнутый контур (К).
Впоследствии [566, 2)] мы увидим, что этот результат, полученный с по-
мощью физических соображений, позволяет дать и некоторую аналитическую
характеристику функций и и о.
3) Тепло, поглощенное газом. Рассмотрим некоторую массу, например,
1 моль газа. Состояние газа характеризуется тремя величинами: его объе-
мом V, Давлением р и абсолютной температурой Т. Если считать газ иде-
альным, то эти три величины оказываются связанными между собой урав-
нением Клапейрона:
pV — RT,
где R есть постоянная. Таким образом, любая из величин р, V и Т может
быть выражена через две другие. Поэтому для определения состояния газа
достаточно знать две из этих величин. Пусть это будут, например, V и р.
Тогда т о ч к а с абсциссой V и ординатойр служит изображением состояния
газа. Если состояние газа меняется от начального состояния, отвечающего
точке А, до конечного состояния, определяемого точкой В, то весь про-
цесс изменения характеризуется кривой (A)s(АВ), устанавливающей
последовательность непрерывно меняющихся состояний *.
* И здесь, и впредь мы имеем в виду так называемые к вазистацио-
нарные процессы, т. е. представляем изменение состояния газа происхо-
дящим настолько медленно и сопровождающимся настолько хорошим пере-
мешиванием, что вся масса газа одновременно проходит через всякое
промежуточное состояние.
44 гл. XV. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА {554
Поставим теперь себе задачу установить, какое количество тепла U (кал)
поглощается данной массой газа во время всего этого процесса, характери-
зуемого кривой (АГ). С этой целью, как обычно, рассмотрим некоторый «беско-
нечно малый» элементарный процесс, переводящий газ из состояния (V, р, Т)
в бесконечно близкое состояние (VdV, рdp, Т-[- dT). Ему отвечает
элемент кривой (АГ) (рис. 17). Определение того элементарного количества
тепла dU, которое при этом ему было сообщено, мы однажды уже произвели
[при выводе формулы Пуассона, 361, 3)]. Воспользуемся полученным там
выражением:
dU=^Vdp+^-p dV.
Для того чтобы найти общее количество тепла U, сообщенное газу в те-
чение всего процесса его изменения, характеризуемого кривой (АГ), остается
лишь «просуммировать» Элементы dU
вдоль этой кривой:
('*)
^Vdp + ^pdV.
(23)
Итак, количество тепла U непо-
средственно выражается криволиней-
ным интегралом второго типа.
Если бы мы выражали элементар-
ное приращение тепла dUне через dV
и dp, а через d¥n dT, или через dp и dT,
то и тогда дело свелось бы к криволи-
нейному интегралу,‘который, однако,
пришлось бы брать по кривой, л ежащей,
соответственно,в плоскости VTили рТ.
4) Действие тока на магнит. Закон Био и Савара, характеризую-
щий действие тока на магнит, имеет «дифференциальную» форму. Согласно
этому закону, элемент ds проводника, по которому идет ток силы I, дей-
ствует на отстоящую от него на расстояние г «магнитную массу» т с силой,
величина которой равна
Im sin w ds
----> <24)
У=
где <р (0 < <р < я) есть угол между вектором г, соединяющим магнитный по-
люс с элементом тока, и направленным в сторону течения тока
элементом ds проводника. Направление же этой элементарной силы перпенди-
кулярно к плоскости, определяемой векторами г и ~ds, и идет в ту сторону,
с которой вращение от г к ds на угол <р кажется происходящим против
часовой стрелки. [Ср. 356, 8).]
Поставим себе задачей охарактеризовать магнитное поле тока,
идущего по конечному замкнутому проводнику (Д) произвольной формы и
произвольно расположенному в пространстве; иными словами, установить силу,
с которой весь этот проводник в целом действует на «магнитную массу» т,
помещенную в любой точке М пространства. Получение закона Био и С а-
в а р а в «интегральной» форме затрудняется, однако, тем обстоятельством,
что отдельные элементарные силы, о которых была речь выше, по-разному
направлены и складывать их надо геометрически.
В подобном случае обычно переходят, к проекциям векторов на оси какой-
либо прямоугольной системы координат в пространстве, ибо проекции эле-
ментарных сил складываются уже алгебраически,
5551	§ 3. УСЛОВИЯ НЕЗАВИСИМОСТИ ИНТЕГРАЛА ОТ ПУТИ	45
Для упрощения выкладок используем аппарат векторной алгебры. Если
переписать выражение (24) для величины элементарной силы dF в виде
ml . .
р- • г ds sin<p,
ml
то легко заметить, что оно лишь множителем отличается от величины
векторного произведения г X ds. Так как и направление dF, опре-
деляемое законом Био и Савара, совпадает с направлением этого произ-
ведения, то можно написать
-гл ml <—* у,
d/? = p-(r X ds)-
Рассмотрим теперь произвольную (правую) прямоугольную координатную
систему Oxyz. Если через х, у, г обозначить координаты (начальной точки)
элемента ds, а через £, т;, С— координаты рассматриваемой точки М про-
странства, то проекциями вектора г на оси будут
х — 5, у—ц, z — С;
вектор же ds имеет проекции
dx, dy, dz.
В таком случае проекциями dF будут произведения множителя соответ-
ственно, на
(у —dz — (z — С) dy, (z — C)dx — (x —$) dz,
(x—5) dy — (y — i]) dx.
Таким образом, суммируя по всем элементам кривой (Д'), окончательно
получим выражения для проекций искомой силы F на оси в виде криволи-
нейных интегралов по пространственной кривой (/<):
Fx==w/ C(j>-^)dz-(z-O^
**	Ч	г
W
Fy — ml
(
(х — 0 dy — (у — т;) dx
F	»
. )
причем направление на кривой определяется направлением течения тока.
Это и дает решение нашей задачи.
§ 3. Условия независимости криволинейного интеграла
от пути
555.	Постановка задачи, связь с вопросом о точном диффе-
ренциале. Пусть в некоторой связной области (D) заданы две не-
прерывные функции
Р=Р(х, у) и Q—Q(x, у).
(z — i)dx—(х—t) dz
rs
46
ГЛ. XV. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА 1556
Рассмотрим криволинейный интеграл второго типа
\Pdx-\-Qdy.	(1)
(АВ)
Здесь А и В — какие-нибудь две точки из области (D), a (AS)—
произвольная соединяющая их кусочно-гладкая * кривая, которая це-
ликом лежит в этой области.
Основная задача настоящего параграфа состоит в выяснении ус-
ловий, при которых величина этого интеграла оказывается не
зависящей от формы пути (АВ), т. е. однозначно определяется
начальной и конечной точками А и В, где бы эти точки не лежали.
Поведение интеграла (1) определяется свойствами дифференциаль-
ного выражения
Pdx-VQdy,	(2)
стоящего под знаком интеграла. Напомним, что мы уже имели дело
с подобного рода выражением, когда речь шла о дифференци-
руемой функции F (х, у) от двух переменных и о (полном)
дифференциале ее [179]
dF = 4r dx-}-~ dy,	(3)
дх 1 ду	'
которое отождествляется с выражением (2) при
Однако далеко не каждое выражение вида (2) есть «точный диф-
ференциал», т. е. не для каждого такого выражения существует
«первообразная функция» F (х, у), для которой это выражение слу-
жит (полным) дифференциалом. И вот оказывается, что интеграл (1)
не зависит от пути именно в тех случаях, когда его подинтеграль-
ное выражение есть точный дифференциал! Сформулируем это фун-
даментальной важности утверждение в виде теоремы, доказательству
которой будут посвящены ближайшие два пп°:
Теорема 1. Для того чтобы криволинейный интеграл (1) не
зависел от формы пути интегрирования, необходимо и доста-
точно, чтобы дифференциальное выражение (2) было в рассмат-
риваемой области дифференциалом от некоторой (однозначной **)
функции двух переменных.
556.	Дифференцирование интеграла, не зависящего от пути.
Допустим сначала, что интеграл (1) не зависит от пути.
* Мы ограничимся в этом параграфе рассмотрением только таких путей
интегрирования; этим заведомо обеспечивается существование интеграла (1).
** Читателю впоследствии [562] станет ясной необходимость подчерки-
вания однозначности первообразной функции.
556]	$ 3. УСЛОВИЯ НЕЗАВИСИМОСТИ ИНТЕГРАЛА ОТ ПУТИ
47
В этом случае интеграл однозначно определяется заданием точек
Л(х0,_у0) и В(хьу^, в связи с чем его обозначают символом
В	(Xi, >i)
Pdx-]-Qdy или § Pdx-]-Qdy.
А	(х0, Vo)
Здесь указаны только начало и конец пути интегрирования; сам
путь не указан, но он безразличен — можно интегрировать
по любому, конечно, без сделанного предположения о независимости
от пути такое обозначение не имело бы определенного смысла.
Если точку А(х0,ул) фиксировать, а точку В заменить произ-
точкой М(х,у) области (D), то полученный интеграл пред-
вольной
ставит собой некоторую функ-
цию от т о ч к и М, т. е. от ее
координат х, у; в области (D):
. 	(х, У)
F(x,y)= Pdx-]-Qdy. (4)
(хо, J>o)
Займемся теперь вопросом об
ее частных производных как
по х, так и по _у.
Взяв произвольную точку
в области (£)), при-
дадим Xi приращение Дх и
перейдем к точке С (xt -|- Дх, у]), которая при достаточно малом Дх
будет также принадлежать (D) вместе со всем отрезком ВС
(рис. 18). Соответствующие значения функции будут
(xi, У1)
Р(Х1,У1)= $ Pdx-]-Qdy,
(*о. То)
(•*1 + Ьх, yt)
F(Xj + Дх,_У1)=	Pdx-]-Qdy.
(*о, З’о)
Первый из этих интегралов мы возьмем по произвольной кри-
вой (К), соединяющей точки Л и В, а для второго интеграла путь
интегрирования составим из этой же кривой (К) и из прямолиней-
ного отрезка ВС. Таким образом, приращение функции F будет
F(Xi4-Дх,>1) — /7(х1,_У1)= $ Pdx-]-Qdy = § P(x,y)dx',
(ВС)	(ВС)
интеграл, содержащий Qdy, обращается в нуль, так как отрезок ВС
перпендикулярен к оси у.
48
ГЛ. XV. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА (556
Оставшийся интеграл непосредственно приводится к обыкновен-
ному определенному интегралу: для этого в подинтегральной функ-
ции нужно заменить у на ух (из уравнения у=У\ прямой ВС) и
в качестве пределов интегрирования по х взять абсциссы точек В
и С. Окончательно
Xi + Дх
A(xi4-Дх, —F(x1,y1) = (R) P(x,y\)dx.
Применяя к полученному обыкновенному интегралу теорему о сред-
нем и деля обе части равенства на Дх, найдем
+	р	0 д х, у	(о 0	1).
Устремим теперь Дх к нулю. В силу непрерывности функции
Р(х,у), правая часть равенства, а с нею и левая, стремится к Р(хьУ1).
Следовательно, в точке (xb yi) частная производная функция F по х
существует и выражается равенством
^Ь) = Р(х1,_У1).
Аналогично устанавливается и формула
Так как точка (Xi,yi) была взята произвольно внутри области (£)),
то для всех точек этой области будем иметь
dF (х, у) п, ч dF(x, у)	.
-^ = Р(Х,У), —^-; = Q(x,y).
Поскольку эти частные производные непрерывны, функция F(x,y)
имеет дифференциал’.
dF—^dx4-d~dy = Pdx4-Qdy,
совпадающий с подинтегральным выражением для интеграла
(1) [179]*
Таким образом, для криволинейного интеграла, не зависящего
от пути, нам удалось установить результат, вполне аналогичный
теореме о дифференцировании обыкновенного определенного инте-
грала по переменному верхнему пределу [305, 12°].
Вместе с тем доказана необходимость условия, сформули-
рованного в теореме предыдущего п°. Если интеграл (1) не
* Отсюда, между прочим, вытекает и непрерывность самой функ-
ции F(x, у) по обеим переменным.
557]	§ 3. УСЛОВИЯ НЕЗАВИСИМОСТИ ИНТЕГРАЛА ОТ ПУТИ	49
зависит от пути, то выражение (2) действительно
будет точным дифференциалом: сам интеграл (4) при сде-
ланном предположении и дает нам однозначную первообразную функ-
цию для подинтегрального выражения!
557.	Вычисление криволинейного интеграла через первооб-
разную. Предположим теперь, обратно, что выражение (2)
представляет собой (полный) дифференциал от не-
которой однозначной функции Ф(х,_у), так что
Рассмотрим какую-нибудь кусочно-гладкую кривую (К), соединяю-
щую две данные точки: А с координатами хА, уА и В с координа-
тами хв, ув. Пусть параметрическое представление ее будет
и при изменении параметра от а до р кривая описывается в направ-
лении от А к В. Таким образом,
?(а) = хл, ф(а) = ул; ?(р) = хв> ф(Р)=_ув.
Вычисляя теперь криволинейный интеграл вдоль кривой (/С) путем
сведения его к обыкновенному интегралу [по формуле (6) п° 547],
получим
I= \ Pdx-\-Qdy —
(ю	₽
= И р (О, Ф (0) (0 + Q (0> Ф (0) Ф' (0} dt
а
или, принимая во внимание (5),
₽	₽
1= J Ш + g ¥(t)}dt= 5 ^Ф(?(0- Ф(0)Л
а	а
•— по правилу дифференцирования сложной функции.
Окончательно
7 == Ф (? (t), ф (0) | = Ф (? (?), ф (?)) - Ф (т (а), ф (а)) =
= Ф (хв, ув)	Ф (хА, _Уд).
Итак, при наличии первообразной функции
Ф(7И)==Ф(Х, у)
50 гл. XV. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА (558
криволинейный интеграл вычисляется по простой формуле:
5 Pdx-{- Qdy = $(xB, ув) — Ф(хА, УА) =
(АВ)
<хв, YB)
(ХА, *А)
(6)
= Ф(х,у)
или, короче,
5 Pdx+Qfl!y = ®(5) — ф(Д) = ф(Л1)|д.	(6*)
(АВ)
Эта формула вполне аналогична основной формуле интегрального
исчисления [308], выражающей обыкновенный определенный инте-
грал через первообразную. Подчеркнем, однако, еще раз, что она
приложима только к таким интегралам, для которых подинтегральное
выражение есть точный дифференциал.
Одновременно эта формула показывает, что в рассматривае-
мом случае интеграл (1) не зависит от выбора кри-
вой АВ *, чем устанавливается и достаточность условия, ука-
занного в теореме п° 555. Таким образом, эта теорема теперь пол-
ностью доказана.
558. Признак точного дифференциала и нахождение перво-
образной в случае прямоугольной области. Теперь естественно
возникает вопрос о том, по какому признаку можно установить,
является ли предложенное дифференциальное выражение (2) точ-
ным дифференциалом или нет. Ответ на этот вопрос позволит окон-
чательно выяснить и условия независимости криволинейного инте-
грала от пути.
Для того чтобы получить признак в простой и удобной для про-
верки форме, мы впредь будем дополнительно предполагать, что
в рассматриваемой области (О) существуют и не-
л	'	дР dQ
прерывны обе частные производные и
При этом предположении искомый признак получается сразу.
Если выражение (2) есть дифференциал некоторой функции ф(х,_у),
так что имеют место равенства (5):
дх' ч~ду ’
то
дР__ д2Ф dQ _ д*Ф
ду дхду’ дх дудх'
* Ибо, именно ввиду однозначности функции Ф, ее значения Ф (Л)
и Ф (В) вполне определяются заданием точек А и В.
558]	§ 3. УСЛОВИЯ НЕЗАВИСИМОСТИ ИНТЕГРАЛА ОТ ПУТИ
5
Предположенная непрерывность частных производных
дР
dQ
дх
и
обеспечивает равенство двух смешанных производных [190],
вательно,
df dQ
ду дх'
следо
(а:
Таким образом, это замечательное по простоте соотношение ока-
зывается необходимым условием для того, чтобы выражение (У
было точным дифференциалом.
Обращаясь к исследованию достаточности условия (А), мь
ограничимся сначала случаем, когда область (D) представляет собой
прямоугольник; пусть, для определенности, это будет конечный
замкнутый прямоугольник [а, Ь; с, </]. В предположении, что выпол-
няется условие (А), мы непосредственно дадим для этого случаг
построение первообразной.
Задача состоит в том, чтобы определить в прямоугольнике (а, b
с, dj функцию Ф(х,у), которая удовлетворяла бы двум уравнениям
д£=р(*.у)>	(б*:
Действительно, ввиду непрерывности функций Р и Q отсюда уже
следовало бы, что выражение (2) является для упомянутой функции
полным дифференциалом [179].
' Взяв любые значения х0 и х в [а, Ь], проинтегрируем первое иг
уравнений (5*) по х от х0 до х при любом фиксированном значении у
из [с, d]; мы найдем
Ф (х, у) = \р (х, yydx-уФ (х0, у)-
хо
Если теперь во втором из уравнений (5*) положить х = хв и про-
интегрировать его по у между любыми значениями _у0 и у из [с, d]
то получится, что
У
ф (*о> У) — $ Q (Хй, у) dy-уф (х0, у о).
Таким образом, искомая функция Ф(х,у) необходимо имеет вид
•»	У
ф(*> y) = \P(x, y)dx + \Q(x9, y)dy-yc, (7
Хо	у»
где С=Ф (х0, _ye) = const.
Остается теперь проверить, что функция, определяемая формулой (7
(какова бы ни была постоянная С), в действительности удовлетворяет
52 ГЛ. XV. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА (559
обоим уравнениям (5*). Относительно первого это очевидно, ибо
производная по х первого слагаемого в (7) справа равна Р(х, у)
[305], а последние два слагаемых не зависят от х. Продифференци-
руем теперь равенство (7) по у, причем к первому интегралу справа
применим правило Лейбница [507]:
дФ С дР , . „,	.
57= J ^dx^^x.,y\
*о
В силу (А), вместо можно сюда подставить тогда
сведется к разности Q(x, у) — Q(xg, у), а производная
жется равной просто Q(x, у), что и требовалось доказать.
интеграл
дФ
57 ока-
Заметим, что если бы мы начали с интегрирования по у, то при-
шли бы к такому выражению для искомой первообразной:
X	у
^(х, у) = \Р(х, yg)dx-\-\d(x, y)dy-\-C,	(8)
хц	Уо
лишь по форме отличающемуся от прежнего.
Полезно дать себе отчет в том, что, фиксируя значение перво-
образной в какой-нибудь точке области, мы тем самым выбираем по-
стоянную в общем выражении первообразной и получаем уже вполне
определенную и однозначную первообразную.
559.	Обобщение на случай произвольной области. Рассмотрим
теперь произвольную (конечно, связную) область (£>), ограниченную
одной или несколькими кусочно-гладкими кривыми и при этом конеч-
ную или простирающуюся в бесконечность. Эту область мы впредь
будем предполагать открытой. В таком случае каждая ее точка
является внутренней [163] и принадлежит ей вместе с некоторой, ска-
жем, прямоугольной окрестностью. Так как к последней прило-
жимы рассуждения предыдущего п°, то при выполнении усло-
вия (А) в окрестности каждой точки области (£)) для
выражения (2) существует первообразная и даже беско-
нечное множество первообразных, разнящихся одна от другой на по-
стоянную. Однако согласование всех этих первообразных так, чтобы
получилась однозначная первообразная для всей области (£)),
оказывается не всегда возможным! Вопрос здесь зависит от характера
самой области.
Чтобы обеспечить существование такой однозначной перво-
образной в общем случае, приходится наложить на область (£)) свое-
образное ограничение. Его можно сформулировать так: какой бы про-
стой замкнутый контур, лежащий в области (D), ни взять, огра-
ниченная извне этим контуром область должна также целиком
принадлежать области (D). Иными словами, область не должна со-
559]
§ 8. УСЛОВИЯ НЕЗАВИСИМОСТИ ИНТЕГРАЛА ОТ ПУТИ
53
держать «дырок», даже точечных. Связную область, обладающую этим
свойством, называют односвязной.
Если речь идет о конечной области (т. е. не простирающейся
в бесконечность), то понятие односвязности можно сформулировать
еще проще: область должна быть ограничена единственным
замкнутым контуром. На рис. 19 представлены примеры одно-
связных и неодносвязных областей, из них а), г), д) конечны, а б),
в), е) простираются в бесконечность.
Пусть же рассматриваемая область (£)) будет односвязной;
сначала мы предположим ее конечной, так что она попросту ограни-
чена единственной кусочно-гладкой кривой (/С). Построение перво-
образной для области (О) мы будем производить постепенно, исходя
из содержащихся в (О) областей, разлагающихся на прямо-
угольники.
Задавшись произвольно малым числом е^>0, мы можем каждую
точку М контура (/С) окружить таким квадратом со стороной
<^е, чтобы в его пределах контур выражался явным уравнением
одного из двух типов [ср. 223]; лишь в угловой точке мы будем
иметь стык двух подобных кривых.
По лемме Боре ля [175], можно, сохранив лишь конечное число
этих квадратов, покрыть ими весь контур (К). Этой конечной цепью
квадратов извне ограничивается некоторая замкнутая область (D),
целиком лежащая в (D) и очевидным образом разлагающаяся на пря-
моугольники. Она будет связной *, а тогда уже и односвязной вместе
с (D); ей заведомо будут принадлежать все точки области (D),
отстоящие от контура на расстояние е.
* Если две точки Мо и М, принадлежат (D), то их можно соединить ло-
маной (I), целиком лежащей в (D) [163]. Эта ломаная, вообще говоря, может
и выходить за пределы (Д), попадая внутрь каких-либо из упомянутых в тек-
сте квадратов. Но часть ломаной, содержащаяся в таком квадрате, всегда мо-
жет быть заменена соответствующей частью его обвода. Таким путем и полу-
чается соединяющая точки Л10 и ломаная (£), целиком лежащая в ф).
54 ГЛ. XV. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА [559
Мы покажем ниже, как строится первообразная для области (£)).
Чтобы иметь дело с определенной первообразной, мы фиксируем ее
значение в какой-нибудь точке 7И0, принадлежащей (D). Заметим,
что две первообразные, определенные для двух налегающих одна
на другую областей, в общей их части могут разниться лишь
на постоянную (так как их разность имеет нулевые частные произ-
водные, 183). Следовательно, если эти первообразные совпадают хоть
в одной точке, они тождественны во всей упомянутой общей части.
Отсюда ясно, что, устремляя е к нулю, мы, действительно, постепенно
распространим определение первообразной на всю область (О) с со-
хранением ее однозначности.
Чтобы построить первообразную для области (О), мы представим
себе эту область разложенной на прямоугольники, которые примы-
таких смежных прямоугольника d^ и rf2 изображены на рис. 20, б.
В каждом из них мы умеем строить первообразные, пусть это будут
Ф1 и Ф2. Вдоль отрезка оф, общего прямоугольникам dv и rf2, они
могут разниться лишь на постоянную; это становится ясным, если
вспомнить, что каждая из них разнится вдоль оф разве лишь посто-
янным слагаемым от какой-либо первообразной, построенной для за-
штрихованного прямоугольника, которая существует в силу предыду-
щего п°. Изменяя одну из первообразных, Ф1 или Ф2, на надлежащую
постоянную, можно, следовательно, добиться их совпадения вдоль
отрезка а^.
Начнем с построения первообразной для того из прямоугольни-
ков, где лежит точка 7И0, причем озаботимся, чтобы в этой точке
первообразная имела именно наперед фиксированное значение. Затем
построим первообразные для примыкающих к нему прямоугольников,
так, чтобы переход через их общие границы не нарушал непрерыв-
ности, и т. д.
Постараемся теперь уяснить себе, в чем же сказывается усло-
вие односвязности области (D), а с нею и ф). Ряд прямоуголь-
ников на рис. 20, а при замысловатости контура (К) может и р а з-
560]	§ 3. УСЛОВИЯ НЕЗАВИСИМОСТИ ИНТЕГРАЛА ОТ ПУТИ
55
ветвиться, как на рис. 21, а: это не помешает непрерывному
распространению первообразной вдоль отделенных друг от друга
отрогов. Но если область имеет «дырку» (см. рис. 21, б) и два
ответвления вновь смыкаются, то для первого замыкающего пря-
моугольника выбор первообразной с сохранением непрерывности
перехода на обоих стыках оф и 78 сразу — может оказаться не-
возможным!
Случай области (D), простирающейся в бесконечность, исчерпы-
вается аналогично, исходя из конечных подобластей, с постепенным
распространением первообразной на всю область (D).
560.	Окончательные результаты. Все сказанное в двух предше-
ствующих пп° может быть суммировано в виде следующего предло-
жения:
Теорема 2. Для того чтобы во всей области (В) выраже-
ние (2) было дифференциалом от некоторой однозначной функ-
ции двух переменных, необходимо, а в предположении одно-
связности области (D) и достаточно, выполнение условия (А).
В. связи с этим условие (А) часто называют «условием интегри-
руемости» выражения (2).
Если вспомнить теперь теорему 1, то непосредственно получается
и следующая заключительная
Теорема 3. Для того чтобы криволинейный интеграл (1), где бы
в области (D) ни были взяты начальная и конечная точки А и В
пути интегрирования, не зависел от формы этого пути, необхо-
димо, а в предположении односвязности области
(D) и достаточно, выполнение условия (А).
Таким образом, мы нашли, наконец, в условии (А) удобный и легко
проверяемый критерий независимости криволинейного интеграла от пути
С помощью этого критерия, например, легко расклассифицировать инте-
гралы, предложенные в задачах 3), 4), 5), 6) п° 549, и предвидеть из
особенности, указанные в замечании.
Ниже мы встретим важные приложения полученных результатов
К особенностям случая неодносвязной области мы вернемся в п° 562
56 гл. XV. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА 1561
561.	Интегралы по замкнутому контуру. До сих пор мы рас-
сматривали криволинейный интеграл (1)
Pdx-^Qdy
(АВ)
и изучали тот важный класс случаев, когда этот интеграл не зависит
от пути интегрирования. Обратимся теперь к рассмотрению интеграла
§ Р dx -f- Q dy,
(L)
(9)
взятого по любому простому замкнутому контуру (Z.) в пределах
области (О), и поставим вопрос об условиях, при которых
этот интеграл всегда
обращается в нуль. Оказы-
вается, что этот вопрос совершен-
но эквивалентен вопросу, решен-
ному выше: если при данном диф-
ференциальном выражении (2) ин-
теграл (1) не зависит от пути, то
интеграл (9) всегда равен нулю,
и обратно.
Действительно, предположим
сначала независимость интегра-
ла (1) от пути. Если (Z.) есть лю-
бой простой замкнутый контур
в области (£)) (рис. 22), то произвольно взятыми на нем точками
А и В разложим его на части {АМВ) и (АДЩ). Так как интегралы
по этим кривым должны быть равны:
(АМВ) (ANB)
то отсюда
(2.) (AMB) (BNA) (АМВ) (ANB)
(10)
(11)
Пусть теперь, обратно, дано, что интеграл (9) по простому замк-
нутому контуру всегда равен нулю. Взяв две точки А и В, соединим
их двумя путями {АМВ) и (ДДЩ); из них составится замкнутый контур
{L)={AMBNA). 
Легким будет случай, когда линии {АМВ) и {ANВ), кроме то-
чек А и В, общих точек не имеют; тогда контур (Z.) сам себя
не пересекает, т. е. оказывается простым.
Если же кривые {АМВ) и {ANB) взаимно пересекаются, то замк-
нутая кривая {L) уже не будет простой.
562]	§ 3. УСЛОВИЯ НЕЗАВИСИМОСТИ ИНТЕГРАЛА ОТ ПУТИ	57
Однако, как показывает следующая лемма, можно все же огра-
ничиться рассмотрением интегралов по п р о с т ы м (т. е. не пересека-
ющим себя) замкнутым контурам.
Лемма. Если интеграл (9) равен нулю, по какому бы просто-
му (т. е. не пересекающему себя) замкнутому контуру его ни
взять, то он будет нулем и при всяком замкнутом контуре,
хотя бы и самопересекающемся.
В силу леммы, установленной в п° 550, достаточно доказать это
утверждение для любой замкнутой ломаной, хотя бы и самопере-
секающейся. Пусть (Z.) и будет такая ломаная, определенным обра-
зом направленная. Исходя из некоторой ее точки Л1о и следуя на-
правлению ломаной, опишем часть ломаной до первого самопе-
ресечения—в точке Mi. Отбросив получившуюся замкнутую ломаную
(Lt), продолжим путь /И07И1 до нового самопересечения, что позволит
выделить еще одну замкнутую ломаную (Z.9), и т. д. После конечно-
го числа шагов ломаная (L) окажется распавшейся на конечное число
не пересекающих себя замкнутых ломаных
(Lt), (L& ...,
вдоль по которым интеграл заведомо нуль. Значит, он равен нулю
и вдоль ломаной (L), что и требовалось доказать.
Таким образом, нами доказана полезная
Теорема 4. Для того чтобы криволинейный интеграл (1) не
зависел от пути, необходимо и достаточно, чтобы интеграл, (9)
ио любому замкнутому контуру был равен нулю. При этом
условие остается достаточным и в том случае, если ограничиться
лишь простыми (т. е. не пересекающими себя) замкнутыми кон-
турами.
Теперь ясно, что об обращении в нуль интеграла (9) по замкну-
тому пути можно судить с помощью того же критерия, который в
теореме 3 был установлен для независимости интеграла (1) от пути:
Теорема 5. Для того чтобы интеграл (9), по какому бы
замкнутому контуру в пределах области (D) его ни взять, обра-
щался в нуль, необходимо, а в с лу чае односвязности об-
ласти (D) и достаточно выполнение условия (А). Это условие
остается необходимым и в том случае, если ограничиться лишь
простыми (т. е. не пересекающими себя) замкнутыми контурами.
Ниже [601], располагая более развитым аппаратом (двойные инте-
гралы, формула Грина), мы вернемся к вопросам, рассмотренным в
настоящем параграфе, и некоторые из установленных здесь резуль-
татов получим вновь и притом более экономным образом.
562.	Случай неодносвязной области или наличия особых точек.
Вся теория, развитая в настоящем параграфе и связанная с использова-
нием условия интегрируемости (А), основана на предположении, что
1) рассматриваемая область (О) одно связна, т. е. лишена «дырок»,
58
ГЛ. XV. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА (562
и 2) функции Р и Q вместе со своими производными ~ и в области
(D) непрерывны. Если эти условия нарушены, то высказанные
выше утверждения, вообще говоря, перестают быть верными. Разобрать-
ся в представляющихся при этом особенностях и составляет цель этого п°.
Отметим, что «особые» точки, в которых нарушены условия не-
прерывности 2), тоже могут трактоваться, если их выключить из области,
как своего рода точечные «дырки». Таким образом, вопрос сводится
к рассмотрению области (D), в которой выполнены все тре-
бования непрерывности и условие (А), но зато имеется
одна или несколько «дырок», точечных или нет. Впрочем, для
Рис. 23.
нулю. Если же точка М
может оказаться и отлич
определенности в дальнейшем изложении мы предпочтем ограни-
читься именно случаем точечных «дырок», т. е. особых точек.
Общий случай трактуется совершенно ана-
логично.
Предположим сначала, что область (О)
содержит одну особую точку М (но не
имеет других «дырок»). Возьмем в этой
области простой замкнутый контур (Z.) и
рассмотрим интеграл (9)
5 Pdx-{- Qdy.
(i)
Если этот контур не охватывает особой
точки, то интеграл по-прежнему равен
лежит внутри контура (L), то интеграл
ным от нуля.
Весьма замечательно, однако, что все интегралы, взятые в по-
ложительном направлении [548] по всевозможным контурам ука-
занного типа, окружающим точку М, равны между собой.
В самом деле, рассмотрим два кусочно^гладких контура и (Z.2),
окружающих точку М. Можно считать их взаимно не пересекающи-
мися, ибо в противном случае мы ввели бы третий контур (Д3), охва-
тывающий оба контура (Z.j), (Z,2) и не пересекающий их, и рассмотрели
бы отдельно пары контуров (Zj), (Z,3) и (А2), (L3).
Кривые (Lt) и (Z,2) вместе составляют контур кольцеобразной
области (Д), заключенной между ними (рис. 23). С помощью двух
разрезов (AiA2) и (В^В^ разобьем эту область на две уже односвяз-
ные части (Д') и (Д"). Тогда мы имеем право писать:
$ + S + $ + S —0
(Ax^Bi) (BtB2)	(A2AD
И
J + $ + $ + $ =0.
(Bi.Ni.A0 (AxAa) (AaATaBa) (BsBl)
562]	§ 3. УСЛОВИЯ НЕЗАВИСИМОСТИ ИНТЕГРАЛА ОТ ПУТИ	59
При складывании интегралы, взятые по разрезам в противоположных
направлениях, взаимно уничтожатся, и мы получим
j 4~ J —
откуда, наконец,
5 = S или $ = $ >
(А1М1В1АГ1А1) (AsMzBsNsAz) (Lt) (i2)
причем последние интегралы берутся оба в положительном напра-
влении. Наше утверждение доказано.
Обозначим общее значение всех подобных интегралов через а; его
называют циклической постоянной, отвечающей особой точке М *.
Покажем теперь, что если (L) — любой замкнутый контур в
области (О), хотя бы и пересекающий себя, но не проходящий через
особую точку М, то
Pdx + Qdy = па,	(12)
где п есть целое число (положительное, отрицательное или нуль).
Это очевидно для многоугольного контура, так как он распадается
на конечное число не пересекающих себя замкнутых многоугольных
контуров, вдоль каждого из которых интеграл равен нулю или
if: а. В общем же случае мы снова воспользуемся леммой, установ-
ленной в п° 550 (и замечанием к ней) и прибегнем к предельному пере-
ходу, исходя из вписанной в кривую ломаной. Так как выражение
вида па (при а 0 и целом и) может стремиться к конечному пре-
делу лишь того же вида (с тем, что число п в конце концов пере-
стает изменяться), то формула (12) оказывается верной для любого
контура (Т).
Перейдем теперь к рассмотрению интеграла по кривой, соеди-
няющей точки А(ха, у о) и B(xlt _у() области (D), но не проходящей
через особую точку. Если (АВ)а есть одна из таких кривых, а (АВ)—
любая другая, то (АВ) и (ВА)а вместе составят замкнутый контур,
так что, в силу (12),
Pdx-}- Qdy Pdx A- Qdy— па,
(AB)	(BA)V
откуда
Pdx-}-Qdy= J Pdx -|- Qdy -}- na.
(AB)	(AB)0
* Совершенно так же определяется и циклическая постоянная, отвечающая
настоящей — неточечной — «дырке».
60
ГЛ. XV. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА [562
Здесь интеграл реально зависит от пути инте-
грирования, но лишь в смысле прибавления целого кратного
циклической постоянной а. Присоединяя к кривой (АВ)й то или иное
число петель, окружающих точку М (рис. 24), можно добиться
того, чтобы множитель п принял любое наперед выбранное целое
значение.
Иными словами, в рассматриваемом случае символ
(•ч.л)
Р dx —Q dy =	Р dx —Q dy
(АВ)	(х0, >о)
при заданных А и В уже не является (если о уЬ 0) однозначным; он
определен с точностью до слагаемого вида па, где л = 0, ± 1, ±2, ...
Если точку В заменить пе-
ременной точкой М (х, у), то
интеграл
(X, у)
F(x,y) = Pdx-^-Qdy
(Х0. _Уо)
по-прежнему представит
первообразную функцию
для выраженияPdx A-Q dy,не-
прерывную (исключая, конечно,
точку М), но многозначную.
Важно дать себе отчет в существенном отличии рассматриваемого
случая от изученного выше [556, 558, 559J. И там можно было бы
говорить о «многозначности» первообразной, поскольку последняя со-
держала в своем выражении произвольную постоянную. Однако
стоило лишь фиксировать эту постоянную, чтобы получить одно-
значную функцию во всей рассматриваемой области; никакой при-
нудительной связи между отдельными «ветвями» многозначной перво-
образной там не было. Здесь же «ветви», разнящиеся на крат-
ное циклической постоянной, уже нельзя рассматривать
обособленно, ибо при вращении вокруг особой точки они непре-
рывным образом переходят одна в другую *.
Для иллюстрации всего изложенного здесь в качестве примера
положим
Р
ст-
,2-
Эти функции с их производными непрерывны во всей плоскости
за исключением начала координат 0(0, 0), которое, таким образом,
* С подобным обстоятельством мы имеем дело в случае многозначных
функций комплексной переменной [ср., например, 458]; нетрудно усмотреть,
что и то, и другое связано со свойствами плоскости.
562]	§ 3. УСЛОВИЯ НЕЗАВИСИМОСТИ ИНТЕГРАЛА ОТ ПУТИ	61
является единственной особой точкой. Непосредственно проверяется,
что условие интегрируемости везде (разумеется, кроме начала коор-
динат) выполнено:
дР _dQ ys~xs
ду дх (х2 -фу2)2 ‘
Легко вычислить, что интеграл
С х dy—у dx
J Xs + у2 ’
(I.)
взятый в положительном направлении по любой окружности с цент-
ром в начале, равен 2z. Такова здесь циклическая постоянная, отве-
чающая начальной точке.
Первообразная для дифференциального выражения
х dy —у dx
х2 -фу2
легко угадывается: это — полярный угол 0, в чем легко убедиться,
если подставить сюда x = rcosO, = г sin 0. Следовательно, общий
вид первообразной будет 0-ф-С (С= const). Однако с каким бы зна-
чением полярного угла 0 мы не исходили в данной точке плоскости,
отличной от начала, если заставить точку сделать л оборотов во-
круг начала в ту или другую сторону, угол 0, непрерывно из-
меняясь, получит при возвращении точки в исходное положение
приращение ± 2 пт, кратное циклической постоянной. Таким образом,
если рассматривать здесь первообразную во всей плоскости или в ее
части, содержащей внутри начало координат (конечно,
само начало исключается), то приходится считаться с многозначностью,
как с неотъемлемым ее свойством: ветви ее, разнящиеся на целое
кратное 2z, в известном смысле неотделимы.
Изложенное исследование читатель без труда распространит и на
случай, когда налицо несколько особых точек или «дырок». Пусть,
например, имеется k особых точек
7И1,	..., Mk.
Если А и В — две (отличные от особых) точки области и через
(А2?)о обозначена какая-либо определенная кривая, соединяющая
эти точки (и не проходящая через особые точки), то общая форма
интеграла по любой подобной же кривой (АВ) будет
Рdx —|— Qdy —	Рdx —|— Qdy —|— n^ci —J— zzgCg—...
(AB)		(AB)0
Здесь	(i = l, 2, k) есть циклическая постоянная, отвечающая
62
ГЛ. XV. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА [563
особой точке Mt, т. е. величина интеграла
\ PdxQdy,
(^)
взятого в положительном направлении по простому замкнутому кон-
туру (Z.(), содержащему внутри себя особую точку и не содер-
жащему других особых точек. Коэффициенты пь п* ..., nk незави-
симо друг от друга могут принимать
„1	любые целые значения.
/	(г)	563. Интеграл Гаусса. В некоторых
‘вопросах математической физики прихо-
\	дится рассматривать криволинейный ин-
теграл первого типа:
г/'МЩР	g== С cos (г, n)rf„,
связываемый с именем Г а у с с а. Здесь
д------------------—	через г обозначена длина
Рис. 25.	г = Г(^-5)2 + (у-^
вектора, соединяющего внешнюю точку
А (;, rt) с переменной точкой М (х, у)
кривой (L) (рис. 25), через (г, п) — угол между этим вектором и нормалью к
кривой в точке М.
.	cos (г, п)
Так как точка А неизменна, то подинтегральное выражение ——-
представляет собой функцию от координат х, у точки М. Представим интеграл
Гаусса в форме криволинейного интеграла второго типа. Если (х, п) и
(х, г) суть углы между положительным направлением оси х и направлениями
радиуса-вектора и нормали, то, очевидно,
(г, п) = (х, п) — (х, г),
так что
cos (г, п) — cos (х, n) cos (х, г) 4* sin (х, n) sin (х, г) =
х— 5	,	\ । У — Ч • /
== —~ COS (х, П) 4- —sin (х, я).
Подставляя это в интеграл Г а у с с а, приведем его к виду
g = \ ртг5 sin + “7^ cos ”)] ds-
(I)
Если же воспользоваться формулой (15) п° 353, то и получим искомое выраже-
ние интеграла g в виде криволинейного интеграла второго типа:
С у — ч . х — $
£= ±	dx----~р~ dy,
(I)
где двойной знак отвечает тому или иному выбору направления нормали.
563J	§ 3. УСЛОВИЯ НЕЗАВИСИМОСТИ ИНТЕГРАЛА ОТ ПУТИ	63
а	г> У—д л	х— £
Функции Р =г8 и Q = р—, Равн0 как и их производные, непре-
рывны во всей плоскости ху за исключением точки А, где г = 0. Во всех
точках, отличных от Д, удовлетворяется условие интегрируемости. Действи-
тельно,
д (х — ^\ _ г8 — 2 (у — т])8 _ (х —$)8 —(у —ц)8
ду \ г8 / г*	г1 ’
А (_-у— = _г8 —2(х —£)8 _(х —£)8 —(у —т))8
дх\ г2 )	г*	г* '
так что эти производные равны.
Если кривая (£) замкнута, но не охватывает точки А (и не проходит
через нее), то необходимо g=0. Если же замкнутая кривая (L) охватывает
точку А, то интеграл Г ау сса может быть и отличным от нуля, но, как мы
видели в предыдущем п“, его значение должно быть одним и тем же для всех
таких кривых. Для выяснения этого значения возьмем в качестве кривой (L)
окружность радиуса с центром в точке А. Тогда
г— R и cos (г, п) — 1
(если считать, что нормаль и радиус-вектор имеют одно и то же направление),
так что
g — 4-	= 4 • 2л/?=2л.
1\ J
Итак, для каждой замкнутой кривой (L), внутри которой находится точка
А, будет
С cos (г, п) . п
g = \ ———- ds — 2я,
если нормаль направить во внешнюю сторону, как мы это сделали в случае
окружности.
Полученные результаты можно было бы легко предвидеть, если предвари-
тельно установить геометрический смысл интеграла Гаусс a: g есть мера угла,
под которым видна из точки А
кривая (L) (если угол, описывае-
мый радиусом-вектором,идущим из
А, при обходе кривой брать со
знаком).
Для обнаружения этого обстоя-
тельства, предположим сначала, что
кривая (L) пересекается с каждым
исходящим из А лучом не более
чем в одной точке (рис. 26). Пусть,
далее, нормаль п к кривой напра-
влена в сторону, противоположную
точке А, так что
л
у-
Возьмем на кривой (L) элемент ds
и определим угол, под которым
этот элемент виден из точки А. Если М есть (например, начальная) точка
этого элемента, то опишем вокруг А окружность радиусом AM и спроекти-
руем на эту окружность элемент ds. Пусть элемент окружности, который
64 гл. XV. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА [564
служит проекцией элемента ds, будет da. Так как угол между ними (считая
оба элемента приближенно прямолинейными) равен углу (г, и), то
da = cos (г, п) ds.
С другой стороны, очевидно,
da = rdy,
где dtf есть центральный угол, отвечающий дуге da, т. е. именно тот угол,
под которым элемент ds виден из точки А. Отсюда имеем для этого элемен-
тарного угла видимости выражение
, cos (г, п) .
dy =----ds.
Наконец, суммируя все элементарные углы, мы получим, что угол видимости
для всей кривой (L) как раз и выражается интегралом g.
Если кривая пересекается лучами, исходящими из точки А, более чем в
одной точке, но может быть разбита на части, каждая из которых пересекает-
ся этими лучами уже лишь в одной точке, то нужно лишь просуммировать
интегралы Г а у с с а, относящиеся к этим частям.
Выберем на кривой (L) определенное направление, а нормаль будем направ-
лять, например так, чтобы угол м7ежду положительно направленной касатель-
7С
ной и нею был 4*	• Тогда в одних частях кривой нормаль окажется направ-
ленной в сторону, противоположную точке А, и интеграл Г а у с с а даст угол ви-
димости с плюсом, в других же частях
нормаль будет направлена в сторону точки А,
и угол видимости получится с минусом.
В общем интеграл Гаусса в этом случае
даст алгебраическую сумму углов
видимости. Впрочем, именно эту сумму и
называют углом видимости для всей кри-
вой (А), понимая, таким образом, под углом
видимости полную меру вращения луча
зрения от начала к концу кривой.
Если кривая замкнута и окружает точ-
ку А, то непосредственно ясно, что угол
видимости кривой есть 2л. Если же замкну-
тая кривая не охватывает точку А, то углы
видимости, взаимно уничтожаясь благодаря
разнице знаков, в сумме дают нуль. Для
простого случая, изображенного на рис. 27, кривая (L) распадается на две
части: (Aj) и (Аг), видные из А под одним и тем же углом; но для кривой (AJ
этот угол получается с плюсом, а для (А2) — с минусом.
Все это полностью согласуется со сказанным выше.
Замечание. Г еометрическая трактовка интеграла Г а у с с а позволяет
усмотреть, что в случае, когда замкнутая кривая (А) проходит через точку А
и в этой точке имеет касательную, значение интеграла будет л.
Если точка А будет угловой и угол между односторонними касательными
в ней равен а, то таково же будет и значение интеграла Г а у с с а. Для ана-
литического обоснования указанного результата следовало бы сначала выделить
из (А) некоторую окрестность точки А, а затем перейти к пределу, сжимая
эту окрестность.
564. Трехмерный случай. Все проведенное выше исследование
может быть повторено и для трехмерного случая.
Пусть в некоторой трехмерной области (V) определены и непре-
рывны три функции: Р(х, у, z), Q(x, у, z), Р(х, у, z); станем
564]
§ 3. УСЛОВИЯ НЕЗАВИСИМОСТИ ИНТЕГРАЛА ОТ ПУТИ
65
рассматривать криволинейный интеграл
Р dx -|— Q dy ~j- R dz	(13)
(AB)
по произвольной лежащей в этой области кривой (АВ). Рассуждения
пп° 556 и 557 переносятся на рассматриваемый случай непосред-
ственно и без изменений. Таким образом, и здесь имеет место тео-
рема, аналогичная теореме 1 п° 555: вопрос о независимости интег-
рала (13) от пути интегрирования приводится к вопросу о том,
будет ли дифференциальное выражение
Pdx-\- Qdy Rdz	(14)
точным дифференциалом, т. е. будет ли существовать такая («перво-
образная») функция Ф(х, у, z), полный дифференциал которой
дФ ,	. дФ , I дФ .
т- dx -4- s- dy -4- 5- dz
дх 1 ду 1 dz
совпадает с выражением (14).
Отметим попутно, что если такая функция существует, то ин-
теграл (13) выражается разностью двух ее конечных значений;
Pdx-\-Qdy-\-Rdz = $(B) — ®(X) = O(Af)|J (15)
(АВ)
[ср. 557 (6*)].
Затем, как и выше, встает вопрос о признаках точного диффе-
ренциала. Допустим существование в области (V) непрерывных про-
изводных
дР дР_ dQ dQ, dR dR
ду ’ dz ' dz ’ дх ' дх' ду '
Тогда, если выражение (14) есть дифференциал некоторой функции
Ф(х, у, z), так что имеют место равенства
	р=№ дх	, Q =	дФ ду'	P —— K~dz ’	(16)
TO					
	дР_ д2Ф дР	д2Ф	dQ	д2Ф dQ д2Ф	
	ду дхду’ dz	дх dz'	dz	dydz ’ dx dydx’	
	dR_	д2Ф	dR_	_ д2Ф	
	дх	дгдх’	dy	dz dy '	
Все эти производные, по предположению, непрерывны; а тогда [191]
имеют место равенства
dP_dQ dQ__dR dR_dP
ду~~дх’ dz~~dy> dx~dz‘
3 Г. М. Фихтенгольц, т. Ill
66 гл. XV. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ, ИНТЕГРАЛ СТИЛТЬЕСА (564
Таким образом, какова бы ни была область (V), условия (Б) яв-
ляются необходимыми для того, чтобы выражение (14) было
точным дифференциалом, а следовательно, и для того, чтобы
интеграл (13) не зависел от пути.
Переходя к вопросу о достаточности этих условий, мы
ограничимся здесь случаем, когда область (V) есть прямоугольный
параллелепипед
(V) = [a, tr, с, d; е, /].
Здесь мы повторим построения п° 558.
Для определения функции Ф(х, у, г) из условий (16), проинтег-
рируем первое из них по х между ха и х(а^х9, х^Ь), считая
у и z произвольно фиксированными в соответствующих промежутках.
Мы получим
Ф (х, у, z) — ^P (х, у, г) dx-j-Ф (х0, У> •?)•
Полагая во втором из уравнений (16) х — х0 и интегрируя по у от
у о ДО у. (с^уй, y^d), найдем
у
Ф (х0, у, z) = $ Q (х0, у, г)4у4-Ф (х0, у0, г).
Jo
Наконец, интегрируем третье уравнение (16), полагая в нем х — хй
и у — у0, по z от г# до z (e^z^, z^f )-.
Ф (х0, уй, z) = \R (х0, у0> z) dz 4- Ф (х0, у0, г0).
«о
Если постоянное значение Ф(х0, у0, z0), которое, очевидно, остается
произвольным, обозначить через С, то окончательно придем к такому
выражению для искомой функции:
*	у
Ф(х, у, z) = \P(x, у, z)dx-^\Q(x0, у, z)dy-\-
*0	Jo	г
4-	(х0, Уо, Z) dz 4- С. (17)
го
Применяя, в случае надобности, правило Лейбница, теперь легко
проверить, что эта функция, действительно, удовлетворяет всем
условиям (16).
Это непосредственное построение первообразной убеждает нас в
том, что, по крайней мере, для параллелепипедальной области (V)
условия (Б) дос таточны для того, чтобы выражение (14)
585]	& з. УСЛОВИЯ НЕЗАВИСИМОСТИ ИНТЕГРАЛА ОТ ПУТИ
67
было точным дифференциалом, а значит и для того, чтобы
интеграл (13) не зависел от пути.
Распространение на общий случай возможно и здесь, с тем лишь,
что область (V) удовлетворяет некоторому условию (аналогичному
односвязности плоской области). Но так как на этот раз про-
ведение всех рассуждений представляет трудности, мы от него от-
казываемся. Ниже [641], после ознакомления с поверхностными ин-
тегралами и формулой Стокса, мы к этим вопросам вернемся.
565. Примеры. 1) Будет ли криволинейный интеграл
(x24-y2)(xdx4-y dy)
U)
по любому замкнутому контуру равен нулю?
Ответ утвердительный, так как подинтегральное выражение явно пред-
ставляет собой полный дифференциал от функции -^-(х24-у2)2-
2) Не прибегая к условию (А), выяснить, зависит ли от пути интегриро-
вания интеграл
J xdy—ydx.
(АВ)
Ответ: зависит (вообще говоря), ибо подобный же интеграл по непересе-
кающему себя замкнутому контуру выражает удвоенную площадь ограничен-
ной этим контуром области [551] и, следовательно, отличен от 0.
3) Установить существование первообразной и найти ее для следующих
дифференциальных выражений:
(а)	(4х’у2 — Эу2 + 5) dx + (Зх4у2 — бху — 4) dy,
(б)	(Юху — 8у) dx (5х2 — 8х + 3) dy,
(в)	(4х’у* — 2у2) dx + (Зх4у2 — 2ху) dy,
(г)	[(х+У + 1) ех — еУ] dx + [ех — (х 4-у +1) еУ] dy.
Решение. С помощью условия интегрируемости выясняется, что в слу-
чаях (а), (б), (г) мы имеем точный дифференциал, а в случае (в) нет.
(а)	По формуле (8), полагая хо=у0 = 0, имеем
Ф (х, у) 5<7х + ^(Зх4у2 — бху — 4) dy 4- С =
= 5х 4- х4у’ — Зху2 — 4у 4- С.
То же получается и по формуле (7):
? £
Ф (х> У) = Ji (4х’у* — Зу2 4- 5) dx 4- \ (— 4) dy 4- С =
= х4у* — Зху2 4- 5х — 4у + С.
(б)	Выгодно, взяв хо=уо = О, вычислять по формуле (8), ибо тогда пер-
вый интеграл обратится в нуль:
У.
Ф (х, У) = \ (5х2 — 8х 4- 3) dy 4- С = (5х2 — 8х 4- 3)у 4" С.
3*
68
ГЛ. XV. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА (565
(г) По любой из указанных формул получим:
Ф (х, у) = (х 4- у) (ех — еУ) 4- С.
лх п	дР dQ
4)	Доказать, что условие	равносильно тождеству
Р (х, у) dx + \ Q (х0, у) dy = $ Р{х,у0) dx 4- $ Q (х, у) dy
jo	хо	Jo
(в предположении непрерывности функций Р, Q, и .
5)	Иногда разыскание первообразной (если условие интегрируемости вы-
полнено) оформляют иначе, чем это сделано в 558. Покажем это на примере 3 (а).
Из условия
6Ф
^_=4хУ-3^ + 5,
интегрируя по х, найдем для Ф выражение х4у3— Зху3 4- 5х с точностью до
«постоянной интегрирования». Эта последняя не зависит от х, по которому мы
интегрировали, но может зависеть от «параметра» у, поэтому мы возьмем ее
в виде ср (у). Итак,
Ф -- х4_у3 — Зх_у2 + 5х 4- <р.
Условие
<?Ф
= Зх4у2 — бху -• 4
дает нам, при подстановке, вместо Ф его выражения
^ = — 4
rfy
откуда <р = —4у4~С- Окончательно
Ф = х4у3 — Зху2 4- 5х — 4у 4- С.
6)	Если тот же прием применить к примеру 3) (в}, не обращая вни-
мания на нарушение условия интегрируемости, то для опре-
деления ср получим условие
da п
-х = 2ху.
dy J
Оно явно противоречиво, ибо справа стоит выражение, содержащее х,
в то время как ср от х не зависит!
7)	Интересно в общем виде выяснить, какую роль в осуществлении ука-
занного приема играет условие интегрируемости.
Интегрируя по х равенство
дФ
найдем, как и в частном примере,
Ф (х, У) = Р У)ах + ч (У)’
хо
565]	s 3. УСЛОВИЯ НЕЗАВИСИМОСТИ ИНТЕГРАЛА ОТ ПУТИ	69
Второе равенство
даст затем для определения ср (у) условие
= у) —Р (х, у) dx = Q (х, у) — dx. (18)
*0	*о
Если последнее выражение фактически от х не зависит (т. е. при у = const
не меняется с изменением х), то простая квадратура по у приводит к выраже-
нию для ср. Если же выражение (18) содержит х, то полученное для ср условие
противоречиво, ибо ср не должно зависеть от х. Таким образом, успех
зависит исключительно от того, свободно ли от х или нет выражение (18),
а это проще всего установить по тому, обращается ли в нуль или нет
частная производная от выражения
(18) по х. Но производная эта равна
dQ дР ,
-5---: таким образом, выполнение
дх	ду ’	’
условия (А), и только оно, гарантирует
успех!.
8)	Какому условию должна удов-
летворять функция F (х, у), чтобы
выражение
F (х, у) (х dx -|-у dy)
было точным дифференциалом?
„ dF dF
Ответ-, х %- —у х—.
ду J дх
9)	Вывести формулы (7) и
п° 558 для первообразной, воспользо-
вавшись выражением первообразной через криволинейный интеграл [556 (4)] и
выбрав в качестве пути интегрирования один раз ломаную АСМ, а другой
раз ADM (рис. 28).
10)	Чтобы дать другой пример применения общей формулы (4) п’ 556 для
разыскания первообразной, решим наново по этой формуле задачу 3) (а), взяв
(8)
в качестве пути интегрирования прямолинейный отрезок, соединяю-
щий начало координат с произвольной то.чкой (х’, у') плоскости (мы иначе
обозначаем ее координаты, чтобы не путать их с координатами х, у пере-
менной точки пути интегрирования).
В интеграле
(*', у')
F(x',y') = \ (4х’у* — Зу2 5) dx -|- (Зх4У— бху — 4) dy
(0. 0)
у'х , . у'х	.
нужно у заменить на (ибо у = -~- как раз и будет уравнение пути ин-
тегрирования) и тем свести дело к вычислению обыкновенного определенного
интеграла по х от 0 до х'. В результате получим
, ,, С /7у'2хв	9у'2х2 . , 4у'\
У)= \	-----х*-----=
== х'4у3 — Зх'у2 -|- 5х' — 4у',
что с точностью до обозначений совпадает с найденным выше выражением.
70 ГЛ. XV. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА [565
11)	Установить область, в которой выражение
Р dx-}- Q dy = y У х2 4-У2 — х dx-j-УУх2-} у2х dy * ♦
является полным дифференциалом, и найти первообразную для этой области.
Решение. Имеем (при у ф 0):
дР _	1	у _^У Ух^ + у2 + х
2Уу~^уу-х	2У^+У ’
dQ _________1_______/ х \ _ У У х2+у2 + х
2У^+У	’
причем в первом случае знак плюс или минус берется в соответствии со зна-
ком у. Таким образом, условие интегрируемости выполняется лишь для _у>0.
Ограничиваясь, в силу этого, верхней полуплоскостью, воспользуемся для
восстановления первообразной тем же приемом, что и в 10), но уравнения пря-
молинейного отрезка возьмем в параметрической форме:
x = x't, y=y't (Osg^sgl).
Тогда
' «У)
F (•*’> У') = J Р dx + Q dy -
(0,0)
= j (х’У У х'2 + у'2 — х' + у' У У х'2 4-у2 4-х') yTdt =
= (х'У У х'2 +у'2 — х' -f-у У У х'2 +у2 + х'\
О
12)	Положим
Pdx + Qdy = 1 у ydlr (А с> АС-В2>0).
2 Ах2 -|-2й х_у 4~ Су2 '	'
Проверить выполнение условия (А) и найти циклическую постоянную, отве-
чающую особой точке (0, 0).
Указание. Проще всего вычислить криволинейный интеграл по эллипсу
Ах2 4- 2Вху 4- Су2 = 1,	(Е)
ибо тогда
Pdx-{-Qdy — ^- ? х dy—у dx
(Е)	(Е)
сведется [551 (10)] попросту к площади этого эллипса, которая нам изве-
стна [339, 6)]. Ср. 549, 9).
13)	Если соблюдено условие интегрируемости, криволинейный интеграл
иной раз может оказаться не зависящим от пут и, а первооб]-ая функ-
ция однозначной — даже при наличии особой точки! Г ер: для
выражения
xdx-\-ydy
х2+у2	>
* Символом V обозначен, как обычно, арифметический корень.
566]
$ 3. УСЛОВИЯ НЕЗАВИСИМОСТИ ИНТЕГРАЛА ОТ ПУТИ
71
имеющего особой точкой начало координат, первообразной будет, например,
функция In(х8-j-j^8), однозначная и непрерывная вместе с произ-
водными во всей плоскости (исключая начало). Читатель легко уяснит себе
что это связано с фактом обращения в нуль циклической постоянной, отве-
чающей началу.
14)	Проинтегрировать дифференциальное выражение
2 (х^у х* + za) dX хУа	( х2 + г3 ху} dZ'
Решение. Легко проверяются «условия интегрируемости»:
dP_dQ________z_ &Q_dR_ j_. dR dP _ \ z2 — x2
dy ~ dx~ x2y2 ’ dz ~ dy — xy2 ’ dx~~ dz x2y ' (x2 + z8)8 '
Вычисление проведем по формуле, аналогичной формуле (17), но с переста-
новкой ролей х и z, и полагая при этом z0 = О, а х0 и у0 > 0. Тогда сохра-
нится лишь один из трех интегралов, и мы сразу найдем:
z
Ф(х, у, z) = £ (-Л-г-А.) rfz-j-С = arctg А_А + с.
о
566.	Приложение к физическим задачам. Вернемся в свете изложенной
теории к некоторым ранее рассмотренным задачам из области механики и фи-
зики.
1)	Работа силового поля. В п° 554 мы видели, что работа силового поля
при перемещении материальной точки с массой 1 вдоль по траектории (К) вы-
ражается криволинейным интегралом [см. 554 (18)]:
A=jXdx+Ydy,	(19)
где Х—Х(х, у) и К--Х(х, у) суть проекции напряжения поля на коорди-
натные оси.
Весьма естественно заняться выяснением условий, при которых работа сил
поля зависит лишь от начального и конечного положений точки, но не от формы
траектории. Этот вопрос, очевидно, равносилен вопросу о независимости значе-
ния криволинейного интеграла (19) от пути интегрирования. Поэтому искомым
условием является равенство
dX __dY
dy dx’
(20)
в предположении, конечно, что область, охватываемая полем, односвязна и что
особые точки отсутствуют.
То же условие можно выразить и в такой форме: работа сил поля при
перемещении материальной точки из одного положения в другое не за-
висит от формы траектории в том и только в том случае, когда эле-
ментарная' работа
X dx + Y dy
служит полным дифференциалом от некоторой однозначной функции
U(x,y). Эту функцию обычно называют силовой или потенциальной', в случае
ее существования само поле получает наименование потенциального.
Работа потенциального поля при перемещении точки из положения
Л (х0, у0) в положение В (xn уд равна [см. 557 (6)] просто соответствующему
приращению силовой функции:
(xi, Уд — U (х0, у„) — U (В) — U (Л).
72 ГЛ. XV. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА [566
В качестве примера рассмотрим поле ньютоновского притяжения. Если
в начале координат О поместить массу р., а в точку А — массу 1, то эта по-
следняя будет притягиваться к центру О с силой ?, равной по величине
г2 ’
где r==yrx2-j-y2 есть расстояние точки А от начала. Так как косинусы уг-
X V
лов, составляемых этой силой с осями, будут-— и — -у, то проекции си-
лы F на оси выразятся так:
Х=-^(
г8 ’ г3
Непосредственно ясно, что ньютоновское поле является потенциальным,
поскольку выражение
~^dx-^dy	(21)
служит дифференциалом для функции
U=^-,
г ’
которая и играет здесь роль потенциальной функции; ее называют ньютонов-
ским потенциалом (поля точки О). Несмотря на наличие особой точки (на-
чало координат), функция эта однозначна: интеграл от выражения (21) по
замкнутому контуру будет нулем, даже если контур охватывает начало («цик-
лическая постоянная» здесь равна нулю!).
При перемещении точки из положения А в положение В силы поля произ-
ведут работу
А = -^—^,
Г В	ГА
где гА и гв суть расстояния точек А и В от центра. При удалении точки В
в бесконечность работа превратится в-—; она будет равна как раз вели-
ГА
и	>
чине ньютоновского потенциала —, если точка перемещается из бесконечно-
г А
сти в положение А.
Примерами не потенциальных полей могут служить поля, образованные
силой
k
F = kr или F — ~ (й = const),
направление которой составляет угол-)--^- с направлением радиуса-вектора г.
Все сказанное здесь легко переносится и на случай пространствен-
ного силового поля.
2)	Плоское установившееся течение несжимаемой жидкости. Если
через и, v обозначить слагающие по осям вектора-скорости, то, как мы вывели
в п° 554, 2), количество жидкости, втекающей в единицу времени через замк-
нутый контур (/<) внутрь, равно
Q= \ о dx — udy
W
566]
§ 3. УСЛОВИЯ НЕЗАВИСИМОСТИ ИНТЕГРАЛА ОТ ПУТИ
73
|см. 554 (22)]. В случае несжимаемой жидкости и при отсутствии источников
и стоков этот интеграл всегда будет нулем. Отсюда следует, что слагающие
н, v вектора-скорости необходимо подчинены условию
дх ду ‘
Тогда подинтегральное выражение v dx— и dy имеет первообразную функ-
цию ® (Л1) = <р (х, _у), которую в гидромеханике называют функцией тока.
Если взять любую кривую (АВ), соединяющую точки А я В, то, как из-
вестно [554 (22)], количество жидкости, протекающей через нее в единицу вре-
мени в определенную с т о р о н у, выражается интегралом
Q = ( v dx — и dy,
(Ай)
причем направление на кривой (АВ) должно быть таким, чтобы нормаль,направ-
ленная в упомянутую сторону, составляла с положительно направленной каса-
тельной угол-]--^-. Теперь мы видим, что эта величина попросту равна раз-
ности ср (В) — <р (А) значений функции тока на концах кривой!
3)	Тепло, поглощенное газом. Рассмотрим вновь [554, 3)] вопрос о коли-
честве тепла, полученном данной массой (скажем, 1 молем) идеального газа при
изменении его состояния. Если самый процесс изменения состояния газа ха-
рактеризуется кривой (К) на плоскости V, то, как мы видели в п° 554, 3),
упомянутое количество тепла выразится криволинейным интеграло.м
[см. там (23)]:
(мы сохраняем прежние обозначения):
Если, как это делается обычно, считать теплоемкости cv и ср газа (при
постоянном объеме и при постоянном давлении) неизменными, то условие ин-
тегрируемости здесь явно нарушено. Действительно, ввиду того что срфст
будет	л ,	л ,
др \Rpj ~ R dV ) — R •
Отсюда следует, что количество тепла U не является функцией от
состояния газа и зависит от того процесса, который к этому состоянию при-
вел. Даже при циклическом процессе, возвращающем газ в его первоначальное
состояние, газ может приобрести (или потерять) некоторое количество тепла.
Если выражение элементарного количества тепла
dU^-ApdV+^Vdp
1\	и
1	pV
умножить на -у, где	есть абсолютная температура газа, то придем к
выражению
dU________________________	\ &Р
~Т ~Ср V + С® ~р ’
которое явно представляет собой полный дифференциал. Первообразной здесь
служит функция
3 = ср In V + со In р.
74 ГЛ. XV. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА (567
Криволинейный интеграл
(К р)
С Л/
' т
(Го-Ро)
уже не зависит от пути интегрирования, соединяющего постоянную точку
(Уо<Ро) с переменной точкой (V, р)к лишь постоянной отличается от указан-
ной выше функции S. Этим интегралом определяется некоторая физическая вели-
чина (так называемая энтропия), уже являющаяся функцией состояния газа
и играющая важную роль в тепловых расчетах.
§ 4. Функции с ограниченным изменением
567. Определение функции с ограниченным изменением. На-
стоящий параграф представляет некоторое отступление от основной
линии этой главы. Он посвящен ознакомлению читателя с важным
классом функций (указанным в заголовке), который был введен в
науку Жорданом (С. Jordan). Этот класс функций будет играть
основную роль в том обобщении понятия определенного интеграла,
которым мы займемся в следующем параграфе. Впрочем, и во многих
других вопросах математического анализа класс функций с ограни-
ченным изменением имеет важное значение.
Пусть функция f (х) определена в некотором конечном промежутке
[а, Ъ\, где а Ь. Разложим этот промежуток произвольным образом
на части с помощью точек деления:
а = х0<х1<х,< ... <х,<х,+1< ... <^хп = Ь
(подобно тому, как мы это делали при составлении интегральных
или римановых сумм, устанавливая понятие определенного интеграла).
Из абсолютных величин приращений функции, отвечающих отдельным
частичным промежуткам, образуем сумму
Л— 1
®=£1Ж+1)—Ж)1-	0)
i=0
Теперь весь вопрос в том, будет ли множество этих чисел, отве-
чающих различным способам дробления промежутка [а, Ь\ на части,
ограничено сверху или нет.
Если суммы (1) в их совокупности ограничены сверху, то го-
ворят, что функция f(x) в промежутке [а,Ь] имеет ограни-
ченное изменение (или ограниченную вариацию). При этом
точную верхнюю границу этих сумм называют полным изме-
нением (или полной вариацией) функции в указанном промежутке
и обозначают символом
ь
\f(x) — sup {ц}.
а
567]	$ 4. ФУНКЦИИ С ОГРАНИЧЕННЫМ ИЗМЕНЕНИЕМ	75
Можно применять это понятие и' в случае функции не ограниченного
изменения, но тогда полное изменение будет равно -{-ос.
По самому определению точной верхней границы, в обоих слу-
чаях, надлежаще выбирая подразделения промежутка [a, ft], можно
достигнуть произвольной близости сумм v к полному изменению
ь
Иными словами, можно выбрать такую последовательность
а
подразделений, чтобы полное изменение служило пределом для
последовательности соответствующих сумм v.
Иногда ставится вопрос об ограниченности изменения функции
/(х)вбесконечном промежутке, например, в промежутке [а, оо].
Говорят, что функция f(x) имеет ограниченное изменение в про-
межутке [а, ос], если она является функцией с ограниченным
изменением в любой его конечной части [и, Д] и полные измене-
А
ния f(x) ограничены в их совокупности. Во всех случаях мы
а
полагаем	,	Л
Н-со	А
V/w = sup {V/w}-	(2)
а	а
Отметим, что в этих определениях никакой роли не играет вопрос
о непрерывности функции /(х).
Примером функции с ограниченным изменением в конечном или
бесконечном промежутке [a, ft] может служить любая ограничен-
ная монотонная функция. Если промежуток [a, ft] конечный, то
это сразу следует из того, что '
V= s’ |/(xI+1) -f(Xi) I = I"£	“№)] | = IA*) -/(«) I.
i=0	i=0
b
так что и V/w = l/(ft)—/(и) |. Для промежутка [а, -]- оо], оче-
а
видно, будет
4-СО
V/W = suP ]|/(Д)—/(а) !} = ]/(+оо)—/(а)|,
А>а
а
разумея под /(-1- оо), как обычно, предел lim /(Л).
А->-{-оо
Дадим теперь пример непрерывной функции, которая, однако, не
будет функцией с ограниченным изменением. Положим
f(x) = xcos£- (для х^О),/(0) = 0
76 ГЛ. XV. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА [568
и рассмотрим, например, промежуток [0, 1]. Если за точки деления этого про-
межутка принять точки
0<2гё<2ге —1<‘,‘ <3<2<1,
то, как легко убедиться,
v = v„=l+^+...+^ = /7„
и [см. 365, 1)]
1
V / W = sup {о} = +
о
568. Классы функций с ограниченным изменением. Мы уже
упоминали о том, что монотонная функция имеет ограничен-
ное изменение. Можно следующим образом расширить этот класс
функций:
1°. Если функция f(x), заданная в промежутке {а, Ь}, такова,
что этот промежуток может быть разложен на конечное число
частей
\ak, ak+l] (й = 0, 1, ... , т — 1; ай = а, ат = Ь),
в каждой из которых f(x) монотонна*, то она имеет в [а, Ь}
ограниченное изменение.
Разбив произвольным образом промежуток [а, Ь\ на части, соста-
вим сумму v. Так как от присоединения каждой новой точки деле-
ния сумма v может разве лишь увеличиться **, то, присоединив к
точкам деления все точки ak, о которых была речь выше, мы полу-
чим сумму v V. Если выделить из суммы v те слагаемые, которые
относятся к промежутку \ak, afc+1], то, обозначая их сумму значком (k)
наверху, будем иметь
так что
_	т-1
1№+1)-Ж)|.
k = 0
Так как произвольная сумма v не превосходит этого числа, то оно
и будет полным изменением функции.
* Про такую функцию говорят, что она кусочно-монотонна в про-
межутке [а, 6].
** Если между X/ и xi+l вставлена точка х', то слага емое | f (xt-+1) —/(х,) |
заменяется суммой
I/ (Х;+1) - f (х') | + |/(х’) -/ (хг) | ^ |/ (х/+1) -f (Xi) |.
568J	$ 4. ФУНКЦИИ С ОГРАНИЧЕННЫМ ИЗМЕНЕНИЕМ	77
2°. Если функция f(x) в промежутке [а, Ь\ удовлетворяет
условию
\f(x)-f(x)\^L\x-x\,	(3)
где А = const, а х и х — любые точки промежутка*, то она
имеет ограниченное изменение, причем
ь
V f(x)^L(b — a).
а
Это следует из неравенства
п —1	л—1
ч = 5 I f (х<-+1 — f (xi) I	L 2 0^+1 — Xi) — L(b — a).
i = 0	i = 0
В частности,
3°. Функция f(x) будет в промежутке [а, функцией, с огра-
ниченным изменением, если она имеет в нем ограниченную произ-
водную'. \f'(x)\^L (где А = const).
В самом деле, по теореме о среднем в этом случае
\f(x)—f(x)\ = \f'(t)(x — x)\^L\x — x\ (x^l^X),
так что выполнено условие Липшица (3).
На основании этого замечания можно, например, утверждать ограничен-
ность изменения функции
/(х) —x2sin J (х^0),/(0)=0
в любом конечном промежутке, ибо производная ее
/' (х) — 2х sin — n cos (xz£ 0), f (0) = 0
ограничена. Любопытно отметить, что в каждом промежутке, содержащем
точку 0, эта функция «бесконечно колеблется», т. е. бесконечное число раз
переходит от возрастания к убыванию, и наоборот.
Обширный класс функций с ограниченным изменением дается сле-
дующим предложением:
4°. Если f(x) в конечном (или даже в бесконечном) проме-
жутке [а, представима в виде интеграла с переменным верх-
ним пределом:
f(x) = c + \^(t)dt,	(4)
а
* Это условие обычно называется условием Липшица (R. Lipschitz).
78 гл. XV. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА. (568
где ср (t) предполагается абсолютно интегрируемой * а этом про-
межутке, то f (х) имеет в нем ограниченное изменение. При этом
ь	ь
а	а
Пусть [а, Ь\ — конечный промежуток; тогда
® = Ё 1/(^/+1) —Ж-) I = .£ I t ? (О dt I <
i=0	i=0 xt
„-IJCf-l-l	ft
J i?(wM mow
1—0 X{	a
откуда и следует наше утверждение.
Если же речь идет о бесконечном промежутке [a, -J- оо], то до-
статочно заметить, что
А	А	4- оо
$ 1?(0М< § МОИ-
а	а	а
Замечание. Можно доказать, что как в случае конечного, так
и в случае бесконечного промежутка на самом деле имеет место
точное равенство
&	ь
Vf(.x^= $ I ? (О I dt.
а	а
Если же функция <р(() в промежутке [а, Ь] интегрируема, но не
абсолютно, то полное изменение f(х) заведомо бесконечно. Мы
не будем останавливаться на этом, но поясним лишь последнюю часть
замечания примерами.
Пусть /(x) = x2sin^j (х 0), / (0) = 0, так что
Г (x) = ?(x) = 2xsin^ —	(х#;0), f (0) = ч (0) = 0.
Тогда, например, для 0^х^2
У(х)=Л?(0Л,
* Т. е. интегрируемой (хотя бы в несобственном смысле) вместе со своей
абсолютной величиной | (01.
569]
S 4. ФУНКЦИИ С ОГРАНИЧЕННЫМ ИЗМЕНЕНИЕМ
79
но в п* 482 мы показали, что интеграл этот — неабсолютно сходящийся. Поль-
зуясь той же идеей, что и там, разложим промежуток [О, 2] точками
V-  75=.	'• ™ *
для соответствующей суммы v, очевидно, будет
Л = 1	Г	* = 1
откуда и следует, что
2
О
Аналогично этому легко показать, что функция
X
'.	С sin t ..
f(x)= \—— dt
в промежутке [0, -f- сю] имеет неограниченное изменение [ср. 476].
569. Свойства функций с ограниченным изменением. Промежу-
ток [a, ft], в котором здесь рассматриваются все функции, предпо-
лагается конечным.
1°. Всякая функция с ограниченным изменением ограничена.
В самом деле, при а х' ft имеем
V' = | /(У) - f (а) ] + |/(ft)	< VЛ*)>
откуда
ь
1Ж) I < |/(x') -/(a) I +1 у (a) I < |/(a) | + V/(x).
a
2°. Сумма, разность и произведение двух функций f(x) и g(x)
с ограниченным изменением также являются функциями с огра-
ниченным изменением.
Пусть s(x)=/(x) + g(x). Тогда
I« Ог+1) — « (X/) | < |/(xi+1) — f(Xi) | +1 g(xj+1) — g(Xt}|
80
ГЛ. XV. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА 1569
й, суммируя по значку I,
215(^+1) —
i
b	b
< 1Ж-+1) -ж-) ।+—§ (*«•) к V/w+V ж).
i	i	a	a
откуда следует
V
a	a	a
Положим теперь p(x)=f(x)g(x) и пусть для a^x^b
|/(х) | < К, | g(x) К L (К, L — const)
[cm. 1°]. Очевидно,
1Ж+1) — P(Xi)\ =
= I/(W (Ж+i) — ЖЛ + g{xi) \f(x^ —f(Xi)\ | <
<К- I Ж+1) - g(Xi) | + L • |/(x/+1) -f(xi) |,
откуда уже легко получить, что
ь	ь	ь
VРЮ^кУ g(x) 4- L V f(x).
а	а	а
3°. Если f(x) и g(x) суть функции с ограниченным изменением
f(x)
и, сверх того, \g(x)\^ay>0, то и частноебудет функ-
8 \х)
цией с ограниченным изменением.
Ввиду свойства 2°, достаточно доказать ограниченность измене-
ния функции h (_к)=^—. Имеем
| k (хм) - Л (х,) I =	to*.) - в to) I .
так что
ъ	ь
V
а	а
4°. Пусть функция f(x) определена в промежутке [а, Ь] и
а<^с<^Ь. Если функция f(x) имеет ограниченное изменение
в промежутке [а, Ь\, то она имеет ограниченное изменение и
569]	§ 4. ФУНКЦИИ С ОГРАНИЧЕННЫМ ИЗМЕНЕНИЕМ	81
в каждом из промежутков [а, с] и [с, Ь], и обратно. При этом
b	с	b
V / w=V / w+V л*)-	(5)
а	а	с
Пусть f (х) имеет ограниченное изменение в [а, Ь\. Разложим на
части каждый из промежутков [а, с] и [с, Z>] порознь:
jo = a<jt< ... <jm = c, г0 = с<г,< ... <£„ = &;	(6)
этим будет разбит на части и весь промежуток [а, &]. Составим
суммы отдельно для промежутков [а, с] и [с, Ь]:
= s I/Сум) -fbk) I, *2=s I f Ы -fW I;
k	i
соответствующая сумма для промежутка [а, Ь\ будет v = vt -J- v*
Таким образом
ь
V7c*)
а
и, следовательно, каждая из сумм vlf v$ порознь ограничена, т. е,
функция f (х) оказывается с ограниченным изменением в промежут-
ках [а, с] и [с, £]. Выбирая подразделения (6) так, чтобы суммы
и стремились к соответствующим полным изменениям, в пределе
получим
ebb
V л*>+V f <•*) < V/ и-	(7)
аса
Допустим теперь, что /(х) имеет ограниченное изменение в каж-
дом из промежутков [а, с] и [с, &]. Произведем произвольное разбие-
ние промежутка [а, Ь] на части. Если точка с не входит в состав
точек деления, то мы ее дополнительно введем, отчего, как мы знаем *,
сумма v может лишь увеличиться. Сохраняя прежние обозначения,
будем иметь
с	b
+ V/(•*)+ V-Я*)-
а	с
Отсюда сразу вытекает ограниченность изменения /(х) в проме-
жутке [а, Ь\ и неравенство.
Ь	с	Ъ
Va*)<Va*)+Va*).	(8)
а	а	с
* См. сноску ** на стр. 76,
82 ГЛ. XV. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА (570
Наконец, из (7) и (8) следует {б).
Из доказанной теоремы, в частности, вытекает:
5°. Если в промежутке [а, Ь\ функция f(x) имеет ограничен-
ное изменение, то для а^х^Ь полное изменение
X
g(x) = y f(t)
а
будет монотонно возрастающей (и ограниченной) функцией от х.
Действительно, если а V х" Ь, то
х"	х'	х"
V/(o=V/(o+Vao>
а	а	х‘
так что
X”
g(x")-g(x’) = y	(9)
х'
(так как по самому определению полного изменения оно не может
быть отрицательным числом).
Теперь становится ясным, что определение полного изменения
в бесконечном промежутке [а, —о©] вместо (2) может быть
дано в следующей форме:
4-00	А
V/w = Jim V/W-	(2*)
А->-|-оо
а	а
С помощью этого замечания теоремы настоящего п° легко обоб-
щаются и на случай бесконечного промежутка.
570. Критерии для функций с ограниченным изменением. Пусть
функция f (х) определена в конечном или бесконечном промежут-
ке [а, Ь].
6°. Для того чтобы функция f(x) имела в промежутке [а, А]
ограниченное изменение, необходимо и достаточно, чтобы для
нее в этом промежутке существовала монотонно возрастающая
и ограниченная функция F(x), такая, что в любой части [х', х"],
(х'<^х") промежутка [а, 6] приращение функции f по абсолют-
ной величине не превосходит соответствующего приращения функ-
ции F:
|/(*") ~Ж) I < > (*") - F (V) *
* Можно было бы, впрочем, ограничиться и неравенством без знака абсо-
лютной величины:
f(x")-f(x)^F(x")-F{x).
ИО]	§ 4. ФУНКЦИИ С ОГРАНИЧЕННЫМ ИЗМЕНЕНИЕМ	83
[Функцию F(x), обладающую этим свойством, естественно было бы
назвать мажорантой для функции f(х).]
Необходимость следует из того, что для функции /(х)
с ограниченным изменением роль мажоранты может играть, например,
функция
X
а
монотонно возрастающая и ограниченная в силу 5°. Неравенство
х"
I/(х”) —f(x') I < g(x") — g(х') = V f (f>
х'
вытекает из самого определения полного изменения функции.
Достаточность для случая конечного промежутка видна сразу
из неравенства
v = У, | f (xi+1) — f (х,) | < У [F (x/+1) — F (x,)] = F (b) — F (a),
i = 0
а для бесконечного — получается предельным переходом.
Очень важной является другая форма критерия:
7°. Для того чтобы функция f (х) имела в промежутке [а, Ь\
ограниченное изменение, необходимо и достаточно, чтобы она
представлялась в этом промежутке в виде разности двух моно-
тонно возрастающих и ограниченных функций:
f(x) = g(x) — h(x).	(Ю)
Необходимость. В силу 6°, для функции f (х) с ограничен-
ным изменением существует монотонно возрастающая и ограниченная
мажоранта F(x). Положим
g(x) = F(x), ft(x) = F(x)-/(x),
так что (10) выполнено. Остается убедиться в монотонности функ-
ции h(xy, но при х'<х"
h (х") - h (х') = [F (х") - F (x')] - [/(*") -f{x’)}	0
по самому определению мажоранты.
Достаточность ясна из того, что при наличии равенства (10)
функция
F(x) = g(x)-\-h (х)
служит мажорантой, ибо
|/(x")-/(x')|^[g(x")-g(x')J + [ft(x") -ft(x')] = F(x")-F (х').
84
ГЛ. XV. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА (571
В виде упражнения предлагается читателю:
1) опираясь на установленные критерии, наново доказать утвер-
ждения 1° — 4° предыдущего п°;
2) для рассмотренных в п° 568 классов функций с ограниченным
изменением непосредственно установить наличие монотонной мажо-
ранты и возможность представления в виде разности монотонных
функций.
По поводу теоремы 7° сделаем дополнительное замечание.
Так как функции g и h обе ограничены, то путем прибавления к ним
одной и той же постоянной всегда можно добиться того, чтобы они
обе стали положительными. Точно так же, прибавляя к функ-
циям g и h какую-либо возрастающую в строгом смысле, но ограни-
ченную функцию (например, arctg х), придем к такому разложению
вида (10), где обе функции будут уже строго возрастающими.
Установленная в 7° возможность сведёния функций с ограничен-
ным изменением в некотором смысле к монотонным функциям не
должна создавать у читателя иллюзий относительно «простоты» пове-
дения функций с ограниченным изменением: ведь бесконечно
колеблющаяся функция	i
/(х) —х'2 sin(х?ё0), /(0) = 0,
которая была рассмотрена в п° 568, тоже допускает представление
в виде разности двух монотонных функций!
Тем не менее, именно в связи с представлением (10), некоторые
свойства монотонных функций переносятся и на функции с ограни-
ченным изменением. Так, если вспомнить, что для монотонной огра-
ниченной функции /(х) при любом х = х0 существуют односторон-
ние пределы, слева и справа,
/(х0-О)= Нт /(х), /(Хо4-О)= Нт /(х)	(11)
х —► хо — 0	jc -♦ jc0 -|- О
[71, 1°], то, применяя это свойство к каждой из функций g и h,
заключим, что и
8°. Для функции /(х) с ограниченным изменением в проме-
жутке [а, Ь} в любой точке х = х0 этого промежутка суще-
ствуют конечные односторонние пределы (11)*.
571. Непрерывные функции с ограниченным изменением.
9°. Пусть в промежутке [а, Ь} задана функция f (х) с ограни-
ченным изменением. Если f(x) в некоторой точке х = х0 непре-
рывна, то в этой же точке непрерывна и функция
g(X)=\Jf®.
а
* Конечно, если х0 есть один из концов промежутка, то речь может идти
только об одном из этих пределов.
571]
§ 4. ФУНКЦИИ С ОГРАНИЧЕННЫМ ИЗМЕНЕНИЕМ
85
Предположим, что х9<^Ь, и докажем, что g(x) непрерывна
в точке х0 справа. С этой целью, взяв произвольное е 0, разло-
жим промежуток [х0, Ь\ точками
*oOi< <ZXn = b
на части так, чтобы оказалось
п — 1	b
v= 2 |/(хг+1)-/(х;)|> V/(0-e-	(12)
Г= 0	л-0
Опираясь на непрерывность функции /(х), можно предположить
при этом, что Xi уже настолько близко к х0, что выполняется нера-
венство .
1/(*1) —/(*о) I О
(в случае надобности, можно было бы вставить еще одну точку
деления, отчего сумма v разве лишь увеличилась бы). Тогда из (12)
следует, что
b	п — 1
V/(0 < е +	1 <
i = 0
п- 1	b
<2е+ 2|/(х/+1)-/(х;)|^2еД-V /(0
i=l	Xi
стало быть,
Xi
х0
или, наконец,
g(*i) — g(Xo)<2e.
Отсюда и подавно
0 < g(*o + 0) — g(x0) < 2s,
следовательно, ввиду произвольности е,
g(xo + O) = g(xo).
Аналогично доказывается, что (при х0^>а)
g(x0— O)=g(xo),
т. е. что g(x) в точке х0 непрерывна слева.
Из доказанной -теоремы вытекает такое следствие:
10°. Непрерывная функция с ограниченным изменением пред-
ставима в виде разности двух непрерывных же возрастаю-
щих функций.
86 гл. XV. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА (571
В самом деле, если вернуться к доказательству предложения 7°
(в части, относящейся к необходимости) и в качестве моно-
тонной мажоранты взять именно функцию
X
f(t),
а
непрерывную в силу 9°, то и получится требуемое разложение.
В заключение покажем, что для непрерывной функции в оп-
ределении полного изменения:
ь
\f/(x) = sup {г>}
а
supremum можно заменить пределом как в том случае, когда полное
изменение конечно, так и в том, когда оно бесконечно.
11°. Пусть функция f(x) непрерывна в конечном промежут-
ке [а, Ь}. Разложив этот промежуток. на части точками
х0 = а<х,< ... <^хп — Ь
и составив сумму
п — 1
« = 0
будем иметь
ь
Пт V— \/f(x),	(13)
А -»0	’
а
где X — max (х/+1 — х;) *.
Как уже отмечалось, сумма v не убывает от добавления новой
точки деления **. С другой стороны, если эта новая точка попадает
в промежуток между xk и xft+1, то увеличение суммы v, проистекаю-
щее из появления этой точки, не превосходит удвоенного ко-
лебания функции /(х) в промежутке [xk, xft+1].
Заметив это, возьмем какое-либо число
ь
A<Vf(x)
а
и найдем сумму V* такую, что
(14)
* Здесь имеется в виду предельный переход такого же типа, как и для
римановых сумм или сумм Дар бу [259, 30].
** См. сноску ** на стр. 76.
5721	$ 4. ФУНКЦИИ С ОГРАНИЧЕННЫМ ИЗМЕНЕНИЕМ
87
Пусть эта сумма отвечает следующему способу деления:
xo = a<^xt<^ ... <^Хт = Ь.
Выберем теперь столь малое 8^>0, что
|/(х")~/(-*')!<
у* — А
4т
лишь только [х" — х' | 8 (это сделать можно ввиду равномерной
непрерывности функции /). Докажем, что для любого способа деле-
ния, которому отвечает Х<^8, будет
v>A.	(15)
В самом деле, имея подобный способ деления (I), составим новый
способ (II), получающийся из (I) добавлением всех точек х*. Если
способу (II) отвечает сумма va, то
Vq^V*.	(16)
С другой стороны, способ (II) получается из (I) путем (самое
большее) Пг-кратного добавления по одной точке. Так как каждое
,	v* — А
добавление вызывает увеличение суммы v, меньшее, чем ——, то
о* — а
Отсюда, а также из (16) и (14), следует, что
v* — А	А + v* \ .
р->А.
Итак» при Х<^8 выполнено (15); но, поскольку всегда
ъ
f(x),
а
о действительно имеет место (13), что и требовалось доказать.
572. Спрямляемые кривые. Понятие функции с ограниченным
изменением находит себе применение в вопросе о спрямляемости
кривой линии, в связи с которым названное понятие и было впервые
введено Жорданом. Изложением этого вопроса мы хотим заклю-
чить настоящий параграф.
Пусть кривая (/<) задана параметрическими уравнениями
х = ?(0, ^ = ф(0.	(17)
где функции ср (0 и ф(<) предположены только непрерывными. Допу-
стим при этом, что кривая не имеет кратнщх точек.
Взяв вершины вписанной в кривую ломаной в точках кривой,
отвечающих значениям параметра
<tn=T,	(18)
88 ГЛ. XV. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА [572
будем иметь для периметра ломаной выражение
п — 1
Р= S И? &+1) - ? <А)]2+[ф &+1) - ф
i — 0
Как мы знаем [247], длина s рассматриваемой дуги кривой опре-
деляется как точная верхняя граница множества всех периметров р.
Если эта граница конечна, кривая и называется спрямляемой.
Достаточные условия спрямляемости мы указали уже в первом томе
[278]. Нижеследующая теорема устанавливает самые общие — необхо-
димые и достаточные условия для этого.
Теорема Жордана. Для спрямляемости кривой (17) необходимо
и достаточно, чтобы функции (/) и ф (t) обе имели ограниченное
изменение в промежутке [£0, Г].
Необходимость. Если кривая спрямляема и имеет длину s,
то при любом подразделении (18) промежутка [4, Т\ имеем
Р =	К[? (*,+1) - ? (Q]2 + [ф &+1) - ф (QJ2 5,
» = о
откуда, в силу очевидного неравенства
I <? (^-+1) - <р (QI	Г [? а/+1) - ? О2 + [ф Gi+1) - ф (Q12,
следует, что
л — 1
У, I <Р &+1) — <Р &) I < s>
< = 0
так что функция ср (t), действительно, имеет ограниченное изменение.
Аналогичное заключение применимо и к функции ф (Z).
Достаточность. Допустим теперь, что обе функции <р(t) и
ф (0 имеют ограниченное изменение. Ввиду очевидного неравенства
п — 1
Р= s У &+о - ? &)12 + [ф &+о - Ф (*/)Т <
» = 0
л— 1	л— 1
< S I? (W-? (^)i+ S 1ф(М-фо
i=0	1 = 0
можно утверждать, что все числа р ограничены сверху, например, числом
г	т
V ?ю+V ф(о>
/о	Л>
а отсюда по доказанному выше уже вытекает спрямляемость кри-
вой (К).
573]
§ 5. ИНТЕГРАЛ СТИЛТЬЕСА
89
Присовокупим еще два важных замечания.
Из только что сказанного явствует, что вся длина s кривой (17)
удовлетворяет неравенству
т	т
to	to
Рассматривая переменную дугу 5 = 5(t), отвечающую промежутку
[4, t] изменения параметра, применим написанное неравенство к про-
межутку [t, £ —]—Д£], где, скажем, Д£^>0. Тогда
/+«	t^lt
0<Д5< V ?(0+ V ж
t	t
Так как при бесконечно малом Д/ обе вариации справа [в силу 571
9°], а с ними и Д5, также бесконечно малы, то мы приходим к заклю-
чению: для непрерывной спрямляемой кривой переменная дуга s(t)
является непрерывной функцией параметра.
Так как эта функция монотонно возрастает от 0 до длины 5 всей
кривой, то, каково бы ни было натуральное число п, можно себе
£
представить кривую разделенной на п частей длины — [теорема
Коши, 82]. Если плоскость покрыта сеткой квадратов со стороной
8
—, то каждая из упомянутых частей не может встретить больше четы-
рех таких квадратов. Таким образом, сумма площадей всех квадратов,
8а
встречающих нашу кривую, во всяком случае не превосходит 4л • -j
и может быть сделана сколь угодно малой: кривая имеет площадь
нуль.
Отсюда — такое интересное следствие: область, ограниченная
с пр я м л я е мой кривой (или несколькими такими кривыми), за-
ведомо квадрируема, т. е. имеет площадь [337].
§ 5.	Интеграл Стилтьеса
573.	Определение интеграла Стилтьеса. Интеграл Стилтьеса
(Th. J. Stieltjes) является непосредственным обобщением обычного
определенного интеграла Римана [295]. Определяется он следующим
образом.
Пусть в промежутке [а, Ь] заданы две ограниченные функции
f (х) и g(x). Разложим точками
a = xo<xi<x2< ... <хп_1<хп = £	(1)
промежуток [а, Ь] на части и положим X = шах Дхг. Выбрав в каж-
дой из частей [х;, х/+1] (1 = 0, 1, .... п—1) по точке вычислим
90 ГЛ. XV. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА (573
значение /($,-) функции f(x) и умножим его на соответст-
вующее промежутку [xit x/+i] приращение функции g(x)
д£ (х.) = g (*i+i) — g
Наконец, составим сумму всех таких произведений:
л-1
(2)
i = 0
Эта сумма носит название интегральной суммы Стилтьеса.
Конечный предел суммы Стилтьеса <з при стремлении
X —тахДх,- к нулю называется интегралом Стилтьеса функ-
ции f (х) по функции g(x) и обозначается символом
ь	л-1
fix)dg(x) = lim а = lim £ Ag(Xg) *.	(3)
л	X —* 0	X —►(), __q
Иной раз, желая особенно отчетливо подчеркнуть, что интеграл
рассматривается в смысле Стилтьеса, употребляют обозначение
ь	ь
(S) ^/(x)<Zg(x) или S/(x)dg(x).
а	а
Предел здесь понимается в том же смысле, что и в случае обык-
новенного определенного интеграла. Точнее говоря, число I называется
интегралом Стилтьеса, если для любого числа е^>0 существует
такое число 8^>0, что лишь только промежуток [а, Ь\ раздроблен
на части так, что Х<^8, тотчас же выполняется неравенство
I ° — I е>
как бы ни выбирать точки в соответствующих промежутках.
При существовании интеграла (3) говорят также, что функция
fix) в промежутке [а, Ь} интегрируема по функции g(x).
Читатель видит, что единственное (но существенное) отличие дан-
ного выше определения от обычного определения интеграла Римана
состоит в том, что /(?,) умножается не на приращение Дх,- незави-
симой переменной, а на приращение Ag(x;) второй функции. Таким
образом, интеграл Римана есть частный случай интеграла Стил-
тьеса, когда в качестве функции g (х) взята сама независимая пере-
менная х:
g(x) = x.
* Мы для определенности предполагали а < Ь; нетрудно аналогично рас-
смотреть и случай, когда а > Ь. Впрочем, он непосредственно приводится
Ь	а
к предыдущему ввиду равенства	j	J.
а	6
574]
§ 5, ИНТЕГРАЛ СТИЛТЬЕСА
91
574.	Общие условия существования интеграла Стилтьеса.
Установим общие условия существования интеграла Стилтьеса,
ограничиваясь, впрочем, предположением, что функция g(x) моно-
тонно возрастает.
Отсюда следует, что при а<^Ь теперь все Ag(x;)^>0, напо-
добие того, как раньше было Дх,^>0. Это позволяет слово за сло-
вом, заменяя лишь Дх,- на Ag(x,), повторить все построения пп°
296 и 297.
Аналогично суммам Д а р б у, и здесь целесообразно ввести суммы
п—1	л—1
i — 0	i — 0
где m-i и М; означают, соответственно, нижнюю и верхнюю точные
границы функции f(x) в i-м промежутке [xit xI+i]. Эти суммы мы
будем называть нижней и верхней суммами Дар бу—Стилтьеса.
Прежде всего, ясно, что (при одном и том же разбиении)
s sg а гС 5,
причем $ и 5 служат точными границами для стилтьесовых сумм с.
Сами суммы Дарбу — Стилтьеса обладают, как и в простей-
шем случае [296], следующими двумя свойствами:
1-е свойство. Если к имеющимся точкам деления добавить
новые точки, то нижняя сумма Дарбу — Стилтьеса может
от этого разве лишь возрасти, а верхняя сумма — разве лишь
уменьшиться.
2-е свойство. Каждая нижняя сумма Дарбу — Стил-
тьеса не превосходит каждой верхней суммы, хотя бы и отве-
чающей другому разбиению промежутка.
Если ввести нижний и верхний интегралы Дарбу — Стил-
тьеса:
= sup {$} и I* — inf {<S},
то оказывается, что
s	5.
Наконец, с помощью сумм Дарбу — Стилтьеса легко устана-
вливается для рассматриваемого случая основной признак
существования интеграла Стилтьеса:
Теорема. Для существования интеграла Стилтьеса необ-
ходимо и достаточно, чтобы было
lim (5 — $) = 0
X —о
или
п — 1
Нш У <вгД^(х,) = 0,	(4)
92 ГЛ. XV. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА (575
если под ы;, как обычно, разуметь колебание Л1г — функции f(x)
в i-м промежутке [х{, х,-+1].
Все доказательства, как указывалось, копируются с соответствую-
щих доказательств, проведенных в пп° 296, 297, и мы можем предо-
ставить их читателю.
В следующем п° мы применим этот критерий к установлению важ-
ных парных классов функций f(x) и g(x)> для которых интеграл
Стилтьеса существует.
575.	Классы случаев существования интеграла Стилтьеса.
I.	Если функция f(x) непрерывна, а функция g(x) имеет огра-
ниченное изменение, то интеграл Стилтьеса
ь
\f(x)dg(x)	(5)
а
существует.
Сначала предположим, что g(x) монотонно возрастает: тогда при-
меним критерий предыдущего п°. По произвольно заданному г^>0
ввиду равномерной непрерывности функции f (х) найдется такое
8 О, что в любом промежутке с длиной, меньшей 8, колебание f (х) бу-
дет меньше g • Пусть теперь промежуток [а, Ь} произвольно
разбит на части так, что К = max Дх,- 8. Тогда все <о,-	g(а)~ и
S	< g<i-g-^)- • S - S (*<•)]=е>
откуда и следует выполнение условия (4), а стало быть и существо-
вание интеграла.
В общем случае, если функция g(x) имеет ограниченное изме-
нение, она представима в виде разности двух ограниченных возра-
стающих функций: g{x)== gi{x) — gti(x) [575, 7°]. В соответст-
вии с этим преобразуется и сумма Стилтьеса, отвечающая функ-
ции g(x):
п— I	п— 1	л — 1
0=2 /&) Д^(^) = S (х>) ~ S	Д& <х^ = 01 — 0.2.
i=0	i = 0	i=0
Так как по уже доказанному. каждая из сумм о, и о2 при Х->0
стремится к конечному пределу, то это справедливо и относительно
суммы о, что и требовалось доказать.
Можно ослабить условия, налагаемые на функцию f (х), если одно-
временно усилить требования к функции g(x):
575]
§ 5. ИНТЕГРАЛ СТИЛТЬЕСА
93
II.	Ес да функция f(x) интегрируема в [а, Ь] в смысле Ри-
мана, a g(x) удовлетворяет условию Липшица:
\g{x) — g(x)\^L{x — х]	(6)
(Z. = const, a х х b),
то интеграл (5) существует.
Для того чтобы опять иметь возможность применить установлен-
ный выше критерий, предположим сначала функцию g(x) не только
удовлетворяющей условию (6), но и монотонно возрастающей.
Ввиду (6), очевидно, Ag(x,) sg АДх,, так что
п— 1	п — 1
У ^AgtXi) С L У 0>;Дх?
1 = 0	1 = 0
Но последняя сумма при X —- 0 и сама стремится к 0 вследствие ин-
тегрируемости (в смысле Римана) функции /(х) [297], а тогда
стремится к нулю и первая сумма, что доказывает существование
интеграла (5).
В общем случае функции g(x), удовлетворяющей условию Лип-
шица (6), представим ее в виде разности
g (х) = Ах — [ Ах — g (х)] = gi (х) — gi (х).
Функция gt (х) = Lx, очевидно, удовлетворяет условию Липшица
и в то же время монотонно возрастает. То же справедливо и для
функции gi(x) = Lx — g(x), так как, в силу (6), при a<zx<^x<zb
gi(х) — gi(х) = L (х — х) — [g(x) — g(x)] Ss 0
и
I gi (x) — gi (x) I sC L (x — x) +1 g(x) — g(x) I sC 2A (x — x).
В таком случае- рассуждение завершается, как и выше.
III.	Если функция /(х) интегрируема в смысле Римана, а
функция g(x) представима в виде интеграла с переменным верх-
ним пределом:
X
g(x) = c-[-^(t)dt,	(7)
а
где ср (t) абсолютно интегрируема в промежутке [а, Ь], то
интеграл (5) существует.
Пусть ср (А) 5= 0, так что g(x) монотонно возрастает. Если ср (f)
интегрируема в собственном смысле и, следовательно, ограничена:
| <р (f) | гС L, то для a sC х х «С b имеем
!#(*) — ДО)1 =
sC А (х — х).
94 гл. XV. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА [575
Таким образом, в этом случае g(x) удовлетворяет условию Лип-
шица, и интеграл существует в силу II.
Предположим теперь, что <р(/) интегрируема в несобственном
смысле. Ограничимся случаем одной особой точки, скажем Ь. Прежде
всего, по произвольно взятому е 0 выберем т] 0 так, чтобы было
ъ
$	(8)
Ь-ц
где 2 — общее колебание функции /(х) в рассматриваемом проме-
жутке.
Разобьем промежуток [а, А] по произволу на части и составим
сумму
п— 1
1=0
Она разлагается на две суммы .S = .£'+ £"> из коих первая отве-
чает промежуткам, целиком содержащимся в промежутке £а, b — yj,
а вторая — остальным промежуткам. Последние наверное содержатся в
промежутке \Ь — т], Ь], если только k = max Дх,<^-у; тогда,
в силу (8),
ь ,
2"<2 С ?(0Л<у.
С другой стороны, так как в промежутке £а, b — yj функция <р (t)
интегрируема в собственном смысле, то по доказанному при достаточно
малом X и сумма % станет меньше у. Отсюда следует (4), что и
требовалось доказать.
В общем случае, когда функция y(t) абсолютно интегрируема
в промежутке [а, Ь}, мы рассмотрим функции
T1(O=ij<£>i+i<o, <р>(о=ша1рцо,
очевидно, неотрицательные и интегрируемые в названном промежутке.
Так как
*Р (0 = <Р1 (О —?«(0,
то вопрос сводится, как и выше, к уже рассмотренному случаю.
Замечание. Пусть функция g(x) непрерывна в промежутке
[а, Ь} и имеет, исключая разве лишь конечное число точек, произ-
576|	$ 5. ИНТЕГРАЛ СТИЛТЬЕСА	95
водную £ (х), причем эта производная * интегрируема (в собственном
или несобственном смысле) от а до Ь\ тогда, как известно [470°, за-
мечание], имеет место формула типа (7):
£(-«) = £ (0)4-$^ (0^-
а
Если g(х) абсолютно интегрируема, то к функции g(x) полно-
стью приложимо изложенное в Ш.
576.	Свойства интеграла Стилтьеса. Из определения интеграла
Стилтьеса непосредственно вытекают следующие его свойства:
*
1°. \dg(x) = g(b) —g(a\,
а
ь	ь 	ь
2° $ [/1 (х) ± А (х)] dg(x) =	(х) dg(x) ±	(х) dg(xy,
а	а	а .
b	b	ь
3°. 5 /(х) d [gt (х) ± g, (х)] — 5 /(х) dgi (х) ± 5 f (х) <fgs (х);
а	а	а
b	b
4°.	V(x)rf[/g(x)] = kl \f(x)dg(x) (k, 1= const).
a	a
При этом в случаях 2°, 3°, 4° из существования интегралов в пра-
вой части вытекает существование интеграла в левой части.
Затем имеем
Ь	с	Ь
5°. $/(х) rfg(x) = \f(x) dg(x) + \f(x) dg(x),
a	a	c
в предположении, что a с b и существуют все три интеграла.
Для доказательства этой формулы достаточно лишь озаботиться
включением точки с в число точек деления промежутка [а, Ь] при
ь
составлении суммы Стилтьеса для интеграла \fdg.
а
По поводу этой формулы сделаем ряд замечаний. Прежде всего,
ь
из существования интеграла J/dg следует уже существование
а
с	b
обоих интегралов ^fdgu \fdg.
а	с
* Если ее значения в точках, где она не существует, выбрать по про-
изволу.
96 гл. XV. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА (576
Для своеобразного предельного процесса, с помощью которого
из стилтьесовой суммы получается интеграл Стилтьеса, имеет
место принцип сходимости Больцано — Коши. Таким образом, по
ь
заданному е^>0 ввиду существования интеграла dg найдется та-
а
кое В 0, что любые две суммы а и а Стилтьеса, которым отве-
чают X и	разнятся меньше чем на е. Если при этом в состав
точек деления включить точку с, а точки деления, приходящиеся на
промежуток [с, Ь], брать в обоих случаях одними и теми же, то раз-
ность а — а сведется к разности <з( — в! двух сумм Стилтьеса, от-
носящихся уже к промежутку [а, с], ибо прочие слагаемые взаимно
уничтожатся. Применяя к промежутку [а, с] и вычисленным для него
стилтьесовым суммам тот же принцип сходимости, заключим о суще-
С
ствовании интеграла \fdg. Аналогично устанавливается и суще-
ь
ь
ствование интеграла \fdg.
с
Особенно заслуживает быть отмеченным тот не имеющий прецеден-
с	b
тов факт, что из существования обоих интегралов \fdg и \fdg,
а	с
b
вообще говоря, не вытекает существование интеграла \f dg.
а
Чтобы убедиться в этом, достаточно рассмотреть пример. Пусть в про-
межутке [—1, 1] функции /(х) и g(x) заданы следующими равенствами:
О при — 1х О,
1 при 0<Xsg 1;
£(*) = {
О при — 1 < х с О,
1 при Osgxsg: 1.
Легко видеть, что интегралы
о
f(x)dg(x),
— 1
1
dg(x)
оба существуют и равны 0, ибо соответствующие им суммы Стилтьеса все
равны 0: для первого это следует из того, что всегда /7(х) = 0, для второго—
из постоянства функции g(x), благодаря чему всегда Ag(x;) = 0.
В то же время интеграл
1
$ /(x)dg(x)
577]	§ 5. ИНТЕГРАЛ СТИЛТЬЕСА	97
не существует. Действительно, разобьем промежуток [—1,1] на части так,
чтобы точка 0 не попала в состав точек деления, и составим сумму
п — 1
’= U /(5.)Дд(хг).
1=0
Если точка 0 попадает в промежуток [ага, xft+1], так что xk < 0 < xk+i, то
в сумме а останется только одно k-e слагаемое; остальные будут нули, потому
что ^g(Xi)—g(xi+1)~g(Xi) = O для l^zk. Итак,
’ =/(?*) fe- (.Xk+1)—g (xft)] =/(?*).
В зависимости от того, будет ли 6*^ 0 или «*>0, окажется а = 0 или а = 1,
так что о предела не имеет.
Указанное своеобразное обстоятельство связано с наличием разрывов в
точке х = 0 для обеих функций /(х) и g(x) [см. 584, 3) и 4)].
577.	Интегрирование по частям. Для интегралов Стилтьеса
имеет место формула
ь	ь	ь
\f(x)dg(x)=f(x)g(*) — \g(x)df(x),	(9)
а	а	а
в предположении, что существует один из этих интегралов; суще-
ствование другого отсюда уже вытекает. Формула эта носит название
формулы интегрирования по частям. Докажем ее.
ь
Пусть существует интеграл \gdf. Разложив промежуток [a, ft]
а
нд части [xit xI+1] (Z = 0, 1, ... , п—1), выберем в этих частях про-
извольно по точке £г, так что
Хя_1	хп
b
Сумму Стилтьеса для интеграла \fdg
а
а = S f — £(*/)]
«=0
можно представить в виде
а = S /Gi-i) g^i) ~ 5 /(?,)g&i) =
i=i ,	«=о
n — I
= - te(«)/(%) 4- S g(*i) [/&) -/&_!)] - gW/Gn-i)}.
4 Г, М, Фихтенгольц, т. III
98j
ГЛ. XV. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА (578
Если прибавить и отнять справа выражение
/(*) g(x) | ba ==f(b)g(b) -f(a)g(a),
то а перепишется так:
° =/(x)g(x) | ba - {g(a) [/(%) -/(а)] +
+ S S(xt) [/&) -/&_,)] + g<J>) [f(b)	}.
i=i
Выражение в фигурных скобках представляет собою стилтьесову
6
сумму для интеграла \gdf (существование которого предположено!).
а
Она отвечает разбиению промежутка [a, Z>] точками деления
а	Ч	-С... £n_i Ь,
если в качестве выбранных из промежутков [$,•_!, cj (Z= 1, ..., п— 1)
точек взять xit а для промежутков [а, %] и [$„_], 6], соответственно,
а и Ь. Если, как обычно, положить X == max (х,+1 — х,), то теперь
длины всех частичных промежутков не превзойдут 2Х. При X —О
ь
сумма в квадратных скобках стремится к § gdf, следовательно, су-
а
b
шествует предел и для а, т. е. интеграл \fdg, и этот интеграл опре-
а
деляется формулой (9).
Как следствие нашего рассуждения, особо отметим тот любопыт-
ный факт, что если функция g(x) в промежутке [а, Z>] интегри-
руема по функции /(х), то и функция f(x) интегрируема по
функции g(x).
Это замечание позволяет добавить ряд новых случаев существо-
вания интеграла Стилтьеса к тем, которые были рассмотрены в 575,
переменив роли функций f и g.
578.	Приведение интеграла Стилтьеса к интегралу Римана. Пусть
функция /(х) непрерывна в промежутке [а, &], a g (х)'монотонно возрастает
в этом промежутке, и притом в строгом смысле *. Тогда, как показал Лебег
ь
(Н. Lebesgue), интеграл Стилтьеса (s) ^/(х) dg(x) с помощью полета-
ет
новки v—g(x) непосредственно приводится к интегралу Римана.
* Последнее мы предполагаем исключительно в целях некоторого упро-
щения изложения.
$ 5. ИНТЕГРАЛ СТИЛТЬЕСА
99
На рис. 29 изображен график функции v =g (х). Для тех значений х = х',
при которых функция g(x) испытывает скачок (ибо мы вовсе не предполагаем
g(x) обязательно непрерывной), мы дополняем график прямолинейным верти-
кальным отрезком, соединяющим точки (x',g(x'—0)) и (х', g (х' + 0)). Так
создается непрерывная линия, которая каждому значению v между
vt=g(a) и V=g(b) относит одно определенное значение х между а и ft. Эта
функция x=g~1(v), очевидно,
будет непрерывной и мо-
нотонно возрастающей в ши-
роком смысле; ее можно
рассматривать как своего рода
обратную для функции
v=g(x).
Именно, если ограничиться
лишь теми значениями v, кото-
рые функция v = g(x) действи-
тельно принимает при измене-
нии х от a aob, yox — g~l(v)
является обратной для нее в
обычном смысле, т. е. относит
v именно то значение х, при
котором g(x) — v. Но из про-
межутка значений v
[g(x' — 0), g(x'4-0)],
связанного со скачком функции
g(x), лишь одно значение
v — v'=g(x') имеет себе соответствующим значение х = х’; другим значе-
ниям v в упомянутом промежутке никакие значения х, очевидно, не отвечают.
Но мы условно относим и им то же значение х = х'; геометрически это и выра-
зилось в дополнении графика функцииy=g(x) рядом вертикальных отрезков.
Докажем теперь, что
ь	v
(S) 5 f (х) dg (х) = (R) 5 f fe"1 (»)) dV,
a	vq
(10)
где последний интеграл берется в обычном смысле, его существование обеспе-
чено, так как функция g-1 (я), а с нею и сложная функция/^1 (о)), непрерывна.
С этой целью разложим промежуток [a, ft] на части с помощью точек деления
e = x0<x1 <...<x(<x;+t <...<x„ = ft
и составим стилтьесову сумму
л— 1
° = £ f (*i)	(*/+i) —£ (*/)] *•
i=0
Если положить t'i = g(x1) (i — 0, 1, ..., n), то будем иметь
«о <	< ••• < Vi <«г+1 <... <пя= К
Так как Xj = g~1 (v,), то
п—\
° = £ f te"1 (»/))	(Дг,< == vi+1 — Vi).
i==0
* Для простоты выбирая в промежутке [х/, х/+1] именно точку Х{.
4*
ICO гл. XV. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА [579
Это выражение имеет вид римановой-суммы для интеграла
v
/(S'-1 (»)) dv.
Отсюда, однако, нельзя еще непосредственно заключить, переходя к пре-
делу, о равенстве (10), ибо даже при Дхг—-0 (X—0) может оказаться, что
Дг»/ к нулю не стремится, если, например, между безгранично сближающи-
мися xt и х,-+, будет заключено значение х = х', где функция g(x) испы-
тывает скачок. Поэтому мы будем рассуждать иначе.
Имеем
V	п-1 ®»+1
5 f (v)) dv=£ $ / (Г1 (v)) dv
Vq	i=0 vi
И
n-1
®= S Ji f(xi)dv,
i~0 -Vf
так что
V	л-1 ®*4-l
о-f/(£-*(«))2 $	(«))и».
Vq	1=0 vi
Предположим теперь Дхг настолько малыми, чтобы колебания функции/(х)
во всех промежутках [х,-, х,-+1] были меньше произвольного наперед задан-
ного числа е > 0. Так как
при vt sg v < vi+1, очевидно, xt sg g~l (v) vi+i,
то одновременно и
В таком случае
\f(.xi)—f(g~i (»)) I <«•
v
| ° — 5 f^g~l (»)) dv | < e (V—1»0).
®o
Этим доказано, что
v
lim о = f (g~* (v)) dv,
откуда и следует (10).
Несмотря на принципиальную важность полученного результата, он не
дает практически удобного средства для вычисления интеграла Стилтьеса.
Как осуществлять это вычисление в некоторых простейших случаях, мы
покажем в следующем п°.
579. Вычисление интегралов Стилтьеса. Докажем следующую
теорему:
1°. Если функция f(x) интегрируема в'смысле Римана в про-
межутке [a, b\, a g(x) представлена интегралом
g{x) = c-\-\^{0dt,
579
§ 5. ИНТЕГРАЛ СТИЛТЬЕСА
101
где функция <р (Q абсолютно интегрируема в [a, Z>], то
ь	ь
&)\f(x)dg(x)==№ ^f(x)y(x)dx.	(11)
а	а
Интеграл справа существует [298, 482]. Существование интеграла
Стилтьеса при сделанных предположениях уже было доказано
[575, III].
Остается лишь установить равенство (11).
Без умаления общности можно предположить функцию <р (х) поло-
жительной [ср. стр. 94].
Составим, как обычно, сумму Стилтьеса
л — 1	п — 1 Х1 -]- 1
а = S	teto+i) — g (Xf)] = S 5	dx'
i=0	i=0 X;
Так как, с другой стороны, можно написать
b	п — 1 xi 4-1
\f{x)<f(x)dx= У, f(x)<f(x)dx,
a	i=0 х,
то будем иметь
b	п — 1 xi -J-1
а—$/(x)y(x)rfx= У $ [/0,-)— / (х)]? (х) <7х.
a	i = 0 xi
Очевидно, для х, х х,Ч1 будет |/($z)—/(х)|йС<ог, где и,- озна-
чает колебание функции /(х) в промежутке [xz, х/+1]. Отсюда выте-
кает такая оценка написанной выше разности:
ь	п-\ xi +1	п-1
а —	(х) ср(х)dx	4{x)dx— У о); Ag(x;).
a	i = 0	x-t	i==0
Но мы уже знаем [575, III], что при X —0 последняя сумма стре-
мится к 0, следовательно,
ь
lim а = /(х) ф (х) dx,
х-о
что и доказывает формулу (И).
В частности, из доказанной теоремы вытекает [если учесть заме-
чание в конце п° 575] такое следствие, удобное для непосредствен-
ного применения на практике:
2°. При прежних предположениях относительно функции f(x)
допустим, что функция g(x) непрерывна во всем промежутке
[а, Ь\ и имеет в нем, исключая разве лишь конечное число точек,
102 ГЛ. XV. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА {W
производную g (х), которая в [а, Ь] абсолютно интегрируема *.
Тогда
ь	ь
(S) $/(x)dg(x) = (R) \f(x)g'(x)dx.
а	а
(12)
Интересно отметить, что интеграл справа в формуле (12) фор-
мально получается из интеграла слева, если, понимая символ dg(x)
буквально как дифференциал, заменить его выражением g'(x)dx.
Обращаясь к случаям, когда функция g(x) оказывается разрывной
(что для практики, как увидим, представляет особый интерес), начнем
с рассмотрения «стандартной» разрывной функции р (х), определяе-
мой равенствами
Р(Х)=/ 0 "Р"	’>
r v 7	(. 1 при ху> 0.
Она имеет разрыв первого рода — скачок — в точке х = 0 справа,
причем величина скачка р ( -1- 0) — р(0) равна 1; в точке х = 0 слева
и в остальных точках функция р (х) непрерывна, функция р (х — с)
будет иметь такой же разрыв в точке х — с справа; наоборот,
р(с — х) будет иметь подобный разрыв в точке х = с слева, при-
чем величина скачка будет равна — 1.
Предположим, что функция /(х) непрерывна в точке х — с, и
ь
вычислим интеграл (S)J /(x)rfp(x — с), где а^с<^Ь (при с = Ь
а
этот интеграл равен нулю).
Составим сумму Стилтьеса:
л— 1
1 = 0
Пусть точка с попадет, скажем, в А-й промежуток, так что xk^c<^xkiA.
Тогда Др(хй — с)—1, а при I k, очевидно, Ap(xz — с) = 0. Таким
образом, вся сумма а сводится к одному слагаемому: а=/($А). Пусть
теперь Х->-0. По непрерывности /(Q->/(c). Следовательно, суще-
ствует (при а с Ь)
ь
(S)^/(x)dp(x — c) = lima=/(c).	(13)
* См. сноску на стр. 95.
§ 5. ИНТЕГРАЛ СТИЛТЬЕСА
103
Аналогично можно убедиться в том, что (при а с Ь)
ь
(S) 5 f(x) dp (c — x) =—f(c)	(14)
а
(при с —а этот интеграл обращается в нуль).
Теперь мы в состоянии доказать теорему, в некотором смысле
более общую чем 2°, а именно, отказаться от требования
непрерывности функции g(х):
3°. Пусть функция f(x) в промежутке [а, Ь] непрерывна, а
g(x) имеет в этом промежутке, исключая разве лишь конечное
число точек, производную g (х), которая абсолютно интегри-
руема в [а, Ь]. При этом пусть функция g(x) в конечном числе
точек
a==^<^cl<^...<Zck<Z-..<icm — b
терпит разрыв первого рода. Тогда существует интеграл Стил-
тьеса и выражается формулой
ь	ь
(S) J/(x)dg(x) = (R)	(х)rfx4-/(а) [g-(а + 0) — g(a)]-f-
а	а
т~- 1
+ S /(Q) [g{ck + 0) - g(ck - 0)] +
Й = 1
+ /(*)[^)-g(^-0)]. (15)
Характерно здесь наличие внеинтегральной суммы, где фигурируют
скачки функции g(x) в точках а или Ь — односторонние *.
Для упрощения записи введем обозначения для скачков функции
g(x) справа и слева:
4 = £(q + 0) — g(ck)	(6 = 0, 1, ..., т — 1),
<4=g(ck)~ g(ck — 0)	(k= 1, 2,	т\,
очевидно, для	— 1, <44~a* = £(c* + 0) — g(ck— 0).
Составим вспомогательную функцию:
&W= У, 4р(х — ck)— У яйр(сй— х),
й=0	й = 1
которая как бы вбирает в себя все разрывы функции g(x), так что
разность gi(x) = g(x) — gi(x)> как мы сейчас установим, оказывается
уже непрерывной.
* Если на деле в какой-либо из этих точек скачка нет, то соответствую-
щее слагаемое суммы обращается в нуль.
104 ГЛ. XV. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА J580
Для значений х, Отличных от всех ck, непрерывность функции
g% (х) не вызывает сомнений, ибо для этих значений непрерывны обе
функции g(x) и gt(x). Докажем теперь непрерывность g%(x) в точке
сДЛ<от) с пр а в а. Все слагаемые суммы gY (х), кроме члена а*р (х—ск),
непрерывны при x — ck справа; поэтому достаточно изучить поведе-
ние выражения g(x) — а£р (х— ck). При x — ck оно имеет значение
g(ck); но таков же и его предел при x->cft4-0:
lim [g(x) — at p (x — cb)]=g(ck + 0) — at = g(ck).
x-Cft+0
Аналогично проверяется и непрерывность функции g%(x) в точке
(А 0) слева.
Далее, если взять точку х (отличную от всех ck), в которой функ-
ция g(x) имеет производную, то вблизи этой точки gx (х) сохраняет
постоянное значение, следовательно, в ней и функция g<i(x) имеет
производную, причем
gi(x) = g'(x).
Для непрерывной функции g%(х), по предыдущей теореме,
существует интеграл Стилтьеса
ь	ь	ь
(S) $ f (х) dgi (х) = (R) f (х) gi (х) dx = (R) f (х) g' (х) dx.
а	а	а
Точно так же легко вычислить и интеграл [см. (13), (14)]
Ь	m —1	ъ
(S) /(х) dgi (х) = 2 at • (S) J f (х) dp (х — cft) —
a	k = 0	а
— У, а* •(S) 5 f (*)(ck — x) =
A = 1	a
m — 1	m
= E Ж) + 2 atf(ek) —f(a) [g(a + 0) - g(a)] +
A=0	k=\
m — 1
+ у /(Q)	+ 0)-g(cft-0)] +/(/>) te(*)-^-0)].
*=i
Складывая почленно эти два равенства, мы и придем к равен-
ству (15); существование интеграла Стилтьеса от/(х) по функции
g(х) = gj (х) -1- gj (х) устанавливается попутно [576, 3°].
580. Примеры. 1) Вычислить по формуле (11) интегралы:
я
2	Т	1
(a) (S) ( x’dln (1 -f-х), (б) (S) ( xdsinx, (в) (S) xdarctgx.
§ 5. ИНТЕГРАЛ СТИЛТЬЕСА
105
2	2
С	(•	X3
Решение, (a) (S) х3 d In (1 -|- х) = (R)	dx —
О	'о
= X3 — X + In (1 + х)) I — In 3 и т. д.
Ответы: (б)	—1; (в) 0.
2) Вычислить по формуле (15) интегралы:
з	(° ПРИ х — ~~ Ь
(a) (S) xdg(x), где g(x) = 2	1 при —1<х<2,
—1	| — 1 при 2 х sg 3;
2
(б) (S) \x3dg(x), где g(x) =
б
— 1 при 0 tg х < у,
1	3
О приу-^хс-у,
„	3
2 при х = -^-,
3
— 2 при у < х < 2.
Решение, (а) Функция g(x) имеет скачок 1 при х = — 1 и скачок —2
при х = 2; в остальных точках g’(x) = 0. Поэтому
з
(S)	xdg(x) = (—!)• 14-2 • (—2)=—5.
1	3
(б) Скачок 1 при х = у и —2 при х = у (значение функции g при
з
х=~2 не влияет на результат); в прочих точках g'(x) = 0.
Имеем:
2
S, 1 \ а / q \ а
х2^(х) = Щ ’И-Дт)
о
3)	Вычислить по формуле (15) интегралы:
2	2	2
(а) $ xdg(x), (б) $ x3dg(x), (в) $ (ха 4- 1) dg(x),
—2	—2	-2
где
g(X) =
х-]-2при —2sgxs=:—1,
2 при — I < х < О,
х24-3 при О^х<2.
106 ГЛ. XV. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА (58®'
Решение.
Производная
Функция g(x) имеет скачки, равные 1, при х = —1 и х — 0.
1 при—2s£x<—1,
g' (*) =
0 при — 1 < х < 0,
2х при 0 < х 2.
Поэтому
2	—12
I xdg(x) = \ х dx 2 i х2 dx-j- (—1) • 1 -|-0-1 = 2-g-,
— 2	—2	о
Аналогично
2	2
xs dg(х) = 11 -у- и (х3 + 1)^(х) = 15-^-.
— 2	—2
4)	Предположим, что вдоль отрезка [а, Ъ] оси х расположены массы, как
сосредоточенные в отдельных точках, так и распределенные непрерывно. Не
делая различия между ними, обозначим для х > а через Ф (х) сумму всех
масс, расположенных в промежутке [а, х]; сверх того, положим, Ф (а) = 0. Оче-
видно, Ф (х) — монотонно возрастающая функция. Поставим себе задачей найти
статический момент этих масс относительно начала координат.
Разобьем промежуток [а, £] на части точками
а — х0 < Xj < ... < х, <х/+1 < ...<хп = Ь.
На отрезке (х,-, х,+1] при «>0 содержится, очевидно, масса Ф (xf+I) — Ф(х,)=
= ДФ (х,). Точно так же на отрезке [a, xt] содержится масса Ф (xt)— Ф (х0) =
= ДФ (х0). Считая массу во всех случаях сосредоточенной, например, на пра-
вом конце промежутка, получим для искомого статического момента прибли-
женное выражение
п 1
м ~ S х«+1 Дф (х«)-
i = 0
При стремлении к 0 всех Дх;, в пределе придем к точному результату:
ь
М = (S) х дФ (х).	(16)
а
Можно было бы и здесь, как это было разъяснено во втором томе по от-
ношению к обыкновенному определенному интегралу [348], сначала установить
«элементарный» статический момент dM = х d<b (х), отвечающий отрезку оси
от х до х dx, а затем «просуммировать» эти элементы.
Аналогично для момента инерции / тех же масс относительно на-
чала найдем формулу
1= (S) jjx2d®(x). а	(17)
а
Важно подчеркнуть, что интеграл Стилтьеса дал возможность
объединить одной интегральной формулой разнородные случаи непрерывно
распределенных и сосредоточенных масс!
§ 5. ИНТЕГРАЛ СТИЛТЬЕСА
107
Пусть непрерывно распределенные массы имеют линейную плотность р (х);
кроме них пусть в точках х = с1, с2, расположены сосредоточенные
массы mlt т2, ..т^. Тогда, исключая эти точки, функция Ф (х) имеет произ-
водную
Ф'(х) = р(х).
В каждой же точке х = с;(/=1, 2.... А)	функция испытывает скачок, рав-
ный именно массе ту, в этой точке сосредоточенной.
Если теперь разложить интеграл (16) по формуле (15), то получим
ь	ь	k
M = (S) jx d<b (x) = (R) j xp(x)dx-|- У, Cjtnj.
a	a	j= 1
Всмотревшись в правую часть, легко в первом члене узнать статический мо-
мент непрерывно распределенных масс, а во втором — статический момент
сосредоточенных масс. Аналогичный результат получится и для интеграла (17).
5)	Чтобы лучше уяснить себе содержание предыдущего упражнения, пред-
лагается:
(а)	составить выражение Ф (х) и построить график его для следующего
распределения масс: массы величины 1 в точках х=1, 2 и 3 и непрерывно
распределенные массы с плотностью 2 в промежутке [1, 3];
(б)	то же — для такого распределения: массы величины 2 при х = 2 и 4 и
непрерывно распределенные массы с плотностью 2х в промежутке [0, 5];
(в)	выяснить распределение масс, если Ф (х) равна функции g(x) задачи 3).
Ответы, (а) В промежутке [1, 3] имеем
	0	для х= 1,
	2х—1	для 1 < х < 2
Ф (х) =		
	2х	для 2=gx<3
	7	для х =3.
(б) В промежутке [0, 5] имеем
	Xs	для	0s	g х< 2,
Ф(х) =	X2	+ 2 для	2<	gx< 4,
	X2	+ 4 для	4s	gXsgO.
(в) Массы величины 1 в точках х = —1 и 0, в промежутке [—2, —1]
непрерывно распределенные массы с плотностью 1, в промежутке [0, 2] —
массы с плотностью 2х.
Рис. 30.
6)	Рассмотрим другой вопрос, в котором интеграл Стилтьеса играет
такую же роль, как и в упражнении 4). Предположим, что на балку (рис. 30),
покоящуюся на двух опорах*, кроме непрерывно распределенной нагрузки
* Это предположение мы делаем лишь ради простоты.
108
ГЛ. XV. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА (580
действуют и сосредоточенные силы. Расположим ось х вдоль по оси балки, а
ось у вертикально вниз (см. рис.). Не делая различий между действую-
щими силами, обозначим для х>0 через F (х) сумму всех сил, приложенных
на отрезке [0, х] балки, включая и реакции опор; далее, пусть F(0) — 0. Силу
F(х) называют перерезывающим усилием в сечении х балки. При
этом силы, направленные вниз, будем считать положительными, а вверх —
отрицательными.
Поставим задачей определить так называемый изгибающий мо-
мент М в произвольном сечении х = с балки. Под этим разумеют сумму мо-
ментов всех сил, действующих на правую (или на левую) часть балки, отно-
сительно этого сечения. При этом, когда (>ечь идет о правой части балки,
момент Считают положительным, если он вращает эту часть по часовой
стрелке (для левой части—обратное правило).
Так как на элементе (х, x-j-dx], скажем, правой части балки приложена
сила F(x-\-dx)— F (x) — dF (х), создающая элементарный момент
dM = (x—t)dF(x),
то, «суммируя», получим
I
М = М (5) = (S) ((х — 5) dF(x).
е
Аналогично, исходя из левой части балки, можно было бы получить (учиты-
вая изменение положительного направления для отсчета моментов)
6
М (5) = (S) J (5 — х) dF(x).	(18)
Легко непосредственно усмотреть, что оба выражения изгибающего мо-
мента в действительности тождественны. Их равенство равносильно условию
I
xdF(x) — ZF(l) = 0,
которое является следствием из условий равновесия
i
F(l) = 0, ^xdF(x) = 0,
выражающих равенство нулю суммы всех сил и суммы моментов (относи-
тельно начала) всех сил, действующих на балку.
Если интенсивность непрерывно распределенной нагрузки обозначить
через q (х), то, исключая точки, где приложены сосредоточенные силы, будет
Пусть сосредоточенные силы Fj<J = 1,2,..., k) приложены в точках x = xj.
Тогда, очевидно, перерезывающее усилие именно в этих точках имеет скачки,
соответственно равные Fj. Далее, применяя, например, к интегралу (18) фор-
мулу (15), получим
М(6) = $ (S — х) q (х) dx + 2 (5 — xj)pj-
.3801
§ 5. ИНТЕГРАЛ стилтьеса
109
В двух слагаемых -правой части легко узнать моменты, порожденные по-
рознь непрерывной нагрузкой и сосреДоточенними силами: интеграл Стил-
тьеса охватывает их единой интегральной формулой.
Установим еще один факт, интересный для теории сопротивления мате-
риалов. Произведя в формуле (18) интегрирование по частям, получим
5
М (6) = J (g — х) dF (х) = (5 — х) F (х)
е в	£
— F(x)rf(e —х)= F(x)dx.
Отсюда ясно, что всюду, за исключением точек приложения сосредото-
ченных сил, имеет место равенство
7)	Пример. Пусть балка длины 1 — 3 несет (рис. 31) «треугольную»
нагрузку с интенсивностью -у х; кроме того, пусть к ней приложены сосре-
доточенная сила, равная 3, в точке Ас=1, и реакции опор, обе равные—3
(они устанавливаются по закону рычДга). Определить перерезывающее уси-
лие F (х) и изгибающий момент М (Й.
Ответ.
F(x) =
«(£) =
0 при х = 0,
х3 — 3 при0<х<1,
х2 при 1 sg х <; 3
0 при х = 3;
15s —35 при O=s=e=sg 1,
5s — 3 при 1 <?g3.
8)	Формула (15) может оказаться полезной и для вычисления обычных
интегралов (в смысле Римана). Проиллюстрируем это на следующем об--
щем примере.
Пусть <р (х)—«кусочно-полиномиаль-
ная» функция в промежутке [a, b\, s>to
означает, что промежуток разлагается на
конечное число частей точками
а =50 < < ... < 5^ = А
так, что в каждой из частей функция
<р(х) представляется полиномом не вы-
ше л-й степени. Заменив значения функ-
ции <р(х) и всех ее производных в точ-
ках а и b нулями, обозначим через
Рис. 31.
b^(j = O, 1,..., ft; i = 0, 1,..., л) вели-
чину скачка i-й производной <?’’’ (х)в /-й
точке х = 5а
Пусть, далее,/(х)— любая непрерывная функция; положим
Л (*) = $/ (*) и» вообще, Fs (х) = Fs_i (х) dx (s > 1).
ПО ГЛ. XV. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА [580
Тогда имеет место следующая формула:
*
J/(x)<p(x)dx =
а
k	k	k
=- Ё л (ц а/’ + 2 о »/’—•+(- Dft+1 S di)
j=0	/=0	/=0
Действительно, последовательно находим
ь	ь	ь	ь
(R) $ f (х) ? (х)dx =(S) 5 ? W dFt (х) = <р (х) Ft (х) — (S) J (х) dv (х);
а	а	а	а
двойная подстановка исчезает, а интеграл
ь	ь
J л (х)	(х) = 2 Л (?;) «/’ + J Л (х) (X) dx-,
a	j	а
аналогично
ь	ъ
F, (х) (х) dx = - 2 F2 (gy) 8;1’ - F3 (х)	(х) dx
a	j	а
И Т. Д.
9)	Установим, в заключение, с помощью формулы (11) одно полезное
обобщение формулы интегрирования по частям для
обыкновенных интегралов. Именно, если и (х) и v (х) обе абсо-
лютно интегрируемы в промежутке [a, b], а (/(х) и И(х) определяются
интегральными формулами:
U(x) = U (а)	и (t) dt,
а
V(x)=V(a)+]v(t)dt,
а
то справедлива формула
ь
U (x)v (х) dx= U (х) V (х)
а
ь ь
— V (х) и (х) dx.
а а
(19)
Для доказательства, по формуле (И) заменим интеграл слева интегралом
Стилтьеса и проинтегрируем по частям [577]:
ь	ь
J i/(x) v (х) dx = 5 и<х') d v W = и(х) v W
a	a
b b
V (x) dU(x).
§ 5. ИНТЕГРАЛ СТИЛТЬЕСА
111
Остается еще раз применить формулу (11) к последнему интегралу, чтобы
прийти к (19).
Здесь функции и (х), v (х) играют -как бы роль производных от функций
U(x), V (х), не будучи ими на деле. При непрерывности функций «(х)
и v (х) мы возвращаемся к обычной формуле интегрирования по частям, ибо
тогда наверное	(х) = ц (х), v4x)=v(x).
581. Геометрическая иллюстрация интеграла Стилтьеса. Рассмотрим
интеграл	ъ (S) \f{t)dg(t),	(20) а
предполагая функцию f(t) непрерывной и положительной, a g(f)— лишь мо-
нотонно возрастающей (в строгом
смысле); функция g(t) может иметь
и разрывы (скачки).
Система параметрических
уравнений
x=g(f), y—f{t) (21)
выражает некоторую кривую (К),
вообще говоря, разрывную (рис.
32). Если при некотором < =
функция g(t) испытывает скачок,
так что g(t0 — 0) < g (t0 -f- 0), то
этим предельным значениям х =
= g(f) отвечает одно и то же
предельное значение у рав-
ное /(/0). Дополним кривую (А) всеми горизонтальными отрезками, соеди-
няющими пары точек
te (ta - о), f(toy> и (g (t0+о), /(/<,)),
отвечающие всем скачкам функции g(f) (см. рис.). Таким образом, соста-
вится уже непрерывная кривая (Z.). Покажем, что интеграл (20) пред-
ставляет площадь фигуры под этой кривой, точнее, площадь фигуры,
ограниченной кривой (£), осью х и двумя крайними ординатами, отвечаю-
щими абсциссам g{a) и g(b).
С этой целью разложим промежуток [а, Ь\ на части точками
а =/0</1<...<Т/<Тг+1 <...<<„ = 6
и в соответствии с этим промежуток [g (a), g(6)] на оси х — на части точ-
Ками	g (а) < g (<i) < ... < g (ti) < g (</+1) <... < g (b).
Введя наименьшее и наибольшее значения т, и А1,- функции f(t) в г'-м про-
межутке <i+j], составим нижнюю и верхнюю суммы Стилтьес а—Д арбу
5 = J] mi Ag (ft), $ = Jg Mt Ag {tt).
i	i
Легко видеть теперь, что они представляют площади фигур, составленных
из входящих и из выходящих прямоугольников, между которыми содержится
рассматриваемая криволинейная фигура.
Так как при стремлении к 0 всех Ai, обе суммы стремятся к общему
пределу (20), то отсюда следует [336], что наша фигура квадрируема и пло-
щадью ее служит действительно интеграл (20).
112 ГЛ. XV. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА (582
*•
582. Теорема о среднем, оценки. 1°. Пусть в промежутке [а, й]
функция f(x) ограничена:
m^f (х)^М,
a g(x) монотонно возрастает. Если существует интеграл Стил-
тьеса I от f (х) по g(x), то имеет место формула
ь
1 = (S) ^/(х) dg(x) = [х [g(b) — g(а)], где т р, < М. (22)
а
Это и есть теорема о среднем для интегралов Стил-
тьеса.
Для доказательства будем исходить из очевидных неравенств для
стилтьесовой суммы а:
т W) — g(a)] < а < М [g(b) — g(a)}.
Переходя к пределу, получим
—	g-(a)]	(23)
или *
_ 1
/Я	—'м-----7Т М.
g(b) — g(a)
Обозначая написанное отношение через р, придем к (22).
Если функция /(х) в промежутке [а, Ь] непрерывна, то обычным
путем убеждаемся в том, что р есть значение функции в некоторой
точке этого промежутка, и формула (22) приобретает вид
ь
^'\f{x)dg{x)—f^}[g{b) — g{a)\, где а^Л^Ь. (24)
а
2°. В практике интегралов Стилтьеса наиболее важным яв-
ляется случай, когда функция /(х) непрерывна, а функция g(x)
имеет ограниченное изменение. Для этого случая справедлива такая
оценка интеграла Стилтьеса:
ь
|5/(х)^(х)|^ЖУ,	(25)
а
где
&
М— max |/(х)|, V=\Jg(x).
a=~xs$b
* Мы предполагаем g(b)>g(a), ибо случай g(b) = g(a) [т. е. g(x) —
= const] не представляет интереса: тогда обе части формулы (22) — нули.
§ 5. ИНТЕГРАЛ СТИЛТЬЕСА
113
Действительно, для суммы Стилтьеса а будет
Н = I §/&) Ag(xO| J |/&) 11 Д^(х/)|
< М. | g(xw) -g(x,) | < М V,
I
так что остается лишь перейти к пределу, чтобы получить требуе-
мое неравенство.
3°. Отсюда вытекает, в частности, и опенка близости суммы а
к самому интегралу Стилтьеса / (при прежних предположениях
относительно функций / и g). Представив а и I в виде
xi+i
а = £/0,.)Д£(х,) = £ $ /0,)^(х),
i	i х.
Xi+1
I=X J
i xl
и почленно вычитая эти равенства, получим
Xi + 1
°-1=Х $ V&)~f(x)]dg(x).
i xt
Если, как обычно, обозначить через <о,- колебание функции f(x)
в промежутке [хь х;+1], так что
|/(U— /(х)|^<ог Для Xi^X^Xi+l,
хш
то, применяя оценку (25) к каждому интегралу в отдельности,
xi
будем иметь
*й-1	xi + l
§ [/Gi) — f (*)] dg(X) |	<»; V SW-
xi	xi
Если промежуток [а, Ь\ раздроблен на столь мелкие части, что
все <ог е, где е 0 — произвольное наперед взятое число, то за-
ключаем, что
ь
|<з —	g(x).	(26)
а
Эти оценки будут нами использованы в следующем п°.
114 ГЛ. XV. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
583. Предельный переход под знаком интеграла Стилтьеса.
1 °. Пусть функции fn (х) (я — 1, 2, 3, ...) непрерывны в проме-
жутке [а, й] и при п-+оо равномерно стремятся к пре-
дельной функции
f(x) = lim /л (х)
[очевидно, также непрерывной, 436], a g(x) — функция с ограни-
ченным изменением. Тогда
ь	ъ
lim \fn(x)dg(x) = \f(x)dg(x).
П-¥СО а	а
Доказательство. По заданному е0 найдется такое N,
что при л>М будет для всех х
1А(*)—/(*)1<е-
Тогда, в силу (25), для п^> N
ъ	ь
15 fn (*) dg(x) — \f(x) dg(x) । =
a	a
b	b
= J [fn (x) — f(x)] dg(x) e V g {X),
a	a
что, ввиду произвольности e, и доказывает теорему.
2°. Пусть теперь функция f(x) непрерывна в промежутке [а, Ь],
а функции gn(x) (л=1, 2, 3, ...) — все с ограниченным измене-
нием в этом промежутке. Если полные изменения этих функ-
ций в их совокупности ограничены:
ь
V(л=1, 2, 3, ...)
а
и Sn (.х) при п-+ оо стремятся к предельной функции
g(x)= lim gn(x),
TO
b	b
lim \f(x) dgn(x) — dg(x).
n-*<na	a
Доказательство. Прежде всего убедимся в том, что предель-
ная функция g(x) сама также будет иметь ограниченное изменение.
Разложив промежуток [а, Ь} произвольным образом на части точками
§ 5. ИНТЕГРАЛ СТИЛТЬЕСА
115
будем иметь (при любом п)
ь
21Sn<х.+1) — Sn {Xi) \^\f g„(x)^ V.
i	а
Переходя к пределу здесь при п—► оо, получим
'£l\g(xi+1) — g(Xi)\^ V,
i
откуда и
ь
V S(x)^sz V.
а
Составим суммы Стилтьеса
0 = ^f(Xi) ^g(Xi), а„ = 2/(хй bgn (xt).
i	i
Если предположить, что промежуток [a, при этом разложен на
столь мелкие части, что колебание функции f(x) в каждой из них
будет уже меньше произвольного наперед взятого числа е^>0, то,
в силу оценки (26), при всех п
ь	ь
|°n — \f(x)dgn(x)\^tV, | a — Jj/(jc)rfg(jc)! ^sV. (27)
а	а
С другой стороны, если разбиение, выбранное под указанным
условием, фиксировать, то, очевидно, ая -> а при п -> оо, так что
найдется такое N, что для будет
1°« — а1<®‘	(28)
Тогда для тех же значений п будем иметь, в силу (27) и (28),
ь	ь	ь
| \fdgn — $ fdg\| fdgn — | + | — ° 1 +
а	а	а
b
+ |o-$/</g|<(2V'+1)S,
а
откуда, ввиду произвольности е, и следует требуемое заключение.
584. Примеры «дополнения. 1) Предполагая функцию g (х) монотонно
возрастающей в строгом смысле, можно доказать относительно
числа Е, фигурирующего в формуле (24), более точное утверждение:
а<;<Ь.
116
ГЛ. XV. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА [584
Действительно, обозначив через ти М наименьшее и наибольшее значе-
ния функции /(х) в промежутке [а, Ь\ и считая т<М*, легко найдем такую
часть [<*,₽] этого промежутка, в которой границами f(x) служат числа т'>т
и М' < ЛТ, так что [ср. (23)]
т [g (₽) — g («)] < tn' [g (₽) — g (a)] =< i S) $ sg
AT fe (₽) - g (a)] < M [g (P) - g (a)].
Написав для промежутков [в, а] и [Р, ft] неравенства вида (23) и склады-
вая их с предыдущими, получим взамен (23) более точные неравенства:
т [£ (b) — g- (в)] < / < М [g (ft) — g (в)],
так что число
_ I
11	g(b)—g(a)
лежит строго между т и М; а тогда найдется и $ строго м е ж д у а и Ь, для
КОТОрОГО [Л = /($), и т. д.
2)	Используя формулу (11) п° 579, формулу интегрирования по частям и
теорему о среднем для интегралов Стилтьеса [577; 582, Г], очень легко
наново установить вторую теорему о среднем для обыкновен-
ных интегралов [306].
Итак, пусть/(х) интегрируема (в смысле Римана), а g(x) монотонно
возрастает ** в промежутке [а, 6]. Введем функцию
F(x) — ^f(x)dx
а
(а^х^ by,
она, как мы знаем, будет непрерывна [305, 1Г].
Теперь последовательно имеем
й	ь	й
$ f (x)g (х) dx = \)g(x)dF(x)=g (х) F (х) |a — $ F (x) dg (x) =
=g (ft) F (ft) - F (E) [g (ft) - g («)] = g (a) F (£) + g (ft) [F (ft) - F (E)] =
e	й
=g («) J/PO dx + g(.b) j f W dx (a ==£ E ft),
a	«
что и требовалось доказать.
Если g (х) монотонно возрастает в строгом смысле, то на основании
сделанного в 1) замечания можно точнее сказать относительно Е: a<E<ft.
3)	Доказать, что, если в точке х = с одна из функций fug непре-
рывна, в то время как другая в окрестности этой точки ограничена, то
с	b
существование интегралов (S) и (S) влечет за собой существование и
а	с
й
(s) J [см. 576, 5”].
а
* При т = М функция /(х) сводится к постоянной, и значение может
быть вообще взято произвольно.
** Случай, когда g(x) монотонно убывает, легко приводится к этому.
§ 5. ИНТЕГРАЛ СТИЛТЬЕСА
117
С этой целью заметим, что, если при составлении стилтьесовой суммы а
мы будем включать точку с в состав точек деления, то сумма а будет слагаться
из двух аналогичных сумм для частичных промежутков [а, с] и [с, J]; при
с	ь
Х = шахДхг —О она будет стремиться к сумме интегралов J fdg -f- $ fdg.
а	с
Пусть теперь точка с не входит в число точек деления. Присоединяя к ним
точку с, мы от а перейдем к новой сумме а, про которую мы уже знаем,
что при X —»0 она имеет указанный предел. Таким образом, достаточно
показать, что разность а — а будет вместе с X стремиться к 0.
_ Пусть точка с попадает в промежуток [л>, х^+1]; тогда сумма 5 отли-
чается от суммы а лишь тем, что вместо слагаемого
f^k)\g(.xk+l)—g(xk)\
в ней имеется два слагаемых:
/(£')& (0-£(-rft)] +/(Г) fe(xft+1)-g(c)],
где £' и $' выбираются произвольно под условиями xk с и csg s’ х*+1.
Положив для упрощения $' = 5’ = с, сведем последнее выражение к
[g(*ft+1)— £'(**)].
так что
а — а = [/(£*)—/(c)] [g(xft+1)~g(xft)].	(29)
Когда X —* 0, то один из множителей правой части бесконечно мал, в то
время как второй ограничен; следовательно, а — а —0, что и требовалось
доказать.
4)	Если обе функции /(х) и g(x) оказываются разрывными в одной
и той же точке х = с(а^с^Ь), то интеграл Стилтьеса
ь
\f(x)dg(x)	(30)
а
заведомо не существует.
Для доказательства будем различать два случая. Пусть сначала a<ccb,
и пределы g (с — 0) ng (с 4-0) не равны. Тогда при построении суммы
Стилтьеса мы точку с не станем вводить в число точек деления; пусть,
скажем, xk < с < х^+1. Выбрав один раз s* ф с, а другой раз взяв с в каче-
стве составим две суммы а и 5, разность которых сведется к выражению
(29). Сближая точки деления, будем иметь
g —g (xft) -> g (c 4- 0) — g (c — 0) ф 0.
Кроме того, точку можно выбирать так, чтобы и разность /($ft)—/(с) была
по абсолютной величине большей некоторого постоянного положительного
числа. Тогда разность а — а не стремится к 0, так что интеграл сущест-
вовать не может.
Если же g(c — 0) = g(c4-0), но их общее значение отлично от g(c)
[«устранимый разрыв»] *, то, наоборот, включим с в число точек деления;
пусть c = Xfe. Если/(х) имеет, например, разрыв в точке х = с справа,
то, как и только что, составим две суммы а и а, разнящиеся лишь выбором
* Сюда относится и случай, когда либо с = а и ^(«4"°) отлично от
g(a), либо с — Ь и g(b — 0) отлично от g(b).
118
ГЛ. XV. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА [584*:
для а точка взята произвольно между xk = c и хА+1, а для а в каче-
стве 5* взята с. Попрежнему имеем (29), и рассуждение завершается аналогично.
Упражнения 3) и 4) проливают свет на тот замечательный факт, о кото-
ром говорилось в конце п° 576.
5)	Пусть f(x) непрерывна, a g(x) имеет ограниченное изменение в про-
межутке [а, &].
Опираясь на оценку (25), доказать непрерывность интеграла Стил-
тьеса
I(x) = \f(t)dg(t)
а
по переменному верхнему пределу х в точке х0, где функция g(x) не-
прерывна.
Заключение сразу вытекает из неравенства
17 (х0Дх) —/(х0) | =
Хй + Ьх
max fix)-
V £<*)>
а $ Ь
ха
если принять во внимание, что в точке ха должна быть непрерывна и
X
вариация^^g(x) [571, 9°].
а
6)	Если 5 есть кдасс непрерывных в промежутке [a, й] функций, а ® —
класс функций с ограниченным изменением в этом промежутке, то, как известно,
каждая функция одного класса интегрируема по каждой функции другого
класса. Доказать, что ни один, ни другой из этих классов не может
быть расширен с сохранением упомянутого свойства.
Это, ввиду 4), почти очевидно относительно класса 5. Действительно,
если функция f(x) имеет точку разрыва х0, то она заведомо не интегри-
руема, например, по функции с ограниченным изменением р(х— х0) [573],
имеющей ту же точку разрыва.
Пусть теперь g(x) в промежутке [в, Z>] имеет бесконечное полное
изменение; в этом предположении построим такую непрерывную функцию
/(х), для которой интеграл (30) не существует.
Если разделить промежуток [в, Z>] пополам, то хоть в одной из половин
полное изменение функции g(x) тоже будет бесконечно; разделим эту
половину снова пополам и т. д. По этому методу определится некоторая
точка с, в каждой окрестности которой g(x) не имеет ограниченного
изменения. Для простоты пусть с — Ь.
В таком случае легко построить последовательность возрастающих и
стремящихся к b значений х = в„:
а = в0
так, чтобы ряд .
ОО
S I g(ai+i)—д(в«)1
1 = 0
расходился. Для этого ряда затем можно подобрать такую последова-
тельность стремящихся к 0 чисел //>0 (i = l, 2, 3,...), чтобы и ряд
00
У! /«|д(а;+1)—2WI	(31)
i = 0
584]
5 5. ИНТЕГРАЛ СТИЛТЬЕСА
119
все же расходился [ср. 375, 4) и 7)]. Теперь определим функцию f(x),
полагая
/(fli)=/<sign |g(a/+l) —	(х=0, 1, 2, ...),
/(*) = 0,
а в промежутках (а/, а,-+1) считая f(x) линейной:
/(х) =/(«,) +	(х_ а.)	(i = 0, 1, 2, ...).
а«+1 “/
Очевидно, /(х) будет непрерывна. В то же время, ввиду расходимости
ряда (31), при п —-<зо и
п—1	п— 1
°п = У	У /<|g(«i+i)—g(e»)R + °о>
i=0	i=0
так что интеграл от f по g действительно не существует.
Доказанное утверждение можно сформулировать и так: если интеграл
Стилтьеса (30) для данной функции f существует по любой g из ®,
то f необходимо принадлежит %; аналогично, если этот интеграл по
данной функции g существует для любой f из 8, то g необходимо при-
надлежит ®.
7)	В первой теореме о предельном переходе под знаком интеграла
Стилтьеса [583, 1°] мы поставили требование, чтобы последовательность
функций {fn (х)} стремилась к предельной функции /(х) равномерно.
Можно, однако, заменить это требование более общим условием, что эти
функции ограничены в их совокупности:
|/я(х)|^Л4
(Л1 = const, а^х^Ъ, п = 1, 2, 3, ...)
[Только при этом нужно еще наперед предположить непрерывность
предельной функции /(х).]
При доказательстве достаточно рассмотреть случай, когда g(x) возрастает
в строгом смысле [см. замечание в п° 570]. Но для этого случая
можно воспользоваться преобразованием, проведенным в п° 578 [см. (10)]:
ь	v
(s) $ /я (*) dg (х) = (R) J fn <g~l (»)) dv,
а
b	И
(s) J	dg (х) = (R) J /(g"1 (v)) do
a
и, имея дело уже с римановыми интегралами, просто применить теорему
А р ц е л а [526].
8) Укажем, в заключение, другую трактовку понятия интеграла
Стилтьеса, связав его с понятием аддитивной функции от промежутка
[ср. 348].
Пусть для каждой части [а, Р] данного промежутка [а, 6] определено
число G([a, ₽]), причем, если промежуток [а, р] точкой 7 разложен на части
[“> 7] и [7, Р], то и
G([a, ₽]) = G([«, 71)+G([7, ₽]).
Тогда G([a, ₽]) есть аддитивная функция от переменного
промежутка [а, р]. Предположим, что кроме нее для промежутка [а, Ь]
* Напомним, что signz есть + 1, 0 или —1 в зависимости от того,
будет ли z > 0, = 0 или < (X Во всех случаях
zsignz = |z|.
120 ГЛ. XV. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА [585*
задана и функция точки/(х). Разложим теперь, как обычно, проме-
жуток [a, Z»] точками
и - х0 <С хг <^ ... <С xn_i <С хп - b
на части [х,-, хг+1] (i = 0, 1, ..., п—1), в каждой части произвольно выберем
по точке и, наконец, составим сумму
п — 1
«= 5 f&)G(\xit xi+1]).	(32)
i = 0
Предел этой суммы при X = max (х,+1 — х(-) —► 0 и есть интеграл Стилтьеса,
который естественно — учитывая процесс его построения — обозначить так:
ь
$/(х) G(dx).	(33)
а
Если определить вторую функцию точки g(x), положив
g(x) = G([e, х]) для х> a, g(a) = О,
то, ввиду аддитивности функции G, во всех случаях
<?([», ₽!) = £(₽) -£(«),	(34)
так что сумма (32) сведется к обыкновенной стилтьесовой сумме
п — 1
’= У /(WlgUi+i) — £(*<•)],
i —О
а предел (33) — к обыкновенному интегралу Стилтьеса
ь
(s)\f(x)dg(x).
а
Обратно, если существует последний интеграл, то, определив функцию от
промежутка равенством (34) (причем легко проверить, что она окажется адди-
тивной), можно свести обыкновенный интеграл Стилтьеса к интегралу (33).
585.	Сведёние криволинейного интеграла второго типа к ин-
тегралу Стилтьеса. После того как читатель освоился с интегралом
Стилтьеса, полезно теперь вернуться к рассмотрению криволи-
нейного интеграла второго типа [546]:
5 f(x, y)dx [или § f(x, _y)dyj.	(35)
(АВ)	(АВ)
Представим себе, что кривая (АВ) задана параметрически уравне-
ниями
х = ?(0> _У = ф(О
и описывается именно в направлении от А к В, когда t монотонно
изменяется от а до р. Пусть для определенности а<^р. Тогда точ-
кам Ai (i = 0, 1,..., и), взятым на кривой для образования интеграль-
ной суммы, будут отвечать возрастающие значения параметра t;
®---С
585]
S 5. ИНТЕГРАЛ СТИЛТЬЕСА
121
а выбранной на дуге АгА;+1 точке М,— значение ^ = тг,
(/ = 0, 1, п—1). Сама же интегральная сумма, например, для
первого из интегралов, напишется в виде
°=£/(?	ф«»д?(О-
i
Непосредственно ясно, что она представляет собою стилтье сову сумму,
так что криволинейный интеграл второго типа по самому
определению отождествляется с частным случаем интеграла
Сти лтьеса:
„	Л
5 f (х, J) dx = (s)	(0, ф (О) d'f (0.
(АВ)	а
Аналогично и
J f(x, у) dy = (S) $/(? (0, ф (0) </ф (0.
(АВ)	а
Отсюда с легкостью получаются очень общие условия существо-
вания криволинейного интеграла (35); достаточно предположить
функцию f (х, у) непрерывной, а функцию ср (t) [или ф (0, смотря
по случаю] имеющей ограниченное изменение [575, 1°].
В частности, если кривая АВ спрямляема [572], а функции
Р(х, У) и Q (х, у) непрерывны, то существует интеграл
Р	Р
Pdx 4- Q dy = Р (ср (0, ф (0) dy (0 + $ Q (? (0, ф (0) Фф (0.
(АВ)	а	а
Теперь, если учесть сказанное в 579 о вычислении интегралов
Стилтьеса [особенно, см. 2°], то можно наново получить фор-
мулы (4), (5) или (6) п° 547, и даже при более общих предположе-
ниях, чем раньше.
Далее, легко обобщить теперь окончательный результат п° 551:
площадь фигуры (D), ограниченной непрерывной с пр ямляе мой
кривой, выражается любой из формул (9), (10) или (И) указан-
ного п°. При этом ничего не придется менять в рассуждениях, ибо
лемма п° 550 (и замечание к ней) непосредственно обобщается на
случай спрямляемой кривой; см. также 572, заключительное
замечание.
Наконец, и вся теория независимости криволинейного интеграла
от пути [§ 3] также непосредственно распространяется на случай
интегралов, взятых по любым спрямляемым путям.
ГЛАВА ШЕСТНАДЦАТАЯ
ДВОЙНЫЕ ИНТЕГРАЛЫ
Рис. 33.
§ 1.	Определение и простейшие свойства
двойного интеграла
586.	Задача об объеме цилиндрического бруса. Наподобие того,
как задача о площади криволинейной трапеции привела нас к понятию
простого определенного интеграла [294], аналогичная задача об объеме
цилиндрического бруса приведет нас к но-
вому понятию — двойного (определен-
ного) интеграла.
Рассмотрим тело (V), которое сверху
ограничено поверхностью
z=f(x, у),	(1)
с боков — цилиндрической поверхностью
с образующими, параллельными оси z, на-
конец, снизу — плоской фигурой (Р) на
плоскости ху (рис. 33). Требуется найти
объем V тела * *.
Для решения этой задачи мы прибег-
нем к обычному в интегральном исчисле-
нии приему, состоящему в разложении искомой величины на элементар-
ные части, приближенному подсчету каждой части, суммированию и
последующему предельному переходу. С этой целью разложим
область (Р) сетью кривых на части (РД, (Р2), ..., (Рп) и рассмотрим
ряд цилиндрических столбиков, которые имеют своими основаниями
эти частичные области и в совокупности .составляют данное тело.
Для подсчета объема отдельных столбиков возьмем произвольно
в каждой фигуре (Р,) по точке: ($f, rti). Если приближенно принять
каждый столбик за настоящий цилиндр с высотой, равной апликате
/(^•> г./)> то объем отдельного столбика оказывается приближенно равным
'	/(?/, т(1-)-Рг,
* Если функцию f(x,y) предположить непрерывной, а плоскую область
(Р) —квадрируемой, то самое существование объема для данного слу-
чая легко вытекает из соображений, изложенных в пп° 341 и 337.
587]	? 1. ОПРЕДЕЛЕНИЕ И СВОЙСТВА ДВОЙНОГО ИНТЕГРАЛА	123
где Pt означает площадь фигуры (Р<). В таком случае приближенное
выражение объема всего тела будет
t= 1
Для повышения точности этого равенства будем уменьшать раз-
меры площадок (Р{), увеличивая их число. В пределе, при стремлении
к нулю наибольшего из диаметров всех областей (/>), это равенство
делается точным, так что
V=lim	(2)
i = 1
и поставленная задача решена.
Предел этого вида и есть двойной интеграл от функции f(x,y)
по области (Р); он обозначается символом
Эджмир,
(Р)
так что формула (2) для объема принимает вид*
V=\\f(x, y)dP.	(2»)
(Р)
Таким образом, двойной интеграл является прямым обобщением
понятия простого определенного интеграла на случай функции двух
переменных. Он играет важную роль также при определении различ-
ных геометрических и физических величин.
587.	Сведёние двойного интеграла к повторному. Продолжая
трактовать двойной интеграл геометрически, как объем цилиндриче-
ского бруса, мы дадим здесь же указания относительно его вычисле-
ния путем сведёния к повторному интегралу.
Во втором томе мы уже имели дело с задачей вычисления объема
тела (V) по его поперечным сечениям [342]. Напомним относящуюся
сюда формулу. Пусть тело ограничено плоскостями х — а и х — Ь
(рис. 34). Допустим, что сечение тела плоскостью, перпендикулярной
к оси х и отвечающей абсциссе х (a sg х Ь), имеет площадь Q (х).
Тогда объем тела, в предположении его существования, выразится
формулой
V=\Q(x)dx.	(3)
&
* Выводу этой формулы нетрудно придать и вполне строгую форму;
см. замечание в п° 590.
124
ГЛ. XVI. ДВОЙНЫЕ ИНТЕГРАЛЫ
[587
Применим теперь эту формулу к вычислению объема цилиндриче-
ского бруса, о котором была речь в предыдущем п°. Начнем с про-
стого случая, когда в основании бруса лежит прямоугольник [a, b; с, d]
(рис. 35).
Сечение бруса плоскостью х = х0 (а х0 6) есть криволиней-
ная трапеция Для нахождения ее площади спроектируем эту
фигуру на плоскость yz; мы получим конгруентную с ней трапецию
(ибо проектирование происходит без искажения). Итак,
Q (х0) = пл. офЗу = пл. «1Р13171.
Но уравнение линии уД на плоскости yz, очевидно, будет
z у) (с < d).
Пользуясь известным выражением площади криволинейной трапе-
ции в виде определенного интеграла, будем иметь
d
Q(x0) = ^/(x0) j)dy.
С
Так как наше рассуждение относится к любому сечению, то вообще
для а х b
d
Q(x) = \f(x,y)dy*.
Подставляя это значение Q(x) в формулу (3), получим
b d
V—^dx \f (х, y)dy.
a c
* Эта функция от x к тому же непрерывна [506], что мы и пред-
полагали при выводе формулы (3).
588}
§ 1. ОПРЕДЕЛЕНИЕ И СВОЙСТВА ДВОЙНОГО ИНТЕГРАЛА
125
Но мы имеем для объема V и выражение (2), следовательно,
& d
\\f(x,y)dP=\dx\f(x,y)dy	(4)
(Р)	а с
— двойной интеграл приведен к повторному.
Аналогичный результат можно получить и для более общего слу
чая, когда область (Р) на пло-
скости ху представляет собой
криволинейную трапецию, огра-
ниченную двумя кривыми:
У=Уо(х), У=У(х)
(a^x^b)
и двумя ординатами х = а и
х = Ь (рис. 36). Разница по
сравнению с рассмотренным
случаем состоит в следующем:
раньше при любом фиксирован-
ном х = х0 изменение у происхо-
дило в одном и том же промежутке [с, d], а теперь этот промежуток
[Уо (•*»)> Г (хе)]
сам зависит от х9, так что
У(*о)
Q(xe)= f(x*,y)dy.
Уо (*о)
Окончательно получим
b Y (х)
V=\\f(x, y)dP—\dx f(x, y)dy*.	(5)
(О	а ,Уо (ж)
Познакомив читателя с понятием двойного интеграла и с его
вычислением в геометрической трактовке, мы перейдем теперь к более
общему изложению вопроса с «/исто аналитической точки зрения.
588 Определение двойного интеграла. Впрочем, и здесь нам
не Обойтись без геометрии или, по крайней мере, без геометри-
ческого языка [160—163]. Мы будем говорить о «двумерной
области» (Р), где определена рассматриваемая функция двух пере-
менных, «кривыми» делить ее на частичные «области», будем брать
«площади» этих «областей» и т. п. На деле это — «области» и «кри-
вые» из арифметического двумерного пространства, их «точ-
ками» служат пары чисел. Но обыкновенно все эти «образы»
заменяются для удобства соответствующими им настоящими геометри-
* И здесь внутренний интеграл представляет собой непрерывную функ-
цию от х [см. 509].
126
ГЛ. XVI. ДВОЙНЫЕ ИНТЕГРАЛЫ
(588
ческими образами, не делая никакой разницы между ними. В частности,
под «площадью области» из арифметического двумерного пространства
разумеется всегда площадь соответствующей геометрической области.
Напомним, что для квадрируемости области, ограниченной какой-
либо кривой, необходимо и достаточно, чтобы эта кривая имела
площадь 0 [337]. Широкий класс таких кривых образуют гладкие
кривые или кривые, состоящие из конечного числа гладких кусков
(так называемые кусочно-гладкие кривые)*. Мы будем пред-
полагать впредь, что как контур области (Р), так и кривые,
которыми мы разлагаем ее на части, все имеют площадь О
(например, принадлежат к указанному классу); этим обеспечивается
существование всех нужных нам площадей.
Вернемся теперь к понятию двойного интеграла, фактически уже
введенному в п° 586, и дадим в развернутом виде общее его опре-
деление.
Пусть в области (Р) определена функция f(x, у) **. Разобьем
область (Р) сетью кривых на конечное число областей (Pt),
(Ра),..., (Р„), площади которых будут Р1( Р4,..., Р„. Хотя проще
всего эти частичные области представлять себе связными, но для
облегчения дальнейшего изложения выгодно не исключать
для них возможности быть и несвязными. В пределах г-й
элементарной области (Р,) возьмем по произволу точку ($,-, т]г), зна-
чение функции в этой точке /(?,, ?],•) умножим на площадь Рг соот-
ветствующей области и все подобные произведения сложим. Полу-
ченную сумму
п
°= S/О/. tn)Pi
i=l
будем называть интегральной суммой для.функции f(x, у)
в области (Р).
Обозначим через К наибольший из диаметров*** частичных
областей (Pf).
Конечный предел1* 1 интегральной суммы а при Х->0 назы-
вается двойным интегралом функции f (х,у) в области (Р)
и обозначается символом
/=$$/(*, y)dP.
(Р)
Функция, имеющая интеграл, называется интегрируемой.
* Можно, не нарушая указанного свойства, допустить даже наличие
конечного числа особых точек.
•• Никаких предположений о непрерывности ее мы при этом не делаем.
*** Напомним, что диаметром точечного множества называется точ-
ная верхняя граница расстояний между двумя произвольными точками мно-
жества. В случае плоской замкнутой области, ограниченной непрерывной
кривой, диаметром служит попросту наибольшая хорда. См. 174.
** Читатель легко сам установит точный смысл этого нового «предела».
5 1. ОПРЕДЕЛЕНИЕ И СВОЙСТВА ДВОЙНОГО ИНТЕГРАЛА	127
589. Условия существования двойного интеграла. Интегрируе-
мая функция необходимо должна быть ограниченной. Действи-
тельно, в противном случае при любом заданном способе разложения
области. (Р) на части можно было бы за счет выбора точек (;;, т^)
сделать интегральную сумму произвольно большой.
Обращаясь к рассмотрению условной интегрируемости
данной функции f(x, у), мы будем поэтому наперед предполагать ее
ограниченной:
m^f(x,y)-^M.
Как и в случае функции от одной переменной, здесь также удобно
ввести так называемые нижнюю и верхнюю суммы Дар бу:
п	п
«=5ад 5=2 ад.
1=1	Z=1
где т{ и М{ означают, соответственно, точные нижнюю и верхнюю
границы значений функции f(x, у) в области (Рг).
При данном способе разложения области (Р) на части, незави-
симо от выбора точек (;г, т],-), будут выполняться неравенства
s -С о sg 5.
Но за счет надлежащего выбора этих точек можно значения /(?,, гД
сделать сколь угодно близкими к тДМ^, а вместе с этим сумму о
сделать сколь угодно близкой к s (S’). Таким образом, верхняя и
нижняя суммы Дар б у являются, соответственно, точными
верхней и нижней границами интегральных сумм, отвечающих
тому же способу разложения области.
Для сумм Дарбу, как и в линейном случае, могут быть уста-
новлены следующие свойства.
1-е свойство. При дальнейшем дроблении частей (PJ, с до-
бавлением к старым линиям деления новых, нижняя сумма
Дарбу не убывает, а верхняя — не возрастает.
2-е свойство. Каждая нижняя сумма Дарбу не превос-
ходит каждой верхней суммы, хотя бы отвечающей и другому
способу разложения области (Р).
Доказательство проводится аналогично прежнему [296]; лишь в
тех случаях, когда там говорилось о точках деления, здесь при-
ходится говорить о линиях деления.
Есть, однако, один момент, на котором нам хотелось бы задер-
жать внимание читателя. В линейном случае каждая новая точка
деления отчетливо разлагает один из старых промежутков на два;
общей частью двух промежутков является тоже промежуток. В пло-
ском случае положение усложняется тем, что две кривые могут пере-
секаться между собой во многих точках (и даже в бесконечном мно-
жестве точек). Поэтому связная частичная область может новой
128
ГЛ. XVI. ДВОЙНЫЕ ИНТЕГРАЛЫ
[590
кривой рассекаться и на несвязные части; точно так же и общей
частью двух связных областей может оказаться несвязная
область. Вот почему мы с самого начала не исключали
из рассмотрения разложения основной области на
несвязные части!
Далее устанавливаются понятия нижнего и верхнего интегралов
Д а р б у.
/* = sup{s}, =
причем оказывается, что
s Д '-С /* '-С
st*
Наконец, путем буквального воспроизведения доказательства для
линейного случая [297] и здесь получается
Теорема. Для существования двойного интеграла необходимо
и достаточно, чтобы было
limbs'— s) = 0
х—>-0
или в других обозначениях
п
lim 2 0^ = 0,	(6)
х-»о -^i
где о>(. есть колебание Aft- — mt функции f (х, у) в частичной
области (Р,).
590. Классы интегрируемых функций. С помощью установлен-
ного выше признака интегрируемости легко доказать:
I. Всякая непрерывная в области (Р) функция f (х, у) инте-
грируема.
Действительно, если функция f непрерывна в (замкнутой)
области (Р), то по свойству равномерной непрерывности каждому
е^>0 отвечает такое 8^>0, что в любой части области (Р) с диа-
метром, меньшим чем 8, колебание функции будет меньше чем е.
Пусть теперь область (Р) разложена на части (Р(), диаметры кото-
рых все меньше 3. Тогда все колебания о>г<^е, и
'^iPi^'ZPi^P,
i	i
откуда и следует выполнение условия (6). Этим интегрируемость
функции доказана.
Замечание. Теперь легко уже придать полную строгость вы-
воду формулы (2*) для объема цилиндрического бруса. Это делается
совершенно так же, как и при выводе интегральной формулы для
площади криволинейной трапеции [329] — с привлечением входящих
и выходящих тел, объемы которых выражаются суммами Д а р б у.
590J	§ I. ОПРЕДЕЛЕНИЕ И СВОЙСТВА ДВОЙНОГО ИНТЕГРАЛА	129
Для того чтобы несколько расширить класс функций, для кото-
рых установлена интегрируемость, мы будем нуждаться в-следующей
лемме.
Лемма. Пусть в области (Р) задана некоторая кривая (L),
имеющая площадь 0. Тогда каждому е^>0 отвечает такое
8^>0, что, лишь только область (Р) разложена на части с диа-
метрами, меньшими 8, сумма площадей, тех из них, которые
имеют с (L) общие точки, будет меньше е.
По предположению, кривую (Z.) можно погрузить в многоугольную
область (Q) с площадью, меньшей чем е. Сделать это можно так,
чтобы кривая (£) и контур (К) упомянутой области не имели общих
точек. Тогда расстояние *
между переменными точками
обеих кривых достигает свое-
го наименьшего значения
8>0.
Разложим теперь область
(Р) по произволу на час-
ти так, чтобы диаметры их
были 8. Те из них, кото-
рые задевают кривую (Z.),
необходимо целиком бу-
дут лежать в области
(Q), следовательно, об-
щая их площадь меньше е.
61х
Рис. 37.
II. Если ограниченная функция f (х, у) имеет разрывы разве
лишь на конечном числе кривых с площадью 0, то она интегри-
руема.
Зададимся произвольным числом е^>0. По предположению, все
«линии разрыва» функции f(x,y) можно заключить внутрь много-
угольной области (Q) с общей площадью е. На рис. 37 эта
область покрыта штриховкой. Границей ее служит конечное число
ломаных (Z.), которые, очевидно, сами имеют площадь 0.
В замкнутой области, получающейся из (Р) выделением внут-
ренности области (Q), функция f(x, у) сплошь непрерывна,
значит и равномерно непрерывна. Следовательно, по задан-
ному е найдется такое число 8t^>0, что во всякой части этой
области, диаметр которой меньше 81( колебание функции f(x, у)
будет е.	4
Теперь, в силу леммы, можно найти и такое 82^>0, что всякий
раз, как область {Р) произвольными кривыми разлагается на части
с диаметрами, меньшими чем 83, сумма площадей тех из них, которые
задевают совокупность ломаных (Z.) — границу выделенной много-
угольной области (Q), — наверное будет е.
* См. 336, сноска.
5 Г, М. Фихтенгольц, т. III
130	гл. XVI. ДВОЙНЫЕ ИНТЕГРАЛЫ	[591
Пусть 8 будет наименьшее из двух чисел 8Ь 82. Разложим
область (Р) на части (PJ, (Р9), ..., (Рп), диаметры которых
меньше 8, и рассмотрим соответствующую сумму
S-л-
i
Разобьем ее на две суммы:
У Pi' + У ^i"Pi",
i'	i"
предполагая, что значок I' отвечает таким областям (Р;>), которые
целиком лежат вне выделенной области (Q), а значок I"— всем
прочим. Оценим каждую из этих сумм в отдельности.
Так как все (Р,-) лежат в области, полученной из (Р) выделе-
нием (Q), и диаметры их <^8^8^ то все од- е, так что
2>гРг<е£Рг<еР.
V	v
С другой стороны, если через 2 обозначить колебание функции
f (х> У) в0 всей области (Р), то будем иметь (так как <ог sC 2)
2®<”Рг'<2уРр'.
Здесь У Pi» есть сумма площадей тех из областей (Р;), которые
1) либо целиком лежат в выключенной области (Q), 2) либо заде-
вают границу (£) этой области. Общая площадь первых меньше е,
ибо Q<^s; то же можно сказать и об общей площади вторых, по-
скольку область разложена на части с диаметрами, меньшими чем
8^89. Итак, ^Pi"< 2s, так что
у, <s>i»Pt» < 22s.
Окончательно, при К <8, оказывается:
2>Рг< (Р 4-22)е.
I
Так как правая часть этого неравенства произвольно мала вместе с е,
то выполняется условие (6) и т. д.
591.	Нижний и верхний интегралы, как пределы. В двумерном слу-
чае также имеет место
Теорема Дарбу. Для любой ограниченной в (Р) функции f(x, у)
выполняются предельные равенства
I* — lim з, /* == lim S
/.-.о л-«а
[ср. 301].
$ 1. ОПРЕДЕЛЕНИЕ И СВОЙСТВА ДВОЙНОГО ИНТЕГРАЛА	131
Мы наметим доказательство .(например, для верхних сумм), так как оно
в одном пункте существенно разнится от рассуждения, приведенного для
линейного случая.
Как и там, по заданному г>0, сначала разложим с помощью сетки кри-
вых область (Р) на части так, чтобы для соответствующей суммы S' было
Упомянутая только что сетка кривых — обозначим их в совокупности через
(Z)— имеет площадь 0. Тогда, по лемме предыдущего п°, найдется такое
8>0, что, как бы область (Р) ни разложить на части (Р,) с диаметрами < 8,
сумма площадей тех из них, которые задевают хоть одну из кривых (Z),
будет < где 2 — полное колебание функции f в области (Р).
Обозначим через S сумму, отвечающую произвольному такому
разложению, и сравним ее с суммой S", которая получится, если мы к имею-
щимся налицо кривым делениям присоединим целиком всю сетку (£). По
1-му свойству сумм Д а р б у [589], S" S', так что и подавно
Разнятся же суммы S и S” лишь теми слагаемыми, которые отвечают
частям (Р^, рассекаемым кривыми (£). Так как сумма площадей этих
частей < 2Q , то легко сообразить, что
Окончательно,
/*sSS</*-H,
что и завершает доказательство.
Теперь критерий существования интеграла приводится к равенству
/* = /*•
С его помощью, как и в линейном случае, устанавливается, что для интег-
рируемости функции достаточно выполнения при любом е>0 неравенства
S — з < е
хотя бы для одной пары сумм Дарбу.
592.	Свойства интегрируемых функций и двойных интегралов.
1°. Если произвольным образом изменить значения интегри-
руемой в (Р) функции f (х, у) вдоль какой-либо кривой (L) с пло-
щадью 0 (с тем лишь условием, чтобы и измененная функция
оставалась ограниченной), то вновь полученная функция также
интегрируема в (Р), и ее интеграл равен интегралу от f(x, у).
Для доказательства нужно составить интегральные суммы для
измененной и исходной функций. Они могут разниться лишь теми
слагаемыми, которые относятся к областям (Р{), задевающим кри-
вую (L). Но, по лемме п° 590, общая площадь этих областей стре-
мится к нулю при X—>0, откуда уже легко заключить, что обе инте-
гральные суммы стремятся к общему пределу.
5»
132
ГЛ. XVI. ДВОЙНЫЕ ИНТЕГРАЛЫ
(592
Таким образом, существование и величина двойного интеграла
не зависят от значений, принимаемых подинтегральной функцией
вдоль конечного числа кривых с площадью 0.
2°. Если область (Р), в которой задана функция f(x, у), кри-
вой (L) (с площадью 0) разложена на две области (Р) и (Р’)> то
из интегрируемости функции f(x,y) во всей области (Р) следует
ее интегрируемость в частичных областях (Р) и (Р"), и обрат-
но— из интегрируемости функции в обеих областях (Р) и (Рг)
вытекает интегрируемость в области (Р). При этом
\\f{x, y}dP=\\f(x, y)dP+\\f(x, y)dP.
(P)	(P')	(P")
Разложим области (P) й (P") произвольным образом на части;
тем самым и (Р) разложится на части:
(р& та..... та
Если значком I' отметить части, содержащиеся в (Р), а значком I"—
части, содержащиеся в (Р')> то
S “Л = У. + У, *»i"Pt"-
Пусть функция f(x, у) интегрируема в (Р), так что при Х->0 стре-
мится к нулю сумма слева; тогда каждая из сумм справа и подавно
стремится к нулю, так что наша функция интегрируема также в (Р')
и (Р').
Обратно, если имеет место последнее обстоятельство, так что
при К -> 0 стремятся к нулю обе суммы справа, то и сумма слева
также стремится к нулю. Однако нужно помнить, что она построена
не для произвольного разбиения области (Р) на части: ведь мы исхо-
дили из разложения порознь областей (Р') и (Р").
Чтобы от произвольного разложения области (Р) перейти к раз-
ложению этого частного вида, достаточно присоединить к линиям
деления кривую (L). Соответствующие им суммы будут разниться
лишь слагаемыми, отвечающими тем элементарным областям, которые
задевают кривую (£). Но, по лемме п°590, их общая площадь стре-
мится к нулю при Х->0, и обе суммы разнятся на бесконечно
малую. Таким образом, условие (6) выполняется в полной общности,
и функция f(x, у) оказывается интегрируемой в (Р).
Наконец, доказываемая формула получается переходом к пределу
при X -> 0 из равенства
S ч) pi=Ж v)м Pi-
Аналогично, из рассмотрения интегральных сумм с помощью пере-
хода к пределу получаются и следующие три свойства;
§ 1. ОПРЕДЕЛЕНИЕ И СВОЙСТВА ДВОЙНОГО ИНТЕГРАЛА	133
3°. Если умножить интегрируемую в (Р) функцию f (х, у) на
постоянную k, то полученная функция также будет интегри-
руема, и при этом
k f(x, y)dP = k'\) \f(x, у) dP.
(P)	(P)
4°. Если в области (P) интегрируемы функции f(x, у) и
g(x, у), то интегрируема и функция f (х, y)±g (х, у), причем
y)]dP=^f(x, y)dP±\\g(x, y)dP.
(P)	(P)	(P)
5°. Если для интегрируемых в (Р) функций f (х, у) и g(x, у)
выполняется неравенство f(x, y)^g(x, у), то
$ \f(x, У) dP^ $ g(x> У) dP.
(Р)	(Р)
Далее,
6°. В случае интегрируемости функции f(x, у) интегрируема
и функция \f(x, у) |, и имеет место неравенство
(Р)	(Р)
Интегрируемость функции \f | следует из простого замечания, что
колебание й, этой функции в любой области Pt не превосходит соот-
ветствующего колебания о)г функции /. Действительно, тогда
и стремление к нулю второй суммы влечет за собой стремление к
нулю первой.
Доказываемое же неравенство получается предельным переходом
из неравенства
|£ж	^)1л.
7°. Если интегрируемая в (Р) функция f (х, у) удовлетворяет
неравенству
т ^f(x, у)^М,
то
тР	\f (х, у) dP < МР.	(7)
(Р)
Это получается предельным переходом из очевидного неравенства
чУР^МР.
134
гл. XVI. ДВОЙНЫЕ ИНТЕГРАЛЫ
[593
Если разделить все части неравенств (7) на Р:
Н/(х, y)dP
т^-^-—р----------
и через р. обозначить среднее отношение, то получим другую запись
неравенства (7)
y)dP=vP (/га<р^Л1),	(8)
(Р)
которая выражает так называемую теорему о среднем зна-
чении.
Предположим теперь, в частности, что функция f(x, у} непре-
рывна в (Р), и возьмем в качестве т и М ее наименьшее и наи-
большее значения в области (Р) — по теореме Вейерштрасса,
173, они существуют! Тогда по известной теореме Больцано—
Коши, 171, непрерывная функция f(x, у), принимающая значения
т и 7И, должна пройти и через каждое промежуточное значение.
Таким образом, во всяком случае в области (Р) должна найтись
такая точка (х, у), что р=/(х, J), и формула (8) принимает вид:
JJ/(x, y)dP=f(x, у)-Р.	(9)
(Р)
Это — особенно употребительная форма теоремы о среднем.
Так же легко переносится на рассматриваемый случай и обоб-
щенная теорема о среднем значении [304, 10°]; предо-
ставляем это читателю.
593.	Интеграл как аддитивная функция области; дифферен-
цирование по области. Рассмотрим (замкнутую) плоскую область (Р)
и содержащиеся в ней частичные (замкнутые) области (р). Мы будем
предполагать все области квадрируемыми (по обстоятельствам
они могут подлежать и другим ограничениям). Если каждой час-
ти (р) области (Р) сопоставляется некоторое определенное число
Ф=Ф((р)),
то этим определяется «функция от области (р)ъ для указан-
ных (р). Примером такой функции от области может служить пло-
щадь области, непрерывно распределенная по ней масса, статические
моменты этой массы, непрерывно распределенная нагрузка или вообще
действующая на нее сила и т. п.
Если при произвольном разложении области (р) на взаимно
не налегающие части
(?) = (?') + (?')
всегда оказывается, что
Ф((р)) = Ф((р')) + Ф((р'))^
593]	$ 1. ОПРЕДЕЛЕНИЕ И СВОЙСТВА ДВОЙНОГО ИНТЕГРАЛА	135
то функцию Ф((р)) от области называют аддитивной. Все
функции, приведенные выше в виде примера, обладают этим свой-
ством аддитивности. Аддитивные функции от области пред-
ставляют особую важность, ибо часто встречаются при изучении
явлений природы.
Пусть в квадрируемой области (Р) задана интегрируемая функ-
ция точки f (M)—f (х, у); тогда она будет интегрируема в любой
квадрируемой же части (р) области (Р), так что интеграл
Ф((Р)) = У)ЛР	(10)
(Р)
также есть функция от области (р). Ввиду 592, 2° и она будет,
очевидно, аддитивной функцией.
Обратимся теперь к «дифференцированию функции Ф ((р)) по
области». Пусть М — фиксированная точка области (Р), а (р) —
любая содержащая эту точку частичная область. Если отно-
шение
Ф((Р))
Р '
где р есть площадь области (р), стремится к определенному ко-
нечному пределу	при безграничном убывании диаметра
области (р), то этот предел называется производной от
Ф((р)) по области в точке М. Если Ф((р)), например, есть
масса, непрерывно распределенная по плоской фигуре (р), то f(M)
есть не что иное, как плотность распределения масс в точке М\
если Ф((р)) означает силу, действующую на фигуру (р), то f(M)
выражает удельное давление в точке М, и т. п.
Особый интерес для нас представляет случай, когда функция от
области выражается интегралом вида (10), где f(x, у)—непре-
рывная в области (Р) функция. Мы покажем, что производной по
области в точке М от интеграла будет подинтегральная функ-
ция, вычисленная именно в этой точке, т. е.
у).
Действительно, взяв область (р), о которой говорится в определении
производной, имеем по теореме о среднем [см. (9)]
ф ((р)) =f(x, у)-р,
где (X, J) есть некоторая точка области (р). Если диаметр области (р)
стремится к нулю, то точка (X, у) безгранично сближается с (х, у)
и, по непрерывности
У)-»/(х, у),
что и требовалось доказать.
136
ГЛ. XVI. ДВОЙНЫЕ ИНТЕГРАЛЫ
[593
Таким образом, двойной интеграл (10) по переменной области
является в особом смысле «первообразной» для подинтегральной
функции точки: он восстанавливает функцию области, для которой
эта функция точки служит производной по области. Естественно
встает вопрос, в какой мере однозначно вообще «первообразная»
определяется своей производной.
В этом направлении можно доказать такое предложение: две
аддитивные функции от области, ((р)) и Ф4 ((р)), имеющие
во всех точках основной области (Р) одну и ту же производную
по области, тождественны.
Если перейти к рассмотрению разности Ф ((р)) = Ф) ((р))— ®j((p))>
дело сведется к доказательству того, что аддитивная функция
области Ф((р)), производная которой во всех точках области (Р)
равна нулю, и сама тождественно обращается в нуль.
Действительно, по самому определению производной, каково бы
ни было число е^>0, каждую точку М области (Р) можно окру-
жить такой окрестностью, чтобы для любой заключенной в ней
части (р) этой области, содержащей М, было
I Р
С помощью леммы Бореля [175], примененной к системе этих
окрестностей, удается затем разложить область (Р) на конечное число
взаимно не налегающих областей:
(Р) = (pj -|- (ра) +... 4- (pk)
так, чтобы для каждой из них было (z= 1, 2, ..., k)
|	1 < е или | Ф ((рг)) | <рге.
Ввиду же предположенной аддитивности функции Ф((р)) имеем
i
Отсюда, в связи с предыдущим неравенством,
|ф((р))1<Е1ф(^))КРе-
i
Но е здесь произвольно, значит Ф((Р)) = 0. Этим и доказано наше
утверждение, поскольку вместо (Р) могла быть взята и любая ча-
стичная область (р).
Сопоставляя все сказанное, мы приходим к такому заключитель-
ному утверждению: двойной интеграл (10) по переменной области
представляет собой единственную аддитивную «первообраз-
ную'» для стоящей под знаком интеграла функции точки *.
* Эта функция предполагается, как и выше, непрерывной.
5SH|.	§ 2. ВЫЧИСЛЕНИЕ ДВОЙНОГО ИНТЕГРАЛА	137
Поэтому, например, без вычислений ясно, что по заданной плот-
ности р (Af) = р (х, у) распределения масс в точке М вся масса,
распределенная по фигуре (Р), выразится интегралом
т = р (х, у) dP;
(Р)
если q (Al) = q (х, у) есть удельное давление в точке М, то
вся действующая на фигуру (Р) сила будет
F = ^9(x, y)dP,
(Р)
и т. п.
Замечание. Выше нам приходилось уже говорить об адди-
тивных функциях от промежутка [348; 584, 8)]. Так как
такая функция всегда представляет собой разность двух значений
некоторой функции точки, то не было надобности для «линей-
ного» случая развивать теорию вроде изложенной выше для «пло-
ского» случая. Однако в теореме о дифференцировании определен-
ного интеграла по переменному верхнему пределу [305, 12°] чита-
тель легко усмотрит аналог доказанной только что теоремы о
дифференцировании двойного интеграла по области, а рассуждения
п° 348 можно трактовать как доказательство того, что интеграл
есть единственная аддитивная функция от промежутка, служащая
«первообразной» для данной функции точки.
§ 2. Вычисление двойного интеграла
594. Приведение двойного интеграла к повторному в случае
прямоугольной области. С этим вопросом в геометрической трак-
товке и при некоторых частных предположениях мы уже имели дело
в п° 587.
Рассмотрим теперь его средствами анализа и притом в самой об-
щей форме; начнем мы с простого случая, когда область интегриро-
вания представляет собой прямоугольник (Р) = [a, b; с, d].
Теорема. Если для функции f(x,y), определенной в прямо-
угольнике (Р) = [а, Ь\ с, d\, существуют двойной интеграл
\\f(X,y)dP	(1)
(Р)
и — при каждом постоянном значении х из [а, Ь] — простой ин-
теграл
d
I(x) = ^f(x, y)dy (a^x^b),	(2)
138
ГЛ. XVI. ДВОЙНЫЕ ИНТЕГРАЛЫ
1594
то существует также повторный интеграл
Ь d
dx \f(x, y)dy
a c
(3)
и выполняется равенство *
b d
$$/(*> У) dP = $ dx J f(x, y) dy.	(4)
(P)	a c
Доказательство. Разобьем промежутки [a, b] и [c, d], опре-
деляющие прямоугольник (Р), на части, вставляя точки деления
хй = а Xi . <^Xj xi+l . <^хп = Ь,
Jo — с ji <^ • • • <ZУь	1 <С •  • Ут — d.
Тогда прямоугольник (Р) разложится
на частичные прямоугольники
(рис. 38)
(Л-.*) = кп */+ь Уь, Л+d
(i = 0, 1, ..., я —1;
А = 0, 1, ..., т— 1).
Обозначим через mt k и
Л4г> k, соответственно, точные
нижнюю и верхнюю границы
функции f(x,y) в прямоуголь-
нике (Рг ft), так что для всех
точек (х, у) этого прямоуголь-
ника
Wi.	y)^Mik.
Фиксируя х в промежутке [xt, x,+i] по произволу: х = ^, и ин-
тегрируя по у от yh до _уй+1, будем иметь [304, 8°]
-'’fe + 1
k Ду* < 5 f у) dy < Mit h &yh,
?k
где ^yk=yk+l — yk; интеграл по у существует, так как предполо-
жено существование интеграла (2) по всему промежутку [с, d}. Сум-
мируя подобные неравенства по k от 0 до т — 1, получим
т — 1	d	т — 1
У, mi. а &) = $/&> y)dy^ 2
й=0	С	*=0
* Читатель легко усмотрит в этом утверждении видоизменение известной
теоремы о двойном и повторном пределах [168].
594]
S 2. ВЫЧИСЛЕНИЕ ДВОЙНОГО ИНТЕГРАЛА
439
Если умножить все части этих неравенств на Дх,-= х;+1Xj
и просуммировать по значку i от 0 до п—1, то найдем
п—1	т —1	п—1	п —1	т —1
У S тцк Ьук < у I ($,-) LXi У Дхг £ Л4;, к by,?
i—0	ft=0	i=0	i = 0	fe = O
Посредине мы получили интегральную сумму для функции /(х).
Что же касается до крайних членов, то они представляют собою не
что иное, как суммы s и 5 Дарбу для двойного интеграла (1).
Действительно, так как Дх,Дул есть площадь прямоугольника
(Л,л)> то> например, имеем
л—1 т —1	л—Im—1
£Дхг£ т11к^ук=^ у tni,k^xi\yk = ^itnikPitk = s.
i = 0	fc = О	i = 0 k = 0	i, к
Таким образом, окончательно
П—1
s-C У 1&)Ьх{^&
Если теперь все Дх,- и Лук одновременно устремить к нулю, то
ввиду существования двойного интеграла (1), обе суммы s и S бу-
дут стремиться к нему, как к пределу. В таком случае и
л — 1
liш 2 /&)Дх,- = $ $f (х, у)dP,
i =0	UP)
т. е. двойной интеграл (1) представляет собой в то же время и ин-
теграл от функции I (х):
ь	ь а
J \f(x’ y)dP = ^I(х) dx = J dx\f(x, у) dy,
(P)	a	a c
что и требовалось доказать.
Меняя роли переменных х и у, наряду с (4) можно доказать и
формулу
d ъ
5 y)dP = \) dy \f(x, у) dx,	(4*)
(P)	c a
в предположении, что при у — const, существует интеграл
ь
^f(x,y)dx.
а
140	гл. XVI. ДВОЙНЫЕ ИНТЕГРАЛЫ	[594
Замечание. Если вместе с двойным интегралом (1) суще-
ствуют оба простых интеграла:
а	ь
J f (х, У) dy (х = const) и \f(x, у) dx (у = const),
с	а
то имеют место одновременно обе формулы (4), (4*), откуда
b	d	d b
^dx^fix, y)dy = ^dy §/(-£,	y)dx.	(5)
a	с	c a
Этот результат	мы	установили -выше	[528],	не пользуясь пред-
положением о существовании двойного интеграла.
Применение формулы (4) или (4*) обусловлено существованием
двойного интеграла и одного из простых. Если функция f (х, у)
непрерывна (случай, который обычно встречается на практике),
то существование всех упомянутых интегралов обеспечено; по отно-
шению к двойному, например, это следует из 590, I. В этом случае
любой из упомянутых формул можно пользоваться для фактиче-
ского вычисления двойного интеграла, так как вычисление
простых интегралов представляет гораздо более простую задачу.
При доказательстве формулы (4) всего естественнее было раз-
ложить прямоугольник (Р) прямыми, параллельными осям, на прямо-
угольные элементы с площадями Ax,Ayfe. Желая в самом символе
двойного интеграла указать на происхождение его от деления
области на части прямыми, параллельными осям, вместо (х, y)dP
(Р)
часто пишут
^/(х, y)dxdy Г или §§/(*, y)dydx].
(Р)	(Р)
Больше того, имея в виду сведёние двойного интеграла, распро-
страненного на прямоугольник (Р) —[a, b; с, d], к повторному, и
самый двойной интеграл часто обозначают символом, сходным с по-
вторным:
bd	db
\\f(x,y)dydx или ^f(x,y)dxdy.
ас	с а
При этом обозначении друг другу соответствуют «внешний интеграл»
и «внешний дифференциал», так что стоит лишь поставить скобки,
чтобы получить тот или другой из повторных интегралов:
§{§/(*, .У) dy\ dx или
а с
${$/(-*> y)dx]dy.
с а
595J	$ 2. ВЫЧИСЛЕНИЕ ДВОЙНОГО ИНТЕГРАЛА
141
595. Примеры. 1) Вычислить интеграл, распространенный на прямо-
угольник (Р) = [3, 4; 1, 2]:
2 4
С С dxdy
J J (х+у)2-
Решение. По
ndx dy
(х+уУ
(P)
формуле (4*) пишем
2	4
Jdx
(х + уУ
Найдем сначала
ndx dy
(х + у)1
(Р)
внутренний интеграл:
4
dx
J
1
у+з
отсюда
2
dxdy	С Г
+	} Ь + 3
(Р)
2) Вычислить интегралы
з 5
Зу — 2у3) dx dy,
1 Ъ 1 25
+Тр=1п24
(а)
, f f Xs dx dy
<»> '.= H l+/
1
1
/ _ С С у dxdy
’ J b’(i+*3-m3/a
Решение.
3	5
(a) Iv = \dy\
(в)
3
— 2у3) dx = jj (195у — бу3) dy = 660.
(6)
в) Проще представить Za по формуле (4) в виде
1 1
8	(l-|_X2_|_^)3/2’
ибо сразу получаем:
1
f ydy__________________________1________1
(1+x2+/)3/a “	K?+2’
так что
/,= t (	1-	1 \dx =
^\Г*2+1	V x^2]
= in х + У^Т1 1 _ln 2+/2
x+/xa + 2 о 1 + /3 '
142
ГЛ. XVI. ДВОЙНЫЕ ИНТЕГРАЛЫ
(595
Если прибегнуть к другому повторному интегралу, то квадратуры ока-
жутся несколько более сложными:
1 1 1
, С , С dx	С dx
lt= \ У dy \ ------J— \ ----------:-J- =
J J (l+x8+v2)’/2’	} (1 +x24-V2) /2
_	1______х_____]*—>________1____
“Т+У у14-x4 s 6+7" 1*-о— (1 + у»8)V2+У2’
/ = V УаУ	1 in /2+7-11’ =
‘ J (1+№)/2+№	2	/2+/+110
____Lm (/3- 1)(/2~+ 1)
2	(/3+1И/2- 1) '
Легко преобразовать этот ответ к прежнему виду.
3) Найти объем V тела, ограниченного снизу плоскостью Ху, с боков пло-
скостями х=0, x — а, у = 0, у = Ь, а сверху эллиптическим параболоидом
,-У +7
2р 2q ‘
Решение. Прежде всего по формуле (2*)
V= { {	+
dP.
Самое же вычисление интеграла произведем по формуле (4*):
Ь а
v={dy{
ь
Г /а’
J \6р
4) То же для тела, ограниченного плоскостью ху, поверхностью х2 +
4- z2 = R2 (z > 0) и плоскостями у = 0 и у — Н.
Решение. Если за основание тела принять прямоугольник [— R, R;
0, Н] на плоскости ху, то
HR	R
V= ? ( /R2 — x2dxdy = 2H /2?3 —х8 dx = ^^.
о -я	о
(Конечно, проще было бы рассматривать тело, как цилиндр, имеющий
основанием полукруг на плоскости xz.J
5) То же для тела, ограниченного плоскостями z = 0, х = а, х = Ь, у = с,
y=d(b> а > 0, d>c>0)H гиперболическим параболоидом z = (т > 0).
л .. (d2 — c2)(b2 — а2)
Ответ. V=-----------Р-------
4т
6) Доказать, что
1 I	1
j (хУ)ху dx dy=^yv dy.
$ 2. ВЫЧИСЛЕНИЕ ДВОЙНОГО ИНТЕГРАЛА	143
Подинтегральная функция в двойном интеграле, если при ху — 0 припи-
сать ей значение 1, будет непрерывна во всем квадрате (0, 1; 0, 1].
Имеем
11 11
(ху)*? dx dy = ^dy (ху)хУ dx.
Делая во внутреннем интеграле подстановку ху = t (при у — const. >• 0), а
затем интегрируя по частям, последовательно получим для двойного инте-
грала выражение
1 у	у	1
Л = 1п	[о — In dy.
у
Двойная подстановка обращается в 0, так как интеграл ( t*dt при у—»0
'о
есть бесконечно малая первого порядка *. Что же касается последнего инте-
грала, то, ввиду тождества
(Я’=^1п^+Л
1
он приводится к интегралу (у? dy.
0
7) Доказать, что (при любом г == const.)
Я Я	я
"2 "2	2"
J cos (2г sin <f> sin 6) da dO = { ( cos (z sin X) dX Is.
t> "o	1 i
Для этой цели каждый из интегралов разложим в ряд по степеням г. По
отношению к простому интегралу это уже было сделано в 440, 13):
Я
2	оо
jj cos (z sinX) dX =у { 1 + 2 (~
Подинтегральная функция в двойном интеграле разлагается в ряд
ОО
cos (2z sin <f> sin fl) — 1	(— 1)*	sin8* f sin8i fl,
i=l
• Ведь lim — f t* dt — lim tf — 1.
у—о У j t-o
144
ГЛ. XVI. ДВОЙНЫЕ ИНТЕГРАЛЫ
(595
равномерно сходящийся для всех значений tf и в в квадрате
^0, yj О, Интегрируя его почленно в этом квадрате, получим*
гс п
У у
cos (2z sin ср sin 6) dcp d0 =
0 0
тс тс
co	2 2
+ 2 (— O’’	§ § sin2' <p sin2’ 0 dcp d0.
i = l	о 0
Но [см. 312 (8)]
It TC	ГС	ГС
У У	У У
j sin2' $ sin2''0 dcp dQ — j d0j sin21 cp sin21 0 dy —
rc	rc
C • 22 A M C  2/ Г* (2Z— I) 1118
= \ sm210d0- \ sm2/<pdcp =	J ’
так что после простых преобразований
1? тс
У У	оо
С j cos (2z sin ср sin 0) dcp d0 = |l 4- 2 —•
0 0	1 = 1
Легко проверить теперь [см. 390, 3)}, что, действительно,
1+У	у , ** !«
Xj 22* [il]4 I v ’ 28*(М)8 J •
i=l	й=1
Таким образом, значение предложенного двойного интеграла может быть
выражено через бесселеву функцию с нулевым значком:
1t 1?
J У
С (*
\ \ cos (2z sin ср sin 0) dcp d0 =	[Jo (z)]8.
8)	Доказать, что при любом А(0<Л<1)
1? ГС	ГС
*2* *2*	У
С С d<fdQ = к С d\ = 2L F(k}
J J 1 — й8 sin2 ср sin2 0	2 \ у 1 _ ks Sins х 2
* Без дальнейших пояснений читатель распространит и понятие равно-
мерно сходящегося ряда и теорему о почленном его интегрировании на слу-
чай, когда члены ряда зависят от двух переменных.
595]
§ 2. ВЫЧИСЛЕНИЕ ДВОЙНОГО ИНТЕГРАЛА
145
Указание. Оба интеграла разложить по степеням k; для интеграла
справа это разложение нам уже встречалось [440, 13)].
9)	Доказать, что если функция f(x) интегрируема в промежутке [а, 6],
а функция g(y) интегрируема в промежутке [с, d\, то функция /(х) g(y)
от двух переменных будет интегрируема в прямоугольнике (Р) = [а, Ь; с, 3|.
У к аз а н и е. Вопрос можно свести к интегрируемости в (Р) порознь
функций /(х) и g.(y), рассматриваемых как функции от двух
переменных*. Для того же, чтобы установить это, удобно воспользо-
ваться облегченным критерием интегрируемости, указанным в конце п° 591.
Заметим, что при этом
d ь
\\f{x)g{y)dxdy = \ dy { §/(x)g(y)dx}==
(Р)	с а
d	b	b	d
= $ Д(у) { $ f{x) dx} dy — 5/(X) dx • $ g(у) dy,
с	a	a	c
так что двойной интеграл приводится здесь к произведе-
нию двух простых интегралов.
Иной раз, наоборот, оказывается полезным представить произведение
двух простых интегралов в виде двойного интеграла. Ниже мы приводим
некоторые примеры применения этой идеи.
10)	Доказать неравенство:
ь	ь
\/(х) dx. \
J	J	J	\л)
а	а
где /(х) — положительная непрерывная функция.
Без умаления общности можно предположить, что a<Z>. Так как инте-
грал не зависит от обозначения переменной интегрирования, и можно
в любом из интегралов букву х заменить буквой у, то левая часть нера-
венства перепишется так:
(Р>	(Р)
где (Р) = [а, Ь\ a, J], Отсюда
z=± С ? [ZW dxdv = И f’W+fty)dxdv
2 Ш/СуН/WJ	П 2/(x)/(y) dXdy-
(P)	(Pi
В силу очевидного неравенства 2 АВ sg Д3 -f- Ва подинтегральная функция 5= 1,
так что ]см. 592, 7°]
/=£(£> —а)3,
что и требовалось доказать.
11)	Неравенство Буняковского. Мы уже имели дело с этим нера-
венством [321]. В виде упражнения дадим новый вывод его для случая функ-
ций /(х) и g(x), интегрируемых в [а, А] в собственном смысле.
Рассмотрим интеграл
в =	If (X) g (у)—f (у) g;(x.)]2 dx dy,
(Р)
* Если теорему n°299, II распространить на функции от двух переменных.
146	ГЛ. XVI. ДВОЙНЫЕ ИНТЕГРАЛЫ	|595
где (Р) есть квадрат [a, b; a, Z>]. Раскрывая скобки, имеем [см. 9)]
ь	ъ	ь	ь
B=\f‘(x)dx-\gt(y)dy — 2^f(x)g(х) dx  J f(y)g(у) dy +
a	a	a	a
b	t>
+ $/а(У)4У'\gs(x)dx
a	a
или, наконец, снова пользуясь независимостью интеграла от обозначе-
ния независимой переменной:
ь	ь	ь
B==2{$/2(x)dx-$g2(x)dx—[$/(x)g(x)dx]2}.
а	а	а
Так как в интеграле В подинтегральное выражение неотрицательно^ то и
В 5= О, откуда и следует требуемое неравенство
ь	ь	ь
[$/(*) dx]2 J/2 (х) dx • $ g2 (x) dx.
a	a	a
Замечание. Из него, в частности, вытекает и неравенство предыду-
щего упражнения ^если f заменить на //, agHa ]7у)’
12)	Неравенство Чебышева. Сходными рассуждениями доказывается
неравенство
ь	ь	ь	ь
\p(x)f(x) dx-^p(x)g(x)dx^p(x)dx-^p(x)f(x)g(x}dx,
а	а	а	а
которое принадлежит П. Л. Чебышеву. Здесь р (х) есть положитель-
ная интегрируемая функция, а /(х) и g(x) — монотонно возрастаю-
щие функции.
Пусть а < Ь. Рассмотрим разность
ь	ь	ь	ь
Д = $g(x)/(x)g(x)dx- jjp(x)dx —(x)/(x)dx- Jp(x)g(x) dx.
a	a	a	a
Заменяя во вторых множителях обоих членов букву х на у, представим эту
разность Д в виде
ь ь
Д = И р р <*)— S (У)] dx dy.
а а
Обменяем теперь ролями х и у.
ь ь
b*=^\p(x)p(y)f(y)\g(y) — g (х)] dx dy.
аа
595]
S 2. ВЫЧИСЛЕНИЕ ДВОЙНОГО ИНТЕГРАЛА
147
Наконец, если взять полусумму обоих выражений, получим
ь ь
д = у § § P(x)p(y)[f(x)—f(y)][g(x) — g(y)]dxdy.
а а
Так как обе функции fug монотонно возрастают, то обе квадратные
скобки одного знака, т. е. подинтегральное выражение всегда неотрица-
тельно, а тогда и А $= О, чем и доказано требуемое неравенство.
Легко видеть, что оно остается в силе и в том случае, когда, обе функ-
ции f и g убывают. В случае, когда одна из них убывает, а другая возрастает,
неравенство меняет смысл.
13)	Пусть функция f(x, у) непрерывна в прямоугольнике (Р) =
= [а, Ь; с, d]. Обозначая через (х, у) произвольную точку в этом прямоуголь-
нике, рассмотрим функцию, выраженную двойным интегралом:
ху
F(x, у) = $$/(«, ») dv du.
a c
Если представить его в виде повторного интеграла:
X У
F (х, у) =^du f(u, v) dv,
а с
то, дифференцируя сначала по х, затем по у, последовательно получим *
dF %	daF
-д— = \ f(x, v) dv, -д—д- = fix, у).
дх J	дх ду J '
С
Мы пришли к аналогу теоремы о дифференцировании простого интеграла по
переменному верхнему пределу. Точно также установим, что и
&F
14)	Пусть f(x, у) интегрируема в прямоугольнике (Р) = [а, Ь\ с, d]. Если
для этой функции (которую на этот раз мы не предполагаем обязательно не-
прерывной) существует «первообразная» функция Ф(х, у), в том смысле, что
д>Ф(х,у) ..	.
' дхду
ТО
JJj f(x> У) dx dy = $ (b, d) — Ф (b, c) — Ф (a, d) + Ф (a, c).
Это — аналог формулы, выражающей обыкновенный определенный инте-
грал через первообразную.
• Следует учесть, что подинтегральная функция \/(«, ®) dv для внеш-
с
него интеграла есть непрерывная функция от и [506].
148
ГЛ. XVI. ДВОЙНЫЕ ИНТЕГРАЛЫ
[595
Наметим доказательство. Разложим прямоугольник [в, Ь\ с, d], как и в
п° 594, на частичные прямоугольники
[а:/, х,-+1; ук, у^] (г = 0, 1, .... п — 1; k = 0, 1, ..., т— 1).
Дважды применяя к выражению
ф Ук+1) — ® (*i+i, Ук) — Ф (xb yk+l) + Ф (xit yk)
формулу конечных приращений *, представим его в виде
фху&к, \ik) ^x^yk=f(iik, уць)^х^ук,
где Xi ^xi+l, yk^^ik^yk+t- Суммируя по i и k, получим
Ц Vk) ^yk = Ф (b, d) - Ф (b, с) - Ф (a, d) + Ф (a, c).
i, k
Наконец, перейдем к пределу.
Как видим, схема рассуждений — та же, что и при доказательстве основ-
ной формулы интегрального исчисления, выражающей простой определенный
интеграл через первообразную [310].
В заключение приведем два поучительных примера, устанавливающих
взаимную независимость условий теоремы п° 594.
15)	Если х — рациональное число, то, представив его в виде несократи-
мой дроби с положительным знаменателем, будем обозначать последний
через qx. Определим в квадрате (Р) = [0, 1; 0, 1] функцию f(x, у), положив:
/(х, _у) = —	—, если х и у оба рациональны,
Чх Чу z
f(x, у) —0	—в прочих случаях.
Функция будет разрывна во всех точках квадрата, имеющих рациональные
координаты, а в остальных — непрерывна.
Так как, каково бы ни было е > 0, лишь в конечном числе точек
может быть />е, то условие интегрируемости, установленное в п° 589, вы-
полняется, и двойной интеграл
\\f(x,y)dP
(Р)
существует; он равен 0.
При иррациональном значении у функция /(х, у) обращается в 0 для
всех х, так что и
1
f (х, у) dx = 0.
б
Если же у рационально, то /(х, _у) = 0 для иррациональных значений х, а для
рациональных х имеем: f (х, у) = — -f- —. Эта функция от переменной х в
Чх Чу
любом промежутке ее изменения имеет колебание > —, следовательно, для
о Чу	л
нее по хне существует интеграла. Значит, не может быть речи
и о повторном интеграле
1 1
&У \f{x, у) dx.
б б
* Ср. преобразование выражения W при доказательстве теоремы о пере-
становке двух дифференцирований в п° 190.
596J
§ 2. ВЫЧИСЛЕНИЕ ДВОЙНОГО ИНТЕГРАЛА
149
Аналогично устанавливается, что не существует и интеграл
1 1
dx f(x, у) dy.
16) Положим теперь f(x,y) = 1 во всех точках квадрата, для которых обе
координаты х,у рациональны и притом qx = qy, и f(x, у) —0 в прочих точках.
Так как в любой части квадрата колебание функции f равно 1, то
двойной интеграл
tyf(x,y)dP
на этот раз не существует.
В то же время при постоянном у функция f(x, у) либо тождественно
равна 0 (если у иррационально), либо может быть отлична от 0 лишь для к о-
вечного числа значений х (если у рационально). В обоих случаях
1
) f (х, У) dx = О,
значит, существует и повторный интеграл
1 1
dy (х, у) dx— 0.
Точно так же существует и интеграл
1 1
t dx f (х, у) dy = 0.
6 б
[Ср. 5281]
596. Приведение двойного интеграла к повторному в случае
криволинейной области. Рассмотрим область (Р), ограниченную
снизу и сверху двумя непрерыв-
ными кривыми:
у = у0(х), у = У(х)
(а С х С Ь),
а с боков — двумя ординатами:
х = а и х — Ь (рис. 39). Тогда
аналогично теореме п° 594 имеет
место следующая
Тёорема. Если для функции
f (х, у), определенной в области
(Р), существует двойной инте-
Рис. 39.
грал
\\f(X,y)dP
(Pl
и — при каждом постоянном значении х из [а, Ь] — простой
интеграл	у
1(х)= 5 f{x,y)dy,
То I*)
150
ГЛ. XVI. ДВОЙНЫЕ ИНТЕГРАЛЫ
|596
то существует также повторный интеграл
b Ytxy
^dx f(x, y)dy
а уо (X)
и выполняется равенство
Ь
$$/(•*> y)dP=\dx f(x, y)dy.
(Pi	a ya(x}
(6)
Доказательство строится на сведении этого случая к рассмотрен-
ному в п° 594. Именно, заключим область (Р) в прямоугольник
(Р) = [а, Ь\ с, d],
полагая с— min _у0(х), a d— max Y(x) (см. рис. 39), и опре-
а^х^Ь	а^х^Ь
делим в этом прямоугольнике функцию /* (х, у) следующим об-
разом:
/*(х, у)=-
Покажем, что
п° 594.
/(х, у), если точка (х, у) принадлежит
области (Р),
0 в прочих точках прямоугольника (Р).
эта функция удовлетворяет условиям теоремы
Прежде всего, она интегрируема в области (Р), ибо здесь она
совпадаег с интегрируемой по условию функцией f(x, у)', очевидно,
поэтому
y)dP = \\f(x, y)dP.
tPi	(P)
С другой стороны, f* (x, у) = 0 вне (P) и, следовательно, ин-
тегрируема и в остальной части (Q) = (Р) — (Р) прямоугольника (Р) *,
причем
$$/*(*, y)dQ=0.
«?)
Тогда, в силу 592, 2°, функция f* интегрируема во всем пря-
моугольнике (Р) и
$ $7* (X, y)dR = \ \f(x, у) dP.	(7)
(Я)	(Р)
При постоянном значении х в [a, Z>] существует интеграл
d	Уо(х)	d
\f*(.x,y)dy— J f*dy-\- j f*dy-\- J f* dy,
c	c	Ил)
* Значения ее на границе этой области роли не играют, см. 592, Г.
§ 2. ВЫЧИСЛЕНИЕ ДВОЙНОГО ИНТЕГРАЛА
151
ибо существует каждый из трех интегралов справа. Действительно,
так как в промежутках [с, у0(х)) и (Y(x), d] изменения^ функция
/*(х, _у) = 0, то первый и третий интегралы существуют, будучи
равны нулю. Второй же интеграл совпадает с интегралом от функ-
ции f (х, у):
Г(х)	F(jrt
$ /* (х, у) dy= j / (х, у) dy,
У а (»)	А’о (X)
поскольку /* (х, у) =f (х, у) для у в [_у0 (х), У (х)]. Окончательно,
d	¥(х)
$/*(х, y)dy= 5 f(x,y)dy.
С	Уч{х)
(8)
В силу упомянутой теоремы, для функции f* существует и по-
вторный интеграл, который равен двойному [см. 594 (4)]:
ь d
5 J f* (х> y)dR—\ dx (x, у) dy.
(Л)	а с
Принимая же во внимание (7) и (8), видим, что эта формула рав-
носильна формуле (6).
Если область (Р) представлж
другого типа и ограничена кривыми
х=х0(у), х=Х(у) (c^y^d)
и прямыми у = с, y—d, то вме-
сто (6) придем к формуле
\\f(x,y)dP =
(Р)
а х(у)
= dy Дх, >) dx, (6*)
С JTo(j)
в предположении, что, наряду с двойным интегралом, при у = const,
существует простой интеграл по X.
Замечание. Если контур области (Р) пересекается лишь в
двух точках как параллелями оси ординат, так и параллелями оси
абсцисс (как, например, в случае, изображенном на рис. 40), то при
выполнении указанных условий применимы обе упомянутые формулы.
Из сопоставления их получается равенство
ь	Г(лг)	d	Х(у}
\dx f(x, y)dy = \dy f(x, y)dx,	(9)
e	y0(x)	C 00
152
ГЛ. XVI. ДВОЙНЫЕ ИНТЕГРАЛЫ
[597
которое представляет и самостоятельный интерес. Это — аналог фор-
мулы (5) п° 594.
Если функция f (х, у) в области (Р) непрерывна, то интегралы,
двойной и простой, существуют, и формулу (5) или (5*), смотря по
типу области (Р), можно использовать для вычисления двойного
интеграла.
В случае более сложного контура область (Р) обычно разла-
гается на конечное число частей рассмотренного типа. [Например, фи-
yi	гура (Р) на рис. 41 рассекается
менты. В связи с этим и здесь
пользуются часто символом
прямо х = а на три такие части:
(Pi), (Р2) и (Р3).] Тогда и иско-
мый интеграл, в силу 592, 2°,
представляется суммой интегра-
лов, распространенных в отдель-
ности на эти части; каждый из
них вычисляется как указано.
В общем случае также, по-
скольку мы свели дело к теореме
п° 594, в основе умозаключений
лежит разбиение рассматриваемой
фигуры на прямоугольные эле-
I обозначения двойного интеграла
^/(х, У)dxdy;
(Р)
произведение dxdy напоминает о площади элементарного прямо-
угольника. Само собою понятны и обозначения
b Y(x}
fdydx или
в jo (х)
riX(y)
fdxdy.
с х9 (j)
597. Примеры. 1) Вычислить двойной интеграл
/ = ^у2/р2 —х2 dP,
(Р)
где (Р) есть круг радиуса Р с центром в начале координат (рис. 42).
Решение. Контур области (Р) имеет уравнение х2-|-у2 = Р2, откуда
у = ± У R2 — х2. Очевидно, у — 4- У R~ — х2 есть уравнение верхней по-
луокружности, а у = — УR2— х2 является уравнением нижней полу-
окружности. Таким образом, при постоянном х из промежутка [— R, Р] пе-
ременная у изменяется от —У R2— х2 до 4- Р2 — х2. По формуле (6)
(с учетом четности по у подинтегральной функции)
R + х2	R	УЯ2-х2
1= dx $ у2 У R2 — x2 dy = 2	У R2 — x2dx	$ у2 dy.
— R	— R	0
597]
§ 2. ВЫЧИСЛЕНИЕ ДВОЙНОГО ИНТЕГРАЛА
153
Вычисляем внутренний интеграл:
VfP-xt е	2
С у2 dy = -L(#2 —х2)2 .
о
Затем (снова с учетом четности)
R	R
-R	б
Совершенно аналогично проводится и вычисление по формуле (6*).
2) Вычислить
АГ= (х2 +>i) dx dy,
(Л)
если область (Д) ограничена двумя параболами: у — х3 и у2 = х.
Решение. Полезно сделать чертеж хотя бы грубо, чтобы получить
общее представление об области. Решая совместно уравнения парабол, на-
ходим точки их пересечения: (0, 0) и (1, 1) (рис. 43).
Если внешнее интегрирование производить по у, то промежутком изме-
нения у будет, очевидно, [0,1]. Взяв произвольное значение у в этих пределах,
видим по чертежу, что х изменяется от х=у3 до х= YУ • По формуле (6*),
1 /у
/<=(dy	(x24-y)rfx.
о j-a
Вычисляем внутренний интеграл:
/У	_ з
(•	v-з	|х=Уv	4 •—	1
\ (x2+y)dx = -¥+y/x	' =-5-у2 —	— у3,
J	о	|x=V2	о	о
У3
а затем — и внешний:
1 з
о
154
ГЛ. XVI. ДВОЙНЫЕ ИНТЕГРАЛЫ
[597
3) Вычислить интеграл се
'	v J=\\xydxdy,
(О
где (D) есть область, ограниченная осями координат и параболой +
4- У у = 1 (рис. 44).
Решение. Имеем:
I	(1-/Г)2	I
J=\xdx \ у dy — -^- \ х(1—У х )4 dx —	.
,)	•)	v	ZoU
0	0	О
4) Вычислить интеграл
X2
-у dx dy, где (С) есть область, ограни-
ТсГ У
ченная прямыми х = 2, у = х и гиперболой ху=1.
Решение. Нанесем эти линии на чертеж (рис. 45). Совместным реше-
нием уравнений легко получить, что прямая х — 2 пересекает прямую у = х
в точке (2, 2), а гиперболу х_у=1—в точке ^2, прямая же у = х и
гипербола (в пределах первого квадранта, где и лежит рассматриваемая
область) пересекаются в точке (1, 1).
Если остановиться для вычисления интеграла I на формуле (6), то вне-
шнее интегрирование по х придется произвести в промежутке [1, 2]. При
фиксированном х в этом промежутке пределы изменения у суть У = ~£
и у — х. Итак,	2 х
С (* х2
7= 1 dx J / dy‘
х
Но
X
так что
2
SQ
(Xs — х) rfx = -j-.
1
$ 2. ВЫЧИСЛЕНИЕ ДВОЙНОГО ИНТЕГРАЛА
155
В то время как в предыдущих примерах вычисление по обеим форму-
лам (6) или (6*) представлялось одинаково простым, в данном случае дело
обстоит иначе: вычисление по формуле (6*) здесь было бы сложнее. Тем
не менее мы выполним его, ибо поучительно дать себе отчет в причине ука-
занного обстоятельства.
Прямая, параллельная оси х, пересекает контур области в двух точках,
так что формула (6*) приложима. Но кривая, ограничивающая нашу область
слева, — она отвечает кривой х = х11(у) общей теории, — здесь состоит из
двух частей: куска прямой и куска гиперболы, которые выражаются раз-
личными уравнениями. Иными словами, упомянутая функция х0 (у) задается
различными формулами в различных частях промежутка £-!•, 2^ изменения у.
Именно,
1	1
. .	—, если	1,
xeCy) = J У	2
у, если 1 sg у 2.
Справа область ограничена прямой х = 2.
Поэтому интегрирование по у удобнее разбить и представить / в виде
1	2	2	2
./= J J rfx+ j7dx-
11 I У
2 у
Так как
f Xs л _ 8	1 f Xs л ____ 8 у
JJ^dx —Зу»—3/> J	’
1	У
у
то
1	2
"2
С подобными обстоятельствами приходится считаться; из двух возмож-
ных путей вычисления двойного интеграла, естественно, выбирают более
простой.
5) Вычислить интегралы:
(а) Л = И cos <х +-^ dx dy> <б> Z« = И (2х +-У) dx dy>
(Qi)	«Ы
(в) /8 — $ $ (х + бу) dx dy,
«2а)
где (QJ есть треугольник, ограниченный прямыми
х — 0, у = х, у — тс,
(<?2) — треугольник, ограниченный осями координат и прямою х-|-_у = 3, а
(Qi)— треугольник, ограниченный прямыми
у = х, у = 5х, х = 1.
156	ГЛ. XVI. ДВОЙНЫЕ ИНТЕГРАЛЫ	1597
Указание. В случаях (а), (б) безразлично, какой из формул (6), (6*)
пользоваться; в случае же (в) удобнее пользоваться формулой (6) (почему?
сделать чертеж!)
27	1
Ответ, (а) Д = -2; (б)	(в) 73 = 254.
Z	О
6) Вычислить интеграл
7= $ $У 4ха —У dx dy,
распространенный на треугольник, который образован прямыми у = 0, х=1,
у — X.
1 х ___________
Решение. По формуле (6) I=^dx\y 4х2 -—у2 dy, внутренний инте-
о и
грал равен
х	_
f /Зх2—_у2 dy =	У4х2—/ + 2х2 arcsinI= (Ку- + хг,
j	Z	£Х у=-0	\ £ О /
О
и
окончательно
/=1(К1
3 \ 2
Можно было бы вести вычисления и по формуле (6*), но в этом слу-
чае мы натолкнулись бы на более трудные квадратуры. Подобное
обстоятельство также следует учитывать при выборе пути для вычисления.
В связи с трудностями, которые иной раз представляет расстановка
пределов интегрирования в случае криволинейной области, полезны следую-
щие упражнения:
7) Переменить порядок интегрирования в повторном интеграле [по фор-
муле (9)]:
4	12х
(a) \dx $ f(x, у) dy,
о 3>2
1 Зх
(В) $ dx ( f(x, у) dy,
О 2х
1	2+V7—бу—у*
(б) dy	/(х, у) dx,
— 7	2-/7— бу —у*
1	V3—y*
(r)\dy J /(х, y)dx,
0 ^2
2 J
считая f(x, у) непрерывной функцией.
(а)	Решение. Область интегрирования определяется совместными не-
равенствами:
О sg х sg 4, Зх2 sg 12х.
Отсюда прежде всего ясно, что крайними значениями у будут 0 и 48. Решая
же последние неравенства относительно х, при фиксированном у найдем,
1	1 Г У *
что х меняется от -г^у до I/ ~ .
1Z	f о
* Оба эти числа не выходят за пределы промежутка [О, 4]!
§ 2. ВЫЧИСЛЕНИЕ ДВОЙНОГО ИНТЕГРАЛА
1'57
Еще проще усмотреть этот результат из рис. 46, где изображена область,
ограниченная прямой _у=12х и параболой _у = 3ха, которые пересекаются в
точках с абсциссами 0 и 4. Отметим, что по оси х взят другой масштаб,
чем по оси у.
Ответ. dy § fdx.
(б)	Указание. Область интегрирования
ограничена окружностью
(х-2)а + (у + 3)2 = 4а.
6	-3 + /124-4х-л*
Ответ. § dx J	f.dy.
— 2	—3—V124-4X —x-i
(в)	Решение.	Область	интегрирования
определяется совместными неравенствами:
Osgxsgl, 2xsg_ys=:3x,
откуда выясняются крайние значения для у: 0 и 3.
Решая последние неравенства, видим, что ^rsgXigX. Но для _у>2
О	Z
предел -у уже выходит из промежутка [0, 1], которым во всяком случае
ограничено изменение х. Следовательно, при 0s£y^2 переменная х изме-
няется от " до -=£- а при 2sg_y=g3 — от до 1.
о 2	о
Значительно проще этот результат получается геометрически, если
сообразить, что область интегрирования есть треугольник, ограниченный
прямыми _у = 3х, _у = 2х и х=1 (сделать чертеж!).
Ответ. Получаем сумму двух повторных интегралов:
2
2	2 У 3	1
j dy § fdx + j dy $ fdx (Cp. 4) и 5) (в)).
V	Г”
(г) Ответ. Получаем сумму трех повторных интегралов:
1 _
2 fix f 2	1 f3 f3 — x2
\ dx V fdy-f ( dx\fdy-f dx ( fdy.
0	0	О	У 2	0
2
158
ГЛ. XVI. ДВОЙНЫЕ ИНТЕГРАЛЫ
[597
8)	Записать в виде одного повторного интеграла выражение:
1	у	3	1
(а)	$ dy j /(х, у) dx + f dy J f(x, y) dx,
7	3	9	10-.У
(6)	j dy J f(x, y) dx + j dy	f (x, y) dx.
У	7
Ответ.
1	з/7	з io-x
(a) \dx J fdy, (6) j dx C fdy.
Ox	|	9
7
(Рекомендуется во всех случаях делать чертежи.)
9)	Показать, что употребительная формула интегрального исчисления
ь
P=^f(x)dx,
а
выражающая площадь криволинейной трапеции, ограниченной осью х, орди-
натами х = а, х = Ь и кривою y=f(x) (где
/3= 0), является следствием очевидного равен-
ства
Р— dx dy.
(Р>
Указание. Воспользоваться форму-
лой (6).
10)	Установить формулу
ь	х	ь ь
5 dx j f(x, y)dy = ^ dy f(x, y) dx, (10)
a	a	ay
где fix, у) есть произвольная
прерывная в треугольнике (Д),
прямыми у = а, х = Ь, у = х.
Указание. См. рис. 47; воспользоваться формулой (9),
нять оба повторных интеграла, к которым приводится двойной ин-
теграл по области (Д).
Доказанная формула обычно связывается с именем Дирихле; она
имеет различные приложения, особенно — в теории так называемых инте-
гральных уравнений Вольтерра (G. Volterra).
11)	С помощью формулы (10) легко доказать, что
функция, не-
ограниченном
т. е. прирав-
$ 2. ВЫЧИСЛЕНИЕ ДВОЙНОГО ИНТЕГРАЛА
159
Последовательное применение этой формулы приводит к результату:
X	*П — 1	/1	X
J <и^ J dtn_,... J fit) dt = ^±^ J (x-ty-'fit) dt,
a	a	a	a
n
который выше [511, 13)] был установлен другим путем.
12)	Вычислить интеграл
/= J хР~гуЧ~1 dx dy,
х=*0, ji&O
х+.У=е1
в предположении, что р 5= 1 и q 2s 1 *.
Имеем по формуле (5)
1	1-х	1
I=AxP~'dx	y4~ldy = ^	хР-*(1— x)4dx=~ В(р, ?+1).
о	о	4 о
Окончательно,
С С хр~М-1 dx dy = Г Г ...
JJ Х У У T(p + q + \y
x=sO, j>=sO
*+.У==1
Эта формула принадлежит Дирихле.
13)	Аналогично вычисляется более общий интеграл
J= f J	(1 — х —у)г~1 dx dy,
х^О, _у>0
х+>«1
в предположении, что 1, q ^5 1, г :> 1 *.
Сначала, как и выше,
1	1—х
J= (xP-»dx	ут1(1 — х—уТ* dy.
8	б
Затем внутренний интеграл преобразуем подстановкой _у = (1—x)t в ре-
зультате:
1 1
J = XP~l (1 — Х)Ч+Г~1 dx t9-1 (1 — 0^' л =
= В(р, 9 + г)В(9, 0 = ^^.
14)	Вычислить интеграл, представляющий дальнейшее обобщение пре-
дыдущего:
С С хР-^ч-Ц! — х—yf-'dxdy
К==	’ J (ax + ₽j + 7)Р+«+г
хго, j’^o
x+jsl
(где a, рО, 7>0 и, кроме того, р5=1, q^l, r^i).•
-* Это ограничение мы устанавливаем здесь лишь для того, чтобы из-
бегнуть обращения подинтегральной функции в бесконечность; впоследствии
[617, 14)] оно будет ослаблено.
160
ГЛ. XVI. ДВОЙНЫЕ ИНТЕГРАЛЫ
1597
Переходя к повторному интегралу, получаем
- С ^-1 dx	(1— -у— уГ1
/<_ ХР dx j (ад. 7)р+9+г аУ>
о	о
а затем, после подстановки у = (1—x)t, изменяем порядок инте-
грирований:
С (1______ог-1 df С __хР 1 ~х)?+г 1_____dx
* yt ц i) at	^+q+rax.
о	о

Для вычисления внутреннего интеграла воспользуемся уже известным ре-
зультатом [534, 2)[. Тогда
г(р)г(? + г) 1 С (1 — 0г~‘
Л Г(р + ? + г) > + 7)₽	^ + 1)?+г
о
и, снова прибегая к тому же результату, окончательно:
Г(р)Г(? + г) 1	Г(?)Г(г)	1	_
Г(/>-Н + г) > + 7)₽ ' Г(?+г) '(3 + 7)«7г
_ Г (/>) Г (g) Г (г)1
г (р + Я + г) (а + 7)₽ (₽ + 7)? 7Г ’
15)	Пусть функции /(х, у), g(x, у) непрерывны в ограниченной замк-
нутой области (£>), причем наименьшее и наибольшее значения функции g
пусть будут т и 7И; пусть ?(и) означает функцию, непрерывную для
^и^М.
Обозначим через ф («) интеграл
5$ f(x,y)dxdy,
m^g^u
распространенный на ту часть области (D), в которой выполняется указан-
ное внизу неравенство *.
Тогда имеет место формула Каталана (Е. Catalan)
м
И f(x,y)<f(g(x,y))dxdy=\<f(u)d^(u),
m^g^M	т
где интеграл справа понимается в смысле Стилтьеса.
Так как непрерывную функцию f всегда можно рассматривать как раз-
ность двух положительных непрерывных функций, то при доказательстве
этой формулы мы можем просто считать функцию f положительной.
Разложив произвольно промежуток [т, М] на части:
т = и0 С ut <... < ut < ui+1 <... < ип = М,
* Мы предполагаем, что уравнение g(x, у) = а выражает замкнутую
кривую, так что упоминаемая в тексте часть области ограничена двумя та-
кими кривыми.
§ 2. ВЫЧИСЛЕНИЕ ДВОЙНОГО ИНТЕГРАЛА	161
соответственно этому разложим и предложенный интеграл (обозначим его
через /):
/== S $ $ f-4{g)dxdy= J] <p(g(Sf, -qf)) J J fix, y) dx dy.
i^O	i=0	ar^“i+1
Мы воспользовались здесь обобщенной теоремой о среднем значении; (Е*, т;*)
есть некоторая точка области, где щ sg g sg u/+1, так что, полагая
g(£f, 1lF) = uz'> будем иметь u^uf ^и;+1. Итак, окончательно,
п— 1
7=2 ?(«*) [ф(иж)-ф(и;)].
>=о
В сумме справа узнаем сумму Стилтьеса. Переходя к пределу при
max Ди, —* 0, установим требуемый результат:
AI
Z=(s) $ ?(и)</ф(«).
т
Если для функции ф (и) существует непрерывная (или хотя бы абсолют-
но интегрируемая) производная ф’ (и), то интеграл Стилтьеса заменяется
обыкновенным:
AI
1= <р (и) ф' (и) du.
т
16)	Для примера покажем, как по методу Каталана, из элементарной
формулы Дирихле [см/12)] может быть выведена более общая формула,
принадлежащая Лиувиллю (J. Liouville).
Возьмем, в частности,
fix, у) — хР~1у9~\ g(x, у)=х+у,
а за область (£>) выберем треугольник х^О, у^О,	Тогда по
формуле Дирихле при 0 < и «£ 1
ф (и) =	х?~1уЧ~1 dx dy — иР^ч J	dx dy =
х^О, ySzO	х>0,
=	(Р) Т (?)	„+д
T(p + q+i)“
и, воспользовавшись преобразованием Каталана, будем иметь
1
J J ^>уг*т(х+у)ф:йу=2^|т(в)^=
JC=sO, J&O	о
5?(и) мР+?”da-
о
Это и есть формула Лиуеилля.
17)	Найти объем тела, ограниченного
(а)	плоскостями х = 0, у> = 0, г = 0, цилиндром х^-\-у2 = Я2 и гипербо-
лическим параболоидом z = xyr (в первом октанте);
6 Г. М, Фихтенгольц, т. III
162
ГЛ. XVI. ДВОЙНЫЕ ИНТЕГРАЛЫ
|597
(б)	плоскостями х = 0, _у = 0, 2 = 0, х4-2у=1 и поверхностью z =
— x2+j+U
(в)	плоскостями у = 1, z = 0, параболическим цилиндром у = х2 и пара-
болоидом z — x2-}-y,
(г)	плоскостями ,у = 0, 2 = 0, у = —х и эллиптическим цилиндром
X2 Z2
—+ —= 1
f са —
' R
Ответ, (а) И= х dx у dy =	А4;
о 6
2	1- 1у
(б) R=(dy С (x2+y+l)dx =4;
•J	V
о	О
1	1
г»	/»	оо
(В) v= \dx\ (х2+/) dy=^;
-1 X*
b
— х
а а
. . С . С с ,,—з-----s j obc
(г) V=\dx 1 — у а2— х2 dy = -$-,
о о
18) То же для тела, ограниченного:
у®
(а)	эллиптическим цилиндром ^2 + ja"= 1 и плоскостями 2 = 0 и z =
= Хх -|- |лу + h (Л > 0);
(б)	цилиндрами az=y2, x2-f-_y2 = r2 и плоскостью 2 = 0;
(в)	частью поверхности xyz — a2, вырезан-
ной из нее плоскостями z =р, z = q (0</><
С q), х = г, х = s (0 < г < s), проекцией этой
части на плоскость ху и проектирующим ци-
линдром.
-Va3-x3
а а
Ответ, (a) V= dx
а	— —V а3 — jc2
а
Рис. 48.	(Хх -|- цу + dy = Ttabh = Ph,
(если Р есть площадь эллипса; результат геометрически очевиден);
Г Vr3-J3	Г
Л (•	с	4 (•	_______
б)	И=- J dy \ У2 rfx = ± у2 Vr2-y2 dy^-d--
0	0	о
s	рх
(в	) У= f dx С — dy = a2 In — In	—,
j	J xy	p	r
r	21
qx
$ 2. ВЫЧИСЛЕНИЕ ДВОЙНОГО ИНТЕГРАЛА
163
19)	Найти объем V тела, вырезанного цилиндром х2-\-у2 — 2ах из пара-
болоида вращения у2 -|- z8 = 4ах.
Решение. Имеем:
2а V 2ах—х3 __________
V=4^ dx	У 4ах—у2 dy.
О о
Полагая 68==4ах в известной формуле
У Ь2—_у2б?_у = -|-arcsin^--]“^r У &3—У3>
вычислим первообразную функцию У 4ах —у3, а с ее помощью найдем
внутренний интеграл:
V2ax—x*	________
У 4ах —у2 dy — 2ах arcsin т/	У 4а2 — х8.
Путем интегрирования по частям получим далее:
2а
х arcsin
о
__	2а
х . а С
-т- dx = -s- \
4а 2 J
о
а /п ,	. х х -----------=\ 12а на*
= -^2a8arcs>n^ —^/4а«-х’) q
3
—==~rfx =
у 4а2 — х2
Наконец,
2а
4- ? х У4a2 — x2dx = -^-a2
Z J	о
О
20)	Найти объем V тела, вырезанного цилиндром х2 4-у2 = Rx из сферы
л;«+_у»4-z8 = /?’ (рис. 48)*.
Решение. Имеем:
у= 4	УR2 — х2 —у2 dx dy,
где (Р) есть полукруг в первом квадранте плоскости ху, ограниченный ли-
ниями х = 0 и х84-у»8 = /?х, кили
R V Rx—x»
5	/Л2— ха — y2dy-
о о
• Это тело иногда называется телом В и в и а н и (Viviani), по имени
итальянского математика XVII в., который впервые его рассматривал.
164
ГЛ. XVI. ДВОЙНЫЕ ИНТЕГРАЛЫ
[597
Но
VRx—x2
/А2 — х2— y2dy =
_^ — х2 arcsin У . У у ™----------р---~2
“ 2 аГСМПГ^=^ + '2	~Х ~У Ь=Э
=л 7 х arcsin У"+у кw—*) Vх-
Интегрируя по частям, найдем:
R	______ R ± i
1 С ZD2 2Ч . -1/" х . nR3 YR C 3R2x2—x2 ,
X)arcSiny R + ^dx = 12— TF ' 7? + x'
О	0
С помощью, например, подстановки x = Rt2 легко найти значение послед-
него интеграла:
. 2R2lA R  (— — I— —R3
12 2R у R ^]5	2J — U5 12,) ° ’
так что
R	________
т $ (*а-x2)arcsin у тгЬdx=&~Й) *’•
о
Далее, без труда найдем
R
'Yr\(R-x)Yx dx — ~R3,
о
так что, окончательно,
v=4(t-4)^=t*-r,-4^*-
2
Замечание. Так как объем полусферы есть -^-тс/?8, то объем ее
о
$
части, получающейся после удаления тела Вив и а ни, равен д-7?’. Любопытно,
что он выражается через радиус R без привлечения каких бы то ни было
иррациональностей.
21)	Вычислить интегралы
Ii = \\ydxcly, 1а=\\ х dx dy,
(A)	.	(Л)
где (А) есть область, ограниченная аркой циклоиды
х — a (t — sin t), у — а (1 — cos t) (0 < £ s< 2я)
и осью X.
* Ниже мы укажем го.р,аздо б.олее простой способ вычисления
этого объема 1611, 6)].
§ 2. ВЫЧИСЛЕНИЕ ДВОЙНОГО ИНТЕГРАЛА	165
Решение. Своеобразие этой задачи состоит в том, что контур области
задан параметрическими уравнениями. Однако ордината у» точки циклоиды пред-
ставляет собой все же однозначную и непрерывную функцию абсциссы х: у~
=у(х), так что, переходя к повторному интегралу, по общей формуле имеем
J'(x)
Д = t dx ydy = i \ у2 (х) dx.
0	0	о
Чтобы освободиться от неизвестной нам функции у (х) и вернуться к из-
вестным функциям, сделаем подстановку x — a(t — sinf). Тогда у(х) надле-
жит заменить на а (1—cos<)» и мы получим
2п	2п
Д f e2(l —cosi)2 da(t — sini)= (1 —cos^)3 dt — ^- -a*.
о	0
Аналогично,
Д = ЗЛ’.
22)	Вычислить интеграл
ЛГ= И ху dx dy,
(В)
где область (В) ограничена осями координат и частью астроиды
х = a cqs3 t, у— a sin31 ^0 t sg 40.
Ответ.
oU
598. Механические приложения. Все геометрические и механические ве-
личины, связанные с плоским непрерывным распределением масс вдоль
некоторой фигуры (Р) и представляющие аддитивные функции об-
ласти, в принципе выражаются двойными интегралами, распространенными
на эту фигуру. В п° 593 мы уже подробно останавливались на этом вопросе.
В частности, мы видели, что сама величина распространенной массы выра-
жается по заданной плотности распределения р (7И) = р (х, у) так:
m = §jj р dP.	(11)
(Р)
Здесь доы имеем в виду дать краткие указания относительно того, как
обычно получают формулы подобного типа. Порядок идей здесь тот же, что
и при применении простого определенного интеграла [см. 348].
Выделяя элементарную часть (dP) фигуры (Р), делают упрощающее вы-
кладки предположение, — например, что масса всего элемента сосредоточена
в одной точке или что плотность распределения масс в пределах элемента
постоянна, — которое позволяет дать для элемента dQ искомой величины Q
приближенное выражение вида
dQ = q(M) dP,
верное до бесконечно малой порядка, высшего чем dP, Тогда точное
значение Q выразится формулой
q(M)dP.
IP)
Обосновать это можно двояко (как и в 348).
166
ГЛ. XVI. ДВОЙНЫЕ ИНТЕГРАЛЫ
[598
Прежде всего, суммируя приближенные выражения для элементов dQ,
можно получить приближенное же значение величины Q в виде интегральной
суммы, а переходя к пределу — точное значение Q уже в виде предела
суммы, т. е. интеграла.
С другой стороны, самое выражение для элемента dQ позволяет заклю-
чить, что q (М) есть «производная по области» величины Q (в точке М),
а отсюда, в силу изложенного в п° 593, снова вытекает тот же результат.
Легко сообразить, например, что элементарные статические моменты и
моменты инерции относительно осей координат будут
dMx = ур dP, dMy = хр dP,
dlx=y°p dP, di у = x2p dP;
отсюда для самих моментов сразу получаем
— ЭД ур dP, Му	= ЭД	хр dP,
ее	гг	(12)
1Х — ЭД Угр	<у=ЭД	Х*Р	dP
<Р)	(Р)
Теперь обычным образом получаются координаты центра тяжести фигуры:
В случае однородной фигуры: р = const эти формулы упрощаются:
ЭД х dP у dP
р > 1=	5
(14)
В отдельных простых случаях удается с помощью двойных интегралов
исчерпать подобные же вопросы по отношению к телам, именно — к ци-
линдрическим брусам.
Пусть дан такой брус, ограниченный поверхностью z = z(x, у), ее проек-
цией (Р) на плоскость ху и проектирующим цилиндром, образующие кото-
рого параллельны оси z. Если, например, требуется определить статический
момент Мху однородного бруса (для простоты предположим объемную
плотность равной единице), то мы представляем себе этот брус состоящим
из ряда элементарных столбиков, с основанием dP и высотой z. Статический
момент столбика относительно плоскости ху равен его массе или — что
в данном случае то же — объему z dP, умноженному на расстояние его центра
тяжести от этой плоскости, т. е. на -^-z. Итак, элементарный статический
момент есть
dMxy = ±-z2dP,
откуда, суммируя по всем столбикам, получаем
5 5z*dP-
V)
(15)
$ 2. ВЫЧИСЛЕНИЕ ДВОЙНОГО ИНТЕГРАЛА
167
Аналогично могут быть установлены и формулы
Mzx = §yzdP, Муг=^ xzdP.	(15а)
(Р)	(Р>
Отсюда легко получить выражение для координат 6, tj, С центра тяжести
бруса:
№ xz dP
Точно так же выводятся и формулы для моментов инерции бруса /2 от-
носительно оси z и 1уг, 1гх относительно плоскостей координат:
4 = У (хг +у2) z dP, 1гх = ysz dP, 1уг — 55 x*z dP, (16)
(P)	(P)	(P)
причем ясно, что 1г = 1гх + IyZ-
Если бы пространственная плотность р распределения масс, не сводясь
к постоянной, зависела бы лишь от х, у (т. е. все же вдоль столбика
была бы постоянной), то по-прежнему можно было бы обойтись двойным
интегралом. Однако, в общем случае, при зависимости р и от z, двойного
интеграла уже было бы недостаточно и пришлось бы обратиться к т р о ft-
но м у интегралу [см. 649].
599.	Примеры. 1) Пусть фигура (Р) представляет собой криволинейную
трапецию, ограниченную кривой y=f(x), отрезком оси х и двумя ордина-
тами х = о и х = Ь, и пусть плотность распределенных по этой фигуре масс
будет 1. Определить статические моменты Мх и Му.
Переходя в формулах (12) к повторным интегралам, будем иметь:
а У(х)	ь
Мх = у dP = dx у dy = у У2 (х) dx,
(Р)	а О	а
Му — 55 х dP = 5 х dx 5 dy =} х f (х) dx
(P)	a 0 a
или, короче,
ь	ъ
Mx — у ya dx, My— xy dx,
a	a
и мы возвращаемся к выражениям статических моментов, уже полученным
нами раньше [351].
Предоставляем читателю повторить эти выкладки для моментов инерции
1Х ® /у-
2)	Цилиндрический брус (V) имеет в основании плоскую фигуру (Р),
а сверху ограничен произвольной плоскостью (А). Доказать, что объем V
тела равен произведению площади Р основания на длину k перпендикуляра
к основанию, проходящего через центр тяжести тела до пересечения
с плоскостью (К).
168
ГЛ. XVI. ДВОЙНЫЕ ИНТЕГРАЛЫ
|599
Если оси расположены, как обычно (рис. 49), и уравнение плоскости (К)
имеет вид
z = ах + by + с,
то по формуле (2*) п° 586
(ax + by + c)dP = a^ xdP + b^ydP + c Ц dP =
(Р)	(Р)	(Р)	(Р)
= (a£ + bii + c)P=Pk.
3)	Доказать, что если в плоскости фигуры (Р) взяты две параллельные
оси х и х' на расстоянии й, причем первая из них проходит через центр
тяжести фигуры, то моменты инерции фигуры относительно этих осей свя-
заны соотношением
Ix. = Ix + h2m,
где т— масса фигуры.
Выбрав ось х за ось абсцисс, имеем
1Х, =1^ (у — h)2 р dP = Ix — 2hMx + h2m.
(Р)
Так как, по предположению,Мх = 0, то мы и приходим к требуемому равенству.
4)	Полярным моментом инерции материальной точки называется произ-
ведение массы точки на квадрат расстояния до полюса. Легко понять, чтб
разуметь под полярным моментом инерции плоской фигуры.
Рис. 49.
Рис. 50.
Поместив полюс в начале координат О, доказать, что полярный момент
7O=/* + Zj,.
5)	Пусть в плоскости ху задана произвольная фугура (Р). Найти общее
выражение для момента инерции этой фигуры относительно любой оси Ои,
составляющей с осью Ох угол 0 (рис. 50).
Если принять ось Ои и перпендикулярную к ней ось Оо за новые коор-
динатные оси, то, как известно, новые координаты и, -о будут связаны со
старыми х, у зависимостями
u = х cos 0 4-j sin 6, v = — xsin04-ycos0.
599]
§ 2. ВЫЧИСЛЕНИЕ ДВОЙНОГО ИНТЕГРАЛА
169
Поэтому
/и = ЭД ®2 р dP = cos2 6 • ЭД у2 р dP — 2 sin в cos 0 •
(Р)	<Р)
4- sin2 6 • ЭД xs р dP.
<Р)
как мы видим, моменты
кроме них здесь встре-
Коэффициентами при cos2 0 и sin2 0 являются,
инерции 1Х и 1у относительно осей координат, но
чается еще величина
Х^=ЭД *УР dp,
(Р)
которую называют центробежным моментом [см. ниже, задачу 7)] или про-
изведением инерции. Итак,
1а = !х cos2	2КХу sin 0 cos 0 4- Jу sin2 0.	(17)
Для наглядной иллюстрации изменения момента инерции фигуры при
вращении оси Ои поступают следующим образом. На оси Ои откладывают
отрезок
ON=-±=
Vln
(см. рис. 50) и рассматривают геометрическое место полученных таким
путем точек N. Если координаты точки N обозначить через х, у, то
x = CWcos0 =-^Л, у — ON sin 0 = - feJL-
Деля соотношение (17) на /а, получим уравнение упомянутого геометри-
ческого места:
!хх2 — 2Кхуху 4- 1уу2 = 1.	(18)
Распространяя неравенство Бу н я к о в с ког о на случай двойных инте-
гралов, легко видеть, что дискриминант
так что кривая (18) есть эллипс. Его называют
эллипсом инерции.
Если Кху = 0, уравнение (18) получает форму
Рис. 51.
осью
которая показывает, что в этом случае оси коор-
динат служат осями эллипса инерции (главными
осями инерции).
6)	Относительно центробежного момента Кху
установить:
а)	если одна из осей, например ось у, будет
самой фигуры (Р) и для расположенных на ней масс*, то NXy = 0;'
(б	) если яачало координат является центром ^яжести фигуры и
через точку Ot (а, Ь) проведены оси Otxt и О^, параллельные прежним
(рис. 51), то
симметрии для
* Так что р (— х, у) = р (х, у).
170
ГЛ. XVI. ДВОЙНЫЕ ИНТЕГРАЛЫ
[599
Формула приобретает особенно простой вид, если Kxy = Q, именно:
^=а’Р- <19>
7)	Пусть плоская фигура (Р) (рис. 52), по которой непрерывным обра-
зом расположены массы, вращается с угловой скоростью « вокруг оси у.
Определим общую величину развивающейся при этом центробежной силы F
и ее момент М относительно
оси z*.
Для элемента р dP центро-
бежная сила равна
df=<o2xp dP
(направлена в одну сторону при
х>0 и в другую при х<0),
а момент ее относительно оси z
dM — ^xy^dP.
Отсюда, суммируя:
F= о? И х р dP = а>гМу,
(Р)
М = <о’ xy?dP = ^K
Рис. 52.	ЭД	у
Трким образом, при <о=1, величина Кху является моментом центробеж-
ной силы; отсюда и название «центробежный момент».
Для того чтобы действие центробежной силы на ось вращения было
равно нулю, необходимо и достаточно выполнение равенств
Му = 0, Кху = 0.
сила не производит никакого действия на ось вращения лишь при условии,
что осью вращения служит одна из главных центральных осей инерции
фигуры.
8)	Рассмотрим тело, полученное от вращения плоской фигуры (Р) (рис. 53)
вокруг оси у, которая ее не пересекает. Определить его объем V и поло-
жение центра тяжести С*.
* Моменты относительно других осей очевидно равны 0,
$ 2. ВЫЧИСЛЕНИЕ ДВОЙНОГО ИНТЕГРАЛА
171
Решении. Возьмем сначала элементарное кольцо, описанное элементом
dP фигуры, его объем можно принять равным объему цилиндра высоты 2гсх
с основанием dP, так что
dV=2wc-dP
и
V= 2п ЭД х dP = 2пМу = 2х$ • Р,
(>)
где Му — статический момент нашей фигуры относительно оси у, а Е—рас-
стояние центра тяжести С фигуры от этой оси. Таким образом, мы снова
получили теорему Г ульдина [351J, но на этот раз для фигуры, ограни-
ченной любым контуром.
Статический момент элементарного кольца, о котором только что была
речь, относительно плоскости хг, очевидно, равен
dM = у dV = 2пху dP,
так что
М = 2я ху dP = 2it/(Xy.
Следовательно, координата у = tj* центра тяжести С* равна
9)	Применить эту формулу к частному случаю, когда фигура (Р) является
прямоугольным треугольником (рис. 54).
При обозначениях чертежа
.. bh/ . 1 ,\ М(За-Н)
МУ—2 1в+т&)=-6-2
(так как положение центра тяжести треугольника известно). Учитывая
уравнение наклонной стороны треугольника:
у=^-(а+ь—•*)»
найдем и Кху =	• Отсюда, в силу (20), 1* = 4- • V	ь .
J	Z4	4 o(J -f- и
h
Как видим, эта координата отлична от координаты т] = ---центра
тяжести самого треугольника.
10)	Показать, что если вращающаяся фигура имеет ось симметрии,
параллельную оси вращения (рис. 55), то необходимо •>]* = •>], т. е. центры
тяжести тела и плоской фигуры ^ежат на одной высоте.
172
ГЛ. XVI. ДВОЙНЫЕ ИНТЕГРАЛЫ
(599
Указание. Это следует из (20) и (19), если учесть, что	—0
[см. 6) (а)].
11)	Показать, что при тех же предположениях момент инерции I
тела, полученного от вращения рассматриваемой фугуры, относительно оси
вращения выразится формулой I = 2л$ (?2Р	31 у1).
12)	Применить формулы (15) и (15а) к следующему частному случаю:
пусть основанием бруса служит прямоугольник [0, а; 0, Ь], сверху же брус
ограничен эллиптическим параболоидом:
х2 , V2
Z~2p^~2q'
а _______ 2a2q 3b2p b
Т’ 11 — a2q + b2p ’Т’
За2? + 2&2р
a2q -|- b2p
Ответ. $ —
.___9а4?2 + 10a2b2pq + 964р2	1
a2q -|- Ь2р	6Qpq ‘
13)	Найти центр тяжести цилиндрического отрезка [334, 8),
рис. 56],
Решение. При обозначениях чертежа уравнение секущей плоскости
будет z — ky, где ft = tga. Роль (Р) здесь играет полукруг радиуса а, огра-
ниченный полуокружностью х2 -|-у2 = а2. Имеем:
а V аа — Xs	а	з
Л4гх —yzdP=k	y2dx dy = у f (а2—х2)2 dx = ^-ka-,
(Р)	—а 5	о
—а
Так как объем
z2dP = А С yz dP = ^ft2a4,
(Р)
2
ka\
О
Af^ = O.
TO
q	q
г = 0,	l=^r.ka.{
14)	To же для части эллипсоида
1
a2 + b2 + c2 L
содержащейся в первом октанте (рис. 57),
599J
§ 2. ВЫЧИСЛЕНИЕ ДВОЙНОГО ИНТЕГРАЛА
173
Решение. Область (Р) ограничена координатными осями и эллипсом
у = ^У а2—х2
(OsSxsja); уравнение поверхности эллипсоида в явном виде будет
V а2 Ь2 •
По формуле (15),
ь]/1- ~
ат а2
1	(	С	/	х2	Vs \
М = — c-\dx I (1-------------j-—	=
2	У	J	\	а2	Ь2]
о	о
а	3
= зт5(“,-‘!)Т‘,х=Г6Л’-
о
Аналогично
Myz = a2bc. мгх — аЬ2с.
В то же время объем
V=~abc,
о
так что
t 3	3 ,	«	3
5=Та- ч=_6, С=_с,
15)	Для кругового цилиндра высоты h и радиуса а найти момент инерции
относительно любой плоскости, проходящей через его
ось (рис. 58).
Решение. Выбрав координатные оси, как ука-
зано на чертеже, по второй из формул (16) имеем
а Та2 — х2
y2zdP'=h dx	y2dy —
~а -Va2 — x2
а	3
= ~h f(e2 —х8)2 dx = ~hal.
о J	4
16)	Найти момент инерции 1г для эллипсоида
Решение. Можно ограничиться одним октантом эллипсоида (рис. 57),
с тем, чтобы результат умножить на 8. В таком случае областью (₽) будет
квадрант эллипса
а2 “ Ь2
174
ГЛ. XVI. ДВОЙНЫЕ ИНТЕГРАЛЫ
1600
Имеем
ь
5	1	у2 \	4
у8 1 —	) dy = -т=- Ttaft’c.
\	о8 /	15
Аналогично
4
lyz — ~[5"
и, наконец,
4
Ц = Ьх + {у* = 15 " аЬс + &2)-
§ 3. Формула Грина
600. Вывод формулы Грина. В настоящем п° мы установим фор-
мулу, связывающую двойной и криволинейный интегралы.
Рассмотрим область (D) — «криволинейную трапецию» (рис. 59),
ограниченную контуром (Z), состоящим из кривых
(PQ): у=у0(х) (а^х^Ь)
и
(RS): y=Y(x) (as^bs^x)
и двух отрезков PS и QR, параллельных оси у.
Предположим, что в области (О) задана функция Р(х, у), непре-
рывная вместе со своей производ-
ен дР
ной -у—,
ду
Вычислим теперь двойной ин-
теграл
J j ^-dxdy
(D)
по формуле (6) п° 596; мы получим
Ь У(х)
И^dxdy=\dx J
(D)	а уо(*)
вычисляется с помощью первооб-
Внутренний интеграл здесь легко
разной функции Р(х, у), именно:
\у = У(х)
У == Р -У) L = v w — Р (Х> Y — Р (Х> Уй (*))•
600]
§ 3. ФОРМУЛА ГРИНА
175
Таким образом,
ь	ь
j §lfrdxdy~ §Р<Х’ Y(x))dx~ \р(х’
(Р)	а	а
Каждый из этих двух интегралов может быть заменен теперь кри-
волинейным интегралом. В самом деле, вспоминая формулу (7)
п° 547, видим, что
ъ
fp(x, Y(x))dx — Р(х, y)dx,
a	(SP)
Ь
Р (х, у) dx.
^Р(х, y0(x))dx= \
а	(А
Отсюда
f С dx dy — Р(х, у) dx — Р (х, y)dx =
\D)	(SR)	(PQ)
— P(x, y)dx-\- P(x, y)dx.
(s'ri	wj’p)
Желая ввести в рассмотрение интеграл по всему контуру (£)
области (D), прибавим к правой части полученного равенства еще
интегралы
Р (х, у) dx и Р (х, у) dx,
(PS)	(RQ)
очевидно, равные нулю, ибо отрезки (PS) и (PQ) перпендикулярны
к оси х [см. 547]. Мы получим
? \ ~£~dxdy= Pdx-{- ? Pdx-y- Pdx-\~ ? Pdx.
CD)	(PS)	(ЗД	(RQ) (QP)
Правая часть этого равенства представляет собой интеграл, взя-
тый по всему замкнутому контуру (£), ограничивающему область (D),
но в отрицательном направлении. В соответствии с соглаше-
нием, установленным нами насчет обозначения криволинейный интег-
ралов по замкнутому контуру [548], мы можем окончательно перепи-
сать полученную формулу так:
№^-dxdy = -Ap(x, у)(Ьс.	О)
(D)	(Z)
Хотя формула эта выведена в предположении правой ориентации
осей, но, как легко убедиться, она сохраняется без изменения и при
176
ГЛ. XVI. ДВОЙНЫЕ ИНТЕГРАЛЫ
[60Э
левой ориентации (лишь положительное направление обхода контура
станет иным).
Выведенная формула справедлива и для областей более сложного
вида, чем рассмотренная: достаточно предположить, что область (D)
разлагается прямыми, параллельными оси у, на конечное число
криволинейных трапеций указанного вида. Мы не будем останавли-
ваться на доказательстве этого, ибо оно проводится совершенно
так же, как и в п° 551 при обобщении формулы, выражающей
площадь криволинейным интегралом.
Аналогично устанавливается и формула
§ dxdy =*= §QU»	(2)
(О)	(L)
в предположении, что функция Q непрерывна в области (О) вместе
со своей частной производной При этом сначала за область (О)
принимается криволинейная трапе-
ция вида, изображенного на рис.
60. Она ограничена кривыми
(PS): х = х0(у) (с ?szy^d)
(QR): х = Х(у) (c^y^d)
гается прямыми, параллельными
нейных трапеций этого вида.
и двумя отрезками (PQ) и (RS),
параллельными оси х. Затем фор-
мула обобщается, как и выше, на
случай области, которая разла-
оси х, на конечное число криволи-
Наконец, если область (О) одновременно удовлетворяет условиям
обоих случаев, т. е. разлагается как на конечное число тра-
пеций первого типа, так и (независимо от этого) на ко-
нечное число трапеций второго типа, то для нее спра-
ведливы обе формулы (1) и (2), конечно, в предположении непре-
рывности функций Р, Q и их производных-^-, Вычитая форму-
лу (1) из (2), получаем
yPdx-[-Qdy= 1 \
(i)	да
дР\, л
dx dy.
(3)
и
Это и есть формула Грина (G. Green)*.
Формулы п° 551, выражающие площадь криволинейными интегра-
лами, легко получаются отсюда, как частные случаи. Например, по-
* Иногда ее связывают с именами Гаусса или Римана.
600]
§ 3. ФОРМУЛА ГРИНА
177
лагая Р = —у, Q = 0 и воспользовавшись очевидным равенством
= придем к формуле (7) п° 551,
Как и в п° 551, здесь можно придать условиям, при которых
справедлива формула (3), более обозримую форму. Именно, можно
Хоказать, что формула Грина имеет место для любой области
(D), ограниченной одним или- несколькими кусочно-гладкими кон-
турами.
Пусть (Z.) будет общий контур нашей области. Повторяя рас-
суждения п° 551, впишем в (L) ломаную (А) (имеющую две наперед
фиксированные вершины) и рассмотрим ограниченную ею много-
угольную область (Д). Предположим, для простоты, что функции Р
и Q определены, непрерывны и имеют непрерывные же производ-
dP dQ	, zn.
ные -з—,-з— и вне области (£)), скажем, в некотором — содержа-
С/V (/Л
щем (£>) внутри себя — прямоугольнике (/?)*. Можно считать,
что и (Д) содержится в (/?). Так как многоугольная область, оче-
видно, может быть разложена на трапеции как одного, так и дру-
гого типа, то к ней формула Грина приложима:
Р(х, y)dx~ Q(x, y)dy= —^dxdy. (4)
(*А)	(А)
Когда длина наибольшей из сторой ломаной Л стремится к нулю, левая
часть равенства (4) стремится к левой части равенства (3), в силу
леммы п° 550 (и замечания к ней).
С другой стороны, как мы видели в п° 551, ломаную (Л) можно
выбрать так, чтобы она лежала вне многоугольной области (А) и
внутри многоугольной области (В), соответственно входящей и
выходящей по отношению к (D), площади которых разнятся произ-
вольно мало:
В — А<г.
Можно считать, что (А) и (В) содержатся в упомянутом раньше
прямоугольнике (R). Имеем, полагая для краткости-^-—~ =f:
f dxdy I -C
(A) - (A)
fdxdy — fdxdy =
(D)	‘(A)
\f\dxdy-j- \f\dxdy^2 H \f\dxdy <2Ms,
(D)-(A)	(А)-И)	(B) — (A)
* На деле для верности формулы это предположение несуще-
ственно.
178
ГЛ. XVT. ДВОЙНЫЕ ИНТЕГРАЛЫ
[601
где М есть наибольшее значение |/| в (R). Отсюда ясно, что и
правая часть равенства (4) при упомянутом предельном переходе
стремится к правой части формулы (3). Таким образом, справедли-
вость этой формулы установлена.
601. Приложение формулы Грина к исследованию криволи-
нейных интегралов. Рассмотрим односвязную [559] открытую
область (G) и предположим, что в ней заданы функции Р и Q, не-
dP дО
прерывные вместе со своими производными — и , Поставим вновь
[561] вопрос:
какому условию должны удовлетворять функции Р и Q, чтобы
обращался в нуль криволинейный интеграл
\ Р dx	Q dy,	(5)
(Z)
взятый по любому простому замкнутому контуру (L), лежа-
щему целиком в (О)?
Так как мы предположили основную область (G) односвяз-
ной, то область (О), ограниченная извне контуром (£), сама также
принадлежит (G), так что мы можем применить к ней формулу Гри-
н а*; тогда криволинейный интеграл (5) заменится двойным интегралом
©
Для того чтобы подобный интеграл всегда был равен нулю, очевидно,
достаточно предположить, что
дР __ dQ
ду дх '
(А)
Необходимость же условия (Л) может быть установлена проще всего,
если, предположив интеграл (6) равным нулю, прибегнуть к диффе-
ренцированию по области [593]: подинтегральная функция, как «про-
изводная» от интеграла (6), и сама тождественно обращается в нуль.
Таким образом, с учетом леммы п° 561, мы получили новое дока-
зательство того, что условие (А) необходимо и достаточно для
обращения в нуль интегралов вида (5), взятых по любому замк-
нутому контуру, если только основная область G односвязна
[561, теорема 5]. В силу теоремы 4 п° 561 при том же предполо-
жении относительно области условие (А) оказывается также
необходимым и достаточным для того, чтобы криволинейный
интеграл	р
\ Р dx -|- Q dy
________________ (/в)
* Обращаем внимание читателя на то, как здесь использована одно-
связность области (G).
$ 3. ФОРМУЛА ГРИНА
179
по-кривой (АВ), соединяющей точки А и В, не зависел от формы
пути интегрирования [560, теорема 3].
Формула Грина позволила установить это непосредственно,
минуя все рассмотрения, связанные с интегрированием точных диф-
ференциалов. При этом по новому освещена и роль предположения
об односвязности основной области.
Теперь, наоборот, отсюда с помощью рассмотрений п° 556 может
быть вновь установлена достаточность условия (А) (необхо-
димость его ясна непосредственно!) для интегрируемости выраже-
ния Р dx Q dy (теорема 2, п° 560).
602.	Примеры И дополнения. 1) Проверить формулу Грина на функ-
циях
(а)	р=—+	Q=A.3 + y8;
(б)	р==	Q = x2+ys
в круге радиуса 1 'с центром в начале координат.
Указание. В обоих случаях	~ = 0, так что двойной интеграл
обращается в нуль. Криволинейный же интеграл, взятый по окружности
х = cos t, у = sin t (0 sg £ sg 2л),
лишь в случае (б) равен нулю, а в случае (а) равен 2л.
Дело в том, что формула Грина выведена в предположении непре-
рывности рассматриваемых функций и их производных, а здесь — в обоих
случаях — это условие в начале координат нарушается. В случае (а) форму-
ла Грина оказалась на деле неприложимой; любопытно, что в случае (б),
несмотря на указанное обстоятельство, она все же верна [ср. 565, 13)].
2)	Преобразовать формулу Грина к виду
(а) §	+ dxdy=" § Pdy—Qdx,
(D) Х	(I)
либо же
(fi) § S	dxdy = ? [Pcos(x, v)+ Qsin(x, *)] ds
ID)	(£)
(где к означает направление внешней нормали).
Указание. Заменить Р на— Q, a Q на Р; использовать формулу (15)
п” 553 для преобразования криволинейного интеграла второго типа в криволи-
нейный интеграл первого типа. Обратить внимание на направление нормали!
3)	С помощью формулы Грина доказать формулы:
, . Г С . . .	С ди .
(а)	\ \ Ди dx dy = \ ds,
(D)	(£)
(б)	J J vbudxdy=—$ $ (-g £ + dxdy+ Ь d8,
(D)	(D)	(t)
(в)	(vA«—a&v)dxdy — ^v^—u^jds,
180
ГЛ. XVI. ДВОЙНЫЕ ИНТЕГРАЛЫ
[602
если положить
J дх2 ду2 ’
д/ df \ \ df . , ч
= -5cos (л> '*) + f Э1П м).
dv дх	ду
Указание, (б) получается из 2) (б), если положить там P — v ,
Q = v^', (а) есть частный случай (б) при » = 1; переменив в (б) роли и, v
и вычитая результат из (б), получим (в).
4)	Функция и, непрерывная вместе со своими производными и удовлетво-
ряющая в рассматриваемой области (G) уравнению Ди = 0, называется г а р-
монической в этой области.
В предположении, что функция и в области (G) имеет непрерывные про-
ди ди д2и д2и
изводные	, доказать следующее утверждение: для того
чтобы функция и—и(х, у} была гармонической, необходимо и достаточно,
чтобы, каков бы ни был простой замкнутый контур (L), выполнялось условие
С ди , п
\ -з- ds = 0.
.1 dv
Указание. Воспользоваться формулой 3) (а).
5)	Если функция и=и(х,у)— гармоническая в замкнутой области (D\
то ее значения внутри области однозначно определяются ее зна-
чениями на контуре (L).
Иными словами, если две гармонические в области (D) функции ultn„
имеют на контуре (L) области одни и те же значения, то они тождественны
во всей области.
Вводя в рассмотрение разность и = и1 — us, сведем вопрос к доказатель-
ству того, что гармоническая в области (D) функция, обращающаяся в нуль
на контуре (L) области, тождественно равна нулю во всей области.
Положим в формуле 3) (б) v — u. Учитывая наложенные на и условия,
получим
Отсюда следует, что во всей области (D)
ди _ ди _ п
дх ду ’
значит, и сводится к постоянной и, обращаясь в 0 на (Z), равна 0 повсюду,
что и требовалось доказать.
6)	Пусть и есть гармоническая функция в области (G), (ха, у0) — какая-
либо внутренняя точка этой области и (К#)—окружность радиуса Р с цент-
ром в точке (ха, у0) *. Тогда имеет место важная формула:
«(х0, Уо) =	«(х, у) ds,	(7)
(#/?)
так что значение гармонической функции в центре равно •.среднему* ее
значению на окружности. Докажем это.
* Радиус Р предполагается настолько малым, чтобы окружность (Kr) це-
ликом лежала в области (G).
602]
§ 3. ФОРМУЛА ГРИНА
181
Положим v = lnr, где г='уг(х—х0)г-\-(у—у0)а; нетрудно проверить,
что v является гармонической функцией в области, полученной из плоскости
исключением точки (х0, у0). В этой же точке функция обращается в беско-
нечность.
Окружив точку (х0, у0) окружностью радиуса р (р < У?), применим к
области (О), содержащейся между окружностями (KR) и (йр), формулу 3) (б);
контур (i) составляется из (Л^) и (fep) вместе. Так как в этой области обе
функции и, v — гармонические, то слева имеем нуль. Справа уничтожается
интеграл
С ди .
\ v -5— as,
.) dv ’
(1)
ибо, например, на окружности (Кр) » = In R — const., а [ввиду 4)]
Г ди , п
\ -з— d s — 0.
J дч
(Kr)
С другой стороны имеем
da d In г |	1	. г_ .
^=~dr\r~R=-Rm
__ d In г 1________________1
dr |r = p__________________р
на (fep),
так что окончательно получаем:
1 С	.	1	С	.
— \ и ds = -к- \ и ds.
Р J R J
(*р)	(Kr)
При достаточно малом р функция и на окружности (fep) сколь угодно мало
отличается от значения и(х0, у0) в центре, так что при р —0 левая часть
имеет предел 2тс • и (х0, у0). Переходя к пределу, установим требуемое ра-
венство.
7)	Из результата, доказанного в 6), вытекает интересное следствие: если
функция и(х, у) непрерывна в замкнутой области (D), ограниченной кон-
туром (L), и является гармонической внутри зтой области, та своего
наибольшего (наименьшего) значения функция не может достигать
внутри области, за исключением случая, когда она сводится к по-
стоянной.
Действительно, если бы упомянутая функция и (х, у), не сводясь к посто-
янной, достигала, скажем, наибольшего своего значения во внутренней
точке (х0, у0), то легко бы было бы придти к противоречию с форму-
лой (7).
Теперь мы может усилить и результат в 5), предположив, что функция и
непрерывна в замкнутой области (£)) и гармонична лишь внутри области.
И здесь достаточно установить, что функция и тождественно равна 0, если об-
ращается в нуль на контуре. А это вытекает из того соображения, что в про-
тивном случае она достигла бы своего наибольшего или наименьшего значения
внутри области вопреки сделанному выше замечанию.
182
ГЛ. XVI. ДВОЙНЫЕ ИНТЕГРАЛЫ
{603
§ 4. Замена переменных в двойном интеграле
603. Преобразование плоских областей. Предположим, что нам
даны две плоскости, отнесенные одна — к прямоугольным осям х и у,
а другая — к таким же осям $ и ц. Рассмотрим в этих плоскостях
две замкнутые области: область (D) на плоскости ху и область
(Д) на плоскости Ц. Каждая из этих областей может быть и неогра-
ниченной, в-частности может охватывать и всю плоскость. Контур
или границу области (если область не охватывает всей плоскости)
мы будем предполагать простой кусочно-гладкой кривой; обозначим
его символом (5) для области (D) и символом (£) для области (Д)
(рис. 61).
Допустим, что в области (Д) дана система непрерывных функций:
Х = х($, 11), 1
,=яе. I	°’
которая каждой точке (Е, ij) области (Д) относит одну определенную
точку (х, у) области (D), причем ни одна точка (х, _у) из (О) не
будет пропущена, так что каждая такая точка отнесена хоть одной
точке (I, ij) из (Д). Если различным точкам (5, ij) отвечают различ-
ные же точки (х, у) (что мы впредь и будем предполагать), так что
каждая точка (х, у) отнесена лишь одной точке (?, ij), то формулы (1)
однозначно разрешимы относительно £ и ij. Переменные ц в свою
очередь являются однозначными функциями от х, у в области (D):
1 = 1(х,у), |
, ч 1	(1а)
ij = ij(x, _v). J
Таким образом, между областями (D) и (Д) устанавливается взаимно
однозначное или одно-однозначное соответствие. Говорят также, что фор-
мулы (1) осуществляют преобразование области (Д) в область (D),
а формулы (1а) дают обратное преобразование области (D) в об-
ласть (Д).
603]
9 Л ЗАМЕНА ПЕРЕМЕННЫХ В ДВОЙНОМ ИНТЕГРАЛЕ
183
Если названные области заполняют соответствующие плоскости,
то мы имеем дело с преобразованием одной плоскости в другую.
Наконец, если обе плоскости совпадают, т. е. если точки (х, у) и
(В, •«]) рассматриваются как точки одной и той же плоскости, то на-
лицо преобразование плоскости в самое себя.
Мы будем предполагать, далее, что функции (1) и (1а) не только
непрерывны, но и имеют непрерывные частные производные (первого
порядка). Тогда, как известно [п° 203, (4)],
Р(х, у) Р(Е, ч)
0(5, 1) ' D(x, у)~ 11
так что оба функциональных определителя отличны от нуля и, по
непрерывности, сохраняют постоянный знак.
Из того факта, что определитель
дх дх
-	У). -	го)
ду ду	1 '
dZ ди]
отличен от нуля в области (Д), уже следует, что внутренней
точке (В®, т]о) области (Д) отвечает в силу формул (1) внутренняя
же точка (х0, Jo) области (D), ибо — по теореме о существовании
неявных функций [п° 208] — этими формулами в целой окрестности
точки (х0, _у0) переменные В и -г) определяются как однозначные
функции от х и у. Аналогично, внутренней точке области (£)) от-
вечает всегда внутренняя точка области (Д). Отсюда уже ясно,
что точкам контура (2) отвечают именно точки контура (S), и об-
ратно.
Если взять в области (Д) простую кусочно-гладкую кривую (Л),
то с помощью преобразования (1) она перейдет в подобную же
кривую (£) в области (О). Действительно, пусть уравнения кривой (Л)
бу'уг:	*=(«).	ч=ч(0
(asgjtsgjp или a^sf^P),	(3)
причем (ограничиваясь гладким куском кривой) можно функции В ((),
-»)(t) считать имеющими непрерывные производные не обращаю-
щиеся одновременно в нуль. Подставляя эти функции в фор-
мулы преобразования (1), мы получим параметрические уравнения
соответствующей кривой (£):
л=х(5(0, i)(0) = ^(O> y=y^(t)>	(4)
Легко видеть, что эти функции также имеют непрерывные произвол-
y(0 = gV(0+^V(0, УИ=^Г(<)+^4'(').	(5)
184
ГЛ. XVI. ДВОЙНЫЕ ИНТЕГРАЛЫ
[604
которые к тому же не могут одновременно обратиться в нуль, так
что особых точек на кривой (Е) нет. Действительно, в противном
D (х, у)
случае, ввиду неравенства нулю определителя
из (5)
следо-
вало бы, что одновременно £' = 0 и -rft=O, что невозможно.
Если точка (;, tj) на плоскости Ц описывает замкнутый
контур (Л), скажем, в положительном направлении, то соответ-
ствующая точка (х, у) опишет также некоторый замкнутый же
контур (£) на плоскости ху, но направление его может оказаться
как положительным, так и отрицательным. Вопрос этот зависит,
как мы увидим ниже [606, 1°], от знака якобиана (2).
Задание пары значений переменных 5 и i) из области (Д) одно-
значно определяет некоторую точку в области (D) на плоскости ху
(и обратно). Это дает основание и числа £, т; называть координатами
точек области (D). По сути дела, уравнения (1)* дают нам пара-
метрическое представление плоской фигуры (Ь), являющееся част-
ным случаем параметрического представления поверхностей, о кото-
ром уже была речь [228].
Как и там, кривую, составленную из точек области (О), у кото-
рых одна из координат сохраняет постоянное значение, называют
координатной линией. Например, полагая в (1) т) = т)0, мы получим
параметрическое представление координатной линии:
Х = Х$, 7)0), у=у$, 7]0)
(роль параметра здесь играет Sj). Неявное уравнение той же
линии получим, полагая т) = т)0 во втором из уравнений (1а):
“П (X, у) = 7]о.
В связи с тем, что координатные линии, вообще говоря, будут
кривыми, числа £, tj, характеризующие положение точки на плоско-
сти ху, и в этом случае (как и в случае кривой поверхности) называют
криволинейными координатами точки.
Придавая координате т) различные (возможные для нее) постоян-
ные значения, мы получим целое семейство координатных линий на
плоскости ху. Фиксируя значение координаты В, мы получим другое
семейство координатных линий. Дри наличии взаимно однозначного
соответствия между рассматриваемыми областями различные линии
одного и того же семейства не пересекаются между собой, и через
любую точку области (О) проходит по одной линии из каждого се-
мейства.
Вся сетка координатных линий на плоскости ху является изобра-
жением сетки прямых £ = const. и т] = const, на плоскости 1ц (рис. 61).
604.	Примеры. 1) Простейшим и важнейшим примером криволинейных
координат являются полярные координаты г, в. Они имеют наглядное геомет-
* Если присоединить к ним еще уравнение z = 0.
604]	§ 4. ЗАМЕНА ПЕРЕМЕННЫХ В ДВОЙНОМ ИНТЕГРАЛЕ	185
рическое истолкование, как полярный радиус-вектор и полярный угол, но
могут быть введены и формально, с помощью известных соотношений:
x = r cos.6, |
у = г sin 6 )
(r=s0).
Если значения г и 0 откладывать по двум взаимно перпендикулярным
осям, считая, скажем, г — абсциссой, а 0 — ординатой (при правой ориента-
ции осей), то каждой точке полуплоскости
гЭ=0 по указанным формулам отвечает одна
определенная точка на плоскости ху.
Читателю наверное приходилось иметь дело
с относящимися к этому случаю координатными
линиями: прямым г = const, отвечают круги ра-
диуса г с центром в начале, а прямым 0 = const,
отвечают лучи, исходящие из начала под углом
0 к оси х (рис. 62).
Однако в данном случае формулы преобра-
зования, вообще, не будут однозначно разреши-
мы: изменение величины угла 0 на (где
k — целое) не отразится на значениях х и у.
Для того чтобы получить все точки плоско-
сти ху, достаточно ограничиться значениями
г > о, о 0 < 2л.
Каждой точке (х, у), отличной от начала, отвечает одно значение г > 0 и одно
значение 0 в указанных пределах. Но неустранимое нарушение однозначности
соответствия связано с началом координат: точке х=у/ = 0 отвечает на
плоскости г0 вся ось 0 (или, если угодно, отрезок ее от 0 = 0 до 0 = 2л).
Рассмотрим на плоскости г0 замкнутый прямоугольник [0, R; 0, 2л| или
С“₽Т (рис. 63); легко видеть, что на плоскости ху ему отвечает замкнутый
круг, описанный вокруг начала
О радиусом R — OA. Но весь
контур этого круга отвечает
одной лишь стороне аЗ упомя-
нутого прямоугольника; сторо-
нам оа и (обеим!) отвечает
один и тот же радиус О А круга;
наконец, всей стороне о-/ отве-
чает лишь точка О. Здесь явно
не соблюдены указанные в пре-
дыдущем п° условия!
Однако если сдвинуть сто-
рону оу на малую величину
р = оо’, а сторону -р^на е = рр', то
новому прямоугольнику о’оф'у
будет отвечать на плоскости ху фигура О'АВ'С, полученная из круга удале-
нием малого круга радиуса р и сектора с центральным углом е, с соблюдением
уже всех требований. При перемещении точки на плоскости г0 по отрезкам
оф', 8'7’, -('o’, °'® соответствующая точка на плоскости ху опишет по порядку
неполную окружность АВ' (радиуса R), отрезок В'С,неполную окружность СО"
(радиуса р) и отрезок О'А. Заметим попутно, что положительному обходу на
плоскости г0 отвечает положительный же обход на плоскости ху.
Якобиан в данного случае равен
Р (х, у) 1 cos 0 — т sin 0 I 
D\r, 4)	|sin4 г008 0 | Г’
оы сохраняет (если исключить начало) положительный знак.
186
ГЛ. XVI. ДВОЙНЫЕ ИНТЕГРАЛЫ
[604
2)	Рассмотрим преобразование плоскости в самое себя, определяемое
формулами
__	$	_ т;
Х Е2 I т,2 > У rs I -г2
(5 и т] не равны одновременно нулю).
Если совместить оси х и 5, у и т), то преобразование это имеет нагляд-
ное геометрическое истолкование. Так как
2i2	1 х у
+.У — гГП--2>	,
+ Т ’	5	7] ’
то ясно, что соответствующие точки лежат всегда на одном луче из начала,
причем их расстояния от начала в произведении дают единицу.
е=
Преобразование это называется инверсией. Оно однозначно обратимо:
- » =....................................У- -
,2 ’	‘ г2 -U U2
(снова х и у не равны одновременно нулю).
Координатными линиями будут окружности, проходящие через начало:
vs — Хх = о, хг + у2 ——у = 0,
60	lo
(!*&)	-Olo^O)
центры которых лежат, соответственно, на осях х и у (рис. 64). При 58 = О
получается ось у(х = 0), а при 7]о = О— ось х(у = 0).
Квадрату 1;	11 на плоскости 5т;, например, отвечает заштрихо-
ванная область на рис. 64. Направления обхода контуров здесь не совпадают.
§ 4. ЗАМЕНА ПЕРЕМЕННЫХ В ДВОЙНОМ ИНТЕГРАЛЕ
187
Так как
дх _ ду _ к]3 — 62 дх _ду___	2£<
d^~di~ (62 + ^)3’
то якобиан
Р(*,У)_	1 ^А
0(5,7])-	(б3 + ^)3^и-
3)	Если исходить из формул преобразования
х = 52 —т]3, у = %ъ,
то при любых 5, т] отсюда однозначно
формулы относительно 5, >], найдем:
i=±yry*a+ys+*
получаются х, у. Разрешая же эти
где знаки 5 и т] связаны условием $7] ==-£-54 Таким образом, каждой точке
(х,у), исключая начало, отвечают две точки (6, -»j), симметричные относительно
начала. Чтобы восстановить однозначность,
Рис. 65.
можно, например, ограничиться верхней
частью плоскости бц (со включением положи-
тельной части оси 5, но без ее отрицательной
части).
Рис. 66.
Координатными линиями здесь будут софокусные (с фокусом в начале) и
соосные параболы (рис. 65):
У2 = 46?(6?-х) и у2 = 4^(х-Н§)
(So	ho^O)»
188
ГЛ. XVI. ДВОЙНЫЕ ИНТЕГРАЛЫ
[604
Значению £о = О отвечает отрицательная часть оси х, а значению т]0 = 0 — ее
положительная часть, Якобиан
D (х, у) _ I 2g — 2ц
D (5, т]) — 12ц 2g
= 4(^ + f)>0,
если исключить начало.
4)	Иногда удобно наперед задаться сеткой координатных линий
и по ним установить систему криволинейных координат.
Рассмотрим, например, два семейства парабол (рис. 66):
у2 = 2рх и х2 = 2qy;
каждое из них в отдельности заполняет всю плоскость ху (если исключить
оси координат).
Естественно ввести g = 2p и i) = 2q в качестве криволинейных координат.
Из равенств _y2 = gx и х2 = ту имеем
Х = у/>гД y! = y-'g2T) И	7] = у(Х, JI^zO).
Якобиан здесь равен
D (х, у) _	2 2 1	3 3	1	1 2 з	’з	_ 1
Ч)	2 зз у £ Т|	1 3	3 у£ I	з •
5)	Будем исходить из семейства софокусных
сечений
Xs V2
2i-4-—2---— 1
x2“k2 —с2
и соосных конических
(6)
(эллипсов — при к > с, гипербол — при 0<к<с; рис. 67).
Через каждую точку (х, у) плоскости, не лежащую на осях, проходят
один эллипс и одна гипербола из этого семейства. Действительно, левая
часть получаемого из (6) уравнения
(А2)2 — А2 (х2 + у2 4- с2) + с2х2 = 0
имеет знак 4* ПРИ X = 0, знак —при А = с и снова знак 4- при больших К.
Следовательно, уравнение это имеет два положительных корня: один
1>си другой |л<с*; это доказывает наше утверждение.
Если предыдущее уравнение рассматривать как квадратное уравнение
относительно К2, то по известному свойству корней имеем
К24-(Л2 = Х24-У 4-с2, ).2[Г° = с2х2,
а отсюда легко выразить х и у через к и ц:
X — ч-	у = ч- У (Х2~ g2) (g2~
* Чтобы не путать этих корней,- мы для большего сохраняем обозначе-
ние А, а меньший обозначаем через р.
605]	§ 4. ЗАМЕНА ПЕРЕМЕННЫХ В ДВОЙНОМ ИНТЕГРАЛЕ	189
Ограничиваясь первым координатным углом, мы должны сохранить здесь
лишь положительные знаки. Числа X, р можно рассматривать, как криволи-
нейные координаты точек этого угла; их называют эллиптическими координа-
тами. Координатными линиями
в этом случае будут как раз
исходные конические сечения.
Подчеркнем, что X изменяет-
ся от с до 4- оо, ар. — от О
до с. Для крайних значений мы
получим:
при Х = с — отрезок оси х
от х = 0 до х = с,
при р = с — отрезок оси х
от х = с до х — + оо,
при р = 0 — положитель-
ную часть оси у.
Наконец, легко вычислить
якобиан:
О(х, у)_
Z)(X, р)
м2____________>2
= —		<0
/(K2_c2)(c2_p2)
605.	Выражение площади в криволинейных координатах. Пред-
положим, что на плоскости ху задана некоторая область (D), огра-
ниченная кусочно-гладким контуром (S) без кратных точек. Пусть
формулы (1) устанавливают взаимно однозначное соответствие между
этой областью и областью (Д) на плоскости Si), ограниченной подоб-
ным же контуром (2)-
Мы сохраним все предположения п° 603 относительно этого пре-
образования областей и, сверх того, еще предположим, что суще-
ствуют и непрерывны в области (Д) смешанные производные второго
порядка для какой-либо из функций (1), скажем:
dsy дгу
dz ду и
(в силу непрерывности, они будут иметь равные значения, 190)*.
При этих предположениях поставим себе задачей выразить пло-
щадь D рассматриваемой области на плоскости ху в виде двойного
интеграла, распространенного на область (Д) на плоскости Ь].
Мы будем исходить из формулы, выражающей площадь (D) кри-
волинейным интегралом, взятым по контуру (5) области (D)
D— § х dy	(7)
(S)
[см. 551, (10)].
* Отметим здесь же, что эти дополнительные предположения несуще-
ственны для справедливости .окончательного результата и введены лишь
для облегчения доказательства.
190
ГЛ. XVI. ДВОЙНЫЕ ИНТЕГРАЛЫ
(605
План дальнейших преобразований таков: сначала мы перейдем,
пользуясь параметрическими уравнениями контура, от криволинейного
интеграла (7) к обыкновенному определенному интегралу. Затем пре-
образуем этот последний опять к криволинейному интегралу, но взя-
тому на этот раз уже по контуру (S) области (Д). Наконец, поль-
зуясь формулой Грина, заменим полученный криволинейный инте-
грал двойным интегралом по области (Д).
Во исполнение этого плана нам нужны параметрические уравнения
контура (5). Так как в дальнейшем мы имеем в виду перейти к кон-
туру (£), то и сейчас мы предпочитаем исходить именно из уравне-
ний этого контура. Пусть (3) дает параметрическое представление
кривой (£); тогда (4) даст, очевидно, такое же представление для
кривой (S), поскольку [как мы упоминали в п° 603] именно она соот-
ветствует на плоскости ху контуру (S). Пределы а и р изменения t
мы выберем так, чтобы при переходе от а к р кривая (5) описыва-
лась в положительном направлении.
Тогда, согласно формуле (5) п° 547,
3
D— х (t) у (f) dt
а
или, если принять во внимание (4) и (5),
х(Ц0, Т)(О)[^(О + ^7)'(О]^.	(8)
а
Сопоставим этот интеграл с криволинейным интегралом
$ *6 Tj)	(9)
(J)
взятым по контуру (2) в положительном направлении. Если
пожелать свести последний по обычному правилу к обыкновенному
определенному интегралу, то пришлось бы подставлять сюда вместо I
И т) функции и i](f) из параметрических уравнений кривой (S),
и мы вернулись бы к интегралу (8).
Впрочем, нужно иметь в виду еще одно обстоятельство. При изме-
нении t от а до р описывается в положительном направлении контур
(5) — так мы выбрали эти пределы. Но контур (£) при
этом может описываться как в положительном, так и в отрицательном
направлении; таким образом, интегралы (8) и (9) могут на деле раз-
ниться знаками. Во всяком случае,
=	+	(Ю)
(2)
§ 4. ЗАМЕНА ПЕРЕМЕННЫХ В ДВОЙНОМ ИНТЕГРАЛЕ
191
причем (подчеркнем это еще раз) знак плюс имеет место, если
положительному обходу контура (S) отвечает положительный
же обход контура (S), и знак минус — в противном случае.
Остается, наконец, преобразовать полученный криволинейный
интеграл в двойной. Для этого надлежит воспользоваться формулой
Г р и н а
J р(?, -4)(R+Q(e, -4)^=5$
(S)	W
где полагаем
Р0, т]) = х^, Q(5,
Так как
dQ___дхду ।	д2у
dt~ di	dr
dP___dx dy ।	d'-y
di) di; d? ' X d$ di; ’
а смешанные производные второго порядка от у равны между собой,
то
dQ dP______D (х, у)
d£ di] ~ D (5, ij) ’
и мы приходим к формуле
(4)
Мы видели в п° 603, что при сделанных предположениях якобиан
J($, 7]) =
Р(х, у)
D& 1))
сохраняет в области (Д) определенный знак. Этот же знак имеет и
интеграл. Но перед ним еще стоит двойной знак ±; так как в ре-
зультате должно получиться существенно положительное число D, то
ясно, что знак neped интегралом совпадает со знаком якобиана.
Если ввести этот знак в подинтегральную функцию, то там получится,
очевидно, абсолютная величина якобиана, так что окончатель-
ное выражение для площади будет
D== S S 1§1Нг)1‘О71== $ S|J($’
(А)	’	(А)
(П)
Это и есть та формула, которую мы желали установить.
Подинтегральное выражение
192
ГЛ. XVI. ДВОЙНЫЕ ИНТЕГРАЛЫ
[606
обычно называют элементом площади в криволинейных координа-
тах. Мы видели, например, что в случае перехода к полярным коор-
динатам- якобиан равен г; следовательно, элемент площади в поляр-
ных координатах есть г dr (Z9.
606.	Дополнительные замечания. 1°. Если сопоставить правило,
по которому выбирался знак, плюс или минус, в формуле (10), с тем
фактом, что этот знак необходимо совпадает со знаком якобиана, то
получится интересное следствие: если якобиан сохраняет положи-
тельный знак, то положительные направления обхода контуров
(S) и (Е) соответствуют друг другу по формулам преобразова-
ния', если же якобиан имеет отрицательный знак, то положи-
тельному направлению на одном контуре соответствует отри-
цательное направление на другом.
Очевидно, это же имеет место и по отношению к любой паре
взаимно соответствующих простых замкнутых контуров (А) и (Л),
лежащих в областях (D) и (Л). Полученный результат легко прове-
ряется на примерах, приведенных в п° 604.
2°. Применяя к формуле (11) теорему о среднем [592, (9)], полу-
чим соотношение
D = \J& ^)|.Д,	(12)
где (;, т]) есть некоторая точка из области (Д), а Д — площадь этой
области.
Сопоставим это соотношение с формулой Лагранжа
Z(?)—/(а)=/'С)(Р —а)	(*<Г<?)-
Если _£=/(:) есть монотонная функция, то она взаимно однозначно
связывает промежуток	с промежутком /(a)sgx^/(!5) (или
/ф)^х^/(а), если f (х)— убывающая функция). Обозначим длины
этих промежутков через 8 и ф тогда формула Лагранжа приво-
дит к равенству
d=\f'®\-b,	(13)
сходному с равенством (12).
Если в формуле (13) «сжимать» промежуток (8) в точку 4, то
в результате получим соотношение
0)1 = Нт 4,
так что абсолютная величина производной является как бы коэффи-
циентом искажения (или коэффициентом растяжения) прямой $
в данной ее точке при преобразовании ее в прямую х.
§ 4. ЗАМЕНА ПЕРЕМЕННЫХ В ДВОЙНОМ ИНТЕГРАЛЕ	193
Точно так же из формулы (12) путем «сжатия» области (Д) в точку
0, т;) получаем
Р6 ^)1 =11Шу*,
так что абсолютная величина якобиана играет роль коэффициента
искажения или коэффициента растяжения плоскости £т) (в данной
ее точке) при преобразовании ее в плоскость ху.
Это замечание указывает на глубокую аналогию между производ-
ной и якобианом [ср. главу шестую].
3°. Формула (11) показывает, что при безграничном уменьшении
площади Д также безгранично уменьшается и соответствующая ей
площадь D. Отсюда уже легко установить, что преобразование обла-
стей, изученное в п° 603, обладает и следующим важным свойством:
кривую (Л) с площадью нуль в области (Д) оно переводит в не-
которую кривую (L) в области (D), также имеющую площадь
нуль.
4°. Формула (И) выведена в предположении взаимно однозначного
соответствия между областями (О) и (Д), а также непрерывности
функций (1), (2) и их частных производных. Однако на практике
обычно приходится сталкиваться со случаями, когда эти предполо-
жения нарушаются в отдельных точках или вдоль отдельных кривых.
Если упомянутые точки и кривые на обеих плоскостях могут быть
заключены в произвольно малые по площади области (d) и (8), то по
выделении их формула уже становится применимой:
D — d = ЭД | J(;, -г;)|did-ц.	(11*)
(Д) - (б)
Пусть якобиан в области (Д) сохраняет ограниченность:
|J($, 7))1^M
тогда интеграл в (11*) разнится от интеграла в (11) на величину
ЭД|7(£, 7j)|cfU7i^Af8.
(«)
Переходя в (11*) к пределу при d и 8->0, восстановим формулу (11).
Для иллюстрации вернемся к примеру 1) в п° 604 и к фигурам,
изображенным на рис. 63. Непосредственно к прямоугольнику (Д) =
= [0, R; 0, 2к] и к кругу (О) радиуса R с центром в начале фор-
мулы (И), которая для этого случая принимает вид
* По сути дела мы дифференцируем интеграл (11) по области в точке
(5, т|) [593].
7 Г, М, Фихтенгольц, т, III
194
ГЛ. XVI. ДВОЙНЫЕ ИНТЕГРАЛЫ
J607
применить нельзя. Но если выключить заштрихованные области (пло-
щади которых вместе с р и s стремятся к нулю), то к получающимся
областям эту формулу применить можно; остается перейти к пределу.
607.	Геометрический вывод. Формула (11) выведена нами с по-
мощью хотя и простых, но формальных и не наглядных рассуждений.
Мы считаем полезным привести другой вывод этой формулы, не вполне
строгий, но зато совершенно прозрачный с геометрической стороны.
Этот вывод принадлежит М. В. Остроградскому.
Рассмотрим снова преобразование плоскости Ь) в плоскость ху,
которое задается формулами (1). Выделим на плоскости Ь] бесконечно
малый прямоугольник ЩЩЩЩ со сторонами di и </т], параллельными
осям I и т] (рис. 68, а). Изображением этого прямоугольника в пло-
скости- ху служит криволинейный четырехугольник PiP^P^Pi
(рис. 68, б); определим его площадь.
Вершины прямоугольника имеют координаты
П1(£, Щ (? 4" di, -»i), П3($4-<Я, + </?]), Щ(;, Tj-f-rfT));
в таком случае соответствующие вершины криволинейного четырех-
угольника будут иметь такие координаты:
Pdx (5, т(), y(i, 7j)),
Р2(х ($ + <#, 7j), y(i-\~di, rj),
P8 (X (i 4- di, 7) + flfTi), у ($ + di, t| 4- (Zt;)),
Pi (x (S, 7j + dT]), у (?, 1) 4- dfify.
Если ограничиться членами первого порядка относительно di, dy, то
приближенно можно взять точки:
Pdx, у), р^х-1-^di,
Л (*4-^4-^. y+^di+^y
Pilx + ^d-* у + ^\
где x — x(i, ц), y—y(i, т]) и, вообще, все производные вычислены
в точке (?, т;). Так как проекции отрезков PiP% и Р3Р4 на обе оси
§ 4. ЗАМЕНА ПЕРЕМЕННЫХ В ДВОЙНОМ ИНТЕГРАЛЕ
195
соответственно равны, то отрезки эти равны и параллельны, так что
(с точностью до малых высшего порядка) четырехугольник Р^Р^Р^Р^
есть параллелограмм.
Его площадь равна удвоенной площади треугольника Рр\Рг.
Из аналитической же геометрии известно, что удвоенная площадь
треугольника, вершины которого находятся в точках (хь (х%, уг),
(х3, Уз)> равна абсолютной величине определителя
Xg Х|	Х3 Х3
Уз —У1	Уз —Уз
Применяя эту формулу к нашему случаю, получим, что искомая пло-
щадь (снова — с точностью до малых высшего порядка) равна абсо-
лютной величине определителя
Итак,
дх ... дх ,
~д^
^dr,
д; ' dq 1
D (х, у) ,, ,
площ.
Разлагая фигуру (Д) на плоскости прямыми, параллельными
осям, на бесконечно малые прямоугольники (и пренебрегая «неправиль-
ными» элементами у контура), мы одновременно разложим и фигуру
(£>) на плоскости ху на криволинейные четырехуголь-
ники рассмотренного вида. Суммируя полученные выражения для
площадей их, вновь приходим к формуле (11).
Приведенное рассуждение, таким образом, подчеркивает важную
геометрическую идею: сущность формулы (11) состоит в том, что
для определения площади фигуры (D)
эта фигура разлагается не на
прямоугольные, а на криволинейные
элементы с помощью сетки коор-
динатных линий.
В некоторых простых случаях эта
идея позволяет находить выражение
«элемента площади» в криволинейных
координатах почти без вычислений.
Например, в случае перехода
к полярным координатам можно рас-
суждать так. Элементарному прямо-
угольнику со сторонами dr и й9
в плоскости г9 на плоскости ху отвечает фугура, ограниченная ду-
гами окружностей радиусов г и г -|- dr и двумя лучами, исходящими
из начала под углами 9 и 9-|-d9 к оси х (рис. 69). Принимая при-
196	ГЛ. XVI. ДВОЙНЫЕ ИНТЕГРАЛЫ	1608
ближенно эту фигуру за прямоугольник со сторонами dr и г dd,
сразу получаем искомое выражение г dr d® элемента площади.
608.	Примеры. Вычислить площади фигур, ограниченных кривыми!
(а)	(х2 +у2)2 = 2а2 (х2 —у2)
(лемниската),
(б)	(х2-J-y2)2 = 2axs,
(в)	(х2+у2)3 = а2(х4+у4).
Решение. Наличие двучлена х2-]-у2 во всех случаях наталкивает на
мысль перейти к полярным координатам, полагая
х = г cos 6, у — г sin в
и вычисляя искомую площадь по формуле
D=^rdrdQ.	(14)
(А)
(а)	Вид лемнискаты над знаком (рис. 70). Кривая симметрична относи-
тельно координатных осей (это легко усмотреть и из уравнения кривой, ибо
Рис. 70.
оно не меняет вида при замене хна — х илиу на —у). Поэтому достаточно
определить площадь части (JD) фигуры, содержащейся в первом координат-
ном угле, а затем учетверить ее.
Полярным уравнением лемнискаты служит
г2 = 2а2 cos 26,
причем (если ограничиться первым координатным углом) 6 надлежит изменять
лишь от 0 до — ввиду того, что cos 26 должен быть положительным. Таким
образом, область (Д) на плоскости гб, отвечающая (Z)), ограничена кривой
r = e)^2cos26
(образ лемнискаты), отрезком оси г (который отвечает отрезку оси х) и отрез-
§ 4. ЗАМЕНА ПЕРЕМЕННЫХ В ДВОЙНОМ ИНТЕГРАЛЕ
197
ком оси в от 6 = 0 до 6 = -4- (образ одной лишь начальной точки—с нару-
шением взаимной однозначности соответствия) *.
Имеем
4	а У 2	cos 29	4
(*	(*	С	а?
D = 1 d9 I г dr = аа i cos 2В d& = ,
о	в	о
так что вся искомая площадь есть 2а8.
(б)	Полезно наперед составить себе общее представление о виде кривой.
Кривая симметрична относительно
оси х (уравнение не меняется от
замены у на —у), расположена
вправо от оси_у (х не может быть
отрицательным); пересекает ось х
при х = 0 и х = 2а. К тому же
кривая ограничена: из самого урав-
нения ясно, что
так что
х1^2ах‘,
х^2а,
а так как и у* ij 2ахг, то и
| у |	2а. Эскиз кривой дан на
рис. 71.
Полярное уравнение кривой будет: г = 2а cos3 6, где 6 изменяется от—
до -%. Ввиду симметрии можно написать
X	1С
Т	2а cos8	9	2
df) I rdr — 4a‘ \ cos3 6 rf6 = na*.
•'	♦)	О
0	0	0
(в)	Кривая симметрична относительно обеих осей. Хотя начальная точка
х=_у = 0 формально «принадлежит» кривой, ибо удовлетворяет уравнению,
но эта точка является изолированной; действительно, прих>=_у>0
•легко получаем из уравнения кривой
(2х8)3 2аах4, откуда х$=-^,
так что вблизи начала точек кривой нет **. Исключим начало из рассмотрения.
Легко видеть, что кривая ограничена: при х ~.sу, очевидно, х’ ij; 2а8х4, х3 sS 2аа
и т. д. Кривая имеет примерно вид, изображенный на рис. 72.
* См. по этому поводу замечание 4’ в п° 406.
♦* В этом, разумеется, можно было бы убедиться и с помощью критерия
о* 236.
198
ГЛ. XVI. ДВОЙНЫЕ ИНТЕГРАЛЫ
[608
Полярное уравнение кривой: г2 = a2 (cos4 6 -j- sin4 0). Учитывая симметрию,
имеем
Я	«
2 a J^cos* 6 + sin* ®	2
D — 4 </0	г dr— 2а2 \ (cos4 0 г]- sin4 0) rfO =
о	о	о
2*
/»	Я
= 4e2 \ sin4 0 rfO = — па2.
4
2)	Показать, что формула (14) непосредственно приводит к уже известной
формуле для вычисления площади сектора в полярных координатах [338]:
£> = у \ r‘d&,
где под г разумеется та функция от 0, которая фигурирует в полярном
уравнении кривой.
Все задачи 1) можно было бы решить и непосредственно по этой формуле.
3) Найти площади фигур,
ограниченных кривыми:
/а) (^.л.УУ-^У
( ' \as+ b2l ~ с2-’
/ Vs «»2 \ 2
l .у8? —
i2+ Ь2] ~~ с2’
•2	,,2 \ 2	г2,,
с3 ’
Решение. В тех случаях,
когда в уравнении кривой фигу-
X2 , V2
рирует двучлен	, реко-
мендуется вводить собобщен-
ные> полярные координаты,
которые с декартовыми свя-
заны формулами *
х = ar cos 0, y — br sin 0.
Геометрический смысл этого преобразования сводится к сжатию плоскости
к координатным осям с последующим переходом к полярным координатам.
Якобиан преобразования равен abr.
(а)	Кривая ограничена; симметрична относительно начала (ибо ее урав-
нение не изменяет вида при одновременной замене х на —х и у
на —у,); две симметричные петли лежат одна в первом координатном угле,
а другая — в третьем (ху^гО); начало есть единственная точка пересечения
с осями.
* При применении этих координат мы сталкиваемся с таким же нарушением
однозначности соответствия, как и в случае полярных координат. См. 606, 4°.
§ 4. ЗАМЕНА ПЕРЕМЕННЫХ В ДВОЙНОМ ИНТЕГРАЛЕ
199
У равнение образа нашей кривой на плоскости г0 будет ♦
г* = sin 0 cos 0.
с*
С учетом симметрии имеем
7 V sin 9 сов 9
{*	р	агЬ* е	гм
D = 2\M I	abrdr = —j- I sin 0 cos 0 d0 =	.
J	J	L J	2c’
(б)	Кривая ограничена, симметрична относительно осей; начало служит
лишь изолированной ее точкой. Имеем
«_	________________ л
2 У a2 cos2 0	62 sin2 9	V
D == 4ab J dft C r dr = 2ab (a’ cos3 0 -|- b* sin3 0) d§ =
= £а*(а’ + П
(в)	Кривая ограничена, симметрична относительно осей; начало есть един-
ственная ее точка пересечения с осью у, но с осью х она пересекается еще
в’ _
в точках х = ± —. Для петли, лежащей вправо от оси у, будем иметь
а о я -а л
r = —cos0, — у sg 0 sC , так что
D = 4ab
г:	а „
У ТС05в
2
С 5 n jn п alb
I cos’ 8 с?0 = — . —j-
J	2 c’
(г)	Кривая ограничена, симметрична относительно оси у, лежит вверх от
оси х. Начало есть единственная точка пересечения с осями, так что кривая
состоит из двух петель, лежащих в первом и во втором координатных углах.
Уравнение кривой в новых координатах:
в’й	,
г — —г cos’ 0 sin 0.
с“
Ответ. D =
4)	Найти площадь петли кривой:
(а) (х + у)* = ахгу, (б) (х у)3 = аху, (в) (x-j-y)s = ax‘ya.
Решение. Если рассматривать лишь части кривых, содержащиеся
в первом координатном угле (так что х 3= 0, у 0), то все они оказываются
ограниченными, в чем можно убедиться подобно 1) (б). Кривые проходят
через начало, не имея других точек пересечения с осями. Отсюда ясно, что
именно эти части представляют собой петли, о которых говорится в задаче.
В предыдущих примерах переход от сложного уравнения кривой в декар-
товых координатах к простому уравнению в криволинейных координатах
строился по существу на использовании тождества cos’ 0 -|- sin’ 0=1. Двучлен
• Легко усмотреть, что кривая является как бы сдавленной лемнискатой.
200
ГЛ. XVI. ДВОЙНЫЕ ИНТЕГРАЛЫ
[608
х-|-у тоже подсказывает мысль об использовании этого же тождества:
положим (только для х 0 и у 01)
х = r cos* 6, у = г sin* 6.
Якобиан преобразования будет *:
/«Iе?8’0 ~2r®n0cos0| = 2r sin 6 cos 6.
|sm*0 2rsin0cos0|
(а) Уравнение петли в новых координатах
г = a cos4 0 sin* 0.
Далее,
к	я
2	a cos * в sin8 в	2
(•	С	С	а3
D = 2 I sin 0 cos 6 dO I r dr — a* i cos’ 0 sin8 0 d6 gyg.
о	0	0
л*	дЗ
<б)Д = бб- <B)° = T260-
5)	Укажем теперь другой подход к выбору системы криволинейных коор-
динат, который часто оказывается полезным при определении площади криво-
линейного четырехугольника. Если обе пары кривых, представляю-
щих противоположные стороны этого четырехугольника, входят в состав каж-
дая — своего семейства кривых, заполняющих плоскость (и зависящих
от одного параметра), то именно эти
два семейства естественно принять
за сетку координатных линий. Их па-
раметры обычно и дают удобную для
данного случая систему криволиней-
ных координат.
Разъясним этот прием на примере.
Пусть требуется найти площадь фигу-
ры, ограниченной параболами
ys = px, ys — qx, х2 = ау, х3 = Ьу,
где 0 < р < g и 0 < а < & (рис. 73).
Здесь удобно рассмотреть два
семейства парабол:
у* = $х (p^^q)
и
х* — т\у
каждое из которых заполняет нашу фигуру, и из них составить сетку коорди-
натных линий. Это равносильно тому, что параметры их 5 и т; мы принимаем за
криволинейные координаты. Все это уже нам знакомо по п° 579, 4); из напи-
санных уравнений имеем: х = ]/£? и y = /ri2v, так что якобиан
_1_
3’
Отсюда сразу получаем
О = у(9 —р)(й —в).
* Здесь снова находит себе применение сказанное в 606, 4°.
608]
5 4. ЗАМЕНА ПЕРЕМЕННЫХ В ДВОЙНОМ ИНТЕГРАЛЕ
201
6)	Подобным же методом предлагается определить площадь четырех-
угольника, ограниченного
(а)	гиперболами ху=р, xy = q и прямыми у —ах, у-=Ьх;
(б)	гиперболами ху—р, xy — q и параболами у3 — ах, у3 = Ьх;
(в)	параболами х3 = ру, х3 — qy и прямыми у = ах, у = Ьх;
(г)	прямыми х-[-у=р, x-\-y = q и у = ах, у = Ьх.
При этом во всех случаях предполагается, что Q<p<iq и 0<a<fr,
(а)	Решение. Сетка координатных линий:
xy = i (p^^q), У =	(а^т^Ъ).
Отсюда

Наконец.
? й
р «
(б)	Указание. Положитьху — ?, у3 =^x(p^i^q,
биан J=4-. Ответ. D=~(q — п)1п —.
81]	З	а
(в)	Ответ. D = ^-(q3—ps)(b3—а3).
яко-
(г)	Ответ. 0 =
2	2	2
7) Найти площадь астроиды х3 -f-у3 = а3.
, Решение. Параметрические уравнения астроиды:
лг = a cos8t, у— a sin81 (0 si t si 2л).
Если заменить здесь а через r(Osgr^a), то получим семейство подобных
астроид, заполняющих нашу фигуру:
х = г cos81, у = г sin81.
При постоянном t, очевидно, эти уравнения дадут пучок лучей из начала.
Воспользуемся же этими формулами, как формулами преобразования; оче-
видно, в основе здесь лежит по существу та же идея, что и в двух преды-
дущих задачах. Якобиан
J= 3r sin31 cos31.
Окончательно,
•я
У
(*	ч
D — 6a3 I sin31 cos31 dt = na3.
V	°
8) Рассмотрим преобразование, которое определяется формулами
л: — “	, у= уйи (и 2=0, ПЭ=О).
202
ГЛ. XVI. ДВОЙНЫЕ ИНТЕГРАЛЫ
[608
Очевидно, всегда х^у^О, так что точка (х,у) лежит в угловом прост-
ранстве между положительным направлением оси х и биссектрисой у — х
первого координатного угла. Обратно, каждой точке (х, у») из этого углового
пространства отвечают вообще две пары неотрицательных значений и, v,
являющиеся корнями квадратного уравнения
z2 — 2хг + у2 = 0.
Можно восстановить однозначность соответствия, если условиться всегда
считать u>:v, т. е. и точку («, v) брать в пределах аналогичного углового
пространства на плоскости uv; тогда
и = х-\-]^ х2—у3,	v = x— х2—у2.
Легко вычислить якобиан преобразования
Z=±(T/i
4 \ У v У и/
Любопытную особенность имеют здесь координатные линии. При и — const
получаем:
у2 = и (2х — и) = 2и^х — уj,
и аналогично при v = const.
у2 = v (2х — v) — 2v l^x —	.
Таким образом, мы в обоих случаях получаем одно и то же (!) семейство
парабол	.
у2 = 2/Цх —
ось которых совпадает с осью х, а директриса — с осью у. Каждая такая
Рис. 74.
парабола касается прямой у = х
в точке (/?, р).
Кажущийся парадокс разрешается
просто: при и—р ио, меняющемся
от 0 до р, описывается часть этой
параболы от ее вершины до упомя-
нутой точки касания, а при о=р и
и, меняющемся от р до со, описы-
вается остальная часть пара-
болы, простирающаяся в бесконеч-
ность (рис. 74).
Если на плоскости ху взять фи-
гуру (Di), ограниченную осью х и
двумя параболами:
у2 = 2р (х —£-), y* = 2q (х —
(0<р<<7),
то на плоскости uv ей будет отвечать прямоугольник (Дх) = [р, q; 0,р], причем
отрезкам прямых и—р и v=p будут отвечать две дуги первой параболы,
смыкающиеся в точке касания. Аналогично, фигуре (_О2) (на плоскости ху), огра-
ниченной тремя параболами, а именно, кроме указанных двух еще параболой
у2 = 2r ( х — у)
(г > q),
608]
§ 4. ЗАМЕНА ПЕРЕМЕННЫХ В ДВОЙНОМ ИНТЕГРАЛЕ
203
будет отвечать на плоскости uv прямоугольник (д2) = [?, г; р, q], и снова —
отрезкам прямых u—q и v = q будут отвечать две дуги одной и той же па-
раболы,
С помощью указанного прео{разования теперь, например, легко определить
площадь фигуры (О2). Имеем
q г ____	_
^=4$ ^V'T-V'v)auav=
Р Q
= 4 К/7- Vp)(Гг?- V¥)-(Vr - Vq)(ZF- =
V
=	+Г7 + /r).
О
Аналогично можно было бы попытаться найти и Dlt но мы встретимся в этом
случае с несобственным двойным интегралом, у которого подинтегральная
функция обращается в оо вдоль отрезка осин. О подобных интегралах—речь
впереди [см. 617, 8)].
9) Для того чтобы площади фигур (Д) и (£>), получаемых одна из другой
с помощью преобразования (1), всегда были равны между собой, очевидно,
необходимо и достаточно условие
I D <х’ У) I — 1
' I |-Ь
Поставим себе задачей найти общий вид преобразований плоскости
сохраняющих площадь.
При этом мы можем в предыдущем условии отбросить знак абсолютной
величины и написать его в виде
D(x, у)
£(И)
(15)
ибо к этому случаю всегда можно ввести дело, обменяв в случае необходимости
РОЛЯМИ $ И 7).
Кроме того, для простоты мы будем предполагать, что одна из входящих
ду
в якобиан четырех частных производных, например отлична от нуля в о
всей рассматриваемой области. Тогда можно разрешить второе из уравнений (1)
относительно т; и, подставив полученное выражение в первое уравнение (1),
представить рассматриваемое преобразование в виде
x = x(?,/(S,y))=g(6,y). J
Характеристикой функций / и g мы и займемся. Именно, мы докажем, что
условие (15) равносильно такому:
df___ dg
ду д?
(17)
Прежде всего, по правилу дифференцирования неявных функций получаем
_ 1	df __ а
Л) ду~1' di dq df ’
(18)
204
ГЛ. XVI. ДВОЙНЫЕ ИНТЕГРАЛЫ
[609
Затем, дифференцируя g, как сложную функцию, находим
dg___________________________ дх . дх df
di ~~ di ’’’ drf di‘
Отсюда и из второго равенства (18) исключаем
ду dg дх ду дх ду   D (х, у)
дц di di dq d-ц di D(i, ц)
Наконец, вычитая почленно первое равенство (18), придем к тождеству
dyfdg df\D(x,y)
ohg \ di ду) D(i, у) ’
которое и доказывает наше утверждение.
На основании теоремы 2 п° 560 теперь мы видим, что общий вид функ-
ций f и g, при которых преобразование (16) сохраняет пло-
щадь, дается формулами
при произвольной функции U.
609. Замена переменных в двойных интегралах. Рассмотрим
двойной интеграл
\\f(x,y)dxdy,	(19)
(£>)
где область (D) ограничена кусочно-гладким контуром (S’), а функция
f(x,y) непрерывна в этой области или, самое большее, допускает
разрывы вдоль конечного числа кусочно-гладких кривых (сохраняя
и в этом случае ограниченность).
Предположим теперь, что область (£)) связана формулами (1):
х — x(i, ц), у=_у($, т|)
с некоторой областью (Д) на плоскости Ь], с соблюдением всех усло-
вий, при которых мы выводили в п° 605 формулу (11), выража-
ющую площадь фигуры (D) в криволинейных координатах *. Поста-
вим себе целью, заменяя переменные в интеграле (19), представить
его в виде интеграла, распространенного на область (Д).
Для этого разобьем область (Д) с помощью некоторой сетки
кусочно-гладких кривых на части (Д,) (1 — 1, 2,..., л); тогда область
(D) соответствующими (тоже кусочно-гладкими) кривыми разобьется
на части (£),) (рис. 75, а, б). В каждой части (D{) выберем про-
извольно по точке (xt. _уг); наконец, составим интегральную сумму
для интеграла (19):	„
3 = S/C*i> У^О1’
________________ i=l
* Мы предполагаем, таким образом, также существование и непрерывность
d2y d2y „
смешанных производных второго порядка и Ср. сноску на стр. 189.
609]
§ 4. ЗАМЕНА ПЕРЕМЕННЫХ В ДВОЙНОМ ИНТЕГРАЛЕ
205
которая имеет этот интеграл своим пределом при стремлении наи-
большего из диаметров областей (Dt) к нулю.
Применив к каждой части (£);) формулу (12) п° 606, будем иметь
£),==[/($*, ТЛ1А 2,., я),
где 0*, т]*) есть некоторая определенная точка области (А,-). Заменяя
в сумме а каждое О; этим выражением, получим
o^f^yi) |УМ|А(.
i
В то время- как точка ($*, -q*) дается теоремой о среднем и
в ее выборе мы не вольны, точка (хг, yt) берется в области (О,)
совершенно
ложим
произвольно. Пользуясь этим
Xt = X®, tf), y^ytf, <),
произволом, no-
т. е. выберем в качестве точки (х;, у,) ту точку области (£);), кото-
рая отвечает точке ($*, -q*) области (АД Тогда сумма а примет вид
°=£/(*	у G?> О) I J&, ) I А,;
i
в этом виде она, очевидно, является интегральной суммой для инте-
грала	.. ,
5	(5, -q), у (5, -q)) I JG, -q) | d^	(20)
(A)
Существование этого интеграла вытекает из того, что подинтеграль-
ная функция либо непрерывна, либо же (сохраняя ограниченность)
допускает разрывы лишь вдоль конечного числа кусочно-гладких
кривых, которые служат на плоскости Ц изображениями кривых
разрыва функции f(x, у).
206
ГЛ. xvt. ДВОЙНЫЕ ИНТЕГРАЛЫ
[610
Если заставить теперь диаметры всех областей (А,) стремиться
к нулю, то по непрерывности функций (1) и диаметры всех обла-
стей (£),•) также будут стремиться к нулю. Тогда сумма а должна
стремиться как к интегралу (19), так и к интегралу (20), ибо для
обоих одновременно служит интегральной суммой. Таким образом,
\\f(x,y)dxdy=;\\f(x($, -q), у ($, т]))| J($, Tj)|ded-ц. (21)
(О)	(А)
Эта формула и решает поставленную задачу — о замене перемен-
ных в двойном интеграле. Формула (11), очевидно, является ее част-
ным случаем и получается отсюда при f (х,у)=1.
Итак, для того чтобы осуществить замену переменных в
двойном интеграле (19), нужно не только подставить в функ-
цию f вместо х и у их выражения (1), но и заменить элемент
площади dxdy его выражением в криволинейных координатах.
С помощью соображений, аналогичных приведенным в п° 606, 4°,
и здесь легко установить, что формула (21) сохраняет справедли-
вость в ряде случаев, когда условия, наложенные на преобразова-
ние (1), нарушаются в отдельных точках или вдоль отдельных линий.
610. Аналогия с простым интегралом. Интеграл по ориенти-
рованной области. Формула замены переменных в двойном интеграле
весьма сходна с формулой замены переменной в обыкновенном опре-
деленном интеграле:
ъ	₽
J/(x)dx=$/(x(£))x'(5)dt	(22)
а	а
Однако в формуле (22) отсутствует знак абсолютной величины,
что уже несколько нарушает аналогию. Это расхождение объясняется
просто. Обыкновенный определенный интеграл берется по ориен-
тированному промежутку 302: ведь а может быть и меньше
и больше Ь, равно как и а может быть и меньше и больше р.
В то же время двойной интеграл мы до сих пор рассматривали лишь
по неориентированной области.
Можно, однако, и в случае двойного интеграла перейти к рас-
смотрению ориентированных областей. Ориентация области
создается тем, что ее контуру придается определенное направление
обхода — положительное или отрицательное (548); одновременно та-
кое же направление обхода придается и всем замкнутым простым;
кривым в пределах области. Если выбирается положительное направ-
ление обхода, то говорят, что область положительно ори-
ентирована, в противном же случае — что она отрицательно
ориентирована.
Естественно условиться для ориентированной области (О) в ка-
честве площади брать ее обыкновенную площадь со знаком плюс,
611J	§ 4. ЗАМЕНА ПЕРЕМЕННЫХ В ДВОЙНОМ ИНТЕГРАЛЕ	207
если область ориентирована положительно, и со знаком минус — в
противном случае. При разложении области (£)) на части (DJ эти
части, как указывалось, ориентируются согласно с ориентацией всей
области; соответственным образом снабжаются знаками и их пло-
щади.
Теперь для ориентированной области (D) можно по об-
разцу п° 688 построить понятие двойного интеграла
J J/(x, j)dxdy,
причем этот интеграл совпадает с определенным раньше, если область
имеет положительную ориентацию, и отличается от него знаком
в случае отрицательной ориентации.
Эта новая точка зрения на двойной интеграл позволяет прежде
всего формулу (11) п° 605, выражающую площадь в криволинейных
координатах, переписать без знака абсолютной величины при яко-
биане:
сЧ^ЖЛЛ|=5(р<6’,|)Л‘'’1’
если только ориентацию областей (D) и (Д) произ-
водить согласованно. Это прямо следует из замечания 606, 1°.
При том же условии формулу (12) п° 606 можно напи-
сать также без знака абсолютной величины:
D = JC, ^)-Д,
и в такой форме она служит естественным обобщением формулы
Лагранжа.
Наконец, теперь и общая формула (21) может быть написана
для согласованно ориентированных областей (£))
и (Д) в виде
5у)dxdy=\\f (х(£, к;) у ($, -q)) J0, ng)dl dt\.
(D)	(A)
Таким образом, стоило лишь поставить простые и двойные интегралы
в одинаковые условия, чтобы аналогия стала полной!
Впрочем, в дальнейшем изложении мы все же вернемся к обыч-
ной точке зрения и будем рассматривать двойные интегралы, распро-
страненные на неориентированные области.
611. Примеры. Так как преобразование переменных в двойном интеграле
часто имеет целью упрощение области интегрирования, то здесь снова нахо-
дит себе приложение все указания, сделанные по этому поводу в п° 608. На-
ряду с этим естественной целью преобразования является также упрощение
Подинтегральиого выражения.
208
ГЛ. XVI. ДВОЙНЫЕ ИНТЕГРАЛЫ
[611
1) Если область представляет собой круг (с центром в начале) или его
сектор, то выгодно перейти к полярным координатам. Для примера
предлагается наново решить задачи: 1); 17) (а); 18) (б) п° 597,
Для второй из них имеем
2тг7?
V — ху dx dy = J rs cos 0 sin 0 dr dQ =s
2«	R
C	CT?4
= \ sin0cos0rf0- \ r3rfr = --g-«
•J	J	о
Если при этом и в состав подинтегрального выражения входит сумма
х34-у>2, то тем больше оснований ждать упрощений от применения полярных
координат.
2)	Найти объем части шара (радиуса /?), вырезаемой из него прямым кру-
говым цилиндром (радиуса г < /?), ось которого проходит через центр шара.
Решение. Принимая центр шара за начало координат, а ось цилиндра
за ось z, будем иметь
2тс г
V= С V/?2 —х2—>2 dxdy = t /?» —p2.pdpd0 =
0 О
= ^-р?’—(Т?2-^].
3)	Найти объем тела, ограниченного параболоидом вращения az = xa-j-ya
и плоскостью г = а.
п	па>
Ответ.
4)	Найти положение центра тяжести для кругового сектора радиуса /?
с центральным углом 2а.
Решение. Выбрав за полярную ось (и ось х) биссектрису центрального
угла, будем иметь
а К
С С	2
Л4д,= \ \ г2 cos 0 rfr rfO =-g-/?’sin а.
—а 0
Если разделить это выражение на площадь сектора Р — то найдется
абсцисса $ центра тяжести:
О а
Так как центр тяжести, ввиду симметрии, лежит на биссектрисе, то поло-
жение его установлено.
5)	Найти массу круга (радиуса /?), плотность которого в каждой точке
равна расстоянию Этой точки от контура круга.
Ответ, т — -^-7?’.
О ;
Приведем еще ряд примеров, где выгодно использовать полярные коор-
динаты.
6)	Найти объем «тела В и в и а н и> [597, 20) ].
Решение. Мы имели уже
etlj
§ 4. ЗАМЕНА ПЕРЕМЕННЫХ В ДВОЙНОМ ИНТЕГРАЛЕ
209
где (Р) есть полукруг в первом квадранте плоскости ху, построенный на
радиусе Р сферы, как на диаметре (рис. 48). Наличие выражения x2+ys в
подинтегральной функции подсказывает переход к полярным координатам.
Полярное уравнение контура (Р), т. е. полуокружности, будет г =-R cos 9
при изменении 0 от 0 до у. Таким образом,
я	я
"2* JRcosO	~2
И=4 ? dO ( У— -rdr = 4-Я8 (1 — sin8 0) d0 =
Л Л	** л
оо	о
Как видим, выкладки здесь, действительно, очень упростились*.
7)	Найти (а) положение центра тяжести и (б) полярный момент инерции
для одного лепестка лемнискаты
(х2+у2)2=2а2(х2 — у1).
Решение, (а) Полярное уравнение кривой:
г2 = 2а2cos29 (—
\ 4	4/
Имеем последовательно:
я ________ ж
4 cos20	_ 4	3
Му =	? г2 cos 0 dr d0 = У-— а8 cos 0  cos 2 20 d0 =
z Л Л	о л
ж	0	я
“"Г	“
я
—	”4"	£
= ii^-a8 (1— 2 sin2 О)2 cos0d0
V	J
и далее, полагая У 2 sin 0 = sin и:
Я
"2“
4 С	тс
Му = — а8 \ cos4 <а do = — а8.
Так как площадь одного лепестка Р = аа [339, 12)], то 6 = -—, чем и
определяется положение центра тяжести.
(б) Имеем
Я
~4~ а/2 cos 26
Z°=§ J r8drd0 = -^-.
« о
Г
* Не исключена возможность и того, что упрощение подинте-
грального выражения оказывается связанным с таким услож-
нением области интегрирования, что переход к полярным коорди-
натам в конечном счете невыгоден.
210
ГЛ. XVI. ДВОЙНЫЕ ИНТЕГРАЛЫ
[611
8)	Найти полярный момент инерции кардиоиды г = а (1 -[- cos 0) относи-
тельно полюса.
35
Ответ. /0 = яа4.
9)	Установить для «тела Вивиани» положение центра тяжести. [См. 6).]
Решение. Из соображений симметрии ясно, что центр тяжести лежит
на оси х. Вычислим статический момент:
Му2 = 4 $ \xzdx dy = 4 § х У Л* — х2 —у2 dxdy —
(Р)	<Р)
п
2	Rcos 6 _______
= 4(cos0rf0 ( У Л2—г2-г2 dr.
Внутренний интеграл:
У? cos 6
у Л2 —г2 • г2 dr = -£- (2г2—Л2) У л2 — г‘+
О
. А4	Г I r=/?cos0	/?4 Г	ТЕ
4--ё-arcsin—	— —g-1 cos 0 (2 cos2 0 — 1) sin 0 4--—0
о	A. ] r=ts0	о l	2
так что
Отсюда, наконец,
t — Myz ________________________	q
V ~ 5(3к — 4)
10)	Найти объем тела, ограниченного эллиптическим цилиндром
плоскостью z = 0 и одной из следующих поверхностей:
(а)	плоскостью z — ~кх ру -|- й (й > 0),
.	№ v*
(б)	эллиптическим параболоидом —- = —(с>0),
(в)	гиперболическим параболоидом cz = ху (с > 0).
Решение. Вопрос сводится к вычислению интеграла, распространен-
ного на эллипсе плоскости ху, в связи с чем целесообразно перейти к
обобщенным полярным координатам, положив
х = ar cos 0, y — br sin 0;
якобиан преобразования при этом будет J — abr.
611]
§ 4. ЗАМЕНА ПЕРЕМЕННЫХ В ДВОЙНОМ ИНТЕГРАЛЕ
211
Например, для случая (б) получим
те
~2 1
.. с С С [ хг . у* \ . .	„ . С С / a2 cos2 9
(О)	о о
Аналогично найдем и для других случаев:
aabs *
(a) V=r.M, (б)	.
Ъг sin20 \	.
----s— r3dr dv =
92 1
• к /а2 , &\
= аЬс -г + “Г •
8	\р2	q 1
11)	Найти объем трехосного эллипсоида
jt-2 V2 Z2
_ 4-	4-— = 1
а2 ft2 ^с2 ь
Указание. Прибегнуть к обобщенным полярным координатам
~	4	,
Ответ, -j- наос.
О
12)	Вычислить интеграл г г . ,
Z = \ ху dxdy,
(D)
распространенный на петлю кривой
/ X2 у2 \2 _ х2у
\ а‘ "* Ъ*) — с8
в первом координатном угле. [Ср. 608, 3) (г).]
w	л 1 а10*8
Указание то же. Ответ.	.
840 с12
13)	Вычислить интегралы:
(а) /1 = S V V* +Уу dx dy, (б) 4 = И xnyndx dy
(А)	„	(А)
(п — натуральное), где (А) есть область, ограниченная осями координат и па-
раболой Yx + Y у — i-
Решение. Параметрические уравнения кривой: х = cos4t, у = sin41
^0 yj. Естественно рассмотреть семейство парабол, подобно располо-
женных (относительно начала): x=pcos4Z, _y = psin4Z (Osgpsg 1). Вводя
Р и t в качестве нов'ых переменных, будем иметь J = 4р cos’ t sin8t, так что
те
~2 1
С С —	2
= \ I Y f ' 4р cos81 sin81 df dt = -jg-,
V 1
Z2 = 4 \ \ pSrt+1 cos4rt+31 sin4rt+3 td? dt =
те
T
2 C	9
= —ГТ \ COS4"+81 sin4n+e t dt =—r-T
» + 1 J	«+ 1
[(4n + 2)ll]2
(8n + 6)l! •
* ff случае (в) тело состоит из четырех симметричных частей, из которых
две расположены под плоскостью ху, а две—’Под нею.
212
ГЛ. xvr. ДВОЙНЫЕ ИНТЕГРАЛЫ
[611
Последнее выражение может быть преобразовано к виду
(2п+ 1)!
(л 4- 1) (2л + 2) (2л + 3)... (4п + 3) ’
При и=1 отсюда, в частности, получается решение задачи 3) п’ 597.
14)	Вычислить интеграл
(В)
где (В) есть область, ограниченная осями координат и параболой
У казание. Положить х = ар соз4Л у = bp sin4р 1,
2
Ответ. К—^аЬ.
15)	Найти интеграл
(* (* х2 sin ху . .
)
(О)
где (D) есть область, ограниченная четырьмя параболами х2 = ау, х2 = Ьу,
у2—рх, у2 = qx (0 <: а < b, Q < р < q).
Решение. Прибегнув к замене переменных, указанной в 604, 4)
ср. 608, 5)], преобразуем интеграл к виду
г 9
L = т] sin di dt\.
а р
Теперь легкое вычисление дает:
___sin pb — sin ра _ sin qb — sin qa
—	p	q	1
Аналогично угадывается подходящая система криволинейных координат
и в следующих случаях:
16)	Найти интеграл
I— И ху dx dy,
(А)
если (А) есть четырехсторонник, ограниченный кривыми:
(а) у = ах3, y = bxs, у2=рх, y2 = qx;
(б) у* = ах2, у2 == Ьх2, у —ах, у =
У казание. Ввести новые координаты ?, т;, положив
(а) у = ix3, у2 =
(б)_у’=5х2, у = грс.
611]
§ 4. ЗАМЕНА ПЕРЕМЕННЫХ В ДВОЙНОМ ИНТЕГРАЛЕ
213
Ответ.
(а)	1=^(а Ъ-Ь 5)^-р5)-,
(б)	/=^(&4-а4)(а-1»-₽-10).
17)	Пусть (D) будет треугольник, определяемый неравенствами х^О,
у>?0, x-j-ysgl. Предполагая р3= 1, q^l, непосредственно установить
формулу Лиувилля [597, 16)] *
1
J J V (х 4-у) xP~l_y9~l dx dy = В (р, q) f <f (и) ир+Ч~1 du,
(О)	б
где tp (и) есть непрерывная функция в промежутке [0,1].
Доказательство. Положим
х = «(1—о), у = uv
или
и = x-4-v, v =—.
*+У
Этими формулами устанавливается взаимно однозначное соответствие между
треугольником (£)) на плоскости ху и квадратом (Д) = [0,1; 0,1] на пло-
скости uv. [Исключение составляет лишь точка х = 0, _у = 0, которой отве-
чает отрезок оси о.] При этом
Заменяя переменные, получим, что двойной интеграл равен
. 1 1
j <р («) «Р+?—1 V?-1 (1 — »)Р-‘ du dv
или
1 1
vi~l (1—v)p~l dv • j tp («) «Р+?-1 du.
Так как первый множитель как раз и есть В (q, р) = В(р, q), то требуемый
результат установлен.
18)	С помощью той же замены переменных можно доказать и более
общую формулу:
С С	хР_1у9_1
J J	(ах + р> + 7)Р+ч^^ =
— ВС \ С У («) ЦР+9"1 du
— \Р> Я) ] (ад	I «
о
(где р, g^sl; а, ₽2=0, 7 > 0; <р(«) непрерывна). При этом надлежит вос-
пользоваться известным результатом: 534, 2).
* Выше она была выведена из формулы Дирихле, которая является
ее частным случаем (при ? = 1).
214
ГЛ. XVI. ДВОЙНЫЕ ИНТЕГРАЛЫ
[612
19)	К формуле Лиувилля приводится формула
1 1 1
j /(«?) (1 — “)р~1 Р1’ (1 —	da d$ = В (р, q) \f(v) (1 — »)₽+?-> dv,
если применить подстановку
р=1-л
1 —у
1 *
причем х$:0, у 5^0, x-f-ysSl- Якобиан J = -j-----
20)	Доказать с помощью замены переменных тождество (при любом
z — const.)
те те
~2 ~2
j cos (2г sin sin 0) dtp df) =
[ср. 595, 7)].
Доказательство.
Замена переменных в двойном интеграле по
формулам
u-4-v	. и — v
T =	9 = -^-
приводит его к виду
у Г V [ cos (z cos и) cos (z cos v) 4-
(A)
+ sin (z cos и) sin (z cos v)] du dv,
где (Д) есть косо поставленный квадрат, изобра-
женный на рис. 76. Но интеграл от второго сла-
гаемого равен нулю (подстановка и = к — и'),
а интеграл от первого слагаемого, распространенный на квадрат (Д), непо-
средственно приводится к удвоенному подобному же интегралу, взятому
по квадрату £о,	0, yj. Отсюда уже легко получить требуемый ре-
зультат.
§ 5. Несобственные двойные интегралы
612.	Интегралы, распространенные на неограниченную
область. Понятие двойного интеграла обобщается на случай неогра-
ниченной, т. е. простирающейся в бесконечность области, или на
случай неограниченной функции, подобно тому как это сде-
лано в главе тринадцатой по отношению к простым интегралам.
Остановимся сначала на случае неограниченной области (Р).
Примером такой области может служить вся плоскость или часть ее,
лежащая вне некоторого круга или другой ограниченной плоской
• Впрочем, точка х = 0, у=1 здесь требует оговорок.
612]
§ 5. НЕСОБСТВЕННЫЕ ДВОЙНЫЕ ИНТЕГРАЛЫ
215
фигуры, какой-либо угол и т. п. Что касается границы этой области,
то она предполагается имеющей площадь 0 (например, состоящей из
кусочно-гладких кривых) в каждой ограниченной своей части. Пусть
в области (Р) задана некоторая функция f{x, у), которую будем
предполагать интегрируемой в обычном смысле слова в каждой огра-
ниченной и квадрируемой части области (Р).
Проведя вспомогательную кривую {К') (тоже с площадью 0),
отсечем от области (Р) ограниченную и связную ее часть.(Р'),
в которой интеграл	/{х, уух4у	(1)
(Р')
по предположению существует. Станем теперь удалять кривую {К)
всеми ее точками в бесконечность, так, чтобы наименьшее рас-
стояние Р от начала до точек этой кривой возрастало до бесконеч-
ности. Тогда отсекаемая ею переменная область (Р') постепенно бу-
дет охватывать все точки области (Р): каждая точка из (Р) будет
принадлежать (Р') при достаточно большом Р.
Предел {конечный или бесконечный) интеграла (1) при Р—>оо
называют {несобственным) интегралом от функции f{x,y) в не-
ограниченной области (Р) и обозначают символом
5 § У) dx dy — lim J J f {x, y) dx dy.
(P)	P-HOOjpz)
В случае существования конечного предела интеграл (2)
называется сходящимся, в противном случае—расходящимся.
Функция, для которой интеграл (2) сходится, называется интегри-
руемой (в несобственном смысле) в области (Р).
В случае положительной функции f{x, у) достаточно, рас-
смотрев какую-нибудь1 определенную последовательность уда-
ляющихся в бесконечность кривых
(КД №), .... {Кп),...
ими областей
(Л). (А), .... {Рп),...,
существование конечной границы
/==supK j f{x, y)dxdy\,
(2)
й отсекаемых
предположить
v п'
уже вытекала сходимость интеграла (2;
чтобы отсюда
Действительно, какую бы область (Р') ни отделить кривой {К')
от (Р), при достаточно большом п эта область целиком будет содер-
жаться в (Р„), так что
J $/(*> y)dxdy ? f{x, y)dxdy
216
ГЛ. XVI. ДВОЙНЫЕ ИНТЕГРАЛЫ
(612
и, тем более,
J У) dx dy «с I.
<Р'У
(3)
С другой стороны, по заданному s^>0 можно найти такое п0,
чтобы было
$5 f^x' y)dxdy^>I—е.
При достаточно большом R*, в свою очередь, область (Р') охватит
(РЛо), следовательно, и подавно
$ y)dxdy^I — г.
(Р'}
(4)
Неравенства (3) и (4) в совокупности доказывают, что число I удо-
влетворяет определению двойного интеграла.
С помощью этого соображения легко доказывается теорема о
сравнении интегралов, аналогичная теореме п° 474. Далее, если
сохранить относительно функции f(x, _у) прежние предположения, то
из сходимости интеграла от \f(x, j)[, распространенного на
неограниченную область (Р), вытекает сходимость подобного же
интеграла для функции f(x, у).
Для доказательства этого рассмотрим две неотрицательные функ-
ции:
очевидно,
у (д. )_ ( ?(х’ -У)’ если f(x’
+	( 0 в противном случае,
у .	( —f{x, у), если f(x, _у)=^0,
| 0 в противном случае.
Из интегрируемости функции \f(x, _у)| вытекает сходимость инте-
гралов для функций
/+ (х, у) \f(x, у) | и /_ (х, у) sg \f(x, у) |,
а следовательно, и для функции
/(jc, y)=f+(x, y)—f.(x, у).
Весьма замечателен тот факт,
интеграла от функции f(x, у),
* Мы все время сохраняем за R
стояния точек кривой (/С) от начала.
что и обратно: из сходимости
распространенного на неограни-
его значение, как наименьшего рас-
613)	§ 5. НЕСОБСТВЕННЫЕ ДВОЙНЫЕ ИНТЕГРАЛЫ	217
ченную область (Р), вытекает сходимость интеграла и для
\f(x, у)|. Этому предложению нет аналога в теории простых несоб-
ственных интегралов: мы знаем [475], что там могли существовать и
неабсолютно сходящиеся интегралы.
Доказательство мы дадим в следующем п°.
613.	Теорема об абсолютной сходимости несобственного двой-
ного интеграла. Каждый сходящийся интеграл
\\/(х, y)dxdy	(5)
(Р)
необходимо и абсолютно сходится, т. е. одновременно с ним
сходится и интеграл
y)]dxdy.	(6)
(Р)
Допустим противное. Взяв последовательность областей
{(Л>)}> так> чтобы они, расширяясь, постепенно охватывали всю
область (Р), будем иметь
lim $5 \f(x, y)\dxdy = + оо.
п —► ОО jp )
71
Не умаляя общности, мы можем допустить, что при каждом зна-
чении п выполняется неравенство
\f{x,y)\dxdyZ>^\\ \f(x,y)\dxdy-}-2n.
(P»+D	• (Ря)
Этого можно достигнуть, разрежая (в случае надобности) последо-
вательность {(Ря)}, т. е. извлекая из нее частичную последователь-
ность и наново нумеруя ее.
Обозначая через (р„) разность областей (Ря+1) и (Ря), очевидно,
будем иметь
55	>)ldx^>255 \f{x,y)\dxdy-\-2n.
Но
]/(х, у)|=/+(х, J)+A(x, у),
так что
5	5 \f(x> У) I dxdy — Ц f+(x, y)dxdy-}-§§ f_(x, y)dxdy.
(ря)	(Ря)	(ря)
Пусть из двух интегралов справа ббльшим будет, например, первый.
Тогда
5 5 Л (х> -У) dx dy > 5 5 \f(x>y)\dxdy^-n.
<pn>
218
ГЛ. XVI. ДВОЙНЫЕ ИНТЕГРАЛЫ
(613
Заменяя двойной интеграл слева достаточно близкой к нему
нижней суммой Дарбу, сохраним неравенство *
У > $ 5 \КХ> УУ \dxdy-\- п.
i	(PJ
Можно в этой сумме оставить лишь те слагаемые, которым отвечают
т(„	0; обозначив совокупность соответствующих элементов
(Рл*) через (рп), получим, тем более,
55 /(*> У) dx dy =
Срп)
= 5$А('Г> y)dxdy>\ \ \f(x, y)\dxdy + n.
~ (Р»>
Обозначим через (Ря) область, составленную из (Ря) и (/»„); так
как
55 f^x’ y)dxdy^ — 55 \f(x>y)\dxdy,
<ря> <ря>
то, складывая почленно это неравенство с предыдущим, найдем
55 f(x> y)dxdy~^>n.
Область (ря), а с нею и (Ря), можно деформировать так, чтобы
из последней получилась связная область (Ря), и притом по пло-
щади столь мало разнящаяся от (Ря), что все же сохраняется нера-
венство
55 /(*• y)dxdy^>n.
(Р'п>
Этого легко достигнуть, соединяя оторванные части области узкими
«коридорами» с произвольно малой общей площадью.
Отсюда уже ясно, что интеграл (5) сходиться не может, вопреки
предположению; это противоречие и доказывает теорему.
Заметим, что принципиальная разница между одномерным и дву-
мерным случаями связана именно с заключительной частью проведен-
ного рассуждения. Несвязную линейную область, состоящую из от-
дельных промежутков, уже нельзя произвольно малой деформацией
превратить в связную (т. е. в цельный промежуток).
* Здесь (р^) суть элементарные части, на которые разбита область (ра),
a mjp — соответствующие точные нижние границы функции /+ (х, у).
6141
§ 5. НЕСОБСТВЕННЫЕ ДВОЙНЫЕ ИНТЕГРАЛЫ
219
Доказанная теорема вместе с замечаниями предыдущего п° сводит
вопрос о сходимости и вычислении несобственного интеграла от
произвольной функции к такому же вопросу для положительной
(неотрицательной) функции. Последним вопросом мы в последующем п°
преимущественно и займемся.
614. Приведение двойного интеграла к повторному. Ограни-
чимся сначала предположением, что функция f(x, у) неотрицательна.
Если эта функция задана в неограниченной области любой формы,
то, полагая ее дополнительно вне этой области равной нулю, всегда
можно свести дело к случаю неограниченной же прямоугольной
области. Пусть, скажем, речь идет о бесконечном в одном направле-
нии прямоугольнике [a, ft; с, -]-оо] (а, ft, с — конечные числа, причем
ft^>a). Будем предполагать, что в каждом конечном прямоугольнике
[a, ft; с, d] (при любом d^>c) существуют как двойной интеграл,
так и простой интеграл по у — оба в собственном смысле,
так что [594] имеет место формула
'	. ь а
55 f dx dy —^dx^fdy.	(7)
[a, b\ c, d\	a c
Желая установить подобную же формулу для бесконечного пря-
моугольника, т. е. для случая d = -ф- оо, предположим, что сходится
повторный интеграл
Ь оо
/=5 dx § fdy.
а с
Так как при любом d^>c имеем
55 fdxdy^I,
[a, й; с, d|
то по сказанному в 612 отсюда уже следует сходимость двойного
интеграла
55	f dx dy = lim 55 f dx dy,	(8)
[a, b; c, -j-oo]	<*-°° Ci
который, очевидно, не превосходит 1. Остается лишь доказать, что
на деле двойной интеграл равен I.
00
Если интеграл dy представляет собой функцию от х, инте-
С
грируемую в собственном смысле, следовательно, ограниченную
некоторой постоянной L, то и подавно
d
5/(х> y)dy ^ L.
С
220
ГЛ. XVI. ДВОЙНЫЕ ИНТЕГРАЛЫ
(614
В таком случае по теореме II п° 526
6 d
1= lim ^dx^fdy.
^-*4-°°а с
Сопоставляя это с (7) и (8), приходим к требуемому результату.
Установленный факт сохраняет силу и в том случае, если инте-
грал I сходится, как несобственный. Пусть, например, b является
ОО
единственной особой точкой для функции \f dy от х. Тогда по
С
доказанному, при 0 т; ft — а,
Ь—7]	4-00
J J f dxdy= dx § f dy,
[a, b — tj; c, 4-oo]	a	c
(9)
и обе части равенства при ц—>0 стремятся к I. Принимая же во
внимание, что
fdxdy^	fdxdy,
[а. 6; с, +°о]	]а, b — tj; с,4-оо]
снова заключаем о равенстве двойного и повторного интегралов по
прямоугольнику [а, Ь; с, -{- оо].
Заметим, что если бы несобственный повторный интеграл имел
бесконечное значение, то, как видно из предыдущих двух соотно-
шений, таково же было бы и значение двойного интеграла.
Итак, имеем подобно (7)
Ъ со
fdxdy —\ dx $ fdy,
[а, b; с, 4-о°]	а с
(10)
причем из существования повторного интеграла справа уже вытекает
существование двойного интеграла. Равенство сохраняется даже в том
случае, когда интеграл справа равен оо.
Обратимся, наконец, к рассмотрению прямоугольника [а, -|- оо;
с, -{- оо ], простирающегося в бесконечность по двум взаимно пер-
пендикулярным направлениям. И здесь будем предполагать, что в каж-
дом конечном прямоугольнике [a, b; с, d] (при любых bа и d^>с)
существуют в собственном смысле двойной интеграл и простой
интеграл по у.
Для рассматриваемого случая также может быть установлена
формула
fdxdy— J dx J fdy,	(11)
la, 4-00; c, 4-00]	a c
615]	g 5. НЕСОБСТВЕННЫЕ ДВОЙНЫЕ ИНТЕГРАЛЫ	221
в предположении, что повторный интеграл справа сходится. Это
легко получается из (10) переходом к пределу при 6->Ц-оо, напо-
добие того, как выше мы (10) получили из (9). И здесь двойной
интеграл оказывается равным -|- оо, если таково значение повторного
интеграла.
Скажем теперь несколько слов относительно случая, когда функ-
ция f (х, у) меняет знак; ограничимся для определенности форму-
лой (10). В конечном прямоугольнике [a, b; с, d} (при d^>c) мы
сохраняем прежние предположения, но, наряду со сходимостью по-
вторного интеграла от самой функции:
b -|"°о
§ dx f(x, y)dy,
а с
мы на этот раз допустим сходимость повторного интеграла и от ее
абсолютной величины:
Ь	—J-оо
\dx § \f(x,y)\dy.
а с
Тогда подобные же повторные интегралы будут существовать и
для функций f+(x, у) и f_(x, у), упомянутых в конце п° 612.
Применяя к этим неотрицательным функциям порознь доказан-
ную формулу (10) и вычитая результаты, убедимся в справедливости
этой формулы и для данной функции f(x, у).
615. Интегралы от неограниченных функций. Пусть функция
f (•*> У) задана в ограниченной области (Р), но сама оказывается
неограниченной в окрестности отдельных точек Mlt Ж2,...; в любой
части области (Р), не содержащей этих точек, мы предполагаем
функцию интегрируемой в собственном смысле слова.
Выделим теперь особые точки Afi, Мг,окружив их кри-
выми (A,), (Аа),,.. Если удалить из области (Р) ограниченные этими
кривыми окрестности особых точек, то мы получим область (Р'), для
которой по предположению интеграл
[\f(x,y)dxdy	(1*)
(R)
сходится. Станем «стягивать» кривые (Aj), (As),... в указанные точки
так, чтобы наибольшее из расстояний точек этих контуров (k)
до соответствующих точек М — обозначим его через р — стремилось
к нулю *. Заметим, что при этом и площади рассматриваемых окрест-
ностей (меньшие чем тера) также будут стремиться к нулю.
* Вместо этого можно было бы предположить стремящимися к нулю
диаметры всех областей, ограниченных контурами (А).
222	ГЛ. XVI. ДВОЙНЫЕ ИНТЕГРАЛЫ	(615
Интеграл ^несобственный) от неограниченной функции f(x, у)
по области (Р) определяется как предел интеграла (1*) при
Р-0:
J §/(х, у) dx dy — lim f(x, у) dx dy.	(2*)
(P)	p * 0 (p)
Особые точки могут лежать и вдоль некоторых особых линий,
которые мы всегда будем предполагать имеющими площадь 0.
В этом случае приходится окружать эти линии «сжимающимися»
к ним окрестностями, и принципиально здесь нет ничего нового.
Однако точная характеристика подразумевающегося здесь предель-
ного процесса требует еще некоторых пояснений. Пусть особая
линия (/) окружена окрестностью с контуром (А). Если взять
точку А на (А), то из расстояний этой точки от различных точек В
на (/) существует наименьшее, рд; с другой стороны, если
изменять положение А на (k), то из всехврд найдется наибольшее, р.
Это число в некотором смысле и характеризует степень удаленности
контура (А) от кривой (/), и предельный процесс направляется усло-
вием: р —0. (При наличии нескольких кривых под р разумеется
наибольшее из подобных чисел.) Здесь также можно доказать, что
вместе с р стремится к нулю и площадь рассматриваемой окрест-
ности.
Наконец, определение несобственного интеграла легко распро-
страняется на случай неограниченной области и определенной в ней
функции, которая на конечном расстоянии имеет особые точки.
Замечание. Если бы при построении несобственного инте-
грала, кроме особых точек (или линий), мы стали выделять и неко-
торые такие точки (или линии), которые на деле не являются осо-
быми, то это обстоятельство никак не могло бы отразиться ни на
существовании, ни на величине того предела, которым представляется
интеграл. В самом деле, пусть, например, к особым точкам доба-
вляется неособая точка А и, сверх того, что необходимо по точному
смыслу определения несобственного интеграла, — мы выделяем еще
окрестность этой точки А. Но вблизи А функция ограничена, и
интеграл по упомянутой окрестности, вместе с площадью ее, стре-
мится к 0.
На все перечисленные случаи несобственных интегралов пере-
носится то, что было изложено в пп° 612—614.
Прежде всего, и здесь справедлива замечательная теорема о том,
что несобственные двойные интегралы если сходятся, то, по
необходимости, — абсолютно. Доказательство строится так же,
как и в п° 613.
Что касается вопроса о сведёнии двойного интеграла к повтор-
ному, то здесь также достаточно ограничиться случаем, когда,
областью (Р) служит (конечный) прямоугольник [a, b; с, d]. Можно
доказать, ш о для неотрицательной функции f (х, у) имеет место
6161
§ 5. НЕСОБСТВЕННЫЕ ДВОЙНЫЕ ИНТЕГРАЛЫ
223
формула (7) — в предположении существования повторного интеграла
(существование двойного отсюда уже будет вытекать).
Впрочем, следует при этом уточнить еще предполагаемое распо-
ложение особых точек* функции. Начнем со случая, когда они
лежат на горизонтальной прямой (например, у == d) или, более
обще, на кривой, выражаемой явным уравнением вида
V =у (х)	(а^х^ Ь).
Для этого случая доказательство — такое же, как в п° 614 при
d — -|- оо. Отсюда перейдем к случаю, когда особые точки лежат
еще и на некоторой вертикальной прямой (например, х = Ь),
рассуждая, как и выше при Ь— оо. Если рассматриваемая функ-
ция меняет знак, то приходится еще предположить существование
повторного интеграла для \f(x, у)).
Обобщение на случай нескольких кривых или прямых или на
случай бесконечного прямоугольника с особенностями на конечном
расстоянии — очевидно.
616.	Замена переменных в несобственных интегралах. Пусть
в плоскостях ху и имеем, соответственно, ограниченные
области (£)) и (Д), связанные формулами преобразования:
или обратными им:
Х — Х$, 7)), 1
v—y& iq) J
5 = Н(х, у), 1
7i=7i (х, у), J
(12)
(12а)
с соблюдением всех условий, о которых подробно говорилось
в п° 603.
Пусть, далее, в области (£)) задана функция f(x, у), непрерыв-
ная всюду, за исключением конечного числа отдельных точек или
даже кривых **, где она обращается в бесконечность.
Покажем, что при этих условиях равенство
5	(•*> y)dxdy = ^f(x 0, tj), у 0, 7j))| J(5, 7j) | dldTj (13)
(D)	(A)
имеет место, если только сходится один из этих интегралов; сходи-
мость другого отсюда уже будет вытекать.
о*Действительно, если особые точки и особые линии первого инте-
грала в области (£)) выделить их окрестностями, то соответ-
* В любом частичном прямоугольнике, где нет особых точек, формула
вида (7) предполагается верной.
** Все кривые, о которых идет речь в настоящем п°, предполагаются
кусочно-гладкими.
224
ГЛ. XVI. ДВОЙНЫЕ ИНТЕГРАЛЫ
[616
ствующими окрестностями в области (А) выделятся особые
точки и особые линии второго интеграла. Пусть при этом получатся
область (£)') на плоскости ху и область (Д') на плоскости fy. Тогда
по формуле (21)п°609
$$/(*» У) dxdy — \ \f(x ($, 71), у G, Т])) IJG, Ч) I dy. (14)
(О')	(Д')
Предполагая непрерывность соответствия между областями (D) и (А)
в обе стороны *, легко видеть, что при «сжимании» окрестностей
на плоскости ху к окруженным ими точкам или линиям такой же
процесс будет происходить и с окрестностями на плоскости и
обратно. Отсюда ясно, что, переходя в предыдущем соотношении
к пределу, из сходимости одного из интегралов мы действительно
можем заключить о сходимости другого и вместе с тем о наличии
равенства (13).
Можно было бы допустить даже, что в отдельных точках обла-
сти (А) или вдоль отдельных лежащих в ней линий (не пересекающих
ранее рассмотренных в этой области особых линий) обращается
в бесконечность якобиан J($, т;), а с ним и подинтегральная функция
второго из интегралов. Хотя соответствующие точки и линии на пло-
скости ху не являются особыми для первого интеграла, но их выде-
ление, по замечанию предыдущего п°, не создает затруднений, так
что и при новых допущениях заключение остается в силе.
Заметим еще, что и в рассматриваемом случае часто приходится
сталкиваться с нарушением непрерывности или взаимной однознач-
ности соответствия в отдельных точках или вдоль отдельных линий.
В подобных обстоятельствах приложимы соображения п° 606, 4°
[ср. конец п° 609].
Наконец, обратимся к случаю, когда хоть одна из областей (D),
(А) является неограниченной.
Если обе эти области простираются в бесконечность, причем
точки их, находящиеся на конечном расстоянии, связаны соответ-
ствием (12) или (12а), то, отделив (соответствующими) кривыми огра-
ниченные части этих областей, (Z/) и (Д'), мы при соблюдении
указанных выше условий будем иметь равенство (14). Так как упо-
мянутые кривые, очевидно, могут удаляться в бесконечность лишь
одновременно, то остается лишь перейти в (14) к пределу, чтобы
получить (13), причем снова из сходимости одного из интегралов
следует сходимость другого.
Пусть теперь, скажем, область (D) простирается в бесконечность,
а область (А) нет, и точки области (D) связаны соответствием со
всеми точками области (А), за исключением отдельной точки (или
кривой), которая, так сказать, отвечает бесконечно удаленной части
• Мы имеем в виду непрерывность функций (12) и (12а).
617]	$ 5. НЕСОБСТВЕННЫЕ ДВОЙНЫЕ ИНТЕГРАЛЫ
225
контура области (D). Отделив кривой ограниченную часть обла-
сти (Ь), мы соответствующей кривой в области (Д) выделим упомя-
нутую точку (или кривую) и тем получим области (О') и (Д'), к ко-
торым уже приложимы прежние рассуждения, и т. д.
Заметим, что замена переменных наряду с переходом к повтор-
ному интегралу является весьма удобным средством для установле-
ния существования несобственных двойных интегралов. Многочислен-
ные примеры тому читатель найдет в следующем п°.
617. Примеры. 1) Установить условия сходимости интегралов (т>0):
(Э) И (х2+Л
dx dy
(ха+/)'"’
(в)
Решение. В полярных координатах эти интегралы сведутся к следующим:
2л 1	1	оо	1
. ч С С Г dr „ С dr	п £ dr , . г. С г dr
(а). \ dO \	—2я \	,	(б) 2п \	(в) 2к \
(10*	о	I	о
Очевидно, условия сходимости будут:
(а)т<1, (б)т>1, (в) т<1.
2)	Аналогичный вопрос по отношению к интегралам (а, Э, т>0)
С С dxdy ... С С dxdy
W JJ (х*+_?₽)"” W J J (x*+y9y”
Jt>0, у 5=0	jr&o, J15=0
X® -f- =S 1	Xa + y9 Э: 1
/в)	H dxdy________________
w	JJ	(1— Xя— y$)m '
X&O, y^zO
-с®+_уР=~1
Указание. Прибегнуть к подстановке
£2	2 £
x = r®cos® 0, y = r₽ sin^ fl.
Ответ, (a) — 4- -i- > m; (6) —	< m; (в) m < 1.
dp	dp
Те же ответы получатся и в случае, когда изменение переменных в за-
дачах 1), 2) ограничивается сектором между лучами в = в0 и 6 = 9Х.
3)	Если область (Dt) изменения переменных х, у есть криволинейный тре-
угольник АОВ (рис. 77), ограниченный отрезком АО оси х, дугой ОВ пара-
болы у = х! и дугой ВА окружности x2-f-ya = l, то интеграл
СС dxdy
П Xs+у2’
8 Г. М. Фихтенгодьц, т. Ш
226
ГЛ. XVI. ДВОЙНЫЕ ИНТЕГРАЛЫ
|617
длякоторого начало по-прежнему служит особой точкой,
все же существует (хотя не существует для круга!). Действительно, при пере-
ходе к полярным координатам интеграл пре-
образуется к виду *
г	1	г
С	С	dr	С	.	cos2	в
\ dO \	— — \	In	- .	dO,
j	J	r	J	sm 6	’
0 sin 0	0
cos2 6
откуда и вытекает сказанное.
4)	Аналогично, взяв в качестве области
(Da) треугольник АОС (тот же рисунок), можно
установить существование интеграла
С С dx dy
И 1-Х2 -у*’
О>2)
для которого особыми будут точки А и С. Так как
ных координатах уравнение линии АС будет г = ц- , то
женный интеграл сводится к следующему:
в поляр-
предло-
2 cos 6 +• sin в	4	2
С .А С г dr f sin 20	If sin <f>
\rfe \	Ь=Н=-рТ+йГ20й=-2 ,Vn'------
0	0	о	0
1+ sin <р
Q/
Рис. 78.
который явно существует.
5)	На сравнении с интегралами, рассмотренными в 1), основан следующий
признак сходимости'.
Если (£)) есть: (а) ограниченная область, содержащая начальную точку,
или (б) простирающаяся в бесконечность область, не содержащая начальной
точки, то интеграл от функции f(x,y)
в (D) сходится, коль скоро f(x, у)
в (D) может быть представлена в виде
f(x v)==
' у> (X2 + у2)т ’
где tp ограничена и, соответственно
случаю, (а) т<1 или (б) т> 1.
Легко перефразировать этот при-
знак для случая, когда начальная точ-
ка заменена любой точкой (х0, у0).
6)	Проверить сходимость двой-
ного интеграла от функции
«а_____________________Г2
J J'	(х2	у»2)2 ’
распространенного на: (а) треугольник
ОВС (рис. 78), (б) квадрат ОАВС,
(в) бесконечную полосу YCBE, (г) бесконечный треугольник EBG, (д) бес
конечный квадрат EBF.
* Через 8 обозначен угол луча ОВ с полярной осью.
617]	§ 5. НЕСОБСТВЕННЫЕ ДВОЙНЫЕ ИНТЕГРАЛЫ
227
Ответ. В случаях (а), (г) интеграл не сходится (тем более это справед-
ливо для случаев (б), (д)!); в случае (в) интеграл сходится, он равен
7)	Пусть функции /(х) и g(y) абсолютно интегрируемы — первая
в промежутке [в, 6], а вторая — в промежутке [с, d] (каждый из этих проме-
жутков может быть как конечным, так и бесконечным). Доказать, что тогда
сходится и двойной интеграл
ь	d
$ J /(*) g(y) dxdy — £ f(x) dx - ( g(y)dy
[a, S; c, d]	a	c
[cp. 605, 9)].
Вопрос легко приводится к случаю неотрицательных функций; этим пред-
положением мы и ограничимся.
Если, скажем, оба промежутка конечны, и единственными особыми точ-
ками являются, соответственно, Ь и d, то, как мы уже знаем, существует
собственный двойной интеграл (8 и s>0)
Ь—S	d —s
И f (х) g (у) dx dy — ( f(x)dx- ( g(y)dy;
[a, ft —6; с, d — <]	а	с
остается лишь перейти к пределу при Й—*0, s-*0.
Указанные условия относительно функций /и g оказываются и необходи-
мыми для существования двойного интеграла, исключая тот случай, когда
один из интегралов
ь	d
J|/(x)|dx, $|g(y)|dy
а	с
равен нулю.
8)	Найти площадь фигуры (Dt), ограниченной параболами у* =
= 2р(х—и y* — 2qCx—(0</><7) и осью х [см. 608, 8)].
Решение. Воспользовавшись криволинейными координатами, приве-
денными в указанном месте, имеем:
Р 9	_ _
ЧЖ-Ут)**-
о Р
Р	9	pi
= 4- / \ -^=г • \ Y и du — t Yvdv- \
4 U	'	х’ J
о	Р	о	Р
7?=-} = 4^—^pq •
у ц ) о
Вычисление площади привело к несобственному интегралу (осо-
бая линия — отрезок оси и). После того как замена переменных распро-
странена и на случай несобственных интегралов, законность проведенной
выкладки не может вызывать сомнения.
9)	Вычислить интеграл (0 < с < а)
1 с
=	— ха — (сг — х*)у* Ус*—х* dxdy.
8*
228
ГЛ. XVI. ДВОЙНЫЕ ИНТЕГРАЛЫ
(617
Применим подстановку
v ______ uv
/Гр? ’ y~V^ly+u2) — v2 ’
где (и, v) изменяется в бесконечном прямоугольнике [0, 4*	0, с]; яко-
биан равен--—- 	— 	- , Имеем:
Y 14-u2/ c2(i + «2)—v2
с со _______ ОО	с
С С vVo2—v2 . f du С /----------------
Т+й2— ^^""лГ/й2' \ vVa2 — V2 dv =
= -j[aa-(e8-c2)21,
Здесь оказалось выгодным интеграл собственный свести к не-
собственному, который легче вычисляется.
10)	Двойной интеграл
ОО 00
P = j е~~х2~у2 dx dy
существует, ибо существует повторный:
00	00	ОО	00	ОС
Р=Д dx e~x2~y2dy=\ e~x2dx-^ е~~yadj={^ е~
о о	о	6	1 &
Его легко вычислить, если перейти к полярным координатам; первый
квадрант на плоскости ху преобразуется при этом в полосу на плоскости гО,
ограниченную прямыми 0 = 0, г = 0 и 0 = -^-. Таким образом,
ft
2 оо	со
Поэтому
00	,
e~x2dx = ^~.
о
Этот замечательный по простоте прием вычисления принадлежит Пуас-
сону.
11)	Если в том же интеграле Р перейти к эллиптическим коор-
динатам [604, 5)] по формулам
ro'-y-f)., x,+j,,=x,+(l,_e,
D (х, у) _	р.2 —X2
D (X, (л) ”~/(Х8 —с2)(с8 —р2)’
617J
§ 5. НЕСОБСТВЕННЫЕ ДВОЙНЫЕ ИНТЕГРАЛЫ
229
то получим
со с
г_(Х2+(хг_с2)(ха_
..	........ ' ф^Х=-г
/(Xs —са)(с2 —И2)	4
или
СО 19
С е~х X2 rfX
J /X2 —с2
<?~хз rfX
V X2 —с2
е 1x3 |л8 ф __ я	с3
/ с2—р.2	4
Если взять с = 1 и сделать подстановку Х = ]Ли4-1, р=)^г>, то при-
дем к любопытному соотношению:
e~v dv
/и(1 —и)
СО
С e~v dv
J /о(1 +«)
12)	С помощью обобщенных полярных координат
х = ar cos 0, у = br sin 0 (Osgr^l, 0	0	2л)
легко найти- значение двойного интеграла
aS ‘ Z?2 l
dx dy
= ~а6.
Если же перейти к эллиптическим координатам, о которых только что
шла речь (взяв с2 = а2 — Ьг, так что данный эллипс отвечает X = а), то для
того же интеграла получим
J=ab\	..X2 —|л2 ... .
J J ^(л2 —Х2)(а2 —р2)(Х2 —с2) (с2—р2)
Таким образом,
с а
( £ ____________________ X2—— [Л2______________ //X /7п = —
J Y(a2 — X2) (а2 — р2) (X2 — с2) (с2 — р2) И 2 •
Полагая здесь а — 1, с = k<Z 1, к' —	— ks, наконец X — Y1 — Л'8 sin2 ф,
ц = к sin <р(0<р, фг£-^-}, сведем этот интеграл к следующему:
Я ft
С V о — *'*sin* Ф) + (1 — fe3 sin2 <р) — 1
о о — A8 sin2 <р) (I — Л'2 sin2 ф)	2 ’
230
ГЛ. XVI. ДВОЙНЫЕ ИНТЕГРАЛЫ
(617
что может быть представлено в виде
х
2"
с
3 /1 — A2 sina ср
2	2
? Y1 — ft'2 sin2 Ф d'b 4- —------------—- -
? Y1 —ft'2 sin2 ф
It	It	It
~2	’З	У
rf<P	С	йф	я
Yi — k2 sin2 cp Y1 — ft'2 sin2 ф 2 ‘
X Y1 — ft2 sin2 cp dcp —
о	о
Читатель узнает в этом уже встречавшееся нам соотношение Л е-
жандра [см. 511, 12) и 534, 10)].
13)	Приведем вывод известного соотношения между эйлеровыми инте-
гралами 1-го и 2-го рода, принадлежащий Якоби.
Так как (при а > 0 и Ь > 0)
СО
Г(а)=Л e-yya~ldy,
00
T(b) = [e-Xx^ dxt
о
то, очевидно,
г (а) Г (6) =Г $ е-х-ухь~1уа-1 dxdy
О о
Положим здесь
х = и(1—»), y — uv,
так что первому квадранту на плоскости ху отвечает полоса на плоскости uv,
ограниченная прямыми » = 0, « = 0, ®=1. Якобиан преобразования равен и.
Поэтому
1 СО
Г(а)Г (6)=Д e~uua+b~l -^(l— о)*-1 dudv =
О о
оо	1
= С e-uu“+i>^ du-\va~Yi — v)»-1 dv = T(a + b)3(a, b),
о	о
что и требовалось доказать.
14)	В предыдущем изложении нами был выведен ряд формул, область
применимости которых теперь может быть расширена. Это относится, на-
пример, к формуле Дирихле:
dx dy
Г(Р)Г(<7)
Г.(д-Н +1)
* + 1
[597, 12)] и к более общей формуле Лиувилля:
ср (х 4"J) xP~iy9~l dx dy
Г(Р)Г(?) С
Г(р + ?) &’
ср («) иР|+9-1 du

«171
§ 5. НЕСОБСТВЕННЫЕ ДВОЙНЫЕ ИНТЕГРАЛЫ
231
{611, 17)], которые сохраняют силу при любых р и q>Q. При этом доказа-
тельства остаются те же.
Можно пойти и дальше: в формуле Лиувилля мы до сих пор пред-
полагали функцию <р (ju) непрерывной при изменении и от 0 до I, теперь же
можно допустить и обращение ее в бесконечность в одной или нескольких
точках этого промежутка, лишь бы интеграл справа был абсолютно
сходящимся (иначе интеграл слева не будет сходиться вовсе).
Наконец, можно в формуле Лиувилля распространить двойной интег-
рал на бесконечную область, определяемую неравенствами
х^О, у^О, x-f-y^l,
если только интеграл справа взят в промежутке от 1 до + оо (снова в пред-
положении его абсолютной сходимости).
£-я
а
мулы
Все это не требует никаких существенных изменений в доказательстве.
15) Если в формулах Дирихле и Лиувилля заменить р и q на
q	/ $ \а / ч	.
, а затем произвести подстановку х = J , у = j , то эти фор-
получат более общий вид:
» Все постоянные a, b, а, р, р, q предполагаются здесь положительными.
232
ГЛ. XVI. ДВОЙНЫЕ ИНТЕГРАЛЫ
[617
Для примера предлагается установить условия сходимости и вычислить
интегралы (zn>0):
С f	хР~'у9-'
(а)	\ \	-/	„	. dx dy,
x. у &0
•«>	И
x, у S О
x“ + j'₽S=l
(„> CC	. ixi,_
J J	(1—x°—yP)”1
x, y^O
*“+>₽« 1
в (A I)
Ответ, (a) --------------—(при условии ~ + 4"> m
B(£ тА
...	\« p I /	P , q \
(o) --------------— (при условии — -p-тг < tn I;
•Ц«—f—f)
i r (4) r(f)r
(в) -5---—--------------— (при условии m< 1).
? r(f+f+‘-“)
[Ср. задачу 1).]
16)	Выведенная в n’ 597, 15) формула Каталана:
Al
5 $	/(х> У) Ч к (х, j)| dx dy = $ <f (и)	(u),
j):SAl	m
где
'P (и) = U f(x, У) dx dy,
”»« g(x, y)z~u
с введением несобственных интегралов может быть обобщена на случай
4-00	м
М = 4- оо, если только \ понимать и здесь, как lim (.
т
17)	Найти значение интеграла
L — In sin (х—y)dx dy,
(А)
где А есть треугольник, ограниченный прямыми у — 0, х = п,у х=х (рис. 79, а).
617]
§ 5. НЕСОБСТВЕННЫЕ ДВОЙНЫЕ ИНТЕГРАЛЫ
233
Полагая
преобразуем область (Л) в треугольник (А) на плоскости ut, ограниченный
прямыми u — t, u-j-t— 2п, t = 0 (рис. 79, б). Так как якобиан преобразова-
ния равен -g-, то
In sin t dt du
du,
если через (E) обозначить треугольник, ограниченный прямыми u = t, и = л,
<= 0 (см. рисунок). Далее можно написать:
In sin t dt du = In sin t dt — — ~ In 2.
18)	Вычислить (при любых натуральных тип) интеграл
/ = \
Рт(Х)Ра(у)
К1— х3 — у3
dx dy,
где Рп означает n-й многочлен Лежандра.
Решение. Напомним, что многочлен Лежандра с нечетным (четным)
значком содержит лишь нечетные (четные) степени х. Отсюда ясно сразу, что
/=0, если только хоть один из значков т или п будет нечетным.
Пусть же оба они — четные: т = 2р, п = 2м. Рассмотрим интеграл
Ра,(х)^
/1— X3 — у3
1	/1 - ха
С	С	v3P
dxdy=\ Ps, (X) dx	\	< F
J.	•>_ У 1 — x3—у3
-1	-Г1-Х2

По известной формуле
те
а	а	*2
С —fL.-. dy = 2 £ =2а3Р sin^e dO = ка3Р	,
J /аа— у3	i	b	(2/ОН	’
— а	0	0
234
ГЛ. XVI. ДВОЙНЫЕ ИНТЕГРАЛЫ
[617
так что наш интеграл приведется к
1
* ~~~^!!1)!1 (х) •(I ~х2)Р dx’
следовательно, он равен 0 при р <ч [по основному свойству многочленов
Лежандра; 320 (8)]. Отсюда — предложенный интеграл / = 0 при
п = 2ч ф т — 2р. Остается случай, когда л = т = 2р. В этом случае
/ = С £	dx dy == С С
J J V 1 — ха — у2	J J
х3+>2-^1	x*+y*s~l
1
=	5 P8p(x)(l-x»Xdx = (-l)H

dx dy —

— (	И(2И)!!^ J p>Jx!pv<x*dx —<—	4,._4-|
[320 (10)]. Итак, окончательно,
’ 0,	кроме случая n=m = 2p,
i i\2’o» (п—ОН 1	о
[(-о 2тс -д. 2и + ?> если n = m = 2p.
Предоставляем читателю убедиться в законности проделанных операций
19) Вычислить интеграл (Л и у в и л л ь)
/?(Х)=Н е V	у* dxdy (Х>0).
о о
Пользуясь правилом Лейбница, найдем его производную по параметру К:
d/?_
dk
??	j-1 dxdy*
зг х у
Заменим здесь одну лишь переменную х, полагая (при у — const.)
dx dz
, так что — =-----; получим
ху	X Z
* Предоставляем читателю убедиться в существовании интеграла J? и
в дозволительности применения правила Л е й б н и ц а. Последнее обосновы-
вается такими же соображениями, как и в случае простого интеграла.
617J
$ 5. НЕСОБСТВЕННЫЕ ДВОЙНЫЕ ИНТЕГРАЛЫ
235
Интегрируя это простое дифференциальное уравнение, найдем К — Се~*\
Постоянная С определится, если положить к=0:
/}(([)=С = г(1)г(4) = —= А
ш ш six у3
о
Итак, окончательно,
рз
20)	Вычислить интеграл
00 00
О О
cos 2fe К-ТУ
е х у--------. А  dx dy
(где k = const.).
Так как подинтегральная функция по абсолютной величине не превос-
ходит функции
е~*~У
V ху’
заведомо имеющей интеграл по первому кваппанту [см. 7)], то су-
ществование интеграла А обеспечено.	у
Обозначая через (D) ту часть первого квад-
ранта, где х^у (на рис. 80 она заштрихо-
вана), имеем, очевидно,
. О С С cos2fe Уху , ,
Л =2 \ \ ег*~У----—L	-dxdy.
J J	Уху
(D)	г у
Произведем' теперь замену переменных по фор-
мулам	__ Q
и=х+у,	® = 2К XV,
Рис. 80.
точка (и,») описывает аналогичную (D) область (Д) на плоскости uv,
так что и^у. При этом
D (и, ®) _ х—у _ 2 К иа — Ра и D (х, у) _ у
D(x,y)~~	у	D(u,v)	2К«2 —®2 ’
Получим после подстановки
(Д1
COS kv . . о
е “	 ' dudv — 2
У и2 — у2
е adu
cos kv
у и2— V2
dv.
Для вычисления внутреннего интеграла положим
у = и sin в, dv = и cos в di = У и2 — v2 di,
и он сведется к интегралу [440, 12)]
я
т
cos (feu sin в) di — ~ (^“).
236
ГЛ. XVI. ДВОЙНЫЕ ИНТЕГРАЛЫ
[617
Пользуясь известным результатом [524, 3)], найдем окончательно:
00
А = п \ e~uJa (ka) du = — *	.
3 ov V*2+i
0
21)	Вычислить интеграл
В = { t g—oVjC2+J’3 C0g C0Sj„] (fx ду,
0 0
где a, $ и — постоянные и a > 0.
Очевидно,
4-00 4-00
...dxdy,
— 00 —00
Перейдем к полярным координатам, полагая
х = г cos в, у = г sin 0;
одновременно для облегчения выкладок положим также
$ = р cos ср, vj = р sin ср.
После подстановки и легких преобразований получим
2тс оо
В = d9 e~a/'cos[rpcos(0—ср)] • rdr +
2-гс оо
+ db e~ar cos[rp cos(0 ср)] • rdr|.
Полагая 0ч^ср = Х и пользуясь периодичностью, сведем оба повторных инте-
грала к одному и тому же:
те
2тс со	2	оо
В — -j- \ d\ \	е-аг cos (гр cos X)  г dr	= l	d\ 1 e~ar cos (rp	cos X) • r dr,
4 о б	V	S
Легко вычислить (например, интегрируя по частям), что
ОО
ё	а2 — Ь2
e-^cosbr-rdr =	+ &2)3 (а > 0).
О
В таком случае
к
~2
D _ f а2 — р2 cos2 X ________ л а я	а
b — ) (а2 4-р2 cos2 X)2 dA “ Т	Г " "2	Г'
»	(аг+р2)2	(°2 + 52 +’I2)2
617J
S 5. НЕСОБСТВЕННЫЕ ДВОЙНЫЕ ИНТЕГРАЛЫ
237
Можно и в общем виде показать (пользуясь тем же приемом), что если
интеграл
? (У^2 + У3) cos cosjii) <Zx dy
сходится, то он всегда оказывается зависящим только от У l;3-}- ц2, т. е.
имеет вид / СКЕ2 + ц2).
22)	Пусть (D) означает треугольник ОАВ (рис. 81), характеризуемый
неравенствами Osgxsga и у^х, а /(х)— произвольная непрерывная
от 0 до а функция. Приводя двойной интеграл
г г f(y) dx dy
'' /(а— Х)(Х — у)
(О)
к повторному двумя способами, доказать формулу
ах	а
С dx
(15)
f(y)dy
о
о
о
[По сути дела, это частное применение формулы Д и-
рихле, 597, 10), но на этот раз — к несобственным
интегралам; особые линии здесь: х — а и _у = х.]
Воспользуемся формулой (15) для решения одной интересной задачи,
принадлежащей Абелю.
Пусть <р (х) есть данная функция, непрерывная вместе со своей про-
изводной в промежутке [0, а], причем <р(0) = 0. Требуется определить
непрерывную в этом же промежутке функцию f(x) так, чтобы при всех х
выполнялось условие
Т(х)=Г^М
(16)
[Такого типа уравнение, где искомая функция стоит под знаком интег-
рала, называется интегральным. Уравнение Абеля представляет один
из первых примеров интегральных уравнений; для интегральных уравнений
теперь существует широко развитая теория.]
Умножив обе части равенства (16) на	, проинтегрируем его
У Я — х
по х от 0 до любого а (0 < a sg а); ввиду (15) найдем
<р (х) dx
У а — X
Ц f(y)dy.
Если взять и слева и справа производную по а, используя уже известный
нам результат 511, 14), то и придем к выражению искомой функции:
У а — х
71
dx.
238
ГЛ. XVI. ДВОЙНЫЕ ИНТЕГРАЛЫ
[617
Остается проверить, что полученная функция удовлетворяет поставленным
требованиям. Непрерывность ее по а легко устанавливается с помощью указан-
ной в 511, 14) подстановки. Если же эту функцию подставить в уравнение (16),
то, опираясь на формулу (15), найдем
XV	х
5	-.ДДг dt = Д’ (0 dt=? W I? (°)=°ь
71 J у х—у J У у — t	J
что и требовалось доказать.
В заключение остановимся еще на двух-трех примерах, выясняющих
некоторые принципиальные моменты.
23)	Покажем, прежде всего, что для несобственных интегралов (даже от
неотрицательных функций) теорема п’ 594, позволяющая из существования
двойного интеграла заключить о существовании повторного, вообще не
имеет места.
Пусть в квадрате [0, 1; 0, 1] функция f(x, у) определена следующим
образом:
Ьп, если х = -т~1 и 0<у^^
fix, у) =	1
(п=1, 2, 3, ...; т=1, 2,... , 2л-«),
. О в прочих точках.
При у яа. const, может существовать лишь конечное число значений х
для которых /^£0. Значит,
1 1 1
\f[x,y)dx = Q и f dy \f(x, у) dx — 0.
Теперь, если х = const, и не имеет вида	, то /=0 и
1 1
\ f(x> y)dy — Q. Если же х = const = —т<^ 1 , то Д(х> y)dy =
± °
2»	1 j
= J/4y=l. Отсюда ясно, что повторный интеграл	y)dy
о	оо
не существует.
[Для функции f(x, y)-\-f(y, х), очевидно, не существует уже ни один
из повторных, интегралов!]
Что же касается двойного интеграла, то прежде всего замечаем, что
особые точки заполняют отрезок [0, 1| на оси х. При любом е>0
в прямоугольнике [0, 1; е, 1] функция f может быть отлична от 0 лишь на
конечном числе отрезков прямых х = —» для которых
Поэтому
И f{x,y)dxdy = Q't
[0. 1; «, 1]
переходя к пределу при е —► 0, видим, что и
И
10. 1; 0, Ц
dx dy = 0.
617]
§ 5. НЕСОБСТВЕННЫЕ ДВОЙНЫЕ ИНТЕГРАЛЫ
239
24)	Нетрудно установить, что двойные интегралы
(а) J J е~х? sin х dx dy, (б) J J sin (х2 +_у2) dx dy
оба не сходятся (в смысле данного в п° 612 определения).
В случае (а) явно не существует интеграл от абсолютной величины под-
интегральной функции, ибо иначе имел бы конечное значение повторный
интеграл
оо	оа	оо
। •	1 j С j С I sin XI .
| яп х | dx \ е ХУ dy = \ J—-—1 dx,
чего на деле нет [477]. Отсюда, ввиду 613, и вытекает утверждение
В случае (б), если через (7<л) обозначить квадрант круга радиуса 7?
с центром в начале, то, переходя к полярным координатам, будем иметь
2 R
sin (х2у2) dx dy =	<70 sin г* • г dr =	(1—cos/?2),
о
При возрастании 7? до бесконечности это выражение определенного предела
не имеет, что также решает вопрос.
Любопытно отметить, что в каждом из рассмотренных примеров повтор-
ные интегралы оба существуют (и даже равны между собой):
00	00	00	00
1 dy \ е~хУ sin х dx = I sinxdx у e-*'1 rfy =
0	0	0	0
[522, 2’],
CO CO	00	00
( dy C sin (x2+y2) dx— dx ? sin (x2 + y2) dy =	[522, 5”].
oo	bo
Таким образом, для функций переменного знака одно существование
повторного интеграла еще не обеспечивает существования двойного интеграла
(напомним, что в 614 мы дополнительно требовали существования повтор-
ного интеграла для абсолютной величины функции!).
25)	Если бесконечный прямоугольник [0, + оо; 0, -f- оо] исчерпывать не
произвольными бесконечно расширяющимися областями (как этого тре-
бует определение п° 612), а специально прямоугольными обла-
стями вида [О, А; О, В], то в обоих рассмотренных выше случаях окажется,
что для интеграла
Ц ...dxdy
10, Л; О, В]
при А, В —* 4- оо существует определенный конечный предел.
240
ГЛ. XVT. ДВОЙНЫЕ ИНТЕГРАЛЫ
(617
Это сразу видно относительно интеграла
И sin (х2 + №) dx dy =
10, А; 0, В]
А	В	А	В
= \ sin х2 dx • ( cosy2 dy -f- \ cos x2 dx • \ siny2 dy,
который при указанном предельном переходе стремится к пределу-^- [522, 5°],
Рассмотрим теперь интеграл
•	л ____Вх •
sin х , г е sin х .
----dx — \ -------------dx.
X	х
Первый из интегралов справа (при Л — -}'00) стремится к -g-, а второй
(при А, В —-[-оо) имеет пределом 0, ибо по абсолютной величине не пре-
восходит интеграла
р	1 _ р- Ав
С е Bxdx =----5 
J	о
Итак, здесь окончательно в пределе получается -g- .
Подобные пределы, связанные со специализацией предельного
перехода, напоминают «главные значения» несобственных интегралов [484].
Их можно рассматривать и в случае произвольной простирающейся в беско-
нечность области, если вне ее положить функцию равной нулю. Некоторые
математики считали целесообразным именно эти пределы класть в основу
самого определения понятия несобственного двойного интеграла (что суще-
ственно разнится от принятого в нашем изложении определения). При
такой точке зрения оба рассмотренных в 24) интеграла оказались бы схо-
дящимися и притом неабсолютно.
Замечание. Сходное положение вещей имеет место по отношению
к двойным рядам. Так как мы там исходили всегда из бесконечной
прямоугольной матрицы, то представлялось естественным исчерпывать
се постоянно расширяющимися конечными прямоугольными же матри-
цами, что и было нами положено в основу определения суммы двойного ряда [394].
Поэтому-то двойные ряды могли быть как абсолютно, так и неабсолютно
сходящимися. Существует, однако, и другая точка зрения, согласно которой
от бесконечной матрицы конечные куски отделяются кривыми произвольной
формы, лишь бы удаляющимися всеми точками в бесконечность. Эта точка
зрения сближается с той, на которой построено данное выше [612] опреде-
ление несобственного двойного интеграла. Если стоять на ней, то и двойные
ряды окажутся сходящимися лишь абсолютно, подобно несобственным
интегралам.
* Совпадение этого предела с общим значением повторных интегралов,
которое имеет место в обоих случаях, конечно, закономерно [ср. 168].
ГЛАВА СЕМНАДЦАТАЯ
ПЛОЩАДЬ ПОВЕРХНОСТИ.
ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
§ 1. Двусторонние поверхности
618. Сторона поверхности. Установим сначала важное для даль-
нейшего изложения понятие стороны поверхности.
В ряде случаев это понятие интуитивно ясно. Если поверхность
задается явным уравнением вида z=f (х,у), можно говорить о верх-
ней стороне или о нижней стороне поверхности *. Если поверхность
ограничивает некоторое тело, то также легко представить себе ее
две стороны — внутреннюю, обращенную к телу, и внешнюю,
обращенную к окружающему тело пространству.
Исходя из этого интуитивного представления, постараемся теперь
дать точное определение понятия стороны поверхности.
Рассмотрим гладкую поверхность (5), замкнутую или ограни-
ченную кусочно-гладким контуром. Так как на поверхности нет осо-
бых точек, то в каждой точке поверхности имеется определенная ка-
сательная плоскость, положение которой непрерывно изменяется
вместе с точкой касания.
Взяв на поверхности определенную точку 7И0, проведем в ней
нормаль, которой припишем определенное направление — одно из
двух возможных (они отличаются одно от другого знаками направ-
ляющих косинусов). Проведем по поверхности замкнутый контур,
исходящий из Al# и возвращающийся в 2Й0, причем предположим, что
он не пересекает границы поверхности. Заставим точку М обойти
этот контур и в каждом из последовательных ее положений будем
приписывать нормали то из двух направлений, в которое непре-
рывно переходит направление, выбранное нами в начальном поло-
жении Af0. При этом может случиться одно из двух: либо после
обхода контура мы вернемся в точку Мо с тем же направле-
нием нормали, либо же — с направлением, противоположным исход-
ному.
* Мы часто будем пользоваться подобным выражением, подразумевая
при этом, что сама ось z направлена вертикально вверх.
242
ГЛ. XVII. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
[618
Если для какой-либо точки 2Ив и какого-либо проходящего через
нее контура МЛАМО имеет место последнее обстоятельство, то и для
любой другой точки Afj легко построить замкнутый контур, который,
выходя из и возвращаясь в нее же, приведет нас в эту точку
с направлением нормали, противоположным исходному. Таким, напри-
мер, будет контур MiMqAMqMi, если под разуметь какую-
нибудь проходящую по поверхности кривую, соединяющую Afj с 7И0,
но не пересекающую границы поверхности, а под A40Af, — ту же кри-
вую в обратном направлении.
В этом случае поверхность называют односторонней. Классическим
примером такой поверхности является так называемый лист М ёбиу с а
(рис. 82). Модель ее можно получить, если прямоугольный кусок
бумаги ABCD, перекрутив один раз, склеить так, чтобы точка А
совпала с С, а В с D. Если полученное перекрученное кольцо начать
красить в какой-либо цвет, то
В,	можно, не переходя через его
A	D границы, покрасить все кольцо
этим цветом- Мы впредь по-
к*	добные поверхности исключим
И3 РассмотРения-
Предположим теперь, что
какова бы ни была точка
Рис. 82.	и каков бы ни был
замкнутый контур, проходящий
через Мй и не пересекающий границы поверхности, после обхода его мы
неизменно возвращаемся в исходную точку Мо с исходным же направле-
нием нормали. При этих условиях поверхность называется двусторонней.
Пусть же S—двусторонняя поверхность. Возьмем на ней любую
точку Мй и нормали в этой точке припишем определенное направле-
ние. Взяв какую-либо другую точку Mi поверхности, соединим А40 и
Mi произвольным путем (К), лежащим на поверхности и не пере-
секающим ее границы, и заставим точку М перейти из 2И0 в Mi по
этому пути. Если при этом непрерывно изменять направление нормали,
то точка М придет в положение Mi с вполне определенным направ-
лением нормали, не зависящим от выбора пути (К). Действительно,
если бы, приходя в точку Mi из точки Мй по двум различным путям
(КО и (К2)> мы получали в точке Mi различные направления нормали,
то замкнутый путь Мо (Ki) Mi (КС1) Af0 приводил бы нас в точку
Мо с направлением нормали, отличным от исходного, что противоре-
чило бы определению двусторонней поверхности.
Таким образом, на двусторонней поверхности выбор направления
нормали в одной точке однозначно определяет выбор направления
нормали во всех точках поверхности. Совокупность всех точек
поверхности с приписанными нормалями в них по указанному
правилу направлениями и называется определенной стороной
поверхности.
619]
§ 1. ДВУСТОРОННИЕ ПОВЕРХНОСТИ
243
619. Примеры. 1) Простейшим и наиболее важным примером двусто-
ронней поверхности является поверхность, выражаемая явным уравнением
z = z(x, у), в предположении, что функция z непрерывна в некоторой пло-
ской области (D) и допускает в ней непрерывные частные производные
dz
P-dJc И * =
dz
В этом случае направляющие косинусы нормали к поверхности имеют
выражение [234 (11)]
1	— Р	— Я
COS Л. =---- г	, COS U =----;  	.	,
±/1+р2 + ?2	l+/?+-F
1
cos ч = -—— '	.
± / 1+Р2 + <72
Выбрав перед радикалом определенный знак, мы тем самым устанавливаем
во всех точках поверхности определенное направление нормали. Так как на-
правляющие косинусы, в силу, сделанных предположений, будут непрерыв-
ными функциями координат точки, то и установленное направление нормали
будет также непрерывно зависеть от положения точки. Отсюда ясно, что вы-
бор знака neped paduKaAOM в формулах для cos X, cos р, cos э определяет
сторону поверхности^ том именно смысле, какой выше приписан
этому понятию.
Если выберем перед радикалом знак плюс, то во всех точках поверхности
1
COS V = —====•
/ 1+Р8 + -7!
будет положительным, т. е. угол, составленный с осью z Нормалью соответ-
ствующей выбранной стороне, будет острым. Таким образом, сторона поверх-
ности, определяемая указанным выбором знака, оказывается верхней сто-
роной. Напротив, выбор знака минус в выражениях,направляющих косинусов
нормали характеризует нижнюю сторону поверхности (нормали составляют
с осью z тупые углы).
2) Рассмотрим теперь, более обще, произвольную простую незамкн у-
т у ю гладкую поверхность (S), заданную параметрическими уравнениями
х = х(и, v), y—y(u,v), z — z(u,v),	(1)
причем параметры и, о изменяются в некоторой ограниченной области (Д)
на плоскости uv. Требование гладкости означает, что функции (1) непре-
рывны в (Д) вместе со своими частными производными и
что на поверхности нет особых точек. Помимо этого (что осо-
бенно важно подчеркнуть), мы предположили поверхность простой, так
что на ней нет кратных точек, и каждая точка поверхности полу-
чается лишь при одной паре значений параметров и, о.
Если через А, В, С обозначить, как обычно, определители матрицы
/ хи У и zu \
\ х'„ у; z;
то, по предположению, всегда Аг В3 -[- С1 > 0, и направляющие косинусы
нормали к поверхности выразятся известными формулами [234, (17)]:
,	А	В	]
COS Л =----г	• , COS U=-.	.
дг+в’4-с* ±Уаз+вз+с* .
с
COS V =---- -	.
+ Y А» + В* + С3
244	ГЛ. XVII. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ	[620
И в этом случае выбор знака перед радикалом характеризует сто-
рону поверхности, так что поверхность оказывается двусторонней.
Действительно, раз знак выбран, формулы (2) каждой точке поверхности (так
как ей отвечает одна лишь пара значений и, »1) сопоставляют одно опре-
деленное направление нормали, которое при передвижении точки изменяется
непрерывным образом.
При нарушении предположения об отсутствии кратных точек уже нельзя
безоговорочно утверждать, что поверхность двусторонняя. Тогда кратной точке
Л40 поверхности отвечают, по меньшей мере, две различные пары u0, v0 и и,,
значений параметров, и может случиться, что при этих значениях формулы
(2), даже если знак перед радикалом выбран одинаково, определяют про-
тивоположные направления нормали в точке Л40. Если это действи-
тельно так, то поверхность наверное будет односторонней. В самом
деле, соединим точки т„ (u0, v0) и тх (и1( vt) на плоскости uv кривою т^;
тогда на поверхности (S) в соответствии с ней мы получим замкнутую
кривую, исходящую из Л1о и возвращающуюся в Л40; выйдя из Л40 с одним
направлением нормали, мы после обхода этой кривой вернемся в Л40 уже
с противоположным направлением!
3) Если гладкая поверхность (S) оказывается замкнутой и ограничивает
некоторое тело, то наличие у нее двух сторон — внешней и внутрен-
ней — ясно непосредственно. Допустим, что эта поверхность выражается
уравнениями (1). Хотя на этот раз предположение о взаимно однозначном
соответствии между точками поверхности и точками области (Д) не осуще-
ствимо в полной мере, но выбор знака в формулах (2) все же опреде-
ляет сторону поверхности. Суть дела именно в том, что случай,
о котором только что была речь, здесь заведомо невозможен.
620. Ориентация поверхностей и пространства. Пусть (S) будет
незамкнутая гладкая двусторонняя поверхность, ограниченная
простым контуром (£); выберем определенную сторону этой
поверхности. Припишем теперь контуру (I) определенное направление
обхода в качестве положительного по следующему правилу,
обход должен казаться происходящим против часовой стрелки
наблюдателю, движущемуся в этом направлении по контуру так, что
нормаль к поверхности, отвечающая выбранной стороне,
пронизывает его от ног к голове. Слова «против часовой стрелки»
означают, точнее говоря, что наблюдатель должен видеть непосред-
ственно прилегающую к нему часть поверхности слева от себя.
По тому же правилу одновременно устанавливается положительное
направление обхода для каждого простого замкнутого контура, ле-
жащего на поверхности и ограничивающего некоторую ее часть *.
Направление обхода, обратное положительному, назовем отрица-
тельным. В совокупности все это и составляет содержание поня-
тия ориентации поверхности.
Если исходить из другой стороны поверхности, то нормали из-
менят свое направление на обратное, изменится положение наблю-
дателя, в связи с чем по нашему правилу придется переставить
положительное и отрицательное направления обхода контура (£) и
* Только с этой частью и надлежит считаться ири определении поло-
жительного направления на контуре.
620)
§ 1. ДВУСТОРОННИЕ ПОВЕРХНОСТИ
245
других контуров, лежащих на поверхности: поверхность изменит свою
ориентацию. Таким образом, если всегда держаться установленного
правила, выбор стороны поверхности определяет ее ориентацию
и, обратно, выбор положительного направления обхода контура
поверхности однозначно определяет ее сторону?
В случае замкнутой гладкой поверхности (5), ограничивающей
некоторое тело, речь может идти о внешней или о внутренней
по отношению к этому телу стороне поверхности. Установить для
любого простого замкнутого контура положительное направление об-
хода с помощью сформулированного выше правила на этот раз не
удается. Причина этого — двоякая. Прежде всего такой контур мо-
жет просто «не разделять» поверхность (как, например, в случае
любых параллелей или меридианов на торе), и тогда поверхность
примыкает к контуру с обеих сторон: наше правило ничего не дает.
Но если даже контур «разделяет» поверхность на две области, то
он обе их «ограничивает» в равной мере, и в зависимости от того,
какую из них выбрать, наше правило приводит к тому или другому
из двух направлений на контуре, как к положительному. Ограничи-
ваясь контурами, «разделяющими» поверхность, мы станем вместе
с контуром указывать и область, тогда положительное направление
устанавливается уже вполне однозначно *. Этим и определяется
ориентация поверхности — та или другая, в зависимости от
выбранной стороны.
Если условиться принять для каждой такой поверхности за по-
ложительную ориентацию ту, которая отвечает внешней сто-
роне поверхности, а за отрицательную — противоположную ей, то
этим создается некая определенная ориентация самого про-
странства. Это вполне аналогично тому, как выбор положитель-
ного направления (можно было бы сказать — положительной
ориентации) на любом лежащем на плоскости простом замкнутом
контуре характеризовал ориентацию плоскости [548].
Та ориентация пространства, которая сейчас была определена и
 в основу которой в конечном счете было положено вращение против
часовой стрелки, называется правой. Если вместо этого ис-
ходить из вращения по часовой стрелке, то получится левая
ориентация пространства. Для избежания путаницы мы
впредь в тех вопросах, где ориентация пространства играет роль,
всегда будем предполагать правую ориентацию пространства.
Нужно сказать, что и самое расположение координатных осей
в пространстве ставится в связь с установленной ориентацией
* Если рассматривать на плоскости незамкнутый или замкнутый контур,
определенным образом направленный, то в первом случае о любых двух
точках на контуре можно сказать, какая из них предшествует и какая сле-
дует, а во втором случае это можно сделать, лишь если вместе с точками
указать и ограничиваемую ими дугу кривой. В этом можно усмотреть ана-
логию со сказанным в тексте.
246
ГЛ. XVII. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
|621
пространства. При правой ориентации оси располагаются так, что вра-
щение от оси х к оси у кажется происходящим против часовой
стрелки, если на них смотреть из положительной части оси z (это
сохраняет силу и при круговых перестановках букв xyz) (рис. 83, а);
при левой ориентации упомянутое вращение происходит по часовой
стрелке (рис. 83, б). В пер-
вом случае координатная си-
стема Oxyz называется правой,
а во втором — левой. В согла-
сии с заключенным выше усло-
вием мы в указанных случаях
впредь будем пользоваться
правой координатной системой.
Рис. 83.
идеи
на ней
о
621. Выбор знака в форму-
лах для направляющих коси-
нусов нормали. Дадим сейчас
важное для дальнейшего прило-
связи между выбором стороны
той или другой ориентации.
жение изложенной выше
поверхности и созданием
Рассмотрим вновь простую незамкнутую гладкую поверхность S
и выберем определенную ее сторону (а с нею — и ориен-
тацию!). Пусть (Л) будет контур области (А) на плоскости uv,
а (I) — соответствующий ему контур нашей поверхности. Допустим,
что положительному обходу контура (Л) отвечает по-
ложительный же обход контура (Z.)*. Тогда и для любых
соответствующих друг другу контуров (X) в области (Д) и (/) на по-
верхности (S) имеет место то же самое: положительный обход (X)
влечет за собой положительный обход (/)**.
При этих условиях для характеристики выбранной сто-
роны поверхности в формулах (2) для направляющих косинусов
нормали перед радикалом нужно взять знак плюс.
Для доказательства этого достаточно установить, что хоть в од-
ной точке направление, определяемое этими формулами со знаком
плюс, совпадает с нужным направлением нормали. Возьмем на поверх-
ности какую-нибудь
тй(п0, ®о) в области
скажем, определитель
внутреннюю точку
(Д). Пусть в этой
Л4Й; ей отвечает точка
точке отличен от нуля,
с== х'а уй
Xv у-о
*	Этого всегда легко добиться, заменив в случае надобности параметр
и на — и.
*	* Так как о направлении обхода контура можно судить по направ-
лению, в котором описывается любая его часть, то высказанное утверждение
очевидно для контура (X), имеющего общую часть с (Л), а затем легко
переносится и на общий случай.
622]
§ 1. ДВУСТОРОННИЕ ПОВЕРХНОСТИ
247
Тогда найдется столь малая окрестность точки т9 на плоскости uv,
ограниченная контуром (X), что соответствующая ей окрестность точки
на поверхности (S), ограниченная контуром (Г), проектируется
на плоскость ху взаимно однозначно. Обозначим контур этой про-
екции на плоскость ху через (k) (рис. 84).
Если в рассматриваемой точке и в*ее окрестности определитель
С^>0, то положительному обходу контура (X) отвечает положитель-
ный же обход (т. е. при выбранном расположении осей обход про-
тив часовой стрелки) контура (k) [см. 606, 1)]. Как видно из
чертежа, для того чтобы соответствующий этому обход контура (/)
на поверхности тоже казался происходящим против часовой
так что нормаль в точ-
стрелки, на него нужно смотреть сверху,
ке Ж» в этом случае должна
быть направлена вверх,
т. е. должна составлять с
осью z острый угол. Это
именно и имеет место по
формулам- (2), если в них
взять знак плюс, ибо при
С^> 0 тогда и cos v 0. На-
оборот, при С<^0 нормаль
должна составлять с осью z
тупой угол, что также
осуществляется на деле при
указанном выборе знака, ибо
при С 0 и cos v < 0.
Если гладкая поверхность (5) оказывается замкнутой и ограни-
чивает некоторое тело [ср. 619, 3)[, то для нее имеет место анало-
гичное обстоятельство. Допустим, что мы остановились на
определенной стороне поверхности и что положи-
тельному обходу одного какого-нибудь контура (Хв)
в области (Д) отвечает положительный обход опреде-
ляемого им контура (4) на поверхности (5), если связать
(/#) с той областью на (S), которая отвечает ограниченной контуром (Хо)
области на плоскости uv. В таком случае предложение, доказанное
выше для случая незамкнутой поверхности, будет справедливо и теперь.
622. Случай кусочно-гладкой поверхности. Развитые в п° 620
идеи дают также удобное средство для распространения понятия сторо-
ны поверхности на случай кусочно-гладкой поверхности. Соображения, из-
ложенные в. п° 618, в этом случае непосредственно неприложимы, так
как вдоль «ребер», соединяющих гладкие куски поверхности, опреде-
ленной касательной плоскости не существует, и при переходе через них
о непрерывном изменении направления нормали говорить не приходится.
Пусть дана кусочно-гладкая поверхность (S), состоящая из глад-
ких кусков (Si), (&), ..., примыкающих один к.другому по ребру —
248
ГЛ. XVII. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
[623
общей части их контуров. Предположим прежде всего, что каждый
из этих кусков в отдельности является двусторонней поверх-
ностью. Но этого, разумеется, недостаточно для того, чтобы всю
поверхность (S) можно было рассматривать, как двустороннюю; ведь и
поверхность Мёбиуса легко составляется
из двух гладких двусторонних кусков.
На контуре (Kt) каждого куска (5{)
(Z=l, 2, ...) выберем в качестве поло-
жительного одно из двух направлений;
этим, как мы видели, фиксируется сторо-
на поверхности (S,). Если этот выбор
можно произвести так, чтобы всегда об-
щая часть двух примыкающих конту-
ров * описывалась в обоих случаях в
противоположных направлениях
рис 85	(рис. 85), то лишь тогда поверхность
(S) является двусторонней. Сторона по-
верхности (S) определится, как совокупность сторон ее частей, вы-
бранных указанным образом.
Если хоть в одном случае направление обхода
на противоположное, то для соблюдения нашего
то же сделать и со всеми контурами. Тогда и
выбранные стороны всех кусков (S/) заменятся
противоположными им; их совокупность составит
вторую сторону поверхности.
Для того чтобы освоиться с установленными
соглашениями, предлагается читателю: 1) осущест-
вить их на примере поверхности куба (рис. 86),
подобрав надлежащие направления обхода конту-
ров всех шести составляющих плоских кусков,
2) дать себе отчет в том, какие затруднения встре-
тились бы, если бы попытаться то же сделать для
контура заменить
условия придется
поверхности Мё-
биуса, разложенной на два или более двусторонних куска, и, нако-
нец, 3) показать, что данное выше определение стороны не зависит
от того, на какие гладкие куски разложена поверхность.
§ 2. Площадь кривой поверхности
623. Пример Шварца. Понятие площади кривой поверхности
имеет известную аналогию с понятием длины кривой линии. Длину
(незамкнутой) дуги мы определяли как предел периметра вписанной
в дугу ломаной — при условии, что длины всех ее сторон стремятся
к нулю. В случае же кривой поверхности (тоже, скажем, незамкнутой)
естественно было бы рассматривать вписанную в нее многогранную
* Эта часть может состоять и из отдельных кусков.
623)
§ 2. ПЛОЩАДЬ КРИВОЙ ПОВЕРХНОСТИ
249
поверхность и определять площадь кривой поверхности,
как предел площади этой многогранной поверх-
ности — при условии, что диаметры всех граней стремятся к нулю.
В конце прошлого столетия, однако, была обнаружена не-
пригодность этого определения. Именно, Шварц (Н. A. Schwarz)
показал, что упомянутый предел не существует даже для простого
случая поверхности прямого кругового цилиндра! Мы приведем этот
поучительный пример.
Пусть дан такой цилиндр радиуса R и высоты /7. Впишем в него
многогранную поверхность следующим образом. Разделив высоту ци-
линдра на т равных частей,
проведем через точки деления
плоскости, перпендикулярные
к оси цилиндра, так что на его
поверхности получится т -|- 1
окружностей (включая сюда и
окружности обоих оснований
цилиндра). Каждую из этих
окружностей разделим на и
равных частей так, чтобы
точки деления вышележащей окружности находи-
лись над серединами дуг нижележащей окружности.
Возьмем, далее, треугольники, образованные хордами всех этих
дуг и отрезками, соединяющими концы хорд с теми точками деления
выше- и нижележащих окружностей, которые расположены как раз
над или под серединами соответствующих дуг (рис. 87). В своей
совокупности эти 2тп равных треугольников и образуют нужную
нам многогранную поверхность (£т,л); модель ее представлена на
рис. 88.
 Подсчитаем теперь площадь а каждого из треугольников. За ос-
нование примем хорду, длина которой равна
2R sin
Л
250
ГЛ. XV1T. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
f623
Для нахождения высоты АВ треугольника (см. рис. 87) заметим, что
ДД = /ДС24-5С2, где
АС = ОС — ОА = r(i — cos -V ВС= — .
\	п I ’	т
Таким образом, площадь одного треугольника равна
a = R sin £	(1 - cos £)’ +	,
а площадь всей многогранной поверхности будет
£т n=2mna = 2Rn sin j/”Rimi ^1 — cos H*.
Когда тип неограниченно возрастают, то диаметры всех тре-
угольников стремятся к нулю, но площадь 2m, л предела не имеет.
В самом деле, допустим, что тип возрастают так, что отношение
стремится к определенному пределу q:
.. т
hm = q.
ns ’
Имеем
lim п sin - = тс,
п
а с другой стороны, в силу сделанного допущения,
lim т (1 — cos —= lim m2 sin1 Д = lim ~ q.
\	nj	2п 2 п’ 2 ’
Следовательно,
lim2m.„=2TCR y^-q^kP,
и мы видим, что предел этот существенно зависит от величины q,
т. е. от способа одновременного возрастания тип. При q = Q, и
только в этом случае, названный предел равен 2r.RH (величине пло-
щади, выведенной в школьном курсе геометрии), но вместе с q он
может равняться даже бесконечности. Таким образом, при независи-
мом друг от друга возрастании чисел т и п до бесконечности для
площади 2m, п определенного предела, действительно, не существует,
и поверхность цилиндра, если стоять на точке зрения упомянутого
определения, оказывается лишенной площади.
Важно дать себе отчет в том, чем отличается положение вещей
в случае ломаной, вписанной в кривую, и в случае многогранной
поверхности, вписанной в кривую поверхность. Будем для простоты
считать кривую и кривую поверхность, о которых идет речь, глад-
кими. Тогда лишь только хорды, составляющие ломаную, достаточно
малы, направление каждой из них сколь угодно мало разнится от
524|	§ 2. ПЛОЩАДЬ КРИВОЙ ПОВЕРХНОСТИ	251
направления касательной в любой точке соответствующей дуги. По-
этому такая бесконечно малая хорда и может со все возрастающей
точностью служить заменой соответствующего элемента дуги. Напро-
тив, сколь угодно малая многоугольная площадка, вершины которой
лежат на кривой поверхности, может оказаться вовсе не близкой по
своему расположению в пространстве к касательной плоскости к по-
верхности; в таком случае заменять элемент поверхности она, понятно,
не может. Это обстоятельство прекрасно иллюстрируется только что
рассмотренным примером: касательные плоскости к цилиндрической
поверхности все вертикальны, а треугольные грани вписанной
поверхности при большом q становятся почти горизонтальными,
образуя мелкие складки.
624.	Определение площади кривой поверхности. Все сказанное
приводит к мысли наперед потребовать от вписанной в данную
кривую поверхность многогранной поверхности не только того, чтобы
диаметры ее граней стремились к нулю, но и того, чтобы р а с п о л о-
жение этих граней в пространстве безгранично при-
ближалось к расположению касательных плоскостей
к поверхности.
Однако полное осуществление этой мысли далеко не просто, и
мы вынуждены от него отказаться [ср. п° 627]. Мы дадим опреде-
ление понятия площадь кривой поверхности, основанное на другой
идее, впрочем, тоже представляющейся вполне естественной.
Мы будем рассматривать. незамкнутую гладкую поверхность
(5), ограниченную кусочно-гладким контуром (£). Представим, себе
эту поверхность разложенной с помощью сети кусочно-гладких кри-
вых на части
(Si), №),.... (5„)
и в каждой части (5,) произвольно выберем по точке (/ = 1,2,..., и).
Спроектировав ортогонально элемент (Si) на касательную плоскость
к поверхности в точке 2Иг, мы получим в проекции плоскую фигуру
(Tt) с площадью 7\.
Назовем площадью поверхности (S) предел S суммы этих
площадей 7} (1=1, 2, ..., и) при условии, что диаметры всех
элементов (5,) стремятся к нулю.
Если через X обозначить наибольший из упомянутых диамет-
ров, то можно написать
5= Нт У Tt.
Х-»0 i
Читатель легко восстановит точную характеристику этого предель-
ного процесса как на «языке е-8», так и на «языке последователь-
ностей».
Поверхность, имеющая площадь, называется квадрируемой.
252	ГЛ. XVII. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ	(625
625.	Замечание. Для того чтобы сформулированное определение
получило точный смысл, мы установим следующее вспомогательное
утверждение:
•Каждая часть (S') поверхности (S) с достаточно малым диа-
метром проектируется на касательную плоскость в любой
точке М этой части в займ но однозначно.
Таким образом, если диаметры всех элементов (St) поверхности,
о которых была речь в предыдущем п°, достаточно малы, то их про-
екции (7)) на соответствующие касательные плоскости ’представляют
собою вполне определенные плоские фигуры, ограниченные кусочно-
гладкими кривыми и заведомо квадрируемые: сумма У Т{ имеет смысл.
Перейдем к доказательству. Пусть поверхность (S) задана
параметрическими уравнениями
х = х(и, v),y=y(u, v), z — z(u, v),	(1)
где (и, v) изменяется в области (Д), ограниченной кусочно-гладким
контуром (Л), на плоскости uv. При этом пусть между точками (5)
и (Д) установлено взаимно однозначное соответствие, и точкам кон-
тура (Л) отвечают точки контура (L) поверхности.
Для устранения некоторых трудностей, связанных с точками кон-
тура, удобно заранее распространить функции (1) с сохранением
их дифференциальных свойств [261] на некоторую более широкую
область (А), с тем, чтобы получить гладкую же поверхность (S), слу-
жащую как бы продолжением поверхности (5).
Каждую точку Af0 поверхности (S) можно окружить таким кус-
ком (s) поверхности (S) [или (S), если речь о точке контура], чтобы
этот кусок выражался явным уравнением одного из трех типов
[228] и притом проектировался на соответствующую координатную
плоскость в некоторый круг. Можно предположить, сверх того,
что нормали в двухточках (е) никогда не оказываются
взаимно перпендикулярными (этого легко добиться умень-
шением диаметра области). Тогда мы утверждаем, что кусок (s) по-
верхности проектируется на касательную плоскость в любой
его точке М взаимно однозначно.
Для доказательства допустим противное. В таком случае найдутся
на ($) три точки Afi, А13 такие, что хорда AfiAf2 будет парал-
лельна нормали к поверхности в точке 7Й3 (рис. 89). Пусть при
этом сама поверхность ($) выражается, скажем, явным уравнением вида
z=f(x, у),
где точка (х, у) на плоскости ху описывает круг (k). Проведем
через хорду AfiAf2 плоскость, параллельную оси z\ она пересечет
нашу поверхность ($) по некоторой дуге AfiAf2*. Как мы знаем [112,114],
* Здесь играет роль то обстоятельство, что отрезок в который
проектируется хорда AfjAfg на плоскость ху, целиком принадлежит кругу (й).
626)
§ 2. ПЛОЩАДЬ КРИВОЙ ПОВЕРХНОСТИ
253
на этой дуге найдется точка в которой касательная парал-
лельна хорде. Но тогда нормаль к поверхности в точке Ж*, наверное,
будет перпендикулярна к этой хорде, а значит, и к нормали в точке Ж3_,
что противоречит допущению, и т. д.
Для того чтобы, опираясь на это,
доказать теперь высказанное вначале
утверждение, мы поступим так. Для
каждой точки Жо поверхности (S)
заменим упомянутую выше ее «окре-
стность» (s) более узкой «окрестно-
стью» ($') так, чтобы контуры
их не имели общих точек.
Точке Жо и куску поверхности (s')
на плоскости uv отвечают точка тп
и ее окрестность (§'); ничто не ме-
шает не причислять к ($') и (§') их
контуров, т. е. считать их откры-
тыми. Применив к системе {(§')}
открытых областей, покрывающих
всю область (Д), лемму Б о р е л я
[175], мы выделим конечное по-
Рис. 89.
крытие, а, возвращаясь к поверхности (S), отсюда уже легко по-
лучить конечное число кусков
О')> (^)...............(s'm)>
в совокупности докрывающих всю поверхность (5). Наряду с ними рас-
смотрим и соответственные более широкие области, упомянутые вначале:
(si), («в), .... (sm).
Возьмем для каждого I точную
куска (si) от точек части (5) —
нижнюю границу расстояний точек
(«,) поверхности и обозначим через т;
наименьшее из этих чисел. Пусть диа-
метр части (S') нашей поверхности
меньше числа т). Если какая-либо ее
точка попадает в некоторое опреде-
ленное (sj), то вся часть (S') цели-
ком содержится в соответственном
(s;) и, следовательно, вместе с (.$/)
обладает требуемым свойством.
626.	Существование площади
поверхности и ее вычисление. По-
кажем, что при сделанных выше пред-
положениях поверхность (1) квадрируема, и установим удобную
формулу для вычисления ее площади.
Пусть (S') — какая-либо часть (S), обладающая тем свойством,
которое сформулировано в начале предыдущего п°, а Ж' (х', у’, z') —
254
ГЛ. XVH. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
[626
любая ее точка. Перенеся начало координат в эту точку, перейдем
к новой системе координат именно, за плоскость Ь] возьмем ка-
сательную плоскость к поверхности в точке ЛГ, а за ось С — соот-
ветственную нормаль (рис. 90). Формулы преобразования координат
имеют вид:
$ = (х — х’) cos ах —|— (у —у') cos pt -|- (z — z') cos -j-j,
т] = (x — x’) cos a2 -|- (y —y’) cos -|- (z — z’) cos -[2,
. C = (x — x') cos X' (y —y') cos p.' (z — z') cos V,
где ab pi, ..., v' означают углы между новыми и старыми коорди-
натными осями, в соответствии с таблицей
	X	У	z
£	ai	₽i	7i
	аг		7»
C	X'	и'	У
Так как (S') проектируется на плоскость в некоторую область
(Г) взаимно однозначно, а, с другой стороны, точки (У) связаны
взаимно однозначным соответствием с точками некоторой части (Д')
области (Д), то и между точками (Т) и (Д') имеет место такое же со-
ответствие. Оно осуществляется первыми двумя из формул преобразо-
вания, если под х,у, z разуметь функции (1). Пользуясь выражением
площади в криволинейных координатах [605], имеем
Но якобиан
(Д')
(2)
Д(£, ч)
D (u, v)
х'и COS 04 -j-yu COS Pl -|-z'u. COS fi X^ COS eq COS Pl -|-z'v COS Yi
Xu COS 0Ц -\~Уи COS P, z'u COS x’t, COS (Xj 4~y '-o cos pi 4" cos Ъ
есть определитель, отвечающий произведению матриц
1 Хи Уи %и\
^Х® у<и
cos cos Pi cos Yi'
cos aa cos p2 cos
6261
§ 2. ПЛОЩАДЬ КРИВОЙ ПОВЕРХНОСТИ
255
да по известной теореме алгебры равен сумме произведений соответ-
ствующих определителей второго порядка
Ут
cos Pi cos 7i
cos ps cos 7a
Xu у u
Хт Ут
cos 7i cos оц
cos 7a cos Oj
cos at
cos ota
cos pi
cos Pa
= A cos X' В cos jx' -J- C cos /.
Zu %u
Zts Xt
ДОы воспользовались
ментов определителя
здесь тем, что алгебраические дополнения эле-
COS «1 COS Pl
cos a2 cos Pa
cos X' cos jx'
cos 7i
cos 7a
cos v'
= 1
в точности равны самим элементам. Это следует, например, из того,
что каждый из координатных ортов
(COS Я), COS pl, COS 71),	(cos«2, COS Pa, COS 7a), (COsX', COS [x', COS’/)
Представляет собой векторное произведение двух других [ср. 664 (2)].
С другой стороны, если через А', В, С обозначить значения
определителей А, В, С в точке М, то
v	Д'	,	В’
А’а+В,г + С,г	±/Д'а +В'2 + С” ’
,	С'
cos V =---7======
± /Д'а+ В’а + С,а
(знак берется во всех случаях один и тот же). Поэтому
I D (£, т|) I _ \АА' + ВВ'+СС\
I В (U, V) I — у Д'» _|_ £'2 _|_ с-г *
Справа мы имеем непрерывную функцию четырех независимых
переменных и, v, ttr, v' в области (Д)Х(Д)*- При и' = и, v’ = v
она обращается в
Кд’+в’ + с4
И отличается от этого выражения на величину а = а(«, v, и’, v'), ко-
торая ввиду равномерной непрерывности упомянутой функции,
лишь только расстояние точек (к, v) и («', v’) достаточно мало, ста-
новится произвольно малой независимо от положения точки (и', v').
Тогда из (2) получается
Г = $$	+	dv 4- е'Д',
(Д')
* Так мы обозначаем четырехмерную область точек («, v, и’, v'), для
Которых (и, v) и (и’, V) по отдельности принадлежат двумерной области (Л).
256
ГЛ. XVII. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
(624
где е' бесконечно мало одновременно с диаметром Д или, если угодно
одновременно с диаметром <$'. Применив этот результат к каждой иг
частей (Si) (1=1, 2,	п), на которые мы разлагаем поверхносп
(5), мы придем к ряду равенств подобного же типа
Tt = 55 /А2-}-В2 + С2 du dv	еД;
здесь (Д() есть соответствующая (Si) часть области (Д). Суммируем
2^ = 55	+ + dv + е,
i	(А)
где величина
I
очевидно, будет бесконечно малой одновременно с X. Таким образом,
для J] Т, при X -> 0 действительно существует предел
t	___________
S=55K^2 + B24-C2 dudv,	(3J
(А)
который по определению и есть площадь поверхности.
Если матрицу
«возвести в квадрат» и составить определитель
Хи ~Ь_У«2 “4~ zu XUXV “ЬД'и.Ро “Н ZUZV
ХиХъ УиУт> “j- ZUZV Х-о	Zvs
то по известной теореме алгебры он окажется равным именно А2 -ф-
Обычно полагают
х'и + У и + z'u = Е, x'ux'v-\-y'uy'v-\-z'uz'v — F,
x'v + J? + z'£ = О
— это так называемые гауссовы коэффициенты поверхности, играю-
щие важную роль в дифференциальной геометрии. В этих обозначениях
A24-S2 + C2 = Z:G — Е\
так что формула (3) может быть написана и так:
•S = $ 5 KfG —F2 du dv.	(3*)
9 2. ПЛОЩАДЬ КРИВОЙ ПОВЕРХНОСТИ
257
Выражение
1/>-|-5а + СМп dv = Keg—F3 du dv	(4)
называют элементом площади в криволинейных координатах.
Мы ограничивались до сих пор случаем незамкнутой глад-
кой поверхности. Если поверхность не подходит под этот случай,
но разлагается на конечное число незамкнутых гладких кусков, то
ее площадью назовем сумму площадей отдельных кусков. При этом
легко показать^что так определенная площадь на деле не зависит
от того, как данная поверхность разложена на куски нужного типа.
Если вся данная поверхность характеризуется параметрическими урав-
нениями, то площадь ее в указанном общем случае по-прежнему вы-
ражается формулой (3) или (3*).
Остановимся в заключение на том простейшем частном случае,
когда поверхность (5) задается явным уравнением
z=f(x, у),
те (х, у) изменяется в области (О) на плоскости ху. Переменные
х и у играют роль параметров и и v. Полагая, как обычно,
по матрице
1	0 р\
О 1 q]
составляем определители А—— р, В — — q, С=1, так что в рас-
сматриваемом случае
5 =	+	(5)
(О)
Вспоминая, что для острого угла v нормали с осью z будет
1
COS V = ,--- ------: ,
/i+ps + ?2
можно написать формулу для площади и так:
(О)
Наконец, если не требовать специально, чтобы угол v был острым, то
MSrSSj- <5б>
ф)
[Ср. формулу (7) п° 544 для длины дуги кривой, заданной яв-
ным уравнением _у=/(х).]
9 Г. М. Фихтенгольц, т. Ш
258
ГЛ. XVII. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
[627
627. Подход через вписанные многогранные поверхности. Хотя мы
и отказались от мысли положить в основу самого определения понятия
площади кривой поверхности вписанные в нее многогранные поверхности, но
сейчас мы вернемся к этому и покажем, по крайней мере, как можно строить
вписанные многогранные поверхности, площади которых заведомо стремятся
к площади данной кривой поверхности.
Мы займемся, в основном, случаем, когда область (Д) представляет собой
прямоугольник со сторонами, параллельными координатным осям.
Выберем определенную сторону поверхности (S) и тем самым устано-
вим положительное направление обхода ее контура. Можно считать, что это
направление соответствует положительному обхо-
ду контура прямоугольника (Д). Мы знаем [621],
что при этих условиях направляющие косинусы
нормали к поверхности задаются формулами
Рис. 91.
V	л2 + в- -|- с2 ’
в
cos |Л = - -	....—,
/д2 + в24-с2’
с
cos м =  
/д24-в2-1-с2
с положительным значением радикала.
Разложим теперь прямоугольник (Д) с помощью
параллелей его сторонам на частичные прямоуголь-
ники, а затем каждый из них диагональю разложим
еще на два прямоугольных треугольника (рис. 91, в).
Таким образом мы осуществим триангуляцию
области (Д). Пусть одним из элементарных тре-
угольников будет Л с вершинами в точках
т0 (щ, ®0), nij («0 + A, v0),	(«0, v0 + А),
где А и А — числа одного знака. На поверхности
(S) им отвечают точки
Мо (х0, у0, г0), Mi (Xi, yit Zi), М3 (х2, у2, z3),
определяющие в пространстве некоторый ДЛ4ОМ1Л!2 (рис. 91, б). Из всех
таких треугольников составится многогранная поверхность (S), вписанная в (S);
ее мы и будем рассматривать. Если обход контура каждого такого треуголь-
ника производить именно в направлении M0MiM3Mg, что отвечает положитель-
ному обходу контура треугольника Л тдггцт^ то этим определится сторона
многогранной поверхности (£), в согласии с условиями, установленными в п° 622.
Если Л M0MtM3 спроектировать на плоскость ху, то получится &NgNiN3
с вершинами в точках
4 (*<,, уо), Ni (хи yi), N3 (xt, у3).
Площадь этого последнего треугольника по величине и по знаку (с учетом
его ориентации!) выразится, как известно из аналитической геометрии, опре-
делителем	. .	,
0 __ 1 *! Х0 У1 Хо
ху	2 |Ха — Хд у3 — Уо Г
По формуле конечных приращений
Xi—Xg=X(Ug + h, Vg) — X(Ug, Vg) = (Ug -|- 0Л, Vg) • А =
= 14 («0, »о) + е11 • h,
628]
§ 2. ПЛОЩАДЬ КРИВОЙ ПОВЕРХНОСТИ
259
где величина произвольно мала вместе с Л, независимо от поло-
жения точки (и0, ®о)*. Точно так же
У1	— y<> = (y'u + si) -h,
Х2— Х0 = (х; + е8)-Й, у2—b = (y; + s4)-*>
где все производные вычислены при u = u0, v = v0, а буквой е со значками
здесь (и впредь) обозначаются величины, произвольно малые вместе с й и А,
независимо от положения точки (иэ, о0). Теперь величина
может быть переписана в виде
’*	1 хи + г1 Л/ + ег
ажу ---“9"
2	x» + e« Ут> + е4
= 1йА (С+О = (С + ч)Л
(6)
где 8 есть площадь Л	Аналогично получим и для проекций на дру-
гие координатные плоскости:
Ъуг = И + £в) • 8> агх = (Я + *?) •	(6а)
Площадь а самого	вычислится теперь по формуле
а = 1/’а2	аа
и — у иху -j- чуг т »zxt
и для нее легко получить выражение
а = {У А^ + Ва + С^ + е8}  8.	(7)
Нетрудно сообразить, что отношения
ауг	агх аху
а ’	а ’ а
выразят направляющие косинусы нормали к плоскости треугольника
в соответствии с его ориентацией. Ввиду (6), (ба) и (7), они
при й и А —>0 стремятся к направляющим косинусам (5) нормали к поверх-
ности, и притом равномерно для всех граней. Очевидно также,
что при указанном предельном переходе и диаметры всех граней по-
верхности (Е) равномерно стремятся к нулю, что и требо-
валось доказать.
Наконец, суммируя равенства вида (7), легко усмотреть, что площадь
миогогранной поверхности (Е)
E	= S/As + Ba + ^.8 + Ses-8
при й и А —0 стремится именно к площади (3) кривой поверхности.
Эти построения естественно распространяются на случай, когда область
(Д) составлена из прямоугольников. Триангуляция же произвольной области
потребовала бы довольно кропотливых (хотя и вполне элементарных) сообра-
жений; на этом мы останавливаться не будем.
628. Особые случаи определения площади. Пусть снова задана глад-
кая поверхность без кратных точек. Она имеет площадь (SV выражаемую
формулой (3) или (3*). Представим себе, что на поверхности (S) выделена не-
которая ее часть (s), ограниченная кусочно-гладкой кривой (/); ей в области
* Мы испольвуем здесь равномерную непрерывность производной х’и.
Аналогичные соображения приложимы и в дальнейшем.
260
ГЛ. XVII. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
|629
(Л) отвечает часть ее (6), ограниченная также кусочно-гладкой кривой (X).
Площадь части (S') поверхности, полученной выделением фигуры (з), и пло-
щадь самой фигуры (з), очевидно, будут равны, соответственно,
S' = U У EG—F2du dv, s = $ $ У EG—F2du dv.
(Д)-(5)	(«)
Если фигура (з) на поверхности будет теперь стягиваться в точку
или в линию, то это же будет происходить и с плоской фигурой (8), и
площадь ее 8 будет стремиться к нулю. С нею будет стремиться к нулю и з,
так что
limS’ = S.	(8)
Представим себе теперь, что та же поверхность задана иным представ-
лением:
х = х*(и*, v*), у =у* (и*, v*), z = z*(u*,v*),
при котором в отдельной точке или вдоль отдельной линии появляется «осо-
бенность» (в частности, обращаются в бесконечность производные фигурирую-
щих в этом представлении функций). Выделив эту точку или линию с помощью
ее окрестности (з), площадь (S') остающейся части выразим, как обычно:
S’= Ц У E*G* — F*2 du* dv*,
если звездочкой отмечать все величины, относящиеся ко второму представле-
нию. Но мы уже знаем [см. (8)], что — при стягивании (з) в упомянутую точку
или линию — S' должна стремиться к S; следовательно, для получения S мы
можем перейти к пределу в предшествующей формуле, стягивая в точку или
в линию область 8*. Но тогда снова получится формула обычного вида
S = $$ У E*G* — F*2 du* dv*,
(Д*)
лишь интеграл может оказаться несобственным.
Даже в том случае, когда поверхность (S), вообще гладкая, имеет в от-
дельной точке или вдоль отдельной линии неустранимую, т. ё. не зави-
сящую от способа ее представления, особенность, мы все же будем пользо-
ваться интегралом (3*), если только он существует, хотя бы как несобствен-
ный, для выражения ее площади. Ясно, что при этом мы площадь S на деле
определяем, как предел площади S', т. е. равенство (8), которое мы выше
доказывали, здесь служит просто расширением нашего первоначального
определения.
629. Примеры. 1) Найти площадь участка поверхности, вырезаемого:
а) цилиндром x3-f-Js = ^s (х, _у>0) из гиперболического параболоида
г = ху;
Vs	X* V®
(б)	цилиндром ^2 + ^2 ==с2 из эллиптического параболоида г ==--[-	;
(в)	цилиндром (х2 +_у3)3 = 2а2ху из гиперболического параболоида
ху = az;
(г)	цилиндром х3+_у3 = р3 из сферы х3 4-у3 4- z2 — R2 (р < Л).
(а) Решение. Имеем р=у, q = x, так что по формуле (5)
S =	$ $ У1 -1-х3+j3 dx dy.
X. V>0
Х3-Н'3’5Я3
26'
629J	§ 2. ПЛОЩАДЬ КРИВОЙ ПОВЕРХНОСТИ
Переходя к полярным координатам, найдем
2 R	з_
S = d6 j r/F+F dr = ~ [(14-7?2)2 — 1].
(б)	Указание. Воспользоваться обобщенными полярными коорди-
натами.
Ответ: S = ~nab [(1 + с2)5/2 — 1].
О
(в)	Указание. Перейти к полярным координатам. Уравнение направ-
ляющей Килиндра в полярных координатах будет г2 = a2 sin 29. Получим
те
2*	2
S =А а2 С [(1 -I- Sin 29)2 — 1] М.
О	1
Подстановка в —	X .
„ О 2 . /10 л \
Ответ. Я = ~а21—-----1 •
(г)	Ответ. S = 4я/? (/? — //?2 —р2).
2)	Найти площадь частей сферы х2 4-у2 -f- z2 = R2, вырезанных из нее
цилиндром x2-{-y2 — Rx (верхнего и нижнего оснований «тела Виви ан и»,
см. 597, 20), рис. 48).
Решение. Имеем для верхнего основания
z=v^-^-y2,
V 1+р2 + ?2 = г-....R =•
/Л2 — х2 —у2
и, следовательно,
S = 2tf ? t - dxdy —
J .J V R2 — x2 — y2
<D)
причем областью интегрирования служит круг, ограниченный окружностью
х2 + у2 = Rx.
Переходя к полярным координатам, получим [ср. 611, 6)]:
те	те
2 Ц cos 9	2	R cos 9
S = 2R С М ? . rrfr ,. = 4/? С М (	, rdr —.
J 6 /У?2 —г2	VR2 — г2
Выполняя интегрирование, окончательно найдем S = 4/?2(-^—1).
Так как площадь поверхности полусферы равна 2л7?2, то площадь той
части полусферы, которая остается по выделении «тела В и в и а н и>, будет
равна 47?2 и, следовательно, выражается через радиус R без привлечения
каких-либо иррациональностей; ср. в связи с этим замечание, сделанное
в а* 597, 20) по поводу формулы для объема «тела Вивиани».
262
ГЛ. XVII. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
(629
Замечание. Конечно, можно было бы и не заменять интеграл по про-
межутку— =g6sg удвоенным интегралом по промежутку Osgflsg-^.
Но, вычисляя сразу интеграл от-до нужно помнить, что выра-
жение внутреннего интеграла
У? cos 9
С г dr
А	У ^3_Г2
[—)/> —г2]
r = R cos 6
= R—R У siiiM
r = 0
нам придется писать в одном виде: /?(1—sin 6) для 0 sg0sg-у, и в другом:
/?(1 + sin в) для—g-sg6sg0 (ибо радикал всегда положителен, а синус
имеет в одном случае знак плюс, а в другом знак минус). Не приняв этого
во внимание, получили бы неправильный результат.
3)	Найти площадь: (а) части поверхности конуса у2 -|-z2=x2, лежащей
внутри цилиндра x2+y2 = R2; (б) части поверхности конуса z2 = 2xy (х,у>0),
заключенной между плоскостями х = а и у = Ь; (в) части той же повеохности,
лежащей внутри сферы x2-\-y2-}-z2 = a2.
R
V К2-у2
Указание, (а) 5 = 8^2 С dy С х dx _
о J Ух2—у2
Ъ а ________ ______
(б) S=/2 dy § (]/у+]/^рх = у (а-|-6)/2^.
О о
(в) Пересечение поверхностей лежит в плоскостях х -|-у = ± а. Далее,
s=2,/r $$ (УуУт)"'?-
х, у ^0
а	а — х	а
= 4y2^yxdx ? -4^ = 8/2 ( yx(a-x)dx = ny2- а2,
п к Уу х
4)	Доказать, что площадь S любой фигуры, лежащей на одной (скажем
верхней) полости конуса вращения
x2+j2	z2
a2	с2	’
пропорциональна площади ее проекции на плоскость ху.
Указание. Исходить из явного уравнения z — ^-Ух2 +у2 и вос-
пользоваться формулой (5).
5)	Дана поверхность z = arcsin (shxshj); найти площадь ее части, со-
держащейся между плоскостями х=а и x = b(0<a<zb).
629]
§ 2. ПЛОЩАДЬ КРИВОЙ ПОВЕРХНОСТИ
263
Решение. Имеем
__ ch х sh у ________ sh х ch у
Р ~ /1 — sh2 х ’ 4 ~ V I—sh2xsh2J ’
/1+/>2 + <72
ch х ch у
/1 —sh2xsh8y '
Область интегрирования определяется условиями
а^х^Ь, | sh х • shy |	1.
Сделаем Лдстановку shx = 5, shy = iq; тогда для новых
жутками изменения будут
переменных проме-
Таким образом,
sh ь
$ =
sh а
sh а «£ $ -С sh b,
dri
V1—еу
she
In
sh Ь
sh а ‘
6) Найти площадь поверхности цилиндра х2Ц-у2 = /?х, заключенной
внутри сферы х24-Уа + z2 = /?2 (боковую поверхность «тела Виви ан и»).
Решение. Уравнение передней части поверхности у=]/’7?х—х2.
Область изменения независимых переменных (х, г) ограничена осью г и
параболой z=p<7?8—Rx. Так как
_ 2 Х ду=0
д* V Rx — х2’ &
то
R VR»-Rx
л г, С С	dz dx
5=	\ V .......>•.	=
J J______/Rx — х2
0 -VR*-Rx
R
= 4RVR -^L- = 47?2.
Vх
(Cp. 347, 4).]
7) Найти площадь боковой поверхности ко-
нуса высоты с, основанием которого служит
эллипс с полуосями а и Ъ (а > Ь); высота проходит через центр основания.
Решение. Если начало координат взять в вершине конуса и плоскость
ху провести параллельно основанию (рис. 92), то уравнение поверхности
будет
‘-УШИ.
е
264
ГЛ. XVII. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
[629
и искомая площадь
где (Е) есть эллипс
V
_ а. г— <: 1
а2 "Г J2 -- *>
и для краткости положено
а ’ р— Ь
Переходя к обобщенным полярным координатам, получим
Л
V
S = lab У a2 cos2fi + ₽2 sin2 6 <70.
Результат легко приводится к полному эллиптическому интегралу второго рода:
S = 2ayV+^E(k), где й =
8)	Найти площадь поверхности, образованной вращением кривой y=f(x)
вокруг оси	/(х)^0).
Решение. Нетрудно сообразить, что уравнение поверхности вращения
будет
/ + г2 = [/(х)]\
а уравнение верхней половины ее
?=К [/ (X)F-J2.
Отсюда
= f(x)f'(x)	= —у
У[/(х)]’-у”
n+p’ + ^=/(x)/|W,-=?.
Таким образом, искомая площадь выражается интегралом
где область (D) на плоскости ху ограничена линиями х — а, x—b, y=f{x)
и у = — f(x).
Переходя к повторному интегралу, найдем
»	/И
S = 2 \ f(x) У 1 4- [/' (X)l! dX \  г.
а	— j
6291
$ 2. ПЛОЩАДЬ КРИВОЙ ПОВЕРХНОСТИ
265
и так как внутренний интеграл равен л, то получается уже известная нам
формула [344, (22)]:
ь
S = 2n\f(x) / 1 + [/ (х)]3 dx.
а
Как читатель, вероятно, и сам заметил, в задачах 2) — 8) мы все время
имели дело с теми особыми случаями вычисления площадей, о которых была
речь в п° 628.
9)	Решить задачу 2), используя параметрическое представление сфери-
ческой поверхности через сферические координаты:
х = 7? sin ср cos 0, у = 7? sin ср sin 0, z = R cos ср
(О *1 ср -С л, 0 ' 0	2л).
По матрице производных
/ 7? cos ср cos 0 7? cos ср sin 0 — 7? sin ср\
\— 7? sin ср sin 0	7? sin ср cos 0	0 /
легко найти гауссовы коэффициенты сферы:
E = RS, F—0, G = 7?2sin2cp, так что У EG— F3 = 7?2 sin ср.
Ограничимся рассмотрением четверти изучаемой поверхности, лежащей
в первом октанте. Для точек «кривой В и в и а н и>, т. е. кривой пересечения
сферы и цилиндра (в пределах первого октанта), будет ср-|-0 = -^-.
Действительно, подставляя выражения х и у через ср и 0 в уравнение
цилиндра х2 у3 = 7?х, получим sin ср = cos 0, и так как для рассматриваемых
точек, очевидно, 0=^0^-^- и О^ср-<-^~, то отсюда и следует, что
<Р + 6 = у.
Установив, на основании сказанного, пределы изменения параметров ср
и 0, получим по формуле (3*)
2
S = 47?2
i'9
о
известному уже результату, избежав на этот
Как видим, мы пришли к
раз разрывов подинтегральной функции.
10)	Рассмотрим так называемую общую винтовую поверхность [229, 5)|,
которая описывается кривою
X =?(«), z = cp(u), [=р(и)>0]
(расположенной в плоскости xz) при винтовом движении ее вокруг оси г
и вдоль оси г. Уравнения ее (если угол поворота обозначить через о) будут:
х = ср (ц) cos о, у = ср (и) sin v, г = ср (и) -[- со.
По матрице производных
/ ср’ (u) cos о (и) sin v Ф’ (и) V
\— ср (и) sin v ср' (и) cos о с /
составляем гауссовы коэффициенты поверхности:
£=[=?'(и)]2+UW> F=c.<P'(«), G= [ср(и)]3 + с*.
266
ГЛ. XVII. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
(629
Таким образом, выражение
VEG—F2 = У {[? («)]’ + с2} {[<?' (а)]2 + №’ («)]’} - с2 [<И («)]’
оказывается зависящим только от и, что, вообще говоря, упрощает вычисления.
11)	Воспользоваться этими результатами для определения площади части
(а) обыкновенной винтовой поверхности
X = и cos V, у = и sin V, z = cv, •
вырезанной из нее цилиндром х2Ц-у2 = а2 и плоскостями z = 0 и г = 2лс
(так что 0 v sg 2л);
(б) винтовой поверхности	________
.	*	sin а , , 1 Г 1 -4- sin и •
x = tgacosu, y=tgasin®, z — ——5—4- In I/ —!------------f-v,
2 cos2 a r cos а
отвечающей изменению параметров в прямоугольнике
0^®^2я.
4 ’
(а)	Р е ш е н и е. В данном случае
у EG—F2 = У а2 + с2,
так что
2л
5 =
:2 а + У<
Г,п--------С
У а2 -]- с2 du do = 2л
(б)	Ответ. 3 = уп.
12)	Если в задаче о винтовом движении кривой положить с = 0, так что
поступательное движение отсутствует, то получится поверхность вращения:
х = <р (и) cos v, у = <р (a) sin v, z = ty (и)
(asg;ар, 0 и 2л).
Тогда
У EG- F2 = ? (а) у (У (а)]2 +	(а)]2,
и площадь этой поверхности выразится формулой
₽ _____________________
S = 2л J ? (а) У И (а)]2 + [ф' (a)]2 du.
а
Эта формула обобщает результат задачи 8), но не потребовала введения
несобственных интегралов. [Ср. 344, (21).]
13)	Оправдать выведенную в 346 [(25)] формулу для площади части
цилиндрической поверхности, исходя из>общей формулы (3*).
14)	Иногда бывает удобно задавать поверхность в полярных или сфери-
ческих координатах г, ff, <р, которые с обыкновенными прямоугольными коор-
динатами связаны известными формулами:
х == г sin <р cos 6, y = r sin ср sin 6, z = rcos?
(г 'S 0, 0 <р л, 0 sg 0 sg 2п).
При этом предполагается, что полярный радиус-вектор г задан в виде функ-
ции от углов <р и 0:	г = г(<р, 6)
(полярное уравнение поверхности). Найти выражение площади кривой по-
верхности для этого случая.
629]
§ 2. ПЛОЩАДЬ КРИВОЙ ПОВЕРХНОСТИ
267
Решение. Можно воспользоваться общим выражением (3*), но лишь
в качестве параметров взять <р и 9. Написанные выше формулы как раз и
дают параметрическое представление поверхности, если мыслить, что вместо
г подставлено его выражение через ср и 6 из полярного уравнения поверхности.
По матрице производных
дг
дб
cos 6 — г sin О
cos 6
sin ср
sin ср -|- г cos ср) sin 6
-зг- sin 0 4- г cos 0 ) sin ср
ЯА	•	1	*
дг
COS ср — Г Sin ср
дг
wcos,p
легко составить
дг дг
d<f ЙО
„ 1дг\а . . . s
+r2sms<p,
EQ-P = [(г- + (*)')	+ (-g-)p.
Таким образом, окончательно имеем
MJ/	<”
где (А) есть область изменения аргументов <р, 6.
Элемент площади в сферических координатах будет таков:
+	гйсрйв.
15)	Вычислить площадь поверхности
(xa-|-y2 + z2)2 = 2a2xy.
Решение. Здесь как раз удобно использовать формулу (9). Полярное
радиуса /?, касающуюся в начале координат
плоскости ху. Требуется найти площадь ее части, содержащейся внутри
конуса za = Axs -f- By3, с вершиной в начале (рис. 93).
268
ГЛ. XVII. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
(629
Решение. Воспользуемся и здесь формулой (9), исходя из полярного
уравнения сферы: г = 2/? cos ср. Имеем
S = П 47?3 sin ср cos ср dcp d0,
(Д)
где область (Д) интегрирования по ср и в ограничена кривою
{A cos2 6 -|- В sin2 0) sin2<p = cos2<p.
Если свести дело к определению площади той части поверхности, которая
Л
лежит в первом октанте, то при любом 0 между 0 и -%- угол у изменяется
от 0 до угла <р0 = ср0 (6), для которого
tg2 ? ° = A cos2 0 4- В sin2 0 '
Очевидно,
те
у
S = 16/?2 \ d0 \ sin <р cos <р dcp.
I	• а	1	• з 1	1
\ sin ср cos <р dcp = sma ср0 =	j— - ь -—s-g
J • тт	2	2	1 + Л cos2 0 4- В sin2 6	’
и окончательно
Л
V
С _ОП2 С
J (Л + 1) cos2 В.+ (В + 1) sin20 “ у- (д + D (в + 1)'-
Любопытно, что эта площадь совпадает с площадью эллипса, имеющего
полуосями хорды DC и ЕС (см. рисунок).
17) Доказать, что площадь поверхности
(х2 _|_у _|_ г2)2 = сЛг2 4-	f Z3
совпадает с площадью поверхности эллипсоида
х2 у2 z2 _
а2 ' Ь2 ‘ с2 1
если взять
а=к с=_±.
а ’ р	7
Доказательство. В сферических координатах уравнение поверх-
ности:
г2 = a2 sin2 ср cos2 0 4- Р3 sin2 ср sin2 0 4- 7s cos2 Ср,
и по формуле (9) площадь ее равна
Л л
тт _________________________________
Sx = 8 У (a4 cos3 0 4- Р1 sin3 8) sin3 <р 4" I4 c°s3 <р sin ср dcp d0.
629]
9 2. ПЛОЩАДЬ КРИВОЙ ПОВЕРХНОСТИ
269
С другой стороны, если исходить из обычного параметрического пред-
ставления эллипсоида:
х = a sin ср cos 9, у — b sin ср sin в, z = с cos ср
(О ’С ср 'С л; 0	6 :< 2л),
то определители матрицы производных окажутся равными
А = cb sin2 ср cos 9, В — ас sin2cp sin О, С = ab sin ср cos ср,
и по формуле (3) площадь поверхности эллипсоида выразится так:
Л Л
___________________________________________________________
S = 8 \ \ (csbs cos2 0 4- с2а2 sin2 9) sin2 ср -f- asba cos2 cp sin cp rfcp M.
Мы видим, что выражения для St и 5
если положить
cb = а2, са — ft2,
или
а=А Ь = ^-,
а '	0 ’
действительно отождествляются,
ай==72
e = J±,
что и требовалось доказать.
18) Определим теперь площадь поверхности трехосного эллипсоида:
А*® V® Z®
^ + ^ + -?-=1 (">*>«>«)•
Переписав для первого октанта уравнение поверхности в явном виде:
Положим для краткости
5 = 8
Тогда искомая площадь выразится, по формуле (5), интегралом
JJ V *
х, у^.0
270
ГЛ. XVII. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
1629
Путем подстановки — = $,	преобразуем его к виду:
s=8a6 н
еДЛо У 1-£2-12
Е2+*12«1
Желая использовать здесь формулу преобразования двойного интеграла,
принадлежащую Каталану [см. 597, 15) и 617, 16)], заметим, что кривая
есть не что иное, как эллипс
...g__.+ .....<_=1
а2—1	us — 1 *’
U2 — а2	И2 —₽2
так что четверть его площади
Е.У0	didli =Т К(«2-“2)(«2-^)'
1/ 1-а252-₽2т>2 _
V 1-£2 —7)2
Тогда, по формуле Каталана,
ОО
S = 2itaZ>f ud —.....— ы-~-1—.....—
J У (и2 —а2)(«2 — ₽2)‘
Займемся преобразованием этого эллиптического интеграла.
Прежде всего проинтегрируем по частям *:
4- оо
С . и2 — 1
\ ud	— —
У (а2—а2)(а2 —₽2)
_ (	И(Ы2—.1)
I У (а2 —а2)(а2 —₽2)
Затем выполним подстановку
(и2—1)<7и	)
У (и2 —а2) (а2 — ₽2)/
а , acos<p ,
U	, du —-----;—й  и<р,
sm<p ’	sin2 ср т
изменяя ср'от (х = arcsin а до 0. Тогда, с одной стороны,
и (иг — 1)________________________________________а2 — sin2 о _______
У (а2 — а2) (а2 — ₽2)	а sin <р cos <?У 1 — кг sin2 <р *
* Заметим, что здесь ни двойная подстановка от внеинтегрального чле-
на, ни определенный интеграл от 1 до -]-оо в отдельности не имеют
смысла. Налицо, при а = -[-оо, неопределенность вида оо — оо!
629]
$ 2. ПЛОЩАДЬ КРИВОЙ ПОВЕРХНОСТИ
271
й
если положить k = ~- (k < 1). С другой же,
_	(и8 — l)du_______/ а8 _ \ do _
Y (u8— а2) (ц8— р2)	\ sin2 ср /Y а2—г р2 sin2 ср
= //а2-?2 sin2 ср I-?2	\ . =
\ sin2 <р	/а2 — sin2 ср/ 7
— L У 1—fe2sin2? _ I—?2	1
~ \“ Sin2 ср	а у 1—fc2sin2cp,
так что интеграл под знаком двойной подстановки представится в виде
а Y 1—A2 sin2 ср 1—Р8С	d<{
' sin8 ср ? a J у 1— k2 sin2 ср ‘
Интегрируя в первом члене по частям, последовательно преобразуем
это выражение так:
,-----------(• COS2 ф
— a Ctg ср •	1 — Й8 sin2 ср —Д2а Jy===dcp-
 е	ctgcp./l—fe2sin2=p-
“ • J у 1 — k2 sm8 ср
1 С 1 — k2a2 sin2 ср ,
—:-- \ —	T do = — a ctg <p • у 1 — к2 sin2 ср 
“ ' Y 1 — Й2 s*n2 ?
1 —a2
— -....-\---- ~T — a \ у 1 — /г2 sin2 ср d<
“ J Y 1 — *2 sin2cp J
Затем объединяем оба внеинтегральных члена:
a2 — sin2 ср	„—
•--------- ' т ---------— a Ctg ср • У 1 — k2 sm2 ср —
a sin ср cos ср YI — к2 sin8 ср
 (a2	₽8 cos8 cp — 1) sin cp ♦
rfcp
— а
acoscpj/- i—*8sin2cp •
Двойная подстановка по ср от рс = arcsin а до 0 дает для этого выражения
такой результат: ]^(1 — a2) (1—(З2). Учитывая двойную подстановку и для
Интегралов, окончательно получим формулу
- = 2те8 +	{ c2F(у, к) + (а2 - с2) Е (р, к)},
У а2— с2
данную впервые Лежандром. Здесь-
а V Ь2 — с2
-	• Г	v г.
и. = arcsin ------, к — -г- -
а ’ Ь у а2 —с2
19)	Г а у с с ввел для поверхностей понятие полной кривизны в данной
точке, совершенно аналогичное понятию кривизны для плоских кривых ]250].
* Этим мы, наконец, уничтожаем ту неопределенность при <р = 0, кото-
рая отмечалась выше.
272
ГЛ. XVII. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
(629
Пусть дана поверхность и на ней точка. Возьмем любую часть (S) поверх-
ности, окружающую эту точку, и рассмотрим всю совокупность нормалей
в различных точках (S). Описав вокруг начала сферу радиусом единица, ста-
нем проводить из начала лучи, параллельные упомянутым нормалям; они выре-
жут на поверхности сферы некоторую ее часть (£). Площадь ее £ есть мера
телесного угла, заполненного всеми проведенными лучами; это — аналог угла <>,
о котором была речь в определении, данном в п° 250. Предел отношения
при стягивании (S) в данную точку и называется полной кривиз-
ной поверхности в этой точке. Поставим себе задачей вычислить его.
Предположим, что поверхность задана уравнением
z=f(x, у),
причем функция f имеет непрерывные производные первого и второго по-
рядков	~df _df —d2f _ d2f ,d2f
? dx' dy ' r dx2 ’ S dx dy ’ dy2
и, кроме того, определитель
D(x,y) ~rt~S
(Ю)
где (U) — проекция (d), a (и)— проекция на
для соответствующих точек (х,у, z) и
ностей один и тот же.
Преобразуем второй интеграл к переменным
Р
V 1 +р2 +
( z' = cos \
отличен от нуля (в рассматриваемой точке и вблизи нее).
По формуле (56) имеем
dxdy ______________________________С f dx' dy'
I cos vl ’ " J J I cos v | ’
(Z>)	(O)
плоскость ху, угол же ч
(x', у', z') обеих поверх-
х, у. Так как, очевидно,
_	__________Ч
q2 ’ Л	Г1+р8 + 92
= 1 \
/1+р2 + ?2 г
то
D (х', у')______________________	1
D(p, q) -(1+р2 + 92)2-
Если учесть еще (10), то окончательно получим
D(x', у')_	П — з2
D(x,y) ~ (\+p2 + q2)2 ’
В таком случае по формуле замены переменных:
| rt — s’ |	dx dy
(1 + P2 + 92)2 I cos v | *
(O)
Дифференцируя как S, так и S по области (D) [593], легко получить
теперь, что	s |rf-s’|
(l+p’-l-g’)’ *
Это и есть искомое выражение для полной кривизны.
2=
629|	g 2. ПЛОЩАДЬ КРИВОЙ ПОВЕРХНОСТИ	273
20)	Формула (50 может быть весьма просто получена, если исходить —
для случая явного задания поверхности (3) — из другого определения площади
кривой поверхности.
Разложим поверхность (5) на части (3,) (7 = 1, 2,	, и); в соответствии
с этим ее проекция (D) на плоскость ху разложится на части (Di). В неко-
торой точке (М^ площадки (S,) проведем к поверхности касательную пло-
скость и спроектируем площадку (Si) на эту плоскость параллельно
оси z. Обозначая через Г/ площадь полученной плоской фигуры, очевидно,
будем иметь
D{= Ti' | COS |,
если Ч{ есть угол нормали к поверхности в точке Mi с осью z. Если под
площадью S поверхности разуметь предел суммы площадей именно этих
плоских фигур, то сразу придем к результату
5 = НтУ Tf = limy..	fXdy ,
Ai *	| cos | j J cosm ’
i	i	(O)
поскольку написанная сумма явно представляет собой интегральную сумму
для последнего интеграла.
Подчеркнем, что измененное определение площади кривой поверхности, хотя
и весьма просто приводит здесь к окончательной формуле, имеет существен-
ный недостаток: оно формально связано с выбором координатного триедра
(проектирование параллельно оси zl) и приложимо лишь к частному типу
поверхностей.
21)	Пусть от параметрического задания
х — х(и, v), у=у(и, v), z = z(u, у) ((и, v) из (Д))
гладкой поверхности (S) с помощью формул *
и —U (и*, о*), v = V (и*, о*)	((и* о*) из (Д*))
мы переходим к другому ее представлению
х — х* (и*, о*),	У—У* (и*, v*), z = z* (и*, v*),
в котором она также не имеет особенностей. Легко показать непосред-
ственно, что формула (3) для площади (S) поверхности преобразуется при
этом в аналогичную же формулу
3 =	/Л*2 + В*2 + С*2 du* dv*
(Д*)
(все величины, относящиеся к новому представлению, мы отмечаем звездоч-
ками).
Действительно, полагая
Р(и, у)
D(u*,v*)'
имеем по известному свойству функциональных определителей
А*—АЦ В* —ВЦ С* = С1.
* Функции U и V предполагаются непрерывными вместе со своими част-
ными производными.
274
ГЛ. XVII. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
[63Э
Отсюда, между прочим, ясно, что / в (Д*) отлично от нуля, ибо иначе поверх-
ность в новом представлении имела бы особенности. Теперь по формуле замены
переменных сразу получаем
С ( у Аа + В2+ С^ du dv =
(А)
что и требовалось доказать.
J J у Аг + В2 + С2 • 111 du* dv* =
(А*)
В*2 -L С*2 du* dv*,
§ 3. Поверхностные интегралы первого типа
630. Определение поверхностного интеграла первого типа.
Поверхностные интегралы первого типа представляют собой такое
же естественное обобщение двойных интегралов, каким криволиней-
ные интегралы первого типа являются по отношению к простым
определенным интегралам.
Строится это обобщение так. Пусть в точках некоторой двусто-
ронней гладкой (или кусочно-гладкой) поверхности (S), ограниченной
кусочно-гладким контуром, определена функция f (М) = f (х, у, z).
Разобьем поверхность (S) с помощью сети произвольно проведенных
кусочно-гладких кривых на части (ЗД (32), ... , (3„). Взяв в каждой
части (S,) (1 = 1, 2, ... , п) по произволу точку Mi(xit yit z,), вычи-
слим в этой точке значение функции
Л-> г,)
и, умножив его на площадь 3) соответствующей части поверхности,
составим сумму всех таких произведений:
п	п
° = 2/(Л1г)5г= 2 Ж, У>>
i = l	i=l
которую мы будем называть — по сходству со многими ранее рассмот-
ренными суммами — интегральной суммой.
Конечный предел этой интегральной суммы при стремлении диа-
метров всех частей (3,) к нулю называется поверхностным
интегралом первого типа* от функции f (Af) = f (х, у, z)
по поверхности (3) и обозначается символом
I=\\f(M)dS=\\f(x, у, z)dS,	(1)
(S)	(•$)
где dS напоминает об элементарных площадях 3,-.
* В отличие от поверхностных интегралов второго типа, рассматриваемых
ниже [634].
631}	§ 3. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ ПЕРВОГО ТИПА	275
631. Сведёние к обыкновенному двойному интегралу. Ограни-
чимся случаем простой незамкнутой гладкой поверхности (3) без
кратных точек.
Какова бы ни была функция f(x, у, z), определенная в точках
поверхности (S) и ограниченная:
|/(х, у, z)[^L,	(2)
имеет место равенство
$$/(*> У> z)dS=
($) ____________________________________________
= ^/(х(«, v), у (и, v), z(u, v^EQ—Pdudv (3)
(A)
в предположении существования одного из этих интегралов (что вле-
чет за собой и существование другого).
Таким образом, для сведёния поверхностного интеграла первого
типа к обыкновенному двойному нужно лишь заменить коорди-
наты х, у, z их выражениями через параметры, а элемент пло-
щади dS—его выражением в криволинейных координатах.
Обратимся к доказательству высказанного утверждения.
Как уже отмечалось, разложению поверхности (5) на части с по-
мощью кусочно-гладких кривых отвечает подобное же разложение
области (Д), и обратно. Точно так же, если к нулю стремятся диа-
метры частей (3), то это справедливо и по отношению к диаметрам
частей (Д), и обратно.
Разложим же соответственным образом поверхность (3) на части
(3(), (5g), ... , (Зл), а область (Д) на части (Д,)> (Да), ... , (Дя) и вы-
берем в каждой части (3,) по точке (хг, yt, zt), а в части (Д,) — по
точке («г, которые также отвечали бы одна другой, так что
Xi = x(Ui, v^, yi=y(ui, v^, Z, = Z(Ui, vi).	(4)
Составим теперь интегральную сумму для интеграла (1):
о= %f(Xi, У и Zi)Si.
i = l
По общей формуле (3*) п° 626 будет
3/==^	EQ—F*dudv.
&)
Применив же теорему о среднем, получим
Si=[VEG-Ei]a=F.-^l,
V=7!.
I
где (ult Vi) есть некоторая точка области (Д,).
276
ГЛ. XVII. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
[631
С помощью этого выражения для 5,- и вспоминая (4), мы можем
переписать сумму а так:
п
а =	Vi), y(Ui, vt), z(Ui, t»,))[/eG—/*]и=,т - A.-
i=i	-
v = v.
I
В этом виде она напоминает интегральную сумму для второго из
интегралов (3):
п
О*=	^)> y(^i> vt) z(Ui, Vi)) [/£О-Я]„=„. • Дг.
£=1 *
*—1	V — V.
I
Различие между суммами в и о* заключается в том, что в последней
и сложная функция /(...) и корень jA.. всякий раз вычисляются
для одной и той же (произвольно взятой) точки (иг, v^, а в пер-
вой— функция /(...) берется в точке (иг, vt), а выражение К--
в точке (wf, vt) (которая называется теоремой о среднем и не
произвольна).
Рассмотрим разность между обеими суммами:
-_____
<3-----<3
= S/G• -Я[Veg-/*]«=£:- [Keg-/*]
; .1
Пусть г^>0— произвольно малое
прерывности функции KEG—/*,
областей (Д,) будет
[]/jEG —/*]а=57 —
V — V.
I
Учитывая (2), легко приходим
и = и. I А/.
•0=г^	I
число. В силу (равномерной) не-
при достаточно малых диаметрах
[KE'G—/*]„=„
v=v.
к оценке
е.
|я — а* |<^е£Д,
так что
lim (я — а*) = 0.
Отсюда ясно, что из существования предела для одной из этих
сумм следует существование равного ему предела и для другой.
Этим и доказано наше утверждение.
В частности, двойной интеграл справа в (3), а значит и поверх-
ностный интеграл слева, существует в предположении непрерывности
функции f(x, у, z) вдоль поверхности (5).
Если поверхность (5) задана явным уравнением:
Z = z (х, у),
то формула (3) принимает вид
$ \f(x, У- *)	$ \f(x> У> z (х, у)) К1	+ q* dx dy, (5)
(S)	(D)
где (D) означает проекцию поверхности (<S) на плоскость ху.
632]
§ 3. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ ПЕРВОГО ТИПА
277
Так как 1	= |с^'<| (где v> как обычно, есть угол
между нормалью к поверхности и осью z), то формулу (5) можно
написать и так:
/(х, у, z) dS= А f(x, у, z (х, у))
(О)
Мы предполагали до сих пор поверхность (S), на которую был
распространен интеграл, гладкой и незамкнутой. Наши результаты
легко распространяются и на случай кусочно-гладкой поверх-
ности, как незамкнутой, так и замкнутой.
632. Механические приложения поверхностных интегралов первого
типа. Г. С помощью названных интегралов можно определять массы, моменты,
координаты центров тяжести и т. п. величины для материальных поверх-
ностей, вдоль которых распределены массы с определенной в каждой точке
поверхностной плотностью.
Так как здесь нет ничего нового по сравнению со случаем плоского рас-
пределения масс, рассмотренным выше, то мы остановимся на этих вопросах
только в упражнениях.
2°. Притяжение простого слоя. Поверхностные интегралы первого типа
естественно входят в рассмотрение при изучении притяжения масс, распреде-
ленных на поверхности.
Пусть по поверхности (S) непрерывным образом распределены массы с
заданной в каждой точке М (х, у, г) поверхности плотностью р (Л4) = р (х,у, г)* ••.
Пусть, далее, в точке А (5, »], С) (вне поверхности) находится единица массы.
Требуется определить, с какой по величине и по направлению силой У7 притя-
гивается точка А поверхностью (S), если в основу положен ньютонов закон
притяжения (закон всемирного тяготения).
Если бы точка А притягивалась одной лишь материальной точкой
М (х, у, г) с сосредоточенной в ней массой т, то величина силы притяжения
была бы равна
где г есть расстояние AM, т. е.
г == /(х-5)2 + (у-< + (г-О2.	(6)
Так как эта сила направлена от А к М, то ее направляющие косинусы
будут
X — $ у — И) z — С
г ’ г ’ г
и, следовательно, проекции силы притяжения F на оси координат выразятся
так:
„ х — 6 „ у — тп	z — С	...
Рх = т-уГ~, Гу^т-г—А, Fz = m-^-.	(7)
• В этом случае говорят о простом слое (в отличие от двойного слоя,
который мы не рассматриваем).
•• Как обычно, «постоянную тяготения», т. е. множитель пропорциональ-
ности в формуле Ньютона (зависящий от выбора единиц), мы заменяем
единицей, чтобы упростить запись.
278
ГЛ. XVII. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
[632
В случае системы притягивающих материальных точек эти выражения
заменились бы суммами подобных выражений; наконец, при непрерывном рас-
пределении масс по поверхности появятся вместо сумм интегралы.
Применяя обычный прием изложения, можно было бы рассмотреть эле-
мент dS поверхности с массой р dS, как бы сосредоточенной в одной из его
точек М (х, у, г). Оказываемое им на точку А притяжение будет иметь про-
екции на оси [ср. (7)]:
dFx=t~$dS, dFy = Py-^dS, dFz = ?Z-^dS,
где г означает расстояние AM, выражаемое формулой (6). Теперь остается
лишь «просуммировать» эти выражения, что приведет к следующим формулам
для проекций силы F притяжения простого слоя на осн:
(S)
г’
dS,
z — t
(8)
Этим сила F определена полностью как по величине, так и по направ-
лению.
Если бы притягиваемая точка А и сама лежала на поверхности (S), то
проекции притяжения на оси по-прежнему выражались бы интегралами (8), но
на этот раз интегралы эти были бы несобственными, поскольку вблизи
точки А подинтегральные функции все перестают быть ограниченными.
3°. Потенциал простого слоя. В случае одной притягивающей точки
М (х, у, г), как мы видели, проекции притягивающей силы на оси имеют
выражения (7). Легко усмотреть, что эти проекции являются частными произ-
водными по 6, 1] и С от функции
которая называется ньютоновским потенциалом на точку А поля точки М.
[Ср. 566, 1).]
В случае поля, созданного системой материальных точек, потенциал выра-
зился бы суммой дробей этого вида, причем производные потенциала по 6, i], С
по-прежнему давали бы проекции силы притяжения на оси.
Отсюда естественно приходим к такому выражению для потенциала
простого слоя, расположенного по поверхности (S), с плотностью р, на
точку Д:
IF (6, т),С) =
И-
(S)
Возникает лишь вопрос, сохраняется ли для этого потенциала фундамен-
тальное свойство:
dW_ dW_p
"Эе х’	It” *’
(Ю)
где Fx, Fy, Fz суть проекции силы F притяжения простого слоя на оси и
определяются формулами (8).
Если точка А не лежит на поверхности, так что никаких нарушений
непрерывности нет, то легко показать, что к интегралу (9) при дифференци-
ровании его по Е, ij или С применимо правило Лейбница (для этого пона-
добилось бы лишь повторение уже знакомых нам рассуждений). Таким путем
оправдываются и для рассматриваемого случая распределения масс соотно-
шения (10).
633]
§ 3. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ ПЕРВОГО ТИПА
279
633. Примеры. 1) Вычислить поверхностные интегралы:
распространенные на поверхность (S) эллипсоида:
*•2	ч»2 w2
+ + = 1 (»>»>«>»).
Решение, (а) Если воспользоваться представлением эллипсоида:
х = a sin? cos9, у —6 sin? sin 9, z = c cos?
(0«g?sgit; 0sg9«g2it),
to [629, 17)] элемент поверхности представится в виде
dS = abc gff V COS.8-9- + sin2 ? sin.* e- + sin ? d? d9.
F a3 ' b3 c3
С другой стороны, подинтегральная функция
-» /~х3 у* , z* 2 __/ sin* ? cos2 9 sin* ? sin2 9 cos2 ?
V a* + b* +c4 Г a3 H b3 * c2 *
По соображениям симметрии вычисление приводится к первому октанту,
так что
тт
I	С /sin2®cos2 9 sin2® sin29 , cos2?\ .	.
A = Sabc \ \	-----4------------b —5-X) sin ? d? d9 =
4 a /1 , 1 1 Ц
= — л abc -т4- м T т .
3	\a3 1  b3 c2 )
(б) Аналогично,
я n
,	_ , С Г	sin ® d? d9
Ia = 8abc | I-----------------—i-------------------5- .
J J (e2 sin2 ? cos2 9 b3 sin2 ? sin2 9 4- cs cos2 ?)2
Вычисляя внутренний интеграл по ?, положим cos? = z:
1
Г___________________________dz___________________________________1
I	3 в2 cos2 9 4- b3 sin2 9 X
J {(в2 cos2 9 4- b3 sin2 9) — (a3 cos2 9 4- b3 sin2 9 — c2) z2} 2
(a3 cos2 94-й2 sin2 9) — (a2 cos2 9 4- b3 Bin2 9 — c2) z2
2___________1_________
c a3 cos2 9 4- b3 sin2 9’
280
ГЛ. XVII. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
[633
и окончательно
2
2)	Вычислить интеграл
L = у (j2z2 + z2x2 + х2/) dS,
(S)
где (S) есть поверхность, отсекаемая от верхней части конуса z2 = A2(x24_3's)
цилиндром Xs У2— 2ах = 0.	_______
Решение. Переписав уравнение поверхности в виде z = k Ух2-|-У2>
имеем dS — У1 -|- k2 dx dy, и по формуле (5)
L = УТ+k2 У [k2 (х2 4-у2)2 4-х2у2] dxdy,
GO)
где (D) есть круг, ограниченный окружностью х2 4-Js — 2ах = 0 на плоскости
ху. Переходя к полярным координатам, найдем
1 = 1- (80/г2 4- 7) па* У1+&.
3)	Вывести формулу (принадлежащую Пуассону):
п 2тс
j f(m sin су cos 0 4~ и sin ? sin 0 4~ Р cos<p) sin <p dbd^ =
1
= In J f(u Ут2 4- n2 4-P2) da
(где m2 4~ n2 4~p2 > 0 и f(f) есть непрерывная функция для
111 sS /m24-n24-/).
Решение. Обозначим интеграл слева через
Р; его легко представить в виде поверхностного
интеграла
Р = f(mx 4- пу 4- Рг)
(S)
распространенного на сферу (S), описанную вокруг
начала радиусом 1.
Переходя к новой системе координат uvw,
возьмем за плоскость vw именно плоскость
тх пу pz = 0 и направим ось и перпендикулярно к ней (рис. 94); тогда
mx + ny+pz
У т2 4- п2 4-р2
В координатах uvw тот же интеграл напишется так:
P = ^f(u У m2 + n2+p2)dS-
Рис. 94.
281
633]	§ 3. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ ПЕРВОГО ТИПА
Если параметрическое представление сферы (S) взять в виде
и = и, 0=1^1-— u2 cos и, w = У1 — u2 sin а
(—l^u^l; 0<<о<2л),
то dS — du dw, и окончательно
2я 1	1
• p = j $/(a/m2 + n2+p2)rfu «Ао = 2л j/(a/ т* + га2 + р2) du.
Полагая м = cos X (0 X л), часто пишут формулу Пуассона в виде
it 2те
j f(m sin р cos 6 -f- n sin ? sin 6 + p cos p) sin p d0 dp =
= 2л /(]Лm2 4- n2 -f-р2 cosX) sinX dX.
4)	Пусть вдоль поверхности (S) распределена масса с плотностью р =
— ₽ (х, У> 2)- Найти выражения в виде поверхностных интегралов, распростра-
ненных на (S): (а) общего количества т массы; (б) статических моментов и
моментов инерции ее Муг, Мгх, Мху, 1уг, 12Х, /уг относительно координатных
плоскостей; (в) координат i), С центра тяжести массы.
5)	Найти массу поверхности сферы, если ее поверхностная плотность в
каждой точке равна (а) расстоянию этой точки от вертикального диаметра,
(б) квадрату этого расстояния.
(а)	Решение. Взяв за начало координат центр сферы и направив ось г
по вертикали, перейдем к сферическим координатам су и 0, полагая
х = 7? sin р cos 0, у — R sin р sin 0, z — R cos у,
где R — радиус сферы. Тогда
dS = R2 sin р dp d0, p = ]^x2 -f-y2 = R sin ep,
хак что
2к я
т — J р dS — R* sin2 ср dtp d0 = л2/?3.
g
(б)	Ответ: m = -^^Ri.
6) При тех же предположениях (а) и (б) относительно распределения масс
найти положение центра тяжести верхней полусферы.
(а) Решение. Если выбрать оси, как и только что, то по соображениям
симметрии сразу ясно, что $ = т| = 0.
Вычислим статический момент:
Я
2л 2~
Мху = \ \ zp dS = R*	sin2tp cos?dp d0 = -|- л 7?’.
(S)	0 0
Мы уже знаем [см. задачу 5)] полную величину массы: т = -^- л27?3, значит,
H=^y = ±R,
т Зл
282
ГЛ. XVII. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
[633
з
(б)	Ответ. При том же расположении осей $ = щ = О, С — — /?.
О
7)	Найти (а) положение центра тяжести однородной (р = const) кони-
ческой поверхности
г = ~У х2+у3 (x2+j2</?2),
R
(б) ее моменты инерции относительно координатных плоскостей.
Решение, (а) Очевидно, $ = -») = 0. Далее, имеем
Л2	/
1 + -^dxdy = -^dxdy
(1=У h2 R2),
и, следовательно,
Я
Mvy = ^sP § §	4-j2 dx dy=^~ р С г8 dr = |- ithlRp.
Так как m — nlRp, то ?==— h.
О
7?
,,ч	,	С С . ,с 2яй2/ С . . nh2lR
(б)	lxy= \ \ pz2dS=-^-p \ г2 dr — р.
<S)	о
Аналогично
, _ 7 — гс//?*
'уг — 1ХХ —	. р.
8) Дан прямой круговой цилиндр радиуса R и высоты h. Предполагая его
боковую поверхность однородной (р = 1), найти (а) притяжение, испытываемое
со стороны поверхности центром основания, (б) потенциал этой поверхности на
центр основания.
Решение, (а) Если принять центр основания за начало координат, а ось
цилиндра — за ось z, то, очевидно, Fx= Fy = Q. Представив цилиндр пара-
метрически:
х = R cos 0, у = R sin 0, z = z,
имеем dS — R dz d6, так что
2п h
0 о (^2 + z3)2
1
/ТгЧЙ’
(б) Имеем
2я Л	_________
9) Для конической поверхности задачи 7) найти (а) потенциал этой поверх-
ности на центр основания конуса и (б) на его вершину, а также (в) притяже-
ние, испытываемое центром основания и (г) вершиной конуса.
ЙЗ]
§ 3. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ ПЕРВОГО ТИПА
283
Решение, (а) Полагая I == У Ra 4* Л2, будем иметь
R
Я „У х‘ + у’ + (2 - Л)а	J
X -т’.у a	и
R	R
2п С lar — Rha . . 2я7?Ла С	dr
= -т- О \  —---_ ."  иГ —г” ---------;1 р \ •	... ....—
Z. yisra — 2Rhar + haRa	1 $Уlara— 2Rhar + haRa
= У lara — 2Rhar + haRa Г=/? +
l	|r—0
4- 2”^- In [Z2r — Rha + У la (lara — 2Rhar + haRa)]	=
- 2lt/?P (p _ м 4. 2^8P 1 n * I+A
— z (R «)+ p ln A Z_A«
(6) W=
Ip f f dx dy
R j j У xa+ya +T2
= 2it7?p.
(в) По соображениям симметрии Fx — Fy = Q. Далее,
Fic==1R: §	------jdxdy =
Х»+.У2==Я2	+ (2 _ A)SJ 2
= 2MRv $--------
0 [lara — 2Rhar + haRa]T
Интеграл приводится к сумме трех интегралов:
К	R
1 С	dr	, R(ha — Ra) f l‘r — Rha
p \	:	г '	/«	\	з^“г
® (lara — 2Rhar 4- Rahay	° (lara — 2Rhar 4- W)2
R
2R*ha C	dr	_
I* J	3.“
о (Fra — 2Rhar +Raha)2
1 . R l + R , ha~Ra	..	2 ,n . ..
— Z3 n h l — Л+ RhR	Л)	p (Л4-Л).
Собрав все результаты, окончательно получим:
р____2nhR? . R l + R 2лр (7? 4- Л)
р 111 h T=~h I •
(г) На этот раз несобственный интеграл оказывав тся расходящимся:
р -В* С С dxdy
Is	х24-^2
 Ха+.У2==Я»
284
ГЛ. XVII. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
(633
10) Предполагая, что плотность масс, распределенных по поверхности ко-
нуса, равна расстоянию точки до вершины, найти (а) потенциал поверхности
на вершину, (б) притяжение, испытываемое вершиной со стороны поверхности.
Ответ, (a) W=nRl = S; (б) Fx = Fv = 0, Fz — ^~-.
11) Найти силу притяжения точки однородным (р = const) сферическим
слоем.
Решение. Пусть центр сферы лежит в начале координат, а притягивае-
мая точка А .(массы 1) находится на положительной оси z на расстоянии а от
центра. Проекции Fx и Fy силы притяжения на оси х и у, очевидно, равны
нулю. Далее, имеем
ИН-'3
(S)
(г — расстояние между точкой А и произвольной точкой М сферы). Если
перейти к сферическим координатам:
х = /? sin <f cos 0, y — R sin <p sin 0, z — R cos ?,
to
dS = R3 sin ? d<? dd, Rs -{-a3 — 2Ra cos?
и
P __ o—ns* C (7? cos? —a) sin? dtp
5 (R3 + a3 — 2Aja cos?)2
Подстановкой R3-\-a3— 2/?acos? = £2 преобразуем это выражение
7?4-a
C [R3 — a3 Л.,	Rs-aa ,п
а2 р J k t3 ldt а2 ₽ |Я —«I 'Я 7'
I R-a\
Рассмотрим теперь два предположения.
(1)	Пусть a<zR; в таком случае — a\=R — а, в квадратных скобках
стоит нуль и
/^ = 0.
Итак, точка, находящаяся в ну три однородного сферического слоя,
не испытывает со стороны последнего никакого притяжения.
(2)	Если же a>R, то |R—о|=—(R — а), так что

Поэтому точка, находящаяся вне однородного сферического слоя,
испытывает со стороны последнего такое же притяжение, какое испы-
тывала бы, если сосредоточить всю массу m = 4nR3p = Sp слоя в его
центре.
Остановимся особо на случае a = R. В этом случае точка А лежит на
сфере, и интеграл (И) становится несобственным. После очевидных
упрощений он принимает вид

ТС
/Тр
sin ?</?
Y1 — cos ?
= —2яр.
Б34]	$ 4. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ ВТОРОГО ТИПА	285
При приближении а к R со стороны меньших или больших значений
имеет предельные значения, соответственно, 0 и — 4яр. Таким образом, притя-
жение испытывает разрыв непрерывности при прохождении притягиваемой
точки через поверхность сферы, причем величина притяжения для точки на
сфере есть среднее арифметическое упомянутых предельных значений.
12)	Найти потенциал однородного сферического слоя на произвольно взя-
тую точку.
Решение. При прежних обозначениях имеем
W(a) = £ (₽ = 2^₽ 5  Sin;frfiF' - =
Jj	r	J /Я24-оа — 27?acos<?
(о)	0
= -^-р J <#==—р(Я4-а —|Я —в|).
I К-«|
Если а < R, то
U7(e) = 4x/?p,
так что внутри однородного сферического слоя его потенциал постоянен.
Напротив, при а > R будет
4 ’ а ’
т. е. потенциал, созданный сферическим слоем во внешнем простран-
стве, не изменится, если всю массу его сосредоточить в центре.
Для случая a=R несобственный интеграл, выражающий потенциал,
имеет значение
№(Я) = 4*Яр.
Как видим, при переходе точки через сферическую поверхность потенциал
сохраняет непрерывность.
§ 4. Поверхностные интегралы второго типа
634. Определение поверхностного интеграла второго типа.
Это новое интегральное образование строится по образцу криволи-
нейного интеграла второго типа.
Там мы исходили из направленной (ориентированной) кривой
И разложив ее на элементы, каждый такой элемент, соответственно
направленный, проектировали на координатную ось. Проекция
получалась тоже направленной, и мы брали ее длину со знаком
плюс или минус в зависимости от того, совпадало ли ее направление
с направлением оси или нет.
Аналогичным образом рассмотрим теперь двустороннюю
поверхность (3), гладкую или кусочно-гладкую, и фиксируем какую-
либо из двух ее сторон; как мы видели [620], это равносильно
выбору на поверхности определенной ориентации.
Для определенности предположим сначала, что поверхность задана
явным уравнением
z = z (х, у),
286
ГЛ. XVII. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
[634
причем точка {х, у) изменяется в области (D) на плоскости ху,
ограниченной кусочно-гладким контуром. Тогда выбор возможен
между верхней и нижней сторонами поверхности. В первом случае
замкнутой кривой на поверхности приписывается направление про-
тив часовой стрелки, если смотреть сверху, во втором —
обратное направление.
Если поверхность разбита на элементы и каждый такой, соответ-
ственно ориентированный, элемент спроектировать на плоскость ху,
то направление обхода контура проектируемой фигуры определит и
направление обхода контура проекции. Это направление будет совпа-
дать с вращением против часовой стрелки, т. е. отвечать ориентации
самой плоскости ху, если фиксирована была верхняя сторона по-
верхности (5); в этом случае мы площадь проекции будем брать со
знаком плюс. В случае нижней стороны вращение будет обрат-
ным, и площадь проекции будем брать со знаком минус [стр. 610].
Пусть теперь в точках данной поверхности (5) определена неко-
торая функция f (Ж) == f (х, у, г). Разложив поверхность сетью
кусочно-гладких кривых на элементы
(50, (50, .... (50,
выберем в каждом элементе (SJ по точке М((х{, у{, z^). Затем вы-
числим значение функции /GW/)==/(xf, .У/, zi) и умножим его на
площадь Dt проекции на плоскость ху элемента (SO, снабжен-
ную знаком по указанному выше правилу. Составим, наконец, сумму
(тоже, своего рода, интегральную сумму)
° = £ /(МО Dt = £ f(Xi, yt, Zi) Dt.	(1)
Конечный предел этой интегральной суммы при стремлении диа-
метров всех частей (S0 к нулю называют поверхностным
интегралом {второго типа) от
f (Ж) dxdy=f {х, у, z) dx dy,
распространенным на выбранную сторону поверхности (S),
и обозначают символом
I=\\f{M)dxdy — ^f{x,y, z)dxdy,	(2)
(S)	(S)
(здесь dxdy напоминает о площади проекции элемента поверх-
ности на плоскость ху).
Впрочем, в этом символе не содержится как раз указания на то,
какую именно сторону поверхности имеют в виду, так что это ука-
зание приходится делать всякий раз особо. Из самого определения
635]	§ 4. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ ВТОРОГО ТИПА
287
следует, что при замене рассматриваемой стороны поверхности проти-
воположной стороной интеграл меняет знак.
Если поверхность (S) не имеет указанного специального вида, то
определение поверхностного интеграла строится совершенно так же,
лишь площади £)г проекций приходится брать не все с одними и теми
же, а возможно и с разными знаками, если одни элементы поверх-
ности оказываются лежащими, так сказать,
вверху, а другие — снизу (рис. 95).
Если элемент лежит на цилиндриче-
ской части поверхности, с образующими,
параллельными оси г, то проекцией его
служит направляющая цилиндрической по-
верхности; мы будем предполагать, что
эта кривая имеет нулевую площадь, и
в таком случае о знаке ее говорить не
приходится.
Однако здесь может встретиться
и такой случай, когда элемент лежит
частью сверху, частью снизу, либо
когда элемент не проектируется на
плоскость ху взаимно однозначно.
Так как на деле роль подобных «неправильных» элементов
ничтожна, то слагаемых, отвечающих этим элементам, мы в интеграль-
ную сумму включать не будем. Ниже мы убедимся в том, что это
•соглашение не вносит никаких осложнений ни в вычисление, ни в
использование поверхностных интегралов.
Если вместо плоскости ху проектировать элементы поверхности
на плоскость yz или zx, то получим два других поверхностных
интеграла второго типа:
У> z)dydz или ^/(х, у, z)dzdx. (2*)
(S)	<«)
В приложениях чаще всего встречаются соединения интегралов всех
этих видов:
Pdy dz + Q dz dx 4- R dx dy,
(«)
где P, Q, R суть функции от (x, у, z), определенные в точках по-
верхности (S). Еще раз подчеркнем, что во всех случаях поверх-
ность (S) предполагается двусторонней и что интеграл рас-
пространяется на определенную ее старо ну.
635. Простейшие частные случаи. 1°. Возвратимся вновь к инте-
гралу (2) для случая, когда поверхность (S) задана явным урав-
нением
z = z(x, у) ((х, у) из (D)),
288
ГЛ. XVII. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
(631
причем функция z непрерывна вместе со своими частными произвол
dz	dz
r dx ’ dy
Если интеграл (2) берется по верхней стороне поверхности
то в интегральной сумме (1) все Dt положительны. Подставляя в эт]
сумму вместо Z[ его значение г(х{, _уг), приведем ее к виду
° = 'ZtfiXi, yit z (х^ y{)) Db
z=i
в котором легко узнать интегральную сумму для обыкновенной
двойного интеграла
$ (х, У> z (х, У)) dx dy.
(D)
Переходя к пределу, установим равенство
5	(х, у, z)dxdy—^f (х, у, z (х, _у)) dx dy, (3
(S)	(D)
причем существование одного из этих интегралов влечет за co6of
существование другого. В частности, оба интеграла наверное суще
ствуют, если функция f непрерывна.
Если интеграл распространить на нижнюю сторону поверх
ности (S), то будем иметь, очевидно,
У> z)dxdy ——§$/(-*> У> z(x> y))dxdy. (3*
(S)	(D)
Замечание. Можно было бы во всех случаях сохранить фор
мулу (3), если только двойной интеграл справа считать распростра
ненным на надлежаще ориентированную область (D) [см. 610’
Покажем теперь (для рассматриваемого случая), что поверхностны!
интеграл второго типа приводится и к поверхностному интегралу пер
вого типа. Рассмотрим снова сумму (1), в предположении, что фикси
рована верхняя сторона поверхности, так что все > 0. По фор
муле (2) п° 625
(Ъг> cos>*
где v есть острый угол между нормалью к поверхности и осью г
Применив теорему о среднем значении, получим
или Di — SiCOSVi;
COS'*/
здесь v* означает угол с осью z нормали к поверхности в некоторо!
635]	§ 4. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ ВТОРОГО ТИПА	289
(отнюдь не произвольно выбираемой) точке элемента (£,). Подставляя
в а это значение Dit получим
0= f^Xi> У1’ Zi) C0S N*Si-
i= 1
Эту сумму естественно сопоставить с суммой
3=2 f(Xi’ У1’ Zi) C0S
i = l
где отвечает уже произвольно выбранной точке (xt, yit z{); послед-
няя сумма является, очевидно, интегральной суммой для поверх-
ностного интеграла первого типа
f(x, у, z) cos v dS.
(S)
Ввиду непрерывности функции
1
cos м =---	--,
/1+^ + 9’
если поверхность (S) разложить на достаточно малые элементы, то
колебание этого косинуса в пределах отдельного элемента станет
меньше любого наперед заданного числа е 0. Предполагая функцию f
ограниченной: |/| ^М, оценим разность обеих сумм а и 3:
Iа — 51 < 2 \f(xi> Ук zt) 11 cos — cos IS» <AlSs;
»= i
»аким образом, a — a —► 0. Ясно, что для обеих сумм предел суще-
ствует одновременно и притом один и тот же. Так мы приходим
к равенству
У’ z) dx dy = $$/(*, У> z) cos vdS,	(4)
(S)	(S)
причем из существования одного из интегралов вытекает существова-
ние другого. Мы видим снова, что, в частности, оба интеграла суще-
ствуют в предположении непрерывности функции /.
Заменяя верхнюю сторону поверхности нижней, мы тем самым
меняем знак левой части равенства (4). Если одновременно с тем
под ч разуметь угол с осью z нормали, направленной вниз же, то
косинус, а с ним и интеграл справа, также изменит знак, так что
равенство сохранится.
2°. Если (S) есть часть цилиндрической поверхности с образующими,
гираллельными оси z, направляющая которой на плоскости ху имеет
10 Г. М. Фихтенгольц, т, III
290
ГЛ. XVII. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
[63(
нулевую площадь, то все ее элементы имеют нулевые проекции, таи
что в этом случае
§ \f(x, у, г) dx dy = 0.	(5;
(S)
Очевидно, здесь также имеет место формула (4): так как cos v = 0
то и правая часть этой формулы будет нулем.
636.	Общий случай. Обратимся к общему случаю простой незамк-
нутой гладкой поверхности. В интегральную сумму
=	У1> ^)Di>
как мы условились, не включены слагаемые, отвечающие «неправиль-
ным» элементам, которые либо лежат на поверхности частью сверху
а частью — снизу, либо не допускают взаимно однозначной проекции
на плоскость ху. На это обстоятельство условно указывает штри>
у знака суммы.
Разумея вообще под v угол, составленный с осью z нормальк
к поверхности, направленной в соответствии с выбранной сторо
ной поверхности, мы будем иметь всегда равенство, верное вплоп
до знака (v* имеет тот же смысл, что и выше):
Di = S; cos v*.
Таким образом,
а' = 27(х,-, у/( Zi) cos vf Si.
Эту сумму сопоставим с суммой
У = 27(хг, yif z^ cos Vj
(v,- отвечает выбранной точке). Как и выше, легко убеждаемся в том
что
Нт (а' — ?) = 0.	(6
Если к сумме а' присоединить еще сумму
3" = 5’7(х/> У1’ гг) cos Vi S£,
сбответствующую отброшенным «неправильным» элементам, то полу
чится полностью интегральная сумма о для поверхностного интеграл;
первого типа
$ У> z) cos vdS.
(S)
Можно доказать [мы предпочитаем сделать это ниже, в 637], чт
при стремлении к нулю диаметров всех элементов (SJ сумма
з"-»0.	» (7
636}	§ 4. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ ВТОРОГО ТИПА	291
Тогда в связи с (6) мы снова получаем равенство (4), в предположе-
нии, что существует один из фигурирующих в нем интегралов (суще-
ствование другого отсюда уже вытекает).
Исходя из параметрического представления поверхности (S), можно
свести интеграл в (4) справа, а с ним, по доказанному, и интеграл
слева — к обыкновенному двойному интегралу, распространенному на
область (Д) изменения параметров. Именно, так как
cos v — ±  г С —, dS =	А2 4- В* 4- С2 du dv,
то имеем
J $/(x, у, z)dx dy = ±<^\if (x (и, v), у (и, v), z(u, v))Cdudv. (8)
(S)	(A)
Двойной знак отвечает двум сторонам поверхности (.S'); в частности,
если ориентация плоскости uv отвечает ориентации поверхности (£),
-связанной с выбором определенной ее стороны, то надлежит взять
знак плюс [621]. И здесь существование одного из этих интегралов
влечет за собой существование другого.
Аналогичные рассмотрения могут быть проведены и для других
поверхностных интегралов второго типа, связанных с проектированием
на другие координатные плоскости. Объединяя все эти результаты,
можно написать
J J Р dy dz -|- Q dz dx -|- R dx dy =
($)
= Ц (P cos Q cos p. —R cos v) dS. (9)
(S)
Это — общая формула, сводящая поверхностный интеграл, второго
типа к поверхностному интегралу первого типа. Здесь Р, Q, R обо-
значают ограниченные функции, определенные в точках поверхности
(S), a cos k, cos р, cos v суть направляющие косинусы нормали, на-
правленной в соответствии с выбранной стороной поверхности.
Приведем, наконец, общую формулу, сводящую поверхностный
интеграл второго типа к обыкновенному двойному интегралу:
Р dy dz -[- Q dz dx R dx dy =
ts>
= ±\\(PA+QB + RC)dudv. (10)
(A)
В правой части подразумевается, что в функции Р, Q, R вместо
х, у, z подставлены их выражения через и, v. По поводу знака можно
повторить прежние замечания.
10«
292
ГЛ. XVII. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
[637
Все полученные результаты непосредственно распространяются
и на более общий случай поверхности — замкнутой или нет, — состав-
ленной из конечного числа простых незамкнутых гладких частей, при-
мыкающих одна к другой.
637.	Деталь доказательства. .Обратимся к доказательству соотноше-
ния (7). Мы утверждаем, что по любому наперед заданному е>0 найдется
такое т) > 0, что, лишь только диаметры всех элементов будут меньше i],
в «неправильных» элементах повсюду будет выполняться неравенство
| COS v I < е.	(П)
Допустим противное; тогда существуют такое е0 >0 и такая последова-
тельность «неправильных» элементов (sft) с убывающими до нуля
диаметрами, что в некоторой точке каждого (s*) будет
|с08м|₽=ео-	(12)
Если через (8ft) обозначить элемент области (Д), отвечающий (sft), то и диа-
метры элементов (8ft) также стремятся к нулю. С помощью леммы Боль-
цано—В ейерштрасса [172], из последовательности {(8*)} можно выделить
такую частичную последовательность, элементы которой стягиваются к неко-
торой точке (иа, v0) области (Д); впрочем, без умаления общности можно
предположить это относительно самой последовательности {(8ft)}.
Для угла \ == ч>0, отвечающего значениям и — и0, v = va параметров и, v,
необходимо должно быть
cosm0 = 0.	(13)
Действительно, в противном случае мы имели бы для этих значений пара-
метров
Но тогда в окрестности точки (иа, о0) можно было бы рассматривать и, v
как однозначные функции от х, у и, подставив их выражения через х, у
в функцию z — z(u, v), представить поверхность явным уравнением
z=f{x, у)*.
Кроме того, в этой окрестности, если выбрать ее достаточно малой, cosv
сохранял бы определенный знак. Так как (8ft) при достаточно больших k
неминуемо попали бы в эту окрестность, то им не могли бы отвечать «не-
правильные» элементы (sft).
Итак, равенство (13) установлено. В таком случае, при достаточной
близости (8ft) к точке (иа, va), мы имели бы для этих областей сплошь
| COS v I < е0,
вопреки предположению (12). Полученное противоречие и доказывает наше
утверждение, связанное с неравенством (11).
Пусть теперь диаметры элементов, на которые разложена поверхность (S),
все будут меньше i]. Тогда для «неправильных» элементов (если они вообще
имеются) выполняется неравенство (11), и соответствующая им сумма о"
будет по абсолютной величине меньше, чем TWSe, если через М обозначить
верхнюю границу для |/|. Отсюда и следует (7).
* Если точка (и0, va) принадлежит контуру области (Д), то сказанное
остается справедливым для общей части упомянутой окрестности этой точки
с областью (Д). См. Дополнение к первому тому [262].
638]
§ 4. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ ВТОРОГО ТИПА
293
638.	Выражение объема тела поверхностным интегралом. Объем
тела выражается интегралом, распространенным на ограничивающую
это тело поверхность, наподобие того, как
площадь плоской фигуры выражается
интегралом, взятым по контуру фигуры
[551]. Рассмотрим тело (V), ограничен-
ное кусочно-гладкими поверхностями
(5t) z = zl>(x,y),
(S2) z = Z(x, у)
и цилиндрической поверхностью (53), об-
разующие которой параллельны оси z
(рис. 96). Направляющей этой поверхно-
сти служит кусочно-гладкая замкнутая кри-
вая (К) на плоскости ху, ограничивающая
плоскую область (D). В частном слу-
чае на кривой (К) может выполняться
и равенство z0(x, y) — Z(x, у); тогда поверхность (53) вырож-
дается в линию.
Объем V тела, очевидно, равен разности интегралов
V=^Z(x, у)dxdy — 55(х> У)dxdy.
(D)	(D)
Вводя поверхностные интегралы, можно это равенство переписать
так [см. (3) и (3*)]:
V= 5 5 z dx dy 4~ 5 5 zdxdy,
№)	(Si)
причем интегралы берутся по верхней стороне поверхности (S2)
и по нижней стороне поверхности (51). Прибавим к правой части
интеграл
55 zdxdy,
(«8>
распространенный на внешнюю сторону цилиндрической поверх-
ности (53). Этот интеграл, в силу (5), равен нулю, а потому прибав-
ление его не нарушает равенства. Итак, окончательно,
V= zdxdy,
(S)
(14)
где интеграл распространен на внешнюю сторону поверхности
(S) = (51) 4~ (<%) + (53), ограничивающей тело.
Формула (14) установлена нами лишь для цилиндрических брусов,
определенным образом ориентированных. Но, очевидно, она верна для
294
ГЛ. XVII. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
(638
гораздо более широкого класса тел, которые могут быть разло-
жены на части изученного вида с помощью цилиндрических поверх-
ностей с образующими, параллельными оси z. Действительно, осуще-
ствив это разложение, мы можем применить к каждой части фор-
мулу (14) и затем сложить результаты. Так как интегралы, распро-
страненные на вспомогательные цилиндрические поверхности, равны
нулю, то мы вновь приходим к формуле (14).
Мы покажем сейчас, что эта формула имеет место для широкого
класса наичаще встречающихся тел, именно, для тел, ограничен-
ных произвольными кусочно-гладкими поверхно-
стями.
Пусть (V) — такое тело. Прежде всего выделим все «ребра» на
его поверхности (S) о помощью конечного числа прямоугольных парал-
лелепипедов *, и притом так, чтобы не только их общий объем был
произвольно мал, но произвольно малой была бы и площадь заклю-
ченной в них части поверхности (5), а вместе с тем и распространен-
ный на эту часть интеграл
Возьмем теперь любую точку А1о(«о, х»0) поверхности, не лежа-
щую на «ребре». Так как она не является особой, то в ней отли-
чен от нуля хоть один из определителей
А, В, С. Если С 0, то, как известно,
в окрестности точки Л10 соответствующий
кусок поверхности (S) выражается явным
уравнением вида
г=/(х, у).
При А Ф 0 или В Ф 0 придем к явным же
уравнениям других видов:
x = g(y, г) или y = k(z, х).
Рис. 97.
Таким образом, точка 7И0 может быть окружена таким параллелепи-
педом, который вырезает из тела (V) «призматический брус», огра-
ниченный пятью плоскостями и куском поверхности одного из этих
трех видов (рис. 97).
Применяя лемму Б о р е л я [175] к нашей поверхности **, мы выде-
лим из всей этой бесконечной системы параллелепипедов конечное
их число. В результате, за выключением параллелепипедальной по-
лосы, выделяющей «ребра», остальная часть (Ц) тела (V) разобьется
на конечное число «призматических брусов» и просто параллелепи-
педов. -Если бы удалось доказать справедливость формулы (14) для
всех этих элементарных тел, то путем сложения легко было бы убе-
* Здесь и ниже мы имеем в виду параллелепипеды с гранями, соответ-
ственно параллельными координатным плоскостям.
** Которая, как нетрудно видеть, представляет собой замкнутое
множество.
638]	§ 4. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ ВТОРОГО ТИПА	295
литься и в ее верности для их суммы (V,), а затем с помощью пре-
дельного перехода (связанного со сжиманием окрестностей «ребер»)
и для исходного тела (V).
Но для брусов первого вида, а тем более для параллелепипедов,
формула уже доказана выше. Остановимся теперь для примера на
«призматическом брусе» (V) второго вида, ограниченного плоскостями
х = х^ y=yw у=уь z = z^ z = Zi и поверхностью (s): x = g(y, z).
Подражая процессу, которым мы пользовались в п° 551 для рас-
ширения условий применимости формулы для площади плоской фи-
гуры, мы на этот раз вместо вписывания ломаной в кривую станем
вписывать в поверхность ($) многогранную поверхность (а). Как мы
знаем [627], с помощью надлежащей триангуляции прямо-
угольника
(О = 0о> Уъ zn> zi]>
представляющего собой проекцию нашего тела на плоскость yz, это
можно сделать так, чтобы нормали к граням поверхности (а) были
Сколь угодно близки по направлению к нормалям к поверхности
в точках соответствующих ее участков. Заменив поверхность (s)
многогранной поверхностью (о), мы вправе написать для измененного
тела V формулу
V=^zdxdy,	(15)
(5)
где через (S) обозначена вся поверхность, ограничивающая много-
гранник (V)- Действительно, этот многогранник легко разлагается
на части такого типа, для которого наша формула уже доказана.
Остается теперь в (15) перейти к пределу (при безграничном умень-
шении ребер многогранной поверхности и сближении направлений
нормалей к ее граням и к данной кривой поверхности), чтобы по-
лучить (14).
Для доказательства сближения правых частей названных формул
Мредставим их разность в виде
55 z dx dy — 55 z	dy + «>
(S)	W
tae а обозначает интегралы по тем частям боковых поверхностей
тел (У) и (V), которыми эти поверхности разнятся. Очевидно, что
«—►О. Разность же интегралов можно переписать, переходя к инте-
гралам первого типа, сначала в виде
5 5 z cos v ds — 5 5 z cos v d<3,
(«) (®)
296
ГЛ. XVII. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
[638
а затем, снова возвращаясь к интегралам второго типа, — в виде
(5)	(»)
Здесь cos X, cos v, cos X, cos v — направляющие косинусы внешних
нормалей к обеим поверхностям. Заметим, что на (s)
1	1
cos X = r
есть непрерывная функция, не обращающаяся в нуль, и, следова-
тельно, ограничена снизу положительным числом;
при достаточном же сближении нормалей к поверхностям (s) и (о)
то же справедливо и относительно cos X для многогранной поверх-
ности (о).
Наконец, вводя уравнение x — g(y, z) многогранной поверхно-
сти (о), можно переписать это выражение в виде обыкновенного
двойного интеграла, распространенного на прямоугольник (d):
cosv I	Г cosv I ) , ,
—г-	— I z —F	„ У dy dz.
co&KAx=g(y,Z) L cosXJjc= г(л J
Учитывая не только сближение соответствующих точек поверхно-
стей (s) и (о), но и сближение нормалей в них к этим поверхностям,
теперь уже ясно, что в упомянутом предельном процессе написанный
интеграл стремится к нулю, чем и завершается доказательство.
Наряду с формулой (14) объем тела выражается и формулами
V—^xdydz или V—^у dzdx,	(14*)
(S)	(S)
которые получаются простым изменением роли осей. Складывая все
три, можно получить и более симметричную формулу:
V = у х dy dz -]-j dz dx -j- z dx dy.	(16)
(S)
Во всех случаях интеграл берется по внешней стороне поверх-
ности (5), ограничивающей тело.
Вводя вновь направляющие косинусы cos X, cos р, cos v вне;ш-
ней нормали, перепишем последнее выражение в виде поверхностного
интеграла первого типа:
V = у Г ? (х cos X -\-у cos р z cos v) dS.	-(17)
(•S)
639)
$ 4. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ ВТОРОГО ТИПА
297
639. Формула Стокса. Пусть (S) снова будет простая гладкая
двухсторонняя поверхность, ограниченная кусочно-гладким конту-
ром (А). Точки поверхности с помощью формул
х — х(и, v), у=у(и, у), z = z(u, v)
связаны взаимно однозначным соответствием с точками плоской об-
ласти (Д), ограниченной кусочно-гладким же контуром (Л), на пло-
скости wv. При наших предположениях всегда А8 В8 Ц- (?	0.
Выбрав определенную сторону поверхности, а в соответствии
с этим и ориентацию на ней [620], для определенности будем
считать, что положительному обходу контура (Л) отвечает обход
контура (Z.) в положительном направлении. Тогда, как мы устано-
вили в 621, формулы
4-Ka2 + bs+c2	+Ка24-в2+с8
 с
cos v =-- ----------
+ У Аа + В*-\-С2
(18)
характеризуют именно выбранную сторону поверхности (S).
После этих замечаний мы обращаемся к выводу формулы, связы-
вающей поверхностный интеграл с криволинейным и служащей обоб-
щением уже известной нам формулы Грина [600].
Пусть в некоторой пространственной области, содержащей внутри
себя поверхность (Д’), задана функция
Р = Р(х, у, z),
непрерывная в этой области вместе со своими частными производ-
ными. Тогда имеет место формула
Рdx = ( ? dzdx — -J^dxdy,	(19)
(1)	(S)
причем направление обхода контура (L) соответствует той стороне
поверхности (S), на которую распространен интеграл справа.
Прежде всего преобразуем криволинейный интеграл по кривой (L),
заменив его интегралом по кривой (Л):
\pdx=^P.(^dU-}-d£dvy	(20)
(i)	(Л)
Равенство это легко проверить, если ввести параметрическое пред-
ставление кривой (Л), а через него — и кривой (L): оба интеграла
сведутся к одному и тому же обыкновенному интегралу по пара-
метру.
Теперь к интегралу в (20) справа применим формулу Грина:
W	(А)
298
ГЛ. XVII. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
[639
Так как последнее подинтегральное выражение в развернутом виде дает
(дР dx ,дР ду ,дР дг\ду , „ d2x  
\дх да ' ду du ' dz du) dv ‘ dvdu
__(dP дх .дР ду ,дР dz\dy______~ д* * *х _
\дх dv ' ду dv * dz dv) du du dv
__dP (dz dx	dz dx\	dP (dx dy
dz \du dv	dv du)	dy \du dv
дх dy\
dv ди)’
то мы приходим к двойному интегралу
(А)
По формуле же (10) его легко преобразовать в поверхностный интеграл
fcdzdx-^dxdy,
(SI
последний берется по выбранной стороне поверхности, ибо именно
эту сторону характеризуют формулы (18). Этим и завершается дока-
зательство равенства (19)*.
Эта формула установлена нами для гладкой поверхности; но
ее легко распространить и на случай кусочно-гладкой (само-
непересекающейся) поверхности: стоит лишь написать ее для каж-
дого гладкого куска в отдельности и почленно сложить полученные
равенства.
Путем круговой перестановки букв х, у, z получаются еще два
аналогичных равенства:
£ Qdy = J jj dxdy — ~fdy dz,
(Z)	(S)
R dz — И dy dz — dz dx,
d)	(S)
где Q и R — новые функции от x, у, z, удовлетворяющие тем же
условиям, что и Р.
Складывая все три равенства (19) и (19*), получим искомый ре-
зультат в наиболее общей форме:
Pdx+Qdy + R dz = (M_^dxdy +
(l)	(SI
(19*)
%-®****- р')
* Следует отметить, что при выводе нами использованы существование
др \ д^х д^х
и непрерывность производных \и , dii дй * к0Т0Рые в окончатель-
ном результате не участвуют. На деле формула имеет место и без этих
предположений.
640]	§ 4. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ ВТОРОГО ТИПА	299
Это равенство и называется формулой Стокса (G. G. Stokes).
Еще раз подчеркнем, что сторона поверхности и направ-
ление обхода контура взаимно определяются по правилу,
установленному в п° 620.
Если в качестве куска поверхности (5) взять плоскую область (£))
на плоскости ху, так что z = 0, то получится формула
Pdx+Qdy=^ $-^dxdy,
. )	IS)
в которой читатель узнает формулу Грина; таким образом, по-
следняя является частным случаем формулы Стокса*.
Отметим, наконец, что поверхностный интеграл второго типа в
формуле Стокса может быть заменен поверхностным интегралом
первого типа. Тогда эта формула примет вид
Jpdx+Qdj + Rdz=JU(g-^)cosX4-
(i)	(S)
причем cos X, cos p., cos v означают направляющие косинусы нормали,
отвечающей именно выбранной стороне поверхности.
640. Примеры. 1) Вычислить интеграл
1= П +-VS)dx аУ>
 (S)
распространенный на нижнюю сторону круга лг -|-у2 = R3.
Указание. Так как поверхность, по которой берется интеграл, совпа-
дает со своей проекцией (£>) на плоскость ху, то, учитывая сторону,
имеем
I = —Ц (х2 + у3) dx dy.
W
Ответ. I — —
2)	Вычислить интеграл
J = \^x3y3zdxdy
<S)
по верхней стороне нижней половины сферы х2у’-|-z2 = R3.
* Для облегчения запоминания формулы Стокса укажем, что первое
влагаемое в интеграле справа — то же, что и в формуле Г р и н а, а остальные
получаются из него, круговой перестановкой букв х, у, z и Р, Q, R.
300
ГЛ. XVII. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
1640
У казание. Проекцией полусферы на плоскость ху служит круг (£>),
ограниченный окружностью х24-у2 = Я2. Уравнение нижней полусферы z =
= — У R? — —Уг' Поэтому
J=— § § х2у2 У R2 —х2 —у2 dx dy.
CD)
2я
Ответ. J = — xt^R7-
Юэ
3)	Вычислить интеграл
АГ= x4 s dy dz + у2 dz dx 4- г2 dx dy,
распространенный на внешнюю сторону сферы
(х - а)2 4- (у - Ь)2 + (z — с)2 = R2.
Решение. Остановимся на вычислении интеграла
/<3 = И z2 dx dy.
(S)
Так как явное уравнение сферы будет
z — с = ± V R2 — (x — a)2 — (y — b)2
(где плюс отвечает верхней полусфере, а минус — нижней), то удобно пред-
ставить подинтегральную функцию г2 в виде
z2 = (z — с)2 + с2 4- 2е (z — с).
Сумма первых двух членов, будучи проинтегрирована по верхней стороне
верхней полусферы и нижней стороне нижней полусферы, дает резуль-
таты разных знаков, которые взаимно уничтожаются. Последний же член,
который сам меняет знак при переходе от верхней полусферы к нижней, дает
при интегрировании по ним равные результаты, так что
К3 = 4с ?	У R2 — (х — а)2 — (у — b)2 dx dy = |- лс R\
(x-a)S-Ky-ft)2==/?8
Аналогично получаются и другие два интеграла
ЯГ1 = И х2 dy dz, Kt — \\yadz dx.
(S)	-	(S)
Ответ. K= я/?’ (a 4~ + c).
4)	Найти интегралы
(а) Л = Ц dx dy, (б) /2 — И z dx dy, (в) It == ( f z2 dx dy,
(S)	(S)	(S)
распространенные на внешнюю сторону эллипсоида
Xs	Z*
^.^4-4=1,
а2 ' b2 с2
4
Ответ, (а) /х = 0; (б) /4 = д-яа&с; (в) /3 = 0.
640)
§ 4. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ ВТОРОГО ТИПА
301
5)	Вычислить интегралы
(a) Lt = И ха dy dz, (б) La=\\yz dz dx
(S	)	(S)
по верхней стороне верхней половины того же эллипсоида.
V2
Решение, (а) х=±а I/ 1—~,
з
£i=4аз $ И1 ~ ?)2 dy dz'
(Di)
Vs za
где (Dt) есть первый квадрант эллипса = 1. Переходя к обобщен-
ным полярным координатам, легко найдем
2
О
Можно столь же легко получить этот результат, исходя из параметриче-
ского представления нашей поверхности:
X = а sin <р cos 0, у — b sin ср sin 0, z = с cos <р	(22)
^)ss?=g^-; 0sgo=g2r^.
Так как А — be sins <р cos 0, то по формуле (10)
Z,, = а3Ьс
2	2я
С	с	2
\ sin5 ср aftp \ cos4 0 dO = — гс агЬс.
(Верхней стороне поверхности отвечает знак плюс в упомянутой формуле).
(б	) Пользуясь и здесь параметрическим представлением, заметим, что
jB = ас sin2 <р sin 0. Поэтому
Г	2я
La — abc* \ sin’ ср cosep dep \ sin’ 0 d0 = — айс’.
V	о
6) Найти интеграл
№
(S)
dz dx
У
dxdy
z
по внешней стороне эллипсоида, о котором была речь выше.
Указание. Интеграл — несобственный, поскольку подинтегральное вы-
ражение обращается в бесконечность (в сечениях эллипсоида плоскостями
координат). С помощью параметрического представления приходим к собст-
венному двойному интегралу.
_	. (аЬ , Ъс , са\
Ответ. *4—4~ —4-у).
7)	Если выражение (16) для объема V тела преобразовать по формуле (10)
в обыкновенный двойной интеграл, то получим
у \ \ (Ах -f- By 4- Cz) du dv.
W
(23)
302
ГЛ. XVII. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
[640
Учитывая значения А, В, С как определителей, легко результат этот предста-
вить в виде
х у
Z
Z'u
Z'v
da dv.
При этом знак плюс ставится, если А, В, С имеют знаки направляющих
косинусов внешней нормали; в противном случае ставится знак минус.
8)	Вычислить по этой формуле объем V эллипсоида
t zi_ 1
дЗ -Г £2 .+ с2 —
исходя из параметрического представления (22) (0 sg л; 0	0	2тс).
4
У Казани в. Определитель равен abc sin <р. Отпет. V = — ъаЬс.
9)	Если поверхность, ограничивающая тело, задана полярным уравнением:
г = г(<р, 0),
то, как в 629, 14), можно перейти к параметрическому представлению поверх-
ности, причем роль параметров играют <р, 0.
Предлагается, исходя из этого представления, вывести из формулы (23)
изящное выражение для объема:
V == г8 sin у dy df),	(24)
где (А) есть область изменения параметров у, 0.
10)	Вычислить объем тела, ограниченного поверхностью
(x»+^ + z2)s==2a8xy.
Решение. Исхода из полярного уравнения поверхности
г — a sin <р У sin 20>
используем формулу (24). Будем иметь:
те	те
"2	2"	£	£
V =	а* \ sin4 <р dy \ sin 2 0 cos 2 0 d0.
О J	)
Вычисляя первый интеграл по формуле (8) из 312, а второй — по формуле в
534, 4), (а), окончательно найдем:
V 48 °	\4Г
11)	Проверить формулу Стокса (21) для функций
Р = хУ, C? = l, /? = г,
если контур (£) есть окружность х8 -f-у1 = as, z = 0, а поверхностью (S) слу-
жит полусфера Xs + ys -J-za = a3 (z>0). При этом на поверхности возьмем
верхнюю сторону, а контуру придадим направление против часовой стрелки
(если смотреть сверху).
Ицтеграл
5х2_у8 dx 4- dy 4~ z dzt
)
640]
S 4. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ ВТОРОГО ТИПА
303
очевидно, приводится к одному первому члену
2тг
\ x2ys dx — — ае \ sin1 fl cos2 0 dfl = — a".
J	J	о
(i)	о
Далее, имеем
—dQ — 0 дР дР-н
дх ду- y’ dy dz~"’ dI~dJ<:
Вычисляя интеграл
— 3^ x2y2dxdy —— 3	xsy2dxdy =— ae,
.	(S)	хУУа1
придем к тому же результату.
12)	Проверить формулу Стокса для функций
Р — У, Q — z, R = x,
если (L) есть окружность
x = acos.2/, у = аУ2 sin t cos/, z = a sin21 (0 t я),
a (S) — ограниченный ею круг.
(Круг этот получается в пересечении плоскости х 4- z = а и сферы хг 4-
4-_у2 4-z2 = а2; его радиус равен
Криволинейный интеграл
Я
(у dx 4-г dy 4- х dz = а1 \ (— У 2 sin2 / 4- 2cos8 / sin /) dt=— У2Г паг
(l)	о	1
поверхностный же
— dx dy 4- dy dz 4- dz dx
(S)
оказывается равен сумме площадей проекций упомянутого круга на коорди-
натные плоскости, взятой с обратным знаком, т. е. —2-j-cos 45° =
= — У 2 ла2.
13)	Проверить формулу Стокса, положив
P=_y24-z2, Q = z24-x2, /? = х24-у
и взяв в качестве (S) поверхность, вырезанную цилиндром х1 4- у2 = 2гх из
сферы х‘ 4- у2 4- z2 = 2Rx (R > г, z>0).
Поибегнув к параметрическому представлению кривой
x = r (1 4-cos/), y» = r sin/, z = y2r(R — r) 1 4-cos/ (0</?<2л)*,
* Если положить x — r —rcost, y = rsin/, то геометрический смысл
гараметра / ясен; подставляя эти выражения в уравнение сферы, найдем и
1висимость z от /.
304
ГЛ. XVII. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
[640
для криволинейного интеграла найдем довольно сложное выражение в виде
обыкновенного интеграла:
2те
j {[г2 sin2t + 2r (/? — г)(1 4- cos 0] (— r sin t) -f-
+ [2r (R — r) (1 4-cos t) 4- rs (1 + cos f)2] rcosf4~
4-	[r2 (1 4-cos Q2 4-ra sin2.1 У(-sin t)} dt.
£• t 1 vvb l	J
Но первое и третье слагаемые в фигурных скобках имеют вид / (cos t) dcos t,
и интегралы от них, ввиду периодичности косинуса, равны нулю. Выполнив
остающуюся выкладку, получим 2л/?г2.
Поверхностный же интеграл
2^ § (у— z)dy dz-\-(z—х) dzdx-}-(x—у) dxdy,
распространенный на верхнюю сторону упомянутой поверхности, преобра-
зуем сначала в интеграл другого типа:
2	[(у — z) cos X 4" (г — х) cos [j. 4* (х —у) cos v] dS.
Так как
то, подставляя эти выражения, произведем упрощение и сведем искомый ин-
теграл к следующему:
2jJ(z-y)dS.
В силу симметрии поверхности относительно плоскости xz, интеграл J у dS
оказывается нулем. Остающийся же интеграл снова преобразуем к интегралу
второго типа:
(S)
(S)
) dx dy = 2nRr2.
(S)
14)	Проверить формулу Стокса
( (z2 — х2) dx 4- (х2 — у2) dy 4- (у2 — z2) dz =
L)
= 2 f J х dx dy 4-у dy dz 4~ z dz dx,
(S)
взяв за (S) винтовую поверхность
x = wcoso,. y = usino, z —co
(fl ^u^b;	2ir),
Mt}	§ 4. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ ВТОРОГО ТИПА	305
ограниченную двумя винтовыми линиями и двумя прямолинейными отрезками
в совокупности образующими контур (£).
Ответ. Если поверхностный интеграл распространить на верхнюю
сторону указанной поверхности, а криволинейный взять в соответствующем
направлении, то оба интеграла равны г.с (Ь‘г— а2).
641. Приложение формулы Стокса к исследованию криволиней-
ных интегралов в пространстве. Пусть в открытой области (Г)
заданы функции Р, Q, R, непрерывные со своими производными
дР дР. dQ dQ, дР дР
ду ’ дг ' дг' дх' дх' ду ’
С помощью формулы Стокса легко установить условия, необ-
ходимые и достаточные для того, чтобы обращался в нуль ин-
теграл
\ Pdx-YQdy + Rdz,	(25)
(i)
взятый по любому простому (т. е. не пересекающему себя) замк-
нутому кусочно-гладкому контуру (L), лежащему в (Т).
Впрочем, для того чтобы возможно было использовать формулу
Стокса, нужно наперед наложить на трехмерную область (7),
к которой относятся наши рассмотрения, естественное ограничение.
Именно, нужно потребовать, чтобы, каков бы ни был простой за-
мкнутый кусочно-гладкий контур (£) в области (Т), на него
можно было «натянуть^ кусочно-гладкую (самонепересекающуюся)
поверхность (5), имеющую (L) своим контуром и также цели-
ком содержащуюся в (Т). Это свойство аналогично свойству од-
носвязности плоской области; при наличии его пространствен-
ную область (Г) также называют («поверхностно»*) одно-
связной. Упомянем для примера, что тело, ограниченное двумя
концентрическими сферическими поверхностями, будете этом смысле
односвязным, а тор нет.
Пусть же область (Т) будет (поверхностно) односвязной. Натя-
нув на контур (£), как сказано, поверхность (S), заменим по фор-
муле Стокса криволинейный интеграл (25) поверхностным интег-
ралом
(£)
Для обращения его в нуль, очевидно, достаточны условия
?B = dQ дР^дР
дх ду’ ду дг ' дг дх’
* В отличие от другого типа односвязности пространственной области, о
которой речь будет ниже [632].
306
ГЛ. XVH. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
[641
Эти условия в то же время и необходимы, в чем легко убе-
диться (наподобие п° 601), если рассматривать плоские фигуры (S),
лежащие в плоскостях, параллельных поочередно той или .иной из
координатных плоскостей.
Читатель видит, что мы использовали здесь формулу Стокса
совершенно так же, как в п° 601 с аналогичными целями была ис-
пользована формула Грина.
Легко доказать, что те же условия (Б) будут необходимы и
достаточны для того, чтобы интеграл
Р dx	Q dy “I- R.	(26)
(АВ)
не зависел от формы кривой (АВ), соединяющей любые две
точки А и В области (Г), в предположении, конечно, что эта
область поверхностно односвязна.
Необходимость. Если предположить интеграл (26) незави-
сящим от пути, то (как и в п° 561) отсюда следует обращение в
нуль интеграла (25) по простому замкнутому контуру (L), а значит
и выполнение условия (Б).
Достаточность. Из (Б) вытекает обращение в нуль инте-
грала (25) по простому замкнутому контуру (L). Отсюда (как и в
561) легко получается равенство
S = S	(27)
(A/В) (АЯВ)’
если только кривые (AIB) и (AIIB) не имеют общих точек, кроме
А и В. Если же это не так, и взятые кривые пересекаются, то
здесь вопрос оказывается более простым, чем в плоском случае:
в связной пространственной области (7) всегда можно взять такую
третью кривую (АШВ), которая уже не пересекалась бы ни с одной
из прежних. Тогда
< = s , $ = s .
(A/В (АШВ) (А//В) (АШВ)
откуда и следует (27).
С этим исследованием можно связать и вопрос о том, будет
ли дифференциальное выражение
Р dx 4- Qdy -\-Rdz	(28)
полным дифференциалом от некоторой однозначной функции
трех переменных. Необходимость условий (Б), для того что-
бы это было так, проверяется непосредственно, см. п° 564. Но в то
641)	§ 4. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ ВТОРОГО ТИПА	307
время как там достаточность условий (Б) была установлена
лишь для случая, когда основная область (Г) есть прямоугольный
параллелепипед, теперь нетрудно сделать это и в общем случае
(поверхностно) односвязной области. Первообразная может быть
написана сразу в виде криволинейного интеграла
(X. У, Z)
F(x,y, z)= § Pdx-\- Qdy -\-Rdz,
(*o. Уо, го)
который — при соблюдении условий (Б) — не зависит от пути. Итак,
для области (Г) указанного типа, условия (Б) оказываются необ-
ходимыми U достаточными для того, чтобы выражение (28)
было точным дифференциалом.
ГЛАВА ВОСЕМНАДЦАТАЯ
ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
§ 1.	Тройной интеграл и его вычисление
642.	Задача о вычислении массы тела. Пусть дано некоторое
тело (V), заполненное массами, и в каждой его точке М (х, у, г)
известна плотность
p = p(M) = p(x,y, z)
распределения этих масс. Требуется определить всю массу т тела.
Для решения этой задачи разложим тело (V) на ряд частей:
(Ц), (Ц), ... , (У„)
и выберем в пределах каждой из них по точке
АШ-ъ, Q-
Примем приближенно, что в пределах части (У,) плотность постоянна
и равна как раз плотности р($г, т];, С,) в выбранной точке. Тогда
масса mi этой части приближенно выразится так:
=	71»> Q
масса же всего тела будет
т = У, р i\t, С,) V,
i=l
Если диаметры всех частей стремятся к нулю, то в пределе это
приближенное равенство становится точным, так что
да = lim У р T\it Q ‘Vt,	(1)
j=i
и задача решена.
Мы видим, что решение задачи и здесь привело к рассмотрению
предела своеобразной суммы — типа интегральных сумм раз-
личного вида, с которыми мы многократно имели дело на протяже-
нии всего курса.
643]	§ 1. ТРОЙНОЙ ИНТЕГРАЛ И ЕГО ВЫЧИСЛЕНИЕ	309
Подобного рода пределы приходится часто рассматривать в ме-
ханике и физике; они получили название тройных интегралов.
В принятых для них обозначениях полученный выше результат за-
пишется так:
т —	р (х, у, z)d V.	(2)
(Ю
Теории тройных интегралов и их важным приложениям посвящена,
в основном, настоящая глава. Так как целый ряд предложений, уста-
новленных для двойных интегралов, переносится вместе с их доказа-
тельствами на случай тройных интегралов, то мы обычно будем
довольствоваться лишь формулировкой этих предложений, предоставляя
читателю перефразировать прежние доказательства.
643.	Тройной интеграл и условия его существования. При
построении общего определения нового интегрального образования—
тройного интеграла, основную роль играет понятие объема тела,
наподобие того как понятие площади плоской фигуры лежало в
основе определения двойного интеграла.
С понятием объема мы уже знакомы по первому тому и сталки-
вались с ним не раз. Условие существования объема для данного
тела заключается в том, чтобы ограничивающая его поверх-
ность имела объем 0 [341]. Только такие поверхности мы и
будем рассматривать, так что существование объемов во всех нуж-
ных нам случаях тем самым обеспечивается. В частности, как мы
знаем, в состав указанного класса поверхностей входят кусочно-
гладкие поверхности.
Пусть теперь в некоторой пространственной области (V) задана
функция f(x,y, z). Разобьем эту область с помощью сети поверх-
ностей на конечное число частей (УД (У2), ... , (У„), имеющих соот-
ветственно объемы Уь Уъ,..., Vn. В пределах z-го элемента (У;)
возьмем по произволу точку tq,-, СД значение функции в этой
точке /(?,-, т](Д,) умножим на объем У,- и составим интегральную
сумму
° = 2 Ж Ч, Q Уг.
1 = 1
Конечный предел I этой суммы, при стремлении к нулю наи-
большего из диаметров всех областей (У,) и называется трой-
ным интегралом функции f(х, у, z) в области (У). Он
обозначается символом
z)dV—\$/(*>.У z)dxdy dz.
(Ю	(V)
310	ГЛ. XVIII. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ	[644
Конечный предел подобного вида может существовать только для
ограниченной функции; для такой функции вводятся, кроме
интегральной суммы а, еще суммы Дарбу:
п	п
s=^miVit
1=1	i=l
где
zw; = inf{/}, M,= sup{/}.
(ty	(Ир
Обычным путем устанавливается, что для существования интеграла
необходимо и достаточно условие
lim (5— s) = 0
или
lim. 2 ^iVi = О,
i = l
где fOi — Mi — т{ есть колебание функции f в области (ИД [Заме-
тим, что при существовании интеграла обе суммы $, 5 также имеют
его своим пределом.]
Отсюда непосредственно следует, что всякая непрерывная функ-
ция f интегрируема.
Можно несколько расширить эти условия, а именно: интегри-
руема всякая ограниченная функция, все разрывы которой лежат
на конечном числе поверхностей с объемом 0.
Доказательство этого утверждения [ср. 690] основано на следую-
щей лемме:
Если область (V), содержащая поверхность (5) с объемом 0
разложена на элементарные области, то сумма объемов тех и:
них, которые задевают поверхность (S), стремится к нулю
вместе с диаметрами всех частичных областей.
644.	Свойства интегрируемых функций и тройных интегралов
Достаточно перечислить эти свойства [доказываются они аналогично
изложенному в 592].
1°. Существование и величина тройного интеграла не зависят
от значений, принимаемых функцией вдоль конечного числа поверх-
ностей с объемом 0.
2°. Если (У) = (У') + (И")> то

(V)	(Р)	(V”)
причем из существования интеграла слева вытекает уже суще-
ствование интегралов справа, и обратно.
644)
§ 1. ТРОЙНОЙ ИНТЕГРАЛ И ЕГО ВЫЧИСЛЕНИЕ
311
3°. Если k = const., то
kfdV=k
(V)	(Ю
причем из существования интеграла справа следует и существо-
вание интеграла слева.
4°. Если в области (V) интегрируемы две функции Jug, то
интегрируема и функция f±S> причем
\\W±g)dV=\\\fdV±\\\gdV.
(V)	(И)	(Ю
5°. Если для интегрируемых в области (У) функций fug вы-
полняется неравенство f^g, то
(Ю	(Ю
6°. В случае интегрируемости функции f интегрируема и
функция |/|, и имеет место неравенство
(Ю	(И)
7°. Если интегрируемая в (V) функция f удовлетворяет нера-
венству
m^f ^М,
то
mV^\\\fdV^MV.
(И
Иными словами, имеет место теорема о среднем значении
=	(/и р. гС Л4).
(И
В случае непрерывности функции f эту формулу можно написать
в виде	р е.. „
\\\fd.V=f(X,y,z) V,	(3)
(Ю
где (X, у, S) есть некоторая точка области (V).
Далее, легко распространяется на трехмерный случай и содержа-
ние п° 693: так же, как и там, устанавливается понятие функции
вт (трехмерной) области, в частности, аддитивной функции.
Лажным примером такой функции (см. 2°) является интеграл по пе-
ременной области (у)-.
^(.(J>)) = \\\fdv.	(4)
312
ГЛ. XVIII. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
|645
Вводится аналогично прежнему понятие производной функ-
ции Ф ((©)) по области в данной точке М’, так называется
предел
lim
при стягивании к точке М содержащей ее области (©).
8°. Если подинтегральная функция непрерывна, то производной
интеграла (4) будет как раз
значение подинтегральной
функции в этой точке, т. е.
f(M)=f(x,y, z).
Таким образом, при сделан-
ном предположении интеграл (4)
служит для функции f в не-
котором смысле «первообраз-
ной» и, как доказывается ана-
логично плоскому случаю,
единственной аддитив-
ной первообразной.
645. Вычисление тройного
интеграла, распространенно-
го на параллелепипед. Изло-
по области в точке М (х, у, г) от
жение вопроса о вычислении тройного интеграла начнем с того
случая, когда тело, в котором определена функция f(x, у, г), пред-
ставляет собой прямоугольный параллелепипед (T)—[a,b;c,d;e,f]
(рис. 98), проектирующийся на плоскость уг в прямоугольник
(R) = [c,d;e, /].
Теорема. Если для функции f(x, у, г) существует тройной
интеграл
\\\f(x,y,z)dT	(5)
(Г)
и — при каждом постоянном х из [а, й] — двойной интеграл
l(x) = \\f(x,y,z)dR,	(6)
(«)
то существует также повторный интеграл
ъ
dx f (х, у, z) dR,	(7)
a (R)
и выполняется равенство
ь
\\\tf(x,y,z)dT=\dx\\f(x,y,z)dR.	(8)
(Л	a (R)
645]	$ 1. ТРОЙНОЙ ИНТЕГРАЛ И ЕГО ВЫЧИСЛЕНИЕ	313
Доказательство аналогично проведенному в п° 594. Разде-
лив промежутки [a, b}, [с, d] и [е, /] на части с помощью точек
хл — а х{ х, хп — Ь,
Уй — С	• • <У} <^ -  <^Ут = d,
Zt=f,
тем самым разложим параллелепипед (7) на элементарные параллеле-
пипеды
(7), /, *) = [*,•> xi+i, у}, уJ+i, zk, zft+1]
(z = 0, 1,..., п— 1; / = 0, 1,..., т — 1; k = 0, 1,..., I— 1)
и одновременно прямоугольник (/?) — на элементарные прямоуголь-
ники
(fy, л) = [Л’Л41’> zk> 2ft+i]
(где j и k пробегают те же значения, что и только что).
Положив
mt, у, A = inf {/}, j k~ sup {/},
<Ti,hk>
имеем в силу 644, 7°,
m,. j, lAyj^Zk	J7’z) dy dz < Mit k^yj^zk
для всех значений x из [x,, х;+1]. Фиксируя произвольное значение
x=ki в этом промежутке, просуммируем подобные неравенства для
всех значений j и k; мы получим неравенства
Е Е т‘. i, k^y^zk < 1 (У = У> z) dy dz <
J *	</?)
^ЕЕ^-.лаАу/Д^-
J к
Наконец, умножим эти неравенства почленно на Дхг и просумми-
руем на этот раз по значку I:
222«и. АДх;ДууДгА ==£ Е a*z < Е Е Е м‘. j.
i J к	i	i j k
Крайние члены представляют собой суммы Дарбу для интеграла
(3) и стремятся к нему, как к пределу, при стремлении к нулю всех
разностей Дхг, Дуу, ДгА. Значит, к тому же пределу стремится и
интегральная сумма, стоящая посредине. Этим доказано одновременно
как существование интеграла (7), так и равенство (8).
314	ГЛ. XVIII. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ	[646
Если предположить еще существование простого интеграла
f
\f(x,y,z)dz	(9)
е
при любых значениях х из [а, Ь] и у из [с, d], то двойной интег-
рал в равенстве (8) можно заменить повторным [594] и окончательно
получим:
b d f
\\\f(x,y,z)dT=\dx^dy\f(x,ytz)dz.	(10)
(Г)	асе
Таким образом, вычисление тройного интеграла приводится к
последовательному вычислению трех простых интегралов. Роли пере-
менных х, у, z в формуле (10), разумеется, могут быть произвольно
переставлены.
Предлагаем читателю убедиться самому, что из существования
тройного интеграла (5) и простого интеграла (9) вытекает формула:
\\\f(x,y,z)dT=\\dxdy\)j\x,y,z)dz,	(11)
(Л	(Q) е
где Q = [a, b; с, d]. И здесь роли переменных можно переставлять.
В частности, для случая непрерывной функции f(x, у, z),
очевидно, имеют место все формулы (8), (10), (11) и им подобные,
получающиеся перестановкой переменных.
646.	Вычисление тройного интеграла по любой области. Как
и в п° 596, общий случай интеграла, распространенного на тело (V)
любой формы, может быть легко приведен к только что рассмотрен-
ному. Именно, если функция f(x, у, г) определена в области (V),
то вместо нее следует лишь ввести,
функцию f * (х, у, z), определенную
в объемлющем (V) прямоугольном
параллелепипеде ('/), полагая
'	(0	вне (V).
Этим путем и получаются все при-
водимые ниже формулы.
Рис. 99.	Мы остановимся на случаях, пред-
ставляющих наибольший интерес.
Пусть тело (V) содержится между плоскостями х = хй и х — Х
и каждою параллельною им плоскостью, отвечающею фиксированному
значению х(хй^х^Х), пересекается по некоторой фигуре, имею-
щей площадь; через (PJ обозначим ее проекцию на плоскость:-уz
647|	$ 1. ТРОЙНОЙ ИНТЕГРАЛ И ЕГО ВЫЧИСЛЕНИЕ	815
(рис. 99). Тогда
X
W\f(x,y,z)dV= \^х\\ f(x,y,z~)dydz	(8*)
(И	x0 (Рж)
в предположении существования тройного и двойного интегралов.
Это — аналог формулы (8).
Пусть, далее, тело (V) представляет собой «цилиндрический
брус», ограниченный снизу и сверху, соответственно, поверхностями
z = z(x,y) и z — Z(x,у),
проектирующимися на плоскость ху в некоторую фигуру (D), огра-
ниченную кривой {К) с площадью 0; с боков тело (V) ограничено
цилиндрической поверхностью с образующими, параллельными оси z,
и с кривой {К) в роли направляющей
(рис. 96). Тогда аналогично формуле
(11) имеем
\\\f(x,y,z)dV=
=	$ f(x,y, z)dz; (П*)
(D)	z0(x,y)
при этом предполагается существова-
ние тройного интеграла и простого —
внутреннего — интеграла справа.
Если область (D) представляет со-
бой криволинейную трапецию, ограни-
ченную двумя кривыми (рис. 100)
v = y0(x) и у=У(х) (х0 ==: х ==: X)
И прямыми х — ха, х = Х, то тело (V) подходит под оба типа, рас-
смотренных выше. Заменяя двойной интеграл — то ли в формуле (8 *),
то ли в формуле (11*) — повторным, получим
X У(х) Z(x, у)
$$\f(x, у, z)d V= $ dx $ dy $ f(x,y,z)dz.
(V)	Xo >o(x)	z0(x, y)
(10*)
Эта формула обобщает формулу (10)
Как и в простейшем случае, который был рассмотрен в преды-
дущем п°, и здесь непрерывность функции f(x,y,z) обеспечивает
ирвложимость всех формул (8*), (И*), (10*) и им подобных, полу-
чающихся из них перестановкой переменных х, у, z.
647.	Несобственные тройные интегралы. В случаях, когда об-
меть интегрирования простирается в бесконечность или подинтег-
Нвьная функция перестает быть ограниченной вблизи особых точек,
316
ГЛ. XVIII. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
[64
линий или поверхностей, несобственный тройной интеграл получаете
с помощью дополнительного предельного перехода, исходя из соб
ственного интеграла. Своеобразие многомерного случая по сравнении
с линейным случаем уже было отмечено в связи с изучение»
несобственных двойных интегралов, и сейчас к этому добавит!
нечего.
Несобственные тройные интегралы также являются необходимс
абсолютно сходящимися. Это обстоятельство сводит вест
вопрос о существовании и вычислении таких интегралов к случаи
положительной (неотрицательной) подинтегральной функции.
Ограничиваясь этим предположением, можно, как и в случае двой
ных интегралов, установить связь между тройным интегралом и раз
ного типа повторными интегралами. Остана
f	вливаться на этом мы не будем.
648.	Примеры. 1) Вычислить интеграл
ЛВжЬк	, С С С dx dydz
j||||k	J~ni<r+x+,+T)<-
распространенный на тетраедр (V), ограничивав-
У мый плоскостями x — Q, _у«=0, z = 0 и х-Ру4
4-z=l (рис. 101).
Решение. Проекцией тела на плоскость ху
/г	служит треугольник, образованный прямыми х=0
р 101	у = 0 и х4-у=1. Ясно, что границами измене
‘	‘	ния х служат числа 0 и 1, а при постоянном л
в этих границах переменная у изменяется от 0 дс
1 —х. Если же фиксированы и х, и у, то точка может перемещаться пс
вертикали от плоскости z = 0 до плоскости х4-у + 2=1; таким образом
пределами изменения z будут 0 и 1—х—у.
По формуле (10*) имеем
1	1—х 1—х—у
I dx dy ( TT—i  i Я •
J ? О+’К+З' + г)"
Последовательно вычисляем интегралы, начиная с внутреннего:
'	(14-^+у + г)’	2[(1+х4-^	4_|’
о
1-х
1 С Г ' 1	1Ъ _ Ч 1 з—
2 \ [(1 4- X 4-у)2	4 J ау — 2 U 4- 1	4
наконец,
648]	$ 1. ТРОЙНОЙ ИНТЕГРАЛ И ЕГО ВЫЧИСЛЕНИЕ
317
2) Вычислить интеграл
z dx dy dz,
У® 2^	- -
где (V) есть верхняя половина эллипсоида	+ ~2'С 1.
х1 у#
Решение. Проекцией тела на плоскость ху является эллипс
1. Поэтому пределами изменения х являются числа — а и а, при фиксиро-
ванном же х переменная у изменяется от — У а1—х3 до 4"|" У а*— х3.
Тело ограничено снизу плоскостью ху, а сверху — поверхностью эллипсоида,
так что при фиксированных х и у пределами изменения г служат
По той же формуле (10*)
° А
\ (ва —х’)2 dx* = ~ abc3.
<Ju Л	Я
Вычисление можно было бы провести и другим путем. Именно, по фор-
муле (8*), лишь меняя в ней роли переменных х и z, будем иметь
С	с
I — dz \ § z dx dy = ( z dz dx dy,
d	«	ir2)
где (/?ж) есть проекция на плоскость ху сечения эллипсоида плоскостью
Z=z (проектирование происходит без искажения). Но двойной интеграл
JS dxdy
Оу
• Ввиду четности подинтегральной функции.
318
ГЛ. XVIII. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ	(648
есть не что иное, как площадь этой проекции. Так как контур проекции
имеет на плоскости ху уравнение
т. е. представляет собою эллипс с полуосями
то, как мы уже знаем,
/ za\
Следовательно,
i «.С Л - г*\ а я
Г = паЬ \ z 11-----з- аг = —.
J \ с2 /	4
о
Выкладка значительно упростилась, но лишь потому, что удалось ио
пользовать известную нам величину площади эллипса.
3) Вычислить интеграл
£==Ш
(V)
у* z*
где (Г) есть весь эллипсоид-^4-^ +^-^1.
Решение. Применяя второй способ, указанный при решении преды
дущей задачи, получим
“	* а	с 2
L = dx dy dz 4-	~ dy dz dx 4- dz dx dy.
-°	(Ч) -ь (%) -с сУ
Отсюда
а	b
—а	— &
с
nab С . !.	г‘\ .	4
—г- \ гг 1-----s- ] dz —	• nabc
с2 J \	с2/	5
— с
4) Вычислить интеграл
7 = J J J z dxdydz,
(А)
где тело (Д) ограничено конической поверхностью г2 = (хг 4~>2) и пло
скостью z — h (рис. 102).
648]
S 1. ТРОЙНОЙ ИНТЕГРАЛ И ЕГО ВЫЧИСЛЕНИЕ
319
л2 1
(х* -Ь У2) ] dx dy
Решение, (а) Проекция (О) конуса на плоскость ху есть круг
х* -\-ys ^R2. По формуле (И*)
л
I— dxdy	zdz = ~
•А
или, переходя к полярным координатам,
2® к
i f л Г/ы «. . r.R^h2
1 = 2rA rf8 \ (/?	r*>rdr = ——
о о
(б) При другом способе решения можно написать
л
1 = £ z dz f dx dy,
о (D)
где (D) есть проекция на плоскость ху сечения конуса плоскостью, ей парал-
лельной и лежащей на высоте z над нею. Эта проекция
1	Rz
есть круг радиуса так что двойной интеграл,
представляющий его площадь, равен Отсюда
* ,
, С . nRW
1 р’
5)	Вычислить интеграл
7<= j j j х dx dy dz,
<V)
г.
Рис. 102.
7
где (V) есть призма, ограниченная плоскостями
*=0, у = 0, z = 0, y = h и x-\-z—a.
У к а з а н и к. Воспользоваться формулой (8*); (Рх) есть прямоугольник
во сторонами h и а — х.
Ответ: K=s-.
о
6)	Найти значение интеграла
z2 dx dy dz,
где (Г) есть общая часть двух сфер (рис. 103):
Решение. Пересечение их поверхностей происходит по плоскости z =
•4^-. Сечения тела (Г) плоскостями, параллельными плоскости ху, суть круги.
320
ГЛ. XVIII. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
(648
Переходя и здесь к повторному интегралу — простому от двойного, найдем.
что
J=ti \ z2(2/?z— z2)rfz4~’c \ z2 (7?2 — z2)dz
7)	Вычислить интеграл
S = j (х 4-3’ + z)2 dx dy dz,
где (V) есть общая часть параболоида х2 -j-y2^az и сферы х2 4~3’s 4~ г’ === За2
Решение. Прежде всего, раскрывая под-
интегральное выражение, видим, что интеграль
от членов 2ху, 2xz, 2уг по соображениям сим-
метрии исчезают *. Таким образом,
S = J	(х2 4-у2 + z2) dx dy dz.
По формуле (8*) (с перестановкой ролей д
и z)
S = f dz j J (x! 4-3»2 + z2) dx dy 4-
0	x3+y2^2az
aV~3
\ dz И	(х2 + у2 + z2) dx dy
а № + У2 =5 За2 — z3
Двойные интегралы легко вычисляются с помощью перехода к поляр
ным координатам:
V 2az
2л j (г2 4- z2) г dr = 2л (a2z2 4- az’),
2л (	(г2 4- г2) г dr = у л (9а1 — z1).
Отсюда
a	a V~3
5 = 2л (a2z2 -j-az’)dz 4-у л (9а1—zi)dz =
* Это можно обосновать (прибегнув к повторным интегралам) свой
ствами лишь простых и двойных интегралов.
648}
§ 1. ТРОЙНОЙ ИНТЕГРАЛ И ЕГО ВЫЧИСЛЕНИЕ’
321
8)	Вычислить интеграл
7 = j | J (x2 + ys + z2) dxdy dz,
где (Г) есть общая часть конуса у?2 4-z2 =<х2 и сферы х2 4-у* 4* z2=== ^?2 (х ^0).
Ответ. / =	(2 —У"2).
п\ ГТ	I Z \3	(Х \2 1 I У\2
9)	Пусть дан конус ( —I ==	+ \~\ ;
плоскостью z = e он пересекается по эллипсу,
проекция которого на плоскость ху имеет урав-
(X \2	/ у \2
— 1 4- (-у 1 = 1. Рассмотрим'тело (V), ле-
жащее в первом октанте и ограниченное упомя-
нутыми конической поверхностью и плоскостью
z = c, а также двумя координатными плоскостями
х = 0 и у = 0 (рис. 104).
Предлагается вычислить распространенный на
это тело интеграл
Д =
~ dx dy dz.
z
(а)	Интегрируя сначала по z, затем по у и, наконец, по х, находим пре-
делы изменения:
для х: 0 и а, для у: 0 и b ^/~ 1 — ~,
Тогда
и последовательно
»]Л-(£)2
1/" г	Л ___Г / х \21
Л=1«>Г7.
11 Г. М. Фихтенгольц, т. Ш
322	гл. XVIII. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ	(648
(б)	Выкладки немного упрощаются, если интегрировать в обратном
порядке. На плоскость yz наше тело проектируется в виде треугольника, огра-
ниченного прямыми у = 0, z = c иу = г. Поэтому пределы изменения будут
для z: 0 и с, для у\ О и — г,
с
для х: Она
и искомый интеграл перепишется так:
В этом случае
с 1
.	1 а*Ьг С -о .	1
dz=x>a b v с-
(10) Найти интегралы
(а)	z™ dx dy dz, (б) Za = хт dx dy dz,
где тело (¥)<—то же, что и в предыдущей задаче (т— натуральное).
У Казани е. Интегрирования расположить в том же порядке, как и в 9) (б)
Во втором случае интеграл
ь
~7г	m +1
приводится к известному интегралу
_	, . . к abcm+l
Ответ, (a)
2
5 cos^+Mrffl [300, 1)].
о
(б) 1г =
ат+1Ьс(т—1)1! я
т + 3 (т + 2)!! 2"
аот+1&с (т —1)1!
 т 4- 3 (т 4- 2)1!
(при т четном),
(при т нечетном).
«49]
5 1. ТРОЙНОЙ ИНТЕГРАЛ и ЕГО ВЫЧИСЛЕНИЕ
323
11) Вычислить интеграл
н= (И	r ^^ydz.-^ («>₽>7>0).
J J	V а!х*4-ву 4-7*2*
Х.у ,ZS:0	1	1
** +.У3+ **==₽*
Решение. Имеем
R VR’-x3 Уф-х* ->»
// = ? х rfx	у dy ?	Z dZ ц» у-;
(J	0	0	/ а*Х*4-₽*у*4-752*
, У ^2 —X3—>2
\	... dz = ±- [Y7*дз 4- (а* — 7*) Xs 4- (₽’ — 72)у3 — Vа2х2 4-р2у21,
•К₽2_Х2	3
-A- j [...] ydy = -3p-^J_ f) [^ 4- (*a - П*2Р-
1	— a*
~ 37*(P*-72) [78*’ + («a-7’)*8]2 +зЙХ’
и, наконец, после элементарных (хоть и длинных) преобразований
и _ Я5	Pl + 7а 4~ аЭ
15 (₽-И) (т 4-“)(“ + ?) •
12)	Показать, что употребительные формулы для вычисления (а) объема
цилиндрического бруса, ограниченного поверхностью z = «(x, у),
V == И z dx dy
<Р)
В (б) объема тела по поперечным сечениям:
ь
V = j Q (х) dx
а
суть следствия основной формулы:

У Казание. Применить к последнему интегралу формулы (11*) и (8*)*.
649.	Механические приложения. Естественно, что все геометрические
и механические величины, связанные с распределением масс в пределах неко-
торого тела (V) в пространстве, в принципе выражаются на этот раз трой-
ными интегралами, распространенными на тело (У). Здесь также проще всего
иользоваться принципом «суммирования бесконечно малых элементов» [ср.
348—356 и 598].
* Дальнейшие примеры на вычисление тройных интегралов можно позаим-
ствовать из п° 675, где рассматриваются интегралы n-й кратности, взяв там п=3.
11*
324	ГЛ. XVIII. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ	(649
(12)
Обозначим через р плотность распределения масс в произвольной точке
тела (V); она является функцией от координат точки; эту функцию мы будем
всегда предполагать непрерывной. Суммируя элементы массы dtn = pdV=
= р dx dy dz, для величины всей массы будем иметь
"* = j	pdxdydz
{ср. 642].
Исходя из элементарных статических моментов
dMyz = xdm — Xf dV, dMzx =y dm =yp dV,
dMxy — z dm — Zf dV,
найдем самые статические моменты:
Л1.уг = ((( хр dV, Mzx
(Ю

(13)
(Ю
а по ним — и координаты центра
т
тяжести:
т
У-?"*7
т
(И)

В случае однородного тела, р = const, получаем проще:
V ’ и
t

V
Сами собой понятны и формулы
осей координат:
^=H№2+zS)?rflz>
(Ю
для моментов инерции относительно
/у=ИИг2+х2>₽^’
(V)
{x*+ys)?dv
(15)
или относительно координатных плоскостей:

(16)
Наконец, пусть массы, заполняющие тело (V), оказывают притяжение н<
точку Л (?, т), С) (массы 1) по закону Ньютона. Сила притяжения со сто'
роны элемента dtn = pdV массы имеет на оси координат проекции*
^ = ^=^р«/И, dFv=^^pdV, dFz = Z-^~pdV,
Л	рЦ Г '	у	рЗ Г ’	*	рЗ *	*
где
г = V (х - 5)2 + (у - Т])2 + (Z - 0»
* См. сноску ** на стр. 277.
650|	§ L ТРОЙНОЙ ИНТЕГРАЛ И ЕГО ВЫЧИСЛЕНИЕ
325
есть расстояние элемента (или точки, в которой мы считаем сосредоточен-
ной его массу) от точки А. Суммируя, для проекций полной силы F при-
тяжения на оси координат получим
(Ю
г3 г
(П)
5 р dv-
(V) J
Аналогично определяется и потенциал нашего тела на точку:

(18)
Если точка А лежит вне тела, то все эти интегралы оказываются соб-
ственными. В этом случае можно дифференцировать интеграл W по любой
из переменных 5, т;, С под знаком интеграла на основании соображений, сход-
ных с теми, которыми мы пользовались в отношении простых интегралов
[507]. В результате мы и получим, что
ft ~ Гх’ дг, — ГУ’ ft ~~
(19)
В случае же, когда точка А сама принадлежит телу (V), в этой точке
Г = 0, и подинтегральные функции в (17) и (18) вблизи нее перестают быть
ограниченными. Ниже [663] будет показано, что эти интегралы, как несоб-
ственные, все же существуют, и для них выполняются основные соотноше-
ния (19).
650.	Примеры. 1) В 598 для статических моментов однородного цилин*
дрического бруса (при р = 1) мы имели формулы:
Муг = ^zxdxdy, Мгх = zy dx dy, = z~dx dy.
(P't	(P)	(P)
Вывести их из общих формул (13) предыдущего п°.
Имеем, например,
z(.e, у)
Мху = J И z dV = ( ( dx dy ( z rfz;
(V)	(P)	8
Ho	z(x,y)	z=z(x,y)
Z dz = ~ z2
О	2=0
что и приводит к требуемому результату.
В 598 взамен вычисления последнего интеграла были привлечены сообра-
жения из области механики (относительно статического момента элементар-
ного столбика).
2)	Аналогично, в предположении, что площадь поперечного сечения
тела (V), параллельного некоторой плоскости, задана в функции расстояниях
сечения от этой плоскости: Р (х), в 356 1) была выведена для статического
момента формула	ъ
М = х Р (х) dx.
а
Ее также можно получить, как следствие из общей формулы.
326
ГЛ. XVIII. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
[650
Именно, по формуле (8*)
ь
M = J (J xdy=jxdxjj dy dz',
(V)	а (PJ
но внутренний интеграл как раз и выражает площадь сечения, которая на-
перед дана.
Замечание. Эти примеры привлекают наше внимание к тому факту,
что некоторые из механических величин, относящихся к простран-
ственному распределению масс, выражались (правда, при простейших
предположениях) двойными и даже простыми интегралами. Эта иллю-
зия понижения кратности интеграла,- как читатель видит, проистекает из того,
что при представлении тройного интеграла в виде двойного от простого или
простого от двойного внутренний интеграл в простых случаях оказывается
уже известным из геометрических или механических соображений и не
Нуждается в вычислении.
3)	Использовать задачи 2), 4), 10) п’ 648 для определения положения
центров тяжести рассмотренных там тел.
4)	Найти центр тяжести тела, ограниченного поверхностями параболоида
Xs + у* = 2az и сферы х2+jy2-[-z2=3c2
Решение. Статический момент относительно плоскости ху проще
всего вычислить по формуле, упомянутой в 2), с заменой лишь х на z. Пло-
щадь R (z) поперечного сечения равна тс-2аг для z от 0 до а и тс (Зе2— z2)
для z от а до d /3. Таким образом,
МХу = 2тсе \ z2dz -|- тс
б
а У~3
(•
\ (Зе2 — zs)dz = —г,а\
•) **
а
Так как объем тела уже известен: V= —-(6 У 3 — 5) [343, 6)], то С =
и
5	—
= оо(6 У 3-{-5)а. По соображениям симметрии: 5 = 71 = 0.
ОО
5)	Найти массу и определить положение центра тяжести сферы
х2-Н2 + z2 sg 2az,
если плотность в точках сферы обратно пропорциональна расстоянию этих
точек от начала координат:
_________k______
?~~У xl-j-y2-j-z2 *
Решение. По формуле (12) п° 648 масса
f С С
+’
Преобразуя тройной интеграл аналогично (8*), можно представить его в виде
йростого интеграла от двойного:
«50]
9 1. ТРОЙНОЙ ИНТЕГРАЛ И ЕГО ВЫЧИСЛЕНИЕ
327
~где (Rz) есть круг радиуса )/’2ez — г*. Внутренний интеграл без труда
числяется, если перейти к полярным координатам;
он оказывается равным
2я V 2аг — z3
С С rdrdfi „	.
\ \ 3 = 2к^2аг ~г)-
J J V г» -L 9^
Отсюда
< г. о
т = -Q- ляа2.
о
Аналогично вычисляется и статический мо-
мент
ь С С С zdxdydz 16 . .
Mxv — K	\ \ \		- = т-g- nka-.
у	j J J	Y х2 4- у2 4-z2	15
JC2+^ + z2=S2az V
ВЫ-
центра тяжести,
4
Таким образом, С = —а. Остальные две координаты
видно, равны 0.
6)	Та же задача, но при другом законе распределения масс:
к
оче-
Р ха+.У2 + га ’
лриводит к результатам:
т = 2nka,
Mx = nkas, С = 4
л ’	2
'-sis*'
В дальнейших задачах плотность р распределения масс предполагаем
постоянной.
7)	Найти притяжение центра основания цилиндра всей массой цилиндра
(рис. 105).
При обозначениях рис. 105 имеем [см. 648, (17)]
л
И dXdy \ ----------PZrfZ.£ =
х2+>2^₽2 О (x2+y+z2)2
( 1 1 \..
р ...... :----7=====^ \dxdy =
„ W 4- У2	Y Xs 4- Vs 4- й2 /
= 2лр(7?4-й — Y R'+h*)-,
остальные две слагающие притяжения равны 0, так что притяжение на-
правлено вертикально вверх.
8)	Найти притяжение конусом его вершины (рис. 106).
Ответ, F= Ft = (I — й).
328
ГЛ. XVIII. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
|65(
9)	Найти притяжение, испытываемое любой точкой А (массы 1) со сто-
роны сферы (рис. 107).
Решение. Обозначим радиус сферы через R, а расстояние О А через а
Оси координат расположим так, чтобы положительное направление оси г
проходило через точку А. Тогда
мп—
R
dx dy dz —
dx dy
J .1
X^+y^R^-Z^ [л.2+>,з_{_(2_д)2]2
Внутренний интеграл легко вычислить путем перехода к полярным коорди-
натам,
он равен
Затем,
Fz = 2тср
Ho
—R
-R
’2 — 2az-\-a2j‘
,2 — 2az + a2_
dz.
R
Z-а	С .	/ X ,
-—dz= у sign (z — a) dz —
-R
— 2R, если Ofl,
— 2a, если a
С помощью подстановки t = f/rR2— 2az-\-a2 легко вычислить и второй
интеграл:
-R
________= dz =
2az -|- а2
о оз
*5—»—2R, если a ^R,
За2’	’
4
--5- а, если a^R,
О
R
R
1
1
R
— R
z — a
z— a
z — a
650)
§ 1. ТРОЙНОЙ ИНТЕГРАЛ И ЕГО ВЫЧИСЛЕНИЕ
329
Окончательно получаем, что
4	1
—, если a^R,
F —
г~\	4
—пер, если a^R.
О
В то же время, очевидно, Fx= Fy = 0. Итак, во всех случаях притяжение
направлено к центру сферы.
При этом точка, находящаяся вне сферы (a$zR), испытывает со сто-
роны последней такое же притяжение, какое испытывало бы, если бы
4
в центре сферы была сосредоточена вся ее масса m = ^-r,R3p. С другой
О
стороны, так как по отношению к точке, лежащей внутри сферы (в < R),
притяжение не зависит от R (и имеет такую же величину, как и в случае
/? = а), то ясно, что наружный сферический слой не оказывает на внут-
реннюю точку никакого действия.
10)	Найти потенциал цилиндра на центр его основания.
Указание. Здесь проще начать с интегрирования по х и у, причем
двойной интеграл вычислить с привлечением полярных координат:
а	а
W= { р dz Н dxdy- — = 2др (/^4-2з_г) dz =
= pnT?2 • In h +	4- рпл (/ 7?2 + ha — h).
f\
И) Найти потенциал конуса (а) на его вершину и (б) на центр его осно-
вания.
У казание — то же.
Ответ, (а) 1Г=пй(/—й)р;
mi wz яЯ!Л3 R (I + Я) , п/?2й ,D ..
(б)	1F=—pin	+ -72- Р (/? — К).
12) Найти потенциал сферы на произвольную точку А.
Решение. При обозначениях задачи 9) имеем
______dx dy_____
У x* + y* + (z—a)s
R ________________
= 2np J (уR2— 2e«-f-a2 — \z — a\)dz.
-R
Различая случаи a R, имеем далее
R
J У R2 — 2az + a2 dz= ±[(R + a)* — | R — a |3] =
~R
, 2	1
-|^.±4-27?a (a^R),
4a24-2/?2	(a^R),
a
330	ГЛ. XVIH. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ	(65С
Я	( 2Ra	(a^R),
\ lz — a I dz — <
Л	I а24-/?2 (asgtf).
Таким образом,
г	4	1
у «/?»₽• у
М	Г	2 X
12л/?2-х- т.а2)	р (а /?).
Мы видим прежде всего, что потенциал на точку, лежащую вне сфе-
ры, таков же, как если бы вся масса сферы была сосредоточена в et
центре.
Вторая же из полученных формул приводит к такому следствию. Еслг
рассмотреть полую сферу с внутренним радиусом Rt и внешним радиу-
сом /?21 то ее потенциал на точку, лежащую в полости (а < R,), предста-
вится в виде разности
!	2	\	I	2	\
1Г= 1Г2 — W\ = [2nRI — 4t«zs р — 2л/?2 —4^s р =
\	о	/	\	о	}
= 2л(/?2-/?2)р
и не зависит от а. Потенциал полой сферы в пределах полости сохраняет
постоянную величину.
z
Рис. 108.
13) При обозначениях рис. 108 найти моменты инерции тора: Iz и 1Х
[См. 648 (15).]
Указание. Имеем
4 = 2pUz $ J U8 + У3) dx dy,
0	tf?=S*2 + .y2=S/?|
а
lx — 2р j dz J J (ys + 2s) dx dy,
0	Я’^+У^Я2
где R, — d—a2 — z3, /?2 = d j/^a2— z2. Двойные интегралы вычисли
ются переходом к полярным координатам
Ответ. — atd (4ds За2) р, Ix — ~ a2d (4d2 -]* 5а2) р.
455OJ	$ 1. ТРОЙНОЙ ИНТЕГРАЛ И ЕГО ВЫЧИСЛЕНИЕ
331
14) Пусть тело (V) вращается вокруг оси z с угловой скоростью и.
Тогда для элемента dm = fdV, отстоящего от оси вращения на расстояние
г = У х3 4- у3, линейная скорость будет t> = r<o, а следовательно кинети-
15) Поставим теперь задачей вычислить момент инерции рассматривае-
мого тела (V) относительно произвольной оси и (рис. 109), составляющий
е координатными осями, соответственно, углы а, ₽, 7.
Для расстояния МЬ = Ъ произвольной точки M(x,y,z) тела от оси
имеем 82 = г2— d3, где, как известно из аналитической геометрии,
Г3 = х3 Уг +	— х cos а у cos ₽ z cos 7 *.
Так как cos2 а 4- cos2 ₽ 4“ cos2 7=1, получаем отсюда
В2 — х3 (cos2 ₽ 4- cos2 7) 4- ys (cos2 7 4- cos2 a) -|- z2 (cos2 a 4- cos2 fl) —
— 2yz cos ₽ cos 7 — 2zx cos 7 cos a — 2xy cos a cos P-
Теперь ясно, что
/а =	82p dV = Ix cos2 a 4-1 у cos2 ₽ 4- Iz cos2 7 —
(ю
— 2Kyz cos ₽ cos 7 — 2KZX cos 7 cos a — 2Kxy cos a cos p,
где
=	Кгх — ( И zxp dV, KXy = W\xy^dV.
(Ю	(k)	(V)
Последние интегралы носят название произведений инерции или
Центробежных моментов [ср. 599, 5)].
Если пожелать наглядно изобразить распределение моментов инерции
тела относительно различных осей, проходящих через начало, то аналогично
|ому, как мы это делали для плоской фигуры, следует на каждой оси и от-
ложить отрезок
CW = -4
Ьусть
„	COS a v cos 8 cos 7
X= CWcosa =	Y=——=. Z——==
V lu	V lu'
* Последнее соотношение есть запись того факта, что точка М лежит
плоскости, проходящей перпендикулярно к оси на расстоянии d от начала.
332	гл. XVin. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ	(650
будут координаты конца N этого отрезка. Тогда из найденного для /в вы-
ражения легко получить уравнение геометрического места точек Nt
/хХ2 + 1у Г + 4Z2 - 2Kyz YZ — 2KzxZX— 2KxyXY= 1.
Так как ON не обращается в бесконечность, то эта поверхность вто-
рого порядка необходимо является эллипсоидом; она носит название эллип-
соида инерции. При исследовании движения твердого тела важную роль
играют оси эллипсоида инерции, называемые главными, осями инерции1, если
точка О есть центр тяжести тела, то соответствующие оси инерции назы-
ваются главными центральными осями инерции.
Будет ли та или другая из координатных осей главной осью инерции,
зависит от центробежных моментов. Например, для того чтобы ось
х была главной осью инерции, необходимо и достаточно выполнение условий
л^=о, KZX = Q.
В частности, они выполняются, если массы расположены симметрично от-
носительно плоскости уг.
16) Рассмотрим, в заключение, вопрос о центробежной силе,
развивающейся при вращении твердого тела вокруг оси.
Если тело (И) вращается вокруг оси г с угловой скоростью ш, то на
элемент dm = p dV тела будет действовать элементарная центробежная сила
величины
dF — tiflr dm = w2rp dV,
где г есть расстояние элемента от оси вращения. Ее проекции на коорди-
натные оси будут
dFx = ^xPdV, dFy = ^2ypdV, dFz = 0,
так что проекции результирующей центробежной силы F выразятся
интегралами
Fx = <*2\\\xt>dV=^Myz, Fy = ^Mzx, FZ = Q,
(Ю
где Myz, Mzx — статические моменты нашего тела. Если через J, •/;, С обоз-
начить координаты центра тяжести тела, то эти формулы перепишутся так:
Fx — Fy = т, Fz -- 0.
Отсюда видно, что упомянутая результирующая центробежная сила F
в точности такова, как если бы вся масса тела была сосредоточена в
его центре тяжести.
Элементарная центробежная сила, о которой выше была речь, имеет
следующие моменты относительно координатных осей:
dMx = z dFy = «2угр dV, dMy — z dFx — <a2zxp dV, dMz = 0.
Следовательно, результирующие моменты относительно этих осей будут:
Mx = ^\\\yzPdV=<^.Kyz, Му = <ь2Кгх, Мг = 0.
(V)
Для того чтобы центробежные силы взаимно уравновешивались и не
оказывали никакого действия на вал (а через его посредство — на подшип-
ники, в которых он укреплен), необходимы и достаточны условия:
M^ = 0, Л1гх=0, Куг=0, Kzx = 0.
651J
t 2. ФОРМУЛА ГАУССА - ОСТРОГРАДСКОГО
333
Первые два означают, что центр тяжести тела должен лежать на осиz;
пусть это и будет начало О. Последние же два показывают, что ось z должна
быть одной из главных осей инерции. Итак, центробежная сила не произ-
водит давления на подшипники лишь при условии, если ось вращения со-
впадает с одной из главных центральных осей инерции вращающего-
ся тела.
§ 2.	Формула Гаусса — Остроградского
651.	Формула Остроградского. В теории двойных интегралов мы
ознакомились с формулой Грина, связывающей двойной интеграл
по плоской области с криволинейным интегралом по контуру области.
Ее аналогом в теории тройных интегралов служит формула Остро-
градского, связывающая тройной интеграл по пространственной
области с поверхностным интегралом на границе области.
Рассмотрим тело (V) (рис. 96), ограниченное кусочно-гладкими
поверхностями ,
($i) z = z^(x,y}
№) z=Z(x, у) ( ° j
' и цилиндрической поверхностью (Sa), образующие которой парал-
' лельны оси z. Направляющей здесь служит кусочно-гладкая замкну-
тая кривая (R) на плоскости ху, ограничивающая область (О) — проек-
цию тела (V) на эту плоскость.
Допустим, что в области (V) определена некоторая функция
dR
R (х, у, z), непрерывная вместе со своей производной во всей
области (Г), включая ее границу. Тогда имеет место формула
dx dy dz —	R dx dy,
(1)
причем R есть поверхность, ограничивающая тело, и интеграл справа
распространен на внешнюю ее сторону.
Действительно, по формуле (11*) п° 645,
dR , , , И j J	С dR-.i
dx dy dz= \ \ dx dy	\	-^dz =
Ю)	г0 (X, у)
= ^R(x, у, Z(x, y))dxdy — ^R(x, у, z9(x, v))dxdy.
(О)	(О)
Если ввести в рассмотрение поверхностные интегралы, то, в силу
формул (3) и (3*) п° 635,
\ dx dy dz = R (х, у, z) dx dy R (х, у, z) dx dy,
J (V)	№)	(V
причем первый из интегралов справа распространен на верхнюю
334
ГЛ. XVIII. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
1651
сторону поверхности (53), а второй — на нижнюю сторону поверх-
ности (51). Равенство не нарушится, если мы прибавим к правой его
части интеграл
R (х, у, z) dx dy,
(S2)
распространенный на внешнюю сторону поверхности (53), так как
этот интеграл равен нулю [635, (5)]. Объединяя все три поверхност-
ных интеграла в один, мы и придем к формуле (1), которая пред-
ставляет собой частный случай формулы Остроградского.
В приведенном рассуждении читатель, вероятно, уже усмотрел
сходство с тем, с помощью которого в п° 638 была выведена фор-
мула (14) для объема тела (У): эта последняя получается из фор-
мулы (1) при R(x, у, z) = z.
Как и там, легко понять, что формула (1) верна для более широ-
кого класса тел, которые могут быть разложены на части изученного
типа. Можно доказать также, что формула (1) справедлива вообще
для тел, ограниченных произвольными кусочно-гладкими поверхностями.
Доказательство проводится в основном так же, как и в п° 638,
при расширении условий применимости формулы для объема. К этому
добавим только одно замечание. Если рассматриваемое тело (У) пред-
ставляет собой «призматический брус», ограниченный, скажем, справа
поверхностью x = g(y, z), то изложенное в п° 638 рассуждение
переносится на настоящий случай лишь в предположении, что функ-
ции R и ~ определены и непрерывны и в некоторой области справа
от упомянутой поверхности (ибо вписанная многогранная поверхность
может и выйти несколько за пределы рассматриваемого тела)*.
Аналогично формуле (1) имеют место и формулы:
dx dy	Р dy dz,
dx d_y d^ = Q d^ dx,
J (V) У	IS)
(2)
(3)
если функции P и Q непрерывны в области (У) вместе со своими
дР dQ
производными и
Сложив все три формулы (1), (2), (3), мы и придем к общей
формуле Остроградского:

dx dydz= Р dy dz -f- Q dz dx	R dx dy. (4)
* На деле для верности формулы это предположение несущест-
венно.
652]	§ 2. ФОРМУЛА ГАУССА - ОСТРОГРАДСКОГО	335
Она выражает общего вида поверхностный интеграл второго типа,
распространенный на внешнюю сторону замкнутой поверхности, через
тройной интеграл, взятый по телу, ограниченному этой поверхностью.
Если привлечь к рассмотрению поверхностные интегралы первого
типа, то получим другой, весьма употребительный и легко запоми-
наемый вид формулы Остроградского:
IV)
= (Р cos X -{- Q cos р. + R cos v) dS, (5)
(S)
где X, |i, v суть углы, составленные внешней нормалью к поверх-
ности (S) с координатными осями.
Замечание. Формулы Грина, Стокса и Остроград-
ского объединены одной идеей: они выражают интеграл, распро-
страненный на некоторый геометрический образ, через интеграл, взя-
тый по границе этого образа. При этом формула Грина относится
к случаю двумерного пространства, формула Стокса — также к
случаю двумерного, но «кривого» пространства, а формула Остро-
градского — к случаю трехмерного пространства.
На основную формулу интегрального исчисления
ь
\Г (х) dx=f(b) —f(a)
а
мы можем смотреть, как на некоторый аналог этих формул для
одномерного пространства.
652.	Приложение формулы Остроградского к исследованию
поверхностных интегралов. Пусть в некоторой открытой области (Г)
трехмерного пространства заданы непрерывные функции Р, Q, R.
Взяв любую замкнутую поверхность (5), лежащую в этой области и
ограничивающую некоторое тело, рассмотрим поверхностный интеграл
Р dy dz -{- Q dz dx -{- R dx dy =
kS)
— 5 5 (P c°s X -{- Q cos fi -{- R cos v) dS. (6)
(5)
Какому условию должны удовлетворять функции Р, Q, R,
чтобы интеграл (6) всякий раз оказывался равным нулю?
Эта задача аналогична задаче об обращении в нуль криволиней-
ного интеграла по замкнутому контуру [601, 641], которая легко
разрешалась с помощью формулы Грина или Стокса. Здесь же
йы прибегнем к формуле Остроградского, предполагая, конечно,
836
ГЛ. XVIII. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
(653
что для функций Р, Q, R существуют и непрерывны те производ-
ные, которые фигурируют в этой формуле.
Однако для того чтобы иметь право преобразовать интеграл (6)
по формуле Остроградского, необходимо и в настоящем случае
наложить некоторое ограничение непосредственно на основную об-
ласть (Г). Именно, нужно потребовать, чтобы, лишь только обла-
сти (Т) принадлежит простая замкнутая поверхность (S), огра-
ничивающая извне тело (V), то и это тело также целиком со-
держится в указанной области. Область, обладающую этим свой-
ством, называют («пространственно») односвязной [ср.
641]. Сущность этого типа односвязности состоит в отсутствии «дыр»,
хотя бы и точечных; по отношению к телу, не простирающемуся
в бесконечность, можно было бы попросту потребовать, чтобы его
границей служила одна-единственная замкнутая поверхность
[ср. 659]. Поэтому, например, в отличие от сказанного по поводу
«поверхностной» односвязности в 641, здесь тор будет односвязным
телом, а полая сфера — нет.
Формула Гаусса—Ос тр о г р а д с к о г о сразу приводит к ис-
комому условию:
. д/?__о
дх ' ду ' dz
(В)
Достаточность его очевидна, а необходимость легко
доказывается с помощью дифференцирования тройного интеграла по
области [644, 8°].
Аналогично случаю криволинейных интегралов, вопрос об обра-
щении в нуль интеграла по замкнутой поверхности оказывается рав-
носильным вопросу о независимости интеграла по незамкнутой по-
верхности, «натянутой» на данный контур, от формы поверхности.
Останавливаться на этом не станем.
В заключение заметим, что если требование непрерывности функ-
ций Р, Q, R и их производных нарушено в одной или нескольких
точках области (Т), то и при выполнении равенства (В) интеграл (6)
может оказаться отличным от нуля. Но в этом случае нетрудно
установить, что интеграл (6) имеет одно и то же значение для всех
замкнутых поверхностей (S), охватывающих определенную особую
точку [ср. 562].
Все эти обстоятельства иллюстрируются на примере интеграла
Гаусса, которому мы посвящаем следующий п°. -
653.	Интеграл Гаусса. Так называется интеграл
G=^ cos^n).^
(s)
где г есть длина радиуса-вектора, соединяющего постоянную точку А (;, т;, С)
с переменной точкой М (х, у, г) поверхности:
г=V (^-5)2+О’-’1)3+(г-(;п
653]
t 2. ФОРМУЛА ГАУССА — ОСТРОГРАДСКОГО
337
а через (г, п) обозначен угол между этим радиусом-вектором и нормалью к
поверхности в точке М При этом поверхность (S) предполагается двусто-
ронней, и нормаль п отвечает определенной ее стороне.
Если направляющие косинусы нормали суть cosX, cos р., cost, то
cos (г, п) = cos (х, г) cos X -|- cos (у, г) cos и + cos (z, г) cos ч =
х— $	, , у — -п , z — Z
— -----COS X 4- --L COS р ч---cos ч.
г ~ г 11 г
Таким образом, интеграл Г а у с с а перепишется так:
(S)
= И dy dzdz dxdx dy.
(S)
Здесь
p = ^, Q=^,
так что
dP_ 1	3(x — 5)2 dQ _ 1	3(> — y])2 dP_ 1	3(z — Q2
dx r3 r3 ’ dy r3 r3 ’ dz r3 r3
Легко проверить выполнение условия (В) во всем пространстве, исклю-
чая точку А (;, 7], С), в которой функции Р, Q, Р терпят разрыв. Следо-
вательно, интеграл Г а у с с а, взятый по замкнутой поверхности, равен нулю,
если поверхность не охватывает точки А. Для всех же поверхностей, со-
держащих эту точку внутри себя, интеграл сохраняет одно и то же значе-
ние. Его легко найти, если за поверхность (S) взять, например, сферу, опи-
санную радиусом Р вокруг точки А. Здесь радиус-вектор точки сферы со-
храняет постоянную длину, а направление его совпадает с направлением
внешней нормали к сфере, так что cos (г, п) = 1. Имеем:
(S)
таково значение интеграла Г а у с с а для всех поверхностей, окружающих
точку А.
Все эти результаты легко устанавливаются и непосредственно, если ис-
ходить из геометрического смысла интеграла Г а у с с а, как меры телесного
угла *, nod которым поверхность (S) видна из точки А.
Для доказательства этого предположим сначала, что поверхность (S) пере-
секается с каждым лучом, исходящим из точки А, не более, чем в одной точке.
Пусть нормаль п направлена в сторону, противоположную точке А. Взяв эле-
мент (dS) поверхности (S), выберем точку М на нем и проведем через эту
точку сферу с центром в точке А. Если спроектировать элемент (</3)изДна
* Телесным углом называется часть пространства, ограниченная
некоторой конической поверхностью; вершина конуса является вершиной
угла. Если вокруг вершины описать сферу единичного радиуса, то упомяну-
тая коническая поверхность вырежет на ней фигуру, площадь которой и слу-
жит мерой телесного угла.
338	ГЛ. XVIII. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ	(654
упомянутую сферу, то площадь проекции будет*:
cos (г, n) dS,
так что площадь фигуры, вырезанной исходящими из А лучами зрения на
сфере единичного радиуса, будет:
Это и есть (телесный) угол видимости элемента (rfS). Мерой же угла видимости
всей поверхности (8) служит сумма всех элементарных углов, т. е. интеграл G.
Если поверхность (S) пересекается с лучами, исходящими из А, более чем
в одной точке, но может-быть разложена на части, каждая из которых пе-
ресекается этими лучами уже лишь в одной точке, то нужно лишь просум-
мировать интегралы Г аусса, относящиеся к этим частям.
Обычно выбирается определенная сторона поверхности, и направление нор-
мали п согласуют с этим выбором. Тогда для одних участков поверхности эта
нормаль окажется направленной в сторону, противоположную Л, и угол види-
мости получится с плюсом; для других же участков, где нормаль направлена
в сторону А, этот угол получится с минусом. Интеграл Гаусса будет алге-
браической суммой этих углов видимости.
Из геометрического истолкования интеграла Г аусса непосредственно
ясно, что если поверхность (8) замкнута и точка А лежит внутри ограни-
ченной ее области, то б = 4я. Наоборот, если точка лежит вне этой области,
то углы видимости разных знаков взаимно уничтожаются и 0 = 0.
Если точка А лежит на самой поверхности (8), то интеграл Г аусса
становится несобственным. Легко понять, что если поверхность (8)
в точке А имеет определенную касательную плоскость, то 0 = 2л.
654.	Примеры. 1) Преобразовать по формуле Остроградского
поверхностные интегралы:
(a)	Ii = \ х2 dy dz + уг dz dx z2 dx dy,
(S)
(6)	I2 = \ ( Ух2 -j-y»2 -f- z2 (cos X -j- cos p -|- cos •*) dS,
(S)
(в)	1г = \ ( x dy dz dz dx z dx dy,
(S)
считая, что поверхность (8) ограничивает тело (V).
Ответ.
(а) /1==2$ (x+y + z)dV,
(в) /, = ЗУ[ср. 638(16)!].
* При этом мы приближенно считаем как элемент (dS), так и его про-
екцию плоскими и пользуемся формулой для ортогональной (а не цен-
тральной) проекции. Но для бесконечно малого элемента (dS) и допускаемая
здесь относительная погрешность будет бесконечно мала.
654]
f 2, ФОРМУЛА ГАУССА - ОСТРОГРАДСКОГО
339
2)	Доказать с помощью формулы Остроградского формулы:
(а)
(6)
(в)
Ц5
»Ди dx dy dz =
С C (* (du dv du dv , ди dv\ . . . . С С , ди „
= ”\Р	vihdS'
С t (о Ди — и До) dx dy dz = ? ( [v — и dS,
J (V)	(S)
если положить
йТ~ dx2^ dy2‘dz2'
df df ,	.  df . df .	.
~ cos (x, n) 4- -4- cos (y, n) 4- -4 cos (z, n)
dn dx 4 ' ' 1 dy	' 1 dz ' ’ '
в этой области. Доказать,
выполнением, условия
и разуметь под я внешнюю нормаль к поверхности.
Указание. Решение этой и ближайших задач вполне аналогично
решению задач 3), 4), 5), 6), 7) п° 602.
3)	Функция и, непрерывная вместе со своими производными и удовлетво-
ряющая в области (V) уравнению Ди = 0, называется гармонической
в этой области. Доказать, что гармоническая функция характеризуется
(5)
для любой содержащейся в области (V) простой замкнутой поверхно-
сти (S).
4)	Доказать следующее утверждение:
Если функция и—гармоническая в замкнутой области (V), то ее
значения внутри области однозначно определяются ее значениями на
поверхности (8), ограничивающей эту область.
5)	Пусть и есть гармоническая функция в области (V), (х0, у„, z0) —
какая-либо внутренняя точка этой области и (8^)— сфера радиуса 7? с
центром в точке (х0, _у0, z0). Тогда имеет место формула:
и(ха, у„ 2о)=-4^> И и(х, у, z)dS.
(SR)
Доказать это.
Указание. См. доказательство в 602, 6); лишь в качестве вспомога-
тельной гармонической функции здесь следует взять ® = где
г= / (х —х0)2 + (у> —Уо)2 + (z — z0)2 •
6)	Доказать, что функция и(х, у, г), непрерывная в замкнутой обла-
сти (V) и гармоническая внутри области, не может достигать своего
наибольшего (наименьшего) значения внутри области (если только не
сводится к постоянной),
Пользуясь этим, усилить результат в 4) наподобие того, как это сделано
в 602, 7).
340	ГЛ. XVIII. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ	J654
7)	. Доказать, что жесткая замкнутая поверхность, подвергнутая всесто-
роннему равномерному давлению, остается в равновесии.
С этой целью установим, что равны нулю главный вектор и главный
момент (относительно какой-либо точки) всей системы приложенных к по-
верхности сил.
Выделим элемент (dS) поверхности. Если через р — const, обозначить
давление, т. е. силу, действующую на единицу площади, то элементарная
сила, действующая на (rfS) по нормали к этому элементу, будет иметь про-
екции на оси
•—pcosXrfS,	—pcospirfS, —pcosvrfS	(7)
(знак минус поставлен потому, что давление направлено внутрь поверх-
ности, а X, jj, v суть углы внешней нормали с координатными осями).
Проекции Rx, Ry, Rz главного вектора получаются из проекций (7) эле-
ментарных сил суммированием их:
Rx = — р\ ( cos X dS, Ry= — р\ V cos р- dS, Rz = — p\ C cos v dS.
(S)	(S)	(S)
Но все эти интегралы равны нулю, что видно из формулы Ое троград-
ского, если положить в ней
P=l, Q = R = (y, Q=\, P = R = 0-, /? = 1, P=Q = 0.
Итак, главный вектор давлений равен нулю.
Для определения главного момента системы элементарных сил, скажем,
относительно начала координат, просуммируем составляющие по осям мо-
ментов этих элементарных сил *:
p(zcospi—у cos у) dS, p(xcosv—zcosX)dS, p(ycosX—xcospJrfS.
Таким образом, проекции главного момента давлений относительно начала будут!
Lx=p\ ^(zcosp.—у cos'») dS, Ly=p\ j(xcosv— zcosX)dS,
(S)	(S)
Lz=p\ J (y cosX —xcos|x) dS.
(S)
Если в формуле О с тро гр а дек ого взять Р = 0, Q=pz, R=—РУ, го
получим, что Lx = 0. Так же легко установить, что и Ly = Lz — 0. Главный
момент давлений (относительно начала) равен нулю. Этим и завершается
доказательство.
8)	В качестве последнего примера применения формулы Остроград-
с к о г о выведем один из основных законов гидростатики —закон Архимеда.
Известно, что давление жидкости на погруженную в нее площадку напра-
влено по нормали к площадке и равно весу столба жидкости, основанием кото-
рого служит эта площадка, а высотой — глубина погружения площадки. Допу-
стим теперь, что в жидкость погружено твердое тело (V); на каждый элемент
(dS) его поверхности (S) по указанному закону давит жидкость. Требуется
определить равнодействующую элементарных давлений и ее точку приложения.
* Напомним, что если слагающие силы по осям суть X, У, Z, и прило-
жена она в точке (х, у, z), то момент силы относительно точки (5, •>], С) имеет
следующие проекции на оси:
Lx = (y — t\)Z — (z — tyY, Ly = (z—C)X—(x — t)Z,
Lz = (x-i)Y-(y-ri)X.
6541
S 2. ФОРМУЛА ГАУССА - ОСТРОГРАДСКОГО
341
Для решения этой задачи выберем координатную систему, совместив
плоскость ху со свободной поверхностью жидкости, а ось z направив верти-
кально вниз.
Пусть удельный вес жидкости равен р, а глубина погружения элемента
(dS) есть z; тогда испытываемое этим элементом давление будет;
pz dS,
а составляющие его по осям
— pz cos X dS, — pz cos p dS, — pz cos ч dS.
В таком случае для проекций главного вектора на оси имеем:
Rx — — р J z cos X dS, Ry = — р J J z cos р dS,
(S)	(S)
Rz = — p § z cos v dS.
is>
С помощью формулы Остроградского, как и в предыдущей задаче,
легко получить
Kx = Ry = 0, Rz = — Р	— РК
(У)
Таким образом, главный вектор давлений направлен вертикально вверх и
равен весу вытесненной телом жидкости.
Рассмотрим теперь моменты элементарных сил относительно центра тя-
жести С ($, -у), С) тела (здесь и дальше имеется в виду центр тяжести
геометрического тела при равномерном распределении масс; он
может не совпадать с центром тяжести физического тела). Составляю-
щие элементарных моментов по осям будут
pz [(z—C)cosp— (у-—ц) cosvj, pz [(x — 6) cosч— (z— QcosX],
pz [(.У — ’l) cos X — (x — g) cos p],
а для составляющих главного момента (относительно точки С) получим:
Lx = р z [(z — С) cos р — (у — •>;) cos ч] dS,
\S)
Ly = р t J 2 [(-С — ?) cos ч — (z — Q cos X] dS,
(S)
Lz = p j J z [(y> — i]) cos X — (x — £) cos p] dS.
(S)
Применяя к первому интегралу формулу О с т р о г р а д с к о г о, найдем:
(У)
= рП § 01— У) dV = p
(У) J
(У)
ибо интеграл \)jydH есть статический момент тела относительно пло-
(V)
скости xz и равен v]V. Аналогично устанавливается, что Ly — 0; непосред-
ственно получается, наконец, что и £г=0.
342	ГЛ. XVIII. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ	[655
Итак, главный момент давлений относительно центра тяжести тела
равен нулю. Сопоставляя это утверждение с ранее доказанным предложением
о главном векторе, приходим к такому заключению: на тело, погруженное
в жидкость, со стороны последней действует сила, равная весу жидкости,
вытесненной телом; эта сила приложена к центру тяжести (геометри-
ческого) тела и направлена вертикально вверх.
§ 3. Замена переменных в тройных интегралах
655. Преобразование пространств и криволинейные коорди-
наты. Идеи, развитые в п° 603 в связи с преобразованием плоских
областей, естественно переносятся и на случай пространственных
областей.
Пусть имеем пространство, отнесенное к системе прямоугольных
координат xyz, и другое пространство с системой координат
Рассмотрим две замкнутые области (D) и (Д) в этих пространствах,
ограниченные соответственно поверхностями (5) и (2), которые мы
всегда будем предполагать кусочно-гладкими. Допустим, что эти
области связаны между собой взаимно однозначным непре-
рывным соответствием, которое осуществляется формулами:
Х — Х$, ТГ], С),
У=У& С),
z — z$, т], С).
(1)
При этом, необходимо, точкам поверхности (%) отвечают именно
точки поверхности (S), и наоборот.
Пусть функции (1) имеют в области (Д) непрерывные частные
производные; тогда и якобиан
D [х, у, г)	(ty.
D (5, -г), С)	к ’
также является непрерывной функцией в (Д). Мы и здесь [ср. п° 603]
будем считать, что этот определитель всегда отличен от нуля,
сохраняя определенный знак.
Если в области (Д) взять кусочно-гладкую поверхность:
£ = £(«, V), 7] = 7](ZZ, v), С = С(«, г»)	(3)
(предполагая, что параметры изменяются в некоторой области Е на
плоскости uv), то формулы (1) преобразуют ее в кусочно-глад-
кую же поверхность в области (D). Эта поверхность будет иметь
уравнения
X = X (£ (U, V), 7] (и, v), С (и, т)) = х (и, о), у ==у (и, v), z = z (и, v). (4)
Ограничимся случаем гладкой поверхности (2): на ней особых точек
нет, так что определяем:
D (и, v)’ D(u,v)’ D (и, v)	'
656]
§ 3. ЗАМЕНА ПЕРЕМЕННЫХ В ТРОЙНЫХ ИНТЕГРАЛАХ
343
одновременно в нуль не обращаются. Проверке подлежит лишь отсут-
ствие особых точек и на поверхности (3).
По формуле (6) п° 204 имеем линейные равенства относительно
величин (4):
D (у, z)	D(y, z)		D (t), C)	\D(y, z)	O(C, 5) ,
D (и, v)	D (i, C)	D (u, v)	1 D (C, g) 1 D(y, г) 1 D (6, tj)	D (u, v) 1 . D(i, -n) D (u, v) ’
D (z, x) _	D (z, x)	D(v, C)	I D (z, x)	D(C, 5) ,
(u, v)	D 0), C)	D (u, v)	1 D(C, 5) i O(z. x) 1 D(t, -n)	D (u, v) । . 0(5, *1) D (u, v) ’
D (x, y) _ D (x, y)		О 01, C)	1 D (x, y)	D(f., £) ,
D (u, v)	Db, C)	D («, v)	1 O(C, 5) i D(x,y) rD(i, t))	D (u, v) ' . 0(5, •»;) D (u, v)‘
Определитель, составленный из коэффициентов при этих величинах,
т. е. из алгебраических дополнений к элементам определителя (2), —
по известной теореме алгебры равен квадрату этого последнего и,
следовательно, вместе с ним отличен от нуля. Если бы левые
части написанных равенств в какой-нибудь точке (и, -о) одновременно
обратились в нуль, то нулями были бы и все три определителя (5),
что противоречило бы допущению.
Числа 5, ц, С, однозначно характеризующие положение точки
в пространстве xyz, называются криволинейными координатами
этой точки. Точки пространства xyz, для которых одна из этих
координат сохраняет постоянное значение, образуют координатную
поверхность. Всего будет существовать три семейства таких коор-
динатных поверхностей; через каждую точку области (О) проходит
по одной поверхности каждого семейства.
Впрочем, все это будет так лишь в предположении строгой однознач-
ности соответствия между областями (D) и (А). На
практике эта однозначность часто нарушается.
656. Примеры. 1) Цилиндрические координаты.
представляют соединение полярных координат в пло-
скости хусобычнойдекартовойаппликатойг(рис. НО).
Формулы, связывающие их с декартовыми, имеют вид
х — р cos 0, у = р sin 6, г = z.	(2)
Эти формулы отображают область
0 sg р < -]- со, 0 sg 0 < 2я, — оо <; z < Ц- оэ
на все пространство xyz. Отметим, однако, что прямая р — 0, z = z отобра-
жается в одну точку (0, 0, z); этим нарушается взаимная однозначность соот-
ветствия.
344
ГЛ. XVIII. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
[656
Координатные поверхности в рассматриваемом случае будут:
(а)	р== const. — цилиндрические поверхности с образующими, параллель-
ными оси z; направляющими для них служат окружности на плоскости ху
с Центром в начале;
(б)	6 = const—полуплоскости, проходящие через ось z;
(в)	z = const — плоскости, параллельные плоскости ху.
Якобиан преобразования:
J=
cos в
— р sin в
О
sin 6	О
р cos 6 О
О	1
cos в sin 6
— sin 6 cos в
Исключая случай р=0, якобиан сохраняет положительный знак.
2) Сферические координаты, называемые иначе полярными координа-
тами в пространстве, связаны с декартовыми формулами:
где
х = г sin ср cos в, у = г sin ср sin 6, г —г cos ср,
О г < + оо, 0 ср 5g: л, 0 =< 6 < 2п.
Геометрический смысл
Рис. 111.
величин г, <р, 6 ясен из рис. 111: г есть радиус-век-
тор ОМ, соединяющий начало (п о л ю с) с данной
точкой М; ср—угол, составляемый этим радиусом-
вектором с осью z (полярной осью); в —
угол, составляемый с осьюх проекцией OP = г sin ср
радиуса-вектора ОМ на плоскость ху (перпенди-
кулярную к полярной оси).
В этом случае мы снова сталкиваемся с нару-
шением взаимной однозначности соответствия:
плоскость г = 0 пространства губ отображает-
ся в начало координат x=y = z = 0, прямая
<р = 0(п) , г = г отображается в одну точку:
x=y = 0, z —г.
Координатные поверхности составляют три семейства:
(а)	г = const— концентрические сферы с центром в начале координат;
(б)	<р = const — круговые конусы, осью которых служит ось z;
(в)	в = const — полуплоскости, проходящие через ось г.
Якобиан этого преобразования»
7=
sin ср cos 6
Г COS ср cos 6
г sin ср sin в
sin <p sin 6
r COS ep sin в
r sin ср cos 6
COS ср
— r sin ср
о
= г2 sin ср.
Якобиан сохраняет знак плюс, за исключением упомянутых выше слу-
чаев, когда г = 0, либо ер = О(п), и якобиан обращается в нуль.
3) Преобразование пространства самого в себя по формулам:
__	6	т)	_ С
Х— + Т)8 + с2 - У—	> z~ е2+1)з-|-с>
(с2 -f- т)2 + С2 > 0) однозначно обратимо:
,	X	_ у	г— г
xa+v24-z2 ’	’1— x2+yc24-z2 ’	x2+y2 + z2'
Оно, как и в случае плоскости [604, 2)], называется инверсией и имеет
наглядно геометрическое истолкование; предоставляем читателю установить
его, равно как и найти отвечающие этому преобразованию три семейства
координатных поверхностей.
657]	§ 3. ЗАМЕНА ПЕРЕМЕННЫХ В ТРОЙНЫХ ИНТЕГРАЛАХ	345
4) Эллиптические координаты.. Рассмотрим семейство софокусных и со-
основных поверхностей второго порядка:
v+l?bi-.+vb>=1 «к*<‘>.	«
состоящее из эллипсоидов (при X > k), однополостных гиперболоидов (при
k > X > h) и, наконец, двуполостных гиперболоидов (при 0 < X <; й).
Через каждую точку (х, у, z) пространства, не лежащую на координат-
ных плоскостях, проходит по одной поверхности каждого типа. Действи-
тельно, левая часть уравнения, получаемого из (2):
X2 (Xs — й2) (Xs — й2) — (X2 — й2) (X2 — Л2) х2 — X2 (X2 — й2) у2 —
— X2 (X2 —Л2) г2 = 0,
имеет знак минус при X = 0, знак плюс при Х = й, снова знак минус при
X == k и, наконец, знак плюс при больших X. Отсюда следует, что уравнение
имеет три положительных корня: один X > k (что отвечает эллип-
соиду), второй р < й, но > h (он дает однополостный гиперболоид), третий
ч < h (двуполостный гиперболоид).
Используя свойства корней написанного выше уравнения, которое мы
можем рассматривать как кубическое уравнение относительно X2, а именно:
X2 4- р2 + = х2 + у2 + z2 + й2 + й2,
Х2р2 -J- р2ч2 -J- ч2\2 = (й2 + й2) х2 -J- k2y2 + h2z2 + й2й2;
Х2р2ч2 = й2й2х2,
найдем:
х = + v = + К(^-й2Ж-й2) (й2-р
hk' у	й]Л й2 —й2 ’
—-ь У~ k"> № ~ Iх2)
~~	kV й2 — й2
Если ограничиться первым координатным октантом, то в этих формулах над-
лежит сохранить лишь положительные знаки. Числа X, р, ч можно рассмат-
ривать, как криволинейные координаты точек этого угла. Их и называют
эллиптическими координатами. Три семейства координатных поверхно-
стей— это и будут семейства эллипсоидов, однополостных и двуполостных
гиперболоидов, о которых была речь выше.
Якобиан преобразования имеет вид:
j _	(X2 — р2) (X2 — Ч2) (р2 — ч2)____
— У (X2 — й2) (X2 — й2) (р2 — й2) (й2 — р2) (й2 — ч2) (й2 — v2) ’
657.	Выражение объема в криволинейных координатах. Воз-
вращаясь к предположениям и обозначениям п° 655, поставим себе
задачей выразить объем (ограниченного) тела (£)) в пространстве xyz
тройным интегралом, распространенным на соответствующее тело (А)
в лространстве
* Как и в п° 605, мы и здесь предполагаем дополнительно существова-
ние и непрерывность частных производных, скажем,
x'iv -4.... Лч>
это облегчает доказательство, хотя не существенно для верности самого
результата.
346	ГЛ. XVIII. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ	[657
Искомый объем выражается прежде всего поверхностным интегра-
лом второго типа [см. 613 (14)]:
D — \^zdxdy,
’(А)
распространенным на внешнюю сторону поверхности (5). Отсюда
постараемся перейти к обыкновенному двойному интегралу.
Будем исходить из параметрических уравнений (3) поверхности (5)
(и, v изменяются в области (2?) на плоскости uv). Тогда уравне-
ния (4) выразят, очевидно, поверхность (S).
Полагая
г___D (х, у)
D (и, v)’
по формуле (8) п° 636 имеем:
£) = § ^zCdudv.
(£)
При этом интеграл берется со знаком плюс, если ориентация поверх-
ности (S), связанная с рассмотрением внешней ее стороны,
соответствует ориентации плоскости uv, что всегда можно предпо-
ложить [620, 621].
Так как х, у зависят от и, v через посредство переменных
5, т), С, то, по известному свойству функциональных определителей,
[204, (6)]:
r_D(x, y)D&-n) , D (х, y)D(i\, I) , D(x, y)D(Z, g)
D(g, i))D(u, v)~T~D(y), t)D(u, v)''D(t, g) D(u, v)‘
Подставляя выражение С в полученный выше интеграл, найдем:
n— С { ЛР(х, у)Р($, g) । D(x,y)D^, С) ,
JJ Р(6, ц)О(и, v)'D(yi, C)D(u,v)^
(£)
I P (x, y) D (C, g) ~b
D(C, 5) D(u, «)J	W
Сопоставим этот интеграл с поверхностным интегралом второго
типа, распространенным на внешнюю сторону поверхности (Е):
+ЖЛ4 (7>
(2)
Если его преобразовать, исходя из параметрических уравнений (3),
к обыкновенному двойному интегралу, по формуле, аналогичной
формуле (10) п° 636, то придем как раз к интегралу (4). Единствен-
ное различие между этими интегралами может заключаться лишь
в знаке: если ориентация плоскости uv соответствует ориентации
657)
§ 8. ЗАМЕНА ПЕРЕМЕННЫХ В ТРОЙНЫХ ИНТЕГРАЛАХ
347
поверхности (2), связанной с рассмотрением внешней ее стороны,
то интегралы равны, в противном же случае они разнятся знаками.
Наконец, от интеграла (7) по формуле Остроградского
можно перейти к тройному интегралу по области (Д):
(А)
Подинтегральное выражение равно:
dz D(x, у) ,dzD (х, у) .dzD (х, у) .
di D(n, С) * ify £>(С, 6) + di D(i, ii) +
I Д d D(x,y) . d D(x, y) , d D(x, y)~|
I di D(ii, C)"T* dn D(i, i) “1“ ft D& ,,)]•
Сумма, стоящая здесь в первой строке,		равна якобиану:
D (х, у, z)	 D(i, ч, i)	dx dx dy dy ft di]	dx di ду di ’
в чем легко убедиться, разлагая	dz dz dz di dij di этот определитель по элементам	
последней строки; сумма же в квадратных скобках, как показывает
непосредственное вычисление, равна нулю *.
Таким образом, приходим к формуле:
(А)
Если вспомнить, что по предположению якобиан сохраняет знак,
который он сообщает и интегралу, то станет ясно (так как мы здесь
считаем Z)^>0), что знак перед интегралом должен совпасть со зна-
* Очевидно,
d D(x, у)	dsx dy ,	dx d2y	dsx dy	dx dsy
di D(n, i)	— dijdi di +	di; didi	didi di;	di diidi’
d D (x, y)	dax dy ,	dx d-'y	dsx dy	dx d '2v
di} D(i,i)	— didij ft +	di ft ft;	di	didt] ’
d D(x, y)	dsx dy	dx dsy	d2x dy	dx day
X D(i, 7i)	didi dii+	ft di]di	drtdi di	dij didi'
Складывая эти равенства почленно, получим справа тождественно нуль.
348	гл. XVIII. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ	{658
ком якобиана. Это дает нам право переписать полученный результат
в окончательной форме:
Mniwvsrl'0’1* (8>
или, обозначая якобиан для краткости через т], С):
т), QldUTiiZC.	(8*)
(д)
Подинтегральное выражение
=	.7),
обычно называют элементом объема в криволинейных координа-
тах.
658.	Дополнительные замечания. 1°. На поверхностях (Е) и (S)
мы фиксировали определенные стороны, именно, внешние по отно-
шению к ограниченным ими телам. В связи с этим для названных
поверхностей установлены и определенные ориентации [620]. Если
точка на поверхности (S) опишет простой замкнутый контур, раз-
деляющий поверхность, и мы остановимся на любой из
двух ограничиваемых им областей, то соответствующая
ей по формулам (1) точка на поверхности (S) опишет подобный же
контур, причем на этот раз нам не придется производить выбор из
двух областей, ибо этот выбор осуществится сам со-
бою по тому же закону соответствия (1). Если напра-
вление обхода первого контура с точки зрения ориентации поверх-
ности (S) было, скажем, положительным, то направление обхода
второго контура, если исходить из ориентации поверхности (S), мо-
жет оказаться как положительным, так и отрицательным.
В первом случае мы будем говорить, что ориентации обеих поверх-
ностей соответствуют одна другой по формулам преобразования, а
во втором — что они не соответствуют.
Так как мы с самого начала считали ориентацию поверхности (8)
отвечающей ориентации плоскости uv, то тот или другой случай
имеет место в зависимости от того, будет ли ориентация поверх-
ности (Е) отвечать ориентации плоскости uv или нет. С этим, в
свою очередь, был связан выбор того или иного знака перед инте-
гралом в формуле для объема. Но в конце обнаружилось, что упо-
мянутый знак совпадает со знаком якобиана.
Сопоставляя все сказанное, мы приходим к заключению:
В зависимости от того, сохраняет ли якобиан положитель-
ный или отрицательный знак, ориентации обеих поверхностей
(Е) и (S) оказываются соответствующими одна другой по фор-
мулам преобразования (1) или нет.
659)
S 3. ЗАМЕНА ПЕРЕМЕННЫХ В ТРОЙНЫХ ИНТЕГРАЛАХ
349
2°. Применяя к формуле (8*) теорему о среднем, получаем соот-
ношение	„	, - - - , .
D = \J& t),Q1 A,	(9)
где (V, т), С) есть некоторая точка из области (А), а А — объем этой
области. Отсюда легко вывести, что при стягивании области (А) к
точке (£, т), С) будем иметь [ср. и 644, 8°]:
|/($,73,01 = lim
так что абсолютная величина якобиана есть коэффициент рас-
тяжения пространства (в данной его точке) при преобразовании
его в пространство xyz.
3°. Формула (8) [(8*)] выведена при известных предположениях
(взаимно однозначное и непрерывное соответствие между областями
(D) и (А) и т. д.). Однако, как и в 606, 4°, можно показать, что
нарушение этих условий в отдельных точках или вдоль отдельных
линий и поверхностей не мешает формуле- быть верной, лишь бы
якобиан оставался ограниченным или, по крайней мере, интегрируе-
мым (хотя бы в несобственном смысле).
659.	Геометрический вывод. Вывод формулы (6) можно по-
строить и. на чисто геометрических соображениях (которые и здесь
впервые сформулировал М. В. О с т р о г р а д с к и й, ср. 609). Беско-
нечно малому прямоугольному параллелепипеду в пространстве
с измерениями dt\, dX. сопоставляется элементарное тело в про-
странстве xyz между координатными поверхностями «$» и «$-[-</$»,
«71» и «т]	«С» и «С4-/С», которое приближенно можно рассмат-
ривать как косоугольный параллелепипед. Его объем равен ушесте-
ренному объему тетраедра с вершинами в точках:
Р,(х, у, г),	+
г+§д+
и по известной из аналитической геометрии формуле выражается
(по абсолютной величине) определителем:
о5	дх .	dx jr
di	(Л)	1	di
%dl di	dz .	dz di^
___D (х, у, z) „ ,
~ 0(5, 1], С)
350	гл. XVIII. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ	1660
Суммируя эти отдельные «элементы объема», приходим к фор-
муле (6).
Таким образом, существо дела и здесь в том, что для опре-
деления объема тела оно разлагается на элементы не с помощью
взаимно перпендикулярных плоскостей, а с помощью сетки коор-
динатных поверхностей.
В простых случаях выражение для «элемента объема» в криво-
линейных координатах может быть получено непосредственно.
Для примера в случае цилиндрических координат рассмотрим
элементарную область (в пространстве xyz), ограниченную двумя цилиндри-
ческими поверхностями радиусов р и p-J-rfp, двумя горизонтальными плоскостями,
лежащими на высотах г и z dz,
и двумя полуплоскостями, проходя-
щими через ось z и наклоненными к
плоскости xz под углами в и 6 4- йв
(рис. 112а). Считая приближенно эту область прямоугольным параллелепипедом,
без труда находим, что измерения его суть dp, р rffl и dz, так что объем его
равен р dp d0 dz, а якобиан, представляющий отношение этого объема
к объему dpdOdz элементарного параллелепипеда в пространстве p0z, равен р.
Аналогично в случае сферических координат рассмотрим эле-
ментарную область (в пространстве xyz), ограниченную сферами радиусов г и
гdr, конусами и <р+«/<р и полуплоскостями 0 и 0-|-rf0 (рис. 1126).
И эту область можно принять за прямоугольный параллелепипеде измерениями
AD — dr, AB — rd<? и, наконец, АС. Так как дуга АС равна своей проек-
ции MN, а последняя описана радиусом 0A4 = rsin<p и отвечает центральному
углу dd, то AC — rsin<pd0. В силу этого объем рассматриваемой области
равен г3 sin у dr d<? dd, а якобиан есть r3sin<p.
Оба эти результата, найденные из элементарно-геометрических сообра-
жений, согласуются со сказанным в 656, 1) и 2).
660.	Примеры. 1) Вычислить объем тела, ограниченного поверхностью
(а) (х3+у3 + z3)2 = e3z,
(б)	(х3 +у»а -$-z3)s = a3xyz,
(в)	(х3 4- у3 4- z3)n = хзп~1.
56OJ	§ 3. ЗАМЕНА ПЕРЕМЕННЫХ В ТРОЙНЫХ ИНТЕГРАЛАХ	351
Решение, (а) Тело расположено симметрично относительно плоскостей
yz и zx, ибо х и у входят в уравнение только в квадратах. Далее, поскольку
левая часть уравнения всегда положительна, необходимо и z^O, т. е. все
тело лежит вверх от плоскости ху. Эти замечания позволяют ограничиться
вычислением объема четверти нашего тела, лежащей в первом октанте.
Наличие в уравнении выражения x2-)-y2-)-z2 подсказывает нам переход
к сферическим координатам. Подставляя в уравнение (а) поверхности выра-
жения
х = г sin cos 0, у = г sin <р sin 0, z == г cos v,
8 /---
придем к уравнению поверхности в сферических координатах: г = ау с08?1
Так как первый октант характеризуется неравенствами O^tp^-^,0^0^
я
то, учитывая значение якобиана J=rasin!p [656, 2)], будем иметь:
(б)	Тело лежит в первом, третьем, шестом и восьмом октантах, для кото-
рых, соответственно:
х Ss 0, у	О, z Ss 0; х -0, у 0, z 0;
х sg 0, у	0, z -0; х :> 0, у sg 0, z sg 0;
Оно состоит из четырех частей, которые попарно симметричны относительно
одной из координатных осей (ни левая, ни правая части уравнения не изме-
няются при одновременном изменении знаков любых д в у х из величин х,у, z).
Переходя к сферическим координатам, получим:
2	2 о у ein2 f cos <р sin 9 cos в
V— 4 I М, l d<f	i	г2 sin <р dr =
о о	«
те	те
7	2*
4	(*	а?
= а’ \ sin’ <р cos ® dv • \ sin 0 cos 0 rf0 — -s-.
o J	J	О
0	0
(в)	Формулы перехода к сферическим координатам здесь проще взять в
виде
х = г cos <р, у - г sin cos 0, z = г sin <р sin 0.
Тогда уравнение поверхности примет форму г = cos2zl 1 <р.
Ответ. V = --т, я——.
3 (Зп — 1)
2)	Найти объем тела, ограниченного поверхностью
(a)	(x*4-y2)24-z1=y,
(б)	(х2-|-у2)’-|-ze = 3zs.
(а)	Решение. Хотя тип задачи и несколько отличен от предыдущих,
нр и здесь выгодно применить сферические координаты. Уравнение поверх-
ности примет форму:
г’ (sin1 у -f- cos1 <р) = sin sin 0.
352	ГЛ. XVIII. ТРОЙНЫЕ И МНОГОКРАТНЫЕ интегралы	(60
Учитывая симметрию, будем иметь:
it it у sin у sin
2	2 V sin* 4- cos* <р
У=4	г8sin<рdr'=
о о	о
Я
2	оо	_
__ 4 С cos2 ср d<?		 4 С t2 	 к У 2
3 ' sin4 ш -f* cos4 <₽	3.' 1+^4_3
о	о
(б)	Указание.
It
*2	1
т. n (* cos3 ср sin ср da С и du
V = 2п \ - т —X-J- = It \ 5-J---5 —
.) sm6 ср	cos’ <р	J 3«2 — За 4-1
о	о
2т?
(если положить n = cos2<p). Ответ. V-
3/3
3)	Найти объем тела, ограниченного поверхностью:
.2 у z/2 _ х^у
? + &2~t'c2J ~~h2’
.2	.,2	~2 \ 2	у.2	„2
1г^Ь2^ с2/ ~ а2 Ь~ ’
?_ , /	z2/ _ [х2 z
2 + b2 +c2J “Да2 + Ь2/ с *
vs z%
(а)	Решение. При наличии выражения 4- — в уравнении пс
верхности часто бывает полезен перехрд к обобщенным с ф ерич е с к и j
координатам* по формулам:
х = ar sin ср cos 0, y = br sin ср sin 6, z = cr cos <p;
якобиан в этом случае равен J = abc г2 sin ср. Имеем (с учетом симметрии'
я я a2b sin3 <р cos2 9 sin 9
*2	2*	йз
V= 4 rf0 rfcp	abc г2 sin ср dr =
о	о	о
Я	я
Т	У
4 a7h^c	(*	(*
= -5—jv	\ cos6 6 sin3 6 rfG i sin10 9 rfc
3 A9 J	’
о	0
так что окончательно
__ it a'b'e
И —192~F~'
* Которые аналогичны обобщенным полярным координатам на плоскост!
660]
§ 3. ЗАМЕНА ПЕРЕМЕННЫХ В ТРОЙНЫХ ИНТЕГРАЛАХ
353
(б)	Ответ. V = ~abc.	(в) Ответ. V = ~abc.
4	' '	60
4)	Найти объем тела, ограниченного поверхностями
x*+y‘ + zs=l, x2+3»24-z2=16, z2 = x2+j2, z = 0, j = 0, у = х.
Указание. Эти поверхности определяют промежутки изменения для
Сферических координат:
1з<Гз<4; <р sg, О<0<~(или
4 т 2 ’	4 \	4]
Тело состоит из двух обособленных кусков (в первом и третьем координат-
ных октантах).
_	21 /2я
Ответ. V = —4------.
4
5)	Вычислить объем тела, ограниченного поверхностью
2_	2	2_
(х\з . (у\з , [z \ з
\ а / ‘\Ь ) ' \с)	‘
Решение. Введем новые координаты по формулам:
х — ar sin3 ср cos3 0, y = br sin3 ср sin3 0, z = cr cos’ ср
(Osjrg:!, 0cp<1 и, 0^0 ^2x).
В этом случае якобиан
J = 9 abc r2 sin5 cp cos2 cp sin2 0 cos2 0,
так что
1	тс	2те
С	С	С	4
V= 9 abc I г3 dr \ sin5 ср cos2 <р <&р \ sin2 0 cos2 0 rf0 = 5= я abc.
J	е)	е)
0	0	о
6)	Найти объем тела, ограниченного поверхностями
(х у -j- z)2 = ay, х — 0, у — 0, z = 0.
У КАЗАНИ Е. Положить
х = г sin2 ср cos2 0, у — г sin2 <р sin2 0, z = г cos2 ср
(г^О, O^cp^-J, 0<6<-^.
Якобиан
J=4г2 sin’ ср cos ср sin 0 cos 0.
а8
Ответ. V=^.
60
7)	Найти объем косоугольного параллелепипеда, ограниченного шестью
плоскостями:
+ b1y + clz = ± Л(,
агх 4- Ьзу -j- caz — + Л2,
ер? 4- ьзУ + счг = — йз,
предполагая, разумеется, что определитель
а1 Й1
отличен от нуля.
Оз Ь% са
°а Й5 са
12 Г, М. Фихтенгольц, т, П1
354	гл. XVIII. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ	[660
Решение. Введем новые переменные

т] = агх 4- Ь^у + c2z,
С = а3х 4- Ъзу + c8z
(—	— й2^>)^й2, —- й3	С sg й3).
_	D (х, у, г)
Определитель ^~С)'
ной величине определителя
проще всего найти, заметив, что он равен обрат-
Ще, ч, 0
D (х, у, z)
. Имеем
А1	Й2 Аз
j d* j drl j
— hi	—hz	—hz
~ПдГ-
8)	Найти объем тела, ограниченного
(а) цилиндром
{а3х 4- Ь^у 4- Cjz)2 4- (а2х 4- Ь2у 4- c2z)2 = R-
и плоскостями
а3х 4- Ь3у 4- czz — 0 и а3х 4- Ьау 4- c8z = й;
(б) эллипсоидом
(а,х 4- bty 4- М2 4- (e2x 4- йзУ 4- c2z)2 4- <а2х 4- Ь.у 4- c8z)2 = /?2
(при прежнем предположении, что определитель Д^О).
. nR*h л .	4 п/?3
Ответ, (a)	(б)
9)	Применение цилиндрических координат к вычислению объема тела
приводит к интересной формуле.
Рассмотрим тело (И), ограниченное кусочно-гладкой поверхностью, и пред-
из оси z полуплоскость, отвечающая 6 = const, пере-
секает тело по некоторой плоской фигуре (Qj),
при изменении 6 от а до р (рис. 113). Тогда
положим, что исходящая
Рис. ИЗ.
V= J Ц р dp dO dz = j d0 j j p dp dz,
<Ю	« (Qj)
причем фигуру (Qe) удобно отнести к прямоуголь-
ной системе координат pz, вращающейся вместе
с упомянутой плоскостью вокруг оси z*.
Теперь легко видеть, что двойной интеграл
(р dp dz представляет статический момент
(Qe)
фигуры (Qj) относительно оси z, который равен
произведению площади Q (6) этой фигуры на
расстояние рс(0) ее центра тяжести С от оси z:
И р dp dz = Q (в) рс (0).
* Вместо того, чтобы тождественную с ней фигуру относить к непод-
вижной плоскости pz в пространстве ₽0z.
660)	$ 3. ЗАМЕНА ПЕРЕМЕННЫХ В ТРОЙНЫХ ИНТЕГРАЛАХ	355
Подставляя это выражение для объема, придем к окончательной формуле:
И=$<?(8)Рс(в) М.
Л
Эта формула была указана П. П. Кусковым. Она особенно удобна для опре-
деления объема тел получающихся при винтовом движении плоской фигуры
(постоянной или деформирующейся), как-то: винтовых нарезок, пружин и т. п.
Если тело (И) есть попросту тело вращения неизменной фигуры (Q),
не пересекающей оси z, вокруг этой оси, то Q = const, рс = const, <х = 0,
₽ = 2я, и формула принимает вид:
У= Q • 2яр(-.
Она выражает известную теорему Г ульдина [351], гласящую, что объем
тела вращения плоской фигуры около не пересекающей ее оси равен про-
изведению площади этой фигуры на длину окружности, описанной центром
тяжести фигуры. Таким образом, формула Кускова является естественным
обобщением этой классической теоремы (и, наоборот, легко может быть из
нее получена).
10)	Объем трехосного эллипсоида
х3 . у3 । z2	,	.
а2 + £2 + С8 — 1 (Д > Ь > С)
4
многократно вычислялся; он равен -^-tzabc. Попробуем, однако, к вычисле-
нию этого объема привлечь эллиптические координаты)., р, ч [655, 4)]. Если
положить
й2 = а2 — b3, k3 = a3 — c3,
то сам данный эллипсоид получается при Х = а.
Первому октанту эллипсоида отвечает изменение X от k до а, р от h до
k, ч до 0 до h. Поэтому
Л  * а
1 С . С . О	(X2 — р2)(Х2 — v2)(p2 — Vs)
-к-И — \ дч \ dp \ 	 	—	7	-... - "	'	rfX.
8 S К k К (>-2 — Л2) (X3 — k3) (р2 — Л2) (й2 — р2) (Л2 — ч2) (й2 — v2)
Но, как указано, этот объем равен
• —r.abc =	a Y (а3 — Л2) (а2 — й2).
Таково, следовательно, значение написанного выше сложного интеграла;
Найти это значение иным путем представило бы значительные трудности.
В заключение дадим два интересных применения основной формулы (8),
Позволяющих установить связь понятий площади кривой поверхно-
сти идлиныкривой с принципиально более простым понятием объема
тела.
11) Пусть задана гладкая поверхность (S):
х — х(и, v), у=у(и, v), z — z(u, v),
причем в области (Д) изменения параметров и, v эти функции имеют непре-
рывные производные второго порядка.
12*
356	гл. XVIII. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ	[660
На нормали к поверхности в каждой ее точке Af отложим, симметрично
в обе стороны от поверхности, отрезок длины 2г >0. Эти отрезки заполнят
некоторое тело (Иг) *, в котором содержится и за-
данная поверхность (рис. 114).
Обозначая через х, у, г координаты точки Af
поверхности, а через X, Y, Z—координаты любой
точки Р на упомянутом отрезке нормали в ней,
будем иметь, очевидно,
х х + у л2-j-в2 + с2 ₽’
Y=y  В	р,
У А2 + В2 + С2
„	!	С
Z—Z-\--л	р,
ул2+в2+с2
где А, В, С имеют обычное значение, а р означает расстояние МР (с соот-
ветствующим знаком, так что — rsgpsgr). Параметры (и, V, р) служат, таким
образом, криволинейными координатами для точек упомянутой области (Vr).
По формуле (8) объем Vr этого тела равен
4$$
Но
*й + а1(«> ®)р Уй + “s (и, v) р z'a+a3(u,v)f
D(X, Y, Z) _	®)Р K+Ps(«> ®)Р 4 + ₽s(«> »)Р
D Р)	А В С
УА2 + В2+ С2 УА2+В2 + С2 УА2+В2 + С2
= У А2 -ь В2 + С2 + Т! («, г») р + Та («> ®) Ра,
где а„ а2, о8, Pt, Р2, ₽8, Yj, fa означают некоторые непрерывные функции от
и, и. Очевидно, при достаточно малом г (так как | р | sg г) это выражение
будет иметь знак первого слагаемого, т. е. станет положительным. Поэтому
Vr= j rfP \\{УA2+B2 + C2+‘fl? + ls?2}dudv =
-г (А)	____________
= 2r f j У A2 -J- В2 -J- С2 du dv -f- Lr2 (L = const.).
(Д)
Отсюда легко вытекает окончательный результат
liin^= j УA2 + B2 + C2dudv;
в последнем интеграле мы узнаем площадь S кривой поверхности. Таким
образом эта площадь может быть получена, исходя из
объема.
* Можно доказать, что при достаточно малом г упомянутые
отрезки между собой не пересекаются, так что каждая точка тела лежит на
одной нормали.
660]	$ 3. ЗАМЕНА ПЕРЕМЕННЫХ В ТРОЙНЫХ ИНТЕГРАЛАХ	357
12) Пусть задана гладкая кривая
x—x(f), y=y(t), z — z(t~)
причем функции х, у, z имеют и непрерывные вторые производные. В пло-
скости, нормальной к кривой в любой ее точке М, вообразим себе круг ра-
диуса г > 0 с центром в М. Из всех таких кругов составится некоторое
тело (Vг) *, содержащее кривую.
Не умаляя общности, можно предположить, что на рассматриваемом
участке кривой всегда х^2-|- у)3>0. Тогда, желая построить в упомянутой
плоскости, нормальной к кривой, прямоугольную систему координат, мы мо-
жем принять за оси координат две взаимно перпендикулярные нормали
с направляющими косинусами
у’	х' п	x'z'
у Х'-уу- у Х'з+уз ух’з+у’зух'3+y'a+z’2 ’
y'z'	У х'а 4- у'3
Ух'а-\-у'а Ух’2+у'2У^ ’	Уx'a+y'a+z'a ’
Обозначив соответствующие координаты через и, v, мы можем выра-
зить координаты X, Y, Z любой точки Р тела (уг) так:
Здесь t, и, v играют роль криволинейных координат точки Р, так что
ШО (X, Y, Z) \	.
у...—1—dtdudv.
I и, v) |
Легко видеть, однако, что
D (X, Y, Z) _
D(t, ut v)
*' + “i(0« + ₽i(0»
У
= У х'а4-у'а
x’z'
У + <Ч + (t)v
_______X'
У х'*+у'3
y'z'
«' + <»» (0«+М0 V
0
у х'3 +/•
у х’3 4-у'8 ух'3 4-у'2 4- Z'2 ух'а 4-у'8 У х'3 4-у'3 4-z'2 Уx'3+y'3+z'3
— У X'3 4-у'а 4- Z'3 4- a (f) U 4- ₽ (t) V,
* И здесь можно доказать, что — снова при достаточно малом г—
эти круги попарно не имеют общих точек, так что каждая точка тела при-
иадлежит лишь одному из них.
558	гл. XVIII. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ	[661
где а„ ..., р,— непрерывные функции от t. Это выражение сохраняет поло-
жительный знак при достаточно малом г (так как | и |,	Тогда
т	_____________
Vr = \ dt	И { Ух'3 +y'‘ + z'2-jra (t) м-Ь₽ (t) v } dudv =
4	+
T ______________
= nr3 J У x’3 + у’3 + z’a dt J J (Ku + Lv) du dv,
4	e24-'O2<r3
- где К и L — постоянные. В первом интеграле узнаем длину s дуги, второй
же интеграл обращается в нуль. Поэтому
Vr — лг2з, s = -^4.
лг
Длина дуги получается из объема еще более непо-
средственно, даже без предельного перехода!
661. Замена переменных в тройных интегралах. С помощью
выражения объема в криволинейных координатах нетрудно установить
и общую формулу замены переменных в тройных интегралах.
Пусть между областями (D) и (Д) пространств xyz и суще-
ствует соответствие, охарактеризованное в п° 655. Считая соблю-
денными все условия, при которых была выведена формула (8), мы
покажем теперь, что имеет место следующее равенство:
S S У’ z) dx dz —
(О)
=И *1> о» у & *i’ с)>z С” ’i’।। d- drid* <10)
(A)
вполне аналогичное формуле замены переменных в двойных интегралах.
При этом функцию f(x,y,z) мы предполагаем непрерывной или, самое
большее, допускающей разрывы вдоль конечного числа кусочно-
гладких поверхностей (но во всяком случае сохраняющей ограничен-
ность). Таким образом, существование обоих интегралов в равенстве
(10) не вызывает сомнений; нужно установить лишь самое равенство.
Для доказательства поступаем так же, как и в п° 609. Разложив
кусочно-гладкими поверхностями области (О) и (Д) на (соответству-
ющие друг другу) элементарные части (О;) и (Д,) (/=1, 2, ..., и),
применим к каждой паре областей (£){), (Д,) формулу (7); мы получим
Di = \J^i,	у|Д,-;	(ii)
где (?г, т)г, у есть некоторая точка области Дг, не зависящая от на-
шего выбора. Возьмем соответствующую точку (xi( yb zt) области
(Pi), т. е. положим
= •£(£/> У>	Tj,-, у, Zi = z(ii, т];, У, (12)
662]	$ 3. ЗАМЕНА ПЕРЕМЕННЫХ В ТРОЙНЫХ ИНТЕГРАЛАХ	359
и составим интегральную сумму для первого из интегралов (10):
i
Подставив сюда вместо J;, 2г выражения (12), а вместо Dt — вы-
ражение (10), придем к сумме
°=£/(*&.	у&>	z&’ 0)1 /(С с7)| дг,
i
которая, очевидно, уже является интегральной суммой для второго
из интегралов (10).
Устремим к нулю диаметры областей Д/( вследствие чего в силу
непрерывности соответствия устремятся к нулю и диаметры областей
(Р^. Сумма о должна стремиться одновременно к обоим интегралам,
откуда и следует требуемое равенство.
Как и в случае двойных интегралов, формула (10) имеет место
и при нарушении сформулированных выше при доказательстве фор-
мулы (8) предположений в отдельных точках или вдоль конечного
числа кусочно-гладких линий и поверхностей, лишь бы якобиан
сохранял ограниченность.
Можно пойти дальше в расширении условий применимости фор-
мулы (10), допуская и несобственные интегралы. Мы предоставляем
читателю перефразировать для рассматриваемого случая изложенное
в п° 617. Подчеркнем еще раз, что при указанных там условиях
формула имеет место в предположении существования одного из
интегралов (10), существование другого отсюда уже будет вытекать.
В заключение упомянем, что формулы (8) и (10) могли бы быть
.написаны и без знака абсолютной величины при якобиане. Для того
чтобы иметь право на это, следовало бы ввести понятие об ориенти-
рованном теле (в связи с ориентированием его границы), затем в за-
висимости от его ориентации приписывать тот или другой знак его
объему и распространенному на тело интегралу. Подробности предо-
ставляем читателю, отсылая его к п° 616 и к замечанию 1° в п° 658.
662. Примеры. 1) Вычислить интеграл
где (V) есть тело, ограниченное сверху поверхностью
(x2+y2-f-z2)2 = a2xy,
а снизу плоскостью z = 0.
Решение. Перейдем к сферическим координатам. Уравнение поверх-
ности примет вид
rs = a2 sin2 ? sin 0 cos 6,
360
ГЛ. XVIII. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ	{662
а интеграл, с учетом симметрии тела относительно оси г, преобразуется так:
Z л
2	2 asiny V^sinflcosG
1 — 2 df) dy § г3 sin <р cos <р sin 8 cos 6 dr =
оо	о
те	те
~2	2"
д4	С	С	а*
= I sin3 6 cos3 6 <Z0 1 sin5 <p cos <p dtp =	.
о	0
2) Вычислить интеграл
«= Ш -X!KdX-dy-—- (.>p >-!><>)
J J J / «лг' + ₽У+1"г>
X, V, Z>0
*2+.y2 + z2==7?2
[cp. 648, 11)].
Решение. В сферических координатах
те те
2 1R
w f f С___________r< sin8 ? cos ? s'n Qcos e dr d<y dO
J J J Y a2 sin2 <p cos2 6 + p2 sin2 tp sin2 0 72 cos2 <? '
0 0 0
Удобно произвести подстановку sin2<p = n, sin2 8 = v. Тогда
1 1 R
И==±А C C r4______________u dr da dv__________
4 ' ' J/ a2U(l—n) + ₽2M® + 72(l—U)
0 0 0
1 1
/?5 (•	, (•	dv
= -nn\ u du \	---=
20 J J Y [72 + (a2 — 72) U] + (₽2 — a2) UV
о 0
_ R5 ₽7 + 7a +
“15 (₽ + 7)(Y + a)(a + ₽)-
3) Вычислить интеграл
„__ С f f хУг dx dy dz
x2+y2 + z2>
(V)
где (V) есть трехосный эллипсоид
Решение. Если перейти к обобщенным сферическим координатам
по формулам
х = ar sin <f cos 0, у = br sin <p sin 8, z — cr cos<p,
J = abc r2 sin <p,
то интеграл перепишется в виде
те те
~2 "2 1
[ f f t____________________________sin3 <р cos у sin 6 cos 6 rfr dtp rffl_
AT == a2b3c2 J J J r a2 sin2 <p cos2 8 b2 sin2 <p sin2 0 -f- c2 cos2 <p *
0 0 0
361
662)	§ 3. ЗАМЕНА ПЕРЕМЕННЫХ В ТРОЙНЫХ ИНТЕГРАЛАХ
Подстановка sin2<p = u, sin2 9 = г». Окончательный результат:
,,	а*Ь2с2	,, ,, с . „ », а , .... Ь )
К— р-;--э------.... ...--«vrs-----sT i b 2C2 In -Г- 4- c2e2 In-k a2b2 In — }.
8 (a2 — bs) (№ — с2) (c2 — a2) I b 1 с л a J
4)	Вычислить повторный интеграл
1
co co yz
\dz \y dy e*»2 x2dx.
1	‘1 "o
Решение. Заменяя его тройным интегралом
S S S	йУ dz,
прибегнем затем к подстановке
u-j-v_______a-J-® + w
и ’	u-J-®
= 1
u(u-{-v)‘
Интеграл приведется к такому:
5 $ $	е“+’>+® du dv dw,
и, v, ®&0
который вычисляется легко.
е
Ответ: —1.
5)	Вернемся к вычислению двойного интеграла:
В — ё~а	cos xi cosуц dx dy
[ср. 617, 21)]. Так как при &>0
[ „	4ва.д -ffb
I е	d4 = ~^~e
[497, 8)], то, полагая Ь = аугх*+у11, получаем?
________	_ “ пз «2 (*«+>«)
e-e/^+F== 2 Се «2 аз.
те J
о
362	гл. XVIII. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ	(662
Подставляя это в интеграл В и меняя порядок интегрирований, найдем
со	оо оо	а3(х3-}-^2)
Д =	df) е 463 cosxjcosyqdx dy
о	оо
или, если перейти к переменным и = -^ и v = -^:
00	/ 00	оо
г, 8 с —I с -и2	20U; Г _va 2007] .
В = —== \ е	02 dO J \ е “cos----du \ е	cos --1 dv =
/кв2 J	| J	a J	в
о I о	о
оо О2
V м3 \ 2 / J
О
[519, 6) (а)]. Интегрируя по частям, нетрудно уже получить окончательный
результат:	в
(в2 + ^+Г|2)2
Перестановка интегрирований обосновывается существованием трой-
ного интеграла.
6)	Найти массу и определить положение центра тяжести сферы
x2+y2 + z2^2ez
при следующем законе распределения масс:
_ k
P — /x2+/ + z2
[ср. 650, 5)].
У Казани в. Перейти к сферическим координатам.
7)	Найти притяжение, испытываемое произвольной точкой пространства
ео стороны однородной сферы [Ср. 650, 9).]
Решение. Перейдя к сферическим координатам, найдем
2it я R
р ___рг3 (г cos <р — а) sin <р dr d<? df)
0 0 0	(г2 -j- а3 — 2аг cos <р) 2
Но, определяя притяжение сферическим слоем [633, 11)], мы уже нашли зна-
чение двойного интеграла
2л я
И (г cos <р — а) sin ? d<f df) _(0 при а < г,
т- 4тс
° ° (г2-)-в! — 2ercos<p) 2	' д2 ПРИ а>г-
В таком случае при в>/?
В
J r3dr = —1к/?’р.1,
о
а при а < Ц	а
= —	J r2dr = -yK?e.
о
662J
§ 3. ЗАМЕНА ПЕРЕМЕННЫХ В ТРОЙНЫХ ИНТЕГРАЛАХ
363
8)	Найти потенциал однородной сферы на произвольную точку [ср.
У казание. Перейти к сферическим координатам и использовать ре-
зультаты задачи 12), 633.
9)	Решить наново задачи, относящиеся к притяжению и потенциалу
сферы, при более общем законе распределения масс:
1Р=/(г).
где f— произвольная функция расстояния точки от центра.
Отметим, что заключения, сформулированные нами в 650, 9) и 12),
остаются в силе и в настоящем случае.
10)	Найти моменты инерции 1г и 1Х тора [ср. 650, 13)].
Указание. Учитывая, что тор получается от вращения круга (см.
рис. 108), положение точки в этом теле естественно определить, во-первых,
углом <р, который составлен меридиональным сечением с плоскостью хг, и,
во-вторых, обыкновенными полярными координатами р, 6—в пределах самого
сечения.
Тогда
х = (d + р cos 8) cos <р, у — (d р cos 6) sin ср, z = р sin 8,
J = р (d + р cos 6),
причем р изменяется от 0 до a, a <? и 8—от 0 до 2к.
И) Вычисление потенциала однородного (р = 1) эллипсоида
х3 vs z2
на его центр приводит к эллиптическому интегралу.
Введем сферические координаты, но, взяв на этот раз ось х за полярную ось:
х = г cos ср, у — г sin ср cos 8, z = г sin у sin 9.
Будем иметь
dx dy dz ______________________________
К x84-y84-zr “
где
It	It
J	У
. C .	. (*
J sm cP 4 J В cos8 8 C sin2 8 ’
о о
cos8 <f i sin8 cp cos8 cp sin8 cp
~ a3 b3 ' G— a8
Внутренний интеграл равен —Полагая, далее,	——— соз<р = /,
2 у ВС	я
получим эллиптический интеграл первого рода
Va2-c2
2п abc
Y а3—с3
а3 — Ъ3
а3 —с3
= 8
364	ГЛ. XVIII. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ-	[663
который, в свою очередь, с помощью подстановки t == sin \ приводится
к форме Лежандра:
^0
,v. 2л abc f d>.	2х abc „. .
W  ——----- \ —	n7" — — ------ zzr г (^Q,
/a2 — cs J V 1— AgsinU	/a2—c3
о
где для краткости положено
. у а2 —с3 .	-.Га2 — Ь3'
К» = агс sin-------, k0 = у .
663. Притяжение со стороны тела и потенциал на внутреннюю
точку. Вернемся теперь к общим выражениям (17) и (18) п° 649 для проек-
ций на координатные оси притяжения телом точки А (j, tj, С) и потенциала на
эту точку, но остановимся специально на том случае, когда сама точка А
принадлежит телу. Это снова даст повод использовать замену переменных.
Легко убедиться, прежде всего, в существовании упомянутых несобствен-
ных интегралов. Достаточно перейти к сферическим координатам, выбрав за
полюс точку А, чтобы эти интегралы преобразовались в собственные. Если
вырезать из тела (У) сферу (о0) радиуса га с центром в А, то получим
2те « го
ИГ-МН
(»о)	ООО
г2 sin <р dr dy dd__
-
-я г©
\ \ \ p r sin у dr dy d6;
Р
аналогично
2те я Го
{ С Р dv = р cos 0 sin2 <р dr dy db
(Do)	6 0 0
и т. д. Подинтегральные функции здесь оказываются непрерывными *.
Гораздо более тонких соображений требует установление для рассматри-
ваемого случая соотношений (19) п’ 649. Здесь также оказываются полез-
ными сферические координаты.
Прежде всего из предыдущих равенств получаются неравенства
(13)
^о)	(L = maxp),
™
(”о)
которыми мы ниже воспользуемся.
Придании теперь g приращение h и наряду с точкой А (?, т;, С) рассмот-
рим точку At (; + й, >], С). Обозначая по-прежнему через г расстояние AM
от точки А до произвольной точки Af(x, у, z) тела, через rt обозначим
расстояние AtM. Нужно доказать, что при й—>0 и разность

стремится к нулю.
• Плотность р мы считаем непрерывной функцией от координат.
6631
« 3. ЗАМЕНА ПЕРЕМЕННЫХ В ТРОЙНЫХ ИНТЕГРАЛАХ
365
д==
Выделим из тела (V) сферу (»0) радиуса 2 | h | с центром в А (рис. 115);
тогда Д представится в виде суммы четырех членов:
(®о)	(®о)
I
ру.
г8
Второй и третий
при г0 = 2 I h |:
(Ю-(»<>>
члены сразу оцениваются с помощью неравенств (13) и (14)
1 С С С Р dv 2nL (2А)«
тгт \ \ \ 1-----=== —2 г = ЗяД л ,
I*I J ' J г " IЛI 1 "
(»о)
(»о)
Чтобы удобнее оценить первый член, окружим точку сферой (v^ радиуса
dv ^2и£.2|Л| = 4я£|Л|.
Рис. 115.
31 Л |; в ней целиком содержится сфера (о0). Тогда, снова пользуясь нера-
венством вида (13), будем иметь
(®о)	<•»!>
Наконец, обращаемся к последнему члену. Если ввести функцию
ле,’!, о=у,
то выражение в фигурных скобках есть не что иное, как
/е+*, о-/(г, т), о _
д	7$ Vm Ч> '»/»
что по формуле Тейлора может быть заменено через
Ад'де+ол, (о<в<1).
Но в нашем случае
Г a	1.
/£«(»» Ч» У	fi,
366
ГЛ. XVIII. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
[664
поэтому	4
1Л’8(; + 0Л, 1, С) 1^-5,
'2
где г2 есть расстояние А3М от точки М до точки А3 (; + 0й, ц, С).
Из треугольника АМА3 (см. рис.) имеем AaAf>>AAf— АА3. Но точка
М лежит вне сферы (о0) рис. 21 h |, а АА3, очевидно, меньше | h |, так
что АА3< -у AM и А3М>-^-АМ, т. е. г2>--^-г. Учитывая все это, при-
ходим к такой оценке:
x — S
г3
(V) —(»о)
Возьмем теперь сферу (У,), с центром в А, столь большого радиуса /?,
чтобы в ней целиком содержалось тело (V). Тогда полученное выражение
в свою очередь оказывается меньшим, чем
2ic те 7?
16£|Л|	^ = 16£|Й|Н §	=
(Vi)-(io)	о <J 2 | Л |
= 64те£ • | й | (In/?—In 2 | Л I)-
Окончательно
|Д|^С1|Л|+С2|й|1п2|Л|,
где Ct и C3 — постоянные, которые нетрудно подсчитать. Отсюда ясно, что
Д вместе с h стремится к нулю, т. е.
dW
д3
Аналогично устанавливаются и другие два из соотношений (19) п°649. Нако-
нец, подобными же соображениями можно доказать и непрерывность
dW dW dW	.
производных	~^г даже для точек А, принадлежащих телу (V).
§ 4.	Элементы векторного анализа
664.	Скаляры и векторы. Применение интегрального исчисления к во-
просам математической физики и механики часто удобнее проводить в век-
торной форме. Поэтому читателю полезно ознакомиться с некоторыми основ-
ными понятиями векторного анализа, которые приводят к векторной интер-
претации интегральных образований и связывающих их формул интегрального
исчисления.
Мы предполагаем, что читатель уже знаком с понятием скаляра или
скалярной величины, которая вполне характеризуется своим числен-
ным значением (как, например, объем, масса, плотность, температура) и с по-
нятием вектора или векторной величины, которая для полного
своего определения требует еще указания на направление (перемещение,
скорость, ускорение, сила и т. п.). Говоря о векторе, мы, как обычно, будем
представлять себе изображающий его направленный отрезок. Условимся
обозначать векторы буквами со стрелками над ними: X n v, ... ; те же
буквы без стрелок: А, г, v, ... будут означать длины векторов:
Л = |35|, r = |F|, v = |v|,
а буквы со значками, например Ах, rv, vn, ... —векторов X г\ 7, ... проек-
ции, соответственно, на оси х, у, п, ... Проекции A# А?} Аг вектора Л на
6651	« 4. ЭЛЕМЕНТЫ ВЕКТОРНОГО АНАЛИЗА	36V
координатные оси вполне его определяют и по длине (численному значе-
нию) и по направлению.
Мы считаем также, что читатель владеет и основными сведениями из
векторной алгебры. Ограничимся напоминанием, что скалярным произве-
дением векторов Я и 3 называется скаляр (число)
X • В = АВ cos (X, В),
которое через проекции на оси выражается так:
А • В — АХВХ + АуВу + AZBZ.	(1)
Векторное произведение векторов А и S есть вектор с длиною
АВ | sin (А, В) |, перпендикулярный к обоим сомножителям и направленный
в ту сторону, с которой вращение от А к В (на угол, меньший 180°) ка-
жется происходящим против часовой стрелки; его обозначают че-
рез ~А X В. Проекции векторного произведения на оси будут
AyBz AzBy, AZBX AXBZ, AxBy AyBx,	(2)
если, как мы это впредь и будем предполагать, в основу положена правая
система координат [620].
665.	Скалярное и векторное поля. Если с каждой точкой М опреде-
ленной пространственной области (которая может охватывать и все про-
странство) связана некоторая скалярная или векторная величина, то говорят,
что задано поле этой величины, соответственно, скалярное или векторное.
В ближайших пп° нам все время придется иметь дело с такими полями.
Примером скалярного поля может служить поле температуры или элек-
трического потенциала. Если положение точки М определять ее координа-
тами по отношению к некоторой произвольно выбранной координатной си-
стеме Oxyz, то задание поля скалярной величины U равносильно просто
заданию числовой функции О (х, у, г). Мы всегда будем предполагать, что
эта функция имеет непрерывные частные производные по всем переменным.
Если эти производные не обращаются одновременно в нуль, то уравнение
U(x, у, z), = C С = const
определяет некоторую поверхность (без особых точек), вдоль которой вели-
чина U сохраняет постоянное значение; такая поверхность называется по-
верхностью уровня. Вся рассматриваемая область заполнена этими поверх-
ностями, так что через каждую точку ее проходит одна и только одна по-
верхность уровня. Ясно, что поверхности уровня между собой не пересекаются.
Примером векторного поля может служить силовое поле или поле скоро-
стей; подобные поля нам уже встречались. Если положить в основу некоторую
систему координат Oxyz, то задание поля векторной величины Ж может
быть осуществлено путем задания ее проекцией на оси
Ах (х, у, z), Ау (х, у, z), Az (х, у, г)	(3)
как функций от координат точки М, с которой величина А связана. И эти
функции мы будем предполагать имеющими непрерывные производные. При
изучении векторного поля важную роль играют векторные линии', векторной
линией называется кривая, направление которой в каждой ее точке М совпав
дает с направлением вектора А, отвечающего этой точке. Если вспомнить
[234]. что направляющие косинусы касательной к кривой пропорциональны
дифференциалам dx, dy, dz, то получится, что векторная линия характери-
зуется равенствами
Ах ~ Ау ~"Ах'
868	ГЛ. XVin. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ	(666
В предположении, что вектор Я не обращается в нуль, можно доказать, опираясь
на «теорему существования» из теории линейных систем дифференциальных
уравнений, что вся рассматриваемая область заполняется векторными линиями,
причем через каждую точку ее проходит одна и только одна такая линия.
Векторные линии между собой не пересекаются.
Иногда приходится рассматривать поверхности, составленные из векторных
линий; их называют векторными поверхностями. Векторная поверхность
характеризуется тем, что в каждой ее точке Af соответствующий вектор A (А1)
лежит в плоскости, касательной к поверхности в этой точке (или тем, что
проекция Ап вектора А на нормаль п к поверхности во всех ее точках равна
нулю). Если взять в рассматриваемой области какую-нибудь линию, отличную
от векторных линий, и через каждую ее точку провести векторную линию, то
геометрическое место этих линий и даст нам векторную поверхность. В случае,
если упомянутая «направляющая» линия является замкнутой, получается трубко-
образная векторная поверхность, которая и называется векторной трубкой.
666.	Градиент. Пусть задано скалярное поле U(M) = U(x, у, z). Век-
тор g с проекциями на оси
dU dU dU
дх' ду’ dz	(4)
называется градиентом величины U (в соответствующей точке) и обо-
значается так:	—	, „
g = grad U.
Это формальное определение имеет тот недостаток, что использует коорди-
натные оси и оставляет открытым вопрос о независимости понятия градиента
от их выбора.
Чтобы убедиться в этой независимости, вспомним данное еще в первом
томе [184] определение производной от функции по заданному
. dU
направлению Г. , которая выражает скорость возрастания функции
по направлению I. Мы имели там формулу
dU dU , dU о , dU
-5J- = 5— COS а 4- 5— COS 8 -+- з— cos 1,
dl дх ' ду г 1 dz 1
где cos a, cos р, cos у суть направляющие косинусы направления Z; если через
X* обозначить единичный вектор, проведенный в этом направлении, то ее
можно переписать и так:
= gfad U- X == gradzZ/_
Наибольшего значения эта производная, очевидно, достигает в том случае,
когда направление Z совпадает с направлением градиента, причем это наи-
большее значение равно
. й гм	т Г(dU\s , (dU\2 । /dU\*
Это приводит нас к такому определению [ср. 184]: градиентом скалярной
величины U в данной точке называется вектор, который по численному
значению и по направлению характеризует наибольшую скорость возраста-
ния величины U. Здесь уже координатная система не упоминается вовсе.
Легко усмотреть, что направление градиента совпадает с направлением
нормали к поверхности уровня U{x, у, z) = C, проходящей через данную
точку.
Итак, скалярное поле £/(М) порождает векторное поле
градиента grad U.
666]	§ 4. ЭЛЕМЕНТЫ ВЕКТОРНОГО АНАЛИЗА	369
Г а м и л ь т о н (W. R. Hamilton) ввел в рассмотрение символиче-
ский векторе проекциями
А А А
дх ’ ду ’ dz
на оси координат, который он назвал «наблой» и обозначил через V. Поль-
зуясь этим обозначением, можно написать, что
grad U= VU.
Действительно, если упомянутый «вектор» формально «умножить» на ска-
ляр U, то и получится вектор с проекциями (4)!
Примеры. 1) Обозначая через г радиус-вектор ОМ, соединяющий не-
которую постоянную точку О с переменной точки М пространства, а через
г — его длину, положим
ЩЛ4) = ?(г),
где <р — какая-нибудь скалярная функция от положительного скалярного аргу-
мента г, имеющая производную постоянного знака. Поверхностями уровня,
очевидно, будут сферы радиуса г с центром в О, так что направление гра-
диента совпадает с радиальным или прямо противоположно ему, смотря по
тому, будет ли <р’(г)>0 или <0. Легко видеть, что
gradtp(r) = <p' (г)-у.
В частности,
grad у = — р г (с == const).
Если поместить в точке О массу т и рассмотреть поле ньютоновского
притяжения, то его напряжение ? в точке М будет
и, таким образом,
-я лт
F=&zA—.
Вопрос о том, может ли данное векторное поле быть рассматриваемо
как поле градиента для некоторой скалярной величины, имеет большую важ-
ность. По существу он для нас не нов; мы вернемся к нему ниже [670].
2) Рассмотрим поле температуры U. Взяв элемент поверхности (dS)
с определенным образом направленной нормалью и, подсчитаем количество dQ
тепла, протекшего через этот элемент в направлении п за бесконечно малый
промежуток времени dt. Тепло течет от более нагретых частей тела или
среды к менее нагретым, и притом тем быстрее, чем быстрее убывает
температура. Обычно принимают, что упомянутое выше элементарное коли-
чество тепла dQ пропорционально dS, dt и, наконец, |	. Обозначая через
/г>0 коэффициент пропорциональности («коэффициент внутренней тепло-
проводности» для данного места), можно написать
dQ = — kdSdt^-
дп ’
в согласии со сказанным выше количество тепла dQ оказывается положи-
di/
тельным именно в том случае, когда отрицательно, т. е. когда в напра-
влении п температура U убывает.
370
ГЛ. XVIII. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
[667
Если ввести так называемый вектор потока тепла
~q =— k grad U,
то выражение для dQ можно переписать короче:
dQ — dSdtqn.
Рис. 116.
стационарным, так
667.	Поток вектора через поверхность. Пусть теперь задано некоторое
векторное поле А (Л4), т. е. заданы три функции (3). Возьмем поверхность (3)
и, выбрав определенную ее сторону, обозначим через cos k, cosf», cosv направ-
ляющие косинусы соответственно направ-
ленной нормали п. Тогда поверхностный
интеграл
(п) (Лд-cos 1 + Aj,cosp+ A2cos v) dS,
(S)
который короче можно написать так'.
j AndS,
(S)
называют потоком вектора А через по-
верхность (S) в указанную сторону.
Обратимся к примерам.
1) Самое название «поток» связано с не-
которой гидромеханической задачей. Рас-
смотрим движение жидкости в пространстве;
в общем случае мы не предполагаем его
скорость движения v зависит не только от
положения точки М, к которой она относится, но и от времени t. Поставим
себе задачей вычислить количество жидкости, протекающее через поверх-
ность (3) в определенную сторону за бесконечно малый промежуток времени
dt. Через элемент (dS) поверхности протечет количество жидкости, которое
заполнит собой цилиндр с основанием dS и высотой vndt (рис. 116), где нор-
маль п предполагается направленной именно в выбранную сторону. Если
через р обозначить плотность жидкости, которая также может зависеть и
от положения точки, и от времени, то масса протекшей через dS жидкости
будет
р dS vndt.
что
Для всей поверхности (3) получим
dt ( J pon<ZS.
(S)
Количество же протекшей жидкости Q, отнесенное к единице времени,
выразится интегралом
Q=Upv„dS;	(5)
(S)
читатель узнает в нем «поток вектора» pv через поверхность (3)!
2) Аналогично можно говорить и о потоке тепла. Легко видеть,
что [при обозначениях п° 641, 2)] за время dt через поверхность (S) проте-
чет количество тепла, равное
Л у qndS.
6681
9 4. ЭЛЕМЕНТЫ ВЕКТОРНОГО АНАЛИЗА
371
Если отнести количество протекшего тепла к единице времени, то получим
S 5 4ndS,
(3)
т. е. «поток вектора» ~q через поверхность (8). Отсюда и название вектора
~q——k grad U
— «вектор потока тепла».
Замечание. Так как оба рассмотренных в 1) и 2) процесса мы не
предполагали установившимися, то на деле величина Q сама, вообще говоря,
зависит от времени. Она имеет характер скорости и точнее может быть
названа с к о р о с т ь ю возрастания количества протекшей через (S) жид-
кости (или протекшего тепла) в рассматриваемый момент времени.
3) Если рассматривается поле ньютоновского притяжения [о котором
была речь в 666, 1)]
-я т —
F= — г
то поток этого вектора через поверхность (8)
'^Lds
dV.
(6)
(S)	(S)
оказывается связанным с телесным углом, под которым поверхность (S)
видна из точки О [653].
668. Формула Остроградского. Дивергенция. Возвращаясь к общему
случаю векторного поля А, рассмотрим тело (V), ограниченное замкнутой
поверхностью (8); через п будем обозначать внешнюю нормаль к поверх-
ности. Тогда по формуле Остроградского [651 (5)], если положить в
ней Р—Ах, Q = Ay, Р=Аг, можно преобразовать поток вектора А через
поверхность (8) вовне в тройной интеграл:
xcos X -[- Ay cos + Дгсоз v) dS =
(5)	(3)
Стоящее под знаком тройного интеграла выражение называется ди-
вергенцией (или расходимостью) вектора А (в соответствующей
точке) и обозначается символом
Л дх + ду + дг '
Таким образом, формула Остроградского перепишется в виде
=	(7)
в каком она чаще всего и" применяется.
Введенная только что величина, дивергенция, есть скаляр; но ее
определение формально связано с выбором координатной системы. Для того
чтобы освободиться от этого недостатка, поступим следующим образом.
Окружим точку М каким-нибудь телом (V) с поверхностью (8) и напишем
372	ГЛ. XVIII. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ	[669
формулу (7); если обе части разделить на объем V тела и перейти к пре-
делу^ стягивая тело (V) в точку М, то [644, 8°] справа как раз и получится,
div А в точке М. Итак,
div3 — lim ---------- (8)
это равенство также может служить определением дивергенции, причем в
этой форме определение уже не зависит от выбора координатной системы.
На этот раз векторное поле А порождает скалярное
поле дивергенции div А.
Заметим, что определение (6) дивергенции может быть с помощью сим-
волического вектора V Гамильтона записано так:
div "А = V • А;
это станет ясно, если вспомнить выражение (1) скалярного произведения
двух векторов.
Пример. Остановимся на движении несжимаемой жидкости
(р = 1) при наличии источников (или стоков). Производительностью источ-
ников, заключенных внутри замкнутой поверхности (S), называется количе-
ство вытекающей через (S) жидкости, отнесенное к единице времени, т. е.
поток вектора-скорости v
[см. 667, 1)]. Если источники распределены непрерывно по рассматри-
ваемой области, то вводится понятие плотности источников. Так называют
предельное значение производительности источников в теле (V), окружаю-
щем точку М, рассчитанное на единицу объема, т. е.
5 J
Пт ----------
(V) — М V
Но, как мы только что видели [см. (8)[, этот предел равен div 5; итак, div's
и есть плотность источников.
Аналогичное рассмотрение можно провести и для теплового потока при
наличии источников тепла, лишь вместо вектора-скорости пришлось бы
взять вектор потока тепла.
669. Циркуляция вектора. Формула Стокса. Вихрь. Пусть снова дано
какое-нибудь векторное поле А (М). Интеграл
SAxdx Aydy Azdz = j A{dl,
)	(i)
взятый no некоторой кривой (I) в пределах рассматриваемой области,
называется линейным интегралом от вектора А вдоль кривой (L). В слу-
чае замкнутой кривой этот интеграл называют циркуляцией вектора
А вдоль (/).
Если поле А есть силовое поле, то линейный интеграл выражает работу
сил поля при перемещении точки ПО' кривой (Z) [ср. 554].
669]
S 4. ЭЛЕМЕНТЫ ВЕКТОРНОГО АНАЛИЗА
373
Представим себе некую поверхность (S), ограниченную замкнутым кон-
туром (/). Тогда по известной уже читателю формуле Стокса [639 (21 *)]
циркуляция вектора А вдоль этого контура может быть выражена поверх-
ностным интегралом:
0 . С С (1дАг дАу\ у . (дАх
й (3)
дАд . дАу дАх\ )
-j-5 cos у. +	----г* cos v] dS.
дх	\дх ду J
Вектор с проекциями на оси
дАг__дАу дАу^дА^ дАу дАх
ду dz * dz дх ’ дх ду	'
называется вихрем или ротором вектора А и обозначается сим-
волом *	-♦
го1Д.
Таким образом, в векторной форме формула Стокса запишется так:
A[dl = И rot„ Л dS.
(?)	(3)
(10)
Циркуляция вектора вдоль замкнутого контура оказывается равной по-
току вихря через поверхность, ограниченную этим контуром. При этом на-
правление обхода контура и сторона поверхности должны соответствовать
друг1 другу, как это разъяснено в п°620.
Данное выше определение понятия «вихрь»
страдает обычным недостатком: в нем исполь-
зуется определенная координатная система. Взяв
любое направление и, исходящее из данной
точки М, окружим ее в перпендикулярной к п
плоскости площадкой (а) с контуром (X) (рис. 117).
Тогда по формуле Стокса
(	rot„ A da;
(М	(»)
разделив обе части равенства на площадь а упо-
мянутой площадки и «стягивая» последнюю к
данной точке, в пределе получим **
j Ад1\
rot„X= lim —------------
(а) — М °
Таким образом, удается определить проекцию вектора rot А на любую
ось, а значит, — и сам вектор, без всякой ссылки на предварительно выбран-
ную координатную систему.
Подчеркнем, что здесь векторное поле Л*порождает вектор-
ное же поле вихря rot А С помощью гамильтонова вектора V можно
просто записать и определение вихря: rot A—N х А [см. выражения (2) для
проекций векторного произведения!].
* От английского слова rotation — вращение; употребительно и обозна-
чение curl И—от английского слова curl, означающего «завиток».
** Легко усмотреть здесь своеобразное дифференцирование по
области; обосновать его предоставляем читателю.
374
ГЛ. XVIII. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
[670
П р и м е р. Рассмотрим произвольное движение некоего твердого тела.
Если фиксировать в нем точку О (рис. 118), то, как доказывается в кине-
матике, для любого
ляется формулой
момента времени поле скорости v точек тела опреде-
v = v° + <о X Л
где v° есть споступательная скорость», т. е. скорость
точки О, <о — мгновенная сугловая скорость», а
г —радиус-вектор, соединяющий точку О с произ-
вольной точкой М тела. Проекции этого вектора
на оси произвольной системы Oxyz будут [см. (2)]
+	“ун-
если, воспользовавшись выражениями (9), подсчи-
тать проекции вихря для этого поля, то получим
2<лх, 2а>у, 2и>г, так что <o=-^-roto.
Таким образом, с точно'стью до числового множителя, ротор поля ско-
рости v дает как раз мгновенную угловую скорость; с этим связано и самое
название сротор».
670. Специальные поля. В этом и следующем п° для простоты
мы ограничимся рассмотрением полей, связанных с прямоуголь-
ными пространственными областями, в частности со всем трех-
мерным пространством.
1) Потенциальное поле. Векторное поле А называется потен-
циальным, если существует скалярная величина U, для которой
А служит градиентом; -♦_______grad £7.
Это равенство распадается на следующие три [см. (4)]:
д _dU_ , _dJJ . _dU
х~ дх' *~ду' г~дг
и равносильно утверждению, что выражение Axdx -|- Aydy -|- Azdz
является полным дифференциалом от функции U(x, у, z). Перво-
образная функция U называется потенциальной функцией
(или скалярным потенциалом) поля А.
Перефразируя уже известное нам [564 и 641; см. условия (Б)],
можно сказать, что
для того чтобы поле А было потенциальным, необходимо
и достаточно, чтобы во всей рассматриваемой области выпол-
нялись равенства
дАг дАу дАх dAz дАу дАх
ду	dz ’ dz	дх ' дх	ду *
т. е. чтобы rot А обращался в нуль.
670]	$ 4. ЭЛЕМЕНТЫ ВЕКТОРНОГО АНАЛИЗА	375
Таким образом, понятие потенциального поля оказывается
совпадающим с понятием «безвихревого» поля.
Опираясь на сказанное в п° 564 и 641, можно охарактеризовать
потенциальное поле и тем, что циркуляция по простому замкну-
тому контуру всегда будет нулем, а линейный, интеграл по кри-
вой, соединяющей любые две точки поля, оказывается не завися-
щим от формы кривой.
Сама потенциальная функция U, с точностью до произ-
вольного постоянного слагаемого, определяется линей-
ным интегралом
Axdx Aydy Audz = Atdl,
(l)	(0
взятым от некоторой фиксированной точки Л1о до переменной точки
М рассматриваемой области по любой соединяющей эти точки кривой (/).
Все эти факты получают естественное истолкование в терминах
работы для случая потенциального силового поля. Таким будет,
как известно, поле ньютоновского притяжения как в случае отдель-
ных притягивающих центров, так и при непрерывном распределении
притягивающих масс.
2)	Соленоидальное поле. Векторное поле А называется солено-
идальным, или трубчатым (от греческого слова aokev — трубка),
если существует векторная величина В, для которой А служит вихрем:
A = rotB.	(11)
Это равенство распадается на следующие три [см. (9)]:
д __дВ2___дВу	. __дВх__дВг	. ___дВу	дВх	/юч
*	ду	dz ’	? dz	дх ’ г дх	ду *	' '
Сам вектор В называют векторным потенциалом поля А.
Докажем теперь следующую теорему, дающую легко проверяемое
условие соленоидальности:
для того чтобы поле А было соленоидальным, необходимо и
достаточно, чтобы во всей рассматриваемой области выполня-
лось равенство	div А_0
Необходимость проверяется непосредственно вычислением:
если А — rot В, то [см. (12)]
div А = div rot В = -Д	4- £ №* —	4~
дх \ ду dz ] ' дух dz дх ) Г
___________дВх\____
। dz\dx
Достаточность. Пусть имеет место равенство (13). Поста-
раемся найти хотя бы частное решение (Вх, Ву, Вг) уравнений (12).
376	ГЛ. XVIII. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ	[670
В целях упрощения положим с самого начала Вг = 0. Тогда первые
два из уравнений (12) примут вид
dBv дВх
____L—Д _____2— л
dz ~х’ дг
и при интегрировании по z дадут следующие выражения для Вх и Ву.
г	г
ву = — \Ах(х,у, z) + <р (х, у), Вх — $ Ау (х, у, z) dz,
Z0	г0
где гй — произвольное из допустимых значений z, а <р (х, у) — еще
подлежащая определению функция двух переменных. Дифференцируя
интегралы по правилу Лейбница, найдем
z	г
дВу__ С дАх , , dy дВх_____ С дАу ,
dP—	+	~ду—})~д}Аг-
г0	Zf)
Используя равенство (13) для того, чтобы удовлетворить последнему
из уравнений (12), получим такое условие на функцию <р
^ = Ах(х,у, z№),
откуда <р легко определяется интегрированием по х (с точностью до
произвольного слагаемого, зависящего от _у).
Итак, наше утверждение доказано. Представляет интерес еще
установить, какая степень произвола остается при определении вектор-
ного потенциала В из уравнения (И). Если Д(о) есть какое-либо фи-
ксированное его решение, то общее решение В определяется условием
rot (5— _S(o)) = O и, в силу 2), пред-
ставится в виде
5 = Д(0) + С,
I где С есть любой потенциальный
уЗД-'*"	вектор.
—	с00бражений п°652 явствует,
Рис 11д	что условие (13), характеризующее со-
леноидальное поле А, равносильно
требованию, чтобы поток вектора А через любую замкнутую
(и ограничивающую некоторое тело (V)) поверхность (S) был равен
нулю.
Рассмотрим теперь в качестве тела (V) отрезок векторной
трубки (рис. 119) между двумя произвольными ее сечениями
(<Si) и (5г); боковую поверхность отрезка трубки обозначим через
(<93). Тогда — в случае соленоидального поля, — по сказанному,
{»+И+1Й^=о.
(St) (S,)	(5,)
670]	8 4. ЭЛЕМЕНТЫ ВЕКТОРНОГО АНАЛИЗА	377
причем нормаль направлена вовне по отношению к телу. Вдоль по-
верхности (<S3), очевидно, Ап = 0(665); если в сечении (S,) изменить
направления нормалей (так, чтобы они — в некотором смысле — были
направлены согласно с нормалями в (S2), см. рис. 119), то придем
к равенству:	^AadS=^ AndS.
($1)	(«а)
Таким образом, мы получаем следующее свойство соленоидального поля:
поток вектора через поперечные сечения векторной трубки со-
храняет постоянную величину, ее называют интенсивностью
векторной трубки.
Легко показать, что указанное свойство вполне характеризует со-
леноидальное поле. Это сразу следует из формулы (8) для расходи-
мости вектора А, если в качестве тела (V), окружающего выбран-
ную точку Ж, взять именно отрезок векторной трубки: тогда
^X„dS=0, а с ним и 6лгД = 0.
(S)
Если вернуться к приведенной выше гидромеханической интер-
претации векторного поля, то окажется, что в случае несжимаемой
жидкости и при отсутствии источников (div v = 0) расход
жидкости через поперечное сечение векторной трубки имеет одно и
то же значение для всех сечений.
3)	Разложение произвольного векторного поля. Мы покажем те-
перь, что произвольный вектор А всегда может быть представ-
лен в виде суммы потенциального вектора А и солено-
идального вектора А':
A = A'-j-A'
(rot Д'= 0, div Д'= 0).
Положим сразу же Д'—grad®, где Ф — еще подлежащая опре-
делению скалярная функция; равенство rotД'=п^^Ф = 0 этим
-уже обеспечено. Теперь А’ = А — grad®, так что Ф нужно выбрать
под условием
div Д' = div А — div grad Ф = 0.
Но
divgrad®=^ + ^- + ^ = A®,
если, как обычно, под Д Ф разуметь оператор Лапласа. Таким обра-
зом, для определения Ф имеем дифференциальное уравнение в част-
ных производных второго порядка
Д Ф = div Д,
которое всегда имеет решения (и даже бесчисленное множество их).
378	ГЛ. XVIII. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ	[671
671. Обратная задача векторного анализа. Она состоит в разыс-
кании векторного поля А по наперед заданным его расхо-
димости divA — F (F — скалярная функция) и вихрю rot А = В. Ввиду
2), ясно, что для разрешимости задачи во всяком случае необходимо
условие: div 5 = 0; предположим это условие выполненным.
Естественно (если вспомнить 3)) искать решение А в виде
суммы решений А' и А" таких систем:
(1) rot А' = 0, div A' — F, (2) rot А" = В, divA" = 0.
(1) Из первого уравнения, в силу 1), А'= grad®. Для определе-
ния Ф обратимся ко второму уравнению:
div grad Ф = F или ДФ = 5,
так что Ф есть одно из решений уже знакомого нам дифференциаль-
ного уравнения.
(2) Ввиду того, что (по предположению) div 5 = 0, в силу 2),
уравнение первое рассматриваемой системы имеет решение *. Обозначая
через А” какое-нибудь фиксированное частное решение этого урав-
нения, общее его решение можно написать в виде А" = А” С,
где С — произвольный потенциальный вектор, C=grad®. Остается
удовлетворить еще и второму уравнению системы (2), т. е. опреде-
лить Ф из условия
div А" = div A” -J- ДФ = 0 или ДФ =— div А".
Поставленная задача решена. Установить теперь степень произ-
вола в определении искомого вектора А. Легко сообразить, что два
решения разнятся таким вектором О, который удовлетворяет двум
уравнениям:	.. - п , х а
J	div 0=0, rot 0=0.
Второе из них дает: 0=0, rot 0=0, а из первого получаем тогда,
что Д77= 0: И есть произвольная гармоническая функция.
Однозначно вектор А получается, если установлены и «гранич-
ные условия», которые приводят к однозначному определению упо-
мянутой гармонической функции.
Результаты двух последних п° распространяются и на области
общего вида, удовлетворяющие — это нужно подчеркнуть — требова-
ниям односвязности того или другого типа, смотря по случаю.
672. Приложения. В заключение этого параграфа мы приведем
различные примеры использования понятий векторного анализа и
основных интегральных формул в векторной форме. Начнем с примеров
на применение формулы Остроградского и связанных с нею понятий.
* Обращаем внимание читателя на изменение обозначений — по срав-
нению с 2).
672]
§ 4. ЭЛЕМЕНТЫ ВЕКТОРНОГО АНАЛИЗА
379
Г. Уравнение неразрывности. Рассмотрим вновь движение жидкости при
отсутствии источников, но не будем, вообще говоря, предполагать
ее несжимаемой. Считая, что жидкость сплошным образом заполняет прост-
ранство или определенную его часть, вырежем из жидкости, произвольное
тело (V), ограниченное поверхностью (S). Количество жидкости Q, вытекаю-
щее вовне из этого тела, рассчитанное на единицу времени, как мы знаем,
выразится формулой (5). Подсчитаем это же количество иначе. Если учесть
изменение плотности р за промежуток dt на величину^dt, то масса pd/
элемента (dV) тела изменится на ^dtdV, а масса всего рассматриваемого
тела на

Такое количество жидкости должно за промежуток времени dt протечь
внутрь тела; изменив его знак, получим количество жидкости, вытекаю-
щей за этот промежуток вовне. Наконец, если отнести количество выте-
кающей жидкости к единице времени, то найдем
Чтобы удобнее было приравнять оба выражения для Q, преобразуем по-
верхностный интеграл (5) по формуле Остроградского (7) также
к тройному интегралу. Таким путем мы получим
S |^+div(pw)|dK=0.
Так как это равенство имеет место для любого тела (V) в пределах рас-
сматриваемой области, то, в силу 644, 8°, отсюда следует, что тождест-
венно	а	~
+ div (pv) — 0.
Это равенство и известно под наименованием уравнения неразрывности.
2°. Основное уравнение движения идеальной жидкости. Пусть на
жидкость в общем случае действуют как внешние, так и внутренние силы.
Внешние силы мы считаем пропорциональными массе, так что, если /%сть
сила, действующая на единицу массы, то на элемент жидкости (dV) будет
действовать сила fdV F-
Что же касается внутренних сил, т. е. сил, действующих на выделенное
из жидкости тело (V7) со стороны остальной жидкости, то идеальная жидкость
характеризуется именно тем, что эти силы приводятся к нормальному по
отношению к поверхности (S) этого тела давлению, направленному внутрь
тела. При этом самая величина р давления, приходящегося на единицу пло-
щади, зависит не от ориентации той бесконечно малой площадки, к ко-
торой давление приложено, а лишь от ее координат. Таким образом, на
элемент поверхности (dS) действует сила, проекции которой на оси будут
—pdS cos X, —р dS cos р, —pdS cos v,
если через cos X, cos p, cos v обозначить направляющие косинусы Внешней
нормали к поверхности. На все тело (V) будет действовать сила, опреде-
ляемая проекциями
— HpcosX dS, — И р cosр dS, — Ир cosvdS,
W	W	IS)
380	ГЛ. XVIII. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ	(672
или — если снова прибегнуть к преобразованию по формуле Остроград-
ского, — интегралами
чр-
Сила, приходящаяся на долю элемента (dV) жидкости, будет иметь проекции
-d£dV, -dPdV, -dPdV,
дх ’ ду	dz
и следовательно, как вектор, представится в виде
— dVgrad р.
Если теперь через а обозначить отвечающее элементу (dV) ускорение,
то по закону движения Ньютона
р dVa = Fр dV— dVgrad р,
откуда окончательно
a — ~F--^-gradp.	(14)
Это и есть основное уравнение движения идеальной жидкости в век-
торной форме. Оно распадается на три скалярных уравнения, если перейти
к проекциям на три оси координат.
3°. Уравнение теплопроводности. В качестве последнего примера приме-
нения формулы Остроградского рассмотрим вопрос о тепловом состоя-
нии тела под действием внутренней теплопроводности при отсутствии источ-
ников тепла.
Если выделить тело (V), ограниченное поверхностью (S), то, как мы ви-
дели в 667, 2), количество тепла, вытекающего из тела через поверхность (S)
вовне, рассчитанное на единицу времени, будет равно
Q— — Ийgrad„ UdS
(S)
(мы сохраняем прежние обозначения). Изменив знак в этом выражении и пре-
образуя его к тройному интегралу, для количества тепла, вытекающего
внутрь тела, найдем выражение
div (й grad t/)dV.	(15)
Это тепло повлечет за собой изменение температуры внутри тела (V) и
может быть подсчитано иначе. Увеличение температуры U на dU— dtee
промежуток времени dt потребует сообщения элементу (dV) тела количества
тепла
с dt/p dV= c^dtp dV,
где с означает теплоемкость тела в рассматриваемой точке. Все тело (И)
за время dt поглотит количество тепла
(Ю
672J
§ 4. ЭЛЕМЕНТЫ ВЕКТОРНОГО АНАЛИЗА
381
если же отнести его к единице времени, то получим
Приравнивая выражения (15) и (16), придем к равенству
§	~ div Srad } dV>
которое выполняется для любого тела (V), взятого в рассматриваемой области.
Отсюда, как и выше в 1°, заключаем, что в этой области имеем тождественно:
ср = div (й grad U).
Это и есть уравнение теплопроводности.
В случае однородной среды оно принимает вид
dU
dt
k
где а3— — и А означает оператор Лапласа:
... d3U . d*U , d3U
^~дхз+ дуз+ дг3’
Наконец, при стационарном распределении температуры U она не за-
висит от времени и удовлетворяет уравнению Лапласа
Д£/=0,
т. е. является гармонической функцией координат точки.
Перейдем к примерам приложения формулы С т о к с а и связанных с нею
понятий. Эти приложения относятся к движению жидкости.
4°. Рассматривая внутри жидкости линию или поверхность в некий мо-
мент времени, мы будем интересоваться тем, какой образ составится из
тех же жидкихчастицв другой мо-	у*—ч.
мент. В этих исследованиях важную роль	В& \
будет играть такое вспомогательное утвер- —	\
ждение: производная по времени от цир- / А
куляции скорости по замкнутому жидко- В^ 1	I
му контуру равна циркуляции ускорения	у J________У
по этому же контуру.	. jjf	п
Рассмотрим какой-нибудь контур (Z.o) =	'
= (Л0В0) в момент времени^. Выберем за	р
параметр, определяющий положение точки	нис’
Мо на нем, скажем, дугу e== Л0М0 (рис. 120); если в момент t жидкий кон-
тур (Ло) = (Л 0В0) перешел в (£) = (ЛВ), то положение точки М, в которую
перешла точка Мо, определится уравнениями вида
X = <? (a, t), у = <р (а> 0> г = Х (а> 0 (0 «£ ° =6 о).
Циркуляция скорости
I	а
J= vxdx + М? + v»di = (v* 57 + Vy	de iyi)
382
ГЛ. XVtU. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
может быть продифференцирована по t по правилу Лейбница:
dJ _ С !дух дх .
dv? ду
dt да
ди,дг\ . .
С / дгх .	д2у .	д2z \ . С ( дх . ду . дг\ , ,
4- \ в, 3-5- 4- uv -3-3- 4- у, 5-3- da = \	—к av	4- а, 3- ] da 4-
0	У	у\хда'?да'гда “
СТ
Первый из полученных двух интегралов дает циркуляцию ускорения
5 axdx -|- aydy -|- azdz.
(I)
Второй же непосредственно вычисляется, так как подинтегральное выраже-
ние есть производная по а от
у (уX 4- Уу + Vz) = у У2;
он равен
что в случае замкнутого контура (L) обращается в 0.
Итак, окончательно:
axdx 4- aydy 4- azdz,
(I)
(18)
что и требовалось доказать.
5°. Пусть мы имеем дело с идеальной жидкостью в смысле 2’.
Кроме того, сделаем еще два предположения: 1) сила F имеет потенциал,
т. е.
F^gradf/;
2) плотность р есть однозначная функция от давления *:
Введем величину
₽ = ?(/»)•
Ф(р) =
dp .
?(Р)’
* Жидкость, удовлетворяющая последнему требованию, иногда назы-
вается «баротропной».
6721	§ 4. ЭЛЕМЕНТЫ ВЕКТОРНОГО АНАЛИЗА	383
тогда
д<Ь _ др  1 др
дх dpdx р ~дх
и аналогично
дФ  1 др дФ  I др
ду	р ду ’ dz	р dz'
так что
grad Ф=-i-grad р.
Мы имели уже основное уравнение гидродинамики (14). Теперь оно на-
пишется в виде
"2 = grad (U— Ф).
Если подставить это в полученное выше равенство (18), то окажется
~ = \ d (U—Ф) = 0, так что J=const.
(i)
Таким образом, циркуляция скорости по любому замкнутому жидкому
контуру постоянна во времени. Это есть теорема Томсона (W. Thomson).
Отсюда, как простое следствие, получается интересное предложение
Лагранжа: если рассматриваемая масса жидкости не имеет вихрей в
некий определенный момент времени, то она не может иметь вихрей и
во всякий другой момент. Действительно, отсутствие вихрей равносильно
обращению в нуль циркуляции скорости вдоль любого замкнутого контура
1670, 1’]. Если это обстоятельство имеет место однажды, то по теореме
Томсон а то же будет и всегда.
6°. Теперь мы в состоянии доказать две важные теоремы Гельмгольца,
относящиеся к «вихревым> линиям и трубкам *. При этом мы все время
сохраняем предположения, указанные в начале 5°.
_ Теорема о сохранении вихревых линий. Частицы жидкости, обра-
зующие вихревую линию в некий момент времени, и во все время дви-
жения образуют вихревую линию.
Нам проще доказать это сначала относительно вихревой поверх-
ност и. Пусть (So) будет такой поверхностью в момент времени t0; тогда
В каждой ее точке вихрь скорости
2 = rot®
(будет лежать в касательной к (So) плоскости, т. е. 2„ = 0. Если взять на по-
верхности любой замкнутый контур (Хо), ограничивающий часть (а0) поверх-
ности, то пр,формуле Стокса (14)
$ vxdx 4- Vydy 4- vgdz = J J QndS0 = 0.
(X«)	(Oq'
* Вихревой линией или поверхностью (в частности, трубкой)
Называется, соответственно, векторная линия или поверхность (трубка) для
Ноля вихря.
384	гл. XVIII. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ	(673
В момент времени t жидкая поверхность (So) перейдет в поверхность (S),
ее часть (з0) — в (а), а жидкий контур (Хо)— в контур (X). Но по теореме
Томсона и сейчас
( vxdx vydy -\-vzdz= О,
так что (снова по формуле Стокса)
$$2„dS = 0.
(’)
Ввиду произвольности (а) отсюда легко заключить, что вдоль (S) тождественно
2„ = 0,
так что и поверхность (S) оказывается вихревой.
Так как вихревую линию всегда можно рассматривать как пересечение
двух вихревых поверхностей, то теорема доказана. В частности, отсюда сле-
дует и сохранение вихревых трубок.
Теперь уж совсем легко получается
Теорема о сохранении интенсивноста вахревых трубок. Интен-
сивность любой вихревой трубки во все время движения остается посто-
янной.
По формуле Стокса интенсивность вихревой трубки, т. е. поток вихря
через поперечное сечение трубки, приводится к циркуляции скорости по
контуру этого сечения [ср. 670, 23]. В таком случае требуемое заключение
прямо следует из теоремы Томсона [3°).
Этими примерами применения введенных понятий и основных формул
интегрального исчисления мы и ограничимся.
§ 5. Многократные интегралы
673. Задача о притяжении и потенциале двух тел. Потребности
анализа и его приложений не исчерпываются уже изученными типами
определенных интегралов: простыми, двойными и тройными.
Проиллюстрируем это на примере задачи о притяжении
двух тел. Будем обозначать через Хц уь координаты точек
первого тела, (Ц), а через х2, у2, z2, — координаты точек второго
тела, (У2). Пусть в функции от этих координат заданы и плотности
распределения масс в обоих телах: р2 == pt (хь уь Zi) и р2=р2 (х2, _у2, z2).
Если в каждом из тел выделить по элементу с массой, соответственно,
Ptdxtdyidzt и p2dx2dy2tfe2, то второй из них действует на первый по
закону Ньютона с силой *
p1p2rfx1d'y1rfzirfx2rfy2rfz2
г2	’
* 1.2
где Г1>2 есть расстояние между элементами:
П,2 = V 0^2 -^l)2 + (У2 -У1)2 + (г2 г1)2-
* Коэффициент пропорциональности в ньютоновой формуле закона
всемирного тяготения мы, как обычно, полагаем равным L
673}
$ 5. МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
385
Так как эта сила направлена от точки (xit уь Zi) к точке
(х2, уз, Zi), то ее направляющие косинусы будут	Уа А,
г1,а г1,а
*8 —. Поэтому проекция, скажем, на ось х силы притяжения пер-
Г 1,2
вого элемента вторым равна
PiPs (*г — Xi)
'1.3
Проекция же Fx результирующей силы, с какой второе тело притя-
гивает первое, получается суммированием найденных выражений по
всем элементам обоих тел, т. е. выражается шестикратным
интегралом
р»р«(^«—~ dXidyjdztdXidyidZz,
распространенным на шестимерную область ( V) = ( Vj) X ( Va) то-
чек (х1( уь zt, Хз, уз, гз), где (xt, yt, zt) взято из (Ц), а (хз, yit z2)
из (Vs). Так же выражаются и другие две проекции.
Аналогично этому величина
fi^dx^yjdz^XtdysdZj
есть потенциал одного элемента на другой. Суммируя эти выражения,
получим потенциал одного тела на другое, снова в виде шестикрат-
ного
интеграла:
dXidy^dzidXi/iyidZi.
ri, з
Если оба тела тождественны, то подобный интеграл, деленный на 2
(ибо иначе каждая пара элементов учитывалась бы дважды!), даст
нам потенциал тела на себя.
Предложим себе для примера вычислить потенциал на себя одно-
родной (р! = р8 = 1) сферы х2 у2 z4 R2, т. е. интеграл
S


Вычисление можно провести так. Потенциал сферы xss -f- z8 R2
на элемент dx^dy^dzi с координатами xb yb zt, отстоящий на рас-
стояние ri = Ух8	-j- z\ от центра, мы уже знаем [650, 12)]; он
выражается Тройным интегралом и равен *
2	\
2irR2----g- w8 j dx^dy^dzi.
* Следует учесть, что масса точки, на которую здесь вычисляется по-
тенциал, есть не 1, a dx^y^dZi, кроме того роль а, которое фигурирует
в выведенной раньше формуле, здесь играет гР
13 Г, М. Фихтенгольц, т. III
386	ГЛ. XVIII. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ	(674
Остается еще просуммировать подобные выражения по всем элементам
сферы х, -(-yj + z\ R2, т. е. взять еще один тройной интеграл:
(2тс^2 — У кг *) dxidyi^i-
»?+>’1 + гГ=^2
Это легко выполнить, переходя к сферическим координатам. Оконча-
тельно получим:
Жо = Ц*2Я5.
В данном случае вычисление шестикратного интеграла свелось к
вычислению двух тройных интегралов, из которых один к тому же
был уже известен.
Перейдем теперь к установлению относящихся сюда общих поня-
тий, хотя в большинстве случаев придется ограничиться ссылкой на
аналогию с изученными выше видами интегралов.
674. Объем «-мерного тела, «-кратный интеграл. Наподобие
того, как при определении простого, двойного, тройного интеграла,
мы пользовались понятием длины отрезка, площади плоской фи-
гуры, объема пространственного тела, в основе определения «-крат-
ного интеграла лежит понятие объема* «-мерной области. Для
простейшей «-мерной области — «-мерного прямоугольного параллеле-
пипеда
[а1; Ь{, а* ; aw bn]	(1)
объемом называется произведение его измерений
(61 — аО (62 — а2)... (6„ — а„).
Само собою ясно, чтб разуметь под объемом тела, составленного из
конечного числа таких параллелепипедов. Элементарно можно пока-
зать, что объем не зависит от того, каким образом тело разложено
на параллелепипеды.
Рассматривая такие «параллелепипедальные» тела, входящие в дан-
ное «-мерное тело (V) и выходящие из него, можно обычным обра-
зом построить понятие объема V для тела (V) [ср. 340].
Мы будем иметь дело только с телами, для которых объем сущест-
вует; он заведомо существует для тел, ограниченных гладкими
или кусочно-гладкими поверхностями**, в частности, для
* Мы решили сохранить этот термин, хотя смысл его, разумеется,
меняется вместе с п: речь идет об „«-мерном объеме®. Можно было бы за-
менить его одним из слов: „протяженность®, „мера® и т. п.
** Г ладкой поверхностью называется здесь образ в «-мерном про-
странстве, определяемый п параметрическими уравнениями си — 1 пара-
метрами, причем фигурирующие в уравнениях функции параметров должны
быть непрерывны вместе с частными производными, и определители (и—1)-го
порядка матрицы производных не должны одновременно обращаться в нуль.
674]	5 5. МНОГОКРАТНЫЕ ИНТЕГРАЛЫ	387
простейших: знакомых намл-мерных областей — «-мерного симплекса
Х| О, Х% 0, . . . , Хп О, Х^ —[— Xj —[—... —|— хп	h
и «-мерной сферы
х[ -[- х| -J- хя sgi г3;
ниже мы вычислим их объемы [650, 1) и 2)].
Пусть в области ( V) задана функция « переменных f (xj, х2, ... ,
хя); тогда, разлагая эту область на элементарные части и повторяя
другие столь привычные уже нам операции [ср. 643], придем к по-
нятию «-кратного интеграла
п
1= $... $/(хъ хъ, ... , х„) dxtdXi ... dxn.	(2)
(V)
В случае непрерывной подинтегральной функции он наверное суще-
ствует.
Вычисление такого интеграла приводится к вычислению интегра-
лов низшей кратности, вплоть до простых. В случае, когда область
интегрирования (V) представляет собою прямоугольный параллелепи-
пед (1), имеет место формула, аналогичная формуле (10) п° 645:
bl	bi
I = dxt J dXi ... J f(xb ха, ... , хл)dxn.	(3)
«ч	«я
Для областей более общего вида, характеризуемых неравенствами
X? -с Ха -с Х1г Ха (Х1) -с Xg (Xj),...
, х%(хъ ..., х^) ==Sx„Хп(хъ ..., х^О,
применима формула, аналогичная формуле (10 *) п° 646
Xi Х>(ж,)	Хп<х‘...хл-1>
I—^dXi dxt... J /(xb xs,..., xa)dxn. (4)
*? .....
Подобным же образом (для соответствующего вида областей,
который в каждом случае нетрудно установить) имеют место и дру-
гие формулы, аналогичные формулам (8 *) и (11 *) п° 646, где
вычисление «-кратного интеграла приводится к последовательному
вычислению Интегралов низших кратностей, в сумме дающих п.
Все 9то доказывается совершенно так же, как для случаев
л =2 или «==3, без привлечения каких бы то ни было новых идей,
так что нет надобности на этом задерживаться. Без дальнейших
пояснений очевидно, как определяются несобственные «-кратные
интегралы и как на них распространяются упомянутые выше формулы.
13*
388
ГЛ. XVIII. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
(675
Замечание. Можно было бы для функции от п переменных
установить понятие и об интеграле, распространенном на
(и—1)-мерную поверхность [см. замечания к примерам 3) и
16) п° 676]. Ввиду сложности предмета, мы не можем здесь на этом
останавливаться. Отметим лишь, что М. В. Остроградским —
в обобщение формулы (4) п° 651 — было установлено соотношение,
связывающее такой интеграл, взятый по замкнутой поверхности,
с неким n-кратным интегралом, распространенным на ограниченное
ею тело.
675. Замена переменных в л-кратном интеграле. Этот вопрос
мы рассмотрим несколько подробнее. Пусть даны две «-мерные
области: (D) в пространстве х,х<, ... хп и (А) в пространстве BjB2..Ап,
ограниченные каждая одной непрерывной — гладкой или кусочно-глад-
кой — поверхностью. Предположим, что между ними с помощью
формул	t ,
JCl---К, (Bi, B2, ... , Bn),
X2 = X% ($i, B2, .. . , Вл),	(5)
jcn—xn (Bj, B2, .. , Вя)
устанавливается взаимно однозначное соответствие. Тогда, при
ных предположениях относительно производных и сохранения
обыч-
знака
якобианом
	дх.	дх2 dit	dxn ” di,
	дх,	дх2	дхп
D(ii, .... in) ~~	Я»	ЙВз	" di2
	•	• •	• •
	дх,	дх2	dxn
			
	din	din	
интеграл от непрерывной в (D) функции f (jq, х2, ..., хп) может
быть преобразован по формуле
п
... $/(Х1, .... xn)dx, ... dxn —
(D)
п
= S ... J/^iCBb ..., Вл), ...,x„(Bi,.... B„))| J[dBi ... dB„, (6)
w
которая совершенно аналогична формулам преобразования двойных
и тройных интегралов [609 (21); 661 (8)].
Доказательство этой формулы мы проведем по методу
математической индукции. Так как для п = 2 и л = 3 она уже была
675J
$ 5. МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
389
установлена, то достаточно, предположив справедливость
подобной формулы преобразования для (и—^-крат-
ного интеграла, доказать ее для интеграла и-кратного.
Без умаления общности можно предположить, что какая-либо из
частных производных сохраняет знак (иначе пришлось бы лишь
разложить область (Д) на части, для которых это справедливо);
х	dx,
пусть это будет производная
Выделив в предложенном интеграле (2) интегрирование
перепишем этот интеграл в виде
__	п — 1
Al	.
ПО Х1г
, xjdxs ... dx^,
(7)

здесь (DXl) означает область изменения переменных х2,	х„, от-
вечающую фиксированному значению хР
Разрешив первое из уравнений (5) относительно переменной
выразим ее в функции от х2, $2, ,..,
$1---(Ху ?2, ..., ?п)
и подставим это выражение в остальные формулы. Таким путем мы
получим новые формулы преобразования:
Х2----X 2 (^i (Xj, ?2, .. . , ?л), ?2, ...» $я)----Х2 (Х1, ?2, • • • , £д),
(8)
Хп — Хп ($i (Ху $2, .,., 5д), ?2, ... , $„) — Хп (Хц, $2, ... , £л).
Преобразуем, исходя из этих формул, (я — 1)-кратный внутренний
интеграл в (7) к переменным Е2, ..., что по предположению можно
сделать по формуле, аналогичной (6). Мы придем к интегралу
^dXiJ ... \f(xb x2(xb S2, ..., Q, ...
..., ^Я(Х1, $2, ...,	A 
где
дхп
^$2
У*__ D	хя)___	....
~ D&, ...» W “ .... •
дха дхп
din dia
(9)
390	ГЛ. XVIII. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ	[675
Поставим теперь в нем интегрирование по xt на первое место:
.......................
{ ... [d^ ... dln $ f(xb x2(Xi, .................
(Д>)	*10(£2.U
• • • > %п (*1> ^i> • • • г £д)) 1 J* I dXy
и во внутреннем интеграле перейдем от переменной х^ к переменной
по первой из формул (5) (при фиксированных ?2, ..5Л). Мы получим
.....................................Ы
$... $<й2... <йл	•••> Q»
<Л‘>	....5п)
х2Сь е2,.... U .... *л&, ?2,....
или, возвращаясь к n-кратному интегралу:
п
(Д)	I «« I
Чтобы придти к (6), остается только убедиться в тождестве
Но, дифференцируя сложные функции (8) по ?2, ..., 5Л и используя
для выражения производных от функции правило дифференциро-
вания неявной функции, найдем
dxi dxt
dXj__dxi , dxj ____dx,	dtk
dik~~ dik^~d^d^ ~ &Ч
(/, k = 2, ..., и).
Поэтому, если в определителе J к элементам k-Vi строки (k — 2,..., n)
прибавить соответственные элементы первой строки, умноженные на
dxj
-—то он примет вид
Ж
dxt	дх3	дхп
		
		
	дх.	дхл
	- -	
	•	д£2
Л	дХ2	дхп
		
	д1а	’ din
676)	$ 5. МНОГОКРАТНЫЕ ИНТЕГРАЛЫ	391
откуда и ясно, что он равен J* ~. Этим и завершается доказа-
тельство.
Заметим, что мы молчаливо предполагали (и—1)-мерные области
(DXl) и (ДХ1) ограниченными всякий раз одной непрерывной, гладкой
или кусочно-гладкой, поверхностью (в соответствующем пространстве).
Раздробив предварительно область (D) и одновременно с нею (Д) на
части, всегда можно добиться того, чтобы сказанное было верно, по
крайней мере, для каждой части в отдельности. Формула (6), справед-
ливая для этих частей, будет справедлива и для всей области в целом.
Обычным образом формула замены переменных распространяется
и на случай несобственных интегралов.
676. Примеры. 1) Найти объем Тп «-мерного симплекса [162]
(Гп):	..., хя>=0, х,-|-хг-[• ... хп h.
Решение. Имеем
л
Та =	( dxldxi ... dxn =
(Г„)
Л A — Xi	h — xi — .. . —
== dxt dxt ...	dxn.
Заменяя в этих простых интегралах последовательно переменные по
формулам
Xi == Л$1, ха —	..., хл —
причем нет надобности пользоваться общей форму-
лой (6), придем к результату
1 l-5t 1-Е1-...-Ея_!
Tn=>h*\dlt С dt, ...	\ dtn =
= Лп ( ... J dit ... dt„ = anA”,
512=0..... t==0
5i+-.. + ln;Sl
если через ая обозначить значение интеграла, подобного предложенному, но
отвечающего й=1.
С другой же стороны, имеем (попутно используя полученный результат)
«л=^л S • • • S d5i...d5n_i =
0	5120,...,5Я .2=0
и
392
ГЛ. XVIII. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
1676
Найденное рекуррентное соотношение (с учетом того, что а1=1) дает нам
1
“л — л! ’
так что окончательно
2)	Найти объем Vn л-мерной сферы [162]
(/„): xl + xl+ ...
Решение. На этот раз речь идет о вычислении интеграла
п
Vn =	$ . . . 5 dXtdXb ... dxn.
х*+х»+...+х%&1»
Полагая
at, = 7??!, х2 = Тй3, .... хл = 7йл*,
легко получить, что Vn = $nRn, где числовой коэффициент рл выражает
объем л-мерной сферы радиуса 1.
Для определения рл преобразуем
п
?л —	§ . • • §	•” ^п —
е?+ •.. + i&si
1
— dZn ^ . . . ^	... й?$л_1.
Внутренний интеграл представляет объем (л — 1)-мерной сферы радиуса
п— 1
У1—5Л и, следовательно, равен рл_( (1 — 6Д) 2 . Подставляя, придем
снова к рекуррентному соотношению
Л
У
₽» = 2₽ЛД sinMdO
о
или [см. 534, 4) (б)]
г
_	\ 2 )
₽л — ₽»-1. /Г /„ 4- 2\ •
\ 2 J
* И здесь также не нужна общая формула (6): представив крат-
ный интеграл по формуле (4) в виде повторного, можно затем последова-
тельно заменять переменные в каждом из простых интегралов в отдельности.
393
676]	$ 5. МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
Так как р1 = 2, то легкое вычисление дает
л
Искомый же объем равен
л
Для случаев п четного и нечетного получаются формулы
[/ — psm [/	_ (2rc)m
гт ~ т\* ’ im+1 — (2m + 1)!! К ’
В частности, для Vlt Vs, Vs, естественно, находим хорошо известные зна-
чения 27?, пЦ3,
3)	Вычислить (несобственный!) интеграл
dxi ... dxn_t
yi-xf- ... -х3п_х
(n>2).
Решение. Преобразуем предложенный интеграл так:
S=	dxt,,, dxn_t X
л*+ ...+л£_2==1
-*л-2
X	(	__
--——м----------]А ~Х1~ "• — хп-2~ хп- 1
Внутренний интеграл здесь равен я, так что [см. 2)]
Замечание. Любопытно отметить, что вычисленный только что ин-
теграл, с точностью до множителя 2, выражает площадь поверх-
ности л-мерной сферы ... -[-хД=1. Не входя в подробности,
упомянем, что в случае явного задания поверхности
л„=/(х1...х^),
394
ГЛ. XVIII. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
|676
где точка (хь , xn_t) изменяется в (и — 1)-мерной области (Е), площадь
этой поверхности выражается интегралом *
л- 1
(£)
| dxt ... dxn_i.
В частности, для полу с.ф еры
2 I
п — 1
имеем
rfx! ... dxn i
п
dXj ... dxn i
Х& 1
— 1
Таким образом, площадь поверхности n-мерной сферы радиуса 1 равна
в случае сферы радиуса R площадь, очевидно, будет
2^п_^п~1=2-
Г
n
У
^n~l-
Этот результат принадлежит Якоби.
4)	Доказать формулу Дирихле:
1 ,
dxt ... dxn
Л
п
Г(р,) - Г(р„)
Г(Р1+ ••• + /’» + О
(Pi, —. Ря>0).
Применим метод математической индукции, опираясь на то, что при
п — 2 формула уже была установлена [(697, 12); 617, 14)]. Допустим ее вер-
ность для (л — 1)-кратного интеграла. Переписав левую часть формулы в виде
xfr ‘ dxn $ • • • $	х*» 1 ... х^лд dXl ... dxn_lt
* Она по строению совершенно аналогична формуле (4а) 329 для длины
дуги плоской кривой и формуле (5) 626 для площади кривой поверх-
ности, где в обоих случаях имеется в виду явное задание.
395
676]	$ 5. МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
произведем во внутреннем интеграле подстановку •
*1-(1~••• > ХП-1-(1 Хп) 5д-1
и затем применим к (п — 1)-мерному интегралу формулу Дирихле.
Мы получим
если заменить интеграл его выражением через Г:
г (Рп) Г (Pt + • • • Ч~ Pn-i Ч~ 1)
Г (Р1 + ••• +Рл-1 +Рд+ 1) ’
то придем к требуемому результату.
5)	Формулу Дирихле легко обобщить:
••• х„п ' dxt ... dxn =
(<Ч, аь Pi > 0).
Эта формула приводится к уже доказанной, если перейти к новым пере-
менным =	‘(< = 1, ..., п) *.
В частности, при pi = ... = pn = l,al = ••• =ал = 2, al = ... = an = R,
отсюда снова получается формула для объема Vn п-мерной
сферы ** [(см. 2)].
* См. сноску на стр. 392.
** Следует лишь иметь в виду, что в, связи с ограничением положи-
тельными значениями переменных формула Дирихле непосредственно
дает лишь объема.
396	ГЛ. XVIII. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ	(676
6)	Особо отметим формулу Дирихле для случая п = 3:
J J ) xP~1y9~izr~1 dx dy dz =
x, у, г & О
. W Г (4) г Ш Г (y'l
г4+|+т+1)’
(р, q, г>0),
которая полезна при определении объемов, статических моментов, моментов
инерции и центробежных моментов для однородных тел указанной формы.
Например, для части эллипсоида ( — ) + гу) +(7)	1 (“ = ₽ = Т = 4>»
содержащейся в первом октанте, получаем (считая плотность равной 1):
Гг ШТ
.	abc I \ 2 Л те
при р = q = г = 1	V= -g-	4- = _ abc,
ы
9	,	м	a'bc	г (1) [г (4)Г те 2А
при р = 2, ? = г=1 Муг = —%-г (3)	= |g abc,
гШГг ШТ
„	.	,	a*bc	х к 2 7 L \2 /] те ..
при р = 3, q = r=\	1уг=-^---Ш =30^.
Ы
в^гШ[г(1>13 1
при р=1, q — r — 2 Куг = —--abV, и т. д.
ГЫ
7)	Доказать формулу Лиувилля (plt р2, ..., рп > 0):
п
J ... $	<р(*!+ ••• +xn)xPli~lx^~l ... xpn~l dxtdx2 ... dxn =
xi; •••• *„s=° ,
+ ... + Xn 1
B= Г(Р1)Г(Р2)	Г(р„) С (р(и)цР1+Рг+ +pn-ldu,
Г(/’1 + /’2+ ••• +p«)
в предположении абсолютной сходимости простого интеграла справа.
676]
$ в. МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
397
Для п — 2 эта формула уже известна [597, 16); 611, 17); 617, 14)]. До-
пустим ее справедливость для (п—1)-кратного интеграла. Левую часть дока-
зываемой формулы перепишем так:
п— 1
•••	1 dxi ••• dxn-i х
<Р (Х1 + • • • + Хп) ХпП dxtl‘
Если положить
Ф(0= J чЦЛ-Хп) idxn,
то внутренний интеграл здесь заменится через ф(х1+ ... + -*n-i)i а тогда
по формуле Лиувилля, примененной к (п — 1)-кратному интегралу, по-
следний представится так:
Г (Pi) ... Г (Рд-i)
1’(Р1+ ••• +/’л-1)
f Ф(0<Р1 + '”+р'*-1 ’л.
Подставляя Вместо ф (0 его выражение, мы заменим полученный повторный
интеграл двойным:
J $	<?(t + xn)tPl +"' +Р'*-1	1 dtdxn.
t, х э=о
Остается лишь применить к последнему уже доказанную формулу, чтобы
придти к требуемому результату.
8)	Отсюда легко получить более общую формулу:
(все числа а,-, а/, pt предполагаются положительными).
895	гл. XVIII. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ	(676
Эта формула, например, позволяет вычислить следующие интегралы, уста-
навливая попутно и условия их существования *:
р—‘—р	— 1 хРа 1
(а) \ ... \ -------—— -------dxi ••• dxn =
..хя^о
хМ+...+х“'^1
। r(g)-r(r:)r<i->‘>
-“"Г (1-и + ^+...+?»)
\	®1	ал/
(при [л < 1);
при |х<^- + ••• + -);
ад/
где для краткости положено
т=^ + ..- +
а1
Рп
а«‘
* Поскольку абсолютная сходимость интеграла справа в формуле Л и у-
в и л л я имеет место одновременно со сходимостью интеграла слева.
676]
$ 5. МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
399
9)	Доказать с помощью математической индукции формулу:
л
?	xf1 —1 ... хр“ rfx, ... dx„
... \ т(х. + ...+х»)------!--------=----- ,1+ 2Р ~
.... Ж Jo	(«Л + - + «л + *)Р1+-+Рл
= г».г».) t	____т
Т(Л, + ... + я«)^ ’ (Од„ + „р.,,, (0„„+ »/«
(«!...ап О, b > 0)
[см. 611, 18); воспользоваться 534, 2)].
10)	Покажем, следуя Коши, как вычисление кратного интеграла
xPi-1 ... хРп-1е+•••+апхп>
(ft0 4- btXt +... + bnxnyi
(pb <ц blt ? > 0)
может быть приведено к вычислению простого интеграла.
По известной формуле [531 (13)]
____________1_____________
(ft0 + Ьгх1 4~ ••• 4“ Ьпхп)ч
__!_\ е~«(*о + *1*1 + - + *я*я) ,,9~1
T(7)J
Подставляя это в интеграл /Си изменяя порядок интегрирований, представим
его в виде
e-boauq-\du х
или, наконец, если для интегралов в фигурных скобках снова использовать
указанную формулу:
Г fa) -Г(ря) С е-Мц?-1
г (7) .	J (at + b^..,(ап + Ьпи)рп’
Результат этот имеет место и при Ьо — О, но в предположении, что р, 4-...
.••4-Рл>7.
11)	Приведем вычисление интеграла
(atXi-^-anxn)ik dxt ... dxn,
x’+...+x'=£i
где2й — четное натуральное число, a alt..., ап — произвольные Вещественные
числа.
400
ГЛ. XVIII. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
[676
Имеем, прежде всего, по формуле для степени многочлена
(alXl 4- ... + anxnyk =	xj .2 Jl„! а1‘''1 а*П ‘ Х^
Х14-.„4-Хя = 2й
Если интегрировать по сфере xj-f-...-|-х*	1, то интегралы от членов, для
которых хоть один из показателей X — нечетное число, оказываются нулями.
Таким образом,
,	V	2/г!	2 а
Isft= 2	^1...2(хяГа1|Х1-а^яХ
Р1 + — + !1л = &
X $ ••• § xpi... Xanv-n dXi ... dxn.
ж«+...+^1
Но по обобщенной формуле Дирихле [см. 5)] написанный интеграл имеет
значение *
г(н+4)-г(и,.+4-)
r(-J + A+l)
Полагая здесь
2Р г ’
после преобразований получим:
_(2А— 1)1!
2ft
8	9	___.
ajP-i ... а^п —
Этот интеграл (правда, другим путем) впервые вычислил Н. Я. Сонин.
Заметив, что интеграл
п
i2fe+i =	$	$ (“ixi + ••• + a«x»)2ft+1^xi ••• dxn
4+...+4«‘
равен всегда нулю, Сонин получил затем, с помощью разложения показа-
* При этом следует учесть, что формула Дирихле предполагает огра-
ничения Xj^O, ..., ХдЭ^О; поэтому результат, который она дает, должен
быть еще умножен на 2П.
676J	§ 5. МНОГОКРАТНЫЕ ИНТЕГРАЛЫ	401
тельной функции в ряд и почленного интегрирования, значение и такого инте-
грала:
п
J ••• Jj e	” ndxt ... dx„ =
*1 + — 1
00
=JV—-У------------------A$\
k\ г (4+*+1V2
fe = O	/
где для краткости положено
Р=Г^+-+^.
При четном п — 2т этот результат может быть переписан в виде
п
00	00	-77-
У 1	У (-1? р-р\^_(2к)2
Zi h\ (k + и)! k 2 } ~ (if)m Zi fel (k + m)l \ 2 )	“	«. ?? p/’
fe = O	k=0	(|.p)2	2
t. e. выражается через бесселеву функцию co значком m = -^- [395,14)] от мни-
мого аргумента. Нужно сказать, впрочем, что, если ввести в рассмотрение и
бесселевы функции с дробным значком, то полученный результат сохранит
силу при нечетном п.
12)	Перейдем теперь к примерам применения к вычислению кратных ин-
тегралов общей формулы (6) замены переменных.
Естественно начать с обобщенного полярного преобразования по фор-
мулам
х, = г cos <рj,
хг = г sin <pt cos tf2,
x3 = rsin?1sin?2cosif3,
xn_j = г sin <fi sin ср3. . sin <pn_s coscpn_n
xn = r sin <px sin <pa. . sin!f„_a sin !ря_1Ф .
Если в пространстве х1ха...хп рассматривается сфера х‘ Ц-х| 4-... +
+ х*</?2, то ей в новом пространстве ...'рп_1, очевидно, можно поста-
вить в соответствие прямоугольный параллелепипед
..., 0'f’n-2"Siте,
если же берется только часть сферы, отвечающая ограничениям Xi^O,
Xj^zO, ...,хд^0, то изменение всех углов <рь ..., ограничивается
[. 711
О’ Т г
Якобиан преобразования
j___ ^(^11	•••! Хп)
~~ D(r, <fi, <ря-1)
.Вычисляется непосредственно по определению очень кропотливо. Поэтому мы
402	гл. XVIII. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ	(676
вычислим его обходным путем. Формулы (10) легко приводят к системе урав-
нений:
Л = г’-(х« + х|4-... + х’) = 0,
F2 == г2 sin2 ?, — (х2 + -.. + х2) = 0,
Fa = г* sin2 ?, sin2 <р2 — (х2 -j-... + х2) = 0,
F„ = r2 sin2?! — sin®?n-i— х2 = 0,
для которой, обратно, система функций (10) и будет решением. В таком случае
по формуле п° 210, 8),
D (FFit • ••> Fn)
D(xt, x2, ..., x„) _ D(r, ?lt ..., <p„_i)
D(r,4lt .... ?„_t) < V D(Fit F2, Fn)'
D (xb x2....x„)
Оба последних определителя вычисляются сразу, ибо приводятся к произве-
дениям диагональных членов; они равны соответственно
Д(Л.	Fn)
D(rt.....?n-i)
= (— 1)Я2Я гга~1 sin2/,_’?i cos ?! sin2"-8 ?2 cos ?2 ... sin ?„_j cos ?я_1,
== 2ягя sin" 1 ?i cos ?! sin" 2 ?2 cos ?2 ... sin ?„_, cos ?„_i.
Таким образом, окончательно,
J= -fifa-^2’ Хя) = rn-' sin»-2 ?i sin"”3 ?2 ... sin?„_2.
D(r, ?i, ...,	2
Рассмотрим для примера интеграл
G= J ... J f(yx} + ... + x*)dxt ...dxn.
*j + — + JCB^:#2
Если прибегнуть к полярному преобразованию, то его вычисление непосред-
ственно приведется к вычислению п отдельных, один от другого не зависящих,
интегралов:
R	я	я
G=^rn~1f(r)dr -j sinn-2?irf?i ...j sin2 ?„_s rf?„_, X
я	2л
X 5 sin ?Л—2 ^?Л-2 J ^?Я-1«
о	о
Если использовать для вычисления интегралов от степеней синуса формулу из
534, 4) б):
676]
t в. МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
403
то после упрощений получим
г(тН
так что вопрос свелся к вычислению одного простого интеграла по г.
В этом, как частные случаи, содержатся результаты упражнений 2) и 3).
В свою очередь, полученный результат содержится в формуле Лиувилля 8).
13)	Если возвести формулы (10) в квадрат, заменить х*, х|,..., х8 через
х1( х8,	х„* а г8, sins<f>!, ..., sin8!f„_j— через ult us. и„, то придем
к такой системе соотношений:
X1 = U1(1 — иг),
ха = и1иа(1—и3),
(11)
хп-1 — uiui ••• ип-1 (1	«л),
x„ = u1ns... ип.
Преобразование (И), таким образом, в некотором смысле равно-
сильно полярному преобразованию (10). В случае п = 2 его применил Якоби
для доказательства известного соотношения между функциями В и Г [617 (13)1.
Предлагается непосредственно установить формулу Лиувнл-
ля 7), применив к интегралу в левой части преобразование (11). Симплексу
X, О, Х2 0....  g:	0, X, + ...-[- х„ 1
при этом отвечает куб [0, 1; ...; О, 1] в пространстве п, ... ип. Якобиан пре-
образований равен
1 —«а “±(1 — иг) ••• «а ... Мя-1(1—«л) «а ... «л
— «1 Ml —“з) ••• «1«3	(1 — «л)	«1«» ••• «л
0	—«Л ...
О	0	... Uj	... Пд—а (1	«л)	«1 • • • «л-&«л
О	0	... Hi ... Пд_1	Ux ... Пд_1
Если к элементам каждого столбца прибавить соответственные элементы всех
последующих столбцов, то все элементы ниже диагонали заменятся нулями,
а диагональные элементы окажутся равными
1, «о .......«1	••• «л-i-
Таким образом, окончательно
и?-2 Un_i.
По формуле (6) наш интеграл приводится к следующему:
л
1 “ Г
J ... J <р(«1)и1Р1+Р8+-+р»-’(1— и2)Р1-’ X
о о
X «Л+-+р»-1... (\—unfn-l~XuPn~Xdut ... dun,
* Конечно, в таком случае эти переменные могут принимать лишь неот-
рицательные значения.
404	ГЛ. XVIII. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ	1676
а этот уже представляется в виде произведения простых интегралов;
остальное ясно.
14) То же преобразование переменных позволяет получить и видоизме-
ненную формулу Лиувилля, где л-кратный интеграл оказывается распро-
страненным на бесконечную область:
J ... J <p(Xi4-xs + ... + x„) xf1 ’xfa *...
х^п xdxt dxa ... dxn =
= Г(р1)г(ра).„г(ря) C (tt)uP1+Pa+...+P„-lrf«;
г(Р1+л + --+Рл) T
при этом предполагается, что интеграл справа сходится абсолютно.
Эта формула обобщается так же, как и предшествующая [ср. 8)[:
л
С помощью последней формулы можно установить, например, что
л
X®1+ ..• + *“ л
xf1 '-..хРап ldxt...dxn
(x^H-.-. + x^X
«1 ---“л
,	г(^ ...Г
1_____________\°i )	\ая1
Pl-	Т1Р±+ 1 Рп\
ai	ап/ \«1	“л/
при + +
.	“1	“л/
676|
§ 5. МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
405
15) Доказать формулу (также принадлежащую Л и у в и л л ю):
1 1
j... j<p(ViV2 ••• v«)(l —	— v2)Pa-1...
... (1—on)p»-1vp*vP1+P2 ... vPnl+'"+Pn~ldvt ... dvn =
_ гу>ог(р8)... г(рд) г _ Pi +Ра+ ...+рл_ 1 du
T(Pi+p» + • + Рп) J
Указание. Формула выводится из соотношения, данного в 7), если
заменить там ч/(и) на <р (1 —и) и положить
Х1 = (1— V1)v2 ... vn,
х2 = (1 — vs)v3 ... vn.
хп-1=(У— vn^)vn,
Xpi === 1	®П‘
Якобиан преобразования в этом случае имеет значение
.	,	а л —2 л-1
/=(— l)nV2V3... Vn-lvn •
16) Рассмотрим, вместе с Каталаном, интеграл (и 3=3):
§ ••• § /(«л+ ••+»№)	~| х4J
*J+...+4=i
n— 1
dx^ •'« dxn^j
Ю-*?—^-i;
при этом, полагая
M = fXmf +... + ma>
считаем функцию /(«) непрерывной для |и|<:Л4.
Прибегнем к линейному ортогональному преобразованию всех
переменных, включая и хп, по формулам
4-	btua +... 4- Мл-i + !А,
ха = оаи14- batia 4* ••• 4" ^2u»-i ~Ь hun,
хп ==0^1, + bnua 4-... 4- knun _i 4-
* В первой форме этот интеграл по сути является поверхностным
интегралом
J... j/(m1x14-mnxn)rfS,
[1аспространенным на поверхность единичной сферы в n-мерном пространстве
ср. замечание к (3)].
406
ГЛ. XVIII. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
[676
где ns коэффициентов подчинены
л(«+ 1)
—• условиям
а1 + а1 + — + «„= 1.	+ ••• + апЬп = 0,
'J + '* + - + '»= 1. Vi + Ы +... + kaln = 0.
Из них следует, что
«| + И| + ... + ^ = 4 + х| + ... + х’ = 1,
и мы берем за новые независимые переменные иь .... ип_ъ полагая
ип = +/1— uj —...—
Произвол в выборе коэффициентов настолько велик, что мы вправе конкретно
положить
а‘=м-	</==1>2.....л>
и даже дополнительно потребовать, чтобы определитель, составленный из
коэффициентов преобразования, был равен Ц- 1. При таком предположении, как
известно, алгебраическое дополнение, отвечающее какому-либо элементу
определителя, равно самому элементу. С учетом этого якобиан
	7| ч а*1я •вГ ОЧ1 С$ а | а •«Г а | а 1м а
Д(х„ х„_1) _ D («1, .... «»_,)	’ О •*	.	,	№ ~	• 1 1	:	: Г	:	: я | а а 1-	•	• i	:	:	1 1	:	: а~	.	.	а 1 а а I а	.	. а 1“	.	.	. »•	•	• •	• 1 . *•	•	м I	::	L Д	•	•	№ : • *1* Ф	•	•	8 a j?	•	•
оказывается равным
, . И1 , . U,
1п + ап~и7 + Ь^
Таким образом,
, Un-i   хп
П «Л «Л
К =2 С ... С /(AfuJ—z-------dUl "• dUn~l —
2	—«i-!
“1 + — + “zi — 1 =51
,	n — 2
= 2
du^ ... dua t
у(1_ар_Ц|_..._Ы2_1
“1
Внутренний интеграл, как легко получить из 3), равен
л—1
2	л
г
676]
$ в. МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
407
так что окончательно
—
К = 2-?n-lf	2 du-
Полагая здесь u = cos X (0 sg X sg к), можно написать результат и в виде
л— 1 р
К= 2---- I f (]AnJ+ ••• + '«’ cosX) sin "“21 rfX.
ГЫ J
о
При п = 3 отсюда получается известная формула Пуассона, которую
мы вывели в 633, 3) и, по существу, тем же методом преобразования координат.
17)	Известная уже нам формула Каталана [см. 597, 15) и 616, 16)]
непосредственно—путем повторения тех же рассуждений — переносится на
n-мерный случай
п
5 ••• J /U1.......хп) <Р (g(x,.xn)) dxt ... dxn —
m^g(xl..
М	М
= (S)^ ?(u)d|(«) = (R) ^(u)^f-du,	(12)
т	т
где
л
Ф(“)= J ... j /(Xj, ..., хя) dXi ... dxn.	(13)
m^S.g(x1.xn)^u
+oo	M
Здесь M может быть и + <ю, причем \ понимается как Пт ( .
„	м -»оо „
ОТ	ffl
Предполагается для примера по методу Каталана получить из формулы
Дирихле 4) формулу Лиувилля 7).
18)	Н. Я. Сонин обратил внимание на то, что формулу Каталана
иной раз можно использовать в другом плане.
Предположим функцию f(xlt ..., хя) однородной [187] степени®,
а функцию g(х,,..., х„) — однородной же, но первой степени; например,
функция g может иметь вид
Xi + ... + х„ или ]/х’ + ...+ х’.
Пусть, далее, т = 0. Тогда, полагая в (13)
Xi—ufu
хл—н£я
408	ГЛ. XVIII. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ	|67в
(Якобиан J— ип) и учитывая, что неравенство 0sgg-(x1(..., хя)^и перейдет
при этом в неравенство 0^g(5x,..., Ея)^ 1, мы получим, что
Л
I (И)=ц««	]	/(?>,..., е„)	... de„.
....
Подставляем это в (12) (лишь вместо $ снова пишем х):
j ••• ) f(xu .... x„)<[>(g(xx,.... x„))rfxj ... dxn =
.......x^s-M
J ••• j f{xu .... xn)rfxx ... dxn- U(w)rfan4
^g(Xi....*„)=S1	i>
Теперь, если удается выбрать, во-первых, функцию <р и, во-вторых, пре-
дел М так, чтобы интеграл слева легко вычислялся, то отсюда получается
выражение для интеграла
Л
J ... j /(х1( ..., x„)rfxx ... rfx„.
0tSg(xt.....xnI=Sl
Если, например, ограничиваясь неотрицательными значениями хх, ..., хя,
взять
g(xlt ..., хя) = хх4- ... -|-хя,
/(хх, ..., хя) = х^1 —' ... х^»-1 (рг>0),
<р(и) = е~“, Л4 = -|-оо,
то з окажется равным рх+ ... +ря— п, и мы получим формулу Дири-
хле (4)]:
Л
$ ... $ xPi 1 ... x„n 'dxt...dx„ =
х'........хп-°
0==*1 + ... +*„^1
ОО	00
5 e~X1 хр-1 rfxx ...	х^~' dxn
о о
(Pi + •••	+Рп)	ир1+	•• • +рп-1 du
Г (Pi) - Г(ря)
г (Pi + ••• +р»4-1)'
19)	Предлагается тем же приемом осуществить приведение интеграла
п
р ?	Хр1~ 1 ... ХРп~ 1
\	\	*	//1*	// у
3 " J (*л+...+м»)’ х” я’
...хг^°
0==*1 + • • •
в предположении, что
Pi > 0, bt> 0, рх + ... 4-ря > q > 0.
6761
§ в. МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
409
Указание, Взять <р(и) = е~а, М = -}-со; воспользоваться результатом
10) при в1= ... = о„ = 1 и &о = О.
Ответ.
Г(р1) ... Г(ря) С ________________u«-'du
Г(Р1+ 4-Рл —?+1)г(?) J (1 + &iU)P1 ... (1+&„и)р»'
20)	Н. Я. Сонину принадлежит также следующее обобщение формулы
Каталана:
п
j J ?(*i, •••> xn,g(xlt ..., xn))dxl ... dxn =
m^g{xl....xn)^~M
где
Ф(£,С)= J ...	X„, C)rfXj ...
m^g(xi....xn)^f
[Формула Каталана отсюда получается, если функции <р(хъ ...,хя, с)
придать частную форму: f(xlt хя)<р(с).]
. Приведем доказательство автора.
В очевидном равенстве
5	’ Хп.^0 dxl... dxn —	... J dxi... dxn^ F (Хц.. *>.хя,£) dt
m m=Sg^M	m
ПОЛОЖИМ
f [<Wi, —	если m^g(xt......xn)^t,
I 0, если g(xn .... xn)>t;
тогда получим
.	C.^CX!, .„,х„,0^ ^ dXn==
m m^g^i
C j j C <Wi-..., x„, t) ..
= \ ... \ dx, ... dx„ \  --—  dt,
J J	J
m:=gsSAI	g
Если вычислить внутренний интеграл справа, то отсюда
п
5 ... j<p(xH .... X„, g)dX! ... dxn =
m^g^M
М .-----"----j,
= Ф(7И, М)— dt ... (	... dxn. (14)
т m^g^t
410	ГЛ. ХУНТ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ	(676
С Другой стороны, по правилу дифференцирования сложной функции
«полная производная»
Применяя к вычислению второй производной справа правило Лейбница,
заменим ее через
С С д<? (Xj, ..., хп, t) ,	,
} " \ dt dXl "• dXn'
Проинтегрируем теперь это равенство по t от тдоЛТ; принимая во внимание,
что Ф (m, т) = 0, найдем:
м
Ф(М,М) — J dt J ... J fe (£1’ -, x„, f) dx^ . . dx^
m
M
чшл <15’
m
Если сопоставить (14) и (15), то и получится доказываемая формула.
21)	Применим формулу Сонина к вычислению интеграла:
„	О1*1+---+аЛ*Л
г	f	*1+ ••• +*n ,1
S= j ••• ) e	dx! ••• dxn-
Здесь
? (*1, •••,*/!, С) = <? C
g(xlt ..., xn)—1/rxst+ ... +%*,
m = 0, M = 1,
? ..OlJgl+•••+«„Xn
Ф (<, c)= J ... J e c dxt ... dxn.
Имеем, очевидно,
-----Z-,	а1х1+..,4-дяхя
^ ... J e c dxt ... dxn =
*1+ ••• +хп^
676]	$ 5. МНОГОКРАТНЫЕ ИНТЕГРАЛЫ	411
Воспользовавшись результатом упражнения 11), легко получить разложение
п оо
Ф(<, с) = « 2 У -------
k=0 ft! Г
1
tfk+n
где
Отсюда
п
дФ (t, с)
dt
= *»->•
3k
Л=0 ft! Г
1
так что по формуле С о н н н а
fe=0 .ft! Г
ср. II)].
22) Вычислить интеграл (л^О):
п
гк 2я2
п(р02	2
5 =
п
1
{ср. 617, 19)].
Дифференцируя (при X > 0) по параметру X под знаком интеграла и заменяя
в результате одну переменную xt через
получим, что
п — 1
L"^+"'+'n-,+'+^r^r77Vx
dX - П \ ... р	X
L_1 'LzZ-i "^=2-1
X *2	••Хп— 1 - 2 П йхз dxn^ldz
т. е.
rf/? D
л=-'г/г-
Отсюда
R = Ce~n\
412	ГЛ. XVIII. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ	[676
Так как при Х=0 интеграл /? сохраняет непрерывность, то
с=я (°)=Г (L) г т (1^1) =	(2.)^
[531, 6°]. Окончательно:
л —1
/? = -4=(2л) 2 е~лХ.
V «
23)Лиувилль остроумно использовал этот интеграл для вывода теоремы
умножения для функции Г, принадлежащей Г а у с с у [536].
Умножив обе части полученного равенства на 1р~г (р > 0), проинтегрируем
его по X от X = 0 до X = -f-<®. Справа получится
2 . I XP-»e-n^rfX = -^-^—Г(р).	(16)
Уа J
°.
Слева же перенесем интегрирование по X на первое место (по порядку выпол-
нения):
л — 1
оо оо	1_। л — 1 _ ।
J ...J е~(х‘+‘... dx, ... dxn_, X
о о
X р " Xn-l.W-ldl.
Внутренний интеграл подстановкой ------------ =t приводится к
Xj ... Хя_!
а тогда остающийся (л—1)-кратный интеграл распадается на произведение
отдельных простых интегралов:
оо	p-f-l _ ।	оо	р-|-л— 1 _
" dx, ... С е~Хп~1.хпЛ dxn_,=
о	(Г
__£р	. г (р + г 1 \
п \п )	\ п )\ п )’
Приравнивая это произведение выражению (16) и заменяяр через ла (а > 0),
мы и придем к формуле Гаусса:
л — 1
Г(а)г[а + 1) ... Г[а + ^-)= (2"Ц._Г(па)
\	/	\ rtr J па-----------
в ее обычном виде.
676]
$ в. МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
413
24) Пусть fi(x), fs(x), fn(x) будут ограниченные функции, интегри-
руемые в конечном промежутке [о, &]. Доказать, что
п	fl C^i) fl (^2) • • • fl (хп) fs(Xl) /2(^2) fi(xn)	2 rfXxrfXa ... dXn =	
'ь	ь' 1	с	с я!	J ... J а	а			
			
	ffl(Xl) fn. (хз) ••• fn(xn)	.—	6	6	6 \f*dx ^fjsdx...\f1fndx a	a	a b	b	b ^ftfidX ^ffdx	^fsfn^x a	a	a
			b	b	b Ifnfidx If^dx...^* a	a	a
Определитель справа называется определителем Грама (J. P.Gram).
Разложив промежуток [в, Ъ] на т (> п) равных частей, введем в рассмотре-
ние значения всех п функций в точках деления:
(< = 1, 2, ..., п; j = Q, 1, ..., т— 1).
Возведем в квадрат прямоугольную матрицу, составленную из этих чисел. По
известной теореме соответствующий ей определитель *
I^W’I
оказывается равным сумме квадратов определителей упомянутой исходной
матрицы:	v
где суммирование распространено на всевозможные сочетания из т (> л)
значков 0, 1, ...,т—1 по я. Если от сочетаний перейти к размещениям,
то каждый член воспроизведется я! раз; можно не избегать и равенства знач-
ков J, ибо этому случаю отвечает нулевой член. В результате можно написать:
т— 1 т — 1	tn — 1
_ л — а\П
Если каждое слагаемое кратной суммы слева умножить на I ——I и
Ь — а
одновременно каждый элемент определителя справа на - т , то получится
равенство вроде доказываемого, но лишь с интегральными суммами вместо ин-
тегралов. Чтобы завершить доказательство, остается перейти к пределу при
т — со.
* Для краткости мы записываем в виде |	| определитель, у которого
в пересечении i-й строки и А-го столбца стоит элемент aik.
ГЛАВА ДЕВЯТНАДЦАТАЯ
РЯДЫ ФУРЬЕ
§ 1. Введение
677. Периодические величины и гармонический анализ. В на-
уке и технике часто приходится иметь дело с периодиче-
скими явлениями, т. е. такими, которые воспроизводятся
в прежнем виде через определенный промежуток времени Т,
называемый периодом. Примером может служить установив-
шееся движение паровой машины, которая по истечении опре-
деленного числа оборотов снова проходит через свое начальное
положение, затем явление переменного тока, и т. п. Различные
величины, связанные с рассматриваемым периодическим явлением,
по истечении периода Т возвращаются к своим прежним зна-
чениям и представляют, следовательно, периодические функции
от времени t, характеризуемые равенством
ср(^+7) = ср(О,
Таковы, например, сила и напряжение переменного тока или —
в примере паровой машины — путь, скорость и ускорение крейц-
копфа, давление пара, касательное усилие в пальце кривошипа
и т. д.
Простейшей из периодических функций (если не считать по-
стоянной) является синусоидальная величина-. A sin (ш£ -|- а),
где <о есть «частота», связанная с периодом Т соотношением:
® =	О)
Из подобных простейших периодических функций могут быть
составлены и более сложные. Наперед ясно, что составляющие
синусоидальные величины должны быть разных частот, ибо, как
легко убедиться, сложение синусоидальных величин одной и той
же частоты не дает ничего нового, ибо приводит опять к си-
нусоидальной величине, притом той же частоты. Наоборот, если
сложить несколько величин вида
у0 = Ло, Ji == sin (y>t -f- <Xi)> Уг = А3 sin (2w< -f- оц),
y3 = Л3 sin (Зо>£аз)> •• • »
(2)
677)
S 1. ВВЕДЕНИЕ
415
которые, если не считать постоянной, имеют частоты
ш, 2ш, Зш, ... ,
кратные наименьшей из них, <о, и периоды
т.'^т.
-Г,
3 1г "
то получится периодическая функция (с периодом 7"), но
уже существенно отличная от величин типа (2).
Для примера мы воспроизводим здесь (рис. 121) сложение
трех синусоидальных величин:
sin 14- sin 2t 4- sin 3/;
। 2	1 4
график этой функции по своему характеру уже значительно
разнится от синусоиды. Еще в большей степени это имеет место
для суммы бесконечного ряда, составленного из величин
вида (2).
Теперь естественно поставить обратный вопрос: можно_ ли
д а иную периодическую функцию <р (0 периода Т представить
в виде суммы конечного или хотя бы бесконечного множества
синусоидальных величин вида (2)? Как увидим ниже, по отноше-
нию к довольно широкому классу функций на этот вопрос можно
Мать утвердительный ответ, но только если привлечь имен-
но всю бесконечную последовательность величин (2).
418
ГЛ. XIX. РЯДЫ ФУРЬЕ
[677
Для функций этого класса имеет место разложение в «тригономет-
рический ряд»:
(4 === zIq —|— Д^ sin (oif —|—	—|— Д3 sin (2<о^ —|— tXg) —|—
-j- Д3 sin (3o)f -j- аз) 4“ • • •= До 4“ У, Дд sin (л wt ал)> (3)
п— 1
причем До, Д1( ар Д2, «а, ... суть постоянные, имеющие осо-
бые значения для каждой такой функции, а частота <о- дается
формулой (1).
Геометрически это означает, что график периодической функции
получается путем наложения ряда синусоид. Если же истол-
ковать каждую синусоидальную величину механически как представ-
ляющую гармоническое колебательное движение, то можно также
сказать, что здесь сложное колебание, характеризуемое функцией
<р(0, разлагается на отдельные гармонические колебания.
В связи с этим отдельные синусоидальные величины, входящие
в состав разложения (3), называют гармоническими составляющими
функции <р(7) или просто ее гармониками (первой, второй и т. д.).
Самый же процесс разложения периодической функции на гармоники
носит название гармонического анализа.
Если за независимую переменную выбрать
Х = О)Г = у-,
то получится функция ОТ X:
тоже периодическая, но со стандартным периодом 2т. Разложение
же (3) примет вид
f (х) = Д3 —1~ Д1 sin (х —сц) —[— А% sin (2х —ctg)
+ Д3з1п(Зх4-а3)4-... = Д04- У, Д„8щ(лх-|-а„).	(4)
п— 1
Развернув члены этого ряда по формуле для синуса суммы
и положив
До = «о, Д„8ша„ = а„, Ancosan — bn (п—1, 2, 3, ...),
мы придем к окончательной форме тригонометрического разложе-
ния:
/(х) == а0 (at cos х 4- bY sin х) 4- (a* cos 2х 4- b3 sin 2х) 4~
4- (а3 cos Зх 4~ b3 sin Зх) 4- • • • =
ОО
— 4~ У (апcos пх 4-	(5)
д=1
678]
§ 1. ВВЕДЕНИЕ
417
в которой мы всегда и будем его рассматривать *. Здесь функ-
ция от угла х, имеющая период 2тс, оказывается разложенной
по косинусам и синусам углов, кратных х.
Мы пришли к разложению функции в тригонометрический ряд,
отправляясь от периодических, колебательных явлений и связанных
с ними величин. Важно отметить, однако, уже сейчас, что подобные
разложения часто оказываются полезными и при исследовании функ-
ций, заданных лишь в определенном конечном промежутке и вовсе
не порожденных никакими колебательными явлениями.
678.	Определение коэффициентов по методу Эйлера — Фурье.
Для того чтобы установить возможность тригонометрического раз-
ложения (5) для заданной функции f(x), имеющей период 2тс, нужно
исходить из определенного набора коэффициентов а0, аь Ьи ..., апЬп,...
Мы укажем прием для определения их, который во второй половине
: XVIII века был применен Эйлером и независимо от него в начале
1 XIX века — Фурье.
Будем предполагать функцию f(x) интегрируемой в проме-
.. жутке [— тс, тс] — в собственном или в несобственном смысле-,
в последнем случае мы дополнительно будем предполагать, что
функция абсолютно интегрируема. Допустим, что разложение (5)
имеет место, и проинтегрируем его почленно от —тс до тс; мы по-
лучим
Тс	00	тс	тс
§ f(x) dx = 2тс ай -|- У, cos пх dx -ф- Ьп $
—ТС	Л=-1	—тс	—тс
Но, как легко видеть,
ТС
С	. sin пх I« Л
\ cos пх dx —--------------- — О
J	Л I -Тс
—тс
(6)
и
С . J	COS пх I « Л
\ s\nnxdx =------------=0
J	п -тс
Поэтому все члены под знаком суммы будут нулями, и окончательно
найдем
ТС
=	(7)
—тс
Для того чтобы установить величину коэффициента ат, умно-
жим обе части равенства (5), которое мы все время предполагаем
* От этого разложения, разумеется, легко перейти в случае надобности
обратно к разложению вида (4).
14 Г. М, Фихтенгольц, т, III
418
ГЛ. XIX. РЯДЫ ФУРЬЕ
[678
выполненным, на cos тх и снова проинтегрируем почленно в том
же промежутке:
те	те
$ f(x) cos тх dx =ай $ cos тх dx-\-
— -к	— тс
00 Г тс	«
+ 2 а« S cos пх cos тх 4" S sin пх cos тх dx 
/1== 1	— тс	— я
Первый член справа исчезает ввиду (6). Далее имеем [ср. 308, 4)]
ТС	тс
sin пх cos тхdx — -у [sin (л-ф- zw)x-[-sin(n—m)x]dx — G\ (8)
— тс	—тс
тс	тс
cos пх cos тх dx — у	[ cos (п -]- т)х-{- cos (и—m)x\dx — Q, (9)
— Л	— тс
если п т, и, наконец,
тс	.тс
С « j	С	14- cos 2тх	,
\	cos1	тх dx =	\	——---------------dx = tt.
— тс	— тс
(10)
Таким образом, обращаются в нуль все интегралы под знаком суммы,
кроме интеграла, при котором множителем стоит именно коэффициент
ат. Отсюда этот коэффициент и определяется:
ТС
ат = ~ f(x) cos mxdx
— тс
=	3,...).
(И)
Аналогично, умножая предварительно разложение (5) на sin тх
и затем интегрируя почленно, определим коэффициент при синусе:
ТС
bm = ~ f (х) sin тх dx
(т = \,'1, з,
(12)
При этом, кроме (6) и (8), мы опираемся еще на легко проверяемые
соотношения:
ТС
$ sin пх sin тх dx — 0,	(13)
— Л
если п т, и
$ sin2 тх dx — тс.
(14)
679]	s 1. ВВЕДЕНИЕ	419
Формулы (7), (11) и (12) известны под названием формул Эйлера —
Фурье', вычисленные по этим формулам коэффициенты называются
коэффициентами Фурье данной функции, а составленный с их
помощью тригонометрический ряд (5) — ее рядом Фу рье. Рядами
Фурье мы исключительно и будем заниматься в настоящей главе.
Дадим теперь себе отчет в том, какова логическая ценность про-
веденных рассуждений. Так как мы исходили из предположения, что
тригонометрическое разложение (5) имеет место, то вопрос о том,
отвечает ли это действительности, естественно, остается откры-
тым. Но убедительны ли те соображения, с помощью которых по
примеру Эйлера и Фурье мы определили коэффициенты разло-
жения (5), даже в предположении, что оно осуществляется? Мы
пользовались повторно почленным интегрированием ряда,
а эта операция не всегда дозволительна [434]. Достаточный условием
для ее применимости является равномерная сходимость ряда.
Поэтому строго установленным можно считать лишь следующее:
если функция f (х), имеющая период 2т, разлагается в равно-
мерно сходящийся тригонометрический ряд (5)*, то последний
необходимо будет ее рядом Фурье.
Если же предполагать наперед равномерности сходимости, то
наши соображения не доказывают даже и того, что функция может раз-
лагаться только в ряд Фурье [ср. ниже 759, 760]. Каков же смысл
приведенных соображений? Их можно рассматривать лишь как наве-
дение, достаточное для того, чтобы в поисках тригонометрического
разложения данной функции, по крайней мере, начать с ее ряда
Фурье, обязуясь (уже со всею строгостью!) установить, при каких
условиях он сходится и притом — именно к данной функции.
Пока же это не сделано, мы имеем право лишь формально
рассматривать ряд Фурье данной функции f(x), но не можем о нем
ничего утверждать, кроме того, что он «порожден» функцией f(x).
Эту его связь с функцией f обычно обозначают так:
ОО
f(x) ~ у] (дп cos пх -[- bn sin пх),	(5 а)
п = 1
избегая знака равенства.
к679. Ортогональные системы функций. Изложенное в предыду-
щем п° является образцом рассуждений, которыми часто приходится
пользоваться в математическом анализе при изучении многих разло-
жений.
* Заметим, что равномерная сходимость сохранится и при умножении всех
членов ряда на ограниченные функции cos тх, sin тх [429]. Равномерную
сходимость можно было бы заменить здесь ограниченностью частичных
(Сумм ряда [528].
14*
420
ГЛ. XIX. РЯДЫ ФУРЬЕ
[679
Назовем две функции <р (х) и ф (х), определенные в промежутке
[a, Z>], ортогональными в этом промежутке, если их произведение
имеет интеграл, равный нулю:
' ь
$ ср (х) ф (х) dx = 0.
а
Рассмотрим систему функций {<рл(х)}, определенных в промежутке
[а, />] и интегрируемых в нем вместе с их квадратами; тогда, как
мы знаем [483, 6)], и произведения этих функций, взятых попарно,
также интегрируемы. Если функции данной системы попарно ортого-
нальны:
ь
\(?n(x)<?m(x')dx = 0	(15)
а
(п, т — 0, 1, 2, ..,; п ф т),
то ее называют ортогональной системой функций. При этом мы
всегда будем предполагать, что
ь
5<p«(x)tZx = Xm>0,	,	(16)
а
так что в составе нашей системы нет ни функции, тождественно
равной нулю, ни какой-либо другой ей уподобляющейся, в
некотором смысле * функции, интеграл от квадрата которой оказывает-
ся нулем.
При соблюдении условий Хл=1 (л = 0, 1, 2, ...) система назы-
вается нормальной. Если же эти условия не выполнены, то при
{tpn (х))
_ [, которая уже заведомо
г J
будет нормальной. Обратимся к примерам.
1) Важнейшим примером ортогональной системы функций как раз
и является тригонометрическая система
1, cos х, sin х, cos 2х, sin 2х, ..., cos пх, sin пх, ...	(17)
в промежутке [ — тс, тс], которую мы рассматривали выше; ее ортого-
нальность следует из соотношений (6), (8), (9) и (13). Однако нор-
мальной она не будет ввиду (10) и (14). Умножая тригонометрические
функции (17) на надлежащие множители, легко получить нормальную
систему:
1 cosx sin х cosnx sin rax	.,
/2тс ’у тс’ /л’	’ Y п ’	/ тс ’	V ’
* См. ниже, 733.
679]
$ 1. ВВЕДЕНИЙ
421
2) Отметим, что та же система (17) или (17*) в урезанном про-
межутке [0, тс] уже не будет ортогональной, ибо
1С
§ sin пх cos тх dx ф О,
о
если п и т — числа разной четности. Наоборот, каждая из частичных
систем, состоящая либо только из косинусов:
либо только	1, cos л:, cos 2л:, ..., cos пл:, ...,	(18) из синусов: sin х, sin 2л:, ..., sin пл:, ...	(19)
в отдельности, будет в этом промежутке ортогональной, что легко
проверить.
3) Несущественно разнятся от только что рассмотренных такие
системы:	,	пх	2пх	гапх 1, COS -у, COS -у-,..., COS-у—,(18*)
и	. пх	. 2пх	. гапх	„.j.. sin-у, sin-у-,...,	sin-j—,...	(19*)
Каждая из них представляет собой ортогональную систему в про-
межутке [0, /].
4)	Чтобы дать пример более сложной ортогональной системы, состоящей из
тригонометрических же функций, рассмотрим трансцендентное уравнение:
tg £ = (с = const).	(20)
Можно доказать, что оно имеет бесконечное множество положительных корней:
61, 6з, •.., 6д, •..;
графически эти корни получаются, как абсциссы точек пересечения тангенсо-
иды -г] = tg £ и прямой ч) = с$ (рис. 122). Составим систему
sin у х, sin у х,..., sin у х,...
Легко вычислить (при а^₽), что
i
Г .	. „ .	1 (sin (а — ₽)Z	sin(a-]-₽)/l
\ Sin ах Sin $Х dx = -Н- -! 1-а1------- I о f==
J	-	2 ( а — р	а -|-р J
, Ptga/ — ata В/
— COS al COS В/ —- „-ft.- .
as — Ва
£ £
Если положить здесь а = у, ₽= -у (при notin'), то, используя уравнение (20),
получим:
СЕ Е
\ sin у х • sin -у х dx = 0 (п ф т).
422
ГЛ. XIX. РЯДЫ ФУРЬЕ
[679
Этим установлена ортогональность указанной системы в промежутке
[О, /].
Аналогичное заключение можно сделать относительно системы
если
COS у х, cos у x, cos -j- x, ...,
£2» • • •»	• • •
есть последовательность положительных корней уравнения
ctg $ = с$ (с = const).
Однако ни та, ни другая система не будут нормальными.
5) Важный пример ортогональной системы в промежутке [—1,1] до-
ставляют многочлены Лежандра:
Р.(х) = 1,Р.(х) = 51д',*^-|>* („1, 2. 3, ...)
[см. пп° 118, 320]. Так как
Р2п^х
2
2л+1 ’
то для получения нормальной системы нужно было бы эти полиномы
умножить, соответственно, на т/~га-]---- (n = 0, 1, 2, ...).
6) Наконец, рассмотрим еще один пример, связанный с бессе л ев ыми
функциями. Мы ограничимся для простоты письма функцией Jo (х), но все ска-
занное будет справедливо и для функций Jn (х) при п > 0.
В теории бесселевых функций устанавливается, что Jo (х) имеет бесчи-
сленное множество положительных корней:
?1> ?2> •••	•••
679|	S i. введений	423
Переписав уравнение, которому удовлетворяет функция Jt(x), в виде
d Г dzl
— I х —- = — xz,
dx |_ dxj
легко получить, каковы бы ни были числа а и
d Г dja (ах)1	, , , .
^с[Х-^Г\=~ах^лх}’
£ Г х	_ ^xj (? j
dx[_ dx J r °'r '
Умножая первое из этих равенств на J0($x), а второе — на Ja (ах), и почленно
вычитая одно из другого, найдем:
(3» — as) xJe (ах) Ja (Зх)	[ах4 (Зх) J'a (ах) — 3xJ0 (ах) (fix)).
Отсюда, если а
1
С i i \ г zo \ j аЛФ)Л(а)—ЗЛ>(°)Л(₽)
х/0 (ах) J, (Зх) dx =	.	(21)
Если положить здесь a = £n)3 = £m (при п^т), то придем к соотношению
I
§ Х/о М Jo ^Х =
О
которое показывает, что система функций {]^х Jo ($ях)} ортогональна
в промежутке [0, 1]*. Эта система не будет нормальной.
Пусть в промежутке [a, Z>] дана какая-нибудь ортогональная си-
стема {<р„(х)}. Зададимся целью разложить определенную в [а, Ь] функ-
цию f(x) в «ряд по функциям <р» вида:
/(х) = со®о (х) 4-	(х) -j-... -f-	(х) 4- • ••	(22)
Для определения коэффициентов этого разложения, допуская его
возможность, поступим так, как мы это сделали в частном случае
Выше. Именно, умножив обе части разложения на <рт(х), проинтег-
рируем его почленно:
$ f (*)	(*) dx = сп J <р„ (х) <pm (х) dx.
а	п = 0	а
* Обобщая понятие ортогональности функций и ф, вводят понятие орто-
гональности с весом р(х), связывая его с выполнением равенства
ь
р (х) <р (х) ф (х) dx =0.
а
Если воспользоваться этой терминологией, то можно сказать также, что система
функций {Je($nx)} будет ортогональна с весом х.
424
ГЛ. XIX. РЯДЫ ФУРЬЕ
(680
В силу ортогональности [см. (15) и (16)], все интегралы справа,
кроме одного, будут нулями, и легко получается:
ь
ст = г-	(23)
t)
а
(т=0, 1, 2, ...)
[Формулы (7), (И), (12) являются частными случаями этой формулы.]
Ряд (22) с коэффициентами, составленными по формулам (23),
называется ' {обобщенным) рядом Фурье данной функции, а
сами коэффициенты — ее {обобщенными) коэффициентами Фурье
относительно системы {<рга(л:)}. Особенно просто выглядят формулы
(23) в случае нормальной системы; тогда
ь
cm=\)f{x)<?m (х) dx	(23*)
а
(т —0, 1, 2,
Конечно, здесь могут быть повторены те же замечания, какими
мы закончили предыдущий п°. Обобщенный ряд Фурье, построен-
ный для данной функции f {х), связан с нею лишь ф о р м а л ь но.
И в общем случае связь между функцией f{x) и ее (обобщенным)
рядом Фурье обозначают так:
СО
f{x)^Xcn<?n(x).	(22*)
о
Сходимость этого ряда к функции f{x), как и в случае тригономет-
рического ряда, подлежит еще исследованию.
680. Тригонометрическое интерполирование. Можно естествен-
ным образом подойти к вопросу о представлении заданной функции
ф{х) тригонометрическим рядом, отправляясь от тригонометри-
ческого интерполирования, т. е. приближения к функции
f {х) с помощью тригонометрического многочлена
(х) = + У, (a* cos kx + sin kx),	(24)
k=i
значения которого в ряде точек совпадают с соответствующими
значениями функции.
Именно, всегда можно подобрать 2л-|-1 коэффициентов: а0, аи
..., ага, тригонометрического многочлена n-го порядка (24)
так, чтобы его значения были равны значениям функции f{x) в 2/z —[— 1
наперед указанных точках промежутка (— тс, тс), например в точках
— /X {I = — п, — п -ф-1,..., — 1, 0, 1,..., п — 1, п),
680]
§ 1. ВВЕДЕНИЙ
425
2л
где X—. Действительно, для определения этих 2л 1 коэф-
фициентов мы имеем столько же линейных уравнений:
п
«о+ S (ал cos k\t + sin klt)=/($,-)
A = 1
(i = —Л, — л-t-l.л).
Для решения этой системы нам придется вспомнить одно элемен-
тарное тригонометрическое тождество *:
п
1	। V -и
-о + 7 cos th.
(25)
(26)
„ . 1 .
2	sin у Л
Сложим почленно все равенства (25). Ввиду нечетности синуса
коэффициент при
п
У, sin k'ii = 0.
i=—п
и о коэффициенте при ak, ибо по
п
То же можно сказать
косинуса	п
cos = 1 4- 2 cos = 0
i = — п	i — 1
четности
(27)
в силу тождества (26), если взять в нем /г = ЛХ = 2п^ 1'
•.=4 2 /<ц-
i=—n
Поэтому
(28)
Чтобы определить am (1 лг л), умножим равенства (25), соот-
ветственно, на cos m<i и снова почленно сложим. Коэффициент при
«о будет нулем ввиду (27); равен, очевидно, нулю и коэффициент
при по нечетности синуса. Что же касается коэффициента
при аА, то он представится так:
ДЛЯ
cos М,-cos/л£г = у cos (^ 4~ т) + у 2 cos — тУ'1>
l= — n	i = — n	i — — n
h~
при k т обе суммы справа ввиду (27) обратятся в нуль, а при
k = m первая сумма будет нулем, в то время как вторая получит,
* Его легко получить, если умножить левую часть на 2 sin у h и каж-
дое произведение 2 sin у h cos ih заменить разностью sin
— sin [i — j) h. [Ср. 307 (2).]
426
ГЛ. XIX. РЯДЫ ФУРЬВ
[680
очевидно, значение . Таким образом, лишь коэффициент при
а.т оказывается отличным от нуля, именно, равным	Теперь
уже легко найти
п
=	2 cos (К'Ж'О-	(29)
i=—п
Совершенно аналогично, умножая равенства (25) на sin пЛ1 и скла-
дывая, найдем	п
рт=2^рт 2 sin	л)-	(30)
i——n
Читатель несомненно заметил в примененном приеме сходство с
методом Эйлера — Фурье для определения коэффициентов тригоно-
метрического ряда. Однако здесь наши выкладки безупречны, ибо легко
проверить, что полученные значения неизвестных действительно удов-
летворяют уравнениям (25). Впрочем, это и без проверки ясно из
простых алгебраических соображений. Мы видели, что система (25)
может иметь, если вообще имеет, лишь единственное решение,
которое дается формулами (28), (29), (30), каков бы ни был на-
бор правых частей. Но в таком случае ее определитель необ-
ходимо отличен от нуля, и сама система является определенной.
Итак, тригонометрический многочлен а„(х) с найденными значениями
коэффициентов удовлетворяет поставленным требованиям и может
служить для интерполирования нашей функции в промежутке [ — тс, тс].
Предположим теперь, что заданная функция в этом промежутке
интегрируема (на этот раз — в собственном смысле!). Если мы
станем увеличивать п до бесконечности, то интерполяционный мно-
гочлен a„(jt) будет меняться, совпадая с f(x) на все более и более
«густом» множестве точек. Он не только будет «удлиняться», но и
уже вошедшие в игру его коэффициенты будут изменяться. Чтобы
лучше разобраться в их поведении, представим себе промежуток
[ — тс, тс] разложенным на 2л -j- 1 равных частей с помощью точек
деления xt = (21 — 1)
( — лI л -|- 1). Точки являются
как раз серединами этих частичных промежутков, а длины последних
2тс
все равны ДлГ;- = 2ге_^^ =Х. Если переписать формулы (28), (29) и
(30) в виде
п	п
а°=4 2	а'"=т 2 ^')cos
i=—n	i = — n
n
Pm = 4 2 /Gi) Sin
/=г— n
6811
§ 2. РАЗЛОЖЕНИЙ ФУНКЦИЙ В РЯД ФУРЬЕ
427
то суммы в правых частях окажутся интегральными суммами,
отвечающими именно указанному разбиению промежутка. Теперь ясно,
что при п -> оо
ТС
^fWx,
— тс
*/n r
тс
-i- f(x) cos mx dx,
—TC
TC
— TC
sin mxdx,
так что предельными значениями коэффициентов интерполяцион-
ного тригонометрического многочлена являются соответствую-
щие коэффициенты Фурье нашей функции. Можно сказать, что
интерполяционный многочлен «в пределе» как бы переходит в ряд
Фурье!
Этот процесс, разумеется, тоже может рассматриваться лишь как
наведение. Он ничего не доказывает относительно связи между функ-
цией и ее рядом Фурье, но, в свою очередь, достаточно мотивирует
интерес именно к этому ряду. В последующих параграфах мы и зай-
мемся, наконец, непосредственно изучением поведения ряда Фурье
для разных классов функций.
§ 2. Разложение функций в ряд Фурье
681. Постановка вопроса. Интеграл Дирихле. Пусть f(x) бу-
дет функция с периодом 2те, абсолютно интегрируемая, хотя бы и
в несобственном смысле, в промежутке [ — те, те], а следовательно, и
в любом конечном промежутке. Вычислим постоянные (ее коэффици-
енты Фурье):
«	тс
ат — ~	f (и) cos mu du, bm — ~^ /(и) sin mudu (1)
— ТС	— тс
(т—0, 1, 2, ...)	(т = 1, 2, ...)
и по ним составим ряд Фурье нашей функции
ОО
f (*) ~ Y + У (flm cos mx + bm sin mx).
m = l
(2)
Читатель замечает здесь маленькое отступление от обозначений п° 678:
коэффициент а9 мы определяем теперь по общей формуле для ат
при т = 0, в разрез с формулой (7) упомянутого п°, но зато сво-
бодный член ряда пишем в виде у.
428
ГЛ. XIX. РЯДЫ ФУРЬЕ
[681
Заметим здесь же (этим замечанием мы будем пользоваться
и в последующем), что для функции F(u), имеющей период 2ir, ве-
личина интеграла
§ F (и) du
а
по промежутку длины 2тс не зависит от а [ср. 314, 10) и 316]. По-
этому и в формулах (1), определяющих коэффициенты Фурье, ин-
тегралы могут быть взяты по любому промежутку длины 2тс; напри-
мер, можно было бы написать
2тс	2ic
ат = — \ f (-v) cos тх dx, bm = — f(x) sin mx dx (1*)
о	о
(m = 0, 1, 2, ...)	(m=l,	2,	...)
и т. п.
Для того, чтобы исследовать поведение ряда (2) в какой-нибудь
определенной точке х — хй, составим удобное выражение для его
частичной суммы	п
sn Uo) — у + (ат cos тх* + bm sin тхй).
/п = 1
Подставим вместо ат и Ьт их интегральные выражения (1) и подве-
дем постоянные числа cos тх}, sin тхй под знак интеграла:
ТС
= J f(u)du +
— ТС
п тс
-[- 2 у \ f (и) [cos mu cos тх0 -[- sin mu sin тх№] du =
т= 1 —тс
тс	п
= у § /00 {у + 2 COS ОТ (й — Хо)р«.
— тс	т= 1
Воспользовавшись для преобразования выражения в фигурных
скобках формулой (26) п° 680, будем иметь:
j «	sin(2n+l)t=^“
т+ У cos от (и — х0) =-----------——--------,
и окончательно
ТС
f sin(2n+l)^-^
s* (Хо) = -!/(«) ——у—— du.	(3)
J 2 sln ~2
— тс
Этот важный интеграл носит имя Дирихле (G. Lejeune-Dirichlet).
682]	§ 2. РАЗЛОЖЕНИЕ ФУНКЦИЙ В РЯД ФУРЬЕ	42S
Так как мы имеем здесь дело с функциями от и периода 2л, то
промежуток интегрирования [— к, л] по сделанному выше замечанию
можно заменить, например, промежутком [х0—Xo-j-it]:
Хо+1С
Г	sin(2«+l)t^
Sn (Хо) — — I / («) ---------------du.
/ л	1	о  и Хо
J	2sin-T~
*0 —
Подстановкой t—u — преобразуем этот интеграл к виду:
тс
Sn (*0) = — | f (Хо + О------dt.
J	2 sin t
— 1C
тс 0
Затем, разбивая интеграл на два: § -р § и приводя второй интеграл
О —тс
путем изменения знака переменной тоже к промежутку [0, л], придем
к такому окончательному выражению для л-й частичной суммы ряда
Фурье:
1 I	sin (n-|--=-)<
М*о)=т | [А*о + Э+Л*о-Э]—----------------i~-dt. (4)
I	2 sin 1
2
о
Таким образом, дело сводится к исследованию поведения именно
этого интеграла, содержащего параметр п. Своеобразие представля-
ющейся здесь задачи заключается в том, что здесь не может
быть использован предельный переход под знаком интеграла*, ко-
торый до сих пор (см. главу XIV) служил нам единственным сред-
ством для разыскания предела интеграла, содержащего параметр.
И с таким положением вещей нам в этой и в следующей главах
придется сталкиваться систематически.
682.	Первая основная лемма. Прежде чем продолжить наше ис-
следование, докажем следующее важное для дальнейшего утвержде-
ние, которое принадлежит Риману:
Если функция g(t) абсолютно интегрируема в некотором
конечном промежутке [а, t>], то
ь
lim (g(0 sin pt dt = Q
* В данном случае подинтегральное выражение при п —> со вовсе не
имеет предела.
430
ГЛ. XIX. РЯДЫ ФУРЬЕ
(682
и, аналогично,
ь
lim \ g (t) cos pt dt = 0.
p—00 '
Доказательство достаточно провести для первого из этих пре-
делов. Заметим предварительно, что, каков бы ни был конечный про-
межуток [а, 0], имеем такую оценку:
а
IC .	, ,, I I cospa — cospB I ~ 2
I J sin pt dt | = I -it-—-(5)
s
Допустим сначала, что функция f(x) интегрируема в собственном
смысле. Разобьем промежуток [а, Ь] на п частей точками
а=4<9<---<9<9+1<---<^ = ^	(6)
и в соответствии с этим разложим и интеграл
Ь	n — \ii+i
g(t) sin pt dt— 2 § g(t) sin pt dt.
a	i=0
Обозначив через /и,- точную нижнюю границу значений g(t) в i-м
промежутке, можно преобразовать это выражение так:
ь
\g(t) sin pt dt =
a
n— I 'i+1
= У 5 te(O — mt\ sinpidi-]- У mt $ sin pi di.
1=0	1=0 t.
Гели о>г есть колебание функции g(f) в i-м промежутке, то в его
пределах g(t)—	с учетом неравенства (5) теперь легко по-
лучить для нашего интеграла оценку:
b	n—i	п—1
| £(9 sin ptdt | <	+ y
a	i=0	‘ 1=0
Задавшись произвольным числом e^>0, выберем сначала дроб-
ление (6) так, чтобы было
1=0
682L	S 2. РАЗЛОЖЕНИЕ ФУНКЦИЙ В РЯД ФУРЬЕ	43
это сделать можно именно ввиду интегрируемости функции g [297]
Теперь, так как числа mt тем самым уже определены
можем взять
и для этих значений р получим
ь
|$g(/) sin pt dt [ г,
a
что и доказывает наше утверждение.
В случае, если функция g(t) интегрируема в несобственном смысл»
(но обязательно абсолютно!) достаточно ограничиться предполо
жением, что в промежутке [а, Ь\ имеется лишь одна особая точка
например точка Ь*.
Пусть	— а. Разлагая интеграл на два:
b	b — vi	ь
а а Ь — т]
для второго интеграла справа имеем при любом р оценку:
ь	ь
| $ #(0 sin ptdt\^	| g(f) | dt,
Ь — ц	b — ц
что если выбрать т] достаточно малым. Что же касается ин
теграла
5 g(t)smptdt,
а
то при р -> о° он стремится к нулю — по уже доказанному, та:
как в промежутке [а, b — т;] функция g(f) интегрируема в с об ст
венном смысле слова; написанный интеграл по абсолютной ве
личине также станет «Су при достаточно большом р. Этим и завер
шается доказательство.
Мы обращаем внимание читателя на то, что уже здесь пределы
к которым стремятся интегралы, установлены помимо предель
ного перехода под знаком интеграла.
* Иначе можно было бы разложить промежуток на конечное число ча-
стей, содержащих лишь по одной особой точке, и применить рассужденш
к каждой части в отдельности.
432
ГЛ. ХГХ. РЯДЫ ФУРЬЕ
[683
Если вспомнить формулы (1), выражающие коэффициенты Фу р ье,
то в качестве первого непосредственного следствия отсюда полу-
чается утверждение:
Коэффициенты Фу рье ат, Ьт абсолютно интегрируемой
функции при т -> оо стремятся к нулю.
683.	Принцип локализации. Вторым непосредственным же след-
ствием доказанной леммы является так называемый „принцип лока-
лизации".
Взяв произвольное положительное число 8<^тс, разобьем интеграл
тс	8	тс
в (4) на два: = Если второй из них переписать в виде:
О	0	8
X Г/(*,, +0+/(*.-О
"у 2 sin t
то станет ясно, что множитель при синусе является абсолютно
интегрируемой функцией от t в промежутке [8, те], ибо знаменатель
2 sin у t в этом промежутке в нуль не обращается. В таком случае
по лемме этот интеграл при п -> оо стремится к нулю, так что и
самое существование предела для частичной суммы ряда Фурье,
$„(х0), и величина этого предела целиком определяются поведением
одного лишь интеграла
б
Г*	• I ,
1	sin	f
р»(5) = ^ I №o + 0+m-0]-..........V !  dt. (7)
J	2 sin у t
o
Но в этот интеграл входят лишь значения функции f(x), отвечаю-
щие изменению аргумента в промежутке от хй — 8 до ха -|- 8. Этим
простым соображением и доказывается „принцип локализации", со-
стоящий в следующем:
Теорема Рамана. Поведение ряда Фурье функции /(х) в
некоторой точке хй * зависит исключительно от значений, при-
нимаемых функцией в непосредственной близости рассматривае-
мой точки, т. е. в сколь угодно малой ее окрестности.
Таким образом, если, например, взять две функции, значения ко-
торых в произвольно малой окрестности точки х0 совпадают, то как
бы они ни разнились вне этой окрестности, соответст-
вующие этим функциям ряды Фурье ведут себя в точке х0 одина-
ково: либо оба сходятся, и притом к одной и той же сумме, либо
* Мы понимаем под этим сходимость или расходимость ряда в точке х0,
а также наличие для него (в случае сходимости) той или иной суммы.
684]
§ 2. РАЗЛОЖЕНИЕ ФУНКЦИЙ В РЯД ФУРЬЕ
433
оба расходятся. Этот результат покажется еще более разительным,
если подчеркнуть, что самые коэффициенты Фурье рассматриваемых
функций, зависящие от всех их значений, могут оказаться совершенно
различными!
Эта теорема обычно связывается с именем Римана, ибо является
следствием более общей его теоремы, доказанной в 1853 г. Следует,
однако, отметить, что идея „принципа локализации“ содержится в од-
ной работе Остроградского 1828 г. по математической физи-
ке, а также отражена в исследованиях Лобачевского 1834 г. по
тригонометрическим рядам.
684.	Признаки Дини и Липшица сходимости рядов Фурье.
Возвращаемся к прерванному исследованию поведения частичной суммы
sn(xa) РяДа Фурье, для которой мы получили интегральное выраже-
ние (4). Отметим, что упомянутое равенство имеет место для каждой
функции f (х), удовлетворяющей поставленным условиям. Если, в част-
ности, взять f(x)=l, то и s„(x)=l, и из (4) получим, что
ТС
2 С sin(n+4V
l=- I —1dt.
я I 2 sin 1
V 2
о
Умножая обе части этого равенства на постоянное число So —
предполагаемую сумму нашего ряда, точное значение
которой мы установим ниже, и вычитая результат из (4), найдем:
ТС
/ 1 \
sin p
<р(0 -> dt,	(8)
2 sin 4 t
о	z
где для краткости положено
<р(О=/(хо4_0-|-/(*в— 0 — 2>%.	(9)
Если мы хотим установить, что действительно является суммой
ряда, то для этого нужно доказать, что интеграл (8) при д->оо
стремится к нулю.
Обратимся к выбору самого числа So. Практически важны те случаи,
когда (а) функция f(x) в точке х0 непрерывна, либо (б) f(x) имеете
этой точке с обеих сторон разве лишь разрывы первого рода (или
скачки), так что оба предела /(хо + О) и f(x^— 0) существуют.
Этими случаями мы впредь ограничимся и раз навсегда полагаем:
в случав (a): Sa—f(x0),
в случае 1б¥ S’ —+°)+/(*„—0)
о случае МАЛ ----------%
434
ГЛ. XIX. РЯДЫ ФУРЬВ
[684
В различении случаев (а) и (б) нет надобности, если в точке х0,
где налицо разрыв первого рода, выполняется равенство
=/ (x<i 4~ Q) + / (хо — 0)
Точки, где это условие соблюдено, иногда называют регулярными.
Отметим, что так как
(a) lim f(xa ± f) —f (л:0) или (б) lim f (хй ± t) —f (лг0 ± 0),
/-« + о	/—+о
смотря по случаю, то при указанном выборе числа So всегда будет
lim <р (0 = 0.	(10)
/-+о
Имея это в виду, сформулируем теперь
Признак Дини. (U. Dini) Ряд Фурье функции f (х) в точке х0
сходится к сумме S», если при некотором /г^>0 интеграл
существует.
Действительно, при этом
с НЦ£>1 л
О
предположении существует и интеграл
(8) в виде
4* / 1\
---j— • sin	dt,
Если переписать выражение
1С
11
-J ' 
о
то непосредственно по основной лемме ясно, что оно при п -> оо
Lt
.	<р(0	т(0	2
стремится к нулю, так как функция а с нею и •---------------—
sin
абсолютно интегрируема. Этим и завершается доказательство.
В развернутом виде интеграл Дини может быть написан так:
А
в случае (а): ( 1/(^ + О+/(^-О-2/(хо) |.^
о
, случае (в): ( 1Г<*. + О	Q-ZQe. + ЩI д,.
684]	$ 2. РАЗЛОЖЕНИЕ ФУНКЦИЙ В РЯД ФУРЬЕ	435
Очевидно, достаточно предположить существование порознь ин-
тегралов (смотря по случаю)
А	А
! f ~Ь 0 f fo») I и !/(•*» 0 /(-*•«) I &	(11)
и	и
или
A	A
C	/(*<> +0)1 и C |/(xo-O-/(xo-0)| dt
о	0
Отсюда можно получить ряд частных признаков, используя различные
известные признаки существования интегралов. Например, ограничи-
ваясь случаем (а), укажем
Признак Липшица (R. О. Lipschitz). Ряд Фурье функции f (х)
сходится в точке х0, где она непрерывна, к сумме /(х0), если
для достаточно малых t выполняется неравенство
|/(Хо±0-/(Хо)|^^,
где L и а — положительные постоянные (asgl).
В случае а = 1 имеем попросту
f(x0±t)—f(x0) | г
так что интегралы (И) существуют как собственные [480]. Если же
а<^ 1, то
|/(х0 ± 0—/(х0) I	L
I t | K tl~*'
и так как справа стоит интегрируемая функция, то интегралы (11)
все же существуют, хотя бы как несобственные [482].
В частности, условие Липшица при а=1 заведомо будет вы-
полнено, если для функции f(x) в точке х0 существует конечная
производная f (х0) или, по крайней мере, конечные односторонние
производные
Л(х0) = lim <(x° + 0-/(^o) , /дХо)= нт /(хо-0-/(хо),
<-►+0	r	/ —+0	— ‘
хотя бы и различные между собой («угловая точка»). Таким образом,
в точке х0, где функция /(х) дифференцируема или, по край-
ней мере, имеет обе конечные односторонние производные, ряд
Фу р ь е сходится, причем сумма его равна f(xe).
Легко перефразировать признак Липшица и для случая (б).
Как частное следствие отсюда, укажем и здесь, что в точке х0
436	ГЛ. XIX. РЯДЫ ФУРЬВ	[685
разрыва первого рода для сходимости ряда Фу рве достаточно
предположить существование конечных пределов:
lim /(-Vq + O— /(-Vq + O)	lim /(-^о—o—/(-Vp —0)
/ — + о	t	’	+ 0	—t ’
причем на этот раз суммой ряда будет -	°)
Упомянутые пределы в некотором смысле уподобляются односто-
ронним производным, лишь значение /(х0) функции в точке х0 заме-
няется, соответственно, ее предельными значениями справа или слева
от этой точки.
Наиболее часто на практике приходится иметь дело с функциями
f(х), имеющими период 2л и дифференцируемыми или же
кусочно-дифференцируемым и. * Как видим, для таких функ-
ций ряд Фурье всегда сходится к самой функции f(x), за исклю-
чением «точек стыка» различных функций, где суммой ряда будет
/(х„4-0) +/(х„-0)
2
685. Вторая основная лемма. Для построения дальнейших при-
знаков мы будем нуждаться еще в одном вспомогательном утвержде-
нии, впервые установленном Дирихле:
Если функция g(t) монотонно возрастает, оставаясь ограни-
ченной, в промежутке [0, h], где h^>0, то
ь
lim
р—»со
g(t)
s^dt = ^g(+0).
(12)
Доказательство. Прежде всего, рассматриваемый интеграл
может быть представлен в виде суммы двух интегралов:
л	л
g(+0) §^л+^(0-£(+0)]^л.	(13)
б	о
Если первый из них с помощью подстановки pt = z преобразовать
к виду	ph
gk+^A^dz,
о
* Функция f(x') называется кусочно-дифференцируемой в
промежутке [а, 6], если этот промежуток разлагается на конечное число
частичных промежутков, внутри которых функция дифференцируема, а на
концах не только имеет предельные значения, но и односторонние произ-
водные, при условии замены на этих концах значений функций упомянутыми
предельными значениями. Можно представить себе кусочно-дифференцируе-
мую функцию как бы «склеенной» из нескольких функций, дифференцируе-
мых (а следовательно, и непрерывных) в замкнутых частичных промежут-
ках с тем лишь, что в «точках стыка» (равно как и на концах а и b основ-
ного промежутка) ее значения устанавливаются особо.
685]
§ 2. РАЗЛОЖЕНИЕ ФУНКЦИЙ В РЯД ФУРЬЕ
437
то сразу ясно, что при р-+-\-оо он стремится к y-g(-|-0), и^°
Таким образом, весь вопрос сводится к доказательству того, что
второй из интегралов (13) стремится к нулю.
По произвольно заданному е^>0 найдется такое 8^>0 (можно
считать 8<^/г), что
— £(+0)<Ч для
Разобьем теперь упомянутый только что интеграл на два:
г л
(J (0 - £(+ 0)] dt = л + 4
о 6 7
К интегралу Д применим формулу Бонне [306]; мы получим, что
8	р8
/1 = [£(&)-£(+0)] JS-Y^^ = [g(8)-^(+0)] \ ^dz.
л	РЛ
Но первый множитель е, а второй равномерно ограничен при всех
значениях р. Действительно, из сходимости несобственного интеграла
оэ
С sin г ,	,	_ „ч ,
Д -j-dz следует, что непрерывная (при г^О) функция от г
д
имеющая при	конечный предел, будет ограничена при
всех значениях» z:
| dz\^L . (Z. = const),
о
так что
р8
I С sin Z ,
Ij—*
РЛ
р5 pi)

Итак, для интеграла 4 имеем независимо от р оценку
|/1|<2£е.	(14)
Что же касается интеграла 4 то при р -> оо (и фиксирован-
ном 8) он стремится к нулю по лемме п° 682, так как множитель при
438	гл. XIX. РЯДЫ ФУРЬЕ	[686
sin pt есть интегрируемая в собственном смысле функция (ведь
/>г8!). Этим и завершается доказательство.
686. Признак Дирихле — Жордана. Обратимся теперь к выводу,
нового признака сходимости рядов Фурье, основанного на другой
идее.
Признак Дирихле — Джордана. Ряд Фурье функции f(x)
в точке х0 сходится к сумме Sn, если в некотором промежутке
[х0 — h, х0 + h] с центром в этой точке функция имеет огра-
ниченное изменение.
Мы видели в п° 683, что поведение частичной суммы s„(x0) при
л->оо определяется поведением интеграла рп(8) [см. (7)], где за 8,
в частности, можно взять и то число h, о котором была речь выше.
Перепишем интеграл p„(ft) в виде
А	1	.	.	I , 1 \ ,
1	-у«	ап	(« + -=- f
pn(ft) = v I [/(Xo + O+Axo-^Ol-A-----------—7	dt.
•* I	1 .	t>
J	smTz
6
Сумма в квадратных скобках, по предположению, есть функция
-р
с ограниченным изменением; частное же —।— представляет собой воз-
sin-2*
растающую функцию. Таким образом, и произведение их имеет огра-
ниченное изменение и, следовательно, представляется в виде разности
двух монотонно возрастающих функций. Поскольку лемма предыду-
щего п° приложима к каждой из них в отдельности, она приложима
и к их разности, и мы сразу получаем, что
lim p„ (ft) =1 • -J [ftx0 + 0) +/(х0 - 0)]	+
п—* 00
Этим все доказано, ибо в точке непрерывности полученное выраже-
ние само собою обращается в /(х0).
Нужно сказать, что первоначально сформулированные самим
Дирихле условия разложимости функции в ряд Фурье носили
более частный характер. Именно, он установил следующее предложение:
Признак Дирихле. Если функция f(x) периода 2те кусочно-
монотонна в промежутке [—те, те] * и имеет в нем не более, чем
конечное число точек разрыва, то ее ряд Фурье сходится
* Под этим разумеется возможность разложить промежуток [—к, к] на
конечное число частичных промежутков, внутри которых по отдельности
функция монотонна.
686]	$ 2. РАЗЛОЖЕНИЕ ФУНКЦИЙ В РЯД ФУРЬЕ	439
к сумме /(хо) в каждой точке непрерывности и к сумме
f 0*0 "Ь Q) "Ь f (*0-0) А Ч
J	J— 2	--------~ 6 кажд°й точке разрыва.
С тех пор высказанные здесь условия известны под именем
«условий Дирихле».
Так как функция, удовлетворяющая этим условиям, очевидно,
имеет ограниченное изменение в любом конечном промежутке, то
этот признак формально перекрывается предыдущим признаком.
Изложенных признаков вполне достаточно для удовлетворения
практических потребностей анализа и его приложений. Другие пред-
ложенные признаки представляют, главным образом, теоретический
интерес; на них мы не имеем возможности останавливаться.
Коснемся в заключение вопроса о взаимоотношении признаков
Дини и Дирихле—Жордана. Можно показать, что они несрав-
нимы между собой, т. е. не вытекают один из другого. Рассмотрим
сначала функцию / (х), которая в промежутке [— тс, тс] опреде-
ляется так *:	.
f(x)=—г—। при х^О,
'"Щ
1/(0) = 0.
Эта функция непрерывна и кусочно-монотонна и, значит, удовлетво-
ряет условиям Дирихле. В то же время интеграл Дини, относя-
щийся к точке х = 0:
1/(0 тН/(- 0-2/(0) |
t
о
dt = 2
явно расходится при любом h ~^> 0.
С другой стороны, если в промежутке [—тс, тс] определить функ-
цию равенствами *:
/(х) = х cos-^- при х^О,
7(0) = О,
то в точке х — 0 заведомо выполняется условие Липшица:
|/(х) -/(0) |	| х I,
а следовательно и условие Дини. Однако на этот раз функция
/(х)ни в какой окрестности точки х = 0 не имеет ограниченного
изменения [567].
* На остальную'часть числовой оси функция распространяется по закону
Периодичности: /(х-|-2гс)=/(х).
440
ГЛ. XIX. РЯДЫ ФУРЬЕ
(687
687. Случай непериодической функции. Вся построенная выше
теория исходила из предположения, что заданная функция опреде-
лена для всех вещественных значений х и притом имеет период 2тс.
Между тем, чаще всего приходится иметь дело с непериоди-
ческой функцией f (х), иной раз даже заданной только в проме-
жутке [— тс, тс].
Чтобы иметь право применить к такой функции изложенную тео-
рию, введем взамен нее вспомогательную функцию /*(х), определен-
ную следующим образом. В промежутке [—тс, тс] мы отождест-
вляем f* с /.
f*(x)=f(x)	(—tc<^xsCtc),	(i 5)
затем полагаем
/*(—тс)=/*(тс),
а на остальные вещественные значения х распространяем функцию
/*(х) по закону периодичности.
К построенной таким образом функции /*(х) с периодом 2тс
можно уже применять доказанные теоремы разложения. Однако если
речь идет о точке х0, лежащей строго между —тс и
тс, то [при. проверке условий этих теорем нам пришлось бы иметь
дело ввиду (15) лишь с фактически заданной функцией /(х). По
той же причине и коэффициенты разложения можно вычислять по
формулам (I), не переходя к функции /*(х). Короче говоря, все до-
казанное выше непосредственно переносится на заданную функ-
цию f(x), минуя вспомогательную функцию /*(х).
Особого внимания, однако, требуют концы промежутка x = ±ir.
При проверке для функции /*(х) условий какой-либо из теорем
пп° 684, 686, скажем в точке х = тс, нам пришлось бы иметь дело
как со значениями вспомогательной функции f* (х) слева от х = тс,
где они совпадают с соответственными значениями данной функ-
ции. f(x), так и со значениями /* (х) справа от х = тс, где они
совпадают уже со значениями /(х) справа от х — — тс. Поэтому,
если бы мы пожелали перефразировать для случаев точек х = ±тс, на-
пример, признак Дирихле — Жордана, то нам в обоих случаях
следовало бы потребовать, чтобы /(х) имела ограниченное изменение
как слева от х = тс, так и справа от х=—тс. При этом в качестве
значения So в обоих же случаях надлежало бы взять
/*(тс + 0)+/*(тс-0) _/»(-п + 0)+/»(-тс-0)_
—	2	2
_/("+0)+/(тс-0)
2
Таким образом, если заданная функция f(х) даже непрерывна
при х = ±тс, но не имеет периода 2тс, так что /(тс)7?:/(—тс),
688]	$ 2. РАЗЛОЖЕНИЕ ФУНКЦИЙ В РЯД ФУРЬЕ	441
то при соблюдении какого-либо из достаточных для сходимости ряда
Фурье условий суммой этого ряда будет число
/( —д)+/(д)
2
отличное как от /(—л), так и от /(л). Для такой функции разло-
жение может иметь место лишь в открытом промежутке (— л, л).
Следующее замечание заслуживает серьезного внимания читателя.
Если тригонометрический ряд (2) сходится в промежутке (—л, л)
к функции f(x), то ввиду того, что его члены имеют период 2л, он
сходится всюду, и сумма его S(x) оказывается тоже периодиче-
ской функцией от х с периодом 2л. Но эта сумма вне указан-
ного промежутка вообще уже не совпадает с функцией f(х)
(если последняя была задана на всей вещественной оси). Ниже [690]
это замечание будет проиллюстрировано многочисленными примерами.
Отметим, наконец, что вместо промежутка [—л, л] можно было
бы взять любой промежуток [а, а 2л] длины 2л.
v 688. Случай произвольного промежутка. Предположим, что
функция f (х) задана в промежутке [— I, Z] произвольной длины
2/(/^>0). Если прибегнуть к подстановке
х = — (—
те 4	7 ’
то получится функция от у в промежутке [—л, л], к кото-
рой уже приложимы рассмотрения предыдущего п°. При соблюде-
нии определенных условий, как мы видели, можно разложить ее
в ряд Фурье:
ОО
f Hr)= “г + 2 cos пу +bn sin ny>h
/1 = 1
коэффициенты которого определяются формулами Эйлера — Фурье:
1С	я
ап=1J cos nydy’ bn=:^\ Л-?)sin nydy-
—те	—	те
(n= 0, 1, 2 .. .)	(n=l,	2,	...)
Вернемся теперь к прежней переменной х, полагая
тех
у=—•
Тогда мы получим разложение заданной функции /(х) в тригоно-
метрический ряд несколько измененного типа:
ОО
/(х)=4- 2 (ап cos + bn sin .	(16)
л=Г
442
ГЛ. XIX. РЯДЫ ФУРЬЕ
[689
Здесь косинусы и синусы берутся от углов, кратных не х, а -j-.
Можно было бы и формулы для определения коэффициентов этого
разложения преобразовать той же подстановкой к виду
i	i
а„ = — \ /(х) cos —— dx, bn — -j- \ f(x) sin—j— dx. (17)
-z	-i
(л = 0. 1,2,...)	(n=l,2....)
В отношении концов промежутка х = ±1 сохраняют силу заме-
чания, сделанные в предыдущем п° относительно точек х = ± тс.
Конечно, промежуток [—I, Z] может быть заменен любым другим
промежутком длины 2/, в частности, промежутком [0, 2/]. В послед-
нем случае формулы (17) должны быть заменены формулами
2Z	21
а„ = Ц- ^/(х) cos ~Xdx, bn = ~ f f(x) sin dx. (17*)
b	о
(л = 0, 1, 2,...)	(л = 1, 2, ...)
При всех оговорках относительно концов промежутка или отно-
сительно точек разрыва функции, мы все же установили факт огром-
ного принципиального значения: произвольно заданная в произволь-
ном промежутке функция в очень широком классе случаев*
оказывается разложимой в тригонометрический ряд, т. е. пред-
ставляется единым аналитическим выражением — тригонометрическим
рядом — во всей области определения функции. В п° 690, в частно-
сти, мы найдем большое число примеров такого разложения функций,
первоначально заданных в различных частях промежутка различными
аналитическими выражениями. Аппарат тригонометрических рядов
оказывается универсальным средством для «склеивания» функций,
окончательно стирая грань между функциями, допускающими
единое аналитическое представление во всей области определе-
ния, и функциями, определенными с помощью нескольких анали-
тических выражений [ср. 46, 3°; 363 5); 407, замечание I; 497,
11) и др.].
689. Разложения только по косинусам или только по синусам.
Начнем со следующего замечания: если заданная в промежутке
[—тс, тс] интегрируемая (в собственном или несобственном смысле)
функция f(х) будет нечетной, то для нее
$ f(x)dx — 0.
* Включающем, например, функции кусочно-дифференцируемые или ку-
сочно-монотонные и т. п.
6891	S 2. РАЗЛОЖЕНИЕ ФУНКЦИЙ В РЯД ФУРЬЕ	443
ТС
В этом легко убедиться, представив интеграл J в виде суммы ин-
— л
тс О
тегралов: §-]~ J и заменив во втором из них х на — х. Таким же
О — те
путем устанавливается, что в случае четной функции /(х):
f (x)dx — 2^f(x)dx
— те	О
[ср. 312, 9) и 314].
Пусть теперь /(х) будет абсолютно интегрируемая в промежутке
[—тс, тс] четная функция. Тогда произведение /(х) sin пх окажется
нечетной функцией, и по сказанному
те
bn — -i- /(х) sin пх dx = 0.
(п=1,2?...)
Таким образом, ряд Фу р ье четной функции содержит одни лишь
косинусы:
/(х) ~	2 а“ cos пх' (18)
п=1
Так как /(х) cos пх в этом случае тоже будет четной функцией
то, применив сюда второе из сделанных выше замечаний, можем,
коэффициенты ап разложения написать в виде
те
2 С
ап — — I f (х) cos пх dx.	(19)
о
(п = 0, 1, 2, ...)
Если же функция /(х) будет нечетной, то нечетной будет
и функция ”/(х) cos пх, так что
те
ал —/(х) cos nxdx — Q.
— те
(л=0, 1, 2, ...)
Мы приходим к заключению, что ряд Фурье нечетной функции
содержит одни лишь синусы:
2 bn sin пх.	(20)
л=1
444
ГЛ. XIX. РЯДЫ ФУРЬЕ
[689
При этом ввиду четности произведения /(х) sin пх можно писать:
1С
2 (*
bn = — \ f(x) sin nxdx.	(21)
о
Отметим попутно, что каждая функция f(x), заданная в проме-
жутке [— тс, тс], может быть представлена в виде суммы четной
и нечетной составляющих функций:
/(х)=/1(х)+/2(х),
где
Очевидно, что ряд Фурье функции f(x) как раз и составится
из разложения по косинусам функции j\ (х) и разложения по синусам
функции /2 (х).
Предположим, далее, что функция /(х) задана лишь в про-
межутке [0, тс]. Желая разложить ее в этом промежутке в ряд
Фурье (2), мы дополним определение нашей функции для значе-
ний х в промежутке
[— тс, 0) по произволу, а затем при-
меним сказанное в 687. Подчеркнутый
выше произвол в определении функ-
ции дает возможность получить таким
путем различные тригонометрические
ряды. Если в какой-нибудь точке х0
между 0 и тс наша функция удовлетво-
ряет одному из признаков, установлен-
ных в пп° 694, 696, то все эти ряды бу-
дут в точке х0 сходиться к/(х0) или в слу-
чар пазпывя к -^(хо + °)+/(*о—0)
Час раорЫоа К —	%	,
Можно использовать произвол в опре-
делении функции в промежутке [— тс, 0)
так, чтобы получить для /(х) разложение
только по косинусам или толь-
ко по синусам. Действительно, пред-
ставим себе, что для 0 х «С тс мы полагаем
f(-x)=/(x),	(22)
так что в результате получится четная функция в промежутке
[—тс, тс] (рис. 123, а), к тому же имеющая даже период 2тс. Ее
разложение, как мы видели, будет содержать одни только косинусы.
Коэффициенты разложения можно вычислять по формулам (19), куда
входят лишь значения первоначально заданной функции /(х).
689]
§ 2. РАЗЛОЖЕНИЕ ФУНКЦИЙ В РЯД ФУРЬЕ
445
Аналогично, если дополнить определение функции /(х) условием
(для 0<^х^тс)
/(— х) = — /(х),
(23)
так, чтобы она оказалась нечетной (рис. 123, б), то в ее разло-
жении будут участвовать только члены с синусами. Коэффициенты
его определяются по формулам (21).
Таким образом, заданную в промежутке [0, к] функцию при
соблюдении известных условий оказывается возможным разла-
гать как в ряд по косинусам, так и в ряд по синусам!
Особого исследования требуют, впрочем, точки х = 0 и х = тс.
Здесь оба разложения ведут себя по-разному. Предположим
для простоты, что заданная функция /(х) непрерывна при х = 0 и
х = тс, и рассмотрим сначала разложение по косинусам. Условие (22)
прежде всего сохраняет непрерывность при х = 0, так что при
соблюдении надлежащих условий ряд (18) при х = 0 будет сходиться
именно к / (0). Т ак как, далее,
/(-тс4-0)=/(тс-0)=/(тс),
то и при х=тс имеет место аналогичное обстоятельство.
Иначе обстоит дело с разложением по синусам. Не вдаваясь
в соображения относительно нарушения непрерывности условием
(23) и т. п„ мы просто заметим, что в точках х = 0 и х = тс сумма
ряда (20) явно будет нулем. Поэтому она может дать нам значения
f (0) и f (тс), очевидно, лишь в том случае, если и эти значения
равны нулю.
Если функция f (х) задана в промежутке [0, Z] (Z 0), то, прибегнув
к той же замене переменной, что и в 688, мы сведем вопрос о раз-
ложении ее в ряд по косинусам:
ОО
а0 1 V1	пг.х
йп cos—~
ti = 1
или в ряд по синусам:
ОО
2b*sin ——
п = 1
к только что рассмотренному. При этом коэффициенты разложений
вычисляются, соответственно, по формулам:
i
ап = ~ \ /(х) cos -у- dx	(24)
(л = 0, 1, 2, ...)
или
I
sin dx.	(25)
о
(л=1,2,...)
446
ГЛ. XIX. РЯДЫ ФУРЬЕ
[690
690. Примеры. Функции, которые ниже приводятся в виде примеров,
как правило, относятся к классу дифференцируемых или кусочно-дифферен-
цируемых. Поэтому самая возможность их разложения в ряд Фурье — вне
сомнения, и мы на этом вопросе останавливаться не будем.
1)	Разложить функцию
/ (х) = е“*	(а = const, а 0)
в промежутке (—те, те).
По формулам (1):
1
а0= —
п
ап
9 sh ап
ап
а„ — — \ еах cos пх dx
те )	те
1 a cos пх + п sin пх
еах
1 2л .
----»— » Sh «те,
1Г л2—'
Ъ„ = —— ? еах sin пх dx =
ТС J	тс
a sin пх — п cos пх
а2 + п2
еах
g—CVK

= (-!)'
=<.- 1)л~14
тс
2п к
—:—г sh ап.
J- ла
Итак, для —те<х<те будем иметь
2
е°* = — sh an
[a cos пх — п sin пх] .
V (-1)"
£ а2 + и2
п— 1
Если бы мы исходили из промежутка (0, 2те), то получилось бы разложение
с иными коэффициентами — в этом случае нужно было бы пользоваться форму-
лами (1*). Впрочем, новое разложение легко вывести и из уже найденного.
2)	Разложить функцию
/г(х) = -5-
в промежутке (0, 2те).
По формулам (1*):
2л
1 С
ао = — \
те 1
— X ,7	1
2	dX ~ 2те
1
тех—2~ Х
2л
г
О
2л
1 С
а« = —' \
те л
2— cos пх dx —
1 . .sin пх
= 2^<те-х)-Г-
2л
2я
,	1 (* те — X .	,	1 .	. cos пх
&"=те-\ -2-«ППХаГХ=-^(те-х)^г-
2 тс
2тг
-5— \ sin nxdx — 0.
2пте У	’
(п=1,2, з,...)
2л
If л 1
-х—\ cos nxdx = —.
2пте )	п
о
О
О
690]
I 2. РАЗЛОЖЕНИЕ ФУНКЦИЙ В РЯД ФУРЬЕ
447
Таким образом, мы приходим к замечательному по простоте разложению,
содержащему одни лишь синусы:
ОО
тс — х V sin пх	п ч
-2- = 2~Г-(0<Х<2’с)-
п=1
При х=0 (или 2те) сумма ряда равна нулю, и равенство нарушается.
Не будет равенства и вне указанного промежутка. График суммы ряда
5(х)(рис. 124) состоит из бесчисленного множества параллельных отрезков
и ряда отдельных точек на оси х.
3)	Ввиду особой важности разложения, полученного в предыдущем упраж-
нении, мы дадим элементарный вывод его, не опирающийся на общую теорию.
Пусть 0<x<2ic. Воспользовавшись формулой (26) п° 680, которую мы
можем написать так:
»	sin (2n + 1)
7 cos kx = -------------------
о . X
*= 1	2 sm -у
имеем последовательно:
X п
sin kx	1’ V г.1 л
—~k—= V 2, cos kt dt
6 * = 1
* sin (2л 4- 1) ~
-------------~dt =
о 2 sin у
1_1	t ;fsin(2n+l)4-
t sin (2n + 1) у dt +	------------ dt.
b
Но при n —► -f- оо второй член в последней части равенства стремится к 0 по
основной лемме п° 682*, а третий член подстановкой и = (2n	1) ~
* Множитель в квадратных скобках, если при < = 0 приписать ему значе-
ние 0, оказывается функцией, аналитической в этой точке, ибо в окрест-
ности ее разлагается в степенной ряд:
1	* 1	1 f , 37 „ .
„ . t — 12 1 + 5760*
2 sin-s-
448
ГЛ. XIX. РЯДЫ ФУРЬЕ
[690
преобразуется к виду
(2л + 1)у
С sin и ,
\	----da
и
и,
+ °°
С sin и , те
очевидно, стремится к \ —— du — ^-.
Отсюда
lim
п —► оо
п
2 sin kx
~k~
*=1
что и требовалось доказать.
4) Из разложения в 2) уже без вычислений можно получить и другие
интересные разложения. Заменяя в нем х на 2х и деля обе части равенства
на 2, найдем:
ОО
те X ___ VI sin2ftx
4-~Т-' L 2k
*=1
(О < х < те),
вычитая же одно разложение из другого, получим:
ОО
те _ VI sin (2k—1)х
2k^\
Л=1
(О < X < те).
Если через 8(х) обозначить сумму последнего ряда, то S (0) = S (те) = 0.
Изменяя знак х, для промежутка (—те, 0) по нечетности синуса найдем, что
Рис. 125.
о
2 ’
S(x) =— для прочих же значений х сумма 8(х) получается по закону пе-
Л
риодичности, так что, в частности, для промежутка (2те, Зте) снова S(x) = -^-,
и т. д. График функции 8 (х) изображен на рис. 125; рисунок же 126 харак-
теризует постепенное приближение к этой разрывной функции частичных
сумм ряда.
те
Если положить в рассматриваемом разложении х = -^-, то получим уже
известный нам ряд Лейбница [404(16)]
те
¥
1 —
690]
§ 2. РАЗЛОЖЕНИЕ ФУНКЦИЙ В РЯД ФУРЬЕ
449
„	п	те
При х = -^~ и х = -~- получаются ряды:
• о	о
It , , 1	1	1,1,1	It .	1,1	1,1
4~ +5	7	11 + 13+17	“ 2/3	1	5 + 7	11 + 13
Сочетая полученное здесь разложение с разложением в 2), легко прийти
к ряду для функции /(х) = х:
ОО
2/	<чИ_1 sin пх .	\
(— 1)" (—«<*<«).
П = 1
Непосредственно мы получаем его лишь для 0<х<к, но равенство явно
имеет место для х = 0 и, кроме того, обе его части, очевидно, представляют
Мечетные функции, так что окончательно разложение оказывается верным
16 Г. М. Фихтенгольц, т. III
450
ГЛ. XIX. РЯДЫ ФУРЬЕ
[690
для всего промежутка (—те, те). График суммы ряда при изменении х
от —оо до + оо легко себе представить по рис. 127. На рис. -128
приведен график частичной суммы:
. . „ I .	sin 2х . sin Зх sin 4х . sin 5х\
У = s6(x) = 2 (япх-----------3---------h—g-J.
5)	Опираясь на разложение в 2), доказать, что на всей вещественной оси
00	„	( х — Е(х) для нецелых х,
1	1 yi sin 2пте х  I
2	те	п	j — дЛя целых х.
п — 1	(Л
6)	Разложить (четную!) функцию f(x) = xs в ряд по косинусам в
промежутке [— те, те].
690]
S 2. РАЗЛОЖЕНИЕ ФУНКЦИЙ В РЯД ФУРЬЕ
451
По формулам (19):
1 'См
уво=-^х = у,
1С	Я
„	2 С „» j 2 „ sin пх I" 4 С
<2П = — \ Xs cos пх dx = — Xs-----\ х sm пх dx —
Я J	я п [О ПК )
о	о
я
4 созлх	I*	4	С	, ... 4
— -—х---------------\	cos пх dx = (— 1)п —=	(и > 0),
пп п	|о	п3п	J	' ' п3	'	”
так что
ОО
"2 I л V / 14„cosnx .	.
№ = — + 4 2, (—(~я<х<я).
п = 1
График суммы ряда, состоящий из бесконечного числа примыкающих
одна к другой параболических дуг, изображен на рис. 129.
Полагая в полученном разложении х = я илих = 0, придем к известным
результатам:
, которые, впрочем, и непосредственно вытекают один из другого.
7)	Разложить функции:
(a)	(х) = cos ах по косинусам в [— л, я],
(б)	ft (х) = sin ах по синусам в (— я, я)
(число а здесь предполагается не целым).
15*
452
ГЛ. XIX. РЯДЫ ФУРЬЕ
(690
(а)	Имеем
ТС
1	1 С , sin ат.
~—ап = — \ cos ах dx =--------
2 0 л А	ап
ап = — \ cos ах cos пх dx =
те J
о
тс
1 С ,	,	. , ,	,	2а sin ал ,	_.
= — \ [cos (ап) хcos (а — ri)x]dx = (— l)n—a-----j—— (n > 0) ,
1Z j	Cl --fl 7t
0
так что
оо
n cosax 1 । V / „-flcosnx ,	. 4
2^ = 2~a+l	(-^х^л).
п = 1
(б)	Ответ.
ОО
л Sing£= у „ ПЕШИХ (_те<Х<те).
2 sm ал	’ а2 — п-
Л = 1
Отметим попутно, что при х = 0 из (а) получается:
ОО
1 - 1 । 2 V ад_____________________
sin ал аг. и (ал)2 — (пп)2
п— 1
или, если положить ал = х:
(здесь z — любое число, отличное от кратного л). Мы вновь пришли к раз-
ложению функции . 1 - на простые дроби. Полагая же в (а) х = л, мы мо-
жем восстановить разложение на простые дроби функции ctgz. [Ср. 441, 9).]
Весьма замечательно, что столько важных математических фактов полу-
чается просто как следствие отдельных тригонометрических разложений!
8)	Разложения функций
(а) fi (х) — ch ах по косинусам в [— л, л],
(б) /2 (х) = sh ах по синусам (— л, л)
проще всего получить из разложения в 1) функции f(x) = eax, для которой
они служат четной и нечетной составляющими [689]. Они имеют вид:
ОО
л ch ах 1 . V i	а	,	\
тг-т—=о-+ / (— 1) -г~1—5 cos их (—п^Х^п),
2 sh ап 2а 1	' а2 + и2	'
п = 1
оо
те shax	V / пи-i п	/	х
-к--с-= 7 (—1)	—5-i—gSinnx	(—те<х<те).
2 sh ап	а- 4-
л = 1
690]
§ 2. РАЗЛОЖЕНИЕ ФУНКЦИЙ В РЯД ФУРЬЕ
453
Как следствие отсюда можно получить разложения на простые дроби
функций — и cth z.
Перейдем к примерам разложений функций, заданных в промежутке от 0
до я, по косин у в ам или по синусам [689].
9)	Функцию f(x) = x в промежутке [0, л] разложить по косинусам.
По формулам (19):
1С
1	if. п
T"o=-\xdx=y,
2	С	2 sin пх 1	2 (’	.
ап = — \ х cos пх dx = — х-----------I-------\ sin пх dx =
л	1	л П |0 пл J
___„ cos ПЛ — 1
ГГП
т. е.
4
a2k~ 0, a2k-l— ______________ 1	(£=1>2, 3,
(л>0),
Искомое разложение имеет вид:
л 4 VI cos (2k — 1) х
2"~ V Zi (2k — I)2
ft = 1
(0 •< x •< л).
График суммы ряда представлен на рис. 130 [ср. разложение в 4) той же
функции по синусам и график на рис. 127]. На рис. 131 изображена аппрок-
симирующая кривая:
л 4 /	1	1
У — $5 (х) = у — — (cos х -]- cos Зх -]- -gj cos5х
Комбинируя полученный результат с разложением в 6) функции х2 по
косинусам, легко установить:
ОО
Зх2 — блх 2л2 Vi cos их
12 	— Z л2
л = 1
(0 < х л).
454
ГЛ. XIX. РЯДЫ ФУРЬЕ
(690
Впрочем, так как обе части равенства не меняют своего значения при за-
мене х на 2те— х, то на деле равенство сохраняется и в более широком
промежутке [0, 2те].
Рис. 131.
10)	Функцию f(x) = х2 в промежутке (0, те) разложить по с и н у с а м.
Ответ.
ОО
X2 = 2 ^л sin пх1
где
те А _ 2те	8
—1_ те(2й—I)3’
Предоставляется читателю составить график для суммы ряда и сопоставить
его с графиком на рис. 129.
11)	Разложить функцию f(x) = eax в промежутке от 0 до те (а) в ряд
по косинусам и (б) в ряд по синусам.
Ответ.
(а) еах
'Оо
е«те — 1 2а у, (—1)леа11— 1
яте те	а2 п2
п = 1
cos пх
(О X - ' те),
ОО
(6)^ = 1 2tl-(-l)^-]^sinnx
л = 1
(О < х < те).
12)	Разложить функции
(а)	/, (х) = sin ах по косинусам в [0, те),
(б)	/2 (х) = cos ах по синусам в (0, те).
(а) Решение. Предположим сначала, что а— число не цел ое.
690]
§ 2. разложение функций в РЯД ФУРЬЕ
455
Тогда
1	1 С .	.	1 — cos ак
-х- а0 = — \ sin ах ах =-------------------------
2 те j	те
1С
2 е	.
ап = — \ sin ах cos пх dx = — \ [sin (а -|- л) х 4* sin (а — л) х| dx —
^[l-^-iy.cosaz]^-^
Искомое разложение можно написать в виде:
00
1 — cos ал [, , „ V! cos 2йх ) ,
smax==___|i+2a 2^-^^} +
k = \
со
। q 14-созате V cos (2Хг—1)х
+ те Z —
k = 1
(О si X si л).
Пусть теперь а — целое число. Здесь снова придется различать слу-
чаи, когда а = 2т есть четное число или а = 2т— 1 нечетное число.
При а —2т
л л	8m	1
«о — 0, агк — 0, aik_, —	(2ш)3_(2А_1)2,
так что
cos (2k —I) х *
(2m)s —(2А—I)2
(0 si X si л).
Аналогично при а = 2т—1
ОО
sin<2„- 1)х-1 [1 + 2 (2„-1) 2 (2„
k — 1
(О si х si л).
(б) Указание. Следует различать те же случаи, что и в (а).
13) Доказать, что для х в [0, л]
СО
2cos(2A— 1)х	1	,	_ . . . . _	„ „
’ (2й-1)« = 96 "~ 2х)	+ 2пХ ~ 2х )’
*= 1
Указание. Разлагая в ряд Фурье функцию /(х), приведенную
в правой части, при повторном интегрировании по частям учесть, что
/(0)=/(л) = 0.
* Легко показать, что если в левой части заменить синус его абсолют-
ной величиной, то разложение будет иметь место на всей вещественной оси.
456
ГЛ. XIX. РЯДЫ ФУРЬЕ
|690
14) Рассмотрим теперь примеры разложения функций, интегрируемых
в несобственном смысле. Пусть требуется разложить по косинусам в
промежутке (— л, к) четную функцию
/(х) = 1п 2 cos у.
На концах промежутка функция обращается в оо, но сохраняет (абсолют-
ную) интегрируемость.
По формуле (19):
It
л	"2
1	1 С	х	9 С
а0 = — \ In 2 cos -5- dx = In 2 -|--\ In cos t dt — 0
2	7C J	2	K J
о	0
[cm. 492, Г], а для zz>0
It
„	2 С , о x	.	2 , „ x sin nx I ,
an — — \ In 2 cos -q- cos nx dx — — In 2 cos 7г- • ------------------- 4-
Л J	Z	Л	z n
0	0
dx = (—1)"
л .	X
. „ Sin nx COS Tf
— \-----------£_ dx
Пп У . X
О ЯПу
(замена x на л — х). Для вычисления последнего интеграла представим
подинтегральную функцию в виде суммы:
х . [ , 1 \	. !	1 \
sin их cos у sm (ra-|-yl х smlra —ylx
sin у	2 sin у х	2 sin у х
а каждое из слагаемых, в силу тождества (26) п’680, заменим, соответ-
ственно, суммой:
п	га— 1
у + 2 cos или	COS IX.
i=l	»=1
Окончательно
/_ ПЛ-1
—	(n=i, 2,3,...),
и искомое разложение имеет вид:
ОО
! п х V /	1^-1 COS ПХ	,	.
In2cosy=	(—*<*<*)
л = 1
Можно считать, что это равенство имеет место и при х = ±я, если
в этом случае обеим его частям приписать значение — ос. Если под знаком
1п вместо косинуса написать его абсолютную величину, то равенство будет
справедливо для всех вещественных значений х!
690]
§ 2. РАЗЛОЖЕНИЕ ФУНКЦИЙ В РЯД ФУРЬЕ
457
Заменяя в установленном равенстве х на п — х, придем к другому
интересному разложению:
ОО
1 О . X V COS ПХ	п .
— In 2 sin -£- = У —-—	(0 < х < 2л).
п = 1
Относительно распространения этой формулы можно сделать те же заме-
чания, что и выше.
Приведем в заключение примеры разложения «склеенных» функций, ко-
торые в разных частях промежутка задаются разными аналитическими вы-
ражениями *
15) Пусть
{О, если — п < х < О,
х, если Ой£Хй£л.
Разложить эту функцию в полный ряд Фурье.
Имеем по формулам (1):.
It
1	1 С . л
\ xdx=T,
5
If	.	1 sin пх I11 If. . cos лп — 1
a„ =— \ xcos nxax~— x--------------\ svnnx dx =----5.
nJ	и n |o лп J	n2n ’
t. e.
A	2
*2fe —°,	“ (2/e_I)27:-
Аналогично
__ COSOT	1
n n '	' n '
Разложение будет таково:
,, . л 2	, . sin2x 2	„ , sin3x
f(x) = -.----cosx+smx — —~-----cos 3x4------=----
4 л	2 9л	3
sin 4x	.	,
----4---...	(— л < x < л).
16) Функции
( 1 для 0 x < h,
(a)	AW =
( 0 для h < x л;
(б)	Л(х) = |1-ГЛдля0^^2Л>
(	0 для 2Л < X л
разложить в промежутке от 0 до л по’ к о с и н у с а м.
* Впрочем, здесь Нет ничего принципиально нового по сравнению с уже
изученными примерами: ведь, скажем, сумма ряда в 2) также может рассмат-
риваться, как функция, «склеенная» из ряда линейных функций (ср. рис. 124).
458
ГЛ. XIX. РЯДЫ ФУРЬЕ
[680
л	л
. . 1 If. h	2 С ,	2 sin гай
(а) -а- ай = — \ dx == —, а„ = — \ cos пх dx =-
' ' 2 0 л ) л’	"J	п га
о	о
оо
, . . 2й ( 1 , V sin nh 1 ,n __ __ .
/i(x)=v{t+2тсо8л4
п = 1
, 1
исключая, впрочем, точку х — п, где сумма ряда равна -%.
(б) у а0
4h
2 С* /. х\ ,	2 1 — сов2гай 2 sin2 гай
а„ — — \ 1 — тгг cos пх dx =----------------------=--------jt— ,
п л J \	2й/	л 2га2й л л2й ’
(О '5 х л).
17) Доказать, что
. .	cos5x , cos7x
(a) cos х-----5— + —^------
cosllx ,
П г
К	Л	_ 11
—— при Osgx<^-,
2/3	3
11	и
---— При Х = ~г,
4/3	3
Л и 2и
О при -5"<Х<-^,
о	О
2л
при x = v,
О
2л
при < X л.
о
(б)
sin 5л: . sin Тх
sin х — , 52  + -у-------
sin 11х
Н2 *
И	_	11
--X при Os£Xsi~.
2/3	3
18) Пусть функция /(х) определена равенствами:
/(х) =
Л	11
C0SX для 0^
и
— cos х для < X К.
Разложить ее по косинусам.
690]
§ 2. РАЗЛОЖЕНИЕ ФУНКЦИЙ В РЯД ФУРЬЕ
459
Ответ.	т
I fe=l
19) Доказать, что сумма ряда
СО
(cos х 4- sin х) + V	J -J—i [cos (4А + 1) х — sin (4й -|- 1) х —
fe=0
— cos (4k 4- 3) х — sin (4k 4* 3) x]
равна я sin x для тя < x < тл 4-y, rccosx для тя4-у < x < (иг 4* 1)”
и (— l)my для х = тя или fffl4-yj"
(m = 0,± 1, ±2, ...).
20) Вокруг трех вершин правильного ше-
стиугольника (через одну) радиусами, рав-
ными стороне а шестиугольника; описаны ок-
ружности; из их внешних дуг составляется
трилистник (рис. 132). Написать поляр-
ное уравнение трилистника, если за полюс
принят центр шестиугольника, а полярная	рис 132.
ось проведена через центр одного из кругов.
У к а з а н и в. г =/(6) (—я<8<г.), где четная функция /(0) опре-
деляется равенствами:
/(9) =
2а cos в для
о
Разложить эту функцию по косинусам.
Ответ.
--7^- г = 4- + Г) \ cos 30 — -=Д=- cos 60 4* cos 90 —...
За 2*2-4	5-7	‘8-10
(— я si 0 sg я).
21)	Использовав уже известные разложения, доказать, что
ОО
(а)	х sin х = 1 — у cos х 4- 2	(— ч<х^х);
п—2
00
(б)	xcosx= — уsinx4-2 V (—sinnx (— я<х<я);
п — 2
оо
X 1	ЖЛ (__ iyi
(в)	sin х In 2 cos у = у sin х 4* У _<  sin пх (— ъ < х < я);
л=2
оо
X 1	1	ЖЛ	л
(г)	COSXln2coSy = у — у COSX4- 2, ~	..COS ПА' (— Я < X < я).
л=2
460
ГЛ. XIX. РЯДЫ ФУРЬЕ
[690
22)	Если заданная в промежутке [0, 2л] функция f (х) удовлетворяет
условию
(а) /(2г. — x)—f(x) или (б) /(2л— х)= —/(х),
то в первом случае все &л = 0, а во втором — все а„ = 0.
Доказать это [либо исходя из формул (1), либо опираясь на четность
или нечетность периодически продолженной функции].
Замечание. Теперь ясно, что особенности разложения в промежутке
[0, 2л] функцийЯ 2 и ln2sin-^- [2) и 14)] можно было бы предвидеть, так
как
л — (2л — х)_ л — X
2	—	2~ ’
In 2 sin	2~ = In 2 sin .
23)	Доказать, что если в промежутке [—л, л] функция f(x) удовлетво-
ряет условию
(а) /(х + л) = /(х) или (б) /(х-|-л) = —/(х),
то в первом случае =	— а во втором asm =/>sm = 0.
24)	Ограничиваясь функциями, заданными в промежутке [0, л], доказать,
что условие
(а)	/(л — х)=/(х) влечет равенства eam_i=0 (при разложении поко-
си н у с а м) или Ь2т — 0 (при разложении по синусам);
(б)	/(л — х)=—/(х) влечет равенства а2т = 0 (при разложении по ко-
си ну с а м) или 62т_1 = 0 (при разложении по синусам).
Замечание. На этом основании можно было бы предвидеть особен-
ности разложений по синусам функций ------~ и -j- в 4), функций sin 2тх и
sin (2m—1)х по косинусам в 12), а также разложений в 13), 17) и 18).
25)	Подражая рассуждениям п° 689 установить, что функцию /(х), задан-
[_ Л 1	.
0, *2" I, можно в нем с обычными оговорками разло-
жить по косинусам или по синусам одних лишь четных кратных или одних
нечетных кратных х. Вывести формулы для коэффициентов, приложить
их к примерам.
26)	Пусть задана функция /(х), имеющая период 2л, и ат, Ьт — ее коэф-
фициенты Фурье. Требуется выразить через них коэффициенты Фурье
Ьт «смещенной» функции /(х-|- Л) (Л = const).
Используя замечание в 681 насчет интеграла от периодической функции
имеем:
It	It -|~й
а0 = —\ /(х + Л)сГх = — \ /(x)rfx = a0,
л J	К J
— тс	.	_ _|_Д
тс	« + Л
~ат — — ^ / (х 4- Л) cos mx dx =	/ (х) cos т (х — Л) dx =
— тс	— тс -\-h
тс -I- h	тс-рЛ
If	If
= cos mh— \ / (x) cos mx dx -]- sin rnh— \ /(x)sinmxrfx =
— тс-|-Л	— tc-J-Л
— am cos mh bm sin mh
и, аналогично,
bm = cos mh — am sin mh.
691]
§ 2. РАЗЛОЖЕНИЕ ФУНКЦИЙ В РЯД ФУРЬЕ
461
691. Разложение In Г (х). В качестве более сложного примера мы устано-
вим, следуя Куммеру (Е. Е. Kummer), разложение в ряд Фурье функ-
ции In Г (х) в промежутке (0, 1].
Пользуясь сделанными в п° 688 замечаниями о разложении функции в
промежутке (О, 2Z] (в нашем случае 21 = 1), ищем разложение в виде:
ОО
In Г (х) = -^ 4- 2 (ап cos 2ллх + bn sin 2ллх),
л=1
причем коэффициенты его могут быть установлены по формулам, аналогичным
формулам (17*) п° 688:
г	1
ап = 2 j In Г (х) cos 2ллх dx,	bn = 2 In Г (х) sin 2ллх dx.
(n = 0, 1, 2, . ..)	(Л=1, 2, . . .)
Впрочем, как мы покажем, коэффициенты ап можно определить почти
без вычислений. В самом деле, логарифмируя известное соотношение [531,5°]
мы найдем
1пГ(х)4-1пГ(1 —х) = 1п 2л—ln2sin?tx.
Ряд Фурье функции In Г(1 —х) получается из ряда Фурье функции
1пГ(х) заменой х на 1—х, так что члены с косинусами сохранятся, а члены
с синусами изменят знаки. Складывая, получим
ОО
а04- 2 2алсо8 2ллх.
я=1
С другой стороны, легко написать ряд Фурье для функции, стоящей в пра-
вой части равенства, если использовать известное разложение функции
X
— In 2 sin -g- [690, 14)], но заменив лишь х на 2лх:
ОО
In 2тс —]—	— cos 2ллх.
п= I
Таким образом, получаем сразу
уа0 = 1п/2л, ап = ~	(л=1, 2,...).
Гораздо большего труда потребует вычисление коэффициентов Ьп. Мы
будем исходить из формулы для In Г (х) [540]
ОО
которую подстановкой е z = t преобразуем к виду:
о
462
ГЛ. XIX. РЯДЫ ФУРЬЕ
[691
Подставляя это выражение в формулу для Ьп и переставляя интегрирования
по х и по t, получим:
1 1
р dt f Г1 /х-i	л
b„ = 2 \ ,—- \ —=----— — х 4- 1 sin 2ллх dx.
' In t 1 —t 1
о о
Для обоснования нашего права переставлять интегрирования заметим
следующее. Выражение
[1 — tx~l , , 1 sin 2ллх
теряет непрерывность как функция двух переменных лишь при /=0* Но
интеграл от этого выражения по переменной t сходится равномерно
относительно х в [0, 1], ибо (при 0<т< 1)
sin
1—t	(1
2илх I „
।	-1 dt <
In t I
1	1 I sin 2плх I „	1	1	„
1 --T I In Z I X	1 -T I in z I
По известной теореме [521] перестановка допустима.
Продолжаем вычисление. Имеем:
1	1
\ sin 2ллх dx = 0, х sin 2пт.х dx = — Ч— ,
J	J	2лл	’
о	о
1 1
tx~l sin 2ллх dx = у- ех 1п * sin 2ллх dx =
о
_ 1п /  sin 2илх— 2л к cos 2ллх	1п , | *=1 _ (1—t) 2лл
t [In2/ 4" 4л2к2]	j х=0	t [in2/4* 4л2 л21 ‘
Отсюда
2лл
/ [In2/ 4- 4nV]
1 1 dt
2лл J In t ’
Полагая здесь / = e~2ra,t“, окончательно приведем выражение для Ьп к виду;
В частности,
откуда
nbn — bt = — (tr2"" — е~зп*“) — = — In п
те J	и 11
* Легко проверить, что при t = 1 непрерывность фактически не нарушается.
692]
§ 3. ДОПОЛНЕНИЯ
463
(интеграл Фруллани, 495). Таким образом, определение всех коэффициен-
тов приводится к определению первого из них.
Вспомним интегральное выражение эйлеровой постоянной [535|:
Но первый интеграл вычисляется непосредственно, он равен 6; второй же
равен — In 2л (снова — интеграл Фруллани). Окончательно получаем:
ТС
bi=— (С 4-In 2л),
ТС
откуда затем
5„ = ^-(С + 1п2пл).
Итак, искомое разложение имеет вид:
ОО
In Г (х) = In /2л + cos	(С + 1п 2лл) sin 2тглх
п=1
(0<х<1).
§ 3. Дополнения
692. Ряды с убывающими коэффициентами. До сих пор мы
исходили из наперед заданной функции и разлагали ее в ряд Фурье,
пользуясь установленными для этого достаточными условиями. В не-
многих простых случаях удается, наоборот, по заданному тригономет-
рическому ряду установить, что он сходится к некоторой абсо-
лютно интегрируемой функции и является ее рядом Фурье. Мы из-
ложим относящиеся сюда исследования Юнга [W. Н. Young].
Речь будет идти о рядах вида:
оо	оо
(С)	+ 2 У, COS чх, (S) 2 У,sin w>
V=1	V = 1
причем мы раз навсегда предположим, что коэффициенты у, поло-
жительны и стремятся к нулю, монотонно убывая. Как мы
знаем [см. конец п° 430], в любом замкнутом промежутке, не содер-
жащем точек 2Ая(А = 0, ±1, ...), оба ряда сходятся равномер-
но. Обозначим сумму ряда (С) через f(x), а сумму ряда (S) через
g(x); обе функции имеют период 2тс и непрерывны повсюду, исклю-
чая точек вида 2kit. В этих исключительных точках ряд (С) может
464
ГЛ. XIX. РЯДЫ ФУРЬЕ
[692
и расходиться* *. Так как функция f четна, a g нечетна, то доста-
точно ограничиться промежутком [0, и].
1°. Если функция f (или g) абсолютно интегрируема, то
ряд (С) [или (S)] представляет собой ее ряд Фурье**.
(а) Умножив разложение функции g на sinтх (т = 1, 2, 3, ...):
ОО
g(x) sin тх — У, q., sin vx • sin тх,
V = 1
мы получим равномерно сходящийся в промежутке [0, л] ряд.
Действительно, так как
п
2 sin vxsin тх
i=i
то
I sin тх I	тх
J— = т~,
. X	X
sin-x-	—
2	л
и сюда приложим признак Дирихле [429]. |^Мы использовали здесь
элементарные неравенства
|sinz|«s;z (z^O), sinz^>-|-2'> (o<z<y).j
В таком случае ряд можно почленно проинтегрировать от 0 до it,
и мы получим:
2 ё
qm = — \ g(x) sin тх dx.
а
(б) Переходя к функции /, умножим ее разложение на 1 — cos тх:
f (х) (1 — cos тх) —
СО
= y q0 (1 — cos тх) -ф- Ччcos (1 — cos тх).
V=1
СО
* Если ряд У сходится, то оба ряда (С) и (S) сходятся равномерно
1
к непрерывным функциям, для которых и служат рядами Фурье [678]. Все
дальнейшее представляет интерес лишь в случае, если упомянутый ряд рас-
ходится.
** Эта теорема есть частный случай одной общей и очень трудно дока-
зываемой теоремы [см. 750, 751]; мы предпочли для рядов рассматриваемого
простого типа здесь же исчерпать этот вопрос.
692]	§ з. дополнения	465'
Этот ряд также будет по признаку Дирихле равномерно сходя-
щимся в промежутке [0, и]. Чтобы убедиться в этом, достаточно
заметить, что
«	sinfn + lp
4+ У COS	(1)
v = 1	2 sin х
и потому
п
1	ч I V	/1	х _ I—cos тх _
у (I — cos тх) -j- 2, cos — cos тх} '-----------х~"
v=I	sift ~2~
Tmsxs I 9	1	23
—к----= -г т*кх -г пгт?.
2х 4	4
и
^Использовано неравенство: 1—cos z <4 &. j
Интегрируя почленно от 0 до it, находим:
It	It
2 С	2 С
Чй — Чт = — \ f(x)dx—— \ f(x) cos mxdx.
(m = l, 2, 3, . ..)
Перейдем здесь к пределу при т —. оо. При этом по предполо-
жению qm —-0, а также стремится к нулю и последний интеграл —
по основной лемме п° 682. Таким образом, получаем сначала
It
4’0=-|’ f(x)dx,
а затем и вообще
Я
2 Р
qm = — \ f (х) cos тх dx,
чем и завершается доказательство.
2°. Если ряд
ОО
= Q	(2)
V=1
сходится, то оба ряда (С) и (S) определяют абсолютно инте-
грируемые функции {и, следовательно, являются их рядами
Фу р ь е).
466
ГЛ. XIX. РЯДЫ ФУРЬЕ
(692
Так как рассуждения для обоих рядов однотипны, то мы огра-
ничимся случаем ряда (С). Полагая
Qn — у 4“ 4“ • • • 4“ Чп>
будем иметь последовательно:
ОО	ОО	п
2Qn 1	। V 1 v
n(n-H) — 2 ft “г ^л(л-Н) Z
/1=1	/1=1	v=l
оо оо	оо
=yft4- 2 ft 2 Tpr'+i) =Tft4" 2 ^r=lft4-Q; <3)
v — 1 n=v	y = l
мы переставили здесь два суммирования [393] и использовали оче-
видные равенства:
ОО	оо
У—т—г-гг = 1 и вообще У	\	.
Li п (л +1)	Li	п (п 4-1)
Л=1	л=»
Пусть теперь
ТС _	_ к
п + 1	п
Для этих значений х представим f(x) в виде:
(п	\ оо
у7о 4- 2 ft Cos + 2 ft cos w
V = 1	/	V = n +1
Первая сумма оценивается по абсолютной величине числом Qn. Для
оценки второй применим к выражению
v=n-|-nt
У у, cos чх
4-1
лемму Абеля [383]. Так как
то
ч=п-\-т
У </„ cos NX ^-^-<^qn+l<~qn<i(n+l)qn.
»=«+!	sinyx
§ 3. ДОПОЛНЕНИЯ
467
Та же оценка в пределе сохраняется и для всей второй суммы, так
что окончательно
!/(•*) I 'S Qn+ («-}- 1)?я
В таком случае [см. (3) и (2)]
It
«	оо га
5 \f(x)\dx = У \f(x)\dx^
О	п=\ it
га 4-1
оо
2м»”+1)	(-§-*>+2Q) >
га=1
так что функция f(х) действительно абсолютно интегрируема.
Остается применить 1°.
Как мы увидим ниже [732J, сходимость ряда (2) является одно-
временно и необходимой для того, чтобы ряд (S) был рядом
Фурье, так что в отношении ряда (S) полученный результат даль-
нейшему улучшению не подлежит. Иначе обстоит дело с рядом (С):
здесь упомянутое условие отнюдь не необходимо. Мы приведем для
этого случая еще и другое достаточное условие, которое не покры-
вается прежним.
3°. Если и разности &q,i = q,l— yv+1 монотонно убывают с
возрастанием v, то функция f(x) неотрицательна и интегри-
руема [а ряд (С) является ее рядом Фу р ь е].
Подвергнем частичную сумму
п
Сл(х) = у?»+	cos (х>°)
V = I
преобразованию Абеля [383]. Учитывая (1), найдем:
Г л-1
С„(х) =---Ц—J У Д^. sin	+
2sinyX[ "о	'
+ Чп‘sin (л + у) х ••
Полученную сумму мы снова подвергнем преобразованию Абеля.
Если для краткости положить Д<7„ — Дд\,+1 = и учесть, что
т
2sin (ч+у) х~
»=о
1 — cos(m-f- 1) х
о 	।
2 sin у х
468
ГЛ. XIX. РЯДЫ ФУРЬЕ
[692
то Сп (х) приведется к виду:
Сл(х)
п — 2
= —Ц  У ДЧ -(1 — COS У + 1х) 4-
4 sin2	х м=q
+ Д7л л •
1 — cos пх
4 sin2 у к
sin ( п 4-	' х
\	2 1
о •	1
2 sin х
~УЯп •
Так как последние два члена стремятся к нулю при п->-\-<х>,
то, переходя к пределу, получим для f (х) разложение по неот-
рицательным и непрерывным функциям:
ОО
/(x)=2A^-1~C0S(l + 1)*
„ =0	4 sin2 Y х
(коэффициенты неотрицательны по предположению). Отсюда
ясно, что и функция f(x) неотрицательна.
Для доказательства интегрируемости этой функции восполь-
зуемся следствием из п° 518 и замечанием к нему, перефразиро-
ванным для рядов. Можно написать:
/(х) dx= У &q4 l-cosfr-H)* dx>
1=Q й 4 sin2 у x
если только сходится этот ряд.
Так как
cos Хх
то непосредственно получаем:
С 1-^.4-..1)х^=к0 + 1)
О*5	4 sin2 у х
[ср. 309, 5) (б)], так что
л	оо
и(х)йх = у20 + !)дЧ-
о'	»=о
Остается лишь убедиться в сходимости ряда справа.
Мы видели в 375, 3), что если ряд
СО
2 а,	(4)
v=0
693]
§ 3. ДОПОЛНЕНИЯ
469
с монотонно убывающими положительными членами сходитс’я, то
необходимо выполняется условие
va, -> 0.
Отсюда следует, далее, что ряд
ОО	оо
У, (V +1) (а, — а,+1) = 2 (V + 1) Да,
4=0	4=0
сходится и имеет ту же сумму, что и ряд (4); это видно из тож-
дества
У, (v + 1) («4 — а,+1) = у «4 — пап.
v =0	у =0
Если теперь взять а, = Д^„ то оказывается, что
ОО	оо
У (*+1)АЧ= s Д?4^^о,
ч=0	у = 0
и окончательно
о
Теорема доказана.
Например, условию этой теоремы удовлетворяет ряд
со
2 cos ПХ.
In л ’
л = 2
этот пример поучителен в том отношении, что теорема 2° к нему
не применима, так как ряд
ОО
У —Ь-
n In л
л = 2
расходится [367, 69)].
Замечание. Если в рядах (С) и (S) заменить переменную х
на х -(- it, то получатся ряды с знакопеременными коэффициентами,
убывающими по абсолютной величине. Для таких рядов доказанные
теоремы также сохраняют силу.
693. Суммирование тригонометрических рядов с помощью
аналитических функций комплексной переменной. В ряде случаев,
исследуя коэффициенты рядов вида (С) или (S), можно установить,
что эти ряды сходятся (исключая, быть может, отдельные точки)
и являются рядами Фурье для своих сумм (см., например, преды-
дущий п°), но во всех этих случаях естественно возникает вопрос,
470
ГЛ. XIX. РЯДЫ ФУРЬЕ
[693
как найти суммы этих рядов или — точнее — как выразить их в ко-
нечном виде через элементарные функции, если они, вообще, в таком
виде выражаются. Еще Эйлер (а также Лагранж) с успехом
применял для суммирования тригонометрических рядов в конечном
виде аналитические функции комплексной переменной. Идея метода
Эйлера состоит в следующем.
Допустим, что при некотором наборе коэффициентов {q4} ряды
(С) и (S) сходятся к функциям f(x) и g(x) повсюду в промежутке
[О, 2тг], исключая разве лишь отдельные точки. Рассмотрим теперь
степенной ряд с теми же коэффициентами, расположенный по степеням
комплексной переменной z:
СО
(5)
V = 1
На окружности единичного круга | z | = 1, т. е. при z = eix, этот
ряд по предположению сходится, исключая отдельные точки:
СО	00
2’9’о + у ^е',‘* = у?’о+ У ^(cos vx-j-Zsinvx) =
V = 1	V=1
=/(*) +^(*).	(6)
В таком случае, по известному свойству степенных рядов ряд (5)
заведомо сходится при | z |	1, т. е. внутри единичного круга,
определяя там некоторую функцию <р (г) комплексной переменной.
Используя известные нам [см. § 5 главы XII] разложения элемен-
тарных функций комплексной переменной, часто удается свести к ним
и функцию <p(z). Тогда для z — rexi (г 1) имеем:
ОО
и по теореме Абеля [456], лишь только ряд (6) сходится, его сумма
получается как предел
f (*) + lg (*) = Пт <р (reix).	(7)
Г-+ 1
Обычно этот предел равен попросту ср (eix), что и позволяет вычис-
лить в конечном виде функции f(x) и g(x).
Пусть, например, предложены ряды
оо	оо
VI cos мх VI sin мх
м	м ’
V = 1
Доказанные в предыдущем п° утверждения приводят к заключению,
что оба эти ряда сходятся (первый — исключая точки 0 и 2тс) и слу-
€93]
§ 3. ДОПОЛНЕНИЯ
471
жат рядами Фурье для определяемых ими функций f(x) и g(x).
Но что это за функции? Для ответа на этот вопрос составим ряд
По сходству с логарифмическим рядом [458] легко устанавливается
его сумма:
<?(*) = — 1п(1 — г) = 1п -~z (И<1),
следовательно,
/(*)+	=	2к).
Теперь легкое вычисление дает:
1_____ 1	__• I . sin х ________
1—eix (1—cosx) — isinx 2'	2(1—cosx)
так что модуль этого выражения есть-----, а аргумент
2sinT
Поэтому
1 I	t . X । • X
In = —ln 2 sin т +1 "T~
и, таким образом, окончательно
f(x) = — ln2siny, g(x) = ^—~~ (0<^х<^2тс).
Результаты эти нам знакомы [690, 14) и 2)] и даже были однажды
получены с помощью «комплексных» соображений [461, 6) (б)]; но
в первом случае мы исходили из функций f и g, а во втором — из
аналитической функции <р. Здесь же впервые нам отправной
точкой послужили сами ряды. Дальнейшие примеры подоб-
ного рода читатель найдет в следующем п°.
Подчеркнем еще раз, что нужно наперед быть уверенным в схо-
ди м о с т и рядов (С) и (S), чтобы иметь право определить их суммы
с помощью предельного равенства (7). Одно существование предела
в правой части этого равенства еще не позволяет сделать заключе-
нйе о сходимости упомянутых рядов. Чтобы показать это на при-
мере, рассмотрим ряды
оо	оо
2 c°svx и 2sinvx>
. V— 1	»—1
472
ГЛ. XIX. РЯДЫ ФУРЬЕ
|694
заведомо расходящиеся для 0х2тс. Между тем, если со-
ставить соответствующий им ряд
то при стремлении точки z — ге1Х вдоль по радиусу единичного круга
к точке е1Х на окружности, его сумма будет иметь вполне определен-
ный предел
1	1 ___. sin х
1 — etx~~2~l 2(1—cos х)
(0<x<2it).
Если сходимость рядов (С) и (S) наперед не установлена, то
равенство (7) можно рассматривать только как наведение: получив
с его помощью функции fug, следует затем вычислить их коэф-
фициенты Фурье и лишь в случае совпадения с коэффициентами
данных рядов прибегнуть к известным признакам сходимости рядов
Фурье.
694. Примеры. Во всех задачах сходимость предложенных рядов
предоставляется установить читателю.
I) Просуммировать ряды:
, . , , cos х , cos 2х ,	, cos пх ,
(а) 1Н- — + —+... + г—+„,
sin х , sin 2х .	, sin пх ,
(б)_г + __
Решение. Здесь *
со
<р(г)=1+ 2 ?Г = ег-
V=1
так что
<Р (е,х) == ecos Л'+'sinх_ ecosx jcos (sjn i sin (sin
Отсюда
(a) f (x) = ecos x cos (sin x), g (x) = ecos x sin (sin x).
2) Просуммировать ряды
. . cos x cos 3x , cos 5x .. sin x sin 3x . sin 5x
(а) -у,	—ду	I j, •••. б) -у,	gj | gj
...	cos 2x , cos 4x	, . sin 2x	sin 4x , sin 6x
(B) 1----2!~+~4!------(Г) “2!------------4Г + ~бГ
У Казани e. Функция <p (z) равна
Slnz = 7j—-31 +	•••
в случаях (а), (б); она равна
* Мы сохраняем обозначения предыдущего п°.
694]
§ 3. ДОПОЛНЕНИЯ
473
в случаях (в), (г). Использовать разложения синуса и косинуса от комплекс-
ного аргумента на вещественную и мнимую части [359]:
sin (а -|- ₽z) = sin а ch р -|-<’cos а sh Р>
COS (а 4* р() = COS а ch Р — i sin a sh p.
Ответ.
(a) sin (cos x) ch (sin x), (6) cos (cos x) sh (sin x);
(в) cos (cos x) ch (sin x), (r) sin (cos x) sh<(sin x).
3) Просуммировать ряды:
CO	' co
w i+2	<«> 2 <-1)M diTr
n = 1	n—1
co	co
<> 2<-1>'sS+ <r> 2
n = 2	ra=2
(д) У (—l^^-j-cosnx, (e) У (—l^^-j-sinnx;
n=2	/1 = 2
co
<«> 2 <-)'' <n+0?» + 2>.
n=0
co
W 2	(»+?)“+2) -
n— 1
(а), (б). Решение. Соответствующий этим случаям ряд
z z$ zs
? (г) = 1 + 172 — 2^3	3^4 ~ ‘
непосредственно не дает известной нам элементарной функции, но если,
использовав очевидное равенство
11 1 •
п (tl 4- 1) п п 4~ 1 ’
преобразовать его следующим образом:
( z% z^	\	( z z% z^	)
1+ {г-т + т~- } + {^¥ + ‘з -T+ •" J ’
то, вспоминая логарифмический ряд [459], легко уже найдем, что
<Р (2)= 1 +1П(1 +г) + у[1п (14-г)-г] = {1+^ In (1 +2).
Подставим теперь сюда z — eix = cos х 4- i sin x. Имеем:
1 4- 2 = (1 4- cos x) 4- i sin x — 2 cos fcos 4- i sin ,
474
ГЛ. XIX. РЯДЫ ФУРБЕ
[694
так что (для 0 < х < тс) модуль этого выражения есть 2cosy, а аргумент
In (1 4-г) = In 2 cos у 4- «у.
Окончательно,
ср («'*) = [(1 4* cos х) — i sin х] • |jn2cosy 4* i у].
Отсюда для — л < х < л
X 1
f(x) — (1 4- cos х) In 2 cos у 4~у x s’n x>
1	X
g (x) = у x (1 4- cos x) — sin x In 2 cos у.
(в) — (з). Указание. Во всех случаях, используя соответственно ра-
венства
1	! / 1	1 \ п 1 / 1	. I \
га2—1	2 \ л — 1 га + 1 ] ’ га2 — 1	2 \ га — 1 + л 4-1 / ’
1 _ । 1
(л41)(л42)-л+1 л + 2’
свести дело к логарифмическому ряду.
X X
Ответ, (ж) (cos х 4* cos 2х) In 2 cos у у (sin х + sin 2х) — cos х,
X X
(з) (sin х 4" sin 2Л‘) in 2 cos — у (cos х 4* cos 2х) — sin х.
[По поводу (в) — (е) ср. 690, 21).]
4) Просуммировать ряд:
СО
2
cos (2л — 1) х
п
Указание. <р (г) = у In (1-]-г2).
Ответ. Ограничиваясь промежутком 0<х<ж, имеем
cos х In 2 cos х 4- х sin x
/(*) =
для 0sgx<y,
It
cos x In 2 | cos x | 4- (x —") sin x для у < x тс.
5) Просуммировать ряды:
. , cos 2x , cos 3x , cos 4x ,
(a) -пт+~27Г+“зТТ +-’
/хч cos2x , cos3x , cos4x ,
W 1 .2-3 + 2-3-4 + 3-4-5 +'"
694}
§ 3. ДОПОЛНЕНИЯ
475
У Казани е. Используя разложения
1 1
(п— 1)п И (я—l)n(n-f-l)
«на простые дроби», свести дело к In-,-.
Ответ, (а) (1 — cos х) In 2 sin	Х sin х + cos х,
х 3	1
(б)	(1 — cos х) In 2 sin -у + -j- cos х—
в обоих случаях для 0 < х с 2те.
6) Просуммировать ряды:
СО	со
2 (_1Г. y»gSi'>--. («> 2	,l"£'z,')x.
Л=1	л=1
<-> 2 тай?-
п—\
(а), (б). Решение. Составив ряд
со
2 (-D"-1
22Л-1
2я^П>
узнаем в нем разложение арктангенса:
t 1 , 1 + zi
arctg z == ^- In -г—!—г,
6	27	1—zt’
которое имеет место для | z |	1, исключая z = ±i [459].
Положим здесь z = eix, ограничиваясь промежутком Osgxsg®, но исклю-
чая х = -^-. Имеем:
1 -J- zi . cos х   /те	х \
1 — zi	* 1 -]- sin х	1	\4	2 / ’
I . Ix \ I	, те
так что модуль этого выражения есть tg I-g-l1, а аргумент равен
или —в зависимости от того, будет лих<у или х>-”-. Следова-
тельно,
arctgz = ±A + /.|in|tg^ + ^|.
Итак,
те „	те
-j- ДЛЯ 0 < X < у,
/(*) =
ТС тс
___ для ~2~ х Тсу
476
ГЛ. XIX. РЯДЫ ФУРЬЕ
[694
и для тех же значений х
, ,	1 , I . 7 те , X \ I 1 , . . ! те . х\
g(x) = yln|tg	|= — lntg2 (т + т).
(в) Указание. Сочетая только что полученный результат с резуль-
татом упражнения 4), найдем:
-г---i- (cos х In 2 cos x x sin x) для 0 x <Z -5-,
/W =	n	j
----,	-9-	(cos x In 2	I cos x I	(x — те) sin x)	для	-у < x < n
'	4-Z	Z
7)	Просуммировать ряды:
, .	, 1 cos Зх . 1  3 cos 5x , 1 • 3 • 5 cos lx ,
(a)	cosx + y-_+—+...;
, 1 sin 3x , 1  3 sin 5x ,
(6)	slnx + ___ + ___ + ...:
. . cos x 1 cos Зх 1 • 3 cos 5x 1 • 3 • 5 cos 7x ,
W 1.2 + 2” 3-4 ‘M 5-6 '2-4-6 7-8 +”’’
, . sin x , 1 sin 3x , 1 • 3 sin 5x ,
Г) + У 3-4 '2^4 5-6 +’"
Решение. Для случаев (а) и (б):
, . V (2n —3)!! z2'1-*
?(Z) = 2 (2n —2)!! 2^1 = аГСЯП Z
n = 1
[459]. Далее, для О^х^те:
arcsin eix = arcsin cos x-/ in ( jy [	sjn x _j_ sjn x).
У 1 + sin x
Это легко проверить, установив, что синус выражения справа действи-
тельно равен е‘х. Впрочем, нетрудно и вывести это выражение, найдя
и, v из уравнений
sin и ch v — cos х, cos и sh v = sin x.
Итак,
.. ,	. cosx
f(x) = arcsin	—,
V 1 + sin x	(0 ==r x sg те).
g (x) = In (J/' 1 sin x У'sin x)
Для случаев (в) и (г) получается ряд:
z , 1 z3 , 1 • 3 z5 , 1 • 3 • 5 z7 ,
1-2+ 2 3-4 + 2-45-6 + 2-4-67-8 +-----
_	, 1 z3 , 1 -3z5 , 1 - 3-5 z> ,
1'2 3'2-45 '2-4-67
— arcsin z + у (/1 — 2a — 1)
695]	§ з. дополнения	477
[460]. Отсюда для 0 sj х sS те
/(х) = a resin—— cos х-у' 2sin х cos + -7-^ — cos х,
у 1 -|- sin х	' 2	4 /
g (х) = In (у^ 1 4-sin х jAsin х) — 2 sinx sin	-f- sin х-
695. Комплексная форма рядов Фурье. Рассмотрим снова про-
извольную функцию f(x) с периодом 2 те, абсолютно интегрируемую
в любом конечном промежутке, и связанный с нею ряд Фурье:
СО
fix)+ ^ат cos /их + sin тх.	(8)
т — 1
Его коэффициенты определяются формулами
те	те
ат = -L / (и) cos mu du, bm = ±-^f (и) sin mu du. (9)
—те	— те
(т = 0, 1, 2,. . ,)	(т=1, 2,.. .)
Если заменить теперь cos/их и sinтх их выражениями через
показательную функцию от чисто мнимого аргумента [457]:
cos/их=-g- (emxi	е~тХ1),
sin тх = (emxl — e~mxi) = у (e~mxi — emxi),
то получится ряд
со
т = \
Его короче можно записать так:
+ со
7(x)~ S ckekxi,	(10)
k =— co
полагая
Со == ~2 ai’ ст == ~2~(.ат	с-т == "2*	4“	00
(ni=l, 2, 3, ...)
так ЧТО *
с-т==^т-	(12)
Это и есть комплексная форма ряда Фурье функции f(x).
* Напомним, что если г есть комплексное число, символ z означает
сопряженное с ним число.
478
ГЛ. XIX. РЯДЫ ФУРЬЕ
1695
Если г соблюдены достаточные условия сходимости ряда (8) к
функции f(x\ то к той же сумме сходится и ряд (10), если только
(как явствует из самого способа его получения) процесс суммирова-
ния его понимать как разыскание предела при п —► -|- со симметрично
составленной суммы
п
S c^mxi-
т ——п
Впрочем, если сходятся порознь ряды
СО	со
2 cmemxi и
т=0	т — 1
то упомянутый предел получается путем сложения их сумм.
Коэффициенты ст разложения (10), определяемые формулами (11),
если учесть формулы Эйлера — Фурье (9), могут быть записаны
единообразно:
п
f (и) e~nai du.	(13)
— тс
(л = 0, ±1, ±2, . ..)
Эти коэффициенты могли бы быть получены и непосредственно, по-
добно коэффициентам ат и Ьт [678], если, допустив, что функция f (х)
разлагается в ряд (10) (так что вместо ~ можно поставить = ), умно-
жить обе части равенства на e~nxi и проинтегрировать от — тс до тс,
причем справа выполнить интегрирование почленно.
Если имеем комплексную функцию
/(x)=/!(x)4-Z/2(x),
где /1,	— вещественные функции рассмотренного типа, то естест-
венно рядом Фурье функции f назвать формальную сумму рядов
Фурье функций fi и /а, из которых второй предварительно по-
членно умножен на I. В комплексной форме ряд Фурье функции f
имеет вид (10), где коэффициенты сп, как и только что, выражаются
формулами (13). [Но в общем случае, конечно, нельзя утверждать
сопряженности коэффициентов ст и с_т.]
Иногда разложение функции в ряд Фурье естественно и непосредст-
венно получается именно в комплексной форме. В качестве примера вспомним
производящую функцию для функций Бесселя и ее разложение [395, 14)]:
е	— 2j JnWzn.
/1=ж—-СО
695j	§ 3. ДОПОЛНЕНИЯ	479
Нетрудно видеть, что это разложение имеет место для всех комплексных
значений а, отличных от нуля. Положив здесь z = eix, найдем:
 • +“
e««sin^= 2 Jn(a)enxi\	(14)
л = —оо
комплексная функция
ea£sino; _ sjR cos х) _]_ / sjn sjn х)	(15)
оказалась разложенной в ряд типа (10), который сходится равномерно
относительно х * (по свойству степенных рядов) и потому заведомо будет ее
рядом Фурье.
Вспомнив, что
/-m(a) = (-l)mJm(a)
[395, 14)], перепишем полученное разложение в виде:
СО
/»(«)+ S +
т—1
= Л (а) + 2 У л* (°) cos + 2i X (a) sin (2k — 1) x. (16)
*=1	ft=i
Если приравнять отдельно вещественные и мнимые части выражений (15) и (16).
то придем к интересным разложениям:
ОО
cos (a sin х) = Jo (а) 4- 2 У] Jlk (a) cos 2kx,
fe"=i
СО
sin (о sin х) = 2 2 Л/г-i (°) sin (2й—1)х.
fe=l
Отсюда, заменяя х на х-|--^-, можно вывести и другие два разложения:
ОО
cos (a cos х) == J„ (а) + 2	(— 1)* J2*(a)cos2fex,
* = !
ОО
sin (a cos х) = 2 У] (— l)fe-1 (a) cos (2k — 1) х.
k=i
* Мы имеем в виду ряды
порознь.
480
ГЛ. XIX. РЯДЫ ФУРЬВ
J696
Наконец, если применить к вычислению коэффициентов разложения (14)
формулы (13), то получим известные интегральные выражения для бесселевых
функций:
J„(e) = 6J-C e(asinx—пх}1дх __ J_ fcos(esjnx—nx)dx,
»)	TC J	*
— тс	0
которые нам не раз встречались.
696- Сопряженный ряд. Тригонометрический ряд
оо
у+2 ат cos тх -|- bm sin тх	(17)
т~ 1
с произвольными вещественными коэффициентами можно формаль-
но* рассматривать, как вещественную часть степенного ряда
СО
(ат~ЬтГ)2т,	(18)
т — 1
расположенного по степеням комплексной переменной z, при z = ext.
Действительно, тогда
2'm — emxi = cos тх —j— Z sin mx
и
(am — bml) zm — (am cos mx -|- bm sin mx)
4~ i (— bm cos mx am sin mx).
Мнимая же часть формально представляется рядом
СО
( — bm cos тх + ат sin тх).	(19)
m = I
Ряд (19) называется сопряженным с рядом (17).
Особый интерес представляет ряд, сопряженный с рядом Фурье
некоторой (имеющей период 2ir и абсолютно интегрируемой) функ-
ции f(x). В частности, можно параллельно с вопросом о сходимости
самого ряда Фурье (17) поставить и вопрос о сходимости сопря-
женного с ним ряда. Впрочем, в последнем случае дополнительной
трудностью служит то обстоятельство, что наперед неясно, какой
суммы естественно ждать от сопряженного ряда.
Начнем, как и в п° 691, с составления удобного выражения для
частичной суммы s„(x0) ряда (19) при х = х0. Подставляя вместо
* Формально — потому, что мы ничего не знаем о сходимости
написанных рядов.
6961
$ 3. ДОПОЛНЕНИЯ
481
коэффициентов а0, at, Ьь ат, Ьт, ... их интегральные выражения
[см. (9)], найдем последовательно:
п к
s п (х0) =2 у f(ti) [ — sin mu cos mxa -|-cos mu sin mx0] du —
m = l —n
те	n
= — у /(«)2 S*nz?/(H — xa)du.
— it	m = l
Если сумму под знаком интеграла преобразовать по формуле
"	cosyf — cos (« + 4-^ t
У sinz»/=--------------j----;,
2 sin ±1
то выражение для s„(x0) примет вид
. * cosl- (и — x0) — cos (n +4-') (u — x0)
sn (xa)= — \ f (u)----------------j-----------------d"-
-«	siny(u — x0)
Этот интеграл является аналогом интеграла Дирихле. .
Переходя к промежутку [х0 — тс, х04-тс] и воспользовавшись под-
становкой и — x0 = t, как и в п° 681, получим
. £	cos-^-Z— cos (п + t
sn (х0) = _ 2. V /(Хо 4-1) —Л-----3-----£L_ dt =
-«	sin у t
. Ji cos — cos (я + 4-V
= - i V W---------------1----1— dt’ (2°)
»	sinyf
где для краткости положено
ф(0=/(хв + 0— f(xa-t).	(21)
Если предположить сходимость интеграла
5’o=-i^JTL^	<22>
хотя бы и не абсолютную, то можно написать:
1 р	c°s(n4-4-V
8а (Хо) - So = у \ ф (0 —dt
S 2sin-l-T
и пытаться установить стремление к нулю последнего интеграла при
л — -[-оо: тогда So и окажется суммой ряда (19). Ограничимся
16 Г. М. Фихтенгольц, т. III
482
ГЛ. XIX. РЯДЫ ФУРЬЕ
|696
указанием достаточного условия для этого, построенного по типу приз-
нака Дини [684]:
Сопряженный ряд для ряда Фурье функции J(х) в точке
хй сходится к сумме S$, если интеграл
л
JbKOl,#	(Л>0)
существует.
Ввиду того что	j
НО	Т*
2 tg у f	tg -у t
из сделанного предположения прежде всего вытекает даже абсолют-
ная сходимость интеграла (22). Аналогично устанавливается абсолют-
ная сходимость интеграла
С 2 sin у t
а отсюда по основной лемме п° 682 следует, что sn (х0) — So —• О,
что и требовалось доказать.
Очевидно,	достаточно	сделать	предположение	о	существовании
порознь интегралов
л	,	л
С |/(х0+<)-/(х0)| dt	и	j	|/(хо-О-/(хо)|	dt
О	о
или более частное предположение о выполнении условия Липшица:
|/(xo±O-/(Xo)|^Cfa	(0<а<1).
Отметим, что все эти условия предполагают непрерывность
функции f (х) в точке х0 или, по крайней мере, совпадение пределов
/(х0 ± 0). Впрочем, можно и в общем случае доказать, что при наличии
скачка функции f (х) в рассматриваемой точке х0, т. е. при условии
/(Хо + О)-/(хо-О)^О,
сопряженный ряд (19) в этой точке заведомо расходится*, так что
предположение о непрерывности функции f(x) в точке х0 оказы-
вается необходимым. В этом усматривается любопытное рас-
хождение в положении вещей по отношению к рядам (17) и (19):
ведь для ряда Фурье (17) наличие скачка само по себе не слу-
жило препятствием к сходимости.
В более детальное исследование ряда, сопряженного с рядом
Фурье, мы вдаваться не будем.
* А также, очевидно, расходится и интеграл (22)1
697]	§ з. дополнения	483
697. Кратные ряды Фурье. Можно рассматривать ряды Фурье
и для функций нескольких переменных. Чтобы дать об этом пред-
ставление, достаточно ограничиться случаем функции двух переменных.
Пусть для всех вещественных значений хну задана функция f(x,y).
Мы предположим ее имеющей период 2тс как по х, так и по у, и
интегрируемой (в собственном или несобственном смысле) в квадрате
(Q) == [ — тс, тс; — it, тс].
Подражая разложению (10), напишем для нее двойной ряд
4-со
7(х,у)~ 2 тл>т^+т>)‘,	(23)
п, т=—со
где коэффициенты 7Ъ|1 определяются формулами, аналогичными (13)
Ъ, н = 4^ J J / Iх, У) е^х+«4•’ dx dy.
(т, 11=^ ± 1, ±2, ...)
Это и есть ряд Фурье функции f(x, у) в комплексной форме.
Его коэффициенты могли бы быть получены обычным приемом, если,
заменяя знак ~ в написанном выше соотношении на =, умножить
обе части «равенства» на е~<ПХ+тУ>1 и проинтегрировать по квадрату
(Q), выполняя для ряда это интегрирование почленно.
В вещественной форме ряд Фурье выглядит на этот раз до-
вольно громоздко. Если в комплексном ряде объединить сопряженные
члены, то получим:
СО
/(х, у)~ У, [а„ т cos пх cos ту -|- bn т cos пх sin ту
п, т—0
-|- сп т sin пх cos ту -|- dn т sin пх sin ту\, (24)
где
ао.о j | f{x, у)dxdy,
(Q)
о — 2^2	f (x, y)cos nx dx dy, a0, m= И /(x, y) cos my dx dy,
, «?>,	(Q)
yi=l, 2, 3, . . .)	(m=l, 2, 3, ...)
Ьй, m —	f {X, y) sin my dx dy,
(Q)
2, 3, ...)
Cn, 0 — -^2	f (X, y) sin nx dx dy,
(<?)
1,	2, 3 ...)
16
484
ГЛ. XIX. РЯДЫ ФУРЬЕ
[698
\ \ f (х, у) cos пх cos ту dx dy,
(Q)
f(x, у) cos пх sin ту dx dy,
(Q)
? /(x, y) sin nx cos my dx dy,
(Q)
f (x, ' y) sin nx sin my dx dy.
(Q)
(25)
и, наконец, при т, п=\, 2, 3, ...
____1_
ап, т те2
”л, т — п2
________1_
сп, т — я2
“«• т — IX2
Впрочем, обычно ряд (24) пишут в виде "
СО
/(х, у) ~ у, т [ani т cos пх cos ту -ф- т cos пх sin ту 4-
п, т = 0
-|- сп т sin пх cos ту -ф- dn< т sin пх sin ту], (24 *)
разумея под множителем /.„ т четверть, если п = m = Q, поло-
вину, если из значков п, т лишь один равен нулю, и единицу,
если ни один из них не нуль. Зато коэффициенты ап т, bn_ т, сп> т, dn т
все вычисляются по формулам (25).
Вопрос о сходимости ряда (24) [или (24 *)] решается путем иссле-
дования его частичной суммы т (ха, у0), для которой можно полу-
чить интегральное выражение вроде интеграла Дирихле:
у0) =
.	sm пфу iism ифу »
= 4^2 \ \ f (*o + lt> Уч> + ---------j-----j-------— du dv.
(Q)	Sin у и stay v
Мы не будем этим заниматься. Заметим лишь, что функция f(x,y) за-
ведомо разлагается в точке (х0,_у0) в ряд Фурье, если выполнены усло-
вия: 1) частные производные f'x^f'y повсюду существуют и ограни-
чены, 2) в окрестности данной точки существует вторая производная
fxy (или fyx), которая к тому же в данной точке непрерывна.
§ 4. Характер сходимости рядов Фурье
698. Некоторые дополнения к основным леммам. Переходя
к изучению самого характера сходимости рядов Фурье, мы оста-
новимся сначала на достаточных условиях равномерной сходи-
мости этих рядов.
Для этого нам, прежде всего, необходимо сделать дополнение
к первой основной лемме п° 682. Именно, вводя в рассмо-
698]
§ 4. ХАРАКТЕР СХОДИМОСТИ РЯДОВ ФУРЬЕ
485
тренные там интегралы различные параметры, мы будем интересо-
ваться теперь вопросом о равномерном относительно этих пара-
метров стремления интегралов к нулю.
1°. Пусть функция g(f) определена и абсолютно интегри-
руема в промежутке [Д В]; тогда оба интеграла
ь	ь
g(f) sin pt dt, g(t) cos pt dt
a	a
при р-+-\-<ж> стремятся к нулю равномерно относительно
переменных а и Ь, которые принимают произвольные значения
в промежутке [Д 5].
Достаточно рассмотреть первый из интегралов. Ввиду равномерной
непрерывности функций
А
можно разбить по заданному s^>0 промежуток [А, 5] точками
X =	<^<...<^<1:^1 <...<•£„ = 5
на столь мелкие части, чтобы было
•4 + 1
5	(i = 0, 1,..., л—1).
, 'ч
Для интегралов вида
g(t) sin pt dt,	(1)
/=0, !, 2..n)
так как их конечное число можно установить общее Д 0,
такое, что для р Д все они по абсолютной величине уже будут е.
Но, как легко видеть, интеграл
ь
J g (f) sin pt dt,
a
каковы бы ни были а и Ь, разнится (при любом р) меньше, чем на 2е,
от одного из интегралов (1). Следовательно, при />^>Дон независимо
от а и b по абсолютной величине будет <^3е, что и требовалось
доказать.
2°. Можно утверждать, далее, что и интегралы
 b	ь
5 g (х±0 sin Pt dt, § g(x +1) c.osptdt
a	a
486
ГЛ. XIX. РЯДЫ ФУРЬЕ
1698
при р00 стремятся к нулю равномерно относительно
параметров а, b и х, подчиненных лишь условиям
А^х±а, х±Ь^ В.
Действительно, например, первый из них подстановкой
х ± t — и
может быть представлен в виде
х ± Ь
§ g (и) sin р (и — х) du —
хн_ а
x±b	х+Ь
= cospx § g(u) sin ри du — sin px § g(u)cospudu,
X±a	x±a
так что вопрос приводится к предыдущему случаю (1°).
3°. Наконец, если ввести в подинтегральное выражение еще
произвольный множитель -[ (0 с ограниченным изменением в [А, В],
то и интегралы
ь	ь
J g(x ± 0 у (0 sin pt dt, g(x ± 0 7 (0 cos pt dt
a	a
при p —>-f-оо также стремятся к нулю равномерно.
Так как ^(0 представляется в виде разности двух монотонно
возрастающих функций, то достаточно предположить самое ?(0
возрастающей. В таком случае, по второй теореме о среднем [306]
ь
$g(x±07(0 sinptdt =
а
т	b
= Т (а)§ g(x ± 0 sin ptdt-\~i (b) § g(x Н; 0 cos pt dt
a	‘c
(a -C; t -С b).
Ввиду ограниченности функции у(0, вопрос и здесь приводится
к уже рассмотренному случаю (2°).
Перейдем теперь ко второй основной лемме [п° 685];
ее мы дополним лишь следующим замечанием:
4°. Пусть функция g(f) непрерывна и монотонно возрастает
в промежутке [А, В], содержащем внутри себя промежуток
[а, £]. Тогда интеграл
ь
\g(x±t)^dt
о
699]
§ 4. ХАРАКТЕР СХОДИМОСТИ РЯДОВ ФУРЬЕ
487
(где 0<^h^a — А и В — Ь) при р-J-00 стремится к пре-
делу ^g(x) равномерно относительно х в промежутке
[а, Ь}.
Проследим применительно к данному случаю доказа-
тельство, приведенное в п° 685. Первый из интегралов (13), п° 685,
который сейчас напишется так:
h	ph
, ч С sin/rt .. z ч C sin г .
g(x) \ —f-dt=g(x) \ — dz,
стремится к пределу ~ g(x) равномерно относительно x
в [a, b} ввиду ограниченности g(x). С другой стороны, равномерная
непрерывность функции g(x) в [Д, Z?] дает нам возможность по
заданному г^>0 выбрать независимо от х, изменяющегося
в пределах от а до Ь, число 8^>0 так, чтобы было
|g-(x±O — £(-*0|<О при 08.
Разбивая второй из интегралов (13) п° 685, как и там, на сумму
Л “НА» имеем оценку (14) независимо не только от р, но и от х
Наконец, /а стремится к нулю равномерно относительно х,
в силу 3°. Отсюда в совокупности и вытекает требуемое заключение.
699. Признаки равномерной сходимости рядов Фурье. Теперь
нетрудно уже установить удобные признаки, по которым можно
было бы судить о равномерной сходимости ряда Фурье в неко-
тором промежутке [а, Ь] к самой функции f(x). Эту функцию
естественно прежде всего предположить непрерывной в названном
промежутке [см. 431]. Сформулируем на первом месте видоизмененный
Признак Дини. Ряд Фу рье функции f(x), непрерывной
в промежутке [а, Ь], сходится к ней равномерно в этом
промежутке, если при некотором й^>0 для всех х из [а, Ь]
интеграл	ь
^dt	.(2)
о 1
сходится, и к тому же равномерно, относительно х (при
t=0).
Напомним, что в этом случае
<Р (О = / (х + 0 +/ (х — t) — 2/ (х)
. Р Sin [л + t
sn(x)-f(x) = ~ I <р(0---
J 2sii4*
dt.
(3)
488
ГЛ. XIX. РЯДЫ ФУРЬЕ
[699
По произвольно заданному s^>0, в силу сделанного предполо-
жения, найдется такое не зависящее от х число 80, что
д л я в с е х х из [а, Ь]
а
О
8	я
Тогда интеграл (3) представится в виде суммы	При
о	а
этом, очевидно, каково бы ни было п,
для всех указанных значений х одновременно.
Обращаясь к интегралу
. I , 1 \,
sin n-hv t
?(0-.	, dt,	(4)
2 sint
мы видим, что
интегралы
||/(x±o-
а
-----Ц------sin (п 4- 4-V dt
2 sin -±-t v 1
n-+<x> к нулю равномерно относительно х
справедливо и
стремятся при
в [а, Ь\, в силу пункта 3° предыдущего п°. То же
для интеграла	ж
а
ввиду ограниченности функции /(х) в промежутке [а, Ь]. Таким
образом, существует такой не зависящий от х номер N, что
для n^>N и интеграл (3) по абсолютной величине станет <е,
каково бы ни было х из [а, &]. Этим все доказано.
* Мы воспользовались неравенством
2 /п	те \
sin z > — ? 0 < Z < — '
те \	2 j
699J	§ 4. ХАРАКТЕР СХОДИМОСТИ РЯДОВ ФУРЬЕ	489
Отсюда, в частности, вытекает
Признак Липшица. Ряд Фурье функции f(x) сходится
к этой функции равномерно в промежутке [а, Ь], если
в некотором более широком промежутке [А, В] (А а b В)
выполняется условие
\f{x')—f(x)\^C\x’ — x\\
где х, х' — любые принадлежащие [А, 5] точки, а С и а — поло-
жительные постоянные (а^1).
Действительно, если за h выбрать наименьшее из чисел В — b
и а — А, то интеграл (2) при всех х в [а, Ь] мажорируется следую-
щим сходящимся интегралом:
о
Очевидно условие Липшица (при а=1) выполняется, а сле-
довательно, равномерная сходимость к функции f (х) осуще-
ствляется в промежутке [а, Ь], если в более широком проме-
жутке функция f (х) имеет ограниченную производную f (х).
Впрочем, это условие содержится как частный случай и в сле-
дующем:
Признак Дирихле — Жордана. Ряд Фурье функции f(x)
сходится к этой функции равномерно в промежутке fa, б],
если в некотором более широком промежутке [А, 5] функция f(x)
непрерывна и имеет ограниченное изменение.
Следуя рассуждениям в п° 686, представим интеграл
ТС
Р	sin [п +	.
М*)=4 I 1/(* + 0+/(х-0]—----------------^-dt
I	2 sin 1
о
h	it
1	f I 1 С «
в виде суммы интегралов: — \ -|- — \ , выбирая положительное число я
о л
меньшим а — А и В — Ь, независимо от значений х в [а, Ь].
Относительно второго из этих интегралов сразу ясно, что он при
п -> оо стремится кО равномерно относительно х, в силу 3°.
Из первого же интеграла, полагая
1
2	sin t
1
2 sin у t
490
ГЛ. XIX. РЯДЫ ФУРЬВ
[700
мы прежде всего выделим часть
[/(х + 0+/(х-0]
1
о •	1 >
2 sin у t
1 1
t
sin	у)
которая, также в силу 3°, равномерно стремится к нулю *.
Обратимся, наконец, к интегралу
1 ?	sin I л 4- -у 11
V \ [/(х + 0 +/(х - 0] - t dt.
&
1 ак как в промежутке [Л, £?] функция f (х) представляется в виде
разности двух непрерывных возрастающих функций:
/(х)=/1(х)~/,(х),
то, применяя к каждой из них предложение 4°, убеждаемся, что
этот интеграл стремится к пределу — -• у2/(х) = f(х) равно-
мерно же. Этим и завершается доказательство.
В частности, если функция f(x), заданная в промежутке
[— тс, тс], непрерывна в этом промежутке и имеет в нем огра-
ниченное изменение, а также удовлетворяет условию
/(—тс)=/(тс),
то ее ряд Фур ье во всем промежутке сходится к ней ра.в но-
ме р но.
Для доказательства достаточно распространить функцию по закону
периодичности, с периодом 2тс, на всю числовую ось, а тогда за
промежуток [Л, В} взять любой, содержащий внутри себя проме-
жуток [—тс, тс].
700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
Переходя к исследованию поведения ряда Фурье функции/(х) вблизи точки
разрыва этой функции, мы начнем с рассмотрения одного частного ряда, для
которого интересующее нас явление выступает с наибольшей простотой и
отчетливостью.
Мы знаем, что ряд
_ V sin (1k — 1) х „ f .	, sin Зх , sin 5x ,
2 2	2S--1 -2 {sinx + -y+—+.
1
сходится к сумме
(ТС	л
, если 0 < х < тс,
О, если х = 0, ± тс,
тс	п
—2", если —ж; х <; 0
(5)
* См. сноску на стр. 447.
700]
§ 4. ХАРАКТЕР СХОДИМОСТИ РЯДОВ ФУРЬЕ
491
[см. 690, 4)]; в точке х — 0 эта функция претерпевает скачок и справа, и
слева:
o(+0)-a(0) = y, а(0) —а (—0) = у.
Изучим поведение частичной суммы ряда *
л
•и.,«=2 2	.
*=1
Ввиду ее нечетности достаточно рассматривать эту сумму лишь в про-
межутке [0, и]. Больше того, очевидное тождество
sin (2k — 1) ^у х' ) = sin (2k — 1)	-х'
показывает, что ®2л-1 (х) симметрична относительно точки х = у
°ал-1
---°2Л-11 2
это позволяет ограничить исследование промежутком |^0, у
Для суммы с2п_! (х) легко получается выражение:
®2л—1 (х) — 2 j [cos « + cos За + cos (2п — l)u]du =	du
(6)
или, если положить 2nu=t:
inx
®2л-1(-«) = ^	dt.	(7)
0 Sin 2п
Последнее выражение можно написать
тс 2тс
в виде суммы:
kr. 2пх
..+ f
(А — 1) тс	sin
где k = E^^. Полагая вообще для i == 0, 1..п—1
(i 1) тс	тс
1 С sin<	, 1 Г sinz .	.
_	—^^-dz = (-1}ч
sm 2h	« sm ~2iT
°2Л-1 W =
(8)
имеем, очевидно,
»i>0 и vi+l<vi.	(9)
Таким образом, окончательно:
°2Л-1 (X) = », — »i +.I)*’1	+ (— 1)*vk,	(8 *)
• Очевидно, о2л W = °2л-1 W-
492
ГЛ. XIX. РЯДЫ ФУРЬЕ
1700
где через (—1 )kvь обозначено последнее, «неправильное», слагаемое; оно
имеет знак (—1)®, а по абсолютной величине меньше vk.
Отсюда непосредственно вытекает ряд заключений о поведении суммы
ТС
a2zi-i (x)i если п фиксировано, а х изменяется от 0 до -g-:
1)	сумма a2n_j (х) положительна, обращаясь в нуль лишь при х = 0;
2)	она имеет экстремумы в точках
тп
Хт==2п	2.... «).
Наконец, из представления экстремального значения
’2я-1 (хт) = »о — + ••• + (— О'”
с учетом неравенств (9) получается также, что
[ТС "|
0, -g- максимальные
значения a2n-i (х) слева направо убывают, а минимальные — возрастают.
Все эти утверждения иллюстрируются рис. 133, где для примера изобра-
жен график функции аи (х).
Остановимся теперь на наибольшем максимуме функции a2«-i (х), т- е- на
первом ее максимуме, считая от х = 0. Он принимается функцией в точке
* Утверждение 2) об экстремумах функции ®2Л_1 (х) легко получается
и из рассмотрения производной
d . . sin2nx .
[«-(ад
700]
§ 4. ХАРАКТЕР СХОДИМОСТИ РЯДОВ ФУРЬЕ
493
и равен по величине |см. (7)]
п
= а2л_! (xW) = 1 dt.
« Sin 2н
Здесь в обозначение введен номер п, ибо на этот раз мы намерены проследить
за поведением функции именно при изменении п. Очевидно, х^ монотонно
убывает при возрастании п и стремится к 0 при л—«--J-co. Для облегчения
исследования самой величины перепишем выражение для нее в следую-
щем виде:
те
М|»_ fsjli
J “S
Так как второй множитель в подинтегральном выражении с возрастанием п
равномерно (относительно t) и притом убывая* стремится к единице,
то, очевидно, и убывая стремится к пределу:
lim f ^Ldt^fj...	(10)
л-»4-со	t
0
Итак, имеем:
4) первый (наибольший) максимум функции asn_i (х) достигается при
значении х — х^, которое монотонно убывая стремится к нулю при
безграничном возрастании п, а самый максимум при этом монотонно
убывая стремится к пределу |л1г выражаемому формулой (10).
Аналогичное утверждение можно было бы сделать вообще относительно
fe-го (k фиксировано!) экстремума функции: оно достигается при значении
x^ = k-~
которое стремится к 0 при п — оо, -а величина k-го экстремума при
этом монотонно стремится к пределу
14 =
kit
С sin *л,
J ~Tdt'
о
а именно — убывая, если речь идет о максимуме (k — нечетное), и
возрастая — в случае минимума (k — четное).
Для иллюстрации мы приводим рис. 134, где сопоставлены графики пер-
вых шести сумм о2Л-1(х) при п= 1, 2, 3, 4, 5, 6.
* Мы используем здесь тот факт, что функция при возрастании z
от 0 до у и сама возрастает.
494
ГЛ. XIX. РЯДЫ ФУРЬЕ
|700
Числа р.*, как явствует из рассуждений, проведенных в п° 439, попере-
менно то больше, то меньше числа
СО
С sin£ тс
Т dt=2-
о
Разности р* = р.*—-у имеют следующие значения:
Р1 = 0,281*; р2= —0,153; Рв = 0,104; р4= — 0,073; р5=Ц063; ... (11)
Теперь мы в состоянии уже достаточно полно охарактеризовать сходи-
мость частичн ых сумм a2„_j (х) ряда (5) к его сумме а (х); ограничимся для
определенности промежутком [0, л].
Если точки разрыва х = 0 и х = те выделить сколь угодно малыми
окрестностями [0, 8) и — 8, те], то в остающемся промежутке [8, те—В],
в силу доказанного в предыдущем п°, ряд сходится равномерно. Иными
словами, графики частичных сумм (х) при достаточно больших п сколь
„ л
угодно тесно примыкают к прямой = сразу на всем протяжении этого
промежутка. Вблизи же точки х = 0 (их = те), где функция а(х) скачком
переходит от значения -g- к значению 0, равномерность приближения есте-
ственно должна нарушиться, ибо а2Л_! (х) от близких к значений при
х — 8 (или те — 8) непрерывным образом переходят к значению 0
при X = 0 (или те).
Весьма замечательно, однако, что нарушение равномерности
не исчерпывается только сказанным; к этому факту мы при-
влекаем внимание читателя. В непосредственной близости к оси у справа,
прежде чем резко устремиться к начальной точке (0, 0), графики функций
* Ср. 412, 4).
701]
$ 4. ХАРАКТЕР СХОДИМОСТИ РЯДОВ ФУРЬЕ
495
У
п
г
б)
Рис. 135.
О
О
.п
а)
о2Я_х(х) колеблются около прямой _у = -у, причем «амплитуды» этих колеба-
ний вовсе не имеют тенденции бесконечно уменьшаться при п —► со. Наоборот,
как мы видели, высота первого, и наиболее высокого, горба над упомянутой
прямой стремится при этом к величине pt = 0,281; за первым горбом, пере-
двигаясь справа налево с возрастанием п и сгущаясь к оси у, следуют даль-
нейшие впадины и горбы, причем расстояния их вершин от прямой У — при
«—►со стремятся, соответственно, к дальнейшим величинам р2, р3, ... и т. д. из
ряда (11). Аналогичная картина имеет место вблизи прямой х = п слева. Точно
также вблизи оси у слева снова по-
вторяется та же картина с тем лишь
изменением, что все рассматривае-
мые величины получают обратные
знаки.
Можно сказать, что «предель-
ным геометрическим образом» при
п —► <ю для кривых у =	(х)
является не ломаная, изображен-
ная на рис. 135, а (как естественно
было бы ожидать!), а ломаная рис.
135, б с соответственно удлинен-
ными — примерно на 0,281:	=
=18°/о—вертикальными отрезками.
Этот своеобразный дефект сходимости впервые был в самом конце
прошлого века отмечен, также на частном примере тригонометрического разло-
жения, Гиббсом (J. W. Gibbs) и в связи с этим известен под названием
явление Гиббса. Мы увидим сейчас, что это явление в некотором смысле
имеет место в общем случае.
701. Случай произвольной функции. Рассмотрим периодическую, с
периодом 2я, абсолютно интегрируемую функцию /(х), с изолирован-
ной точкой разрыва первого рода х = х0. Тогда в некотором промежутке
[х0 — Д, х0 4* А] (д > 0) не будет других точек разрыва; для простоты пред-'
положим, что в этом промежутке функция имеет ограниченное изменение.
Введем теперь функцию а (х — х0), которая отличается от изученной в пре-
дыдущем п° функции сдвигом вправо на х0, и составим с ее помощью функцию
<Р(Х)=/(Х) -/(Х° + 0) +/(Х°~°)-1 [/(х„ + 0) _/(хв-0)1 а (х —х„).
Если условиться за значение /(х0) в точке разрыва х = хй принимать
/(хо4-0)+/(хо — 0)
- х	-----то, как легко проверить:
? (х0 + 0) = (х0 — 0) = (х0) = 0.
Функция <р(х) в точке х = х0 оказывается непрерывной: с помощью
функции с удалось компенсировать разрыв функции /1 Функция <р будет не-
прерывна и в прочих точках промежутка [х0 — Д, х„-|-Д], если взять Д<я;
кроме того, вместе с функциями f и а функция <р также будет иметь в на-
званном промежутке ограниченное изменение.
Теперь мы можем написать:
/ W =/(*о) 4“ I/ (*о + °) —/ (хв — 0)] а (X — Хо) -I- <р (X).
Заменив здесь каждую из функций а(х— х0) и <f(x) ее разложением в ряд
496
ГЛ. XIX. РЯДЫ ФУРЬВ
|701
Фурье, мы получим, очевидно, и разложение заданной функции в ряд
Фурье. Частичная сумма sm (х) последнего ряда представляется в виде:
sm (*) =/(*о) + /(Хо + 0^~/(х°~0)- ат (х — х0) +	(х).
7U
Здесь, при т = 2п — 1 или 2п,
„ /г ri— V sin(2/s—1)(х —х„)_
ат(х х0)—	2k^\
k = \
п
= 2	_1 [cos х0 sin (2fe — 1) х — sin xc cos (2 k — 1) x],
*= 1
a (x) означает соответствующую частичную сумму ряда для <р.
Так как ср(хо) = 0 и функция tp(x) в точке х0 непрерывна, то при доста-
точно малом Д в с е ее значения в промежутке [х0 — Д, х0 Д] будут сколь
угодно малы. В то же время в этом промежутке срт (х) стремится к ср (х)
равномерно, следовательно, при достаточно большом т и значения<рт(х)
будут сколь угодно малыми. Таким образом, поведение сумм sm (х) в
основном определяется уже известным нам поведением сумм ат (х — х0); на-
личие слагаемого срт (х) вносит в него лишь незначительные искажения, тем
меньшие, чем ближе х к х0 и чем больше т.
Если при нечетном т = 2п — 1 положить
£ffl=x°+^==x°
а при четном /п = 2п:
г	.	. те
ТО
lim =
т —► оо
Наряду с этим, если учесть (10),
lim sm (5m) =/(х0) + ^+ °)-Г>Г<-го-0).
т->оо	те
так как, очевидно, при т—
?m (5m) = [<Pm (5m) — <Р (5m)] + <P (5m) — 0.
Заменяя /j., на-^--[*Р1 и вводя величину скачка D=f (хо-|-О) — f (х0 — 0),
можно пёреписать полученный результат и так:
lim sm (5m) =/(х0 0) -f- — pt.	(12)
т -* оо	76
Аналогично, полагая
5т = Х0 —	или Х0 ——,
в зависимости от того, будет ли т нечетным или четным, получим:
Пт sm(5m)=/(x0—0) —(13)
Таким образом, и в рассматриваемом общем случае предельное
значение колебания сумм sm (х) в окрестности точки разрыва х0 оказы-
вается больше самой величины | D | скачка функции/(х) на
2 [ О |
702]
$ 4. ХАРАКТЕР СХОДИМОСТИ РЯДОВ ФУРЬЕ
497
т. е. на те же 18% ее. И здесь также для получения предельного геометри-
ческого образа для графиков сумм sm (х) недостаточно к кривой у —
=/(х) присоединить отрезок вертикальной прямой х = х0, соединяющий
точки с ординатами /(х0— 0) и /(хо-фО), но приходится этот отрезок
соответственным образом удлинить и вверх и вниз. Можно сказать, что
идля произвольной функции осуществляется явление
Гиббса!
Замечание. Исследования, связанные с явлением Г и б б с а, приводят
и к другим интересным результатам. Так, с их помощью могут быть уста-
новлены формулы, определяющие для функции/(х) с ограниченным измене-
нием ее односторонние пределы /(хо±0) и величину скачка в любой точке
х0 непосредственно по ее ряду Фурье. Для этой цели могут
быть использованы, например, формулы (12) и (13): вычитая их почленно,
найдем
^ = о7~' 6m tsm (’m) sm (£/n)]>
m -* co
после чего уже легко определяется и /(хо±0). Различные формулы этого
типа были установлены Ф е й е р о м (L. Fejer).
702. Особенности рядов Фурье; предварительные замечания.
Во всех признаках сходимости рядов Фурье, относящихся к непре-
рывным функциям, кроме самой непрерывности неизменно требовалось
что-нибудь еще: то ли существование некоего интеграла, выполнение
неравенства, наличие конечной производной, то ли ограниченность
изменения функции, ее кусочная монотонность. Естественно возникает
вопрос: не будет ли достаточно для сходимости ряда Фурье одной
непрерывности породившей его функции? Еще в 1876 г. дю Буа-
Реймонд (Р. du Bois-Reymond) дал отрицательный ответ на этот
вопрос, построив пример непрерывной функции с расходящимся
в некоторых точках рядом Фурье.
Лебег (Н. Lebesgue) в 1906 г. построил пример такой непре-
рывной функции, к которой ее ряд Фурье сходится повсюду, но
не равномерно.
Мы хотим дать здесь примеры осуществления как «особенности
дю Буа-Реймонда», так и «особенности Лебега», следуя при
их построении по пути, указанному Ф е й е р о м.
Элементами построения в обоих случаях служат конечные триго-
нометрические многочлены (тип означают натуральные числа):
Рт.
, .___[cos тх . cqs (т -ф 1) х .	. cos(m-|-n — 1) xl
П. w — [ п ~1	г • • • Н	i J —
[cos (m-фи 4- 1)х ,	! cos(m%2n— 1)х , соз(/п-ф2и)х
L 1	1 п — 1	П
.	, ч__[sinmx . sin(m-|- 1)х .	. sin(m-|-n — 1)х]
.т, п W — [ п ~Г п _ j ~Г • • • Н	j	J —
___[ sin (m -ф и -ф 1) х .	! sin (m -ф 2n —1)х . sin (m -ф 2n) х ~
L 1 “Г • • • “г п — ।	~1 й
Установим предварительно некоторые свойства этих многочленов.
498
ГЛ. XIX. РЯДЫ ФУРЬЕ
(702
1°. Прежде всего, существует такая постоянная М, что
и	(14)
каковы бы ни были значения переменной х и значков т и п.
Для доказательства этого преобразуем многочлены Р и Q, объ-
единяя в каждом члены с одинаковыми коэффициентами. Так, полагая
в первом (при v=l, 2......п)
+ cos(m + n+20£ = 2 sin {т _!_п)х
приведем его к виду:
п
Рот,„(х) = 2 sin (т + «)х	-^7^-
V = 1
Аналогично
п
QOT.„(x) = —2cos(m + «)x У
V = 1
Так как множители при сумме, которая фигурирует здесь в обоих
случаях, явно ограничены, то вопрос сводится к ограниченности
самой суммы. Мы уже имели случай [690, 3)] представить ее в
виде:
о
Второе слагаемое справа здесь ограничено ввиду равномерного
стремления его к нулю при п—> оо [698, 1°], а третье — ввиду схо-
оо
С sin и ,	„	,
димости интеграла \ -^-аи. Отсюда и вытекает требуемое заклю-
чение.
2°. Иначе обстоит дело с частичными суммами многочле-
нов Р и Q (т. е. суммами любого числа последовательных членов
их, начиная с первого). Если для многочлена Рт п(х) взять сумму
первых п его членов, то при х = 0 она получит значение
1	+у+ ••• 4“»
702]
$ 4. ХАРАКТЕР СХОДИМОСТИ РЯДОВ ФУРЬЕ
499
растущее вместе с п до бесконечности [36.5, 1)]. Так как,
очевидно,
— = ln(v+ 1) — In v,
то для Нп получается известная оценка:
/7„>1пл.
Частичные суммы многочлена	при х = 0 все обращаются
в нуль. Однако если мы вычислим сумму первых п его членов в
близкой к нулю (при больших т и п) точке х =
найдем:
ТС
2(m-|-n) *
то
2 (т п)
Но по известному неравенству sin z z при	так что
эта сумма сказывается большей, чем
1 \
т -\-п)
= Нп
п
т-\-п
1п п — 1,
и также бесконечно возрастает в'месте с п. В этом, соб-
ственно, уже содержится как бы зародыш обеих особенностей — дю
Буа-Реймонда и Лебега.
3°. Если же мы, взяв любое положительное число е, ограничим
изменение переменной х промежутком [е, 2тс — е] *, то все частичные
суммы обоих многочленов оказываются ограниченными (по абсолют-
ной величине) одной и той же постоянной £(е), не зависящей от т
и п. Достаточно доказать это относительно выражений вида
cos (р ± X) х
sin (р ± X) х
(15)
ибо, как легко видеть, упомянутые частичные суммы в общем случае
представляют собой разности двух подобных выражений.
Остановимся для примера на выражении
i
2	cos (р 4- X) х
X
х = 1
* Или — что не составляет разницы — промежутком от 2йя-|-е до
2 (А Д-1) л — е, где k — любое целое число.
500
ГЛ. XIX. РЯДЫ ФУРЬЕ
|703
и для его оценки воспользуемся леммой Абеля [383]. Множи-
тели у при возрастании значка X убывают, оставаясь положитель-
ными. Что же касается множителей cos (р-]~ X) х, то сумма любого
числа их
sin (р + Х0 + 4-) х — sin (р + у) х
У, COS (Р + X) X =--------------------:-------------------
“1	2sin|-
по абсолютной величине не превосходит постоянной------
sinY
Отсюда
заключаем, что и
cos (р -f- X) х
X
1
sinT
То же справедливо и относительно других выражений (15). Таким
образом, в качестве упомянутой границы Л(е) можно взять постоян-
2
ную --—.
sinT
Все эти свойства будут использованы в следующем п°.
\
703. Построение особенностей. Возьмем теперь последователь-
ность положительных чисел {аА}, для которой ряд сходится,
и две бесконечно возрастающие последовательности натуральных
чисел {mk}, { nk } и построим два ряда:
ОО
У akPmk.nk(.x) = ^{x)	(I)
1
И
оо
У akQmk, пк (х) = (*)•	(Н)
* = 1
Оба ряда абсолютно и равномерно сходятся, ибо ввиду (14)
мажорируются сходящимся рядом М У] ak. Следовательно [431], функ-
ции Ф(х) и Ф(х) заведомо будут непрерывными.
Выбор чисел ak, mk и nk мы подчиним следующим двум тре-
бованиям:
1)	mkJri mk + 2nk (для А=1, 2, 3, .,.),
2)	ak In nk -]- ос при А -> ос.
703|	§ 4. ХАРАКТЕР СХОДИМОСТИ РЯДОВ ФУРЬЕ
Можно, например, положить
501
а* = ^> от* = л* = 2<
Ввиду 1) два различных тригонометрических многочлена акРть, nk (х)
или ahQmk, пк (х)> входящих, соответственно, в ряд (I) или (II), не
содержат членов с одинаковыми кратными х. Если теперь просто
подряд написать все члены последовательных многочленов, входящих
в (I) или (II), т. е. раскрыть все скобки, то получатся два тригоно-
метрических ряда (один по косинусам, а второй по синусам), кото-
рые и будут рядами Фурье функций Ф(х) и Ф(х). В са-
мом деле, если, например, умножить обе части равенства (I) на
cosрх и проинтегрировать от 0 до 2тс, то ввиду равномерной
сходимости ряда интегрирование в нем можно будет выполнить
почленно. Затем, каждый интеграл
2ч
akPmh. nk(x) COS рХ dx
О
заменится конечной суммой интегралов, причем все они будут
нулями, кроме того случая, когда в состав akPmki nk (х) входит
cos рх. Таким путем мы и убедимся в том, что коэффициент при
cos рх будет коэффициентом Фурье.
Обратимся теперь к вопросу о сходимости этих рядов Фурье
и ее характере. Если изменение х ограничить промежутком [е, 2 я — е],
то оба эти ряда сходятся и даже равномерно, наподобие ря-
дов (I) й (II). Это видно из того, что любая частичная сумма, ска-
жем ряда Фурье для функции Ф (х), отличается от некоторой
частичной суммы
4 — 1
2а акРщк, пк О')
* = 1
ряда (I) на некоторую частичную сумму
гочлена
asPms. ns (X),
тригонометрического мно-
которая в силу 702, 3°, по абсолютной величине не превосходит
asL (е) и при безграничном возрастании з равномерно стремится
к нулю.
Ввиду произвольности е, таким образом, сходимость рядов Фурье
для функции Ф (х) и Ф (х) обеспечена при всех значениях х в (0,2к).
При х = 0 (или 2 я) первый ряд, однако, уже расходится, и
налицо — «особенность дю Буа-Реймонда»! Действительно, если
502	гл. xix. ряды фурье	(704
его /и-ю частичную сумму вообще обозначить через sm (х), имеем
sznA + nA-l (-*0	smk-i (X)=	5
[cosmjx ।	, cos(m* + n*—1)х]
_	.	J,
так что [см. 700, 2°]
(0)	(0) ==	ak
что, в связи с требованием 2), свидетельствует о нарушении основ-
ного условия сходимости ряда [376].
Что же касается ряда Фурье функции Ф (х), состоящего из
одних синусов, то он, конечно, сходится и при х=0 (или 2it). Но
на этот раз в окрестности точки х = 0 сходимость не будет
равномерной, и мы имеем здесь осуществление «особенности
Лебега»! Чтобы убедиться в этом, обозначим вообще через sm(x)
его т-ю частичную сумму и вычислим разность
+Л^- 1 (-^)	С^) 
[sinmAx !	! sm(mk + nk — l)xl
••• +~--------г-------J
в точке х = -ТГ-.——г; в силу 700, 2°, она оказывается большей,
чем
(1пи* —1),
и растет до бесконечности вместе с k.
Ценою некоторого усложнения построений удается определить
такую непрерывную функцию Ф (х) с периодом 2я, что ее ряд
Фурье имеет точки расходимости в любой части промежут-
ка [0, 2тс].
До сих пор, однако, не решен вопрос, может ли ряд Фурье
непрерывной функции быть всюду расходящимся. Правда, пример
всюду расходящегося ряда Фурье был дан с помощью тонкого
построения акад. А. Н. Колмогоровым, но его пример относится
уже к функциям более сложной природы и притом использует более
общее, чем обычное, определение понятия интеграла (принадлежащее
Лебегу).
§ 5. Оценка остатка в зависимости от дифференциальных
свойств функции
704.	Связь между коэффициентами Фурье функции и ее
производных. Рассмотрим функцию /(х) с периодом 2 к, имеющую
производные до k-ro порядка (й^1) включительно. Первые k—1
из них, разумеется, будут непрерывными функциями; относительно
А-й производной предположим покуда, что она (абсолютно) интегри-
705J	$ 5. ОЦЕНКА ОСТАТКА	503
руема. Обозначая по-прежнему через ат, Ьт коэффициенты Фурье
функции f(x), для производной (х) (/=1, 2, k) коэффи-
циенты Фурье мы будем обозначать через а^, b{jj.
Интегрируя по частям, найдем (для. т—\, 2, 3, ...)
кат — f (х) cos тхdx—f (х)	1	f (х) sin тхdx,
— те	— те
так что
аналогично
Если полученные формулы применить к коэффициентам ат, Ь'т и
выражения последних через а?т, Ь’п подставить в. формулы для ат,
Ьт, то окажется, что
а’	Ь”
т	и	т
О,^, —---г- . и^. —  — _
m	тг > "т	
Продолжая этот процесс, мы индуктивно установим окончатель-
ные формулы, в которых приходится различать случай четного
и нечетного k-.
при k = 2h-.	=	bm = (-\)h-?r, (la)
a<*>
при A = 2A-J-1:	am = (-l)ft+1^r, bm = (-(16)
Поставим себе задачей, пользуясь этими формулами, установить
оценку для остатка ряда Фурье Л-кратно дифференцируемой
функции, при тех или иных условиях, налагаемых на Л-ю производ-
ную. В начале предыдущего параграфа мы изучали вопрос о равно-
мерной сходимости ряда Фурье, т. е. о равномерном стремлении
его остатка к нулю; здесь, правда, при более тяжелых предположе-
ниях, мы оказываемся в состоянии оценить даже быстроту этого
стремления, установив порядок малости остатка в зависимости от
дифференциальной природы функции.
705.	Оценка частичной суммы в случае ограниченной функ-
ции. Предварительно мы дадим оценку для частичной суммы sn(x)
ряда Фурье, равно как и для частичной суммы sn (х) сопряжен-
ного с ним ряда, предполагая функцию f (х) только ограниченной:
|/(х)|<7И;
под М здесь можно разуметь, например, точную верхнюю гра-
ницу для |/(х)|.
504
ГЛ. XIX. РЯДЫ ФУРЬЕ
(705
По известной формуле [см. 681, (4)]
Я
1 Г	sin
s„(x)=4 I [/(x + 0+/(x- 01-------~-^~dt.
!	2sin-i-Z
o'	2
Отсюда последовательно имеем *:
It	7t
, fflsin("+4VL
I (*)	— 1 1-------j---dt<^M I !----------!<// =
.)	2 sin	J	‘
о	0
(n+4)’	i (n+y),t
,,	С	I sin и I ,	. (* , .	du
= M	\ J----1 du <Z M \ du + M	\ — =
J u	J 1 J и
0	0	1
= Л4 Г1 + In + я] <Z M (ln л+ 1 + ln 2it).
Если под А разуметь достаточно большую постоянную, то (при
п 2) последнее выражение в скобках окажется меньшим, чем 4 In л,
так что окончательно получим
I sn (X) I 21Л4 In л** (л 2).	(2)
Переходя к сопряженному ряду, вспоминаем, что [696, (20)]
, Р	coslf-— COS
s„(x) = -4 I [/(x + 0-/(x-0]----------4----2-^-dt.
I	2 sin 4/
о	2
Поэтому
* См. сноску на стр. 488.
** Например, можно взять
Но это, конечно, не есть наилучшее из возможных значений постоянной А •
706]	§ 5. ОЦЕНКА ОСТАТКА	505
Рассуждая далее, как и выше, придем к аналогичной оценке:
| sn (х) | AM In л (n>s2),	(3)
где А есть новая ^постоянная, вообще отличная от прежней, но подобно
ей не зависящая от выбора функции f(x). Впрочем, конечно, можно
было бы в обоих случаях пользоваться одной и той же постоянной —
наибольшей из двух.
Разность Rn(x)=/(x)— sn(x) (это будет остатком ряда
Фурье лишь в том случае, если он сходится к функции /) оцени-
вается аналогично (2):
IRn(*) 1 ММ Inп (n5s2).
Действительно,
I Rn (*) I	l/С*) I +1 sn (х) | ==s М + AM In п,
так что стоит лишь надлежаще увеличить постоянную А, чтобы
придти к требуемому неравенству.
Читателя не должен удивлять тот факт, что справа в неравенстве
стоит величина, растущая до бесконечности вместе с п. Мы знаем
ведь, что для некоторых ограниченных (и даже непрерывных,
см. 703) функций /(х) величина Rn(x), действительно, может бес-
конечно возрастать, а наше неравенство должно охватывать все
ограниченные интегрируемые функции!
706.	Оценка остатка в случае функции с ограниченной fe-й
производной. Обратимся теперь снова к рассмотрению функции f(x)
с периодом 2тс, имеющей производные до А-го (fe^l) порядка вклю-
чительно, причем на этот раз предположим k-ю производную огра-
ниченной:
и интегрируемой в собственном смысле.
Установим следующий важный результат, принадлежащий акад.
С. Н. Бернштейну: при сделанных предположениях существует
абсолютная постоянная А такая, что (для п ^2)
|Д„(х)| AMk^-.	(4)
При доказательстве мы будем различать случаи четного
инечетногоА.
1°. Пусть k = ’2h. Выражение для остатка ряда Фурье функ-
ции f(x) *
СО
Rn = Rn(x)= У, ат cos mx-\-bmsin. тх,
m=n-|-l
* При сделанных предположениях ряд Фурье будет повсюду сходиться
к функции f(x) [684].
506	ГЛ. XIX. РЯДЫ ФУРЬЕ	(706
если воспользоваться формулами (1а), может быть написано в виде:
ОО
/?„ = (— 1 )ft 2 C°S тХ + Ь{т Sin тХ^
m = n4-l
В скобках имеем zn-й член ряда Фурье функции /(Л)(х); вводя
частичную сумму ат = ст(х) этого ряда, можем заменить названный
член через ат— ат1:
СО
Rn=(-i)h 2
m=n + l
е
Раскрыв скобки и по-другому объединив члены [ср. 383], мы придем
к ряду:
ОО
(— 1)feRn = — (И_р !)Г+ 2 (m®	(m-|-
m=n4-l
Для обоснования указанного преобразования заметим, что
Пт —ь- = 0;
это следует из неравенства
I ат I АМк 1п т,	(6)
которое получится, если неравенство (2) применить к функции (х).
Из (5) и (6) вытекает, оценка:
|/?д| Л In и . у /1	1
Мк (п +1 )^ '	\mk (m-f-l)*/
m=n4-l
Последнюю сумму снова преобразуем к виду [ср. 371]:
ОО
2 (Ш+
m = n4-l
Если воспользоваться неравенствами
In (z/z —1) — In tn = In fl +-M << —
v 1 7	\	1 m) m
и
co
2	1	1	J.
mA+1	k	nk
707]	$ 5. ОЦЕНКА ОСТАТКА	507
[см. 373, а)], то последовательно получатся для нее оценки
in (п +1) I V 1 In (я +1) , у 1
(я 4- l)ft "г” m (m + l)ft (я 4~ О* ~7" h tnk+l
m=»4-l	m=n4-l
^Inn ,	1	, 1	1 In n 4- 2
\ ^F l nk+i i" £	”^F \ nk
Возвращаясь к получаем для этой величины такую оценку:
. п ।	, 2Д In я 4- 2А ____о,
I Rn I < мк---— (п 5= 2),
откуда, конечно, надлежаще изменив А, легко прийти уже к (4).
2°. Теперь предположим k = 2h-\-l. Опираясь на формулы (16),
перепишем Rn так:
СО
Rn=(— i)ft 2 i sin тх ~cos тх)-
m=n4-l
В выражении, стоящем в скобках, мы узнаем на этот раз т-й член
ряда, сопряженного с рядом Фурье функции /(А)(х) [670].
Так как и для его частичной суммы ат = ат(х) также имеем оценку
I 1 < AMk \пт
[см. (3)], то дальнейшие рассуждения ничем не разнятся от приведен-
ных выше.
707.	Случай функции, имеющей Л-ю производную с ограни-
ченным изменением Рассмотрим сначала функцию /(х) с периодом
2тс, которая сама имеет в промежутке [—тс, тс] ограниченное измене-
ние. Переходя к интегралам Стилтьеса и воспользовавшись фор-
мулой интегрирования по частям [677], представим коэффициент ап
функции f (х) в виде:
1 z ч С ( г ч . Sin пх
en=-(s) ^/(x)d—
—X
= /(х)8ШЯХ
47 ля
К	я
------— (s) sin nxdf(x).
— я---—я
(7)
Внеинтегральный член исчезает, что же касается последнего инте-
грала, то, оценивая его обычным для интеграла Стилтьеса образом
[582, 2°], получим:
sin nxdf(x)
— Я
sg шах | sin пх| • у /(х).
508
ГЛ. XIX. РЯДЫ ФУРЬЕ
|707
Таким образом, окончательно
|а„К— V--,
I ЛI л п ’
если через V обозначить полное изменение функции f (х) в про-
межутке [— к, и]. Так же оценивается и коэффициент Ьп.
Если две переменные величины а и р, зависящие, скажем, от одной
и той же независимой переменной, обладают тем свойством, что их
отношение остается ограниченным:
|	1 -С М (М = const),
то этот факт записывают следующим образом *:
Р = О(а).
Пользуясь этим обозначением, мы можем выразить доказанное свой-
ство коэффициентов Фурье а„, Ьп функции с ограниченным измене-
нием так:
a„=o(-V bn=0[—V
я \п )’ п \ п )
Пусть теперь для функции f(x) с периодом 2тс существует
k-я (k 1) производная fw (х), которая в промежутке [—тс, тс]
имеет ограниченное изменение; тогда для коэффициентов Фурье
функции f (х) справедлива оценка:
KI,	(и=1, 2, 3, ...),
где Vk есть полное изменение функции	в промежутке
[— тс, тс].
Это сразу вытекает из сопоставления, доказанного только что
с формулами (1а) и (16) п° 704.
Итак, на этот раз
=	(8)
Зная порядок коэффициентов Фурье, теперь нетрудно уже оце-
нить и остаток ряда Фурье: при тех же предположениях, для
остатка Rn(x) ряда Фурье функции f(x) имеем неравенство:
|Ял(*)к4.
* Ср. это обозначение с обозначением о (а), которое мы ввели в п° 60.
7081
§ 5. ОЦЕНКА ОСТАТКА
509
Действительно,
СО
оо
<2Ц V 1	1 Vk
' тс	mft+1 Ли п* ’
т =п+1
Таким образом, несколько более тяжелое ограничение (по сравне-
нию с предыдущим п°), которое мы наложили на Л-ю производную
функции, повлекло за собой улучшение оценки остатка Rn{x\. в чи-
слителе исчез In л!
Замечание. Подчеркнем еще раз, что в рассуждениях настоя-
щего и предшествующего пп° существенную роль играла периодич-
ность самой функции f(x) и ее производных. Если первона-
чально функция была задана лишь в промежутке [— л, тс], то
нужно потребовать выполнения условий:
/(—тс)=/(тс), /'(—тс)=/'(тс), •••> Ж(-тс)=/(Ж),
разумея здесь под производными односторонние производные. Лишь
тогда будут обеспечены непрерывность и существование последо-
вательных производных для периодически продолженной
функции, а вместе с тем и справедливость установленных выше
оценок.
708.	Влияние разрывов функции и ее производных на поря-
док малости коэффициентов Фурье. Мы видели, что наличие у функ-
ции ряда непрерывных производных обеспечивает быстрое убывание
коэффициентов Фурье и, как следствие, быструю сходимость ряда
Фурье.
Однако в математической практике часто встречаются случаи, когда
разложению в ряд Фурье подлежит функция, которая в пределах
от — тс до тс как бы «склеивается» из нескольких функций, имеющих
каждая в своем промежутке определенное число производных. В точ-
ках «стыка», таким образом, создаются скачки как для самой
функции, так и для ее последовательных производных. Эти разрывы
понижают порядок малости коэффициентов Фурье, а вместе с этим,
как легко понять, и порядок малости остатка ряда Фурье. Обра-
тимся к детальному исследованию этого вопроса.
1°. Пусть функция f(x) будет непрерывна в промежутке [—тс, тс),
исключая «точки стыка»

(9)
в которых она имеет разрывы первого рода, т. е. претерпевает скачки
=f(\> + 0)	- 0) (р = 1, 2, ..., т).
510	гл. xix. ряды фурье	|708
К их числу должна быть присоединена и точка Ев = —тс, если раз-
ность
8q0)==/(—тс0) —/(тс — 0)
отлична от нуля, ибо в этой точке появится разрыв при периодиче-
ском продолжении функции.
Предположим, далее, что повсюду, исключая лишь указанные точки,
существует конечная производная f (х), скажем, абсолютно интегри-
руемая в промежутке [—тс, тс]. Для выражения коэффициента ап
функции /(х) мы снова перейдем к интегралу Стилтьеса и про-
интегрируем по частям [см. равенство (7)]. Если выделить в послед-
нем интеграле слагаемые, отвечающие скачкам функции/(х) [579, (15)],
то получим
Я
а„ — ~ ^ / (х) cos пх dx —
— те
т	те
=-----—У B/’sinnL—— /'(x)sinnxrfx
ПТС **	и Птс J v 7
|Л= 1	— к
или, короче,
где положено
И=1
а через Ъ'п, как и раньше, обозначен коэффициент Фурье для функ-
ции /’(х). Аналогично можно установить, что
В , а'
=	(12)
где
03)
11=0
а а'п также означает коэффициент Фурье для /'(х).
Наложим теперь на производную f'(x) требование, чтобы она
имела ограниченное изменение в промежутке [—тс, тс]. Так
как ее коэффициенты Фурье при этом предположении имеют поря-
док О [707], то формулы (10) и (12) можно переписать и так:
«.=£ + <>(1),	(14)
г’*=4”+°(й-	“5>
708]
$ 6. ОЦЕНКА ОСТАТКА
511
Эти формулы с отчетливостью показывают, как наличие точек разрыва
у функции, несмотря на существование производной во всех прочих
точках, сразу понижает порядок малости коэффициентов Фурье.
Пусть теперь, наоборот, известно, что коэффициенты Фурье не-
которой функции f(x) имеют вид (14) и (15), причем величины Ап,
Вп определяются формулами (11) и (13), где {8/’} есть данный набор
т 4-1 чисел. Тогда функция f(x) необходимо имеет разрывы первого
рода именно в точках (9) и претерпевает в них скачки, соответ-
ственно равные 2>'0> (р.= 1, 2, ... , ту, кроме того, для нее суще-
ствуют пределы f{—тс4~0), /(тс— 0)*, и их разность равна 8'^’.
В прочих же точках функция непрерывна.
Для того чтобы в этом убедиться, составим вспомогательную
функцию /(х), например, из линейных в (?и, $и+1) функций так, чтобы
она в указанных точках претерпевала как раз указанные скачки. Для
ее коэффициентов Фурье имеем аналогично (14) и (15):
а„=^4-оШ, ^„=^4-оШ.
п п 1	\п?)' а п 1	\пг]'
где А„ и Вп имеют прежние значения. Тогда для разности / (х) —/(х)
получится разложение вида
ОО
а0 4* an cos 4“ Рл sin пх>
п— 1
где
ал> Рл = О ,
т. е.
1ал!> 1?лК§ (K=const).
00
Этот ряд, мажорируемый сходящимся рядом 2/<2“2> сходится по-
1 _
всюду равномерно. Отсюда уже ясно, что разность /(х)—f(x)
представляет собой непрерывную функцию с периодом 2тс и, сле-
довательно, /(х) имеет те же скачки и в тех же точках, что и /(х).
♦ Мы и здесь и впредь всегда подразумеваем, что
/^«g-l/^+oj+z^-o)],
равно как
/(- «)=/00=2- [/(- * + 0) +/(тс - 0)],
гак что все точки разрыва оказываются регулярными [см. 684].
512
ГЛ. XIX. РЯДЫ ФУРЬЕ
[708
2°. Теперь предположим сверх сказанного, что первая производная
f’(x) имеет предельные значения
/'(—* +°), /'(^±0),
и, кроме того, что повсюду (исключая «точки стыка») существует
вторая производная f" (х), которая к тому же в промежутке [— те, те)
имеет ограниченное изменение.
Используя уже доказанное, можно утверждать, что тогда
Д' Ь'' А' / 1 \
• п п П ।	/ 1 \
dfl 1"	1	1	С/ 1 о ] .
и п	п '	\п?) ’
Ьп=вЛ+а1=^+о{^,
п п ‘ п п 1 \п*/’
если через А'п, В'п. обозначить аналогично (11) и (13) величины
л=—8p’sin«^	(16)
Ц=1
(п=\, 2, 3, ...),
Вп = ~ 2 SP>c°sn^,	(17)
и=0
где
^’=/'(^ + 0)-/'(^-0) (^=1, 2, ... , т),
=/' (-*+0)-/' (те- 0).
Подставляя же эти выражения для а'п и Ь'п в формулы (10) и (12),
окончательно получим для рассматриваемого случая:
«.=4"-4;+о(±),	а»»
».=т’ + ^’ + °(й-	<19>
И здесь также можно доказать в некотором смысле обрат-
ное утверждение. Пусть коэффициенты Фурье некоторой функции
f(x) имеют вид (18) и (19), причем величины Ап, Вп, А'п, В'п. опре-
деляются формулами (11), (13), (16), (17) при данном наборе чисел
{8^°’}, Тогда про функцию f (х) можно утверждать, что она
непрерывна и имеет непрерывную производную f (х) повсюду в (— те, те),
исключая точки где и функция и ее производная претерпевают
скачки, соответственно равные 8^” и 8^’; кроме того,
/(_1т + 0)-/(те-0) = 8-
Г(-те + 0)-/(те-0) = 8-‘-.
TO8J
§5. ОЦЕНКА ОСТАТКА
553
Доказательство, как и выше, осуществляется с помощью построе-
ния вспомогательной функции f(x), которую на этот раз можно со-
ставить из квадратичных функций так, чтобы она и ее производная
имели именно указанные скачки в указанных же точках. Легко усмот-
реть, что разность f(x) — f (х) будет разлагаться в ряд Ф у р ь е с коэф-
фициентами порядка О . Тогда не только этот ряд, но и ряд, по-
лученный из него почленным дифференцированием, с коэффициентами
порядка О будут сходиться равномерно и, следовательно,
разность f(x)—f(x) будет периодична (с периодом 2тс) и непре-
рывна вместе со своей производной. Отсюда и вытекает требуемое
утверждение.
3°. В общем случае пусть f, f, ... , непрерывны в (— тс, тс),
исключая точки $ (р = 0, 1, ... , т), где все эти функции претерпе-
вают скачки, соответственно равные
С, 8^, ... , й'*"1’ (р = 0, 1, ... , т).
Кроме того, предположим, что повсюду (исключая «точки стыка») су-
ществует производная /(fe) и имеет в промежутке [— тс, тс] ограни-
ченное изменение. Введем обозначения:
т
Ап= — v 2 8®sin«'p.>
(i = 0,1.л — 1; п=1, 2, 3, ...)
т
^t)=i 2 cos/zv-
tx=O
Тогда имеют место формулы (соответственно, при k нечетном и k
четном):
Если же известно, что имеют место подобные формулы, то отсюда,
обратно, можно (как и выше) сделать заключение о точках разрыва
и величине скачков самой функции и ее । k — 1 производных.
)7 Г, М. Фихтенгольц, т. III
514
ГЛ. XIX. РЯДЫ ФУРЬЕ
[709
709.	Случай функции, заданной в промежутке [0, тс]. Как мы
знаем, если функция /(х) задана лишь от 0 до тс, то при соблюдении
надлежащих условий ее можно разлагать в этом промежутке как в ряд
по косинусам
/(_г) = у- 5ал cos пх (О^хг^тс),	(22)
так и в ряд по синусам
/(х)= J] bn sin пх (0<^х<^тс)	(23)
1
[689]. Такого рода разложения чаще всего встречаются на прак-
тике. Результаты предыдущего п° могут быть приложены и к рас-
сматриваемому случаю, если представить себе функцию f(x) продол-
женной и на промежуток [— тс, 0) (а) четным образом — для получе-
ния ряда по косинусам или (б) нечетным образом — для получения
ряда по синусам.
Пусть точками промежутка (0, тс), где функция f(x) и ее произ-
водные до (k—1)-й включительно имеют скачки, будут
0<^1<^«<С ••• <0/71 <Л>
а сами величины скачков попрежнему обозначены через
, С-,) (Р=1. 2, ... , т).
В случае продолжения функции четным образом скачки в точках £
воспроизводятся и в точках — $ , но с обратными знаками,
при продолжении же функции нечетным образом скачки воспроизво-
дятся в точках — с сохранением знаков. Далее, для четной
функции
/(+0)—/(—0) = 0, /(—тс4~ 0) —/(тс — 0) = О,
для нечетной же функции скачки
/(+0)-/(-0) = 2/(4-0),
/(_ + 0) -/(тс - 0) = - 2/(тс - 0)
вообще могут быть отличными от нуля. Наконец, отметим еще, что при
дифференцировании четная функция переходит в нечетную, а нечетная —
в четную. Если учесть все эти замечания, то для коэффициентов ап
и Ьп разложения нашей функции, соответственно, по косинусам или
709]
$ 5. ОЦЕНКА ОСТАТКА
515
по синусам получатся формулы вида (20) и (21), но с такими значе-
ниями для и В„}:
а(п=—4 28*’sin"^
ii=i
5»’—4 {2 cos <+ °) ~ c°s (л—°)} •
ii=i
(24)
В связи с этими формулами сделаем следующее важное замечание.
Пусть функция f(x) непрерывна во всем промежутке [0, л] вместе со своими
производными до (к— 1)-го порядка включительно; кроме того, пусть суще-
ствует и k-я производная и имеет в этом промежутке ограниченное изменение.
Тем не менее, вообще говоря, нельзя утверждать относительно коэф-
фициентов ап и Ьп разложений. (22) и (23), что они будут порядка О gri)
[ср. 707 и формулы (8)!]. Действительно, хотя все суммы в этом случае
будут нулями, этого нельзя сказать про суммы
= 2 {/<*> (0) — cos пл (”)}•
п те
Продолжение функции нечетным образом искусственно создает разрыв при х =
= 0 или нарушает периодичность у самой функции и ее производных четного
порядка, а продолжение четным образом делает то же с производными нечет-
ного порядка!
Поэтому, если требуется разложить упомянутую-функцию /(х) в проме-
жутке [0, л] в быстро сходящийся ряд, с полным использованием дифферен-
циальных свойств функции, целесообразно продолжить ее на промежуток
[—л, 0] с помощью многочлена (2fe—1)-й степени г (х), определяемого
из условий
}	г (0) = f (0), г' (0) = Г (0).г1*"11	(0) = У1*-1’ (0),
Г (— л) = f (л), Г’ {— л) = f (л).Г1*"* '(—*)= fk~l> (л).
[Построить такой многочлен можно, например, по способу, указанному в п° 257.]
Таким путем мы сохраним дифференциальные свойства функции для всего про-
межутка [—л, л].
Пусть для 0 sgxsg л, скажем,/(х) = х — Для того чтобы осуще-
, ствить разложение этой функции с коэффициентами порядка О j, мы про-
должим ее с помощью многочлена
, .	л , . Г	12 ,	30	201	12	.	30 .	20 ,	, л
г (х) = X --гг + X*---т Xs--о X------. =--;	X6---; X1--s Xs	+ X — Н-.
' '	2 *	(	л4	л’	л2]	л4	л8	л8	* 2
Если для продолженной таким образом функции составить обычный ряд
Фурье, то для функции /(х) = х — ~ в промежутке [0, л] и получится
искомое быстро сходящееся разложение:
12	1 т , 1440
-т-ул-----лл COS (2v — 1)ХЧ-------7-
л2 (2v — 1)’ J '	' * л4
^sin2vx-
Изложенный здесь прием указан А. С. М а л и е в ы м,
17*
516
ГЛ. XIX. РЯДЫ ФУРЬЕ
(710
710. Метод выделения особенностей. Пусть функция /(х)впро-
межутке [0, it] задается рядом (22) по косинусам или рядом (23) по
синусам углов, кратных х*, причем коэффициенты этих разложений
имеют вид (20) или (21), где А^, определяются формулами (24).
Ряды эти сходятся плохо, и мы знаем, что причиной тому служат
разрывы самой функции и ее производных. Акад. А. Н. Крылов
предложил для этого случая своеобразный метод выделения осо-
бенностей, благодаря чему достигается улучшение сходимости ряда.
Сущность этого метода, собственно говоря, уже содержится в пре-
дыдущем изложении. Она состоит в построении такой вспомогательной
(кусочно-полиномиальной) функции f(x) с известным тригоно-
метрическим разложением, которая как бы впитывает в себя
все особенности данной функции /(х), ясные из ее разложения. Вы-
читая из функции /(х) эту вспомогательную функцию и соответственно
этому ив данного разложения — разложение вспомогательной функции,
мы тем самым выделяем плохо сходящуюся часть данного
разложения, так что остающийся ряд уже сходится быстро.
Проще всего, впрочем, этот результат получается, если научиться и е-
поср е дственно суммировать, пользуясь уже известными разложениями,
эти плохо сходящиеся части.
Г. Пусть задан ряд по косинусам (22), причем
«п=—
п * \ns)’
где
т
Ап = — ^^1 Сц sin	(25)
11=1
Точки
0 < ^ < < ... < 5т < л
даны, равно как дан и набор чисел {Ср.}. Установим непосредственную сумму
ряда
ОО
g (х) = 2 cos пх'
71=1
Простые преобразования приводят к результату:
т со	со	т
р.=1	п=1	п—1	р. = 1
* Часто встречающийся на практике случай, когда разложение произво-
,Л „	ях
дится в промежутке [0, Z] по косинусам или по синусам углов, кратных -у,
„	„ тех
получается из рассмотренного в тексте случая простой заменой х на —.
710]
$ 5. ОЦЕНКА ОСТАТКА
517
причем сумму
? (X) = 2	2 Sitln(x + M
п = 1	п=\
легко вычислить, если вспомнить известное [690, 2)] разложение
2 sin nz
п ’
п=1
которое имеет сумму —-
< z <; 0. Таким образом,
при 0 < г < 2л и, очевидно,
л-)-2 о
—при—2л <
«Рр. (*) =
л 4-х— 6ц. л — х —8м	. .	,
—Г- ---&-----------&= —Л-|-8ц дЛя Х<8ц.
л — х 4- 8и. л — х — 8,,
----------------= ДЛЯ х >
Отсюда g (х) = const = 7ц внутри каждого из промежутков (8ц, 8ц+1) (р- =»
= 0, 1...т) * и претерпевает в точках 8ц (р. = 1, 2, ..., т) скачки, в точ-
ности равные Сц. Мы имеем, следовательно, 7ц— 7ц-1 = Сц (|*== 1, 2,..., т),
откуда
и
Ъ = 7о+5 <ъ;	(26)
Х=1
кроме того, так как (0) = — + то
т	т	т
7o=s(O)=2 (~"+w=422	(27)
Ц=1	Ц = 1	(1=1
Таким образом, функция g(x) вполне определена.
Пусть, например, имеем разложение:
“ sin п у
g W = 2- —~— cos пх.
п— 1
Здесь
л 2	. л
Ап =------Ci sin п -н-,
причем Ci — — у, 81 = у. Тогда
____________________________	1 л л п __________ л
~Я'1'2 ‘2“Z
* Для удобства мы полагаем 8о = О и 6m+i = it.
518
ГЛ. XIX. РЯДЫ ФУРЬЕ
[710
или, непосредственно,
ТС
00 sin и -х-
’• = 6<0)=2-Т-
П=1
затем
-1Г
— 1 — 4 ’
7i=t<>4-ci=—-j.
Итак, окончательно, функция g(x) равна при	и равна —
л
при -% < ХС- л.
2°. Рассмотрим теперь ряд по синусам (23), причем
где
т
ВП— — СцСОВ/^и + со — Ст-иСозпл}. '	(28)
р=1
На этот раз зададимся целью непосредственно просуммировать ряд
h (х) = sin пх-
71=1
Имеем:
й(х)=	Sin”(x + ?IJL) | sinn(x —(
[1=1 n=l	n = l
co	oo
. 2c0 sin nx________Г yi sin n (x -|- TC) . sin n(x — tc)"| __
"* TC n TC I	n ‘ n J
я=1	ri=l
m
=2 л
p.=i
причем
, . л — (x 4- л) л -I- (x — д)
<p(x)=-------^2~!— -------!—— — x	для всех x;
( ® — (* + 5p.)	” + (^~M
I 2	2	—
I n — (•* Ч~ У । 71 — — 5ц) _
12^2
Очевидно,
Л(+О) = со, Л(л —0) = cm+I;
Л(5ц + 0) —Л(5ц —0) = С(1 (ц=1, 2, ..., т).
710]
$ 5. ОЦЕНКА ОСТАТКА
519
Вместе с тем повсюду (исключая точки разрыва) существует производная
Л' (х) = const = f, где
ш
7 — ~ (ет+1 — со —	.	(29)
ц=1
Функция Л(х) внутри каждого из промежутков (£и, 5^.,.,) оказывается
Рис. 136.
линейной функцией с коэффициентом 7 при х:
h (х) = 7Х + 8^ при Хр.
([л = 0, 1, ..., m),
причем
80 —Со> = со Ч* си ••• »	= со 4“ ci Ч” •• • 4“ сгп‘	(30)
Легко выполнить построение графика функции Л(х) (рис. 136). Прямая,
соединяющая точки
т
(0, с0) и (л, cffl+1 — 2	’
1
очевидно, будет иметь угловой коэффициент 7. Остальное построение ясно
из рисунка.
Пусть, например,
тс
Sin п
sinnx,
Л(х) =
п
Я
ТС
cos/г -% t
co==cs=O,
1
— х
тс
i 1	1 ,
— X — 1 = — (х — Тс)
тс	тс '	'
результатом, чтобы
1 е
<1—1, Si—2-.
л
при -2
улучшить сходимость ряда
л
2" ’
так что
R -	‘
Вп------
Здесь (рис. 137)
Л(х) =
Воспользуемся эт
ОО
... .	2 V п л .
/(х) =— — 2, z>3_1 cos п у sin пх.	(31)
л=2
620
ГЛ. XIX. РЯДЫ ФУРЬЕ
[7ГО
Так как
п _ £.	1	= 1 ,	1
п3— Г-' п ' 1__ 1 п п (п2— 1)’
п3
то в данном случае
Если из функции f(x) вычесть только что найденную функцию h (х), то для
разности /(х)— Л (х) получится разложение
2 VI C0S ” 2
Я Z п(п3 — 1) Sin"X>
/1=1
коэффициенты которого будут уже порядка O^j!
3°. Возвращаясь к ряду по косинусам (22), предположим теперь, что
а —	— — Д- О ( 1 'l
где Ап выражается формулой (25), а В'п получается из (28) заменой постоян-
ных с0, с,...cm+1 другими постоянными с'о, с[, ..., Так как мы уже
умеем [см. 1°] выделять часть тригонометрического ряда, зависящую от чле-
нов первого порядка, то обратимся к членам второго порядка.
Пусть (заменяя для упрощения обозначений В’л через Вп)
ОО
п= 1
Очевидно, gt (х) есть непрерывная функция от х. Продифференцировав этот
ряд почленно, получим новый ряд
ОО
gl(x) = 2 ^sinnx>
/1—1
который мы уже умеем суммировать [2°]. Так как последний ряд равно-
мерно сходится в любой замкнутой части промежутка [0, тс],, не содержа-
щей ни концов этого промежутка, ни точек разрыва* *, то (исключая эти
точки) его сумма действительно представляет производную функции gx (х).
Итак, в силу 2°,
gi (х) = ix + 8р. для ?р < х < 5р+1,
(IXsssO, 1, ... , /и)
где у и 8р определяются формулами (29) и (30). Интегрируя, находим (г уче-
том непрерывности!):
gi (х) = у 7Х2 + 8рХ + ер для Ер х Ер+1.
(р. = 0, 1, т)
оо
Л ~	• „	v sin nz
* Это вытекает из известных свойств ряда 7----------------.
1
7101
S 5. ОЦЕНКА ОСТАТКА
521
В точках деления 5и+1 значение функции gt(x) получается одновременно по
двум формулам, так что
~2~ Н- ^р.^+1 Н" ~	^+1	Н- ep.+i"
Отсюда (если вспомнить,’ что 8ц+1 = 8^	cp.+i):
ер.+1 = ер.	Сри+15|Д.+ 1-
Если известно е0, то по этой формуле последовательно найдутся е,................
Что же касается е0, то оно определится равенством:
со
eo = gl(O) = -2^.
л=1
Сумма этого ряда может быть найдена и в конечном виде, если вспомнить
выражение Вп и воспользоваться известным [690, 9)] разложением:
со
2 cos пх
п2
71=1
Зх2 — блх -|- 2л2
12
(0 -С х -С 2л).
Например, если дано
“ 1 — cos п у
& (х) = 2, --------------cos пх,
то здесь
в i t
#п=—1 +COS Пу, с0== —у, С1==у,
Л	тс
cs = 0, £j = y,
Для определения
Л	Л
положим в упомянутом выше разложении сначала х = 0, а затем х = у;
5л2 _	л2 _
в результате найдем Ео = -5й". Тогда е1 = е0— с1;1 =—Окончательно
00	00
gl(x) =
4°. Теперь в ряде по синусам (23) положим
где Вп выражается по-прежнему формулой (28), а А'п строится по образцу
(25) —с заменой с на с'. И здесь достаточно ограничиться лишь членами
второго порядка.
522
гл. xix. ряды фурьв
(710
Рассмотрим же ряд (снова: Ап вместо А^)
со
(х) = sin пх<
/1=1
представляющий, очевидно, непрерывную функцию. Дифференцируем:
ОО
h’i (х) = 2 V cosnx = 8(х)
n=l
[см. Г]. Как и выше, легко убедиться, что (исключая концы промежутка и
точки Ец) g(x) действительно будет производной от Aj(x). В силу Г,
А[(х) = 7(1 для £ц < х < Ец+1 ((х = 0, 1.т),
где уц определяются формулами (26) и (27). Отсюда
Mx)=vH для Ец<х<Ец+1.
При этом 80 == О [так как Л1(0) = 0], а остальные 8ц определятся последо-
вательно из условия непрерывности функции ht(x) в точках Ец+1:
Vm-i + 8ц = 7ц+1Ец+1 + 8ц+1	(р. = 0, 1, ..., т— 1),
что дает
==	ср.+1£|х+1-
Пусть, например, дан ряд
hi (х) = sin х —g- sin Зх ~ sin 5х —... ,
который можно представить и в виде
°° sinn-J
hi (х) = 2, —“г— sin пх-
П = 1
Здесь
Tt	71	71	ТС	ТС®
5i=-y, ci= 2’ 'io:=‘4'> 'il==	~4< ®о=о> ®1==‘4‘
[ср. пример в Г], так что
-j-x,	если
2
7С , ТС3 ТС ,	v	7С
—-4 х + -3- = -^-(тг —х), если ysSx^Tt.
5°. Можно было бы подобным же образом просуммировать и части три-
гонометрического ряда, связанные с членами более высокого порядка в раз-
ложении коэффициентов. Вместо создания общих схем практичнее в каждом
данном конкретном случае проделывать то, что мы делали выше при рас-
смотрении рядов общего вида.
Вернемся для примера снова к ряду (31); полагая на этот раз
« =1+>+__L__
/Is—1 п ^п3^п3(п2 — 1)’
710)
S 5. ОЦЕНКА ОСТАТКА
523
представим bn в виде
.	2	л	1	2	тс	1	2	л 1
0П =-----cosn-x- • ------cosn-x- • -т----cos я„-----------гг.
" л	2	п	л	2	я’	л	2	я’(я2—1) ’
в соответствии с чем функция/(х) разобьется на три слагаемых. Первое из
них, h (х), есть функция, уже вычисленная в 2°. Рассмотрим второе слагаемое:
2 у Cosn 2 .
g(x) = — — 2i ....п» smnx-
п—1
Дифференцируя дважды, найдем:
оо	”
2 -V C0SnT
/1—1
sin пх.
Последняя функция только знаком отличается от h (х):
g" <х) =
Л
Л	Л
если Ojgxjg-^-,
л
если -g- х s;; л.
Отсюда, интегрируя, получим:
-^х2 + 7°
-^(Х-П)2 + Ъ
_	л
для 0 х
л
для х л.
g' (*) =
Приравнивая два значения g'(-получающиеся отсюда, установим, что
Ъ=7о- Значение же ?0 легко определить, непосредственно полагая х = 0 в
разложении g'(х): 70 = ^, Еще раз интегрируя и принимая во внимание,
что g (0) = g (2л) = 0, найдем:
g(x) =
~i*3+7ox
— (х — ”)’ + То (X — л)
для OsgxsSy,
Л
ДЛЯ -у X fig л *.
Таким образом, функция g(x) определена вполне, и мы имеем окончательно
f (х) = h (х) + g (х) + т (х),
* Приравнивая два получающиеся отсюда значения	снова нахо-
дим, что То = ^.
ГЛ. XIX. РЯДЫ ФУРЬЕ
[711
где функция <р(х), хотя и неизвестна в конечном виде, но задается разлог
гкением
2 V C0S”T
<₽(х) = У	——sin их,
т 4 ' л и3 (и2 — 1)	’
л=2
коэффициенты которого будут уже порядка О и очень быстро убывают.
§ 6. Интеграл Фурье
711. Интеграл Фурье как предельный случай ряда Фурье. Мы
хотим воспроизвести здесь в существенных чертах те замечательные
по их прозрачности, хотя и лишенные строгости, соображения, кото-
рые привели Фурье к его интегральной формуле *.
Если функция f(x) задана в конечном промежутке [—I, Z], то
при определенных условиях, которые нас здесь не интересуют, ее
можно представить в этом промежутке тригонометрическим рядом:
со
л, ч д0 । v	тях « < тпх
f (x)=-% + 2 cos ~i—ьb*sin ~r<
m= 1
где
I	t
1 f j:, , тли ,	.	1 С л, . . тли ,
am=j- \/(h)cos —j-~du, bm = —	—j—du
—l (m=0, 1, 2, ...)	—l	(m=l, 2, ...)
[cm. 688]. Подставляя вместо коэффициентов am и bm их выражения,
можно переписать ряд в виде
I	оо	I
=	2 Т	§/(«)cos ™(u — x)du. (1)
— I	m = \	—I
Пусть теперь	функция	f(x)	будет	определена во всем бесконеч-
ном промежутке	(— оо,	оо).	В этом случае, каково бы ни было х,
соответствующее значение /(х) выразится разложением (1) при лю-
бом Z^>| х|. Переходя здесь к пределу при /—►-(-со, попытаемся
установить «предельную форму» этого разложения.
Про первый член правой части равенства (1) естественно считать,
что он стремится к нулю **. Обращаясь же к бесконечному ряду,
* Эта формула, независимо от Фурье, была получена и Коши.
** Это становится очевидным, например, если предположить, что ин-
+°°
теграл \ f (и) du сходится.
— ОО
711]
$ 6. ИНТЕГРАЛ ФУРЬЕ
525
мы можем рассматривать множители -у под знаком косинуса как
дискретные значения
я	2л	тл
— ~Y > • • • ’ zm — ~i~ i	•
некоей переменной z, непрерывно меняющейся от 0 до -{-со; при
этом приращение
^zm == zm-tl	zm == >
очевидно, стремится к нулю при I —► -ф- со. В этих обозначениях
наш ряд перепишется так:
ОО	I
— 2 Д2,я»-1 $ f w c°s (и—
m=l	— I
Он напоминает интегральную сумму для функции
1 V
— \ / (и) cos z (и — х) du
— СО
от z в промежутке [0, -}-оо]. Переходя к пределу при Z->-f-oo,
вместо ряда получим интеграл; таким путем и приходим к интеграль-
ной формуле Фурье:
4~ОО -j-oo
/(х) = -i dz	f (и) cos z(u — х) du.
О	—оо
Можно представить эту формулу, раскрывая выражение косинуса
разности, и в виде
СО
f(x) — [a (г) cos zx -|- b (г) sin zx] dx,
и
где
4-оо	4-со
1 С	1 С •
a (z) = — \ f (и) cos zu du, b(z) = — \ f (и) sin zu du.
— 00	— 00
Здесь ясно обнаруживается аналогия с тригонометрическим разложе-
нием: лишь параметр т, пробегающий ряд натуральных значений, за-
менен здесь непрерывно изменяющимся параметром г, а бесконечный
ряд — интегралом. Коэффициенты a (z) и b (г) также по своей струк-
туре напоминают коэффициенты Фурье.
Конечно, все эти соображения имеют характер лишь наведения;
действительные условия справедливости формулы Фурье еще
626
ГЛ. XIX. РЯДЫ ФУРЬВ
|712
подлежат выяснению. Но и при проведении строгих рассуждений мы
будем следовать основным этапам рассуждений, связанных с рядами
Фурье.
712.	Предварительные замечания. Относительно функции f(x)
предположим теперь, что она абсолютно интегрируема в бес-
конечном промежутке (— оо, оо). В этом предположении рас-
смотрим интеграл
А 4~со
J(A) — у \ dz f(u) cos z {и — хй) du,
О —оо
где А есть произвольное конечное положительное число, а х0 — лю-
бое фиксированное значение х. Этот интеграл представляет аналог
частичной суммы ряда Фурье: из него интеграл Фурье
4~со 4-°°
-i-	( dz /(и) cos z (и — х0) du	(2)
О —оо
получается в пределе при А —►	оо.
Так как функция f(x) и при любом конечном В^>0 также аб-
солютно интегрируема в промежутке [—В, В], то по теореме IV*
п° 497 будем иметь:
АВ	в	А
^dz § f(u) cos z (и — x^)dii = $ f (h) discos z (u— xa)dz==
о-в	— BO
в
(*	/, 4	sin z (u— x0)	,	/o,
= \	----u-x	du-	(3)
J	*♦ ~~~
-В
Но интеграл
Ц- со
f (и) cos г (и — х0) du	(4)
— ОО
мажорируется сходящимся по предположению интегралом
$ 1/(й)| du
и, следовательно, сходится равномерно относительно z (как
при и = -j-oo, так и при и — — оо) для любого промежутка его
в
значений. Таким образом, интеграл § f(ti) cos z (и — х0) du при
—в
В — + оо стремится к своему пределу (4) равномерно. Поэтому,
переходя в равенстве (3) к пределу при В —-f-oo, в интеграле
713]
§6. ИНТЕГРАЛ ФУРЬЕ
527
слева предельный переход можно выполнить под знаком инте-
грала [теорема I п° 493] *. Отсюда для J (А) получается выражение
в виде интеграла
4-со
г/»\ ll и \ sin А (а —	.
dW=~ \ /(«) a’du,
— СО
напоминающего интеграл Дирихле [681] и в действительности
играющего такую же точно роль. Элементарным преобразованием его
легко привести к виду
4-00
•/И)=± $ /(хо+О^-л=
— оо
4-00
= 4	[/(Xo + 0+/(xo-f)]S^dt	(5)
Для дальнейшего изложения нам понадобится следующее очевид-
ное дополнение к основной лемме п° 681:
Если функция g(t) абсолютно интегрируема в бесконечном
промежутке [а, -|-оо], то
4-00
lim \ g(Osinprf(ft = O
Р-4-оо а
(равно как и
lim	S (О cos Р* dt — 0).
Р-Н-оо а
Доказательство можно скопировать с доказательства самой леммы
п° 681 (для случая, когда функция f(x) имеет особую точку).
713. Достаточные признаки. Умножив обе части равенства •
ОО
j = |JmnA£^	(Л>0)
на постоянное число So — предполагаемое значение инте-
грала (2), вычтем результат почленно из равенства (5). Мы по-
лучим
00
J(A)-5o = | С	(6)
* Ср^теорему IV п’ 508, где подинтегральную функцию мы предполагали
непрерывной. Здесь мы такого предположения не делаем.
528
гл. xix. ряды фурьв
[713
если, как и в п° 683, положить для краткости
? (О =/(Хо + о +/(Хо - о - 2S0.
И здесь мы ограничимся случаями, когда (а) функция f(x)
в точке хл непрерывна, либо (б) имеет в этой точке с обеих сторон
разве лишь разрывы первого рода. При этом мы полагаем:
в случае (а) З’о=/(х#),
в случаев 9_______/(хо + °)+/(хо —0)
в случае од —-------------,
В этом предположении имеем теперь
Признак Дини. Интеграл Фурье функции f(x) в точке хп
сходится и имеет значение 8$, если при некотором h^>Q сходится
интеграл	д
Представим интеграл (6) в	виде	суммы интегралов:
оо	Л	оо
_Ц=_Ц+1С.
л J	те	J	1	тс	J
0	О	Л
Первый из них при А—--ф-оо стремится к нулю — в силу основной
леммы п° 682. Что же касается второго, то, подставляя вместо ср(/)
его выражение, разобьем этот интеграл в свою очередь на два сла-
гаемых:
ОО	оо
1 f/(Xo + <)-b/(x0-0 sin	2 F
те J	t	те Л t
h	h
Ввиду предположенной абсолютной интегрируемости функции f
будет абсолютно интегрируемой и функция
f (хо ~Ь О +/(-Ч> — 0
t	’
а тогда первое слагаемое при А—«--ф-оо стремится к нулю уже
в силу того дополнения к основной лемме, которое сделано в конце
предыдущего п°. Наконец, стремление к нулю интеграла
СО	со
Л	АЛ
непосредственно очевидно по самому определению несобственного
интеграла.
714f
§ 6. ИНТЕГРАЛ ФУРЬЕ
529
Отсюда, как и в п° 684, могут быть получены более простые
частные признаки. Упомянем для примера, что достаточным является
существование для функции /(х) в точке ха конечной производной
или, по крайней мере, конечных односторонних производных.
К интегралу Фурье приложим также и
Признак Дирихле—Жордана. Интеграл Фу рье функции f(x)
в точке х0 сходится и имеет значение Se, если в некотором
промежутке [х0 — h, х0 -j- h] с центром в этой точке функ-
ция f(x) имеет ограниченное изменение.
Если интеграл
ОО
АЛ) =4 № + О+/(х0-О]4^л
** J	*
представить в виде суммы интегралов
h	оо
-Ц+-Ц,
л J 1 те J ’
□	Л
то про второй из них мы только что установили, что он при А —* оо
стремится к нулю. Первый же стремится к
| 1	+ 0) +/(х0 - 0)] =
— на этот раз на основании леммы п° 685. Действительно, функция
+	— О в промежутке [О, Л] значений t имеет ограни-
ченное изменение и, следовательно, представляется в виде разности
двух возрастающих функций, к каждой из которых в отдельности
лемма приложима.
714. Видоизменение основного предположения. В основе наших рас-
суждений до сих пор лежало предположение, сделанное в начале п° 712, что
функция f(x) абсолютно интегрируема во всем бесконечном про-
межутке от —со до -j-00- Затем уже, налагая дополнительно различные
условия на поведение функции в непосредственной окрестности интересующей
нас точки х0, мы и получим те или иные достаточные признаки представи-
мости функции в этой точке интегралом Фурье.
На практике, однако, указанное выше основное предположение иной раз
представляется стеснительным, и мы сохраним лишь допущение, что
Г. Функция f(x) абсолютно интегрируема в каждом конечном
промежутке,
а условие на бесконечности заменим следующим:
2°. Для | х | Н функция f(x) монотонна* и притом
lim /(х) = 0.	(7)
* Точнее говоря, она монотонна для х^/Уи для — Н по отдель-
ности.
530
ГЛ. XIX. РЯДЫ ФУРЬЕ
[714
Вспомним, что в рассуждениях п° 712 существенную роль играла равно-
мерная относительно z сходимость при и = + оо иприи=—оо интеграла (4)
4-.СО
J f(u) cos z (u—xa)du.
—oo
Так как для z^a>0
и
\ cosz (u — x0) du
_2
a ’
то по признаку 2° n° 515 мы и сейчас можем заключить о равномерной отно-
сительно z сходимости этого интеграла, но, как видим, на этот раз лишь для
значений z а, где а — любое, но фиксированное положительное число.
Это вынуждает нас ввести в рассмотрение вместо 7(Д) интеграл
А 4-со
1 С С
J(A,a) = —\dz I /(u)cosz(u—x0)du	(Л>а>0),
а	—оо
из которого интеграл Фурье получается при двойном предельном переходе:
при А — -j-оо и в — 0. Для интеграла J(А, а) уже можно получить совер-
шенно так же, как это сделано в п“ 712, выражение
ОО
7(Д, «) = 1 С \f(xa + t)+f(x0-t)]s^dt-
** А	*
оо
J 1/4*0 + 0 +/(*о~S^-dt, (8)
так что
оо
у . . к л If /л\ sin At ,,
J (Л, а) So = — \ <р (t) —-— dt —
к j	t
оо
- V 'i К4*о + о +/4*« -01 dt- (9)
о
Докажем прежде всего, что
ОО
lim ( [/(*о + 0+/4*о—01 ^« = 0.	(Ю)
а->0 J	*
Представим наш интеграл в виде
Д оо
714)
§ 6. ИНТЕГРАЛ ФУРЬЕ
531
где Д во всяком случае предположено столь большим, чтобы было xt— Д<
<—Н, х0-|-Д>//. Сразу ясно, что
д А
так что при а —О этот интеграл стремится к 0, каково бы ни было Д.
Обращаясь ко второму интегралу, имеем по второй теореме о среднем
значении 1487], с учетом соотношения (7),
со	Д'
С v* / sir dt , а\ С sm dt j,
\ 7(x0±f)—Л=/(х0±Д) \ dt —
ab*
'	. ч С sin Z ,	л.
=/(хв±Д)\ — dz (Д'>Д).
аА
Так как второй множитель здесь есть ограниченная величина (мы не раз об
этом упоминали), а первый ввиду (7) может быть сделан сколь угодно малым
за счет Д, то это же справедливо и относительно всего выражения. Соотно-
шение (10), таким образом, установлено, и поведение выражений (8) или (9),
как и раньше, оказывается зависящим лишь от интеграла, содержащего А.
Мы выше доказывали предельное равенство
СО
lim t [/(xo + O+/(xo-Ol^«=O
А—4-оо J	I
(где Л — некоторое фиксированное положительное число), опираясь на абсо-
лютную интегрируемость функции /в бесконечном промежутке. Это же
можно установить и пользуясь нашими новыми предположениями. В самом
деле, считая Д > Л, имеем:
оо Д со
А А А
Второй из интегралов справа можно трактовать так же, как и аналогичный
интеграл, содержащий параметр в; первый же интеграл при А — -f- оо стре-
мится к 0 по основной лемме п° 682.
Теперь уже ясно, что признаки Дини и Дирихле — /К о р д а н а [713]
остаются в силе и при новых предположениях относительно функции f(x).
Из всего сказанного выше, в частности, вытекает такое условие приложи-
мости формулы Фурье: если функция f(x) имеет ограниченное изменение
во всем бесконечном промежутке [— оо, оо] и, сверх того, выпол-
няется предельное равенство (7), то в каждой точке х0 интеграл Фурье
сходится и имеет значение So.
Действительно, при сделанных предположениях функцию f(x) можно
представить в виде разности двух ограниченных возрастающих функций
/1(х) и ft(x), имеющих как при х—►-J-оо, так и при х — — оо равные
[в силу (7)] пределы
/1 (+ оо) = Л (+ со) = с',	А (— со) =/а (— со) = с".
532
ГЛ. XIX. РЯДЫ ФУРЬЕ
1715
Введем теперь взамен j\ и /2 функции
{fi (х) — с' Для х Э5 0>	(ft (х) — С для х Э: О,
<р2 (х) = {
fl (х)-с" ДЛЯХ<0,	(/2(х)— с" длях<0.
Тогда по-прежнему
/(Х)=<р1 (х) — <р2 (х),
но на этот раз
lim <р2 (х) = lim <р2 (х) = О,
х-»±оо	х-» + со
так что для каждой из функций <рь <р2 выполнены условия 1) и 2); кроме того,
в любой точке к ним применим, очевидно, признак Дирихле — Жордана.
715.	Различные виды формулы Фурье. Предполагая выполнен-
ными достаточные условия применимости формулы Фурье, будем
считать для простоты, что в рассматриваемой точке х функция f(x)
непрерывна или, если разрывна, то удовлетворяет условию
у f(x + °)+/(х — 0)
т. е. что рассматриваемая точка является регулярной [684]. Тогда
во всяком случае имеем:
/(х) = ~ f dz ^/(н)созг(н — x)du.	(11)
0	— со
Ввиду того, что внутренний интеграл явно представляет собой
четную функцию от z, эту формулу можно переписать и так:
4-00 -J-co
/(х) = 2^ dz f (и) cos z (и— x)du.	(12)
— СО
Легко показать далее, что при сделанных в п° 712 [или п° 714]
общих предположениях относительно функции f(x) существует и
интеграл
4~ОО
f (и) sin z (а — x)du.
—оо
Этот интеграл, к тому же, является непрерывной функцией от z* и,
очевидно, нечетной. Хотя нельзя ручаться за существование для этой
функции несобственного интеграла от — оо до -]- оо, но он наверное
♦) Если в основу положены предположения п° 714, то исключение может
представиться лишь при z = 0.
715]
S 6. ИНТЕГРАЛ ФУРЬЕ
533
существует в смысле главного значения [484], причем
4-	со + °о
V. р. dz § f (и) sin z (и — x) du = 0.
— CO — 00
Умножая это равенство на ~ и складывая с (12), придем к соот-
ношению
+ СО	00
/(х) = ^ J dz § f(u)eis(a~x} du,	(13)
— со	— со
где наружный интеграл понимается в смысле главного значения.
В этом виде формула была впервые представлена Коши.
Возвращаясь к формуле (11), напишем ее в виде
ОО	+ со
f (х) = -i-	cos zxdz f (и) cos zu du -ф-
0	— co
oo	+00
-ф- -i- ? sin zx dz	/(zz)sin zudu.
0	— oo
Если f (и) есть четная функция, то
4~ со	00	4-00
§ f (и) cos zu du = 2 jj f (и) cos zu du, § f (u) sin zudu — 0,
— oo	0	— co
и мы получим упрощенную формулу, содержащую лишь косинусы
00	00
2	С	С
/(х) = —	\ cos zx dz \ f(ii) cos zu du.	(14
о	0
Аналогично, в случае нечетной функции f(x) мы приходим к фор-
муле, содержащей лишь синусы:
00	00
' 2 С	С
/(х) = — \ sin zx dz \ f (и) sin zu du.	(15^
Пусть теперь функция f(x) задана лишь в промежутке [0, -ф- оо)
и удовлетворяет в этом промежутке условиям, аналогичным тем
которые раньше были поставлены по отношению ко всему проме-
жутку (— оо, -ф- оо). Тогда, распространяя функцию f(x) на про-
межуток (—оо, 0) с помощью равенств (х^>0):.
/(—х)=/(х) или /(— х) = — /(х),
534
ГЛ. XIX. РЯДЫ ФУРЬЕ
[716
мы получим в первом случае четную, а во втором — нечетную
функцию в промежутке (— оо, -ф- оо). Для положительных значений х
(при соблюдении соответствующих достаточных условий) мы можем,
таким образом, пользоваться как формулой (14), так и формулой (15).
Если в точке х —О предположить функцию f(x) непрерывной,
то формула (14) и в этой точке приложима, ибо и продолженная
четным образом функция сохранит здесь непрерывность. Формула
же (15) вообще в точке х —О неприложима: она воспроизводит
значение /(0) лишь в том случае, если это значение есть нуль.
Эти соображения вполне аналогичны сказанному в п°689 о рядах
Фурье.
716. Преобразование Фурье. Предположим, что формула Фурье
(12) имеет место для всех значений х в промежутке (—оо,	—
за возможными исключениями в конечном числе точек. Эту формулу
можно себе представить, как суперпозицию. таких двух Формул *:
+ °О	т-
F(z)=-1= \ f{u)e^du, f(x)=-±= \ F (z)e~iX!! dz. (16)
у ZTC J	у Ztt J
— 00	r — co
Функция F (z), сопоставляемая no первой формуле функции f(x),
называется ее преобразован и ем Фу рье. В свою очередь, по
второй формуле функция /(х) является (обратным) преобра-
зованием Фурье (разница в знаке при i!) для функции F(x).
Заметим, что функция F будет, вообще говоря, комплексной даже
при вещественной /; впрочем, можно было бы здесь и исходную
функцию f предположить комплексной.
Равенство
4- оо
f(x) = -±=- J F (z) е~1хг dz,
где функция f(x) дана, можно рассматривать, как интегральное
уравнение относительно неизвестной функции F(z), стоящей под
знаком интеграла. Решение уравнения доставляется формулой
+00
F(^) = -A^ J f(ii)eizadu.
'	— 00
Естественно, эти равенства можно и поменять ролями.
Обратимся теперь к формуле (14); если она выполняется для
всех положительных значений х с теми же исключениями, что и
* Последний интеграл, если сделаны лишь те предположения относи-
тельно f(x), о которых была речь выше, понимается в смысле главного
значения.
716|
§ 6. ИНТЕГРАЛ ФУРЬЕ
535
выше, то ее можно представить, как суперпозицию двух — на этот
раз вещественных и совершенно симметричных!—формул
Fc (г) = J/ -2- j /(и) cos zn du,
__. оо
f(x)=l/ — \ Fc(z) cos xzdz.
(17)
Аналогично и формула (15) может быть разложена на две:
Fs (г) — С f (и) sin zu du,
(18)
sin xz dz.
о
Функции Fc(z) и Fs(z) называются, соответственно, косинус-
преобразованием или с и ну с-пр е о бр а з о в а ни е м Фурье
для функции f (х). Как видим, функция f по Fc (или Fs) получается
совершенно так же, как и FC{FS) по /. Иными словами, функции f
и Fc (Fs) взаимно являются косинус-(сйнус-)преобразованиями.
Коши назвал пары функций f и Fc или f и Fs, соответственно,
сопряженными функциями первого и второго рода. И здесь также
каждое из равенств (17) [или (18)] можно рассматривать как инте-
гральное уравнение, в котором функция вне интеграла дана, а функция
под знаком интеграла разыскивается; решение дается другим равенством.
Сопоставляя функции F, Fc и Fs, можно сказать следующее.
В случае четной функции f(x) имеем
F(z)=Fe(z)
(на значения z<^0 функция Fc(z) распространяется четным обра-
зом), а в случае нечетной /(х):
F(z) = ZFs(z)
(на значения z<^0 функция Fs(z) распространяется нечетным
образом). В общем случае функция /(х) разлагается на сумму чет-
ной и нечетной функций:
g(Х) = /(х) +2/(~ х) , h (х) =	.
Тогда *
F(z) = Qe(z)-\-tHs(z).
* Gc(z) обозначает косинус-преобразование для функции g(x), а
Я, (г) — синус-преобразование для функции Л(х).
536
ГЛ. XIX. РЯДЫ ФУРЬЕ
(716
В связи с этим обстоятельством достаточно ограничиться приме-
рами косинус- и синус-преобразований.
1) Пусть функция /(х) = е-ОА‘ (а>0, х>=0); тогда ее косинус-преобра-
зованием будет функция
|^^coszxdz = y
а синус-преобразованием — функция
___со	__
W = У I е-а‘ sin ZX dz =
Так как е ах интегрируема в промежутке [0, + ooj,
место и взаимные соотношения:
то должны иметь
2а
тс
cos zx
&+~Z2
dz = e~ax
(x^O)
и
£
тс
C z sin zx
\ a2 + zs
о
dz — e~ax
(*>0),
или
COS xz
a2 + z2
dz = ^~ e ax,
2a ’
z sin xz
a* + z*
dz = ^ e~ax.
Мы узнаем в этих интегралах известные уже нам интегралы Лапласа
[522, 4°].
Таким образом, в лице пар функций
е-ах ~\f —___а  и е~ах 1/"—_____________- 
’ К * «2 + х3	’ У я а3 + х3
мы имеем здесь примеры сопряженных функций первого и второго
рода (по Коши). Если бы интегралы Лапласа нам не были известны,
то Изложенная теория открыла бы путь к их вычислению.
2) Рассмотрим теперь функцию, определенную равенствами
/(х) =
1 для О х < а,
~ для х = а,	(а>0).
О для х 2> а
В этом случае
Г-- а	г—
„ , .	1 / 2 С . т / 2 sin ах
^(х)= у — \ coszxtfz = у —-у—
Если, желая и на этом примере проверить формулу Фурье, мы
найдем косинус-преобразование для полученной функции, то придем
717]	§ 6. ИНТЕГРАЛ ФУРЬЕ	537
к «разрывному множителю» Дирихле [497, 9)]
СО
2 С sin az
— \ ------cos zx dz
тс У Z
значение которого действительно совпадает с исходной функцией /(х)! Ана-
логично	а
t \ т /* 2 С . л ч /~ 2 1 — cos ах
Fs (*) = |/ — \ Sln zx dz — у —---------
и т. д.
Многочисленные примеры преобразований Фурье читатель найдет
в п°718.
717. Некоторые свойства преобразований Фурье. Представляет
интерес изучение свойств преобразований Фурье F(x) функции f(x),
исходя из тех или иных предположений относительно этой последней.
Прежде всего, если функция f (х) абсолютно интегрируема
в промежутке [— оо, -|- °°]> то функция
1 V
Д(х) = -^ \ f(u)elxadu	(19)
— со
непрерывна во всем этом промежутке и стремится к нулю при
х—>-± оо.
Непрерывность следует из того, что написанный интеграл равно-
мерно сходится при и = ±оо относительно х, ибо мажорируется
сходящимся интегралом ц_га
\f(u)\du,
— со
не содержащим параметра х. Доказательство копируется с доказа-
тельств теорем 1 п°518 и 2 п°520 с ссылкой на теорему 1* п°510
(вместо теоремы 1 п°506). Что же касается поведения функции F
на бесконечности, то оно устанавливается на основании заключи-
тельного замечания п° 712.
Предположим теперь, что xnf(x), где п — натуральное число,
также абсолютно интегрируема в промежутке [—оо, -J- оо].
Тогда функция F(x) имеет п последовательных производных
Г(х), ...,Д(л)(х),
которые при х -> ± оо все стремятся к нулю.
Последовательно дифференцируя интеграл (19) по параметру х
под знаком интеграла, получим:
F(*>(x) = -^=- J f{u) иkeixa du.
— со
{k « 1, 2, ..., п)
538
ГЛ. XIX. РЯДЫ ФУРЬЕ
р!8
Этот интеграл сходится равномерно относительно х ввиду наличия
мажорирующего интеграла
Н-ОО
5 \f(u)uk\du,
— со
чем и обосновывается право на применение правил Лейбница.
Доказательство копируется с доказательства теоремы 3 п°520 с
ссылкой на теорему 3* п° 510 (вместо теоремы 3 п° 507). Пове-
дение производных на бесконечности и здесь устанавливается с по-
мощью заключительного замечания п°712.
Итак, дифференциальные свойства функции F (х) в основном
определяются поведением функции /(х) на бесконечности. Наоборот,
по дифференциальным свойствам функции f(x) можно в некоторой
степени судить о поведении функции F(x) на бесконечности. Именно:
если функция f(x) и ее последовательные п—1 производные
стремятся к нулю при х->±оо, а п-я производная /<я) (х) абсо-
лютно интегрируема в промежутке [— оо, -J- оо], то
lim x"F (х) = 0.
X —► ± СО
Это непосредственно следует из выражения для F(x):
+«>
F (х) =-L.	$ /») («) eixa du,
— со
которое получается последовательным интегрированием По частям.
718. Примеры и дополнения. 1) Показать, что косинус-преобразование
функции е совпадает с нею же самой.
Действительно, по формуле п° 519, 6) (а):
Дифференцируя это равенство по х, придем к заключению, что синус-
-|*2
преобразование функции хе тождественно с нею самой.
2)	Установить формулу:
(а)
2 С sm2z
— \ —=— cos 2zx dz =
r. J z2
tin2
1—x, если Osgxsg 1,
О, если x 1.
2 C, /14-z2	.	1— e~x . n.
(6)	— \ In -—-----cos xz dz =-—— (x 0).
7181
| 6. ИНТЕГРАЛ ФУРЬЕ
539
У казание. Вычислить косинус-преобразование функции от х, указан-
ной справа, и воспользоваться сопряженностью обеих функций, (условия
применимости формулы Фурье выполнены!).
3)	Решить интегральное уравнение:
00
i g (z) sin zx dz = f (x)
для случаев, когда
(V sin x для 0 < x s£ л,
2
О для %2гл,
или
	тс -yCOSX для	0 X с тс
(б) /(Х) =	тс для	X = тс,
	0	для	X > Л.
Указание. Решением будет синус-преобразование для функции
„	. . sin л х	... х sin л х
Ответ, (a) -j (б) п -г.
4)	Показать, что функция ----- является одновременно своим собствен-
У х
ным косинус- и синус-преобразованием.
Имеем, например,
_________ со	_ 00
Г 2 С sin xz	. -\ГЪ	1 С sin<	..	1	.___
I/ — \ —dz — I/ —	•	—= \ -7=-	dt — —~	[522,	5 ].
г п^ Уг	г п	Yx^yt Ух
5)	Использовать синус-преобразование функции
1
е2г-х + 1
для получения нового интеграла.
По формуле п° 519, 8) (б) упомянутое преобразование будет
1 /1_________1 \
' I	2	2 /
\ в — е /
Так как исходная функция удовлетворяет условиям применимости формулы
Фурье, то она, в свою очередь, является синус-преобразованием только
что приведенной функции.
Учитывая значение интеграла
sinxz . л ,
340
ГЛ. XIX. РЯДЫ ФУРЬВ
(718
отсюда легко получить, что
С sin xz . _______________ п е~х — ё ~х
J ~~г_	dz ~~2 егХ + е~*х
° е* 2 — е 2
или, наконец, при других обозначениях
СО
С sin ах .	1 ,, а .	Л.
\ —г---dx = -н- th (а > 0).
\ sh пх 2	2 4	’
6)	Показать, что для функции
1 1
]Л2кх
синус-преобразование тождественно с нею же самой.
У Казани в. Воспользоваться формулой п° 519, 8) (а).
7)	Проверить формулу Фурье (14) для функций cos-^-x2 и sin-y-x2
(которые, кстати сказать, не удовлетворяют тем предположениям,
при которых формула Фурье была нами выведена!):
Имеем:
1	2	A	1
cos	z2 cos xz dz = ——
2	|<2it
22 + хг
1
)Л2^
z2 —xz
или, полагая z = x4-w и учитывая известные значения интегралов Фре-
неля [522, 5°]:
1
/2^
cos 4- (u2 — xs) du = —-I— J cos 1
2	/2it I 2
cos у «2 du 4-
+ sin у x’ t sin у «2 du
1	!	1	. . . 1	,
—cos -к- x2 4- sin x2
/2 \	2	2
Аналогично
С • 1 2 и
\ sin -%- z2 cos xz dz
о
1
/2
'	1 2	• 1 Л
cos -у х2 — sin -у х21.
Теперь уже непосредственно ясно, что косинус-преобразованиями полу-
ченных функций являются именно исходные функции, а это и равносильно
справедливости формулы Фурье.
8)	Проверить (а) формулу Фурье (14) для функции
/(x) = cix =
(интегральный косинус),
.V
718|
§ 6. ИНТЕГРАЛ ФУРЬЕ
541
(б) формулу (15) для функции
оо
. .	. С sin г! ..
g(x) = Sl X —-\ —у-Й
X
(интегральный синус).
Установленные нами условия применимости формул не соблюдены!
(а) Решение. По формуле п° 497, 19) (а):
О для х < 1.
Далее,
__________ со	со	со
1 Г 2 С _ . .	.	С cos xz .	С cos t .,
I/ — \ Fc (г) cos xz dz — —\ —-—dz=— \ —-—dt — cix.
0	I	x
(б) Указание. Использовать 497, 19) (б).
9) Проверить обе формулы
Фурье (14) и
(15) для функции -i, где
В силу 539, 3),
coszx
zs
Xs-1
,, , ,	”8 *
Г (s) cos у
а затем
cos zx
Г (s) cos у $ zl~S
dz
1	Tt	Xs
т> z \	713	2 т, /Г ч я (1 —8) ‘
Г (s) cos у Г (1 — s) cos —iy—-
Это и равно —j [если учесть ф о р м у л у дополнения для функции Г,
531, 5°]. Х
Аналогично проверяется и формула (15).
10) Проверить формулу Фурье (14) для функции Бесселя с нуле-
вым значком, Jo (х).
Мы имели в 524, 5):
“	(	0 при х> 1,
\ W cos zx dz =  при X < 1.
tf	( V 1 — X2
Поэтому
1Г
со	co	1	2
2 С , С . . .	,	2 С cos ох 2 J , . . .
— \ cos их du у JQ (z) cos zu dz-=- — \	du = — \ cos (x sin <p) dv.
J	J	К J У 1 __U8	Я J	Т/ T>
что действительно равно Jo (x) [ср. 695].
1
542
ГЛ. XIX. РЯДЫ ФУРЬЕ
(718
11) Рассмотрим (при n = 0, 1, 2, ...) функцию /(х), определяемую ра-
венствами
/(х) =
Ее косинус-преобразование равно
_ 1
ДЛЯ Osg X < 1,
для х> 1.
п
(1 -г2)
2 cos zx dz
или, если косинус разложить в ряд и почленно проинтегрировать:
/=’с(х) = 1/-| У (-1)^ Ь2’(1-г2)Л 2dz.
V = о	о
Но, в силу 534, 1),
_ (2м—1)1! (2л—1)1!
— 2v+n+1 (м-J-л)1
Поэтому, вспоминая разложение бесселевой функции со значком п [395, 14)],
окончательно получим:
__	со	___
(2п —1)1!
» = 0
Так как для исходной функции условия приложимости формулы Фурье
выполнены, то косинус-преобразованием для функции Fc (х) должна быть
именно исходная функция. Это приводит нас к интересному интегралу:
Jn («)	.
‘ „ - cos zx dz —
zn
(2n—1)!!(1	%2)
0
£
2 при 0^x< 1,
при x > 1.
При л = 0 отсюда получается уже известная формула [524, 5)].
12) В выражении интегрального логарифма
г
Чй <0<г<,>
положим z = e *(х>0) и t = e мы получим:
.. _х С du
h е х==— \ —г
х
718]
§ 6. ИНТЕГРАЛ ФУРЬЕ
541
Так как при х > 1
а при 0 <хс 1
то | li е~х | интегрируема от 0 до + оо, и обе формулы Фурье (14) и (15)
заведомо приложимы.
Найдем косинус-преобразование функции 11 е~х-.
Интегрируя по частям, приведем его к виду.
_	( с-* sin2X dz = - 1/— arctg Х
У л х j z	У п х
о
[522, 2°]. Отсюда, обратно,
00
С arctgz . л
I —cos zx dz =--------2" ‘le (х > 0)
о
— нами найдено значение нового интеграла!
Аналогичным путем, использовав синус-преобразование, найдем другой
интеграл:	ю
f ln(l+zs) .	.	, п.
\	i—!_—sin zx dz — — л li e x * (xz> 0).
о
13) Доказать, что в формуле Фурье
СО -{-со
/(х) = — f dz V /(u)cosz(u— x)du
л .1 J
О — со
при соблюдении каких-либо из указанных выше достаточных условий внутрен-
ний интеграл может быть заменен интегралом по любому конечному про-
межутку	ь
^f(u) cosz (и — х) du,
а
лишь бы только точка х лежала между а и ft.
* Промежуточный интеграл
со
С	cos xz — 1 .
\ е z---------dz
J z
легко вычисляется дифференцированием по параметру х.
644
ГЛ. XIX. РЯДЫ ФУРЬЕ
[718
Указание. Взамен /(«) рассмотреть новую функцию, равную/(и)
при a < и <. b и нулю — для прочих значений и.
14) Пусть функция f(x) монотонно убывает (в широком смысле) в про-
межутке (0, + ос) и стремится к нулю при х—>-|-оо; в окрестности точки
х = 0 предположим эту функцию интегрируемой*. Доказать, что тогда ее
синус-преобразование Fs (х) для х > 0 является неотрицательной
функцией.
Из сделанных предположений прежде всего вытекает существование
интеграла
со
(х) = 1/" JL f(z) sin xz dz
[476, 482]. Его можно представить и в виде суммы ряда
<д+1) -те
___ СО X
Fs (х) = т/" —	/ (z) sin xz dz,
п — 0 mt
~х
члены которого попеременно положительны и отрицательны и, к тому же,
по абсолютной величине убывают (ряд «лейбницевского типа», 381). Отсю-
да— требуемое заключение.
15) Пусть /(х)—ограниченная монотонно убывающая функция
в [0, + оо], стремящаяся к нулю при х—►-(-оо. Предположим, сверх того,
что для нее при х > 0 существует отрицательная и притом монотонно воз-
растающая (в широком смысле) производная /' (х). Доказать, что тогда
косинус-преобразование Fc (х) есть неотрицательная функция, инте-
грируемая в промежутке [0, + оо].
Имеем, если 0 < а < А <	оо:
л	л
5 \f'(x)l^x = — ^f'(x)dx=f(a)—f(A),
а	а
так что, ввиду ограниченности функции /(х), производная /' (х) интегри-
руема в промежутке [0, -(- оо]. Отсюда же следует, что
/'(х) —О при х—> + 00.
Интегрируя по частям, получим:
СО
f (z) cos xz dz —
о
sin xz dz;
если к последнему интегралу применить доказанное в 14), то окажется, что
Fc(x)=sO.
* Возможно, в несобственном смысле, если в точке х = 0 функция /(х)
обращается в бесконечность.
719]
§ 6. ИНТЕГРАЛ ФУРЬЕ
545
Так как для функции /(х) выполнены условия приложимости формулы
Фурье, то при х = 0 получаем
ОО СО	оо
/(4-0)= т/"А dz /(u)cosz«rf«= т/"А ( Fc(z)dz,
71 о о	“	71 о
в чем содержится и утверждение об интегрируемости функции 2% (z)!
Замечание. Подчеркнем, что ни одна из этих двух теорем не верна
для преобразования другого типа. Для функции /(х), рассмотренной в при-
мере 2) п° 716, соответствующее косину с-преобразование
р	sin ах
Fc(x)-y _
меняет знак. Еслй же взять f(x) = e~ax (пример 1) того же п°), то
с и н у с-преобразование
хотя и сохраняет знак плюс для х > 0, но не интегрируемо в про-
межутке [0, 4- ос].
719. Случай функции двух переменных. Формула Фурье
может быть распространена и на случай функции нескольких пере-
менных f(xb хг, ..., хп). Мы остановимся подробнее на функции
двух переменных f(xb х2), которук? мы предположим определенной
во всей плоскости (—оо, -ф- оо; —оо, -j-оо) и к тому же диф-
ференцируемой по каждой из переменных в отдельности.
Пусть, далее, при любом фиксированном х2 функция /(хь х2)
абсолютно интегрируема по х1 в промежутке [—оо, А оо] и,
аналогично, при любом фиксированном хх она абсолютно инте-
грируема по х2 в том же промежутке. Применяя при фиксированном
х2 к функции f (хь х2) от одной переменной Xj уже известную
нам формулу Фурье* (И), получим:
ОО + 00
f (хъ х2) — — \ dzi \ f (иь х2) cos («1 — х^ diti.
О — co
Аналогично и функция х2) от переменной х2 при фиксирован-
ном «1 в свою очередь представляется формулой:
СО	00
f (и1> Xi) — — dzt f («!, п2) cos z3 (гг2 — х2) du3.
0	— оо
* Условия применимости этой формулы здесь соблюдены в силу сделан-
ных предположений. Конечно, эти предположения можно было бы видоизме-
нить.
18 Г, М, Фихтенгольц, т. III
546
ГЛ. XIX. РЯДЫ ФУРЬЕ
[7J9
Подставляя, придем к искомой формуле:
СО	4“ СО	со
f (хр х2) = —'2- J d.Zi § cos zx (tii — xi) diti dz<i X
0	— co	0
4- co	CO	4“ OO	co
X	f (jh, «2) cos z2 (zz2 — x2) diii = dzi duY dzt X
— co	0	— co	0
+ co
X \ f («!> “a) cos Zi (ill — xi) cos г2 (ut — x2) zZzz2.
— co
Так же, как это было сделано в 715, и здесь можно перейти
к формуле, содержащей показательную функцию:
f(Xi, хг) =
со	4"00	4-°°	4*оо
= 4^5 dzi dill dZs f(iii,Ui)eilzaai~Xl)+2!‘{a2~X!‘}]diii, (20)
— со	—со	— со	— со
если только интегралы по zt и по г2 понимать в смысле главного
значения.
Если функция f(Xi, х2) оказывается четной как по х1э так и
по х2, то все промежутки интегрирования можно свести к проме-
жутку [0, 4“ 00] и сохранить лишь косинусы:
со
/(хьх2) = -^- \ cos ZiXidzi \ cos Zitiidiii \ cosz2x2d^2X
СО
X $ /(«!> па) cos z2w2dzz2. (21)
о
В случае нечетности вместо косинусов повсюду здесь надлежит
поставить синусы.
Обе формулы имеют место и для функции f(xit х2), заданной
лишь в первом квадранте [0, 4~	0> 4~°°]> так как 66 можно про-
должить на всю плоскость по желанию четным или нечетным обра-
зом (для формулы, содержащей синусы, исключение составляют точки
на осях!).
Во всех этих формулах порядок интегрирований должен быть
таков, как указано (разве лишь с перестановкой значков 1 и 2).
Если удается обосновать перестановку двух про-
межуточных интегрирований, то формулы приобретают
720]
§ 7. ПРИЛОЖЕНИЯ
547
особенно симметричную форму. Формула (20) в этом случае ока-
зывается эквивалентной двум таким:
+ со 4“ со
F (z,, z2) —dui	/{иьи^е^г^+г^биг,
— со — со
/(xi,x8) = 2^-	dzt	/7(z1,z2)e-i<2i*i+^2)dz8;
— ОО — СО
функция F(ziy z2) называется преобразованием Фурье функции
f{xb х2).
Аналогично этому и формула (21) распадается на две формулы,
имеющие на этот раз совершенно одинаковый вид:
СО	со
2 С	С
Fc(Zi,zi) = — XdUi \ f(uit ui) cos Zi«i cos z^ du*
CO co
2 С C
f (xit x2) = — \ dzt \ Fc (zb z3) cos z^ cos ztXi dz*.
Здесь Fc(Zt, zi) представляет собой косинус-преобразование функ-
ции f(x\, х^; очевидно, и f(xu xi) служит косинус-преобразованием
для функции Fc(zlt Zi).
Перенести все сказанное на с и ну с-п р ео б р а з о в а н и я предо-
ставляем читателю.
§ 7. Приложения
720. Выражение эксцентрической аномалии планеты через ее сред-
нюю аномалию. Разложёние функции в ряд Фурье приводит к удобному
аналитическому представлению функций, которое часто оказывается выгод-
ным для вычислительных целей. Изложенный ниже важный при-
мер этого рода мы заимствуем из теоретической астрономии.
Мы уже имели дело с уравнением Кеплера-.
E = M-|-esinE (0<е<1),	(1)
которое связывает эксцентрическую аномалию Е планеты с ее
средней аномалией М [83; 452, 2)]. В силу этого уравнения Е являет-
ся однозначной и дифференцируемой функцией от М, к тому же — нечетной.
Увеличение М на 2л влечет явным образом н увеличение Е на 2л. Отсюда
ясно, что sinE будет периодической функцией от М с периодом 2л и раз-
лагается в ряд по синусам дуг, кратных М-.
СО
sin Е = У bn sin пМ.
п= 1
Остается определить коэффициенты Ъп.
18»
548
ГЛ. XIX. РЯДЫ ФУРЬЕ
(720
По формулам (21) п° 689
те
bn — sin Е sin пМ dM =
те
. „ cos пМ	1 С ..dsinE ,,,
= — sin Е • --- 4---------\ cos пЛ4—; dM.
п |л1=о 1 п j dM
Внеинтегральный член обратится в нуль, так как при Л4 = 0 (или л) также
и Е = 0 (или л). Заменяя в последнем интеграле переменную М переменной
Е, для которой промежуток изменения будет тот же, и учитывая само урав-
нение Кеплера, получим далее:
те	те
1 С	1 с
-у- Ъп = — I cos пМ cos Е dE —----- \ cos (пЕ — ле sin Е) cos Е dE=
&	fl J	fl J
о	о
Г те	те
= 2^ \cos(n+l£ — nz sin E)dE 4- cos (n—IE — ns sin E)dE .
L о	о
Согласно известной интегральной формуле, выражающей функцию Jm(x)
Бесселя,
те
cos (тЕ — х sin Е) dE = Jm (х)
[см., например, п° 695]. Таким образом,
[Л1+1 (пе) + Jn-i (пе)1-
С другой стороны, легко установить тождество
[Лг+1 (*) + Jn-i (•*)! — Jn (•*)•
Поэтому
2
*» = — /„(«),
так что
оо
. „	2 V 1 , , ч •	,,
sin Е = — У —- Jn (ле) sin лЛ4
Л— 1
и, наконец,
оо
Е = М + 2 У -L Jn (т) sin пМ.
п = 1
Полученное выражение эксцентрической аномалии Е через среднюю ано-
малию М играет важную роль в небесной механике. Ранее нами уже было
найдено разложение величины Е по степеням эксцентриситета е с коэффици-
ентами, зависящими от М [452, 2)]. Но оно годилось лишь для значений
721J
§ 7. ПРИЛОЖЕНИЯ
549
концами в точках х = 0 и х = 1
е<0, 6627... и, например, не могло быть применяемо для кометных орбит с боль-
шим эксцентриситетом; установленная формула свободна от этого недостатка.
721. Задача о колебании струны. Наиболее важные приложения ряды
(и интегралы) Фурье имеют в области математической физики. Желая осве-
тить эти приложения примерами, мы начнехм с классической задачи о коле-
бании струны, которая сыграла важную роль в самой постановке вопроса
о возможности тригонометрического разложения функции.
Под струной мы разумеем свободно изгибающуюся и невесомую нить.
Пусть такая струна, длины I, закреплена i___... _ __ ___ .. С .. ..
оси х и под действием натяжения
И располагается в равновесии
вдоль этой оси (рис. 138). Пред-
ставим себе, что в момент 7 = 0
струна выводится из положения
равновесия и, вдобавок, точки ее
снабжаются некоторыми скоростя-
ми в вертикальном направлении.
Тогда точки струны начнут коле-
баться в вертикальной же плос-
кости *. Если допустить, что каж-
дая точка М струны с абсциссой
дая точка М струны с абсциссой х колеблется строго вертикально, то ее
отклонение у в момент времени Z jsO от положения равновесия будет функ-
цией от обеих переменных х и t:
у=у(х, t).
Задача и состоит в определении этой функции.
Ограничимся рассмотрением лишь малых колебаний струны, при
dy .
которых величины у и малы (так что струна незначительно отдаляется
от положения равновесия и остается пологой); это дает нам право прене-
брегать квадратами этих малых величин.
Возьмем элемент ds = M'N' струны в момент времени t (см. рис.);
его длину, в силу сказанного, можно считать равной его первоначальной
длине dx = MN в начальный момент, ибо
- /	/ а,.\2
dx = dx.
ds
Раз мы пренебрегаем изменениями длины, то и натяжение струны мы можем
считать неизменным.
На выделенный элемент струны действует в точке М' натяжение Н,
направленное влево по касательной в этой точке, а в точке N' — такое же
натяжение, но направленное вправо по касательной. Если через а и а обо-
значить соответствующие углы наклона касательной, то сумма вертикальных
составляющих этих сил (а только их нам и нужно учитывать) будет
lAdx.
Здесь мы снова воспользовались правом отбрасывать квадраты малых вели-
чин (например, положили
sin а = —	—. = tg а =	.
•вГ 1 ।	&	ti у / >
И (sin а — sin а) = 77
. ду
а затем приращение функции заменили ее дифференциалом.
* Плоскость рис. 138 мы и предполагаем вертикальной.
550
ГЛ. XIX. РЯДЫ ФУРЬЕ
[721
Если обозначить черезр «линейную» плотность струны, то масса элемента
будет
р ds = р dx.
Тогда по закону движения Ньютона произведение массы элемента р dx на
d2v
ускорение должно равняться найденной выше силе, действующей на этот
элемент:
. д3у „ д3у .
р dx •	= Н dx.
r cia дх3
Полагая
окончательно получим такое дифференциальное уравнение
в частных производных:
ai
Ос3 дх3'
(2)
которое и описывает изучаемое явление.
Кроме этого уравнения, искомая функция у—у (х, t) должна удовлет-
ворять еще ряду требований, прежде всего — так называемым предельным
или граничным условиям:
у (0, f) = 0, у (I, t) = 0,	(3)
выражающим факт закрепления концов струны. Затем, если функции f(x)
и g(x)* (OsgxsgZ) характеризуют отклонения и скорости точек струны
в момент t — 0, то должны выполняться и начальные условия:
У (х, 0) = / (х),	= g (х).	(4)
Таким образом, задача сводится к разысканию такой
функции^(х, Z), которая удовлетворяла бы уравнению (2)
и условиям (3) и (4).
Начнем, следуя по пути, указанному Фурье, с разыскания частных
решений уравнения (2), удовлетворяющих, сверх того, предельным условиям
(3), но отличным от нулевого решения (начальные условия мы
пока оставляем в стороне). Упомянутые частные решения мы станем искать
в виде произведения двух функций, из которых одна зависит только от х,
а другая — только от Z:
у = Х(х) Г (Z).
Уравнение (2) в этом случае принимает вид
XT" = а3Х"Т,
где штрихи означают производные по той переменной, от которой функция
зависит, или
Так как левая часть этого равенства не зависит от х, а вторая — от Z, то
общее значение их по необходимости не'зависит ни от х, ни от t и сводится
* При х = 0 или х = 1 обе функции, очевидно, должны обращаться в
нуль.
721]	§ 7. ПРИЛОЖЕНИЯ	551
к постоянной, которую мы возьмем в виде — а8Ха (при X > 0). Тогда уравне-
ние (5) распадается на два:
Т" + а*кгТ = 0, Х" + Х8Х=0;	(6)
их решения ( «общие интегралы> ) имеют вид:
Г=A cos akt 4- В sin akt,
Х=С coskx D sinXx.
Для того чтобы функция у = XT удовлетворяла предельным условиям (3), им
должна удовлетворять функция X. Полагая х = 0, сразу видим, что С = 0;
полагая же х = 1 и учитывая, что D уже не может быть нулем, придем
к условию
sin Х/ = 0,
откуда kl — пк при натуральном п. Таким образом, X может иметь одно из
следующих значений:
Х1=-^-, Х2 = 2у-, кп — п-^-, ....	(7)
Полагая при Х=Х„
AD = an, BD — bn,
придем к такой последовательности частных решений:
уп = (ап cosaXn<-|-6„ sinaX„f) sinXnx
(rt=l, 2, 3, .
Нетрудно видеть, что поставленным требованиям будет удовлетворять
и сумма этих решений, взятых в любом числе. Это наталкивает на мысль рас-
смотреть бесконечный ряд, составленный из всех таких решений,
и положить
СО
у = У, (ап cos aknt -|- bn sin aknt) sin кпх.	(8)
л = 1
Мы примем пока, что этот ряд сходится и что сумма его удовлетворяет
уравнению (2); выполнение условий (3) очевидно. Теперь лишь обращаемся
мы к нач а льным у слов иям (4) и постараемся распорядиться постоян-
ными ап, Ьп так, чтобы удовлетворить и им. Допустим, что для ряда (8)
законно почленное дифференцирование по t, так что
СО
= ^ (— алаХл sin аМ + bnaln cos aknt) sin кпх.	(9)
л = 1
Полагая в (8) и (9) t = 0, приходим к условиям
У, ап sin k„x=f(x), ^aknbnsmknx =g(x).	(10)
Отсюда, если только функции f и g удовлетворяют условиям разложимости
в ряд Фурье, по формулам (25) п° 689 и определяются, наконец, искомые
* Если бы мы взяли постоянное значение отношений (5) в форме а2Х!, то
предельным условиям могла бы удовлетворять только функция X, тождест-
венно равная нулю.
552
ГЛ. XIX. РЯДЫ ФУРЬЕ
(721
коэффициенты:
2 С	2 С
an = —j~\f(x)sm\nxdx, ba = ^--j-\g (х) sin\nx dx. (II)
о	" о
Мы получили, таким образом, по крайней мере формально, полное
решение поставленной задачи в виде ряда (8) с коэффициентами, вычислен-
ными по формулам (11)!
Правда, вопрос о том, будет ли оно действительно решением,
пока остается открытым. Для того чтобы ответить на него, наложим теперь
требования на функции f и g; именно, пусть функция g будет дифференци-
руема, а функция f дважды дифференцируема, причем производные f" и g'
предположим имеющими ограниченное изменение в промежутке [0, /]. Тогда
имеют место такие оценки *:
Оба разложения (10) в действительности имеют место во всем промежутке
[0, /]; сходится и разложение (8), причем определяемая им функция удовлет-
воряет как предельным, так и начальным условиям (почленное дифференци-
рованное по t теперь оправдывается равномерной сходимостью ряда (9)!).
Несколько сложнее удостовериться в том, что эта функция удовлетворяет
самому дифференциальному уравнению **.
Заметим, что ряды (10) сходятся и за пределами промежутка [0, /]; обо-
значая их суммы по-прежнему через/(х) и g (х), мы получаем, таким образом,
распространения этих функций на весь бесконечный промежуток (—оо, 4-оо)
с сохранением их дифференциальных свойств, за исклю-
чением разве лишь точек вида kl при целом k. Ряд для g (х), равномерно сходя-
щийся в любом конечном промежутке, можно почленно проинтегрировать,
так что
— cos	= ~<Г gl (Х>’
1
где gi(x) есть одна из первообразных для функции g(x). Раскрывая скобки
в (8), можно переписать это выражение в виде
ОО	со
У = ~2" { 2 а“ sin X/l +2'ап Sin ~~ af) “
1	1
оо	оо
— у, ьп cos Xn (х + at) 4- У bn cos Х„ (х — at) } =
* Это следует из общих формул (21) п° 708 и замечания п° 709, замена
промежутка [0, л] промежутком [0, /], конечно, несущественна. При этом
естественные условия
/(0) =/(/)-о, g(0)=g(/) = 0,
связанные с закреплением концов струны, как раз и влекут за собой равен-
ство нулю величины, обозначенной там через Вп.
** Почленным дифференцированием установить это можно было бы, лишь
наложив чрезмерно тяжелые ограничения на функции f и g, чтобы повысить
порядок малости коэффициентов ап и Ьп.
722]
§ 7. ПРИЛОЖЕНИЯ
553
Дважды дифференцируя по t и по х, теперь уже легко убедиться в выполне-
нии уравнения (2)!
Решение рассмотренной здесь задачи можно было бы получить и непо-
средственно в последней форме, но решение в форме тригонометрического
ряда (8) имеет преимущество, ибо позволяет вскрыть важные физические
особенности изучаемого явления. Объединяя в (8) оба члена в скобках, пере-
пишем разложение так:
ОО
2	.	. птс . [ппа , ,
Д„ sin — х sm (— t+an
п— 1
Рис. 139.
Мы видим, что полное колебание струны слагается из
ряда отдельных колебаний
.	. Птс . /пла , ,	\
Уп = Ап sin -у X sin (—j- t + a„J .
Участвующие в таком элементарном колебании точки
струны все колеблются с одной и той же частотой или,
если угодно, с одним и тем же периодом, которому от-
вечает тон определенной высоты. Амплитуда колебания
каждой точки зависит от ее положения; она равна
. I . пл Г
Ап яп у- х .
Вся струна разбивается на п равных участков, причем
точки одного и того же участка находятся всегда в
одной и той же фазе, а точки соседних участков—в прямо противоположных
фазах. На рис. 139 изображены последовательные положения струны для слу-
чаев п=1, 2, 3, 4. Точки, отделяющие один участок от другого, находятся
в покое; это — так называемые «узлы». Середины участков («пучности»)
колеблются с наибольшей амплитудой. Описанное явление носит название
стоячей волны; отсюда и сам метод Фурье обычно называют методом
стоячих волн.
Основной тон определяется первой составляющей у/, ей отвечает
частота =	= -уТ/ — и период Л = 2Z1/ JL .Остальные
тона, од-
новременно с основным издаваемые струной, или обертоны, характеризуют
определенную «окраску» звука, или его тембр. Если нажать пальцем в се-
редине струны, то сразу заглохнут как основной тон, так и нечетные обертоны,
для которых там была пучность. Четные обертоны, для которых на середину
струны приходится узел, все сохранятся; среди них роль основного будет
играть второй обертон, с периодом rs = -^- Tlt и струна станет издавать ок-
таву первоначального тона. Все это можно прочитать по полученному реше-
нию нашей задачи!'
722. Задача о распространении тепла в конечном стержне. Пусть
имеем тонкий однородный стержень длины Z, расположенный между точками
х= 0 и х —Z по оси х. Сечение стержня, площади а, мы считаем на-
столько малым, что всем точкам сечения в каждый момент можно припи-
сать одну и ту же температуру. Боковая поверхность стержня предпола-
гается изолированной от окружающей среды *. В начальный момент/ = 0
* Вместо стержня можно было бы представить себе бесконечную стену
между плоскостями х = 0 и х — 1, в предположении, что в каждой перпенди-
кулярной к оси х плоскости сохраняется один и тот же тепловой режим.
554
ГЛ. XIX. РЯДЫ ФУРЬЕ
(722
дано распределение температуры и вдоль стержня, характеризуемое функ-
цией/(х) (0	кроме того, указан тепловой режим, поддерживаемый
на концах стержня. Задача состоит в определении температуры точек стержня,
как функции от абсциссы точки х и времени Z:
и = и (х, t).
Рассмотрим элемент стержня между сечениями х и x-j-dx. Количество
тепла, которое за бесконечно малый промежуток времени dt пройдет через
левое сечение внутрь элемента, выразится так [ср. 666, 2)]:
— Ай dt,
дх ’
где k есть «коэффициент внутренней теплопроводности» стержня; знак минус
объясняется тем, что тепло переходит от более нагретых мест к менее нагре-
тым. Аналогично этому через правое сечение вовне проходит за тот же про-
межуток времени количество тепла
. / ди . д2и . \
~ka^ + ^dXldt'
изменив здесь знак, мы получим количество тепла, прошедшего через упомя-
нутое сечение справа налево, т. е. внутрь элемента. Таким образом, общее
количество тепла, накопившегося в выделенном элементе за промежуток вре-
мени dt, будет:
, д2и . ..
кв dx dt.
Это количество можно подсчитать и иначе, исходя из того, что им обусловлено
ди „ г-	,
повышение температуры на dt. Если через сир обозначить, соответственно,
теплоемкость и плотность вещества стержня, то затраченное на это тепло
выразится так:
, ди ..
сра dx • -fa- dt.
Приравнивая оба выражения, придем к основному дифференциальному урав-
нению теплопроводности:
ди . д2и
---— as-----
dt дх2’
(12)
где для краткости положено

[Впрочем, это уравнение
можно было бы получить из общего уравнения
ди , .
= а2 Ьи,
dt ’
выведенного для пространства в п° 612, 3°, если считать и не зависящим ни
от у, ни от z.j
(а) Предположим сначала, что на обоих концах стержня поддерживается
постоянная температура-, скажем, 0. Это приводит к таким предельным
условиям:
u(0, t) — u(l, А)=0 (ZSsO).
722J	§ 7. приложения	555
Выше мы упоминали уже о начальном условии:
и(х, 0)=/(х) (OsgxsgZ),	(13)
причем в связи с предельными условиями необходимо предположить /(0) =
=/(Z) = 0. Для разыскания функции ы(х, Z), удовлетворяющей уравнению
(12) и всем поставленным условиям, применим метод Фурье.
Пусть, как и выше, и = ХТ, так что уравнение принимает вид:
ХГ = а'2Х"Т или = а8
1 А
если постоянное значение этих отношений положить равным — а8Х8(Х>0),
то уравнение разобьется на два:
Г + а2Х2Г = 0, откуда T = Ce~a2W	G4)
и
X"-f-X8X=0, откуда X— A cosXx-f-B sin Хх.	(15)
Для того чтобы функция XT удовлетворяла предельным условиям, необхо-
димо, чтобы было
Д=0, XZ = nir (где л=1, 2, 3, ...),
так что X может принимать лишь значения (7), как и в предыдущей задаче *.
Полагая ВС = Ьп, получим такой, ряд частных решений:
un = bne~a^ sinX„x.
(л=1, 2, 3, ...)
Общее решение возьмем в форме ряда
и—	bne~a2*nt sin Х„х.	(16)
п— 1
Желая удовлетворить начальному условию, мы должны положить:
со
2 sin-у-х=/(х) (OsgxsgZ).
п= 1
Если функция /(х) непрерывна и имеет ограниченное изменение, то для осу-
ществления этого разложения достаточно взять:
i
.	2 С . плх .
bn — — \ f(x) sm —— dx.
На этот раз установление того факта, что формальное решение (16)
является и действительным решением, не представляет затруднений.
Наличие множителя
е~а^=е 12
позволяет дифференцировать ряд (16) почленно — по t и дважды по х, ибо
получающиеся ряды сходятся равномерно относительно x(0^x^Z) и отно-
сительно t (t а > 0).
* См. сноску на стр. 551.
556
ГЛ. XIX. РЯДЫ ФУРЬЕ
1722
б) Пусть теперь на конце х — 1 поддерживается постоянная температура
п0, а второй конец х = 0 изолирован, так что через него никакого движения
тепла не происходит. Этим предположениям отвечают предельные условия:
(17)
Начальное условие сохраняем в прежнем виде.
Удобнее, впрочем, ввести взамен и новую неизвестную функцию v, поло-
жив u = u0-\-v. Для v имеем, очевидно, такое же уравнение:
dv . d-v
dt а dx- ’
Предельные условия заменятся более простыми:
t>(U)=o, ^ojUq.
'	’ dx
Наконец, начальное условие преобразуется так:
v (х, 0) = /(х) — и0.
Полагая, как обычно, v = XT, получим для Т и X прежние выражения
(14) и (15). Так как
= —ХД sin \х 4- \В cos Хх
dx	1	’
то второе предельное условие даст 5 = 0, а из первого получим:
cos XZ = 0,
так что на этот раз X может принимать значения
^i=='2T->	= 3	, ••• , Х„ = (2л— l)-^",...
Окончательно приходим к таким частным решениям:
vn =	- а2 X"'cos X „X,
(Л=1, 2, 3, ...)
из которых и составляем общее решение
v = 2jOne cosX„x.
1
Начальное условие в этом случае приводит к разложению
ОО
2 ап cos (2л — 1)	= f (х) — и„
1
не стандартного вида [ср. задачу 25) п° 690]. Легко, однако, показать, что
при соблюдении обычных требований относительно функции f(x) это разложе-
ние в действительности имеет место при
I
2
а"~ I
о
/(х) cos (2л - 1) ’g dx-| и0
723J
S 7. ПРИЛОЖЕНИЯ
557
Итак, окончательно
. v, -any
и — иа 4- 7] апе cos Х„х
1
при только что указанных значениях коэффициентов; то, что это—действи-
тельно решение, проверяется, как и в случае (а).
В частности, если / (х) = О, имеем разложение:
оо
4«o'V 1	у ~
и = «О---ДГ=Л е C0S
1
По этой формуле, при «о = ЗОО и а2 = 0,139*, и были вычислены значения и
для различных t и х, и по ним построены приведенные на рис. 140 графики
распределения температур в стерж-
не в различные моменты времени.
723. Случай бесконечного
стержня. Решим теперь ту же
задачу о распространении тепла
для случая стержня, бесконечного
в обе стороны, скажем, располо-
женного вдоль оси х (или для всего
пространства, если только во всех
точках каждой перпендикулярной
к оси х плоскости температура
одна и та же). Дифференциальное
уравнение остается тем же; н а-
чальное условие
и(х, 0)=/(х)
на этот раз должно выполняться
во всем промежутке (— оо, оо),
а предельных условий,
естественно никаких нет.
Как и в прежних случаях по-
лучается частное решение уравне-
ния в виде
и = (a cos Хх -f- b sin Хх) е~ “2ха/;
но здесь нет оснований из всех
положительных значений пара-
метра X выбирать какие-либо.
Поэтому, считая и постоянные а и
Ъ зависящими от X:
а = а (X), b = b (X),
* Имеется в виду чугунный стержень длиной 5 см\ для этого
случая
? = 0,0072 ~, с = 0,13	k = 0,00013-,
см”	кг- С ’ см-°C-сек*
так что а2 = 0,139.
ГЛ. XIX. РЯДЫ ФУРЬЕ
(723
естественно для получения общего решения вместо суммы прибегнуть к ин-
тегралу:
и = [а (X) cos Хх -j- b (X) sin Хх] e~a2Wdk.	(18)
Для того чтобы это — пока формальное — решение удовлетворяло на-
чальному условию, функции а (X) и й(Х) должны быть подобраны так, чтобы
для всех х было
ОР
[а (X) cos Хх 4- b (X) sin Хх] d\=f (х).
о
Предположим теперь, что функция /(х) удовлетворяет условиям приложи-
мости формулы Фурье, которую напишем в виде
1“( +“ 1
/(х) = —\ < cos Хх \ /(z) cosXz dz 4- sin Хх \ /(z) sin Xz dz > d\.
0 I -'co	—CO	J
Отсюда ясно, что функции а(Х), #(Х) можно определить формулами:
1 + °° 1 +°°
а(Х) = — § /(z)cosXzdz, bQ.) —— J f (z) sinXz dz.
Я —co	—co
В таком случае решение (18) примет вид:
и = —Je~a2X2,dX J /(z)cosX(z — х) • dz.
” 0	—со
Если функция /(х) абсолютно интегрируема в промежутке [— оо, 4- оо],
то [521, теорема 5] здесь можно переставить интегрирования по X и по z:
и = — { f(z) dz \e~aSy'"t cos X(z — x) dX.
7C J	X
— co	0
Внутренний интеграл непосредственно вычисляется согласно 6) (а) п° 519; он
оказывается равным
,--(г-*>3
_1_1/ Л 4“3* .
2а V t
Таким образом, окончательно решение задачи представляется в виде простого
интеграла:
-f-00	_ (z — х)а
« =----/(2)е	4о2/ dz.	(19)
2а у nt J
— оо
Дифференцированием по t и по х (дважды) под знаком интеграла легко убе-
диться, что это — действительно решение.
Рассмотрим еще случай «полубесконечного», т. е. бесконечного в одну
сторону стержня, например лежащего вдоль положительной части оси х
724]
§ 7. ПРИЛОЖЕНИЯ
553
(или, если угодно, полупространства х^О). Пусть на конце х = 0 поддер-
живается температура 0. Для этого случая может быть использовано прежнее
решение (19), если только продолжить функцию f(x) (здесь заданную лишь
для значений х между 0 и 4- с») на отрицательные значения х так, чтобы
было
+°о	_ г~
J f(z)e iaSt dz = 0.
-со
Ввиду четности показательного множителя, очевидно, достаточно продолжить
функцию f(x) нечетным образом. Тогда решение новой задачи запишете*
так:
со Г _ (z — x)2	_
1 С z./ \|	4а-7
н =---т=\/(г) е — е
2аУт |_
(z+x-p -1
4“2' dz.
Если потребовать, чтобы при х = 0 было н = н0, то, вводя новую неиз-
вестную функцию v = h— «0, легко получить:
оо	— -у)а	(-? 4~ *)а ~[
,	1 С гл/ \ л	4аа/	4аа/ I .
Ц = «о + П ,/—\ 1/(г) —«о!- е	[dz.
2а у nt J	1	J
Отметим частный случай, когда при этом f(x) = 0; решение примет вид:
а = иа
Для но = 300 и а2 = 0,139* по этой формуле при различных х и t были
вычислены значения и, и по ним построены графики распределения темпера-
туры в стержне в различные моменты времени. Эти графики, изображенные
на рис. 141, интересно сопоставить с графиками на рис. 140.
724.	Видоизменение предельных условий. Вернемся к задаче о распро-
странении тепла в конечном стержне, рассмотренной в 722, но видоизменим
предельные условия. Именно, предполагая по-прежнему, что на конце х — С
поддерживается температура 0, будем считать, что на конце х = 1 имеет месте
свободное излучение в окружающую среду температуры 0. Количество тепла,
подводимого за промежуток времени dt к этому концу, будет [см. 722[:
. dull, t) .t
— Ла----> dt,
дх
а количество излучаемого тепла по закону Ньютона [ср. 359, 3)] равно
Лан (/, f) dt,
где Л есть «коэффициент внешней теплопроводности».Следовательно, на конце
х = 1 должно выполняться такое условие:
ди(1, t) , „
-k—^- = hu(l,t).
* Что отвечает стержню из чугуна; см. сноску на стр. 557.
560
ГЛ. XIX. РЯДЫ ФУРЬЕ
[724
Если рассмотреть теперь частное решение — вида и = ХТ, то получим, как и
в п° 722:
T—Ce~aSW,
X— A cos Хх + В sin Хх.
Рис. 141.
£ X
sin-^-=/(x);	(20)
его можно рассматривать как обобщенный ряд Фурье функции fix)
в промежутке [0, /[ и, пользуясь ортогональностью функций
[679, 4)], обычным образом определить коэффициенты Ъп-.
f (х) sin	dx
srn2-^- dx
о
725)
§ 7. ПРИЛОЖЕНИЯ
561
Мы оставим открытым вопрос об условиях, которые надлежало бы нало-
жить на функцию f(x), чтобы обеспечить равенство (20), и ограничимся
формальным решением поставленной задачи.
725.	Распространение тепла в круглой пластине. Мы рассмотрим теп-
ловую задачу еще для одного случая—круглой пластины радиуса /? с центром в
начале координат. Предположим пластину настолько тонкой, что по высоте ее
температура не меняется, а верхнюю и нижнюю ее поверхности будем счи-
тать изолированными. Больше того, мы ограничимся изучением случая, когда
температура и будет зависеть только от полярного радиуса-вектора г (но не
от полярного угла 9): для этого достаточно предположить, что таковы же
начальные и предельные данные. [Можно было бы и здесь вместо
пластины с изолированными поверхностями рассматривать круговой цилиндр,
бесконечный вниз и вверх.]
Взяв общее дифференциальное уравнение теплопроводности:
du „.
з- =а2Ди
dt
[672, 3°], мы прежде всего, ввиду независимости и от z, перепишем его в
виде
ди __ . [dsu , dsu\
dt ~ \dxs ~'ду*)'
Переходя на плоскости ху к полярным координатам, мы должны заменить
выражение в скобках следующим:
dsu . 1 d1u . 1 du
drs + r*№+~rdr
[см. 222, 1]. Наконец, учитывая, что и не зависит от 6, приходим к такому
уравнению:
dt \дг*+ г dr)'	1 '
Пусть начальное распределение температуры будет задано
в виде
й(г, 0) = <р(г) (О^г^Л),
а предельное условие сводится к
«(/?, <) = 0.
Прибегнем и здесь к методу Фурье. Станем искать частное решение урав-
нения (21) в виде
и = /?(г) Т(0:
тогда для определения этих функций получатся уравнения
7*а2Х2Т=0 и R" + уЯ' + X2 Я = 0.
Из первого из них Т—Се~а2''21. Второе же, если положить r = -l- z и
Л
R z = J (z), перейдет в уравнение Бесселя:
7"4- —7'4-7=0.
Z
562	гл. xix. ряды фурье	[725
Отождествим же J с функцией Бесселя с нулевым значком, т. е. поло-
жим /? (г) = Jo (Хг). Предельное условие дает
Jo(X/?) = O.
Мы уже упоминали в 679, 6), что функция Jo (х) имеет бесчисленное множе-
ство положительных корней (п— 1> 2,3,...); таким образом, для X возможен
ряд значений
Им отвечают частные решения вида
чп = спе-аЧп( Ja(kar),
из которых, как обычно, составляется общее решение:
« = ^<v-a2A"4(V)-
Остается определить коэффициенты сп. Неиспользованное еще начальное
условие дает в этом случае
1
Мы уже видели в 679, 6), что система функций {J0(5„x)} ортогональна
в обобщенном смысле — с «весом» х* в промежутке [0, 1]; оче-
видно, система ('/?")} будет ортогональной в промежутке [0, /?] с «ве-
сом» г. Обычным образом определяя коэффициенты этого обобщенного
ряда Фурье, найдем
( Г<Р (г) Jo dr
О
Я
§ rJ^^dr
о
И здесь мы удовольствуемся полученным формальным решением.
Читатель видит, что последние два примера уже выходят за пределы
обыкновенных рядов Фурье. Мы привели их, желая создать у читателя
правильную ориентацию в вопросе о приложении рядов Фурье в математи-
ческой физике. Они там играют важную роль, но, конечно, далеко не исчерпы-
вают потребностей математической физики: достаточно небольшого изменения
условий задачи, чтобы оказалось необходимым прибегнуть к разложениям уже
другого рода. Это обстоятельство нисколько не умаляет значения рядов
Фурье и развитой для них теории, потому что ряды Фурье навсегда
останутся простейшим и важнейшим примером «ортогонального разложения»;
по образцу его строятся все другие подобные разложения, теория которых
теснейшим образом переплетается с теорией рядов Фурье.
* См. сноску на стр. 423.
726]
§ 7. ПРИЛОЖЕНИЯ
563
726.	Практический гармонический анализ. Схема для двенадцати
ординат. Разложение функции в ряд Фурье, или гармонический анализ,
оказывается нужным во многих чисто практических вопросах машиноведения,
электротехники и пр. Но в этих случаях очень редко приходится непосред-
ственно пользоваться формулами Эйлера — Фурье:
2я	2я
<z0 = ~ \ f(.x)dx*,	<х„ = — £ f (х) cos пх dx,
и	о
2л
bn — — \ f(x) sin пх dx
(22)
(п= 1, 2, 3, ...)
для вычисления коэффициентов разложения. Дело в том, что функции, кото-
рые нужно подвергнуть гармоническому анализу, обыкновенно задаются
таблицей своих значений или графиком. Таким образом, аналитиче-
ского выражения функции в нашем распоряжении нет; иногда к самому гар-
моническому анализу прибегают именно для того, чтобы таким путем полу-
чить хотя бы приближенное аналитическое выражение для функции. В этих
условиях для вычисления коэффициентов Фурье нужно обратиться к при-
ближенным методам. Разумеется, на практике приходится пользоваться лишь
немногими первыми членами тригонометрического разложения. Коэффициенты
ряда Фурье в большинстве случаев быстро убывают, а с ними быстро падает
и влияние далеких гармоник.
Обычно дается (или снимается с графика) ряд равноотстоящих ординат,
т. е. ряд значений функции у, отвечающих равноотстоящим значениям аргу-
мента х. По этим ординатам величины (22) можно приближенно вычислить,
пользуясь методами, изложенными в главе IX (§ 5). , Но вычисления здесь
оказываются довольно громоздкими, и для того чтобы упростить и, так ска-
зать, автоматизировать их, придумано много различных приемов, один из
которых мы и изложим.
Пусть, скажем, промежуток от 0 до 2л разделен на k равных частей и
пусть известны ординаты
У о, У1, У г, , Ук-i, Ук=Уч,
отвечающие точкам деления
°>	2.^,...,(й-1)^,2л.
Тогда по формуле трапеций [322] имеем (конечно, лишь приближенно!):
„ __ 1 2л Г 1	.11
0 —2^ ’	+
Ввиду периодичности нашей функции Уь—Уы и значение аЛ можно напи-
сать и так:
ka^ =уа +.У14“ J’s + •••	(23)
* Мы возвращаемся здесь к обозначению свободного члена в тригоно-
метрическом разложении через аа (а не
564
ГЛ. XIX. РЯДЫ ФУРЬЕ
[726
Аналогично,'применяя формулу трапеций к другим интегралам (22), найдем!
1 2л Г	2л .	4л '
ат = — • у po+bcosm-^4-y>2cosm-^+...+
.	2 (k — 1) л
+5’*-! COS тk 
или
*	1	2л ,	4л ,	,
-2-am=5’o+5’iCosrn у+5’2cosmy + ... +
,	2(й —1)л
+ 5’*-i cos т к
а также
k ,	. 2л ,	. 4л	.	2 (k — 1)л
у ьт =У1 sm my+yFs ЯП m У +... +5^-1 sm т —>—^-1—.
Положим сначала й=12 и будем исходить из двенадцати ординат
Уо, У1, У2, .... Уп,
отвечающих двенадцати равноотстоящим значениям аргумента:
л л л 2я 5л 7я 4я Зя 5л Пл
°’ ~б’ Т’ Т’ Т’ IP Т’ Т’ 1Г’
или в градусах
0°, 30°, 60°, 90°, 120’, 150°, 180°, 210°, 240°, 270°, 300°, 330°.
Все множители, на которые придется умножать эти ординаты, по
мулам приведения сведутся к следующим:
±1; ± sin 30° = ± 0,5; ± sin 60’ = ± 0,866.
(24)
(25)
фор-
Именно, легко проверить, что
6«i = (уг + 5’ю —yt —Л) sin 30° + (54 + 5’и — 5’в —Ут) sin 60° + (у» — 5’в)
6а2 = (У1 +5’5 +5»? +5’11— 5’2—У 4—5’в—У1 о) sin 30’ + (5’в + 5’в—5’в—5’в)
6в3 =5’о+5’4+5’в— 5’2—5’в— 5’ю	(26)
6*1 = 01+5’5 —5’7 —5’и) sin 30’ + 02 + 5’4 —5’в —5’ю)sin60° + О2 —5’в)
6*2 = 01 + У 2 + У 7 + 5’в—5’в — 5’в —У io —5’и) sin 60°
6*з =5’1+5’5+5’в— 5’в— Ут— Уи, и т. д.
Например,
6а, =5’0 +5»! cos 30° +5^ cos 60° + 513 cos 90° + yt cos 120’ +5>6 cos 150° +
+ 5,5 cos 180° +5’; cos 210° + 54 cos 240° +513 cos 270° +
+5110 cos 300° +5'11 cos 330° =5'0 + yt sin 60° +57, sin 30° —
—уt sin 30° —yt sin 60° —ye —у, sin 60° —yt sin 30° +5’10 sin 30° +
+5’и sin 60°,
что совпадает с написанным выше выражением.
Для того чтобы свести выкладки (особенно — умножения) к минимуму,
их производят по определенной схеме, предложенной Рунге (С. Runge).
727)
§ 7. ПРИЛОЖЕНИЯ
565
Сначала выписывают в указываемом ниже порядке ординаты и над
каждой парой подписанных одна под другой ординат производят сложение
и вычитание:
ординаты
Уо У1 Уз Уз Уз Уз Уз
У и Узо Уз Уз У1
суммы Ua и2 «3 и. иа
разности vt vs v3 v4 v.
Затем аналогично выписывают эти суммы и разности и снова подвергают их
сложению и вычитанию:
	суммы	разности
	Ui и% и3	»i vt va
	we ^5 ^4	V3 Vt
суммы-	so s2 s3	суммы	01 a2 a3
разности	d6 dt d.,	разности	81 S2
Теперь, получив после всех этих сложений и вычитаний ряд величин s, d, а, 8,
мы можем следующим образом выразить через них искомые коэффициенты:
12а0 — s0 + Sj s2 + s3,
6ax = d0 4- 0,866 dL 4- 0,5 d3,
6a2 = (s0 — s3) 4- 0,5 (Sj — s2),
6a3 — da d.,t
6bi = 0,5 Sj 4- 0,866a2 4* °з,
6*2 = 0,866 (8,4-83),
6*s = Si — o3 и T. д.
(27)
Нетрудно убедиться, что эти формулы в точности соответствуют фор-
мулам (26).
727. Примеры. 1) На рис. 142 изображена диаграмма касательных уси-
лий (на пальце кривошипа) для некоторой паровой машины *. В связи с
вопросом о крутильных колебаниях вала представляет интерес выделить гармо-
нические составляющие касательного усилия Т, как функции от угла <р пово-
рота кривошипа. Сняв с графика двенадцать равноотстоящих ординат, произ-
ведем гармонический анализ по указанной схеме:
T 1	— 7200	— 300 7000	4300	0	-5200 —7400	
T i		250 4500	7600	3850	-2250	
и	— 7200	— 50 11500	11900	3850	-7450 —7400	
V		— 550 2500 —	-3300 —	3850	-2950	
	— 7200	— 50 11500	11900		— 550	2500	— 3300
	— 7400	— 7450 3850		V I	— 2950 — 3850	
s	— 14600	— 7500 15350	11900	a	— 3500 —1350	— 3300
d	200	7400 7650		8	2400	6350	
* Подобные диаграммы строятся на основе индикаторных диаграмм
€ учетом сил инерции.
566
ГЛ. XIX. РЯДЫ ФУРЬЕ
(727
Теперь по формулам (27):
12а0 = — 14600 — 7500+ 15350+ 11900 = 5150;
ба1 = 200 + 7400 • 0,866 + 7650  0,5 = 10433;
6а3 = (— 14600 — 11900) + (— 7500 — 15350)  0,5 = — 37925;
6а3 = 200 — 7 650 = — 7450;
6bt = — 3500 • 0,5 — 1350 • 0,866 — 3300 = — 6219;
6*3 = (2400 + 6350) • 0,866 = 7578;
6*3 = — 3500 + 3300 = — 200;
а0 = 429,
а, = 1739;
а3 = —6321,
а3 = — 1242,
*, = — 1037,
*2= 1263,
*3 = —33.
Таким образом,
T=429+ 1739 cos <р —1037 sin <р —6321 cos 2<р + 1263 sin 2<р —
— 1242 cos 3<р — 33 sin 3<р +...
Объединим члены, содержащие косинус и синус одного и того же угла:
Т = 430 + 2020 sin (<р + 121°) + 6440 sin (2<р + 281°) +
+ 1240 sin (3<р + 268°) + ...
Мы видим, что наиболее сильное влияние здесь оказывает вторая
гармоника.
2)	Для того чтобы дать себе отчет в том, с какой, примерно, точностью
пол} чаются коэффициенты Фурье функции по двенадцати ординатам ее
727J
S 7. ПРИЛОЖЕНИЯ
567
графика, мы приложим изложенный метод к некоторым аналитически задан-
ным функциям и сравним приближенные результаты с точными,
Сначала рассмотрим функцию f(x), которая в промежутке [0, 2гс] задается
формулой
у = f (х) = 2^2 (х3 — Зях2 2л2х),’
а для остальных значений х определяется по закону периодичности
/(х + 2л)==/(х).
График функции представлен на рис. 143.
Вычислим табличку:
	0	я	я т	я	2я 3	5к "6"	Я	7 г т	4я 3	Зя т	5я т	Ня 6	2п
У =	0	0,400	0,582	0,589	0,465	0,255	0	-0,255	-0,465	—0,589	-0,582	—0,400	0
При этом можно использовать легко проверяемое тождество:
/(2п-х) = -/(х).
По схеме Рунге по этим значениям у найдем:
*, = 0,608, *3 = 0,076, /<3 = 0,022;
все числа uit а с ними и все коэффициенты ап оказываются нулями [690,22)].
В то же время формулы (22) непосредственно дают (с помощью трех-
кратного интегрирования по частям):
Ът =	\	— Зях2 2л2х) sin тх dx = —,
568
ГЛ. XIX. РЯДЫ ФУРЬЕ
[727
так что
= 4 = 0,6079, й2 = 4» = 0,0760, й3 =-2, = 0,0225.
л2 .	4л2	9л'
Совпадение превосходное!
3)	Однако далеко не всегда получается столь точный результат. В виде
второго примера мы возьмем функцию с периодом 2л, которая в промежутке
[0, 2л] определяется так:
y=/(X) = -L(X — я)2.
Ее график дан на рис. 144.
Пользуясь очевидным тождеством:
/(2л —х)=/(х),
составим табличку:
	0	п "6	п "з	X 2"	2х т	5х V	X	7х 6	4х 3	Зх Т	5х “Г	Нх 6	2х
У =	1	0,694	0,444	0,250	0,111	0,028	0	0,028	0,111	0,250	0,444	0,694	1
Тогда по схеме Рунге
а0 = 0,338;	= 0,414; а2 = 0,111; а3 = 0,056;
числа же V, и коэффициенты Ьт — на этот раз нули [690, 22)]. Точные зна-
чения коэффициентов будут:
2л
а0 = - J-j ( (х — л)2 dx = 4 = 0,333,
j	Z
0
2 к
1 С	4
ат = -j \ (х— л)2 cos тх dx — -^^ (т Дэ 1),
в частности,
4	14
а, = Л = 0,405; в1=-^=ь0,101; as =	-= 0,045.
1 л2 ’л2	’	9л2
Таким образом, если для первых двух коэффициентов относительная
погрешность не превосходит 1,5—2%, то для последующих она достигает
10% (а2) и даже 20% (<х3)! Ниже [730] мы еще вернемся к вопросу о точ-
ности полученных нами приближенных формул. Но уже и сейчас ясно, что
для повышения этой точности нужно брать больше ординат.
728]
5 7. ПРИЛОЖЕНИЯ
569
728. Схема для двадцати четырех ординат. Положим теперь, что даны
или сняты с графика двадцать четыре ординаты:
Уо, У1, Уз....Уаз,
отвечающих значениям аргумента:
„ тх тс тс	23тс
’ 12 ’ Т ’ Т ’ •••’“12’
или
0°, 15°, 30”, 45”, ..., 345°.
На этот раз все множители, на которые при приближенном вычислении
коэффициентов Фурье приходится умножать ординаты, сведутся к таким:
± 1, ± sin 30”, ± sin 45°, ± sin 60°, ± sin 75°.
Не вдаваясь в подробности (ввиду полной аналогии с предыдущим), при-
ведем сразу схему вычислений, также предложенную Рунге. После опыта,
который уже имеет читатель, эта схема ему будет понятна без пояснений.
Вот она:
ординаты.
Уо У1 Уо Уз Уз Уз Уо У? Уз Уо Ую Уп Ую
Узз Уза Уо1 Уоо Ую J’is У17 Ую Ую Ун У13
суммы-
разности
Uo Ui U2 U3 H4 U5 U& U-j Us £Zjo
t’l V2 V8 Vi Vt Vi Vs'Va Vi0 Vtt
	суммы «0	«1	«2	«3 «4 «5 «в «12 «11 «10 «9 «8 «7		V1 V11	разности »2	Vi vs va Vio Ve Va V,
суммы	Ро Pl Р2 Рз Pi Ръ Рв	суммы	Г1	rs r3 rt ra re
разности	4о 41 4a 4з 41 4з	разности	81	^2 ^3 ^4 ^5
	суммы		разности
	Po Pi Pa Рз		Si s3 s3
	Ps Po Pt		S5 S4
суммы	1 «i •«Г © •ee	суммы	ffli m2 m3
разности	Zo h	разности	«1 «2
Отметим, что с величинами q и г нет надобности проделывать сложения
и вычитания.
570
ГЛ. XIX. РЯДЫ ФУРЬЕ
[729
Теперь через полученные указанным путем величины k, I, т, п, q и г
коэффициенты Фурье выразятся следующим образом:
24а0 = k0 4- kt + k2 4-
12^1 = [q0 + 0,5?4 4- 0,6124 (qt 4- ?s)] 4“ [0,8660?2 4- 0,7071?, 4"
4-0,3536(?j —?5)],
12a2 = /0 4- 0,8660/4 4- 0,5/2,
12a, = (qe - q4) 4- 0,7071 (?, - q3 - q3),
12a4 — (k0 — k3) 4- 0,5 (fej — fe2),
12a5 = [?0 4- 0,5?4 4- 0,6124 (^'4- ?,)] — [0,8660?3 4- 0,7071?, 4-
4-0,3536 (?4-?5)l,
12a0 =: Iq	12r
12*4 = [0,5r2 4- re 4- 0,6124 (Г1 4- rs)] 4- [0,7071г, 4- 0,8660r4 —
- 0,3536 (Г4 —r6)],
12*2 = 0,5m 4 4- 0,8660m2 4- m„
12*, = (r3 - r„) 4- 0,7071 (r, 4- r, - r5),
12*4 = 0,8660 («4 4" n2),
12*5 = [0,5r2 4- re 4- 0,6124 (Г1 4- r6)[ — [0,7071 r, 4- 0,8660r4 —
- 0,3536 (r4 —r6)],
12*e =//’, — и т.д.
(28)
Дальнейшие коэффициенты по двадцати четырем ординатам получаются
с все меньшей и меньшей точностью.
Обращаем внимание читателя на одну подробность. Для получения
коэффициентов at и а5 нужно отдельно вычислить те выражения, кото-
рые поставлены в квадратные скобки, а затем сложить их (для нахож-
дения а,) и вычесть (для нахождения а3). Аналогичное замечание —
относительно вычисления коэффициентов *4 и *3.
1 став, прои Т {	29. Примеры. 1) Возвращаясь к диаграмме касательных усилий, пред- анной на рис. 142, снимем с нее двадцать четыре ординаты и наново зведем гармонический анализ, пользуясь новой схемой: —7200 —4150 —300 3250 7000 7450	4300	2750	0 —2650 —5200 —7700 —7400 —5150 250 2300 4500 6800	7600 6400	3850	650 —2250 —4850		
и V	—7200 —930С 1000 U {	—50 5550 11500 14250 11900 9150	3850 -2000 —7450 —12550 -7400 —550 950 2500 650 —3300 —3650 —3850 —3300 —2950 —2850 —7200 — 9300 — 50 5550 11500 14250 11900 —7400 —12550 —7450 —2000 3850 9150	
	р Q V	1	14600 —21850 —7500	3550 15350 23400 11900 200	3250 7400	7550 7650 5100 1000 —550	950 2500	650 —3300 —2850 —2950 —3300 —3850 —3650
	S		— 1850 —3500 —2350 —1350 —3000 —3300 3850 2400 4250 6350 4300
7301
s 7. ПРИЛОЖЕНИЯ
571
р 1	—14600 —21850		—7500 3550 15350	S |	3850 4300	2400 4250 6350
	11900	23400				
k	—2700	1550	7850 3550	т	8150	8750 4250
1	—26500	—45250	—22850	п	—450	—3950
Отсюда по формулам (28):
а0 = 427,	^== 1685,	а2 = —6426,	а3 = —1175,	а, = — 783,
а6 = —163,	а„ = —304,	^= — 938,	Ъг = 1325,	&6 = — 87,
bt= — 318,	£5 = —398,	&0=325.
Итак, получается разложение:
Т = 427 4- 1685 cos <р — 938 sin ? — 6426 cos 2<р + 1325 sin 2<р —
— 1175 cos 3<р — 87 sin 3<p— 783cos4<p — 318 sin 4<p — 163 cos5<p—
— 398 sin 5<p — 304 cos 6<p 4- 325 sin 6<p 4-...
или, объединяя и округляя:
Т = 430 + 1930 sin (<р + 119°) + 6560 sin (2<р + 282°) +
-4-1180 sin (3<р -J- 266’) + 845 sin (4c + 248°) + 430 sin (5<? + 202°) +
+ 445 sin (6?	317°) + ...
Сравнивая это разложение с разложением той же величины Т, произве-
денным в п° 727, 1), видим, что в первых трех гармониках получается более
или менее удовлетворительное совпадение.
2) Предлагается читателю вычислить двадцать четыре ординаты кривой
У = -^(х~
тс
о которой была речь в п’ 727, 3), и, пользуясь указанной схемой, найти при-
ближенные значения коэффициентов а0, at, а2, а3, ait as, ав.
Ответ. а0 = 0,334;	0,407; а2 = 0,104; а3 ===(),047; а4 = 0,028; <х5== 0,019;
а0 = 0,014, в то время как верные знаки будут:
а0 = 0,333; <х1== 0,405; а2 = 0,101; а3= 0,045; а4 = 0,025;
а6== 0,016;	= 0,011.
Кроме приведенных схем для приближенного вычисления коэффициентов
тригонометрического разложения функции, существуют и другие: для шест-
надцати или тридцати двух ординат (обычны в морском деле при изучении
девиации компасов), для тридцати шести ординат (употребительны в электро-
технике) и т. д. Придуманы также вырезные шаблоны, автоматически
устанавливающие расположение вычислений. Во всех этих случаях сущность
приемов, с помощью которых достигаются упрощения при практическом
вычислении коэффициентов Фурье, остается та же, что и выше.
730. Сопоставление приближенных и точных значений коэффициен-
тов Фурье. Если функция у —f(x) задана в промежутке [0, 2тс] аналити-
чески и дважды дифференцируема, то погрешности найденных выше прибли-
женных формул для коэффициентов Фурье могут быть установлены, как
обычно [730]. Мы зададимся здесь другой целью, именно, мы выведем соот-
ношения, связывающие приближённое значение данного коэффициента
с точными значениями этого же и других коэффициентов. Эти соотно-
шения не приводят к оценкам для погрешностей, но все же проливают свет
на весь вопрос в целом и создают в нем надлежащую ориентацию.
572
ГЛ. XIX. РЯДЫ ФУРЬЕ
[730
Итак, предположим, что для рассматриваемой функции y=f(x) в про-
межутке [0, 2к] имеет место разложение Фурье:
ОО	оо
у> = л()4- Ап cos пх 4- 2 вп s'n пх-
п=1	п=1
Мы умышленно обозначаем здесь коэффициенты Фурье большими буквами,
чтобы отличить их от приближенных значений их, которые будут обозначаться
2/тс
малыми буквами. Полагая в написанном равенстве х = -^-(1 = 0, 1, ..., k—1),
мы вычислим те частные значения функции у,, которые фигурируют в фор-
мулах (23), (24) и (25), дающих приближенные значения коэффициентов:
, , V л 2/даг , V г> • 2штс
п—1	п—1
Подставим эти величины в первую из этих формул; переставляя сум-
мирования, найдем:
оо	А— 1	оо	k — 1
».=4{+2А’ 1 “т+22
п = 1 i = 0	п = 1	< = 1
Но, как легко видеть, суммы
*-1	_	*-1
2	21/мг	VI	.	2fnit
C0S~T" ’	2 sm-r
l	= 0	i=l
равны 0, за исключением того случая, когда «кратной и
первая сумма получает значение k (вторая сумма и в этом случае равна 0).
Отсюда сразу получается
ао =	+ Ak +	+ Ask +	(29)
Подставляя выражения для _у, в формулу (24) и снова переставляя сум-
мирования, получим последовательно:
А — 1	оо	k — 1
2	f . V .2m” , V . V ,2тл .2ял .
=	2 Cos«-fc-+ 2	2 COSZ-y-COSl-^-h
i—0	п—1	z = 0
оо k— 1
VI . 2zzm . ,2ял)
п = 1	i = 0
А —1	оо	А —1
4b2-T+242'»i2-4^+
z = 0	n=l	z=0
k — 1	со	k — 1
2. 2 (я — т) л ] , VI и Г V • . 2 (я + и) л .
cosi jH~j + 2s42 smi k +
i — 0	n = 1	i — 1
A-l
i = i
730]
§ 7. ПРИЛОЖЕНИЯ
573
И здесь также отличными от нуля (и при этом—равными k) будут лишь те
суммы косинусов, у которых множитель п±т оказывается кратным k,
т. е. для значений п вида pk±m (р—-целое). Если для определенности счи-
тать 2т k, то придем к такому ряду для ат:
ат — Лт + Ak_m Ak+m +	-J- ...	(30)
Совершенно аналогично получается, что
Ьщ —Вт Bk_m	Вk_m -f-...	(31)
Это и есть те формулы, которые мы хотели установить.
Мы усматриваем из них, что, скажем, ат отличается от Ат суммой неко-
торых коэффициентов А с большими номерами, если только k
велико, ат, наоборот, не слишком велико. Становится ясным,
что важную роль в вопросе о точности приближений играет быстрота
убывания коэффициентов Фурье, которая, как мы знаем [706—708],
в свою очередь, связана с дифференциальными свойствами
функции, продолженной навесь промежуток (—оо, -f- оо).
Это обстоятельство хорошо иллюстрируется примерами 2) и 3) п° 727: обра-
щаем внимание читателя на угловые точки графика во втором из них!
Полагая А = 12, мы будем иметь в частности (ограничиваясь для при-
мера коэффициентами при косинусах):
а0 = Ло 4*-^12 Ч-•••> ai = Ч- Ai +
в2 — ^2 Ч- -^10 Ч* ••> а3 — Ч* Л Ч- •••
и наряду с этим
as> = А Ч" А Ч~ •••> ав = 2Л, Ч- •  •(')»
и т. д. Отсюда видно, что за пределами первых двух-трех гармоник нельзя
ждать сколько-нибудь удовлетворительной точности.
Результаты сразу улучшаются при переходе к k = 24:
аО = ^о+ ^24 + •••> а1 — -А1 Ч* -^23 Ч* •••>
ав = Л Ч- л18Ч- •••, И т. д.
Здесь, вообще говоря, можно ждать хорошей точности для первых семи-
восьми гармоник.
ГЛАВА ДВАДЦАТАЯ
РЯДЫ ФУРЬЕ (продолжение)*
§ 1. Операции над рядами Фурье. Полнота и замкнутость
731. Почленное интегрирование ряда Фурье. Предположим
функцию f(х), как обычно, абсолютно интегрируемой в проме-
жутке [— к, к]. Пусть ее ряд Фурье будет
СО
2 ап cos пх -j- bn sin пх.	(1)
п = 1
Введем в рассмотрение для — те х к функцию
X
F(x)= J[/(x)-|]dx,
О
(2)
очевидно, непрерывную и с ограниченным изменением [486, 7°; 568, 4°];
к тому же она имеет период 2те, ибо
F (к) — F (— к) = § f (х) dx — теа0 = 0.	(3)
—11
В таком случае, по теореме п° 686, эта функция во всем промежутке
разлагается в ряд Фурье:
ОО
F (х) — -j- cos пх 4" sin пх	(4)
П =я 1
(который к тому же, согласно 699, равномерно сходится к ней).
* Глава XIX была посвящена, главным образом, разложению функций в
сходящиеся ряды Фурье; в ней эти ряды изучались как вычислитель-
ный аппарат. В настоящей же главе мы становимся на более общую точку
зрения и изложим ряд важных вопросов, представляющих преимущест-
венно теоретический интерес.
731|
§ 1. ОПЕРАЦИИ НАД РЯДАМИ ФУРЬЕ
573
Между коэффициентами рядов (1) и (4) существует простая связь.
Действительно, если воспользоваться обобщенной формулой интегри-
рования по частям, установленной в п° 580, 9), то будем иметь (для
л^1):
*1С
Ап — -i- F (х) cos пх dx —
— -гс
1 с, sinnx
= — F (х)----------
it v ' П
f (х) sin пх dx,
то есть
Аналогично, на этот раз с учетом равенства (3), получим
Для нахождения же Ао положим в (4) х = 0:
Подставив в разложение (4) найденные значения коэффициентов,
можем переписать его в виде
о°
р 2 ап sin их +	(1 — cos пх)
п= 1
Отсюда, если учесть равенство (2), имеем
X	X	оо X
( /(х) dx — С ~ dx-{- 2 § [ancos ях-j-^n sin nx]dx. (6)
О	0	n=1 О
Очевидно, и для любого промежутка [х', х"], где — к х’ х" те,
имеет- место подобное же соотношение:
х”	х"	оо х”
f(x) dx= -^dx -]- 2 § (an cos nx sin их] dx.
x'	xr	n—\ X*
Таким образом, интеграл от функции /(х) получается почлен-
ным интегрированием соответствующего ей ряда Фурье. Тот
факт, что почленное интегрирование ряда Фурье оказывается
всегда допустимым, тем более замечателен, что мы установили
его, даже не делая предположения о сходимости са-
мого ряда (1) к функции /(х)!
576
ГЛ. XX. РЯДЫ ФУРЬЕ (ПРОДОЛЖЕНИЕ)
[731
Ясно, что в качестве основного промежутка вместо [— тс, тс] мо-
жет быть выбран любой другой промежуток длины 2тс. Точно так же
все сказанное относится и к рядам, содержащим одни лишь косинусы
или одни лишь синусы [689] и рассматриваемым в промежутке [0, тс].
Интегрированием известных тригонометрических разложений могут быть
получены другие разложения. Член в (6), если угодно иметь тригономет-
рическое же разложение, следует перенести в другую часть равенства. Не-
которого внимания требует к себе свободный член : получить его в ко-
нечном виде удается либо непосредственным суммированием ряда (5), либо
же интегрированием по формуле
А_1
2 ~2я
- 1С
Поясним это примером. Если проинтегрировать разложение
ОО
2 sin пх тс— х tc. _	_ п \
_	(0<х<2я)
n=l
[см. 6S0, 2)] от 0 до х, то получим:
СО
21  COS ПХ	ТС	I
-----2	= тг X-г X2 .
п2-----------------2	4
п= 1
Отсюда
ОО
2 cos пх 1 , я .	.. ~	~ „ .
—г-=_х2-ух + с	(0^х^2я),
п = 1
причем с определяется либо как сумма ряда
ОО
2_1__я^
п2 6 ’
П=1
либо как интеграл:
2к
1 С [тс	1	. Тс3
тс- \ -тс- х--гХ1 ах = -~-.
2тс J \2	4	/	6
о
Таким образом, мы приходим к разложению, которое независимо было по-
лучено в 690, 9). Аналогично разложение в 7) (а) получается из разложения
в 7) (б) и т. д.
Замечание. Подчеркнем, что проведенным рассуждением попутно
установлен такой факт: какова бы ни была абсолютно интегрируемая
в промежутке [—я, я] функция f(x), ряд
п — 1
(5*)
где Ьп — коэффициенты при синусах в ее ряде Фурье, необходимо схо-
дится [ср. 692, 2°]. Ниже, в 758, мы воспользуемся этим замечанием.
732]	§ 1. ОПЕРАЦИИ НАД РЯДАМИ ФУРЬЕ	577
732. Почленное дифференцирование ряда Фурье. Пусть в про-
межутке J— к, к] задана непрерывная функция /(хХудовлетво-
ряющая условию /(—те)=/(к) и имеющая (исключая разве лишь
отдельные точки в конечном числе) производную /'(х); пусть, далее,
эта производная сама оказывается абсолютно интегрируемой в на-
званном промежутке. Тогда
7(x) = $/'(x)dx+/(0)
о
[310, 481] и, как мы только что видели, ряд Фурье (1) функции
f (х) получается из ряда Фурье функции f (х)
ОО
2 а'п cos пх -|- b'n sin их	(7)
п = 1
почленным интегрированием, так как при наложенных на/(х)
условиях свободного члена в последнем разложении не будет:
те
= ~ ^r(x)dx=l[/(z)-/(-«)] = 0.
— те
В таком случае, очевидно, и обратно—ряд (7) для производной f'(x)
может быть получен из ряда (1), отвечающего данной функции
f(x), почленным дифференцированием.
Мы обращаем особое внимание читателя на ту роль, которую здесь
играет предположение о периодичности функции f(х). При
нарушении этого условия свободный член у ряда Фурье для /' (х)
был бы отличен от нуля, и уже по одному этому упомянутый ряд не
мог бы быть получен из ряда (1) почленным дифференцированием!
Например, в случае разложения (а — не целое)
ОО
л sin ах V е	п
-----= У (— 1)л  -------- sm пх
2 sm ал 4	7 а8 — ns
я=1
[664, 7) (б)] почленное дифференцирование приводит к ряду
оо
2	as — ^COSnx’
П = 1
который заведомо никаким рядом Фурье быть не может, ибо его
коэффициенты даже не стремятся к нулю [682].
Замечание. До сих пор мы говорили о возможности получения
ряда Фурье (7) для производной f (х) путем почленного диффе-
ренцирования ряда Фурье исходной функции /(х). При этом вовсе
19 Г, М, Фихтенгольц, т. 111
578	ГЛ. XX. РЯДЫ ФУРЬЕ (ПРОДОЛЖЕНИЕ)	1733
не было речи о сходимости ряда (7) к функции /'(х); эту схо-
димость надлежит устанавливать особо, пользуясь теми или другими
достаточными признаками [684, 686].
Нужно отметить, что, ввиду появления при дифференцировании
cos пх и sin пх натуральных множителей п, порядок малости коэф-
фициентов понижается и ухудшаются шансы на сходимость. Между
тем, при решении с помощью рядов Фурье задач математической
физики часто приходится дифференцировать эти ряды, и даже неод-
нократно. Для обеспечения сходимости получаемых рядов иногда ока-
зывается полезным предварительное выделение плохо сходя-
щихся частей по методу А. Н. Крылова [710]. При этом
сумма выделенной части, известная в конечном виде, дифференци-
руется непосредственно, а для остающегося ряда стараются добиться
столь высокого порядка малости коэффициентов, чтобы и после диф-
ференцирования получить все же равномерно сходящийся ряд.
733. Полнота тригонометрической системы. Если непрерывная
в промежутке [—тс, тс] функция f(x) имеет коэффициенты
Фурье, все равные нулю, то и сама функция сводится тожде-
ственно к нулю. Действительно, в этом случае, как ясно из равен-
ства (6), при всех х будет
\f(x)dx-*Q,	(8)
о
откуда, дифференцируя по х, именно ввиду непрерывности под-
интегральной функции [305, 12°] и получим тождественно
/(х) = 0.
Иными словами, кроме функции, тождественно равной нулю,
не существует непрерывной функции, которая в промежутке
[—тс, тс]* была бы ортогональна [679] ко всем функциям триго-
нометрической системы
1, cos х, sinx, cos 2х, sin2x,..., cos их, sin их,...	(9)
Этот именно факт и выражают, говоря, что тригонометрическая
система полна — в классе непрерывных функций.
Если две непрерывные функции /(х) и /а(х) имеют одни и те
же коэффициенты Фурье, то они необходимо тождественны, ибо их
разность /1 (х) —/2 (х) будет иметь коэффициенты Фурье, сплошь
равные нулю. Таким образом, непрерывная функция однознач-
но определяется своими коэффициентами Фурье. Это лишь
другая формулировка свойства полноты тригонометрической си-
стемы.
* Или в каком-нибудь другом промежутке длины 2л.
733J
5 1. ОПЕРАЦИИ НАД РЯДАМИ ФУРЬЕ
579
Если обратиться к рассмотрению и разрывных функций, то положение
вещей может оказаться другим. Функция, которая, скажем, лишь в конечном
числе точек отлична от нуля, уже не равна нулю «тождественно», но в то же
время, очевидно, будет ортогональна к любой из функций (9), как, впрочем,
и ко всякой интегрируемой (в собственном или несоб-
ственном смысле) функции. Можно представить себе функции, от-
личные от нуля даже в бесконечном множестве точек и все же обла-
дающие последним свойством. Такова, например, функция/(х)
[ср. 70, 8), 300, 1)], равная —, если х есть несократимая дробь вида
± С л^, а в прочих точках промежутка [— л, л] равная 0.
Однако функция, которая в рассматриваемом промежутке ортогональна
ко всякой вообще интегрируемой функции, не отличается «существенно»
от нуля; мы будем называть такую функцию эквивалентной нулю.
Теперь можно доказать, что абсолютно интегрируемая в промежутке
[—л, л] функция f(x), коэффициенты Фурье которой все равны нулю,
необходимо эквивалентна нулю.
Действительно, если g(x)—произвольная функция, интегрируемая в соб-
ственном смысле, то, в силу 579, Г,
(R) $/(*)£ (х) dx = (S) $ g (х) dP (х),
— те	— те
х
где F(х) = f (х) dx. При сделанных предположениях Л(х) = 0 [см. (8)],
так что /(х) ортогональна к g(x).
Отсюда легко перейти к случаю, когда g (х) интегрируема в несоб-
ственном смысле. Пусть, например, точка л будет ее единственной осо-
бой точкой. Тогда, полагая g*(x)—g(x) в [—л, л — ej (е>»0) и g*(x) = 0
в (л — е, л], по доказанному будем иметь
те —е	те
f-gdx= f • g* dx = 0.
— те	— те
Остается лишь перейти к пределу при е—>0.
Расширяя несколько понятие «полноты», можно утверждать теперь, что
тригонометрическая система (9) полна в классе абсолютно интегрируе-
мых функций. Смысл этого таков: кроме функций, эквивалентных нулю,
не существует абсолютно интегрируемой функции, которая в промежутке
[—л, л] была бы ортогональна ко всем функциям (9).
Наконец, если две абсолютно интегрируемые функции имеют одни и те
же коэффициенты Фурье, то их разность эквивалентна нулю. Если не счи-
тать такие функции «существенно» различными, то в некотором смысле
можно сказать и здесь, что абсолютно интегрируемая функция однозначно
определяется своими коэффициентами Фурье.
Замечание. Все сказанное сохраняет свою силу и порознь для
систем
1, cos х, cos 2х,..., cos их,...
или
sinx, sin2x,..., sin/гх,...,
но лишь в промежутке [0, л].
19’
580	ГЛ. XX. РЯДЫ ФУРЬЕ (ПРОДОЛЖЕНИЕ)	[734
734. Равномерная аппроксимация функций. Теоремы Вейер-
штрасса. Если какую-либо функцию f(x) в промежутке [а, &]
«аппроксимируют»* с помощью другой, g(x), то качество этой
аппроксимации можно, в зависимости от обстоятельств, оценивать по-
разному. Но, естественно, в основу во всех случаях кладется рас-
смотрение разности
r(x)=f(x) — g(x).
Если мы одинаково заинтересованы в малом отклонении одной из
функций от другой во всех отдельно взятых точках, то
за меру приближения принимают их максимальное отклонение в
промежутке, т. е. число
8 = sup | г (х) |.
а^х^Ь
В этом случае говорят о равномерной аппроксимации
функции f(x) с помощью функции g(x).
Мы приведем две фундаментальные теоремы Вейерштрасса,
относящиеся к равномерной аппроксимации непрерывных
функций, во-первых, с помощью тригонометрических многочленов и,
во-вторых, с помощью обыкновенных (алгебраических) многочленов.
Теорема 1. Если функция /(х) непрерывна в промежутке
[— it, it] и удовлетворяет условию
/(-it)=/(it),'
то, каково бы ни было число е^>0, найдется такой тригоно-
метрический многочлен
Т(х) — а0 + 2 (а/п cos тх + ?»»sin тх}>
т = 1
что равномерно для всех значений х в упомянутом проме-
жутке будет
|/(х)-Т(х)|<е.	(10)
Построим прежде всего такую кусочно-линейную функцию
<р(х), чтобы повсюду в [—-к, it] выполнялось неравенство
|/(х) —<р(х)|<у.	(11)
Для этого разобьем промежуток [—it, к] точками
— it == х0 Xi <^... <^ хг хг+1 . <Z xk = 1С
на столь малые части, чтобы в каждой из них колебание функции /
* То есть приближенно воспроизводят.
734]	§ 1. ОПЕРАЦИИ НАД РЯДАМИ ФУРЬЕ	581
было ~. Функцию ср (х) определим в промежутке [— тс, тс], полагая
ее в каждом отдельном промежутке [xit xi+1] равной линейной
функции
f (*,)+(*-*«•)>
Л1+1 Л1
которая на концах промежутка совпадает с /(х). По сути дела речь
идет о вписывании ломаной линии в кривую, выражаемую уравнением
y—f(x). Если через /и, и Л1; обозначить наименьшее и наибольшее
значения функции f в z-м промежутке, то по условию 7Иг —	<^ -|-, и
так как в этом промежутке значения обеих функций f и ср содер-
жатся между mt и Л1;, то выполнение неравенства (11) во всем про-
межутке [-— тс, тс] удостоверено^
Функция ср (х) подобно f (х) непрерывна в промежутке [— тс, тс]
и удовлетворяет условию
ср(— тс) = ср (тс);
но, сверх того, она, как кусочно-монотонная функция, имеет в этом
промежутке ограниченное изменение [568, 1°]. При этих условиях,
согласно признаку Дирихле—Жордана [690], ср(х) разлагается
в равномерно сходящийся ряд Фурье:
ОО
<р (х) = 0С0	2 ат cos тх + Sin тх-
т= 1
Следовательно, если в качестве многочлена Т(х) взять n-ю частичную
сумму этого ряда при достаточно большом п, то он будет отли-
чаться от ср (х) меньше, чем на :
14>(х)— 7-(х)]<-1	(12)
сразу для всех рассматриваемых значений х.
Из (11) и (12) вытекает (10).
Возьмем теперь последовательность {е*} убывающих до нуля по-
ложительных чисел и для каждого числа s = построим многочлен
7'=7'ft(x), о котором была речь в доказанной теореме; тогда полу-
чится последовательность {7*(х)} тригонометрических многочленов,
которая сходится к функции f(х) равномерно в промежутке
[—тс, тс]. Переходя обычным образом [427] от последовательности
к бесконечному ряду, получим другую формулировку теоремы, оче-
видно, равносильную прежней: при указанных в теореме 1 усло-
виях функция f(x) разлагается в равномерно сходящийся
ряд, членами которого являются тригонометрические многочлены.
582
ГЛ. XX. РЯДЫ ФУРЬЕ (ПРОДОЛЖЕНИЕ)
(734
Из теоремы 1 уже легко выводится
Теорема 2. Если функция f(x) непрерывна в промежутке
[а, й], то, каково бы ни было число е^>0, найдется такой це-
лый алгебраический многочлен
Р kx)= со	cix ~г cixi • • • ~Ь спхП<
что равномерно для всех значений х в [а, Ь] будет
|/(х)-Р(х)|О	(13)
Простой подстановкой
+ а)
можно свести дело к рассмотрению промежутка [0, тс], ибо многочлен,
целый относительно х', очевидно, будет целым и относительно х.
Чтобы не усложнять обозначений, будем считать, что первоначально
данный промежуток и есть [0, к].
Распространим теперь функцию f(x) на весь промежуток [ — тс, к],
Функция сохранит непрерывность и, очевидно, будет удовлетворять
условию /( — я) =/ (it). В таком случае по теореме 1 найдется такой
тригонометрический многочлен Т(х), что для всех значений
х между — к и тс будет
|/(х)-7-(х)|<|.	(14)
Если заменить каждую из тригонометрических функций, входящих
в состав Т, ее разложением по степеням х [404], то и функция Т
представится в виде суммы повсюду сходящегося степенного ряда:
СО
T(x)=^cmxm.
m=0
В промежутке [ — я, тс] этот ряд сходится равномерно; поэтому,
если отождествить многочлен Р(х) с и-й частичной суммой этого ряда,
при достаточно большом п, то для всех х в промежутке [ — тс, тс]
будет
|7-(х)-Р(х)|<-1	(15)
Остается сопоставить (14) и (15).
Как и выше, доказанной теореме можно дать другую формули-
ровку: функция f (х), непрерывная в промежутке [а, Ь], разла-
гается в этом промежутке в равномерно сходящийся ряд,
членами которого являются целые алгебраические многочлены.
735]
5 1. ОПЕРАЦИИ НАД РЯДАМИ ФУРЬЕ
583
735. Аппроксимация функций в среднем. Экстремальные свой-
ства отрезков ряда Фурье. При аппроксимации функции f(x) в
промежутке [а, Ь] с помощью другой функции g(x) можно стать и
на другую точку зрения, предпочитая вместо равномерной близости
этих функций требовать, чтобы функции были близки лишь «в сред-
нем». В этом случае за меру близости их можно взять их сред-
нее отклонение
а
=	$ \r(x)\dx
а
или, чего мы и будем держаться в последующем, среднее квад-
ратичное отклонение
Вместо этого выражения, впрочем, удобнее рассматривать более про-
стую величину:
ь
Д = г’ (х) dx = (b — а) 8"2.
а
Обратимся вновь к рассмотрению произвольной ортогональ-
ной в промежутке [а, Ь] системы функций {'-pm(x)} (/и = 0, 1, 2,...),
интегрируемых с их квадратами [679]. Пусть f(x)— заданная в том
же промежутке функция, также интегрируемая с квадратом, ил—
фиксированное натуральное число. Поставим себе такую задачу: из
всех линейных комбинаций первых п-j-l функций ср
(х) — уосро (х) -Н1Ч>1 (х) + • • • + Ж (•*)	(16)
при произвольном наборе коэффициентов 70, 71,..., найти ту, ко-
торая осуществляет наилучшее — в смысле среднего квадрати-
ческого отклонения — приближение к функции/(х). Иными словами,
требуется добиться наименьшего значения для величины
ь
дя= $[/(*) — <Jn(x)]2dx.
а
Подставив сюда вместо ап(х) ее развернутое выражение, по-
лучим:
ь	а	ь
(х) dx — 2 2 Im $/(*) dx +
a	/п=0	а
п b	b
+ S I’m. S w dx + 2 S IftTm $ <x) (*) dx-
a	k<jn a
584	ГЛ. XX. РЯДЫ ФУРЬЕ (ПРОДОЛЖЕНИЕ)	[735
Последняя сумма исчезает ввиду ортогональности нашей системы.
Вводя постоянные
ь
^т=\Чт(х)Лх
а
и (обобщенные) коэффициенты Фурье функции f(x)
ь
ст = у — \ f (х)	(х) dx,
,''ГП V
а
можно переписать выражение для Д„ в виде
Ь	п	п
ba=\f4x)dx — 2 У ХтсЛ+ у Хт^т.
а	т—0
Чтобы под знаком суммы получить полные квадраты, нужно ввести
туда еще члены Хтс„. Добавив их с плюсами и с минусами, оконча-
тельно получим:
6	п	п
bn = \f*(x)dx- у Х„Л + у Хот(Ти-ст)*.
a	т=0	т=0
Теперь ясно, что Дп достигает своего наименьшего значения
тогда, когда обращается в нуль последняя сумма, а это будет при
То = со> = 1п = Сп-
Таким образом, из всех многочленов вида (16) именно отрезок
(обобщенного) ряда Фурье
sn (х) = со?о (х) ci?i (х) + • • • сп?п (х)
доставляет величине наименьшее возможное для нее зна-
чение	ь	ь
8„ = $ \f (х) - (X)]2 dx =	(x) dx - 2 Xm^. (17)
a	a
Снова наше внимание приковывается к коэффициентам Фурье как,
в некотором смысле, «лучшим» из всех возможных! Важно отметить
при этом, что коэффициенты, оказавшиеся «лучшими» при фиксиро-
ванном п, сохраняют свою роль и при ббльших значениях п, к ним
лишь присоединяются еще новые коэффициенты!
Равенство (17) называют тождеством Бесселя. Из него по-
лучаются неравенства
п	ь
У ^тСт^Л(х)бХ
т=0	а
735]	$ 1. ОПЕРАЦИИ НАД РЯДАМИ ФУРЬЕ	585
и (если перейти к пределу при п оо)
оо	Ъ
(18)
m=0	а
Это — неравенство Бесселя. Любопытно, что ряд в (18) оказы-
вается всегда сходящимся, лишь бы функция f(x) была интегри-
руема с квадратом.
При возрастании п величина Вл убывает, поскольку в ее выра-
жении (17) добавляются новые отрицательные слагаемые. Чем
больше п, тем ближе сумма s„(x) «в среднем» подходит к рассма-
триваемой функции f(x). Естественно возникает вопрос: можно ли
за счет увеличения п добиться сколь угодно малого
среднего квадратического отклонения, т. е. стремится
ли к О при л—>оо?
Если это выполняется, то говорят, что сумма sn (х) сходится к
функции f(x) «в среднем» (что — подчеркнем это — вовсе не пред-
полагает «точечной» сходимости sn(x) к f(x) в обычном смысле
слова). Из тождества Бесселя ясно, что тогда (и только тогда),
имеет место равенство [ср. (18)]:
со	Ъ
У, ^тс*т = \Л (х) dx.
т=0	а
Следуя В. А. Стеклову, мы будем называть его уравнением
замкнутости. Обычно, впрочем, его называют формулой Пар се-
ва ля (М. A. Parseval), по имени ученого, который еще в начале
XIX века рассматривал подобную формулу для тригонометрической
системы (без какого-либо обоснования).
Если уравнение замкнутости выполняется для каждой функ-
ции /(х), интегрируемой с квадратом, то саму систему {<ря (х)}
называют замкнутой.
Применим теперь все сказанное в частности к тригонометри-
ческой системе (9). Вместо сумм вида (16) придется рассматривать
тригонометрические многочлены
п
Sn(x) = Л + 2	COS тх +	sln тх
т=1
и исследовать осуществляемое ими приближение «в среднем», которое
характеризуется величиной
Дл= $ [/(x)-S„(x)pdx.
— те
586
ГЛ. XX. РЯДЫ ФУРЬЕ (ПРОДОЛЖЕНИЕ)
|736
Оказывается, что при фиксированном п наименьшее значение
этой величине доставляет соответствующий, отрезок ряда
Фурье	п
sn(x) =	2 ит cos mx-\-bm sin тх.
т=1
Само же это наименьшее значение дается равенством
те
= § I/ (*) — 8п (x)]s dx =
— те
те	[	п
= \^(х)Фх-к	2 (<& + ^)
— те	(	т—\
(19)
(«тождество Бесселя»). Из него вытекает, как и в общем случае,
сходимость ряда, составленного из квадратов коэффициентов Фурье:
оо	те
4+2 I ^dx
т—\	—те
(«неравенство Бесселя»).
Для рассматриваемой конкретной системы (9) мы в состоянии
полностью решить поставленный в общем случае вопрос, что и будет
выполнено в следующем п°.
736.	Замкнутость тригонометрической системы. Теорема Ляпу-
нова. Имеет место следующая замечательная теорема, строгое дока-
зательство которой (для случая ограниченной функции) впервые было
дано А. М. Ляпуновым.
Теорема. Какова бы ни была интегрируемая с квадратом
функция f(x), всегда
lim Вп = 0,
П-ь-СО
и выполняется «уравнение замкну тостик
со	те
4+2 (x)dx-
т=1	—те
(20)
Доказательство мы разобьем на несколько этапов.
1°. Если функция f(x) непрерывна в промежутке [ — л, тс] и удо-
влетворяет условию /(— ic)=/(tc), то по первой теореме Вейер-
ш т р а с с а существует такой тригонометрический многочлен Т (х) (по-
'рядок которого мы здесь обозначим через N), что
|/(х)-7-(х)|<1/Г^.
736J	§ 1. ОПЕРАЦИИ НАД РЯДАМИ ФУРЬЕ	587
где е — произвольное наперед заданное положительное число. Тогда
в
$ [/(х)-Т(х)]Чх<е.
— те
По экстремальному же свойству отрезка ряда Фурье [735], по-
скольку Т(х) при желании можно рассматривать как тригонометри-
ческий многочлен любого порядка n^N, и подавно, при n^N
= $ [/ (х) — s„ (x)]3dx < е,
—те
так что 8„->0 при и-*оо.
2°. Для того чтобы распространить это заключение и на другие
случаи, установим одно вспомогательное неравенство.
Если интегрируемая с квадратом функция /(х) представляется в
виде суммы f'(x)-\-f'(x) двух подобных же функций, то, обозначая
штрихами относящиеся к ним величины, будем иметь
/(X) - sa (X) = \f (X) - sn (X)] + \Г (X) - S" (X)],
откуда
\f (х) - sn (х)]2	2 ][/'(х) - sn(х)]3 + [Г (X) - &(х)П*
и, далее,
те
$ [/(х) —8„(х)]Чх<
—те
^2^5 [Г (•*) —sk(x)]’dx-l- 5 [/"(х) —8]](х)]Мх|
I—те	—те	'
или, короче:
8„^2{8; + Q
Заметим, наконец, что из тождества Бесселя [см. (19)], применен-
ного к функции f, следует
8"=^ \f”*dx.
—те
Таким образом, окончательно
8лг=;2! 8],-j- $ /"’dxk	(21)
’ —те	’
Это и есть нужное нам неравенство.
* Мы пользуемся здесь элементарным неравенством
(a + ft)s=g2(a2-|-ft8).
688
ГЛ. XX. РЯДЫ ФУРЬЕ (ПРОДОЛЖЕНИЕ)
1736
3°. Пусть теперь функция /(х) будет интегрируема в собствен-
ном смысле (а значит ограничена) в промежутке [ — те, те]. Изме-
няя в случае надобности значение функции на одном из концов
промежутка, можно считать, что /(— те)=/(те). Построим вспомога-
тельную функцию ср (х), как мы делали это при доказательстве первой
теоремы Вейерштрасса [734], причем дробление промежутка на
этот раз выберем так, чтобы было
i
где е — наперед взятое по произволу положительное число, ш,- — ко-
лебание функции f в z-м частичном промежутке, а 2—полное коле-
бание функции f во всем промежутке от —те до те [297].
Мы положим
/"=/-?.
В силу 1°, Вп->0 при л->оо, так что, начиная с некоторого места,
С другой стороны, так как в z-м частичном промежутке
|/"(х)| = |/(х)-?(х)|^шг,
ТО
те	л7"4“1
— ir	I Х[	i	i
Теперь, ввиду (21), уже ясно, что для достаточно больших п будет
8»<e>
и т. д.
4°. Пусть, наконец, функция /(х) будет интегрируема в несоб-
ственном смысле, но обязательно с квадратом. Для простоты
предположим, что при этом единственной особой точкой для f
(и для /2) будет х = те. Тогда по заданному е^>0 можно найти
такое ij ]> 0, что будет
те
J т<~.
те — т]
Положим в этом случае
f\x) — ПрИ ~—
[	0 при х^те — т)
737]
§ 1. ОПЕРАЦИИ НАД РЯДАМИ ФУРЬЕ
589
и, наоборот,
« — •»!>
Очевидно,
(х) при
С другой стороны, к функции f, интегрируемой в собственном
смысле, приложим только что доказанный результат. С помощью (21)
заключаем, что и здесь 8Я -> 0. Этим завершается доказательство
теоремы Ляпунова.
Пользуясь установленной в предыдущем п° терминологией, можно
сказать, что тригонометрическая система является з амкну-
той.
737.	Обобщенное уравнение замкнутости. Пусть даны две
функции f(x) и ср(х), интегрируемые в промежутке [ — те, те] с квад-
ратами. Как известно [483, 6)], тогда функции /-[-ср и /—ср также
будут интегрируемы с квадратами. Если обозначить, соответственно,
через ат, Ьт и am, j3m коэффициенты Фурье функций / и ср, то
для функций /-ь ср, очевидно, коэффициентами Фурье будут
zt ®m> ^>т zt Pm"
Применив уравнение замкнутости порознь к функциям /-[-ср и
/ — ср, получим:
2 t(a« +а-)2 + (*т + М] =| J l/+<pN*
т— 1	— те
И
оо	те
(Arp!8 -|_ 2 [(ат - ат)2 + (Ът - ₽„)’] =1 5 [/- срР dx.
m=l	—я
Если почленно вычесть эти два равенства одно из другого, то, при-
нимая во внимание тождество
(а-уЬ^ — (а — Ь)г = ^аЬ,
придем к обобщенному уравнению замкнутости
оо	те
+ 2 (V» + Ш = -Ц / (*) <Р (х) dx.	(22)
т=\	—те
Уравнение (20) получается отсюда при ср ==/. Эту общую формулу
также называют формулой Парсеваля.
590
ГЛ. XX. РЯДЫ ФУРЬЕ (ПРОДОЛЖЕНИЕ)
(737
Обобщенное уравнение замкнутости (22) теснейшим образом свя-
зано с вопросом о почленном интегрировании рядов Фурье. Под-
ставляя вместо коэффициентов am, j3m их интегральные выражения:
л	те
am — <р (х) cos тх dx,	<р (х) sin тх dx,
— те	—те
(т=0, 1,2,...)	(m=l,	2,	3,	. .,)
перепишем равенство (22) в виде
те	со те
-у- ср (х) dx -{- (ат cos тх -{- bm sin тх) ср (х) dx =
—те	т=1 —те
те
= §/(•*)? (x)dx.
—те
Отсюда ясно, что упомянутое равенство совершенно равносильно
утверждению: ряд Фурье функции /(х) (интегрируемой с квад-
ратом) по умножении всех его членов на произвольную функцию
ср(х) (также интегрируемую с квадратом) можно в промежутке
от —к до к интегрировать почленно (в том смысле, что в резуль-
тате этого получится интеграл от произведения обеих функций!).
Конечно, промежуток [—гс, гс] здесь может быть заменен любой
его частью [х', х"], ибо это попросту сводится к замене, скажем,
функции ср другой функцией, которая совпадает с ср в промежутке
[х', х"] и равна нулю вне этого промежутка. При ср = 1 мы воз-
вращаемся к тому утверждению, которое было установлено в 731,
впрочем, с одним ограничением: функция f все же здесь предпо-
лагается интегрируемой с квадратом.
Формулу (22) можно доказать и при несимметричных условиях,
налагаемых на f и <р, облегчая эти условия для одной из функций, но зато
отягчая их для другой. Так, Юнгом (W. Н. Young) была высказана следую-
щая теорема: формула (22) имеет место в предположении, что функция
f(x) абсолютно интегрируема в промежутке [—л, л], а функция <р (х)
имеет ограниченное изменение.
Доказательство опирается на одно свойство частичных сумм (х)
ряда Фурье функции ® (х), которое будет установлено лишь впоследствии
[744, 5°|:эти суммы'равномерно ограничены, т. е. для—
х - я и п = 1, 2, 3, ...,
| ал (х) | sg Z. (L = const).
Примем это свойство пока без доказательства.
Не умаляя общности рассуждений, можно предположить, что точки раз-
рыва функции <р (х) все являются регулярными [658], так что всегда
„ _*? (х +°) + ? (х — °).
Ч (х)----------о---------»
737]
.§. 1. ОПЕРАЦИИ НАД РЯДАМИ ФУРЬЕ
591
в таком случае по теореме Дирихле — Жордана [686] будем иметь для
всех значений х
lim а„ (х) = о (х),
п"—>со
и одновременно
lim /(х) а„ (х) = / (х) <р (х).
П-^-СО
Ес ли f (х) ограничена:
| / (х) | Л1 (М — const),
так что и
| f (х) аа (х) | «£ ML (п — 0, 1, 2, ...),
то по теореме А р ц е л а [526] заключаем, что
lim ( f (х) сп (х) dx = (f (х) <f (х) dx.	(23)
»-оо Л	2,
Справедливость этого равенства может быть установлена и для случая
неограниченной (но абсолютно интегрируемой) функции /(х). Пусть ее
единственной особой точкой будет х = «. Тогда сначала по заданному е>0
возьмем >] > 0 так, чтобы было
J |/(x)|dx<e;
вместе с этим будут выполняться и неравенства
те
J f (х) <? (х) dx < 1л,
те — 7)
J f(x)tn(x)dx
<Ь
(последнее — каково бы ни было п). В промежутке же [—л, л — tq], где функ-
ция /(х) ограничена, имеем аналогично (23):
те—7)	те — 7)
lim V f (х) an (х) dx = V f (х) <р (х) dx.
-4	-4
Отсюда уже легко получается и само равенство (23).
Доказанное равенство есть лишь другая форма записи для формулы
(22), ибо
те	те	р	п
V J /(X)	(х) dX = 1	/(X)	+ 2 «т
— те	—те	*-
cos тх -]- pm sin тх
dx —
п.
~+ 2 ^атат + Ьт^т).
т=\
Обобщенное уравнение замкнутости, установленное при иных условиях,
чем раньше, снова может быть перефразировано, как утверждение, относя-
щееся к почленному интегрированию ряда Фурье (и притом в двух раз-
личных формулировках в связи с несимметричностью условий, нала-
гаемых здесь на функции f и <р). Заметим, что на этот раз предложение п° 731
получается как следствие уже с полной общностью.
592
ГЛ. XX. РЯДЫ ФУРЬЕ (ПРОДОЛЖЕНИЕ)
[738
738.	Умножение рядов Фурье. Пусть даны две функции f и ср
с их рядами Фурье:
ОО
2 ат cos тх -ф- bm sin тх,
т = 1
ОО
ф (х)	+ 2 arn cos тх +	sin тх.
т = 1
Задача, которую мы сейчас ставим перед собой, состоит в том, чтобы
написать ряд Фурье для произведения /ср этих функций:
ОО
f(x) <р (х) ~	У Ат cos тх -ф- Вт sin тх,
т—\
т. е. выразить его коэффициенты через данные коэффициенты а, b
и а, р.
Предположим, что функции / и ср интегрируемы с их квадра-
тами *, так что для них имеет место обобщенное уравнение замкну-
тости (22). Тогда оно непосредственно приводит к выражению для
коэффициента Ло:
1С	00
Л0 = Т $	=	+ 2	+W-
— ч	т = I
Нетрудно и определение коэффициентов Ak, Вк (при k =
— 1, 2, 3, ...) тоже свести к использованию формулы (22). Выра-
жение для Ak	п
Ak = -i- /ср cos kx dx
—те
отличается от выражения для Ло тем, что ср заменено на ср cos kx.
Постараемся же найти коэффициенты Фурье для этой последней
функции:
те	те
ср (x) cos &х • cos тх dx = -^--	ср (х) cos (т -ф- k) х dx -ф-
— те	—те
те
ср (х) cos (т — k)x dx
— те
— 2
я
— \ ф (х) cos kx • sin тх dx — -L-
л j	2
— те
(Pm+fc + Р
* Вместо этого можно было бы предположить функцию / абсолютно инте-
грируемой, а <р — имеющей ограниченное изменение.
739]	§ 1. ОПЕРАЦИИ НАД РЯДАМИ ФУРЬЕ	593
причем эти формулы годятся не только для m^k, но и для т k,
если условиться полагать
<*-л = «л> ₽-л = — Ра-
Теперь, снова по формуле (22),
ОО
^к =	2 ^ат “Ь am-k) + &т (Pm+A + Pm-*)]-
т—1
Аналогично получается, что
ОО
Вк =	+ у 2 [«/»	- ?»>-а) - Ьт (*т+к - ат-*)]-
т=1
Этими формулами и решается поставленная задача.
Интересно отметить, что те же выражения для коэффи-
циентов А, В могут быть получены путем формаль-
ного перемножения рядов Фурье для функций f и
если в последующем заменить произведения косинусов и синусов их
суммами или разностями и объединить подобные члены. Это обстоя-
тельство тем более замечательно* что здесь мы вовсе не предпола-
гаем даже сходимости перемножаемых рядов.
739.	Некоторые приложения уравнения замкнутости. Уравнение
замкнутости находит многообразные приложения как в самой теории рядов
Фурье, так и в других областях анализа. Мы рассмотрим в виде примера
некоторые из них.
Г. Абсолютная сходимость рядов Фурье. С. Н. Бернштейну при-
надлежит следующая теорема: если функция f (х) с периодом 2л удовлетво-
ряет условию Липшица
1	л	Л
с показателем то сходится ряд
ОО	00 
П—1	П=1
где ап, Ьп— коэффициенты Фурье функции /*.
Заметим прежде всего, что, если
00
/(х)~у + 2| ат cosmx -|- Ьт sinmx,
т = 1
то
оо
/(х±й)~^ +
2	cos s'n cos тх 4*
т= 1
+ (bm cos mh Т ат sin mh) sin тх]
* Это влечет за собой сходимость порознь рядов £ | ап | и 2 j Ъп | и сле-
довательно, абсолютную сходимость соответствующего ряда Фурье.
594
ГЛ. XX. РЯДЫ ФУРЬЕ (ПРОДОЛЖЕНИЕ)
[739
690, 26)]. В таком случае
ОО
f(x-\-h) — f(x — h.)~2 2 sin rnh (bm cos mx — am sin mx)
m— 1
и, но уравнению замкнутости,
-i- § [/(* + *)— fix— ft)]8rfx = 4 p2m sin8 mh.
— it	m—\
Если учесть теперь само условие Липшица, то интеграл слева опе-
нится числом Ch2a, где С — постоянная. Взяв произвольное натуральное
число N, положим h — тогда
СО
2 P^sin22W<CliV‘2a
/п== 1
(здесь С, означает новую постоянную), а следовательно, и подавно
., К
Но для т>-^~, очевидно,
и можно утверждать, что
2 Рт^2СЛ-8“.
„ N
В частности, если выбрать N=2’ (•»=!, 2, 3, ...), имеем
г’
2	р^гсх-г-8-.
/п==2',-14-1
Но по известному неравенству 133 (5а)
/2Сх .2-’»-2 2 l’ = УС12^2
739J
§ 1. ОПЕРАЦИИ НАД РЯДАМИ ФУРЬЕ
595
Суммируя все подобные неравенства при м = 1, 2, 3, ..получим
оо	_ 00	* _Л
'< + °О.
т—2	v = l
ибо при а > -j ряд справа сходится. Теорема доказана.
Полученный результат предельно точен: примером можно показать, что
1
при а=у он уже не имеет места.
2°. Доказательство некоторых неравенств. Уравнение замкнутости
применяется к доказательству ряда полезных неравенств.
Начнем с неравенств, указанных впервые В. А. Стекловым и с успехом
использованных им в математической физике. Пусть функция f(x) непрерывна
в промежутке [0, л] и имеет в нем (за исключением разве лишь конечного
числа точек) производную f (х), интегрируемую с квадратом. Тогда, если вы-
полняется одно из двух условий
(а)	|/(x)rfx = 0
или
(б)/(0) =/(л) =0.
имеет место неравенство
jf/'(x)]Mx^b/(x)ptfx,	(24)
о	о
причем равенство осуществляется в случае (а) лишь для функций вида
f (х) = A cos х, а в случае (б)—для функций вида /(x)=Bsinx.
Начнем со случая (а). В этом случае в разложении функции /(х) в про-
межутке [0, л] по косинусам отсутствует свободный член:
00
f (х) ~ У] ап cos пх.
л=1
Так как при четном продолжении функции /(х) на промежуток [—л, 0]
выполняется условие /(—л)=/(л), то по правилу п° 732
00
/' (х) ~ — 2 пап sin пх.
п= 1
Теперь согласно уравнению замкнутости, которое, как легко видеть, имеет
место в промежутке [О, л] и для ряда по косинусам и для ряда по синусам,
будет
Я	00
д [/(x)]2rfx=2a«
О	п=1
и одновременно
я	00
-M[/'(x)]»dx==2"2a£
О	л = 1
596
ГЛ. XX. РЯДЫ ФУРЬЕ (ПРОДОЛЖЕНИЕ)
[739
Отсюда непосредственно и вытекает неравенство (24), причем ясно, что
равенство может иметь место, лишь если
а„ = 0 при п^2,
т. е. если f (х) = at cos х.
В случае (б) аналогично рассмотрим для функции f(x) ряд по синусам:
СО
Л*)~ 2 bn s>n пх.
п= 1
При нечетном продолжении функции f (х) на промежуток [ — я, 0], именно
в силу условия (б), сохранится непрерывность при х = 0 и выполнится тре-
бование /(—	так что снова приложимо^правило п° 732:
00
f (х) ~ 2 nbn cos пх.
п— 1
Применение уравнения замкнутости и здесь сразу решает вопрос.
Впоследствии Виртингер (W. Wirtinger) установил несколько более
общее неравенство. Предположим, что функция f(x) непрерывна в промежутке
[ — те, те] и имеет в нем (за исключением разве лишь конечного числа точек)
производную f (х), интегрируемую с квадратом. Тогда, если выполнены
условия
/( —те)=/(те) и J /(x)dx = 0,
— те
имеет место неравенство
5 ]/'(x)]2rfx>= 5 [/(x)]2rfx,	(25)
— та	—та
причем равенство осуществляется для функций вида f (х) = A cos х 4*
4- В sin х.
Доказательство, как и выше, сводится к применению уравнения замкну-
тости к рядам
ОО
f (х) ~ 2 ап cos пх + Ьп sin пх
п= 1
и
00
f (х) ~ У] п (bn cos пх — ап sin пх).
п = 1
Неравенства Стеклова получаются из (25), если, в частности, положить
функцию / (х) (а) четной или (б) н е ч е т н о й.
Ниже мы приводим пример установления более сложного неравенства.
3°. Изопериметрическая задача-, требуется среди всевоз-
можных замкнутых плоских кривых, имеющих данную
длину L, найти ту, которая ограничивает фигуру наи-
большей площади.
Известно, что решением является окружность; приведем чисто аналитиче-
ское доказательство этого факта, принадлежащее Г у р в и ц у (A. Hurwitz),
причем ограничимся рассмотрением гладких кривых.
739]
§ 1. ОПЕРАЦИИ НАД РЯДАМИ ФУРЬЕ
597
Итак, пусть замкнутая гладкая кривая (L) длины £ задана параметрически,
причем в роли параметра фигурирует длина дуги s, отсчитываемая от некото-
рой точки:	x = x(s), y=y(s) (O^s^L).
п	j 2лл	Л
Переходя к параметру t-—^--, изменяющемуся от 0 до 2л, перепишем эти
уравнения в виде
х — <? (0, У — Ф (О (0 sg sg 2л);
особо отметим выполнение условий
<р (0) = <р (2л) и ip (0) = ф (2л).
В силу 732, ясно, что из рядов Ф у р ь е, в которые разлагаются функции
<Р (0 И ф (0:
<р(0=у+2 ат cos mt + bm sin mt,
m = l
со
>K0 = -y+ 2 COS mt + dm sin mt,
m.= l
ряды Фурье для их производных получаются почленным дифференцирова-
нием:
00
<р' (0 ~ 2 mbm cos mt — rnam sin mt,
m—l
co
Ф' (0 ~ 2 cos mi — rncm sin mt.
m=l
Применяя здесь уравнение замкнутости, получим:
2тс	оо
~	2 m2<a®+4),
О	m = l
2те	оо
-М[<но]’л=2 т’(4+4)-
О	т=1
Так как
, L* *
[<?' (OF W (012==(s/)2 —	(26)
то отсюда
оо
£2 = 2л2 2 т* (а3т + ?т + еат + <).	(27)
m=l
С другой стороны, площадь F фигуры, ограниченной рассматриваемой
кривой, по известной формуле [526 (9)] выразится так:
2л	2тс
F = ? хdy = х^ dt = V <р (0 4»' (0 dt *	(28)
 (I) О	О
* Если предположить (что мы вправе сделать), что при изменении пара-
метра t от 0 до 2л кривая описывается в положительном направлении.
598
ГЛ. XX. РЯДЫ ФУРЬЕ (ПРОДОЛЖЕНИЕ)
(739
Воспользовавшись на этот раз обобщенным уравнением замкнутости, пред-
ставим выражение для площади в виде
F —л £ т (ат^т ^тст)-
т = \
(29)
В таком случае, вычитая из равенства (27) равенство (29), умноженное на 4п,
получим:
' 00
2 т!(<+^+4+<)-
уп= 1
L2 — 4пР= 2 л2
со
2/й (&т$гп ЬтСгп) =
m —1
/оо	со
= 2*4 2 0"а«1 —2 (mc'n + W’ +
00
+ 2 («’-D (»« + <)
т—2
и, так как все слагаемые суммы в фигурных скобках неотрицательны, всегда
будет выполняться «изопериметрическое неравенство»
£2 — 4лА^0,
то есть
Знак равенства имеет место — и одновременно площадь F получает наи-
большее из возможных для нее значений — лишь в том случае, если все
слагаемые — нули, т. е. если
= тот, Ьт = тст, bm — dm = 0.
(m = l, 2, 3, ...)	(m=2, 3, ...)
Это равносильно соотношениям
= q= — blt am = bm = cm = dm = O для т^2.
Но тогда
х = -у а0	«1 cos t bt sin t,
у = c0 — bx cos 14- «1 sin t,
откуда
(x— -’-а0) 4*(у —y«o) =«? + &.?>
и наша кривая есть не что иное, как окружность! Этим и доказано
экстремальное свойство круга.
740]	§ 2. ПРИМЕНЕНИЕ МЕТОДОВ СУММИРОВАНИЯ К РЯДАМ ФУРЬЕ 599
Заметим, впрочем, что если воспользоваться неравенством (25)*, то изо-
периметрическое неравенство можно установить, уже не прибегая
к у]Гавнению замкнутости. Действительно, мы можем, не умаляя
общности, предположить, что центр тяжести кривой лежит на оси у, т. е. что
2я
J <р(/)Л = 0.	(30)
о
Тогда из (26) и (28) имеем
2тс	2п	2п	2те
L* ?	ее
2^-—2Г= \ [<р'2 + ф'2]Л —2 \ <[4/Л=\ [<р —	—<р8] Лэ=0
0	0	0	о
— именно в силу неравенства (25), с учетом условия (30). При этом равен-
ство может осуществиться, лишь если <р (t) = A cosf 4- В sin t и <р' (t) =<р(0»
откуда <p(Z)=/lsinT— BcosZ-f-C, и т. д.
§ 2. Применение методов обобщенного суммирования
к рядам Фурье
740. Основная лемма. Для того чтобы в дальнейшем изложении
избежать повторений, мы предпошлем ему некоторые общие сообра-
жения, составляющие существо ряда последующих доказательств.
Рассмотрим интеграл общего вида (<^>0)
tydt,	(1)
о
содержащий параметр X. Областью изменения параметра пусть будет
некоторое множество Л = {Х}, имеющее точку сгущения ш, конечную
или нет. Относительно функции Ф((, X) предположим, что она опре-
делена для значений t в [0, а] и значений X из Л, и при постоян-
ном X интегрируема по t в собственном смысле. Кроме того, наложим
на функцию Ф(£, X) следующие три требования:
1°. Ф((, X)s=0.
2°. Каково бы ни было X из Л,
$Ф(£, X)d(=l **
о
и, наконец,
* Которое, очевидно, имеет место и при замене промежутка [ — я, те]
промежутком [0, 2те].
** Достаточно было бы предположить, что
lim V Ф (t, X) dt = 1,
х-ш J
но мы в этом обобщении не заинтересованы,
600
ГЛ. XX. РЯДЫ ФУРЬЕ (ПРОДОЛЖЕНИЕ)
1740
3°. При любом 3, 0<^8<^а, величина
М (8, к) = sup Ф (t, к)
при к —• <о стремится к нулю.
Функцию Ф, удовлетворяющую этим условиям, для краткости
будем называть положительным ядром.
Лемма. Если Ф (t, к) есть положительное ядро, a g(f)—
произвольная, абсолютно интегрируемая функция, для которой
существует предел g(-j- 0), то
limJ(k) = §(-{-0).
X—*U)
Доказательство. Ввиду 2°,
Д( + 0) = ^(+0)Ф(6 к)Л;
о
вычитая это равенство почленно из (1), получим:
JW - g(+0) = $ [g(0 - g(+0)] ф (t, к) dt.
о
Задавшись произвольным числом е 0, возьмем теперь 8 (0 <4 о а)
так, чтобы при 0<^f^8 было
1^(0-д(+о)|<4-,
и разобьем предшествующий интеграл на сумму двух интегралов:
а	8	а
$ = S + S —71 + J2-
0	0	б
Для первого из них, принимая во внимание 1° и 2°, сразу получаем
оценку;
1-лМ 1^(0—д(+о)]ф(х k)^<-^j®a, к)^<-|-,
о	о
и притом независимо от к. С другой стороны,
1^(0 — д(4-0)|Ф(/, k)rf^
б
.^Ж(8, к)5^(0-^(4-0)1 Л. (2)
о
741]	$ 2. ПРИМЕНЕНИЕ МЕТОДОВ СУММИРОВАНИЯ К РЯДАМ ФУРЬЕ 601
В силу 3°, Л —0, так что для значений X, достаточно близких к ю,
будет | ЛI , а вместе с этим и
RW-£(+о)|<е>
что и требовалось доказать.
К сказанному сделаем еще такое дополнение. Предположим, что
функция g, кроме переменной t, зависит еще от одной переменной х
(О^х^а):
g=g(t, х),
но при постоянном х удовлетворяет прежним условиям. Тогда, если
1) g(t, х) равномерно ограничена при всех t и xi
\g(t, x)\^L
и 2) стремление g(t, х) к g(4-0, х) осуществляется равно-
мерно относительно х, то и интеграл
JQ., x)=\g(t, x)$(t, \)dt
о
при X — <о стремится к пределу g(4~0, х) равномерно от-
носительно х.
Действительно, в силу 2) число 3, о котором была речь в пред-
шествующем рассуждении, можно выбрать независимо от х.
Далее, так как, в силу 1),
\g(t> *) —£(4~°> -v)|^2£,
то неравенство (2) можно заменить таким:
| Л|^2£аЛ4(8, X),
где справа уже нет никакой зависимости х. Отсюда ясно, что для
значений X, достаточно близких к ш, неравенство | ЛI <С а с ним
и неравенство
R0-» *) —g(4-°> х)I<е>
будет выполняться сразу для всех значений х, что тре-
бовалось доказать.
741. Суммирование рядов Фурье по методу Пуассона—Абеля.
Пусть f(x) снова означает функцию с периодом 2л, абсолютно
интегрируемую в любом конечном промежутке. Рассмотрим ее ряд
Фурье
00
Ж~4°-4- 2 ат cos тх 4- sin тХ	(3)
т=1
602
ГЛ. XX. РЯДЫ ФУРЬЕ (ПРОДОЛЖЕНИЕ)
(741
и при произвольном фиксированном х применим к нему метод обоб-
щенного суммирования Пуассона — Абеля [418]. С этой целью
умножим члены этого ряда по порядку на гт(т = 0, 1, 2, ... ),
где 0<^г<^1, и составим ряд
ОО
/(г, х) = а£-+- rm (ат cos тх	bm sinтх).	(4)
т = 1
Так как коэффициенты ат, Ьт при т -> оо стремятся к нулю [656],
то они ограничены в их совокупности:
|a«L \bm\^K (К=const),
ОО
так что ряд (4) мажорируется просто прогрессией 2/СУ, гт и заве-
о
домо сходится.
Чтобы облегчить исследование поведения его суммы f(r, х) при
г —► 1, представим ее в виде интеграла. Если заменить в (4) коэф-
фициенты ат, Ьт их интегральными выражениями
те
ат =	/(и) cos mu du,
—те
(m = 0, 1, 2 ...)
те
Ьт = f (и) sin mu du,
—те
(т = 1, 2, ...)
то получим сначала
те	оо те
f(r, х) = ~ f(u)du-)-^- 2 г/” § f(u)cosm(u—x)du,
—те	т — 1 —те
а затем
те	оо
f(r, *) = “	+ 2 rmcosm(u —
- те	т— 1
Переход этот мотивируется ссылкой на следствие, установленное
в п° 510: равномерно (относительно х) сходящийся ряд в фигурных
скобках, по умножении его членов на абсолютно интегрируемую
функцию, можно интегрировать почленно. Так как сумма упомянутого
ряда нам известна [см., например, 741, 2)]:
-[- rm cos т (и — х) =
т=1
j____________1 — Г2
2 1 — 2r cos (и — х) + г2 ’
то окончательно приходим к такому выражению:
те
f(r, x) = 2jc f (и) J _ 2r cos + r2 du.
—те
(5)
741]	§ 2. ПРИМЕНЕНИЕ МЕТОДОВ СУММИРОВАНИЯ К РЯДАМ ФУРЬЕ 603
Этот замечательный интеграл, называемый интегралом Пу ас с она
(S. D. Poisson), играет важную роль во многих вопросах анализа.
Фактически и ряд (4) и интеграл (5), к которому этот ряд при-
водится, были рассмотрены Пуассоном задолго до появления
идеи «обобщенного суммирования», но рассуждения автора не были
достаточно строгими. Точную теорию интеграла Пуассона дал
Шварц (Н. A. Schwarz).
Теорема. Пусть для функции f(x) в рассматриваемой
точке х существуют пределы справа и слева f(x±b). Тогда
If	I _f.2
!im f(r, х) = lim х-\ f(u)-.—х---------г-х—.du =
r_i-o v ’ r-»i—о 2те J v ’ 1 — ?rcos(u — x)4-r2
/(x + 0)+/(x-0) .	(6)
В частности, в точке непрерывности этот предел равен f(x).
Если же функция f(x) везде непрерывна*, то f(r, х) стре-
мится к f (х) равномерно относительно х.
Доказательство. Преобразуя интеграл Пуассона (5)
так же, как мы в свое время преобразовали интеграл Дирихле [681],
получим:
те
/(г, х)=1 J 1/(^+0+/(х-01—	dt. (7)
Желая применить к этому интегралу лемму предыдущего п°, мы
положим
/ (х 4~ 0 4~ / (х — 0 &
а в качестве ядра возьмем функцию
Ф(*, г) = -—.-.	(8)
' ' л 1 — 2r cos 14- г2	4 '
(ядро Пу ас с она). Здесь роль параметра к играет г, область его
изменения есть промежуток [0, 1), а <о=1. Покажем, что функ-
ция Ф удовлетворяет всем требованиям, предъявленным в преды-
дущем п° к положительному ядру.
Прежде всего Ф(7, г)^>0 [см. требование 1°]. Действительно,
при г < 1 числитель дроби (8), очевидно, положителен; то же
заключение легко сделать и о знаменателе, если представить его
в виде
1—2г cosf-]-r2 = (l — г)’ 4г sin2 g-.	(9)
* Напомним, что мы предполагаем функцию f(x) имеющей период 2п.
604	гл. XX. РЯДЫ ФУРЬЕ (ПРОДОЛЖЕНИЕ)	(741
Если, далее, положить в (7) /=1, то и /(г, х) = 1, и мы полу-
чаем, что
те
1 Р 1__________________________га
л \ 1—2r cos £-[- г2 dt 1»
т. е. выполняется требование 2°. Наконец, при 8 t тс (если
число 8 произвольно выбрано между 0 и тс) будет sin sin^- >
так что [см. (9)]
1 — 2r cos t г2 4r sin2 .
Отсюда
.	11 ___ г2
м (8, г) =ДТ ф г) к------------г •
" 4r sin2 ъ
Очевидно, М (8, г) —> 0 при г —♦ 1 (и фиксированном 8); выполнено
и требование 3°.
В таком случае на основании упомянутой леммы имеем
Нш /(г, x) = lim ^±-0. +/(^~0 =/(£±0)_±/(^.-0.^
r—1-O	/->4-0
что и требовалось доказать.
Пусть теперь функция /(х) будет везде непрерывна. Тогда
она необходимо ограничена: \fа вместе с этим и
|/(х-Н)+7(х —Q |-сд-
Кроме того, ввиду равномерной непрерывности функции f(x)
выражение
/ (х 4- /) 4- / (х — t)
2
стремится при 7—>-[-0 к своему пределу /(х) равномерно
относительно х. Этим на основании дополнительного замечания
предыдущего п° оправдывается и заключительное утверждение
теоремы.
Итак, доказанная теорема учит, что в точке х, где функ-
ция f(х) непрерывна или, в крайнем случае, имеет разрыв
первого рода, ряд Фу р ье (3) суммируем по методу Пу а с-
с она — Абеля, причем «обобщенной суммой» ряда оказывается
/(х) или +
смотря по случаю.
742]	§ 2. ПРИМЕНЕНИЕ МЕТОДОВ СУММИРОВАНИЯ К РЯДАМ ФУРЬЕ 605
Замечание. Если функция f(x) первоначально была задана
лишь в промежутке [—it, it], то, переходя обычным образом [687]
к периодической функции, легко усмотрим, что для — it х it
все остается по-старому, а для х = ч-тс пределом интеграла
Пуассона, или «обобщенной суммой» ряда, будет
/(_я + о)+/(я_о)
2
742. Решение задачи Дирихле для
изученный в предыдущем п°, может быть
называемой задачи Дирихле для одного
Интеграл Пуассона,
круга.
использован при решении так
простого, но важного частного
случая. Напомним, что функция и — и (х, у) называется гармонической
в некоторой области, если она в этой области непрерывна вместе со своими
ди ди дги д2и
производными	д-^2, ^2 и удовлетворяет уравнению в частных
производных
dsu д2и _
дх* + ду3~ U
(Ю)
(уравнение Лапласа). Рассмотрим конечную область (О), ограниченную
замкнутым контуром (L). Тогда задача Дирихле для этой области форму-
лируется следующим образом: на конту-
ре (L) произвольно задана непрерывная
функция точки; требуется же найти
такую непрерывную в замкнутой обла-
сти (D) и гармоническую внутри нее
функцию и = и (х, у), которая на кон-
туре совпадала бы с заданной функ-
цией *. Мы дадим решение этой задачи
для случая, когда область (D) есть круг,
описанный вокруг начала радиусом 1 (к это»
му, очевидно, легко приводится и случай
произвольного круга).
Итак, пусть на окружности (L) на-
званного круга задана некоторая непрерыв-
ная функция точки. Если положение точки
на окружности определять полярным уг-
лом 0 (рис. 145), то это равносильно зада-
нию непрерывной (и, очевидно, имеющей
период 2л) функции /(0). Нам удобно и внутри круга (D) перейти к поляр-
ным координатам г, 0, заменив уравнение (10) соответственно преобразо-
ванным уравнением
д2и , 1 Ув 1
dr*+r* д&>+г 00
(10*)
[см. 222, 1)]; нам предстоит, таким образом, найти непрерывную при г sg 1
функцию и = и(г, 0), которая при г<1 удовлетворяла бы уравнению (10*),
а при г = 1 совпадала бы с /(9).
В порядке наведения начнем с простейших (не считая постоянной)
решений уравнения (10*):
rn cos «0, rnsinnO (п=1, 2, 3, ...);
* В п° 602, 7) было установлено, что своими контурными значениями
гармоническая функция определяется однозначно.
6С6
ГЛ. XX. РЯДЫ ФУРЬЕ (ПРОДОЛЖЕНИЕ)
(742
найти их можно было бы по методу Фурье [701]. Нетрудно проверить
непосредственно, что эти функции уравнению удовлетворяют. Умножив их на
произвольные множители Ап, Вп и присоединив еще постоянный член Ло,
составим ряд
СО
и (г, 0) = До-[- (Ат cos m9 -\~Вт sin
т — \
который формально* также удовлетворяет уравнению (10*). Наконец,
учитывая граничное условие: и (1, 6) =/(0), получим
Д04~ Лщ cos т0sin т0 =/(9),
m = l
откуда, как обычно, заключаем, что До, Ат, Вт суть коэффициенты Фурье
функции /(0):
До=='^>	= Вт — Ьт-
Окончательно приходим к такому, пока формальному, решению постав-
ленной задачи:
оо
и(г, 0) = -^-]- 2 rm (ат cos тО bm sin m0).	(11)
т — 1
В этом ряде легко узнать ряд Пуассона для функции/(0), который, если
угодно, можно заменить и интегралом Пуассона:
Я
1	(•	1 _ Г2
и (г, 0) = 75— \ /(«) ;-5--- ---jr-1 г du.	(11*)
' ’ ' 2it J 7 ' 1 — 2г cos (« — 0) + г
—те
Остается убедиться, что построенная функция в действительности
удовлетворяет всем требованиям.
Прежде всего, так как коэффициенты ат и Ът ограничены в их совокуп-
ности, то нетрудно видеть, что если рассматривать лишь значения rsgr0, где
r0< 1, но может быть взято сколь угодно близким к единице, ряды, получен-
ные из (11) почленным дифференцированием по г или по 9 (однажды или
дважды), все будут сходиться равномерно как относительно г, так и отно-
сительно 0. В таком случае они и дадут последовательные производные функ-
ции и (г, 0), и эта функция внутри круга, т. е. при r< 1, будет удовлетворять
преобразованному уравнению Лапласа, поскольку ему удовлетворяют по
отдельности все члены ряда.
Внутри круга функция и (г, 0) непрерывна по совокупности переменных
(г, 0); это вытекает из равномерной сходимости ряда (11) сразу по обеим
переменным (при rsgr„<: 1) по теореме 1 п° 431, которая легко распростра-
няется и на случай функций двух переменных. Установим теперь, что функ-
ция и (г, 0), при приближении точки М (г, 0) изнутри круга к точке М' (1, 90)
на окружности, стремится именно к /(0о). Действительно, ввиду непрерывности
функции/(0) по произвольно взятому е > 0 найдется такое 8 > 0, что при
19 — 90 / < В будет
|/(9)-/(90)1<4.
* Если допустить возможность беспрепятственного почленного
дифференцирования.
743]
§ 2. ПРИМЕНЕНИЕ МЕТОДОВ СУММИРОВАНИЯ К РЯДАМ ФУРЬЕ
607
С другой стороны, в силу того, что и (г, 9) при г—1—0 стремится к /(9)
равномерно относительно 9 [741], число 8 можно считать и столь малым,
что при | г — 1 | < 8 будет
|Ц(Г, 0)_/(в)|<у
при всех 9. Итак, окончательно при | г — 1 | < 8 и | 9 — 0О ] < 8 имеем:
|и(г, 9)-/(90)|<е,
что "и завершает доказательство.
743. Суммирование рядов Фурье по методу Чезаро— Фейера.
Как известно [681], частичная сумма sn (х) ряда Фурье (3) может
быть представлена интегралом Дирихле
те
1 \.
о- (Ц—х)
------du.
^(и—Х)
s„(x)
В таком случае среднее арифметическое первых п таких сумм напи-
шется в виде:	„
о„ (х) =
 — ------j— --------du
J0 2 sin у (и — х)
или после упрощения [ср. 418, 2)]:
те
2
впМ—2пп
— те
 П ,	X
sin у (и — х)
/(«) -4-------------
sin у (и — х)
du.
Этот интеграл называют интегралом Фейера (L. Fejer) по имени
ученого, впервые успешно применившего метод средних арифметиче-
ских к обобщенному суммированию рядов Фурье. Фейеру принад-
лежит также следующая теорема (см. теорему Шварца).
Теорема. Пусть для функции f(x) в рассматриваемой
точке х существуют пределы справа и слева /(х + О). Тогда
те
2
lim о„(х)= lim Д- |/(«)
л —со	rc-*cczzl7: I
. п .	.
sin у (и — х)
. 1 ,
sin у-(и — х)
du =
^/(х + 0)+/(х-0),	(12)
В частности, в точке непрерывности этот предел равен f(x).
Если же функция f(x) везде непрерывна*, то сумма зп(х)
стремится к f(x) равномерно относительно х.
* См. сноску на стр. 603.
608
ГЛ. XX. РЯДЫ ФУРЬЕ (ПРОДОЛЖЕНИЕ)
(743
Доказательство. Подобно интегралу Дирихле и интегралу
Пуассона, интеграл Ф е й е р а может быть представлен в виде:
те
а« i У +0 +f<-x - 01
о
(13)
Этот случай также подходит под общую схему п° 740, если поло-
жить, как и в 741,
A£±£).+./^-0.=g(0>
а за ядро принять функцию
/  п А2
, / sin v t \
Ф0, л) = — —£_
Пл I .	1	/
ysiH -g- tj
{ядро Фейер а).
Легко убедиться в том, что это действительно положитель-
ное ядро, как оно было определено в п° 740 (вместо X здесь на-
туральный параметр л; ш = -|-оо). В самом деле, что
Ф(6 л) Sa 0,
непосредственно очевидно. Если в (13) взять /=1, то одновременно
и s„=l, а также а„=1, так что
те
f! . и Л2
/ SUl-yf \
-2- ^=1,	(14)
т. е. для ядра Ф е й е р а выполняется требование 2° п° 723. Что же
касается требования 3°, то легко получить оценку
(8, и) = sup Ф(6 я)=^^—Ц->
откуда и следует, что М (В, л) —► 0 при п — оо.
В таком случае, применяя лемму п° 740, получим предельное
соотношение (12).
Наконец, заключительное утверждение теоремы обосновывается
как и в случае теоремы Шварца.
На этот раз из доказанной теоремы явствует, что в точке х,
где функция f(x) непрерывна или, в крайнем случае, имеет раз-
рыв первого рода, ряд Фурье (3) суммируем по методу средних
арифметических, причем «.обобщенной суммой» ряда будет
/(х) или /(x + 0)+/(f^0)>
соот ветственно.
744|
« Т. ПРИМЕНЕНИЕ методов СУММИРОВАНИЯ К РЯДАМ ФУРЬЕ
609
Опираясь на теорему Фробениуса (4211, из этого утверждения,
как следствие, можно получить аналогичное утверждение гг 741.
относящееся к суммированию по методу Пуассона — Абеля.
Если функция f(x) задана лишь в промежутке [— г., с], то по
поводу нес можно повторить замечание, сделанное в конце
п 741.
744. Некоторые приложения обобщенного суммирования рядов
Фурье. Мы имеем здесь в виду привести некоторые следствия из тео-
ремы Фейера (хотя для той же цели, иной раз — ценой небольшого
усложнения рассуждений, — могла бы служить и теорема Шварца).
Первые два из них иллюстрируют то любопытное обстоятельство,
что обобщенное суммирование может послужить основанием для утвер-
ждений, относящихся к суммированию в собственном смысле!
Г. Если ряд Фурье (3) сходится в некоторой точке х,
где функция f(x) непрерывна или имеет обыкновенный разрыв,
то сумма ряда необходимо равна
/(х) или /(xiOl+JTx-O),
соответственно.
Действительно, именно такова по теореме Фейера будет «обоб-
щенная сумма» ряда, полученная по методу средних арифметических.
Ввиду же регулярности этого метода (420], поскольку ряд имеет сумму
в обычном смысле, эта сумма должна совпадать с «обобщенной
суммой».
2*. Из теоремы Фейера как следствие может быть получена теорема
Дирихле - Жордана о сходимости ряда Фурье для функции с ограни-
ченным изменением |70в|.
Если /(х) есть функция с ограниченным изменением во всем промежутке
(— я, я], то в любой точке х для нее существуют пределы /(х ± 0), и «обоб-
щенной суммой» ряда Фурье будет	——. С другой сто-
роны, известно Р07]. что для функции с ограниченным изменением коэффи-
циенты Фурье ая, Ья будут порядка О ( -), а тогда по теореме X а р д и
\ Л /
(422) отсюда следует, что ряд (3) сходится в обычней смысле н притом к той
же умме.
Этим, впрочем, не покрывается еще теорема Д я р и х л е — Жордана,
которая в формулировке п* 686 имеет, так сказать» «локальный» характер.
Ограниченность, изменения там требуется лишь по етнолвеиию к произвольно
малой окрестности рассматриваемой'точки. Но мы звмем (683), что именно
значения, принимаемые функцией в этой окрестности, и определяют поведение
ряда Ф у р ь е и величину его суммы в данной точке. Поэтому, ничего не меняя
по существу, мы могли бы изменить значения функции вне упомянутой окрест-
ности так, чтобы получилась функция с ограниченным изменением во всем
промежутке |— я, я], а к этой функции уже применимо сказанное выше.
3*. Если функция /(х) непрерывна в промежутке (—я, я) и к тому же
удовлетворяет условию
20 Г. М. Фяхтевгольц, т. Ill
610
ГЛ. XX. РЯДЫ ФУРЬЕ (ПРОДОЛЖЕНИЕ)
[744
то она может быть распространена на всю числовую ось, как периодическая
(с периодом 2л) и повсюду непрерывная функция, В таком случае последова-
тельность фейеровских сумм {оп(х)} сходится к f(x) равномерно для
всех х в промежутке [—л, я]. Так как каждая такая сумма есть тригоно-
метрический многочлен, то отсюда очевидным образом получается
теорема Вейерштрасса об аппроксимации периодической непрерывной
функции [734].
4°. Из теоремы Ф е й е р а непосредственно может быть получено утвержде-
ние о полноте тригонометрической системы в классе не-
прерывных функций [ср. 733]. В самом деле, если непрерывная в про-
межутке [—л, г.] функция /(х) оказывается ортогональной ко всем функциям
тригонометрической системы, так что равны нулю все ее коэффициенты
Фурье, то ап(х) = 0. В то же время, по крайней мере в открытом проме-
жутке (—л, я), ап (х) — f (х) при п —• оо; следовательно,/(х)== 0 внутри про-
межутка, а по непрерывности — и на концах его.
Присовокупим еще следующие замечания, хотя и не связанные с теоремой
Ф е й е р а, но относящиеся к фейеровски.м суммам.
5°. Если функция f(x) оказывается ограниченной и при изменении в
промежутке [—л, л] содержится между т и М, то между теми же
границами содержатся и все фейеровские суммы ап (х).
Это сразу получается из оценки интеграла (13) с учетом (14):
Для частичных сумм ряда Фурье s„ (х) подобное утверждение уже не
имеет места: здесь сказывается тот факт, что «ядро Дирихле»
sin [ п 4- у \t
sin^!!
в отличие от «ядра Ф е й е р а», меняет знак. По отношению к этим суммам
нельзя ручаться даже за существование общих для них всех границ.
Однако если коэффициенты ап, Ьп функции f(x) будут порядка
О , то и частичные суммы sn (х) все же оказываются равномерно
ограниченными. Именно, если при всех я=1, 2, 3, ... имеем
п|а„|^Л, п\Ьп\^В,
то можно утверждать, что
т — (Л -f- В) sn (х) М -f- (Л -f- В).
745]	§ 2. ПРИМЕНЕНИЕ МЕТОДОВ СУММИРОВАНИЯ К РЯДАМ ФУРЬЕ 611
Действительно, применяя к настоящему случаю соображения п° 422,
получим:
Л
у, k (ак cos kx 4- Ьк sin kx)
sn (x) = ®л+1 (x) 4- ----.
Но
| k (ак cos kx 4- bk sin kx) | sg A 4- B,
в то время как по доказанному
m “g an+1 (x) sg M.
Отсюда и вытекает требуемое утверждение.
Если, например, рассмотреть разложение [690, 2)]
ОО
те — х VI sin пх /Л _ п ч	Z1 е.
—2~=2i	(а<х<2я)>	о5)
1
то здесь т = — -J, Л4 = -^-, /1 = 0, В = 1. Поэтому можно утверждать, что
частичные суммы этого ряда по абсолютной величине равномерно ограничены
числом у 4-1 [ср. 702].
Из доказанного утверждения можно сделать и более общее заключение:
частичные суммы ряда Фурье функции с ограниченным изменением бу-
дут все равномерно ограничены [ср. 737]. Это следует из того, что для
названной функции коэффициенты Фурье ап, Ьп заведомо будут порядка
О (1) [707].
745. Почленное дифференцирование рядов Фурье. Если ряд
Фурье (3) функции f (х) продифференцировать почленно, то полу-
ченный ряд
ОО
У т (bm cos тх — ат sin тх),	(16)
т = 1
вообще говоря, -будет расходящимся, даже если в рассматриваемой
точке х для функции f(x) существует конечная производная /'(х).
Примером может служить только что упомянутый ряд (15): почлен-
ное дифференцирование приводит к повсюду расходящемуся ряду
ОО
У cos тх.
1
Однако имеет место следующее интересное предложение, принад-
лежащее Ф а т (Р. Fatou): если в точке х существует конечная
производная f (х), то ряд (16) суммируем по методу Пуас-
сона — Абеля и именно к сумме f (х).
20*
612
ГЛ. XX. РЯДЫ ФУРЬЕ (ПРОДОЛЖЕНИЕ)
[745
Для доказательства продифференцируем по х ряд Пуас-
сона (4):
ОО
Фе ’ = S tMm (Ьт C0S тх — ат sin тхУ>	(17)
т — I
почленное дифференцирование здесь допустимо в силу равномер-
ной относительно х сходимости полученного ряда. Тот же резуль-
тат получится, если продифференцировать по х интеграл Пуас-
сона (5):
df(r,x)__\ С . 2г(1 — г8) sin (и — х) ,
дх “2л У w [1 — 2r cos (u — x) + r2]8	’
причем в этом случае можно дифференцировать под знаком инте-
грала по теореме 3* п° 510. Последний интеграл преобразуем так:
df(r, х)_ 1 С f( . „ 2г(1 — г2) sin Г
дх “2л 3 м ' П —2rcos/ + r8]8
— те
__ С f(x-\-t)—f (x — t) 2 (1 — г8)sin81
Г л \	2sin/ [1 — 2rcost + r8J8
Положим
2 sin/ . *
если переписать это выражение в виде
_./л A	. /(х — 0— /(х)1 t
В'' 2 [ t "г"	— t J ’ sin/ ’
то станет ясно, что
£(+о) =/(*)•
Покажем, далее, что функция
 ( > ’ Л [1—2г cos /+ Г818
является положительным ядром в смысле п° 740. Прежде
всего, очевидно,
Ф(/, г)>0.
Положим в (18), в частности, /(x)=sinx. Тогда
fi \	•	й/(г, х)	у(х-|-/)—f(x — /)
/ (G x) = r sin х, - \ ’ ' = г cos х, У- ,------ == cos х.
OJC	& SHI I
746]	§ 3. ЕДИНСТВЕННОСТЬ ТРИГОНОМЕТРИЧЕСКОГО РАЗЛОЖЕНИЯ
613
Подставляя все это, по сокращении на г cos х, получим, что
_1_ С 2(1—г8) sin* Z
it j [1—2г cos <г8]*
Наконец,
1 2(1—г8)
я Г, . « 8 I8 ’
14r sin* -g-T
так что заведомо 7И(8, г) —О при г—1.
Применяя теперь лемму п° 740, видим, что интеграл (18), который
служит суммой ряда (17), стремится к f (х) при г—* 1. А это и
означает, что ряд (16) суммируется по методу Пуассона — Абеля
к /'(х), что и требовалось доказать.
Замечания. L Доказанная теорема может быть обобщена на
случай повторного дифференцирования: если в рассматриваемой
точке существует конечная производная (х)(р^>1), то ряд,
полученный из (3) р-кратным дифференцированием, суммируем
к f(p\x) по методу Пуассона — Абеля.
II. Для суммирования по Ч е з а р о уже не имеет места утвержде-
ние, аналогичное теореме Фату. Если, впрочем, усилить требования
к производной и предположить непрерывность ее в рассматри-
ваемой точке, то суммирование по Пуассону — Абелю может быть
заменено суммированием по Чезаро.
§ 3. Единственность тригонометрического разложений
функции
746. Вспомогательные предложения об обобщенных производ-
ных. Чтобы ниже не прерывать изложения важного вопроса, указан-
ного в заголовке, мы предпошлем ему ряд вспомогательных соображений.
Пусть в некотором промежутке [а ,Ь\ задана функция f(x). Возьмем
значение х между а и Ь: а<^х<^Ь; тогда для достаточно малых
Л^>0 имеет смысл разность Дд/7(х)=/7(х-ф-й)— F(x— ti). Если
существует конечный предел-
Я'1(х)= lim
л-+о 2Я
его называют обобщенной («симметрической») производной функ-
ции F(x) в точке х. Лишь только существует производная F (х)
в обычном смысле, необходимо существует и обобщенная производ-
ная Я'1 (х), ей равная; это непосредственно видно из следующего
соотношения: при h—♦~|~0
ДлГ(х)_ 1 ГГ(х4-Л)-Г(х)_1 F(x-ft)-F(x)-| р ,
2й “ 2 |_ Л ‘	J—W-
614	ГЛ. XX, РЯДЫ ФУРЬЕ (ПРОДОЛЖЕНИЕ)	[746
Однако обобщенная производная может существовать в некоторых
случаях, когда обыкновенной производной нет. Примером тому служит
функция
F (х) = х sin (х ф 0), F (0) — 0;
известно [102, 1°], что в точке х = 0 производной она не имеет;
обобщенная же производная ее в этой точке равна нулю.
Рассмотрим, далее, вторую разность
М F (х) = ДЙДЙ F (х) = bhF (х + К) - bhF (х — /г) =
= [F (х + 2h) — F (х)] — [F (х) — F (х — 2й)] =
'= F (х 4- 2h) — 2F (х) + F (х — 2/г).
Если существует конечный предел
Fl"l(x) = lim
л—4-0 4Л
его называют обобщенной второй производной функции F(х)
в рассматриваемой точке х. И здесь можно доказать, что в случае
существования обычной второй производной F' (х) существует и равна
ей обобщенная производная. Действительно, если к двум функциям
от h, &hF (х) и 4/г2 применить формулу Коши*:
№hF (х)	F' (х + 26Л) — F' (х — 20й)
W =	40й	’
то, в силу сказанного выше'об обобщенной (первой) производной
ясно, что . при h —► 0 полученное выражение стремится к F" (х).
Пример функции
F (х) = х3 sin (х Ф 0), F (0) = 0
[см. 101, 2°] показывает, что обратное утверждение неверно: суще-
ствование обобщенной производной Я"1 (х) не влечет за собой обяза-
тельно существования обычной производной F” (х).
Следующая теорема устанавливает, что обобщенная вторая произ-
водная в некоторых случаях может играть ту же роль, что и обык-
новенная
Теорема Шварца. Если для непрерывной в промежутке [а, Ь]
функции F(х) обобщенная вторая производная Я"1(х) суще-
ствует в ну три промежутка и равна нулю, то F(х) будет
линейной функцией (совсем так, как если бы было дано, что обык-
новенная производная F” (х) = 0!).
* Предположение о существовании второй производной F" (х) в точке х
уже включает предположение о существовании первой производной F' (х)
в окрестности этой точки.
746]	§ 3. ЕДИНСТВЕННОСТЬ ТРИГОНОМЕТРИЧЕСКОГО РАЗЛОЖЕНИЯ 615
Для доказательства возьмем произвольное число е 0 и построим
вспомогательную функцию
<р(х) = ± {^(х) — F(a) —	(х — а)| +
-}- е (х — а) (х — Ь),
причем наши рассуждения будут в равной мере относиться к обоим
знакам перед скобками. Тогда внутри промежутка имеем
<pl"l (х) = 2е,	(1)
ибо для функции F обобщенная вторая производная равна нулю’
а для квадратичной функции — ее обыкновенной второй производной *•
Функция <р(х) на концах промежутка [a, Z>] обращается в нуль.
Покажем, что внутри промежутка она не может принимать положи-
тельных значений. Действительно, в противном случае <р (х), как не-
прерывная функция, достигала бы своего наибольшего (положитель-
ного) значения в некоторой внутренней точке хй. Но тогда мы
имели бы
<р (х0 ± 2/г) =< ср (х0), Дл<р (х«) О
и, наконец,
<pl”l(xe)=lim^^<0
л-4-0 4Я
вопреки равенству (1)1
Итак, <р(х)=^0 для всех х, т. е.
± |Д(х) — F (а) —s (х — а) (Ь — х)<
е (Ь — а)2,
и притом, какой бы знак, плюс или минус, ни взять перед скобками.
Поэтому и
|F(x)— F(a) —	(х- a) |<e(Z> - а)2.
Ввиду произвольности е отсюда следует, что левая часть неравенства
есть нуль, так что
cz \ ш \ । F(b) — F(a),	.
F (х) = F(а)----’ь_ак ’ (х — а),
что и требовалось доказать.
Иной раз условие (х) = 0 оказывается удовлетворенным повсюду,
за исключением отдельных «точек неизвестности», где про выполнение
его ничего не дано. Тогда находит применение
* Ясно, что если две функции F и О в рассматриваемой точке имеют
производные F1”1 и G1"1, то для их суммы или разности F±G также суще-
ствует обобщенная вторая производная, равная, соответственно, ±
616
ГЛ. XX. РЯДЫ ФУРЬЕ (ПРОДОЛЖЕНИЕ)
(747
= 0.
Обобщенная теорема Шварца. Пусть для непрерывной в про-
межутке [а, й] функции F (х) производная F["l(x) существует и
равна нулю повсюду внутри промежутка, за исключением конеч-
ного числа «.точек неизвестности»
аО1О«< ••• <хт<Ь-
Если в каждой из этих, точек выполняется хотя бы облегченное
условие .
lim -4^—=. О,	(2)
л-4-0
то функция F(x) все же будет в промежутке [а, Ь] линейной.
По предыдущей теореме функция F (х) наверное будет линейной
функцией от х между двумя исключительными значениями, так что,
скажем, в промежутке [х^, хД имеем
F (х) = cx-\-d,
а в смежном промежутке. [хг, х,+1]
F (х) —с'х-r-d'.
При этом в точке х — х, оба выражения совпадают:
F(xi)=cxl-\-d — c'xi-\-d'.	(3)
Условие (2) для x = xt дает
fFtXi + Zhy-FtXi} F(Xi-2K)-F(xi)
Л+ot 2Л	-2Л
Но левая часть здесь выражает попросту разность угловых коэффи-
циентов прямых y — cx-\-d ау = с'х-|-d'. Итак, с = с', а тогда из (3)
и d—d', т. е. оба прямолинейных отрезка составляют на деле про-
должение один другого. Так как сказанное относится к любым двум
смежным отрезкам, то график нашей функции во всем промежутке
[a, будет прямая, и функция оказывается линейной.
747. Риманов метод суммирования тригонометрических рядов.
Важную роль в дальнейшем играет развитый Риманом метод сум-
мирования тригонометрических рядов:
оо
у + 2 вл cos пх + bn sin пх-	(4)
Л=“1
Этот метод не предполагает вовсе, что ряд (4) является рядом
Фурье для какой-либо функции, и может быть приложен к совер-
шенно произвольному тригонометрическому ряду, лишь бы коэффи-
циенты его были ограничены в их совокупности:
|а„|,	(1 = const).	(5.)
747]
§ 3. ЕДИНСТВЕННОСТЬ ТРИГОНОМЕТРИЧЕСКОГО РАЗЛОЖЕНИЯ
617
Формально проинтегрировав ряд (1) почленно дважды, получим ряд:
р _ а0*а	«Л cos ях + bn sin пх
г
При выполнении условия (5) этот ряд мажорируется сходящимся рядом
и, следовательно, в любом промежутке изменения х сходится равно-
мерно и определяет непрерывную функцию F(х). Если для нее
в данной точке х существует конечный предел
]im ЬМ
т. е. обобщенная вторая производная	то последнюю и
называют «обобщенной суммой» ряда (1) в смысле Римана.
Если для примера применить этот метод к ряду
<30
у + 2 cos пх'
1
то здесь

Вспоминая [664, 9)], что для 0 «С х sg: 2тс суммой рЯда, стоящего
х J ха	пх । те2
справа, будет-------2~’т~'б'’ имеем
Поэтому для 0 х 2тс, очевидно, Я"1 (х)'== F" (х) — 0, и «обобщен-
ной суммой» ряда оказывается нуль [ср. 418 и 420].
Легко проверить, что
Д1 cos пх — — 2 cos пх (1 — cos 2ий) = — 4 cos пх ,sin4 nh
и
Д* sin пх = — 4 sin пх sin* nh.
Отсюда
«о 1 V >	it, \ /sinnftX4
—4Д8  = У +	(«л COS ПХ + Ьп Sin ПХ) ]	(7>
П=1
Таким образом, метод суммирования Римана сводится
^умножению членов ряда (4) на множители вида
/ sin nh \4	,	_
(- . I и к предельному переходу при й->0.
•618
ГЛ. XX. РЯДЫ ФУРЬЕ (ПРОДОЛЖЕНИЕ)
[747
В такой форме метод Нимана может быть приложен и к совер-
шенно произвольному ряду
Если ряд
У, и»-
п—О
л=0.
по крайней мере для достаточно малых h, сходится, и его сумма ср (й)
при h 0 стремится к пределу U, то это и будет «обобщенной
суммой»,исходного ряда.
Читатель видит, что метод Римана подходит под общую схему
п° 426. Роль параметра х в этом случае играет h (при ш = 0),
а множители *
... /sin лй
удовлетворяют обоим сформулированным там требованиям. Это оче-
видно по отношению к первому.
lim 7п(й) = Пт
ft—»-0	h->Q \ пп J
Что же касается второго, то, учитывая, что
nh
/sinnft)2 Zsin(n—1)й\2 С r/sinz)2]'’ ,
(Я-1)й ) = з LJ dz
(л—1)Л
К sin пй\2
nh /
nh
sin(n—f ll7sinzVTI
(n-\)h / j / JI
(n-1) Л
будем иметь
оо
170 (Л) I + JlbW—b-iWIxzz
Д— 1
sin (n— 1) Л\2 I
(n—\)h 7 |
и
00
* Под T^(h) мы разумеем просто единицу.
747]	§ 3. ЕДИНСТВЕННОСТЬ ТРИГОНОМЕТРИЧЕСКОГО РАЗЛОЖЕНИЯ 619
Существование этого интеграла легко проверить, ибо
Г 7 sin z\*T n .	7	sinz\ 1 I 1 \
L(“) J =2sinz(cosz“_r)F==0^)
при z—► oo.
Таким образом, метод обобщенного суммирования Римана ока-
зывается регулярным. Этот факт применительно к тригонометрическим
рядам и формулирует
Первая теорема Римана. Если тригонометрический ряд (4)
в точке х сходится к сумме S, то функция Р (х), полученная из
него формальным почленным интегрированием дважды, имеет
в этой точке обобщенную вторую производную, равную S'.
fA."\(x)=S:
Заметим, что для случая ряда Фурье выражение
Д^(х)
4Л»
легко преобразуется к виду интеграла изученного в п° 740 типа и
притом С «положительным ядром». Таким путем для риманова метода
суммирования может быть установлена теорема, совершенно анало-
гичная теореме Шварца [741] и теореме Фейера [743], на чем
мы останавливаться, однако, не будем: для нас метод Римана важен
как мощное орудие исследования тригонометрических рядов общего
вида *. На этом пути нужна будет и
Вторая теорема Римана. Если коэффициенты ап, Ьп ряда (4)
стремятся к нулю, то независимо от сходимости
ряда выполняется условие (2):
Положим при любом фиксированном х
щ — Ц, ип-= ап cos пх 4- bn sin пх.
Тогда вопрос приводится к доказательству соотношения
! н°+ 2	Н = 0,	<8
I Л=1	J
По условию теоремы пя->0, т. е. для произвольно заданной
s.0 найдется такой номер N, что при n^N будет | ип | е. Пред
* Сам Риман вовсе не занимался обобщенным суммированием рядш
Он развил свою теорию для решения поставленной им задачи—дать полну]
характеристику функций, разлагающихся в тригонометрический ряд общее
вида. Мы не имеем возможности излагать здесь эти исследования Риман:
620
ГЛ. XX. РЯДЫ ФУРЬЕ (ПРОДОЛЖЕНИЕ)
{748
ставим теперь интересующее нас выражение в виде суммы двух выра-
жений:
Имеем:
I I е
ОО
V! /sin пй\а
Z \пй/
Легко показать, что множитель при s ограничен независимо от й.
Мы видели, например, что
ОО
1 V! sin2 nh _it — ft
"ft Zi n2" ~~7T
n = l
[494, 4)]. Следовательно,
I&
e.
Что же касается выражения «Si, то оно, очевидно, стремится к нулю
вместе с h и становится при достаточно малом й по абсолютной ве-
личине меньшим, чем s. Отсюда в совокупности и вытекает утверж-
дение (8).
748. Лемма о коэффициентах сходящегося ряда. Доказываемое
ниже предложение, полезное в дальнейшем, представляет и самостоя-
тельный интерес.
Лемма Кантора (G. Cantor). Если тригонометрический
Ряд (4)
ат cos тх -|- bm sin тх
п=1
сходится, по крайней мере, для значений х в некотором проме-
жутке (</) —[а, р], то коэффициенты ат, Ьт ряда необходимо
стремятся к нулю при т-><х>.
Представим общий член ряда в виде
ат cos тх -|- bm sin тх = рот sin т(х — am),
где pm==Kam + ^m- Требуется доказать, что рт->0.
Допустим противное; тогда для бесконечного множества значе-
ний т будет выполняться неравенство
(9)
где 8 есть некоторое постоянное положительное число.
749]	§ 3. ЕДИНСТВЕННОСТЬ ТРИГОНОМЕТРИЧЕСКОГО РАЗЛОЖЕНИЯ 621
Мы индуктивно построим последовательность вложенных один
в другой промежутков {(«/„)} и возрастающих значков {тп} (и=1,
2, 3, ...) таких, что
I Prn„ sin тп (х — аИл) | > у для х из (</„).	(10)
В качестве тх возьмем первый из номеров т, удовлетворяющих,
кроме неравенства (9), еще неравенству *
md it.
При изменении х в промежутке (</) функция sin т^ (х — amj) хоть
однажды примет значение ± 1, а тогда по непрерывности найдется и
такой содержащийся в (d) промежуток («/Д во всех точках которого
эта-функция по абсолютной величине будет и, следовательно,
во внимание к (9),
I Pm1 sin тх(х — aOTi)|> 4 для х из (dj.
Если и mn_i уже определены, то совершенно аналогично
тому, как это сделано только что, определяется значок тп и строится
содержащийся в (йя-1) промежуток (d„) так, что выполняется (10).
При этом легко осуществить и требование тп^>тп_х.
Возьмем теперь точку х& содержащуюся во всех (rf„) (а такая
точка, хотя одна, всегда найдется). В ней неравенство (10) будет
иметь место при всех zi, а тогда, ввиду нарушения необходимого
условия сходимости, ряд (4) при х = хй расходится — вопреки пред-
положению. Этим лемма и доказана.
749. Единственность тригонометрического разложения. Мы по-
дошли, наконец, к одному из фундаментальных вопросов, которые
являются целью настоящего параграфа. Если ф у н к ц и я /(х) в п р о-
межутке [—it, it] разлагается в некий тригонометри-
ческий ряд (4)г то будет ли эго разложение единст-
венным? Вопрос этот тем более законен, что выражение коэффи-
циентов ряда формулами Эйлера — Фурье, как мы помним [678],
не имело логически безупречной мотивации. Следующая тропрмя дает
на него утвердительный ответ;
Теорема Гейне—Кантора. Если два тригонометрических ряда
ОО
У 4- 2 ат cos тх -р bm sin тх	(4)
т=1
И
оо
ат cos тх 4- sin тх	(11)
_______________ Л1=1
* Через d мы обозначаем длину промежутка (d) = [а, 0].
622	гл. XX. РЯДЫ ФУРЬЕ (ПРОДОЛЖЕНИЕ)	[749
сходятся к одной и той же сумме f(x) во всех точках про-
межутка [—тс, тс] (даже за возможным исключением конечного
числа точек неизвестности-» хь х%, xk), то эти ряды тож-
дественны, т. е.
ат — ^т>	Ьт = $т-
(m=0, 1, 2, . . .)	(л>=1, 2, 3, . . .)
Почленно вычитая ряды (4) и (11), сведем доказываемую теорему
к теореме об единственности тригонометрического разложения нуля:
Если тригонометрический ряд (4) сходится к нулю в проме-
жутке [—тс, тс] (исключая разве лишь конечное число точек не-
известности»), то все его коэффициенты должны быть нулями:
ат = 0, Ьт = 0.
Докажем это последнее утверждение.
По лемме предыдущего п° коэффициенты ат и Ьт стремятся
к нулю', в частности, отсюда вытекает, что они ограничены в
совокупности.
Рассмотрим риманову функцию F (х) [см. (6)], при наших предпо-
ложениях непрерывную. За выключением «точек неизвестности» ее
обобщенная вторая производная	повсюду равна нулю по
первой теореме Римана [747]. По второй же теореме Римана
[747] * даже в «точках неизвестности» выполняется облегченное усло-
вие (2).‘ Тогда на основании обобщенной теоремы Шварца [746]
можно заключить, что функция F(x) линейна:
«о*2 yiamcosmx+&msinmx_ . ,
~4 L т* — сх-\-а.
1
Важно подчеркнуть, что это равенство на деле имеет место на
всей числовой оси, ибо сказанное о промежутке [— тс, тс] справедливо
и для любого конечного промежутка. Переписав полученное равенство
в виде
аох2 __	__ d . у ат cos тх + Ьт sin тх
4	' Zd т? ’
1
из периодичности функции, стоящей в правой части равенства, сразу
заключаем, что ао = с = О. Итак, имеем разложение нуля:
ОО
g___d । 1g ат cos тх -|- Ьт sin тх
1
* Она здесь применима именно потому, что коэффициенты ат и Ьт
стремятся к нулю!
750]	$ 3, ЕДИНСТВЕННОСТЬ ТРИГОНОМЕТРИЧЕСКОГО РАЗЛОЖЕНИЯ 623'
но на этот раз — в равномерно сходящийся ряд! В таком
случае [678] коэффициенты его с необходимостью выражаются фор-
мулами Эй лер'а— Фурье, и мы приходим к требуемому заключе-
нию: ат = Ьт = 0.
Замечание. Можно было бы следующим образом избежать-
ссылки на лемму Кантора.
Пусть х — любая точка, отличная от «точек неизвестности», так
чТо ряд (4) при этом значении х сходится, и его общий член, разу-
меется, стремится к нулю:
ат cos тх -[- bm sin тх -> 0.	(12}'
Подставляя в ряд (4) вместо х значения х-)-8 и х — 8 и почленно
складывая, придем к разложению
ОО
Оо 4- 2 (am C0S тХ + sin тх) cos т^>
т=1
которое сходится к нулю при всех значениях 8, кроме разве лишь
конечного числа их (если речь идет о любом конечном промежутке
изменения 8). Но по отношению к этому тригонометрическому ряду
с переменной 8 мы уже знаем, что его коэффициенты стремятся
к нулю, и к нему (без всякой ссылки на лемму Кантор а!) приме-
нимы изложенные выше рассуждения, так что ао = О и
ат cos тх -4- bm sin тх = G.	zi
(ш=1, 2, з....)	'
Равенства эти имеют место не только для точек х, отличных от
«точек неизвестности», но, в силу непрерывности функций косинус
и синус, просто везде. Дифференцируя по х, получим еще и ра-
венства
bm cos тх — ат sin тх-O',	(14}
из (13) и (14), наконец, вытекает, что ат = Ьт = 0.
750. Заключительные теоремы о рядах Фурье. Итак, если для
какой-либо функции f (х) в промежутке [— тс, тс] возможно разложе-
ние в тригонометрический ряд, то только одним способом. Каков
же этот единственный способ? Обязательно ли это
будет ряд Фурье функции /(х)*?
Нам известны такие — даже непрерывные — функции, которые не
разлагаются в ряд Фурье [703], но до сих пор мы оставляли откры-
тым вопрос, не может ли подобная функция быть разложена в три-
гонометрический ряд с другими коэффициентами, отличными от коэф-
фициентов Фурье.
* Конечно, в предположении, что функция/(х) абсолютно интегри-
руема, ибо, говоря о ряде Фурье, мы всегда здесь имеем в виду (как и
выше) именно ряд Фурье абсолютно интегрируемой функции.
624	гл. XX. РЯДЫ ФУРЬЕ (ПРОДОЛЖЕНИЕ)	[750
Все эти вопросы тем более естественны, что мы, с другой стороны,
легко можем построить тригонометрический ряд, повсюду сходящийся
(следовательно, однозначно определяющий некоторую функцию) и в
то же время заведомо не могущий быть рядом Фурье.
Таков, например, ряд
00
V! sinnx
Ал In п *
п==2
Этот ряд даже равномерно, сходится в любом замкнутом проме-
жутке, не содержащем точек вида 2 k- (k = 0,± 1, ±2, ...) [430],
и определяет там непрерывную функцию; но и в точках вида 2kr. он
также сходится, очевидно,, к нулю. В то же время этот ряд вообще
не является рядом Фурье, ибо здесь нарушено необходимое
для этого условие, установленное в конце п° 731 [см. там заме-
ОО
чание]: ряд п расходится! [367,6)].
2 '
Поставленные вопросы получают окончательное разрешение в тео-
реме настоящего п° и в ее обобщении, которое мы изложим в сле-
дующем п°.
Предпошлем одно замечание, принадлежащее Лебегу (Н. Lebes-
gue).
Лемма. Если непрерывная в промежутке [а, Ь] функция F (х)
имеет повсюду внутри этого промежутка обобщенную вторую
производную Я"1(х), содержащуюся между границами т и М:
т	/4"1 (х) гС М,
то и любое отношение вида—заключено между теми же
границами, в предположении, конечно, что промежуток [х0 — 2h,
х0 2й] целиком содержится в [а, Ь].
Рассмотрим функцию
<? (X) =/(х0) + (х - х0)	+
которая представляет собой целый многочлен второй степени. Непосред-
ственной проверкой убеждаемся, что он принимает те же значения,
что и /(х), в трех точках: хв—2й, х0, х0 + 2й, так что в этих
точках разность
Х(х)=/(х) —<р(х)
обращается в нуль. Функция X (х) непрерывна, в промежутке [хв — 2h,
Хо -|- 2й] и имеет внутри него обобщенную вторую производную:
кП(х)=/Г](х)-^^
750J
§ 3. ЕДИНСТВЕННОСТЬ ТРИГОНОМЕТРИЧЕСКОГО РАЗЛОЖЕНИЯ
625
(для многочлена <р обобщенная вторая производная будет попросту равна
обыкновенной второй произаодной). Своих наибольшего и наименьшего
значений X (х) достигает в двух точках: xt и хг, внутри промежутка
[Хо — 2й, Хь 2й] *. Легко показать^ что в этих точках имеем соответ-
ственно XI"i (xi) О, XI"! (х2)	0 [ср. рассуждение на стр. 615], откуда
чем и доказано высказанное утверждение.
Теперь, наконец, мы в состоянии доказать следующую замечатель-
ную теорему:
Теорема дю Буа-Реймонда (Р. du Bois Reymond). Если функ-
ция f (х), ограниченная и интегрируемая (в собственном
смысле) в промежутке [— тс, тс], разлагается в этом промежутке
в тригонометрический ряд:
ОО
/(х) = -у -]- ап cos nx-\-bn sin пх,	(15)
л—1
то ряд этот необходимо я&ляется ее рядом Фу р ье.
Из сходимости ряда прежде всего вытекает ограниченность коэф-
фициентов ап, Ьп [лемма п° 748]. Введя риманову функцию F (х),
ЦРМ
имеем для выражения —разложение в тригонометрический ряд (7):
аа . v /	, L .	, /sin пй\а
4^2 — 2	^а" C°S пх~^~ sln пхУ (”	) »
л=1	'
который (при постоянном й) сходится равномерно относительно х,
ОО
ибо мажорируется рядом вида L В таком случае [678] коэф.;
1
фициенты этого ряда необходимо являются коэффициентами Фурье
для его суммы:
ао = ~
К
С W>(x)
J 4йа
dx,
1
COS ПХ----yrs— dx,
4й2	’
(16)
sinnftx* 1
. nh )	тс
(л=1, 2, 3,
sin пх
ЦР(х)
4й2
dx
* Даже если одно из этих значений есть нуль, то и оно достигается
внутри — в точке х0.
21 Г. М, Фихтенгольц, т. III
626
ГЛ. XX. РЯДЫ ФУРЬЕ (ПРОДОЛЖЕНИЕ)
|7М
Заметим, что разложение (15) можно считать осуществляющимся
и вне промежутка [—те, те], если функцию fix) периодически про-
должить на всю числовую ось. Следовательно, по первой теореме
Римана [747] для всех значений х будем иметь
Fl"4x)=f(x).
Ввиду ограниченности функции /(х):
по предшествующей лемме, одновременно и
для всех значений х и h.
Перейдем теперь к пределу при Л->0 в равенствах (16), причем
в правых частях их, по теореме А р ц е л а [526], это можно сделать
под знаком интеграла. Мы получаем, таким образом:
Щ = fix)dx, ап — -^- fix) cos пх dx,
— п	—«
bn = -i- f(x) sin пх dx
"	(л= 1, 2, 3, ...)
(18)
что и требовалось доказать.
751. Обобщение. Мы откажемся теперь от предположения о г р а-
ниченности функции fix) и допустим даже существование ко-
нечного числа точек, в которых разложение (15) может не иметь
места. И при этих облегченных условиях справедлива
Обобщенная теорема дю Буа-Реймонда. Если функция fix),
абсолютно интегрируемая в промежутке [—те, те], разлагается
в этом промежутке, исключая разве лишь конечное число точек,
в тригонометрический ряд (15), то последний необходимо являет-
ся ее рядом Фу р ье*.
Начнем с того, что функцию fix) периодически распространим
на всю числовую ось **. Впрочем, взамен fix) удобнее рассматри-
вать функцию
<р(х)=/(х) —	.
* Это обобщение принадлежит Валл е-П у с с е н у (Ch. J. de la Vallee
Poussin).
** Если функция fix) не удовлетворяет условию: /(—те)=/(те), то пред-
варительно, чтобы добиться выполнения этого условия, нужно изменить зна-
чение функции на одном из концов промежутка [—л, те], скажем, на том,
где не имеет места разложение (15).
781]	§ 3. ЕДИНСТВЕННОСТЬ ТРИГОНОМЕТРИЧЕСКОГО РАЗЛОЖЕНИЯ 621
Для нее в любом конечном промежутке (за возможными исключениями
в конечном числе точек) имеет место разложение уже без свобод-
ного члена:
ОО
<р (х) = 2 ancos пх + ^nsin«x.
П=1
Мы докажем, что, во-первых,
К
§ <f(x)dx — 0
—к
и, во-вторых, для и=1, 2, 3, ...
п	п
ал— <р (х) созях dx, bn — i <р (х) sin пх dx; (19
— ТС	—тс
отсюда уже будут следовать требуемые соотношения (18).
Ограниченность коэффициентов [по лемме п° 748] и здесь позво-
ляет ввести в рассмотрение риманову функцию
Ф (х) = — Д" C0S ПХ + Ьп ПХ
на этот раз периодическую (с периодом 2ic).
Возьмем промежуток [а, [3], не содержащий ни упомянутых выше
исключительных точек, ни особых точек функции <р(х); таков же
очевидно, будет и промежуток [а — 8, [3	8] при некотором, доста
точно малом, 8. Ввиду ограниченности функции <р, как и выше, за
д? ф (х)
ключаем об ограниченности выражения —— при а «с х sg [3, /г=с8
К тому-же
При любом у из [а, р] по теореме А р ц е л a [526] имеем:
г Д 2 Ф (х)	|
lim \—-rrg—dx= \ <p(x)dx.
л->о J 4Л	J
а	а
Если положить
V
Ф!(у)= \®(t)dt,
О
21»
628
ГЛ. XX. РЯДЫ ФУРЬЕ (ПРОДОЛЖЕНИЕ)
(731
то последнее соотношение можно представить в виде
Й I	4й3
Так как выражение в фигурных скобках ограничено, при а ^.у С
Р и h 8, то, снова применяя теорему Ариела, имеем:
X	х	у
lim $ {...} dy = § dy J<p (0 dt
ft-° a	a	a
(a x £< P).
Полагая, далее,
X
Ф2 (x) = 5	(у) dy,
0
сможем написать полученное соотношение так:
lim
л-*о
I 4Й2
^Ф2(»)
4Л2
дл ф1 (“) 1	С	г
(* ~ а) —w—} = J	J <р (О dt-
a a
Но ®g(x), очевидно, имеет Ф(х) своей обыкновенной второй произ-
водной, так что
lim
л-о
4й2
Д? Ф» (а)
Ф(х), Ит--й-7< = Ф(а).
л-о 4"
Если через 7 обозначить еще (очевидно, существующий) предел
Д2 Ф. (а)
lim Л „
л-о 4Л2
то окончательно найдем:
х у
\dy ^{f)dt = ^{x) — Ф (a) — 7 (х — a).
a a
Легко видеть теперь, что повторный интеграл
х у
^dy ^(t)dt
о о
(при —it	отличается от предыдущего на линейную функ-
цию. Таким образом, функция
х у
1Г(х) = Ф(х) — \dy \<?(t)dt	(20)
О о
7511
§ 3. ЕДИНСТВЕННОСТЬ ТРИГОНОМЕТРИЧЕСКОГО РАЗЛОЖЕНИЯ
629
оказывается линейной в каждом промежутке вида [а, р]. Значит, в
каждой точке х, отличной от особых точек функции <р и от исклю-
чительных точек, где не имеет места разложение (15), будет
Ф* 1"’(х) = 0.
С другой стороны, во всех точках х без исключения выпол-
няется условие типа (2): выражение
Д^(х) Д|Ф(х) 1	£	j x^h £
S dy\^t)dt + -^h $ dy\^t)dt
х 0	х О
стремится к нулю при h—► 0. Действительно, для первого слагаемого
справа стремление к нулю следует из второй теоремы Римана
[в силу леммы п° 748], а по теореме о дифференцировании интег-
рала по переменному верхнему пределу [305, 12°] то же Заключение
оказывается справедливым и для суммы двух других слагаемых.
В таком случае, на основании обобщенной теоремы Шварца
[746], имеем в любом конечном промежутке, а следовательно, и для
всех вообще значений х:
ЧТ (x) — cx-\-d.	(21)
Пусть теперь
ОО
2аясозлх ?nsin пх,>
1
дважды интегрируя почленно [731], получим:
X	у	ОО
$ dy § <р (0	-?в C0S WXntPn Sin ПХ • .	(22)
0	0	1
Сопоставляя (20), (21) и (22), придем к разложению
°0*2 | сх | d — 2 (ал — an) cos ПХ + (Рл — sin пХ
1
которое справедливо для всех вещественных значений х без исклю-
чения.
Так как правая часть представляет собой непрерывную и периоди-
ческую, а значит, ограниченную функцию от х, то необхо-
димо с —0, а также
00 = -^- <f(x)dx = 0.
—«
630
ГЛ. XX. РЯДЫ ФУРЬЕ (ПРОДОЛЖЕНИЕ)
[751
Теперь оказывается, что ряд
п — а„) cos пх (ря — bn) sin пх
л2
повсюду сходится к 0, и притом равномерно. Отсюда [678 или
749] следует, что все его коэффициенты суть нули, так что выпол-
няются условия (19):
п
1 с , ,	,
ап = ап = — \ <р (x)cos пх ах,
—к
к
Ьп = фп = ^	<р (x)sin nxdx,
—It
чем и завершается доказательство.
Таким образом, мы подвели, наконец, фундамент под всю изло-
женную выше теорию тригонометрического разложения функций и
обосновали то исключительное внимание, которое уделялось именно
рядам Фурье.
ДОПОЛНЕНИЕ
ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
752. Различные виды пределов, встречающиеся в анализе.
Понятие предела пронизывает весь курс анализа, но в разных его
частях принимает весьма различные формы.
Мы начали с изучения простейшего случая — предела варианты,
пробегающей нумерованную последовательность значений [22, 23]; при-
менительно к нему и была подробно развита теория пределов
(глава 1). Затем понятие предела было обобщено на случай пре-
дела функции от одной или от нескольких переменных [52, 165] *.
Предельный процесс усложнился, но в общем сохранил свой характер.
Интегральное исчисление привело нас к рассмотрению пределов
интегральных сумм Римана и Дарбу [295, 296, 301]. Здесь пре-
дельный процесс оказался связанным с дроблением на части данного
промежутка и, по сравнению с ранее изученным, представил уже зна-
чительное своеобразие.
К этого типа пределам в известной мере примыкают пределы,
с которыми мы столкнулись в главе X при определении понятий дли-
ны дуги (предел периметра вписанной ломаной, 330), площади плос-
кой фигуры (предел площади входящих и выходящих прямоугольных
фигур, 336) и т. п.
Наконец, в третьем томе читатель встретил еще другие предель-
ные образования, получаемые в результате других предельных процес-
сов, отличных от указанных выше.
Все упомянутые разновидности предела принципиально мо-
гут быть сведены к пределу в ар и анты. Эту мысль мы под-
черкивали на протяжении всего изложения, входя поначалу в под-
робности [53, 166, 295], а затем ограничиваясь уже лишь упомина-
нием о возможности перефразировки определения предела «на языке
последовательностей». Конечно, сведёние сложных предельных процес-
сов к простому пределу варианты представляет интерес само по
себе. Но для нас оно было важно еще и в том отношении, что осво-
бождало от необходимости всякйй раз вновь устанавливать элемен-
тарные теоремы из теории пределов.
* Мы все время имеем в виду определения предела на языке <е-8>.
632
ДОПОЛНЕНИЕ
[753
Хотя подобным путем и восстанавливается единство всех встре-
тившихся нам видов предела, однако самая необходимость «ана-
томирования» для этого переменной, выделение из множества ее зна-
чений особых нумерованных последовательностей, несомненно, содер-
жат в себе элемент искусственности. Общего определения предела
переменной это все же не создает.
Цель настоящего дополнительного параграфа и состоит в том, что-
бы установить общую точку зрения на предел, которая охвати-
ла бы как частные случаи все встречающиеся в анализе различ-
ные виды предела, и на ее основе наметить контуры общей тео-
рии пределов.
Излагаемые ниже идеи впервые были высказаны С. О. Шатунов-
ским, а затем американскими учеными Муром (Е.Н. Moore) и Сми-
том (Н. L. Smith). [Заметим, впрочем, что принадлежащая им поста-
новка вопроса отнюдь не является единственно возможной.]
753. Упорядоченные множества (в собственном смысле). Изу-
ченные выше образцы переменных, имеющих пределы, подсказывают
мысль, что для того чтобы вообще имело смысл говорить о пре-
деле переменной, ее область изменения не может оставаться «аморф-
ной» и должна быть определенным образом направлена или упо-
рядочена. В связи с этим мы установим сначала в общей форме
основные понятия, относящиеся к упорядоченным множествам.
Пусть имеем множество ^=={P}, состоящее из элементов Р ка-
кой угодно природы. Если для определенной пары различных
элементов Р, Р' согласились считать, что один из них (например, Р')
следует за другим (Р), то обозначают это так: Р' с- Р, и говорят,
что для пары Р, Р' установлен порядок. Правило, устанавли-
вающее порядок для всевозможных пар различных элементов аР или
только для некоторых из этих пар, во всяком случае должно подчи-
няться следующим двум требованиям:
I) если Ру S- Р2, то не может быть одновременно Р2 £- Рд;
II) если Ру$- Pt и Р2 S- Р3, то необходимо Ру £- Р3 (т. е. отно-
шение «следует» обладает транзитивным свойством).
Если по некоторому правилу для всех пар различных элементов,
взятых из еР, установлен порядок с соблюдением требований I, II, то
множество аР называется упорядоченным (или, точнее, упорядо-
ченным в собственном смысле, в отличие от упорядоченных в обоб-
щенном смысле множеств, которые будут рассмотрены в следующем п°).
Вот примеры упорядоченных множеств:
1) Любое множество вещественных чисел {х} естественным
образом упорядочивается, если расположить эти числа в порядке воз-
растания (х' £- х, когда х'^>х)* или убывания (х' %- х, когда х'<^х).
* Отправляясь от этого простого примера и стало привычным обозначать
отношение «следует» знаком , сходным со знаком > («больше»).
754]
ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
633
Тот же пример в геометрической форме может быть представлен
так: любое множество точек на горизонтальной прямой упорядочи-
вается, если из двух точек следующей считать ту, которая лежит
правее (или — левее).
2) Рассмотрим теперь какое-нибудь множество = {Ж (х, у/)},
состоящее из некоторых точек Ж (х, у) двумерного (арифметического)
пространства. Это множество можно упорядочить, скажем, следующим
образом:
Ж' (У, У) М (х, у), если х^>х', а при х — х, если у~>у'.
Во всех этих случаях легко проверить соблюдение требований I и II.
Для облегчения использования введенного понятия при рассмотре-
нии предела переменной, мы будем дополнительно предпола-
гать, что в рассматриваемом множестве еТ5 нет «последнего»
элемента (который следовал бы за всеми остальными). Таким
образом, какой бы элемент Р из еТ5 ни взять, всегда найдется элемент
Р’, следующий за Р: Р <=- Р.
754. Упорядоченные множества (в обобщенном смысле). Как
увидим в дальнейшем, чаще всего приходится поступаться предполо-
жением, что для каждой пары элементов рассматриваемого мно-
жества zfi установлен порядок, и довольствоваться тем, что такой
порядок установлен (с соблюдением условий I и II) лишь для неко-
торых пар. В подобных случаях, однако, мы будем требовать еще
выполнения такого условия:
III) для любых двух элементов Р, Р множества zP в этол
множестве найдется элемент Р', следующий за обоими
Р' F Р, Р' F Р.
[При этом безразлично, установлен ли порядок для самих элементое
Р и Р или нет.]
Это условие само по себе уже делает невозможным существование
в zP последнего элемента.
Легко видеть, что всякое множество, упорядоченное в собственной
смысле, если только оно лишено последнего элемента, необходимс
удовлетворяет и условию III. Действительно, каковы бы ни 6ыле
элементы Р и Р из zP, для них в данном случае порядок устано-
влен; пусть, скажем, Р %- Р. Так как Р — не последний элемент
то в найдется элемент Р' S Р; по транзитивному свойству отно-
шения одновременно и Р” Р, что и требовалось доказать.
Если хотя бы для некоторых пар элементов множества zP устано
влен порядок, с соблюдением всех трех условий I, II, III, мы также
будем называть множество 5s упорядоченным (в обобщенной
смысл е)*.
* Говорят также о «частично упорядоченном», «полуупорядочением» иле
«не вполне упорядоченном» множестве.
634
ДОПОЛНЕНИЕ
(754
Приведем теперь примеры таких множеств.
3)	Рассмотрим множество 3? вещественных чисел х, для которо-
го а служит точкой сгущения [52]; пусть само число а при этом не
принадлежит №.
Условимся считать, что
х £- х, если । х' — а |	| х — а |,
так что следующим будет то из значений, которое ближе к а.
Требования I, II явно соблюдены. Если в № не встречается зна-
чений х, равноотстоящих от а, но лежащих по разные стороны от а,
то множество № будет упорядочено в собственном смысле. Если же
такие пары значений имеются, то для них нашим соглашением, очевид-
но, порядок не будет установлен.
Проверим теперь выполнение требования III. Возьмем любые числа
х и У из №. Так как они оба отличны от а, и а служит для №
точкой сгущения, то в У необходимо найдется такое х", которое
будет ближе к а, чем х и У; тогда У' %- х и У' У.
Таким образом, множество № во всяком случае является упоря-
доченным в обобщенном смысле.
4)	Пусть № будет числовое множество с точкой сгущения оо.
Его можно упорядочить с помощью условия
У %- х, если j У | if— | х |.
Все требования I, II, III выполнены. Если в № нет пар значений
х, разнящихся лишь знаками, то множество будет упорядочено
в собственном смысле. Если же такие пары имеются, то для них
порядок не установлен, и можно говорить об упорядоченности лишь
в обобщенном смысле.
5)	Возьмем теперь любое множество е^ = {Л1(х, у)} точек дву-
мерного пространства с точкой сгущения Af0(a, b) [153]. Предполо-
жим, что обе координаты а и b конечны; пусть точка Мй множеству
<М не принадлежит.
Установим соглашение, что
М(У,	у),
если
тах(|У — а\, |У — b | )<^тах (| х — а\,	— b | ).
Подобно 3), все требования I, И, III здесь выполнены. Проверим,
например, условие III. Пусть даны две точки М (х, у) и М' (У, у')
из &#; так как обе они отличны от Л40, то
a = max(|x — а |, |_у — Z>|)^>0
и
а'=:П1ах(]У — а\,	— b |)0.
Пусть 8 будет наименьшим из этих чисел; ввиду того, что для
754J
ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
635
<Ж служит точкой сгущения, в <М найдется такая точка Nt’ (х", у"),
что | х” — а |	8 и |_у" — b |	8. А тогда
М'^-М и М' ь- М,
Г»
что и требовалось доказать. Итак, установленным соглашением мно-
жество действительно упорядочено (в обобщенном смысле).
Если какая-либо из координат точки 7Ив, скажем а, равна оо, то
можно модифицировать наше соглашение, например, заменив | х — а |
на Ар ит.д.
6)	Приведем в виде примера еще другие способы упорядочения
множества о котором была только что речь (а и b считаем ко-
нечными).
Можно условиться так:
М'(х', /)£- М(х, у),
если
I х' — а | +1 у' — b | < | х — а Ц-1у — b |,
или же так:
М	У') 5- М (х> У)>
если
/(х'-а)2 + О'-&)а</ (х-а)’ + О-&)а.
Предлагаем читателю проверить соблюдение в обоих случаях требо-
ваний I, II, III.
7)	Пусть есть множество «целочисленных» точек (т, п), где
т и п — натуральные числа, с точкой сгущения (-|-оо> -J-00)- Анало-
гично 5), это множество можно упорядочить по правилу
(tri, ri) (и, л), если min (tri, ri) min (т, п).
Проще — такой закон упорядочения:
(mr, tt) <— (т, ri), если т’ т и ri п.
И здесь требования I, II, III соблюдены.
8)	Возьмем теперь примеры из другой области. Пусть элементами
рассматриваемого множества будут всевозможные разбиения R
данного промежутка [а, на конечное число частей с помощью точек
деления	 .
a = x9<^xi<^...<^xi<^x;+l<^...<^xa = b.
Если через X обозначить наибольшую из длин этих частей,
то естественно расположить различные разбиения R в порядке убы-
вания X; тб из разбиений будет следующим, которому отвечает
меньшее X.
Соблюдение условий I, II очевидно. Легко проверяется и усло-
вие III: каковы бы ни были два разбиения, отвечающие значениям
X и X', всегда можно осуществить разбиение на еще более мелкие части,
которому отвечало бы число X", меньшее и X и X'.
63»
ДОПОЛНЕНИЕ
[755
Множество таким образом, оказывается упорядоченным, но
лишь в обобщенном смысле: для двух различных разбиений с одним
и тем же X порядок не установлен.
9)	Для рассмотренного только что множества	можно
установить порядок другим соглашением: разбиение R' следует за
разбиением R, если оно получено из R добавлением к его точкам
деления еще новых точек деления. Это также приводит к упорядоче-
нию лишь в обобщенном смысле: порядок не установлен, например,
для двух разбиений R и R’, имеющих сплошь различные точки
деления.
755. Упорядоченная переменная и ее предел. Рассмотрим теперь
переменную х с областью изменения Ж. Можно представить себе,
что непосредственно эта область SP упорядочена (в собственном или
обобщенном смысле) или — более общо — что значения х из Ж по-
ставлены в однозначное соответствие элементам Р некоторого упоря-
доченного множества	состоящего из объектов любой при-
роды. В этом случае и сама переменная х называется упорядо-
ченной.
Сообразно с упорядочивается и множество значений х = хр\
именно, считают, что
Хр> с— Хрг если Р Р (в ёТ5).
Это есть воспроизведение в общей, форме того, что мы имели для
варианты х„, значения которой ставились в соответствие числам
натурального ряда — «номерам» — и располагались по возрастанию их
хп’ S- если л' п.
Умея различать элементы Р множества мы различаем и значе-
ния х = Хр нашей переменной по этим «пометкам» Р. В этих усло-
виях мы допускаем (как и в случае варианты) возможность и равных
значений с различными «пометками».
Подчеркнем особо, что, говоря об упорядоченной переменной, мы
по существу не связываем с этим никаких представлений о располо-
жении ее значений в пространстве или во времени. Сле-
дующее значение не занимает «более далекого места», чем пре-
дыдущее; следующее значение не принимается переменной
«позже» предыдущего и т. д. Если же, тем не менее, обычно
позволяют себе употреблять выражения вроде «начиная с некоторого
места» или «с некоторого момента изменения» и т. п., то делается
это лишь для образности языка.
Определение предела упорядоченной переменной х = хр
(или — как иногда говорят — предела упорядоченного мно-
жества {хр}) совершенно аналогично определению предела варианты
(или последовательности):
756]
ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
637
переменная х = хр имеет конечный предел а, если для каж-
дого числа е^>0 найдется такая «пометка» Р, из что для
всех Р$- Pt соответствующие значения х = хр удовлетворяют
неравенству
| х — а | = \хР — а | в.
В определении п° 23 роль Рг играло, очевидно, Ntt ведь соотно-
шение п"г~ Nt равносильно неравенству n~^>Ne
Точно так же дается определение и бесконечного предела:
переменная х — Хр имеет предел оо, если для каждого числа
Е^>0 найдется такая «пометка» Ре из аР, что
] х | = | Хр |	Е,
лишь только Р Ре.
Легко перефразировать последнее определение для случая, когда
речь идет о бесконечности определенного знака, -[- оо или — оо.
При этом пишут, как обычно:
limx = a(oo, 4-®°> —во) "или х->а(оо, -[-оо, —°0)-
Обратимся к примерам.
756. Примеры. Начнем с примера переменной х, у которой область
изменения непосредственно упорядочена.
1)	Пусть = будет любое множество вещественных чисел
с точкой сгущения а, упорядоченное по убыванию | х — а | [см. при-
мер 3) п° 754]. Очевидно, соответствующая переменная х имеет пре-
делом а: какое бы е^>0 ни взять, в & найдется х„ отличное от а,
такое, что | х, — а | в, а тогда для х S- хв и подавно | х — а | в.
Аналогично, если = {х} имеет точку сгущения оо и множе-
ство это упорядочить по возрастанию | х | [см. пример 4) п° 754],
то х -> оо.
Чаще встречаются, однако, случаи, когда значения переменной
поставлены в соответствие «пометкам» Р из некоторого упорядочен-
ного множества «Р. Приводимые ниже примеры этого рода имеют
особую важность: они показывают, что изученные в нашем курсе
различные виды пределов действительно могут быть рассматри-
ваемы как частные осуществления изложенного выше общего
определения.
2)	Рассмотрим понятие предела функции [52]
lim/(x) = A	(1)
х-+а
ограничиваясь для простоты случаем конечных а и А.
Пусть функция f{x) определена в области ^’ = {х}, имеющей
точку сгущения а; значение а само в SC не входит или, по крайней
мере, не учитывается при определении предела (1). Эта функция и
есть здесь та переменная, о пределе которой идет речь, х же играет
638
ДОПОЛНЕНИЕ
[756
роль «пометки» Р. Условимся понимать указание х-± а в том
смысле, что область Ж изменения х упорядочена по убыванию
|х— а| [754, 3)]. Тогда соответственным образом упорядочивается и
множество значений функции {/(х)}, и равенство (1) — в согласии
с общим определением — приобретает определенный смысл. Именно,
оно означает, что по заданному е^>0 всегда найдется такое значе-
ние хе из ST, что неравенство
|/(х) —Л|<е	(2)
выполняется для х хе, т. е. лишь только | х а |	| хе — а |.
Положив | х, — а | = 8, последнее условие можно записать так:
| х — а |	8. Обратно, если неравенство (2) имеет место при
| х — а К 8, то, взяв хе под условием | х, — а |	8, можно утвер-
ждать, что (2) выполняется для х<—хе. .Таким образом, новое опре-
деление предела функции равносильно прежнему [52].
3)	Определение предела функции двух переменных
lim f{M) = lim f(x, у)— A	(3)
Л1-»Л10	x-*a
может быть выражено в терминах упорядоченной переменной совер-
шенно аналогично.
Пусть функция f{M)=f{x, у) определена в области =
— {М (х, _у)} с точкой сгущения 7И0 (а, Ь); сама эта точка при опре-
делении равенства (3) в расчет не берется. Точки М (х, у) из
играют роль «пометок». Упорядочив множество так, как это сде-
лано в п° 754, 5) {именно в этом смысле мы уславливаемся пони-
мать указание М ->- М» или х-+ а, у мы тем самым упорядо-
чиваем и множество значений функции {f{M)} = {f{x, у)}. Тогда
равенство (3) приобретает смысл — в согласии с общим определением
предела упорядоченной переменной.
И здесь сразу видно, что новое понимание равенства (3) равно-
сильно прежнему [165].
Определение предела по существу останется тем же, если вместо
закона упорядочения множества <^= {М(х, у)}, указанного в 754, 5),
положить в основу те правила, которые были проведены в 6).
4)	Для переменной хт_ п, зависящей от двух натуральных знач-
ков т и п, понятие предела
lim xm> п = А
т-*х>
П-fCO
строится на таком законе упорядочения пар (т, п)'
{тг, п')£~{т, л), если пнп(лг', п') min {т, л)
[см. 754, 7)]. Оно совпадает с тем определением, о котором была
речь в конце п° 165.
757]
ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
639
Тот же результат получился бы, если бы мы исходили и из более
простого, также упомянутого в 7), правила упорядочения
(т',	п), если т’^>т, п'^>п.
Распространение всего сказанного на случай функций от несколь-
ких переменных не представляет затруднений.
5)	Обратимся, наконец, к вопросу о пределе сумм Римана или
Дарбу для заданной в промежутке [а, &] ограниченной функции f(x).
Эти суммы связаны с разбиением R промежутка [а, Ь] на части с по-
мощью произвольных точек деления
a==x0<Xi< ... <хг<хм< ••• <Zxn = b>
причем предельный процесс направляется тем, что Х->0, где Х =
— тахДх,-. В 754, 8) мы уже упорядочивали множество всевозмож-
ных разбиений промежутка на части =={/?} по убыванию X. Соот-
ветственно этому упорядочиваются и значения сумм Дарбу, $ и 5.
Для построения римановой суммы а, кроме разбиения промежутка
на части, нужно еще выбрать в каждой части по точке. Таким обра-
зом, риманова сумма характеризуется набором не Только точек
деления, но и промежуточных точек; эти наборы (а с ними и рима-
новы суммы) также можно упорядочить по убыванию X.
Теперь уже ясно, что пределы
lim a,	lim s,	lim 5
Х-*0	Х-U)	х—о
подходят под общую схему, развитую здесь.
Заметим попутно, что те же, по существу, пределы получились бы
во всех случаях, если бы в основу упорядочения множеств {о}, {«},
{S} было положено и правило 9) п° 754. В виде упражнения пред-
лагается читателю доказать это, опираясь на результаты пп° 297 и 301.
Аналогично исчерпывается вопрос о пределах, рассмотренных при
определении длины дуги [330], площади плоской фигуры [336] кри-
волинейных, двойных и поверхностных интегралов [544, 550, 589,
631, 635] и т. д.
757.	Замечание о пределе функции. Говоря о пределе (1), мы
условились одним лишь вполне определенным образом упорядочивать
множество 35 = {х} [754, 3)], а с ним и множество значений функ-
ции {/(х)}. Определение предела этой последней, построенное на
рассмотрении упомянутого «стандартного» закона приближения х к а,
оказалось равносильным тому определению, которое было дано в п° 52
«на языке е-8».
Можно было бы, однако, отказаться от «стандартизации» закона при-
ближения х к а, предоставляя х изменяться вдоль множества 35 или лю-
бой из его частей, сохраняющих а в качестве точки сгущения и упорядо-
ченных по произвольному правилу, но так, что а является их пределом.
Значения функции /(х) всякий раз упорядочиваются сообразно с х.
640
ДОПОЛНЕНИЙ
[758
Таким образом, равенство (1) можно понимать и так:
по какому бы закону независимая переменная х ни стреми-
лась к пределу а, функция f(x) всегда стремится к одному и
тому же пределу А.
Это определение сближается с определением п° 53 «на языке
последовательностей», лишь произвольная последовательность
значений х, стремящаяся к а, здесь заменена вообще произвольным
упорядоченным множеством, имеющим предел а.
Для доказательства равносильности только что приведенного опре-
деления и данного в предыдущем п° достаточно установить, что из
существования предела (1) в смысле п° 52 следует сформулированное
выше утверждение. Пусть же для любого е 0 найдется такое 8	0,
что неравенство (2) выполняется, лишь только |х— а|<^8. По
какому бы закону х ни стремилось к а, по самому определению пре-
дела должно существовать такое значение х, что для х £- х будет
|х— а|<^8; тогда для тех же значений х выполнится и неравен-
ство (2), т. е., действительно, f (х) -> А.
Такое же замечание можно было бы сделать и относительно
функций двух (или нескольких) переменных.
758.	Распространение теории пределов. Обратимся, наконец,
к распространению утверждений, доказанных в главе I для варианты,
на общий случай упорядоченной переменной. Это распро-
странение осуществить нетрудно, если шаг за шагом проследить по-
строение теории пределов для варианты.
Всякий раз, когда там была речь о выполнении какого-либо соот-
ношения для значений х„ с номерами п, ббльшими некоторого 7V,
здесь придется говорить об его выполнении для значений х=хр
с «пометками» Р, следующими за некоторым Р'.
Например, докажем утверждение, аналогичное 26, 1°:
Если упорядоченная переменная хр стремится к пределу а и
а~^>р	то и хР^у>р (xp<^q), по крайней мере, начиная
с некоторого места.
Взяв е а — р (е q — а), найдем такое Р, что для Р$- Р
будет | хР — а | е; для тех же Хр, очевидно, и
хр ]> а — е^>р (хР а -|- е q).
Так же обобщаются и утверждения 26, 2° — 4°. Последнее, впрочем,
перефразируется так: если переменная х имеет (конечный) предел а,
то она является, ограниченной, по крайней мере, начиная
с некоторого места [ср. 55, I, 4°].
При доказательстве единственности предела [26,5°] при-
ходится своеобразно воспользоваться условием. III [754].
Допустим (рассуждая от противного), что одновременно хр->а,
Xp->Z>, причем а<^Ь. Если взять г между а и Ь, то, с одной
СТОРОНЫ, Хр Г ДЛЯ Р Р, С Другой же СТОРОНЫ, Хр^> г для Р Р’.
758}
ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
641
Но именно в силу III найдется такая «пометка» Р, что сраз у и Р Р
и Р£-Р"; тогда одновременно хР<^г и хр^>г, что и осуществляет
требуемое противоречие.
На упорядоченную переменную следующим образом распростра-
няется определение монотонной переменной: переменная хр на-
зывается монотонно возрастающей (или возрастающей
в широком смысле), если Р' Р всегда влечет за собой
Хр,^>Хр (или Хр,^Х^.
Примером такой переменной может служить монотонно возрастаю-
щая функция f (х), если ее значения упорядочены по возрастанию
независимой переменной х, или частная сумма положитель-
ного двойного ряда
S ai,
i,k=l
если считать
при т'^>т и п'~^>п.
Так же устанавливается понятие монотонно убывающе4
переменной.
Во внимание к известным свойствам сумм, Дариу s и 5 [296],
если только упорядочить разбиения промежутка так, как это сделано
в примере 9) п° 754, очевидно, нижняя сумма s окажется монотонно
возрастающей переменной, а верхняя сумма 5—монотонно убываю-
щей. Этого нельзя сказать, если взять другой способ упорядочения
[754, 8)].
Теперь легко обобщить теорему п° 34 о монотонной варианте:
Монотонно возрастающая переменная х—хР всегда имеет
предел. Если переменная ограничена сверху, то этот предел ко-
нечен, в противном случае он равен -[- ое.
Предполагая переменную ограниченной, положим a = sup{xp}
так что все хр^а и, с другой стороны, каково бы ни было числе
е О, найдется такая «пометка» Ре, что хр а — е. Но тогда, липп
только Р^-Р„, будем иметь xp^>xp, следовательно, и подавно
хр^>а— е. Таким образом, для P^-Pt выполняется неравенство
|хр—а|<^е, откуда хр-+а.
Если переменная хР не ограничена, то для каждого числа Е^>С
найдется такое РЕ, что хРе^>Е. Тогда для Р^-Ръ и подавне
хр^>Е, так что хр-»Ц-°°- Теорема доказана.
В этой теореме, как частные случаи, содержатся теорема
п° 34 о пределе монотонной варианты и теорема п° 57 о существова-
нии предела для монотонной функции, а также теорема п° 394 о схо-
димости положительного двойного ряда. Проведенное здесь рассужде-
ние, как читателю ясно, в общей форме лишь, воспроизводит те, ко-
торые были осуществлены в указанных местах для доказательстве
порознь частных теорем.
642
ДОПОЛНЕНИЕ
|758
Заметим, что из доказанной общей теоремы сразу вытекает и
существование конечных пределов для сумм s и 5 Дарбу, но лишь
если стоять на точке зрения правила 9) п° 754; совпадение их с пре-
делами, рассмотренными в 301, еще подлежало бы доказательству.
В качестве более сложного примера остановимся на доказательстве
принципа сходимости [ср. 39]:
Для того чтобы упорядоченная переменная хр имела конеч-
ный предел, необходимо и достаточно, чтобы для каждого числа
е]>0 существовала такая «.пометка-» Рг, что неравенство
| хР — Хр-1<^е
выполняется, лишь только Р$- Рг и Р Pt.
Перефразируя рассуждение п° 39, прежде всего установим необ-
ходимость этого условия. Если хр — а, то по числу е/2 найдется
такое Р, что для Р^-Р будет \хр — а |	е/2. Пусть Р^-Р и Р Р,
тогда сразу |хр— а |<Ч/2 и |а — Хр-|<[е/2, так что \хр — Xp-|<j;
за Ре в этом случае можно взять Р.
Для доказательства достаточности предположим условие
выполненным.
Произведем в области всех вещественных чисел сечение по сле-
дующему правилу. В класс А отнесем каждое вещественное число а,
для которого — начиная с некоторогоместа—
х^>а.
В класс А' отнесем все остальные вещественные числа а'. Легко ви-
деть, что это правило действительно определяет сечение. Мы остано-
вимся лишь на доказательстве непустоты обоих классов
При произвольном е^>0 найдется, по предположению, соответст-
вующее ему Рс такое, что лишь только Р^~ Pt и Р Рс, тотчас же
|хр— хр-|<^е или Хр- — е<^хр<^Хр--фе.
Отсюда уже ясно, что (при Р Ре) хр — е есть одно из чисел а,
а хр- -ф- е — одно из чисел а'; последнее, собственно, опять требует
использования условия III: если бы хр--|~® было одним из а, так что
неравенство хр^>хр- -ф-е выполнялось бы, скажем, для Р^~ Р, то, взяв
(в силу III) Р так, чтобы сразу было Р$-Р, и Р Р, имели бы
одновременно xp<^Xp-\-s и хр^>хр -|- е!
По теореме Дедекинда [9] существует пограничное между обо-
ими классами число а
а^а^а.
В частности, при Р Р,
хр — е^а^хр -ф- е, то есть |хр-— a е,
откуда и следует, что хр—»а.
Эта теорема находит себе интересные применения. Она не только
содержит, как частные случаи, уже известные нам теоремы пп°
759J
ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
643
39 и 58, но приводит и к новым результатам. Так, с ее помощью
принцип сходимости распространяется на функции нескольких пере-
менных, на двойные ряды и т. п. Оно дает также условие спрямля-
емости дуги [330]. Предоставляя читателю самому сформулировать
это условие, обращаем внимание на то, что условие явно выполняется
для части дуги, если выполняется для всей дуги; таким образом,
сейчас можно было бы в два слова доказать утверждение, которое
раньше потребовало от нас длинных рассуждений [247].
759.	Одинаково упорядоченные переменные. Для обобщения
таких утверждений, в которых участвуют одновременно две (или не-
сколько) переменных, введем понятие одинаково упорядочен-
ных переменных. Так называются две переменные х и у, кото-
рые могут быть упорядочены с помощью одного и того же упо-
рядоченного множества <>75 = {Р}, с элементами которого их значения
ставятся в однозначное соответствие (соответствующими мы
будем считать их значения хр, ур с одинаковыми «пометками» Р).
Если, например, имеем две функции f(x) и g(x) от одной и той
же независимой переменной х, с упорядоченной областью изменения
37, то эти функции будут одинаково упорядоченными переменными.
Соответствующими будут те их значения, которые определяются од-
ним и тем же значением х (оно и играет роль «пометки» Р).
Вот другой пример. Пусть для функции f(x) и g(x), определенных
в некотором промежутке [а, &], построены интегральные суммы
а = 2/(гг)Дх,- и т==2^^)Дх«--
i	I
Здесь соответствующими следует, очевидно, считать суммы, опреде-
ляемые одним и тем же набором точек деления хг и промежу-
точных точек $г; этот набор играет в рассматриваемом случае роль
«пометки» /> если упорядочить их, а с ними и суммы а, т, по убы-
ванию X —тахДх;, то снова получим одинаково упорядоченные пе-
ременные.
Соединяя теперь две переменные х, у знаками равенства или зна-
ками арифметических действий, мы будем предполагать эти перемен-
ные одинаково упорядоченными и подразумевать, что речь
идет о соответствующих значениях их, хр и ур, с одинаковыми «по-
метками». Обращаясь с этими пометками, как раньше обращались
с номерами п значений варианты, легко воспроизвести все прежние рас-
суждения, относившиеся к вариантам.
Для примера докажем предложение, обобщающее лемму 2 п° 29:
Если переменная хр ограничена (по крайней мере, начиная
с некоторого места), а одинаково с нею упорядоченная переменная
о-р — бесконечно малая, то и их произведение будет бесконечно
малой.
644
ДОПОЛНЕНИЕ
[760
Пусть же
| хр | М,
скажем, для Р^~ Р. Задавшись произвольным е 0, по числу
найдем такое Р', что для Р^~ Р' будет
I < М-
В согласии с условием III, существует такое Ро, что
Ро F Р и Ро Р’.
Если Р Ро, то (в силу II) одновременно
Р^-Р и Р^Р",
так что выполняются сразу оба предыдущих неравенства, а тогда
| хра.р | = | Хр | • | ар | М • = е,
что и доказывает наше утверждение.
После приведенных примеров читателю ясно, что вся теория пре-
делов (с сохранением основных линий в доказательствах) действительно
переносится на общий случай упорядоченных переменных.
760.	Упорядочение с помощью числового параметра. Во всех
встречавшихся нам случаях применения в анализе понятия предела
упорядочение множества <35 = {Р} «пометок» для значений перемен-
ной Хр осуществлялось однообразно. В общем виде применявшийся
способ упорядочивания может быть описан следующим образом.
Каждому элементу Р из ставится в соответствие значение t
некоторого параметра, причем и многим Р может отвечать одно и то
же f; множество всех таких Р обозначим через Предположим,
что все t'y>Q и существуют сколь угодно малые значения t, для
которых не пусто.
Условимся теперь что из двух элементов Р считается следу-
ющим то, которому отвечает меньшее значение параметра t
(т. е. расположим элементы Р «по убыванию параметра»). Для двух
элементов Р, которым отвечает одно и то же t, так что они входят
в одно и то же множество aPt (равно как и для соответствующих
им значений х), порядок не устанавливается. При этом будут со-
блюдены все условия I, II, III. Это очевидно по отношению к I, II;
проверим выполнение III. Пусть Р и Р — любые два элемента из
множества а?5, и им отвечают значения t и f параметра. По предпо-
ложению, найдется такое значение t", меньшее, чем t и ?, для
которого aPt„ не пусто. Тогда любое Р' из Pt„ будет следующим
и за Р, и за Р.
Читатель легко проверит, что «се известные ему случаи использо-
вания понятия предела подходят под эту схему. Для варианты хп
761]	ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ	64t
с «пометкой» п, можно принять t = Если речь идет о функции
f(x) и ее пределе при х—*а, то множество «пометок» х упорядочи-
вается по убыванию параметра t=\x— а |. Также и в случае функ-
ции f(M)=f(x, у) двух переменных, где роль «пометки» играет точ-
ка М(х, у), определяя предел функции при \х-^а, у^ Ь, можно
охарактеризовать процесс с помощью любого из параметров
= max {] х — а |, |у — b |},	= | х — а | -j-1у — b |
или
/3= / (х — а)3 -ф- (у — Ь)\
Для сумм Дарбу
s='£imikxi, S='%lMibxi
i	i
«пометкой» служит набор точек деления; при переходе к суммам
Римана
i
к нему присоединяется еще набор точек £;. В обоих случаях эти
«пометки» упорядочиваются с помощью параметра £ = тахДхг. При
определении длины дуги параметром служит наибольший из диаметров
частичных дуг и т. д.
Во всех случаях, когда область изменения переменной х или —
вернее — множество «пометок» = {Р} упорядочены указанным выше
образом с помощью числового параметра t, очевидно, определение
предела (мы ограничиваемся случаем конечного предела) может быть
дано в следующем виде: число а является пределом х, если каж-
дому числу е^>0 отвечает такое 8^>0, что
| х — а | <4
лишь только соответствующее ему значение параметра /<^8.
Упорядочением с помощью числового параметра • мы пользо-
вались и в третьем томе. Однако этот простой способ упорядочи-
вания все же не покрывает потребностей математического анализа в
его более высоких ветвях. В качестве примера такого упорядочения,
которое вообще нельзя осуществить подобным путем (с привлече-
нием числового параметра), можно привести правило 9) п° 754: это
станет ясным из рассмотрений следующего п°.
761.	Сведёние к варианте. Во всех конкретных случаях, когда
мы сталкивались с понятием предела, до сих пор оказывалось воз-
можным в некотором смысле свести вопрос к пределу варианты.
Эта возможность выражения понятия предела на «языке последова-
тельностей» играла важную роль в предыдущем изложении. Исследуем
646
ДОПОЛНЕНИЕ
[761
теперь, как обстоит дело в общем случае упорядоченной пе-
ременной х — хр.
С этой целью введем понятие конфинальной подпосле-
довательности для данного упорядоченного множества =
Так мы будем называть последовательность
Pi,	Рп, ...	(4)
элементов, извлеченных из а?5, если выполнено следующее условие:
какой бы элемент Р' из «Т5 ни взять, элементы Рп для достаточно
больших номеров оказываются следующими за Р':
Рп^- Рг (для n N).
Если переменная х упорядочена с помощью «пометок» Р из
то, при наличии конфинальной подпоследовательности (4) для мно-
жества аР, соответствующую извлеченную из & последовательность
значений х
* • . ,	• • • >	(б)
где хп = хРп, будем называть конфинальной подпоследо-
вательностью для =
Прежде всего встает вопрос о самом существовании хоть
одной подпоследовательности (4), конфинальной для аР, или, что
то же, подпоследовательности (5), конфинальной для
Нужно сказать, что во всех случаях, когда упорядочивание мно-
жества еР осуществляется с помощью некоторого числового пара-
метра t (как это разъяснено в предыдущем п°), построение подобной
подпоследовательности не представляет труда: взяв последователь-
ность {£„}, tn “*• 0 так> чтобы все множества были непусты,
выберем из каждого efitn по элементу Р„: составленная из них после-
довательность {Р„} очевидно и будет искомой.
В общем случае, однако, для упорядоченного множества = {Р} мо-
жет и не существовать ни одной конфинальной подпоследовательности.
Рассмотрим, для примера, множество eff={R} различных раз-
биений данного промежутка [а, Ь} на конечное число частей *, при-
чем упорядочивание этого множества произведем по правилу 9) п° 754.
Допустим, рассуждая от противного, что для существует конфи-
нальная подпоследовательность
Ri> Ri> • • •, Rn> • • •
разбиений. Каждому Rn отвечает конечный набор точек деления.
Легко построить такой промежуток [аь ЭД (а at Ь), чтобы
в нем не лежала ни одна точка деления из Rp Затем построим
промежуток [аъ ЭД (aj Oj Ь* Ь^, свободный от точек деления R*,
* Эти /?, как указывалось, могут служить «пометками», например, для
сумм Дарбу некоей функции, определенной в [а, £[.
762]
ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
647
и т. д. до бесконечности. На л-й стадии окажется построенным про-
межуток [ап, bn\ (an_i<Zan<Z^n<Zbn-t)’ в котором не содержится
точек деления Rn. Если озаботиться при этом, чтобы было Ьп — an-+Q,
то, по лемме о вложенных промежутках [38], найдется единственная
точка c = lima„ = lim bn, которая принадлежит всем промежуткам
[ал, &„]. Эта точка, очевидно, не совпадает ни с какой точкой деле-
ния ни одного /?„. Если взять теперь любое разбиение R' промежутка
[а, Ь], в котором среди точек деления фигурирует с, то по правилу
9) 754 ни одно Rn не может считаться следующим за R\ вопреки
определению конфинальной подпоследовательности. Это противоречие
и доказывает, что на деле такой подпоследовательности нет.
[Отсюда-то, между прочим, и следует, что указанный способ
упорядочивания множества <& = {R} не поддается параметриза-
ции в смысле предыдущего п°!]
Предположим теперь, что множество «пометок» аР, а с ним
и область изменения 37 упорядоченной переменной х, вообще содер-
жит конфинальные подпоследовательности. В этом случае (и — по-
нятно — только в этом случае) вопрос о пределе переменной х
обычным образом сводится к вопросу о пределе 'варианты:
для того чтобы переменная х имела предел а, необходимо и
достаточно, чтобы к этому пределу стремилась каждая вари-
анта хп, пробегающая конфинальную подпоследовательность для37.
Действительно, если х -► а (где мы, для определенности, предпола-
гаем а конечным), то при любом е^>0 имеем:
|	— а | е, лишь только Р £- Ре
Но если взята любая конфинальная подпоследовательность (4), то
для достаточно больших п, по определению, будет Ра Pt, так что
|х„ — а\ = \хРп — а|<е.
Это и значит, что варианта хп—>а.
Обратно, пусть каждая такая варианта стремится к а. Для того
чтобы доказать, что тогда х -► а, допустим противное: для некоторого
е 0, какое бы ни взять Р' из аР, найдется Р £- Р такое, что | хр — а | ^е.
Возьмем какую-нибудь конкретную конфинальную для S7 подпосле-
довательность {Рд}. Согласно сказанному, по каждому Р'п найдется
в о?5 элемент Рп Р„', для которого
|х„ — а| = |хРл — a (л= 1, 2, 3, ...).
Легко показать, что и подпоследовательность {Р„} будет конфиналь-
ной для о?5, а значит подпоследовательность {хП} — конфинальной
для 37, а тогда предыдущее неравенство противоречит допущению.
762.	Наибольший и наименьший пределы упорядоченной пере-
менной. Рассмотрим упорядоченную переменную х, значения которой
снабжены «пометками» Р из еТ5. При любом Р составим множество
648
ДОПОЛНЕНИЕ
|762
Жр из тех значений х, которые следуют за хр, т. е. отвечают «по-
меткам» Р' Р, и найдем его точные границы
sup Жр и inf Жр
(которые могут оказаться и бесконечными). Каждая из них является
упорядоченной переменнойспометкамиР и притом первая —
монотонно убывающей, а вторая — монотонно возрастающей (в смысле
п° 758). В таком случае, по теореме о монотонной переменной, су-
ществуют определенные (конечные или нет) пределы
М* = lim (sup Жр), М* = lim (inf ^р) *.	(6) •
Их, в общем случае, и называют, соответственно, наибольшим
или наименьшим пределом переменной х и пишут
214* = lim х, ЛД = Итх.
Равенство этих пределов есть условие, необходимое и доста-
точное для существования предела переменной х в обычном
смысле [755].
Действительно, если существует конечный предел
a = limx,	(7)
то для любого е 0 найдется такая «пометка» Ре, что
а — е хр а -|- е для Р Р8.	(8)
Тогда и
а — е sg inf М* -С М* -С sup -C a -[- e,
так что, ввиду произвольности е,
М* — М*=а.
Обратно, если имеет место это равенство (при а конечном), то,
ввиду (6), снова по е^>0 найдется такое Рс, что
а — е inf Жр^ -С sup а е,
так что выполняется (8), а отсюда следует (7).
Предоставляем читателю провести рассуждения для случая
а — ± оо.
Числа М* и М*, в случае их конечности, могут быть охаракте-
ризованы их свойствами, которые вполне аналогичны свойствам 1 и
II, изученным в 42. Для примера остановимся на М *.
* То обстоятельство, что рассматриваемые переменные могут принимать
и несобственные значения ± оо, не создает затруднений.
762]	ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ	649
Если взять по произволу число е^>0 и «пометку» Р(1, то суще-
ствует такое Ре Ро, что
М * — e sup М* -]- е.
Отсюда, по определению точной верхней границы, следует
I свойство числа М*: для всех Р^- Pt будет
хР<М* + е.
II свойство числа М*-. найдется хоть одно значение хр‘
(где Р Ро), такое, что
хрР>М* — s.
Пусть теперь множество <& = {Р} допускает конфинальные под-
последовательности (4), которым отвечают конфинальные для Ж под-
последовательности (5) значений нашей переменной. Если какая-либо
из таких последовательностей имеет предел, то его называют ч а-
стичным пределом переменной х [ср. 40 и 59].
В этом случае можно доказать, что наибольший и наименьший
пределы 714* и М*, определенные выше, являются в то же время, соот-
ветственно, наибольшим и наименьшим из всех частич-
ных пределов переменной х [как и в 40 или 59].
Действительно (если снова ограничиться наибольшим преде-
лом в предположении его конечности), из свойства I сразу ясно, что
ни один частичный предел не может превзойти М*. Для того чтобы
построить конфинальную для подпоследовательность (5), стремя-
щуюся к М* (и тем показать, что М* само служит частичным пре-
делом), мы исходим наперед из некоторой подпоследовательности
р\, piр;,....
конфинальной для 3\ А затем, с помощью свойств I и II [ср. 40],
индуктивно строим подпоследовательность(4)так, чтобы, во-первых, было
РРг-Р'п
(так что и (4) будет конфинальной для 4Т5!) и, во-вторых, чтобы хп —
= хр удовлетворяло двойному неравенству
М* —
где еп — произвольно взятая положительная варианта, стремящаяся к 0.
Очевидно, последовательность (5), конфинальная для SC, будет иметь
своим пределом 714*.
Можно указать еще один пример наибольшего и наименьшего пре-
делов из уже знакомой читателю области. Так, очевидно, верхний
и нижний интегралы Дарбу 7* и [296, 301] являются, соответ-
ственно, наибольшим и наименьшим пределами для интегральной суммы
(суммы Римана) а = (U ^xt ПРИ — max ^xi 0-
АЛФАВИТНЫЙ УКАЗАТЕЛЬ
Абель 237
Абсолютная сходимость рядов Фурье
593
Аддитивная функция от области пло-
ской 134, 165
---------пространственной 311
---------, определение ее по произ-
водной 136, 312
------промежутка 119, 137
Аппроксимация функции в среднем
583
---равномерная 579
Архимеда закон 340
Арцела 119, 591, 626, 627
Астроида 35
Бернштейн 505, 593
Бесселевы функции 144, 235, 401, 411,
422, 478, 541, 548, 561
Бессель 584, 585, 586
Био и Савара закон 44
Буняковского неравенство 146, 169
Бэта-функция 213, 230
Валле-Пуссен 626
Вейерштрасс 580, 610
Вектор 366
—	потока тепла 370
Векторная линия, поверхность 367,
368
—	трубка 368, 376
Векторное поле 367
—	произведение 45, 367
Вивиани тело 163, 208, 210, 261, 263,
265
Винтовая поверхность 265
Виртингер 596
Вихревая линия 383, 384
—	поверхность 383
— трубка 383, 384
Вихрь 373
Вихря поток 373
Вольтерра 158
Вращение плоской фигуры 170
Вращение тела 331, 332
Вращения поверхность 264, 266
— тело 170, 355
Гамильтон 369
Гамма-функция 159, 161, 230, 392,
394—403, 407, 411, 461, 541
Гармоники 492
Гармоническая функция в круге 605
------- области плоской 180
----------пространственной 339, 381
Гармонические колебания 492
Гармонический анализ 492
----практический, схема на 12 орди-
нат 563
------—, схема на 24 ординаты 568
Гаусс 62, 336, 412
Гаусса—Остроградского формула 333
Гауссовы коэффициенты поверхности
256
Гейне—Кантора теорема 621
Гельмгольц 383
Гиббс 495, 497
Главное значение несобственного ин-
теграла 240, 533
Градиент 368
Грам 413
Грина формула 174
Гульдина теорема 171, 355
Гурвиц 596
Дарбу верхние и нижние интегралы
128
----------как пределы 130, 649
----Стилтьеса суммы 91
— суммы для интеграла двойного 127
---------- тройного 310
Двойной интеграл 123, 126
----, выражение через первообраз-
ную 147
------ как аддитивная функция обла-
сти 135
----, классы интегрируемых функ-
ций 128
----несобственный 214, 221
АЛФАВИТНЫЙ УКАЗАТЕЛЬ
651
Двойной интеграл, приведение к пов-
торному 123, 137, 149
— —, свойства 131
----, условия существования 128,131
— ряд, сопоставление с двойным ин-
тегралом 240
----Фурье 483
Двусторонняя поверхность 242, 248
Декартов лист 36
Диаметр точечного множества 126
Дивергенция 371
Дини признаки 434, 487, 528, 531
Дирихле — Жордана признаки 438,
489, 529, 531, 609
—	задача для круга 605
—	интеграл 423
—	лемма 436, 486
—	разрывный множитель 536
—	.условие 439
— формулы 158, 231, 237, 394, 407
Дифференциал точный, интегрирова-
ние 50, 52, 65, 68
•---, признаки 50, 65, 178
----, связь с криволинейным инте-
гралом 46, 65, 66, 306
Дифференциальное уравнение гидро-
динамики 379, 382
----колебания струны 550
----теплопроводности 380, 554, 561
Дифференцирование по области 135,
312
— ряда Фурье, почленное 577, 611
Длина дуги 14, 358, 643
Дю Буа-Реймонд 497, 625, 626
Жидкий контур 381, 383
Жордан 74, 87, 88
Жордана — Дирихле признаки 438,
489, 529, 531, 609
Замена переменных в интегралах
двойных 204
---------несобственных 223
---------тройных 358
---------л-кратных 388
Замкнутая ортогональная система
функций 585
Замкнутости уравнение 585, 586, 589,
590
Замкнутость тригонометрической си-
стемы 586 -
Изгибающий момент 108
Изопериметрическая задача 596
Инверсия 186, 344
Инерции главные оси 169, 170, 332
— момент плоской фигуры 166
Инерции момент полярный 168
----поверхности 277
----прямолинейного отрезка 106
----тела 324
——цилиндрического бруса 167
Интегральная сумма 12, 20, 90, 126,
274, 286, 308
Интегральное уравнение 158, 237,
534, 535, 539
Интегральный косинус 540
—	логарифм 542
—	синус 541
Интегрирование по частям для инте-
гралов Стилтьеса 97
---------обыкновенных интегралов
ПО
— рядов Фурье, почленное 574,590,591
— точных дифференциалов 51,52,65,68
Интегрируемая функция 90, 127, 310
Интегрируемости условие (для диф-
ференциальных выражений) 46, 50
Источники 372
—, плотность 372
—	, производительность 372
Кантор 620
Кантора — Гейне теорема 621
Кдталзн 405
Каталана формула 160, 232, 270, 407,
409
Квадрируемая поверхность 251
Квази-стационарный процесс 43
Кеплера уравнение 547
Кинетическая энергия вращающегося
тела 331
Колмогоров 502
Конфинальная подпоследовательность
646
Координатные линии 184
—	поверхности 343
Косинус-преобразование Фурье 535,
545
Косинус-преобразование Фурье для
функции двух переменных 547
Котангенс, разложение на простые
дроби 452
Коши 524, 533, 535
Кратные интегралы 126, 309, 386
----Фурье 545
—	ряды Фурье 483
Кривизна поверхности, гауссова 272
Криволинейные координаты в про-
странстве 343
---- на плоскости 184
----, элемент объема 348
----, элемент площади 192, 257
652
АЛФАВИТНЫЙ УКАЗАТЕЛЬ
Криволинейный интеграл второго ти-
па 20, 21
•--------, вычисление черев перво-
образную 49, 65
---------,	дифференцирование 46
---------, независимость от пути
29, 46, 55, 65, 121, 178, 306.
---------,	поведение в случае не-
односвязной области 57, 70
---------по замкнутому контуру 25,
56, 67. 178, 305
---------, приближение интегралом
по ломаной' 301
---------, сведение к интегралу
Стилтьеса 120
---------, сведение к обыкновенно-
му интегралу 22
---------, связь с криволинейным
интегралом первого типа; 38
----первого типа 11
	, сведение к обыкновенно-
му интегралу 13
Крылов 516, 578
Куммер 461
Кусков 355
Лагранж 383,, 470.
Лаплас 381, 536, 605
Лебег 98, 497, 502, 624
Левая координатная система 26, 246
Левая ориентация плоскости 26
----- пространства 245
Лежандр 230, 271
Лежандра многочлены 233, 422
Лейбниц 234, 278, 376, 410, 448
Лемниската 196
Линейный интеграл 372
Липшиц 77, 93, 435, 489, 593
Липшица признаки 435, 489
Лиувилль 234, 405, 412
Лиувилля формулы 161, 213, 214, 231,
396, 403, 407
Ляпунов 586
Малиев 515
Масса кривой 11, 17
—•— поверхности 277, 281
— плоской фигуры 137, 165
— тела 308, 323
Мёбиус 242, 248
Многократные интегралы 387
-----, замена переменных 388
-----, сведение к повторному 387
Монотонная переменная, возрастаю-
щая и убывающая 641
Мур 632
Наб да 369*
Направление на замкнутом контуре
Напряжение поля 40
Начальные условия 550, 555, 556, 557,
560, 561
Неравномерная сходимость рядов
Фурье 495, 497
Неразрывности уравнение 379
Несобственный двойной интеграл 215,
222, 240
-------, абсолютная сходимость 217,
222
-------, замена переменных 223
------, приведение к повторному
-------, признаки сходимости 226
—	тройной интеграл 315
Нечетная функция 442, 533, 535, 546
Нормальная ортогональная система
функций 420
Нь/отона закон притяжения 18, 72,
277, 324, 364, 371, 384
Объем в криволинейных координатах
345( 349*
	—, выражение поверхностным инте-
гралом 293; 333
—	, различные формулы 301
— тела по. поперечным сечениям 323
—, формула Кускова 355
— цилиндрического бруса 122, 323
— «-мерного параллелепипеда 386
---симплекса 391
--- тела 386
— «-мерной сферы 392
Ограниченного изменения функции
74
-------, классы 76
— •----, критерии 82
-------непрерывные 84
-------, ограниченность	частичных
сумм ряда Фурье 611
-------, порядок коэффициентов
Фурье 508
т------, свойства 79
Односвязность плоской области 53,
178
— пространственной области 305, 336
Односторонняя поверхность 242
Ориентация плоскости 26
— поверхности 244, 245
— —, связь со стороной поверхности
245
— пространства 245
Ориентированная область, интеграл
по ней 207, 359
АЛФАВИТНЫЙ УКАЗАТЕЛЬ
653
Ортогональная система функций 420,
583
Ортогональные функции 420
----с весом 423, 562
Особенностей выделение как метод
улучшения сходимости 516, 578
Особенности рядов Фурье 497
Остаток ряда Фурье, оценка 505,
508
Остроградский 333, 335, 371, 379, 388
Остроградского—Гаусса формула 333
Парсеваль 585, 589
Первообразная функция 46, 60, 65,
136, 147
Перерезывающее усилие 108
Периодическая функция 414
----, интеграл по периоду 427
Плотность линейная 11
— объемная 308, 324
— поверхностная 135, 277
Площадь винтовой поверхности 265
— кривой поверхности 248, 251, 356
-------, особые случаи 259
-------, параметрическое задание
252, 273
-------, явное задание 257, 273
— плоской фигуры в криволинейных
координатах 189, 194
-------, выражение криволинейным
интегралом 32, 121, 176
— поверхности вращения 264, 266
----n-мерной сферы 393
— цилиндрической поверхности 266
Поверхностные интегралы второго
типа 285, 287
---------, независимость от формы
поверхности 336
--------- по замкнутой поверхности
335
---------, сведение к двойному 288,
291
---------, связь с поверхностными
интегралами первого типа 289, 291
----в «-мерном пространстве 388,
405
---- первого типа 274
---------, сведение к двойному 275*
Поверхность вращения 264, 266
— уровня 367
Поле векторное 367
— магнитное 44
—	ньютоновского притяжения 72,
369, 371
— силовое 40, 71, 372
—	скалярное 367
Поле скорости 42, 370, 374
— температуры 369
Полное изменение функции 74, 82,
86
Полнота тригонометрической системы
578, 610
Положительное ядро 600, 603, 608,
610, 612, 619
Полярное уравнение поверхности
266
Полярные координаты в пространстве
344
------ в «-мерном пространстве 401
•--- на плоскости 184
----обобщенные 198
----, элемент площади 192, 195
Потенциал векторный 375
— ньютоновский, созданный матери-
альной точкой 72
----, — поверхностью 278
----,— сферическим слоем 285
----, — сферой 329
— — , — телом 325, 364
----,— эллипсоидом 363
----тела на сам'о себя 385
---------другое тело 385
Потенциальная функция 71, 374
Потенциальное поле 71, 374
Поток вектора через поверхность
370
— тепла 370
----, вектор 371
Правая координатная система 26,
246
— ориентация плоскости 26
---- пространства 245
Предел упорядоченной переменной
636
-------наибольший, наименьший 648
-------, условие существования 642,
Предельные условия 550, 555, 556,
557, 559, 561
Преобразование плоских областей
182
-------, сохраняющее площадь 203
— пространственных областей 342
Приложения к механике и физике:
интеграла двойного 137, 165—173,
208
— криволинейного второго типа
41, 43, 44, 72, 73, 382
-----первого типа 11, 17, 42
— многократного 384
— поверхностного 277, 281, 370,
379, 380
— Стилтьеса 106, 108
654
АЛФАВИТНЫЙ УКАЗАТЕЛЬ
интеграла тройного 308, 324—332,
340, 362, 364, 379, 380
— Фурье 558
рядов Фурье 551, 555, 557, 560, 565,
570
Притяжение материальной точки кри-
вой 19
------поверхностью 277
------ сферическим слоем 284
------сферой 328
------телом 325, 364
— тела телом 385
Произведение инерции 169, 331
Производная обобщенная, первая и
вторая 613, 614
— по направлению 368
---- области 135, 312
Простой слой 277
Пуассон 228, 280, 407, 603, 606
Пучности 553
Работа силового поля 40, 71, 372
Равномерная сходимость рядов Фурье
419, 487
Расходимость 371
Расходящихся рядов суммирование,
см. Суммирование рядов обобщен-
ное
Регулярная точка 434
Риман 429, 432, 619, 631
Римана метод суммирования 616,
618
Ротор 373, 374
Рунге 564, 569
Силовая функция 71
Силовое поле 40, 71, 372
Синус-преобразование Фурье 535,
545
------ для функции двух перемен-
ных 547
Синус, разложение обратной величи-
ны на простые дроби 452
Скаляр 366
Скалярное поле 367
— произведение 367
Смит 632
Соленоидальное поле 375
Сонин 400, 407, 409
Сопряженные функции первого и
второго рода 536
Сопряженный тригонометрический
ряд 480
Спрямляемая кривая 11, 88, 89
Среднее значение, теорема 112, 116,
134, 311
Среднее квадратичное отклонение
583
Статические моменты кривой 18
------- поверхности 281
----плоской фигуры 166
---- прямолинейного отрезка 106
---- тела 324
----цилиндрического бруса 166
Стеклов 585, 595
Стилтьеса—Дарбу суммы 91
—интеграл 90
----, вычисление 100
----, геометрическая иллюстрация
111
----, интегрирование по частям 97
----, классы случаев существования
92, 98
----, непрерывность по верхнему
пределу 118
— —, оценка 112
----, предельный переход 114,
119
----, приведение к обыкновенному
98
----, свойства 95
----, теорема о среднем 112, 116
----, условие существования 96
Стилтьеса сумма 90
Стокса формула 297, 373
Сторона поверхности 241,	242,
248
Стоячих волн метод, см. Фурье ме-
тод
Струны колебание 549
Суммирование рядов обобщенное,
метод Римана 619
— тригонометрических рядов в ко-
нечном виде 469
-------обобщенное, метод Пауссо-
на —Абеля 601
---------) — Римана 616
---------, — Чезаро — Фейера 607
Сфера, притяжение и потенциал 328,
329
Сферические координаты 266
----обобщенные 360
----, элемент площади кривой и
поверхности 267
Сферический слой, притяжение и по-
тенциал 284, 285
Сходимость интеграла Фурье, при-
знак Дини 528, 531
-------, — Дирихле — Жордана 529,
531
— рядов Фурье абсолютная 593
— -----неравномерная 495, 497
-------, признак Дини 434
АЛФАВИТНЫЙ УКАЗАТЕЛЬ
655
Сходимость рядов Фурье, признак
Дирихле 438
-------, — Дирихле — Жордана 438
-------, — Липшица 435
------- равномерная 419
--------, признак Дини 487
--------, — Дирихле — Жордана
489
--------, — Липшица 489
Телесный угол 272, 337
Тепла распространение в круглой
пластине 561
-------стержне бесконечном 557
--------конечном 553, 559
--------- полубесконечном 559
------- теле 370
Тепло, поглощенное газом 43, 73
Теплопроводности уравнение 380,554,
561
Томсон 383
Тригонометрическая система функ-
ций, замкнутость 586
-------, полнота 578, 610
Тригонометрический многочлен 424,
580, 585
— ряд 416
----, лемма о коэффициентах 620
----, не являющийся рядом Фурье
624
----сопряженный 480
Тригонометрическое интерполирова-
ние 424
Тройной интеграл 309
---- как аддитивная функция обла-
сти 311
----, классы интегрируемых функ-
ций 310
----, несобственный 315
----, приведение к повторному 312,
314
----, свойства 310
----, условие существования 310
Угол видимости кривой 63
----поверхности 338, 371
Узлы 553
Улучшение сходимости рядов Фурье
Умножение рядов Фурье 592
Упорядоченная переменная 636
---- , предел 636
— — , сведение к варианте 645
Упорядоченное множество 632,
633
Фату теорема 611
Фейер 497, 607
Фурье 417
— интеграл 524
— коэффициенты 419, 432, 586
----обобщенные 424, 560, 562
----.порядок малости 509
----, экстремальное свойство 584,
586
— метод 5б0, 553, 555, 560, 561,
606
— преобразование 534, 537
— — для функции двух переменных
547
— ряд 419, 427
---- двойной 483
——, комплексная форма 477
----обобщенный 424
— формула, различные виды 525,
532
— — для функции двух переменных
545
Центр тяжести кривой 18
---- поверхности 277
----плоской фигуры 166
---- тела 324
----цилиндрического бруса 167
Центробежная сила 332
Центробежный момент 169, 331
Циклическая постоянная 59, 70
Цилиндрические координаты 343,
354
Цилиндрический отрезок 172
Циркуляция вектора 372
Частичная сумма ряда Фурье, ограни-
ченность 610
--------- , оценка 503
----сопряженного ряда, оценка
504
Чебышев 146
Четная функция 443, 534, 535, 546
Шатуновский 632
Шварц 248, 603, 614, 616, 629
Эйлер 417
Эйлера метод суммирования 470
----Фурье формулы 419
Эйлерова постоянная 463
Эквивалентная нулю функция 579
Экстремальное свойство отрезков
ряда Фурье 584, 586
656	АЛФАВИТНЫЙ УКАЗАТЕЛЬ
Элемент площади в криволинейных
координатах 192, 195, 257
-------полярных координатах 192,
195
-------сферических координатах 267
— объема в криволинейных коорди-
натах 348, 350
------- сферических координатах
350
------- цилиндрических координа-
тах 350
Эллипс 35
—	инерции 169
Эллипсоид 172, 173, 268, 269, 363,
396
Эллипсоид инерции 332
Эллиптические интегралы 270, 363
— координаты 189, 228, 229, 345,
355
Энтропия 74
Юнг 463, 590
Ядро положительное 600, 612, 619
—	Дирихле 610
—	Пуассона 603
—	Фейера 608
Якоби 230, 394, 403
Якобиан как коэффициент растяже-
ния 193 349